Автор: Блохинцев Д.И.
Теги: физика математическая физика квантовая механика переводная литература издательство знание
Год: 1944
Текст
БЛОХИНЦЕВ
Д. И. БЛОХИНЦЕВ
ВВЕДЕНИЕ
В КВАНТОВУЮ
МЕХАНИКУ
ВВЕДЕНИЕ
В КВАНТОВУЮ
МЕХАНИКУ
ОГИЗ • ГОСТЕХИЗДАТ • 1944
Д. И. БЛОХИНЦЕВ
ВВЕДЕНИЕ
КВАНТОВУЮ
МЕХАНИКУ
Допущено Всесоюзным комитетом
по делам высшей школы при СНК СССР
в качестве учебника для университетов
огиз
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 4 4 ЛЕНИНГРАД
Scan AAW
Редактор Э. Г. Ананиашвили. Подписано к печати 8/VI 1944 г. 30,25 печ. л., 35,9 авт. л.
48 700 тип. зн. в печ. л. Тираж 3000 экз. Л52973. Цена книги 18 р. Зак. № 1626.
1-я Образцовая типография треста „Полиграфкнига“ Огиза при СНК РСФСР.
Москва, Валовая, 28.
ОГЛАВЛЕНИЕ
Введение......................................................' • Т
Глава I. Основы квартовой теории.................................... 9
§ 1. Энергия и импульс световых квантов.................... 9
§ 2. Фотоэффект и эффект Комптона......................... 19
§ 3. Атомизм.............................................. 13
§ 4. Теория Н. Бора..................................... 19
§ 5. Теория излучения А. Эйнштейна........................ 18
§ 6. Формула Планка....................................... 22
Глава II. Волновые явления при движении частиц..................... 28
§ 7. Волны де-Бройля. Групповая скорость.................... 28
§ 8. Диффракция электронов, атомов и молекул 28
Глава III. Основы квантовой механики............................... 81
§ 9. Статистическая интерпретация воли де-Бройля........... 31!
§ 10. Вероятность местоположения частицы..................... 34
§11. Принцип суперпозиции состояний......................... 39
§ 12. Вероятность импульса частицы........................... 38
§ 13. Средние значения функций от координат и функций
от импульса.................................................. 49
§ 14. Гейзенбергово соотношение неопределенностей............ 42
§ 15. Доказательство соотношения Гейзенберга для общего
случая . .................................................... 49
§ 19. Статистические ансамбли квантовой механики. Ансамбли
чистые и смешанные . . ................................. 51
§ 17. Понятие состояния в квантовой механике и измерение . . 55
Глава IV. Изображение механических величин операторами ... 60
§ 18. Линейные самосопряженные операторы..................... 90
§ 19. Общая формула для среднего значения величины и для
среднего квадратичного отклонения ........................... 94
§ 20. Собственные значения и собственные функции операторов
и их физический смысл. «Квантование».................... 95
§ 21. Основные свойства собственных функций.................. 97
§ 22. Общий метод вычисления вероятностей результатов изме-
рения ....................................................... 71
§ 23. Условия возможности одновременного измерения разных
механических величин ... ........................... 74
§ 24. Операторы координаты и импульса частицы............... 75
§ 25. Оператор момента импульса частицы................. 77
§ 26. Оператор энергии и функция Гамильтона.......... . 81
§ 27. Гамильтониан........................................... 83
1*
4
ОГЛАВЛЕНИЕ
Глава V. Изменение состояния во времени........................... 85
§ 28. Уравнение Шредингера.................................. 85
§ 29. Уравнение непрерывности............................... 89
§ 30. Стационарные состояния..............•................. 92
Глава VI. Изменение во времени механических величин............. 94
§ 31. Производные операторов по времени................ 94
§ 32. Уравнения движения в квантовой механике. Теорема Эрен-
феста............................................. 96
§ 33. Интегралы движения .................................. 99
Глава VII. Связь квантовой механики с классической механикой
и оптикой............................................. 101
§ 34. Переход от квантовых уравнений к уравнениям Ньютона . 101
§ 35. Переход от временного уравнения Шредингера к класси-
ческому уравнению Гамильтона-Якоби......................... 105
§ 36. Квантовая механика и оптика.......................... 108
Глава VIII. Основы теории представлений.......................... 111
§ 37. Различные представления состояния квантовых систем . . 111
§ 38. Различные представления операторов, изображающих ме-
ханические величины. Матрица............................... 113
§ 39. Матрицы и действия над ними.......................... 115
§ 40. Определение среднего значения и спектра величины, пред-
ставляемой оператором в матричной форме.................... 120
§ 4К Унитарные преобразования............................. 122
§ 42. Уравнение Шредингера и зависимость операторов от вре-
мени в матричной форме..................................... 124
Глава IX. Теория движения частицы в поле потенциальных сил . 126
§ 43. Введение............................................. 126
§ 44. Гармонический осциллятор............................. 127
§ 45. Осциллятор в энергетическом представлении............ 133
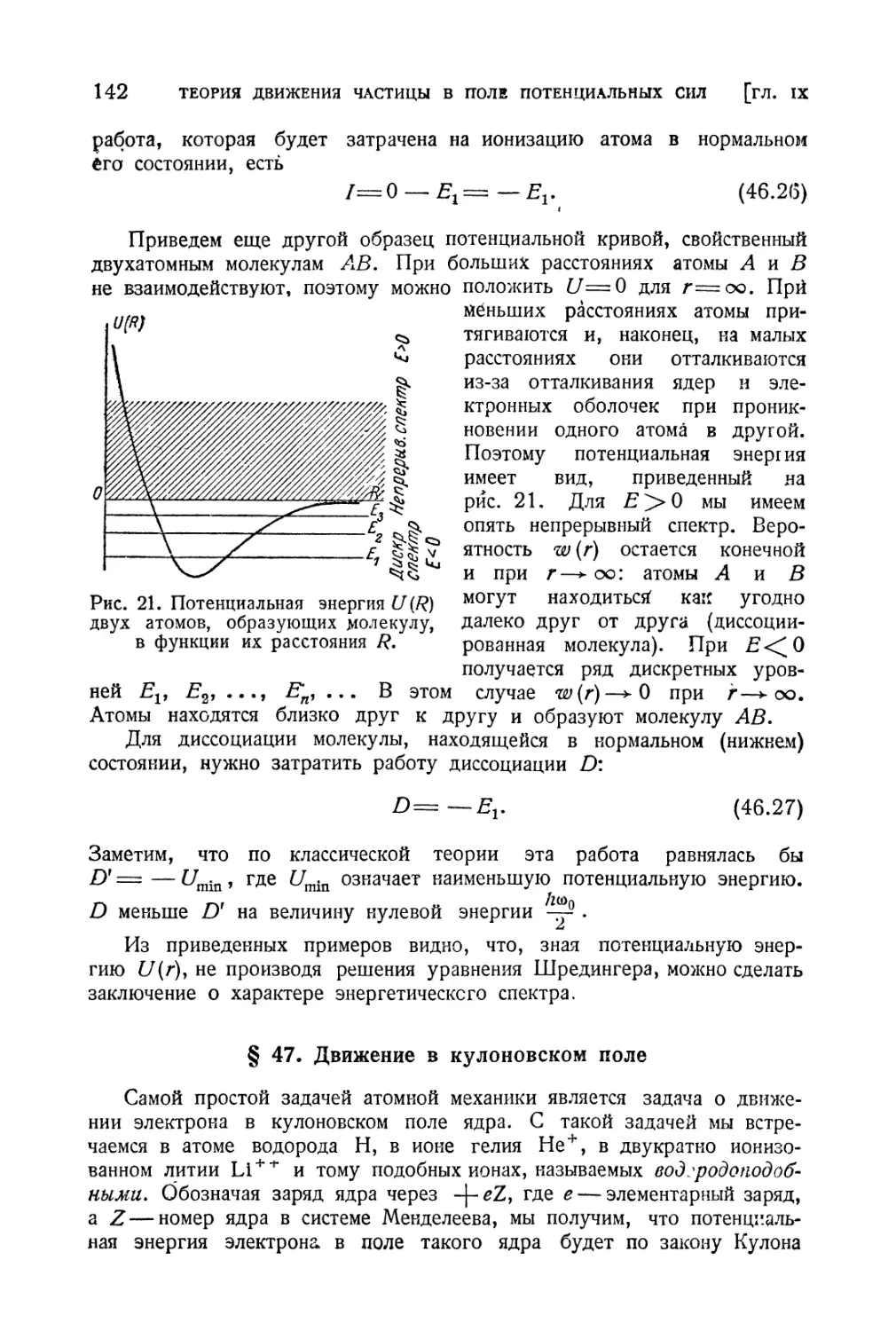
§ 46. Движение в поле центральной силы..................... 136
§ 47. Движение в кулоновском поле.......................... 142
§ 48. Спектр и волновые функции атома водорода............. 147
§ 49. Движение электрона в водородоподобных атомах........ 155
§ 50. Токи в атомах. Магнетон Бора ........................ 158
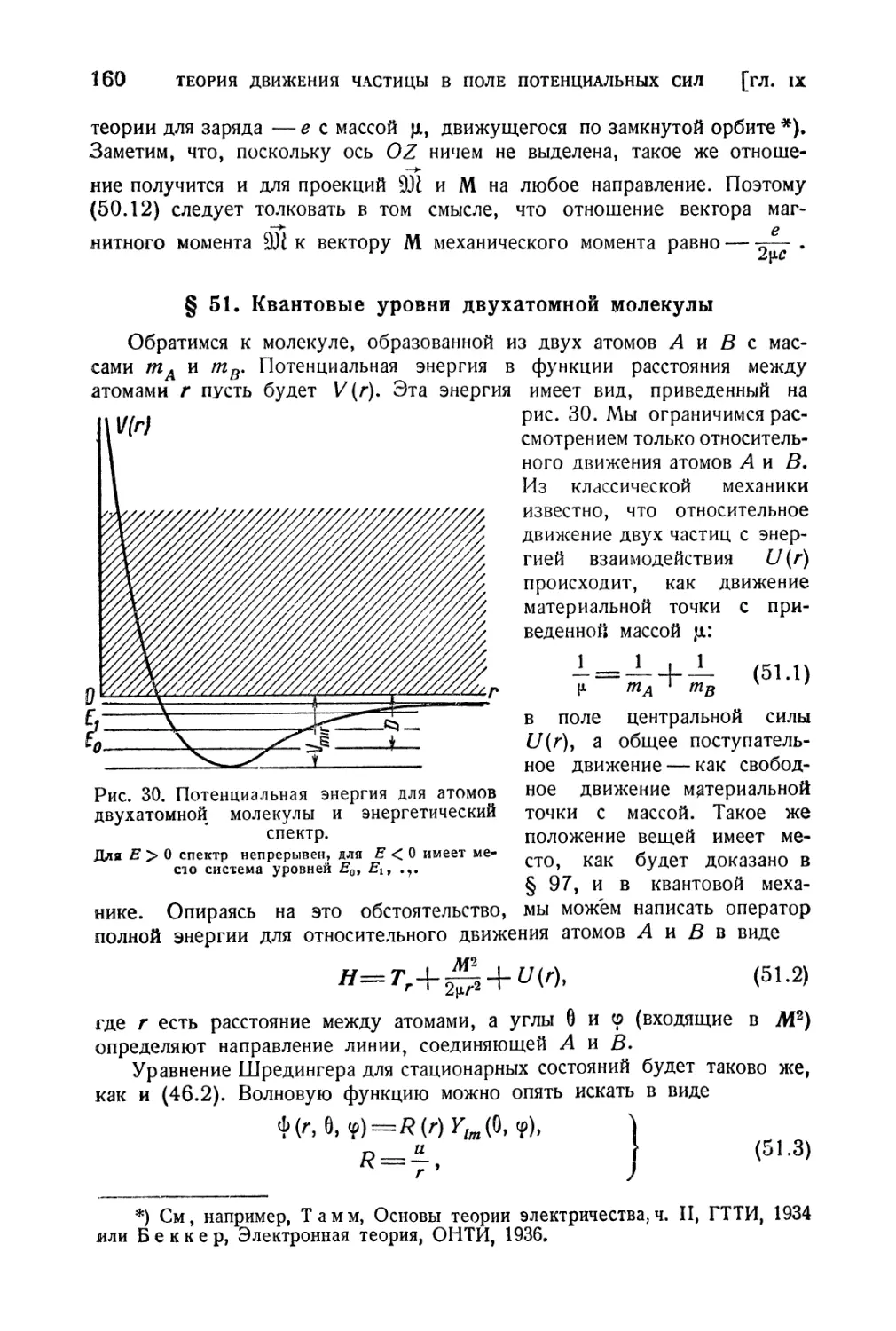
§ 51. Квантовые уровни двухатомной молекулы................ 160
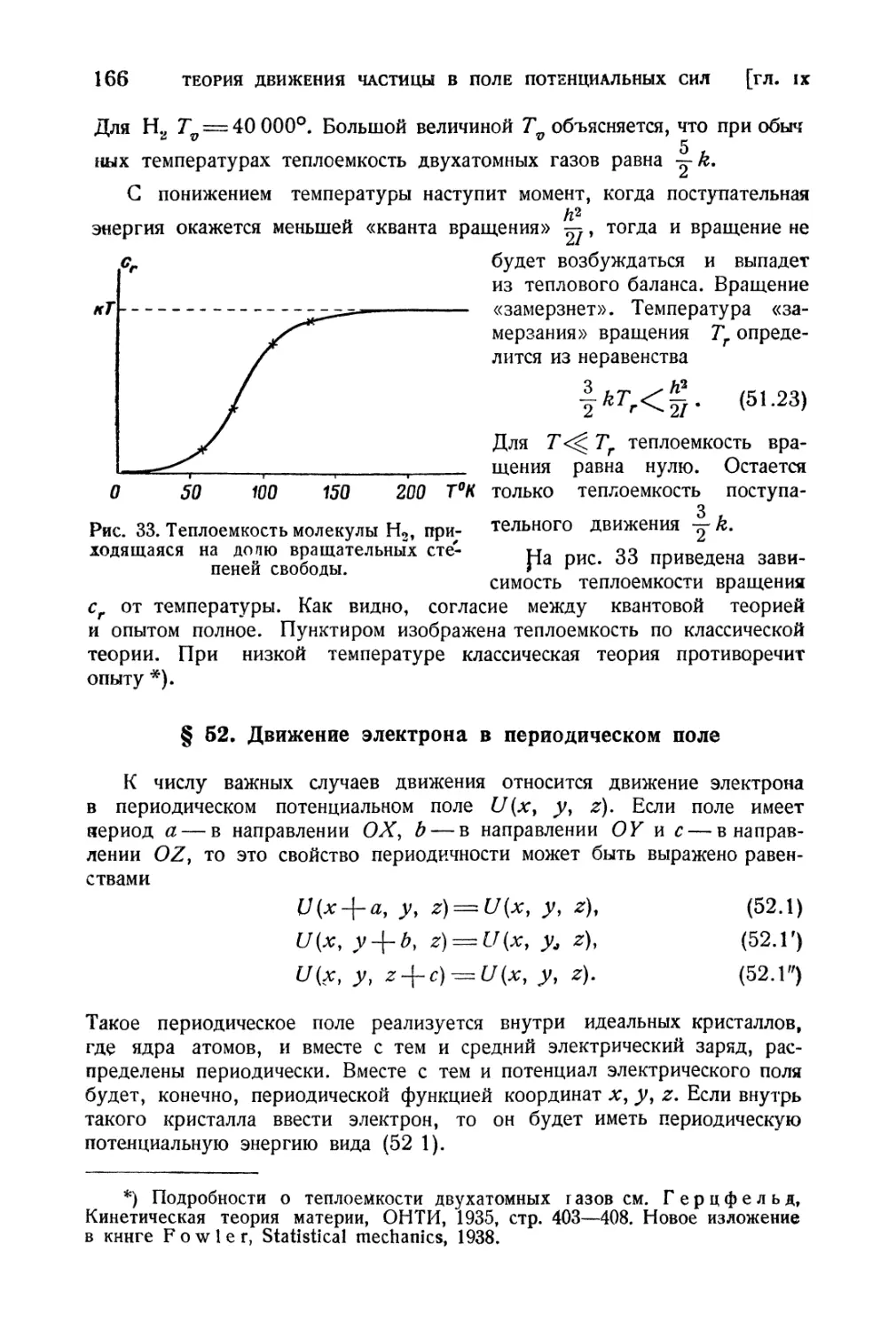
§ 52. Движение электрона в периодическом поле.............. 166
Глава X. Движение заряженной частицы в электромагнитном поле 175
§ 53. Произвольное электромагнитное поле................... 175
§ 54. Движение заряженной свободной частицы в однородном
магнитном поле............................................. 180
Глава XI. Собственный механический и магнитный моменты элек-
трона (спин)..................................................... 182
§ 55. Экспериментальные доказательства существования спина
электрона............................................. 182
§ 56. Оператор спина электрона............................. 185
§ 57. Спиновые функции..................................... 188
§ 58. Уравнение Паули...................................... 192
§ 59. Простой эффект Зеемана . . ‘ ‘..................... 195
ОГЛАВЛЕНИЕ а
§ 60. Свойства полного момента импульса.................... 199
§ 61. Нумерация термов атома с учетом спина электрона. Муль-
типлетная структура спектров .............................. 203
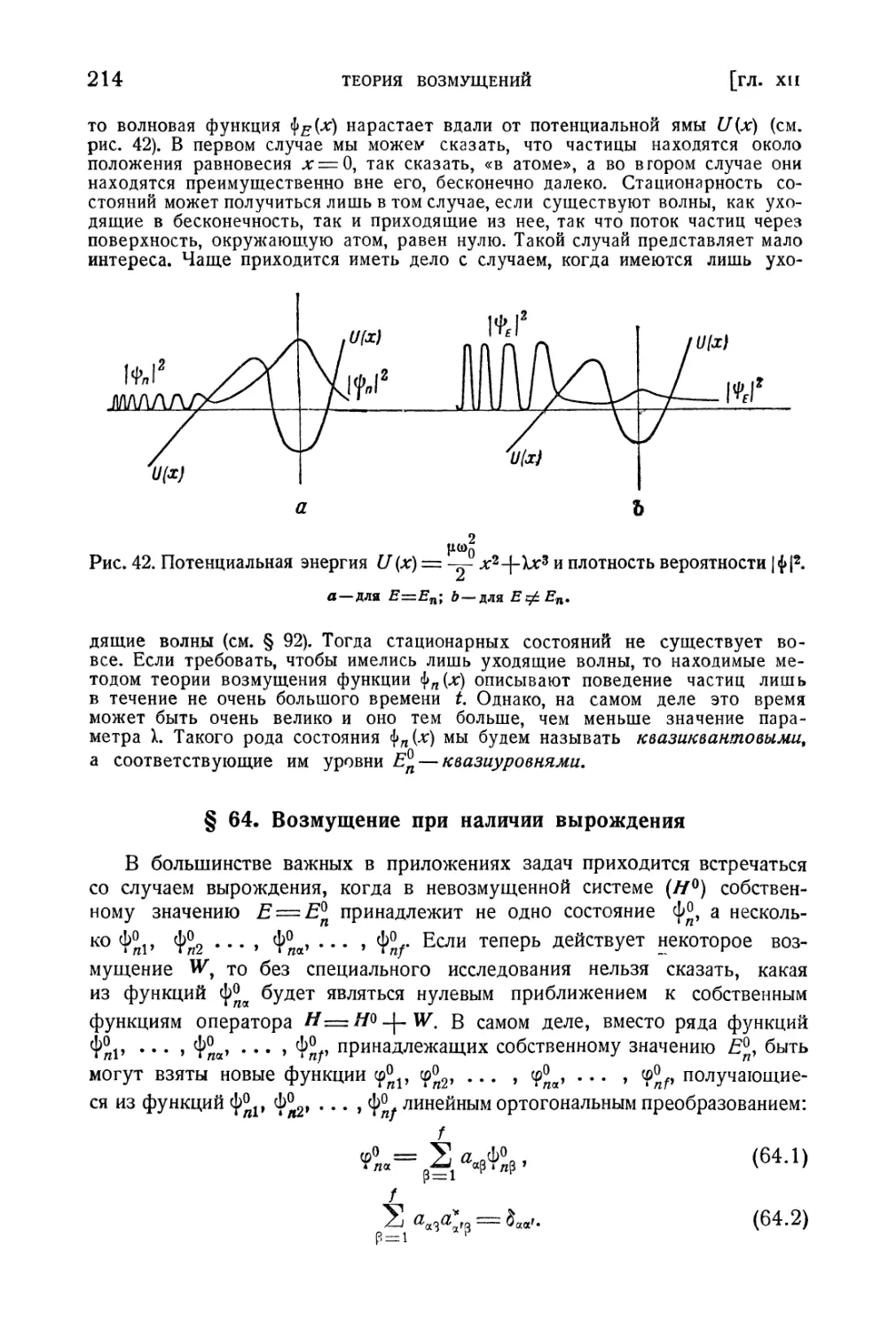
Глава XII. Теория возмущений.................................... 207
§ 62. Постановка вопроса................................... 207
§ 63. Возмущение в отсутствии вырождения................... 210
§ 64. Возмущение при наличии вырождения.................... 214
§ 65. Расщепление уровней в случае двукратного вырождения . 219
§ 66. Замечания о снятии вырождения........................ 222
Глава XIII. Простейшие приложения теории возмущений............ 225
§ 67. Ангармонический осциллятор........................... 225
§ 68. Эффект Штарка........................................ 227
§ 69. Эффект Штарка в атоме водорода....................... 231
§ 70. Сложный (аномальный) эффект Зеемана.................. 234
§ 71. Наглядное толкование сложного эффекта Зеемана .... 240
Глава XIV. Теория возмущений для непрерывного спектра и тео-
рия столкновений ..........................\.................... 241
§ 72. Теория возмущений для непрерывного спектра........... 241
§ 73. Постановка вопроса в теории столкновений частиц .... 247
§ 74. Расчет упругого рассеяния приближенным методом Борна . 252
§ 75. Упругое рассеяние атомами быстрых заряженных частиц . 257
Глава XV. Теория квантовых переходов............................. 262
§ 76. Постановка вопроса................................... 262
§ 77. Вероятности переходов под влиянием возмущения, завися-
щего от времени............................................ 265
§ 78. Переходы под влиянием возмущения, не зависящего от
времени.................................................... 269
Глава XVI. Излучение, поглощение и рассеяние света атомными
системами............................................. 270
§ 79. Введение............................................. 270
§ 80. Поглощение и излучение света................ 272
§ 81. Связь с коэффициентами Эйнштейна.............. 277
§ 82. Принцип соответствия...............................' 280
§ 83. Правила отбора для дипольного излучения.............. 283
§ 84. Интенсивности в спектре излучения ................... 288
§ 85. Дисперсия ......................i.................... 289
§ 86. Комбинационное рассеяние............................. 296
§ 87. Учет изменения фазы электромагнитного поля волны внутри
атома...................................................... 299
§ 88. Фотоэлектрический эффект............................. 302
Глава XVII. Прохождение частиц через потенциальные барьеры . ЗОЭ
§ 89. Постановка проблемы и простейшие случаи........ 309
§ 90. Кажущаяся парадоксальность «туннельного эффекта» ... 314
§ 91. Холодная эмиссия электронов из металла......... 316
§ 92. Трехмерный потенциальный барьер. Квазистационарные со-
стояния .................................................. 319
§ 93. Теория радиоактивного а-распада................ 324
§ 94. Ионизация атомов в сильных электрических полях .... 328
6
ОГЛАВЛЕНИЕ
Глава XVIII. Задача многих тел.................................... 331
§ 95. Общие замечания о задаче многих тел................... 331
§ 96. Закон сохранения полного импульса системы частиц . . . 335
§ 97. Движение центра тяжести системы частиц........... 337
§ 98. Закон сохранения момента импульса системы частиц . . . 340
Глава XIX. Простейшие применения теории движения многих тел . 345
§ 99. Учет движения ядра в атомах........................... 345
§ 100. Система частиц, совершающих малые колебания...... 347
§ 101. Движение атомов во внешнем поле . . •................ 352
§ 102. Определение стационарных состояний атомов методом от-
клонения во внешнем поле..................................... 354
§ 103. Неупругие столкновения электрона с атомом. Определение
стационарных состояний атомов методом столкновений . . 359
§ 104. Замечания о законе сохранения энергии в квантовой ме-
ханике .............................•........................ 364
Глава XX. Системы из одинаковых частиц............................ 366
§ 105. Принцип неразличимости частиц........................ 366
§ 106. Симметричные и антисимметричные состояния............ 370
§ 107. Частицы Бозе и частицы Ферми. Принцип Паули .... 373
§ 108. Волновые функции для системы частиц Ферми и частиц
Бозе......................................................... 380
Глава XXI. Вторичное квантование и квантовая статистика .... 383
§ 109. Вторичное квантование................................ 383
§ 110. Гипотеза о столкновениях. Газ Ферми-Дирака и газ Бозе-
Эйнштейна ................................................... 391
Глава XXII. Многоэлектронные атомы............................... 398
§ 111. Атом гелия........................................... 398
§ 112. Приближенная количественная теория атома гелия .... 407
§ 113. Обменная энергия..................................... 411
§ 114. Квантовая механика атома и периодическая система эле-
ментов Менделеева........................................ 415
Глава XXIII. Образование молекул.................................. 423
§ 115. Молекула водорода ................................... 423
§ 116. Природа химических сил............................... 434
§ 117. Силы Ван-дер-Ваальса................................. 437
Глава XXIV. Магнитные явления..................................... 441
§ 118. Парамагнетизм и диамагнетизм атомов...........• • 441
§ 119. Ферромагнетизм....................................... 444
Глава XXV. Заключение............................................. 448
§ 120. Формальная схема квантовой механики.................. 448
§ 121. Границы применимости квантовой механики.............. 453
Дополнения........................................................ 457
Предметный указатель.............................................. 481
ВВЕДЕНИЕ
В последние десятилетия наука об атомных явлениях образовала не
только одну из самых значительных глав современной физики, но и полу-
чила самое широкое и общеизвестное применение в современной технике.
Уже самый поверхностный взгляд в эту замечательную область явле-
ний обнаруживает новые черты, существенно отличные от тех, которые
свойственны макромиру.
Первое, с чем мы встречаемся в микромире, это — атомизм. Про-
стейшие элементарные частицы характеризуются вполне определенными
признаками (зарядом, массой и пр.), одинаковыми для всех частиц одного
сорта. Эта одинаковость носит характер тождественности.
Ничего подобного не существует в макромире. Макроскопические
объекты представляют собой совокупности большого числа элементар-
ных частиц. Закономерности макроскопических явлений, это — законо-
мерности, свойственные совокупностям большего числа частиц. Макро-
скопическое рассмотрение есть как раз такое рассмотрение, в котором
принципиально игнорируется атомизм. Макроскопические объекты, как
бы «стандартно» ни были они изготовлены, все же могут отличаться
друг от друга, хотя бы и очень мало.
Все это показывает, что было бы абсолютно неправильным рассматри-
вать микрочастицы по образцу макроскопических тел. Даже материаль-
ная точка классической механики есть абстрактный, идеализованный образ
вовсе не микрочастицы, а тела, состоящего из большого числа микро-
частиц, размеры которого малы в сравнении с фигурирующими в задаче
расстояниями.
Атомизм проводит резкую грань между объектами микрофизики
и объектами макрофизики. Новые опытные факты показывают, что и
законы движения микрочастиц резко отличны от законов движения
макроскопических тел: микрочастицы обнаруживают волновые свойства.
Если пропускать поток микрочастиц, например, электронов, через
кристалл, то частицы распределятся на экране так же, как распреде-
ляется интенсивность рентгеновских волн, подходящей длины волны. Мы
получаем чуждое классической механике явление диффракции частиц.
В свое время мы покажем, что предположение о движении частиц
по траекториям, каковы бы они ни были, несовместимо с явлением диф-
фракции частиц. Поэтому принципы классической механики, в которой
понятие траектории является одним из основных понятий, непригодны
для анализа движения микрочастиц. Само слово «микрочастица» или
8
ВВЕДЕНИЕ
«частица» в применении к индивидуумам микромира вызывает в нашем
представлении, повидимому, гораздо больше аналогий с материальными
точками классической механики, нежели это отвечает действительности.
Классическая механика оказывается лишь некоторым приближением,
пригодным для описания движения тел большой массы, движущихся
в достаточно плавно изменяющихся полях (макроскопических полях).
В области микромира на смену классической механике приходит меха-
ника квантовая. Таким образом, предметом рассмотрения квантовой меха-
ники является движение микрочастиц.
Квантовая механика является статистической теорией: она пользуется
методами математической теории вероятностей и предсказывает лишь
вероятности результатов измерений над отдельными микрочастицами
(в частности, конечно, возможны и достоверные высказывания с вероят-
ностью, равной 1). Так, с помощью квантовой механики можно пред-
сказать, как распределятся в среднем на фотопластинке электроны,
отраженные от поверхности кристалла, но относительно места попадания
каждого из электронов может быть сделано лишь вероятностное суждение:
«с такой-то вероятностью будет обнаружено там-то»,
С подобным же положением дел мы встречаемся и в статистической
механике. Однако, между квантовой механикой и классической статисти-
ческой механикой есть глубокое различие.
В основе классической статистической механики лежит ньютоновская
механика, допускающая описание истории каждой из частиц, так что в
принципе возможно дать «биографию» каждого отдельного экземпляра.
A priori, в области микрофизики мы вовсе не лишены права спрашивать,
почему один электрон обнаружился в одном месте фотопластинки,
а другой в другом месте, но мы не знаем средств для решения подоб-
ных вопросов.
Современная квантовая механика, в противоположность статистической
механике, не построена на основе какой-либо теории индивидуальных
микропроцессов. В квантовой механике состояния микрочастиц с самого
начала определяются измерительными операциями, производимыми с по-
мощью макроскопических аппаратов. В частности, когда мы говорим
о повторении «одного и того же опыта», то имеется в виду повторе-
ние макроскопических условий для микрофизических явлений. Таким
образом, в квантовой механике атомные явления изучаются с точки зре-
ния измерений, производимых аппаратами, в которых принципиально
игнорируется атомизм (макроскопические аппараты).
В круге, ограниченном такой постановкой вопросов, квантовая меха-
ника является вполне законченным и стройным зданием, подобным дру-
гим величайшим созданиям человеческой мысли.
ГЛАВА I
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
§ 1. Энергия и импульс световых квантов
Представление о прерывном испускании и поглощении света конечными
порциями — квантами — впервые было высказано А. Эйнштейном на
основании планковской теории распределения энергии в спектре черного
излучения. Энергия е такого кванта света пропорциональна (цикличе-
ской) частоте колебаний света (о и выражается уравнением
б = Ло), (1.1)
где h = 1,05-10"27 эрг-сек. — постоянная Планка*). Это представ-
ление получило законченную форму после того, как А. Эйнштейну
удалось показать, что помимо энергии е кванту света следует еще при-
£
писать импульс /? = — , направление которого совпадает с направлением
распространения света.
Если ввести волновой вектор к, компоненты которого равны
&x=y-cosa, —ycosp, ^=y-cosY, где A — длина волны, a cos а,
cos р и cos у — направляющие косинусы нормали к световой волне, то
формула для импульса кванта света может быть написана в векторной
форме
р = Лк. (1.2)
Формулы (1.1) и (1.2) являются основными уравнениями квантовой
теории света и связывают энергию е и импульс р кванта света с часто-
той волны (О и длиной волны X.
Глубокий смысл квантовой теории света заключается не в том, что
мы представляем себе свет как газ, состоящий из частиц с энергией
/го) и импульсом /гк (такое представление полезно ввиду наглядности,
но односторонне), а в том, что обмен энергией и импульсом между
микросистемами (электрон, атом, молекула и т. п.) и светом происхо-
дит путем порождения одних и уничтожения других квантов света.
Эта мысль получает свое точное выражение в применении закона
сохранения энергий и импульса к какой-нибудь системе, взаимодействую-
*) В старой литературе под постоянной Планка обычно разумели величину
в 2тс раз большую, т. е. равную 6,61-10“27 эрг-сек.
10 ОСНОВЫ КВАНТОВОЙ ТЕОРИИ [гл. I
щей со светом (точнее, вообще с каким-либо электромагнитным излу-
чением). Ради наглядности вместо взаимодействия мы будем говорить,
более образно, «столкновение».
Обозначим через Е и Р энергию и импульс системы до «столкновет
ния» с квантом света, а через Е' и Р'—ее энергию и импульс после
«столкновения». Далее, через Л(о и Лк —энергию и импульс кванта
света до «столкновения» и, наконец, через Л(о' и Лк' — те же величины
после «столкновения».
Точный смысл слова «столкновения» здесь означает, что в резуль-
тате взаимодействия энергия и импульс электромагнитной волны частоты
и направления к уменьшились соответственно на Л(о и Лк (квант
света исчез), а энергия и импульс другого электромагнитного колеба-
ния частоты со' и направления к' увеличились на Лсог и Лк' (появился
квант света). Образно мы и говорим, что квант света (Л<о, Лк)
столкнулся с системой и изменил свою энергию и импульс до
(Л(о', Лк'), т. е. выражаемся так, как если бы квант света был час-
тицей.
В принятых нами обозначениях закон сохранения энергии и импульса
формулируется в.виде
Л(о4-£, = Л(о'+^', (1.3)
ЛкЦ-Р = Лк' 4-Р'. (1.4)
Эти уравнения обнимают все три основных процесса: поглощение,
испускание и рассеяние света *).
Если со' —О (тогда и к' —0), то уравнения (1.3) и (1.4) отно-
сятся к поглощению кванта света Лео; если <о —0 (к = 0), то эти же
уравнения определяют излучение кванта Лео'.
Если же (о, со' =7^=0, то эти уравнения относятся к рассеянию света,
.когда квант Л<о, Лк превращается в квант иной энергии Лео' и иного
импульса Лк'.
§ 2. Фотоэффект и эффект Комптона
Справедливость основных уравнений квантовой теории света (1.3)
и (1.4) обосновывается экспериментально.
Уравнение (1.3) впервые было применено А. Эйнштейном к фото-
электрическому эффекту. Представим себе, что на поверхность металла
падает монохроматический свет частоты (и. При этом из металла начнут
вылетать электроны. Так как для извлечения электронов из металла сле-
дует затратить некоторую работу % (ее называют работой выхода элек-
тронов из металла), то первоначальную энергию электрона в металле
следует считать равной — /. Квант света при фотоэффекте поглощается
*) Теория допускает также многократные процессы, происходящие путем
поглощения, испускания и рассеяния двух, трех и большего числа квантов
сразу. Эти процессы значительно менее вероятны. На опыте их не удава-
лось наблюдать. Поэтому можно ограничиться рассмотрением одного кванта
света.
§ 21 ФОТОЭФФЕКТ И ЭФФЕКТ КОМПТОНА 11
полностью, т. е. /ио' — 0. Энергия же электрона Е после поглощения
кванта света равна —, где — масса электрона, a v — его скорость
после вылета из металла. Следовательно, уравнение (1.3) в рассматри-
ваемом случае гласит *):
(2.1)
Это и есть знаменитое уравнение А. Эйнштейна для фотоэф-
фекта.
В то время как по классической теории энергия фотоэлектронов
должна была бы зависеть от интенсивности света, согласно квантовой
теории их энергия определяется частотой света, именно, она линейно зави-
сит от частоты света со. Этот фундаментальный вывод квантовой ’теории
был проверен опытами Р. Милликэна, полностью подтвердившего указанный
вывод теории **).
Совокупность уравнений (1.3) и (1.4) была экспериментально обос-
нована А. Комптоном, изучавшим зависимость частоты рассеянных рент-
геновских лучей от угла рассеяния. В качестве веществ, рассеивающих
лучи, А. Комптон брал вещества, в которых электроны слабо связаны
с атомом (парафин, графит). Так как энергия кванта рентгеновских
лучей велика, то при расчете можно игнорировать энергию электрона
в атоме (по крайней мере для электронов в верхних оболочках атома)
и рассматривать электроны как свободные, покоящиеся частицы. Соответ-
ственно этому начальную энергию электрона Е и его импульс Р будем
считать равными нулю.
После столкновения с квантом рентгеновских лучей энергия элек-
трона может оказаться очень большой, поэтому мы применим формулы
теории относительности, учитывающие зависимость массы частицы от ее
скорости. Согласно теории относительности кинетическая энергия элек-
трона, движущегося со скоростью V, равна
£' = —^_°с2 — тас2, (2.2)
где /п0 — масса покоя и с — скорость света, а импульс равен
*) Уравнение (1.4) в этом случае не имеет значения, так как оно просто
утверждает, что импульс кванта света передается1 всему куску металла в
целом.
**) Подробности опытов Р. Милликэна см. в книге Дж. Гарнвелл и
Дж. Ливингуд, Экспериментальная атомная физика, ОНТИ, 1936, § 75. См.
также книги Т артаковский, Кванты света и Р. Милликэн, Электрон.
12
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
[гл. I
Подставляя эти значения в (1.3) и (1.4) и имея в виду, что Е = 0,
Р = 0, мы получим:
й<о = Л<.)’4-/пос2 [р==— 1] > (2-4)
Лк = Лк'+^^, £=-. (2.4’)
Здесь (о и к — частота и волновой вектор падающего излучения, a o>f
и к' — эти же величины для излучения рассеянного.
Из первого уравнения непосредственно следует, что (о > о'. Сле-
довательно, рассеянное излучение должно обладать большей длиной
волны, нежели падающее. Этот вывод подтверждается опытами Компто-
на, в то время как по классической теории частота рассеянного света дол-
жна равняться частоте падающего (рэлеевское рассеяние).
Из уравнений (2.4) следует один важный вывод: свободный электрон не
может поглощать, а может только рассеивать свет. Действительно, полное
поглощение означало бы, что со'= 0 (и kr = 0). Тогда из второго уравнения
следует, что к и v одинаково на-
р / правлены. Поэтому его можно запи-
। сать в скалярной форме:
i Х\ л*=-Й^.
: \
j Комбинируя это уравнение с первым
। сэ х. уравнением (1.6)f получаем, что для
_ _ \ Ък X _ _А_ поглощения
I / 1____! = ?
! // yi — р Vi —Р
। / Оно имеет два корня (5=1 и [5 = 0,
’ что приводит к k = 0 или k = оо (cd = О
или со = оо ). В первом случае квант
вообще отсутствует, во втором его
энергия равна оо. Этим и доказы-
' __ вается невозможность поглощения.
Рис. 1. Параллелограмм Комптона. Рассмотренный нами выше фото-
эффект, при котором квант поглощается
целиком, возможен лишь по той причине, что электрон связан с металлом, что
выражается в необходимости затратить работу % для его вырывания.
Для того, чтобы иметь возможность проверить уравнения (2.4),
Комптону предстояла задача определить из них, как зависит частота
рассеянного света <о' от угла рассеяния 6. На рис. 1 линия ОА изобра-
жает направление распространения пучка первичных рентгеновских лучей.
Направление ОС есть направление, по которому наблюдают рассеянные
электронами лучи. Построенный на рис. 1 параллелограмм дает сложе-
ние импульсов падающего кванта Лк, рассеянного ЛК и электрона Pf.
Угол 0 есть угол рассеяния, а угол а есть угол между импульсом пер-
вичного кванта и импульсом получившего толчок электрона, так назы-
ваемого «электрона отдачи». Для нахождения связи между углом 6
и величиной рассеянного кванта Лео* спроецируем второе из уравнений
(2.4') на две взаимно перпендикулярные оси ОА и ОВ. Замечая, что
АТОМИЗМ
13
§ 3]
, . . (О . 1 . . (О'
| к | = — , а I к [ = — , мы получим:
Л<о W , m^v
— — — cos 0 ч—~== cos а,
с с и 1 — f2
м W . п тли
О = — sin 0----sin а.
с Ki— ?2
Исключая из этих уравнений, путем несложных алгебраических выкла-
док, р и угол а, мы получим:
, 2Л , . 9 О
(О--(О = ---5- (0(1) Sin2 тг •
mQc2 2
2ъс , 2пс
Заменяя здесь (о через -у-, (о через , легко находим изменение
длины волны Дк = к' — к:
Ak=-^sin2-l. (2.5)
т$с £
Эта формула была впервые получена А. Комптоном. Меняя угол, под
которым наблюдалось рассеянное излучение, и измеряя в нем изменение
длины волны Дк, Комптон и By (Woo) сравнили результаты своих изме-
рений с предсказаниями теории по формуле (1.7) и получили полное
согласие с теорией*).
Поэтому опыты Комптона показывают полную справедливость пред-
положения о существовании импульса у кванта света, величина которого
определяется формулой (1.2).
Заметим, что наблюдения в камере Вильсона позволяют в некоторых
случаях установить направление рассеянного при комптон-эффекте кванта,
а также путь и энергию электрона отдачи и тем самым позволяют как
бы воочию видеть сложение импульса электрона и кванта шсвета, при-
веденное нами на рис. 1**).
§ 3. Атомизм
В микромире мы встречаемся с рядом простейших, элементарных
частиц. Такими частицами являются: (протоны, нейтроны, электроны и
позитроны (в последнее время открыты мезотроны, частицы, примерно
в 100 раз более тяжелые, нежели электроны). Масса, заряд и другие
свойства всех экземпляров элементарных частиц одного рода одинаковы
и не могут быть подвергнуты изменениям. Они являются неизменными
признаками, характерными для каждого рода элементарных частиц.
В существовании элементарных частиц выражается атомизм, свойственный
микромиру и составляющий его важнейшую, отличительную, черту.
Сложные частицы, образованные из элементарных частиц (например, моле-
кулы, атомы, ядра атомов), также обладают атомистическими свойствами.
Эти атомистические свойства обусловлены двумя обстоятельствами.
Во-первых, каждый сорт сложных частиц образуется из вполне опреде-
*) Подробности опытов см. в книге Тартаковский, Кванты света,
ГИЗ, 1928.
**) Тартаковский, loc. cit.
14
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
[гл. I
ленных элементарных частиц (например, атом водорода образуется из
одного протона и одного электрона). Во-вторых, внутренние состояния
сложных частиц прерывны: для каждой сложной частицы существует
своя последовательность вполне определенных возможных состояний,
каждое из которых отделено от другого скачкообразными изменениями *).
Благодаря этому далеко не всякое воздействие моэйет перевести
сложную систему, например, из состояния с наименьшей энер-
гией (так называемое «нормальное» состояние) в соседнее («возбужден-
ное»).
Если энергия внешнего воздействия недостаточна для того, чтобы
вызвать переход системы из нормального состояния в возбужденное,
то по прекращении внешнего воздействия система окажется в том же
состоянии, в каком она была до применения этого воздействия (в «нор-
мальном» состоянии). В силу этого атомные системы, подвергаясь какому-
либо внешнему воздействию, остаются в широких пределах такими же,
какими они были до воздействия (или переходят в новые, вполне опреде-
ленные состояния). Именно такая
п скачкообразность в изменении со-
/;\ стояний сложных атомных систем
А / ; была той физической (правда, в
/[ \ / ! явном виде неизвестной) причиной,
I I i / ! которая позволяла химикам гово-
/ \ \ / ! рить о неделимости атомов, а фи-
/ ; V/ • зикам (в кинетической теории) —
А / ! !' рассматривать атомы как неизмен-
/ц / 1 Г ные материальные точки. Эти неиз-
/ i ; • менность и неделимость соблюдают-
/ \ J ; ся, лишь пока внешние воздействия
У ; ! : не достигнут той степени интен-
!--------1--------!----- сивности, при которой окажутся
Ц,= 4,9 2Vr=9,& возможными переходы сложной
Рис. 2. Результаты опыта Франка и частицы в соседние состояния.
Герца. Подчеркнем еще, что в макро-
скопической области никакой пре-
рывности состояний не наблюдается. Первоначально одинаковые макро-
скопические системы (насколько вообще можно достигнуть одинаковости
в макромире) с течением времени могут оказаться совершенно различ-
ными, даже если внешние воздействия были невелики. Таким образом,
прерывность состояний сложных атомных систем является одной из важ-
нейших особенностей микромира.
Эта прерывность доказывается прямыми опытами. Франк и Герц
пропускали поток электронов через пары ртути. Оказалось, что проте-
кающий ток в зависимости от энергии электронов имеет максимумы
и минимумы, изображенные на рис. 2. Первоначально, пока энергия
*) Это утверждение не относится к движению сложной частицы как целого.
Состояния движения сложной частицы как целого могут как угодно мало
отличаться друг от друга.
АТОМИЗМ
1
§ 3]
электронов не превосходит 4,9 eV, пучок электронов проходит чере^
пар ртути, не теряя энергии (на самом деле при столкновении элек-
трона с атомом ртути как с целым происходит некоторый обмен энер-
гией; однако, ввиду того, что масса атома ртути во много раз пре-
вышает массу электрона, удар происходит практически упруго, и этим
обменом энергий можно пренебречь), и поэтому ток растет с
ростом напряжения. Но как только, достигается энергия в 4,9 eV, ток?
падает, благодаря тому что электроны начинают терять энергию
при столкновении с атомами ртути, изменяя их внутреннее состо-
яние.
Этим и доказывается прерывность возможных значений внутренней
энергии атома ртути: энергия состояния атома ртути, ближайшего
к нормальному, превышает его энергию на 4,9 eV *).
Штерну и Герлаху удалось показать, что и вращательный импульс
(момент количества движения) атомов имеет, подобно энергии, также
только некоторые дискретные значения. Штерн и Герлах измеряли маг-
нитный момент атомов. Этот магнитный момент обусловлен внутриатом-
ными токами, и так как последние вызываются движением электронов,
то между магнитным моментом атома и вращательным импульсом сущест-
вует связь, которая будет нами рассмотрена в §§ 50, 59. Сущность
опытов Штерна и Герлаха заключалась в том, что они пропускали узкий
пучок атомов в неоднородном магнитном поле. Если атом имеет магнитный
момент 2)1, то в магнитном поле напряженности SK он имеет потенци-
альную энергию, равную
{/=- — SOfcosa,
где а — угол между направлением магнитного поля и направлением
магнитного момента атома. Сила, действующая на атом со стороны
неоднородного поля (если оно меняется по направлению оси OZ),
равна
„ dU т дЗС
г — — -^- = Шс—V— cos а.
dz dz
Градиент поля был направлен перпендикулярно к пучку атомов, и, сле-
довательно, сила F вызывала отклонения атомов от первоначального на-
правления движения. Если бы были возможны все ориентации магнит-
ного момента атома относительно магнитного поля, как это следует из
классических представлений, то сила F принимала бы все значения
™ то D ,
от — UK до -f- дл . Различные атомы отклонились бы различно,
и при попадании пучка на экран мы получили бы размытое изобра-
жение щели, ограничивающей пучок. На самом деле получается два
*) Подробности об опытах Франка и Герца см. в книге Д. Гарнвелл
и Д. Ливингуд, Экспериментальная атомная физика, ОНТИ, 1935 или.
Хвольсон, Куос физики, дополнительный том.
16
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
[гл. I
резких изображения щели (рис. 3). Этот результат опыта показывает,
что возможны лишь две дискретные ориентации магнитного момента
атома: cos а = 4- 1.
Вычисление, далее, показывает, что величина отклонения пучков
соответствует значению магнитного момента атома ЭЛ, равному
ЭЛВ = = 9 • 10-20 CGSE,
2рс
где е — заряд электрона, р—его масса, с — скорость света. Это значе-
ние было впервые теоретически найдено Н. Бором из элементарной
а Ь
Рис. 3. Расщепление пучка
паров натрия в магнитном
поле:
а — в отсутствии поля; Ъ — в при-
сутствии поля.
квантовой теории и называется магнето-
ном Бора. Оно является как бы квантом
магнитного момента.
Явление, открытое Штерном и Герлахом,
называют пространственным квантова-
нием, так как речь идет о дискретности
ориентаций магнитного момента относитель-
но магнитного поля. На основании упомяну-
той связи между вращательным импульсом
и магнитным моментом можно сказать, что
опыты Штерна и Герлаха доказывают так-
же прерывность возможных значений враща-
тельного импульса.
Впоследствии (гл. XI) мы покажем, что
наблюдавшийся Штерном и Герлахом магнит-
ный момент атома обусловлен не орбиталь-
ным движением электрона (как это перво-
начально думали), а собственным магнитным
моментом, присущим самому электрону *).
С интересующей сейчас нас общей точки
зрения мы можем сказать, что опыты Штер-
на и Герлаха показывают, что магнитный
момент атома в целом имеет квантовые,
дискретные значения, и таким образом приносят новое доказательство
прерывности, свойственной возможным состояниям атома **).
§ 4. Теория Н. Бора
Для того, чтобы описать рассмотренные в предыдущем параграфе
прерывные свойства атомных систем, Н. Бор предложил видоизменить
классическую механику, введя в законы движения постоянную Планка h.
Видоизменение заключалось в том, что Н. Бор предположил, что не
*) Это относится к первым опытам Штерна и Герлаха с Н и Ag в нор-
мальных состояниях. В общем случае магнитный момент атома обусловлен
как орбитальным движением электронов, так и собственным магнитным момен-
том этих электронов.
Подробности опытов Штерна и Герлаха см. в книге Гарнвелла
и Ливингуда.
ТЕОРИЯ Н. БОРА
17
§ 4]
все движения, допускаемые классической механикой, реализуются в атом-
ных системах, а лишь некоторые избранные. Бор предложил особый
рецепт выбора, который мы не предполагаем здесь рассматривать *).
С помощью этого рецепта удалось успешно найти возможные значения
энергии атома водорода, но прием Н. Бора оказался несостоятельным
Для более сложных атомных систем (например, для атома Не). В при-
менении к энергии атома гипотеза Бора (или, как ее называли, посту-
лат Бора) означала, что энергия атома Е может принимать лишь пре-
рывные, квантовые значения
E = Elt EZ,ES, Еп, ... (4.1)
Современная теория, как мы увидим, не нуждается в таком постулате
и вообще не считает дискретность состояний обязательным признаком
квантовой системы. Тем не менее постулат Бора является правильным
и до сего времени, так как он может рассматриваться как прямое вы-
ражение опытных фактов.
Постулат Бора противоречил классической теории излучения, так
как по этой теории возбужденный атом излучает непрерывно, и, сле-
довательно, его энергия может оказаться лежащей между дозволенными
уровнями энергии. Поэтому Бор встал на квантовую точку зрения (§ 1),
согласно которой энергия излучается порциями — квантами света. Тогда,
объединяя закон сохранения энергии с постулатом Бора о дискретности
состояний атомов, мы получим написанный впервые Бором закон, связы-
вающий частоты (о^, которые может испускать и поглощать атом
(спектр атома), с квантовыми уровнями Еп, свойственными данному
атому. Именно, мы получаем **):
hvmn = Em-En. (4.2)
Это уравнение есть не что иное, как закон сохранения энергии при
излучении и поглощении света, и в старой теории Бора представлял
один из постулатов его теории («правило частот» Бора).,
Разделив уравнение (4.2) на постоянную Планка, мы найдем, что
частоты, поглощаемые или излучаемые квантовыми системами, всегда
могут быть представлены в виде разности двух частот:
F Е
(й =(О ----(О ; О) — (0 — -Л (4.3)
тп т п* tn fa * h '
Эти частоты называются спектральными термами.
Еще задолго до теории Бора чисто эмпирически было установлено
Ритцем, что наблюдаемые частоты атомов могут быть представлены как
разности термов («комбинационный принцип» Ритца). Поэтому (4.3)
можно рассматривать так же, как выражение эмпирического правила
Ритца.
*) Теория Бора подробно изложена в книге Бриллуэн, Атом Бора,
ОНТИ, 1935.
**) Для поглощения полагаем в (1.3): со' = 0, Е' — Ет> Е~Еп<Ет>
Для излучения <or = <own, Е'~Еп, Е~Ет, о> = 0.
2 Блохинцев
18
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
[гл. I
Правило частот Бора еще ничего не говорит об интенсивности
испускания или поглощения той или иной частоты. Вычисление этих
интенсивностей представляло для теории Бора непреодолимую трудность.
Были возможны лишь качественные суждения.
§ 5. Теория излучения А. Эйнштейна
Квантовая теория излучения А. Эйнштейна носит до некоторой
степени феноменологический характер *), тем не менее она позволяет,
опираясь на современную квантовую механику, решить вопрос об интен-
сивностях излучения и поглощения света.
С квантовой точки зрения интенсивность испускания или поглощения
электромагнитного излучения определяется вероятностью перехода атома
из одного состояния в другое. Вопрос об интенсивностях сводится
к вычислению этих вероятностей.
Рассмотрим два состояния какой-нибудь системы, например, атома.
Одно обозначим буквой т, а другое буквой п. Энергия первого состояния
пусть будет Ет, а второго Еп. Для опре-
деленности предположим, что Ет^Еп^
так что состояние т принадлежит более
высокому квантовому уровню Ет, нежели
состояние п, принадлежащее квантовому
уровню Еп.
Опыт показывает, что система может
сама собой перейти из высшего состоя-
ния т в низшее п, испуская квант света
Лео = Ет — Еп(^частота со — >
имеющего, кроме того, определенную
поляризацию и распространяющегося
внутри телесного угла d(2 (рис. 4). Любую
поляризацию для определенного напра-
Направление распространения
(угол частота два незави-
симых направления поляризации
L и 12.
вления распространения света мы можем
представить как сложение двух независимых поляризаций и 12,
перпендикулярных друг другу. При переходе Ет—>Еп может быть
излучен квант света либо с поляризацией 1Р либо с поляризацией 12.
Поляризацию мы будем отмечать индексом а (а = 1, 2). Вероят-
ность перехода т —► п в 1 сек. с излучением кванта частоты
£ _______g
= т h—~ ’ в телесном Угле с поляризацией а мы обозначим
через
dWr = a^dQ.
(5.1)
Эту вероятность называют вероятностью «спонтанного» (самопроизволь-
*) Предположения А. Эйнштейна получают полное обоснование в современ-
ной квантовой электродинамике. См. Г е й т л е р, Квантовая теория излучения,
ГИТТЛ, 1940.
§ 5] ТЕОРИЯ ИЗЛУЧЕНИЯ А. ЭЙНШТЕЙНА 19
ного) перехода. Возможности такого перехода в классической теории
соответствует излучение возбужденного осциллятора.
Если имеется излучение, окружающее атом, то оно оказывает воз-
действие на атом в двух отношениях. Во-первых, это излучение может
поглощаться, причем атом будет переходить из низшего состояния п
в высшее т. Вероятность такого перехода в 1 сек. обозначим через dWa.
Во-вторых, если атом находится в возбужденном состоянии /п, то внеш-
нее излучение может способствовать переходу атома в низшее состояние
п так, что вероятность излучения увеличится на некоторую величину dWr.
Эту добавочную вероятность мы будем называть вероятностью индуциро-
ванного (или вынужденного) перехода. Оба типа переходов имеют
аналогию в классической теории: осциллятор, находящийся под влиянием
внешнего излучения, может как поглощать, так и излучать энергию в
зависимости от соотношения фазы его колебаний и фазы световой волны.
Согласно сказанному, полная вероятность излучения равна
dWr=dW'r-\-dW"r,
Вероятность поглощения dWa и вероятность вынужденного излуче-
ния dW"r, по предположению Эйнштейна, пропорциональны числу кван-
тов света как раз того сорта, о поглощении и излучении которых идет
речь. Определим это число.
Излучение может быть, вообще говоря, не монохроматическим,
иметь различное направление распространения и разную поляризацию.
Для определения характера излучения мы введем величину ра (о>, Q) d®
дающую плотность энергии излучения, имеющего направление в преде-
лах телесного угла d&, поляризацию а и частоту, лежащую в пределах
со, Так как энергия кванта равна Ла), то число квантов света,
частота которого лежит в пределах со, со —с/со, который распространяется
в телесном угле d& и имеет поляризацию а, равно (на 1 см*)'.
ра (со, 2) rfo) dQ
Ла)
На основании замечания о пропорциональности между числом квантов
и вероятностями поглощения и вынужденного излучения мы можем
положить:
?«(«>> (5-2)
dW"r = bM^ (5.3)
Величины мы назовем дифференциальными коэффициен-
тами Эйнштейна. Они зависят только от рода систем, излучающих
и поглощающих свет, и могут быть вычислены методами кванто-
вой механики (см. § 81). Однако, Эйнштейну удалось сделать неко-
торые общие заключения о свойствах этих коэффициентов без их вычи-
сления.
Рассмотрим условия, при которых осуществляется равновесие между
излучением и поглощением. Пусть чш; ло атомов, находящихся в воз-
2*
20 ОСНОВЫ КВАНТОВОЙ ТЕОРИИ [гл. I
бужденном состоянии /п, есть пт, а число атомов, находящихся в ниж-
нем .состоянии, пусть равно пп. Тогда число квантов света, излучаемых
в 1 сек. при переходах т —>п, будет равно
а число поглощаемых в 1 сек. квантов при переходах п —► т будет
равно
nndWa.
В условиях равновесия число актов поглощения должно равняться числу
актов испускания, т. е.
nndW^n^dW^dW"^.
Подставляя сюда dW'r из (5.1) и dW", dWa из (5.2) и (5.3),
найдем после сокращения на
Пп Ьп* Р« (“> Й) — «А [*«« Р« (®> й) + «та] (5-4)
(причем <о = в>тп).
Представим теперь себе, что мы имеем дело с тепловым равновесием.
Тогда числа атомов пп в различных состояниях тг, т будут функциями
температуры Т. Вместе с тем и плотность излучения р (to, 2) должна
быть функцией температуры. Это будет плотность излучения, находя-
щегося в равновесии с веществом при температуре Т, т. е. плотность
черного излучения.
Свойства черного излучения, как известно, не зависят от конкретных
свойств вещества, с которым оно находится в равновесии. Поэтому все
выводы, которые будут сделаны на пути исследования черного излучения,
имеют общее значение. Именно этим обстоятельством и воспользовался
Эйнштейн, чтобы установить соотношения между коэффициентами
в общем виде.
Отношение между числами атомов, находящихся в различных состоя-
ниях, мы можем определить из статистики. Обычно (см., например, § 48)
какому-нибудь квантовому уровню Еп отвечает несколько различных
состояний квантовой системы. Число таких состояний fn называют ста-
тистическим весом или степенью вырождения.
Согласно каноническому распределению, справедливому как для
классических, так и для квантовых систем, число атомов. ДГЛ, находя-
щихся в состоянии с энергией Еп, будет равно
J?n
Nn — const. -fn е kT, (5.5)
где k—постоянная Больцмана. Если нас ийтересует число пп атомов,
находящихся в каком-либо одном из состояний, принадлежащих энергии
Еп, то на основании того же распределения будем иметь:
n„=^=const.-e kT. (5.5')
§ 5]
ТЕОРИЯ ИЗЛУЧЕНИЯ А. ЭЙНШТЕЙНА
21
Подставляя пп и пт из (5.5') в (5.4) и сокращая на общую постоян-
ную, получим:
__ЕП __Ет
* ^b^?^tQ,T) = e Т)-[-аЦ, (5.6)
причем мы ввели в р в качестве аргумента еще и температуру, так как
при тепловом равновесии, как уже указывалось, плотность равновесного
излучения зависит от температуры. При Т~> оо плотность излучения р
должна неограниченно возрастать, т. е. р—> оо.
Из (5.6) при Т—> оо получаем первое важное соотношение
bm=bn . (5.7)
па та ' '
На основании этого соотношения, замечая еще, что Ет— En = h®,
мы получаем из (5.6):
ап 1
----- (5-8)
Uma kT 1
е —l
Чтобы определить отношение , Эйнштейн остроумно пользуется тем
Ьща
обстоятельством, что при высоких температурах, т. е. при
полученная квантовая формула (5.8) для плотности равновесного излу-
чения должна переходить в классическую формулу Рэлея-Джинса. В
самом деле, классическая формула для плотности равновесного излучения
выводится в предположении, что излучение частоты <о может иметь
сколь угодно малую энергию. По квантовой же теории наименьшая
энергия такого излучения есть Лео. Если kT^h®, то величиной А(о
можно пренебречь, и тогда основная предпосылка классической теории
h
будет выполнена. Из (5.8) при разлагая в ряд ekT, получаем:
ра(о>, Й, 7') = ^.^’. (5.9)
га' ' hn h& ' 7
та
С другой стороны, классическая формула Рэлея-Джинса дает для плот-
ности равновесного излучения следующее выражение:
Ра(“>й> T) = ^kT. (5.Ю)
Как мы пояснили, для kT^h® обе формулы (5.8) и (5.10} должны
совпадать. Поэтому, сравнивая (5.9) с (5.10), находим:
Ай>3 ,
= 5-9-0" ? h(ti = E„, — Е„.
та
Эта важная формула позволяет вычислять один коэффициент по дру-
гому, так как полученное отношение не зависит от рода вещества (как
это и должно быть), а зависит только от частоты излучения.
(5.П)
22
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
[гл. I
Вставляя найденное отношение в (5.8), получаем окончательную
формулу для плотности равновесного излучения:
М“.Й. n = S- (5.12)
ект-1
§ 6. Формула Планка
Интегрируя ра(со, Q, Т) по всему телесному углу (Й = 4тт) и сумми-
руя по обеим поляризациям (а = 1, 2), мы получим плотность излучения
р(о), 7), приходящуюся на интервал частоты о), независимо от
направления распространения и поляризации. Согласно (5.12) равновесное
Рис. 5. Распределение
энергии в спектре чер-
ного излучения для
различных темпера-
тур.
По оси абсцисс отложены
длины волн в р..
излучение изотропно, и плотность для обеих
поляризаций одинакова. Поэтому мы получаем:
р((о, Т) = 8тгра (со, Й, 7), (6.1)
т. е. плотность равновесного излучения частоты
(о при температуре Т равна
Р(“’ • (6-2)
ект-1
Эта формула дает спектральное распределение
энергии в спектре черного излучения и впервые
была установлена Планком *). На рис. 5 приве-
дены графики этого распределения для разных
температур Т. В области hax^kT закон Планка
совпадает с классическим законом Рэлея-Джинса,
который для р (со, Т) гласит:
m2
Ркл>. <6-3)
В области больших квантов Л(о|>&7,
в виду, что ekT^> 1, из (6.2) получаем:
. /гео3 —
р(“> т>=^е •
имея
(6-4)
Формула Рэлея-Джинса выводится из рассмотрения света, как непрерыв-
ных волн. Формула (6.4) может быть получена, если свет рассматривать
как газ, состоящий из частиц с энергией, равной г — hw. Первая картина
<есть волновая картина света, вторая — корпускулярная картина. Обе
картины являются недостаточными: формула Планка не соответствует
ни той, ни другой.
*) Заметим, что в старой литературе формула Планка пишется иначе.
Различие заключается в том, что: 1) вместо нашей постоянной h употребляется
(введенная Планком) в 2л, раз большая постоянная; 2) вместо циклической ча-
стоты со употребляется обычная у = Заметим еще, что р (со, Г)бЛо —
= р (v, Т) dv, т. е. р (v, Т) = 2яр (со, Т).
§ 7]
ВОЛНЫ ДЕ-БРОЙЛЯ, групповая СКОРОСТЬ
23
Легко видеть, что волновая картина применима в той области, где
кванты света малы, а число их велико; напротив, корпускулярная картина
справедлива в той области, где кванты велики, а число их невелико.
Действительно, число квантов в 1 см3 в рэлеевской области <^kT)
в интервале частот от <о1 до ©j есть
1 тсМ h ' ' '
а в области /z(o2|>&T (виновская область) оно равно
2 ЙО)3
Ш п —----
= (6.5')
Отношение dN2 к dNt равно
dN2 hvl
dNx
dN<>
при (09 —> oo << 1.
r 2 dN\
(6.6)
ГЛАВА II
ВОЛНОВЫЕ ЯВЛЕНИЯ ПРИ ДВИЖЕНИИ ЧАСТИЦ
§ 7. Волны де-Бройля. Групповая скорость
Мы не предполагаем здесь следовать историческому развитию квантовой
механики и, в частности, излагать тот, сам по себе не лишенный инте-
реса, путь аналогий между механикой и оптикой, который привел де-
Бройля и позднее Шредингера к установлению исходных пунктов вол-
новой (или, как теперь чаще называют, квантовой) механики *). Если не
касаться тех сторон первоначальной теории, которые в настоящее время
имеют лишь историческое значение, то основная мысль де-Бройля заклю-
чается в распространении основных законов квантовой теории света (1.1)
и (1.2) на движение частиц.
Именно, с движением всякой свободно движущейся частицы, имеющей
энергию Е и импульс р, де-Бройль связывает плоскую волну
ф(г, К = kr\ (7.1)
где г — радиус-вектор произвольной точки пространства, t — время.
Частота этой волны о и ее волновой вектор к связаны с энергией
и импульсом частицы теми же уравнениями, которые справедливы для
квантов света, т. е.
£ = (7.2)
p=/zk. (7.3)
*) Читатель, интересующийся этой стороной дела, найдет прекрасное из-
ложение идей де-Бройля в книге последнего: Введение в волновую механику,
ДНТВУ, 1934.
24
ВОЛНОВЫЕ ЯВЛЕНИЯ ПРИ ДВИЖЕНИИ ЧАСТИЦ
[гл. п
Это — основные уравнения де-Бройля. Мы имеем здесь дело с истори-
ческим ходом идей, обратным тому, который ведет к квантовой теории
света. Для света мы имели первоначально волновую картину и в кван-
товой теории дополнили ее корпускулярной, вводя представления об
импульсе и энергии кванта света. Напротив, для частиц (электронов,
атомов ит. п.) мы имеем в качестве исходного пункта классическое
представление о движении частиц и по идее де:Бройля, переходя к кванто-
вой теории, дополняем эту классическую, корпускулярную картину пред-
2гс
|к|’
ставлениями волновой теории, вводя частоту со и длину волны 1 =
волн,
ассоциированных с движением частицы.
Подставляя в (7.1) (о и к из (7.2) и (7.3), мы получим новое вы-
ражение для волны (7.1), в котором будет в явной форме установлена
связь частоты и длины волны с корпускулярными величинами: энергией
частицы Е и ее импульсом р:
ф(г, t) — Ce h' (7.Г)
Такую волну мы будем называть волной де-Бройля. Вопрос о природе
этих волн и о толковании значения их амплитуды С мы отложим до
следующей главы, так как этот вопрос вовсе не является простым.
На первый взгляд может показаться, что движение волны (7.1) не
может иметь никакой связи с механическими законами движения частиц.
Однако, это не так. Чтобы усмотреть эту связь, обратимся к рассмотре-
нию основных свойств волны де-Бройля. Ради упрощения расчетов вы-
берем направление оси ОХ совпадающим с направлением распространения
волны; тогда вместо (7.1) мы будем иметь:
ф(х, 1) = Се^^х\ (7.4}
Величина (о/ — kx представляет собой фазу волны. Рассмотрим некоторую
точку х, где фаза имеет определенное значение а. Координата этой
точки определится из уравнения
а — ю/ — kx,
откуда видно, что значение фазы а будет с течением времени переме-
щаться в пространстве со скоростью и, которую мы получим, диффе-
ренцируя предыдущее равенство по t:
(7.5)
Эта скорость называется фазовой. Если эта скорость зависит от k, а,
следовательно, и от длины волны к ^так как , то имеет ме-
сто дисперсия волн. В отличие от электромагнитных волн, для волн
де-Бройля существует дисперсия в пустом пространстве. Это обстоя-
тельство вытекает из уравнений де-Бройля (7.2) и (7.3). Действительно,
между энергией Е и импульсом р существует связь. Для скоростей
частицы v<^c, т. е. в области применимости ньютоновской механики,
25»
§ 7] ВОЛНЫ ДЕ-БРОЙЛЯ. ГРУППОВАЯ СКОРОСТЬ
энергия свободно движущейся частицы равна*)
тде т — масса частицы. Подставляя это значение Е в (7.2) и выражая р*
через № [с помощью (7.3)], мы получим:
«=&,*’• (7.7,.
и, следовательно, н = “ есть функция k.
Перейдем теперь к установлению связи движения волны с движением,'
частицы. Для этого мы рассмотрим не строго монохроматическую
волну (7.4), имеющую вполне определенную частоту (о и длину волны
А = , а почти монохроматическую волну, которую мы будем называть
группой волн. Под группой волн,.более обще, мы будем разуметь сумму
волн, мало отличающихся друг от друга по длине волны и направлению,-
распространения. Для простоты мы рассмотрим группу из волн (7.4),
распространяющихся в направлении ОХ. Согласно данному определению-
группы мы можем написать для, колебания ф (х, f) следующее выражение:
ДД?
ф(х, 0= j c(k)e* i^'at~kx'> dk, (7.8)
k0 — bk
. 2л
где = есть волновое число, около которого лежат волновые числа
Ао
волн, образующих группу (Д6 предполагается малым). Ввиду того, что
мало, мы можем разложить частоту со, которая есть функция k [ср. фор-
мулу (7.7)] по степеням k — kQ. Тогда мы получим:
“ = —*о)+ •••
k = kQ -р (k — kQ).
Взяв k—kQ в качестве новой переменной интегрирования Е и считав
амплитуду с (k) медленно меняющейся функцией k, найдем, что ф (х,
может быть представлено в виде
ф(х, f) = c(^0)e‘W-M) f е V'**™ *J
—\k
*) В классической (нерелятивистской) физике энергия всегда определяется
вплоть до аддитивной произвольной постоянной, так что формулу (7.6) можно
было бы написать в виде
рч
Е = --—const
2/га0
Поэтому и абсолютное значение частоты волн де-Бройля произвольно. Эта
произвольность не отражается, однако, ни на одном физическом выводе теории.
26
ВОЛНОВЫЕ ЯВЛЕНИЯ ПРИ ДВИЖЕНИИ ЧАСТИЦ
[гл. II
и, выполняя простое интегрирование по 5, найдем:
ф(х, /) = 2с(&0)
ei(u)0t-k0x) —,
= с (х,
(7.9)
Ввиду наличия под знаком sin малой величины Д&, с (х, I) будет медленно
меняться в функции времени t и координаты х, поэтому r(x, t) можно
рассматривать как амплитуду почти монохроматической волны, а (<о0/ —
— kQx) — как ее фазу. Определим точку х, где амплитуда с (х, t) имеет
максимум. Эту точку будем называть центром группы волн. Очевидно,
искомый максимум будет находиться в точке
Отсюда следует, что центр группы будет перемещаться со скоростью V,
которую мы найдем, дифференцируя предыдущее равенство по t\
именно,
v=№\ • (7.10)
\dkjQ v
Эту скорость мы будем называть групповой скоростью (в отличие от
скорости фазы, равной ^). Если бы рассматриваемые волны не обла-
ко /
дали дисперсией, то мы имели бы V=u. В случае волн де-Бройля
ввиду наличия дисперсии Вычислим, пользуясь (7.7), групповую
скорость V:
у___dm____hk
dk ’
но согласно (5.3) hk —р, с другой стороны, р = т^и, где v — скорость
частицы. Поэтому мы приходим к важному выводу:
(7.И)
итак, групповая скорость волн де-Бройля равна механической скорости
частицы v.
Полученные нами соотношения (7.10) и (7Л1) могут быть легко выведены
для распространения волн в любом направлении по отношению к осям ОХ,
OY, OZ. Предоставляя этот вывод читателю, приведем здесь лишь окончатель-
ный результат:
У дт дЕ
х dkx дрх
= vx>
Vy=
dm___дЕ___
dkx dpz~Vz'
дт_дЕ__
dk—d^-vy
или в векторной форме:
V — Vkm = \рЕ — v.
(7.10')
Вычислим для двух случаев длину волны \ волн де-Бройля. Из (7.3)
§ 7]’ ВОЛНЫ ДЕ-БРОЙЛЯ. ГРУППОВАЯ СКОРОСТЬ
27
следует, что
(7.12)
___2гс_____2тсй
k р
Ограничиваясь случаем малых скоростей
п Р2
Е=~~, мы получим:
__ 2тс/г
V 2т^Е
с и пользуясь равенством
(7.12')
Эта формула позволяет вычислять длину волны X, зная массу тъ и энергию
частицы Е. Применим эту формулу специально к электрону. В этом
случае /я0 = 9-10“28г. Выражая энергию электрона в eV, для чего
положим E~eV, где е — заряд электрона, а V—ускоряющая электрон
разность потенциалов, измеренная в вольтах, мы найдем:
x = ’|/'vA- <7-13)
Для V=1 eV получаем 1=12,2 А, для У= 10 000 eV получаем
1 = 0,122 А. Вычислим еще длину волны для молекулы водорода, имею-
щей энергию 6-10~14 эргов, что равно средней энергии молекулы водо-
рода при температуре 300°. Масса молекулы равна 2*1,66 • 10~24 г. Под-
ставляя эти величины в (7.12), найдем 1=1 А.
Как видим, длина волны 1 волн де-Бройля очень мала, и тем меньше,
чем больше энергия частицы и ее масса. Практически, например, совсем
не удается получить длину волны 1, равную длине волны видимого
света, так как уже с электронами, обладающими энергией в 1 eV,
весьма трудно экспериментировать, а при 1=10~5 см мы имели бы
дело с электронами, энергия которых равна всего лишь 1,2-10~4 eV.
Идея о связи движения частицы с движением волны была столь
чужда установившимся в механике представлениям, что казалась чистой
фантазией, и только опыт мог заставить принять ее как ценный вклад
в науку. В каких же явлениях следовало искать подтверждения или,
напротив, опровержения представления о волновых явлениях при движе-
нии частиц? Независимо от природы волн существует совокупность
явлений, присущих только волнам. Это — явления диффракции и интер- 1
ференции. Оба явления обусловлены сложением волн с определенными
фазами и амплитудами, и их существование вытекает из самой природы
волнового движения. Поэтому для проверки идеи де-Бройля следовало
обратиться к опытам, в которых можно было бы обнаружить эти явления,
оперируя с частицами. Из оптики известно,, что явление диффракции
только в том случае заметно, когда расстояние между штрихами
диффракционной решетки сравнимо с длиной волны диффрагирующих
волн. Если делать опыты с электронами, то согласно приведенному выше
расчету длина волны волн де-Бройля по порядку величины равна 1 А,
а для атомов еще меньше. Поэтому условия для наблюдения диффрак-
ции электронов примерно таковы же, как и условия для наблюдения
диффракции рентгеновских лучей, так что подходящей диффракционной
28
ВОЛНОВЫЕ ЯВЛЕНИЯ ПРИ ДВИЖЕНИИ ЧАСТИЦ
[гл. П
решеткой могут быть лишь кристаллы, где расстояние между «штри-
хами» — атомами кристалла — по порядку величины равно 1 А. Опыты,
подтвердившие правильность точки зрения де-Бройля, будут кратко
изложены в следующем параграфе.
§ 8. Диффракция электронов, атомов и молекул
Переходя теперь к изложению опытов, доказавших правильность
идеи де-Бройля, мы начнем с классических опытов Дэвиссона и Джермера.
Дэвиссон и Джермер изучали рассеяние пучка электронов на поверхности
кристаллов. Наблюдая интенсивность пучков в зависимости от угла
рассеяния, можно было заметить, что распределение электронов по
углам весьма сходно с
Рис. 6. Схема опыта
Дэвиссона и Джермера.
распределением интенсивности волн при диффрак-
ции. На рис. 6 схематически изображен опыт
Дэвиссона и Джермера. Электронная пушка слу-
жила источником пучка электронов. Фарадеев
цилиндр соединялся с гальванометром, и по току
можно было судить о количестве электронов,
рассеянных поверхностью монокристалла под
углом 9 к первоначальному пучку, который падал
перпендикулярно к поверхности. Получающаяся
картина рассеяния электронов весьма сложна, а
за деталями опыта Дэвиссона и Джермера мы
отошлем читателя к специальным монографиям *).
Электроны небольшой энергии не проникают
глубоко внутрь кристалла, поэтому значительная
доля рассеянных электронов рассеивается поверх-
ностным слоем кристалла так, что диффракция происходит в основном
от плоской диффракционной решетки, образованной атомами кристалла,
расположенными на его поверхности. Согласно элементарной теории
диффракции положение диффракционных максимумов определяется
формулой:
nk = ^sin9, (8.1)
где п — порядок диффракционного максимума, X — длина волны диффра-
гирующих лучей, d — постоянная плоской поверхностной решетки
кристалла, а 6 — угол между нормалью к решетке и направлением*
рассеянного пучка. Зная энергию первичных электронов, падающих на
кристалл (в опытах Дэвиссона и Джермера энергия электронов могла
изменяться примерно от 30 до 400 eV). Дэвиссон и Джермер могли
для каждой энергии вычислить длину волны А по формуле де-Бройля
(7.13) и вычислить из формулы (8.1) положение максимума для* рас-
сеянных, «диффрагированных» электронов **). Другой способ проверки
*) См., например, П. С, Тартаковский, Экспериментальные основания
волновой теории материи, ГТТИ, 1932.
**) Впоследствии выяснилось, что для электронов малой энергии, в противо-
положность быстрым электронам и рентгеновским лучам, показатель преломле-
§ 81 ДИФФРАКЦИЯ ЭЛЕКТРОНОВ, АТОМОВ И МОЛЕКУЛ
29
формулы де-Бройля мог заключаться в проверке справедливости (8.1)
для электронов разной энергии. Подставляя в (8.1) X из (7.13), мы
найдем, что в случае правильности формулы де-Бройля должно иметь
место равенство
]/ Vsin 6 = const. (8.2)
(если угол 9 отвечает положению максимума интенсивности рассеянных
электронов). И тот и другой путь привели Дэвиссона и Джермера
к заключению о полной справедливости формулы де-Бройля (7.12),
связывающей длину волны к с импульсом электронов р.
Диффракцию рентгеновских лучей удается наблюдать не только
от монокристаллов, но и от поликристаллических образований, например,
от кристаллических порошков (метод Дебая-Шеррера). Г. П. Томсон
впервые применил этот метод к наблюдению диффракции электронов.
В этом методе первичный пучок электронов пропускается через толщу
пленки, имеющей поликристаллическую структуру (во избежание силь-
ного поглощения электронов пленки берутся очень тонкими, около
10"5 см). В такой пленке
хаотическим образом. В
этом методе луч пронизы-
вает кристалл, и мы имеем
дело с пространственной
диффракционной решет-
кой. Условие Брэгга для
пространственной решетки
гласит:
пк = 2d sin ср, (8.3)
где d—постоянная про-
странственной диффракцн-
онной решетки, р — угол
между лучом и плоскостью
решетки, п, \ имеют преж-
отдельные монокристаллики расположены
Рис. 7. Схема опыта Томсона-Тартаковского.
нее значение. Если какой-либо из кристалликов пленки удовлетворяет
этому условию (см. рис. 7), то на фотопластинке Р мы получим пятно Q в
точке падения на пластинку диффрагированного луча KQ- Так как кри-
сталлики расположены хаотически, то среди них найдутся и такие, что их
положение будет отличаться от положения кристаллика К лишь поворотом
вокруг оси SO, совпадающей с направлением падающего пучка.
В результате на пластинке вместо пятна Q мы получим кольцо с радиу-
сом OQ, Вообще каждому пятну при диффракции от монокристалла
в методе Дебая-Шеррера соответствует диффракционное кольцо. Легко
вычислить диаметр (D) этих колец. Если расстояние от пластинки до
пленки есть L, то
ния кристалла отличен от 1. Это обстоятельство нужно учитывать при расчете
диффракции медленных электронов.
30
ВОЛНОВЫЕ ЯВЛЕНИЯ ПРИ ДВИЖЕНИИ ЧАСТИЦ
[гл. 1!
при малых углах ср; комбинируя это равенство с (8.3), получим:
"1 D
ПК = а 777
Подставляя вместо 1 ее выражение через энергию электронов по формуле
де-Бройля (7.13), мы найдем, что
Z)j/y= const. (8.4)
Справедливость этого соотношения была полностью подтверждена
наблюдениями Г. П. Томсона, а также П. С. Тартаковского *)•
В настоящее время достигнуто значительное усовершенствование
методики, и диффракция электронов находит столь же успешное при-
менение для анализа строения кристаллов (особенно их поверхностей).
как и диффракция рентгеновских лучей.
На рис. 8 мы приводим картину диф-
Рис. 9. Диффракция атомов
Не на кристалле LiF.
Рис. 8. Диффракция электронных лучей от
тонкой серебряной пластинки (по Г. Марку
и Р. Вирлю)*
Скорости электронов (36 kV ускоряющего напря-
жения) соответствует волна де-Бройля в 0,0645 А.
Экспозиции 0,1 сек.
фракции электронов от серебряной пленки («электронограмма») се-
ребра, полученную Марком и Вирлем. Таким образом реальность
диффракции электронов не вызывает в настоящее время никаких сомнений.
Вопрос о применимости формулы де-Бройля (7.12) к частицам,
более сложным, нежели электрон, к атомам и молекулам является
весьма принципиальным. Действительно, возможность применения ее
к сложным системам означает, что волновые явления не являются результа-
том особенностей строения той или иной частицы, а имеют общую значи-
мость, выражают общий закон движения частиц. Штерн и Эстерман поста-
вили своей задачей проверить формулу де-Бройля для атомов и молекул.
*) См. П. С. Т а р т а к о в с к и й, loc. cit.
§ 9] СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛН ДЕ-БРОЙЛЯ 3t
Для этой цели/ Штерн и Эстерман исследовали отражение 'Не и Н2
от кристаллов L1F. Меняя температуру «печи», служившей источником
узкого пучка атомных или молекулярных лучей, экспериментаторы имели
возможность менять энергию исследуемых частиц, а вместе с тем и длину
волны де-Бройля. Интенсивность рассеянного кристаллом пучка измеря-
лась с помощью очень чувствительного манометра.
Опыты Штерна и Эстермана вполне подтвердили применимость,
формулы де-Бройля к указанным сложным частицам. На рис. 9 при-
ведено распределение интенсивности в рассеянном пучке атомов Не,
отражающихся от кристаллов LiF при Г=295°. Угол 0° отвечает
правильному отражению пучка Не от кристалла. Для этого угла имеем
резкий максимум. Если учесть то простое обстоятельство, что размеры
атома не меньше расстояния между ионами решетки LiF, то уже наличие
правильного отражения невозможно объяснить с точки зрения корпус-
кулярной механики. Помимо максимума, отвечающего правильному
отражению, имеется еще два диффракционных максимума (спектры
первого порядка). Положение их хорошо согласуется с вычисленным
по формуле де-Бройля*). Подобный же результат получен для моле-
кул Н2. Следовательно, формула де-Бройля имеет общую значимость..
Г Л АВ А III
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
§ 9. Статистическая интерпретация волн де-Бройля
Физический смысл волн, связанных по идее де-Бройля с движением
частиц, был раскрыт не сразу. Вначале были попытки рассматривать сами *
частицы как образования из волн, распределенные в некоторой области
пространства. Интенсивность волны де-Бройля рассматривалась в этой
концепции как величина, характеризующая плотность среды, из которой
образована частица. Это понимание волн де-Бройля имело совершенно^
классический характер. Основанием для него служило то обстоятельство,
что в некоторых, весьма частных случаях, оказалось возможным
(теоретически) построить волновые образования, движение которых
совпадает с движением частицы, движущейся по законам классической
механики. Примером таких образований может служить рассмотренная
выше группа волн. Как было показано в § 7, центр группы волн
движется как частица. Однако, движение такой группы волн все же не
вполне совпадает с движением частицы. Дело в том, что сама форма
группы волн с течением времени изменяется. .Именно, как будет показано
в § 34, размеры группы возрастают: группа волн расплывается. Необхо-
димость такого расплывания можно легко понять из факта существования
дисперсии волн де-Бройля в пустоте. Отдельные волны, из которых. •*)
•*) См. П. С. Тартаковский, loc. cit.
32
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
образована группа, распространяются с различной скоростью. Благодаря
этому группа волн будет расплываться. Таким образом, построенная
из волн де-Бройля частица будет неустойчива: даже при движении
в пустом пространстве размеры ее будут все время возрастать не-
ограниченно. Эта неустойчивость будет особенно разительна, если
обратиться к случаю, когда частица движется в неоднородном прост-
ранстве, переходя из одной среды в другую. Примером такого случая
являются классические опыты по диффракции частиц. Когда, например,
в опыте Томсона-Тартаковского пучок частиц проходит тонкую фольгу,
то он разделяется на систему конусообразных диффрагированных пучков.
Если рассматривать частицу, в данном случае электрон, как образование
из волн, то первоначально мы должны отождествить с электроном
падающую волну, размеры которой определяются диафрагмами прибора,
а после прохождения фольги — всю систему диффрагированных волн.
Каждый диффрагированный пучок должен был бы представлять некоторую
долю электрона. Представим теперь себе, что мы поставили два прибора,
регистрирующие попадание электронов (например, фотопластинки), при-
чем в первый прибор направлен только первый диффрагированный пучок,
а во второй прибор — только второй диффрагированный пучок. Тогда,
если отождествлять с частицей всю систему диффрагированных волн,
то мы должны притти к заключению, что каждый из приемных аппаратов
примет лишь часть частицы. Это и есть крайнее нарушение устойчивости
частицы, приводящее изложенное понимание волн де-Бройля к резкому
противоречию с опытом.
В самом деле, частица всегда действует как целое, и обнаруживается
в приборе вся частица, а вовсе не ее доля. В рассмотренном примере
электрон попал бы либо на первый прибор, либо на второй (но не
частью на первый и частью на второй). В том факте, что простейшие
частицы всегда действуют как нечто целое, и заключается атомизм,
наблюдаемый, в явлениях микромира. Поэтому представление о частицах
как об образованиях из волн де-Бройля, противоречит атомизму и должно
быть отвергнуто.
Равным образом нельзя допустить, что сами волны являются образо-
ванием из частиц или, трчнее говоря, возникают в среде, образованной
частицами. Именно, опыт показывает, что диффракционная картина,
возникающая на фотопластинке, не зависит от интенсивности падающего
пучка частиц, а, следовательно, и от плотности частиц в единице объема.
Чтобы получить одну и ту же диффракционную картину, можно умень-
шать интенсивность, но увеличивать экспозицию: важно лишь общее
число прошедших частиц. Этот факт определенно показывает, что
каждый из электронов диффрагирует независимо от других*).
Поэтому существование волновых явлений нельзя связывать с наличием
одновременно большого числа частиц.
*) При очень больших плотностях в задающем пучке, благодаря кулонов-
скому взаимодействию может получиться дополнительное рассеяние. Это,
однако, имеет второстепенное значение для рассматриваемого вопроса: важно,
что при малых плотностях не получается исчезновения волновых Явлений.
§ 9] СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛН ДЕ-БРОЙЛЯ 33
Чтобы еще более подчеркнуть это обстоятельство, заметим, что
волновые явления в движении микрочастиц проявляются и в таких
случаях, когда говорить о среде, образованной совокупностью частиц,
совсем не приходится. Действительно, такие свойства проявляют элек-
троны, движущиеся в атомах, где число их совсем не велико (один
в водороде, два в гелии и т. д.).
Правильное толкование волн де-Бройля было найдено М. Борном
на совсем другом пути. Чтобы уяснить основную мысль Борна, пред-
ставим себе, что мы производим диффракцию электронов и регистрируем
попадание «диффрагированных» электронов на фотопластинке. Пусть
первоначально пропущено небольшое число электронов. Каждый из
электронов, проходя через диффракционный прибор (например, через
фольгу), попадает в какое-либо совсем неопределенное место фото-
пластинки и производит там фотохимическое действие. Прохождение
немногих электронов даст на фотопластинке картину попаданий, по-
хожую на мишень, простреленную плохим стрелком. Только при боль-
шом числе попаданий выявляется регулярность в распределении элек-
тронов на фотопластинке и, наконец, образуется распределение, пол-
ностью отвечающее распределению интенсивностей при диффракция
волн (например, система диффракционных колец, изображенная на рис. 8).
Такое поведение частиц привело Борна к статистическому толкова-
нию волн де-Бройля, позволяющему сочетать атомизм частиц с волно-
выми явлениями. Согласно статистической интерпретации интенсивность
волн де-Бройля в каком-либо месте пространства пропорциональна
вероятности обнаружить частицу в этом месте. Так, например,
если один диффрагированный пучок направляется на одну фотопла-
стинку, а второй на другую, то при большом числе прошедших через
аппарат электронов число электронов, попавших на каждую из пла-
стинок, пропорционально интенсивности волн де-Бройля, распростра-
няющихся в направлении каждой из фотопластинок.
Есчи фотопластинку поместить так, что направление от диффрак-
ционного аппарата к пластинке совпадает с направлением диффракционного
минимума (в этом направлении волны гасят друг друга), то частицы
вовсе не будут попадать на такую фотопластинку. Если же речь идет не
о большом числе электронов, а об одном, то интенсивность волн де-
Бройля указывает лишь вероятность попадания электрона, но вовсе не
обязывает электрон к тому или иному определенному поведению.
В таком понимании волны де-Бройля не имеют ничего общего с вол-
нами, известными из классической физики. Во всех «классических»
волнах абсолютное значение амплитуды волны определяет физическое
состояние. Если, например, амплитуда колебаний воздуха в одном случае
всюду в два раза больше, чем в другом, то это означает вчетверо
ббльшую энергию колебаний и вместе с тем другое физическое со-
стояние среды. В случае волн де-Бройля интенсивности определяют
вероятности местонахождения частицы. Поэтому важно лишь отноше-
ние интенсивностей в различных частях пространства, а не сама
их абсолютная величина. Это отношение показывает, во сколько раз
3 Блохинцев
84
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
в одном месте пространства вероятнее обнаружить частицу, нежели
в другом. Поэтому, если в одном случае интенсивность волн де-Бройля
всюду вдвое больше, чем в другом случае, то физическое состояние
частиц все же одно и то же, так как при таком увеличении амплитуды
волн отношения интенсивностей в различных областях пространства
остаются неизменными. Волны де-Бройля дают, таким образом, лишь
статистические сведения о движении частиц. В соответствии с этим эти
волны следует рассматривать как волны вероятности; они определяют
вероятность обнаружения частицы в каком-нибудь месте пространства,
в какой-нибудь момент времени*).
§ 10. Вероятность местоположения частицы
Мы можем теперь математически формулировать статистическую
интерпретацию волн де-Бройля. Для этого заметим, прежде всего, что
слово «волны» мы употребляем сейчас весьма условно. Только в очень
специальных случаях состояние частиц будет описываться простыми пло-
скими волнами. В общем случае то, что мы сейчас называем волнами
де-Бройля, может представлять собой весьма сложную функцию коор-
динат х, у, z и времени /. Тем не менее и для этих сложных случаев
мы будем употреблять термин волновая функция и обозначать послед-
нюю буквой ф **):
ф = ф(х, у, z, /). (Ю.1)
Величины х, у, z мы будем называть координатами частицы. Со-
гласно изложенному в § 9 точный смысл в х, j/, z вкладывается сле-
дующей измерительной операцией: величины х, у, z определяются
как координаты той точки, в которой обнаруживается частица.
Так, например, это будут координаты пятнышка на фотопластинке,
получившегося в результате попадания на пластинку частицы, или, на-
пример, координаты, определяющие положение щели, через которую
прошла частица, и т. п.
Интенсивность волн, а вместе с тем и вероятность местонахождения
частицы определяются квадратом амплитуды колебания ф2. Имея, однако,
в виду, что ф может быть комплексной величиной, а вероятность должна
быть всегда величиной положительной, мы будем брать за меру интен-
*) Впоследствии мы увидим, что, зная волну де-Бройля, описывающую
состояние частиц, можно найти вероятность не только местоположения ча-
стицы, но и вероятность любого результата измерения любой механической
величины, относящейся к рассматриваемой частице.
**) Укажем здесь, что для двух простых случаев мы уже знаехМ волновую
функцию. Именно, для частиц, движущихся с заданным импульсом р, волно-
вая функция ф есть монохроматическая плоская волна (7.1). Далее, нам
известна функция для почти монохроматической волны, т. е. для группы волн
(7.8). В ближайшем изложении мы будем оперировать с произвольными волно-
выми функциями, оставляя пока в стороне вопрос о том, как такие функции
могут быть определены для заданных физических условий (ср. § 28). Считая
такое определение возможным, мы будем говорить, что ^-функция описывает
(статистически) состояние частицы.
§10] ВЕРОЯТНОСТЬ МЕСТОПОЛОЖЕНИЯ ЧАСТИЦЫ 35
сивности не ф2, а квадрат модуля ф, т. е. величину
| ф | = ф*ф,
где через ф* обозначена величина, комплексно сопряженная ф*).
Далее, следует заметить, что вероятность найти частицу в области
точки х, у, z зависит, конечно, от размеров выбираемой области. Рас-
сматривая бесконечно малую область х, x-j- dx; у, у dy\ z, z-j- dz,
мы можем считать ф внутри нее постоянной, а поэтому вероятность
найти частицу — пропорциональной объему этой области. Обозначим
этот элемент объема через dv = dx dy dz.
Обозначая саму вероятность (бесконечно малую) найти частицу
в элементе объема dv в окрестности точки х, у, z и в момент вре-
мени t через dW(x, у, z, t), мы можем записать статистическую трак-
товку волн де-Бройля в виде следующего равенства:
dW(x, у, z, t)~ | ф (аг, у, z, /)|2afo. (10.2)
Это равенство позволяет по заданной волновой функции ф (х, у, z, t),
описывающей состояние частицы, вычислить вероятность местонахожде-
ния этой частицы dW(x, у, z, t). Величину
чо(х, у, z, /) = ^=|ф(х, у, z, 0|8 (Ю.З)
будем называть плотностью вероятности.
Вероятность найти частицу в момент времени t в объеме V согласно
теореме сложения вероятностей равна
W(V, t) = \dW=\w-dv = С|ф|2^. (10.4)
V V V
Если произвести интегрирование по всему объему, то мы получим
вероятность того, что в момент времени t частица находится где-нибудь.
Это вероятность достоверного события. В теории вероятностей принято
вероятность достоверного события считать равной 1. Если принято это
соглашение, то интеграл от |ф|2 по всему объему следует приравнять 1:
У|ф(х, у, z, t) |2 dv = 1. (10.5)
00
Это условие называется нормировкой, а функция ф, удовлетворяющая
этому условию, называется нормированной.
Нормировка может не удаться, если интеграл, взятый по всему объему
от ф, расходится, т. е. функция ф квадратично не интегрируема. В физически
реальных условиях движение частицы всегда происходит в ограниченном про-
странстве. Это ограничение обусловливается геометрическими размерами при-
боров и конечной скоростью движения частиц. Поэтому вероятность найти
частицу отлична от нуля лишь в конечной области пространства, так что функ-
ция ф должна быть интегрируема. Однако, в ряде случаев приходится все же
*) В дальнейшем звездочка всегда будет означать комплексно сопряжен-
ную величину.
3*
36
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
пользоваться некоторыми идеализациями, которые ведут к неинтегрируемым
функциям. Простым примером таких функций является плоская волна (7.1).
В то время, как в действительности параллельный лучок всегда ограничен
диафрагмами с боков и спереди своим фронтом, при достаточно больших
размерах пучка, когда краевые эффекты не играют роли, мы можем рассма-
тривать пучок как плоскую волну. Последняя же предполагается занимающей
все пространство.
Из (7.1) следует, что | <[> |2 = | С |2 = const. Это означает, что частицу
одинаково вероятно найти в любом месте. Нормировать к 1 в этом случае
нельзя. В дальнейшем мы дадим рациональную нормировку и для этого случая.
Второе замечание относится к зависимости от времени. Нормировка имеет
смысл лишь постольку, поскольку она сохраняется во времени, т. е. равен-
ство (10.5) должно иметь силу для всех моментов времени (иначе нельзя
сравнивать вероятности, относящиеся к различным моментам времени). При
рассмотрении законов изменения волновой функции во времени будет пока-
зано (гл. XII, § 28), что нормировка действительно не меняется, т. е. инте-
грал (10.5) от времени не зависит.
§ 11. Принцип суперпозиции состояний
В данных физических условиях частица может находиться в различ-
ных состояниях в зависимости от способа, каким она в эти условия по-
падает. Обращаясь к простейшему случаю свободного движения частицы
без действия внешних сил и без взаимодействия с другими частицами,
мы можем иметь дело с состояниями движения, различающимися как
величиной, так и направлением импульсов. Каждое из этих состояний
может быть реализовано само по себе. Однако, существуют и более
сложные случаи. Примером может служить диффракционный опыт Дэвис-
сона и Джермера, в котором падающий на кристалл пучок разбивается
на систему диффрагированных пучков. После взаимодействия с кри-
сталлом движение, происходит опять-таки в пустом пространстве, но пред-
ставляется уже целой совокупностью волн де-Бройля, отличадощихся
друг от друга направлением распространения.
Бросая на поверхность кристалла пучок определенного направления
и определенной длины волны к, мы не можем получить какую-нибудь
одну из диффрагированных волн, а получаем сразу всю совокупность
этих волн (вместе с падающей), находящихся к тому же в определен-
ных фазовых отношениях друг к другу (и поэтому способных к интер-
ференции). Вся эта совокупность волн представляет собою единое вол-
новое поле и изображается одной волновой функцией ф. Однако, такое
волновое поле является совокупностью простых волн де-Бройля фр,
каждая из которых сама по себе может описывать возможное состояние
движения частицы в пустом пространстве. В этом можно убедиться,
если выделить с помощью диафрагмы из всего волнового поля ф один
из диффрагированных пучков и затем вторично подвергнуть его диф-
фракции.
Мы говорим, что состояние, возникающее при диффракции частиц
на поверхности кристалла, является суперпозицией (наложением) со-
стояний свободного движения, описываемых простыми волнами де-Бройля.
Этот случай суперпозиции является частным выражением общего прин-
§ 11] ПРИНЦИП СУПЕРПОЗИЦИИ состояний 37
ципа суперпозиции состояний, составляющего одну из основ квантовой
механики.
Этот принцип может быть сформулирован следующим образом: если
какая-либо система {частица или их совокупность) способна на-
ходиться в состоянии, изображаемом волновой функцией фр и
в другом состоянии ф2, то она может находиться и в состоянии,
изображаемом волновой функцией ф, такой, что
ф = С1Ф14-С2ф2,
где сг и с2 — произвольные числа {амплитуды частных состояний ф1
и ф2). Отсюда следует, что если имеется ряд возможных состояний
системы, отличающихся друг от друга значением какой-либо механи-
ческой величины (импульса, энергии, момента импульса и т. п.), кото-
рые изображаются волновыми функциями фр ф2, фл, ..., то
согласно принципу суперпозиции существует сложное состояние:
ф=£1ф1 + с2ф2+ • • • • • • О1-1)
где cv с2, ..., сп, ... —произвольные амплитуды.
Если состояния, входящие в суперпозицию, отличаются друг от
друга бесконечно мало, то вместо суммы (11.1) мы будем иметь ин-
теграл.
Важным примером суперпозиции последнего рода является пред-
ставление произвольного волнового поля ф {х, у, z, t) в виде супер-
позиции волн де-Бройля*)
Фр(х, у, z, *)= —кл А . (11.2)
Именно, волновую функцию любого состояния можно написать в виде
4-оо
ф(х, у, z, f)==[^\c{px, ру, рг, О-фр(х> Л z’ ^PxdpydPz-. (11-3)
— 00
где с{рх, ру, pz, t)'—амплитуда волны де-Бройля, имеющей импульс
Р(РХ, Ру’ Рг)-
В самом деле, (И.З) есть не что иное, как разложение ф(х, у, z, t)
в тройной интеграл Фурье. Чтобы в этом убедиться, обозначим
Ру' Рг' ^ = С(РХ' ру’ Рг’ е ‘ (И-4)
Тогда на основании (11.2) формула (П.З) может быть записана
в виде
, , СП* / A dPxdPydPz М1
ф(х, у, Z, O=Jjj <f(Px’ ру' Рг' л • 4S/ <П-5)
— 00 ' ’
*) Множитель (2я/г)—8А» введен из соображений нормировки, целесообраз-
ность которой вскоре выяснится {см. (12.6)].
38 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ [гл. >н
Отсюда по известной теореме Фурье об обращении интеграла (11.5)
мы находим для каждой функции ф амплитуды ср, а вместе с тем и с,
именно:
, л fTc,, „ -1г^+ог+!2. dtd.ydz
р,, р„ Hr11' у’ г' ’
— 00
Таким образом мы видим, что любое состояние можно рассмат-
ривать как суперпозицию волн де-Бройля, т. е. состояний с задан-
ным импульсом частицы рх, ру, pz.
§ 12. Вероятность импульса частицы
Мы показали, как на основе статистического толкования волн
де-Бройля можно определить вероятность местонахождения частицы.
Сейчас мы увидим, что принцип суперпозиции позволяет расширить
статистическое толкование так, что оказывается возможным определить
не только вероятность тех или иных значений координат частицы, но
и вероятность ее импульса р.
Формулу де-Бройля
л (11 । 2тс \
р = йк | к | = — 2
мы будем рассматривать как определение величины р, которую в кван-
товой механике мы будем называть импульсом частицы *). С этой
точки зрения измерительные операции, которые определяют р, таковы же,
как и измерительные операции, необходимые для определения направ-
ления распространения волны и длины волны X. Поэтому прибором,
измеряющим импульс частиц, может служить диффракционная решетка.
По распределению интенсивностей в диффракционной картине можно
определить X и направление первичной волны. Так как диффракция
частиц происходит независимо для каждой из частиц, то мы имеем
право приписать импульс р каждой из частиц в отдельности.
Чтобы рассмотреть теперь вопрос об определении вероятности того
или иного значения импульса частицы, обратимся к опыту по диф-
*) В связи с данным нами определением импульса микрочастицы может
возникнуть вопрос: почему вообще величину р = hk следует называть импуль-
сом? Ответ на этот вопрос заключается в том, что определенная таким образом
величина р на самом деле обладает свойствами, вполне аналогичными свой-
ствам импульса ркл- в классической механике (ср. §§ 32, 33, 96). В § 34 по-
казано, что классический импульс ркл> (подчиняющийся уравнению Ньютона)
есть среднее квантового импульса
Ркл.= Р*
В частности, для состояния с определенным значением р имеем ркл.— Р-
Благодаря этому р может быть измерено, скажем, по отдаче при ударе, как
это делается в классической механике для определения ркл.
Мы, однако, предпочли чисто классическому определению определение
р = hk, взяв тем самым в основу новую измерительную операцию, невозмож-
ную в классической области.
§ 12]
ВЕРОЯТНОСТЬ ИМПУЛЬСА ЧАСТИЦЫ
39
фракции частиц (например, электронов) на поверхности кристалла.
Суперпозиция волн де-Бройля, образующая волновое поле ф (х, у, z, t)
при диффракции на поверхности кристалла, схематически изображена
на рис. 10, где показаны падающая (/), отраженная (г) и одна из диф->
фрагированных (d) волн. В соответствии с реальными условиями пред-
положено, что первичная волна
представляет собой ограничен-
ный диафрагмой пучок. Такими
же пучками являются и вторич-
ные волны.
Каждый из пучков мы можем
представить в виде волны
де-Бройля фр (х, у, z, t) с ам-
плитудой с (р), медленно меняю-
щейся в направлении, перпенди-
кулярном к пучку*). Всеволно-
вое поле ф представим как
суперпозицию полей, принадле-
жащих отдельным пучкам:
ф = 2с(Р)Фр (12.1)
р
(где сумма взята по всем пуч-
кам).
В целом состояние ф являет-
ся состоянием с неопределенным
импульсом частиц, так как оно
представляет собой суперпози-
цию состояний фр с различными
импульсами частиц. Поэтому,
если мы будем производить изме-
рение импульса частицы, то мы
можем получить в каждом
отдельном измерении одно из
значений р, содержащихся в
Рис. 10. При ограниченном первичном
пучке i отдельные частные волны r, d
и т. д. пространственно разделяются.
суперпозиции (12.1).
Какова вероятность того, что мы получим значение импульса, рав-
ное р? Диффракционная решетка разложит нам волновое поле на моно-
хроматические (в действительности — почти монохроматические) пучки,
так же как она разлагает белый свет на отдельные спектрально чистые
компоненты. Чтобы* подсчитать число частиц, имеющих импульс р, по-
ставим цилиндр Фарадея и будем определять число частиц, попадающих
в него при различных его положениях. Вблизи поверхности кристалла
*) Вне пучка с(р) = 0. Таким образом в отличие от (11.3) рассматриваемые
сейчас амплитуды являются функциями координат. Но ввиду медленности из-
менения с(р) они близки к истинным амплитудам Фурье, фигурирующим
40
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. 111
мы имеем сложное волновое поле, представляющее собой результат
интерференции всех пучков. Вдали же от кристалла пучки разделяются.
Вероятность того, что в цилиндре обнаружится частица, согласно ста-
тистической интерпретации ф (jv, у, z, t) будет пропорциональна
| ф (х, у, z, t) |2. Если мы поставим цилиндр Фарадея достаточно далеко
от кристалла, то отдельные пучки уже разделятся друг от друга и
I ф (х, у, z, t) |2 сведется к
1ф(х’ л z< ^)I2=Ic(p)I2I фр (х> л z)l2 (12-2)
(для одного из пучков). Имея в виду значение фр (11.2), получаем:
|ф(х, у, z, (12.3)
Следовательно, |с(р) |2 пропорционально вероятности обнаружить электрон
в цилиндре Фарадея, если он расположен так, что в него направлена
волна фр . Такой волне принадлежат электроны, имеющие импульс р. По-
этому величина | с (р) |2 пропорциональна вероятности обнаружить в состо-
янии ф электрон с импульсом р.
Имея в виду (11.4) и то, что вероятность обнаружить импульс
частицы лежащим в интервале рх, Px~\-dpx, ру, py-\-dpy\ р2, pz-{-dp2
должна быть пропорциональна dpxdpydpz, мы приходим к следую-
щему выражению для искомой вероятности:
dW(px, ру, р2) = \с(рх, ру, р2, t) '\idpxdpydp2 (12.4)
и для плотности вероятности
™ (Рх> Ру’ Рг’ 0 = к <Рх’ Ру’ Рг’ (12.5)
Написанные формулы содержат определенный выбор нормировки вероят-
ностей для импульса.
Пользуясь тем, что ру, pz, 0 есть согласно (11.6) компонента разло-
жения в ряд Фурье ф (х, у, z, t), нетрудно доказать, что
4-00 Н-00
j j j \С (Рх, Ру, Pz, О I2 dPxdpydpz = j j j I ? (Px, Ру, Рг, t) I2 dpxdPydpz =
— oo — 00
= J J J | <[> (x, y, z, f) I2 dx dy dz. (12.5»
— 00
Левая часть есть вероятность найти любое значение импульса частицы (досто-
верное событие), правая часть есть вероятность найти частицу в любом месте
пространства (также достоверное событие). Поэтому сделанный выбор нор-
мировки вероятностей целесообразен: вероятности достоверных событий оди-
наковы. В частности, если вероятность найти частицу в любом месте пола-
гается равной 1, то и вероятность найти любой импульс будет также равна 1.
§ 13. Средние значения функций от координат и функций
от импульса
В предыдущем мы нашли вероятность местоположения частицы
(10.3) в состоянии ф и вероятность импульса частицы (12.5) в этом же
состоянии. Это позволяет нам тотчас же написать средние значения
§ 13] СРЕДНИЕ ЗНАЧЕНИЯ 4Т
любой функции от координат частицы F(x, у, z) и любой функции от
импульса частицы F(px, Ру, р?) для состояния, изображаемого волновой
функцией ф. Именно, из (10.3) и (12.5) согласно определению среднего
значения случайной величины имеем:
F(x, у, z) = § F(x, у, z)l ф(х,у, z)\2dxdydz =
= § (х,у, z) F(x,y, 2)ф(х, у, z)dxdydz (13.1}
при условии
j |ф(*, У у z)|2 dxdy dz=\ (13.2)
и
F(PX, РуРг) = \F<PX, Ру' Pz) \С(РХ, Ру Pz) I2 dPxdPydPz =
= J C* (Px> py Pz) F(PX’ Py' Pz) C (px> Py Pz) dPXdPydPz 033)
при условии
Jk(Ar, py, P2) \^dPAP^Pz=)- (13-4)
(Здесь интегралы взяты по всей области изменения переменных х, у, z
или pv, ру, pz соответственно.)
Формулы (13.1) и (13.3) допускают весьма важное преобразование,
основанное на свойствах интегралов Фурье. Пусть F(x, у, z) есть целая
рациональная функция от х, у, z и F(px, ру, pz)— целая рациональная
функция от рх, ру, pz.
Тогда формулы (13.1) и (13.3) могут быть переписаны в следующем
виде:
F(x,
= ^c*{px,Py,pz)F^ih^, ih^, ih^) c(PX<Py>Pz'>dpxdpydp2, (13.5)
P(Px,Py,Pz) =
= j\*(x, y, z)F^—ih~, —ihty —ih^if[x,y,z)dxdydz. (13.6)
Эти формулы означают, что аргументы функции F следует заменить
символами дифференцирования по указанным аргументам и умножения на
+ /Л и выполнить полученную операцию под стоящей позади F функ-
цией. Так, например, для вычисления среднего значения компоненты
импульса рх поступаем так: F(px, ру, р^—рх- Следовательно,
Рх= J с*{рх, Ру, pz)pxc (рх, Ру, рг) dpxdPydpz, (13.7)
или по формуле (13.6), заменяя рх на —получим
рх=— § ф* (х, у, z) th dx dydz. (13.8)
Подобным же образом среднее значение р2х можно вычислить либо по
42 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ [гл. 111
формуле (13.3):
= Р* (Рх, Ру, PJ р\с (рх, ру, Рг) dpxdpydpz, (13.9)
или, заменяя
на
г(—(,3-10)
по формуле (13.10):
Р2Х —— A2 ]*$(*,Д', z) ^dxdydz. (13.11)
Доказательство эквивалентности (13.1), (13.3) и (13.5), (13.6) соответ-
ственно приведено в дополнении I.
§ 14. Гейзенбергово соотношение неопределенностей
Мы перейдем теперь к рассмотрению одного из наиболее важных
в принципиальном отношении пунктов квантовой механики. Из преды-
дущего мы видели, что квантовая механика описывает поведение микро-
частиц статистическим образом. Именно, знание волновой функции ф,
изображающей состояние частицы, позволяет предсказать вероятность
того или иного положения частицы и того или иного значения ее им-
пульса (а также, как мы подробнее увидим впоследствии, и вероятности
других, более сложных механических величин). Иными словами, знание'
ф-функции позволяет предсказать вероятности результатов различных
измерений, производимых над частицами.
В классической механике, обращаясь к движению частиц, мы можем,
поставить вопрос по-иному. Именно, мы можем интересоваться траекто-
рией частиц и движением частиц по таким траекториям. A priori мож-
но было бы думать, что и в области микромира существуют такие тра-
ектории, а квантовая механика рассматривает лишь некоторое среднее
статистическое из таких движений пс траекториям, подобно тому как
это делается в статистической механике. Простые соображения показы-
вают, что это не так. В области микромира механические величины
находятся в иных отношениях, нежели в области макромира, в области
классической механики.
С понятием движения частицы по траектории неизбежно связано
предположение о существовании у частицы в каждый момент времени
определенной координаты х и определенного импульса р. Первая ука-
зывает положение частицы, а вторая величина (р) указывает, как изме-
няется это положение в течение бесконечно малого интервала времени dt:
x-\-dx = x-[-^ dt, (14.1)
р
где т — масса, а — скорость частицы.
Мы можем указать вполне определенно те измерительные манипуля-
ции, которые должны быть произведены, чтобы получить числа, одно из
§14] ГЕЙЗЕНБЕРГОВО СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ 43
которых мы назовем координатой частицы х, а другое — ее импульсом р.
Указанием этих манипуляций вкладывается смысл в величины х и р.
Так, величину х мы получим, отмечая деление масштаба, совпадающее
с положением рассматриваемой частицы. Мы получим и ту величину,
которую мы назовем импульсом р, если измерим одним из известных
способов массу частицы т и ее скорость последнюю — измеряя
время, в течение которого частица проходит от одного деления мас-
штаба к другому, достаточно близкому. Тогда p = mv. Можно указать
и другие способы измерения р и х, которые эквивалентны изложенному.
Так или иначе, но в макромире пара величин х, р может быть опре-
делена, по крайней мере в принципе, для каждого момента времени.
Обратимся теперь к микромиру. Основываясь на опытах по диф-
фракции микрочастиц, мы будем считать правильным соотношение де-
Бройля
Это соотношение связывает импульс микрочастицы р с длиной волны
де-Бройля 1. Если под 1 понимать именно длину волны, то, какова бы
ни была природа волн, эта величина не может быть функцией коорди-
нат х. Выражение «длина волны в точке х равна 1» не имеет никакого
смысла, ибо по своему определению длина волны есть характеристика
синусоидальной волны, неограниченно простирающейся в пространстве
(от х — —оо до х = -|-оо), 1 есть «функция» формы волны, а не
функция координаты какой-либо точки. Поэтому в (14.2) правая часть не
может быть функцией координаты х. Следовательно, не может быть
функцией координаты х и левая часть равенства (14.2), т. е. импульс р.
Мы приходим к заключению, что коль скоро соотношение де-Бройля
(14.2) признается правильным, то импульс частицы р не может быть
функцией координаты частицы х. В области микромира выражение:
«импульс частицы в точке х равен р» также не имеет смысла. Стало
быть, если соотношение де-Бройля справедливо, то не может сущест-
вовать таких измерительных манипуляций, которые позволили бы одно-
временно определить координату частицы х и ее импульс р. Вместе
с тем манипуляции, применяемые в области значимости соотношения де-
Бройля (область микромира) для измерения координаты частицы х и ее
импульса /?, должны быть взаимно исключающими друг друга: можно
измерить либо х, либо р.
Мы указывали, что под координатой микрочастицы в сущности
понимается координата того места, где обнаруживается действие частицы
(например, координата «пятнышка» на фотопластинке при экране). Им-
пульс же р может быть измерен путем определения длины волны в диф-
фракционном опыте. Нетрудно видеть, что оба измерения являются
действительно исключающими Друг друга. Допустим, что мы имеем дело
с пучком микрочастиц (скажем, электронов), который мы подвергаем диф-
фракции на диффракционной решетке (скажем, на монокристалле). Пусть по
распределению интенсивностей диффрагированных пучков на экране мы
44
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
установили, что длина волны в нашем пучке равна 1 и, следовательно, им-
2тс/г т-г
пульс частиц равен р= — . При этом нам совершенно ничего неиз-
вестно о координатах частиц. Однако, попадая на экран, частицы
распределяются некоторым, в среднем вполне определенным, образом,
и, отмечая положение точек попадания, мы вместе с тем определяем
координаты частиц. Но теперь было бы уже неправильным говорить
о том, что импульс частиц равен попрежнему р. В результате взаимо-
действия с экраном он претерпел изменение.
Действительно, если мы соберем все частицы, упавщие на экран
в области х, x-\-dx, то волновая функция этих частиц ф(х) должна
обращаться в нуль (точнее, становиться малой) вне интервала Дх. Такая
волновая функция не может быть, конечно, монохроматической, сину-
соидальной волной, а представляет собой целый набор монохроматических
волн, которые в области х, x-\-dx
Рис. 11. Иллюстрация к измерению ру
и у: диффракция от щели в экране.
усиливают друг друга, а вне этой
области гасят друг друга. Если
бы мы теперь подвергли вторично
эти отобранные частицы диффрак-
ции, то диффракционный аппарат
показал бы нам, что состояние
ф (х) представляет собой не моно-
хроматическую волну, а целый на-
бор волн. Вместе с тем мы конста-
тировали бы, что импульс этих
частиц р имел неопределенное значе-
ние, соответственно тому, что ф (х)
не есть волна определенной длины,
а представляет собой суперпози-
цию монохроматических волн.
Приведем еще один пример,
иллюстрирующий взаимоисключаю-
щий характер операций, приме-
няемых для измерения импульса и
координаты частицы. Представим себе, что имеем состояние частицы,
описываемое плоской волной де-Бройля ф . Пусть волна распространяется
по направлению оси ОХ. Это состояние обладает той особенностью,
что импульс частицы имеет вполне определенное значение, именно:
РХ=Р> Py = Q< Рг = °- <14-3)
Таким образом, исходя из этого состояния, мы предполагаем импульс
известным из предварительных измерений.
Положение частицы (ее координата) в этом состоянии, напротив,
совсем неизвестно: | ф |2 == const., и, стало быть, все положения ча-
стицы равновероятны. Попытаемся фиксировать хотя бы одну из коор-
динат частиц, например, у. Для этого поставим экран со щелью, рас-
положив его плоскость перпендикулярно к направлению распростране-
ния волн так, как это показано на рис. 11. Пусть ширина щели есть d.
§ 14] ГЕЙЗЕНБЕРГОВО СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ 45
Если частица пройдет через эту щель, то в момент прохождения ее
координата фиксируется положением щели с точностью до ширины
щели d. Так как импульс вдоль оси OY известен (ру = 0), то на пер-
вый взгляд кажется, что мы определили и импульс ру, и координату у.
Однако это не так. В приведенном рассуждении пропущено то обстоя-
тельство, что около щели будет иметь место диффракция: волны будут
отклоняться от первоначального направления распространения. Вместе
с тем импульс частиц при внесении экрана со щелью изменится и
не будет таким, каким он, был до внесения экрана.
Среднее значение импульса ру по оси OY останется неизменным:
/^ = 0, так как диффракция около щели происходит симметричным об-
разом. Оценим по порядку величины возможные отклонения импульса от
этого среднего значения кру. Если мы будем отклонять луч от оси ОХ,
то скоро он займет положение, соответствующее первому диффракцион-
ному минимуму (дальше пойдет первый диффракционный максимум и т. д.).
Обозначим угол, образованный осью ОХ и указанным лучом, через а.
Тогда наибольшая интенсивность волн будет приходиться на область от
— а до-|-а. Угол а определится из того условия, что в этом направ-
лении лучи, исходящие от краев щели, гасят друг друга (разность
фаз тг). Если длину волн обозначим через X, то для интересующего
нас угла получим известное соотношение
sina = ^. (14.4)
Ширина щели d есть не что иное, как неточность &у, допускаемая при
измерении координаты у.
Далее, р sin а есть проекция импульса на ось OY. Так как основная
интенсивность волн де-Бройля падает в область углов от —а до -|-а,
то при измерении импульса ру большинство результатов измерения
будет лежать в интервале от —у sin а до -\-р sin а, т. е. разброс из-
меряемых значений около среднего значения ру = 0 равен ^ру=р sin a.
Так как по соотношению де-Бройля />=-у, то, подставляя в (14.4)
. a * <
дру вместо —— и &у вместо d, мы получим:
hp^y — nh.
(14.5)
Это соотношение показывает, что чем точнее определяется положе-
ние частицы (чем меньше Ду, т. е. чем уже щель), тем в большей сте-
пени становится неопределенным импульс (тем больше Д/^), и наоборот.
Соотношение (14.5) называется соотношением неопределенностей
Гейзенберга для координаты и импульса частицы*).
*) Заметим, что в нашем выводе этого соотношения мы воспользовались
тем, что длина волнцт X, а вместе с тем и полный импульс частицы р не ме-
няются при диффракции. Следовательно, при таком рассмотрении наибольшее
значение Ьру есть р = > что соответствует частице, движущейся вдоль
экрана. Поэтому может показаться, что мы можем, ограничившись точно-
46
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
Выведем теперь, независимо от конкретного способа измерения х и
р, соотношение Гейзенберга для частиц, состояние которых представляется
группой волн. Как было показано в § 7, группа волн
d)(x, t)= j c{k)-e~i^t-kx'>dk (14.6)
k0 — bk
может быть представлена в таком виде [см. (7.9)]:
sin Г t — х )
ф(х, t) = 2c(kQ)e-i^-kx) - - (14.7)
Интенсивность | ф |2 в такой группе волн для некоторого момента вре-
мени t изображена на рис. 12. Удвоенное расстояние от точки максимума
Рис. 12. Интенсивность | <[> |2 в группе волн в функции х для некоторого мо-
мента времени t.
| ф |2 до первого минимума мы можем принять за меру, определяющую раз-
меры группы. Обозначим его через 2Дх. Из (14.7) следует, что Дх=
Иными словами,
ДхД& —тг. (14.8)
Это чисто волновое соотношение, справедливое для любых волн, пока-
стью кру—р, добиться сколь угодно большой точности в определении коор-
динаты у, уменьшая ширину щели. Это, конечно, противоречит соотношению
Гейзенберга (14.5). На самом деле это не так. Наше рассмотрение прибли-
женно. Оно пригодно при условии, что длина волны X меньше ширины щели.
С уменьшением ширины щели характер волнового поля за экраном услож-
няется. Этому полю уже нельзя приписать определенной длины волны X так,
как мы это делаем. Разбор этого случая показывает, что соотношение (14.5)*
остается верным.
В следующем параграфе мы покажем соотношение Гейзенберга для лю-
бого волнового поля. Тем самым будут уничтожены всякие сомнения, связан-
ные с допущениями элементарного вывода, имеющего лишь иллюстративное
значение.
§ 14J ГЕЙЗЕНБЕРГОВО СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ 47"
зывает, что произведение линейных размеров группы волн Дх на интер-
вал волновых чисел Д£ тех волн, из которых построена группа, есть
величина постоянная и равная тг.
В частности, если мы желаем послать очень короткий радиосигнал (ма-
лое Дх), то неизбежно в нем будут представлены с заметной интенсивностью
весьма отличающиеся по длине волны отдельные монохроматические волны.
Поэтому такой сигнал будет принят приемниками, настроенными на различные
волны. Напротив, если мы желаем, чтобы нас принимали приемники, настро-
енные лишь определенным образом, то мы должны посылать очень монохро-
матические сигналы, а стало быть, согласно (14.8) — достаточно длинные.
Возвратимся теперь к квантовой механике. По уравнению де-Бройля
p = hk,
и поэтому
Др = Л Д/г. (14.9)
Разумея под группой волн (14.6) группу волн де-Бройля, умножим на
постоянную Планка h уравнение (14.8), тогда на основании (14.9) мы
получим:
ДрхДх = тг/г, (14.10)
т. е. мы получаем соотношение Гейзенберга для р и х.
Если мы будем производить измерение координат частиц, находя-
щихся в состоянии, описываемом группой волн де-Бройля (17.6), то
в момент времени t среднее значение результатов измерения координат
“ d<A , „
будет х = • г, но значения результатов отдельных измерений будут
разбросаны около х, преимущественно в интервале Если же мы
будем в том же состоянии измерять импульс частиц р, то среднее значе-
ние будет равно p=pQ = hkQ и отдельные значения будут сосредото-
чиваться около pQ в интервале Др = +Л Д/г.
Соотношение Гейзенберга (14.10) показывает, что чем уже группа,
т, е. чем определеннее значение координат частиц {малое Дх), тем
менее определенно значение импульса частиц (большое Др), и наобо-
рот. Из него следует, что если в результате измерения мы . получаем
частицу, имеющую вполне определенное значение импульса (Дрх = 0), то
размеры группы (Дх), описывающей состояние частицы, должны быть
бесконечно велики: координата частицы совершенно неопределенна. На-
оборот, если в результате измерения мы получаем частицу с определен-
ным значением координаты (Дх = 0), то импульс такой частицы совер-
шенно неопрецелен (Дрх= оо ).
Невозможность одновременного применения понятий импульса и коорди-
наты к микрочастицам приводит к несостоятельности предположения
о возможности существования траекторий микрочастиц. Вместе с тем
отпадает и упомянутое выше предположение о том, что квантовая ме-
ханика, быть может, рассматривает лишь некоторое среднее из таких
траекторий, аналогично классической статистической механике.
Исходя из опытов по диффракции, можно сделать это последнее
положение еще более убедительным. Дело в том, что диффракционная
48
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
картина, возникающая на экране, зависит от полного числа штрихов
в диффракционной решетке п. На рис. 13 изображено распределение
интенсивностей при диффракции плоской волны, проходящей через экран
перпендикулярно его плоскости, для случаев, когда в экране имеется
одна щель (а), две такие же щели (Ь) и, наконец, шесть щелей (с).
Допустим, что частицы движутся по некоторым траекториям так, что
в каждый момент времени обладают определенным значением импульса
и координат. Диффракционную картину мы должны тогда понимать как
результат некоторого статистического распределения частиц по различным,
возможным траекториям. При предположении, что частицы имеют траек-
(а)
(Ъ)
Рис. 13. Диффракция от различного числа щелей.
торию, мы должны считать, что каждая из них проходит через какую-то
вполне определенную щель экрана и, следовательно, взаимодействует
лишь с несколькими щелями п\ попадающими в сферу действия ее сил.
Если радиус действия сил есть а, а постоянная решетки есть d, то
п, = ~. Следовательно, диффракция (отклонение частиц под влиянием
взаимодействия с экраном) должна была бы определяться не полным
"числом штрихов в решетке п, а числом ri, т. е. не числом штрихов
в решетке, а характером сил взаимодействия между частицей и штриха-
ми, в первую очередь, радиусом действия этих сил. Например, если
диффракция сперва происходит через одну щель (рис. 13, я), а потом
открывается вторая щель, то если расстояние между двумя щелями больше
радиуса действия сил, то прохождения частиц через каждую щель сле-
дует считать независимыми. Мы получили бы диффракционную картину
ту же, что и от одной щели (а), но более интенсивную. На самом же
деле должна получиться совсем иная картина (рис. 13, Ь).
§ 15] СООТНОШЕНИЕ ГЕЙЗЕНБЕРГА ДЛЯ ОБЩЕГО СЛУЧАЯ 49
Опыт подтверждает независимость диффракционной картины от сфе-
ры действия сил. Например, в опытах Штерна и Эстермана по диф-
фракции Не на кристаллах LiF (§ 7) радиус действия а меньше посто-
янной решетки d. Далее, картина диффракции Не и Н2 и, наконец,
рентгеновских лучей одна и та же, несмотря на полное различие взаимо-
действия этих лучей с решеткой LiF. Она определяется в первую оче-
редь чисто геометрическими причинами: расположением ионов Li и F
в кристалле («штрихами» решетки). Это позволяет рассчитывать диффрак-
цию по уравнению Брэгга, в которое входит лишь длина волн X, а не
природа диффрагирующих частиц. Поэтому явление диффракции час-
тиц нельзя согласовать с предположением о существовании траекторий.
§ 15. Доказательство соотношения Гейзенберга
для общего случая
Перейдем к доказательству соотношения Гейзенберга для любого
состояния частицы, описываемого какой-либо волновой функцией ф (х).
Простоты ради ограничимся одним пространственным измерением: обоб-
щение на большое число измерений будет совершенно тривиальным.
Итак, пусть нам дано какое-либо состояние частицы, изображаемое вол-
новой функцией ф (х)*). Волновую функцию мы будем считать нормиро-
ванной к 1 в области от — оо до -|- оо .
Для того, чтобы установить соотношение Гейзенберга в строгой
форме, нам следует прежде всего выбирать меру для отклонения отдель-
ных результатов измерений импульса р и координаты х от их средних
значений р и х. Иными словами, точнее определить, что мы разумеем
под А/? и Дх (см. предыдущий параграф).
В качестве такой меры мы выберем употребляемые в статистике сред-
ние квадратичные отклонения Др2 и Дх2 (иначе называемые средни-
ми квадратичными ошибками). Эти величины определяются следующим
образом. Пусть х есть среднее значение какой-либо величины х. Если
в каком-либо индивидуальном измерении мы получим значение х, то
Дх =х—х будет отклонением результата измерения от среднего зна-
чения х. Среднее значение этого отклонения, очевидно, всегда равно
нулю:
Дх = х—х=х — х = 0.
Поэтому за меру отклонения индивидуальных измерений от среднего
берут не Дх, а Дх2 — среднее от квадрата индивидуальных отклонений.
Основываясь на этом пояснении, мы можем написать:
Дх2=х2 —(х)2, (15.1)
Д^2 — (р)2. (15.2)
*) Время t мы можем не выписывать явно, так как все дальнейшее спра-
ведливо для любого момента времени.
4 Блохинцев
50
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
Не уменьшая общности доказательства, мы можем взять для дальней-
шего подходящую систему координат. Именно, выберем начало коор-
динат в точке х. Тогда х=0. Далее, пусть эта система координат
движется вместе с центром распределения х. Тогда и р=0. В этой си-
стеме координат получим вместо (15.1) и (15.2)
Д*2=х2, (15.Г)
Др2 =р2. (15.2')
Согласно (13.1) и (13.11) имеем:
4- оо
J ф*(х)х2ф(х)dx, (15.3)
— 00
Д^==^2=_Л2 (15.4)
Наша задача заключается в установлении связи между Др2 и Дх2. Для
этой цели рассмотрим вспомогательный интеграл:
4-о°
/(£) = J |М(*) + 4?Г dx^Q, (15.5)
— 00
где $ — вещественная вспомогательная переменная. Раскрывая квадрат
модуля, получаем:
-}-оо 4-оо
— 00 —оо
4~ оо
— 00
Обозначая
4-00 ___
A= J х2|ф|2Лс =Дх2, (15.6’)
—оо
+00
B= — f х^-(ф*ф)й?х= Сф*ф<7х=1, (15.6")
J ах j
— 00
+°0 ___
С= I dx= — Г dx=^ (15.6'")
J dx dx J T dx2 h2 v 1
— 00
(здесь произведено интегрирование по частям), мы находим
1$) = А& — В^ + ОО. (15.7)
Так как I (£) всюду положительно (при вещественном S), то это
означает, что корни уравнения
/(£) = 0
(15.7')
§ 16] СТАТИСТИЧЕСКИЕ АНСАМБЛИ КВАНТОВОЙ МЕХАНИКИ 51
комплексны. На основании известной теоремы о корнях квадратного
уравнения это может быть лишь при условии, что
4АС^В2. (15.8)
Подставляя в .это неравенство значение Л, В, С из (15.6', 6", 6'"), мы
приходим к искомому соотношению для Дх2 и Др2:
(15.9)
Это и есть соотношение Гейзенберга в наиболее общем и строгом виде.
Вместе с тем доказано," что нет таких состояний, которые обладали бы
тем свойством, что среднее квадратичное отклонение результатов изме-
рения для импульса Др2 и для соответствующей ему координаты Дх2
равнялось бы нулю *).
Напротив, мы видим, что чем меньше среднее квадратичное откло-
нение для одной из этих величин, тем больше оно для другой. Отсюда
следует, что нельзя придумать такой опыт, который позволил бы дать
физическое определение паре р, х, ибо возможность реализации такого
опыта предполагает существование таких состояний, в которых одновре-
менно Др2 = 0 и Дх2 = 0, что противоречит соотношению Гейзенберга,
о_ 2тс7г
основанному, в конечном счете, на уравнении де-Бройля р = -у- .
§ 16. Статистические ансамбли квантовой механики.
Ансамбли чистые и смешанные
Волновая функция частицы (или, более обще, какой-нибудь системы)
позволяет предсказать вероятности результатов измерений различных
механических величин, относящихся к рассматриваемой частице (или
системе) **). Волновая функция ф дает, таким образом, статистическое опи-
сание состояния квантовых систем.
Ясно, что такие предсказания могут быть проверены лишь при
повторении одного и того же опыта большое число раз. Поэтому,
хотя мы и говорим о волновой функции одной частицы (или одной
системы), целесообразно представлять себе большое число таких частиц
*) Наше доказательство относилось лишь к тем состояниям, которые
изображаются интегрируемыми функциями. Если состояние изображается не-
интегрируемой функцией, то Дх2 = оо • При этом Д/?2 = 0 лишь для моно-
хроматических волн. В остальных случаях Д/?2 > 0. Поэтому для неинтегриру-
/ Л2 \
емых функций соотношение (15.9) выполнено тривиальным образом ( °о > ].
Соотношение Гейзенберга выполнено и для монохроматических волн. Это сле-
дует из того, что монохроматическую волну можно рассматривать как предел
группы волн при kp — h \k—> 0. Установленное же нами соотношение (14.5)
не зависит от величины Д&.
**) В предыдущем мы изложили лишь способ определения вероятности
координат и импульсов для одной частицы. В дальнейшем мы дадим общие
методы определения вероятности любых величин для любых систем.
4*
52 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ [гл. III
(или, в общем случае, систем) N, которые независимы друг от друга
и служат просто для повторения опыта (серия независимых опытов).
Такой набор частиц (или систем) мы будем называть ансамблем.
Результаты измерения какой-либо величины в различных опытах
серии будут, вообще говоря, разными. Квантовая механика позволяет
предсказать вероятность каждого результата измерения именно в такой
серии независимых опытов. Средние же значения величин, фигурирую-
щих в квантовой механике, суть именно средние результатов измерений,
произведенных в такой серии независимых опытов. В частности, среднее
квадратичное отклонение импульса Др2 в соотношении неопределенно-
стей Гейзенберга (15.9) есть среднее квадратичное отклонение ре-
зультатов измерения импульса, найденных в серии независимых опытов
над частицами некоторого ансамбля, а Дх2 есть среднее квадратичное
отклонение результатов измерения координаты, найденных в серии неза-
висимых опытов, произведенных над частицами того же ансамбля (но
не над теми же частицами).
Таким образом, соотношение неопределенностей Гейзенберга
относится к результатам измерений, произведенных над части-
цами ансамбля.
Согласно (15.9) соотношение Гейзенберга доказывается для любой
волновой функции ф, изображающей состояние частиц. Поэтому для
любого ансамбля справедливо соотношение неопределенностей Гей-
зенберга:
-------№
(15.9)
и оно может рассматриваться как наиболее фундаментальное свойство
ансамблей, изучаемых квантовой механикой.
В проведенном нами сейчас рассуждении явно предполагалось, что
все частицы ансамбля описываются одной волновой функцией ф. Такой
ансамбль называют чистым. Может, однако, представиться и более общий
случай. Именно, мы можем вообразить себе, что часть частиц находится
в состоянии фр а другая часть N2 — в состоянии ф2. Полный ансамбль
образует совокупность N= Nr -f" N2 частиц. Подансамбль представляет
собой чистый случай (фх), подансамбль N2 частиц представляет другой чистый
случай (ф2). Полный ансамбль характеризуется двумя волновыми функциями
фх и ф2 и двумя числами = , р2 = ^2, указывающими пропорцию,
в которой смешаны чистые состояния. Такой ансамбль, образующийся
путем смешивания нескольких чистых ансамблей, будем называть смешан-
ным. Поскольку соотношение Гейзенберга выполнено для каждого
из чистых подансамблей из числа образующих смешанный ансамбль,
то оно выполнено и для всего смешанного ансамбля в целом. Таким
образом, соотношение (15.9) справедливо и для чистых, и для смешанных
ансамблей, т. е. справедливо всегда.
Перейдем теперь к более подробной характеристике различия между
чистым ансамблем и смешанным. Для этого обратим внимание читателя
§ 16] СТАТИСТИЧЕСКИЕ АНСАМБЛИ КВАНТОВОЙ МЕХАНИКИ 53
на то, что из одних и тех же частных состояний может быть образо-
ван как чистый ансамбль, так и смешанный. Допустим, например, что
мы имеем два состояния фх (х) и ф2 (х). Тогда мы можем представить
себе новое состояние ф (х), являющееся суперпозицией состояний
Ф1 и ф/
ф(х) = с1ф1(х) + с2ф2(х). (16.1)
Ансамбль, описываемый функцией ф (х), будет чистым ансамблем (по
определению). Состояния Фх и ф2 входят в ф с определенными ампли-
тудами и фазами (фазы включены в q и с2, которые могут быть ком-
плексными). Мы можем сказать, что ансамбль ф образуется из фх и ф2
когерентным образом. Это выражается в том, что в вероятность
местонахождения частицы w (х) входив интерференционный член
С1С* Ф1 (*) ф* (*):
®(х)МФ(*)12М<лПФ1(*)12 + 1с2|2|Ф2(*)12 +
+ cic* Ф1 (*) Ф* (•*) + ^саФТ (*) Ф2 {*) (16.2)
Если же из состояний фх (х) и ф2 (х) образовать смесь с вероятностями
рх и pv,, то вероятность w (х) будет вычисляться так: вероятность найти
частицу около х, если она находится в состоянии фх, есть | фх |2, и
вероятность найти состояние фх есть pv следовательно, вероятность
найти частицу около х в состоянии фх в нашем ансамбле равна р11 фх |2.
Подобным же образом для состояния ф2 найдем р21 ф212. Полная вероят-
ность найти частицу около х в нашем ансамбле будет
^(х)=;р1|ф1(х)|2+р2|ф2(х)|2. (16.3)
Интерференционный член здесь уже отсутствует. Таким образом, разли-
чие между чистым случаем и смесью в отношении частных состояний ана-
логично различию в сложении когерентного и некогерентного света:
при вычислении вероятности в чистом случае складываются ампли-
туды, а в смешанном — интенсивности. В первом случае имеется интер-
ференция, со втором ее нет.
В общем случае, если мы имеем частные состояния фх, ф2, ...,
фл, . . ., то смесь из этих состояний будет даваться двумя строками *):
фр ф2, .... ф„> ••• (16.4)
PvPv •>Рп> ••• (16.4')
Числа ррр2, .. .,Ph, • • . суть вероятности присутствия в смеси состоя-
ний фх, ф2, ..., фл, ... соответственно. Из этих же состояний может
быть образован чистый ансамбль, описываемый функцией ф, представ-
ляющей собой суперпозицию:
Ф = ^1Ф1+С2Ф2+ • • • +Сяф„, (16.5)
в которой отдельные частные состояния когерентны между собой.
*) Нейманом было показано, что вместо волновой функции можно ввести
особый статистический оператор (или, иначе, «матрицу плотности»), который
позволяет дать совершенно единое описание как чистых, так и смешанных
ансамблей. См. Дирак, Основы квантовой механики или (полнее) Neuman,
Mathematische Grundlagen der Quantenmechanik.
54
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. III
В первом случае для вероятности w(x) получаем выражение
п
соответствующее сложению интенсивностей, а во втором случае эта
вероятность равна
^(х) = |ф«=21сп|2-1Ф„(х) р +
п
+ 2 #Ж(*)Фт(*) (16-2')
т уЬп, п
и соответствует сложению амплитуд (16.5). Часто в этом последнем
случае говорят об «интерференции вероятностей».
Приведем пример чистого ансамбля и смеси. Допустим, что мы про-
изводим опыт по упругому рассеянию электронов на атомах газа. Если
плотность газа достаточно мала, то электрон будет рассеиваться лишь
на одном атоме. Иначе говоря, условия (давление газа, толщина слоя
газа, через который проходит пучок электронов) предполагаются такими,
что можно ограничиться одним столкновением электрона и пренебречь
многократными. Если, к тому же, плотность электронов в падающем
пучке мала, так что их взаимодействием можно пренебречь, то мы
имеем дело сразу с воспроизведением большого числа независимых
опытов по рассеянию одного электрона на одном атоме. Допустим
сперва, что электроны в падающем пучке имеют все одинаковый
импульс р0 (монохроматический пучок). Волновая функция ФРо электрона
представится в виде суперпозиции падающей волны фРо и волны, рас-
сеянной атомом срРо:
Фро = Фро + <Рро • (16.6)
В приведенном примере мы имеем дело с чистым ансамблем, харак-
теризуемым одной волновой функцией ФРо. Мы можем теперь пред-
ставить себе, что электроны в первичном пучке имеют некоторое из-
вестное нам распределение по импульсам, например, максвелловское, так
что вероятность того, что импульс лежит в области pQx , Px-{-dpQXl
Ру> Ру + ^у P^f + есть
__рр
dP=const. • е '2mkT dp\dp^ydp^z, (16.7)
где т— масса электрона, а Т—температура. В этом случае наш ста-
тистический ансамбль описывается не одной волновой функцией ФРо
(16.6), а набором такого рода функций (отличающихся значением на-
чального импульса р0) и вероятностей dP (16.7) начальных импульсов р0.
Каждый подансамбль частиц, описываемый волновой функцией ФРо,
является чистым. Чистые ансамбли смешаны в пропорции, определяемой
вероятностью dP (15.2). Мы имеем дело со смесью. Такого рода смесь
имеет место в опытах Штерна и Эстермана по диффракции Не на
LiF (§ 7), где скорости атомов Не в первичном пучке распределены
по Максвеллу.
§ 17] ПОНЯТИЕ СОСТОЯНИЯ В КВАНТОВОЙ МЕХАНИКЕ И ИЗМЕРЕНИЕ 55
Напротив, в опытах Девиссона и Джермера мы имеем дело с моно-
хроматическим пучком электронов, состояние которого задается одной
волновой функцией, а поэтому там — чистый ансамбль. Конечно, и
в этом опыте, строго говоря, мы могли бы промерить распределение
первичных электронов по скоростям и тогда убедились бы, что они не
вполне монохроматичны, и стало быть, имели бы дело со смесью. Но
ввиду того, что чистые состояния, мало отличные друг от друга, ведут
к одним и тем же (точнее мало отличным) результатам измерения, то
смесь из очень близких чистых состояний можно рассматривать как
чистый случай.
§ 17. Понятие состояния в квантовой механике и измерение
В физике состояние объектов определяется путем измерения вели-
чин, характеризующих эти объекты. Измерения производятся с помо-
щью аппаратов, которые в конечном счете являются макроскопиче-
скими устройствами. Сами объекты измерения в макроскопической
области являются макроскопическими телами. Вместе с тем в макроско-
пической области измерения, по крайней мере в принципе, могут быть
проведены без нарушения состояния измеряемого объекта. Иначе го-
воря, вмешательство аппарата может быть сделано сколь угодно малым.
Иное положение дел имеет место в квантовой области. Здесь мы
имеем дело с измерениями, производимыми над атомными объектами,
над микрочастицами. Аппараты же попрежнему представляют собой
макроскопические устройства, т. е. рассматриваются как системы, под-
чиняющиеся законам макроскопической (классической) физики. В такой
постановке проблемы, характерной для квантовой механики, измерение
не является индифферентным по отношению к состоянию» измеряемых
объектов: влияние измерения в квантовой области» вообще говоря,
не может быть сделано сколь угодно малым.
Переходя к более подробному анализу этого обстоятельства, мы
начнем сперва с классификации измерений. Мы будем различать два
рода измерений: «повторимые» и «предсказуемые» *). Для первого рода
измерений характерно то, что повторение измерения ведет к резуль-
тату» совпадающему с результатом предыдущего измерения (риш,
конечно, нет других причин, которые сами по себе могут изменить
измеряемую величину за промежуток времени, протекающий между двумя
измерениями).
Предсказуемые измерения, отличаются от повторимых тем, что
измеряемая величина меняется в процессе самого измерения так,
что повторение измерения не ведет к прежнему результату**).
Заметим, что это изменение измеряемой величины не является не-
определенным, а может быть указано из результатов измерения. Отсюда
и название «предсказуемое» измерение.
*) Иногда говорят: «измерения назад» и «измерения вперед».
**) Таким образом «повторимое» измерение есть частный случай «пред-
сказуемого».
56
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
[гл. Ш
Приведем пример, иллюстрирующий эти два способа измерения.
Так как нас интересует сейчас принципиальная сторона дела, то мы
можем рассмотреть опыт, который практически трудно осуществим, но
в принципе возможен («мысленный эксперимент»). Именно, пусть мы
измеряем импульс электрона по частоте рассеянного им света. Для всех
рассуждений достаточно воспользоваться законами сохранения импульса и
энергии. Кроме того, простоты ради, ограничимся одним пространствен-
ным измерением (ОХ). Обозначим импульс электрона до столкновения
с квантом света через рх, а после столкновения — через р', частоту
падающего света — через у, а рассеянного через у'. Энергия соответствую-
щих квантов света будет Лу и Лу'. Их импульс будет у и — (для
света, рассеянного назад). Тогда закон сохранения энергии дает
Лу — Луг = (17.1)
а закон сохранения импульса
/zv । Л/ 7'7 Рх Рх* (17.2)
Отсюда легко находим
Рх = тйС v + v' (17-3)
Рх^: А» mGC v-|-v' + 2ОТоС2 (> + >') (17.3')
(Ду = у — у'). Первый член справа в каждом из этих равенств обуслов-
лен эффектом Допплера, а второй — эффектом Комптона.
Если частоты у и у' малы*), то рх=р'х, т. е. импульс до измерения
равен импульсу после измерения. Опыт будет повторимый. Если же у вели-
ко, то благодаря эффекту Комптона р’х=^рх. В результате измерения по-
лучается новое (однако, вполне определенное) значение.измеряемой вели-
чины. Повторение этого опыта приведет к новому результату (до опыта
р'х, после опытар" ит. д.). Это — опыт предсказуемый **). В §§ 102,
103 приведены еще примеры повторимых и предсказуемых опытов по
измерению внутренней энергии атома.
Из приведенного деления опытов следует, что необходимо различать
между результатом измерения какой-либо величины в исходном состоя-
нии и значением этой же величины после измерения (в приведенном
*) Достаточно, чтобы v было мало в системе, в которой электрон по-
коится.
**) Заметим, что такое деление опытов возможно уже и в классической
теории и само по себе не содержит ничего квантового. Так, если мы изме-
ряем импульс частицы рх по отклонению в поле сил, направленных перпен-
дикулярно к оси ОХ, то рх есть интеграл движения и потому опыт повторим.
Если же мы измеряем импульс рх полем сил, направленных параллельно ОХ
(тормозящий потенциал !), то в конце опыта рх = 0 (по сути самого метода).
Это предсказуемый опыт,
§ 17] ПОНЯТИЕ СОСТОЯНИЯ В КВАНТОВОЙ МЕХАНИКЕ И ИЗМЕРЕНИЕ 57
выше примере рх и р'х соответственно). Только для повторимых опытов
необходимость в таком различии отпадает (рх =р'х)-
После этих предварительных замечаний рассмотрим детальнее те из-
менения в состоянии микрочастиц, которые вызываются измерением. Мы
проведем наши рассуждения применительно к импульсу микрочастицы рх
и ее координате х. Пусть нам дано некоторое состояние частицы, изо-
бражаемое волновой функцией ф (х). Выбор ф (х) следует считать про-
диктованным некоторым предшествующим измерением при помощи ма-
кроскопического прибора.
Нам нет сейчас необходимости ближе знать характер этого измере-
ния*). Допустим, что мы измеряем теперь компоненту импульса ча-
стицы по оси ОХ. Пусть мы получили значение импульса, равное р
(мы сейчас имеем в виду результат измерения в исходном состоянии).
Если наш опыт — повторимый, то то же самое значение импульса полу-
чится и после опыта. Если же опыт — предсказуемый, то после опыта
получится иное, хотя 'и вполне определенное значение импульса, ска-
жем р'. Так или иначе, в обоих случаях мы получаем состояние с оп-
ределенным значением импульса (р или р').
Состояние с определенным значением импульса есть волна де-Бройля
(мы возьмем ее для момента £ = 0). Поэтому после произведенного
измерения состояние нашей частицы описывается новой функцией:
1 ip- 1 ip—
* ил« *. (17-0
которая, вообще говоря, не совпадает с ф (х). Таким образом, в ре-
зультате измерения импульса мы получаем новое состояние. В частно-
сти, производя теперь, например, измерения координаты частицы, мы
можем получить такие значения х, которые вообще нельзя было бы
получить, производя измерения этой величины в исходном состоянии
ф(х).
Из этого примера ясно видно, что измерение, даже повторимое,
меняет состояние микрочастиц [исключение представлял бы случай из-
мерения импульса в состоянии с заданным импульсом: ф(х) = фр(х)].
Поэтому, если мы желаем проверить вероятностные предсказания,
вытекающие из задания волновой функции ф (х), то мы должны обя-
зательно обратиться к серии независимых измерений над частицами, на-
ходящимися в состоянии ф (х), т. е. к ансамблю.
Измерения, последовательно производимые над одной частицей, не
будут все относиться к измерениям в состоянии ф (х), так как уже пер-
вое измерение изменит, вообще говоря, состояние частицы [например,,
переведет ф(х) в ф^(х) или фрг (х)].
Обращаясь теперь к измерениям над ансамблем частиц, проследим,
как меняется сам ансамбль в результате производимых измерений. Для.
определенности положим, что речь идет а повторимых измерениях им-
пульса. Произведя всего N измерений на N независимых частицах.
*) По поводу определения <р-функции из измерений#см. § 28»
58 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ [гл. ш
(т. е., попросту говоря, повторяя опыт N раз), мы получим, допустим,
в N1 случаях p—pv в N2 случаях р—р2, в N3 случаях р=р3
и т. д. Тогда состояния частиц после измерения представятся вол-
новой функцией
N2 частиц—волновой функцией
1 ip-^
ф (х) = —=е h (17.6)
и т. д. Каждая из этих подсовокупностей частиц характеризуется одной
волновой функцией и представляет собой чистый ансамбль. Весь же ан-
самбль из N== -(- N2 -J- ... частиц представляет собой смесь состоя-
ний фр1, ф^а, ... Вероятности этих состояний будут ~ . [если N
велико *)]. Согласно § 12 эти вероятности пропорциональны |с(р)|2, т. е.
^ = w(P1)=|C(P1)|2; ^ = w(A) = |C(A)|2;..., (17.7)
где с(р) есть амплитуда волны де-ьроиля ^р(х; в состоянии у уч*
Таким образом мы видим, что измерение переводит чистый ан-
самбль в смешанный. Этот вывод справедлив не только для измерения
импульса, но и для измерений любых величин* **). Если мы теперь об-
ратимся к какому-нибудь подансамблю полученной смеси, например,
к частицам Д/р имеющим импульс px=pv т. е. сосредоточим наше
внимание на одном определенном результате измерения, то мы можем
выразить эффект измерения импульса так: измерение импульса из чи-
стого ансамбля ф (х) с неопределенным значением импульса (Др2 =^= 0)
выбирает ансамбль ф^ с определенным значением импульса. Таким об-
разом, в результате Измерения возникает новое состояние: из ф (х)
возникает ф^ (х), представляющее* новый чистый ансамбль (мы сейчас
имеем в виду один определенный результат измерения p=pj. Этот
новый чистый ансамбль (или чистый случай) характеризуется тем, что
Др2 = 0, а Дх2=оо, т. е. это есть ансамбль с совершенно неопреде-
ленным значением координат частиц, но с определенным значением им-
пульса. Все это нужно понимать так, что если мы теперь на этих ча-
стицах повторим измерение импульса, то мы опять получим р=р13
если же мы произведем измерение координаты, то мы получим, что все
значения х равновероятны, в то время как в исходном состоянии ф(х)
вероятность наблюдения х, x-\-dx была | ф (х) |2 dx. Отсюда ясно, что
измерение меняет состояние частицы и вместе с тем переводит один
статистический ансамбль в другой.
’ АГ ’ * ” и т- п- СУТЬ частости. При большом N мы, как всегда,
отождествляем частости с вероятностями.
**) Исключение представляет тот случай, когда измеряемая величина
имеет определенное значение в исходном состоянии.
§ 17] ПОНЯТИЕ СОСТОЯНИЯ В КВАНТОВОЙ МЕХАНИКЕ И ИЗМЕРЕНИЕ
59
Совершенно подобное же мы получим с измерением координаты х
(а в общем случае и любой механической величины). В состоянии ф (х)
Дх2^=0. Поэтому в разных измерениях мы будем получать значения
x = xv х2, х3, ... Состояние с определенным значением x = xt изоб-
ражается волновой функцией
Эта функция равна 0 для всех х, кроме х = х1 (когда она равна оо).
Собрав вместе одинаковые результаты измерения, мы получим частиц
с х = хр М2 с х —х2 и т. д. У нас возникает смесь, в которой сме-
шаны состояния ... в пропорциях ~ , ... Согласно § 10
^=w(a:1) = |ф(atJ |3, ^ = от(х2) = |ф(х2)|3, ..(17.9)
т. е. измерение координаты в чистом случае ф (х) приводит к смеси
состояний ф^(х). Сосредоточиваясь на определенном результате изме-
рения x = xv мы можем опять сказать, что измерение х из чистого^
ансамбля ф (х) выбирает ансамбль с определенным значением х (фЛ1 (х)),
т. е. переводит состояние ф(х) в фХ1(х).
Наше обсуждение предполагало повторимое измерение. В этом
случае пропорция чистых состояний в возникающей смеси определяется
вероятностями результатов измерения в исходном состоянии (величинами
|с(р)|2 или |ф(х)|2). Мы не будем здесь столь же подробно рассматри-
вать случай предсказуемых измерений. В этом случае, разумеется, также
получается смесь. Однако, пропорция чистых состояний в такой смеси
не определяется непосредственно вероятностями в исходном состоянии.
Чтобы вычислить получающуюся в результате предсказуемого измере-
ния смесь, необходимо еще учесть те изменения измеряемой величины,
которые получаются благодаря действию измерительного аппарата (за-
мена р на /?').
В заключение обратим внимание читателя на то, что взаимоисклю-
чающий характер измерений импульса р и координаты х выражается
очень ясно в том, что измерение р и измерение х переводят ансамбль
ф(х) в различные ансамбли: в смесь фРт(х) и смесь фХп (х) соответ-
ственно. Измерять можно либо импульс, либо координату, но нельзя из-
мерять их одновременно, ибо нельзя перевести частицы сразу в два
различных состояния фРт (х) и ф*п (х).
Новые ансамбли (смесь ф и смесь фх), как и исходный (ф), на ос-
новании изложенного в § 16 подчиняются соотношению неопределенно-
стей Гейзенберга? Таким образом мы видим, что измерения не могут
привести к ансамблю с определенным значением координаты и импульса
частццы. По классической теории, напротив, если даже взять ансамбль
частиц, в котором средние квадратичные Др2 и Дх2 не равны нулю,
то все же путем измерений можно было бы выделить новый ансамбль,
в котором Д/?2 = 0 и Дх2 = 0. В квантовой теории такого рода ан-
самбли возникнуть не могут: измерения р и х носят взаимоисключаю-
щий характер.
60 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гЛ. IV
ГЛАВА IV
ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ
§ 18. Линейные самосопряженные операторы
Как мы видели, в квантовой области не существует таких состоя-
ний, в которых импульс и координата частицы имели бы одновременно
определенные значения. Это обстоятельство находит свое отражение
и в формальной стороне теории: математический аппарат квантовой меха-
ники резко отличается от аппарата классической механики, в которой
задание пары величин р, х обладает полным смыслом. Переходя к из-
ложению этого аппарата, мы в качестве исходного пункта используем
выражения для среднего значения функций координат или импуль-
сов, в состоянии ф(х, у, z)y приведенные в § 13. Именно, мы имели
для среднего значения функции координат частицы (13.1) .
F(x,y, z) = § ф*(х,д, z) F(x,y,z) ф(х,.у,г) dxdydz (18.1)
и для среднего значения функции импульсов (13.6)
F(px,Py,Pt) =
=Jd>* (х,у, z) f(^ — , — ih^, — ih ^) ф (х,у, z)dxdy zfe.(18.2)
Эти формулы получают совершенно одинаковый вид, если проекции
импульса рх, ру, pz изобразить операторами
/>=— ih£-, P==-ih^-, p==-ih4- (18.3)
х ох У ду' z dz ' '
и соответственно этому обозначению написать (18.2) в виде
F^Px^PyyPz) = $ Ф* U,У, z) F(PX ,Py,Pz)ty (х,у, z) dx dy dz. (18.4)
Таким образом мы приходим к изображению функций от импульса
F(р^ ру, рг) оператором F(PX ,Ру,Рг )•
Этот результат подсказывает, что и другие более сложные механи-
ческие величины L(px, pyi pz, х, у, z), зависящие как от координат, так
и от импульсов, также должны изображаться операторами. И в самом
деле, оказывается, что все взаимоотношения между механическими ве-
личинами в квантовой области могут быть выражены на языке операто-
ров определенного класса. В этом заключается фундаментальное значение
введения операторов в квантовую механику.
Чтобы ограничить класс операторов, встречающихся в квантовой
механике,- обратимся сперва к общему определению оператора. Незави-
симо от конкретного вида под оператором L будем разуметь символ,
показывающий, каким способом каждой из рассматриваемого класса
функций и(х) сопоставляется другая функция г>(х). Это символически
записывается в виде умножения и на L:
v = Lu, (18.5)
§ 18] ЛИНЕЙНЫЕ САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 61
В этом равенстве под L можно разуметь, например, умножение на
х(£ = х), дифференцирование по х ^L= или извлечение корня
(L — V ) и т. п.
Из всего разнообразия мыслимых операторов для изображения ме-
ханических величин в квантовой области употребляется один определен-
ный класс операторов, именно так называемые линейные самосопряжен-
ные (иначе — эрмитовские) операторы.
Оператор L называют линейным, если он обладает следующим
свойством:
L(qrZi -\-c2u2) = c1-Lu1 -\-c2-Lu2i (18.6)
где иг и и2— две произвольные функции, а сг и с2— произвольные
числа. Ясно, что V не является линейным оператором; напротив,
есть оператор линейный.
Линейный оператор L называют самосопряженным (эрмитовским),
если имеет место равенство:
У u*i(x)-Lu2(x)-dx = у и2(х)- L*u*(x)-dx, (18.7)
где интеграл взят по всей области изменения переменной х, а и* и и2
суть две произвольные функции весьма широкого класса*). Если пере-
менных много, то под dx следует разуметь dxdydz...
Значение условия самосопряженности, как мы увидим позднее, за-
ключается в том, что только подчиняющиеся этому условию опера-
торы могут изображать вещественные (немнимые) физические вели-
чины.
Поясним свойство (18.7) на примере оператора импульса Рх — —ih .
Имеем
-}-оо -]-оо 1
J «2— — 1йи*и2^ +
— 00 —оо 00
* +00
+ ~^dxz=z J urP*xu\-dx
—oo
1так как n*(zt oo)==zz2(i+: оо) = 0]. Таким образом Рх есть линейный и само-
сопряженный оператор. Легко видеть, что оператор есть линейный, но не
самосопряженный; в самом деле,
+00 л +00 * +л°° *
J uidxdx=- }u^dX^+ J U*tedx-
—00 — 00 — 00
*) Они должны быть интегрируемы и иметь производные, исчезающие на
границах области интегрирования.
62 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
Пользуясь введенной терминологией, мы можем так формулировать
основную идею, на которой основано применение операторов в кванто-
вой механике:
Каждой механической величине L сопоставляется линейный
самосопряженный оператор L. Символически запишем это сопостав-
ление в виде
L—+L. (18.8)
Имея в распоряжении некоторые операторы, мы можем построить из
них другие. Способы построения из простых операторов более сложных
вытекают из значения самих операторов и могут быть сформулированы
в несложных алгебраических правилах. Рассмотрим два линейных и са-
мосопряженных оператора А и В. Будем называть суммой этих двух
операторов такой оператор С, что
Сф = Дф-|-#ф. (18.9)
Символически запишем это в виде
С=ДЦ-^. (18.10)
Например, если A = i-^, а В — х, то из (18.9) следует
С = i з—р х.
дх 1
Несколько сложнее определится умножение. Под произведением двух
операторов А и В будем разуметь такой оператор С, что
С$ = А(В$), (18.11)
т. е. сперва следует подействовать на ф оператором В, а потом на
этот результат подействовать оператором А. Если тот же окончатель-
ный результат может быть достигнут оператором С, то С и будет
произведением А и В. Символически это запишем так:
С = АВ. (18.12)
Пример: A = i-^, В — х, тогда
C& = A(Bb) = i~(x$) = ty + ix
отсюда следует, что
с=/+^^==/(1+х^)-
Существенно, что произведение операторов зависит от порядка мно-
жителей. В приведенном примере имеем:
С'ф=В(Дф) = гх|^ , т. е. C — ix~.
т ' т' дх ох
Поэтому, если, имеются два оператора А и В, то кроме произведения С
существует еще другое произведение:
С'=ВА. (18.12')
Установленные правила позволяют производить с операторами сло-
жение, вычитание и умножение так же, как это делается в обычной
§ 18] ЛИНЕЙНЫЕ САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 63
алгебре, за исключением одного пункта: вообще нельзя менять порядка
сомножителей. Например, оператор
С=(А — В) (А-{-В) = А2 — ВА-\-АВ — В2,
но не равен А2 — В2.
Такая алгебра, в которой нельзя менять порядок множителей, назы-
вается алгеброй некоммутативных величин, а сами величины неком-
мутативными (неперестановочными).
Если оба произведения С и С равны:
АВ — ВА — Ъ, (18.13)
то операторы А и В называются коммутирующими (перестановочны-
ми). В противном случае их называют не комму тирующими. При умно-
жении линейных самосопряженных операторов следует иметь в виду,
что произведение не будет, вообще говоря, также самосопряженным опе-
ратором. Именно,
ДВ = 1(АЯ-]-ВД)4-±(ДВ — ВА). (18.14)
Пользуясь самосопряженностью каждого из операторов А и В, с по-
мощью (18.7) можно доказать, что оператор
Г=^-(ДВ4-ВД). (18.15)
будет самосопряженным, а оператор
G=^(AB—BA) (18.16)
не будет обладать этим свойством, кроме случая коммутирующих опе-
раторов, когда G = 0. Так как всякий оператор коммутирует сам с собой,,
то из сказанного следует, что любая (целая и положительная степень)
линейного самосопряженного оператора А
Д" = Д.Д...,.Д (18.17)
п
будет оператором такого же рода.
Пользуясь изложенными правилами, мы можем, исходя из известных
нам операторов проекций импульса Рх, Ру, Рг (18.3) и операторов
координат частицы х, у, г*), построить более сложные операторы L,
изображающие в квантовой механике величины, аналогичные классическим
.функциям от координат импульсов L (рх, ру, pz, х, у, z).
Вопрос о том, какую именно физическую величину изображает тот или
иной оператор, решается свойствами и способами наблюдения этой вели-
чины. В тех случаях, когда изображаемая оператором L квантовая вели-
чина обладает свойствами, аналогичными свойствам некоторой классической
величины L, — для обеих величин употребляют одно и то же название.
*) Поскольку волновая функция рассматривается как функция координат
частицы х, у, z, постольку действие «операторов» х, у, z сводится просто*
к умножению функции на х, у или z, действие оператора F (х, у, z) — к ум-
ножению на F(x, у, z).
64 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
Разумеется, не все линейные и самосопряженные операторы, образован-
ные из Ру, Рг и х, у, z, будут изображать величины, имеющие про-
стой физический смысл и подчиняющиеся простым законам. Так же обстоит
дело и в классической теории. Так, величина имеет смысл кинетической
энергии и подчиняется закону сохранения (в отсутствии внешних сил),
величина же рх3 не имеет какого-либо общего правила поведения и
поэтому не играет никакой роли в механике.
§ 19. Общая формула для среднего значения величины и
для среднего квадратичного отклонения
Формулы (18.1) и (18.2) дают среднее значение соответственно функ-
ций координат и функций импульса для произвольного состояния ф.
В квантовой механике принимают, что эти формулы имеют общее
значение, т. е. что они справедливы для любой механической величины £,
изображаемой оператором L. В соответствии с этим среднее значение из
результатов измерения величины L в состоянии ф определяют с помощью
формулы
L = j ф*.£ф.у, (19.1)
где под dx разумеется элемент объема в пространстве независимых пе-
ременных и интеграл взят по всей области изменения этих переменных.
Ясно, что (18.1) и (18.2) являются частным случаем (19.1). Чтобы полу-
чить (18.1) из (19.1), следует положить L — F(x, у, z), а под Ура-
зуметь dxdydz. Чтобы получить (18.2), следует положить
£ = F — ш-г-, — ш, — th-к-] .
\ дх ду’ dz)
На основании свойства самосопряженности оператора £, мы можем на-
писать (19.1) в эквивалентной форме:
Z= (19.Г)
[для этого полагаем в (18.7) «* = ф*, «2 = ф]. Из сравнения (19.1)
и (19.1') следует, что
£ = £*, (19.2)
т. е. среднее значение величины, изображаемой самосопряженным опе-
ратором, вещественно.
Мы получим более детальные сведения о величине £, если вычислим по-
мимо ее среднего значения L еще и среднее квадратичное отклонение Д£2,
указывающее, насколько в среднем отклоняются результаты отдельных
измерений от среднего значения. Вычислим Д£2. Для этого следует по-
строить оператор, изображающий величину Д£2. бтклонение от сред-
него определяется, как Д£ = £ — £. Стало быть, оператор, изображаю-
щий его, будет
Д£ = £ —£.
(19.3)
§ 20] СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ 65
Так как квадрат отклонения Д£2 = (£— £)2, то оператор для Д£2 будет
(Д£)2==(£ —£)2i (19.4)
Пользуясь общим определением среднего значения (19.1), мы найдем:
AZ2==J$*.(AI)2(|>.rfx. (19.5)
Таким образом, зная оператор £, мы можем вычислить и Д£2.
Величина ДА2 должна быть положительной. Это легко доказать, поль-
зуясь самосопряженностью оператора £. Так как L есть число, то опера-
тор Д£ есть также оператор самосопряженный. Поэтому, пользуясь (18.7)
и полагая в (19.5) = (Д£ф) = iz2, находим:
Д/2 = J (Д£ф) (Д£*ф*) dx = J | Д£ (19.6)
так как | Д£ф |2 0, то из (19.6) следует, что
‘Д£2^0, (19.7)
т. е., как и должно быть, среднее квадратичное отклонение всегда
положительно или равно нулю.
§ 20. Собственные значения и собственные функции операторов
и их физический смысл. «Квантование»
Формулы предыдущего параграфа дают выражение для среднего
значения £ и среднего квадратичного отклонения Д£2. Эти формулы
еще ничего це говорят о том, каковы будут значения величины £ в от-
дельных измерениях.
Чтобы найти возможные значения величины £, обратимся к таким
состояниям в которых интересующая нас величина имеет только
одно значение £. В таких состояниях среднее квадратичное отклоне-
ние Д£2 = 0. Стало быть, для этих состояний на основании (19.6)
имеем:
J | Д£ф£ |2 dx~ 0. (20.1)
Так как под интегралом стоит существенно положительная величина,
то из (20.1) следует:
|Д£ф£|2 —0.
Но модуль комплексного числа равен нулю только тогда, когда само число
равно нулю. Поэтому мы получаем:
Д£ф£ = О
или, имея в виду значения оператора Д£ (19.3) и то, что в рассматривае-
мом состоянии £=£, мы находим окончательно
= (20.2)
Ввиду того, что £ есть оператор, найденное нами равенство является
дифференциальным уравнением для определения волновой функции
5 Блохинцев
66 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гЛ. IV
того состояния, в котором представляемая оператором L величина имеет
значение L.
На первый взгляд это уравнение определяет ф£, но ничего не го-
ворит о возможных значениях L. Однако, это не так. Дело в том, что
не любые решения уравнения (20.2) могут нас удовлетворить, а только
конечные, непрерывные и однозначные во всем интервале изменения
независимых переменных. Первое из этих требований есть требование
конечного значения вероятности | ф |2, второе определяет однозначную
связь состояния в одной области пространства с состоянием в соседней,
а третье требование есть требование того, чтобы волновая функция
в каждой точке пространства имела только одно определенное значение *).
Эти необходимые и весьма скромные требования, предъявляемые
к решениям уравнения (20.2), ведут к тому, что во многих случаях
решения, обладающие указанными свойствами, существуют не при всех
мыслимых значениях А, а лишь при некоторых избранных значениях L =
— А,; £2,..., Lny...
В математике задача о нахождении указанных решений носит назва-
ние задачи о нахождении собственных функций ф£ уравнения и соб-
ственных (иногда говорят характеристических) значений параметра
уравнения L. Вместо «уравнения» мы чаще будем говорить о собствен-
ных функциях и собственных значениях оператора L, которым и
определяется вид уравнения (20.2). Мы будем считать, что никаких иных
значений величины L нельзя наблюдать на опыте, кроме тех, которые
получаются в состояниях с определенным значением L (т. е. в которых
\LP = 0). Иными словами, совокупность собственных значений опера-
тора L: Lp Ь2, ..., Ln, ... и дает те значения механической вели-
чины L, которые могут наблюдаться на опыте.
Соответствующие состояния определяются собственными функциями
Фр Ф2> • • • >Ф«, ’ • • В каждом из этих состояний ДА2 = 0 и величина L
имеет только одно значение Л2, ... £л, ... соответственно. Сово-
купность возможных значений величины мы будем называть спектром
этой величины.
Спектр может быть дискретным, когда возможны только отдельные
значения Lv L2, ... Ln, ... г либо состоящим из отдельных полос,
так что возможные значения L лежат в интервалах: ==С L L2,
”) Как показало дальнейшее развитие квантовой механики (релятивистское),
предъявленные нами требования к ^-функции на самом деле чрезмерно
жестки. Так, например, достаточно требовать интегрируемости | ф |2, а не ко-
нечного значения <[> (интегрируемость | <[> |2 означает требование конечности
не по отношению к плотности вероятности | <[> |2, а по отношению к вероятности
найти частицу в любом конечном объеме, равной J | ф |2rZV). Далее, не обяза-
тельно требование однозначности ф, а достаточно требования однозначности
вероятности (так как сама функция ф не является наблюдаемой величиной).
Однако, в рассматриваемых в этой книге задачах эти менее жесткие требова-
ния сами собой приводят к указанным в тексте более жестким требованиям.
Прэтому мы будем придерживаться их. См. по затрагиваемому вопросу статью
W. Р a u 1 i, Handb. d. Phys., т. XXIV, I, стр. 123.
§ 21] ОСНОВНЫЕ СВОЙСТВА СОБСТВЕННЫХ ФУНКЦИЙ 67
вообще Ln^. L^Ln+v либо, наконец, непрерывным, когда
все значения L оказываются возможными. Когда возможные значения
величины являются дискретными, то говорят, что величина идоеет кван-
тованные значения.
В примитивной теории Бора отсутствовали методы, позволяющие в об-
щем виде решить вопрос о возможных значениях той или иной величины,
в частности, найти квантовые значения. Современная квантовая механика
полностью решает этот вопрос, сводя его к чисто математической за-
даче нахождения собственных функций и собственных значений операторов,
изображающих механические величины.
Из самосопряженности оператора L следует, что наблюдаемые зна-
чения L будут: вещественны:
Ln = L*n или L = Z*. (20.3)
В самом деле, собственное значение Ln (или L) можно рассматривать
как среднее значение величины L в собственном состоянии фя (или ф£
соответственно). Но среднее значение величины, изображаемой самосопря-
женным оператором, вещественно [ср. (19.2)].
Этим полностью разъясняется значение самосопряженности операто-
ров: ^самосопряженные операторы изображают вещественные вели-
чины.
§ 2L Основные свойства собственных функций
Обратимся к рассмотрению важнейших свойств собственных функций
самосопряженных операторов. Сперва ограничимся случаем дискретного
спектра. Пусть мы имеем какие-либо две функции иг и и2. Эти функции
будут называться ортогональными, если
^u\u2dx = 6, (21.1)
причем интеграл взят по всей области изменения переменных. Для про-
стоты мы обозначаем все переменные одной буквой х.
Теорема, которую мы желаем доказать, заключается в том, что соб-
ственные функции фЛ и §]п самосопряженного оператора £, принадлежа-
щие различным собственным значениям Ln и Lm, ортогональны между
собой, т. е.
(21.2)
В силу предположения о том, что фл и фт являются собственными
функциями, мы можем написать:
LK = Ln$m> L^n = Ln^n- (21.3)
Из первого уравнения получим комплексно сопряженное:
= (21-Зг)
[напомним, что согласно (20.3) — Умножая второе из уравне-
ний (21.3) слева на а (21.3') на фя, вычтем одно из другого. Тогда
получится:
5*
68 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гл. IV
Интегрируя это равенство по всей области изменения переменных, будем
иметь
\K-^ndx-^n-L^^dx==(Ln-Lm^^ndx.
В силу самосопряженности L левая часть равна нулю [следует в равен-
стве (18.7), определяющем самосопряженность, положить =
— а2], следовательно,
Так как Ln=^= Lm, то отсюда следует справедливость (21.2).
Функции дискретного спектра всегда интегрируются квадратично,
поэтому мы можем нормировать их к 1:
(21.5)
Это последнее равенство можно объединить с равенством (21.2) в одно:
(21.6)
где символ Ьтп определяется следующим образом:
I (21.7)
о^ = О, если п^т. \ v
Системы функций, удовлетворяющие (21.5), мы будем называть орто-
гональными и нормированными системами функций.
В значительном большинстве случаев, встречающихся в квантовой
механике, собственному значению Ln оператора L принадлежит не одна
функция фп, а несколько собственных функций^ фл2, ...,
..., . Такие случаи называются вырожденными. Если значению
L — Ln принадлежит / собственных функций, то говорят о наличии
f-кратного вырождения. Физический смысл «вырождения» заключается
в том, что какое-нибудь определенное значение величины L = Ln может
быть реализовано в разных состояниях.
Доказанная нами теорема об ортогональности собственных функций
относится лишь к функциям, принадлежащим к разным собственным
значениям. В случае вырождения функции (k— 1, 2, ..., /) отно-
сятся к одному и тому же собственному значению Ln:
^nk = Ln\k, k=l, 2, ..f. (21.8)
Поэтому они не будут, вообще говоря, ортогональными. Однако, можно
доказать *), что эти функции могут быть всегда выбраны так, что они
будут также ортогональны между собою:
(21-9>
Поэтому условие (21.6) можно считать всегда выполненным, если под
т и п в общем случае разуметь не один индекс, а всю совокупность
*) См. дополнение II.
§ 21] ОСНОВНЫЕ СВОЙСТВА СОБСТВЕННЫХ ФУНКЦИЙ 69
индексов, характеризующих собственную функцию (например, вместо
т — два индекса т и k\ вместо п также два индекса п и k).
В том случае, когда оператор L имеет непрерывные собственные
значения, доказанные теоремы непосредственно неприменимы. Однако,
и в этом случае собственные функции обладают свойствами, аналогич-
ными свойствам функций дискретного спектра.
Собственные функции непрерывного спектра нельзя перенумеровать
числами. В этом случае функции зависят от собственного значения L,
как от параметра, так что мы можем написать:
ф£(х)=ф(х, £), (21.10)
где через х обозначены переменные, в которых выражен опера-
тор L,
Свойства ортогональности собственных функций непрерывного спектра
проще всего могут быть выражены с помощью особого символа S (L1 — Z),
называемого функцией Дирака или ^-функцией. Этот символ опреде-
ляется формулой:
ь
— L)dLf — 0, если точка L-—L лежит вне ин-
fl
тервала (а, Ь); ц)
У У(ЛГ) 5(ЛГ — L) dL' если точка U — L лежит внутри
а
интервала (а, Ь), ,
где f(L') — любая (достаточно гладкая) функция. Можно доказать*),
что функции непрерывного спектра ф (х, L) могут быть нормированы
так, что
j ф*(х, £')ф(х, £)rfx = 5(L' —L), (21.12)
что выполняется аналогично (21.6), ибо из (21.11) следует пола-
гая /(£')= 1], что §(£'— L) = 0 всюду, кроме точки = где S
обращается в бесконечность. Таким образом, символ 8 (И— L}
играет ту же роль, что и символ Ьтп в случае дискретного
спектра.
В математике доказывается, что система собственных функций one
ратрра очень широкого класса является не только системой ортогональ-
ных функций, но системой полной.
Это означает, что любую функцию ф(х), определенную в той же
области переменных и подчиненную тем же граничным условиям, что
и собственные функции фп(х), можно представить в виде ряда из этих
собственных функций:
Ф(*) = 2^ЯФЯ(-Р). (21.13)
*) См. дополнение Ш.
70 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гЛ. IV
Пользуясь ортогональностью функций фп, мы можем определить коэффи-
циенты сп и таким образом найти ряд, представляющий ф (х) *).
Для этого умножим (21.13) на ф^(х) и проинтегрируем по всему
пространству:
f 'К (х) Ф (*)dx = S сп j (х) Ф„ (х) dx.
В силу ортогональности и нормировки функций фл, интегралы, стоящие
под знаком суммы, равны Ьтп [см. (21.6)]; таким образом,
К (*) Ф (•«)dx = 2 спьтп=ст.
w п
Отсюда, меняя обозначение т на и, получаем:
c„=J ф;(*)Ф(*и*- (21.14)
Таким образом, зная ф и систему ортогональных функций фя, мы мо-
жем найти все амплитуды сп, встречающиеся в ряде (21.12). Частным
случаем таких разложений по ортогональным функциям являются ряды
Фурье.
В случае непрерывного спектра имеет место разложение в интеграл,
подобный интегралу Фурье. Именно, в этом случае
ф(х) = р(Л)ф(х, L)dL. (21.15)
Для определения коэффициентов c(L) умножим (21.15) на ф*(х, L')
и проинтегрируем по х:
j ф* (х, L') (х) dx — § c(L)dL* § ф* (х, £')ф(х, L)dx=^
= ^c(L)dL-b(U — L) = c(U).
Меняя здесь обозначение L! на £, получим окончательно:
c(£)=j<|>*(x, L}ty(x)dx. (21.16)
Найденные нами представления любой функции в виде разложений
(21.13) и (21.16) по собственным функциям операторов приводят к очень
важному выводу: любое состояние, изображаемое волновой функцией
ф (х), может быть представлено в виде суперпозиции (21.13) или (21.16)
*) Мы ограничиваемся указанием способа нахождения коэффициентов сп
ряда (21.13). Относительно понятия полноты, системы ортогональных функций
и сходимости написанного ряда к функции ф(х)см. Курант и Гильберт,
Методы математической физики, т. I, ГТТИ, 1933, гл. II, § 1. Сам термин
«полнота системы» функций (иногда говорят «замкнутость» системы) легко
может быть уяснен из следующего соображения. Пусть мы имеем последо-
вательность ортогональных функций, совпадающую с последовательностью
но не содержащую, скажем, функции <1ц(п=1). Эта система функций
(<|>2, •••» •••)» как и система (<[ц, ф2, <|>3, ..., <[>л, ...), будет ортогональ-
ной, но не полной, так как по ней нельзя представить в виде ряда любую
функцию (именно, нельзя представить <|ц). Доказательство полноты системы как
раз и заключается в доказательстве отсутствия подобных пропусков.
§ 22] ВЕРОЯТНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ 71
состояний, относящихся к определенному значению какой-либо механи-
ческой величины. В самом деле, состояния фп или ф (х, L) по самому
своему определению суть состояния, в которых некоторая механическая
величина L имеет определенное значение Ln (либо соответственно L).
А выражения (21.13) и (21.16) представляют ф(х) в виде суммы (либо
интеграла) этих частных состояний.
§ 22. Общий метод вычисления вероятностей результатов
измерения
В предыдущем было показано, как находить среднее значение L
любой величины, изображаемой оператором Д, и как находить возмож-
ные значения Lv ..., ... такой величины. Теперь мы перейдем
к вычислению вероятности того, что в некотором состоянии ф (х) в ре-
зультате произведенного измерения механической величины L будет
обнаружено значение Lt=Ln. Основная идея вычисления базируется на
принципе суперпозиции состояний. Пусть собственные функции опера-
тора L будут фл(х). На основании свойства полноты и ортогональности
этих функций мы можем представить волновую функцию ф в виде супер-
позиции
Ф(*)=5СЛ<*)- (22.1)
п
Для сопряженной функции получим:
ф*(х)=24Х(-*) (22.Г)
т
(где т пробегает те же значения, что и п).
Подставляя эти выражения для ф и ф* в формулу для среднего
значения величины L в состоянии ф, мы найдем:
(22-2)
пт*1
так как фй есть собственная функция оператора £, то
4,=^- (22.3)
Пользуясь (22.3) и ортогональностью функций ф^, и фл, мы получаем
вместо (22.2)
1=22 - 2#A-
п т п
т. е.
1 = 2 (22.4)
п
Далее, умножая (22.1) на (22.Г) и интегрируя по всему пространству,
получаем:
1=22^„ J ^„^=2^4*™ =2к I2
пт т п' п
или
2К1г=1- (22.5)
п
72 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
С другой стороны, если через w(Ln) обозначить вероятность того, что
случайная величина L имеет одно из возможных значений £п, то по
общему определению среднего имеем:
А = 3>(АП)АЯ (22.6)
п
при условии
5>(А„)=1. (22.7)
Сравнение (22.6) и (22.7) с (22.4) и (22.5) показывает, что
w(AB) = |cn|2. (22.8)
Т. е. вероятность найти значение механической величины L равным
одному из ее возможных значений Ln равна квадрату модуля ам-
плитуды собственного состояния фп. Иными словами, эта вероятность
определяется интенсивностью | сп |2, с которой собственное состояние фл
представлено в состоянии ф.
Для вычисления вероятностей того или иного значения величины,
имеющей непрерывный спектр, поступаем совершенно аналогично тому,
как было сделано в случае дискретного спектра. Именно, разложим
рассматриваемое состояние ф по собственным функциям ф (х, L) опера-
тора L:
ф (х) = у с (L) ф (х, L) dL; (22.9)
при этом ф(х, L) нормировано к 8-функции, а ф к 1.
Вычислим опять среднее значение L в состоянии ф:
с* (Г) ф* (х, Г) dL! • L J с (L) ф (х, £) dL dx,
и так как ф (х, L) есть собственная функция, то
£ф(х, £) = £ф(х„£);
подставляя это в предыдущее выражение для L и меняя порядок интег-
рирования, получим:
Z=yjc*(A')c(A)z/A'dA.A J ф*(х, А’)ф(х, L)dx
и в силу (21.12):
Z = J J с* (£’) с (A) dL' dL AS (А' — А).
На основании свойств 8-функции отсюда следует
А= У | с (А) I2 А <7А. (22.10)
Подобным же образом получаем
1 = J ф*фйх = рх J с* (А') Ф (х, A’) dL' • J с (А) ф (х, A) dL =
== f [ с* (А') с (A) dL'dL-8{L’ — А) = ( | с (А) |2 dL,
А==у ф*-Аф-</х=Н
т. е.
У |с(А) |2</А= 1.
(22.11)
§ 22]
ВЕРОЯТНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
73
Если вероятность того, что значение непрерывной, случайной величины
лежит между L и L-\-dL есть w(£)d£, то по общему определению
среднего значения
при условии
L = ^w(L)LdL
^w(L)dL=l.
(22.12)..
(22.13)
Сравнивая (22.12) и (22.13) с (22.10) и (22.11), получаем:
w(L)dL~\c(L)\2dL. (22.14)
Таким образом и в случае непрерывного спектра мы приходим к стати-
стической интерпретации интенсивностей собственных состояний | с (L) |2 *).
Приведенные выше формулы справедливы лишь для чистого ансамбля,
характеризуемого одной волновой функцией ф (х). Для смешанного
ансамбля предыдущие формулы должны быть несколько обобщены.
Пусть мы имеем смешанный ансамбль, образованный из чистых
ф2, ..., фа, ..., смешанных в пропорции Pv Р2, ..., Ра, ...
Тогда, если вероятность найти значение Ln некоторой величины L в чи-
стом ансамбле фа есть (LJ, то полная вероятность найти L~Ln
в смешанном ансамбле будет равна
(22.15)
Подобным же образом для величины, имеющей непрерывный спектр,
будем иметь:
w (L) dL=^ Pawa (L) dL, (22.16)
a
причем
wa(Z-) = ka(Z.)|\ (22.17>
где can и ca(L) суть амплитуды собственных функций оператора L
фл(х) или соответственно ф(х, L) в разложении фа(х). В соответ-
ствии с формулами (22.15) и (22.16) среднее значение величины L
в смешанном ансамбле есть
1 = 2 (22.18)
«
где есть среднее значение L в чистом ансамбле фа:
ь;=5ф:^ф^ (22.19)
*) Заметим, что формула (22.12) содержит как частный случай формулы
(12.4) для вероятности импульса. Действительно, с(рх, ру, рг) есть амплитуда
состояния фр, состояния с определенным импульсом, иными словами, — соб-
ственного состояния оператора импульса. Поэтому с(рх, ру, р2) и e{L)
в (22.14) имеют один и тот же смысл. Дря перехода от (22.14) к (12.4) доста-
точно разуметь под L три компоненты импульса р*, ру, pz и соответственно
под dL произведение dpxdpydpr
74 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
§ 23. Условия возможности одновременного измерения разных
механических величин
Мы видели, что в квантовой области не существует таких состояний
частиц, в которых импульс и соответствующая ему координата одновре-
менно имели бы определенное значение. В таком же взаимо исключаю-
щем друг друга отношении находятся и многие другие величины.
В самом деле, чтобы существовали состояния, в которых две величины
L и М одновременно имели бы определенные значения (ДА)2 —О,
(АЛ/)2 = 0, нужно, чтобы волновая функция такого состояния была
общей собственной функцией операторов L и М. Между тем уравнения
для собственных функций операторов L и М
L^l=L^l и (23.1)
имеют, вообще говоря, различные решения
Поэтому в состояниях-ф£, с определенным значением L (ДА2 = 0),
’величина М не имеет определенного значения (ДЛ42 0) и, наоборот,
в состоянии фдр с определенным значением М. (ДЖ2 = 0), величина L
не имеет определенного значения (ДЛ2^>0).
Только в особых случаях две величины L и М имеют одновременно
определенное значение (для этого нужно, чтобы Можно по-
казать, что условием того, чтобы две величины L и М всегда могли
иметь одновременно определенные значения, является коммутативность
их операторов L и М. Иначе говорз^ должно иметь место операторное
„равенство*):
LM = ML. (23.2)
Напротив, если
(23.3)
то величины L и М не имеют одновременно определенных значений
(кроме, может быть, исключительных).
Две величины, изображаемые коммутирующими операторами,
по крайней мере в принципе могут быть измерены одновременно.
Две величины, изображаемые некоммутирующими операторами, не
могут быть измерены одновременно. Измерение одной из таких ве-
личин L ведет к состоянию ф£. Измеряя в этом состоянии 7И, мы по-
лучим некоторое новое состояние не совцадающее с исходным ф7.
Иными словами, измерение одной из таких величии меняет состояние
системы таким образом, что значение другой величины становится не-
определенным.
Мы видим, что и в общем случае мы встречаемся с влиянием изме-
рительного аппарата на состояние системы, подобным рассмотренному
выше на примере измерения импульса и координаты (ср. §§ 14, 17).
Поэтому всякий аппарат, применяемый в квантовой области для изме-
рения механических величин, относящихся к микрочастицам, должен быть
♦) См. дополнение IV.
§ 24] ОПЕРАТОРЫ КООРДИНАТЫ И ИМПУЛЬСА ЧАСТИЦЫ
75
тщательно рассмотрен с точки зрения анализа значения получаемых с его
помощью результатов измерения и тех изменений в состоянии системы,
к которым он может приводить. Примеры такого анализа приведены
в §§ 102, 103. Всякого рода догматические суждения, йе основанные
на анализе конкретного устройства аппарата, могут йривести к ошибоч-
ным выводам.
§ 24. Операторы координаты и импульса частицы
Поскольку волновая функция рассматривается нами как функция
координат частицы, постольку оператор координаты частицы х есть само
число х. Действие функции координат частицы F(x, у, z) как опера-
тора сводится просто к умножению ф (х, у, z) на F (х, у, z).
При этом же выборе переменных *) в волновой функции операторы
проекций импульса частицы в соответствии с § 13 будут:
p'=~lhh- <24-»
или в векторной форме:
— ihV, (24. Г)
где V есть оператор градиента (набла).
Операторы проекций импульса и координат подчиняются определен-
ным правилам перестановки, которые очень облегчают расчеты с ними.
Пусть ф(х, у, z) есть волновая функция; тогда имеем:
х (Р ф) ==х ( — ih ) = — ihx ~ ,
v \ дх/ дх'
Рх (*Ф) = — ih (*Ф) = —ihx
Вычитая вторую строку из первой, находим: (хРх — Ф = ihty,
т. е. хРх — Р*х — ih, (24.2)
и аналогичным образом ypy—pyy=ih, (24.2')
zPz — Pzz = ih. (24.2")
Эти правила перестановок носят название перестановочных соотноше-
ний Гейзенберга.
Легко видеть, что xPy — Pyx—0, (24.3)
уРг-Ргу = 0, (24.3')
zPy — Pyz=Q (24.3")
и т. д.
*) Возможность другого выбора независимых переменных в волновой
функции рассмотрена в гл. VIII,
76 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
Подобным же путем можно установить более общие перестановочные
соотношения для любой функции F(x, у, z) и операторов импульса.
Именно:
dF
FPx-PxF=ih°£, (24.4)
FP„-~PvF=ihd-f, (24.4')
у у ду х
dF
FPz — PzF=ih°-F. (24.4")
Из этих соотношений следует, что импульс нельзя измерить одновре-
менно с функцией от координат, если последняя содержит ту коорди-
нату, проекцию импульса вдоль которой хотят измерить.
Определим теперь собственные значения и собственные функции опе-
ратора проекции импульса на какую-нибудь ось (например, ОХ). Со-
гласно изложенному в § 20 уравнение для собственных функций опе-
ратора импульса имеет вид
РХ$ = РХ^ (24-5)
где рх—собственное значение. Имея в виду значение получаем:
(24.5')
Это уравнение легко интегрируется, и мы получаем:
£РхХ
= h , (24.6)
где N — постоянное число. Для того, чтобы это решение было всюду
конечным (непрерывность и однозначность этого решения очевидны),
достаточно, чтобы рх было любым- вещественным числом. Поэтому спектр
собственных значений Рх получается непрерывным:
— оо °0- (24.7)
Множитель /V можно выбрать так, чтобы функция была нормиро-
вана к S-функции. Для этого нужно положить N= (2тг/г)-1/3 *) так, что
окончательно нормированные и ортогональные собственные функции
оператора Р будут
1
(24-8’
( Фр- (•*) 'Ы (X) dx = b (р’х — Рх). (24.9)
J X
То, что мы получили в качестве собственных функций импульса фРа>
плоские волны де-Бройля, не может быть неожиданным. То, что волна
де-Бройля есть состояние с определенным значением' импульса, было
в сущности исходным пунктом (§ 7).
*) См. дополнение III, формулу (20).
§ 25]
ОПЕРАТОР МОМЕНТА ИМПУЛЬСА ЧАСТИЦЫ
11
§ 25. Оператор момента импульса частицы
Под моментом импульса частицы (моментом количества движения)
в классической механике понимают векторное произведение импульса
частицы р на радиус-вектор г, проведенный от некоторой избранной
точки (например, центра сил) к частице:
М = [рг]. (25.1)
Значение этой величины в механике определяется тем, что она является
интегралом движения в поле центральных сил.
В квантовой механике момент импульса изображается оператором
— [Рг], (25.2)
—►
где Р—оператор (векторный) импульса (24.1), а г — радиус-вектор.
Основанием к такому выбору оператора момента импульса является не
просто внешняя аналогия с классическим выражением (25.1), но то, что
изображаемая оператором М величина является также интегралом дви-
жения в поле центральных сил (ср. § 33) и обладает свойствами, ана-
логичными свойствам момента импульса в классической механике.
Операторы проекций момента импульса на оси координат, соот-
ветственно значению векторного произведения (25.2), суть:
М* = Ргу - Pvz = th (г - у ^),
My = P^-p^ = ih(zTx-xT2) '
М,~Рх — Р y=zih(x"—У ,
г У х' \ ду dx / '
и, наконец, оператор квадрата момента импульса есть
' v 1 | \ ду dz} '
(25.3)
(25.4)
Найдем правила перестановки для компонент момента импульса. Эти
правила понадобятся нам в дальнейшем, а сейчас они могут служить
иллюстрацией приемов алгебры операторов. Вычислим коммутатор
G~-MyMz — MrMv. Подставим сюда вместо Му и Мг их выраже-
ние (25.3). Вычислим сперва МуМг:
Мумг = (Ргх — Pxz) {Рху — Рух) = РгхРху — PzPxy —
— 4- PxzPyx — уРгхРх—zyP‘~x — x~PzPy -|- zPyPxx
(так как у и Р7, Рх, z и Pv Ру перестановочны). Подобным же
образом
МгМу = yPfx — zyp* - х^РгРу 4- zPyxPx,
Вычитая из первою равенства второе, найдем:
— Л1гА1, ~уРг (хРх — Рхх) -|~ zPy (Рхх — хРх).
78 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гЛ. 1V
Пользуясь теперь (19.4), получаем:
ММ, — М,Мv = ih(yPz — Pz) = ihM .
у z z у z у ' X
Меняя циклически x, у, z, получим все три перестановки:
МуМ2 — M,My=ihMx, (25.5)
МгМх — MxM2=ihMy, (25.5')
ММ — MM==ihM„. (25.5")
Таким образом, операторы компонент момента импульса некомму-
тативны.
Напротив, каждая из компонент импульса коммутирует с ква-
дратом полного момента импульса*.
МХМ2 — М2МХ = 0, (25.6)
МуМ2 — М2Му = 0, (25.6')
М,М2 — 7И2Мг = О. (25.6")
Доказательство этого положения предоставляем читателю.
Из этих правил перестановки следует, что проекции момента импуль-
са Мх, Му, М, не могут быть одновременно измерены. В состоянии,
в котором одна из проекций имеет определенное значение (ДЖ2 = 0),
другие две проекции не имеют определенного значения (ДЛ42^>0,
Д2И2^>0). Напротив, любая из проекций и квадрат полного момента
могут быть измерены одновременно.
Определим теперь возможные значения проекции момента импульса
на какое-либо произвольное направление и возможные значения абсо-
лютной величины момента (точнее — значения 7И2). Для решения этой
задачи удобно перейти к полярной системе координат, взяв избранное
направление за ось OZ. В этой системе координат
x — r sin 0 cos ср, y = r sin 0 sin ср, z — г cos 0, (25.7)
где 0 есть угол между осью OZ и радиусом-вектором г, а ср — угол,
отсчитываемый в плоскости ху от оси ОХ.
Несколько громоздкое преобразование формул (25.3) из декартовой
системы координат в полярную приводит к следующему результату:
z7z(sin<p^4-ctg0c°s<p^), (25-8>
Му==— ih (coscp ^4- ctg 6 sin <p J0, (25.8')
(25-8">
M^-h?^, (25.9)
где есть так называемый оператор Лапласа для сферы:
Vi —+ (25.10)
0» ? sin 6 дв \ eft J [ sm2 0 '
§ 25J
ОПЕРАТОР МОМЕНТА ИМПУЛЬСА ЧАСТИЦЫ
79
Так как операторы (25.8) и (25.9) действуют только на углы 0,
то волновую функцию достаточно рассматривать в зависимости лишь от
этих углов, т. е.
Ф = Ф(О, ср). (25.11)
Уравнение для определения собственных значений оператора М2 согласно
(20.2) (полагаем там L — M2, L = M2) будет
М2ф = Ж2ф. (25.12)
Вставляя сюда Л12 из (25.9) и обозначая
* = (25.13)
мы получим уравнение (25.12) в виде
J-slfsinO^)+^4fl^+x<I’ = 0- (25.14>
sin 0 дО \ д§ J 1 sin2 0 д<р2 « * \ f
Это уравнение мы должны решить для всей области переменных
6, ф (О 0 тг, 0 ср 2тг), причем интересующие нас решения должны
быть конечными, непрерывными и однозначными. Уравнение (25.14)
хорошо известно. Это — уравнение для шаровых функций. Подробности
об этих функциях и о решении уравнения (25.14) приведены в допол-
нении V. Здесь мы ограничимся лишь кратким резюме.
Оказывается, что решения этого уравнения, удовлетворяющие по-
ставленным условиям, существуют не при всех значениях 1, а лишь при
1 —/(/4-1), (25.15)
где / — целое положительное число.
При каждом таком значении / имеется 2/ —р 1 решений, которые
представляют собой шаровые функции. Мы обозначим их так:
<?) = / Л|ст|(^6)^, (25.16)
где число пг — целое число и ограничено следующими значениями т:
±1, ±2, ..., ±/; /=1, 2, 3, ... (25.17)
(всего 2/4~1 значений). Знаком \т\ обозначено . абсолютное значение
числа т. Функция т I (cos 6) определяется так:
J-^LL Л т |
(E)==(l-^) 2 '^Р№ £ = cosO, (25.18)
причем Pz(£) есть так называемый полином Лежандра:
(25.19)
Множитель, стоящий перед р\т\ выбран так, чтобы ортогональные
функции Yt т были, кроме того, и нормированными к 1 на поверхности
80 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [гл. IV
шара, т. е. *):
it 2тг
(25.20)
о о
Используем теперь этй известные математические результаты для
нашей задачи. Как уже было сказано, уравнение (25.14) имеет одно-
значные и конечные решения лишь при значениях А = I (l-\- 1). Поэтому
собственные значения оператора квадрата момента импульса будут
ТИ2 = Л2/(/-|-1); Z=0, 1, 2, ..., (25.21)
а соответствующие собственные функции суть
К(9. <р)—гп = о, ±1, ±/. (25.22)
Собственному значению (25.21) принадлежат всего 2Z —I собствен-
ная функция, отличающиеся значением числа т. Таким образом, мы
имеем дело с случаем вырождения (см. § 21). Сущность этого выро-
кдения легко уяснить себе, если обратить внимание на то, что собствен-
ные функции оператора квадрата момента импульса М2 являются также
собственными функциями оператора проекции момента импульса на ось
В самом деле, уравнение для собственных функций оператора есть
= (25.23)
подставляя сюда Mz из (25.8"), получим:
— ik^- = Мг$.
Если сюда подставить ф//и, то, имея в виду, что пропорционально е1т\
мы найдем:
т. е. уравнение (25.23) удовлетворяется функцией причем собствен-
ные значения оператора равны
Mz — hm, т = 0, ±1, ±/. (25.24)
Отсюда следует, что состояния при заданном полном моменте 7I42
(дано /), различающиеся индексом т, суть состояния с различными про-
екциями момента на ось OZ.
Полученный нами результат показывает, что возможные значения
абсолютной величины момента импульса (25.21) и возможные значения
проекции момента импульса на произвольную ось OZ (25.24) имеют
квантованные значения. Никакие другие значения, кроме приведенных, не
могут оказаться результатом измерения. В состояниях, в которых /И2 и
Mz имеют определенные значения, Мх и не имеют определенного
значения (кроме случая I— 0, когда М2 = Мх — My — Mz==0)f так как
*) Координаты 0 и ср отмечают точки поверхности шара. Элемент поверх-
ности шара равен sin 0 d® dy, а не dO
§ 26] ОПЕРАТОР ЭНЕРГИИ И ФУНКЦИЯ ГАМИЛЬТОНА 81
функции (25.22) не являются собственными функциями операторов
и Му [(25.8), (25.8')], в чем можно убедиться непосредственно. Это же
вытекает из факта некоммутативности Мх, Му, Mz.
Разумеется, что возможные значения Мх и Му таковы же, как и Mz
(25.24), ибо направление OZ ничем не выделено, и чтобы убедиться
в справедливости нашего утверждения, достаточна представить себе, что
ось ОХ или OY принята за полярную ось OZ. Поэтому, если мы будем
измерять Мх или Му, то мы получим всегда одно из значений km
(пг~0, -4- 1, Ч- 2Э .-4- /), но при этом возникает новое состояние
с определенным значением, скажем, Мх. Это состояние будет состоянием
с неопределенными Му и т. е. одновременные измерения компонент
момента импульса взаимно исключаются: измерение одной компоненты
делает неопределенным значение другой.
§ 26. Оператор энергии и функция Гамильтона
а) Оператор кинетической энергии Т. Опыт показывает, что ки-
нетическая энергия микрочастиц связана с импульсом таким же образом,
как и для макроскопических тел *), т. е. кинетическая энергия Т ча-
стицы, имеющей массу р и импульс р, равна
г=Й=5<',’+'?+Й>- <26'Ч
Этот опытный факт заставляет написать оператор кинетической энергии
в виде
—►
D2 1
т=т*=^р‘+р>+р> <26-2’
Вставляя сюда значение операторов Рх, Pyi Pz из (24.1), находим:
/>2
T=—~^t (26.2')
/ д2 д2 . д2 \
где V2 есть оператор Лапласа 4" 3^2) • ® сиду такого вы-
бора оператора Т его собственные значения Т будут равны (26.1), если
под р , рг разуметь собственные значения операторов импульса
рх р р л
В самом деле, уравнение для. собственных функций Ф (х, д/, z) опе-
ратора Т есть
(26.3)
и удовлетворяется функцией, представляющей плоскую волну де-Бройля:
фг(х’у’ * • (26-4>
Эта же функция является собственной функцией операторов импульса,
*) Это обстоятельство в сущности уже использовано в основных соотно-
шениях де-Бройля (см. § 7).
6 Блохинцев
82
ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ
[гл. IV
так что кинетическая энергия Т измерима одновременно с импульсами
рх, Ру' Pz (разумеется, операторы 7, Рх, Ру, Рг коммутируют между
собой). Оператор Т может быть легко написан в любой криволинейной
системе координат. Для этого достаточно написать оператор Лапласа V2
в соответствующей системе. В частности, в полярной системе координат
оператор V2 имеет вид:
V2
р6-5»
где ? следует взять из (25.10).
Подставляя V2 из (26.5) в (26.2') и имея в виду (25.9), мы получим:
т=т'+^. <26-6>
где Л12 есть оператор квадрата момента импульса, а Тг есть
Т — — (26.7)
г 2рг2дг\ дг ) ' '
Оператор Р может рассматриваться как оператор кинетической энергии,
УИ2
соответствующей движению по радиусу-вектору, а оператор —2 —
как оператор кинетической энергии трансверсального движения *).
Ь) Оператор полной энергии Н. Заметим сперва, что доператор
потенциальной энергии U, поскольку последняя есть функция только
координат частицы х, у, z, есть просто U(х, у, z). В классической ме-
ханике полная энергия
Подобным же образом
полную энергию, есть
энергий, т. е.
есть сумма потенциальной и кинетической энергий,
и в квантовой механике оператор, изображающий
сумма операторов кинетической и потенциальной
Н=Т+и (х, у, Z).
(26.8)
Вид потенциальной энергии U{x, у, z\ так же как и в классической
механике, заимствуется из опыта и характеризует силовое поле, дей-
ствующее на частицу.
Заметим, что в квантовой механике нельзя сказать, что полная энер-
гия есть сумма кинетической и потенциальной энергии. Кинетическая
энергия есть ^функция импульсов, а потенциальная — функция координат.
Координаты же и импульсы не могут быть одновременно измерены. По-
этому нельзя измерить полную энергию, измеряя порознь кинетическую
и потенциальную**).
*) (26.6) вполне отвечает представлению кинетической энергии в класси-
ческой механике в виде
Р2Г М*
2|i 2|хг2 ’
где рг — проекция импульса на радиус-вектор.
**) Операторы Т и Z7, разумеется, не коммутируют, в чем легко убедиться,
пользуясь правилом перестановки (24.4). Отсюда следует, что Т и U не мо-
гут быть определены одновременно для одного и того же состояния ф.
ГАМИЛЬТОНИАН
83
§ 27]
Полная энергия должна измеряться непосредственно, как одно целое.
Возможные значения полной энергии частицы зависят от вида U (х, у, z),
т. е. от рода частицы и от силового поля, в котором она движется.
Нахождение этих значений составляет одну из важнейших задач кванто-
вой механики и будет рассмотрено позже.
Полную энергию, выраженную через импульсы и координаты, в клас-
сической механике называют функцией Гамильтона. Оператор энергии Н
у нас выражен через операторы импульса [через (26.2)], поэтому опера-
тор И мы будем также называть оператором функции Гамильтона или
коротко — гамильтонианом.
§ 27. Гамильтониан
Понятие функции Гамильтона в классической механике, на самом
деле, болеб обще, нежели понятие энергии. Значение функции Гамиль-
тона заключается в том, что из нее могут быть получены уравнения
движения в произвольной системе координат. Таково же, как мы вскоре
увидим, и значение гамильтониана в квантовой механике. Вид функции
Гамильтона (и соответственно гамильтониана) определяется природой час-
тиц и силовых полей и для разных случаев различен.
Следует различать два важных случая: когда силы не зависят от
скорости частицы и когда они зависят от нее. В первом случае сила F
является функцией только координат частицы и времени и может быть
представлена как градиент некоторой функции U (а;, у, zt t), которую
мы назовем силовой функцией *):
F= — V/7 (а;, у. z, t). (27.1)
Если силы не зависят от времени, то /7(х, у, z) есть не что иное, как
потенциальная энергия частицы. В этом случае функция Гамильтона
совпадает с полной энергией частицы и равна T-\-U (х, у, z). Соответ-
ствующий гамильтониан есть (26.8) и совпадает с оператором полной
энергии. В более общем случае функция Тамильтона есть сумма кинети-
ческой энергии Т и силовой функции U: H=T-]-U(х, у, z, t). Так
как U не является теперь потенциальной энергией, то и- И не есть пол-
ная энергия системы.
В полной аналогии с классическим выражением функции Гамильтона,
гамильтониан напишется в квантовой механике для этого случая в виде
Я=Т+67(^Л z. t), (27.2)
где U — силовая функция.
Остается рассмотреть случай сил, зависящих от, скорости частицы
В микромире единственными известными силами такого рода являются
силы, возникающие в электромагнитном поле (сила Лоренца). Поэтому
достаточно рассмотреть гамильтониан для движения заряженной частищ1
(заряд е, масса g) в произвольном электромагнитном поле.
*) Чаще в механике под силовой функцией понимают — U. Заметим еще
что, представляя силу как градиент от U, мы исключаем вихревые поля (слу
чай, когда rotF^O). Однако, такого рода силы, не зависящие от скорости
в механике микрочастиц неизвестны.
6*
84 ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ [ГЛ. IV
Как известно из теории поля, произвольное электромагнитное поле <§
(напряженность электрического поля), 3% (напряженность магнитного поля)
может быть описано с помощью скалярного потенциала V и векторного
потенциала А, причем
(2^.3)
$F=rotA. (27.4)
Классическая функция Гамильтона Н, приводящая к правильным урав-
нениям движения в электромагнитном поле, имеет вид
Я=Ч(р—7А)8 + ^’ <27^>
где р (рх, руУ pz) есть вектор обобщенного импульёа [так, что р — —- А =
= gv, где v — скорость частицы, но р jjlv! *)].
Оказывается, что в квантовой механике мы получаем правильный
—
гамильтониан, если под р будем разуметь оператор импульса Р=—11$,
т. е. оператор гамильтона для этого случая есть
//=±(р-±А)2 + еИ. (27.6)
Если помимо электромагнитных сил ^имеются еще и другие силы, описы-
ваемые силовой функцией 67, то общим выражением для гамильтониана
будет
Я=2Т 7А)2 + ₽У+У. (27.7)
Раскроем теперь в явном виде оператор (р—f’A) • Имеем:
(?-?Нл-иГ+('|,1Й+
+ (Л-|^У- <27-8)
По определению произведения операторов
-7Л») =
=^-7У’И.-7^А+5^-
Далее, на основании (24.4), имеем:
АЛ=“г’А^г’
поэтому
*) См. дополнение VI.
§ 28]
УРАВНЕНИЕ ШРЕДИНГЕРА
85
Повторяя вычисления для остальных двух членов в (27.8) и складывая
результаты, мы находим:
Н= ^-Р* — ~ кР^- div А -4- тА А2 + е У 4- U. (27.9)
2 р. pt’ 1 2рс 1 2ре2 11 ' '
Чтобы получить выражение гимильтониана в произвольной криво-
линейной системе координат qv q2, q3, достаточно преобразовать полу-
ченный нами для декартовой системы координат гамильтониан в такую
систему, следуя обычным правилам дифференциального исчисления [при-
мер такого преобразования дает формула (26.5)]. Вид гамильтониана
в криволинейной системе координат не находится в таком простом от-
ношении к классической функции Гамильтона, какое имеет место в де-
картовой системе координат (замена р на оператор Р). Это обстоятель-
ство не является случайным. Декартова система в квантовой механике
выделена среди всех других координатных систем тем, что в этой си-
стеме кинетическая энергия выражается суммой квадратов компонент
импульса рх, ру, р„, так что, измерив импульс, мы можем вычислить
•кинетическую энергию.
В криволинейной системе координат кинетическая энергия выражается
в виде квадратичной функции обобщенных импульсов рА:
з
Т== 3 (27.10)
Z, k — i
причем' коэффициенты a.k являются функциями координат. Измерение
(& = 1,2, 3) еще не определяет кинетической энергии, так как нужно еще
знать aik. Последние суть функции координат qk (&=1, 2, 3) и по-
этому не могут быть определены одновременно с импульсами pk. Таким
образом, только в декартовой системе координат измерение импульсов
есть в то же время и измерение кинетической энергии.
Об уравнениях квантовой механики в криволинейной системе коорди-
нат см. дополнение VII.
ГЛАВА V
ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ
§ 28. Уравнение Шредингера
Пусть в какой-нибудь момент времени (/ — 0) дана волновая функция
ф (v, 0), описывающая состояние частицы (буквой х мы обозначаем всю
совокупность координат частицы). С помощью этой волновой функции
мы можем вычислить вероятность результатов измерения различных механи-
ческих величин для момента времени t = 0 в ансамбле частиц, находящихся
в состоянии ф (х, 0). В этом смысле мы говорим, что волновая функ-
ция ф(х, 0) определяет состояние частицы в момент времени / = 0.
Допустим теперь, что мы намерены, произвести измерения не в мо-
мент времени/=0, а позднее, в момент ^^>0. За это время состояние
86 ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ [гл. V
частиц, вообще говоря, изменится и будет изображаться некоторой
новой волновой функцией, которую мы обозначим через ф (х, /).
Каким образом связаны волновые функции ф (х, 0) и ф (х, ?)? Со-
стояние в начальный момент времени должно определять состояние
в последующие моменты времени. Поэтому из волновой функции ф (х, 0)
для t = 0 должно определяться . и значение ф (х, /) в более поздние
моменты времени.
Рассмотрим функцию ф в момент времени Д/, бесконечно близкий
к / = 0. Тогда
ф (х, Д/)=ф (х, 0) + (^)/=0 Д*+ • • -
Согласно сказанному, _ должно определяться из ф(х, 0), т. е.
где L (х, 0)—некоторая операция, которую следует произвести над ф (х, 0),
чтобы получить
Так как момент t = 0 взят совершенно произвольно, то будем иметь
d-^=L(x,t^(x,f). (28.1)
Вид оператора £, который можно назвать оператором смещения
во времени, не может быть определен из изложенных выше положений
квантовой механики и должен быть постулирован.
Мы можем, однако/ сказать, опираясь/ на принцип суперпозиции
состояний, что этот оператор должен быть линейным. Далее, оператор L
не может содержать ни производных, ни интегралов по времени. В са-
мом деле, если бы он содержал первую производную по /, то это озна-
чало бы просто, что оператор L есть не тот оператор, который мы
хотим разуметь: оператор L выражает первую производную по t через
ф(х,/). Если бы он содержал высшие производные по /, то (28.1)
означало бы уравнение для ф более высокого порядка, чем первый, и,
следовательно, для определения состояния в последующие моменты вре-
мени нужно было бы знать при t = 0 не только ф'(х, 0), но и производные по
времени от ф: (g) , . *), т. е. волновая функция ф не опре-
деляла бы состояния системы, что противоречит нашему основному
предположению (ф определяет состояние системы). Наличие интеграла
по t означало бы, шчто для последующего играет роль значение ф на
целом отрезке времени, т. е. история процесса. Таким образом L может
содержать t лишь как параметр.
*) Так, например, уравнение для колебаний струны есть уравнение второго
порядка по времени. Для определения состояния струны в момент t — 0 нужно
знать не только отклонение струны а(х, t) для = 0, но и скорости ее точек
да (х, t) . -
-^-'при t =
§ 28]
УРАВНЕНИЕ ШРЕДИНГЕРА
87
Правильный выбор оператора L подсказывается рассмотрением свобод-
ного движения с определенным значением импульса^. Волновая функция
для такого движения есть волна де-Бройля:
t) = Ne Л ,
где
„2 । „2 i „2
Рх + ру+ Рг ,
2И
Непосредственная Подстановка показывает, что эта волна удовлетворяет
уравнению
Это последнее уравнение можно переписать в виде:
если под оператором Н разуметь гимильтониан для свободного движе-
ния частицы:
А2
Н=Т=~2^
Отсюда следует, что для свободного движения оператор смещения
ih
В квантовой механике делается обобщение этого частного резуль-
тата, именно, принимают, что оператор смещения L всегда равен
(28.2)
где И есть гамильтониан (оператор функции Гамильтона), вид которого
для разных случаев рассмотрен в § 27.
В соответствии с этим постулатом уравнение (28.1) для волновой
функции ф может быть теперь записано в виде:
(28.3)
Это уравнение носит название уравнения Шредингера. Оно обра-
зует одну из основ квантовой механики *) и обоснование свое находит
не столько в теоретических и исторических обстоятельствах, привед-
ших к установлению этого уравнения, сколько в согласии с опытом
квантовой механики, опирающейся на это уравнение.
*) Во многих курсах стремятся «вывести» уравнение Шредингера. На са-
мом деле, это уравнение ниоткуда не выводится, а образует основу новой
теории. Поэтому мы предпочитаем постулировать это уравнение, ограничившись
приведеннымй выше доводами в пользу такого постулата.
88 ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ [ГЛ. V
В раскрытом виде уравнение Шредингера (28.3) в отсутствии магнит-
ного поля, в соответствии с значением оператора Н [см. (27.2) и (26.2')],
гласит:
+ (28.4)
[при наличии магнитного поля следует взять Н из (27.9)].
Наиболее важной особенностью уравнения Шредингера является
наличие мнимой единицы перед производной . В классической физике
уравнения первого порядка по времени не имеют периодических реше-
ний— они описывают необратимые процессы, например, диффузию,
теплопроводность*). Благодаря мнимости коэффициента при урав-
нение . Шредингера, будучи уравнением первого порядка по времени,
может иметь и периодические решения.
По этой же причине волновая функция ф является, вообще говоря, комп-
лексной величиной. В классической теории волн также применяют комплекс-
ное написание волны в виде
и = const. • Лх),
но в итоге имеют дело лишь с Действительной или мнимой частью п. Напри-
мер, фактическое смещение частиц будет
и1 = const. • sin т— kx).
Введение i здесь просто необязательный расчетный прием. Иначе обстоит
дело в квантовой механике. Если взять вместо волны де-Бройля <|» ее дейст-
вительную или мнимую часть, например,
. (Et — Рхх—РУУ—Ргг}
ф' = N Sin -------; -------- ,
т h 1
то для фг нельзя найти уравнения первого порядка по времени, которое было
бы совместимо с соотношениями де-Бройля:
В связи с уравнением Шредингера остановимся еще на проблеме
измерения волновой функции. Очевидно, что вся постановка вопроса
«найти ф(х,/), если дано ф(х, 0)» имеет смысл лишь в том случае,
если ф (х, 0) может быть однозначно сопоставлено с некоторыми опре-
деленными физическими условиями. Такое сопоставление не является
тривиальным, так как на опыте мы не можем определить ф (ибр вол-
новая функция содержит некоторый произвол, ф и ф' = const. • ф опи-
сывают одно и то же состояние), а можем определить лишь вероятности
тех или иных результатов измерения. Последние же определяют лишь
квадрат модуля функции или квадраты модулей амплитуд разложения
функции по собственным функциям какого-нибудь оператора. Такого
рода измерения лишь сужают возможный выбор ф, но вовсе не опре-
деляют ее.
*) Конечйо, характер решения дифференциального уравнения зависит еще
и от краевых условий. Проводя указанное противопоставление, мы имеем
в виду случаи, когда ни U (х, у, z), ни краевые условия не зависят от времени.
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
89
§ 29]
Таким образом, в общем случае мы встречаемся здесь с некоторой
трудностью. Однако, обычная постановка вопроса в квантовой меха-
нике такова, что эта трудность отпадает. Именно, обычно начальное
состояние частицы или системы частиц задается измерением ка-
ких-либо механических величин £, М, N, ... Тогда, поскольку эти
значения определены, постольку мы можем утверждать, что начальное
состояние будет собственным состоянием операторов L, М, N, ...,
принадлежащим собственным значениям Ц /И, N, ... Этим самым
волновая функция определена (разумеется, вплоть до несущественного
постоянного множителя). Например, если начальное состояние частицы
фиксируется измерением ее импульса p(£=pJC, М=ру, N=pz), то
начальная волновая функция ф (г, 0) = фР (г), где фр есть плоская волна
де-Бройля. Зная ф (г, 0), мы можем из уравнения Шредингера опреде-
лить ф (г, /), а с помощью этой функции могут быть предсказаны
вероятности измерений в момент времени /.
§ 29. Уравнение непрерывности
Из уравнения Шредингера следует закон сохранения вещества, вы-
. ражаемый уравнением непрерывности:
| + divj = O, (29.1)
где р—- средняя плотность вещества в точке х, у, z, a j—средняя
плотность тока.
Для того, чтобы получить это уравнение, возьмем уравнение Шре-
дингера сначала для простого случая потенциальных сил (28.4)
(29-2)
Уравнение для комплексно сопряженной функции будет
-/Л¥= -^2-Н + £/Ф*- (29.2-)
Умножая уравнение (29.2) на ф*, а (29.2') на ф и вычитая один
результат из другого, получим:
lh (ф* S+ф^?*)=- s (ф*рф - Фт-
Это равенство может быть тотчас же переписано в виде
^(Ф*Ф)=|Шу(Ф*7Ф-Ф?Ф*); (29-3)
ф*ф есть плотность вероятности w:
^=ф*ф. (29.4)
Если через J обозначить вектор
j=g(4>Vd>* — ф*7ф), (29.5)
90 ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ [гЛ. V
то уравнение (29.3) запишется в форме
5+dlvJ = 0. (29. в)
Отсюда следует, что вектор J есть вектор плотности тока ве-
роятности. Уравнение (29.6) получает более наглядное толкование,
если заметить, что ^ = ф*ф может рассматриваться также как средняя
плотность частиц. Тогда J следует рассматривать как средний поток
частиц через 1 см2 в 1 сек. В соответствии с этим уравнением (29.6)
нужно толковать как закон сохранения числа частиц. В частности,
интегрируя (29.6) по некоторому конечному объему V и применяя
теорему Гаусса, получаем:
~ рш dv = — J div J dv = — J JNds, (29.7)
v v s
где последний интеграл взят по поверхности 5, охватывающей объем V.
Распространяя интегрирование по всему пространству (V—> оо) и имея
в виду, что волновые функции ф, а вместе с тем и плотность тока J
обращаются на бесконечно удаленной поверхности в нуль*), мы на-
ходим:
= (29.8)
ОО 00
т. е. полная вероятность найти частицу где-либо в пространстве
не зависит от времени. Следовательно, число частиц остается неизмен-
ным. Вместе с тем (29.8) утверждает, что нормировка волновых функций
не меняется с течением времени — положение, о котором мы уже упо-
минали в § 10.
Умножим J и w на массу частицы р:
р[1=|1.ге) = |Х|ф|2, \
Д(1 = ^(фТф* —ф*¥ф). J (29-9)
Тогда р^ имеет смысл средней, плотности вещества (массы), .a —
средней плотности тока вещества (массы). Из (29.6) следует, что
эти величины подчиняются уравнению непрерывности
+ div = О, (29.10)
т. е. изменение средней массы в некоторой бесконечно малой
области обусловлено втеканием или вытеканием этой массы через
поверхность, ограничивающую эту область.
*) В случае, когда функции <[> не интегрируемы, интеграл j JNds может
и не обратиться в нуль даже по бесконечно удаленной поверхности, физи-
чески это означает существование потока частиц из бесконечности или
в бесконечность.
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
91
§ 29]
Подобным же образом, умножая и J на заряд частицы е, получим
среднюю плотность электрического заряда и среднюю плотность эле-
ктрического тока:
ре=е-^ — е | ф|2, 1
Je=~ (ф¥ф* — ф*Уф), j (29.11)
для которых опять-таки получается уравнение непрерывности
^4-divJe=0. (29.12)
Уравнения (29.10), и (29.12) выражают закон сохранения массы и эле-
ктричества в квантовой механике.
Если представить волновую функцию ф в виде
ф = ш?/0, (29.13)
где и— действительная амплитуда, а 0 — действительная фаза» то под-
становка (29.13) в (29.5) дает
J=^-u2V0; (29.5')
так как и® есть плотность гш, то величина yV0 может быть интерпре-
тирована как средняя скорость в точке х, z:
v = yV9 (29.14)
А а
и величина — 0 как — потенциал скорости.
Из формулы (29.5') с особенной ясностью видно, что плотность токов J
отлична от нуля лишь в том случае,х когда' состояние описывается ком-
плексной функцией ф (иначе 0 = 0).
При наличии магнитного поля «Я?, описываемого вектором-потенциа-
лом А = rot А), формула для плотности тока J должна быть видо-
изменена*). Именно, при наличии магнитного поля вместо (29.5) полу-
чается выражение для плотности тока, носящее название тока Гордо-
на-Шредингера'.
i=% [W - Ф**Ф] Аф*ф. (29.5")
Чтобы получить это выражение, следует подставить в уравнение Шре-
дингера (28.3) гамильтониан (27.9) для движения в произвольном элек-
тромагнитном поле. Производя эту подстановку, находим уравнение
Шредингера для этого случая:
“ Й ~ А’Ф + “Л’ м + 2-J А’Ф +
+ ^Уф+^ф (29.15)
*) Видоизменение обусловлено тем, что при наличии магнитного поля
операторы Рх, Pyt Рг суть операторы обобщенного импульса, а не обычного
(произведение массы на скорость). Так же обстоит дело и в классической
механике. Ср. дополнение VI, формулу (10).
92 ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ [гл. V
и для сопряженной функции
— /А^ = — ^У2ф — — АУф*—div Аф* 4- Д А2ф* +
dt 2jx т \кс ‘ т 1 2нг2 т 1
(29 Л 6)
Умножим опять первое уравнение на ф*, а второе на ф и вычтем
один результат из другого. Тогда получается:
/А = _ g div (ф*Уф - фУф*) + {div А (ф*ф) 4-
4-А(ф*?ф + фУф*)у.
Выражение в фигурных скобках может быть преобразовано следующим
образом:
div Аф*ф + А (ф*Уф + фУф*) = div Аф*ф +'AV (ф*ф) = 2 div (Аф*ф).
Подставляя этот результат в предыдущее выражение для —и деля
на th, получаем;
'ЦРН div [фУф* - ф*Уф] - ДАф*ф} = 0. (29.16')
Это и есть уравнение непрерывности при наличии магнитного поля,
описываемого вектор-потенциалом А.( Выражение в фигурных скобках
должно быть плотностью тока J. Как видно, оно совпадает с (29.14).
§ 30. Стационарные состояния
В отсутствии переменных внешних полей гамильтониан Н не зави-
сит от времени и совпадает с оператором полной энергии Н (х). В этом
случае уравнение Шредингера
»А^*>==Я(х)ф(хД) (30.1)
имеет важные решения, получающиеся путем разделения переменных
хи/:
ф(х,/) = ф(х)/(/). (30.2)
Подставляя (30.2) в (30.1) и обозначая постоянную разделения пере-
менных через Е, мы получаем:
ih^—Ef, (30.3)
Я(х)ф(х) = £ф(х). (30.4)
Первое уравнение сразу решается:
/(/) = const.^-ZA • (30.5)
Что же касается второго уравнения, то, как видно, оно совпадает
с уравнением для собственных функций оператора энергии //*). Если
*) Уравнение (30.4) получается из общего уравнения (20.2), если там по-
ложить L — H, L = E.
§ 30] СТАЦИОНАРНЫЕ состояния 93
обозначить эти функции через фл(х), а собственные значения через Ел
(для определенности мы берем случай дискретного спектра энергии), то
окончательно решение (30.2) напишется в виде
F t
Отсюда следует, что состояния с определенным значением энергии
Еп (АС2 = 0) гармонически зависят от времени с частотой, равной
(30.7)
Этот результат распространяет соотношение де-Бройля F = A(0, при-
менявшееся первоначально к свободному движению, на любые системы.
Состояние (30.6), с определенным значением энергии, по причинам,
которые сейчас выяснятся, называют стационарными. Уравнение же
^30.4) называют уравнением Шредингера для стационарных состояний.
В силу линейности уравнения (30.1) его общее решение ф(х, t)
может быть представлено как суперпозиция стационарных состояний
с произвольными, нд постоянными амплитудами, именно:
Ф {х, о=5 Wе “• <30-8)
п
Амплитуды сп определяются из начальной функции ф (х, 0). В самом
деле, в силу ортогональности функций фл имеем:
гл^ф(х,0)фл(х)б/х. (30.9)
Вычислим вероятность местоположения частицы wn (х, t) и плотность
тока JJx, /) в n-ом стационарном состоянии. Согласно (29.4) и (29.5)
имеем:
{х, о = I Ф„ (х, t) |2 = ф* (X, 0 ф„ (X, f),
(X, t} = ^{ Ф„ (х, t) Гф* (х, t} - ф* (х, 0 ¥ф„ (X, 0}.
Подставляя сюда фл (х, t) из (30.6), находим, что
^(x,/) = w„(x, 0), (30.10)
JJx, 0 = 0). (30.11)
Т. е. в стационарных состояниях вероятность местоположения
частицы и плотность тока не зависят от времени.
Отсюда же [имея в виду (29.11)] следует, что в этих состояниях
средняя плотность электрических зарядов ре и средняя плотность элек-
трических токов не зависят от времени.
Таким образом система, находящаяся в состоянии с определенной
энергией Еп (ДС2 = 0), с точки зрения электрической представляет
собой систему статически распределенных зарядов и постоянных токов.
Такая система не должна изЛучать. Это приводит нас к важному вы-
94
ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ ВЕЛИЧИН
[гл. VI
воду, который в примитивной теории Бора постулировался: атом, на-
ходящийся в каком-нибудь квантовом состоянии Еп, не излучает*).
Характеристика стационарных состояний будет более полной, если мы
обратим внимание читателя на то, что в стационарных состояниях вероятность
w (L) найти какое-нибудь значение L любой механической величины (не за-
висящей явно от времени) не зависит от времени. Вместе с тем и среднее
значение L является постоянным. Для доказательства этого положения вос-
пользуемся формулой (28.14)
w{L) = \c(L) |2,
где с (L) есть амплитуда в разложении <[> (х, t) по собственным функциям <[>£ (х)
оператора £, представляющего величину L. Согласно (21.16) имеем для ста-
ционарного состояния <|>л (х, t) (30.6):
c(L) = j t}dx = e h J<|>2 (x)|a(x)dx
и, следовательно,
w (L) = | c (L) |2 = | j ф* (X) Ф„ {x)dx = const (30.12)
Г Л А В A VI
ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ ВЕЛИЧИН
§ 31. Производные операторов по времени
Уравнение Шредингера позволяет установить простые правила, сле-
дуя которым можно вычислить изменение среднего значения той или
иной механической величины за бесконечно малый промежуток времени.
Иными словами, вычислить производную ho времени ~ L от среднего
значения L некоторой величины L.
Физический смысл этой производной таков. Допустим, что в момент
времени t имеется состояние, описываемое волновой функцией ф (х, /).
Произведем измерения величины L В этом состоянии. Мы получим
результаты отдельных измерений £", А"1, ... Среднее из большого
числа измерений будет L(t) и вычисляется по формуле
= /)• f)-dx. (31.1)
Другую серию наблюдений мы проведем в момент времени f = / -}- Д/,
близкий к I. Мы получим новую серию результатов **). Среднее
*) Это утверждение, как будет объяснено в гл. XVI, § 80, на самом деле
приближенно.
**) Измерение значения какой-либо величины точно в .данный момент
времени может привести к изменению состояния микрочастицы. Поэтому
производство двух серий измерений в момент t и момент подробно
следует представлять себе следующим образом. Имеется ансамбль из боль-
ПРОИЗВОДНЫЕ ОПЕРАТОРОВ ПО ВРЕМЕНИ
95
§ 31]
значение из этих результатов будет другое, так как за время I
состояние изменится ,и те же результаты А', А", А'", ... будут
получаться с иной степенью вероятности. Кроме того, может случиться,
что сама величина явно зависит от времени т;ак, что и возможные зна-
чения А', А", А'", ... будут изменяться с течением времени. Обозначим'
средний результат измерений в момент через А (/-j-Д/), тогда
(Г) = Нт • (31.2)
ас д/ О с
Вычислили эту производную. Дифференцируя (31.1) по времени, полу-
чаем:
Ф* J <31-3>
дк
Очевидно, что первый член есть среднее значение и равен нулю,
если А явно не зависит от времени. Два последних члена мы упростим,
пользуясь уравнением!Шредингера (28.3). Именно, из (28.3) имеем:
dt ih
5=—
dt ih т
Подставляя это в (31.3), находим:
ет = S - и <"•« (Д'Я +a J “х-
Первый интеграл преобразуем, пользуясь самосопряженностью опера-
тора Н. Обозначая я*, £ф = #2, на основании свойства само-
сопряженности (18.7) получаем:
J (Я*ф*) (£<|>) dx = J и2-Я*«* • dx=J u^Httfdx = j <!>* (Я£ф) dx.
Подставляя это в выражение для , находим:
<31л>
Оператор — (LH—HL) обозначим через
[Я, £] = 1(£Я-Я£) (31.5)
шого числа независимых экземпляров N, находящихся в состоянии ф(х, t).
Мы разбиваем N на две большие группы N1 л N".Jb момент t мы производим
измерения в первой группе частиц N' и получаем A(t) [при этом состояние
этих экземпляров, вообще говоря, изменится и оно уже больше не описы-
вается функцией ф (х, Q]. Затем в момент мы произведем измерения
в группе N4 нетронутых первым измерением экземпляров. Из этих измерений
и получается
96 ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ ВЕЛИЧИН [ГЛ. VI
и будем называть квантовой скобкой Пуассона*). Это обозначение
позволяет написать (31.4) в форме
(31.6)
Мы видим, что производная по времени от среднего значения L есть
среднее от некоторой величины, изображаемой оператором
“+[«. ч-
Поэтому этот последний оператор следует принять за оператор
производной по времени ~ от величины А, изображаемой опера-
тором L:
а<ч=ж+["’ Ч- <31-7»
Это определение оператора, изображающего производную по вре-
dL
мени , ведет к тому, что
“м*. (31S)
т. е. производная по времени от среднего равна среднему от
производной по времени.
Если величина L не зависит явно оу времени, то и формулы (31.6)
и (31.7) упрощаются:
^ = [НГТ], (31.9)
dt
^ = [Н, £]. (31.10)
§ 32. Уравнения движения в квантовой механике.
Теорема Эренфеста
Найдем теперь законы изменения импульсов и координат с тече-
нием времени^
Импульсы и координаты являются величинами, не зависящими явно
от времени. Поэтому согласно (31.10) операторы производных этих
величин по времени выражаются просто через квантовые скобки Пуас-
сона, т. е. в конечной счете через операторы самих этих величин
и гамильтониан И, характеризующий рассматриваемую механическую
систему.
*) Эта терминология заимствована из классической механики. См. дополне-
ние VI, формулу (4).
§ 32] УРАВНЕНИЯ ДВИЖЕНИЯ В КВАНТОВОЙ МЕХАНИКЕ 97
Обозначим операторы декартовых координат х, у, z и соответ-
ствующих импульсов рх, ру, pz соответственно через X, Y, Z
и Рх, Ру1 Pz*\ Гамильтониан Н будет функцией этих операторов
и, вообще говоря, времени i:
Н~Н(РХ, Ру, Рг, X. г, z, /). (32.1)
Обозначим далее через операторы производных коор-
динат по времени, т. е. операторы проекций скорости на оси коорди-
dPx dPy dPz
нат, а через ~тг > ’ ~ti--операторы производных по времени
ИI Ul UI
от проекций импульса.
Подставляя в (31.10) вместо L операторы Xt Y, Z\ Рх, Ру, Pz,
получим искомые операторные уравнения:
g = [/7, X]; У]; § = [Я Z]; (32.2)
tZP,,. _ _ dPv dP~
а,—-нр.' -^=^Н-Р,У- ИГ=1н-рЛ <32-2')
Эти операторные уравнения вполне аналогичны классическим уравнениям
Гамильтона и поэтому называются квантовыми уравнениями Гамиль-
тона **).
В классической .механике первая группа уравнений (производные от
координат) устанавливает связь между скоростью и импульсом, а вторая
группа (производные от импульсов) выражает законы изменения импульса
во времени. Такое же значение имеют и квантовые уравнения Гамиль-
тона. Для того, чтобы в этом убедиться, следует раскрыть явно вид
скобок Пуассона в (32.2) и (32.2'). Ради простоты рассмотрим случай,
когда магнитные силы отсутствуют. В этом случае гамильтониан имеет
вид [см. (27.2)]
у; z' <32-3>
Рассматривая волновую функцию как функцию координат частицы
х, у, z и времени /, имеем следующие выражения для операторов:
Х=х, Y=y, Z = z,
Р,= ~лт,- (32.4)
Вычислим теперь оператор Имеем
[Я, Х^^ХН-НХ^^ХР^-Р^Х), (32.5)
*) Мы ограничиваемся рассмотрением движения в декартовой системе
координат. Об уравнениях в криволинейной системе координат см. дополне-
**) Ср. дополнение VI, уравнение (7).
7 Блохинцев
98 ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ ВЕЛИЧИН [ГЛ. VI
так как X коммутирует с Ру, Pz, U(х, z, /). Правило перестановки
операторов X и Рх (24.2) дает|
Р\Х= Рх (РхХ) = Рх (ХРх -ih) = (Р^) Рх - ihPx=
= {ХРх — th) рх — ihPx = ХР2х — 2ihPx. (32.6)
Подставляя это в (32.5), находим:
= (32.7)
Для у, z, очевидно, получим подобный же результат, поэтому
dX Рх dY Pv dZ Pz
-ЙГ=—> Zh=—> = (32.8)
dt pi dt pi dt |i ' '
т. e. оператор скорости равен оператору импульса, деленному на
массу' частицы pt. Иными словами, связь между операторами скорости
и импульса такова же, как и связь между нами в классической механике. dP Найдем теперь оператор . Из (32.2) соответствующими величи- и (24.4) имеем:
[Я, />,]= k(PxU—UPx) = ihK x x' - — ~~ дх 9 (32.9)
т. е. dPx dU dPy _ dU dPz dU . (32.10)
dt дх ’ dt dy 9 dt dz
dU dU dU — , — 5- , — суть дх ду dz J не что иное, как операторы проекций
силы. Так что (32.10) можно переписать также в виде
dPx —F , dt x’ dt У9 dPz dt (32.11)
т. e. оператор производной по времени от импульса равен оператору
силы. Поэтому (32.10) можно рассматривать как уравнения Ньютона
в операторной форме.
_ dx dp~
Если мы вычислим среднее значение от величин —, и т. д. в
каком-нибудь состоянии ф, то из (32.8) и (32.10) на основании (31.8)
получаем:
_ (32-12’
= )=—Ш = р (32.13)
dt dt дх * ' '
и т. д. Иначе говоря, производная по времени от средней координаты
х равна среднему импульсу, деленному на массу частицы, и производная
от среднего импульса рх равна средней силе F.
$ 33] ИНТЕГРАЛЫ ДВИЖЕНИЯ 99
В раскрытой форме равенства (32.12) и (32.13) гласят:
f $*x$dx = - [^-P^.dx, (32.12')
tit I [1 1
(32.13')
Эти равенства носят название теорем Эренфеста. Они показывают,
что для средних значений импульсов и координат остаются в силе
уравнения классической механики.
§ 33. Интегралы движения
В квантовой механике мы имеем те же интегралы движения, что
и в классической. Величина L будет интегралом движения, если
£1-°- <33-’>
Особый интерес представляет случай, когда величина L не зависит
явно от времени; тогда вместо (33.1) имеем:
= L] = 0, (33.2)
т. е. для интегралов движения (не зависящих явно от времени) кван-
товая скобка Пуассона равна нулю.
Из формул (33.1) и (33.2) следует, что среднее значение интегралов
движения не зависит от времени:
J(Z) = o. (зз.з)
Покажем теперь, что и вероятность w (Ln, t) найти в момент времени t
какое-нибудь значение интеграла движения, равное, скажем, £п, не
зависит от времени**).
Так как операторы L и Н коммутируют, то они имеют общие
собственные функции фя(х):
(зз.4)
(33.4')
Разложим произвольное состояние ф (х, t) по «собственным функциям фп
Эти функции суть функции стационарных состояний, поэтому [ср. (30.8)
<!>(*, 1)-=^с$п{х}е » (33.5)
П V
ИЛИ
Ф (х, t)^cn(/) ф„(х), (33.6)
п
*) Речь идет об интегралах движения, не зависящих явно от времени..
7*
100 ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ ВЕЛИЧИН [гл. VI
где
сп Ю = спе'^ = сп (0) е~(33.7)
Разложение (33.6) есть разложение ф(х, t) по собственным функциям
оператора L, поэтому
w(Ln, /) = |ся(/)|2 = рл(0)|2 = const. (33.8)
Вид интегралов движения зависит от рода силового поля, в кото-
ром движется частица. Для свободного движения силовая функция
£7(х, у, z, /) = 0, и гамильтониан будет равен
Я= Т=1 (Р2 + р2 + ру (33.9)
Как и в классической механике, в этом случае интегралом движения
является импульс, действительно:
[Н, РЖ]==[Я, Ру] = [Н, PJ = O, (33.10)
dPf = 0, = ^ = 0. (33.11)
dt dt dt
В поле центральной силы имеет место закон площадей — момент
импульса есть интеграл движения, В самом деле, в поле централь-
ной силы потенциальная энергия U есть функция расстояния от центра
силы: U=U(r). Поэтому для этого случая гамильтониан Н может быть
написан в виде [ср. (26.6)]
H=Tr+^ + UW- (33.12)
Операторы квадрата момента импульса М2 и его проекций М2
согласно (25.8) зависят только от углов 6, ср, .поэтому не действуют
на функции от г. Кроме того, оператор Л12, входящий в (33.12), ком-
мутирует с Мх, Му и М2 [см. (25.6)]. Поэтому все четыре названных
оператора коммутируют с //(33.12) так, что
[Н, Л12] = о, ^=0, (33.13)
dMx dMv dM,
[Н, МХ]—[Н, Му]—[Н, М,]=0, ^ = ^ = -^ = 0. (33.14)
Таким образом, момент импульса в поле центральных сил есть интеграл
движения.
Применим теперь равенство (33.1) к гамильтониану. Полагая
L-Н, получаем:
+да"]=1- <ззл5)
Если гамильтониан не зависит явно от времени, то
~ = 0. (33.16)
§ 34] ПЕРЕХОД К УРАВНЕНИЯМ НЬЮТОНА 101
Но в этом случае гамильтониан совпадает с оператором полной энер-
гии,. Поэтому (33.16) утверждает, что полная энергия в поле сил,
не зависящих от времени, есть интеграл движения. Иначе
говоря, (33.16) выражает закон сохранения энергии в квантовой
механике.
Согласно изложенному выше о свойствах интегралов движения
уравнение (33.16) следует понимать в том смысле, что ни среднее зна-
чение энергии Е, ни вероятности найти отдельные возможные значения
энергии Е = Еп не/зависят от времени*).
ГЛАЁА VII
СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ
МЕХАНИКОЙ И ОПТИКОЙ
§ 34. Переход от квантовых уравнений к уравнениям Ньютона
Доказанные в § 32 теоремы Эренфеста утверждают, что во всяком
состоянии ф для средних значений механических величин имеют место
уравнения Ньютона **):
v-Tt^p* <341)
d,-. dU cP dU
i№=~ii или (341>
Представим себе, что ф заметным образом отлично от нуля лишь
в очень малой области Дх, Такое состояние мы будем называть волно-
вым пакетом. ' Если бы среднее значение х изменилось согласно
классическому уравнению Ньютона и форма пакета не менялась бы, то
движение пакета | ф |2 мы могли бы рассматривать как движение мате-
риальной точки, подчиняющейся ньютоновской механике. Вообще говоря,
такого движения по квантовой механике не получается, так как, во-
первых, волновой пакет расплывается и, во-вторых, чтобы движение
центра тяжести пакета х совпадало с движением материальной точки
в поле Z7(x), нужно, чтобы
— — . (34.2)
дх дх
г Последнее равенство, вообще говоря, не имеет места. Рассмотрим все
же подробнее те условия, при которых приближенно движение пакета
совпадает с движением материальной точки. Среднее значение х коор-
*) О законе сохранения энергии в квантовой механике см. § 104.
**) Мы ограничиваемся одним измерением. Обобщение рассуждений на
пространственный случай не представляет никакого труда.
102 СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ [гл. VH
динаты х, т. е. координата центра тяжести пакета, определяется фор-
мулой
х = У ф*хф dx. (34.3)
Среднее значение силы есть
— = — JV <344>
Положим х = х-]~£, тогда
-^=-[ф*(х+е)^±^ф(х + ^. (34.4')
С/»Ии Ъг (J sb
Допустим, что Щх) есть достаточно медленно меняющаяся функция х
в области, где | ф |2 заметным образом отлично от нуля. Тогда
jh- можно разложить в ряд по степеням Е. Производя это раз-
дх
ложение, получим
_вд_ f
дх дх J ‘ т И дх2 J т т
(М5)
Но
j ф*ф dl = $ф*ф</х=1,
j ф*$ф = § ф*(х — х) ф dx ~ 0,
j ф*£2ф dZ =5 Ф*(* ““ *)2 Ф dx =
Поэтому
(34.6)
дх дх 2 дх3
Из второго уравнения (34.1') имеем:
^=_^_1йМ>.дл (34.7)
dt2 дх 2 дх%
Если поле изменяется медленно, то, выбрав достаточно малую ширину
пакета Дх2, мы можем в этом уравнении пренебречь всеми членами,
кроме первого. Тогда мы получим уравнение Ньютона:
(34.7')
дх v '
которое будет справедливо для того промежутка времени для кото-
рого отброшенные в уравнении (34.7) члены малы, т. е. по крайней
ПЕРЕХОД К УРАВНЕНИЯМ НЬЮТОНА
§ 34]
мере при условии
^(x)L 1 dW(x)
дх 2
Дх2.
103
(34.8)
Величина Дх2, определяющая размеры пакета, есть функция времени и,
вообще говоря, растет со временем (см. ниже): пакет расплывается.
Поэтому, если даже неравенство (34.8) выполнено в начальный момент
времени, то, начиная с некоторого момента /, оно может нарушиться.
По и выполнение неравенства (34.8) еще не означает, что состояние
частицы совпадает с классическим *).
Действительно, если взять очень узкий пакет (Дх2 мало), то средняя
потенциальная энергия частицы по квантовой механике практически равна
потенциальной энергии материальной точки, находящейся в центре вол-
нового пакета:
u= j % и(х). (34.9)
Но этого нельзя сказать о кинетической энергии Т. Действительно,
=1+-^ • (3410)
В силу соотношения Гейзенберга
T~z^h2
Др2 -= ,
г 4Дх2 ’
поэтому в (34.10) первый квантовый член может оказаться гораздо
большим классической энергии частицы, движущейся с импульсом р.
Квантовым членом в (34.10) можно пренебречь, если
или Дх2 Э> — , (34.11)
2|х 2р. Р2
Таким образом движение частицы можно считать происходящим по за-
конам классической механики в течение времени /, если в течение этого
времени можно одновременно удовлетворить неравенствам (34.8) и (34.11).
Обстоятельства, благоприятствующие этим неравенствам, суть: 1) боль-
шая кинетическая энергия частицы Т; 2) поле Z7(x), представляющее
собой медленно меняющуюся функцию координат х.
Таким образом, переход от квантовых уравнений движения к
ньютоновским получается при переходе к большим кинетическим
энергиям частиц и плавным полям.
Рассмотрим расплывание пакета для свободного движения частицы. Сред-
нее квадратичное отклонение Дх2 есть среднее от величины Дх2 —х2— х2,
*) Для всех функций U (х) вида: U — а Ц- Ьх -|- сх2, как следует из (34.7),
движение центра тяжести пакета точно совпадает с классическим движением
материальной точки в поле Щх). К числу таких случаев относятся: а) свобод-
ное движение, Ь) движение в однородном поле, с) гармонический осциллятор-
и некоторые другие (например, в однородном магнитном поле получаются те
же результаты, что и для осциллятора).
104 СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ [гл. VII
где х—координата центра пакета. Согласно (34.7) имеем:
= t/, х = vt 4- х0, (34.12)
т. е. центр пакета движется инерциально со скоростью v. Производные ве-
личины Дх2 по времени вычисляются по общей формуле (31.7). Полагая там
£ = Дх3, находим:
+ [Я, =-<+[Я, х2],
и так как для свободного движения оператор Я=~Р2, то*)
[Я, х2] = х2] = 2^ (xW - PW) = хР+Р*.
гг * d\x2
Таким образом оператор —- равен
^Дх2 хРЦ-Рх dx2 хР^-Рх п—
dt pt dt |i
Вычисляем теперь вторую производную
^2Дх2__ д (d\x2\ . Г ^Дх2~1 __ d2x. Гн хР + Рх1
dt2 ~ dt\ dt /“^L ’ dt + |i J’
[я,^±^] = {(XP+PX) pt-РЦхР+Рх)^2-^.,
t. e.
d2Ax2 2P2 d2(x)2 2P2
dt2 — |12 d& |12 2v <34-14)
Ввиду того, что P2 коммутирует с Zf, все высшие производные от Дх2 равны
нулю. Таким образом разложение Дх2 в ряд Тейлора по степенЯхМ t имеет вид
М = Дх2+ (хР+Рх -2vx ) 1' (^-2Р) t*. (34.15)
Переходя от операторов к средним значениям, получим:
= (^хр+рх —*,x'}t + (^~р) I3, (34.16)
Дх^ — величина, обязательно положительная, поэтому из (34.16) следует, что
Дх, с ростом t неограниченно растет (может быть, переходя через минимум),
т. е. пакет расплывается. Во многих случаях [в зависимости от вида ф(х, 0)]
член с't исчезает. Тогда (34.16) получает особенно простой вид:
Дх^ = Д^+ Дг/21\ (34.17)
где Д^2 — среднее квадратичное отклонение скорости:
Дс/2 — z^ = v2 — v2.
И2
*) Во всех дальнейших расчетах пользуемся формулой Рхх = хРх — ih.
§ 35] ПЕРЕХОД К УРАВНЕНИЮ ГАМИЛЬТОНА-ЯКОЬИ 105
Расплывание такого пакета в точности совпадает с растеканием роя частиц
в классической,механике, если их начальные положения и скорости распреде-
ленй около средних значений с квадратичными отклонениями Дхр и At/2. Од-
нако, в классической механике можно взять рой, в котором Ах2 и At/2 —0.
В квантовой механике этого сделать нельзя в силу соотношения неопределен-
ностей Гейзенберга.
§ 35. Переход от временного уравнения Шредингера к классиче-
скому уравнению Гамильтона-Якоби
В предыдущем мы установили связь квантовых уравнений движения
с уравнениями Ньютона и этим самым — связь квантовой механики
с классической. Эта связь может быть обнаружена еще другим спосо-
бом, а именно, можно показать, что классическое уравнение Гамильтона-
Якоби является предельным случаем временного уравнения Шредингера.
Чтобы доказать это, напомним сперва уравнения Гамильтона-Якоби. Для
простоты ограничимся рассмотрением движения одной частицы массы g,
в потенциальном поле СЦх, у, z, t). Уравнение Гамильтона-Якоби пи-
шется для функции действия So (х, у, zy t), которая обладает тем свой-
ством, что
Р* дх ' Ру ду ’ Р* dz ’ \ )
где рх, ру, рг суть проекции импульса частицы на оси координат.
Само уравнение Гамильтона-Якоби для рассматриваемого случая
гласит:
+(>)’+ Л ')• <з5.2)
Так как функция Гамильтона Н(рх, ру, pz, х, у, z, t) равна
н(Рх, Ру’ Рг’ х’ У’ z’ = + U^X’ У> Z' <35-3)'
то из (35.1) и (35.2) следует, что уравнение Гамильтона-Якоби может
быть' написано в виде
Если функция Гамильтона не зависит явно от времени, то она равна
энергии частицы Е. Тогда из (35.4)1 следует
d4f=E, S0=Et — s0(x, у, z). (35.5}
Равенства (35.1) показывают, что траектории являются линиями,
ортогональными к поверхностям 50= const. Если Н не'зависит от вре-
мени явно, то форма этих поверхностей не меняется с течением времени
106 СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ [ГЛ. VII
^(траектории будут линиями, ортогональными к поверхностям 50 = const.).
На рис. 14 показаны эти поверхности и возможные траектории ча-
стицы.
Частица, находящаяся в момент времени / —0 в точке а, будет
двигаться в дальнейшем по траектории а, Ь. Представим себе рой ча-
Рис. 14. Траектории и поверхности
постоянной функции действия.
стиц, имеющих различные началь-
ные координаты х0, yQ, z$.
Пусть в элементе объема AV
имеется ДМ = р A V частиц, где
р — плотность частиц. К моменту
времени t все эти частицы пере-
местятся в некоторую другую об-
ласть пространства, но число их,
конечно, не изменится. Поэтому,
если следить за движением эле-
мента объема A V, связанного с
этими частицами, то число частиц
в нем остается неизменным. Обоз-
начая локальную производную че-
D
рез , получим:
DkN । ПДУ n
Но, как известно, локальные производные от р и ДУ фавны
Пр др . DW . TZ
= + -^-dlvvAK
где v—скорость движения частиц. Комбинируя эти выражения с пре-
дыдущим равенством, мы получаем уравнение непрерывности
g+dlv(pv) = O. (35.6)
На основании (35.1)
V=| = |VSO. (35.7)
Поэтому (35.6) можно переписать в виде
~-div(pVS0) = 0 или g=l{VpV50 + pP50}. (35.8).
Таким образом рой частиц движется, как жидкость. Занимаемый им
объем не «расплывается», а только деформируется.
Уравнения (35 8) можно рассматривать и иначе. Если мы разделим
ддг
число частиц A7V в объеме A V на общее число частиц М, то можно
рассматривать как вероятность найти частицу в объеме А У, а плотность
р — как плотность вероятности.
ПЕРЕХОД К УРАВНЕНИЮ ГАМИЛЬТОНА-ЯКОБИ
107
§ 35]
Покажем теперь, что временное уравнение Шредингера
= (35.9)
ведет приближенно к тем же результатам, что и рассмотренное уравне-
ние Гамильтона-Якоби. Для этого представим сперва волновую функцию ф
в виде
<35Л°)
где S—некоторая новая искомая функция. Замечая, что
дх h дх *’ дх2 h2\dx) ‘ h дх2
мы получим, подставляя (35.10) в (35.9), уравнение для функции
Разложим теперь 5 по степеням ih\
5= So -j- (th) Sx + (/A)2 S2 + ... (35.12)
Подставляя (35.12) в (35.11) и сравнивая одинаковые степени h,
мы получаем уравнения:,
(35..3)
dSj__ 1 f9 dS0 I 9 dSj । 9 dSp dSj । Г2 о I__________
dt 2|i 1 dx dx * dy dy * dz dz "* 0 J
=1{2VSOV51 + V2SO} (35.13')
И T. Д.
Первое из этих уравнений в точности совпадает с уравнением Га-
мильтона-Якоби (35.2), а второе, как легко видеть, совпадает с уравне-
нием непрерывности (35.8). В самом деле, вероятность найти частицу
в окрестности точки х, у, z есть
р = |ф|2 (35.14)
Отсюда
Vp = 2VS1^+-,
д?___9 д£г 25i
dt~2 dt е *
Поэтому, умножая первое из уравнений (35.13) на г251, мы получаем
уравнение непрерывности (35.8).
Шм остается выяснить вопрос об области применимости полученного
приближенного решения уравнения Шредингера. Получая первое из урав-
нений (35.13), мы отбросили член V2S; это возможно сделать, если
(35.15)
108 СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ [гл. VII
Пользуясь (35.1) это неравенство можно записать в виде
g>£|dlvp|. (35.1В)
Это неравенство утверждает, что кинетическая энергия должна быть
велика, а изменения импульса | div р | малы. Для одного измерения получим:
(35.1£'>
Вводя длину волны де-Бройля находим:
(35.17)
т. е. длина волны должна медленно меняться в функции координаты *).
§ 36. Квантовая механика и оптика
Исторически одним из истоков квантовой механики послужили парал-
лели, установленные Гамильтоном между геометрической оптикой и ме-
ханикой. Эти забытые аналогии были привлечены де-Бройлем в совре-
менную физику, и с их помощью были сделаны первые шаги квантовой
(волновой) механики**). Часто- говорилось, что Шредингер построил
механику, аналогичную волновой оптике.
Аналогии часто помогают решению той или иной физической проблемы,
но все же остаются только аналогиями. Окончательно написанное Шре-
дингером уравнение не совпадает ни с одним из ранее известных урав-
нений для распространения волн. Эти последние — всегда уравнения вто-
рого порядка по времени, в то время как уравнение Шредингера —
первого порядка по времени. Существуют.и другие отличия.
Тем не менее все же представляет интерес сравнить уравнение Шре-
дингера с уравнениями волновой оптики. Допустим, что мы имеем не-
которую однородную среду, в которой распространяются волны со ско-
ростью v. Тогда уравнение для смещения f в таких волнах будет
V2/—-2^ = °. (36.1)
J v2, dt£ ' '
Для волны, имеющей частоту колебаний со, можно положить
f=ue-Mr (36.2)
тогда из (36.1) получаем^
¥2и4-&2и = 0, /г2 = ^ (36.3)
*) Из изложенного следует, что в случае медленного изменения X волно-
вая функция ф (х) может быть приближенно определена через классическую
функцию Гамильтона-Якоби So и классическую плотность р по формулам
(35.10), (35.12) и (35.14). На этом основан приближенный мет^д нахождения вол-
новых функций и квантовых уравнений (мет^д Вентцеля-Брйллуэна-Крамерса).
Изложение этого метода см. в статье Pauli, Hndb. d. Phys., т. XXIV, I.
**) См. де-Бро г ль, Введение в волновую механику, ДНТВУ, 1934.
КВАНТОВАЯ МЕХАНИКА И ОПТИКА
109
§ 36]
2^
(& = -у—волновое число, к — длина волны). Уравнение (38.3) строго
применимо для однородной среды*). Однако, оно описывает явления
диффракции и интерференции и в том случае, если считать скорость v
функцией координат. Поэтому его можно рассматривать как волновое
уравнение и для неоднородной, среды. В этом случае k2 будет функцией
координат. Условно будем и в этом случае называть k волновым числом,
а Л — -г- — длиной волны.
к
Введем показатель преломления п(х,у, z):
ь
n(x,^^) = J = ^, (36.4)
где Хо— длина волны в пустоте. Тогда уравнение (36.3) можно написать
в виде
V2zz-]-/^2zz = 0. (36.5)
Если неоднородности малы так, что показатель преломления п мало ме-
няется на протяжении длины волны, то из волнового уравнения (36.5)
можно получить основное уравнение геометрической оптики.
Для этого положим:
« = (36.6)
где а — амплитуда, Ло0— фаза волны. Если длина волны мала, то kQ
велико. Разложим а и 0 по обратным степеням Ло:
0 0О+ Г-01 + —2 • • • (36.8)
«о k0
Подставляя (36.7) и (36.8) в (36.6), а (36.6) в (36.5) и собирая оди-
наковые степени Ло, получим уравнение (36.5) в виде
— йоао (V0o)2 + ^йп2аа 4- О (Ао) = О,
где O(kQ) означает члены порядка kQ и ниже**).
*) Уравнение для распространения волн в неоднородной среде (например,
электромагнитных волн в среде с переменной диэлектрической постоянной)
выглядит на самом деле сложнее, нежели (36.3).
**) Вычисляя члены, обозначенные через О (#0), читатель легко убедится,
что мы пренебрегаем членом &оГ29о по сравнению c#q(V0o)2. Беря (для про-
стоты) одно измерение, мы можем написать условие справедливости нашего
приближения в виде
° \ дх J I дх2 I
Замечая, что
ПО СВЯЗЬ КВАНТОВОЙ МЕХАНИКИ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ [гл. VII
Отсюда
(V0o)2 = zz2. (36.9)
Это и есть основное уравнение геометрической оптики, определяющее
поверхности постоянной фазы
0О (х, у, z) — const. (36.10)
через показатель преломления п (х,у, z). Лучи будут линиями, ортогональ-
ными к этим поверхностям.
Сопоставим с уравнением (36.9) уравнение Гамильтона-Якоби (35.2)
для функции действия So. Производя там подстановку SQ = Et— sQ,
мы можем написать (35.2) в виде
(Vs0)2 = 2|х [Е — U(x, у, £)]. (35.11)
Сравнение этого уравнения с (36.9) показывает, что задаче о распро-
странении лучей малой длины волны (большое £0) в неоднородной среде
с показателем преломления n(x,y;z) может быть сопоставлена задача
о движении материальной точки в поле сил с потенциальной энергией
U(x,y, z), причем роль показателя преломления играет величина
V2}i(E—U), а фазы — величина s0. Траектории частиц суть линии,
ортогональные к поверхностям s0 (х, у, 2*) = const. Поэтому траектории
совпадают с лучами света в среде, показатель преломления которой п
пропорционален р<2р(£'—U). Таким образом, классическая механика
материальной точки аналогична геометрической оптике.
Если уравнение (36.3) рассматривать как уравнение волновой оптики,
то можно сказать, что волновая (квантовая) механика аналогична
волновой оптике. В самом деле, уравнение Шредингера
Подстановкой
Ъ = ие h (36.12)
сводится к уравнению
+ ^и==0. (36.13)
Пусть теперь в некоторой области пространства силы отсутствуют:
(7= С= const. Обозначим волновое число в этой области через kQ.
Тогда
^=J(£-C) (36.14)
мы получаем:
т. е. изменение длины волны должно быть мало. Это совпадает с ранее полу-
ченным условием (35.17) для перехода от уравнения Шредингера к уравнению
Г амильтона-Якоби.
§ 37] ПРЕДСТАВЛЕНИЯ СОСТОЯНИЯ КВАНТОВЫХ СИСТЕМ 111
(обычно полагают С=0). Вводя показатель преломления волн по отно-
шению к этой области пространства
мы можем написать уравнение (36.13) в виде
V2a + ^2«=:(), (36.13'>
что совпадает с (36.3).
Простейшие задачи по расчету преломления и отражения волн при-
ведены в § 89.
ГЛАВА VIII
ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
§ 37. Различные представления состояния квантовых систем
Как мы видели, для квантовой механики характерно то, что одно-
временное употребление ряда механических величин (рх и х, Т и Ur
Мх и Му и т. д.) теряет всякий смысл, так как не реализуется таких
состояний системы ф, в которых приведенные величины одновременно
имели бы определенное значение. Поэтому в отношении каждой кван-
товой системы все измерительные аппараты могут быть разбиты на
группы, в каждую из которых включаются аппараты, измеряющие одно-
временно определяемые величины. Одновременное употребление аппа-
ратов разных групп исключается: свойства аппаратов одной группы
противоречат свойствам аппаратов другой группы. Так, например, если
мы имеем дело с частицей, координаты центра тяжести которой суть
х, у, г, то мы легко можем выделить две группы аппаратов: к первой
группе можно отнести аппараты, определяющие координаты х, у, z и
любые функции от них F{x, у, z) (например, потенциальную энергию U)f
а ко второй группе — аппараты, измеряющие импульс рх, ру, pz и лю-
бую функцию этих импульсов F(px, ру, рг) (например, кинетическую
энергию Т). Возможны и другие группы аппаратов.
До сих пор мы изображали состояние частицы волновой функ-
цией ф (х), беря в качестве переменной координату частицы х (про-
стоты ради мы всюду употребляем далее лишь одну координату х).
Координата х определяется измерительным аппаратом, исключающим
возможность измерения импульса рх (будем писать просто р). Предста-
вим себе, что мы интересуемся не координатой, а импульсом частицы р.
Для измерения следует взять другой аппарат, исключающий измерение х.
Между тем волновая функция ф у нас взята как функция х. Нельзя ли
представить состояние так, чтобы волновая функция была функцией
импульса р?
В первом случае мы будем говорить, что состояние отнесено к ап-
парату, измеряющему координату х, во втором случае — к аппарату г
112 ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ [гЛ. VIII
измеряющему импульс р. Коротко говорят: состояние дано в -пред-
ставлении или состояние дано в «р» -представлении.
Найти «р»-представление легко. Пусть нам дана волновая функция
Ф(-М) ( «х»-представление). Разложим эту функцию по собственным
функциям оператора импульса ф^ (х) (т. е. в интеграл Фурье), тогда
= (37.1)
С (р; 0 = J Ф (*, t) ф* (xj dx. (37.2)
Если мы знаем амплитуды с (р, /), то мы знаем и ф (х, /), задание с (р, t)
вполне определяет ф (х, /). Поэтому с (р, t) можно рассматривать как
волновую функцию, данную в функции импульса р и изображающую
физически то же состояние частицы, что и функции ф(х, t). Формулу
(37.1) следует рассматривать как преобразование волновой функции от
«р»-представления к «х»-представлению, а (37.2) — как преобразование
от «х»-представления к «р»-представлению.
Рассмотрим теперь представление состояния, когда за независимую
переменную взята энергия частицы Е. Пусть, для определенности,
Е имеет дискретный спектр значений: Ev Е2, ..., Еп, ... Соответствую-
щие собственные функции обозначим через фг (х), ф2(х), • •., фл(х), . •.
Волновую функцию ф (х, t) мы можем представить в виде ряда
Ч(-М) = 2с„(0фя(х), (37.3)
п
са^=^{х,^^п(х)йх. (37.4)
Опять-таки задание всех амплитуд сп (t) вполне определяет ф (х, /). Об-
ратно, задание ф(х, t) определяет cn[t). Поэтому совокупность всех cn(t)
можно рассматривать как волновую функцию, описывающую то же со-
стояние, что ф (х, Z), но в представлении, в котором за независимую
переменную взята энергия Е *).
С этой точки зрения формула (37.3) есть преобразование волновой
функции от «Е»-представления к «х»-представлению. Формула (37.4)
есть формула обратного преобразования. Из формул (37.1), (37.2),
(37.3) и (37.4) следует, что вероятность найти какое-либо зна-
чение независимой переменной равна квадрату модуля волновой
функции в соответствующем представлении. В самом деле, пусть
имеется некоторое состояние ф(х,/), тогда вероятность w(x, t) найти
значение координаты, лежащее между х и x-\-dx, будет
w (х, t) dx — | ф (х, t) \2dx. (37.5)
Вероятность w (р, t) dp найти импульс р между р и р -j- dp будет
w (р, /) dp = | с (р, t) \2dp. (37.6)
Вероятность найти энергию w (Еп, t) равной Еп будет
«(£я,п=к„Ю12М‘(£я>*)1г- (37.7)
*) Мы могли бы, в полной аналогии с с(р, t), написать ctt (t) (п = 1, 2, 3,...)
£ виде са(0 = с(Е, f) (Е=Еь Е2,..., Е„,...).
§ 38]
ПРЕДСТАВЛЕНИЯ ОПЕРАТОРОВ МЕХАНИЧЕСКИХ ВЕЛИЧИН
ИЗ
§ 38. Различные представления операторов, изображающих
механические величины. Матрица
Для того, чтобы изображение состояний ф в разных независимых
переменных получило полную законченность, нужно еще найти способ
представления операторов в тех же переменных. Между тем до сих
пор мы рассматривали операторы L как «функции» х, считая, что L
имеет вид этом слГ4ае оператор L действует на
функции от х вида ф (х) и производит новую функцию <р (х) соответ-
ственно формуле
<P(x) = l(—ih^, х)ф(х). (38.1)
Поэтому можно сказать, что мы брали оператор L в «х»-предста-
влении.
Найдем теперь оператор L в энергетическом представлении («/:»-
представление), считая, что энергия имеет дискретный спектр значений Еп.
Соответствующие собственные функции пусть будут фл(х). Тогда функ-
ции сриф можно представить в виде
ф(х)=5сЖ(х)> (38.2)
п
(38.3)
п
Совокупность сп есть ф в «/^-представлении, а совокупность Ьп есть ср
также в «/?»-представлении. Оператор L производит из ф новую функ-
цию ср, а вместе с тем из сп новые амплитуды Ьп. Если мы найдем
оператор, который бы непосредственно выражал 'Ьп через сп, то feM
самым мы найдем оператор L в «^-представлении. Для этой цели под-
ставим ф и ср из (38.2) и (38.3) в (38.1). Тогда м*ы получаем:
2Мп(-у)=2^-^ФпИ- (38.4)
п п
Умножая (38.4) на ф*(х) и интегрируя по всему пространству х, мы
получим в силу ортогональности функций фл(х)
= 5 Lmncn, (38.5)
п
где
= (38.6)
Зная все величины Lmn, мы можем по формуле (38.5) найти все
амплитуды (функцию tp в «/^-представлении) по заданным сп (т. е.
по функции ф в «Ё»-представлении). Поэтому совокупность всех
величин Lmn следует рассматривать как оператор L в «Е» -представ-
лении.
8 Блохинцев
114
ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
[ГЛ. VIII
Эту совокупность Можно расположить в виде квадратной таблицы
^11 ^12 Лз • • • ^1п
^21 ^22 ^23 • * * ^2п
(38.7)
L =
L/ril Lm% • • • Lmn
имеющей бесконечное число строк и столбцов. Такая таблица называется
матрицей. Сами величины Lmn называются матричными элементами..
Каждый матричный элемент имеет два индекса *). Первый есть номер
строки, второй — номер столбца. Безразлично, как мы располагаем в та-
кой матрице строки и столбцы. Но в каждом расчете необходимо, ко-
нечно, соблюдать одно определенное расположение. Мы условимся ну-
меровать строки и столбцы в порядке возрастания собственных значений:
Е% Е% ... Еп ...
Можно найти представление операторов £ и в том случае, когда
независимая переменная имеет непрерывный спектр значений. Обратимся
в качестве примера к «р»-представлению. В полной параллели с (38.2)
и (38.3) имеем:
ф(х) = Р(р)ф/,(х)ф, (38.2')
|(x) = J b(p)typ{x)dp, (38.3')
с(р) и Ь(р) суть функции ф и (р в «р»-представлении. Найдем связь
между f(p) й Ь(р). Вставляя (38.2F) и (38.Зг) в (38.1), получаем:
J b(p)^p{x)dp=^c(p)-L^p(x)-dp. (38.4')
Умножая это на (х) и интегрируя по х, в силу ортогональности
функций фр(х) получаем:
j b(p)b{p' — p)dp = ^c(p)dp j ф*,-£фр-^х
ИЛИ
ь (/>') = J Lplpc (р) dp, (38.5')
где
Lp,p = L(p',p) = Ji,;- (x)-L'bp(x)-dx. (38.6')
*) Часто применяются другие обозначения матричных элементов, введен-
ные Дираком, именцо, пишут:
(т | L | п) вместо Lmn,
или еще подробнее:
(Em\L |£д) вместо
Lmtr
В этом последнем обозначении указывается не только оператор (£), которому
принадлежит матричный элемент, но и представление, в котором он берется (£),
и, наконец, номера собственных значений т и л, которым принадлежит матрич-
ный элемент. Такое обозначение особенно удобно в случае вырождения (§ 21),
когда волновые функции характеризуются несколькими индексами.
§ 39] МАТРИЦЫ И ДЕЙСТВИЯ НАД ними 115
Величина L есть оператор L в «р»-представлении. Она зависит от
двух переменных р' и р, пробегающих рдни и те же значения. L
попрежнему будем называть матричным элементом оператора L
в «р»-представлении, а всю совокупность значений Lpfp—матрицей. Ясно,
что в этом случае мы не можем изобразить Lp,p в виде таблицы. Тем
не менее и в этом случае р' будем называть номером строки, а р — но-
мером столбца.
Мы видим, что в произвольном представлении операторы изобра-
жаются матрицами **). В «х»-представлении мы имели 'операторы в виде
дифференциальных операторов. Однако, можно показать (см. § 39),
что и в этом представлении операторы можно записать в матричной
форме.
§ 39. Матрицы и действия над ними
В матрицах мы отличаем среди всех элементов так называемые диа-
гональные элементы. Диагональными элементами называются матричные
элементы, ном‘ер строки которых равен номеру колонны, т. е. элементы
вида Lnn. В случае непрерывного спектра диагональными элементами
называют элементы вида Lpp. Если матрица имеет только диагональные
элементы, то ее называют диагональной матрицей. В случае дискрет-
ного спектра такая матрица имеет вид
Ln 0 0 ...
О £22 0 ...
о’ V 0
О ...
О ...
(39.1)
Важным случаем диагональной матрицы является единичная матрица i
с элементами Ьтп, равными
(39.2)
Эта матрица имеет, следовательно, вид
1
о
о
о
о
о
1
о
1
о
о
о
о
(39.2")
*) В самом деле, под Е или р можно разуметь любую величину £, имею-
щую дискретный или соответственно непрерывный спектр значений. Более
обще под Е или р можно разуметь целую совокупность независимых, одно-
временно измеримых величин £, М, N...
Более полное изложение теории представлений и преобразований от одного
представления к другому читатель найдет в книгах: Дирак, Основы кван-
товой механики, ГТТИ, 1935; Френкель, Волновая механика, т. II, ГТТИ,
1935.
3*
116 ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ [гл. VIII
Из определения матричных элементов единичной матрицы (39.2) следует,
что единичная матрица остается единичной в любом представле-
нии» ибо равенство (39.2) имеет место для любой системы ортогональных
функций фя(х). Элементы диагональной матрицы L всегда могут быть
записаны в виде:
^тп = ^тП- (39.3)
Часто наряду с какой-либо матрицей £, обладающей элементами Lmn,
приходится рассматривать родственные ей матрицы. Среди таких отме-
тим сперва комплексно-сопряженную Матрицу L*. Элементы этой
матрицы комплексно сопряжены соответствующим элементам исходной
матрицы:
(A*) mr = L* (39.4)
Далее, из данной матрицы можно образовать транспонированную мат-
рицу L. Эта матрица образуется из исходной путем взаимной замены
строк и столбцов. Элементы этой матрицы определяются формулой
^mn=Lnm- (39.5)
Если мы возьмем матрицу, комплексно-сопряженную транспонированной
(т. е. £*), то мы получим матрицу, которую называют сопряженной
к исходной и обозначают через L+. Ее элементы определяются фор-
мулой
(£+U^(L*)mn-=An*m. (39.6)
В том случае, когда сопряженная матрица равна исходной:
L+—L (т. е. Lmn = L*nm\ (39.7)
то матрица называется эрмитовской или самосопряженной. Это опре-
деление вполне соответствует нашему прежнему определению эрмитов-
ского или самосопряженного оператора (18.7). В самом деле, если опе-
ратор L — эрмйтовский, то мы имеем для его матричных элементов:
L = -dx=z f ф-L*^*-dx = L*
тп J ‘ m 1 л J 1 л \V\ ппг
Рассмотрим теперь алгебраические операции над матрицами. Об-
ратимся сначала к сложению матриц. Пусть дан некоторый оператор С,
являющийся суммой рператрров А и В. Тогда под суммой матриц А и В
м!ы будем разуметь матрицу оператора С. Легко найти элементы этой
матрицы. Имеем:
Cmn=^*m-Ciln-dx^^*m.Ai}n.dX + \ K-^n'dx, (39.8)
следовательно,
= + (39.9)
т. е. матричный элемент суммы операторов равен сумме соответ-
ствующих элементов каждого из входящих в сумму операторов.
Весьма важным в смысле приложений является правило умножения матриц.
§ 39] МАТРИЦЫ И ДЕЙСТВИЯ НАД ними 117
Для установления этого правила вычислим матричный элемент опера-
тора С, являющегося произведением двух операторов А и В. Поль-
зуясь определением матричного элемента, получаем:
Стп=\(39.10)
Величина В$п сама является некоторой функцией и может быть разло-
жена в ряд по ортогональным функциям ^(х):
к
где
h=\mndX=Bkn.
Подставляя это разложение в (29.10), получим:
гтл Jk • 5 BknAmk.
К R k
Следовательно,
Cmn^AmkBkn. (39.11)
k
Это и есть правило умножения матриц: чтобы получить матричный
элемент Стп матрицы, представляющей произведение операто-
ров А и В, нужно элементы т-ой строки матрицы А умножить
на элементы п-го столбца матрицы В и сложить. Правило сло-
жения матриц (39.9) и правило умножения матриц позволит по данным
матрицам операторов Д, В, ... находить матрицы, представляющие
различные функции от Д, В, ... В этом и заключается основное при-
менение этих правил.
Кроме того, правило умножения позволяет в несколько иной форме
представить формулу (38.5), выражающую результат действия опера-
тора L на волновую функцию. Именно, эту формулу можно рассмат-
ривать как матричное произведение. Для этого представим саму волновую
функцию в «£»-представлении в виде матрицы^ с одним столбцом:
ct 0 0
с2 0 0
Таким же образом представим и функцию ср:
by 0 0 ...
0 0 ...
Ьт 0 ........
т
(39.12)
(39.13)
118
ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
[ГЛ. VIII
Теперь легко видеть, что (38.5) может быть написано в виде матрич-
ного произведения
с? = £ф, (39.14)
где ср есть матрица (39.13), ф— матрица (39.12), a L — матрица
(38.7). В самом деле, например, Ьт есть элемент /n-ой строки и пер-
вого столбца матрицы (39.13). Он должен получиться согласно (39.11)
путем перемножения элементов w-ой строки матрицы (38.7) на эле-
менты первого столбца матрицы ф (39.12). Но это как раз и дает
уравнения (38.5). Сопряженную волновую функцию c*v с*, ..., с*, ...
можно записать в виде матрицы, сопряженной к (39.12), именно в виде
матрицы с одной строкой:
4 (% ... 4 ...
О 0 ... О ...
(39.12')
С записью волновых функций в виде матриц (39.12) мы встретимся в
теории магнитного момента электрона.
Заметим еще следующий результат из правила умножения матриц.
Матрица С+, сопряженная к произведению С двух матриц А и В,
должна писаться в виде
С+ =(АВ)+ =Я+А + . (39.15)
В самом деле, элементы С+п по определению сопряженной матрицы
равны С*^. Из (39.11) имеем:
С+тп = С*пт = Е А'Л = = Е + U
k k k
Совершенно аналогичным путем [заменяя суммы на интегралы, символ
Ътп на 8(р'—/?)] получаем соответствующие формулы для непрерывных ма-
триц.
Именно, вместо (39.2) имеем единичную матрицу
3=с8(/-р). (39.2')
Элементы диагональной матрицы запишутся теперь в виде
Lp<p = L(p')i{p’— р). (39.3')
Свойство самосопряженности выразится формулой
Lp'p = Lppl. М
Матричный элемент суммы двух матриц А и В будет равен
= Aprp -|- Bpfp) (39.9')
а матричный элемент произведения двух матриц А и В будет равен
Cp'p=^Apip"Bp,'pdp". (39.11')
Приведем примеры непрерывных матриц. Рассмотрим сначала опера-
тор координаты х в «р»-представлении. Согласно определению мат-
§ 39] МАТРИЦЫ И ДЕЙСТВИЯ НАД ними 119
ричного элемента имеем:
f I г -'т
xpfp—j $p'x^pdx — j *e dx —
= dx~~ ih^-Цр — pr). (39.12")
i dp 2ith J dp r '
Далее, по формуле (38.5'), определяющей действие оператора £, дан-
ного в матричной форме, на волновую функцию, имеем:
b (р')=J xp,vc (р) dp= — § (р’ —р)с (р) dp.
Производя здесь интегрирование по частям, находим:
Ь(р') = [ — ih-Цр’— p)c(p)]t*4-iAjS(p' — Р) d-^-dp
или
= (39.13’)
т. е. оператор х в «р» -представлении может быть дан либо в виде
матрицы (39.12), либо в виде дифференциального оператора /Л ~
(39.13). Последний результат нам уже знаком (ср. § 13).
Оператор & в своем собственном представлении может быть изоб-
ражен диагональной матрицей
хХ1Х = х'Ъ(х — х'), (39.14')
а оператор любой функции И(х) матрицей
Vx,x= И(х')8(х —х'). (39.15')
В самом деле, по формуле (38.5'), заменяя там обозначения b на ср,
с на ф, р на х, получаем:
ср(х') — J Улф(х)^х=^ У(х')8(х — х')ф(х)б/х
или ср (х)= И(х) ф (х), (39.16)
т. е. действие функции И(х) в «х»-представлении сводится к умноже-
нию ф(х) на И(х). Результат опять-таки известный.
Подобным же образом оператор Р может быть дан в матричной
форме
px4=4-iA^S(x—х'). (39.17)
Имеем:
?(*')=J Лг'хф (х) dx=th J 5 (X — х') ф (X) dx.
Интегрируя здесь по частям, получаем:
<Р(Х)=-Г/!^Ф(Х), (39.18)
т. е. матричное представление (39.17) оператора Р эквивалентно диф-
ференциальному Р = —
120
ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
[гл. VIII
§ 40. Определение среднего значения и спектра величины, пред-
ставляемой оператором в матричной форме
Формула (19.1) для среднего значения величины, изображаемой
оператором L в состоянии ф(*, ^)» может быть легко
переписана в матричной форме. Пусть фп(х) суть собственная функ-
ция, принадлежащая n-му собственному значению величины, которая
берется за независимую переменную (например, энергия). Представляя
ф(х, t) в виде ряда
ф(х, /) = 3Сйфл(*. о (40.1)
п
и подставляя ф(х, t) и ф*(х, t)
= t) (40.Г)
в формулу
L = J(p*(x, ^)’Ьф(х, t)-dx,
мы получаем:
L = ^^mcn\rm-^n-dx,
пт и
т. е.
= S ^icm^mncn* (40.2)
п т
Это и есть выражение для среднего значения L величины Lmn, если
представляющий ее оператор L дан в матричной форме. Рассматривая
совокупность сп как матрицу ф с одним столбцом (39.12), а совокуп-
ность Ст — как сопряженную матрицу ф+ с одной строкой (39.12'), мы
можем по правилу матричного умножения записать (40.2) в виде
А = ф+£ф. (40.3)
Спектр величины (совокупность ее возможных значений) и собственные
функции представляющего ее оператора L определяются согласно (20.2)
из уравнения
£ф£=£ф£.
Подставляя в это уравнение ф в виде (40.1), умножая слева на ф^ и
интегрируя по х, получим:
5Х Jrm-^n-dx = L^cn J ^ndx
п J J
ИЛИ
^Lmncn = Lcn. (40.4)
п
Это — бесконечная система линейных однородных алгебраических урав-
нений для определения амплитуд собственной функции сп и собствен-
ных значений оператора Ln,
Как известно из алгебры, система однородных линейных уравнений
только в том случае имеет решение, отличное от нуля, когда опреде-
§ 40]
СРЕДНИЕ ЗНАЧЕНИЯ
121
литель, составленный
В нашем случае этот
столбцов * *):
из коэффициентов уравнений, обращается
определитель имеет бесконечное число
в нуль
строк и
^12 118 • • •
^22 L ^23 • • • ^2п
= 0.
(40.5)
^п2 ^пЗ • * * ^пп L, . .
I
L
Это уравнение накладывает ограничения на возможные значения L. Оно
является уравнением бесконечно высокой степени L (трансцендентным) и
будет иметь бесконечно большое число корней: L — Lv L2, ...,
La, ... В алгебре доказывается, что корни такого уравнения обяза-
тельно действительны. Совокупность значений La, при которых разре-
шима система уравнений (40.4), и будет совокупностью собственных
значений оператора L. Подставляя в (40.4) один из корней уравнения
(40.5), например, La, мы найдем соответствующее этому корню ре-
шение:
£ = Дх> Cl===Cl(^a)f С2==С2(1'а)> •••> ^ = ^n(Ax)» ••• (40.6)
Совокупность найденных таким образом значений cv с2, ..., сп, ... и
будет собственной функцией оператора £, принадлежащей a-му собст-
венному значению L = La.
Эта же волновая функция в «х» -представлении будет **)
Ф«(^)=2сп(£в)ф„(х). (40.6')
п
В своем собственном представлении, всякая величина изображается
диагональной матрицей, В самом деле, если фл(х) есть собственная
функция оператора £, то его матрица имеет элементы:
Lmn = J ¥m-L'h'dx^(40.7)
где Ln есть n-ое собственное значение оператора L. Поэтому задачу о
нахождении собственных значений оператора L можно рассматривать как
задачу о приведении матрицы оператора £, данного в произвольном
представлении, к диагональному виду. (40.7).
Так как коммутирующие операторы имеют общую систему собст-
венных функций, то их матрицы могут быть одновременно приведены к
диагональному виду.
*) Такой определитель следует рассматривать как предел определителя,,
образованного для системы конечного числа N неизвестных сп, при —>• оо.
Уравнение (40.5) имеет смысл, если такой предел существует. Пример такого*
уравнения читатель найдет в книге Уиттекера и Ватсона, Современ-
ный анализ, ч. II, стр. 240.
*fe) Функция фа(х) может быть непосредственно получена путем решения,
дифференциального уравнения £ф = L$. Решение уравнений (40.4) и (40.5) обыч-
но не проще решения указанного дифференциального уравнения. Однако*,
при приближенном решении уравнений (ср. § 64, гл. XII) уравнения в матрич-
ной форме оказываются весьма полезными.
122 ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ [гл. VIII
§ 41. Унитарные преобразования
Рассмотрим преобразование какого-нибудь оператора О от одного произ-
вольного представления к другому. Пусть в йервом представлении оператор G
изображается матрицей G', элементы которой нумеруются собственными зна-
чениями L^=Lr, L2, ..., Ln, ..., Lm, ... оператора L («/.«-представление).
Во втором представлении пусть тот же оператор G изображается матрицей
элементы которой нумеруются собственными значениями М = М2, ...,
Afa, ..., Afp, ... оператора М («Л4»-представление). Для определенности мы
предполагаем, что L и М имеют дискретный спектр. Если оператор G дан
первоначально в «.^-представлении = и собственные
функции операторов L и М суть (х), с[>2 (*), • • •, Фп (А • •W, — и ?i (*“)»
?2(х)’ •• > ?а(4 •••, <Рр(*)> — соответственно, то матричными элементами опе-
ратора G в «/«-представлении будут
Gmn = J с (X) а ( - ih , х^ К (х) dx, (41.1)
а в «7И»-представлении
= — ih^< x^<f?(x)dx. (41.2)
Спрашивается, какова связь между матрицей G' с элементами Gmn и матри-
цей G" с элементами Gap? Разложим собственные функции оператора М по
собственным функциям оператора £:
T₽W = Sln(-v)5„?i S^(x)SXa, (41.3)
п т
причем
ФпМ SL = У Фт W Т« (x)dx. (41.4)
Подстановка (41.3) в (41.2) на основании (41.1) дает
— S S (41.5)
т п
Совокупность величин Sn^ можно рассматривать как матрицу S, строки кото-
рой нумеруются собственными значениями величины Z, а столбцы — собствен-
ными значениями величины М. Наряду с матрицей S рассмотрим сопряженную
матрицу S+, элементами которой являются
($ + )ат $та’ (41.6)
так что S+ =§* и, следовательно, строки матрицы нумеруются собственными
значениями Л4, а столбцы — собственными значениями L На основании (41.6)
формула преобразования от Gmn и G^ (41.5) может быть написана
в виде
— S S ($+)атРтп$п$ (41.7)
т п
или, на основании правила умножения матриц, в матричном виде
G" = S+G'S. (41.8)
Таким образом матрицу S и сопряженную ей матрицу S+ можно рассматри-
вать как матрицы, с помощью которых совершается преобразование опера-
тора от одного представления («А») к другому «714»), Матрица S обладает важ-
ным свойством. Перемножая функции у*(х) и ?р(х) и интегрируя результат
§ 41] УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ 123
по х, на основании ортогональности собственных функций мы получаем
S 5 ~ (41.9)
т п
ИЛИ
= Ч (41.10)
т. е. в матричной форме
$+$=!. (41.11)
Подобным же образом, разлагая функции фл(х) по функциям ?з(х), можно
убедиться, что
S $та (^+)ал == $тп> (41.12)
а
т. е.
SS+ = 1. (41.1V)
Матрица, удовлетворяющая 'условиям (41.11) и (41И V), называется унитар-
ной. Так как произведение S+ на $ или $ на S+ дает единичную матрицу,
то S+ есть матрица, обратная S, т. е.
S+* = S-i. (41.13)
Заметим, что унитарная матрица не является эрмитовской, так гкак для
эрмитовской матрицы вместо (41J3) мы имели бы $+=$. На основании из-
ложенного мы можем сказать, что преобразование оператора от одного пред-
ставления к другому совершается с помощью унитарной матрицы $ с элемен-
тами (41.4). Само преобразование (41.8) называют унитарным. Имея в виду
(41.13), мы можем также переписать его в виде^
G,, = S-1GfS. (41.14)
Задачу о приведении матрицы к диагональному виду можно рассматривать
как задачу о нахождении такой матрицы S, с помощью которой преобразова-
ние (41.14) дает диагональную матрицу G". В самом деле, умножая (41.14)
слева на матрицу S, мы получаем:]
SG" = GfS (41.15)
или, в раскрытом виде,
S $таРа$ — S (41.16)
а , п
Если матрица (7ар диагональна, то
Smfiaa = S ^тп $паС (41.17)
т
Так как. собственные значения (Заа нам неизвестны, то нам следует опустить
индекс а, и мы получим:
$тР — S @тп$1и (41.18)
т
что совпадает с уравнением (40.4), если положить G = L, S = C.
Заметим одно важное свойство унитарного преобразования: унитарное
преобразование оставляет неизменным сумму диагональных элементов
матрицы. Эту сумму называют следом {или «шпуром») матрицы и обозна-
чают т£к:
SpG = SGn„. (41.19)
п
Из (41.7) имеем:
S ^аа = S S S ($+)ат@тп$па = S S @тп S (^+)а/п^Да 3
а а т п т п а
— S S ~ (41.20)
т п п
т. е. след матрицы есть инвариант унитарного преобразования. Этим
свойством часто пользуются в приложениях.
124 ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ [гл. VIII
§ 42. Уравнение Шредингера и зависимость операторов от вре-
мени в матричной форме
Уравнение Шредингера (28.3) может быть переписано в матричной
форме, если разложить ф(х, /) в ряд по собственным функциям фл(х)
какого-либо оператора. Подставляя в (28.3) ф fa t) в виде ряда
ф(х, 0 = 5с„(0фл(х),
п
умножая слева ^на ф^ (х) и интегрируя по х, находим:
^^Г = Е^»А» /«=1, 2,-3, (42.1)
где (V2.2)
есть матричный элемент гамильтониана И. Это уравнение по заданным
в начальный момент гп(0) [т. е. по ф(х, 0)] определяет cn(t) [т. е.
ф (х, 0].
Пусть Н есть оператор полной энергии. Возьмем в качестве функ-
ций фл(х) собственные функции оператора Н. Тогда cn(t) суть ампли*
туды стационарных состояний, а матрица Н бужа диагональной:
Hmn^\Vm-H^n.dx = Enhmn. (42.3)
Подставляя эти значения Нтп в (42.1), находим уравнение Шредингера
для этого случая
de
ih~7 = Em<m- (42.4)
Отсюда
__. Emt
Ст^ = ст(°)е h > (42.5)
т. е. амплитуды стационарных состояний гармонически зависят
от времени. Это совпадает с выводами § 30.
Применим теперь уравнение Шредингера в матричной форме к вы-
числению производной оператора по времени. Дифференцируя по вре-
мени среднее значение (40.2), находим
a_Q__^=yy с* cj-vv/r
dt - at 7^6 4 tn dt £-4 £-4 at гппьп\ Z 4 т^тп at ’
т п т п т п
из (42.1) имеем:
- ihd-w = S ^k.
k k
т-r dW
Подставляя эти производные в выражение для , получаем:
< %- +и Е X £ -
т п т п k
ih EEE ^mkck ^тасв'
m n k
§ 42] УРАВНЕНИЕ ШРЕДИНГЕРА В МАТРИЧНОЙ ФОРМЕ 125
Учитывая, что в силу самосопряженности оператора
__ тт
11 mk 11 km'
а так же то, что индексы пг, п и k пробегают одни и те же значения,
мы можем (переменив во втором члене обозначение k на я, а в третьем k
на пг) переписать предыдущее уравнение в форме:
=S S < %5 сп+тп ЕЕ c'm {Е н*п - Е
m п пг п ‘ k k '
По правилу умножения матриц
^mkHkn = {LH)^, ^HmkLkn = (HL)mn
так, что
тг = #=SS ^Тг+a <LH“ m> Jс- <42-6'
пг п У >
где
1 (LH— HL)mn= ± £ ^mkHkn- HmkLkn) == [Я, L]mn (42.7)
k
есть матричный элемент скобки Пуассона. Из сравнения с формулой
для среднего (42.2) следует, что матричный элемент оператора скоро-
dL
сти —г, есть
dt
(Й)„, = тг+["'Ч"- t42'8»
Формулы (42.6) и (42.8) представляют собой формулы (31.4\ и (31.7)
соответственно в матричном представлении. ~
Рассмотрим важный частный случай. Пусть гамильтониан Н не зави-
сит от времени, так что Н есть оператор полной энергии. Возьмем
специально энергетическое представление («£»-представление). Тогда
матрица И будет диагональной:
Hkn = EkPkn' Hmk — •
Предполагая еще, что оператор L не зависит явно от времени, мы по-
лучим из (42.7) и (42.8):
или
(dt )(42.9)
где
= [(42.10)
есть боровская частота. В частности, матрица оператора скорости будет
иметь элементы
126 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
где хтп— элементы матрицы координаты х. Соотношение между ско-
ростью и координатой получается совершенно таким же, как для осцил-
лятора, колеблющегося с частотой (&тп.
Формула (42.9) становится совершенно очевидной, если применить
так называемый гейзенберговский способ представления оператора.
Этот способ заключается в том, что матрица какого-нибудь оператора L
строится с помощью волновых функций стационарных состояний, взя-
тых для времени /:
Ф«(*> 0=(М*)« л.
Ясно, что это можно сделать, так как ф„(х, t) так же, как и фя(г),
образуют полную ортогональную систему функций. Стало быть, в гей-
зенберговском представлении матричный элемент оператора L опреде-
лится по формуле
Lmn (0 = J Ф*я (*> • Цп = Lmne*>™‘. (42.12)
Отсюда для оператора, не зависящего явно от времени
Эта формула отличается от (42.9) только тем, что зависимость от вре-
мени перенесена с волновых функций на операторы.
Согласно (42.12) матричные элементы операторов, явно не завися-
щих от времени, в гейзенберговском представлении гармонически зави-
сят от времени, с частотами Бора
ГЛ АВ А IX
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ
§ 43. Введение
В этой главе мы рассмотрим простейшие задачи атомной механики,
относящиеся к движению частицы в поле потенциальных сил. Вообще,
если силы не зависят от времени, то основной задачей атомной меха-
ники будет задача о нахождении стационарных состояний системы. Дей-
ствительно, в этом случае согласно (30.8) произвольное состояние ф (x, t)
может быть представлено как суперпозиция стационарных состояний
с постоянными амплитудами с^.
(43.1)
п
ФЯ(*>О = ФЯ(*Н Л> (43.2)
где фл(х) суть волновые функции стационарных состояний, а Еп — со-
ответствующие значения энергии. Волновые функции фя(х) суть еобст-
§ 44] ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 127
венные функции оператора энергии Н и определяются согласно (30.4)
из уравнения Шредингера для стационарных состояний
Н<Ъ = Е^. (43.3)
Задача о нахождении стационарных состояний есть вместе с тем задача
о нахождении спектра энергии Е.
Особое значение этой задачи для атомной механики заключается
в том, что в противоположность классической механике квантовая меха-
ника приводит во многих случаях к квантованию энергии, т. е. к ди-
скретному спектру значений ее Ev Е2, ..., Еп, ... Эти значения часто
называют квантовыми уровнями или уровнями энергии.
Если система (например, электрон в атоме, молекула и т. п.), об-
ладающая таким спектром энергии, подвергается извне слабому воздей-
ствию, то ее квантовые уровни не меняются (точнее, меняются мало)»
Однако, благодаря внешнему воздействию система может переходить из
одного уровня в другой так, что ее состояние может измениться значи-
тельно. Вероятности этих переходов мы вычислим значительно позднее.
Нахождение же возможных значений энергии позволит нам сразу
сказать, каковы возможные изменения энергии^ рассматриваемой нами
системы, если между ней и какой-либо другой системой или внешним
полем установлена слабая связь*). Так, если найденные уровни энер-
гии будут Е2, Еп, ...,Ет, ..., то обмен энергий возможен
лишь порциями:
= (43.4)
§ 44. Гармонический осциллятор
В классической механике гамильтонова функция одномерного гар-
монического осциллятора имеет вид
о 2
^=27 + 7^ (44-В
Здесь рх — импульс частицы, р— ее масса, х— отклонение от положе-
ния равновесия, а а)0 — собственная частота (циклическая) осциллятора.
Заметим, что гармонический осциллятор, поскольку речь идет о меха-
нических колебаниях, является идеализацией, так как значение потен-
|1С0?
циальной энергии U — -%- х2 означает, что по мере удаления от по-
ложения равновесия сила неограниченно возрастает. Во всех реальных
случаях, начиная с некоторых значений амплитуды, начинаются заметные
отступления от гармоничности, а при больших значениях х сила вза-
имодействия стремится к нулю (a U—к постоянной величине). Однако,
для небольших амплитуд х можно вполне пользоваться представлением
о гармоническом осцилляторе.
*) Если связь между системами сильна, то мы имеем одну целую систему.
Если велико внешнее поле, то уровни в системе заметно меняются. Поэтому
предположение о слабости связи является важным.
128 теория движения частицы в поле потенциальных сил [гл. IX
Теория гармонического одномерного осциллятора имеет большое
значение в приложениях, так как подходящим выбором координат («нор-
мальные координаты») движение любой системы частиц, совершающих
малые колебания, может быть сведено к движению совокупности неза-
висимых осцилляторов *).
В квантовой механике под одномерным осциллятором мы будем ра-
зуметь систему, описываемую оператором Гамильтона /f, равным, в пол-
ной аналогии с (44.1),
|1(0л
+ (44.2)
тде Рх — оператор импульса, а X—оператор координаты**). Соответ-
ственно этому гамильтониану уравнение Шредингера в «х»-представле-
нии для стационарных состояний осциллятора имеет вид
Л3 d^ , р>о .
-17®+т'’«=Ч.
(44.3)
Для решения этого уравнения введем безразмерные величины
(44.4)
Обозначая дифференцирование по $ штрихом и рассматривая ф как
функцию S, после элементарных преобразований мы сможем написать
уравнение (44.3) в виде
ф" + (Х — £2)ф = 0. (44.5)
Нам следует найти конечные, непрерывные и однозначные решения
этого уравнения в интервале — оо -}- оо. Такие решения урав-
нение (44.5) имеет не при всех значениях параметра X, а лишь при
Х = 2п+1, п = 0,1,2,3, ..., (44.6)
причем соответствующие собственные функции фге равны
= ’(44.7)
где Нп (£) есть полином Чебышева-Эрмита я-го порядка ***), определяе-
мый формулой
Н •
(44.8)
*) См. § 100. Кроме того, теория квантовых гармонических осцилляторов
находит важное применение в квантовой теории света (см. Г а й т л е р, Кван-
товая теория излучения, ГИТТЛ, 1940).
**) Может возникнуть вопрос: почему имеет смысл называть систему
€ гамильтонианом (44.2) гармоническим осциллятором? Ответ заключается в том,
что система, описываемая гамильтонианом (44.2), излучает и поглощает только
одну частоту <о0 (см. § 83, А) и при h —> 0 переходит в классическую систему
с гамильтоновой функцией (44.1) (ср. §§ 34, 35).
***) Подробности, касающиеся решения уравнения (44.5) и в особенности
требования (44.6), даны в дополнении VIII.
§ 44]
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
129
при этом множитель перед е^2 выбран так, что функция фя(Е) нормиро-
вана по Е к 1:
4-оо -f-оо
J ф’(£) <£== J (&)<£==!. (44.9)
— 00 ~оо
Таким образом, одного требования непрерывности и конечности ф ока-
зывается достаточно, чтобы параметр I получал лишь дискретные зна-
чения (44.6). Но согласно (44.4) этот параметр определяет энергию.
Комбинируя (44.4) и (44.6), находим, что возможные значения Еп суть
£'п = А0)0(я-|-2-) , я = 0,1,2, 3, ... (44.10)
Эта формула показывает, что энергия осциллятора Е может иметь лишь
дискретные значения (44.10). Число л, определяющее номер квантового
уровня, называют главным квантовым числом.
Окончательно мы запишем собственную функцию, принадлежащую
л-му собственному значению и данную в «х»-представлении, в виде
е 2
(44.11)
V хо
где $ = — .* Эти функции нормированы так, что
хо
4-о°
j ty\(x)dx==A.
— 00
Пользуясь формулами (44.7) и (44.8), выпишем несколько собственных
функций вида (44.11)
|0(x)=7J==e-x’/2*!, я = 0, (44.12)
ф1(х)= 1^-^* л=ъ (44.12')
V 2х0 У-к 0
^^=—=±==^^(4^-2), п = 2. (44.12")
у 22«2х0Тгк ' *о 7
Первая функция не обращается в нуль нигде (кроме х==+оо). Вто-
рая обращается в нуль при х — 0. Точку, где волновая функция об-
ращается в нуль, будем называть узлом. Третья функция обращается
в нуль при х = + ^^ И имеет, стало быть, два узла. Мы замечаем,
что число узлов равно номеру функции п. Это свойство справедливо
для любого к*). Таким образом квантовое число равно числу узлов * 9
*) Всегда номер собственной функции равен числу узлов. Общее доказа-
тельство этой теоремы смотри у~Р. Куранта и Д. Гильберта, Методы
математической физики, ГТТИ, 1933, т. 1, стр. 429—434.
9 Блохинцев
130
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
собственной функции. Эти волновые функции изображены на рис. 15,а.
Вид функций ф„(х) аналогичен виду функции £7я(х), изображающей
кб'лебание закрепленной на концах струны. Для сравнения на рис. 15,&
приведена функция Un(x) для основного тона (п = 0), первого обертона
(л=1) и второго обертона (л = 2).
Обнаруживающаяся аналогия между колебаниями струны и волновой
функцией осциллятора не является случайной. Она обусловлена двумя
Обстоятельствами. Во-первых, в обоих случаях дело идет об одном из-
мерении. Во-вторых, колебания струны суть собственные колебания.
Согласно общей теореме об узлах собственных функций (см. примеча-
ние на стр. 129) число узлов функции ф„(х) и функции ип(х) должно
быть одинаково.
Чтобы получить еще более полное представление о квантовых со-
стояниях осциллятора, мы приводим
Рис. 16. Диаграмма квантовых уров-
ней (Еп) и потенциальной энергии
P-Wo
U (х) = -^-хг для гармонического ос-
циллятора.
на рис. 16 потенциальную функцию
осциллятора U (х) = х2- По оси
ординат отложена потенциальная
энергия, а по оси абсцисс откло-
нение х. На этом же рисунке
горизонтальными линиями изоб-
ражены уровни энергии Еп (44.10)
для разных п. Такие диаграммы,
на которых изображается одно-
временно энергетический спектр
и потенциальная энергия, упот-
ребляются довольно часто. Они
позволяют произвести простое срав-
нение с классической картиной дви-
жения. Рассмотрим, например,
уровень Ех. Согласно классической
механике частица, имеющая энергию, Ех, могла бы быть обнаружена
лишь в области АВ. В самом деле, А и В суть точки, где потенциаль-
ная энергия равна полной. В этих точках кинетическая энергия Т равна
нулю, так как E=T+U, .T=E—U. (44.13)
§ 44]
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
131
Точки А и В называются точками поворота. Очевидно, О А — ОВ
естп амплитуда колебания частицы, имеющей энергию Ег.
Вычислим вероятность w(x)dx найти частицу в области х, x-\-dx
по классической механике. Эта вероятность пропорциональна вре-
мени dt, в течение которого частица проходит отрезок dx. Если пе-
риод колебаний есть Г=—, то мы можем положить:
= (44.14)
где v— скорость частицы. Выразим v как функцию х. Имеем:
X = a sin (!)0/, (44.15)
где а — амплитуда колебаний:
Из (44.15) имеем:
v = a®Q cos соо/, (44.16)
т. е. опять-таки по (44.15):
® = а<°0(1 —З)7’- (44.17)-
Следовательно,
dx = А у , - а < х < + а. (44.18)
Эта вероятность изображена на рис.
дает, как и следует ожидать, на точ-
ки поворота А и В.
Вероятность найти частицу в об-
ласти х, x-\-dx по квантовой меха-
нике равна (для п = 1)
wKB.(x) dx = (х) dx,
причем (bj следует взять из (46.12').
Следовательно,
wKB. (х) dx = -Le-*8/x * (44.19)
У2гс ф0
График этой вероятности также
изображен на рис. 17. Как видно,
квантовая вероятность также имеет
максимумы около классических точек
3
поворота (точно, для Е1 = -%
Рис. 17. Сравнение квантовой ве-
роятности (^кв.) местонахождения
частицы (для п = 1) с классической
(®кл.)-
А, В—точки поворота; Аг, Вг — точки
максимума .
0Д=0В = 1/ —,аОЛ'=ОВ' = 1/ —),но в отличие, от клас-
г |ХС1)0 г Р-СОф
сического случая вероятность найти частицу отлична от нуля и за
точками поворота. Это обстоятельство не представляет в квантовой
дш
132
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
механике какого-либо противоречия, так как равенство (44.13) в кван-
товой механике не имеет силы: кинетическая энергия Т и потенциальная
U не являются одновременно измеримыми величинами.
Особенно сильно подчеркивается различие между квантовым и класси-
ческим случаем, если рассмотреть состояние с наименьшей энергией.
По классической теории наименьшая энергия осциллятора есть £ —О
и соответствует покоящейся в положении равновесия частице. Вероят-
ность ^кл-(^) в этом случае имеет вид, приведенный на рис. 18. Она
всюду равна нулю, кроме точки х = 0. По
квантовой теории наименьшая энергия осцилля-
тора есть
Р _ ^о.
она называется нулевой энергией. Вероят-
ность wKB.(x) в этом случае равна
Рис. 18. Классическая и
квантовая вероятности для
состояния осциллятора с
наименьшей энергией Ео.
Она также приведена на рис. 18.
Выясним детальнее свойства нулевой энер-
гии. Очевидно, что эта энергия не может быть
отнята от осциллятора, ибо по своему суще-
ству она есть минимальная энергия, которую может иметь осциллятор.
Ее можно отнять, лишь изменяя сам осциллятор, именно, уменьшая ча-
стоту <о0, т. е. путем изменения коэффициента упругости. Существо-
вание нулевой энергии является типичным для квантовых систем и пред-
ставляет собой прямое следствие соотношения Гейзенберга
--- --- А2
Др2 • Дх2 > j(44.20)
В самом деле, средние значения р и х в состоянии с определенным
значением энергии равны нулю:
х = j фяхфяйх = j(|)2xrfx = 0 (44.21)
(что следует из нечетности подинтегральной функции),
P=^nPx^ndx= —ih\=°- (44-22)
Поэтому для осциллятора соотношения Гейзенберга (46.20) можно пере-
писать в виде
(44.20')
С другой стороны, средняя энергия осциллятора равна
= (44.23)
§ 45]
ОСЦИЛЛЯТОР В ЭНЕРГЕТИЧЕСКОМ ПРЕДСТАВЛЕНИИ
133
Из сопоставления (44.20е) и (44.23) непосредственно видно, что, умень-
шая потенциальную энергию, мы увеличиваем кинетическую, и на-
оборот. В частности, состояние с наименьшей потенциальной энергией
U=0 есть состояние с бесконечно большой кинетической энергией
Т=оо. Объединяя (44.20е) и (44.23), получаем:
Р2
2И
Б
(44.24)
Отсюда легко найти минимальное значение Е. Именно, из
получаем:
Л = 0
min Е> -у ,
(44.25)
т. е. нулевая энергия есть наименьшая энергия, совместимая с со-
отношением Гейзенберга.
Примером частиц, совершающих малые колебания, могут служить
атомы в молекуле или в твердом теле. Экспериментально удается до-
казать наличие нулевой энергии и нулевых колебаний атомов путем
наблюдения рассеяния света кристаллами. Рассеяние света обусловлено
колебаниями атомов. По мере уменьшения температуры амплитуда ко-
лебаний согласно классической теории должна неограниченно уменьшаться,
а вместе с тем должно исчезать и рассеяние света. Между тем опыт
показывает*), что интенсивность рассеяния света по мере уменьшения
температуры стремится к некоторому, предельному значению,, указыва-
ющему на то, что и при абсолютном нуле колебания атома не прекра-
щаются. Этот факт и подтверждает существование нулевых колебаний.
§ 45. Осциллятор в энергетическом представлении
Обратимся к представлению, в котором за независимую переменную
взята энергия осциллятора Е. В этом представлении оператор полной
энергии Н будет диагональной матрицей с элементами
Нтя==*ЕяЬтп, (45.1)
тп п тпг у /
или на основании (44.10):
Л®0 2 0 0 0 ...
н= 0 3 ь 2 0 0 ... (45.2)
0 0 уА<оо о ...
*) См. R. W. J a m е s, G. W. В г i п d 1 е у, R. G. W о о d, Proc. Roy. Soc.,
125, 401 (1929).
134 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Любое состояние осциллятора ф (х, t) можно представить как супер-
позицию стационарных состояний (ср. § 30):
__
ф(х,0=2с„(Ч)ф„(х)в (45.3)
п
где фя(х) даётся формулой (44.11), а Еп— формулой (44.10). Сово-
купность всех сп будет волновой функцией в «Е» -представлении.
Вероятность найти в состоянии ф (х, t) значение энергии Еп равна
w(fn) = p„(/)|2 = |C„(0)P. (45.4)
Эта вероятность не зависит от времени, что соответствует тому, что
энергия есть интеграл движения.
Найдем оператор координаты X в «f»-представлении. По общей
теории он должен изобразиться матрицей с элементами
xmn=\$mx$ndx- (45.5)
Подставляя сюда ф^ и фя из (44.7), получаем:
+оо ____
Xmn==XQ (^) (^) (45.6)
J г Иш0
— 00
фигурирующий здесь интеграл может быть вычислен и равен
для т = п—
I V —2 для = [
( 0 в остальных случаях. J
(45.7)
Пользуясь этим результатом, мы можем написать (45.6) с помощью
символа атп в следующем виде:
хтп==‘ х\ ~2 ^п~ 1»W~F ^п+1, • (45.8)
Приведем матрицу X. Из (45.8) видно, что отличны от нуля лишь со-
седние с главной диагональю элементы, именно:
¥=х
о
(45.91
В гейзенберговском представлении элементы матрицы оператора X будут
§ 45] осциллятор в энергетическом представлении 135
равны [см. (42.12)]
xmn^ = * * * * * xmn-eia,mnti (45.10)
где
= (45.11)
Так как хтп^=0 лишь для т — п+Л, то все матричные элементы ко-
ординатй осциллятора колеблются с одной и той же частотой, равной
собственной частоте осциллятора со0.
Вычислим теперь среднее значение координаты осциллятора х для
произвольного состояния. По общей формуле (42.2) имеем:
224 (t)хтпсп(0 = 22ст(0)хтп(0• сп (0). (45.12)
т п т п
На основании сказанного о матричных элементах хтп (/) среднее зна-
чение х будет гармонической функцией времени с частотой о)0. Иначе
говоря, х зависит от времени так же, как зависит от времени коорди-
ната классического осциллятора*):
x(t) — a cos (со0^ ?>)• (45.13)
где а — амплитуда, ср.— фаза.
Матрица оператора импульса в «^-представлении может быть
найдена либо путем вычисления интегралов
Pmn = ^Mndx^ —ih dx' (45.14)
либо, более просто, на основании квантовых уравнений движеййя. Сог-
ласно этим уравнениям
dX Р dt ' (45.15)
т. е. (—} Ртп И \ dt Jmn‘ (45.16)
Пользуясь формулой (42.11), находим:
Рта 1®тпР’%тп1 (45.17)
или ртп=№>лт~п)хтп- (45.18)
Разумеется, вычисление интегралов (45.14) ведет к тому же
результату.
*) Этот же результат мы можем получить непосредственно из теоремы
Эренфеста. Уравнение (34.7) для осциллятора принимает вид
d*x 2 —
11 dF
откуда путем интегрирования находим:
х = a cos (coq^+<р).
136 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [гЛ. IX
§ 46. Движение в поле центральной силы
Поле центральной силы характеризуется тем, что потенциальная
энергия частицы в таком поле зависит лишь от ее»расстояния г от не-
которого центра (силового центра). Законы движения в поле централь-
ной силы образуют фундамент атомной механики: решение общей зада-
чи о движении электронов в атоме опирается в той или иной мере на
результаты, относящиеся к движению одной частицы в поле централь-
ной силы.
Обозначая через {/(г) потенциальную энергию частицы, мы можем
написать оператор полной энергии И в виде (33.12)
+ (46.1)
где NP есть оператор квадрата момента импульса, а Тг—оператор ки-
нетической энергии для радиального движения.
Из общей теории интегралов движения (§ 33) следует, что инте-
гралами движения в поле центральной силы будут: полная энергия Е и
момент импульса (т. е. 2И2, Мх, Му, Mg). Мы поставим себе задачу най-
ти стационарные состояния частицы, движущейся в поле U(r).
Уравнение Шредингера для стационарных состояний ф в нашем слу-
чае гласит:
ЛФ+^Ф+^ИФ^Ф- (46.2)
Волновую функцию ф естественно искать как функцию полярных
координат г, 6, ср. Мы должны найти однозначные, непрерывные и конеч-
ные решения ф уравнения (46.2) во всей области изменения переменных
г, 0, ср, т. е. в области 0 ^ г оо, 0 6 тг, 0^ р<2тг. Так как
операторы НиМ2 коммутируют, то они должны иметь общие собствен-
ные функции, поэтому мы можем написать второе уравнение для ф:
М2ф = 7И2ф. (46.3)
Собственные значения 7И2 согласно §25 равны №1(1так что вме-
сто М2ф мы можем подставить в (46.2) величину №1(1-(- 1)ф. Тогда
мы получаем уравнение
ЛФ + Ф + W Ф = <46-2'>
Это уравнение содержит явно лишь одну переменную г. Полагая теперь
ФШ) = /?(г)-Г//и(О,(р), (46.4)
где Ylm (6, гр) есть собственная функция оператора 7И2, мы одновременно
удовлетворяем и уравнению (46.3), и уравнению (46.2'), если функция
R (г) удовлетворяет уравнению
+ + R = ER- (46.5)
§ 46] ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНОЙ силы 137
Это уравнение получается путем деления (46*2) на Ylm. Мы будем
называть его уравнением Шредингера для радиальной функции
Напомним (см. § 25), что функции Ylm являются также собственны-
ми функциями одной из проекций момента импульса, именно — при на-
шем выборе координат проекции Мг. Поэтому в поле центральной силы
полная энергия, квадрат момента импульса и проекция момента импульса
на некоторое произвольное направление OZ являются величинами, одно-
временно измеримыми.
Возможные значения энергии Е определяются из уравнения (46.5)’
и зависят от вида U(г). Они, кроме того, могут зависеть от величины
момента импульса М2 (через число /), но они не могут зависеть от про-
екции момента импульса (и, следовательно, от числа т)\ Мг не вхо-
дит в уравнение (46.5). Это объясняется тем, что мы имеем дело с по-
лем, обладающим центральной симметрией, так что все направления в-
пространстве физически равноправны и поэтому энергия не может за-
висеть от ориентации в пространстве момента импульса. Для дальней-
ших выводов мы должны более подробно определить вид U(г).
Во всех реальных физических системах взаимодействие на бесконеч-
но больших расстояниях бесконечно мало. Это означает, что асимптоти-
чески (при г —► оо) потенциальная энергия принимает постоянное зна-
чение:
U (г) r->oo = const. = С, (46.6)
где С—произвольная постоянная, определяющая уровень потенциаль-
ной энергии в бесконечности.
Мы увидим, что характер решения уравнения (46.5) существенно за-
висит от того, больше ли полная энергия Е, чем значение потенциаль-
ной энергии в бесконечности (С) или меньше. Так как С есть произ-
вольная постоянная, то в тех случаях, когда специально не оговоренот
мы будем полагать ее равной нулю и различать два случая: Е>0 и
£<0.
Определим еще вид Щг) вблизи центра сил (при г—> 0). Мы будем
считать, что U (г) имеет в нуле полюс, порядок которого меньше 2:
д
Щг)„0=£, а <2. (46.7>-
Сделанные нами предположения о виде U(r) охватывают весьма широ-
кий круг задач атомной механики. Так, например, в проблеме движе-
ния валентного электрона в атоме речь идет о движении электрона в
поле ядра атома, окруженного оболочкой более близких к ядру элек-
тронов.
При малых расстояниях действие этих электронов несущественно,,
основное поле будет кулоновским полем ядра. Потенциальная энергия,
А
электрона в кулоновском поле имеет вид — и поэтому входит в класс
(46.7). В случае взаимодействия двух атомов при малых расстояниях
наибольшее взаимодействие есть отталкивание ядер по закону Кулона»
138 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Д
'Т. е. потенциальная энергия имеет опять-таки вид у. В обоих приме-
рах U имеет при г=0 полюс первого порядка.
Для исследования решения уравнения (46.5) представим это реше-
ние в виде
Я(г) = ^. (46.8)
'Подставляя это выражение для R в (47.5) и замечая, что согласно
<26.7) .
у» р — г2 —(г2 — — — — —? (46 9)
Лгк— 2и дг\Г дг)~ 2р. г dr2' 1 '
мы получаем такое уравнение для и:
h2 d2u . h4(l+\) . тг „ /ла 1ПЧ
“2^4-----------^u + Uu = Eu- (46Л°)
Рассмотрим сначала асимптотические решения этого уравнения при
Г —> оо. Пренебрегая для больших г членом с и U(r) [мы считаем
С в (46.6) равной нулю], мы получаем простое уравнение:
— гг^ = Еи. (46.И)
2|i dr2 ' '
Обозначая
№==^- ДЛЯ- £>0 и Х2 = ^для £<0, (46.12)
злы получаем общее решение (46.11) в виде
u = Cieikr-[- C2e~ikr, Е> 0, (46.13)
и = + С2 eXr, Е < 0, (46.14)
где Cj и С2 суть произвольные постоянные. Согласно (46.8) асимпто-
тическое решение уравнения (46.5) имеет вид
R = C1 ^т]-С8 , £>0, (46.15)
R = C^ + C^, £<0. (46.16)
В первом случае Е^>0 решение R конечно и непрерывно при любом
значении постоянных. Как видно, оно представляет собой суперпозицию
сходящихся и расходящихся сферических волн. Вероятность найти ча-
стицу в этом случае не исчезает даже для больших г. Именно, вероят-
ность, найти частицу между г и r*-[-dr пропорциональна |/?|2 и объему
шарового слоя 4тгг2^г*):
w (г) dr | R |2 4тгг2г/г = 4тг | Cxeikr -ф- С2е~ikr \2dr.
*) Более детальное исследование (см., например, В. А. Ф о к, Начала кван-
товой механики, КУ БУЧ, 1932) показывает, Что сделанное нами пренебреже-
ние в уравнении (46.10) потенциальной энергией U (г) законно лишь в том
случае, если U (г) при г—► оо стремится быстрее к нулю, нежели В слу-
§ 46] ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНОЙ силы 139
Такие состояния соответствуют апериодическим орбитам в клас-
сической механике, когда частица движется из бесконечности- к центру
сил и уходит опять в бесконечность.
Иное положение вещей имеет место при £<^0. В этом случае не-
обходимо положить С2 = 0, иначе R становится оо при г—► оо. Поэ-
тому нужное решение в этом случае будет
= (46.16')
Для этих состояний
w (г) dr 4тг | Сг |2 е~2Хг
и при больших г w(r)—> О, т. е. частицу можно найти лишь вблизи
центра сил. Такие состояния соответствуют периодическим орбитам
в классической механике, когда частица движется около силового центра.
Исследуем теперь поведение решений вблизи центра (г—* 0). Будем
искать и (г) в виде степенного ряда
tt(r) = rr(l+^r-|-tz2r2+ ...). (46.17)
Подставим это выражение для и в уравнение (46.10). Тогда низшей
Степенью г будет Л“2 или гт~а. Мы видим, что если а<^2, то низ-
шей степенью будет г^~2. Член с И“2 будет наибольшим (при г—>• 0);
поэтому, игнорируя величины высшего порядка, мы найдем, что резуль-
татом подстановки (46.17) в (46.10) будет
[Y (Y—1) — Z(Z-{-l)]rT"2-j-члены высшего порядка —0. (46.18)
Чтобы это равенство было соблюдено тождественно при всех (беско-
нечно малых) значениях г, необходимо, чтобы
Y(Y~1) = /(/4-1). (46.19)
Отсюда
Y = Z-(-l или Y = — (46.20)
Следовательно, при г—>0 решение /?, равное имеет вид
/? = (1 4“ V2 4“ • * •) 4“ С‘2г”’/~1(1 4”
+ v2+---)> (46.21)
где С[ и С' — произвольные постоянные.
Для того, чтобы функция оставалась конечной, необходимо поло-
жить ^2 = 0. Таким образом, собственная функция R при малых г имеет
вид
R = с;и(1 +^r4-6Z2r24- ...). (46.22)
При г—+ оо это частное решение перейдет либо в (46.15) (если 7?>0),
В
чае кулоновского поля С7(г)г_>со = —, и асимптотические решения (46.15) и
(46.16) несколько видоизменятся, но не стол^ существенно, чтобы это
видоизменение отразилось на справедливости наших дальнейших рассуждений*
140
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
либо в (46.16) (если Е<^0). Полагая С' = 0, мы выбираем частное
решение уравнения (46.10). Поэтому коэффициенты Cj и С2 в (46:15)
или в (46.16) будут находиться уже во вполне определенном отношении
друг к другу [абсолютная же величина этих коэффициентов не имеет
значения, так как уравнение (46.10) есть однородное уравнение]. Это
отношение зависит теперь только от параметров уравнения (46.10), в
частности, от Е. Следовательно, при С2' —0 имеем:
^ =/(£), (46.23)
где f—некоторая функция Е, зависящая от вида уравнения (46.10),
т. е. от U(г).
Если энергия частицы Е>0, то оба частных решения в (46.10)
Q
конечны, и поэтому при любом отношении ~ решение (46.16) есть до-
*С,
пустимое решение, — в частности, и при том , которое получается из
f
требования С2 = 0. Поэтому мы не должны накладывать какого-либо
Q
нового ограничения на отношение . Вместе с тем параметр Е может
ci
иметь любое значение. Отсюда следует, что если энергия £Г^>0,
то энергия не квантуется, а принимает все значения от 0 до оо.
Таким образом при Е>§ мы имеем непрерывный спектр энер-
гии. Другое положение дел имеет место при £<^0. Из требования
конечности функции R в нуле (С'=0) не следует С2 = 0, так что
в общем случае при R конечном в нуле решение будет возрастать
в бесконечности неограниченно. Чтобы получить решения конечные и
в бесконечности, нужно дополнительно потребовать С2 —0. А это нала-
гает ограничение на возможные значения энергии Е, так как тогда из
(46.23) следует
^=f(E) = 0.
(46.24)
Это будет некоторое трансцендентное уравнение для Е. Корни этого
уравнения
E=EV Е2, ..., Еп, ... (46.25)
и будут собственными ^качениями оператора энергии, так как только
при этих значениях Е решение R конечно и при г=0, и при г=оо.
Следовательно, при E<^Q получается дискретный спектр возможных
значений энергии. Мы получаем в этом случае систему квантовых
уровней (46.25).
Рассмотрим теперь подробней несколько наиболее типичных видов
потенциальной энергии U(r). Во всех случаях мы будем считать, что
потенциальная энергия имеет (если имеет вообще) при г=0 полюс
1 ГТ X
порядка ниже -%. Потенциальную энергию в бесконечности условимся
считать равной нулю. На рис. 19 изображена потенциальная энергия U
I 46]
ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНОЙ СИЛЫ
141
Uld,E
Рис. 19. Потенциальная
энергия для случая оттал-
кивания от центра. Энер-
гетический спектр (Е > 0)
непрерывен.
в функции расстояния от центра г для случая отталкивания частицы.
В этом случае полная энергия частицы положительна*). При Е^>0
спектр энергии непрерывен. Следовательно,
в случае отталкивающих сил возможны все
значения энергии от 0 до -|-оо. Это обоз-
начено на рисунке штриховкой. На рис. 20
изображена потенциальная энергия для случая
притяжения. В этом случае мы должны раз-
личать две возможности: Е^>0 и Е<^0.
В первом случае спектр будет непрерыв-
ным (штрихованная часть рисунка). Вд втором
случае мы получаем дискретный спектр зна-
чений Е2, ..., Еп, ... Эти кванто-
вые уровни изображены на рис. 20 гори-
зонтальными линиями. Приведенный спектр,
состоящий из прерывного и сплошного, является как раз тем энергети-
ческим спектром, который свойственен электрону, взаимодействую-
Рис. 20. Потенциальная энергия для
случая притяжения к центру.
Энергетический спектр для Е > 0 непреры-
вен, для Е < 0 состоит из отдельных уров-
ней Fj, Е^ ...» Еп. I есть энергия ионизации.
но, чтобы энергия его электрона была больше 0,
щему с ядром или положительным
ионом (притяжение по закону Ку-
лона).
Дискретные уровни отвечают,
как было показано выше, движе-
нию электррна в атоме (вероят-
ность найти электрон вдали от
атома исчезающе мала). Напро-
тив, сплошной спектр отвечает
ионизованному атому, так как эле-
ктрон в этом случае может ока-
заться как угодно далеко от атома.
Энергия, необходимая для иони-
зации, так называемая работа ио-
низации /, легко может быть по-
лучена из приведенной на рисунке
диаграммы. Действительно/ энер-
гия, которую имеет электрон в
нормальном, невозбужденном со-
стоянии атома, есть Ev Для того,
чтобы атом был ионизован, нуж-
поэтому наименьшая
*) В классической механике Это следует из того, что кинетическая энер-
гия Т > 0, и если U > 0, то и Е > 0. В квантовой механике положение дел
совершенно такое же:
Е— I ф*.р2 ф• tZt'—। dv.
Первый член есть кинетическая энергия и обязательно положителен, так как
положительны собственные значения оператора Р2. Если U > 0, то и Е > 0.
142
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
работа, которая будет затрачена на ионизацию атома в нормальном
его состоянии, есть
1=0 — Ег = — Ег (46.2(5)
Приведем еще другой образец потенциальной кривой, свойственный
двухатомным молекулам AJB. При больших расстояниях атомы А и В
не взаимодействуют, поэтому можно положить U=0 для г=оо. Прй
Рис. 21. Потенциальная энергия U(R}
двух атомов, образующих молекулу,
в функции их расстояния R.
мёныпих расстояниях атомы при-
тягиваются и, наконец, на малых
расстояниях они отталкиваются
из-за отталкивания ядер и эле-
ктронных оболочек при проник-
новении одного атома в другой.
Поэтому потенциальная энергия
имеет вид, приведенный на
рис. 21. Для £>0 мы имеем
опять непрерывный спектр. Веро-
ятность w (г) остается конечной
и при г—> оо: атомы А и В
могут находиться! как угодно
далеко друг от друга (диссоции-
рованная молекула). При £<^0
получается ряд дискретных уров-
ней Ev Е2, ..., Е*п, ... В этом случае w(r)—^0 при г—> оо.
Атомы находятся близко друг к другу и образуют молекулу АВ.
Для диссоциации молекулы, находящейся в нормальном (нижнем)
состоянии, нужно затратить работу диссоциации Z):
D = — Ех.
(46.27)
Заметим, что по классической теории эта работа равнялась бы
D' = — Umin, где Z7min означает наименьшую потенциальную энергию.
D меньше D1 на величину нулевой энергии .
Из приведенных примеров видно, что, зная потенциальную энер-
гию Z7(r), не производя решения уравнения Шредингера, можно сделать
заключение о характере энергетического спектра. § *
§ 47. Движение в кулоновском поле
Самой простой задачей атомной механики является задача о движе-
нии электрона в кулоновском поле ядра. С такой задачей мы встре-
чаемся в атоме водорода Н, в ионе гелия Не*, в двукратно ионизо-
ванном литии L1*'** и тому подобных ионах, называемых вод гродопод об-
ними. Обозначая заряд ядра через -\-eZ,y где е — элементарный заряд,
a Z—номер ядра в системе Менделеева, мы получим, что потенциаль-
ная энергия электрона в поле такого ядра будет по закону Кулона
§ 46] ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНОЙ силы 143
равна
U(r)=—-^-. (47.1)
Для того, чтобы найти квантовые уровни для рассматриваемого движе-
ний электрона, нужно решить уравнение Шредингера для радиальной
функции R. Полагая
R = y, (47.2)
мы получим, как было показано в § 46, для и уравнение (46.10).
Подставляя туда U из (47.1) и разумея под' ц массу электрона, по-
лучаем подлежащее решению уравнение
h2d2u . 7z2Z(Z-|-l) Ze2 „
— 0-7Г-2 + 0--НГ-2 u —J— u — Eu. (47.8)
2|x dr2 ‘ 2|i r2 r \ 7
Рассматриваемый нами случай соответствует притяжению (рис. 20).
Поэтому согласно общей теории движения в поле центральных сил мы
будем иметь непрерывный энергетический спектр для Е 0 и дискрет-
ный для £’<^0. Мы поставим себе задачу найти этот дискретный спектр
и соответствующие собственные функции R. В целях удобства реше-
ния введем вместо г и Е безразмерные величины
/* /?
Р = г и (47Л)
где
а = —, = 0,529-10-8 см, £1 = ^г = ^ = 13,55 eV. (47.5)
и,#2 1 Ла '
Подстановка (47.4) в (47.3) приводит к тому, что в уравнении не
будет содержаться атомных постоянных ц, е, h. Именно, вместо (47.3)
получаем:
+ [2е +у«=0. (47.6)
В соответствии с изложенным в 'предыдущем параграфе об асимптоти-
ческом поведении функции и мы будем искать и в виде
и(р) = е-“Р/(р),a = j/—2е , (47.7)
где /(р) — новая искомая функция.
Подставляя и(р) из (47.7) в (47.6), мы найдем уравнение для функ-
ции /(р). Именно, после несложных вычислений получаем:
(47.8|
dp2 dp 1 L р Р2 J \ 7
Решение этого уравнения будем искать в виде ряда по степеням р.
Из общей теории мы знаем, что конечное при г—0 решение уравне-
ния (47.3) таково, что ряд по степеням г должен начинаться с члена rz+1
Из (47.7) тогда следует, что конечное в нуле решение (47.8) должно
144 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [гЛ. IX
начинаться с р4*1. Поэтому /(р) будем искать в виде
/(P) = P,+1 1 (47.9)
где — пока неизвестные коэффициенты ряда.
Ряд (47.9) должен быть таков, чтобы функция R(r), которую мы
можем теперь согласно (47.2) и (47.7) написать в виде
/?(p)==CW) (47.2')
не нарастала бы до ©о при р —> оо. Для нахождения коэффициентов
ряда подставим (47.9) в (47.8) и соберем одинаковые степени р. Эта
подстановка дает:
2 {‘W0'+*+2)(v-H+i)-/(/+i)]+
+ a,[2Z—2a(v4-/4-l)]} р’+'=0. (47.10)
Чтобы ряд (47.9) был решением уравнения (47.8), нужно, чтобы (47.10)
было удовлетворено тождественно при всех значениях р от 0 до оо.
Это возможно лишь в том случае, если коэффициенты при каждой
степени р были равны нулю, т. е. когда
+1 [(v+1+2) (v +1 +1)—1)] +
+ ^V[2Z — 2a(v + /+l)l = 0 (47.11)
для всех значений V. Эта формула дает рекуррентное соотношение
между и av+1:
а —________2g 1) 2Z----------a У — Q 123 (47 12]
v+1 — [(> + ^+2)(* + /+1) — ^+01 ” ’ ’ ’ ’ •••
Первый коэффициент а0, конечно, произволен, так как уравнение одно-
родно. Дав ему какое-либо значение, найдем из (47.12) at; по ах най-
дем а2 и т. д. Вычисляя все av, мы получим искомое решение в виде
ряда по степеням р.
Нетрудно видеть, что полученный ряд будет сходиться при всех
значениях р, но при больших р растет столь сильно, что R—
при р—^оо будет стремиться к бесконечности*). Следовательно, как и
*) Полагая \ — s~2l-1, перепишем (47.12) в виде
av+i —v + i (V_|_S4_i) а<-
Cl 1
Отсюда видно, что отношение > —г—т при v —► оо. Далее, мы можем
y-J-1
взять такое v = vr, что
V+ 2----------------------------------1 1
- 2
§ 47]
ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ
145
следовало из общей теории § 46, конечное при р = 0 решение не
будет, вообще говоря, конечным при р = оо. Однако, решение будет
заведомо конечно и при р = оо , если ряд оборвется на каком-нибудь чле-
не. Тогда/(р) будет многочленом и будет стремиться к нулю при р —>оо.
Такое решение будет собственной функцией уравнения, так как оно
конечно всюду во всем интервале от р = 0 до р = оо и само собой,
разумеется, однозначно.
Легко видёть, что обрыв ряда на каком-нибудь члене, например,
номера v = nr, может произойти лишь при особом значении параметра
уравнения а. Действительно, положим, что коэффициент аПт еще не
равен нулю. Чтобы следующий коэффициент а^.+1 обращался в нуль,
необходимо, чтобы
2a(nr+Z4-l) — 2Z = 0,
т. е.
а =—г4-гт- (47.13)
«г -М+1 ' ’
Ясно, чт*о при этом условии не только а„г+1, но и все последующие
коэффициенты обращаются с нуль, ибо они все пропорциональны а„г+1.
Таким образом, (47.13) есть необходимое и достаточное условие, чтобы
решение /(р) обращалось в многочлен, а вместе с тем функция /?(р)
оставалась бы всюду конечной. Полагая
п = пг-^1-\-\ (47.14)
и подставляя в (47.13) значение а из (47.7), получим:
e=-f2- (47.13-)
Имея в виду выражение Е через е (47.4), мы получаем, что конечные
и однозначные решения R существуют лишь при следующих значе-
ниях энергии электрона'.
_____ZM|*2 1
— W п* 1
где число п принимает согласно (47.14) значения
/г=1, 2, 3, ... , пг=0, 1, 2, 3, ...
(47.15)
(47.16)
где
е>0, у(1+е)< 1.
Начиная с этого значения v, коэффициенты^ растут быстрее, нежели коэф-
фициенты ряда, определяемые рекуррентной формулой
^+1 — „II b'l'
Ряд же б этими коэффициентами дает
Д ( р) = еа б+е)?.
Поэтому /(р) растет быстр е Д(р), и, следовательно, функция, (47.2‘) бу-
дет стремиться к оо при р—► оо.
Ю Блохинцев
146 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Число п определяет, как мы видим, энергию электрона и называется
главным квантовым числом.
Полученная формула для квантовых уровней Еп электрона, движу-
щегося в кулоновском поле, найдена впервые Бором на основе полу-
классической квантовой теории. В этой теории, где квантование носило
характер искусственного рецепта, приходилось специально оговаривать
невозможность значения п = 0. В квантовой механике это значение
исключено само собой, так как I принимает значения 0,1,2,...,
а пг есть номер члена ряда (47.9) и имеет наименьшее значение 0,-
Прежде чем перейти к подробному рассмотрению полученных кван-
товых уровней Еп> рассмотрим еще вид собственных решений R (р).
Z
Для собственных решений а = —, поэтому формула (47.12) упро-
щается:
а = 2Z —(Z-F-vH-D а ,4712г
V+1 п (v_|_i)(2/4-v4-2) V’
Вычисляя один коэффициент за другим и подставляя их в (47.9), по-
лучим /(р):
ц— а о1+1 (1_______п~1 * (\ I 1 /2j^P \2 г
°Р V 1!(2/-|-2)\ п )' 2 1 (2/-J-2) (2Z3) ( п ) '
_!_-----------~ 1 2).,. 1__(47 17)
-Г— (и-1)!(2/ + 2)(2/ + 3)...(2/ + лг) ( п J J *
Отсюда видно, что целесообразно ввести новую переменную:
= Г. (47.18)
п па ' 7
Объединяя все постоянные множители в один фактор ATw/, мы получим
из (47.2'), что функция /?л/(р), принадлежащая квантовым числам п
и /, будет равна
Rn№ = ^~* 5 tf). (47.19)
где через 1%^ обозначен многочлен, стоящий в фигурных скобках
в формуле (47.17). Такое обозначение связано с принятым в матема-
тике. Дело в том, что многочлен в (47.17) выражается через произ-
водные многочленов Лагерра, которые определяются формулой
= (47.20)
Тогда под многочленом Lsk (£) понимают многочлен
= (47.21)
Полагая здесь k±=n-\-l и $=2/-|-1, легко убедиться, что мы полу-
чим многочлен, заключенный в фигурные скобки в формуле (47.17).
Формулы (47.20) и (47.21) легко позволяют вычислять функции Rnl.
Множитель Nnl в (47.19) мы будем выбирать так, чтобы функция Rnl
§ 48] СПЕКТР И ВОЛНОВЫЕ ФУНКЦИИ АТОМА ВОДОРОДА 147
была нормирована к 1:
J 1. (47.22)
О
Полная собственная функция согласно (47.4) будет равна произведе-
нию Rnl на собственную функцию оператора момента импульса, т. е.
Фв/Я1(/-Л,<р) = /?„Дг)Гйя(0,<Р). (47.23)
Энергия Еп, как следует из (47.15), зависит лишь от главного кванто-
вого числа п. Если это число задано, то из (47.14) вытекает, что ор-
битальное число I может иметь лишь такие значения:
/=0, 1,2,..., п — 1 (nr=n— 1, п — 2, .. ., 0). (47.24)
Далее, как мы знаем, магнитное число т при заданном / пробегает
значения
/и = 0, ± 1, ±2, .. ., ±/. (47.25)
Подсчитаем теперь, сколько различных волновых функций принадлежит
квантовому уравнению Еп. При каждом / мы имеем 2Z —1 функций,
отличающихся числом т. Но I пробегает значения от 0 до п -— 1,
поэтому полное число функций будет
л—1
2 (2/-4-1) = л2. (47.26)
1=0
Таким образом, каждому квантовому уровню Еп принадлежит л2
различных состояний. Мы имеем дело со случаем (п2 — 1 )-кратного
вырождения.
§ 48. Спектр и волновые функции атома водорода
Из формулы (47,15), подставляя в нее значения универсальных по-
стоянных е, р. и Л, мы можем вычислить квантовые уровни электрона,
движущегося в кулоновском поле ядра номера Z. На рис. 22 приве-
дены эти уровни для атома водорода (Z—1).
Числа по вертикали слева дают энергию уровней в электрон-вольтах
(энергия отсчитывается при этом не от 0, а от нижнего уровня Ег).
Как видно, по мере роста главного квантового числа п уровни распо-
лагаются теснее, и при /г = оо Е& — 0; далее идет область непрерыв-
ного спектра £^>0, соответствующая ионизованному атому. Энергия
ионизации атома водорода равна
13,55 eV. (48.1)
Чтобы понять значение чисел, нанесенных на правой вертикали, на-
помним, что частота света (о, излучаемого при переходе из уровня Еп1
в уровень Епчю, согласно квантовой теории света определяется из
Ю*
148 теория движения частицы в поле потенциальных сйл [гл. IX
уравнения Бора*):
h^ = Enim Еп1ут1. (48.2)
Подставляя сюда энергию Еп1т из (47.15), получим:
п'<п- (48.3)
Эта формула (при Z=l) дает частоту света, излучаемого или погло-
Рис. 22. Схема квантовых уровней атома водорода.
частоты.
водорода
щаемого атомом водо-
рода. Величина на-
зывается спектраль-
ным термом. Разности
термов дают
Для атома
терм равен
Еп ___
h
n=l, 2, 3...
1 (48.4)
Величина R
« = 3 = 5'27'Х
х 1015сек.-х (48.4')
называется постоян-
ной Ридберга-Ритца и
впервые теоретически
была вычислена Бором.
В спектроскопии вели-
чину термов чаще ука-
зывают не жв частотах
Е
— , а в волновых чи-
слах, показывающих,
сколько длин волн 1
укладывается в 1 см.
Если циклическая часто-
та света есть (о, то обыч-
. 1
обычно в у, так что
(0 ГЛ
ная частота v = ^. Эту-то частоту и измеряют
спектроскопическое > спектр, (волновое число) равно обыкновенной часто-
те v, деленной на скорость света с:
___ 1 V _________ (О
VcneKTp. = Y = 7 = 2^ СМ
Постоянная Ридберга-Ритца в волновых числах равна
1,09-Юь см~1.
2rJi3c
(48.4")
*) Это будет доказано. Пока мы опираемся на изложенное в § 2.
§ 48] СПЕКТР И ВОЛНОВЫЕ ФУНКЦИИ АТОМА ВОДОРОДА 149
Термы водорода в этих же единицах равны
Числа, нанесенные на диаграмме уровней водорода (рис. 22) справа,
дают величину спектральных термов в обратных сантиметрах. Линии,
соединяющие уровни по своей длине, пропорциональны энергии кванта
света, излучаемого или поглощаемого при переходе электрона между
этими уровнями. Указанные на этих линиях числа дают длину волны X
света в А.
Все частоты, относящиеся к переходам, кончающимся одним и тем
же нижним уровнем, образуют так называемую спектральную серию.
Отметим наиболее важные серии водорода. Переходы на уровень п — \
(нижний) образуют серию Лаймана, Частоты серии Лаймана вычисля-
ются по формуле
д=2, 3,... (48.5)
Среди этих спектральных линий линия п — 2 имеет наибольшую длину
волны 1=1215,68 А. Она находится в ультрафиолетовой части спектра.
Переходы на уровень п = 2 соответствуют излучению видимого
света. Совокупность этих спектральных линий образует знаменитую
серию Бальмера, Частоты этой серии суть
v = « = 3, 4, ... (48.6)
Формула (48.6) была найдена Бальмером в 1885 г. на основе анализа
эмпирических данных о спектре водорода. Впоследствии эта формула
сыграла исключительную роль в расшифровке спектров и послужила
пробным камнем для квантовой теории атома. Спектральные линии серии
Бальмера обозначаются буквами
(/2 = 3), (/2 = 4), Нч (/2 = 5) и т. д.
Кроме серии Бальмера и серии Лаймана на диаграмме приведены и дру-
гие серии, соответствующие переходам на уровни /2 = 3,4 и 5 (серии
Ритца-Пашена, Брэккета и Пфунда соответственно). Линии этих серий
лежат в инфракрасной области спектра.
Спектры водородоподобных ионов Не+, Li++ и т. п. имеют такой
же вид, как и рассмотренный спектр водорода, но все линии переме-
щаются в область более коротких длин волн, так как в этих случаях
постоянную Ридберга следует увеличить в Z2 раз. Именно, согласно
(48.3) и (48.4") частоты для этих ионов будут вычисляться из формулы
у = Л'<«. (48.7)
Обратимся теперь к более детальному анализу квантовых состояний
и соответствующих собственных функций фл//я(г, 0, <р) (47.23). Любое
определенное состояние, задаваемое тройкой квантовых чисел /2, /, т»
150
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
представляет собой собственное состояние трех одновременно измеримых
величин: энергии, квадрата момента импульса и проекции момента
импульса на некоторое направление OZ. Все эти три величины имеют
в состоянии определенные значения, именно:
£ --- ---1 /4о е\
2/z2 л2’ (48.8)
= 7 = 0, 1, 2,..., п—1, (48.9)
Mz — hm9 = 0, + 1, + 2, ...,-Р Z. (48.10)
Таким образом, динамическое значение квантовых чисел n, Z, т
Рис. 23. Полярные координаты.
заключается в том, что глав-
ное число п указывает кван-
товый уровень Еп, орби-
тальное число Z — величи-
ну момента импульса Af]
и, наконец, магнитное чи-
сло т—величину проек-
ции момента импульса Mg
на некоторое произвольное
направление OZ*).
Квадрат абсолютного
значения фп(т(г, 0, <?)
(«координатное представ-
лением) дает вероятность
того, что при определении
положения электрона в
квантовом состоянии п, I,
т он будет обнаружен в
окрестности точки г, 6, ср. Точнее эта вероятность определяется так:
<Wnlm (г» <?) r4r Sin 6^0 = I $п1т I2 ГЫГ Sitl 0 <48 Л 1) ‘
Чтобы нагляднее представить себе характер этой вероятности, мы при-
водим на рис. 23 полярную систему координат. Полярная ось OZ выде-
ляется тем, что она есть как раз то направление, на которое проецин
руется момент импульса Mz—hm. Обозначая через z/Й элемент телесного
угла sin 6 db dy в области 6, ср и пользуясь формулой (47.23) для §п1т>
мы можем написать вероятность (48.11) в форме
(г, 0, <р) r*dr dQ = R2nl (г) r*dr | Ylm (О, <р) |2 d&. (48.12)
Если мы проинтегрируем (48.12) по всем углам б/й, то мы получим
вероятность найти электрон между двумя сферами радиусов г и r-\-dr.
*) Число Z называют орбитальным квантовым числом по той причине, что
в старой боровской теории оно определяло при заданной энергии форму
орбиты; т называют магнитным по той причине, что оно играет существенную
роль в магнитных явлениях (см. §§ 59, 70).
§ 48] СПЕКТР И ВОЛНОВЫЕ ФУНКЦИИ АТОМА ВОДОРОДА 151
Обозначим эту вероятность через
^nt<r}dr=Rnl{r)^dr.
(48.13)
На рис. 24 даны эти вероятности для различных состояний. Числа на
кривых показывают значение чисел n, l\nr—n—Л—1). Например, 31
означает n = 3, /=1 (nr=l). По
абсциссе отложено расстояние от
центра ? = ~ [см* (47.18)]. Из
графиков легко видеть, что чис-
ло пг (которое называют радиаль-
ным квантовым числом) равно чис-
лу узлов волновой функции Rnl.
При этом мы имеем не узлы в точ-
ках, а узловые поверхности, ибо Rnl
обращается в нуль при некотором
г — /, а это означает поверхность
шара радиуса г'. Стало быть, в
состоянии, характеризуемом числа-
ми п, I, имеется пг — п— I—1
узловых поверхностей, имеющих
форму шара.
Выясним теперь значение вве-
денной ранее длины а. Из вида
функций /?я/(р) (47.19) следует,
что при больших г(р —* оо) ради-
альная функция Rnl принимает вид
Zr =
с) d- состояния (1=2) и состояние 4]
Рис. 24. Распределение заряда в пер-
вых состояниях водорода.
Абсцисса — г в радиусах водорода, ордината —
вероятность найти электрон между г и г + dr.
Поэтому при больших значениях г вероятность будет равна
2Zr
Wnl^=N^le Па(^-)2П-
(48.15)
Отсюда следует, что длина есть длина’ определяющая размеры
атома, так как для г вероятность юп1 (г) практически равна нулю.
Приведем более подробный расчет для самого цижнего квантового
состояния (n—1). В этом случае из (47.19) имеем:
z
Яю(р) = Мо* < (48.16)
Следовательно,
w10(r) = rf0a?e а(^). (48.17)
Zr
Максимальное значение этой вероятности получается при р = — = 1.
152
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Отсюда следует, что в состоянии п — 1 (Z = т — 0) наиболее вероятно
найти электрон при
„___ а № 0,529 А_8
го |i£2Z Z Ю (48.18}
Эта величина есть в точности радиус первой орбиты Бора, величина кото-
рого впервые была получена Бором из старой теории квантования в 1913 г.
Так как нижняя орбита по теории Бора — круговая, то по этой
теории вероятность найти электрон
в состоянии п — 1 отлична от нуля
лишь на шаре радиуса Сог-
ласно же новой квантовой меха-
нике она отлична от нуля во всем
пространстве. На рис. 25 сопо-
ставлены вероятности по старой
теории (-Докл.) и по новой (wKB.).
для состояния п = 1 атома водоро-
да. Приведенное соответствие меж-
ду ^кл. и -г^кв. наблюдается и для
других состояний: оно является
далеко неполным, что видно уже
из того, что в квантовой механике
Рис. 25. Сравнение шкл (г) и шкв. (г) в нижнем состоянии момент им-
для состояния п = 1 (Z = т = 0).’ пульса Л42 — 0 (Z = 0)^ в то время
как по старой теории в этом же
состоянии = Несмотря на неполноту указанного соответствия,
оно делает все же картину распределения вероятности более наглядной
и указывает на связь между квантовой и классической механикой, ко-
торая и в самом деле существует (ср. гл. VII).
Обратимся теперь к распределению по углам. Если проинтегриро-
вать (48.11) по г от 0 до оо, то мы получим вероятность w//n(0, ср)
того, что электрон окажется лежащим где-то в телесном угле dQ (см.
рис. j23) около луча (0, ср). В силу нормировки функций Rnl получаем:
(6, <р) == I Ylm (0, <?) I2 d&. (48.19)
Из вида функции 7^(0, ср) следует, что вероятность не зависит от
угла ср и равна
wZ/r (0) = [Р\™ । (cos О)]2 dti. (48.20)
Следовательно, распределение по углам обладает симметрией тела вра-
щения около той оси, на которую фиксирована проекция момента
импульса (у нДс эта ось есть ось OZ).
На рис. 26 мы изобразили графики вероятности для различных
состояний Z, т. При этом принята полярная система координат 6, wlm,
так что величина wlm откладывается по радиусу-вектору. Дчя сравнения
приведены орбиты по Бору, расположенные надлежащим образом. При
Z = 0, = 0 вероятность
= № = i (48.21)
§ 48] СПЕКТР И ВОЛНОВЫЕ ФУНКЦИИ АТОМА ВОДОРОДА 153
не зависит от угла 6, и поэтому мы имеем сферическую симметрию.
Состояние, в котором момент импульса равен нулю (Z = Q), называют s-co-
стоянием, соответствующий терм называют s-термом; s-состояние
характеризуется, следовательно, шаровой симметрией. Соответствующих
орбит по Бору нет. Это обстоятельство представляло одну из трудностей
теории Бора, так как приходилось сопоставлять с оптическим s-термом
состояния с I— 1 (т = О, Ч- 1), в то время как опыт однозначного
Рис. 26. Угловое распределение электронов (0) для S-, /?-, d- и /- состояний
показывал, что электрон в s-терме не обладает орбитальным механи
ческим (и магнитным) моментом.
Состояние с /=1 t(m = O, ±1) называется p-состоянием, а соот-
ветствующий терм — р-термом. Вероятность в этом случае определяется
функциями Р\ (cos 0) и Р[ (cos 6). Подставляя значения этих функций
из (25.1G), имеем:
Wi.il (O) = -^sin«0, (48.22)
cos20- (48.22'>
На рис. 26 изображены вероятности w10, а также соответствую-
щие орбиты по теории Бора. Из рисунков видно, что если по боров-
ской теории в случае, например, = 1 вероятность найти электрон
отлична от нуля лишь в плоскости орбит (0 = -^-) , то по квантовой
механике она не равна нулю и для других значений угла 0 (на конусах
О—const) Соответствие замечается в том, что максимум вероятности
154
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [гЛ. IX
лежит при 0 = ~. Подобное же соответствие имеется и для т — О
(максимум при 0 = 0).
Состояние с I — 2 (m — Q, +1, + 2) называется d-состоянием,
а терм — d-термом. На рис. 26 приведена и вероятность w21 для / — 2,
т— 1. Из формул для шаровых функций (25.16) легко получить
w2> х (6) = ( cos 9)]2 = || sin20 cos26. (48.23)
При /=2 и т—\ мы имеем по
Рис. 27. Узловые поверхности дейст-
вительной части функции (г, 0, ср):
пг—п—I—1 сфер, 1—1 т[ конусов, | т |
плоскостей.
Бору совокупность орбит, нормали
к которым образуют конус с осью
OZ и углом раствора, равным 60°.
На конусе с раствором 60° лежит
и максимум вероятности по теории
Бора. По квантовой механике этот
максимум приходится на угол 45°.
Вид вероятностей wZw (6)
(рис. 26) позволяет нам создать
некоторое представление о форме
атома в различных состояниях. Эта
форма определяется значением ор-
битального числа /, а магнитное
число т, как видно, определяет
ориентацию атома в пространстве.
Из приведенных выражений для
вероятностей wZ/w(0) видно, что
функция Р™ с / —0 не имеет
узлов, с /=Ч и /?г = 0 имеет
одну узловую поверхность (плос-
кость б — -2-), с I = 2 и т=1 —
опять одну узловую поверхность
( плоскость 6 — j. Вообще урав-
нение
P'w(cos6) = Q
дает I — | т | действительных корней 02‘ • • •> 0/—|m |- Эти углы и суть
углы раствора конусов (б = const ), которые образуют узловые поверх-
ности. Часть волновой функции зависящая от угла ср, именно
ех/я<?, не имеет узлов, но ее действительная часть cosmp или мнимая
(/ sin /иср) имеют т узлов: <рр ^2,...,Фт, которые в пространстве даюг
узловые плоскости, проходящие через полярную ось.
На рис. 27 изображено семейство узловых поверхностей функции
состоящее из шаров (узлы функции Рл/), конусов (узлы функции Рр)
и плоскостей (узлы функции cosz^'p или ыпту). Число шаров равно лг,
конусов/—| т | и плоскостей | т |. Всего имеется nr + I——
sz=nr-]-l—n—1 узловых поверхностей. Таким образом, мы опять
§ 49] ДВИЖЕНИЕ ЭЛЕКТРОНА В ВОДОРОДОПОДОБНЫХ АТОМАХ 155
имеем иллюстрацию к общей теореме, упомянутой в примечании на
стр. 129.
Приведенные на рис. 27 узловые поверхности характеризуются той же
геометрией, что и узловые поверхности колеблющегося тара. Поэто-
му функции ^nim(ry 0, ср) имеют сходство с функциями, изображающи-
ми колебание шара, подобно тому как собственные функции осцилля-
тора фл(х)имеют сходство с функциями, изображающими колебание струны.
§ 49. Движение электрона в водородоподобных атомах
Существует ряд атомов, имеющих один валентный электрон: это
атомы щелочных металлов Li, Na, К, . • . Мы будем называть их водо-
родоподобными. В этих атомах имеется группа внутренних электронов,
а внешний, валентный электрон движется в поле ядра и этих внутрен-
них электронов.
Строго говоря, мы имеем дело в этом случае с многоэлектронной
проблемой. Однако, в перечисленных атомах имеемся одна особенность,
позволяющая приближенно свести задачу к задаче о движении одного
электрона в поле центральных сил. Дело в том, что если удалить из
такого атома валентный электрон, то оставшиеся электроны образуют
электронную оболочку, характерную для инертных газов. Например,
ион Ll+ имеет электронную оболочку, аналогичную электронной оболочке
атома Не. И опыт, и теория показывают, что электронная оболочка
электронного газа образует весьма прочную систему, имеющую сфери-
ческую симметрию и мало деформирующуюся внешними воздействиями.
Поэтому приближенно можно поступить так* считать, что внешний
валентный электрон вообще не влияет на внутренние электроны, и таким
образом рассматрив ть движение внешнего электрона в поле ядра и
внутренних электронов.
В силу сферической симметрии распределения последних поле, созда-
ваемое ими, будет центральным *). Найдем потенциальную энергию
внешнего, валентного электрона U (г) в поле ядра атома и внутренних
электронов. Обозначим через V(r) потенциал этого поля, тогда
U(r) = — eV(r). (49.1)
Пусть, далее, р (г) есть средняя плотность электрического заряда, созда-
ваемая внутренними электронами **). Тогда полный электронный заряд
[ — eN(r)]> заключенный внутри сферы радиуса г, будет равен
г
— eN(г) — 4к ( р (г) r2dr. (49.2)
б
Учитывая еще заряд ядра мы можем представить полный заряд
*) Подчеркнем еще раз, что это верно лишь приближенно, так как внеш-
ний электрон на самом деле будет поляризовать внутреннюю электронную
оболочку.
**) Вероятность р(г) может быть вычислена методами квантовой механи-
ки. Так, для Li+ речь будет итти о движении двух электронов в поле ядра.
Задача здесь такова же, как и в случае атома Не. Последняя рассмотрена
в § 111 Кроме того, р (г) может быть измерена и экспериментально (см. § 75).
156
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ГЮЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
в рассматриваемой сфере в виде
eZ*(r) = е [Z — W (г)], (49.3)
где через Z* обозначен эффективный номер ядра на расстоянии г.
Отсюда по теореме Гаусса получаем, что поле Sr равно
= (49.4)
а потенциал IZ(r) равен
г
V(r)=— e^^fi-dr. (49.5)
ОО
Из (49.3) следует, что действие электронной оболочки сводится к экра-
eZ
нированию поля ядра , причем это экранирование различно для
различных расстояний от ядра. Вблизи ядра его поле не экранируется.
В самом деле, при г—>0
г
hm — — 4тгр (0) 11m f г2 dr.
r->0 r r->o r J
Поэтому в этой области
о ________________________________eZ
Or r2 »
а потенциал
V(r) = ^ +const. (49.6)
Напротив, в областях r^>a, где a—радиус электронной оболочки,
W)r>a=AT,
где N—полное число электронов в оболочке, имеем
_ e(Z-N)
о г-- г
и потенциал будет равен
V(r)^=g(Z~^, (49.7)
что соответствует потенциалу ядра, заряд которого уменьшен на заряд
электронов оболочки.
Часто, делая еще более грубое приближение, игнорируют зависи-
мость эффективного номера Z* (г) от г и берут какое-нибудь наиболее
подходящее постоянное значение для
Z* = Z—ДГ(г0). (49.8)
Однако, такое приближение очень грубо и не ведет к хорошим ре-
зультатам*). Полученная нами потенциальная энергия £7(г) = — eV (г)
*) Конечно, применимость или неприменимость того или иного приближе-
ния зависит еще и от того, какую степень точности желают получить
§ 49] ДВИЖЕНИЕ ЭЛЕКТРОНА В ВОДОРОДОПОДОБНЫХ АТОМАХ 157
для валентного электрона водородоподобного атома принадлежит к классу
рассмотренных в § 47 полюс порядка у). Так как то мы имеем
дело со случаем притяжения. Отсюда следует, что энергетический
спектр водородоподобного атома
будет состоять из непрерывного
спектра (Е > 0), отвечающего
ионизованному атому, и дискрет-
ного (£<0), образующего сово-
купность квантовых уровней атома.
Мы не будем заниматься реше-
нием радиального уравнения (46 5)
для этого вида потенциальной
энергии. Оно может быть ре-
шено лишь численным интегриро-
ванием Ограничимся лишь изложе-
нием результатов
Самым существенным обстоя-
тельством является то, что энер-
гия Е зависит в этом случае не
только от главного квантового
числа л, но и от радиального пг.
Это нетрудно понять. В уравнение
(46 5) для функций /?, из кото-
рого определяются и квантовые
уровни Еп, входит орбитальное
квантовое число I. Поэтому Е
будет, вообще говоря, зависеть
от числа Z. Кроме того, значение Е
зависит от номера собственной
функции уравнения (46.5), т. е.
2s (л =2,1=0)
2p(n=2)L = 1]
1s(n = 1,l=0)
Рис. 28. Снятие «/»-вырождения в во-
дородоподобных атомах.
Припечены три первых уровня атома калия.
Уровни 2//, 2s, сливающиеся в водороде, в
калии разделены.
от радиального числа пг. Таким образом, в общем случае собственные
значения Е зависят от двух квантовых чисел, пг и Z, или так как
П — пг-\- Z-J- 1, то можно сказать, что зависит от п и Z. Следователь-
но, полная нумерация уровней и собственных функций будет такая:
Z = o 1, 2, ..., п-1,
/п = 0,± 1, ... , ±Z,
Е=Еп1, п= 1,2,3,...,
(49.9)
а не Еп, как в случае кулоновского поля. То, что в кулоновском поле
энергия зависит лишь от п, есть специальная особенность этоТо поля,
которая имеет свои основания *). В случае кулоновского поля числа пг
и Z входят в выражение энергии в виде суммы n = nr-\-1-\- i.
Таким образом, в кудоновском поле, как уже и отмечалось, имеет
место вырождение («I»-вырождение), заключающееся в том, что энергия при
*) См. Вс 'А. Фок, Докл. Акад. наук, 1935, № 2, стр. 169.
158 ТЕОРИЯ ДВИЖЕНИЙ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
заданном главном числе п не зависит от величины момента импульса
(/). В общем случае центрального поля U(r) это «/»-вырождение снято,
и термы с одним и тем же главным квантовым числом п, но с разными
орбитальными числами I имеют разную величину. На рис. 28 приведе-
ны уровни для водородоподобного атома калия. Как видно, например,
главному числу п = 2 принадлежит два уровня 1=0 (5-терм) и /=1
(р-терм). В случае водорода эти уровни сливаются вместе.
Что касается магнитного квантового числа ш, то оно, как уже объяснялось
(§ 48), определяет ориентацию атома в пространстве, и поэтому энер-
гия атома (в отсутствии внешних полей) не может зависеть от этого
числа.
§ 50. Токи в атомах. Магнетон Бора
Вычислим плотность электрического тока, текущего в атоме, если
электрон находится в стационарном состоянии-, с определенным значением
проекции момента импульса Mz=hm. Волновая функция такого состо-
яния равна
Ф„;т (г, о, l(cosO)^. (50.1)
Согласно (29 11) плотность электрического тока в состоянии будет
выражаться формулой
J=- f (50.2)
(мы берем перед е ’внак —, считая заряд электрона равным — е,
2 = 4,778 • 10“"10 единиц CGSE). Удобно найти вектор J в полярных
координатах г, 6, ср. Для этого заметим, что в полярной системе про-
*7 д 1 д \ д п
екции оператора градиента V суть , у у] > у81д"д • Следовательно,
проекции вектора J на радиус, меридиан и широту равны соответственно
<50'3)
л = -2т'Ст-й«тг-}=°' <50Л>
Первые два результата получаются сразу, если вспомнить, что Р} т I и
Рп1 СУТЬ Действительные функции переменных 6 и г, а последний сле-
дует из того, что пропорциональна eim^. Таким образом, в стацио-
нарных состояниях проекции тока на радиус и меридиан равны нулю
(что очевидно и из геометрических соображений; если, например, Jr=^=0,
то заряды будут либо растекаться либо накапливаться) и ток течет вдоль
широтных кругов (рис. 29). Это течение вполне соответствует сред-
нему току по классической механике для совокупности орбит, имею-
щих один и тот же полный момент импульса /И2 и одну и ту же проекцию
этого момента на ось OZ.
| 50]
ТОКИ В АТОМАХ. МАГНЕТОН БОРА
159
Теперь, основываясь на формуле (50.5)
найти магнитный момент атома. Сила
площадку da, направленную в мери-
диональной плоскости (рис. 29), равна
dI = J^d3. (50.6)
Магнитный момент, создаваемый этим
током, равен
= = (50.7)
где S — площадь, обтекаемая током di.
Эта площадь равна тгг2 sin2 6 (см. рис. 29).
Поэтому
|ф ,,Л. (508)
jirsm 01 *п1т । \ ’
Чтобы получить полный момент
следует просуммировать по всем трубкам
тока Тогда мы получим:
Яйг=- $J21Trsin9(50-9)
Но 2тгг sin 9 da есть объем трубки.
Так как внутри трубки величина | §п1т |2
постоянна, то интеграл в (50.9) есть
для плотности тока, нетрудно
тока di, протекающего через
Рис. 29. Токи в атоме при за-
данных вращательном моменте
Л42 и его проекции Mz.
просто интеграл от | §п1т |2 по всему объему. Этот интеграл в силу
нормировки равен 1, следовательно, проекция магнитного момента на
ось имеет значение
(50.10)
где
5ЛВ = = 9 • 10"21 единиц CGSE, (50.11)
т. е. она имеет квантовое значение, равное целому числу магнето-
нов Бора (см. § 3). Знак — обусловлен отрицательным зарядом
электрона.
Произведенный расчет показывает, таким образом, что в состояниях
с Mz=^=0 в атоме течет электрический ток. Этот ток создает магнит-
ный момент (50.10), так что атом представляет собой в целом маг-
нитный диполь. Отношение проекции магнитного момента к проек-
ции механического момента Мг равно
% =______
Мг 2\lc
(50.12)
и в точности совпадает с отношением этих величин по классической
160 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
теории для заряда — е с массой g, движущегося по замкнутой орбите *).
Заметим, что, поскольку ось OZ ничем не выделена, такое же отноше-
ние получится и для проекций 9)1 и М на любое направление. Поэтому
(50.12) следует толковать в том смысле, что отношение вектора маг-
нитного момента 9)1 к вектору М механического момента равно — .
§51. Квантовые уровни двухатомной молекулы
Обратимся к молекуле, образованной из двух атомов Л и В с мас-
сами тА и тв. Потенциальная энергия в функции расстояния между
атомами г пусть будет V(/j. Эта энергия имеет вид, приведенный на
Рис. 30. Потенциальная энергия для атомов
двухатомной молекулы и энергетический
спектр.
Для Е > 0 спектр непрерывен, для Е < 0 имеет ме-
сто система уровней Ео, Eit .,.
рис. 30. Мы ограничимся рас-
смотрением только относитель-
ного движения атомов Л и В,
Из классической механики
известно, что относительное
движение двух частиц с энер-
гией взаимодействия U (г)
происходит, как движение
материальной точки с при-
веденной массой р:
(51.1)
И тА 1 тв ' ’
в поле центральной силы
£7(г), а общее поступатель-
ное движение — как свобод-
ное движение материальной
точки с массой. Такое же
положение вещей имеет ме-
сто, как будет доказано в
§ 97, и в квантовой меха-
нике. Опираясь на это обстоятельство, мы можем написать оператор
полной энергии для относительного движения атомов Л и В в виде
+ т <51.2)
где г есть расстояние между атомами, а углы 6 и ср (входящие в М2)
определяют направление линии, соединяющей А и В.
Уравнение Шредингера для стационарных состояний будет таково же,
как и (46.2). Волновую функцию можно опять искать в виде
ф(г,0,<Р)=/?(г)Кйв(0,<р), 1
р____ц Г (51.3)
v »• * I
*) См, например, Тамм, Основы теории электричества,ч. II, ГТТИ, 1934
или Беккер, Электронная теория, ОНТИ, 1936.
§ 51]
КВАНТОВЫЕ УРОВНИ ДВУХАТОМНОЙ МОЛЕКУЛЫ
161
(51.4)
причем для и будем иметь уравнение
2|irf/*2 1 L 2lx/'2 J
й2/(/+1)
Член —2^—~ можно рассматривать как дополнительную потенциальную
энергию, так что всю потенци-
альную энергию для движения
по радиусу можно определить
в виде
Рис. 31. Связь колебания и вращения в
двухатомной молекуле.
= (51.5)
и переписать уравнение (51.4)
в виде
-£S+^W« = ^-(51-4’)
График функции Wt(r) плп
разных / изображен на рис. 31.
В отсутствии вращения
(Z —0) WQ(r) = U(r), и мы
имеем случай, рассмотренный
в § 46 (рис. 19). Если враще-
ние не сильно (/ невелико), то
W[(r) все еще не сильно отли-
чается от U(г). Последняя кри-
вая лишь несколько искажается.
Если, наконец, / очень велико,
то кривая принимает вид,
приведенный на рис. 31 (слу-
чай /|>1). Мы знаем, что
для 1 = 0 молекула имеет ди-
скретный спектр при Е 0 и
непрерывный при £^>0. При
сильном вращении Wt(r} всюду
”” ; , ./ положительно. Тогда из доказанной в
§ 46 теоремы следует, что £г>0 и спектр, стало быть, будет не-
прерывным Молекула будет диссоциировать на атомы А и В. Эта
диссоциация является результатом действия центробежной силы, которая
развивается при вращении молекулы
Рассмотрим случай, когда вращение невелико, так что Wt мало
отличается от Щг}— по крайней мере в области минимума U(г) (г — г0).
Разложим Wt(r} по степеням отклонения от положения равновесия
г—rv Положение равновесия зависит от I и определится из мини-
мума UZz(/j:
d_ dU _ /г2/(/-4-1) _ п
dr dr 2jxr3
(51.6)
11 Блохинцев
162
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ
[гл. IX
Отсюда находим r—rv Далее, имеем:
wt (г) = - 4-1 (qgp )г< (7- - rf, (51-7)
причем Wt(r} = U(r()+h^±V. (51.8)
Введем обозначения:
(^?)Г=Г=’ХО)Ь ^1=^ x = r — rt. (51.9)
Подстановка ^(г) из (51.7) в (51.5) в обозначениях (51.9) даёт
-К^+[уИ+гЦ^1,+т^г]“=£“- <51-5'>
Обозначая через Е' величину
£' = £—(51.10)
мы перепишем уравнение (51.5') в виде
— ££+4^2« = £’«- (51.5")
Это — уравнение для стационарных состояний осциллятора (44.3), обла-
дающего собственной частотой Согласно (44.10) его собственные
значения Е' суть
£'==A(D,(n-J-l) , п — 0, 1, 2. (51.11)
а собственные функции согласно (44.11)
и„(х)=е-Ч*’Н„®, (51.12)
л0
Пользуясь (51.10), находим полную внутреннюю энергию молекулы:
Ещ-U{r^ 4- (и 4-1) + , (51.13)
п = 0,1,2,..., / = 0,1,2,..., (51.13')
а собственные функции молекулы
0> <P) = ^««(r)rto(0> ?)• (51Л4>
Эти волновые функции описывают вращение молекулы и ее колебания.
Энергия молекулы Еп1 оказывается равной сумме энергии колебаний с
частотой (Dj и энергии вращения молекулы:
£ «ЗД+Ц. (51.15)
27 Z
Имея в виду, что №1(11) есть квадрат момента импульса Atf, мы
видим, что выражение для энергии вращения молекулы в квантовой
механике таково же, как и в классической, так как согласно
§ 51] КВАНТОВЫЕ УРОВНИ ДВУХАТОМНОЙ МОЛЕКУЛЫ 163
(51.9) /z есть момент инерции молекулы*). Формула (51.15) показывает,
что энергия вращения квантуется, причем расстояние между соседними
уровнями равно
=« у (/ + 1) (51.16)
(если пренебрегать слабой зависимостью момента инерции от Z, т. е.
растяжением молекулы под влиянием центробежной силы).
Полученные нами решения, конечно, приближенны. Мы пренебрегли
ангармоничностью колебаний молекулы, отбросив внешние члены в раз-
ложении Wt(r) по степеням г—rv Это допустимо, если отклонения
г—rt малы в сравнении с'расстоянием между атомами rt (или г0). Из
.теории рсциллятора следует, что среднее значение х2 ==~- (п + уJ
[чтобы в этом убедиться, достаточно вычислить матричный элемент х2^,
пользуясь матрицей хтп (45.8)]. Поэтому
\x\=v^=yr^ .
и условие справедливости нашего приближения может быть написано
в виде
1*1^1 ,С1
— <! или у —у п + (51.17)
т. е. приближение тем лучше, чем больше масса атомов молекулы, чем
больше частота колебаний (о0 и чем больше расстояние между атомами
г0. Кроме того, уровень колебаний должен быть не очень высок (п мало).
При больших п и I связь между колебаниями и вращением молекулы
становится сильной, и все наше приближение делается несостоятельным.
Напротив, при малых п и I мы можем вообще пренебречь зависимостью
rz от / и брать вместо /z и (ор /0 и <о0 для Z = 0.
Величины /0 и (00 обычно таковы, что «квант» энергии колебаний
Л2
А(оо гораздо больше «кванта» энергии вращения Так^ например, для
молекулы водорода
/?2
^ = 8,75-10-12 эрг., -=1,15-10-14 эрг.
Благодаря этому обстоятельству энергетический спектр молекулы
состоит из системы уровней колебательных (разные значения числа л)
и вращательных (разные /), последние лежат очень близко друг к другу.
Схема энергетического спектра молекулы приведена на рис. 32.
Пунктирная линия на границе с непрерывным спектром есть 2?=0
и соответствует энергии диссоциирующей молекулы. Это значение
энергии может быть достигнуто при любом п для достаточно боль-
ших Z.
*) Напомним, что по классической механике энергия вращения равна «
>1*
164 ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Энергия диссоциации молекулы Z), находящейся в нормальном со-
стоянии (zz = / = O), равна, как было показано еще в §48,
D=U9—^. (51.18)
Важнейшая область явлений, в которой обнаруживается квантование
движения молекулы, — это спектры молекул. Пусть возможные уровни
энергии электрона в молекуле суть EN. Тогда полная энергия молекулы
и ее оптического электрона равйа
/(Z4-l)4-const. (51.19)
Написав в таком виде энергию, мы предполагаем, что связь между
в молекуле слаба, так что
приближенно можно пред-
ставить энергию в виде сум-
мы энергии электрона и
энергии атомов. Тем не
менее эта связь все же су-
ществует, и даже при сла-
бой связи изменение состоя-
ния электрона (переход
с уровня En на другой
Е^} будет сопровождаться
изменением состояния ато-
мов. Поэтому, если молеку-
ла поглощает квант света
Лю, то чисть этой энер-
гии пойдет на возбуждз-
ние электрона, а другая
часть на возбуждение
движения атомов молекулы. Обратно, квант частоты Асо может быть из-
лучен не только за счет энергии электрона, но и за счет энергии дви-
жения атомов молекулы. Поэтому, чтобы получить частоты (о излучае-
мого и поглощаемого молекулой света, в правиле частот Бора
h(d = E — Е
следует под Е разуметь энергию всей молекулы в целом. Подставляя
сюда Е из (51.19), получим:
Aw = En, — En+ А(оо (п< - п) + [/' (/' + 1) -1 (/ + 1)]. (51.20)
Обозначая частоту , обусловленную переходами электрона,
через мы можем переписать (51 20) в вице
“=4«+“«(»,-")+24(.''+ 4-('+44 • (5|-21)
движением электронов и движением атомов
i=i
1=0
E-Q
п
ь=г-
1=1'
ь=0'~
1=1';
п=2
3
4
--------------1-----1-------------ц +
(п=0)
Рис. 32. Схема вибрационных (л) и ротационных
уровней (/) двухатомной‘молекулы.
§ 51]
КВАНТОВЫЕ УРОВНИ ДВУХАТОМНОЙ МОЛЕКУЛЫ
165
обычно гораздо больше <оо и тем более Поэтому рядом со
спектральной линией, отвечающей чисто электронному переходу (частота
v^w), при наблюдении в спектроскоп будет наблюдаться ряд линий,
очень близких, почти сливающихся друг с другом*). Такой спектр назы-
вают полосатым. Он характерен для двухатомных молекул (атомы имеют
спектр, состоящий из довольно далеко отстоящих друг от друга линий,
иногда, правда, расщепляющихся на небольшое число соседних). Линии
в полосах обусловлены изменением вращательного движения молекул.
Поэтому эти полось! часто называют ротационными. Кроме линий, об-
условленных изменением вращения (число Z), будут получаться линии,
обусловленные изменением колебательного движения (число п). Эти линии
часто называют вибрационными.
Таким образом, сложность молекулярных спектров обусловливается
тем, что в обмене энергией молекулы со светом участвует, вообще
говоря, вся молекула в целом: не только состояния оптического элект-
рона, но и состояния колебания и вращения молекулы претерпевают
изменение. Теория молекулярных спектров образует ь настоящее время
довольно широко разработанную, но все же далеко не законченную
область атомной механики **).
Помимо молекулярных спектров квантовый характер движения моле-
кулы обнаруживается на теплоемкости двухатомных газов. Согласно клас-
сической теории теплоемкость, приходящаяся на одну степень свободы,
равна у , где k — постоянная Больцмана, равная 1,36 -10“16 эрг/град~
Двухатомная молекула имеет всего шесть степеней свободы, поэтому по
классической теории ее теплоемкость должна быть постоянной и равняться
k
6 — = 3&. Между тем опыт показывает, что при средних температурах
5 <
теплоемкость действительно постоянна, но равна -% к, а при низких па-
дает до — k. Этот факт находит полное объяснение в квантовой теории.
Если при температуре Т средняя энергия поступательного движения
молекулы — kT меньше Аа)0, то колебания молекулы не возбуждаются
(точнее, возбуждаются редко). Молекулу можно рассматривать в этом
случае как жесткую и считать число ее степеней свободы равным как
бы не 6, а 5. Говорят, что колебацие «замерзает». Температура замер-
зания 7^, очевидно, определится из неравенства
|АГф<Л®0. (51.22}
*) Конечно, будут эти линии сливаться или нет, — зависит от разрешаю-
щей силы спектроскопа.
♦*) О молекулах см. подробно в книгах: К. В. Никольский, Квантовая
механика молекулы, ГТТИ, 1934; Крон иг, Полосатые спектры и строение
молекул. См. также § ,115 настоящей книги.
166
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Рис. 33. Теплоемкость молекулы Н2, при-
ходящаяся на допю вращательных сте-
пеней свободы.
Для Н2 7^ = 40 000°. Большой величиной 7^ объясняется, что при обыч
ных температурах теплоемкость двухатомных газов равна -%k.
С понижением температуры наступит момент, когда поступательная
№
энергия окажется меньшей «кванта вращения» , тогда и вращение не
будет возбуждаться и выпадет
из теплового баланса. Вращение
«замерзнет». Температура «за-
мерзания» вращения Тг опреде-
лится из неравенства
(51.23)
Для Т<^ТГ теплоемкость вра-
щения равна нулю. Остается
только теплоемкость поступа-
3 <
тельного движения k.
J4a рис. 33 приведена зави-
симость теплоемкости вращения
сг от температуры. Как видно, согласие между квантовой теорией
и опытом полное. Пунктиром изображена теплоемкость по классической
теории. При низкой температуре классическая теория противоречит
опыту *).
§ 52, Движение электрона в периодическом поле
К числу важных случаев движения относится движение электрона
в периодическом потенциальном поле Z7(x, у, z). Если поле имеет
период а — в направлении OX, b — в направлении ОУ и с — в направ-
лении OZ, то это свойство периодичности может быть выражено равен-
ствами
U(x-\-a, у, z) = U(x, у, z), (52.1)
£7(х, ? + z) = U(x, ул z), (52. Г)
Щх, у, z-\-c) — U(x, у, z). (52.1")
Такое периодическое поле реализуется внутри идеальных кристаллов,
где ядра атомов, и вместе с тем и средний электрический заряд, рас-
пределены периодически. Вместе с тем и потенциал электрического поля
будет, конечно, периодической функцией координат х, у, z. Если внутрь
такого кристалла ввести электрон, то он будет иметь периодическую
потенциальную энергию вида (52 1).
*) Подробности о теплоемкости двухатомных газов см. Герцфельд,
Кинетическая теория материи, ОНТИ, 1935, стр. 403—408. Новое изложение
в книге Fowler, Statistical mechanics, 1938.
§ 52] ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРИОДИЧЕСКОМ ПОЛЕ
167
Строго говоря, в этом случае мы имеем дело с проблемой многих
электронов. Замена такой проблемы более простой задачей о движении
одного электрона во внешнем поле является приближением. Оно, наверно,
справедливо для больших скоростей рассматриваемого электрона (и до
той поры, пока нас не инте-
ресуют неупругие столкнове-
ния электрона). Что же ка-
сается применения такого при-
ближения к движению элек-
тронов самого кристалла, то
до сих пор не дано обосно-
вания такой возможности, хо-
тя вытекающие из расчетов
следствия позволяют истолко-
вать множество явлений.
На рис. 34 изображена
потенциальная энергия элек-
трона в кристалле в функции
х при условии, что ось ОХ
V(jc о,о)
и X
Рис. 34. Кривая потенциальной энергии
электрона в кристалле (в функции одной
координаты х).
Пунктиром изображена волновая функция (модули-
рованная волна).
проходит через центры ато-
мов, образующих кристалл. В точках ...—2а, —а, -[-2а, ...
расположены центры атомов*. В этих точках U имеет полюс первого
/ e*Z \
порядка I---— J .
Для выяснения возможных уровней энергии электрона в периодическом
поле и собственных функций энергии нужно решить уравнение Шредин-
гера, которое мы возьмем сперва в «х»-представлении. Это уравнение
гласит:
— +t/ф = £(!),
(52.2)
где pi— масса электрона, a U—потенциальная энергия, подчиняющаяся
условию периодичности (52.1). Ставя себе целью лишь выяснение самых
основных свойств движения в периодическом поле, мы ограничимся одним
измерением. Тогда вместо (52 1) и (52.2) будем иметь:
U(x-\-a) = U(x), (52. Г")
<52-2')
Для исследования этого уравнения перейдем к «/?»-представлению.
Положим для этой цели
4-о° k
ф(х)=У c(k)e^dk, k = kx=p^, (52.3)
где рх — импульс по оси ОХ. Соответственно разложим потенциальную
энергию U в ряд Фурье
4-оо _ 2™пх
и(х)^^ипе Un=U*_n. (52.4)
— 00
168
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [ГЛ. IX
Коэффициенты этого ряда Un суть не что иное, как U(х) в «р»-пред
ставлении. Подставим (52.3) и (52.4) в (52.2'):
-}-оо -f-оо 4-оо z (ft—
Л2 С е'Ьх С р 4 Л 7
k2c(k)e dk-\-?U c(k)_-------- dk =
2H--U V2u "Л J/2k
4-со
= Е \ c(k)el^dk. (52.5)
Л W
е-Шх
Умножая это уравнение на и интегрируя по х от — оо до -f- оо?
мы получим 3-функции:
4-ро 4-оо 4-jso
£ j &2c (k)b(k — k')dk^-^un J c(k)t(k — ~ — k'}dk =
^ — 00 —оо —00 j
= Е J c(k)b(k — k')dk. (52.5')
—oo
Выполняя, наконец, интегрирование по k и меняя обозначение k' на k*
получаем:
4-°°
g^(fe)4-X^(^+2-^)=£C(A!). (52.6)
—оо
Это уравнение есть не что иное, как уравнение (52.2') в «р»-представ-
лении. Особенностью его является то, что в него входят лишь те г(^),
аргументы которых отличаются друг от друга величиной 2ттю/а (n — Of
—f~ 1, —I— 2, ...).
Величины c(k), с (&-|- Ям/а) суть неизвестные, которые нам нужно
вычислить. Все они связаны между собой уравнениями вида (52.6), кото-
рые легко получить, если менять в (52 6) k на 2nzn/a, где юг — целое
число. Перенося в (52 6) член с Е налево, мы без труда можем напи-
сать уравнения для всех связанных между собою функций с (k 2тип[а)':
+ 1>4‘ + 7+т)=0’
— GO
m = 0 V. & — e\ c (k\+-
* 2|i J 7
+е\И*+?)=о. (5М
4-00
' +Е^(а-?+2-г)=0’
— со
.............................Й Т. Д. >
§ 52] ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРИОДИЧЕСКОМ ПОЛЕ 169
Это — система алгебраических линейных однородных уравнений для
бесконечного числа неизвестных f m = 0, -Ы, +2, ...
Для того, чтобы эта система имела отличные от нуля решения, необ-
ходимо, чтобы ее определитель Д равнялся нулю. Этот определитель
зависит от Е и k (и всех коэффициентов Un) и является вообще транс-
цендентной функцией от Е. Поэтому уравнение
Д(£, k) = 0 (52.8)
имеет бесконечное число корней E — Ev Е2, .Ер ..., каждый
из которых является функцией волнового числа k. Отсюда следует, что
энергетический спектр частицы, движущейся в периодическом поле, будет
состоять из отдельных областей
Е = Е}(й), 7=1, 2, 3, (52.9)
в каждой из которых энергия есть функция волнового числа k. Эта
области называются зонами дозволенной энергии или просто зонами.
Покажем, что в пределах каждой зоны энергия есть периодическая
функция волнового числа k с периодом —. для доказательства заменим
2к
в системе уравнений (52.7) всюду k на k± — . Тогда, как непосред-
ственно видно из (52.7), такая замена означает просто иной порядок
написания уравнения (52.7), т. е. система уравнений переходит сама
в себя. Поэтому и корни Е останутся неизменными, так что
£;( А ±7 )=£/*). (52.10)
Таким образом, энергия есть в самом деле периодическая функ-
ция k и, следовательно, может быть выражена рядом Фурье:
00
EJ № = S Ерп cos (52.11)
т=0
где коэффициенты Ejm зависят лишь от в/да потенциальной энергии
i7(x), т. е. от *).
На рис. 35 приведены типичные кривые зависимости от Е} (k) для
двух первых зон Е} и Е2. В первой зоне энергия меняется от минималь-
ного значения Е[ до максимального Е'[, во второй от Е'2 до Е”. Интер-
вал Е от до Е'2 не реализуется и образует запрещенную зону.
Таким образом, спектр состоит из отрезков непрерывного спектра (по-
лос) от Е'х до E"v от Ё2 до Ё2 и т. д. Как правило, запрещенные об-
ласти суживаются по мере увеличения номера зоны, вплоть до слияния
в непрерывный’ спектр в пределе у=оо.
*) Мы написали ряд по cos. Общий ряд Фурье содержит как cos, так и sin
Однако, легко видеть из (52.7), что замена Л на —k не может изменить коэф-
фициентов уравнения (52 7). При такой замене они опять переходят сами в
себя. Поэтому Е должно быть четной функцией k.
по
ТЕОРИЯ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ [гл. IX
Общий вид собственных функций может быть также легко получен.
Каждому собственному значению £ = £.(&) принадлежит определенное
решение системы (52.7). Данному значению (52.7) принадлежит Cj(k)
с вполне .определенным значением k, либо отличающимся от него на
2и
целое число — . Если мы хотим записать с(k) в виде одной функции,
Рис. 35. Энергетический спектр и энергия в функции волнового числа k для
электрона, движущегося в периодическом поле.
то мы можем это сделать с помощью 5-функций следующим образом:
4-оо
c)k(k')=cf(k') £ b(k+2^ — k'\. (52.12)
п=— 00 7
Это и есть решение, принадлежащее собственному значению Ej(k) и
взятое в «р»-представлении (так как k'= . Отсюда получим ф в
«х» -представлении:
V° eik'x V"? / 2тш \ eWx
— оо л
Производя здесь интегрирование по k\ получим;
4-°° i ( Л4-— ) х
= + <52,3>
Вынося здесь eikx за знак суммирования, получим:
^jk{x)=e^aJk{x), (52.14)
где ЯуЛ(х) есть некоторая периодическая функция х с периодом а\
и/&(х-|-а) = «л(х). (52.15)
ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРИОДИЧЕСКОМ ПОЛЕ
171
§ 52]
ф^(х) (52.14) есть собственная функция оператора энергии в «х»-пред-
ставлении, относящаяся к собственному значению Е} (k), т. е. к /-ой
зоне и волновому числу, равному k. Она представляет собой плос-
кую волну (eikx), модулированную в такт периодичности потен-
циальной энергии. На рис. 34 изображена действительная часть такой
функции (пунктирная кривая). Точками на оси ОХ отмечены положения
ядер атомов [полюса функции С/(х)]. Около этих точек функция фуДх)
близка к тем, которые свойственны изолированным атомам.
Из решения (52.13) непосредственно следует, что состояния с опре-
деленным значением энергии (Д£2 — 0) суть (как и всегда при наличии
поля) состояния с неопределенным значением импульса р. Именно в со-
стоянии с энергией Ej(k) возможны значения импульса р, равные
п = 0, +1, ±2, ... (52.16)
с вероятностью
<52J7>
для pn = h • Среднее значение импульса р в состоянии
вообще говоря, не равно нулю.
Докажем теперь теорему о движении группы волн в периодическом
поле, подобную теореме о движении группы волн в отсутствии поля
(§ 7). Зависимость от времени функций ф/Лг(х), как представляющих
стационарные состояния, будет гармоническая с частотой <d=—:
Л
(х, t) = (х)е * . (52.18)
Образуем из этих состояний группу, ограничиваясь функциями, принад-
лежащими одной определенной зоне (/). Соответственно этому предпо-
ложению индекс / опустим совсем.
По определению группы имеем:
Ло+Д*
ф(х, t)= j c{k)e^kx~^ uk(x)dkt (52.19)
где Д£— малый интервал. Полагая
k=k0^8, ш(й)=®(£о)+(^)оа4-...
и считая c(k) и uk(x) медленно меняющимися функциями k (в области
+ Д^), мы получим вместо (52.19)
ф(х, 0 = c(A0)afto(x)^C*»*-“,‘>/) j е I \dkJo J dh. (52.19')
— Д&
Вынесенные за знак интеграла множители являются быстропеременными
функциями х и t. Интеграл по 8, напротив, медленно меняется, если Д/г
172 теория движения частицы в поле потенциальных сил [гл. IX
мало. Поэтому этот интеграл можно рассматривать так же, как мы де-
лали в § 7, как амплитуду группы ф (х, t).
Повторяя в точности все рассуждения § 5,,Мы найдем, что максимум
амплитуды . («центр» группы) перемещается с групповой скоростью,
равной
”=(S)=4C-ff’); <52-20'
Отсюда следует, что средний импульс такой группы равен
<52'21)
Пользуясь выражением для Е (52.11), мы можем написать выражение
для среднего импульса в группе состояний в у-ой зоне и около kQ = k
в следующем виде:
7 = — j X Ejm т sin (mak)- (52.22)
т — \
Отсюда видно, что на границах зоны (& = -+—) средний импульс
/7 = 0. Легко непосредственно убедиться из вида функций ф^(х) (52.13),
что в этих случаях мы имеем стоячие модулированные волны. Для
значений k ™ средний импульс вообще не равен нулю. Следовательно,
состояния с определенной энергией в периодическом поле суть состоя-
ния со средним импульсом, вообще говоря, не равным нулю.
Если О1раничиться в ряде (52.11) двумя первыми членами (пг = О
и т— 1), то получим*
Е. (k) = EJQ 4-E.t cos (ka). (52.11 ’)
В центре зоны (около k = 0, см. рис. 35) можно разложить (52.1 Г)
по степеням А?, тогда найдем:
E^k^E^E^ (1-^4-...). (52.11")
Для свободного движения энергия равна
£,=const. + ^ (52.11'")
(см. § 7). Поэтому (52.1 Iя) можно переписать в виде
Ej (k) = const. 4- , (52.23)
где р* есть так называемая эффективная масса:
1___________1 (d*Ei \ (52.24)
Л2 ~№\ d№
Соответственно, импульс равен
7=jAA, (52.25)
§ 52]
ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРИОДИЧЕСКОМ ПОЛЕ
173
т. е. отличается от импульса свободной частицы коэффициентом
Подобным же образом можно представить энергию и на краях зоны
= Возьмем, например, окрестность точки & = Поло-
жим k = —— Е. Тогда
а
cos (ak) = cos (я — £а)——cos (Ea).
В этой области
Ej(k)=Ej0-EA(l—^+... ),
т. е.
£/(ft)=const+^, k, (52.23Т
где ji** есть эффективная масса на краю зоны. Из (52.24) следует, что
р**= — pi*,
г. е. эффективнее массы в середине и на краю зоны имеют противо-
положные знаки.
Доказанные в этом отделе теоремы имеют исключительное значение
в современной теории металлов *). Не имея возможности входить в де-
тали этой обширной в настоящее время теории, мы ограничимся самыми
краткими -замечаниями **). Теорема о движении группы в периодичес-
ком поле показывает, что в периодическом поле электрон движется с
неизменным средним импульсом, вообще говоря, не равным нулю (это
впервые было показано Ф. Блохом в 1927 г.). Поэтому омическое со-
противление металла может быть вызвано только тем, что реальный
металл не является средой с идеально периодическим полем. Отступле-
ния от строгой периодичности поля вызывают рассеяние электронных
волн [фд (х)] и приводят к изменению среднего импульса электрона
p/k, чем и вызывается омическое сопротивление. Эти отступления от
периодичности обусловлены двумя причинами: 1) тепловыми колебаниями
атомов металла, 2) наличием посторонних вкраплений в кристалле и
случайными микродеформациями По мере уменьшения температуры ме-
талла уменьшается амплитуда колебания атомов, а вместе с тем умень-
шается рассеяние электронных волн и, следовательно, падает сопротив-
ление. В хорошо приготовленном кристалле вторая причина может играть
малую роль, поэтому сопротивление металла будет стреми*гь^я к нулю
(или очень малой величине) по мере понижения температуры ***). По
*) Мы должны были бы обобщить эти теоремы на три измерения. Однако,
это обобщение тривиально, своди1ся просто к увеличению числа переменных
(х, у, z вместо х, kx, ky, kz вместо k) и все теоремы сохраняют свою силу.
**) Подробно современная теория металлов изложена в книге Бете и Зом-
мерфельд, Теория металлов, ОНТИ, 1938
***) При этом мы не имеем в виду «сверхпроводимости». Последнее явле-
ние заключается в резком, скачкообразном падении сопротивления некоторых
металлов до нуля и до сих пор не получило теоретического обьяснения.
174 теория движения частицы в поле потенциальных сил [гл. IX
классической теории оно должно было бы возрастать («замерзание элек-
тронного газа»).
Построенная на основе этой качественной картины количественная
теория омического сопротивления металлов приводит к хорошему согла-
сию с опытом (см. сноску на стр. 173).
Отметим еще одно интересное обстоятельство.' Несмотря на то, что
опыты Толмэна твердо установили, что проводимость металлов обуслов-
лена движением электронов, оказалось, что в некоторых металлах знак
эффекта Холла таков, как если бы проводимость была обусловлена поло-
жительно заряженными частицами. Эта аномалия полностью объясняется
с точки зрения квантовой механики. Можно показать, что если прово-
димость металла обусловлена электронами, находящимися на краю зоны,
то / дело будет обстоять так, как если бы это были не электроны, а
положительно заряженные частицы.
Представим себе, что на электрон, находящийся на крад) зоны, дей-
ствует электрическое поле $. Сила, действующая на электрон, равна
е&. Эта сила вызовет изменение среднего импульса, которое по тео-
реме Эренфеста равно
Согласно (52.22) получаем:
dp d ( ^d^_\ Н d2E dk
dt dt\hdk' h dk2 dt *
С другой стороны, работа, произведенная полем за 1 сек., равна
dE a q 1 dE dEdk
— = e&v— eg -г = ~l.?*
dt и h dk dk dt
Отсюда
dk e8
di — ~ir*
Имея в виду, что согласно (52.23')
d2E d2E _ h2
dk2 d^2 pi**1
мы получаем:
% = (52.26)
Обычное положение дел таково, что pi* положительно. (Это видно уже
из того, что с уменьшением величины периодического поля U —-> О,
т. е. при переходе к свободному движению Ji* —► pi.) Но из (52.25)
следует, что pi** = — pi* 0.
Следовательно, согласно (52.26), электрон, находящийся на краю зоны,
движется так, как если бы он имел заряд е'\
1 Р-
е & ц** ’
т. е. заряд, по знаку противоположный заряду е (\ак как
§ 53]
ПРОИЗВОЛЬНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
175
ГЛАВА X
ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ЭЛЕКТРОМАГНИТНОМ
ПОЛЕ
§ 53. Произвольное электромагнитное поле
Рассмотрим теперь движение частиц с зарядом е и массой р в произ-
вольном электромагнитном п'оле. Пусть напряженность электрического
поля есть (§, а напряженность магнитного поля Эти напряженности
мы выразим через скалярный потенциал V и векторный потенциал А:
(53.1)
—rotA. (53.2)
Гамильтониан для этого случая приведен в § 23 и равен (27.7)
//=!> — ±(АР)—^-dlvA + ^A2 + rV4-f7, (53.3)
2р. }JL£' 1 2р.б? 1 2|1С2 1 1 ’ ' 7
где U—силовая функция и присоединена на тот случай, если по-
мимо электромагнитных сил имеются еще и другие силы.
Мы не будем сейчас искать стационарные состояния, так как в про-
извольном электромагнитном поле они не всегда существуют. Ограни-
чимся установлением уравнений движения и из них выведем некоторые
общие заключения.
Для установления уравнений движения мы можем опираться на об-
щую теорию, изложенную в § 32. Согласно (32.2) и (32.2') дело сво-
дится к вычислению квантовых скобок Пуассона для координат х, у, z
и импульсов Рх, Р < Pz, причем под оператором И следует разуметь
гамильтониан (53.3) *).
о dX / dY dZ
Вычислим сперва оператор скорости напишутся тогда
но аналогии^. Имеем:
= [Н, х] = 1 [Л, х] - £ [АЛ Л], (53.4)
первую скобку мы уже вычисляли (32.5), и она дает результат ~х-
[см. (32.5, 6, 7, 8)]. Для второй имеем:
[АЛ х] = [АхРх, х] = 1 (хАхРх - А^) =
= Vh МЛ - Ах (хРх - ih)] = Ах. (53.^
*) Дальнейший расчет аналогичен классическому, рассмотренному в до
волнении' VI.
176 ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ [ГЛ. X
Следовательно,
~ = [Н, х\ = Црх—-дА ^=[Н,у}=-(р' — — А V
е } \ ( е \Л ' (53.6)
-£=[Н, z] = -(p—-A.).
dt L J ji \ z c z)
Эти операторные уравнения в точности совпадают с первой группой
классических уравнений Гамильтона (см. дополнение X, формула 6),
если под Р разуметь величину, а не оператор.
Вторая группа уравнений получается несколько более сложным пу-
о dPx .
'тем. Вычислим —~ •
dt
- [Н, Ря]=~~ [АР, PJ + g [div A, PJ +
+ tA2’ U> <53-7>
Вычислим все эти скобки, начиная с последних:
(53.8)
е2 дА2 е2 / дАх дА? дАг \
2цс2 [A2’ = 2|хс2 дх = дх ах г~дх )’
the the/д2Ах д2А? д'Аг \
2jj£ А» 2ji£ дх 2{хД дх2 ’ дудх ’ дгдх/ ’
е е fdA* , (М„ . dAz \
- [ал pj=„;г‘.+р.)
Следовательно,
^Рх _ ди _ dV
dt дх е дх
ihed&vK 1
г С “Ч " 2к дх | ' (53-9)
Чтобы получить производную не от обобщенного импульса, а от
обыкновенного, равного согласно (53.6)
н —р_______L д
И at сл*’
(53.10)
нужно из (54.9) вычесть . Для этого вычислим -у . Имеем
£ ал = L дА , £ г н А (53.11)
с dt с dt * с L
Подставляя сюда Н из (53.2), находим:
~[Н. А,] = 5-ДА AJ-^[АР. AJ. (53.12)
Далее, вычисляем эги скобки:
[Я AJ = 2 Рх + д-^-Ру + ^Рг)-^Ах, (53.13)
[АЯ Аж]=А^ + Д^ + А^. (53.14)
§ 53]
ПРОИЗВОЛЬНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
177
Отсюда получаем:
е dAx е дА* , е (дАк / е \ , дАу / е \ .
~с dt ~с # + рИ дх Vх ~с “Ь ду у У ~с Ау) +
+ (рг~ -ЛгН— (53.15)
1 dz \ z с z) ( 2рс х ' '
Вычитая теперь (53.15) из (53.9), находим:
_ _dU_ ( 1 dAx
дх \с dt
е / дАх dAz
це \ dz дх
Но
1 дАх дУ
с dt дх~
д div А
VM
ddivAX /c-o Ч/-.Х
O’3-16)
dAy dAx _
~dx d^~^z'
d fdAK дЛ„\ d fdA
X’
dAx dA~
—Л_____z- — w
dz dx лУ'
z dAx \ —>
~dx dy \ dy dx J dz\ dx dz ) ro^x^*
Имея еще в виду (53.10), получаем из (53 16)*
d2X dU г । & ( ^Y | / с о 1 7\
~ dY dZ .
Операторы скорости — и не перестановочны с полем SK (если оно
не однородно). Поэтому в (53.17) лучше произвести симметризацию:
ih dSKz
ih dSKу
Р dz
z dt
dZ
^y^di~
Отсюда следует, что
суу л/ Z 1 [ dY । dY ?rj> _______dZ dZ | ।
^zdt~ ^y~dF~^YCzdt “» dt Му dt dt +
+ grotj£. (53 18)
Подставляя (53.18) в (53.17), получаем:
d^X dU , о , е dY ,
dt* дх +е®^+ 2с \^^dt “Г
+ (53.19)
Выражение
<53-2»>
12 Блохинцев
178 ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ [ГЛ. X
следует рассматривать как оператор силы, Лоренца, действующей
в поле 5% на частицу с зарядом е. В самом деле, классическое
выражение для силы Лоренца имеет вид
Остальные два уравнения для осей OY и 0Z, очевидно, напишутся
путем циклической подстановки х, у, z.
Переходя от операторного равенства (53.19) к уравнению для сред-
них значений, для чего умножаем (53.19) слева на ф* (х, у, z, t), а
справа на ф (х, у, z, t), и интегрируем по всему пространству, мы по-
лучаем теорему Эренфеста для движения в электромагнитном поле:
(РХ dU , -ъ । е U dY . dY
dfi дх “Ь 2c\\^^dt “Ьat
<53-21>
Это уравнение вполне аналогично классическому уравнению Ньютона
hS=-"+«^+7{^'s'-^S}- (53-21'>
Рассмотрим теперь специальный случай движения в однородном эле-
ктрическом и магнитном поле. В этом случае $ и ffC не зависят от
dX dY dZ о
координат и поэтому коммутируют с операторами —, — и —. В силу
этого для однородных полей вместо (53.21) получаем:
= (53.22)
х, Уч z СУТЬ координаты центра волнового пакета. Сравнение с (53.21)
показывает, что в однородном электромагнитном поле центр пакета дви-
жется по законам классической механики как частица с зарядом е и
массой ji.
Если магнитное поле отсутствует, то вместо (53.22) получаем:
= х=^2+^ + х0, (53.23)
т. е. равномерно ускоренное движение центра волнового пакета. За-
метим, что в однородном электрическом поле не существует стационар-
ных решений [соответствующие4 волновые функции обращаются в бес-
конечность при х = + оо (смотря по направлению поля $х)]. Действи-
тельно, согласно (53 23) центр волнового пакета для / = должен
лежать в бесконечности: поле «сдувает» частицы в сторону падения
потенциальной энергии.
§ 53] ПРОИЗВОЛЬНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 179
В магнитном поле существуют стационарные решения (см. § 54).
Они существуют также при одновременном наличии электрического
и магнитного полей, если они перпендикулярны друг к другу.
Из (53.1) и (53.2) следует, что если вместо потенциалов А и У мы введем
новые А' и У', связанные с прежними формулой:
A' = A + V/, (53.24)
<53.25)
где /—произвольная функция координат и времени, то потенциалы А' и У’
описывают то же поле, что и А и У. Действительно,
7= — - ~—viz'=7— 4 £ v/+1 F,
с dt с dt ' с dt
Таким образом, потенциалы А, V вплоть до преобразования (53. 24, 25) про-
извольны. Но потенциалы входят в гамильтониан Н. Поэтому может пока-
заться, что физические выводы могут зависеть от произвола в выборе А и У.
На самом деле это не так. Физические выводы зависят лишь от поля £, Ж *
а не от потенциалов А, У. В частности, в уравнение движения (53 21) входят
лишь напряженности полей, а не потенциалы. Это пример, иллюстрирующий
правильность приведенного утверждения.
Предоставляем самому читателю прямой подстановкой показать, что если
найдено решение уравнения Шредингера
= (53.26)
где Н—гамильтониан (53.3), то решение фг уравнения Шредингера
(53.26')
где Я' отличается от Я. заменой А и У на А' и У' по формулам (53.24) и
(53.25), будет получаться из ф по формуле
<53-27*
так как f— действительная функция, то
1Ф'|2—1Ф12> (53.28)
J’ = {W* ~ Г?*'} - AI f I2 {F<|>* - $*?<[>} -
-^А|фр = Л (53.29)
Г**'
ie
(так как ?<(.' =
Т. е. вероятность местонахождения частицы и плотность тока остаются
неизменными при преобразовании потенциалов (53.24) и (53.25), оставляющем
неизменным электромагнитное nc^ie. Подобным же образом и все другие фи-
зические величины остаются теми же.
Это свойство уравнения Шредингера называется электромагнитной
инвариантностью*),
*) Этим же свойством обладают классические уравнения Гамильтона (см.
дополнение VI).
12*
180 ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ [ГЛ. X
§ 54. Движение заряженной свободной частицы в однородном
магнитном поле
Направим ось OZ по направлению магнитного поля. Тогда компо-
ненты поля будут —0, —
Вектор-потенциал А возьмем в виде
Ах=—&С.у, Ay — Az = §. (54.1)
Тогда из уравнения (54.2) получается как раз нужное поле (чем и
оправдывается выбор А):
.^х = о, ^ = 0, 5^=,—^ = ^. (54.2)
Других полей мы не предполагаем (£7=0, У== 0), поэтому на осно-
вании (53.3) уравнение Шредингера для стационарных состояний на-
пишется в виде
- Г?’* - ? I + 2$. <54'3>
В этом уравнении мы можем сразу разделить переменные, если по-
ложим
ф(х, у, z) = el^x+^^(y), (54.4)
где а и [J — некоторые постоянные.
Подставляя (54.4) в (54 3), находим уравнение для функции tp (у):
ИЩ . вЫ . ^^2 г /^21
- d? + W ^ус? + г - -2Г Г <54-5)
(54.6)
Это последнее уравнение легко приводится к уравнению для осцилля-
тора. Для этого положим-
, hac
У=У~^
еЖ
0)0 *
Тогда после простых преобразований получаем вместо предыдущего
уравнения новое уравнение
й2 rf2T р<0^
(54.6')
(54.6")
(54 7)
Это и есть уравнение для осциллятора массы р, частоты <оо [см. (44 3)].
Отсюда на основании известных решений для осциллятора мы можем
сразу написать нужные нам решения:
^(У) = б-2^Ь (5<8)
'= /т* “ /тЙ>). (54 9)
8==Л0)0(л_|-^)1 й==0,1, 2,... (54 10)
§ 54] ЗАРЯЖЕННАЯ ЧАСТИЦА В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ 181
Стало быть, собственные функции частицы в поле будут
*Нп®, (54.11)
а квантовые уравнения определятся формулой
(«+1)+(54.12)
где п = 0, 1, 2, ...
Последний член есть не что иное, как кинетическая энергия движе-
ния по оси OZ (вдоль поля), первая же часть
(54.12')
представляет собой энергию движения в плоскости x, у, перпендикуляр-
ной к магнитному полю. Эту энергию можно записать в виде потен-
циальной энергии тока, обладающего магнитным моментом ЭЛ в магнит-
ном поле (О, О, Именно, положим
Еп(0) = — (3W)== — аЛ^ = 9Лв(2/х+1)^. (54 13)
Из этой формулы мы видим, что проекция магнитного момента ЭЛг на
направление магнитного поля есть целое кратное от магнетона Бора
Полученное квантование энергии свободной частицы, движущейся
в магнитном поле, является важным следствием квантовой механики,
так как приводит к наличию диамагнетизма у электронного газа, в то
время как по классической теории диамагнитные свойства у электрон-
ного газа должны отсутствовать *).
Собственные функции (54.11). вполне соответствуют классическому
закону движения в магнитном поле. Именно, по классической теории
мы имеем круговое движение в плоскости х, у с частотой <оо (как раз
эта часть энергии квантуется) и свободное движение по оси OZ **)
Действительно, волновая функция (54.11) означает, что обобщен-
ный импульс по оси ОХ равен p*x=^ha и по оси OZ равен pQz = hfi.
По оси OY мы имеем гармоническое движение с частотой <о0 около
ерх
положения равновесия yQ — . Согласно классической механике импульс
по оси ОХ также постоянен, и это не противоречит тому, что по
оси ОХ также происходит гармоническое колебание около некоторого
в л .
положения равновесия х0, так как рх~№х— ~ Ах, а не рстИ.
Обобщенный импульс рх определяет положение равновесия и
поэтому от него не зависит энергия движения Еп (^).
См., например, Бете и Зоммерфельд, Электронная теория металлов,
ОНТИ, 1938; Ф. Блох, Молекулярная теория магнетизма, ДНТВУ, 1934.
**) См дополнение IX, где приведен соответствующий расчет по клас-
сической механике.
182 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
То обстоятельство, что по квантово-механическому решению как
будто получается гармоническое движение только по оси OY, в то
время как классическое круговое движение означает гармоническое
колебание и по оси ОК, и по оси ОХ ^с разностью фаз связано
с тем, что волновая функция (х, у, z) (54.11) описывает состояние
с неопределенным положением равновесия колебаний по оси ОХ.
Так как энергия Еп($) не зависит от а, то мы имеем бесконечно
высокое вырождение, соответствующее различным возможным положе-
ниям точки равновесия х0. Поэтому энергии Еп($) принадлежит не
только найденное нами решение но и все волновые функции вида
Н~оо _Еа
фяр (х, у, z)— j с (а) 2Hn(Z)da,
— 00
где с (а) — произвольная функция а.
В частности, можно подобрать с (а) так, чтобы решение соответ-
ствовало определенному положению точки равновесия по оси ОХ (х0).
ГЛАВА XI
СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ
ЭЛЕКТРОНА (СПИН)
§ 55. Экспериментальные доказательства существования
спина электрона
Изложенная в предыдущем теория движения заряженной частицы
в магнитном поле является далеко не полной. Дело в том, что помимо
механического и магнитного моментов, создаваемых движением центра
тяжести электрона, электрону необходимо приписать собственный ме-
ханический и магнитный моменты, как если бы он являлся не материаль-
ной точкой, а вращающимся заряженным волчком. Этот механический
и магнитный моменты называют спиновыми (в отличие от механического
ц магнитного моментов, создаваемых движением центра тяжести элек-
трона, которые мы будем теперь называть орбитальными). Само явле-
ние называют спином электрона *).
Мы изложим кратко те опытные факты, из которых следует суще-
ствование спина электрона**). Одно из наиболее простых и прямых
указаний на существование спина электрона получается из опытов
Штерна и Герлаха по пространственному квантованию (§ 3). Штерн и
*) От английского глагола to spin, означающего «вертеть» (веретено).
**) Подробное изложение этих фактов читатель найдет в книге Вве-
денский и Ландсберг, Введение в современную теорию магнетизма,
ГИЗ, 1929.
§ 55] ДОКАЗАТЕЛЬСТВА СУЩЕСТВОВАНИЯ СПИНА 183
Герлах наблюдали расщепление надвое пучка атомов водорода, заведомо
находящихся в s-состоянии. В этом состоянии механический, а вместе
с ним и магнитный момент равен нулю. Между тем факт отклонения
пучка атомов в магнитном поле показывает, что эти атомы обладают
в s-состоянии магнитным моментом. Расщепление только на два пучка
показывает, что проекция этого магнитного момента может прини-
мать только два значения. Результаты измерений показывают, что абсо-
лютная величина этого момента равна магнетону Бора ЭЛ5. Таким
образом, в s-состоянии атома, имеющего лишь один электрон, суще-
---- 2р{
а---Ь с
---- К—i—
ствует магнитный момент ЭЛ, про-
екция которого Ч-ЭЛ5 на магнит-
ное поле принимает лишь два
значения.
Существование этого магнит-
ного момента в состоянии, где орби-
тальный момент заведомо отсутст-
вует, можно объяснить, если пред-
положить, что этот магнитный мо-
мент свойственен самому электрону.
Это предположение опирается еще
и на следующие важные обстоя-
гр
1s
Рис. 36. Мультиплетная структура
уровня 2р.
Переходы (Ь) и (с) образуют две близкие ли-
нии (дублет)
тельства. Спектральные линии даже
тех атомов, которые имеют один оптический электрон, оказываются бо-
лее сложными, нежели это следует из изложенной выше теории движения
электрона в поле центральных сил Так, например, в атоме Na вместо
одной спектральной линии (а) (см. рис. 36), отвечающей переходу
2р—>ls, наблюдаются две очень близкие линии (/?, с), исходящие из
двух4 близких уровней. Это — так называемый дублет Na (линии
5895,93 А и 5889,96 А)
Таким образом, р-терм Na следует считать состоящим из двух
близких уровней*. Подобная структура спектральных линий наблюдается и в
других атомах и носит название мультиплетной структуры спектров.
Теория движения электрона в поле центральных сил показывает,
что -терм (п = 2, 7=1) состоит из трех сливающихся уровней
(/^ = 0, ЧМ), но вовсе не из двух близких. Расщепление трех уров-
ней может получиться лишь во внешнем поле, а дублет (/?, с) наблю-
дается в отсутствии поля.
Предположение, что электрон имеет собственный магнитный момент 9Ла
позволяет сразу объяснить происхождение двойного расщепления термов
одновалентных атомов В атоме, во всех состояниях (р, d,.. ), кроме
состояния s, где орбитальный момент равен нулю, существуют электри-
ческие токи (ср. § 52) Эти токи создают внутреннее магнитное поле.
В зависимости от ориентации спинового магнитного момента электрона
(вдоль этого поля или против него) получается два состояния с не-
сколько различной энергией, так что каждый из уровней р, </,... рас-
щепляется на два близких уровня (см. § 61).
184 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
Рис 37.
Схема
опыта
Эйнштей-
на и де-
Как мы увидим, расщепление спектральных линий атомов в магнит-
ном поле (эффект Зеемана, § 70) также требует предположения о суще-
ствовании спина электрона и только на его основе может быть
объяснено.
Обратимся теперь к собственному механическому моменту электрона.
Обозначим его через s. Если бы проекция этого момента sz на любое
направление OZ определялась бы целым числом постоянных План-
ка msh (как это имеет место для орбитального момента), то сле-
довало бы ожидать по крайней мере трех ориентаций спина /и =0, -4- 1»
В самом деле, упомянутый результат опыта Штерна и Гер-
лаха, а также двойное расщепление уровней р, d, ...
показывают, что возможны только две ориентации спина
электрона. Эти факты привели юлландских физиков Улен-
бека и Гаудсмита к предположению, что проекция собст-
венного механического момента электрона sz на лю-
бое направление измеряется полущелым числом постов
янных Планка и может принимать лишь два значения
= (55.1)
Это предположение Уленбек и Гаудсмит дополняют, в
соответствии с опытными данными, предположением о нали-
—>
чии у электрона собственного магнитного момента ЭЛ,
проекция которого ЭЛ2 л<а любое направление может при-
нимать также только два значения:
9Иг=±9Лв = ^. (55 2)
Из (55.1) и (55.2) следует, что отношение спинового магнитного момента
е
к спиновому механическому моменту равно — — :
ii = -ycs, (55 3)
в то время как для орбитальных моментов получается отношение
-- (см § 50).
Существование отношения (55.3) между магнитным моментом и
механическим было обнаружено еще в 1915 г. в опыте А. Эйнштейна
и де-Гааса. Вкратце сущность этого опыта сводится к следующему.
Ферромагнитный стержень / (см. рис. 37) подвешивается на нитях так,
чго может вращаться вокруг своей оси. Если изменить направление
продольного магнитного поля то изменится и направление намагни-
чивания стержня, т. е. его магнитный момент ЭЛ. Так как магнитный
момент пропорционален механическому
^ = -2^М> (55 4)
§ 56]
ОПЕРАТОР СПИНА ЭЛЕКТРОНА
185
то изменится и механический момент М электронов всего стержня *)^
В результате стержень придет во вращение и будет закручивать нить.
Из этого кручения можно определить М, а вместе с тем и проверить
отношение ~. Для электронов это отношение должно быть отрица-
тельным (заряд электрона равен —е) Это и получилось из опыта г
показывая таким образом, что намагничивание куска ферромагнетика
обусловливается движением электронов. Однако, отношение получилось
равным
не
е
2\i.c
, а-----. Для орбитального движения при самых
общих предположениях и классическая, и квантовая теория ведут к зна-
е
чению — ~.
2р.г
Поэтому результат опыта казался загадочным. Если же
считать, что намагничивание обусловлено не орбитальным движением
ЭД х е
эпектрона, а его спином, то отношение должно быть равно — —, что
и получается на опыте. Это предположение позволило не только
объяснить результаты опыта Эйнштейна и де-Гааса, но и заложить
основы современной теории ферромагнетизма (см. § 119).
Заметим, что в настоящее время существование спина электрона
может рассматриваться как следствие из релятивистской теории элек-
трона, развитой Дираком. Однако, изложение этой теории выходит за
рамки нашей книги **).
§ 56. Оператор спина электрона
Обратимся теперь к математической формулировке гипотезы У лен-
бека и Гаудсмита.
В соответствии с общими принципами квантовой механики собствен-
ный механический момент электрона (для краткости будем просто гово-
рить спин электрона) должен изображаться линейным самосопряженным
оператором. Обозначим операторы проекций спина на оси координат
через sy, s2. Чтобы определить вид этих операторов, мы потребуем,
чтобы эти операторы подчинялись тем же правилам перестановки, что
*) Заметим, что формулу (55 4) мы пишем теперь для суммарного момента
всех электронов. Поскольку она справедлива для каждого электрона стержня,
то она будет справедлива и для всей их совокупности Подробнее об этом
см. в книгах И. Е. Тамм, Основы теорий электричества, ч.П, ОНТИ, 1934,
Введенский и Ландсберг, loc cit.
1*) См. Дирак, Основы квантовой механики, ОНТИ, 1937, § 72. Дирак
показал, что из релятивистского уравнения для движения электрона авто-
матически вытекает, что электрон должен обладать магнитным моментом (56 2)
и механическим моментом (56 1), и таким образом дал теоретическое обосно-
вание гипотезе Уленбека и Гаудсмита. Однако, физическая природа спина
электрона остается все же невыясненной По этой причине вместо «вращение»
электрона говорят «спин» электрона Надлежащее понимание спина электрона,
вероятно, окажется возможным лишь на основе теории структуры электрона.
Если, например, электрон представляет собой некоторое образование из^
электромагнитного поля, то невозможно применять к нему термин «вращение>
в том же смысле, как оно применяетсяк твердому телу.
186 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
и компоненты орбитального момента Afx, М2 *). Тогда, заменяя
в (25.5) М на s, получаем:
sxsy — sysx = ihsz, '
sysx—s,sy = ihsx, ►
«л—-
(56.1)
Проекция спина на любое направление (по исходной гипотезе) может
принимать только два значения: i• Поэтому операторы sx, sy, sz
должны изображаться двухрядными матрицами, так как двухрядная
матрица, будучи приведена к диагональному виду, содержит лишь два
диагональных члена и, стало быть, имеет только два собственных зна-
чения. Полагая
h h h /СГ/С.
= sy=2°y' (56-2)
мы можем сказать, что операторы <зг (спиновые матрицы) должны
быть двухрядными матрицами вида
& & to k-д а to h* to to ^11 ^12 ^21 ^22 > = f12 ^21 C22 , (56.3)
имеющими собственные значения h2 и сокращая на , получаем. & 4~ 1. Подставляя (56.2) в (56.1)
0^ — 0^=2гаг,
0А“ °А=2А-
(56.4)
(56.4')
(56 4")
Ввиду того, что собственные значения ох, oz равны Чк 1, то
собственные значения операторов ах, aj, суть -f- 1- Стало быть, в своем
собственном представлении эти последние матрицы должны иметь вид
1 о
О 1
1 О
О 1
1 О
О 1 ’
а2
(56.5)
т. е. они являются единичными матрицами S:
1
О 1
(56.6)
Единичная матрица остается единичной во всяком представлении
•(см. § 39). Поэтому матрицы о£, имеют вид (56.5) во всяком
возможном представлении. Рассмотрим теперь комбинацию
2/ (°Х°У + j = 2i°x°y + ®у2А-
*) Опираясь на теорию групп, можно доказать, что правила (56 1) являют-
ся единственно возможными См , например, Pauli, Handb d Phys , т. XIV, I.
§ 56]
ОПЕРАТОР СПИНА ЭЛЕКТРОНА
187
На основании (56.4) это можно переписать в виде
(°А — °У + °У = в№ — °г°У + °Х ~ Wy
=»Х~в^;
но есть единичная матрица, поэтому
q2(5 z=zq (J2.
у z •
Следовательно,
(56-7)
т. e. матрицы a , как говорят, антикоммутируют.
Комбинируя (56.7) с (56.4) и применяя циклическую перестановку
<?х, а находим:
^у=—^х = 1^ ]
V* = — = гЧ> 7 (56.8)
а а = — a а = Zj . I
x^z ”y- J
Найдем теперь явный вид матриц ах, о^, аг. Пусть, скажем, матрица^
приведена к диагональному виду. Так как ее собственные значения
равны -4- 1, то диагональный вид az будет
(56.9)
Можно показать, что в этом же
и. av будут иметь вид
У 0 1
1 о
представлении остальные две матрицы
»,= • 0 • <56-9'>
Для доказательства образуем произведения <зг<зх и аха2. По правилу мат-
ричного умножения (§ 39), имеем
<№= 1 0| И11 М = 1 в11 в»|,
I 6 —1 | I #21 #22 I I —#21 —#22 I
а а I ДИ ^12 I U | __ I а11 — #12 I
Х Z I #21 #22 I I 0 1 I I #21 #22 I
На основании (56 8) имеем:
I #11 #12 I ___ _I #11 #12 I __ | — #11 #12 |
I—‘#21 —#22l I #21 #22 1 I #21 #22 1
или
#11= —#11, #12— #12» #21— #21» #22 —#22»
т. е.
#ц 0, #22 ~~ 6*
Поэтому матрица имеет вид
<^=1 ° Н <56jo>
| #21 О |
Образуем теперь а2х
02 I 0 ^12 I I 0 #12 | __ I #12 #21 0 |
Х I #21 О I I #21 j j 0 #12 #21 I
Сравнивая с (56 5), получаем, что #12#21 —1. Матрица должна быть самосо-
пряженной^ е. #12 —#21- Стало быть, | #1212=1.
188 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
Отсюда получаем:
I 0 I
О I*
где а — действительное число
Подобным же образом находим, что
I 0 |
О I*
(56.11)
(56 11')
Перемножая теперь на а потом на и пользуясь (56.8), получим:
I £*(*-£) О I___________________| £-*(*-?) О I
откуда
л
т. е. а — р = —, Таким образом, все соотношения удовлетворены при произ-
вольном значении а Поэтому без всяких ограничений мы можем взять а —О,
ц—------Подставляя эти значения в (56.11) и (56.1 Г), получаем (56.9').
Согласно (56 2) из (56 9) и (56 9') получаем матрицы операторов
s*, s , sz в представлении, в котором sz - диагоналей (^-представление):
Заметим, что значки 1 и 2, нумерующие матричные элементы матриц
а и s, приобретают теперь (поскольку выбрано представление) опреде-
ленное значение значок 1 относится к первому собственному значению
$z (+4)»а 2—ко вт°р°му (—4)*
Образуем теперь оператор квадрата спина электрона. Из (56 12)
имеем:
Вводя квантовые числа ms и ls1 определяющие значение проекции
спина на любое направление OZ и его квадрат соответственно, мы мо-
жем написать формулы для квантования спина в полной аналогии с фор-
мулами (45.5) для орбитальногр момента:
S2 = A2/x(/,-l-1), (56 14)
sz=hms, ^=±1. (56 15)
§ 57. Спиновые функции
Мы видим, чю в квантовой механике состояние спина должно ха-
рактеризоваться двумя величинами* абсолютным значением | s | (или s2)
и проекцией спина на какое-либо направление sz. Первая величина (s2)
предполагается для всех электронов одинаковой, поэтому речь можег
итти лишь об одной переменной sz. Таким образом, наряду с тремя
§ 57]
СПИНОВЫЕ ФУНКЦИИ
189
переменными, определяющими движение центра тяжести электрона (х, у, z
или рх, pz и т. п.), появляется еще одна переменная sz, опреде-
ляющая спин электрона. Поэтому можно сказать, что электрон имеет
четыре степени свободы *).
Соответственно этому волновую функцию ф, определяющую состоя-
ние электрона, следует считать функцией четырех переменных: три отно-
сятся к центру тяжести электрона, а четвертая — к спину (у2). Напри-
мер, в координатном представлении для электрона следует писать:
ф = ф(х, у, z, sz, t). (57.1)
Так как спиновая переменная имеет только два значения (±у)» то
можно сказать, чго вместо одной функции мы получаем две:
ф1==ф(х,л z, +4- *), (57.2)
ф2 = ф (х, у, z, — t). (57.2')
Эти функции мы будем иногда писать в виде матрицы с одним столбцом
Ф1 0
ф2 О
а сопряженную функцию — в виде матрицы с одной строкой
0 0‘
(57.3)
(57.3')
Такой способ написания позволит воспользоваться правилами § 39 (39.12).
Ясно, что волновые функции фх и ф2 будут только в том случае
различны, если существует реальная связь между спином и движением
центра тяжести. Такая связь существует и представляет собой взаимо-
действие магнитного момента спина с магнитным полем токов, создаваемых
движением центра тяжести заряженного электрона. Это взаимодействие
обусловливает мультиплетную структуру спектров (см. § 55). Поэтому,
если мы игнорируем мультиплетную структуру спектров, то мы можем
вообще пренебречь взаимодействием между спином и орбитальным дви-
жением. В этом приближении
tbjx, у, г, /)==ф2(х, у, z, /) = ф(х, у, z, f). (57.4)
Однако, чтобы и в этом случае отметить, что речь идет о частице,
*) Спиновые переменные sx, sy, sz отличаются от всех известных нам
квантовых величин тем, что они принимают лишь два значения. Это связано
с предположением о строго определенном значении полного момента электро-
на (s2).
Если бы считали s2 переменными, то мы получили бы не одну, а две сте-
пени свободы, как и должно быть для волчка. Поэтому можно думать, что
рассматриваемый в современной физике спин электрона представляет лишь
одно из возможных состояний вращения электрона (другие значения s2 могут,
например, требовать большой энергии вращения). Этот вопрос следует пока
считать открытым.
190 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
обладающей спином, пишут функцию (57.1) в виде соответствующих
разделению переменных:
ф(х, у, z, sz, 0 = ф(х, у, z, t)-S^sz), (57.5)
где через Sa(sz) обозначена спиновая функция. По существу это про-
стой значок, указывающий состояние спина частицы.
Значение этого «значка» или иначе «спиновой функции» таково:
индекс а принимает два значения, которые обычно полагают равными
и —г|2 (вместо 1 и 2). Первое значение (или 1) озна-
чает, что проекция спина на некоторое^ избранное направление OZ равна
у. Второе значение индекса а означает состояние спина с другим
возможным значением проекции спина да это же направление, именно
— —. «Аргумент» s2 «функции» рассматривают как независимую
переменную, могущую принимать два значения: + —. Тогда
S+1/a(4) = l, S+1/,(-A) = 0, (57.6)
. 1 , h
так как по смыслу значка в состоянии а= + у > sz= ту» и в этом
. h
же состоянии не может быть sz = — у, поэтому соответствующая
функция равна нулю. Подобным же образом
(|)=0, 5_,/>(-|) = 1. (57.6')
Запись в виде (57.1) и, как частный случай, в отсутствии взаимодейст-
вия спина и орбитального движения, в виде (57.5), позволяет рассмат-
ривать спин sz как динамическую переменную, подобную любой другой
механической величине.
Введенные «волновые» функции спина Sa($J обладают свойством орто-
гональности и нормировки. Чтобы в этом убедиться, возьмем произведение
где 5* означает, как всегда, функцию, сопряженную с а д, р .
Просуммируем это -произведение по всем возможным значениям спиновой
переменной sz (таких значений только два: . Тогда непосред-
ственно из (57.6) и (57.6') (имея в виду, чго 5* = S) следует, что
(57-7>
sz
Функция \(^) может быть записана и в матричной форме (58.3). Именно,
5+‘/.= 1 0 0 0 0 0 1 0 , (57.8)
1 0 0 1
0 0 • ^.,.= 0 0 (57.8')
§ 57]
СПИНОВЫЕ ФУНКЦИИ
191
Вычислим теперь результат действия любого
типа
г __ ^12
ь I L
Ь21 ь22
спинового оператора,
(57.9)
на волновую функцию. Значки 1, 2, если оператор L взят в «^«-пред-
ставлении, означают номера собственных значений Согласно
формуле (38.5), определяющей действие оператора, данного в матрич-
ной форме, на волновую функцию, мы будем иметь, что оператор а
делает из функции Ф(ф1}ф2) НОВУЮ функцию Ф(срп ср2) по правилу
epi = Лцф14-112^2, (57.10)^
(р2 — ^21Ф1 ^22^2* (57.10}/
Отличие (57.10) от (38.5) заключается лишь в том, что в (57.10) мы
имеем двухрядные матрицы и соответственно функцию из двух компо-
нент, а в (38.5) мы разумели матрицу с неограниченным числом эле-
ментов Lmn и функцию ф с бесконечным числом компонент сп(с1, с2, ...)»
Представляя Ф в виде матрицы (столбца) (57.3), мы можем записать
два уравнения (57.10) и (57.10') в виде одного матричного:
Ф = £Ф (57.11)
[см. (39.14)]. В самом деле, (57.11)
в развернутом виде означает
Ф =
° = £:
?2 0 ^2
11 ^12
21 ^22
Ф1 о = (Л1Ф1+м2) о
Ф2 0 (М1 + М2) о
(57.1V)
что совпадает с (57.10) и (57.10'). В дальнейшем под символом типа £ф9
если взят оператор, зависящий от спина, мы будем разуметь именно
такого рода произведения, которые в сущности представляют два урав-
нения (57.10, 10') в виде одного матричного.
Среднее значение любого спинового оператора L в состоянии фх, ф2
согласно общей формуле (40.2) есть
L(x, у, z, ^) = 'pUn4’1 + + + (57.12)
Так как функции фх и ф2 зависят еще и от координат центра тяжести
электрона, то мы написали £(х, у, z, t), имея в виду, что получаю-
щееся по (57.12) среднее есть среднее от L при заданном положении
центра тяжести электрона. Среднее в состоянии фп ф2 при любом по-
ложении электрона получится по формуле
L(t) = ^L(x, у, z, t}dxdydz. (57.13)
Формулы (57.12) и (57.13) с помощью представления ф в виде матрицы
с одним столбцом могут быть записаны в виде
£(х, у, z, t}==4*LW, (57.12')
L (/) = J Ф+LWdx dy dz. (57.13')
192 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНЭ [гл. XI
В частности,
ф* ф;
ajx, у, z, t)=^,x4 = ** *2
Подобным же образом
0 +Ф2Ф1 0 _
о о о “
==Ш + Ш- (57.14)
О 1
1 О
°>(х> У> z> ^) = Ч,+о)1Ч,х= —+ (57.14')
у, Z, /) = ф+агФ = ф^1 — ф2ф2- (57.14")
§ 58. Уравнение Паули
Рассмотрим теперь движение электрона в электромагнитном поле,
’учитывая наличие спина. Согласно основной гипотезе (§ 56) электрон
обладает магнитным моментом
Жв = — -s= — <3, (58.1)
° pc 2jj.£ ' '
где а — вектор-оператор с компонентами о^,, (56.9) и (56.9').
Благодаря наличию этого момента электрон в магнитном поле SK {Жх,
приобретает добавочную потенциальную энергию, равную
энергии магнитного диполя в поле St:
ДС7=—(ЗН^Д). (58.2)
Оператор этой энергии согласно (58.1) есть
^=^ЗД=|Й)=|(’Л+’Л+8ЛЛ <58-3>
Поэтому гамильтониан (27.7) для движения заряженной частицы в элект-
ромагнитном поле при учете спина должен быть пополнен добавочным
^членом (58.3) так, что он будет равен
Я=1(Р+|АР-е1/+1/+2^(а^) (58.4)
’(мы положим заряд электрона равным —е).
Уравнение Шредингера для волновой функции ф (фх, ф2) теперь
“будет гласить
ih?=7 АУФ -е w +Ж ф- (58-5)
Это уравнение носит название уравнения Паули. Заметим, что под ф
мы разумеем столбец (57.3), поэтому в (58.5) записано в сущности два
уравнения для двух функций и ф2 в виде одного матричного.
Определим теперь плотность тока. Для этого запишем (55.5) в виде
/Л^ = Я0Ф+^(5^)Ф, (58.6)
где через Н$ обозначены члены, не содержащие операторов j. Напишем
УРАВНЕНИЕ ПАУЛИ
193
§ 58]
уравнение для сопряженной функции Ф+, которую мы будем мыслить
в виде строки (57.3):
- ih + g ((aj£) Ф)+. (58.6')
Символ ( )+ означает, что в соответствующей матрице столбцы и строки
переставлены и элементы взяты сопряженными.
Умножая теперь (58.6) на Ф+ слева, а (58.6Г) на Ф справа и вы-
битая одно уравнение из другого, мы получаем:
ih£ (Ф+Ф) = Ф+ЯОФ — (Я0*Ф)+Ф+^ {Ф+ (аЯ’)Ф —
— ((а^)Ф+)Ф). (58.7)
Согласно (39.15) имеем
((с^)Ф)+=Ф+ (аг^) (58.8)
в силу самосопряженности оператора а+—а. Поэтому член в фигурных
скобках равен нулю. Остальные, не содержащие операторов а, после
вычислений, совершенно аналогичных приведенным в § 29 при получе-
нии формулы Гордона-Шредингера, дают *)
+ -gdlv {ф^-ф^ + ф^-ф^} -
-^<нУ[а(ф;ф14-ф;ф2)]. (58.9)
Переписывая это уравнение в форме уравнения непрерывности для
плотности вероятности w и плотности потока частиц J, мы находим:
w(x, у, Z, /) = Ф:Ф1 + Ф2Ф2) (58.10)
л=^№Ф;-Ф^Ф1)+(Ф2тф;-ф^ф2)]+^а(ф;ф1+ф‘ф2), (58.ii)
или
w(x,'_y, z, /) = ф+ф, J=g[TV¥+—Ч,+7Ф] + ^АФ+Ф. (58.12)
Эти формулы показывают, что вероятность местонахождения электрона
и плотность токов аддитивно слагаются из двух частей, каждая из ко-
торых относится к электронам с одной определенной ориентацией спина.
Формула для нормировки вероятности имеет вид
J(Ф1Ф1 + Ф2Ф2) dxdydz—\ или j Ф+ФаСгdy dz—\. (58.13)
Величины
(х, у. z, /) —w2(x, у. z, /) —ф*ф2 (58.14)
*) Пользуясь матричной записью, мы все время оперируем с четырьмя
функциями Ф2» Ф1,,Ф2 сразу. Рекомендуем читателю, впервые знакомящемуся
с матричными методами, написать уравнения (58.6) и (58.6') в развернутом
виле (четыре уравнения) и путем умножения первых двух на и ф2, а двух
вторых на фх и ф2 получить тот же результат,
13 Блохинцев
194 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
„ I ft
суть вероятности найти электрон в точке х, у, z в момент t с s — —
Л
h
или s9— —тг соответственно.
z 2.
Величины
wx = j dy dz,
W2 = \ ty dz
(58.15)
„ f ft
суть вероятности найти электрон со спином sz = или со спином
sz=—соответственно. Плотность электрических зарядов ре и плот-
ность энергетического тока Je согласно (59.12) будут равны
рв = — e’P+’P, Je = g! Ф+VlP — ЧФР+ ] — А (1Р+,Р), (58.16)
ре и не описывают полностью всех источников электромагнитного поля
в случае электрона. Нужно учесть еще магнитный момент электрона (58.1),
создающий магнитное поле. Из (58.1) и общей формулы (57.12) полу-
чаем выражение для средней плотности магнитного момента (намагничи-
вания I):
1 (X, у, z, t)= — е£с (ф+аФ). (58.17)
Согласно уравнению Максвелла для магнитного поля имеем урав-
нения:
rot^ = ^J,, divB = 0, B = .^4-4nI. (58.18)
Из этих уравнений и определится магнитное поле, создаваемое электро-
ном, находящимся в состоянии Ф, если под Je и I разуметь (58.16) и
(58.17). Вводя в первое уравнение вместо SK индукцию В, получим:
rotB = y {Je4-crotl}. (58.18')
Таким образом, вместо намагничения I можно рассматривать ток, экви-
валентный этому намагничению, именно:
Jf==crotl=—*Arot(4;+<jlP), div^ = 0. (58.19)
"г
Полный электрический ток, соответствующий и орбитальному, и спино-
вому движению, есть
Je=gi[4'+V’P — 4W+] — A (’Р+’Р) — grot(T+a»P). (58.20).
Для вычисления компонент спинового тока следует воспользоваться
формулами (57.14) и (57.14’).
ПРОСТОЙ ЭФФЕКТ ЗЕЕМАНА
195
§ 59]
§ 59. Простой эффект Зеемана
Рассмотрим атом с одним валентным электроном, находящийся во
внешнем однородном магнитном поле. Электрон атома будет подвер-
гаться одновременно действию этого магнитного поля и действию элект-
рического поля ядра и внутренних электронов. Это поле будем считать
центральным и потенциальную энергию электрона в нем» обозначим че-
рез U (г).
Магнитное поле направим по оси OZ и возьмем векторный потен-
циал А в виде
. SK л , А /КПП
Ах=------Ay^=-Y-^x, Л2=0. (59.1)
Магнитное поле по формуле «Я? = rot А получается правильное:
^ = ^ = 0, (59.2)
Подставляя это значение А в гамильтониан (58.4), получаем урав-
нение Паули:
dt 2р. 1 х ' 2?с дх ду / 1
+ 2^ +-^ Ф Ф- <59-3>
Членом с при малых полях мы можем пренебречь *). Далее, оператор
= = <59-4)
есть оператор компоненты орбитального момента. Обозначая еще через
Я°=-^2 + Щг) (59.5)
гамильтониан электрона в отсутствии магнитного поля, мы получаем:
/й^ = Я°Ф + ^(Мг+Ла2)Ф. (59.6)
Из этого уравнения следует, что, поскольку мы пренебрегаем <^2, по-
стольку член, выражающий действие магнитного поля, может рассматри-
ваться как потенциальная энергия At/ магнитного диполй с моментом
— 2^ (А1 hаг) в магнитном поле
- Я = ^(Л!2 + Лаг). (59.7)
Мы будем искать стационарные состояния. Для этого представим
волновую функцию в виде
Т(х, у, z, /) = Ч;(х, у, z)e h, (59.8)
*) Как будет показано в § 118, пренебрегаемый член определяет слабые
диамагнитные явления.
13*
196 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
где Е— энергия стационарного состояния. Подставляя ее в (59.6),
найдем:
Я0,р+1^(Л,г+Ч)’Р=^Р- (59-6')
Возьмем представление, в котором матрица диагональна -предста-
вление), тогда
1 0 db -4~ б.. I
11 = -гуН (59.9)
г 0 — 1 ф2 — ф2| ' 1
и, стало быть, уравнение (59.6’) распадается на два уравнения для ф,’
и ф2 порознь:
(59.10)
Я°^+-^(Я-Л)ф2 = ^ф2. (59.10')
Решение этих уравнений получается тотчас же, если заметить, что
в отсутствии магнитного поля мы имеем два решения:
’P»ta==(^0Z")’ E="einl ДЛЯ Спина Sz~ +4’ (5911)
/ о \ h
)> для спина S2=(59.11’)
\ Т nlm ‘
причем а
= <?). (59.12)
Так как Mz<bnlm = ' т0 эти же Реш^ния есть решения уравнений
<59.10) и (59.10'), но только принадлежат другим собственным значе-
ниям. Подставляя (59.11) и (59.1 Г) в (59.10) и (59.10'), получаем два
решения:
ч';». *.==+4' <59|3>
п.. £=£•;„ (seis')
т. е. волновые функции (поскольку пренебрегли членом с ^f2) не изме-
няются: атом не деформируется магнитным полем. Энергия же начинает
зависеть от ориентации момента относительно поля, т. е. от магнитного
числа tn', совпадавшие в отсутствии магнитного поля уровни теперь
расщепляются (снимается «тп»-вырождение).
На рис. 38 дано расщепление <$- и р-термов. Расщепление р-терма
получается из (59.13) и (59.13'), если перебрать возможные значения т
при /—1 (т. е. —-1-1,0). Расщепление 5-терма (/ = 0, /п = 0) полу-
чается лишь благодаря спину электрона. Это — важный результат
теории сйина: как раз это расщепление наблюдали Штерн и Герлах
в своих опытах.
Благодаря расщеплению уровней увеличивается число возможных
переходов, а вместе с тем и число наблюдаемых спектральных линий.
§ 59]
ПРОСТОЙ ЭФФЕКТ ЗЕЕМАНА
197
Это явление носит название простого эффекта Зеемана (в отличие
от сложного, см. § 70). Как будет показано в § 83,В, при оптических
переходах число т может изменяться только на ± 1 или 0. Кроме
того, спиновый магнитный момент очень слабо взаимодействует с полем
световой волны. Поэтому идут в расчет лишь те переходы, при которых
спин не меняется. Эти переходы изображены на рис. 38 линиями
m=+t
т~ о
т-~1
Is
Рис.
Без поля (Н= О) В поле (МФО)
38. Расщепление s- и /z-термов в сильном магнитном поле (с учетом’
1 спина).
(а, Ь,
с) и (a1, с'). Частоты этих переходов вычисляются по формуле
En4fmt — En„lrfm„ EQn,lf — EQn„lff eSK
=--------д-------=----------------Г 2^(т ~ ”*)• (59.14>
Обозначая частоты в отсутствии поля через со0, а при наличии поля
через (о, мы получаем:
® = (59.15)
Так как т—т!1 — ± 1, 0, то имеем три частоты: одну неизменную
. , еЗК
и две — смещенные на -+• •
Это расщепление на три линии (нормальный триплет Зеемана) как
раз таково, как оно получается из классической теории эффекта Зеемана.
В классической теории, как известно*), явление Зеемана объясняется
прецессией орбиты в магнитном поле с частотой, равной частоте Лармора
— Квантовая формула (59.15) не содержит постоянной План-
ка h, и поэтому результат должен совпадать с классическим (он не может
измениться, если положить й — 0). Это совпадение имеет место.
Покажем, что и в квантовой механике явление Зеемана обусловлено
прецессионным движением момента импульса вокруг направления магнит-
*) См. Лоренц, Теория электронов или Беккер, Электронная
теория.
198 СрБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
ного поля. Вычислим для этого производные по времени от орбитального и
спинового моментов. По общей формуле (31.10) имеем:
dMx _ dMv dMz
* \ H Ml - - г H M 1 - Г H Ml , (59.16)
at at dt dsx _ ds i, _ dsz dt dt S^’ dt
(59.17)
Подставляя сюда гамильтониан из (59.6)
н=нй+S(м*+Ч)=н°++20а (59.18)
——> —>- —>
и замечая, что HQ коммутирует с М и s и то, что М и 5 коммути-
руют между собою (так как М действует на функции от 0, у, функции от sx, sy, sz), мы находим: , a s — на
аМх OL dMv OL dM,
-dT-0’
dsx dsv %OL dsz
dt ih szsx)y dt ih (SySz SxSy^' Пользуясь (25.5) и (56.1), получаем: = 0. dt
dMx dMv dMz (59.19)
~dF==~0^ -df- + OLM*’ ~d^Q’
dsx ds» ds7 -^ = + 2ОЛ, -^=0. (59.20)
Переходя от этих операторных формул к средним значениям и имея
6 виду, что OL есть просто число, мы находим:
dMx — dMv — dM~ -^=-oLMy, -^=OLMX, -^=0, (59.21)
dsx — dsu — ds~ -^=-20^, ^ = 0. (59.22)
Из этих уравнений следует, что проекции орбитального и спинового
момента на направление магнитного поля являются, каждая порознь,
интегралом движения. Компонента же орбитального момента, перпенди-
кулярная магнитному полю, вращается с частотой Лармора OL. Такая же
компонента спинового момента вращается с удвоенной частотой 20 L
[в силу аномального отношения магнитного момента к механическому,
см. (58.1)]. Действительно, из (59.21) имеем:
d2Mx dMv 2 _ __ 1 dMx
^=-0^=-^ «,= -0^- (59-23>
Отсюда
Mx — Asin(OLt-f-a), Му= — Л cos (О^а), Af2 = const. (59.23')
Подобным же образом из (59.22) получаем:
sx~ Bsin (2О^-{- Р), sy= — В sin (2О£/-[~ Р), Г, = const. (59.24)
§ 60] СВОЙСТВА ПОЛНОГО МОМЕНТА ИМПУЛЬСА 199
§ 60. Свойства полного момента импульса
Мы видели, что и орбитальный момент М, и спиновый s представ-
ляют собой величины, принимающие лишь квантовые дискретные значения.
Рассмотрим теперь полный момент импульса, являющийся суммой орби-
тального и спинового моментов.
Оператор полного момента определим в виде суммы операторов
орбитального момента М и s:
7 = М (60.1)
J==Mx + sx, Jy = My-\-sy, Jz = Mz-ySz. (60.17
Покажем, что операторы компонент полного вращательного момента
подчиняются тем же правилам коммутации (25.5), что и компоненты
орбитального момента Мх, Му, Мг. Для этого заметим, что М и s
коммутируют, так как оператор М действует на координаты, а оператор
s на йих не действует. Поэтому
JxJv — JVJX=(Мх+sr) (М,+sy) — ЦЛу + sy) CM , + sj
= M xMy — MyMx 4- sxsy — sysx=i hMx -|- ihs2 (60.2)
[последнее в силу (25.5) и (56.1)]. Таким образом,
АА JVJX = i'hJzy (60.3)
JvJz — J;Jv=ihJx, (60.3')
(бо.з")
(два последних равенства получаются из первого циклической переста-
новкой).
Найдем теперь оператор квадрата полного вращательного момента /2.
Имеем
/2=(л1-1-7)2=м2 4- 7 4- 2м 7=
= ^4-52 + 2(МА+МЛ + Л!А). (60.4)
Оператор J2 коммутирует с любой проекцией J. Например, рас-
смотрим проекциюша OZ Jz = Mz-\- sz. Так как Мг коммутирует с Л!2,
s2 и sz с М2, s2, то достаточно доказать, что Jz коммутирует с 2 (Ms).
J4 - jy2 = 2 (Мzsx + Mysy + Mzsz) {Мг+sz) -
— 2 (Мг -j- s2) (Mxsx+Mysy + Mzsz).
Раскрывая здесь скобки, получаем:
•>4 - JZJ2 = 2 {(Л1Д - MZMX) sx + (MyMz - MzMy) sz +
+mx (»a—»Л)+isysz—vP };
подставляя сюда выражение в круглых скобках из (25.5) и (56.1),
находим:
J2 J J J2
2 { - ihfAysx + ihfAxsy + №х (— ihsy) + Му (+ ihsr)} = 0.
200 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. Xi
Подобным же образом доказывается утверждение для остальных двух
компонент. Таким образом,
J2^ —JxJ2 = 0, (60.5)
—J/2 = 0, (60.5')
J2JZ — JzJ2 = 0; (60.5")
эти равенства — такого же вида, как и (25.5). Отсюда следует, что
оператор J2 и оператор любой проекции (но одной), например, Jz,
одновременно могут быть приведены к диагональному виду, и, стало быть,
величины J2 и Jz принадлежат к числу одновременно измеримых.
Легко видеть также, что оператор J2 коммутирует с операторами
М2 и s2. Действительно, обращаясь к формуле (62.4), мы непосред-
ственно видим это свойство оператора J2, так как 7И2 коммутирует
с М2, Al*, Af , Af2 и sx, sy, sz и s2. Равным образом s2, являясь еди-
ничной матрицей [умноженной на ^h2, см. (58.13)], коммутирует с
$ и sz. Поэтому
.АМ2 —Ж/2 = 0, (60.6)
J2S2_S2J2 =0. (60.6')
Следовательно, J2, Л12 и s2 представляют собой также одновременно
измеримые величины. Из (60.4) имеем:
(is) = |(J2-Afa-S8). (60.7)
Так как (Ms) образуется из величин одновременно измеримых, то
скалярное произведение (Af s) одновременно измеримо с J2, М2 и s2.
Замечая, что
(ЛВ)-Р= (/Г), (60.8)
мы получаем из (61.7) еще скалярное произведение (J s):
(77)=у(/2—m2+s2). (60.9)
Ниже мы покажем, что квадрат полного момента J2 и его проекция Jz
на любое направлению квантуются аналогично орбитальному моменту,
но полуцелыми числами. Именно,
/2=А7(;41), 7=1, 1, А, (60.10)
«У=±А, ±А............±7> (6o.il)
причем квантовое число у, определяющее собственные значения полного
момента, может быть выражено через орбитальное число I и спиновое ls
(58.14) по формуле
+ или ]=\1— /Д (60.12)
Из формул для собственных значений J2 (60.10), М2 (25.21) и ss
§ 60]
СВОЙСТВА ПОЛНОГО МОМЕНТА ИМПУЛЬСА
201
(56.14) получаем важные в спектроскопии выражения для собственных
значений (М s) и (J s):
(лТ7)=^[/(;4-1)-^+1)]. (60.13J
(Js) = % [J (j + 1) -1 (I + 1) + ls{ls 4- 1 )]• (60.14).
Эти формулы мы применили позднее к теории сложного эффекта Зее-
мана.
Обратимся теперь к доказательству формул (60.10) и (60.11). Уравнение
для собственных функций J2 имеет вид
/2ф—(60.15}
где под Ф следует разуметь столбец
Ф = (60.16)
ф»
Пользуясь (60.4), (56.13) и (56.12), находим уравнение (60.15) в раскрытой форме
1 0 Ф1
0 1 Фа
. „ („ л 0 1
+ 2 2 J 0
+^4
Л.М А 1° —1
~Г'ту 2 р 0
1 0 IN-/2
о-1 г ф,
Производя здесь умножение и сложение матриц, получаем:
м 2ф1+4 Л2Ф1+ЛЖгфх4- Л (Afx - iMy} фа о
М2фг + 4 Л2Ф. - W, + * (Мх + iMy) ф, 0
0
Л,
0
и, наконец, сравнивая элементы, получаем два уравнения:
М2фх + 4 Л2Ф1 + + Л (Мх-/Л,) фг = /2ф1г
ЛТ2ф2+4 ^2-ЛМ^-{-Л(Мх+1Му)^ — ^
Эти уравнения легко решаются, если положить
Ф1 = йГ//я(0- ?). Ъ =
(60.17}
(60.18)
(60.19)
(60.19^
(60.20)
где Y[m (в, <р) есть шаровая функция, а а и b — неопределенные коэффициенты.
Тогда имеем:
М 2фг = (Z -4- 1) ([>!, iW/h = hm^b (60.21)
МЦ2 == hH (/+1) ф2, a (W +1) & <б0-21
и, далее,
{Мх - iMy) Ytm = - V(l + m)(l~m+\) Y,t (60.22,
(M, + iMy) Yln = - /(/ - m) (I+m +1) Г,, w+1. (60.22')
Эти последние два равенства получаются из свойств шаровых функций*)
♦) См. дополнение VI, формулу (33.34).
202 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
Подставляя <[>t и из (60.20) в уравнения (60.19) и пользуясь (60.21)
и (60.22), после сокращения первого уравнения на h2Yim, а второго на
получим:
(/+1) 4-4-а — У(74-m4-!)(/—«) Ь = hz, (60.23)
/U4-1)+4 — /”~1]z’~ V(Z4-/n4-i)(z—от)«—м>, (60.23')
где
JT2
Х = (60.24)
Чтобы эти уравнения имели отличные от нуля решения, необходимо, чтобы
их определитель равнялся нулю. Это дает нам уравнение для определения к:
К/4-1) + |+«-* -У(/4-от4-1)(/-/и)
—/(/4-от4-1)(/—от) /(/4-1)4-1—от —1 —к
(60.25)
Отсюда находим два корня
Х=(/ + тУл(/ + у). (60.26)
Сравнивая это с (60.24), получаем искомые собственные значения
(60.27)
(60.27r)
Первое значение отвечает сложению орбитального и спинового моментов,
а второе — вычитанию их. Подставляя значение К, в уравнения (60.23) и решая
их, находим а и Ьу а вместе с тец и собственные функции (61.20). При этом
мы еще нормируем их так, что а2-{-Ь2=\.
Несложные выкладки приводят к следующим функциям: для собственного
значения (60.27): _________ ________________________
/Z~I- т —I— 1 т. , >w /“ I »»
21 | | Фз— у 2Z I 1 га*1 (60.28)
и для собственного значения (60.27'):
Ь = j/= j/^Z+^r r'-т+,‘ (60-28,)
Решения, как мы видим, вырождены. В самом деле, при заданном Z можно
брать разные числа zzz = 0, dz 1, zt 2, ..., zt Z, а собственное значение J2 от m
не зависит. Причина этого вырождения заключается в том, что при заданной
абсолютной величине вращательного момента J2 возможны его различные
ориентации в пространстве. Чтобы в этом убедиться, покажем, что решения
(60.28) и (60.28') являются также собственными функциями оператора Jz проек-
ции полного момента J на OZ.
Действительно, уравнение для собственных функций оператора Jz есть
Л = <60,29)
или, в раскрытом виде,
(Лг4-5г) Ф =
Ф1 _ Г Ф1 |
Фз г ФгГ
1 °Н
о —11/
^61] МУЛЬТИПЛЕТНАЯ СТРУКТУРА СПЕКТРОВ
Отсюда, пользуясь (60.21), получаем:
(60.30)
(60.31)
т. е. наши решения принадлежат собственному значению
Jz=h •
Обращаясь к решениям (60.28) и (60.28'), мы видим, что в первом решении т
может пробегать значения т — — (Z-f-1) (при этом ^ = 0), —Z, —Z-f-1,...»
О, 1, 2,..., Z, а во втором решении — значения т~ — I, —Z-J-1, О,
1, 2,..., (/—1) (при т~1 = ф2 = 0). Вводя теперь квантовой число
+ или j= I/ — ls I = | Z—yj, мы можем написать (60.27) и
(60.27') в виде (60.10). И, наконец, введя обозначение — на основании
сказанного о возможных значениях т при заданном Z, получаем формулу (62.11).
§ 61. Нумерация термов атома с учетом спина электрона.
Мультиплетная структура спектров
Состояние электрона в поле центральных сил м-ы характеризовали
тремя квантовыми числами n, Z, т. Квантовые уровни Еп1 такого электрона
определялись двумя квантовыми числами n, Z. При этом мы совсем игно-
рировали спин электрона. Если учесть еще и спин, то каждое состояние
?) окажется в сущности двойным, так как возможны две
ориентации спина
sz = hms, ms = ±~. (61.1)
Таким образом, к трем квантовым числам, определяющим состояние
цейтра тяжести электрона, присоединяется четвертое ms, определяющее
спин электрона. Обозначим волновую функцию электрона с учетом спина
через (г, 6, ср, $г). Так как взаимодействие спина с орбитальным
движением мы сейчас не учитываем, то согласно (57.5) эта функция
может быть представлена в виде
^mms о, <р) = (г, о. ф) \ (SJ (61.2)
(причем значок а функции S мы на этот раз заменяем значком т^. Со-
ответствующий квантовый уровень есть
Е=Еп1. (61.3)
Четверка квантовых чисел может принимать следующие значения:
я=1, 2, 3,..., O^Z^n—1,
— Z^Czzz^Z, ms~ i Tjr • (61.4)
204 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ, XJ
Для каждого терма Еп1 мы имеем 2/ 1 состояний, отличающихся
ориентацией орбитального момента, каждое из которых, в свою очередь,
распадается на два состо5шия, отличающихся спином. Всего 2 (2Z—1)
состояний. Таким образом, налицо 2 (2Z-f- 1)-кратное вырождение.
Если учесть теперь слабое взаимодействие спина с магнитным полем
орбитальных токов, то энергия состояния будет зависеть еще от ориен-
тации спина s относительно орбитального момента М. Мы не будем
здесь излагать расчет этого взаимодействия, так как поправка на взаимо-
действие спина и орбитального движения оказывается такого же порядка,
как и поправка, происходящая от зависимости массы электрона от скорости.
Поэтому правильный расчет расщепления уровней требует в этом слу-
чае релятивистского уравнения для движения электрона, рассмотрение
которого выходит за рамки этого курса *). Ограничимся качественным
анализом этого расщепления и оценкой его величины. Магнитный момент
электрона движется в поле орбитального тока SKV Его энергия в этом
поле равна
(ЖВД). (61.5)
—
Величину магнитного поля мы можем оценить как магнитное поле
диполя, эквивалентного орбитальным токам, т. е. диполя с моментом
Это поле равно **)
(61.6)
—> —>
где г есть радиус-вектор, соединяющий диполи 2RZ и Поскольку
нас интересует только порядок величины Д7?, то мьг можем считать
5^z % , где а есть длина порядка внутриатомных расстояний (10~8 см).
Тогда
A£%^^cos(9)lB, Я’,). (61.7)
Величины моментов 9Jtz, по порядку равны магнетону Бора (9-10""20
CQSE)> a cos (9)1, SK) в силу свойств спина может принимать только
два значения 4- (смотря по ориентации спина: по полю или против
него). Подставляя в (61.7) численные значения, получаем &Е -4- 8 10~15
эрг. Эта величина мала в сравнении с разностью энергий между уров-
нями, отличающимися числами n, Z, и поэтому возникающие новые
спектральные линии близки друг к другу. В частности, для упоминавше-
гося в § 54 дублета Na (линии 5896 А и 5890 A) Д£ = 2,8 • 10“15 эрг,
*) См. Дирак, Основы квантовой механики. Расчет расщепления приве-
ден в книге Бете, Квантовая механика простейших систем.
**) См., например, И. Е. Тамм, Основы теории электричества, т. I, стр. 70.
§ 61]
МУЛЬТИПЛЕТНАЯ СТРУКТУРА СПЕКТРОВ
205
L
।
0
Таким образом, различием в ориентациях спинового магнитного
момента по отношению я внутреннему магнитному полю атома
можно объяснить происхождение мультиплетности спектральных
линий.
Из изложенного явствует, что для атомов с одним оптическим элек-
троном возможны только дублеты (двойные линии), соответственно двум
ориентациям спина электрона. Этот вывод теории вполне
подтверждается спектральными данными *). г
Обратимся теперь к нумерации уровней атома с
учетом мультиплетной структуры. При учете спиново-
орбитального взаимодействия ни орбитальный момент 7И,
->
ни спиновый s не имеют определенного значения в со-
стоянии с определенной энергией (они не коммутируют-
с оператором Гамильтона). По классической механике
мы имели бы прецессию векторов М и s вокруг век-
тора полного момента J:
J=M + s, (61.8)
как это показано на рис. 39 **). Полный момент J
остается при этом постоянным. Соответствующее поло-
жение имеет место и в квантовой механике. При учете
спинового взаимодействия только полный момент J
имеет определенное значение в состоянии с заданной
энергией (он коммутирует с оператором Гамильтона //).
Поэтому при учете взаимодействия спина с орбитой
состояний следует классифицировать по значениям пол-
ного момента J.
Как было показано в предыдущем параграфе, полный момент кван-
туется по тем же правилам, что и орбитальный момент. Именно, если
ввести квантовое число /, определяющее полный момент J, то
Рис. 39. Сложе-
ние спинового и
орбитального
моментов и их
прецессия во-
круг направле-
ния полного мо-
мента J.
J2=A7(/+n,
<61.9>
а проекция J на произвольное направление OZ имеет значения:
j^-hm^ (61.10)
при этом
(6i.ii)
если спиновый момент параллелен орбитальному, и
j=\l — (61 12)
♦) Подробности см. в книге Фриш, Атомные спектры, ОНТИ, 1935.
**) Подробности полуклассической теории см. в книге Бриллуена,
Атом Бора, ДНТВУ, 1935.
206 СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ МОМЕНТЫ ЭЛЕКТРОНА [ГЛ. XI
если они антипараллельньь Подобным же образом квантовое число
определяющее проекцию J, есть
(61.13)
Так как Z, пг — целые, a ls и т3— полуцелые, то
1 3 5 .1.3 . .
J 21 2’ 2,‘”> — 2 ’ — 2 * ’ * (61.14)
В зависимости от ориентации спина энергия терма будет различной»
именно, она будет разной для j— I и j= | I — у |. Поэтому
в этом случае уровни энергии следует характеризовать значе-
ниями главного числа п, значением орбитального числа I и числом
j9 определяющим полный момент, т. е. в этом случае
Е=ЕП1/. (61.15)
Волновые функции будут зависеть от спиновой переменной sz и раз-
личны для разных у:
(61Л6)
(В этом случае переменные г, 6, ср и sz не разделяются.) Квантовые
уровни при заданном /, разлйчающиеся величиной у, близки друг/
другу, так как это есть как раз различие на энергию взаимодействия
спина с орбитальным движением для двух разных ориентаций спина.
Четверка чисел n, Z, у, mj может принимать следующие значения:
п=1, 2, 3,..., (61. 17)
0<Z<n—1, (61.17')
j=l+ls ИЛИ IZ-/J, /,= |, (61.17")
(61. 17"')
Величину орбитального момента I обозначают в спектроскопии бук-
вами (как мы это уже поясняли)
5 (Z=0), р (Z=l), d (Z = 2), f (Z = 3),...
Главное квантовое число п ставят впереди буквы. Справа внизу указы-
вают число у*. Поэтому, например, уровень (терм) с п = 3, 1—\,
3
j — ~2 обозначают так: 3/73/9. Иногда ставят еще один значок: 32/?3/з—
двойка слева вверху указывает, что терм З2р3/О принадлежит к числу
дуплетных (двойных). В случае одного оптического электрона это
указание излишне, т. е. там все уровни дуплетные — и J=
«= | Z— Zy|, кроме, конечно, 5-уровней, где 1 — 0).
§ 62]
ПОСТАНОВКА ВОПРОСА
207
При рассмотрении гелия мы встретимся с случаем более сложной
мультиплетной структуры. Так, благодаря наличию двух электронов
имеются одиночные термы (сингулетные) и тройные (триплетные) (см. § 12)о
Чтобы различать эти случаи, значок,
указывающий мультиплетность уровня,
все же сохраняют. Итак, уровень» обо-
значаемый по обычнзму способу
9 2,64 эл в /п \ л л
2 -----------!—
(61.15) через спектроско-
пически обозначается через 32/?з/2.
На рис. 40 приведена схема уров-
ней водородоподобного атома (т. е.
атома с одним оптическим электроном)
с учетом мультиплетной структуры.
Там же приведены квантовые числа и
спектроскопические обозначения.
Каждому из рассмотренных уров-
ней Enlj принадлежит 2/—|— 1 состоя-
ний, различающихся числом т^ т. е.
ориентацией полного момента J в про-
странстве. Только при наложении внеш-
2,1 эле
(1s) o^L-OJ-1^
Рис. 40. Мультиплетная структура
2/7-терма атома натрия.
(Линии 5889,963 А и Г89',930 А образуют.
него поля эти сливающиеся уровни
могут разделиться (см. теорию слож-
ного эффекта Зеемана, § 70). В отсут-
ствии такого поля мы имеем (2у—[— 1)-
кратное вырождение. Так, 251/гтерм имеет вырождение 2: два состоя-
известный дублет натрия —желтые линии^
Di и Di ) 2у-терм далеко отодвинут от
2/7-термов, как эго и должно быть в во-
дородоподобных атомах («Ь-вырождение
сияю).
ния, отличающиеся ориентацией спина. 2рз//герм имеет 4-кратное вырож -
1 3
дение, соответственно ориентациям J: ± т? , ±-о •
J & &
ГЛАВА XII
ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 62. Постановка вопроса
Лишь в очень немногих случаях задачу о нахождении квантовых,
уровней системы (т. е. о йахождении собственных значений и собствен-
ных функций оператора энергии //) удается разрешить с помощью
изученных в математике функций. В большинстве проблем атомной ме-
ханики таких простых решений не существует. Поэтому очень важен
весьма обширный класс случаев, когда рассматриваемая задача может
быть приближенно сведена к задаче, относящейся к более простой си-
стеме, для которой собственные значения Е^п и собственные функции фр
известны. Такая возможность представляется в тех случаях, когда опе-
ратор энергии Н рассматриваемой системы мало отличается от оператора
ЕЕ более простой системы.
208
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. XII
Точное значение слов «операторы мало отличаются» выяснится из
дальнейшего. Сейчас мы укажем те случаи, которые относятся к кругу
задач, могущих быть решенными приближенно. Допустим, что нам изве-
стны волновые функции и квантовые уровни электронов, движущихся
в атоме. Нас интересует, как изменятся квантовые уровни и волновые
функции, если атом поместить во внешнее электрическое или магнитное поле.
Достигаемые на опыте поля обычно малы в сравнении с внутриатом-
ным кулоновским полем *). Действие внешнего поля можно рассматри-
вать как малую поправку или, как мы будем говорить, возмущение
(этот термин заимствован из небесной механики и применялся перво-
начально для обозначения влияния одной планеты на орбиту другой).
Таким же путем могут быть учтены слабые взаимодействия электронов
внутри атомов, например, магнитные, а в иных случаях даже и кулонов-
ские. Общие методы решения подобных задач и составляют предмет
теории возмущений.
Мы ограничимся пока рассмотрением таких случаев, когда оператор
энергии Н обладает дискретным спектром. Пусть данный нам гамиль-
тониан И равен
(62.1)
Добавок IF будем рассматривать как малый и будем называть энергией
возмущения (или иногда кратко — возмущением). Далее, мы предпола-
гаем , что собственные значения Е® оператора Н и его собственные функ-
ции известны, так что
(62.2)
Наша задача заключается в нахождении собственных значений Еп опера-
тора Н и его собственных функций. Эта задача, как мы знаем, сводится
к решению уравнения Шредингера
Н$ = Е$. (62.3)
Уравнение (62.3) отличается от уравнения (62.2) согласно (62.1)
одним членом 1Уф, который мы считаем малым.
Для приближенного решения задачи методом теории возмущений
пишут прежде всего уравнение (62. 3) в таком представлении, в кото-
ром за основную переменную берут собственные значения Е^ операто-
ра Я, т. е. уравнение (62. 2) берут в «£'°»-представлении. Если перво-
начально оператор И (62. 1) и вместе с тем уравнение (62.3) даны,
как это чаще всего и будет, в координатном представлении, то нужно
от этого представления перейти к «f0»-представлению. Напомним этот
переход. Будем всюду явно писать только одну координату х (в случае
надобности под х можно разуметь любое число переменных так же, как
и под значком п у волновой функции можно разуметь ряд квантовых
чисел). Пусть в координатном представлении («х»-представление) соб-
*) В случае электрического поля можно достигнуть полей, сравнимых
с внутриатомными. Ср. опыты Траубенберга по Штарк-эффекту в сильных
полях, § 94.
§ 62] ПОСТАНОВКА ВОПРОСА 209
ственные функции оператора HQ будут ф^(х). Разложим искомую функ-
цию ф(х) по функциям ф^(х):
(62.4)
п
Тогда совокупность всех сп есть не что иное, как функция ф в «F0»-
представлении.
Подставляя (62.4) в уравнение (62. 3), умножая его на ф^ (х) и интег-
рируя по х, получим:
ЪНтпсп = Есп, (62.5)
п
где Нтп есть матричный элемент оператора Н в «Е0»-представлении:
(62.6)
Матрица,, образованная из элементов Нтп, есть оператор Н в «£0»-
представлении. Имея в виду (62. 1) и (62. 2), получаем:
^тп = ^Нй+ ^)^dx=^-H^dx-\-
+ ^.W^n-dx^l^mn+Wmn, (62.6')
где Wmn есть матричный элемент энергии возмущения в «Z:0»-представлении:
= (62.7)
Матрица, образованная из элементов Wmn, есть оператор W в этом же
представлении. Подставляя (62. 6') в (62. 5), получим:
2^mn+^m„]cn = ECm. (62.8)
п
Перенося все члены налево, находим:
+ ^тт - + 3 Wmrfn = °- (62.9)
nj=m
где п и т пробегают все значения, которыми нумеруются функции не-
возмущенной системы ф°.
Пока мы никак не использовали предположение о малости W, и
уравнение (62. 9) справедливо точно. Задача теории возмущения заклю-
чается в том, чтобы использовать предположение о малости величин W .
Чтобы явно выразить степень малости W, положим:
W=Xw, (62.10)
где 1 — малый параметр. При X = 0 оператор Н переходит в //°. Тогда
уравнение (62. 9) запишется в виде
2 (62.11)
прт
Это уравнение мы будем решать по степеням X, считая X малой величи-
14 Блохинцев
210 ТЕОРИЯ ВОЗМУЩЕНИЙ [гл. хв
ной. При Х = 0 из (62.11) получается просто уравнение (62.2) в «£0»-
представлении:
(4,— Е}ст = 0, (62.12)
имеющее решения:
Е[й}=Еат, с^=\. (62.13)
При малых значениях X естественно ожидать, что решения уравне-
ний (62.11) будут близки к решениям уравнений (62.12), т. е.
к (62.13). Это предположение мы можем выразить явно, если пред-
ставим собственные функции ст уравнения (62.11) и его собственные
значения Ет в виде рядов по степеням малого параметра X:
c„=i"’+^’+i,4’ + --- <62Л4>
И
Е = £(о) 4- Xf (1) 4- Х2£(2) 4- ... (62.15)
При Х = 0 (62.14) и (62.15) переходят в (62.13), причем В0 должно
равняться Е^т. Оказывается4, что решение уравнений (62.11) существен-
но зависит от того, вырождены ли состояния системы HQ или нет. Если
они вырождены, то каждому собственному значению Еп принадлежит
несколько собственных функций если не вырождены, — то только
одна функция. Эти два случая мы рассмотрим порознь.
§ 63. Возмущение в отсутствии вырождения
Пусть каждому собственному значению Е® невозмущенного уравне-
ния (62.3) принадлежит лишь одна собственная функция ф®, соответст-
венно— одна амплитуда Подставим в уравнение (62.9) ряды (62.14)
и (62.15) и соберем члены с одинаковыми степенями. Тогда получается
И - Е•] +ф_-£«] <<_«> + Ей,-£'п1 +
+ S «..«Г}
п^т
+[4,-£°]42)+ 2 ®да,41’} + -=о- (63.1)
п^т
Это представление уравнения (62.9) позволяет легко разрешить его
методом последовательных приближений. Мы получим нулевое прибли-
жение, если положим Х = 0; тогда получаем
[£^ —£<°)]cW==:0, т—\, 2, 3, kt... (63.2)
Это — уравнение для невозмущенной системы HQ. Пусть нас интересует,
как меняется уровень Е* и собственная функция под действием воз-
§ 63] ВОЗМУЩЕНИЕ В ОТСУТСТВИИ ВЫРОЖДЕНИЯ 211
мущения W. Тогда из решений (62.2) мы берем &-ое:
Е(0) = £ь c°m = bmk, (63.3)
т. е. все с^ = 0, кроме =
Решение (63.3) мы будем называть решением в нулевом приближе-
нии. Это решение мы подставляем в уравнение (63.1) с тем, чтобы
найти следующее, первое приближение. Подстановка дает
5 + (63-4)
т ф п
где через О(Х2) обозначены члены порядка к2 и выше. Ограничиваясь
первым приближением, мы должны считать эти члены малыми и отбро-
сить их. Тогда получаем:
3 (63.4')
m^zn
Если мы возьмем из этих уравнений уравнение номера m = k, то получим:
^4-£(1) = 0. (63.4")
Отсюда находим поправку к Ek первого приближения:
£(1) = ^- (63.5)
Из уравнений с m=^=k находим поправки к амплитудам с®, именно,
если m=^k, то (63.4') дает
+ = (63.4'")
Отсюда
<£> = m^=k- (63.6)
/и pv pv ' ' '
nk cm
Найдем теперь второе приближение; для этого следует учесть члены
с л2. Подставим первое приближение (63.'5) и (63.6) в (63.1), тогда
найдем:
( т
+ 1 + 0 №) = 0. (63.7)
п 7= т ck сп '
где через О (I8) обозначены члены порядка к8 и выше. Пренебрегая эти-
ми членами, получим уравнение для определения Е^ и № (второе
приближение). При этом уравнение номера m — k получается в виде
—£(2)+E>Z~o- = O- (63.7')
lepn ck п
14*
212
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. XII
Отсюда находим поправку к энергии во втором приближении:
F(2)____ wkn wnk
Fq— f° ’
k^zn
Из уравнений с т k найдем с<?>;
„(2) = _ Wkk Wmk I У Wkn Wnk
(63.8)
m=^=ky n=^k. (63.9)
Эту процедуру можно продолжать и дальше, переходя все к более
высоким и высоким приближениям. Мы ограничимся вторым приближе-
нием и выпишем результат. Согласно (62.15), (62.16) и (63.3), (63.5),
(63.6), (63.8) и (63.9) имеем:
А=^ + ^ + *2Е + О (П
nj=.k
С =1, с==\ а,”>* .-I-
гс 1 т 77 О ___ 2?0 *
т
-- --^kk^mk 1 I с
ММ г
(63.10)
V>kn™nk
(63.11)
Из этих формул видно, что предположение о малости оператора W
в сравнении с //° означает малость отношения
I ^wnm
/?0___ /?0
I п т
1, п т;
(63.12)
при выполнении этого условия поправочные члены в (63.10) и (63.11)
малы и собственные значения Ek оператора Н и его собственные функ-
ции cm(k) близки к собственным значениям и собственным функциям
оператора //°. Условие (63.12) — это условие применимости теории воз-
мущений. На основании (62.11) это условие может быть записано так-
же в виде
Гр|Г%Ц<<1, п=£т, (63.13)
I I
где IFWZ7 суть матричные элементы оператора возмущения.
Пользуясь (62.4) и (63.6), а также (63.5), мы можем написать наше
решение в «х»представлении:
М = Е (63.14)
m^zk^k 23 tn
= = (63.15)
Из последней формулы видно, что поправка к уровням в первом при-
ближении равна среднему значению энергии возмущения в невозму-
щенном состоянии (ф°).
§ 63]
ВОЗМУЩЕНИЕ В ОТСУТСТВИИ ВЫРОЖДЕНИЯ
213
Из условия пригодности метода теории возмущения (63.13) непосредственно
видно, что успех приближенного расчета зависит от того, какой именно кван-
товый уровень мы рассчитываем. Так, например, в кулоновском поле разности
энергий соседних уровней выражаются формулой
£
Л2
1
(и + 1)2
_ ± 2л — 1 О
~"л2 (Л Zt I)2 1 •
При малых л эта величина может быть гораздо больше Wfl п ± г. Для боль-
ших же л она стремится к нулю, как 1/л3, и условие (63.13) может оказаться
несоблюденным. Поэтому метод теории возмущений может быть пригодным
для расчета поправок для нижних квантовых уровней и непригодным для
расчета поправок для высоких квантовых уровней. Это обстоятельство нель-
зя не иметь в виду при приложении теории возмущений к конкретным проб-
лемам.
Второе, что следует отметить, — это некоторые особые случаи, когда
условие (63 13) соблюдено и тем не менее квантовые состояния систем Н и
/7° радикально отличаются. Дело в том, что энергия возмущения W может
оказаться такого вида, что существенно изменит асимптотическое поведение
потенциальной энергии U (х). Допустим, что к гармоническому осциллятору
приложено возмущение lF=Xx3. Уравнение Шредингера будет:
/г2
2pdx2
х2^ХхЧ==£6.
(63.16)
При 1 = 0 мы имеем уравнение для гармонического осциллятора, имею-
щего дискретный спектр энергии Еп = й(о0 ( л у ) . Матричные элементы
возмущения
wnm —
при малом X могут быть как угодно малы в сравнении с Ет— En~h^{ni — п).
Тем не менее при всяком X уравнение (63.16) имеет непрерывный спектр и
только при Х = 0 оно имеет дискрет-
ный спектр собственных значений.
Действительно, потенциальная энер-
JJLCOq X2
гия U (х) — —2 1- Хх3 имеет вид,
приведенный на рис. 41. При всяком
значении Е для больших отрицатель-
ных х, U(х) < Е, т. е. асимптотическое
значение потенциальной энергии мень-
ше Е. Поэтому энергетический спектр
должен быть непрерывным.
Спрашивается, какой смысл име-
ют в этом случае приближенные функ-
ции фл(х) и уровни Е®, которые мы
можем вычислить из <|>® и Е® мето-
Рис. 41. Кривая потенциальной энер-
рко®
гии U (х) — — Хх3 (пунктирная
JJUOq
кривая Щ{х) = — )л
дом теории возмущения, пользуясь
малостью параметра X? Оказывается,
что при малых X найденные методом
теории возмущения функции ф?1(-г)отли'
чаются тем, что они велики вблизи потенциальной ямы U(х) и малы вне ее. На
рис. 42 повторена (а) кривая потенциальной энергии U (х) рис. 41 и, кроме того,
(Ъ) нанесен квадрат модуля волновой функции |ф(х)|2. Такое положение дел
имеет место, если энергия Е = En^z Е®- Если же энергия Е не равна Еп,
214
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. XII
то волновая функция <[»£(*) нарастает вдали от потенциальной ямы U(x) (см.
рис. 42). В первом случае мы можем сказать, что частицы находятся около
положения равновесия х = 0, так сказать, «в атоме», а во втором случае они
находятся преимущественно вне его, бесконечно далеко. Стационарность со-
стояний может получиться лишь в том случае, если существуют волны, как ухо-
дящие в бесконечность, так и приходящие из нее, так что поток частиц через
поверхность, окружающую атом, равен нулю. Такой случай представляет мало
интереса. Чаще приходится иметь дело с случаем, когда имеются лишь ухо-
|Ш0
Рис. 42. Потенциальная энергия U(x) = -^- x2-f-kr3 и плотность вероятности |ф|2.
а—для Е=Еп; Ь—-для Е Еп.
дящие волны (см. § 92). Тогда стационарных состояний не существует во-
все. Если требовать, чтобы имелись лишь уходящие волны, то находимые ме-
тодом теории возмущения функции <|>л(х) описывают поведение частиц лишь
в течение не очень большого времени t. Однако, на самом деле это время
может быть очень велико и оно тем больше, чем меньше значение пара-
метра X. Такого рода состояния <|>п(х) мы будем называть квазиквантовыми,
а соответствующие им уровни — квазиуровнями.
§ 64. Возмущение при наличии вырождения
В большинстве важных в приложениях задач приходится встречаться
со случаем вырождения, когда в невозмущенной системе (//°) собствен-
ному значению Е — Е^ принадлежит не одно состояние ф®, а несколь-
ко ф®р ф^2____, ф®а, ... , ф^. Если теперь действует некоторое воз-
мущение то без специального исследования нельзя сказать, какая
из функций ф^а будет являться нулевым приближением к собственным
функциям оператора //о цл. В самом деле, вместо ряда функций
фор ... , ф®а, ... , ф^, принадлежащих собственному значению Е®, быть
могут взяты новые функции ф^2, ... , ср®а, ... , получающие-
ся из функций фОр ф®2, ... , фо линейным ортогональным преобразованием:
f
= U (64.2)
§ 64] ВОЗМУЩЕНИЕ ПРИ НАЛИЧИИ ВЫРОЖДЕНИЯ 215
Функции (р®а, будучи линейными комбинациями функций ф^, будут
также решением уравнения Шредингера
Н^п=Е^а, (64-3)
принадлежащим собственному значению f®, и при добавочном условии
(64.2) оу дут ортогональными, если функции ф®а ортогональны. Функции
срО* суть поэтому также возможные функции нулевого приближения, но
неизвестно, какие коэффициенты следует взять, чтобы получить
правильное нулевое приближение.
Для решения этого вопроса обратимся к уравнению (62.9). Нам,
однако, следует теперь его несколько модифицировать, уточнив обозна-
чения. При наличии вырождения собственные функции оператора име-
ют по крайней мере два индекса (п, а). Поэтому в этом случае (62.4)
следует написать подробнее, заменяя индекс п на два: л, а. Тогда мы
получим:
ф(х) = 2с„Ха(х)- (64.4)
П, а
Соответственно этому уравнение (62.10) получится (заменяя п на л, а;
т на /л, Р) в виде
"Ь 2 пасп* = ®' (64.5)
где
(64.6)
есть матричный элемент энергии возмущения и получается из (62.7)
увеличением числа квантовых чисел, нумерующих состояния. Е^т есть
энергия /n-го квантового уровня для невозмущенной задачи. Эта энергия
от квантового числа а не зависит (вырождение).
Допустим, что мы теперь желаем найти квантовый уровень возмущен-
ной системы Ek, близкий к Е%, и соответствующие собственные функ-
ции фйа(х). Ограничимся решением этой задачи в первом приближении
для уровней и в нулевом приближении для функций.
В отсутствии вырождения мы полагали для функций нулевого при-
ближения, что они просто совпадают с невозмущенными. Соответственно
этому в нулевом приближении ^а=1, а остальные равны 0. Этого
нельзя сделать при наличии вырождения, ибо, отбрасывая в нулевом
приближении возмущение W, мы получим из (64.5):
(£•0 —Е)ст о = 0;
это дает ^=^=0 для Е = Е^т, но при этом не одно а все при.
надлежащие собственному значению именно ст^ для р — 1, 2,...
Таким образом, в нулевом приближении не одна амплитуда, а целая
группа отлична от нуля. Поэтому правильным нулевым приближением для
216
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. XII
функций k-ro уровня будет
а=1, 2,...,/,
cW = 0 (n^k).
(64.7)
В этом приближении мы возьмем из числа уравнений (64.6) те, кото-
рые содержат не равные нулю с^. Это будут уравнения:
[^+^-3^+ 2 = (64.8)
® 7= 3
Поскольку мы ограничиваемся нулевым приближением к &-му уровню, мы
можем опустить индекс k (держа его просто в уме), положив при этом
= ь = (64.9)
40) = Ф а=Т, 2,...,/а. (64.9')
Тогда уравнения (64.8) запишутся в виде
/к
+ 2 ^Л0) = °> ? = 1, 2,...,Д. (64.10)
У Е® мы сохранили число k, чтобы подчеркнуть все же, что речь идет
о группе из Д-состояний, принадлежащих уровню
Для того, чтобы уравнения (64.10) имели отличные от нуля реше-
ния, необходимо, чтобы определитель системы (64Д0) обращался в нуль,
т. е.
Д(£) =
^2 •••
^21 f»4-if22-e ... И72/л
= 0. (64.11)
......... El-Wfkfk-E
Это — алгебраическое уравнение степени fk для определения Е. Часто
оно называется вековым *) уравнением. Из него мы получим fk корней:
E — EkV Ek2,..., Ek^..., Ekfk* (64.12)
Так как матричные элементы WQa предполагаются малыми, то эти корни бу-
дут близки между собой. Следовательно, мы получаем важный результат, при
наложении возмущения вырожденный уровень (Е^) распадается на
ряд близких уровней (64.12). Вырождение снимается. Если некоторые
из корней (64.12) равны, то вырождение снимается лишь частью.
Для каждого из корней Еы (64.12) мы получим свое решение для
амплйтуд с^ из уравнения (64.10). Чтобы отметить, что решение
с!^, ..., ..., принадлежит уровню Eka, мы введем в с^°> еще
*) Название «вековое уравнение» заимствовано из астрономии.
§ 64] ВОЗМУЩЕНИЕ ПРИ НАЛИЧИИ ВЫРОЖДЕНИЯ 217
один индекс а так, что решение уравнений (64.10) для Eka запишется
в виде
*<?>. Ф--., <$>•••. < а=1, 2,..., Д (64.13)
(если бы мы еще удержали индекс Л, то полная нумерация для с(°) была
бы (64.13) есть приближенная (в нулевом приближении) волновая
функция оператора Н в «£°»-представлении. В «х»-представлении ре-
шение (64.13) запишется в виде
fk
(64.13')
Таким образом, каждому уровню E=Eka принадлежит теперь своя
функция <рЛа, которая и является функцией нулевого приближения для
возмущенной системы (И).
Отличие функций (64.13) от функций (64.1) заключается в том,
что в (64.1) коэффициенты произвольны [вплоть до условия ортого-
нальности (64.2)], а коэффициенты в (64.13) определенны. Следова-
тельно, функции нулевого приближения <рАа представляют собой частный
случай функций невозмущенной задачи Заметим, что если вычис-
лить следующие приближения, то нетрудно убедиться, что условием
пригодности метода теории возмущения будет опять-таки (63.12), кото-
рое теперь для вырожденного случая будет гласить:
1^ (64.14)
В § 40 было показано, что задача нахождения собственных значений и
собственных функций любого оператора £, заданного в матричной форме, сво-
дится к решению уравнений (40.4) и (40.5). Разумея в (40.4) под оператором L
оператор потной энергии Я, мы должны в случае вырождения разуметь в
(40.4) под индексом п два индекса: п, а, под т— также два индекса: т, f. В ре-
зультате из (40.4) мы получаем уравнения
— Ест$> (64.15)
которые совпадают с (63.5), так как
(64.i6>
Уравнение (40.5), соответствующее системе (40.4), в нашем случае запишется
несколько сложнее (по форме), так как строки и столбцы матрицы оператора
Н нумеруются двумя квантовыми числами п и а. Именно, при каждом п имеется
fn разных значений а (/„-кратное вырождение). Число fn возрастает с увели-
чением п. Для первого уровня Д = 1 (вырождения не бывает).
Расположить элементы Нт^пл в матрицу не представляет труда. Так,
можно нумеровать какой-нибудь ’столбец парой (и, 1), а следующие столбцы
номерами: (л, 2), (л, 3),..., (л, /„), затем пойдут столбцы с номерами(п4-1,1)г
(«4-1, 2),... до («4“1> /я+i) и т- д- Подобным же образом нумеруем строки:
(т, 1), (т, 2),..., (т, fm) и т. д. При такой нумерации элементов матрицы
Ятр, уравнение для определения собственных значений Е может быты
218
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. XII
написано в следующем виде [это и есть уравнение (40.5) для нашего случая]:
^11,11 — El #11, 21* • • #11, 2ft • • • #u, ki....#11, kfk • •
#21,11 i #21,21—£«..^21, 2/j : ••• #21, kl.....#21’ kf^ **
H2f*,n ‘kl.............kfk* *
11 #Л1, 21............... .Hkl, kl— E. . . Hkl, kfk
H”^ 11 ^P’21 .................ftl
Hkfk^...................
= 0.
(64.17)
Обведенные пунктирными прямоугольниками матричные элементы относятся к
одному и тому же квантовому уровню. Так, например, в первом прямоуголь-
нике (один элемент)—к уровню k—\, во втором — к уровню & = 2, в третьем
ж Л-му уровню. Если мы пренебрежем матричными элементами, относящимися
к различным уровням, т. е. элементами типа Нт^ (т а) [эти элементы
♦согласно (64.16) равны Ла], то уравнение (64.17) упростится и примет вид
^i^l °..:...................................
0 : #21, 21 — Е ... #21, 2/3 • 0 ...........
0 i................. :......................
0 :#2/2, 21 ••• #2/2, 2/3 ..................
° ........................... ' ^ki.kx — E ---H'lMf
о............................ ; ..................... k
о............................ . ..................... •=..
° ........................... : Hkfk,kl •••HkffrWk —Е
= 0.
(64.18)
Такую матрицу называют ступенчатой. Ее определитель №(Е) разбивается
на произведение определителей меньшего ранга, именно *):
Д0(^=|Я11-Е|.
#21, 21 — Е .. . /721, 2/2
^2/2’ 21 • • • ^2<2 ,2ft Е
^ki, ki — Е.. kfk
(6119)
Hkfk, ki---Hkfktkfk—E
*) Этот результат получается сразу, если раскрывать определитель (64.18)
iSio обычному правилу раскрытия: произведение элементов на миноры.
§ 65] РАСЩЕПЛЕНИЕ УРОВНЕЙ 219
Обозначая входящие сюда определители через получим:
ДО (Е) = ДА (Е) • Д/2 (£)... Д/Д5 (Е) = 0. (64.20)
Уравнение (64.20) будет удовлетворено, если Afi(E) = 0, или Д^(£) = 0, паи
вообще Дд(£)=0. Корни этих уравнений и дают в первомJ приближении
энергии первого, второго и вообще £-го уровня. Уравнение
Д/Аг (^) = 0 (64.21)
тождественно с уравнением (64 11), установленным другим путем.
В § 40 мы объясняли, что задача нахождения собственных значений опе-
ратора может рассматриваться как задача о приведении к диагональному
виду его матрицы. Из изложенного мы видим, что принимаемое в теории воз-
мущения первое приближение заключается в том, что мы пренебрегаем мат-
ричными элементами, относящимися к разным уровням, и таким образом за-
дачу о приведении к диагональному виду бесконечной матрицы сводим к при-
ведению к диагональному виду конечных матриц [отдельных матриц в сту-
пенчатой матрице (64.18)].
§ 65. Расщепление уровней в случае двукратного вырождения
Рассмотрим частный случай снятия вырождения возмущением, когда
интересующий нас уровень невозмущенной системы двукратно вырож-
ден. Пусть собственному значению Е® оператора принадлежат две функ-
ции (Д = 2): ф^ и ф^2. Любые две функции и <р^2, получающиеся
из ф^ и ф®2 путем ортогонального преобразования, будут также соб-
ственными функциями оператора //°, принадлежащими уровню Это
преобразование мы можем записать в виде [см. (63.1)]:
(65Л>
(Р“2 = Мм +«22%- <65Л')
Чтобы удовлетворить условию ортогональности (64.2), положим:
а11— cos 6-^, а12 —sin 1
6Z21 —— sin 6-^Р, а22 = cos J ( • )
причем 6 и р здесь два произвольных угла. Таким образом,
«о =cos -4- sin <1)0 ]
ф^2 = — sin 6 • е1? ф^ cos 0 • £“*4^2 ) (Ьо.З)
представляют собой наиболее обшие выражения для волновых функций,
принадлежащих двукратно вырожденному уровню Е°.
Ортогональность и нормировку этих функций легко проверить непо-
средственно и убедиться также, что коэффициенты (65.2) удовле-
творяют условию ортогональности (64.2). При ^=6 — 0 из (65.3) по-
лучаются исходные функции ф®р ф®2. Пусть теперь наложено некоторое
возмущение W. Нулевое приближение будет выражаться функциями,
220
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. XII
являющимися функциями невозмущенной системы, т. е. функциями
(65.1), но с вполне определенными коэффициентами; иначе говоря, значе-
ния углов 6 и р будут зависеть от вида возмущения W. Для определе-
ния этих углов будем искать прямо коэффициенты ct и с2 в суперпозиции
<Р = С1Фм + С2Фи- (65‘4)
Согласно изложенной выше теории, эти коэффициенты определяются из
уравнения (64.10), которое в рассматриваемом частном случае гласит:
[^+^i-£]q+^2=o. 1 _
[£0 + И723 _ Е] с2 + 1Г2Л = 0, / (Ь5-5)
где TF11, IF12, 1^21 > ^22 — матричные элементы энергии
^23 = 5 wib-dX’
Вековое уравнение (64.11) имеет тогда вид
Д (Е) — 8 ^12 — 0
1Г22 —е —v’
где е — поправка к энергии k-ro уровня:
г = Е — Е*
k
возмущения:
(65.6)
(65.6')
(65.6")
(65.7)
(65.8)
Раскрывая определитель (65.7) и решая получающееся
уравнение, мы найдем два корня:
±
квадратное
(65.9)
Из уравнений (65.5) находим:
е1__ ^12
С2 Wu-e'
Полагая ^2=1^12 и подставляя в (65.10) первый корень 1 • e21? (sp знак-{-):
£1 — 1 W12\eW
с2 W22 — Wn 2 (t^ii - «W + 1^12 I2
а для второго корня (г2, знак—):
С} 1 W\2 | eW
W22—Wu 2 4 j/ HIF13I2
ctg
, получим:
tg 0 • е2^.
(65.10)
(65.11)
(65.12)
(65.12')
§ 65] РАСЩЕПЛЕНИЕ УРОВНЕЙ 221
Таким образом, получаются следующие решения (в «х»-представлении):
р ____ /70 I ^11+^22 . - (1ГП--- Ж2)2 . .2
^1—2 Г V 4 Г1 ^12 Ь {6513)
= COS 6 • 4" sin 0 • е~® • Ф^2
Р — Р» _|_ ^и+^22 , |2 1
£«-£И 2 V 4 Г' ^12' > (65.13')
(рЛ2 = —sin 0 - • ф^ 4- cos 6 • • ф^2,
причем
tg 9 =--------------JУ1-2!.—... , (65.14)
(65Л5)
Весьма важным является частный случай, когда
Wn=W22, W12=W2l. (65.16)
Для этого случая имеем:
^>-^+^1+^12, )
(65.17)
<р«=^(% + Ф22)-]
==£» + Гп- 1Г12, )
(65.17')
(%-%)>
Преобразование (65 3) есть поворот. Мы можем получить прямую геомет-
рическую аналогию, если будем считать ₽ = 0 (это требует, чтобы Й^12= IF21).
Тогда коэффициенты а действительны. Частные значения коэффициентов а —
коэффициенты с — также действительны. Вместо 65.4) мы можем написать,
полагая = с2 — л:
? = Еф? + ч^ (65.18)
(индекс k мы будем держать в уме). Если потребовать, чтобы
£2_р (б519)
то средним значением энергии возмущения W в состоянии (65.18) будет
($ф?4-71Ф2)-^1+^-^. (65.20)
Согласно (65.6) получим:
W= 1ГПЕ2 + 21Г12^ + 1722тЛ (65.21)
Это уравнение можно рассматривать как уравнение кривой второго порядка
222 ТЕОРИЯ ВОЗМУЩЕНИЙ [гл. хп
на плоскости (£, tq). Таким образом, среднее значение W есть квадратичная
форма от амплитуд т), представляющих состояние <р.
Введем теперь вместо системы координат %, т) новые координаты т/,
отличающиеся от первых поворотом на угол 0;
£ = cos(Mr — sin0«7)\ tq = sin 0 - cos 0 • (65.22)
Подставляя в (67.18), получим:
<Р = £’<??+ ^2»
= cos 0 • 4>J 4-sm 6 • ’ (65.23)
<f>2 =— Sin 0 • Cpj-P cos о
Относительно функций и матрица W должна быть диагональной. Дейст-
Рис. 43. Геометрическая ил-
вительно,
^22 == У ?2 ’ ^?2 ’ dx ~ £2>
T;.irT°.rfx== ^i=o.
(65.24)
Поэтому среднее значение W в состоянии
представится теперь в ином виде:
(65.25)
т. е. в новых переменных S', т/ средняя
энергия является кривой второго порядка, от-
несенной к главным осям (рис. 43).
Таким образом, задача о приведении ма-
люстрация приведения к диа- трицы IV к диагональному виду совпадает
тональному виду матрицы с геометрической задачей о приведении к ка-
второго ранга. ионическому виду кривой второго порядка
(отнесение к главным осям). В более общем
случае $ и т) комплексны, поэтому полного совпадения задач нет, но аналогия
сохраняется, если £ и т) и в этом случае рассматривать как координаты точки.
§ 66. Замечания о снятии вырождения
Мы показали, что при включении возмущения вырождение, свойст-
венное невозмущенной системе, снимается: сливающиеся уровни рас-
щепляются. Чем обусловлено это расщепление? Для ответа на этот
вопрос обратимся прежде всего к причинам существования вы-
рождения.
Мы видели, что, например, уровни электрона в поле центральных
сил вырождены 2/ 1 раз (если не считать спинового вырождения).
Это вырождение обусловлено тем, что энергия электрона в поле цен-
тральных сил не зависит от ориентации момента импульса относительно
поля. Математически это выражается тем, что гамильтониан в этом слу-
§ 66] ЗАМЕЧАНИЯ О СНЯТИИ ВЫРОЖДЕНИЯ 223
чае обладает симметрией вращения, именно, гамильтониан
Я° = —J-2V24-t7(r) (г=/х2+д/24-г2) (66.1>
остается неизменным при повороте системы координат, когда координаты
х, у, z переходят в х\ у', z'. В самом деле, при повороте
Х2 4-3,2 _|_22^х-2 4-у2 4-z'2 ; (66.2)
¥2=^4-^4_^=^4-Л-+Л; (66.21)
дх2‘ду2 ‘ dz2 дх'" 1 ду'" 1 дгл
последнее равенство вытекает проще всего из того, что
V2 = (V)2,
так как V есть векторный оператор, а квадрат вектора не меняется при
повороте. Таким образом,
Я°(х, у. z)=H0(xf, у, zf).
(66.3)
Если наложенное возмущение не обладает сферической симметрией, то
энергия электрона будет зависеть от ориентации момента и произойдет
расщепление уровней. Вместе с тем для оператора /7° равенство (66.3)
уже не будет иметь места. Этот пример показывает, что наличие вырож-
дения связано с той или иной симметрией поля, а снятие вырождения —
с нарушением этой симметрии.
Приведем еще пример. Пусть мы имеем осциллятор в плоскости х, у,
обладающей одинаковыми частотами со0 для колебаний по ОХ и по ОУ.
Уравнение Шредингера для такого осциллятора имеет вид
Л2 /W . д2Ф\
дх2 + о>У7
2
ф(Х2 4-з,2)ф = £ф.
(66.4)
Гамильтониан в этом уравнении остается неизменным при повороте
системы координат вокруг оси OZ. Таким образом, он обладает сим-
метрией вращения. Согласно сказанному следует ожидать вырождения.
Оно действительно имеется. В самом деле, уравнение (66.4) решается
сразу разделением переменных:
ф(Х) J) = <|>1 (x)c|>2(j),
E=EX^-EV
(66.5)
Подставляя (66.5) в (66.4), обычным путем получаем два уравнения:
Л2 д2<(ц ,
— fa2 + Т = ^1»
Л2 d2<J>2 jioJq
-27^ + ^2=^2-
(66.6)
(66.6'>
224 ТЕОРИЯ ВОЗМУЩЕНИЙ [гл. XII
Эти уравнения для осцилляторов имеют известные функции и известные
собственные значения, именно:
Ф1(*) = К(*)> £,=/4 («1+4). Я1 = 0, 1, 2,..., (66.7)
Ф2М = Ф„3М, ^ = /4(^ + 1), n2 = 0, 1, 2,... (66.7')
Отсюда
ЗМ»,МШ £’П1Пз = ^(°о(«1 + «2 + 1)- (66.8)
Введем «главное квантовое число»
n = ^i + «2 4“ Ъ п2 — п— пг — 1. (66.9)
Тогда
Л = |Я,МФВ-Я,_1(Л En = h^n, п=\,2,... (66.10)
Каждому уровню Еп будет отвечать п функций (п2 = 0, /?2 = 1, ,
п2 — п—1). Следовательно, вырождение действительно имеется.
Допустим теперь, что возмущение Ж заключается в изменении коэф-
фициента упругости для колебаний вдоль оси OY. Тогда частота коле-
баний по оси ОУ изменится. Пусть она будет равна сог Гамильтониан
возмущенной системы тогда получит вид
„___ «2 / & д2 \ |1<о+
П~ 2|i"Г 2 "Г 2 ’
^) = |(“?-‘0о)Л
W здесь — возмущение. В рассматриваемом примере решение возму-
щенной системы может быть получено точно. Дело, очевидно, сводится
к замене в (66.7) со0 на а)г В результате решение получит вид
.у)
En.n, = h<Wl + At0l«2 + IF + ?
(66.9')
фЯ1Лз (*> У) = фп. (*) <РЯ- п, -1 (у)->
Еп, П1 = А®0«1 + Л(01 (« — Г'
г (66.10')
2 2 )
Как видим, уровни с различным значением числа пг и одним и тем
же п будут иметь разную энергию. Один уровень Еп невозмущенной
системы расщепился на уровни Еп 0, Еп р ... , Еп п_г (числом п).
Вырождение снялось.
Резюмируем вывод из этих примеров. Если гамильтониан /7° (х, у, z)
остается инвариантным (неизменным) по отношению к некоторому пре-
образованию координат (х, у, z—> х', у', z'), то собственные значения
Е® вырождены. Если возмущение нарушает указанную инвариантность,
то, хотя бы частью, вырождение снимается.
§ 67] АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 225
ГЛАВА XIII
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ
§ 67. Ангармонический осциллятор
Гармонический осциллятор является идеализацией реальных механи-
ческих систем. Действительная потенциальная энергия частиц никогда
не представляется функцией а изображается гораздо более
сложной функцией U(х). Первое выражение справедливо лишь для
малых х. Чтобы уточнить выражение потенциальной энергии U(х), мы
можем кроме члена х2 учесть еще и более высокие члкены разло-
жения U(x) по степеням отклонения х:
7/(х) = ф х2-|-).лЛ (67.1)
Коль скоро добавочные члены остаются малыми, мы имеем дело с гар-
моническим осциллятором, несколько возмущенным наличием отступле-
ний от кривой, свойственной идеальному гармоническому осциллятору.
Такой осциллятор мы будем называть ангармоническим.
Найдем квантовые уровни ангармонического осциллятора, считая
добавочные члены в (67.1) малыми (1 мало). Решим эту задачу методом
теории возмущений, опираясь на уже известные решения для гармони-
ческого осциллятора. В качестве возмущения W у нас фигурируют
добавочные члены в выражении для потенциальной энергии *):
UZ(x) = lx3(67.2)
Квантовые уровни невозмущенной системы (1=0) суть уровни гармони-
ческого осциллятора; его собственные функции обозначим через
(я+4) , ф"(х). (67.3)
В данном случае вырождения нет: каждому уровню принадлежит лишь
одно состояние Матричным элементом энергии возмущения W будет
^ = 5^-W^n-dx = ^mx^ndx = l^)mn, (67.4)
где через (х3)тп обозначены матричные элементы для х3.
*) Мы можем считать, что спектр возмущенной системы останется все
же дискретным, так как Хх3 есть поправочный член и он вообще негоден для
больших х. Таким образом, из вида поправки (67.2) не следует делать заклю-
чения, что асимптотическое поведение U(x) радикально изменилось, как это
предполагалось в § 63, где добавочный член 1х3 формально рассматривался
как пригодный и для больших х.
15 Блохинцев
226 ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ [гл. XIII
Согласно формуле (63.10) энергия &-го уровня возмущенной системы
во втором приближении равна
+ >• Пь + • (67.5)
flpk С п
Таким образом, нам достаточно вычислить матрицу (x3)wn.z Эту
матрицу мы могли бы непосредственно вычислить из формулы (67.4)
с помощью функций фо [см. (44.11)]. Однако, мы поступим более
просто. Матрица хтп нам известна [см. (45.8)]. По правилу умножения
матриц мы можем вычислить из матрицы 'хтп матрицу (х3)тп. Именно,
ЖХ = У ХЫ (x2)ln = У Xkl У Х1тХтп = L £ XklXlmXmn- (67‘6)
I 1т 1т
Подставляя сюда значение матричных элементов xkl, х1т, хтп из
(45.8), получаем:
+/Ж1Жf + (67.7)
Ввиду наличия 8 двойной ряд по I и т просто суммируется, и мы
получаем:
> V...+
+ /• (67.8)
Отсюда следует, что (х3)^ = 0, и поэтому поправка к Е® в первом
приближении равна нулю. Поправка второго приближения, содержащая
сумму по /г, также просто вычисляется, так как из суммы остается
согласно (67,8) только четыре члена: /г = ^-РЗ, n = k±\. Кроме
того, (x3)kn = (x3)nk. Поэтому, подставляя (67.8) в (67.5) и принимая
во внимание (67.3), находим:
+ + ‘ = <М.2,... (67.9)
Это и есть искомое приближенное выражение для энергии квантовых
уровней осциллятора с учетом поправочного ангармонического члена кг3.
Легко найти условие применимости нашего приближения. Матричный
элемент энергии возмущения Х(х3)Лл для больших квантовых чисел k
по порядку величины согласно (67.8) равен
—
Разности уровней Е^— Е^п Лш0. Таким образом, условие применимости
§ 68]
ЭФФЕКТ ШТАРКА
227
теории возмущения (33 13) сводится к
h_ \3/2 0*
ио)0 / 7zcoQ
(67.10)
Наше приближение применимо, следовательно, для не слишком высоких
уровней, именно:
(^оу/з^о^
(67.10')
Это условие в переводе на язык классической механики означает, что
амплитуда колебания должна быть не слишком большой.
Формула (67.9) находит свое применение для вычисления колебатель-
ных уровней молекулы. В § 51, рассматривая двухатомную молекулу,
мы ограничились вторым членом разложения потенциальной энергии
Щх) по степеням отклонения (х) от положения равновесия и соответст-
венно этому получили для молекулы гармонические колебания. Если бы мы
учли и следующий член разложения, что, вообще говоря, приходится
делать, то колебательные уровни молекулы определились бы форму-
лой (67.9), а не (67.3).
§ 68. Эффект Штарка
Эффектом Штарка называют найденное И. Штарком расщепление
спектральных линий' атомов в электрическом поле. Картина расщепления
Рис. 44. Эффект Штарка бальмеровской серии при больших полях (по Рауш-
фон-Траубенбергу).
Поле возрастает снизу вверх, максимальное значение равно 1,14 миллиона вольт, белые ли-
нии— линии постоянного поля. Одновременно сняты 'нёвозмущенные (без поля) водородные
линии они изображаются средними линиями каждой картины расщепления, которые на ри-
сунке проходят почти прямолинейно. При сравнении штарковских линий, соседних с несме-
щенными линиями, ясно видно, что линия, лежащая с красной (левой) стороны, всегда уда-
лена от несмещенной линии гораздо дальше, чем соседняя фиолетовая линия (квадратичный
эффект Штарка). Это особенно хорошо заметно у линии Н$. Далее, видно, что все ’линии
перестают существовать при определенной критической напряженности поля Н раньше,
чем Jfg, раньше, чем Н , и т. д., — красные компоненты каждой линии раньше, чем фио-
летовые/Явление исчезновения линий объяснено в § 94.
изображена на рис. 44, где дано расщепление спектральных линий
водорода /Ур, Н, Hv (линии серии Бальмера). Опыт показывает,
что действие электрического поля на атом водорода и на другие атомы
15*
228 ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ [гл. X1II
весьма различно. В водороде расщепление спектральных линий пропор-
ционально первой степени электрического поля а во всех остальных
атомах оно пропорционально второй степени поля ($2)- В сильных полях
(порядка 105 V)cm) появляется дополнительное расщепление, пропор-
циональное высшим степеням Кроме того, по мере увеличения поля,
как было наблюдено Рауш-фон-Траубенбергом, спектральные линии
уширяются и, наконец, вовсе исчезают. Это последнее явление мы рас-
смотрим позднее в § 94. Сейчас мы будем рассматривать поля, меньшие
105 V/CM.
Из сравнения величины внутриатомного электрического поля
<£о = ^ =5,13-10» V/CM
(а—радиус первой орбиты Бора) с внешним полем (<£?<^105 V/сл)
следует, что в широких пределах действие внешнего поля можно рас-
сматривать как возмущение. Этйм мы и воспользуемся для нахождения
квантовых уровней и волновых функций атомного электрона при наличии
внешнего поля Обозначим потенциальную энергию оптического
электрона в атоме через U(r). Если теперь еще имеется внешнее одно-
—>
родное электрическое поле напряженности <§, то электрон будет иметь
некоторую добавочную потенциальную энергию W. Эту энергию легко
вычислить.
Возьмем ось OZ за направление электрического паля <£. Тогда
потенциальная энергия электрона в поле будет равна
W=e£z = — Dzg, (68.1)
где Dz = — ez есть компонента электрического момента на ось OZ*).
Полная потенциальная энергия электрона будет равна
^(г) = 6Г(г)_|-^. (68.2)
Уравнение Шредингера для стационарных состояний будет иметь вид
_|>Ф + [Щг) + ^]Ф==£ф. (68.3)
Возмущение W относится к случаю, рассмотренному в § 63. Именно,
даже как угодно малое поле $ меняет асимптотическое поведение
потенциальной энергии. Если ^ = 0, то U'—► 0 при z •+ оот а если
^=^=0, то U1—» Ч- оо при. z—» -4- оо. Поэтому мы можем применить
теорию возмущения (при малых X) лишь в смысле, разъясненном в § 63.
Таким образом, применяя теорию воз.мущения, мы будем находить
квантовые значения энергии Еп, для которых электрон находится вблизи
атома достаточно большое время («квазиквантовые» состояния). Рассмат-
ривая в этом смысле W как возмущение, мы будем считать состояния
электрона в атоме в отсутствии внешнего поля известными.
*) Заряд электрона мы считаем равным — е и начало координат берем
в центре атома.
§ 68]
ЭФФЕКТ ШТАРКА
229
Рассмотрим сначала водородоподобный атом. Энергию квантовых
уровней атома в отсутствии поля обозначим через:
£ = 0<Z</z—1, /г=1, 2, 3, ... , (68.4)
а соответствующие волновые функции через
Фк = ^/(г)^(СО5б)е/Я1?> (68.5)
Каждый уровень Е?п1 вырожден 2Z —j— 1 раз в силу различных возмож-
ностей для ориентации орбитального момента Mz. Поскольку мы рас-
сматриваем определенный уровень п, I, то мы можем'опустить индексы
/г, Z, сохранив лишь т. Тогда для краткости функции, принадлежащие
уровню Ё^ обозначим через
(68-6)
Наиболее общая функция, представляющая состояние с энергией
E°ni, будет
?= 2 ‘Л (68.7)
т— — 1
Вычислим, каково будет среднее значение проекции электрического
момента Dz в таком состоянии. Имеем:
v т т'
<68-8»
т т'
где
(68.9)
есть матричный элемент электрического момента Dz. Из (68.1) следует,
что матричные элементы энергии возмущения W равны
— (Dz)mmfS. (68.10)
Вычислим (Dz)mmf. Подставляя в (68.10) волновые функции ДО^из (68.5)
и имея в виду, что z = г cos 6, получим:
(Dz)mm< = — е ( R^drlpfPf cos 6sin 6 d§ j e‘(m-m’^d<f. (68.11)
О П о 0
Если то этот интеграл равен нулю, так как е1^т~т'^ есть
периодическая функция ср. Если же т=-т\ то второй интеграл в (68.11)
есть нечетная функция cos 6 и поэтому равен нулю. Таким образом
=0. Вместе с тем в любом .состоянии, принадлежащем уровню
среднее значение электрического момента Dz (68.9) равно нулю.
Согласно (68.1) равна также нулю и энергия возмущения. Отсюда сле-
дует, что в водородоподобйых атомах не может быть расщепления
230
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ
[ГЛ. XIII
уровней в электрическом поле, пропорционального полю, так как сред-
ний электрический момент равен нулю. Расщепление, пропорциональное
высшим степеням поля, конечно, будет иметь место. В самом деле,
функции электрона в поле будут отличны от ^п1т (Ф^т — нулевое
приближение!) В первом приближении мы можем положить:
$nlm — tynlm + Unlm +•••> (68.12)
где ип1т— некоторый добавочный член, пропорциональный первой
степени поля (§.
Расчет показывает, что в этом приближении, когда уже учитывается
деформация атома, средний электрический момент Dz не равен нулю,
а пропорционален полю
~Dz = ag. (68.13)
Этот момент есть результат поляризации атома в поле. Потенциальная
энергия этого момента в поле S равна
W=—(68.14)
что соответствует работе поляризации:
б
при увеличении поля от нуля до
Вместе с тем смещение квантовых уровней будет пропорционально
квадрату поля о2. В расчет величины а, носящей название поляризуе-
мости, мы входить не будем*).
Иное положение вещей имеет место в атоме водорода, где помимо
вырождения, связанного с различными ориентациями орбитального
момента, имеется еще «/»-вырождение. Каждому квантовому уровню
Е® принадлежит п2- функций вида (68.5), различающихся как числом /
(/—0, 1,..., п—1), так и числом tn. Удерживая в памяти номер
уровня л, мы можем выписать функции, принадлежащие уровню £°, в
виде
ф^, Z —0, 1, 2, ..д—1; //г —0, + 1, (68.15)
всего п2 таких функций. Наиболее общим состоянием, принадлежащим
уровню теперь будет
<р== "s 2 <68Л6>
/=0 т— —I
*) См., например, Бете, Квантовая механика простейших систем, стр.
202—215, где дан расчет а для Не. Заметим, что формула для поляризуе-
мости а может быть получена из теории дисперсии (§ 85), если там положить
частоту внещнего поля w = 0.
§ 69] ЭФФЕКТ ШТАРКА В АТОМЕ ВОДОРОДА 231
Средний электрический момент Dz в состоянии ср, ввиду участия
в суперпозиции (68.16) функций с различными значениями /, не равен
нулю (см. расчет в следующем параграфе). Поэтому и средняя добавоч-
ная энергия в поле в состоянии ср
(68.17)
будет, вообще говоря, не равна нулю и пропорциональна полю. В резуль-
тате смещение уровней будет пропорционально полю, что к наблюдается
на самом деле. Таким образом, сущность различия в поведении в элек-
трическом поле атома водорода и водородоподобных атомов заключается
в том, что в первом случае в группе состояний, принадлежащих уровню
Е®, имеется электрический момент, а во втором случае в группе состоя-
ний атома, относящихся к уровню Е^, электрический момент отсутст-
вует и появляется только в результате поляризации (деформации) атома.
§ 69. Эффект Штарка в атоме водорода
Вывод общей формулы для расщепления уровней водорода в элек-
трическом поле читатель найдет во многих курсах*). Мы ограничимся
разбором примера, на котором легко выяснить всю сущность дела.
Именно, мы рассмотрим расщепление второго квантового уровня атома
водорода (п = 2) (первый уровень не вырожден и потому не рас-
щепляется). Таким образом, мы берем наиболее простой случай.
Указанному квантовому уровню принадлежат четыре состояния,
характеризуемые следующими волновыми функциями:
Ф2ОО ----^?20 (И *^0
Ф2Ю = (Г) ' ’
Ф21,—1 — ^?21(Г) 1,е
Согласно (25.18)
(s-терм),
> (р-терм).
(69.1)
(69.2)
Далее, из (47.19) получаем радиальные функции Rnlt
где а — радиус
(69.3)
орбиты Бора, а и
тели. Пользуясь тем,/что х = г sin 9 cos
1
-7— — нормирующие множи-
у ба3
ср» У = гsin9 sin ср, ^ = rcos07
*) См. Бете, Квантовая механика простейших систем, стр. 180.
232
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ
[гл. ХШ
мы можем написать функции (69.1) в виде
$200 = $1 = R20 =f(r),
$210=$2= y/r^^ = F(r)z,
ф,,—ф« = ,/In х + д'_о/Н (69-4>
Т2П тз у 8тс ^2i л *\г) у2 ’
Ф„,-,=Ф!=/
Г "
/
Наиболее общим состоянием, принадлежащим уровню Е®, будет
<р=2сХ (69-5>
ос=1
Чтобы определить приближенно квантовые уровни и волновые функции
при наличии внешнего электрического поля <§ согласно теории возму-
щения, нужно решить уравнения (64.10), которые в нашем случае гласят:
[£*2 & ^apfa = 0>’ а, 1,2, 3,4. (69.6)
(69.7)
Из представления функций в форме (69.4) легко видеть, что все инте-
гралы (69.7), за исключением двух, именно,
Г12==1Г21 = ^ \f(r)F(r)z*dv, (69.8)
в силу нечетности подинтегральной функции относительно z равны нулю.
Интеграл же (69.8) легко вычисляется в полярных координатах. На осно-
вании (69.4) и (69.3) имеем:
_ ОО тг 2тс г _ г
ООО
Имеем
я 2я я 2я
J Jz2 sin 9 d§ dy = r2 J J cos2 9 sin 91/9 d<p — ~ r2.
0 0 0 0
Вводя переменную , получаем окончательно
TF12=U72i = ^-fe“?(l — = (69 8')
0
§ 69]
ЭФФЕКТ ШТАРКА В АТОМЕ ВОДОРОДА
233
Напишем теперь систему уравнений (69.6) в явном виде. На основании
сказанного о матричных элементах РГа9, получаем:
(£<>- Е)с2+ 1Г2Л = 0,
(££-£)Cs = 0,
(E°-E)Ci = 0.
(69.67
Определитель этой системы Д2(£*) должен равняться нулю (см. § 66):
е°2—е ^2 0 0
Д2(£) = 1Г21 0 £« — Е 0 о о ° 1 О CN -—'
0 0 0 £2° — Е
= (£•» — Е) 2 [(£« — Е)2 — Wf2] = 0. (69.9>
Отсюда находим корни Ev Е2, Е3, Et, которые равны энергии возму-
щенных уровней:
£! = £!!+^12, Е2 = Ц—№12, Е2 = Е, = Е^ (69.10)
Таким образом вырождение снято только частью: четверной уровень рас-
щепляется лишь на три разных *). Картина этого расщепления приведена
на рис. 45.
В результате вместо одной спектральной линии, отвечающей переходу
—> Е® [переход изображе
три линии, отвечающие пе-
реходам:
(а)Е3,Е^Е^
W Е.-+Е*,
(с) Е2-+ £0.
Это и есть штарковское явле-
ние расщепления спектральных
линий в электрическом поле.
[Заметим, что ради простоты
мы рассчитали расщепление
первой линии ультрафиолетовой серии Лаймана, на самом деле Штарк
изучал расщепление линий серии Бальмера (видимый свет).]
Из (69.10) и (69.8) следует» что разница &Е в уровнях энергии Ег
и Е2 равна б^л, т. е. &Е = 3• 10“8-$ eV, если $ дано в V/cm. Рас-
щепление маленькое, даже для — Ю4 V)cm, ^Е—3-\0~4: V, а раз-
ность £0 — £0 ю eV.
на рисунке
Г"-------г
L2
СЗ
стрелкой а] мы получим
£•;—*—
Без поля
Рис. 45. Расщепление уровня п = 2 атома
водорода в электрическом поле.
9 Без поля мы имели гамильтониан, обладающий сферической симметрией
При наличии поля еще остается симметрия вращения вокруг направления поля.
234
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. XIII
Вычислим теперь волновые функции ср в нулевом приближении, отно-
сящиеся к уровням Ev Е2, Е3 и Е^. Для этого нужно найти амплитуды сл
из уравнений (69.6'). Подставляя в (69.6') Е==Е3 = Е4 = Е%, находим,
что с3 и £4=7^= 0, a ct = с2 — 0. Следовательно, для несмещенных уров-
ней наиболее общее состояние описывается функцией:
? = + ' Е = Е2> (69.11)
с3 и с4 произвольны (вырождение не снято). Подставляя в (69.6') Е = Е1 =
= E0-|-U712, получаем г?3 = г4 = 0, с1 = с2. Поэтому уровню Ег отве-
чает волновая функция
<Р1 = уУ (Ф? + ^)> ^=^+^12- (69-12)
Подобным же путем вычисляем для г?3 = с4 = 0 и ct =— с2, и вол-
новая функция имеет вид
= Ф§), £2=^-IF12. (69.12')
(Множитель взят
из соображений нормировки <рх и <р2 к 1.) Таким
образом при наличии поля £ волновые функции стационарных состо-
яний*) будут <р2 и <р3 — ф|, <р4 == фо. Мы предоставляем читателю
самому убедиться, что, как и должно быть по общей теории, матрица
возмущения W в новом представлении
(69.13)
будет диагональной матри щей Зеа£ 0 0 0 — Зеа<§ 0 0 0 0 0 0 • (69.14)
Отсюда следует, что полу 0 000 ченную картину расщепления уровней мы мо-
жем пояснить еще и так: уровни Е3 и Е± не смещаются потому, что
в состояниях (р3 и <р4 электрический момент равен нулю. Смещения же
уровней Ег и Е2 определяются тем, что в состояниях cpt и <р2 момент
равен Зае$ и — Зае$ соответственно, т. е. в первом случае он ориен-
тирован против поля, а во втором случае — по полю.
§ 70. Сложный (аномальный) эффект Зеемана
Рассмотренная в § 59 теория расщепления спектральных линий в маг-
нитном поле (простой эффект Зеемана) является далеко не полной, так
как не учитывает мультиплетной структуры спектральных линий. Введем
теперь в рассмотрение и эту структуру.
*) Точнее «почти стационарных». Ср. §§ 92, 94.
§70] СЛОЖНЫЙ (АНОМАЛЬНЫЙ) ЭФФЕКТ ЗЕЕМАНА 235
Гамильтониан Н атомного электрона, находящегося в магнитном поле,
согласно (67.8) равен
я=яо+^(я+ч)=77°+^(^+25г) (70-1)
(при этом мы игнорируем члены с $%2 как малые). /7° есть гамильтониан
в отсутствии внешнего магнитного поля:
//° = -^V2 + t/(r). (70.2)
Учитывая мультиплетную структуру спектра, мы должны дополнить этот
гамильтониан членами энергии взаимодействия спина с орбитальным
движением (они, как объяснялось в § 6, обусловливают структуру спек-
тров). Далее, напомним замечание в § 61, согласно которому поправки на
зависимость массы электрона от скорости (релятивистский эффект) такого же
порядка, как и взаимодействие спина с орбитой. Все эти дополнитель-
ные члены в энергии электрона, обусловливающие мультиплетную струк-
туру, обозначим через
(70.3)
Мы не будем раскрывать явно вид этого оператора и ограничимся
указанием аргументов, от которых он зависит. Появление в WQ опера-
торов импульса электрона ясно уже из того, что внутреннее магнитное поле
создаваемое орбитальным движением электрона, зависит от скорости
электрона, а следовательно, и от его импульса *). Таким образом, пол-
ный гамильтониан должен быть написан в виде
7/—/7°4~ Wo+ Wj W=_F(Mg + 2sg). (70.4)
Мы будем различать два случая: первый, когда магнитное поле настолько
велико, что энергия электрона во внешнем поле W гораздо больше энер-
гии W°, обусловливающей мультиплетное расщепление, и второй, когда
энергия во внешнем поле W гораздо меньше энергии (малые маг-
нитные поля).
Уточним понятие «сильного» и «слабого» поля. Заметим, что энер-
гия W0, которой мы пренебрегаем по порядку величины, равна разности
энергий уровней в дублете (см. рис. 40). Обозначим эту величину
через
(70-5)
По закону Био и Савара это поле равно:
<= 7 '"1Й
где v — скорость электрона, аг — радиус-вектор, проведенный от электрона
к точке, где наблюдается поле
236
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ
[гл. XIII
Расщепление, создаваемое
eh
порядку величины
соответствует условию
магнитным полем, равно согласно (59.13) по
Поэтому рассмотренное в § 59 приближение
(70.6)
Если, например, = 5,3• 10~15 эрг. (линии Dr и Z?2 в Na, см. рис. 40),
то (70.6) дает SK j>5*104 гаусс. Напротив; слабое поле SK опреде-
ляется из неравенства т. е.
(70.7)
В первом случае (сильные поля!) мы можем пренебречь величиной , "UZ0
по сравнению с W. Тогда мы получаем случай, уже рассмотренный
в § 59 (простой эффект Зеемана). В случае слабых полей расстояние
уровней в мультиплете jp гораздо больше поэтому в нулевом
приближении мы можем пренебречь энергией электрона во внешнем
поле W по сравнению с IF0 и рассматривать в качестве гамильтониана
невозмущенной системы
H=HQ+
(70.8)
a W— как возмущение. Получающаяся в этом случае картина расщепле-
ния уровней- и соответственно спектральных линий гораздо сложнее рас-
смотренной в .§ 59. Само явление носит название сложного (иногда
говорят аномального) эффекта Зеемана,
Чтобы рассмотреть это расщепление, заметим, что квантовые уровни
невозмущенной системы [гамильтониан (70.8)], как объяснялось в § 61,
будут вырождены 2у—|— 1 раз, соответственно возможным ориентациям
полного момента J. При наличии внешнего поля такой уровень должен
расщепляться, так как разным ориентациям J будет отвечать разная энер-
—
гия магнитного момента во внешнем магнитном поле &С. Для того, чтобы
найти это расщепление, мы должны определить собственные значения
энергии возмущения W. Для этого напомним (ср. § 61), что состояния
невозмущенной системы с учетом мультиплетности характеризуются
четырьмя квантовыми числами n, Z, ту Поэтому матричные элементы
энергии возмущения W будут иметь вид Wnijm^n'upm'j. Если мы огра-
ничимся первым приближением, то, как излагалось в § 64, нужно пре-
небречь матричными элементами энергии возмущения, относящимися к раз-
ным уровням невозмущенной системы. Так как у йас эти уровни нуме-
руются числами /г, Z, /, то в нулевом приближении рассмотрению под-
лежат только элементы
Wmpn'j = Wnlj'mj, nljnij» (70.9)
Пригодность такого приближения обеспечивается малостью магнитного
поля. Так как матричные элементы Wmpn имеют порядок величины
§ 70]
СЛОЖНЫЙ (АНОМАЛЬНЫЙ) ЭФФЕКТ ЗЕЕМАНА
237
Т0 Условие (70.7) можно переписать в виде
Enlj — Enip
(70.10)
что является как раз условием применимости теории возмущения. При
этом мы взяли разность энергий в пределах мультиплета (разные j и f,
но одинаковые п и Z). Ясно, что для разных п и I (70.10) выполнено,
если выполнено для одинаковых пи/.
На основании сказанного дело сводится к приведению матрицы Wm^'j
к диагональному виду. Для этого выразим энергию возмущения W- через
проекцию Jz на ось OZ полного момента J. Имеем:
W=^(M,-|-2s2) = O£(< + s2)> (70.11)
где OL есть частота Лармора. Рассмотрим теперь произведение SZJ2.
Эту величину можно представить в виде
= S' (+ Jp - Jz (sxJx + syJy + VJ +
+ («Л - -W A+(V, -
или
5гЛ=/г(« J) + Q, (70.12)
Q=(«Л - W Jx+(V, ~ Jy- <70-13>
Пользуясь теоремой о сложении вращательных моментов, мы можем
согласно (60.4) переписать (70.12) в виде
«г<Л = .7г1(.72 —M2-H2)4-Q. (70.12')
Если мы возьмем теперь такое представление, в котором J2 есть диа-
гональная матрица, то тогда (70.12') можно разделить на J2 (ибо диа-
гональная матрица ведет себя как обыкновенная величина, а не как
оператор). Поэтому в этом представлении из (70.12') получаем:
(70.13')
и, следовательно, энергию возмущения W можно написать в виде
^=ОЛ{1 + } +OL%. (70.14)
Матричные элементы оператора Q отличны от нуля лишь в том случае,
когда j
Действительно, оператор Q может быть представлен в виде
(70.15)
где
Тле= ^2$у' Чу = ^2$Х 4g~ ^Х$у JySX (ft ЛЬ)
238 ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ [гл. XIII
(индексы получаются циклической перестановкой). Пользуясь правилами пере-
становки компонент момента (§ 60), легко доказать, что
+ + = (70.17)
ZzYx lz*^z~z^ (70.18)
(из последних равенств вытекают еще и другие путем циклической переста-
новки х, у, z). Если теперь взять три проекции орбитального момента Мх,
Му, Mz и три координаты х, у, z, то нетрудно видеть, что для них имеют
место совершенно аналогичные алгебраические равенства, именно:
Мхх 4- Муу + Mzz = 0, (70.17')
Мzx — xMz = i hy, Mzy—yMz =z — ihx, Mzz — zMz — 0. (70.18')
Сравнение (70.17') и (70.18') с (70.17) и (70.18) показывает, что структура
матриц Jx, Jy, Jz в отношении Тз такова же, как и структура мат-
риц Мх, Му, Mz в отношении матриц х, у, z. В § 83, В показано, что един-
ственные отличные от нуля матричные элементы х, у, z имеют вид xt р
у1 / zi (где I—орбитальное число). Диагональные элементы Хц, уц,
zn равны нулю. Но I есть как раз номер собственного значения Таким
образом, диагональные матричные элементы х, у, z равны нулю в представ-
лейии, в котором М2 диагоналей. Поэтому должны равняться нулю и диаго-
нальные элементы ух, чу, yz в представлении, в котором J2 диагоналей,
т. е. матричные элементы
(lx) 0; = (lz) fmj, Jmj—Q. (70.19)
Так как, кроме того, Jx, Jy, Jz коммутируют c J2, то их матричные элементы,
не равные нулю, имеют вид
(Zr) jm3, jnij, (Jy) Jmj, jmj, (Jz) jm3, Jmj . (70.20)
Из (70.19) и (70.20) следует, что матричные элементы Q вида Qjmjtjm'j равны
нулю (в чем легко убеждаемся, образуя Q из у и J по правилу умножения
матриц).
Таким образом, в интересующую нас матрицу возмущения, эле-
менты которой относятся к одному и тому же значению полного мо-
мента у, оператор Q не дает никакого добавления. Иными словами,
все элементы матрицы W образуются за счет части
жащей Q, т. е. за счет оператора
W, не содер-
J2_Jf2_52
2J2
(70.21)
Так как Jz, М2, s2 и J2 коммутируют друг е другом, то их матрицы
могут быть одновременно приведены к диагональному виду. Вместе с тем
приводится к диагональному виду и матрица оператора W1 (с элементами
)• Чтобы получить ее диагональные элементы, достаточно под-
ставить вместо Jz, М2, S2 и J2 собственные значения этих операторов»
Имея в виду, что
Jz=hmp
ЛР = й2/(/-|~ 1),
*2=а2Ш+1)>
(70.22)
§70] сложный (аномальный) ЭФФЕКТ ЗЕЕМАНА 23&
мы получаем
W = hOjtn. { 1 + /+ В } . (70.23)
L 7 t 1 2/(j 4-1) 1 '
Ри£. 46. Расщепление уровней 25^з, 2А/а, 27>з/3 ПРИ сложном эффекте Зеемана-
правку W к энергии уровня Епу через &Ejim}, мы
(70.23) в виде
hEjimj = hOjITLjg,
где g означает «множитель Ланде» и равен
1 । JU +1)-1 +1) + ls(ls +1)
g~ 1 ! W+l) '
Так как nij пробегает все значения от —j до /,
из (70.25), каждый уровень Enjt расщепляется в слабом
на 2/—1 уровней.
На рис. 46 приведена схема расщепления уровней:
8^(/=у, / = о), 2А/а(; = 1, /=1) и 8А/ж(/=® , /=1) ,
можем написать
(70.24)
(70.25>
то, как видно
магнитном поле
240 ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ ВОЗМУЩЕНИЙ [гл. XIII
—>
При большем поле SK /сложное расщепление упрощается и полу-
чается рассмотренное выше (рис. 38). Это явление (упрощение расще-
пления спектральных линий в магнитном поле при переходе от слабых
полей к сильным) наблюдается на опыте и носит название эффекта
Пашена-Бака.
§ 71. Наглядное толкование сложного эффекта Зеемана
Полученная нами формула (70.23) для расщепления квантовых уров-
ней в слабых магнитных полях может быть наглядно истолкована в тер-
минах векторной модели. В магнитном поле квадрат полного враща-
тельного момента J2 и его
I*
I
Рис. 47. Прецессия полного
момента J вокруг направле-
ния магнитного поля.
проекция на магнитное поле Jz являются
интегралами движения. Вектор же полного
момента J не является интегралом движе-
ния. Именно, вектор J прецессирует вокруг
направления магнитного поля так, как это
показано на рис. 47.
Если связь между орбитальным движе-
нием и спином велика, то относительная
ориентация вектора спина s и вектора ор-
битального момента Mz сохраняется, но оба
они прецессируют вокруг полного момен-
та J. Добавочная энергия IF в магнитном
поле равна энергии магнитных диполей с
моментами—Д-М. и — — sb поле
1 |ic
= +^(Л + *г)- (71.1)
Нам нужно найти среднее значение вели-
чины IF. Jz имеет постоянное значение.
Напротив, sz есть переменная величина,
поэтому для вычисления среднего значе-
среднее значение sz, имея в виду, что век-
ния W нужно вычислить
тор s участвует в двух прецессионных движениях: вокруг вектора J и
вместе с J вокруг направления магнитного поля (OZ).
Так как
^ = 5C0S(^, S),
(71-2)
то нам нужно вычислить среднее значение cos(^f, s). Из рис. 47 видно,
что
cos (^f, s) = cos (s, J) • cos (J, Ж), (71.3)
т. e.
= s cos (s, J) • cos (J, $%). (71.4)
§ 72] ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА 241
Но
cos (J, j£)= , (71.5)
и из треугольника со сторонами J, М, s получаем:
sJ cos (s, J) = (sJ) = | (J2 — M2 -j- s2). (71.6)
Из этих формул получаем
^=A(J2-A(2+s2)- (7k7)
Подставляя sz в выражение (71.1) для энергии W, находим
>=4-OJ4 + ^)-+OiJ,(l+^=^±^) . (71.8)
Если в этой формуле разуметь под Jz, J2, Л42, s2 их квантовые зна-
чения (70.22), то из (71.8) мы получим квантовую формулу (70.24).
ГЛ АВА XIV
ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА
И ТЕОРИЯ СТОЛКНОВЕНИЙ
§ 72. Теория возмущений для непрерывного спектра
Мы обратимся теперь к тому случаю, когда невозмущенная система
имеет непрерывный энергетический спектр. Обозначим гамильтониан этой
системы через ТУ0, собственные функции, принадлежащие уровню энер-
гии Е,— через фд. Уравнение Шредингера в этих обозначениях имеет
вид
ЯОфО=£-фОв (72.1)
Допустим, что на эту систему действует возмущение W. Уравнение
Шредингера для возмущенной системы тогда имеет вид
(Я°+ W) ф = £ф. (72.2)
Если возмущение таково, что оно не нарушает непрерывного характера
спектра оператора Н, т. е. оператор HQ имеет также непрерывный
спектр, то все действие возмущения сводится к изменению вида соб-
ственных функций, принадлежащих уровню Е. Вместе с тем задача
теории возмущения сводится в этом случае к нахождению функций фЕ,
которые при малом возмущении W могут мало отличаться от функ-
ции фо. Возможен однако и другой случай, когда возмущение УУ при-
водит к образованию разрывов в непрерывном спектре. Тогда в задачу
теории возмущения входит не только определение измененных волно-
16 Блохинцев
242 ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [гл. XIV
вых функций, но и определение положения и величины разрывов
в первоначально непрерывном энергетическом спектре Е.
Оба эти случая мы рассмотрим на простом примере частицы, сво-
бодно движущейся вдоль оси ОХ. Уравнение Шредингера в этом случае
имеет вид
<72-3>
и имеет собственные функции и собственные значения
рх
е 1 h п2
|0=_L_, £(/>) = 4- . (72.4)
Возмущенное уравнение напишется в виде
+ = I72-5*
так что 1Г(х) есть добавочная потенциальная энергия. Значок штрих
у Е присоединен на тот случай, если спектр возмущенной системы
изменится. Без всяких ограничений мы можем положить
Е’ = Е + $, (72.6)
Ф = Ф°М+ «(*). (72.7)
Однако, считая возможным применить теорию возмущений к решению
уравнения (72.5), мы будем считать, что 11 s | Е, | и (х) | | (х) |
и будем пренебрегать произведениями е1Г, ей, uW как величинами
второго порядка малости. Тогда подстановка (72.6) и (72.7) в (72.5),
учитывая (72.3), дает
<72-8>
Представим и(х) в виде суперпозиции невозмущенных состояний
+оо
«(*) = J и(р’)фо,(х)йГр'. (72.9)
— 00
Подставляя теперь (72.9) в (72.8), умножим (72.8) на (х) и проин-
тегрируем по х. Имея в виду, что
^ф°*ф°,4^ = §(/—/>),
мы получим:
^«(р')-£«^)=е8(/-р)-^р (72.10)
[уравнение (72.8) в «/?»-представлении]. Здесь
Г 1 Г i(p—p')x
WP'P = J W • W(x) rpW-dx = ^W{x} e ^(72.11)
§72] ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА 243
ecib матричный элемент в «/ъ>-представлении. Из (72.10) находим:
и (р') = £° . (72 12)
’ Е(р’) — Е{р) ' 7
В точке р' =р знаменатель (72.12) обращается в нуль. Если мы возь-
мем е^О, то мы получим и (р') оо -Ъ(р'—р), и наше решение ни
в коем случае не будет приближением к dA Поэтому следует поло-
жить с• 0j т. е.
W , 2|лИ/ г
«(/)= -г5^И= -(7+W^ • <72.13>
Подставляя это значение и(р'\ в (72.9) и (72.7), мы находим:
Ф (Х)^фо(х)_(72.14)
тр\ / тр\ / j Е(р')— Е(р) ' 7
Интеграл здесь перечеркнут, что означает, что при интегрировании
мы должны исключить точку р'~р, так как в этой точке формула
(72.13) теряет смысл. К тому жег
функция фо (х) (р’=р) уже выде-
лена из интеграла особо*).
Необходимым условием состоя-
тельности нашего метода решения
является малость добавка в (72.14),
т. е.
1Ф,(*)—ф® WK
<|ф0(х)|. (72.15)
Из (72.13) видно, что и(р') вбли-
зи резонансной точки р—р' будет
тем меньше, чем больше р, т. е.
Следовательно, наше приближение
Рис. 48. Кривые для энергии возму-
щения W (х).
чем больше энергия частицы Е,
пригодно при больших энергиях
частицы.
В произведенном расчете мы считали, что матричный элемент WP’j>
является конечной величиной. Это будет иметь место в случае, если №(х)
достаточно быстро исчезает при |х|—> оо, т. е. для этого возмущение
должно быть сосредоточено в некоторой области пространства (рис. 48).
В этом случае, как следует из наших расчетов, энергетический спектр
*) Точный смысл знака -у может быть определен следующим образом:
p'}dp' = lim | f F(p,p')dp'-{- j F(p, p') dp'
—*oo
Определенный таким способом предел носит название главного значения
интеграла.
244 ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [гл. XIV
остается непрерывным*), если добавок и мал. Если возмущение IF(x)
распространяется на все пространство так, что Wp'p бесконечно, то
в первоначально непрерывном спектре могут образоваться разрывы.
В качестве примера приведем возмущение вида
1F(x) = acos(^J = |{^ * 1 * }, (72.16)
где 1 и q—некоторые параметры. Вычисляя теперь матричные эле-
менты Wp’p по формуле (72.11), мы получаем:
wpp, = | + (72.17)
Подставляя это значение Wppi в (72.14), мы ввиду наличия S-функций
сразу выполняем интегрирование и находим:
6 (х) — 4° (х)__М____________________[____^р-2дМ \ (72 18)
Vp\x) 2 \E(p-+2q) — Е(р) ‘ Е (р — 2q) — Е (р) / *
При малых 1 это будет пригодное приближение, но оно отказывается
служить в точках
£(p±27) = Z:(p), р = ^q, (72 19)
так как в этих точках при любом X добавок к ф^ обращается в беско-
нечность.
Чтобы построить приближенно решение для р — + 7, воспользуемся
тем, что уровню Е(р) принадлежат всегда две функции ф® и ф^_р. Са-
мое общее решение, принадлежащее уровню Е(р), будет
= + (72.19’)
где а и р — неопределенные коэффициенты. Если в (72.7) подставить
теперь <р вместо ф£, то, повторяя все выкладки, мы получим вме-
сто (72.8):
<72-s'>
Подставляя сюда и из (72.9), умножая на ф^, и интегрируя по х,
найдем вместо (72.10):
U (р') (Е(р') — Е (р)) = г (а$ (р—р') +
+ (Р +р'))- №Р'р + №р', ->) (72.Ю')
*) Если возмущение изображается кривой b (рис. 48), то при достаточно
глубоком минимуме могут образоваться дискретные уровни (на рисунке это
изображено пунктиром). Наш приближенный метод не дает этих уровней, так
как он применим лишь для больших энергий Е.
§72] ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА 245
и, наконец, вставляя сюда значение Wpip и WP't __р из (72.17),
получим:
и(р')(Е (/>') — Е(р)) — е [аЗ(р —/>') +
+ №(р +/>')] — у [а {5(2^-|-р— Р')^г^Ъ—2q-\~P — р')} +
-Н {S(2<7-/>-//) + §( — 2q — p — //)}]. (72.10”)
Если то мы можем положить s = 0, и взять либо а=\у
р = 0, либо а=0, р = 1. В первом случае получим прежнее решение
(72.18), во втором случае получим решение ф^, приближенное к фЬр.
Для p—-\-q имеем из (72.10)
а <р') [£(/’’) — £' (?)] = е [aS (^ — р') + (q +/>')] —
— 4 {<*[5(3? —/) + §( — q — р')] +
+ №(?— />') + 5( — 3? — /)]} • (72.10"')
Для p' — q левая часть равна нулю и должна равняться нулю также
и правая. Имея в виду, что при d(£) = 0, мы получаем:
а(О)[еа-^] = О (72.20)
и для р’= —q
5(0)[е? —|а]=0. (72.20')
Сокращая на 3(0), получаем систему уравнений:
со й 1 7 о со -со 1 и>| й о (72.21)
для определения а и (5. Легко видеть, что для р — —q из (72.10")
получается опять эта же система (72.21). Система (72.21) однородна.
Из равенства нулю ее определителя получаем:
е= ± 2-, (72 22)
а соответствующие решения а и имеют вид
а —для е = -}А (72.23)
и
а — — ₽ для е == — А. (72.23')
В результате, для импульса р — + мы имеем решения:
f-£(±?) + b W*)==«(n?-HU’ (72 24)
E^E{±q)-^, 'Ь^*)==<*(Ф^-Фи- (72.24*)
246
ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА
[ГЛ. XIV
Рис. 49. Образование разрывов (запрещен-
ных полос) в непрерывном спектре при на-
ложении периодического возмущения.
Иными словами, в точке р— + # энергия претерпевает разрыв. Для
импульсов, лежащих вдали от р = -4- ^7, как было показано, е — 0 и,
стало быть, Е = Е(р). На рис. 49 изображена кривая энергии Е
в функции р\ пунктиром для невозмущенного движения, а сплошной
линией для возмущенного. В точках p = ^q получается разрыв вели-
чины X. Другие разрывы р — -+- 2</, отмеченные на рисунке, получатся
при расчете во втором приближении. (Вообще разрыв получается в точках
- ’ получается спектр типа, рас-
смотренного в § 52, именно,
спектр, состоящий из зон доз-
воленной энергии от Е— О
до E=E(q) —~ и от
Е = E(q) до следующе-
го разрыва и т. д. и из
зон запрещенной энергии от
Е=Е(р) —~ до Е=
= Е (q) -р и т. д. Эти за-
прещенные участки энергии
отмечены на оси ординат
штриховкой. При малой вели-
чине возмущенного поля
X —> 0 разрывы становятся
очень узкими. Следовательно,
спектр частицы, движущейся
в периодическом поле при малой амплитуде поля, является как бы обра-
щением дискретного спектра, характерного, например, для атомов. В ди-
скретном спектре «дозволены» только некоторые значения энергии Е1У
Е2,..., а остальные значения «запрещены». В рассматриваемом случае
широкие участки энергии «дозволены», а некоторые узкие полоски
исключены.
На рис. 49 помимо вычисленного нами разрыва в сплошном
спектре Е показано еще плавное изменение Е в функции р вблизи этих
точек разрыва. Это изменение могло бы быть получено и из нашего
расчета, если бы мы учли, что решение (72.18) не годится не только
в точках р — zb гДе оно просто обращается в бесконечность, но и
во всех точках, где
\E{p±‘2q)~ Е(р) | = 1, (72.25)
так как в этой области
нечен, но велик. Таким
решений в/окрестности
импульсов р дббавок к
образом, следовало бы
точек p — zbq> Этот
Е хотя и не беско-
исследовать поведение
расчет мы опускаем *).
*) Этот расчет имеется, например, в книге Бриллуэна, Квантовая ста-
тистика, ОНТИ, 1934, §§ 95—97.
§ 73]
СТОЛКНОВЕНИЯ ЧАСТИЦ
247
Существенно, что наличие этих разрывов сказывается на виде функ-
ции Е(р) вблизи разрыва и таким образом меняет число состояний
(которое мы можем считать пропорциональным dp), приходящихся
на интервал энергии dE. Именно, для невозмущенной задачи ,
а для возмущенной ^=осв точках разрыва энергии. Этот результат
может быть получен и без специального расчета. В § 52 мы показали
в общем виде, что для частицы, движущейся в периодическом поле,
групповая скорость
_±dE______dE
V h dk dp
на краях зон равна нулю. То, что в нашем примере групповая ско-
рость на краю зоны равна нулю, следует уже просто из того, что на
краях зон мы имеем не бегущие (е h) волны, а стоячие (72.24)
и (72.24').
В дальнейшем мы рассмотрим приложение теории возмущения в не-
прерывном спектре к проблеме столкновения частиц. При этом мы будем
иметь дело с локализованным в некоторой области возмущением, т. е.
со случаем, когда непрерывный спектр невозмущенной системы не нару-
шается возмущением.
§ 73. Постановка вопроса в теории столкновений частиц
Теория столкновения частиц образует в настоящее время одну из
весьма обширных глав атомной механики*). В нашем курсе мы не имеем
возможности подробно излагать эту теорию и ограничимся лишь осве-
щением самой постановки вопроса в теории столкновений и разбором
приближенного метода М. Борна для упругих столкновений. Представим
себе некоторую частицу А, которую для определенности будем считать
атомом, и падающий на нее поток частиц В, которые для определен-
ности будем считать электронами. Поток частиц В пусть падает по
направлению OZ (рис. 50). Электроны В, сталкиваясь с атомом, могут
претерпевать изменение своего состояния в двух отношениях. Во-первых,
они изменяют направление своего движения, во-вторых, они могут от-
дать некоторую часть s своей энергии Е атому Л* **) В этом случае
мы говорим о неупругом столкновении, *или неупругом рассеянии.
Если е —0, то столкновение называют упругим (упругое рассеяние)
В опыте интересуются числом электронов (частиц В), проходящих в 1 сек.
' *) См., например, монографию Мотт и Мэсси, Теория атомных столк-
новений, ОНТИ, 1936.
**) Если атом Л первоначально находился в возбужденном состоянии, то мо-
жет быть и такой случай, когда он отдает свою энергию электрону В В этом
случае первоначальная энергия электрона может увеличиться на некоторую
величину s. Такие удары называют ударами «второго рода».
248
ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА
[гл. XIV
через площадку dS (рис. 50), поставленную перпендикулярно к лучу,
проведенному из центра рассеивателя А. Обозначим поток частиц, про-
ходящих через эту площадку и имеющих энергию Е— е, через dNz.
Это число dN& пропорционально размерам площади dS (поскольку она мала)
Рис. 50. Столкновение частиц по квантовой механике.
А— рассеивающий атом, В— падающий пучок частиц.
и обратно пропорционально квадрату расстояния до рассеивателя (г).
Кроме того, dN&, очевидно, пропорционально потоку частиц в первич-
ном пучке N. Таким образом,
dNt=Nq(i,b, , (73.1)
где N—число частиц, проходящих через площадь в 1 см2 в 1 сек.
в первичном потоке, а #(е, 6, ср) — некоторый множитель пропорциональ-
ности между dNn и N. Величина — есть телесный угол dQ, под кото-
рым видна площадка dS из центра рассеивателя А. Отношение
определяет вероятность рассеяния в угол dQ с потерей энергии е. Это
отношение равно
у=?М> <?)<&• (73.2)
Из (73.1) следует, что q имеет размерность площади (так как
№ = 4;, то М = И
и называется дифференциальным эффективным сечением (атома А)
для неупругого рассеяния в угол dQ с потерей энергии £. Это назва-
ние обусловлено тем, что, представляя (73.2) в виде
jv(i СЛ2) dw (е, 0, <₽), (73.2')
мы можем сказать, что вероятность rfw(s, 0, <р) получить dNz частиц,
потерявших энергию е и рассеянных в угол такова же, как вероят-
§ 73]
СТОЛКНОВЕНИЯ ЧАСТИЦ
249
ность при хаотическом обстреле площади в 1 см2, попасть в площадку
размером #(е, 0, ср) dQ см2. Величина
Qe=$ = J<7(e,9,<?)^, (73.3)
п
где интеграл взят по полному телесному углу 4тт, дает так называемое пол-
ное эффективное сечение для неупругого столкновения с потерей энер-
гии N£=Q£N есть число (рассчитанное на 1 сек.) частиц, потеряв-
ших при столкновении энергию s при первичном потоке N частиц
через 1 см в 1 сек.
Из этих формул следует, что вычисление дифференциального эф-
фективного сечения q позволяет полностью ответить на вопрос о рас-
пределении по углам и по энергиям претерпевших столкновение частиiи
Задача теории столкновения сводится к вычислению а.
Рис. 51. Столкновение частицы В с атомом А по классической механике (слу-
чай отталкивания).
Оставляя на время вопрос о методах вычисления этой величины в кван-
товой механике, рассмотрим, в каких случаях следует для расчета столкновения
применять квантовую механику, а в каких случаях—классическую механику.
Для этого рассмотрим, как протекает столкновение, если применять законы
классическо'1 механики. На рис. 51 изображен атом А с центром в О. Вокруг
него проведена сфера радиуса а, вне которой силы между атомом А и падаю-
щей частицей В малы. Эту сферу мы будем называть сферой действия*).
*) Эта сфера не всегда может быть определена. Например, для закона
Кулона U , и ни о какой сфере говорить не приходится. Сферу дей-
ствия можно определить лишь в том случае, когда силы достаточно быстро*
убывают.
250
ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА
[гл. XIV
Частица В, двигавшаяся первоначально вдоль оси BZ, попадая в эту сферу,
будет претерпевать отклонение так, как показано на рис. 51 (приведен случай
отталкивания А и В). Опустим из центра атома перпендикуляр на первона-
чальное направление движения частицы BZ. Пусть длина этого перпендику-
ляра есть р. Его называют параметром удара (или прицельным расстоя-
нием) Частица, имеющая определенный параметр удара, отклонится на вполне
определенный угол 0 так, что р = р (0), 0 = 0 (р). Частицы, имеющие параметры
удара между р и р-|-^р, отклонятся на углы, лежащие между б и
(угол ? мы сейчас, не рассматриваем, предполагая сферическую симметрию
поля атома Л). Если представить себе поток первичных частиц, проходящих
через площадку в 1 см\ то из них отклонятся на углы 6, O-j-dO те, которые
проходят через кольцо, образованное кругами радиуса р [и p-^dp. Площадь
этого кольца есть 2крс1с (рис 51). Таким образом, вероятность отклониться на
углы, лежащие между О и будет равна
= (73'4i
Стало быть, величина 2npdp есть эффективное дифференциальное сечение для
отклонения на углы 0, 0 -|- dO (при любом угле <р). Очевидно, что точность,
с которой определяется параметр удара р, должна быть такова, чтобы мы
могли решить, в какой части сферы действия пролетает частица, так как от
этого зависит величина отклонения ее траектории; иначе говоря, во всяком
случае должно соблюдаться неравенство dp<^a.
В классической механике dp можно брать сколько угодно малым. Иначе
обстоит дело в квантовой механйке из-за квантования момента импульса. Если
мы обозначим через М момент импульса, через р. — массу частицы и через v —
ее скорость, то
M=pvp и (73.5)
В квантовой механике момент импульса принимает лишь дискретные значения,
причем приращение dM, которое мы теперь обозначим через АЛТ, по порядку
величины равно h. Таким образом, вместо (73.5) мы должны написать*)
Др = А . (73.5')
НУ
Следовательно, условие dp а теперь гласит:
До % -- < а. (73 6)
рс/ есть импульс частицы р. Но есть длина волны де-Бройля X, поэтому
(73.6) можно переписать в виде
X < 2тся. (73 7)
*) Мы производим здесь качественную оценку. Формула (73.5Г) не озна-
чает, что параметр удара представляет собой квантующуюся величину.
Будучи, по существу, координатой, параметр удара, рассматриваемый как
оператор, имеет непрерывный спектр (0 р оо). Более детальное рассмотре-
ние показало бы, что дискретность момента ведет к тому, что максимумы ве-
роятности найти частицу с данным моментом Л12 — Л2 (/-f-1) / на расстоянии р
от центра образуют дискретную последовательность. Др в (73 5Г) есть, по по-
рядку величины, расстояние между этими максимумами. См. Мотт и Мэсси,
loc. cit.
§ 73]
СТОЛКНОВЕНИЯ ЧАСТИЦ
251
Иными словами, классическую механику можно применять в том случае, когда
длина волны падающих частиц к много меньше сферы действия а. Длина
волны X электронов с энергией в несколько электрон-вольт равна по по-
рядку 10~8 см. Такого же порядка и сфера действия а. Поэтому при расчете
столкновения электронов с атомами нельзя обойтись без применения квантовой
механики. Напротив, для а-частиц (масса 10~24 г, 109 см/сек) получается
длина волны Х^10“13гл/, так что можно применять классическую механику
(если исключить из рассмотрения силы, радиус сферы действия которых по-
рядка 10~13 см, что имеет место как раз для ядерных сил).'
Рассмотрение столкновения лишь с одним атомом, вместо рассмотрения
столкновения с совокупностью атомов, образующих газ или жидкое или, на-
конец, твердое тело, само по себе является абстракцией, пригодной далеко
не всегда. Рассматривая лишь один атом, мы предполагаем, что частица до
столкновения с атомом движется свободно. В этом — самая сущность поста-
новки проблемы о попарном столкновении. Чтобы оценить, когда такая по-
становка вопроса* возможна, рассмотрим средний путь (свободный пробег),
который частица В пробегает без столкновения в совокупности атомов, обра-
зующих тело.
Для определенности рассмотрим лишь упругие столкновения. Введем кри-
терий того, что частица В не взаимодействовала с атомом А (двигалась сво-
бодно). В качестве такого критерия будем считать некоторый угод отклоне-
ния 0о. Если угол отклонения 0 < 0о, то мы будем считать, что частица не
отклонилась — двигалась свободно, если 0 > 0о, то, напротив, будем считать,
что взаимодействие имело место. Эффективное Qo для отклонения на углы,
большие 0о, равно
Qo=J9(O, 9, <p)d9. (73.8)
20
Знак 20 показывает, что при интеграции мы исключаем малые отклонения
(О < М- Представим теперь себе поток N частиц В, проходящих через пло-
щадку в 1 см2. При прохождении длины dx этот поток пронижет объем (1 см2) dx.
Если через п обозначить число атомов в 1 см3 тела (газообразного, жидкого
или твердого), то в указанном объеме поток частиц В встретит# (1 cM2)dx
атомов А. Вероятность столкновения с одним из атомов А одной из частиц В
при прохождении слоя dx равна
CM2)ix = Q6ndx. (73.9)
1 см£
Обозначим через N(x) величину потока неотклоненных частиц на глубине х
внутри вещества. Согласно (73.9) убыль этого потока при прохождении слоя
х, x-}-dx будет = — JV(x) Qon. (73.10)
Отсюда находим N(x) = Nl)e-Q«nx. (73.11)
Стало быть, величина w(x) = e-Q“nx (73.12)
есть вероятность пройти путь х без столкновения. Следовательно, средний
свободный путь I равен
00
I = Ох (/ -L . (73 13)
Для того, чтобы мы и в самом деле могли считать частицу, проходящую путь /,
252 ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [гл. XIV
свободно движущейся относительно какого-нибудь из атомов тела, нужно,
чтобы свободный пробег был больше сферы действия а. Иначе частица все
время будет находиться в сфере действия того атома, с которым ей пред-
стоит столкнуться. Таким образом, условие применимости теории попарных
столкновений как в классической, так и в квантовой механике есть
Z>a. (73.14)
Если сфера действия а не может быть определена, то применение теории
попарных столкновений становится по меньшей мере сомнительным (во всяком
случае, для тех столкновений, для которых I мало).
В квантовой механике условие (73.14) должно быть дополнено еще одним
условием специально квантового характера. Нас интересуют изменения им-
пульса (и энергии) частицы при столкновениях. Состояние с определенным
значением импульса р есть волна де-Бройля с длиной волны к =
Из условия (73.14) следует, что нам нужно рассматривать движение свобод-
ной частицы на протяжении свободного пробега Z, т. е..мы должны иметь дело
с группой волн, размеры которой не превышают Z. В такой группе, вообще
говрря, Др2 Ф 0 — это состояние с неопределенным импульсом. Чтобы можно
было пренебречь этой неопределенностью (и оперировать тогда с монохрома-
тической волной), нужно, чтобы
Z>X. (73.15)
В случае невыполнения условий (73.14) и (73.15) необходимо рассматривать
столкновение сразу со всей совокупностью атомов А или искать особые об-
ходные пути, которые позволили бы обойти трудности такой прямой поста-
новки задачи.
§ 74. Расчет упругого рассеяния приближенным методом Борна
Ограничиваясь исследованием упругого рассеяния, мы можем не рас-
сматривать внутренней структуры атома А *). Действие атома А на па-
дающие частицы В можно в этом случае рассматривать как действие
силового центра. Если атом обладает сферической симметрией, то поле,
создаваемое этим атомом, будет полем центральных сил. Имея в виду
именно этот случай, обозначим потенциальную энергию частицы В в поле
атома А через U(r) (г—расстояние от центра А до В). Энергию ча-
стицы В обозначим через В. Если считать, что Z7(r) = 0 при г— со,
то мы должны взять В О, так как нас интересует такой случай, когда
частица В с энергией В движется из бесконечности к атому А. Согласно
общей теории движения в поле центральных сил такие состояния ча-
стицы В возможны лишь для В^>0.
Обозначая волновую функцию частицы В через ф(х, у, z), мы мо-
жем написать для нее уравнение Шредингера в виде
+ = (74.1)
(ц— масса частицы В). Потенциальную энергию U(r) мы будем считать
*) Напротив, при расчете неупругдх столкновений неизбежно приходится
рассматривать структуру атома Л, так как при неупругом столкновении изме-
няется квантовое состояние этого атома.
§ 74]
РАСЧЕТ УПРУГОГО РАССЕЯНИЯ МЕТОДОМ БОРНА
253
достаточно быстро убывающей с возрастанием расстояния г от атома А.
Введем волновое число
= (74-2)
где Р — импульс частицы. Обозначим далее
gt/(r)=V(r). (74.3)
Тогда уравнение (74.1) можно переписать в виде
Г2ф k4> = V(r) ф. (74.1r)
Решения этого уравнения, принадлежащие энергии E(k2), очень
сильно вырождены и имеют весьма разнообразную форму.
Мы должны взять такие решения, которые соответствовали бы по-
ставленной физической задаче, т. е. чтобы для больших расстояний от
атома А решение ф было бы совокупностью плоской волны, пред-
ставляющей поток падающих частиц В, и расходящейся волны,
представляющей рассеянные частицы [в общем решении уравнения
(74.Г) могли бы, например, присутствовать еще и сходящиеся
ВОЛНЫ].
Соответственно этому представим ф в виде суперпозиции:
ф = ф°-|-^, (74.4)
где фа представляет поток падающих частиц, а и — поток рассеянных.
Считая, что падающие частицы движутся вдоль оси OZ, мы возьмем
ф° в виде
L3—\ см3. (74.5)
Выбранная нормировка функции ф° означает плотность падающих частиц
|фо|2—1 см~2: одну частицу на единицу объема. При этом поток по
формуле (29.5) будет равен
Jz = — I <Ь» |2 = VI <1>° [2 = V (сек-1 -см-г), (74.6)
где v — ~ — есть скорость частиц. Функция й. изображающая со-
стояние рассеянных частиц, для больших расстояний г от центра атома
должна иметь вид расходящейся волны:
и(т, 0) = Л(О)^, (74.7)
Г->ОО г
где А (0) есть амплитуда рассеянной волны, а 8 — угол между г и OZ.
т. е. угол рассеяния.
Вычислим теперь поток рассеянных частиц на большом расстоянив
от атома. Из формулы для потока частиц (29.5) и из (74.7) следует^
254 ТЕОРИЯ' ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [гл. XIV
что поток рассеянных частиц будет равен *):
J — и* ^}=-|Л(0) |з.1===^ИЖ., (74.8)
г 2р. I dr dr) |i 1 ' 1 1 г2 г2 ' т
Отсюда поток через площадку dS будет
dN=JrdS~v | А (0) |2 dQ, (74.9)
и, следовательно, из (74.6) и (73.2) находим:
<7((») = ^ = М(9)|2. (74Л0>
Таким образом,, для вычисления эффективного сечения q (0) доста-
точно знать амплитуду рассеянной волны А (0). Чтобы найти
рассеянную волну д, мы будем считать V(r) в (74. Г) возмущением
и применим для решения уравнения (74.1') методы'теории возмущений**).
Подставляя (74.4) в (74.Г) и пренебрегая членом Vu как членом вто-
рого порядка малости, мы получим:
V2zz + ^2«== (74.11)
Нам нужно теперь найти решение этого уравнения, имеющее асимпто-
тическую форму (74.7). Вместо разложения и по невозмущенным функ-
циям мы применим для решения (74.11) более прямой метод. Именно,
рассмотрим функцию
ф(г, /) = Ф0(г)е^, (74.12)
где г — радиус-вектор точки х, у, z, a t будем рассматривать как
время, соответственно этому о) — как некоторую частоту. Будем, далее,
рассматривать Ф как скалярный потенциал, создаваемый электрическйми
зарядами, распределенными в пространстве с плотностью
p(r, jf) = p0(r)eto/. (74.13)
Из электродинамики известно, что потенциал удовлетворяет уравнению
Даламбера
(74.14)
где с — скорость распространения электромагнитных волн. Решение
уравнения (74.14) известно: именно, если брать волны, излучаемые
зарядом p(r',/)flto' (dv'~ dx’dy’dz1), расположенным в точке г', то.
*) См. (50.3). Остальные компоненты в поле центральных сил будут
равны нулю [Л (0) действительно!]. Заметим еще, что если бы в (74.7) мы взяли
е+ikr вместо e~tkr, то мы получили бы сходящийся поток.
**) Мы будем, кроме тогр, предполагать, что V(r) убывает с расстоянием
быстрее, нежели —(см. примечание в § 46 на стр. 138). Матричный элемент
V(г) будем считать конечным, так что из изложенного в § 72 следует, что
спектр Е останется непрерывным.
§74] РАСЧЕТ УПРУГОГО РАССЕЯНИЯ МЕТОДОМ БОРНА 255
электрический потенциал в точке г в момент времени t равен
Гр(г-
ф (г> /) = J х |Г>_Г|'~—7 (74.15)
где | г1 — г | есть расстояние от точки г', где расположен заряд
до точки наблюдения г. Подставляя в (74.15) Ф из (74.12) и р из
(74.13) и сокращая на eiwt, получаем:
Г -Z~|r'-r|
Фо(г) = уо(Г}^—.q------dv'. (74.16)
Если мы подставим в уравнение Даламбера Ф (74.12) и р (74.13) и со-
кратим на то получим:
¥*Ф0 + ^Ф0=-4"Р0. (74.17)
Сравнивая это уравнение с (74.11), мы видим, что (74.11) и (74.17)
совпадают, если положить
Фо = «, ^ = k, Po = iw°. (74.18)
Отсюда на основании (74.16) заключаем, что
есть решение уравнения (74.11). При этом у нас уже автоматически
учтено, что и содержит лишь расходящиеся волны, так как решение
(74.15) есть решение для излучаемых, а не «всасываемых» зарядами волн.
Найдем теперь вид zz(r') вдали от атома А. Для этого обозначим
единичный вектор в направлении падающего пучка (ось OZ) через п0>
а единичный вектор в направлении вектора г через и. Преобразуем
сначала | гг — г|. Из треуголь-
ника, приведенного на рис. 52,
имеем:
г' — г |3 = г2 —J— № — 2 (иг) г,
где г=|г|, / —|г’|. Отсюда
для г г1 получаем?
1г' —г| =
= г—(пг')4-о(<-), (74.20)
где О (~} означает члены по- Рис. 52. Пояснение к выбору векторов
г п, п0 и т. д.
рядка - и выше.
Подставляя | г' — г| из (74.20) в (74.19) и пренебрегая еще в зна-
менателе величиной пг’ по сравнению с г, мы получаем выражение
256
ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА
[ГЛ. XIV
для и, справедливое для больших расстояний г от атома *):
а (г) — — 1?^ je-«*"r'y(r')<|>o(r')rft>'. (74.19')
Подставляя сюда ф° (г') из (74.5) и имея в виду, что гг —г'п0, мы
получаем:
«(г)~ —e~ik (п“По) r'V(r')dv'. (74 21)
Сравнивая (74.21) с (74.7), мы видим, что амплитуда рассеянной волны
равна
А — — ~ Je'* <“»-»> r,K(r')rf»’. (74.22)
Введем вектор
К = £(п0 —п), Л"=&|п0 —п| —2&sin у = у sitiy . (74.23)
Тогда, имея в виду (74.3), получаем:
А (9) = - i If eiKr'U(r') dv', (74 24)
т. e. амплитуда рассеянной волны пропорциональна компоненте Ф^рье
в разложении потенциала по плоским волнам е^г. Подставляя это зна-
чение Л(0) в (74.10), находим эффективное сечение:
= (ЙГ [J (74 25)
Эта формула, как следует из ее вывода, приближенна. В теории стол-
кновения это приближение (первое приближение теории возмущений)
обычно называют борцовским. Мы не можем входить подробно в вопрос
о точности борновского приближения и пригодности его в тех или
иных случаях *♦). Укажем лишь на то, что интенсивность рассеянной
волны |«(Г)р вблизи рассеивающего центра должна быть мала
в сравнении с интенсивностью волны падающей |ф0(г)]2. Из форму-
лы (74.15) легко оценить отношение |zz|2 к | ф012> взяв значение этих
функций в центре атома (Jr — 0). Считая, что силы — центральные,
так что V{rf)= У(г!), и полагая в (74.15) г = 0, dv9 =/2dr'cosO'dQ'd(p\
kr1 = kr' cos 6’, после элементарного интегрирования по углам 6 и у
находим
(74.26)
При k—>0 интеграл справа стремится к 0. Поэтому при достаточно
большой энергии частицы (большое £) метод Борна будет всегда
пригоден. * **)
♦) Т. е. для где а—радиус сферы действия.
**) См, Мотт и Мэсси, loc, eft.
§75] УПРУГОЕ РАССЕЯНИЕ БЫСТРЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ 257
§ 75. Упругое рассеяние атомами быстрых заряженных частиц
Полученная нами формула для дифференциального эффективного
сечения применима для расчета упругого рассеяния достаточно бы-
стрых частиц. Далее наш вывод неявно предполагал, что атом и до
удара, и после удара покоится. Если скорость падающих частиц велика,
а скорость атома до удара есть тепловая скорость, то последней можно
пренебречь. Пренебречь же скоростью после удара можно лишь в том
случае, если масса сталкивающейся частицы р много меньше массы
атома М. Предполагая, что все эти условия соблюдены, вычислим рас-
сеяние частиц с массой р и зарядом ev Обозначим через—£р(г") =
— — ер (/') плотность электрического заряда, создаваемого роем элек-
тронов атома в точке г" (предполагаем сферическую симметрию р),
а через Z — атомный номер. Тогда электрический потенциал в точке г
будет
.. Ze r?(r”}dv"
gj > (75-о
а потенциальная энергия частицы в таком поле будет равна
гт/ \ / \ %еех С? (г") du” m
/7(г) = (г) = —1 — eet J |Г„_Г| > (75.2)
Подставляя это значение U(r) в (74.24), мы получаем:
А (0) = — Г f eiWdv' f . (75.3)
v ’ Л2 4к J ? 1 /г2 4к J J |г" — г ’ | v 7
Входящие сюда интегралы рассмотрим порознь. Для этого заметим, что
интеграл
Г р*Кг'
<75-4)
может рассматриваться как потенциал, создаваемый в точке г" электри-
ческими зарядами, распределенными в пространстве с плотностью
р (г') = е‘Кг'.
Потенциал ср (г') удовлетворяет уравнению Пуассона:
(Г') = _ 4тгр (Гг) = — 4пе/Кг'. (75.5)
Из этого уравнения сразу находим ср (гг):
?(r')=7lqr. |К|2=/^+^+^. (75.6)
Из сопоставления (75.4) с первым интегралом в (75.3) следует, что
С./Кг' С е‘Кг' 4«
л=J V - J ти w • (757)
17 Блохинцев
258 ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [гл. XIV
Для второго, двойного интеграла получаем:
/, = f <,.»*' J "
= J ^'P(r")^p- = |-^-3 Jrfwp(r)e'Kr. (75.8)
Для выполнения интегрирования в (75.8) возьмем полярную систему
координат с полярной осью, параллельной К, тогда
dv = г2 dr sin 6 dft dtp, Кг = Kr cos 6.
Получаем:
оо 2я тс
J dvp (г) е/Кг = J р (г) r2dr J dtp J elKr cos esin 0 tZO.
0 0 0
Вводя переменную cos 0 — В, легко выполняем интегрирование по В и ср
и получаем:
J dvp (г) ezKr = р--p(r)r2rfr. (75.9)
b
Подставляя (75.9) в (75.8) и (75.7) в (75.3), мы находим окончательное
выражение для Л (6):
л<0)= (75ло>
о
Имея в виду, что
К2 — 4k2 sin2 ~ sin2 у ,
где v — скорость частицы, и обозначая
/=’(0) = 4тг [5^2-3 р (г) А/г, (75.11)
J А Г
о
находим окончательно:
Л(0) = ^ {^-F (0)} cosec2 4 . (75.12)
Величину F(0) называют атомным фактором. Эта величина, как мы
видим, определяет рассеяние электронов по углам. Заметим, что эта же
величина определяет и рассеяние рентгеновских лучей.
Из (75.12) находим дифференциальное эффективное сечение для
упругого рассеяния электронов с энергией Е в область угла 0:
?(0) = 4^{Z-F(0)}2cosec^. (75.13)
§ 75]
УПРУГОЕ РАССЕЯНИЕ БЫСТРЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ
259
Чтобы эта формула стала более конкретной, сделаем простое предпо-
ложение о плотности ер заряда электронного роя. Именно, предположим
(чго соответствует выводам квантовой механики), что р экспоненциально
спадает с увеличением рассеяния от центра атома:
Р=РО* °,
где а—«радиус» атома. В целом атом нейтрален, поэтому
(75.14)
(75.15)
Z п
отсюда находим Следовательно,
Р 8яа3 е
(75.16}
Вычислим теперь атомный фактор:
^(6)===4те J р (г)
®° е
о
легко вычисляется:
r2dr =
о
где £ — Кг. Последний интеграл
оо__________со _
г
о
Отсюда
Ка^-е~^=^-2.
7
l_j_X2a2
О ’
1 4Z?2a2sin2
(75.17)
о
Z
и, следовательно,
1
4 ' 4p2t^ I
2 1 в
-г I cosec4
14-4A2^2sin2_y
(76.18)
Для быстрых частиц Aj#|>1, поэтому в (75.18) для не слишком малых
углов рассеяния можно пренебречь вторым членом выражения в скобках
по сравнению с единицей. Тогда получается:
, о
а (0) = л 9 — cosec4
(75.19)
Эга формула в точности совпадает с формулой для упругого рассеяния
частиц с зарядом е и массой |Л в кулоновском поле ядра с зарядом Ze.
Впервые эта формула была получена Резерфордом еще на основе
классической механики.
Совсем иной результат получается для малых углов рассеяния. В те
время как из (75 19) при 6 = 0 получаем #(0) = оо, из (75.18) сле-
дует, что при 6 = 0 7(0) = const.
17г
260 ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ НЕПРЕРЫВНОГО СПЕКТРА [ГЛ. XIV
То обстоятельство, что для больших углов рассеяния рассеяние по-
лучается таким, как в кулоновском поле голого ядра, может быть на-
глядно истолковано таким образом. Большие отклонения получаются за,
счет частиц, пролетающих близко от ядра, благодаря чему на них поле
роя электронов не действует. Малые отклонения получаются, напротив,
мри далеких пролетах частиц. В этом случае заряд ядра почти полностью
экранируется отрицательным зарядом электронного роя. Тогда поле
очень сильно отличается от кулоновского.
А. Рассеяние а-частиц
Рис. 53. Рассеяние а-частиц при прохожде-
нии золотой фольги в 0,001 мм толщиной.
Сплошная кривая изображает q (9) в полярной диа-
грамме. Числа на лучах дают наблюденное число
рассеянных частиц. О А — направление падающего
пучка
Для а-частиц заряд е1=-]-2е, масса p = 4jiH =6,64-10~24 г, где
gH — масса атома водорода. Если атомный вес атома А гораздо боль-
ше 4, то мы можем непосредственно применить наши формулы к рас-
чету рассеяния а-частиц атомами, а-частицы, излучаемые радиоактив-
ными элементами, имеют скорость v 109 см)сек. Поэтом^ из (65.4)
получаем волновое число &=^1012 — Размеры атома а=^10“8 см.
Сл&мяйпельпо, ka 104, так что вплоть до очень малых углов
(sin у 10”4—10~5)мож-
но пользоваться формулой
(75.19) вместо (75.18). Таким
образом, для а-частиц имеем:
?«(°)==^cosec44 <75-2°)
(длч sin-^>-i). На рис.
53 изображено число рассеян-
ных а-частиц для разных
углов 0 при рассеянии на
золоте.
Как уже упоминалось, фор-
мула (75.20) была впервые по-
лучена Резерфордом из классической механики путем рассмотрения гипербо-
лических орбит а-частиц в кулоновском поле атомного ядра. Эта
формула послужила в свое время ключом к открытию ядерной струк-
туры атома *) и носит название формулы Резерфорда. Так как вплоть
до самых малых углов 0 экранирование заряда ядра роем электронов
не играет роли (F(0) 0), то формула (75 20) есть квантовая формула
для рассеяния а-частиц в чисто кулоновском поле точечного заряда Ze.
Таким образом, рассеяние в кулоновском поле оказывается одинаковым
ио квантовой и по классической механике **).
sin
См. классическую книгу Э. Резерфорд, Строение атома, ГИЗ, 1923.
**) Формула (75.20) получена нами в борновском приближении и для
у . Формулу для рассеяния в кулоновском поле можно получить точно
§75] УПРУГОЕ РАССЕЯНИЕ БЫСТРЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ 261
В. Рассеяние электронов
Для электронов ;л=10“27г, так что борцовское приближение при-
менимо лишь для электронов с энергией в несколько сот электрон-вольт.
Для 500 eV скорость электронов v = 1,3 • 109 см^ек, k — 1,3 • 109 сл""\
т. е. ka 1. Поэтому пренебрегать атомным фактором в (75.18) нельзя.
Эффективное сечение #(0) в этом случае равно
^(0) = 4^{Z-F(0)}2cosec4|- (75.21)
На рис. 54 изображены кривая рассеяния электронов в Не, вычисленная
теоретически, и результаты измерений Даймонда.
Весьма замечательным обстоятельством является возможность опре-
делить из наблюдений над рассеянием электронов распределение элек-
трического заряда в атоме. В самом деле, наблюдая рассеяние электронов
для разных скоростей v и углов 0, мы получаем ^(в)—дифференциальное
эффективное сечение, а из (75.21) находим тогда атомный фактор F(ty>
который есть функция числа К=~ sin[см. (75.11)]. Соответственно
этому будем рассматривав F как
функцию /С. Из (75.11) имеем:
K-F{K) __ * 71
' 4я
= j sin (Кг) • р (г) г dr. (75.22)
о
Отсюда по теореме Фурье по-
лучаем*
4тгг2р (г) =
= -\K-F(K)&m(Kr}-dK (75.23)
71 о
[причем мы воспользовались тем,
что K-F(K) есть нечетная функ-
ция К]-
Определяя' атомный фактор
F(K) из опыта, мы находим из
(75.23) р(г). Величина р(г) есть
средняя плотность электрического
заряда в атоме, создаваемого роем
Рис. 54. Упругое рассеяние в гелии
(по Мотту).
А — теоретическая кривая с атомным полем
Хартри, В — резерфордовское рассеяние; С—
рассеяние рентгеновского излучения такой
же длины волны. Крестики — намерения
Дайцонда.
электронов. Таким образом, эта вели-
(см Мотт и Мэсси, Теория атомных столкновений, ОНТИ, 1936, гл. ИI).
Оказывается, что она точно и для всех углов совпадает с резерфордовской
формулой. В случае одинаковых частиц, например, рассеяние а-частиц в Не,
квантовая, механика дает иной' результат. Опыт подтверждает в этом случае
вывод квантовой механики (см. Мотт и Мэсси, loc. cit., § 4 и § 4,1).
262
ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ
[гл XV
чина может быть получена из опыта. С другой стороны, эту же величину
можно вычислить теоретически, так как вероятность того или иного
положения электрона в атоме определяется через волновую функцию
Рис. 55. Плотность электрического за-
ряда в Не (4ярг2) в функции расстоя-
ния г.
1—по рассеянию электронов; 2—по рассея-
нию рентгеновских лучей; 3 — теоретическая.
рая получается из волновой функцг
совпадение максимумов иэкспоненц
| ф |2. Как мы уже отмечали, атом-
ный фактор F(K) может быть так-
же определен из опытов по рас-
сеянию рентгеновских лучей. Это
опять позволяет найти р.
Весьма интересно сравнить пред-
сказание квантовой механики с
результатами опыта в отношении
такой деликатной величины, как
распределение среднего заряда вну-
три атома. Опыт превосходно под-
тверждает теорию *). На рис. 55
в качестве иллюстрации мы приво-
дим величину 4тгрг2 по измерениям
рассеяния рентгеновских лучей и
электронов в Не и теоретическую
кривую для этой же величины, кото-
ф для Не (см. § 112). Замечательно
льного спадания р при г —> оо.
ГЛАВА XV
ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ
§ 76. Постановка вопроса
Одной из важнейших задач квантовой механики является вычисление
вероятностей перехода системы из одного квантового состояния в дру-
гое. Это — как раз та проблема, которая оказалась неразрешимой
в рамках примитивной квантовой теории Бора. Вопрос о вероятности
перехода из одного квантового состояния в другое может быть обри-
сован следующим образом. Пусть известно, что в момент времени t~ О
система находилась в некотором состоянии фл(х), характеризуемом
определенным значением какой-либо механической величины L = Ltl (или,
может быть, нескольких величин А, /И, N, ...). С течением времени,
благодаря внешнему воздействию или в силу внутренних причин состоя-
ние системы может измениться. В результате к моменту t она будет
находиться в состоянии фл(х, /). Если теперь произвести измерение
величины L в этом состоянии, то, вообще говоря, мы сможем найти
любое значение А, например, L = Lm. Если мы нашли L — Lm, то го-
*) См. обзор I. Howard М с Millen, Rev. Mod. Phys., т. II, 1939,
стр. 84.
ПОСТАНОВКА ВОПРОСА
263
§ 76]
ворят, что система совершила переход из состояния с L = Ltl в со-
стояние с L — Lm. Пусть вероятность найти значение L — Lm в со-
стоянии фя(х, t) есть Так как при / = 0 7*^(0) —О для пгп
и равно 1 для т = п, то Pmn(t) называют вероятностью перехода из
состояния (х) с L = Ln в состояние4 (х) с L — Lm *).
Наиболее важными задачами из теории квантовых переходов являются
задачи на вычисление вероятности перехода из состояния с одной энер-
гией Еп в состояние с другой энергией Ет или, как говорят, вероят-
ности перехода с одного квантового уровня на другой. В связи
с этим заметим, что если частица (или в общем случае система) нахо-
дится под действием зависящего от времени внешнего поля, то понятие
потенциальной энергии, а вместе с тем и полной энергии лишено
смысла (это не относится к кинетической энергии). Поэтому в общем
случае вопрос о переходе частицы с одного квантового уровня на
другой получает смысл лишь тогда, когда причина, вызывающая пере-
ход, действует в течение конечного промежутка времени, скажем, от
t = 0 до t—T. Вне этого промежутка полная энергия является инте-
гралом движения и может быть определена путем надлежащих измере-
ний (см. §§ 102 и 103), Решение уравнения Шредингера, определя-
ющего ф(х, t) по ф(х, 0), представляет большие трудности. Резуль-
таты, имеющие общее значение, могут быть получены лишь в тех слу-
чаях, когда переходы с одного уровня на другой вызываются сла-
быми воздействиями, так что эти воздействия можно рассматривать как
возмущение.
При этом условии уравнение Шредингера может быть написано
в виде
= W(x, /)ф, (76.1)
где HQ (х) есть оператор полной энергии системы в отсутствии возму-
щения, а УУ(х, t)— возмущение. При малом W HQ(x) можно рас-
сматривать как оператор полной энергии, и поэтому в этом специаль-
ном случае включение и выключение W(x, /) приобретают второсте-
пенное значение.
Для нахождения вероятности перехода Pmn(t) с уровня Еп на уро-
вень Ет удобно написать уравнение (76.1) в «^-представлении. Раз-
ложим ф(х, t) по собственным функциям ф^(х) оператора полной
энергии Н°:
ф(х, 0==S<^«$*(*)* h ; (76 2)
k
* i — t
подставляя ф в таком виде в (76.1), умножая на §т(х)е h и инте-
*) Подчеркнем, что система сама по себе перешла не из фя(х) в Фт(х),
а из фл(х) в фл(х, t). Лишь производя измерение, мы получаем из фл(х, t\
какое-либо из состояний с определенным значением Z, например, фот(х).
264 ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ [гл. XV
грируя по х, мы получим обычным способом уравнение (76.1) в «^«-пред-
ставлении:
ih = £ Wmk (t) е^ск (/) (76 3)
k
(причем принято во внимание, что HQ<bk = Ektyk), Здесь Wmk (t) есть
матричный элемент энергий возмущения:
(0=J <*) • ™(х> i) Фл W • dx> (76-4)
Е ___Еъ
a (3>mk — боровская частота —- для перехода Ет —+ Ek, В началь-
ный момент предполагается, что система находится в состоянии Е — Еп.
Следовательно, при / — О
ck (0) 1, если k = nt и ^(0) —0, если k=^n. (76.5)
Вероятность найти систему в состоянии Е — Еть момент времени /*)
равна | ст (/) |2. Поэтому вероятность перехода из Еп в Ет к моменту t
равна
^«W = M0l2- .(76.6)
Таким образом, дело сводится к определению величин ck(t) из урав-
нений (76.3) с начальными данными (76.5).
Мы будем рассматривать W(x, t} как малое возмущение. Для реше-
ния уравнения (76.3) заметим, что если совсем игнорировать VV, то
величины ck(t) будуч постоянными. Поэтому в качестве нулевого при-
ближения для W можно взять их начальное значение (76.5):
W = bnk. (76.7)
Подставляя эти значения в правую часть (76.3), мы найдем уравнение
для первого приближения (/):
(t)
lh ~Г = Е e‘W^=Wmn V) e‘Wmnt- (76‘8)
k
Отсюда
t
c” & = И Ю e‘Wdx + (76-9)
0
Подставляя это первое приближение для c^(t) в правую часть (76.3),
мы найдем уравнение для второго приближения’
/М2) (+\
ih = £ Wmk W e‘mnAtc^ (76-1 °>
k
Так как c^(t) суть опять известные функции времени (76.9), то, ин-
*) См. § 22.
§ 77]
ВОЗМУЩЕНИЕ, ЗАВИСЯЩЕЕ ОТ ВРЕМЕНИ
265
тегрируя (76.10) по времени, мы найдем с№ (/), т. е. второе прибли-
жение. Эту процедуру можно продолжать и дальше, и она веде г к точ-
ному решению для ст (/). Однако, вообще говоря, придется брать много
приближений или ограничиваться малыми отрезками времени /. Если же-
W(x, t) мало, то достаточно ограничиться первым или вторым прибли-
жением.
В дальнейшем мы рассмотрим различные специальные случаи возму-
щений и систем.
§ 77. Вероятности переходов под влиянием возмущения,
зависящего от времени
Определим теперь вероятность перехода системы из квантового
уровня Еп в Ет под действием возмущения IF(x, /), зависящего от
времени. Допустим, что возмущение равно нулю для /<^0 и для
Считая, что Wmn(t) столь малы, что первое приближение пригодно и
для t—I\ мы получаем из (76'.8) амплитуду (/) для в виде
Т Ч-оо
с(т YR j" Ю — jfi J wmn (T) (77.1)
0 —QO
(Заметим, что для t"^>T от времени не зависят, так как энергия
есть интеграл движения )
Полученное выражение для (/) имеет простое значение. В самом
деле, возмущение W(x, t) может быть разложено в интеграл Фурье
+ QO
W(x, t)== \ W(x, a>)e-™dw. (77.2)
—сю
Отсюда по теореме Фурье получаем:
+ оо
W(x, й>) = A J* W{x, f)e,№tdi. (77.3)
— 00
Матричный элемент возмущения (76.4) на основании (77.2) может быть
написан’ в виде
J ФХ (*) • =
«= j j (X) • W(x, a) (x) • dx =
— 00 —00
+ oo
= f (77.4)
— 00
266 ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ [ГЛ. XV
где Wmn (со) есть матричный элемент компоненты Фурье частоты со.
Применяя к (77.4) теорему Фурье, находим:
Ч-оо
^=4, J Wmn(t)e^dt. (77.5)
— 00
Сравнивая это с интегралом в (77.1), мы видим, что
^ = TnW^mn)-
При этом наше приближение законно, если мало [это — необ-
ходимое условие, так как с^)(0) = 0]. Согласно (76.6) и (77.6) веро-
ятность перехода из состояния Еп в состояние Ет будет равна
4л:2
Pthn = -f^\^mn^mnW- (77.7)
Эта формула содержит важный результат. Как мы видим, Ртп^=^
только тогда, когда Wmn ((dwJ Ф 0, т. е. переход из уровня Еп в уро-
вень Е возможен лишь в том случае, когда в спектре возмущения
Е ____________________________Е
содержится частота — —з. Иными словами, переход носит
резонансный характер. Положение выглядит так, как если бы кван-
товая система • являлась совокупностью осцилляторов с собственными ча-
стотами, равными частотам Бора со tn. При действии внешнего перемен-
ного воздействия возбуждаются только те осцилляторы, частоты которых
совпадают с частотами, присутствующими во внешнем воздействии. Ниже
мы произведем важные приложения формулы (77.7) к оптическим
вопросам.
Формула (77.7) выведена для переходов в дискретном спектре. Для
переходов в непрерывном спектре она должна быть несколько видо-
изменена. Рассмотрим необходимые видоизменения для переходов из
дискретного спектра в непрерывный, считая, что система имеет и тот и
другой спектр (таков, например, спектр атомов).
Состояния непрерывного спектра характеризуются непрерывными па-
раметрами. Мы обозначим их через а, [5, у. (В качестве таковых могут,
например, фигурировать три компоненты импульса частицы рх, ру, pz.)
Пока будем явно писать лишь один из этих параметров и обозначим
его через а. Энергия будет функцией этих параметров Е = Е (а). Соот-
ветствующей волновой функцией будет Фа(л;). Тогда в (76.2) наряду
с суммой по состояниям, дискретного спектра появится еще интеграл по
состояниям непрерывного спектра (интеграл по а):
<Ь(х, t)=^lck{t)<bk(x}e h -НМОФЛ*)* Л da- • (77-8)
£ u
Считая, что функции фа (х) нормированы к 8 (а -— а1) и повторяя вы-
§77] ВОЗМУЩЕНИЕ, ЗАВИСЯЩЕЕ ОТ ВРЕМЕНИ 267
кладки, ведущие от (76.1) к (76.8), мы найдем, что
£ . Е^-Еп х
c^^ = Th\W^U Л dz, (77.9,
О
если система первоначально находилась в состоянии Еп, причем
^яЮ = 5Ф:(х)-1Г(х, t)^n{x)-dx. (77.10)
4
Дальнейшие расчеты зависят от предположений о характере зависи-
мости IF(x, t) от времени. Мы предположим, что оно монохроматично
(при переходах в дискретном спектре обязательно нужно учитывать
немонохроматичность реальных возмущений, в случае же переходов
в непрерывный спектр это не обязательно и реальное возмущение можно
считать монохроматическим). Итак, будем считать, что
1Г(х, t)=W(x)e^+W*(x)e-1^. (77.11)
<77-12)
где 1Гад и W* суть матричные элементы компонент Фурье от W(x, t).
Подставляя (77.12) в (77.9) и интегрируя по времени, мы находим:
-г[Е (а)—+ М t
1 eh — 1
А цу ---------------1
ih а« /
-L[£(a)-^ + ^]
- (Г (а) — En—hu}
1 eh — 1
ih W an i *
-[£(а)-£д-Ь>]
Так как o^>0, £'(a)^>0, £я<^0, то первый член мал, а второй
велик для E\ti} = En-\-h®. Поэтому мы ограничиваемся вторым членом
и получаем для вероятности перехода из Еп в интервала, аЦ-^акмо-
менту времени t\
К12^=|ад ~[Е («)-£в-Йи>]< е — 1 (77.13)
i [F («) - Еп - Ы]
Вероятность же перехода из Еп в a, a-\~da в 1 сек. равна
sin /t^(q)—
р fa. — dn — 2 I IT I2____________J_________da (77.14)
Г<таа — dt аа ~2 I W*n I ^(а) ——Ь) V 7
Последний множитель в (77.14) для больших^/отличается от S-функции
только множителем у. Поэтому вероятность P^da можно написать
в виде
P„(a)rfa=J|<|4[f(a)-5„-fta>]da. (77.15)
268
ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ
[ГЛ. XV
Если состояние непрерывного спектра характеризуется несколькими
параметрами а, р, у, то подобным же образом получим для вероятности
перехода из состояния Еп в область a, a-{-da\ 0, Y» Y~b^Y
в 1 сек.:
РЛ(а, Р, y)rfatZpafy =
О ip
= -'| W^Tj„|2 8[£(а, ₽, Y)-^-A®]rfa^rfy. (77.16)
Нетрудно также получить вероятность переходов в непрерывном
спектре. Именно, беря начальное состояние фао9оТо [т. е. £а^(0) =
= § (а — а0) § — ?о) (Y — Yo)3> аналогичным путем получим для вероят-
ности перехода в 1 сек. из а0, ^0, у0 в интервала, a-{-da; р,
х> y+^y:
^о3от.(а’ =
=4“| М)-£(«о> K^-h^dad^d^. (77.17)
Эти формулы показывают опять-таки резонансный характер перехода,
так как найденные вероятности отличны от нуля лишь для переходов,
для которых
Л<о = £(а, У)-^в=^,а (77.18)
или
й<о = Е(а, Р, Y) — Е[а0, 0О, = воМо, (77.18')
т. е. частота внешнего воздействия равна частоте Бора для воз-
можного перехода.
В точке резонанса вычисленные вероятности обращаются в беско-
нечность. Одрдко, по соседству с этой точкой они равны нулю*). Поэтому
вероятность перехода в сколь угодно малый интервал энергий, содер-
жащий точку резонанса, получается конечной. Чтобы в этом убедиться,
достаточно взять вместо параметров а, р, у, нумерующих состояния
непрерывного спектра, какие-либо новые параметры, в число которых
входит энергия. Пусть это будут параметры Е, а} Ь. Они суть функ-
ции у. Имеем:
dad$d4 = $(E, a, b)dEdadb. (77.19)
р(£, а, Ь) называют плотностью состояний на интервал энергии»
на интервал а» на интервал Ь.
Подставляя это значение da, d$, dy в выражение для вероятностей
(77.16) или (77.17) и интегрируя по Д, мы получим нуль, если интер-
вал интегрирования не содержит сточки резонанса, и конечное число,
если содержит эту точку. Именно, из (77.16) и (77.17) получаем*
P„(E, a, b)dadb = ^\ WEabn\^(E, a, b)dadb, (77.20)
a, b)dadb=%\ WEabM\^(E, а> b)dadb, (77.21)
*) Это не совсем точно, так как согласно (77.14) мы имеем дело лишь
с приближением к 8-функции, а не саму 3-функцию. См. § 102.
§ 78]
ВОЗМУЩЕНИЕ, НЕ ЗАВИСЯЩЕЕ ОТ ВРЕМЕНИ
269
причем здесь разумеется то значение £*, которое следует из условий
резонанса (77.18) или (77.18') соответственно.
В частном случае, когда за параметры a, у взяты три компоненты
импульса частицы рх, ру, pz, целесообразно рассматривать импульс ко-
нечного состояния в полярной системе координат /?, 0, ср. Тогда имеем
dpxdpydpz-=p2dp dQy dQ — sin 0 d0 dy. (77.22)
Энергия частицы
Л 2
есть Е=*~, так что p2dp —р2 dE — \ip dE.
Внося это в (77.22) и сравнивая с (77.19), находим*
р (f, 0, <p) = p(F)sinO, p(£) = gp=^-(2g)3^V.. (77.23}
Подставляя это в (77.20) и (77.21), находим:
Рп (Е, О, Ф)dQ = % | 1Г£9тя |2 р (£) dQ, (77.24}
9-
О, WE^I2p(E)dQ. (77.25)
Эти формулы дают вероятность перехода в 1 сек. из состояния п или
а0, р0> То в состояние с энергией Е, причем импульс частицы попадает
в телесный угол dQ.
§ 78. Переходы под влиянием возмущения, не зависящего
от времени
Если возмущение не зависит от времени, то мы можем искать ста-
______________________/5* /
ционарные решения ty(x)e Л уравнения Шредингера и, следова-
тельно, свести задачу к решению уравнения
W(Х) ф (Х) = £ф (х)>
методы приближенного решения которого были уже рассмотрены. Однако
можно ставить вопрос и в духе теории квантовых переходов. Обе
постановки вопроса эквивалентно ведут к одним и тем же результатам *).
Чтобы получить вероятность перехода под влиянием возмущения,
не зависящего от времени, достаточно в формулах (77.16) и (77.17)
положить со = 0. Тогда условия (77.18) и (77.18') гласят:
Е(а, р, y)=:F„ или Е(а, ₽, ^) = Е(ай, р0, Ь), (78.1)
т. е. переходы возможны лишь без изменения энергии. Это следует из
общей теории, так как энергия в рассматриваемом случае есть инте-
грал движения. Следовательно, переходы под влиянием возмущения, не
зависящего от времени, могут быть лишь такого рода, что происходит
*) Ср. § 103, где рассмотрено столкновение методом переходов с § 74,
где та же задача решена методом стационарных состояний.
270 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
перераспределение энергии между частямй системы или изменяются
какие-либо другие механические величины (например, направление им-
пульса частицы).
В непрерывном спектре формула для вероятности перехода в 1 сек.
из состояния E(aQ, £0, у0) в состояние £*0, a, a-\-~da; b, b-\-db на
основании сказанного получается прямо из (77.21):
b)dadb, (78.2)
и если взять за а, р, у импульсы, то
... 8, «)</а= 2Г'| ^р.р.р. !"р(Е«)Й. (78.3)
Эти формулы совпадают по виду с (77.21) и (77.25) и отличаются от
них лишь резонансным условием (78.1), выражающим закон сохране-
ния энергии.
Заметим, что в случае не, зависящего от времени возмущения не
Имеет большого смысла рассматривать переходы только между дискрет-
ными состояниями, так как условие равенства энергий начального и
конечного состояний в этом случае может соблюдаться лишь в исклю-
чительных случаях.
ГЛАВА XVI
ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА
АТОМНЫМИ СИСТЕМАМИ
§ 79. Введение
Вопросы, связанные с проблемами взаимодействия света и микро-
частиц в их полном объеме выходят за рамки квантовой механики. Они
не могут быть рассмотрены без привлечения дополнительных принципов,
касающихся законов возникновения и исчезновения электромагнитного
поля. Однако, мы можем продвинуться довольно далеко, опираясь на по-
луфеноменологическуютеорию излучения Эйнштейна, существенно базирую-
щуюся на законах сохранения энергии и импульса при взаимодействии между
квантовыми системами и полем электромагнитного излучения. В самом деле,
поведение квантовой системы в заданном электромагнитном поле вполне
входит в круг механических задач. Поэтому мы можем, опираясь на
теорию квантовых переходов, вычислить вероятность того, что под
влиянием падающего света атом перейдет в возбужденное состояние
или, напротив, из возбужденного в более низкое. В первом случае энер-
гия атома увеличится на величину Ет— Еп, если Еп — энергия исход-
ного состояния, а Ет — энергия возбужденного, во втором — на эту же
величину уменьшится. Рассмотрим сначала первый процесс.
§ 79]
ВВЕДЕНИЕ
271
Если мы будем считать, что добавочная энергия атома Ет— Еп займ*
ствована от электромагнитного поля, то тем самым вероятность перехода
атома из состояния Еп в Ет мы отождествляем с вероятностью погло-
щения порции энергии света, равной Ет — Еп, т. е. как раз с той ве-
личиной, которая фигурирует в теории Эйнштейна (вероятность погло-
щения кванта света). Чтобы это отождествление было возможно (не
противоречило квантовой механике), необходимо, чрэбы переход атома
из Еп в Ет был возможен лишь в том случае, когда разность энергий
Ет—Еп равна энергии кванта действующего света /до, т. е. когда
соблюдено условие частот Бора
h® = Em — Еп. (79.1)
Из теории квантовых переходов мы знаем, что это как раз имеет место,
так как переход Еп—+Ет возможен лишь тогда, когда в спектре
Е — Е
внешнего воздействия присутствует частота <0 = -^-^—? = (!>тл. В на-
шем случае это означает, что в спектре падающего света должна со-
держаться эта частота, иными словами, должны иметься кванты света
с энергией
s = hv = Em-En. (79 2)
Более того, мы знаем, что переход Еп —* Ет целиком осуществляется
той частью возмущения, которая гармонически зависит от времени
с частотой <йтп. Таким образом, если мы представим себе, что падаю-
щий свет разложен на совокупность монохроматических волн, то пере-
ход Еп —► Ет полностью реализуется за счет той волны, которая имеет
частоту (дтп и соответствующие кванты e = h(j)mn.
Переход атома под влиянием света из возбужденного состояния Ет
в низшее Еп, если опять применять закон сохранения энергии, нужно
будет рассматривать как излучение кванта света е = Ет — Еп. Вероятность
этого перехода мы также можем вычислить. Она будет совпадать с ве-
роятностью вынужденного излучения в теории Эйнштейна (вероятность
излучения под влиянием излучения).
Мы не можем, однако, в рамках механики рассматривать третий
процесс — спонтанное излучение атома, происходящее и в отсутствии
внешнего воздействия — в отсутствии, следовательно, падающего света.
Если атом находится в возбужденном состоянии в отсутствии внешнего
воздействия, то квантовая механика утверждает, что он будет сколь
угодно долго находиться в этом состоянии. Состояния с определенной
энергией, как мы знаем (§ 30), стационарны, а энергия есть интеграл
движения. Между тем опыт показывает, что атом сам собой будет пере-
ходить в нормальное состояние, излучая свет.
Это противоречие не должно вызывать удивления. Мы с самого
начала рассматриваем чисто механическую проблему: движение электрона в
заданном внешнем поле (например, в электростатическом поле ядра) и не
учитываем того обстоятельства, что движущийся электрон создает электро-
272 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
магнитное поле, которое действует и на него самого. Короче говоря,
мы игнорируем обратное действие поля электрона на самый электрон.
С такого же рода положением мы встречаемся и в классической
механике Если мы рассматриваем движение заряженной частицы, например,
црд влиянием квазиупругой силы, то мы получим ответ, что частица,
имевшая в начале энергию Е, будет сохранять это значение энергии
и в дальнейшем. Если же мы учтем, что заряженная движущаяся частица
создает электромагнитное поле, которое действует на нее, то мы обна-
ружим, что частица на самом деле будет терять свою энергию — излу-
чать свет. Классическая теория дает, как известно *), следующую формулу
dE
для энергии излучаемой в 1 сек. частицей, гармонически колеб-
лющейся с частотой <о0 и обладающей электрическим моментом Вкл:
тде (Окл>)2 означает среднее по времени от (DKJI )2. Обратное действие
этого излучения тормозит частицу, так что она постепенно останавли-
вается.
Эта задача об излучении с учетом обратного действия выходит по
существу за рамки механики, относясь уже к электродинамике. В этой
книге мы не предполагаем касаться проблем квантовой электродинамики,
далеких еще от полного решения **). Мы обойдем этот пункт, постули-
руя, в соответствии с теорией Эйнштейна, что такое спонтанное излу-
чение существует.
Имея возможность на основе квантовой механики вычислить вероят-
ность поглощения света, ^ы, опираясь на устанавливаемое в теории
Эйнштейна универсальное соотношение (5.11) между вероятностью по-
глощения и вероятностью спонтанного излучения, сможем вычислить и
эту последнюю величину. Нам теперь остается только реализовать эту
программу.
§ 80. Поглощение и излучение света
Для решения задачи о поглощении или излучении света согласно
изложенному в предыдущем параграфе нам следует подсчитать вероят-
ность перехода атома с Одного квантового уровня на другой под дей-
ствием падающего света. Для этого следует прежде всего определить
взаимодействие оптического электрона в атоме со световой волной.
Предположим, что мы имеем дело с поляризованным светом, эле-
—>
ктрический вектор которого есть $ (х, /). Помимо электрического поля
имеется еще и магнитное Ж (х, 0, однако, действием последнего на
*) См, например, Тамм, Основы теории электричества, ОНТИ, 1934»
ч. II, стр. 243.
**) Квантовая теория излучения дает возможность обосновать ^теорию
Эйнштейна. См. по этому поводу’ книги Дирак, Основы квантовой меха-
ники, ОНТИ, 1937, и Гайт л ер, Квантовая теория излучения, ГИТТЛ, 1940.
§ 80] ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА 273
электрон в сравнении с действием электрического поля можно прене-
бречь #). Действие электрического поля существенно различно, смотря
по тому, меняется заметным образом поле <§ (x,t) на протяжении
атома или нет. Легко дать критерий, по которому можно различить эти
два случая. Пусть падающий свет монохроматичен (или почти монохро-
матичен) и имеет длину волны, равную к. Тогда электрическое поле
<§ t) равно
^(x,f) = ^ocos((o0< — (80.1)
/ 2яс\ т_т
|(оо=—1. Нас, разумеется, интересует поле не во всем пространстве,
а только внутри атома. Пусть размеры атома равны а *) **). Возьмем начало
гп 2ях
координат в центре атома. Тогда в пределах атома фаза волны -у- ме-
, 2тш
няется на величину порядка Ч—и если размеры атома гораздо меньше
длины волны падающего света, то изменением фазы внутри атома можно
пренебречь, так что в каждый момент времени поле внутри атома может
быть описано выражением
S(x,t) = So cos (“</) (80. Г)
и, следовательно, одинаково во всех точках пространства внутри атома.
Условие малости размеров атома в сравнении с длиной волны соблю-
дается в очень широких пределах. Достаточно, чтобы Х5>> 10~8 см
10~8 см). Ультрафиолетовый и видимый свет имеют длины волн,
в тысячи раз большие 10~8 см, так что условие для такого света
вполне соблюдено. Иначе обстоит дело в области рентгеновских лучей,
так как в этой области длина волны далеко не всегда превосходит
размеры атома***). Задача о действии таких лучей в этом случае сложнее
*) Сила, действующая на электрон со стороны магнитного поля, есть сила
Лоренца
F=7[V^].
где v — скорость электрона, с — скорость света. Сила действия электричес-
кого поля есть е<§. В световой волне и одинаковы, поэтому действие
магнитного поля в — раз меньше. Скорости электрона в атоме в 100 раз
меньше с, поэтому магнитное действие в 100 раз слабее.
**) а есть радиус области, где волновые функции заметно отличаются от 0.
***) qacT0 интересуются действием рентгеновских лучей на внутренние
электроны (Л>оболочка) Размеры /С-оболочки для элементов с большим атом-
ным номером гораздо меньше оболочки, образуемой внешними электронамиг
Это позволяет расширить область длин волн, для которых можно пренебречь
изменением фазы поля.
18 Блохинцев
274 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
Мы начнем с рассмотрения первого случая, когда длина волны гораздо
больше размеров атома. При этом мы освободимся от частного пред-
положения о монохроматичности света, считая все же, что фигурирующие
в спектре длины волн велики в сравнении с размерами атома. Внутри
атома будет тогда действовать электрическое поле света, одинаковое
на всем протяжении атома, но зависящее от времени, обозначим его
через
S= S(t). (80,2)
При сделанных нами предположениях легко, не прибегая к общему
гамильтониану для электрона во внешнем электромагнитном поле,
определить вид взаимодействия электрона с электрическим полем света
(80.2). Поле (80.2) выводится из скалярного потенциала ср (г, t) =
— — $г = —(SХх $zz>h так что силовая функция для элек-
трона, находящегося в точке г, в этом поле будет равна
W(г, t) = — е<р = + е (Sr) = — SD, <80-3)
где D = —ет есть электрический момент электрона, если г есть радиус-
вектор, проведенный от ядра к электрону*). Вводя еще единичный
вектор 1, параллельный направлению поля $ (£) = 1.$ (/), мы можем на-
писать (80.3) в виде
IT (г, /)=—<£(/)• (1D). (80.4)
Если через /7° обозначить оператор полной. энергии электрона, то
уравнение Шредингера для волновой функции ф(г, t) будет
г-Л^=Я»ф + Г(г, Оф. (80.5)
Величину W (г, t) будем рассматривать как возмущение, что оказывается
возможным при всех практически достижимых интенсивностях света**).
Мы поставим теперь задачу вычислить вероятность перехода атома
под влиянием светового поля из квантового уровня Еп (ф = фл) в квантовый
уровень Ди(ф = ф/и). Для того, чтобы можно было полностью применить
к этой задаче теорию квантовых переходов, развитую в § 77, мы
сделаем предположение, что поток света начал действовать в момент
времени t = 0 и был прекращен в момент времени t=T. Если Т
гораздо больше периода колебаний световых волн, то такое включение
и выключение не повлияет на спектральный состав падающего света.
*) Направление электрического момента считают от отрицательного заряда
к положительному, а вектор г направлен обратно: от положительного ядра
к отрицательному электрону.
**) Так, поле солнечного света равно ~ 0,1 CQSE, в то время как атомное
-> е2
поле £ равно— % 107 CGSE.
§ 80] ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА 275
Согласно (77.7) вероятность перехода Ртп из состояния Еп в состо-
яние Ет к моменту времени f, равному или большему Г, выражается
в виде
4<2 I 12
Рт = Wmri ((0^я) , (80.6)
тп ft* тп \ тп' | > \ f
где Wmn есть коэффициент Фурье для частоты ®тп от матричного
элемента энергии возмущения W(г, /). Согласно (80.4) имеем:
W = JK • ^(Г, t)t>n.dv^ -S ю-J Ф^ (1D) фя^=
= - s (0 (ID^), (80.7)
где ХУтп есть матричный элемент вектора электрического момента,
имеющий компоненты
Dmn=— |
Dmn = —6 Ф-^ФлdV' 1 (80-8)
Dmn=— e J Фт*Фл^- J
Из (80. 7) следует, что компонента Фурье от Wmn (/) равна компоненте
Фурье от $ Ю» умноженной на —ID^ (так как не зависит, от
времени). Таким образом, мы получаем, что
Wmn (®mn) =S (<%,) • (ID^), (80.9)
где через $ (<o^n) обозначена компонента Фурье от <§ (t), принадлежа-
щая частоте т. е. величина 1
тп1
-{-со 2*
S = J S (0 e-lu,mnfdt = J S (/) е~ ivimntdt. (80.10)
— оо 0
Следовательно, вероятность перехода из Еп в Ет согласно (80. 6) равна
ртп= I2 ’ ।ID™ I2- <8ол
Квадрат компоненты Фурье электрического тока | $ I2 мы можем
выразить через количество протекшей за время Т .энергии. В самом
деле, плотность электромагнитной энергии равна (знаменатель 4тг>
а не 8тг, так как имеется еще равная электрической магнитная энергия).
Поток энергии равен (где с — скорость света). Отсюда вся про-
текшая через 1 см2 энергия равна
-J-00 4"0О -}-00 4-00
£=£ J ^>2{t)dt= £- J dt J s (®)e+'loZd® J ^(й)’)е_‘‘ш'^й).(80.12>-
— 00 —CO —QO —00
*8*
276 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
Интегрируя сначала по t и замечая, что
4-оо
J —а>'),
— 00
найдем, что
Е— ^2тг J ^(й>)^*(о)')8(<о — w')d<od<o' =
—00 I
= -^J |<^(о))|2^<о=с JI <f> (а>) I2
—оо
[так как <8 (о>) = ^?* (— со) ввиду действительности ^?(/)]. Если через
£*((0) обозначить протекшую энергию ца интервал частоты afa), то
00
Е= J E(®)d(s);
о
сравнение с предыдущей формулой показывает, что
Е(а>) = с | S (ш) |2. (80.13)
Таким образом,
Ртп = S 11D«„I2 ~~• (80.14)
ТПП I тпл Q \ /
Количество протекшей энергии £(to) равно, очевидно, плотности лучистой
энергии р (to), на интервал частоты dto, умноженной на скорость света и
время протекания энергии Т, т. е.
Е (to) = p(to)cT. (80.15)
На основании (80.14) и (80.15) мы можем определить вероятностьр тп
перехода из состояния Еп в Ет в единицу времени. Для этого нужно
разделить Ртп на время, в течение которого действует свет, т. е. на Т:
Р
л = Стп
Ртп р •
)
С помощью (80.15) находим, что вероятность перехода в единицу
времени будет равна
Pmn=4^|lDmn|2p (%„).- <80Л6)
Обозначив еще угол между вектором электрического^ момента Dmn и
направлением поляризации светового поля 1 через 0^, мы получим
окончательную формулу для ртп в таком виде:
Ртп= Wcos20ro„p(«>m„). (80.16')
§ 81] СВЯЗЬ С КОЭФФИЦИЕНТАМИ ЭЙНШТЕЙНА 277
Из этой формулы мы видим, что для вычисления вероятности пере-
хода достаточно знать матрицу электрического момента Ътп,
целиком определяющуюся свойствами рассматриваемой атомной
системы. К этому важнейшему обстоятельству мы еще вернемся в даль-
нейшем, а теперь установим связь вычисленной нами вероятности ртп
с коэффициентами Эйнштейна, рассмотренными нами в § 5.
§ 81. Связь с коэффициентами Эйнштейна
Согласно теории Эйнштейна вероятность поглощения кванта света
h® — Em— Еп, имеющего поляризацию а и распространяющегося в
телесном угле в 1 сек. [см. (5.2)], равна
dv>a = (81.1)
Мы же получили вероятность ртп в предположении, что волна плоская,
распространяющаяся в некотором вполне определенном направлении
Соответственно этому у нас в формулу для вероятности входит лишь
спектральное распределение, а не распределение по углам. Общая связь
между ра((о) и ра(ю, Й) есть
р«(")=ур«(®- 2)^2- <81.2)
Так как ра (со) конечно, а ра (со, й) в нашем случае отлично от нуля лишь
для одного вполне определенного направления, то плотность ра (со, й)
должна в отношении угла й носить характер S-функции:
ра(со, Й) = ра(<о)8(Й). (81.3)
Интегрируя (81.3) по dQ и пользуясь (81.1), находим вероятность
поглощения в 1 сек. для волны, распространяющейся в определенном
направлении (без раствора лучей):
= (81 4>
На основании закона сохранения энергии вероятность поглощения кванта
свега hwmn должна быть равна вероятности перехода атома из состояния
Еп в Ет ,т. е. wa=pmn. Сравнивая (80.16) и (81.4), находим, что
коэффициент Эйнштейна b™t для абсорбции света равен
bm = I D,„„ I2 cos2 0m„. (81.5)
Нам нужно теперь подробнее разобраться в значении той или иной
поляризации света. Формула для вероятности перехода ртп (80.16)
получена в предположении, что свет поляризован в направлении 1,
образующем угол Qmn с направлением электрического момента Dmn.
В коэффициентах же Эйнштейна Ь™а индекс а (а = 1,2) указывает на
принадлежность поляризации к одной из выбранных за независимые
(lj или 12). Мы можем без всяких ограничений выбрать в качестве пер-
278 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
вого направления 11(а=1) направление, перпендикулярное к лучу я
лежащее в плоскости луча и вектора а в качестве второго 12 (а =2)—
направление, перпендикулярное к этой плоскости (см. рис. 56).
Полагая 1 = 1Р получаем = угде Осесть угол между
вектором поляризации Т)тп и направлением распространения поглощаемоге
излучения. Из (81.5) тогда получаем:
П = (81-5')
Полагая 1 = 12, получаем 0^ = —, т. е.
% = (81.5")
Пользуясь формулой (5.11), определяющей отношение коэффициента
спонтанного излучения к коэффициенту индуцированного излучения
Ьп =Ьт Гем. (5.7)1, мы можем
п тп пл L '
х № написать вероятность dw'r спонтан-
ного излучения кванта света Л(о =
Ч, ч = Ет— Еп в телесный угол
и поляризации а в виде
dw’==a” dQ dQ =
т/ / —-^bmdQ, (81.6)
/ / Em — Еп иг
^6 / /С ' где (0 = —- = ®тп. На осно-
/ вании (81.5) и (81.5') получаем:*
/ / / 3
///
/// ^2
/// 6 для света, поляризованного парал-
лельно 1р и
dw'r2 = V (81.7')
Рис. 56. Выбор независимых поляри-
заций (11э 12). для света, поляризованного парал-
лельно 12.
Чтобы получить полную вероятность спонтанного излучения при
переходе из состояния Ет в состояние Еп, нужно проинтегрировать
dwrl по всем направлениям распространения. Производя эту интеграцию,
получаем:
< = (81.8)
Если уровни Ет и Еп вырождены, то одна и та же частота штп может
излучаться путем различных переходов из Ет в Еп, Суммируя (81. 8)
по всем этим переходам, мы получим полную вероятность излучения
§ 81]
СВЯЗЬ С КОЭФФИЦИЕНТАМИ ЭЙНШТЕЙНА
279
частоты в 1 сек. Мы ее обозначим через
л з
(81-9)
Величину Апт называют также коэффициентом Эйнштейна для спонтан-
ного излучения частоты &тп. Наряду с А^ вводят соответствующий коэффи-
циент для поглощения изотропного, неполяризованного излучения частоты
(81.10)
4я
где сумма взята по обеим поляризациям (а =1,2) и по всем переходам из
уровня ЕЛ в уровень Ет, fn означает степень вырождения уровня Еп. Инте-
грал взят по всем направлениям распространения света. Подобным же образом
можно ввести коэффициент В" для индуцированного излучения:
В"т = 8^й dQ’ <81 1 »’>
4те
где fm — степень вырождения уровня Ет. Пользуясь свойствами ^а, и
а^ легко доказать , что
fmBnm—fnB™ Anm = h~m^ Впт. (81.11)
J т т J П п > fn ПаС" "I '
Величина определяет продолжительность жизни атома в возбужденном
состоянии.
Если к моменту времени t мы имеем Nm атомов, находящихся в воз-
бужденном состоянии Ет, то среднее число атомов, спонтанно перехо-
дящих в нижнее состояние Еп, будет за время t равно
dNm=-A”mNmdt,
откуда N —№е~Ат* — № (81.12) т т fn 1
где Т (81.13) тп ап ' ' Лт
Из этих формул следует, что хтп есть средняя продолжительность
жизни атома в возбужденном уровне Ет.
Из (81. 9) получаем:
T"‘"~4<0L2Id™!2"
3>c*h
(81.14)
Оценим эту величину для видимого света ®тп 4-1016; Ътп по
порядку величины равно — еа. где а — размеры атома, так 4To|Dmzz|^
280
ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА
[ГЛ. XVI
^2-10~18. Отсюда находим т^^Ю-8 сек., т. е. ^пп^Ттп —
= — «= Ю-is сек. *).
®тп
Вычислим теперь среднюю энергию, излучаемую в 1 сек. в элемент
телесного угла при переходе т—+п. Так как при каждом переходе
излучается энергия h®mn — Ет — Еп, то средняя энергия, излучаемая в
угол t/й, будет за 1 сек. £ обозначим ее через d j:
<8115>
а полное излучение за 1 сек. получим, интегрируя по всем углам Й:
dE 4<Л„
«“jrlD-J1- (81.16)
Как распределение излучаемой энергии по углам (81.15), так и пол-
ная энергия, излучаемая в 1 сек , совпадают с соответствующими фор-
мулами для классического осциллятора, обладающего собственной часто-
той (t)Q==:(i)mn и средним электрическим моментом:
(D^7 = 2 |D„JS. (81.17)
Кроме того, и поляризация света такая же, как у классического осцил-
лятора (именно, излучается свет лишь с поляризацией llf см. рис. 56).
§ 82. Принцип соответствия
Рассмотрим излучение заряженной частицы (заряд — e)t движущейся
«согласно законам классической механики. Для простоты ограничимся слу-
чаем одного измерения. Период движения пусть будет т0 = — . Обо-
значая координату частицы через x(t), мы разложим ее в ряд Фурье.
x(t) = ^>xkeiWkt, (82.1)
k — —оо
(i)^ = (0q^, k = 4— 1,4~~ 2,..., x^ = x_^
G)o будет основной частотой, a cak — частотами обертонов. Пола! ай
xk = \xk\e^, (82.2)
мы можем записать (82.1) в форме
X(t)= 2 21 Xk I cos (akt + (рй). (82.1')
k = i
*) Именно это обстоятельство позволяет рассматривать возбужденные
состояния атома как стационарные (по крайней мере, приближенно). См. по
этому поводу § 104.
§ 82]
ПРИНЦИП СООТВЕТСТВИЯ
281
Электрический момент частицы D пусть равен ex(t), т. е.
D(t)= +S Dke‘Wkt = £ 2 | Z)A I cos (а>А /-f" ?л)> (82.3)
ft = -oo Л = 1
где
= exk.
Интенсивность излучения частоты соЛ, его распределение в пространстве
и его поляризация определяются членом
^. = 2PJC0S(°>^ + ?^ (82-4)
Средняя энергия, излучаемая таким диполем в телесный угол //й, равна
d{c^J2 sin20dQ> (82-5)
а полное излучение равно
= 75—)2 (82.6)
dt Зсз 1 ' ’
где
ЩЛ2 = 41 Dk |2 [cos («V + Л P = 21 Dk p. (82.7)
Таким образом, мы получаем вместо (82.5) и (82.6)
d( —) =-^11 Dh |2 sin2 6 dSL, (82.5')
\ dt / 2ксЗ 1 *' ' '
Ш = |Т). I2. (82.6')
dt Зсз *1 ' 1
Из сопоставления этих формул с (81.15) и (81.16) следует, что мат-
ричный элемент электрического момента Dmn является полным аналогом
классических компонент Фурье. Эту аналогию мы можем продолжить,
если рассмотрим изменение по времени электрических моментов Отп,
взяв их в гейзенберговском представлении. Мы считали Dmn не завися-
щим от времени и зависимость от времени переноси чи на волновые функ-
ции, напротив, можно считать волновые функции не зависящими от
времени, а зависимость от времени перенести на операторы (матрицы)г
как это было в общем виде для любой механической величины пояс-
нено в § 43. Тогда мы имеем
D„a(t)=D„(O)el^=Dmie1^. (82.8)
Соответствующее представление в классической теории означает, что
временные множители е‘Шк в (82.3) мы включаем в £>Л:
Dk (t) = Dk(Q) eta>lct=Dk e‘Wkf. (82.8')
Таким образом, классически движущаяся частица в отношении излучае-
мого ею поля может быть характеризована однорядной последователь-
282 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
ностью гармонически колеблющихся диполей (82.8')^
, D2elwJ, DneiWnt, ... (82.9')
с частотами
й)1 = <оо, ф2 = 2(о0, о)и==«(о0, ..., (82.1(F)
представляющими основной тон и обертоны системы.
Квантовая же система характеризуется в отношении излучения также
совокупностью гармонически колеблющихся диполей, но образующих
гораздо более богатое4 многообразие. Именно, всю совокупность этих
осцилляторов можно представить матрицей электрического момента
п п р1^ n pi^nt
UU ••• •••
D21e',U1,/D22 ... D2„e^ ...
D(0= . . . . .......... .... (82.9)
г\ г\ ГЧ
umle Um2e ••• umne
с частотами
P ______________________________________P
(82.10)
также образующими матрицу
0 (012 ... й)1я ...
<о21 0 ... ш2и ...
(82.10")
0) , (D о ... СО . . .
ml m2 тп
Диагональные элементы Dnn (/) матрицы D (/) не зависят от времени,
так как Фяя = 0, и представляют собой средний электрический момент
атома в п-м квантовом состоянии. Недиагональные элементы опреде-
ляют излучение атома и колеблются с боровскими частотами.
Таким образом, мы приходим к комбинационному принципу Ритца,
выраженному в (81.10), согласно которому частоты атомов выражаются
Е
как разности термов , в противоположность выводу классической тео-
рии о кратности всех частот некоторой основной частоте (о0«
Еще задолго до открытия квантовой механики Н. Бором было высказано
предположение, согласно которому амплитуды классических осцилляторов De
могут служить для определения интенсивностей и поляризации излучения кван-
товых систем. Это предположение носило название принципа соответствия.
Однако, до создания квантовой механики применение этого принципа было весьма
неоднозначно и, по меньшей мере, двусмысленно. В самом деле, в теории Бора
квантовые движения представлялись как движения по квантованным орбитам.
Классические амплитуды Dn относятся к движению по какой-либо одной опре-
деленной орбите. Они будут получены, если мы разложим в ряд Фурье радиус-
вектор г(0 частицы, движущейся по n-ой орбите. Излучение же происходит
при переходе из одного квантового состояния в другое, говоря на языке ста-
рой боровской теории, при переходе с одной орбиты (п) на другую (тп). Какое
§ 83] ПРАВИЛА ОТБОРА ДЛЯ ДИПОЛЬНОГО ИЗЛУЧЕНИЯ 283
из двух движений следует разложить в ряд Фурье, чтобы получить коэффи-
циенты Фурье Dfc, определяющие излучение, — на это нельзя было дать ответа.
Однако, применение принципа соответствия к переходам на уровнях с боль-
шими квантовыми числами (п 1), сопровождающимися малыми изменени-
ями квантового .числа (| п — т | = | k | п\ было вполне рационально. При боль-
ших квантовых числах п квантовые орбиты лежат очень близко друг к другу,
образуя практически почти непрерывную последовательность классических
неквантованных орбит. Для переходов между такими орбитами, поскольку
изменение числа п мало, можно было однозначно пользоваться принципом
соответствия, считая, что интенсивность излучения определяется классическими
компонентами Фурье поскольку ввиду малого различия в w-ой и /и-ой
орбите безразлично, какое из этих двух движений подвергнуть разложению на
гармонические составляющие для определения амплитуд отдельных тонов
и обертонов, т. е. величин D^.
Существенным затруднением д^я теории Бо^а являлась невозможность
вычислить интенсивность излучения для малых квантовых чисел и для боль-
ших их изменений. В этой типично квантовой области переходов принцип
соответствия отказывался служить, и попытки распространить его и на малые
значения п вели к двусмысленным результатам, в лучшем случае позволяв-
шим сделать не количественные, а лишь качественные высказывания о харак-
тере излучения.
В предыдущем мы, исходя из теории Эйнштейна, пришли к заклю-
чению, что квантовая система поглощает и излучает, как совокупность
классических гармонических осцилляторов с компонентами Фурье электри-
ческого мрмента, равными Ътпе1^тп* • Следовательно, для вычисления
поглощения или излучения света квантовой системой нужно вычислить по-
глощение или излучение классических осцилляторов с моментами
Вычислив энергию, поглощаемую или излучаемую в 1 сек., и разделив
ее на величину поглощаемого или излучаемого кванта света h® — Em— Еп,
мы получим вероятность соответствующего квантового перехода в 1 сек.
Это утверждение может рассматриваться как современная форма
принципа соответствия *).
§ 83. Правила отбора для дипольного излучения
Может оказаться, что некоторые из электрических моментов Ътп
равны нулю. Тогда переход т —> п под действием света не реализуется,
и соответствующая частота ®тп не поглощается и не излучается, не-
смотря на то, что уровни Ет и Еп существуют. В таком случае гово-
рят о правиле отбора, т. е. о правиле, которое как бы отбирает из числа
всех мыслимых переходов Ет-^-Еп только некоторые, в действитель-
ности реализующиеся. Следует иметь в виду, что переход невозможен
лишь под действием таких возмущений W, матричные элементы кото-
рых пропорциональны Dm„. Так, например, какой-нибудь переход
*) Более подробную и общую формулировку этого принципа читатель най-
дет в статье Pauli, Handb. der Phys., XXIV, 1. Можно также показать (см.
там же § 12), что при больших квантовых числах т и п и при | k I =
~\т— п\<^т, п матричные элементы = приближенно
равны классическим компонентам Фурье’ —exk(t) =—exk(0)edw<t9 так что
старая форма принципа соответствия целиком укладывается в новую.
284 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
т л, невозможный под действием света, вполне может быть реали-
зован в результате столкновения с электроном.
Сейчас мы рассмотрим свойства матриц ХУтп для важнейших случаев
и выведем правило отбора для поглощения и излучения света.
А. Правила отбора для осциллятора
Пусть мы имеем осциллятор с массой ц, собственной частотой (о0 и
зарядом е. Квантовые уровни Еп такого осциллятора определяются
формулой
En = h^ (» + у) , га = 0,1,2,3,... (83.1)
Элементы матрицы электрического момента должны равняться
Dmn = еХтп#'*™'* = exmne‘W° > (83•2)
где хтп суть элементы матрицы координаты. В § 46 мы вычислили
матрицу координаты и нашли, что элементы ее отличны от нуля лишь
для = n + 1. Поэтому мы получаем правило отбора:
Dmn^Q лишь при /п —п-Р 1, (83.3)
а соответствующие частоты будут равны (own = (o0(/n— п) —Ч-(о0,
т. е. собственной частоте осциллятора.
Пользуясь (46 9) и обозначая DQ = exQ = e ]/^~ , мы *<ожем на-
писать матрицу £>(/) в гейзенберговском представлении в виде
0 Ойе-‘^у^ £>ое1ш»у1/2 0 0 DQe^y^ 0 ... 0 ...
D(0 = 0 О0е-'ш»Уз77 0 0 ...
. (83 4)
Таким образом, осциллятор может поглощать и излучать только
собственную частоту <о0 (так же как и в классической механике).
Установленное правйло отбора справедливо не всегда. Мы должны
вспомнить, что наши расчеты взаимодействия со светом базировались на
предположении, что длина волны света 1 гораздо больше размеров си-
стемы а. Только при этом условии взаимодействие со светом выра-
жается через матрицу электрического момента. Размеры осциллятора
определяются его амплитудой. По порядку величины она равна
Поэтому правило отбора (83.3) применимо лишь
при условии
т. е. для не слишком больших амплитуд колебания.
§ 83] ПРАВИЛА ОТБОРА ДЛЯ ДИПОЛЬНОГО ИЗЛУЧЕНИЯ 285
Следует заметить, что реальные осцилляторы при больших амплиту-
дах колебания (большие п) становятся ангармоническими, и это уже само
по себе может послужить причиной нарушения простого правила отбора.
В. Правила отбора для оптического электрона
атома
Рассмотрим матрицу электрического момента для электрона, движу-
щегося в поле центральных сил. В этом случае волновые функции ста-
ционарных состояний имеют вид
Фяйя(б 6> <f) = Rnl(r)P?(cosb)e>”4. (83.6)
Нам нужно вычислить матрицу электрического момента относительно
этой системы функций. Так как матрицы компонент электрического мо-
мента отличаются от матриц координат электрона только множителем
— е, то мы будем вычислять эти последние. Кроме того, оказывается
удобным вычислять матрицы не от х, у, г, а от комбинаций
£ = х-\-1у — гып§-е1\ = х — (у— г sin 0-6?“% С = г. (83.7)
Пользуясь функциями (83.6), получаем:
оо п 2тс
Knlm, П'1’т!= \ RnlRn’l^dr \Р” • Р»'sin® б rfOj е' dy,
о о о
оо тс 2~
n-ZW = J RniRn’l'Pdr j ppp-'sin® 6 P <P~'? ,
0 0 о
00 тс 2-t
n4,m, = j RnlRn4<r*dr J P^sm 6 cos 0 d^e‘ ? dy.
0 0 о
(83.8)
Интегралы по <p берутся, очевидно, сразу:
2n 2тс
= j cf<p = $ml> m. (83 9)
О о
Вводя обозначения
RntRnWr3clr-= Ini* nrit, (83 10)
о
j Pf P™' sin2 0 M = S’™', (83.11)
о
j P™' Sin 6 cos 6 rfO = C™', (83.12)
0
286 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
мы можем переписать матричные элементы (83.8) в виде
tri —~ (83.13)
^nlmjriViri== 2тйп1,пЧ’- '^m,iri-\-\> (83.14)
* ^m,fri> (83.15)
Эти формулы дают нам сразу правила отбора для изменения магнит-
ного числа т. Матричные элементы $ отличны от нуля лишь для iri —
= т 1, элементы 7] — для rri = пг — 1 и элементы z для rri = пг.
Таким образом, возможны лишь переходы, при которых магнитное чи-
сло пг изменяется по правилу
rri — пг = + 1 или 0.
Исследуя интегралы S™”1' и мы можем установить еще правило
отбора для орбитального квантового числа /. Для этого следует уста-
новить условия, при которых эти интегралы не обращаются в нуль.
Рассмотрим сперва интеграл Off*'. Нас интересует лишь тот случай,
когда rri = m\
С™=J ppp™ COS 0 sin 0 db. (83.16)
Вводя переменную x = cosO, получим:
у
С"[,т= \ Pft(x)-P'"(x)x-dx. (83.16')
На основании свойств шаровых функций имеем:
хР? (х) = а1тР^ (х) + Ь1тР^ (х), (83.17)
где а1т и Ь1т — некоторые коэффициенты*).
Имея в виду, что функции Р™ ортогональны между собой, и под-
ставляя (83.17) в (83.16), найдем, что Cfi™ имеет вид
ЦГ = “ьМ + М', 1-1, (83.18)
и, следовательно, С™?1 не равны нулю при f = / -+- 1.
Подобным же образом для интегралов (83.11) получаем (при
^=±=/«4- 1):
____________________________________________
£ Р”}^1 х2Р” (x)dx. (83.16*)
-1 ‘
Пользуясь формулой для шаровых функций **)
(1 _ р? {Х)=а1тР^ (х) + 1(А (83-17')'
*) См. дополнение VI [формула (30)].
**) См. дополнение VI [формула (31)].
§ 83] ПРАВИЛА ОТБОРА ДЛЯ ДИПОЛЬНОГО ИЗЛУЧЕНИЯ 287
получим, что
= 1'-Н1тЪ+1, V. (83.19)
Применяя предыдущую формулу для (1—х2)1/з (х), подобным же
образом найдем:
Sm.m-1 = ац т_^ Zr+1. (83.197
Эти формулы показывают, что S™”1' =^= 0 лишь для Г = Z -4- 1.
Таким образом, мы получаем правило отбора для орбитального
квантового числа
Г — /=±1. (83.20)
Правил отбора для радиального числа пг=п — I—1 не сущест-
вует. Последнее найденное нами правило отбора показывает, что опти-
ческие переходы (для т. е. для дипольного излучения) возможны
лишь между состояниями, являющимися соседними в отношении изме-
нения вращательного момента M2 = №l(l-\- 1).
Мы объясняли, что в спектроскопии состояние с 7=0 называют s-
термом, состояние с 7=1 р-термом, состояние с 1 = 2 tZ-термом и т. д.
Спектроскопистам было давно известно, что оптические переходы со-
вершаются лишь между s- и р-, р- и tZ-, d- и /-термами. Как мы ви-
дим, квантовая механика дает объяснение этому факту: только для та-
ких переходов электрические моменты (диполи) Dm/Z отличны от нуля.
Рассмотрим еще подрббнее правило отбора для магнитного числа т в
применении к простому эффекту Зеемана. В § 59 нами было установлено, что
квантовые уровни атомов в магнитном поле расщепляются, причем если поле
направлено по оси OZ, то a priori возможные частоты излучения опреде-
ляются из формулы (60.15):
tbnitnrfVm' = <*>о + OL (тг — т), (83.21}
где <о0 — частота в отсутствии поля Соответствующие состояниям Еп1т
функции равны (83.1) (атом в магнитном поле в первом приближении не
деформируется). Поэтому и матричные элементы Dnim, n'Vm' останутся такими
же, как и в отсутствии внешнего поля Поэтому мы можем применить к
оптическим переходам, при наличии магнитного поля, правила отбора, выве-
денные нами в предположении отсутствия какого-либо внешнего поля. На
основании этих правил следует, что возможно излучение и поглощение не
всех частот, предписываемых формулой (83.21), а только трех:
ел —если iri— т — + и со = со0, если = т. (83.22)
Это — кай раз то расщепление (нормальный триплет Зеемана), которое мы
уже обсуждали в § 60. Установим теперь поляризацию соответствующих
спектральных линий.
Для несмещенной линии (яг' = /п) отличен от нуля лишь электрический
момент по оси OZ. Следовательно, излучение несмещенной частоты обуслов-
лено диполем, направленным вдоль магнитного поля Электрический век-
тор излучения диполя лежит в одной плоскости с самим диполем. Поэтому
излучение частоты будет поляризовано так, что плоскость поляризации будет
проходить через направление магнитного поля. Для = матричные
288 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
элементы z и т) равны нулю [см. (83.13), (83.14) и (83.15)]. JHa основании (83 7)
тогда получаем:
ynlmt n4ft т 4-1 = пФ, /«4-1 % • (83.23
Подобным же образом для т1 = т — 1 получим:
“Г‘ Т
Уп1т, пЧ\ т~Л = Xnlmt пЧ\ т- 1 -е
(83.23']
Эти формулы показывают, что фаза диполя по оси OY смещена на zt ~ по
сравнению с фазой диполя по оси ОХ. Поэтому переход т—► т-]-1 со-
ответствует возбуждению колебаний поляризованных по правому, а пере-
ход т —► т — 1 по левому кругу. Соответственно этому излучение с ча-
стотой (о — tog -f- поляризовано по правому кругу, а с w — w0 — Ol — по
левому.
Таким образом, и частоты, и поляризации для простого эффекта Зеемана
согласно квантовой теории таковы же, как по классической теории Лоренца.
Преимущество квантовой теории в этом вопросе заключается в том, что она
позволяет помимо этих выводов дагь относительную (а если сформулированы
условия возбуждения, то и абсолютную) величину интенсивностей для всех
компонент зеемановского триплета ю —со0, (Ogziz'O^.
§ 84. Интенсивности в спектре излучения
Если атом находится в возбужденном состоянии (лтг), то возможен
спонтанный переход атома в низкий уровень (п) с излучением кванта
dE
света В § 81 мы получили выражение для энергии — , излуча-
емой возбужденным атомом в единицу времени (81.16). Чтобы получить
полную наблюдаемую интенсивность излучения, следует умножить эту
величину на число атомов Nm, находящихся в возбужденном состоянии (пг).
Это число зависит от условий возбуждения. Если, например, возбу-
ждение тепловое и светящееся вещество находится в тепловом рав-
новесии при температуре Г, то
_Ет
Nm — C(T)e ”, (84.1)
где С—некоторая функция температуры, зависящая от рода излучате-
лей. Если возбуждение производится ударами электронов и реализовано
равновесие, то число Мт найдется из условий этого равновесия, число
переходов в 1 сек. в возбужденные состояния под влиянием ударов
электронов должно равняться числу переходов в 1 сек. в низшие со-
стояния, происходящих благодаря спонтанному излучению и частью бла-
годаря столкновениям с электронами.
В общем случае, не уточняя вида можно написать для интен-
сивности 1тп излучения частоты о)^, вызванного переходом из состоя-
ния (т) в состояние (/г):
4<о4
I =дг_^|В I2. (84.2)
*тп /и 3 ‘ тп 1 ' '
§ 85]
ДИСПЕРСИЯ
289
§ 85. Дисперсия
Задачей теории дисперсии является расчет рассеяния света. При
взаимодействии со средой свет не только поглощается, но и рассеи-
вается, меняя направление своего распространения, а в общем случае —
и частоту.
Одной из наиболее простых задач теории дисперсии является вычи-
сление показателя преломления для газа. Согласно классической теории
поля, по известному соотношению Максвелла, показатель преломления
среды п равен ]/*е, где s — диэлектрическая постоянная. Диэлектриче-
ская постоянная в свою очередь связана с поляризуемостью среды а
соотношением £=1-|-41та так, что
(85. V
Если N—число атомов в 1 см3, а — коэффициент поляризуемо-
сти отдельного атома, то а = и, следовательно,
л2—1=4тгЛ$. (85.2)
Коэффициент атомной поляризуемости определяется из формулы
Р=Й (85.3)
где р есть электрический момент атома, a S — переменное электриче-
ское поле световой волны. Задача сводится к вычислению
В классической теории оптический электрон рассматривался как ча-
стица, движущаяся под влиянием квазиупругой силы. Соответственно
этому предположению для коэффициента поляризуемости [J получалось
выражение
(85.4)
Н ш0 —
где е — заряд электрона, pi — его масса, о)0 — собственная частота оп-
тического электрона, а а) — частота внешнего поля*). «Если в атоме
имеются электроны, обладающие различными собственными частотами <оо,
(ор (о2, ..., ... и число электронов с частотой <dk есть fk, то вме-
сто (85.4) следует иметь в виду более общую формулу
? = (85.5)
И А “Л —ю2
Число fk можно также рассматривать, как число осцилляторов в атоме,
обладающих собственной частотой (0^,. Формула правильно описывает
дисперсию в смысле зависимости [J (а стало быть, и показателя прелом-
ления) от частоты падающего света со. Однако, удивительным образом
опыт приводил к тому, что числа fk оказывались меньшими единицы.
*) См. Беккер, Электронная теория, § 25.
19 Блохинцев
290 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
Мы перейдем теперь к изложению квантовой теории дисперсии, ко-
торая приводит для когерентного рассеяния к той же формуле (85.5),
что и классическая теория. Но при этом величины fk уже не являются
числами электронов k-ro сорта, а имеют совсем другой смысл. Поэтому
мы будем называть fk иначе, а именно, согласно установившейся тер-
минологии — силой осциллятора.
Квантовая теория позволяет вычислить силы осцилляторов fk в пол-
ном согласии с опытными данными.
Задача о дисперсии света в квантовой теории может быть постав-
лена в полную параллель с квантовой теорией излучения и поглощения
света. Подобно тому, как в этих последних случаях разыскивается ве-
роятность поглощения или излучения кванта света, так и в случае дис-
персии можно искать вероятность того, чго первоначальный квант света
(падающий пучок) изменит в результате взаимодействия с атомом на-
правление своего импульса, а в общем случае и свою энергию.
Мы, однако, базируясь на принципе соответствия, пойдем более
простым и более близким классической теории путем. Именно, мы най-
дем электрический момент р(/), который возникает в атоме, находя-
щемся в переменном поле световой волны. Свет мы будем предполагать
монохроматическим, частоты со. Ограничиваясь опять случаем, когда
длина волны \ много больше размеров квантовой системы а, мы можем
написать электрическое поле световой волны $(/) внутри системы (ато-
ма или молекулы) в виде
S — So cos (85 6)
Пусть атом до включения светового поля находился в одном из
своих квантовых уровней Еп, собственная функция, соответствующая
этому состоянию, пусть будет ф^(г, 0).
При наличии светового поля состояние атома будет иным (в нем
будут возникать вынужденные колебания). Пусть это состояние описы-
вается функцией фл(г, /). Эта функция должна удовлетворять уравне-
нию Шредингера
/Л^ = Явфл+Ия, (85.7)
где есть оператор полной энергии системы (в отсутствии светового
поля), a W—возмущение, вызываемое световой волной. Согласно
(85.6) W равняется
Ц7=еЭог cosco/. (85.8)
Для решения уравнения (85.7) представим фл в виде
фл (г> 0 — Фл (г) e~lu3nt -\-ип (г) е~1 <шп—«>) * <ип (г) +<о) (85.9}
Е
где <ол*=-^, а ип и vn суть искомые поправки к Функция ф®
есть функция стационарного состояния невозмущенной системы:
№®» = £лф». (85.10}
§ 85]
ДИСПЕРСИЯ
291
Подставим (85.9) в уравнение (85.7) и в первом приближении
пренебрежем произведениями Wun, Wvn (так как эти члены будут про-
порциональны (§2 и уже относятся ко второму приближению). Тогда мы
получим:
h (<DW — (о) ипеш-\-Н (<ол (о) vne~£uii —
=№ипе^ + HQvne~^ 4- е (Эог) -е‘“ ф°. (85.11)
Приравнивая здесь коэффициенты при компонентах Фурье, мы получим
уравнения для ип и vn:
h^n-W)Un = H<>Un + e-^ фо, (85.12)
M®„ + ®K = /*4 + ^4°- (85.12')
Для решения этих уравнений разложим и и v в ряды по ортого-
нальным функциям ф®:
«я=^4/Ф?> (85.13)
(85.13')
Подставляя эти выражения для ип и vn в (85.12) и (85.12') и имея
в виду, что функции фо удовлетворяют уравнению /7°ф^ = £Офр мы
находим:
h 4/ К- ®) Ф1 = *Цг Ф°> (85-14)
h S Вп{ (о>„ -«,+ «>) ф<> = ф°. (85.14')
Умножим теперь эти уравнения на ф^ и проинтегрируем по всему про-
странству. Тогда в силу ортогональности функций ф°р ф£* получим:
h (“я — °>А — “) ЛяА = т J ФГ (<£оГ) ^ndv ’ (85.15)
h (“я — «А + ®) = 4 j ФГ Й #Г) <№>. (85.15’)
Отсюда находим Ank и Bnk'
л (85.16)
пк (^»А — ’ D __ <§>^kn
(85.16')
2й(«>пА4-ш)’
где
Еп — Ek
®„А~“л “a— h
суть собственные частоты атома, a D^n есть матричный элемент вектора
электрического момента.
292
ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА
[ГД. XVI
Из (85.16) и (85.16') следует, что примененный нами метод решения урав-
нений (85.14) и (85.14') пригоден лишь тогда, когда частота падающего света со
не совпадает ни с одной из собственных частот атома <ortA, т. е. вдали от ре-
зонанса. Необходимая степень удаления от w = u>nk определяется условием:
I SI 2/г | (&ak zt to
Только при этом условии Ank и Bnk 1. Чтобы получить и область резонанса,
необходимо учитывать затухание осцилляторов Dkae^knf.
Подставляя найденные значения Ank и Bnk в (85.13) и (85.13'), а
ип и vn в (85.9), мы получаем приближенное выражение для (г, /):
% (r. i) = W (D - e E (r) -
(85ЛГ)
Вычислим теперь в первом приближении электрический момент рпп (t),
который индуцируется полем $ (/) в состоянии Это состояние при
наложении по/тя переходит в фл(г, /). Средний электрический момент
в этом состоянии равен
рпп=—/)г-ф„(г, t}dv = — ej |ф„(г, t) \*-r-dv. (85.18)
Согласно (85.17) | фл (г, /) |2 с точностью до членов первого порядка
по (§0 равно
|Ф„ (г. tl Р = I«I’ - '4г S «*« ~
k
у £0Р,„ ф0..0_^у foDL _
2Л
Подставляя это в (85.18) и замечая, что
—4'И’г‘Вл’=1)л,
получим:
(^ОРЛ„)РАД
(0/z& + <d )
(85Л9)
__п еМ у*
Ряя И) Unn ~2h -2-i \ — (О
е—ш „ ((^оВ&д) Едй
2/г k + w * ^nk — <*>
Мы видим, что электрический момент рпп(£) складывается из двух ча-
стей: из не зависящего от времени момента Dnn и из индуцирован-
§ 85]
ДИСПЕРСИЯ
293
ного дополнительного момента, линейно зависящего от поля. Dnzz
есть не что иное, как средний электрический момент атома (или моле-
кулы) в состоянии п. Так как он не зависит от времени, то в диспер-
сии света он никакого участия не принимает. Индуцированный момент
меняется периодически во времени, и притом с частотой, равной частоте
падающего света <о. Более того, фаза колебаний этого последнего мо-
мента находится в определенной связи с фазой электрического вектора
падающего света. Этот добавочный момент и ответственен за когерент-
ное рассеяние — дисперсию. Обозначим его через рглл(/):
Согласно (85.19) этот индуцированный момент может быть написан (по
компонентам) в виде
(РлЛ = 31 { + Wo/‘W + Mo/"}, ]
(p^=W»/“Wo/“Wo/“'}- f <85-20)
(Р’ИЛ = ^ { Mo/'0* + J
где через Э? обозначена действительная часть от стоящего за этим
знаком выражения.
Совокупность величин образует тензор атомной поляризуемости
(85.21)
имеющий типичные компоненты вида
Рлу— — у У* / (Рл&)х । <Pnk>x I , (85.22)
причем (D^, (D*^ и т. п. суть проекции векторов Dnk, D*n на
оси ОХ и OY. Остальные компоненты тензора р получаются из (85.22)
заменой значков х, у на все возможные пары из х, у, z. Так как
то тензор (85.22) является эрмитовским:
(85.23)
и, следовательно, диагональные члены $хх, р р^ действительны.
В общем случае, при комплексных $х2;, р^, фаза индуциро-
ванного момента и его направление не совпадают с фазой и напра-
влением электрического поля световой волны Е (/). Если все ком-
поненты тензора р действительны, то направление р'пп не совпадает
с направлением поля, но фазы их одинаковы.
Для сравнения с классической теорией рассмотрим частный, но весьма
важный случай, когда тензор Р сводится к одному скаляру, т. е. когда
294 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
= = = ПРИ этих условиях и фаза
индуцированного момента, и его направление совпадают с фазой и
направлением поля световой волны.
В этом специальном случае проще всего выяснить основное разли-
чие с классической теорией дисперсии. Из (85.22), при сделанном до-
пущении, имея в виду, что ®kn =— получаем*
f = ₽„=₽„ = ?» = |£-'^^-. <S5.2+>
k nk
где
и предположено (изотропность системы), что
l(Dnft)J2 = l(Dn^l2 = l(»^|2-
Полученную формулу (85.24) для поляризуемости мы можем напи-
сать в виде, совершенно аналогичном классической формуле (85.5),
именно:
(85-5')
И V шпк — “2
где
1 %nk 1 Dnk l~wkn (85 25)
J nk h e2h * \ • ‘
fnk
Величину fnk в квантовой теории принято называть силой осцил-
лятора. Она просто связана с вероятностью спонтанного перехода Akn .
Именно, на основании (81.9) имеем:
Лк
2*Ч„ П'
Таким образом сила осциллятора fnk определяет интенсивность спон-
танного излучения.
Величины fnk могут быть вычислены, если известны волновые функ-
ции системы *).
Мы видим, что величины fnk имеют в квантовой теории совсем иное
значение, нежели в классической, где соответствующая величина fk
имела смысл числа электронов &-го сорта и поэтому была целым чи-
слом. Силы осцилляторов fnk в согласии с опытом не являются целыми
числами. Можно, кроме того, доказать, что их сумма равна 1 **).
Согласно квантовой теории, как следует из (85.5'), сумма дисперсион-
1
ных членов вида —«------ имеется налицо уже для одного электрона,
“лЛ —“2
находящегося в состоянии ф°. Это находится в прямой связи с тем
*) См. Бете, Квантовая механика Простых систем, ОНТИ, 1935.
**) См. Бете, loc. c:t.
§ 85] дисперсия 295
обстоятельством, что квантовая система в отношении взаимодействия со
светом ведет себя как совокупность осцилляторов с моментами Отпе‘Ютпп?г
хотя бы даже речь шла лишь об одной частице.
Если атом может находиться не только в состоянии ф£, но и в дру-
гих (смешанный ансамбль), то, чтобы получить полную поляризуемость £,
нужно поляризуемость, обусловленную атомами, находящимися в со-
стоянии (J/J, умножить на вероятность нахождения атома в состоянии
и сложить полученные выражения. Обозначая через вероятность того,
что атом находится в состоянии мы получим для поля-
ризуемости а 1 см3 газа выражение
‘85 26’
п к nk
где N—число атомов в 1 см3. Показатель преломления в функции
частоты падающего света согласно (85.2) и (85.26) равен
й!(в)=1_^ууф (85.27)
Iх X-jX-d (О". (О3
п k пк
Часто среди всех членов суммы, входящей в (85.27), один или несколько
преобладают над всеми остальными. Это реализуется в тех случаях,
когда частота (о не слишком удалена от резонансной частоты ®nk.
Рис. 57. Дисперсионные кривые для положительной и отрицательной дисперсии.
Сила осциллятора fnk может принимать и отрицательное значение.
Если атом находится в возбужденном состоянии (и), то среди состоя-
ний k будут и такие, для которых (0Ля<^0(Ek<^E^. В этом случае
дисперсионная кривая имеет необычный ход — получается отрицатель-
ная дисперсия. На рис. 57 изображен ход дисперсионной кривой в об-
296 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
ласти аномальной дисперсии для обычного (классического) случая (fnk 0)
и для случая отрицательной дисперсии (/^<^9).
Экспериментально определение сил осцилляторов является не простой
задачей. Для иллюстрации согласия теории с экспериментом приведем
данные Ладенбурга и Карста *) для отношения сил осцилляторов водо-
родных линий серии Бальмера На и Эти авторы нашли, что
5,9:1 4,66:1. Теоретически получается /а:Д = 5,37:1.
§ 86. Комбинационное рассеяние
Мы вычислили в предыдущем параграфе электрический момент ,
индуцируемый светом в /г-ом состоянии атома. Рассмотрим теперь, какой
добавочный электрический момент ртп индуцируется светом в квантовой
системе при переходе ее из одного состояния т в другое п. Эта за-
дача легко может быть "решена на основе результатов предыдущего
параграфа. Формула (85.17) дает состояние фл(г, /), врзникающее из
фО(г)е~*ш^ под действием света. Совершенно такую же формулу мы
можем написать для состояния фт(г, /), возникающего под действием
того же света из состояния ф^ (г) е~~Вместо (85.18) мы теперь
будем иметь для момента pmn(t), отвечающего переходу из т в /г,
следующую формулу:
Ртп^=—е!|К(г> Огфп(г, (86.1)
Подставляя сюда значение функций фп (г, /) из (85.17) и ф^ (г, /), ко-
торая также получается из (85.17) заменой значка п на т, мы получим:
= + (86.2)
где
1 ^mk | ^kn I ov
b (36-3>
k
_________£ J (^pDfen) Pgift I ^kn 1 /gg g..
mn 2hlu\ <oaft + «> “ — «> J ’ ' ‘ ’
k
Мы видим, таким образом, что помимо уже рассмотренного нами выше
электрического момента D^, зависящего от времени периодически
с частотой появляются еще два дополнительных, индуцированных
светом, электрических момента (86.3) и (86.3'), частоты колебаний ко-
торых суть комбинационные частоты ® — Электрический
момент Т)тп, как мы знаем, определяет спонтанное излучение и погло-
щения для переходов Ет~^±.Еп. Полученные нами дополнительные мо-
менты D<+) и обусловливают рассеяние падающего света, но с из-
*)R. Ladenburg u. А. С а г s t, Zs. f. Phys., 48, 192 (1928).
§ 86]
КОМБИНАЦИОННОЕ РАССЕЯНИЕ
297
мененной частотой. Эти измененные частоты представляют собой сумму
или разность частоты падающего света со и одной из собственной частот
Ет—
системы со
тп /г
Чтобы определить интенсивность этого рассеянного света, мы при-
меним принцип соответствия, согласно которому атом излучает и погло-
щает свет как совокупность осцилляторов. Согласно (86.2) мы имеем
теперь три таких осциллятора. Первый из них нами уже рассмотрен
в § 81, а вторые два
D(+) и D<—) (86.4V
тп тп ' '
согласно формуле (81.16) для средней энергии, излучаемой осциллято-
ром в 1 сек., дают следующие интенсивности для излучения частоты
со' — ®тп (о и (o" = (oZW7Z — со соответственно:
=। D(+> |2 (8б.5)
4(«>mn —<>)*_. D(-)i2 (86 5’)
dt 3c3 1 «« 1 ’ • ’
где D<+) и определяются выражениями (86.3) и (86.3r) и зависят
от интенсивности падающего света. Обращаясь к закону сохранения
энергии, мы можем интерпретировать полученное рассеяние с изменен-
ной частотой на основе представления о световых квантах. Пусть атом:
E^hu)
находится в состоянии п,
имея энергию Еп. С атомом
«сталкивается» квант света
частоты со (энергия е —/до).
В результате столкновения
часть энергии кванта может
пойти на возбуждение атома
(переход в состояние Еп^>Ег^\.
Тогда рассеянный квант будет
иметь энергию, равную
г" = = h® — (Ет — Еп)
(а) ы‘^ы-ытп (Ь)
(рис. оо, а), и частоту (красная компонента) (Фиолетовая компонента)
ю'' = “ —“>“тл>0-
Если атом находится в состоя- Рис. 58. Схема переходов при комбинацией-
нии Ет Еп, то рассеянный ном Рассеянии света,
квант может получить энер-
гию от атома, который перейдет в низшее состояние Еп. В этом случае
энергия кванта рассеянного света е' будет равна (рис. 58, Ь)
г'— Тио’= ha>-\-(Em —Еп),
а частота будет равна (о'=со-4“<»^л> ^тп^®- Интенсивности частоты сог и со"
298 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
и даются формулами (86.5) и (86.5'). Мы видим, что применение за-
конов сохранения энергии между квантовой системой и излучением не
допускает рассеяния частот (о"<^О. Этот вывод не следует автомати-
чески из формулы (86.5) и является специальным требованием, по-
скольку мы остаемся в рамках принципа соответствия *).
Чтобы определить абсолютные интенсивности рассеяния частот <ог и о",
следует умножить (86.5) на число Nm атомов, находящихся в состоянии т,
и (86.5?) на число Nn атомов в состоянии п. Частоты (o' ^>(о; поэтому
их часто называют «фиолетовыми» компонентами рассеянного комбина-
ционного излучения, а со" со называются «красными» компонентами.
Следовательно, окончательно для интенсивностей фиолетовых компонент
имеем:
Г = N 1 DS) Is» (86.6)
а для интенсивности красных компонент
ID<-)I8. (86.6'}
Отношение этих интенсивностей равно
£. = I I2 . (86 У)
Z" |D<->P *
Комбинационное рассеяние было экспериментально установлено Ра-
маном (Раман-эффект) на жидкостях и одновременно с ним Л. И. Ман-
дельштамом и Г. С. Ландсбергом на твердых телах. В обоих случаях
частоты <отп являлись колебательными частотами. В опытах Рамана это
были частоты колебаний молекул жидкости. В опытах Л. И. Мандель-
штама и Г. С. Ландсберга частоты ®тп являлись частотами молекуляр-
ных колебаний кристалла. В применении к этим опытам особо важный
' ж
вывод из формулы для отношения заключался в том, что интенсив-
ность фиолетовых компонент должна расти с температурой. В самом
деле, число возбужденных колебательных состояний кристалла Nm ра-
стет с температурой Т по закону
дг;
е kT -1
соответственно этому должна возрастать и интенсивность фиолетовых
компонент в спектре комбинационного рассеяния. Этот вывод ^теории
вполне подтверждается экспериментально.
Частоты колебаний молекулы определяются ее структурой. Поэтому
исследование молекулярных колебаний является мощным средством изу-
*) В квантовой теории радиации этот вывод получается сам собою. См., на-
пример, Г. Плаче к, Релеевское рассеяние и Раман-эффект, ОНТИ УССР,
§ 87] ИЗМЕНЕНИЯ ФАЗЫ ЭЛЕКТРОМАГНИТНОЙ волны 299
чения строения молекул. Частоты эти лежат в инфракрасной области,
а многие из колебаний молекул вообще не сопровождаются изменениями
электрического момента (оптически неактивные колебания). Обе эти при-
чины крайне затрудняют прямое исследование частот колебаний моле-
кулы. Комбинационное рассеяние в значительной мере облегчает эти
трудности. Изучая комбинационное рассеяние, мы можем иметь дело
с видимым светом и по изменению его частоты определить частоты мо-
лекулярных колебаний, независимо от того, являются ли они оптически
активными или нет. Изучение комбинационного рассеяния молекул в на-
стоящее время образует большую область физической науки.
Подробности, относящиеся к этому явлению, читатель может полу-
чить из цитированной выше книги Г. Плачека.
§ 87. Учет изменения фазы электромагнитного поля волны
внутри атома
Все наши расчеты в предыдущем предполагали, что мы имеем дело
со светом, длина волны 1 которого больше размеров системы а.
Нетрудно модифицировать всю теорию взаимодействия атома со
светом таким образом, чтобы освободиться от предположения X а.
Для этого нужно исходить из гамильтониана (27.9), описывающего по-
ведение электрона в произвольном электромагнитном поле (при этом мы
можем пренебречь малым взаимодействием спина электрона с полем
световой волны).
Для световой волны вектор-потенциал Можно всегда выбрать так,
что divA = 0 и скалярной потенциал V—0. Таким образом, поле
световой волны будет вычисляться по формуле
^ = rotA. (87.1)
Пренебрегая, кроме того, в (27.9) величиной А2 (как величиной вто-
рого порядка малости), мы можем написать гамильтониан (27.9) в виде
«=£+ И+Д а₽="ч-^аХ <87-2>
Возмущение (в первом приближении) равно
ИЧП *) = jJA^=-^AV- (87.3)
Представим вектор-потенциал в виде интеграла Фурье
А (г, /) = j* Ао (со) -krW(D, (87.3')
где к — волновой вектор *). Тогда компонента Фурье от матричного эле-
*) Мы будем считать, что направление отдельных частных волн в (87.3)
и их поляризации одинаковы.
300 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
мента возмущения, принадлежащая частоте cowzz, равна
^ЯИ1(‘»Я1Я)=-^А0(«>лм)|ф>-^.¥ф„.^. (87.4)
На основании (87.1)
^тп
где есть компонента Фурье от электрического поля. Поэтому
l^n("mn)l2== 1 I2. (87.5)
I1 чпп J I
Внося это выражение в формулу для вероятности перехода (80.6) и
переходя от | d?o (Ч^л) I2 к плотности излучения так же, как это дела-
лось в § 80, мы получим вероятность перехода в 1 сек. в виде
Ртп=^, OmB(k)|2p(<o„J, (87.6)
где
D«n (k) = ~ J Ф>-‘’кГ •(87.7)
Формула (87.6) вполне аналогична (80.16'), и из нее можно получить
коэффициенты Эйнштейна для случая коротких волн.
Различие между (80.16') и (87.6) заключается в том, что в первой
формуле Dwrz имеет значение электрического момента, не зависящего от
характера излучения, определяемого свойствами атомной системы, в то
время как вектор Dmzz(k) зависит от волнового вектора излучения к.
Поэтому коэффициенты Эйнштейна получатся иными, нежели для
дипольного излучения (их общие свойства, установленные в § 5,
конечно, останутся неизменными). Вместе с тем разпределение излу-
чения по углам, его поляризация и зависимость от частоты также
изменятся.
Сделанный нами в § 82 вывод о том, что квантовая система взаимо-
действует с излучением, как совокупность осцилляторов, остается в пол-
ной силе и для излучения любой длины волны. Отличие случая длинных
волн (к а) от случая коротких волн (X < а) заключается лишь в том,
что в первом случае квантовую систему можно рассматривать как сово-
купность диполей с моментами &тпе1Штп*, в то время как в случае ко-
ротких волн нельзя игнорировать изменение фазы волны внутри системы,
и квантовая система с точки зрения взаимодействия с радиацией упо-
добляется системе осцилляторов с частотами и>тп, размеры которых
меньше размеров длины волны. В эюм случае уместнее говорить о сово-
купности токов и зарядов, распределенных в пространстве и зависящих
от времени периодически с частотами ютп. Для длинных волн можно
пренебречь изменением фазы в пределах атома и разложить eikr в (87.7)
по степеням kr: = 1 -f- i (кг) . Так как функции ф^ и ф^ от-
§ 87] ИЗМЕНЕНИЯ ФАЗЫ ЭЛЕКТРОМАГНИТНОЙ волны 301
личны от нуля заметным образом лишь в пределах атома, то это раз-
ложение есть разложение по степеням ka=-^--отношению размеров
атома а к длине волны X. Из (87.7) тогда получаем
f f«(kr)v«*,+... =
rmn J rmnj
= DU>+D£> + ... (87.8)
Первый член DO) есть
1 тп
D W = — f • dv = — V, (87.9)
mn ^mnj m n l^mn mn ' 7
где Pmn — матричный элемент оператора импульса. На основании кван-
товых уравнений движения имеем:
Утп==№>тпГтп' (87Л0)
где гтп есть матричный элемент радиуса-вектора. Следовательно,
D(^ = D«n- (87.11)
Т. е. при длинных волнах в первом приближении мы получаем из (87.6)
формулу (80.16') для дипольного излучения. Если DOTZZ=^0, то сле-
дующим членом можно пренебречь. В тех же случаях, когда
в силу правил отбора 0^ = 0, второй член в (87.8) определяет
излучение.
Можно показать, что это излучение носит характер квадруполь-
ного излучения. Таким образом, для переходов, для которых запре-
щено дипольное излучение, существует квадрупольное излучение. Уста-
новленные ранее (§ 83) правила отбора являются приближенными. Разу-
меется, что интенсивность квадрупольного излучения много меньше
интенсивности дипольного (если последнее существует). В самом деле,
D ^примерно в раз меньше неисчезающего дипольного момента.
Поэтому вероятность перехода с квадрупольным излучением по порядку
/2тса\ 2
величины в I -у \ раз меньше вероятности перехода с дипольным излу-
чением. Соответственно этому время жизни атома в возбужденном со-
/ X \2
стоянии, коль скоро дипольное излучение невозможно, в I раз
больше времени жизни для незапрещенного дипольного перехода, кото-
рое мы оценили в § 83 примерно в 10-8 сек. Отсюда для види-
мого света (\^5-103A и а^\ А) время жизни т в возбужденном
состоянии, из которого возможен переход в нижнее состояние
только путем квадрупольного излучения, равно примерно 10~2
сек. Такие состояния атомов называют метастабильными состо-
яниями.
302 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [ГЛ. XVI
§ 88. Фотоэлектрический эффект
В этом параграфе мы рассмотрим теорию фотоэлектрического
эффекта на атомах. Задача, стоящая перед нами, заключается в вычис-
лении вероятности ионизации атома действием световой волны и в опре-
делении углового распределения вылетающих электронов. Таким обра-
зом, речь идет о переходе электрона из нормального уровня (нижний
уровень дискретного спектра) в уровни непрерывного спектра.
Энергию нормального уровня обозначим через EQ (Ео < 0), а соот-
ветствующую волновую функцию через ф0(г). Волновые функции не-
прерывного спектра, принадлежащие энергии Е, ввиду большого вырож-
дения можно брать весьма различным образом, лишь бы они образовы-
вали полную систему ортогональных функций. Мы возьмем такие функ-
ции, которые фигурировали у нас в теории упругих столкновений,
т. е. суперпозицию плоской волны, с определенным импульсом элек-
трона р (рх, ру, р2), и волны, рассеянной атомом. Для больших рас-
стояний от атома такие волновые функции будут иметь вид (ср. § 74):
^PvPz (г) = COnst- {е ‘ * + fPxPsPz ?) . (88-1)
где k — волновое число. Такого типа функции являются одной из воз-
можных форм волновых функций стационарных состояний непрерывного
спектра. Энергия Е состояния (88.1) будет равна
<88-2>
Функции (88.1) будем считать нормированными к Ъ(рх—р'х), Щру—p'v),
i(p2—p'z). Возмущение, вызывающее переходы, согласно (87.3) возьмем
в виде
“AV, (88.3)
где А — вектор-потенциал световой волны. Волну мы предположим мо-
нохроматической и возьмем А в виде
А= j Aoe-'(w/-kr) ( (88.4)
где к есть волновой вектор волны. Так как волна поперечная, то
div А = 0, т. е.
Аок = О. (88.5)
Для вычисления интересующей нас вероятности перехода мы- можем
прямо применить формулу (77.24), так как последняя как раз выве-
дена для переходов из дискретного спектра в непрерывный под влия-
нием возмущения, гармонически зависящего от времени.
Разумея в (77.24) под Еп энергию нормального состояния атома EQ,
под импульсом рх, ру, рг (р, 6, ср) — импульс фотоэлектрона, мы должны
§ 88] фотоэлектрический эффект 303
согласно (88.3), (88.4) и (77.12) взять в качестве матричного элемента
возмущения величину
WE, е,Ф:о= ^,Ру,Рг: 0= -g| Ао J rm.^.dxdydz. (88.6}
Тогда вероятность перехода электрона в 1 сек. из состояния Яо в со-
стояние Е=Ец-\-/г<а> с импульсом, лежащим в телесном угле dQ, будет
равна
Ро (Е, 6, <р) dQ = о + W* I о I2 • (88-П
причем сюда входят лишь такие значения импульса рх, ру, рг, которые
удовлетворяют резонансному условию
е=тг,=^+р}+р^=е>+'“‘- <88-8>
Переходы в другие уровни Е невозможны. Замечая, что EQ=—Ц
где I—работа ионизации, мы можем переписать (88.8) в виде
п2
£- = Лш—/. (88.9)
Это есть уравнение Эйнштейна для фотоэффекта на атоме.
Для того, чтобы получить окончательное выражение для Р^Е, 0, ср),
необходимо вычислить матричный элемент (88.6). Для этой цели необ-
ходимо знать волновую функцию исходного состояния ф0 и функции
непрерывного спектра ^PxPyPz. Допустим, что мы интересуемся фото-
эффектом с /С-оболочки (тогда — Е$ = I есть ионизационный потенциал
ЛГ-оболочки). Эта оболочка расположена близко к ядру атома, и поэтому
(игнорируя взаимодействие двух /С-электронов) можно взять для
функцию нижнего уровня для движения в кулоновском поле. Это
будет (п — 1—т — 0)
Фо=Фюо=(^з) е а, (88.10;
где Z — номер элемента, а а — радиус первой боровской орбиты.
Такая функция будет весьма близко аппроксимировать истинную.
Мы ограничимся весьма грубым приближением для функций непрерыв-
ного спектра. Именно, мы будем попросту игнорировать изменение
плоской волны вблизи атома благодаря действию его поля и соответ-
ственно этому вместо точной функции возьмем невозмущенную действием
атомного поля плоскую волну
(p0DX + Ру V ~\~PZZ}
е1 л
ж— <8811>
(нормирована по р к 5-функции). Такое приближение мало годится для
аккуратного расчета, однако все же в нем еще сохраняются существен-
304 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [гл. Xyi
ные черты явления. Оно будет тем лучше, чем больше энергия фото-
электрона, т. е. оно пригодно для Е^>— Е$ = 1. При таком предполо-
жении о функциях непрерывного спектра матричный элемент (88.6)
может быть вычислен без большого труда. Подставляя (88.10) и
(88.11) в (88.6), мы получим:
Рис. 59. Расположение век-
торов Ао, Кир при фото-
эффекте.
tfz ihe 1 / Z V/s
С /(kr-И
X е V h A0(Ve a)dxdydz. (88.12)
Пусть волна распространяется по направле-
нию оси ОХ, а электрический вектор (по-
ляризация) направлен по оси OZ. Тогда ОХ
есть направление вектора k, a OZ — вектора
Ао. Тогда Ао —0, 0, Ао, и, следовательно,
тут _________the 1 ( % \^3 д Z к/
w= 0 - — (2лЛ)5/> -) До - X
X С г 1 Г — б а dxdy dz.
(88.12')
Расположение векторов к, р, Ао дано на рис. 59. Для выполнения
интегрирования в (88.12') возьмем вектор Лк — р за полярную ось сфе-
рической системы координат 6, Ф.
Если ось OZ в этой системе имеет углы 0', Ф', то
z = (r)2 — rcos (OZ, г).
cos угла между OZ и г, если вектор г имеет полярные координаты
0, Ф, будет
cos (OZ, г) == cos 0-cos 0' Ц- sin 0 sin 0' cos (Ф' — Ф).
Угол между Лк — р и г есть 0. Поэтому (88.12') можно записать
в виде
(88-12"’
где
fldr § jsin0rZ0 к л|гс080 « {cos 0 cos 0'4“
0 0 0
Ц-sin 0 sin 0' соз(Ф’ — Ф)}. (88.13)
Интеграл по Ф от соэ(Ф — Ф') дает, очевидно, нуль, поэтому
00 I р I о —
J=cos0' f fldr fsin0 6Z0£Zlk Л » °S a ,COs0. (88.13')
о 0
§ 88]
ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
305
Вводя переменную $ = cos 0 и обозначая | к — ~ | г через q, мы получим:
°? +1 . ._7г
J=cos0' \ fudr \ $ dz,eiq' а
о —1
и, выполняя здесь простые интегрирования, найдем окончательно
16ш I к — £-1
7=cos0' Г^-Ч--------ГП“2 • (88.13")
[e2"nk 7Г| J
Остается выразить cos0r через углы в той системе координат, где за
полярную ось принято направление распространения света (ось ОХ,
вектор к). Пусть угол между плоскостью, образованной векторами р и
к — у и плоскостью ZX, будет ср (см. рис. 59). Угол между Лк и
Лк — р, пусть есть 0'. Обозначая еще угол между ОХ и р через 0,
мы получим из сферического треугольника со сторонами 0', 0' и ~:
cos 0' = sin 0' cos ср
и из треугольника со сторонами Лк, р, Лк — р:
sin 0r = sin 0 cos ср р—-
Ч Лк — р |
Поэтому
г I а 16тс/р
J= sin 0 cos ср —j—r
|§+1к-’Г
На основании (88.13")
(88.14)
ш „ .0 = -—-ЛгГ—„ i2T2sin8cos?- (88-15)
|_ я2 * I Л I J
Далее,
r?2
Из закона сохранения энергии (88.10), считая, что (это—условие
применимости нашего приближения), мы найдем:
ръ______h<&
2р.с с
= hk.
Обозначая через v скорость электрона , получаем ЛЛ = — р, и, стало
быть,
НН('->'+£).
Мы оперируем с нерелятивистской теорией, поэтому пригодность наших
20 Блохинцев
306
ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА
[ГЛ. XVI
формул ограничена не только со стороны малых скоростей I j ,
но и со стороны больших. Необходимо, чтобы скорость фотоэлектрона
I/2
была значительно меньше скорости света с. Поэтому членами порядка
следует пренебрегать (учет их находится за пределами применимости
нерелятивистской теории). Поэтому
|k_E|2
I h I h“ \ c J
Заметим, что мы еще можем отбросить член по сравнению с
| л ]2 I л 12 м2 ^2
к — v- . В самом деле, к — 4- а а =—. Следовательно,
| h | | h I Л2 pic2
2pi Z2pic4
Л2"2Л2~ ’
(88.16)
Z2_Z2piM_
д2
Но согласно формуле Бальмера
—____р —т
эквивалентно Таким образом,
Z2
т р —
имея в
Z2
роны, мы должны опустить в (88.15) член
Подставляя (88.16) в (88.15), мы найдем
для искомого матричного элемента:
_ 8ксЛ 1 /ZV/8'Z .
^да;о— (2лЛ)Ц^ « «
виду быстрые
в знаменателе.
окончательное
Л4 sin 0 cos у
f 1----— cos О
\ с
фотоэлект-
выражение
. (88.17)
Подставляя, наконец, это значение матричного элемента в выражение
для вероятности (88.7), мы получим:
Рй (Е, 9, v)dti = dQ 8(2(1f^- A2 (-Y (Ла>) /зsin2 9 cos2 у . (88.18)
° ‘ p6(i_£cos0y
Вместо Л2 можно ввести поток световой энергии. Из (88.4) получаем
—>•
электрическое поле S
1 дА со л , , , , ч
—7-^ = —-Ло sin (о)^—кг).
—>•
Величина магнитного поля Ж такова же, и так как оно перпендику-
лярно то вектор Пойнтинга S равен по величине
S=£<^=£^sin*H-kr).
Среднее значение его равно
- ®2^п
8кс
8кс —
Л2 —— 5
о (О2
(88.19)
§ 88]
ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
307
Подставляя это в (88.18), найдем:
sin2 0 cos2 <р
(88.20)
Объединяя все постоянные в одну b и замечая, что р6 —(2g£')3 =
= (2рьЛй))3, мы получим:
Ро(£, 0, (р) dQ sin2flcos2y Sd&, (88.21)
(!-4 cose)
где
64 (2н)’/з/гб Z* .
° y?c 6z5‘(2pi)3,
(88.22)
Рис. 60. Сдвиг вперед макси-
мума фотоэффекта.
^тах <УГОЛ межяУ направлением
распространения света и направ-
лением максимума фотоэмиссии)
V
в функции (3=— (по Зоммер-
фельду).
Из полученной нами формулы следуют самые основные черты фотоэлект-
• (рической эмиссии. Во-первых, число фотоэлектронов пропорционально
интенсивности падающего света 5, скорость же фотоэлектронов зависит
согласно (88.10) лишь от частоты падающего света со, т. е. мы полу-
чаем как раз те особенности фотоэффекта, которые представляют прин-
ципиальные трудности для понимания с точки зрения классических кон-
цепций. Далее, формула (88.21) дает угло-
вое распределение фотоэлектронов. Так как
угол 6 отсчитывается от направления рас-
пространения света, а ср — от электрическо-
го вектора, и максимум фотоэмиссии лежит
при ф = 0, т0 это означает,
что наибольшее число фотоэлектронов
(рис. 59) летит в направлении OZ, т. е.
в направлении электрического вектора све-
товой волны.
При увеличении частоты падающего све-
та скорость фотоэлектронов возрастает так,
что начинает играть роль множитель
(1—£_COs0^ 4 в (88.21), в силу чего
максимум фотоэмиссии сдвигается в направ-
лении меньших 0, т. е. в направлении
распространения света. Этот вывод нахо-
дится в согласии с опытом. На рис. 60 изображены результаты
опыта. По оси ординат отложен косинус угла 0 между направлением
распространения света и направлением максимальной эмиссии, по оси
абсцисс отложена скорость фотоэлектронов, причем за единицу ско-
рости взята скорость света, cos 0ОТ = 0 отвечает направлению вдоль
электрического вектора волны, a cos 0m=l—направлению вдоль луча
света. Как видно, результаты расчета хорошо совпадают с данными
опыта (кружки). С помощью формулы (88.22) мы можем получить и
20*
308 ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА [гЛ. XVI
абсолютную величину фотоэффекта. Обычно в таких случаях вычисляют
коэффициент поглощения для падающего света т. Для нахождения его
поступаем следующим образом.
Представим себе, что на слой вещества толщиною Дх падает поток
света 5. Тогда, если в 1 см3 вещества содержится п атомов, то
в объеме 1 см2 X Д* в 1 сек. произойдет в среднем
1 см2 • Дх • п § Ро (Е, 6, <р) dQ
ионизаций атомов. Поглощенная при этом энергия будет равна этой
величине, умноженной на Aw (так как при каждой ионизации погло-
щается квант света Aw). С другой стороны, в этот же слой в 1 сек.
входит энергия <9 X 1 Таким образом, убыль потока энергии S’
при прохождении тонкого слоя Дх равна
AS = — han Ьх j Ро (Е, 9,'<р) dQ.
Подставляя сюда Р0(Е, 0, ср) из (88.21), мы получим:
AS = — han ^xba~'hS f > sln ^cos y dQ.
J (i_Zcos9j4
Полагая
z=bnha-^ Г _sin29cos2? dQ, (88.23)
J (1 —cos 0 j
мы получим:
Д5= —tS Дх;
отсюда следует, что т есть коэффициент абсорбции. Число атомов
в единице объема пропорционально плотности вещества р, именно:
лг = 6,06- 102в -Р
А
где А — атомный вес вещества. Подставляя это в (88.23) и обозначая
6,06-1023 .. р sin2 0 cos2 <р
Ь' = -2—л--I "7----------Vt-
А \ (л v л\4
J \ 1 — cos о )
мы получим величину так называемого массового коэффициента аб~
сорбции - в виде
т hr
p <&l
(88.24)
Эта зависимость от частоты также подтверждается опытами над погло-
щением рентгеновских лучей. Следует впрочем иметь в виду, что (88.24)
выведено для поглощения в /^-оболочке. На самом деле поглощение
происходит сразу несколькими оболочками. Мы не будем рассматривать
относящиеся сюда усложнения и отсылаем интересующегося читателя
к специальной литературе *).
*) М. Stobbe, Ann. d. Phys., 7, 661 (1930); A. S о m m e г f e 1 d und
C. S chur, Ann. d. Phys., 4, 409 (1930).
§ 89]
ПОСТАНОВКА ПРОБЛЕМЫ И ПРОСТЕЙШИЕ СЛУЧАИ
309
ГЛАВА XVII
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ
§ 89. Постановка проблемы и простейшие случаи
Если мы имеем две области пространства, в которых потенциальная
энергия частицы меньше, нежели на поверхности, разделяющей эти об-
ласти, то мы говорим, что области разделены потенциальным барьером.
Простейшим примером потенциального барьера может служить
барьер в одном измерении, изображенный на рис. 61. По оси ординат
отложена потенциальная энергия U (Зс) в функции координаты частицы х.
В точке xQ потенциальная энергия имеет максимум Um. Все про-
странство — оо х -|- о° делится в этой точке на две области:
x<^xQ и х^>х0, в которых U<^Um. Значение термина «потенциаль-
ный барьер» сейчас же выяснится,
если мы рассмотрим движение ча-
стицы в поле U (х) на основе
классической механики. Полная
энергия частицы Е равна
E=^-\-U(x), (89.1)
где р — импульс частицы, a pi —
ее масса. Решая (89.1) относитель-
но импульса, получим:
Р {X) - ± /2ц[£—Щх)]. (89.2)
Знаки 4z следует выбрать в зави-
симости от направления движения
частицы. Если энергия частицы Е больше «высоты» барьера U , то
частица беспрепятственно пройдет барьер слева направо, если начальный
импульс р^>0, или — в противоположном направлении, если начальный
импульс р<^0.
Допустим, что частица движется слева, имея полную энергию Д
меньшую Um. Тогда в точке xr U(x1) = E, р(х1) = 0, частица оста-
новится. Вся ее энергия обратится в потенциальную, и движение нач-
нется в обратном порядке: хг есть точка поворота. Поэтому при E<^UJn
частица, движущаяся слева, не пройдет через область максимума потен-
циала (х = х0) и не проникнет во вторую область х>х0. Подобным
же образом, если частица движется справа налево, имея Е<^ит, то
она не проникнет в область за второй точкой поворота х2, в которой
[7(х2)=Я (см. рис. 61). Таким образом потенциальный барьер яв-
ляется непрозрачной перегородкой для всех частиц, энергия которых
меньше Um (напротив, он «прозрачен» для частиц, обладающих энер-
гией E^U^. Этим и разъясняется название «потенциальный барьер».
Совсем иначе происходит движение частиц вблизи потенциальных
барьеров, если речь идет о движениях микроскопических частиц в микро-
310
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ
[ГЛ. XVII
скопических полях, т. е. о движениях, при рассмотрении которых нель-
зя игнорировать квантовые эффекты (пренебрегать постоянной Планка).
В этом случае, как мы сейчас увидим, в противоположность выводам
классической механики, частицы с энергией Е, большей высоты барьера
частично отражаются от барьера, а частицы с энергией, меньшей Um,
частично проникают через барьер.
Для того, чтобы в этом убедиться, мы рассмотрим совсем простой
случай барьера, изображенный на рис. 62. Именно, мы будем считать,
что потенциальная энергия частицы U(x) всюду
। ™ равна нулю, кроме области 0 /, где она
; имеет постоянное значение, равное Um. Такой
т барьер представляет собой, конечно, идеализа-
цию, но на нем особенно просто можно про-
следить интересующие нас стороны дела. Мы
0~ ь х можем себе представить, что такой прямоуголь-
Рис. 62. Самый простой НЬ1Й баРьеР возникает путем непрерывной дефор-
потенциальный барьер, мации плавного барьера, изображенного на
рис. 61.
Будем искать стационарные состояния частицы, движущейся в поле
такого барьера. Обозначая потенциальную энергию через £7(х), мы
получим уравнение Шредингера в виде
(89-3)
Обозначая в дальнейшем дифференцирование по х штрихом и вводя
оптические обозначения
= (89.4)
где п(х) — показатель преломления (см. § 36), мы перепишем уравне-
ние (89.3) в виде
ф’ + А;2л2(х)ф = 0. (89.5)
Уравнение (89.5) распадается на три уравнения для трех областей про-
странства:
ф«4-А;2ф = 0> х<0, t7(x) —0, (89.5')
ф"-ф-^/гД (х)ф = 0, 0<х</, U{x) — Um, (89.5")
ф"4-А;2ф = 0, х>/, £7(х) = 0. (89.5"')
Решения в этих областях могут быть написаны сразу:
ф (х) — ф, (х) = Ае0^ + Be~ikaX, (89.6)
ф (х) = фп (х) = aeik^x -ф- fy-lk<**x, (89.6')
ф (х) = фш (х) = ае‘к«х-\-Ье~‘каХ, (89.6")
где А, В, a, jJ, а и b — произвольные постоянные. Однако, это — общие
решения трех независимых уравнений (89.6), (89.6') (89.6") и они,
§ 89] ПОСТАНОВКА ПРОБЛЕМЫ И ПРОСТЕЙШИЕ СЛУЧАИ 311
вообще говоря, не образуют какой-либо одной волновой функции, опи-
сывающей состояние частицы, движущейся в силовом поле U(x). Для
того, чтобы они давали действительно одну функцию ф (х), мы должны
соблюсти краевые условия, которые мы сейчас установим.
Для этого будем рассматривать U(x) и, следовательно, п(х) как
плавную функцию х. Интегрируя тогда уравнение (89.5) около точки
х = 0, получим:
+д н-д
j ty'dx + У я2 (х) ф dx — 0.
--Д — А
Отсюда
ф’( + А) — Ф'( — Д)= — J »2(x)<b(x)dx. (89.7)
— д
Переходя к пределу Д->0, получаем краевое условие:
ф-( + О) = ф'(-О). (89.7')
Далее, согласно общему требованию о непрерывности волновых
функций имеем второе краевое условие:
ф(-[-О) = ф( —0). (89.7")
Точка х —0 ничем не выделена, поэтому условия (89.7') и (89.7") дол-
жны быть соблюдены в любой точке, в частности, и при х = /.
Чтобы решение (89.6) трех уравнений (89.5) можно было рассмат-
ривать как предел решения одного уравнения при переходе от плав-
ного изменения U(x) к скачкообразному, нужно, чтобы эти решения
в точках х = 0 и х — 1 удовлетворяли краевым условиям (89.7') и
(89.7"), т. е.
^(oWnP), ф;(О)=ф;1(О), ।
Фп(0=Фш(0, Фп (О=фадо- )
Подставляя сюда значение функций из (89.6), получаем:
Л —В = C/L —J—
ik0 (А — В) = ikonm (а — ₽),
QgikoTivnl-== deL^a^ Ьв
ik^m (ae£k°nrni — ^e~£k°nml) = ikQ (ae£k°l — be~£k°l).
Мы имеем четыре уравнения для шести постоянных. Произвол в выборе
постоянных объясняется тем, что могут быть волны, падающие на барьер
слева, а мргут быть — падающие на него справа.
Если мы, например, возьмем Л, В^О, # = 0, то Aeik*x может рас-
сматриваться как падающая волна, Be~ik°x— как отраженная, a aeik°x—
как проходящая. Если бы мы взяли то это означало бы, что
есть eih,e падающая волна с другой стороны барьера. Эти возможности
(89.8)
I (89.9)
312
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
соответствуют в классической механике случаям движения частиц к ба-
рьеру слева, либо справа.
Мы рассмотрим для определенности случай падения частиц слева.
Тогда мы должны взять # = 0. Кроме того, без всяких ограничений мы
можем принять амплитуду падающей волны за единицу: Я=1. Урав-
нения (89.9) принимают тогда вид:
(а-Р),
+? 0—ikofiml ae^Q^ I
пт (aeik°nm! — ) = ae[k*1.
Из этих алгебраических уравнений находим а, р, В и а\
а==_____________2e~ik^l(l+nm)____________
e-ikanml ц _|_ л^)2 _ e^mt (1 _
о__________________2е1к“Пт1 (1 — пт)_____
Р е~^т1 (1 _|_ Лт)2 gOWml (] _ 2 ’
—ikQnml__g^onml
e~ik°nml (1 + пт^ — ?*»"”>' (1 — лт)2 ’
. --------------^пт_________________
g-ikonml 0 _ g'lWml (1 _ „m)2 •
(89.10)
(89.11)
(89.12)
(89.13)
(89.14)
Если энергия частицы E больше высоты барьера Um, то показатель
преломления пт действителен. В этом случае интенсивность отраженной
волны | В [2 равна
1^12 ______________4(1 ПтР s*n _____________________ zgg j дх
(1 + «J4+ (1 - - 2 (1 -пД) cos (2A0«m/) ’
а интенсивность проходящей волны
U + «J4+(1 — nm)4 — 2 (1 — л 2) cos (2£0лт/)
Вычислим по формуле для плотности тока поток частиц в па-
дающей волне (Уо), отраженной (Jr) и проходящей (JJ. *Из (89.6) имеем:
Jo = k01А |2 = k0, Jr=— A0|B|2, Jd=A0|a|2. (89.16)
Отношение потока падающих частиц к потоку отраженных
4' = ^МТ- = |ВР = « (89.17>
называют коэффициентом отражения. Отношение потока падающих
частиц к потоку проходящих
Т: = Ш" = И! = О (89.18)
называют коэффициентом прозрачности барьера.
§ 89] ПОСТАНОВКА ПРОБЛЕМЫ И ПРОСТЕЙШИЕ СЛУЧАИ 31$
Из закона сохранения числа частиц (уравнение непрерывности для J)^
следует, что
(89.19>
(приведенные выше выражения для R и D позволяют непосредственно^
убедиться в справедливости этого равенства).
По классической механике, если Е>Ц , должно иметь место =
D=l: барьер совершенно прозрачен. Йз(89.15) следует, что | В |2 =^= 0г
поэтому в квантовой механике /?^>0, D<^\. Частицы частью
отражаются так же, как отражаются световые волны на грани-
це двух сред.
Если энергия частицы Е меньше высоты барьера Um, то по класси-
ческой механике имеет место полное отражение 29 = 0, /? = 1. При,
этом частицы совсем не проникают внутрь барьера. В оптике такой,
случай отвечает полному внутреннему отражению. Согласно геометри-
ческой оптике лучи света не проникают во вторую среду.
Более тонкое рассмотрение на основе волновой оптики показывает,
что в действительности световое поле при полном отражении все же
проникает в среду, от которой происходит отражение, и если эта среда
представляет собой очень тонкую пластинку, то свет частично проходит
через нее. Квантовая механика в случае Е (случай отражения)
приводит к выводу, анологичному выводу волновой оптики (см. аналогии
в § 36). Действительно, если E<^Um, то показатель преломления
пт является чисто мнимой величиной [см. (89.4)]. Поэтому мы положим
= = (89'20»
Внося это выражение для пт в (89.14), вычислим теперь ]я|2. Тогда,
считая еМ «т I * 1, получаем:
д = I g I2 = | „jjs *~2*°1 Ят 11 • (89.21)
Обозначая первый дробный множитель через Z)o (он не очень отличается
от 1) и имея в виду значение kQ, получаем:
о ________
D= Dfj- й . (89.22>
Таким образом, при Е Um, в противоположность выводам классиче-
ской механики, частицы проходят через барьер.
Явление прохождения через потенциальный барьер получило образ-
ное название туннельного эффекта.
Очевидно, что туннельный эффект будет имедъ заметное значение
лишь в тех случаях, когда D не слишком мал, т. е. когда
(89.23)
Нетрудно видеть, что с туннельным эффектом мы можем встретиться
лишь в области микроскопических явлений. Так, например, для
314 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
U— Е10-"11 эрг (около десяти электрон-вольт), р 10~27 г (мас-
са электрона) и /=^10-8 см. из (89.22) получим D^e~~\ Но если
мы возьмем, например, I — 1 см. то из той же формулы получим
D^£-1°8. Увеличение массы частицы и превышение Um над Е еще
более уменьшат D. Подобным же образом можно показать, что рас-
смотренное выше отражение исчезает с ростом энергии частицы — кван-
товая механика переходит в классическую.
Формулу (89.22) для коэффициента прозрачности D. выведенную нами
.для прямоугольного барьера, мы можем обобщить и на случай барьера
произвольной формы. Мы произведем сейчас это обобщение простым,
хотя и не строгим путем.
Пусть мы имеем потенциальный барьер U(х), изображенный на
рис. 61. Представим его приближенно в виде совокупности прямоуголь-
ных барьеров с шириной dx и высотой U(x). Эти барьеры на рисунке
заштрихованы. Частица, имеющая энергию Е. вступает в барьер в точке
х — хг и покидает его в точке х — х2. Согласно (89.22) коэффициент
прозрачности для одного из этих элементарных барьеров равен
о ___________
7
[потенциальная энергия U(x) должна быть достаточно плавной, чтобы
dx можно было взять достаточно большим]. Коэффициент прозрачности
для всего барьера должен равняться произведению коэффициентов про-
зрачности для всех элементарных барьеров (как раз это предположение
не является вполне обоснованным в наших рассуждениях). Тогда пока-
затели в формуле для D' сложатся и мы получим *)
х3
- | j /2М<7(х)-Е] Ох
D=Doe х‘ . (89.24)
§ 90. Кажущаяся парадоксальность «туннельного эффекта»
Прохождение частиц через потенциальные барьеры представляется на
первый взгляд парадоксальным. Эту парадоксальность усматривают в том,
что частица, находящаяся внутри потенциального барьера при полной
энергии Е. меньшей высоты барьера Um. должна иметь отрицательную
кинетическую энергию Т—~, ибо полная энергия, как это имеет место
в классической механике, является суммой энергий кинетической и потен-
циальной:
о2 .
*) Эта формула может быть обоснована для достаточно гладких барьеров
на основании метода Бриллуэна-Вентцеля-Крамерса (при этом получается
Dq — 4). См. Pauli, Handb. d. Phys,t XXIV, 1, § 12. См. также книгу Г а м о в,
Строение ядра и радиоактивность.
§ 90]
«ТУННЕЛЬНЫЙ ЭФФЕКТ»
315
м2
В области, где U(x)"^>E, ^-<^0, что бессмысленно, так как импульс
2|Х
р есть действительная величина. Как раз эти области, как мы знаем
из классической механики, недоступны для частицы. Между тем согласно
квантовой механике частица может быть обнаружена и в этой «запрет-
ной» области. Таким образом, получается, будто квантовая механика
приводит к заключению, что кинетическая энергия частицы может быть
отрицательной, а импульс частицы мнимым. Это заключение и называют
парадоксом «туннельного эффекта».
На самом деле здесь нет никакого парадокса, а само заключение
неверно. Дело в том, что, поскольку туннельный эффект есть явление
квантовое [при h—>0 коэффициент прозрачности D (89.24) стремится
к нулю], постольку он может обсуждаться лишь в рамках квантовой
механики. Полную же энергию частицы можно рассмотреть как сумму
кинетической и потенциальной энергий только на основе классической
механики. Формула Е= ^-\-U(x) предполагает, что мы одновременно
знаем величину как кинетической энергии Т, так и потенциальной
U(x). Иными словами, мы приписываем одновременно определенное зна-
чение координате частицы х и ее импульсу р, что противоречит кван-
товой механике. Деление полной энергии на потенциальную и кинети-
ческую в квантовой механике лишено смысла, а вместе с тем и несо-
стоятелен и парадокс, основанный на возможности представить полную
Энергию Е как сумму кинетической (функция импульса) и потенциаль-
ной энергии (функция координат).
Нам остается лишь посмотреть, не может ли все же оказаться так,
что путем измерения положения частицы мы обнаружим ее внутри
потенциального барьера, в то время как ее полная энергия меньше
высоты барьера.
Обнаружить частицу внутри барьера действительно можно, даже
если Е < Uоднако, коль скоро фиксируется координата частицы х,
при этом создается согласно соотношению неопределенности дополни-
тельная дисперсия в импульсе (Др2), так что уже нельзя утверждать,
что энергия частицы, после того как определили ее положение, равна Е.
Отсюда следует заключение, что аппарат, приспособленный для
измерения положения частиц, необходимо должен обладать некоторым
запасом энергии, который он был бы в состоянии передать частице.
Из формулы для коэффициента прозрачности следует, что частицы про-
никают заметным образом лишь на глубину /, определяемую равенством
(88.23). Чтобы обнаружить частицу внутри барьера, мы должны фик-
сировать ее координату с точностью Дх I. Но тогда неизбежно воз-
никает дисперсия импульса Др2 > ~ . Подставляя сюда из
(89.23), находим:
2р. т
(90.1)
316
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
т. е. изменение кинетической энергии частицы, вносимое вмешательством
измерения, должно быть больше той энергии, которой ей недостает до
высоты барьера Um.
Приведем пример, иллюстрирующий роль измерительного аппарата. Пусть
мы желаем определить координату частицы, находящейся внутри потенциаль-
ного барьера, таким путем, что будем посылать узкий пучок света в направ-
лении, перпендикулярном к направлению движения частицы. Если пучок рас-
сеется, то, значит, на его пути попалась частица.
Как объяснялось выше, точность нашего измерения должна быть такова,
чтобы Дх < Z; с другой стороны, нельзя создать пучок света, ширина кото-
рого была бы меньше длины световой волны X. Таким образом Дх > X, а сле-
довательно, длина волны света должна быть меньше Z, т. е.
V^(Um-E) ’
С
так как X = — , где у — частота световых колебаний, ас — скорость света, то
отсюда следует, что
/z2v2 > 2 pc2 (Um — Е).
Фигурирующие в нерелятивистской механике энергии должны быть меньше
собственной энергии частицы |i£2, поэтому
hv>Um — E,
т. е. энергия применяемых в световом пучке квантов света должна быть
больше, нежели разность между высотой потенциального барьера и энергией
частицы.
Таким образом, этот пример иллюстрирует положение о необходимости
применить для измерения координаты аппараты, обладающие достаточно боль-
шой энергией чтобы можно было локализовать частицу.
§ 91. Холодная эмиссия электронов из металла
Если к металлу приложить большое электрическое поле (порядка
10б волып\см} так, чтобы он являлся катодом, то такое поле вырывает
электроны: получается электрический ток. Это явление впервые наблю-
далось Милликэном и Эйрингом и получило название «холодной эмис-
сии». Оно может быть легко истолковано на основе квантовой теории
прохождения частиц через потенциальный барьер и притом, в общих
чертах, в согласии с опытом.
В этом параграфе мы рассмотрим теорию этого эффекта, представ-
ляющую одно из наиболее простых приложений теории прохождения
через потенциальный барьер. Обратимся сначала к картине движения
электронов в металле в отсутствии внешнего электрического поля.
Чтобы удалить электрон из металла, необходимо затратить некото-
рую работу. Следовательно, потенциальная энергия электрона в металле
меньше, нежели вне металла. Наиболее простым образом этот факт
может быть выражен, если мы примем потенциальную энергию электрона
U(х) внутри металла равной 0, а вне металла равной 0, так что
потенциальная энергия имеет вид, изображенный на рис. 63. Схемати-
зируя таким образом истинный ход потенциальной энергии, мы в сущ-
ности оперируем со средним полем в металле. На самом деле, потенциал
§ 91]
ХОЛОДНАЯ ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
317
внутри металла меняется от точки к точке с периодом, равным постоянной
кристаллической решетки. Наше приближение соответствует гипотезе сво-
бодных электронов, так как, поскольку U(x) = 0, то внутри металла
нет никаких сил, действующих на электрон.
Здесь мы не можем обсуждать вопрос о степени правильности такого
приближения*). Ограничимся лишь указанием на то, что рассмотрение
электронов в металле как свободно движущихся частиц («электронный
газ») позволяет уяснить многие явления в металлах и поэтому, в опре-
деленных рамках, является законным. Распределение по энергиям элек-
тронов этого газа таково, что
подавляющее большинство электро-
нов имеет энергию Е<^С (при
абсолютном нуле температуры
электроны заполняют все уровни
энергии от E—Q до Е — г^^С,
где е0 есть так называемая нулевая
энергия;, см. § 110). Поток элект-
ронов металла, падающий изнутри
металла на его поверхность, обо-
значим через Jo. Так как элект-
роны имеют энергию Е С, то
этот поток полностью отражается
от скачка потенциала С, имеющего
№
Металл ! Вакуум
Рис. 63. Поле на границе металла.
Сплошная линия—в отсутствии внешнего
поля, пунктирная линия — при наличии внеш-
него поля &. При наличии поля образуется
барьер О ВС'.
место на границе металл — вакуум.
Представим теперь себе, что наложено электрическое поле S, направ-
ленное к поверхности металла. Тогда к потенциальной энергии элек-
трона U(х) (рис. 63) добавится потенциальная энергия электрона в по-
стоянном поле Si равная —е$х (е — заряд электрона). Полная потен-
циальная энергия электрона будет теперь равна
U'(х) — U (х) — eSx=C— ^x(x>0), )
U'(x) = 0 (x<0). J 1 '
Кривая потенциальной энергии примет теперь иной вид. Она изобра-
жена на рис. 63 пунктиром. Заметим, что внутри металла нельзя создать
большого поля, поэтому изменение U(х) произойдет лишь вне металла.
Мы видим, что образуется потенциальный барьер. По классической
механике электрон мог бы пройти через барьер лишь в том случае,
если его энергия Е"^>С. Таких электронов у нас очень мало
(они обусловливают малую термоионную эмиссию). Поэтому никакого
электронного тока по классической механике при наложении поля полу-
читься не должно **). Однако, если поле S достаточно велико, то барьер
*) См., например, Бете и Зоммер,фельд, Электронная теория ме-
таллов.
**) Если поле понижает высоту барьера, то, если высота последнего С
станет меньше то же самое будет иметь место и по классической механике.
Но это будет колоссальный ток: электроны хлынут лавиной через барьер.
На самом деле имеет место постепенное нарастание тока с ростом поля.
318
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
будет узок, мы будем иметь дело с резким изменением потен-
циальной энергии и классическая механика будет неприменима: электроны
будут проходить через потенциальный барьер.
Вычислим коэффициент прозрачности этого барьера для электронов,
имеющих энергию движения по оси ОХ, равную Ех. Согласно (89.24)
дело сводится к вычислению интеграла
S = ( /2ц|1Г (х) —£] dx,
Х1
где xt и x2— координаты точек поворота. Первая точка поворота есть
(см. рис. 63), очевидно, х1 = 0, так как для всякой энергии ЕХ<^С
горизонтальная прямая Ех, изображающая значение энергии движения
по ОХ, пересекает кривую потенциальной энергии в точке х — 0.
Вторая точка поворота х2 получится, как видно из чертежа, при
Ех — С— е$х;
отсюда
следовательно,
С-Ех
S — J /2ц [С— е^х — Ех] dx. <91-2)
о
Введем переменную интегрирования Е= х. Тогда мы получим
5 = /2/ (С~^ ( /Г=Т = 2 /2/ . (91.3)
49 ./ о еф
0
Таким образом, коэффициент прозрачности D для электронов, обладаю-
щих энергией движения по оси ОХ, равной Ех, равен
_£ (с~Е^)3/а
D(Ex) — DQe 3 h es . (91.4)
Коэффициент этот несколько различен для разных Ех, но так как
С> Ех, то средний (по энергиям электронов) коэффициент прозрачности
будет иметь вид
___ _________________________________
D — D^e s , (91.5)
где Z)o и <§Q— константы, зависящие от рода металла. Ток холодной
эмиссии будет равен
= (91.6)
Эта зависимость тока от поля вполне подтверждается опытом.
§ 92]
КВАЗИСТАЦИОНАРНЫЕ СОСТОЯНИЯ
319
§ 92. Трехмерный потенциальный барьер.
Квазистационарные состояния
нам встретятся такие случаи, когда
Рис. 64, а и Ь. Потенциальный барьер,
ограничивающий замкнутую область
(Г<Г0)‘
Рассмотренные в §§ 90 и 91 задачи о прохождении через потен-
циальный барьер отличались той особенностью, что в них речь шла
о потоке частиц, приходящих из бесконечности и встречающих на
своем пути потенциальный барьер. В дальнейшем (теория радиоактив-
ного распада, автоионизация атомо
речь будет итти о потоке частиц,
выходящих из некоторой ограни-
ченной области пространства (ядро
атома, атом), окруженной потен-
циальным барьером.
Пусть шар с центром в О и
радиусом г0 (рис. 64, а) есть та
поверхность, на которой потенци-
альная энергия U (г) принимает
максимальное значение, так что для
'<?« и<ит и ДЛЯ r>r0
U<^Um. Соответствующий пример
графика U(г) дан на рис. 64, Ь. Допустим, что нас интересует про-
хождение через барьер частиц, первоначально находившихся внутри
него. Соответственно предположению, что частицы, падающие извне,
отсутствуют (нет «бомбардировки»), мы должны взять вне барьера лишь
уходящие волны
ф = С^^, А>0. (92.1)
Это условие мы будем называть условием излучения. Ясно, что*
уравнение Шредингера
(92-2}
в этом случае может иметь лишь нестационарные решения. Действи-
тельно, применим закон сохранения числа частиц к сфере радиуса г:
V ) S = — j J^dQ. (92.3)
Из (92.1) имеем: Jr 2 V ‘ dr и, стало быть, Л hk\C\2 (92.4)
дг т J г2
4 к ?*=- V |С|МЙ<0, (92.5)
т. е. среднее число частиц в объеме сферы V убывает так, что ф не
может гармонически зависеть от времени.
320
ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
Задачу о истечении частиц из барьера можно решать, исходя из
уравнения (92<2) с начальным условием ф (г, 0) таким, что функция
ф (г, 0) отлична от нуля лишь внутри барьера (чтобы выразить тот
факт, что при t — О частица находилась внутри барьера). Можно, одна-
ко, исходить из другого условия, до некоторой степени противопо-
ложного, именно считать, что истечение частиц происходит уже давно
и значительная часть их уже находится вне барьера. Такой подход
к решению мы рассмотрим подробнее. Он удобен тем, что до-
пускает разделение переменных г и t в уравнении (92.2). Поло-
жим сразу
,Et
<|> (г, /) = ф(г)ег h . (92.6)
При этом величина Е будет комплексной, и ее нельзя рассматривать
как энергию частиц (см. об этом ниже).
Мы положим*)
Е=Е0+^. (92.7)
Тогда среднее число частиц в объеме Уо,
заключенном внутри барьера, согласно (92.6)
и (92.7) будет
ф*(г)ф(г)^,
т. е.
N(t) = e-^N(0). (92.8)
Рис. 65. Потенциальный барь-
ер, ограничивающий замкну-
тую область (г < /1) и имею-
щий простую прямоугольную
форму.
Потенциальная кривая О, n,
Um соответствует потенциальной
яме, получающейся из барьера
отодвиганием г8 в бесконечность.
Fp — уровни в такой яме.
взяв форму барьера U(r),
для простоты, состояния с
Тогда, полагая
Величину X будем называть константой
распада. Подстановка (92.6) в (92.2) дает
_gvs$4-t/(rH = (£0 + ^) ф. (92.9)
Чтобы выяснить принципиальную сторону
дела, мы рассмотрим схематичный пример,
изображенную на рис. 65. Рассмотрим далее,
орбитальным моментом, равным нулю: / = 0.
(92.10)
мы получим из (92.9)
^+t/(r)«=(£0+z4)«.
(92.11)
*) Из (92.6) и (92.7), видно что если взять X — 0, то мы получили бы стаци-
онарные состояния, что противоречит согласно (92.5) условию излучения.
§ 92] КВАЗИСТАЦИОНАРНЫЕ состояния 321
Согласно нашему предположению о виде U(r) уравнение (92.11)
разобьется на три:
= 0 (0<г<г1), (92.12)
и" — q2u = 0 (rr < г < г2), (92.12')
и” + ^2«=0 (г2<г), (92.12")
где
А2 = ^(е0 + Ф), ?2=^((/ж-Е0-/4). (92.13)
Решения этих уравнений имеют вид
И, = A'e-ikr+Beikr (0 < г < «ц =ae?r-[-?e~?r (г, <Zr<i um — ae~ikr-]-belkr (rz<Zr)- 7i), 7а)» (92.14) (92.14’) (92.14")
Из условия конечности ф в нуле следует, что
А’ = — В, и{ — А sin kr. (92.15)
Кроме того, условие излучения дает й = 0 (только уходящие волны).
Краевые условия на границах г—гх и г = г2, как. мы установили
в § 89, сводятся к равенству функций и их первых производных:
A sin krx = (92.16)
kA cos krx — q (aeV* — ^-^r<) для r=rp (92.16')
ae^-\-^e~4^ = ae~ ikr\ (92.17)
q{a.e^— $e~4r*) = ikae~ikr* для r = r2. (92.17')
На этот раз мы имеем четыре однородных уравнения для четырех коэф-
фициентов Л, a, jJ, а. Поэтому необходимо, чтобы определитель Д
системы уравнений (92.16), (92.17) обращался в нуль. Несложные вычис-
ления дают:
А (А)=е~<1 tg kr, - 1) tg Ar, + 1) , (92.18)
где l означает ширину барьера r2 — rv (92.18) есть трансцендентное
уравнение для k. Определим его корни приближенно, считая ql J>> 1,
Тогда в нулевом приближении можно отбросить член с е'"'*1, и мы полу-
чаем
tg Ar,-f-1 — 0. (92.19)
Это — точное уравнение для нахождения собственных значений для потен-
циальной ямы (0, L7J, изображенной на рис. 65 и получаемой из
потенциального барьера рис. 65 при г2 = оо. В такой потенциальной
яме имеются дискретные уровни энергии (для Если корни
уравнения (92.19) обозначить через &02, ..., &Оп, . .., то энергия
этих уровней будет [согласно (92.13)] равна
= «=1,2,3,... (92.20)
21 Блохинцев
322 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
Корни действительны*), так что 1=0, и по порядку величины
равны у-. В этом случае мы имеем стационарные состояния. При ко-
нечной ширине барьера асимптотическое поведение потенциальной энер-
гии таково, что U(r)r__,оо<£, и вместо дискретного спектра (92.20)
мы получаем непрерывный. Однако, условие излучения выбирает из
непрерывного спектра уровни, близкие к EQn, но они не будут теперь
стационарными (1яУ=0). При малых \п они будут почти стационарными.
Это — квазистационарные уровни, упоминавшиеся в § 63. Определим
величину считая ее малой. Для этого разложим е^1 в (92.18) по
степеням Д£ = &— &0, где kQ — один из корней уравнения (92.19) для
стационарных состояний потенциальной ямы, а в член с подставим
k — kQ; замечая, что
— A tekr —
dk~ q> Ъ*г1— qQ>
поручим:
4^(1 +9°Г1) д*+ • • • =°-
Qq + «о Мо
Отсюда находим Д/г.
При этом малую поправку к действительной части kQ мы можем
опустить, как не представляющую интереса. Мнимая же часть будет
равна
ka)=^(ik)=ik0
4е-2?°Ч<7р
(9о + ^о)2 (1Н-Wj)
(92.21)
Пренебрегая также малой поправкой к действительной части k в (92 13),
мы можем положить Из (92.13) получаем:
/Ху.
2kQh9
(92.22)
(92.23)
Сравнивая это с предыдущим выражением для Д£, мы находим:
к = А .....
Н<7о+*о)2(1+П>
Имея в виду, что ~ есть скорость частицы vQ внутри барьера и
что kQ у = (г0 — радиус ямы), мы получаем из (92.23) и (92.13):
, Г>п -~У2^(СГт-£)1
А==2/0б
(92.24)
*) Для достаточно глубокой ямы (Um —* оо) tf_ —» со, и вместо (92.19)
имеем taAz-1 = O, kai\ — *n, л —0, 1, 2, 3,...
§ 92]
КВАЗИСТАЦИОНАРНЫЕ СОСТОЯНИЯ
323
Эта формула имеет простое наглядное толкование. — есть число ударов
го
частицы о внутреннюю стенку барьера в 1 сек., а экспоненциальный
множитель есть коэффициент прозрачности.
Отметим еще некоторые особенности рассмотренной задачи. Мнимое зна-
чение волнового вектора к приводит к тому, что интенсивность излучаемой
волны — e~~ikr неограниченнб растет по мере удаления от потенциального
барьера:
ae~ikr e-‘kcr+^r
. ис с>
Фш = —— = а----------------.
Рост ф1П вытекает из требования, чтобы имелось только излучение, и от-
вечает тому факту, что на больших расстояниях находится частицы, вылетев-
шие раньше, еще тогда, когда интенсивность | фг |2 внутри самого барьера
была больше. Однако, в нашем методе решения мы не учли того обстоятельства,
что излучение на самом деле когда-то началось (а не длилось все время от
t ——оо) и что к моменту начала излучения | р было конечно. Поэтому наш
вывод о том, что фш -> оо при гоо, вывод, относящийся к частицам, выле-
тевшим очень давно, неверен, и само найденное решение справедливо лишь
для небольших г, именно — для
Далее, отметим, что в связи с формулой (92.7) в литературе часто говорят
о мнимой энергии. Следует и четь в виду, что такое выражение имеет лишь
чисто формальный смысл. Найденное нами состояние
ф(г, /) = <Ыг)г А 2 (92.25)
не есть стационарное состояние с определенным значением энергии (стацио-
нарные состояния гармонически зависят от времени).
Чтобы определить вероятность найти то или иное значение энергии
в этом состоянии, нужно разложить функцию (92.25) по собственным функциям
оператора энергии Н. Так как U(г) > 0, то собственные значения этого опера-
тора ^ = Лсо>Ои, кроме того, они образуют непрерывный спектр 0^/?< оо.
Обозначая соответствующие собственные функции через фш(г), мы получим:
00
ф (г, f) = С с (со) фш (г) dto, (92.26)
Это представление ф (г, t) справедливо согласно сказанному выше о ф1П лишь
Для малых г. При малых же г ф0(г) совпадает с одной из собственных функций
оператора энергии, именно — сфШо(г) — • Поэтому для малых г имеем:
Отсюда
0° 2 л * л
р — t
Ф (Г, t) = фШо (г) 1 с (<0) eiwtdu> — Фо (г) е
О
1 t-iiat
О
, 1 1
2к1 ~’ Г
z((0 —Wo) — у
(92.26*)
(92.27)
и, следовательно,
ic^)i2
(<o-«.o)a+Y
(92.28)
21*
324 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVH
и так как £=/г<о, то вероятность найти Е лежащей между Е nE-\-dE в со-
стоянии (92.25) фудет равна
I с ( [2 — Л_________________ (99 29)
4,<(е_£о)!+№-
т. е. уровень £0, как говорят, имеет ширину. Обычно эту ширину &Е опре-
деляют как такую разность | Е—£0|, для которой вероятность найти Е вдвое
меньше вероятности найти Eq, т. е.
(92.30)
Если ввести длительность жизни частицы в состоянии ф0, определяемую
тю формуле 1=-^-, то мы получаем:
Д£.т=А (эг-зо1)
— соотношение между длительностью жизни т и шириной уровня Отсюда
мы видим, что утверждение, что $астица находится в стационарно^ состоянии
конечное время т, ведет к тому, что само значение энергии фиксируется лишь
с ограниченной точностью.
§ 93. Теория радиоактивного а-распада
Известно, что многие радиоактивные элементы распадаются, испуская
а-частицы. По вылете из атомного ядра а-частица, имея/ двукратный
положительный заряд (-(- 2е), ускоряется в кулоновском поле атомного
ядра, заряд которого обозначим через Ze (под Z будем подразумевать
номер элемента после вылета а-частицы, Z — Z' — 2, если Z1 есть но-
мер элемента до радиоактивного распада).
Большая прочность а-частицы позволяет предполагать, что она су-
ществует в ядре в виде самостоятельного объекта, являясь одним из
простых образований, из которых строится атомное ядро*). Ясно, что
а-частица может длительно находиться в атомном ядре лишь в том слу-
чае, если область вблизи атомного ядра является минимумом потенциаль-
ной энергии а-частицы. Кулоновская потенциальная энергия а-частицы,
2Ze2 .
равная -у—, где г—расстояние от ядра до частицы, по мере приближе-
ния к ядру, как это изображено на рис. 66 пунктирной кривой, все
время возрастает монотонно. Поэтому минимум энергии вблизи ядра
может получиться лишь в том случае, если на близких расстояниях на
а-частицу действуют какие-то иные силы помимо электрических. Природа
этих сил в настоящее время неизвестна. Известно лишь, что они весьма
велики и действуют лишь на очень малых расстояниях. Именно этими
силами и обусловливается смена кулоновского отталкивания на резкое
*) Это предположение не является обязательным. Возможно, что перед
вылетом из ядра а-частица образуется из более простых частиц: нейтронов и про-
тонов. Мы будем считать в дальнейшем, что она существует в ядре постоянно.
§ 93]
ТЕОРИЯ РАДИОАКТИВНОГО Я-РАСПАДА
325
притяжение вблизи ядра, изображенное на рис. 66 сплошной кривой.
Такое поведение потенциала называют образованием потенциальной
ямы или кратера. При наличии таких сил я-частица, находящаяся
в области г<^г0, т- е* в поле притягательных сил, будет длительно
удерживаться внутри ядра.
Как же происходит я-распад? Долгое время это оставалось загад-
кой. Еще Кельвин предполагал, что частицы, испускаемые радиоактив-
ным элементом, как бы кипят внутри потенциального кратера. Время
от времени одна из частиц получает избыток энергии над средней, пре-
одолевает барьер и, вылетев за
полем, приобретая большую
энергию. Эта картина весьма
подходила бы по крайней
мере для качественного пони-
мания явления, если бы не
опыт Резерфорда, показав-
ший, что дело обстоит иначе.
К изложению этого опыта мы
сейчас и перейдем.
Резерфорд бомбардировал
атомы радиоактивного урана
я-частицами тория С'. Энер-
гия а-частиц тория С' равна
13*'10~в эрг. Такие частицы,
него, ускоряется отталкивательным
Рис. 66. Кривая потенциальной энергии
а-частицы в функции расстояния от ядра
(г, Um, г'). Та же кривая схематизирована
(/*, Um, /*о) (резкое падение после г0).
преодолевая кулоновское от-
талкивание, могут весьма
близко подойти к ядру. Оце-
ним расстояния наибольшего
сближения гг Очевидно, что гх
2Z'<?2
есть то расстояние, при котором потенциальная энергия частицы ---------
ri
будет равна исходной кинетической, т. е. ------= П>-10 6 эрг. Z' есть
номер урана и равен 92. Поэтому мы находим, что г1 = 3’10“12 см.
Наблюдение показывает, что рассеяние таких частиц строго такое,
каким оно должно быть при действии на а-частицу кулоновского поля.
Это означает, что ядерные силы начинают действовать на я-частицу на
расстояниях, меньших, нежели 3-10”"12 см. Поэтому а-частицы, заклю-
ченные в ядре, находятся внутри области, радиус которой меньше
3. см.
С другой стороны, уран сам является радиоактивным элементом и
^спускает а-частицы. Измерение ’ энергии этих частиц показывает, что
она равна'6,6 • 10”6 эрг.
Эти а-частицы вылетают из ядра, т. е. с расстояний; меньших
3>10~12 см. Тогда, ускоряясь в кулоновском поле1 они должны были
6м приобрести энергию, равную высоте потенциального барьера
(см. рис. 66) и во всяком случае ббльшую, нежели 13-10“6 эрга.
326 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVI!
Получается же так, как если бы они вылетали с расстояния г=6-10“12 см.
Таким образом, опыт приводит к парадоксальному положению вещей:
либо нужно предположить, что кулоновское электрическое поле ядра
действует на падающие извне а-частицы, но не действует на вылета-
ющие из ядра, либо считать, что закон сохранения энергии не выпол-
няется при радиоактивном распаде.
Решение этого парадокса было дано Г. Гамовым, который указал
на вытекающую из квантовой механики возможность туннельного эф-
фекта через потенциальный барьер, разделяющий область притяжения
(г<^г0) от области отталкивания (г^> г0).
В самом деле, тогда парадокс полностью решается: частица, нахо-
дящаяся внутри ядра, может иметь энергию, меньшую, нежели высота
барьера, и все же пройти через него. Частица же, пролетающая извне,
ввиду малой прозрачности барьера лишь в очень редких случаях будет
захватываться ядром (так как время пребывания ее около ядра очень
мало). Поэтому рассеяние а-частиц, падающих извне, будет обуслов-
ливаться кулоновскими силами, действующими за пределами барьера.
Предположенная малая прозрачность барьера согласуется с тем фактом,
что периоды радиоактивного а-распада весьма велики.
Применяя теорию прохождения через потенциальные барьеры, легко
облечь изложенную идею в математическую форму и найти выражение
для константы радиоактивного распада 1. Напомним, что эта константа
определяется следующим образом. Если имеющееся к моменту времени t
число нераспавшихся атомов равно N, то в течение времени dt среднее
число распавшихся атомов dN будет равно
dN=-\-N-dt, N (t) = AT (0) (93.1)
Для вычисления, константы распада X мы можем применить кванто-
вую теорию просачивания частиц через замкнутые барьеры, изложен-
ную в предшествующем параграфе. Согласно этой теории а-частицу
внутри ядра следует рассматривать как находящуюся в «квазистацио-
нарном» состоянии. Обозначая скорость частицы в этом состоянии через vt,
радиус барьера через г0 и, наконец, его коэффициент прозрачности
иерез Д мы получим:
(93.2)
Остается лишь вычислить D. Ввиду более сложной формы барьера
вместо (92.24) мы получим [см. (89.24)]:
Га
—V2? [U(r)-£J dr
\ = X . (93.3)
Из рис. 66 следует, что первая точка поворота есть г0 (радиус
ядра), вторая (г2) определится из условия
—- = Е, гъ=-р-. (93.4)
г 2
ТЕОРИЯ РАДИОАКТИВНОГО 3-РАСПАДА
327
§ 93]
Таким образом,
2Ze*
Е
Го
— —Edr. (93.5)
Вводя
сюда новую переменную $ = — , мы получаем:
Г2
<S = 2Zs2
— 1<й,
(93.5':
Jo
г3
и, полагая, наконец, еще $ = cos2a, мы без труда вычислим вышена-
писанный интеграл:
COS2«0 — w
и r2 2Ze2
(93.6)
Воспользуемся тем, что отношение — меньше единицы, и разложим
Г2
и0 и sin 2я0 в, ряд по степеням у (достаточно ограничиться двумя пер-
выми членами). Тогда мы получим:
(93.7)
/2Ё
—. Итак, выражение для
константы
распада (93.3) раскрывается следующим образом:
2 Ко
(93.8)
или
<пу______. 8<?уТ 1/~7ГГ I hP9
InX— hv + Л V £ °+ 2|хг*‘
(93.9)
замечательным выводом из этой формулы является зависи-
Наиболее
мость между X и скоростью а-частицы v. Подобная зависимость еще
задолго до теории Гамова была установлена на опыте Гайгером и
Нэттолом.
Далее, мы видим, что In X зависит от номера элемента Z (Z* — Z — 2)
и радиуса ядра.
Из опыта известно, что константы распада варьируют в очень ши-
роких пределах: от 10""5 сек.”1 до 1011 сек."*1. Если бы в таких же
пределах приходилось варьировать параметры, определяющие X,
328 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVI5
то теория была бы наверно неправильной. Замечательным следствием
формулы (93.9) является то, что если по эмпирическим данным для X
определять радиусы ядер, то окажется, что они все лежат в разумных
границах, примерно от 5-10“12 см до 9-10“12 см. Значительное
различие в величине X для разных элементов определяется не раз-
личием в радиусах ядер, а различием в энергии вылетающих частиц.
Слабую зависимость X от г0 и резкую от v следует рассматривать как
подтверждение теории *).
§ 94. Ионизация атомов в сильных электрических полях
Подобно тому как сильное электрическое поле вырывает электроны
из металлов (холодная эмиссия, § 91), оно вырывает их также и из
отдельных атомов газа. Явление это называют иногда «автоионизацией»
атомов и его причину легко понять, если рассмотреть вид потенциаль-
ной энергии электрона в атоме при наличии внешнего электрического
поля. Пусть потенциальная энергия электрона в отсутствии внешнего
поля есть U(г). Внешнее электрическое поле S пусть направлено по
оси OZ. Тогда вся потенциальная энергия электрона равна
U’(r)==U(r) + eSz. (94.1)
Рассмотрим вид потенциальной кривой на оси OZ (х-—у = 0, г— \z |).
В отсутствии внешнего поля ($ = 0) If = U (г) и имеет вид, изобра-
Рис. 67. Сложение атомного поля и
внешнего. В области образуется
потенциальный барьер.
женный на рис. 67 пунктиром. До-
полнительная потенциальная энергия
во внешнем поле e$z изобразится
прямой аа!. Кривая полной потен-
циальной энергии получающая-
ся сложением, проведена на рис. 67
сплошной линией а'Ь1 и ab. Мы
видим, что около точки г0 образуется
потенциальный барьер, разделяю-
щий пространство на две области:
внутреннюю z">z§ и внешнюю
z<^z§, в каждой из которых потен-
циальная энергия U меньше Т7'(,г0)“
= Um. На чертеже приведены также
два уровня энергии Е и Е. Если
энергия Е = Е" > Um, то электрон
не будет удерживаться вблизи атома, а будет удаляться в область отри-
цательных z. Если же энергия электрона Е = Е' <^Um, то согласно
законам классической механики электрон останется во внутренней об-
ласти. По квантовой механике в этом случае просачивание через барьер
*) Подробности теории радиактивного распада см. в книге Г а м о в а,
Атомное ядро и радиоактивность.
§ 94] ИОНИЗАЦИЯ АТОМОВ В СИЛЬНЫХ ЭЛЕКТРИЧЕСКИХ полях 329
все же будет иметь место. Таким образом, здесь создается положение
вещей, вполне аналогичное тому, которое имеет место при радиоактив-
ном распаде.
Теперь уже совсем легко видеть причину ионизации атомов полем.
При включении поля получается барьер, через который электроны про-
никают во внешнее пространство. Если высота барьера Um меньше
энергии электрона, то частицы будут проходить («над барьером») и
по классической механике. Поэтому и классическая механика приводит
к возможности ионизации атома внешним электрическим полем. Раз-
личие заключается лишь в том, что по законам квантовой механики
эта ионизация должна наступать при меньших полях, нежели это
предписывается механикой классической, так как согласно кванто-
вой механике для возможности ионизации не нужно, чтобы барьер
оказался меньше энергии электрона. Ясно, однако, что при малых
полях барьер будет очень широким и прозрачность его будет
очень мала.
Явление автоионизации можно наблюдать таким образом: допустим,
чго мы наблюдаем какую-либо спектральную линию, обусловленную
электронным переходом из состояния Е’ в Ео (см. рис. 67). По мере уве-
личения электрического поля эта линия будет смещаться (Штарк-эффект),
и если поле достигнет столь большой величины, что прозрачность
барьера будет велика, то электрон в состоянии Е' будет чаще выле-
жать из атома, проходя через барьер (ионизация), нежели падать в ниж-
нее состояние (£*0), излучая свет. Благодаря этому спектральная линия
будет слабеть, пока, наконец, совсем не исчезнет. Это явление на-
блюдал Рауш-фон-Траубенберг на бальмеровской серии атомного
водорода *).
Для того, чтобы иметь возможность проследить Действие электриче-
ского поля различной напряженности, Рауш-фон-Траубенберг устраивал
так, что различные части спектральной линии обусловливались светом,
исходящим от атомов, находящихся в полях различной силы. Именно,
в объеме светящегося газа электрическое поле возрастало в направле-
нии, параллельном щели спектроскопа (до некоторого предела, достигнув
которого оно вновь падало). На фотографии (см. рис. 44) приведены
результаты его опытов. Буквами , у, 5, е обозначены линии серии Баль-
мера (77р — переход и = 4—>п = 2, — переход /г = 5—>п = 2,
— переход п==6-—>п = 2 и /7е — переход п = 7 —>п = 2). При-
ложенное электрическое поле растет снизу вверх. Белые линии на фо-
тографии суть линии одинаковой напряженности поля. Из фото-
графии видно, что линии сперва расщепляются. Это расщепление увели-
чивается по мере роста поля (из расщепления линии легко видеть
положение линии максимальной напряженности поля). При некоторой
напряженности поля спектральная линия исчезает.
*) Заметим, что наблюдение числа электронов, вырываемых полем, в дан-
ном случае затруднено, так как в условиях газового разряда трудно устано-
вить, за счет каких именно причин возрастает электронный ток.
330 ПРОХОЖДЕНИЕ ЧАСТИЦ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ [ГЛ. XVII
Сравнение линий [J, у, 8, е показывает, что они исчезают в после-
довательности е,, 8, у (при достигнутых полях р полностью не исчезает).
Это есть последовательность возрастания энергии возбужденного состоя-
ния. Из рис. 67 явствует, что чем выше энергия электрона, тем меньше
при заданном поле ширина и высота барьера, т. е. тем больше его
прозрачность. Таким образом, наблюдающаяся последовательность в ис-
чезновении спектральных линий вполне соответствует нашему толкова-
нию этого явления как результата туннельного эффекта. То обстоя-
тельство, что красные компоненты расщепленных линий исчезают раньше
фиолетовых, также прлучает полное разъяснение при более детальном
рассмотрении волновых функций электрона. Именно, состояния, отвечаю-
щие линиям, смещенным в красную сторону, обладают тем свойством,
что в них интенсивность электронного облака больше в области барьера,
нежели в состояниях для фиолетовых компонент. Благодаря этому
ионизация протекает более благоприятным образом.
Сформулируем несколько детальнее те условия, при которых сле-
дует ожидать исчезновения спектральной линии в электрическом поле.
Пусть вероятность оптического перехода электрона в нижнее состояние
будет (т — время жизни в возбужденном состоянии). Время жизни
электрона в возбужденном состоянии есть т 10“8 сек. Вероятность
перехода электрона в нижнее состояние в 1 сек. будет . Вероят-
ность туннельного эффекта (ионизации) будет равна (так же, как и
при расчете радиоактивного распада) числу ударов электрона о внут-
реннюю стенку потенциального барьера в 1 сек., умноженному на коэф-
фициент прозрачности D. Число ударов о барьер по порядку величины
равно гр- , где v — скорость электрона, а г0 — радиус барьера, при-
мерно равный радиусу орбиты а. Скорость равна, опять-таки по порядку
величины, v = | Е |, где | Е | — энергия электрона, ар. — его масса.
Следовательно,
v __
— 1016 сек.-1
«з
(^2 Й2 \ _
так как Е~ — — , Следовательно, вероятность автоиони-
2а ’ р.£2 /
зации равна 1016 D сек."”1. Чтобы преобладала автоионизация (условие
исчезновения спектральной линии), нужно, чтобы ~ < D-1016, т. е*
£)>10“8.
Количественная теория автоионизации была дана Ланчосом *) и на-
ходится в очень хорошем согласии с опытом.
*) См. С. Lanczos, Zs. Phys., 68, 204 (1931). См. также Г. Бете,
Квантовая механика простейших систем, ОНТИ, 1935, стр. 193—197.
§ 95] ОБЩИЕ ЗАМЕЧАНИЯ О ЗАДАЧЕ МНОГИХ ТЕЛ
331
ГЛАВА ХУШ
ЗАДАЧА МНОГИХ ТЕЛ
§ 95. Общие замечания о задаче многих тел
Квантовая механика одной частицы во внешнем поле может быть
просто обобщена на случай движения многих частиц. Для этого так же,
как и в классической механике, достаточно рассматривать систему из Af
частиц как одну частицу с 3N степенями свободы (если не считать спина
частиц; с учетом спина будем иметь 4М степеней свободы). Все общие
положения квантовой механики, имеющие силу для системы с несколькими
степенями свободы, могут быть сразу же перенесены на систему, состоя-
щую из N частиц. Тем не менее существуют некоторые специфические мо-
менты, свойственные системам из многих частиц и заслуживающие
специального рассмотрения.
Среди этцх специфических моментов особо важные выясняются для
систем, состоящих из одинаковых частиц. В дальнейшем нам придется
подробно остановиться на них. Свойства систем из одинаковых частиц
образуют одну из наиболее замечательных глав квантовой механики.
Однако, пока мы оставим в стороне эти особенности систем с одина-
ковыми частицами и обратимся к некоторым вопросам, общим для систем
любых частиц.
Всегда ли можно рассматривать совокупность частиц как механи-
ческую систему с соответственно большим числом степеней свободы?
Ответ должен быть отрицательный. Рассмотрение системы частиц с коор-
динатами xxyyzv XnV2^2, ..., xNyNzN, как механической системы
с ЗМ степенями свободы, возможно лишь при условии, что между части-
цами не действуют запаздывающие силы (или при приближенном рас-
смотрении таких сил). Иначе говоря, все силы взаимодействия должны
зависеть лишь от мгновенных значений механических величин, относя-
щихся к нашим частицам (например, от их координат и скоростей
в данный момент времени), а не от их значений в прошлом, как это бы-
вает при действии запаздывающих сил. Это условие не является особен-
ностью квантовой механики. Оно таково же и в классической механике.
Поясним это условие на примере электромагнитных сил. Пусть рас-
стояние между частицей номера j и частицей номера k есть Гд. Тогда
время, в течение которого распространится электромагнитное возмуще-
ние от одной частицы к другой, равно т = “ , где с — скорость света.
Для того, чтобы можно было считать силы мгновенными, необходимо,
чтобы за время т расстояние между частицами мало изменилось. Если
относительная скорость частиц вдоль rik есть v то изменение rjk за вре-
А Vjk'rjk п
мят есть — = . Следовательно, наше условие гласит:
vjktrfk
-----т. е. v/k
С
332 ЗАДАЧА МНОГИХ ТЕЛ [ГЛ. XVII!
Следовательно, относительные скорости частиц должны быть гораздо
меньше скорости света с. Короче говоря, это всегда можно сделать,
если мы ограничиваемся нерелятивистской областью скоростей.
Если v с, то сверх того, что мы должны будем учитывать и ре-
лятивистские, и квантовые эффекты, мы должны будехМ вместе с меха-
ническими уравнениями для частиц рассматривать, еще и уравнения
электромагнитного поля, которые управляют распространением взаимо-
действия от одной частицы к другой.
Относящиеся сюда вопросы выходят за рамки этой книги и вообще
полностью они не разрешены современной теорией *).
Поскольку же v<^.c, мы можем рассматривать квантовую механику
системы частиц как механику одной частицы с многими степенями сво-
боды.
Если у нас имеется N частиц с координатами xkykzk (& = 1, 2,
3, ..., N) и с массами mk> то волновая функция ф в этом Случае
будет, как всегда, функцией координат всех степеней свободы нашей
системы и времени т. е. функция 37V—j— 1 аргументов **):
Ф = Ф(*1>•••> х»Ук’гь............хК’Ух’г& (95л)
Она определяется таким образом в пространстве 3N измерений, так
называемом пространстве конфигурации системы. Название этого фик-
тивного пространства проистекает от того, что задание координат точки
в этом пространстве есть задание трехмерных координат (xk, yk, zk)
для всех частиц (k — 1, 2, 3, N) нашей системы и, следовательно,
определяет расположение (конфигурацию) всех частиц системы в трех-
мерном пространстве. Поэтому точку пространства конфигураций с
32V координатами (xvyvzv ..., xN,yNizN) называют изображающей
(систему) точкой.
Обозначим бесконечно малый элемент объема в пространстве кон-
фигураций через б/й:
d$ = dx1dy1dz1 ... dxkdykdzk ... dxNdyNdzN. (95.2)
Тогда величина
•••» •’W*»**» •••> Х^У^ zN)d&— (95.3)
есть вероятность того, что изображающая точка лежит в элементе
объема dQ пространства конфигураций в момент времени /, т. е. ве-
роятность конфигурации системы, при которой в момент t координаты
первой частицы лежат между xlt x1-\-dx1, yv Уг-^-dy^, zv
Zj-l-fifei, &-ой частицы — между xk, xk-\-dxk, yk, УьЛ~^У^
zk + dzk и т- Д-
*) См. Гайт л ер, Квантовая теория излучения, ГИТТЛ, 1940; Дирак,
Основы квантовой механики, гл. XIV.
**) Чтобы не усложнять излишним образом дела, мы не рассматриваем
сейчас спина частиц.
§ 95] ОБЩИЕ ЗАМЕЧАНИЯ О ЗАДАЧЕ МНОГИХ ТЕЛ 333
Наряду с элементом объема (95.2) рассмотрим элементы объема в
подпространствах типа dQk, d§kp ... и т. д., определенные по формулам
d& — dxkdykdzkdQk, (95.4)
d& — dxkdykdzkdXjdyjdZjd§kj и т. п. (95.4')
Интегрируя (95.3) по координатам всех частиц кроме £-ой, т. е. по dQk,
мы найдем вероятность того, что координаты 6-ой частицы лежат
между xk, xk -j- dxk, yk, yk -|- dyk, zk, zk 4- dzk при любом положении
других, иными словами, мы найдем вероятность того, что &-ая частица
находится в данном месте пространства. Обозначая эту вероятность
через ^(хА, yk, zk, получаем:
та (хА, yk, zk, t) dxkdykdzk = dxkdykdzk d$k. (95.5)
Подобным же образом величина
™ хр У Г zp t^dx^y^z^xfiy^Zj—
— dxkdykdzkdxjdyflz1 § <|>*ф dQk/ (95.5')
есть вероятность того, что &-ая частица находится около точки xkykzk^
/-ая частица одновременно ' около точки х}у -Zj. Таким образом, зная
волновую функцию ф, заданную в пространстве конфигураций, можно
определить вероятность данной конфигурации системы (95.3), вероят-
ность положения любой из частиц (95.5) и, наконец, вероятность того
или иного положения пары частиц (95.5') и т. п. Равным образом по общим
формулам квантовой механики, разлагая ф по собственным функциям
какого-либо из интересующих нас операторов, можно вычислить и вероят-
ности того или иного значения любой механической величины.
Мы будем считать, что волновая функция ф(хр ..., ^, /) также, как
и волновая функция одной частицы, подчиняется уравнению Шредингера
(95.6)
причем Н означает здесь гамильтониан для системы частиц. Последний,
в полной аналогии с классической гамильтоновой функцией для систе-
мы N частиц с массами rqv — , tnk> .. ., mN
N 2
uk(x&y&zk' *)} + ^2 Ukj(xk,yk'xpуpzjh
где Uk (xk1 yk, zk, t) — силовая функция &-ой частицы во внешнем поле,
a Ukf (хк, ... z^ — энергия взаимодействия &-ой и /-ой частиц, на-
пишется в виде
я= S {- {Хк'yk’°} +
+ S хрУр2^ (95-6'>
334
ЗАДАЧА МНОГИХ ТЕЛ
[ГЛ. Х¥Ш
где
= + Л
k дх2ь ду\' dz2k'
Очевидно, что этот гамильтониан представляет собой простое обобще-
ние гамильтониана для одной частицы *).
Из уравнения (95.6) следует уравнение непрерывности для вероят-
ности w в пространстве конфигураций. Чтобы получить его, умножим
(95.6) на ф* и вычтем сопряженную величину. Имея в виду значение
гамильтониана (95.6'), мы» получим:
«Фф*Ф)=-§ {ф*^ф-ф^ф* }•
Полагая
где — оператор с проекциями
полученную формулу в виде
мы
можем
N
S+2>v.j.=o.
k—1
(95.7)
написать
(95.8)
д д д~
d*k дгк'
Это уравнение показывает, что изменение вероятности конфигурации w
обусловливается потоком этой вероятности. Ток есть функция коор-
динат всех частиц (и времени) и имеет смысл плотности тока, обуслов-
ленного движением &-ой частицы при заданных координатах всех осталь-
ных (TV—1) частиц. Чтобы получить плотность тока &-ой частицы
при любом положении остальных, следует интегрировать (95.7) по всем
координатам, кроме координат &-ой частицы:
ik(xk^y^zk> • • •» х&У& zk* • • •» zn> (95.9)
Этот ток также удовлетворяет уравнению непрерывности, но уже в трех-
мерном пространстве. Именно, интегрируя (95.9) по dQki мы получаем:
J 5? w ’ ’ ’ ’ Zn' d&k ~
= zn> t)dQk=Jt™(xk>yk>zk> 0-
Далее,
Sj У div*<3k’<iQb — У 4- У div*3k<dQk.
Так как dQk [см. (95.4)] как раз содержит координаты всех частиц
*) Можно было бы выписать гамильтониан при наличии магнитного поля
и с учетом спина. Он равен сумме гамильтонианов отдельных частиц плюс
члены, определяющие взаимодействие частиц между собой.
§ 96]
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
335
кроме &-ой, то интегралы вида можно преобразовать
верхностные и если ф исчезает в бесконечности, то они равны
Так как, напротив в интеграле j дифференцирование и
грирование идут по различным переменным, то
J = divA = divAjA.
Таким образом, мы получаем закон сохранения для каждой из частик
/) = 01
сформулированный уже в трехмерном пространстве (xk) yk) zk).
в по-
нулю.
инте-
(95.10)
§ 96. Закон сохранения полного импульса системьг частиц
В классической механике, как известно, полный импульс системы
частиц, находящихся под действием лишь внутренних сил, остается
постоянным. При этом центр тяжести системы движется по инерции пря-
молинейно и равномерно. Если же имеются внешние силы, то изменение
полного импульса в 1 сек. равно результирующей всех внешних сил, дей-
ствующих на частицы системы. Мы покажем, что эти положения клас-
сической механики сохраняют свою силу и в квантовой области. Определим
для этой цели оператор полного импульса всех частиц системы Р,
Под оператором полного импульса всей системы частиц мы будем под-
разумевать сумму операторов импульса Pk всех частиц k — 1, 2, ..., JVi
) N N
р = 2 рк=—«2 V,. (96.1)
—►>
Вычислим оператор производной импульса Р по времени. Согласно об-
щим формулам квантовой механики
—
^ = L(HP— PH). (96.2)
Подставляя сюда Н из (95.6) и замечая, что Р коммутирует с операто-
N
ром кинетической энергии частиц Т= — У. — мы получим, что
7% ( N N N
(2*4+ 2 *4/) (2 v*)-
N N N )
-(2 Vft) ( S £4+ S }. (96.2’)
336
ЗАДАЧА МНОГИХ ТЕЛ
[ГЛ. Х¥Ш
Далее, замечаем, что
N М
Uk (S vA) - ( 2 V J Uk = - VkUk. (96.3)
A = 1 A=1
Наконец, вычислим перестановку оператора 3 и взаимной энергии
k—1
частиц 2 При этом мы сделаем предположение, что силы между
k=j
частицами зависят лишь от взаимных расстояний между частицами гк^
так, что Ukj—Ukj(rkj). Тогда на Ukj действуют только те операторы У &
N
из суммы 2 для которых k' = k или k' — Jt т. е. на Ukj дейст-
зует пара: V*-|-Vy. Имеем:
но
^k^kj
w
Следовательно,
+ V7) - (V* + Vy) UkJ = - VkUk/ - Vz£7a/,
dUkj r __dUkjTkJ
drkJ * drkj rkJ '
dUWv _ dUk]Tkj
drkJ J H drkJ rkI *
W/+VA>=0-
(96.4)
(96.5)
Это есть выражение закона о действии и противодействии. Из него
следует, что перестановка операторов (96.4) равна нулю.
Таким образом, получается:
N
~dt ~ (xk> Уюz ю (96.6)
k—i
т. e. оператор производной полного импульса по времени равен опе-
ратору результирующей силы, действующей со стороны внешних полей
на нашу систему.
Эта теорема является полным аналогом классической теоремы о дви-
жении центра тяжести системы. Различие заключается лишь в том, что
в квантовой механике она формулируется не для самих механических
величин, а для изображающих эти величины операторов и, следова-
тельно, для средних значений величин.
Если внешние силы отсутствуют (Uk — 0), то из (96.6) следует, что
dP
dt
= 0,
(96.7)
т. е. полный импульс системы частиц, взаимодействующих между
собой, в отсутствии внешних сил сохраняется.
Напомним, что операторное равенство (96.7) означает, что: 1) среднее
значение полного импульса не меняется с течением времени, 2) вероятно-
сти w(P') того или иного значения Р* также остаются неизменными.
§ 97]
ДВИЖЕНИЕ ЦЕНТРА ТЯЖЕСТИ СИСТЕМЫ ЧАСТИЦ
337
§ 97. Движение центра тяжести системы частиц
Докажем важную для приложения теорему об отделении движения
центра тяжести от относительных движений частиц, образующих систему.
Для этого преобразуем гамильтониан системы частиц //, подверженных
действию лишь внутренних сил:
//= — (97.1)
где
N N
°=44* " (9Л2>
к новым координатам: координатам центра тяжести системы X, Y, Z
и 3N—3 относительных координат. Удобно взять так называемые ко-
ординаты Якоби, которые определяются следующим образом:
е ___w1xf4-w2x2
2 ' 3’
. __ ^1*! 4-^-4-«у*/
/ —|— /л2 —|— ... —/Иу 7+1 ’
(97.3)
t ___ >W1X1 4- • • • 4- mNxN /__
N mi 4- • • • 4- тн
Совершенно такие же формулы имеют место для осей ОУ к OZ:
m1y14-...+m/y/
г1~ yj+v г1лг—к>
. ___miz^ 4- • • + mjzj „ ___
(97.3')
Эти формулы представляют собой обобщение обычных формул для
координат центра тяжести и относительных координат двух частиц.
Координаты Якоби являются ортогональными. С помощью обычных пра-
вил перехода от дифференцирования по одним переменным к дифферен-
цированию по другим переменным можно доказать, что *)
N-1
(97.4)
*) См. дополнение X.
22, Блохинцев
338
ЗАДАЧА МНОГИХ ТЕЛ
[ГЛ. XVIII
где V2== (i- , д2 1 д2 - 1 д2 ' (97.5) (97.6)
42 , 1 - *4 1 1 дХ* ' 1 дГ2 г dZ^ ’
М есть масса всей системы, a — приведенная масса центра тяжести
j первых частиц и (/-{-1)-ой:
и
N
М= S тк,
k — \
1 — 1 I 1
k—\
N
Ed _____ d__ d
dxk ~ ^N~"dX'
(97.7)
(97.8)
(97.9)
Из этих формул следует, что гамильтониан (97.1) может быть написан
в виде
//= —— V2 V' — ?2 I
п 2Л1
+ ^-р Ъ •••> Чанр Ср (97Л°)
причем оператор
i i (97 11)
1 27И ~ ’ (?У2 “Г д?Ч '
есть оператор кинетической энергии центра тяжести всей системы,
а оператор
N— 1
t,=-Y.^2, <97.12)
есть оператор кинетической энергии относительного движения ча-
стиц. Существенно, что в энергию взаимодействия W координаты
центра тяжести не входят. Преобразуя Е1? ..., Е^-р т]р .fyy-p
...» к любым новым относительным координатам, qv q ? .
<7здг-з, мы не изменим оператора Т. Поэтому вообще вместо (93.6)
можно напирать
Я===-^¥2 + Я«-^’ ^-з), (97.13)
где //• есть гамильтониан для относительного движения и не со-
держим координат центра тяжести. Далее, на основании (97.4) и (96.1)
§ 97] ДВИЖЕНИЕ ЦЕНТРА ТЯЖЕСТИ СИСТЕМЫ ЧАСТИЦ 339
получаем новое выражение для оператора полного импульса:
p.=~u‘zz- <97-14>'
Волновую функцию Ф будем рассматривать как функцию координат
центра тяжести X, У, Z и относительных координату, у, ^ЗЛМ.
Уравнение Шредингера с гамильтонианом (97.8) допускает разделение
переменных, если положить
ЧЧХ, У, Z, qv q2, qiN_3, t) =
= Ф(Х, Y,Z,t)^(qvq2,...,q3N_s,t). (97.15)
Подставляя (97.15),в уравнение Шредингера, получим:
ih <Ь + ih$ д± = — ф ?*Ф + ФЯ,-ф. (97.16)
Разделив это на Фф и приравнивая порознь члены, зависящие от
X, У, Z и у, у, ..., Уд^д, мы найдем два уравнения:
— (97.17)
ihd±=H$. (97.18)
Первое из уравнений относится к движению центра тяжести, вто-
рое — к относительному движению. Как мы видим, первое есть урав-
нение движения^ свободной частицы с массой М: центр тяжести в от-
сутствии внешних сил движется, как свободная материальная точка.
Простейшее, частное, решение уравнения (97.17) есть волна де-Бройля
Ф(Х, y.Z, = Р» Pz\ (97.19)
Она же, как следует из (97.9), есть собственная функция оператора
полного импульса Рх, Ру, Pz, принадлежащая собственным значениям
рх, Ру PZ' есть собственное значение кинетической энергии движе-
ния центра тяжести системы:
Е = ^Р2х+Ру+р2>
Длина волны 1 этих волн, как это следует из (97.14), такая же,
как и для элементарной частицы, равна
l = “=W' = 07.20)
где V—групповая скорость движения центра тяжести.
Вывод этот важен, так как, особенно подчеркивает, что волны
де-Бройля не являются какими-то колебаниями, связанными с природой
(например, структурой частиц), а выражают в квантовой области общий
закон движения свободных частиц или закон движения центра тяжести
системы, не подверженной действию внешних сил.
22*
340
ЗАДАЧА МНОГИХ ТЕЛ
[ГЛ. XVIII
§ 98. Закон сохранения момента импульса системы частиц
Пусть мы имеем систему из М частиц. Обозначим операторы про-
екций момента импульса 6-ой частицы на оси координат через
М*, Mkz'.
'»4)' ,9sj,)
«:=-4x*sy7--v‘.s-J f98-1"’
где xk, Z'k — координаты 6-ой частицы.
Соответственно этому операторы проекций полного момента им-
пульса всей системы частиц Mxf Myf Mz определим по формулам
",= 2 м;.
м2= 2^-
г г
(98.2)
(98.2’)
(98.2")
Покажем, что оператор производной по\ времени от момента импульса
равен моменту сил, действующих на систему (точнее, оператору мо-
мента сил). Согласно общему определению производной оператора мы
имеем:
(98.3)
Гамильтониан Н согласно (95.6) равен
+ Е
kzbJ—\
(98.4)
Для вычисления перестановки операторов в (98.3) мы должны иметь
в виду, что каждое слагаемое М* в операторе действует лишь на
те члены в 77, которые содержат координаты 6-ой частицы.
Операторы коммутируют с оператором Мх- Действительно, как
мы знаем, оператор кинетической энергии можно представить в виде
-—^=7Гл+^,
2/па * 2mkrl
(98.5)
где ТГк— оператор той части кинетической энергии частицы, которая
отвечает движению частицы по радиусу-вектору гЛ, a (Affe)2 — квадрат
§ 98]
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
341
момента импульса &-ой частицы. Мк коммутирует и с Trk, и с
поэтому Мх коммутирует с —9^”^ а*
Вычислим .теперь перестановку Мк и Uk. Имеем:
UM * — MkUk — — ih(uk(yk-^----zk~ \ —
k x x к I k\kdzk kdyk) \"kdzk kdykJ k)
Наконец, найдем еще перестановку:
>. х. / ^Ubf dUki\
Uk Мх —MkUkf — ~ ih (у -±L — zk-^-) =
KJ X X KJ ^Zk A J
iduKj( zk~zj Уи — УЛ
—г‘—>
ч dUki 1 •
Подставляя (98.6) и (98.7) в (98.3), мы найдем:
(98.7)
dMx уч [ dUk dUk \ уч 'dUbj 1
“dT ~ V* ~дГк ~~ Zk ~дук ) + к•
Последняя сумма равна нулю, в чем убеждаемся сразу, переменив ме-
стами индексы k и j. Поэтому получаем:
dMx _у< dUk
dt Z* \Ук дгк
- Wk\
к^кГ
(98.8)
Стоящее справа -выражение есть не что иное, как оператор проекции
на ось ОХ суммы моментов внешних сил, действующих на систему.
Совершенно таким же образом получаем:
dMy dt * II Zftdxk Wk\ Xkdzk )’ (98.8\
N
dM2 dt A=1 (x d^- у k dyk -V '* dxk)' (98.8":
Таким образом, мы получаем теорему, известную из классической меха-
ники: изменение момента импульса в 1 сек, равно моменту внешних
сил, действующих на систему. Эта теорема в квантовой механике,
подобно теореме о полном импульсе, формулируется для операторов.
Если момент внешних сил равен нулю, то полный момент импульса
системы сохраняется:
dMx dMy dMz
dt dt dt
Следовательно, в отсутствии внешних сил ни среднее значение момента
342
ЗАДАЧА МНОГИХ ТЕЛ
[ГЛ. XVIII
импульса Мх, Му, Mz, ни вероятности w (AQ, w(tW^), w(Af) найти
то или иное значение какой-либо из проекций момента не меняются
с течением времени.
Если учесть спин частиц, то оператор полного момента импульса
должен быть определен по формулам
N
Мх= 2(М* + «*), (98.10)
k — \
N
(98.10')
N
М = S(Af* + s*). (98.10")
k—1
где skx, sy, skz— операторы (двухрядные матрицы) проекций собствен-
ного механического момента &-ой частицы. Теорема о сохранении пол-
ного момента импульса остается в силе и в этом случае. Если нет сил,
действующих на спины, то доказательство этой теоремы ничем не отли-
чается от приведенного выше, так как при таком предположении га-
—>
мильтониан системы коммутирует со всеми операторами sk.
Так как операторы Mkx, М*, Mkz, skx, s*, skJ принадлежащие разным
частицам (разные k), коммутируют между собой, то из известных пра-
вил перестановки для компонент орбитального момента (25.5) и спино-
вого момента (57.1) одной частицы легко получить правила переста-
новки для полного момента импульса системы частиц:
М^Лу — МуМх = ihMz, (98.11)
MyMz- ihMx, (98.11')
мгмх— ihMy, (98.11")
М2МХ — 0, (98.12)
JA2lAy — М^ЛГ2-- 0, (98.12')
М2Мг — мгм2= 0, (98.12")
где М2 есть оператор квадрата полного момента импульса:
M2 = M2x + M2y + M2z. (98.13)
Пользуясь этими правилами перестановки, докажем, что полный
момент импульса квантуется по формулам
— (93.14)
A1z-hm, (98.15)
причем J есть либо целое число 0, 1, 2, . .., либо полуцелое 2/2, 3/2,
5/2, ..., в зависимости от числа частиц и их спина. Для электрона
спин равену. Тогда целое J /получим для четного числа электронов,
а полуцелое — для нечетного числа электронов.
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
343
§ 98]
Формула (98.15) доказывается сразу, если заметить, что отдельные члены
в сумме (98.11") коммутируют между собой и, следовательно, могут быть
одновременно приведены к диагональному виду так, что собственное значение
Mz равно сумме собственных значений Mz-j-sz. Но собственные значения
последних суть hmk, где mk — целое или полуцелое число, смотря по значению
спина частиц. Таким образом,
N N
Mz = 2 hmk = hm, tn= (98.15)
kz=A k — \
Для определения собственных значений М2 введем операторы
4 = + В = МХ~ iMy. (98.16)
Пользуясь (98.12), получаем:
AMZ — — hA, BMZ —MZB hB. (98.17)
Напишем эти равенства в виде произведений матриц, беря представление,
в котором Mz диагонально. Тогда получаем:
Amfm"hm'r — hrn'Am'm" — — hArn'm” ,)
V (98.18)
— hm'Bm'm" — — hBm'm" J
или
Am'm" (tn” — m'4-1) — 0, Bm'm" (tnff — m' —-1) — 0. (98.19)
Отсюда следует, что единственные неисчезающие элементы А и В суть
А т~\ и т+1- Оператор квадрата полного момента 2И2 можно выразить
через операторы А и В двояким образом, именно:
Af2 = АВ + M2Z — hMz, (98.20)
№=BA-\-M2z+hMz. (98.20')
Отсюда
Ь2 / h \2
АВ=1№-^-[мг-^) , (98.21)
й2 I h \ 2
+ ‘ (98.21')
Беря диагональный элемент (т, т) от этих равенств, получим:
№ i 1 \2
(АВ)тт = Ат, Вт.1г т = АР + 'L _й2 ( т _ „ ) , (98.22)
<ВА)тт = Вт,т+1 ^+1>m = ^ + z-^(m4-2) . (98.22-)
Будем теперь считать величину М2 заданной. Тогда возможные значения | пг [
неизбежно ограничены. В самом деле,
собственное значение + не может быть отрицательным. Обозначим
нижнее значение т через т\ а верхнее через т” Тогда из (98.22) и (99.22’)
следует (так как Ат\ т'—1 = 0, Вт’—х,т' — 0 и Лот^4-1, ^”=0, Вт”, «"4-1 — 0):
м2+^=й2
ЗАДАЧА МНОГИХ ТЕЛ
344
Отсюда
[гл. XVIII
(98.23)
(98.23')
Разность ти-т,4-1 есть число целое, равное числу различных возможных
Mz при данном М2. Обозначим т" — tri = 2/4“ 1. Тогда из (98.23) и (98.23')
получаем:
и+'=2/
или
M2 = /zV(J4-l).
В силу полной равноправности положительных и отрицательных значении М£
мы Должны положить тп — — т'. Вместе с (98.15') это нам дает
1 3
где т — 0, zt 1, ± 2, ..., ± J или m = ± ± -у , ..., zt 7.
При доказательстве мы пользовались только правилами перестановки
операторов проекций импульса (98.12) и (98.13). Так как таким же правилам
перестановки подчиняются порознь проекции оператора полного орбитального
момента
> N
М{ = (98-24)
*=1
и полного спинового момента
у N
Ms=^s^, (98.25)
k—1
то их собственные значения определятся формулами
Л1| = Л2£(£+1), Z = 0, 1, 2, 3, ..., (98.26)
M2s=h*Ls(Ls-\-\), Ls = 0, 1, 2, 3, ... или 1/s. »/2, 5/2, ... (98.27)
Отсюда и из (98.14) следует, что оператор скалярного произведения
ЪММ^ЛР — М^ + М2 (98.28)
имеет собственные значения
(ММ5) = /г2 {J(J+ 1) - L (L + 1) + Ls (Ls+ 1)}, (98.29)
так что формула (60.13) для одной частицы является частным случаем (98.29).
Повторяя рассуждения § 70, можно легко вывести формулу для множителя
Ланде для системы частиц:
г=»ол„ {, + 2V+4-^+.l>+'-<W}, (98.ЗО)
так что (70.23) будет частным случаем (98.30) для одной частицы. (98.30)
дает расщепление уровней в магнитном поле для системы электронов (слож-
ный атом).
§ 99]
УЧЕТ ДВИЖЕНИЯ ЯДРА В АТОМАХ
345
ГЛАВА XIX
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ
§ 99. Учет движения ядра в атомах
При рассмотрении движения оптического электрона в атоме мы?
предполагали ядро атома неподвижным, рассматривая его как источник
центральных сил. Такое приближение тем лучше, чем больше масса
ядра т. Пользуясь доказанной выше теоремой о центре тяжести, легко
учесть поправки, обусловленные конечностью массы ядра. Уравнение для
определения энергии Е и собственных функций будет, с учетом:
движения ядра, писаться в виде
/ _ t Л ]____/г2 / д2 д2 । д2 \)
I 2/и1\<?х, ‘ ду% dz\' 2т2'Эх2 «Ъ'г ^г2' '
+ У(г)ф = £Ч', (99.1)
где тг —масса ядра, xlf ylt —его координаты, т2 — масса электрона
х2, № z2 — его координаты, г есть расстояние между ядром и электроном:
Г2 = (Х1 _ Хг)2 {ух _у2)2 + {Zx _ (99.2>
Вводя координаты Якоби, согласно (97.3) получим:
£, = х,-^^х, = Х (99.3).
»,=Л-Л=Л (99.3')
!),=,,-гг = г, = (99.3")
так *что тп, Zi в этом случае суть просто относительные координаты
ядра и электрона, X. У, Z—координаты центра тяжести электрона и
ядра. В этих координатах гамильтониан уравнений (99.1) перепишется
согласно (97.5) в виде
t д2Ф ( #>Ф\ h2/d2lV . (W . д2Ф\ 1
2М\дХ2 Иd/2 Н ^72 J 2|Л ^2 7Г ду2 i dz2 J i
+ Щг)ф = £ф, (99.Г)
где
41=,^1 = ± + (99.4)
Разделим переменные X, У, Z и х, у, z так же, как это делалось,
в § 97 [см. (97.10)]:
PzZ)
Ч*(Х, Y, Z, х, у, ^) = е v, z). (99.5)
Это решение означает свободное движение центра тяжести атома с
346 ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
импульсом рх, ру, pz. Для функции ф (х, y,t z}, описывающей относи-
тельное движение, получим:
где
«=£-аг +
Уравнение (99.6) совершенно одинаково с уравнением для движения
частицы с массой pt в заданном силовом поле £/(/*). е имеет смысл внут-
ренней энергии атома (энергии относительного движения), а полная
энергия Е складывается из энергии относительного движения е и энер-
гии движения центра тяжести атома Когда мы решали задачу о
движении электрона в атоме, то мы имели дело с таким же уравнением,
.как и (99.6), но вместо приведенной массы р стояла масса этектрона.
Поэтому нам нет надобности заново решать задачу о движении элект-
рона в атоме с учетом движения ядра. Достаточно, чтобы найти е и
ф (х, у, z), заменить во всех прежних формулах массу электрона на
приведенную массу pt. Так как масса ядра тх во много раз больше
массы электрона т2, то из (99.4) следует, что р т2, так что вызы-
ваемые движением ядра поправки кейф будут малы. Если считать
массу ядра бесконечно большой, то р. =/тг2 (масса электрона). При
этом условии в § 48 нами было найдено значение постоянной Ридберга R
(мы обозначим ее теперь через /?оо и массу электрона через /п2), равное
««=» <99-8»
Мы видим, что для того, чтобы получить истинное значение постоянной
Ридберга, определяющей оптические частоты электрона, движущегося
в кулоновском поле, нужно заменить т.2 на приведенную массу pi. Так
как pt для различных атомов различно, то это обстоятельство позволяет
определить из спектральных наблюдений массу электрона. Это было
сделано ХаустойОм с помощью аккуратных измерений линий /7а и
водорода и сравнения их с соответствующими линиями иона Не+. Так,
например, для частота Vh для водорода равна
Vh=^h(22 32) =зб^н,
где /?н — постоянная Ридберга для водорода. Для иона гелия и для
того же квантового перехода имеем:
л п П 1 \ 20 п
VHe = 4/<Не ^22 — 32 ) ~ 36 ^Не’
где /?не — постоянная Ридберга для Не+. Множитель 4 появляется по
той причине, что величина термов атома (см. § 40) пропорциональна
квадрату заряда ядра Z2. Заряд же ядра Не вдвое больше заряда
§ 100] СИСТЕМА ЧАСТИЦ, СОВЕРШАЮЩИХ МАЛЫЕ КОЛЕБАНИЯ 347
ядра Н . Из предыдущих формул следует, что
(99.10)
Подставляя
(99.9*)
где Цне и |1н суть-приведенные массы иона гелия и водорода. Согласий
(99.4) имеем:
1 J_ । J_ _1__J L±
Нн m H w2 ’ Р-Не WZHe m2 ’
где mн — масса ядра водорода, a tn^— масса ядра гелия,
это в предыдущую формулу, мы получим:
* mHe4-mH ’ тн '
Отсюда видно, что, определив спектроскопически у и зная атомные
веса Н и Не, мы можем вычислить отношение — , т. е. «атомный
вес» электрона. Указанным путем Хаустон нашел
— = 0,000548, — = 1838,2 +1,8. (99.11)
,?2н т2
Этот же эффект является средством для определения масс изотопов.
В самом деле, линии, соответствующие одинаковым квантовым перехо-
дам, у разных изотопов несколько различны из-за различия в приведен-
ных массах. Таким путем была установлена масса тяжелого водорода
(дейтона): ш0 = 2шн-
§ 100. Система частиц, совершающих малые колебания
Рассмотрим сначала систему из двух одинаковых частиц, совершающих
малые колебания. Обозначим отклонение первой частицы от положения
равновесия через а второй — через х2. Потенциальная энергия
U(xv х2) для малых отклонений может, быть разложена в ряд
2 2
U(x-V х2)==~ х?-]- • • • (100.1)
Здесь у. — масса частиц (одинаковая для обоих), о>0 — частота-колебаний
частиц в отсутствии взаимодействия между ними, \хгх2 — энергия взаи-
модействия частиц (для малых хг и х2).
Оператор полной энергии частиц, имеющих потенциальную энергию
(100.1), имеет вид
I 2___
2p.2xf ‘ 2 Х' 2цдх| V
(100.2)
Из классической механики известно, что для системы частиц, совер-
шающих малые колебания, можно ввести так называемые «нормальные
348
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
координаты» #2, в которых потенциальная энергия U выразится в виде
суммы квадратов qv q2, а кине+ическая энергия — в виде суммы квад-
ратов соответствующих импульсов, так что мы будем иметь дело с
двумя независимыми нормальными колебаниями. В рассматриваемом част-
ном случае эти нормальные координаты связаны с хг и х2 формулами
*1 = + *2 = -7=(<71 —?2)- (ЮО.З)
ул ул
Эта особенность нормальных координат сохраняется и в квантовой ме-
ханике. Введем в (100.1) вместо xt и х2 нормальные координаты q^ и q2.
Для этого заметим, что
дф дф дхг , дф дх2 1 / дф . дф \
дхг dq± дх2 dq± У 2 \ дхг дх2)’
^ф_ 1/^Ф । । д2ф \
dq? 2\dxf дх^ дххдх2) ’
подобным же образом
д2Ф _ 1 /д2ф . д2ф 2 д2ф
dq2 2 \dxi дх\ дххдх2
Следовательно,
^ф । ^ф_^ф । ^ф
дх? дх2 dq\ dq?2
На
основании этого равенства получаем:
где
Н=
2рА<^ ' 2 2 ^2’
ро)2 — |Л0)2 х, рй)2 = 110)2------------------
(100.4)
(100.5)
осцилляторов
Из (100.4) следует, что гамильтониан двух связанных
в нормальных координатах представляется в виде суммы гамильтонианов
для двух независимых осцилляторов, одного с частотой Wj и другого
с частотой а)2 (тот же результат, что и в классической механике).
Найдем квантовые уровни и соответствующие им собственные функ-
ции системы 'связанных осцилляторов. Оператор содержит координаты
<71 V <?2 и’ следовательно, волновая функция ф должна рассматриваться
как
ний
функция qx и q2. Уравнение Шредингера для стационарных состоя-
вшей системы имеет вид
й2 dty Н«>1 ,, Л2 . Н“2 2 t Р!
2ц 2 2ц дд'У 2
(100.6)
Это уравнение легко решается разделением переменных. Для этого
положим:
Ф С71» ^Ь)==Ф1 (100.7)
и
+ (100.8)
§ 100] СИСТЕМА ЧАСТИЦ, СОВЕРШАЮЩИХ МАЛЫЕ КОЛЕБАНИЯ 349
Подставляя (100.7) и (100.8) в (100.6)' д^ля результат на <1^ (^) ф2 (</2)
и приравнивая порознь постоянным Ег и Е2 члены в левой части, за-
висящие от qx и q2 соответственно, получим:
h2 |1<о? Q t
(100£”
(100-9'>
2|i dq2 2
Первое из этих уравнений есть уравнение для осциллятора с часто-
той шр а второе — для осциллятора с частотой <о2. Поэтому собствен-
ными функциями уравнений (100.9) будут
_________________________ _________________________
а собственными значениями
En=hw1 4-у) , «, = 0, 1, 2, ... (100.11)
Подобным же образом для уравнения (100.9') имеем:
—
(100.10’)
^л, = Л®2(«2+|). «2 = 0, 1, 2, 3, ... (100.11’)
Отсюда следует, что собственные функции исходного уравнения (100.6)
имеют вид
Фп.яЛр (100.12)
а соответствующие собственные значения оператора энергии равны
£Л1Я,=Мл144) • (100.13)
Нулевая энергия системы равна
^00 = ^+^ (100.14)
Вероятность найти нормальные координаты лежащими в интервалах
9i, 9i+^9i и q2, q2-\-dqz равна
(9i, 92) dq^dq^ = ф^„2(91, 92) dqxdq2. (100.15)
Если мы желаем определить вероятность того, что координаты частиц
лежат в интервалах хг, x1-4-dx1 и х2, x2-j-dx2, то для этого до-
статочно заметить, что
dqxdq2~dx1dx2,
350
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
и выразить в (100.15) qx и через xt и х2. Тогда получим:
w (Xj, х2) dxxdx2 —
= + — x^dxtdx2. (100.16)
Сходные результаты получаются для системы с любым числом сте-
пеней свободы. Пусть мы имеем N частиц, совершающих малые коле-
бания около положений равновесия. Обозначим отклонения &-ой частицы
от положения равновесия через xk, yk, zk. Тогда потенциальная энер-
гия равна
N
и==~2 X (А‘ЬХ1Хк^В1кУ1УьЛ~С,к?1гк+ Dikx/yk^
(Ю0.17)
причем величины Aik, Bik, Clk, Dlk, Eik, Fik суть вторые производ-
ные потенциальной энергии по смещениям. Так, например,
А d2U
ik dx-tdxk
Из классической механики известно*), что в этом случае можно ввести
нормальные координаты qs, 5=1, 2, ..., 3^ такие, что гамильтонова
функция, распадается на сумму гамильтоновых' функций гармонических
осцилляторов.
Нормальные координаты qs и декартовы xk, yk, zk связаны орто-
гональным преобразованием:
2, м (100.18)
k
где ask, ysk суть коэффициенты преобразования. В нормальных коор-
динатах qg —> гамильтониан нашей системы
(-£V2J + tE (^М+---+вМ) (100.19)
£=1 л hk=l
преобразуется к виду
/ Л2 д2 , |10>2. \
«=Е-2-^+т4 <100'20’
где р. — некоторая эффективная масса, а — частоты нормальных ко-
лебаний. Уравнение Шредингера для стационарных состояний имеет вид
/ Л2 д2 \1
1-5=1 \ / _
= (?1. > ?злг)- (100.21)
*) См., например, М. Борн, Теория твердого тела.
§ 100] СИСТЕМА ЧАСТИЦ, СОВЕРШАЮЩИХ МАЛЫЕ КОЛЕБАНИЯ 351
Очевидно, что это уравнение распадается на 3N уравнений для 3N
независимых осцилляторов, если представить Ф в виде произведения
функций от <7Р <?2, ..., #злг. Уравнение для осциллятора, представляю-
щего 5-ое нормальное колебание, будет
-Гв-£? + т^(^)==^"!,(^ (100-22}
"г* U4S "
Отсюда
(100-23>
E„, = hog(nt+±), ^ = 0,1,2, .. (100.24)
Собственные же функции и собственные значения всей системы осцил-
ляторов определяются выражениями
... п* ... ?2> • • •» ’ #32у) =
= К (Л(<h) • • фл,(?,) • • • <|>3jvtaw), (100.25>
Еп,па... п,•..n3N=f^i (я1+у) + • • 4“Аю, (”j4_4')4“ • • • 4~
4-йа)злг(^4-|), (100.26Х
где и2, ..., и?, ..., излг—целые положительные числа, включая
нуль. Нулевая же энергия системы равна
£0= 4(о>14-о>24- • • • 4-^4- • • • 4-«W (Ю0.27)
Перебирая всевозможные значения чисел ns в (100.26), мы получим
все квантовые уровни системы колеблющихся частиц. Из (100.26) сле-
дует, что для определения этих уровней достаточно знать частоты нор-
мальных колебаний <ог
Примером систем, имеющих квантовые уровни вида (100.26), могут
служить молекулы и твердые тела. И в тех, и в других атомы совер-
шают малые колебания около положений равновесия *).
Заметим, что при больших амплитудах колебаний следует учесть
высшие члены в разложении потенциальной энергии, именно, члены вида
А, . d3*Z г. у г-L и т. п. Колебания тогда будут нелинейными, и
3! dxtdykdzt i^k 1 \ j j >
наши результаты будут иметь лишь приближенное значение. В частности,
формула (100.26) будет справедлива лишь для малых квантовых чисел ns^
*) Квантование энергии колебаний атомов в твердом теле находит свое
выражение в квантовом характере теплоемкости твердого тела, которая при
достаточно низких температурах меньше той, которая полагалась бы по клас-
сической теории (3k, где k — постоянная Больцмана), именно, теплоемкость
твердого тела убывает с уменьшением температуры пропорционально Г3.
Расчет теплоемкости твердого тела на основе квантовой теории см. в книге
Г ерцфельд, Кинетическая теория материи, или более новое изложение в
книге Fowler, Statistical mechanics, Cambridge, 1938.
352
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
§ 101. Движение атомов во внешнем поле
Рассмотрим движение системы частиц (атома, молекулы) во внеш-
нем поле сил. В целях большей конкретности мы ограничимся систе-
мой из двух частиц с массами и тп2 и координатами xlf yv и
•^2’ 3^2»
Обобщение на случай большего числа частиц совершенно три-
виально.
Обозначим энергию взаимодействия частиц через — х2, —у2,
— z2), энергию первой частицы во внешнем поле через U(xv уг, zj,
а энергию второй — через U(x2, у2, z2). Уравнение Шредингера для
волновой функции системы Ф^рУр^, х2,у2,^2,/) будет иметь вид
ih~£t Vi<F+ЦФ+С/аФ+ ГР. (101.1)
Введем в это уравнение вместо координат частиц хр ур и х2, у2,
координаты центра тяжести X, X, Z и относительные координаты
х, у, z [см. (99.3)]. Переходя в (101.1) к этим новым координатам
и замечая что по (99.3)
х1 = Аг+?1х,
Л = Р+Г1Л
__ m2
Ч1
Х2-ЗС
Уъ = У~ ЪУ> ‘
= Z y2z,
y2=-5—.
12 -f- m2
(101.2)
(101.3)
мы получим:
“жZ+T,z)¥+
+ ^2(Х—у2х, х—Т2у, z—Y2*)lP+(101.Г)
где
V2_J!l JI I Л V2___J, Л I Л
X dX2 i^2idZ2’ x — dy2^ dz2 *
Переменные X, X, Z и x, y, z в этом уравнении ввиду наличия поля
(Ц и £72) не разделяются. Поэтому в общем случае исследование этого
уравнения весьма затруднено.
Предположим, однако, что размеры системы малы. Это означает, что
мы ограничиваемся рассмотрением таких систем и таких состояний Ч;,
когда волновая функция Ф достаточно быстро убывает с увеличением
относительно расстояния r= K^2+j2-|-22 двух частиц. Пусть это убы-
вание таково, что вероятность найти частицы на расстоянии г^>а друг
от друга практически равна нулю. Тогда а можно рассматривать как
размер нашей системы (например, «радиус» атома, «длина» молекулы
и т. п.).
В этом случае в уравнении (101.1') играют роль лишь такие обла-
сти х, у, z. для которых г<^а. При таком предположении мы можем
§ 101] ДВИЖЕНИЕ АТОМОВ ВО ВНЕШНЕМ ПОЛЕ 353
разложить Ц и Ц по степеням х, у, z (если Ц и U2 достаточно
гладкие функции). Это разложение мы напишем в виде
^(ЛГ+yjX, У+YiJ, Z4-YiZ) + fZ2(X—y2x, У— ^у, Z—^z) =
= U^X, Y, Z) + U.(X, Y,Z) + d-^x + ...+d-^Z + ...=
= V(X, У, Z)-|-wpC, У, Z, x,y, £)+ (101.4)
где V(A\ Y, Z) есть потенциальная энергия центра тяжести системы.,
а через w обозначен член (или члены), содержащий х, у, z. Этот член
связывает движение центра тяжести с относительным движением. Урав-
нение Шредингера (100. Г) теперь можно написать в виде
й"=[-23й’’х+ V’ + ir(W)] Ч' +
+ w(X, У, Z, х,у, z)4. (101.5)
Пусть в отсутствии внешнего поля собственные функции для внут-
реннего движения будут (х, у, г), а собственные значения энергии
Очевидно, что ф° есть решение уравнения
О01-6)
Если мы учтем влияние внешнего поля, то к этому уравнению доба-
вится член w(X, Y, Z,x,y, z), и мы получим уравнение
— г)ф4-та(Х, Y, Z, х, у, z) ф = Ей. (101.7)
В это уравнение координаты центра тяжести X, Y, Z входят как па-
раметры, и от них будут зависеть как волновые функции, так и соб-
ственные значения этого уравнения.
Во многих случаях w (X, У, Z, х, у, z) можно рассматривать как
возмущение. Это обстоятельство позволяет решить уравнение, если
известны решения уравнения (101.6). Обозначим собственные функции
уравнения (101.7) и его собственные значения через
= r-Z)’ En = En{X,Y,Z). (.101.8)
Разложим теперь Ф (х, у, z, X, У, Z, /) по собственным функциям фл.
Тогда получается:
Ч(х,у, Z, X, Y, Z, /) = 2Ф„(Х У, X, t)tya(x,y, z, X, Y, Z). (101.9)
п
Подставляя это разложение в уравнение (101.5), умножая на ф^(х, у, z,
X, У, Z) и интегрируя по х, у. z, получим (в силу ортогональности
функций фл) уравнения для функций Фл:
— S ЪК+1^Х’ Y У, Х)]фт~
— (2а„ЛгФ„ + ^тяФл), (Ю1.9’)
2ЛТ ' тп п тп п 1 ' 1
п
23
Блохинцев
354
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
где
amn = ^m-^n-dxdydz, (101.10)
bmn = \rm^n-dxdydz. (101.10')
Эти два последних члена отличны от нуля лишь в том случае, если
функции фл зависят от координат центра тяжести X, У, Z и приводят
к возможности переходов системы из одного состояния в другое. Дей-
ствительно, если при t — О все Ф„ —0, кроме то при / = 0
-^^±=0, и с течением времени из состояния Флг будет возникать супер-
позиция (101.9).
Если не зависят от X, Y, Z, то атп и Ьтп равны 0. Если эта
независимость имеет место, хотя бы приближенно, то мы можем пре-
небречь величинами атп и Ьтп в (101.9') и тогда получим:
к,г)]Фв. (101.11)
Это есть уравнение для движения центра тяжести системы в по-
тенциальном поле с потенциальной энергией, равной
Un = V(Xt У, Z)-\-En(X, У, Z), (101.12)
при условии, что внутреннее состояние системы есть п-ое квантовое
состояние. Уравнение (101.12) таково же, как уравнение для движе-
ния материальной точки.
§ 102. Определение стационарных состояний атомов методом
отклонения во внешнем поле
В этом параграфе мы рассмотрим теорию опытов, в которых опре-
деляют стационарное состояние атома, подвергая пучок атомов отклоне-
нию внешним полем. Обратимся к важнейшему опыту такого рода —
к опыту Штерна-Герлаха. Этот опыт обычно рассматривают как опыт
по определению магнитного момента атома. Будучи рассматриваем более
непосредственно, этот( опыт является опытом по определению энергии
атома во внешнем магнитном поле.
Из теории движения атомного электрона при наличии магнитного
поля (§ 59) следует, что, поскольку пренебрегается высшими степенями
магнитного поля, постольку действие магнитного поля можно выразить
через добавочную потенциальную энергию (59.7), равную энергии маг-
нитного диполя (орбитального и спинового) в магнитном поле. Поэтому
мы можем применить к интересующему нас случаю теорию предыду-
щего параграфа. Из расчетов в § 59 следует, что в упомянутом при-
ближении волновые функции электрона ^п1т не зависят от магнитного
поля, а собственные значения энергии равны (59.13):
= + (« = ±П. (102.1)
§ 102] ОПРЕДЕЛЕНИЕ СТАЦИОНАРНЫХ состояний 355
При этом мы считали поле Ж однородным. Если оно достаточно плавно
(для макроскопических полей нужная плавность всегда обеспечена), то
его можно рассматривать так же, как функцию координат центра атома
X /, Z без того, чтобы нарушилась справедливость (102.1) *).
Таким образом, мы можем написать
Enlm(X, К,2) = ^ + |(т±1ДОЛ4 (102.2)
Волновые функции ^п1т от X, К, Z зависеть не будут, так как они
не зависят от поля 5%. Стало быть, мы имеем дело со случаем, когда
вместо общих уравнений (100.9) для волновых функций Ф, описываю-
щих движение центра, тяжести, можно написать уравнения (101.11).
Эти уравнения в нашем случае будут гласить:
ihd^r=-&i ^nlm + Enlm(X, Y, Z)*ntm. (102.3)
Так как масса атома М велика, а внешнее поле SrC всегда плавно ме-
няется от точки к точке, то мы имеем налицо как раз те условия, при
которых применимо приближение классической механики. Положив
____________ ___ (^> 2",/)
Ф„/М(Х y,Z,/) = r₽„to(X Y,Z,t).e * , (102.4)
где Snlm— функция действия, а рп1т — плотность атомов в простран-
стве, мы получим для Snlm 41 ^п1т в первом приближении классические
уравнения
= + (Ю2.5)
Т + ^1у(рп/т^) = 0. (102.6)
Первое уравнение есть уравнение Гамильтона-Якоби и утверждает, что
частица будет двигаться по классическим траекториям. Второе уравне-
ние есть уравнение непрерывности и утверждает, что рой частиц будет
двигаться так, чтобы поток частиц, проходящий через любое сечение
трубки, образованной траекториями, был постоянен (ср. § 35).
Обратимся теперь к чертежу (рис. 68). Пусть на протяжении от
D до Р действует магнитное поле, направленное по оси OZ. В D ще-
дана диафрагма, через которую поступают атомы. Ширина щели
в диафрагме пусть есть AZ0. Пучок атомов, входящий в £), будет
расщепляться. Те из атомов, которые окажутся в состоянии с магнитным
моментом /7^ = 0, будут двигаться без действия сил. Из уравнений
*) Для этого достаточно, чтобы поле Ж мало менялось в пределах раз-
меров атома а, т. е. должно соблюдаться условие
\дЖ |Ж I
•^>1 дХ а ’ j дУ а * j dZ а|*
23*
356
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
(102.5) и (102.6) мы получим проходящий без отклонения пучок. Атомы,
находящиеся в каком-либо другом состоянии с образуют откло-
ненные пучки (на рис. 68 приведены два таких пучка).
Существенно, что магнитный момент рт меняется от состояния к
состоянию скачкообразно. Благодаря этому пучки, вообще говоря, раз-
деляются так, что по месту падения атомов на экран (или фотоплас-
тинку) Р мы можем решить, в каком из возможных состояний нахо-
дятся атомы, т. е. определить их
стационарные состояния., Траекто-
рии, принадлежащие пучкам, легко
вычислить из уравнений (102.5),
(102.6), учитывая расположение
диафрагмы Z), ее форму и началь-
ное распределение скоростей атомов.
Можно и прямо воспользовать-
ся уравнениями Ньютона:
дл d2X___ dEnim
dt2 дХ ’
_____дЕп1т
dt2 ~ дУ '
Рис. 68. К теории опытов Штерна-
Герлаха.
MdS <102-7)
Будем считать, что магнитное поле &С зависит лишь от z (по крайней
мере на большей части отрезка DP). Тогда ид (101.7) получаем:
X=vt-\-X^
к=У0,
' ___ 1 дЕп1т >2 | у
2М dZ
(102.8)
(102.8')
(102.8")
где v — скорость атомов (мы предполагаем,, что они первцначально дви-
жутся параллельно ОА, и, кроме того, градиент поля в пределах
области движения атомов считаем почти постоянным). Обозначая длину
DP через I и пользуясь (102.2), мы получим отклонение
~ 1 eh . , -. d$K I2
Z„. -- Z« =------ X-VS П"4” 1 ) j ~9 •
m 0 2M 2}lc ' — 7 dZ v2
(102.9)
Произведенный нами расчет лишь приближенный. В действительности
атомы, проходящие диафрагму, не будут двигаться по классическим
траекториям: пучок будет расползаться.
Чтобы учесть это явление, следует сделать еще один шаг в при-
ближенном решении уравнения (108.3), учтя члены в Snlm и рп1т, содер-
жащие первые степени h (см. § 35). Мы не будем этого делать, а
ограничимся лишь оценками.
§ 102]
ОПРЕДЕЛЕНИЕ СТАЦИОНАРНЫХ СОСТОЯНИЙ
357
Пусть ширина пучка в направлении OZ есть AZ0. Тогда скорости
атомов в направлении OZ в силу соотношения неопределенности
AZ0-A^>A (102.10}
не могут равняться нулю (как это допускалось в классическом расчете).
Если среднее значение pz = 0, то
^•Mvzy А, т. е.
из (102.10) следует, что
h
При прохождении через поле в течение
разброса в скоростях v2, ширина пучка
(102.10')
времени /, благодаря наличию
AZ возрастает и будет равна
, ht
vt J> т, л-~
z ' /W-AZ0
(102.11)
Для того, чтобы мы были еще в состоянии решить, к какому из состоя-
ний Еп1т или Enimi относится атом, падающий на экран Р, необходимо,
чтобы | Z/n' — Zm\^> ^Zr т. е. на основании (102.8")
I дЕп1т, дЕп1т I ht
2M\dZ ~dZ~\^ M^Zq
(102.12)
или
ciF r)F
-~^z.----------t^h. (102.13)
Но так как в силу слабой зависимости Enimr и Еп1т от Z
I- Е„, J > | JZ, - 4zJ ,
то последнее неравенство можно записать также в виде
| Enltri Enim И
(102.14)
т. е. для того, чтобы различать стационарные состояния атома (Enimi
или Еп1т), измерение должно производиться в течение достаточно боль-
шого времени t:
(102.15)
К этому обстоятельству мы еще вернемся в § 104.
В заключение теории опытов по определению стационарных состоя-
ний атомов методом отклонения пучка атомов во внешнем поле рассмот-
рим более сложный случай, когда первоначальная волновая функция
представляет состояние с неопределенным значением энергии.
По общей теории вероятность получить цри измерении в таком
состоянии значение энергии Еп равна | сп |2, где сп — амплитуда в разло-
жении ф по собственным функциям оператора энергии *). Покажем, как
*) Для простоты мы обозначаем все квантовые числа {п, I, т) одной
буквой п.
358 ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
относится это общее утверждение к определению энергии методом
отклонения пучков. Если система находится во внутреннем состоянии
фп (х» У* то полная волновая функция, с учетом движения центра
тяжести, будет равна
Ф(Х У, Z, х,у, z) = $n(X, У, Z)<bn(x,y,z), (102.16)
причем Фп определяется из уравнений (102.3) [или вообще из (101.41)].
Если состояние ф есть суперпозиция фп, то в силу линейности уравне-
ний квантовой механики общая функция имеет вид
Ф(Х, К, Z, х, у, г)=^спФп(Х, У, Z)-&n(x,y, z). (102.17)
п
Непосредственно на опыте мы измеряем не внутреннюю энергию
атома, которая нас интересует, а положение атома А, У, Z. Опреде-
ляем вероятность того, что атом находится в области
X X-\-dX, У, Y-YdY, Z, Z-\-dZ.
Эта вероятность равна
w(X У, Z)dXdYdZ = dXdYdZ j |Ф|2^хdy dz =
~^i\cn?‘\®n?dXdYdZ. (102.18)
n
Измерение энергии атома En заключается в том, что мы решаем,
к какому из пучков (см. рис. 68) относится атом. Каждый пучок опи-
сывается своей функцией Ф„(Х У, Z). Для того, чтобы наш опыт был
действительно опытом по измерению энергии атома, нужно, чтобы раз-
личные пучки были разделены друг от друга, иными словами, функции
Фл (X У, Z) должны быть отличны от нуля в различных областях про-
странства [для этого должно быть обязательно выполнено условие
(102.15)].
Определим теперь, какова вероятность того, что атом принадле-
жит пучку т. Для этого нужно проинтегрировать (102.18) по объему
этого пучка. Мы обозначим этот объем через Vm\
wm=(w(X, У, Z)dXdydZ=^[cni2-lj^fe^dXdydZ. (102.19)
т Ущ
Если пучки разделены, то все интегралы равны (нулю кроме интеграла
( \^m\tdXdY dZ,
4.
равного в силу нормировки Фт единице. Таким образом,
™т = Ы2- (102.20)
Но есть как раз вероятность того, что энергия атома равна Ет
(так как атомы с различной энергией принадлежат разным пучкам). По-
этому рассмотренное нами определение энергии атома находится в пол-
ном согласии с интерпретацией величин |гп|2 как вероятностей найти
§ 103] НЕУПРУГИЕ СТОЛКНОВЕНИЯ ЭЛЕКТРОНА С АТОМОМ 359
значение энергии атома Еп. При этом измерительным аппаратом служил
сам атом: внутренняя энергия Еп определялась по положению центра
тяжести атома. Далее, отметим, что в процессе измерения энергия не
подвергалась изменению. Поэтому рассмотренный нами опыт принадле-
жит к числу «повторимых» (ср. § 17).
Обратим внимание еще на одно важное обстоятельство. В § 17 мы
утверждали, что измерение всегда превращает чистый ансамбль в сме-
шанный. Легко убедиться, что в рассматриваемом случае это превраще-
ние на самом деле имеет место. Определим вероятность найти электрон
в окрестности точки х, у, z при Заданном положении центра тяжести
атома X, F, Z. Имеем:
w(x,^, z, X, Г, Z) = |Ф|2 =
=22 (*, У> К (X, у, z) Ф„ (X, Y, Z) Ф*т (X, У, Z). (102.21)
и, т
В области, где Фл и перекрываются, мы имеем интерференцию
состояний фя, Ьт и для определения w важны фазы сп, с*т. В области,
где Фл и Ф^ не перекрываются (измерение!), мы получаем:
w(x,y, z. X, К, Z) = |Ф|2 =
= SKI2-| Ы*,У, г)\2-\Фп(Х, Y,Z)\2, (102.21')
п
т. е. фазы сп выпали. Вероятность w образуется теперь некогерентно
из как это характерно для смешанного ансамбля (ср. § 16).
§ 103. Неупругие столкновения электрона с атомом. Определение
стационарных состояний атомов методом столкновений
Одним из простых приложений теории движения многих тел является
расчет неупругих столкновений с атомами. С такого рода столкновения-
ми мы встречаемся в опытах Франка и Герца (§ 3). Однако, наш расчет
нельзя будет непосредственно применить к этим опытам, так как мы
будем предполагать, что сталкивающийся электрон имеет энергию, зна-
чительно превышающую энергию электрона в атоме (при этом условии
можно будет применить теорию возмущений). Оператор полной энергии
двух электронов*) имеет вид
Я(гр Г2) = Я(Г1)4-Я(Г2)+ W(rv г2) =
= Я° (Г1, r2)+W(rp г2), (103.1)
+ (1.03,2)
2u ^2’
, (ЮЗ.З)
Г(Г1,Г2)=:Я(Г2)+-^—
*) Движение атома в целом мы можем игнорировать ввиду большой вели-
чины массы ядра по сравнению с массой электрона.
360
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
Здесь U (л) означает потенциальную энергию атомного электрона в поле
остова (ядра и остальных электронов атома). -------г есть кулоновская
I Г1 Г2 I
энергия взаимодействия атомного электрона с электроном, летящим
извне. U(r2) есть энергия этого последнего электрона в поле остова
атома. Остальные члены имеют само собою понятное значение.
Кинетическую энергию летящего извне электрона мы считаем столь
большой, что все его взаимодействие с атомом W будем рассматривать
как возмущение. Тогда уравнение Шредингера для невозмущенного
движения будет иметь вид
Я°(гр г2)ф0(Г1, г2) = £фо(Г1),гг). (103.4)
Оно имеет решение
(103.5)
£ = + (^3.6)
где фо — волновая функция стационарного состояния электрона в атоме,
принадлежащая энергии Е? а фРо— волна де-Бройля, описывающая
свободное движение летящего извне электрона с импульсом р0.
Нас интересует вероятность перехода нашей системы из двух элект-
ронов в какое-нибудь другое состояние:
ФиГ1’Г*) = ^<Г1)'МГ2)’ (103-7>-
Для вычисления этой вероятности^применим теорию Квантовых пере-
ходов под влиянием возмущения, не зависящего от времени (§ 78).
Таким возмущением является у нас энергия W (103.3). Вычислим сначала
матричный элемент этого возмущения для перехода П, р0 —> т, р.
Имеем:
^p,npo = Jf r2) г2) (103.8)
(здесь dvx, dv2 означает интегрирование по координатам первого и
соответственно второго электрона). Вычислим сначала интеграл по dvv
Введем:
рил(г1)=-«^’(п). (103.9)
Эту величину будем называть матричным элементом плотности заряда
для перехода п —> т (очевидно, что рпп есть среднее значение плотности
в состоянии фо). Учитывая ортогональность функций ф^ и ф®, мы по-
лучаем:
f(П) • ФП(П) { 47 (r3) + i^^i} - U(r2) bmn -
_gJ = Vmn(rt). (103.10)
Последняя величина может рассматриваться как матричный элемент
§ 103]
НЕУПРУГИЕ СТОЛКНОВЕНИЯ ЭЛЕКТРОНА С АТОМОМ
361
потенциальной энергии сталкивающегося электрона (2) в поле ядра и
атомного электрона (1).
Если т = п, то столкновение будет упругим. Vnn совпадает с той
энергией возмущения, которая фигурировала у нас в § 75 в теории
упругого рассеяния электронов. Подставляя Vmn(r2) в (102.8) и имея
в виду, что
. РоГ2 . рГ8
. е h е' h
Фро (гг) (2.хЛ)’/з ’ (2яЛ)3/а ’
(103.11)
мы получим:
1 С ,(р°-р)п- <
Wmp,nPa=^dv2Vmn(r2)e * =^L_^n(K), (103.12)
где через К обозначен вектор
K_PorzP = ko-k,
(103.13)
где к0 и к — волновые векторы электрона до и после столкновения.
Для вычисления вероятности перехода в 1 сек. из начального со-
стояния £п, ро, ро, рО в конечное Ет, р, dQ (dQ — элемент телесного
угла, в котором лежит направление импульса электрона р после столк-
новения) применяем формулу (78.3). Плотность состояний на интервал
полной энергии системы, обозначенная в (78.3) через р (£*), будет у нас
такая же, как и для одной частицы [см. (77.23)], так как
^=Ф.+С)=О-
Следовательно, р(В) = рр. Поэтому согласно (78.3) и (103.12) имеем:
РЯр0(/и, Р)^=^(2^1Ляя(К)|гИР^. (103.14)
Чтобы вместо вероятности перехода в 1 сек. получить эффективное
сечение <?(р0, р, 6, у) для перехода р0—dQ, нужно иначе норми-
ровать функции падающего электрона. Именно, их нужно нормировать
так, чтобы поток через 1 см2 в 1 сек. равнялся 1. Для этого вместо
(103.11) нужно взять
• Рогя
е h
где Vq — скорость падающего электрона:
t’o=LT=7- (Ю3.15)
Функции (103.11) и (103.1 Г) отличаются множителем
362
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
Так как в вероятность (103.14) начальная функция входит в квадрате,
то, переходя от нормировки (103.11) к нормировке (103.1 Г) (для пада-
ющих частиц), мы получим в (103.14) множитель (2тгА)3 —. Вместе с тем
Ро
вероятность РлРо(/^, р) примет размерность площади. Так как принятая
нами нормировка для падающей волны — как раз та, которая, прини-
мается для расчета эффективного сечения (поток: одна частица в 1 сек.
через 1 см2), то полученная вероятность совпадает с эффективным се-
чением. На основании сделанных замечаний получаем эффективное се-
чение в виде
qnpa (т, р) = £ G^)21 Fmn (К) P dQ. (103.16)
При этом условие резонанса, совпадающее с законом сохранения энергии,
в случае возмущения, не зависящего от времени, гласит:
Рп Р2
е,, + ти=г„ + 2< (103.17)
Для упругого рассеяния т = п, р—р^ и формула (103.16) в точности
совпадает с выведенной в § 74 методом стационарных состояний. Для
неупругого рассеяния вид атомного фактора Fmn несколько иной [см.
(103.12)]. Кроме того, в q входит множитель р/р0, смысл которого
легко уяснить. qdQ есть отношение потоков падающего и рассеянного
в угол dQ. В это отношение потоков входит отношение скоростей,
которое как раз равно р/р0 и выпадает для упругого рассеяния. Обоз-
начая р через ртп, К через Кт7г=-^-, часто пишут (103.16) в форме
Чтп^ <?)dQ=P~^- К«)|2<Й- <103Л6')
‘Отсюда, интегрируя по всем возможным углам рассеяния dQ, мы получим
эффективное сечение для любого стрлкновения, при котором энергия
электрона меняется на величину Ет— Еп, а атом переходит из состоя-
ния Еп в
= (103.18)
Если Еп — нижнее нормальное состояние атома, то соударяющийся
электрон может только возбуждать атом (Ет^>Eh). В этом случае
Qmn называют эффективным сечением для возбуждения атома. На
рис. 69 приведена типичная зависимость этого сечения от энергии
электронов. На основании закона сохранения (103.17) мы можем, из-
о 2
Р2, PQ
меряя изменение энергии падающих электронов ’ определить
разности Ет — Еп и тем самым установить энергетический спектр атома.
Это и было впервые проделано в опытах Франка и Герца.
Если, как это обычно делают, принять границу (/п = оо) между
дискретным и непрерывным спектрами атома за нуль при отсчете энер-
§ 103] НЕУПРУГИЕ СТОЛКНОВЕНИЯ ЭЛЕКТРОНА С АТОМОМ
363
гии атомного электрона, то, определяя ту потерю энергии первичных
ч —2
Р2 А)
электронов — — —
, при которой начинается ионизация атома (появ-
ляются вторичные электроны), мы можем также измерить., энергию
состояния атома, в котором он находился до столкновения. В самом
деле, в этом случае из (103.17) имеем:
, _I F _Л2_£о
'» 2|) 2|1 “Г 00 —2|1 2|х"
(103.17')
Рис. 69. Зависимость эффективного
сечения (Qmn) для возбуждения
ударами электронов от энергии
электронов Е.
Таким образом, следовательно, мы можем определить стационарное
состояние атома. Отличие этого измерения от измерений отклонением
атомов внешним полем заключается в
том, что состояние атома после из-
мерения меняется (например, про-
исходит ионизация атома), в то время
как в опытах по отклонению оно
остается неизменным. Таким образом,
рассматриваемое нами измерение энер-
гии относится к числу «предсказуе-
мых» (ср. § 17).
Обратим внимание на то обстоя-
тельство, что при измерении энергии
атома методом столкновений требует-
ся, как и в методе отклонения, не-
которое минимальное время. Дейст-
вительно, измерение основывается на законе сохранения энергии (103.17).
Этот закон выражается наличием S-функции в вероятности перехода
[ср. § 77, формулы (15), (16) и (17), при этом в них следует поло-
жить А(о = О].
На самом деле мы имеем дело не с S-функцией, а с приближенным
ее выражением (77.14):
= 4 g-V • (103.19)
которое лишь при t —оо переходит bS(Z? — EQ). Функция S' (Е—£0)
отлична от нуля заметным образом для всего интервала разности
&(Е— EQ^ для которого
Д(£—Eq)-h,
и становится малой лишь для
ЦЕ—E^yt^h, (103.20)
т. е. имеется неопределенность в разности начальной энергии Е(}
и конечной Е, связанная с длительностью промежутка времени t между
началом измерения (начало взаимодействия падающего электрона с ато-
мом) и концом измерения (определение энергии падающего электрона
после столкновения).
364 ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ ДВИЖЕНИЯ МНОГИХ ТЕЛ [ГЛ. XIX
Предположим теперь, что энергию падающего извне электрона и до
и после столкновения мы знаем точно. Тогда из (103.20) следует со-
отношение для длительности измерения t и неопределенности Д (Е*и—
б* разности начальной и конечной энергии измеряемой системы (атома):
Д(£я — En,)-t^h. (103.21)
Чтобы определить уровни нашей системы^ (опыт Франка и Герца), фик-
сируем еще и конечную энергию. Для этого будем отмечать те случаи,
когда в результате столкновения атом ионизуется (Еп* 0), и измерять
энергию вылетающего из атома электрона. Тогда вся неопределенность
перенесется на начальное состояние, и из (103.21) мы получим:
A(FJ./>Zh (103.2V)
Чтобы можно было знать, . какую из энергий Еп или Ет имел атом
до столкновения, нужно, очевидно, чтобы А (Еп) | Еп — Е^ [, т. е.
IEn-Eml-t^h, (103.22)
т. е. для того, чтобы отличить, в каком из состояний находился атом
до опыта, нужна достаточная длительность измерения (при этом энергия
после опыта предполагается известной). Если же ограничиться опреде-
лением энергии только до опыта (в исходном состоянии) или только
после опыта, то соотношение (103.2Г) не имеет места.
§ 104. Замечания о законе сохранения энергии в квантовой
механике
В классической теории закон сохранения энергии утверждает, что
энергия замкнутой системы остается неизменной, так что, если обозна-
чить энергию такой системы в момент / = 0 через EQ, а в момент t
через £*., то
E^ = Ef (104.1)
В квантоврй механике закон сохранения энергии формулируется весьма
аналогичным образом. Именно, согласно § 33 энергия является интегра-
лом движения, и вероятность w (Е, t) найти в момент t значение энергии,
равное Е, не зависит от времени:
^-9=0. (104.2>
at
Закон сохранения энергии в только что высказанной форме предполагает
возможность определения энергии в данный момент времени без того,
чтобы подвергнуть ее неконтролируемому измерению. В классической
механике возможность такого измерения не вызывает сомнений. В кван-
товой механике, напротив, такого рода возможность ввиду того, что
вмешательство прибора, вообще говоря, меняет состояние системы, не
является самоочевидной.
§ 104] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В КВАНТОВОЙ МЕХАНИКЕ 365
Рассмотренные в §§ 102, 103 измерительные устройства для опре-
деления энергии показывают, что энергия без нарушения ее величины
(«повторимый» опыт) может быть измерена лишь с точностью
(104.3)
где т — длительность измерения. Однако, это не представляет трудности
для закона сохранения энергии, так как энергия является интегралом
движения, и мы располагаем как угодно большим временем, чтобы
произвести длительное измерение. Так, например, если мы проведем
измерение в течение времени т, а затем предоставим систему самой себе
на время Т, а затем вновь определим энергию, то закон сохранения
энергии (104.2) утверждает, что результат этого второго измерения
с точностью ДЕ ~ совпадает с результатом первого измерения. Если
же не требовать неизменяемости энергии при ее измерении, то никаких
ограничений на точность кратковременного (мгновенного) измерения
энергии не наложено, так как соотношение (104.3) содержит лишь не-
определенность ДЕ ‘разности энергий до опыта и после опыта [ср.
(103.21)]. Поэтому можно получить сколь угодно точное значение
о величинё энергии в данный момент времени, если ограничиться зна-
нием ее величины либо до опыта, либо после опыта. Так, например,
можно определить значение энергии в момент / = 0 после опыта и
в момент t—T до опыта. Тогда закон сохранения энергии утверждает,
что оба значения энергии будут равны друг другу.
В заключение вопроса об энергии укажем на то, что соотношения между
неопределенностью ДЕ значения энергии Е в данный момент времени t и точ-
ностью фиксации этого момента ДЕ
ДЕД^/г, (104.4)
подобного соотношению
ДрхДх^/г, (104.5)
в квантовой механике не существует. Мы имели бы соотношение (104.4)
если бы энергии Е можно было бы сопоставить оператор ih ~ подобно тому,
как импульсу рх сопоставляется оператор — in . На самом же деле опе-
ратор энергии Н есть «функция» операторов импульса и координат: Н~
= И (Рх, Ру, Pz, х, у, z\ Однако, в частных случаях можно получить соотно-
шение (104.4), если вложить надлежащий смысл в ДЕ и ДЕ
Приведем примеры. Пусть мы имеем группу волн, движущуюся с груп-
повой скоростью v и имеющую размеры Дх (см. §§ 7 и 14). Введем время
Дх
Atz=z —, в ч течение которого группа проходит через какую-нибудь точку
пространства х. Имея в виду, что
Д£=д(^)=С'ДА (104.6)
мы получим из (104.5):
Дх
vbp — = (104.7)
366
СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ
[гл. XX
Здесь &Е—дисперсия энергии, а М— время прохождения группы через
фиксированную точку пространства.
Другим примером соотношения (104.4) может служить соотношение, полу-
чающееся для так называемой длительности жизни состояния. Пусть в на-
чальный момент времени t~ 0 мы имеем некоторое состояние, описываемое
волновой функцией
ф (х, 0) = с (0) ?0 (х), с (0) = 1. (104.8)
В более поздний момент времени мы получим состояние
ф (х, t) = c (t) <fo (х) 4- и (х, t). (104.9)
Если теперь c(t)—► 0 при > оо, а и(х, t) и <р0(х) ортогональны (или почти
ортогональны), то мы можем сказать, что частица покидает состояние <р0.
Если при t — амплитуда | cQ (t) | уже значительно меньше 1, то мы можем
назвать Af длительностью жизни состояния <р0. Ясно, что в этом случае cQ(t)
не есть гармоническая функция времени. Амплитуда состояний с определен-
ной энергией (&E=Q) зависит от времени гармонически. Поэтому <р0(х) есть
состояние с неопределенной энергией (ЛЕ > 0). Таким образом, АЕ М > 0.
ЬЕ Ы имеет размерность h и при переходе к классической теории (h —> 0)
> 0. Поэтому мы можем написать:
АЕА;>у/г, (104.10)
где у — некоторый неопределенный численный коэффициент *). Пример такого
соотношения между дисперсией энергии и длительностью жизни состояния
мы имели в теории радиоактивного распада [ср. (92.30)].
ГЛАВА XX
СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ
§ 105. Принцип неразличимости частиц
Мы перейдем теперь к рассмотрению свойств систем, состоящих из
одинаковых частиц. Одинаковыми частицами мы будем называть частицы,
имеющие одинаковые массу (/п), заряд (е), спин (s) и т. д., так что
в равных условиях (внешнее поле, присутствие других частиц) такие
частицы ведут себя одинаковым образом. о
С точки зрения атомизма естественно, но не необходимо считать, что
все экземпляры частиц одного рода (электроны, протоны, нейтроны и
т. д.) между собой тождественны. В самом деле, измерение величин,
характеризующих частицы (т, е, s), производится, конечно, лишь с не-
которой точностью (Д/n, Де, As), и всегда законно предполагать, что,
по крайней мере в пределах точности измерения, разные экземпляры
могут отличаться друг от друга.
Одинаковы или неодинаковы все экземпляры одного рода, это
можно было бы решить лишь в том случае, если бы поведение сово-
купности одинаковых частиц качественно отличалось от поведения сово-
*) Значение этого коэффициента зависит от выбора меры для дисперсии
энергии ДЕ и для длительности состояния Af, и также от ?0. Вообще говоря,
этот коэффициент по порядку величины близок к 1.
§ 105]
ПРИНЦИП НЕРАЗЛИЧИМОСТИ ЧАСТИЦ
367
купности различных, хотя бы и сколь угодно мало различных частиц.
Именно к такому качественному отличию свойств совокупности одина-
ковых частиц от свойств совокупности различных частиц приводит кван-
товая механика. Поэтому, опираясь на квантовую механику и опыт,,
можно решить на первый взгляд нерешимый вопрос о том, тождест-
венны ли друг другу все представители частиц одного рода или нет.
Чтобы уяснить себе, каким путем решается этот вопрос, мы должны
обратиться сначала к изучению наиболее простых особенностей сово-
купностей, состоящих из одинаковых частиц. Пусть мы имеем N одина-
ковых частиц. Координаты, принадлежащие &-ой частице, обозначим
буквой qk, так что под qk следует разуметь три координаты, опреде-
ляющие положения центра тяжести частицы (xk, yk, zk) и, может быть, еще
четвёртую, определяющую спин частицы (sk), если она таковым обладает.
Обозначим массу частиц через т, энергию во внешнем поле через
U(qk, t), а энергию взаимодействия &-ой и /-ой частиц через W(qk, q})a
Тогда гамильтониан системы таких частиц будет равен
w
H(qv q2,...,qk,...,qp..., qN,t)=^ Г + ^(^> 01 +
N
Aj' ^=/' = 1
Предположение об одинаковости частиц выразилось здесь в том, что
массы частиц, энергия во внешнем поле U и энергии взаимодействия W
для всех частиц взяты одинаковыми. Эта особенность гамильтониана
сохраняется в любом внешнем поле: на одинаковые частицы любое*
внешнее поле действует одинаковым образом.
Для проведения общих выводов не очень удобно опираться на спе-
циальный вид гамильтониана (105.1)*). Поэтому мы должны выразить
тот факт, что гамильтониан описывает систему одинаковых частиц, без
того, чтобы прибегать к явному его виду.
Исходя из (105.1), легко уяснить себе, в чем заключается обяза-
тельная и наиболее общая особенность гамильтониана системы одинако-
вых частиц. Если в гамильтониане (105.1) мы переставим местами ко-
ординаты &-ой частицы (qk) и у-ой частицы (</у), то гамильтониан не
изменится. В самом деле, такая перестановка обозначает просто пере-
становку слагаемых в суммах, входящих в гамильтониан:
H(qx,q2,... ,qk,...,qp ...,qN, t) =
= H(qx,qi,...,qp...,qk,...,qN,e} (105.2)
для всех пар (/, k) из N частиц, образующих систему. Если бы среди Д/
частиц была бы хоть одна отличная, то это равенство не имело бы
*) Написав гамильтониан Н в форме (105.1), мы исключили непотенциаль-
ные поля (например, магнитное поле), также исключили взаимодействие, мо-
гущее зависеть от скоростей частиц (магнитные силы). Все это могло бы
быть учтено и нисколько не изменило бы хода дальнейших рассуждений.
368 СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ [гл. XX
места как раз для перестановки этой отличной частицы с любой другой.
Таким образом, равенство (105.2) и выражает самое общее свойство
гамильтониана, относящегося к совокупности одинаковых частиц.
Коротко это свойство может быть сформулировано так: гамильто-
ниан системы одинаковых частиц инвариантен (симметричен) от-
носительно перестановки координат любой пары частиц.
Ввиду того, что нам в дальнейшем придется часто встречаться
с перестановками, нам удобно ввести новый оператор — оператор пе-
рестановки частиц PkJ. Под этим оператором мы будем подразуме-
вать символ, указывающий на то, что координаты Aj-ой* и /-ой частиц
должны быть переставлены. Например, если мы имеем функцию
qk,...,qp...), то
Pk/f(...,qk,...,qp...)=f(...,qp..., qk,.. .). (105.3)
Этот оператор, очевидно, принадлежит к числу линейных операторов,
так как для того, чтобы переставить координаты в сумме двух функ-
ций, нужно переставить их в каждой из функций.
С помощью оператора Pkj равенство (105.2) можно написать в виде
PkjH{qlt. ..,qk,...,q.,...,qN,t) =
= H(q1,...,qk,...,qp...,qlf,t)PkJ (105.4)
для всех пар k, j. Таким образом, оператор Pkj коммутируем с га-
мильтонианом системы одинаковых частиц. Действительно, если мы
применим к некоторой функции ф оператор PH. то в силу (105.2)
это все равно, что применить к ф оператор HP. ибо оператор Р
оставляет неизменным согласно (105.2) гамильтониан Н.
Опираясь на это свойство гамильтониана, докажем важную вспомо-
гательную теорему относительно волновых функций, описывающих со-
стояние систем из одинаковых частиц. Пусть волновая функция системы
Af частиц есть (qr...., qk...., q^...., qN. /); она должна удовлетво-
рять уравнению Шредингера
lh-------------------------= Я(?П. . ., qk, .. ., qp ..qN, t) X
X• •> qj,...,qN,t). (Ю5.5)
Переставим в этом уравнении координаты &-ой и /-ой частиц. Для
этого подействуем на обе его части оператором Pkj\
ih^t(Pkp)=Pkjm. (Ю5.5')
В силу того, что гамильтониан Н для одинаковых частиц симметричен
относительно перестановки частиц, мы можем на основании (105.4)
переставить в (105.5') операторы Pkj и Н. Тогда мы получим:
ih^(Pkp)=H{Pkp}. (105.6)
Из сопоставления (105.6) с исходным уравнением (105.5) следует, что
§ 105] ПРИНЦИП НЕРАЗЛИЧИМОСТИ ЧАСГИЦ 369
если Ф (^,.. ., qk,..., qj,.. ., qN, t) есть решение уравнения Шре-
дингера (105.5), то и
У' = (qv q}, -.., qk, .... (105.7)
есть также решение этого уравнения, и, следовательно, ЛРГ наряду с Ф
представляет одно из возможных состояний системы. Оно отличается от
прежнего Ф тем, что &-ая частица находится теперь в состоянии, ранее,
занимавшемся j-ой частицей, а /-ая занимает теперь состояние &-ой.
Продолжая перестановки, мы можем получить новые возможные состоя-
ния системы Ф", Ф"г, отличающиеся друг о г друга распределением
частиц по состояниям.
Утверждая, что первая частица находится в состоянии а (первое
место в волновой функции), вторая частица — в состоянии Ъ (второе
место) и т. д., мы встречаемся с одной характерной трудностью. Дело
в том, что, становясь на атомистическую точку зрения, считая разные
Рис. 70. Нумерация частиц по их положениям в пространстве.
а—в классической механике; b—в квантовой. В области, заштрихованной
дважды, нумерация спуталась.
экземпляры частиц одного рода одинаковыми, мы можем различать чд-
стицы только по их состоянию — например, по их положению в простран-
стве, по величине их импульса, энергии и т. д. Разумеется, что с тече-
нием времени состояние частиц может измениться, и они могут обме-
няться своими состояниями. Поскольку в классической механике принци-
пиально возможно проследить за траекторией частиц, постольку, отметив
частицы, например, по их положению в ромеит времени / = 0, мы
можем в любой момент сказать, находится ли в данном месте та частица,
которую мы назвали первой, или та, которую назвали второй. Между
тем, в квантовой области этого сделать нельзя. Если бы мы отметили
частицы по их положению в момент / —0, то волновые пакеты, относя-
щиеся к различным частицам, быстро бы растеклись и перекрылись, так
что, обнаружив в момент t 0 где-либо какую-нибудь из частиц, мы уже
никак не могли бы сказать, какая же это из частиц — первая или вторая.
Эти рассуждения иллюстрируются рис. 70. Ш рис. 70, а изобра-
жены положения частиц и в момент t—.Q и дальнейшие движе-
24 Блохинцев
370 СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ [гл. XX
ния их по классическим траекториям. На рис. 70, b изображены вол-
новые пакеты частиц в момент Z = 0 около хг и х2 (заштрихованные
области) и их дальнейшее рассеяние. Следует отметить, что заштрихо-
ваны только те области, где |Ф|2 имеет большую величину, так что
в незаштрихованных областях пакеты также перекрываются, только зна-
чение | Ф |2 там мало. Найдя частицу в области пространства, где вол-
новые пакеты перекрываются, мы уже не можем решить, с какой из
двух частиц мы имеем дело. Аналогичные рассуждения можно привести
и в тех случаях, когда частицы отмечаются не по их положению в про*
странстве, как в приведенном примере, но по каким-либо другим меха-
ническим величинам.
Таким образом, в квантовой области единственный способ, по кото-
рому можно различать одинаковые частицы — различие по состояниям,—
отказывается служить. В этой связи мыслимо предположение, что встре-
чающиеся в природе системы устроены так, что вообще проблема раз-
личения одинаковых частиц является надуманной, т. е. что состояния
совокупности одинаковых частиц всегда таковы, что можно говорить
лишь о состоянии всей совокупности в целом, а не о распределении
частиц по состояниям. Это предположение оправдывается на самом деле.
Его мы формулируем в форме принципа неразличимости частиц: в сово-
купности одинаковых частиц реализуются лишь такие состояния,
которые не меняются при обмене одинаковых частиц. Это означает,
что вероятность найти при измерении какой-либо механической величи-
ны Л, относящейся к системе одинаковых частиц или к ее части, значе-
ние, равное Z/, не меняется при обмене частиц их состояниями.
Высказанный принцип не вытекает из изложенных ранее положений
квантовой механики, но, как мы увидим, он вполне подходит к ней и
обязателен, если мы хотим получить из квантовой механики выводы,
согласующиеся с опытом.
§ 106. Симметричные и антисимметричные состояния
Пусть , qk, . ., . ., q^, t) есть волновая функция,
описывающая состояние системы из N одинаковых частиц. Тогда, если
мы обменяем состояниями, скажем, &-ую и у-ую частицы, то получим
новое, как следует из теоремы (105.7), возможное состояние системы,
описываемое волновой функцией Чр (^, . ., q^ ..., qk, .. , qN,t)*
Принцип неразличимости частиц утверждает, что это новое состояние
неотличимо от прежнего, т. е. Ф' и Ф описывают фактически одно и
то же состояние системы.
Волновые функции, описывающие одно и то же физическое состоя-
ние, могут отличаться друг от друга Только постоянным множителем.
Следовательно, из принципа неразличимости вытекает, что
qp qk, . qN, /)=Wi................qk.....qP • • -,qN, t).
где X — некоторый постоянный множитель. Это равенство с помощью
§ 106] СИММЕТРИЧНЫЕ И АНТИСИММЕТРИЧНЫЕ состояния 371
оператора перестановки может быть написано в виде
PkJW = W. (106.1)
В уравнении слева (106.1) на функцию действует оператор Pkj-t а справа
стоит эта же функция, умноженная на число X. Следовательно, уравнение
(106.1) есть уравнение для собственных функций Ч; и собственных зна-
чений X операторов перестановки Pbj.. Мы можем поэтому сказать, что
условие (106.1), накладываемое принципом неразличимости на возмож-
ные состояния системы заключается в том, что волновые функции У,
описывающие состояние системы, должны быть собственными функциями
операторов Pkj (для любых k, /). Нетрудно определить, каковы эти
собственные функции и собственные значения X. Для этого применим к
(106.1) еще раз оператор перестановки PkJ. Имеем:
Р| ф = Х/> Ф. (106.2)
«у 'V/
Два раза применяемый оператор перестановки Pk^ не меняет функции ЧЛ
Поэтому в (106.2) слева стоит просто ф( .., qk, ..., fy, ...), а
справа в силу (106.1) Х2Ч* (..., qk, qp ...), так что (106.2) пе-
реписывается в виде
Ф=Х2Ф,
т. е.
Х2=1. (106.3)
Отсюда получаем собственные значения оператора перестановки Pkj\
Х=±1, (106.4)
а соответствующие собственные функции обладают в силу (106.1) сле-
дующими свойствами:
РА/Ч'=+Ф, Х= + 1 (106.5)
или
Pkj^=z— Ф, Х= —1, (106.6)
т. е. собственными функциями оператора перестановки Pkj являются
функции, которые при перестановке координат &-ой частицы (^) и
координат /-ой частицы (#у) либо не меняются (106-5), <либо меняют
свой знак на противоположный (106.6). Первые функции (106.5) мы
будем называть симметричными, а вторые (106.6) антисимметрич-
ными относительно перестановки частиц номера k и j.
Таким образом, возможные состояния системы из N одинаковых
частиц должны описываться волновыми функциями Ф(^р .. , qk, ...,
Яр 0, которые либо меняют свой знак при перестановке лю-
бой пары частиц (&, /), либо остаются неизменными. Из соображений
равноправности всех чаСтиц нетрудно предвидеть, что возможные функ-
ции Ф таковы, что они либо симметричны во всех парах одинаковых час-»
тиц, либо антисимметричны во всех парах частиц, так что не может.
24*
372
СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ
[гл. XX
быть функций, которые в части частиц симметричны, а в другой—
антисимметричны *). Окончательно из принципа неразличимости частиц
следует, что возможны только два класса состояний для одинаковых
частиц:
(А,/-любые) (106.7)
-—симметричные во веек частицах и
-К (*,/-любые) (106.8)
— антисимметричные во всех частицах.
Мы сейчас покажем, что переходов между этими состояниями быть
не может: если в какой-то момент времени система находится в сим-
метричном (Ч^) или антисимметричном (Ч^) состоянии, то она всегда
находится в симметричном или соответственно антисимметричном состоя-
нии. Для доказательства ,этого важного положения достаточно восполь-
зоваться уравнением Шредингера и тем обстоятельством, что гамильто-
ниан обязательно симметричен относительно одинаковых частиц. Урав-
нение Шредингера
ih~ = HW (106.9)
нам удобно переписать в форме
dW=±HWdit
1 th ’
(106.10)
где dt будет означать приращение волнодой функции за время dt.
Допустим, что в момент времени / = 0 Ф есть симметричная функция
координат частиц (Ф — Ф). Тогда в силу симметрии И величина Н1]^
будет также симметричной функцией координат частиц, а следователь-
но, и приращение функции d^V будет симметричной функцией от коор-
динат частиц.
С помощью оператора перестановки эти рассуждения могут быть
записаны так:
антисим-
Л/(ЯФ,)=яед)«яФ.
отсюда с помощью (106.10) следует:
______________ pkj(d^=dy
*) Если встречаются перестановки и того и другого рода, то Ф = 0. Дей-
ствительно, пусть Ф симметрична при перестановке k и /, j и i, но
метрична при перестановке i и k. Тогда имеем:
9/...
= —•••, gj,
Отсюда
2Ф(..., qb .... qjt ...) = 0, т. е. Ф4..., qt, .... qk,..., ...)=0,
Подобным же образом проводится доказательство в предположении, что две
перестановки антисимметричны, а третья симметрична.
(106.11)
—ф(..., ft,
Яь ...) = — Ф( Я]..Як....?/.•••) =
=—Ф(..., qit.... q^ Яр
§ 107] ЧАСТИЦЫ БОЗЕ И ЧАСТИЦЫ ФЕРМИ. ПРИНЦИП ПАУЛИ 373
для всех пар k, j. Наше доказательство, таким образом, утверждает,
что функция, симметричная в какой-то момент времени (/ — ()), остается
симметричной и в соседние моменты Времени, как в прошлые, так и
будущие, ибо доказательство одинаково применимо и к и
Следовательно, симметрия функции остается неизменной для
всех моментов времени от t~ — оо до f °о. Совершенно ана-
логичным образом проводится соответствующее доказательство для анти-
симметричных функций. Пусть в момент / = 0 функция Ф, описываю-
щая состояние системы, антисимметрична (ф —Фд). Тогда
Далее
Pkj W -H{PkjWa) = - ЯФв,
из (106.10) тогда следует:
(106.12)
т. е. приращение антисимметричной функции Фа само антисимметрично.
Поэтому, если система находится в состоянии, описываемом антисим-
метричной функцией Фа, то она всегда остается в таком состоянии.
Доказанная теорема показывает, что деление состояний на два класса
носит «абсолютный» характер: если какая-либо система в какой-либо
момент времени обнаружена в состоянии того или иного класса (ф^ или
4JJ, то она никогда не перейдет из одного класса в другой. Такой
переход невозможен, каю бы мы ни меняли внешнее поле, так как вся-
кое внешнее поле одинаково действует на одинаковые частицы, и, сле-
довательно, при любом изменении внешнего поля гамильтониан остается
симметричным.
Нам надлежит теперь решить вопрос о том, в каких случаях и
какую из двух возможностей (Ч; — ф^ или ф = Фа) следует применять
для описания состояния системы и? одинаковых частиц.
§ 107. Частицы Бозе и частицы Ферми. Принцип Паули
Как мы видели, квантовая механика на основе принципа неразличи-
мости одинаковых частиц ведет к двум классам состояний, абсолютно
не смешивающихся между собой. Поэтому выбор того или иного класса
состояний для какой-либо системы частиц может быть продиктован только
природой частиц, образующий систему, а не характером внешнего поля
или каким-либо подобным обстоятельством.
Эмпирически установлено, что в природе существуют частицы, при-
надлежащие обоим классам. При этом наблюдается следующее правило’
частицы, обладающие спином, равным целому числу постоянных
Планка'.
s — hm, т — 0, 1, 2, (107.1)
описываются симметричными функциями (Ф^). Мы будем называть
374 СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ [гл. XX
такие частицы частицами Бозе, а совокупности таких частиц—ансамбля-
ми Бозе-Эйнштейна, по имени физиков, разработавших статистику для
таких частиц.
Напротив, частицы, имеющие спин, равный полуцелому числу постоян-
ных Планка:
з — hm, т = ^, у, у, (107.2)
описываются антисимметричными функциями (Ч^). Мы будем назы-
вать такие частицы частицами Ферми, а совокупность таких частиц
ансамблями Ферми-Дирака, по имени физиков, построивших статис-
тику для частиц такого рода *).
Примером частиц Бозе являются ядра гелия (а-частицы), атомы водо-
рода, атомы гелия и многие другие. К числу частиц второго рода .принад-
лежат простейшие частицы — электроны, позитроны, протоны и нейтроны,
все они обладают спином, равным полуцелому числу постоянных Планка.
До сих пор не установлено с полной достоверностью существование
простейших частиц с целым спином (107.1)**), поэтому возможно, что
простейшие частицы всегда имеют спин, равный $ =. Тогда частицы
Бозе были бы исключительно частицами сложной структуры.
То, что сейчас известно об этих частицах, согласуется с таким пред-
положением: а-частицы и Многие другие ядра, принадлежащие к числу
частиц Бозе, являются сложными образованиями. Это же, разумеется,
относится и к атомам.
Предполагая, что простейшие частицы суть частицы Ферми (что
вполне подтверждается опытом), легко понять, почему перечисленные
выше частицы Бозе будут описываться симметричными функциями (Ч^).
Рассмотрим для примера атом водорода. Атом водорода представляет
собой систему из двух частиц Ферми: протойа и электрона. Суммар-
ный механический момент атома водорода в нормальном состоянии скла-
дывается из механического момента (спина) протона и из спина электрона.
Так как каждый из них имеет момент, равный -4-у > то суммарный
*) В недавней работе Паули показал, что это правило может быть обос-
новано теоретически. Однако, мы не имеем во;можности обсуждать здесь его
аргументацию и отсылаем читателя к оригиналу: W. Р а и И, Bericht iioer die
allgemeitien Eigenschaften Elementarteilchen, Huitieme Conseil de physique,
Solvay,
**) Предполагается, что полутяжелая частица (масса около 100—200 масс
электрона), так называемый «мезотрон», имеет спин, равный h. Существо-
вание такой частицы вытекает из исследований космических лучей.
Однако, предположение о ее спине не может еще считаться вполне обосно-
ванным.
Что касается кванта света, то его вращательный момент (спин) должен
измеряться целым числом h. Было бы, однако, весьма неуместно проводить
параллели между квантом света и простейшими частицами до тех пор, пока
мы не рассматриваем процесс рождения и уничтожения этих частиц (см. по-
следнюю главу этой книги).
§ 107] ЧАСТИЦЫ БОЗЕ И ЧАСТИЦЫ ФЕРМИ. ПРИНЦИП ПАУЛИ 375
момент атома водорода в нормальном состоянии может быть равен 0
или 4£Л, т. е. измеряется целым числом постоянных Планка.
Рассмотрим теперь ансамбль из атомов водорода. Координаты про-
тона k-ro атома обозначим через Qk, а координаты электрона k-ro
атома через Zk. Тогда волновая функция, описывающая ансамбль, состоя-
щий из Матомов водорода, будет иметь вид
’F=’F(Qi, QpZj, Q^i). (107.3)
Будем рассматривать каждый из атомов водорода как одну частицу
(это можно сделать во всем том круге явлений, где можно игнориро-
вать возможность возбуждения электрона атома водорода). Тогда обмен
состояниями двух атомов водорода — k-ro и /-го — означает одновре-
менную перестановку вЧ; и координат ядер Qk, Q}., и координат элек-
тронов принадлежащих &-му и /-му атомам. Но так как мы счи-
таем протоны и электроны * частицами Ферми, то волновая функция ф
должна быть антисимметрична относительно перестановки любой пары
ядер (Qfc и Qy Равным образом она должна быть антисимметрична и
при перестановке любой пары электронов и $у.). Таким образом,
при перестановке'k-ro и /-го протона ф меняет знак, при перестановке
&-го и /-го электрона она также меняет знак. Следовательно, при пере-
становке атомов водорода, когда сразу переставляется и пара протонов,
и пара электронов, ф не изменится вовсе, т. е. относительно переста-
новки атомов ъо до рода Ф симметрична, и атомы водорода, поскольку они
рассматриваются как простые частицы, принадлежат к числу частиц Бозе.
Подобным же образом можно провести рассуждения и для а-ча-
стицы, которая состоит из двух протонов и двух нейтронов? Суммар-
ный механический момент а-частицы должен быть целым числом Л, так
как он должен составляться из ^етырех спинов, каждый из которых
равен . В самом деле, механический момент а-частицы равен 0.
Нетрудно провести рассуждения с волновой функцией для а-частиц,
подобные проведенным нами для атома водррода. Исходя из того, что
волновая функция для системы а-частиц должна быть Антисимметрична
относительно перестановки протонов и относительно перестановки ней-
тронов, легко притти к заключению, что относительно перестановки
а-частиц волновая функция должна быть симметрична, т. е. а-частицы
должны относиться к числу частиц Бозе.
После этих замечаний о сложных частицах типа Бозе мы обратимся
к рассмотрению основной особенности часТиц типа Ферми. Эта фунда-
ментального значения особенность заключается в том, что частицы этого
рода подчиняются так называемому принципу Паули, который еще за-
долго до разработки квантовой механики был сформулирован В. Паули
на основании анализа эмпирических данных о спектрах сложных атомов.
Принцип этот (в элементарной форме) гласит: в одном и том же
квантовом состоянии не может находиться более одного электрона.
Поясним этот принцип примером. Квантовое состояние -электрона,
движущегося в поле центральных сил, характеризуется тремя квантовы-
376 СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ [гл. XX
ми числами /I, Z, т, определяющими энергию электрона (/г), его орби-
тальный момент (Z) и одну проекцию орбитального момента на какое-
либо направление (ш), а также четвертым квантовым числом у) ,
определяющим проекции спина электрона sz на то же направление. Пол-
ностью квантовое состояние задается четырьмя числами я, Z, т, ms. Принцип
Паули утверждает, что в таком состоянии либо вообще нет электрона,
либо есть только один. Более же одного электрона там быть не может.
В состоянии с одними и теми же квантовыми числами, относящимися
к движению центра тяжести электрона (и, Z, /п), можно поместить
, 1
два электрона с противоположными направлениями спина ms = ± v •
Приведенная формулировка принципа Паули проста, но страдает
тем недостатком, что она приближенна. В самом деле, когда мы поме-
щаем второй электрон в состояние с заданными числами /г, Z, т, то все
это состояние в результате взаимодействия первого электрона со вторым
изменяется. Поэтому в элементарной формулировке не вполне ясно, в
какое именно состояние нельзя поместить более одного электрона. Тем
нё менее, ввиду того, что состояние электронов из-за их взаимодей-
ствия во многих случаях меняется незначительно, уже элементарная фор-
мулировка принципа Паули оказывается весьма плодотворной.
Сформулируем принцип Паули так, чтобы освободиться от только
что указанного затруднения. Для этого заметим, что электрон (или дру-
h \ Л
гая частица со спином -% ) есть частица, обладающая четырьмя степеня-
ми свободы: три относятся к движению его центра тяжести, четвертая
есть спин. Поэтому для указания состояния отдельного электрона, при-
надлежащего системе или одинокого, достаточно измерить четыре вели-
чины Lv L2, s, которые должны обладать следующими свойствами:
а) все они должны быть одновременно измеримы; Ь) первые три долж-
ны характеризовать движение центра тяжести и быть независимыми;
с) четвертая должна определять состояние спина электрона. После изме-
рения получится состояние bLLiL3S (^), в котором заданы четыре
величины Lv L2, s. Ради краткости мы обозначим определенное зна-
чение четверки таких величин одной буквой п, так что
= (^)- (107.4)
Приведем примеры таких четверок. Можно взять за три величины ком-
поненты импульса рх, ру, pz, а в качестве четвертой величины, опреде-
ляющей спин электрона,—например, проекцию спина на направление
импульса электрона sp. Тогда Lr—px, L2 — py, L3—pz, S=LSP' Под-
черкнутая нами независимость трех величин Lv L2, L3 исключает, па-
пример, такой выбор £1=pjc, L2—Py, L3—p^, так как в этом случае
£3 есть функция Lv Другой выбор величин может, быть, например, та-
ким: в качестве Lx возьмем энергию движения электронов, в поле ядра
Еп1т (^1 = ^п1тУ за ^2 возьмем момент импульса электрона (£2 — Л4),
за £3 — проекцию момента импульса на какое-либо направление
(£8—ЛЦ и, наконец, для определения спинового состояния возьмем
§ 107] ЧАСТИЦЫ БОЗЕ И ЧАСТИЦЫ ФЕРМИ. ПРИНЦИП ПАУЛИ 377
проекцию sz спина на ось OZ. При первом выборе величин £р £2, £8,
s после измерения получается состояние
^n^k) = ^PxPyPzsp (?*)> (107.5)
при втором выборе —
= (107.5')
Эти состояния, возникающие в результате измерения, не будут во-
обще стационарными состояниями, что явствует уже просто из того, что
в системе электронов ни импульс отдельного электрона, ни энергия от-
дельного электрона не являются интегралами движения. Для нас сейчас
существенна другая сторона дела. Введя в рассмотрение состояния от-
дельного электрона фп(д^), возникающие в результате измерения, про-
изведенного на электроне системы, мы освободились от употребления
неясного термина «состояние электрона в системе», хак как состояние
системы характеризуется одной волновой функцией ф , qk,..., qN, t)
и выделить там состояние одного электрона вообще невозможно. Если
мы производим измерение величин, относящихся к отдельному электрону
(£1} £2, £3, 5), то по крайней мере в момент времени ^ = 0, в который?
было произведено измерение, состояние электрона будет
(&)•
Таким образом, вместо «состояния отдельного электрона в системе» мы
оперируем с состоянием отдельного электрона, возникающим в результате
произведенного над ним измерения. Эти замечания позволяют нам фор-
мулировать принцип Паули в самой общей форме, не прибегая к не-
точным словам «квантовые состояния отдельного электрона».
В этой общей форме принцип Паули гласит: в каждый момент
времени при измерении любых четырех величин Lv Ls, s, харак-
теризующих состояние электрона, каждое значение четверки вели-
чин Lly L2, s может быть получено только для одного элек-
трона системы.
Теперь мы докажем, что эмпирически установленный принцип Паули
есть следствие принципа неразличимости частиц в квантовой механике.
Именно, частицы, описываемые антисимметричными волновыми функ-
циями (частицы Ферми), подчиняются принципу Паули.
Сначала мы проведем доказательство, простоты ради, для ансамбля,
состоящего только из двух частиц. Обобщение на любое число частиц
будет уже совершенно просто.
Допустим, что состояние частиц характеризуется антисимметричной
функцией q2> t) (qv q2 означают, как и раньше, совокупность
всех координат, включая спин, первой и соответственно второй частицы).
Допустим, что мы измеряем для первого электрона совокупность четы-
рех величин, характеризующих полностью его состояние. Их значение
мы обозначим одной буквой nv Значение тех же величин для второго
электрона обозначим через п2.
378
СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ
[гл. XX
Состояние первого электрона, когда измеряемые величины имеют
значение nv пусть описывается волновой функцией ф (t/J, соответ-
ственное состояние второго электрона фЛз(#2). Так как речь идет об
измерении механических величин, то функция фЛ1(^) является собствен-
ной функцией операторов этих величин, и, следовательнд, функции
для разных значений пг образуют ортогональную систему функций:
• (W7.6)
То же самое, конечно, относится и к функции фПа(^2). При этом, так
как под п2 разумеются те же механические величины, что и под nv то
фЯа — такие же функции, как и фЛ1, с той лишь разницей, что они
относятся ко второму электрону, так что у них в качестве аргумента
вместо qx стоит q2.
Разложим функцию Ф(#1? qv t), описывающую состояние системы,
то собственным функциям измеряемых на электронах величин, т. е. по
и Получим:
Ф(?1, д2, 0=52 с (/4, Я2)Ф»,(?1)'ФЯ.(^)» (Ю7.7)
где
c(nv п2, t) = jT(?P ?2. (107.8)
при этом, написав в (107.7) сумму по пг и п2, мы предположили, что
измеряемые величины принимают лишь дискретные значения. Если бы
они принимали непрерывные значения, то следовало бы вместо суммы
писать интегралы. Это не изменило бы дальнейшего хода рассуждений.
Поэтому ради определенности мы сохраним обозначение через сумму.
Сумма по пх и п2 распространена по всем значениям пг и /г2; кроме
того, пг и п2 пробегают одинаковые значения (так как речь идет об
одних и тех же механических величинах как для первого, так и для
второго электрона).
Согласно общей теории величина
w(zzn п2, Z) = |r(^, п2, /)|2 (107.9)
есть вероятность того, что в момент времени t на первом электроне
будет получено значение измеряемых величин, равное а на втором—
значение тех же величин, равное п2. Переставим в Ф(^1, #2, t) первый
и второй электроны. По предположению мы имеем дело с частицами
Ферми, так что функция Ф изменит при этой перестановке свой знак.
Следовательно,
ф(?2. 0, (107.10)
Я1 fh
т., е.
”2’ (?2)фл,(?1) =
Ях Ля
=—”2’(io7.il)
Ях th
§ 107] ЧАСТИЦЫ ВОЗЕ И ЧАСТИЦЫ ФЕРМИ. ПРИНЦИП ПАУЛИ 379
Если мы теперь изменим обозначения, заменив пА на п2, а п2 на пи
все останется по прежнему, так как суммы распространены по всем
значениям пг и п2, и они пробегают одни и те же значения. На осно-
вании этогЪ замечания мы можем переписать (107.11) в виде
22 с («2. л1> t) К (9г) Фя, (ft) =
Ла tli
= «2- О'кОШЛК (107.12)
Л1 Ла
Эти ряды по ортогональным функциям могут равняться друг другу
только при условии, что коэффициенты при одинаковых функциях
равны между собой, т. е.
б(пр п2, /) = —с(п2, пи t). (107.13)
Для ^ = ^2, мы получаем, что:
c(nv nv t) =—c\nv nu t), (107.13')
hq функция, равная самой себе с обратным знаком, равна нулю. Сле-
довательно,
с(п, п, /) = 0. (107.14)
Подставляя это в (106.9), находим, что если значения и п2 оди-
наковы, то вероятность n2i t) равна нулю:
w(/z, п, t)=0. (107.15)
Тем самым наше предложение доказано: вероятность того, что одно-
временно в системе двух электронов будут измерены на обоих электро-
нах одни и те же значения одной и той же совокупности механических
величин, характеризующих состояние электрона, равна нулю. Следова-
тельно, такой результат измерения невозможен, что и составляет содер-
жание принципа Паули.
Обобщение на N частиц проводится без труда путем таких же
рассуждений, как те, что были нами только что проведены для двух
частиц. Волновая функция системы Ф(д4, ..., Яр qN,t)
разлагается в этом случае следующим образом:
*P(ft, •••> ft, •••, Яр •••> Яю *) =
=2---2---S---Sc("i- •••• •••’ пр •••>
Л& nj nN
ХФт(^) ••• Ф/Uft) ••• Фл/ft) ••• Ф»^Д (Ю7.П
где
с(Лр .... пк, rij, ..., nN, t)==
= J • • • Jrfft • • • dqN4(ft, ... ,qN, t) (ft) ... <|>^ (qN). (107.8’)
Вероятность найти значения измеряемых величин равными пА на первом
380 СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ [гл. XX
электроне, nk-—на &-ом, rzy— на /-ом, tiN— на ЛЛом, равна
w(nn ..., nki ..., пр ..., nN.
= |с(л„ .... Пк, .... пр .... п№ /)р. (107.9')
Производя в (107.7') перестановку &-ой и /-ой частиц и меняя сумми-
рование по на суммирование по п}. и наоборот, мы в полной ана-
логии с (106.11) и (106.12) получим:
с(пр пр nk, nN,t)=
= —с(пи nk, rtj, nN, t), (107.13")
откуда следует, что
с(пи ,np ..., nk, nNlt) — O для nk — np (107.14')
Следовательно,
w(zzn nk, np .nNi t)~0 для nk — np (107.15')
Так как это доказательство применимо к любым парам частиц (k, /) из
числа 7V частиц, то все nk должны быть различны, иначе w = 0. Таким
образом, вероятность найти в системе частиц Ферми хотя бы пару
частиц, для которых результаты измерений всех величин, характеризую-
щих состояние частицы (я*), одинаковы, равна нулю.
Итак, принцип Паули, в самом деле, является следствием принципа
неразличимости частиц и квантовой механики. Он соблюдается не только
для электронов, но и для всех частиц Ферми, т. е. для всех частиц,
описываемых антисимметричными функциями. В частности, принципу
Паули подчиняются электроны, позитроны, протоны и нейтроны.
§ 108, Волновые функции для системы частиц Ферми
и частиц Бозе
Рассмотрим несколько подробнее волновые функции, обладающие
свойством симметрии илй антисимметрии в частицах. Начнем с анти-
симметричных функций, принадлежащих частицам Ферми. Сначала
обратимся к случаю двух частиц. Антисимметричная функция «двух
частиц может быть разложена по собственным функциям
и Фл9(^2)> принадлежащим отдельным частицам:
V ?2> ^)==SSC^1’ (108.1)
я2
(108.1) мы можем представить в ином виде, разбив сумму на две части,
в одной пусть ^^>«2, а в другой [ni“rt2 выпадает, так
как с(пи nv tf) = 0]:
(41, 2 2е("1’ й2> К^1)К+
W1 > «я Лз
+ 2 2с(К1, (108Л')
Пх < Пч Пч
§ 108] ВОЛНОВЫЕ ФУНКЦИИ ДЛЯ ЧАСТИЦ ФЕРМИ И ЧАСТИЦ БОЗЕ
381
Меняя во второй сумме индексы суммирования на й п2
мы получим:
Чг(?1. 9а, 0= 2 2c<rai- и2- 0<Ь„|(4’1)Ф„,(?2)4-
+ 2 2с(л2> (Ю8.1")
Ла < П1 тц
и, наконец, переставляя nt и п2 в г(л2, nv /), мы получим на основа-
нии (107.13):
Ч'(«Ъ <72, *) =
=2 2С(Я1’п2’/НФ«,(?1)ФЯз(^)—ФЯ,(?2)ФЯ2(^Н; (Ю8.2)
Л1 Пг Пг
выражение в скобках мы можем представить в виде определителя и
записать ЧИ в виде
’PG/v ?2,/)= 2 2С(Я1’и2> ^)- К(ft) 4>«ж(4,2>| (Ю8.3)
К (?1) Ф«,М •
Таким образом, антисимметричная волновая функция представляется
в виде суммы (или интеграла) определителей вида
<»B1«,(ft,ft)==l • (Ю8.4)
Если мы имеем дело с М частицами, то подобным же образом легко
получить, опираясь на (107.13), в общем случае
ф(?р • ’ як>•.-яР• • я&0=S- • -Sc(»i....,«*,• • ,п,...,nN,t}x
Л1>л2>..г> nN
X Фя1,...» л*,...» л,,...» • i4k> • • * > #/> • • • ’ #лгЬ (108.5)
где
Фд1, ...Лл, (^1> • • • • ••>?/,
К (ft)... ф«. (ft) • • • К (я}) • • • фл, (як)
фл. (ft) • • • фл, (Як) фл. (Я/) • • фл, (Як)
Флк(^1) ’ • -Фи/е(^а ‘ ’ •ФлцД?/)* • * Фл& (fty) (
Флуу (ft) . • • Флуу (Як) • ' • Ф«уу (ft) • • • Флуу(^уу)
Раскрывая определитель, мы можем написать Ф также в виде
Фяр ... пк, ... Uj, ... nN {Qv •••> 4k^> ••• 9/» • • • ^дг) —
= S(± 1) Pфл. (Яг) • • • фл* (Як)• • • Ф», (Я;).. .флуу (Як)- (Ю8.6')
р J
Здесь сумма взята по всем перестановкам частиц qv qN, при-
чем знак + или — берется перед слагаемыми в (108.6'), смотря по тому,
382
СИСТЕМЫ ИЗ ОДИНАКОВЫХ ЧАСТИЦ
[гл. XX
получается ли некоторое расположение величин q из расположения
в порядке возрастающих номеров qv q2, ...,qk, qk4.i> qN путем
четного числа парных перестановок или путем/' нечетного числа парных
перестановок.
Приведенное представление антисимметричных волновых функций
в виде суммы определителей очень важно в практических приложениях
теории при приближенном решении задачи о движении многих тел»
Допустим, что нас интересуют волновые функции стационарных состоя-
ний двух электронов в атоме. Такие функции найти, вообще говоря,
довольно трудно. Напротив, функции одного электрона найти значи-
тельно проще. Допустим, что эти функции мы знаем — пусть это будут
функции (^) и (<?2). Если взаимодействие электронов не сильно,
то волновая функция системы двух электронов будет такова, что со-
стояние каждого из электронов будет мало отличаться от состояния
одного электрона в атоме в отсутствии другого электрона. Если же
один электрон мы помещаем в квантовое состояние, характеризуемое
величинами (квантовыми числами) то вероятность найти какое-нибудь
иное значение в этом состоянии равна нулю. Подобным же образом,
помещая второй электрон в состояние я2, мы должны будем утверж-
дать, что вероятность найти п'2 равна нулю. Если мы теперь имеем дело
сразу с двумя электронами в атоме, то в случае слабого взаимодейст-
вия между электронами состояние при помещении второго электрона
должно мало измениться. Это означает, что если теперь вероятность
найти Yun2 = ri2 и будет отлична от нуля, то она все же бу-
дет мала, а стало быть, все с(п'х (108.3) малы кроме с (nv п2, t).
Пренебрегая всеми с кроме c(nvfi2)t\ мы получим из (108.3) волно-
вую функцию Ф° для двух электронов атома в нулевом приближении:
’Р0 (41, Чг, t) = c(nv,n2, t)
(9i) (9г)
фл»(91)
(108.7)
и так как общий множитель c(nv п2, t) не играет роли, то
’Р» = Ф„,л,(9р 92). (108.8)
Аналогично и в случае многих частиц, при условии слабого взаимодей-
ствия между ними, функцией нулевого приближения для системы ча-
стиц Ф° является Фи, „к „} ПЛГ(9П ..., qk, ... 9/. • > 4N)
(108.6), если фЛ1 (9,), <ЬЛа(92), . ., §nN(.q^ суть функции электронов без
учета взаимодействия.
Таким образом, представление антисимметричной волновой функции
в виде определителя (108.4) или (108.6) дает приближенный способ
для представления волновых функций системы слабо взаимодействующих
частиц через функции отдельных частиц в отсутствии взаимодействия
между нимц.
Для частиц Бозе мы имеем другое разложение волновой функции
Системы частиц Ф ио произведениям функций отдельных частиц:
§ 109] ВТОРИЧНОЕ КВАНТОВАНИЕ 383
Ф». (?i) Ф«, (^2) • • -Фл№*)- • •'Mfyb • -флдг^лг)- Переставляя в разложе-
нии волновой функции системы
’Н?!, qk, Чр qN,t) = ^i...^c(n1, ...
Пх ПЦ
• •, «лр t)• фи. (ft).. -фи* (qh)• •.ф^(qj)•'h, ^N) (i08.9)
координаты &-ой и /-ой частиц и замечая, что функция Ф для частиц
Бозе при этом не должна измениться, мы, сравнивая коэффициенты при
одинаковых произведениях, найдем, что
c(«i, ..в, nk, пр ...,nN, t) =
= -[-с(п1, ...» Пк, (108.10)
Для двух частиц будем поэтому иметь:
44ft, ft) = 2 c(ft.ft) {фи. (ft) фи, (ft) + фя, (ft) фл. (ft)}. (108.11)
> «2
Если взаимодействие между частицами слабо, то приближенное выра-
жение для волновой функции состояния двух частиц, близкого к со-
стоянию невзаимодействующих частиц, в ротором одна из частиц нахо-
дится в состоянии /гр а другая в п2 имеет вид
- фи. (ft) фи, (ft) + фи, (ft) фи. (ft). (108.12)
В случае 7V частиц на основании сходной аргументации получим:
^=2ф„1(у1)...фнЛ(^)...ф„>(?/). .^nN(qN), (Ю8.13)
где 2 означает сумму по всем 7V! перестановкам координат частиц
р
Я& • • • > Як*
ГЛАВА XXI
ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА
§ 109. Вторичное квантование
Ансамбли одинаковых частиц могут быть рассмотрены особым мето-
дом, носящим название вторичного квантования.
Сущность этого метода заключается в том, что в качестве незави-
симых переменных для описания ансамбля берут не координаты частиц
(«метод конфигурационного пространства»), а число частиц в отдель-
ных состояниях. Для того, чтобы выполнить такое преобразование от
одних переменных к другим, сначала вместо координат частиц qv Я^* • - >Як
берут за независимые величины некоторые другие переменные, изобра-
жаемые операторами Lv L2i LN (например, собственную энергию
384
ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА
[гл. XXI
частиц, равную кинетической энергии плюс потенциальная энергия во
внешнем поле). Собственные значения этих операторов пусть будут
£Я1, ..., а собственные функции ф„, (91), фл> (?2), ..., фЯлг (qN).
Состояния отдельной Л-ой частицы будут тогда нумероваться кванто-
выми числами пк.
Обозначим через Hk оператор полной собственной энергии &-ой
частицы (или ее гамильтониан), а через Wkj взаимодействие &-ой и /-ой
частиц. Тогда уравнение Шредингера для системы из N частиц имеет
вид
(109.1)
Разложим волновую функцию Ч; по собственным функциям операто-
ров £:
ф = 2 • • *2 с (Лг • • • > Флх (*71) Фла (Ю9.2)
П\ nN
Величина (лр л2, ..nN, /) |2 есть вероятность того, что в мо-
мент t первая частица имеет L — Lnx, вторая L = Ln, и т. д., или,
иначе, вероятность того, что первая частица находится в состоянии nv
вторая в л2 и т. д. Подставляя (109.2) в (109.1), умножая результат
слева на ф^ (^) ф;,(%). . -Ф^^) и интегрируя по qv q,, ...,qN, по-
лучим:
лг
S EwткпкС mz, • • • > • • • i
N
+2 •••
k&J nk nj
.nk, np mN,ty, (109.3)
при этом (Нк)ткпк и (Wkj}mkmj, nknj суть матричные элементы
(Нк)ткпк = [ ф*г/( (qk) • Hk (qk) фп& (qk) dqk, (109.jt)
( ^hj)mkmj, fikn, =
=j (<Ik) ¥mj (?/)• Wkj {qk, q/) tynk (qk) фл, {qj}-dqkdqr (109.5)
Уравнение (109.3) есть, очевидно, уравнение (109.1) в «£»-пред-
ставлении. Амплитуды с суть симметричные функции аргументов
mv т2, ..., mN для частиц Бозе (см. § 108) и антисимметричные функ-
ции этих же аргументов для частиц Ферми (см. § 108).
В силу одинаковости частиц матричные элементы (109.4) и (109.5)
зависят лишь от значения квантовых чисел пгю nk, Пр а не от но-,
мера частиц k, j. Обозначая какое-нибудь значение тк через w,
nk через л, подобным же образом т. через т\ tij через п’, координаты
§ 109] ВТОРИЧНОЕ КВАНТОВАНИЕ 385
&-ой частицы через q, а /-ой — через q'9 мы можем написать (109.4)
и (109.5) в виде
= - g J <!>; (?) V®4>„ (?) dq + J <!? (q) U(q, t) фл (q) dq =
= g f Ж (?) V<|>„ (?) dq + J (q) (q) U(q, i) dq = Hmn, (109.6)
( Wkj)mkmj, nwij = J К (?) К- № W(q, q') ф„ (?) фл' (?') dq dq' =
= Wmm',nn'. (109.7)
Рассмотрим теперь дальнейшие преобразования для случая частиц
Возе. Так как амплитуды с являются симметричными функциями аргу-
ментов пг1, т2, .. ., mN, то их значения зависят лишь от того, сколько
аргументов имеют значения mv сколько т2, . .., и т. д., а не от того,
какая именно из частиц имеет т = т1 или <т — т2, т. е. они являются
функциями числа частиц в каждом из состояний. Обозначим эти числа
через Nv N2, ..., Nm, ..., Nn, ... и т. д. Следовательно, например,
Nm равно числу чисел mk среди аргументов с, значение которых равно/я.
Чтобы преобразовать с от переменных т к переменным /V, мы должны
изменить нормировку.
В самом деле, если рассматривать с как функцию чисел N, то
(NvN29 .. .)|2 есть вероятность найти частиц в состоянии 1, N2—
в состоянии 2 и т. д. Эта же вероятность выразится через с(т19
т2, ..., mN) в виде
|c(NpN2, ...)|2 = S|c(otvz«2, «v)|2,
где сумма взята по c(mvm2, ..., mN), имеющим Nx чисел tnk, рав-
ных 1, Л/2 чисел mk, равных 2, и т. д. Так как в силу симметрии все
эти с равны между собою, то
I |2 ЛП I J2
p(WvNt> •••)] =jv1!7v0'!... |c(^i,^a. •••> ^лг)| •
Таким образом,
с (Nv N2, ...) = ) 1г с (mv mN). (109.8)
Подставляя теперь в (109.8) вместо с (mv т2У ..., mN) амплитуды
c(NvN2, ...), мы можем выполнить суммирования по частицам k и j\
Для этого воспользуемся (109.6) и (109.7) и заметим, что с(пг1Ут2, ...,
nky ..., mN, t) отличается от с (mv т2, .. ., mk9 . .., ntN, t) тем, что
число частиц в состоянии mk — m уменьшилось на 1, а число частиц
в состоянии nk = n увеличилось на 1. Подобным же образом с(/пр
т2У • • •» nks • • • iпр • • •> mN ’ отличается от с (т1У т2У ..., mk, ...,
nij, ..., mN, t) тем, что число частиц в состояниях mk = m и nij — m*
уменьшилось на 1, а в состояниях nk — n9 увеличилось на 1.
25 Блохинцев
В86 ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА [ГЛ. ХХ5
На основании этих замечаний получаем:
.XHN,.......Л1„.....N„......N„....Nn’......<)} =
=s ад. x
y^C(Nv A/ZWL—1, Nm4 •••» •••> №/, /)-{"•
+4EE NmNmt Wmmt
, nn’ X
x ^1!...(Хя,-1)!...(^-1Л...^я+1)!---(АГя*+!)!.,.у/. c .
...» Nm—\, .... Nm— 1,.’., W„4-l, ...,№- + 1, ...,/). (109.9)
_ ( N\ \V.
Деля это на -уту ।-----) > получим:
ih^c(Nv .... Nm, Nm,, N„, Nn,, ...» t) =
-Е^(Ч+1)1/з.........................^-1,...,
• • •, Nn + 1..Nn,......t) + £ (Nn + 1 yi> (Nn, + l )V. X
X Wmm,,nn, c{Nv .... Nm— 1, Nm, — 1, .... /V„+l, ...
Л/лг+1, (109.10>
Это и есть искомое уравнение, в котором за независимые переменные
взяты числа частиц в отдельных состояниях. Это уравнение может быть
записано в очень удобной форме, если ввести операторы ^~/0л и
которые меняют Nn на Д/ЛЧ- 1*):
e^f{Nn)=f{Nn—\), e-'V(^)=/(Afn4-l). (109.11)
Вместо целесообразнее ввести связанные с ними операторы
an = N^e~‘^. (109.12)
п п 1 п п ' '
*) Явное выражение этих операторов несущественно. Можно, например»
взять По формуле Тэйлора имеем:
^=1
Полагая А — zt 1, получаем (109.11). При этом, однако, имеет место дополнитель-
ное условие:
г"''0«/(О) = Ог а не /(—1)!
§ 109] ВТОРИЧНОЕ КВАНТОВАНИЕ 387
Эти операторы, очевидно, обладают следующими свойствами;
«Х=^я, ana*n==Nn+\, (109.13)
—= (109.14)
С помощью этих операторов уравнение (109.10) может быть написано
в виде
ih ••• 0=Яс (Wn ..., , (109.15)
где
S S a*ma*m,Wmm.,пп,апап,. (109.16)
т, п т,т' тцп'
Этот гамильтониан можно написать в другой форме, которая соот-
ветствует классическому гамильтониану некоторого волнового поля.
Пусть волновая функция одной частицы есть ф (д'). Разложим эту функ-
цию по собственным функциям фл(<?) оператора £:
Ф(?) = 2«„ФП(?)- (Ю9.17)
п
Будем теперь рассматривать амплитуды ап не как числа, а как опера-
торы со свойствами (109.13) и (109.14). Таким образом, и сама функ-
ция ф рассматривается не как функция, а как оператор
Ф(?)=2«ЯФ„(?)> (109.17')
п
т. е. волновая функция одной частицы как бы «квантуется». Отсюда
и название метода вторичное квантование [следует ясно представлять
себе, что на самом деле волновой функцией у нас является не Ф
(109.17'), a c(NpW2, ...,/)} С помощью квантованной волновой
функции Ф(^) (109.17') гамильтониан (109.16) может быть написан
в виде
^=gJv»F*(?)V’P(?)^+JФ*(<?)Ф(<7)
+ 4 J Ф* (q) ф* (?') • W(g, д') Ф (д) Ф (д') dq dq\ (109.18)
Эквивалентность (109.18) и (109.16) очевидна, если учесть (109.6) и
(109.7).
Представим теперь на время, что стоящие в (109.18) Ф(<?) суть не опера-
торы, а обычные функции, и будем, для определенности, разуметь под нашими
частицами частицы с зарядом е. Тогда величину 7(g) —-- | ?<[> (qj |2 можно рас-
сматривать как плотность кинетической энергии, е ] <[> (q) |2 = о (q) — как плот-
ность заряда. Полагая далее
U(qft) = eV(q)t
25*
388 ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА [ГЛ. XXI
где V(q) есть электростатический потенциал, и имея в виду, что W(q, q')~ —— ,
rqqr
где rqqt есть расстояние между точками q и q', мы можем написать (109.18)
в виде
= J T(q)dq + J p(q) V(q)dq±l dq'dq. (109.181)
’Это выражение можно рассматривать как классическое выражение для энер-
гии заряженной жидкости, плотность которой пропорциональна | ф (q) |2, а плот-
Если в (109.18') разуметь теперь под <[> опять оператор (109.17') и надле-
жащим образом расположить Ф* и Ф, то мы получим из (109.18') квантовый
гамильтониан дая системы одинаковых частиц (109.18). Этот переход от
(109.18') к (109.18) служит также основанием для того, чтобы назвать наш метод
методом «вторичного квантования».
Заметим, что переход от неквантованной волновой функции (109.17)
к квантованной (109.17') может быть сформулирован непосредственно без об-
ращения к операторам ап. Действительно, из (109.14) и (109.17) следует:
Ф (q) Ф* (д') — Ф* (q’) Ф (?) = 3 — атап) Фп (?) С (?') =
т, п
= S С (?') (?) = S С С?1) Ьп (?)-
/и, п п
где сумма распространена по всем собственным функциям. Такая сумма, как
можно доказать, равна 3(^' — q). Поэтому квантование волновой функции
можно записать в виде
Ф (q) Ф* (^ — Ф* (qr) Ф (q) = 3 (?' — q), (109.19)
Мы провели преобразование для частиц Бозе. Можно также про-
вести соответствующее преобразование для частиц Ферми, которое,
однако,, несколько более кропотливо в виду того, что при переста-
новке частиц c(mvm2i, ..., mN,t) меняет свой знак. Кроме того,
ясно, что числа частиц в состояниях Nm могут иметь только два зна-
чения 1 или 0 (иначе, в согласии с принципом Паули, см. § 108,
с = 0). Выполняя сходные преобразования*), мы получим из (109.3)
опять уравнение (109.15), но операторы а* будут определены не-
сколько иначе, именно:
0„, ,...)= ±/(М, (109.20)
</(М, .... 1„, ...)= 0, (109.20')
«Я/(М. •••• 0„, ...)=0, (Ю9.21)
1„, ...)=±/(М, .... 0а, ...), (109.21')
причем знак или — берется, смотря по тому, четное или нечетное
число занятых (Nk = 1) состояний предшествует состоянию /г, если со-
*) См., например, Дирак, Основы квантовой механики, § 80, или ориги-
нальную работу Jordan u. Wiegner, Zs. f. Phys., 47, 631 (1928);
V. Fock, ibid., 75, 622 (1932).
§ 109] ВТОРИЧНОЕ КВАНТОВАНИЕ 389
стояния расположить в порядке возрастания /г*). Далее,
a*nan=Nn (° или 1), «Х=1—Ч- (109.22)
+ = (109.22')
Представление гамильтониана (108.18) остается также в силе, если
под ап в (109.17) разуметь оператор, обладающий свойствами (109.20),
(109.21). Переход от классической энергии (109.18') к (109.18) остается
также в силе, однако вместо (109.19) получается новое условие квантова-
ния Ф:
Ф (q )Ф* (q') + Ф* (?') Ч; (?) = §(?' — ?). (109.19')
Обратимся теперь к вычислению вероятностей перехода под влия-
нием возмущения в ансамбле одинаковых частиц. Рассмотрим в качестве
примера переходы под влиянием слабого взаимодействия между частицами.
При этом в качестве величин, описывающих состояние частиц, целесо-
образно взять их собственную энергию Lk — Hk. Тогда матрица Нтп
будет диагональной. Обозначим возможные значения энергии частиц
через е^. Кроме того, 77^ = Следовательно, уравнение (109.15)
получает вид
ih ....t) = у дг (дг N -L
т
+ пп’а„ав.с(Д/р Л/2,..., t). (109.23)
тт', пп'
Очевидно, что есть энеРгия Е всех частиц без учета взаи-
т
модействия. Вместо c(Nv N2 ,..t) удобнее ввести c(A/p N21..., /) =
— -т S
— b(NvN2, ..., t)e m . Подставляя это в (109.23), находим:
ih db(Nb N2,
dt
— тт fem + Ewi'—en— 6л'У
= £« A a*ma*m,Wmm<,nn'anan,b(NvN2,...,t). (109.24)
mtn\ nn1
Пусть теперь начальное состояние есть b (Л/J, . J, ,..., 2V£,, ...
. . . , 2VJ, ..., №п, , ..., 0) —1 [все остальные b(Nv N2,..., 0) = 0].
*) Можно ввести вигперовскую функцию >/г, равную zt 1:
П (1-2^),
т^п
тогда в (109.20) и в (109.21') вместо можно писать 1).
390 ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА [ГЛ. XXI
Подставляя в правую часть начальное значение Ь, находим:
ih^b(N^,N^.........=
од .
..., Д^,4-1, ..., 1, м,—1, (109.25)
При этом мы берем такое b(Nv N9,...), чтобы справа в резуль-
тате действия операторов а*т, а*т„ ап,ап, получилось как раз #(A/J,...,
А^, ..., А/^г, ... ,М, ..., , 0) = 1, так как все остальные
амплитуды b в первом приближении равны нулю. Дальнейший расчет
зависит от рода частиц. Возьмем, например, частицы Бозе. Подставляя
в (109.25) операторы я*, ап (109.12) и выполняя обозначенную ими
операцию, мы получим:
— ’Г еп—enf) t ------------------ --------
Интегрируя (109. 25') по времени и вычисляя обычным образом (ср. § 78)
1 о d W2
вероятность перехода в 1 сек. Ртт^пп1= —, мы найдем:
Ртт,,„п, = №т№т, (л/о + 1) (дго + !) 2? | wmm,t пп,\Ч (em + ет, -
— е„—е„-). (Ю9.26)
Подобным же образом, разумея в (109.25) операторы (109.20),
(109.21), получим для частиц Ферми:
О<гг
Ртт,,пп, =Л/»(1 -Л^)(1 -№nl) + -
— е„ —е„-). (109.27)
Эти формулы показывают, что вероятность перехода из начального
состояния т, т' в конечное ц, п' зависит не только от числа частиц
в начальном состоянии А^, но и от числа частиц в конечном
состоянии М, Это совершенно новый результат квантовой теории,
не имеющий места в классической механике. Для частиц Бозе вероятность
перехода тем больше, чем больше число частиц в конечном состоянии.
Для частиц Ферми вероятность перехода равна нулю, если состояние,
в которое происходит переход, занято (А/0 = 1 или А^,= 1). Это и
есть новое выражение принципа Паули.
Изложенный в этом параграфе метод вторичного квантования, как
и следует из его вывода, совершенно эквивалентен методу конфигура-
ционного пространства. Однако, есть одна особенность, позволяющая
расширить область применения метода вторичного квантования. Как видно
из уравнения (109.15), в него не входит явно полное число частиц
§ 110] ГАЗ ФЕРМИ-ДИРАКА И ГАЗ БОЗЕ-ЭЙНШТЕЙНА 391
рассматриваемого ансамбля 7V= 2 Мп- ^но является теперь постоянной
т
интегрирования и входит лишь в качестве начального данного
т
Ясно, что с течением времени М не меняется, ибо операторы а* и а
входят в (109.16) всегда в такой комбинации, что уменьшение частиц
в каком-нибудь одном состоянии обязательно сопровождается соответ-
ствующим увеличением числа частиц в другом состоянии. В современ-
ной физике приходится иметь дело с явлениями рождения и уничтоже-
ния частиц. Эти явления выходят, строго говоря, за рамки квантовой
механики. Однако, метод вторичного квантования ввиду того, что в него
не входит явным образом полное число частиц, оказывается весьма пригодным
для описания такого рода явлений (см. гл. XXV). Если кванты света,
фотоны, рассматривать как частицы, то можно процессы испускания
и поглощения света рассмотреть как процесс перехода кванта света из
некоторого нулевого состояния (0), которое отличается тем, что фотоны,
находящиеся в нем, не могут быть обнаружены экспериментально (так
как, находясь в состоянии с наименьшей, нулевой энергией, они не
могут отдавать свою энергию), в состояние с большей энергией, и обратно.
Число фотонов в нулевом состоянии предполагается бесконечно большим
(Nq = оо ), так что может быть порождено (испущено) как угодно
много фотонов. Основанная на этой мысли квантовая теория излучения
была развита Дираком *).
§ 110. Гипотеза о столкновениях. Газ Ферми-Дирака
и газ Бозе-Эйнштейна
В классической кинетической теории предполагается, что вероятность
перехода частиц, в результате столкновения, из некоторого состояния
тит' (энергии частиц и е^г) в другое состояние пип' (энергии
частиц гп и еяг) пропорциональна числам частиц в начальных состояниях
Nm и Nm>:
Ртт’, пп1 z= ^тт', пп' ‘ (110.1 )
Если Nm и Nmr —среднее число частиц в состояниях т и т', то пред-
полагается в соответствии с (110.1г), что среднее число переходов из
т, т' в п, п' равно
Ртт\ пп1 ^тт’, пп1 (И0.1)
При этом Атт^ nnt = Апп\ mmi (обратимость элементарных процессов).
На основании квантовой механики мы должны для газа, состоящего
из одинаковых частиц, сделать другое предположение о среднем числе
переходов под влиянием столкновений. Как было показано в предыду-
щем параграфе, вероятность перехода зависит не только от числа ча-
стиц в исходных состояниях, но и от степени населенности конечных
*) Дирак, Основы квантовой механики, §§ 64—67.
392 ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА [ГЛ. XXI
состояний, именно, вместо (110.1') в согласии с (109.26) и (109.27) мы
имеем для вероятности столкновения в случае частиц Ферми:
Ртт', пп1 = Лтт^ KmNm' (1 — Nn) (1 — №0 (110.2)
(ЛГт, MnS Mi» Мг' = 1 или 0). В этой формуле явно выражен прин-
цип Паули: если одно из конечных состояний занято Nn — 1 или Nnt — 1,
то перехода быть не может. Подобным же образом, для частиц Бозе
имеем:
Рmm’, rmr Аяш', пп' МЛ-(Ч + 1)(№-+1). (ИО.З)
Здесь множители (A/^-J-l) и (№'4~1) не имеют столь наглядного зна-
чения, какое имеют множители (1—АГ), (1—Nni) в случае частиц
Ферми. Однако, необходимость наличия таких множителей была нами
доказана (§ 109). Мы можем сказать, что частицы Бозе имеют тенден-
цию к ассоциации: они переходят в наиболее населенные состояния *).
Равенство величин Ammtf ппг и Апп>1 тт> (обратный переход) вытекает
в квантовой механике непосредственно из того факта, что Атт\ пч>
пропорционально квадрату модуля матричного элемента энергии взаимо-
действия Wmm\ nnf, a Wmm^ nn,z==z
В соответствии с(110.2)и (110.3) для газа из одинаковых частиц в кван-
товой механике для среднего числа переходов под влиянием столкнове-
ний берут вместо (110.1) выражение
Ртт^ пп’ = А тт^ пп, N)nNn(y ± (1± ЛГЛ), (110.4)
причем знак — берут для частиц Ферми, а знак для частиц Бозе.
Формулу (110.4) мы будем рассматривать как новое предположение
о среднем числе столкновений частиц, основанное на квантовой меха-
нике **). Очевидно, что (110.4) превращается в классическое выраже-
ние (110.1), если среднее число частиц в каждом из состояний мало
в сравнении с единицей.
Найдем теперь распределение по энергии частиц при тепловом равно-
весии в газе частиц Бозе или Ферми. При тепловом равновесии число
переходов в состояния п и п' в результате столкновения частиц, на-
ходившихся в состоянии т и т\ должно равняться числу обратных
*) Это приводит к замечательному свойству газа из частиц Бозе: при
низкой температуре наступает своеобразная конденсация этого газа, даже
если предположить, что газ — совершенно идеальный, так что силы взаимо-
действия бесконечно малы. См. A. Einstein, Berichte der Preuss. Akad., 3,
1925.
*S’J) Мы называем (110.4) «предположением», так как в выражении для
вероятности перехода (110.2) разумеются истинные значения населенности
уровней Nm, Nm\ Nn, Nn’> а в (110.4) стоят средние значения Nm, Nm’> Nni Nn'-
Равенство NmNm' (1 ± Nn) (1 zt (1 zt Nn) (1 zLNn’) не является
очевидным и не выполняется заведомо при всех условиях.
§ ИО]
ГАЗ ФЕРМИ-ДИРАКА И ГАЗ БОЗЕ-ЭЙНШТЕЙНА
393
переходов [принцип детального равновесия). Из (110.4) тогда получаем
(в силу равенства Атт^ nni = Апп\ mm'Y
1 ± Ч) (1 '± №') = ВД, (1 ± (1 ± (И0.5)
Далее, при равновесии среднее число частиц в каждом из состояний Л^_
будем считать только функцией энергии этого состояния гт [Nm — N (£/л) |.
На основании закона сохранения энергии при столкновениях [ср. (109.26)
и (109.27)] имеем:
4“ £^'~ £л 4~ £«г* (110.6)
Из (110.5) получаем, что
\±Nm' \+Nn
—11^—= С, (110.5')
1 zt Nn'
где С—некоторая постоянная, могущая зависеть [на основании сделан-
ного предположения oN и закона сохранения (110.6)] лишь от суммы
£л« + £^ (ИЛИ £л + £«' = £лИ + £^0- Таким образом,
. Nmf
С’(£/?г + £тО-
(110.5")
Обозначая ---= мы перепишем (110.5") в виде
1 zt Nm
+ (П0.7>
Дифференцируя это равенство один раз по и другой раз по
и деля один результат на другой, найдем:
? (^) ? (M 0 ’
(110.8)
где 9 — некоторая постоянная, не зависящая от г. Интегрируя теперь>
(110.8) по ew, находим:
= (110.9)
где а — постоянная интегрирования. Отсюда находим для среднего числа
частиц в состоянии с энергией гт\
(110.10)
(знак — для частиц Бозе, знак для частиц Ферми). При большой
энергии частицы (е—>оо) закон распределения по энергиям должен сов-
падать с классическим законом Больцмана
__ _Еш
N(em) = const. •<? кТ,
(110.11)
394
ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА
[ГЛ. XXI
где k — постоянная Больцмана, а Т—абсолютная температура. Пере-
ходя в (110.10) к пределу ew—>оои сравнивая с (110.11), находим,
•что Q = kT. Таким образом, окончательно
1
е7П
(110.12)
Постоянная интегрирования а определится из условия равенства числа
частиц во всех состояниях полному числу частиц в рассматриваемом
экземпляре газа:
(полз)
ш
Совокупность частиц, подчиняющихся закону распределения (110.12)
со знаком (-|~), носит название газа Ферми-Дирака, а со знаком (—) —
газа Бозе-Эйнштейна. Закон (110.12) явно написан для дискретных
состояний.
Введем число состояний на интервал энергии dz. Обозначим его
через Vp (е) dz, где V—объем всего газа. Тогда, суммируя (110.12)
по всем квантовым состояниям, энергия которых попадает в интервал
s, е MbI получаем среднее число частиц газа, имеющих энергию между
з, e-j-t/e (закон распределения по энергиям):
F (s) dz = -Vp(s)rfe ,
и деля на У, получаем то же число для единицы объема газа:
/(e)<fe^-p(s)rfe . (110.14)
Вместо (110.13) теперь следует написать:
ОО оо
(7(e) ds = —(110.15)
о 1 1
N
где п — у — плотность числа частиц *).
Распределение (110.14) со знаком (Ц-) носит название распределе-
ния Ферми-Дирака, а со знаком (—)—распределения Бозе-Эйн-
штейна. Наиболее существенной особенностью распределения Ферми-
Дирака является существование нулевой энергии газа. Чтобы в этом
*) Очевидно, что р(е) не может зависеть от объема газа, так как иначе
функция распределения также зависела бы от него. Такая независимость p(s)
от V всегда имеет место, если объем газа V значительно больше X3, где
Л — длина волны в преобладающем числе занятых состояний.
§ 110] ГАЗ ФЕРМИ-ДИРАКА И ГАЗ БОЗЕ-ЭЙНШТЕЙНА 395
убедиться, положим а =— ; тогда имеем:
/(е) = -т^-. (И0.16)
ое 0 +1 е 0 +1
При 0 —> О (низкие температуры) е0 должно быть больше нуля (если
энергию е отсчитывать от нуля так, что е 0), иначе при 0 —О
/(e)—-> 0 и нельзя удовлетворить первому равенству (110.16). Далее,
мы видим, что при 0—->0 /(е) = р(е) для е<^80 и /(е)0 для е^>е0,
т. е. при абсолютном нуле все состояния в газе Ферми-Дирака заняты
вплоть до состояний се — е0, остальные же состояния свободны. Энергия
частиц, занимающих состояния оте = 0 до s — е0, и есть нулевая
энергия газа. Более подробное рассмотрение показывает, что такое
распределение очень мало меняется с температурой, если только тем-
пература остается такой, что 0 = ^Г<^ео. е0, очевидно, есть макси-
мальная энергия частицы в газе Ферми-Дирака при абсолютном
нуле температуры.
Мы вывели распределения Ферми-Дирака и Бозе-Эйнштейна, ис-
ходя из гипотезы о столкновениях (110.4). Эти же распределения мо-
гут быть найдены из общих положений термодинамической статистики
(ансамбль Гиббса) без каких-либо предположений о кинетике про-
цессов *).
Отличие расчетов, базирующихся на квантовой механике, от рас-
четов, базирующихся на классической механике, заключается в разном
способе подсчета числа возможных состояний. В квантовой механике
состояние характеризуется заданием симметричной или антисимметричной
волновой функции Ч;, и различные перестановки частиц по отдельным
состояниям не дают нового состояния (Ф переходит сама в себя или
меняет знак). С точки зрения классической механики каждая такая пере-
становка означает новое состояние частиц. Классическая статистика,
базирующаяся на таком подсчете состояний, не является самостоятель-
ной статистикой, а представляет собой предельный случай квантовой
статистики, в которой число состояний исчисляется по числу различных
волновых функций (можно показать, что классическая статистика полу-
чается из квантовой, если число частиц в объеме средней длины
волны ).3 много меньше единицы). Что касается квантовой статистики,
то различают две статистики — статистику Ферми-Дирака (для
частиц, подчиняющихся принципу Паули, — антисимметричные Ф)
и статистику Бозе-Эйнштейна (симметричные Ф, частицы Бозе).
В своих принципиальных основах эти две статистики, конечно, не
различаются.
Применим статистику Ферми-Дирака к электронам проводимости
в металле. Последние приближенно можно рассматривать как свобод-
*) См. М. А. Ле онт о вич, Лекции по статистической физике (стекло-
графическое издание), МГУ.
396 ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ СТАТИСТИКА [ГЛ. XXI
ные частицы*). Подсчитаем число состояний на интервал энергии р(г).
В объеме металла Л3 = V состояния свободных частиц будут стоячими
волнами. Удобнее рассматривать бегущие волны, считая металл бесконечно
большим, но мы будем предполагать, что в каждом объеме А3 — V
состояние полностью повторяется («условие периодичности»). Такое
рассмотрение вполне законно, если где \ есть длина волны пре-
обладающего числа занятых состояний. Волновые функции будут пло-
скими бегущими волнами вида
ei (^+М+^)
^==~ (2я£)3/»
(110.17)
(нормированы к 1 в L3), причем kx, ky, kz имеют значения
► --- -----л
L '
. 2-/2,
k^~ir
(110.18)
Благодаря такому выбору kx, ky, kz состояние в объемах Л3 повторяется.
Состояния у нас нумеруются числами nx, пу, nz. Эту тройку чисел
и следует теперь разуметь под одним индексом т, фигурировавшим
в (110.12).
Образуем сумму 2 ^nx^ny^nz (Ал = Ч-1) по состояниям, кото-
рые попадают в интервал энергии е, г -1- dz. На основании (110.18)
имеем:
^пх^пг= (2)8 Д^Д^Д^,
следовательно,
22 = (2тс)3 bkxbkybkz — С dkx dky dkz —
E>e + rfe £> *+* s, e-J-rfe
= 7X3 ff k^d~dzd^=^k^d^dz. (110.19)
(2я)3 J J dz (2k)3 dz v '
£, S~[-ds.
Л2
Замечая, что для свободных частиц е = — k2 и что каждому значению к
соответствуют два состояния с различной ориентацией спина электрона,
мы получаем:
vP(£^£==W^£,/^£- (110-20>
Подставляя это значение р(г) в (110.14), находим закон распределения
свободных электронов:
/<£^£=?wTMF~ • (110-21)
г й +1
*) Строгое доказательство возможности такого приближения и установле-
ние границ его применимости до сих пор еще не произведены.
§ 110]
ГАЗ ФЕРМИ-ДИРАКА И ГАЗ БОЗЕ-ЭЙНШТЕЙНА
397
Вычислим максимальную энергию s0 для 0 = 0. Так как при
0=0 /(е) = 0 для е е0, то из (110.16) и (110.21) имеем:
бо «о
о о
Отсюда
Величина максимальной энергии электрона е0 для металлов
(п 1022 см~3) получается равной нескольким электрон-вольтам. Такого
же порядка величины средняя нулевая энергия электронов е (0) [точно
е (0) = 3/5 е0]. По классической теории средняя энергия электронов дол-
жна быть гораздо меньше (3/2 kT). Более детальное исследование по-
казывает, что е0 очень мало зависит от температуры, если только по-
следняя много меньше TQ = ~. Эта температура для электронного газа
составляет ^ 10 000°. Для температур T^>TQ можно доказать, что
распределение Ферми-Дирака переходит в максвелловское распределение
dz — const, е 0 e'Ms. (110.24)
Температуру То называют температурой вырождения газа. Применение
статистики Ферми-Дирака к электронному газу позволило преодолеть
многочисленные принципиальные затруднения классической электронной
теории металлов и в настоящее время является исходным пунктом со-
временной теории *).
В качестве примера распределения Бозе-Эйнштейна рассмотрим чер-
ное излучение. Будем считать кванты света (фотоны) частицами. Соотно-
шение между энергией е и волновым числом k для этих частиц есть
z = h® = hck, т. е. ^ = (Ас)"1. Так как состояния фотона представ-
ляются плоской волной, то число состояний на интервал энергии будет
(109.19). При этом еще нужно умножить (109.19) на 2, так как для
каждого значения к возможны две независимые поляризации. Следова-
тельно, из (110.19) получаем:
p(s)ds = ~ (^-У^-ds. (110.25)
г' (2гс)3 \ he/ he \ • f
Таким образом, закон распределения фотонов по энергии получается
в виде
*) Литература по квантовой теории металлов весьма обширна. Укажем
на Электронную теорию металлов Бете и Зоммерфельда и очень
хороший обзор R. Peierls, Ergebnisse d. exakten Naturwiss., 1932.
398
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XXII
Полное число фотонов неопределенно ( = оо), поэтому условие (110.15)
для определения а не может быть использовано. Энергия в единице
объема в интервале dz будет равна ер (г) dz. Имея в виду, что е =
перейдем к плотности излучения zz(to) на интервал частот du\ u(($)d(ti —
==ер (г) hd®. На основании этого получаем:
й(ю)^ = ^ »----. (110.26')
Л+я+1
При /го) 0 закон распределения должен переходить в классический
закон Рэлея-Джинса (§ 6). Чтобы получить этот закон, следует взять
а = 0. Таким образом, получаем:
, . Тгю3 1
е* 4-1
т. е. формулу Планка*).
(110.26")
ГЛАВА XXII
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
§ 111. Атом гелия
Атом гелия, второй атом периодической системы, является наиболее
простым из многоэлектронных атомов. Однако, уже на нем классическая
механика потерпела полный крах. Попытки рассчитать его методами
классической механики (с учетом квантовых условий Бора) привели к
выводу о невозможности применения классической механики к атомным
системам с двумя и большим числом электронов. Было сделано предпо-
ложение о существовании некоторого рода «немеханических действий».
Современная квантовая механика в проблеме многоэлектронных систем
не встречает никаких принципиальных трудностей (вычислительные труд-
ности довольно значительны).
Мы начнем с качественного анализа возможных состояний атома гелия,
опираясь при этом на общую теорию систем, состоящих из одинаковых
частиц, изложенную в § 105—108. Определим прежде всего вид опе-
ратора Гамильтона Н для электронов атома гелия. Взаимодействия
в атоме гелия можно разбить на две группы. В первую входят значи-
тельные кулоновские взаимодействия между ядром и электронами, во
вторую — слабые магнитные взаимодействия, обусловленные взаимодей-
ствием спинов электронов между собой и с орбитальным движением**).
*) Применяя метод Гиббса, можно непосредственно вывести формулу
(110.26), не прибегая к классическому закону Рэлея-Джинса.
**) В эту же группу следует отнести поправки, обусловленные зависимо-
стью массы электрона от скорости (ср. §§ 61 и 70).
§ И1]
АТОМ ГЕЛИЯ
399*
Мы обозначим координаты электронов через yv zx (rj и x2,v
у2, z2 (г2), а их спины через s2 и s2. Оператор энергии кулоновских
взаимодействий будет равен
у _______2g2 2g2 g2
“ Ъ г2 +
(111.1),
где первые два члена представляют энергии взаимодействия первого*
и соответственно второго электрона с ядром атома, имеющим заряд
-|-2g, а третий член определяет энергию кулоновского взаимодействия
электронов (рис. 71).
Оператор магнитных взаимодействий мы обозначим через Он
будет зависеть от спинов электронов, их положения и скоростей
W—W(sv s2, rp r2, — ih\, (111.2>
Учитывая еще кинетическую энергию обоих электронов, мы можем
написать полный гамильтониан электронов атома гелия в виде
Я(Г1, r2, S1) s2) = -gvf-^-^-^ + £+Vy. (111.3)
Последний член, как мы знаем (ср. § 60), очень мал и обусловливает
мультиплетную структуру спектров. Ограни-
чиваясь в дальнейшем качественным анализом
мультиплетного строения уровней гелия, мы
вовсе отбросим этот член и будем исходить
из гамильтониана
H(rv г2) =
А2 2е2 2е2
2Г
I g2
+ -. (111.4)
В этом приближении, когда игнорируются
Рис. 71. Взаимодействия
в атоме Не.
малые спиновые взаимодействия, переменные,
относящиеся к движению* центров тяжестей
электронов и к их спину, разделяются. Выби-
рая в качестве спиновых переменных проекции спинов на некоторое
направление (например, OZ): szl и sz?, мы можем (ср. § 57) написать
полную волновую функцию двух электронов атома гелия в виде
г2, $г.) = Ф(Г1, г2).£($г1, 5г2), (111.5)
где через S(szl, sz2) обозначена часть волновой функции Ф, зависящая
от спинов.
Оператор Гамильтона И (И 1.4) [а также и точный (111.3)] сим-
метричен относительно обоих электронов ввиду их тождественности.
Поэтому к рассматриваемому случаю применимо утверждение общей
теории (§ 108), согласно которому волновая функция Ф (111.5)
должна быть антисимметричной или симметричной относительно ча-
400 МНОГОЭЛЕКТРОННЫЕ АТОМЫ [гл, XXII
стиц, в зависимости от того, подчиняются ли они принципу Паули
или нет.
Опыт показывает, что электроны подчиняются принципу Паули
(впервые именно для электронов он и был установлен). Следовательно,
волновая функция (111.5) должна быть антисимметричной относительно
перестановки электронов, т. е.
/’пДОр Г2- Szl’ Sz2> = — ’Р(г1, Г2, ^1, S2„). (111.6)
Оператор перестановки мы можем представить в виде произведения
двух операторов перестановки Р'2 и из которых первый перестав-
ляет координаты центра тяжести электронов гг и г3, а второй — спины
электронов szl и sz2. Тогда (111.6) с помощью (111.5) можно написать
в вице*)
/>;2Ф(Г1, r2).p;2s(Srf, 5г2)=-Ф(Г1, г2)-5(5г1,5г3). (ни)
^Отсюда мы получаем две возможности: либо
р;2Ф(Г1> г2)=+Ф(Г1, г2), (1И.8)
и тогда
^)=~S{szV 5г„), (111.9)
«либо же
р;2Ф(Г1, г2)=-Ф(гр г2), (1П.8')
и тогда
(Szl> S (^1. ^)- (111 -9')
Первая возможность означает, что координатная функция симметрична,
а спиновая антисимметрична, вторая возможность означает, что коорди-
натная функция антисимметрична, а спиновая — симметрична. Поэтому
мы получаем два класса волновых функций для возможных состояний
атома Не, именно:
^), (111.10)
Фц-Ф^П, Г2)^(5г1, ^2), (111.10')
тде значками а и 5 обозначены симметричные и соответственно антисим-
метричные функции.
Рассмотрим теперь подробнее спиновые функции Sa и 3^. Поскольку
мы игнорируем взаимодействие спинов, каждую функцию можно было
бы написать в виде произведения спиновых функций, рассмотренных
в § 57 (57.6), (57.6'), относящихся к каждому электрону в отдельности,
т. е. в виде
*) Утверждение (111.6) справедливо и в тех условиях, когда не пренебре-
гается спиновым взаимодействием. Дальнейшее, напротив, базируется на
^приближении (111.5).
§ 1И]
АТОМ ГЕЛИЯ
401
где значки ах и а3 и* указывают, как направлен спин электрона-по
оси OZ или против нее. Но функция (111.11) не является ни симмет-
ричной, ни антисимметричной функцией спинов электронов. Легко, однако,
построить из функций (111.11) антисимметричные функции Sa и сим-
метричные 5^.
Рассмотрим сначала случай, когда спины электронов противоположны
друг другу. Тогда волновая функция (111.11) имеет вид
s^==S+^S_^sz2), (111.12)
но возможно и другое состояние, когда спин первого электрона про-
тивоположен оси OZ, а спин второго направлен по оси OZ:
sz2)^S_lll(szl)S+lfl(sz2). (111.12')
Оба состояния отвечают суммарному спину по оси OZ, равному нулю,
и оба принадлежат одной и той же энергии Е. Поэтому этой же
энергии может принадлежать и любая суперпозиция этих состояний.
Среди них единственная, описываемая антисимметричной функцией Sa,
имеет вид 5)
Sa(s,v {$+4, (^l)5_I/a(S?2)-S_1/,(sH)S+./>(^)}.. (111..13)
Таким образом мы определили вид антисимметричной спиновой функции.
Если спины электронов параллельны, то антисимметричные состояния,
очевидно, невозможны. В этом случае мы можем иметь состояния спина
электронов
s; (^i. =*+•/, <^) $+•/. (^2). < 111 л 4>
(111.14')
Эти состояния с самого начала симметричны по спину электронов. Кроме
того, из функций (111.12), (111.12') можно образовать еще одну сим-
метричную в спинах электронов функцию, именно:
^"Чр {5+‘M^i)5->/a(^) + 5_./i(^2)5+./1(sil)}. (111.14")
V *
♦) Множитель присоединен из соображений нормировки Sa к 1. В са-
мом деле, функции S=bx/a(<yJ нормированы к 1 согласно (57.7). Если мы обра-
зуем произведение
szd ^2)
х h К
и просуммируем по обоим спинам = zt у , = zt у , то мы, как легко
убедиться, пользуясь (57.7), получим 1.
26 Блохинцев
402
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[ГЛ. XXI!
Таким образом мы имеем всего три симметричные по спину функции
3^, S" и S'J'. Первые две относятся к суммарному спину 1, но в со-
стоянии спин направлен по оси OZ, а в состоянии S'J — против оси
QZ, Несколько менее ясно то обстоятельство, что состояние У"
у
также относится к суммарному спину 1, но только он ориентирован
перпендикулярно оси OZ. В этом можно убедиться проще всего сле-
дующим образом. Мы берем в качестве спиновых переменных проекции
спина на ось OZ. Если* речь идет о состоянии, в котором спин ориен-
€Z
1 оара^Не
орто=Не
Полный спин-0 Полный спин-1
тирован | OZ, то эти переменные
szl и sz2 Должны иметь неопреде-
ленное значение -4- у . т. е. со-
стояние со спином | OZ должно
записываться в и sz2 перемен-
ных так, чтобы фигурировали все
возможные значения szl и sz2. Кроме
того, мы ищем состояние, симметрич-
ное в спинах. Тогда (111.14") есть
единственный способ написать вол-
новую функцию этого состояния*).
На рис. 72 приведено схема-
Рис. 72. Схема сложения спинов двух
тически расположение спинов для
найденных нами состояний.
электронов.
На схеме отмечены принятые в тексте обо- ТаКИМ образом, СОСТОЯНИЯ, СИМ-
Значения волновых функций соответствую- 1 1 ’
щих состояний. метричные в координатах центров
тяжести электронов Фу, суть состоя-
ния с суммарным спином электронов, равным нулю. Состояния, антисим-
метричные в координатах центров тяжести электронов Фй, суть состоя-
ния с параллельными спинами электронов (суммарный спин равен 1).
*) Утверждение о принадлежности состояний S”s и к спину 1 (сло-
жение спинов электронов) может быть проверено прямым вычислением. Если
обозначить операторы спинов электронов, определяемые матрицами (56.12),
через и s2> т0 оператор полного спина представится матрицей
Sp = ^2 -j- 2Sj <$2*
Собственная функция S оператора $2 должна удовлетворять уравнению
^.S = ^(Z5+1).S,
где ls — число, определяющее полный спин. Из этого уравнения можно убе-
диться, что ls имеет всего два значения: ls = Q (антипараллельные спины)
или ls = 1 (параллельные спины). Далее непосредственной подстановкой в это
же уравнение функций 5^ и можно убедиться, что эти функции суть
функции, принадлежащие ls—\.
Простые выкладки, нужные для доказательства этих предложений, предо-
ставляем сделать самому читателю.
§ 1 1 L] ATOM ГЕЛИЯ 403
Таких состояний имеется три, соответственно трем квантовым ориен-
тациям суммарного спина. Уровни атома гелия распадаются поэтому на
два класса: на уровни с антипараллельными спинами и на уровни с
параллельными спинами.
Если мы учтем, что от ориентации спина по отношению к орбиталь-
ному движению хотя очень мало, но все же зависит энергия квантового
уровня, то мы должны будем притти к заключению, что уровни с анти-
параллельными спинами будут одиночные (сингу летные}, а уровни с
параллельными спинами будут распадаться на три близких, соответ-
ственно трем возможным ориентациям суммарного спина относительно маг-
нитного поля, создаваемого орбитальным движением. Таким образом эти
уровни будут тройные (триплетные} *).
Самым замечательным свойством этих двух классов состояний гелия
является то, что между ними невозможны (почти невозможны) квантовые
переходы. В самом деле, спиновые взаимодействия очень малы, и если
их совсем игнорировать, то гамильтониан электронов атома гелия, даже
при действии внешних полей, например, светового поля, будет симмет-
ричным относительно координат электронов, так как внешнее поле оди-
наково действует на оба электрона. Таким образом,
H(rv r2} = H(r2, rj. (111.15)
Изменение какой-нибудь волновой функции Ф (гр г2, sz2, t} дается
уравнением Шредингера, которое мы напишем в виде
dt > r2> 5Z1> t) = H (tj, r2) Ф (r„ r2, szV $г2, t) dt (111.16)
подобно тому, как мы это делали в § 106. Если Ф(гр г2, $г], sz2, t)
есть в какой-то момент симметричная функция координат электронов гр г2>
•ю приращение этой функции согласно (111.16) ввиду (111.15)
будет также симметричным. Подобным же образом, если Ф (гр г2, sz2, t}
антисимметрично, то и поиращения будут антисимметричными. Сле-
довательно, симметричное в координатах состояние остается симметрич-
ным при всех возможных изменениях. Равным образом, антисимметричное
состояние также остается антисимметричным. Следовательно, невозможны
переходы из состояний Фт (111.10) в состояния Фп (111.10') и обратно.
Заметим, что следует иметь в виду отличие доказанной сейчас тео-
ремы от общей теоремы § 106. Функции Фт и Фп являются антисиммет-
ричными функциями в частицах, поэтому между состояниями Фт и Фп
с точки зрения общей теоремы § 106 возможны переходы. Мы доказы-
ваем сейчас невозможность перехода между Ф1 и Фп при условии, что
игнорируются взаимодействия со спином. Поскольку эти взаимодействия
все же существуют, то переходы между Ф1 и Фп на самом деле возмож-
ны, но ввиду малости взаимодействия со спином они будут очень мало
вероятны.
*) Расчет величины этого расщепления см. в книге Бете, Квантовая ме-
ханика простейших систем, § 23.
26*
404
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[ГЛ. XXI!
В качестве иллюстрации приведем оценки для действия световой
волны. Энергия взаимодействия световой волны с зарядом электрона, по
порядку величины, будет равна
W' = ega,
где а — размеры атома, е — заряд электрона, а $—электрическое поле
световой волны (еа есть электрический момент атома). Взаимодействие
же световой волны с магнитным моментом электрона, по порядку вели-
eh
чины, равно произведению магнитного момента электрона на магнит-
ное поле волны
W=e^~ &С-,
2цс
так как £ и SK в световой волне равны, то
W" _ h
W' 2рса *
h h
— есть, по порядку величины, импульс электрона в атоме, а — — его
скорость v. Итак,
W" _ v_
W' с
Это отношение составляет менее 1/100. Поэтому весьма мало вероятно,
что свет вызовет переход, при котором
изменится направление спина
электрона*). Иными словами,
будут преобладать переходы
без изменения спина, т. е.
переходы между состояниями
с одинаковой симметрией в
координатах электронов. Это
и утверждает только что
доказанная теорема.
Следовательно, если гелий
находится в состоянии с па-
раллельными спинами (анти-
симметричное в координатах
состояние), то весьма мало
Рис. 73. Расположение спинов в орто- и
пара-гелии.
Орто-Не
вероятно, чтобы его состояние изменилось на состояние с антипарал-
лельными спинами (симметричное в координатах), и наоборот. Положение
вещей таково, как если бы существовало два сорта гелия — с параллель-
ными и с антипараллельными спинами. Первый сорт гелия называют
орто-гелием, а второй — пара-гелием (см. схему на рис. 73). Для
*) Следует еще учесть, что вероятность перехода пропорциональна ква-
драту энергии возмущения, поэтому отношение вероятностей будет 10-4.
§ 111]
ATOM ГЕЛИЯ
405
тогр, чтобы перевести один сорт в другой, нужно изменить направление
спина одного из электронов. Ввиду малости магнитного момента спина
эго изменение произвести весьма трудно. Легко видеть, что энергети-
чески нижнее состояние гелия должно быть состоянием пара-гелия.
В самом деле, мы неоднократно указывали на* то, что нижнее состояние
характеризуется волновой функцией без узлов. Но антисимметричная
функция Фд(гр г2) имеет узел (узловую поверхность при г1 = г2).
В самом деле,
фа(г1> г8)=—Ф(г2,.Г1);
при гх = г2 = г получаем:
Фа(г, г) = —Фа(г, г),
т. е. Фа(г, г) = 0. Поэтому ^функцией нижнего состояния должна быть
симметричная функция Ф^(г1? г2). Следовательно, это будет состояние,
антисимметричное в спинах, т. е. состояние пара-гелия. Таким образом,
гелий в нормальном состоянии есть пара-гелий.
В связи с этимч возникает вопрос: как получить орто-гелий? Если
освещать светом, то практически будут получаться возбужденные со-
стояния опять-таки с антипараллельными спинами, т. е. пара-гелий.
Таким путем мы не добьемся никакого результата. Иначе обстоит дело,
если бомбардировать гелий электронами. В этом случае мы имеем
дело с тремя одинаковыми частицами: два электрона атома гелия и
один падающий извне. Поэтому данный нами анализ состояний
для двух одинаковых частиц будет в этом случае непригоден.
Физически дело сводится к тому, что падающий электрон может
стать на место атомного, а атомный вылететь из атома. Так как в
пучке падающих электронов есть электроны со всяким направле-
нием спина, то в результате такого обмена в атоме могут оказаться
электроны с одинаково направляемым спином: пара-гелий превратится
в орто-гелий.
Доказательство существования двух гелиев (точнее двух классов
состояний гелия) позволило полностью истолковать всю совокупность
спектроскопических данных, относящихся к спектру гелия и к его по-
ведению в различных условиях. На рис. 74 мы приводим схему1 уровней
атома гелия. В пара-гелии суммарный спин равен нулю. Мультиплетная
структура отсутствует. Линии являются одиночными (сингуледными).
Соответствующие термы обозначаются буквами с присоединением слева
вверху значка 1 (например *Р). Напротив, термы орто-гелия распа-
даются на три близких между собою. Спектральные линии орто-гелия соот-
ветственно этому расщеплению уровней состоят из трех близких линий
(триплеты). Термы орто-гелия обозначаются присоединением слева вверху
значка 3 (триплет), например, 8S, 3Р. На рис. 75 отмечено состояние
орто-гелия 2 как Мвтастабильное. Дело в том, что это состояние есть
низшее состояние орто-гелия. Переход в нижнее состояние есть переход
в состояние 1 пара-гелия и связан с изменением направления спина. Он мало
406
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XXII
вероятен, и атом гелия, оказавшийся в таком состоянии, будет находиться
в нем весьма долго, несмотря на наличие запаса энергии в 19,77 eV.
вольт
24,47-
24-
Лара-гелий. .
,pi
PDF
Ь 0.744
22-
18-
16-
14 —
12-
10-
8 ~
6-
4-
2~
<$о
S
20,55-
20-
19,77 ~
6
Орто-гелий ~
Ргл Зро Рз21 I
А Рг 4 f исм
-2
-1?
—---- 'V
5f — 5
4f ~4
~-3
Рис. 74. Схема спектральных термов гелия.
0
На этом мы закончим качественный анализ состояний атома Не и
перейдем к приближенной количественной теории.
§ 112] ТЕОРИЯ АТОМА ГЕЛИЯ 407
§ 112. Приближенная количественная теория атома гелия
Для расчета квантовых уровней атома гелия мы применим метод,
который, хотя и не является лучшим с точки зрения достигаемой точ-
ности расчетов, но зато отличается простотой и наглядностью. Уравне-
ние Шредингера для определения квантовых уровней атома Не и вол-
новых функций стационарных состояний имеет вид
Я(Гр Г2, 5г1, s^(rv г2, ^1, ^) = ЕФ(Г1, г2, 5г1,5г2), (112.1)
и так как мы пренебрегаем спиновыми взаимодействиями, то это урав-
нение, пользуясь (111.5), можно сократить на Тогда мы
получим:
Я(гх, г2)Ф(гр г2) = £Ф(Г1, г2),, (112.2)
причем оператор полной энергии дается формулой (111.4). Этот опера-
тор можно написать в виде
Я(г„ г2) = Я0(Гр r2)+ W(r12), (112.3)
где
Л2 _2 Л2 _2 2d?2 2d?2
Яо(гр г2)=-^¥-^¥2-^-^ = Я0(г1)4-Я0(г8)) (112.4)
^(Г12)=Г- (112.5)
'12
Оператор /70(гр г2) есть оператор полной энергии, описывающей
движение двух электронов в поле ядра без взаимодействия их между
собой. 1Г(г12) есть энергия взаимодействия электронов. Наше прибли-
жение будет заключаться в том, что эту энергию взаимодействия мы
будем рассматривать как малую поправку и в качестве нулевого при-
ближения будем брать движение невзаимодействующих электронов в поле
ядра*). .
Волновые функции и квантовые уровни для такого движения извест-
ны, так как это есть движение в кулоновском поле. Пусть первый
электрон находится в состоянии фя(гх), энергия Еп, а второй элек-
трон— в состоянии (г2), энергия^. Тогда в качестве функции нуле-
вого приближения, принадлежащей энергии Еп-\-Ет, можно взять
ФИП. Г2) = ф„<г1)фт(г2). (112.6)
В самом деле,
Я0(Гр Г2)Ф1(Г1, Г2)=:://о(Г1)Фй(Г1)Фт(Г1) + ^о(Г2)Фп(Г2)фт(г2)^
=Еп фв (Г1) Ф« (г2) + Ет Ф„ (г,) (г2),
т. е.
яо(гр г2)ф, (ГР гг) = (£„ + £’т)ф1(г1, г2). (112.7)
Однако, энергии Еп~\-Ет принадлежит, очевидно, и другое состояние,
*) В конце концов оказывается, что энергия взаимодействия не очень мала
(поэтому приближение не является особенно хорошим), но все же она меньше
разности энергии низших уровней примерно в три раза.
408 МНОГОЭЛЕКТРОННЫЕ АТОМЫ [гл. ххп
когда первый электрон находится в состоянии Еп, а второй в состоянии Е .
Волновая функция этого состояния есть
Ф2(гр Г2) = фя,(г1)фя(г2). (112.6')
Подобно тому как мы нашли (112.7), мы найдем, что
Я0(гр г2)ф2(гр г2) = (£„ + £от)ф2(г1, г2). (112.7')
Такцм образом, уровню Еп-[-Ет невозмущенной системы принадлежат
два состояния и ф2, отличающихся обменом состояний электронов (1)
и (2). Мы имеем дело с вырождением. Это вырождение называют обмен-
ным. Согласно общей теории возмущений (§ 64) правильная волновая
функция нулевого приближения должна быть суперпозицией вырожден-
ных состояний*):
Ф(гр г2) = <;!<!>! (г„ r2) + c2(|z2(rp г2). (112.8)
Амплитуды сх и г2 и квантовые уровни Е возмущенной системы опре-
делятся из основных уравнений теории возмущения. Так как мы ограни-
чиваемся рассмотрением двукратного обменного вырождения (функ-
ции фх и ф2), то мы можем прямо применить теорию для двукратного
вырождения, изложенную в § 65. Для определения амплитуд и г2
тогда получаются уравнения (65.5), которые в нашем случае гласят:
(^+^и-^1 + ^2 = 0, У
где Е°т есть энергия невозмущенного движения:
Епт=Еп + Ет (112.10)
(в обозначениях § 65 индексы п, т обозначены одной буквой k), а вели-
чины IFU , IF12, 1F22, W21 суть матричные элементы энергии возмуще-
ния W [см. (65.6)1. Так как в (65.6) имеется в виду интегрирование
по всем переменным, от которых зависят волновые функции, то в нашем
случае формулы (65.6) гласят:
1ГП = ф; Wi^dv^v» (112.11)
Г12 = j ф* W^dvxdv2, (112.11')
где dvA — dxrdyydzv dv^ — dx^dy^dz^ a W есть энергия возмуще-
ния £112.5).
*) Строго говоря, мы должны были бы снабдить волновые функции
тремя индексами (л, Z, т), так как, как мы знаем, уровню Еп принадлежит
всего л2 различных состояний (вырождение в кулоновском поле!). Соответ-
ственно этому для правильного расчета уровней Не в качестве функции нуле-
вого приближения следует брать суперпозицию состояний, отличающихся не
только обменом электронов, как мы это сделали, но и всех состояний, при-
надлежащих уровням Еп и Ет и отличающихся вращательными моментами
и их ориентациями. Мы, однако, будем вести расчет так, как если бы уров-
ни Еп не были вырождены. Это делается только для того, чтобы выявить
особенности задачи, вытекающие исключительно из того факта, что мы имеем
дело с двумя одинаковыми частицами.
§ И2]
ТЕОРИЯ АТОМА ГЕЛИЯ
409
Уровни энергии возмущенной системы Е определяются из векового
уравнения (65.7), которое полностью сохраняет свой вид:
rV£ir^12e =0’ 012.12)
И'21 W 22 g
где в теперешних обозначениях поправка к энергии равна
+ (112.13)
Прежде чем решать это уравнение, установим некоторые специаль-
ные особенности матричных элементов (112.11). Подставляя в (112.11),
(112.1Г), вместо и ф2 их значения из (112.6) и W из (113.5), мы
получаем:
U7- — (* dv.dv. =+ Г22. (112.14)
J Г12
Далее, легко видеть, что W\2 равно UZ21. В самом деле,
1^12 = е8
^<г1Нт(Г1)Фя(г2)^(г2)
---------------------dvxdv2,
(112.15)
с другой стороны,
IF21 = J . 1Гф1 • dv^=e2 J —-----------------------dv^. (112.16)
Так как переменные интеграции Г](хр yv zj и г2(х2, у2, г2) пробе-
гают одни и те же значения, то мы можем заменить переменные инте-
грации xv yv zt на x2, j/2, ,z2, a x2, y2, z2 на xv yv zx (это просто
новое обозначение), и так как г12 = г21, то при такой замене IF12 про-
сто совпадает с W^p Следовательно,
^12= ^21= ^*2= > (Н2Л7)
т. е. величины IF12 действительны. Мы положим
ГП=1Г22 = /С, W12=W21 = A, (112.18)
К и А суть действительные величины. В этих обозначениях вековое
уравнение (112.12) принимает вид
КТ = (112.19)
откуда получаем
(/<— е)2 = Л2, е==:/С±Д. (112.20)
Уравнения (112.9) с помощью новых обозначений запишутся в виде
(К— е) С1 + Ас2 = 0, (К — е) с2 + Асг = 0 . (112.9>
Подставляя сюда первый корень (е) из (112.20), находим с1~с2. Под-
410
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XXIГ
ставляя второй корень е, находим
(112.8) будет
ф/г1> + <М,
сх — — с2. Следовательно, решение
^=^л + £и+/С+Л, (112.21)
Еа — Еп-\-Ет-\-К—А (112.22)
1
(множитель у= введен для нормировки).
Таким образом, благодаря обменному вырождению получается два
рода состояний; симметричные Фд, и антисимметричные Фд [напомним,
что согласно (112.6) и (112.6') при перестановке координат электро-
нов переходит в ф2]. Существование этих двух родов состояний
находится в полном согласии с общей теорией § 106. Мы знаем, что
первые состояния суть состояния пара-гелия, а вторые — состояния орто-
гелия. (112.21) и (112.22) суть, следовательно, приближенные выра-
жения для функций пара- и орто-гелия.
Излагая качественную теорию атома гелия, мы указали на то, что
нормальное состояние должно описываться симметричной функцией (пара-
гелий). Этот результат также содержится в решениях (112.21) и (112.22).
В самом деле, нижнему уровню Ех принадлежит лишь одна волновая
"функция фюо(г1)- Поэтому, чтобы образовать нижнее состояние атома
гелия, имеется лишь одна возможность — поместить второй электрон
в это же состояние (отсюда уже из элементарного понимания принципа
Паули следует, что второй электрон должен иметь спин, противополож-
ный спину первого). Следовательно, в нижнем состоянии ф! = ф2 и
Фа — 0. Таким образом, для нижнего состояния имеем единственное
решение
Фу — (г1> гг) — Фюо (ri) Фюо (гг)» (112.23)
В = 2Е14-АГ4-Л. (112.23')
Разность энергии пара- и орто-состояний согласно (112.21) и (112.22)
равна 2А. Следовательно, система уровней гелия распадается на две
энергетически различные системы уровней пара- и орто-гелия. Каждому
уровню атома гелия Еп-^-Ет, которые получаются без учета взаимо-
действия электронов, соответствуют при учете взаимодействия два уров-
ня— уровень пара-гелия Еп -j- Ет К—А и уровень орто-гелия
ЕаАгЕт-]~ А. Так, например, если один электрон находится в
нижнем состоянии Ev а второй в следующем верхнем Е2 (энергия
Е1-^Е2)1 то, учитывая обмен «электронов и их взаимодействие, мы
получим два уровня Ег -{- £2 К 4" и 4" ^2 + К— А- Это расщеп-
ление, а также уровень 2ЕХ К4" изображены на диаграмме рис. 75.
Эта диаграмма дает менее многообразное расщепление, чем при-
веденное в полной спектроскопической схеме рис. 74. Это объясняется
тем, что мы игнорировали (для простоты) то обстоятельство, что уровни
невозмущенной проблемы (например, Е2) вырождены (кроме первого).
£олее полный расчет показал бы, что расщепление уровней получается
§ 113]
ОБМЕННАЯ ЭНЕРГИЯ
411
не только благодаря обменному вырождению, но и благодаря снятию
«7»-вырождения. Последнее ясно уже из того, что «7»-вырождение суще-
ствует только в кулоновском поле ядра. Присутствие второго электрона
неминуемо должно его снять. Учет этого снятия «7»-вырождения дает более
богатую картину расщепления уровней, совпадающую со схемой рис. 75.
Отсылая читателя, интересующегося вычислительными вопросами, к
специальной литературе*), ограничимся здесь указанием на положение
дел с теоретическим расче-
том уровней Не. Расчеты
гелия по методу, изложен-
ному у нас, приводят к
дадеко не идеальному со-
гласию с опытом. Именно,
поправка е оказывается на
10—2О°/о отличной от той,
которая следует из экспе-
риментальных измерений.
В настоящее время сущест-
вуют гораздо более со-
вершенные методы расчета.
Хиллераас получил (в вось-
мом приближении) значе-
ние для основного уровня
гелия (ионизационный по-
тенциал) величину I—
= 198 308 см~г (мы при-
водим величину энергии
в обратных сантиметрах,
в
<\J
£
2Е.+К+Д
ЕлЕ+К-Д
:з
Рис. 75. Схема обменного расщепления уров-
ней гелия.
2
g г
s &
Ч» is
г
так как это принято в
спектроскопии), в то время как экспериментальное значение ионизацион-
ного потенциала Не равно 7=198 298 43 6 слГ1. Совпадение теории
и эксперимента поразительное, особенно если иметь в виду, что в рас-
чет не входят никакие произвольные постоянные, которые можно было
бы «подгонять» к опытным данным.
Вычисление возбужденных термов благодаря «7»-вырождению го-
раздо сложнее, и достигнутая там точность значительно меньше при-
веденной для основного терма.
§ 113. Обменная энергия
Рассмотрим теперь подробнее значение поправки е = КА, обус-
ловленной кулоновским взаимодействием электронов. Для этого вместо
волновых функций и введем новые величины
= ртт(г2) = - *I ф,л (r2)I 2> (113.1)
?тп (Г1) = — (г,) (г,) , (Г2) == — ефт (r2)<I>X (Г2). (113.2)
*) См. Бете, Квантовая механика простейших систем, §§ 11—24.
412
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[ГЛ. XXII
Первые две имеют простой физический смысл. Именно, рл/г (rj , оче-
видно, означает среднюю плотность электрического заряда в точке гр
создаваемую электроном, находящимся в состоянии (rj. Подобным
же образом ртт (г2) означает среднюю плотность электрического заряда
в точке г2, создаваемого электроном, находящимся в состоянии (г2).
Две последние величины р/и„(г1) ир/7гл(г2)не имеют такого простого
смысла. Это—плотности зарядов, обусловленные тем, что каждый из
электронов может находиться частью в состоянии частью в со-
стоянии фт(г2). Мы будем называть их обменными плотностями. Эти
величины могут быть комплексными, поэтому название «плотность заряда»
употребляется здесь весьма формально. С помощью введенных плотно-
стей величина К на основании (112.18) и (112.14) может быть напи-
сана в виде
J dv^, (113.3)
а величина А на основании (112.8) и (112.15) в виде
Ртл(Г1) Pmn(r2) dv^dv^ . 13 4ч
Величина К имеет простое и наглядное значение. В самом деле, ин-
теграл в (114.3) есть не что иное, как взаимная кулоновская энергия
двух зарядов, один из которых распределен в пространстве с плот-
ностью ряп, а второй — с плотностью pmw. Образно мы могли бы
истолковать эту энергию как энергию кулоновского взаимодействия
двух электронов, заряды которых размазаны в пространстве. Поэтому
эту часть энергии взаимодействия электронов называют кулоновской
(в узком смысле слова). Другая часть (А) не может быть наглядно ис-
толкована. Формально А можно рассматривать как электростатическую
энергию двух зарядов, распределенных с плотностями ртп и
Эту часть энергии взаимодействия электронов называют обменной энер-
гией. В этом смысле говорят, что энергия взаимодействия двух
нов состоит из. двух частей — кулоновской К и обменной А.
На самом деле следует иметь в виду, что как К, так и
ловлены кулоновским взаимодействием (при г = 0 и АГ— 0, и
Различие между кулоновской энергией (в узком смысле слова)
ной А основано на приближенном представлении функций системы Фа
и в виде -4=(ф!±ф2). Тем не менее, это разделение энергии взаи-
V й
модействия на кулоновскую и обменную части оказывается очень пло-
электро-
А обус-
Л = 0).
и обмен-
дотворным и поэтому получило право на существование.
Согласно теории возмущений поправка к энергии s должна просто
равняться средней энергии возмущения в соответствующем состоянии.
Это утверждение легко проверить для рассматриваемого нами случая.
Энергией возмущения является кулоновская энергия взаимодействия элек-
еъ
тронов —. Чтобы вычислить среднее значение этой энергии в неко-
S ИЗ]
ОБМЕННАЯ ЭНЕРГИЯ
413
тором состоянии Ф(гр г2), нужно умножить — на вероятность положе-
ния первого электрона в области dvx и второго в области dv2, т. е.
на | Ф |2 dv^dv^ и проинтегрировать по всем возможным .положениям
электронов, т. е. вычислить интеграл
~= ^-|Ф|М^3. (113.5)
'12 J '12
Подставляя Фа или Ф^ из (112.21) и (112.22) вместо Ф, мы находим:
I- (г1 {ШЖО+Ш+Ш ^1^2. (И3.6)
Г12 Z J Г12
что в силу (112.6) и (112.6') равно
— =
Г12
Т; е. поправка е есть просто средняя энергия кулоновского взаимо-
действия электронов в состоянии Фу или Фа.
Этот расчет позволяет нам глубже взглянуть на происхождение
обменной энергии. | |2 dvxdv2 есть вероятность того, что первый
электрон находится в области dvx и в состоянии п, а второй — в области
dv2 и в состоянии т. Аналогично | Ф212 dvxdv2 есть вероятность того,
что первый электрон находится в области ^dvx и в состоянии т, а вто-
рой — в области dv2 и в состоянии п. Если бы состояния и ф2 были
независимы, то мы получили бы, что вероятность первому электрону
находиться в области dvx. а второму — в области dv2^ независимо от
того, в каких состояниях эти электроны находятся, равна (считая
и ф2 равновероятными)
^2—уШ11ЖФ2|2Ж^2« (И3.7)
Квантовая механика ведет к тому, что состояния и ф2 не незави-
симы и фактически реализующееся состояние есть
Ф = ^=(Ф1± Ф2)« (113.8)
й ф2 находятся при этом в определенных фазовых соотношениях, и
мы получаем в выражении • для вероятности нахождения частиц в облас-
тях dvx и dv2 интерференционный член
dP'n == | Ф | ^dvrdv2 = dPn ± (ф1ф* ф1ф2) dv^dv^, (113.9)
который и приводит к существованию обменной энергии.
Легко видеть, что обменная энергия вовсе не связана специально
с кулоновским взаимодействием электронов. Предположив любое дру-
414
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XX П
гое взаимодействие наших частиц lF(r12), мы все равно получили
бы среднюю энергию IF (г12) в виде двух частей: IF — энергии в узком
смысле слова, которая получилась бы, если бы в (113.3) вместо —ввести
Г12
IF(r12), и обменной энергии Д, которая получилась из (113.4), если
опягь-таки вместо — ввести туда IF(r12). Таким образом, всякое класси-
ческое взаимодействие Wдвух одинаковых частиц ведет к обменной
энергии.
Обменная энергия не имеет никаких аналогов в классической меха-
нике. Открытие ее существования является одним из фундаментальных
и новых результатов квантовой теории.
Название «обменная энергия» выяснится гораздо полнее, если мы
рассмотрим состояния Ф, в которых распределение частиц по состоя-
ниям п и т фиксировано. Для этого обратимся к временной зависимости
состояний Фа и Фг Так как это — стационарные состояния, то
Ф^-р^ + Фг)*
Фа = ^(Ф1 + Ф2)й
2(£0 + K-A)t
+ К + Л) t
(113.10)
Обозначим
“о-—Г"’
(113.11)
и рассмотрим вместо и Фа состояние, являющееся их суперповицией
(это будет уже не стационарное состояние):
4-ф2(е_,8/—е1^ (113.12)
или
где
Ф=С1 (Оф^зЮФ,, (113.13)
бг(/) — е ^cosS/, c2(t) — e Zw<>zsin8Z. (113.14)
Согласно статистическому значению амплитуд q и с2, | сх |2 есть вероят-
ность нахождения системы в состоянии фх (т. е. первый электрон в /г,
а второй в /п), а |с2|2— вероятность того, что система находится в со-
стоянии ф2 (т. е. первый электрон в w, а второй в п). Имеем:
[ С1 (/) р = cos2 8/, | с2 (t) |2 = sin2 8/; (113.15)
отсюда взятое нами состояние Ф (113.12) таково, что при t — 0 первый элек-
трон находится в состоянии фл, второй в состоянии ф^. Спустя время т =
получим | 12 = 0, | с212= 1, т. е. первый электрон перейдет в состоя-
ние ф^, а второй в фп — произойдет обмен состояниями. На основании
§ 114] ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА 415
(113.11) мы видим, что это время обмена можно выразить через обменную
энергию. Именно, мы получаем, что
(113.16)
Отсюда следует важный вывод: время обмена состояниями обратно
пропорционально обменной энергии.
Интересно посмотреть те условия, при которых обменная энергия
столь мала, а время обмена столь велико, что обменом можно совсем
пренебречь. Обменная энергия зависит от плотности ртп (г) —
— Фт(г) фя(г), следовательно, она зависит от того, насколько перекры-
ваются функции состояний и Если ^ = 0 там, где фл^АО, или
там, где = 0, то ртп = 0 и обменная энергия вовсе отсутствует.
Этот крайний случай является, однако, идеализацией. Тем не менее мы мо-
жем вывести из него важное заключение: если состояния и таковы,
что I Ф/и I2 и I Фп I2 сосредоточены в разных частях пространства, то об-
менная энергия мала (стремится к нулю).
Допустим теперь, что состояния суть состояния электрона в атоме,
но энергии Еп и Ет предположим сильно отличающимися: Ет^>Еп.
Тогда функция сосредоточена в области, очень близкой к ядру,
а довольно широко распространяется от ядра. Так как обе функции
нормированы к 1, то это означает, что мало там, где заметно
велико. Следовательно, плотность ртп опять-таки мала. Таким образом,
обменная энергия мала и обменом можно пренебречь, если идет речь
либо об обмене состояниями, сосредоточенными в разных частях про-
странства, либо об обмене состояниями, сильно отличающимися по энергии.
Последнее обстоятельство оправдывает, например, то, что во многих
случаях можно пренебречь обменом оптического электрона с электро-
нами внутренних оболочек.
§ 114. Квантовая механика атома и периодическая
система элементов Менделеева
Задачей атомной механики в проблеме построения теории периоди-
ческой системы является расчет движения электронов в атомах на осно-
вании заданной массы и заданного заряда ядра*). Поставленная таким
образом задача представляется чрезвычайно трудной математически из-за
большого числа электронов в атомах (до 92 в уране) и, несмотря на
существование специальных приближенных методов для решения много-
электронных проблем, решена только частично лишь для наиболее про-
стых атомов. Заметим, что в классической механике даже проблема дви-
жения трех тел не получила до сих пор общего и полного решения.
В атомной механике, к счастью, положение лучше и многие практически
важные результаты могут быть получены уже весьма грубыми и прибли-
*) Вопрос о массе ядра и его заряде относится уже к теории атомного
ядра; изложение этой теории выходит за рамки нашей книги. Интересующе-
муся читателю можем указать на монографию Бете иБечер, Физика ядра.
416
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XXII
женными методами. Причиной такого упрощения является дискретность
состояний электронов в атомах. Благодаря этому на основе принципа
Паули и теории движения одного электрона в поле центральной силы
удается достигнуть существенных результатов в понимании распределения
электронов в атомах и, вместе с тем, периодичности в химических свойст-
вах элементов.
Впервые закономерности периодической системы элементов с точки
зрения атомной механики были рассмотрены Н. Бором *), а позднее,
с учетом спина электрона, — Стонером. Как известно, классические
исследования Резерфорда и Мозли показали, что номер элемента Z в
периодической системе элементов равен заряду ядра атома, выраженному
в единицах элементарного заряда е. Вместе с тем, для нейтрального
атома число электронов в его электронной оболочке равно также Z.
По современному, хорошо обоснованному экспериментально, пред-
ставлению ядра атомов образуются из незаряженных частиц — нейтро-
нов (заряд 0, масса 1,00845, если массу кислорода принять за 16) и
протонов (заряд-]-е, масса 1,00807). Число протонов в ядре равно
также Z. Атомы с одинаковым числом протонов, но отличающиеся друг
от друга числом нейтронов, имеют один и тот же номер Z, но разный
атомный вес А. Такие атомы называются изотопами. Химические свой-
ства зависят от числа электронов в нейтральном атоме, т. е. от Z, по-
этому изотопы химически равноценны **) и совокупность изотопов, при-
надлежащих одному и тому же Z, представляет собой один и тот же
химический элемент. Оказывается, что атомный вес А 2Z, так что
число протонов и нейтронов в ядрах приблизительно равно друг другу.
Благодаря этому расположение элементов в порядке возрастания атомного
веса (как это делал впервые Менделеев) ведет (за немногими исключениями)
к тому ike расположению, что и расположение по заряду ядра
Чтобы разобраться в распределении электронов в элементах, мы
будем представлять себе каждый последующий элемент образованным
из предыдущего путем прибавления к ядру одного протона (и надле-
жащего числа нейтронов) и соответственно прибавления одного электрона
к электронной оболочке атома. Далее, мы будем игнорировать взаимо-
действие электронов и внесем, где будет нужно, поправки на это
взаимодействие.
Нейтрон можно рассматривать как нулевой элемент периодической
системы (Z = 0), образующий нулевой период. Первым элементом будет
водород (Z=l). Ядро водорода образовано из одного протона***).
*) См. Н. Бор, Три статьи о спектрах и о строении атома, ГИЗ, 1923.
**) Речь идет о свойствах валентности. В кинетике реакций имеет значение
не только число электронов, но и масса атома. Поэтому нельзя сказать, что
изотопы с химической точки зрения вполне тождественны. Однако различия,
возникающие из-за изотопии, все же крайне малы, если не считать, например,
изотопов водорода, для которых массы сильно различны, именно, равны 1,2 иЗ.
***) Кроме того, имеются изотопы водорода, встречающиеся в естествен-
ных условиях в незначительных количествах; именно: Z=l, А = 2 (дейтон)
и Z=l, А = 3. Первый из них удается получить в довольно больших коли-
чествах («тяжелая вода»).
§ 114] ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА 417
Нормальное состояние единственного электрона атома водорода характе-
ризуется квантовыми числами zz = 1, Z = 0, z/г = О, — -Ч- Соответ-
ствующая волновая функция будет ^ntmm (#), где через q обозначены
координаты центра тяжести электрона и спиновая координата.
Увеличивая заряд ядра на-|-1, мы получим ядро гелия. В состояние
п = \, Z = 0, т = 0 можно поместить второй электрон, если спин его
противоположен спину первого электрона (для одного ^=-[--^-,для
другого —у). Точнее говоря, мы должны из функций
1 (<7i) и Ф
о, 0,+у ‘1,0,
1 (#2) образовать антисимметричную волновую
Т
функцию так, как это делалось в § 108. Два электрона гелия занимают
все возможные состояния, принадлежащие /г=1. Эта группа состояний
^zz=l, Z = 0, m = 0, ms = ЧЬ ) называется К-оболочкой (рентгено-
скопическое обозначение термов). Таким образом ^оболочка заполнена,
вместе с тем закончен первый период периодической системы, состоящий
всего из двух элементов Н и Не.
Увеличивая заряд ядра еще на -f- 1 и добавляя один электрон, мы
перейдем к Li. При этом приближенной волновой функцией должна
быть антисимметрическая комбинация из
Фл1//И1/И₽1 (#1) * фл^з/Яа/Я^ (#2) * Флз^з/Из^З (?3)>
принадлежащая наименьшей энергии (нормальное состояние Li). Следуя
таким образом далее, мы можем сказать, что в нашем приближении
волновая функция многоэлектронного атома, номера Z, будет являться
антисимметричной комбинацией из функций ^nkikmkm6k каждая из
которых описывает движение одного электрона в кулоновском поле
ядра, с зарядом -\-eZ. На основании (108.6') мы можем написать эту
функцию в виде
Ф •••> = 2 — 1) ^rhhmimg! '^nzlzmzmsz (qz)- (11 4.1)
Р
Эта функЦйя равна нулю, если для двух электронов числа /г, Z, т,
совпадают (принцип Паули!). Так как нас интересует нормальное состоя-
ние атома, то числа /гр Zp nv lz должны быть выбраны так, чтобы
энергия всей системы электронов
z
(114.2)
к = 1 '
была наименьшей. Если под функциями tynkikmkm8k разуметь волновые
функции для движения в кулоновском поле ядра (полное игнорирование
взаимодействия электронов), то энергия отдельных состояний Еп1 зависит
лишь от п. На самом деле существует зависимость Еп1 от Z, так как
электроны движутся не только в поле ядра, но и в поле других элек-
27 Блохинцев
418 МНОГОЭЛЕКТРОННЫЕ АТОМЫ [гл. XXII
тронов*). Эта зависимость более слабая, но все же для достаточно
больших п может оказаться, что состояния с большим п и малым I
могут иметь меньшую энергию, нежели состояния с меньшим тг, но
с бблыиим /. Такой случай, как мы увидим, впервые встречается
для калия.
Итак, для Li приближенная волновая функция имеет вид (114.1)
при Z = 3. Так как /С-оболочка уже заполнена, то третий электрон
должен быть помещен в состояние тг = 2, Z = 0, m = 0, т5— +* 1/9.»
Группа состояний с тг = 2 называется L-оболочкой. Таким образом, в
Li начинает заполняться L-оболочка. Всего в L-оболочке имеется
2тг2 = 2*22 = 8 состояний. Два из них принадлежат 5-терму (7 = 0,
т = 0, 77^ = 4--^, и шесть—/7-терму (/ = 1, т = 0, -4- 1, —
Увеличивая далее заряд ядра и прибавляя электрон, мы перейдем
от Li к Вё, от Be к В и т. д. через С, N, О, F до Ne. В неоне все
8 мест А-оболочки заняты. Мы получаем опять инертный газ и вместе
с тем заканчиваем второй период периодической системы. Дальнейшие
электроны могут быть помещены лишь в состояния с п — 3. Это —
так называемая М-оболочка. В Ж-оболочке имеется всего 2 • З2 — 18
состояний (7 = 0, 7=1, 7 = 2). Группа состояний с 7 = 0 и 7=1
вполне аналогична L-оболочке и заполнится на протяжении от Na до Аг.
Мы получим третий период периодической системы. Увеличивая заряд Аг
на е и добавляя электрон, мы получим калий. Если бы мы поместили
электрон калия в 7И-оболочку, то состояние этого электрона характе-
ризовалось бы 7=2 (дАтерм). Однако, и в оптическом, и в химическом
отношениях атом К вполне схож с атомами Li и Na, которые имеют
внешний валентный электрон в 5-терме. Поэтому мы должны поместить
электрон калия в состояние п = 4, 7 = 0, начав новую оболочку (ААобо-
лочка), не закончив заполнение 7И-оболочки. Это означает, что со-
стояние /г = 4, 7 = 0 имеет меньшую энергию Е^, нежели состояние
л = 3, 7 = 2 (L1^), что вполне может быть, если учесть взаимодействие
электронов. Таким образом мы получаем в калии распределение элек-
тронов, вполне аналогичное их распределению Na (см. таблицу).
*) Представление волновой функции Ф системы электронов в виде анти-
симметричной комбинации произведений функций отдельных электронов
является, конечно, приближенным. Можно поставить вопрос: как найти такие
функции ^П1тт^ чтобы функция Ф наилучшим образом представлялась в виде
(114.1)? На этот вопрос отвечает метод Хартри-Фока (см. Бете, Квантовая
механика простейших систем, или Френкель, Волновая механика, ОНТИ(,
1935, ч. II). Сущность метода Хартри-Фока заключается в разыскании таких
которые обращают в минимум полную энергию системы:
Е— ... dqz,
при условии
^Ф*Ф (ig1 в' , dgz — j.
§ И4]
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА
419
Распределение электронов в атомах
Элемент К L М Основной терм Ионизаци- онный по- тенциал (в электрон- вольтах) *)
1,0 15 2,0 2s 2,1 2р 3,0 35 3,1 3/7 3,2 3d 4,0 45 4,1 4/7
Н 1 1 . 25ъ 13,539
Не 2 2 — — — — -— — — 24,45
Li 3 2 1 — — — — — 25v., 5,37
Be 4 2 2 — — — — — — 9,48
В 5 2 2 1 — — — — — 2А/2 8,4
С 6 2 2 2 — — — — — 3Р„ 11,217
N 7 2 2 3 — — — — — 4 5»/, 14,47
О 8 2 2 4 — — — — — 3А 13,56
F 9 2 2 5 — — —i — — 2А/2 18,6
Ne 10 2 2 6 — — — — — 21,5
Na 11 1 — 25./2 5,12
Mg 12 2 — — — — 150 7,61
Al Si 13 14 Конфигурация 2 2 1 2 — 2/4 3Р0 5,96 7,39
P 15 неона 2 3 — — — 4 5% 10,3
S 16 2 4 — — — 3А 10,31
Cl 17 2 5 — — — 2 А/, 12,96
Ar 18 2 6 — — — 15,69
К 19 1 251/з 4,32
Ca 20 — 2 — 45„ 6,09
Sc 21 1 2 — 2£)з/3 6,57
Ti V 22 23 Конфигурация аргона 2 3 2 2 3А 4 А/, 6,80 6,76
Cr 24 5 1 — ’А 6,74
Mn 25 5 2 — 6 5\2 7,40
Fe 26 6 2 — 5Д 7,83
Co 27 7 2 4 А, 7,81
Ni 28 8 2 — 3А 7,606
Cu 29 10 1 — 2 51/, 7,69
Zn 30 10 2 — 45О 9,35
Ga 31 10 2 1 2 А/, 5,97
Ge 32 10 2 2 3Р„ 7,85
As 33 10 2 3 45з/„ 9,4
Se 34 10 2 4 3А
Br 35 10 2 5 2 А/2 11,80
Kr 36 10 2 6 13,940
*) 1 электрон-вольт = 23 ккал.
27*
420
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. XXII
Продолжение
Элемент Конфигура- 7V О р Основной Ионизаци- онный по-
ция внутрен- них слоев 4,2 4,3 4/ 5,0 55 5,1 5р 5,2 bd 6,0 65 терм тенциал (в электрон- вольтах) *)
Rb 37 Sr 38 Y 39 Zr 40 Nb 41 Mo 42 Ma 43 Ru 44 Rh 45 Pd 46 Конфигура^ ция крип- тона 1 2 4 5 6 7 8 10 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 j 1 1 1 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2SVa 'lsQ 2 3Л «£>/. 6 л. 4 /ч 4,16 5,67 6,5 7,35 7,7 7,7 8,5
Ag 47 Cd 48 In 49 Sn 50 Sb '51 Те 52 J 53 X 54 Конфигурация палладия II 1 II 1 II 1 2 2 2 2 2 2 2 1 2 3 4 5 6 1 1 1 1 1 1 1 1 — 2^ 2Р‘Л 3Л 4 зл 2Рз/а 7,54 8,95 5,76 7,37 8,5 10, 12,078
Cs 55 Ba 56 La* 57 Ce* 58 Pr* 59 Nd* 60 II* 61 Sm* 62 Eu* 63 Gd* 64 Tb* 65 Dy *66 Ho* 67 Er* 68 Tu* 69 Yb* 70 Cp* 71 *) 1 9J Слои от 1^ до bd содержат 46 электронов 1ектрон-вольт = 23 к> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 кал. Слои от 55 ДО 5/7 содерж ат 8 элект- ронов 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2S./2 2^Ч з//, 4КЧ 6ь/а «А 8//’/, 'Ки 4 к 2D^ 3,88 5,19
§ 114]
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА
421
Продолжение
Элемент Конфигура- ция внутрен- них слоев О р Q Основной терм Ионизаци- онный по- тенциал (в электрон- вольтах) *)
5,2 М 5,3 5/ 6,0 6s 6,1 6,0 6,2 6d 7,0 Is
Hf* 72 Таг 73 W 74 Re* 75 Os* 76 Ir* 77 Pt 78 Слои от Is до Ър содер- жат 68 элек- тронов 2 3 . 4 5 6 7 8 — 2 2 2 2 2 2 2 — — — 3 F 1 2 4A/o 6A 6^/2 5 A 4 ^/2
An 79 Hg 80 T1 81 Pb 82 Bi 83 Po 84 Am* 85 Em 86 Слои от 1s до 5d содержат 78 элек- тронов 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 1 2 3 4 5 6 — I 1 I 1 1 n 1 2SVa ^0 2 Аз 8 A. «А/, 9,20 10,39 6,08 7,39 8,0 10,689
Vi* 87 Ra* 88 Ac* 89 Th* 90 Pa* 91 U* 92 *) 1 9Jj Конфигурация эманации [ектрон-вольт = 23 ккал. 1 2 3 4 1 2 2 2 2 2 2 Аз 2 Аз 8 A 4 Аз 8 A
1
В таблице указаны не только распределения электронов и основные
термы, действительно полученные из спектров, но и те, которые были
определены на основании заключений по аналогии; последние отмечены
звездочкой после символа элемента. Однако, надежность этих выводов
по аналогии весьма велика.
Следующий элемент есть Са (Z — 2Q). Опять-таки спектроскопические
данные указывают на необходимость поместить электрон Са в s-терм
(N-оболочка). В дальнейших элементах происходит заполнение 7И-обо-
лочки [от Sc (Z=21) до Zn (Z=s=30)J. Далее заполняется TV-оболочка
до криптона (Кг, Z = 36), и этим заканчивается следующий период
(мы получаем инертный газ). Таким образом, для инертных газов (кроме Не)
характерна конфигурация из 8 электронов: два в s-состоянии и шесть
в р-состоянии.
Следующий за Кг элемент — рубидий (Rb, Z — 37). Он аналогичен Na
и К- Поэтому внешний электрон Rb помещается не в TV-оболочке, а
422
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
[гл. ХХП
начинает новую оболочку (п = 5, О-оболочка). Электрон Sr (щелочно-
земельный) находится опять в О-оболочке, так что Sr аналогичен Са.
В следующих за Sr элементах заполняются О-оболочка и свободные
места в /V-оболочке (см. таблицу). С цезия начинает заполняться Р-обо-
лочка (п = 6).
Элементы группы редких земель (от La, Z = 57, до Hf, Z=72,
включительно) обладают очень сходными химическими свойствами, так
как они все имеют сходное распределение электронов в О- и /^-оболочках.
Рис. 76. Периодическая система элементов по Н. Бору.
Как мы видим, сходство химических свойств определяется сходством
в строении внешней электронной оболочки. Открытая Менделеевым
периодичность в химических свойствах с точки зрения атомной механики
объясняется повторяемостью в структуре этих внешних оболочек. Так
инертные газы Ne, Аг, Кг, X и Em имеют одинаковые оболочки из
восьми электронов. Щелочные металлы имеют один электрон в s -терме
сверх оболочки инертного газа. Щелочно-земельные металлы имеют два
§ И5]
МОЛЕКУЛА ВОДОРОДА
423
электрона сверх оболочки инертного газа (терм1^). Галоиды F, С1,
Вг, J, Ат имеют оболочки, в которых недостает одного электрона до
оболочки инертного газа. Таким образом, квантовая механика позволяет
объяснить важнейший химический закон — закон периодичности химичес-
ских свойств.
На рис. 76 (стр. 422) приведена таблица Менделеева в форме,
приданной ей Н. Бором.
ГЛАВА XXIII
ОБРАЗОВАНИЕ МОЛЕКУЛ
§ 115. Молекула водорода
Теперь мы рассмотрим на основе квантовой механики молекулу
водорода Н2.
Молекула Н2 обладает типичной гомополярной связью. Поэтому,
рассмотрев этот простейший случай гомополярной молекулы, мы можем
рассчитывать на выяснение природы сил, обусловливающих гомополярные
валентные связи. Для того, чтобы вычислить силу взаимодействия между
двумя атомами водорода, нужно определить их потенциальную энергию
U(R) как функцию расстояния между центрами атомов (между ядрами) R.
Эта энергия U(/?) складывается из двух частей: из энергии кулоновского
еъ
взаимодействия ядер и из энергии электронов Е, которая зависит
от расстояния между ядрами и поэтому входит в потенциальную энергию
взаимодействия двух атомов. Итак, мы можем написать, что искомая
энергия U(R) равна
U(R)=e^ + E(R). (115.1)
Та^им образом, задача сводится к определению энергии электронов
E(R). Для больших расстояний R между атомами, очевидно, можно
пренебречь влиянием одного атома на движение электрона в другом атоме,
поэтому для R —+ оо энергия электронов просто равна сумме энергий
электронов в каждом из атомов водорода.
В дальнейшем нас будет интересовать молекула водорода в нижнем
энергетическом состоянии. Соответственно этому при разведении атомов
на бесконечное расстояние друг от друга, мы получим атомы водорода
в нормальном состоянии. Обозначим энергию атома водорода в нормаль-
ном состоянии через (А’о равна 13,55 eV). Тогда для интересующих
нас состояний молекулы энергия для больших R равна 2£0. Мы положим:
Е (/?) = 2£0 + г(/?). (115.2)
Очевидно, s (/?) будет означать изменение энергии электронов при
сближении атомов водорода. Эту величину нам и следует определить.
424
ОБРАЗОВАНИЕ МОЛЕКУЛ
[ГЛ. XXIII
Вся энергия электронов Е (7?) определится из уравнения Шредингера
как собственное значение оператора Гамильтона для нашей системы
электронов. Этот оператор Гамильтона легко написать:
^V2—-V2 — ——Л- —
2|* 1 2|л 2 Гл Гь1 Га2 ”Г Г12 •
(115.3)
Здесь кроме очевидных операторов кинетической энергии обоих элект-
ронов входят: а) потенциальная энергия первого электрона (1) и пер-
вого ядра (— —Ь) потенциальная энергия второго электрона (2)
и ядра (— —с) потенциальная энергия первого электрона (1) и
\ Г'
второго ядра ( —— d) потенциальная энергия второго электрона (2)
и, наконец, е) энергия взаимодействия обоих
и первого ядра
(11
„(2)
"Т
у*
\ia
/ g>2 \
электронов — ) . Рис. 77
\ /*12 /
поясняет примененные здесь
обозначения для расстояний
ГаГ> ГЫ> ГЬ2' rafr г12-
Если волновую функцию
системы наших
мы обозначим через
Ф(Гр г2),
Схема решения
для
нов
электро-
— R--+
Схема решения
Рис. 77. Схема взаимодействия в молекуле Н2
Сплошные линии соединяют частицы, между кото-
рыми взаимодействие учтено в решении или <Ь2.
Пунктирные линии соединяют частицы, взаимодей-
ствие между которыми в нулевом приближении
игнорируется.
то уравнение Шредингера
для определения Ф и Е
будет иметь вид
Я(Г1, г2)Ф = £Ф, (115.4)
где Н дается выражением
(115.3).
Решить уравнение (115.4)
можно лишь приближенно.
Мы будем здесь следовать
методу Гайтлера и Лондона,
которые впервые рассмотрели
интересующую нас задач/.
Их метод не является самым
лучшим в смысле достигаемой точности, но зато он отличается большой
простотой и наглядностью и весьма близок к методу, применяемому при
решении задачи об атоме Не § 112.
В качестве исходного приближения для волновой функции в этом
методе принимаются волновые функции невзаимодействующих атомов
водорода. Иными словами, нулевое приближение есть решение для да-
леко раздвинутых друг от друга атомов Н (7?—> оо). Соответствующее
§ 115] МОЛЕКУЛА ВОДОРОДА 425'
значение энергии системы есть 2В0. Мы можем считать расстояния
большими до тех пор, пока изменение энергии электронов при сбли-
жении атомов мало в сравнении с разностью между нижним уровнем 2Е&
и ближайшим высшим Ео Ех:
| е (/?) I < I (£- Fo) I. (115.5)
Последняя величина составляет 10,15 eV. Для таких расстояний вели-
чину s(/?) можно рассматривать как поправку к энергии невзаимодейст-
вующих атомов 2В0, а саму волновую функцию системы электронов Ф—
как функцию, близкую к вотновой функции невзаимодействующих ато-
мов водорода.
Для того, чтобы произвести подсчет таким путем, т. е. исходя из
удаленных друг от друга атомов водорода, мы должны подробнее рас-
смотреть гамильтониан нашей системы (115.3). Обозначим через На(\}
часть гамильтониана Н (115.3), равную
ЯД1)= — , (115.6)-
а 2ц 1 гл' ' ’
а через ЯА(2)— другую его часть, равную
Ь2 z,2
Очевидно, что гамильтониан На(1) есть гамильтониан, соответствующий?
движению первого электрона (1) вокруг ядра (я), а Нь(2) есть гамиль-
тониан для движения второго электрона около ядра (Z>). Полный гамиль-
тониан Н может быть написан в виде
Я=Яо(1)-|-Я&(2)-|-IF(1, 2), (115.3').
где
р2 р2 Р2
Г(1,2)=-^-^—(115.8).
га2 ГЬ1 '12
Обратимся к случаю больших расстояний R. Пусть первый электрон
находится в атоме (а) (около ядра а), а второй — в атоме (Ь) (около
ядра Ь). Тогда величиной IF(1, 2) можно пренебречь, так как эта ве-
личина есть энергия взаимодействия второго электрона с ядром (а) плюс
энергия взаимодействия первого электрона с ядром (Ь) и, наконец, плюс
энергия взаимодействия обоих электронов. Если атомы далеки друг от
друга, то все эти три величины малы. Поэтому приближенно в урав-
нении (115.4) величину IF(1, 2) можно отбросить, и мы получим урав-
нение:
[ЯД1) + ЯЙ(2)]Ф=ЯФ. (115.9)
Это уравнение описывает два невзаимодействующих атома водорода при
условии, что первый электрон находится в атоме (а), а второй в атоме (Ь).
Решение этого уравнения тотчас же может быть написано. Это — не
что иное, как произведение волновых функций для нормального состоя-
ния атома водорода. Действительно, пусть фд(га1) есть волновая функция*
нормального состояния атома водорода (я) для первого электрона,
426
ОБРАЗОВАНИЕ МОЛЕКУЛ
[ГЛ. XXIII
Ф^(г&2) — волновая функция нормального состояния атомов (Ь) для
второго электрона; тогда в силу (115.6) и (115.7)
(115.10)
Я&(2)<Ьй(ги)=£0фй(гм). (115.10')
В качестве решения уравнения (115.9) мы можем взять
Ф1(Г1, r2) = <|)a(ral)d>ft(ri2). (115.11)
^Соответствующее ему значение энергии Е будет 2£’о.
Если бы не было вырождения, то решение (115.11) и было бы ну-
левым приближением. Однако, на самом деле в рассматриваемой задаче
имеется обменное вырождение. Очевидно, что кроме решения (115.11)
возможно и такое решение, когда на первом атоме (а) находится второй
электрон (2), а на втором атоме (Ь) находится первый электрон (1).
Чтобы усмотреть это решение, разобьем гамильтониан (115.3) на отдель-
ные слагаемые следующим образом:
Я=/7а(2) + Яй(1)+1Г(2, 1), (115.3")
где
(115.6')
га2
«суть гамильтонианы для атомов водорода, когда второй электрон (2)
.находится в атоме (а) и соответственно когда первый электрон находится
в атоме (Ь). Далее,
z»2 z>2 z>2
Г(2, 1)= — е~ — ~ + (И5.81)
га\ ГЬ2 г12
есть взаимодействие электронов и электронов и ядер, принадлежащих
разным атомам. При достаточно большом расстоянии между атомами (а)
и (Ь) этой величиной можно пренебречь, и уравнение (115.4) превра-
тится в упрощенное:
[Яв(2)4-Я,(1)]Ф = ЕФ. (115.9')
Это опять подобно (115.9) есть уравнение для двух невзаимодействую-
щих атомов водорода, и его решение будет
ф2(Г1, г2) = фа(га2)фй (/„), (115.1 Г)
т. е. отличается от (115.11) перестановкой (обменом) электронов. Разу-
меется, что соответствующее значение энергии Е есть опять-таки 2Е$.
Таким образом, для больших R уравнение (115.4) имеет два решения
(115.11) и (115.1 Г), принадлежащих энергии 2Е0. Эти два решения
иллюстрируются схемой, изображенной на рис. 77. При учете взаимо-
действия между атомами 1Г(1, 2) и IF(2, 1) решение Ф не будет, ко-
нечно, совпадать ни с ни с ф2, но нулевое приближение к Ф будет
§ 115]
МОЛЕКУЛА ВОДОРОДА
427
линейной комбинацией из и ф2 как всегда, при наличии вырождения.
Поэтому мы можем положить:
Ф==С1Ф1 +С2Ф2 + ?> (115.12)
где сх и с2 — подлежащие определению коэффициенты, а ср — малый (по-
скольку расстояния R не очень малы) добавок к нулевому приближению.
Рассматривая ср как малый добавок, мы будем пренебрегать произ-
ведениями IF(1, 2) ср, IF(2, 1)ср, еср, так как W и s сами рассматри-
ваются как малыек величины. Вставляя (115.12) в (115.4) и пользуясь
обозначением (115.12), мы получим:
= 2f0 (CjCpj 4- с2ф2) е 4- с2ф2) 4-
4-(2£’04-е)<р. (115.13)
Здесь мы произведем разбиение на части согласно (115.3) и (115.3'):
€1[ЯО(1)4-Я6(2)4-17(1, 2)]ф14-С2[Яо(2)4-Яй(1)4-17(2, 1)] ф24-
4- [На (1) 4- Нь (2)] ? 4- 17(1, 2) ср = 2Ей (С1фх + с2ф2) 4-
4-е(С1ф14-С2ф2) + (2£0 + 4<р. (115.14)
Пользуясь тем, что и сЬ2 суть решения уравнений (115.9) и (115.9')
с E—2Eq и пренебрегая произведениями PFcp, еср, мы найдем:
[Яв (1) 4- Яй (2)] <р - 2£о(р = [г - I7( 1, 2)] 4-
+ [s-W> 1)]с2ф2. (П5.15)
Это — неоднородное уравнение для определения поправок к волновой
функции ср и к собственному значению е. Однако, у нас еще не опре-
делены коэффициенты сг и г2, входящие в правую часть уравне-
ния (115.15).
Для определения их заметим, что если бы справа в (115.15) стоял
нуль, то мы имели бы для ср однородное уравнение, совпадающее
с (115.9), которое имеет решение d>j. Согласно известной математиче-
ской теореме неоднородное уравнение имеет решение лишь в том случае,
если его правая часть ортогональна к решению однородного уравнения.
Иными словами, должно иметь место равенство
J{[e— 17(1, 2)]^ + [8—17(2, 1)]с2ф2} <М^2 = 0, (115.16)
где dvr = dx1dy1dz1, dv2 — dx2dy2dz2. Это дает нам одно уравнение
для двух коэффициентов сг и с2. Легко получить и второе. Для этого
в (115.13) член Ну представим в другом виде, именно:
/Zcp = [/7J2) + //,(l)]cp-pi7(2, 1)ср;
пренебрегая опять IFcp, как величиной второго порядка малости, мы
получим вместо (115.15):
[На (2) 4- Hb (1)] ®- 2£о® = [г - 17(1, 2)] С1фх 4-
4~[е—17(2, 1)]с2ф2. (115.15')
Левая часть совпадает с уравнением (115.9'), которое имеет решение ф2.
428
ОБРАЗОВАНИЕ МОЛЕКУЛ
[гл. ХХШ
Опять-таки правая часть неоднородного уравнения для ср должна быть
ортогональна к решению однородного уравнения ф2. Это и дает нам
второе уравнение:
J {[g— U7(l, 2)j^i + [s— W(2, 1)]с2ф2} ф2^^2 = 0. (115.16')
Для дальнейшего введем сокращенные обозначения:
К= j VT(1, 2)ф1(!)1б?и1^2= J ¥Г(2, 1)ф2ф2</гу^2, (115.17)
А = j 1Г(1, 2) ф3ф1^1^2== JVT(2, Пф^аЦ^. (115.18)
Приведенные здесь равенства интегралов вытекают из того, что IF(1,2)—
= />i'2IF(2, 1) и ф2 = Р1'2ф1, так что интегралы отличаются лишь обо-
значением подинтегральных переменных и поэтому равны. Функции фх
и ф2 неортогональны между собой, поэтому мы введем еще третий
интеграл *):
Sz=\ft$2d'Oldv2. (115.19)
С помощью этих обозначений (115.15) и (115.15')'записываются в виде
(е —tf)C1-|-(sS2_ Л)с2 = 0, (115.20)
(eS2 — Л)С!-|-(е — К)с2 = 0. (115.20’)
Отсюда находим сначала уравнение для е:
(г — КУ — (г£2 — Л)2 — 0. (115.21)
Это уравнение дает два корня:
= (115.22)
£2 = f+^- (115.22')
Подставляя эти значения в (115.19), найдем две системы решений для
с2, г2. Именно, для £==£-[
г1=-г2 (115.23)
и для е = е2
q = r2. (115.23')
Следовательно, наши решения могут быть написаны в таком виде:
£й=2£о + гЕ^. Фв = ф!-ф2 (115.24)
(антисимметричные решения) и
Е^Ей + *±Л, ф^=ф1 + ф2 (115.24')
(симметричное решение).
*) и ф2 ортогональны лишь для 7?= со. Для /? —О S = l.
§ 115]
МОЛЕКУЛА ВОДОРОДА
429
Рассмотрим теперь подробнее значение полученных поправок к энер-
гии. Для этого выпишем подробное значение интегралов (115.17) и
(115.18). Подставляя в (115.17) 1Г(1, 2) из (115.8) и из (115.11),
мы получим *):
к=.[ {- £-£+£}к
^2 £>2
так как член — не содержит координат второго электрона, а----
гЬ\ га2
координат первого, и так как в силу нормировки
j Ф2 Ча1) dvx = 1,
то, обозначая через р^(2)=—среднюю плотность электриче-
ского заряда, создаваемую электроном (2) в атоме (#), через рд(1) =
=— — среднюю плотность электрического заряда, создаваемую
электроном (1) в атоме (я), мы сможем выразить К в новой форме:
Р, (2) dv2 + С £ ра (1) dv1 + [ (115.25)
J ra2 J rb\ J '12
Первый интеграл есть средняя потенциальная энергия электрона (2) ато-
ма (Ь) в поле ядра (я), второй интеграл — та же величина для первого
электрона (1) атома (а) в поле ядра (Ь) и, наконец, третий интеграл
есть средняя потенциальная энергия электронов (1) и (2), находящихся
в разных атомах. Таким образом, К есть не что иное, как средняя
энергия электростатического взаимодействия атомов кроме взаимо-
действия ядер, которое мы считаем отдельно [см. (115.2)].
Интеграл (115.18) представляет собой обменную энергию. Под-
ставляя в (115.18) значение 117(1,2) и и ф2, мы получим:
А = I К ~ К + £ ** (^2) Чы) dv,dv2.
JI ra2 rbl -12)
Обозначая обменную плотность так, как мы это делали при рассмотре-
нии атома Не, через
рбй(1)=— «ШШ-
мы можем написать А в виде
A = s Jiрйй (2) + 5 Ji?аЬ (1} dV1+; (115.26)
последний член есть обменная энергия электронов, совершенно такого
же вида, как та, что была нами получена при рассмотрении атома. Раз-
личие заключается в том, что там речь шла об обмене электронов, со-
стояния которых различались энергией электронов, а здесь состояния
*) Если подставить U7(2, 1) из (115.8) и ф2 из (115.11), то читатель сможет
непосредственно убедиться в справедливости равенства двух интегралов
в (115.17).
430 ОБРАЗОВАНИЕ МОЛЕКУЛ [ГЛ. XXIII
и Фа различаются положением электронов у атома (а) или у атома (Ь).
Обмен электронами происходит между атомами (а) и (Ь).
Первые два члена представляют собой поправки к обменной энергии,
происходящие из-за неортогональности волновых функций, именно:
J ФЛ) Ф» (Г61) = J Ф« (^2) Ф6 Ы ^2 • (115.19')
При R —> оо волновые функции фд и ф6 в силу экспоненциального
убывания с увеличением расстояния от ядер (а) и (Ь) столь мало пере-
крываются отлично от нуля вблизи ядра (а), а — вблизи ядра (#)],
что S очень мало и стремится к 0. Напротив, при/? = 0 ядра (я) и (#)
совпадают. Тогда фл и ф& суть волновые функции одного и того же
атома водорода. В силу нормировки фа и ф^ при R — Q S равно 1.
Поэтому
0<5=^1. (115.27)
Равным образом и S’2 (115.19) также заключено в этих пределах. Та-
ким образом, полученные нами формулы (115.24) и (115.24') для энер-
гии двух атомов водорода совпадают по своему физическому смыслу
с соответствующими (115.21), (115.22) формулами для энергии атома Не,
именно, поправки складываются из энергии кулоновского взаимодейст-
вия К и из обменной энергии А. Некоторое различие обусловлено лишь
неортогональностью волновых функций (члены с S и S2). Мы можем
теперь написать энергию U(R) двух атомов водорода для антисимме-
тричного состояния Фд и симметричного Ф .
На основании (115.1), (115.2) и (115.24), (115.24') имеем:
и____I — I
Эти формулы можно переписать в виде:
t4 = 2£-0+(| (115.28)
4 = 2^o+(J + ^)+^—52 (И5.28')
£>2
Тогда члены представляют собой среднюю кулоновскую энергию
двух атомов водорода, находящихся на расстоянии R между собой.
А — обменная энергия. Последний член, пропорциональный S2, включает
поправки на неортогональность волновых функций, послуживших нам
в качестве нулевого приближения.
С помощью формул (115.25) и (115.26) может быть вычислена и ку-
лоновская, и обменная энергия. Для этого достаточно подставить в эти
интегралы выражение для волновой функции нормального состояния водо-
§ 115]
МОЛЕКУЛА ВОДОРОДА
431
рода. Эта функция известна и есть просто экспоненциальная функция:
4(/j = -?2__e «
Т У4тагЗ
(115.29)
[например, фв(гл) и фл(гл2): каждая
Рис. 78. Энергия взаимодействия двух
атомов водорода для триплетного 3S и
сингулетного состояний. В последнем
состоянии образуется устойчивая моле-
кула Н2.
где г — расстояния электрона от ядра, а о, — радиус первой орбиты
Бора. Чтобы получить функции фд(гл1), (г&2) и т. д., нужно вместо г
в предыдущую формулу подставить гаХ или гЬ2 и т. д., так как эти
величины есть как раз расстояния какого-либо из электронов до одного
из ядер (см; рис. 77).
Мы не будем производить здесь вычисления этих интегралов. Заме-
тим лишь то, что как интеграл К, так и А содержат волновые функции,
относящиеся к различным атомам
из этих функций экспоненци-
ально убывает с увеличением гаХ
и г62]. Поэтому оба интеграла
К и А отличны от нуля лишь
постольку, поскольку волновые
функции, а, стало быть, и
электронные оболочки атомов
взаимно перекрываются.
В результате оба интеграла
убывают с увеличением расстоя-
27?
ния между атомами 7?, как е а .
На рис. 78 изображена взаимная
энергия атомов Ua(R) и US(R)
как функция расстояния между
атомами R, получающаяся в ре-
зультате вычисления кулонов-
ской К и обменной А энергий *).
Величина 2£*0 принята за О
отсчета энергии. Расстояние R
измерено в единицах боровского
радиуса, так что по оси абс-
• п В
цисс отложено не R, а — .
• Как видно из рисунка, для антисимметричного состояния (Фд) энер-
гия Ua(R) отвечает отталкиванию двух атомов водорода, так что мо-
лекула Н2 образоваться не может. Напротив, для симметричного состоя-
ния энергия US(R) имеет минимум при RQ— 1,4-<2 = 0,74-10~8 см,
так что атомы водорода будут в этом случае иметь тенденцию нахо-
диться на расстоянии /?0 друг от друга. В симметричном состоянии,
следовательно, образуется устойчивая молекула водорода Н2. Мы сейчас
свяжем эти два рода состояния с направлениями спинов электронов. Это
*) По поводу вычисления интегралов К и А см. Б е т е, Квантовая меха-
ника простейших систем, стр. 360—361.
432
ОБРАЗОВАНИЕ МОЛЕКУЛ
[ГЛ. XXIII
совсем нетрудно сделать, если вспомнить результаты, полученные нами
для атома Не § 112. Полученные нами волновые функции для моле-
кулы Н2 зависят лишь от координат центров тяжестей электронов гх и г2.
Полная волновая функция Ф должна еще зависеть и от спинов электро-
нов szl и sz2. Так как взаимодействием спинов с орбитальным движением
и взаимодействием спинов между собой мы пренебрегали, то волновая
функция Ф представляется как произведение функции Ф от координат
центров тяжести электронов на функцию S от спинов szl и sz2. Так
как электроны подчиняются принципу Паули, то волновая функция Ф
должна быть антисимметрична при перестановке электронов. Так же как
и в случае атома Не, мы имеем две координатные функции Ф: симме-
тричную Ф^ и антисимметричную Фа.
Чтобы в обоих случаях вся функция Ф была антисимметрична, нужно,
чтобы для Ф = Фу спиновая функция S(szl, ^2) была антисимметрична
по спину Напротив, для антисимметричной функции Ф = ФбГ
опиновая функция должна быть симметрична (£=Д). Очевидно, что
опиновые функции Sa и Д будут совершенно такими же, как и полу-
ченные нами в § 112. Именно, Дописывает состояние с антипараллель-
ными спинами (см. § 112). Таким образом, состояние Ф^ с энергией US(R)
есть сингулетное состояние (противоположно направленные спины). Такое
оостояние в молекулах обычно обозначают знаком 12. Состояние Фд
с энергией Ua(R), напротив, есть триплетное состояние (параллельные
.спины). Это состояние обозначают знаком 32.
Обращаясь к кривым для Ua и Us рис. 78, мы можем выразить
приведенный там результат так: два атома водорода, имеющих элек-
троны с противоположно направленными спинами (^-состояние), притя-
гиваются и образуют молекулу. Два атома водорода, имеющих элек-
троны с параллельными спинами (32-состояние), отталкиваются.
Притяжение или отталкивание атомов водорода зависит от знака
обменной энергии А (так как энергии Ua и Us отличаются лишь зна-
ком А). Таким образом, образование гомополярной молекулы Н2 опре-
деляется обменными силами, и этим объясняется то, что ни в классиче-
ских теориях, ни в примитивной квантовой теории Бора нельзя было
построить теорию гомополярной связи. Мы обратимся теперь к некото-
рым подробностям, касающимся потенциальной энергии US(R) молекулы
водорода Н2. На рис. 78 кривая US(R) изображена отдельно от кривой
триплетного состояния Ua (R). Зная аналитическое выражение для Us (/?),
мы можем найти положение равновесия (точку /? = /?0) из уравнения
^5) = о. (115.30)
Разлагая далее US(R) по степеням отклонения от положения равно-
весия (R = Rq)j мы получим:
и. (Я)=и, (Я,)+1 @ (R - ад+
§ 115]
МОЛЕКУЛА ВОДОРОДА
433
Это разложение справедливо для малых отклонений (/? — /?0). Если
было бы достаточно, в смысле точности, ограничиться только членом
разложения с (R— 7?0)2, то мы имели бы дело с гармоническим осцил-
лятором. Частота этого осциллятора может быть получена следующим
образом. Потенциальная энергия осциллятора, обладающего массой ц
и частотой о)о и совершающего колебания, около положения равнове-
сия /?0, равна
U(R) = const. 4- ф (R — Rtf.
Сравнивая это с предыдущей формулой для Ц.(/?), мы находим:
Отсюда
Заметим, что так как речь идет об относительном движении ядер, то
под g следует разуметь приведенную массу двух атомов водорода, т. е.
если через шц обозначить массу атома водорода, то
1 2
- = — . (115.33)
С помощью формулы (115.32) мы можем найти частоту молекулярных
колебаний <оа по кривизне потенциальной кривой US(R) в точке
равновесия Ro. Третий член в (115.31) дает поправку на отклонение
от гармоничности.
Для больших энергий колебания эта поправка будет играть возра-
стающую роль. Если энергия колебаний Е будет больше значения
потенциальной энергии US(R) на бесконечности [на рис. 78 US(R)
положено равным нулю, так что речь идет о то моле-
кула вообще не будет колебаться, а диссоциирует. Энергия Z),
необходимая для диссоциации, по классической механике была бы
равна —Us(Rq}-
Чтобы получить правильное значение энергии диссоциации молекулы,
нужно еще учесть, что в самом нижнем состоянии молекула имеет по-,
ложительную нулевую энергию колебаний (см. рис. 78). Эту энер-
гию нужно вычесть.
Таким образом D равно
D = -^(7?o) + ^;
таким путем мы можем найти и энергию диссоциации.
Итак, произведенный расчет позволяет найти: 1) положение равно-
весия /?0, 2) частоту молекулярных колебаний <оо и 3) энергию диссо-
циации D молекулы Н2. Все эти величины известны из опыта. Величи-
на /?0 входит в момент инерции молекулы/, который равен и
28 Блохинцез
434
ОБРАЗОВАНИЕ МОЛЕКУЛ
[гл. XXIII
Теоретическое значение Эксперимен- тальное значе- ние
0,735-10-8 см 4280 см~1 4,37 eV 0,753-10-8 см 4390 см-' 4,38 eV
может быть определен по спектральным данным из формулы Деландра
(ср. § 43). Частота колебаний <оо опять-таки определяется из спектраль-
ных данных. Величина работы диссоциации может быть определена и
оптически, и химически. Ниже мы приводим таблицу, в которой даны
результаты вычислений Хиллера-
аса *) для Н2 и опытные данные.
Эти данные показывают прекрасное
согласие, особенно если учесть то,
что первые две величины (/?0 и <о0)
очень чувствительно зависят от
формы кривой /7у(/?). Кроме того,
отметим, что достигнутая' Хиллера-
асом точность не является предель-
ной и могла бы быть еще повышена.
Достигнутый квантовой механикой
успех в расчете молекулы Н2, основанном лишь на том факте, что эта
молекула состоит из двух протонов и двух электронов (без привлечения
каких-либо произвольных констант), является одним из крупнейших успе-
хов современной квантовой теории.
§ 116. Природа химических сил
В химии различают два рода связей, приводящих к образованию
молекул: ионные (гетерополярные) и гомополярные. Ионная связь реали-
зуется в тех случаях, когда молекулу можно представить себе как
образование из положительных и отрицательных ионов (пример NaCl).
Гомополярная связь реализуется в тех случаях, когда деление на ионы
провести невозможно. Типичным случаем гомополярной связи являются
молекулы из одинаковых атомов (пример Н2).
Теорию ионных связей разрабатывали еще и до квантовой механики,
и не без успеха. Основная идея ионной связи (валентности) принадлежит
Косселю. Согласно этой идее гетерополярная валентность элемента опре-
деляется числом электронов, которое нужно отнять (у электроположи-
тельного элемента) или прибавить (к электроотрицательному элементу)^
чтобы получить ион, имеющий электронную оболочку ближайшего
инертного газа. Так, от Na нужно отнять один электрон, чтобы полу-
чить оболочку Ne. К С1 нужно прибавить один электрон, чтобы полу-
чить оболочку Аг. Таким образом Na+ и С1“ являются как бы заря-
женными атомами инертных газов.
При этих условиях основную роль в ионной связи должно играть
кулоновское притяжение разноименно заряженных ионов, поскольку
электронные оболочки инертных газов химически неактивны. Однако,
известно, что одни электростатические силы не могут обеспечить устой-
чивого равновесия. Поэтому помимо кулоновского притяжения зарядов
*) Сводные данные о молекуле Н2 см. у Б е т е, Квантовая механика про-
стейших систем, стр. 370.
§116]
ПРИРОДА ХИМИЧЕСКИХ СИЛ
435
е1
ионов —у необходимо ввести еще некоторое отталкивание на близких
расстояниях. Эти отталкивательные силы в классической теории не могли
быть рассчитаны, но введение их казалось эмпирически обоснованным,
поскольку атомы инертных газов отталкиваются друг от друга на малых-
расстояниях. Отталкивательные силы брались в виде
а
j-m ’
где а и пг — эмпирически определяемые константы. Полная потенциальная
энергия двух ионов имеет поэтому вид *)
Щг)=-у + ^. (116.1)
Если на указанном пути удавалось подойти к проблеме гетерополярной
связи, то проблема гомополярной связи оставалась совершенно темной.
Попытки рассчитать молекулу Н2 никогда не приводили к удовлетвори-
тельному результату. Из изложенной выше квантовой теории молекулы
Н2 ясна и причина этих неудач. Главную роль в образовании молекулы
Н2 играют обменные силы, существование которых является особенностью
самой квантовой механики. Сами по себе эти силы не требуют привле-
чения какого-либо нового взаимодействия частиц. Они возникают из того
же кулоновского взаимодействия электронов в молекуле Н2. Кроме того,
как мы видели, для построения правильной теории молекулы Н2 необ-
ходим учет принципа Паули, т. е. принципа неразличимости частиц.
Незнание этих сторон дела и являлось причиной невозможности решить
проблему строения даже простейшей молекулы до открытия квантовой
механики.
Напротив, успешное решение проблемы молекулы Н2 средствами
квантовой механики послужило исходным пунктом для квантовой теории
гомополярной валентности. Не имея здесь возможности входить в под-
робное освещение этого вопроса, ограничимся немногими замечаниями **).
Для Н2 мы получили два состояния: с параллельными и антипараллель-
ными спинами. На рис. 79 изображено распределение плотности элект-
рического заряда электронов р для этих двух состояний. Плотность
электрического заряда в точке г вычисляется из волновой функции
Ф(гр г2) по формуле
p(r)= — Ф(г, r’)dv'. (116.2)
Если спины атомов параллельны, то Ф = Фд. В точке г = гг = 0
(узловая плоскость). Благодаря этому плотность р в области между
атомами имеет минимум (рис. 79, а). Напротив, в состоянии с парал-
*) Заметим, что квантовая механика дает иной вид отталкивательного члена,
лучше согласующийся с опытом.
**) Подробное изложение этого вопроса читатель найдет в книгах: М. Б о р н,
Химическая связь и квантовая механика, ДНТВУ, 1932; Г. Гельман, Кван-
товая химия, ОНТИ, 1937.
28*
436
ОБРАЗОВАНИЕ МОЛЕКУЛ
[гл. ХХШ
дельными спинами Ф = Ф^ узловой плоскости не имеется и плотности
зарядов обоих атомов как бы сливаются (рис. 79, Ь\ Слияние плотностей
(образование гомополярной связи) мы сопоставляем валентному штриху
Н — Н. Образование минимума плотности — отсутствию такой связи.
Можно показать, что силы гомополярной связи обладают свойствами
насыщения — признаком, характерным для валентных сил. Нетрудно
видеть, что присоединение третьего атома Н к молекуле Н2 не приво-
дит к созданию обменных сил между электронами молекулы и третьим
атомом. В самом деле, обозначим волновую функцию электронов моле-
кулы (^тома а и Ь) через Ф^(гр r2)Sa($p s2). Волновую функцию
электрона третьего атома (с) обозначим^ через фс(г3) &/а ($3)- Спин тре-
тьего электрона мы взяли направленным по оси OZ. Можно было бы
взять и противоположное направление. Важно лишь то, что спин треть-
а—распределение плотности зарядов в двух отталкивающихся атомах Н(32); Ъ—распределе-
ние плотности зарядов в молекуле Н2 fE).
его электрона противоположен спину одного из электронов молекулы.
Чтобы получить функцию всей системы, нужно из Ф^а и ф^ образо-
вать антисимметричную в частицах функцию (учет принципа Паули).
Единственная антисимметричная функция, которую можно построить из
ФД, и фД есть
Ф(гр r2, r3, s2> 53)=^{Ф,(Г1,г2)фс(г8)5о(5р *<№($<,) +
4-Ф/Гр Гз)Фв(г2)5а(^8, '1)&/,($2) +
+ Ф/г2, г8) (г,) sa (s2, s3) &/„(*!)}• (116.3)
Функции ^(Sp s2) согласно (111.13) имеют вид
-L {s4i (S1) (s2) - &/. (s2) (S1)}.
r *
Исходя из свойств ортогональности и нормировки спиновых функций
Sx(s) (а==±^-) (40.15), легко убедиться, что все три спиновые функ-
§ 117] СИЛЫ ВАН-ДЕР-ВААЛЬСА 437
ции, фигурирующие в суперпозиции (116.3), ортогональны между
собой. Поэтому, если мы возьмем | Ф |2 и просуммируем по всем зна-
чениям )всех трех спинов, чтобы получить вероятность w (гр г2, г3)
положения электронов в окрестности точек гр г2, г3, то мы получим:
«’(п, Г2, г3)= £ 1Ф12 = | {1ф5(п. г2)121Фс(г8)1г-Ь
«?2» $3
+ 1фЛ1, r3)l2l W 12 + 1ф.(г2, гв)Р|фс(г8)12}- (116.4)
Обозначая, как мы это делали в предыдущем параграфе, плотность за-
ряда электрона, находящегося на атоме (а), через ра, на атоме (£)— че-
рез р6, наконец, на атоме (с) — через ре, а обменную плотность через
раЬ, мы можем, пользуясь значением (115.24'), (115.11), (115.1 Г),
написать полученную вероятность конфигурации электронов в виде
Г2> r8) = l {[pa(r1)p&(r2) + 2PaS(r1)pa&(r2)]pc('-3) +
+ [Ро ('l) ?b ta) + 2Ра6 (П) ?ab (^)] ?е W +
+ [Ра (>2) ?b W + 2Po6 W ?ab (''в)] ?c (П)} > (116.5)
где
pe(ri)=—рИг1)=— pc(''i)=—еФ2Ы (И6.6)
и
Pab (Л) = — е^а (Ла) Ы’ (116.6')
Из этого выражения мы видим, что для третьего атома (с) не возникает
обменной плотности (типа рас, рЬе), а следовательно, и обменных сил
с атомами (а) и (Л), образующими молекулу. Кулоновское же взаимо-
действие остается. Поэтому третий атом будет отталкиваться. Этим
и доказывается способность обменных сил к насыщению и правомочность
сопоставления валентного штриха слиянию плотности электрических за-
рядов двух атомов.
Заметим, что никакого строгого разграничения между гомополярной
и ионной связью на самом деле провести нельзя. Это — просто два
крайних случая. В типичном случае гомополярной связи заряд распре-
делен симметрично между обоими атомами. Если атомы неодинаковы,
то такая симметрия нарушается. Если, наконец, симметрия нарушается
резко, так что заряд электронов сосредоточивается преимущественно
около одного из атомов, то мы получим случай ионной связи.
§ 117. Силы Ван-дер-Ваальса
В предыдущем нами были рассмотрены валентные силы. Эти силы,
будучи связаны с ориентацией спинов электронов, обладают свойством
насыщения. Кроме того, эти силы действуют на коротких расстояниях.
Они определяются степенью перекрытия электронных плотностей, при-
надлежащих взаимодействующим атомам. Так как по мере удаления от
атома электрическая плотность убывает экспоненциально с увеличением
438 ОБРАЗОВАНИЕ МОЛЕКУЛ [ГЛ. XXIП
расстояния от центра атома, то и валентные силы убывают экспонен-
циально с увеличением расстояния между атомами.
Помимо этих валентных сил между атомами и молекулами действуют
еще особые силы, имеющие всегда характер сил притяжения. Это —
силы Ван-дер-Ваальса. Замечательным свойством этих сил является то,
что они действуют между электрически нейтральными системами и си-
стемами, не обладающими электрическим моментом. Так, например, они
действуют между атомами Не, распределение заряда в которых обла-
дает шаровой симметрией, так что эти атомы не обладают ни дипольным,
ни квадрупольным, ни каким-либо высщим электрическим моментом.
Второе важное свойство этих сил заключается в том, что эти силы не
зависят от температуры. Природа этих сил оказывается также квантовой
(как это впервые выяснил Лондон).
Эти силы можно получить, если рассмотреть взаимодействие доста-
точно удаленных друг от друга атомов. На большом расстоянии между
атомами валентные силы, вычисляемые из первого приближения теории
возмущения, оказываются уже очень малыми. Напротив, на этих рас-
стояниях оказывается уже невозможным игнорировать второе прибли-
жение, в котором учитывается деформация электронных оболочек ато-
мов. Объясняется это тем, что дополнительные поправки к энергии
взаимодействия атомов, вычисляемые во втором приближении, убывают
о 1
с ув сличением расстояния R между атомами пропорционально , в то
время как энергия валентных связей убывает пропорционально е а • При
больших R второе приближение оказывается больше первого.
Производя для больших расстояний подсчет энергии во втором при-
ближении, можно получить силы Ван-дер-Ваальса. Не входя в эти рас-
четы, мы поясним основную идею квантовой теории сил Ван-дер-Ваальса
на простом примере, позволяющем точное решение задачи. Вместо
реальных атомов рассмотрим два одномерных осциллятора с собственной
частотой <оо (такая модель атома фигурирует в классической теории
дисперсии). Обозначим координату электрона в первом атоме через xv
а его импульс через координату электрона во втором атоме
через х2, импульс через р2. Расстояние между «атомами» пусть будет R.
Электрический момент первого атома есть exv а второго ех2. Если
расстояние R между этими атомами достаточно велико, то энергия
взаимодействия этих атомов может быть представлена как потенциальная
энергия взаимодействия двух диполей с моментами ехг и ех2. Эта энер-
гия равна
(117.1)
Если осцилляторы покоятся, то л'1=х2 = 0 и их дипольные моменты
равны нулю. Так как, кроме того, оба «атома» электрически нейтральны,
то никакого взаимодействия между ними не получается.
Согласно классической теории, взаимодействие возникает лишь между
колеблющимися осцилляторами. Не вдаваясь в расчет этого взаимодей-
§ 1'17]
СИЛЫ ВАН-ДЕР-ВААЛЬСА
439
ствия, мы можем предсказать, что его величина будет зависеть от
температуры Т. Это ясно уже из того, что при Г=0° абс. колебаний
нет и х1=х2 = 0. Иное дело получается по квантовой механике. Даже
при абсолютном нуле имеются нулевые колебания, которые приводят
к тому, что средняя энергия взаимодействия рассматриваемых нами
осцилляторов не равна нулю.
Для вычисления этой энергии обратимся к расчетам § 100, где как
раз рассмотрен интересующий нас случай взаимодействия двух одномер-
ных осцилляторов, обладающих частотой соо и массой pi. Энергия вза-
имодействия осцилляторов была предположена в виде 1хгх2 [см. (100.2)].
В нашем случае энергия взаимодействия осцилляторов выражается фор-
мулой (117.1). Стало быть, полагая в формулах § 100
(117.2)
мы можем воспользоваться всеми результатами этого параграфа. Сейчас
нас интересует наименьшая нулевая энергия наших осцилляторов. Эта
энергия равна
F0==^L_]_ ^1=1^4-^), (117.3)
где ©! и о)2 определяются из формулы (100.5)
0)? = (1)2 4- — , (1)2 _ ш2-L Ф
1 V 1 и JJL
Отсюда, считая ~ , находим:
f 1 , X 1 / X \2 . 1
(1)х = (00 1 -]---2-— [ -^2 j |>
L И) 8\^о/ j
Г1 х I / * \2 г 1
(1>2-(Од II 2 о I 2 I *1 * * ’ I
L 8 Х^о/ J
и, следовательно,
। 1 X2
®1 + ®2 = 2«)0-т—(117.4)
Имея в виду значение X для нашего случая (117.2), находим из (117.3)
и (117.4) нулевую энергию двух дипольно взаимодействующих осцил-
ляторов:
(/?) = Лю0 у —3 • #6 4“ • • • (117.5)
И шо
Мы видим, что нулевая энергия оказывается функцией расстояния 7?
между осцилляторами — «атомами» и, стало быть, играет роль потен-
циальной энергии взаимодействия этих «атомов».
Отбрасывая несущественную аддитивную постоянную йо)о, получаем
для этой энергии выражение
440 ОБРАЗОВАНИЕ МОЛЕКУЛ [ГЛ. XXIII
Мы видим, что эта энергия обусловлена притягательными силами
(знак—!). Эти силы можно рассматривать как силы Ван-дер-Ваальса
для наших идеализированных атомов. Квантовая природа этих сил ясна
уже из того, что при Л = 0 £7=0, так что в предельном случае клас-
сической механики эти силы равны нулю.
Таким образом, ван-дер-ваальсовское притяжение есть результат
уменьшения нулевой энергии при сближении осцилляторов. Формулу
(117.6) мы можем преобразовать, введя в нее коэффициент атомной
поляризуемости [5 для постоянного поля. Из теории дисперсии мы знаем,
что коэффициент атомной поляризуемости для осциллятора массы р. и
частоты <о0 равен (§ 85) *)
Н <0q — «о2
полагая здесь <о = О, получаем коэффициент поляризуемости для по-
стоянного поля
л е2
? = —2- (117.7)
Внося его в формулу для потенциальной энергии ван-дер-ваальсовской
силы (117.6), получаем:
U(R) = -^±., (117.8)
где
е = Ь)0, (117.9)
т. е. разности между квантовыми уровнями осциллятора. Так как в фор-
мулу для ван-дер-ваальсовых сил входит коэффициент поляризуемости,
получаемый из теории дисперсии, то эти силы в последнее время иногда
называют дисперсионными.
Расчет, проведенный во втором приближении для реальных атомов,
приводит в основном к тому же результату, что и полученный нами
(117.8) для модели атома в виде линейного осциллятора. Именно, кван-
товая формула для потенциальной энергии сил Ван-дер-Ваальса для
реальных атомов гласит:
U(R)= — k1^, (117.10)
где р — атомная поляризуемость в постоянном поле, /—ионизационный
потенциал атома, a k — некоторый численный коэффициент, по порядку
величины равный 1.
Это выражение для ван-дер-ваальсовского взаимодействия хорошо
согласуется с экспериментальными данными, заимствуемыми из изучения
отступлений газов от закона Клапейрона **).
*) Эта формула—классическая. Квантовая формула (85.6) для осциллятора
ведет к тому же результату, в чем предлагаем «убедиться читателю самостоя-
тельно, воспользовавшись матрицей хпк для координаты осциллятора и фор-
мулой (85.25).
**) См. Бете, Квантовая механика простейших систем, § 63. Там же обзор
литературы.
§ 118]
ПАРАМАГНЕТИЗМ И ДИАМАГНЕТИЗМ ATOMQB
441
ГЛАВА XXIV
МАГНИТНЫЕ ЯВЛЕНИЯ
§ 118. Парамагнетизм и диамагнетизм атомов
Основной и простейшей задачей атомной механики из области магнит-
ных явлений является вычисление магнитных моментов атомов, помещенных
во внешнее магнитное поле. Мы уже вычисляли элементарным способом
магнитный момент орбитальных токов в атоме (§ 50). Обратимся теперь
к общим методам.
Наиболее общим образом операторы проекций магнитного момента мо-
гут быть определены как производные (с обратным знаком) от оператора
полной энергии (точнее гамильтониана) по проекциям магнитного поля:
<n81>
В частности, для одного электрона гамильтониан Ну описывающий дви-
жение электрона в магнитном поле, имеет вид
//=i(^ + 7A)2 + f7W+^s^ <118-2>
(знак перед вектором-потенциалом А взят потому, что мы считаем
заряд электрона равным —е). Направим ось OZ по направлению маг-
нитного поля и возьмем вектор-потенциал в форме
Л=------2“Л Ау = ~2~х> (118.3)
Дифференцируя тогда Н m$% = fflzy мы найдем:
Оператор, стоящий в прямых скобках, есть оператор проекции на OZ
момента истинного импульса*). Далее, Рух— Рху есть оператор про-
екции на OZ момента обобщенного импульса Mz. Пользуясь (118.3),
представим (118.4) в виде
i <«. +. 2s-> - v +л=
Как мы видим, оператор состоит из двух частей: не зависящей от магнит-
ного поля и зависящей от него. Рассмотрим их порознь. Первая часть
^==-5^4+^) (118-6)
*) Напомним, что в магнитном поле не ip, а — fР4- — а) есть one-
И и \ 1 с /
ратор скорости.
442
МАГНИТНЫЕ ЯВЛЕНИЯ
[ГЛ. XXIV
имеет собственные значения, которые мы уже находили в теории эф-
фекта Зеемана. Действительно, энергия возмущения в магнитном поле
W——Собственные значения W различны, смотря по тому,
имеем мы дело с сильными магнитными полями (простой эффект Зеемана)
или со слабыми (сложный эффект Зеемана). В последнем случае собст-
венные значения W даются формулой (70.23). Эти собственные значения
отличаются от собственных значений ЭЛг множителем — 3%. Поэтому из
(70.28) находим:
где ntj есть магнитно-квантовое число, j—число, определяющее пол-
ный механический момент, I — орбитальный, ls — спиновый. Потенциаль-
ная энергия этого момента во внешнем магнитном поле есть как раз W.
Она может принимать как положительные, так и отрицательные значе-
,1,3
ния, смотря по значению ^у = +-2> ip •••> 1-
При термодинамическом равновесии будут предпочитаться отрица-
тельные значения W и, следовательно, положительные значения 9Л\
В результате получится средний момент, направленный по полю, т. е.
случай парамагнетизма. Существенно, что ЭЛ^ не может равняться нулю.
Следовательно, одноэлектронные атомы всегда парамагнитны. Вто-
рой член в (118.5)
(Ив-»)
представляет собой магнитный момент, который всегда направлен (как
непосредственно видно) против поля. Тдким образом, этот момент обу-
словливает диамагнетизм. Ок никогда не может быть равен нулю, так
как x2+j/2>0, и поэтому диамагнитный эффект имеет место во всех
-атомах. Однако, легко видеть, что момент ЭЛ" значительно меньше 9Л'г
и может быть пренебрежен в сравнении с последним. Действительно,
eh е2
9Л^ по порядку величины равняется магнетону , а ЭЛ" а2,
где а — размеры атома. ЭЛ*|>9Л" для всех полей 3%, для которых
Все практически достижимые поля удовлетворяют этому условию.
Если мы имеем несколько электронов в атоме, то если их число
четное, полный момент импульса может оказаться равным нулю. Вме-
сте с тем, будет равен нулю и магнитный момент 9Л^, обусловливаю-
щий парамагнетизм. Такой атом будет диамагнитным. Так, например,
в атоме гелия, в основном состоянии, как мы знаем, орбитальный мо-
мент равен нулю, а спиновый компенсирован благодаря противополож-
ному направлению спинов. Поэтому 9Л^ = 0. Гелий должен быть диа-
§ 118]
ПАРАМАГНЕТИЗМ И ДИАМАГНЕТИЗМ АТОМОВ
443
магнитным, что и наблюдается в действительности. Диамагнитную вос-
приимчивость гелия можно вычислите, имея в виду, что для двух элек-
тронов ЭЛ" будет равно
(118.10)
Средние значения х2, у\ в силу сферической симметрии основ-
ного состояния гелия и симметрии электронов в нем равны между со-
^•2 —
бой и равны -у , где г2 — средний квадрат радиуса-вектора. Таким
образом,
др" —___— г2
~ 2^2 3 г ’
Диамагнитная восприимчивость, рассчитанная на один атом, будет равна
<Ж'' 2г2 -
у=___?=г2
(118.11)
С помощью волновых функций для электронов атома гелия (112.23)
можно вычислить среднее значение г2 и получить численное значение
магнитной восприимчивости.
Вычисление 4 с помощью волновых функций дает 4 = —1,87-10~6.
Экспериментальное значение / = —1,88-10“6. Заметим, что выражение
(118.8) для диамагнитного момента совпадает с тем, которое получается
из классической электронной теории *). Однако, только квантовая меха-
ника позволяет вычислить х2 -(-.у2, исходя из констант, характеризую-
щих атом.
Если мы имеем дело с многоэлектронным атомом, то вместо (118.7) мы
получим на основании изложенного в § 98 [см. формулу (98.30)]:
he т h -J- ^+l)-IU+D+^(^+in (11812)
- - 2|5 тЛ1 ‘ ----------Л74Й)-----------/ ’ °18Л2)
где J есть число, определяющее полный момент импульса всех электронов,
L — число, определяющее полный орбитальный Момент, a Ls — число, опреде-
ляющее полный спиновый момент. | m.j J и определяет проекцию полного
момента на магнитное поле. Если J—0, что может быть лишь для атомов
с четным числом электронов, то 30^ = 0 и атом будет диамагнитным, причем
N
Е <118.13)
где АГ—число электронов. Если J $£ 0, то величиной можно пренебречь
в сравнении с Атомы с J ф 0 будут парамагнитными.
*) Ср., Беккер, Электронная теория, § 29.
444
МАГНИТНЫЕ ЯВЛЕНИЯ
[ГЛ. XXIV
§ 119. Ферромагнетизм
Происхождение постоянного магнетизма ферромагнитных веществ
представлялось до последних лет совершенно загадочным. Сущность
явления заключается, как известно, в том, что ферромагнитные тела
могут оставаться намагниченными и в отсутствии внешнего магнитного
поля «Я?. Для объяснения свойств ферромагнетиков Вейсс предложил
теорию, объясняющую постоянный магнетизм наличием внутреннего маг-
нитного поля 3%р которое и заставляет ориентироваться элементарные
магниты, даже если внешнее поле равно нулю. Теория Вейсса позволяет
объяснить многие свойства ферромагнетиков, однако происхождение
внутреннего поля 3^. оставалось неразъясненным.
Для приведения теории Вейсса в согласие с опытом приходится до-
пускать, что поле 3%. имеет колоссальную величину: 106 гауссов. Пря-
мые опыты *) показывают, что такого магнитного поля внутри ферро-
магнетика на самом деле не существует. Гейзенбергу удалось показать,
что силы, ориентирующие элементарные магниты, — обменные силы.
Этим была объяснена природа загадочного вейссового поля. Гейзенберг,
в согласии с данными опыта Эйнштейна и де-Гааса (см. § 55), предпо-
лагает, что намагничивание ферромагнитных тел обусловлено не орби-
тальным движением электронов, а магнитным моментом спина. Далее,
ферромагнетизм, повидимому, следует отнести не за счет валентных
электронов («электроны проводимости»), а за счет электронов внутрен-
них, незаконченных оболочек атомов ферромагнетиков (см. распределе-
ние электронов в Fe, Ni и Со по таблице на стр. 419).
Для простоты допустим, что в каждом из атомов, образующих кри-
сталл, имеется лишь один такой электрон. Взаимодействие такого элек-
трона с соседними атомами можно считать малым и роэтому можно
рассматривать волновую функцию всех электронов, обусловливающих
ферромагнетизм (числом 7V), как соответствующую системе невзаимодей-
ствующих электронов.
Для нумерации состояний заметим, что положение центров атомов
в кристалле (узлы решетки) определяется вектором
т = п^-\-п^-}-пйлй, (119.1)
где nv п2, п3— целые числа, а ар а2 и а3 — основные векторы ре-
шетки. Таким образом, положение каждого атома определяется тройкой
чисел ni9 п2, п3. Ради краткости эту тройку будем обозначать одной
буквой п и называть номером атома. Пусть волновая функция А-го
электрона, находящегося на л-ом атоме, есть
где S—спиновая функция.
*) Дорфман пропускал пучок быстрых электронов через намагниченную
ферромагнитную фольгу. Поле в 106 гауссов должно было бы отклонять эле*
ктроны, чего на самом деле не наблюдалось.
§ 119]
ФЕРРОМАГНЕТИЗМ
445
Поскольку мы пренебрегаем взаимодействием с соседними атомами,
постольку волновая функция всего кристалла в целом будет антисим-
метричной комбинацией вида (108.6') из произведений функций Фл,
относящихся к отдельным электронам. Выбор значков а (-[- 1/2 или
— г/2) у каждой из функций Sa будет означать выбор определенного
распределения спинов (направленных по оси OZ или против нее) среди
атомов кристалла. Если спины всех электронов ориентированы в одном
направлении, например, по OZ, то мы будем иметь дело с полным
насыщением (максимальное намагничивание). Рассмотрим такое состоя-
нхе, когда все спины направлены по OZ, за исключением одного, на-
правленного против OZ. Пусть такой спин находится на атоме но-
мера I, Тогда согласно сказанному выше волновая функция Ф всех
N электронов имеет вид
Ч'< -Ж ’Hi (^) S+v. (sz) ф2 (r2) 5+.,а (s2) ... (г) S_t/, (s,) ...
р -ШЧМ (П9.2)
Учтем теперь взаимодействие электронов с соседними атомами. Для
этого применим теорию возмущений. Мы имеем дело со случаем вы-
рождения, так как, очевидно, электрон со спином, направленным про-
тив оси OZ, может находиться на любом из атомов. Поэтому правиль-
ная функция нулевого приближения будет линейной суперпозицией из Фр
Ф=У ярфр, (119.3)
л=1
причем амплитуды надлежит еще определить. Для этого заметим,
что оператор полной энергии Н электронов равен
N N
£ им, (119.4)
= 1 пт п£т~\
N №
(И9.5)
/1=1
где Н„ — оператор полной энергии /z-го электрона, находящегося на
^2
n-ом атоме,-------энергия взаимодействия /z-го и яг-го электронов, а
гпт
Un(rm)— энергия взаимодействия /гс-го электрона с /z-ым ионом (/г 7^ аи).
Все члены в Н кроме /7° будем рассматривать как возмущение. Под-
ставляя в уравнение. Шредингера /7Ф = £Ф вместо Ф приближенную
функцию (119.3) и имея в виду, что
(119.6)
где — энергия электрона в атоме, мы получим:
I’ п^т-1 тЛ ' J V
v
(119.7)
446 МАГНИТНЫЕ ЯВЛЕНИЯ [гл. XXIV
Умножим теперь это уравнение на Ф*, проинтегрируем результат по
координатам всех электронов и просуммируем по двум значениям спина
sz = 4- у каждого из электронов. При этом мы будем считать функ-
ции (г) и (г), относящиеся к различным атомам, ортогональными *).
Далее при суммировании по спину следует иметь в виду ортогональ-
ность функций Sa (sz) (ср. § 57). В результате мы получим вместо
(119.7)
М- Ео • я,-}- hv \ау — = Еа„ (119.8)
где Iiv есть обменный интеграл (матричный элемент энергии возму-
щения):
= Ц* ф, (г,) фр (г2) ф* (г2) ф* (rj + Ut (г,) + UV (r2) 4-
+ UV (ra) + Ц (rj ) d^dvv (119.9)
Волновые функции c]>z(r) быстро убывают с увеличением расстояния
г от центра атома. Поэтому обменный интеграл Z/f быстро убывает с
увеличением расстояния между атомами I и Z'. Благодаря этому при
решении уравнений (119.8) можно ограничиться матричными элемен-
тами 1ц1, относящимися к ближайшим соседям. Так как в кристалле все
ближайшие соседние атомы равноправны, то обменный интеграл имеет
для них одно и то же значение /. Таким образом, уравнения (119.8)
можно написать в виде
(£_^0)^4-/^[az—^] = 0, (119.9')
где сумма распространена по атомам соседним атому Z. Число ближай-
ших соседей и их расположение зависят от типа кристаллической решет-
ки. Для простой кубической решетки соседние с атомом Z(Zn Z2, Z3) атомы
имеют числа Z', равные Zj + 1, Z2, Z3; Z1? Z2 +1, Z3; Zp Z2, Z3 +1.
Легко видеть, что уравнения (119.9') решаются подстановкой
at=aiMt = const. • е (119.10)
где qv q2, q3 — некоторые безразмерные величины. В самом деле, под-
становка (119.10) в (119.9') дает
Е— NEq = 21 [3 — cos qt — cos q2 — cos ^3], (119*11)
откуда
E(<h’ ft) = ^0 +2713- c°sft — cos?2 — c°S7s]- (И9.12)
Замечая, что lxa, l2a, l3a, где a — постоянная решетки, суть коорди-
наты узла решетки, мы видим, что (119.10) может рассматриваться
как плоская волна с волновым вектором к= — ~ . Веро-
ятность найти спин, направленный цротив OZ, есть | az|2 = const., т. е.
*) На самом деле они ортогональны только приближенно.
§ П9]
ФЕРРОМАГНЕТИЗМ
447
все положения спина равновероятны. Таким образом, амплитуды а1г
определяющие состояние спина, весьма аналогичны волновой функции
свободно движущейся частицы, имеющей заданный импульс. Эта анало-
гия еще усугубляется тем, что, по крайней мере для малых к, энергия
(119.12) может быть написана в виде
const. + 2^2+...,
(119.13}
Л2
где^ = /<22, т. е. в виде, совпадающем с выражением энергии для
свободной частицы. Величину ц* можно рассматривать как эффектив-
ную массу. Существование такой аналогии между распространением в
кристалле спина определенной ориентации и движением свободной ча-
стицы приводит к тому, что, имея в виду состояние (119.3), говорят
о спиновой волне.
Если в кристалле имеется не один, а несколько (г) спинов, ориен-
тированных против оси OZ, то расчет протекает аналогичным образом,
но усложняется тем, что при наличии многих спинов, ориентированных
против оси OZ, могут встретиться пары соседних атомов со спинами,
направленными против OZ. Для этих пар обменные интегралы не равны
нулю. Однако, при небольшом числе г такие случаи будут встречаться
редко, и полное решение может рассматриваться как совокупность не-
взаимодействующих спиновых волн вида (119.9) (или, с корпускулярной
точки зрения как «спиновый газ»). Энергия будет суммой энергий для
каждой из спиновых волн. Если мы обозначим вектор q для &-ой спи-
новой волны через q*, то вся энергия спинового газа, будет
г
Е=ЛЖ0 + 2/ У [3 — cos qlk— cos q2k — cos q3k\. (119.14}
k—\
Из этой формулы следует, что при отрицательном / ферромагне-
тизма быть не может, так как при I <^0 энергия имеет минимум при
наибольшем г. Поэтому при тепловом равновесии первоначальная ори-
ентация всех спинов по оси будет стремиться расстроиться. Напротив,
при положительном обменном интеграле минимум энергии будет дости-
гаться при наименьшем г, так что если некоторая часть спинов ориен-
тирована против оси OZ, то эти спины будут иметь тенденцию ориен-
тироваться по оси OZ (число г будет уменьшаться). Поэтому положи-
тельное значение обменного интеграла является необходимым условием
ферромагнетизма (только в этом случае состояние с наименьшей энер-
гией может быть состоянием, в котором все спины электронов направ-
лены одинаково). Причиной, приводящей к ориентации спинов в одну
сторону, являются, таким образом, не фиктивное магнитное поле
Вейсса, а обменные силы. Ферромагнетизм есть явление квантовое.
Наконец, мы видим, что ферромагнетизм не является свойством от-
дельных атомов, а представляет собой свойство кристалла, что на-
ходится в согласии с тем фактом, что ферромагнитных газов не
существует.
448
ЗАКЛЮЧЕНИЕ
[ГЛ. XXV
Для вычисления намагничения ферромагнетика при какой-либо тем-
пературе Т следует найти, методами статистики, среднее значение г.
Тогда магнитный момент куска ферромагнетика, содержащего N элек-
тронов, будет, очевидно, равен
= (119.15)
где есть магнитный момент одного электрона (магнетон Бора). За
соответствующими вычислениями и другими подробностями мы отсылаем
читателя к специальной литературе *).
ГЛАВА XXV
ЗАКЛЮЧЕНИЕ
§ 120. Формальная схема квантовой механики
Излагая основные положения квантовой механики, мы не стремились
к строгой дедуктивной последовательности. Логическая стройность де-
дуктивного изложения неизбежно влечет за собой абстрактность, кото-
рая скрадывает опытные основания того или иного обобщающего поло-
жения. Напротив, в заключение книги весьма уместно коротко резюми-
ровать основные положения квантовой механики.
Движение микрочастиц характеризуется рядом величин: координатой
частицы х, импульсом р, энергией Е, моментом импульса М и т. д.
Эти величины определяются путем определенных измерительных опера-
ций. Так, например, под х, строго говоря, разумеют координату точки
экрана, фотопластинки и т. п., в которую попадает электрон или дру-
гая частица. Говоря о координате электрона в атоме, мы имеем уже
дело с косвенным определением: если бы можно было поставить в атом
фотопластинку, то координата электрона (пятно на фотопластинке) мо-
гла бы оказаться в таком-то месте. И, на самом деле, определяем ее
косвенным путем. Импульс частицы может быть, например, определен
путем измерения длины волны (в диффракционном опыте).
Задачей квантовой механики являются определение возможных зна-
чений той или иной величины (определение спектра) и вычисление ве-
роятностей того или иного результата измерения. Исходным пунктом
теории является выбор математического аппарата для количественной
формулировки соотношений между различными величинами и вероятно-
стями результатов измерения этих величин. Как мы видели, таким ап-
паратом является аппарат линейных, самосопряженных операторов.
Именно, соотношения между квантовыми величинами можно выразить на
языке таких операторов, а вероятности наблюдения тех или иных зна-
чений величин можно получить из волновой функции Ф. Аргументами
этой функции могут являться значения любых одновременно измеримых
*) Ф. Блох, Молекулярная теория магнетизма, ЦНТВУ, 1934.
§ 120]
ФОРМАЛЬНАЯ СХЕМА КВАНТОВОЙ МЕХАНИКИ
449
величин А, Л4, N, ... Эти величины могут пробегать как дискретные,
так и непрерывные последовательности значений *).
Поскольку задание Ф позволяет вычислить вероятности результатов
всевозможных измерений, совместимых с физической природой системы,
постольку мы говорим, что волновая функция Ф определяет состоя-
ние квантовых систем. Сами механические величины L, 714, N, ...
изображаются линейными самосопряженными (эрмитовскими) операторами
£, М, N, ...
Основное свойство состояний выражается в принципе суперпозиции
состояний если два состояния системы изображаются волновыми
функциями Фх и Ф2, то существует и третье состояние, изобра-
жаемое волновой функцией
Ф^аФ^Я^, (120.1)
где а и b — произвольные числа. Так как ни одно физическое выска-
зывание квантовой механики не меняется, если волновую функцию
умножить на постоянное число, то
Ф и aW (I)
изображают одно и то же физическое состояние. В связи с этим вол-
новые функции берут обычно нормированными к 1 или к 8-функции.
Ввиду того, что конкретный вид условия нормировки зависит от того
представления, в котором мы берем волновую функцию, то мы сейчас
запишем это условие в символическом виде
(Ф, ф)—1 или 8-функции, (120.2)
разумея под (Ф, Ф) либо интегралы
Ч'* (М) Ч; (М) dM,
если аргумент М непрерывен, либо сумму
^Ф*(Л4)Ф(ЛГ),
если он дискретен **). Если функция нормирована, то число а (120.1)
должно иметь вид
а = е\ (120.3)
где а — вещественная фаза. Нормированные волновые функции опреде-
ляются лишь с точностью до постоянной фазы.
*) Если волновая функция дана в импульсном представлении, то мы ее
обозначали через с (рх, ру, pZi t\ если она дана в дискретном, например, энер-
гетическом представлении, то мы обозначали ее через сп (п~ 1, 2, 3, ...).
Сейчас, однако, удобнее обозначать ее одной и той же 'буквой Ф, независимо
от того, в каком представлении она дана. В этом обозначении мы будем иметь:
С(РХ, Ру, Рг, () = ^(Рх, Ру, Рг, *),
ca(t) = c(En, t) = V(En, t), Ea=E1,Ei,... и т. п.
**) Например, M=zx> тогда нормировка будет J Ф*(х)Ф (х) dx=\, или,
например, Л4==Е, где Е дискретно (Е=Еп, и—1, 2, 3, ...). Тогда Ф(Л1) =
= Ф (£) = Ф (£л) = Гд, и условие нормировки будет 21 са |2 = 1.
п
29 Блохинцев
450
ЗАКЛЮЧЕНИЕ
[ГЛ. XXV
Принцигъ суперпозиции состояний образует первое важнейшее поло-
жение квантовой механики и возникает как обобщение фактов, обнару-
живающихся в диффракции частиц.
В качестве второго фундаментального пункта волновой механики
целесообразно взять определение среднего значения из результатов
измерения какой-либо величины L в состоянии Ф. Так как подобно
условию нормировки конкретный вид среднего L зависит о г представ-
ления, в котором берется оператор L и Ч^-функция, то мы запишем
формулу для среднего значения в символическом виде:
£ = (Ф, £Ч;), (П)
разумея под (Чт, £Ч;) либо выражение
j Ф*(Ж).£(М)Ф(2И).<Ш,
если аргумент М непрерывен и оператор £ дан в дифференциальной
форме, либо выражение
Ф* (М') (М") dM'dM",
если аргумент М непрерывен и оператор £ дан в матричной форме,
либо, наконец,
52ф*(/И')л^Ф(М'),
М» М”
если аргумент М—дискретный. Все эти три выражения эквивалентны
друг другу *).
Определение среднего позволяет найти возможные значения вели-
чины L в состояниях, в которых L имеет только одно определенное
значение. Эти состояния характеризуются равенством нулю среднего
квадратичного отклонения
Д£2 = 0. (120.4)
Как было показано в § 20, требование (120.4) ведет к уравнению для
собственных функций оператора £:
= (Ш)
(оператор £ и функции Ф взяты в «/И»-представлении). Уравнение (Ш)
есть либо дифференциальное, либо интегральное, либо бесконечная си-
стема алгебраических уравнений, смотря по природе величины М. Это
уравнение определяет собственные функции Ф£(Л4) оператора £ и его
собственные значения L. Мы принимаем, что собственные значения и
суть те значения величины L, которые могут наблюдаться на опыте.
Совокупность возможных значений L образует спектр величины L.
Собственные функции Ф£(Л4) самосопряженного оператора £ обра-
зуют полную и ортогональную систему функций:
(Фг,ФА,) = W или (Фг, Фд,,) = §(£' — Г). (120.5)
*) См. гл. VIII, § 38—41.
§ 120] ФОРМАЛЬНАЯ СХЕМА КВАНТОВОЙ МЕХАНИКИ 451
Поэтому волновая функция Ф любого состояния может быть представ-
лена в виде суперпозиции состояний Ф£(ТИ) с заданным значением L:
ЦТ (М) = S ’Р (О ’Рд W или lP(W= J Т (L) (Ж) dL, (120.6)
смотря по тому, дискретны или непрерывны возможные значения L. Ф (7И)
и Ф (L) суть волновые функции одного и того же состояния, но данные
в различных представлениях («7И»-представлении и «А»-представлении).
На собственную функцию Ф7 (714) можно смотреть как на функцию, произ-
водящую преобразование от «714»-представления к «/^-представлению *).
Если в формулу для среднего (II) подставить Ф(714) из (120.7), то
ввиду ортогональности функций Ф£(ТИ) получим:
L = ^\4s{L)\2L или Z = у|Ф(£)\2-L-dL (120.7)
(смотря по тому, непрерывна или дискретна величина L). Следовательно,
из определения среднего вытекает, что
|Ф(£)|2 или |Ф(/.)|2^/. (120.8)
есть вероятность найти в состоянии Ф значение L (или /,, L-^dL). Так
как L есть произвольная величина, то вообще, если волновая функция
дана в каком-то «7И»-представлении, то j Ф (714) |2 (для непрерывного
|Ф(714)|2 dM} суть вероятности найти М (или 7И, 714dM} в состоя-
нии Ф.
Четвертый существенный пункт квантовой механики относится к за-
висимости состояний от времени; именно, изменение волновой функции
за время t определяется из уравнения Шредингера
ih~ = H4, (IV)
где Н—гамильтониан, характеризующий природу рассматриваемой кван-
товой системы. Гамильтониан Н всегда складывается из двух частей:
оператора кинетической энергии системы Т и оператора U, определяю-
щего взаимодействия внутри системы и взаимодействие системы с внеш-
ним полем. Вид оператора кинетической энергии Т определяется из того
обстоятельства, что, измеряя декартовы импульсы pxk, pyk, pzk (k —
номер частицы системы) и кинетическую энергию частиц Г, мы можем
убедиться, что связь между р/г и Т такова же, как и в классической
механике. Отсюда получаем, что оператор Т равен
Г = (120.Э)
k
где nik— масса &-ой частицы. Зная вид Т в декартовых координатах,
мы можем получить Т и в любых криволинейных координатах. Вид U /
определяется из опыта. Квантовая механика, так же как и классическая,
не предсказывает характера внешних сил и сил между частицами. Задание
*) Ср. § 41, где такую функцию Sna — ^(2) мы определили как матрицу
унитарного преобразования.
29*
452
ЗАКЛЮЧЕНИЕ
[гл. XXV
масс частиц tnk и вида U есть определение рода системы, а вместе
с этим и свойственного ей гамильтониана
(120.10)
При наличии магнитных сил (сил, зависящих от скоростей частиц)
оператор кинетической энергии получается из (120.9) заменой операторов
Рх = — ih£, P= — ih~, P^- — ih4- (120.11)
х дх У ду 2 dz ' 7
= — ih~ — - Ах, Р1 А ,
* дх с х У ду с У
pz = -ih~ — - Л * (120.1 Г)
z dz с 2’ v '
это — предположение, окончательное оправдание которому можно найти
только в согласии с опытом.
Из уравнения Шредингера (IV) и определения среднего (II) следует
(см. § 31):
£ (L) = (ф, [И, L] Ф) + (ф, Ф ) , (120.12)
где
[Я,1] = ^(£Я— HL). (120.13)
Называя (по определению) оператором производной оператора по вре-
мени такой оператор , чтобы
мы получаем:
г=г + [»Ц- <12О15>
Эта формула позволяет найти интегралы движения и тем самым
притти к выражению для операторов важнейших механических величин,
положив в основу вид гамильтониана (120.10). Именно, из (120.15),
(120.10) и (120.9) следует, что для свободного движения, которое харак-
теризуется £7=0, интегралом движения будет оператор
k k
(ср. § 96). Поэтому этот оператор следует назвать оператором пол-
ного импульса*). Подобным же образом для случая поля центральных
сил (ср. § 98) интегралом движения будет оператор
= (120.17)
k
*) Разумеется, что названия «оператор импульса», «оператор момента им-
пульса», в конце концов, получают свое оправдание во всей совокупности свойств
тех величин, которые представляются приведенными выше операторами.
§ 121J ГРАНИЦЫ ПРИМЕНИМОСТИ КВАНТОВОЙ мехлники 453
поэтому этот оператор может быть назван оператором полного момен-
та импульса [в случае частиц со спином (120.17) следует еще при-
—►- ——>-
соединить где sk — оператор спинового момента]. Из/^игА
можно строить и другие более сложные операторы, физическое значе-
ние которых может быть весьма специальным. Таким образом, вид важ-
нейших операторов может быть определен, если постулировать вид опе-
ратора Гамильтона (т. е. уравнение Шредингера).
Последнее из основных предположений квантовой механики относится
к системам одинаковых частиц и было нами сформулировано в § 105
в форме принципа неразличимости частиц. Согласно этому принципу
обмен любой пары Л, j одинаковых частиц не ведет к физически новому
состоянию. Математически это выражается в форме условия, накладывае-
мого на волновые функции
(v;
где \ — число, одинаковое для всех k,j. Мы показали в § 105, что
это условие ведет к делению состояний на два класса
ф = Фа (антисимметричные), (120.18)
ф = ф^ (симметричные). (120.18')
Далее, из (III) следует, что симметрия волновой функции не может из-
мениться с течением времени (см. § 106). Поэтому принадлежность частиц
к сорту (Фо) или (ФД может определиться только природой частиц.
Частицы, состояние которых описывается волновой функцией ФЛ, суть
частицы Ферми. Они подчиняются ^принципу Паули, который выте-
кает как следствие из (120.18). Частицы, состояние которых описывается-
волновыми функциями Ф^, называются частицами Бозе. Для йих прин-
цип Паули не имеет силы.
Таким образом, мы видим, что в основе квантовой механики лежат,
пять фундаментальных предположений: (I) — принцип суперпозиции состоя-
ний, (II) — определение среднего значения, (III) — толкование собствен-
ных значений, как единственно возможных значений величины, (IV) —
уравнение Шредингера и (V) — принцип неразличимости одинаковых
частиц.
§ 121. Границы применимости квантовой механики
Вполне строго и точно границы применимости физической теории
могут быть указаны лишь на основе более общей теории, включающей
рассматриваемую как частный или предельный случай. В настоящее время
не существует теории микроявлений, более обширной и глубокой, не-
жели квантовая механика. Поэтому границы квантовой механики могут
быть проведены лишь очень ориентировочно. Именно, мы можем навер-
ное сказать лишь то, что квантовая механика неприложима к системам,
состоящим из частиц, движущихся со скоростями, сравнимыми со ско-
ростью света f, т. е. в релятивистской области.
454
ЗАКЛЮЧЕНИЕ
[гл. XXV
Квантовая механика является механикой систем с ограниченным ко-
нечным числом степеней свободы. Она является аналогом классической
механики систем материальных точек. Если скорости движения частиц
становятся сравнимыми со скоростью света, то вообще не приходится
говорить о системе с конечным числом степеней свободы. В самом деле,
в этом случае нельзя не учитывать конечной величины скорости распро-
странения электромагнитных полей. Если за время Д/ расстояние между
частицами r^k изменится на Дгд, то при условии, что относительная
скорость частиц —близка к скорости света, примерно такое же время
нужно для распространения электромагнитного поля на расстояние Д/д.
Поэтому наряду с частицами нужно рассматривать электромагнитное поле,
которое само и создается этими частицами и на них действует. Иными
словами, в систему должны быть включены не только все частицы (что
дает ЗМ степеней свободы для М бесспиновых частиц и 4^ для
частиц со спином), но и электромагнитное поле, состояние которого
определяется бесконечным числом степеней свободы.
Дело осложняется еще тем, что, как показывает опыт, когда энер-
гия световых квантов или частиц превышает собственную энергию
частиц /w0c2 (z/z0 — масса покоя), то частицы могут возникать, рождаться
и, напротив, исчезать. Так, квант «света» с энергией йш 2/лг0<?2 может
изчезнуть и превратиться в пару частиц: электрон (е“) и позитрон (е+)
(электрон с положительным элементарным зарядом) *). Обратно, позитрон
и электрон могут превратиться в квант света.
Эти процессы превращения мы можем написать в виде схемы
Л(о^±е+ 4-е-. (121.1)
Другого рода известные процессы, при которых возникают частицы,
это — процессы радиоактивного распада. Нейтрон (л) превращается в про-
тон (р), и при этом появляется электрон (е“) (и, может быть, еще
гипотетическое излучение — нейтрино). Это превращение мы можем на-
писать в виде схемы
п—> р 4“ 4" Лу. (121.2)
В радиоактивном позитронном распаде мы имеем дело с другим превра-
щением, с превращением протона в нейтрон и позитрон (е+), по схеме
р —> п4~е+ 4"^>- (121.3)
Сопоставление приведенных схем показывает, что нейтрон нельзя рас-
сматривать как сложную частицу, состоящую из протона и электрона,
равным образом нельзя рассматривать и протон, как состоящий из ней-
трона и позитрона. Мы имеем дело не с выбрасыванием готовых частиц,
а с рождением частиц (е+ или е~) при превращениях п^^р.
В процессах (121.1), (121.2) и (121.3) мы не имеем уже ничего
общего с механикой системы частиц: само число частиц подвергается
*) Закон сохранения импульса и энергии требует, чтобы в этом процессе
участвовала еще одна частица, например, ядро атома или второй фотон.
§ 121]
ГРАНИЦЫ ПРИМЕНИМОСТИ КВАНТОВОЙ МвХАНИКИ
455
изменениям. Нанта система обладает, таким образом, неопределенным,
бесконечно большие числом степеней свободы. Квантовая механика не
может быть применена к таким системам, так как она оперирует с задан-
ным, неизменным числом частиц. Проблемы электродинамики и систем
с неопределенным числом частиц выходят, конечно, за рамки механики,
и поэтому изложенная в этой книге квантовая механика образует вполне
замкнутую, самостоятельную теорию. Однако, при больших скоростях
движения частиц указанные немеханические обстоятельства возникают сами
собой, и поэтому оказывается уже невозможным провести разделение
между механикой и электродинамикой: проблемы квантовой электро-
динамики и проблемы систем с неопределенным числом частиц сливаются
с проблемами квантовой механики, образуя одну общую задачу — задачу
построения квантовой теории систем с бесконечно большим числом сте-
пеней свободы. На пути решения этой задачи в настоящее время до-
стигнуты лишь частичные успехи. Во-первых, удалось построить кванто-
вую теорию излучения (без помощи принципа соответствия), в которой
факт существования квантов света (фотонов) является исходным пунктом.
Такая теория впервые развита Дираком *).
Согласно этой теории электромагнитное излучение рассматривается
как совокупность фотонов (фотонный газ), не взаимодействующих между
собой, но взаимодействующих с заряженными частицами. Описывая такой
газ методом вторичного квантования (ср. § 109) и пользуясь тем, что
в этом методе полное число частиц (в данном случае фотонов) явно не
фигурирует, можно процессы испускания и поглощения фотонов заря-
женными частицами изобразить как процессы перехода фотонов из не-
которого нулевого состояния или соответственно в него. При этом фотоны
в нулевом состоянии считаются ненаблюдаемыми **). Эта теория успешно
применяется к процессам, в которых участвует ограниченное число свето-
вых квантов, и в смысле практических результатов равноценна с теорией
излучения, основанной на принципе соответствия.
Тем не менее она имеет то фундаментальное преимущество перед
принципом соответствия, что включает электромагнитное поле в общий
круг идей квантовой физики, будучи по постановке вопросов и по ме-
тодам их решения вполне аналогичной квантовой механике.
Распространение указанной теории не только на процессы поглоще-
ния и испускания радиации, но и на любые электромагнитные процессы,
включая взаимодействие частиц, ведет уже к трудностям. В этих слу-
чаях приходится иметь дело с бесконечно большим числом фотонов.
Вместе с тем оказывается, что так же, как и в классической электрон-
*) См. Дирак, Основы квантовоц механики, гл. XI.
**) Другой, эквивалентный способ построения квантовой теории излучения
заключается в том, что каждая плоская, поляризованная и монохроматическая
волна рассматривается как квантовый осциллятор, так что ее энергия равна
л/гсо 4- е0 (s—нулевая энергия), где п — целое, положительное число, а <о— частота
колебаний волны. В этом способе электромагнитное излучение рассматривается
как совокупность осцилляторов, подчиняющихся уравнениям Гамильтона. Изло-
жение этого метода дано в книге Г айтлера, Квантовая теория излучения
гиттл, 1940. F
456
ЗАКЛЮЧЕНИЕ
[гл. XXV]
ной теории, электромагнитная масса заряженных частиц равна бесконеч-
ности *). Проблема массы частицу оказывается одной из труднейших
и до сих пор не решенных задач теории.
Второе направление развития квантовой теории связано также с име-
нем Дирака. Дираку удалось построить релятивистскую, квантовую те-
орию движения электрона во внешнем электромагнитном поле по схеме,
близкой к схеме нерелятивистской квантовой механики **). Эта теория
позволяет успешно рассчитать превращения света в электроны и пози-
троны и обратно, а также движение быстрого электрона. Однако, эта
теория неполна, так как она относится к движению одного электрона
во внешнем поле, а не к системе электронов. Она неприменима также
к тяжелым частицам, к протонам, нейтронам и ядрам. Процессы рож-
дения пары позитрона и электрона и их уничтожения, хотя и рассчи-
тываются в цей математически, но требуют для физического толкования
неясного и неправдоподобного предположения о том, что нерожденные
электроны существуют в готовом виде, но находятся в особом состоянии,
в котором они недоступны наблюдению ***). Таким образом, применение
методов квантовой механики к системам с бесконечно большим числом
степеней свободы возможно лишь частично и не обходится без введения
специальных, подчас искусственных, допущений, чуждых самой кванто-
вой механике.
Поэтому, без опасения впасть в ошибку, мы можем сказать, что
наибольшую и неопределенную трудность современной микрофизики пред-
ставляют системы с бесконечно большим числом степеней свободы. Для
описания поведения систем, образованных быстродвижущимися частицами,
и для описания рождения и уничтожения частиц требуется новая фи-
зическая теория, которая позволит заглянуть в микромир глубже, чем
это можно сделать, опираясь на круг идей современной квантовой ме-
ханики.
*) См. Г айтлер, loc. cit., § 6.
**) См. Дирак, loc. cit., § 81.
***) Дирак, loc. cit., § 75.
ДОПОЛНЕНИЯ
I
Преобразование Фурье
Напомним сначала интеграл Дирихле, фигурирующий в теории
интегралов Фурье:
ь
1. 1 Г / ч sin mz j .
hm - <p(z)—— dz, (1}
m oo j z
a
где y(z)— произвольная функция. Этот интеграл обладает следующими
свойствами: 1) если а, или а, то этот интеграл равен 0;
2) если а<^0, #^>0, то он равен ср (0) (для непрерывных функций)*).
,, t 1 sin mz
Наличие функции — —-— под знаком интеграл? и взятие предела
(т—> оо) мы-можем обозначить одним символом 5(г), так что предыду-
щий интеграл напишем в виде
р ( =0, если а, или а, £<^0,
j ф(^)о(^) = । _ (р(0), если 0, #^>0. |
а /
Символ 5 (г) часто называют S-функцией (дельта-функция). Общее
определение символа S дано в дополнении III. Переходя к доказательству
эквивалентности формул (13.1), (13.3)ги (13.5), (13.6) соответственно,
мы рассмотрим ради сокращения выкладок случай одного измерения
и докажем справедливость равенства
-{-00 4-00
= J = J Ф*(*) ( — ih-^ )"<Ь(х) dx, (3)
— ОО —СО
где (рх) есть компонента Фурье от ф (х):
+00
Ч(РХ) = (4)
J \zr.n)-
— 00
*) См., например, В. И. Смирнов, Курс высшей математики, ОНТИ,
1937, т. II, стр. 369.
458
ДОПОЛНЕНИЯ
а п — целая положительная степень. Для доказательства подставим в (3)
вместо ср(рх) и их выражения из (4). Тогда имеем:
Ч-оо 4-оо 4-*>
'" = J dp, J ф*« -Pi f Ф W И
— оо —оо —оо
— i-x- $ п —1-х*
Вместо произведения рпхе h можно написать е * • Тогда
получаем:
й=+У Й f
— 00 —00
/ Рах' +оо _..£®х
е h dx' Г ф (л-) ( } е h &х-
— QQ
(6)
Проинтегрируем в последнем интеграле п раз по частям, причем
будем предполагать, что ф(х) и ее производные обращаются в нуль
на границах интегрирования х — 4- оо. Выполняя интегрирование,
найдем:
- +Г?\„ %°° +л°° _,£*?/ Л \я
рпх= j S j й dx’ Jе А (-ih£) ^^dx> м
— оо —оо —оо
переменим теперь порядок интегрирования и будем интегрировать
сначала по рх:
4-00 4-ос
р"= J ф*(хг)г/х' J (—ih-^ni)(x)dx
— 00 —00
+“ ;Рх (х'-Ж)
р *
— оо
df)
2кД
(8)
Введем теперь переменные £=^, z = x' — х. Выполняя в, последнем
интеграле в (8) интеграцию по С в конечных пределах от — т до-}-^»
а затем переходя к пределу т --> оо, мы можем написать (8) в виде
4-оо 4-00
J [(~dx' J dz
— 00 —co
4-ос 4-00
— dx J (x~\-z)S(z)dz. (8')
— 00 — 00
На основании (2) (a — —oo, b = 4~°°)’ ? (z)= Ф* (хЧ~г) име^м-
4-oo
[( — (x)] Ф*
ihdx-
ДОПОЛНЕНИЯ
459
Тем самым доказано (3). Целая рациональная функция от рх имеет
вид F {рх} = ^ап-Р”х- Имеем:
п
F'PX}= И«J?=И ап- f ф* w (—ih ) лф (*)dx=
п П J
= ^*(x)F(—ih^(x}dx. (10)
Таким образом, эквивалентность (13.3) и (13.6) для случая одного
измерения доказана. Обобщение на "три измерения сводится просто
к увеличению числа интегрирований и поэтому совершенно тривиально
[достаточно доказать эквивалентность (13.3), (13.6) для среднего от
Р^с'Р^'Р^ где I— целые и положительные степени].
Справедливость равенства
-j-00 -j- оо
*" = J ^*(x)xn^(x)dx = J (n>
— оо — оо
следует из справедливости (3), если заметить, что по теореме Фурье
+оо {рхх
Заменяя в (3) ф на ср, рх на х и
единицы в показателе формулы (4),
(И) и (4е). Из (11) далее следует
меняя одновременно
мы получаем из (3)
знак у мнимой
и (4) формулы
(12)
Я
— оо
Это — частный случай (13.5) для одного измерения. Обобщение на три
измерения опять-таки тривиально.
II
Собственные функции в случае вырождения
Собственные функции флД;(&=1, 2,..., /), принадлежащие соб-
ственному значению Ln, лийейно независимы, т. е. между ними не
существует соотношений вида
(О
&Х.-1
где —некоторые постоянные. Если бы такие соотношения существо-
460
ДОПОЛНЕНИЯ
вали, то они означали бы, что одна или несколько функций выражаются
через другие, т. е. фактическое число различных собственных функций,
принадлежащих Ln, было бы не /, а меньше. Если функции не
ортогональны между собой, то мы можем ввести новые функции,
получающиеся из tynk линейным преобразованием
%,«= а = 1> 2- •••> /• (2)
А=1
В силу линейности уравнения для собственных функций функции
будут опять-таки собственными функциями оператора L и принад-
лежащими собственному значению Ln.
Из условия ортогональности функций срла:
J Ч*п^Х = (3)
следуют условия для определения коэффициентов aak:
S a*kaw skk'~^
где sw есть
Skk’ = J
Возможность найти коэффициенты aak, удовлетворяющие условиям
(4), следует из геометрической аналогии. Будем рассматривать функции
как единичные векторы jk в пространстве f измерений, a Sk# — как
скалярные произведения (jk, j#Y Тогда (2) можно рассматривать как
преобразование в пространстве / измерений от косоугольной системы
координат к прямоугольной *). Отсюда ясно, что преобразование (2) —
не единственное: получив ортогональную систему координат, мы можем
ее еще вращать любым образом.
Так, например, если функции <bnk уже ортогональны, то
и из (4) тогда следует
ортогональных 2 atka№ —
^nk
Это и есть условия для коэффициентов ортогонального преобразо-
вания системы ортогональных функций в новую систему опять-таки
ортогональных функций фла. Таким образом, собственные функции,
принадлежащие одному собственному значению Ln, определяются лишь
с «точностью» до ортогонального преобразования вида (2) с коэффи-
циентами, подчиняющимися условию (6).
--------------- собственными
*) Подробности об ортогонализации функций см. в книге Курант
и Гильберт, Методы математической физики, т. I, гл. II, § 1.
ДОПОЛНЕНИЯ
461
Ш
Ортогональность и нормировка собственных функций
непрерывного спектра, d-функция
Проинтегрируем уравнение для собственных функций
£ф(х, L) = L<b(x, L)
(1)
по L в малом интервале ДА. Мы получим:
4 + ДА
АДф(х, А) = § Аф(х, L)dL. (2)
i
где
Дф(х, L) = J ф(х, L)dL. (3)
L
Эту величину называют собственным дифференциалом (опера-
тора L). Примером такого собственного дифференциала является рас-
смотренная в § 7 группа волн. Мы докажем, что не сами функции,
а собственные дифференциалы являются ортогональными и могут быть
нормированы. Для этого проинтегрируем подобным же образом сопряжен-
ное уравнение
£*ф(х, А') = А'ф*(х, А’) (4)
по А'; мы найдем:
£'Н-Д£'
£*Дф*(х, Г) = у £'ф*(х, L')dL'. (5)
и
Умножим (2) на Дф*(х, А'), а (5) на Дф(х, А), вычтем один результат
из другого и проинтегрируем по х. Тогда получим:
Сdx {Дф* (х, £') • L Дф (х, L) — Дф (х, L) * А* Дф* (х, А')} =
J £-|-Д££'+Д£'
= Jdxp£ \dL'{L — £')ф*(х, £')$(*, L). (6)
L I'
Левая часть равна нулю в силу самосопряженности оператора £, а справа
при малых ДА и ДА' мы можем вынести А — А' за знак интеграла.
Тогда получим:
(А — А')рх-Дф*(х, А')Дф(х, £) = 0. (7)
Если интервалы ДА и ДА'не перекрываются, то А^=А'. Отсюда следует
У^х-Дф*(х, А')Дф(х, А) = 0, (8)
т. е. ортогональность собственных дифференциалов. Если ДА и ДА'
462
ДОПОЛНЕНИЯ
совпадают, то интеграл (8) не равен нулю. Нетрудно показать, что он
будет первого порядка малости относительно ДА. В самом деле, ин-
теграл
7= рх.Дф*(х, £)Дф(х, L} (9)
можно заменить интегралом
l3
Г— jrfx-A$*(x, А)^ф(х, L)dL, (10)
Li
причем Lx и выбраны так, что участок (А, А-ф-ДА) лежит внутри
участка (Ар А2). В силу ортогональности собственных дифференциалов
интеграл по участкам (Ап А) и (А —|— ДА, А2) ничего не добавит к интегралу
(9). Поэтому (9) и (10) равны. Но при ДА—^0 (10) стремится к 0
как ДА. Поэтому, выбирая подходящий нормировочный множитель, можно
всегда сделать так, чтобы
т. е.
рх-Дф*(х, А)Дф(х, А) = ДА (И)
при ДА —► 0.
Формулы (8) и (И) можно объединить в одну, выражающую норми-
ровку и ортогональность собственных дифференциалов:
У^хДф*(х, А’)Дф«хА) = ДА или 0 (12)
в зависимости от того, совпадают интервалы А, A-f-ДА и А', А*-|-ДА
или нет. Освобождаясь от одного интегрирования (по dL) в (12), мы
можем написать (12) в виде
^х-Дф*(х, А')ф(х, А)=1 или 0, (12')
смотря по тому, попадает ли точка L' — L к интервал А', А'-|-ДА или
нет. Условие ортогональности и нормировки (12) или (12') может быть
с помощью особого символа сформулировано для самих функций. Для
этого поменяем в (12) порядок интегрирования по х и dL'\
Z'+AZ
( dL’^(x, А)ф*(х, L')dx=\ или 0. (13)
V
Введем обозначение
Jф*(х, Аг)ф(х, A)afx = S(A' —А). (14)
Тогда из (13) следует
Z'+AZ
j d£'-8(L' —£) = 1 или 0, (15)
V
смотря по тому, попадет ли точка L' = L в интервал А', А' № или
ДОПОЛНЕНИЯ
463
нет. Это последнее равенство мы будем рассматривать как определение
символа — L), называемого ^-функцией или функцией Дирака
(на самом деле это не функция, а просто обозначение).
Из (15) следует [(21.11)], что
ь
— L)dL' =f(L) или 0, (16)
а
смотря по тому, попадет ли точка L’ — L в интервал (а, Ь) или нет.
Для доказательства (16) достаточно разбить интервал (а, Ь) на столь
малые участки, чтобы в каждом из них можно было вынести функцию
f(L') за знак интеграла (для этого она должна быть гладкой). Во всех
участках результат интеграции в силу (15) будет равен нулю кроме,
однако, как угодно малого, содержащего точку L' = L. В этом участке
интервал от S согласно (15) будет равен 1.
Вместо того, чтобы говорить о нормировке и ортогональности
собственных дифференциалов (12), мы будем говорить, что собственные
функции нормированы к 8-функции (14).’
В качестве примера проведем нормировку собственных функций
оператора импульса Рх. Эти функции суть
.РхХ
^(x) = NPxe » , (17)
где NP(B — искомый нормирующий множитель, могущий a priori зависеть
от рх. Образуем интеграл (14):
+ ос (Рх— Рх)Х
С ф*, (x)tyPx(x)dx=N*, NPx ( е * dx =
J -00
+гт (рх-р^х
=N*,N..h- lira /-----------л—=
Рх m->oo J h
Л —т
„ . р/’х-P)mxl
2 sin------- I
= N*,NPx.h- lim ------Ц(18)
Px m-+co (px — Px)
TT 1 Sin/TZZ
Сравнивая это с множителем Дирихле lim------------, обладающим'
т ->оо 71 z
свойством 8-функции от z [см. дополнение I, формулу (1)], мы находим,
что
(Ч) (x)^Px(x)dx=N*, NPx-2ith-Z(p'x —рх). (19)
J рх 1х
Отсюда определяем нормирующий множитель
I |2 2тгЛ = 1, NPx = (2-ггЛ)-V. (20)
(разумеется, еще можно ’ было* бы включить фазовый множитель где
ф — действительная функция, однако в этом нет никакой'надобности).
464
ДОПОЛНЕНИЯ
IV
Значение коммутативности операторов
Докажем теорему: если два оператора L и М имеют общую полную
систему собственных функций, то их операторы коммутируют. Обозна-
чим общие собственные функции через ф„(х). Тогда имеем:
L'h = ^n, Ж<|>„ = лу>я- О)
Действуя на первое уравнение оператором Л1, а на второе оператором L
и вычитая один результат из другого, получим:
ML'i)n — LnMni)n, LMbn = LnM„<!?n, = (2)
Так как любую функцию можно разложить по функциям фд, то мы
имеем:
(ML —LM)^ = ^cn (ML — LM) фл = О, (3)
п
т. е., применяя оператор ML — LM к любой функции, мы получаем
-нуль. На языке операторов это означает коммутативность операторов:
ML — LM—0. (4)
Покажем теперь, что если операторы L и М коммутируют, то они
имеют общие собственные функции. Уравнение для собственных
функций оператора L будет
£ф = £ф. (5)
Действуя на это уравнение оператором М и меняя порядок ML на LM,
мы получаем:
£(Мф) = £(Мф). (6)
Отсюда следует, что ф' = ТИф есть также собственная функция опе-
ратора £, принадлежащая собственному значению L. Если вырождение
отсутствует, то значению L принадлежит лишь одна функция, а, стало
быть, ф' может отличаться от ф лишь постоянным множителем, т. е.
ф' = ЛМ). Таким образом
А1ф —УИф, (7)
откуда следует, что ф есть также собственная функция оператора М.
В случае наличия вырождения ф' может быть линейной комбинацией
функции фА(&= 1, 2, ..., /), принадлежащих собственному значению L:
ф' = А% = 2 *=1,2, (8)
k=\
Однако, вместо функций фА можно взять их линейные комбинации (см.
дополнение II):
(9)
ДОПОЛНЕНИЯ
465
причем ak могут быть выбраны так, что новые функции ср будут соб-
ственными функциями оператора М'.
Му —Му. (10)
Подставляя сюда ср из (9) и пользуясь (8), найдем путем сравнения
коэффициентов при
2 = & = 1, 2, ..., /. (11)
k=\
Это — система однородных алгебраических уравнений для определения
коэффициентов ak. Она имеет решение лишь в том случае, когда ее
определитель равен нулю:
Мп — М Л412 ... Mlf
^21 М22 М ... Л42у __ Q (12)
Жу1 . . . . . Mff—M
Из этого уравнения найдем корни М19 М2, ..., М^ Для каждого из
этих корней (2Иа) получим свое решение уравнений (11) аа1, ла2, ..., аа/
и, следовательно, согласно (9) свою функцию ср:
?«= S а«А- (13>
k=l
Новые функции сра (а—1, 2, ..будучи линейными комбина-
циями будут собственными функциями оператора L, принадлежа-
щими значению Ц а вместе с тем и собственными функциями dnepa-
тора М, принадлежащими значениям M=Mlf Л42, ..., Л4а, Л^,
соответственно.
V
Шаровые функции У/т(0, ср)
В проблеме нахождения собственных значений оператора момента
импульса М2 мы встречаемся с уравнением для шаровых функций (25.14):
1 (sin04- 1 Я+Хф = О. (1>
sin 0 ди \ / * sm2 0 ду2 1 т ' '
Нам нужно найти собственные функции этого
рывные, однозначные и конечные решения во
переменных 0 0 тг, 0 ср 2тг.
Разделим прежде всего переменные 6 и ср.
ф = 0(0).ф(?).
уравнения (т. е. непре-
всей области изменения
Для этого положим:
(2)
30 Блохинцев
466
ДОПОЛНЕНИЯ
Подстановка (2) в (1) приводит к разделению переменных, если положить
Отсюда у
Фт(^)=^т(?- (4)
Чтобы Фт было однозначной функцией <р, необходимо, чтобы пг было
целым числом
т = 0, ±2, ... (5)
Подставляя (4) в (1) и деля на Фт, получим уравнение для 0:
—Ц (sin 6 0 10 = 0. (6)
sin 0 дб \ ди ) sin20 1 v '
Введем вместо 6 новую переменную
£ = cos6, —dZ=—sin 6^6 (7)
и будем рассматривать 0 как функцию $. Тогда из (6) получается:
(1—£2)0" —2ф' + _^_)0 = о. (8)
Рассмотрим поведение решения 0 вблизи особых точек уравнения
$ = zb 1 • Обратимся сначала к точке £ = 1. Введем переменную
,г = 5— 1. Тогда из (8) получаем:
в"+4Жв'-[яйй)+й!п?]0=о' (9)
Будем искать 0 в виде ряда по степеням z:
0 = 2^, v = a0-j-a1z-j-a2z2-^ ...-j-avzv-j-,.. (10)
Нам нужно сперва определить степень у, с которой начинается ряд.
При z—> 0
0 —
Подставляя это решение в (9) и пренебрегая бесконечно малыми мень-
шего порядка, нежели г?“2, мы получим из (9):
откуда
Y = ±y. (И,
То же значение у получается для разложения вблизи особой точки $ =
= — 1. Чтобы решение оставалось конечным при $ —zb 1> нужно в (10)
взять
т. е. для /п^>0 у=у, для /п<^0 у — —у. Второе решение (11)
обращается в бесконечность. Таким образом, мы можем взять 0 в виде
I ГП I
0^(1—?) 2
(13)
ДОПОЛНЕНИЯ
467
где v — ряд по степеням z. Нам теперь удобнее взять v в виде ряда
по £:
v= 2 b£. (14)
Подставляя (13) в (8), получим:
(1—^2) ^—2 ([/п 1 + 1) — |/7г’| — /7г2) = (15)
Внося сюда ряд (14) и сравнивая коэффициенты при одинаковых сте-
пенях Е, мы получаем рекуррентную формулу для определения коэффи-
циентов Ьч\
(v_[_2)(v+l)^+2=[v(v-l) + 2(|/n|4-l)v-X4-|/n|4-'«2]^(16)
Если ряд (14) оборвется на каком-то члене номера v — k, то v будет
многочленом &-ой степени, и, следовательно, (13) будет конечным, не-
прерывным и однозначным решением, т. е. собственной функцией урав-
нения (1). Из (16) следует, что ряд может оборваться лишь в том слу-
чае, если
k(k— 1) + 2 (|/72 | + 1) — 1 + |/72|+/722 =0,
т. е.
*=(* + И)(*+1 (17)
Полагая
^ + |/72| = Z, (18)
мы получаем:
1=Z(/+1), Z = 0, 1, 2, 3, ... (19)
| т | = 0, 1, 2, ..., Z. (20)
Можно доказать, что никаких других собственных функций уравнения (1)
не существует*).
Решение 0, принадлежащее характеристическим числам Z и /тг, мы
обозначим через
0(£) = р1"И(£), E = cos6. (21)
Если уравнение (15) дифференцировать по Е, то получается уравнение,
в котором \т\ заменяется на \т\ +1. Поэтому, если решение для
т = 0 обозначать через РДЕ), то
I т I а\т\
pi«l($) = (l-£2) 2 -^Рг(£). (22)
РДЕ) есть многочлен степени Z и называется многочленом (или поли-
номом) Лежандра. Коэффициент при нем обычно нормируется так, что
Pz(!)=l. (23)
Из (16) при | /721 == 0 получаем:
_v(v+l)-/(/+l) 2
°v+2— (v 2) (V Ц_ 1)
Отсюда мы видим, что если взять #о + О, то многочлен Pt будет со-
держать лишь четные степени Е, если же />0 = О, Z^ + О, то только
*) См. В е с h е г t, Ann, d. Phys., 83, 906 (1927).
31 Блохинцев
468
ДОПОЛНЕНИЯ
нечетные. Выбирая bQ (при четном Z) или bt (при нечетном Z) так, чтобы
соблюдалось (23), мы можем вычислить все коэффициенты в многочлене Рг
Можно проверить, что получающийся многочлен может быть представлен
формулой
p°t ® = Pt®= ~ (^ -1)'. (25)
Имея в виду (2), (4) и (21), мы получаем собственную функцию урав-
нения (1) в виде
(6, ?) = ^1тР\т 1 (cos 0) eim\ (26)
где Nlm— нормировочный множитель. Вычисление этого нормировочного
множителя, которое мы опускаем *), приводит к значению
кт ч/“U I m D- (2/-|-1)
Nlm—y (Z+| ml)! 4п *
Функции (26) образуют полную систему ортогональных функций на по-
верхности шара 6, ср. Поэтому любая интегрируемая квадратично и одно-
значная функция ф(0, (р) может быть представлена в виде ряда
Ш <?)=s S (28)
2—0 пг — —I
VJS&
ctm= j j ф(9> (9> sin 9 d9 d4’ (29>
В заключение приведем результаты применения некоторых операторов
к шаровым функциям, встречающихся в приложениях:
а) умножение на cos 9 = ? или sin 0 = ^1— $2:
еу i/~(^ 4~ ~Ь 1) — от~~|~1) у ।
,m V (2/4-1) (2Z-4-3) 11+Ьт~Г____________
, (/-]-m)(/ —т) у (30)
~ГУ (2/-1-1)(2/-1) 4-1,т’
(/_ от_|_ 1) (/_ +2) v ,
(2/4-1) (2/4-3) 4+l,»i-lT
-1-1Х<z+OT)(^+”t —!) у I eif (31)
^У (2/+D(2/-l) • Vй'
6) Действие операторов проекций вращательного момента Мх, Му, Мг:
M,Ylm=;hmYlm, (32)
(Мх+Y,m = - h /(/ - m) (14- tn + 1) Yt,m+15 (33)
(Mx - iMy) Ylm = - h V(I + m) (I - m + 1) F;, m_y (34)
Доказательство этих формул пртведено в специальных курсах шаровых
функций. См. также Бете, Квантовая механика простейших систем, § 65.
*) См., например, В. А. Фок, Начала квантовой механики, стр. 124—125.
ДОПОЛНЕНИЯ
469
VI
Уравнение Гамильтона
Пусть qv #2, ..., qs, •.q? суть обобщенные координаты, опре-
деляющие конфигурацию системы, a pv р2, ps, ^-,pf—соответ-
ствующие обобщенные сопряженные импульсы. Функция Гамильтона Н
есть функция этих координат и импульсов и, вообще говоря, времени
Уравнения Гамильтона, как известно, гласят:
dps__ дН dq^_______дН
~di~~d^ dt~fys-
Производная по времени от любой функции F обобщенных коор-
динат, импульсов и времени будет
dt ~ dt' dqs dt “* dps dt *
Пользуясь уравнениями Гамильтона (1), мы можем переписать (2) в виде
<3>
где [Н, F] равно
[Я, n = (4)
L J ^d4sdPs dqsdpsi '
и называется скобкой Пуассона.
Очевидно, что сами уравнения Гамильтона (1) могут быть также
записаны с помощью скобок Пуассона
^ = [Я, М ^=[Я, 5=1,2,...,/ (5>
[для этого полагаем в (3) F=ps и F= Как мы увидим (§ 31), в совер-
шенно аналогичном виде пишутся уравнения движения в квантовой
механике. В частном случае декартовой системы координат и одной
частицы, движущейся в поле сил, выводимых из силовой функции
U(x, у, z, t), имеем:
„2 f л2 I „2
Р X "I -Г V “Г Pz 1 тт/
-----\-Щх, у, z, t) (6)
(9, =х, Чъ=у, qs — z, Р1=РХ, Рг=Ру, Рз=Рг). На основании (5>
получаем отсюда:
^Рх _ гп —= ~ — г/у Xi—^L —£* (7\
dt L ’ Px\ dx dx ’ dt L » J dpx jx * '
и аналогичные уравнения для остальных двух координат и импульсов.
Из (7) находим:
dU
т. е. уравнение Ньютона,
470
ДОПОЛНЕНИЯ
В случае движения заряженной частицы с зарядом е и массой р
в электромагнитном поле, описываемом скалярным потенциалом V и век-
торным А, так что
£ = (9)
^=rotA, (10)
где — напряженность электрического поля, a — магнитного, функ-
ция Гамильтона пишется в виде
"=i(p-?A)a+eK <6’>
Докажем, что вытекающие из этой функции уравнения Гамильтона
dpx dt = — дН дх 9 dpy dt _дН ду ’ dpz dt = — дН dz ’ (7')
dx ~dt __ дН ~ дРх dy ’ dt дН др у ' dz ~dt дН дрг (7")
эквивалентны уравнениям Ньютона для той же частицы, движущейся под
действием силы Лоренца:
P d2x _ d& = e dt ^У (8')
V- d*y _ dt2 = e dt (8й)
P d2z _ dt2 ~e / dx \~di^y~ —36 ) dt 'Л'*) (8"')
Подставляя в (7') и\ (7") Н из (6) и производя дифференцирование,
получим:
dpx___ е
dt
Из (7') получаем:
La \дАУ I-
с у! дх Т-
La дАг cdV
с г; дх дх
dx___ 1
dt |i
(рх
с х ' dt
dz 1 / е
dt u. v z с ‘
Из (10) следует, что
dpx ____ д2х . e dAx
~dU 'A~d^Ar~c~~dt ’
(9')
(10')
(И)
Так как значение вектора-потенциала Ах берется в точке, где находится
заряд е, то полная производная по времени от Ах будет
dAx дАх । дАх dx . дАх dy . дАх dz
-# = -аг+<12>
((> \ / 6 \ ( в
РХ~7АА' \РУ~"7Ау)'\Рг~7Аг
ДОПОЛНЕНИЯ
471
дАх
ду
из (10') и значение из (11) и пользуясь (12), найдем:
^£х__е_дА^_ 4у(дАу
” dt2 с dt е дх ‘ с |_ dt \ дх
“Т" dt \ дх dz ) ] ’
(13>
Отсюда на основании формул (9) и (10), связывающих поле и потен-
циалы, находи^:
<8"">
т. е. первое из уравнений (8'). Подобным же образом получаются
и остальные два уравнения (8") и (8'").
Таким образом уравнения Гамильтона (7') и (7”), вытекающие из
функции Гамильтона (6), эквивалентны уравнениям Ньютона (8).
Потенциалы А и V могут быть выбираемы произвольно, лишь бы
по (9F) и (10г) получалось нужное электромагнитное поле. Если мы
вместо А и V возьмем
A’ = A + V/, V’=V-±d/t, (14>
где f—произвольная функция координат и времени, то =
Подставляя в функцию Гамильтона (6) А' и V вместо А
и V, мы, очевидно, придем к уравнению движения (13), если там под А
и V разуметь А' и V'. Пользуясь (14), убеждаемся, что новый выбор
потенциалов не меняет уравнения (8). Это свойство уравнений Гамиль-
тона называют электромагнитной инвариантностью.
Заметим, что в отличие от уравнения движения (8) функция Гамиль-
тона Н меняется при преобразовании (14). Например, движение водно-
родном постоянном электрическом поле S, направленном по оси ОХ>,
может быть описано потенциалами А = 0, У=— (§х. Вместо этих
потенциалов можно взять по '(14) другие потенциалы, например, Ах —
— А'у = A!z = Q, У' = 0. Предоставляем читателю самому убе-
диться в том, что в обоих случаях мы получаем уравнение Ньютона
для равноускоренного движения, но при первом выборе потенциалов
функция Гамильтона имеет смысл полной энергии частицы, а при вто-
ром она равна кинетической энергии частицы.
VII
Уравнение Шредингера и уравнения движения в криволинейной
системе координат
В § 27 мы объясняли причину, по которой декартова система коор-
динат в квантовой механике занимает особое положение среди всех
других возможных систем: в декартовой системе координат измерение
проекций импульса pxi ру, pz дает нам также значение кинетической
472
ДОПОЛНЕНИЯ
энергии. Поэтому исходные уравнения квантовой механики пишут обычно
в декартовой системе координат. Уравнение Шредингера легко может
быть написано и в любой криволинейной системе координат qx, q2, q3,
поскольку оно дано в декартовой системе. В этой последней оно
гласит:
ih — = —•^-^2Ф(Х>Л + z< z, t) (1)
Ul
[простоты ради, мы пишем уравнение для одной частицы и в отсутствии
магнитного поля*)]. При переходе от декартовых координат к криво-
линейным ф и U будут функциями от qu q2, q3. ВсёМело сводится
к преобразованию оператора Лапласа V2. Пусть квадрат линейного
элемента ds2 в криволинейной системе координат q есть
з
ds2 = <Zx24-rfy2 + </z2= 2 gSkd^sdqk, (2)
J, Ь=1
где gsk— компоненты метрического тензора. Далее, пусть D2 = |jg^||
есть определитель матрицы gsk. Введем еще элементы обратной мат-
рицы gsk, так что
^*==5*, (* = *)> ^ = 0 (^)- (3)
[В (3) по а суммируем от 1 до 3.]
Тогда оператор V2 в этих обозначениях запишется в виде**)
(4)
(где суммировано по s и k), и соответственно этому уравнение Шре-
дингера получает вид
<7з, О _ & 1 ( д ( n„sk d^{qb q2, q3, t) \ \ ,
Ш dt ~ 2^D\ dqs \ Ug dqk J J
+ U(qv q2, q&, 0Ж, 0- (5)
Оператор Гамильтона будет
(6>
Беря скобку Пуассона
Т = ["’ ’j-
dq($ x г
мы получим контравариантную компоненту скорости . Умножая на
массу р, мы получим такую же компоненту импульса Чтобы полу-
чить ковариантную компоненту импульса Ps, преобразуем по фор-
муле перехода от контравариантных к ковариантным компонентам:
= (8)
*) Общий случай см. W. Pauli, Handb, d. Phys,, XXIV, ч. I.
**) См., например, Эйхенвальд, Теоретическая физика, ч. 1, §§ 157—166.
ДОПОЛНЕНИЯ
473
В качестве примера рассмотрим полярную систему координат г, 6,
ср. В этом случае
ds2 = dr2 r2d№ -|- г2 sin2 6 dtp2, = 1, g22 = г2, g33 = г2 sin2 0. (9)
*ru = 1, ^22 = ^> ^3 = 7^й’ (9’)
Гамильтониан будет равен
„ w р2 . 2 д . 1 1 д ( . А д \ . 1 а21 . тт ,1П.
2р. Ldr2”^ г дг^~г* sin 0 d0 \Sin д0 * ’ / ”^r2sin2 0 d?2J
Найдем первую группу уравнений (операторы скорости). Согласно (7)
имеем:
^=[Я, г], = 6], £ = [Я, <р]. (И)
Вычислим сначала первую скобку Пуассона. Для этого заметим, что
В силу этого первая скобка Пуассона (10) дает
1‘й=-“7(г,'--)=₽И- ,,2>
Для второй скобки Пуассона из перестановки
6 —— (sin 6 — ... )-— — fsin9 — ... --— (Ksin0...)
sin 0 dO \ дв / stn0d0 \ dO / /sin 9 d0
получаем:
ji-=— (/5Л..)=Р<9> (13)
dt г2 /sin 0 дв '
и, наконец, для третьей скобки совсем просто получается
----------. А—(14\
г dt г2 sin2 0 '
Переходя по формуле (8) к ковариантным компонентам Pr, Р$ , Р^ мы
получаем на основании (9), (12.13) и (12.14):
Р= — ih — (— г...}, Рь =--— (]/sm6...),
r\dr J /sin 0(^0 (15)
^=-/л4- J
Вычислим теперь вторую группу квантовых уравнений Гамильтона.
-«:=[«, Л). ^ = [«,«1 = <16'
Для этого целесообразно представить (10) в виде
н=^+^+и{г’ ’ (17)
474
ДОПОЛНЕНИЯ
где М2 — оператор квадрата момента импульса, а Рг—первый из опе-
раторов (15). Несложное вычисление скобок Пуассона (16) с помощью
(17) дает
dPr_ М2 dU dPt ________________ ctgQ Г 2 Л21 dU
dt 2pr3 Or’ dt jir2 sinO i ? 4 J дв ’
dP? __ dU
dt dcp
(18)
Из этих трех уравнений два (для Рг и Р ) совпадают по форме
с соответствующими классическими уравнениями Гамильтона. Уравнение
для Ре вместо Р2 содержит Р2 — —. Появление — ~ связано с суще-
ствованием в квантовой механике устойчивых состояний с М2 = О,
в конечном счете с нулевой энергией квантовых систем.
VIII
Решение уравнения для осциллятора
Задача о нахождении квантовых уровней осциллятора приводит к
уравнению
ф"+(Х-^)ф = О. (1)
Нам нужно найти конечные и непрерывные решения этого уравнения.
Исследуем асимптотическое поведение решения (1), т. е. для Е = -Ьоо.
Эти точки одновременно являются особыми точками уравнения. Для
этого положим
ф $) = е№ v$). (2)
Подставляя (2) в (1), находим:
^ + 2/^ + [7+/2 + к — £2]? = 0. (3)
Чтобы функция явилась фактором, определяющим асимптотическое
поведение ф($), нужно выбрать / так, чтобы коэффициент /'-j-/'2 — В2
в особых точках S —+ оо был регулярным, т. е. чтобы член с £2
уничтожался. Это дает
(4)
Стало быть, решение уравнения (1) можно представить в виде
ф(£) = С1е-«3 ^ф-l-c^+W3 (5)
Мы интересуемся конечными решениями ф, поэтому берем частное
решение с2 = 0, т. е. берем ф в виде
(6)
Для функции 27-будем теперь иметь уравнение
г/' —2^' + (Х — 1) 27 = 0. (7)
ДОПОЛНЕНИЯ
475
Точка Е = 0 есть регулярная. Поэтому v можно искать в виде ряда
Тейлора
v= 2 (8>
k=0
Подставляя (8) в (7) и собирая одинаковые степени Е, получим рекур-
рентную формулу для определения коэффициентов ak:
(А + 2)(&+1)аА+2 —2^й + (1-1).аА = 0, (9>
откуда
2k — (1 — 1) ,1П.
а4+2 (^4-2) (А+1)
Если ряд (8) оборвется на члене номера п, то v будет многочленом
/г-ой степени. Тогда решение (6) будет конечным непрерывным и одно-
значным во всей области —o©<^E<^-j~ оо. Такие решения и будут
собственными функциями уравнения (I). Из (Ю) следует, что ряд может
оборваться лишь при тех значениях X, которые определяются формулой
X = 2n+1, л = 0, I, 2, ... (И)
Это и есть формула (37.7), приведенная в- тексте.
Многочлен v(%) с коэффициентами, определяемыми формулой (l(ty
для 1 — 2п 4“ 1, носит название многочлена Эрмита- Чебышева.
Его обозначают обычно через /7Л(Е), и он удовлетворяет уравнению-
(7) при Х = 2п4“1, т. е- уравнению
^-2^; + 2п^л = 0. (12)>
Легко проверить, что этому уравнению удовлетворяет многочлен
Поэтому Нп только множителем отличается от этого последнего мно
гочлена. Следуя обычному определению, мы положим:
(13)
[Нетрудно убедиться, что многочлен (13) имеет коэффициенты, совпа-
дающие с данными формулы (10) при l = 2n-|~l-]
Приведенный в тексте (37.9) многочлен Нп отличается от (13) мно-
жителем УУп, который выбран так, что функция (Е) нормиро-
вана к 1. Именно, в тексте мы даем нормированный полином Эрмита
Нп(£) = /~1)П е? (е-л«). (14)
” V2«л! XT din
Собственное решение уравнения (1), принадлежащее собственному зна-
чению 1 = 2п -J- 1, может быть теперь записано в виде
фп($) = е-№//л($)1 (15)
где под /7Л(Е) будем разуметь нормированный полином Эрмита-Чебы-
шева (14).
476
ДОПОЛНЕНИЯ
Функции фл(Е) ввиду самосопряженности оператора, определяющего
уравнение (1), должны быть ортогональными. В этом легко убеждаемся
непосредственно. В самом деле, для двух функций фл и имеем:
^+(2л+1_тя=о,
^•+(2л<_Н1_е2)фя,=о.
Умножая первое уравнение на фл/, а второе на фл, вычитая и интегри-
руя по Е, получаем:
+ оо 4-00
— 00 —оо
Левая часть есть
Тэ-1 1 Т=о:
— 00 —00
т. е.
V
С помощью интегрирования по частям можно также убедиться, что
+°°
j ФЯ(Р»^=Ъ
—00
следовательно,
4-оо
J фяфл,^ = (16)
т. е. функции фл образуют систему ортогональных и нормированных
функций. Любая функция ф(Е) (с несущественными для нас ограни-
чениями) может быть представлена в виде ряда
Ф(5)= S (17)
где
сп = f 08)
Обратимся теперь к свойствам ненормированных многочленов Эрмита-
Чебышева (13). По формуле Коши производная может быть
представлена в виде интеграла по замкнутому контуру
а& е~р j*(г—o«+i dz< О9)
ДОПОЛНЕНИЯ
477
причем контур обходит точку S. Поэтому из (13) имеем:
Полагая z — Z— t, получим:
,20)
(контур обходит вокруг / = 0). Из последней формулы следует, что
= (21)
п=0
т. е. есть производящая функция для Нп(£).
Производящая функция (19) позволяет установить важное рекуррент-
ное соотношение между полиномами Эрмита. Для этого дифференцируем
(19) по /:
е - (2$ - 2/) = £ Ф Zn-1’
п—\
т. е.
S г ". ® " - SI". ®’=2 ". Ю <’-• (22)
и—0 л=0 л=1
Собирая коэффициенты при одинаковых степенях t, получаем:
25Яя(5) = Яя+1(г)4-2ЛЯя_1($). (23)
Умножая эту формулу на $ и применяя (23), еще раз получим:
2^Я„ (?) = (2л +1) Нп (5) + 1//я+2 (5) + 2л (л -1) Нп_г ($). (24)
Умножим эти равенства на и заменим в них ненормированные
полиномы Эрмита на нормированные [для чего в (23) и в (24) каждый
полином Нт умножаем и делим на у.2тш\ j/T ]. После сокращения
на общие множители получим рекуррентные соотношения для волновых
функций (15). Именно
= (251
Отсюда получаем интеграл, встречающийся в §§ 44, 45. Умножая (25)
на фт(£), интегрируя по $ и принимая во внимание ортогональность и
нормировку функций (16), получим:
(26)
что дает интеграл (45.7)
Подобным же путем, исходя из (25) и ортогональности, можно
вычислить интегралы от любой целой и положительной степени $.
478
ДОПОЛНЕНИЯ
IX
Электрон в однородном магнитном поле
Функция Гамильтона [см. дополнение VI, формулу (6)] при сделан-
ном нами выборе вектора-потенциала А (55.1) имеет вид
2 2
"=s('-+7<+£4 <'»
Отсюда dpx _^_0 dt дх * — —fp -4--ЯГ \ 1 dt ду цс с'^У) ! /<2\ dPz__dH_n dt dz J
dx дН 1 / dt дрх |i Vх ’ е_ \ dy ЬН ру dz дН р^ с У)’ dt др у |л ’ dt дрг и'
Следовательно,
рх = const. = = р^ pz = const. — р^ (4)
'dt2 f («+>>) (5>
Полагая
y=Y __ е&С ’ ®» к ’ (6)
получим:
d2Y dt* '' = -<о^, Y—a sin (о0^ b cos соо^, (7)
и, стало быть, л
у = a sin о СРх (/4-6 cos (8)
Далее,
dx е е f еру. \
V-dt = Px + ^ %у=Рх + 7 & {a sin + b cosgV — , (9)
т. e.
x = —л cos (oo/ -f- b sin (Of/-]-*o> (Ю)
t. e. движение происходит по кругу
(X-X0P+(j/ + ^)2 = fl2 + &2
СРх
еМ
с центром в х = х0, у —
и с радиусом R = |/«2 + Ь2. Энер-
гия движения не зависит от рР.— эта величина определяет положение
центра круга.
Полная параллельность этого классического расчета с приведенным
в § 55 квантовым очевидна.
ДОПОЛНЕНИЯ
479
Координаты Якоби
Согласно формулам преобразования (97.3) имеем:
______mk
dxk Mj’
0xk
1,
dxk
0, A>/+1, (1)
причем
(2)
есть масса первых j частиц. С помощью (1) и (2) находим:
N N N At At N At N At
Едф уч дф ________________уч дф у^ dfy
k=A R k — 1 ;=1 J R /=1 J k — l R
V 1 ___d<(> _ дф
‘ dxy+1J ~d^—d7 ’
(3)
т. e. мы получаем формулу (97.9), приведенную в основном тексте.
Сходным же образом вычисляется оператор кинетической энергии.
Достаточно вычислить оператор
D Ф=У -£ Е (4)
^ткд^к ^тк^^д^Гдхкдхк
С помощью (1) и (2) находим:
D ф _ у 1 (у у д2<!> _____2 у тк д2ф ) __
&М}М;> dkjdtf ^kMj —
n . ( х N г л„. N му А
__у 1 12 у у ть ^ 4» g у тк д I. ।
-U V — I V — £!t_ I \ /c:\
Ф \^k M* + <r3’
Первая сумма no k в (5), как легко видеть (путем изменения порядка
суммирования по j и f) равна нулю. Вторая сумма преобразуется
следующим образом:
A2f } N J
д2Ф _____ уч уч mk д2ф * уч 1 д2ф
J ~ -
N ( N 2 ы
уч 1 I уч f^k д2Ф
^тк[^^.д^
N N— 1
480
ДОПОЛНЕНИЯ
т. е. N—1
D£-Md?N (7)
где pt., есть приведенная масса центра тяжести первых j частиц и
(/4-1)-ой:
~ = лг + —• (8)
Р/ Mj । mJ+1 ' '
Имея в виду, что
= + + <9)
из (7) получаем (97.4):
°-t=i S 77,10>
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоионизация 328, 329
Амплитуды состояний 37
Ангармонический осцилля-
тор 225
Аномальный эффект Зеема-
на 234 и д., 240 и д.
Ансамбли Бозе-Эйнштейна
373, 374
— статистические 51 ид.
----смешанные 51, 52
----чистые 51, 52, 58
— Ферми-Дирака 374
Антисимметричные состоя-
ния 370 и д.
— функции 371
Апериодические орбиты 139
Атом водорода 147
— гелия 398 и д., 407 и д.
Атомизм 13 и д.
Атомный фактор 258
Бальмера серия 149
Барьер потенциальный 309
и д.
Бозе частицы 373, 380,
453
Бозе-Эйнштейна ансамбли
373, 374
----газ 391 и д.
----распределение 394
----статистика 395
Бора магнетон 16, 158 и
д., 448
— постулат 17
— правило частот 17
— теория 16 и д.
Брэккета серия 149
Ван-дер-Ваальса силы 437
и д.
Вековое уравнение 216
Вейсса теория 444
Вероятность перехода 263,
265
Вибрационные линии 165
Водород 416
Водорода атом 147
Водородоподобные атомы
155 и д., 229
— ионы 142
Возмущение 208, 225 и д.,
241 и д.
— в отсутствии вырожде-
ния 210 и д.
— при наличии вырожде-
ния 214 и д.
Волновая функция 34 и д.
Волновое поле 36
Волновой вектор 9
— пакет 101, 370
Волновые функции атома
водорода 147 и д.
Волны де-Бройля 23 ид.,
31 и д.
— модулированные 172
Временное уравнение Шре-
дингера 105 ид.
Время обмена состояниями
415
Вторичное квантование 383
и д., 387
Вынужденные переходы 19
Вырождение 68, 80, 157,
182, 204, 214 и д., 219,
222 и д.
— газа 397
— двукратное 219
— обменное 408, 426
Вырождения степень 20
Газ Бозе-Эйнштейна 391
и д.
— Ферми-Дирака 391 ид.
Гамильтона уравнения 469
— функция 81 и д.
Гамильтона-Якоби уравне-
ние 105 и д.
Гамильтониан 83 и 84, 97,
452
Гармонический осциллятор
127 и д., 433
Гейзенберговский способ
представления операторов
126
Гелий 398 и д., 407 и д.,
417
Гетерополярная валентность
434
Главное квантовое число
129, 146
Гомополярные связи 434
Группа волн 25, 46
Групповая скорость 23 ид.
Двукратное вырождение 219
Двухатомная молекула
160—166
Де-Бройля волны 23 и д.,
31 и д.
8-функция 69, 457, 461, 463
Диагональная матрица 115
Диамагнетизм 441 ид.
Диамагнитная восприимчи-
вость 443
Дипольное излучение 283
и д.
Дискретные уровни энергии
140
Дискретный спектр физиче-
ской величины 66
Дисперсионные силы 440
Дисперсия 289 и д
— отрицательная 295
Диссоциация 433
Дифференциальное эффек-
тивное сечение для неуп-
ругого рассеяния 248, 25&
Дифференциальные коэффи-
циенты Эйнштейна 19
Диффракция атомов и мо-
лекул 30
— плоских волн 48
— рентгеновских лучей 2£>
— электронов 27, 28 и д.
Длительность жизни состоя-
ния 366
Дублеты 205
Единичная матрица 115
Задача многих тел 331 ид.
Закон площадей 100
— сохранения массы и элек-
тричества в квантовой ме-
ханике 91
---момента импульса си-
стемы частиц 340 и д.
---полного импульса си-
стемы частиц 335 и д.
--- энергии 270
------в квантовой механи-
ке 101, 364 и д.
Запрещенные зоны 169
Зеемана эффект 184, 195,
234, 240, 287
---простой 195 и д..
287
---сложный 234 и д.ь
240 и д.
Зоны 169
— запрещенные 169
Излучение 18 и д., 270 и
Д., 272
— дипольное 283 и д.
— квадрупольное 301
— спонтанное 271
— черное 20
Измерение 55 и д. 71, 74
Измерения’ повторимые 55
и д.
— предсказуемые 55 и д.
Изображающая точка 332
Изотопы 4 16
Импульс 100
— световых квантов 9 и д.
— частицы 38 и д., 41, 75,
77
Импульса оператор 61, 75
Индуцированные переходы
19
Инертные газы 421
Интегралы движения 99
и д.
Интенсивности в спектре
излучения 288 и д.
482
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Интенсивность спонтанного
излучения 294
Ионизация атомов 328
Ионные (гетерополярные)
связи 434
Ионы 434 и д.
— водородоподобные 142
Кальций 421
Квадрупольное излучение
301
Квазиквантовые состояния
214
Квазистационарные состоя-
ния 326
— уровни 322
Квази-уровни 214
Квантование 65 и д.
— вторичное 383 и д., 387
— пространственное 16
Квантованные значения фи-
зической величины 67
Квантовые переходы 262
и д.
— уравнения Гамильтона 97
— уровни 127
----двухатомной моле-
кулы 160 ид.
Кванты света 9
Кинетическая энергия 81
Я-оболочка 417
Комбинационное рассеяние
296 и д.
Комбинационные частоты
296
Комбинационный принцип
Ритца 17, 282
Коммутативность операто-
ров 63, 74, 464
Комптона опыты 12 и 13
— эффект 10 и д.
Константа радиоактивного
распада 320, 326
Координаты 34, 40, 75
— Якоби 337, 479
Коэффициент абсорбции
308
----массовый 308
— поляризуемости 289,440
Коэффициенты Эйнштейна
277, 300
---- для спонтанного из-
лучения 2 79
Криволинейная система ко-
ординат 471 ид.
Кулоновское поле 142 ид.
Лагерра полиномы 146
Лаймана серия 149
Ланде множитель 239
Лапласа оператор 78
Лежандра полиномы 79, 467
Линейные операторы 61
— самосопряженные опе-
раторы 60 ид., 449
Лцтий 417
/.-оболочка 418
Магнетон Бора 16, 158 ид.,
448
Магнитная восприимчивость
443
Магнитное квантовое число
150
— поле 180—182
Магнитные явления 441
и д.
Малые колебания 347 и д.
Масса частицы 456
— эффективная 173
Массовый коэффициент аб-
сорбции 308
Матрицы 113 и д., 115
и д.
Метастабильные состояния
3Q1, 405
Метод столкновений 359
и д.
— Хартри-Фока 418
Многоэлектронные атомы
398 и д.
Множитель Ланде 239
М-оболочка 418, 421
Модулированные волны 172
Молекула водорода 423 и д.
Молекулы 423 ид.
Момент импульса системы
частиц 340
----частицы 77 и д., 100,
199 и д
— количества движения
частицы 77
Мультиплетная структура
спектров 183, 203 и д.,
234
Нейтрино 454
Нейтрон 416
Некоммутирующие опера-
торы 63
Непрерывности уравнения
89 и д.
Непрерывный спектр 461
----физической величи-
ны 67
----энергии 140
Неразличимость частиц 366
и д., 453
Неупругие столкновения
электрона с атомом 359
и д.
Неупругое рассеяние 248
АА-оболочка 421
Нормальнее координаты
347, 348
Нормальный триплет Зее-
мана 197, 287
Нормировка 35
— собственных функций
непрерывного спектра 461
Нулевая энергия газа 395
Ньютона уравнение 469
Обменная энергия 411 ид.,
429
Обменное вырождение 408,
426
— расщепление 411
Обменные плотности 412
и д.
— силы 435, 447
Обменный интеграл 446
Одиночные (сингулетные)
уровни 403
Однородное магнитное поле
180-182
О-оболочка 422
Оператор импульса 61, 75
— квадрата момента им-
пульса 77
— кинетической энергии
81
— координаты 75 и д.
— Лапласа 7 8
— момента импульса ча-
стицы 77
Оператор перестановки час-
тиц 368
— полного импульса 339,
452
— полного момента им-
пульса 453
— полной энергии 82
— скорости 98
— смещения во времени 86
— спина электрона 185
— спинового момента 453
— функции Гамильтона 83
и д
— энергии 81
Операторы линейные 61
---самосопряженные 60
и д.
— механических величин
60 и д
— самосопряженные 61
— эрмитовские 61
Опыт Франка и Герца 14,
362, 364
— Штерна и Герлаха 15,
182, 354
— Эйнштейна и де Гааса
184
Опыты Комптона 12, 13
Орбитальное квантовое чис-
ло 150
Орбиты апериодические 139
— периодические 139
Ортогелий 404
Ортогональность собствен-
ных дифференциалов 461
---функций непрерывного
спектра 461
Ортогональные функции 67
Осциллятор 284, 348 и д.,
438 и д., 474 и д.
— ангармонический 225
и д.
— гармонический 127 и д.,
433
---в энергетическом пред-
ставлении 133 ид.
Отрицательная дисперсия
295
Парагелий 404
Парадокс туннельного эф-
фекта 315
Парамагнетизм 441 ид.
Параметр удара 250
Паули принцип 373 и д.,
400, 416, 417, 435, 453
— уравнение 192 ид.
Пашена-Бака эффект 240
Перестановка частиц 368
Перестановочные соотноше-
ния Гейзенберга 75
Периодическая система эле-
ментов Менделеева 415
и д.
Периодические орбиты 139
Периодическое поле 166—
174
Планка формула 22, 23,
398
Плотность вероятности 35
— магнитного момента 194
— равновесного излучения
22
— тока 89 и д.
Повторимые измерения 55
и д.
Поглощение света 272
и д.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
483
Показатель преломления
109, 289, 295
Поле Вейсса 444
— волновое 36
— однородное магнитное
180—182
— потенциальных сил 126
и ц
— центральной силы 136
и д
— электромагнитное 17 5 и д.
Полиномы Лагерра 146
— Лежандра 79, 467
— Эрмита-Чебышева 475
Полная энергия в поле сил
101
Полное эффективное сече-
ние для неупругого рас-
сеяния 249
Полный импульс системы
частиц 335, 339
— момент импупьса 199
и д
Полосатые спектры 165
Поляризуемость 230, 289,
295
Постоянная Планка 9
— Ридберга-Ритца 148
Постулат Бора 17
Потенциальная яма 325
Потенциальный барьер 309
и д.
---трехмерный 319 ид.
Правила отбора для диполь-
ного излучения 283 ид.
---для оптического элект-
рона атома 285
--- для осциллятора 284
Правило частот Бора 17
Предсказуемые измерения
55 и д.
Преобразование Фурье 457
Преобразования унитарные
122 и д
Принцип детального равно-
весия 393
— неразличимости частиц
366 и д , 453
— Паули 373 и д., 400,
416, 435, 453
— соответствия 280 и д.
— суперпозиции состояний
36, 450
Прицельное расстояние 250
Продолжительность жизни
атома в возбужденном со-
стоянии 279
Производные операторов по
времени 94 и д.
Простой эффект Зеемана
195—198, 287
Пространственное квантова-
ние 16
Пуассона скобки 469
Пфунда серия 149
Работа выхода 10
Радиальное квантовое число
151
Радиоактивный а-распад 324
и д.
Расплывание волнового па-
кета ЮЗ
Распределение Бозе-Эйн-
штейна 394
— Ферми-Дирака 394
— электронов в атомах 419
и д.
Распределение энергии в
спектре черного излуче-
ния 22
Рассеяние а-частиц 260
— комбинационное 296 и д,
— света 289
— упругое 362
— электронов 261
---на атомах газа 54
Расщепление обменное 411
— спектральных линий в
электрическом поле 227
и д
— уровней 219 и д.
--- водорода в электриче-
ском поле 231 ид
Резерфорда формула 260
Ридберга-Ритца постоянная
148
Ритца комбинационный
принцип 18, 282
Ритца-Пашена серия 149
Ротационные полосы 165
Рубидий 421
Рэлея-Джинса формула 21
Самосопряженная матрица
Самосопряженные опера-
торы 61
Световые кванты 9 и д.
Серия Бальмера 149
— Брэккета 149
— Лаймана 149
— Пфунда 149
— Ритца-Пашена 149
Сила осциллятора 290
Силовая функция 83
Силы Ван-дер-Ваальса 437
и д
— дисперсионные 440
— обменные 435, J47
— химические 434 и д.
Симметричные состояния
370 и д
— функции 371
Скобки Пуассона 469
Скорость групповая 230 и д.
След матрицы 123
Сложный эффект Зеемана
234 и д., 240 и д.
Смесь состояний 52
Смешанные ансамбли 51, 52
Снятие вырождения 222 и д
Собственные значения опе-
раторов 65 и д , 450
— функции 450
---в случае вырождения
459 и д.
--- непрерывного спектра
461
--- операторов 65
Соотношение неопределен-
ностей 42, 49 и д , 52
Состояние 55 и д.
— квантовой системы 449
Сохранение массы и элек-
тричества в квантовой ме-
ханике 91
— момента импульса систе-
мы частиц 340
— полного импульса систе-
мы частиц 335
— числа частиц 90
— • энергии в квантовой ме-
ханике 101, 364 и д.
Спектр атома водорода 147
и д.
Спектр излучения 288 и д.
— физической величины 66,
120 и д., 450
—-----дискретный 66
------непрерывный 67
Спектральная серия 149
Спектральные термы 17,
148
Спектры полосатые 165
Спин электрона 182 и д.,
240, 416
Спиновые функции 188
Спиновый момент 453
Спонтанное излучение 271,
294
Спонтанные переходы 18
Среднее значение функции
40 и д.
— квадратичное отклонение
49, 64
Средние значения физиче-
ских величин, 64, 120 и
Д , 450
Средний свободный путь
251
Статистика Бозе-Эйнштейна
395
— Ферми-Дирака 395
Статистические ансамбли
квантовой механики 51
и д.
Статистический вес 20
Стационарные состояния 92
и д , 359 и д.
Степень вырождения 20
Стопкновения частиц 10,
247 и д., 391
— упругие 251
Суперпозиция состояний
36 и д , 450
— стационарных состояний
93
Сфера действия 249
Температура вырождения
газа 397
Теория Бора 16 и д.
— Вейсса 444
— возмущений 207 и д.,
225 и д
---для непрерывного спек-
тра 241 ид.
— излучения Эйнштейна
18 ид.
— представлений 111 и д.
— столкновений частиц 247
и д.
Теорема Эренфеста 96 и д.
Термы 17, 148
Ток вероятности 90
-- Гордона-Шредингера 91
Токи в атомах 158 ид.
Трехмерный потенциальный
барьер 319 и д.
Триплет Зеемана 197
Тройные (триплетные) уров-
ни 403
Туннельный эффект 313
Удары второго рода 247
Умножение матриць( 11 7
Унитарные преобразования
122 и д.
Упругие столкновения 251
Упругое рассеяние 252 и д.,
257 и д., 362
Уравнение Гамильтона-
Якоби 105 ид.
484
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнение непрерывности
89 и д.
— Ньютонгг 469
— Паули 192—194
— Шредингера 85 и д., 93,
124, 451
----в криволинейных ко-
ординатах 471 ид.
----временное 105 и д.
----для стационарных со-
стояний 83
— Эйнштейна 11
----для фотоэффекта на
атоме 303
Уравнения Гамильтона
квантовые_469
— движения в квантовой
механике 96 и д.
Уровни энергии 127
— квазистационарные 322
— одиночные (сингулетные)
403
— тройные (триплетные)
403
— с а непараллельными
спинами 403
— с параллельными спи-
нами 403
Условие излучения 319,
321
— периодичности 396
Ферми частицы 373 ид.,
380, 453
Ферми-Дирака ансамбли
374
----газ 391 и д.
----распределение 394
----статистика 395
Ферромагнетизм 444
Формула Планка 22, 23,
398
— Резерфорда 260
— Рэлея-Джинса 21
Фотоэлектрический эффект
10 и д., 302 и д.
Франка и Герца опыты 14,
362, 364
Функции антисимметричные
371
Функции ортогональные 67
— симметричные 371
— собственные 67
— спиновые 188
— шаровые 465
Функция волновая 34 и д.
— Гамильтона 81 и д.
— действия 105
— Дирака 69, 457, 461,
463
— силовая 83
Хартри-Фока метод 418
Химические силы 434 и д.
Холодная эмиссия электро-
нов из металла 316 и д.
Центр группы волн 26
Частицы Бозе 373, 380, 453
— Ферми 373 ид., 380,
453
Черное излучение 20
Чистые ансамбли 51 ид.,
58
Шаровые функции 465
Шпур 123
Шредингера уравнение 85
и д., 93, 451
---- в криволинейной си-
стеме координат 471
----для стационарных со-
стояний 93
Штарка эффект 227 ид.
— эффект в атоме водорода
231 ид.
----квадратичный 227
Штерна и Герлаха опыты
15, 182, 354
Эйнштейна дифференциаль-
ные коэффициенты 19
— и де-Гааса опыт 184
— коэффициенты 277, 300
----для спонтанного излу-
чения 279
— теория излучения 18
и д.
Эйнштейна уравнение 11
----для фотоэффекта на
атоме 303
Электрическое поле 227 и д.,
231 ид.
Электродинамика 455
Электромагнитная инвари-
антность 179, 471
Электромагнитное поле 175
и д.
Электрон в однородном маг-
нитном поле 478
Электронный газ 317
Элементарные частицы 13
Энергия 81 и д.
— в поле сил 101
— возмущения 208
— диссоциации молекулы
433
— кинетическая 81
— нулевая 132
— обменная 411 ид., 429
— световых квантов 9 и ц.
Эренфеста теорема 99
Эрмита-Чебышева полино-
мы 475
Эрмитовские операторы 61
Эффект Зеемана 184
----простой 195 и д., 287
----сложный 234 и д.,
240 и д.
— Комптона 10 и д.
— Пашена-Бака 240
— фотоэлектрический 302
и д.
— Штарка 227 и д.
----в атоме водорода 231
и д.
----квадратичный 227
Эффективная масса 173
Эффективное сечение для
возбуждения атомов 362
----для неупругого рас-
сеяния, дифференциаль-
ное 248
•---для неупругого рассе-
яния, полное 249
Якоби координаты 337, 479
Цена 18 руб.