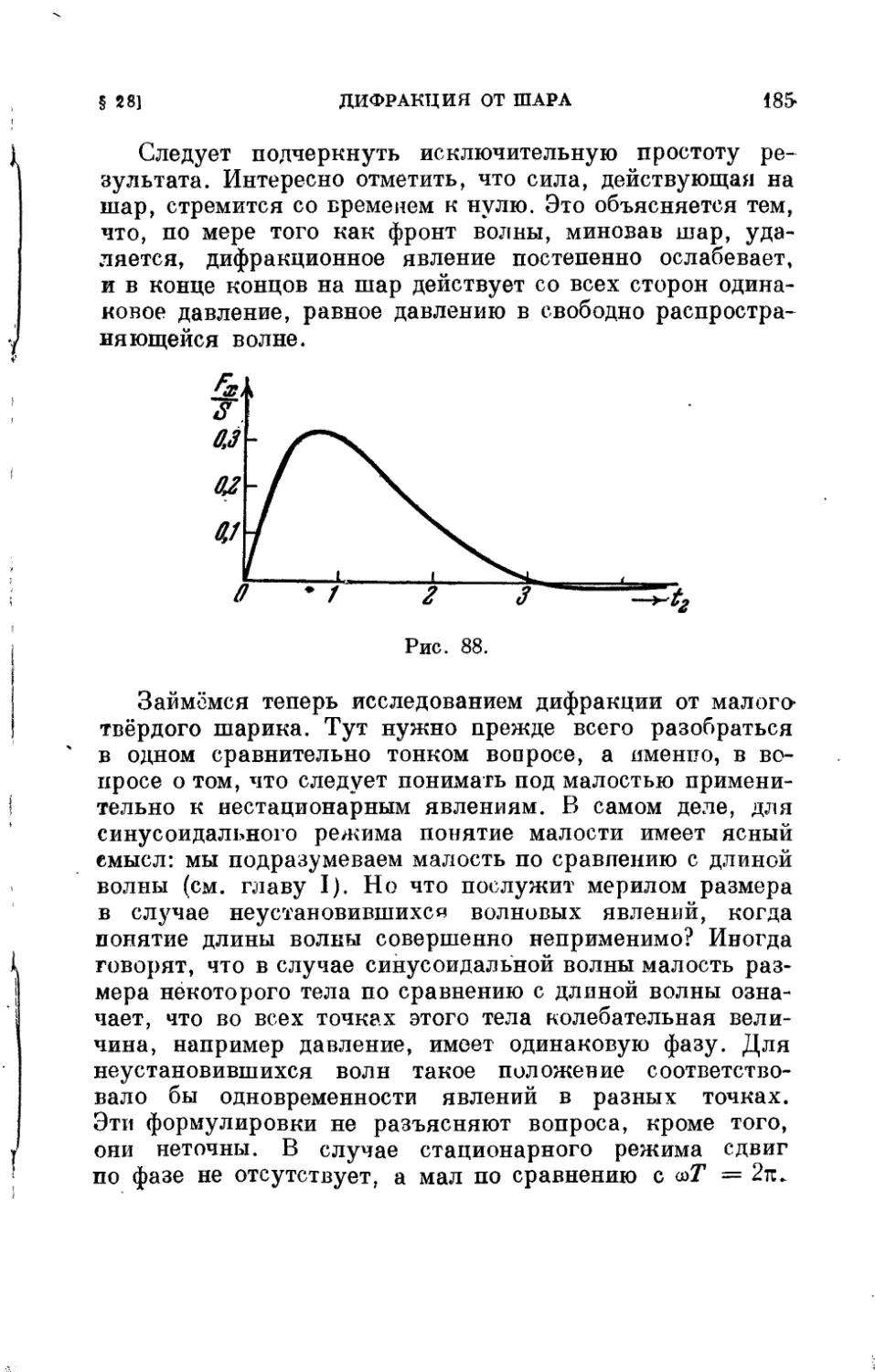
Текст
А. А. ХАРКЕВИЧ
НЕУСТАНОВИВШИЕСЯ
ВОЛНОВЫЕ ЯВЛЕНИЯ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 5 0 ЛЕНИНГРАД
13-5-4
АННОТАЦИЯ
В монографии развиты общие теоретические методы
рассмотрения нестационарных волновых явлений и проведено
исследование наиболее интересных задач из этой области. Получены
новые оригинальные решения задачи дифракции.
Книга представляет интерес для научных работников,
специализирующихся в области акустики и электромагнитных
колебаний, а также для аспирантов и студентов старших курсов
соответствующих специальностей.
редакторы Д. М. Высоновский Техн. редактор С. С. Гаврглов.
и Ё. Д. Щукин.
Подписано к печати 9/Х 1950 г. Бумага 84x108/32- 3,188 бум. л.
10,455 печ. л. 10,02 уч.-изд. л. 38 900 тип. зн. в печ. л. Т-07899.
Тираж 5 000 экз. Цена книги 6 руб. Заказ № 2598.
Отпечатано в 3 типографии ЛРТГШ г. Рига, ул. Ленина 137/139 с матриц 3 типографии
„Красный пролетарий** Главполиграфиздата при Совете Министров СССР, Москва,
Краснопролетарская, 16.
СОДЕРЖАНИЕ
Предисловие 5
Введение 7
Глава I. Основы теории волн
§ 1. Основные понятия 9
§ 2. Математическое описание волн 13
§ 3. Отражение и преломление 16
§ 4. Интерференция и нап авленность 19
§ 5. Излучение и приём 23
§ 6. Дифракция 29
§ 7. Принцип наложения 34
§ 8. Ряд и интеграл Фурье 37
§ 9. Интеграл Дюамеля 40
Глава II. Теория неустановившихся волновых явлений
§ 10. Вспомогательный аппарат 44
§ 11. Одномерная разрывная волна 56
§ 12. Волновые явления в конечной системе 62
§ 13. Шаровая волна; точечный источник 68
§ 14. Простейшие групповые антенны 69
§ 15. Приледение антенны более общего вида к
прямолинейной 73
§ 16. Ближнее поле групповых антенн 78
§ 17. Цилиндрическая волна , 84
§ 18. Реакция на излучатель 86
§ 19. Направленность 94
§ 20. Шаровые антенны 105
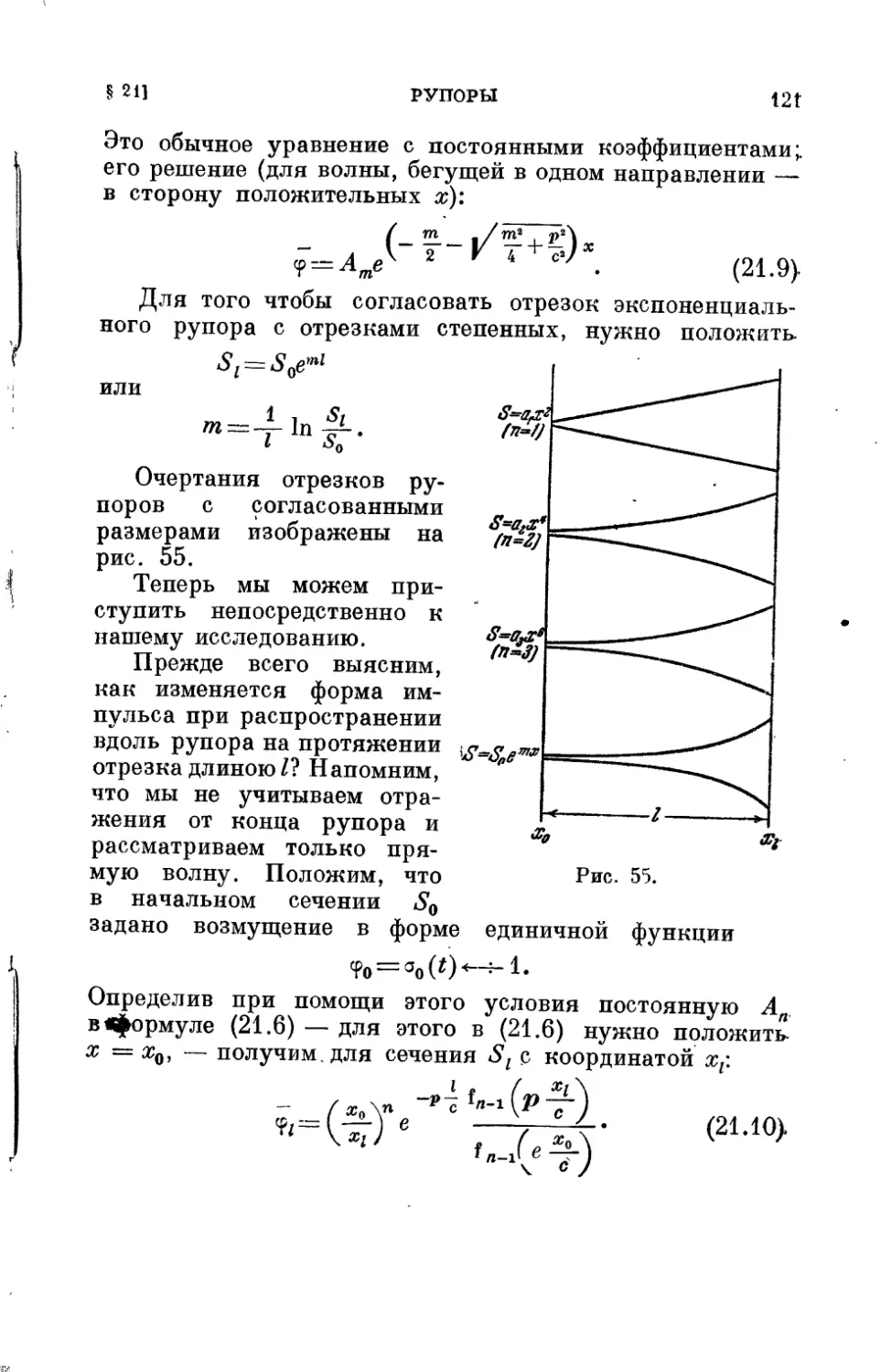
§ 21. Рупоры 118
4 ОГЛАВЛКНИЕ
§ 22. Прием и излучение 133
§ 23. Энергетические соотношения 140
§ 24. Дифракция; общие соображения 151
§ 25. Дифракция от прямолинейного края 159
§ 26. Некоторые задачи излучения 167
§ 27. Преобразование области дифракции 175
§ 28. Дифракция от шара 178
§ 29. Связь между стационарными и нестационарными
решениями 189
Заключение 196
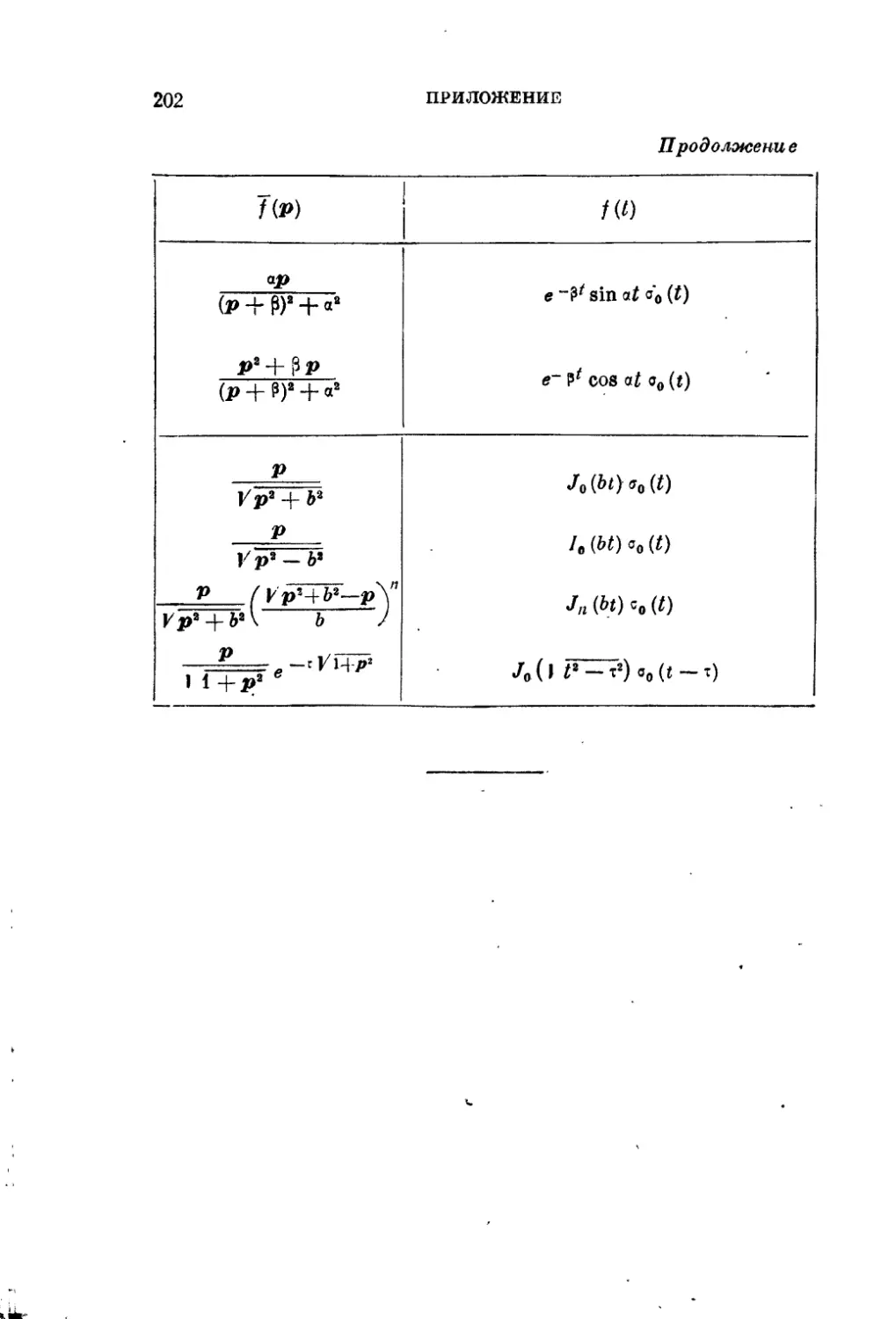
Приложение. Таблица некоторых операционных формул 200
ПРЕДИСЛОВИЕ
Короткая первая глава представляет собою конспект
стационарной теории волн и служит введением ко второй
главе.
Материал второй главы, посвященной собственно
теории неустановившихся волновых явлений, объединяет
результаты, полученные и в большей части
опубликованные мною в течение ряда лет, но изложен совершенно
заново. Некоторую долю содержания второй главы
составляют, разумеется, и общеизвестные вещи.
Конечно, работы остаётся ещё очень много, но я
полагал, что систематическое изложение уже накопленного
материала может представить известный интерес.
Киев, март 1950.
А, Харкевич
ВВЕДЕНИЕ
Понятие о волнах появилось первоначально
применительно к периодическим волновым движениям. Основные
волновые явления — распространение, излучение, приём,
отражение, преломление, интерференция, ди<|факция
волн — предполагаются явлениями периодическими, а
чаще всего рассматриваются для простейшего случая
синусоидальных волн.
Между тем строго периодических явлений не
существует; понятие периодического явления есть математическая
абстракция. Более того, в действительности при
практическом использовании разного рода волн приходится
иметь дело с волнами совершенно непериодического
характера.
Конечно, располагая решением волновой задачи для
синусоидального случая, можно чисто аналитическим
путём распространить это решение на любой более
общий, в том числе и непериодический случай.
Однако этот путь, во-первых, не является
кратчайшим, а во-вторых, не способствует уяснению подчас весьма
своеобразных соотношений, возникающих при
непериодических волновых явлениях.
Прямое исследование непериодических явлений при
помощи некоторых специальных приёмов позволяет быстро
получить вполне наглядные результаты, отличающиеся
иногда поразительной простотой.
8
ВВЕДЕНИЕ
Из нескольких применяющихся у нас терминов для
обозначения непериодических явлений: нестационарные,
переходные, неустановившиеся — выбран последний.
Перед тем как приступить к изложению теории
неустановившихся волновых явлений, необходимо хотя бы
кратко напомнить основные представления и определения
обычной теории волн, чему и посвящена первая глава.
Материал изложен применительно к звуковым волнам,
однако ряд общих положений применим к волнам любой
физической природы, описываемым обычными волновыми
уравнениями.
ГЛАВА I
ОСНОВЫ ТЕОРИИ ВОЛН
§ 1. Основные понятия
Волной называется вообще распределение некоторой'!
величины в пространстве. Если это распределение
движется, то мы имеем дело с бегущей волной, если оно не-|
подвижно, то волна — стоячая. Движение волны совер-1
шается со скоростью, называемой скоростью распростране-j
ния. Скорость распространения зависит от свойств среды. \
Простейшая волна — синусоидальная. При этом
величина, характеризующая волну, распределяется в
пространстве вдоль направления распространения по закону
синуса. Возьмем, например, наиболее доступную
непосредственному наблюдению волну — волну на поверхности
воды (именно к этому явлению, очевидно, был впервые
применён термин «волна»). Величина, характеризующая такую
волну, есть уровень воды в данном месте. Волна на
поверхности воды есть (в простейшем случае) синусоидальное
распределение уровня в направлении распространения
волны. Мы наблюдаем на поверхности воды в
естественных условиях чаще всего бегущие волны, но при
помощи специальных приспособлений можно получить и
стоячие волны; тогда распределение уровня будет
неподвижным.
Расстояние между двумя гребнями или между двумя
впадинами называется длиной волны.
Интенсивность волны характеризуется амплитудой
изменения определяющей величины; в рассматриваемом
случае это будет высота волны, т. е. половина разности
высот гребня и впадины.
10 основы теории волн [гл. i
Для всех волн, которыми мы в дальнейшем будем
интересоваться, скорость распространения не зависит от
амплитуды; с математической точки зрения это означает, что
мы будем рассматривать линейные волновые уравнения.
Проследив движение любой частицы воды на
поверхности, мы заметим, что частица движется вверх и вниз
(точнее—по эллипсу), но в среднем остаётся на месте, тогда как
волна движется. Понятие о движении волны есть понятие
чисто кинематическое; движется поступательно гребень
{или, собтветственно, впадина волны), т. е. место, где
имеется наибольший (или, соответственно, наименьший)
уровень. Проследив движение отдельной частицы воды, мы
можем определить её колебательную скорость; эта
перешенная величина, связанная с амплитудой волны, не
имеет ничего общего с постоянной скоростью
распространения.
Число колебаний частицы в секунду называется
частотою; между частотой /, скоростью распространения с
и длиною волны к существует очевидное и универсальное
соотношение;
Отметив две какие-либо частицы на некотором расстоянии
друг от друга в направлении распространения и наблюдая
их движение, мы замечаем, что движение их
одинаково, с тою лишь разницей, что более удалённая (по
движению волны) частица воспроизводит движение более
близкой частицы с некоторым запозданием т, или с
некоторым сдвигом по фазе <?, причём
т=-, ср = шт = 2тг/х = 2т:^г ,
где d — расстояние между частицами, Т — период
колебания. Величина т есть время пробега волною
расстояния d.
«Эти представления переносятся и на другие виды
волн.
Нас интересуют упругие волны, из числа которых
наибольшее значение имеют звуковые волны в воздухе
4
§ 1}
ОСНОВНЫЕ ПОНЯТИЯ
11
и воде и сейсмические волны, распространяющиеся в
земной коре.
Нужно выяснить, прежде всего, какие величины
характеризуют названные виды волн. При упругих иолнах
волновое движение совершается вереде (воздух, вода, земля).
Значит, это движение может характеризоваться движением
частиц среды,т. е. так же, как и в случае волны на
поверхности воды. Таким образом, упругую волну можно
описывать смещением или колебательной скоростью частицы
среды.
Теперь нужно заметить, что можтго себе представить
колебательное движение частиц среды либо в направлении,
перпендикулярном к направлению распространения, либо
в направлении, совпадающем с направлением
распространения. Первый случай — это так называемая
поперечная волна; волна на поверхности воды есть волна
поперечная. Второй случай—так называемая продольная волна.
Продольные волны возможны в сплошных твёрдых, жидких
и газообразных средах; поперечные волны возможны
только в телах, оказывающих противодействие изменению
формы, т. е. главным образом в твёрдых телах*).
Таким образом, звуковые волны в воздухе и воде
представляют собою продольные волны. Частицы среды
колеблются в направлении распространения; так как
колебания различных частиц различаются по фазе, то в
результате движения оказывается, что в одних местах в
данный момент в единице объёма оказывается больше частиц,
чем в покоящейся среде, а в других — меньше.
Другими словами, в одних местах давление оказывается
больше начального (сгущение), а в других — меньше
(разрежение).
Следовательно, давление в данном месте есть
переменная величина, и интенсивность волны можно выражать
амплитудой давления, а самую волну определясь как
распределение давления в пространстве. В акустике чаще
*) Здесь нет противоречия со сказанным раньше, так как
поперечная волна на поверхности воды возможна именно потому,
что поверхность воды под влиянием силы тяжести стремится
сохранить плоскую форму.
12 основы теории волн (гл. i
всего так и поступают. Можно ввести и другие
определяющие величины: если меняется давление, то меняется и
плотность; для описания волновых явлений можно
привлечь переменную плотность или обратную величину —
удельный объём.
Если звуковая волна распространяется по
цилиндрической трубе или по стержню — мы имеем дело с одномерным
случаем; волновое состояние определяется одной
единственной координатой. Если же волна распространяется
в неограниченной сплошной среде, то это, вообще говоря,
случай трёхмерный, описываемый при помощи трёх
пространственных координат. Однако в теории волн
рассматривают преимущественно три вырожденных случая:
случай плоской волны, случай шаровой волны (с централь-
ной симметрией) и случай волны цилиндрической (с
осевой симметрией).
Плоская волна зависит только от одной координаты;
координатная ось совпадает с направлением
распространения. Поверхности, проведённые для данного момента
через точки, в которых определяющая волну величина
находится в одинаковых фазах, являются плоскостями,
параллельными друг другу и перпендикулярными к
направлению распространения.
Шаровая волна описывается также при помощи одной
координаты, но в этом случае координатой является
расстояние, отсчитываемое в любом направлении от
одной точки — центра волны. Поверхности равных фаз
представляют собою в этом случае концентрические
сферические поверхности. Направление распространения в
каждой точке совпадает с нормалью к этим поверхностям,
т. е. с радиусом-вектором, проведённым из центра в
данную точку.
Наконец, в случае цилиндрической волны
единственной координатой служит также расстояние, но
отсчитываемое не от центра, а от некоторой оси, и притом в
плоскости, перпендикулярной к этой оси. Поверхности
равных фаз представляют собою коаксиальные
цилиндрические поверхности.
Введение названных трёх простейших типов волн
вполне оправдано тем, что, во-первых, к ним с достаточ-
§ 2J МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВОЛН 13
ным приближением приводятся многие практические
случаи, а, во-вторых, более сложные волновые картины могут
быть построены путём наложения простейших (например,
плоских) волн.
§ 2. Математическое описание волн
В математической физике предпочитают выбирать в
качестве величины, определяющей волну, некоторую
скалярную функцию времени и координат. Для звуковых
волн такой величиной является потенциал скорости;
можно, впрочем, пользоваться и давлением, которое здесь
также является скалярной величиной. Между
колебательной скоростью о, давлением р и потенциалом ср
существуют следующие соотношения:
_ fL?. — * дЛ ■
V* -" дх ' Р — Ро dt '
здесь vx—компонента скорости по направлению осих, р0—
начальная плотность среды, t — время.
Волновое уравнение, независимо от физической
природы волн, для трёхмерного пространства записывается
в прямоугольных координатах так:
*!? , *!? , *!?_±^__0 /он
дх2 ^ ду2 ^ dz2 с2 dt2 " К '
То же уравнение в сферических координатах имеет вид:
d2-i 2 d-f , 1 г д ( . п д*\ , 1 d2i 1 1 дЪ л 0 0
а в цилиндрических координатах
1 д / с>?\ 1 &*? д^ 1 <?2? _0 ,р ъ
Tdr\rTr)*r*~d:)2 ^ dz2 ""с"5Г1 —а l ^
Совершенно естественно выбрать (2.1) для описания
плоской волны, (2.2) — для сферической и (2.3) —
для цилиндрической. В первом случае выпадает завис и-
14 основы теории волн 1гл. i
мость от двух координат, уравнение плоской волны
принимает вид:
Для сферической волны из (2.2) выпадают
производные по углам; мы получаем уравнение сферической волны
в форме:
£+?*4*=0. (2.5)
дг* ' г дг с1 dt2 v '
Наконец, в случае цилиндрической волны в уравнении
(2.3) остаются только члены, зависящие от г, и уравнение
цилиндрической волны принимает вид:
дг9^ г дг с2 */■ —а ^'0)
Скорость распространения зависит, как сказано, от
свойств среды; для акустических волн — продольных
волн сжатия — скорость распространения
V Ре
где х — объёмный модуль упругости среды, р0 —
начальная плотность. Модуль упругости зависит от теплового
режима; в акустике сжатие и расширение происходят по
адиабатическому закону; при этом
с
где у = --£-( = 1,4 для воздуха), Р0 — начальное давление.
Си
Обратимся к решениям волновых уравнений для
синусоидальных колебаний.
В этом случае можно "положить
у = е*»*Ф(х,у,г)
и, следовательно,
#2'f 2
_=_оАр.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВОЛН ^
Вводя волновое число
7 о) 2т:
С А
получим волновое уравнение плоской волны в следующем
виде:
£+*'?=<>. (2-7>
Общее решение этого уравнения таково:
где со — круговая частота, а А и i? — постоянные,
определяемые из условий задачи. По физическому смыслу
решение представляет собой две волны, движущиеся
вдоль оси х в противоположных направлениях; первый
член представляет волну, движущуюся в направлении
возрастания х. Если среда однородна и не ограничена
и имеется единственный источник плоской волны, то
второй член решения должен быть отброшен, и постоянная А
зависит только от режима источника.
Обращаясь к уравнению (2.5) сферической волны,
заметим, что оно приводится к форме (2.7), если ввести
вместо ср переменную ср г. Отсюда следует, что решение
уравнения (2.5) для синусоидальных колебаний имеет вид:
ф = dei wt-кП 4- - е* (Ы+кг). (2.9)
Первый член представляет волну, расходящуюся из центра.
Сравнивая (2.8) и (2.9), мы замечаем, что в плоской волне
амплитуда потенциала не зависит от координаты, тогда
как в сферической волне амплитуда убывает с расстоя-
1
нием как —, что ооусловлено расхождением волны.
Решение уравнения цилиндрической волны
представляет существенные особенности. Для синусоидальных
колебаний (2.6) может быть представлено в виде:
16
основы теории волн
[ГЛ. Г
-Это уравнение введением новой переменной кг приводится
к уравнению Бесселя нулевого порядка; для
цилиндрической волны получается решение, выражаемое не в
тригонометрических, а в бесселевых функциях аргумента кг.
Это означает, что волновое движение при
синусоидальной зависимости от времени выражается
несинусоидальной зависимостью от координаты, в отличие от плоской
волны, которая выражается синусоидальными
зависимостями как от времени, так и от координаты. Лишь на
^больших расстояниях от оси цилиндрическая волна
приближается к синусоидальной, как это следует из
асимптотических выражений для бесселевых функций.
Решение уравнения (2.10) здесь не приводится, так как
выбор частных интегралов зависит от условий задачи.
, Перейдём теперь к рассмотрению основных волновых
явлений. Исследование каждого такого явления сводится
к решению волнового уравнения с учётом определённых
граничных условий. Когда потребуется пояснить
физический смысл соотношений, мы будем „ссылаться всякий
раз на представления, относящиеся, в частности, к
звуковым волнам; на общность выводов это не повлияет.
§ 3. Отражение и преломление
Когда волна на пути своего распространения
встречает совершенно непроницаемую для волны плоскость,
происходит полное отражение волны. При этом возникает
отражённая волна, направление которой определяется
правилом: угол падения равен углу отражения. Для звуковой
волны условие непроницаемости состоит в том, что
отражающая плоскость предполагается совершенно жёсткой;
математически это выражается условием
У„=о
на плоскости, где vn — нормальная компонента
колебательной скорости. (Для электромагнитной волны
аналогичные условия возникают, когда волна встречается с
поверхностью совершенного проводника.)
Построение отражённой волны с удобством
выполняется при помощи так называемых фиктивных источни-
§ 3]
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ
17
ков, располагаемых симметрично действительным
источникам относительно отражающей плоскости (рис. 1).
Второй наглядный приём построения отражённой
волны состоит в перегибании чертежа поля по линии,
представляющей на чертеже след отражающей плоскости
(рис. 2). Этим приёмом нам предстоит воспользоваться
в дальнейшем. Пока что заметим лишь, что оба приёма
Рис. 1.
Рис. 2.
дают не только качественную, но и количественную
картину явлений при отражении, если условиться
складывать в каждой точке потенциалы от действительных
и фиктивных источников, или потенциалы в совмещаемых
точках чертежа при его перегибании.
Пусть теперь волна встречается с плоской границей
двух различных сред. И в этом случае имеет место
отражение, однако не полное; амплитуда отражённой волны
меньше, чем падающей. Кроме того, образуется волна,
проходящая из первой среды во вторую. Эта волна
называется преломлённой, так как направление её
распространения не совпадает с направлением распространения
падающей волны. Явление подчиняется следующему правилу:
синусы углов преломления и падения относятся как
скорости распространения в граничащих средах.
Количественные соотношения рассмотрим для
простейшего случая нормального падения плоской волны на
пограничную плоскость. Используя условие на границе*
находим, что степень отражения зависит от соотношения
* А. А. Харкевич
18 основы теории волн [гл. I
так называемых волновых сопротивлений обеих сред.
Для звуковых волн волновое сопротивление
представляет собой отношение амплитуды давления к
амплитуде скорости в плоской волне, выражается соотношением
и, стало быть, зависит от тех же двух констант (х и р0),
что и скорость распространения. Называя коэффициентом
отражения отношение потенциала ср2 отражённой волны
к потенциалу ф2 падающей волны, получаем для этой
величины:
где wx и w2 — волновые сопротивления соответственно
первой и второй среды. Если w2^>w19 то к0 — 1— это и есть
случай полного отражения, с которого' мы начали. Но
полное отражение получается и при обратном
соотношении, т. е. при w2<^wv При этом к.р =—1. Это означает,
что отражённая волна имеет такую же амплитуду, как и
падающая, но противоположную фазу (на границе). Если
же w2 = wl9 то к9 = О, что и естественно, так как среда в этом
случае однородна и понятие границы теряет смысл. Что
касается волны, проходящей во вторую среду
(преломлённой волны), то, исходя из непрерывности потенциала
на границе, получаем для коэффициента прохождения:
^=£=_^_ (33)
где через ср' обозначен потенциал проходящей волны. Таким
обраЗОМ, iTn^wnpj^TjiiflWfftiTBrft тта панйЧ^т слус.угстцьлр ттрруп-
дящей воЛны; при w2^>wx &т~1* а к'у—2.
х—ьсё сказаннйё^выше относилось к случаи? встречи вол-,
ны с неограниченной (бесконечной) плоской границей.
Когда мы перейдём от этого абстрактного случая к
реальным соотношениям и станем рассматривать явления,
возникающие при встрече волны с препятствиями конечных
размеров, то мы столкнёмся с явлением значительно более
сложным — с дифракцией волн.
§ 4) ИНТЕРФЕРЕНЦИЯ И НАПРАВЛЕННОСТЬ 19
§ 4. Интерференция и направленность
Интерференцией называется явление, возникающее при
наложении нескольких колебаний, сдвинутых по фазе.
При интерференции волн получаются типичные
пространственные картины, о которых можно составить
представление, рассмотрев один из простейших случаев:
образование стоячей плоской волны.
Пусть плоская волна претерпевает полное отражение.
В результате этого в поле существуют одновременно две
волны, падающая и отражённая, распространяющиеся
в противоположных направлениях. Таким образом, мы
должны использовать оба члена решения (2.8) уравнения
плоской волны. Перенесём начало координат на
отражающую плоскость. Тогда второй член представляет
падающую волну, а первый — отражённую. Так как
отражение предполагается полным, то А=В, и мы
получаем:
ср = Aet'ot (e?kx -f- e-*kx) = 2 Aef^ cos kx. (4.1)
Это выражение показывает, что в стоячей волне 1)
амплитуда зависит от координаты и 2) колебания во всех точках
пространства происходят синфазно. (Для бегущей волны
дело обстоит как раз наоборот.) Наибольшая амплитуда
наблюдается при cos kx=l и равна удвоенной амплитуде
бегущей волны; это происходит в тех точках, в которых
фазы колебаний для прямой и отражённой волн
совпадают (точнее говоря, сдвинуты на 2mz). Такие точки
называются пучностями. В некоторых же точках
результирующий потенциал от сложения колебаний
противоположного знака (что соответствует сдвигу фазы на (2и-|-1)7г)
оказывается равным нулю. Такие точки называются
узлами. Косинусоидальное распределение потенциала
вдоль координаты остаётся в пространстве неподвижным,
чем и обусловлено название стоячей волны.
Если коэффициент отражения меньше единицы, то
получаются несколько более сложные соотношения,
характеризующиеся тем, что потенциал не достигает двойного
вначения в пучностях и сохраняет конечное значение
20 основы теории волн [гл. i
в узлах. В этом более общем случае соотношения очень
удобно трактовать как наложение бегущей волны на
чистую стоячую.
Важным для практики следствием интерференционных
соотношений является присущее излучателям и
приёмникам волн свойство направленности.
Всякий излучатель обладает неодинаковой
интенсивностью излучения по разным направлениям. Точно так же
всякий приёмник неодинаково реагирует на волны,
приходящие с разных сторон. Это свойство и называется
направленностью, причём, как выясняется, определяющие
направленность закономерности, относящиеся как к
излучателям, так и к приёмникам, покоятся на одних и тех же
основаниях и сводятся к явлению интерференции.
Рассмотрим про-
f(точке стой пример. Пусть
наблюдения даны два синфазных
точечных источника
(1 и 2) на
расстоянии Ь друг от друга
(рис. 3). Точечным
источником мы
называем пока малый
источник, не
обладающий сам по себе
никакой
направленностью, т. е.
излучающий чистую
сферическую волну. Выясним, каков будет результат действия обоих
источников в точке наблюдения, достаточно удалённой,
•чтобы лучи, проведённые к ней из точек 1 и 2, можно было
считать параллельными. (Это^елови^ вполне отвечает
практически важным применениям понятия направлен-^
'нгости; оно расшифровывается""""как ycjij3^ge---Ttfagre^T^~^asr^
|е^шизлучающеи систшы^Ею_^алн.енитп^с^асст
точки в.Шяютш^.,) ШГсередины от^езк8ГТ^===^Еи^ста-
?вйм пё^тен^и^уляр и назовём его осью системы. Угол О
между осью и направлением на точку наблюдения
является аргументом искомой зависимости. Предположим, что
такой же, как 1 и 2, источник помещён посредине отрез-
Рис. 3.
§ 4] ИНТЕРФЕРЕНЦИЯ И НАПРАВЛЕННОСТЬ 21
ка 1—2, и пусть этот источник создаёт в точке
наблюдения потенциал
Устраним этот вспомогательный источник и заметим,
что действительный источник 1 находится дальше на -^- ,
а источник 2—ближе на г- > где d= 6 sin & — разность хода
волны от обоих источников до точки наблюдения.
Следовательно, источники 1 и 2 дадут в этой точке,
соответственно: «
а действие обоих источников вместе получим, складывая
эти два потенциала:
ср = ь + ср2 = <р' (в4+«-*Г) = ?^<• 2 cos (| sin » ). (4.2)
Характеристикой направленности называют обычно
зависимость потенциала от угла &, приведённую к виду
безразмерной функции R(b) так, чтобы Д(0) = 1, т. е.
определяют эту функцию как
д<НЯ8|. (43)
В нашем случае, очевидно,
Д(»)=|сов(увт»)|. (4.4)
Как видим, потенциал в точке наблюдения при движении
этой точки по окружности (или при повороте системы
излучателей) колеблется и для определённых положений
принимает нулевые значения. График функции (4.4) в
полярных координатах имеет вид розетки со многими
лепестками (рис. 4; здесь Ь Х = 2).
Очень важно заметить, что в аргумент кроме sin Ь
входит ещё произведение А& — 2- у. Если kb<^l, то Д(&)^1,
22
ОСНОВЫ ТЕОРИИ ВОЛН
[ГЛ.1
т. е. направленность отсутствует. Это значит, что наша
система уподобляется точечному источнику, если размер Ь
достаточно мал по сравнению с длиной волны. Это
заключение верно и по отношению к более сложным системам,
и мы можем теперь уточнить понятие точечного
источника: точечным источником
мы вправе назвать любую
систему синфазных
источников, если размеры системы
малы по сравнению с длиной
волны.
Картина, изображённая
на рис. 4, не типична. Для
действительных излучателей
(и приёмников) чаще всего на
характеристике направленности имеется один главный
максимум, а добавочные лепестки значительно меньше
(а специальными приёмами эти лепестки могут быть ещё
значительно подавлены). Такого рода зависимость
получается, например, если представить себе источники
равномерно и непрерывно распределёнными по отрезку
прямой длиною I. Для
вычисления действия такой
системы нужно выполнить
интегрирование по Z, которое
даёт
Рис. 4.
Л(») =
sin (-p sin b\
kl
sin Ь
. (4.5)
Рис. 5.
График этой зависимости представлен на рис. 5 (&Z = 20).
Всякий реальный источник может быть представлен
комбинацией точечных источников. Такие комбинации
называются вообще группами. Группы могут быть
дискретными (когда источники мыслятся в отдельных точках
на конечных расстояниях друг от друга) и
распределёнными, или непрерывными (когда источники мыслятся
непрерывно распределёнными по некоторой геометрической
форме). Распределённые группы могут быть линейные,
n£ ^оМ\' btjr^*
4>Ч^{
sA '/
а
ИЗЛУЧЕНИЕ И ПРИЁМ
( }
\ И 1Д
поверхностные и объёмные. Распределение может быть
однородным (т. е. когда все элементарные источники
обладают одинаковой интенсивностью при одинаковой
площади) и неоднородным. Формула (4.5) и рис. 5
относятся к прямолинейной непрерывной однородной группе.
Мы говорили до сих пор только о группах синфазных
источников. Рассмотрим диполь, т. е. комбинацию двух
точечных источников противоположного знака.
Воспользовавшись чертежом^риС. "3, п[5оШЯем аналоГИЧНое-рассуж-
дение, с той лишь разницей, что вместо (4.2) получим:
? == <р' (*4 - е-*т) = tent*™*'2 sin [j sin &) • (4-6)
В данном случае в направлении прежней оси излучения
не будет; поэтому нам следует выбрать за ось диполя
прямую, проходящую через
оба источника. Условившись
отсчитывать угол Ь от этой
новой оси, получим, что при
кЬ <^; 1 характеристика
направленности диполя
Я (») = | cos ^ | (4.7)
(рис. 6). Итак, диполь
обладает направленностью и при
малых по сравнению с длиной волны:'размерах. Вообще же,
составляя группы из различным/образом фазированных
источников, можно получить весьма разнообразные
характеристики направленности. /
§ 5. Излучение и приём
•^
5^>
Источником звуковых волн может являться всякое
колеблющееся тело, соприкасающееся с упругой средой.
Приёмником звуковых волн может служить всякое
способное колебаться тело^помещённое в среду, в которой
распространяются волга. Чаще всего одно и то же
тело может служить как излучателем, так и приёмником;
в первом случае оно приводится в колебание какой-либо
24 основы теории волн [гл. i
механической силой, во втором — воздействием звуковой
волны. Свойства тела как излучателя и как приёмника
находятся в теснейшей связи. Подчёркивая эту связь,
называют устройства, излучающие или принимающие
звуковые волны, — звуковыми антеннами. Многие
свойства звуковых антенн, основывающиеся на общих
волновых соотношениях, описываются совершенно такими же
закономерностями, как и свойства антенн, служащих
для излучения и приёма электромагнитных волн. Однако
различие в природе волн определяет существенное
различие конструктивных форм звуковых и радиоантенн.
Наша задача состоит, конечно, в изучении не только
качественных, но и количественных соотношений. G этой
целью начнём с рассмотрения простейшей модели
звуковой антенны. На первых же шагах мы столкнёмся с
упомянутым выше различием: в то время как в
качестве простейшей формы излучателя электромагнитных
волн выступает диполь Герца, в акустике начинают
обычно исследование антенн с модели, называемой
«пульсирующий шар».
Представим себе шар, центр которого неподвижен, а
радиус периодически изменяется, так что каждая точка
поверхности совершает синусоидальное колебательное
движение в направлении радиуса. Нетрудно видеть, что
в силу симметрии излучаемая волна будет сферической.
Механизм излучения, как и для любого другого
колеблющегося тела, состоит в том, что поверхность излучателя,
смещаясь, сжимает прилегающие к ней слои среды. Эти
слоя воздействуют на соседние, и возмущение
распространяется во все стороны от шара, причём вследствие
инерции среды распространение совершается не мгновенно,
а с уже известной нам конечной скоростью—;скоростью
звука. Займёмся теперь количественным описанием
явлений, вводя по ходу дела необходимые определения.
Полагая, что пульсирующий шар находится в
неограниченной среде, т. е. что существует только расходящаяся
от шара волна, можем выразить эту волну первым
членом (2.9):
(р-^еДих-Ап. (5.1)
§ 5] ИЗЛУЧЕНИЕ И ПРИЁМ 25
Мы можем сразу найти давление р и радиальную
скорость и:
P = ?opt =/«ft,7 -^'""-**•'= /(оРо?; (5.2)
Пусть радиальная скорость поверхности шара задана как
Тогда, обозначая начальный радиус шара через а,
получим:
t,e=^(l+/fta)e* <«*-*%
откуда определяется постоянная А:
"т" 1 4- jka '
следовательно,
Это есть выражение для потенциала через заданную
скорость поверхности шара. Если же режим антенны
определён силой, действующей на единицу поверхности шара*
то при помощи (5.2) находим:
таким образом,
9 г /соре
Возвращаясь к (5.4), введём
<*=р.тъ=:«*™- <5-5>
26
основы теории волн
[ГЛ. I
Это есть так называемая объёмная скорость источника,
т. е. вытесняемый им в единицу времени объём. Эта же
величина называется иногда напряжённостью источника.
При ка<^1> т. е. для шара, малого по сравнению с
длиной волны, получаем:
<P = fe.^* -(5.6)
Как видим, величина а в этом выражении вовсе не
фигурирует, размер шара перестаёт играть роль, действие
излучателя характеризуется исключительно его
объёмной скоростью. Сделанный нами переход есть переход к
точечному источнику, а формула (5.6) выражает
создаваемый таким источником потенциал. Форма и размер
точечного источника не оказывают влияния на его работу,
при условии, что он действительно точечный, т. е. что
он мал по сравнению с длиной волны. Формула (5.6) играет
очень важную роль в дальнейшем.
Теперь введём отношение давления на поверхности
излучателя к его объёмной скорости и назовём это
отношение акустическим сопротивлением излучателя:
В нашем случае
8=Й- М
0 w 1
3 = 5\-—Т' - (5.8)
1+7ь
где w = р0е — уже известное нам волновое
сопротивление среды. Излучаемая мощность есть
или, если
2
W^^R.
Действительная (активная) слагающая R акустического
сопротивления 3 носит название сопротивления излуче-
§ 5}
ИЗЛУЧЕНИЕ И ПРИЁМ
27
ния. Это понятие и его применения совершенно
аналогичны встречаемым в радиотехнике.
В нашем случае
H~s T+ftW • ^У)
Другой важной моделью акустической антенны
является неограниченная плоскость, колеблющаяся в
направлении своей нормали. Соотношения для этой модели
можно получить из предыдущего предельным переходом
при а -»оо. Эти соотношения оказываются весьма простыми:
волна излучается плоская, амплитуды потенциала,
давления и скорости везде одинаковы. Мы получаем
следующие -зависимости:
WUa # WU ^ D W /г лг\\
А = -^; * = Т; 3 = ^ = 5-- (5-10)
Пульсирующий шар является первым и простейшим
представителем семейства шаровых антенн, обладающих
многими замечательными свойствами. Мы не
предпринимаем пока исследования этих свойств; отметим лишь, что
следующим по порядку членом семейства является так
называемый колеблющийся шар, т. е. шар, совершающий
колебательное движение вдоль некоторой оси без
деформации. Оказывается, что такой излучатель обладает
свойствами диполя.
Общий приём исследования любого вида антенн состоит
в следующем: поверхность антенны разбивается на
бесконечно малые элементы, каждому из которых
приписывается объёмная скорость du = vndS, где vn — нормальная
скорость в данной точке. Каждый элемент
рассматривается как независимый точечный источник.
Составляется согласно (5.6) дифференциальное выражение
которое интегрируется по всей поверхности излучателя.
Если антенна излучает в полупространство или в часть
пространства, ограниченную некоторым телесным углом,
то множитель 4ти в знаменателе заменяется множителем
соответственно 2ъ или 2. Для того чтобы найти реакцию
28 основы теории волн [гл. i
поля на излучатель или акустическое сопротивление,
составляют выражение для давления на данный элемент
поверхности и снова интегрируют этр выражение по всей
поверхности. Такие вычисления возможны, если
отсутствует дифракция, т. е. если между любой точкой на
поверхности излучателя и любой точкой в поле можно
провести прямую, не пересекающую излучатель.
Действие антенны в качестве приёмника сводится в
общих чертах к тому, что, будучи помещена в звуковое
поле, она приходит в колебательное движение. Для
выяснения количественных соотношений нужно учесть, что,
с одной стороны, на поверхность антенны действует сила,
которая может быть вычислена как
F=\pdS,
s
где dS— элемент поверхности антенны. С другой же
стороны, движению поверхности препятствует реакция
среды, так как колеблющаяся поверхность действует как
излучатель и создаёт вторичное звуковое поле.
Как уже говорилось, свойства антенны как
излучателя и как приёмника тесно связаны между собою; чтобы
разобраться в этих соотношениях, лучше всего поставить
вопрос о работе антенны в общем виде. Пусть дана система
из двух антенн, 1 и 2. Положим, что система линейна.
Тогда мы можем утверждать, что давления рх и р2 на
поверхностях обеих антенн и их объёмные скорости их и и2
связаны линейными соотношениями:
Pi = cii»i + 'i»»„ I (5 12)
Выясним смысл коэффициентов с12 и с21. Мы имеем:
с =Ы
21 щ I ия=о '
т. е. этот коэффициент показывает, какое давление р2
развивается на поверхности антенны 2, если антенна 1
колеблется с объёмной скоростью uv при условии, что ан-
I 6] ДИФРАКЦИЯ 29
тенна 2 заторможена, т. е. не может совершать никакого
движения. Коэффициент
выражает аналогичные соотношения для работы системы
передачи в обратном направлении, т. е. когда излучает
антенна 2. Наиболее существенным для дальнейшего
является основанное на теореме взаимности*)
утверждение, что коэффициенты с12 и с21 равны друг другу, т, е.
что .
щ
Это соотношение, как i ряд других сходных соотношений,
выводимых из той же теоремы взаимности, как раз и
служит выражением единства приёмно-излучательных свойств
всякой антенны. Относящиеся к этим вопросам
соображения развиваются более подробно применительно к
неустановившимся явлениям в § 22 второй главы.
Напомним ещё раз, что хотя наше изложение
конкретизируется на материале звуковых волн, но многие
основные выводы имеют общий характер, т.е. приложимы к
волнам любой физической природы.
§ 6. Дифракция
Явление дифракции состоит в том, что волна,
встречаясь с препятствием конечных размеров, в той или иной
мере огибает это препятствие.
Это явление требует самого серьёзного внимания, во-
первых, потому, что практическое значение его очень
велико, а во-вторых, вследствие значительных трудностей,
возникающих при его математическом исследовании. Роль
дифракционных явлений становится ясной, если
представить себе, что никакое использование или даже простое
наблюдение каких бы то ни было волн немыслимо без
*) Подробное изложение относящихся сюда вопросов можно
найти в монографии В. В. Фурдуева «Теоремы взаимности»,
ГТТИ, 1948 г.
1*2=0
.Pi
«,=0
(5.13)
30
основы теории волн
[ГЛ. I
встречи с теми или иными предметами. Свободно
распространяющаяся волна недоступна наблюдению и не может
быть использована. С другой стороны, очевидно, что
всевозможные приборы и устройства для наблюдения и
использования волн представляют собою препятствия
конечных размеров, и, следовательно, с явлением
дифракции мы имеем дело всегда. Всё, что говорилось раньше
об отражении и преломлении, относилось к
специальному и притом абстрактному случаю бесконечно
протяжённой границы двух сред. Наблюдая явления,
происходящие при встрече волны с телом конечных размеров и
произвольной формы, мы не можем уже говорить об
отражении; мы говорим в этом случае о дифракционном поле,
образующемся вокруг препятствия, и спереди и сзади.
Мы вынуждены отказаться от простых и удобных
представлений лучевой (геометрической) теории волн; лучи
(как бы мы их ни определяли) искривляются около
препятствия, и, следовательно, само понятие луча теряет
своё значение. Мы должны отказаться также от
привычного представления о геометрической тени; оказывается,
что волновое возмущение той или иной интенсивности
наблюдается также и на поверхности препятствия,
противолежащей источнику. Иначе говоря, переходя к
изучению дифракционных явлений, мы должны отбросить
целый комплекс простейшие представлений и овладеть
пониманием волновых явлений на более высоком уровне.
Следует теперь уточнить понятие о размерах. Во всей
стационарной теории волн для определения тех или иных
размеров применяется переменный масштаб — длина
волны. «Большой» или «малый» нужно понимать как
большой или малый по сравнению с длиной волны.
«Конечный» означает сравнимый с длиной волны.
Абстрактный термин «бесконечный» имеет чаще всего вполне
реальный смысл; речь идёт о величине весьма большой по
сравнению с длиной волны. Если бы такое истолкование не
было возможным, то не имело бы никакого смысла
рассуждать об отражении волы в духе § 3. Практически же
эти рассуждения отнюдь не бесполезны, но их следует
относить к частному случаю встречи волны с границей,
протяжённость которой весьма велика по сравнению с
%
§ 6] ДИФРАКЦИЯ 31
длиной волны. Из этого следует, что результаты § 3 в
реальном случае верны лишь с приближением тем
большим, чем больше протяжённость границы по сравнению
с длиной волны.
В различных отраслях науки и техники мы исследуем
и применяем волны не только различной физической
природы, но и весьма различной длины. Оптика имеет дело
со световыми волнами и ближайшими областями
инфракрасной и ультрафиолетовой частей спектра, т. е. с
волнами, длина которых достигает порядка микрона.
Акустика применяет волны длиною от нескольких сантиметров
до десятка метров, а если включить сюда также ультра-
и инфразвуковые волны в различных средах, то
диапазон длин волн ещё значительно расширится. Длины
радиоволн охватывают огромный диапазон от сантиметров
до километров.
Такое различие в длинах волн определяет и различие
их поведения; так, например, в повседневной жизни мы
не наблюдаем дифракции световых волн, так как они очень
коротки, но зато постоянно наблюдаем дифракцию
значительно более длинных
звуковых и радиоволн.
Обратимся теперь к
физико-математической стороне
проблемы.
Для качественного
понимания дифракционных
явлений весьма полезен принцип
Гюйгенса, состоящий, как
известно, в том, что каждая
точка волны может
рассматриваться как новый точечный
источник. Пользуясь этим
представлением, можно
легко построить фронт распро- Рис. 7.
страняющейся волны (рис. 7),
можно также наметить основные качественные черты
дифракционных явлений. Так, например, если плоская
волна встречается с экраном, снабжённым маленьким
отверстием, то это отверстие будет являться источником
32
основы теории волн
1ГЛ. I
расходящейся по ту сторону экрана волны. Если экран
снабжён целым рядом отверстий, то волны, излучаемые
каждым отверстием, как источником, будут
интерферировать. Мы подходим, таким образом, к объяснению
действия дифракционной решётки.
К сожалению, принцип Гюйгенса в его элементарной
форме не даёт возможности получить количественное
решение дифракционной задачи. Впоследствии Кирхгоф
построил теорию, которая приводит к точному решению
этой задачи; дело сводится к вычислению некоторого
интеграла, под знак которого входят значения потенциала
и его нормальных производных (а также производных по
времени, что не столь существенно), определённые на
произвольной замкнутой поверхности.
Формула Кирхгофа имеет вид:
s
где срд — потенциал в точке А, охватываемой
произвольной поверхностью S, п — внутренняя нормаль к S, г —
расстояние от элемента поверхности dS до точки А.
Хотя формула Кирхгофа сама по себе безупречна,
однако, применение её наталкивается на трудности
принципиального характера. Поверхность, на которой должны быть
известны значения потенциала и его нормальной
производной (так называемая гюйгенсова поверхность), может
выбираться произвольно. Но как бы мы её ни выбирали,
до того, как задача решена, мы не имеем достоверных
сведений о том, что на ней происходит, и, следовательно,
точное решение снова от нас ускользает. Обычный выход
из этого порочного круга состоит в том, что назначают
на гюйгенсовой поверхности предположительные, но по
возможности пратдоподобные значения волнового
возмущения. Само собою разумеется, что получаемое при
атом решение будет приближённым, степень приближения
зависит от того, насколько удачно сделаны исходные
предположения.
Так, например, при решении задачи о дифракции
относительно отверстия в экране поступают обычно так: сов-
§61
ДИФРАКЦИЯ
33
мещают гюйгенсову поверхность с экраном (включая и
плоскость отверстия), замыкают эту поверхность на
бесконечности и предполагают, что в плоскости отверстия
возмущение такое же, как при свободном распространении
волны, а на задней поверхности экрана возмущение вообще
отсутствует. Выполнив вычисления по формуле (6.1), мы
найдём потенциал как функцию координат, причём его
значения на гюйгенсовой поверхности будут отличаться
от первоначально предположенных. Можно было бы
воспользоваться найденными значениями и действовать далее
методом последовательных приближений. Однако при
решении оптических задач обычно ограничиваются
первым приближением, которое, как оказывается, не только
схватывает все существенные детали дифракционного
явления, но и даёт достаточное для практических
надобностей количественное приближение. Естественно, конечно,
стремиться к получению точных решений различных
дифракционных задач. Такие решения известны для
небольшого числа специальных случаев. Так, например,
существует точное решение для дифракции относительно шара.
Здесь задача, формулированная в сферических коорди-
натах, решается при помощи довольно хорошо разрабо^
тайной теории шаровых функций. Вообще, пересматривая"
известные решения дифракционных задач, можно отме-1
тить, что все эти решения получаются специализирован-]
ными, а не общими методами.
Большой принципиальный интерес представляет
принадлежащее Зоммерфельду точное решение задачи о
дифракции плоской волны относительно прямолинейного
края полубесконечного экрана. Потенциал в этом
случае не зависит от координаты, отсчитываемой вдоль края
экрана, и задача приводится, следовательно, к плоской.
Идея решения вкратце такова: условия, существующие
на экране, могли бы получиться в свободном поле при
наличии второго, симметрично расположенного
источника. Однако такого источника на самом деле нет. Но если
ему нет места в действительном физическом пространстве,
то его можно поместить во вспомогательном фиктивном
пространстве. Строится двулистная риманова
поверхность. Один лист физический, другой фиктивный; оба листа
3 А. А. Харкевич
©
основы теории волн
[ГЛ. I
сшиты по линии экрана. Остаётся подобрать
симметричную относительно шва функцию, удовлетворяющую
волновому уравнению на обоих листах. Часть решения,
отвечающая фиктивному листу, в окончательном
результате, понятно, отбрасывается.
За последнее время в области теории дифракции новые
методы созданы академиками Смирновым и Соболевым;
появилось точное решение задачи о дифракции
относительно круглого отверстия.
Вообще же положение оставляет желать лучшего;
хотелось бы располагать достаточно общим и не слишком
сложным методом получения точных решений хотя бы
простейших дифракционных задач.
§ 7. Принцип наложения
Одним из сильнейших орудий исследования линей-
.у ных проблем является принцип наложения или супер-
^ч* ^ позиции.
Применительно к волнам принцип наложения состоит
^ в том, что наличие волнового поля не изменяет свойств
*| среды, и, следовательно, любая другая волна^распростра-
^ няется в среде та!кт как есдд.бы никакого поля вереде не
^*~3®2^ одновременно суще-
^^схщоощих волн получается простым суммированием полей
t каждой отдельной волны; потенциалы, как скалярные
величины, складываются алгебраически; градиенты, как.
<^ векторные величины, складываются геометрически. Мы
уже пользовались неявно принципом наложения в § 4,
когда говорили об интерференции, представляющей собою
результат наложения волн, или в § 5, где излучение неко-
TopoMj^RepxHocTH рассмат^р^-прр*. как нм^бние полей,'
<ч\ создаваемых отдельными элементами __эт.о^ров^х5П^ти.
^? ' Из принципа наложения вытекает""возможностьобТрат-
^ ного действия — разложения, состоящего в том, что мы
можем любое сложное волновое возмущение разложить
на простейшие составляющие, причём выбор характера
этих составляющих полностью зависит от нашего
усмотрения и диктуется исключительно соображениями,
относящимися к удобству исследования.
i
§ 7J ПРИНЦИП НАЛОЖЕНИЯ 35
В начале этого параграфа указывалось, что принцип
наложения применим к линейным проблемам. Следует
рассмотреть этот вопрос подробнее для того, чтобы наметить
границы применимости принципа наложения.
Если законы изменения состояния среды при волновых
возмущениях ш?линеин£г, то можно предвидеть два след-
ствия этой нелинейности*. Во-первых, при наличии волно-
вПгТГвозмущения волновые постоянные среды изменяются
в среднему а это уже является нарушением принщпа
наложения. Во-вторых, нелинейность среды нарушает простой
закон суммирования. Это можно пояснить следующей
схематический выкладкой. Пусть х и у—две величины,
характеризующие волновое возмущение. При линейной
зависимости между ними принцип наложения применим,
и мы имеем при одновременном наличии двух волн:
Уг - кхг; у2 = кх2\ у = у1-\~у2 = к К + жг) = кх-
Если же зависимость нелинейна, то
2/l = /(*i)'> Уа = /(»2); У = /(«)=/(Ж1 + Ж2)^/(Ж1)+/(Ж2)»
т. е. принцип наложения неприменим.
Посмотрим теперь, как обстоит дело для различных
волн. Для электромагнитных волн в пустоте до сих пор
никаких нарушений линейности экспериментально не
обнаружено. Однако если электромагнитные волны
распространяются вблизи несовершенных диэлектриков или
проводников, то возникают характерные нарушения принципа
наложения. К таким явлениям относится, например, так
называемый Люксембург-Горьковский эффект, состоящий
в модуляции передачи одной радиостанции полем другой.
Этот эффект объясняют нелинейностью ионосферы.
Звуковые волны распространяются в заведомо нелипей-.
ной среде. Дело в том, что адиабатический закон сжатия,
по которому совершаются акустические явления, —
закон существенно нелинейный. Мы описываем
акустические явления линейными уравнениями лишь приближённо.
Это приближение оказывается достаточным, если мы
ограничимся рассмотрением так называемых малых
возмущений, т. е. таких возмущений, при которых относительные
3*
36 основы теории волн [гл. д
изменения давления, плотности, объёма и т. д. весьма малы.
При этом условии приращения этих величин
приблизительно пропорциональны друг другу, и мы'вправе
воспользоваться линеаризованными уравнениями акустики,
что упрощает дело. Зная же, в чём состоит приближение,
мы легко можем его оценить.
Математическое применение принципа наложения
сводится в общих чертах к следующему.
Пусть дано уравнение
У=*Р(х),
где *Р — линейный функциональный оператор,
включающий в себя какие угодно дифференциальные и
интегральные операции. Предположим, что решение данного
уравнения оказывается затруднительным, как это часто и
бывает в действительности. Представим величину х в виде
суммы (конечной или бесконечной)
X '=L: ^^ Xft
выбрав слагаемые Х{ таким образом, чтобы уравнение
разрешалось по возможности легко. Найдя слагаемые
решения, получаем окончательный результат простым
суммированием:
Следует ещё раз подчеркнуть, что эра схема применима
лишь при условии, что Ф есть линейный оператор.
Разложение х=-Ъх{, как уже говорилось, произвольно.
Функция х может, например, быть разложена в ряд
по любым функциям или представлена
соответствующим интегральным выражением. Очень большую роль
играют разложения по тригонометрическим функциям,
составляющие основу метода Фурье, которому
посвящен следующий параграф. Применяются, однако, и
другие разложения, например по шаровым функциям,
в частности по полиномам Лежандра. Некоторые
специальные весьма удобные разложения будут обсуждены
ниже.
§ 81 РЯД И ИНТЕГРАЛ ФУРЬЕ 37
§ 8. Ряд и интеграл Фурье
Стационарная теория волн рассматривает
возмущения, описываемые периодическими функциями времени
и координат. Наиболее удобным разложением для
периодических функций является разложение в ряд по
тригонометрическим функциям, называемое рядом Фурье. Если
периодическая функция (пусть для определённости это
будет функция времени t) определена как
f(*) = f(t + nT),
где Т — период, п — произвольное целое число, то
функция эта может быть представлена рядом Фурье следующим
образом:
/(*)= 2^Аи)'> . (8.1)
—со
где
^2
2
Это — так называемая комплексная форма ряда Фурье.
Физический смысл (8.1) состоит в том, что периодическая
функция представляется как сумма синусоидальных
колебаний с частотами, кратными основной частоте
2л
Т
Колебание основной частоты носит название первой
гармоники, колебание двойной частоты — второй
гармоники, и т. д. Величина | ak | даёт значения амплитуд
гармоник; совокупность значений | ak | носит название спектра
амплитуд*).
*) Обычно говорят просто спектр: однако уточнение
терминологии желательно, так как можно говорить и о спектре фаз, и
о спектре мощности и энергии.
(8.2)
38 основы теории волн [гл. i
В координатах (|а|, о) спектр представляет
совокупность точек с координатами (\ak\, &со). Общепринято
графическое изображение спектра при помощи вертикальных
отрезков, длина которых
ак\ пропорциональна
соответствующим | ak |. Такого
рода спектр носит название
линейчатого (рис. 8).
? о Знания одного лишь
о ш L L 9ш L L **& спектРа амплитуд ещ§ не-
достаточно для восстанов-
Рис- 8- ления вида функции / {t)\
как видно из (8.1), для
этого нужно ещё знать спектр фаз cpfe. Однако ответ на
ряд существенных вопросов можно получить при помощи
одного спектра амплитуд. Возвращаясь к сказанному в
предыдущем параграфе, мы видим, что типовая задача
у = Ч?(х)
для случая, когда х есть периодическая функция t,
решается при помощи ряда Фурье следующим образом:
выбирается
и решается уравнение вида
yt = 4f(x^4f[aff^%
после чего общее решение получается также в форме ряда
Фурье:
Таким образом, решение любой проблемы для
простейшего случая чисто синусоидального режима без труда
обобщается на случай произвольного периодического
режима. Вот почему при исследовании колебаний и волн
ограничиваются обычно рассмотрением синусоидального
режима. Если известно поведение некоторой системы в
синусоидальном режиме любой частоты, то тем самым решён
вопрос и о поведении этой системы в любом периодическом
режиме.
§ 8]
РЯД И ИНТЕГРАЛ ФУРЬЕ
39
Хотя мы говорили пока только о периодических
функциях времени, но совершенно аналогичные соображения
относятся к периодическим функциям пространственных
координат. Соответственно изменяется лишь смысл
величин. Например, период надо понимать в этом случае не как
промежуток времени, а как отрезок, за пределами
которого изменения функции воспроизводятся повторно.
Возможно замечательное обобщение ряда Фурье,
позволяющее применить ту же идею разложения по
синусоидальным функциям к непериодическим функциям. Такое
обобщение можно себе представить, если принять во
внимание, что непериодическая функция может
рассматриваться как периодическая, но с периодом, стремящимся к
бесконечности. При этом основная частота стремится к нулю;
к нулю стремится также и интервал между отдельными
спектральными линиями; сумма конечных слагаемых,
которую представляет собой ряд Фурье, должна быть
заменена интегралом. Оформив надлежащим образом эти
рассуждения, мы получим формулу интеграла Фурье (она
дана здесь также в комплексной форме):
4оо
/W= 5^' & (!»)<**'*»> . (83)
-со
где
-Ко
$(/<*>) = [ f(t)e-№dt. (8.4)
—со
Интеграл Фурье представляет любую (с практически
несущественными математическими ограничениями)
непериодическую функцию в виде суммы бесконечного числа
бесконечно близких по частоте и бесконечно малых по
амплитуде колебаний. (Интервал между компонентами
есть dec, амплитуда каждой компоненты | S (/со) | dco.)
Величина \S (/со) j носит название амплитудного спектра
функции/ (t). Однако в отличие от спектра периодической
функции спектр непериодической функции представляет
собою не совокупность дискретных значений, а непрерыв
40 ОСНОВЫ ТЕОРИИ ВОЛН [ГЛ. I
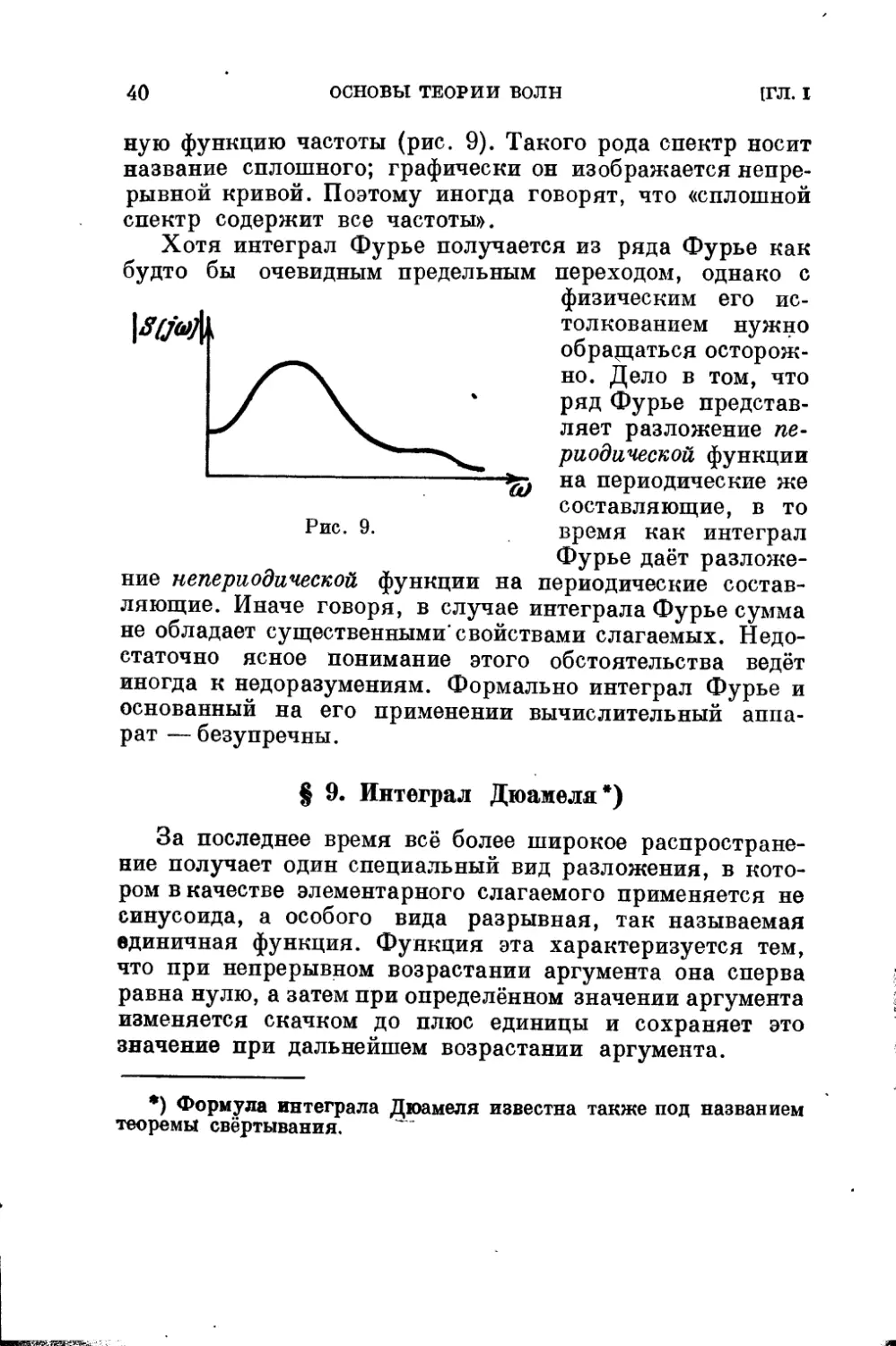
ную функцию частоты (рис. 9). Такого рода спектр носит
название сплошного; графически он изображается
непрерывной кривой. Поэтому иногда говорят, что «сплошной
спектр содержит все частоты».
Хотя интеграл Фурье получается из ряда Фурье как
будто бы очевидным предельным переходом, однако с
физическим его
истолкованием нужно
обращаться
осторожно. Дело в том, что
ряд Фурье
представляет разложение
периодической функции
■^ на периодические же
составляющие, в то
Рис. 9. время как интеграл
Фурье даёт
разложение непериодической функции на периодические
составляющие. Иначе говоря, в случае интеграла Фурье сумма
не обладает существенными'свойствами слагаемых.
Недостаточно ясное понимание этого обстоятельства ведёт
иногда к недоразумениям. Формально интеграл Фурье и
основанный на его применении вычислительный
аппарат — безупречны.
§ 9. Интеграл Дюамеля*)
За последнее время всё более широкое
распространение получает один специальный вид разложения, в
котором в качестве элементарного слагаемого применяется не
синусоида, а особого вида разрывная, так называемая
единичная функция. Функция эта характеризуется тем,
что при непрерывном возрастании аргумента она сперва
равна нулю, а затем при определённом значении аргумента
изменяется скачком до плюс единицы и сохраняет это
значение при дальнейшем возрастании аргумента.
*) Формула интеграла Дюамеля известна также под названием
теоремы свёртывания.
I 9)
ИНТЕГРАЛ ДЮАМЕЛЯ
41
Определение этой функции таково:
n(t ^_| ° [«<*]
СГо (^ — -) — | i [t>%y
Любая данная функция может быть разложена по
единичным функциям. Наиболее наглядно такое
разложение получается предельным переходом. Возьмём
график какой-либо функции / (t) (рис. 10). ~
(9.1)-
Разобьём ось
>ffdt]-№
Рис. 10.
абсцисс на равные отрезки Д£ и впишем в данный график
ломаную линию /(£), как показано на рисунке. На
основании определения (9.1) можем записать аналитическое
выражение для ломаной:
/w=/(P)obW + [/(AO-/(0)]a0(*-AO +
+ [/(Ш)-/(А*)] о0(1--2Д*)+ ••.==
= 2У(Ш)-![(к-1)М]} о0(1-Ш).
лд*=о
Будем переходить к пределу, устремляя Д* к нулю. Тогда
приращение функции / заменится её дифференциалом,
сумма перейдёт в интеграл, переменная суммирования kit
может быть заменена переменной интегрирования т, а
ломаная f(t) совпадёт с данной функцией./(*). Мы получаем:
/«=U('^ww-
(9.2)
42 " ОСНОВЫ ТЕОРИИ ВОЛН [ГЛ. I
Этот интеграл нужно понимать в смысле Стильтьеса, т. е
он применим и в том случае, когда функция f(t) имеет
разрывы. Если f(t) непрерывная (и гладкая) функция,
то (9.2) принимает вид
t
f{t) = fa(t—z)f(x)dx. (9.3)
О
Если же имеются разрывы, т. е. скачкообразные изменения
функции при определённых значениях аргумента, то к
предыдущему выражению нужно ещё прибавить сумму
произведений величин скачков на о0 (t — ik), где %k—абсциссы
точек разрыва. Так, например, если функция f(t) равна
нулю при £<^0, а при г~0 скачком достигает значения
/(0) (как на рис. 10), то, выражая обобщённый диферен-
циал в (9.2) через производную, мы должны записать:
t
f H) = f (0) т0 (*) + Ja0 (t - т) /' (т) dx. (9.4)
0
Применим теперь это разложение к решению общей
линейной задачи на основе принципа наложения. Пусть по-
прежнему задача сводится к решению линейного уравнения
у=Ч?{х)
и пусть х задана как некоторая функция x(t) и выражена
интегралом (9.2). Применяя линейную операцию *Р к обеим
частям уравнения (и полагая, что мы можем применить
её и под знаком интеграла к функциям t), получим:
t
y(t) = \4>[i0(t-^)]dx(x).
о
• Обозначая
h(t) = V[o0{t)},
можем записать:
t
y(t)=[h(t-T)dx(x). (9.5)
О
Это и есть интеграл Дюамеля (в форме Стильтьеса).
Функция h(t) носит название переходной функции.
Она представляет решение задачи для x(t) = aQ(t) и яв-
% 9] ИНТЕГРАЛ ДЮАМЕЛЯ 43
ляется важной и достаточно общей характеристикой
исследуемой системы. Заменой переменных и интегрированием
по частям можно получить из (9.5) несколько
равнозначащих форм, одна из которых может оказаться более
удобной для вычислений в зависимости от вида функций
h и х. Так, например, для случая, когда h и х имеют
разрывы при t = О, можно записать:
t
у (t)=x{0)h (t) + \h (t ->z)x' (x) d-z
о
t
=x (0)h (t) + [h (z)x' {t - т) d-z
о
= h(0)x(t)+[h'{t — z)x(i)dz
о
= h (0)x (t) + [h'(x) x(t-x) dx.
b
Всё сказанное о функциях времени переносится без
каких-либо формальных изменений на функции координат.
В заключение следует сказать несколько 'слов о роли
интегралов Фурье и Дюамеля как инструментов
исследования.
С методической точки зрения оба эти интеграла
совершенно равноценны. В принципе оба интеграла
представляют некоторые разложения на бесконечно малые
слагаемые, имеющие целью решение задачи на основе принципа
наложения. Различие обоих интегралов сводится лишь
к различию вида элементарных слагаемых: синусоида
в интеграле Фурье, единичная функция в интеграле
Дюамеля. Однако это различие практически существенно, так
как приводит к значительному различию в технике
вычислений. В зависимости от характера проблемы либо один,
либо другой инструмент может оказаться более
подходящим с чисто практической точки зрения вычислителя.
(9.6)
ГЛАВА II
ТЕОРИЯ НЕУСТАНОВИВШИХСЯ
ВОЛНОВЫХ ЯВЛЕНИЙ
§ 10. Вспомогательный аппарат.
Исследование вопросов теории неустановившихся
волновых явлений удобно производить при помощи некоторых
специально приспособленных для этой цели методов и
приёмов. Сюда относится прежде всего операционное
исчисление, а также некоторые приёмы анализа разрывных
функций. Всё это составляет вспомогательный
математический аппарат нашего исследования; к описанию этого
аппарата мы и переходим. При этом не ставится цель
подробного и систематического изложения в духе
учебника. Наибольшее внимание уделено общим соображениям;
детали теории операционного исчисления можно
почерпнуть в имеющихся руководствах.
а) Операционное исчисление
Операционное исчисление в его современном виде
основывается на линейном функциональном
преобразовании, именно на так называемом преобразовании Лапласа:
оо
/М:- ^f(t)er**dt*). (10.1)
*) Многие авторы предпочитают определение
оо
f(p)=$f(t)e-ptdt.
о.
Если выбрать такое определение, то все последующие
соотношения примут несколько иной вид.
§ 10] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЫВНЫЕ ФУНКЦИИ 45
В результате этого преобразования функция/ (t)
вещественного переменного t переходит в другую функцию/
(^комплексного переменного р.
Связь между функциями f(t) и/(р), выражаемую (10.1),
сокращённо записывают так:
/Ы+->/(')
и называют f(t) оригиналом, a f(p)—изображением.
На функцию f(t) налагается существенное ограничение:
предполагается, что она равна нулю при t<^0. Это условие
*
можно записать так (обозначая через f(t) произвольную
функцию):
' /(0=7 («к (о- (ю.2)
Таким образом, f(t) может иметь разрыв при t~0.
В дальнейшем рассматриваются только функции вида
(10.2).
Изображение, т. е. f(p), выглядит, конечно, совсем
не так, как оригинал, т. е./(£). Многие трансцендентные
функции t переходят после преобразования в
рациональные функции J9. Так, например, подставив в(10.1) f(t) = e~at,
нетрудно убедиться, что существует такое
соответствие:
e~«t <_,_ Р
РЛа
Изображение единичной функции a0(t) есть единица, и т. п#
Существуют готовые таблицы операционных формул,
в которых сведены изображения весьма разнообразных
оригиналов, в том числе и многих специальных
функций. Краткая таблица такого рода дана в
приложении.
Самое замечательное свойство преобразования (10.1) —
свойство, которое и определяет значение
операционного исчисления для исследований в области
математической физики, — состоит в том, что дифференциальные и
интегральные операции, совершаемые над оригиналами,
46 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
заменяются простейшими алгебраическими операциями
(делением и умножением) над изображениями. А так как
преобразование (10.1) линейно (и, следовательно,
изображение суммы есть сумма изображений), то мы можем
построить изображение дифференциального уравнения,
причём это изображение будет представлять собою
также уравнение, по уже не дифференциальное, а
алгебраическое.
Составление изображения дифференциального
уравнения производится при помощи следующих
операционных формул:
t t
J \f{t){dtY^-^l{p), (10.3)
0 0
7г-кратный интеграл
— p^f (0) - ... -pf-D (0). (10.4)
В формуле (10.4) /^(0) представляют собою значения
функции и её производных до (п—1)-го порядка при £ = 0. Эти
значения образуют систему так называемых начальных
условий. При «нулевых» начальных условиях, т. е. когда
все /(fe) (0) равны нулю, мы имеем просто
д^-^р»7(р). (10.5)
Из всего этого вытекает следующий метод решения
физико-математической задачи:
1. Составляется дифференциальное (или интегро-диф-
ференциальное) уравнение задачи с соответствующими
начальными условиями.
2. На основании формул (10.3) и (10.4), применяемых
почленно к левой части, и при помощи таблиц операционных
формул, применяемых к правой части, строится
изображение уравнения. (В это изображение уже входят
начальные условия, так что операция нахождения постоянных
интегрирования по начальным условиям отпадает.)
§ 101 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЫВНЫЕ ФУНКЦИИ 47
3. Полученное алгебраическое уравнение решается
относительно изображения искомой функции; мы
получаем изображение решения.
4. Зная изображение решения, находим его оригинал,
т. е. бкончательный результат.
Для этой последней операции зачастую достаточно
располагать таблицей готовых формул. Существуют и
общие методы нахождения оригинала по известному
решению. Наиболее употребительный приём состоит в
применении так называемой теоремы или формулы
разложения Хевисайда.
Если изображение представлено в виде
то формула Хевисайда даёт оригинал в следующей форме:
где pk—это п корней характеристического уравнения
Существенно отметить, что формула (10.6) применима
не только для рациональных, но и для трансцендентных
(с простыми полюсами) функций f{p)\ сумма в правой части
(10.6) может оказаться бесконечной и даёт решение в виде
ряда, который, впрочем, во многих случаях суммируется.
Вышеописанная процедура решения
дифференциального уравнения при помощи операционного исчисления
относилась к случаю обыкновенного дифференциального
уравнения (однородного или неоднородного). Эту
методику можно распространить и на случай уравнения в
частных производных. В этом случае преобразование (10.1)
следует применить столько раз, сколько независимых
переменных в уравнении. Мы будем получать последовательно
первое, второе и т. д. изображения уравнения. Все эти
изображения до (т—1)-го включительно (т — число
аргументов) будут дифференциальными уравнениями, (т—1) е
изображение будет уравнением в полных производных,
48 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
и, наконец, (т)-е изображение будет алгебраическим
уравнением, включающим в себя как начальные, так и
граничные условия задачи (также в виде соответствующих
изображений). Для нахождения окончательного
результата необходимо, разумеется, пройти те же т ступеней
преобразования в обратном порядке.
Кроме вышеприведенных основных зависимостей в
операционном исчислении применяется ещё ряд полезных
теорем, которые приведены без доказательства.
Теорема умножения (аргумента):
f{at)+-*-f(£). (10.7)
Теорема смещения:
PfJ§£r+- *""/(<). (Ю.8)
Теорема запаздывания:
f{t-*)oo{t-*)+-*-*-*xT{p). (Ю.9)
Теорема Бореля:
i/i (P) U (р) -+- Wi (* - х) /, (*) dx. (10.10)
v о
Теорема Гринберга:
a-rioo _ _
i[A «>•/, (01 =24;S Мв6£=Й *.<«>.«)
a—/OO
В обеих последних теоремах подразумеваются
соответствия
ti(p)-*■+№', 7t(p)4-/.«).
Теоремы Бореля и Гринберга в некотором смысле
взаимнообратны: первая позволяет найти оригинал,
соответствующий произведению двух изображений, а вторая—
изображение произведения двух оригиналов. Последнее
существенно, например, когда в задачу входит
нахождение мощностей или энергий.
В заключение отметим ещё одно полезное
соотношение: комплексные стационарные решения получаются
I 10] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЫВНЫЕ ФУНКЦИИ 49
из операционных выражений, т. е. изображений, путём
простой замены р на/со, и обратно. Это соотношение вытекает
из полнейшего сходства между интегралом, выражающим
комплексный спектр (см. §8), и преобразованием Лапласа.
Представления и приёмы операционного исчисления
широко использованы в дальнейшем изложении.
б) Анализ разрывных функций
Ниже описываются некоторые приёмы, оказавшиеся
практически удобными и полезными. Это описание не
содержит математического обоснования (которым я и не
занимался). Читатель, которого такое изложение не
удовлетворит, может отказаться от применения этих приёмов
и воспользоваться любыми другими, которые, впрочем,
приведут его к тем же результатам, по всей вероятности
с большей затратой времени и труда.
Вернёмся к определению единичной функции
*<«-Ч ? 1>Л (,0-,2)
Будем называть эту функцию примитивной разрывной
функцией нулевого порядка. Введём теперь функции
отрицательных порядков, определив их рекуррентным
соотношением
t
(0=5°ч.(*)<*т. (Ю.13)
о
Легко видеть, что примитивная разрывная функция
минус первого порядка есть
t
*о
минус второго порядка —
t
°-2 (0 = J а0 СО * dx = у а0 (*),
о
и так далее.
4* А. А. Харкевич
50 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Введём, далее, примитивные разрывные функции
положительных порядков. Определением этих функций
послужит рекуррентное
соотношение
_>, on+i{t)=%[3n{t)\. (10.14)
у
/
(
г*-а-^
>
»
/
у\
t
\а
'
г
1 >*-
Рис. 11.
дельным переходом,
вида;
Это определение расходится
с общепринятым понятием
дифференцируемости
функций. Представление о
свойствах разрывных функций
положительных порядков
может быть составлено пре-
Пусть дана функция следующего
[*<0],
[0<t<a],
t 1
Производная этой функции
{ ° ['«>],
I 0 [t>a]
(см. рис. 11).
При устремлении а к нулю функция f(t) переходит
в пределе в a0(t)\ предельным выражением -J- является
функция a^t). Свойства этой функции могут быть описаны
так: она равна нулю при всех значениях t ф 0; при t = 0
она совершает скачок до значения плюс бесконечность;
при этом, однако, интеграл функции a^t), взятый по
интервалу, включающему точку разрыва, сохраняет
конечное значение, равное единице. Функцию ax(£) называют
- ' ■:&
§ 10) ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЫВНЫЕ ФУНКЦИИ 51
иногда единичным импульсом. Аналогичную функцию
называют также функцией Дирака.
Представление о функции второго порядка, a2(t)9
можно составить аналогичным образом. Эта функция при
t = 0 совершает последовательно два скачка — первый
в плюс бесконечность, второй в минус бесконечность.
Свойства примитивных
разрывных функций различ- ^fi^vj
ных порядков можно
характеризовать ещё следующим
образом: родоначальница семей- _
ства — функция a0(t) — имеет
при t = 0 разрыв самой
функции; функция а^ (t)—разрыв
первой производной; функ- __
ция о_л (*) — разрыв 71-й
производной. Функция <*i{t)
имеет разрыв интеграла; ^ *
функция an(t) — разрыв Рис. 12.
га-кратного интеграла.
Примитивные разрывные функции обладают рядом
простых свойств, непосредственно вытекающих из их
определения. Например,
оя(аж) = зл(аО,
K(*)]e = &o(*),
и так далее.
В дальнейшем нам чаще всего будут встречаться
разрывные функции аргумента и параметра вида Gn (t—т). Эти
функции претерпевают разрыв при t = т. Их можно
дифференцировать как по ty так и по т, причём справедливы
формулы:
5/вяи —(C) = en+i(' — lc)i ' )
d / \ (10-15)
Это соотношение поясняется графиком рис. 12, на
ротором <з0 (i-x) представлена как функция аргумента и как
функция параметра.
4*
52 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
Пусть теперь функция времени и параметра, равная
нулю при t < т, представлена в виде
/(*/с)=/(*,т)о0(*-т),
*
где / — непрерывная функция. Она, так сказать,
обрублена в точке t=z множителем о0 (t—т). Найдём
производные разрывной функции /, применяя к рышеприведённому
выражению обычное правило дифференцирования
произведения. Мы получаем:
/Г(«л)=/Г(*,*)а0(*-т) +
+ /;(*,т)а1(*-т)+/(т)т)а2(*-т),
} (10.16);
/<?(<,*)=/> (<,t)o,(I-t) +
+h~l) (т, т) ъ (*-т) + ... + / (х, х) ая (I - х). J
Приведём ещё разложение в ряд по разрывным
функциям. Разложим сперва в ряд Тэйлора около точки < = х
*
непрерывную функцию /:
?(«,t)=?(t,T)+'-^/;(t,T)+-^£-/r(T,x)+...
Умножим обе части на о0(Г—т) и получим:
/(*,*)=? К *) «о (*—0+/ifcx)«-i (<-«) +
*
+ /Г(Т,Т)<7_2(*-Т)+... (10.17)
Геометрический смысл этого разложения поясняется
графиками рис. 13.
§ 10] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЫВНЫЕ ФУНКЦИИ 53
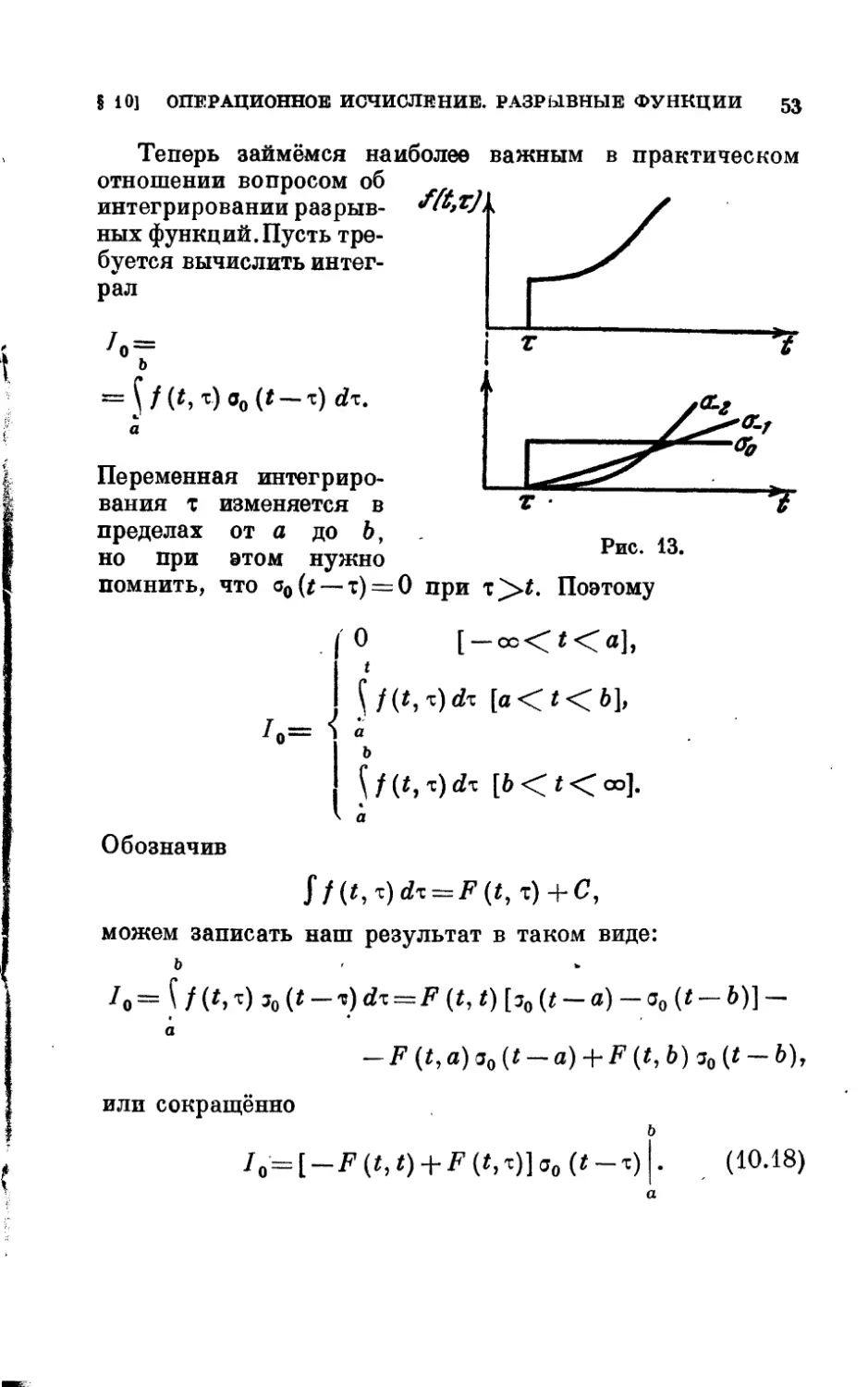
Теперь займёмся наиболее важным в практическом
отношении вопросом об
интегрировании разрыв- *(*»V/k
ных функций. Пусть
требуется вычислить
интеграл
'•7
^/(^ке-*)**.
Переменная
интегрирования т изменяется в
пределах от а до 6,
но при этом нужно
помнить, что a0(t — x) = 0 при т>£. Поэтому
Рис. 13.
ГО
[-со<*<а],
/•= i «
$/(*,*)* [a<t<b],
2
Ь
\f{t,-z)dx [6<«<оо].
Обозначив
ft(t,x)d* = F(t,T)+C,
можем записать наш результат в таком виде:
ъ
Io=U(t^)30(t-^dx = F(t,t)[30(t-a)-e0(t-b)]-
-F(t,a)a0(t-a) + F(t, b) a0 {t-b),
или сокращенно
h = [-F(t,t) + F(t,r)]o0(t-x)
(10.18)
54 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ 1ГЛ. II
Вычислим интеграл с разрывной функцией первого
порядка:
Л= $/(*,*) з^-т)^.
Интеграл этот возьмём по частям:
ь
а
Ъ Ь
' =—/(*,^)а0(« —х)|+ jJ/xC^x)^^ —x)dx.
а а
Последний интеграл * вычисляется по формуле (10.18). н
мы получаем:
ъ ъ
Л= J/(«,х)в1(«-т)Л=-/(«,<) ^(^т)|. (10.19)
а а
Действуя аналогичным образом, получим интегралы,
содержащие разрывные функции высших порядков:
ь
It=[f{t,z)ot(t-z)dt =
= -\f(t,t)a0{t~-x)+f(t,x)a1(t—c)]
(10.20)
= - I/"*"4 (*, 0 «О (* -1) + /(П~2) (*, •=) <h (<-*) +
ь
+ ...+/(*,т)о«_,(«-т)]|. (10.21)
a
Из формулы (10. 19) можно, кстати, получить:
оо -foo
[f{*).3x(t-i)fc = f(t)s0{t), \ f{4)b(t-T)dz = f(t),
0 —ОО
§ 10) ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. РАЗРЕ.1ВНЫЕ ФУНКЦИИ 55
т. е. при помощи разрывной функции первого порядка
всякая функция может быть представлена интегралом от
самой себя.
Наконец, нам понадобится формула интегрирования
выражения, содержащего разрывный множитель в том
более сложном случае, когда имеется некоторая
функциональная зависимость момента разрыва от параметра т.
Требуется вычислить интеграл
ь
/ = $/(^т)о0[*-?(т)]«Ь.
а
Интегрируем по частям:
ь ь
7 = F(*,x)a0[«-cp(T)]U^(<,T)ei[<-<p(x)]<p'(x)dx.
I *J
а а
В последнем интеграле сделаем замену переменных по
формулам
ср(т)~#; т ==&(#).
Тогда
lF{t,*)oi[t-4{x)]d[<t{x)]=$ F[t^(x)]a1{t^x)dx =
« у (а)
ь
= -/ф,?(ОК[*-?('0]
Таким образом, окончательно
ь
I=[f(t,x)<y0[t-9(T)]dx =
а
Ь
= {-FlWi*)] + F(*,*)} blt-li*)]]- (10.22)
а
Эту важную формулу- полезно сравнить с формулой
(10.18), являющейся частным случаем (10.22) при <р(т) — г.
56 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ {ГЛ. II
§ 11. Одномерная разрывная волна
Из §§ 9 и 10 достаточно очевидно, что наиболее удобной
элементарной формой неустановившегося волнового
возмущения является волна, описываемая единичной
функцией. Для случая одномерной (например, плоской) волны
аналитическое представление потенциала может быть
записано в виде
^а°('-7)> (11Л)
где t — время, х — координата, с — скорость
распространения. Наша волна несёт разрыв потенциала на
фронте. Перед фронтом, т. е. там, куда волна ещё не пришла,
потенциал равен нулю; там, где фронт волны уже
прошёл, потенциал равен единице *).
Распространение волны (11.1), |
которую убудем кратко называть ____ I
единичной, происходит очень про- 1—»» I
К , I;
Рис. 14. Рис. 15.
сто: фронт перемещается в направлении оси х со
скоростью с (рис. 14). К этому, в сущности, нечего добавить,
и мы перейдём сразу к рассмотрению отражения
единичной волны.
При отражении с коэффициентом отражения плюс
единица от места отражения распространяется в
противоположном направлении положительная отражённая волна
(рис. 15). Перед её фронтом потенциал равен единице,
*) Следует сразу разъяснить, что наличие разрыва не следует
связывать с какими-либо физическими особенностями
рассматриваемой волны; разрывная волна вводится нами лишь как эле-
§ 11] ОДНОМЕРНАЯ РАЗРЫВНАЯ ВОЛНА 57
жозади фронта—двум (так как потенциалы прямой и
отражённой волн складываются алгебраически).
Если коэффициент отражения равен минус единице,
то отражённая волна имеет обратный знак и, следуя в
обратном направлении, уничтожает потенциал, созданный
нрямой волной (рис. 16).
Если отражение неполное, то потенциал отражённой
велкы меньше по абсолютной величине потенциала
прямой; кроме того, наблюдается преломлённая, или проходя-
Ь
3
Рис. 16. Рис. 17.
щая волна (рис. 17). Количественные соотношения
выражаются формулами § 3 главы I.
Обратимся к более сложному случаю, когда
отражение происходит от реактивного сопротивления. Для
синусоидальной волны это означало бы, что коэффициент
отражения является комплексной величиной, и
следовательно, отражённая, волна получает некоторый сдвиг
фазы относительно прямой волны. В нашем же случае
мы можем представить коэффициент отражения
некоторым операционным выражением, из которого, переходя
к оригиналу, найдём форму отражённой волны. Форма
ментарная форма возмущения; в действительной физической
картине разрывов может и не быть (и чаще всего и не бывает).
Таким образом, разрывная волна есть промежуточное, и скорее
математическое, чем физическое представление. Выбор такого
представления предопределяется математическим аппаратом; мы
видели, что единичная функция играет основную роль при
применении интеграла Дюамеля, операционного исчисления и ана-
иза разрывных функци й.
bi
у
58
ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
волны сохраняется только в двух случаях: при полном
отражении и при отражении от конечного активного
сопротивления. Во всех остальных случаях волна искажается.
Пусть, например, плоская волна,
распространяющаяся в среде с волновым сопротивлением w,
встречается с подвижной совершенно жёсткой стенкой,
обладающей массой М на каждый еж2 своей поверхности. Коэффи-
диент отражения в операционной форме (т. е.
«изображение» коэффициента отражения)
будет
рМ — w
ъ-_
к=
рМ ~\- w
По определению
%
?2=*??1»
НО
Рис. 18.
¥i = 3o(' + 7)
^начало координат перенесено в место отражения), а
изображение прямой волны
— р —
Следовательно, изображение отражённой волны
w
<P2=Ml=-
Р —
М р-
р +
м
По таблице готовых формул и учитывая теорему
запаздывания, находим оригинал, т. е. отражённую волну,
как функцию х и t:
<p,=(2e-s0+7)-i)e. («+?)-
{см. рис. 18).
Рассмотрим другой пример: пусть стенка невесома,
но упруга; её сопротивление на единицу поверхности
пусть будет — »где$ — коэффициент упругости. Тордаана
§ 111
ОДНОМЕРНАЯ РАЗРЫВНАЯ ВОЛНА
59
логично предыдущему
s
Р
-\-w
-р +
?2:
~ г*
Р + :
-:,(1^2Г-> + Э),л(м-:)
Рис. 19.
(см. рис. 19).
Мы говорим о плоской звуковой волне. Всё то же
относится не только к плоской электромагнитной волне, но и
к одномерной электрической
волне, наблюдаемой в электрической
линии. Рассмотренные случаи
отражения соответствуют следующим
режимам линии: холостой ход;
короткое замыкание; включение в
конце линии омического
сопротивления, не равного вслновому;
включение в конце линии
сосредоточенной индуктивности и
сосредоточенной ёмкости. Всё
последующее содержание этого
параграфа в одинаковой мере относится к перечисленным
различным видам волн, объединяемым тем существенным
признаком, что все они являются волнами одномерными
и описываются выражением (11.1).
В практике приходится иметь дело с более сложными
явлениями отражения от нескольких границ. При этом
наблюдаются многократные отражения; волновая картина
до чрезвычайности усложняется с течением времени. Для
того чтобы облегчить рассмотрение хотя бы начальной
стадии развития этой картины, с успехом применяется
простое и наглядное графическое построение, которое можно
назвать волновой сеткой. (Это построение было в своё
время предложено Быоли*) для описания блуждающих
*) См. Бьюли, Волновые процессы в линиях и
трансформаторах, ОНТИ, 1938.
60 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИИ (ГЛ. И
волн в высоковольтных линиях.) Мы поясним идею и
способ этого построения на примере.
Пусть два слоя с разными волновыми сопротивлениями
и, для общности, разными скоростями распространения
заключены между двумя стенками с конечными
сопротивлениями (рис. 20). Пусть единичная волна начинает
распространяться из среды 1 в сре-
I* —*+* h~*\ ДУ 2. Встретившись с границей обеих
сред, волна частично отразится,
частично пройдёт во вторую среду.
w2 p Преломлённая волна отразится
I
Of
с У% от стенки,*снова вернётся к грани-
'/л | - и% це, где опять произойдет частич-
^ р ное отражение, и так далее. Так|
'' как каждый раз при неполном отра-"
Рис. 20. жении падающая волна порождает
две новых (отражённую и
преломленную), то общее число отдельных волн быстро возрастает.
Будем строить график, откладывая координату по
горизонтали, а время—по вертикали вниз (рис. 21). Пусть
единичная волна в начальный момент исходит из левой стенки.
Движение фронта изобразится прямой, наклон которой
определяется скоростью распространения. Волна
доходит до границы и отражается с коэффициентом отражения
Д. ^г — Щ
12 W2-\-Wt
Первоначальная волна была единичная; она несла
потенциал, равный единице. Значит, потенциал отражённой
волнь; равен к12. Эта волна отмечена в левой части
графика. Встречаясь со стенкой, волна к12 отражается с
коэффициентом отражения кг (зависящим от свойств стенки).
Получается новая отражённая волна с потенциалом кхк12.
Вообще при каждом очередном отражении потенциал
отражённой волны получается путём умножения потенциала
падающей волны на соответствующий коэффициент
отражения.
Вернёмся к началу. После первой встречи начальной
единичной волны с границей, кроме отражённой волны
к12, образовалась ещё преломлённая волна к'12 {к'12—
|11) ОДНОМЕР НА Я РА ЗРЫВНА Я ВОЛНА 61
коэффициент прохождения). Волна &'12, встретившись с
правой стенкой, даёт отражённую влево волну к.гк'12;
эта последняя отражается от границы с коэффициентом
отражения к21 и так далее, как показано на графике.
Вшшая~.с^^
менную волновую картину и позволяет легко получить
Рис. 21.
4
ответы не различные вопросы, уводящиеся к двум основ-
1Шм: 1) чт^происходит ^-течением времени в точке с
координатой хТ~2) каково распределениеt потенциала в рро-
с^'рдтетвгтю'Т^
4'Для ответа на первый вопрос мы проводим
вертикальную линию на расстоянии х от начала координат. Точки
пересечения этой вертикали с наклонными волновыми
линиями сразу показывают моменты, когда в данную точку
приходят те или иные волны. Мы можем либо построить
62 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
график изменения потенциала в данной точке, либо
записать результат аналитически. Например, вот что будет
происходить на левой стенке:
? = <»о(0-: ft«(i + *i)*e(*-2b)+
+ *1*i3(l + *i)a0('-U1,+ ...=
ОО
= о0 (t) + к12 (1 + кх) 2 (*! *u)™-' з0 (* - 2т ^'.
т—\.
Для ответа на второй вопрос мы должны провести на
сетке горизонтальную линию, отстоящую на т от начала.
Эта линия является своеобразной итоговой чертой: для
получения потенциала в данной точке в данный момент
мы должны сложить все волны, лежащие выше этой черты.
Точки пересечения волновых линий с итоговой чертой
обозначают мгновенное положение фронтов
соответствующих волн. В этих точках имеется скачкообразное
изменение потенциала.
Если отражение происходит от реактивных
сопротивлений, то соответствующие коэффициенты отражения надо
понимать как изображения, перемножаемые по тем же
правилам, как и вещественные коэффициенты. Понятно,
что определение формы волны, в особенности после
многократного отражения, в этом случае сильно усложняется.
По поводу волновой сетки можно ещё заметить, что
она подсказывает необходимость отказа от волнового
описания явлений и перехода к статистическим воззрениям
для более поздних стадий процесса, когда проследить за
всё возрастающим множеством индивидуальных волн
становится уже невозможным.
f
§ 12. Волновые явления в конечной системе
Некоторые характерные для неустановившихся волн
явления в конечной системе мы поясним на примере.
Пусть дана цилиндрическая труба длиною I, один конец
которой наглухо закрыт, а на втором имеется подвижный
поршень, который при t = 0 начинает вдвигаться с по-
§ 12] ВОЛНОВЫЕ ЯВЛЕНИЯ В КОНЕЧНОЙ СИСТЕМЕ 6$
стоянной скоростью, сжимая заключённую в цилиндре
среду. Выясним, какова реакция со стороны среды на
поршень. Эта реакция, выражаемая давлением на
поршень, вовсе не будет плавно возрастать, как можно было
бы себе представить, отвлекаясь от волнового закона
распространения возмущения. Ведь в первый момент всё
обстоит точно так же, как если бы труба была
бесконечной. В этом случае внутрь трубы излучалась бы плоская
волна, и давление на поршень, движущийся с линейной
скоростью
было бы равно
p = wvQ3Q{t),
т. е. давление, приняв с самого начала значение р0 — wvQi.
в дальнейшем не изменялось бы. Поршень, так сказать,.
«узнает» о конечности трубы лишь тогда, когда к нему
/ приходит отражённая от конца трубы волна. В этот момент,.
спустя время 2т —2— от начала движения поршня,
давление на поршень изменяется скачком, а следовательно,
изменяется скачком и акустическое сопротивление,
определённое нами как отношение давления к объёмной скорости,.
Освоившись с этим представлением, мы могли бы получить
решение поставленной задачи последовательным
рассуждением, которое очень облегчается построением
волновой сетки. Мы приведём здесь, однако, чисто
аналитическое решение задачи, воспользовавшись операционным
р методом (см. § 10 главы II).
Мы имеем одномерное волновое уравнение
* <92з 1 <92-
Найдём первое изображение этого уравнения:
£-^f=-£?(0,*)-f*<?(0,z). (12.2).
Здесь ф (0, х) и у (0, х) —начальные условия, т. е.
значения потенциала и его первой производной по времени-
в начальный момент (при £=0) для любой точки.
64 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ {ГЛ. II
Мы не будем находить второе изображение волнового
уравнения, следуя методике, изложенной в § 10, так как
для решения нашей простой задачи это совершенно
излишне. Мы будем сразу решать обыкновенное
дифференциальное уравнение (12.2).
В нашем случае начальные условия, очевидно,
нулевые, так как мы предполагаем, что до начала движения
поршня никакого возмущения в трубе не было.
Следовательно, наше уравнение является однородным. Его общее
решение имеет, как известно, вид
<р = Лес +Ве с ,
где А и В — величины, определяемые на основании
граничных условий.
Эти условия заданы в нашей задаче следующим
образом: на конце # = 0 задана скорость v~ v0a0(t)f конец
х — l наглухо заделан, что можно выразить
равенством v = 0\x=zl.
Найдём давление и скорость:
v= -& v- ~!Гх = А-Ае ° +Ве V-
Введём граничные условия:
х = 0; v(0)=v0a0(t); v(0)=v0=f(-A + B);
x = l; o(Z) = 0; v(l) = 0= -Ae*>^ + Be **.
Отсюда находим А и В:
-»\ pj
A = v0c- -?—1-; B = vb°-^-L-
2shp с 2shpc
♦
$ 12] ВОЛНОВЫЕ ЯВЛЕНИЯ В КОНЕЧНОЙ СИСТЕМЕ
Для давления получаем:
65
chp
1-х
p=—wv0
ip7
Давление на поршень (х = 0)
р(0)=— wv0cthp~.
Мы оперировали пока с изображениями. Для перехода
к оригиналам, т. е. к функциям времени, воспользуемся
очень удобным в данном случае разложением по
экспоненциальным функциям:
cth^
СО
= 1 + 2 J е-2***.
Легко перейти к оригиналу в виде ряда по единичным
функциям
p(t,0) =
со
= аюв[зь(^+2 2^о(«-2*т)],
fc=l
I
/г ¥т 6т 8т
Рис. 22.
где т== время пробега волны
по трубе (в один конец). Как
видим, при непрерывном
движении уоршня давление на него
возрастает скачкообразно,
каждый раз, когда к поршню
возвращается отражённая от конца цилиндра волна
(рис. 22). Чем короче труба, тем мельче делаются
ступеньки на графике изменения давления и тем больше
приближается ступенчатая ломаная к прямой,
нанесённой на рис. 22 пунктиром и изображающей процесс
о А. А. Харкевич
66 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
сжатия для среды, рассматриваемой как система с
сосредоточенными постоянными (говоря другими словами,
пунктирная прямая изображает процесс сжатия безинерцион-
ной среды, т. е. среды с бесконечно большой скоростью
распространения).
Полезно решить аналогичную задачу, отличающуюся
от предыдущей заданным режимом поршня. Раньше мы
полагали, что поршень движется с предписанной
скоростью v = v0aQ(t). Теперь же пусть к поршню, не
обладающему собственным сопротивлением (т. е. невесомому
и движущемуся без трения), внезапно приложено
постоянное внешнее избыточное давление, так что давление на
поршень (и снаружи и, очевидно, изнутри цилиндра)
выражается так:
Требуется найти движение поршня.
Игнорируя волновые явления, мы могли бы ожидать,
что поршень мгновенно вдвинется в цилиндр, изменив
его объём настолько, чтобы в цилиндре установилось
избыточное давление, равное внешнему. Однако
явление протекает гораздо более сложным образом.
Граничные условия нашей новой задачи таковы: на поршне,
т. е. при х = О, давление равно р(0) = р0е0 (t). На
закрытом конце цилиндра, т. е. при х = /, попрежнему
v = 0.
Мы имеем:
■ _ i _ i
x^l; 0=0; 0=О = |»(-Ле*с +Ве Р с ).
Находим Л и В:
5 12] ВОЛНОВЫЕ ЯВЛЕНИЯ В КОНЕЧНОЙ СИСТЕМЕ 67
и выражение для скорости:
1-х
sh p
v = bL L..
W I
ch р —
с
Скорость поршня получим, положив х = 0:
tT(0) = &-th »-.
4 ' w л с
Применим тот же приём разложения по экспоненциальным
функциям:
— °°
fe=l
е»т + Г
Таким образом, искомая скорость поршня
оо
o(«,0) = g[l+22(-l)*M*-2*r)].
ft = l
На рис. 23 верхний график изображает скорость, а
нижний — перемещение поршня. На этом последнем гра-
Ч
Я\
Рис. 23.
фике пунктирная горизонтальная прямая показывает
среднее смещение поршня — то самое, о котором
говорилось в начале и которое должно было бы вызвать
повышение давления в цилиндре на р0, если бы задача
трактовалась статически.
68 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. il
§ 13. Шаровая волна; точечный источник
Переходя к рассмотрению шаровой волны, заметим
прежде всего, что мы можем несколько упростить
составление волнового уравнения, воспользовавшись тем
обстоятельством, что переход от уравнений для
стационарных синусоидальных процессов к изображениям
уравнения для нестационарных процессов совершается
простой заменой /а> на р, если имеются нулевые начальные
условия.
Сделав такую замену в уравнении (2.5) главы I,
получим изображение уравнения сферической волны:
или, введя переменную срг,
*g?+£>==* (13.2)
откуда для расходящейся из центра волны
? = 4е-*5\ (13.3)
Постоянная А определяется свойствами источника.
Повторяя рассуждения § 5 главы I, мы получим формулу,
совершенно аналогичную формуле (5.6):
г
? = fee с- (13-4)
Здесь, однако, иа представляет собою изображение
объёмной скорости источника.
Рассмотрим простейший случай:
иа = а0(*); йа =1.
Это означает, что при t = 0 источник начинает
действовать; действие его состоит в том, что из него истекает *)
среда с постоянной объёмной скоростью, равной (в приня-
*) Термин «источник» получает здесь совершенно
непосредственный и очевидный смысл.
§ 14]
ПРОСТЕЙШИЕ ГРУППОВЫЕ АНТЕННЫ
69
той системе единиц) одному кубическому сантиметру в
секунду. Потенциал, создаваемый таким источником, как
функция времени и координаты, выражается формулой
<Р=&ао(^-7)
(13.5)
Точка г = 0, в которой находится источник, является
особой: потенциал принимает в этой точке бесконечное
значение. Это не приводит обычно к затруднениям при
вычислениях, так как для бесконечно малых источников
и объёмная скорость бесконечно мала. Изменение
потенциала в пространстве и во времени для рассмотренного
случая представлено графи-
\ чески на рис. 24 и 25.
Рис. 24.
Рис. 25.
Выражение для потенциала точечного источника и
представление об излучаемой им шаровой волне играют
в дальнейшем очень большую роль, так как, основываясь
на принципе наложения, можно всякий источник
конечных размеров представить как совокупность точечных
источников.
§ 14. Простейшие групповые антенны
Рассмотрим свойства групп, начиная с самых простых
дискретных. Пусть, например, даны два одинаковых
точечных источника с напряжённостью иа о0 (t) на некотором
расстоянии 6 друг от друга. Потенциал, создаваемый
70 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
такой группой на,расстоянии г ^ 6, будет
? = ?! + ?»= e[ao(/-7-)+5o(«-7-Tsin&)]
(рис. 26). Совершенно ясно, что запоздание второй
ступеньки зависит от направления на точку наблюдения, и
что при v = 0 обе ступеньки сливаются, так как
возмущение приходит в точку наблюдения от обоих источников
одновременно. По этому поводу следует отметить, что в
случае работы подобной же группы из двух точечных
источников в синусоидальном режиме
(р\ я мы делали некоторые выкладки
(см. § 4). В данном же случае все
соотношения настолько просты,
^ что применение каких-либо вы-
^ ^f числений для получения
абсолютно очевидного результата пред-
Рис. 26. ставляется совершенно
неуместным.
Также легко сообразить, что ряд точечных источников,
расположенных на равных расстояниях вдоль прямой
(прямолинейная дискретная группа), даст потенциал,
график которого, как функции времени, представится
лесенкой со столькими одинаковыми ступеньками, сколько
источников в группе.
Наконец, в наиболее общем случае дискретной группы,
состоящей из любого числа источников различной
напряжённости, расположенных как угодно в пространстве,
мы получим график изменения потенциала в точке
наблюдения также в виде лесенки, но высота ступенек будет
определяться напряжённостями источников и,
следовательно, будет неодинакова, а запаздывание ступенек будет
определяться соответственными разностями ходов. Случай,
когда источники вступают в действие неодновременно,
также не составляет никаких затруднений.
На этом вопрос о дискретных группах можно пока
считать исчерпанным. Нам ещё неоднократно предстоит
отмечать поражающую простоту ряда выводов,
относящихся к неустановившимся волновым режимам.
§ 14]
ПРОСТЕЙШИЕ ГРУППОВЫЕ АНТЕННЫ
71
Обратимся теперь к непрерывным распределённым
группам. Простейшим представителем этого рода групп
является непрерывная однородная прямолинейная группа.
Представление о такой группе можно составить себе
предельным переходом от дискретной прямолинейной группы.
Пусть число отдельных источников, расположенных вдоль
отрезка прямой, увеличивается беспредельно, пока они
не покроют непрерывно весь отрезок. При этом, конечно,
подразумевается, что суммарная напряжённость
источников остаётся конечной. График потенциала будет
представляться лесенкой, ступеньки которой будут становиться всё
мельче, пока в пределе лесенка не превратится в
наклонную прямую. Хотя и этот результат достаточно очевиден,
но мы всё же получим его аналитически; нам пора
привести в действие наш аппарат, так как нам предстоит
рассмотрение более сложных случаев.
Дана непрерывная прямолинейная группа длиною I
с напряжённостью и( на единицу длины, так что общая
напряжённость группы и = и}. Каждый элемент dx,
который мы будем
рассматривать как точечный источник,
обладав г напряжённостью
du = uvdx и создаёт в точке
наблюдения потенциал dcp.
Составив выражение для dcp,
нужно проинтегрировать его
по I; мы получим, таким
образом, потенциал,
наводимый всей групп ой. Это
вычисление мы выполним
двумя способами. Первый состоит в том, что мы пользуемся
формулой (13.4) для изображения потенциала точечного
источника и пишем (рис. 27):
Рис. 27.
,- du —P
r+ct
4кг
- р — — р — sm a- ,
се с dx;
72 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. И
и, переходя к оригиналу, получаем:
где
*' = <_-!
С
(рис. 28). Установившееся значение потенциала для
любого Ь равно
и
По второму способу мы представим потенциал,
наводнит
и
jsAnf t-%
с
Рис. 28
мый элементом группы, сразу в виде разрывной функции
времени на основании формулы (9.1):
, Uidx ( . г х . <Д
4кг
щс
4кг sin О
о
" 4кг1 sin О
— Sin* -^-Sin&
- • о
[f з0 (f) - (V - 4 sin ft ) a0 (V - I sin ft j] .
В рассмотренном простом случае преимущества второго
способа ещё не очевидны; однако для более сложных антенн
упрощение вычислений очень значительно, и мы будем
в дальнейшем пользоваться преимущественно
интегрированием разрывных функций.
§ 151 ПРИВЕДЕНИЕ АНТЕННЫ К ПРЯМОЛИНЕЙНОЙ 7$
§ 15. Приведение антенны более общего вида
к прямолинейной
Рассмотрим прежде всего неоднородную непрерывную
прямолинейную группу. Она характеризуется тем, что
напряжённость отдельных элементов неодинакова и
зависит от координат элементов; другими словами,
напряжённость распределена по длине антенны неравномерно.
Напряжённость элемента может быть выражена как
du = u (x)dz,
где и(х) — функция, выражающая закон распределения
напряжённости. Для однородной группы это есть
постоянная величина, которую мы раньше обозначали через и^
Теперь мы имеем:
7 и (х) dx [ . х . <Д
i
о
о
где U — фикция, определяемая соотношением
\ и (х) dx — U (х) + с.
Мы видим, таким образом, что производная потенциала
по времени воспроизводит в известном масштабе функцию
распределения.
Самый общий вид групповой антенны может быть
приведён к неоднородной прямолинейной. Для такого
приведения достаточно перенести элементы данной антенны
на соответствующим образом выбранную прямую и
определить из чисто геометрических соображений функцию
распределения для получаемой эквивалентной
прямолинейной группы.
4
74 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ ГГЛ. II
Поясним эту мысль на примере плоской линейной
группы. Пусть антенна представляет собой произвольный
плоский контур Z, вдоль которого напряжённость
распределена по закону и(1). Направление на точку наблюдения
обозначено вектором г (рис. 29). Проведём ось х в
плоскости /по направлению проекцииг на плоскость контура L
Каждый элемент dl рассматривается как элементарный
точечный источник с
напряжённостью du =
~u(l)dl. Но очевидно,
что действие этого
источника в точке
наблюдения не изменится от
перемещения источника
вдоль прямой,
перпендикулярной оси х (при
условии, что это
перемещение мало по
сравнению с г). Мы можем, следовательно, перенести все
элементы контура I на ось х и построить таким образом
эквивалентную прямолинейную группу. Каждому
элементу dl на контуре будет соответствовать элемент dx
на прямой. Очевидно, что напряжённости эквивалентного
и действительного источников должны быть равны, т. е.
и (I) dl~u (x) dx,
откуда и определяется функция распределения для
эквивалентной проямолинейной группы
Рис. 29.
и (х) ~ и (I)
dl
dx '
(15.2)
Приведённое рассуждение относится к приведению
линейной группы. Сходным образом осуществляется
приведение поверхностных и объёмных групп. Напряжённости
элементарных источников будут выражаться
соответственно как и {S) dS и и (V) dV, где S — поверхность, V—
объём.
Разберём несколько частных случаев.
§ 15] ПРИВЕДЕНИЕ АНТЕННЫ К ПРЯМОЛИНЕЙНОЙ 75
а) Кольцевая однородная группа
Пусть напряжённость равномерно распределена по
окружности радиуса а и выражается как щ a0(t) на
единицу длины окружности, т. е.
и0
Ul = 2U >
где и0 — общая напряжённость группы. Легко видеть,
что
dl __JL 1
dx ~~ sin a — i/2 j» /£\» '
и, следовательно:
и(х) = иГ
V2ax — x2
U {х) = 2ufl arc sin (J- -1 ^ (15.3)
и, наконец, по формуле (15.1)
<? = fe{ I arc sin (f -1 ) t*o (O - *o (*' - 2tJ] +
+ 4[Jo(0 + a0(^~-2irt)]}, (15.4)
где
tn-=— sinfr.
б) Круговая однородная группа
В этом случае напряжённость равномерно
распределена по площади круга радиуса а. На единицу площади
приходится напряжённость
76 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Мы имеем для функции распределения эквивалентной
прямолинейной группы
/ \ dS
Элемент площади (рис. 30)
выражается как
* га —
А \
Л \
Л I
1
Ч 1
А 1
Л У 1
Л ж I
dS = 2а sin а cfo,
откуда
^5
Рис. du. ц(я) = и8^==2а8]/2ая--ж2,
С/ (#) = 2ks ^У^аж — я2^^
= к£ [(ж — а) У2ах — х2 + a2 arc sin (j- - i Yj (15.5)
и потенциал
+ arc sin g— l)] [*0 (0 -a0 (*' -2т.)] -Ц [ae (0 +
+ о0(*'-2та)]}. (15.6)
в) Шаровая поверхностная однородная группа
Представим себе излучатель в форме сферической
поверхности с равномерно распределённой по ней
напряжённостью. Элемент
поверхности (рис. 31) /М1\у*
будет равен тщ^щ^^^/М1^И^
dS = 2тгА dl — 2ua dx,
так что
dS 0
ах
Рис. 31.
и эквивалентная прямолинейная группа оказывается
однородной. Здесь нужно напомнить, что мы суммируем действио
источников, расположенных на всей поверхности шара,
§ 151 ПРИВЕДЕНИЕ АНТЕННЫ К ПРЯМОЛИНЕЙНОЙ
77
78 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
в том числе и на полушарии, противолежащем точке
наблюдения. Другими словами, предполагается, что
сферическая поверхность, занятая источниками, совершенно
прозрачна для волны. Это конечно, абстрактный случай;
он приведён здесь лишь ради простоты получаемых
соотношений.
Некоторые результаты, относящиеся к групповым
антеннам, представлены на сводном графике рис. 32.
§ 16. Ближнее поле групповых антенн
Два предыдущих параграфа были посвящены
исследованию поля, создаваемого антенной на расстоянии,
большем по сравнению с её размером. Соотношения при этом
упрощаются за счёт того, что
направления на точку наблюдения от
любого элемента антенны считаются
параллельными.
Теперь мы рассмотрим более
общий случай, когда расстояние до
точки наблюдения и размер антенны
соизмеримы и когда, следовательно,
вышеуказанное геометрическое
упрощение отпадает. Естественно, вы-
Рис. 33. кладки и результаты усложняются.
Поле, создаваемое антенной на
расстояниях, сравнимых с её размером, называют обычно
ближним полем.
Начнём с простейшей группы из двух одинаковых
точечных источников, находящихся на расстоянии 6 друг
от друга (рис. 33). Расстояния от точки наблюдения А до
источников 1 и 2 равны, соответственно, гг и г2. Мы должны
не только учесть различие величин потенциалов обоих
источников, обусловленное неодинаковостью расстояний
их до точки наблюдения, но и выразить запаздывание через
разность хода. Таким образом:
*
§ 16J
БЛИЖНЕЕ ПОЛЕ ГРУППОВЫХ АНТЕНН
7&
Остаётся выразить гх и г2 через координаты точки
наблюдения. Выбрав полярные координаты гид (рис. 33),
находим;
гЧ~т+ &rsin&, )
}
(16.2)
От этих более общих соотношений нетрудно вернуться к
частному случаю г^>6 (§ 14). Составим выражение для
разности хода при -=■—► ос .
Y7
— — frrsind —
4
i i
^r^l + AsinftV^(l-^sin&JT]~6sin{L
Прежде чем перейти к более сложным примерам,
проделаем одно вспомогательное вычисление: найдём поле,,
создаваемое неограниченной
излучающей плоскостью. Нам уже известно,
что это поле представляет собой
обычную плоскую волну. Пусть точка
наблюдения А находится на расстоянии
х от излучающей плоскости.
Элементарное возмущение в точке А будет
, u.dS / г \
Рис. 34.
(мы полагаем, что плоскость излучает
в полупространство). Потенциал, наводимый в точке Ат
получим в виде
us С dS ( г\
Выберем элемент площади в форме кольца (рис. 34)
dS = 2nydy.
«о
НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Так как
Г2 = ^ + а;2; Vdy=rdr> 2Tr=dr '
следовательно,
T-BsU(«-T)dr=WeM-iO~'?')==
Потенциал равномерно возрастает; непрерывно
следующие друг за другом от всё более далёких колец
элементарные возмущения равны, так как увеличение
расстояния до кольца компенсируется увеличением его
площади Если нас интересует не потенцал, а давление, то,
используя уже известное нам соотношение, получаем:
Это выражение и представляет собою единичную
разрывную плоскую волну давления.
Теперь рассмотрим несколько более сложный пример:
вычислим ближнее поле круговой антенны. Для понимания
соотношений, которые нам предстоит получить, нужно
заметить что случай, когда проекция точки наблюдения
оказывается в пределах излучающего круга (рис. 35),
существенно отличается от случая, когда эта проекция лежит вне
круга (рис 36). Дело в том, что в первом случае (рис. 35)
в начальной фазе явления в точку А приходят возмущения
от полного кольца, и так обстоит дело до тех пор, пока
кольцо не коснётся границы излучающего круга. До этого
момента всё будет происходить совершенно так же, как и в
только что рассмотренном случае неограниченной
плоскости- потенциал будет равномерно нарастать. В
дальнейшем в точку А будут приходить возмущения от
усеченного кольца, пока, наконец, кольцо не выйдет полностью
за пределы излучающего круга. После этого дальнейшее
нарастание потенциала прекратится. Что же касается
§ 16] БЛИЖНЕЕ ПОЛЕ ГРУППОВЫХ АНТЕНН gl
второго случая (рис. 36), то здесь потенциал будет
создаваться усечённым кольцом с самого начала.
Ещё одно замечание: мы будем вычислять не
потенциал, а давление в точке наблюдения. Казалось бы, это
безразлично, так как потенциал и давление связаны между
собой очень простой зависимостью; можно найти сперва
до тт
потенциал, а потом давление /> = p0^-. Но дело заключается
в том, что, вычисляя непосредственно давление, мы можем
зачастую сильно упростить выкладки, используя
замечательное свойство функции ах (t). Это свойство состоит
в том, что при вычислении интегралов от выражений,
содержащих в качестве сомножителя функцию аг, не
требуется нахождения первообразных функций (т. е.
неопределённых интегралов); такого рода интегралы
вычисляются по формуле
ь ь
U(t^)o1(t-x)dx=-f(tft)a0{t^x)\
а а
(см. формулу (1*0.19)).
Мы пользовались до сих пор выражением для
элементарно^ слагаемого потенциала
^ёЧ'-f)-
" А. А. Харкевич
82 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Теперь же будем исходить из элементарного слагаемого
давления
^=*!М=£*('-т) <16-5>
(мы всё время предполагаем, что скорость изменяется
по закону единичной функции, т. е. что du есть величина,
не зависящая от времени).
В силу связи между <р и р можно ещё сказать, что найти
p(t) при скорости, изменяющейся по закону а0 (£),— это
то же самое, что найти <р (t) при скорости, изменяющейся
как аг(1). Эту же мысль можно выразить ещё многими
способами; например, можно просто напомнить, что
производная суммы есть сумма производных слагаемых.
Перейдём к вычислению, начав со случая рис. 36.
Элемент площади есть усечённое кольцо
dS = 2$ydy.
Давление, создаваемое этим элементом,
Далее,
r2=rl +г/2; rdr = ydy; — = -.$dr.
Нам нужно выразить fi функцией г. Из геометрических
соотношений рис. 36 находим:
у2 + <Р — 22/dcosp = a2,
d — R sin ft, r0 — R cos ft;
исключая у у d и re, находим:
* о г* — a2 — Я2cos20 tAa P.
B —arccos = . (16.6)
r 2Rsmb Vr2 — R2cos2 Ъ '
Теперь определим предельные значения расстояний,
ггт1г2. Из геометрических соотношений получаем:
г, == \/а2 + R2 — 2aR sin tt, ^|
1 ' } (16.7)
31П №. /
rz = y/a2+R* + 2aRsm\
§ 16]
БЛИЖНЕЕ ПОЛЕ ГРУППОВЫХ АНТЕНН
83
Составляем выражение для давления:
s п
(16.8,
Эта формула даёт решение нашей задачи для случая,
когда проекция точки наблюдения лежит вне круга.
Что же касается другого случая (рис. 35), то здесь мы
получаем нужный нам результат следующим рассуждением;
возмущение достигает
точки А в момент t = — .
с
Давление сразу
принимает значение р — wus
и сохраняет это
значение до момента t =— . В
интервале
давление
по закону
1
с ^ ^ с
изменяется
p = vwus${ct),
и, наконец, с момента
t = -? в точку А уже
не приходят больше
никакие возмущения, и
давление остаётся в дальнейшем равным нулю.
Аналитически всё это записывается так:
№ кривой... 12 3 4 5
Ь 90 60 45 30 0е
р = таш {ao(^J)-a0(^-3) + ^(cO[ao(^-?)~
- *rU-
?)]} ■ (I»-»)
G*
84 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Графики p(t) представлены на рис. 37 (верхние кривые
вычислены для aj R = 1, нижние—для a/R — 0,5; р0 = wajSy
Tz=lR/c). Нужно заметить, что решение задачи о
ближнем поле круговой антенны для синусоидального режима
оказывается чрезвычайно сложным.
—^г?
0 Ю*
*m*f
Рис. 38.
с
На рис. 38 представлена картина изобар для t
В этот момент на поверхности круга давления уже нет.
За единицу принято p0=wulS, т. е. давление, создаваемое
неограниченной плоскостью.
§ 17. Цилиндрическая волна
Мы вполне подготовлены сейчас к тому, чтобы
построить выражение для цилиндрической разрывной волны.
Мы не будем решать для этой цели
волновое уравнение; проще сразу
выбрать некоторую простейшую модель
антенны с осевой симметрией и
вычислить создаваемое такой антенной
поле.
Возьмём в качестве антенны
излучающую линию, или, пользуясь
терминологией предыдущих параграфов,
прямолинейную непрерывную
однородную бесконечную группу. Потенциал,
создаваемый в точке А элементом dy (рис. 39), равен
Рис. 39.
§ 171 ЦИЛИНДРИЧЕСКАЯ ВОЛНА 85
Мы имеем:
^ = ^+у«; ^ = * = dr
и результирующий потенциал
со .
X
(17.1)
Этот результат интересен во многих отношениях. Мы
видим, что в отличие от сферической волны (см. § 13)
цилиндрическая волна не несёт разрыва потенциала на фронте.
Потенциал на фронте равен нулю, а в области позади
фронта непрерывно нарастает. Зато первая производная
потенциала на фронте бесконечно велика, а следовательно,
бесконечно велико и давление. (Ещё раз напомним, что
смущаться этим не следует; речь идёт о разрывах
математических, а не физических. Разрывы и скачки, конечные
или бесконечные, обусловлены тем, что мы рассматриваем
случай разрывного же возбуждения волнового явления.
Это есть не более, как вычислительный приём, который при
правильном применении к разумно поставленной
физической задаче не может привести нас к бессмысленным
результатам.) Второе обстоятельство, обращающее на себя
внимание, состоит в том, что, опять-таки в отличие от
сферической волны, потенциал в данной точке поля
цилиндрической волны неограниченно возрастает с течением
времени. Закон убывания потенциала с расстоянием для
сферической и * цилиндрической волны также различен:
для сферической волны потенциал убывает как -, а для
цилиндрической в данный момент как Arch —» или
приближённо при x^>ct как In 2-. Оговорка «в данный момент»
подчёркивает тот факт, что в случае сферической волны
распределение потенциала в пространстве для всего
поля #>зади фронта остаётся неизменным (см. рис. 24).
86 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Характеризующие цилиндрическую волну зависимости
потенциала как от координаты, так и от времени
представлены графически на рис. 40 и 41.
По поводу различных видов волн следует ещё
заметить, что часто говорят, что сферическая и
цилиндрическая волна при
достаточном удалении от
источника переходят в
плоскую волну.
Применительно к
неустановившимся волнам это
верно лишь в том
ограниченном смысле, что
i -ч» i цилиндрический или
5 $ 7z сферический фронт при
Рис. 40. очень малой кривизне
с чисто геометрической
точки зрения мало отличается от плоского. Но из
этого вовсе не следует, что цилиндрическая волна
утрачивает присущие ей закономерности и что они с тем или
2л
. . 2 3 ¥ 5 6 7t
Рис. 41.
иным приближением могут быть замещены
закономерностями плоской волны. Достаточно взглянуть на формулу
(17.1), чтобы убедиться, что никакой предельный «переход
цилиндрической волны в плоскую» невозможен.
§ 18. Реакция на излучатель
При работе излучателя он испытывает реакцию со
стороны им же создаваемого поля. В случае акустического
излучателя реакция проявляется в том, что на поверхность
§ 18]
РЕАКЦИЯ НА ИЗЛУЧАТЕЛЬ
87
.излучателя при его работе действует некоторое давление.
Мы можем также характеризовать реакцию так
называемым акустическим сопротивлением, о котором уже
говорилось в главе 1, § 5. Для синусоидального режима
сопротивление — это, вообще говоря, комплексная постоянная
величина; вещественная часть носит название
сопротивления излучения. Для неустановившихся явлений,
которые мы рассматриваем, давление и скорость являются
функциями времени, а следовательно, их отношение,
которое мы называем сопротивлением, также будет
представляться некоторой функцией времени. Если условиться,
что работа излучателя характеризуется скоростью,
изменяющейся как <т0 (t), то определённое для такого режима
сопротивление носит название переходного. Ясно, что
для t^>0 функция, представляющая изменение давления,
воспроизводит в известном масштабе изменение
сопротивления. Поэтому, в сущности говоря, безразлично,
вычисляем ли мы при таком режиме давление или сопротивление.
Поясним всё это на примере излучателя в форме шара
переменного радиуса. Такая модель фигурировала уже
в § 5 главы I в качестве «пульсирующего» шара. Теперь же
мы должны себе представить, что в момент t = О
поверхность шара начинает двигаться с постоянной радиальной
скоростью va. Таким образом, мы имеем теперь дело с
равномерно раздувающимся («пухнущим») шаром.
Создаваемая при этом волна будет несомненно сферической, и мы
можем сразу записать выражение для изображения
потенциала:
г
А -р-
Найдём изображение давления и скорости
г А кг
(РЩРо 57 5 начальные условия нулевые);
- А (1 , 1ч -Ргг)
Акг\г ' * с )
88 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Это — радиальная линейная скорость частиц,
вычисленная как v = — J-. Если радиус шара есть а, то на
поверхности его мы имеем давление и радиальную скорость
а
А -2>-
Ро=?оРьГав '
ъ-ъЬ^+р'ёУ
Объёмную скорость получим, умножив радиальную
скорость на поверхность:
Отношение давления к объёмной скорости есть
а
£*=£_ w Р с ~w p
-" • О kr,a2 . a S , с •
Давление выражается через скорость и сопротивление
Pu=»m8 = a.J ~^-
а
Если
Ua = U(Po (О,
то
и мы видим, что давление просто пропорционально
сопротивлению, о чём и говорилось выше. Коэффициент
пропорциональности есть и0. Переходя к оригиналу (при
помощи таблицы готовых формул), находим:
ct
w —-
P**-*P*(t)=aose a МО
§ 18] РЕАКЦИЯ НА ИЗЛУЧАТЕЛЬ 89
Умножив это на S, получим полную силу реакции,
действующую на поверхность шара при её движении с
объёмной скоростью ua~u050(t):
J*.
F(t)=Spa(t)^u0we *a0(t).
Мы видим, что в первый момент, т. е. при t — О, сила
реакции равна
F(0) = u0w.
Это очень характерный результат; вспомним, что точно
так же дело обстоит и для бесконечной плоскости,
излучающей при своём движении плоскую волну. В дальнейшем
обнаруживается разница: реакция на плоскость остаётся
неизменной, тогда как реакция на шар, как мы вывели,
убывает по экспоненциальному закону. Но это различие
обусловлено различием в конфигурации полей; в первый
же момент, когда поле не успело ещё развиться и когда
возмущение локализовано в слое, непосредственно
прилегающем к поверхности излучателя, реакция на
излучатель любой формы оказывается одинаковой и определяется
только скоростью и волновым сопротивлением среды.
Мы будем иметь ещё другие подтверждения этого
заключения.
Рассмотрим более сложный пример: определим
реакцию на круговую антенну. В акустике круговая антенна
представляется обычно в виде модели, называемой
«поршневая диафрагма». Это есть плоский, круглый, совершенно
жёсткий (т. е. недеформирующийся) диск, движущийся
в направлении своей нормали в отверстии в бесконечном
плоском совершенно жёстком экране. Предполагается, что
зазор между диском и экраном отсутствует. Такая модель
представляет собой с механической точки зрения систему
с одной степенью свободы. Наша задача состоит в том,
чтобы вычислить полную силу реакции на диск.
Ш Если линейная скорость диска есть v=v050(t)f то
каждый элемент поверхности может рассматриваться как
точечный источник с напряжённостью
da ~v dS.
ЖИНРГШИ5В'Ш";0*^" " «■- *-
*90 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Мы должны сначала найти давление в каждой точке диска,
просуммировав в этой точке действие всех элементов
поверхности, а затем определить силу, интегрируя давление
по всей поверхности. Элементарное давление
Выберем элемент поверхности в виде
dS = rdr da
«(рис. 42). Порядок интегрирования безразличен. Будем
сначала интегрировать по г,
т. е. найдём сначала давление,
создаваемое элементарным
сектором в точке, лежащей
в вершине сектора. При
этом г будет изменяться от 0
до R. Таким образом,
'HPW*('-7)*=
о о
■?$[«■<«>-«•(«-")]*
Рис. 42.
Заметим, что в
подинтегральном выражении г
сократилось. Это означает, что действие всех элементов сектора
в вершине одинаково, так как увеличение расстояния
компенсируется увеличением площади. С подобным
соотношением мы уже встречались в § 16. Для дальнейшего
вычисления выразим R через а. Пусть будет
Л^ср(а); а = ф'"(Д).
Тогда по формуле (10.22)
- Р=1Г\ Ы«) -s.[«-<p(a)]}«fc =
= =р {„„ (ct) + [ф (ct - а)] о0 [ct - ?(a)] 1}
(18.1)
§ 18] РЕАКЦИЯ НЛ ИЗЛУЧАТЕЛЬ
В нашем случае (см. рис. 42)
а = ф (7?) = arccos
91
Д2 + 2/2-
2yR
сЧ% + у2-
■а2
>
-а2
2yct
<Ь (cj) = arccos
R — ср (а) = у cos a + /а2 —у2 sin2 а;
<p(it) = a — у; ср(0) = а + 2Л
Итак,
/> = *да0 {а0 (<?*) — а0 (ct — а + г/) +
+ -arccos—=gL [50(с*-а + у) —
— <%(« —а —у)]}
(рис. 43).
Мы определили давление как функцию времени для
ясчки с координатой у. Заметим, что здесь повторены
(18.2)
Ко
кривой
1
2
3
4
5
6
У/а
О
0,2
0,4
0,6
0,8
1,0
Рис. 43.
по существу выкладки § 16. Наша формула (18.2) могла бы
быть получена из формулы (16.9) как частный случай
последней при г0= 0, т. е. когда точка наблюдения лежит
^а круге. Остаётся последний этап — вычисление силы
реакции.
Элемент силы равен
dF = pdS.
92 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
В данном случае естественно выбрать кольцевой элемент
площади
dS — 2-R,ydyy
и, таким образом,
а
6
-f_ arccos—XJL Ы^-а + У)-
—^- [ Зо («) — з0 (« - «)] +
+ [ — Ф («, а — и)+Ф (ct, а)] з0 («) +
+ [Ф (ct,a — ct) —Ф (ct, ct — a)] з0 (сг —а) +
+ [Ф(а,ы — а)—Ф(м, а)]з0(« —2а) I.
Неопределённьтй интеграл берётся по частям:
Ф (с*,у) = \ arccos —^ ycfy =
^nrrrn~c8*8+yW Ч Cif-У (*'*»-«')]*»
= 2-У2 arccos » ™ + ^-a'arcem* ^ -
-\V- (Л* - «2)я + 2У2 (Л2 + "2) ~*Д
Далее,
Ф (с,«) =- «^ (arccos g_ g ,/ГЗЩ; _ ^);
ф(«, а - ct) = -| а2 +-J (с« - а)2;
Ф(«, ct ---а)= — |- о2.
§18]
РЕАКЦИЯ НА ИЗЛУЧАТЕЛЬ
93
Проделав остающиеся простые выкладки и заменив
линейную скорость объёмной
tm2v0 = Sv0^-u0,
получаем окончательный результат:
~o0{ct-2a)] (18.3)
(рис. 44). Как видим, и в этом случае
F{0)=uGw.
В формуле (18.3) следует ещё отметить, что сила
обращается в нуль через конечный промежуток времени и
оА
о
дальнейшее движение диска с постоянной скоростью не
встречает противодействия со стороны среды. Этот
результат легко понять, если принять во внимание, что
давление на любой элемент поверхности диска составляется
из импульсов, приходящих от всех остальных элементов.
Процесс начинается при t = О и заканчивается, когда
к данному элементу придёт возмущение, посланное
наиболее удалённым элементом. Но наибольшее возможное
расстояние между двумя точками на круге равно диаметру.
Таким образом, процесс суммирования импульсов
давления заканчивается ко времени
2а
t= .
с
Рис. 44.
94 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Труднее понять другое: почему аналогичные
соотношения не получаются для «пухнущего» шара? Ведь, как
мы видели, сила, действующая на поверхность такого шара,
убывает по экспоненциальному закону, т. е. процесс
суммирования, о котором только что шла речь, никогда
не прекращается! Тут суть дела заключается в дифракции.
Решая задачу об излучении шара в целом, мы обходили
вопрос о дифракции. Если же мы стали бы решать задачу
методами этого параграфа (что, кстати говоря, было бы
совершеино нецелесообразно), то нам пришлось бы начать
с рассмотрения взаимодействия двух элементов
поверхности шара. Возмущение, посылаемое каким-либо
элементом, может достигнуть другого элемента только за
счёт дифракции, так как прямолинейного пути между двумя
точками на поверхности шара нет. Но дифрагирующая
волна, достигнув некоторой точки, продолжает огибать
шар; она обогнёт его кругом и начнёт следующий обход
и будет приходить в данную точку неограниченное число
раз, соответственно ослабевая с каждым разом. Таким
образом, в случае шара и не приходится ожидать
прекращения реакции по прошествии какого-либо конечного
промежутка времени.
§ 19. Направленность
В первой главе (§ 4) было показано, что свойство
направленности, присущее излучающим и приёмным
антеннам, имеет чисто интерференционную природу.
Направленность (т. е., например, в случае излучения, зависимость
потенциала в точке наблюдения от направления на эту точку)
определяется исключительно фазовыми соотношениями.
Совершенно ясно, что эти соотношения не могут быть
непосредственно перенесены в область непериодических
волновых возмущений. Такой перенос возможен лишь на
основе спектрального представления непериодического
явления и при помощи математического аппарата
интеграла Фурье. Однако, становясь на этот путь, мы
закрываем глаза на качественно новые черты, отличающие
неустановившееся волновое поле. Поэтому мы попытаемся
разобраться в вопросе заново.
§ 19)
НАПРАВЛЕННОСТЬ
9S
Вспомним, что, вычисляя потенциал, создаваемый
различными типами антенн при возбуждении их единичной
объёмной скоростью (§§ 14 и 15), мы всякий раз получали
выражения, содержащие угол & между направлением на
точку наблюдения и главным направлением, которое мы
называли осью антенны. Вопрос о характере зависимости
от & до сих пор не затрагивался; теперь как раз об этой-та
зависимости и должна пойти речь.
В общих чертах дело обстоит так: при скорости,
изменяющейся как и0ао(0> в точке наблюдения до момента
t'=t— - потенциал равен нулю, затем он начинает па-
растать, и установившееся постоянное его значение равно
Это постоянное значение достигается ко времени, по
истечении которого до точки наблюдения дойдут возмущения or
наиболее удалённых элементов
антенны. Время установления
зависит от разности хода волны
от крайних точек антенны до
точки наблюдения. Разность же
хода зависит, с одной стороны,
от размера антенны, а с другой
стороны, от расположения
точки наблюдения относительно
антенны. Если через а обозначен
размер антенны в плоскости,
проходящей через ось и точку , рИс. 45.
наблюдения (рис. 45), то
наибольшая разность хода составляет d =a sin ft, а время
установления Г:=—= — sin&. Таким образом, при
изменении угла Ь изменяется масштаб времени для
зависимости <р (t).
Наиболее общим образом можно охарактеризовать
эти соотношения как изменение формы кривой <р (t) в
зависимости от изменения 9. Но такая, хотя и правильная,
качественная характеристика положения не позволяет-
9fi ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
ещё подойти к определению направленности. Нам нужно
выбрать определённый параметр, количественно
определяющий форму кривой ф (t), и установить зависимость
этого параметра от угла &. При этом нужно выбрать
параметр, исходя из конкретных технических представлений;
нужно, чтобы на этот параметр по возможности
непосредственно реагировали приборы, применяемые в данной
отрасли волновой техники. Конечно, применяя какие-либо
хронометрические приборы, можно непосредственно
измерять время установления, о котором только что
говорилось. Но мы попытаемся
выбрать параметр так, чтобы
получить определение
направленности, по возможности близкое
к употребительному.
Применительно к стационарным
процессам оперируют
зависимостью от угла той или иной
величины, характеризующей
интенсивность сигнала. В
нашем же случае такой величи-
а{ ной может послужить ско-
—| рость нарастания потенциала
1 . >. или величина, ей
пропорциональная.
Рассмотрим для примера
прямолинейную однородную
группу. Для разных углов Ь мы получаем зависимость <р (t)
в виде семейства линий, представленного на рис. 46(a). По-
до
строим соответствующее семейство дляр*^>■£• (рис. 46 (б)).
Как видим, отдельные линии этого семейства различаются
величиной мгновенного давления. Легко представить
себе и осуществить приборы, непосредственно
реагирующие на эту величину. «С точки зрения» таких приборов
направленность есть зависимость максимального
мгновенного значения наблюдаемой величины от угла д.
Эта формулировка представляет собою определение
направленности, которым мы будем пользоваться и дальше.
Заметим, что это определение не только не расходится
Рис. 46.
4
5 19]
НАПРАВЛЕННОСТЬ
97
с обычным, но включает его в себя как частный случай.
Действительно: в случае синусоидального режима
наибольшее мгновенное значение есть просто амплитуда
синусоиды, а направленность при этом может выражаться
зависимостью амплитуды (или какого-либо среднего
значения) от угла.
Таким образом, вопрос получает необходимую
определённость, и мы можем вычислить характеристику
направленности для прямолинейной антенны в
непериодическом режиме и ^=u0o0(t) в соответствии с
вышеприведённым определением. Мы вывели в § 14 для
прямолинейной антенны:
?=4^M^-^'-Tsin»)]-
Отсюда находим давление:
UQW
4-rl sin ft
[°o (О - «о («'-7 *'*»)]• (19.1.)
Наибольшее значение давления (которое в
рассматриваемом случае сохраняется во всём интервале 00'<С—sin ft)
равно
* 4uW sin Ь
Pmzx — A^j ein ft • (19.2)
В этом выражении уже содержится характеристика
направленности, но возникает специфическое затруднение:
мы не можем привести эту характеристику к
унифицированному масштабу, так как при ft = 0 давление бесконечно
велико. Мы можем выйти из этого положения так: отбросить
несущественный для дела множитель т|- и рассматривать
в качестве характеристики направленности величину
Д = г4-тг, (19.3)
J sin d ч '
которая в отличие от обычной безразмерной
характеристики направленности имеет размерность [L~l]. График
характеристики (19.3) в полярных координатах имеет
необычный вид: он представляется двумя параллельными
7
А. А. Харкевич
98 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
прямыми (рис. 47). Чем больше Z, тем уже характеристика.
Это существенно, поэтому множитель I оставлен в
выражении (19.3).
Сходным образом характеристики направленности
получаются и для других типов антенн. Разница состоит лишь
в том, что кривые давления имеют иную форму и,
следовательно, выражение для /?тах отличается от (19.2).
Дополнительные трудности
возникают с кольцевой
антенной, но в
подробности зтого случая мы
входить не будем.
Мы предполагали до
сих пор, что антенна
возбуждается
скоростью u~u0a0(t).
Положение совершенно ме-
га няется при другом за
. - коне изменения скоро-
и_ £-г*\ сти. При t = О может
* претерпевать разрыв не
Рис. 47. сама скорость, а её
первая, вторая,...,
n-япроизводная, или, другими словами, скорость может в
первый момент нарастать по линейному, квадратичному
закону,..., по кривой п-то порядка.
Все предыдущие рассуждения сохранят, однако, силу
при условии, что приёмный аппарат будет реагировать
не на давление, а на производную давления того же
порядка, что и претерпевающая разрыв производная скорости
антенны. Иначе говоря, для получения желаемой
характеристики направленности нужно заранее знать
характер сигнала и соответственным образом устраивать
приёмник.
Такое положение отнюдь не является специальной
принадлежностью непериодических явлений; напротив,
можно провести полнейшую аналогию с обычными
представлениями теории направленности. В самом деле: обычная
характеристика направленности вовсе не определяет
направленных свойств антенны каким-либо универсальным обра-
4
§ 19]
НАПРАВЛЕННОСТЬ
99
зом. Обычная характеристика направленности относится
также к вполне определённому частному виду сигнала,
а именно к случаю синусоиды определённой частоты.
Определить же строение поля и реакцию приёмника
для любого сложного сигнала можно лишь тогда, когда
сигнал известен. Таким образом мы можем установить
следующее важное, но не всегда ясно понимаемое общее
положение: понятие о направленности, как бы мы её ни
определили, не имеет смысла, если не указан (или не
подразумевается) вид сигнала*).
Для пояснения этого положения рассмотрим пример:
определим характеристику направленности для сигнала
в форме усечённой синусоиды, т. е. для сигнала,
представляющего собою несколько циклов синусоиды. Такой сигнал
может быть аналитически представлен в следующем виде:
B = tt0sin©*[a0(0—о0(* —лГ)], (19.4)
где Г—период (Т= —) , п —число полных циклов.
Вычислим характеристику направленности для
прямолинейной антенны. Элементарное возмущение равно
^sin<o(.-^sin»)[a0^-fsin»)^
Результирующий потенциал
i
*=1гЛ 8ina> ('' -7 8in&) Ь('-7 вШ) -
6
~~ °° (*' ~" 7 sin Ь ~ пТ)] dx =
= ШГВ ] Sin ш С ~т) К С-0 -°о W-пТ-к)] dx,
о
*) Одно интересное исключение из этого положения
разбирается в следующем параграфе.
7*
100 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. I
где
х . ,
т = — sini
с
I
shift.
Выполняя интегрирование, получаем:
? = Й4{(1~СОвв"') К (П-««(*'-»Г)]-
-[l-cosmit'-xJU^it'-^-^it'-nT-^)]}. (19.5)
Это выражение показывает, что явление в точке
наблюдения распадается на три фазы и притом различным образом,
в зависимости от соотношения между т0 и
^.Действительно, если иГ</с0, то мы имеем, вводя <р'=
4r. r
ип1
-ср:
0
=^ о
*'Н
(1 — COS<0*')
[1 —COS СО (t' -
о
Если же пТ^>т0, то
0
— (1 — COSco*')
[*'<0],
[0<«'<п2']>
[nT<t'<4],
[*'<0],
[0<*'<т0],
(19.6)
*P' = J ^NswU'-tJ—созсоГ] [То</'<пГ],
(19.7)
— [l-cosco(r-T0)]
1>Тп
о
[nT<t'<nT + z0],
[п7, + т0<*/<оо].
Напомним, что тгГ есть продолжительность сигнала, а т0—
разность времён прихода возмущений от концов антенны.
В случае пТ<т0, как показывают формулы (19.6), сигнал
расщепляется; в точке наблюдения сигнал наблюдается
в интервалах 0<V<n!F и T0<Ct'<^nT + т0. В интервале же
nT<^t'<^T0 никакого возмущения в точке наблюдения нет.
Этот странный на первый взгляд результат связан с тем,
что мы выбрали сигнал в форме целого числа полных цик-
4
§ 19]
НАПРАВЛЕННОСТЬ
101
лов синусоиды. Ход явления в точке наолюдения
представлен графически на рис. 48. Случай пТ>т0
представляет ту принципиальную особенность, что в интервале
Рис. 48.
?o<t'<CnT в точке наблюдения возмущения, посылаемые
отдельными элментами антенны, суммируются совершенно
так же, как при стационарном режиме антенны. На этом
основании эту фазу явления можно назвать квазистацио-
парной фазой; длительность её, разумеется, конечна и
ограничена вышеуказанным интервалом xQ<^t'<jiT. Те же фазы
102 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
явления, в которых функция выражается как 1—cos tot'
или 1—oos ш (tr—т0), будем называть нестационарными
фазами.
Теперь мы можем непосредственно заняться вопросом
о направленности. Для этого нужно в соответствии с
принятым нами общим определением найти наибольшие
мгновенные значения потенциала (или, что то же,
пропорциональной ему величины ср').
В нестационарных фазах мы имеем, независимо от
соотношения между пТ и т0 (см. (19.6) и (19.7)):
или
^Hecx.^ti-COSO^-^)],
так что наибольшее значение <р' будет
т нест. макс. то •
т2
(19.8)
Что касается квазистационарной фазы, то для неё (см.
(19.7))
SHI СО -~-
Т'квст. = ^ [°0S °> С - То) - COS at] = — Sin Ш (У - Yj ,
*"2
и, следовательно, наибольшее мгновенное значение
sin w y
9 квст. макс. I * (1У.У)
•i
Заметим, что формула (19.9) есть не что иное, как
выражение для обычной (стационарной) характеристики
направленности прямолинейной антенны. Сопоставляя
(19.8) и (19.9), мы видим, что
Sinco^ х
й>-?г СО —
2 2
4
§ 19]
НАПРАВЛЕННОСТЬ
103
т. е. амплитуда квазистационарной фазы не превосходит
амплитуды нестационарной фазы. Это верно, однако, в
отношении амплитуд, но не наибольших мгновенных
значений на протяжении той или иной фазы. Дело в том, что
при уменьшении т0 нестационарная фаза,
характеризуемая функцией (1—cosco*'), усекается при всех
меньших значениях
t' = 1a
переходя в квазистационарную
Т 1
фазу. Наконец, при т0<Су функция (1—cos Ы') уже
не достигает своего максимального значения, равного
а ограничивается значением (1—cosa>i0). При
определённом значении т0 последняя величина сравнивается
с амплитудой квазистационарной фазы; мы составляем
уравнение
1 — COS ШТ0
2
ш2
и, решая его, находим значение т0, при котором
сравниваются наибольшие мгновенные значения потенциала
в нестационарной и квазистационарной фазах:
Тп =
2 *
Итак, характеристика направленности выражается
различным образом в зависимости от соотношения между
т0 и Т. Мы можем записать окончательно:
Д(в) =
sma) °
"2
(19.10)
104 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
При т0<Г0 мы имеем обычную (стационарную) характе-
Li гр
ристику направленности. При ~(ь>~2
Л(») = Л=-
Отсюда
к -у sin &
R sin ft = —г = const.
4
(для данного kl). T
Таким образом, для V>t>- график характеристики
направленности в полярных координатах представляется
двумя прямыми, па-
ft* раллельными оси 0 =
■^ " =0 и
расположенными по обе стороны
от неё на
расстоянии—j . Такого* ро-
да характеристику
мы уже встречали (см.
формулу (19.3) и рис.
47). Указанные
прямые смыкаются со
стационарной характеристикой в точках а)т0 = тг, т. е. при
R =~- Последнее равенство есть уравнение окружности,
на которой лежат точки перехода. Если о)Т0<Гтс при
любых ft, т. е если &Z</it, то характеристика направленности
при всех значениях угла имеет то же выражение, как и
для стационарного режима. Геометрически это выражает-
Sino> -
ся в том, что характеристика направленности R=
полностью лежит вне окружности R = —, не
пересекаясь с нею. На рис. 49 построены графики
характеристик направленности по формулам (19.10).
§ 20] ШАРОВЫЕ АНТЕННЫ 105
§ 20. Шаровые антенны
Существует особый класс звуковых антенн, для
которого вопросы направленности решаются проще. Этот
класс антенн обладает вообще очень интересными
свойствами, и мы рассмотрим их довольно подробно. Речь идёт
о так называемых шаровых антеннах. Однако здесь
подразумевается не непрерывная группа с распределением
источников по сфере, которая упоминалась раньше (§ 15,в)
и для которой сфера является лишь геометрическим
местом источников. Под шаровой антенной мы будем теперь
понимать материальный шар, поверхность которого может
определённым образом деформироваться. Простейший
пример такого рода антенны мы уже имели — это
«пухнущий» шар (§ 18). Как мы сейчас увидим, «пухнущий*
шар принадлежит интересующему нас классу антенн
и является младшим членом некоторого семейства.
Пусть дан шар начального радиуса а, и пусть задано
какое угодно распределение радиальной скорости на его
поверхности. (Речь идёт именно о радиальной скорости,
т. е. о нормальной к поверхности шара составляющей
скорости, так как ясно, что касательные составляющие
излучения не производят.) Задача состоит в нахождении
потенциала, создаваемого шаром при таких условиях.
Общий метод решения этой задачи состоит в том, что
мы составляем волновое уравнение в сферических
координатах и находим его общее решение, выраженное рядом
по сферическим функциям. Затем мы находим
радиальную скорость как
и, наконец, используем граничное условие, состоящее в
том, что на поверхности шара, т. е. при г~а,
радиальная скорость должна равняться заданной. При
этом скорость на поверхности шара также должна быть
представлена разложением в ряд по сферическим функциям.
Мы ограничимся рассмотрением случая осевой симметрии
поля, а следовательно, и распределения скорости на
поверхности шара. В этом частном случае сферические
106 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
функции общего вида Sn вырождаются в простые
полиномы Лежандра Рп (cos ft). Выражение для скорости на
поверхности шара может быть записано в виде
С* = 2«Л(С08&), (20.1)
а потенциал в поле антенны
Здесь 1п и Fn— полиномы, введённые Стоксом. Нетрудно
получить (20.1) из (20.2), если найти
а?
положить г=а и воспользоваться существующим между
in и ¥п соотношением:
(l + z)tn(z)-zin(z)=Fn(z).
Напомним выражения лежандровых и стоксовых
полиномов.
Полиномы Лежандра
Рв 00 = 1 [д = С08д],
Pi 00=1*,
• р2Ы=|(3^-1),
РзЫ=2-(5^3-3^),
Р*00=4 (35^-30^ + 3),
PeOO = -J(63|*»-7V + 15ti),
*
§20)
ШАРОВЫЕ АНТЕННЫ
107
Полиномы Стокса in (z)
f0(*) = l,
* / ч л . 6 , 15 , 15
fs(2) = l + -+78+28,
f Ы-1 + LO, 45 105 105
. , > - , 15 , 105 . 420 . 945 . 945
l5(2) = l + --r-r+-r+-T + -J- ,
Полиномы Стокса F„(z)
F0(z)---z + l,
F1(z) = z + 2 +|,
F2(Z)-z + 4 + ■§+£>
F,(,) = , + 7 +? + 5 +5,
p4(.)=..-,ll+?+¥+?+?.
F5(,) = 2 + 16 + ?-f? + ^ + ^° + 5-7?,
Теперь обратимся к ещё более специальному случаю:
предположим, что распределение радиальной скорости
по шару выражается одним единственным членом
разложения по полиномам Лежандра, т. е. пусть
»а = РЯЫ-
(20.3)
108 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Антенну с таким распределением скорости будем
называть основной антенной п-го порядка. Создаваемый ею
потенциал
ЧР'с)
Из сопоставления (20.3) и (20.4) вытекает заключение
о следующем замечательном свойстве основных антенн:
зависимость потенциала в поле основной антенны от
угловой координаты выражается той же самой функцией
Pn(|x) =Pn(cosO), какой выражается распределение
радиальной скорости на поверхности антенны.
Это положение имеет силу независимо от характера
сигнала. Все приведённые выше формулы предполагают
изменение радиальной скорости во времени по закону о0 (t).
Для возмущения более сложной формы в наши формулы
вошло бы ещё в качестве сомножителя изображение
соответствующей функции времени, но это изображение не
зависело бы от ft. Следовательно, основные антенны
обладают ещё одним, не менее примечательным
свойством:
сигнал в поле основной антенны на данном расстоянии
от неё не изменяет своей формы в зависимости от углового
положения точки наблюдения.
Конечно, оба указанных свойства не являются
независимыми друг от друга; это просто две разные
формулировки для общих закономерностей, присущих основным
антеннам.
Но если сигнал сохраняет форму и лишь изменяет в
зависимости от направления на точку наблюдения свою
величину, то направленность антенны может быть вполне
охарактеризована единственным образом для всех
сигналов, для всех режимов и для всех расстояний. Для этого
мы составляем обычное выражение для нормированной
характеристики направленности
(20.5)
*w=as
ш
(0)
¥
§201
ШАРОВЫЕ АНТЕННЫ
109
и так как Ря (1) = 1, то универсальная характеристика
направленности основной антенны га-го порядка
выражается просто абсолютным значением полинома Лежандра:
Л(») = |Ря(оов»)|.
Необходимо подчеркнуть, что основные шаровые
антенны — единственный известный класс антенн, для
которых возможно введение универсальных характеристик
направленности. Легко убедиться, что общая шаровая
антенна подобным свойством не обладает. Действительно:
формула (20.4) показывает, что потенциал выражается
в общем случае суммою произведений, каждое из которых
зависит как от р, так и от 0; иначе говоря, такую сумму
нельзя представить в виде простого произведения двух
функций, из которых одна зависит только от р, а другая—
только от ft. Следовательно, в зависимости от
направления на точку наблюдения будет меняться и
интенсивность и форма сигнала, и, следовательно, введение
универсальной характеристики направленности делается
невозможным.
Для наглядности вид деформированной поверхности
шаровой антенны и соответствующие характеристики
направленности показаны на рис. 50 и 51. В сущности
на обоих рисунках представлены графики одной и той
же функции P„(cos§) в полярных координатах, но на
рис. 50 эта функция наложена на окружность,
изображающую не деформированный шар, а на рис. 51
абсолютное значение той же функции отложено от центра вдоль
радиуса-вектора.
Основная антенна нулевого порядка — это «пухнущий»
шар, эквивалентный точечному источнику. Антенна
первого порядка— смещающийся шар, эквивалентный диполю.
Антенны высших порядков эквивалентны соответствующим
мультиполям. Отметим, что на поверхности основных
антенн образуются узловые линии, число которых равно
порядку антенны. Для оценки направленных свойств
основных антенн могут оказаться полезными
некоторые приближённые формулы. Так, например, известно
110 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
асимптотическое выражение полиномов Лежандра для
больших п:
РпМ ^"К^£"Ь[(» + |> +Л • (20.6)
71=0
Л=1 -f
11
1 1.
It
\\
^s=-
^"-^
!\
~'-~'
11
II
V
-3 .'(
— О | ||
\^_
"^^ч
*4^
II
\\"
II
/У
п=9 -
/f
\^
Ml
1 У
Рис. 50. Рис. 51.
Первый корень этого выражения определяет границы глав-
§ 20]
ШАРОВЫЕ АНТЕННЫ
111
ного максимума; он вписывается в конус с углом при
вершине
Для /1=4, например, й^ЗО0; это значение отличается
от точного примерно на 0,5°; с повышением порядка
приближение улучшается. Чтобы оценить величину
добавочных максимумов (боковых лепестков), можно
воспользоваться другой известной формулой, дающей значение
полинома Лежандра чётного порядка при *) = 90°
(полиномы нечётных порядков равны при этом значении 0 нулю):
|Р2Я(0)1-1,3254.6;.-. ;(2?2;1)- w
Простые формулы (20.7) и (20.8) позволяют сделать
быструю и грубую оценку направленных свойств антенны.
Укажем ещё два свойства шаровых антенн, вытекающие
из ортогональности полиномов Лежандра. Во-первых,
для основных антенн всех порядков (кроме нулевого)
объёмная скорость равна нулю, т. е. при деформации шар
не изменяет своего объёма. Докажем это. Элемент
объёмной скорости
du = vadS,
но
^ = yoP«(cos8)>
где v0 — радиальная скорость, заданная как функция
/ (или р). Далее, элемент поверхности шара
dS=:2rM28mbdb.
Переходя к переменной jx=cos&, получаем:
+1 +1
и -2:гаЧ JР„(ц)<2р = 2тгаЧ>0 SР„ ЫР0 0*Wf* = О
-1 -1
для всех пфО. При п = 0 интеграл равен двум, и
тг = 4тса2а0.
112 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Во-вторых (это мы оставим без доказательства), для
общей шаровой антенны излучаемая мощность (или
энергия) представляется простой суммой мощностей (или
энергий), излучаемых отдельными основными
составляющими.
Займёмся теперь неустановившимся режимом основных
антенн. Упростим свою задачу, ограничившись
рассмотрением закона изменения по-
. тенциала на весьма большом
f расстоянии от антенны. При
г-+ оо in(p -) —♦ 1. Таким об-
у разом, потенциал на больших
расстояниях выражается более
\2 простой по сравнению с (20.4)
формулой:
/7
?-~РД^~2>^
г—а л
<>:)
.(20.9)
В этом выражении первый
множитель зависит только от
размера антенны и координат
точки наблюдения, второй
характеризует запаздывание
возмущения и, наконец, только
третий множитель содержит
интересующую нас
характеристику формы сигнала в виде
её изображения. Нам нужно,
стало быть, найти оригинал,
соответствующий изображению—-—— . Для этого можно
Рис. 52.
'■('i)
воспользоваться формулой Хевисайда, что требует
нахождения корней стоксова полинома F„ (z). Значения корней
даны в нижеследующей таблице, а графическая
интерпретация этой таблицы — на рис. 52.
20]
ШАРОВЫЕ АНТЕННЫ
Корни стоксовых полиномов F„ (z)
113
п
0
1
2
3
4
5
*i
—1,00
—1,00+
+ /1,00
—1,78
—1,20+
+ /2,90
-3,05
-1,354-
+ /4,81
•
—
-1,00-
— /1,00
-1,11+
+ /1,95
—1,20—
-/2,90
—1,28+
+ /3,86
—1,35—
-/4,81
Ч
—
—
—1,11—
— /1,95
—2,30+
+ /0,89
—1,28—
— /3,86
-3,024-
+ /2,68
Ч
—
—
—
-2,30-
—/0,89
-2,70+
+ >'!J7
-3,02-
— /2,68
Zb
—
—
-—
—2,70—
-/1,77
—3,63+
+ /0,91
*6
—
—
—
—3,63—
-/0,91
Нам удобнее будет оперировать дальше
вспомогательными полиномами
<&B(*) = *»F„(*),
имеющими, очевидно, те же корни, что и Fn(z). Число
корней полиномов ¥п и Фп на единицу больше их порядка.
Теперь мы можем записать на основании формулы
Хевисаида для потенциала, как функции времени,
отсчитанного от момента прихода возмущения в точку
наблюдения:
n+l n_i г —
Для давления получим несколько более простую формулу:
с*
ft=i
Обозначая сумму через
(20.11)
Ч'7)"
А. А. Ха] кевич
114 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ гГЛ. II
поручим, подставляя значения корней и выполняя
вычисления: «
h± (f) = <T*''(cos V—sin *'),
Графики этих функций до 4-го порядка представлены
на рис. 53. Эти графики показывают, что в начальный
момент (в момент прихода возмущения в точку наблюде-
Рис. 53.
ния) давление изменяется скачком от нуля до значения
w-j P„(fO (при скорости на поверхности антенны, равной
единице) независимо от порядка антенны. В дальнейшем
давление спадает и притом тем быстрее, чем выше
порядок антенны. Для антенны нулевого порядка давление
Спадает монотонно, для антенн же более высоких
порядков изменение давления имеет колебательный характер,
причём колебания выражены тем резче, чем выше
порядок антенны.
Можно довольно просто определить наклон графика
в начале, т. е. скорость убывания давления при t = 0.
Для этого достаточно воспользоваться тем
обстоятельством, что если
/(*)--/(О,
то _
\\mf{t) = \\mf{p).
*-> 0 р-ххэ
щ
§ 20] ШАРОВЫЕ АНТЕНПЫ 115
Нас интересует скорость изменения давления, т. е.
производная по времени функции h ( — J . Мы имеем:
d , fet\ с \р с ) __ с \р с
F\pac) "М'т)
или
«<0—^д-
Отделим в изображении целую часть — она
соответствует начальному скачку
Искомое значение наклона даёт дробная часть этого
выражения.
Так как
Фя(*)=*пИ+*,.*"+ . . . +а0,
то при z-»oo имеем:
A'(0)=,_a„ = -(l+^ti))*).
На рис. 53 касательные к кривымArt (£') при *'= 0 отмечены
пунктиром.
Рассмотрим в заключение соотношения на
поверхности антенны. Мы имеем общее выражение для
изображения давления (по формуле (20.4)):
г-* a in\p~7 '
р = 9от=п±е-*-р^-^Рп{\>)- (20.12)
*) Это значение ап вытекает из определения стоксовых
полиномов; оно дано здесь без вывода.
1J6 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Давление на поверхности шара (г- а)
или
Корни Ф„ (z) нам известны, и мы можем сразу применить
формулу Хевисайда:
W (t>\-X:zkln_(4)eZk
которая даёт:
Ро(П = е~х,
р\ (t')=ze~xo,o&x.
Очень интересна следующая интерпретация
соотношений на поверхности антенны: возьмём отношение
давления к радиальной скорости
Это отношение, представляющее так называемое
удельное акустическое сопротивление, не зависит от угловой
координаты:
Ьп v~wFn(z)-
Возьмём теперь обратную величину
w_ = ¥n (z)
Ьп zin(z)
и будем делить числитель на знаменатель. В результате
§20]
ШАРОВЫЕ АНТЕННЫ
117
деления это выражение сможет быть представлено в виде
непрерывных дробей:
h z
7 + 1
w_ _ _3
h~z I.
w 4
до __ J5» j
+i
i
-i+r
i
(20.14)
4+*
7 +
z ^ 3 ,
>
Легко подобрать электрические схемы, проводимость
которых выражается формулами, аналогичными (20.14).
Такие схемы, являющиеся эквивалентными схемами для
антенн различных порядков (с точки зрения соотношений
между давлением и скоростью на их поверхности),
изображены на рис. 54. Параметры, обозначенные на
схемах, таковы: М — индуктивность, численно равная
массе среды в цилиндре длиною а и сечением, равным
единице; С — ёмкость, численно равная гибкости среды
в таком же цилиндре. При таком выборе параметров схема
изображает явления на поверхности антенны следующим
образом: если задать входной ток, изменяющийся по
закону
J = p»(i*H(0.
118 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
то напряжение на зажимах схемы будет численно равным
давлению в данной точке поверхности шара и будет
воспроизводить его изменение во времени.
ЛсрмМ Схема -
С М
с
й\
г ч
>w
\w
№
М\
flopjtM
iw
Схема
C/S С
Рис. 54.
§ 21. Рупоры
Рупором называется волновод в форме расширяющейся
трубы. Мы рассмотрим неустановившиеся волновые
явления в рупорах, основываясь на приближённой теории,
применяемой до настоящего времени. Согласно этой
теории предполагается, что потенциал зависит только от
одной координаты, отсчитываемой вдоль оси рупора.
Иначе говоря, предполагается, что в любом сечении
рупора потенцпал одинаков.
В результате такого (довольно грубого)
предположения уравнение волны в рупоре сводится к одномерному
уравнению следующего вида:
дх* + S дх
c*dt*
= 0.
(21.1)
5 21]
РУПОРЫ
119
Это уравнение отличается от обычного уравнения плоской
волны наличием второго члена, содержащего ^ . Этот
член характеризует убывание потенциала вследствие
расхождения волны. Через S обозначена зависящая от
координаты х площадь поперечного сечения рупора, так что
S=S(z); S' = g.
Решение уравнения (21.1) зависит, разумеется, от
вида функции S(x). Мы ограничимся рассмотрением
наиболее известного семейства так называемых степенных
рупоров, для которых
S ^апх2п.
Используя &ту зависимость, получим уравнение степенных
рупоров в виде
dtf + 'iFx'-^W^0- (21-2>
Первое изображение уравнения (21.2) будет:
?"+??-*»,?? = °- (21-3)
Традиционный приём решения уравнения состоит в том,
что подстановкой
_ j_
приводят (21.3) к уравнению Бесселя. Ив числа возможных
решений выбирают решение, выражаемое в ханкелевых
функциях. Ограничиваясь целыми п, можно выразить
затем решение в элементарных функциях, пользуясь
формулами для бесселевых функций, порядок которых
выражается целым числом с половиной.
Мы воспользуемся другим приёмом. Будем искать
решение для воллы, движущейся в сторону положительных х9
в виде
4 = A.(j>±yebf(p±), (21.4)
120 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
где Ап — постоянная, а / — неизвестная пока функция.
Подставив (21.4) в (21.3), получим:
Г-2/'-^^/ = 0. (21.5)
\ Р-)
Уравнение (21.5) определяет функцию /. Оказывается,
что эта функция есть не что иное, как уже известный нам
полином Стокса (см. предыдущий параграф). Решением
уравнения (21.5) является стоксов полином порядка
п—1; таким образом, для изображения потенциала в
рупоре порядка п мы имеем:
^n = An{pT)~ne-pXcin-i{p^). (21.6)
Нас интересует, конечно, сравнение рупоров различных
степеней. Но для того чтобы такое сравнение имело смысл,
нужно привести все семейство к некоторым согласованным,
размерам. Это можно сделать следующим образом:
вырежем отрезки рупоров длиною / и потребуем, чтобы
площади сечений в начале и конце этих отрезков были
одинаковы для всех рупоров, т. е. пусть
Отсюда можно найти ап и х0:
Х0 — 2п —
I I
)
П, \ (21.7)
Предельным членом семейства степенных рупоров
является, как известно, экспоненциальный рупор:
S^S0emx.
Волновое уравнение для экспоненциального рупора
принимает вид
f" + гщ' - ^ ^ =: 0. (21.8)
§ 21]
РУПОРЫ
12t
Это обычное уравнение с постоянными коэффициентами;
его решение (для волны, бегущей в одном направлении —
в сторону положительных х):
X-fV
? = А^ *'*". (21.9>
Для того чтобы согласовать отрезок
экспоненциального рупора с отрезками степенных, нужно положить
или
ГП:
1 , St
zTlnst
(Ж)
Очертания отрезков
рупоров с согласованными
размерами изображены на
рис. 55.
Теперь мы можем
приступить непосредственно к
нашему исследованию.
Прежде всего выясним,
как изменяется форма
импульса при распространении
вдоль рупора на протяжении \g=semA
отрезка длиною 11 Напомним,
что мы не учитываем
отражения от конца рупора и
рассматриваем только
прямую волну. Положим, что
в начальном сечении S0
задано возмущение в форме единичной функции
<Ро = °о(*)«-*- !•
Определив при помощи этого условия постоянную Ап,
в «формуле (21.6) — для этого в (21.6) нужно положить-
<%
Рис. 55.
30 — dCi
0>
получим, для сечения St с координатой х{\
122 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Заметим прежде всего, что первый множитель
есть величина, постоянная для всех степенных рупоров.
Этот множитель, меньший единицы, характеризует
убывание потенциала за счёт расхождения волны вследствие
увеличения сечения волновода. Второй множитель
выражает запаздывание возмущения, приходящего в сечение
Sty на время пробега волны вдоль отрезка рупора. Это
время равно, очевидно,—. Таким образом, интересующая
нас зависимость заключена в третьем множителе, которым
мы и займёмся. Для различных значений п} подставляя
соответствующие выражения стоксовых полиномов,
получим:
?i =
(**)_
1,
i+
pxt
И)
ML
Р*о
•(•*)
W)
1 + 3—+ з(—Y
1 + 3—+з(—Y
рх„ \ рх„ /
14*
— р*1
-«(-^YW-^-Y
Р%1/
\pxiJ
Ч с J : рх0 \pxj п \pxj )
(21.11)
и так далее.
Для нахождения оригиналов послужит формула Хе-
висайда; нужно лишь знать корни полиномов 1п%
§ 21}
РУПОРЫ
123
Мы имеем:
Корни стоксовых полиномов tn (z)
\ п
1
2
3
«1
—1,00
—1,50+/0,87
-2,33
Ч
-1,50-/0,87
—1,84+/1,75
*з
—1,84-/1,75
Произведя вычисления, найдём:
fc=[5-+(l-J)e"S]*C).
-I,73(l-^)%in0,87|-]}c0(*),
'-{(ifT + t1'64-4'23^4-4'55^2- > (21-12)
-1,95(^-)3]е -2>33£ + [-0,65 + 4,23 J -
-4,55 (?JT+W(-5)i]--t,M*-lf7^ +
+ [-l,92 + 2,25^ + l,28(-j)2-
и так далее.
Для завершения вычислений нужно выбрать какое-
либо численное значение отношения выходного и
входного сечений. Пусть будет
^-=-ieoo.
124 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
ct ct
Введём обозначение — = si, т = -г и составим вспомо-
X, I
гательную табличку:
п
Xi
£
1
0,025
39
2
0,158
5,32
3
0,282
2,42
4
0,398
1,51
Перепишем предыдущие формулы с численными
коэффициентами:
<Pi = "<)(*),
сра = [0,158 ч- 0,842 е-5'35 >0(т), .
ср3 = [0,08 + е-3'65 т (0,92 cos 2,12 х -
-0,87 sin 2,12 т)]о0(х),
ср4 = [0,064 ч- 0,566 е 3,54х +
} (2.1.13)
-2,8т
+ е ' (0,37 cos 2,68 т-1,14 sin 2,68 т)]а0(т)
В тыком виде эти формулы уже могут быть использованы
для построения графиков. Нужно только не забыть
восстановить опущенное при выводе запаздывание; для
этого при построении нужно в этих формулах
подразумевать аргумент не х, а т—1.
Обратимся теперь к экспоненциальному рупору. Для
него мы имеем:
ml
V**,
! = « 2
!•
И в этом выражении первый множитель
ml
е~~2- =
Si
§21J
РУПОРЫ
125
Остающийся второй множитель перепишем, введя обо-
ml
значение -—= л:
ср-=е ' (21.14)
Нам нужно найти оригинал этого выражения. Для этого
необходимо применить специальный приём. Мы
воспользуемся одной готовой формулой*) и после некоторых
преобразований приведём искомый результат к виду:
Эта формула учитывает запаздывание, так как в отличие
от степенных рупоров множитель в изображении (21.14),
выражающий запаздывание, не отделяется и не был нами
опущен. С точки зрения частотных зависимостей это
обстоятельство указывает на наличие дисперсии. Используя
то же численное значение -^ = 1600, найдём:
До
Х=3,7. •
Функцию (21.15) приходится вычислять графическим
методом.
Результаты вычислений по формулам (21.13) и (21.15)
сведены на графике рис. 56. Из этого графика следует,
что конический рупор (п = 1) совершенно не искажает
распространяющегося по нему импульса и является,
следовательно, идеальным волноводом. Все остальные
степенные рупоры вносят искажения тем большие, чем больше п.
Искажения проявляются в том, что потенциал, достигая
в первый момент (то-есть в момент прибытия импульса
к выходному сечению) максимального значения,
одинакового для всех рупоров, убывает затем тем быстрее,
чем больше п. Наихудшим с этой точки зрения
оказывается экспоненциальный рупор. Интересно ещё отметить,
*)А. М. Эфрос и А. М. Данилевский, Операционное
исчисление и контурные интегралы, ДНТВУ, 1937, стр. 156,
формула (286).
126 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. Ц
что с течением времени потенциал стремится к постоянному
значению, тем меньшему, чем больше п. Это предельное
значение можно также рассматривать как меру искажения
импульса.
Рассмотрим теперь то же семейство рупоров с другой
точки зрения, а именно с точки зрения переходного
сопротивления. Вопрос ставится следующим образом: на
Рис. 56.
входе отрезка рупора задаётся определённый импульс
скорости; ищется форма возникающего при этом импульса
давления. Речь идёт о давлении, возникающем в том же
месте, т. е. во входном сечении. Таким образом,
волновые свойства рупора при таком исследовании
непосредственно не затрагиваются; рупор рассматривается как
акустический двухполюсник, и речь идёт о свойствах его,
как нагрузки для того или иного излучателя. Заметим,
что это есть как раз обычная при исследовании рупоров
постановка вопроса.
Нам нужно найти выражение для давления и для
скорости. Из (21.6) получаем:
-£ = PoPy = AnPop(p^yie-p*flt.1(p^-); (21.16)
»=-Й=^*7-Г-"*Ч^> (21.17).
§21] РУПОРЫ 127
Разделив (21.16) на (21.17), получим операционное
выражение для акустического сопротивления рупора в
сечении с координатой х:
£=4
= w-
(21.18)
Если мы теперь найдём оригинал для этого изображения,
то получим функцию времени, представляющую
изменение давления во входном сечении, если в том же сечении
задана скорость, изменяющаяся по закону единичной
функции. Для различных п будем иметь:
W
А
W
е * .
е ~1,5*о ( cos 0,87 ^L - 0,58 sin 0,87 -^),
ct ct
■£- = 0,43 e~2,S2^ + е-1,84~*( 0,57 cos 1,75 SL_
} (21.19)
-0,54 sin 1,75 A\
Ct
или, приводя эти формулы к аргументу т = -у
ДО
А
до
= е
-8 «с
(cos 4,6 т — 0,58 sin 4,6 т),
0,57 cos 4,2
-0,54 sin 4,2 т),
:0,43е 5,6т + е 4,Бт(0,57cos4,2 т-
)> (21.20|
*
128 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Обратимся к экспоненциальному рупору.
Из (21.9) получаем:
-р = АМе Л V -*J» (21-21)
-v=Am^(l + YU^)e^l^i+^X> 121.22)
JL
l^X ^w »* . (21.23)
v *+/i+4-
Для нахождения оригинала последнего выражения
сделаем предварительно некоторые преобразования. Умножим
числитель и знаменатель на
f •!
Это даст
f=-w - ^ = w - 1-^
_р_ \ р_ р
Первый член в скобках умножим и разделим на
V
1 -Г о J
получим:
JL 2 £
а = а, _^= + ^_^L=_J!* . (21.24)
Оригиналом первого члена является бесеелева функция
§ 21] РУПОРЫ 129
нулевого порядка аргумента <&kt (см. таблицы готовых
формул). Оригиналом второго члена является двойной
интеграл той же функции в пределах от 0 до &kt. Третий
член имеет оригиналом просто &kt. Таким образом
искомое выражение имеет вид:
т~=/оК*) + \' ^poW^V- (21-25)
о о
Это выражение неудобно для вычислений, а поэтому мы
выполним интегрирование во втором члене.
Воспользовавшись известными формулами, можем представить двои-
ной интеграл в виде двойной суммы
fct х ОО ОО
6 6 fc=0 i=0
Но последняя сумма легко упрощается и приводится
к виду
ОО ОО ОО
ft=0i-0 n=i
Последнее выражение уже вполне пригодно для
вычислений, так как при не очень больших значениях аргумента
ряд быстро сходится.
По поводу экспоненциального рупора интересно ещё
заметить, что с течением времени переходный процесс
в нём вырождается в затухающее синусоидальное
колебание с критической частотой. Это заключение рытекает из
асимптотического выражения для бесселевой функции:
/o(z)*7oo^"^"sin(z~x)'
Заменяя
а>Л$ = Хт ( = 3,7т),
9 А. А. Харкевич
130 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
можем теперь построить график переходных
сопротивлений всего семейства по формулам (21.20) и (21.25)(рис. 57).
Как видно из графика, сравнительная оценка различных
рупоров по переходному сопротивлению приводит к об
ратным (по сравнению
с предыдущим)
результатам, а именно:
наилучшим оказывается
экспоненциальный
рупор, наихудшим —
конический. Возникает,
естественно, вопрос о
том, какому же рупору
следует отдать
предпочтение в практических
применениях? Но из
предыдущего ясно, что вопрос получает и смысл и
определённый ответ лишь при условии, что мы отдаём
себе отчёт в назначении и способе использования
рупора.
Выражение (21.18) для входного сопротивления
степенного рупора допускает интересную интерпретацию.
Можно показать, что для стоксовых полиномов
справедливо следующее рекуррентное соотношение:
10
ttu
¥
чп
^
71
=>
v/7
*™
W
=о)?¥
С
Рис. 57.
М»)
2л-1
f*-i (*)
.(*)
f*-i (*)
(21.26)
Последовательно применяя это соотношение, можем
представить (21.18) в виде непрерывной дроби:
*п/*п-
'2п — 1
+
2п-
U
Р-
Ъ — 5
х
■ь
1
2/г —7
х
(21.27)
-I-...
§ 2Ь
РУПОРЫ
131
В частности,
W
w
■ h
W
=
1
1
X
3
X
P1T
5
X
+ 1
, *
i
--V+-
1
X '
(21. 28)
и так далее.
Заметим, что
Р— и> = рр0х=^рм;
р-
рж рС '
где М = р0#— масса воздуха, заключённого в цилиндре
высотою х и площадью основания, равной единице,
а С = —-2 — гибкость воздуха в том же цилиндре.
Все эти соотношения и (21.28) дают нам основание
представить входные сопротивления степенных рупоров
электрическими эквивалентными схемами в духе первой
системы электромеханических аналогий (рис. 58). Для
входного сопротивления экспоненциального рупора также
может быть построена эквивалентная схема, имеющая
вид бесконечного фильтра верхних частот (рис. 59).
Обозначенные на схеме параметры имеют следующие
значения: *
М:
9*
С=-
р0с2т
132 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Я-/ М \
о—
о—
*wS
С
-Н-
*>wS
С/3
п=3 Ф
М\
'•wS
— Я f\
C/S С
HI-HI-
'.wS
n=S
С/7 С/3
oj yVS
«У oj if a
Рис. 58.
\wS
С С С
Л\ L 11 t fh
>v§ /va //j
/У?
Рис. 59.
§ 223
ПРИЕМ И ИЗЛУЧЕНИЕ
133
§ 22. Приём и излучение
Вопросы приёма и излучения получают наиболее
полное освещение, если рассмотреть закономерности,
существующие в акустической системе передачи. Под системой
передачи мы будем понимать совокупность двух антенн,
каждая из которых может быть как излучателем, 1ак и
приёмником. Режим системы передачи будем описывать
при помощи величин среднего (по поверхности антенны)
давления и объёмной скорости. Нужно признать, что
такой выбор переменных обусловливает довольно
существенное ограничение общности. Дело в том, что, выбрав
переменные, мы, естественно, предполагаем, что ни одна из
них не является тождертвенным нулём. А это означает,
что мы исключаем из рассмотрения все антенны порядка
выше нулевого, т. е. диполи и вообще мультиполи*).
Однако и при таком ограничении можно получить, как
будет видно, полезные результаты. Формулы, которые
мы выведем, будут годиться для антенны нулевого
порядка, например ь форме раздувающегося шара, для
точечных источников, для неограниченной плоскости и т. п.
Составим уравнения системы передачи в следующем
общем виде:
p1^=^cllu1 + c12u2} I (22.1)
р2=с21и1 + с22и2. |
Здесь р — среднее давление, и — объёмная скорость;
индексы 1 и 2 указывают, к какой из двух антенн относится
данная переменная величина. Коэффициенты eik мы
сейчас определим.
Положим, что антенна 1 излучает с заданной
объёмной скоростью и1$ а антенна 2 закреплена так, что
иа =0. На поверхности антенны 1 давление в результате
её собственного излучения будет
Pn = 3iuv (22-2>
*) Сказанное здесь представляет собою упрощение. Введённое
ограничение требует более тонких формулировок. За
подробностями рекомендуется обратиться к уже цитированному труду
В. В. Фурдуева.
134 ТКОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Волна давления, распространяясь, достигнет антенны 2,
находящейся на расстоянии /. Давление при отсутствии
антенны 2 было бы
P21 = Pllfl(l)>
где Д (I) — безразмерная функция координат
местоположения антенны 2. Функция f± (l) зависит от свойств
антенны 1. Вследствие наличия антенны 2, которая, будучи
© _ (D
<р„тз2щм
Рис. 60.
закреплена, ведёт себя как твёрдое тело, возникает
дифракционное поле. Это поле даёт на поверхности антенны
2 добавочное среднее давление, отношение которого к
давлению р21 мы обозначим через g2 (0). Дифракционное поле
антенны 2, распространяясь обратно к антенне 1, создаёт
на расстоянии / относительное давление g2(l). Так как
скорость антенны 1 задана, то возникает дифракция снова
как от твёрдого тела, что даёт на поверхности антенны
1 добавочное давление, учитываемое множителем gx (0),
и так далее. Всё это рассуждение наглядно представляется
волновой сеткой рис. 60.
р,/,а)дгг(Щ№,аА
221
ПРИЕМ И ИЗЛУЧЕНИЕ
135
Если теперь просуммировать все слагающие среднего
давления на поверхности антенны 1, то получится
J»i=?u{l+/i(J)*,(*)[l + *i(0)] +
+ /i(*)*i(*)*i(I)[l + *i(0)] + -}. (22.3)
Суммируя формально этот бесконечный ряд и учитывая
(22.2), получаем следующее выражение для одного из
коэффициентов:
Cii =
Pi
u2=0
^[1+ш.т^т]. (22.4,
Подытожив подобным же образом давление на поверхности
закреплённой антенны 2, получим:
■•/>,=fti{/i(l)[l + *.(0)] +
откуда
С«П ~—
Р2
_Q / (]\ 1 + *> (0)
w2=0
i-*i(»)ft№ '
(22.5)
(22.6)
Для нахождения двух остальных коэффициентов, с12
и с22, можно сделать обращение системы передачи, т. е.
заставить антенну 2 излучать, а антенну 1 закрепить.
Гораздо проще, однако, получить нужный результат
перестановкой индексов 1 и 2 в формулах (22.4) и (22.6).
В результате уравнения (22.1)спстемы передачи принимают
следующий вид:
Pi-Si\}+h(i) i-gl(i)gi(i) ) Bi +
(22.7)
i
136 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Перед тем, как перейти к приложениям этих
уравнений, уточним определения входящих в коэффициенты
функций / и g.
f(l) есть отношение давления в свободном поле на
расстоянии I от излучающей антенны к давлению на её
поверхности.
g (0) есть отношение среднего давления, возникающего
на поверхности отвердевшей антенны, к давлению в
свободном поле (т. е. при отсутствии антенны).
g (i) есть отношение давления, возникающего
вследствие дифракции от отвердевшей антенны на расстоянии /
от неё, к давлению в свободном поле в месте
расположения антенны.
Все функции / и g для стационарного синусоидального
режима представляют собою функции аргумента /о> и
являются, следовательно, комплексными величинами. В
более общем понимании эти функции являются
изображениями соответствующих функций времени, т.е. функциями
оператора р.
Сопоставляя приведённое выше построение с § 11, можно
сказать, что функции g представляют собою обобщение
коэффициента отражения.
Поясним эти определения на простейшем примере.
Пусть система передачи состоит из двух поршней на
расстоянии / друг от друга в цилиндрической трубе
единичного сечения. В этом случае мы имеем:
'Зх=32=^; /i(Q=/i(*)=«"*T;
*i(0) = ft(0) = 1; 8l{l) = gt(l) =e -*'.
Подставляя эти значения в выражения коэффициентов clk9
получаем уравнения рассматриваемой системы передачи
в виде:
.1 I , W
p1=zwcth p—Ul + г
с
-j—u1 + wctb. p—
(22-8)
shp
с
§ 22) ПРИЕМ И ИЗЛУЧЕНИЕ 137
В качестве одного из применений общих уравнений
определим функцию g(0). Для этого воспользуемся
теоремой взаимности, по которой должно быть
Отсюда
или
с12—с21*
&/.W[i + *i(0)]=3i/i(0[i + *.(0)]
i+*i(0)=етН1+*.(°)ь (22-9)
При помощи этой формулы можно, например, найти
давление, возникающее в результате дифракции на
поверхности антенны 1, если известны её характеристики Qx и Д
и если, кроме того, известны все характеристики
произвольной вспомогательной антенны 2. Выберем, например,
как это обычно и делается, антенну 2 в форме малога
шарика радиуса Ь (малая антенна нулевого порядка).
В этом случае
Подставив это в (22.9), получим:
* + 81{°) = -%£'^Ш1)' (22.10)
Формула (22.10) выражает в общем виде соотношение,
известное для частного случая под названием закона Шоттки.
Положим, что мы хотим знать среднее давление на
поверхности шара радиуса а с учётом дифракции (радиус а
не предполагается малым, а потому дифракцией не пре-
небрегается). Для такого шара
Подставляя в (22.10), находим:
** р —
1+л(0) е с
l + pf
138 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. 1Г
Этот же результат может быть получен классическим
методом разложения решений волнового уравнения по
сферическим функциям путём гораздо более громоздких
выкладок.
В заключение рассмотрим ещё один интересный
пример. Пусть система передачи состоит из малого шарика
{антенна 2) и неограниченной плоскости (антенна 1).
Можно было бы ожидать, что при встрече звуковой волны
•с плоскостью произойдёт простое отражение с удвоением
давления. Это, однако, не так. Для нашей плоскости
сопротивление, рассчитанное на произвольную конечную
площадь 5*, равно
о — w
Oi — ~$* •
Функция fx (I) равна, очевидно, е-* т (как выше, в случае
цилиндрической трубы), так как неограниченная
плоскость излучает плоскую волну, для которой явления в
различных точках поля различаются только запаздыванием.
Применяя (22.10), находим для рассматриваемого случая:
л , /л\ 4 тсс/ 4кcl . ,.*
1 + *i(°) =-£5*"*— -£*- * so (0 •
Этот результат вовсе не очевиден, а потому мы раз"
берём задачу подробно, пользуясь более наглядным
методом.
Напомним прежде всего, что по определению^(0)
представляет собою отношение давления, обусловленного
дифракцией от твёрдой плоскости (в нашем случае
дифракция вырождается в простое отражение), к давлению,
которое было бы на месте плоскости, если бы антенна 2
излучала в свободное пространство. Обозначив дифракционное
(отражённое) давление через р& , а давление свободного
излучения через р21, можем записать:
l + gl(0)=:l + i^ P* + Pd=Jh; .
где через рг обозначено полное давление на плоскости,
-складывающееся из давлений прямой и отражённой волны.
221
ПРИЕМ И ИЗЛУЧЕНИЕ
139
Рассматриваемая система изображена схематически
на рис. 61. 1 означает плоскость, 2— малый шаровой
излучатель, А — сферический фронт волны, исходящей
из 2. Фронт волны пересекается с плоскостью по
окружности радиуса а, увеличивающегося с течением времени.
Вне этой окружности волна до
плоскости ещё не дошла, и
избыточного давления там нет.
Если давление в свободном
поле в точке 0, т. е. у
основания перпендикуляра,
опущенного из 2 на i, обозначено
через р21, то давление в любой
точке на расстоянии г от О
будет:
/> = 2^21^-Л-')'
Рис. 61.
причем множитель -к учитывает
убываниЛдавления вследствие
расхождения волны,
множитель 2 появляется вследствие
удвоения давления при полном
отражении, и, наконец, мно-
житель о0 It J указывает запаздывание вследствие
увеличения расстояния. Чтобы найти среднее давление,
нам нужно умножить давление на элемент площади,
проинтегрировать и разделить на площадь. Элемент площади
выберем в форме кольца
dS* = 2urdr,
или, так как
г2 + /2 = Д2; rdr=RdR,
то
dS* = 2*RdR.
Введя обозначение
R-1
с
dR = cdx,
i
140 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
получим для среднего давления:
оо
о
т. е. тот же результат, который выше был получен
непосредственно из формулы (22.10). Физический смысл этого
результата состоит в том, что сила, действующая на
плоскость, непрерывно возрастает, так как увеличивается
площадь, на которую воздействует давление исходящей
из источника 2 волны.
§ 23. Энергетические соотношения
Мы займёмся теперь энергетическими соотношениями
в неустановившемся акустическом волновом поле.
Исследованию этого вопроса необходимо, однако, предпослать
некоторые общие соображения. Зависимость между
давлением и объёмом принято описывать в акустике адиаба-
• тическим законом:
' ' PVi = const, (23.1)
где Р и V — давление и соответствующий объём для
любого данного состояния газа. Уравнения линейной
акустики выводятся в предположении, что давление и объём
получают малые относительно начальных значений
приращения р и v. Если так, то, обозначая начальные
значения давления и объёма через Р0 и F0, можем записать:
% P*VJ = (P0+ p){Vo + vy,
ИЛИ
откуда
P~--lP*-yt (23.2)
или
Р^Ро VtyTP , (23.3)
г 0
i 23)
ЭН ЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
141
т. е. мы выражаем приближённо связь между Р
нелинейной зависимостью, тогда как точная зависимость,
вытекающая из (23.1), имеет вид
Р = РЛ
(23.4)
Геометрический смысл этих соотношений
поясняется рис. 62, на котором построена адиабата (23.4) и
прямая (23.3), касательная к адиабате в точке (Р0, V0).
Пользование прибли- «.
жёнными зависимостями
(23.2) или (23.3) позволяет
правильно определить в
первом приближении
любые величины первого
порядка, на чём и строится
вывод всех известных со-
отношений^линейной
акустики. Однако для
определения в том же первом
приближении величин
второго порядка линейное
приближение уже непригодно. Попробуем подсчитать
приращение энергии массы газа, сжимаемой
адиабатически от объёма V0 до объёма V± (разумеется, с
соответствующим повышением давления от Р0 до Рг).
Мы имеем:
Д£:
Уг
:J PdV =
Vo
PiVi-PqV.
Y-l
(23.5)
Развёртывая это выражение по степеням малого
отношения -— и сохраняя члены до второго порядка, получаем
для первого приближения:
1 Y \
+тк)=у-т(1-^:У <23-6»
142 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ \.ГЛ. II
Если же мы попытаемся определить ту же величину из
формул линейного приближения, то получим:
*Е = 4Г(Р0 + Р1) {yi-V0)=V0f(l + -^r). (23.7)
Итак, выражение для приращения потенциальной
энергии, содержащее линейный и квадратичный члены
относительно избыточного давления р, получаемое из
линейного приближения, даёт, как и следовало ожидать,
неверное значение квадратичного члена: Тем не менее мы будем
в дальнейшем пользоваться формулой (23.7) и вот по
каким соображениям. При синусоидальных волнах
квадратичный член полностью определяет энергетические
соотношения, так как линейный член при интегрировании
по объёму даёт в среднем нуль. Нас же будет интересовать
главным образом тот специальный случай, когда
квадратичным членом можно пренебречь по сравнению с
линейным, а в этом случае (23.7) и (23.6) совпадают. Можно,
кроме того, отметить, что обсуждённые выше вопросы,
поднятые впервые в советской литературе*), не находят
отражения ни в одном из известных руководств по акустике.
Введём приращение объёмной плотности
потенциальной энергии, для которого из (23.7) получаем:
K-4?-f(«+-rf-)-f + -£. (23.8,
где х = у^о— объёмный модуль упругости среды. Для
малых возмущений,которые мы только и рассматриваем,
^<1, (23.9)
и, следовательно, в выражении (23.8) второй
(квадратичный) член по абсолютной величине много меньше
первого (линейного).
Это ещё не означает, что мы можем всегда отбросить
квадратичный член в выражении для потенциальной
энергии конечного объёма.
*) Б. П. Константинов и И. М. Бронштейн, Phys.
Zs. d. Sowietunion 9, 6,630 (1936); H. Н.Андреев, J. of Physics,
АН СССР 1, 4, 305 (1940).
§ 23) ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ 143:.
Действительно, в общем случае мы должны писать:
AEtt=MpdV +±\P4V. (23.10>
V v
»
Соотношение между обоими членами этого выражения
зависит от характера функции р. Если эта функция знако-
переменна, то первый интеграл может дать сколь угодно
малые значения, так что слагаемым потенциальной
энергии, зависящим от линейного члена, можно пренебречь,,
и мы сохраняем только обычный второй член.
Именно так обстоит дело для синусоидальных волн.
По мере того, как мы увеличиваем объём V, первое
слагаемое (23.10) колеблется около нуля, тогда как второе
неограниченно возрастает.
Если же давление р в пределах данного объёма не
изменяет знака, то, в силу (23.9), мы можем пренебречь
в (23.10) вторым слагаемым, зависящим от квадратичного
члена, и в этом случае мы имеем:
% bEn~l-[pdV. (23.11)
V
Рассмотрим поле, создаваемое неограниченной
излучающей плоскостью. Пусть нормальная скорость задана
в виде
0Л = 0о°о(О-
В поле получающейся при этом плоской волны скорость
и давление будут
т. е. избыточное давление во всех точках поля одинаково,
и следовательно, полагая его малым по отношению к
начальному давлению, мы можем в данном случае, восполь-
144 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГХ I*
зоваться формулой (23.8), отбросив квадратичный член,
что даёт для объёмной плотности потенциальной энергии
Дгп^. (23.12)
Кроме потенциальной энергии в поле находится также
кинетическая энергия. Плотность последней может быть
выражена как
sK=<^. (23.13)
(Эта формула справедлива для покоящейся среды, т. е. в
предположении, что начальной скорости нет.) Выражая
скорость через давление, получим:
8 --?-
Другими словами, кинетическая энергия как раз равна
отбрасываемому нами квадратичному члену в выражении
для потенциальной энергии (это соотношение
общеизвестно, но, как было показано выше, неверно), и,
следовательно, мы можем пренебрегать и кинетической
энергией и писать уже для полного приращения объёмной
плотности энергии *
Дз = Дв„ + е« = -f (l + -£)^ f, (23.14)"
тг, соответственно, для полного приращения энергии в
лекотором объёме
LEc^y[pdV. (23.15)
v
Несколько иначе обстоит дело для шаровой волны.
В качестве источника такой волны выберем шар
переменного радиуса.
Пусть радиальная скорость поверхности шара
va=vQ<s0{t).
'23] ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ 145
В поле шаровой волны скорость и давление будут
p = wv0—e « v « 'o0( с J.
Кинетическая энергия поля
2 cf_ _o-£L
EB = 2icp0\o»r4r = lg^(3-4e a+e ")• (23.16)
a
Приращение потенциальной энергии поля
4£-=t(f+£)«"=■
эди
= a«*V + ^ <* ~ е а > "■= Д^п + ДаЯп. (23.17)
Первый член представляет линейное, второй —
квадратичное приращение потенциальной энергии. Через и0 =
= 4тга21>0 обозначена объёмная скорость источника.
Отметим пре(|Ьльные соотношения. При а —> оо шаровая
волна переходит в плоскую. При этом
Е" ^ Swv*t; _^<-
Если же стремить а к нулю, что соответствует переходу
к точечному источнику, то
Е _ 3 а>"о
До£„^
^ »оо; Т{
к 16 гсас I р
V юл? £к g
2 п 16 тгас
т. е. кинетическая и потенциальная энергии при конечной
объёмной скорости источника стремятся к бесконечности
вследствие особенностей поля вблизи источника, причём
кинетическая энергия в три раза больше потенциальной.
10 А. А. Харкевич
146 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. П
Квадратичные составляющие энергии сосредоточены, как
видно, в области, близкой к источнику; в этой области
они преобладают над линейной составляющей.
Следовательно, выведенные выше приближённые линейные
выражения для энергии не могут применяться в области,
непосредственно прилегающей к точечному источнику.
(Впрочем, и самые уравнения акустики теряют силу в этой
области.)
Полное приращение энергии поля
wu%
Для малых а оба члена сравниваются при радиусе поля
л=с« = _^
В дальнейшем первый член, т. е. линейная составляющая,
неуклонно растёт, тогда как квадратичная составляющая
стремится к постоянному пределу. Следовательно, для
больших радиусов, или, что то же, для больших времён,
квадратичной составляющей энергии поля можно уже
пренебречь.
Перейдём теперь к исследованию энергетического
баланса, т. е. соотношения между энергией поля и работой
источника. Начнём со случая плоской волны, излучаемой
неограниченной плоскостью, движущейся с нормальной
скоростью
»„ ^(МО-
Работа, совершаемая плоскостью, рассчитанная на
площадь S, равна произведению действующей на эту площадь
силы на перемещение:
X t t
A=\Fdz=\Fvdt = S \ (P0 + p)vdt =
do 6
= Sctf(i+-Q. ^ (23.18)
§ 23] ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ 147
■*-£*
Л
С другой стороны,
V
оо
=55^1+йЬ('-т)^=л'т(1+^)- (2319)
о
Баланс сходится. Работа источника растёт со временем,
так как плоскость всё время движется и работает против
силы постоянного давления Р0+р\ энергия поля также
всё время возрастает, так как фронт продвигается со
скоростью с, и объём поля, равный Set, увеличивается.
Отметим одно обстоятельство,
которое может ускользнуть от первого
взгляда. Дело в том, что в
рассмотренном случае линейная часть работы
источника не совершается тем
источником внешней силы, который
приводит излучающую плоскость в
движение. Для уяснения этого рассмотрим
конкретный случай. Пусть излучающая
плоскость делит пополам пространство,
заполненное упругой средой при
начальном давлении Р0. Если'плоскость
начнёт двигаться с постоянной
скоростью v0, то перед нею образуется
положительное избыточное давление p = wv0f а позади неё —
такое же отрицательное избыточное давление. В
результате на плоскость будет действовать сзади сила S(P0—р)у
а спереди S(P0-{-p) (рис. 63). Так как силы эти
противоположно направлены, то результирующая сила будет
F^2pS,
и, следовательно, работа источника внешней силы будет
равна
t
° ъ
О >
ГГ ^ .и.
р
ч "' >
* р
Рис. 63.
А = [ 2Spv0dt = 25 ^ t.
(23.20)
1С*
148 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Для того чтобы свести энергетический баланс, нужно
принять во внимание, что поле образуется по обе стороны
движущейся плоскости (рис. 64). Общая энергия поля
для обоих полупространств получается путём сложения
двух выражений вида (23.19), различающихся знаком
при р. В результате линейный член выпадет,
квадратичный удвоится, и мы получим:
ДЯ = 2Sct -£-=2S -J t. (23.21)
Тем не менее бесспорно, что в переднем полупространстве
имеется приращение энергии, выражаемое линейной
функцией давления. Теперь,
однако, уже ясно, что
работа, равная этому
линейному приращению
энергии, совершена не
внешней силой,
приводящей излучатель в
Т
1
Пт
г
\г.л , J c ci , j я движение, а силой
давления Р0, действующей
Рис 64. на заднюю сторону
плоскости. В переднем
полупространстве прибывает энергии настолько же,
насколько убывает в заднем.
Продолжая наше рассуждение, допустим, что среда
имеется только в переднем полупространстве, в заднем
же — пустота. Но в таком случае для удержания
излучающей плоскости в исходном положении необходимо
приложить сзади опорную силу, равную Р0 на каждую
единицу площади. Какова бы ни была природа этой силы
(сила пружин, сила тяжести и т. п.) — работа, равная
линейному приращению энергии, будет совершена именно
ею. Разница с предыдущим случаем будет состоять лишь
в том, что выпадет множитель 2 из квадратичных
выражений для энергии и работы. •
Возвращаясь к балансу энергии, составим выраженное
для него в несколько более общем виде, для чего выразим
элемент работы источника через объёмную скорость:
dA=FdZ = S(P0+p)dz = (P0 + p)dQ=:(P0 + p)udt-
§ 231 ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ 149
здесь F — полная сила, действующая на поверхность
источника, S — величина поверхности, £ — нормальное
её смещение, dQ = Sd$ — описываемый при перемещении
объём, и =-г — объёмная скорость. Отбрасывая
квадратичный член, получаем:
A = P0}udt. (23.22)
о
Приравнивая (23.22) и (23.15), получим равенство,
выражающее баланс для линейных составляющих работы и
энергии:
t
P^udt^1 [pdV. (23.23)
о v
Это весьма полезное соотношение может быть выведено
и другим путём, а именно, на основе принципа сохранения
массы. Мы представляем себе действие источника так,
что из него истекает сжимаемая среда в количестве и см3
в одну секунду. Масса, вытекшая за время £, равна
M = 9o\udt (23.24)
о
(если пренебречь малым изменением плотности). Эта масса
должна разместиться в окружающем источник
пространстве, что вызовет, понятно, увеличение плотности против
первоначальной. Обозначая приращение плотности через р,
можем записать:
M=$pdV.
Но при адиабатическом*сжатии и при малых
возмущениях
i-= A- JL
P. Y Л '
и, таким образом, мы можем выразить массу через
избыточное давление:
M=-*l- \pdV. (23.25)
150 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. IT
Приравняв (23.24) и (23.25), получим снова (23.23).
Выражением (23.23) нам ещё предстоит воспользоваться в
дальнейшем. Пока что заметим, что оно полезно, в частности,
тем, что позволяет для оценки линейной составляющей
энергии заменить вычисление объёмного интеграла в
правой части вычислением интеграла по времени в левой
части, что иногда значительно проще.
Так, например, мы сразу можем утверждать, чтоГpdV
может быть отброшен в случае синусоидальных волн на
том основании, что, очевидно, в этом случае [и dt в среднем
равен нулю. И, вообще, Гв dt может представлять собою
J 4
очень малую величину, если в есть знакопеременная
функция времени.
Представляет интерес случай, когда источник
является источником не нулевого порядка, как рассмотренные
выше движущаяся плоскость и «пухнущий» шар, а
высшего порядка. Речь идёт об источниках типа мультиполя.
Возьмём, например, основные шаровые излучатели,
для которых радиальная скорость на поверхности задана
как
yo = t>mP«(cos&)>
где Рл — полином Лежандра порядка пу Ь — полярный
угол (предполагается осевая симметрия). Объёмная
скорость равна, вообще говоря,
ио = Г vo dS.
s
Выберем для данного случая
dS = 2i:a2smbdb= — * Sd{co$b). >
Таким образом
41
u0 = SvmfPn{p)dp.
—i
Но в силу ортогональности полиномов Лежандра этот
интеграл равен нулю для всех п =/= 0 (см. § 20). При п == Q
u0 = Sv0.
$241 ДИФРАКЦИЯ; ОБЩИЕ СООБРАЖЕНИЯ 151
Это — уже рассмотренный нами раздувающийсяшар,
источник нулевого порядка. Для всех же шаровых источников
более высоких порядков объёмная скорость есть
тождественный нуль независимо от характера процесса, а
значит, равен нулю и f p dV. Это объясняется тем, что давление
есть знакопеременная функция пространственной
угловой координаты. Так, например, при п = 1 мы имеем
P(cos &)= cosd, и радиальная скорость, а с нею и давление,
изменяются как на поверхности шара, так и в поле, по
закону косинуса. Давление переходит через нуль и
меняет знак на экваториальной плоскости. Аналогично
обстоит дело и для более высоких порядков
излучателей, причём число нулевых поверхностей равно порядку
излучателя.
Итак, мы видим, что для суждения о применимости
к каждому данному случаю линейных выражений для
энергии и работы нужно знать зависимость скорости или
давления как от времени, так и от координат. Если
соотношения наперёд не ясны, то следует начинать с общих
формул вроде (23.10).
Отметим в заключение, что в тех случаях, когда
энергия и работа могут быть выражены через давление или
скорость линейно, к энергетическим соотношениям
применим принцип наложения. Это значит, что мы можем
найти энергию поля для элементарного возмущения, а
затем вычислить энергию любого более сложного
возмущения (выражаемого не знакопеременными функциями)
посредством простого суммирования.
§ 24. Дифракция; общие соображения
Приступая к рассмотрению проблем дифракции,
постараемся сперва составить себе некоторые общие
качественные представления о картине дифракционных явлений.
Прежде всего установим Лдно важное для
дальнейшего положение.
Предположим, что имеется точечный источник,
определяемый объёмной скоростью
ю = в0ао(0>
152 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
т. е. в некоторый момент, принимаемый за начало
отсчёта времён, из источника в окружающее пространство
начинает истекать сжимаемая среда с объёмной скоростью
п0 см3/сек. В результате действия источника плотность
и давление в окружающем пространстве, начальные
значения которых обозначим через р0 и Р0, получат
приращения соответственно р и р. Граница возмущённой области,
т. е. фронт волны, будет передвигаться со скоростью звука,
и ко времени tx возмущённая область пространства, т. е.
поле, достигнет протяжённости гг == ctx в направлении
распространения, захватив объём Vx. В рассматриваемом
простейшем случае единственного точечного источника Vx
представляет собою объём сферы радиуса rv Применяя
к этой картине формулу (23.23), можем записать:
%(udt = $pdV. (24 1)
О V!
Но равенство это справедливо независимо от того, каково
пространственное распределение давления, и от того,
каков объём Vx. Интеграл в правой части должен сохранять
одно и то же значение при том единственном условии, что
те или иные изменения строения поля не влияют на режим
источника. Поэтому мы можем записать
J>dF = const (24.2)
v,
в том смысле, что этот интеграл, взятый по всему объёму
поля на данный момент, не зависит от строения поля. Под
изменениями строения поля понимаются те изменения,
которые могут возникнуть при нарушении однородности
поля вследствие явлений отражения, преломления, ди
фракции и т. п. *т
Поясним это положение примером. Пусть от точечного
источника О (рис. 65) распространяется шаровая волна,
встречающая на своём пути некоторое препятствие D,
которое мы предполагаем совершенно жёстким и,
следовательно, непроницаемым для волны. Если встреча волны
с препятствием уже состоялась и к рассматриваемому
моменту фронт продвинулся в положение ВВ> то позади
\
§ 243 ДИФРАКЦИЯ; ОБЩИЕ СООБРАЖЕНИЯ 153'
образовалось дифракционное поле, фронт которого,
обозначенный линиейСС, нетрудно построить с помощью
принципа Гюйгенса. Направления распространения для обеих
волн, прямой и дифракционной, нормальны к
соответствующим фронтам и отмечены на рисунке стрелками.
Применяя к рассматриваемому случаю высказанное-
выше положение, мы мсжем утверждать, что fpdV,
который мы взяли бы по
всему объёму,
ограниченному сферичес ким
фронтом BBt при
отсутствии препятствия,
будет равен интегралу,
взятому по тому же
объёму, но за вычетом
части, занятой
препятствием (на рисунке
заштрихована). Иными
словами, при внесении
препятствия уменыне- Рис. 65.
ние объёма поля
компенсируется повышением давления в той части поля, где
образуется дифракционная волна.
Но так как в объёме внутри фронта ВВ и вне фронта СС
поле в обоих случаях (т. е. как при отсутствии, так и при
наличии препятствия) одинаково, то мы приходим к
следующему заключению: fpdV для давления, создаваемога
дифракционной волной в объёме, ограниченном её
фронтом, равен значению (р dV для давления, которое имелось
бы в прямой волне в объёме, занятом препятствием,
если бы препятствие было удалено. Этот вывод может
быть получен аналитически при помощи простых
выкладок.
Обозначим: Vв — объём сферы, ограниченной
фронтом ВВ прямой волны, V с — объём, ограниченный
фронтом СС дифракционной волны (объём области
дифракции или дифракционного поля), Vd — объём,
вырезаемый препятствием D из сферы ВВ (заштрихованная
часть на рис. 65); кроме того, обозначим через р давление
0
154 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
{избыточное) в прямой волне, а через рд—давление
в дифракционной волне.
Основываясь на нашем положении, выраженном
формулой (24.2), мы можем составить равенство, в левой
части которого мы запишем значение Г/? dV для свободного
поля, т. е. при отсутствии препятствия, а в правой части —
значение \р dV для поля, искажённого наличием
препятствия:
fPdv= j- Pdv+ ; (p+pjdv,
s-vc
или
или
fpdV = f(p + pd)dV,
vc
$PddV=$pdV, (24.3)
VC~~VD VD
в чём и состоит аналитическая формулировка нашего
утверждения.
Хотя положение (24.2) и его следствие (24.3) не дают
возможности решать дифракционные задачи, они могут
всё же послужить для дальнейшего развития
качественных представлений.
Мы можем теперь утверждать вообще, что если в поле
образовалась по тем или иным причинам зона с давлением,
повышенным против давления в свободно
распространяющейся волне, то обязательно должна образоваться также
и зона с пониженным давлением. Если обозначить
давление в первой зоне через р-\-рх, а во второй — через р — р2,
и если объёмы зон обозначены соответственно через Vx
и F2, то должно быть
fPldV=~fp%dV. (24.4)
vt v2
Если начальные давления в обеих упомянутых зонах
неодинаковы, то, обозначив их через pi и рц, можем
записать (24.4) в более общем виде:
S (ft + Pi) dV=$ (ft, -ft,) dV. (24.5)
v, v,
§ 24]
ДИФРАКЦИЯ; ОБЩИЕ СООБРАЖЕНИЯ
155
Соотношения (24.4) и (24.5) также являются следствиями
(24.3). В некоторых случаях зоны 1 и 2 и распределения
давлений в них симметричны. Тогда, во-первых, рг =
— Р2 = Рд> а> во-вторых, мы можем применить (24.5) к любой
паре симметрично расположенных элементов объёма, что
после сокращения на dV даёт:
Pi + Pd^Pn-Pd-
(24.6)
Под рд подразумевается давление дифракционной волны.
Эти симметричные случаи удобно трактовать как
результат одновременного наличия источника и равного ему
но напряжённости стока (или минус-источника).
Поясним это на
примере. Пусть
плоская волна ВВ
распространяется
параллельно плоскому
жёсткому экрану, в
котором проделано
маленькое отверстие
О (рис. 66). Тогда по
ту сторону экрана
образуется шаровая
дифракционная
волна с фронтом СС и
центром в О. По
предыдущему
необходимо, чтобы по эту сторону экрана произошло
соответствующее понижение давления, что можно представить,
как результат появления в О отрицательного источника
такой же напряжённости.
Таким образом, отверстие О является источником для
нижнего полупространства и стоком для верхнего. Но
этого мало: если проследить развитие явления с момента
прихода фронта к отверстию О, то станет очевидным, что
равенство (24.5) нужно применять для любого момента
к одинаковым объёмам по обе стороны экрана
(пунктирные линии на рис. 66) и чтр не только фронты СС и DD
расположены совершенно симметрично, но и
распределение давлений внутри обеих дифракционных областей
Рис. 66.
156 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
также симметрично. Это, в общем совершенно очевидное,
положение мы оставляем без формального доказательства.
Сказанное справедливо и в более общем случае. Пусть
плоская волна, распространяющаяся слева направо,
встречает плоский жёсткий экран с отверстием произвольной
формы и произвольных размеров (рис. 67). Справа от
экрана образуется «проходящая» »дифракционная волна,
а слева, во-первых, плоский фронт отражённой волны
и, во-вторых, отражённая дифракционная
волна, совершенно симметричная
проходящей.
Интересно, что эти представления
выдерживают предельный переход вплоть до
полного устранения экрана.
Положим, что давление падающей
волны равно единице. Будем неограни-
И- ченно увеличивать отверстие в экране,
пока он не исчезнет вовсе. От такого
предельного перехода у нас останутся:
1) прямая волна с давлением=1; 2)
отражённая волна с давлением =1; 3)
отражённая дифракционная волна с
давлением = — 1; 4) проходящая дифракционная
волна с давлением = 1.
Первые три слагаемых относятся к
полупространству перед экраном и дают в
сумме единицу; то же значение получается
и позади экрана, точнее — позади той
плоскости, где он был. Итак, мы получаем правильную
картину беспрепятственно распространяющейся плоской
волны.
Нам пригодится ещё представление о перегибе поля,
упомянутое в § 3, и помогающее выяснить строение поля
при отражении. Речь идёт о том, что если на чертеже
изобразить распределение давления в поле, а затем
изобразить поле, изменённое вследствие внесения в него
жёсткого неограниченного экрана, то второй чертёж
получается из первого путём перегибания его по линии
расположения экрана. При этом давления в совмещаемых при
перегибе точках чертежа складываются.
FT4
Ь4>
§ 24] ДИФРАКЦИЯ; ОБЩИЕ СООБРАЖЕНИЯ 157
/
О
г
г
Рис. 68.
Несколько примеров такого построения показаны на
рисунках 68, 69, 70 и 71. На этих рисунках буквой а
обозначена картина поля до внесения экрана, а буквой б —
после внесения экрана,
положение которого от- | I
мечено на рисунках
пунктирной прямой.
Если речь идёт о
плоской задаче, то плоскость
перегибается
относительно линии; для
пространственной задачи можно
говорить о перегибе
объёма относительно
плоскости. Так, например,
рис. 70 можно
толковать либо как
изображение плоского поля, либо как проекцию поля
сферической волны, встречающей плоский экран.
Пусть в экране
имеется отверстие,
около ^которого
возникает
дифракционная картина. Еслиэто
отверстие закрыть
экраном, который,
таким образом,
делается
неограниченным, то мы должны
получить простое
отражение:
С точки зрения
перегиба поля это
означает, что
совмещение полей
проходящей и отражённой
дифракционных волн должно давать в сумме поле
простой отражённой волны. Это соображение,
иллюстрируемое рис. 71, может быть выведено непосредственно
из (24.4).
f\(fi
I/
j/
158 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Мы предполагаем, что в поле, т. е. внутри области,
ограниченной фронтом, давление меняется непрерывно.
Если так, то при перегибе поля давление по линии пере-
Рис. 70.
гиба удваивается (т. е. давление удваивается в результате
отражения на самой поверхности жёсткого экрана). Но
в таком случае при «разгибании» поля, что соответствует
г h
Рис. 71.
г
г
6
полному или частичному устранению экрана, давленге
по линии разгиба должно уменьшиться вдвое.
Это последнее соображение поможет нам существенно
упростить формулировку граничных условий
дифракционной задачи, решаемой в следующем параграфе.
§ 25) ДИФРАКЦИЯ ОТ ПРЯМОЛИНЕЙНОГО КРАЯ 159
§ 25. Дифракция от прямолинейного края
Решим для неустановившегося режима классическую
задачу о дифракции от прямолинейного края. Постановка
задачи такова: плоская волна встречается с плоским
жёстким бесконечно тонким полубезграничным экраном,
прямолинейный край которого параллелен фронту волны.
Задача эта является плоской. Угол встречи, то-есть угол
между направлением распространения и направлением
плоского экрана, произволен. Однако мы приведём сперва
решение задачи для двух частных случаев: для случая
скольжения волны параллельно экрану и для случая
нормального падения, после чего переход к общему случаю
не составит затруднений.
а) Случай скольжения волны параллельно экрану
Общая картина явления на плоскости,
перпендикулярной краю, показана на рис. 72. Фронт единичной
волны, распространяющейся
справа налево, уже миновал
край О' экрана, след которого
на плоскости чертежа
обозначен двойной линией.
Дифракционное поле развивается в
цилиндре г <; ct, если время
отсчитывается от момента
прихода фронта волны на край
экрана. Потенциал перед
фронтом (то-есть там, куда волна
ещё не пришла) везде равен
нулю. Позади фронта плоской
волны потенциал равен
единице. Потенциал внутри
круга дифракции неизвестен; задача и состоит в его
нахождении.
Задача сводится к разысканию решения волнового-
уравнения
О
J uk (УЖ\д
Рис. 72.
*2 dt*
да*
-О,
(25.1)
160 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. 1Г
удовлетворяющего граничным условиям. Заметим
прежде всего, что в силу особенностей нашей задачи
речь идёт об однородном решении волнового
уравнения. Вследствие этого, вводя новый безразмерный
аргумент z — Д —\ мы можем свести волновое уравнение
к уравнению Лапласа. С физической точки зрения эт©
означает, что картина рис. 72 с течением времени
увеличивается в линейных размерах пропорционально времени,
т. е. сохраняя подобие самой себе.. Граничные условия
остаются при этом неизменными. В рассматриваемом
случае они таковы:
1) <р=0 на верхней полуокружности; 2) <р—1 на нижней
полуокружности; 3) ~-= 0 на обоих берегах разреза по
линии экрана.
Мы имеем, таким образом, задачу смешанного типа
(граничные условия выражены как через потенциал, так
и через его нормальную производную), осложнённую
наличием разреза. Конечно, и в таком виде задача может
решаться обычными методами теории функций
комплексной переменной. Однако мы предпримем упрощение
постановки задачи, после чего будем решать её элементарными
^средствами.
На основании рассуждений предыдущего параграфа
мы можем утверждать, во-первых, что потенциал на ра-
1
даусе О' А' равен у, а, во-вторых, что если потенциал в
любой точке верхнего полукруга обозначен через <р, т©
для симметрично расположенной точки нижнего
полукруга потенциал должен быть равен 1 — <р. Первое
утверждение вытекает из понятия jo «разгибании» поля.
Действительно, если бы экран иьт неограничен, то
потенциал на О'А' был бы равен единице. Если же экран на
этом участке устранить (что соответствует «разгибанию»),
то потенциал должен уменьшиться вдвое, т. е. измениться
до значения 7)-. Что касается второго утверждения, то он©
.непосредственно следует из формулы (24.6).
§ 251 ДИФРАКЦИЯ ОТ ПРЯМОЛИНЕЙНОГО КРАЯ 161
В результате постановка задачи существенно
упрощается: мы должны искать решение волнового уравнения
для полукруга при следующих граничных условиях (для
верхнего полукруга): а) <р = О — на полуокружности;
Ь) <р = 2 — на радиусе 0'А'\ с) ~- = 0 — на радиусе О'А.
Преобразуем теперь уравнение (25.1). В
рассматриваемом случае очень удобно заменить переменную по
формуле
chz-=-y-, (25.2)
что приводит (25.1) к уравнению Лапласа в декартовых
координатах:
Граничные условия на основании (25.2) принимают
вид:
a) й(0, а)=0 [0<а<тс],
b) ф(*, я) = -*-,
c) фа(2, 0)=0.
Решением уравнения (25.3) может быть, как известно,
произведение тригонометрической функции одного
аргумента на экспоненциальную функцию другого.
Мы будем искать решение в виде ряда
ф(г, a)=^ + ^amcosmaeTmz. (25.4)
т
Сумма по косинусам выбрана для того, чтобы
удовлетворить условию (с). Далее по условиям задачи
( 0 [0<a<ic],
а из (25.4) имеем:
4»(0, а) = ^ +>? «mcosта,
т
11 А. А, Харкевич
162 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ 1ГЛ. II
так что
?+2л
cos та
-{
0 [0<a<ic],
1 [тг<а<2тг].
Для того чтобы получить разложение этой функции
по косинусам, добавим чётное продолжение этой функции
-2я -Я
л
Рис. 73.
гл
а
ь области отрицательных а (рис. 73), а для того чтобы
удовлетворить условию Ь), разложим правую часть в ряд
Фурье по половинным углам. Мы получим: й
4Ч0>«)=т+2а«СО8та===
t 2 ~ cos^-l)-
2 я 2d^ (.
ft=l
If"1 (2Л — 1)
(25.5)
т. е.
т-
2к—1
A-zll
Подставляя эти значения в (25.4), находим:
<|> (z, а) =
1.
/ , оо cos (2ft — ^ | е - —2~
*-4 (2Ar — 1)
[0<а<тг]. (25.6)
Подобранная таким образом функция удовлетворяет
как уравнению (25.3), так и граничным условиям а), Ь)
и с), и даёт, стало быть, решение задачи для верхнего
полукруга. Для нижнего полукруга, т. е. при[—■ тг<^а<С0].
§ 25] ДИФРЛ.КЦИЯ ОТ ПРЯМОЛИНЕЙНОГО КРАЯ 163
нужно вычесть (25.6) из единицы. Не останавливаясь на
формуле (25.6), приведом решение к конечной форме.
Для этого представим ряд из (25.6) в следующем виде:
„ _ ?*zi h
, °о Cos (2A —\)\е 2 , Т {~*+>а)
Av_—J1 =lRey^i^l- «
*^ (— l)fe-1 (2Л — 1) « ^-^ (— l)^^1 (2Л — 1)
=4Re(^-£F+^----)=^Re(arctg^
где обозначено
s = -2 ( —z-f/a).
Далее
arctg (а + /6) - \ (arctg {_%_р + / Arth 1 + f2 + &2).
У нас
z г
а = е 2cos-^; Ъ — е 2 sin-«г-
и, стало быть,
2
TRe(arctge-) =7 arctg {_g_z =- arctg (/ ^-j—, ,
или, переходя к первоначальному аргументу,
?(r, a) = i/lrp4arctgl/ -Lp"- = |. (25.7)
/1 4- cos a
^Т7
Знаки (—) и (-[-) относятся, соответственно, к верхнему
и нижнему полукругам. Формула (25.7) даёт
окончательное решение задачи.
Эквипотенциальные линии, построенные на основании
вычислений по формуле (25.7), изображены на рис. 74.
11*
164 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
б) Случай нормального падения
Волновая картина показана на рис. 75. Единичная
плоская волна приходит снизу. Слева вверху — фронт
проходящей плоской волны. Справа внизу — фронт
полностью отражённой от эк-
£--— ^ д рана волны,
распространяющейся в обратном
направлении. Перед
фронтом прямой волны ф=0,
ГТТ
Рис. 74.
Рис. 75.
позади фронта прямой волны 9 = 1> позади фронта
отражённой волны 9—2. При помощи «разгибания»
устанавливаем, что па О'А' <р = 1. На О'А попрежнему
-~- = 0. Дифракционное явление развивается в круге»
r<^ct, причём граничные условия на окружности r—ct
для верхнего полукруга таковы:
<?(ct, a) = {
(0 [0<в<^],
1 [у<я<4
Как и раньше, перейдём к функции^ (z, а). Граничные
условия задачи имеют вид:
( 0 [0<а<£|, Ь) ф(г,«) = 1;
( 1 Ц<а<я]; c)^(z,0) = 0.
N
§ 2Ь]
ДИФРАКЦИЯ ОТ ПРЯМОЛИНЕЙНОГО КРАЯ
165
Будем попрежнему искать решение в виде (25.4). На этот
раз, чтобы удовлетворить условиям задачи, возьмём
чётно-продолженную функцию
I о [о<«<|].
<К0,а) = <| 1 [|<а<|я],
( 2 [|тг<а<2П]
(рис. 76). Разложение этой функции по косинусам
половинных углов имеет вид
а
♦(0,^1-^2
2^Г£, 003(2*-!)^
"* 2к — 1 '
где
Таким образом,
^ = 1, 1,-1,-1, 1,
2V2 £ <">8(2*-1)т *-^2
= 1_ ilLy^ _*_ -[0<a<ic].. (25.8)
2к- 1
Эта формула даёт решение задачи для верхнего
полукруга в форме бесконечного ряда. И это выражение можно
2\
привести к конечной форме, однако на этот раз нам нужно
подобрать функцию, представляемую рядом
т? / ч , Ж3 ХЪ X1 , X9 ,
166 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Здесь придётся воспользоваться цикличностью ряда по
степеням yj. Мы получим:
F (х) = -^-(arctg yjx — arctg/ /jx).
Подставляя
x — e<
4 (-2+Уа)
проделывая все выкладки и возвращаясь к
первоначальному аргументу, получим решение задачи в следующей
окончательной форме:
2 cos
ср(г, а) = 1 =н - arctg -
IK?3
i-1
г
(25.9)
На рис. 77 изображены эквипотенциальные линии для
рассмотренного случая.
в) Общий случай
В общем случае
нашей задачи плоская
волна падает на экран
под произвольным
углом. На рис. 78
изображена картина явления.
Плоскость экрана
составляет с напрагше-
нием распространения
угол д. Слева — фронт
проходящей снизу
прямой волны. Такой же
фронт имеется и
справа — там, где прямая волна ещё не дошла до экрана
(правее точки А). Левее точки А образовался уже фронт
отражённой волны.
Граничные условия Ь) и с) остаются для^ общего
случая те же, что и для предыдущего частного случая, если
Рис. 77.
§ 26] НЕКОТОРЫЕ ЗАДАЧИ ИЗЛУЧЕНИЯ 167
отсчитывать переменный угол а попрежнему от плоскости
экрана. Что же касается условия а), то для него мы имеем
^ , 0 [0<а<&],
<Р (ct.
'.«) = { 1
[9<а<к].
Выбирая для 0» (0, а) функцию
f 0 [0<а<«],
Ф(0.«)Н 1 [Ь<а<2г.-Ь],
J 1 [Ъ<а<2г.-Ъ],
\ 2 [2тг —»<а<2-]
и действуя аналогично предыдущему, получим решение:
_ 2fc-l x
, °° sin (2ft - 1) 4 cos (2ft - 1)4 e 2
♦(.. «)=i-|2 2ft-i
ft=l
[0<a<w]. (25.10)
В частном случае нормального падения $==?у и (25.10) пере-
Рис. 78.
ходит в (25.8). При скольжении волны параллельно экрану
Ь~тс, и мы получим (25.6). При помощи вышеописанных
приёмов можно представить (25.10) в конечной форме.
§ 26. Некоторые задачи излучения
Задача излучения состоит обычно в нахождении поля
некоторого источника. Обычный приём решения этой
задачи состоит в том, что поверхность излучателя разбивают
168 ТКОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
на бесконечно малые элементы, каждый из которых
рассматривается как точечный источник. Составляют
дифференциальное выражение для потенциала, наводимого
каждым элементом dS в точке наблюдения А,
** = 2^Я '
где R — расстояние от dS до A, vn(t) — нормальная
скорость элемента dS (множитель 2 тг предполагает, что
излучение происходят в полупространство); затем интегрируют
это выражение по зеей поверхности излучателя.
-Однако эта процедура применима безоговорочно лишь
в том случае, когда между любой точкой поля и любым
элементарным источником может быть проведена прямая,
не пересекающая ни излучателя, ни каких-либо
препятствий. Этот случай хотя и имеет значение, но является
всего лишь частным, и притом простейшим. Во всех
остальных случаях мы имеем дело с дифракцией. Это, правда,
не всегда очевидно. Например, излучение раздувающегося
шара в силу центральной симметрии находится
элементарно. Излучение шаровых антенн более высоких
порядков определяется, как мы видели в § 20, одним общим
приёмом без всякого упоминания о дифракции. Тем не менее все
эти задачи по существу дифракционные, и это становится
совершенно ясным именно тогда, когда мы пытаемся
вычислить поле шаровой антенны путём суммирования полей
отдельных элементов её поверхности. К вопросу о
дифракции от шара мы вернёмся в следующем параграфе, а пока
займёмся рассмотрением некоторых задач, решение
которых облегчается материалом предшествующих параграфов.
Именно, мы рассмотрим вопрос об излучении
полуплоскости.
Пусть ограниченная прямой полуплоскость движется
сверху вниз (рис. 79) со скоростью
Это равносильно тому, как если бы нижняя сторона
полуплоскости внезапно покрылась равномерно распределён-
/
%
§26] НЕКОТОРЫЕ ЗАДАЧИ ИЗЛУЧЕНИЯ 169
ными положительными источниками, а верхняя —
отрицательными. Вниз излучается положительная
единичная волна, вверх —
отрицательная. Но
излучение источников одной
стороны попадает на другую
сторону только в
результате дифракции. Область
дифракции заключена в
цилиндре r<^ct, ось
которого совпадает с краем
полуплоскости.
Расставив на чертеже
значения давления, мы убеждаемся, что граничные
условия задачи таковы:,
-p(ct, а):
-1 [о<«<£|,
0 Ц<*<Н,
1 [|*<a<2TCj.
Кроме того, на О'А' давление равно нулю — это следует
просто из условий симметрии. И, наконец, нормальная
скорость на О'А равна заданной величине v. Последнее
условие на основании общей зависимости между
давлением и скоростью может быть записано в следующем виде:
где п — нормаль к плоскости. Но так как
v = v0oQ(t),
то
т. е. мы имеем только начальный импульс (при t =■ 0);
в дальнейшем — = 0.
170 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ 1ГЛ. II
Сопоставляя выясненные нами граничные условия
с*теми, которые относятся к задаче о дифракции
относительно полубезграничного экрана при нормальном
падении (см. § 25 и рис. 77), мы убеждаемся, что обе системы
граничных условий различаются только постоянным
слагаемым, равным единице. Но если так, то и решения обеих
задач различаются на то же слагаемое, так как ясно, что
«функция, удовлетворяющая уравнению Лапласа или
волновому уравнению, не перестанет быть решением этих
уравнений после прибавления к ней любой постоянной
величины.
На основании этих соображений мы можем
воспользоваться формулой (25.9) и сразу выписать решение
рассматриваемой задачи:
1 2 V ~г
p(r,a)^ + wvQ- arctg — (26.1)
1 — cos a
и построить картину изобар (рис. 80), которая отличается
от рис. 77 также постоянным слагаемым, равным единице.
Предыдущий случай сводится к действию источников
разных знаков на обеих сторонах полуплоскости. В
качестве следующей задачи разберём случай, когда обе
стороны полуплоскости покрываются источниками одного^
знака, например положительными. С точки зрения
движения плоскости нужно представить себе плоскость со-
,#
§261 НЕКОТОРЫЕ ЗАДАЧИ ИЗЛУЧЕНИЯ 171
стоящей из двух слоев, движущихся с заданной скоростью
в противоположные стороны. Иначе говоря, слои
раздвигаются, или, попросту, плоскость утолщается,
«пухнет», оставаясь в среднем на месте. Это — плоская
аналогия «пухнущего» шара.
Как вверх, так и вниз излучаются положительные
единичные волны (рис. 81). Условия на О1 А остаются
прежними Что касается ОгА'} то мы ничего не можем
сказать о давлении,
которое там полу- "^
чается, но зато из
полной симметрии
картины
распределения давлений мы
заключаем, что на •
О'А* должно быть у
дп
-0.
Это — очень важный
вывод. Ведь если Рис. 82.
так, то мы не изменим
положения, поместив в О'А' жёсткий экран. А после этого
становится ясным, что задача не принадлежит к числу
дифракционных — это элементарная задача излучения
в полупространство, которую мы сейчас и решим обычным
методом. Вычисление во всём сходно с тем, которое было
проделано в § 16 в связи с вопросом о ближнем поле
круговой антенны. Разница сводится к пределам
интегрирования. Вспомогательное построение изображено на рис. 82.
Мы имеем:
du
dp =р0-
где
Но
о-*)
ди
da = vdS,
v =v0o0(t),
172 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ.-II
и, стало быть,
Выберем элемент площади в виде
dS = adad$ = RdRd§
(рис. 82) и обозначим
с
Тогда давление в точке наблюдения выразится
интегралом
s
со
Г
€
Для р0из рис. 82 находим:
г
os a
ро (т) = arccos
- >
sin2 а
и, таким образом, решение нашей задачи имеет вид:
wvQ — cos a ^ /na ov
р = —- arccos_/-,,, =г- . ^ (26.2)
У(т-;-—
Изобары для рассмотренной задачи изображены на рис. 83*
Мы учли при построении, что в том случае, когда
проекция точки наблюдения лежит на излучающей
полуплоскости, в формуле (26.2) изменяется знак аргумента агсссЯ?.
Рассмотрим ещё одну задачу. Пусть требуется найти
поле, создаваемое полуплоскостью, которая покрывается
источниками только с одной стороны. При ^решении этой
задачи можно воспользоваться тем обстоятельством, что
§ 261 НЕКОТОРЫЕ ЗАДАЧИ ИЗЛУЧЕНИЯ 173
вышерассмотренные задачи не только линейны, но
корректно поставлены, т. е. решения непрерывным
образом зависят от граничных условий. Поэтому искомое
решение можно построить путём наложения решений двух
предыдущих задач. Аналитически решение выразится
полусуммой (26.1) и (26.2). Соответствующая картина
изобар показана на рис. 84.
Займёмся теперь одним специальным вопросом,
связанным с предыдущим, а именно, вопросом о реакции на
излучающую полуплоскость. Дело в том, что благодаря
дифракционному явлению, развивгюцемуся у края
полуплоскости, давление в пределах прилегающей к краю
полосы шириною ct оказывается меньше, чем если бы
такая полоса принадлежала бесконечной плоскости,
движущейся с такой же нормальной скоростью. Давление
в пределах указанной полосы зависит, конечно, от
координаты на плоскости. Соответствующие формулы легко
получить из (26.1) и (26.2), положив в них а — 0. Мы
вычислим полную силу, действующую на полосу шириною ct
и длиною, равной единице, для всех трёх рассмотренных
случаев, схематически изображённых на рис. 85. Мерой
сравнения послужит сила, действующая на такую же
площадку бесконечной плоскости. Эту величину легко
определить; она равна
F0 = 2pS = 2wv^ ct.
174 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ: I1
Множитель 2 учитывает то обстоятельство, что при
движении плоскости перед ней образуется сжатие, а позади
неё — такое же по абсолютной величине разрежение.
Для случая рис. 85,а мы имеем из (26.2) следующее
выражение для распределения давления в пределах
интересующей нас полосы:
/, = _j.arccos(-7rJ.
,++ + + + + + 4-4»
+ 4- + + + + + + +
+++++++++
Интегрируя, найдём величину
силы:
Я J \ CI J
1 •
+++++++++ J в к_1
2wvoct = 0fi8FQ.
Рис. 85.
Для случая рис. 85, б, полагая
а = О в формуле (26.1), получим для давления:
у±.
Г
и для силы:
ct
р = J^l [ arccos (l - 2^ )dr = wvQ ct = 0,5 F0.
о
Наконец, в случае рис. 85, в на одну сторону
полуплоскости действует давление
^1 = ^[агссоз(-^)+агсао8(1-2^)],
а на другую сторону
A = ^[areco.(-^)-.rcco.(l-2f)].
§ 27] ПРЕОБРАЗОВАНИЕ ОБЛАСТИ ДИФРАКЦИИ 17*
Разность давлений
И»0 { А О Г \
ft - Л = -^" ^rcc°s {} - 2-^-)
и обусловленная этой разностью сила
^=|^0^ = 0,25F0.
§ 27. Преобразование области дифракции
Как мы видели, элементарная задача излучения, т. е.
задача нахождения поля некоторого источника, решается
весьма просто; решение может быть записано сразу в форме
интеграла
S
где ул— нормальная скорость элемента поверхности dS>
R — расстояние от dS до точки наблюдения A, Q—те-
лесный угол, в который излучает каждый элемент dS.
Однако эта формула применима только в тех случаях,
когда любой радиус-вектор /?, проведённый из rf5 в i, не
пересекает ни источника, ни каких-либо препятствий,
иначе говоря, когда точка А видна из любой точки
поверхности источника. Если это условие но выполнено —
задача относится к числу дифракционных, и формула
(27.1) неприменима.
Можно предложить особый метод решения
дифракционных задач, общая идея которого состоит в таком
преобразовании цоля, чтобы условие «прямой видимости»
было выполнено, после чего дифракционная задача
сводится к элементарной задаче излучения. Под
преобразованием поля подразумевается некоторая деформация его.
Очевидно, лто преобразование должно быть
инвариантным по отношению к волновому уравнению. С
аналитической точки зрения преобразование состоит в переходе
к новым координатам в волновом уравнении. После тога
как получено решение задачи в новых координатах»
176 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
искомое решение в первоначальных координатах
получается при помощи применённых формул преобразования
координат.
Итак, процедура решения дифракционной задачи при
помощи этого метода состоит из следующих операций:
а) Прежде всего формулируем данную
дифракционную задачу и устанавливаем её граничные условия.
б) Затем ставим вспомогательную задачу, выбирая
подходящим образом деформированную вместе со своими
границами область дифракции. При этом, во-первых,
необходимо, чтобы во вспомогательной задаче выполнялось
условие прямой видимости, а, во-вторых, желательно,
чтобы условия на преобразованных границах
сохранились.
в) Решаем вспомогательную задачу по формуле (27.1).
г) Находим формулы инвариантного преобразования
координат для перехода от основной задачи к
вспомогательной.
д) При помощи формул преобразования получаем из
решения вспомогательной задачи решение основной
дифракционной задачи.
Покажем применение метода на примере,
заимствованном из материала предыдущих параграфов.
Положим, что мы желаем решить задачу о дифракции
плоской единичной волны от края экрана для случая
скольжения волны параллельно экрану Картина
явления для этого случая была изображена на рис. 72.
Преобразуем эту картину следующим образом: сожмём
круг в полукруг путём уменьшения всех углов вдвое.
При этом радиус О'А останется на месте, радиус О'А'
повернётся на 90° по часовой стрелке, фронт плоской
волны — тоже, радиус, соответствующий нижнему
берегу разреза О А, повернётся на 180° в ту же сторону и
займёт положение О'А". Преобразованная таким образом
картина показана на рис. 86. Граничные условия
вспомогательной задачи таковы: ср — 0 на дуге АА!, ср=1
на дуге А'А", -^=0 на обоих радиусах О'А и О'А".
Но эта картина есть не что иное, как картина поля,
получающегося при излучении полуплоскостью слева
I 271 ПРЕОБРАЗОВАНИЕ ОБЛАСТИ ДИФРАКЦИИ 177
от О'. Это поле находится элементарным образом, и
соответствующая задача уже решена в предыдущем параграфе.
Решение выражается формулой (26.2), которую можно
относить как к давлению, так и к потенциалу, так как
обе величины удовлетворяют одному и тому же волновому
уравнению. Поэтому решение вспомогательной задачи,
отвечающей рис. 86, мы можем записать в виде
1 л -— cos p /ПГ7 оч
<р = — arccos , (27.2)
Одна из формул преобразования координат очевидна;
она имеет вид
а = 2р. (27.3)
Остаётся найти формулу преобразования радиусов.
Для этого воспользуемся преобразованием (25.2)
ch z = —,
приводящим волновое уравнение в полярных
координатах (г, а) к уравнению Лапласа (25.3):
дъг ' да2
Мы можем, не изменив этого уравнения, умножить
оба аргумента на одно и то же число. Возьмём
z = 2у,
где
ct
и Р
12 А. А. Харкевич
178 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Таким образом,
chz = ch22/==2ch22/-l,
откуда и получается искомая формула преобразования
радиусов
4 = 2(^у_1. (27.4)
Заменяя теперь в формуле (27.2) р на г и р на а при
помощи (27.3) и (27.4), получим решение нашей
дифракционной задачи
ср(г,а)==— arccos / — Г 1 + ccsа \ л
Переходя от arccos к arctg, можно представить этот
результат в форме (25.7).
Описанный метод может, повидимому, сильно
упростить решение ряда дифракционных Задач. Успех его
применения зависит от удачного выбора преобразования.
§ 28. Дифракция от тара
Классический метод решения задачи о дифракции от
шара сводит дифракционную задачу к задаче излучения
шаровой антенны с соответствующим распределением
радиальной скорости на поверхности шара.
Основная мысль очень проста и сводится к
следующему: если в волновое поле помещён твёрдый шар, то
нормальная скорость на его поверхности равна, очевидно,
нулю. Между тем, если бы шар отсутствовал, то на
сферической поверхности, отмечающей место шара,
существовало бы такое распределение скорости, какое получается
в свободном поле. Следовательно, можно представить
себе поле, получающееся при наличии твёрдого шара,
как результат наложения свободного поля и поля,
создаваемого излучающим шаром, нормальная скорость
каждого элемента поверхности которого равна по величине
и противоположна по направлению нормальной скорости
в той же точке свободного поля. Действительно, при
§28) ДИФРАКЦИЯ ОТ ШАРА 179
соблюдении этого условия результирующая нормальная
скорость на поверхности шара будет равна нулю, в чём
и состоит граничное условие задачи.
Приведём основанные на этих соображениях выкладки.
Решение волнового уравнения для шаровой волны
представляется в форме ряда по сферическим функциям.
При наличии осевой симметрии для любой компоненты
расходящейся волны мы можем записать;
т.-вЛмЧ1-'.^)' (281)
|-«AW^P.^). (28-2)
Пусть задана нормальная скорость va на поверхности
антенны. Разложим и эту величину в ряд по полиномам
Лежандра:
va = v0 + v1 + v%+ ... + vn+... (28.3)
В таком случае
I - —
=«»p,>)V-F»(Hr)>
°» = St
r=a
и мы можем выразить компоненту потенциала через
соответствующую компоненту скорости:
Полное значение дифракционного потенциала выразится
суммой
12*
180 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Теперь займёмся компонентами скорости.
Будем рассматривать дифракцию единичной плоской
волны. Для потенциала такой волны имеем:
ср = е с =^е с =е ^ , (28.6)
где х — координата в направлении распространения,
совпадающая с направлением О = 0. Радиальная скорость
в свободном поле равна
— до у. -rP—V-
а на поверхности шара
а
Эту величину нужно разложить в ряд по полиномам Ле-
жандра:
vM = bp0(u + b1P1{v) + ... + bJP,(ri + --- (28.7)
Должно быть
приравнивая почленно ряды (28.3) и (28.7), получаем:
и для потенциала
г~а со f (рЛ\
Ъ=^~Ъ -6.-Ц4 P.W. (28.8)
Коэффициенты 6rt определяются по формуле:
2го + 1
"l
6Я=^Р$ * (rtP»«*i*=
+i
-^^«"^ЧМ^ (28.9)
2 с
-1
§ 28]
ДИФРАКЦИЯ ОТ ШЛРА
181
Вычисление даёт:
- »• - 7" К» 7Г'**" 7 - (*• I)'*811 »> т] •
-».-8*[-(»тГ*»:+Кр7Гл»г-
~2(l>-|)_38hi>|], j>(28. 10)
-ba = 57[(^7)_lch^7-4(^7r2sh^7 +
+ 9 (* 7)~3ch^ 7 ~ 9 (* £ Г*** т] '
и хтак далее.
Можно дать общую формулу для Ьп> выражая эту
величину при помощи полиномов Лежандра, бесселевых
функций (порядок которых равен целому числу с
половиной) или полиномов Стокса. Так, например, можно
записать
-Ъ =
-(-Цчфт-Х'П-
Следует признать, что неуклюжая формула (28.8) хотя
и даёт полное решение поставленной задачи о дифракции
плоской волны от. твёрдого шара, но не только не
позволяет делать какие-либо общие заключения, но и
непригодна для вычислений. Для нахождения оригинала
практически возможно прибегнуть к численным
методам построения оригинала по известному изображению.
Впрочем, и это потребует большой вычислительной
работы.
К сожалению, решение рассматриваемой задачи в
конечной форме ещё неизвестно. Между тем можно
ожидать, что решение это будет иметь крайне простой вид.
Это предположение основывается, во-первых, на всём
предыдущем материале, из которого явствует, что решения
всех без исключения нестационарных задач имеют чрез-
182 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
вычайно простую аналитическую форму. Во-вторых, это
предположение подкрепляется рассмотрением некоторых
доступных нам простейших аспектов проблемы дифракции
от шара, к чему мы сейчас и перейдём.
Прежде всего вычислим среднее давление,
обусловленное дифракцией, на поверхность твёрдого шара,
помещённого в поле
единичной плоской волны р =
= <70(£ ). Эта
величина выразится, как
8
Выберем
rfS = 2na2sin&dft =
= —2ъаН}х.
Тогда
+1
/
1,0
к
*Лф
Реев
^Р
i
и о v^-*
I I Г
L
:
?
[т\
Я=Щ
Рис. 87.
Рд
ср
С рд dj*.
—1
Пользуясь формулой (28.8), найдём:
а £ . Ч*
» ср
п=0
{'т)1 '
(p)dp.
Но в силу ортогональности полиномов Лежандра все
члены этой суммы обращаются в нуль, кроме члена
нулевого порядка, так что
Рдср= -аЬо
1 + р —
с
1 а 1 . а
chP7 ashPj
*+*— \ * с
Эта формула выражает среднее давление,
обусловленное только дифракционным полем. Если мы хотим найти
полное среднее давление, то мы должны добавить ещё
§ 281 ДИФРАКЦИЯ ОТ ШАРА 183
среднее давление падающей на шар единичной волны.
Для этой величины имеем:
+1 , а
snp —
о J
Полное среднее давление равно
_ _ _ chp — shp — i* с
1 + р- [ i + p-jp- 1+р-
Это — та же самая формула, которую мы получили ранее
(§ 13), исходя из простых и общих соотношений,
основанных на теореме взаимности. Переходя в предыдущих
формулах к оригиналам, найдём закон изменения
средних давлений во времени:
/>.cp = T{[2(l~«-(('+1))-(^ + l)]ao(^ + l) +
+(*i-lK('i-l)}.
J»ocp=j[('i + l)».('i + l)-('i-l)ae(*i-l)].
/>cP = Pacp + ^cP = (1-«~l(l+1))°o(«i + l),
Ct
где Jj ==—. Графики этих функций построены на рис. 87,
Сходным образом можно вычислить силу,
действующую на шар в направлении распространения плоской
волны; эта сила стремится сообщить шару поступательное
движение. Элемент силы (речь идёт о проекции на ось х)
dFx = — pdS cos ft db = 2rfo2p sin » cos bdi\ = 2ъа2рр dji.
В этой формуле также под р понимается полное давление,
т. е. сумма давления падающей плоской волны и дифрак-
184 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
ционного давления. Мы вычислим оба слагаемых силы
отдельно. Для падающей волны
F0 = -2r,a^ e * с ■* ^ = _А. chp|
1 с \ с
Для дифракционного давления по формуле (28.8)
n=0 F„ (р-)_1
Но в этой сумме, опять-таки в силу ортогональности
полипомов Лежандра, выпадают на этот раз все члены, кроме
члена первого порядка (так как Р^) = р.), и мы имеем:
JPd=Tira,61 -
1
• + -!-
P
p
с
ch» —
a\2
I*
Полная сила
a
^ = Fo + ^a = •* , nP^e a ■** Se ~''8in 'Л ('»),
(pf)%2p.^2
где
'.^i-Hf-1
(см. рис. 88).
§ 28] ДИФРАКЦИЯ ОТ ШАРА 18S
Следует подчеркнуть исключительную простоту
результата. Интересно отметить, что сила, действующая на
шар, стремится со временем к нулю. Это объясняется тем,
что, по мере того как фронт волны, миновав шар,
удаляется, дифракционное явление постепенно ослабевает,
и в конце концов на шар действует со всех сторон
одинаковое давление, равное давлению в свободно
распространяющейся волне.
s
аз
| Займемся теперь исследованием дифракции от малого-
1 твёрдого шарика. Тут нужно прежде всего разобраться
4 в одном сравнительно тонком вопросе, а именно, в
вопросе о том, что следует понимать под малостью примени-
! тельно к нестационарным явлениям. В самом деле, для
синусоидального режима понятие малости имеет ясный
смысл: мы подразумеваем малость по сравнению с длиной
волны (см. главу I). Но что послужит мерилом размера
в случае неустановившихся волновых явлений, когда
понятие длины волны совершенно неприменимо? Иногда
1 говорят, что в случае синусоидальной волны малость раз-
I мера некоторого тела по сравнению с длиной волны озна-
J чает, что во всех точках этого тела колебательная вели-
1 чина, например давление, имеет одинаковую фазу. Для
неустановившихся волн такое положение
соответствовало бы одновременности явлений в разных точках.
Эти формулировки не разъясняют вопроса, кроме того,
J они неточны. В случае стационарного режима сдвиг
; по фазе не отсутствует, а мал по сравнению с соГ = 2тс.
Ь
186 теория неустановившихся волновых явлкний [гл. и
Тавтология очевидна:
с к
Что же касается нестационарного режима, то ни
линейного, ни временного масштаба для оценки малости
мы пока не имеем.
Пусть плоская волна встречается с твёрдым шаром.
Положим, что волна синусоидальна. Пусть радиус шара
неограниченно уменьшается. Будет достигнуто
соотношение а = X, а при дальнейшем уменьшении радиуса
будет а^к, и мы будем называть шар малым (по сравнению
с длиной волны).
Пусть теперь с тем же шаром убывающего радиуса а
встречается плоская единичная волна. Ни при каком
конечном радиусе шара не наступит какого-либо качественного
изменения в соотношениях. Критерий одновременности
ничего не даёт; очевидно, что фронт волны проходит шар за
рремя — • Время это, конечно,убывает с радиусом, носравни-
вать егс пока не с чем. Трудность обусловлена тем, что
фронт единичной волны по определению несёт разрыв
давления. Давление в данной точке поля при
проходе фронта через эту точку изменяется скачком, т. е.
бесконечно быстро (на протяжении бесконечно
малого промежутка времени); нарастание давления от
нуля (перед фронтом) до конечного значения (позади
фронта) совершается на протяжении бесконечно
малого отрезка.
Трудность будет устранена, если мы согласимся
считать, что нарастание давления на фронте происходит с
очень большой, но всё же конечной скоростью, или,
другими словами, что фронт имеет хотя и малую, но конечную
глубину. Теперь можно дать разумное определение
малости, а именно: речь идёт о малости тела по сравнению с
глубиной фронта волны. Иначе говоря, тело мало, если время
пробега фронта волны по телу мало по сравнению с
временем нарастания давления. Последняя формулировка
поясняет, в каком смысле следует применять критерий
одновременности.
§ 28) ДИФРАКЦИЯ ОТ ШАРА 187
Все эти соображения можно было бы ещё обобщить,
распространив их на непериодические возмущения
других видов, но в дальнейшие подробности мы уже вдаваться
не будем. Заметим лишь, что приведённые выше
формулировки могут быть истолкованы и со спектральной точки
зрения.
Вернёмся к нашей задаче. Мы собираемся исследовать
дифракцию единичной волны от малого шарика. Это
значит, что мы пренебрегаем разновременностью прихода
волны к разным точкам поверхности шарика. Мы могли бы
получить все нужные результаты из общей формулы
(28.8), переходя к пределу при р >0. Но интереснее
применить физическое рассуждение. Наличие шарика в поле
вызывает следствия двоякого рода. Во-первых, шарик
твёрд, и, следовательно, он не претерпевает объёмного
сжатия, какое претерпевал бы воздух (или вообще
упругая среда), заключённый в таком же сферическом объёме.
Вследствие этого эффект наличия шарика можно выразить
некоторым его излучением как антенны нулевого порядка
(раздувающийся шар). Во-вторых, шарик неподвижен, и,
следовательно, точки его поверхности имеют скорость,
равную нулю, тогда как скорость частиц воздуха в тех же
точках при отсутствии шарика имела бы значение - в
направлении распространения. Вследствие этого эффект
наличия шарика можно представить его излучением как
антенны первого порядка (смещающийся шар). Оба
эффекта нужно сложить.
Представим это рассуждение в аналитической форме.
Для эффекта нулевого порядка
V — х "о—3™ Рос2 '
— — 4 о р
u=pv =Рзта ^г »
где v — приращение объёма, V0 — объём шара, х — объём
188 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ. II
Ж/
dt
dv -> ..
ный модуль упругости среды, к = -, ооъемная
скорость. Наводимый потенциал
— ие
4пг * 3 г р0с2
Для эффекта первого порядка
vr= — cos ft; п — — ,
где vrnvx — радиальная скорость и её проекция на ось г.
Потенциал, создаваемый твёрдым шаром радиуса а,
движущимся со скоростью vx, равен (см. формулу (20.2))
, r-a fx (р — )
i"1-^4e"P~4-^Pi(C0S')-
la2 a i. , i \ -*-£■ „
a -» 0 J p
Складывая ф0 и <px, получаем полный потенциал поля
дифракции:
На поверхности шара, т. е. при г = а, дипольное
.излучение преобладает, и мы имеем:
= — -о- cos ft.
На больших расстояниях
— I р a a2 ~V-7 /1.1 «\
Ф J ~~р в с -о* + •«- COS » ) .
I 29] СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ РЕШЕНИЯ 189
Оригинал выражается функцией ^{t —~). Таким
образом, при встрече плоской волны с малым шариком
возбуждается импульс, разбегающийся от шарика
концентрически, но с неодинаковой интенсивностью в различных
направлениях. Направленность дифракционного
излучения малого шарика для
больших расстояний
выражается нормированной
характеристикой
направленности
Д(») =
6
-3 +Tcosi
(рис. 89). .
Оказывается, что
потенциал равен нулю на
конической поверхности с
углом при вершине
конуса
arccos(~4) = 132°-
Дифракционный потенциал малого шарика очень
мал — он зависит от куба радиуса. Поэтому,
предположив малость шарика, мы вправе пренебречь его
дифракционным полем по сравнению с полем основной волны,
как мы и делали выше (§ 22).
§ 29. Связь между стационарными
и нестационарными решениями
Общая форма волновых уравнений универсальна
в том смысле, что уравнения эти сохраняют силу для любых
волновых возмущений при том единственном условии,
ч#то мы не выходим за пределы линейных соотношений, на
которых основан вывод этих уравнений.
Но решения этих уравнений специализированы. Имея
в виду применение принципа наложения, мы решаем обычно
190 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
волновую задачу либо для синусоидального возмущения —
такое решение называется стационарным, либо для
возмущения в форме единичной функции — такое решение
называется нестационарным.
Так как оба решения представляют собою решения
одного и того же уравнения, то между ними существует
тесная связь. Установив эту связь, мы получаем
возможность выразить стационарное решение через
нестационарное, и обратно.
Предположим, что нам дано обыкновенное
дифференциальное уравнение
тт/ d \ dny dn-xii dv /жЧ
(29.1)
Функция х {t) в правой части представляет собою то, что
выше было названо возмущением. Для стационарного
режима полагаем
x{t) = eiwi
и ищем частное решение в виде
у(1) = Аеяы+*\
что даёт
Я (/«) у = К (/«>)" + а _! (/о))"-1 + ... -!-• oj* + а0] у = е*",
откуда
1 fat
y-H(j<»)e '
Это и есть стационарное решение.
Величину А (со)= L^—А называют обычно частотной ха-
J ч ' |Я(/<о)|
рактеристикой системы, описываемой уравнением (29.1),
1
а величину „ .. — комплексной частотной
характеристикой.
§ 29] СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ РЕШЕНИЯ 191
Для нестационарного режима выбираем возмущение в
правой части в виде
а(*) = °о(0>
а затем строим изображение уравнения (29.1). При
нулевых начальных условиях изображение это имеет вид
откуда
Функцию
1
Г
y^h{t)^+
Н(р)'
1
Н(р) '
выражающую поведение системы под воздействием
возмущения cr0(£), называют обычно переходной функцией.
Для того чтобы выразить частотную характеристику
через переходную, представим решение уравнения (29.1)
в форме интеграла Дюамеля:
t t
у (t) =:[h(t — ц) dx{i) = h{0)x{t) + [ К (%)x{t — т.) dx.
о 6
Для случая х = е^ы получаем:
t
jr^re^1 + Ф (t) = h(0) em + \ A'(T) емиЛ. (29.2)*
Здесь в от^гичие от предыдущего в левой части стоит
полное решение уравнения (29.1) с правой частью езы, т. е.
1 ы г г
кроме частного интеграла „ .. , е дооавлен еще общий
интеграл Ф(£), представляющий собою по физическому
смыслу сумму собственных колебаний. Эти колебания во всякой
реальной системе с течением времени затухают, почему
они и не фигурируют в решении для стационарного, т. е*.
192 ТЕОРИЯ НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ (ГЛ II
установившегося режима. (Само название
«установившийся режим» указывает именно на возможность
пренебречь собственными колебаниями, возникающими при
всяком изменении режима системы.)
Сократим обе части (29.2) на е^г и перейдём к пределу,
устремляя t к бесконечности. Слагаемое Ф(£) выпадет,
л мы получим:
оо
_£- = h (0) + j К (т) е-*"*, (29.3)
о
или, разделяя вещественную и мнимую части,
HW) = R + ix-
ОО
R (ш) = А (0) -}- JI Л' (Т) COS СОТЙТ,
о
оо
X (а>) = — ^ Л' (т) sin arcd*. (29.36)
о
Эти формулы позволяют найти частотную
характеристику по известной переходной характеристике. Мы видим,
что комплексная частотная характеристика представляет
собою не что иное, как комплексный спектр производной
от переходной функции (см. главу I, § 8). Обратная
зависимость могла бы быть получена при помощи формул
обращения, но мы выведем её заново.
Представим для этого единичную функцию cQ(t)
интегралом Фурье. Отделим от а0 (t) постоянную слагающую,
равную половине. Тогда можем записать:
+оо . 4
—ОО
Подставив это разложение в правую часть (29.1), заметим^
(29.3а)
§ 29] СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ РЕШЕНИЯ 193
что постоянная составляющая даст слагающее решения
1 1 г
вида y H(Q\ > и таким образом
11 1 Г РЗЫ
y=hw=jww+ir J тлт*а' (29>4)
—со
или в вещественной форме
со
h(о =4j/W+4-\^sinи+?)d» (29-5)
6
или
М«)=ш+т! ^г1™8»<<^> (29-5a)
6
со
h(t) = i- ( ^i^sincoWco. (29.56)
(О
О
Формула (29.4) или (29.5) служит для нахождения
переходной характеристики по известной частотной.
Аналогичный вывод и с тем же результатом мог быть проделан,
если бы мы исходили не из обыкновенного уравнения, а из
уравнения в частных производных, в частности волнового
уравнения
д2<р-Л-5-=°-
' с2 дЬ1
Разница состоит в том, что возмущение входит в
граничные условия задачи. Однако после «алгебраизации»
уравнения методами § 10 мы приведём задачу к
решению уравнения с правой частью. После возвращения
к оригиналу нестационарное решение выражается обычно
через трансцепдептиые функции, как мы неоднократно
видели выше.
Покажем применение выведенных формул на примере.
Предположим, что мы хотим найти зависимость от
частоты активной составляющей акустического
сопротивления круговой антенны (поршневого излучателя).
13 A. A. Хахшсвич
194 ТЕОРГ.Я НЕУСТАНОВИВШИХСЯ ВОЛНОВЫХ ЯВЛЕНИЙ [ГЛ. II
Переходное сопротивление для рассматриваемой
антенны было вычислено в § 18; мы получили:
»(«> = -£—!«* „Z-^yi-ffi. (29.6)
Эго и есть переходная функция для данного случая. Её
nt оизводная
а(*)-А(*) — ^-5-К1 - (-а-)* - <29-7)
Подставив (29.7) в (29.3а), получим:
2г
о
Н = 1-|т ? |/l-(-£)* cosOTdt,
или, вводя
СТ (О 7
а = Т£' Т = *»
1
Я (<о) = 1 — -^' V71 — а2 cos 2kaa da-
Этот интеграл известен в теории бесселевых функций:
это есть не что иное, как интеграл Пуассона
(И
V *_. J | ,\ „и - 2 cos az da = Jn (z).
В нашем случае
n = i,r(i)-v;,r(n+4)=r(4)=l^
пирнгмая во внимание чётность подинтегральнои функ-
§ 29J СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ РЕШЕНИЯ J9£
цип, находим:
1 J_
-^- (1 —а2) 2 cos azda
о
Итак, окончательно
что и представляет собою общеизвестное выражение
сопротивления излучения поршня.
Л(*)
1
2*
13*
ЗАКЛЮЧЕНИЕ
Заканчивая наше исследование, попытаемся подвести
некоторые итоги.
Во-первых, можно утверждать, что метод решения
линейных физико-математических задач, основанный на
принципе наложения, применяющий разложение
заданных функций по единичным функциям и выражающий
решение интегралом Дюамеля,— метод этот равноценен
спектральному методу, но в определённой категории
случаев приводит к более простым выкладкам.
Во-вторых — и это гораздо более существенно —
формально безупречный спектральный подход к
непериодическим явлениям не может быть связан с
непосредственным физическим пониманием этих явлений, тогда как
аналитические методы, специально приспособленные к
исследованию непериодических явлений, не только не
идут вразрез с физическими представлениями, но
способствуют их развитию. Поэтому оказывается возможным
вести исследование, не разграничивая аналитических
выкладок и качественных физических рассуждений;
такого рода способ изложения неоднократно применён
в данной работе. Далее следует остановиться на уже много
раз отмечавшейся простоте аналитических решений
различных задач теории неустановившихся волновых
явлений. Корни этого важного обстоятельства лежат,
поводимому, довольно глубоко и уходят в методологическую
основу способа исследования.
Во всяком случае очевидно, что, исследуя
неустановившееся явление, мы прослеживаем явление в процессе его
становления и развития. При атом различные
обстоятельства, оказывающие влияние на развитие явления, возни-
ЗАКЛЮЧЕНИИ
197
кают неодновременно и могут поэтому учитываться в
отдельности, поочерёдно, в порядке их временной перспективы.
Каждая деталь явления изучается в процессе своего
развития с момента возникновения.
Спектральный метод этих возможностей не даёт.
Исследуя установившееся явление, мы должны сразу охватить
его в целом, как нечто данное со всеми его деталями, и
лишены возможности выяснить, как же именно это
установившееся явление установилось.
Для того чтобы сделать эти соображения более ясными,
напомним ещё раз в качестве простого примера задачу,
разобранную в § 12. Дана цилиндрическая труба, в
которой возбуждается волна поршнем, движущимся с
заданной скоростью на одном конце трубы; второй конец
трубы наглухо закрыт. Требуется определить силу,
действующую на поршень (или, что то же, входное
сопротивление трубы). Для установившегося периодического
движения мы поступаем так: заменяем в волновом уравнении
с* дР ~ р
i
и решаем полученное обыкновенное дифференциальное
уравнение, используя граничные условия
v{0) = v0; v(l) = 0.
Получается известный результат
Исследуя же неустановившийся режим, мы можем
полностью осмыслить наши выкладки, так как они на
каждом этапе адэкватны происходящему. Мы говорим:
если поршень начал двигаться с постоя! и ;й скоростью,
то от него побежала волна, которая распространяется
совершенно так, как если бы труба была бесконечна.
После встречи с заделанным концом возникает
отражённая волна, которая бежит в обратном направлении.
198
ЗАКЛЮЧЕНИЕ
Достигнув поршня (в этот момент происходит впервые
изменение режима поршня), волна снова отражается,
бежит к заделать м/ концу, вновь отражается, и так
далее. Нам остаётся только записать это рассуждение в
сокращённом виде при помощи принятых знаков и
символов:
4- = 4.(«) + Jb.(«-2i.) + &.(«-4 4-)+..r-
ОО
= °о(0 + 2У°о(*-2*'-7!
что и является решением задачи, или, гсрнсе, записью
решения, к которому мы пришли не аналитическим путём,
а путём элементарного рассуж;ччля, разбирая явление
шаг за шагом.
Тот же результат может быть представлен в форме
изображения
— °° __9- L
-^- = 1-|-2Уе ~'1>с =cth?>-.
W +ad £ С
i-i
Убедительней г* л люстрацией к гысказанпым сообра-
жен и ям может послужить также решение гораздо более
сложной задачи об акустической системе передачи,
рассмотренной в § 22.
Переходя от методологических вопросов к
применениям, можно сказать, что изложенная в этой работе
методика может рассматриваться по только как
специфическое орудие решения нестационарных задач, по и как
методика решения акустических проблем вообще, в том
числе и стационарных. Действительно, найдя
нестационарное решение, которое по самой природе своей обладает
совершенно такой же общностью, как и стационарное, мы
можем сравнительно легко герейтн от одного решения
к другому (если это потребуется), как показано в
предыдущем § 29.
Но область применения изложенных методов не
ограничивается рамками акустики и вообще теории волн. За
последнее время стало ясно, что затронутые проблемы
ЗАКЛЮЧЕНИЕ 199
смыкаются с кругом вопросов сверхзвуковой
аэродинамики. Дело в том, что акустика есть не что иное, как
гидродинамика сжимаемой жидкости для безвихревого
движения. Оказывается, что в то Бремя как в обычной
аэродинамике нельзя отвлечься от турбулентности, играющей
важную роль для движения с дозвуковыми скоростями,
в сверхзвуковой аэродинамике с турбулентностью во
многих случаях можно не считаться, и уравнения
аэродинамики можно свести к уравнениям акустики.
Связанные с этими важными применениями проблемы
требуют дальнейшей разработки.
ПРИЛОЖЕНИЕ
Таблица некоторых операционных фориуд
оо
О
f(p)
1 1
рп
рпе~~^
chpx
shp-
shpz
Р*
thpT
cth px
thpx
P-
f(t)
°o{t-')
*n{t)
OO
OO
c0(/) + 2^o0(t-2kz)
OO
h=l
ПРИЛОЖЕНИЕ
201
Продолжение
f(p)
f(t)
Рч
Р
(п —целое)
(Rem>-1)
Р
р + а
а
р + а
Р
(р+«)"
t^(t)=--'-l(t)
t" '
n\
Mt) = s-„(l)
t"
Г(т + 1)
«o(«
«""«.(О
(1-е-"О "о (О
ар
р2 + аа
Р2
1>2 + а2
а2 -
р2 + й*
sin а t oe (t)
cos а t o0 (t)
(1 — ecsotf) c0(t)
ар
Рг-
р*
р*-
а2
.*'-
а2
а2
а2
sh at c0(t)
chat zQ(t)
(chat—l)*o(*)
202
ПРИЛОЖЕНИЕ
Продолжение
tip) j tit)
1 ap
(p+p)2+*a
p2 + $p
p
Vp2 + ¥
p
P (y^TW^-^W1
Kpa + 62 V ь J
P .. r V l~l »2
■■■■,-■■ .,■■;■■,::, - —' r *| /*
e -?' sin af s'o (£)
e~ P' cos ai e0 (t)
J0(bt)e0(t)
ГЛАВПОЛИГРАФИЗДАТ
при Совете Министров СССР
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
«ГОСТЕХИЗДАТ»
Москва, Орликов пер., 3.
ИМЕЮТСЯ В ПРОДАЖЕ КНИГИ:
Волькенштейн Ф. Ф., Электропроводность
полупроводников. Стр. 352. Ц. 14 р. 25 к.
Гринберг А. П., Методы ускорения заряженных
частиц. Стр. 384 +XVI вкл. (Современные
проблемы физики). Ц. 15 р.
Герман Г. и Вагенер С. Оксидный катод. Перевод
с нем. А. П. Иевлева, в переработке и с
дополнениями Б. М. Царева. Стр. 503. Ц. 24 р.
Ландау Л. и Лифшиц Е, Теория поля. Изд. второе,
переработанное. Стр. 3G4. Ц. 11 р.
Сушкин Н. Г., Электронный микроскоп. Стр. 276.
(Физико-математическая библиотека инженера).
Ц. 10 р. 50 к.
Шинтльмейстер И., Электронная лампа как
прибор для физических измерений. Перераб.
перевод с нем. под ред. и с добавлением Е. Я. Пум-
пера. Стр. 343. (Физико-математическая библиотека
инженера). Ц. 13 р. 85 к.
Книги продаются в книжных магазинах и высылаются
также почтой наложенным платежом без задатка всеми
республиканскими, краевыми и областными отделениями
« Кн и га—п о чтой ».
ГЛАВПОЛИГРАФИЗДАТ
г при Совете Министров СССР
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
«ГОСТЕХИЗДАТ»
Москва, Орликов пер., 3.
Лебедев П. 11., Избранные сочинения. Под ред. п
с предисловием проф. А. К. Тимирязева. Стр. 243.
Ц. 9 р. 80 к.
Морз Ф., Колебания и звук. Перевод со 2-го англ.
издания под ред. проф. С. Н. Ржевкина. Стр. 496.
Ц. 23 р. 25 к.
Льюис В. В., Методы электрического счета
а л ъ ф a jh бета-части ц. Перевод с англ. Н. Н.
Воронова, иод ред. Г. Д. Латышева. Изд. 2-е. Стр. 164.
Ц. 4 р. 80 к.
Гинзбург В. Л., Теория распространения
радиоволн в ионосфере. Стр. 358. Ц. 14 р. 65 к.
Сена Л. А., Столкновения э.лектронов и
ионов с атомами газа. Стр. 216. (Современные
проблемы физики). Ц, 7 р. 50 к.
Стронг Дж. II р ак тика современной ф и з и ч.е-
ской лаборатории. Перевод с англ. под ред.
прсф. В. А. Фабриканта. Стр. 443. Ц. 25 р.
Книги продаются в книжных магазинах и высылаются
также почтой наложенным платежом без задатка всеми
республиканскими, краевыми и областными отделениями
«Книга — почтой».