А. П. ДОМОРЯД
МАТЕМАТИЧЕСКИЕ
ИГРЫ И РАЗВЛЕЧЕНИЯ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1061

ОГЛАВЛЕНИЕ
Предисловие 5
§ 1. Различные системы счисления 9
§ 2. Некоторые сведения из теории чисел 17
§ 3. Сравнения < 21
§ 4. Непрерывные дроби и неопределенные уравнения .... 25
§ 5. Пифагоровы и героновы тройки чисел 34
§ 6. Арифметические развлечения Зо
§ 7. Числовые фокусы • 39
§ 8. Быстрый счет » 45
§ 9. Числовые гиганты t 56
§ 10. Игры с кучами предметов 59
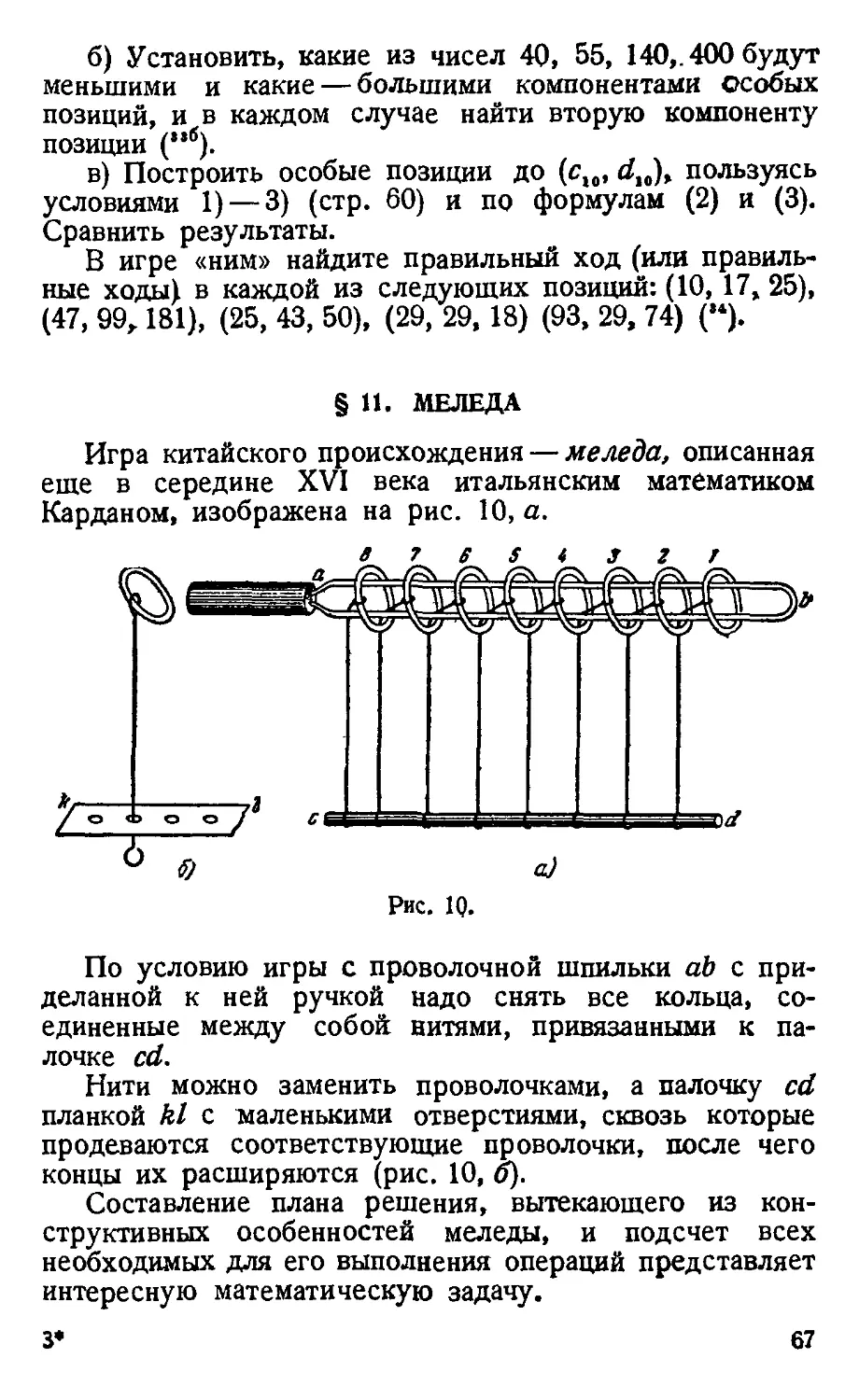
§ 11. Меледа < 67
§ 12. Игра Люка , 70
§ 13. Солитер 71
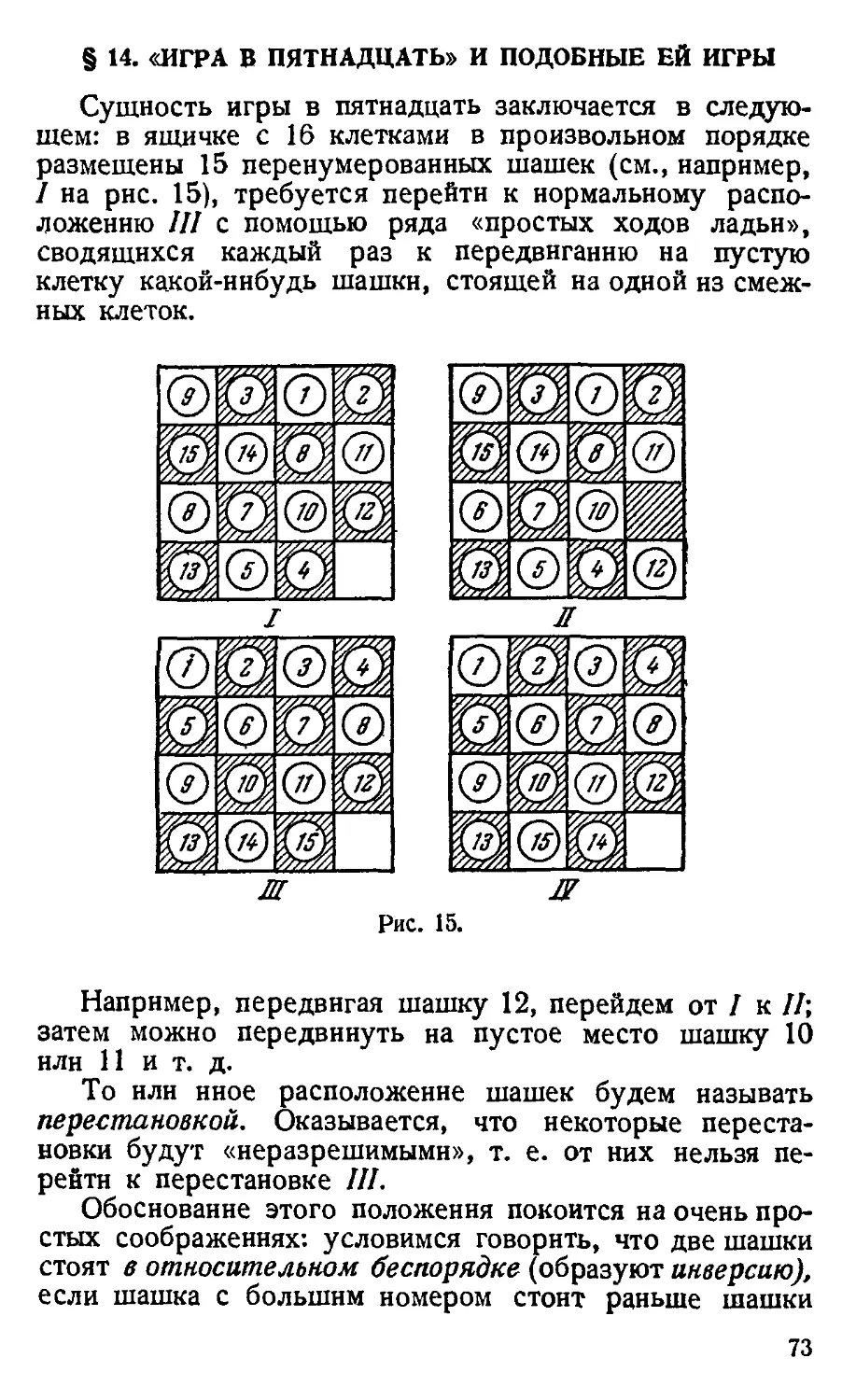
§ 14. «Игра в пятнадцать» и подобные ей игры ........ 73
§ 15. Задачи на определение числа способов достижения цели . 79
§ 16. Магическяе квадраты 89
§ 17. Эйлеровы квадраты . 96
§ 18. Развлечения с домино 98
§ 19. Задачи, связанные с шахматной доской 99
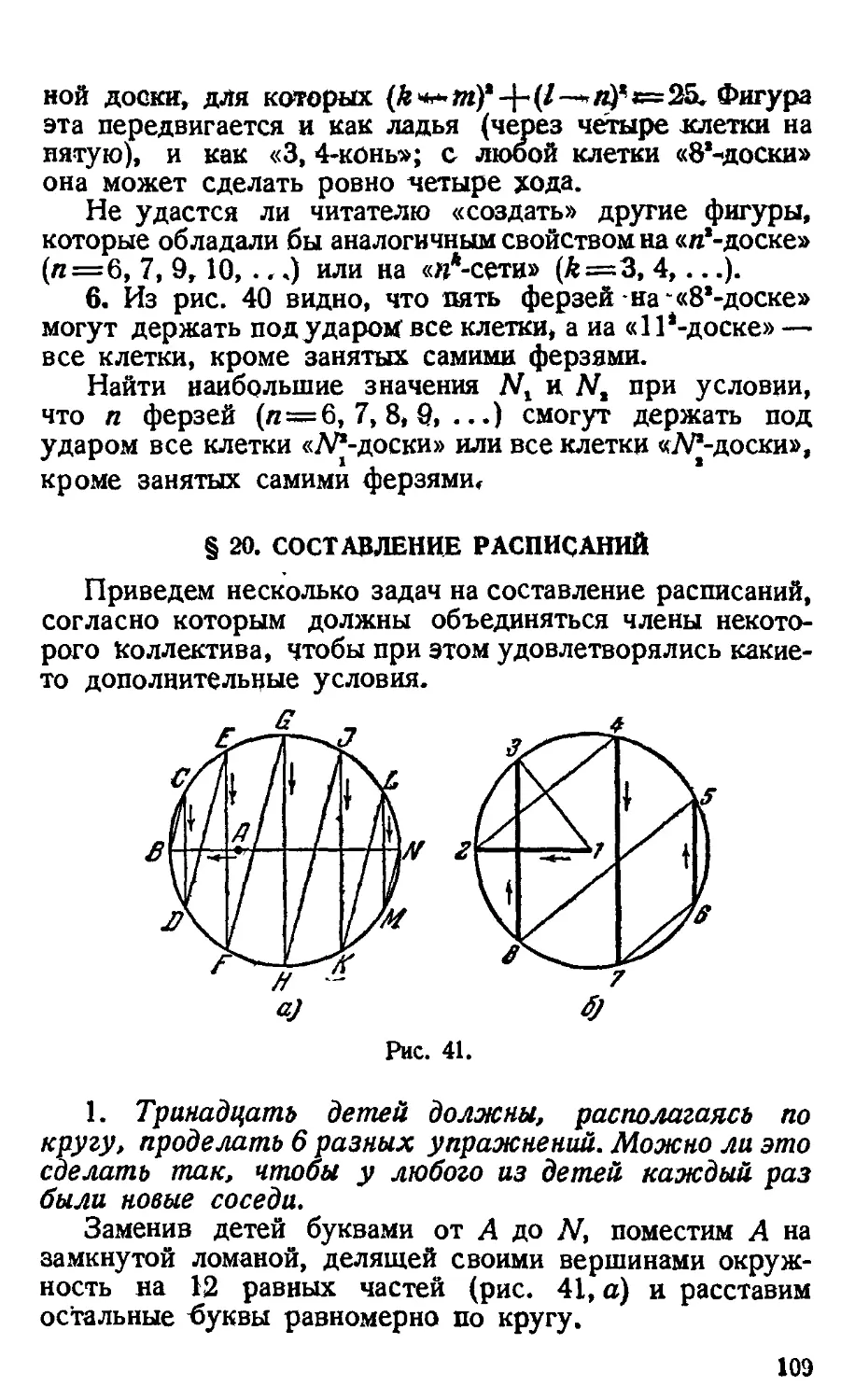
§ 20. Составление расписаний 109
§ 21. «Задача Иосифа Флавия» и ей подобные 112
§ 22. Развлечения, связанные с перемещениями предметов . . .114
§ 23. Простейшие способы построения красивых узоров .... 122
§ 24. Правильные многоугольники из ромбов 127
§ 25. Построение фигур из данных частей 130
§ 26. Составление паркетов 134
§ 27. Перекраивание фигур 142
§ 28. Построение кривых .148
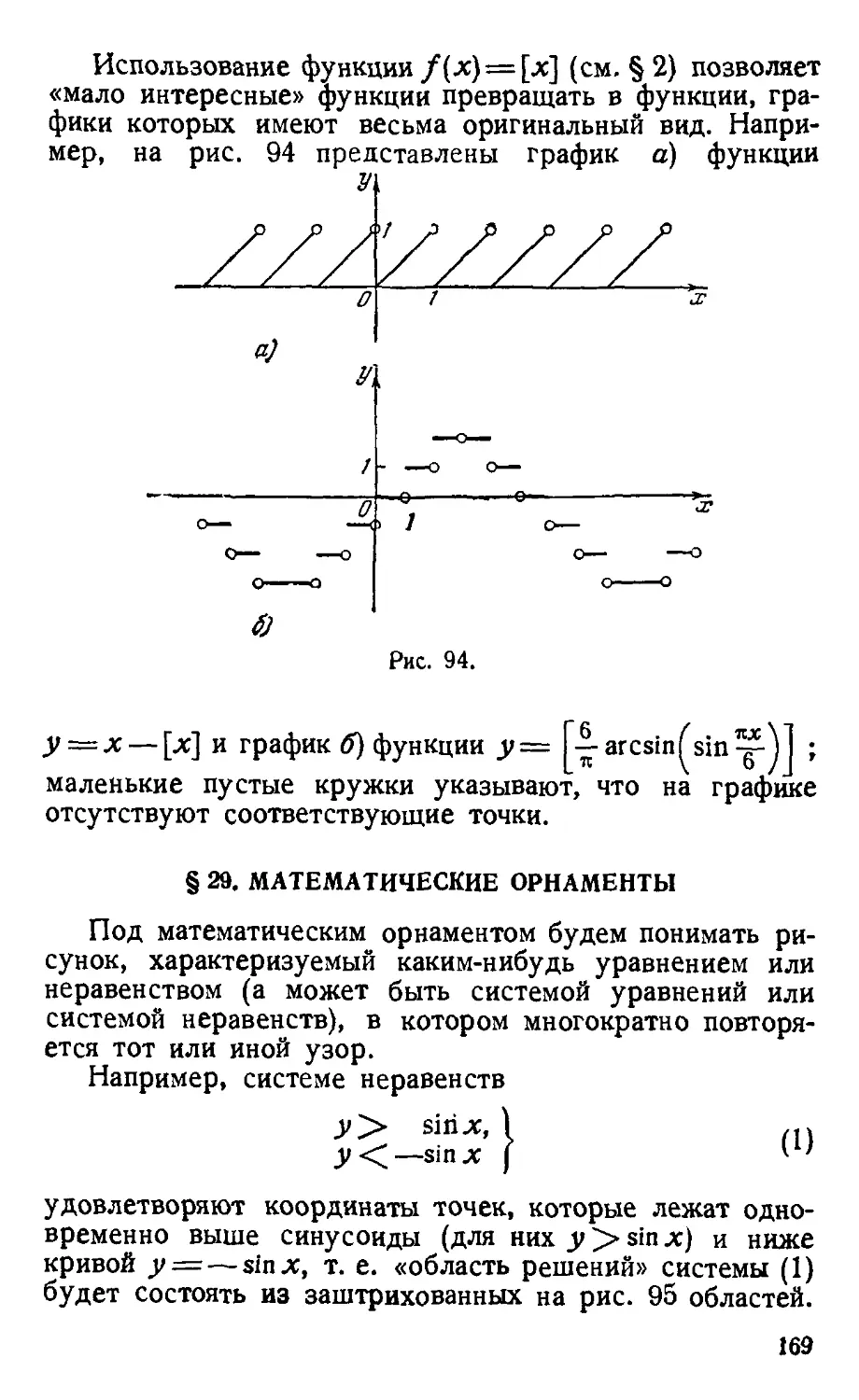
§ 29. Математические орнаменты 169
§ 30. Модели многогранников 173
3

§ 31. Развлечения с листом и с полоской бумаги 182
§ 32. Проблема четырех красок 186
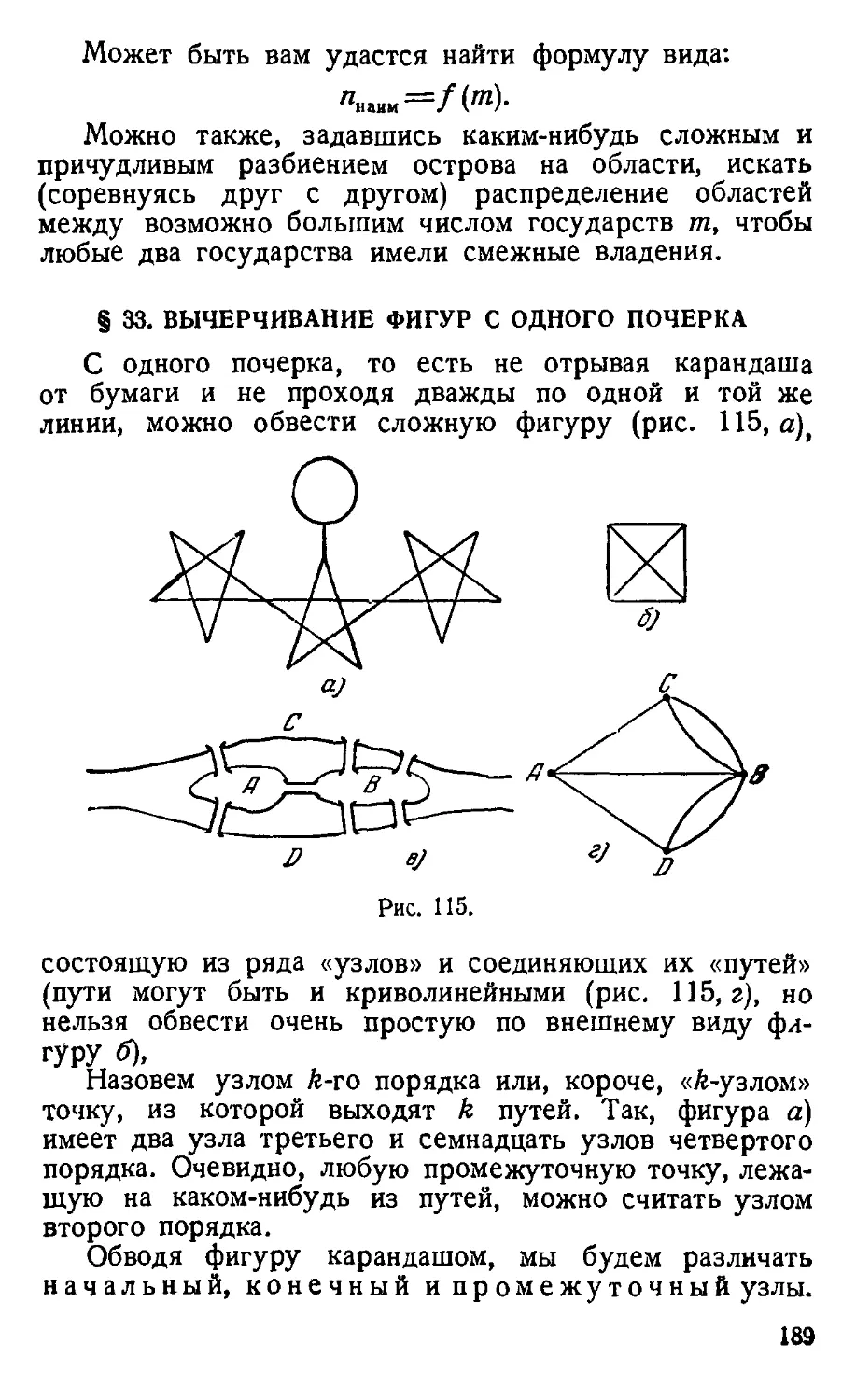
§ 33. Вычерчивание фигур с одного почерка 189
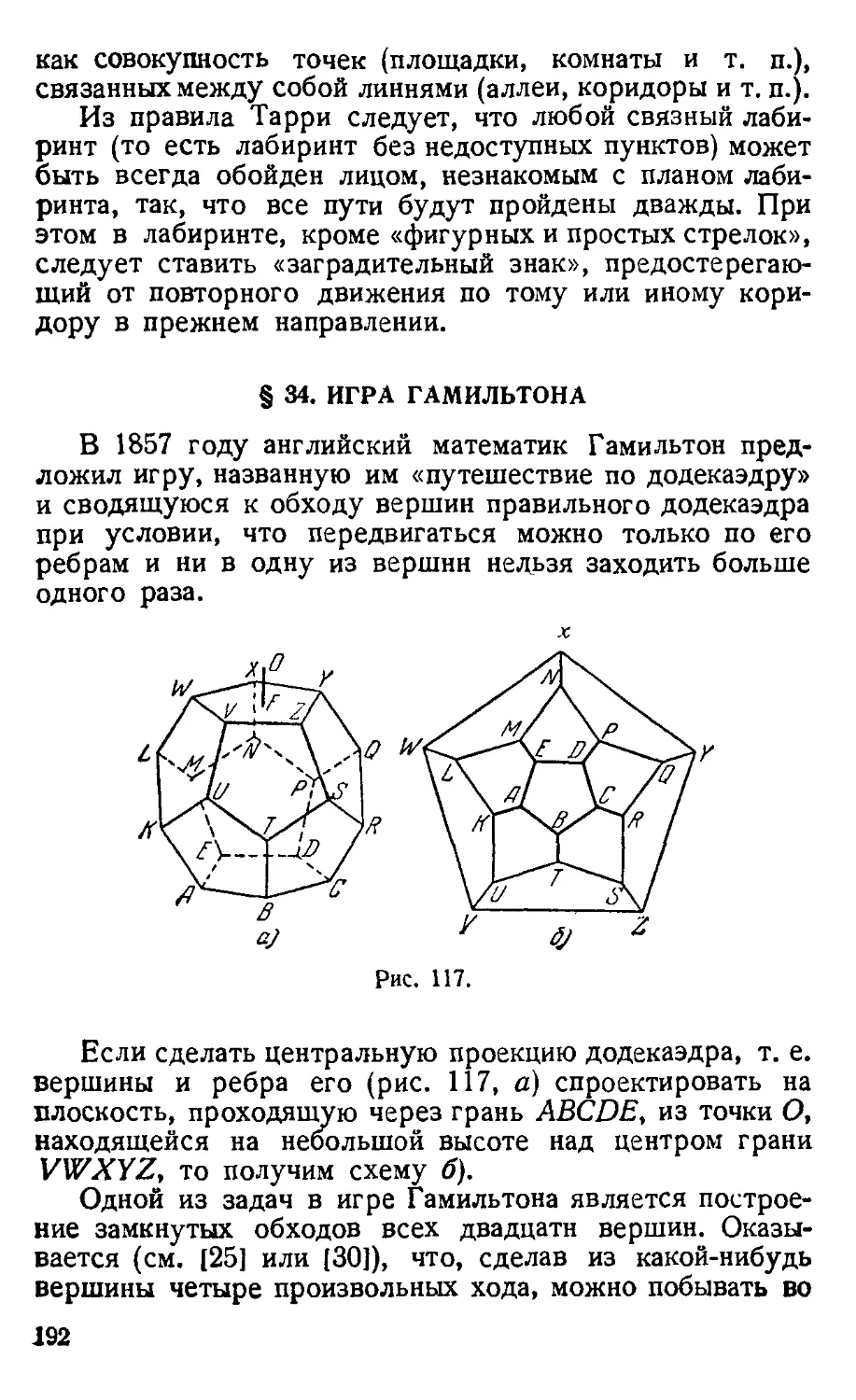
§ 34. Игра Гамильтона 192
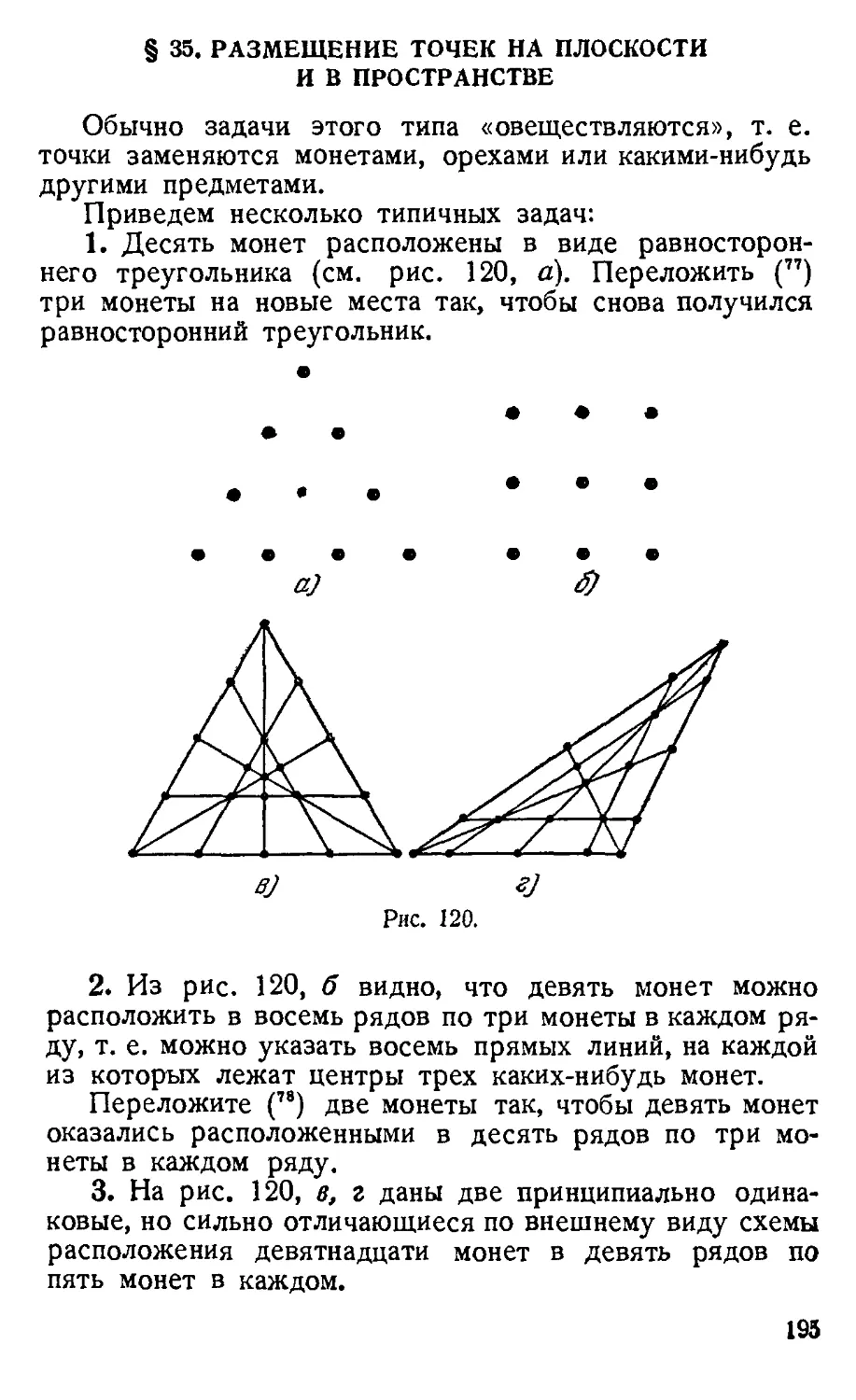
§ 35. Размещение точек на плоскости и в пространстве .... 195
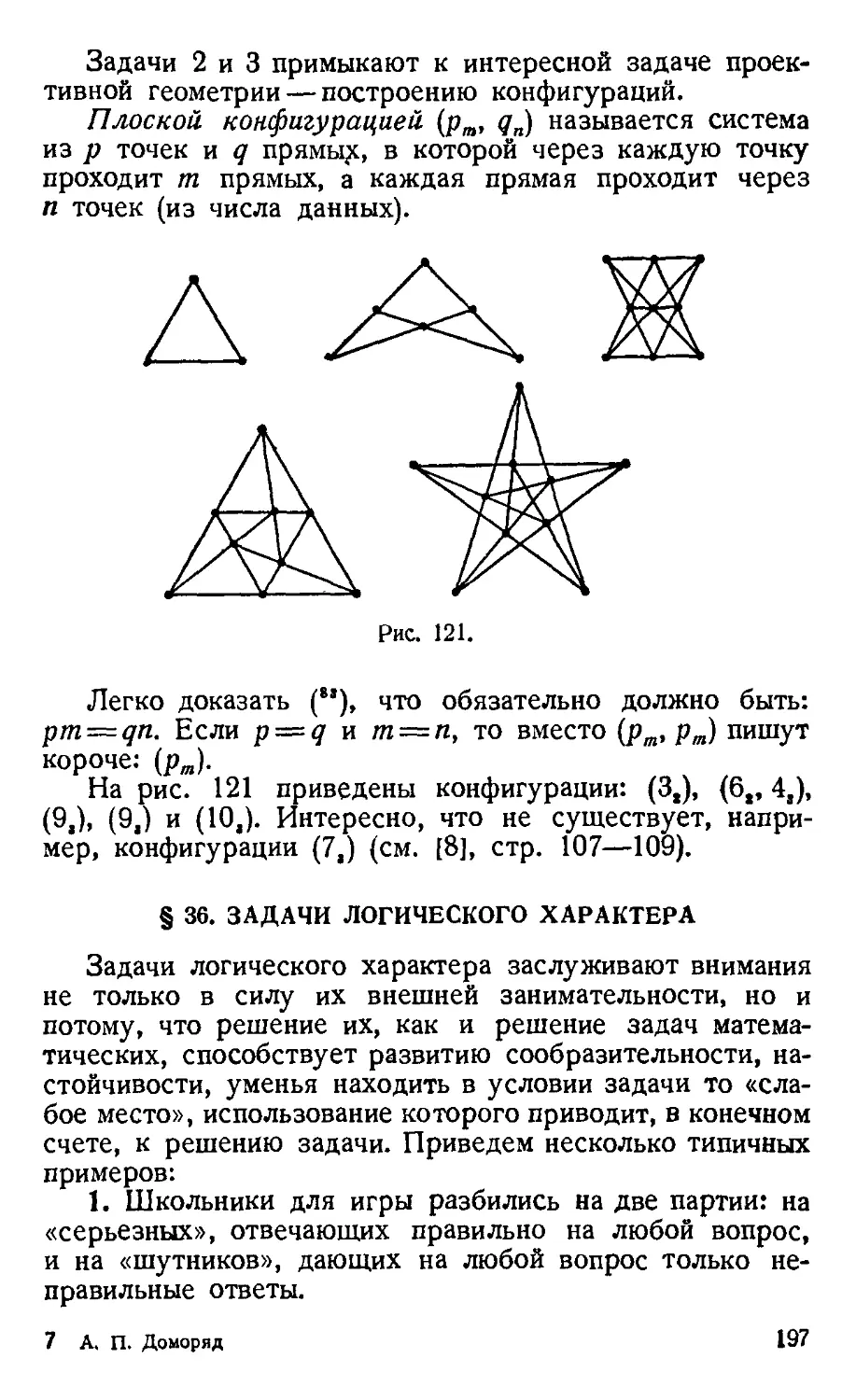
§ 36. Задачи логического характера 197
§ 37. Всякая всячина 206
§ 38. Примечания и ответы к задачам 218
Литература 266

Светлой памяти
дорогих родителей
посвящает эту книгу
Автор
ПРЕДИСЛОВИЕ
Из разнообразного материала, объединяемого
различными авторами под общим названием математических
игр и развлечений, можно выделить несколько групп
«классических развлечений», издавна привлекавших
внимание математиков:
1. Развлечения, связанные с поисками оригинальных
решений задач, допускающих практически
неисчерпаемое множество решений (см., например, «Магические
квадраты»—§ 16, «Задача о шахматном коне»—§ 19
и т. п.); обычно интересуются установлением числа
решений, разработкой методов, дающих большие группы
решений или решения, удовлетворяющие каким-нибудь
специальным требованиям.
2. Математические игры, т. е. игры, в которых двое
играющих рядом «ходов», делаемых поочередно в
соответствии с указанными правилами, стремятся к
определенной цели, причем оказывается возможным для любого
исходного положения предопределить победителя и
указать, как — при любых ходах противника — он может
добиться победы (см., например, § 10).
3. «Игры одного лица», т. е. развлечения, в которых
с помощью ряда операций, выполняемых одним игроком
5

в соответствии с данными правилами, надо достигнуть
определенной^ заранее указанной цели (см., например,
§§ И—14); здесь интересуются условиями, при которых
цель может быть достигнута, и ишут наименьшее число
ходов, необходимых для ее достижения.
Классическим играм и развлечениям посвящена ббль-
шая часть этой книги.
В первых параграфах книги говорится о различных
системах, счисления и о некоторых вопросах теории
чисел, знание которых необходимо для понимания теории
различных математических игр. Впрочем, для многих
читателей эти параграфы могут представить и
самостоятельный интерес.
Теория отдельных игр изложена в книге
довольно полно; в других же случаях даются лишь
результаты и ссылки на источники, где имеется их
обоснование.
Наряду с классическими развлечениями значительное
внимание в книге уделено и развлечениям
«современным» («Быстрый счет», «Перекраивание фигур»,
«Построение кривых», «Модели многогранников» и т. п.).
Особого внимания заслуживают задачи, допускающие
практически неисчерпаемое или даже бесконечное
множество решений («Составление паркетов», «Построение
красивых узоров» и т. д.).
Здесь каждый может попытаться, проявив
настойчивость и изобретательность, получить интересные (свои!)
результаты.
Если такие классические развлечения, как, например,
составление «магических квадратов» могут оказаться по
душе сравнительно узкому кругу лиц, то вырезывание,
например, симметричных фигур из бумаги,
построение красивых узоров, поиски числовых курьезов и т. п.,
не требуя никакой математической подготовки, могут
доставить удовольствие и любителям, и «нелюбителям»
математики. То же можно сказать и о развлечениях,
6

требующих подготовки в объеме 8—10 классов средней
щколы (составление паркетов, построение интересных
кривых и орнаментов и т. п.).
Развлекаясь коллективно, можно проводить конкурсы
на составление оригинальных паркетов, на построение
кривых и орнаментов, на получение красивых
симметричных фигур, вырезаемых из бумаги, и т. д. Каждый
из участников конкурса может «блеснуть» своей
изобретательностью, аккуратностью исполнения,
художественностью раскраски полученных фигур и т. д.
Завершить подобного рода коллективные
развлечения можно составлением альбома или организацией
выставки, где будут собраны лучшие экспонаты.
Многие развлечения и даже отдельные задачи могут
подсказать любителям математики темы для
самостоятельного исследования (использование хода коня вместо
«коротких ходов ладьи» в «игре в 15», поиски
интересных тождеств — см. § 37—, обобщение задачи о
туристах— задача № 13 в § 37 — и т. п.).
В целом книга рассчитана на читателей с
математической подготовкой в объеме 9—10 классов, хотя
ббльшая часть материала доступна
восьмиклассникам, а некоторые вопросы—даже учащимся 5—
6 классов.
Многие параграфы могут быть использованы
преподавателями математики для организации внеклассной
работы.
Разные категории читателей могут по-разному
использовать эту книгу: лица, не увлекающиеся математикой,
могут познакомиться с любопытными свойствами чисел,
фигур и т. п., не вникая в обоснования игр и
развлечений, принимая на веру отдельные утверждения;
любителям математики советуем изучать отдельные места
книги с карандашом и бумагой, решая предлагаемые
задачи и отвечая на отдельные вопросы, предложенные
для размышления.
7

В § 38 даются ответы на помещенные в тексте книги
эадачи и вопросы или указания к их решению, а также
приводятся доказательства отдельных теорем,
упоминаемых в тексте. Ссылки на соответствующий пункт из
§ 38 даются мелкими цифрами, заключенными в круглые
скобки.
Ссылки на книги, в которых читатель может найти
более подробное изложение затронутых вопросов,
даются указанием в квадратных скобках номера источника
(по прилдгаемому списку литературы).

§ 1. РАЗЛИЧНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
У одного любителя математики в тетради были
обнаружены следующие записи:
,3205 (пять и пять — десять; 3217
"г 4775 2 пишем, 1 в 1452
10202 уме и т. д.) 1545
w 435 (пятью семь — тридцать пять; у 104231=273
* 47 3 пишем, 4 в уме и т. п.) 4
4- 37*3 V 47
^2164 X 7
442
421
25553 563
х 3
2131
2131
361
~30
61
"" 60
|14
24,0525...
100
— 74
—
40
30
100 и т. д.
о
II—JL
43 "~ 7
(сокращая на 5)
ос 1
Следовательно, -^=24,0 (52).
Проверка: 0,0(52)=^ = ^
(после сокращения на 52);
94-L- 1_24-14+1_ 361
На первый взгляд все эти действия производят очень
странное впечатление, однако все сделается понятным,
9

если учесть, что все операции выполнялись в
восьмеричной системе счисления.
Дело в том, что в привычном для нас способе записи
чисел отдельные цифры числа N указывают — в
зависимости от занимаемого ими места (позиционный
принцип!)— число единиц, десятков, сотен и т. д. или число
десятых, сотых и т. д. долей, входящих в состав числа N.
Выбирая за основание системы счисления любое
натуральное число k, т. е. считая, что k единиц любого
разряда (а не десять, как это принято в употребляемой
нами десятичной системе) образуют одну единицу
соседнего, более крупного разряда, придем к так
называемой &-ичной системе счисления.
Если £<10, то цифры от k до девяти делаются
излишними (не случайно во всех приведенных выше
примерах отсутствуют 8 и 9!). Если же &>10, то для
чисел от 10 до k — 1 включительно надо придумать
специальные обозначения — цифры; например, в двенад-
цатеричной системе десять и одиннадцать можно
обозначить соответственно через аир.
При записи числа в £-ичной системе удобно указывать
в скобках (справа, внизу) основание системы, написанное
в привычной для нас десятичной системе; например:
1 101ы= 1-2'-)-1.21 + 0-2+1 = 13,
20120(„ = 2.3*+Ь31 + 2-3=177,
а13р(11)=10-12, + Ы21 + 3-124-11 = 17471,
1 «то — l_i_6_i-7 -L 2_477
(О
В последнем примере слева стоит так называемая с и-
стематическая дробь — аналог десятичной дроби.
При больших значениях k цифры от 10 до k — l
можно записывать, пользуясь десятичной системой,
ставя над такими числами-цифрами объединительную
черточку; например:
10 0 6 11(1,)=10.16, + 6-16+11=4203,
ЗТЗ Т2 4Т(б0) = 3.60, +13-60* + 12-60 +
"0) +41 = 695561~
ОЗбШ — ?°4-^—^
(2)
10

Из равенств (1) и (2) видно, что переход от записи
числа в £-ичной системе к записи его в удобной для
нас десятичной системе весьма прост.
Нетрудно решить и обратную задачу: написанное
в десятичной системе натуральное число N записать
в &-ичной системе.
Пусть
Яг=Ьдг-\-сг,
Яп-*=кЯп-1 + Сп-х>
Яп-1 = ^Яп + Сп-1-
Здесь qx и сл — частное и остаток, получающиеся
при делении N на k; вообще qs+t и с, — частное и
остаток, получающиеся при делении qs на к. Каждый из
остатков: с0, с1Г с„ ..., с„_х меньше k, но больше или
равен нулю; 0<Cq„<^k. Отсюда
М= {kqt + cl)k + c(, = qxk* + ctk -f c0 =
+ сп-&-*+...+схк* + схк + сл =
=;= Яп^п-1Сп-х • • •cxcxC* (ft)'
Вычисления удобно вести по схеме, ясной из
следующего примера: выразить 695561 в шестидесятерич-
ной системе счисления:
695561160
"60 11592 160
95 _60_ 193 |60
"60 559 180 3
355 ~540 13
"300 192
556 180
~540 12
161
120
41'
11

Следовательно,
695561 =ЗТЗТ2 4l„0).
Если N=y, то для записи N в А-ичной системе
счисления достаточно в этой системе записать а и Ь;
полученную дробь можно представить в виде
систематической &-ичной дроби, деля в &-ичной системе а на Ь.
При этом число а (считаем, что а<С.Ь) и получающиеся
в процессе деления остатки надо раздроблять —
приписывая к каждому из них справа нуль — в единицы
низших разрядов ( равные -^, -&, ^j, ... J. Представим,
17 4
например, jg в двенадцатеричной системе и у в троичной
системе:
ё=1б2;)==0>"4<»»так как при к==п
15,0 Ц6
14 6 0уП4
60
—60
0
4=^=0,(120102),,,, так как __ll,0f_21
21 0,120102.
120
"112
100
' 21
200
112
~П и т. д.
(последний остаток 11(|) совпадает с исходным числом
а=11<„, следовательно, искомая систематическая дробь
будет бесконечной периодической).
Легко проверить правильность полученного
результата, пользуясь правилом: чтобы превратить чистую
периодическую й-ичную систематическую дробь в дробь
обыкновенную, надо число, стоящее в периоде система-
12

тической дроби, разделить на число, записываемое
столькими цифрами «& — 1», сколько имеется цифр в периоде
(докажите (') это правило, пользуясь формулой для суммы
членов бесконечной убывающей геометрической
прогрессии).
В данном случае k=3t следовательно,
О, (120102),,, = ^=^
Hit *Ч»>
(после сокращения на 10212(„— проверьте!).
Для облегчения умножения и деления чисел в А-ичной
системе полезно иметь таблицу умножения, дающую
попарные произведения чисел, не превышающих k — 1.
Например, при А: = 8 и при А: = 12 имеем
соответственно:
2
3
4
5
6
7
2
4
6
10
12
14
16
3
6
11
14
17
22
25
4
10
14
20
24
30
34
5
12
17
24
31
36
43
6
14
22
30
36
44
52
7
16
25
34
43
52
61
2
3
4
5
6
7
8
9
а
?
2
4
6
8
а
10
12
14
16
18
1а
3
6
9
10
13
16
19
20
23
26
29
4
8
10
14
18
20
24
28
30
34
38
5
а
13
18
21
26
2?
34
39
42
47
6 7 8 9а
10 12 14 16 18
16 19 20 23 26
20 24 28 30 34
26 2? 34 39 42
30 36 40 46 50
36 41 48 53 5а
40 48 54 60 68
46 53 60 69 76
50 5а 68 76 84
56 65 74 83 92
Р
1а
29
38
47
56
65
74
83
92
а1
Например, 5Х6 = 36(8); 5Х7 = 2р(11).
Докажите (!), что извлечение корня квадратного в
любой системе счисления производится так же, как и
в десятичной системе (см. пример в начале параграфа).
Двоичная система счисления
В двоичной системе счисления любое целое число
может быть записано с помощью цифр 1 и 0; это
означает, что любое натуральное число есть сумма различных
степеней двойки:
ЛГ = 2"« +2*>+ ... +2*' («,>«,>.. .>«,>0).
13

На этом свойстве целых чисел основан фокус с
угадыванием чисел: на карточках с «заголовками» 1, 2, 4.
8, 16 (рие. 1) пишутся целые числа так, чтобы любое
число N встречалось лишь на тех карточках, на которых
сумма «заголовков» равна N. Например, 27 (1 -f- 2 -j— 8 -f-
—f—16) должно отсутствовать лишь на карточке с
заголовком 4 и т. п.
2
3
5
7
10
11
м
15
18
IS
гг
гз
гв
27
30
31
1
3
5
7
9
и
13
15
17
13
21
23
25
27
29
31
*
5
6
7
1Z
13
14
15
20
21
22
23
28
23
30
31
8
9
10
11
12
13
п
15
2Ь
25
26
27
28
28
30
31
76
17
18
19
20
21
22
23
2Ь
25
25
27
28
29
30
31
Рис. I.
Предложив кому-нибудь задумать целое число, не
превосходящее 31, и указать точно карточки, на которых
оно встречается, можно сразу «угадать» задуманное
число, сложив числа, стоящие в заголовках указанных
карточек.
Фокус можно «механизировать», написав указанные
таблички на пластинках весом в 1, 2, 4, 8, 16 г. Если
пластинки, содержащие задуманное число, положить на
достаточно чувствительные пружинные весы, то стрелка
остановится на задуманном числе. О другой
возможности механизировать фокус см. [25], стр. 71.
Двоичная система счисления часто используется в
современных электронных вычислительных машинах. Дело
в том, что элементы, с помощью которых изображаются
числа в этих машинах, могут находиться в двух легко
отличимых друг от друга состояниях (например,
положительная и отрицательная электрическая заряженность
участка диэлектрика, намагниченность в двух
противоположных направлениях участка магнитной ленты и т. д.).
Таким образом, каждый такой элемент может быть
14

использован для изображения одного разряда числа,
выраженного в двоичной системе (одно
состояние будет означать нуль в данном разряде,
другое— единицу). Имеет значение и то, что производить
действия только с двумя видами цифр (0 и 1) гораздо
проще.
Двоичная система находит применение и в теории
игр с тремя кучами предметов (см. § 10).
Троичная система счисления
В троичной системе счисления любое целое число
можно изобразить с помощью цифр: 0, 1, 2. Однако,
если ввести «отрицательные цифры», как это делается,
например, при изображении логарифмов с отрицательной
характеристикой, то в силу равенства
2'3m=3m+l — 3m=l-3m+l-\-T'3m
любое число в троичной системе можно изобразить с
помощью цифр: 0, 1, 1, следовательно, имеет место
Теорема. Любое целое число есть алгебраическая
сумма различных степеней тройки, т. е.
w=3"4-3*>+---— з?.—з?«—..., (3)
где «j, а. , Pj, р„ ...—различные целые
неотрицательные числа; отрицательных членов в равенстве
(3) может и не быть.
Например, для числа. 1910 имеем: N=1910 =
= 2121202(!) = 21212112!) = 2122Г111!) = 213П1^,=
= 220'П 11,„ = 3101111(8) =1010"Ш 1(1) = 3' — 3$ — З1 —
— З' + З — 3° (в процессе преобразований тройка
фигурирует временно в качестве цифры).
Отсюда, естественно, вытекает решение старинной
задачи о четырех гирях, с помощью которых можно на
равноплечих весах взвесить любой целочисленный вес
от 1 до 40 килограммов1).
*) Задачу о гирях рассматривал еще в 1202 г. Леонардо
Ливанский (Фибоначчи). Подробный анализ задачи и ее обобщение см. в [30],
стр. 176—178 (дополнение С. О. Шатуновского) и в £25], стр. 76—-90.
15

Действительно, положив на одну чашку весов
гари 3"» кг, З"» кг и т. д., а на другую —3^ кг, 3fr кг,
и т. д. [см. (3)], мы сможем взвесить вес N кг.
Следовательно, набор гирь: 1 кг, 3 кг, 9 кг, ..., 3" кг
позволит взвесить любой целочисленный вес N кг, где
д^<1 + з4-9+...+зп=3"+'—.
При л=3
Задачи
1. Изобразить (,а) в пятеричной системе счисления
числа 2713 и 409 с помощью цифр 0, 1, 2 (допускается
применение «отрицательных цифр»).
2. Проверьте правильность приведенных в начале
параграфа действий двумя путями:
а) выполняя все действия непосредственно в
восьмеричной системе;
б) представив числа, над которыми производятся те
или иные операции, и результаты операций в
десятичной системе.
3. Представьте •=- и -^ в виде систематических
дробей в двоичной, в троичной, в двенадцатеричной и
в шестидесятеричной системах.
Для проверки переведите полученные
систематические дроби в обыкновенные.
4. Представив 676 в двоичной, в троичной и в
пятеричной системах, извлеките из полученных чисел корень
квадратный.
5. Показать (,б), что для перехода от восьмеричной
системы к двоичной достаточно каждую цифру
выразить в виде трехзначного числа в двоичной системе;
например:
и наоборот:
7315(8)= 111 011 001 Ю1(г);
10 000101 110 <г) = 205б(8).
(6

Учитывая это правило и аналогичные правила для
перехода от четверичной, шестнадцатеричнои систем
к двоичной и т. п., покажите, что
И 4 I3(je) = 5515(e) и 773(8)=13323(1).
6. Докажите (*), что при любом &>5 число
123 454 321Ш— точный квадрат.
7< Как определить (') задуманное кем-нибудь
натуральное число N (в пределах до 1000) с помощью
10 вопросов, на которые задумавший число должен
отвечать лишь «да» или «нет»?
8. Не случайно на рисунке 1 каждая из карточек
содержит по шестнадцати чисел.
Вообще, если взять s карточек с заголовками: 1, 2,
4, 8, ..., 2*"*, 2s'1 и любое число т (от 1 до 2s—1)
написать в тех карточках, сумма заголовков которых
равна т, то в каждой карточке окажется по 2s'1 чисел).
Попробуйте доказать эту теорему (').
§ 2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЧИСЕЛ
Если для чисел а и b можно подобрать такое число с,
что а = Ьс, то говорят, что а делится на Ь, и называют
b делителем числа а (в этом параграфе в случаях,
когда не делается специальная оговорка, речь идет о
натуральных числах).
Число р называют простым, если оно имеет только
два Положительных делителя: 1 и р.
Всякое составное (т. е. не простое) число п можно
представить в виде
где plt pit ..., pk — простые числа, a a, J3, ..., а—
некоторые натуральные числа; если при этом среди чисел
Pi» Pf • • •» Pk нет одинаковых, то (1) называется
каноническим разложением числа п на сомножители.
В любом курсе теории чисел доказывается следующая
Теорема. Для любого числа п существует
только одно каноническое разложение (если не
считать разными те разложения, которые отличаются друг
от друга лишь порядком сомножителей).
Иному читателю может показаться странным, что
математики тратят силы на доказательство таких
17

«очевидных» теорем. Однако следующий пример, взятый
из другой числовой области (не из области натуральных
чисел), показывает, что совершенно аналогичная и,
казалось бы, «очевидная» теорема может быть неверна.
Комплексное число вида a -f- Ь V—6, где а и Ь —
любые целые числа, назовем «составным», если его можно
представить в виде
а + b У^б=(с + d V^l) (е -f /У="б),
где с, d, е, f— некоторые целые числа (которые, в
частности, могут быть и нулями) и каждый из
сомножителей отличается от 1 и от — 1. В противном случае
назовем его «простым».
По этому определению числа: 20 — V—6, 7 (здесь
а = 7 и Ь—0) и 6 (а = 6, Ь = 0) будут числами
составными:
20—УГП$ = (2 + ЗУ=6)(1 — 2 V— 6).
6=2-3=(К— б)-(— V— б)-
Но можно доказать, что числа: V— 6, — |/— 6, 2, 3
являются числами «простыми» (см., например, [24],
стр.84—85).Следовательно, «составное» число 6двумя
разными способами разлагается на «простые» множители!
Функции т(л) и S(n)
Обозначим через т(л) число положительных
делителей числа п, а через S(n) — их сумму.
Например, т(10) = 4 и 5(10) = 18, так как у числа
10 имеется только четыре положительных делителя:
1, 2, 5, 10.
Если п=р\р\р\. ..pi — каноническое разложение
числа п, то
х(ф=(« + 1)(р+1)(У4-1)...(а+1), (2)
s<«)=(i4-j\+rf+...+jfl(i+p,+...+p5)X
Х(1+а+...+р1)...(1+л+..-+рХ). (3)
Действительно, делителем числа п будет любое число
вида
*№:■•■#. (4)
И

в котором
0<а'<а; 0<B'sSB; 0<y'<y; ...; 0^о'<о. (5)
Так как а можно выбрать (а-}-1) способом, 8' можно
выбрать (8 4-1) способом и т. д., то для выбора
пары чисел а', 8' существует (а -}- 1) (р -}- 1) способов
(с каждым конкретным значением а! можно объединять
любое из р —|— 1 значений 8'), для выбора тройки чисел
а', В', у' существует («-+-1)(8-}-1)(у-}-1) способов
(любую конкретную пару а', 8' можно объединять с
любым из у -f" 1 значений числа у').
Продолжая эти рассуждения, мы убедимся, что группу
чисел а.', 8', у'» •••, о', удовлетворяющих условиям (5),
можно выбрать (a-f- 1)(8-}-1)(у-{-1).. .(а-}-1) способами.
Следовательно, формула (2) верна. Правильность же
формулы (3) следует из того, что при перемножении
многочленов, стоящих в правой части (3), получается
сумма всевозможных членов вида (4).
Если S(n) = 2n, то число и называется совершенным.
Например, 6 и 28 — числа совершенные, так как
S(6)=12 и£(28) = 56.
Еще Евклид установил, что совершенными будут
четные числа вида
N=2*(2*+1— 1), (6)
где a — натуральное число и 2°1+1 — 1—число простое
(см. {2], стр. 72—74). С другой стороны, четных
совершенных чисел с иным каноническим разложением не
существует.
Пока установлено, что числа вида 2°1+t —1
(называемые числами Мерсенна — по имени французского
ученого XVII века) будут простыми при я=1, 2, 4, 6, 12,
16, 18, 30, 60, 88, 106, 126, 520, 606, 1278, 2202, 2280;
следовательно, пока известны только семнадцать
совершенных чисел.
Первые семь совершенных чисел таковы:
6, 28, 496, 8128, 33550336, 8589 869056,
137 438691328.
До сих пор неизвестно, существуют ли нечетные
совершенные числа.
В средние века математики-мистики уделяли большое
внимание так называемым дружественным числам, то
19

есть таким числам а и Ь, для которых S(a)=^S{b) = a-\-b.
Пользуясь формулой (3), докажите, что 220 и 284 —
дружественные числа; дружественными будут также
числа 18 416 и 17 246.
Функция [х] (целая часть х)
Функция [х] равна наибольшему целому числу, не
превосходящему х (х — любое действительное число).
Например:
[УЛ = 2, Н?]=-4,
[6] = 6.
Функция [х] имеет
«точки разрыва»: при
целых значениях х она
«изменяется скачком».
На рис. 2 дан график
этой функции, причем
левый конец каждого из
горизонтальных отрезков
принадлежит графику
(жирные точки), а
правый— не принадлежит.
Попробуйте доказать ('), что если п\=р\р\р\.. ,р\—
каноническое разложение числа п\, то « = I — +
ГлП Г л"1
+ -j + — + ...; аналогичные формулы имеют
место для р, у» ■ • •> <*•
Зная это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно, пусть
100! = 2ТО.. .97-. Тогда * = [!~ ] + [Щ + [f\ +
Г..
-3 -i -/_'_> } 3 I J" **
Рис. 2.
+ 6 + 3 + 1 = 97иу
100'
64
=
+
Г1001
L 5 J
Г1001
128
+
+ ...=50 + 25 + 12 +
■WO] + ...=20+4 = 24.
Следовательно, 100! делится (2-5)", т. е.
оканчивается двадцатью четырьмя нулями.
20

Задачи
1. Докажите (8), что по формуле (6)- при о=2280
получается 1373-значное совершенное число {lg2s=
= 0,301029996).
2. Пользуясь формулой (3), докажите (*), что для
N = 2" (2а+1 — 1), где 2'+»—1 — простое число, S(N) = 2N.
3. Найти наибольшее натуральное число к, при ко-
101-102...999.1000 - /т
тором ^ ~ будет целым числом (").
4. Показать ("), что 1322314049 613 223140 496 =
= 363 636364* — наименьший точный квадрат,
записываемый в десятичной системе двумя одинаковыми, рядом
друг с другом написанными числами (в других системах
счисления аналогичная задача допускает меньшие решения,
например: 11(|) = 22; 882 882(м) = 7332*; 288 288(„> = 3900').
Поищите точные кубы, записываемые в той или иной
системе счисления двумя одинаковыми, рядом написанными
числами (например: 2' = 11(7); 101101001 101101001U) = 57a).
§ 3. СРАВНЕНИЯ
Если целые числа а и Ь дают при делении на
натуральное число т одинаковые остатки, т. е. a = mql-\-r
и b = mq1-\-r{r, qu qx—целые числа, и 0«sr<ra), то
их называют равноостаточными по модулю т или
сравнимыми по модулю т и записывают это так:
а == b(modт). Например: 27^—13(mod8), так как
27 = 3.8 + 3 и—13 = 8 (—2) +3. Очевидно, разность
а—b сравнимых по модулю т чисел делится на т.
В нашем случае 27 — (—13) = 40; 40 делится на 8.
Предлагаем читателю доказать следующие свойства
сравнений:
если a ==b(modт), с == с? (mod/я), то:
1) a-{-c = &+d(modm), 2) a —c = fr—-d(modm),
3) k-a = k-b(modm) (к— любое целое число),
4) a-c = &-d(modто), 5) а" =зb"(modт), (л—любое
натуральное число). (Учтите, что a = b-\-mt, c = d-\-mt',
где t и t' — некоторые целые числа.)
Из перечисленных свойств легко получается (")
теорема: Если a.=E$(modm)uf{z)=aa-{-a1z-\- ... -\-anzn—
некоторый многочлен с целыми коэффициентами, то
/(a)=/(p)(mod«).
21

С помощью этой теоремы можно вывести признаки
делимости натурального числа N на 7, 9, 11, 13.
Пусть N=ckck_lc„_1.. .<WoUo) = <7ft10* + (7A_110*-4-
+ ... + ^Ю1 + ^lO + c^C^lOOO'-f Cs_l1000*-1 +
+...+C.K)OQ1+C1100o4-C0; здесь С0, С,,..., С,,,—
числа, получающиеся при разбиении числа N справа
налево на грани по три цифры в каждой, s = [у] , а
число С, может оказаться однозначным, двузначным
или трехзначным (например, N= 15032 104 341 = 341 +
-4-104-1000 + 32-1000* + 15.1000*; здесь s = 3, С0 = 341,
С, = 104, С, = 32 и С, = 15).
Вводя обозначения:
<?*** + **-,«*"' + • • • + Сг** + СХХ + С, =/ (*),
C12? + Cs_1z<->+...+Clz + C, = F(z),
будем иметь:
iV=/(10) = F(1000),
fV) = ck + ck_i + ...-\-c1-)rc1Jrcl)=^{N) (сум1„_
цифр числа N),
/(-1)=*.-<\+*.-...+(--1)Ч=<»'(Л0.
Г(-\)=Са-С1 + Сж-...+(-\уС, = '2№
последние две суммы назовем условно алгебраической
суммой цифр и алгебраической суммой трехзначных
граней числа N.
Так как 10=1 (mod 9), то на основании последней
теоремы: /(10) ==/(1) (mod 9) или Л = a (N) (mod 9), т. е.
N дает при делении на 9 тот же остаток, что и a (N),
поэтому N делится на 9 в том и только в том случае,
если <j(N) делится на 9.
Аналогично, из сравнения 10 = — 1 (mod 11) имеем:
/(10)=/(— 1)(mod 11) или N=a'(N){moAl\);
следовательно, N делится на 11, если на 11 делится
алгебраическая сумма цифр числа N (и наоборот!).
Из легко проверяемых сравнений 1000 = —l(mod7),
1000=—1 (mod 11} и 1000=—1 (mod 13) следует:
F(1Q0Q) = F(— l)(mod7), F(1000)=F(—l)(modll)
F{l(№) = F{— 1) (mod 13),
22

или
n=2' (W) (ffl0d 7)> N= 2' (Л0 (mod u).
М=2'(Л/)(тос113),
т. е. Л/1 делится на 7, если алгебраическая сумма
трехзначных граней числа N делится на 7 (и наоборот!);
точно так же формулируются признаки делимости на
11 и на 13.
Аналогичные рассуждения пригодны и для вывода
признаков делимости чисел, записанных в £-ичной
системе счисления, на k — 1 и на fe-j-1: число N делится
на k — 1 (на k-\-l) в том и только в том случае, если
сумма цифр его (алгебраическая сумма цифр) — при
записи N в й-ичной системе—делится на k — 1 (на «-{-1).
Проведите эти рассуждения!
Найдите признаки делимости на пять и на тринадцать
в восьмеричной системе, признаки делимости на два, на
четыре, на семь в троичной системе, признаки делимости на
тринадцать и на восемь в пятеричной системе счисления (").
С помощью сравнений легко решаются задачи
следующего типа: найти остаток, получающийся при
делении числа N=13"+ 48-10s* на 17. Очевидно, надо
найти наименьшее неотрицательное число, сравнимое с N
по модулю 17; применяя свойство сравнений, получим
13"4-48.10" = ( — 4)" — 3-1001' =4.16" — 3< — 2)" =
= — 4( —1)" + 6-16« = — 4 + 6(— 1)' = 2(mod 17),
следовательно, искомый остаток равен двум.
Найдите (14) тем же путем последние две цифры
чисел 293"*, 210»0, 69й + 31м.
Функция Эйлера
Функцией Эйлера <р (п) (п—натуральное число)
называется число чисел, меньших и и взаимно простых
с п. Покажите, что
я = 2
<?(«) = 1
3
2
4
2
5
4
6
2
7
6
8
4
9
6
10
4
12
4
20
8
38
12
(например, у (10) = 4, так как из чисел, меньших десяти,
только четыре числа: 1, 3, 7, 9 взаимно просты с
десятью). Считают <р(1) = 1.
23

Легко доказать ("), что при р простом: <р(р)=р — 1
и у{рк)=рк—р*-\
В теории чисел доказывается, что для взаимно
простых а и b <р lab) = <р (а) <р (Ь). Отсюда следует, что если
n=p"1pl ... р\—каноническое разложение числа п, то
<р(я)=(#-к~№-рГ1) ••• (Pl-PD- 0)
Гаусс доказал, что сумма значений функции Эйлера,
вычисленных для всех делителей числа п, равна числу п.
Например,
<р(1) + <р(2) + <р(5) + ¥(10) = 1+ 1+4 + 4 = 10.
Эйлер доказал, что всегда при взаимно простых к и п
£?<">= 1 (m0(i я); в частности, для простого р, если а
не делится на р, ap~l^\ (modp) («малая теорема
Ферма»).
Рекомендуем читателю проверить на ряде частных
примеров справедливость теорем Эйлера, Гаусса и Ферма
и формулу (1).
Из теоремы Эйлера следует, что «показательное
сравнение» £г=1(то<1л) при взаимно простых k и и
обязательно имеет решение: z = <p(n); однако может
оказаться, что это сравнение будет верным и при
меньших значениях z.
Наименьшее натуральное число z0, удовлетворяющее
этому сравнению, называется показателем, которому
принадлежит к по модулю п. Можно доказать ("), что
z0 обязательно будет делителем числа <р (и). Чтобы найти,
например, наименьший корень сравнения: 60* = 1 (mod 17),
надо испытать все делители числа <р(17) = 16. Так как
60г=9* (mod 17) и 92 = —4 (mod 17), 9* = ( —4)2е=
S — 1 (mod 17), 9" = 1 (mod 17), то 60 принадлежит
показателю 8 по модулю 17.
Если несократимую дробь -^- представить в виде
систематической &-ичной дроби (при k и и взаимно
простых), то число цифр в периоде этой дроби будет равно (")
показателю z0, которому принадлежит k по модулю и.
Например, представляя р= в виде систематической дроби
в шестидесятеричной системе счисления, мы в периоде
24

бесконечной дроби будем иметь 8 цифр. Убедитесь сами,
деля 1 на 17, что ^ = 0, (3 ЗГ 45 52 56 28 П 7)(,„.
Найдите указанным путем число цифр в периодах
бесконечных десятичных дробей, соответствующих обык-
„ 114 6 2
новенным дробям: у t |з» Тз' 13' 19 и пРовеРьте
результаты путем непосредственного деления на 7, на 13 и на 19.
§ 4. НЕПРЕРЫВНЫЕ ДРОБИ И НЕОПРЕДЕЛЕННЫЕ
УРАВНЕНИЯ
Любое положительное рациональное числоу(аиЬ —
натуральные числа) можно представить в виде так
называемой непрерывной (цепной) дроби.
Пусть при делении а на Ь в частном получается
qn= у , а в остатке /\; при делении b на г, в частном
получается qv а в остатке г,; при делении г1 на г,
в частном получается qt, а в остатке г, и т. д. На
каком-то этапе гп_1 обязательно разделится без
остатка на гп (£й=* = 0„).
В теории чисел доказывается, что r„ = (a, b)((a, Ь) —
общий наибольший делитель чисел а и Ь). Процесс
отыскания .общего наибольшего делителя двух чисел с
помощью последовательных делений называют алгоритмом
Евклида.
Обычно деления располагают в компактной форме:
_ а[Ъ_
- rALi.
25

Очевидно,
■я,
! l - а 1
i — •• • —ч»-\
''ж
ft
л 4
?«-
1
1
, 1
tfn-
1
-+£•
Это и есть искомая непрерывная дробь. Ее часто
пишут в виде
I
"Т"о— I 1
~Яп'
где любая из единиц делится на все стояшее под ней
выражение.
Непрерывную дробь удобно также записывать в
условной форме
■£=[?•» <7l' Я Яа-if ЯпЪ
где указываются лишь так называемые неполные частные:
Я» Я и Яг> •••» Яп-о Я,,-
Например,
§=4+1 + ^ =[4,2,3, 2,2],
2 +2"
26

Так как
173 1
156
39 [ 17
— 34 2
17 1 5
_15 '-з~
5 2
_4 2
-2Ц_
2 2
39
4
О
Если оборвать дробь на £-м неполном частном, то,
представив укороченную непрерывную дробь [qt, qx, ...
• • •» Як-v Чк\ в вИДе обыкновенной дроби, получим так
называемую k-ю подходящую дробь ^. Очевидно, ^-=~-
Подходящие дроби обладают-рядом важных свойств
(см. [2] или [28]).
Свойство 1. Числители и знаменатели трех
соседних подходящих дробей связаны рекуррентными
соотношениями:
позволяющими без труда вычислять подходящие дроби
по известным неполным частным.
Подсчитав для дроби -^ ^ = 4 = уИ Qi==4"T-2" =
=Y» мы остальные подходящие дроби можем найти по
формулам (1). Результаты вычисления удобно располагать
в виде таблицы:
к
Як
Рк
Qk
0
4
4
1
1
2
9
2
2
3
31
7
3
2
71
16
4
2
173
39
27

(2)
Например:
Q.=Qi?.+Q.=2.3+i=7
и т. д.
Свойство 2. Всегда
Свойство 3. При любом к имеем:
Рк ^-^(-Р*-1
Qk Qk-i QkQk-i
или
Рк0к-*-0кРк-1 = {-1)*-1- (3)
Отсюда следует, что (Pk, Qft) = l, так как иначе (то
есть при (Л, Q»)>1) выражение РД^ — ЯЛ.»
равное (— 1) , не может делиться на число (Pk, Qk).
Если (а, Ь) = \, то из-?-= 7^ следует а = Рп иЬ =
= Q„, и из (3) при к = п будем иметь:
eQ-.-W-i^-ir1. (4)
Равенство (4) является ключом к решению в целых
числах так называемого неопределенного уравнения
ах-\-Ьу = с, (5)
где а, Ь и с — целые числа, причем (а, &) = 1.
Действительно, переписав (4) в виде
a(-iriCQn_1 + fe(-l)VPn_1 = C)
можно утверждать, что числа
^(-ir'cQ-i. л=(-1)"^»-. (6)
представляют одно из решений в целых числах
уравнения (5). Легко показать (18), что:
1) все остальные решения уравнения (5) получаются
из (6) по формулам: x=x0-\-bt; у*=уа—at, где t —
произвольное целое число;
2) уравнение ах-\-Ъу = с при (а, &)>1 не решается
в целых числах, если с не делится на (а, Ь) (если же с
28

делится на (а, Ь), то, сокращая все члены уравнения (5)
на (а, Ь), придем к уравнению а'х-\-Ь'у = с', где
(а',Ь')=1).
Поясним сказанное выше на примере.
В банке, где сидят пауки и жуки, насчитывается всего
38 ног. Сколько пауков (х) и сколько жуков (у) сидит
в банке, если у паука 8, а у жука 6 ног?
Очевидно, 8x-f-6y = 38 или 4x-}-3j/ = 19. Здесь
а = 4, Ь = 3, с = 19. Для непрерывной дроби-д-=1 + д-
■Q=-y и т?=-$- Следовательно,
° а:0 = (— I1)1"1 • 19-1 = 19, Л = (-1)'.19.1 = -19,
откуда
х=19 + 3г; у= —19 — U.
По смыслу задачи нас интересуют лишь
неотрицательные значения х и у, т. е. должно быть 19-}-3^0
и —19 — 4^0, или — у<^<— ^. При *=—5
имеем: х1 = 4; j/x = 1 (четыре паука и один жук), а
при £= —6 получим: x1 = l; yt = 5 (один паук и пять
жуков).
Укажем еще другой путь решения уравнения (5).
Перепишем его в виде ах — с = — by. Очевидно, надо найти
целые значения х, при которых разность ах — с делится
на Ь, т. е.
ах = с (mod b). (7)
Этому условию удовлетворяет x = m'p(*)-1 (modfe).
Действительно, подставив это значение в сравнение (7),
получим аса*0>~1==С'1 (modfe) (последний переход сделан
на основании теоремы Эйлера).
Например, для уравнения 4х-\-Зу=19 имеем: х==
=5=19-4* (2> -1 (mod З^Ы1"1 (mod 3) или x=l-f 3s;
но тогда у = 5 — 4s. При s = 0 получим xt = 1 и у1 = 5,
а при s = l получим xt = 4 и j/,= l.
Решите любым из указанных способов
неопределенные уравнения:
1) 617х— 125у = 91, 2) 12х + 31j/ = 170
(см. в [22] задачи «ревизия кооператива» и «фокус на
отгадывание дня рождения»).
В непрерывную дробь можно разложить также и
любое иррациональное число а. Выделяя из а целую часть,
29

получим:
«=?.+^ (?.«[■]. ±<L ■,>!).
затем:
«I = ^i + Г (?. = [«Л» а» > 1).
а. = ^+-^ (?. = Ы- *.>1)ит.д.
После и-кратного повторения этой операции полу1
а = [^о» ?,» •••» ?„_,, «Л; так как при любом пап ир
ционально, то процесс никогда не закончится, и мы п
дем к так называемой бесконечной непрерывной дрс
<* = [?<,. ?i. Ях 0в-1» ?»> ...]•
Если а — «квадратичная иррациональность», т. е. а
а-\-ЬУТ . ,
=——~—, где а, о, с, а — целые числа, то непол!
частные, начиная с некоторого номера, будут перис
чески повторяться (см. [2]). Например:
УЗ -1 2
1+—-о~ 1+ 2 +УГ+1
=1
Уз—1
1
1 » 2 + (УТ-1)'
Так как аг = У~3 — 1=о,, то дальше неполные част!
будут периодически повторяться.
В целом будем иметь: V 3 = [1, 1, 2^1, 2, 1, 2,.
Покажите аналогичным путем, что Y 5 = [2, 4, 4, .
и У"7 = [2, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, ...]. Указам
выше свойства подходящих дробей, имеющие мест»
для бесконечных непрерывных дробей, позволяют ле
находить рациональные числа, как угодно близкие к
если известно достаточно много неполных частных.
Действительно, на основании второго свойства п
ходящих дробей а заключено между любыми соседи
30

р р
подходящими дробями т^1* и л*. Но абсолютная
величина разности их равна ~—ту- (свойство третье).
Следовательно, погрешность приближенного равенства а ч=
s=^zl меньше, чем ^—^-, Например, для |/"5 = [2, 4,
4, 4, ...] имеем:
k
4k
Ph
Он
0
2
2
1
1
4
9
4
2
4
38
17
3
4
161
72
4 ...
4 ...
682 ...
305 ...
следовательно, Y Ъ=^^ (погрешность <Сур^\ У^^ут
(погрешность <72.зо5) и т. д.
Найдите (") подходящие дроби для "|/2^=[1, 2, 2, ...]
и для V^3 = [l, 1, 2, 1, 2Г ...], которые отличались бы
от У~2 и от ]/~3 меньше, чем на 10"*.
Разложение ]/»Г в непрерывную дробь дает простой
способ решения в целых числах так называемого
уравнения Пелля:
х% — тух=\. (8)
Пусть Vm = [qt, д„ дг, ... , у,_„ qs, ?„ qlt ...]
(подчеркнут период непрерывной дроби).
Оказывается (см. [2]), что при s четном решениями
уравнения (8) будут пары чисел: (Ps_t, Qs_t), (Р„_„
Q»-i)> (pts-i> Q,s-i) и т- Д-» а при s нечетном —пары
чисел: (Р„_„ Q„_,), (Р„_„ Q„_J, (PM_lf Q,,.,) и т. д.
В [2] дается таблица разложений У~т в непрерывную
дробь при яг < 100, а также наименьшие целые
положительные решения уравнения х* — ту*=1. Для
31

^10 = [3, 6, 6, 6, ...] имеем:
k
Як
Рк
Qk
0
3
3
1
1
6
19
6
2
6
117
37
3 ...
6 ...
721 ...
228 ...
Так как s=l, то решениями уравнения х1— 10у* = 1
будут пары чисел: х1 = Р1 = 19 и y=Ql = 6; хх=*
= р$ = 721_и jy, = Q, = 228 и т. д.
Для "|/32==[5, 1, 1, 1 10, 1, 1, ...] имеем;
k
Як
Рк
Qu
0
5
5
1
1
1
6
1
*
1
11
2
3
1
17
3
4
10
181
32
•
1
198
35
6
1
379
67
7
1
577
102
Так как s=4, то решениями уравнения х1 — 32,у* = 1
будут пары чисел: х1 = Р, = 17 и у1 = Q, = 3; хх = Рч =
= 577 и ^ = Q7=102 и т. д.
Зная, что 1/89 = [9, 2, 3, 3, 18, 2, 3, ...] и "/61 =
= [7, 1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14, 1, 4, 3, ...],
покажите, что наименьшими целыми решениями уравнений
х1 — 89>>* *=1 я х1 — 61_у* = 1 будут соответственно пары
чисел: (500001, 53000) и (1766319049, 226 153980).
В одной статье польского математика Серпин-
ского приводится наименьшее решение уравнения
х1 — 991У=1: .*, = 379 516400 906811 930638014896080
и у, = 12 055 735 790 331 359 447 442 538 767.
Это значит, что У 991j>*-j-l при любом целом
значении у, не превосходящем числа ylt будет числом
иррациональным и, самое меньшее, при у=^у1 получится
рациональное число хх.
Для того чтобы представить себе, как велики числа
хг и ух в последнем примере, заметим, что если бы мы
даже в течение миллиарда миллиардов (1018) лет
вычисляли значения ]/991У + 1 при у = \, 2, 3, 4,..., тратя
32

на каждое вычисление по одной секунде, то каждый раз
у нас корень точно не извлекался бы.
Однако нельзя все-таки было бы утверждать, что
У991.у*-{-1 будет иррациональным при любом
натуральном у: стоило бы, увеличив «испытательный срок»
приблизите льно_в_400_раз, «дойти» до yt и мы обнаружили
бы, что ]/991j/, -\- 1 — число рациональное!
Рассмотрим еще одну задачу, приписываемую
Архимеду и сводящуюся в конце концов к уравнению типа (8).
В найденной в конце восемнадцатого века рукописи
говорится, что Архимед якобы нашел старинную надпись
и послал содержавшуюся в ней задачу александрийским
математикам.
В задаче требуется определить размеры стада коров
и быков, принадлежащих Солнцу. Из первой части
данного в стихах условия задачи (см. [16], стр. 204—206)
следует, что стадо состояло из белых, черных, бурых
и пестрых быков и коров, причем количества быков
(U, X, V, Z) и коров (и, х, у, z) этих расцветок были
связаны соотношениями:
U=^X+Y; X=^Z-\-Y; Z=%2U+Y;
и=^(Х-\-х); x = l(Z-\-z); z=^{Y+y);
y=l£(U-\-u).
Любители вычислений могут найти отсюда (,0):
(/=10366 482*, и =7 206 360*,
Х= 7460514 t, л: = 4893246 t,
Y= 7358060 t, j/=3515820 t,
Z= 4149387 t, z = 5439213 t
(t принимает любые целые значения).
Однако во второй части текста задачи в обращении
к лицу, которое будет решать задачу, отмечается, что
главные трудности в задаче создаются дополнительными
условиями:
«Если сочтешь, скота всего там сколько набралось,
Сколько паслось на лугах мясообильных быков,
Сколько удойных коров и сколько каждого цвета,
2 А. П. Доноряд
33

Не назовет уж никто в числах невеждой тебя.
Все же и к мудрым еще тебя не причислят за это,
Коль не учтешь ты еще разных повадок быков.»
После перечисления повадок быков в заключительной
части текста задачи говорится:
«Если сумеешь все это найти и взором духовным
Стада размеры объять сам и другим передать,
Гордо шествуй вперед, кичася великой победой:
Знай, что, других превзойдя, первый по мудрости ты».
Если учесть повадки быков, то в приведенных
формулах t надо выбрать так, чтобы:
1) сумма U~\-X, равная 17826996 t, была бы точным
квадратом, для чего следует взять £ = 4456 749 s*, где
s — любое натуральное число;
2) сумма Y-\-Z, равная 11 507 4471, была бы «тре-
угольным числом», т. е. числом вида —^—•'.
Подставив вместо t полученное выше выражение,
придем к уравнению: 51285803909 803 д, = в(в + 1).
Если умножим обе части этого уравнения на 8,
прибавим затем к обеим частям по единице и заменим,
наконец, 2л-|-1 на w, то получим уравнение Пелля:
w* — 410 286 423 278 424 s* = l.
Если обозначим через ЛГ численность всего стада
(наименьшее ее значение), когда учтены дополнительные
условия, то окажется (по подсчетам, проделанным в
1880 году Амтором), что
N^77-1010'6".
Вряд ли читателю удастся «взором духовным стада
размеры объять и другим передать»!
§ 5. ПИФАГОРОВЫ И ГЕРОНОВЫ ТРОЙКИ ЧИСЕЛ
Известное соотношение между катетами и
гипотенузой прямоугольного треугольника x1Jry1 = zt можно
рассматривать как неопределенное уравнение с тремя
неизвестными.
Оказывается [2], что всевозможные тройки попарно
взаимно простых целых чисел, удовлетворяющих этому
уравнению («пифагоровы тройки чисел»), получаются по
34

формулам:
у =2av,
z=ax-{-vt,
если вспомогательным переменным и и v придавать
взаимно простые значения разной четности (при
нарушении этого условия будут получаться пифагоровы тройки
чисел, у которых общий наибольший делитель больше
единицы). Например:
и
2
4
3
4
5
3
V
1
1
2
3
2
1
X
3
15
5
7
21
8
У
4
8
12
24
га
6
z
5
17
13
25
29
10
Пифагоровы тройки чисел представляют частный слу«
чай «героиовых троек чисел»—так называются три
целых числа, выражающие
длины сторон треугольника
с целочисленной площадью.
Легко доказать (,l), что
любая из высот «героиова
треугольника» (например,
BD на рис. 3)дает два
прямоугольных треугольника
(ABD и BDC) с
рациональными сторонами,
примыкающих или налегающих друг
на друга.
Взяв прямоугольные
треугольники Д и Д' с
целочисленными сторонами а, Ь,
с и а', Ь', с' (си с' — гипо-
ч а'
тенузы) и умножив все стороны Д на —, получим
треугольник Д, со сторонами а', —, ^-, подобный
треугольнику Д.
2»
&S

Совместив одинаковые катеты треугольников Д, и
Д', можно получить два треугольника с рациональными
сторонами ^ с, с', -j b ± V , при увеличении этих чисел
в а раз получим две героновы тройки чисел: а'с, ас',
\а'Ъ±Ь'а\.
Тем же путем, «уравнивая» катет а с катетом V
(умножая стороны треугольника Д на —) или «уравни-
вая» катет b с катетом а' (при умножении на ~), или
«уравнивая» b с V (при умножении на -А, можно
получить еще шесть героновых троек чисел:
а'с, be', \а'а±Ь'Ь\\ Ь'с, ас', \b'b4rа'а\;
b'c,bc',\b'a±a'b\.
Например, для пифагоровых троек чисел: (3, 4, 5) и
(15, 8, 17) указанным путем легко получить 8
героновых троек чисел: (75, 51, 84), (75, 51, 36), (75, 68, 77),
(75, 68, 13), (40, 51, 77), (40, 51, 13), (40, 68, 84),
(40, 68, 36). Первые две и последние две тройки чисел
после сокращения соответственно на 3 и на 4 дадут:
(25, 17, 28), (25, 17, 12), (10, 17, 21), (10, 17, 9).
Найдите (") героновы тройки чисел, используя
пифагоровы тройки
1) (3, 4, 5) и (5, 12, 13),
2) (7, 24, 25) и (7, 24, 25).
§ 6. АРИФМЕТИЧЕСКИЕ РАЗВЛЕЧЕНИЯ
Существуют арифметические задачи, решение
которых не связано с какой-либо теорией, а требует от
решающего лишь сообразительности и терпения.
К подобного рода задачам можно отнести поиски
интересных соотношений между числами, различных
числовых курьезов и т. п.
Приведем несколько типичных примеров:
1. Между цифрами: 1 2345678 9, не меняя их
последовательности, расставить знаки арифметических
операций и (если понадобится) скобки так, чтобы в
результате получилось то или иное наперед заданное
число N. Например, при N= '/i и при N= 1 имеем: */, =
86

=(123—45): (67+ 89); 1=1 + 2—3+4^5—6 + 7—8+9;
1 = 1 + 23 —45 —67 + 89 и т. п.
Можно задаться целью представить таким образом
возможно большее число натуральных чисел или дробей
(например, дробей вида -g-, где А = 1, 2, 3, ...). Можно,
наоборот, взять какое-нибудь число и искать
всевозможные его представления.
В задачу можно ввести ограничения, разрешив
пользоваться только знаками + и —, или, напротив,
увеличить свободу действий, разрешив пользоваться
радикалами, менять порядок цифр (например, 100:= 67* —
— 4385 —1—уТ) и т. д.
2. Разместить цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 в
приведенных схемах так, чтобы после выполнения
указанных операций получились правильные равенства:
а) _ _• = (например, 12 -483 = 5796 и т. п.)
б) •__ = __■__
в) •_ = __•__
3. Разместить цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы
произведение трех трехзначных чисел: • .
было бы возможно большим (или возможно малым).
4. Разместить цифры: 0, 1,2, 3, 4, 5, 6, 7, 8, 9 так,
чтобы имело место: : =л, где п равно
одному из чисел: 2, 3, 4, 5, 6, 7, 8, 9 (см. [39], 1946, № 3).
5. Некоторые числа можно представить в иной форме,
не привлекая новых цифр; например: 660 = 6! — 60;
1395=15-93; 145=1! + 4! + 5!; 144 = (1+ 4)! + 4! =
= (1+]/Т)!-4!; 387 420 489 = 387+4"-4".
Попробуйте найти аналогичные равенства.
6. Использовав по одному, разу каждую из цифр
1, 2, 3, 4, 5, 6 и каждую из операций: сложение,
вычитание, умножение, деление и возведение в степень,
получить возможно бблыпее число ([36], 1946, № 2, стр. 49).
7. В выражении: 1:2:3:4:5:6:7:8:9 расставить
скобки так, чтобы после вычислений получилось наибольшее
(или наименьшее) из всех возможных чисел.
8. В примерах: 41096-83 = 3 410968 и 8-86 = 688
умножение на двузначное число «упрощено»: вторая
цифра множителя ставится перед множимым, а первая —
после него.
Поищите аналогичные примеры.
37

9. В одной журнальной заметке говорится, что в
пределах первых десяти тысяч существует лишь восемь
чисел, записываемых в двух системах счисления
тремя одинаковыми цифрами.
Наименьшее и наибольшее из них: 273 = 111(1в> =
= 333,,, и 9114 = 222(е„ = Т514 Т4(15); попробуйте найти
остальные.
Не удастся ли вам найти числа: а) записываемые
в трех системах счисления тремя одинаковыми цифрами;
б) записываемые в двух системах счисления четырьмя
одинаковыми цифрами.
10. Любителям математики можно порекомендовать
коллекционирование существующих и поиски новых
числовых курьезов. Приведем несколько примеров,
которые могут подсказать темы для самостоятельных поисков.
а) ШШ44(11Д=ТПТ* ; 4 4l6lOlli) = 7 7\u)
б) 7778* — 2223' = 55 555 555;
в) 888 889* — 111 112а = 777 777 777 777;
г) 999999999* = 12345 678 987 654321 -(1+2 + 3 +
+ 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4+3+2+1).
Как проще всего убедиться в правильности
последних трех равенств?(")
11. Забавные сокращения.
Существуют дроби, величина которых не меняется
при вычеркивании одинаковых цифр и даже групп цифр
u л 19 1 3544
в числителе и в знаменателе. Например: gg = -g-; 7531 =
__344, 2666_266_26_j2_. 143185 _ 1435
— 731 * 6665 — 665 ~'65 — 5 ' 17018 56а-'170560'
4251935 345 425 345 м ,
91819355 ISS^STffiSlSS И Т' Д" МоЖНО ^^ВИТЬ вопрос
об отысканий всех дробей, допускающих такое
«сокращение», оговорив, из скольких цифр составлены
числитель и знаменатель и на каких местах должны стоять
«сокращаемые» цифры. Например, из \^ЬТ_ ==~ {афс)
Юаб
легко получить с=^-j-^; в пределах до десяти
целочисленные значения Ъ и с получаются лишь при а = \,
л л , 16 19 26 49
2, 4, что дает дроби: й, й, й, _.
12. Пользуясь четырьмя четверками (в других
вариантах— пятью пятерками, четырьмя пятерками и т. п.),
38

представить любое целое число от 1 до л, где
л—возможно большее натуральное число. Например: 1=4—
-4+1S 7=^-4 и т. п.
Можно договориться об использовании знака
факториала (21=4!-\-~r-—4), знака радикала (17 = 1/4*+-^-),
ввести «точку перед числом» на уровне строки и «точку
над числом» для изображения десятичных дробей и
десятичных периодических дробей (0,4 = .4; 0,(4) = .4)
(см. [13], стр. 317); например:
19 = х + -^ и т. п.
Если допустить и использование знака логарифма, то,
как это следует из формулы
п=_log4 \ log4V V У •• -УЩ) (проверьте! <"0))>
. v '
2л радикалов
даже с помощью трех четверок можно изобразить любое
натуральное число л.
§ 7. ЧИСЛОВЫЕ ФОКУСЫ
Иногда встречаются люди, выполняющие в уме с
необычайной скоростью операции над многозначными
числами. Такие артисты-вычислители, используя некоторые
искусственные приемы и имеющиеся у них в запасе
различные числовые фокусы, поражают публику рядом
эффектных номеров.
Конечно, даже зная секрет того или иного «номера»,
далеко не все могут с успехом выступать в роли
артиста-вычислителя. Знание секрета помогает лишь в
простейших случаях.
Дадим описание нескольких простых числовых
фокусов.
Угадывание задуманных чисел
Предложив кому-нибудь задумать число и проделать
над ним определенные операции, в ряде случаев легко
по результату вычислений определить задуманное число.
Приведем несколько примеров:
39

1. Предложите кому-нибудь задумать число,
прибавить к нему 3, умножить полученную сумму на 6,
вычесть из этого произведения задуманное число, затем
вычесть еще 8 и, наконец, разделить все это на 5. Если
вам скажут результат, то вы можете сразу назвать
задуманное число. Как следует из равенства [(jc-f-3)-6 —
— х — 8]:5 = х-\-2, для этого достаточно из
полученного результата вычесть два.
2. Предложите кому-нибудь задумать в пределах до
ста два числа х и у (число месяца, возраст человека,
номер обуви, сдачу с рубля и т. п.) и проделать над
ними ряд операций, которые определяются левой частью
равенства
(2 -х -\- 5) • 50 -{-у — 365 = 100л: -{-у — 115 = N.
Тогда, зная лишь N, вы можете- определить хну
(прибавив к N 115 и разбив полученное число на два числа,
отделив две последние цифры).
3. Предложите кому-нибудь задумать число (I),
месяц (т) и год (п) какого-нибудь события, происшедшего
в XX веке (для года взять последние две цифры) и
проделать над /, т, п операции, указанные в левой части
равенства
[(20/+ 222) • 5 +/и] • 100-j-я-{-111 =
= 10000/+100ff2 + « + llllll=M
Для определения задуманной даты надо из N вычесть
111111 и полученную разность разбить на грани,
отделяя— справа налево — по две цифры. Например, если
N=201656, то было задумано 9-05-45, т, е. 9 мая
1945 года. Подобных «фокусов» можно придумать сколько
угодно.
Угадывание результатов действий над неизвестным
числом
Существует ряд фокусов, основанных на том, что
определенные операции приводят к одинаковым
результатам для довольно широкого класса чисел. Иногда это
происходит благодаря исключению задуманного числа
в процессе выполнения действия, иногда — в силу
особенности класса чисел, иногда — благодаря особенности
40

производимых операций. Вот несколько типичных
примеров:
1. Если к любому трехзначному числу N приписать
справа такое же число и разделить полученное
шестизначное число (оно будет равно 100ЬЛ/ = ЛЛ7-1ЫЗ)
на 7, затем полученное частное на Ми, наконец, второе
частное — на 11, то в результате всегда получится 13.
Большинству людей кажется удивительным то, что
все деления происходят без остатка при случайном
выборе N.
2. Так как любое нечетное, отличное от трех,
простое число р можно представить в виде 6k ±1, то
pt4-17 = 36*1±12* + 18» т- е- Р* + 17 ПРИ делении на
12 всегда даст в остатке 6.
3. Если в трехзначном числе abc (здесь а, Ь, с —
цифры числа) а>с, то:
1) в разности abc— cba = a.$y всегда {J = 9 = а-|-у»
2) apY + YPa= Ю89.
Таким образом, зная лишь одну из крайних цифр
числа офу, можно сразу назвать разность между
задуманным числом abc и числом «обращенным», и, ничего
не зная об офу, при любом задуманном числе можно
«угадать» результат сложения: <хру-|-ур<х.
Определение задуманного числа по трем таблицам
Разместив в каждой из трех таблиц подряд числа от
1 до 60 так, чтобы в первой таблице они стояли в трех
столбцах по двадцати чисел в каждом, во второй —
в четырех столбцах по 15 чисел в каждом и в третьей —
в пяти столбцах по 12 чисел в каждом (см. рис. 4),
легко быстро определить задуманное кем-нибудь число N
(N<;60), если будут указаны номера а, {3, у столбцов,
содержащих задуманное число в 1-й, во 2-й и в 3-й
таблицах: N будет равно остатку от деления числа
40<х-{-45[3-|-36у на 60 или, другими словами, N будет
равно наименьшему положительному числу, сравнимому
с суммой (40a -j- 45р -j- 36у) по модулю 60. Например,
при а = 3, р==2, у = 1:
40a-j-45p + 36Y=0 + 30 + 36=6(mod60),T.e.W=6(").
41

Аналогичный вопрос может быть решен для чисел
в пределах до 420, размещенных в четырех таблицах
с тремя, четырьмя, пятью и семью столбцами: если а,
/
/
S
л
51
55
л
г
7
,
52
57
Ш
3
в
53
53
Ш
«
9
ж
59
7
5
а
55
50
I
/
5
•
53
57
Д
г
5
•
54
53
Ш
3
7
•
55
59
Л?
«
в
•
55
63
Рис. 4.
р, 7» & — номера столбцов, в которых стоит задуманное
число, то оно равно остатку от деления числа
280а + \Щ + ЗЗбу +1208 на 420.
Попробуйте это доказать, несколько продолжив
рассуждения, приведенные в § 38 (см. примечание (")).
Фокус с картами
Предложив кому-нибудь вынуть из колоды одну из
тридцати шести карт, можно, быстро просмотрев одну
за другой (не выпуская колоды из рук) оставшиеся
карты, определить название вынутой карты. При этом
не следует и пытаться удержать в памяти, какие из карт
при просмотре оказались в колоде, а достаточно просто
найти сумму 5 оставшихся очков, что при небольшом
навыке делается очень быстро, тем более, что, считая
для простоты туз за одно очко, для 5 будем иметь:
190sSS<C200, а следовательно, при подсчете достаточно
искать (отбрасывая десятки) лишь цифру единиц числа 5.
Если она, например, равна трем, то 5=193,
следовательно, из колоды была вынута семерка, масть
которой легко установить при повторном беглом просмотре
колоды.
/
/
4
7
•
55
5В
П
2
5
в
•
53
59
Ш
3
3
9
ч
•
57
ВО
42

Кто что взял?
Трем лицам А, В я С отгадчик дает соответственно
одну, две и три монеты и оставляет на столе еще 18
монет. А, В а С в его остутствии распределяют между
собой три предмета: вилку, ложку и нож, после чего
владелец вилки берет дополнительно столько монет,
сколько им было получено вначале, а владельцы ложки
и ножа — соответственно удвоенное и учетверенное (по
сравнению с полученным вначале) число монет.
При шести возможных распределениях предметов
между А, В и С: в, л, н; л, в, н; в, н, л; л, н, в; н, в, л;
н, л, в — на столе будут оставаться соответственно:
1, 2, 3, 5, 6, 7 предметов.
Если вы придумаете простой прием для запоминания
вариантов распределения предметов между тремя лицами
в той последовательности, в какой они записаны выше,
то вы сможете с успехом по числу оставшихся монет
угадать, кто взял какой предмет. (Баше указал для этой
цели специальную фразу на французском языке — см. [30],
стр. 54.)
Чтобы аналогично — по остатку монет — определить
владельцев л различных предметов, надо подобрать л
разных чисел: av ах, ...,ап (для начального
распределения монет) и о таких множителей: /га,, тг, ,.., т„, чтобы
при разных способах распределения этих множителей
между числами: alt аг, ..., ап получилось л! неравных,
но, по возможности, мало отличающихся друг от друга
сумм вида:
пи flx + nWflt + • • • + тчап
(alt as, ..., а„ — номера предметов, взятых
соответственно 1-м, 2-м л-м лицом). При л = 4 можно
взять, например, а. = \, at = 2, а, = 3, а4 = 4 и
множители mt:l, 2, 5, 15 (см. [30], § 12).
Извлечение корней из многозначных чисел
Используя ряд простых приемов, нетрудно научиться
быстро извлекать в уме корни нечетной степени из
чисел, являющихся точными степенями двузначных и даже
трехзначных чисел.
43

Вычисляя {/N, надо число N разбить, двигаясь
справа налево, на грани по s цифр в каждой (в левой
грани может, конечно, быть и меньше цифр).
Последнюю цифру корня легко определить,
пользуясь следующими двумя правилами:
I. У чисел л", л*, л", ..., niS+1 на конце стоит всегда
такая же цифра, как и у п.
И. Если л оканчивается цифрой: 0, 1, 2, 3, 4, 5, 6,
7, 8, 9, то п', л', л", ..., л"-1 оканчиваются
соответственно цифрами: 0, 1, 8, 7,_4, 5, 6, 3, 2, 9.
Первая цифра корня {/N легко получается при s=3,
если знать значения л' при 1^л^9, а при s = 5, 7, 9
и т. д. надо запомнить таблицу двузначных логарифмов
первых девяти чисел:
п
lgn
1
0
2
0,30
3
0,48
4
0,60
5
0,70
6
0,78
7
0,85
8
0,90
9
0,95
Примеры: 1. Можно сразу написать ^/314 432 = 68,
применив правило II и заметив, что 6'<314<7\
2. {/JV= (/17 565 568 854 912 = л. Так как 10" < N<
< 2 • 10", то 13,0 < lg N< 13,3, следовательно,
l,85<lgn=-ylgN<! 1,9, т. е. в соответствии с
приведенной таблицей 70<л<80; применяя же правило II,
получим: л = 78.
3. Корень двадцать пятой степени из 46-значного
числа, кончающегося цифрой 8, равен 68 (45<lgAr<46,
следовательно, 1,8 < lg л = ^ lg N < 1,84).
Если Доканчивается одной из цифр: 1, 3, 7, 9, то, зная
лишь две последние цифры числа N, можно найти и две
последние цифры %/N. Например: f/... 53= п= 10z+ 7.
Прикидываем в уме: (7 + Юг)'= 343+ 147 • г ■ 10+...
(два последних слагаемых не влияют на цифру единиц
и цифру десятков).
Так как у N цифра десятков — пять, а у числа 343 —
четыре, то число 147г оканчивается цифрой 1, a z —
цифрой 3, т. е. л =100^ + 37.
44

Этот прием дает иногда артистам-вычислителям
возможность, попросив медленно диктовать справа налево
цифры числа N, давать ответ (при N<i 10'), не дожидаясь
конца диктовки.
Учитывая некоторые побочные обстоятельства, прием
этот можно использовать и тогда, когда последняя
цифра N отлична от 1, 3, 7, 9; он может быть применен
также при s = 5, 7 и т. д.
Отсылая интересующихся к [18], где дано описание
ряда приемов, употребляемых артистами-вычислителями,
дадим здесь описание еще одного способа, позволяющего
найти одну из цифр числа n = l/N, если остальные
цифры л уже известны.
Основан он на следующем правиле ("):
если л' при делении на 11
дает остаток d: 0, 1, 2,- 3, 4, 5, 6, 7, 8, 9, 10,
то л при делении на 11
дает остаток d,: 0, 1, 7, 9, 5, 3, 8, 6, 2, 4, 10.
Как известно из § 3, N^a'(N) (mod 11), где о' (N)—
«алгебраическая сумма цифр» числа N. Поэтому надо
найти a'(N) и определить d, сравнимое с ним по
модулю 11 (0<rf<10).
Если помнить соответствие между d и dt (а артистам-
вычислителям многое приходится держать в памяти!), то
остается по известному rf, найти единственную
неизвестную цифру искомого числа л из условия: й,=ео'(л) (modi 1).
Пример: ^54053028541 =3z81= л (как определяются
все цифры, кроме 2, описано выше).
Так как a'(N) = \ — 4 + 5—8 + 2 — 0 + 3 — 5 + 0 —
— 4 + 5 = — 5 и —5 = 6 (modll), то d=6;
следовательно, а'(л) = 1 — 8 + 2 — 3 = z —10 должно быть
сравнимо с rf,=8 по модулю 11, откуда 2 = 7.
Конечно, все эти вычисления проделать быстро в уме
может лишь человек, обладающий хорошими
вычислительными способностями и прошедший специальную
тренировку.
§ 8. БЫСТРЫЙ СЧЕТ
Стремление к упрощению действий над
многозначными числами привело в начале XVII века к
изобретению таблиц логарифмов, а затем и логарифмической
линейки.
45

В XIX веке стали входить в обиход арифмометры,
в начале XX века — вычислительные машины-автоматы,
а лет пятнадцать назад появились электронные
вычислительные машины, позволяющие решать за несколько
часов задачи, требующие выполнения миллионов
операций над многозначными числами.
В настоящем параграфе описываются значительно
более скромные, доступные каждому средства,
облегчающие и ускоряющие вычисления.
Сокращенное умножение
Перемножая, например, числа 7496 и 3852, выпишем
целиком в соответствующие разряды произведения
каждой цифры множимого на каждую цифру множителя
3 8 5 2
0
0
0
21
0
0
56
12
0
35
32
27
14
20
72
18
8
45
48
18
30
12 !
28874592
7 10 13 10 4 1
В любом из вертикальных столбцов, заключенных
между горизонтальными линиями, стоит (считая сверху
вниз): 1) произведение цифры единиц множителя на
соответствующую цифру (а) множимого; 2) произведения
остальных цифр множителя, перебираемых справа налево,
на стоящие правее а цифры множимого, перебираемые
одновременно слева направо.
Например, в разряде сотен имеем:
8( = 2Х4), 45( = 5Х9), 48( = 8Х6);
здесь а = 4. В разряде десятков тысяч имеем:
0( = 2Х0), 35( = 5Х7), 32( = 8Х4), 27( = ЗХ9);
здесь <х = 0.
46

Складывая затем числа, стоящие в каждом столбце,
и прибавляя к ним отмеченные в уме «десятки»,
полученные при сложении в соседнем справа разряде (см.
числа под дужками), получим, идя справа налево, все
цифры искомого произведения.
Числа, стоящие в строчках, объединенных фигурной
скобкой, можно не выписывать, а выполнять сложение
соответствующих двузначных чисел в уме—для этого
надо, конечно, научиться быстро и безошибочно
складывать двузначные числа.
Например, если мы уже дошли до разряда сотен
(от разряда десятков у нас осталось «4 в уме»), то
произносим (глядя на 2 и 4, затем на 5 и 9, наконец, на
8 и 6); «восемь и четыре—двенадцать; и сорок пять —
пятьдесят семь; и сорок восемь — сто пять, десять в уме»,
(а цифру 5 пишем в разряде сотен).
Попробуйте поупражняться сначала на двузначных,
затем на трехзначных и т. д. числах и вы увидите» что
при некотором навыке можно быстро и безошибочно
находить произведения многозначных чисел.
Сокращенное деление
При делении многозначных чисел легко научиться,
умножая делитель на очередную цифру частного,
одновременно вычитать получающееся произведение (не
выписывая его) из числа N, образованного несколькими
первыми цифрами делимого или какого-нибудь из
промежуточных остатков. Цифры искомой разности
определяются (справа налево) так, чтобы она в сумме с
упомянутым произведением давала число N.
Например: -щ— Цр • Здесь цифры разности: 8, 2, 3
получены так: прикинув в уме, что 5X7 = 35 и что
надо прибавить 8, чтобы получить число,
оканчивающееся цифрой 3, произносим: «тридцать пять и
восемь— сорок три, четыре в уме (в разности записываем
цифру 8); четыре и десять (5><2)— четырнадцать, и
два,— шестнадцать, один в уме (в разности
записываем цифру 2); один и сорок пять (5X9) — сорок шесть,
и три — сорок девять» (записываем в искомой разности
цифру 3).
47

Счеты и палочки Непера
Умножение и деление многозначных чисел сильно
упрощаются при наличии счетов и так называемых
палочек Непера.
Каждая из палочек
Непера дает произведения
стоящей в ее «заголовке»
цифры на 1,2, 3, 4, 5, 6,
7, 8, 9 (см. рис. 5, а); при
этом число десятков
пишется выше, а число
единиц — ниже наклонной
черты, стоящей в
соответствующей клетке.
Положив рядом
несколько палочек так,
чтобы заголовки их
образовывали множимое, и
поместив рядом слева
вспомогательную палочку,
указывающую номера строк,
легко прочитать сразу
произведения стоящего
в заголовке множимого на числа: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Например (см. рис. 5, а),
Рис. 5.
3987X8 =
2/\ 1/ б У 5
= 31896
(цифра десятков, стоящая выше наклонной черты,
прибавляется к цифре единиц в соседней слева клетке).
При перемножении многозначных чисел произведения
множимого на отдельные цифры множителя, получаемые
с помощью палочек Непера, удобно откладывать сразу
(в соответствующем разряде) на счетах.
На рис. 6 показаны отдельные этапы умножения
числа 3987 на 672.
I —на счетах отложены 23 922 сотни (3987X6);
II — к отложенному числу прибавили 27909 десятков
(3987X7);
III — к полученному числу прибавили 7974 единиц
(3987X2).
48

При делении же, например, числа 2225575 на
3987 надо:
1. Отложить на счетах делимое (рис. 7, а).
2. Найти на палочках Непера число, ближайшее
к 22 255, но меньшее его (это будет 19935 = 3987X5),
хо-
-оахгаххх
-ахоохах
-ссгашхх
-оахооос
—азоазх
хгахгаз о
х—
-ооооооос
-ахшхх
-олхоахи
-оооооооооо
+
»
-охахоах
-ахахгах
■ахгаотг
-ахссаг
хахс оса
хсохо ах
—ахгаха
—ооооосос
х
хгхгахо-
-оашхш
+
Л
Рис. 6.
х>
-аххххозх
-ооооососос
-ссаишх
—оосоооос
хахо осос
хахсо ах
хооооооо с
X)
тоэ-
хоо—
-ашха
—arc
—ахах
Ш
и вычесть его из числа 22255; одновременно на верхней
проволоке надо отложить первую цифру (5) частного
(рис. 7, б).
3. Найти на палочках Непера число, ближайшее
к 23 207, но меньшее его (это будет 19935 = 3987X5),
3)—
ю»—
то—
хпхго-
хшь-
-оалхгах
—ахгахах
—ахгагах
—ахахос
--ахаш
—ахгахс
алое
оахс
-оа
-осссс
а)
хгаь
—ахос
-ахшхах
-ашпш.
-ахахшх
-шхахс
го сахах
D-
х>
-аххахс
«хххаха
Сосахо ах
гахо-
4?
хххю-
XD0C-
аха ххю
-am
-coax
-ахахшх
-охоахах
хо—
в—
хаххо-
d
-оашгах
—сахас
-ахаха
ах
чхшга
—ахос
ej
Рис. 7.
XtXO-
то-
ххгахо-
чхш
-чшх
—а
-оссахшх
-озшхах
-оахшхсс
(ХШХШХ
30000000—~-Q
х) ■ ахаш
ХШХШ) с
&
и вычесть его из 23 207, а на второй сверху проволоке
отложить вторую цифру (5) частного (рис. 7, в).
4. Найти на палочках Непера число, ближайшее
к 32725, но меньшее его (это будет 31896 = 3987X8),
и вычесть его из 32 725, а на третьей сверху проволоке
отложить третью цифру (8) частного.
49

В итоге имеем: на верхних проволоках — искомое
частное (558), а на нижних — остаток (829) (рис. 7, г).
Изготовьте — на плотном картоне или на гладкой
фанере — палочки Непера и потренируйтесь, пользуясь
счетами, в умножении и делении многозначных чисел.
Вы увидите, насколько эти простые приспособления
могут- облегчить труд вычислителя.
Изготовить следует два или три комплекта палочек,
так как в множимом могут быть одинаковые цифры; не
забудьте про палочки с заголовком «О»!
Палочки Непера могут принести пользу и при
вычислениях в других системах счисления. На рис. 5, б
изображена палочка для умножения семерки на числа:
1, 2, 3, 4, 5, 6, 7,8,9,10, 11 — в двенадцатеричной системе
счисления (а = 10; р = 11).
Извлечение корня квадратного
Известно, что сумма п последовательных нечетных
чисел (начиная с единицы) равна л1: 14-34-54-...
... + (2л —3) + (2л— 1) = л\
Поэтому вычисление V~N (N— натуральное число)
можно свести к задаче: сумма какого самого большого
числа слагаемых вида 1, 3, 5, 7, 9, 11, ... не будет
превосходить числа N. Эту задачу легко решить на счетах.
Однако при больших N операция эта была бы
утомительна, и лучше, разбив число N на грани, вычислять
последовательно (слева направо) цифры искомого корня.
Если N—трехзначное или четырехзначное число, то
положим:
V~N=№-{-b. (1)
Вместо того, чтобы вычитать из N последовательно
10 а слагаемых суммы:
5 = 1+3 + 5+... + (20а —3)4-(20а —1) = (10а),>
а затем Ь слагаемых суммы:
5' = (20с + 1) + (20о + 3)+... +(20а4г2& —1),
проще вычесть из «старшей грани» числа N всего
лишь а слагаемых: 1 4-3 4^54-...+(2с — 1)=а* (что
равносильно вычитанию из N числа a1 •100=S), а затем
60

уж из оставшегося числа вычитать члены суммы S' (где
первое слагаемое на единицу больше
произведения а на 20).
На рис. 8 показано, как протекает на счетах
вычисление У1369.
Вычитая из первой грани (13) числа: 1, 3, 5,
откладываем на верхней проволоке при каждом выполненном
вычитании по одной косточке.
-шшпд
-апшю:
-O0OO0QGO0C
-агашюс
-агата
-агаша
хо-
■апшссс
—осооссс
шло ооос
хсагао с
ШИШ
ШШЕ1
хо-
-СШПХ
сдахшг ЕШИЗВШШШ ™>
чштгптг
-сштапг
-ашш
-апштсс
яоо
хшэо
ШЗШЮ-
-ооашпг
——<ихис
аис
ло-
——ахшг
ссс
-ошооап:
-апшхп
-ахгаш;
-аштп:
-сшхпхос
-шхххмсс
-ашгавс
-азоооаш
Рис. 8.
Вычитая затем из остатка (469) последовательно числа:
61, 63, 65, 67 ... (61=3X20+1) и откладывая при
каждом выполненном вычитании на второй сверху
проволоке по одной косточке, получим: yT369 = 37.
Для ускорения процесса отдельные цифры искомого
корня можно определять «в уме» и вычитать из
соответствующего остатка сразу сумму нескольких
слагаемых указанного вида.
Например, прикинув в уме, что при извлечении корня
из 1369 второй цифрой будет семерка, вместо вычитания
из остатка (469) чисел: 61, 63, 65, 67, 69, 71, 73 можно
было бы сразу вычесть 7-60 + (1 +3-{-5-{-7-{-9-|-
-{-11-{-13) = 7-60-{-7, = 67.7 и на второй сверху
проволоке отложить семь косточек.
Правда, при этом утратится «автоматизм» в
выполнении операций и весь процесс будет точной копией
обычного способа извлечения корня квадратного на
бумаге.
Если N—пятизначное или шестизначное число, то
а в (1) будет двузначным числом. Для его нахождения
надо извлечь корень из двух «старших граней» числа
N, а затем аналогично предыдущему найти Ь.
51

Например, при вычислении 1^86436, вычитая из 8
числа: 1,3, получим 46 436; затем из 464 вычитаем числа:
41,43,45, 47,49, 51, 53, 55, 57 (41=2X20+1) и,
наконец, из полученного остатка (2336) вычитаем числа: 581,
583, 585, 587 (581 =2X290+!)• На верхних
проволоках у нас получится|/86436 = 294.
Дадим еще описание одного приема извлечения корня
квадратного из чисел, который позволяет сразу находить
рациональное число, очень мало отличающееся от
искомого корня. Пусть
УА=а-\-а^а, (2)
где а — приближенное значение искомого корня, а а —
погрешность приближения, причем известно, что | а | < у
и Y может быть равно у^, j^, щ и т. п.
Из (2) имеем {УА — а)п = а", откуда, возводя
двучлен в п-ю степень, легко получить, например,
при л = 2:
при п — 3:
т/Т а'4-ЗаА , а* • . г .
УА = -3^+А+3^+А = а^+^ (4)
при я = 5:
V А~~ 5а4 -f ^ахА + А* "+" 5а* + ЮахА + А1 " ai + ai' (Ь>
Если за приближенное значение Y А брать первые
слагаемые в этих равенствах, то абсолютная величина
погрешности не будет превышать соответственно чисел:
Та' За'-f Л' 5а*+10а2А + Аг'
Например, УТО=3 + а ^= 3; 0 < a < 0,2 (так как
3,2* = 10,24).
По формуле (3):
(с избытком, так как по формуле (3) всегда а^О, при-
52

чем |<х,|<£-5<0,0067), по формуле (5):
1/ТП ~~ 3'+10-3'-10 +5-3-10»_ 4443 _3 16227758
V™^ 5.3* + 10-3»-10 + 10» —1405 —d'lb^//De-
(с недостатком, так как в этом случае а'^ > 0, причем
К1<ш<°>00000023);
следовательно: 3,16227758 < У ТО < 3,16227782.
Аналогичным путем можно извлекать корни третьей,
пятой и т. д. степени (см. [9], стр. 375—378).
Сложение и вычитание вместо умножения
До изобретения таблиц логарифмов для облегчения
умножения многозначных чисел применялись так
называемые простаферетические таблицы (от греческих слов
«простезис» — прибавление и «афайрезис» — отнятие),
представляющие собой таблицы значений функции ^г-
(см. § 2) при натуральных значениях г (см. [10],
стр. 55—56). Так как при а и b целых
abi
Ла + Ь)
(«-*)'_ !> + *»)'] _ Г(а-*»)']
(числа а-\-Ь и а — b либо оба четные, либо оба нечет-
(а _]_м* (а—Ь)ж
ные; в последнем случае дробные части у-—^—-и ■-. -
одинаковы), то умножение а на b сводится к определению
а -\- Ь, а — b и, наконец, разности чисел ■ ~]Г ' и ■?~ '
взятых из таблицы.
Для перемножения трех чисел можно воспользоваться
тождеством:
аЬс = ±{(а-\-Ь-\-су — (а-\-Ь — с)' — {а-\-с — Ь)' —
-(Ь + с-аУ), (6)
из которого следует, что при наличии таблицы значений
функции 24 вычисление произведения abc можно свести
к определению чисел: а-\-Ь-\-с, а-\-Ь — с, а-\-с—b
b-\-c — а и по ним — при помощи таблицы — правой
части равенства (6).
S3

Приведем в качестве примера такую таблицу для
lsgz-<30. В таблице даны: крупными цифрами —
значения |т , а мелкими — значения k, где
!Н*]+Я'0<*<23'
^\Единицы
Деснгки"^^
0
1
2
0
41,.
333,
1
о,
55,1
'385м
2
0,
72.
443,,
3
1,
91„
506,,
4
2„
114,
5760
5
55
14015
651,
6
^o
170,,
732,
7
14,
20417
820,
8
21.
2430
^l41.
9
зо0
285,,
1016,
Нетрудно, пользуясь формулой (6) и таблицей,
получить:
9-9.9 = 820, — 30, — 30„ —30„ = 729,
17-8-4=10165 — 385^ — 91 „-{-5, = 544 (проверьте!).
О вычислении логарифмов
Дадим еще описание простого приема, позволяющего
вычислять логарифмы чисел с помощью таблицы кубов
натуральных чисел (см. [11]). Возьмите таблицы Бар-
лоу [3], дающие, в частности, кубы всех четырехзначных
чисел, и проверьте приведенные ниже вычисления.
Пусть
lgl3 = C„ CJC,C1...(i) = C, + T}- + g|+gS.+ ...,
т. е. искомый логарифм представлен в виде
систематической троичной дроби.
Тогда
10 3 9 =13,
следовательно, с0=1.
54

Сокращая обе части равенства на 10е» = 10 и возводя
их после этого в куб, получим:
10"+т+г+"==1>3.=2>197>
откуда С! = 0.
Так как при точном возведении числа 2,197 в куб и
при дальнейших вычислениях получились бы очень
«громоздкие» числа, будем дальше вести вычисления с
четырьмя значащими цифрами, определяя так называемые
нижние и верхние границы (Н. Г. и В. Г.) интересующих
нас чисел (всякий раз при округлении чисел в столбец
«Н. Г.» будем записывать их значения с недостатком, а
в столбец «В. Г.» — с избытком).
Дальнейшие вычисления дадут:
10 3
10 3
10 3
10 3
10 3
н. г.
10,60
1,191
1,689
4,818
111,8
10*+Т+- | L397
10 3
10 3
'I0+-O- + —
10 3
10 3
2,726
20,25
8,303
572,4
В. Г.
10,61
1,195
1,707
4,974
123,1
1,866
6,498
274,4
20,67
8,832
с,= 1
са = 0
с4 = 0
с, = 0
с, =2
с7 — 0
са = 0
с0 = 1, с, = 2
си = 0, с,в = 1
cu=2. си = 0
S5

Отсюда:
1 + 35+35+3"° + зтг<1813<1 + з5+3*+35 + 3»° + "-
или
1,113911 <lgl3<l,113979.
Попробуйте, вычисляя таким же способом логарифмы
тех или иных чисел, сверять полученные результаты со
значениями, взятыми из таблиц логарифмов.
§ 9. ЧИСЛОВЫЕ ГИГАНТЫ
В физике, химии, астрономии часто встречаются
числовые «гиганты» и «карлики»; например, расстояния от
Земли до ближайших звезд заключены в пределах от 10"
до 10" км, радиус атома — величина порядка 10~8 см,
число молекул в одной грамм-молекуле вещества
приблизительно равно 6-10" (число Авогадро).
Чтобы лучше ощутить размеры этих чисел, полезны
различные искусственные приемы. Например, наглядное
представление о числе Авогадро дает следующий пример:
при равномерном распределении полного стакана воды
с «мечеными» молекулами в воде пяти земных океанов
в каждом стакане океанской воды окажется ие меньше
пятисот «меченых» молекул (").
Значительно сложнее составить отчетливое
представление о больших и малых числах, встречающихся при
решении различных математических задач. Рассмотрим
несколько примеров.
1. lgx растет с возрастанием х настолько медленно,
что неравенство lgx>100 будет справедливо лишь при
*>10100.
Чтобы получить представление о размерах этого числа,
подсчитайте и убедитесь ("), что оно превосходит число
молекул воды, необходимой для заполнения куба с
ребром в 70 миллионов световых лет (считая, что плотность
воды сохраняется равной единице и что в одном
кубическом сантиметре воды -q-'Ю2* молекул).
Как же представить себе в таком случае размеры
числа АГ==9о0^4,28-10',ов0"100 (проверьте, зная, что
lg9 = 0,95424250943932...), по сравнению с которым даже
численность стада в задаче Архимеда (Af= 77- ю20"*";
66

см. § 4) — число «ультра ультра ...
ультрамикроскопических размеров»!
Но с именем Архимеда связано также число,
значительно превосходящее 9**. В своем сочинении «Псаммит»
(«Исчисление песчинок») Архимед доводит
классификацию чисел до числа 1080 00° 00° 00° 00° 00° (в наших
обозначениях; по классификации же Архимеда — см. [15],
стр. 13 — это число содержит мириаду мириад единиц ми-
риад-мириадного порядка, мириад-мириадного периода;
мириада = 10000).
Однако и этот архимедов гигант уступает
«невзрачному» по внешнему виду числу Q = 4^ . Действительно,
Q = 41"°>4,'»-,°1"> 10»-»1И(проверьте!)(а?а). Чтобыдать
представление о ((длине» числа Q при записи его в
десятичной системе счисления (но, конечно, не о самом числе Q),
в одной книге конца прошлого столетия говорится:
«Представьте себе отрезок такой длины, что световому
лучу понадобился бы квинтиллион (10") лет, чтобы
пройти этот путь. Затем представьте себе шар с
диаметром, равным этому отрезку, наполненный типографской
краской. Всей этой краски не хватило бы, чтобы четко
напечатать это число даже самыми мелкими цифрами,
какие только существуют» (см. [15], стр. 31—32).
Действительно, легко установить ("), что объем
такого шара меньше, чем уЮ1" см3 (проверьте!).
Предполагая, что каждый кубический сантиметр
краски позволит отпечатать 1000 000 000 цифр, мы могли
бы напечатать лишь число, в котором было бы
меньше, чем j-lO1" цифр, а в числе Q цифр больше,
чем 8-10'".
2. Известно, что а* (при а>1) растет с
возрастанием х быстрее, чем х" (л>0), а х" — быстрее, чем
Это значит, что
lira 5 = 0 и lim^=0.
Однако, например, равенство Jim f(x) = Q, где
ж-юо
х1 000 000
f{x) = j 000 до^ , может показаться парадоксальным, если
57

судить по началу таблицы
X
jgt ем ооо
1,000001"
0
0
1
1
1
1,000001
2
21 ооо ооо
1,000002
10»
10° ооо ооо
е к 2,718
10'
Ю7 ооо ооо
е ю ~ 104,"
10»
Ю1а ооо ооо
10»*
10U ооо ооо
^5l0*3,*a0,lOe
Но конец таблицы показывает, что при каком-то
значении х, лежащем в интервале (10", 101*), /(х)=1, а
так как lg/OO11)^ — 29,43.10" (проверьте!), то/(10,4)<
<; Ю-2910°. Число е, фигурирующее в таблице,— основание
так называемых натуральных логарифмов: logeN=\nN,
причем натуральный и десятичный логарифмы одного и
того же числа связаны соотношением: lnN=slgAfX
X 2,3025851.
В высшей математике доказывается, что
e=lim (l+4-)n = 2,7182818...,
n-юо V " /
отсюда \ge=z 0,4342945 и е =^ Ю0'"12'".
Попробуйте доказать ("), что для функции
.„ I у\ 'f»1 lOOOOOl
Т \ t ^0, 000001 1
¥(в" ••••••)>!, НО !р(е"000000)<1.
3. Чрезвычайно быстро растет с возрастанием п фак-
ториальная функция п\. Для оценки скорости роста этой
функции можно воспользоваться неравенствами (см. [26])
У2ме~"п"<п\<У%™п"е-"е12п (формула Стерлинга),
откуда
-jIn(2пл) + nIn п — n< In (л!)<
< 2-1п(2тш)-|-и1пя —" + 12^'
Эти неравенства дают — при больших значениях п —
тесные границы для In (я!). С их помощью легко
убедиться (*°), что после соответствующих перемножений
число 10000! будет «содержать» 35660 цифр, число
1000001 — 456574 цифры и число 10000001 — 5565709
цифр.
58

§ 10. ИГРЫ С КУЧАМИ ПРЕДМЕТОВ
Ниже дано описание трех игр, теория которых
разработана с исчерпывающей полнотой. В каждой из них
большинство исходных положений благоприятно для
игрока, делающего первый ход, т. е. при правильной игре
ему обеспечен выигрыш и лишь исключительные
положения благоприятны для его противника (подразумевается,
что оба игрока знакомы с теорией игры). Таким образом,
играми они могут служить лишь для лиц, незнакомых
с их теорией.
Игра Баше
Из кучи, содержащей сначала п предметов, двое
играющих берут поочередно каждый раз по произвольному,
числу предметов (но не меньше одного и не больше а
предметов за один раз). Выигрывает тот, кто своим
очередным ходом сможет забрать все оставшиеся предметы.
Неблагоприятным для игрока, делающего очередной
ход, будет число предметов в куче (обозначим его
через т), кратное числу а-\-\. Действительно, когда от =
=а-\-\, при любом ходе игрока противник может сразу
забрать все оставшиеся предметы. Если же m=(a-\~l)s
(s — любое натуральное число), то после любого хода
игрока противник, сделав соответствующий ход, может
оставить в куче (a+l)(s—1) предметов, затем —
(a-\-l)(s — 2) предметов и т. д., доведя, наконец, число
предметов в куче до а-\-\, что обеспечит ему выигрыш.
Во всех остальных исходных положениях (когда т=
г=(а-\- l)s-{-r, lsgrsga) первый игрок, взяв г
предметов, обречет своего противника на проигрыш.
Игра эта была уже в 1612 году описана Баше в
несколько иной форме: двое называют поочередно числа
от единицы до десяти и выигрывает тот, кто первый
доведет до ста сумму чисел, названных обоими игроками.
Цзяньшидзы (игра с двумя кучами предметов)
Значительно сложнее теория китайской народной игры
цзяньшидзы («выбирание камней»). Условия ее таковы.
Из двух куч, состоящих из любых предметов, двое
играющих поочередно могут брать либо: 1) произвольное
число предметов из одной кучи (хоть сразу все пред-
59

меты, но не меньше одного), либо 2) одновременно по
одинаковому (тоже произвольному) числу предметов, но
не меньше, чем по одному предмету из каждой кучи.
Выигравшим считается игрок, который при очередном
ходе — так будем называть любую из двух указанных
операций — заберет все оставшиеся предметы.
Назовем позицией {k, I) или (/, k) положение, при
котором в кучах имеется соответственно k и / предметов
(порядок здесь не играет роли). Построим так
называемые «особые» позиции:
(c„dt)y (c^d,), (с2, ds), ...,(с„, dn), ..., (1)
исходя из следующих условий:
1) c0 = d0 = 0.
2) Компонента сп позиции (сп, dn) (я=1, 2, 3,...)
берется равной наименьшему из натуральных чисел,
неиспользованных при построении позиций (с0, d„),
(c^dj, ..., {cn_lt d^J.
3) dn = c„ + n.
Остальные позиции будем называть неособыми.
Вот несколько первых особых позиций: (0,0), (1,2),
(3, 5), (4, 7), (6, 10), (8, 13), (9, 15).
Особые позиции обладают тремя свойствами:
I. Каждое натуральное число входит в одну и только
в одну особую позицию.
Действительно, беря для с„ наименьшее из чисел,
неиспользованных в предыдущих особых позициях, мы
гарантируем, что каждое натуральное число обязательно
войдет в какую-нибудь из позиций (1). Ясно, что сп не
совпадает ни с одной из компонент предыдущих
особых позиций, а так как при k < п dn = сп + п > ck -f-
-\-k — dk~>ck, то и d„ не может совпасть ни с одной из
компонент предшествующих позиций.
П. Любой ход переводит каждую особую позицию
в позицию неособую.
В самом деле, если сделанный ход изменит лишь
одну из компонент особой позиции (сп, dn), то получится
неособая позиция, так как компонента, оставшаяся
неизменной, не может входить в две разные особые позиции;
если же сделанный ход уменьшит одинаково обе
компоненты сп и d„, то разность между ними останется рав-
60

ной л, в то время как у всех остальных особых позиций
(с*> dk) разность между компонентами dk— ck равна k=f=n
(см. условие 3).
III. От любой неособой позиции соответствующим
ходом можно перейти к позиции особой.
Доказательство: если дана неособая позиция
(а, а), где а ф О, то, забирая по а предметов из обеих
куч, можно прийти к особой позиции (0,0). Если же
дана неособая позиция (а, Ъ), где а<СЬ, то возможны
следующие варианты:
1. a = ck; b>ck + k = dk.
Очевидно, достаточно взять из второй кучи b — dh
предметов; это даст особую позицию (сА, dk).
2. a = ck; b<C.ck-\-k, т. е. Ъ — cft = & — а = й<&.
Достаточно из обеих куч взять по ск — сд предметов;
это даст особую позицию (ch, Ь — ck-\-ch) = (ch, A-j-cA) =
3. a = dk. Достаточно из второй кучи взять Ь — ск
предметов; это даст особую позицию (dk, ck) = (ck, dk).
Из свойств II и III следует, что после любого хода
игрока, сделанного им в особой позиции, противник
может свести дело к одной из особых позиций. При
повторении противником этого маневра будут получаться
особые позиции с все меньшими и меньшими
компонентами, пока не получится особая позиция (c0,d0)=(0,0).
А это означает, что противник заберет последние
предметы, то есть победит. Если же позиция неособая, то
подходящим ходом игрок может свести ее к особой.
Поступая так же каждый раз, игрок победит.
Таким образом, при правильной игре обоих партнеров
игроку, делающему первый ход, обеспечен выигрыш,
если исходная позиция неособая, и для него неизбежен
проигрыш, если она особая.
Отметим без доказательства (см. [25], стр. 43—52,
или [32], стр. 426), что ск и dk можно вычислять при
заданном k по формулам:
с^1±р], (2)
dk=[k3-±p.]. (3)
61

Например, прл k =100:
1+У5
2
2
с,„„ =
100
100'
= [100-1,6180327.
= [100-2,6180327.
•]=I61,
,.] = 261.
Из формул (2) и (3) имеем: сА<&
1+Т^5
<«*+!.
т. е.
cft 0,6180327.
= с*—§—<*<(«* + !)—2"
= (са+ 1) 0,6180327.
(4)
dk 0,3819672... =rfft
3-1^5
<A<(rfA + l)
3_/5
2 ^'"^s^t*; 2
= (rfft+l) 0,3819672... (5)
Чтобы быстро находить правильный ход в любой
данной позиции (а, Ь), удобно иметь под руками
достаточно обширную таблицу особых позиций. Если же
такой таблицы нет или ни одно из чисел а и Ъ не
встречается в имеющейся таблице особых позиций, то
следует поступать так: надо выяснить, в каком из интер-
(а + 1)
валов ^ 2 , г ,.;— 2 у, у- 2
(#-{-1) -~—J содержится целое число. Если некоторое
целое число k содержится в первом интервале, то a = ck,
если во втором, то a=^dk. В обоих случаях,
руководствуясь свойством III, можно добиться особой позиции.
Легко показать ("), что некоторое целое число должно
содержаться в одном из этих интервалов, причем в двух
интервалах сразу не может содержаться по целому
числу.
Ним (игра с тремя кучами предметов)
Происхождение этой игры неизвестно, сущность же
ее такова: даны три кучи предметов; двое играющих
могут поочередно брать произвольное число предметов
(но не меньше одного) из одной какой-нибудь кучи
(каждый раз выбор ее предоставляется на усмотрение игрока).
Выигрывает тот, кто, сделав очередной ход, заберет все
оставшиеся предметы.
62

Для уяснения теории игры полезно вспомнить, что
всякое число может быть представлено (и притом
единственным образом) в виде суммы различных
степеней двух.
Например:
17 = 24 + 20,
29 = 2* + 2' +2» +2°,
97 = 2° + 2'+ 2°.
Наз'овем позицию (k, k, /), при которой в кучах
находится соответственно h, k и / предметов, особой, если
каждое из чисел 2s (s = 0, 1, 2, ...) либо совсем не
входит в разложения чисел А, к, I на суммы различных
степеней двух, либо входит в эти разложения всего два
раза.
Если же хотя бы одно из чисел 2s (s = 0, 1,2, ...)
входит в разложения чисел к, к, I один или три раза,
то позицию (k, k, I) будем называть неособой.
Например, позиция (18,21,7) будет особой, так как
18 = 2*-j-21; 21 =2* + 2*+ 2°; 7 = 2х 4- 214- 2°.
Очевидно, что при любом л позиция (0, л, л) (одна куча
разобрана) будет особой.
Теория игры основана на следующих теоремах:
Теорема I. Игрок, делающий очередной ход в
особых позициях (1, 2, 3) и (0, л, л), обречен на проигрыш.
Действительно, при любом ходе игрока в позиции
(О, л, п) противнику достаточно взять такое же число
предметов из другой кучи, чтобы свести дело к
позиции (0, т, т), где т < л; такая тактика приведет его,
наконец, к позиции {0, 0,0), т. е. к выигрышу.
Рассмотрев немногочисленные варианты, читатель
легко убедится, что при исходной позиции (1, 2, 3) также
неизбежен проигрыш игрока, делающего первый ход.
Теорема II. Для любых двух чисел тип можно
подобрать (и притом единственным способом) третье
число р так, чтобы позиция (т, л, р) была особой.
Действительно, достаточно (и необходимо) те степени
двух, которые входят в разложения чисел т и л в
общей сложности один раз, включить в состав числа р,
а степени двух, которые не входят ни в одно из чисел
тип или входят и в т, и в л, в состав числа р не
включать.
63

Например, при m=I9 = 24-}-2,-}-2') и л = 37 = 2!+
4-2*-|-2" в состав р надо включить 25, 2\ 22, 21, что
даст р = 54, образующее с числами 19 и 37 особую
позицию; все же другие числа образуют с 19 и 37
неособые позиции.
Теорема III. Любой ход, сделанный в особой
позиции (k, I, т), приведет к позиции неособой.
Это непосредственно вытекает из теоремы II.
Теорема IV. От любой неособой позиции
соответствующим ходом можно перейти к особой.
Для доказательства рассмотрим следующие два
случая:
1. Наивысшая степень двух входит лишь в одно из
трех чисел или сразу во все три числа; тогда
достаточно наибольшее из этих чисел уменьшить до размеров
числа, образующего с двумя другими числами особую
позицию. Если же в исходной позиции два наибольших
числа одинаковы, то уменьшить можно любое из них
(можно забрать также целиком меньшую кучу
предметов).
2. Пусть наивысшая степень двух, например 2",
входит в разложения только двух чисел; тогда следует
обратить внимание на 2*-1, 2S~* и т. д., пока не
встретим степень двух (обозначим ее через 2Г), которая
входит или в разложение только одного из данных чисел,
или во все три разложения.
Для получения особой позиции достаточно уменьшить
одно из чисел так, чтобы изменилась лишь его
«хвостовая часть» (т. е. часть соответствующей ему суммы
степеней двух, содержащая 2Г и более низкие степени
двух); при этом, в соответствии с разобранным выше
первым случаем, уменьшаться должно число с
наибольшей хвостовой частью; если же одинаковую наибольшую
хвостовую часть имеют два числа, то можно уменьшать
ее у любого из них (или же забрать целиком хвостовую
часть третьего числа).
Примеры: 1.
А=14=2,4-21 + 21,
k = 21 = 24 + 22 + 2°,
/ = 39 = 254-22-}t21 + 20.
Здесь имеем первый случай; достаточно уменьшить
число / так, чтобы получилось число /'= 2* 4-2'+ 21+
64

4-2'=27, т. е. из третьей кучи надо взять 12
предметов.
2.
А = 81=2, + 24 + 2%
k = 121 = 2° + 2' + 24 + 2' + 2°,
/=55 = 2! + 24 + 2« -}- 2' + 2».
Здесь каждое из чисел 2° и 2* входит в разложения
данных чисел по два раза; так как 2* входит во все три
числа, а хвостовая часть наибольшая у числа k, то
следует довести ее до 2'-J-21, что превратит число k
в А1 = 2е -f- 2s -}- 2* -|- 2* = 102, составляющее с h и /
особую позицию.
Итак, взяв из второй кучи 19 предметов, придем
кг особой позиции (81,102, 55).
3.
h = 29 = 2* + 2* + 2' + 2°,
k = 58 = 2' + 2* + 2* + 2*,
/ = 45 = 2'4-2*-J-2'-}-2°.
Это второй вариант второго случая: 2! и 2*
встречаются в разложениях по два раза, а наибольшая
хвостовая часть (2* 4- 2' + 2°) — у двух чисел: h и /.
Следовательно, можно у одного из них уменьшить хвостовую
часть на шесть единиц, доведя ее до 2,-}-214-2')=7,
и это приведет либо к особой позиции (А—6, к, 1) =
= (23, 58, 45), либо к особой позиции (А, к, I—6) =
= (29,58,39). Но можно также просто отбросить
хвостовую часть у числа k, что приведет к особой позиции
{к, к— 10, /) = (29, 48, 45).
Из последних двух теорем следует:
1. Игрок, делающий первый ход в любой особой
позиции, обречен на проигрыш, так как противник всегда
своим ходом может создать другую особую позицию и,
повторяя этот маневр, рано или поздно сведет дело
к позиции (0, л, л) или (1, 2, 3), что обеспечит ему
выигрыш.
2. При любой неособой исходной позиции игроку,
делающему первый ход, надо создать особую позицию,
и выигрыш ему будет обеспечен.
Игру в «ним» можно оформить еще следующим
образом: на шахматной доске ставятся в случайных
3 А. П. Доыоряд
65

ш.
о
ш
Ш
ж.
**
т
ж
1
ш
%
1
ш
местах три шашки; двое поочередно передвигают шашки
по спирали (рис. 9) по направлению к клетке А,
перемещая за один ход какую-нибудь шашку на любое число
клеток (при этом на одной клетке могут оказаться сразу
две и даже три шашки). Игра кончается, когда все
шашки достигнут клетки А, и выигравшим считается
игрок, своим ходом закончивший игру.
Замечание 1. Можно попытаться построить теорию
игр с несколько измененными условиями, разрешив,
например, в игре Баше брать за один ход от трех до
пятнадцати предметов, пока в куче находится больше
пятидесяти предметов, и от одного до десяти
предметов, когда число предметов в
куче не превосходит
пятидесяти.
В игре с двумя кучами
предметов можно, например,
ограничить число забираемых за
один ход предметов или
разрешить забирать одновременно
из обеих куч предметы лишь
в отношении 1:2 и т. п.
В игре «ним» можно ввести
дополнительный ход — взятие
+ поровну из двух или даже из
всех трех куч предметов.
Рис-9- Конечно, далеко не во всех
случаях легко построить
теорию игры, и далеко не всегда оиа будет простой и
красивой; однако, вполне вероятно, что в отдельных
случаях могут получиться интересные результаты.
Замечание 2. Если даже обоим игрокам известна
теория второй или третьей игры, но ограничено время
на обдумывание ходов, то результат игры будет зависеть
от искусства играющих.
Ряд указаний, относящихся к правильному ведению
игры с двумя кучами предметов, имеется в статье
И. В. Арнольда ([38], вып. 7, стр. 16—24), где отмечена
также любопытная связь особых позиций с числами
Фибоначчи.
Попробуйте в игре с двумя кучами предметов:
а) Найти правильные ходы в каждой из следующих
позиций: (27, 37), (14, 90) (47, 69) ("а).
1
Ж
Ш
Ж
66

б) Установить, какие из чисел 40, 55, 140,. 400 будут
меньшими и какие — большими компонентами особых
позиций, и в каждом случае найти вторую компоненту
позиции ("б).
в) Построить особые позиции до (с,0, dia)> пользуясь
условиями 1) — 3) (стр. 60) и по формулам (2) и (3).
Сравнить результаты.
В игре «ним» найдите правильный ход (или
правильные ходы} в каждой из следующих позиций: (10, 17, 25),
(47, 99, 181), (25, 43, 50), (29, 29,18) (93, 29, 74) (").
§ И. МЕЛЕДА
Игра китайского происхождения — меледа, описанная
еше в середине XVI века итальянским математиком
Карданом, изображена на рис. 10, а.
Рис. 1Q.
По условию игры с проволочной шпильки аЪ с
приделанной к ней ручкой надо снять все кольца,
соединенные между собой нитями, привязанными к
палочке cd.
Нити можно заменить проволочками, а палочку cd
планкой Ы с маленькими отверстиями, сквозь которые
продеваются соответствующие проволочки, после чего
концы их расширяются (рис. 10, о).
Составление плана решения, вытекающего из
конструктивных особенностей меледы, и подсчет всех
необходимых для его выполнения операций представляет
интересную математическую задачу.
з*
67

Имея в своих руках меледу (а сделать ее совсем
нетрудно), легко убедиться в том, что:
1. Кольцо / может быть спущено (т. е. его, можно
снять со шпильки и пропустить внутри ее вниз) или
поднято (т. е. его можно, пропустив сквозь шпильку
вверх, надеть на нее) независимо от того, будет ли
в это время любое из остальных колец надето на
шпильку или спущено вниз.
2. Любое из колец с номерами: 3, 4, 5, 6, ... может
быть опущено или поднято в том и только в том
случае, если в это время кольцо с номером на единицу
меньшим будет надето на шпильку, а все кольца с еще
меньшими номерами спущены вниз; при этом
безразлично, в каком состоянии будет любое из колец с
большим, чем у данного кольца, номером.
3. Кольцо 2 может быть спущено или поднято при
любом положении остальных колец только
совместное кольцом }.
В дальнейшем подъем или спуск какого-нибудь
кольца, так же как и совместный подъем или спуск
колец 1 а 2, будем называть ходом.
Пусть меледа имеет я колец: А, В, С, D, .... К, L, М,
имеющих соответственно номера:' п, п—1, п — 2,
я— 3, ..., 3, 2, 1. На схеме кбльца будем обозначать,
ставя соответствующую букву над горизонтальной
чертой, если кольцо поднято, и под чертой, если кольцо
спущено.
Обозначим через uk (k^ri) наименьшее число ходов,
необходимых для спуска (или подъема) колец с номерами
Спуску я-го кольца (см. / на рис. 11) должно
предшествовать положение II, для достижения которого надо
затратить, самое меньшее, и„_2 ходов. Спустив
следующим ходом кольцо А, придем к положению ///,
затратив, в общей сложности, и„_г-{-1 ходов. Легко
убедиться, что:
исходя из положения ///, для спуска кольца В надо
пройти как через одну из промежуточных стадий через
положение IV.
Действительно, для спуска В кольцо С должно быть
надето на шпильку; возникающее сразу после подъема
кольца С положение изображено на схеме V, где
опусканию кольца В мешает кольцо D.
68

Повторяя эти рассуждения, убедимся, что
опусканию D неизбежно должно предшествовать положение VI,
в котором спуску D будет мешать кольцо F; стремясь
к его-спуску, мы должны будем пройти через
положение VII и т. д.
В итоге окажется, что положения IV избежать не
удастся.
Д 8 С D £ f G В J..:/T L М
Л
А
Д
Д
Д
В
В
в
в
в
в
с
с
с
с
с
с
л
л
D
л
D
П
£ У'
£ f
£ F
£ f
£ f
£ Г
G В
G В
G В
G В
G В
G В
J..
J..
J..
J..
J..
.B L M
,
.K L M
.B L M
.B L M
.B L M
A' J... В L M
Рис. 11.
Так как при переходе от /// к IV надо затратить,
самое меньшее, и„_, ходов (столько же, сколько и для
перехода от IV к III), и так как для спуска всех колец
из положения IV, представляющего собой как бы ме-
леду с л—1 кольцами, потребуется еще, самое
меньшее, ип_1 ходов, то
и» = ип-. + 1+«п-, + и„-1 = й„_1 + 2йв_1 + 1. (1)
Очевидно «, = «, = 1. Пользуясь рекуррентным
соотношением (1), получим:
йз = и, + 2«, + 1=4,
«4 = и3 + 2«1 + 1 = 7,
и» = И4 + 2и» + 1 —16 и т. д.
69

Применяя метод математической индукции, легко
убедиться, что
Ив = 1[2"-1-(-1П,
откуда следует, что н„ очень быстро растет с
возрастанием п; например, я21 = 220 = 1048 576.
Задача. В каждом из указанных на рис. 12
положений найти кратчайший путь спуска и кратчайший путь
подъема всех колец и определить соответствующие
числа ходов (").
// tO 8 5 * J t
гг з
W 9
12 И
71 9
12 10
П tO 9
в
0
7
7
7
Т
е
6
-L
5
s
*
*
*
i
2
г 1
J
3 1
г
11 в 7 3 / /
Рис. 12.
Замечание. Если роль колец будут исполнять
пронумерованные игроки^ выходящие из круга,
начерченного на земле, или входящие в него в соответствии
с указанными выше тремя «правилами» спуска и подъема
колец, то получится более живая игра с той же
принципиальной схемой.
Такое видоизменение игры заслуживает внимания
еще и потому, что, освободившись от конструктивных
особенностей меледы, легко изменить условия игры,
подчинив передвижения игроков иным правилам, и при
измененных условиях искать кратчайшее решение задачи.
Конструирование же проволочного аналога игры с
иными условиями представит дополнительную задачу,
решение которой может увенчаться созданием новой
интересной головоломки.
§ 12. ИГРА ЛЮКА
В придуманной французским математиком Люка игре
(он дал ей название «Ханойская башни») требуется
перенести- л -круглых лластинок различных размеров со стол-
70

бика А (рис. 13) на столбик В, пользуясь
вспомогательным столбиком С, причем за один ход можно
переносить только одну пластинку (с любого столбика на
любой другой), но запрещается при этом класть большую
пластинку выше какой-нибудь из меньших.
Надо указать кратчайший путь решения и определить
соответствующее ему число ходов и„.
Так как: для переноса нижней пластинки: на В
необходимо сначала перенести (пользуясь столбшшм В, как
вспомогательным)
остальные пластинки на
столбик С, на что
потребуется по меньшей
мере яя_, ходов, то,
очевидно, «•„=«„_.-f-
откуда, пользуясь
методом математической
индукции ("), легка
получить: ып=2"—г.
jL е
z-^PIIr
/^ШЩ
у
V
ЕиСгАЗ.
Любители математики могут поставить перед собой
целый ряд вопросов частного и общего характера,
связанных с игрой Люка. Обозначим пластинки в порядке
возрастания их размеров номерами: 1,2, 3,4,... Можно
искать, например, наименьшее число ходов, позволяющих
перейти от позиции {А(Ъ, 4, 3), В(7% 5, 1), С (6, 2)} —
в скобках указаны номера пластинок на каждом из
столбиков, считая снизу вверх—к позиции .8(8, 7,6,5,
4, 3, 2, 1) или от позиций
{А (2т, 2т—2, 2т—4,.. .,-6, 4, 2),
В{2т— 1, 2т — 3,...,5, 3, 1)}
или
{А(2т, 2m—l,...,m-\-2, т+1),
В(т,т—1,„..,3,2,1)}
к позиции:
В(2т,2т-^1,2т—2> ...,4,3,2,1),
§ 13. СОЛИТЕР
Игра под названием солитер проводится на доске
с тридцатью тремя клетками (рис. 14). Такую доску
легко получить, прикрыв шахматную доску листом
картона с крестообразным вырезом. На рис. 14 каждая
71

клетка обозначена парой чисел, указывающих номера
горизонтального и вертикального рядов, на пересечении
которых находится клетка.
В начале игры все клетки, за исключением какой-
нибудь одной, заняты шашками.
Требуется снять 31 шашку, причем задаются пустая
«начальная» клетка (а, Ъ) и «конечная» (с, d), на которой
должна оказаться уцелевшая в
конце игры шашка. Правила игры
таковы: любая шашка может быть
снята с доски, если рядом с ней
(в горизонтальном или в
вертикальном направлении) находится
с одной стороны какая-нибудь
шашка («снимающая»), а с
противоположной стороны — пустая
клетка, на которую «снимающая»
шашка должна быть при этом
переведена.
Из теории игры следует (см. [1] или [33]), что
решение будет в том и только в том случае, когда
a==c(mod3) и ft = d(mod3).
Приведем для примера решение задачи, в которой
клетка (44) является и начальной, и конечной.
51
4/
Я
52
*г
зг
73
63
53
43
33
гз
13
74
54
54
44
34
24
/4
г—
75
55
55
45
35
2S
15
5В
45
35
57
47
37
Рис. 14.
1. 64 —44
2. 56 т- 54
3. 44 — 64
4. 52 — 54
5. 73—53
6. 75 - 73
7. 43-63
8. 73 - 53
9. 54 - 52
10. 35 - 55
21. 31-33
22. 43 - 23
23. 51-31
24. 52 — 32
25. 31 - 33
26. 14-34
11. 65-45
12. 15-35
13. 45 - 25
14. 37 - 35
15. 57 - 37
27. 34 - 32
28. 13-33
29. 32 - 34
30. 34 - 54
31. 64 - 44
16. 34 - 36
17. 37-35
18. 25-45
19. 46 - 44
20. 23-43
Здесь в записи каждого хода указаны для «снимающей»
шашки номер исходной клетки и номер клетки, на
которую она ставится (при этом с доски снимается шашка,
стоящая на промежуточной клетке).
Попробуйте снять 31 шашку: а) при начальной клетке
(5, 7) и конечной (2, 4) или б) при начальной клетке (5, 5)
и конечной (5, 2) (").
72

§ 14. «ИГРА В ПЯТНАДЦАТЬ» И ПОДОБНЫЕ ЕЙ ИГРЫ
Сущность игры в пятнадцать заключается в
следующем: в ящичке с 16 клетками в произвольном порядке
размещены 15 перенумерованных шашек (см., например,
/ на рнс. 15), требуется перейти к нормальному
расположению /// с помощью ряда «простых ходов ладьи»,
сводящихся каждый раз к передвнганню на пустую
клетку какой-нибудь шашки, стоящей на одной из
смежных клеток.
Рис. 15.
Например, передвигая шашку 12, перейдем от / к //;
затем можно передвинуть на пустое место шашку 10
нлн 11 и т. д.
То нлн иное расположение шашек будем называть
перестановкой. Оказывается, что некоторые
перестановки будут «неразрешимыми», т. е. от них нельзя
перейти к перестановке ///.
Обоснование этого положения покоится на очень
простых соображениях: условимся говорить, что две шашки
стоят в относительном беспорядке (образуют инверсию),
если шашка с большим номером стоит раньше шашки
73

с меньшим номером; например, в перестановке /// не
имеется ни одной инверсии, в перестановке же / шашка 1
образует две инверсии (с шашками 3 и 9), шашка 2 дает
еще две инверсии с теми же шашками, шашка 3
образует одну инверсию (с 9; инверсии шашки 3 с 2 и 3 с 1
уже нами учтены раньше) и т. п.
Легко подсчитать, что всего в перестановке / имеется
49 инверсий.
Будем считать, что на пустой клетке стоит шашка 16
(фиктивная), и, следовательно, каждый ход сводится
к транспозиции (обмену местами) фиктивной шашки
16 с какой-нибудь соседней с ней шашкой.
В перестановках /, II/, IV ни одна шашка не
образует инверсии с шашкой 16, в перестановке же //
каждая из шашек с номерами: 13, 5, 4, 12 образует с 16
инверсию.
Перестановки с четным числом инверсий (с учетом
и фиктивной шашки 16), например перестановки // и ///,
будем называть четными, а перестановки с нечетным
числом инверсий, например / и IV,--нечетными.
В высшей алгебре доказывается (см. [20]), что
транспозиция любых двух элементов перестановки изменяет
ее тип; следовательно, любой ход в игре в пятнадцать,
представляя собой транспозицию какой-нибудь шашки
с шашкой 16, изменяет тип перестановки (сравнить,
например, переход от / к //); ясно, что четное число
ходов приведет к перестановке исходного типа, а
нечетное— к перестановке противоположного типа.
Если для удобства шестнадцать клеток закрасить
«под шахматную доску», то с каждым ходом будет
меняться цвет пустой клетки, следовательно, будет верна
Теорема I. Неразрешимыми, т. е. неприводимыми
к перестановке III, будут все нечетные перестановки
с пустой, белой клеткой и все четные перестановки
с пустой черной клеткой.
Действительна, от нечетной перестановки с пустой
белой клеткой к перестановке с пустой (тоже белой)
клеткой в правом нижнем углу можно перейти за четное
число ходов, т. е. при этом может получиться лишь
нечетная перестановка, а следовательно, к перестановке ///
мы прийти не сможем. Аналогично доказывается
неразрешимость четных перестановок с пустой черной
клеткой.
74

Верна будет также и более общая
Теорема II. Если считать в игре в пятнадцать
допустимыми не только простые ходы ладьи, но и
перенос любой ишшка на пустую клетку, а также
транспозицию любых двух шашек, то никакая
нечетная перестановка не может быть проведена к
перестановке III четным числом ходов и никакая четная
перестановка не может быть приведена к
перестановке III нечетным числом ходов.
Действительно, при таком изменении правил игры
любой ход, будучи транспозицией каких-нибудь двух
шашек (одна из них может быть и фиктивной), меняет
тип перестановки (докажи-
шашки на пустую клетку -Ш Jg
могут передвигаться лишь Ряс, ie.
ходом коня.
Теорема III. Любая четная перестановка с
пустой белой клеткой и любая нечетная перестановка
с пустой черной клеткой разрешимы, т. е. могут
быть сведены к перестановке III. Остальные же
перестановки могут быть сведены к перестановке IV.
Рассмотрим сначала передвижения пяти шашек
в прямоугольнике из шести клеток. Если обратить
внимание лишь на взаимное расположение шашек при
обходе прямоугольника «по ходу часовой стрелки» (не
считаясь с положением пустой клетки), то
расположения шашек /, //, /// (рис. 16) можно охарактеризовать
одной и той же перестановкой 14 3 5 2 (или, что то
же самое, перестановками 43521, 3521 4 и т. д.).
Легко видеть, что любой горизонтальный ход
(например, ход, переводящий I в II) я вертикальные ходы
в крайних столбцах (например, ход, переводящий /7 в ///)
не изменяют взаимного расположения шашек, а любой
75

вертикальный ход в среднем столбце (например, ход
шашки 4 в расположении /, приводящий к IV) меняет
взаимное расположение шашек, причем перестановка
13 5 4 2, характеризующая новое расположение,
получается из прежней перестановки передвиганием соот-
i i
ветствующего номера на два шага: 1 4 3 5 2. Пользуясь
этим, легко любые три шашки—например 1, 2 и 3 —
поставить рядом друг с другом в порядке возрастания
номеров; так, исходя из перестановки 14 3 5 2, после
передвижения сначала шашки 2, а затем шашки 4 в
среднем столбце (возможность этих ходов надо создать
предварительным круговым передвижением шашек)
придем к перестановке 12 3 4 5 (при другой исходной
позиции могло бы получиться: 1 2 3 5 4).
В соответствии с доказанным, упорядочивание шашек
при любой исходной позиции можно вести, например,
в такой последовательности (не дающей, вообще говоря,
кратчайшего решения):
1) добиться сначала того, чтобы в прямоугольнике
«1, 2, 5, 6, 9, 10» (здесь номера шести клеток,
образующих прямоугольник, указаны в соответствии с
нормальной перестановкой ///) оказались шашки 1, 2 и еще
какие-нибудь три шашки, а одна клетка была бы пустой;
2) передвинуть шашки 1 и 2 на соответствующие им
места;
3) поступая аналогично, последовательно поместить
на свои места шашки:
3 и 4, действуя в рамках прямоугольника «3, 4, 7, 8, 11, 12»,
5 и 6, i » » » «5, 6, 9, 10, 13, 14»,
7 и 8, » » » » «7, 8, 11, 12, 15, 16»,
9 и 13, » » » » «9,10,11,13,14,15»;
4) внутри прямоугольника «10, 11, 12, 14, 15, 16»
окажутся шашки 10, 11, 12, 14 и 15, три из которых:
10, 11 и 12, могут быть передвинуты на свои места,
что приведет либо к перестановке /// (рис. 15), если
исходная перестановка удовлетворяла условиям
теоремы III, либо к перестановке IV.
Можно несколько видоизменить игру в пятнадцать,
взяв шашки с написанными на них буквами, дающими
в обшей сложности какую-нибудь фразу. Если при этом
одна буква будет встречаться два раза, а остальные по
76

одному разу, то при любом исходном расположении
шашек можно рядом ходов привести их к «правильному»
расположению.
Возьмем, например, фразу: «мы навелн порядок»,
приписав буквам: м, ы, я, а, в, е, л, и, п, р, я, д, к,
номера: 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 15,
и распределив 10 н 14 тем или иным способом между
двумя буквами о, мы при любом исходном
расположении шашек на доске получим две перестановки разных
типов, так как они переводятся друг в друга с помощью
одной транспозиции. Следовательно, одна нз
перестановок будет обязательно разрешимой.
а] ф
Рис. 17.
Если бы, например, верхней букве о на рис. 17 мы
приписали 10, а нижней—-14, то получили бы
перестановку четного типа (44 инверсии), распределяя же
номера в обратном порядке, как указано на рисунке,
получим нечетную перестановку (47 инверсий).
Так как пустая клетка в расположении (а) черная,
то, чтобы прийти к расположению б, надо обязательно
верхнюю букву о переводить на четырнадцатую, а
нижнюю— на десятую клетку.
Все сказанное относительно игры в пятнадцать
остается в силе и для «игры в девять», где восемь шашек
перемещаются в квадрате с девятью клетками.
Рассмотрим интересную разновидность игры в
девять, носящую название «хамелеон». Игра проводится
на «доске» с девятью клетками, соединенными
прямолинейными отрезками (рис. 18, а). На восьми шашках
написаны буквы слова «хамелеон», н шашки расставлены
в случайном порядке на каких-то восьми клетках доски.
77

Передвигая шашки по соединительным отрезкам, надо
их разместить так, чтобы при чтении по ходу часовой
стрелки, начиная с клетки 1, получилось слово «хамелеон»,
Перенумеровав клетки «доски» в соответствии б
рис. 18, а, легко убедиться, что любые две клетки
будут соединены друг с другом отрезком прямой в том
Рис 18.
и только в том случае, когда клетки с такими же
номерами в квадрате б) будут связаны простым ходом ладьи.
Так как в слове «хамелеон» две одинаковые буквы е,
а остальные буквы встречаются по одному разу (так же
^_^_^__^_^ как в фразе «мы навели порядок»
встречались две буквы о), то, согласно ска-
"~ занному выше, при любом исходном
— — положении.шашек в квадрате б) их можно
привести к положению в), а
следовательно, и к г), что соответствует
решению игры (сравнить с а)).
Рис. 19. Описание в настоящем параграфе
игры — это игры для одного лица. Однако
и несколько лиц могут состязаться друг с другом в
поисках кратчайших путей перехода от одной из
выбранных позиций к другой.
78

Для усложнения игры в пятнадцать можно запретить
некоторые ходы; например, можно доказать (попробуйте
это сделать) ("), что перегородки, изображенные на
рисунке 19, не мешают переходу от любой исходной
позиции к позиции /// или IV (рис. 15).
Попробуйте исследовать вопрос: будет ли верна
доказанная выше теорема III, если простые ходы ладьи
заменить ходом шахматного коня? Аналогичный вопрос
можно поставить также для квадратной доски с 36
клетками и с 35 пронумерованными шашками, заменив
обычного шахматного коня «2,3-конем», у которого
с каждым ходом юдна координата меняется на две,
а другая—<на три единицы.
§ 15. ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ЧИСЛА СПОСОБОВ
ДОСТИЖЕНИЯ ЦЕЛИ
Задачи о прыгунах
I. Сколькими способами прыгун, стоящий перед
клетками, начерченными на земле (рис. 20), может
достигнуть п-й клетки, если он прыгает слева направо,
приземляясь лишь в начерченных клетках, и длина его
прыжков может быть произвольна.
Рис. 20.
Обозначим через в, число способов достижения s-й
клетки. Для решения задачи следует учесть, что у
прыгуна есть возможность (одна) прыгнуть на я-ю клетку,
не приземляясь на промежуточных. Приземляться на k
промежуточных клетках он может C*_t способами.
Следовательно:
Замечание 1. Очевидно, нами попутно найдено
число различных представлений числа я в виде суммы
79

целых положительных слагаемых (включая и- случай
«суммы», состоящей из одного слагаемого), яричем два
представления считаются разными, если они отличаются
либо самими слагаемыми, либо их порядком.
Замечание 2. Если прыгуну разрешить
приземлиться лишь четное число раз, то в его распоряжении
будет l + C2_t + CJ_!+..., т. е. 2"-2 способов.
II. Сколькими способами прыгун может достигнуть
п-й клетки, если ему разрешено делать лишь
одинарные (на соседнюю клетку) и двойные (через одну клетку)
прыжки?
Обозначим через vs число способов достижения s-й
клетки. Так как на клетку с номером s прыгун может
попасть лишь с клеток с номерами s — 1 и s — 2, а
чтобы добраться до этих клеток, в его распоряжении
имеется соответственно vs_t и vs_t способов, то при
s>2 имеет место равенство
*. = v.-t + v*-M- (2)
Легко непосредственно убедиться, что
z/i = l и v, = 2. (3)
Исходя из (3), можно с помощью соотношения (2)
последовательно определить значения vt, vit vt, ..., т. е.
представить решение задачи в форме таблицы
S
V»
1
1
2
2
3
3
4
5
5
8
6
13
7
21
8
34
9
55
10
89
11
144
12
233
13
377
14
610
Уравнение (2) является частным случаем так
называемых конечно-разностных уравнений:
vx+m = F(vx, vx+l, .... г'я+т_1), (5)
изучаемых в исчислении конечных разностей.
Если известны значения v0, vv vit ..., vm_l, то
с помощью равенства (5), называемого так же
рекуррентным соотношением для функции vx, легко
последовательно найти vm, vm+1, vm+t, ..., т. е. получить
табличное решение уравнения (5). Однако искать этим
80

путем, например, 1>10о» было бы неудобно, и обычно
стремятся представить решение в форме ,бх=/(х).
Легко убедиться ("), что уравнениям (2) и (3)
удовлетворяет функция
«.=*[№Г-№Г]- <6'
Вычисляя с ее помощью значения г»,, г»4, vt, ..., мы
придем к тем же числам, которые получены в таблице (4)
(проверьте!).
Элементарному изложению теории линейных конечно-
разностных уравнений с постоянными коэффициентами,
т. е. уравнений вида
к числу которых принадлежит и уравнение (2),
посвящена интересная книга А. И. Маркушевича [17].
Замечание 3. К решению уравнения (2) приводит
также «задача о кроликах» Леонардо Фибоначчи (см. [17],
стр. 7), в силу чего числа (4) носят название чисел
Фибоначчи. Они обладают рядом интересных свойств (см. [7]).
Отметим здесь лишь связь их с биноминальными
коэффициентами. Из решения второй задачи о прыгуне
следует, что vn равно числу различных представлений
натурального числа п в виде суммы, в которой каждое
из слагаемых равно единице или двум, причем два
представления считаются различными и в том случае,
когда они отличаются друг от друга только порядком
слагаемых. С другой стороны, число представлений,
в которых двойка встречается k раз (0 <; k ^ ЦМ ), равно
C*_ft, так как в этом случае общее число слагаемых
будет равно п — k, а из п — k мест выбрать k мест,
занимаемых двойкой, можно С*_А способами.
Следовательно,
^=i+ci_i+d_2+...+cL7»T (7)
в-|л1
Замечание 4. В первой задаче о прыгуне можно
было бы установить соотношение
«,= !+«.+»•+ ■••+»,-!» (8)
откуда легко прийти (при в1 = 1) к равенству яв=2п~,.
81

Замечание 5. В задаче о прыгунах можно
по-всякому разнообразить условия: например, можно, допустив,
вообще говоря, одинарные, двойные и тройные прыжки,
оговорить, что с клеток, имеющих, например, номера,
кратные пяти (в том числе и из начального положения),
прыжки делаются только одинарные (вязкая почва).
Обозначив при этих условиях через ws число
способов достижения s-й клетки, вместо одного уравнения
будем иметь систему:
'ws—ws^x-\-ws_t-\-ws_t wpus=5k HnpHS=5£;+:l,
■ Щгж='0)3_1-\-п)х_1 при s=5k-\-2,
^=^-1 + ^-» при s=5£-f-3;
причем щ\ = 1, wt=\, w, = 2.
Попробуйте (*°), составляя таблицу значений ws,
убедиться, что в этом случае прыгун может достигнуть
пятнадцатой клетки 1619-ю способами.
Перейдем теперь к задачам, в которых искомая
функция зависит от двух и от большего числа целочисленных
аргументов.
Задача о ладье
Сколькими способами (за наименьшее число ходов)
можно перевести ладью с клетки (О, 0) на клетку
(т, п), если перемещать ее простыми ходами, т. е.
ходами, при которых она перемещается лишь на
соседнюю клетку в горизонтальном или в вертикальном
направлении.
Числа в скобках означают соответственно номер
столбца и номер строки, на пересечении которых
находится клетка, причем левому столбцу и нижней строке
приписывается номер 0 (man — целые неотрицательные
числа).
Обозначим через их%у число способов перехода с клетки
(О, 0) на клетку (х, у). Очевидно, при любых
положительных х и у
**.t = 1 И "t.JF—l- (9)
Так как на клетку (х, у) при х>0 и у^>0 ладья может
попасть лишь с клетки (х — \,у) или с клетки (х,у — 1),
добраться до которых она может соответственно ux_lt у
82

и и
*,?-l
способами, то
Ux.y = Ux.
1,У
Мы получили рекуррентное соотношение для
функции их у, зависящей от двух целочисленных (а в нашей
задаче'и неотрицательных) аргументов.
Если в каждой клетке доски писать соответствующее
ей значение их ,, то в силу (9) и (.10) все клетки левого
столбца и нижней строки можно сразу заполнить
единицами, а затем (см. (10)) постепенно
заполнять остальные клетки,ставя
в них числа, равные сумме двух
соседних (снизу и слева) чисел.
Это даст нам решение (в виде
таблицы) уравнения (10) при
условиях (9) (см. рис. 21).
Задачу о ладье можно решить
более простым путем, что даст
нам попутно и решение
уравнения (10) в виде удобной фор- Рис 21.
мулы.
Заметим, что для перевода ладьи с клетки (0, 0) на
клетку (т, п) надо сделать всего т-\-п ходов: т. в
горизонтальном и л в вертикальном направлениях.
Отдельный способ перевода ладьи можно охарактеризовать
схемой, состоящей из Зукв г я в, указывающей, в каком
порядке надо делать горизонтальные и вертикальные
ходы.
Очевидно, для выбора т мест, занимаемых буквой г
(из имеющихся в схеме т -J-пмест), имеется всего С£+я=
~ "Г I различных возможностей, что и является
решением задачи о ладье. Решением же уравнения (10) при
условиях (9) будет функция
~х,у
х\у\ '
(И)
Задача о пауке
Сколькими способами паук, находящийся в начале
координат, может переползти (кратчайшим путем!)
в узловую точку (k, I, т) пространственной решетки?
(В пространственной решетке любая узловая точка, т. е.
83

точка с целочисленными координатами, связана
стерженьками, параллельными осям координат, с шестью
соседними узловыми точками.) Задача эта является
естественным, обобщением задачи о ладье.
Если обозначить через их< у> г число способов
достижения точки (х, у, z), то при натуральных х, у, z будем
иметь:
их,у, z==ax-i,y, гЛ~их,у-\, гЛ~их,у, г-i- О-*)
К этому разностному уравнению с неизвестной функцией,
зависящей от трех целочисленных аргументов, надо
добавить условия
и _(£±2Н. „ — (* + ») 1. „ _<£+£!! ,13\
их, у, о х\у\ » "*, о, г х\г\ » "о, у, г у\г\ > \1и>
вытекающие из решения предыдущей задачи.
Любой конкретный способ перехода паука с узла
(О, 0, 0) на узел (k, I, т) можно охарактеризовать
последовательностью букв х, у, z, указывающей, в каком
порядке чередуются перемещения паука по направлениям
осей Ox, Оу, Oz; поэтому uktm будет равно числу
способов заполнения k -\-l-\-rri мест k буквами «х», I
буквами «у» и п буквами «z».
Но из имеющихся в нашем распоряжении k-\-l-\-m
мест выбрать k мест для заполнения их буквой «х»
можно . Л, _7""\| способами; каждому из этих способов
(i'+m)\ - л i i
соответствует JT-; возможностей выбрать / мест (из
оставшихся свободными 1-\-т мест) для заполнения их
буквой «у». Следовательно, общее число возможностей
выбрать k мест в схеме (для заполнения их буквой «х»)
и / мест (для заполнения их буквой «у») равно
(k + l + m)\ {l + m)l (k + l-\-m)\
k\(l + m)\ Л я» I k\l\m\ '
Таким образом, решением уравнения (12)
приграничных условиях (13) будет функция их> у> г == EJj^Lti!:.
Многомерные задачи
Задачу о пауке можно обобщить на четырехмерную
решетку, узловые точки которой получаются из узловых
точек трехмерной решетки перемещением ее на одну,
на две, на три и т. д. единицы длины в направлении
84

«четвертой оси» Оа. Нет необходимости направлять
ось Оа перпендикулярно осям Ох, Оу, Oz — для этого
надо было бы «выйти в четырехмерное пространство»,—
а достаточно мысленно представить себе ряд трехмерных
решеток, соответствующие узлы которых соединены
«единичными» стерженьками, «параллельными» оси Ои.
Для трехмерных решеток с конечным числом узлов
это можно осуществить в виде модели, фактически
соединяя «единичными проволочками» соответствующие узлы
«нулевой», первой, второй и т. д. трехмерных решеток.
В такой четырехмерной решетке каждый узел будет
характеризоваться четырьмя целыми числами
(координаты узла).
Сохраняя геометрическую терминологию, часто
совокупность т чисел: с,, с„ ..., ат рассматривают как
координаты точки в «/я-мерном пространстве».
Если считать, что числа с,, с„ ..., ат — целые не
отрицательные, и соседними считать узлы, у которых
лишь одна из координат отличается на единицу, а все
остальные координаты одинаковы, то при ai-^ai-\-...
...-\-ат = п переход из узла О(0, 0, .... 0) в узел
Л (с,, аг, , ат) можно сделать за п ходов (переходя
каждый раз в какой-нибудь соседний узел).
Если ходы, при которых возрастает только первая
координата или только вторая координата и т. д.,
обозначить соответственно буквой .*,, буквой хг и т. д., то
число способов перехода за п ходов из узла 0(0, 0 0)
в узел Л (с,, а„ ..., ат) будет равно числу различных
«перестановок с повторениями» из п элементов:
**1> "*1» •••» -^1> •*!» -^2> •••» Х-, • • •', Хт, Хт, ..., •*„,.
у *• > '
с, элементов аг элементов ат элементов
Повторяя рассуждения, приведенные в задаче о пауке,
покажите, что число это равно —-.—т-~ г(41)-
Примером многомерной задачи может служить задача
о наполнении бочек водой: бочки с номерами 1, 2, ...
..., т — 1, т имеют соответственно вместимость с,, аг,...
■••» ат-\> ащ ведер; сколькими способами можно
наполнить все бочки, если за один прием вода из полного
ведра должна выливаться целиком в одну из бочек?
Число способов, очевидно, равно <д' + д« + -•,• + ?«'• .
85

Задача о шахматном короле
Сколькими способами король сможет перейти
с клетки (0, 0) на клетку (k, I), если он будет
передвигаться в направлении возрастания одной или обеих
(«диагональный ход») координат.
Обозначим искомое число через wkt г. Если при своем
движении король сделает s диагональных ходов
(очевидно, s^k, s=s£/), то число горизонтальных ходов
•будет равно k — s, вертикальных—/ — s, а общее число
ходов будет равно k-\-l — s. Тот или иной способ
перехода короля при s диагональных ходах можно
характеризовать „_ 7jfl~ iiji способами (проверьте,
подсчитав, сколькими способами можно расставить k — s букв г,
I — s букв в и s букв д). Следовательно, при k^l
ш*.'~ ИМ Т(4_|)|((_1)!!!Т"'То|(!_^и|' \lV
где первое слагаемое — число способов достижения
клетки (k, I) без диагональных ходов, второе слагаемое —
с одним диагональным ходом и т. д.
Рекомендуем читателю, опираясь на очевидное
равенство
wxty = V>x.,-x + wx-x,, + V>x-i.,-i (15)
при условии
в»*,. = »..,= !» {Щ
составить таблицу значений функции wXty, заполняя ее
значениями клетки доски, и сверить результаты со
значениями, вычисленными по формуле (14).
Можно, несколько изменив условие задачи, искать
число способов перевода короля с какой-нибудь
конкретной клетки (например, с клетки е2) на ту или иную
клетку шахматной доски за наименьшее число
ходов.
Разобьем доску на зоны, состоящие из клеток, до
которых король может дойти за один ход, за два хода
и т. д. (рис. 22). Пусть, например, для всех клеток первых
трех зон решения уже известны (см. числа, стоящие
в клетках этих зон).
£6

Так как на клетку /5 четвертой зоны можно попасть
лишь с клеток е\, /4, g\ третьей зоны, а до этих клеток
можно дойти соответственно
семью.шестьюитремя
способами, то на клетку /5 король
может попасть шестнадцатью-
способами (7 -|- 6 -\- 3).
Очевидно, до клетки g5
можно добраться десятью
(3 + 6 -j- 1), до клетки Л5—
четырьмя (3+1) способами
и т. д.
Заполняя
последовательно клетки 4-й, 5-й и т. д. зон,
легко убедиться, например,
в том, что в распоряжении
короля имеетея 12, 20, 266 и
357 способов, чтобы добраться соответственно до
клеток а% а7, с8, db.
С d в f д
Рис 22.
Разные задачи
Существует ряд аналогичных задач, в которых для
искомой функции трудно или невозможно составить
разностное уравнение. Так, например, будет обстоять дело,
если короля заменить шахматным конем или если в
задачах о ладье и о пауке запретить некоторые из ходов,
поставив на доске перегородки или уничтожив
некоторые стерженьки в пространственной сетке.
В такого рода задачах зоны, до всех клеток которых
можно добраться за входов (k = l, 2, 3, ...), могут
иметь весьма своеобразный вид, поэтому клетки
различных зон удобно либо нумеровать, либо закрашивать
в разные цвета. При этом, конечно, прежде чем
определять А + 1-ю зону, надо выявить все клетки k-ft зоны.
Крупными цифрами на рис. 23 отмечены клетки,
принадлежащие первым двум зонам в задаче о коне на
неограниченной шахматной доске, мелкими цифрами
указано, сколькими способами конь из клетки А может
попасть в отдельные клетки этих зои.
Очевидно, третьей зоне будут принадлежать те клетки
из числа незаполненных, на которые можно ходом коня
перейти хотя бы с одной клетки второй зоны. Например,
87

Рис. 23. Рис. 24.
и до каждой из них ладья может добраться восемью
способами (*").
Аналогичные вопросы можно поставить в задачах о
короле и о пауке, причем совокупность запрещенных
ходов можно выбирать по-всякому. При этом можно
стремиться к тому, чтобы «Л-зоны» имели какой-нибудь
замысловатый вид.
Легко убедиться, что в задаче о коне пятая, шестая
и т. д. зоны имеют довольно правильный вид, причем
при k 5* 5 для числа Nk клеток k-й зоны имеет место
формула: Nk=l20-\-28(л — 5).
Попробуйте подумать над следующими вопросами:
1. Сколькими способами на неограниченной
шахматной доске король может попасть за четыре хода в
четвертую зону?(")
88

2. Сколькими способами две (три, четыре) нешкя,
стоящие на второй линии шахматной доски, могут быть
доведены до 8-й линии? (") (Имеются в виду различные
способы чередования ходов, делаемых разными пешками,
а также право каждой из них воспользоваться двойным
начальным ходом или отказаться от него.)
3. Не удастся ли вам найти общее решение задачи
о коне, т. е. определить (хотя бы при k 5*5)
зависимость числа способов достижения отдельных клеток
неограниченной шахматной доски от положения, ими
занимаемого.
Аналогичный вопрос можно поставить при тех или
иных значениях р и q для «р, ^-коня», при ходе
которого одна из координат меняется на р единиц, а другая
на q единиц.
§ 16. МАГИЧЕСКИЕ КВАДРАТЫ
Магическим <тг-квадратом-» назовем квадрат,
разделенный на пг клеток, заполненных первыми пг
натуральными числами так, что суммы чисел, стоящих в любом
горизонтальном или вертикальном ряду, а также на
любой из диагоналей квадрата, равны одному и тому же
числу sn= о • Если одинаковы лишь суммы чисел,
стоящих в любом горизонтальном и вертикальном ряду,
то квадрат называют полу магическим. На рис. 25, а
приведен магический квадрат, называемый квадратом
Дюрера по имени математика и художника XVI века,
изобразившего его на известной картине «Меланхолия»;
два нижних средних числа этого квадрата образуют
число 1514 — дату создания картины.
Нетрудно полностью исследовать вопрос о
магических квадратах при л=3. Действительно, s,=
3 (Зг 4- I)
= .J7" =15, и существует лишь восемь способов
представления числа 15 в виде суммы различных чисел
(от единицы до девяти):
15 = 1-{-5 + 9=1-|-6-{-8 =
= 2 + 4 + 9 = 2 + 5 + 8 = 2 + 6 + 7 = 3 + 4 + 8 =
= 3 + 5 + 7 = 4 + 5 + 6.
89

Заметим, что каждое из чисел 1, 3, 7, 9 входит в две,
а каждое из чисел 2, 4, 6, 8 — в три указанные суммы
и лишь число 5 входит в четыре суммы. С другой
стороны, из восьми трехклеточных рядов: трех
горизонтальных, трех вертикальных и двух диагональных — через
каждую из угловых клеток квадрата проходит па три,
через центральную клетку по четыре и через каждую
из остальных клеток по два ряда. Следовательно, число
5 должно обязательно стоять в центральной клетке,
числа 2, 4, 6, 8 — в угловых клетках, а числа 1, 3, 7,
9 — в остальных клетках квадрата.
г
9
*
7
5
3
в
1
в
1В
5
В
«
3
W
В
15
2
11
7
14
13
В
12
1
В
1
В
7
S
3
2
3
4
а]
Рис. 25.
Так как числа 2, 4, 6 и 8 можно расставить лишь
восьмью способами в угловых клетках квадрата так,
чтобы каждая из диагональных сумм равнялась
пятнадцати, а расположение этих чисел вполне определяет
положение чисел 1, 3, 7, 9» то можно утверждать, что
существует лишь восемь девятиклеточных магических
квадратов. Два из них, являющиеся зеркальным
изображением друг друга, приведены на рис. 25, б, в;
остальные шесть могут быть получены из этих квадратов
вращением их вокруг центра на 90°, 180°, 270°. С
возрастанием л число N различных квадратов с л* клетками
быстро растет, и хотя общая формула, выражающая
зависимость N от я, до сих пор не найдена, однако
установлено, например, что существует 880 различных
шестнадцатиклеточных магических квадратов, а уже при
л = 7 число магических квадратов достигает сотен
миллионов.
Для составления магических квадратов с нечетным
числом клеток имеется ряд способов, предложенных
различными авторами. Одним из изящнейших способов
является так называемый метод террас, предложенный
Баше: пг чисел выписываются по порядку (см. рис. 26,
90

тде п=5) в п рядах, параллельных одной из диагоналей
квадрата — в каждом ряду по п чисел, причем среднее
из этих чисел должно стоять в центре квадрата.
Предоставляем читателю, доказать, что параллельное
перенесение всех выступающих за пределы основного
квадрата частей (террас) внутрь квадрата, к
противоположной стороне его, приводит к магическому
квадрату.
Используя зеркальное отражение и повороты на 90°,
180° и 270°, из каждого «квадрата Баше» можно
получить еще семь других магических квадратов.
1'
г
6
3
7
77
«
8
/г
[73
5
9
73
77
27
70
/<s
73
\22
75
73
23
го
24
25
Рис 26.
Для составления магических квадратов с четным
числом клеток удобный способ был предложен Баллом.
Назовем для краткости горизонтальной,
вертикальной и центральной транспозициями (и обозначим через
(а, Р). («» у), (а« *)) Операции, при которых меняются
местами числа а и р, а и у, а и J соответственно
симметричные относительно прямых ВВ\ АА' и центра
квадрата (рис. 27, а).
Легко убедиться, что две центральные транспозиции
(а, й) и (р, у), при которых меняются местами числа а, р,
7, 8 (стоящие в противоположных вершинах
прямоугольника, имеющего прямые АА' и ВВ' своими осями
симметрии), равносильны двум горизонтальным
транспозициям (а, р) и (у, Ь) и двум вертикальным транспозициям
(а, у) и {$, Ь), произведенным друг за другом.
Если заполнить квадрат с (2то)* клетками
натуральными числами от 1 до Am1 включительно, выписывая их
в естественном порядке (заполняя слева направо сначала
3
20
7
77
76
3
25
72
3
27
73
22
74
7
75
2
73
ff\70 е
77\70J3
91

верхнюю, затем вторую, третью и т. д. строки), то легко
доказать (см. [25], стр. 173—176), что:
1. Обе диагонали будут удовлетворять условию
магичности, т. е. суммы чисел, стоящих на каждой
диагонали, будут равны т (4/га* -|-1).
2. Любые два вертикальных (горизонтальных) ряда,
симметрично расположенных относительно прямой ВВ'
(АА'), будут удовлетворять условию магичности, если
в них произвести т. каких-нибудь горизонтальных
(вертикальных) транспозиций.
fi_
+ _-- • ±
+ !_ + _
~_±±1±
1-±±~1 •
-+1_+-
+ Т +
33
4
в
т
гз
г?
ZZZI
т
згзз
гз/г
а ге
35 31
/7 г*
0
ш
&
гз
Ц— +
_±±
_±±1
+ +
«/
а
s
9
*
z
//
7
п
3
/О
3
IS
!3
9
12
г
?J
й'
±_±_-±_+
+ + + ±_
1±1±+_±_
± + ± +*.
±__±+__±
_ + _ + +_±
_±±1_±±1
+ + + +
SS
17
W
гз
зг
w
sz
5Ь
27
л л
Z3
S9
19
37
U
ZI
13
22
3D 31
гз
28 ЗЙ
63
л
_-±11±-
-_J_ + ±1_г
±±_1 ±±
±±±±
±±_ __++
-_J.±±±Iz
- + I I + -
aj
e'J
<U
Рис. 27.
Сущность способа Балла заключается в подборе таких
транспозиций, после выполнения которых все строчки
и столбцы удовлетворяли бы условию магичности, а
элементы каждой диагонали остались бы
(поменявшись, может быть, местами друг с другом) на той же
диагонали.
Условимся горизонтальными (вертикальными)
черточками, стоящими в клетках, симметричных относительно
ВВ' (АА'), указывать на горизонтальные (вертикальные)
транспозиции, которым должны быть подвергнуты
соответствующие числа, а крестиками, стоящими в
вершинах прямоугольника, имеющего центр в центре
квадрата,— на две диагональные транспозиции чисел,
стоящих в вершинах прямоугольника (они, как
было указано выше, заменяют две горизонтальные и две
вертикальные транспозиции, произведенные друг за
другом).
S2

На рис. 27, б, в, г схематично указаны (для m = 3,2,4)
операции, после выполнения которых соответствующие
«естественно» заполненные «4т*-квадраты» — они на
рисунке не приведены—превращаются в квадраты б"), в'), г').
Так как при этом числа любой диагонали остаются
на той же диагонали, а т чисел любого
горизонтального и вертикального ряда меняются местами с
соответствующими числами симметрично расположенного ряда,
то квадраты б'), в') и г') будут магическими.
Советуем читателю убедиться на ряде примеров, что
отыскание схем операций, приводящих к магическим
квадратам, большого труда не представляет и при
данном т. может быть осуществлено, вообще говоря,
многими способами (см. подробнее [25], стр. 176—186).
Следует отметить, что при т четном составление
схемы для перехода от естественно заполненного
квадрата к квадрату магическому проще, чем при т
нечетном, когда в схему неизбежно должны входить наряду
с крестиками горизонтальные и вертикальные черточки.
При четном т схема может состоять из одних
крестиков (см., например, схему г)), что, впрочем, не
является обязательным условием, как это видно, например,
из схемы д).
Расширим несколько понятие магических
«/^-квадратов», считая, что клетки их могут быть заполнены
числами от k-\-l до k~\-nx.
Можно искать магические квадраты, удовлетворяющие
различным дополнительным условиям. Например, еще
в 1544 году Штифель построил магический «7*-квадрат»,
дающий при отбрасывании всех граничных клеток
магический «5-квадрат», заполненный натуральными числами
от 13 до 37, переводимый тем же путем в магический
«3*-квадрат», заполненный числами от 21 до 29 (рис. 28, а).
На рис. 28, б изображен сверхмагический квадрат,
т. е. такой, что если н нему приставить справа такой же
квадрат, то при суммировании по всем «диагональным
направлениям» получатся одинаковые суммы.
Можно построить магический «9*-квадрат»,
распадающийся на 9 девятиклегочных магических квадратов
(см. [30], стр. 106).
По аналогии с магическими квадратами можно строить
магические ««'-кубы», в клетках которых первые п'
чисел (или числа от А-f-l до k-]-n') размещены так, что
93

суммы чисел, стоящих в любом из Зя* рядов,
параллельных какому-либо ребру куба, и по любой диагонали
куба, были одинаковы.
В [30] на стр. 108—109 читатель найдет примеры
магических «4*-куба» и «5'-куба» (магического «З'-куба»
построить нельзя).
Можно ввести понятие магических прямоугольников,
дающих при суммировании по «диагональным
направлениям» и по коротким рядам одинаковые суммы,
отличающиеся от равных между собой сумм чисел, стоящих
в длинных рядах прямоугольника.
\ч\\ч
40
38
39
(3
е
5
4
/
3/
30
33
ts
15
49
г
13
26
Z7
ZZ
37
48
3
14
Z1
ZS
29
36
47
4Z
32
28
Z3
Z4
18
8
41
35
2ff
f7
3*
73
9
48
/2
11
7
44
48
10
16
to
Z4
13
3
23
1Z
20
11
19
8
22
/8
25
21
15
74
16^\23Т\5\7\74\
—г г—! f--|
17 24
£ffi?itl£j
/////
aj
%
Рис. 28.
На рис. 29 изображен магический шестиугольник а)
и «магические звезды» б) и в), дающие при
суммировании по любому из указанных прямолинейных направлений
одинаковые суммы. На рис. 29, г изображена так
называемая центральная проекция правильного додекаэдра
(см. объяснение к рис. 117), начерченная внутри
окружности /. Если составить суммы чисел, расположенных:
1) в вершинах какой-либо грани додекаэдра (19 + 2 +
+ П+8 + 25, 11+8+17 + 5 + 24 и т.п.), 2) вдоль
той или иной пунктирной линии, 3) на окружности,
то каждая из этих девятнадцати сумм будет
равна 65.
Попробуйте поломать голову над следующими
вопросами:
1. Можно ли построить «магические» треугольник и
пятиугольник, аналогичные шестиугольнику а), разместив
в схемы д) и е) соответственно числа от 1 до 7 и от 1
до 11? (").
04

2. У звезды б) не только каждая четверка чисел,
лежащих вдоль сторон, даст в сумме 26, но ту же сумму
образует каждая четверка чисел, стоящих в верщияах
больших ромбов (12 —|— 1 + 7 + 6 и т.п.) и каждая
пятерка чисел, «примыкающих» к вершинам звезды
(34-4 + 8+1 + Ю и тп)>
Рис. 29.
Не удастся ли вам найти существенно иные способы
размещения чисел от 1 до 12 в ту же схему, чтобы
каждая из пятнадцати указанных групп чисел снова да-
дала бы при сложении 26.
3. Числа от 1 до 9 разместить в клетках «З'-квад-
рата» так, чтобы каждая из четырех «угловых сумм»,
состоящих из трех слагаемых, равнялась бы одному и
тому же числу s. Например, для квадрата ж) имеем:
5=14 = 4 + 7 + 3 = 3 + 6 + 5 = 5+8 + 1 = 1+9 + 4.
В [34] показано, что число п существенно различных
решений задачи зависит от s следующим образом:
95

* 112 13 14 15 16 17 18 „ .,_ . ,0
Т| 3 6 10 9 10 6 з- ПРИ S<12 И ПРИ 5>18 за-
дача решений не имеет.
Комбинируя зеркальные отражения и повороты на
90°, 180° и 270°, из каждого из 47 существенно
различных решений можно получить еще 7 несущественно от
него отличающихся решений.
Попробуйте аналогичный вопрос исследовать для
«4!-квадрата» (з) и для «3*-куба» (к), на которых
отмечены клетки, содержащие слагаемые, входящие в одну
из «угловых сумм».
§" 17. ЭЙЛЕРОВЫ КВАДРАТЫ
Если в клетках «и*-квадрата» разместить п элементов
«первого рода»: а,, а„ ..., а„ и п элементов «второго
рода»: bt, Ьг Ь„ (каждый из них берется по п раз),
так, чтобы:
1) в каждой клетке квадрата находилось по одному
элементу каждого рода,
ч\\\\
if
&
3,2
2,23,3
3J
V
1,2
2,1
V
ЗА
4.2
2,3
2,2
V
з,/
t*
3,3
/,2
2,4
4,1
4,4
2,1
!3
3,2
зл
1.1
S.2
4,3
2,2
3,3
V
V
2,53,1
5.4
5,1
2,4
4,2
1,5
4Л
1,2
3,5
5,3
4J
1,4
2,/3,2
^ЩьЩ
55
2±3$\4/gl£Z}£3\
2/£l\4,2\5?\l4\
а]
Я
/////
Рис. 30.
4
2) каждый элемент первого рода был объединен один
и только один раз с каждым элементом второго рода,
3) в каждой строке и в каждом столбце квадрата
имелись все элементы как первого, так и второго рода,
то получится так называемый эйлеров квадрат.
Если третьим свойством будут обладать и диагонали
квадрата, то будем иметь диагональный эйлеров квадрат.
На рис. 30 изображены эйлеровы квадраты при
я=3, 4, 5, причем в клетках указаны лишь индексы
элементов первого и второго рода.
96

Квадрат б) будет диагональным, а квадрат в) даже
будет обладать таким свойством: если к нему
приставить справа такой же квадрат, то на любом из десяти
«диагональных направлений», указанных на рисунке
стрелками, встретится любой элемент первого и второго рода.
Такой квадрат носит название вседиагонального эйлерова
квадрата.
Задачу построения эйлеровых квадратов можно
сформулировать иначе: «Пусть каждый из л* элементов
характеризуется принадлежностью к одному из п классов
и к одной из л категорий, причем любые два предмета
отличаются друг от друга либо классом, либо
категорией, либо сразу и тем и другим.
Требуется разместить предметы в клетках «л'-квад-
рата» так, чтобы в каждом горизонтальном и в каждом
вертикальном ряду стояли бы представители всех
классов и всех категорий.
При л = 4 можно, например, взять 16 фигурных карт
(туз, король, дама, валет) четырех мастей, а при
л> 4 взять л* кусочков картона с нарисованными на них
л разными фигурами (квадраты, треугольники, круги и
т. д.), окрашенными в л разных цветов.
Сам Эйлер безуспешно пытался решить задачу
о тридцати шести офицерах (по шести офицеров разных
званий из шести различных полков). Позже было
доказано, что задача эта неразрешима, т. е. при л = 6
эйлеров квадрат не может быть построен.
Уменьшив на единицу каждое из чисел, стоящих в
клетках эйлерова квадрата, и рассматривая затем пары
чисел, как цифры числа, написанного в л-ичной системе
счисления, мы из любого эйлерова квадрата получим
полумагический квадрат, а из любого диагонального
эйлерова квадрата — магический квадрат.
Рекомендуем читателю получить этим путем из
вседиагонального квадрата в) сверхмагический
«биквадрат».
Любой эйлеров квадрат можно рассматривать как
объединение двух латинских квадратов, т. е. квадратов,
заполненных л элементами (каждый из них берется по
л раз) так, что в каждой строке и в каждом столбце
встречается любой из данных элементов. При этом должны
иметься сочетания каждого элемента одного из латинских
квадратов с каждым из п элементов второго.
4 А. П. Дом оря д
97

§ 18. РАЗВЛЕЧЕНИЯ С ДОМИНО
Как известно, каждая из 28 костей домино разбита
на две половинки, на которых точками нанесены
различные сочетания с повторениями чисел: 0, 1, 2,
3, 4, 5,6. Кость, имеющую на своих половинках k и I
очков, обозначим через (k, I).
Прикладывая кости друг к другу одинаковыми
половинками, можно составить «цепь». Цепь с одинаковыми
половинками на концах можно замкнуть. Разрывая
замкнутую цепь из т костей в том или ином месте, можно
получить незамкнутые цепи.
Можно рассматривать «обобщенное домино», на
половинках костей которого нанесены всевозможные
сочетания с повторениями чисел: 0, 1, 2,..., п— 1, п.
Попробуйте решить следующие задачи:
1. Показать (**), что число костей и сумма всех
очков в обобщенном домино равны соответственно
(л+1) (л+2) п (п + D (я + 2)
2 и 2 •
2. Доказать (*'), что, удалив при четном п из
полного комплекта кость (а, Ь), где а =£ Ь, из оставшихся
костей мы сможем сложить
лишь незамкнутую цепь,
имеющую на концах а и b
очков.
3. Доказать (4В), что прн
п нечетном полный
комплект костей нельзя уложить
в цепь и что самая
длинная цепь будет содержать
не больше чем л'+^ + 3
костей.
4. Распределить 28
костей между четырьмя
игроками так, чтобы до
окончания игры первым игроком ни второй, ни третий
игрок не имели бы возможности положить ни одной
кости (*').
5. Фигура, изображенная на рис. 31, может быть
разбита на 14 квадратов, каждый из которых содержит
четверку одинаковых чисел. Меняя ролями числа: 0, 1,
Рис. 31.
98

|ф
\e\i
\,\,
\з \i
\e\i
\>\>
1*1-
~\\o\* \\s\s
\\Z \2 \\3\3
\\s \s \\2\3
"|M# II* 1*
' \\b\j \\2\7,
N*klUkl
\\A'\\e\3
« 0
3 0
\з\о\
\г \o |
\6\o |
l^kl
1; \° 1
2, 3, 4, 5, б и используя зеркальные отражения от
вертикальной оси фигуры, можно получить 10080 ( = 2-7!)
фигур (включая и данную),
несущественно
отличающихся друг от друга.
Не удастся ли вам найти
фигуру того же вида с
существенно иным разбиением
на 14 квадратов с
четверками одинаковых чисел в
каждом?
6. На рис. 32 кости
домино расположены так, что,
отбросив мысленно правый [7
столбец, состоящий из нулей, *~
мы получим «7*-квадрат», в Рис. 32.
котором сумма очков,
стоящих по любой диагонали и в любом горизонтальном
или вертикальном ряду, равна двадцати четырем.
Не удастся ли вам построить аналогичный^/*—I)1-
квадрат» для обобщенного домино?
§ 19. ЗАДАЧИ, СВЯЗАННЫЕ С ШАХМАТНОЙ ДОСКОЙ
В § 15 были рассмотрены задачи на определение
числа способов передвижения шахматных фигур с одной
клетки доски на другую.
Рассмотрим еще две классические задачи: о ферзях
и о коне и ряд примыкающих к ним вопросов. Одни из
них интересны благодаря тесной связи их с теорией
соединений, другие могут служить источником для
исследований и самостоятельных поисков оригинальных
решений. Много интересных подробностей, относящихся
к задачам о ферзях и о коне, читатель найдет в книге
Окунева Л. Я. [21].
Задача о ладьях
Сколькими способами можно расставить п ладей на
тх-доскеу> так, чтобы они не угрожали друг другу?
Очевидно, ладьи должны стоять в разных строках и
в разных столбцах доски. Любое такое расположение п
фигур на шахматной доске можно охарактеризовать
перестановкой чисел: 1,2, 3,..., п — 2, п—1, п, если
4*
99

условиться, что последовательные числа в перестановке
будут указьгоать номера строк, занимаемых фигурами,
стоящими соответственно в первом,, во втором и т. д.
столбцах.
Так как любой перестановке будет соответствовать
определенное решение нашей задачи, а разным
перестановкам соответствуют, очевидно, разные решения, то
общее число решений рассматриваемой задачи равно л!.
Задача о ладьях сильно усложняется, если
интересоваться лишь решениями, в которых ни одна из ладей
не стоит на диагонали, соединяющей левую нижнюю
клетку с правой верхней. Общее число N таких решений
определяется формулой
N-
==nl{r\-'h+k--'-+Lir1) <см- № стр- 13>;
оно равно числу перестановок из п элементов, в
которых ни один из элементов не занимает своего
«нормального» места.
Разнообразя накладываемые ограничения (например,
требуя, чтобы ладьи стояли лишь на белых полях, или,
сделав «запретной» зоной обе диагонали и т. п.), можно
прийти к более или менее трудным комбинаторным
задачам.
Задача о ферзях
Сколькими способами можно расставить п ферзей
на кп1-доске» так, чтобы они не угрожали друг другу?
Ферзи, стоящие в клетках (р, q) и (s, t), угрожают
друг другу в диагональном направлении тогда и только
--, тогда, когда |р — s] = |# —1\; здесь
р, s — номера столбцов и q,
t—номера строк, на пересечении которых
находятся соответственно клетки (р,
q) и (s, t). В соответствующей
перестановке (см. задачу о ладьях) на р-и
и 5-м местах должны стоять числа q и
t. Перестановка из «чисел тогда и
только тогда будет характеризовать
какое-нибудь из решений задачи,
когда разность номеров мест,
занимаемых любыми двумя числами, отличается по
абсолютной величине от разности этих чисел.
Рис. 33.
100

Легко убедиться, что при л=2 и при л=3 задача
о ферзях неразрешима. Разрешимость задачи при я=4
и при л = 5 легко проверить на рис. 33, а при Л2&6
разрешимость задачи видна из рассмотрения
перестановок, приведенных в таблице:
Вид Перестановка, дающая решение
числа л задачи о ферзях
6^ + 4 2, 4,6,8,..., л — 2, л, 1,3,5,7,..., л — 3,л— 1
6&-J-2 4, л —2, л —4, л —6, ..., 10,8, 6, л,2, п— 1,
1,л — 5, л — 7, ...,5,3,л — 3
6k + b} л>2,4,6,...,л-3,л-1,1,3,5,...,л-4,л-2
6&-J-3 л, 4, л —3, л —5 10, 8, 6, л—1,2, л —2,
1,л —6,л —8, ...,7,5, 3, л —4
Попробуйте доказать, что в каждой из указанных
перестановок разность любых двух элементов отличается
по. абсолютной величине от разности номеров их мест
(см. [21], стр. 23—25). Проверьте это, например, при
£ = 1 и при k = 2.
Вопрос о числе решений задачи о ферзях на «л*-до-
ске» при произвольном л до сих пор не решен, несмотря
на усилия многих математиков. В частном случае (л=8)
установлено, что задача имеет 92 решения. Среди них
«независимых» решений только 12; они характеризуются
перестановками:
15863724 25741863 27581463
16837425 26174835 35841726
24683175 26831475 36258174
25713864 27368514 35281746
Остальные решения получаются из этих двенадцати
путем «отражения всех фигур» от вертикальной средней
линии шахматной доски и путем поворота фигур (взятых
в «начальном» и в «отраженном» положениях) на 90°,
180°, 270° относительно центра шахматной доски.
На рис. 34 в верхнем ряду дано решение,
соответствующее перестановке 15863724, и три решения,
получающиеся из него вращением на 90°, 180° и 270°;
W1

Ш ш ш 3
jsFW*Ar
Ss\^ SSSS \-3*>
.ж
111 if
%г«А
АЛ1
Ж£Ж_М_И
Ш Ш чШ ш
-*К xV-XN ^чУ- 4WV
■-ЧЭ* х«ч> c^*xv sii\w
Мччч ЧШЧЧЧЧЩ Jis*
NSS4? ~X\4S SSl4 ^
Т Ш ^ %
ч%
кЧЧ1 чР чЖ5Ж~
ш Ш ш т
о
Ж
О.
кчч!—Ш—Ш—чМ^
■^ Ш5 ^ "1
iLA^llLJi
„N4f ш ш ш
102

в нижнем ряду даны «отраженное» решение и решения,
получающиеся из него вращением на те же углы.
Таким образом, каждая из указанных перестановок
дает, вообще говоря, всего восемь решений; исключение
представляет последняя перестановка, дающая лишь три
дополнительных решения (проверьте!).
Рассмотренные две задачи могут быть обобщены в
различных направлениях. Например, можно п пар&к или
п ферзей расставлять на «т'-доске» (т^>п) или на
«р, q-доске» (р ^ я, q s* я).
Можно искать решения задачи, при которых,
например, никакие две из расставляемых фигур не будут
связаны друг с другом ходом коня и т. п.
Можно, наконец, взять трехмерную прямоугольную
«я'-сеть» (или даже А-мерную «я*-сеть») протяженностью
в л—1 единиц в направлении каждого «измерения» и
расставлять в ее узлах л* (соответственно я*"1) ладей
или ферзей, не угрожающих друг другу.
При этом будем считать, что ходом ладьи и ходом
ферзя можно попасть с данной узловой точки на любую
узловую точку, у которой лишь одна координата
отличается от соответствующей координаты исходного узла,
а ходом ферзя можно попасть также и на узловые точки,
у которых две координаты отличаются от
соответствующих координат исходного узла на числа, имеющие
равные абсолютные значения. Конечно, можно и по-иному
определить ход ферзя, например, считая, что узлы
Л(а„а„ ...,«*) и B(bltbt bk) соединены ходом
ферзя, если разности bs-~а^ (при s=l,2, ...,k — l,k)
независимо друг от друга принимают одйо из трех
значений: 0, т, — т(т — произвольное целое число), причем
хотя бы одна из этих разностей должна быть отличной
от нуля.
При такой трактовке хода ферзя представлял бы
интерес вопрос определения наименьших значений л (при
различных k), для которых задача о ферзях будет
разрешима.
Заметим, что задача о размещений л слонов (стоящих
на белых и черных полях) на я'-доске оказалась по
трудности средней между задачами о Ладьях и о ферзях.
Число решений ее было установлено сравнительно
недавно советским математиком С. Е. Аршоном ([38], вып.
8, стр. 24—29).
103

Задача о коне
Обойти ходом коня все клетка шахматной доски,
побивав в каждой клетке по одному а только по одному
разу.
Эта задача привлекала внимание многих крупных
математиков, давших ряд приемов для получения ее
частных решений (см. £21], стр. 54—74). Однако до сих пор
не установлено даже, чему равно общее число
решений задачи, хотя и известно, что число это очень
велико.
Обычную шахматную доску можно заменить «я*-доской»
(я =7^=8) или прямоугольной «/я, я-доской». Можно,
наконец, брать и не прямоугольные доски или доски с
«пробелами» внутри.
На рис. 35 приведено несколько решений задачи
о коне со своеобразными узорами, получающимися при
соединении центров клеток, последовательно обходимых
конем, отрезками прямых.
Русский шахматист XIX века Янич нашел решение
задачи о коне, приводящее, если клетки доски
перенумеровать в порядке их обхода, к полумагическому
квадрату с одной и той же суммой (s = 260) по
строкам и по столбца^ (рис. 35, в).
Обычного коня можно заменить «р, q-конем»,
перемещающимся с каждым ходом на р клеток в одном и на q
клеток в другом направлении, причем р и q должны быть
числами разной четности, так как иначе «р, ^-конь»
сможет двигаться лишь по клеткам одного цвета.
Легко убедиться, что «З'-доску» нельзя обойти ходом
обычного коня. Нельзя обойти также и «4*-доску»,
вместе с тем на прямоугольной «3, 4-доске» задача
разрешима.
Естественно, что с возрастанием чисел р и q (или
хотя бы одного из них) задача может оказаться
неразрешимой на «л'-доске», даже при некоторых значениях
л>4.
Интересно исследовать, например, можно ли обойти
«я*-доску» (при л = 5, 6, 7, 8) «2, 3-конем» и «1, 4-конем».
В тех случаях, когда задача окажется неразрешимой,
можно поставить вопрос о минимальном числе клеток,
выпадающем из обхода (например, обычный конь может
обойти все клетки «З'-доски», кроме центральной). В слу-
104

чае же разрешимости можно искать решения с
оригинальными узорами.
Обычная задача о коне равносильна следующей
арифметической задаче: написать 64 различные пары целых
чисел: (ах, 6,), (а„ &,), .... (a,t, &,t) (числа ак и Ьк могут
ев
50
23
tO
St
49
59
S
3
tt
sz
49
22
7
4
47
SB
24
St
S4
9
SO
4S
2
5
S3
tz
2f
S2
t
в
57
40
t4
25
40
33
20
53
44
3t
37
34
t3
23
4t
32
to
5S
25
75
3S
39
54
77
30
43
35
39
27
•7S
29
42
55
t8
Рис. 35.
принимать значения от 1 до 8) так, чтобы для любых
двух соседних пар выполнялось условие
(а„+1-акУ + (Ьк+1-Ьк)' = Ъ
(одна из компонент изменяется на одну, а другая на две
единицы). Если, кроме того, (a,t — «,)+(*•* — &,)*—5,
то из конечной точки обхода можно ходом коня попасть
в начальную точку. Обходы, удовлетворяющие
последнему равенству, называются замкнутыми.
105

Разные задачи
—i—i—i—i—i—i ■ i „
--Г- + + + + + 4--
--4- + + + ++ + -
- + + + + + + + -
--f-f-f-f-f+ -f-
- + + + + + + + -
- + + + + + + + -
--Ы- + + + + + -
-Ll l__l L_J 1 1—I
Рис. 36.
Интересны также задачи, связанные с обходом доски
королем или ладьей, делающей ходы лишь на соседнюю
клетку (простые ходы ладьи).
Так как при любом положении ладьи в ее
распоряжении имеется, самое большее, четыре хода, в то время
как король и конь могут с отдельных клеток делать
до восьми различных ходов, то естественно
ожидать, что задачи, связанные с
ладьей, окажутся наиболее
простыми.
Не удастся ли вам найти,
сколько различных способов
имеется в распоряжении ладьи
для обхода «я*-доски» при
я = 3, 4, 5... или «т, я-доски»
при различных значениях т и
я (может быть, вам удастся
даже найти общее решение
задачи при произвольных т и я).
Следует отметить, что при
нечетных значениях
произведения тп не существует замкнутых обходов «т,и-
доски» ладьей, так как
исходная и конечная клетки будут
обязательно клетками одного
цвета (ладья должна сделать
четное число ходов, чтобы
добраться до конечной клетки) и
не могут быть соединены друг
с другом простым ходом ладьи.
Очевидно также, что для досок
с четным числом клеток
исходная и конечная клетки не могут
быть (для ладьи) одинакового
цвета, чем объясняется, в
частности, неразрешимость
следующей задачи: начав обход из комнаты А (рис. 36),
обойти все комнаты, побывав в каждой по одному разу
и закончив обход в комнате В.
Отметим еще задачи, в которых та или иная фигура
должна пройти через все клетки доски, не обязательно
Рис. 37.
106

останавливаясь в каждой клетке и, может быть, прохода
через отдельные клетки по нескольку раз. Легко,
например, убедиться, что ладья может обойти «я'-даску» за
2я—1 ходов. Для «З'-доски» замена ладьи ферзем не
уменьшает число необходимых для обхода доски ходов.
Однако, если квадратный участок из девяти клеток
расположен внутри большой доски и ферзю разрешается
Рис. 38.
выходить за его пределы, то весь участок можно обойти
уже не за пять ходов, как это имеет место для ладьи,
а за четыре (рис. 37). Аналогичный вопрос можно
поставить при я>3 для «я'-участка», помешенного внутри
большой доски.
Интересно искать такие решения задачи о коне
(короле или ладье), где обход совершается по какой-нибудь
интересной ломаной (см. рис 38). При этом для
незамкнутых обходов можно дополнительно указывать исходную
и конечную клетку.
Вопросы для размышления
1. Для небольших п, k рассмотрите задачу о коне
в случае «я*-сети» (см. стр. 103),считая, что узлы сети
A(ai, а, ак) и B(bit b\, ..., bk) связаны ходом коня,
к It
если 2(а/ — Ь{У — Ь и 21а/—Ь{\ = 3. Аналогичный
вопрос рассмотреть при небольших р и q для <ф, ^-коня»
(см. стр. 104).
2. Слон может пройти через все одноцветные клетки
«8*-доскй» за 17 ходов (рис. 39, а). За какое самое мень-
107

пюе число ходов хзн сможет обойти все одноцветные
клетки «л'-доски» (л=9, 10, 11, ....).
3» Передвигая попеременно белых и черных слонов
(рис. 39, 6), поменять их местами за 36 ходов так, чтобы
Рис. 39.
Рис. 40.
при этом ни разу разноцветные фигуры не угрожали
друг другу (").
4. Показать, что существует всего лишь 8 обходов
«3, 4-доски» ходом коня и все они незамкнутые (")•
5. Интересным свойством обладает фигура, ходом
которой связаны любые две клетки: (k, I) и (т, п) шахмат-
108

ной доски, для которых (А ***»)*-{-(/-•*/*)*«= 25. Фигура
эта передвигается и как ладья (через четыре ялетки на
пятую), и как «3, 4-конь»; с любой клетки «в'-доски»
она может сделать ровно четыре хода.
Не удастся ли читателю «создать» другие фигуры,
которые обладали бы аналогичным свойством на «л'-доске»
(л=6, 7, 9,10, ...) или на ««*-сети» (£=3, 4,...).
6. Из рис. 40 видно, что пять ферзей -на -«8*-доске»
могут держать под ударом: все клетки, а иа «11*-доске» —
все клетки, кроме занятых самими ферзями.
Найти наибольшие значения Nt и Nt при условии,
что л ферзей (л = 6, 7, 8, 9, ...) смогут держать под
ударом все клетки «ЛР-доски» или все клетки «ЛР-доски»,
кроме занятых самими ферзями,
§ 20. СОСТАВЛЕНИЕ РАСПИСАНИЙ
Приведем несколько задач на составление расписаний,
согласно которым должны объединяться члены
некоторого Коллектива, чтобы при этом удовлетворялись какие-
то дополнительные условия.
Рис. 41.
1. Тринадцать детей должны, располагаясь по
кругу, проделать 6 разных упражнений. Можно ли это
сделать так, чтобы у любого из детей каждый раз
были новые соседи.
Заменив детей буквами от А до N, поместим А на
замкнутой ломаной, делящей своими вершинами
окружность на 12 равных частей (рис. 41, а) и расставим
остальные €уквы равномерно по кругу.
109

Обходя ломаную в исходном, указанном на рисунке
положении, а также после поворота ее (вместе с буквой А;
остальные буквы при этом остаются на своих местах)
вокруг центра против движения часовой стрелки на 30°, 60°,
90% 120° и 150°, получим шесть последовательностей букв:
1) ABCDEFOH1KLMNA, 2) ADBFCHEKGMINLA,
3) AFDHBKCMENGLIA, 4) AHFKDMBNCLEIGA,
5) AKHMFNDLBICGEA, 6) AMKNHLFIDGBECA,
в которых по соседству с любой буквой стоят, в общей
Сложности, все остальные буквы.
Попробуйте доказать, что такой прием пригоден и в
общем случае, когда 2я -f-1 детей должны проделать п
упражнений. Может быть, вам удастся найти более
простой прием решения этой задачи.
2. Составить расписание шахматного турнира при
восьми участниках.
Применим прием, аналогичный использованному в
предыдущей задаче: поместив № 1 в центре круга, а
остальные семь "номеров в вершинах вписанного семиугольника,
составим с помощью ломаной линии (рис. 41, б), звенья
которой начерчены попеременно толстыми и тонкими
линиями, расписание на два дня, объединяя сначала номера,
прилегающие к концам толстых, а затем — к концам
тонких линий:
1-й день: 1,2. 4,7 6,5 8,3;
2-й день: 3,1 2,4 7,6 5,8.
Если при- этом лридерживаться указанного
направления обхода и считать, что первый из написанных в
каждой паре номеров играет белыми, а второй — черными,
то каждому из игроков придется сыграть в течение двух
дней и черными, и белыми.
Повертывая ломаную по часовой стрелке вокруг центра
4те 8те 12те
последовательно на у, у и -=- радианов и используя
в последнем случае лишь толстые линии, легко
составить расписание на остальные пять дней:
3-й день: 1,4 6,2 8,7 3,5.
4-й день: 5,1 4,6 2,8 7,3.
5-й день: 1,6 8,4 3,2 5,7.
6-й день: 7,1 6,8 4,3 2,5.
7-й день: 1,8 3,6 5,4 7,2.
110

Указанный прием пригоден, если п (число игроков)
четно; если же л нечетно, то достаточно ввести одного
фиктивного игрока, а того участника, который в этот день
встречается с фиктивным игроком, считать свободным
от игры. Например, уменьшив в полученном выше
расписании все номера на единицу и считая игрока № О
фиктивным, мы получим расписание, при котором
каждый из семи игроков будет играть три раза- белыми и
три раза черными фигурами, имея один свободный от
игры день.
3. Пятнадцать детей каждый день объединяются
для игры в группы по три человека в каждой.
Составить недельное расписание так, чтобы у любого из
детей каждый день были бы новые партнеры.
Задача эта, предложенная (в несколько ином виде)
Киркманом в 1850 году, сразу привлекла внимание ряда
крупных математиков. Приведем одно из ее возможных
решений
1-й деньг а, б, в г, д, е ж, з, и к, л, и н, о, р
2-й день: а, г, ж б, д, з в, и, р к, о, и н, л, е
3-й день: а, к, н б, л, о в, е, в г, з, р ж, д, м
4-й день: а, и, р б, г, к в, д, л ж, о, е н, з, и
5-й день: а, е, и б, ж, н в, з, о г, и, л к, д, р
6-й день: а, з, л б, е, р в, ж, к г, м, о н, д, и
7-й день: а, д, о б, и, и в, г, н ж, л, р к, з, е
Отдельными авторами были даны приемы решения
аналогичных задач при п=5-3*, при л = 3*, при п=
= 63( = 2' —1) и при л = 255( = 2в —1).
Интересно было бы найти для основной задачи и ее
вариантов легко запоминаемые расписания, позволяющие
самим участникам просто осуществлять необходимые
перегруппировки.
Английский математик прошлого века Сильвестр
поставил вопрос (до сих пор, по-видимому, не решенный)
о распределении всевозможных сочетаний по три (их
число = С?5 = 455) в 13 комплексов, каждый из которых
при разбиении на 7 групп давал бы решение задачи
Киркмана.
Решение этого вопроса равносильно составлению
такого квартального (13 недель) расписания, в котором ни
одно сочетание не повторялось бы.
1И

Много интересных подробностей, относящихся к
задаче Киркмана и к ее обобщениям, имеется в [33], т. II,
стр. 97—117.
В рассмотренных задачах и в задачах, им подобных,
можно поставить вопрос (вообще говоря, не легкий!)
о числе существенно различных расписаний, считая,
что два расписания различаются несущественно, если
одно из другого можно получить с помощью
какой-нибудь подстановки (замены одних элементов другими),
произведенной во всем расписании, и с помощью
обмена местами отдельных дней.
Подумайте над следующей задачей.
Задача. Составить (при различных значениях п)
расписание на п-\-\ день для объединения пх
школьников в группы по п человек в каждой так, чтобы
любой из них каждый раз объединялся с новыми
лицами.
Существует простой прием решения этой задачи,
когда п — простое число, но прием этот непригоден при
п составном ([33], II, стр. 94—96).
§ 21. сЗАДАЧА ИОСИФА ФЛАВИЯ» И ЕЙ ПОДОБНЫЕ
Пусть по кругу расположены п элементов и мы,
начав считать от одного из них, будем «отсеивать» каждый
А-й по счету элемент (зачеркивая его, если задача
решается на бумаге; если же по кругу расположены
какие-нибудь предметы, то отсеиваемый предмет будем
откладывать в сторону); отсеяв некоторый элемент, счет
начинают снова со следующего по кругу «уцелевшего»
элемента и т. д.
При этом можно поставить следующие вопросы:
1. Какой элемент будет отсеян в s-ю очередь
(ls^ssg л)? Такую задачу при л = 40 и k = 3 должен
был, по преданию, решить историк Иосиф Флавий
для 5 = 39 и для 5 = 40, чтобы «уцелеть» со своим
другом после тридцати восьми отсеиваний (см. [251,
стр. 122—123).
2. Как должны быть расположены п элементов,
чтобы они отсеивались в заранее намеченном
порядке?
Для решения последней задачи достаточно, выписав в
ряд п первых натуральных чисел, заменяющих данные эле-
112

менты, и двигаясь слева направо, подчеркивать каждое k-e
число, указывая при этом снизу, каким по счету оно
было отсеяно. При этом каждый раз, дойдя до самого
правого неотсеянного числа, надо продолжать счет с
левого конца, что равносильно движению по кругу.
Найдем, например, как должны быть расположены
9 карт одной масти, чтобы, перекладывая одну за
другой верхние карты под низ и выкладывая каждую
четвертую на стол, мы последовательно выложили бы по
старшинству все карты от туза до шестерки.
Пусть в первоначальной стопке карты
перенумерованы сверху вниз:
123456789
(9) (8) (3) (1) (6) (5) (7) (2) (4)
Числа в скобках получились следующим образом:
двигаемся слева направо по верхнему ряду; отмечаем
каждое четвертое число и одновременно пишем
под ним в скобках очередной номер; при дальнейших
движениях слева направо отмеченные числа не
принимаются во внимание (соответствующие карты
выкладываются на стол).
Так как по условию первым должен быть выложен
туз, то его надо положить четвертым сверху, король
должен лежать на восьмом, дама — на третьем и т. д.
и, наконец, шестерка — на первом сверху месте.
Следовательно, порядок карт должен быть таков: шестерка,
семерка, дама, туз, девятка, десятка, восьмерка, король,
валет.
При больших значениях п, особенно если нас
интересует положение какого-то одного элемента, который
должен быть отсеян s-м по счету, существует более
простой прием, не требующий предварительного
определения положения элементов, отсеиваемых раньше
(см. 125], гл. IV).
Обозначим через1 {х} наименьшее целое число,
удовлетворяющее неравенству: {х} ^ х, а ряд чисел
°i = M» °1={°i?}r о8 = К9}, .... an = {a„_1q}, ...
назовем «целочисленной геометрической прогрессией»
со знаменателем q.
Чтобы узнать номер t элемента, который должен
быть отсеян в s-ю очередь (при начальном числе элемен-
113

то» n ъ при отсеивании каждый раз А-го по счету
элемента), надо составить «целочисленную геометрическую
прогрессию», у которой а = к (п'—s) + l и 9 = ^п»
если наибольший из членов этой прогрессии, не
превышающих числа rtk, обозначить через А, то t=nk-\-
+ 1— А.
Для приведенного выше примера с девятью картами
найдем, например, номер карты, которая будет
выложена в пятую очередь на стол. Здесь п=9, & = 4,
k 4
s = 5, q=g—-7=Y' n*33^' Поэтому
al = {4(&-5) + l} = 17,a1 = jl7..|j=23,
а, = |2з4}=31, a4=/3l4}=42>«*;
следовательно, Л = 31 и*=36-{-1— 31 =6, т. е. в
пятую очередь будет выложена на стол шестая карта-
Решите следующие задачи:
"1. Установить (а*) двумя способами, что Иосиф
Флавий и его товарищ должны были занять
соответственно 13-е и 28-е места, чтобы быть «отсеянными» в
последнюю и предпоследнюю очередь.
2. Расположить 36 игральных карт так, чтобы при
перекладывании пяти карт под низ колоды и
выкладывании на стол шестой карты последовательно
появлялись бы по старшинству сначала все карты одной,
затем—другой, третьей и, наконец, четвертой масти (st6).
Построив целочисленную геометрическую
прогрессию, определить, на каком месте должен лежать туз
третьей масти (s = 19), валет четвертой масти (s = 31) и
семерка второй масти (s = 17).
§ 22. РАЗВЛЕЧЕНИЯ, СВЯЗАННЫЕ С ПЕРЕМЕЩЕНИЯМИ
ПРЕДМЕТОВ
В первых четырех задачах этого параграфа надо
прийти к заранее заданным расположениям предметов,
перемещая их по определенным правилам. Некоторые
из этих задач могут послужить для исследований и
обобщений в различных направлениях.
114

В конце параграфа рассматривается задача, в
которой повторное применение некоторой операции
приводит, в конечном счете, к исходному расположению
предметов. Определение числа необходимых для этого
операций связано со свойствами так называемых
подстановок (см. стр. 118), а для решения задачи в общем
виде требуется привлечь теорию чисел.
Перекладывание предметов парами
Четыре черные шашки расположены на прямой
вперемежку с четырьмя белыми. По правилам игры за
один ход мы можем любые две стоящие рядом шашки
переносить (не изменяя их о*о#о*о*
относительного
положения и не разъединяя vx) V о • о • о • • о
на новое место вдоль этой 2)о о • • о • • о
же прямой. Целы игры- #0о*###о 0
за четыре хода
переставить шашки так, чтобы 4/ ••••оооо
слева стояли четыре чер- Рис 42.
ные, а справа — четыре
белые шашки. (Решение указано на рис. 42.) Задача
эта может быть обобщена в следующем направлении:
имеется к видов шашек, по s штук каждого вида.
Исследовать, нри каких значениях k и s можно с
помощью ряда ходов перейти от расположения а) к б)
(рис. 43) (в [25], стр. 189—191, доказывается, что задача
разрешима при любом s>4, если к =2).
«/0© ••• ©0© "• © 0© ••' ©
#00---0©©---©©0---0 * ©©•••©
Рис. 43.
Можно договориться, что за один ход переносятся
не две, а, например, три стоящие рядом шашки; при
этом можно условиться класть их на новом месте
только в прямом, только в обратном или, наконец, и в
прямом, и в обратном порядке. Можно также по-иному
задавать окончательное расположение шашек.
»5

Задача Люка
Шашки расставлены в соответствии с рис. 44.
Требуется белые шашки поменять местами с черными,
причем можно двигать белые шашки только вправо, а
черные — только влево и любая шашка передвигается
|о|о|о|о
Рис. 44.
либо на соседнюю с ней пустую клетку, либо на пустую
клетку, находящуюся непосредственно за ближайшей
шашкой другого цвета.
Отбрасывая после несложного анализа ходы,
приводящие к неразрешимым положениям, легко прийти к
решению, которое записывается так: бччбббччччбббббчччч
чбббббччччбббччб, здесь буквами «б» и «ч» указан
itrpt последовательно передвигаемых шашек.
Собирание монет в группы
Восемь монет расположены в ряд. Надо переложить
четыре монеты так, чтобы получились четыре группы
по две монеты в каждой. При этом каждую переклады-
л^алапаа ваемую монету можно соеди-
ЮФ^(£)\0\£)(О(Ю иять лишь с монетой, отделен-
л,> f,i £. ,у ной от нее двумя монетами
(~\(~\ О О (разрозненными или объеди-
УУ 73 вб «е™™11 в группу).
Почти очевидное решение
Рис. 45. сводится к
последовательному перекладыванию пятой
монеты на вторую, третьей — на седьмую, четвертой —
на первую и, наконец, шестой — на восьмую (см.
рис. 45).
Попробуйте найти решение аналогичной задачи для
рп монет (р^4), которые надо собрать в Р групд по п
монет в каждой, а перекладываемая монета должна
переноситься через п соседних с ней монет (разрозненных
или объединенных — частично или полностью —в группы)
(см. [25]).
116

Рума
В [34] дано описание игры индийского
происхождения, носящей название «Tschuka-Ruma». Приведем ее
в несколько измененном виде.
По кругу расположена 2п-\-1 лунка. В начале игры
одна лунка (рума) пустая, а в каждой из остальных
лежит по п шаров (на рис. 46 л=2).
Цель игры — путем перекладывания шаров собрать
их все в руме.
Назовем ходом игры следующее действие: все шары,
находящиеся в некоторой лунке А, раскладываются по
одному в соседние лунки
(движение происходит по
часовой стрелке). Если число
распределяемых шаров
превышает 2л, то один шар
попадет в лунку А, а
остальные шары снова
распределяются по одному в
соседние лунки.
Первый ход можно де- Рис- 46.
лать из любой лунки. Если
при очередном ходе (в том числе и при первом)
последний из распределяемых шаров попадает в руму, то
следующий ход можно делать из любой лунки, кроме
румы, а если — не. в руму, то следующим ходом должны
распределяться шары из лунки, в которую попал
последний шар, при условии, что эта лунка не была перед
этим пустой, иначе игра считается проигранной.
Легко убедиться, что первый ход (при л =2) должен
быть сделан из лунки 3, так как во всех остальных
случаях мы, делая второй ход, попадем последним
шаром в пустую лунку и проиграем игру. После ряда
попыток можно убедиться, что к цели ведут ходы,
сделанные последовательно из лунок с номерами: 3, 4, 2,
3, 4, 1, 4, 2, 3, 4.
При л = 3 наибольшее число шаров, которое удается
перевести в руму, равно, по-видимому, пятнадцати. При
л = 4 имеется не менее девяти различных решений
задачи.
Интересно было бы создать теорию игры или хотя
бы исследовать ряд частных случаев, в каждом из
117

которых следует либо найти путь (или несколько путей)
достижения цели, либо определить наибольшее число
шаров, которые возможно перевести в руму.
Можно подумать и о различных видоизменениях
игры, помещая, может быть, в начале игры в каждую
лунку по * шаров (s^n), изменяя «правила ходов»
и т. п.
Многократное повторение одной и той же операции
Существует ряд развлечений с картами (которые,
как увидим, можно оформить и иначе), основанных на
том, что, нарушая многократно по какому-нибудь
определенному закону взаимное расположение некоторых
предметов, приходят, в конечном счете, к исходному их
расположению.
Объяснение этого загадочного для непосвященных
явления основано на простых свойствах подстановок.
Если имеется и перенумерованных предметов: с,, alt...
..., ап, то переход от исходного их расположения
к расположению а«„ а*,, ..., а„п (где а,а,... ап —
некоторая перестановка из чисел: 1, 2, ..., п) можно
охарактеризовать так называемой подстановкой А =
= ( "• п п), показывающей, каким числом
\а1а1а, ... а„_, а„ /
(а,) надо заменить число (i), стоящее в верхней строчке
подстановки А.
Элементы а„ аж, .... ап часто бывает удобно
обозначать числами от 1 до п.
„ л (\ 234567 8\
Пусть, например, подстановка •"—(58637 142/
применена сначала к перестановке 1 234567 8,
затем к перестановке, которая при этом получится,
и т. д. Это даст нам:
А А А ^
12345678—*5863714 2—* 72164 538—*4851376 2-
(1) (И) (ПО (IV)
AAA
—*3 2 7 5 6 4 1 8—*6 8 4 7 1 3 5 2—-1 2 3 4 5 6 7 8
(V) (VI) (I) J
Назовем произведением двух подстановок С я D
такую подстановку, которая равносильна подстановкам С
и D, произведенным одна за другой (сначала С, затем D).
118
М1)

Например, если C=(J | J J |).Z?«(J|JJf),
/1 2 3 4 5\
то CZ3=f4 . 2 5 3/" Действительио» в подстановке С
1 заменяется на 2, а в подстановке D 2 заменяется на 4;
следовательно, в подстановке CD 1 заменяется на 4
и т. д.
Убедитесь, что DC=(\ \ \ \ lj) , т. е. DC=£CD.
п ... /1 2 3 4 5 6 7 8\
Легко видеть, что ^ — ( 7 2 16 4 5 3 8/—это
подстановка, переводящая в схеме Q) перестановку I в
перестановку III, перестановку II — в IV и т. д.
Так как шестикратное применение подстановки А
т , ., /1 2 3 4 5 6 7 8\
переводит I в I, то A't^f j о 3 4 5 6 7 8J' то есть
все элементы остаются на своих местах. Такую
подстановку называют тождественной и обозначают буквой Е.
Наименьшее натуральное число s, для которого
В*=Е, называется порядком подстановки В.
Следовательно, порядок подстановки А равен шести.
Для быстрого определения порядка любой
подстановки (особенно, когда число переставляемых элементов
велико) удобно разложить ее на «независимые циклы».
Например, легко подметить, что в подстановке А
элемент I заменяется на 5, элемент 5 — на 7, элемент
7 — на 4, элемент 4 — на 3, элемент 3—на 6, элемент
6 —на 1 (цикл замкнулся).
Другими словами, элементы 1,5, 7,4, 3, 6 уступают
место друг другу в циклическом порядке. Это можно
охарактеризовать «циклической подстановкой» (574361)»
которую часто записывают в виде одной строки:
(15 7 4 3 6) ила (7 4 3 6 J 5) и т. д., где надо помнить,
что каждый из написанных элементов «уступает» место
следующему за ним, а последний элемент — первому
(безразлично поэтому, с какого элемента записывать
циклическую подстановку, существенно лишь сохранять в ней
ту же последовательность элементов).
Кроме того, в подстановке А элемент 2 заменяется
на 8, а 8 — на 2, что дает цикл (2 8), называемый также
транспозицией элементов 2 и 8.
119

Циклы (1 5 .7 4 3 6) и (2 8) называются
независимыми, так как у них нет общих элементов. Итак, А
равна произведению двух циклических подстановок:
Л=(1 5 7 4 3 6) (2 8).
Проверьте, например, чтоБ== (J ^ 41 £™ Уб) =
= (1934) (2) (5 8 7) (6 10) (здесь имеется даже один
одночленный цикл).
Легко доказать ("), что порядок подстановки равен
общему наименьшему кратному порядков независимых
циклов, на которые она распадается. Так, например,
порядок подстановки А равен шести (общее наименьшее
кратное чисел 6 и 2), а порядок подстановки В равен
двенадцати (общее наименьшее кратное чисел 4, 1,3, 2).
В схеме (1) следует обратить внимание на то, что
в каждом из переходов: I —»■ II, II —*- III, III—>-1Уит. д.
которые задаются одной и той же подстановкой А, на
1-е место переносится элемент с 5-го места, на 2-е —
с 8-го, на 3-е — с 6-го, на 4-е—с 3-го, на 5-е — с 7-го,
на 6-е — с 1-го, на 7-е — с 4-го и на 8-е — со 2-го места.
Можно доказать, что это обстоятельств не случайно.
Кроме того, всегда будет иметь место и обратное
явление, т. е. если в серии переходов от одной перестановки
к другой, от нее — к третьей, от третьей — к четвертой и
т. д. все переходы совершаются по одному и тому же
правилу— в смысле изменения порядка мест,
занимаемых элементами,—то все эти переходы можно
охарактеризовать одной и той же подстановкой М,
указывающей, каким элементом заменяется любой конкретный
элемент (").
Установив порядок подстановки М, мы тем самым
найдем, сколько раз следует изменять интересующим
нас способом взаимное расположение элементов, чтобы
снова создалось исходное их расположение.
Интересную иллюстрацию к рассмотренному вопросу
представляет
Тасовка Монжа
Изменение взаимного расположения предметов,
носящее название тасовки Монжа, поясним на следующем
примере: пусть 2я школьников, выстроившись в ряд
(рис. 47, а) и рассчитавшись на первого-второго, сдвоят
ряды (рис. 47, б) и стоящие во втором ряду, сделав
120

«обходный маневр», возглавляемый бывшим:
левофланговым, перейдут (в соответствии со схемой,
изображенной на рис. 47, в) на правый край так, что
левофланговый превратится в правофлангового (на рис. 47 л = 5
и школьники расположены лицом к нам).
В колоде, содержащей 2л карт, тасовка Монжа
осуществляется так: взяв всю колоду лицезой стороной
надо поочЛередю Sepe- «У®©©©©©©®©©
давать в правую руку
одну за другой карты, Q)G)G)®®-
оказываюшиеся к дан- w ч-у w w w
& -^©®©0®|
ному моменту вверху,
кладя их в правой руке
то сверху, то снизу @®®©©0®®®®
тех карт, которые в V4>vwwv-/v>v^^w
правой руке к этому ^ис. 47.
моменту уже
скопились. Очевидно, эту операцию будет характеризовать
подстановка
'1 2 ...л-1 ли + 1л4-2...2л-1 2л
М = ,
\2л2л—2... 4 2 13 ...2л—3 2л—1
При л=1,2, 3, 4, 5, 6, 7,8, 9,10,11,12,13,...
порядок M=s—2, 3,6, 4, 6, 10, 14, 5, 18, 10, 12, 21, 26, ...
Рекомендуем читателю проверить эту таблицу,
подсчитав при разных значениях л соответствующие
значения s.
Например:
*„„ » —я м—( ! 2 3 4 56 7 89 10 11 12 13 14 15 16\
при п — ЪМ— ^6141210864 2 1 3 5 7 9 1113 15/
М=(\ 16 15 13 9) (2 14 11 5 8) (3 12 7 4 10) (6),
т. е. s = 5.
Попробуйте убедиться (на картах или на любых
других перенумерованных предметах), что s-кратное
повторение тасовки Монжа приводит к исходному
расположению элементов.
Можно также выстроить в шеренгу 2л
физкультурников и по схеме, изображенной на рис. 47, произвести
121

s перегруппировок. В результате будет восстановлен
первоначальный порядок.
Существует теорема ([25], стр. 32—36):
Порядок подстановки М равен наименьшему корню
сравнения
2г = —1 (mod 4л + 1),
а если это сравнение решений не имеет, то
наименьшему корню сравнения 2*== 1 (piod4/i-j-l).
Проверьте эту теорему при различных значениях я.
Например, при л = 8 4л-{-1=33; вычисляя различные
степени двух, получим: 2* = — 1 (mod 33), т. е. при л = 8
s = 5.
Если л = 5, то 4лЦ-1=21. Для различных степеней
двух имеем: 24== — 5 (mod 21), 2'== —10 (mod 21), 2е =s
= — 20=1 (mod 21). Следовательно, при л = 5 порядок
подстановки М равен шести.
§ 23. ПРОСТЕЙШИЕ СПОСОБЫ ПОСТРОЕНИЯ
КРАСИВЫХ УЗОРОВ
Вряд ли найдется человек, который не восхищался бы
изумительной формой снежинок, чудесными узорами
кружев и орнаментов, создаваемых большими мастерами,
замысловатыми рисунками на коврах, на тканях, на
полах с красивым сочетанием керамических плиток,
различных по форме и по цвету.
Но создание красивых геометрических образов
доступно каждому, у кого найдется достаточно терпения —■>
было бы желание!
Этот и несколько следующих параграфов посвящены
геометрическим развлечениям разной степени трудности,
целью которых является получение красивых узоров,
орнаментов, кривых и т. п. Начнем с простейшего.
Узоры на клетчатой бумаге
На бумаге «в клетку» каждый может начертить без
большого труда различные замысловатые фигуры; при
этом не обязательно двигаться только вдоль сторон
квадратиков (клеток), но можно проводить также
диагонали квадратиков и прямоугольников, имеющихся на
бумаге (рис. 48).
122

Аналогичные построения можно провести и на бумаге
с треугольными ячейками, которую легко получить из
бумаги «в одну линейку»:
пусть две произвольные
точки А и В (рис. 49) лежат
на однойлинии
разлинованной бумаги; найдем точку С
такую, что АС=ВС=: АВ.
Разрезав бумагу по
прямой АС, получим
самодельную
«линейку»,разбитую по краю на интервалы
длиной а; отложив с ее
помощью на одной из
линий нового листа отрезок
MN= ла (на рис. 49 п = 5)
и разбив его одновременно
на отрезки длиной а,
построим равносторонний
треугольник MNL и через точки деления его сторон
проведем прямые, параллельные сторонам ML и NL.
При составлении орнамента на полученной
треугольной сетке можно разрешить проводить средние линии
SZ-^JSZ
z>
5 zs z
/*J::L s
77^Ш ^
^S^E^ZZ
5 t% Z
/ sz s
sz
zs zs
Рис. 43.
Рис 49.
■треугольников, что равносильно использованию сетки со
стороной треугольников у (см. рис. 50).
Взяв за основу квадратную или треугольную сетку,
попробуйте провести конкурс на получение лучшего
123

узора, причем следует учитывать оригинальность рисунка,
аккуратность исполнения и качество раскраски (следует
договориться о размерах рисунков, например,
прямоугольник 12X20 клеток,
квадрат 10 X Ю клеток,
шестиугольник со сторож
ной 6а).
Циркулем и линейкой
Пользуясь циркулем и
линейкой, можно строить
самые разнообразные
фигуры. Удобно при этом
брать окружность,
разбитую на п равных частей
Рис. 50. (при я = 3, 4, 5, 6, 8, 10
и т. п. сделать это
нетрудно, а при п = 7, 9, И и т. п. и даже при п = 5,
10 можно воспользоваться транспортиром). Для
сокращения труда можно, тщательно выверив построение,
многократно перекалывать острой иглой центр «
вершины правильного многоугольника на чистый лист бумаги.
Рис. 51.
Проводя через точки деления окружности хорды
равной длины, получим разнообразные правильные
звездчатые многоугольники.
Если теперь проводить окружности (или дуги
окружностей) разных радиусов с центрами в вершинах пра-
124

вильных многоугольников и в точках пересечения
окружностей, а затем соединять отдельные пары точек
прямолинейными отрезками, то можно получить бесконечное
множество самых разнообразных фигур,
привлекательность которых возрастает при удачной их раскраске.
В качестве «основы» могут быть использованы, кроме
окружности, и другие фигуры: прямоугольник,
треугольник и т. п. (см. рис. 51).
Симметричные фигуры
Две точки Л и Л' называются симметричными
относительно прямой /, если А я А' лежат по
разные стороны и на одинаковых расстояниях от /,
причем АА' ±_1.
Некоторая плоская фигура называется симметричной
относительно прямой /, если для любой ее точки В
Ч 6) h
Рис. 52.
найдется точка В' (также принадлежащая этой фигуре),
симметричная точке В относительно прямой /. Прямая /
носит название оси симметрии.
На рис. 52 изображены фигуры, имеющие
соответственно одну, две, три, четыре и пять осей
симметрии.
125

Фигуры g несколькими осями симметрии легко
вырезаются из бумаги: сложенный вдвое лист тонкой бумаги
складывается дополнительно п раз в виде «сектора» с
180а
центральным углом —; если обрезать полученный
сектор по какому-нибудь контуру, то, развернув бумагу,
получим фигуру, имеющую п осей симметрии. Если при
этом использовать цветную бумагу, то можно получить
разноцветные ажурные салфетки с причудливыми узорами.
V 5^Э
^-\о^
С \Д
Ч/ х\ /
Ф
Рис. 53.
Назовем точку О центром симметрии п-го порядка
для данной фигуры, если при повороте этой, фигуры во-
Л 360° £ „
круг точки О иа угол она совмещается сама с собой.
Например, иа рис. 52 фигуры б, в, г, д обладают
центрами симметрии соответственно 2, 3, 4 и 5 порядков.
Для построения фигур, обладающих центром
симметрии л-го порядка, можно воспользоваться картонным
(26

шаблоном в виде «сектора» с криволинейным краем
360°
и с углом .
Проведем на бумаге из одной точки О п лучей, об-
360°
разующих утлы —^- . Помещая шаблон поочередно между
каждой парой соседних лучей (так, чтобы точка О'
совпадала с О) и обводя карандашом «наружный край
сектора», получим симметричную фигуру, аналогичную
изображенной на рис. 53, а.
Можно также взять шаблон произвольной формы и
накладывать его одинаковым образом на каждый из
упомянутых выше лучей, например так, чтобы две его точки
А и В находились на каждом из лучей на одних и тех же
расстояниях от точки О (рис. 53,6).
Упомянем еще об одном способе построения
симметричных фигур — путем отпечатывания чернильной кляксы
на обеих половинках согнутого пополам листа. При этом
подчас могут получиться весьма причудливые фигуры
с одной осью симметрии (рис. 53, в).
§ 24. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ИЗ РОМБОВ
Из рис. 54, а видно, что если между концами
семиугольной звезды, составленной из семи ромбов со
стороной а и с острым углом а = у, поместить второй слой
из семи ромбов с углом 8 = 2а = ^, а в выемки новой
звезды поместить семь ромбов с углом у = 3а=-^, то
получится правильный четырнадцатиугольник со
сторонами а.
Взяв восьмиугольную звезду (рис. 54,6), состоящую
из восьми ромбов с углом а' = -^, мы будем иметь во
втором слое квадраты f В' = 2а' = -|-) , а в третьем —
точно такие же ромбы, как и в центральной звезде
(у' = 3а'=тг — а'); все три слоя ромбов образуют
правильный восьмиугольник со стороной 2а.
Попробуйте доказать, что если а=~ и т нечетно
/и
m 1
(га^З), то —g— слоев ромбов образуют правильный
127

2/я-угольник со стороной а, а если га четно (т Ss4), то
тг — 1 слоев ромбов образуют правильный га-угольник
со стороной 2а (**). А так как в каждом слое га ромбов,
то отсюда следует, что при нечетном т. любой
правильный 2га-угольник со стороной Ь можно разбить либо на
2га (га —1) ромбов со стороной у, либо на m(m2~1)-
ромбов со стороной Ь (см., например, в) и г) на рис. 54),
Рис. 54.
Заметим, что разбиение правильного 2га-угольника со
стороной 2а на ромбы со стороной а можно получить,
повертывая правильный «маленький» 2/и-угольник со
стороной а вокруг одной из его вершин последовательно
на углы-,2^., 3-,..., (2га —1) — (см. ABCDEFGH
н ABCDEFGHIK на рис. 54, б, г); при этом поворачи-
»28

ваемый «маленький» 2/и-угольник состоит из таких же
ромбов, как и большой, но ромбов каждого «сорта» в
него входит в четыре раза меньше, чем в большой
2/и-угольник.
Разбиение же правильного 2/и-угольника со стороной
а на ромбы со стороной а (при т нечетном!) можно
получить, повертывая равносторонний т -\- 1 -угольник со
стороной а, в котором два противоположных угла равны
— (/и—1), а каждый из остальных т—1 углов равен
— (/и— 2), вокруг вершины с углом —{т—1)на—,
Рис. 55.
2 ^, ... ,(т — 1)^ радианов (см., например, в 14-уголь-
нике о) восьмиугольник ABCDEFGH и в 10-угольнике
в) шестиугольник ABCDEF).
Для того чтобы при нечетном т получить, в
конечном счете, правильный /и-угольник со стороной 2а, надо
в качестве центральной фигуры взять не звезду,
составленную из т ромбов, а правильный звездчатый
/и-угольник, у которого угол а при вершине равен —, угол р
в «выемке» равен За = — и «глубина выемки» АВ = а
(а) и б) на рис. 55 соответствуют /и = 7 и/и=11).
Докажите, что добавление к такому многоугольнику
5 А. П Доморяд 129

—2~ слоев ромбов всегда приводит к правильному
м-угольнику со стороной 2а ("). При этом все разбиение
m-угольника на ромбы со звездчатым многоугольником
в центре может быть осуществлено с помощью т
маленьких «незамкнутых» правильных многоугольников
(вроде ABCDEFG на фигуре а) или ABCDEFGHIKL на
фигуре б)), переходящих друг в друга при повороте
вокруг центра звезды на угол — .
§ 25. ПОСТРОЕНИЕ ФИГУР ИЗ ДАННЫХ ЧАСТЕЙ
Мозаика
В игре под названием «мозаика» из определенного
набора разноцветных плиток выкладываются различные
фигуры. Обычно в наборы плиток входят квадраты, ром-
Шбы и. прямоугольные треугольники с
острым углом в 45° (рис. 56).
В наиболее простом случае все
плитки должны быть размещены в
соответствии с прилагаемыми к игре
рисунками. Но можно, не придерживаясь
этих рисунков и не ограничивая себя
формой фигуры в целом, искать
оригинальные фигуры, используя при этом
Рис. 56. либо все плитки, входящие в игру,
либо некоторую часть их.
Может быть, кому-нибудь из читателей удастся
придумать новые интересные варианты игры, в которых
наборы плиток будут содержать различные
равнобедренные треугольники, параллелограммы, правильные
многоугольники и т. п. Для осуществления придуманных
вариантов можно использовать плотный картон,
обклеенный цветной глянцевой бумагой.
Если вместо картонных или деревянных плиток
изготовить тонкие разноцветные пластинки из стекла или из
прозрачной пластмассы и допустить налегание плиток
друг на друга, то даже при двухцветной мозаике можно
добиться значительного разнообразия и красочности
рисунков, рассматриваемых «на свет».
130

Фигуры из кусочков квадрата
К числу полезных и увлекательных развлечений
относится составление фигур из семи кусочков квадрата,
разрезанного в соответствии
с рис. 57, а, причем при
составлении заданных фигур
должны быть использованы
все семь кусочков, и они
не должны налегать, даже
частично, друг на друга.
На рис. 58 приведены
симметричные фигуры,
заимствованные из книги В. И. Обреимова [19]. Попробуйте
сложить эти фигуры из частей квадрата, изображенного
на рис. 57, а.
Рис. 57.
Z/^\
И/МЧ
Рис. 58.
Из этих же частей можно складывать и многие другие
фигуры (например, изображения различных предметов,
животных и т. п.).
S*
131

Менее распространенным вариантом игры (см. [23],
ч. 1, стр. 209) является составление фигур из кусочков
квадрата, изображенного на рис. 57, б.
Проведите состязание на придумывание фигур,
которые могут быть составлены из этих кусочков;
победителем будет тот, кто быстрее составит фигуры,
предложенные его «противником».
Не удастся ли вам еще по-иному разбить квадрат на
семь кусочков, так, чтобы из них можно было
составлять разнообразные симметричные фигуры?
При желании игру можно усложнить, придумывая
фигуры, которые должны быть сложены, например, из
шести или из пяти кусочков квадрата, и не указывая, какие
из кусочков должны быть при этом использованы.
Прямоугольники из квадратов
За последние 20 лет на страницах некоторых
математических журналов появился ряд статей, посвященных
вопросу составления прямоугольников из попарно
различных квадратов.
Оказывается, что нельзя составить прямоугольник из п
различных квадратов, если л<9. При я = 9 задача имеет
два решения: можно составить прямоугольник из
квадратов, стороны которых относятся, как 1:4:7:8:9:10:14:15:
:18 (рис. 59), и из квадратов, стороны которых
относятся, как 2:5:7:9:16:25:28:33:36. Составьте(")
прямоугольник из десяти квадратов, стороны которых
относятся, как 3:11:12:23:34:35:38:41:44:45, и
прямоугольник из тринадцати квадратов с отношением сторон: 1:4:
:5:9:14:19:33:52:56:69:70:71:72 (полезно решить
сначала вопрос об отношении сторон для каждого из
составляемых прямоугольников).
Наименьшее число различных квадратов, из которых
можно составить большой квадрат, равно 26. Составьте
большой квадрат, учитывая, что стороны составляющих
квадратов относятся, как 1:11:41:42:43:44:85:168:172:
: 183:194:205:209:5:7: 20:27:34: 61:95:108:113:118:123:
: 136:231, причем первые 13 квадратов образуют
прямоугольник с отношением сторон 608:377, а последние
13 квадратов — прямоугольник с отношением сторон
608:231 (57).
132

В книге Б. А. Кордемского и Н. В. Русалёва [14]
отмечается связь, существующая между вопросом
составления прямоугольников из квадратов и вопросом
распределения токов в замкнутых цепях, составленных из
нескольких проводников.
Интересно заметить, что задача составления
прямоугольного параллелепипеда из конечного числа гопарно
различных кубов неразрешима.
_ 1 /_,
/-^ - ___«
: ::;:::_"" ::::*:_::::::":::±:::
:_::i.:z :__л:: -4----
_:::::::~:i:::::::::::::r«"::::::
Рис. 59.
Действительно, предположим, что задача имеет
решение и v — объем наименьшего из кубов. Так как в
любом прямоугольнике, составленном из попарно различных
квадратов, наименьший квадрат не может примыкать к
стороне прямоугольника (докажите это (")), то
наименьший из кубов (/<",), примыкающих к нижнему основанию
параллелепипеда, будет зажат с боков кубами ббльших
размеров; наименьшей из кубов (/(,), стоящих на дне
образованного ими «колодца», также будет зажат с боков
более крупными (по сравнению с ним) кубами,
образующими «колодец» с меньшим сечением, и т. д.
Среди кубов /С,, Kt, Kv ... найдутся, наконец, кубы,
объем которых меньше v, а это противоречит начальному
предположению.
133

Решите еще следующие две задачи: 1) Разбить куб
на п кубов (среди которых могут быть и одинаковые) при
л=34 и при я = 50("). Попробуйте установить, при
каких значениях п эта задача неразрешима. 2) Докажите (в0),
что при пф2, 3, 5 квадрат можно разбить на и
квадратов (среди которых могут быть и одинаковые).
§ 26. СОСТАВЛЕНИЕ ПАРКЕТОВ
Интересным геометрическим развлечением является
составление паркетов — так для краткости будем
называть покрытие плоскости правильно чередующимися
фигурами одного и того же вида или нескольких данных
видов.
Рис. 60.
Примером простейших паркетов может служить обычная
клетчатая бумага или плоскость, заполненная
одинаковыми правильными треугольниками; объединяя в них тем
или иным способом отдельные ячейки в комплексы, легко
получить множество самых разнообразных
«производных» паркетов. Разнообразие может быть увеличено,
если наращивать одни ячейки за счет других, разбиваемых
134

на части кривыми или ломаными линиями. На рис. 60
приведено несколько неограниченно продолжаемых
(рекомендуем читателю убедиться в этом) производных
паркетов.
Производные паркеты можно строить также из
паркетов, составленных из правильных многоугольников
с разным числом сторон.
Для исследования вопроса о заполнении плоскости
правильными многоугольниками необходимо, в первую
очередь, учесть всевозможные типы «узловых» точек, т. е.
найти различные комбинации
правильных многоугольников, которые
могут сходиться своими вершинами
в одной точке, заполняя без
взаимных перекрытий ее окрестность, и
в каждом случае проверять
возможность неограниченного продолжения
паркета с узловыми точками
найденного типа.
Например, легко убедиться, что
правильные треугольник,
семиугольник и 42-угольник могут дать
узловую точку, но заполнить всю
плоскость правильными
многоугольниками, образующими только узлы
типа (3, 7, 42), невозможно.
Действительно, если в вершине А (рис. 61)
сходятся треугольник ABC, семиугольник S, и 42-угольник
St, то в вершине В к треугольнику ABC и к 42-уголь-
нику должен примыкать семиугольник S„ но тогда
точка С уже не сможет быть узлом типа (3, 7, 42).*
Докажите, что хотя и существуют узлы типа (5,5,10),
но заполнить всю плоскость правильными
пятиугольниками и десятиугольниками невозможно (").
При поисках различных типов узловых точек следует
учесть, что порядок k узловой точки (т. е. число
многоугольников, в ней сходящихся) не может превышать
шести. Кроме того, если в узле k-то порядка сходятся
правильные многоугольники с числом сторон п1, п , пк,
то легко доказать ("), что
Рис. 61.
135

Например, при £ = 3 будем иметь равенство —| \~
я, я,
-{-— = у, которому удовлетворяют такие узлы: (8,8,4),
(12? 12, 3), (10, 5, 5), (12, 6, 4), (6, 6, 6), (3, 7, 42) и т. д.
При k = 4 имеем:—-|-—-|-—-|- — =1; этому условию
удовлетворяют узлы: (6, 3, 4, 4), (6, 3, 6, 3) и т. д.
Исчерпать все паркеты невозможно. Действительно,
взяв, например, треугольную сетку и объединяя
различными способами часть треугольников в шестиугольники,
можно получить бесконечное множество паркетов,
построенных из правильных треугольников и
шестиугольников (рис. 62).
Поэтому целесообразно при построении паркетов
ограничить себя более или менее жесткими условиями.
Например, можно потребовать, чтобы совокупности
многоугольников, окружающих любой узел паркета, для всех
узлов были бы одинаковыми. Требование это не
выполняется для паркетов а), 6) и в), так как на них одни
узлы пятого, а другие — шестого порядка, но
выполняется для паркетов г) и д).
Если наложить еще дополнительное условие,
потребовав, чтобы взаимное расположение многоугольников,
примыкающих к какому-нибудь узлу паркета, было бы
одно и то же для всех узлов, то паркет д) придется
«забраковать», так как к узлу А треугольники и шести-
136

угольники примыкают, чередуясь друг с другом, а около
узла В оба шестиугольника расположены рядом друг
с другом.
Можно потребовать, чтобы все одинаковые
многоугольники паркета были бы однотипными в том смысле,
что любые два одноименных многоугольника паркета
вместе с прилегающими к ним многоугольниками могли бы
полностью быть совмещены друг с другом (см. а), б), в),
137

z) на рис. 63), или можно допустить использование
многоугольников двух различных типов (например, на
паркете д) все квадраты и все шестиугольники однотипны,
а треугольники не все однотипны, так как к одним
треугольникам примыкают три квадрата, а к другим — два
квадрата и треугольник).
Из в), ж), з), и), к) рис. 63 видно, что существуют
пять вариантов окружения правильного шестиугольника
квадратами и правильными треугольниками при
условии, что все шесть вершин шестиугольника должны
быть узлами четвертого порядка и никакие два
шестиугольника не должны иметь даже общей вершины.
Попробуйте исследовать, какие типы
шестиугольников могут одновременно встречаться в неограниченно
продолжаемом паркете, как они будут перемежаться
друг с другом, существуют ли, кроме паркета в),
другие паркеты, в которых все шестиугольники будут одного
типа.
Из сравнения рис. а), б), в), д), е) видно, что из
паркетов, в состав которых входят правильные
двенадцатиугольники, можно получать новые паркеты (если
разбивать двенадцатиугольники на составные части).
Объединяя на паркете е) каждые четыре соседних
треугольника и соответственно каждые два соседних
квадрата в комплексы, получим паркет, у которого все
ячейки и все узлы будут однотипными, но зато появятся
«неправильные ячейки» (прямоугольники, составленные
из двух квадратов).
Отметим интересное свойство равносторонних
шестиугольников, у которых два противоположных утла имеют
по (п — некоторое натуральное число), а остальные
углы равны между собой. Из таких плиток, кроме
паркета а) (рис. 64) с параллельно расположенными
ячейками, можно сложить паркет б), где ячейки заполняют
п «секторов» вида АОВ, сходящихся в центре О (на
рисунке п = 7), и п таких же секторов: BCD, AEF
немного не достающих своими вершинами до центра.
Из правильных пятиугольников в сочетании с
правильными десятиугольниками и звездчатыми пятиугольниками
можно составить интересные паркеты с большим числом
ячеек, но нельзя при этом добиться неограниченной
продолжаемости паркета.
138

Неограниченно продолжаемый паркет можно
составить (") из правильных пятиугольников в сочетании
с ромбами вида г), у которых острый угол равен 36°, а
также из одних равносторонних пятиугольников вида в),
у которых углы при вершинах В и D прямые,
остальные углы по 120° и AB = BC=CD=DE.
Много интересных паркетов с вычурными ячейками
читатель найдет в [31].
Составление паркетов, а тем более их исследование,
доступно лицам с некоторой математической
подготовкой; но раскрашивание уже составленного паркета,
объединение его ячеек в комплексы и даже изменение
формы отдельных ячеек готового паркета не требует
почти никакой математической подготовки.
Двухцветные паркеты
В книге В. И. Обреимова [19] дано описание
квадратных паркетов, которые складываются из квадратных
плиток, разделенных по диагонали на два равных
треугольника (белый и черный).
Беря какой-нибудь комплекс из четырех квадратиков,
например ABCD на рис. 65, можно к нему пристроить
(правее и ниже) три других комплекса так, чтобы
получился шестнадцатиклеточный симметричный паркет, имеющий
горизонтальную (АЕ) и вертикальную (CF) оси симметрии.
Можно брать комплексы не из четырех, а из девяти,
из шестнадцати, из двадцати пяти и т. д. клеток.
139

Так как из п1 квадратиков можно составить 4"
различных комплексов, то при я>2 практически почти
невозможно исчерпать множество симметричных паркетов,
составленных из 4я* квадратов.
Если в симметричном паркете какие-нибудь четыре
квадратика, симметрично расположенные относительно
обеих осей симметрии большого квадрата, например
квадратики а, р, у, 8 на рис. 65, не меняя ориентировки
перемешаемых квадратиков, поменять местами в
горизонтальном направлении (т. е. сделать транспозиции (а, у)
а] г б) е)
Рис. 65.
и (р, 8)) или в вертикальном направлении (транспозиции
(а, р) и (у, 8)), то снова получится симметричный паркет.
Так, горизонтальные транспозиции (а, у) и (р, 8)
переводят паркет а) в паркет б), а последний вертикальными
транспозициями (1,5), (2, 6), (3, 7) и (4, 8) переводится
в паркет в).
Назовем два паркета родственными или
принадлежащими одному классу, если от одного к другому можно
перейти с помощью одной или нескольких транспозиций
параллельных рядов клеток, симметрично расположенных
относительно вертикальной или горизонтальной оси
симметрии паркета. Например, родственными будут
паркеты б) и в) на рис. 65, так как они получаются
друг из друга с помощью транспозиции верхнего и
нижнего горизонтальных рядов.
Не удастся ли читателю определить для п = 2, 3, 4, ...,
на сколько различных классов разбиваются множества
симметричных многоклеточных паркетов, состоящих
из 4я' квадратиков?
Можно составлять также шестиугольные паркеты из
треугольников, раскрашенных в два или в три цвета
(см. рис. 66, а, 0).
140

Составляя из 4 (9,16 и вообще п*) треугольников
вида а) большой равносторонний треугольник ABC
(рис 66, в, где л = 2) или А'В'С (рис. 66, г, где л=3)
и отражая его от стороны ВС (соответственно от В'С),
а полученный ромб ABDC (A'B'D'C) — от АВ и BD
(от А'В' и 5'/)), получим правильный шестиугольник
А*\ ДРУНК
Рис. 66.
с тремя осями симметрии (см. д) и е)), состоящий из 6л*
маленьких двухцветных треугольников.
Если вы попробуете производить отражение в другом
порядке (сначала треугольник ABC от стороны АВ,
а затем полученный ромб от его сторон BE и ВС),
то получится тот же самый шестиугольник (докажите
это!)(").
Разнообразные квадратные паркеты с самыми
причудливыми узорами можно сложить из 4л* плиток с
четырехцветной расцветкой; так как четыре треугольника
с общей вершиной в центре квадрата можно окрасить
шестью существенно различными способами (рис. 66,ж),то
можно договориться либо об использовании квадратов всех
шести сортов, либо ввести какие-нибудь ограничения.
141

§ 27. ПЕРЕКРАИВАНИЕ ФИГУР
Две фигуры (будем под этим понимать две плоские
фигуры или два тела) называются равносоставленными,
если одну из них можно разбить на части, дающие
при ином соединении их друг с другом вторую
фигуру.
Назовем указанный процесс перекраиванием, одной
фигуры в другую.
Теорема I. Если каждая из фигур А и В равно-
составлена с некоторой фигурой С, то фигуры А и В
будут также равносоставлены.
Действительно, если фигура С (рис. 67) сплошными
линиями (а для тел — поверхностями) разбивается на
части, из которых может
быть сложена фигура А, а
пунктирными — на части,
дающие фигуру В, то
совокупность перенумерованных
частей, на которые С
разбивается теми и другими ли-
Рис. 67. ниями, представляет набор
кусочков, из которых при
объединении их в группы: 1, 2; 3, 4, 5 и т. п. можно
сложить фигуру А, а при объединении в группы: 1, 3, 12;
2, 4, 6, 9 и т. п.—фигуру В.
Совершенно очевидна
Теорема II. Любые дверавносоставленные фигуры
равновелики, т. е. имеют одинаковые площади.
Обратная теорема неверна, т. е. из равновеликости
двух фигур не следует, вообще говоря, их
равносоставленность.
Ниже приводится несколько теорем, в которых
говорится о специальных случаях, когда из равновеликости
двух фигур следует их равносоставленность.
Теорема III. Параллелограммы с равными
основаниями и равными высотами равносоставлены (см.
рис. 68, а).
Теорема IV. Любые два равновеликих
прямоугольника равносоставлены.
(Пользуясь условием: ab — cd, показать, что
АВ || CD || LM (рис. 68, б); проведя EKF \\ АВ, легко видеть,
что S1=S[; St = St, а 5, и S', — равносоставлены.)
142

Теорема V. Любые два равновеликих
параллелограмма равносоставлены.
(На основании теоремы III каждый из этих
параллелограммов равносоставлен с некоторым
прямоугольником; остается применить теоремы I и IV.)
Теорема VI. Любые равновеликие треугольник и
прямоугольник равносоставлены.
(Надо учесть, что любой треугольник ABC
равносоставлен с некоторым параллелограммом ADFC, рис. 68, в.)
Рис. 68.
Теорема VII. Любые два равновеликих
многоугольника равносоставлены (теорема Бояй—Гервина).
Действительно, разбив каждый многоугольник (Р и Q)
на треугольники (plt рг, ..., рт и qv qx, ..., qn,
соответственно), достаточно перекроить все треугольники
в прямоугольники (p't, р'г р'т и q\, q't, .... q'n)
с общей высотой h. Прямоугольник с высотой h,
составленный из р[, р'%, ...,р'т (его можно
составить и из q„ q't, ..., q'„), будет равносоставлен с Р
и с Q.
Как видим, теорема, обратная теореме II, верна для
любых многоугольников.
В прошлом веке делались попытки доказать, что
теорема, аналогичная теореме Бояй — Гервина, будет верна
и для многогранников. Но в 1901 году немецкий
математик Ден доказал, что равновеликие куб и правильный
тетраэдр не равносоставлены (доказательство теоремы
Дена и ряд интересных подробностей, относящихся к
вопросу о равносоставленности фигур, читатель найдет
в книге В. Г. Болтянского [5]).
143

Однако, если ограничиться многогранниками
специального вида, то в отдельных случаях из равно великости
следует их равносоставленность. Например,
Теорема VIII. Равновеликие прямоугольные
параллелепипеды равносоставлены.
Обозначим эти прямоугольные параллелепипеды через
Р и Q. Пусть а, Ь, с —ребра Р, а ах, &,, с, —ребра
Q и пусть abc = a1blc1. Возьмем вспомогательный
прямоугольный параллелепипед R с ребрами: alf Ь', с, где
а1Ъ' = аЪ и &'с = &,с,; легко доказать, что Р и # равно-
составлены (у них равны
высоты с и равновелики
основания), так же как и Q с R.
Теорема IX. Любую
призму можно перекроить
в некоторый прямоугольный
параллелепипед.
Действительно, пусть
Р — наклонная призма с
боковым ребром /. Проведем
сечение ABCDE,
перпендикулярное боковым ребрам.
Рис. 69. Тогда из кусков I и II
(рис. 69) составляется
прямая призма Р' с высотой / и основанием ABCDE (если
нельзя провести перпендикулярную к боковым ребрам
плоскость, пересекающую все боковые ребра призмы —
призма слишком широка, и коротка,— то предварительно
ее можно разбить иа узкие призмы с меньшими
основаниями и каждую из них перекроить указанным
способом в прямую призму). По теореме VII, разбивая
многоугольник ABCDE на кусочки: a,, а„ ... , ап, его можно
перекроить в некоторый прямоугольник; следовательно,
из прямых призм с основаниями: а,, а, а„ и
высотой /, на которые распадается Р, можно составить
прямоугольный параллелепипед Р" с высотой А
Теорема X. Любые две равновеликие призмы
равносоставлены. (Это следует из теорем VIII и IX.)
Задачи на перекраивание фигур сопровождаются
иногда указанием числа частей, на которые должна быть
разбита данная фигура. Например:
1. Разбив прямоугольник 9Х16сля* на две части,
перекроить его в квадрат (*").
144

2. Разбив прямоугольник а X Ь см* на две части,
перекроить его в прямоугольник -—-. X си* («—
натуральное число) (,,в).
3. Разбив прямоугольный параллелепипед 8Х8Х
X 27 см' на четыре части, перекроить его в куб с
ребром в 12 см (см. рис. 70).
Попробуйте изготовить картонные модели четырех
частей, пригодных и для составления куба с ребром
12 см, и для составления
параллелепипеда 8X^X18 см'.
4. Разбив прямоугольный
параллелепипед а X b X с см' на
четыре части, перекроить его в па-
ат w 6 («1-4-1) л
раллелепипед ^рХ т(в'+1) X
X ' см* (т. и я — целые) или
в параллелепипед
атп
(т-ИИя+1)
X
/JL-
9
bjm+l) Xcjn+J)
5. На рис. 71 показано, как
должны быть разрезаны на 2 части
коврик (с) и кусок клетчатой
клеенки (б), чтобы из полученных
кусков можно было в первом
случае сшить квадратный коврик, а
во втором — составить шахматную
доску.
Попробуйте придумать
аналогичные задачи, в которых
составные части имели бы по три, по
четыре, по шесть зубцов.
6. Треугольники ASB, BSC, CSD (рис. 72) имеют
общую вершину 5 и равные основания, лежащие на
одной прямой и примыкающие друг к другу (АВ—
= BC=CD).
Докажите, что каждый из них составлен из одного
и того же набора кусочков, занумерованных цифрами:
/, 2, 3, 4 (BK\\CL\\AS; BE\\CF\\DS; BM\\CS;
СЛЛ] BS).
Рассмотрите аналогичный вопрос для я
треугольников (я = 4, 5, 6, ...), имеющих общую вершину и
Рис. ГО.
145

равные, примыкающие друг к другу основания, лежащие
на одной прямой, предполагая, что они разбиваются на
части прямыми, проходящими через вершины оснований
треугольников параллельно боковым сторонам всех
треугольников.
-rf^i-
1
%
%
%
#
%
'4,
'А
■'/,
■i*
'/}.
%
'%
'А
%
%
%
%
%
%
%
1
Й *
%
#
й
Щ
,17
Ф
i)
Рис. 71.
7. Квадрат А (рис. 73) перекроить (") в фигуры В,
С, D, разрезав его в первых двух случаях на три, а
в последнем — на четыре части.
Замечание. В своем математическом кружке вы
можете организовать конкурс на придумывание
интересных фигур, которые могут быть
составлены из определенного
числа частей квадрата или
какой-нибудь заданной фигуры
(круг, правильный
шестиугольник и т. п.).
На рис. 74 показано, как из
шести пронумерованных
кусочков правильного
пятиугольника ABCDE со стороной а
можно сложить
равносторонний треугольник со стороной
:а- 1,993 (см. [39], 1952г., №2,
У Vsi
>HJtg36°
стр. 106). Построения таковы:
1) DK— продолжение BD и DK—DE, т. е. Д EDK=
=ABCD;
2) EL = LK; MN\\AB; CP=DM; BQ = EL, т. e.
EDML = BCPQ и Л QPD = Л LMK= Д LNE;
146

3) ET=z^ = ES=TS=TU=EV, т. е. равносторонний
треугольник SUV равновелик с пятиугольником ABCDE;
4) RW || UV (но RW и АВ не параллельны!),
следовательно, ATUF—ATSR и Д EHV=AEWS. Кроме
Рис. 73.
того, из равновеликости четырехугольников ABRW и
NMFH с соответственно параллельными сторонами
следует, что они при наложении совпадут друг с другом.
В книге Б. А. Кордемского и Н. В. Русалёва [14]
показано, как перекроить квадрат в правильные
треугольник, шестиугольник и пятиугольник, разбивая его
соответственно на пять, пять и шесть кусочков.
Попробуйте перекроить правильный семиугольник в правильный
треугольник или квадрат, правильный шестиугольник
в правильный восьмиугольник и т. п.; при этом следует
147

стремиться к тому, чтобы кусочков было как можно
меньше, а размеры каждого из них не слишком малы.
Может быть, используя теорему I, вам удастся найти
разбиения треугольника (шестиугольника и т. п.) на
кусочки не слишком малых размеров, из которых можно
было бы составить и квадрат, и правильный
пятиугольник (или квадрат и правильный семиугольник и т. п.).
Это привело бы к интересной головоломке: из данного
набора кусочков составить
любой из трех заданных
правильных многоугольников.
Из рис. 75 видно, что
правильный двенадцатиугольник
можно разбить на одинаковые
части так, что из двойного
комплекта кусочков может быть
сложен правильный
двенадцатиугольник, имеющий вдвое
большую плошадь.
Исследуйте вопрос: при
каких значениях пи k правильный
Рис. 75. л-угольник можно разбить на
одинаковые кусочки (число
которых должно быть, по возможности, малым) так, чтобы
из k комплектов таких кусочков можно было бы сложить
подобную фигуру с площадью в k раз большей.
Не удастся ли вам разбить квадрат на п кусочков
так, чтобы при отбрасывании одного, а затем двух из
них (а может быть и трех!) можно было бы каждый раз
из остающихся кусочков складывать квадрат меньших
размеров?
Аналогичный вопрос можно поставить для
правильного треугольника, пятиугольника и т. п.
§ 28. ПОСТРОЕНИЕ КРИВЫХ
Розетки
Любители красивых геометрических фигур могут
заняться построением в полярных координатах кривых,
соответствующих уравнениям вида: r = a-\-bsm—, где
a, b, т, п — некоторые данные числа.
148

В полярных координатах выбираются единичный
отрезок е, полюс О и полярная ось Ох (рис. 76).
Положение любой точки М определяется полярным радиусом ОМ
и полярным углом <р, образованным лучом ОМ и лучом
Ох. Число г, выражающее длину ОМ через е (ОМ=ге)
и численное значение угла <р, выраженного в градусах
или в радианах, называются полярными координатами
мочки М.
Для любой точки, отличной от полюса О, можно
считать 0sgcp<2n и г>0. Однако при построении кри-
270'
Рис. 76.
вых, соответствующих уравнениям вида /-=/(<р),
переменному <р естественно придавать любые значения (в том
числе и отрицательные, и превышающие 2тт), а г может
оказаться как положительным, так и отрицательным.
Для того чтобы найти точку (<р, г), проведем из
точки О луч, образующий с осью Ох угол <р, и отложим
на нем (при /">0) или на его продолжении в
противоположную сторону (при л<0) отрезок \г\е.
Все значительно упростится, если предварительно
построить координатную сетку, состоящую из
концентрических окружностей с радиусами е, 2е, Зе и т. д.
(с центром в полюсе О) и лучей, для которых <р = 0°,
149

l0°, 20°, ... , 340°, 350е; эти лучи будут пригодны и при
<р<0°, и при <р>360°; например, при (р = 740° и при
¥ = — 340° мы попадем на луч, для которого ip = 20°.
(См. на рис. 76 точки УМ (40°,3), N(120° —3), Р(—1230°,2).)
Рассмотрим кривые:
I. /- = sin3:p, II. r=2-~bsin^,f'
III. r=l-f-sin3(f>, IV. r=|- + sin39.
Составим таблицу:
<p
sin Зср
У+sin Зср
1 -|- sin Зср
3 . . „
-j-\- sin 3(f
—30°
—1
—0,5
0
0,5
—20°
—0,87
—0,37
0,13
0,63
—10°
—0,5
0
0,5
1
0°
0
0,5
1
1,5
10°
0,5
1
1,5
2
20°
0,87
1,37
1,87
2,37
30°
1
1,5
2
2,5
¥
sin Зср
у + sin Зср
1 -)- sin Зср
з
у + sin Зср
40°
0,87
1,37
1,87
2,37
50°
0,5
1
1,5
2
60°
0
0,5
1
1,5
70°
—0,5
0
0,5
1
80°
—0,87
—0,37
0,13
0,63
90°
-1
—0,5
0
0,5
(Здесь 0,87 — приближенное значение числа -^- . J
Назовем сектором (а, р) часть плоскости, для точек
которой а<<р<(3. Соединяя точки (0°, 0), (10°; 0,5),
150

aj
SO"
Рис. 77.
151

(20°; 0,87), (30°, 1), (40°; 0,87), (50°; 0,5), (60°,0) плавной
кривой, получим в секторе (0°, 60°) «положительный
лепесток» (1) кривой / (см. рис. 77,а).
Продолжив таблицу до (р = 360° и соединив на
чертеже точки: (60°,0), (70°; —0,5), (80°; —0,87), (90°, —1)
Рис. 78, а и б.
(100°; —0,87), (110°; —0,5), (120°, 0), расположенные
в секторе (240°, 300°), мы получим в этом секторе
«отрицательный лепесток» (2) кривой /.
Легко проследить, что за ним последует
«положительный лепесток» (3) в секторе (120°, 180°),
отрицательный лепесток (4) в секторе (0°, 60°), положительный
152

лепесток (5) в секторе (240°, 300°) и, наконец,
отрицательный лепесток (б) в секторе_(120°, 180°). _
У кривой / лепестки {1) и (4), (2) и (5), (3) и (6)
попарно совпадают. Но из последних трех строчек таблицы
видно, что
1) у кривой II (строчка таблицы, соответствующая
г — -£-\- sin3(p) первый положительный лепесток (1)
располагается в секторе (—10°, 70°) (наибольшее г = 1,5),
Рис. 78, в.
следующий за ним отрицательный лепесток (2) лежит
в секторе (250°, 290°) (наибольшее |г| = 0,5), и т. д.
(см. рис. 77,а),
2) у кривой III будут только положительные лепестки
в секторах (—30°, 90°), (90°, 210°) и (210°, 330°) (рис. 77, б),
3) у кривой IV наименьшее значение г = 0,5 и
лепестки имеют «незаконченный вид» (рис. 77,6).
Совершенно аналогично будет обстоять дело с кривыми
1.5? „1,3
r — a-\-s\n-Z ПрИ а = 0, -^, 1, у.
Здесь угол (р удобно изменять через 18° (от0°до 1080°).
При а = 0 первый (положительный) и второй (отрица-
153

тельный) лепестки разместятся в секторах (0° ,108°) и (288*,
396°), (рис. 78, с), а при а = -^ — в секторах (—18°,
126°) и (306°, 378°) (рис. 78,(5)- Приа=1 будут только
пять положительных лепестков в секторах: (—54°, 162°),
(162°, 378°) и т. д.; то же самое но с «незаконченными
лепестками», будет при а=у (рис. 78, в).
в) г)
Рис. 79.
В общем случае у кривой г = sin ^2 первый положи-
тельный лепесток будет заключен в секторе (0°, ) ,
так как в этом секторе 0°<^^180°. При у<— <1
лепесток будет занимать сектор, больший 180°, но
меньший 360°, а при -^^у Для одного лепестка потре-
154

буется «сектор», превышающий 360° ( на рис. 79 показан
вид лепестков при ~=j, \, у, 4)'
Считая тип взаимно простыми, рассмотрим
уравнение г = sin ~. Нам могут представиться такие случаи:
(з)(Ю
е)
Рис. 80.
1) т четно, п нечетно. Изменяя (р от 0 до ЗбО°л,
получим законченную розетку из 2т лепестков (SQCPn:
180л 0 \ „ _ ^
''~ЦГ== 1тЬ последний из которых будет отрицательным;
поэтому при дальнейшем изменении <р мы снова
«пройдемся» по построенной розетке (нарис. 80,а от = 4, я = 3).
155

2) т нечетно, я четно. Изменяя (р от 0 до я-180°
(целое число окружностей!), мы получим от лепестков
(я-180° :—-~ — т J, но последний из них будет
положительным; поэтому при дальнейшем изменении <р от
я-180° до п>360° будут получаться лепестки,
«диаметрально противоположные» построенным; в общей
сложности, опять получится розетка из 2от лепестков
(на рис. 80, tf от = 5, л = 2).
3) от и л нечетны. При изменении (р от 0° до я-180°
получаются от лепестков, и так как последний из них
будет положительным, то следующий (от + 1)-й лепесток
будет отрицательным и совпадет с самым первым
положительным лепестком; в целом, при изменении (р от
л.180° до л -360° мы получим все от построенных уже
лепестков, но те из них, которые при «первом заходе»
были положительными, станут отрицательными и
наоборот (на рис. 80, в от = 5 и л = 3).
Кривые Лиссажу
Много интересных кривых можно построить и в
декартовых координатах. Особенно просто строятся
кривые, уравнения которых даны в параметрическом виде:
i x = y(t),
где V—вспомогательное переменное (параметр).
В этом случае для построения кривой вычисляют
значения х и у, соответствующие достаточно близким
значениям параметра t (возрастающим или убывающим),
наносят на чертеж точки (х, у) и соединяют их —
в порядке возрастания t — плавной линией. Например,
: = sin It
для уравнений
J x = s\
\ _y = si
sin3r
имеем:
t
X
У
0°
0
0
15°
0,5
0,7
30°
0,87
1
45°
1
0,7
60°
0,87
0
75°
0,5
-0,7
90°
0
—1
105°
-0,5
-0,7
...
...
...
156

Продолжив эту таблицу до * = 360° и нанося —
в соответствии с полученными значениями х и у—
точки Л„, Л,, Л , Л„ на чертеж, легко получить
кривую, изображенную на рис. 81.
Это одна из так называемых кривых Лиссажу,
характеризуемых в общем случае уравнениями:
х = a sin mt, \
y—bsinn(t-\-a.). / * '
Если за параметр t взять время, то фигуры Лиссажу
будут представлять собой результат сложения двух
Д& fig Д/4
Рис. 81.
гармонических колебательных движений, совершаемых
во взаимно перпендикулярных направлениях.
Проверьте, что уравнениям: /. jc=sin3^; _у == sin 5^;
//. x = sin3t; y = cosbt; III. x = s'm3t; yz=sis\4t;
IV. .*=sm(£ — 45°), y = sint соответствуют кривые,
изображенные на рис. 82. Кроме кривых Лиссажу, на
рисунке нанесены квадраты со стороной 2, внутри
которых, касаясь их сторон, располагаются эти кривые.
В общем случае кривая (1) располагается внутри
прямоугольника со сторонами 2а и lb.
При построении кривых Лиссажу полезно определить
заранее точки касания кривой со сторонами соответ-
157

ствующего прямоугольника, а также провести
предварительно внутри прямоугольника вспомогательные прямые:
горизонтальные —на расстояниях b sin 15°, Ь sin 30°,
Ь sin 45е, Ъ sin 60°, Ь sin 75° от начала координат и верти-
Л
Рис. 82, / и П.
кальные — на расстояниях a sin 15°, a sin 30° и т. д. от
начала координат (считая, что <р изменяется через 15° и а = 0),
Кривая Лиссажу будет незамкнутой, если при каком-то
значении параметра кривая «упрется» в вершину пря-
158

моугольника: при дальнейшем возрастании уточка опишет
в обратном направлении ту же кривую (см., например,
кривую / на рис. 82).
Рис. 82, /// и IV.
Найдите, при каком условии кривая / при а = 0
будет незамкнутой ("). Полезно проследить, как замена
уравнений I, например, уравнениями jc = sin3£ у =
= sin b(t-\-3°) превращает незамкнутую кривую в
кривую замкнутую.
159

Циклоиды, эпициклоиды, гипоциклоиды
Любителям математики, несомненно, доставит
удовольствие близкое знакомство с циклоидой,
эпициклоидой и гипоциклоидой — так называются кривые, которые
описывает точка М, находящаяся на окружности радиуса г,
катящейся соответственно по прямой (циклоида), по
неподвижной окружности радиуса R, касаясь ее извне
(эпициклоида), и по неподвижной окружности радиуса R,
касаясь ее изнутри (гипоциклоида).
Уравнения этих кривых в параметрической форме
можно представить так:
( x — c(t — sin £),
циклоида
эпициклоида
гипоциклоида
J x — c(t — s
\ y=r{l—cost),
j x = R[(l-\-m)cosmt — mcos(l-\~ m)f],
\ y = R[{\-\-m)<inmt — /rasin(l + rn)t],
x = R[{\ — m) cos mt -{• m cos (1 — m) t],
R[{m—\)smmt-\-msm\\ — m)t],
где m=-jr (см. [27], том I).
Интересным свойствам этих кривых посвящена книга
Бермана Г. Н. [4], где приводится также внешний вид
эпициклоид и гипоциклоид при разных значениях т.
На рис. 83 изображена эпициклоида (а) при гп=-^- и
2
гипоциклоида (б) при m=-g-.
160

Интересные ломаные
Большие возможности разнообразить вид кривых
связаны с использованием в уравнении кривой знака
абсолютной величины.
Например, уравнениям: y = sinx, y = \sinx[, \у\=*
= sin;t и f j/ f = | sin jc ( соответствуют кривые а), б), в) и
г) на рис. 84.
Рис. 84.
«Кривая», соответствующая уравнению
(2)
представляет собой квадрат ABCD (рис. 85,а), так как,
например, для второй четверти, где х-<0 и j/>0,
уравнение (2) можно переписать в виде —х-\-у=1, а это
уравнение прямой I, от которой надо взять лишь
отрезок ее, лежащий во второй четверти.
Попробуйте убедиться ("), что уравнениям:
1.12*-1| + 12у + 1|+^|*|=-4,
"• l*l + LH+y^{l*-J'l+l*+:vl>-yT+i.
ш. |И+|М-з|-з| = 1
6 Л. П. Доморяд
161

соответствуют правильный шестиугольник,
правильный восьмиугольник и «восьмерка», изображенные на
рис. ЪЬб,в,г, (см. [35], стр. 194—195).
Не удастся ли читателю найти уравнения, дающие
правильные двенадцатиугольник, шестнадцатиугольник и
т. п.? Сложнее, по-видимому, ту же задачу решить для
правильных пятиугольника, семиугольника и т. п.
Рис 85.
Своеобразны также линии, соответствующие
уравнениям вида
у = т arcsin [sin k (х — а)].
Из уравнения у = arcsin (sin х) следует;
1) —y^-^^T и 2) sin.V = sin•*•
При — y ^ х ^ у этим двум условиям удовлетворяет
функция у = х. Графиком ее в интервале (—у, -|Л
будет отрезок АВ ломаной, изображенной на рис. 86.
В интервале ~ ^ х «£ у будем иметь у = п — х,
так как sin(it — x) — smx и в этом интервале
162

ком ВС
Здесь график изобразится отрез-
Так как sin л:—периодическая функция с периодом 2тг,
то ломаная ABC, построенная в интервале (—У'т) '
опять повторится на участках ( у. у) > ( Т' ~2~) и т-д-
Уравнению ,y = arcsin(sinA.x) будет соответствовать
ломаная линия / с периодом у (период функции sin kx)
(на рис. 87 к = 2).
Рис. 87
Добавляя в правой части множитель т, получим
уравнение j; = marcsin(sinftjc), которому при те>0
будет отвечать ломаная вида // (т = -7А> а ПРН га<0 —
ломаная вида /// (те=—2).
Наконец, легко убедиться ("), что, сдвигая
последние ломаные вправо на отрезок а, получим графики
б* 153

функций вида
у = т arcsiti [sin k (х — а)].
Предлагаем читателю убедиться, что уравнению
[y-4arcsin(sinf)][jf + 4arcbin(sinf)]x
X [j>-|arcsin (sin =fifi*)] [у+^втЫа (sin^D)]=0
отвечает совокупность линий, изображенных на рис. 88
(произведение равно нулю только тогда, когда какой-
нибудь из множителей обращается в нуль; приравнивая
поочередно первый, второй, третий и четвертый
множители нулю, получим соответственно уравнения ломаных
а, б, в, г). Дополнительные объяснения к рис. 88 см. в
следующем параграфе.
Вычурные кривые
Интересными особенностями обладают некоторые
кривые, уравнения которых содержат степени с очень
большими показателями (см. статью М. Л. Франка в Г38],
вып. 6, 45—54).
Например, для уравнения у""000 = * имеем таблицу:
(проверьте! ('°а)),
из которой видно, что кривая на очень большом протя-
164
X
У
0
0
ю-«
sfc 0,999986
1
±1
10м
* 1,000023
1Q10O000
St 1,2583

жении почти совершенно не будет отличаться от лома*
ной LMNP (рис. 89).
На рис. 90 изображен график функции y = sva.x-{-
+ 2(sin;t),000000
2 (sin х)шш"
89°45'
89°50'
90°
0,00016
(проверьте! ("") )•
0,032
Из таблицы видно, что второе слагаемое данной
функции очень мало отличается от нуля при значениях х,
П
М
Рис. 89.
даже очень близких к 90° (а также к 270° и т. п.);
поэтому около некоторых точек обыкновенной синусоиды
(Л, Вит. д.) будут иметься очень узкие, направленные
вверх пикообразные выступы, которые при вычерчивании
кривой в сравнительно мелком масштабе будут иметь
вид отрезков AC, BD и т. д.
Рис. 90.
Уравнению У""""" = sin у отвечает кривая, мало
отличающаяся от ломаной ABCDEFGHI (рис. 91) (уже при
х = 0,000001 у ^0,999984).
6* А. П- Доморяд 165

Члены, содержащие степени некоторой периодической
функции с меньшими показателями, могут быть
использованы для изменения вида других, сравнительно
простых кривых.
Попробуйте, пользуясь таблицей значений функции
sinx и легко продолжаемой таблицей;
X
0
5°
10°
15°
20°
25°
sin Зле
0
0,259
0,5
0,707
0,866
0,966
sin5 дх
0
0,0001
0,031
0,178
0,487
0,84
sin' Зл;
0
0,000
0,002
0,044
0,28
0,73
30°
вычертить в крупном масштабе графики функций
y = sinx-{-\(sin3xy
у = sin х — -g-fsin Зл)9.
Влияние дополнительных слагаемых на вид кривой
полезно проследить и в полярных координатах.
У,
L
i
О
7 С
п е и у
/
л
6
2ж т
«
-t
л
Рис. 91.
В интересной статье Н. Ф. Четверухина ([37], 1930 г.,
№5) приводятся некоторые из уравнений, найденных
166

немецким математиком-натуралистом Хабенихтом для
геометрических форм, встречающихся в мире растений.
Рис. 92.
Например, уравнениям r = 4(l+cos3'f) и г = 4(1 -f-
+ cos3(p)-f-4sinf3^> соответствуют кривые,
изображенные на рис. 92.
6»»
167

Уравнения
и
г — 5 -f- 2 cos <р -f- 3 cos" <р
r = 5 + 2coscs-4-3 cos" <p _ sin* 18 у cos1-!
дают контуры «листа сирени» и «листа крапивы».
Советуем читателю построить сначала кривую г=
= 5-|-2cos<p и последить затем сначала влияние члена
3cos"<p, а затем влияние члена —sin* 18ip cos*-^-.
Может быть, кто-нибудь из читателей,
познакомившись со статьей Н. Ф. Четверухина, продолжит
исследования Хабенихта и получит новые интересные результаты.
Весьма своеобразна функция _у == 1 -Ц— jAgcos 2ппх,
принимающая действительные значения (равные единице)
"Э
aj
6J
11 А
г
Рис. 93.
Во всех остальных
только при х = 0, ± — , гЬ— ,
случаях подкоренное выражение будет либо
отрицательным, либо мнимым.
Графиком этой функции будет совокупность точек,
лежащих на расстоянии 1 над осью Ох и отстоящих
друг от друга на —
(см. рис. 93, а).
Если известен график функции y=f(x), то,
сохранив лишь точки этой кривой с абсциссами: 0, ±—, ±—
и т. д., получим график функции .у =/(х) (1 + Klgcos 2ппх)
(см. рис. 93, б, где /(.*) = sin у- и л = 4).
168

Использование функции f(x) = [x] (см. § 2) позволяет
«мало интересные» функции превращать в функции,
графики которых имеют весьма оригинальный вид.
Например, на рис. 94 представлены график а) функции
П
а)
У{
&
Рис. 94.
у — х— [х] и график б) функции у= — arcsinf sin^-j 1 ;
маленькие пустые кружки указывают, что на графике
отсутствуют соответствующие точки.
§ 29. МАТЕМАТИЧЕСКИЕ ОРНАМЕНТЫ
Под математическим орнаментом будем понимать
рисунок, характеризуемый каким-нибудь уравнением или
неравенством (а может быть системой уравнений или
системой неравенств), в котором многократно
повторяется тот или иной узор.
Например, системе неравенств
У>
У<
siax, \
—sin х J
(1)
удовлетворяют координаты точек, которые лежат
одновременно выше синусоиды (для них у > sin х) и ниже
кривой y = ~sinx, т. е. «область решений» системы (1)
будет состоять из заштрихованных на рис. 95 областей.
169

Обозначим через /, (х, у) и /, (х, у) первый и второй
множители в неравенстве
(у — sin х) (у -\- sin х) < 0. (2)
Этому неравенству будут удовлетворять координаты
точек, для которых одновременно/,(х,у) > 0 и/2 (х,у )<0
(они лежат в заштрихованных областях на рис. 95), и
координаты точек, для которых одновременно /, (х,у) < 0
и /г(х,у)^>0 (они заполняют области, отмеченные
звездочками).
Рис. 95.
В целом область решений неравенства (2) будет
состоять из заштрихованных и из отмеченных звездочками
областей. Если в неравенстве
[у — 4arcsln(sinir)] [з>+|-arcsin (sin ^)]Х
"(лг^)]<° (3)
X \У — — arcsin (sin
x[y+i
arcsin sin
множители в левой части обозначить соответственно
через <р,, <р2, <р,, <р4, т0 неравенству (3) будут
удовлетворять координаты точек, в которых либо один из
множителей левой части отрицателен, а остальные —
положительны (это будут, например, «области а» на рис. 88,
где <р,<0, a <pt, <$>,, <pi>0, «области р», где <р4<0, а
«р,, <р2, (рг^>0 и т. п.), либо три множителя в левой части
отрицательны, а четвертый положителен («области а'»,
гДе <Pi> <Р». 94<0 и <рг>0 «области р'», где «р,, <р2, «р4<0,
а 9г^>^ и т- п-)-
В целом область решений нераоенства (3) будет
состоять из заштрихованных на рис. 88 квадратиков.
Увеличивая число множителей в левой части
неравенства, выбирая их так, чтобы кривые и ломаные, на
170

которых они обращаются в нуль, были бы сдвинуты
относительно друг друга на те или иные отрезки, беря
вместо одного сложного неравенства систему простых
неравенств и т. п., можно сильно разнообразить вид
получаемых рисунков.
Предоставим читателю убедиться, что области решений
1) неравенства
(у* — arcsin* (sin х)} (у* — arcsin" sin (х -f* -g-) ) < 0; (4)
2) неравенства
Ф-.Ф-^Ф.ФхФ^О, (5)
где Фк = Ф/1(х,у)—у* — arcsin* sinf^-J--8-) и £ =
= -2, -1, 0, 1, 2;
3) неравенства
bs-sin^][y-sins(^ + -j)] [y_sins(.*-!-)]<0; (6)
4) системы неравенств
-(£)Sarcsins(sin^)<0, (7')
y-(i-)Sarcsin* [smi^-I)] <0; (7')
и 5) системы неравенств
>-(^)aarcsms(sinf)<0, (8')
у_(^Ып-[в1п"^]<0. (8»)
/-(*)' arcsin* [sin &=Щ < 0, (8'")
y-^j'arcsin* [sin^r^j <0 (8"")
состоят соответственно из заштрихованных фигур а),
б), в), г), д) на рис. 96 (на рис. 96, г пунктиром намечены
«широкие» ромбы, дающие решение только неравенства
(7') и «высокие» ромбы, дающие решение только
неравенства (7"); на рис. 96, д большими ромбами /
ограничена область решений неравенства (8'), ромбами //—
171

в;
<
6
д&
I
I
fw
/
ф
; fff Ш 17 ПГ М
^ШжШш£Ш^1ш^Я1яШшж
i а ш if i а ш
1 V
Рис. 96.

область решений неравенства (8") и т. д.; общая часть
этих областей дает цепочку маленьких заштрихованных
ромбиков).
Используя неравенства с высокими степенями
переменных, можно увеличить разнообразие математических
орнаментов. Например, неравенству
(У000001 —sin л) [(2j;)looom —sin(^ —у)]<0 (9)
и неравенству
(/""" — sin^)(j/—iarcsinsin^)<0 (10)
отвечают области решений, чрезвычайно мало
отличающиеся от изображенных на рис. 97, а и 97, б.
Составление математических орнаментов может
служить хорошей темой для состязания в старших классах;
объединяя затем наилучшие орнаменты, можно получить
красочный альбом с красивыми и замысловатыми
рисунками.
§ 30. МОДЕЛИ МНОГОГРАННИКОВ
Пусть в параллельных плоскостях р и о лежат
противоположные ребра правильного тетраэдра,
противоположные вершины куба и правильного икосаэдра (причем
Аб_1_р и CDJ_p)i противоположные грани правильных
октаэдра и додекаэдра (рис. 98).
Ш

Пересекая эти многогранники плоскостью,
проходящей посередине между р и а и параллельной им,
получим в сечении квадрат, два правильных шестиугольника
и два правильных десятиугольника.
Рис. 98.
Если изготовить модели двух половинок каждого из
многогранников и шарнирно соединить их (приклеив
узкую полоску крепкой тонкой бумаги или ткани вдоль
их общего ребра), то получатся модели, наглядно пока-
Рис. 99.
зывающие вид сечений и частей, на которые
многогранники разбиваются «средними плоскостями».
На рис. 99 даны развертки половинок додекаэдра и
икосаэдра.
Интересны и поучительны также модели,
показывающие «переход» от одних правильных многогранников к
174

другим. Из рис. 100, а видно, что правильный октаэдр
ABCDEF можно дополнить до правильного тетраэдра
KLMN, приставляя к четырем его граням по маленькому
тетраэдру.
В свою очередь, приставляя ко всем граням
правильного тетраэдра KLMN одинаковые треугольные пирамиды
KLMV, LMNT, KMNS и KLNU, получим куб. Склеив
отдельно эти пирамиды и соединив их шарнирно друг
с другом по ребрам MN, NL и LM, получим «оболочку»,
при «надевании» которой на тетраэдр KLMN последний
превращается в куб (рис. 100, б).
Рис. 100.
Для куба можно склеить из шести одинаковых
«крышечек» ABCDKL, ADEFMN и т. д. оболочку,
переводящую его в правильный додекаэдр (рис. 101, а). На
рис. 101, б отдельно представлена развертка такой
крышечки; тупые углы у треугольников и трапеций по 108°
Наконец, из двенадцати многогранников, изображенных
на рис. 101, в, можно склеить оболочку, переводящую
правильный додекаэдр с ребром а в правильный
икосаэдр, описанный около додекаэдра. Каждая крышечка
ограничена правильным пятиугольником ABCDE со
стороной а, пятью равнобедренными треугольниками (АКЕ,
EMD и т. п.) с блоковой стороной b = 0,535а и пятью
одинаковыми четырехугольниками {EKSM, DMSL и т. п.);
EK=EM = b; KS=SM^ 0,927а; /КЕМ=\Ж,
/_ EKS = /_ EMS=90е.
На моделях можно познакомиться с разнообразными
по форме призматоидами—так называются выпуклые
многогранники, основаниями которых служат многоуголь-
175

ники произвольного вида, лежащие в параллельных
плоскостях, а боковыми гранями — треугольники (или —
в отдельных случаях — трапеции), все вершины которых
совпадают с соответствующими вершинами оснований.
На рис. 102 изображены призматоид ABCDKLM с
треугольным и четырехугольным основаниями, призматоид
EFHQR с треугольным и «двуугольным» (отрезок QR)
Рис. 101.
основаниями и так называемая правильная антипризма —
так называются призматоиды, основаниями которых
служат одинаковые правильные л-угольники, а боковыми
гранями — равносторонние треугольники, причем «линия
центров оснований» 01Ог перпендикулярна р и
основания повернуты относительно друг друга на угол —.
Развертку призматоида легко построить, если дана
его проекция на плоскость р (или с) и высота к
(рис. 103).
Основания призматоида даются в проекции в
неискаженном виде; для определения же, например, истинного
вида грани CDM надо провести М'Р _|_ CD и отложить
РМх = УМ'Рг-\-к* (см. рис. 102). Аналогичным образом
определяется истинный вид других боковых граней,
примыкающих к основанию ABCD, а затем и граней,
176

примыкающих к основанию KLM (они намечены на
рис. 103 пунктирными линиями).
Вырезав фигуры ALfiLfiMJ)KxA и K'AJJC^MDJC
(оставив по краям необходимый запас для склеивания),
нетрудно склеить затем и сам призматоид.
Рис. 102.
Постройте развертки и склейте модели нескольких
неправильных призматоидов, а также нескольких
правильных антипризм (при л = 5, 6, 7, ...).
Как видно из рис. 104, куб может быть составлен
из трех одинаковых пирамид: LABCD, LMNCD, LAKND,
Рис. 103.
имеющих общее ребро LD (диагональ куба) и
квадратные основания: ABCD, NMCD, AKND; отсюда следует —
без использования формулы для объема пирамиды! — что
объем пирамиды с квадратным основанием, у
которой боковое ребро равно стороне основания а и пер-
а2
пендикулярно плоскости основания, равен •*-.
177

При вращении куба вокруг диагонали LD на 1205 и
на 240° пирамиды LABCD, LNMCD, LAKND переходят
друг в друга.
Сделайте разборную модель куба, склеив эти
пирамиды и соединив «шарнирно» первую со второй по
ребру LC, и первую с третьей — по
ребру LA.
Если пространство заполнить
одинаковыми кубами так, чтобы
любые два соседних куба имели
общую грань, и мысленно
окрасить их — в шахматном порядке —
в белый и черный цвет, то,
проводя через ребра каждого черного
куба ABCDKLMN (рис. 105)
плоскости, проходящие в то же время
Рис- * через центры О,, О, соседних
белых кубов (например, плоскость OxKN), мы разобьем
каждый белый куб на шесть одинаковых пирамид.
Если присоединить к каждому черному кубу
примыкающие к нему белые пирамиды, то пространство
окажется заполненным так называемыми ромбаческама
додекаэдрами.
178

У ромбического додекаэдра 8 трехгранных и 6
четырехгранных углов, и каждая из двенадцати граней —
ромб, диагонали которого относятся, как 1:]/2.
Докажите, что плоскости вида OtKN и KOtN совпадают.
Постройте 5 — 6 одинаковых ромбических додекаэдров
и убедитесь, что они очень хорошо могут быть
«пригнаны» друг к другу.
Если куб ABCDKLMN (рис. 106) разбить на восемь
маленьких кубов плоскостями, параллельными граням и
проходящими через
центр куба, и от
каждого из маленьких
кубов отрезать половину,
примыкающую к
соответствующей вершине
большого куба
(например, семигранник
NXYZPQRSTU,
примыкающий к вершине N),
то от первоначального
куба останется
многогранник с шестью
квадратными и восемью
правильными
шестиугольными гранями,
составленный как бы
из восьми
«полукубиков» с общей вершиной в центре О большого куба.
Точно такой же многогранник можно составить из
восьми «полукубиков», группирующихся около точки N,
если предположить, что описанная выше операция
проделана с каждым из восьми больших кубов, имеющих
общую вершину N.
Следовательно, четырнадцатигранниками,
изображенными на рис. 106, можно «без просветов» заполнить все
пространство. Вы можете наглядно убедиться в этом,
склеив пять таких многогранников одинаковых размеров.
Из твердого картона можно сделать складывающиеся
модели некоторых многогранников. Вырежьте, например,
из картона четыре правильных треугольника и соедините
их шарнирно в две пары, приклеивая к ним полоски
плотной ткани вдоль прямой АВ и вдоль прямой CD
(рис. 107, а).
Рис. 106.
179

Если соединить полученные ромбы тонкой
«замкнутой» натянутой резинкой ONMLKVUTSRQPO, продетой
в отверстия: Ми/., V и U, S и R, Р и Q, то резинка,
укорачиваясь, будет стремиться перевести плоскую
фигуру а) в тетраэдр б) (точки U и V лежат на средней
линии треугольника ABC и т. п.).
Рис. 107.
Для получения складывающейся модели правильного
додекаэдра надо «розетку» из шести правильных,
вырезанных из плотного картона пятиугольников, пять из
которых шарнирно соединены с центральным
пятиугольником ABCDE (рис. 107, в), наложить на такую же
«розетку» с центральным пятиугольником PQRST и через
двадцать отверстий, указанных на рисунке, пропустить
натянутую «замкнутую» резинку.
180

Вопросы для размышления
1. Проводя через каждое из двенадцати ребер куба
плоскость, одинаково наклоненную к граням
соответствующего двугранного угла, мы пришли к ромбическому
додекаэдру (рис. 105).
Проводя через 24 ребра ромбического додекаэдра
плоскости, одинаково наклоненные к соответствующим
его граням, мы придем к многограннику Slt
«описанному» около ромбического додекаэдра; затем из Sx
тем же путем можно получить 5„ из 5, — S, и т. д.
Попробуйте определить вид граней и построить
модели многогранников 5, и 5,.
6J
Рис. 108.
Аналогичные вопросы можно поставить, взяв в
качестве исходного многогранника не куб, а какой-нибудь
другой многогранник (правильный додекаэдр, правильную
пятиугольную антипризму и т. п.).
Что получится, если за исходный многогранник взять
правильный тетраэдр или правильный октаэдр (71)?
2. Если пространство заполнить одинаковыми
параллелепипедами произвольной формы, окрашенными «в
шахматном порядке», то, присоединив к каждому черному
параллелепипеду шесть пирамид с вершинами в центрах
соседних белых параллелепипедов, мы получим
двенадцатигранники, заполняющие пространство без просветов
(рис. 108, а).
181

Отрезая же от каждого большого параллелепипеда
восемь половинок маленьких параллелепипедов, получим
четырнадцатигранники, также пригодные для заполнения
пространства (рис. 108, б).
Попробуйте, зная высоту параллелепипеда h и
проекцию его на плоскость основания, построить развертки
получающихся указанным способом двенадцатигранника
и четырнадцатигранника.
Склеив несколько одинаковых многогранников
каждого типа, убедитесь, что ваши модели могут быть
вплотную «пригнаны» друг к другу.
§ 31. РАЗВЛЕЧЕНИЯ С ЛИСТОМ И С ПОЛОСКОЙ БУМАГИ
На треугольном листе бумаги легко
продемонстрировать, не пользуясь чертежными инструментами, что три
биссектрисы (три медианы, три высоты, три
перпендикуляра в серединах сторон) треугольника пересекаются
в одной точке.
Рис. 109.
Действительно, любую из указанных линий легко
«построить», сложив соответствующим образом лист
бумаги. Если треугольник ABC тупоугольный, то для
получения центра описанной окружности надо взять лист
бумаги в форме AKLBC (рис. 109, а), а для получения
ортоцентра — в форме ABDE с намеченными (сгибами
бумаги) продолжениями сторон АС и ВС.
Еще проще «доказать» теорему о сумме углов
треугольника (рис. 109, б).
Можно также приближенно разделить — без
чертежных инструментов — любой угол ABC на три равные
части, для чего достаточно (рис. 110, а) согнуть бумагу
182

по прямой ВК, проходящей через вершину угла, так,
чтобы углы КВА' и ABC были одинаковы. При
некотором навыке сделать это «на глаз» можно очень точно.
Правильные многоугольники
Если у полоски ABCD с параллельными краями
(рис. 110, б) Z.ABC-=G0°, то, сгибая ее по прямым: ВК,
KL, LM, MN, ... , последним «неполным
треугольником» можно закрыть «письмо-конверт» в форме
равностороннего треугольника. Если же полоску «полусогнуть»
по прямым: ВК, KL, ... , то из нее легко сложить
боковые поверхности различных правильных антипризм
(см. § 30).
Из полоски бумаги с параллельными краями легко
«построить» правильный пятиугольник, «завязав» полоску
0
Рис. ПО.
узлом (рис. ПО, в) и осторожно затянув узел,
сжимая его в виде правильного пятиугольника KLMEF
(рис. 110, г).
Если пропустить затем полоску EFCD, согнув ее по
прямой EF, под трапецию KLMF, то получится «письмо-
конверт» в форме правильного пятиугольника. При
рассматривании на свет такой фигуры, сложенной из не очень
плотной бумаги, ясно вырисовывается правильная
пятиконечная звезда с темной серединой.
183

Рис. 111.
Согнув достаточно длинную полосу ABCD по прямой
АХ (/mAKL=Yj, получим первые три вершины: К, L, М
правильного семиугольника (на рис. 111 надо мысленно
значительно удлинить
полоску за
«криволинейные границы» CD,
затем C1D1 и т. д.).
Сгибая затем
полоску последовательно: по
прямой MN (чтобы NC,
Щ прошла через точку К),
по прямой КР (чтобы
PD, прошла через
точку N), по прямой NQ
(чтобы QCt прошла
через точку Р), по
прямой PR (чтобы RD,
прошла через точку Q,
а РСЬ — через точку I)
и, наконец, по прямой
QL (в результате чего
края полоски должны пройти через точки М и R),
получим правильный семиугольник MNQLKPR, а при
«рассматривании его на свет» увидим несколько
семиугольных звезд.
Лист Мёбиуса
Сблизьте концы АВ и CD полоски бумаги, «скрутите»
слегка ее (чтобы точка С совместилась с В, a D — с Л)
и в скрученном положении склейте концы АВ и CD
(рис. 112). Это даст вам
так называемый лист
Мёбиуса —
одностороннюю поверхность,
которую нельзя окрасить
с двух сторон в разные Рис. 112.
цвета: начав красить в
какой-нибудь ее точке одним цветом и продвигаясь
постепенно все дальше и дальше, мы незаметно придем
в исходную точку с обратной стороны бумаги.
При разрезании листа Мёбиуса по линии,
равноотстоящей от краев, он не распадается на две части,
184

а превращается в «полностью скрученное кольцо»,
а последнее — при разрезании его по «средней линии» —
дает два дважды перекрученных и причудливо друг
с другом сцепленных кольца. Такую «живучесть» листа
Мёбиуса можно использовать для фокуса, производящего
сильное впечатление на неискушенных зрителей.
Любителям математики можно предложить провести
систематическое исследование поведения листа Мёбиуса
и многократно скрученных бумажных колец, разрезаемых
по средней линии или по двум линиям, одинаково
отстоящим друг от друга и от соответствующих краев,
и т. п.
Подробнее о свойствах листа Мёбиуса см. [6],
стр. 117—132.
Построение правильного икосаэдра
Возьмите полосу плотной бумаги шириной в 10—
12 сантиметров, сложите ее в соответствии с рис. ПО, б
и вырежьте несколько равносторонних треугольников.
Каждый из них легко
разделить «на глаз» (и очень
точно!) на шестнадцать
равносторонних
треугольников, сгибая сначала по
средним линиям М'К',
K'L', L'M (надо L
совместить с серединой L'
стороны КМ и прогладить
бумагу по линии М'К'
и т. п.), затем — по
линиям PQ, RS, TQ и т. д.
(см. рис. 113).
Если сделать разрезы
по отрезкам РН, FS, TI, то,
повернув, например, ромб PLQH вокруг вершины Н
против движения часовой стрелки так, чтобы
треугольник HQP оказался под треугольником НМР, и согнув
его по диагонали PQ до совмещения вершины L с
точкой Н, получим пятигранный угол с вершиной Н
(хорошо «скрепленный» загнутым треугольником PQL,
особенно если в центр его капнуть предварительно каплю
клея).
185

Построив аналогичным путем пятигранные углы с
вершинами в точках / и F, получим модель половины
поверхности правильного икосаэдра.
Из четырех-пяти половинок икосаэдра, «надвигая» их
друг на друга так, чтобы каждые две непосредственно
соприкасающиеся половинки имели четыре общие грани,
легко получить достаточно прочную модель правильного
икосаэдра.
Не удастся ли читателю построить прочные модели
правильных тетраэдра, октаэдра и икосаэдра из
нескольких полосок бумаги одинаковой ширины, разбитых на
равносторонние треугольники (см. рис. 110, 6)1 Может
быть удастся построить и модель правильного додекаэдра
из нескольких полосок бумаги, на каждой из которых
были бы «завязаны» расположенные вплотную друг к
другу правильные пятиугольники (см. рис. 110, г).
§ 32. ПРОБЛЕМА ЧЕТЫРЕХ КРАСОК
Допустим, что нам надо раскрасить произвольные
области на плоскости или сферической поверхности
(например, политическую карту мира) таким образом,
чтобы никакие две соседние (т. е. имеющие хотя бы
на небольшом протяжении общую границу) области не
были бы закрашены в одинаковый цвет. Области,
соприкасающиеся лишь в одной или в нескольких точках,
соседними не считаются и закрашивать их в один цвет
можно.
Как показывает опыт, всегда можно обойтись при
этом самое большее четырьмя красками, если, конечно,
отказаться при раскрашивании карт от принятого обычая
закрашивать водные площади, рассматриваемые тоже
как отдельные области, в одинаковый цвет.
Конечно, может случиться, что при неудачном
закрашивании нескольких первых областей окажется необхо-
ходимой пятая краска (например, для закрашивания
центральной области на рис. 114, а, где цифрами обозначены
номера использованных красок), но всегда удается, по
иному окрасив первые области, обойтись четырьмя
красками (см. рис. 114, 6).
Однако пока еще никто не смог строго доказать
(в этом и заключается проблема четырех красок!), что
невозможно так разбить плоскость или поверхность
186

шара на области, чтобы при всех вариантах раскраски
была необходима пятая краска, хотя доказано, что пятью
красками всегда можно обойтись ([24], стр. 90—101).
Интересно, что поверхность тора (рис. 114, в) может
быть разбита даже на семь областей, каждая из которых
будет граничить со всеми остальными областями, и таким
образом обойтись на торе (в общем случае) меньше чем
семью красками нельзя. Однако доказано, что невозможно
разбить поверхность тора на области так, чтобы восьмая
краска была необходима при всех вариантах раскраски.
а) б)
Рис. 114, я и б.
Легко убедиться, что в случае пространственных
областей дело будет обстоять совсем иначе, а именно:
можно взять сколько угодно таких областей, чтобы
любая из них имела с каждой из остальных общую
границу в виде куска некоторой поверхности. Достаточно
взять два ряда длинных брусьев, положенных в разных
направлениях друг на друга (рис. 114, г), и объединить
в отдельные области каждые два одинаково
занумерованных бруска.
Укажем несколько задач и вопросов, примыкающих
по своему характеру к проблеме четырех красок.
1. Склеив модель тела (д), топологически
эквивалентного тору, разбейте его поверхность на семь
областей, каждая из которых граничила бы с шестью
остальными.
2. Посреди двора возвышается большой «мост».
Разбить территорию двора, используя и верхнюю
поверхность моста, и площадь под мостом, на семь участков
так, чтобы любые два участка были смежными. Решение
указать на модели (е), состоящей из листа бумаги
с наклеенной на него в виде моста полоской бумаги.
3. Доказать ("), что произвольное число прямых
разбивает плоскость на области, для раскраски которых
187

достаточно двух красок. А как будет обстоять дело
в пространстве при разбиении его на области
произвольными плоскостями?
4. Доказать ("), что существуют восемь тетраэдров
(не обязательно правильных), которые можно
расположить в пространстве так, чтобы каждый из них имел
с каждым другим общую границу в виде куска грани,
не вырождающегося в линию или в точку.
Ж)
Рис. 114, в — ж
5. Из рис. 114, ж видно, что территорию острова
можно разбить на шесть областей и распределить их
между пятью государствами так, чтобы любые два
государства имели смежные владения. Если потребовать,
чтобы все области, принадлежащие одному и тому же
государству, были окрашены в один цвет, то
использование пяти красок будет неизбежно.
Попробуйте найти при т — 6, 7, 8, 9, ... наименьшее
число п областей, на которые следует разбить остров,
чтобы при распределении областей между т
государствами любые два государства имели смежные владения.
188

Может быть вам удастся найти формулу вида:
Лн»ии=/(т)-
Можно также, задавшись каким-нибудь сложным и
причудливым разбиением острова на области, искать
(соревнуясь друг с другом) распределение областей
между возможно большим числом государств т, чтобы
любые два государства имели смежные владения.
§ 33. ВЫЧЕРЧИВАНИЕ ФИГУР С ОДНОГО ПОЧЕРКА
С одного почерка, то есть не отрывая карандаша
от бумаги и не проходя дважды по одной и той же
линии, можно обвести сложную фигуру (рис. 115, d)t
а.) С
Рис. 115.
состоящую из ряда «узлов» и соединяющих их «путей»
(пути могут быть и криволинейными (рис. 115,2), но
нельзя обвести очень простую по внешнему виду фл-
ГУРУ б),
Назовем узлом А-го порядка или, короче, «А-узлом»
точку, из которой выходят k путей. Так, фигура а)
имеет два узла третьего и семнадцать узлов четвертого
порядка. Очевидно, любую промежуточную точку,
лежащую на каком-нибудь из путей, можно считать узлом
второго порядка.
Обводя фигуру карандашом, мы будем различать
начальный, конечный и промежуточный узлы.
189

Теорема: Если фигуру можно вычертить с одного
почерка, то ни один из нечетных узлов ее не может
быть узлом промежуточным.
Действительно, «2т -\- 1 -узел» может быть лишь
начальным или конечным узлом, так как, пройдя через
него т раз, мы используем 2т путей, а по оставшемуся
пути можно лишь начать или завершить обход фигуры.
Из этой теоремы следует, что нельзя с одного почерка
начертить фигуру, имеющую больше двух нечетных
узлов, в частности нельзя начертить и фигуру б),
имеющую четыре тройных узла.
Рассмотрим известную задачу Эйлера о мостах:
можно ли пройти по семи мостам, соединяющим острова
А и В друг с другом и с берегами С и D реки, пройдя
по каждому мосту по одному лишь разу? (рис. 115, в).
Заменив берег и острова точками, а мосты —
соединяющими их линиями, сведем задачу Эйлера к вопросу
о вычерчивании с одного почерка фигуры г), что
сделать невозможно, так как у нее четыре нечетных
узла.
Докажите (,4), что у любой фигуры число узлов
нечетного порядка четно.
Если от любой точки фигуры к любой другой ее точке
можно перейти по путям, ей принадлежащим, то фигуру
называют связной.
Можно доказать, что любая связная фигура без
нечетных узлов или с двумя нечетными узлами всегда
может быть вычерчена с одного почерка ([25], гл. 8).
Доказательство и поиски способа вычерчивания
любой «вычерчиваемой» фигуры основаны на том, что при
неудачно закончившемся обходе, охватившем не все
линии фигуры, всегда можно найти точку, общую
пройденным путям и путям, оставшимся вне обхода.
Замкнутый путь по непройденным путям, начинающийся и
кончающийся в этой точке, можно включить в первый
вариант обхода, что уменьшит число непройденных
путей. Так следует поступать до тех пор, пока не
получится обход, содержащий все пути.
Очевидно, при наличии двух нечетных узлов один
из них должен быть начальным, а другой — конечным
пунктом обхода; если же все узлы четные, то за
отправную точку можно взять любую точку фигуры и в ней же
закончится весь обход.
190

Если договориться, что каждая линия фигуры должна
быть при вычерчивании пройдена ровно два раза (то
есть каждый путь, связывающий два узла, как бы
заменяется мысленно двумя путями), то кратность каждого
узла удвоится, и любая связная фигура сделается
вычерчиваемой с одного почерка.
Двойное вычерчивание фигуры сразу может быть
доведено до конца, если пользоваться правилом Тарри
([25], стр. 239—242): достигая какого-нибудь узла в
первый раз по некоторому пути /, при возвращении в этог
узел следует избегать
пользоваться путем / до тех пор,
пока будет возможно, то
есть вторично пройти этот
путь лишь тогда, когда все
пути, выходящие из этого
узла, будут пройдены
дважды; при этом нельзя из
какого-нибудь узла выходить
по одному и тому же пути
дважды (второе движение по
любому пути осуществляется
в противоположном
направлении).
На рис. 116 в
соответствии с правилом Тарри
сделано 16 пронумерованных переходов, причем «фигурные
стрелки» ставились на путях, по которым мы подходили
к узлам, где до этого еще ни разу не были (по такому
пути от узла можно отходить, когда все сходящиеся в
нем пути будут пройдены дважды).
При повторном приближении к какому-нибудь узлу
на соответствующем пути ставилась простая стрелка;
по такому пути повторное движение (в обратном
направлении!) можно совершать когда угодно. Например,
вместо пятого «хода» можно было бы прочертить
отрезок от М к D, но восьмой ход ничем нельзя было бы
заменить, так как по DM от узла D одно движение уже
было совершено (четвертый ход), а фигурная стрелка
на DC показывает, что этот путь должен быть пройден
из узла D в последнюю очередь.
Правило Тарри имеет принципиальное значение в
задаче о лабиринтах. Любой лабиринт можно рассматривать
Рис. 116.
191

как совокупность точек (площадки, комнаты и т. п.),
связанных между собой линиями (аллеи, коридоры и т. п.).
Из правила Тарри следует, что любой связный
лабиринт (то есть лабиринт без недоступных пунктов) может
быть всегда обойден лицом, незнакомым с планом
лабиринта, так, что все пути будут пройдены дважды. При
этом в лабиринте, кроме «фигурных и простых стрелок»,
следует ставить «заградительный знак»,
предостерегающий от повторного движения по тому или иному
коридору в прежнем направлении.
§ 34. ИГРА ГАМИЛЬТОНА
В 1857 году английский математик Гамильтон
предложил игру, названную им «путешествие по додекаэдру»
и сводящуюся к обходу вершин правильного додекаэдра
при условии, что передвигаться можно только по его
ребрам и ни в одну из вершин нельзя заходить больше
одного раза.
Если сделать центральную проекцию додекаэдра, т. е.
вершины и ребра его (рис. 117, а) спроектировать на
плоскость, проходящую через грань ABCDE, из точки О,
находящейся на небольшой высоте над центром грани
VWXYZ, то получим схему б).
Одной из задач в игре Гамильтона является
построение замкнутых обходов всех двадцати вершин.
Оказывается (см. [25] или [30]), что, сделав из какой-нибудь
вершины четыре произвольных хода, можно побывать во
192

всех остальных вершинах и двадцатым ходом вернуться
в исходную вершину.
Можно поставить вопрос о числе обходов, задав,
например, первые три и последнюю вершины (в
зависимости от их расположения возможны 0, 1, 2, 4 или 6
обходов), или первые две и последние две вершины и
т. п. При этом можно запретить заход в отдельные
вершины или пользование отдельными ребрами.
Можно рассмотреть игру с двумя участниками,
чертящими поочередно звенья «ломаной обхода», причем
один из участников стремится к завершению полного
обхода (не обязательно замкнутого) всех двадцати вершин,
а другой—к созданию
положения, при
котором часть вершин
окажется необойден-
ной (например,
ломаная SZYXNPDCRQ).
«Чертить»
ломаную игроки могут,
ставя поочередно в
соответст вующие
вершины занумеро- Рис. пь.
ванные белые и
черные шашки. Игра сделается сложнее и интереснее,
если вместо схемы б) взять деревянный додекаэдр с
кольцами, плотно надеваемыми на шпеньки, укрепленные
в его вершинах.
Может быть, читателю удастся построить теорию
игры, доказав неизбежность проигрыша одного из
игроков при правильной игре его противника (надо
рассмотреть, конечно, два варианта, когда игрок,
создающий «тупик», играет белыми или черными).
Путешествие по правильному додекаэдру можно
заменить путешествиями по другим многогранникам.
Интересно, например, что, соблюдая правила игры Гамильтона,
невозможно обойти все вершины ромбического
додекаэдра (см. § 30), так как в последнем имеется шесть
четырехгранных углов и восемь трехгранных, а любое
ребро его связывает «разнородные» вершины.
На рис. 118 приведена пространственная схема, где
существуют незамкнутые и невозможны замкнутые
обходы (почему?) (").
Ж
193

Не удастся ли читателю найти многогранник,
обладающий тем же свойством?
Гамильтон предложил еще вторую игру —
путешествия по граням многогранника, в которой переход с
грани на грань допускается лишь при наличии у них
общего ребра.
Предлагаем читателю убедиться ("), что схема
путей во второй игре Гамильтона, проводимой на
правильном октаэдре и на правильном икосаэдре, ничем
Я
к
р
в
L
О
С
М
R
Л
N
S
}
5
9
13
2
е
W
14
3
У
17
15
*
в
12
Iff
#
Рис. 119.
не отличается от схемы путей первой игры,
проводимой соответственно на кубе и на правильном
додекаэдре.
Задачу о коне из § 19 можно рассматривать, как
задачу обхода по правилам игры Гамильтона всех точек
некоторой схемы: достаточно заменить клетки доски
точками, может быть, и по-иному расположенными, и
соединить линиями точки, соответствующие клеткам,
связанным на шахматной доске ходом коня.
На рис. 119 указаны плоская (а) и
пространственная (б) схемы, соответствующие «3, 4-доске» (в) и
«4*-доске» (г).
194

§ 35. РАЗМЕЩЕНИЕ ТОЧЕК НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
Обычно задачи этого типа «овеществляются», т. е.
точки заменяются монетами, орехами или какими-нибудь
другими предметами.
Приведем несколько типичных задач:
1. Десять монет расположены в виде
равностороннего треугольника (см. рис. 120, а). Переложить (")
три монеты на новые места так, чтобы снова получился
равносторонний треугольник.
а)
$
Рис. 120.
2. Из рис. 120, б видно, что девять монет можно
расположить в восемь рядов по три монеты в каждом
ряду, т. е. можно указать восемь прямых линий, на каждой
из которых лежат центры трех каких-нибудь монет.
Переложите (") две монеты так, чтобы девять монет
оказались расположенными в десять рядов по три
монеты в каждом ряду.
3. На рис. 120, в, г даны две принципиально
одинаковые, но сильно отличающиеся по внешнему виду схемы
расположения девятнадцати монет в девять рядов по
пять монет в каждом.
195

Расположите 19 монет в десять рядов по пяти монет
в каждом ряду (").
Проведите со своими друзьями конкурс на отыскание
таких расположений п точек в т рядов по р точек в
каждом ряду, чтобы отношение — имело по
возможности большое значение (для определенности следует
оговорить, что п не должно превосходить некоторого
числа п0).
Попробуйте исследовать вопросы, аналогичные
построению магических квадратов. Например: можно ли
расставить целые числа от 1 до 19 в узловых точках
схемы (в) на рис. 120 так, чтобы суммы чисел, лежащих
на любой из девяти прямых, были одинаковы.
4. Расположить (80) на плоскости шесть точек так,
чтобы любые три точки были вершинами некоторого
равнобедренного треугольника.
5. Расположить (") в пространстве восемь точек так,
чтобы все 56 треугольников (Q) с вершинами в данных
точках оказались равнобедренными.
Попробуйте изучить вопрос о расположении на
чертеже п точек (при л=7, 8, 9, ...) так, чтобы среди С^
треугольников как можно больше оказалось
равнобедренных. Аналогичный вопрос можно поставить (при л =
= 9, 10, 11, ...) для пространства.
Все эти задачи можно рассматривать и в /п-мерном
пространстве, если понимать под точками /п-мерного
пространства совокупности т действительных чисел,
записанных в определенном порядке, а расстояние между
ТОЧКаМИ . . . г> /п п а \
Л К. а2, ..-, «J и В(р„ р„ ... ,pj
вычислять по формуле:
^ = VK-Pir + (ai-pi)a + ... + K-PJ2.
6. Пользуясь последней формулой, показать (8а), что
в четырехмерном пространстве каждые три из
следующих пяти точек:
0(0,0,0,0), 4(1,0,0,0), В^'^Т-'0'0)'
м ут v± 0\ п/\_ ут ут ут
^\2> 6 ' 3 ' J ^2* b ' 12 ' 4 )'
являются вершинами равностороннего треугольника.
196

Задачи 2 и 3 примыкают к интересной задаче
проективной геометрии — построению конфигураций.
Плоской конфигурацией (рт, дп) называется система
из р точек и q прямых, в которой через каждую точку
проходит т прямых, а каждая прямая проходит через
л точек (из числа данных).
Л А.
А
Рис. 121.
Легко доказать ("), что обязательно должно быть:
pm = qn. Если p = q и т = п, то вместо (рт, рт) пишут
короче: (рт).
На рис. 121 приведены конфигурации: (3,), (6,, 4,),
(9,), (9.) и (10,). Интересно, что не существует,
например, конфигурации (7.) (см. [8], стр. 107—109).
§ 36. ЗАДАЧИ ЛОГИЧЕСКОГО ХАРАКТЕРА
Задачи логического характера заслуживают внимания
не только в силу их внешней занимательности, но и
потому, что решение их, как и решение задач
математических, способствует развитию сообразительности,
настойчивости, уменья находить в условии задачи то
«слабое место», использование которого приводит, в конечном
счете, к решению задачи. Приведем несколько типичных
примеров:
1. Школьники для игры разбились на две партии: на
«серьезных», отвечающих правильно на любой вопрос,
и на «шутников», дающих на любой вопрос только
неправильные ответы.
7 А. П. Доморяд 197

Преподаватель, узнав об этом, спросил у Иванова,
серьезный ли он человек или шутник. Не расслышав
ответа Иванова, он спросил у Петрова и Сидорова,
сидевших рядом с Ивановым: «Что ответил мне Иванов?».
Петров сказал: «Иванов ответил, что он серьезный
человек». Сидоров же сказал: «Иванов ответил, что он
шутник». Кем были Петров и Сидоров? (■*).
2. Шесть школьников, участвуя в воскреснике,
разбились на три бригады. Бригадиров звали: Володя, Петя,
Вася. Володе с Мишей дали двухметровые, Пете с
Костей— полутораметровые, а Васе с Алешей — метровые
бревна, и они каждое
бревно распиливали полностью
на полуметровые поленья.
В стенгазете отметили,
что бригадир Лавров с
Рожковым напилили 26,
бригадир Галкин с Ком-
ковым — 27 и бригадир
Козлов с Евдокимовым —
лиЬт 28 поле"ь^; Как зовУ7
Комкова? (")
Рис- 122- 3. Три приятеля:
Андрей, Борис и Вадим —
сидели без головных уборов друг за другом (рис. 122),
причем Борису и Вадиму было запрещено
оглядываться назад, Борис же видел голову сидящего внизу
Вадима, а Андрей — головы обоих своих приятелей.
Из мешка, содержавшего две белые и три черные
шапки (об этом все трое были осведомлены), каждому
была надета шапка неизвестного (для него) цвета, а
Две шапки неизвестного (для всех) цвета остались в
мешке.
Андрей заявил, что он не может определить цвета
своей шапки. Борис слышал ответ Андрея и сказал, что
и у него не хватает данных для определения цвета
Шапки, находящейся на его голове. Мог ли Вадим на
основании ответов своих приятелей определить цвет
своей шапки? (")
Особо следует отметить задачи, для решения
которых требуется тщательный анализ многочисленных
данных, иногда мало связанных (на первый взгляд) с
искомыми величинами. Например:
198

4. В велогонках приняли участие пять школьников.
Подле гонок пять болельщиков заявили:
I. Сережа занял второе место, а Коля — третье.
II. Надя заняла третье место, а Толя — пятое.
III. Толя занял первое место, а Надя>—второе.
IV. Сережа занял второе место, а Ваня — четвертое.
V. Коля занял первое место, а Ваня — четвертое.
Зная, что одно из показаний каждого «болельщика»
верное, а другое — неверное, найти правильное
распределение мест (").
5. Шестнадцать студентов возвращались после
зимних каникул в Ленинград. Оказалось так, что среди них
было четыре киевлянина: А., Б., В. и Г., четыре
москвича: Д., Е., Ж. и 3., четыре саратовца: И., К., Л. и
М. и четыре ферганца: Н., О., П. и Р.
Оказалось еще, что А., Д., И. и Н. недавно
исполнилось 20 лет, Б., Е., К. и О. — 21 год; В., Ж., Л. и
П. —22 года и Г., 3., М. и Р. —23 года.
Среди них было четыре математика, четыре химика,
четыре геолога и четыре биолога, причем любые четверо
студентов одной специальности были из разных городов
и разного возраста.
Четверо студентов учились на первом, четверо на
втором, четверо на третьем, и четверо на четвертом
курсе, причем .любые «однокурсники» были из разных
городов, разного возраста и разных специальностей.
Наконец, четверо оказались ярыми футболистами,
четверо — боксерами, четверо — волейболистами и
четверо — шахматистами, и каждые четыре любителя одного
и того же вида спорта были из разных городов, разного
возраста, разных специальностей и учились на разных
курсах.
Установить для каждого студента факультет, курс и
любимый вид спорта, если известно, что И. —
волейболист, Е. — футболист, В. — биолог, Г. — математик
первого курса, шахматист, Ж. — химик второго курса,
шахматист и К. — геолог третьего курса, шахматист.
Для большей наглядности удобно составить
таблицу (см. стр. 200).
В клетках этой таблицы надо проставить для каждого
студента: факультет, курс, любимый вид спорта.
В таблице указаны сведения, известные из условия
задачи; остается заполнить (") пустые места таблицы.
7*
199

vJ3o3paCTl
\. 1 20 лет
Город^\)
Киев
Москва
Саратов
Фергана
А.-,-,-.
д.-,-,-.
И.—,—, вол.
н.-,-,-.
21 год
Б.-,-,-.
Е.—,—, футб.
К.геол.,Ш,шахм.
о.-,-,-.
22 года
В. биол.,—,—.
Ж.хим.,Н,шахм.
Л.-,-,-.
п.-,-,-.
23 года
Г.мат.,1,шахм.
з.-,--.
М.-,-,-.
Р.-,-,-.
К логическим задачам можно отнести также задачи
на восстановление стертых цифр и на расшифровку
записей арифметических операций, в которых цифры
заменены буквами.
Решение, их содействует развитию логического
мышления, а составление новых задач такого же типа может
служить темой для «творческого развлечения».
R приведенных ниже четырех примерах можно,
учитывая все обстоятельства, восстановить стертые цифры
и расшифровать значения букв (единственным образом
в каждом из этих примеров) (").
I. Восстановить стертые цифры в записи следующих
операций:
a) "}/******=:*** б) ****** [***
— * **** *8*
***
**
4***
****
***
***
****
****
0 0
И. Найти значения букв в приведенных записях
сложения многозначных чисел:
а) , смех
' гром.
греми.
б) forty
-f- ten
ten
sixty
(одинаковые буквы на протяжении одного примера должны
заменяться одной и той же цифрой, а разные буквы —
разными цифрами).
К задачам этого типа примыкают так называемые
арифметические ребусы, в которых, взяв в качестве
200

«ключа» какое-нибудь слово, состоящее из десяти
разных букв, и заменив мысленно в нем буквы по порядку
цифрами 1, 2-, 3, 4, 5, 6, 7, 8, 9, 0, выписывают в
зашифрованном виде операцию деления двух
многозначных чисел друг на друга. Загадывать ребус лучше всего
группе из нескольких человек, постепенно выписывая (о
промежутками в 2—3 минуты) очередные цифры
частного, произведения этих цифр на делитель и
соответствующие остатки, пока кто-нибудь из решающих не
найдет «ключ» к ребусу.
Пусть в качестве «ключа» взято слово «трудолюбие»
и зашифрована операция деления 240176 на 119.
Выполнив для удобства деление «в цифрах», «ведущий»
записывает операцию в зашифрованном виде:
рдетю л\тти
,руб рет
(1)\_ртю (ТН2)
( тти
щтдл
Сначала надо выписать буквы, отмеченные знаком (1);
при этом решающие уже могут заметить, что тр-тти=
=руб следует: р-т^р и, следовательно /и=1; можно
предугадать также, что следующая буква в частном
будет иметь значение нуль.
После того как будут выписаны буквы, отмеченные
знаком (2), решающие могут заметить, что р = 2 (ртю—
— тти— двузначное число, следовательно р — т=\) и
б=Ь (так как е = 0 и руб-\-р=рде).
Если кто-нибудь, занеся эти буквы в схему искомого
«ключа», догадается, что «ключом» является слово
«трудолюбие», то следующая порция выписанных букв
может, вообще говоря, подтвердить или опровергнуть
его догадку (в данном случае — подтвердить).
Сложность задач такого типа сильно возрастает,
если цифры зашифровывать десятью разными буквами,
не образующими никакого «слова-ключа».
Приведем еще три задачи, в решении которых
преобладает логический элемент. Последняя из них может
служить также интересной иллюстрацией к теории
неопределенных уравнений первой степени.
7* А. П. Доморяд
201

Затрудненные переправы
Три купца А, В, С к их слуги а, Ь, с должны на
двухместной лодке переправиться череэ реку так, чтобы
ни одни из слуг не оставался без своего хозяина в
компании, где присутствует хотя бы один из остальных
купцов.
Одно из возможных решений дается схемой:
переправляются: ) ab be АВ ВС аЬ ас
возвращаются: | b с Bb а а
Если взять п купцов со слугами, то длял = 4и л = 5
задача делается неразрешимой при двухместной лодке,
но имеет решение, если воспользоваться трехместной
лодкой.
Предлагаем читателю показать, как осуществить
переправу: а) при л = 2 (двухместная лодка), сделав три
«прямых» рейса; б) при л=4 (трехместная лодка),
сделав пять «прямых» рейсов; в) при л=5 (трехместная
лодка), сделав шесть «прямых» рейсов (*").
При л=6 и трехместная лодка оказывается
непригодной, но очевидно, при любом значении л можно
обойтись четырехместной лодкой.
Если ввести в условие задачи остров, на который
переправляющиеся через реку могут временно
высаживаться, то при двухместной лодке задача может быть
решена для любых значений л.
Выявление фальшивой монеты
Большую популярность в последние годы приобрели
задачи иа выявление фальшивой монеты, которая
отличается от нормальных монет только своим весом.
В простейшем варианте требуется с помощью k
взвешиваний на равноплечих весах (без гирь) выявить
единственную (более легкую) фальшивую монету из кучи,
содержащей всего л=3* монет.
Здесь достаточно, разбив монеты на три группы по
3*~л монет в каждой, положить любые две группы на
чашки весов, что сразу выявит группу из 3*~1 монет,
содержащую фальшивую монету.
202

Поступая с этой, группой таким же образом, выявим
группу из 3*~* монет, содержащую фальшивую монету
и т. д. Значительно труднее задачи, в условии которых
не указывается, легче или тяжелее фальшивая монета.
Ниже приводится одно из возможных решений задачи:
Среди двенадцати монет есть одна фальшивая. С
помощью трех взвешиваний выявить эту монету и
определить— легче ли она нормальных монет или тяжелее
(см. также [29], ч. I, задача 6).
Если класть при каждом нзирти нянин по четыре монеты
на чашки весов так, как показана во втором и третьем
столбцах помещенной на стр. 204
таблицы (указаны лишь номера,
приписываемые каждой из
монет), то легко убедиться
(проверьте!), что при двадцати четырех
возможных предположениях:
фальшивая монета легкая и ее
номер: I, 2, 3, 4, 5, 6, 7, 8, 9,
10, И, 12 Рис. 123.
и фальшивая монета тяжелая
и ее номер: I, 2, 3, 4, 5, 6, 7, 8, 9, 10, И, 12
(см. нижние строчки таблицы), мы получили бы 24 р а з-
личных варианта результатов взвешивания, указанных
в пронумерованных столбцах таблицы.
Установив при взвешиваниях, какой из этих
вариантов имеет место, мы в нижних двух строчках таблицы
найдем ответ на поставленные в задаче вопросы.
Задачи о монетах в настоящее время обобщаются в
различных направлениях (см., например, [29], ч. I,
задача 5) и представляют пример математического
развлечения, ожидающего построения полной теории.
Для разнообразия можно было бы допустить
использование «m-чашечных» весов (рис. 123, где т = 3),
позволяющих за одно «взвешивание» установить (по
положению узловой точки А), какая из т групп монет легче
(или тяжелее) остальных.
Задачи на разделение жидкостей
Рассмотрим сначала задачу, встречающуюся (в
несколько ином оформлении)- у Шюке (1484 г.) и у Тар-
тальи (1 586 г.).
7** 203

№

взвешивания
1.
2.
3.
№ фалы
нож
монеты
слева
1, 2, 3, 4
1, 2, 3, 5
1, 6, 9, 12
айвой f ле
;гы: \ тя
справа
5, 6, 7, 8
4, 9, 10, 11
2, 5, 7, 10
гкой:
желой:
Возможные результаты взвешивания
— 1
го столбцам
(Обозначения: л — слева легче, т — слева тяжелее
р — слева и справа одинаковый вес)
1
л
л
л
1
2
л
л
т
2
3
л
л
р
3
4
л
т
Р
4
5
т
л
т
5
6
т
Р
л
6
7
т
Р
т
7
8
т
Р
Р
8
9 10
Р
т
л
9
Р
т
т
10
11
Р
т
р
II
12
'Р
Р
л
12
13
т
т
т
1
14
т
т
л
2
15
т
т
р
3
16
т
л
р
4
17
л
т
л
5
18
л
Р
т
6
19
л
Р
л
7
20
л
Р
Р
8
21
Р
л
т
9
22
Р
л
л
10
23
Р
л
Р
11
24
Р
Р
т
12

Из полного сосуда емкостью в 8 литров надо отлить
4 литра вина, пользуясь двумя пустыми сосудами
емкостью в пять и в три литра.
Допустим, что мы отольем сначала в средний сосуд
5 литров. Если дальше избегать явно лишних,
удлиняющих решение действий, то легко прийти к решению,
характеризуемому схемой:
8, 0, 0-^3, 5, 0-^3, 2, 3-^6, 2, 0^6, 0, 2^
— 1, 5, 2^1, 4, 3^4, 4, 0.
Из этой схемы видно, что из большого сосуда
жидкость каждый раз отливают в пустой средний
с о с у,д (наполняя его), а затем возвращают назад
порциями, равными емкости малого сосуда.
В другом способе решения задачи малый и средний
сосуды меняются ролями: жидкость из большого сосуда
отливают в пустой малый сосуд (наполняя его)
и возвращают обратно порциями, равными
емкости среднего сосуда:
8, 0, 0—*5, 0, 3-^5, 3, 0 — 2, 3, 3—*2, 5, 1-—
— 7, 0, 1—7, 1, 0 — 4, 1, 3—4, 4, 0.
Если в общем случае обозначить через а, Ь, с(а —
четное число, а^>Ь~^>с и, конечно, b-\-c~Sz-x\ емкости
трех сосудов, то при взаимно простых Ь и с и при
a~szb-\-c—1 оба способа ведут к цели, что следует
из разрешимости в целых положительных числах
уравнений:
а — Ьх-\-су — ^ и а — ca-\-bv=^-,
отвечающих соответственно первому и второму способам
(см..§ 4).
Но уже при а = Ь-\-с — 2 один из способов может
оказаться непригодным (например, если в первом
способе создается положение (Ь — 1, 0, с — 1), то нельзя
будет из большого сосуда наполнить средний сосуд
и нельзя в большой сосуд влить из малого с литров
вина), но тогда обязательно (см. [25], глава 3) другой
способ приведет к цели. Например, при а=20, й=13
205

и с=9 десять литров вина отделить можно только
вторым способом (").
При а<Ь-\-с — 2 задача может оказаться
неразрешимой, в чем читатель убедится, взяв, например,
а=16, 6 = 12 и с = 7 (")•
§ 37. ВСЯКАЯ ВСЯЧИНА
В настоящем параграфе собраны вопросы из разных
разделов математики; некоторые из них доступны
широкому кругу читателей, другие рассчитаны на лиц,
имеющих математическую подготовку. В ряде случаев
потребуются карандаш, бумага и ... настойчивость.
Отдельные задачи могут подсказать читателю темы для
самостоятельных исследований.
Геометрический вывод формулы
1'4-2' + 3, + --- + (я_1),+я,= п{п+1)(2п + 1)
I
Пусть в п слоях находится (считая снизу вверх) л1,
я—1)*, ..., 3", 2*, I1 кубиков с единичным ребром
на рис. 124 л=5).
Описав около всей стопки кубиков пирамиду OADBC,
у которой ОА=ОВ=ОС= п-f-1 (ее объем равен
з )' П0ЛУЧИМ» что сумма объемов всех кубиков
равна
1, + 2, + 3, + ... + (л— 1),+",=
=j«±i)L_rn + (n_t) + . .> + 3 + 2+1]-
— (л+1)-з з 2 Г" б '
здесь выражение в квадратных скобках равно сумме
объемов призм AFHEPQ /объем= -£-); KPQBML
(объем=^- J и аналогичных призм во всех остальных
206

слоях? (п-{-\).-—сумма объемов маленьких пирамид
(EPKDQ и т. п.).
Рис 124.
Попробуйте аналогичным путем доказать, что:
Г+3' + 5' + 7' + ... + (2л—3)'+(2л—l)» = 2i*!jzJ>(").
Упражнения на развитие «геометрического зрения»
Ниже приводится несколько задач, каждая из
которых пригодна для соревнования под девизом «кто
больше?».
Для решения подобного рода задач нужна
систематичность при учете обнаруживаемых на рисунке фигур
заданного вида; в задаче № 4 необходимо тщательно
продумать, в каком порядке следует перебирать фигуры
указанного вида, чтобы ни одна из них не была
пропущена.
Читатель без труда сможет придумать ряд
аналогичных задач.
207

1. Сколько треугольников, квадратов и.
прямоугольников можно увидеть на рис. 125, а? (•*)
2. Определить число треугольников на рис. 125, <Г(").
3. Сколько треугольников, правильных
шестиугольников и ромбов имеется на рис. 125, в? (*')
4. Сколько квадратов и сколько прямоугольников
можно увидеть на обыкновенной шахматной додже? на
«л*-доске»? на «т, я-доске»?
Рис. 125.
Сколько кубов и сколько прямоугольных
параллелепипедов можно увидеть в кубе с ребром в 10
сантиметров, который разбит плоскостями, параллельными
граням куба, на кубики с ребром в один сантиметр? (**)
5. Сколькими способами можно прочитать слово
«шалаш», двигаясь по прямым, кривым и ломаным
дорожкам (рис. 125, г), если начальная и конечная буква «ш»
не должны совпадать? (")
208

Упомянем еше об игре, которую можно провести
с произвольным многоугольником, ограниченным очень
сложной невыпуклой ломаной (см., например, рис 125, д):
намечая на чертеже ту или иную точку, следует по
возможности быстро определить, где (внутри или вне
многоугольника) лежит данная точка.
Интересные тождества
1. Легко проверить, что (3s,n — 2s" — l)»-j-(4s*" +
-f-4s"),E=(5s,''-f-2s',-f-l)^ Следовательно, по формулам:
a„ = 3stn — 2s"— 1; b„ = 4s,n + 4s"; c„ = 5s*" + 2s" + 1
(где s и n — натуральные числа и s> 1) можно получить
сколько угодно пифагоровых троек чисел (см, § 5).
Углы прямоугольного треугольника со сторонами
а„, Ь„, с„ при достаточно больших значениях п как угодно
мало отличаются от углов треугольника со сторонами
3, 4, -5, так дсак
3__2 1
Попробуйте найти аналогичное тождество,
приводящее к прямоугольным треугольникам с целочисленными
сторонами, «почти подобным» треугольнику со
сторонами 5, 12, 13.
2. Поищите тождества, в которых произведение двух
«громоздких» многочленов равнялось бы многочлену
с небольшим числом членов; например: (jc8—4jc,-J-8jc' —
— lOx' + ax* — 4хг + 2х1 — х-\-±) (.*' _|_ 4л1+ 8*' +
+ Юл' + Ъх1 + 4л* + 2.x' + х + 4"W -х" + Ц лЧ-i-.
3. Тождество а, + (a_ft).=а ^(я 1 Ь)(проверьте1) мож-
но использовать, для «незаконных сокращений»,
приводящих к правильным результатам, например,
37' +13* _ 37 + 13 _ 50
37,+24,—37 + 24~~ 61
И т. п.
209

lie удастся ли вам найти аналогичные тождества, где
бы а числителе к знаменателе «сокращались» показатели
степени у четвертых степеней?
4. Тождество - Л + П"+' = 7'^ГТ "* ~~ П°~
ложительное рациональное число) показывает, что
иногда незаконное «сокращение на знак lg»: -рг —-г- —
может привести к правильному результату. Например:
, 9 9
lgT X
27" =27" (здесь Л* = 2).
lg? ТГ
5. К ряду курьезных равенств приводит тождество
У а+ апа_1 =ау а„а_1 ; например: у2-~=
=>Vh t^S=s УЪ УЦ-* KS"-
6. Незаконно «сокращая на знак sin» сначала
числитель и знаменатель дроби, стоящей в правой части
тождества:
. (n-i-l)a . па
Sin —^ ' -Sin-g
sin а -\- sin 2а -{-•.•+ sin яа = (*'),
sin J
а затем обе части полученного при этом равенства,
придем к тождеству
л + 1 л
2 а'-оа-
a -f- 2а -f-. • • + tia = .
Проверьте это тождество
7. Докажите (,0°), что [3(10*+10*~1+ ...-}-10*-f
_l_ ю+1) л+11* ^ /г» (10"*^1 +10»* + . . .+Ю*+1) +
+ (6я — /г,)(10*-т-Ю*-1-т-... + 10 + 1) + 1.
Это тождество приводит к двум сериям интересных
числовых! равенств: при п— 1 и k=-1, 2, 3, 4,... имеем:
34'=1156; 334, = 11Г556; З334' = 11 115556; 33334* =
= 1111155556 и т. п.; при л=2 и к — \, 2, 3, 4,...
210

имеем: 67* = 4489; 667*=444 889; 6667*=44 448 889;
66 667*=4 444 488 889 и т. п.
Не удастся ли вам найти тождества, приводящие
к аналогичным сериям числовых равенств в других
системах счисления?
Обманы зрения
Попробуйте, соединив перед собой на расстоянии
в 35—50 см концы указательных пальцев так, чтобы
они составляли продолжение один другого, посмотреть
«сквозь пальцы» на удаленную стенку. Вам будет
казаться, что между пальцами зажата маленькая
«сарделька», которая при небольшом раздвигании пальцев
«повиснет» в воздухе.
Рис 126.
Длина «сардельки» будет тем больше, чем дальше
будет находиться рассматриваемый «сквозь пальцы»
предмет. Число «сарделек» можно увеличить, соединяя
попарно несколько пальцев обеих рук.
Объясняется это забавное явление очень просто:
правым глазом мы не увидим часть стены, ограниченную
линиями ABC и KLM (рис. 126, л, б), а левым—часть
стены, ограниченную линиями АВ'С и KL'M. В итоге,
совсем невидимая нами часть стены будет иметь вид
фигуры, заштрихованной на рис. 126, а, б.
211

По той же причине узкая вертикальная щель, выра-»
занная в грани KLMN коробки с примерными
размерами 10X15X30 см* (см. рис. 126, в), будет воспринята
нами как две параллельные щели (или как широкая
шель с вертикальной перемычкой), если мы будем
смотреть сквозь щель двумя глазами на стену со стороны
«отсутствующей грани» ABCD.
Если щель в грани KLMN заменить четырьмя
точечными отверстиями, лежащими в вершинах некоторого
квадрата, а на месте грани ABCD поместить кассету
с фотопластинкой, то, фотографируя с помощью такой
«камеры-обскуры» светлый круг, расположенный на
черном фоне, мы получили бы (при соответствующих
размерах круга) «розетку» (см. рис. 126, г), у которой
интенсивность светлых тонов убывала бы с возрастанием
номера области.
Такая фотография может дать представление о том,
что видело бы четырехглазое существо, смотрящее
сквозь круглое отверстие в грани NKLM на равномерно
освещенную стену (со стороны «отсутствующей грани»
ABCD), если бы зрительные ощущения от каждого глаза в
отдельности «налегали» бы в его сознании друг на друга.
Для разнообразия можно пальцы заменить двумя
полосками картона / и // (соприкасающимися или слегка
раздвинутыми) с тем или иным профилем (рис. 126, д);
вместо' вертикальной щели с параллельными краями
(рис. 126, в) можно брать фигурные щели. Фотографируя
различные объекты и по-разному выбирая точечные
отверстия в камере-обскуре, любители фотографии
могут попытаться получить своеобразные «геометрические
фотографин».
В заключение упомянем об одной любопытной
оптической иллюзии: если смотреть правым глазом через
трубку на какой-нибудь предмет, а ладонью левой руки,
касающейся трубки, заслонить предмет от левого глаза,
то у нас создастся, впечатление, что предмет внден и
левым глазом сквозь «дырку в ладони» (рис. 126, е).
Разные задачи
Приведем сначала несколько простых задач и
вопросов:
1. В одном стакане находилось т см' воды, а в
другом-— п см* спирта. Сначала из первого стакана пере-
212

лили во второй а см* воды, а затем (после тщательного
перемешивания) обратно а см* смеси.
Считая для простоты, что объем смеси равен сумме
объемов смешиваемых жидкостей, определить, чего будет
больше примешано (по объему), спирта в первом
стакане или воды — во втором? (1в1)
2. У Петрова спросили: «Кто изображен на портрете,
висящем на стене?» Петров ответил: «Отец висящего
есть единственный сын отца говорящего». Чей это был
портрет? ('")
3. Сколько всего прапрадедушек и прапрабабушек было
у всех Ваших прапрабабушек и прапрадедушек? ("")
4. Каким покажется угол в 15', если на него
посмотреть через лупу с четырехкратным увеличением? (,0*)
5. На сколько процентов возрастает покупательная
способность населения, когда цены на все товары
снижаются на 20°/о? (,05)
6. Если в первый раз покупательная снособность
населения возросла на 20°/о, а во второй—на 25%, то на
сколько процентов в целом возросла покупательная
способность населения? (1иа)
7. Сколько раз в сутки часовая и минутная стрелки
образуют прямой угол? ("")
8. Когда Коля был молод, как Оля,
Столько лет было тетушке Поле,
Сколько Коле теперь вместе с Олей.
Сколько лет было Коле,
Когда тетушка Поля
Была в возрасте Коли? ('")
9. Летчик вылетел из пункта А и, пролетев на юг
800 км (до пункта В), полетел на восток. Пролетев еще
800 км (до пункта С), он заметил внизу медведя.
Какого цвета был медведь, если известно, что AR=AC? (,ов)
10. А и В продали гурт волов, получив при этом
за каждого вола столько рублей, сколько было волов
в гурте. Желая поделить вырученные деньги поровну,
они брали поочередно по 10 рублей из вырученной
суммы. А получил лишних 10 рублей и в возмещение
присоединил к остатку свой кошелек. Сколько стоил
кошелек? ("")
П. Трое зашли со своими женами в магазин. Каждый
из шести купил по несколько предметов, платя за каждый
из них столько рублей, сколько предметов он купил.
213

Каждый4 муж: потратил! на 45 рублей больше, Чем
его жена; Юрий потратил больше Ольги на 525 рублей^
Логин — больше Нины на 13 рублей. Имена остальных—'-
Александр- и. Татьяна.
Кто на ком женат и сколько- предметов куплена
каждым? ("•)
12. Некто разделил между детьми имевшуюся у него
сумму денег, дав первому из них один рубль, и. -^ часть
остатка, второму — два рубля и -^ часть нового, остатка,
третьему — три рубля и -g- часть нового остатка и т,. д.
Знаяг что' все деньги f$ руб.) оказались-
распределенным» поровну между всеми детьми*, определить S
и числа детей.
Замечательно, что, приравнивая друг другу доли-
каждого из детей, мы получим систему со-вместн*ых
уравнений с неизвестным S, дающую 5=25.
Аналогичным свойством обладает (,1Х) квадрат любого1
натурального числа: выделяя из п* сначала, единицу и , , часть
1
остатка, затем — два и . часть нового остатка и т. д.,
получим ряд одинаковых результатов.
Не удастся ли читателю найти какой-нибудь другой
класс чисел, специфические свойства которого могли
бы послужить источником для серии занимательных задач?
13. Из М в N вышел Павел) и одновременно- с ним
выехал на мотоцикле Глеб (с водителем Юрием).
Проехав часть пути, Глеб пошел дальше пешком, а Юрий
поехал навстречу Павлу и^ забрав его, прибыл в пункт N
одновременно с Глебом.
Зная, что MN=s км, скорость пешехода равна
и км/нас и скорость мотоцикла v км/час, найти время,
затраченное тремя товарищами на путь из М в N (lu).
Эту задачу можно обобщить, считая, например, что
мотоциклист (или два мотоциклиста, перемещающиеся
со скоростями vt км/час и vt км}час) должен помочь
группе из п товарищей добраться одновременно до места
назначения; можно считать также, что один из
помогающих пешеходам мотоциклист может брать сразу двух
пассажиров и т. д,
214

Попробуйте провести исследование различных
вариантов задачи, составляя каждый раз расписание движения
всей группы.
14. Некоторая работа была начата в пятом часу,
а кончена в врсьмом часу, лричем показания часов в
начале и в конце работы переводятся друг в друга, если
поменять местами часовую и минутную стрелки.
Определить продолжительность работы и показать,
что в начале и в конце работы стрелки были одинаково
отклонены от вертикального направления ("').
15. Сколько раз в- сутки показания часов обладают
тем свойством, что, меняя местами минутную и
часовую стрелки, мы придем
к имеющему смысл
показанию часов? ("*)
16. Доказать, что для
каждого натурального к
общее число цифр в
последовательности чисел:
1, 2, 3 10*—1, 10*
равно числу нулей в по- ь»
следовательности чисел:
1, 2, 3,- .... 10*+I —1, Рис 127.
10*+I (ш).
17. Доказать, что плоскую фигуру S произвольной
формы, площадь которой меньше одного квадратного
сантиметра, можно уложить иа клетчатую бумагу с
клетками в 1 см* так, чтобы она не «покрывала ни одной
узловой точки ("•).
18. Можно ли провести прямую, которая пересекала
бы данные прямые: 1Л, /,, lt, /4, случайным образом
расположенные в пространстве? ("')
19. Между прямой / и окружностью С9, касающейся
прямой /, вставлен ряд окружностей: С,, С,, Ct,... (см.
рис. 127) так, что С^, касается окружностей Ck я С,
и прямой /.
Найти радиус окружности £10<Ц), если радиус
окружности С„ равен одному километру, а радиус
.окружности Сх—одному миллиметру (JJ*).
20. Доказать, что луч света, отразившись
последовательно .от трех взаимно перпендикулярных зеркал,
«превратится», в луч, параллельный «лучу падающему», но
направленный в противоположную сторону (,и).
215

21. Как следует направить луч света в
прямоугольном параллелепипеде с зеркальными гранями, чтобы,
отразившись от всех шести граней, он вернулся в
исходную точку? (,м)
22. Летчик, пролетев 2000 км на юг, 2000 км на
восток и 2000 км на север, оказался в исходном пункте.
Откуда он вылетел? (Задача имеет много решений.) (т)
23. Самолет вылетел из Ленинграда и, пролетев а км
на север, а км на восток и а км на юг, оказался на
расстоянии За км восточнее Ленинграда. Найти а ("*).
24. Какую площадь имел бы начерченный на Земле
равносторонний треугольник, если каждый угол его был бы
равен 72°? Здесь речь идет о так называемом
сферическом треугольнике, образованном дугами больших
кругов, проходящих через вершины треугольника ("*).
25. Определить углы равностороннего сферического
треугольника со стороной в 1 километр, начерченного
на идеально гладкой поверхности льда озера ("*).
Головоломки
1. Показать, что от «заплетения» а) на рис. 128
можно перейти, не разрывая веревочных колец, к за-
плетению б) (аналогичные задачи см. в [12]).
2. Как надо сцепить три веревочных кольца, чтобы,
разрезав любое из них, можно было бы два других
кольца разъединить без дополнительных разрывов?
Аналогичный вопрос решить для п веревочных
колец ("■).
3. Если чуть вольно толковать слово «внутри», то
можн о решить следующую шуточную задачу: найти три
совершенно одинаковых тела: А, В, С, которые можно
расположить так, чтобы А было внутри В, В — внутри С
и С— внутри А.
Условиям задачи удовлетворяют три слегка вцтяну-
тые рамки, «вложенные одна в другую» — см. рис. 128, в.
Аналогичную задачу можно решить и в случае п
одинаковых тел. Пусть п змей (их можно представить
себе в виде узких и тонкостенных «конических»
мешочков) расположатся по кругу радиуса R и каждая из них
начнет заглатывать змею, перед ней находящуюся — с
одинаковой «скоростью заглатывания» для всех змей (см.
рис. 129, а, где л = 2).
216

'Л
a) S)
^L_,
Ш
Уа
Лв
V/
ej
,д шт. w/ш
В
(* 7
Рис. 128.
<J
ej
Рис. 129.
217

Когда каждая змея вберет в себя половину своей
жертвы, получится двухслойное кольцо радиуса — (рис.
129, б); когда каждая из змей окажется на 99°/0 внутри
заглатывающей ее змеи, кольцо радиуса -щг будет
состоять из ста слоев и т. д.
4. Завязав сначала бечевку в виде узла г) (рис. 128)
и перейдя от него к узлу д), легко убедиться, потянув
за концы А и В, что в последнем случае на бечевке
никакого узла не осталось.
Следовательно, при закрепленных концах Л и Л
бечевку (е) можно сложить в виде «узла» д).
Попробуйте это сделать!
§ 38. ПРИМЕЧАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
(') Пусть 0, (a-iat...as_1as)m=a.; обозначим число,
стоящее в периоде этой дроби, через N: alat...as_las =Л/.
' (М
тогда «=5+5и-...+!и+9 + &1 + рь+...
I Д*-1 | а* | _g1ft*~1 + g,ft*~,+ ...+g, ,
• • • ~Г ^w-iT^mT • • • — /р Г
. g1y-' + a,y-'+...+g< i ' _£i*i# i _
"1 ps Г • • •'— А* Т Л" Т А«* "Г * • • —
N N .
(в знаменателе s-знач-
& — 1 А —1Л —1...Л —1Л—1Ш
ное число, записанное s цифрами «& — 1»).
(*) Пусть в &-ичной системе извлекается корень
квадратный из четырехзначного числа N=-abcdik) (а, Ъ, с,
а — цифры числа Л/, записанного в й-ичной системе;
ниже значок «&» внизу мы будем опускать). Если
первая цифра а искомого корня найдена, т. е. a* ^.ab =
=a*-f *<(«-ИЛ то
Yabcd = a...
a'b'cd
Очевидно, N=abcd = atkt-\-a'b'cd.
Теперь надо найти наибольшую цифру р, для которой
(aA + p)' = «,A«-j-2aAp-]-p,<N, или (2<х£-|-р)р<Л/—
21В

— ci*k*j=^a'b'cd, т. e» ищется наибольшая цифра %
которая, будучи приписана справа к числу 2а, даст число
(равное 2а& + (3), произведение которого на р не
превысит остатка a'b'cd. Но именно таким правилом мы
руководствуемся и при извлечении квадратного корня в
десятичной системе счисления.
При извлечении корня из- чисел, разбиваемых на три
грани, обозначим через а двузначное число, получающееся
указанным путем при извлечения корня из старших двух
граней-, а через |3—некому» цифру единиц; все
приведенные выше рассуждения останутся в силе. Для чисел,
разбиваемых на четыре грани, сначала ищется корень из
трех старших граней, а затем указанным путем — цифра
единиц искомого корня и т. д.
(й) 2713=41323,,, =41332^=41455(„= И2Щ„.
Проверка: 1Т2ШЫ=51—5*-{-2.&' — 51—2-5—2=
=2713; 409=3114^=12121^.
(ЙУ Пусть Л/=а&с(8>=а-8*-|-£-8-|-е, где каждая из
цифр; а, Ь, с не превышает семи.
Если a = aIa,a,(i)> Ь = Ш,Ы> c=LTf,Y,(l). где каждая
из цифр: а,, a..-а,, р„ р„ р„ у„ у„ 1, равна либо нулю,
либо единице, то
^=(al.2' + a,.2-+a,>.24-(P1.2«-r-p,.2+§,).24-
+ Р.-24 + Р.-2* + Т,-2' +^2 + 1.=ЗД.Ш.Т.Ы*, •
Читая эти равенства справа налево, получим правило
перехода от двоичной системы счисления к
восьмеричной: трехзначные числа, получающиеся при разбиении
на грани (справа налево) числа» записанного в двоичной
системе, дают цифры того же числа, записанного в
восьмеричной системе счисления.
(*) При любом А>5 123454321(JW = 11111V
(*) Так как Л/< 1000 < 1024=2", то для записи
числа Л/ в двоичной системе счисления потребуется не
больше десяти цифр, каждая из которых может быть
либо нулем, либо единицей.
Для определения N достаточно задать десять вопросов.
219

1, Будет ли единицей первая справа цифра числа N,
записанного в двоичной системе счисления? 2. Будет ли
единицей вторая цифра? и т. д.
(•) Легко проверить, что теорема верна при s = 1 и
при s = 2. Применим для доказательства теоремы в
общем случае метод математической индукции:
предположив, что теорема верна при s = n (т. е. для чисел от 1
до 2 —■ 1 мы имеем п карточек, каждая из которых
содержит 2""1 чисел), докажем, что она будет верна и при
S = /l-f-l.
Любое число т, удовлетворяющее условиям: 2"sS
«^m«^2n+1—1, можно представить в виде: т = 2"-\-х,
где 0^лг^2"—1. Все эти 2" чисел попадут в п-\-1-ю
карточку с заголовком 2"; в те или иные из
предшествующих карточек любое из чисел т попадет лишь при
1^лг^2"—1 (в зависимости от слагаемых вида 2", на
которые распадается число х); следовательно, в каждой
из предшествующих карточек появится 2""1 новых чисел
(мы ведь предположили, что теорема верна при s = n).
В итоге каждые из п -J-1 карточек будут содержать по
2" чисел.
(7) Как известно,
л! = 12-3.45 . (и —2)-(й—1)й- (1).
Если перебирать по порядку эти множители, то через
каждые р1 «шагов» будут встречаться множители, кратные
простому числу pj число их равно — , но из них —\
множителей делятся на р\, \—\ —делятся на р\ и т. д.
Следовательно, число множителей в равенстве (1),
в состав которых множитель р1 входит ровно один, два,
три и т. д. раза, соответственно равно числам: — —
220

П Afe=-2-4,ei — 2"80: здесь вычитаемое во много
миллионов раз меньше уменьшаемого. Так как lg2*m=
= 4561-0,301029996 = 1372,997, то 2"" (а
следовательно, и N) содержит 1373 цифры.
П5(Л0 = (1+2 + 2'+...+2'){1+(2*+'-1)} =
=^-2^Г' 2*+, = 2.2в(2'+1 — l) = 2N.
И Щ + [Щ + [Ш] =142 + 20 + 2=164.
— + -уг| = 14 + 2=16; так как числитель равен
(1000!):(100!), то k = 164 —16=148.
(") Если два s-значных числа N, написанных рядом
друг с другом, дают 25-значное число, представляющее
точный квадрат, то это значит, что
1) \0s-i^N<l0s и
2) (lO' + lJ-N—точный квадрат.
Но тогда 10* + 1 должно делиться на квадрат
некоторого целого числа (иначе наименьшее значение N,
удовлетворяющее второму условию, будет 10*+1, что
противоречит первому условию).
Для определения наименьшего значения s, при
котором 10J+ 1 делится на р1, удобно, пользуясь свойствами
сравнений (см. § 3), искать наименьший корень
сравнения: IO^ese—\{тоАрг); например, при /? = 11 имеем:
10* = — 21 (mod 121); 10' =.^-210 = 32 (mod 121);
10* =320 = 78 (mod 121); 10« =780 = 54 (mod 121);
10' =540=56 (mod 121); 10' =560= 76 (mod 121);
10" =760 = 34 (mod 121); 10* = 340=—23 (mod 121);
1010 = — 230= 12(mod 121); 10" = 120 = — 1 (mod 121).
[до11 -1-1 1
—jji— k1 —точный квадрат, если
k — любое натуральное число. Легко проверить,что 4 —
наименьшее значение k, обращающее выражение, стоящее
в квадратных скобках, в одиннадцатизначное число,
равное 13 223140496.
Непосредственной проверкой можно убедиться, что
сравнение вида 10*=. 1 (mod k*), где h—любое простое
221

число, не удовлетворяется при 5<11; следовательно,
1 322 314049613 223 140 496= Г°"^1-4]'=363636 364*~
наименьший точный квадрат, записываемый в десятичной
системе счисления двумя одинаковыми, рядом друг с
другом написанными числами.
(") Если a = p(modm), то а* = р* (mod т), а
следовательно, и aji'zsa$(та&т). Кроме того, очевидно, что
ae = a0 (mod/и).
Складывая почленно последнее сравнение со
сравнениями a,a*sa,p*(modт) (ПРИ s=l, 2, ..., л), получим:
(mod т) или /(а) =/(р) (mod т).
(") Так как 8*=—1 (mod5) то, рассуждая также, как
и при выводе признака делимости на семь в десятичной
системе, получим, что число N, записанное в
восьмеричной системе, делится на пять, если алгебраическая
сумма двузначных граней числа N делится на пять (и
наоборот!). Для получения остальных признаков делимости
достаточно учесть, что 8* = — 1 (mod 13); 5* = —
— 1 (mod 13); 5*~ 1 (mod8); 3 = 1 (mod2);3s-l (mod4);
3*=—1 (mod 7).
(**) Достаточно найти наименьшее положительное
двузначное (или однозначное) число, с которым данное
число сравнимо по модулю 100.
Например, 293"* = (— 7)"* = — 7.49146 = — 7 X
X2401f* = 93-r* = 93(modl00).
Следовательно, 2931м — 93 делится на 100 (293"* при
делении на 100 дает в остатке 93).
(") Среди чисел: 1, 2, 3, 4, ... , / — 2, рк — 1, рк
кратными р будут: р, 1р, Зр, ..., рк~1р=рк (всего рк~1
чисел). Остальные рк—рк~1 чисел будут взаимно
просты с р.
(") Если бы <р (л) при делении на z0 давало бы в
частном q и в остатке г (0<r<lz0), т. е. <f(n) = qzt-±-r,
то из Jfc'^ssl (mod л) следовало бы:
tf2o+r = (A*.)Wsl'.ft'sl (modл),
а это невозможно, так как r<zt.
222

(") Предположим, что числа /пил записаны в Л-ич-
ной системе счисления и от<[л. Если £*«==1 (modл)
(z0 — наименьшее из положительных чисел,
обладающих этим свойством), то и от&г°=/и(тос1я). Это значит,
что, приписав к числу тп справа z0 нулей (что
равносильно умножению тп на &*«) и деля полученное число
на я, мы будем иметь в остатке от, а в частном
некоторую группу цифр: c^f-.c^. Дальнейшее
приписывание к остатку z0 нулей снова даст в частном ту же
группу цифр и т. д.
(") 1) Подставив в уравнение ax-\-by—c xt -f- и вместо
х и yt-\-v вместо у, получим: axt-f-au-\-by<)-\-bv=-c.
Так как аха-\-Ьу0 = с, то au-\-bv должно быть
нулем, откуда аи —— bv, следовательно, аи должно
делиться на Ь. Но а и Ь взаимно простые числа,
следовательно, в должно делиться на&, т. е. u=bt (t может
быть любым целым числом); тогда v=—at. Итак,
удовлетворять данному уравнению будут xt-{-bt и у„—at
при любом целом t.
2) При любых целых хну ах-\-Ьу делится на (а, Ь)
и поэтому не может равняться числу с, которое по
условию не делится на (а, Ь).
(") Так как/2 = [1,2, 2, 2, 2,...] hJ/3 = [1, 1,2, I,
2, 1, 2,..,], то подходящие дроби для ]/2 будут:
J-.3 2. 17 41 99 239 577 1393 3363
1 * 2 ' 5 ' 12' 29' 70 * 169' 408' 985 ' 2378
а для" 1^3:
]_ 2 5 2 1_3 267197265362989 1351 3691
1 ' 1 ' 3 ' 4 » И ' 15 ' 41' 56 ' 153 ' 209 ' 571 ' 780 * 2131' "' *
Следовательно, |/2"^ ^= 1,4142131... и ]Лз^
~£U 1,7320512....причем 1/2-й?|<5^ и
780 *''"•••' i""4'"1 Г " 985 1^985-2378
'780
< '
780-2131
(10) Из первых трех уравнений с четырьмя
неизвестными можно выразить X, Y, Z через U и получить за-
тем: 1602=Ш=Шо=2226=*• где * ~ произвольное
число.
223

Из последних четырех уравнений можн» х, у, z, и
выразить через X, У, Z, V. Если затем взять s = 4657 t,
то получатся приведенные в тексте значения X, Y, Z, U,
х, у, Z, и.
(м) Если ABC—«геронов треугольник» (см. рис. 4),
то длины отрезков: AD, BD, DC рациональны, так как
BD = 2-^, AD=AC1 + *%-BC1 и DC=\AC-AD\.
(") Пифагоровы тройки чисел: (3, 4, 5) и (5, 12, 13
порождают героновы тройки чисел (25,39,56), (25,39,16),
(25/52, 63), (25, 52, 33), (20, 13, 21), (20,13, И), (15,13, 14),
(15, 13, 8).
Пифагоровы тройки чисел (7, 24, 25) и (7, 24, 25) по-
{юждают только три героновы тройки чисел: (25, 25, 48),
25, 25, 14), (175, 600, 527) (четвертый «геронов
треугольник», составленный из двух треугольников, подобных
данным «пифагоровым треугольникам», имеет стороны
7,24 и 25).
(") б) 55 555 555 =10 ООЬ 5555 = (7778 +2223) X
X (7778 — 2223); г) 12345678987654321 = 111111 И1»;
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4+'
+ 3 + 2+1 = 81=9*.
Г)
L//V..VVT
In радикалов
1
= -1о24{1о2442,"} = -Ю21(1) =л.
(**) Если число х, 1 < х < 60, стоит в столбцах
с номерами: a, {J, ■{ в таблицах, изображенных на рис. 4,
то
*===a(mod3), (1)
* = p(mod4), (2)
jc = Y (mod 5). (3)
Из (1) следует:
Л = 3у + а. (4)
224

Подставив это выражение в (2), получим: 3y-\-a==i
s=P(fflod.4), или 9y-|-3a=3p(mod4), откуда j/===3p —
— За==а— p(mod4), или
j, = a —р + 4г. (5)
{При умножении обеих частей сравнения на число
взаимно простое с модулем получается сравнение,
«эквивалентное» исходному — оба они имеют одинаковые корни,
попробуйте это доказать.)
Подставив (5) в (4), получим:
д; = 3(а —p)-fl2z + a = 4a —3p-fl2z. (6)
Из (6) и (3) имеем: 4а —3p+12z = Y(mod5)» или
12а — 9p-f-36z=s3Y(mod5), откуда г = 3у— 12a-f-9p =
= 3Y + 3a-f4p(mod5).
Следовательно, z = 3f-{-3a.-\-4$-{-5t, что после
подстановки в (6) даст:
* = 4а — Зр + 12(3у + 3о+4р + 50 =
= 40а + 45р + 36у + 60г, (7)
или .x===40a-f45p + 36Y(mod60).
(") Пусть из n==dx (mod 11) следует л' =di=d(mod 11),
где 0«sd, «S10 и OsgdsglO, т. е. d,— остаток от
деления л на 11, а d—-остаток от деления л* на 11.
Легко проверить, что при d,, равном: 0, 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, соответствующие значения d будут: 0, 1,
8, 5, 9, 4, 7, 2, 6, 3, 10, т. е. каждому из одиннадцати
значений d соответствует «свое», отличное от других
значение d,.
Если выписать значения d по порядку: 0, 1, 2, 3, 4,
5, 6, 7, 8, 9, 10, то соответствующие значения d, будут:
0, 1, 7, 9, 5, 3, 8, 6, 2, 4, 10.
(") Для проверки достаточно учесть, что: 1. Объем
воды, содержащейся во всех океанах, меньше чем 1,4-10"
литров (?-10" стаканов) — см. статью «Гидросфера»
200
в Б. С. Энциклопедии. 2. В стакане содержится -^ грамм-
молекул воды, следовательно, число «меченых» молекул
ft 1ft** 900 *}
приблизительно равно ——щ—, или у 10м.
-225

(**) Световой год—это расстояние L, «проходимое»
светом за год.
L=365,25 • 24 • 60 • 60 • 3 • 1010 см < 95 • 10" см < 10* см.
Если v — объем куба с ребром 7-10'Z,, а N—число
молекул воды, необходимой для наполнения такого куба,
то
«/<(95• 10м• 7• 10')* смг = (0,665-lO")1 см1 <(•§-)'• Ю"ли*
"<6-Г ■(!)"• w-S-io"-.
("а) Пусть т=4"'; lg т=256- lg 4 > 256- 0,602055 =
= 154,12608 и ях> 1,336-101". Следовательно, Q=
=4m> 41»"-"ти lgQ> 1,336-101**.0,602055 > 0.80434X
ХЮ1М>8.10|И, т. e. Q>10»-iel".
И Радиус шара R=^-L < -^-95- 10м см — см.
примечание ("). Объем шара t»<-|-u-47,5'-101"cAt*<-i X
ХЮ1Мсм\
(") log1,oooool(f"',°')==31 • Ю' logli000001 еъ 31 • 10'. 10« =
= 3,1.10"; (eS?'10V°-' = esl = 10°''"-" = 101*'" = 2,2.10";
loglt...Ml(e"ao')^ 3,2-Ю1*; (е»-10,)1»-, = е" =* 5.86.101*,
(") Пусть, например, «=10000. Из формулы
Стерлинга следует:
lg/г^Тб"4 — 10000lgе + 40000 <lg(10000!)<
<lgyr2lTT0i-100001ge + 40000 + I^6.
Так как lg е =* 0,4342945, lgit=s: 0,49715, lg2=sr 0,3Q103h
12QQQQ—очень маленькое число, то lg (10000!) =
= у(°.49715 + 0,30103 + 4) — 4342,945 + 40000=
==35 659,454, т. е. 10000! —35660-значное число.
(") Если допустим, что существуют два целых числа
k и k тзкие, что а-—^—<«<(«+!)-—^— и
226

3 —Vs 3 — 1^5
a —^— < k' < (a-j-1) —^—, то, складывая почленно
эти неравенства, получим a<C.k-\-k'<ia-\-\, что
невозможно (а и а -\-1 — соседние целые числа). _
~ У"5~-1 У5-1 . ,
Очевидно, между числами а- —*—ка^ [-1
заключено некоторое целое число s. Если s меньше, чем
уТ— 1 . уТ— 1
1 то оно лежит в первом интервале;
а 2 i 2
УТ-1 , уТ- 1 . „ . уТ-1
если же а —* 1-1—о—<s<a —;>—
f-1, то, пере-
3"1<
2 • 2
писав эти неравенства в виде (а-(-1) f 1
<s<а • (l--=P) +1. получим {а +1)^=^>а +
i 1 -^ 3 — У" 5
+ 1 — s>a—j-—, т. е. во втором интервале
заключено целое число а-\-\ — 5.
(") Составим таблицу особенных позиций (ск, dk),
пользуясь тремя правилами, приведенными в начале § 11.
5 б
10 11
12
13
15
16
17
18
19 20
21
22
23
2425._
«*
3 4
11
12
14
16 17
19
22
24
25
27 29
30 32 33 35
37 38 40 ...
<**
5 7
10
15
18
20
23
26128
34
36
41
44 47
52| 54 57 60 62
44-
Правильные ходы: (27,37)—«-(16,26); (14,90)-*(14,23);
(47,69)-^(47,29).
(") Легко проверить, что при а = 40, 55, 140
интервалы (а-0,618..., (а-{-1)-0,61Ъ...) содержат целые
числа: 25, 34, 87, а при а = 400 целое число 153
содержится в интервале (а-0,381... ,, (а-{-!)• 0,ЗЪ1...).
Следовательно, 40 = ctl (d„ = ctb -f- 25 = 65), 55 = c14 (d,t =
= c,4 + 34 = 89), 140 = ce7 (d„ = ct7 + 87 = 227), 400=»
=dw (clM = 400-153 = 247).
(") Правильные ходы: (10, 17, 25) —(8, 17,. 25);
(47, 99, 181)—*(47, 99, 76); (25, 43, 50) —позиция
особенная и все ходы ведут к проигрышу; от позиции (29, 29,18)
можно перейти к (15, 29, 18), или к (29, 29, 0), а от
(93, 29, 74) —к одной из позиций: (87, 29, 74), (93, 23, 74),
(93, 29, 64).
227

С) Рассмотрим для примера положение, при кото*
ром кольца с номерами: 12, 9, 7, 6, 2 спущены, а
остальные надеты на шпильку.
Чтобы спустить 11, надо предварительно спустить 8,
5, 4, 3, 1, после чего останется сделать l-f"ut + Bu
ходов (спустить 11, поднять 1—9, спустить 1—10).
Но чтобы спустить 8, надо пройти, как через одну
из промежуточных стадий, через положение, при
котором 1—7 подняты, а для этого надо: опустить 1, 3, 4
(7 ходов), поднять 6 (один ход), спустить о (u4-f-a,
ходов), поднять 7 (один ход), поднять 1—5 (и, ходов),
на что будет затрачено, в общей сложности, 2u6-f-u4-f-9
ходов. Добавив сюда ы, ходов (для спуска 1—8) и
упомянутые выше 1+и, + Иц ходов, всего получим
uio + at+u» + 2u«+"«+10 ходов,
(") Чтобы убедиться, что формула:
и„ = 2" — 1 верна, достаточно:
1) Показать, что она верна при л=1;2)
предположив, что формула эта верна при л = & {к —
произвольное натуральное число), доказать, что она будет верна
и при n = k-\-\.
Первое следует из того, что одну пластинку со
столбика А на столбик В перенести можно за один ход,
т. е. и, = 1=2' — 1. Допустив же, что иА = 2*—1, мы,
использовав доказанную в § 12 формулу: an = 2an_l-f-l,
получим: uft+t = 2uft-j-1=2(2* — 1)+1 = 2*+1 — 1.
(")
а) 55—57, 75—55, 54—56, 74—54, 53—55, 73—53, 43—63, 51—53,
63—43, 33—53, 41—43, 53—33, 23—43, 31—33, 43—23, 13—33,
15—13, 25—23, 34—32, 13—33, 32—34, 45—25, 37—35, 57—37,
34—36, 37—35, 25—45, 56—54, 54—34, 46—44, 44—24.
б) 53—55, 73—53, 75—73, 65—63, 52—54, 73—53, 54—52, 51—53,
31—51, 32—52, 43—63, 51—53, 63—43, 45—65, 57—55, 65—45,
35—55, 47—45, 55—35, 25—45, 37—35, 45—25, 15—35, 13—15,
23—25, 34—36, 15—35, 36—34, 33—53, 34—54, 54—52.
(") Если передвигать шашки вдоль линии,
изображенной на рис. 130, а и представляющей замкнутое
«кольцо», одна из клеток которого «пустая», то
взаимное расположение шашек на этом кольце не будет
изменяться. Нам надо разместить шашки на кольце —
223

если исходная позиция разрешима!—в таком порядке
(см. рис. 15, III):
1, 2, 3, 4, 8, 12, *, 15, 14, 13, 9, 10, И, 7, 6, 5 (1)
(считая от левой верхней клетки по ходу часовой
стрелки: * — пустая клетка). Будем говорить, что здесь № 2
следует за № 1, №3 —за№ 2, № 15 —за № 12, № 1 —
за № 5 и т. п.
Взаимное расположение шашек на кольце изменяется
лишь тогда, когда В — пустая клетка и на нее
перемешается шашка с клетки А (или наоборот);
передвигаемая шашка при этом сдвигается «по кольцу» на два
(
\
(
к
д
в
\
Л
)
)
©
©
®
©
©
i
®
©
©
@
©
@
©
©
©
®
а)
&
Рис. 130.
места «влево» (или «вправо»). Например, чтобы при
исходной перестановке
5, 7, 14, 11, 13, 15, 1, 2, 9, 8, 6, 4, 3, 10, *, 12 (2)
сдвинуть № 9 на два места «влево», надо создать
круговым перемещением шашек положение б) на рис. 130
и переместить № 9 на пустую клетку. Это даст нам:
2, *, 8, 6, 4, 3, 10, 12, 5, 7, 14, И, 13, 15, 9, 1.
Сместив затем аналогичным способом № 15 на два
места «влево», мы добьемся того, что № 9 будет
следовать за № 13, как в перестановке (1).
Затем так же можно добиться того, что № 10 будет
следовать за №9, № 11 — за № 10, № 7 — за № 11 и
т. д. При этом если перестановка (2) «разрешимая», то
мы придем окончательно к перестановке (1), а если (2)
«неразрешимая» перестановка, то мы придем к
перестановке 1, 2, 3, 4, 8, 12, *, 14, 15, 13, 9, 10, 11, 7, 6, 5,
равносильной IV на рис. 15.
229

("*) При л=1 и при л=2 формула (6) из § 15 дает;
-Ff{(i¥E)*-(L^)*}=1- •-
Затем
•.-.+*.-.=уИС-^)'-(^)'}+
+*Ы(^Г-(Ч2)'Т
-MWX
-1 Л-УУ\
н)
-т о
н)}-^{(-г-;
j+i
так как
i±vi+1=/i±viy h _ , .
2 * V 2 У 2 V 2
(*°) Пользуясь поочередно тремя соотношениями,
связывающими ws, да,_!, w,_», ®,_„ и учитывая, что
w1 = w1 = l и w, — 2, легко получить, последовательно
заполняя клетки нижней строки таблицы:
S
ws
0
1
1
2
1
3
2
4
4
5
7
6
13
7
17
8
30
9
60
10
107
11
197
12
257
13
454
14
908
15...
1619...
(жирным шрифтом напечатаны номера «клеток с вязкой
почвой»).
(*') Тот или иной способ перехода из узла
0(0, 0,..., 0) в узел A {aif а, ат), где
at-\-a,-\-.. .-\-ат = п, можно охарактеризовать схемой
из п букв, среди которых буква л, (показывающая, что
соответствующий ход увеличивает на единицу первую
координату точки) встречается ах раз, буква хх — а% раз
и т. д. и, наконец, буква хт—ат раз. Но выбрать а,
230

мест из л для заполнения их буквой хх можно С£' спо
собами: каждому из этих способов отвечает C0?-ai
вариантов расстановки at букв xt на остающихся
свободными п — аг местах. Следовательно, выбрать а1 мест
для хг и ах мест для xt {из я мест) можно С£' -С?-а,
способами. Каждому из них отвечает ££*-«,-«,
вариантов размещения аг букв х, на остающихся свободными
л—а,—а, местах, т. е. имеется всего С'1 • С?_ Л> -CS-o.-e,
способов для выбора мест, заполняемых буквами х1% х^
и хг.
Рассуждая так дальше, придем к тому, что для
размещения а, букв xlt аг букв xs, ... , ат_1 букв ха_г
(буквы хт займут при этом автоматически остающиеся
свободными ат мест) имеется С£'•£?_<., -С^-в.-а, ...
/-«m-i ' д' (д—gl)!
... ^«-«i-e.-...-««-i — fl]i(„_ai)| д,! (И - д, - а,)! •'•
... (n-ai-at- -am_t)\ = "! способоа
вщ-tlej в1!я1!...в„!
л?
®
<?
*
4
©
;
У?
©
2
г
г
©
i
2
1
4
©
#
2 i
J
©
г
©
<?
*
©
2
©
<?
©
•#
*
©
^
©
/
2
2
6
©
1В
40
8
©
4
2
S
8
43
ts
®
4
©
*
®
Л?
8
©
*
*
1
©
12
Рис, 131.
(") На рис 131 показано, сколькими способами ладья
может добраться за наименьшее число «коротких ходов»
до той или иной клетки шахматной доски «с
перегородками».
231

Для удобства данные, относящиеся к клеткам
четвертой зоны (2, 2, 4, 2, 2), восьмой зоны (10, 2, 2, 2, 4, 8,
2, 2, 2, 10) и двенадцатой зоны (8, 8, 8, 8), обведены
кружками.
(") Из рис. 132 видно, что. четвертая зона состоит
из тридцати двух клеток. Попасть в четвертую зону
король может 320-ю спосо->
бами (сумма чисел, стоящих
в клетках четвертой зоны).
(**) Две пешки со второй
линии на восьмую можно
перевести:
а) за 12 ходов, совсем не
пользуясь правом двойного
хода, g— способами;
б) за 11 ходов, используя
право двойного хода только
для первой пешки (или
только для второй пешки), щ
способами;
в) за 10 ходов, используя для обеих пешек право
двойного хода, =^1 способами. Всего для двух пешек
имеем §; + 2511| + В способов.
Аналогично для трех и четырех пешек будем иметь
J8! . о 17! , „ 16! , _Ш_ гп_гпбпв
соответственно: ggjgy + 3 зущщ + 3 ьЖ + 5J5J5! спосо&ов
24! , . 23! , „ 22! ■ „ 21! , 20!
/
4
го
IS
13
15
10
*
1
4
1
3
6
7
S
3
1
«
10
3
I
г
3
2
1
3
Ю
IS
6
г
1
1
1
г
s
16
7s
7
3
/
/
/
3
7
а
IS"
6
2
1
1
1
2
Б
16
Ю
3
I
г
3
г
i
3
ю
*
/
3
6
7
6
3
1
4
1
«
10
IS
W
IS
w
4>
I
Рис. 132.
И
6161616! "Г 5161616!
5!5!б!б! "Г4 5!5!5!6! "Г"5!5l5!5!
способов.
(**) а) Треугольник построить нельзя, так как в нем
имеется (см. рис. 29, д) шесть направлений, на каждом
из которых суммы трех слагаемых должны быть
одинаковы. Число же 12 можно представить всего лишь
пятью способами в виде суммы трех разных
натуральных чисел, не превышающих семи: 12=1 + 4 + 7 =
—1+5 + 6 = 2 + 3 + 7 = 2 + 4 + 6 = 3 + 4 + 5 (для чи-"
сел 11 и 13 имеется лишь по четыре способа
представления их в виде трех слагаемых, для чисел 10» 14 —
232

по четыре способа, для чисел 9 и 15 — по три способа
и т. д.).
б) Пятиугольник построить нельзя, так как в нем
число, стоящее в центре, должно входить в пять
равных сумм, каждая из которых состоит из трех разных
слагаемых, не превышающих одиннадцати; но легко
непосредственно проверить, что такого числа найти нельзя.
(") 1) В обобщенном домино имеется п-\-\ кость
вида {к, к) и Cl+i= g костей вида (/, т), где
1=£т, а всего — п-)-1 -)-v \. —v ^ " ^ ' костей.
2) Каждое число к встречается п раз в сочетании
с числами т, не равными числу к, и два раза на кости
(k, k). Следовательно, сумма всех очков будет равна
(0+1+2+...+/г)(/г + 2) = и(" + 12)(" + 2).
(*') Если удалить кость (а, Ь) {афЬ) из полного
комплекта обобщенного домино при п четном, то на
оставшихся костях а очков (так же, как и b очков) будет
встречаться нечетное число (л+l) раз (см. (*'), 2).
С другой стороны, очевидно, в любую замкнутую
цепь каждое число очков входит четное число раз;
нечетное число раз некоторое число очков может входить
лишь в незамкнутую цепь, причем это число будет
стоять в .одном из концов этой цепи.
(48) При п нечетном каждое число очков встречается
в обобщенном домино нечетное число (п-\-2) раз. Вне-
замкнутой цепи лишь те числа очков, которые
находятся на концах цепи, входят в цепь нечетное число
раз. Следовательно,, по крайней мере п—1 из чисел:
О, 1,2,3, ... , п—1, п будут фигурировать на костях,
не вошедших в состав цепи, т. е. по крайней мере
^п£— костей домино не могут быть уложены в цепь.
Всех же костей ^ '_—!—'. Следовательно, уложить
,, (л-1-1) (л-4-2) и—1
в цепь можно, самое большее, 2 Т~==
п*+2п + 3
=——2~—■— костей.
233

(*•) Одно из возможных распределений костей: у
первого игрока-(0, 0), (0, 1), (0, 2), (0, 3), (1, 4), (1, 5), (1, 6);
у четвертого игрока —(1, 1), (1,2), (1,3), (0,4), (0, 5),
(0, 6), (2, 2).
Игроки I и IV составляют цепь
(0, 0.) (0, 4) (4, 1) (1, 2) (2, 0) (0, 5) (5, 1) (1, 1) (1, 0)
(0,6) (6,1) (1,3) (3,0)
(игроки II и III не могут вступить в игру, так как у них
нет костей, содержащих нуль очков, или одно очко).
(") Пронумеруем клетки «4, 5-доски» (рис. 39, б)
так, как указано на рис. 133. Вот последовательность
ходов, ведущая к цели:
/
5
9
/J
17
2
6
10
Ц
18
3
7
и
15
/9
t
8
12
15
20
1. 19—14 2—7
2. 18—15 3—6
3. 14— 8 7—13
4. 15—12 6—9
5. 20— 5 1—16
6. 5— 2 16—19
7. 8—11 13—10
8. 12—18 9— 3
9. 11— 1 10—20
10. 17—11 4-10
11. 2—12 19— 9
12. 11—16 10— 5
13. 12— 7 9—14
14. 18—13 3— 8
15. 16— 6 5—15
16. 7—2 14—19
17. 13— 4 8—17
18. 6— 3 15—18
Рис. 133.
(") На рис. 119, а дана плоская
схема, обход которой по правилам
игры Гамильтона (см. § 34)
равносилен обходу «3, 4-доски» ходом шахматного коня. Легко
убедиться, что, начав обход из точек: L, М, R, В, С, Q
(рис. 119, а), нельзя обойти все точки схемы, двигаясь
по отрезкам схемы и имея право заходить в каждую
точку только по одному разу. Возможны обходы:
NBPMAQCKRDLS, PMAQNBRKCSLD,
NBPMAQCSLDRK, PMAQNBRDLSCK,
NQAMPBRKCSLD, AMPBNQCKRDLS,
NQAMPBfiDLSCK, AMPBNQCSLDRK,
каждый из которых характеризуется незамкнутой
ломаной, которая может быть пройдена, конечно, и в
обратном направлении (что мы не будем считать за новый
обход).
234

(!,а) Если выпишем подряд первые сорок
натуральных чисел и будем «отсеивать», идя слева направо,
каждое третье число (подчеркивая его и указывая в
скобках, каким по счету оно было отсеяно), то получим:
j_^^^5^_6^J7^^^_j0n^2131415161718]920
(37) (14) (1) (23) (29) (2) (13) (33) (3) (24) (16) (4) (39) (30) (5) (17) (25) (6) (33) (18)
21^2223242526272829303[323334 35 3j5 37 3JS 39 40
(7) (34) (26) (8) (19) (31) (9) (40) (20) (10) (27) (38) (11) (21) (32) (12) (28) (22) (13) (35)
откуда видно, что элемент № 13 будет отсеян в
предпоследнюю очередь, а № 28 — в последнюю очередь.
k з
2) В нашем случае я = 40, k = 3, q = ^——=~t
nk = \20. При s = 39 aI = k(n — s)-f-1 =4 и
«целочисленная геометрическая прогрессия» будет состоять из
чисел: 4, 6, 9, 14, 21, 32, 48, 72, 108, 162,...
Так как 162>яА; = 120, то Л =108 и t=nk-\-\ —
—А =120 + 1 — 108 = 13, т. е. тринадцатый элемент будет
отсеян в 39-ю очередь.
Если s = 40, а, = 1 и «целочисленная геометрическая
прогрессия» будет состоять из чисел: 1, 2, 3, 5,8, 12,
18,27,41,62,93,140,...
Так как 140>лА = 120, то Л = 93 и *= 120+1 —
— 93 = 28, т. е. двадцать восьмой элемент будет отсеян
в сороковую очередь.
Г6)
(28) (19) (22) (36) (16) (1) (7) (12) (35) (31) (25) (2) (20) (8) (27) (13) (17) (3)
_19 Я)21_22 2324J25 26 27 28 ИЗО 31 J52 JJ3 j|4 J55 36
(23) (30) (9) (32) (29) (4) (14) (21) Щ (10) (34) (5) (26) (24) (15) (33) (11) (6)
Из таблицы видно, что карты должны быть
расположены— считая сверху вниз — в следующем порядке:
пиковый туз (двадцать восьмая карта или, другими
словами, первая карта четвертой масти), трефовый туз
(карта № 19 — первая карта третьей масти), трефовый
валет (карта № 22 — четвертая карта третьей масти)
и т. д.
Так как л = 36, k — 6, q=^-l = ^-, «£ = 216, то
получим следующие «целочисленные геометрические
235

прогрессии»:
при .у = 19: я, = 6-17 + 1 = 103, 124, 149, 179, 215, 258,...
при $ = 31: я1 = 6- 5+1=31, 38, 46, 56, 68, 82, 99, 119, 143, 172,
207, 249,...
при s=17: я, = 6-19 + 1 = 115, 138, 166, 200, 240,...
Так как в этих «прогрессиях» наибольшие числа, не
превышающие числа nk: 215, 207, 200, то
соответствующие значения t будут: 2(216 — 215-j-l),
10(216—207-j-l) и 17(216 — 200 + 1)—см. в таблице
числа, напечатанные жирным шрифтом.
(") Если элементы: ах, я„..., ak расставить на
окружности по хрду часовой стрелки, а затем каждый из них
перевести — против движения часовой стрелки.—на
место соседнего элемента, то это будет равносильно
циклической подстановке С=(а1, аг,..., ak).
Очевидно, Ск=Е, так как после А-кратного
повторения описанной операции все элементы окажутся на
своих прежних местах.
Если подстановка А равна произведению нескольких
независимых циклов: А = Сх-Сг.. .Cs, порядки которых:
кх, кг, ..., ks, то при подстановке Ат все элементы
окажутся на своих прежних местах только в том
случае, если т делится на &,, на кг, на k, и т. д.
Наименьшее значение т, удовлетворяющее этим условиям, равно
наименьшему общему кратному чисел: ях, &,> ... , ks.
(") Пусть в соответствии с указанным в тексте § 22
правилом перехода от одной перестановки к другой, от
нее — к третьей и т. д. при каждом переходе элементы,
стоящие, например, на местах с номерами: а,, а,,..., a.s,
уступают друг другу места в циклическом порядке.
Тогда в состав подстановки М войдет цикл (а', а',..., a's),
где а', а',..., a's — элементы, занимавшие сначала места
С номерами: а,, а,,..., аг
Так же выявляются и другие циклы, входящие в
состав искомой подстановки М.
('*) Обозначим через аА ближайшие к центру углы
ромбов &-го слоя. Если точка А — общая для ромбов
(к — 1)-го и (&-)-1)-го слоев, то a.k_l -J-2 (it—aft) -)- aft+1=2n
(см. рис. 134, а), откуда a.k+l — aA = aA — aft_lt т. e.
236

ai> аи <*■„••• образуют арифметическую прогрессию; раз
2те
ность прогрессии равна at=—,таккака,=2а, (рис. 134,(5),
2я , 2я
откуда аа — а1 = а1=—; следовательно, aft = ft —
Если т нечетно, то am-i =
т — I 2тс
/71
тс (2т — 2)
2т
, Т. е.
aw-i равен углу правильного 2/и-угольника. Другие углы
2
Рис. 134.
2т-угольника состоят из трех углов, сумма которых равна
,0, > 2i m-З | „/ т—\ 2п\
' = ^-3 + 2)=^ = ^.
„ 2я / m , \ я
При от четном a„_i= —f-j — 1 1^-
m
(m-2)
m
2
т. е.
а ш равен углу правильного тя-угольника; в то же
"У -1
время «составной угол» (вроде угла D на рнс. 54, 6)
равен
а_ш_2 + 2(тг— а«__1) =
' =2,+ [|-2-2(|-1)].|=„.
(") Если обозначим ближайший к центру правильного
многоугольника угол ромба А-го слоя через аА, то легко
доказать, что a.k = {2k-\-\)-~ (достаточно установить,
что at = — и аж = — и использовать очевидное равен-
8 А. П. Доморяд
237

ство аА_1-)-аА+1-)-2(тт — аА) = 2тт, откуда следует, что
а,, а„ а,, а4 и т. д. образуют арифметическую
прогрессию). Но тогда а„__з = (2 ^ + 1) ~ =Щ=2, а это
угол правильного /га-угольника. Кроме того, «составной
угол» (вроде угла с вершиной Е на рис. 55, б) равен
а^ + 2(тг-а^__3) = (/«-4)^ + 2 Гп_^2]=п.
2 2 L J
Легко проверить, что каждый из углов «незамкнутого
многоугольника» (вроде многоугольника ABCDEFGHIKL
ее *\ "к (т—2)
на рис. оо, о) равен ——^—-, откуда следует, что
«незамкнутый многоугольник» — правильный (например, если
a — угол при вершине звездчатого многоугольника, то
^/ЛЯС = а-|~(тт — aJrrra+Tt— За = тт — 2a, £BCD =
=a.l-^-(n — a,)=3a-X-TT — 5a = it — 2a и т. д., атт — 2a =
2я я (m — 2)
= тт =—i — угол правильного /га-угольника).
(") Если стороны составляющих квадратов взять
равными 2 см, 5 см, 7 см и т. д., то площади
прямоугольников Slf St, S,, составляемых соответственно из
девяти, десяти и тринадцати квадратов, будут:
4209 смх (2' -f 5г + 7' -j- 9' + 16' -j- 25' -f 28' + 33' + 36'),
10270 см* (3,+ П'-1-12' + 23, + 34' + 35' + 38,+
-j-41' + 44'-j-452),
27495 см* (1»-|-4»+ 5"+ 9"+14*+ 19»+ 33» +52*+
-f- 56' -f 69' -f- 70' -f 71»+ 72').
Так как 4209 = 3-23-61, то стороны
прямоугольника Sx могут быть равны либо 3 см и 1403 см, либо
69 см и 61 см, либо 23 см и 183 см. Первый и третий
случаи не годятся, так как ни одна из сторон Sx не
должна быть меньше стороны большего из
составляющих квадратов (36 см). Поэтому стороны
прямоугольника Sx суть 69 см и 61 см.
Аналогично 10 270 = 2-5-13-79 = 79-130 = 65-158. Но
65 см нельзя представить как сумму длин сторон
квадратов данных размеров. Поэтому стороны S, — 79 см к
130 см. Стороны прямоугольника S, —141 см и 195 см,
так как 27495 = 3-3-5-13-47= 141-195 (другие разбие-
238

ния числа 27495 на два множителя не согласуются
с размерами составляющих квадратов).
Если вместо «квадрат со стороной о» будем писать
«квадрат а», то 5, состоит (считая слева направо) из
квадратов: 36, 33 (верхний ряд); 5, 28 (под 33); 25, 9, 2
(под 36); 7 (под 2 и 5), 16 (под 9 и 7); 5, состоит из
квадратов: 41, 44, 45 (верхний ряд); 38, 3 (под 41);
35, 12 (под 3 и 44); И, 34 (под 45); 23 (под 12 и 11);
S, состоит из квадратов: 71, 72, 52 (верхний ряд); 19, 33
(под 52); 5, 14 (под 19); 70, 1 (под 71); 69, 4 (под 1 и 72);
9 (под 4 и 5); 56 (под 9, 14, 33).
(") «608 X 377-прямоугольник» состоит из квадратов:
209, 205, 194 (верхний ряд), 11, 183 (под 194); 44, 172
(под 205 и 11); 168, 41 (под 209); 1, 43 (под 44); 42
(под 41 и 1); 85 (под 42 и 43).
«608X231-прямоугольник» состоит из квадратов: 231, 95, 61, 108, 113
(верхний ряд), 34, 27 (под 61); 7, 20 (под 27); 136 (под 95,
34 и 7); 123, 5 (под 128); 118 (под 5 и 113).
(") Если бы наименьший квадрат ABCD примыкал
стороной АВ к одной из сторон прямоугольника, то он
был бы либо зажат между двумя более крупными
квадратами, либо «прижат» более крупным квадратом к
соседней стороне прямоугольника; в обоих случаях к
стороне CD наименьшего квадрата не мог бы примыкать
квадрат более крупных размеров.
(••) 1) а* = (^)'-т-17(|),+ 1б(|),,т.е.кубсреб-
ром а можно разбить на 34 куба: куб с ребром у,
17 кубов с ребром у и 16 кубов с ребром у<
2) а* = 2 (у J +48 (-jV, т. е. куб с ребром а можно
разбить на 50 кубов: 2 куба с ребром у и 48 кубов
с ребром -т.
(") Квадрат со стороной а можно разбить на 4
квадрата, на 6 квадратов (один со Стороной у, пять — со
8* 239

стороной 4- J, на 8 квадратов ( один со стороной — ,
семь — со стороной -г-
Но если квадрат можно разбить на s частей, то,
разбивая какой-нибудь один из получающихся при этом
квадратов на четыре части, мы сумеем разбить квадрат
и на s-j-З частей. Следовательно, квадрат можно
разбить на семь (4-J-3), на десять (7-J-3) и т. д. вообще —
на 4-{-3k квадратов. Рассуждая так же, убедимся, что
большой квадрат можно разбить на 6-J-3/ квадратов и
на 8-)-3/й квадратов (k, I, т — натуральные числа).
Но любое натуральное число га, начиная с шести,
можно представить либо в виде 6-J-3/, либо в виде
4-{-3k, либо в виде S-\-3m, так
s&. с как эти числа дают при делении
на три в остатке либо нуль, либо
один, либо два.
(") Все вершины
какого-нибудь правильного
десятиугольника должны быть узлами типа
(10, 5, 5) —см. рис. 135. Но тогда
точки В и Дне могут быть уз-
Рис. 135. лами того же типа, так как тогда
в точке С «сходились бы» два
правильных десятиугольника и один правильный
пятиугольник, что невозможно.
(") Каждый угол правильного /га-угольника равен
180 (от —2) ^ суММа углов, имеющих вершину в узле
10ЛО /„ _ о\
(га,, пг, ... , пк), равна 360°, следовательно, ^ -\-
+ 180°(«,-2) +...+lg01(gzi2U360°. Сокращая'на 180°,
получим: ft-2(i + -^+...+-^-)=2.
(") Из рис. 136, а видно, что из четырех
пятиугольников вида ABCDE (AB = BC=CD=DE; /.В =
= ^D=90°; Z^ = ZC=Z£=120°) можно
составить шестиугольник KCLMNP, у которого
противоположные стороны равны и параллельны, а такими шести-
240

угольниками легко заполнить плоскость. На рис. 136, б
показано, как плоскость может быть заполнена
правильными пятиугольниками и ромбами с острым углом в 36°.
Рис. 136.
(6*) Достаточно доказать, что независимо от того,
будем ли мы отражать треугольник ABC сначала от
стороны ВС или от стороны АВ, произвольная точка М,
Рис. 137. Рис. 138.
принадлежащая треугольнику ABC, приведет, в
конечном счете, к одной и той же пятерке точек: М1У Мх,
М„ М„ Mt (рис. 137).
(«") См. рис. 138.
(6б6) Достаточно провести прямые, параллельные
сторонам прямоугольника и делящие сторону а на п-\-\,
241

а сторону b — на л частей, и провести ломаную в
соответствии с рис. 139 (на рисунке я = 6).
(**) На рис. 140 изображен параллелепипед
am .,Ь(т4-1) ч .
*д_1_ J X—^—л.су>, составленный из двух половинок
Vj и Vt параллелепипеда «аХ^Хс>> (на рисунке т — 4
и PQ = (ww+ М. Проводя через ломаную ABCDEF
— а .
*(
,
=4
£;'
и \
-
Г'>
д
в
am
-~~~~ т+/ "~"-~-^
*~ч
л
Е
f
/
\
/
/ /
V__.^
am
Рис. 139.
/m+7j/n+/J
Рис. 140.
сечение, параллельное ребру PQ, мы разрежем каждую
из половинок V% и Vx на две части; сдвигая правые части
с am
вверх на — и влево на 1т ^_ и ,„_и^ > получим параллеле-
_ атп
ПИПеД(т+1)<Д + 1)- m " и
Аналогично осуществляется перекраивание
параллелепипеда аХЬХс в параллелепипед WTj'X wTh + I)" X
чу с(я+П
(ш 4- 1) (л+1)'
ч ,Ь(т-\-\)., с (л 4- 1) , оч
X , X и (на рисунке д = 3).
(") См. рис. 141.
(•') Чтобы кривая {"zZth
; = a sin mt
^ sin nt пР°шла чеРез 0ДНУ
из вершин прямоугольника, «описанного» около кривой,
надо иметь при каком-то значении параметра t: mt =
= (2А+1).90° и л^=(2/+1)-90°, где к н / — некото-
242

рые целые числа, что возможно лишь при условии, что
найдутся целые числа k и /, для которых ~= % -J-V'
В этом случае при t= Р»+»•«*■ ^ <«+ »■*>" =t,
будем иметь |д;0| = |у0| = 1. Предоставляем читателю
проверить, что точки (xv yj и (xt, yt),
соответствующие значениям параметра ^ = ^0 — Д^ и ^ = i0-f Д^
(Д£—произвольно), совпадут.
(••) I. Уравнение 12у — 11 +12у + 11+1Ц) = 4, если
не использовать знака абсолютной величины, будет
записываться по-разному в каждой из областей: А1У At, At,
Av Л8, А, (рис. 142, а). Например, при У^-* и -*<0
(область Ах) имеем 2у — 1 -\- 2у -\-1 -\- у ' =4, или
уз
у у==\; этому уравнению отвечает прямая /, от
которой надо взять участок ДХ, лежащий в области Аж.
При—~<з'<4' и х^° имеем: 1— 2у + 2у-J- 1 -f-
+ тт:|: = 4, или я = ^у-, а это уравнение прямой т,
243

от которой надо взять лишь отрезок MN, лежащий
в области А,, и т. д.
II. Уравнение |л| + |.у | + у={|*—у | + |*+.У | }==
=уг2_-(-1, если не использовать знака абсолютной
величины, запишется по-разному в каждом из восьми
«секторов» Вк{\ <&<8), на которые плоскость делится
осями координат и биссектрисами координатных углов
(см. рис. 142,(5). Например, в секторе 54, где х<,0,
у^0,х — д»<0,л-{"Д'^0>имеем—хЛ-У-\-Хг={У—xJr
+ (—.K-j,)} = l+yn2, или j, —(1+/2)х==1+У~2;
а это уравнение прямой /, проходящей через точку
(--1,0) под углом 67°30' к оси Ox (tg 67°30' = 1 + V%.
Часть прямой — PQ, лежащая в секторе ВА, дает
сторону PQ правильного восьмиугольника. Предлагаем
читателю убедиться, что так же получаются стороны
правильного восьмиугольника, лежащие в других
секторах.
III. Так как в уравнение ||Jcl~Hl.yl — 3| — 31 ===== 1
хну входят лишь под знаком абсолютной величины,
то достаточно, построив часть «кривой», лежащую в
первой четверти, построить затем «кривые», симметричные
ей относительно оси Ох, оси Оу и начала координат.
При х^О и у^О имеем |*+|.у — 3| — 3[=1,
откуда следует либо -К-Н.У— 3| — 3 = 1, т. е.
LV-3| = 4-*, (1)
либо -К-Н.У — 31 — 3 = —1, т. е.
\у — 3[==2 — х. (2)
244

Уравнение (1) имеет смысл лишь при .х«£4, причем
из него следует либо у— 3 = 4 — х (прямая /, от
которой надо взять участок АВ, где х ^ 4), либоj> — 3 = х — 4
(прямая т, от которой надо взять участок ВС — при
л<4) (см. рис. 142, в).
Уравнение (2) дает: у— 3 = 2 — х (прямая /', от
которой надо взять участок DE, где .к<2), или
у — Ъ = х — 2 (прямая т', от которой надо взять
участок FE, где ;с< 2).
(,0) Пусть y—f(x) — уравнение кривой / и кривая /'
сдвинута относительно / вправо на отрезок л (рис. 143).
Если А'(х, у) —
произвольная точка кривой У
V, а А(Х, Y) —
соответствующая точка
кривой /, т. е. Х=х—<х и
Y=y, то Y=f(X), a
следовательно
это и есть уравнение
кривой /', которому
удовлетворяют
координаты любой ее точки. Рис. 143.
(,оа) Следует воспользоваться семизначными
таблицами логарифмов.
(") 1) Шесть плоскостей, проходящих через ребра
правильного тетраэдра и одинаково наклоненных к
соответствующим граням тетраэдра, образуют в
пересечении друг с другом куб (см. рис. 100, б).
2) Двенадцать длинных диагоналей ромбического
додекаэдра {OiOl и т. п. — см. рис. 105) служат ребрами
некоторого правильного октаэдра. Плоскости,
проходящие через ребра этого октаэдра и одинаково
наклоненные к соответствующим его граням, будут ограничивать
ромбический додекаэдр, изображенный на рис. 105.
(") Предположим, что две краски достаточны для
раскраски областей, на которые плоскость разбивается п
прямыми. Если, проведя п-\- 1-ю прямую, мы по одну
сторону от нее сохраним цвет всех областей (и кусков
245

областей) «я-го разбиения», а по другую сторону
изменим цвет каждой области на обратный, то каждые две
смежные области л-}-1-го разбиения будут окрашены
в разные цвета. Так как при я=1 две краски
достаточны и мы обосновали «переход от я к я-}-1», то
двумя красками можно раскрасить плоскость, разбитую
на области любым числом прямых.
Эти рассуждения сохраняют силу и для
пространства, разбитого на области я плоскостями.
(") Из рис. 144 видно, что любые два из четырех
треугольников ABD, ВСЕ, CAF, DEF имеют общую
границу в виде отрезка
прямой; то же имеет
место и в четверке
треугольников: KLP, LMQ,
MKN, NPQ.
Кроме того, любой
из треугольников
первой четверки частично
перекрывается с любым
треугольником из вто-
^ рой четверки (и, конеч-
Ь# но, наоборот).
Следовательно,если
над плоскостью
чертежа взять точку S, а под
плоскостью чертежа — точку Т, то любые два из восьми
тетраэдров: SABD, SBCE, SCAF, SDEF, TKLP, TLMQ,
TMKN, TNPQ будут иметь общую границу в виде
некоторого куска грани.
С*) Если мы учтем все я, путей, выходящих из
«я^узла», я, путей, выходящих из «я,-узла», и т. д.
и, наконец, все ns путей, выходящих из «я^-узла», то
каждый путь будет учтен дважды; следовательно, общее
• ,- п. 4-72,4-. ..-4-я,
число путей будет равно ———*-^ !—-.
Если бы в числителе этой дроби имелось нечетное
число нечетных слагаемых, то общее число путей было
бы дробным!
(") На рис. 118 семь точек разбиваются на две
группы: К, L, М, N и А, В, С. Схема путей такова, что
Рис. 144.
246

из любой точки первой группы можно перейти
непосредственно только в ту или иную точку второй группы,
и наоборот.
Чтобы обойти все точки, надо начать обход из какой-
нибудь точки первой группы и закончить его в какой-
нибудь другой точке той же группы; но из последней
точки попасть непосредственно в исходную точку
невозможно.
(") Если в правильный октаэдр вписать куб с
вершинами в центрах граней октаэдра, то переход с грани
на грань октаэдра будет возможен в том и только в том
случае, если вершины куба, лежащие на этих гранях,
будут концами какого-нибудь ребра куба.
Аналогичные рассуждения пригодны и для
додекаэдра, вписанного в правильный икосаэдр.
Д
^—•
• • •
• • •
•4
V в)
Рис. 145.
(") На рис. 145, а стрелками показано, куда надо
переложить монеты А, В, С.
(") На рис. 145, б стрелками показано, куда надо
переложить монеты D и Е.
247
О • • о
' ' •)
^*-о а]

С) Решение указано на рис. 145, в.
(,0) Точки надо расположить в вершинах и в центре
правильного пятиугольника (см. рис. 145, г).
(") К шести точкам предыдущей задачи надо
добавить две точки А, и Л,, лежащие на перпендикуляре
к плоскости чертежа, проходящем через центр Alt
причем должно быть: AtA7~ AtA. = АхАг (правда, один из
«треугольников»: /\AlAJAt— будет иметь угол при
вершине 180°).
(") Достаточно показать, что длины отрезков: ОА,
ОВ, ОС, OD, АВ, AC, AD, ВС, BD, CD — одинаковы.
Например:
лс-/^:1)*+№-о)'+(1?-о)'+(о-ог-
_1/ГГТТ1=1
" V 4+Зб+91'
^=/a4)"+ff-¥)'+(f-^)'+(^-o)'=
и т. п.
(") Общее число прямых в конфигурации (рт, qn)
равно q.
Если бы мы учли т прямых, проходящих через
первую точку, затем т прямых, проходящих через
вторую точку, и т. д. и, наконец, т прямых, проходящих
через р-ю точку, то всего мы «насчитали бы» рт
прямых; но при этом каждая прямая будет учтена я раз
(так как одна и та же прямая проходит через п точек),
поэтому -— = q.
248

(*4) Следует учесть, что кем бы ни был Иванов, он
на вопрос преподавателя — серьезный ли он человек
или шутник — мог дать единственный ответ: «я
серьезный человек». Но тогда ясно, что Петров — серьезный
человек, а Сидоров — шутник.
(") Так как из чисел: 26, 27, 28 только число 27
деются на 3, то Галкин с Комковым распиливали полуто-
>аметровые бревнышки, следовательно, их имена: Петя
[ Костя. Но среди бригадиров Кости не было, а Ком-
:ов по условию не бригадир; следовательно, Комков —
Состя.
(") Да, мог. Действительно, из ответа Андрея его
[риятелям должно быть ясно, что на них не может
>ыть двух белых шапок.
Если бы на Вадиме была белая шапка, то Борис
[егко определил бы цвет своей шапки, а так как он
'того сделать не смог, то шапка Вадима черная. Задача
[егко обобщается: можно говорить об я приятелях, си-
[ящих в затылок друг другу, и о 2л+1 шапках (л
белых и п-\-1 черных).
(") Предположив, что Сережа — № 2 (т. е. он занял
второе место), будем иметь: из I — Коля не № 3, из
IV — Ваня не № 4, из V — Коля № 1, из II — Толя не № 1,
Надя № 2, т. е. придем к противоречию: и Сережа и
Надя заняли второе место.
Предположив, что Коля № 3, получим: из I — Сережа
не № 2, из IV — Ваня № 4, из II — Надя не № 3,
Толя № 5, из III — Толя не № 1, Надя № 2;
следовательно, на долю Сережи остается № 1. Итак, по
порядку номеров идут: Сережа, Надя, Коля, Ваня, Толя.
(") Так как известно, что три шахматиста:
саратовец, москвич и киевлянин, а их возраст — 21, 22, 23 года,
то четвертый шахматист — из Ферганы и ему 20 лет
(студент Н.); он биолог (так как остальные три
шахматиста: математик, химик, геолог) и учится на
IV курсе (остальные шахматисты учатся на I, II,
III курсах).
249

Эти сведения заносим под номерами: 1, 2, 3 в
таблицу, где жирным шрифтом записаны условия задачи.
Под номером 4 записываем, что
N. Возраст
Город ^ч
Киев
Москва
Саратов
Фергана
20 лет
А. геол.,
(5)
II, футб.
(17) (28)
Д. мат.,
(6)
III, бокс.
(16) (27)
И. хим.,
(7)
I, вол.
(15)
Н. биол.,
(2)
IV, шахм.
(3) (1)
21 год
Б. хим.,
(4)
IV, бокс.
(18) (29)
Е. биол.,
(13)
I, футб.
(19)
К. геол.,
III, шахм.
О. мат.,
(14)
II, вол.
(20) (32)
22 года
В. биол.,
III, вол.
(22) (30)
Ж. хим.,
II, шахм.
Л. мат.
(8)
IV, футб.
(21) (33)
П. геол.,
(10)
I, бокс.
(23) (35)
23 года
Г. мат.,
I, шахм.
3. геол.,
(12)
IV, вол.
(26) (31)
М. биол.,
(9)
II, бокс.
(25) (34)
Р. хим.,
(11)
III, футб.
(24) (36)
Б.— химик (так как киевляне В. и Г.— биолог и
математик, а студенту К. 21 год и он геолог).
Под номерами 5—14 в таблицу занесены легко
определяемые сведения о специальности остальных студентов.
Затем под номером 15 записываем: химик из Саратова И.—
студент первого курса (так как саратовец К. с III курса,
химик Ж. со II курса, а двадцатилетний Н. с IV курса).
Аналогично определяются (под номерами 16—26) курсы,
на которых учатся остальные студенты.
Двадцатилетний москвич Д.— боксер (№ 27), так как
москвичи Е. и Ж. — футболист и шахматист, а
двадцатилетний И.— волейболист. Дальше — под номерами 28—36 —
указаны любимые виды спорта студентов (например,
250

№ 29: Б.— боксер, так как киевляне А. и Г.^-футболист
и шахматист, а химик И.—волейболист и т. п.).
(") 1) V ****** = ***
— *
***
**
4***
****
б
Сразу видно, что первая цифра искомого корня — 3,
так как квадрат ее — однозначное число и она является
результатом извлечения корня из старшей грани,
состоящей из двух цифр. Вторая цифра искомого корня может
быть только единицей, так как уже 62 X 2 дало бы
трехзначное произведение, а не двузначное (см. две звездочки
в четвертой строке). Наконец, из 62zXz = 4*** следует,
что z (последняя цифра искомого корня) может быть
только семеркой.
— **** *8*
***
****
О
Сразу видно, что частное — 989, так как произведение
делителя на 8—трехзначное, а произведения его на
крайние цифры частного — четырехзначные числа (см. 4-ю,
2-ю и 6-ю строчки схемы деления). Обозначим весь
делитель через 2. Тогда 8z<1000 и 92 5=1000, т. е.
111<2<125. При 2=112 делимое = 989-112= 110768
и деление числа 110768 на 112 в точности происходит
по данной схеме. Но при 2 = 113, 114 и т. д. первый
остаток был бы не двузначным, как это следует из
схемы, а трехзначным числом; например, при 2=113 имеем:
111757( = 989.ПЗ); приг=114: 112746(989-114)
1007 ( = 113-9) 1026 ( = 114-9)
100 101
и т. д. Итак, единственное решение: 110768:112 = 989.
251

3) i смех
' гром
греми
Сразу видно, что г=1. Поэтому рф\\ но р не может
быть и больше единицы, так как при р = 2 даже при
с = 9 при сложении в разряде сотен должно было бы
остаться «два в уме», а это невозможно. Итак, р = 0.
Легко видеть, что .м<9, так как при лг = 9,
рассматривая сложение в разряде сотен, мы получили бы
е = 0, а это невозможно, так как р = 0. Следовательно,
л*<9 и е = м-\-1.
Очевидно, с = 9. Рассматривая же сложение в разряде
десятков, получим: 0 = 8, так как е = м-\-\ и офс = 9.
Итак, имеем:
, 9 мех
~|~ 108м
10 елш
Рассмотрев пять вариантов: м — 2, 3, 4, 5, 6, легко
обнаружить, что только м = Ь не приводит к противоречию,
а дает: 9567 + 1085=10652.
4} /ort;/
, ten
з ^«
sixty
Легко установить, что я = 0 и е = Ъ. Так как г^0> то
i=l (при i = 2 даже при о = 9 при сложении в разряде
сотен должно было бы набраться «три в уме», что
невозможно). По этой же причине о = 9. Итак, имеем:
f9rty
, *50
+ tso
sixty
Следовательно, s=/+l и в разряде сотен
накапливается «два в уме». Но при /=7 и 5 = 8 в разряде
сотен будем иметь, самое большее, 4 -j— 6-f— 6 -f— 1 =
= 17<20. При /=6 и s = 7 в разряде сотен можно
получить: 8 + 8 + 4+1 = 21, или 8 + 8 + 3 + 1 = 20, но
тогда х совпадет либо с i, либо с п.
252

Легко проверить, что при /=3 и 5 = 4 во всех
вариантах х совпадет с одной из «цифр»: s, /, i, п.
Лишь при /=2, s = 3 и /" = 7, * = 8 мы получим
для х значение, не совпадающее ни с одной из
остальных «цифр»: х = 4, а тогда ,у = 6.
Итак, единственное решение: 29 786 -f- 850 -f- 850 =
= 31486.
(go) 1) Переправляются: Аа АВ аЬ
Возвращаются: А а
2) Переправляются: abc АВ BCD abc cd
Возвращаются: с ВЬ ас
3) Переправляются: abc cde ABC CPE bed de
Возвращаютсб: с de cC b d
(") Первый способ дает: (20,0,0)-(7,13,0)-(7,4,9)-
- (16,4,0) - (16,0,4) - (3,13,4) - (3,8,9) - (12,8,0) - (12,0,8).
Так как сложилось положение (Ь — 1, 0, с—1), то
первый способ непригоден.
Второй способ дает: (20,0,0)-(11,0,9)-(11,9,0)-
- (2,9,9) - (2,13,5) - (15,0,5) - (15,5,0) - (6,5,9) - (6,13,1) -
-(19,0,1)-(19,1,0)-(10,1,9)-(10,10,0), т. е. приводит
к цели.
П Первый способ дает: (16,0,0)-(4,12,0)-(4,5,7)-
- (11,5,0) —(11,0,5); он непригоден, так как приводит
к положению (Ь — 1, 0, с — 2).
Второй способ дает: (16,0,0)-(9,0,7)-(9,7,0)-
- (2,7,7)-(2,12,2)-(14,0,2) - (14,2,0) - (7,2,7)- (7,9,0)-
- (0,9,7) - (0,12,4) - (12,0,4) - (12,4,0) - (5,4,7) - (5,11,0).
Так как мы пришли к положению, в котором нельзя
наполнить малый сосуд (из большого сосуда) и нельзя
вернуть в большой сосуд порцию, равную емкости
среднего сосуда, то и второй способ непригоден для
разделения жидкости на две равные части.
(") У описанной пирамиды сторона основания равна
2л -)- 1, а высота — п -j- -^ (если центральные кубики всех
слоев будут находиться в одном столбике).
253

Следовательно,
1« + 3* + 5*+...+(2л — 3)' + (2л— 1)* =
= \ ^_2[(2л-1) + (2я-3)+...
...+5 + 3+l]-4/z.l-T=^:=lil-
(**) Квадратов — 31, треугольников—124,
прямоугольников (в том числе и квадратов) — 87.
(") Тридцать пять треугольников.
(") Треугольников — 78, правильных
шестиугольников — 11, ромбов — 66.
(") 1) Пусть JV,(/n, п) — число квадратов, a N3(m,n) —
число прямоугольников, которые можно увидеть на
«яг, я-доске».
Если и</ги а — сторона клетки шахматной доски,
то на am, /г-доске» имеется: т столбцов шириной а,
в каждом из которых имеется я квадратов со стороной а,
т — 1 столбцов шириной 2а, в каждом из которых
имеется п — 1 квадратов со стороной 2а, т — 2
столбцов шириной За, в каждом из которых имеется я—2
квадратов со стороной За, и т. п., наконец, в одном
столбце шириной та имеется п — т-\-\ квадратов со
стороной та. Следовательно,
N^m, п) = тп + (т— 1)(я — 1) + (/и—2)(я— 2)+ ...
,..+2(я —от + 2) + 1(я —от+1).
Выбрать столбец той или иной ширины на «w, я-доске»
можно m'm2+ ) способами. Выбрав же конкретный стол-
^ и (я 4-1)
бец, в нем можно увидеть —^—- прямоугольников
с основанием, равным ширине столбца (я
прямоугольников с высотой а, п—1 — с высотой 2а и т. д., наконец,
два прямоугольника с высотой (я — 1) а и один — с
высотой ла).
254

Следовательно, Nt(m, п) = т(т2+1)- ^bil. В част-
ности, N(n, n) = n* + (n—iy + (n—2y +.. .+3' + 22+
+ 1.сз»(^+1)(н + 1). ^i(8>8)==204; ^(»,»)=21^;
N,(8,8) = 1296.
2) В основании «105-куба» квадрат со стороной k см
можно выбрать (10 — k-\-\f способами. В столбце
с выбранным основанием имеется 10 — k-j-l «&5-кубов».
Следовательно, в «105-кубе» можно «увидеть» (10—k-\- I)5
'<&5-кубов». Так как k может быть любым числом от 1
до 10, то всего можно увидеть в «105-кубе» 3025
различных кубов (1'4-2'4-35 + 4' + 5'+6* + 754-8,-г-
+ 9* + 105).
Так как выбрать какой-нибудь прямоугольник в
основании «105-куба» можно 3025 ( = N,(10, 10) = 55*)
способами, а взяв столбец с каким-нибудь конкретным
основанием, мы в нем можем увидеть 55 прямоугольных
параллелепипедов с выбранным основанием (10 —{— 9—{—
+ 8+...+ 2-j-1), то в «10*-кубе» можно увидеть
55* различных прямоугольных параллелепипедов.
(") Сорока четырьмя способами.
С") Складывая почленно тождества:
ос 1 а 1 За
sin а sin у = у COS у — у COS у ,
. n . a l За 1 5а
sin 2а SU1 у = у COS у — у COS у ,
а 1 (2л — 1) а 1 (2л-4-1)с
получим:
(sin а-)-sin 2а-)- ... -)- sin па) sin у =
1 а 1 (2л + 1)а . (л+1)а . я«
=у cos у — -j cos—p- = an ^ sin у ,
откуда:
, (л 4- 1) a , ла
Sin ' Sin у
sin a -\- sin 2a + ... + sin/la =
a
Stay
255

(10°) [3(10*+10*-'+...+ 10 + 1) л+ 1]* =
_Гя(10*+'-1) , ,!'_п'00'*+'-2-10*+1 + 1) ,
— [ 3 rlJ — — 9 Г
+ i=n*(iol*+1 + ioJ*+ ... + ю*+1)+
+ (6л —«J)(10*+10*-'+... + l)+l.
С01) Так как после двух переливаний объем
жидкости в первом стакане не изменится, то объем
перешедшего в первый стакан спирта будет равен объему воды,
перешедшей во второй стакан (замечание о «тщательном
перемешивании» надо было бы использовать при
арифметическом— более длинном! — решении, которое
позволило бы, правда, определить и количество примеси
в каждом стакане).
(1И) На стене висел портрет сына Петрова
(вычурный ответ Петрова можно перефразировать так: «Отец
висящего есть я»).
С05). Так как у каждого человека было 8
прапрадедов и 8 прапрабабушек, а у каждого из этих
шестнадцати лиц также было по 16 прямых предков в
«четвертом колене», то искомое число равно 256 (16X16).
Число прямых предков в «восьмом колене» будет
меньше, чем 256, если среди них были, например, случаи
вступления в брак троюродных братьев и сестер и т. п.
("*) 15'; если соединить какие-нибудь точки А а С,
лежащие на сторонах угла ABC, то, глядя через лупу,
мы увидим подобный треугольник А'В'С с такими же
углами, как и у треугольника ABC.
("") На 25"/» (если, например, до снижения цен
килограмм картофеля стоил а рублей, то после
снижения он будет стоить 0,8а рублей и за а рублей можно
будет купить 1,25 кг картофеля).
(10,а) На 50°/0 (если до снижения можно было на
100 рублей купить, например, b кг картофеля, то после
первого снижения можно на 100 рублей купить l,2b кг,
а после второго снижения —1,2-1,25&= l,5b кг).
256

('•') 44 раза (за сутки минутная стрелка делает
24 оборота, а часовая — 2 оборота; следовательно,
минутная стрелка обгоняет часовую 22 раза, а между
двумя «обгонами» стрелки образуют прямой угол два
раза).
("') Пусть в данный момент Коле х лет, а Оле.у лет-
Из условий задачи следует, что тетушке Поле было
х -\-у лет, когда Коле было у лет, т. е. тетушка Поля
на х лет старше Коли или в данный момент ей 2х лет;
х лет назад она была «в возрасте Коли», а Коля —
новорожденным младенцем.
(1М) Летчик увидел белого медведя, так как из
условия: АВ = АС следует, что пунктом А был
северный полюс (А могло быть и невдалеке от южного
полюса— см. примечание С"), но там медведи не водятся).
(1(") Обозначим число волов через 10а-f-Ь(0=<ftsS9).
А а В выручили от продажи 100а" -f- 20ab -f- b* рублей.
Часть вырученной суммы: 100а"-\-20ab они разобрали
поровну, беря поочередно по 10 рублей. В остальной
сумме (Ьг рублей) число десятков должно быть нечетно,
так как когда А забрал последний раз 10 рублей,
осталось меньше десяти рублей.
Так как при 0<ft<9 &, = 0, 1, 4, 9, 16, 25, 36, 49,
64, 81 и только в числах 16 и 36 число десятков нечетно,
то в остатке оказалось 6 рублей. Из уравнения 10 —
— х = 6-\-х найдем, что кошелек стоил 2 рубля.
("') Пусть мужья купили s, х, z предметов, а их
жены соответственно t, y,w предметов. Тогда s* — £* =
= х*— y = z2 — •а>, = 45 или (s + *)(s — t) = {x-\-y)X
ХО*—y) = (z-\-w)(z— ■йу) = 45.
Но число 45 только тремя способами можно
разложить на два множителя: 45 = 45> 1 = 15-3 = 9• 5. Из
уравнений: s-j-£ = 45 и s— t=l найдем: s = 23 и £ = 22.
Аналогично найдем: х = 9, y = Q и z = 7, w = 2.
Следовательно, мужья потратили: Юрий — 529 руб., Алек~
сандр — 81 руб., Логин — 49 руб., а их жены
соответственно: Татьяна — 484 руб., Нина — 36 руб. и Ольга —
4 рубля.
257

(,п) Пусть x рублей — вся сумма денег в общем
случае (когда каждый раз добавляется ——? часть
остатка).
Тогда 1+^1=2Н я + 1 ' 0ТКУда х = пх.
Доля первого из детей (в рублях): 1 -{- _^ = л,
второго 2 +" ~^7 = 2 + (л — 2) = л, третьего
3-| jjqrj—=3-{-(л — 3) = л и т. д. Если
предположить, что первые k детей получили по л рублей, то
доля fc + 1-го будет: fe + l+" ~*^|*+1) = fe+l +
+ л — (k-\-\) = n. Отсюда следует, что каждый из
п детей получит по п рублей.
("*) Если Глеб шел пешком х км (в конце пути),
то Павел столько же прошел пешком в начале пути
(в пункт N они пришли одновременно!).
Пока Глеб шел х км со скоростью и км\час, Юрий
проехал со скоростью v км/час 2s— Зх км (s—2х —
навстречу Павлу us — х км — вдогонку Глебу). Следо-
х и 2su
вательно, 2s — 3x==~v ' 0ТКУда х == v_цЗа и затРаченное
х , s — х s (и + 3v)
время: — = ; Т „ . час.
г и * v v (v -j- Зм)
("*) Окружность циферблата часов разделена на 60
«минутных делений». Пусть начало заседания было
в 4 ч. х мин., а конец — в 7 ч. у мин. Так как часовая
стрелка движется в 12 раз медленнее минутной, то имеем
I х=12(у — 20), 5280
два уравнения: | y=i2(x-35), 0ТКуда Х=Ш =Л"
3300
■^Ш
колено) проверить, что л, — 30 = 30—у0 (см. рис. 146).
("*) Если показания часов сохраняют смысл при
обмене местами часовой и минутной стрелок в
положениях: am ч. х мин.» и «л ч. у мин.», то будем иметь
( X = 12 (V - 5/72), --■„,..„ 60 (д + 12») Ы(п + 12т)
Ь = 12(л-5л), ОТКудаЛ_ 143 >* Ш '
253

Так как /пил изменяются от 0 до 11 включительно,
то для каждой пары чисел т, п (тф^п) мы получим
два момента, когда стрелки можно «безболезненно»
менять местами. За 12 часов таких моментов будет 132
(2-С»), а за сутки —264.
Кроме того, в течение суток часовая и минутная
стрелки 22 раза «совмещаются», т. е. их можно
«поменять местами», не изменяя положения каждой из стрелок.
Рис. 146.
('") Каждое s-значное число п заключено в границах:
10I-1^/i<lQJ. Всех s-значных чисел — 9-Ю1-1, а общее
число цифр в них — 9s-10*-1. Во всех 5-значных числах
цифра старшего разряда не нуль, а в остальных
разрядах и нуль, и каждая из остальных цифр
встречается одинаковое число раз. Следовательно, число ну-
„ эмо*-1 —э-ю*-1
лей во всех s-значных числах равно гт =
= 9(s— 1) • 10*"* (столько же, сколько всех цифр во всех
(s—1)-значных числах).
Если Nt — общее число цифр в последовательности
чисел: 1, 2, 3, ..., 10*— 1,10*, a Nt — общее число нулей
в последовательности: 1, 2, 3 10*+1 —1,10*+1, то
Nt = N, = 9 + 9-2.10+9-3.102-j-...+9.fc.l0*-,+fc+l
(& + 1—число цифр в числе 10*, или число нулей в
числе 10*+1).
259

(п') Наложив произвольным образом фигуру S на
бумагу (рис. 147), осуществим мысленно параллельный
перенос всех клеток, частично ею занятых, на какую-
нибудь клетку ш. При этом занимаемые фигурой участки
могут частично налегать друг
на друга.
В ш обязательно найдется
точка А, не занятая
кусками фигуры S. Точки Л,,
Л„ ..., занимающие в
других клетках такое же
положение, какое Л занимает в со,
°4>. не будут заняты фигурой и
достаточно бумагу под 5
сдвинуть, поместив ее
узловые точки в точки, лежащие
под A, Alt Ах и т. д.
Рис 147.
("') Если даны точка А и две прямые /, и /s,
случайным образом расположенные в пространстве, то
можно, вообще говоря, провести прямую т,
проходящую через А и пересекающую прямые /, и 1Х (нельзя —
в исключительных случаях, когда /, \\1г и Л не лежит
h и 4); до<
в плоскости, проходящей через /,
достаточно
провести плоскости, проходящие через А и /, и
через А и 1г, которые пересекутся по искомой
прямой т.
Выбирая по-разному точку А на /„ мы получим
бесконечное множество прямых: тх, тг каждая из
которых будет пересекаться с прямыми /,, /,, /,.
Прямые ш,, тг, тш, ... образуют так называемую
линейчатую поверхность, с которой прямая /4
пересечется, вообще говоря, в некоторой точке В, лежащей
на какой-то прямой mt. Эта прямая и будет пересекаться
с прямыми llt /,, /„ /4.
("') Пусть /^—радиус окружности С^(0<в< 1000),
О — центр окружности С0 и От — центр окружности Ст
(К як 1000).
Радиусы окружностей С0, Ck, Ск+1 связаны
соотношением
(1)
260

(из треугольника ООкА (см. рис. 148) имеем: (R,-\-Rk)*-
-(#„
или x = 2VR„Ril\ аналогично, из
треугольников OOk+iB и OkOk+1C получим: х-\-у =
= 2}/"#0#А+1 и y = 2VRkRk+1; следовательно,
Выражая длины радиусов в километрах, будем иметь
R„=l, R1 = lO~t. По формуле (1) при £ = 1 получим:
ЫО"» 1
R,-
"(1-10-')2
99Э2
а при k = 2
o___L.fi LV__L
^» 9992" V 999; ~~998' *
Предположив, что
1
(1000 -/л+ 1)2'
1
(2)
■я- (переход от
по формуле (1) получим #«+i==uooo_m).
т к т-\-\), и так как формула (2) верна при т, равном
единице, то она верна при любом т, не превышающем
тысячи, так как при m=1000 она дает: #1000 = 1 и
окружность С1001 построена быть не может.
("*) Пусть направление луча т, «падающего» на
плоскость Оху, характеризуется единичным вектором
261

е=АО={ех, еу, ег) (в скобках указаны компоненты
вектора е, параллельные координатным осям). У луча /»',
отраженного от плоскости Оху (или от плоскости,
параллельной Оху), единичным вектором будет
е, = {ех, еу, —ех) — изменяется лишь знаку компоненты,
параллельной оси Oz (рис. 149).
У лучей от" и от"', получающихся после отражения
луча от' от плоскости, параллельной плоскости Oxz, и
луча от"— от плоскости, параллельной плоскости Oyz,
единичные векторы будут: et = (ex, —еу, —ег) и
е,=(— ех, — <?„, — еж). Следовательно, от" \\ от и
направление луча от противоположно направлению луча от.
("•) Компоненты а, р, у (параллельные ребрам
параллелепипеда) единичного вектора е(а, (3, у),
характеризующего искомое направление луча, при отражении от
граней параллелепипеда не изменяются по абсолютной
величине. Следовательно, при движении воображаемой
точки по «лучу падающему» и по всем отраженным
лучам, суммарные перемещения ее по направлению
каждой из осей Ox, Оу, Oz (считая
положительными перемещения и вверх, и вниз; и вправо, и влево;
и «к нам», и «от нас») будут пропорциональны
числам |<х|, |р|, I"Г 1-
Но к моменту возвращения точки — после отражения
от всех граней — в исходную точку эти суммарные
перемещения будут равны удвоенным длинам ребер: а, Ъ, с
параллелепипеда, следовательно, \а\:\ф\:\ч[==а:Ь:с,
т. е. луч света надо послать параллельно одной из
диагоналей параллелепипеда.
262

Решение задачи почти совсем не усложнится, если
ищется луч света, который, например, до
«возвращения» в исходную точку должен отразиться от левой, от
правой и от задней граней по три раза, от передней —
два раза, от нижней — четыре раза и от верхней — пять
раз. Попробуйте провести соответствующие
рассуждения, считая расстояния исходной точки от левой, от
передней и от нижней граней параллелепипеда
равными а', Ь', с'.
('*') Очевидное решение: А — северный полюс; менее
очевидные решения: А — любая точка в южном
полушарии, лежащая на параллели /', находящейся на
2000 км севернее параллели /, длина которой равна
км (п — любое натуральное число).
('") Так как самолет пролетел а км на восток, а
оказался в итоге на За км восточнее Ленинграда, то
он летел на восток по «параллели <р», радиус которой г,
в три раза меньше радиуса г ленинградской параллели
ff
Рис. 150.
(60° северной широты); следовательно, #cos<p = r,=
==^==^с^602==^ откуда <? = 80°30' (на рис. 150 дана
проекция северного полушария на плоскость,
параллельную оси земного шара). Следовательно, а — длина
дуги меридиана между «параллелью 60°» и «параллелью
anoo/Y ~ ^ „ 40 000 км -20,5 o07Q
оО oU », т. е. а = ogfj = !"/о км.
('") Надо учесть, что сумма углов сферического
треугольника ABC всегда больше 180° и площадь его
263

вычисляется по формуле
где а, р, у — значения углов А, В, С, выраженных в
радианах.
В самом деле, если продолжить ту или иную пару
сторон сферического треугольника ABC (см. рис. 151),
Рис. 151. Рис. 152.
то получатся «сферические двуугольники»: ABA'С А,
ВАВ'СВ, САСВС, площади поверхностей которых
5авл'сл=4гс/?2.^, (1)
Sbab'cb = ^R2-^ (2)
И
Scacbc=Sabc -f- Sabc = 4тг/?*. — .
Если в последнем равенстве заменить Sabc на Sa>b'c,
то получим:
Sabc + Sa>b>c= W.i (3)
(стороны сферических треугольников ABC и А'В'С
попарно одинаковы и хотя эти треугольники не могут,
вообще говоря, быть совмещены при наложении, но
можно доказать, что Sa>b'c = Sabc)-
264

Складывая почленно равенства (1), (2), (3), получим:
откуда
Например, у треугольника DEF, образованного дугами
DE и DF двух меридианов, пересекающихся под
прямым углом, и дугой экватора EF, каждый из углов
равен -^-. Следовательно, SDEF= (у + у+T"wrr) #*=~2~
(как раз одна восьмая площади поверхности всего шара).
("*) Так как радиус земного шара /? ч= 6370 км, а
площадь данного сферического треугольника ABC—
-l/"-n
— ^ = 1_ км*, то, положив /_А = /_В — /_С=ъ
радианов, получим (см. предыдущее примечание):
s "V з
За — тг = -— g= . 6„7Qi рад. Умножая правую часть на
180 ■ 60 ■ 60 , . , г.
для перевода в секунды, получим: /_ А = Z. В =
= 2с^60°0'0",0007.
('") На рис. 152 даны три способа сцепления трех
веревочных колец; первые два способа легко могут
быть использованы и для сцепления п колец, при
котором, разорвав любое кольцо, остальные кольца можно
разъединить без дополнительных разрывов.

ЛИТЕРАТУРА
1. Арене В., Математические игры и развлечения, 1924.
2. Арнольд И. В., Теория чисел, 1939.
3. Б а р л о у, Таблицы квадратов, кубов, корней квадратных, корней
кубичных и обратных величин целых чисел от 1 до 10 000, 1931.
4. Берман Г. п., Циклоида, 1948.
5. Болтянский В. Г., Равновеликие и равносоставлеиные
фигуры, 1956.
6. Бобров С, Волшебный двурог, 1948.
7. Воробьев Н. Н., Числа Фибоначчи, 1951.
8. Гильберт Д. и Кон-Фоссен С, Наглядная геометрия, 1951.
9. Доморяд А. П-, Численные и графические методы решения
уравнений (Энц. Элем. Математики, кн. Н, 1951).
10. Доморяд А. П., Счетные приспособления (Детская
Энциклопедия, т. 3, 1959).
11. Доморяд А. П., О вычислении логарифмов (Уч. зап. Ташкент,
гос. пед, института, вып. VII, 1957).
12. Житомирский О. К- и др., Задачник по высшей геометрии,
ч. I, 1935.
13. Кордемский Б. А., Математическая смекалка, 1954.
14. К о р д е м с к и й Б. А. и Р у с а л ев Н. В., Удивительный
квадрат, 1952.
15. Лит ИМ а и В., Великаны и карлики в мире чисел, 1959.
16. Лурье С. Я-, Архимед, 1945.
17. М а р к у ш е в и ч А. И., Возвратные последовательности, 1951.
18. Меннхеи Ф., Некоторые тайны артистов-вычислителей, 1923.
19. О б р е и м о в В. И., Тройная головоломка, 1884.
20. Окунев Л. Я., Высшая алгебра, 1949.
21. Окунев Л. Я., Комбинаторные задачи иа шахматной доске,
1935.
22. П е р е л ь м а н Я. И., Занимательная алгебра.
23. Перепелкин Д. И., Курс элементарной геометрии, ч. I.
24. радемахерГ. и Теплиц О., Числа и фигуры, 1936.
25. У с п е и с к и и Я., Избранные математические развлечения, 1924.
26. Фихтенгольц Г. М., Курс дифференциального и
интегрального исчисления, т. II, 1948.
27. Фихтенгол ьц Г. М., Математика для инженеров, т. I, 1931.
28. X и и ч и н А. Я., Цепные дроби, 1935.
29. ШклярскиЙ Д. О. и др., Избранные задачи и теоремы
элементарной математики, ч. I — Арифметика и алгебра, 1950.
266

30. Ш у б е р т Г., Математические игры и развлечения, 1923.
31. Шубников А. В., Симметрия, 1940.
32. Я г л о м А. М. и Я г л о м И. М., Неэлемеитариые задачи в
элементарном изложении, 1954.
33. A h г е n s W., Mathematische Unterhaltungen, Bd. I, II.
34. A h r e n s W., Altes und neues aus der Unterhaltungsmathematlk,
1918.
35. Mi tr in о vie D. S., Zbornik matematickin problema, I, 1957.
Журналы и сборники
36. Математика в школе.
37. Математическое образование.
38. Математическое просвещение (1934—1938 гг.).
39. The American Mathematical Monthly.

Александр Петрович Доморяд.
Математические игры и развлечения.
Редактор А. Н. Копылова.
Техн. редактор Н. #. Мурашова.
Корректор JI. О. Сечейко.
Сдано в набор 26/IX 1960 г. Подписано
к печати 14/XII 1960г. Бумага 84x108V,,.
Физ. печ. л. 8,375. Условн. печ. л. 13,74.
Уч.-изд. я. 12v82. Тираж 200 000 9кз.
Т.15024. Цена книги 39 коп. Заказ № 979.
Государственное издательство
физико-математической литературы.
Москва, B-7I, Ленинский проспект, 15.
Первая Образцовая типография
имени А. А. Жданова
Московского городского Совнархоза.
Москва, Ж-54, Валовая, 28.