Автор: Порублев И.Н. Ставровский А.Б.
Теги: компьютерные технологии программирование алгоритмы задачи по программированию
ISBN: 978-5-8459-1244-2
Год: 2007
Текст
Предисловие 13
От издательства "Диалектика" 15
Глава 1. Разминка (понемногу о разном) 17
1.1. Три простые задачи 17
1.1.1. Совпадения стрелок часов 17
1.1.2. Последовательности с одинаковыми суммами 18
1.1.3. Ребус 19
1.2. Знакомство со сложностью алгоритмов 23
1.2.1. Простые и составные числа 23
1.2.2. Понятие сложности алгоритма 25
1.2.3. Характер возрастания сложности 27
1.2.4. Алгоритм Евклида и его современная версия 28
1.2.5. Бинарный алгоритм 29
1.2.6. Понятие сложности задачи 30
1.2.7. Что выбирать? 31
1.3. Несколько технических вопросов 31
1.3.1. Проектирование сверху вниз, подпрограммы
и структурное кодирование 31
1.3.2. Когда уместны безусловные переходы 32
1.3.3. Несколько замечаний о стиле 34
1.3.4. Отладка программы 35
1.3.5. Директивы компилятору 37
1.3.6. Проверка программы 38
1.4. Ввод последовательностей данных 40
1.4.1. Организация данных и вид цикла ввода 40
1.4.2. Изменение источника данных 43
Упражнения 44
Глава 2. Однопроходные алгоритмы 47
2.1. Попутные вычисления 47
2.1.1. Три простых примера 47
2.1.2. Максимальная сумма отрезка числовой последовательности 49
2.1.3. Инопланетная армия 50
2.1.4. Стрельба из двуствольной пушки 53
2.2. Чтение и обработка символов 55
2.2.1. Удаление пробелов 55
2.2.2. Удаление комментариев 57
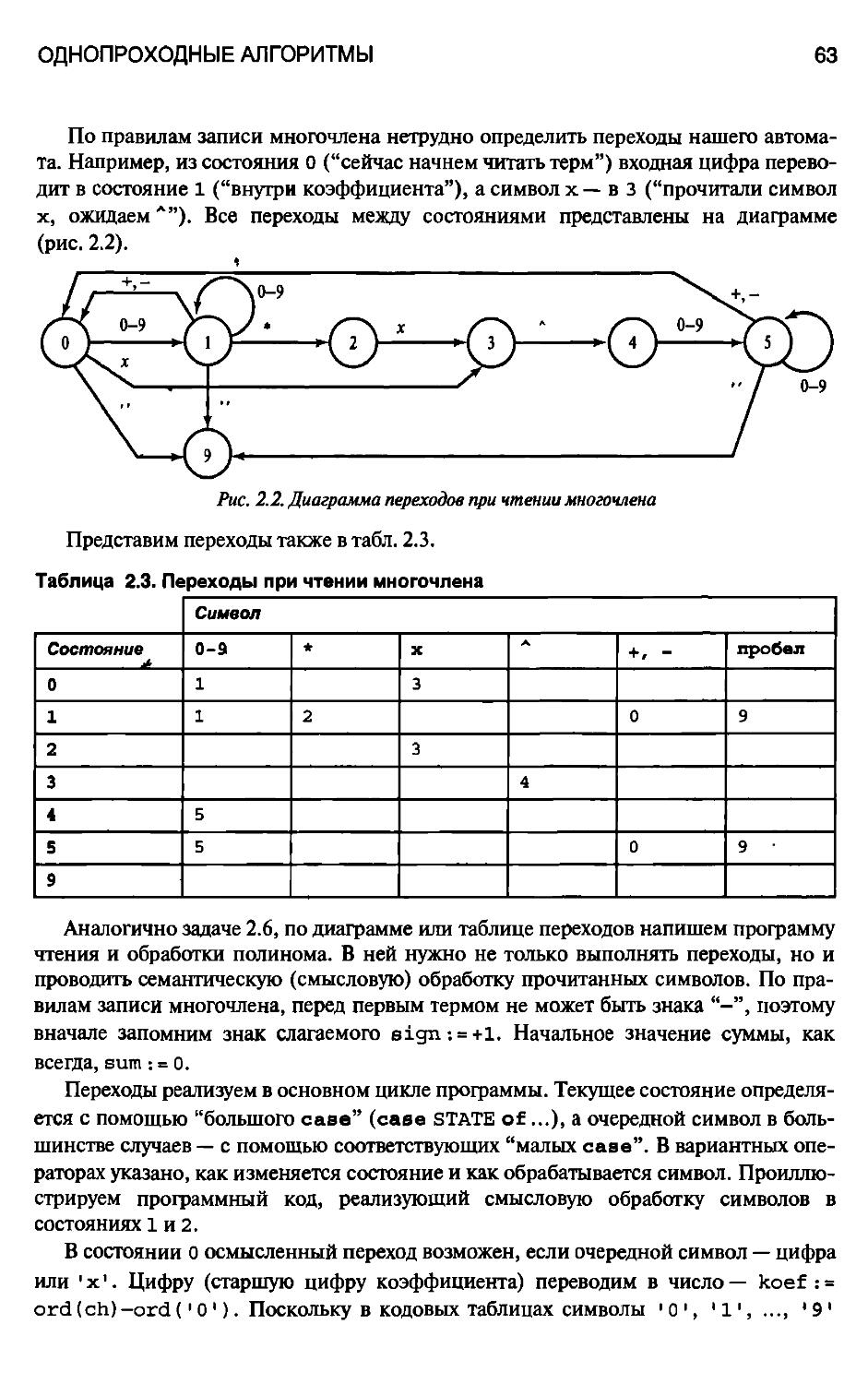
2.2.3. Чтение и вычисление многочлена 59
2.2.4. Языки скобок 67
2.2.5. Линейный поиск подстроки в тексте 72
Упражнения 76
Глава 3. Рекурсия 79
3.1. Основные понятия 79
3.1.1. Рекурсивные определения 79
3.1.2. Простейший пример рекурсивной подпрограммы 80
3.1.3. Глубина рекурсии и общее количество рекурсивных вызовов 81
3.1.4. Косвенная рекурсия 83
3.2. Быстрое возведение в степень 85
3.3. Рисование самоподобных ломаных 88
3.3.1. Снежинка Коха 89
3.3.2. Треугольник Серпиньского 90
3.3.3. Драконова ломаная 93
Упражнения 95
Глава 4. Нестандартная обработка чисел 97
4.1. Длинная целочисленная арифметика 97
4.1.1. Представление длинных чисел 98
4.1.2. Сравнение, сложение и вычитание длинных целых 100
4.1.3. Организация ввода-вывода 102
4.1.4. Умножение длинных целых 103
4.1.5. Деление длинных целых 105
4.1.6. Целая часть квадратного корня длинного числа 107
4.2. Два магических числа 109
4.2.1. Число е 109
4.2.2. Число PI 112
4.3. Остатки от деления 112
4.3.1. Плиты в треугольнике 113
4.3.2. Кратное число с одинаковыми цифрами 115
4.4. Отслеживание циклических повторений 116
4.4.1. Десятичное представление дроби и RO-алгоритм 116
4.4.2. Остатки от деления чисел Фибоначчи 119
4.5. Нули в конце факториала 121
Упражнения 124
Глава 5. Бинарный поиск, слияние и сортировка 127
5.1. Бинарный поиск 127
5.1.1. Идея бинарного поиска 127
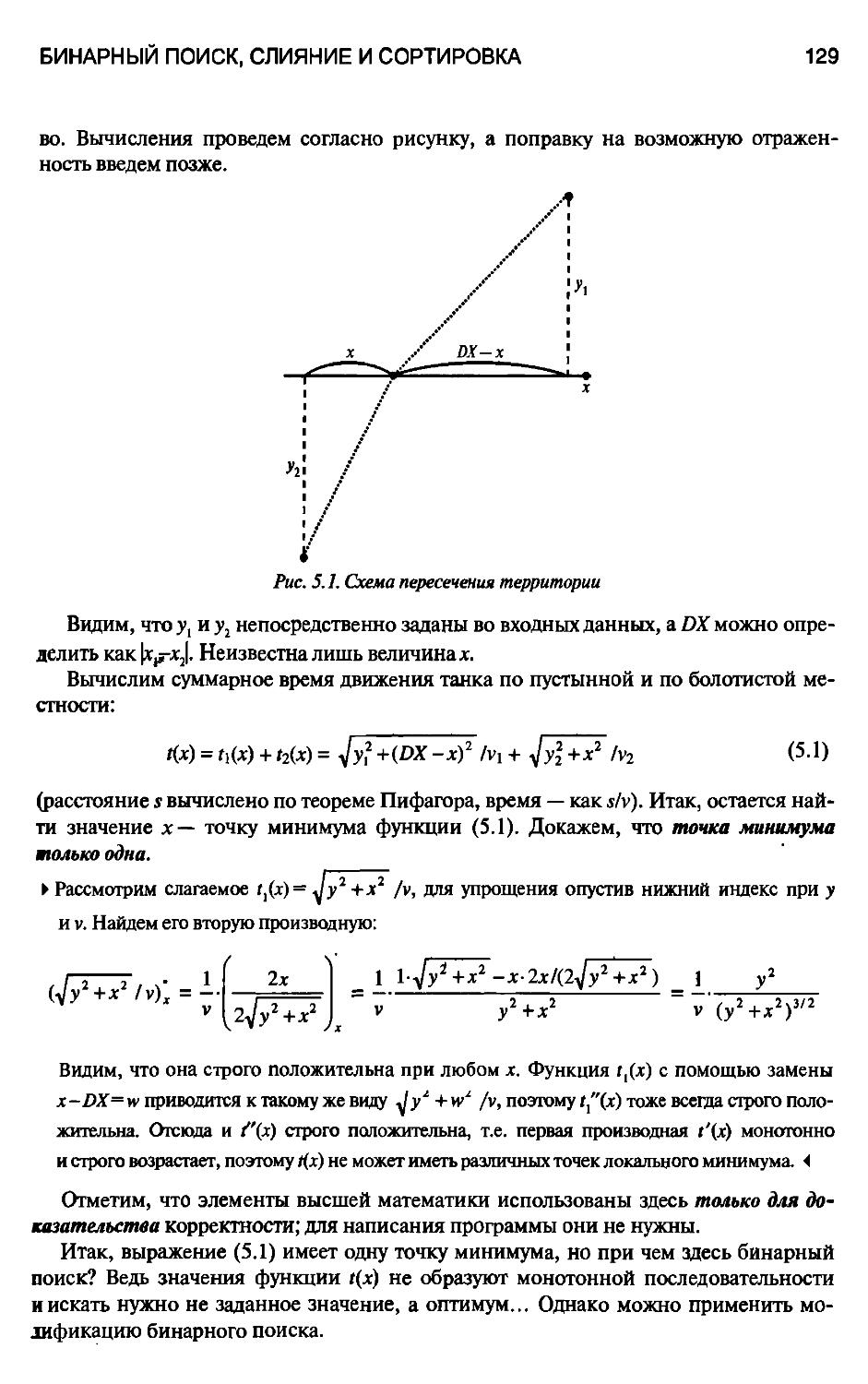
5.1.2. "Оптический танк" 128
5.2. Слияние упорядоченных последовательностей 130
5.2.1. Слияние двух участков массива 130
5.2.2. Слияние файлов 131
5.3. Основные способы сортировки 135
5.3.1. Два простейших алгоритма 135
5.3.2. Сортировка слиянием 137
5.3.3. Быстрая сортировка 140
5.3.4. Пирамидальная сортировка 142
5.3.5. Линейная сортировка подсчетом 145
5.3.6. Поразрядная сортировка 148
5.4. Применение сортировки 150
5.4.1. Проверка уникальности 150
5.4.2. Проход в заборе 151
5.4.3. Транзитивность 153
Упражнения 154
Глава 6. Вычислительная геометрия на плоскости 159
6.1. Точки, векторы, прямые, отрезки 159
6.1.1. Точки, векторы, углы и ориентированная площадь 159
6.1.2. Представление прямых и отрезков 162
6.1.3. Взаимное расположение прямых, отрезков и точек 164
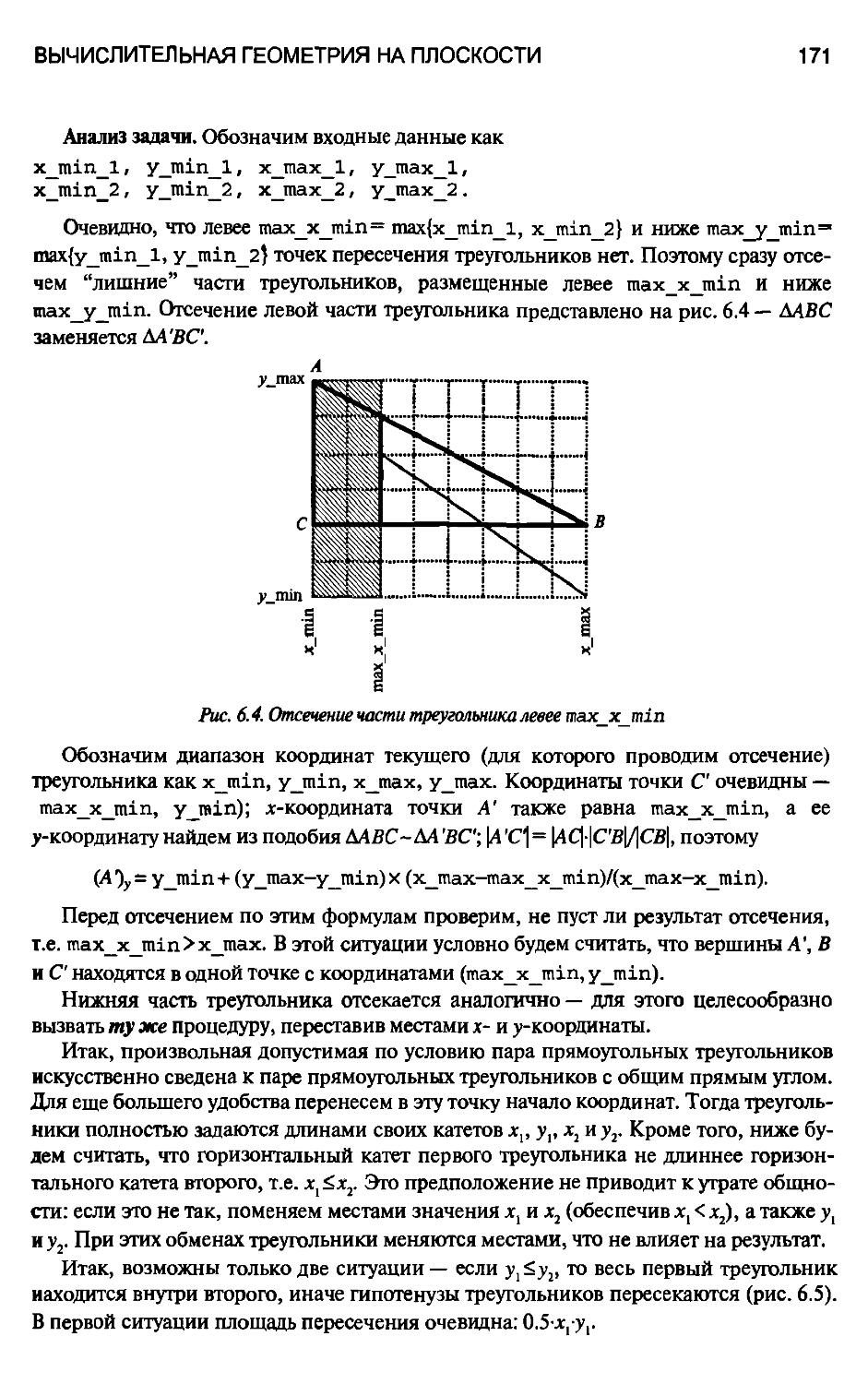
6.1.4. Две задачи о треугольниках 169
6.2. Многоугольники (полигоны) 173
6.2.1. Основные определения 173
6.2.2. Площадь полигона 174
6.2.3. Принадлежность точки полигону 176
6.2.4. Принадлежность точки выпуклому полигону 177
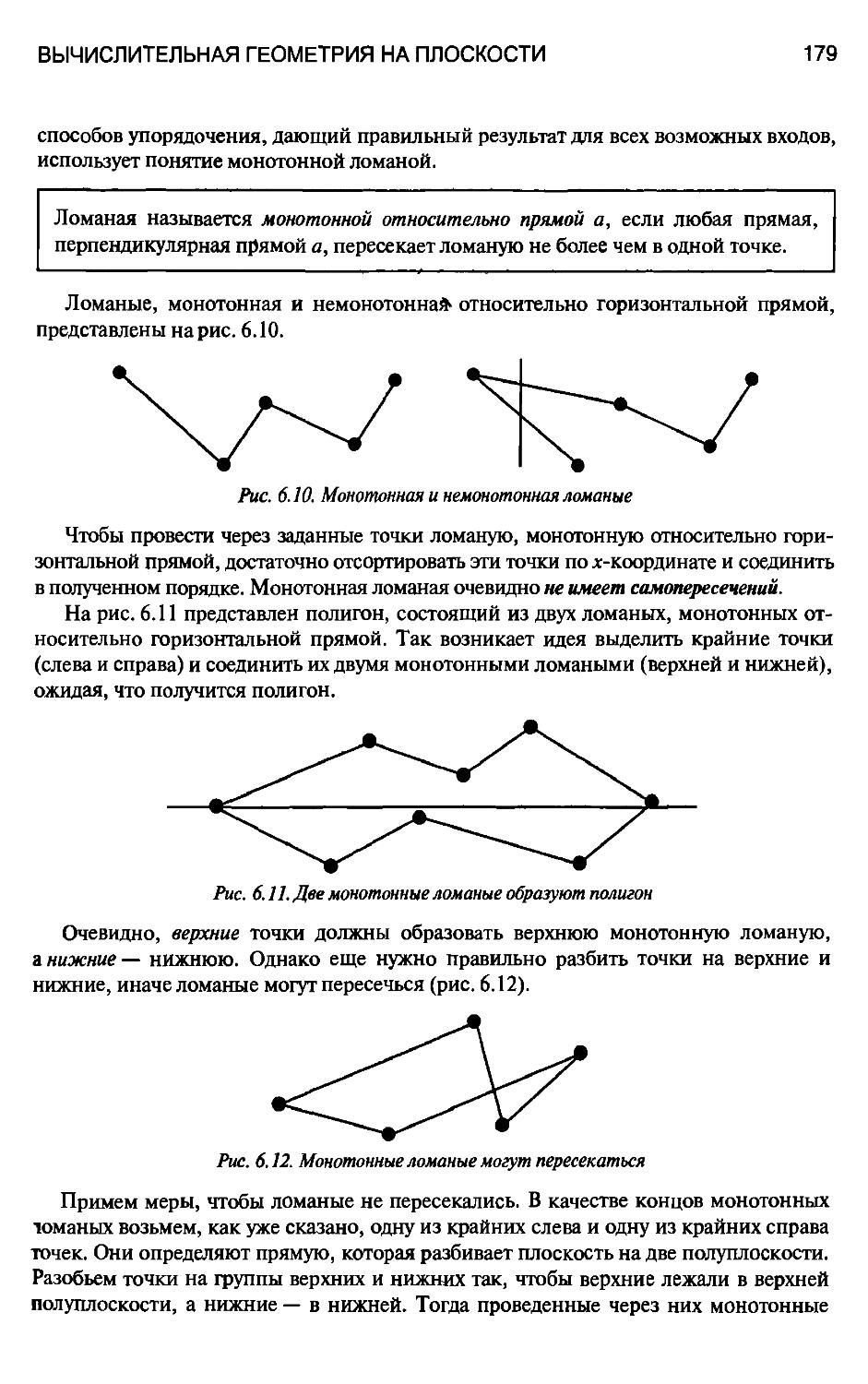
6.2.5. Построение полигонов 178
6.2.6. Сумма и разность полигонов 182
6.3. Окружности и круги 185
6.3.1. Прямая и круг 185
6.3.2. Отрезок и окружность 186
6.3.3. Общие касательные 187
6.3.4. Пересечение двух кругов 188
Упражнения 191
Глава 7. Выметание 195
7.1. Интернет-провайдер 195
7.2. Мера объединения отрезков 199
7.3. Линия горизонта 201
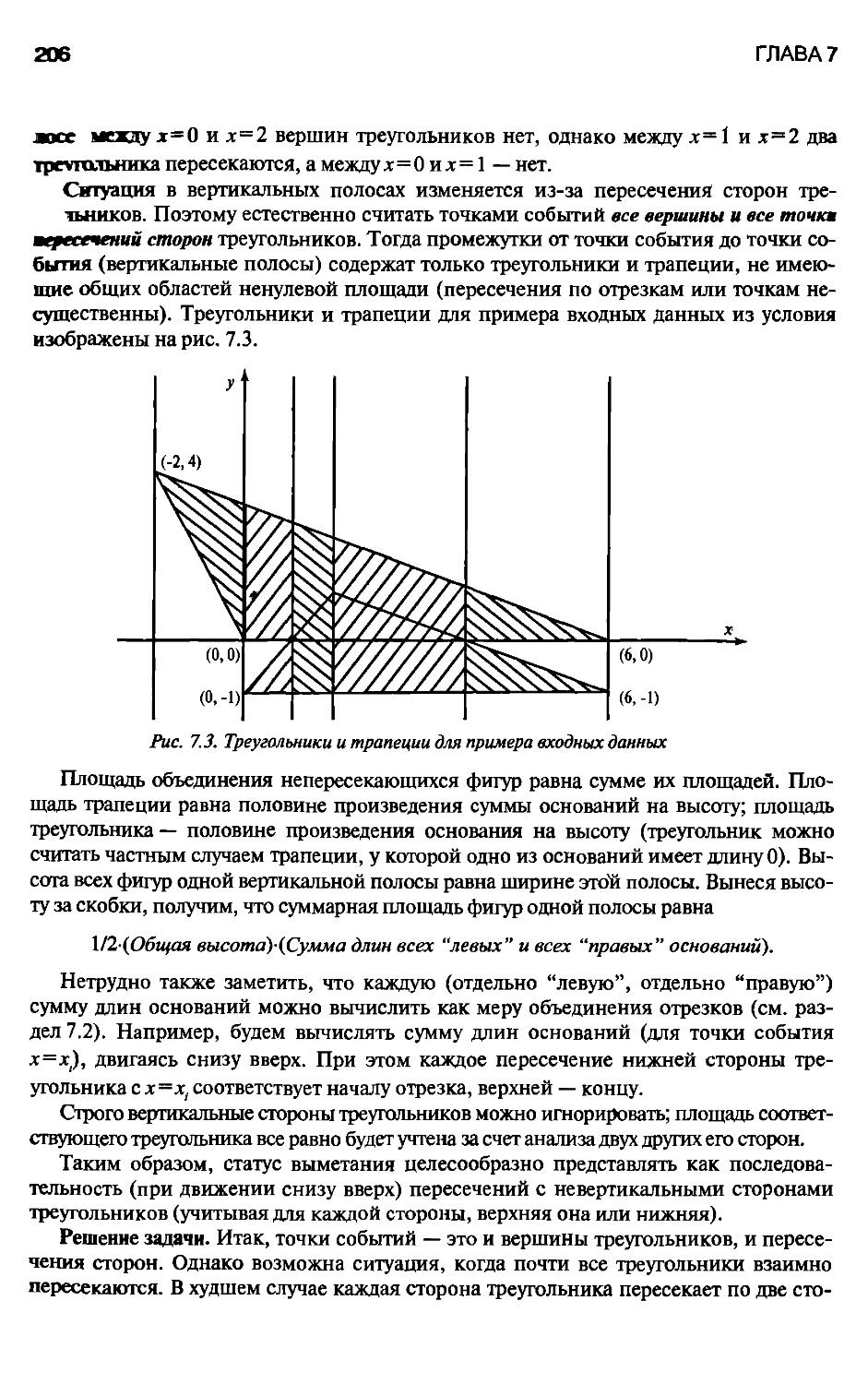
7.4. Мера объединения треугольников 205
Упражнения 209
Глава 8. Графы 211
8.1. Графы и способы их представления 211
8.1.1. Неориентированные графы: основные понятия 211
8.1.2. Ориентированные графы 213
8.1.3. Представления графа 214
8.1.4. Пример: задача о центре дерева 215
8.2. Алгоритмы обхода графов 221
8.2.1. Обход в глубину 221
8.2.2. Обход в ширину 224
8.2.3. Реализация очереди 225
8.3. Применение алгоритмов обхода 226
8.3.1. Построение остовного дерева и остовного леса 226
8.3.2. Расстояния между вершинами 228
8.3.3. Проверка ацикличности и топологическая сортировка
ациклического орграфа 230
8.3.4. Эйлеровы циклы и цепи 233
8.3.5. Обход графа достижимых состояний 236
Упражнения 240
Глава 9. Графы клеток и графы с нагруженными ребрами 243
9.1. Графы на клетчатых полях 243
9.1.1. Фигуры на клетчатом поле 243
9.1.2. Минимальный путь в лабиринте 246
9.1.3. Подсчет клеток в областях 252
9.2. Остовное дерево минимального веса 258
9.3. Алгоритм Дейкстры и его применение 261
9.3.1. Задача с одним источником и положительным весом ребер 261
9.3.2. Максимальный груз 264
9.3.3. Зал Круглых Столов 265
9.4. Скоростная алхимия 270
Упражнения 274
Глава 10. Комбинаторика 279
10.1. "Амебы" комбинаторики 280
10.1.1. Правила суммы и произведения 280
10.1.2. Перестановки, размещения и сочетания без повторений 281
10.1.3. Перестановки, размещения и сочетания с повторениями 282
10.1.4. Размещения и сочетания как отображения 284
10.1.5. Биномиальные коэффициенты 285
10.2. Рекуррентные соотношения и таблицы 286
10.2.1. Пути в квадратных кварталах 286
10.2.2. Правильные скобочные выражения 288
10.2.3. Счастливые билеты 289
10.2.4. Белые и черные кубики 292
10.2.5. Велосипедные гонки 295
10.3. Рекурсия в задаче о русском лото 296
10.4. Включения и исключения 299
10.4.1. Принцип включений и исключений 299
10.4.2. "Батарея, огонь!" 301
10.4.3. Беспорядок в шляпах 303
10.5. Количество раскладок и разбиений 304
10.5.1. Разбиения множества 304
10.5.2. Разбиения множества с учетом порядка классов 305
10.5.3. Разбиения числа на слагаемые 306
Упражнения 307
Глава 11. Перебор вариантов 309
11.1. Порождение подмножеств 309
11.1.1. Все подмножества 309
11.1.2. Подмножества с заданным числом элементов 313
11.2. Порождение последовательностей 315
11.2.1. Размещения ферзей 315
11.2.2. Дерево размещений и его обход 317
11.2.3. Обход дерева с помощью магазина 318
11.2.4. Порождение всех перестановок 320
11.3. Попытки сократить перебор 322
11.3.1. Подмножества положительных чисел с заданной суммой 323
11.3.2. Псевдополиномиальный приближенный алгоритм
поиска подмножества 324
11.3.3. Идея метода ветвей и границ в задаче коммивояжера 325
11.3.4. Решение задачи коммивояжера методом ветвей и границ 326
11.3.5. Упрощенный алгоритм 327
11.4. Послесловие 328
Упражнения 329
Глава 12. Жадные алгоритмы 333
12.1. Знакомство с жадными алгоритмами 333
12.1.1. Быстрый выбор упорядоченных вариантов 333
12.1.2. Сортировка и выбор в динамическом множестве 335
12.1.3. Понятие жадного алгоритма 338
12.2. Матроиды и жадные алгоритмы 339
12.2.1. Понятие матроида 339
12.2.2. Жадный поиск допустимого подмножества с максимальным весом 340
12.2.3. Взвешенный матроид и жадный алгоритм 340
12.2.4. Матричный матроид 341
12.3. Некорректная "жадность" вместо перебора 342
12.3.1. Поспешная укладка рюкзака 342
12.3.2. Распределение заданий 343
Упражнения 344
Глава 13. Динамическое программирование 347
13.1. Принцип оптимальности 347
13.1.1. Путь по клеткам с максимальной суммой 347
13.1.2. Общие замечания по методологии динамического программирования 351
13.1.3. Количество путей с суммой, близкой к максимальной 353
13.2. Монотонная подпоследовательность 358
13.2.1. Поиск монотонной подпоследовательности 358
13.2.2. Бинарный поиск начала подпоследовательности 362
13.2.3. Вложенные коробки 365
13.3. Табличная техника и рекурсия с запоминанием 366
13.3.1. Расстановка скобок в произведении матриц 366
13.3.2. Минимальное количество монет 372
13.3.3. Разбиение алфавита 374
13.3.4. Абзац с блоками разной высоты 376
13.3.5. Максимальное значение выражения 378
13.3.6. Вычеркивание из строки 381
Упражнения 383
Глава 14. Игры двух лиц 387
14.1. Анализ позиций и выбор хода 388
14.1.1. Выигрышные и проигрышные позиции 388
14.1.2. Золотое сечение 390
14.1.3. Ним 394
14.1.4. Таблица ходов 397
14.2. Оценивание позиций: максимальная сумма 398
Упражнения 399
Глава 15. Японский кроссворд 403
15.1. Итерационный анализ линий 403
15.1.1. Постановка задачи и основные идеи решения 403
15.1.2. Ввод, вывод и основные структуры данных 407
15.1.3. Реализация итерационного анализа линий 409
15.2. Анализ линии на основе конечного автомата 410
15.2.1. Описание линии в виде конечного автомата 410
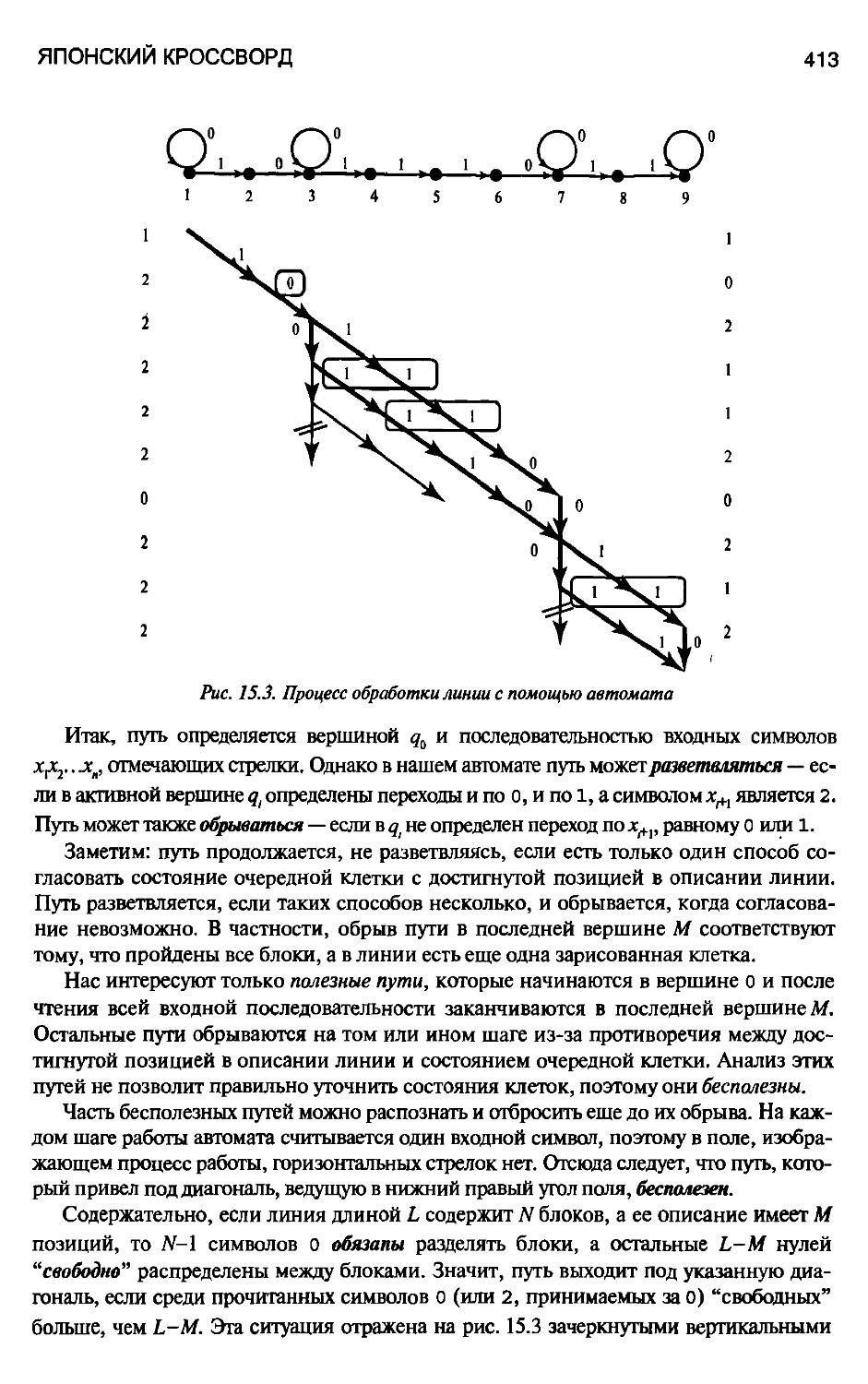
15.2.2. Обработка линии и уточнение клеток 412
15.2.3. Реализация 414
15.3. Решение задачи с помощью перебора 419
15.3.1. Итерационный анализ линий не решает задачу 419
15.3.2. Перебор и исследование состояний клеток с помощью ИАЛ 421
15.3.3. Решение задачи и анализ решения 423
Приложение А. Указания по решению упражнений 427
Глава 1 427
Глава 2 429
Глава 3 431
Глава 4 433
Глава 5 436
Глава 6 440
Глава 7 442
Глава 8 443
Глава 9 446
Глава 10 450
Глава 11 455
Глава 12 459
Глава 13 461
Глава 14 464
Список литературы 469
Предметный указатель 471
#
/>-алгоритм, 117
А
Алгоритм
возведения в степень, 86
индийский, 87
Гаусса, 342
Дейкстры, 262
динамического
программирования, 353
Евклида, 29
жадный, 338; 340
Краскала, 260
недетерминированный, 328
обхода
графа в глубину, 222; 223
дерева поиска, 318
связного графа
в глубину, 221
в ширину, 224
однопроходный, 47
поиска
зацикливания, 117
логарифмический, 127
полиномиальный, 28
приближенный, 324
Прима, 259
псевдополиномиальный, 28; 324;
373
сортировки
быстрый, 140
выбором,136
деревом, 142
пирамидальный, 142
пузырьком, 136
слиянием,137
Флойда-Уоршалла, 229
числовой волны, 247
экспоненциальный, 28
Арифметика
длинная
дробная, 110
целая, 98
Б
Бином Ньютона, 285
Биномиальные коэффициенты, 285
В
Вектор, 160
Выметание, 196
Вычисление булевых выражений
полное и сокращенное, 37
Г
Глубина рекурсии, 81
Граф, 211
ориентированный, 213
ациклический, 230
эйлеров, 234
Графика, 88
черепашья, 88
д
Действие элементарное, 25
Дерево, 213
остовное, 213; 227
минимального веса, 258
сортирующее, 142
Динамическое программирование,
353
Директива компилятору, 37
Директивы компилятору, 37; 67
Дробь
длинная, 110
представление
с плавающей точкой, 110
с фиксированной точкой, 110
3
Задача
NP-полная, 328
коммивояжера, 325
о выпуклой оболочке, 180
о вычеркивании из строки, 381
о кенигсбергских мостах, 234
о количестве
правильных скобочных
выражений, 288
о количестве сюръекций, 305
о коробках, 365
о кратчайших путях в графе, 262
о максимальном
грузе, 264
значении выражения, 378
о минимальном числе монет, 344;
372
о площади полигона, 174
о подмножествах, 309; 313
о подмножестве, 323; 324; 329
о подпоследовательности, 359; 365
о почтовых марках, 331
о разбиении
алфавита, 374
множества, 304
числа, 306
о размещении ферзей, 315
о расстановке скобок, 366
о русском лото, 296
о сокровищнице, 347; 353
о счастливых билетах, 289
о триангуляции выпуклого
многоугольника, 384
о центре дерева, 215
о черных и белых кубиках, 292
об абзаце с блоками разной
высоты, 376
об инверсиях, 303
об остовном дереве минимального
веса, 258
об укладке рюкзака, 331; 343
поиска подстроки, 72
с одним источником, 261
топологической сортировки, 232
труднорешаемая, 328
факторизации, 24
Золотое сечение, 393
И
Игра Ним, 395
К
Код Грея, 312
Конечный автомат, 57; 411
Конструкция forward, 84
Л
Лексический анализ, 62
м
Маршрут
в графе, 212
в орграфе, 213
Матрица, 367
оптимизация умножений, 367
смежности, 214
Матроид, 339
взвешенный, 340
Метод
ветвей и границ, 326
выметания, 196
Кнута-Морриса-Пратта, 72
минимакса, 399
Многоугольник, 173
Множество
тип данных, 23
частично упорядоченное, 80
Монотонная ломаная, 179
н
Направление поворота, 161
О
Обратный ход, 249; 349; 370
Обход
графа
в глубину, 221
в ширину, 224
дерева
в глубину, 317
Определение
рекурсивное, 79
Отображение, 305
Оценка
позиции,399
функции,26
Очередь, 224
с приоритетами, 272
п
Перебор
с возвращениями, 317
сокращение, 20
Перестановка, 281; 303
с повторениями, 283
Площадь
полигона, 174
Подзадачи
аналогичной структуры, 352
независимые, 352
оптимальные, 352
перекрывающиеся, 352
тривиальные, 352
Подпоследовательность, 359
Подпрограмма
рекурсивная, 80
Подстановка, 308
Позиция в игре
выигрышная, 389
проигрышная, 389
Поиск
в графе, 221
дихотомический, 127
логарифмический, 128
Полигон, 173
Порядок
лексикографический, 148
Правило
произведения, 280
суммы, 280
Принцип
включений и исключений, 299
Дирихле, 42
оптимальности динамического
программирования, 352; 353
сокращения перебора с помощью
ограничений, 20
Прямая, 162
Псевдокод, 32
Р
Разбиение
множества, 304
числа, 306
Размер экземпляра задачи, 25
Размещение, 281
с повторениями, 282
Разность Минковского, 184
Расстояние, 160
от точки до прямой, 165
Рекурсия, 79
косвенная, 84; 381
прямая, 84
с запоминанием, 353; 370; 425
С
Самоподобная ломаная, 88
Синтаксический анализ, 62
Скалярное произведение векторов, 161
Скобочные выражения
оптимальная расстановка скобок,
367; 378
Слияние упорядоченных
последовательностей, 130
Сложность
алгоритма, 26
задачи, 30
полиномиальная, 28
Снежинка Коха, 89
Событие
в методе выметания, 196
Сортировка
массива
быстрая, 140
выбором, 136
деревом, 142
пирамидальная, 142
пузырьковая, 136
слиянием, 130; 138
подсчетом, 146
поразрядная, 148
топологическая, 232; 366
устойчивая, 140
цифровая, 148
Состав, 283
Сочетание, 281
с повторениями, 283
Список
ребер, 214
Средства отладки, 64
Статус выметания, 197
Структура смежности, 214
Сумма Минковского, 184
Сюръекция, 305
т
Табличная техника, 368
динамического
программирования, 352
Тождество
Вандермонда, 286
Коши, 286
Точка плоскости, 160
Точки событий, 196
Транзитивное замыкание, 241
Треугольник
Паскаля, 285
Серпиньского, 90
Треугольные числа, 286
Триангуляция, 269
выпуклого многоугольника, 384
Делоне, 269
У
Умножение матриц, 366
Уравнение прямой, 162
Условная компиляция, 67
Ф
Формула
включений и исключений, 300
ориентированной площади, 161
Функция
91 Мак-Карта, 95
возвратов, 73
ц
Цепь
эйлерова, 236
Цикл, 212
гамильтонов, 325
подстановки, 308
эйлеров, 234
ч
Числа
Фибоначчи, 119; 393; 450; 451
Число
Белла, 304
Каталана, 289
простое, 23
составное, 23
Стерлинга второго рода, 304
Я
Японский кроссворд, 403