/
Текст
П.Л.ЛЕБЕЛЕВ •
•г - Bi , • -
•i
*
I
ТЕПЛООБМЕННЫЕ;
СУШИЛЬНЫЕ
И ХОЛОДИЛЬНЫЕ»
УСТАНОВКИ
П. Д. ЛЕБЕДЕВ
С.О'
JVVb
ТЕПЛООБМЕННЫЕ,
СУШИЛЬНЫЕ
И ХОЛОДИЛЬНЫЕ
УСТАНОВКИ
(ТЕПЛОМАССООБМЕННЫЕ
И ХОЛОДИЛЬНЫЕ УСТАНОВКИ)
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебника для специальности «Промышленная теплоэнергетика»
высших учебных заведений
USX
«ЭНЕРГИЯ» • МОСКВА 1972
6П2.2
Л 33
УДК 66.045 (075.8) +621.565(075.8)
Лебедев П.Д.
Л 33 Теплообменные, сушильные и холодильные уста-
новки. Учебник для студентов технических вузов.
Изд. 2-е, перераб. М„ «Энергия», 1972.
Книга состоит из двух разделов. В первом рассмотрены процессы
тепло- и массообмена в различных промышленных теплообменных
аппаратах, выпарных, ректификационных н сушильных установках.
Приведены основные типы, конструкции и схемы этих устройств и да-
ны некоторые методы и примеры нх теплового, гидравлического и ме-
ханического расчетов. Рассмотрено вспомогательное оборудование —
ковденсатоотводчнкн и конденсационные устройства и коэффициенты
совершенства теплообменных аппаратов и теплой спользующнх уста-
новок.
Второй раздел книги посвящен рассмотрению основных типов и
конструкций компрессионных, абсорбционных и пароэжекторных холо-
дильных установок и трансформаторов тепла, указаны области их
применения, приведены основные уравнения н даны примеры их термо-
динамиечского и конструктивного расчета.
Книга соответствует программе курса «Тепломассообменные и хо-
лодильные установки» н предназначена в качестве учебника для сту-
дентов технических вузов по специальности «Промышленная тепло-
энергетика». Она может служить пособием для инженеров и техников,
работающих в области проектирования и эксплуатации промышленных
теплоиспользующнх установок.
3-3-2
6П2.2
ПАНТЕЛЕЙМОН ДМИТРИЕВИЧ ЛЕБЕДЕВ
ТЕПЛООБМЕННЫЕ, СУШИЛЬНЫЕ И ХОЛОДИЛЬНЫЕ УСТАНОВКИ
Редактор В. А. Ефимов
Редактор издательства Л. И. Синельникова
Переплет художника В. И. Карпова
Технический редактор Т. Н. Хромова
Корректор Г. Г. Желтова
Сдано в набор 24/Ш 1972 г. Подписано к печати 27/IX 1972 г. Т-15961
Формат 70Х108V16 Бумага типографская Ьэ 2
Усл. печ. л. 28 Уч.-изд. л. 28,14
Тираж 25 000 экз. Зак. 1128 Цена 1 р. 14 к.
Издательство „Энергия*. Москва, М-114, Шлюзовая наб., 10.
Московская типография № 10 Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Шлюзовая наб., 10.
ПРЕДИСЛОВИЕ
В создание и развитие промышленных тепло- и массообменных ус-
тановок большой вклад внесли отечественные ученые. Благодаря выда-
ющимся работам Д. И. Менделеева и В. В. Морковникова были впер-
вые созданы непрерывно действующие кубовые ректификационные ко-
лонны, что обеспечило нефтеперерабатывающей промышленности Рос-
сии до 1900 г. ведущее место в мире. В 1800 г. в Петербурге впервые
в мировой практике получила применение искусственная сушка под
вакуумом. В 1872 г. И. В. Булыгиным была построена высокоэффектив-
ная лесосушилка на перегретом паре с рециркуляцией сушильного
агента и т. п.
Особенно большой научно-технический прогресс в нашей стране
начался после Великой Октябрьской революции. Подробно с развити-
ем отечественных теплоиспользующих и холодильных установок можно
познакомиться в статье автора в I т. Истории энергетической техники
СССР (Госэнергоиздат, 1957).
Научно-технический прогресс потребовал дальнейшего совершенст-
вования промышленных тепло- и массообменных установок. Благодаря
научным трудам И. А. Тищенко, А. Г. Касаткина, М. А. Кичигина,
А. В. Лыкова, Н. И. Гельперина, А. Н. Плановского, Г. К. Филоненко,
П. Г. Романкова, В. В. Кафарова, И. И. Чернобыльского, Г. Н. Костен-
ко и др. и совмеЛной работе научных сотрудников и инженерно-тех-
нического персонала многих научных учреждений, вузов, конструктор-
ских бюро, проектных организаций и заводов в нашей стране создано
большое количество высокопроизводительных и высокоэкономичных
сушильных, ректификационных, выпарных установок и трансформато-
ров тепла, превосходящих по своим показателям лучшие зарубежные
устройства. ।
В нашей стране установлены и основные требования, предъявля-
емые к модернизации существующих и созданию новых тепло- и мас-
сообменных установок, важнейшими из которых являются следующие:
1. Применение установок непрерывного действия, обеспечивающих
поточность, комплексную автоматизацию и механизацию всего процес-
са производства (в ряде случаев это приводит к отказу от старых тех-
нологических процессов и созданию новых конструкций и схем высоко-
производительных теплоиспользующих установок).
2. Увеличение единичных мощностей аппаратов, т. е. создание мно-
готоннажных, высокопроизводительных автоматизированных агрегатов,
превосходящих по производительности в десятки и сотни раз прежние
установки.
3. Применение новых технологических процессов с использованием
высоких температур и давлений, глубокого вакуума, температур, близ-
1* 3
ких к абсолютному нулю, а также комбинированных способов подвода
тепла с применением токов высокой и промышленной частоты, ультра-
звука или вибрационных эффектов, заданного химического состава
среды, обеспечения магнитного или электрического поля и т. п.
4. Организация одностадийных технологических процессов, т. е. со-
вмещения в одном агрегате нескольких различных производственных
операций, например: фильтрования, сушки, размалывания, обжига,
вулканизации, полимеризации и т. п. (одностадийная обработка мате-
риалов является весьма перспективным средством интенсификации
технологических процессов).
5. Обеспечение во всех технологических процессах гигиеничных и
безопасных условий труда для обслуживающего персонала.
Все эти условия должны соблюдаться при высоком качестве про-
дукта и наилучших технико-экономических показателях работы пред-
приятия. Последние в свою очередь определяются минимально возмож-
ными габаритами установки, минимальным количеством обслуживаю-
щего персонала и наименьшими удельными расходами тепла и электро-
энергии и рациональным включением ее в общую систему управления
предприятием.
Успешное решение всех задач для создания высокопроизводитель-
ных и экономичных теплоиспользующих установок возможно только
при комплексной творческой работе инженеров-промтеплоэнергетиков
с инженерами-технологами и специалистами других отраслей знаний.
Настоящая книга представляет собой второе, переработанное и ис-
правленное в системе СИ, издание книги автора «Теплообменные, су-
шильные и холодильные установки», выпущенной в качестве учебника
издательством «Энергия» в 1966 г.
На межвузовской конференции по промтеплоэнергетике 1971 г. этот
курс было предложено назвать «Тепломассообменные и холодильные
установки».
Эта книга, как и прежняя, базируется на предшествующих курсах
Гидроаэромеханики, Тепло- и массопередачи и Термодинамики и в свою
очередь является базой для курсового проектирования и изучения по-
следующих специальных курсов. Этим определяется ее структура и ха-
рактер изложения материала.
Дополнением к данному учебнику является книга авторам А. А. Щу-
кина по курсовому проектированию теплоиспользующих установок
[Л. 2'1].
Особенностью данного учебника является рассмотрение современ-
ных многообразных промышленных тепло- и массообменных установок
и трансформаторов тепла без акцента на ту или иную отрасль промыш-
ленности. Это позволило сделать необходимые обобщения, провести
классификацию и применить единые методы тепловых расчетов для
процессов и аппаратов различных отраслей промышленности.
Автор выражает большую признательность сотрудникам кафедры
промышленной теплоэнергетики Ивановского энергетического института
за ценные замечания при рецензировании книги.
Особую благодарность автор выражает канд. техн, наук В. А. Ефи-
мову за большой труд по редактированию книги, а также канд. техн,
наук Д. П. Лебедеву и сотрудникам кафедры инженерам А. Г. Вилен-
ской и И. В. Макаровой за участие в пересчете формул и примеров
в систему СИ.
Автор
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ
И КОНТРОЛЮ ЗНАНИИ ПО КУРСУ
«ТЕПЛООБМЕННЫЕ, СУШИЛЬНЫЕ
И ХОЛОДИЛЬНЫЕ УСТАНОВКИ» БЕЗМАШИННЫМ
ПРОГРАММИРОВАННЫМ МЕТОДОМ
Существующая система преподавания и изучения специальных
курсов студентами в высших учебных заведениях имеет ряд существен-
ных недостатков. Многие студенты в течение семестра не пользуются
учебниками или учебными пособиями; лекционный материал изучают
в основном по конспектам и главным образом в период подготовки
к экзаменам. Лектор в течение семестра почти не имеет обратной свя-
зи или информации о том, как курс его лекций воспринимается сту-
дентами. О своих педагогических и методических недостатках он не-
редко узнает только на экзаменах.
Организовать систематический контроль изучения курса всеми
студентами существующими методами не представляется возможным,
да и не предусматривается существующими учебными планами.
В течение последних лет автором настоящей книги и его учениками
успешно проводится преподавание курса «Теплообменные, сушильные
и холодильные установки» с применением систематического безмашин-
ного метода программированного контроля знаний студентов, разра-
ботанного им совместно с сотрудниками кафедры сушильных и тепло-
обменных устройств Московского ордена Ленина энергетического ин-
ститута.
Этот метод отличается строгим планированием всех видов аудитор-
ных и самостоятельных учебных занятий студента по курсу и система-
тическим контролем его знаний в течение всего семестра. В соответст-
вии с разработанной методикой весь учебный материал разбит на са-
мостоятельные, логически законченные разделы, удобные для контроля
знаний.
На основе многолетнего опыта и апробации новой методики обуче-
ния и программированного контроля знаний и составлен данный учеб-
ник. Его содержание полностью соответствует программе, утвержден-
ной Министерством высшего и среднего специального образования
СССР по специальности «Промышленная теплоэнергетика» для всех
вузов страны.
В МЭИ курс «Теплообменные, сушильные и холодильные установ-
ки» читается на седьмом 14-недельном семестре по 4 ч в неделю (56 ч);
по 2 ч в неделю отводится на практические и контрольные занятия
(28 ч); планируется также систематическая самостоятельная работа
студентов по 3 ч в неделю.
Первое групповое занятие начинается с контроля знаний по базо-
вому курсу тепло- и массопередачи, затем на каждой нечетной неделе
5
проводится систематический контроль знаний, а ,по четным неделям —
обычные практические занятия по изучаемой теме.
Для осуществления и развития идей программированного обучения
и контроля мы рекомендуем существенно изменить методику чтения
лекций. Лекции должны содержать только наиболее сложные вопросы
читаемого раздела курса, а описательный материал рекомендуется изу-
чать самостоятельно по учебнику. Особое внимание на лекциях необ-
ходимо уделять новому материалу, появившемуся после издания учеб-
ника.
Большое значение для увеличения объема и улучшения изложения
лекционного материала имеет применение технических средств. 1Лы ре-
комендуем при чтении лекций широко использовать диапроектор днев-
ного света ЛЭТИ для демонстрации конструкций аппаратов и эпиди-
аскоп ЭДИ-454, который позволяет проектировать на экран таблицы,
конструкции аппаратов и формулы (если они даются без вывода), на-
писанные обычной авторучкой на широкой (170 мм) целлофановой ленте
(предварительно или в самом процессе чтения лекций). Пользуясь
таким эпидиаскопом, лектор в ряде случаев может обходиться
без доски и мела, причем изложение материала легко сочета-
ется с изображением необходимых иллюстраций. При этом лектор не
поворачивается спиной к аудитории, видит всех студентов и следит за
их работой. Такое усовершенствование облегчает работу лектора и
дает значительную экономию времени. Доской и мелом целесообразно
пользоваться только для математических выкладок, вывода формул и
изображения простых схем и графиков.
На контрольных занятиях в МЭИ небольшая часть времени отво-
дится разбору наиболее характерных ошибок, сделанных студентами
по предыдущей контрольной работе. Практические занятия посвящают-
ся активному рассмотрению методов расчета теплообменных аппара-
тов, закрепляющих теоретические знания студентов по прочитанным
лекциям, а также рассмотрению отдельных вопросов, возникших у
студентов при изучении лекционного материала по учебнику и конс-
пекту в период подготовки к контрольной работе.
В настоящее время при безмашинном методе программированного
контроля знаний мы применяем кодированный способ комплексных
матричных ответов на заданные вопросы.
Поясним это следующим простым примером.
Вопрос. Напишите цифры, соответствующие критериям Прандтля,
Нуссельта, Рейнольдса и Эйлера;
1) ad/k, 2) wd/v, 3) v/zz;
4) (Тс—Тм)/Тс; 5) Др/(рю1 2)
и выберите в карточке свой ответ среди прилагаемых (обычно десяти)
вариантов матричных ответов.
Такой метод исключает возможность угадывания и дает возмож-
ность проверить, знает ли студент не один критерий (как это делается
при простом выборочном ответе), а большее количество критериев и
т. п., т. е. он позволяет получить большую информацию о знаниях сту-
дентов. Он используется нами для проверки знаний студентов по ха-
рактеристикам работы теплообменных аппаратов, наиболее рациональ-
ной области их применения, по процессам тепло- и массообмена, по
правилам пуска и остановки агрегатов и т. д. Для примера приведем
комплексный вопрос 10 из второй контрольной работы по гл. «Рекупе-
ративные аппараты».
Вопрос 10. На рисунке приведены различные типы ребристых теп-
лообменников (рис. 1-23 из данного учебника).
6
Напишите в числителе цифру, соответствующую тому ребристому
теплообменнику из трех перечисленных, который имеет максимальный
коэффициент оребрения:
1) чугунная трубка с наружным игольчатым оребрением,
2) с продольным внешним оребрением, 3) с гладкими пластинами.
Укажите также соответствующей цифрой в числителе, какой из пе-
речисленных ниже теплообменников при прочих равных условиях будет
иметь больший коэффициент теплопередачи: 4) с насаженными ребра-
ми, 5) с навитыми спиральными ребрами, 6) с ребрами, выполненными
методом холодной прокатки.
Укажите в знаменателе, для каких из перечисленных пар теплоно-
сителей целесообразно применить ребристые теплообменники: 7) вода
— масло, 8) вода — газ, 9) вода — конденсирующийся пар.
Укажите также в знаменателе, какой обычно коэффициент тепло-
отдачи, отнесенный к внутренней или к наружной оребренной поверх-
ности, имеет большее значение: 10) к наружной, оребренной, 11) к
внутренней.
Найдите ответ на этот вопрос в следующей матрице и сопоставьте
с ним ваш зашифрованный ответ:
1) 14/811; 2) 15/811; 3) 16/810; 4) 26/711; 5) 26/811; 6) 25/711;
7) 26/810; 8) 25/710; 9) 36/811; 10) 35/710.
Внесите свои ответы в контрольную карту (см. образец).
Десять таких вопросов задается студенту на контрольном задании,
и, кроме того, он должен дать ответ на пять вопросов в конструкцион-
ной форме, когда ему предлагается записать в соответствующую клет-
ку контрольной карты алгебраическое или простейшее дифференциаль-
ное уравнение, написать размерности отдельных физических величин,
графически изобразить линии процесса по отдельным схемам, дать от-
вет в форме эскиза аппарата и т. п.
Для матричного выборочного ответа по каждому вопросу он должен
обвести кружком одну из десяти цифр, соответствующую по его мне-
нию правильному коду матричного ответа.
При конструкционном ответе он записывает в соответствующий
квадрат формулу, схему или рисует эскиз аппарата или отдельной де-
тали и т. п.
Ниже приводится контрольная карта с заполненными ответами.
Она состоит из десяти ответов по матричному выборочному методу и
пяти конструктивных ответов.
По каждой контрольной работе дается оценка по пятибалльной си-
стеме. Студент допускается к следующим контрольным работам только
при положительной оценке предыдущей работы. Студент, получивший
отличные оценки по всем контрольным работам, может быть освобо-
жден от экзамена по всему курсу или некоторой его части.
Для исключения взаимной информации студентов при одновремен-
ном контроле большого числа групп подготовлено четыре варианта
вопросников.
Во время контрольного занятия студент вносит все ответы только
в контрольную карту.
Проверка ответа по матричному выборочному материалу значитель-
но облегчается применением своего рода «перфорированных» карт-шаб-
лонов из плегсигласа, в которых сделаны отверстия на местах, соответст-
вующих верным ответам. «Перфокарты» накладываются на контроль-
ные карты и позволяют быстро определить правильные ответы.
Большое значение следует придавать последующей статистической
обработке контрольных карт, позволяющей делать строгий, глубокий и
всесторонний психофизиологический анализ восприятия знаний студен-
тами, а также указывающей методические недостатки и ошибки лек-
тора. С этой целью на контрольных занятиях выдается также обычная
7
40-колонная перфокарта с десятью цифрами в каждой колонке, соот-
ветствующими десяти вариантам ответа, среди которых студент кре-
стиком отмечает правильный ответ (правильные ответы на конструк-
ционные вопросы вносит позднее преподаватель)
Эти перфокарты поступают затем в вычислительный центр МЭИ,
где на ЭВМ подсчитывается не только количество правильных, но и ко-
личество ответов, в которых сделаны незначительные ошибки и пред-
ставляется более точная дробная оценка, а также анализируется каче-
ство вопросов (легкие, трудные) и т. д.
Опыт показывает, что применяемые в настоящее время машинный и
безмашинный методы програмированного контроля не дают возможно-
сти проверить знания и умение студентов описывать математически
и физически сложные процессы, делать математические выводы, раз-
бирать и анализировать сложные схемы и т. п. Эти вопросы должны
решаться на практических занятиях и экзаменах. Поэтому разработан-
ный нами метод безмашинного контроля не преследует цели отменить
экзамен. Экзамен при этом имеет свои особенности: в экзаменацион-
ные билеты включаются преимущественно сложные математические
описания и выводы отдельных уравнений, разбор принципов работы
комплексных установок, конструкций аппаратов и т. п.
Предлагаемый метод обучения, кроме совершенствования учебного
процесса, обеспечивает систематический многосторонний и дифференци-
рованный контроль знаний студентов по каждой теме. Экзамен являет-
ся только одним из видов контроля; итоговая оценка учитывает не
только ответ на экзамене, но и все другие виды контроля знаний сту-
дентов и исключает элементы случайности. Поэтому облегчаются про-
ведение экзамена и общая оценка знаний по пройденному курсу.
Коллегия Министерства высшего и среднего специального образо-
вания РСФСР 8 января 1965 г. заслушала сообщение заведующего ка-
федрой сушильных и теплообменных устройств Московского энергети-
ческого института П. Д. Лебедева и одобрила работу кафедры по без-
машинному программированному методу обучения и контроля знаний
студентов.
8
Во исполнение решения коллегии Главные управления направили
высшим учебным заведениям справку об опыте кафедры сушильных и
теплообменных устройств Московского энергетического института и ре-
комендуют учитывать этот опыт работы по совершенствованию учебно-
го процесса в вузе.
Во втором издании данного учебника методика систематического
безмашинного контроля знаний по лекционному поточному курсу, раз-
работанная проф. Лебедевым П. Д. и его сотрудниками, получила даль-
нейшее развитие и совершенствование как в дидактическом, так и в тех-
ническом отношении.
Раздел первый
ТЕПЛООБМЕННЫЕ АППАРАТЫ
И УСТАНОВКИ
ГЛАВА ПЕРВАЯ
РЕКУПЕРАТИВНЫЕ ТЕПЛООБМЕННЫЕ АППАРАТЫ
НЕПРЕРЫВНОГО ДЕЙСТВИЯ
1-1. КЛАССИФИКАЦИЯ ТЕПЛООБМЕННЫХ АППАРАТОВ.
ТЕПЛОНОСИТЕЛИ
Теплообменными аппаратами (теплообменника-
м и) принято называть устройства, предназначенные для передачи теп-
ла от одних тел к другим. В теплообменных аппаратах могут происхо-
дить различные тепловые процессы: изменение температуры, испаре-
ние, кипение, конденсация, расплавление, затвердевание и, наконец, бо-
лее сложные, комбинированные процессы. Количество тел, участвую-
щих в этих процессах, может быть больше двух, а именно: тепло мо-
жет передаваться от одного тела к нескольким другим телам или, на-
оборот, от нескольких тел к одному. Эти тела, отдающие или восприни-
мающие тепло, принято называть теплоносителями.
Классфикация теплообменных аппаратов. Теплооб-
менные аппараты имеют большое распространение во всех отраслях
промышленности и широко применяются в теплосиловых установках.
В зависимости от назначения теплообменные аппараты называются по-
догревателями, конденсаторами, испарителями, паропреобразователями
и т. д.
По принципу действия теплообменные аппараты делятся на поверх-
ностные и смесительные.
В поверхностных аппаратах теплоносители разделены твердыми
теплопроводными стенками, через которые происходит теплообмен меж-
ду теплоносителями. Та часть поверхности стенок, через которую пере-
дается тепло, называется поверхностью нагрева.
В свою очередь поверхностные теплообменные аппараты делятся
на рекуперативные и регенеративные.
Если теплообмен между теплоносителями происходит через разде-
лительные стенки, то теплообменник называют рекуперативным.
В аппаратах этого типа в каждой точке разделительной стенки тепло-
вой поток сохраняет постоянное направление.
Если же два или больше теплоносителей попеременно соприкаса-
ются. с одной и той же поверхностью нагрева, то теплообменный аппа-
рат называют регенеративным. В период соприкосновения с од-
ним из теплоносителей стенки аппарата получают тепло и аккумули-
руют его; в следующий период соприкосновения другого теплоносителя
с той же поверхностью стенок аккумулированное тепло передается теп-
лоносителю. Направление теплового потока во втором периоде изменя-
ется на противоположное.
W
В большинстве рекуперативных аппаратов осуществляется непре-
рывная передача тепла через стенку от одного теплоносителя к друго-
му. Эти аппараты, как правило, являются аппаратами непрерывного
действия. Рекуперативные аппараты, в которых производится периоди-
ческий нагрев или охлаждение одного из теплоносителей, относят
к аппаратам периодического действия.
Регенеративные теплообменники в большинстве случаев являются
аппаратами периодического действия; в них разные теплоносители по-
ступают в различные периоды времени. Непрерывная работа осущест-
вляется в таких аппаратах лишь в том случае, если они снабжены дви-
жущимися стенками или насадками, попеременно соприкасающимися
с потоками разных теплоносителей и непрерывно переносящими тепло
из одного потока в другой.
В смесительных теплообменных аппаратах тепло- и массообмен
осуществляется путем непосредственного контакта и смешения жидких
и газообразных теплоносителей.
В зависимости от назначения производственных процессов в каче-
стве теплоносителей могут применяться самые различные газо-
образные, жидкие и твердые тела.
Водяной пар, как греющий теплоноситель, в теплообменных аппа-
ратах получил большое распространение благодаря ряду его досто-
инств. Его можно транспортировать по трубопроводам на значительные
расстояния (до нескольких сотен метров). Интенсивная теплоотдача
от конденсирующегося водяного пара способствует уменьшению по-
верхности теплообмена. Конденсация водяного пара сопровождается
большим уменьшением его энтальпии; благодаря этому для передачи
сравнительно больших количеств тепла требуются небольшие весовые
количества пара. Постоянство температуры конденсации при заданном
давлении облегчает поддержание постоянства режима и регулирование
процесса в аппаратах.
Основным недостатком водяного пара является неизбежное и зна-
чительное повышение давления с ростом температуры. Например, при
давлении 0,981 • 105 Па* (1 кгс/см2) температура насыщенного пара со-
ставляет 99,1 °C, а температура насыщенного пара 309,5 °C может быть
получена только при давлении 98,1 • 105 Па. Поэтому паровой обогрев
применяется для процессов нагревания только до умеренных темпера-
тур (порядка 60—150°С). Обычно давление греющего пара в теплооб-
менниках составляет от 1,96 - 105 до 11,8 • 105 Па. Для высоких темпера-
тур эти теплообменники очень громоздки (имеют толстые стенки и флан-
цы), весьма дороги и поэтому применяются редко.
Горячая вода, как греющий теплоноситель, получила большое рас-
пространение, особенно в отопительных и вентиляционных установках.
Она приготовляется в специальных водогрейных котлах, производст-
венных технологических агрегатах (например, в печах) или водонагре-
вательных установках ТЭЦ [Л. 44]. Горячую воду, как теплоноситель,
можно транспортировать по трубопроводам на значительные расстоя-
ния (на несколько километров). Понижение температуры воды в хоро-
шо изолированных трубопроводах составляет не более 1 °C на 1 км
Достоинством воды как теплоносителя является сравнительно вы-
сокий коэффициент теплообмена. Однако горячая вода из тепловых
сетей в производственных теплообменниках используется редко, так
как в течение отопительного сезона температура ее непостоянна и из-
меняется от 70 до 130'°C, а в летнее время тепловые сети не работают.
Дымовые и топочные газы применяются в качестве греющего теп-
лоносителя, как правило, на месте их получения для непосредственного
обогревания различных промышленных изделий и материалов, если ка-
* Па=Н/м2.
Н
чество последних несущественно изменяется при загрязнении сажей и
золой. Если же загрязнение обрабатываемого материала недопустимо,
то подогрев его дымовыми газами ведется посредством воздуха, кото-
рый играет роль промежуточного теплоносителя, т. е. дымовые газы
через теплопроводную стенку в рекуперативных теплообменниках от-
дают тепло воздуху, воздух — обрабатываемому материалу. Дымовые
газы могут применяться в теплообменниках для нагрева, выпарки и
термической обработки газообразных, жидких и твердых веществ.
Таблица 1-1
Характеристика некоторых высокотемпературных теплоносителей
Название теплоносителя Химическая формула Температура, *C
отвердевания кипения
Минеральные масла — 0—15 215
Нафталин С1#н, 80,2 218
Дифенил С12н1о 69,5 255
Дифениловый эфир (С,Н,)О2 27 259
Дифенильная смесь (ВОТ) 26,5% дифенила и 73,5% дифе- 12,3 258
Глицерин нилового эфира С.Н, (ОН), —17,9 290
Кремнеорганические соединения (СН,С6Н40)4 —(30-^40) 440
(тетракрезилоксисилан и др.) Нитритнитратная смесь 7% NaNO, + 40% NaNO2 + 143 Выше 550
Натрий +53% KNO, Na 97,8 883
Достоинством дымовых и топочных газов как теплоносителя явля-
ется возможность достижения высокой температуры при атмосферном
давлении, недостатками — громоздкость аппаратуры, обусловленная
низкой теплоотдачей от газов к стенке, сложность регулирования рабо-
чего процесса в теплообменном аппарате, пожарная опасность и срав-
нительно быстрый износ поверхностей теп-
лообмена от золы, а также при чистке аппа-
ратов. Существенным недостатком дымовых
газов является также возможность исполь-
зования их только непосредственно на ме-
сте получения, так как транспортировка их
даже на небольшие расстояния требует
значительных расходов электроэнергии, гро-
моздких каналов и связана с большими теп-
ловыми потерями.
В настоящее время в промышленности
для высокотемпературного обогрева, кроме
дымовых газов, применяют минеральные
масла, органические соединения, расплав-
ленные металлы и соли. Характеристика не-
которых высокотемпературных теплоносите-
лей дана в табл. 1-1.
Если высокотемпературные теплоноси-
тели использовать при температурах ниже
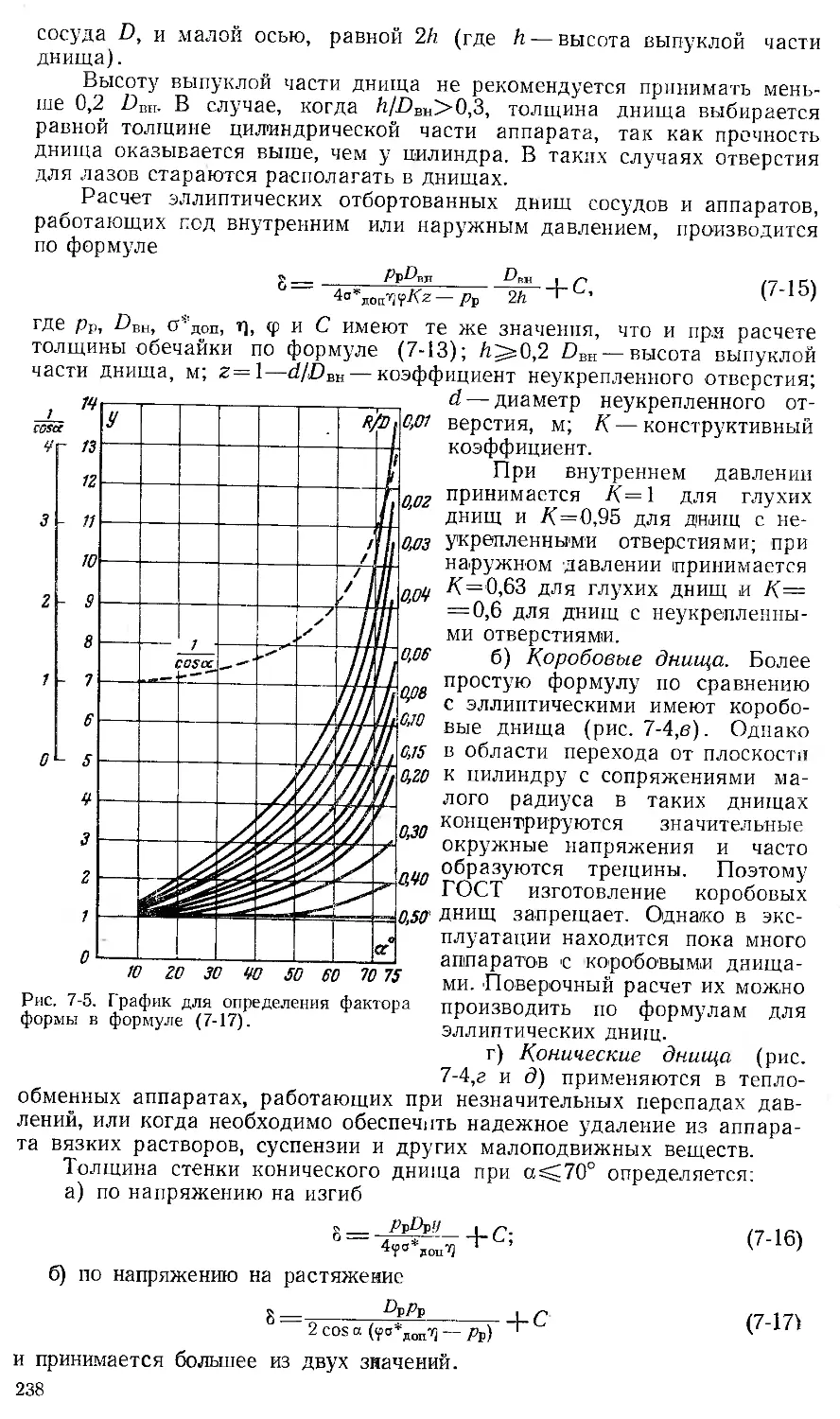
Рис. 1-1. Зависимости между
давлениями и температурами
насыщения для углекислоты
СО2, аммиака NH3 и фреона-12
CC12F2.
точки кипения, то в заполненном ими объеме теплообменного аппарата,
так же как и при дымовых газах, избыточное давление может отсут-
ствовать.
Основными требованиями, предъявляемыми к высокотемператур-
ным теплоносителям, являются: высокая температура кипения при ат-
мосферном давлении, высокая интенсивность теплообмена, низкая тем-
пература отвердевания, малая активность корродирующего действия на
металлы, нетоксичность, невоспламеняемость, взрывобезопасность, тер-
мическая стойкость и дешевизна [Л. 9, 56].
12
Наряду с высокотемпературными теплоносителями имеются низко-
температурные теплоносители и холодильные агенты, которые кипят
при температурах ниже О °C.
На рис. 1-1 приведены зависимости между давлениями и теперату-
рами насыщения для некоторых широко распространенных холодиль-
ных агентов.
В настоящее время для охлаждения используется эффект эндотер-
мической реакции или поглощения тепла при химическом разложении
веществ. Например, при разложении 1 кг хлористого аммония NH4C1 на
NH3 и НС1, которые превращаются в газ, поглощается 3 300 кДж/кг.
Эта величина почти в 1,5 раза превышает теплоту парообразования во-
ды (2 260 кДж/кг).
1-2. КОНСТРУКЦИИ ТРУБЧАТЫХ, ПЛАСТИНЧАТЫХ
И СПИРАЛЬНЫХ АППАРАТОВ ПОВЕРХНОСТНОГО ТИПА
Первые технические теплообменные аппараты представляли собой
варочные котлы с огневым или дымовым обогревом. Позднее стали
делать аппараты с двуслойными стенками, в промежуток между кото-
рыми подавался теплоноситель: греющий пар или горячая вода. Такие
аппараты называют рубашечными. Для повышения интенсивности теп-
лообмена и производительности аппаратов в дальнейшем изготовлялись
аппараты с поверхностью теплообмена в виде изогнутых в змеевик
труб — змеевиковые теплообменники. Однако все указанные аппараты
были мало производительными, трудно регулируемыми и неудобными
в эксплуатации, особенно была трудной их очистка.
Конструкции современных рекуперативных теплообменных аппара-
тов поверхностного типа непрерывного действия весьма разнообразны.
Поэтому в данной книге рассмотрены только наиболее характерные из
них.
Кожухотрубчатые теплообменники (рис. 1-2) представляют собой
аппараты, выполненные из пучков труб, собранных при помощи труб-
ных решеток, и ограниченные кожухами и крышками со штуцерами.
Трубное и межтрубное пространства в аппарате разобщены, а каждое
из этих пространств может быть разделено при помощи перегородок
на несколько ходов. Перегородки устанавливаются с целью увеличения
скорости, а следовательно, и интенсивности теплообмена теплоносите-
лей. Теплообменники этого типа предназначаются для теплообмена
между различными жидкостями, между паром и жидкостями или
между жидкостями и газами. Они применяются тогда, когда требуется
большая поверхность теплообмена.
Трубки теплообменников изготовляются прямыми (за исключением
теплообменников с U-образными трубками, рис. 1-2,г); поэтому они
легко доступны для очистки и замены в случае течи.
Типовые конструкции кожухотрубчатых теплообменников разрабо-
таны НИИХИММАШ.
Б большинстве случаев пар (греющий теплоноситель) вводится
в межтрубное пространство, а нагреваемая жидкость протекает по труб-
кам. Конденсат из межтрубного пространства выходит к конденсатоот-
водчику через штуцер, расположенный в нижней части кожуха. Для
компенсации температурных удлинений, возникающих между кожухом
и трубками, предусматривается возможность свободного удлинения
труб за счет различного рода компенсаторов.
Особенность кожухотрубчатых теплообменников состоит в том, что
проходное сечение межтрубного пространства велико по сравнению
с проходным сечением трубок и может быть больше последнего в 2,5—
3 раза. Поэтому при одинаковых расходах теплоносителей (если тепло
13
обмен происходит без изменения их агрегатного состояния) часто полу-
чаются пониженные скорости теплоносителя и малые значения коэффи-
циентов теплоотдачи на стороне межтрубного пространства, что
значительно снижает коэффициент теплопередачи в аппарате. Для вы-
равнивания проходных сечений иногда применяют усадку концов тру-
бок при закреплении в трубной решетке. Схема такого теплообменника
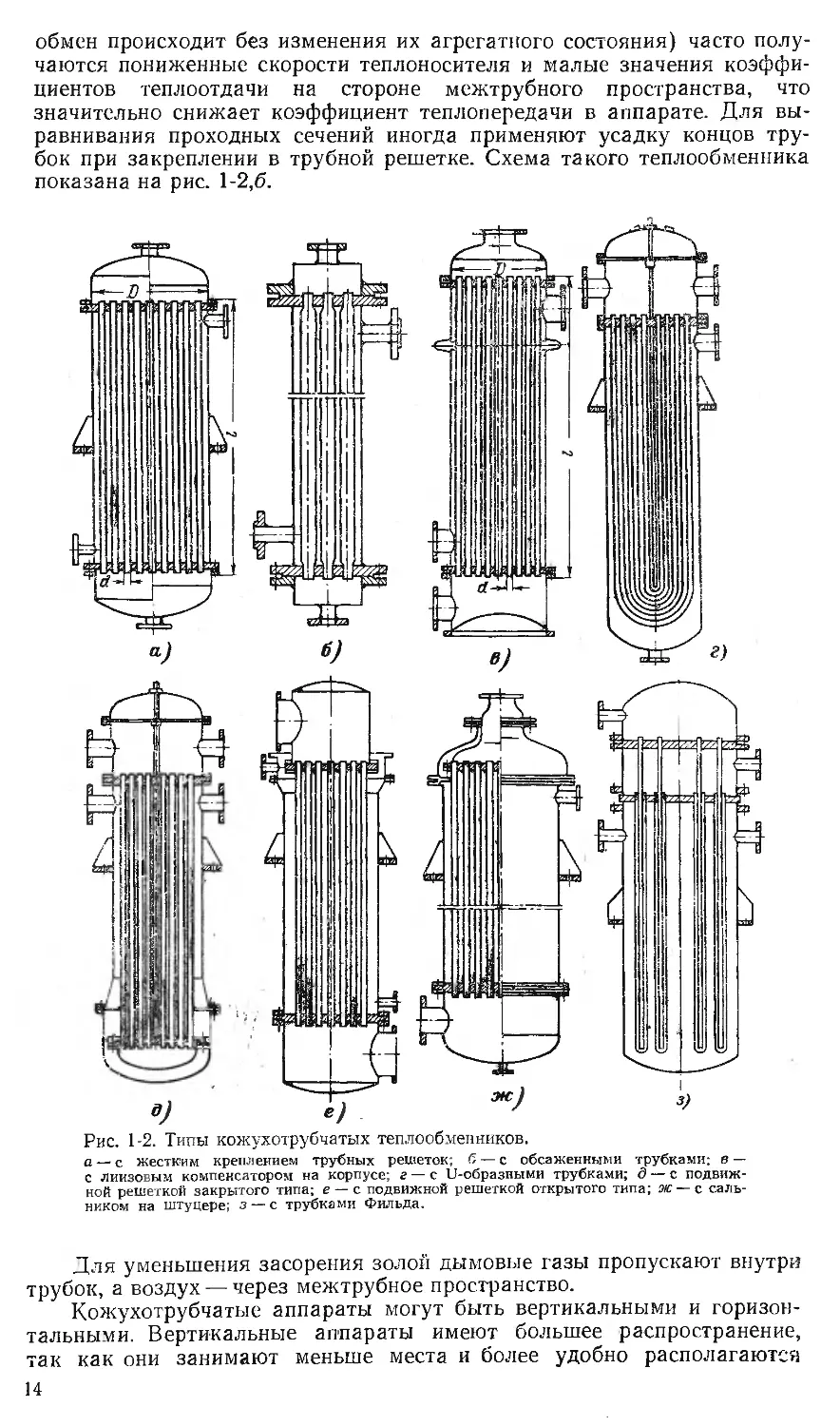
показана на рис. 1-2,6.
Рис. 1 2. Типы кожухотрубчатых теплообменников.
а — с жестким креплением трубных решеток; б — с обсаженными трубками; в —
с линзовым компенсатором на корпусе; г — с U-образными трубками; д — с подвиж-
ной решеткой закрытого типа; е — с подвижной решеткой открытого типа; эю — с саль-
ником на штуцере; з — с трубками Фильда.
Для уменьшения засорения золой дымовые газы пропускают внутри
трубок, а воздух — через межтрубное пространство.
Кожухотрубчатыс аппараты могут быть вертикальными и горизон-
тальными. Вертикальные аппараты имеют большее распространение,
так как они занимают меньше места и более удобно располагаются
14
в рабочем помещении. Для удобства монтажа и эксплуатации макси-
мальную длину трубок для них следует брать не больше 5 м.
Во избежание резкого снижения теплоотдачи от конденсирующегося
пара к стенке в корпусе теплообменника должны быть предусмотрены
краны для выпуска воздуха как из нижней части аппарата над поверх-
ностью конденсата, так и из верхней его части.
Регулирование производительности парожидкостного теплообменни-
ка возможно путем изменения давления (дросселированием греющего
пара), изменения расхода нагреваемого теплоносителя и изменения
(повышения) уровня конденсата в аппарате, т. е. уменьшения активной
поверхности теплообмена. В последнем
случае для контроля уровня конденса-
та необходимо иметь на корпусе водо-
указательное стекло.
Секционные теплообмен-
ник и и теплообменники «труба в тру-
бе». Секционные трубчатые теплооб-
менники (рис. 1-3) при одинаковых
расходах жидкостей имеют меньшую
разницу в скоростях движения тепло-
носителей в трубах и межтрубном про-
странстве и повышенные коэффициенты
теплопередачи по сравнению с обычны-
ми трубчатыми теплообменниками.
Для небольших производительно-
стей целесообразно применение тепло-
обменников типа «труба в трубе», от-
Рис. 1-3 Водоводяной подогреватель
теплосети Мосэнерго.
1—линзовый компенсатор; 2 — разборная
(на резьбе) трубная решетка; 3 — калач;
4 — трубки.
носящихся также к секционным, но конструктивно упрощенным аппара-
там: в наружную трубу вставлена труба меньшего диаметра, отсутст-
вуют трубные решетки и фланцы, все элементы аппарата соединены
сваркой.
Недостатки секционных теплообменников: во-первых, высокая стои-
мость единицы поверхности нагрева, так как деление ее на секции
вызывает увеличение количества наиболее дорогих элементов аппара-
та— трубных решеток, фланцевых соединений, переходных камер, ком-
пенсаторов и т. д.; во-вторых, большая длина пути жидкости по сравне-
нию с одноходовой трубчаткой, что создает значительные гидравлические
сопротивления и вызывает увеличение расхода электроэнергии на рабо-
ту насоса.
Рис. 1-4. Многопоточный разборный теплообменник «труба в трубе».
1 и 3 — первая и вторая распределительные камеры; 2 — решетка теплообменных труб; 4 — решетка
кожуховых труб; 5 — опорная обечайка; 6 — кожуховая труба; 7 — теплообменная труба; 8 — про-
кладка; 9 —задняя камера; 10 — опора.
15
На рис. 1-4 показан многопоточный разборный теплообменник
«труба в трубе», предназначенный для нагрева и охлаждения жидких
и газовых сред в технологических установках заводов нефтяной, химиче-
ской, газовой и других отраслей промышленности. Температура рабочей
среды от —40 до + 450 °C, давление в трубах 2,5—9,0 МПа. Для улуч-
шения теплообмена трубы могут иметь продольные ребра или попереч-
ную винтовую насадку.
Рис. 1-5. Спиральный теплообменник.
1 — разделяющая перегородка; 2 — дистанционные штиф-
ты; 3 — прокладки.
Спиральный теплообменник показан на рис. 1 -5. Два
листа толщиной 3—7 мм (в зависимости от рабочего давления в аппа-
рате) свертывают на специальном станке в спирали, причем при помо-
щи приваренных бобышек между ними сохраняется одинаковое по всей
спирали расстояние от 5 до 15 мм. Таким образом, получаются два ка-
нала и каждый из них имеет полуцилиндрическую часть в центре аппа-
рата и спиральную часть, заканчивающуюся коробкой снаружи. Каж-
дый центральный полуцилиндр и каждая коробка имеют штуцер для
входа или выхода теплоносителя. Спирали изготовляют так, что торцы
листов лежат строго в одной плоскости. Затем их помещают между
дисками, являющимися крышками аппарата, и стягивают болтами. Для
лучшей герметизации и устранения перетекания теплоносителей между
крышками и листами по всему сечению теплообменника помещают про-
кладку из резины, паранита, асбеста или мягкого металла. Такая кон-
струкция обеспечивает возможность чистки поверхностей нагрева и ра-
боту без перетекания теплоносителей при давлениях до 4-103 Па. Для
повышенных давлений и больших производительностей применяют спи-
ральные теплообменники с усложненной, но более надежной конструк-
цией уплотнения торцов спиралей. Спиральные теплообменники бывают
горизонтального и вертикального типов; их устанавливают часто бло-
ками по два, четыре и восемь аппаратов.
Достоинствами спиральных теплообменников по сравнению с много-
ходовыми трубчатыми теплообменниками являются повышенная ком-
пактность (большая поверхность теплообмена в единице объема) при
одинаковых коэффициентах теплопередачи и меньшее гидравлическое
сопротивление для прохода теплоносителей, недостатками их являются
сложность изготовления и меньшая плотность.
Пластинчатые теплообменники бывают различных кон-
струкций; их обычно применяют, когда коэффициенты теплообмена для
обоих теплоносителей одинаковы.
Недостатками изготовлявшихся в прошлом конструкций теплооб-
менников с большими расстояниями (15—40 мм) между пластинами
являлась малая герметичность и применимость лишь для газов из-за
незначительных допустимых перепадов давлений между теплоносите-
16
лями (несколько сотен паскалей или десятков миллиметров водяного
столба).
В настоящее время разработано большое число теплообменников,
поверхность теплообмена которых выполнена из гофрированных пластин
с незначительным расстоянием между пластинами (6—8 мм) (рис. 1-6).
А-А
♦ 1
0’0 0’0 0’0
Б
Г
000000
0 0 0>000
000000
0’0 0’0 0’0
а)
Рис. 1-6. Воздухоподогреватель из гофрированных пластин.
а — элемент пакета; б — модель воздухоподогревателя.
Б
Эти теплообменники очень компактны и по технико-экономическим,
а для разборных конструкций и по эксплуатационным показателям пре-
восходят лучшие трубчатые теплообменники. Однако они пока еще не
могут работать в области
высоких температур и дав-
лений, поэтому в настоящее
время их применяют при
давлениях до 16-105 Па и
температурах до 150 °C при
разборных конструкциях
(между пластинами уклады-
ваются уплотнительные про-
кладки) и до 400 °C — при
неразборных конструкциях
(уплотнение пластин дости-
гается сваркой).
Высокотемпера-
турные рекуперато-
р ы. Для подогрева воздуха
в промышленных печах при
температурах газа 800—
900 °C применяются трубча-
тые рекуператоры из угле-
родистой стали и рекупера-
торы из игольчатых труб
(рис. 1-23). При температу-
рах 900—1000 °C исполь-
зуются термоблочные реку-
ператоры, в которых глад-
кие трубы находятся в про-
фильном чугунном каркасе,
имеющем каналы для дымо-
вых газов. Термоблочные ре-
Рис. 1-7. Вертикальный пленочный конденсатор
поверхностного типа завода «Компрессор».
/ и 2 — указатели уровня жидкого аммиака; 3 — урав-
нительная труба; 4 и 5 — трехходовые вентили с двумя
предохранительными клапанами; 6 и 11 — манометры;
7 — водоприемный бак; 8— обечайка; 9— колпачки
с трубками; W — ресивер; 12 — патрубок для присоеди-
нения к воздухоотделителю.
2—1128
им
17
Рис. 1-8. Вертикальный испаритель типа
ИСВ.
1 — корпус; 2 — греющая секция; 3 — перегородка;
4 — трубка для отсоса воздуха из греющей каме-
ры в корпус вторичного пара; 5 — поплавковый
регулятор питания; 6 — трубопровод химически
очищенной воды; 7 — спускной патрубок для опо-
рожнения; 8 пеноразмывочное устройство; 9 —
лаз; 10 — конденсатоотводчнк; 11 — уровень воды
(«зеркало» испарения).
куператоры, при одинаковой теплопроизводительности имеют в 2—3 ра-
за больший вес, чем игольчатые, но обладают лучшей газовой плотно-
стью [Л. 66]. При температурах газа от 1 000 до 1 200 °C внутри трубок
из легированной стали (со стороны нагреваемого воздуха) устанавли-
вают металлические вставки, которые нагреваются за счет радиацион-
ного потока от наружных стенок и снижают их температуру.
Пленочные конденсаторы поверхностного типа.
В некоторых промышленных установках (например, холодильных) боль-
шое распространение получили
вертикальные пленочные конден-
саторы, один из которых изобра-
жен на рис. 1-7. Пары аммиака
поступают в межтрубное прост-
ранство и конденсируются на
внешней поверхности вертикаль-
ных труб, имеющих длину 3—
6 мм. Охлаждающая вода посту-
пает в бак, дном которого яв-
ляется верхняя трубная решетка,
и из него равномерно распреде-
ляется по трубкам. В каждую
трубку вставляется завихритель,
обеспечивающий спиральное дви-
жение пленки воды по внутрен-
ней поверхности трубки с целью
интенсификации теплообмена за
счет большей скорости при не-
больших расходах воды.
Оросительные конден-
саторы горизонтально-
го типа состоят из нескольких
трубчатых змеевпков, внутри ко-
торых протекает конденсируемый
теплоноситель. Змеевики снару-
жи орошаются водой. Вода сте-
кает каскадно пленкой с горизон-
тальных труб змеевика в поддон,
откуда насосом подается в гра-
дирню и после охлаждения в ней
снова в верхние распределитель-
ные перфорированные трубы или
корыта этого конденсатора. До-
стоинством такого конденсатора
является простота, а недостат-
ком — громоздкость.
Испарители и парооб-
разователи широко применя-
ются для уменьшения и восполне-
ния потерь конденсата. Их можно
разделить на аппараты с естественной циркуляцией воды между труб-
ками и с принудительной циркуляцией воды в кипятильных трубках.
В качестве примера испарителя воды с естественной циркуляцией
на рис. 1-8 представлен вертикальный аппарат типа ИСВ. Естественная
циркуляция в этом аппарате происходит вследствие того, что образую-
щаяся в кипятильных трубках пароводяная эмульсия имеет меньшую
плотность, чем вода в кольцевом зазоре между корпусом и трубной
системой, где ей сообщается значительно меньшее удельное количество
18
тепла на единицу объема. При этом в трубках устанавливается подъем-
ное движение пароводяной эмульсии, а в кольцевом зазоре — опускное
движение воды. Паровые пузырьки по выходе среды из трубок перехо-
дят в паровой объем. Уровень воды в аппарате поддерживается с по-
мощью поплавкового регулятора питания выше верхней трубной решет-
ки. Подача воды производится через пеноразмывочное устройство, пред-
назначенное для того, чтобы размывать шапку пены, образующуюся
над зеркалом испарения при значительной концентрации растворенных
примесей в испаряемой воде. Первичный (греющий) пар поступает
в межтрубное пространство греющей камеры. Для отделения влаги из
вторичного пара в верхней части парового пространства встроено сепа-
рирующее устройство.
В вертикальных испарителях типа ИСВ коэффициент теплопередачи
6 = 3 000=4 000 Вт/(м2-°С) {2 500—3 500 ккал/(м2-ч-°С)].
При термической обработке агрессивных жидкостей паров и газов
(серная, фосфорная, соляная и др. кислоты) поверхности нагрева защи-
щают антикоррозионными покрытиями: фенолформальдегидными или
эпоксидными смолами, полимеризационными пластическими массами,
стеклопластиками. В последние годы термическая обработка агрессив-
ных сред производится также в теплообменниках из непроницаемых
графитовых элементов (труб или блоков), пропитанных фенолформаль-
дегидной смолой, или из графитопласта АТМ-1. Физико-механические
свойства этих материалов приведены в табл. 1-2.
Таблица 1-2
Физико-механические свойства пропитанного графита
и графопласта АТМ-1
Наименование показателей о Пропитанный графит Графопласт АТМ-1
Плотность, (кг/м3)-10~3 Предел прочности при сжатии, МПа То же, кг/смг Теплостойкость, °C Теплопроводность, Вт/(м-*С) . . . Водопоглошение, г/дмг 1,8—1,85 70—100 700—1 000 170 93—116,3 0,07—0,15 1,80—1,85 70—100 700—1 000 130 35—40 0,01—0,1
Вследствие хорошей теплопроводности графита углеграфитовые
теплообменники более компактны по сравнению с теплообменниками
из других неметаллических материалов. Углеграфитовые теплообменни-
ки могут иметь различные конструкции. Их можно изготовлять кожухо-
трубчатыми со стальным кожухом и с трубными досками, крышками и
трубками из углеграфита (рис. 1-9,в), если греющий теплоноситель
неагрессивен, а также полностью из углеграфитовых деталей, например
пластинчатыми, в которых с одной стороны пластины проходит один
теплоноситель, а с противоположной — другой. Получили применение
углеграфитовые теплообменники из цилиндрических и прямоугольных
блоков.
На рис. 1-9,а представлена принципиальная конструкция графито-
вого кожухоблочного теплообменника, предназначенного для нагрева
или испарения кислот насыщенным водяным паром, под давлением
3 -105 Па. Он имеет четыре цилиндрических блока, в каждом из которых
имеются маленькие горизонтальные круглые отверстия, соединяющиеся
с большим вертикальным цилиндрическим отверстием. Блок имеет так-
же большое число маленьких вертикальных отверстий. Греющий пар
поступает в металлический кожух и конденсируется в маленьких гори-
2* 19
Риг. 1-9. Схемы кожухоблочного теплообменника с круглыми графитовыми
блоками и теплообменника с графитовыми трубками, крышками и металличе-
ским корпусом.
а — кожухоблочный теплообменник; б — графитовый блок; в — трубчатый теплообменник;
1 — металлический кожух; 2 — графитовый блок; 3 — металлические фланцы; 4 — анкер-
ная связь; 5—крышки из графита; 6 — трубки из графита.
зонтальных отверстиях. Конденсат стекает по большой вертикаль-
ной трубе, образованной блоками. Агрессивная жидкость (кислота)
проходит по мелким вертикальным трубкам и нагревается. Крыш-
ки теплообменника, соприкасающиеся с кислотой, также выполнены
из графита.
1-3. КОНСТРУКТИВНЫЙ И ТЕПЛОВОЙ РАСЧЕТЫ АППАРАТОВ
ПОВЕРХНОСТНОГО ТИПА
В практике встречаются два случая теплового расчета. Могут быть
заданы теплопроизводительность аппарата, теплоносители и их началь-
ные и конечные параметры; требуется определить поверхность нагрева
и конструктивные размеры аппарата. Этот случай расчета носит назва-
ние конструктивного теплового расчета. В другом случае могут быть
заданы конструкция и размеры аппарата, теплоносители и их начальные
параметры; требуется определить конечные параметры теплоносителей
и теплопроизводительность аппарата. Такой расчет называют провероч-
ным.
Порядок проектирования аппаратов поверхност-
ного типа. Конструктивный тенловой расчет теплообменных аппара-
20
тов производится при проектировании. В этом случае перед тепловым
расчетом необходимо задаться определенной конструкцией аппарата.
После увязки результатов теплового расчета с конструктивными разме-
рами аппарата приступают к гидравлическому расчету, т. е. определяют
гидравлическое сопротивление аппарата, так как может оказаться, что
запроектированный теплообменник из-за большого гидравлического
сопротивления потребует значительного расхода электроэнергии на при-
вод вентилятора или насоса и окажется неэкономичным.
В большинстве случаев интенсификация теплообмена (большие
коэффициенты теплопередачи) и малые поверхности нагрева аппарата
достигаются за счет больших скоростей теплоносителей, однако это
вызывает большие гидравлические сопротивления и требует значитель-
ного расхода электроэнергии на эксплуатацию теплообменника. Поэтому
часто бывает необходимо произвести технико-экономический расчет для
выбора наивыгоднейших скоростей теплоносителей.
В некоторых случаях гидравлическое сопротивление теплообмен-
ного аппарата может быть задано, например, если он должен быть
включен между прямой и обратной линиями теплофикационной сети и
нужно уложиться в располагаемую разность давлений.
После увязки теплового и гидравлического расчетов необходимо
выбрать теплообменник из серийно выпускаемых нашими заводами и
сделать соответствующие дополнительные расчеты, если это необходимо,
в том числе и расчет деталей аппарата на прочность (механический
расчет).
Если аппарат должен работать под давлением более 0,7 • 105 Па, то
его конструктивное выполнение должно соответствовать правилам Гос-
гортехнадзора [Л. 37, 42, 47].
Детальное проектирование теплообменника оправдано и целесооб-
разно только в том случае, если заданным условиям не удовлетворяет
ни один из выпускаемых типов аппаратов. Тепловой расчет теплообмен-
ников очень громоздок, так как он выполняется методом последователь-
ных приближений, когда для определения коэффициента теплообмена
приходится в начале задаваться температурой стенки, а затем в конце
расчета проверять правильность принятого значения и, если получается
большая ошибка, делать перерасчет. Значительную экономию времени
дает расчет теплообменников на электронных вычислительных машинах
(Л. 14].
Конструктивный тепловой расчет состоит в совместном
решении уравнений тепловых балансов, определяющих теплопроизво-
дительность аппарата, и уравнений теплопередачи.
Для аппаратов, работающих без изменения агрегатного (фазового)
состояния теплоносителей, уравнение теплового баланса имеет вид:
Q = G1C1 г]п= G2c2(t"2—t'2). (1 -1)
Для аппаратов с изменением агрегатного состояния одного из теп-
лоносителей уравнение можно записать в виде
Q=Z>i(ii—1'к)т]п= С2сг(^"2—t’z)', (1'2)
для аппаратов с изменением агрегатного состояния обоих тепло-
носителей
Q—Di {ii i'k) т]п—D2 (г2—1цит). (1 -3)
В уравнениях (1-1) — (1-3): Q—тепловая производительность,
кДж/с (ккал/с); Gt и G2 — расходы теплоносителей (воздуха, газов
и т. п.), не изменяющих агрегатное состояние, кг/с; и с2 — теплоем-
21
кости теплоносителей1, кДж/(кг-°С) [ккал/(кг-°С)]; t"b t'2 и t"2—
начальные и конечные температуры теплоносителей, °C; i — энтальпия
пара, кДж/кг (ккал/кг); iK — энтальпия конденсата, кДж/кг (ккал/кг);
г’пит — энтальпия питательной воды, кДж/кг (ккал/кг); т]п— коэффи-
циент, учитывающий потери тепла аппаратом в окружающую среду.
На основе приведенных уравнений определяют расход теплоноси-
телей:
а) без изменения агрегатного состояния теплоносителей
Gi = Q/Ci (i'i—/"1)т]п;
G2=Q/c2(tF2—t'2).
б) при изменении агрегатного состояния одного или обоих тепло-
носителей (кипение, конденсация)
Di = G2c2 (t''2—t'2) I Gi—i'k) T]n!
Di = D2 {i2—1пит) / (Й—Ik) Tin-
Поверхность нагрева теплообменника определяют из уравнений
теплопередачи
Q = kF\K кДж/с, (1-4)
где k — коэффициент теплопередачи, Вт/(м2-°С) [ккал/(м2• ч• °C)]; A/j —
средняя разность температур между теплоносителями, °C; F— поверх-
ность нагрева, м2.
Для трубчатого теплообменника
F = adcvLnz, (1-5)
где tZCp — средний диаметр трубки, м; L — длина трубки, м; п — число
трубок в одном ходу; z — число ходов.
Для пластинчатого теплообменника из нерифленых листов
F=abn, (1-5а)
где F — поверхность пластин с одной стороны, м2; а — ширина пласти-
ны, м; b — высота пластины, м; п — число пластин.
Из уравнения (1-4) следует, что для определения поверхности на-
грева предварительно требуется найти величины коэффициента тепло-
передачи и среднего температурного напора.
Определение среднего температурного напора.
Если температура обоих теплоносителей изменяется вдоль поверхности
теплообмена, то при противотоке и прямотоке
2’31s^7
(1-6)
где А/б — температурный напор (разность температур обоих теплоноси-
телей) на том конце поверхности теплообмена, где он больше; Д/м —
температурный напор на другом конце поверхности теплообмена.
На рис. 1-10 показан характер изменения температур вдоль поверх-
ности теплообмена при противотоке и прямотоке для трех возможных
соотношений полной теплоемкости2 теплоносителей W.
1 Здесь теплоемкости ct и с?, как и в дальнейшем, если особо не оговорено,
являются средними теплоемкостями теплоносителей при постоянном давлении, так как
в большинстве случаев тепловые процессы в теплообменниках можно приближенно счи-
тать изобарными.
2 В предыдущем издании учебника полная теплоемкость тела соответствовала
понятию водяного эквивалента, утратившего свое значение в новой системе СИ.
22
Полной теплоемкостью W некоторого количества теплоносителя G
(кг) или его расхода (кг/ч) с удельной теплоемкостью с кДж/('Кг*°С)
называется количество тепла, необходимое для увеличения его темпе-
ратуры на 1 °C, т. е. W=Gc, кДж/°С.
Если при противотоке значения W=Gc для обоих теплоносителей
одинаковы, то Д^=Л/М=|Л^- В тех случаях, когда Л/б/А^м^4,5 вместо
формулы (1-6) можно пользоваться формулой
+ ди - 0,1 (Д£б - AQ, (1 -7)
что дает ошибку не более 3%, а если Д/б/Д/м^1,8, то расчет можно про-
изводить по формуле
Д/=4-<Д/б + ди- (1-8)
Формулы (1-6) — (1-8) неприменимы, если теплоемкость, расход
или коэффициент теплоотдачи хотя бы одного из теплоносителей сильно
изменяется вдоль поверхности
теплообмена. В последнем случае
Л/ определяют при помощи гра-
фического интегрирования или
разбивают поверхность теплооб-
мена на участки, каждый из ко-
торых рассчитывается самостоя-
тельно при соответствующих Л/ и
коэффициентах теплоотдачи.
В теплообменных аппаратах
противоток имеет ряд преиму-
ществ по сравнению с прямото-
ком, поэтому он получил большее
распространение и его следует
применять во всех случаях, когда
этому не препятствуют требования
технологии или другие обстоя-
тельства. При прямотоке конеч-
ная температура нагреваемого
теплоносителя не может быть вы-
ше конечной температуры грею-
щего, в то время как противоток
свободен от этого ограничения.
При прямотоке предел ис-
пользования тепла греющего теп-
лоносителя определяется тем-
пературой t"i, а при противо-
токе — температурой t\, т. е.
Рис. 1-10. График изменения температур
теплоносителей вдоль поверхности тепло-
обмена при их противотоке и прямотоке.
можно в большей степени использовать энтальпию греющего
теплоносителя. В большинстве практических случаев при противотоке
получается более значительная средняя разность температур, что по-
зволяет иметь меньшую поверхность нагрева аппарата при той же теп-
лопроводности ее или через ту же поверхность передать большее коли-
чество тепла. Обе схемы дают почти одинаковые результаты лишь
в случаях, когда водяные эквиваленты обоих теплоносителей значитель-
но отличаются друг от друга и когда требующееся изменение темпера-
тур теплоносителей значительно меньше температурного напора.
Пример 1-1. В водяном гладкотрубном экономайзере нагревается 6 = 10 000 кг/ч
воды с /'г=40°С до /"2=140°С. Газы при этом охлаждаются с Щ=350 °C до t"i=
= 150°C. Коэффициент теплопередачи для экономайзера #=16,3 Вт/(м2-°С), или
14 ккал/(м2 • ч • °C). Определить поверхность нагрева при противотоке и прямотоке
воды и газов.
23
Решение. Количество тепла, получаемое водой в экономайзере,
10 000-4,187
Q = Gc — =-----здод---(140 — 40)= 1 163 кДж/с = 1,1632МВт.
Средняя логарифмическая разность температур при противотоке
Д/6-Д/и ... (350- 140)-(150 - 40) _
А/л— Д/6 350— 140 154 С-
1п Д/и 1п150—40
Поверхность нагрева экономайзера при противотоке
Q _1,163-10» t с
16,3-154 ~465
Средняя логарифмическая разность температур при прямотоке
(350-40)-(150- 140)
Д^в=---------350^40---------=87>5 С-
1п 150—140
Поверхность нагрева экономайзера при прямотоке
1,163-10» _
F ~ 16,3-87,5 — 820 м*'
Поверхность нагрева при противотоке в данном случае получилась почти в 2 раза
меиыцей.
В большинстве случаев при одинаковых условиях температурный
напор при противотоке имеет наибольшее значение по сравнению с дру-
гими схемами движения тепло-
носителя. Однако при опреде-
лении поверхности теплообмен-
ника имеет значение не только
Д/, но и коэффициент теплоот-
дачи, например при перекрест-
ном токе теплоносителей в теп-
лообменнике с короткими труб-
ками при уменьшении темпера-
турного напора по сравнению
с противотоком увеличивается
коэффициент теплоотдачи и
в результате поверхность теп-
лообмена получается меньше.
При перекрестном токе и
в других более сложных схе-
мах движения теплоносителей
в теплообменнике А? вычис-
ляется по формуле
= Д^прот®др
Рис. 1-11. Коэффициент R) для
раллельно-смешанного тока.
а — с двумя ходами одного из теплоносителей;
с тремя ходами одного из теплоносителей,
ных температур теплоносителей в
противотоком; £ — коэффициент
па-
где Д/прот — средний темпера-
б— турный напор, подсчитанный
по формуле (1-6) для задан-
предположении, что они движутся
перевода, который определяется по
графикам, составленным для конкретных схем движения теплоносите-
лей, в зависимости от условных параметров Р и jR.
24
На рис. 1-11,а дана зависимость ew=f (Р, Р) для параллельно сме-
шанного тока теплоносителей с двумя ходами одного из теплоносителей
в теплообменнике, а на рис. 1-11,6 — для параллельно-смешанного тока
теплоносителей с тремя
ходами одного из тепло-
носителей.
На рис. 1-12,с дана за-
висимость eAt=f{P, R) для
одноходового перекрест-
ного тока теплоносителей
в теплообменнике, а на
рис. 1-12,6 — для двуххо-
дового перекрестного то-
ка теплоносителей при
соединении ходов в про-
тивоточном порядке.
При перекрестном то-
ке теплоноситель может
перемешиваться. Переме-
шивающимися называется
теплоноситель, темпера-
тура которого поперек
данного хода может вы-
равниваться вследствие
перемешивания (напри-
мер, теплоноситель, дви-
жущийся между трубами)
или вообще относительно
равномерна. Непереме-
Рис. 1-12. Коэффициент ед^ ^=f(P, R) для перекрест-
ного тока теплоносителей.
а — для одноходового; б — для двухходового; теплоноси-
тель ti перемешивается, теплоноситель ие перемешивается.
шивающимся называется теплоноситель, температура которого поперек
хода не может выравниваться (например, при движении внутри парал-
лельно включенных труб).
На графиках по значениям Р и R находится поправочный коэффи-
циент ед? = )(ЛЛ):
П . t"2 - t’2 __ it2 р_ t'.-t", _ 8t,
t\-t'2 A t"2 — t'2 St2
где t'i, t"i, t'2 и t"2— начальные и конечные температуры теплоносите-
лей, как это показано на рис.1-11. Р — всегда ^1, a R может быть
больше или меньше 1 в зависимости от соотношения теплоемкостей и
массовых расходов теплоносителей.
Расчеты и графики ^t=f(P, Р) для многочисленных схем тепло-
обмена приведены в работе [Л. 60]. Некоторые графики —f(P, R)
даны в (Л. 11, 18, 48].
При определении расчетной разности температур в случае подогре-
ва жидкости или газа конденсирующимся паром необходимо иметь
в виду, что часто пар, поступающий в теплообменник, бывает перегре-
тым и, кроме того, в самом теплообменнике он не только конденсирует-
ся, но и образующийся конденсат иногда переохлаждается. Для точного
расчета средней разности температур при этих условиях необходимо
общую поверхность аппарата разделить на отдельные части, в которых
передача тепла происходит при различных агрегатных состояниях теп-
лоносителей. Однако практически установить границы этих областей
в теплообменном аппарате иногда бывает трудно. Кроме того, как пока-
зывает ряд опытов, при конденсации перегретого пара у стенок обра-
25
ности
Рис. 1-13. Изменение темпера-
тур греющего пара и подогре-
ваемой воды по поверхности
теплообменника.
/ — область перегретого пара; II—
область насыщенного пара; III —
область переохлажденного конден-
сата; abed — кривая изменения тем-
пературы греющего теплоносителя,
ef — кривая изменения температу-
ры жидкости.
зуется пленка из конденсата, температура которой соответствует темпе-
ратуре насыщенного пара при данном давлении, и наличие начального
перегрева не увеличивает средней разности температур.
Несколько иначе обстоит дело при переохлаждении конденсата,
которое происхоит, если поверхность теплообменного аппарата рассчи-
тана с запасом или если его создают искусственно, задерживая выпуск
конденсата. Переохлаждение конденсата уменьшает среднюю разность
температур между теплоносителями.
Однако при проектировании аппарата и определении средней раз-
температур переохлаждение конденсата также не учитывают и,
если это переохлаждение невелико, счи-
тают, что по всей поверхности греющий
теплоноситель имеет одинаковую темпе-
ратуру. В тех случаях, когда устанавли-
вают специальный теплообменник для
переохлаждения конденсата, этот тепло-
обменник следует рассчитывать как ап-
парат, работающий без изменения агре-
гатного состояния теплоносителей.
На рис. 1-13 показано изменение тем-
ператур теплоносителей вдоль поверхно-
сти теплообмена для случая конденсации
перегретого пара и переохлаждения кон-
денсата. Если температура одного из теп-
лоносителей принимается постоянной по
всей поверхности теплообмена (напри-
мер, при конденсации пара линия Ь'с'),
то при любой схеме движения другого
теплоносителя различие между прямото-
ком и противотоком для расчета теряет-
ся и получается одинаковая средняя раз-
ность температур между теплоносителя-
ми, для которой А/, определяется по
обычным формулам (1-6) — (1-8).
В расчете
обычно принимают температуру со сто-
пара постоянной и
паропреобразователя
роны конденсирующегося
насыщенного пара при данном давлении, хотя в
может поступать как влажный, так и перегретый пар, а в самом аппара-
те возможно некоторое переохлаждение конденсата. Температуру кипе-
ния чистой воды или другой однородной жидкости тоже принимают
постоянной по всей поверхности теплообмена и равной температуре вто-
ричного пара, полагая, что жидкость, поступающая с более низкой тем-
пературой, вследствие незначительности ее объема по сравнению
с объемом кипящей жидкости не понижает температуры последней.
Таким образом, средняя разность температур для паропреобразователя
А^ —
где 1Н1 — температура насыщения конденсирующегося пара, °C; Лй —
то же вторичного пара, °C.
Во избежание чрезмерного увеличения поверхности нагрева тепло-
обменника обычно считают, что средняя разность температур не
быть меньше 15 °C.
Коэффициент теплопередачи для круглой трубы
ляют по формуле из курса «Тепло- и массопередача» [Л. 11]
1 ---, Вт/м2-°С,
аат
равной температуре
паропреобразователь
должна
опреде-
k= —
^св
I ds
2Х 1П dBH
(1-9)
26
где dCp, dBB и dB — средний, внутренний и наружный диаметры трувки, м;
Z — коэффициент теплопроводности материала трубки, Вт/(м-®С); сц
и аг — коэффициенты теплоотдачи для внутренней и внешней стороны
трубки, Вт/(м2*°С); /?3аг — термическое сопротивление, учитывающее
загрязнения с обеих сторон стенки (накипь, сажа и пр.), м2-с,С/Вт.
При вычислении dCp необходимо учитывать следующее правило:
при ctj а2 t/cp -^Н.
при at = а2............dcp=0,5 (dBH+dH);
при ctj oig ••••••• .
Для расчета аппаратов с обычными цилиндрическими трубками,
толщина стенки которых не больше 2,5 мм, можно пользоваться форму-
лой для плоской стенки; ошибка в этом случае составляет не более 1—3%.
Коэффициент теплопередачи для плоской стенки имеет вид:
k = --------, Вт/(м2 • °C),
*__L °cr i D
(1-10)
где бет — толщина стенки трубки, м.
В уравнении (1-9) при б/н/с!вн<1,5 можно принимать lndH/dBH~
«2б/(/Вн+б. При этом ошибка не превышает 1,3% значения 1п^нМш-
Значения /?заг выбирают по экспериментальным данным. Если известны
толщины отложений на внутренней и наружной поверхностях 61 й б2 и
коэффициенты их теплопроводности Zi и Z2 по J?3ar вычисляют по фор-
мулам:
для уравнения (1-9)
П I ^2 .
Кзат ~ Xj dBH Л2 ’
для уравнения (1-Ю)
р ____ &1 1 ^2
«заг— Х1 Т х2 '
Определение конструктивных размеров аппаратов
и коэффициентов теплоотдачи для теплоносителей,
не изменяющих агрегатного состояния. При определении
коэффициентов теплоотдачи для теплоносителей (газов и жидкостей),
не изменяющих агрегатного состояния, прежде всего необходимо за-
даться их скоростями в теплообменнике. В большинстве случаев движе-
ние теплоносителей в теплообменниках осуществляется при помощи
насосов или вентиляторов. Обычно скорости в аппаратах принимаются
в пределах для жидкости 0,5—3 и для газов 5—12 м/с; иногда допуска-
ются и другие скорости.
Скорость теплоносителя и проходные сечения подбираются так,
чтобы значения коэффициентов теплоотдачи были близки, так как при
этом размеры поверхности нагрева получаются наименьшими.
Зная скорость теплоносителя в трубках w м/с, его расход G кг/с и
выбрав величину внутреннего диаметра трубок dBH, м, определяют число
их по формуле
4G
П= ---2---
ndEHwp
(1-И)
в которой р — плотность теплоносителя, кг/м3.
27
Рис. 1-14. Размещение трубок в трубной
решетке трубчатого подогревателя.
а — по вершинам равносторонних треугольников;
б — по концентрическим окружностям.
После этого производят компоновку трубок в сечении теплообмен-
ника и определяют размеры трубной решетки, исходя из следующих
соображений. Толщина стенок трубки для теплообменников обычно со-
ставляет 0,5—2,5 мм. Внутренний диаметр трубок dBH Для облегчения
очистки их от накипи должен быть не меньше 12 мм; для получения
компактных конструкций теплообменников не рекомендуется примене-
ние трубок с dBH больше 38—
57 мм. Шаг трубок s (расстояние
между осями соседних трубок)
обычно выбирают равным (1,3—
1,5) dB, но не меньше dH+6 мм.
Нормальным расположением счи-
тается размещение центров тру-
бок на трубной решетке пэ вер-
шинам равносторонних треуголь-
ников (ромбическое), как пока-
зано на рис. 1-14,с. Размещение
трубок может быть выполнено и
по концентрическим окружностям
(рис. 1-14,6), отстоящим одна от
другой на принятую величину
шага между трубками. Зная чис-
ло трубок, можно по табл. 1-3
определить диаметр окружности, на которой располагаются крайние
трубки.
Как следует из табл. 1-3, при большом количестве трубок ромбиче-
ское размещение дает меньшие размеры трубной решетки.
Таблица 1-3
Значения относительного диаметра трубной решетки D'/s
в зависимости от числа трубок при ромбическом
и концентрическом размещении их
£>'/« /2'1 /2*2 D'/s П*1 /2*2
2 7 7 22 439 410
4 19 19 24 517 485
6 37 37 26 613 566
8 61 62 28 721 653
10 91 93 30 823 747
12 127 130 32 931 847
14 187 173 34 1 045 953
16 241 223 36 1 165 1 066
18 301 279 38 1 306 1 185
20 367 341 40 1459 1 310
Примечание. п\—общее количество трубок, размещаемых на трубной доске по
вершинам равносторонних треугольников [(.ромбическое* размещение (рис. 1-14,а); п'2—об-
щее количество трубок, размещаемых на трубной доске по концентрическим окружностям
(рис. 1-14,6)1.
После нахождения диаметра D' определяют внутренний диаметр
корпуса D по формуле
D—iD'+dB+2k,
где dB— наружный диаметр трубки; k — кольцевой зазор между край-
ними трубками и корпусом, который принимается из конструктивных
соображений 6 мм и больше.
После этого определяют проходное сечение межтрубного простран-
ства и скорость теплоносителя в нем.
Данные табл. 1-3 действительны только для одноходовых теплооб-
менников, когда для размещения трубок используется почти вся актив-
28
ная поверхность трубной доски. Диаметр корпуса многоходового тепло-
обменника определяется с учетом размещения перегородок и произво-
дится обычно графическим путем. С этой целью вычерчивают
в определенном масштабе часть трубной доски и на ней размещают
трубки с учетом мест для перегородок, анкерных связей, каркаса труб-
чатки и т. д.
Длина трубок (расстояние между трубными решетками) выражает-
ся формулой
naevnz
где F— поверхность теплообмена, м2; dcp— средний диаметр трубки, м;
п — число трубок в одном ходу; г — число ходов.
Значение L не должно превышать 6 м.
При расчете пластинчатого теплообменника также задаются ско-
ростью каждого из теплоносителей и определяют необходимые размеры
проходных сечений и число ка-
налов.
При расчете змеевикового
теплообменника определяют сле-
дующие размеры.
Длина одного витка змеевика
I = У ^D2sa+s^
Рис. 1-15. Эскиз к расчету спирального теп-
лообменника.
где Дзм — диаметр витка змееви-
ка, м; s — шаг витков змееви-
ка, м.
Общая длина трубы змеевика
при числе его витков п составит
L—nl, а высота змеевика Н =
= (п—l)s.
Расчет спирального теплооб-
менника [Л. 20] начинают с опре-
деления шага спирали $=&+б,
где Ь — ширина канала, равная
6—15 мм; 6 — толщина листа
(для стали 2—8 мм).
Каждый полувиток спирали строится по радиусам п и г2 (рис. 1-15),
причем для первого полувитка fi=d/2, а для второго r2=^+d/2 и т. д.,
где d— диаметр первого витка спирали I (принимается в пределах
300—800 мм).
Ширина керна
6К=2Г1—Si,
где St — шаг спирали I.
Ось аппарата делит керн на две неравные части (рис. 1-15):
О1Л/=Г1—,(s2/2) и О2А'=Ьк—OtA',
где s2 — шаг спирали II.
Эффективная длина листов спиралей
L3$$ = F/2H,
где F— поверхность теплообмена, м2; Н — высота спиралей, участ-
вующая в теплообмене, м (принимается 375—750 мм по нормали
НИИХИММАШ).
Наружный диаметр спирального теплообменника
D = d -f- 2Ns 4- б, м,
где d — диаметр первого витка, м; N— количество витков спиралей; s —
шаг спиралей, м; б —толщина витков спиралей, м.
29
Келичество витков спиралей
М = 2п = ]/2
где п — число витков одной спирали; s — средний шаг спиралей;
х = 0,5((//х—1).
Выбор расчетных формул для определения коэффициентов тепло-
отдачи внутри трубок и в межтрубном пространстве без перегородок
при продольном обтекании поверхности начинается с вычисления кри-
терия Рейнольдса, который определяет режим движения теплоносителя.
При Re^2 200 устанавливается ламинарный режим движения; 10 000^>
^Re^=2 200 соответствует переходному режиму, a Re>10 000 — турбу-
лентному.
Критерий Re определяется из выражения
Re = w(/3/vffi,
где w — средняя скорость теплоносителя, м/с; — коэффициент кине-
матической вязкости теплоносителя, м2/с, причем индекс ж, как и везде
далее, указывает, что значение величины соответствует средней по сече-
нию температуре теплоносителя; d3— эквивалентный (гидравлический)
диаметр поперечного сечения потока, м, определяемый по формуле
d3=4f!U, (1-12)
где f — площадь поперечного сечения потока, м2; U — смачиваемый
периметр сечения, м.
Для определения коэффициента теплообмена между жидкостью и
стенкой при установившемся турбулентном режиме движения ее
в трубках (Re>10 000) рекомендуется пользоваться критериальным
уравнением
NUjk = = 0,023 Re^’8Pr°’4 ег, (1-13)
где — коэффициент теплопроводности, Вт/(м-°С); Ргж=тж/йж —
критерий Прандтля; — коэффициент кинематической вязкости, м2/с;
ат — коэффициент температуропроводности, м2/с; е/ — поправка, учиты-
вающая отношение длины трубы I к ее диаметру d\ так как в теплооб-
менниках //(/>50, то Ei= 1.
Формула (1-13) применима для всех капельных и упругих жидко-
стей при Re>104 и Рг = 0,72 500 при температуре стенки ниже темпе-
ратуры кипения жидкости и протяженности потока l>30d.
За определяющую температуру, к которой относят физические кон-
станты, следует принимать среднюю арифметическую температуру жид-
кости.
Формула (1-13) может быть представлена в упрощенном виде
а = Вт/(мг-°С), (1-14)
Скорость w подставляется в м/с; коэффициент А является функцией
температуры и свойств теплоносителя. Значения А для воды и воздуха
указаны в табл. 1-4. В тех случаях, когда физические константы заметно
изменяются по сечению потока, более точные результаты дает формула
М. А. Михеева
Nujk = 0,021Reo;W-43 (1-15)
Ил m \ 11Q /
где Prc=vc/Oc — критерий Прандтля, в котором значения физических
констант берутся при температуре стенки.
30
Формула применима при турбулентном течении жидкости или газа
в трубах при значениях 104<Re<2- 10е и 0,7<Рг<700. Так как для га-
зов Pr = const, формула (1-15) упрощается и, в частности, для двух-
атомных газов (Рг—0,71) она принимает следующий вид:
Nu = 0,018Re°-8.
(1-16)
Таблица 1-4
Значение коэффициента А в формуле (1-14)
Температура t, °C А Температура t, °C А
ДЛЯ воды для воздуха ДЛЯ ВОДЫ для воздуха
20 2 000 3,3 110 3 400 2,88
30 2 100 3,24 120 3 500 2,80
40 2 400 3,21 130 3 600 2,78
50 2 600 3,14 140 3 780 2,77
60 2 700 3,11 150 3 850 2,75
70 2 850 3,06 160 3 920 2,73
80 3 000 3,02 170 4 000 2,67
90 3 100 3,01 180 4 100 2,64
100 3 300 2,90
Расчет теплоотдачи при продольном течении в межтрубном про-
странстве без перегородок также производится по формулам (1-13)—
(1-16), но вместо диаметра трубки в критериальные выражения для Nu
и Re подставляется эквивалентный диаметр межтрубного пространства.
При этом вычисленные по формулам значения а умножаются на попра-
вочный коэффициент, равный (51«2М2н)0’18 в интервале 1,3< (SiSz/d2) <6
(где Sj и s2 — шаги труб во взаимно перпендикулярных направлениях;
dH— наружный диаметр труб).
Если сечение потока имеет форму кольцевого зазора, то значение а,
вычисленное по формуле (1-13), следует умножить на величину (cP/с?1)°-18,
где d1 — наружный диаметр внутренней трубки; d2 — внутренний диа-
метр внешней трубки. Эта поправка применима при d2ldi= 1,0-^ 10 *.
При течении в змеевиковой трубе следует вводить поправочный
коэффициент ед, на 'который следует умножить величину а, полученную
по формуле (1-16). Согласно опытам
eK=l+3,54d/£>,
где D — диаметр змеевика; d — диаметр трубки.
При ламинарном течении жидкости в трубах (Re<2 300) необхо-
димо определить значение (GrPr)r. Если эта величина меньше 8-105, то
естественная конвекция не оказывает существенного влияния на тепло-
отдачу, т. е. режим течения жидкости вязкостный. Если (GrPr)r>8-105,
то на вынужденный поток жидкости накладываются токи естественной
конвекции, обусловленные зависимостью плотности от температуры, т. е.
режим течения вязкостно-гравитационный. Соответственно этим усло-
виям и необходимо выбирать расчетные формулы.
Расчет средней теплоотдачи при вязкостном режиме течения жид-
кости в трубах при постоянной температуре стенки (tc = const) можно
производить по следующей формуле [Л. 32]:
кт 1 КС d \1/з / р. \-0.14
Nur = 1,55 ( Рег-т-) е.
у 1 ) \ Р'ж J
(1-17)
* Более точный расчет а кольцевого канала для вязких жидкостей может быть
получен то'формуле (1-15), если в ней изменить коэффициент 0,021 на 0,017 и ввести
поправку (<7г/<71)0,18.
31
где индексы «ж», «с» и «г» означают, что физические свойства жидкости
берутся при средней температуре жидкости '/ж=0,5(^1+^2), темпера-
туре стенки tc и определяющей температуры ^г=0,5(/}Н+/с);
Nur = ac?/2r; P&Tdfl = a = qi(tc — £ж);
n с f 1 I у-1/7/, I о к 1 I \
в = 0,6 (-5---г-) (14-2,5-5-----^-1
— поправка на участок гидродинамической стабилизации, которая вво-
дится, когда перед обогреваемым участком трубы отсутствует участок
гидродинамической стабилизации и (1/Re) • (//d) <0,1; d, I — диаметр и
длина трубы, м; р, ц— плотность и динамическая вязкость жидкости,
кг/м3 и Я-с/м2; 2., с — теплопроводность и теплоемкость жидкости,
Вт/(м-°С) и кДж/(кг-°С); G— расход жидкости G = ptKw1Kndz/4:, кг/с.
Формула (1-17) справедлива при Реж<2 300; Perd//^>20; (GrPr)^
<j8- 105; 0,07<цс/цж<1 500*, где
(GrPr)r = g₽r-^^^-Prr;
здесь ₽г — коэффициент объемного расширения жидкости, 1/°С; vr —
коэффициент кинематической вязкости, м2/с. При вязкостно-гравита-
ционном режиме течения в горизонтальных трубах для расчета средней
теплоотдачи можно пользоваться следующей формулой [Л. 32]:
iNur = 0,8 (Рег 4-Г’4 (Gr Pr)0’1 (JX.V0’14, (1-18)
где
Gr = gpr ; Ре=~;
Vr г
а - t — t— ’ = 0’5 ^н<> “Ь ^«2)1
здесь аг — температуропроводность, м2/с; остальные обозначения ука-
заны в формуле (1-17).
Формула (1-18) справедлива при Re<3000; 20^Ре— ^120;
10®< (GrPr)r< 13 • 10е; 2<Ргг< 10.
В условиях вязкостно-гравитационного течения в вертикальных
трубах при совпадении направлений вынужденной и естественной кон-
векции у стенки (охлаждение жидкости при течении сверху вниз или
нагревание при течении снизу вверх) для расчета средней теплоотдачи
можно пользоваться формулой [Л. 32]
Nur = 0,35 (Рег [(GrPr)r (1-19)
здесь коэффициент теплоотдачи отнесен к температурному напору на
входе, т. е. a=g/(/c—^ж).
Обозначения и размерность физических величин указаны в форму-
лах (1-17) и (1-18).
Формула справедлива при Реж<2 300;
(₽ег -р) < Рег А < 1 100;
20<-i-< 130; 810s<(GrPr)r<4108,
Для газов поправка (Це/Цж)-0,14 ие вводится.
32
где асимптотическое значение числа Пекле
(Рег-р) « 1,5/Gr Pr-j-V’28.
В условиях вязкостно-гравитационного течения в вертикальных
трубах при противоположных направлениях вынужденной и свободной
конвекции у стенок (охлаждение жидкости при течении снизу вверх или
нагревание при течении сверху вниз) для расчета средней теплоотдачи
можно пользоваться следующей формулой:
NUjK=:O,O37Reo*75.Pr0'4 Г—У- (1-19а)
где п=—0,11 при нагревании; п=—0,25 при охлаждении; a=ql{tc—/ж);
0,5 (^Ж1 "Ь •
Формула справедлива при 250^ReHt<2-104 и 1,5-106^GrPr^
< 12-106.
При 2 200<Re<10 ООО, т. е. для переходной области, коэффициент
теплоотдачи более точно может быть определен только по соответст-
вующим экспериментальным кривым для данной жидкости или газа.
Для приближенного определения коэффициентов теплоотдачи при дви-
жении теплоносителей в трубах в области 2 300<Re<10 ООО Б. С. Пету-
хов предлагает определять точку перехода от ламинарного вязкостного
режима к турбулентному (точку, соответствующую расстоянию х от
входного участка трубы) по уравнению
(x/d)p = 1 OOO/j/Re — 2 000.
В этом случае коэффициент теплоотдачи при смешанном движении
определяется по формуле
где ал — средний коэффициент теплообмена на участке трубы длиной хр,
отнесенный к начальной разности температур Д£н и вычисляемый по
формуле для ламинарного вязкостного режима; ат — коэффициент теп-
лообмена на участке длиной I—хр, отнесенный к средней логарифми-
ческой разности температур Д/'л на этом участке и вычисляемый по
формуле для турбулентного режима; Д/л — средняя логарифмическая
разность температур для всей длины трубы.
Расчет теплообмена в пучках гладких труб, обтекаемых попереч-
ным потоком газа, может производиться по формуле ВТИ (Н. В. Куз-
нецова и Э. С. Карасиной), действительной в области значений
6 000<Re<60 ООО:
для шахматных пучков при р2-— <lv,7
Nu=-^-=0,27CzRe°'-e = 0,27Cz (1-20)
s ~~ d
для шахматных пучков при —^->0,7
Nu = 0,295 Cz Re°-e (?3-=^0’25; (1-21)
для коридорных пучков
Nu = 0,177CzRe0-64. (1-22)
Формулы для шахматных пучков справедливы при значениях
1,2<si/d <4,8 и 0,8<s2/d<4.8.
3—1128
33
Формулы для коридорных пучков справедливы при значениях
l,25<Si/d<4,8 и l,19<s2/tZ<4,8.
В этих формулах: d — наружный диаметр труб, м; s2, s'2—по-
перечный, продольный и диагональный шаги труб в пучке, м; w — ско-
рость газа в узком сечении пучка, м/с, отнесенная к средней температуре
газового потока /П=^с+Л/Л; Д/л — средний логарифмический темпера-
турный напор; Cz — поправочный коэффициент, учитывающий влияние
числа рядов труб z в пучке; значения Cz для шахматных пучков выби-
рают по графику на рис. 1-16,а, а для коридорных— 1-16,6.
При обтекании пучков под углом <р<90° коэффициент теплоотдачи а
вычисляется по тем же формулам, что и при поперечном обтекании пуч-
ков, с той только разницей, что ско-
рость газа условно относится к жи-
вому сечению газохода в плоскости
пучка, а не к сечению, нормальному
к оси газохода. Найденная таким
образом величина а должна быть
умножена на поправочный коэффи-
циент е зависящий от угла атаки
и выбираемый по кривым на рис.
1-17, вычерченным по опытным дан-
ным Ф. П. Казакевича.
Для весьма ориентировочных
расчетов при поперечном омывании
Рис. 1-16. График для опреде-
ления коэффициента Cz в фор-
мулах (1-20) —(1-22).
а — для шахматного пучка; б — для
коридорного пучка.
I
Рис. 1-17. График для опреде-
ления поправочного коэффи-
циента е ф при обтекании пуч-
ка под углом Ар.
/ — для коридорного пучка; 2 — для
шахматного пучка.
пучков труб капельными жидкостями могут быть использованы фор-
мулы (1-20) и (1-21), но в них необходимо ввести множитель Рг0-3.
Для увеличения скорости теплоносителя в межтрубном пространст-
ве часто устанавливают перегородки (кольцевые, дисковые и сегмент-
ные), которые удлиняют его путь и в значительной степени направляют
поток перпендикулярно трубам, как показано на рис. 1-18. Коэффициент
теплообмена в пучке труб при наличии перегородок независимо от их
типа можно приближенно в зависимости от расположения трубок опре-
делить по формуле (1-20) или (1-21), умножив затем найденное значе-
ние, как это рекомендует Т. Хоблер [Л. 54], на коэффициент е=0,58-н0,60.
Размеры сегментных перегородок, а также диаметр кольцевых и
дисковых перегородок и расстояние между ними выбирают так, чтобы
скорость теплоносителя во всех сечениях была одинакова. Расчет про-
ходных сечений для кольцевых и дисковых поперечных перегородок
определяют по формулам:
34
а) между корпусом и диском (сечение а на рис. 1-18,6)
б) в вертикальном сечении — между перегородками (сечение b на
рис. 1-18,6)
= 1 ——\
‘ л \ S ]
в) внутри кольца (сечение с на рис. 1-18,6)
где D — внутренний диаметр корпуса, м; £4 и D2 — диаметр кольцевой
перегородки и диаметр дисковой перегородки, м; da — наружный диа-
метр трубки, м; п—число трубок;
s — шаг между трубками, м; h—
расстояние между перегородка-
ми, м; г; — коэффициент заполне-
ния решетки трубками.
Пучок >}
Одноходовой..............0,8—1
Двухходовой..............0,7—0,85
Четырехходовой...........0,6—0,8
Диаметр диска определяют
по формуле
£>2= 1,05s
где п — число трубок в трубной
доске; т] — имеет прежнее зна-
чение.
Площадь прохода теплоноси-
теля между сегментными перего-
родками определяется из выра-
жения
площадь сегмента для прохода
теплоносителя в вырезе перего-
родки (за вычетом площади тру-
бок)
k = (ш~sin? ) ~°-785< Nc.
Рис. 1-18. Перегородки, увеличивающие ско-
рость потока в межтрубном пространстве.
а — сегментные; б — концентрические.
где уо — расстояние между крайней трубкой и стенкой корпуса, м; у —
расстояние между трубками, м; т — количество зазоров между труб-
ками в рядах, расположенных между кромками перегородок; по — коли-
чество рядов трубок, расположенных между кромками перегородок;
Л —расстояние между перегородками, м; D — внутренний диаметр кор-
пуса, м; — центральный угол сегмента, образованный вырезом в пере-
городке; dB— наружный диаметр трубок, м; Nc — количество трубок
в сегментном разрезе перегородки.
Коэффициент теплоотдачи от жидкости к поверхности при стекании
ее пленкой вниз в пленочных конденсаторах (рис. 1-7) определяется из
выражений;
3 * 35
при турбулентном стекании пленки (Re>2 000)
Nur — 0,01 (Ga Pr Re)J/3 ; (1 -23>
при ламинарном стекании пленки (Re <2 000)
Nur = 0,67 (Ga2 Pr3 Re)’/3 ; (1 -24>
Nur = a///2r; Gar = H3^ g/y? ;
Rer — 4Г/р.т; Prr = (сррЛ)г.
где a — коэффициент теплоотдачи, Вт/(м2-°С); H — высота поверхности
теплообмена, м; X — коэффициент теплопроводности, Вт/(м«°С); р —
плотность жидкости, кг/м3; g— ускорение силы тяжести, м/с2; р — дина-
мический коэффициент вязкости, Н - с/м2; ср — теплоемкость жидкости,
Дж/(кГ’°С); Г-=С1П — плотность орошения, кг/(м-с), т. е. количество
жидкости, стекающей в единицу времени через 1 м смоченного перимет-
ра П в сечении, нормальном к направлению движения потока; G — мас-
са жидкости, стекающей по вертикальной поверхности в единицу вре-
мени, кг/с.
Индексы «г» указывают на то, что определяющей температурой для
физических параметров является средняя температура граничного слоя
(пленка) /г='0,5(^с + /ж).
Для случая стекания жидкости пленкой по внутренней поверхности
вертикальных труб смоченный периметр n = ndn (d — внутренний диа-
метр вертикальных труб; п — число труб). В этом случае
Г = G/ndn-, ^&—^Glndn\k.
Для горизонтально расположенных труб оросительных теплообмен-
ников при стекании воды пленкой коэффициенты теплоотдачи с наруж-
ной стороны имеют следующие значения при средней температуре воды
до ее охлаждения 11—25 °C, диаметре трубы 0,012—0,030 м и отноше-
нии шага труб к их диаметру 2—1,7; плотности орошения 820—
960 кг/(м-ч) [Л. 48]:
а = 3740//°’4, Вт/(ма-°С). (1-25)
/
При тех же условиях и отношении шага к диаметру 1,3
а = 5700/7°’5°, Вт/(ма-°С), (1-26)
где Hw= 2in f------плотность орошения кг/(м-с); G — масса воды, по-
ступающей в холодильник, кг/с; I — длина трубы в секции, м, п—число
верхних труб (число секций); наличие цифры 2 в знаменателе объясня-
ется тем, что вода, орошающая каждую трубку, растекается по обе сто-
роны.
Если в аппарате происходит передача тепла от газов, нагретых до
температуры выше 400 °C, то, кроме конвективного теплообмена, следует
учитывать лучистый теплообмен, для чего нужно определить коэффи-
циент теплоотдачи излучением ал. В этом случае
а=ак+ал, Вт/(м2-°С),
где ак — коэффициент теплоотдачи конвекцией; ал — коэффициент теп-
лоотдачи излучением, определяемый как Qn/F(tT—/с); Qn— тепловой
поток от газа к стенке, обусловленный излучением, Дж/с; F— поверх-
ность стенки, м2; /г и /с — средние температуры газа и поверхности стен-
ки, °C.
36
Коэффициент теплоотдачи лучеиспусканием в значительной степени
зависит от содержания СО2 и Н2О в газах и абсолютной температуры
газа в четвертой степени. Значения этих коэффициентов можно подсчи-
тать по приведенным ниже формулам (3-18) и (3-19).
Пример 1-2. Произвести тепловой и конструктивный расчеты основных деталей
секционного водоводяного подогревателя теплосети Мосэнерго (рис. 1-3) при следую-
щих условиях:
схема движения теплоносителей — противоток;
производительность аппарата Q= 1,75 -10е Дж/с (Вт) ='1,5 Гкал/ч;
температура греющей воды 1'1=130 °C и l"i=100°C;
температуры нагреваемой воды 1'2=62°С и 1"г=92°С;
поверхность нагрева выполнена из латунных трубок диаметром dsn/da = 14/16 ммз
теплопроводность материала трубок 7=104,9 Вт/(м - °C);
толщина накипи бн=0,2 мм;
теплопроводность накипи 7П=3,49 Вт/(м-°С);
коэффициент, учитывающий потери тепла в окружающую среду, т)=0,97.
Решение. Определяем средний объемный расход греющей воды при
= 115°С
1,75-10»
Q
Г’~ с (1'1 — l"i) р'т) 4,20-10» (130 —100)-948-0,97 0,0151 м*/с’
Средний объемный расход нагреваемой воды при = 77 *С
Гг- с (Г"2—Г2) р-
1,75-10»
4,19-10» (92—62)-972 °-0143 м’/с.
Q
где р'=948 кг/м3 и р"=972 кг/м3 — плотности воды при соответствующих температу-
рах; с — теплоемкость воды.
Средний температурный напор в аппарате Л1Ор=Д1=Д2=130—92=100—62=38 °C,
поскольку в данном случае водяные эквиваленты теплоносителей почти одинаковы.
Для определения количества трубок в одной секции задаемся скоростью движения
воды в трубках а>1= 1,5 м/с и определяем площадь поперечного сечения трубок в сек-
ции
V, 0,0151 „ „
— т-е-= 0,0101 м2
1,5
Wt
и количество трубок
/г =
4-0,0101
65.
4/.________________
_л2 л-0,0142
По табл. 1-3.находим ближайшее конструктивное число трубок, равное 62 (прк
расположении трубок по концентрическим окружностям). Такому количеству трубок
соответствует диаметр аппарата iy=8s. Принимая шаг по радиусу, s=l,4dH, т. е. s=
= 1,4-0,016 = 0,0224 м и кольцевой зазор £=0,008 м, определяем внутренний диаметр
корпуса:
D=D'+d+2k=8 • 0,022+0,016+2 • 0,008=0,208 м.
Находим скорость движения воды в межтрубном пространстве. Площадь попе»
речного сечения корпуса
izD2 л-0,2082
— -----= 0,034 м2.
4
Площадь, занятая трубками,
4
л-0,0162-62
------------= 0,0125 м2.
Площадь межтрубного пространства
А=Л—/=0,034—0,0125=0;0215 м®.
Скорость воды в межтрубном пространстве
ш2
V2 0,0143 „
0,0215 — 0,67 м/с>
37
Для вычисления коэффициента теплоотдачи от охлаждаемой воды щ находим
критерий Рейнольдса
шАн 1,5-0,014
Re = -^= 0 259-Ю~6 = 81 000 > 10 000,
что соответствует установившемуся турбулентному режиму; поэтому следует пользо-
ваться формулой (1-13), имея в виду, что действительная скорость в трубках
п 64
w'i = Wj -jf - =1,5- -gg = 1.55 м/с.
Для воды можно применить упрощенную формулу (1-14)
И1=Д (w/1)°-8/</02.
Из табл. 1-4 при температуре /Cpi=H5cC находим величину
Л=3 400.
Таким образом,
1 550.3
04 = 3 400 • Q 014» а = 10 ОНО Вт/(м2 • °C) [8 600 ккал/(м2 • ч - * С)].
Коэффициент теплоотдачи аг со стороны нагреваемой воды находим аналогичным
путем. Определяем режим движения воды в межтрубном пространстве
w2dT 0,67-0,023
Re = -Vх = 0,382-lO"^40 000 > 10 °00-
где
D2 — ndl _0,2082 — 62-0,0162
dr = nd^ + D 62-0,0164-0,208 = 0,023 M’
Следовательно, применима та же формула (1-14). .Коэффициент 4=2 950 нахо-
дим по табл. 1-4 при <ср2=77°С. Значит,
0,67°.8
а2 = 2 950 (j р2зб,2 4 600 Вт/(м2 °C) [4 000 ккал/(м2 ч- *С)].
Коэффициент теплопередачи вычисляем по формуле (1-10) для плоской стенки
1 _ 1
k~ 1 аС1 ав 1 1 o,ooi о,ооо2 i “
“1 Хст + Хн + а2 10000 + 90 + 3 + 4600
= 2700 Вт/(м2 °С) [2330 ккал/(м2-ч-°С)].
Поверхность нагрева подогревателя
Q _ 175-106
F~ Ш 2 700-38 -16>8м2-
Длина трубок
F 16,8
L~ ndCJ>n ~~ 3,14-0,015-62 ~5,8 м-
Выполняем подогреватель из двух секций.
Активная длина трубок в каждой секции равна /=£/2=5,8/2=2,9 м, или, округ-
ляя, К=3 м. Таким образом, каждая секция будет состоять из 62 трубок длиной 3 м.
Диаметры всех штуцеров аппарата должны быть одинаковыми, так как расходы
V1=V2-
Приняв скорость воды в штуцере равной 1,5 м/с, получим:
V! 0,0151
= Ш1 1,5 =0-0101 м2
и
. /4-0,0101
dmT=y т-. ^V ------------й----=0,113 м.
Принимаем <7ШТ = 125 мм.
Следует заметить, что по расчетным данным можно было выбрать типовой водо-
водяной подогреватель типа МВН и затем выполнить проверочный расчет.
38
Теплоотдача при конденсации пара. На поверхности,
температура которой ниже температуры насыщения, возможны два
вида конденсации пара: капельная, если конденсат не смачивает по-
верхности. и пленочная, если конденсат смачивает поверхность.
Капельная конденсация обеспечивает наибольшие коэффициенты
теплоотдачи. Она может быть достигнута путем покрытия поверхности
или введения в пар веществ, которые делают поверхность несмачивае-
мой конденсатом (олеаты или пальмитаты меди, цинка или железа
и др.). В теплообменных аппаратах обычно происходит смешанная —
капельная и пленочная конденсация.
При пленочной конденсации сухого насыщенного пара, лишенного
неконденсирующихся газов, и ламинарном течении конденсата на вер-
тикальных трубах и стенках без учета влияния скорости пара на тепло-
обмен, т. е. при к^р"<1, для определения коэффициента теплообмена а
можно пользоваться формулой Нуссельта
»=1-34(^)0'25=1.34(Д^. Вт/(м-.°С). (1-27)
Приближенно можно считать В/ = 5 700+56^ц—0,09^, где tH— тем-
пература насыщения конденсирующегося пара; для более точных рас-
четов значения а, X, р и р, принимают при температуре пленки конден-
сата Ал = V2 • (Лт +А); г —скрытая теплота парообразования, берется
при температуре стенки.
Для определения коэффициентов теплоотдачи от конденсирующе-
гося пара на вертикальных стенках могут быть использованы более точ-
ные расчетные формулы. Для их выбора необходимо определить значе-
ние числа Григуля (приведенная длина)
Z=A177(A—/с), (1-28)
где
- 1/(м-°С).
1 I V2 J rpv 1 v 7
При Z<2 300 имеется ламинарное течение пленки. Коэффициент
теплоотдачи для этих условий можно определить по формуле Д. А. Ла-
бунцова
Л?-78 1
“ = 3’8 /г)]0.22 ’ (1 ’29)
где A4=4/rpv.
Формулу (1-29) можно представить в следующем упрощенном
виде:
° ° I» «. - М1°- ' Вт/(м’-’С). (1-29а)
Коэффициенты Аь А3 и А4 зависят только от физических парамет-
ров жидкости при температуре насыщения. Для воды значения этих
коэффициентов в зависимости от /н приведены в табл. 1-5.
При Z>2 300 в случае пленочной конденсации и смешанного тече-
ния конденсата можно пользоваться формулой С. С. Кутателадзе [Л. 11
и 18] или формулой Д. А. Лабунцова
а==д7Дл? Вт//м2-сС), (1-30)
где Ке=[253 + 0,069(Рг/Ргс)0’25Рг°’5(г—2 300)]4/3; Рг и Ргс—-критерии
Прандтля соответственно при температурах насыщения 7Н и стенки tc.
39
Значения температурных множителей в формулах (1-28), (1-29)
Таблица 1-5
Темпера- тура насы- щения, -с А, А,. Вт/м Лз. Вт/(М'°С) Л-108, м/Вт Темпера- тура насы- щения, t, °C Ль 1/(м-®С) А. Вт/м Лз. Вт/ (м • °C) л4.1о\ м/Вт
20 5,16 1,62 по 60,7 9 180 13 480 6,95
30 7,88 — — 2,06 120 70,3 9 350 13 800 7,65
40 Н.4 -— — 2,54 130 82,0 9 500 14 070 8,47
50 15,6 —. —- 3 06 140 94,0 9 600 14 280 9,29
60 20,9 .— — 3,62 150 107 9 700 14 450 10,15
70 27,1 — — 4,22 160 122 9 730 14 520 11,09
80 34,5 8 400 12 200 4,88 170 136 9 800 14 650 12,04
90 42,7 8710 12 750 5,57 180 150 9 850 14 700 12,90
100 51,5 8 950 * 13100 6,28
В приведенных формулах обозначено:
Д/=ДН—/с— разность температур конденсирующегося пара и стен-
ки, °C; X — коэффициент теплопроводности конденсата, Вт/(м-°С); v —
коэффициент кинематической вязкости конденсата, м2/с; р, — коэффи-
циент динамической вязкости конденсата, Н • с/м2; р' — плотность кон-
денсата, кг/м3; р" — плотность пара, кг/м3; wn— скорость набегающего
потока пара, м/с; г — теплота парообразования, кДж/кг; Н — высота
вертикальной поверхности или трубы, м; все физические параметры
здесь принимаются при /н-
При значениях w^p">\ необходимо учитывать влияние скорости
движения пара на теплоотдачу, а коэффициент теплоотдачи рекоменду-
ется рассчитывать по формуле [Л. 11]
а/ан= 28,ЗП°’08Ми—0,88 ,
' д н
(1-31)
где ан—коэффициент теплоотдачи для неподвижного пара, подсчитан-
ный по формуле (1-29);
г _ ®пР'“к . _ан<
gp"X ’ 1NUa— Л ’
остальные обозначения имеют прежние значения.
Формула (1-31) применима при давлениях водяного пара от 0,05
до 1,0-105 Па, температурных напорах от 2 до 20 °C и Пдс800.
При конденсации водяного пара на горизонтальных трубных пуч-
ках, обтекаемых сверху вниз чистым водяным ларом, значения а по
рядам труб можно определить по методике Бермана [Л. 18].
В приближенных расчетах коэффициента теплообмена для пучка
горизонтальных труб можно воспользоваться формулой Нуссельта,
если положить
а = 0,845 , (1-32)
\yAtnd J ' ’
где d — диаметр трубок, м; п — среднее число труб в вертикальном
ряду.
Коэффициент а для водяного пара можно также определить по пре-
образованной формуле Д. А. Лабунцова
Аг
(1-33)
а= г—__________—
К nd — teT)
где п и d имеют обозначения, указанные в формуле (1-32).
40
Формула действительна при значении числа Григуля Z<3 900, при
определении которого вместо Н — расчетной высоты трубок, следует
подставить произведение nd. Значения коэффициента /42 даны в табл. 1-5.
Коэффициент теплоотдачи при конденсации пара внутри горизон-
тальных труб [Л. 15]
a = C.A^L^d^, (1-34)
где
л- М'°'1
(rv)o.5o<>,» ’
С— 1,26 (для стальных труб); L — длина трубы, м; X, г, р, v и о — физи-
ческие константы жидкости при /н; р" — плотность насыщенного пара.
Значения коэффициента А для водяного пара даны в табл. 1-6.
Таблица 1-6
Значения коэффициента А в зависимости от температуры
конденсирующегося водяного пара
'н- *С 100 ПО 120 130 140 150 160 170 180 190
А 8,42 8,10 7,75 8,42 7,10 6,78 6,47 6,14 5,81 5,49
Все приведенные выше формулы относятся к конденсации насыщен-
ного пара. При конденсации перегретого пара и небольших температу-
рах перегрева а вычисляют по тем же формулам, но вместо г в них под-
ставляют величину
i=r+cn(tn—Д), кДж/кг,
где ta— температура перегретого пара, °C; — температура насыщен-
ного пара, соответствующая давлению в теплообменнике, °C; сп — тепло-
емкость перегретого пара, кДж/(кг-°C).
Значение At при этом по-прежнему равно tR—tc.
В тех случаях, когда из соображений надежности работы аппарата
в него не должен поступать пар высокой температуры, перегретый пар
перед аппаратом увлажняют. Если температура теплопроводящей стен-
ки выше температуры насыщения поступающего пара, то конденсации
перегретого пара происходить не будет и коэффициент теплоотдачи нуж-
но определять по формуле (1-16) или (1-15) в зависимости от условий
теплообмена, который в этом случае происходит за счет понижения тем-
пературы перегрева. Такой случай крайне редок.
Все приведенные выше формулы применимы для случая конденса-
ции только однородного пара, но не смесей паров; конденсация послед-
них происходит по другим законам.
Формулы (1-27)— (1-34) применяются для определения коэффи-
циентов теплоотдачи при конденсации пара на чистых гладких поверх-
ностях (чистые латунные и медные трубы, зачищенные до металличе-
ского блеска стальные трубы). Для окисленных, но не очень загряз-
ненных труб (например, нормальные стальные трубы) значения
коэффициентов теплоотдачи следует принимать на 15—20% ниже рас-
четных.
Коэффициент теплоотдачи при конденсации пара из потока влаж-
ного воздуха (парогазовой смеси) в трубчатых или пластинчатых тепло-
обменниках можно определить по следующей формуле:
«вл = асух+₽гДр/Л/, Вт/(м2-°С), (1-35)
где асух — коэффициент теплоотдачи сухого воздуха, Вт/(м2-°С); fl —
коэффициент массоотдачи при конденсации паров из влажного воздуха,
41
отнесенный к градиенту парциальных давлений {см. (6-1)}; Л/ —раз-
ность температур между влажным воздухом и стенкой, °C; Др — раз-
ность парциальных давлений пара в ядре потока и у стенки, Па; г —
теплота парообразования, кДж/кг.
Коэффициенты тепло- и массообмена асух и р для гидродинамически
стабилизированного течения влажного воздуха (//tZ;>50) в каналах
различной конфигурации можно рассчитывать для ламинарного и пере-
ходного режимов по формуле МЭИ (Ж. Ф. Сергазина).
Ламинарный режим (Re= 1 ОООн-2 ООО):
теплообмен (а)
массообмен (р) Nu = 4,55- 10-3Re°'36(ArPr)04, (l-36a)
Num=4,55- 10~3Re03'6(ArPrm)°-4. (1-366)
Переходный теплообмен (а) массообмен (Р) режим (Re = 2000—10000): Nu = 6,48 • I0~5Re°’82(ArPr)°’4; (1-36b)
Num=6,48 • 10-5Re°>92(ArPrm)0'4. (l-36r)
Турбулентный режим (Re>10 000): теплообмен (а)
массообмен (р) Nu = 0,023Re°’8Pr°-4; (1-36д)
Num = O,O23Re°.8Pr0,4. * m (I-36e)
В этих формулах Num=prfB/Dp; Prm = v/£>c;
Ar = g(f (р — pc)/v2p,
где Dc — коэффициент концентрационной диффузии, определяемый по
формуле (6-10); Dp = Dc/RnT — коэффициент диффузии, отнесенный
к градиенту парциальных давлений; рс и р — плотности влажного воз-
духа у стенки и в ядре потока, кг/м3.
В приведенных соотношениях за определяющий размер принят
эквивалентный диаметр канала d3=$flU (где f и U — площадь и пери-
метр поперечного сечения канала), а за определяющую температуру —
средняя температура влажного воздуха.
Коэффициент теплопередачи k можно определить по формуле (1-10)
для плоской стенки.
Методы повышения коэффициента теплоотдачи
при конденсации пара. В горизонтальных аппаратах с целью
повышения коэффициентов теплоотдачи при конденсации пара рекомен-
довалось расположение трубок по методу Жинаба (рис. 1-19), где цент-
Коридорныи пучок
Рис. 1-19 Схемы расположения труб в конденсаторах пара.
Ромбический пучок
Пучок И^инабо
42
Рис. 1-20 Поправочный
коэффициент ег к коэффи-
циенту теплоотдачи в зави-
симости от содержания воз-
духа в неподвижном паре к.
на верхние трубки ниж-
ры трубок сдвинуты на величину их радиуса относительно трубок сосед-
него верхнего ряда. При этом ожидалась одинаковая толщина пленок
конденсата как на верхних, так и на нижних трубках. Расположение
трубок по методу Жинаба по сравнению с коридорным или шахматным
расположением вызывает увеличение диаметра аппарата, особенно при
незначительных поверхностях теплообмена (меньше 50 м2).
Исследованиями Л. Д. Бермана (ВТИ) было установлено, что ме-
тод Жинаба неэффективен. Вследствие действия сил поверхностного
натяжения происходит выравнивание толщины конденсатной пленки по
периметру трубы и стекание конденсата происходит не в виде струек,
как это предполагалось ранее, а в виде ка-
пель. Опыты показали также, что коэффи-
циент теплоотдачи при конденсации пара
зависит от его скорости в межтрубном про-
странстве, а не от схемы расположения
трубок в трубной решетке.
Различные способы уменьшения толщи-
ны пленки и получения смешанной капель-
но-пленочной конденсации в вертикальных
аппаратах практического применения не
нашли.
Основными мероприятиями по улучше-
нию работы теплообменников при конден-
сации теплоносителей являются: 1) рацио-
нальный отвод конденсата по зонам из сек-
ционных теплообменников для устранения
перетекания конденсата из верхнего корпу<
него корпуса, последовательно с ним включенного; 2) создание доста-
точных проходов для проникновения пара в пучок труб и уменьшения
переохлаждения конденсата; 3) борьба с накипью и другими загряз-
нениями трубок; 4) удаление из аппарата воздуха и других неконден-
сирующихся газов, которые могут ухудшать теплообмен при конденса-
ции. Например, результаты опыта В. А. Гудымчука, представленные
в виде графика на рис. 1-20, показывают, что наличие 1% воздуха в не-
подвижном паре может в 2 раза уменьшить коэффициент теплоотдачи
от конденсирующегося пара к стенке.
Следует заметить, что при выполнении указанных мероприятий
коэффициент теплопередачи в большинстве случаев начинает лимити-
роваться величиной коэффициента теплоотдачи со стороны нагреваемой
жидкости или газа, а также загрязнениями поверхностей нагрева, воз-
можными с обеих сторон стенки.
Теплоотдача при кипении жидкости. Кипение на по-
верхности нагрева наблюдается в том случае, когда температура поверх-
ности tc выше температуры насыщения tH при данном давлении жид-
кости.
На характер парообразования значительное влияние оказывает
плотность теплового потока от поверхности нагрева q или температур-
ный напор, т. е. разность температур At=tc—между теплопередающей
стенкой и кипящей жидкостью.
В зависимости от величин q и Д/ наблюдаются два режима кипения
жидкости. При малых их значениях наблюдается пузырчатое кипение.
Коэффициент теплоотдачи а при пузырчатом кипении растет с увеличе-
нием Д/ (или q), достигая максимального значения при Д/=Д/Кр (или
<? = <7кр) (рис. 1-21). Дальнейшее увеличение Д/ (или q) сопровождается
переходом пузырчатого режима кипения в пленочный. При пленочном
режиме кипения происходит слияние пузырьков, образующихся на по-
верхности нагрева, в подвижную паровую пленку, пар из которой выхо-
дит в виде больших пузырей. При этом а резко уменьшается. В области
43
развитого пленочного кипения а почти не зависит от А/, a q возрастает
приблизительно пропорционально Д/.
Величины qKp и Д/Кр в
ст физических свойств
Рйс. 1-21. Зависимость а и q от
перегрева жидкости А/.
J — область конвективного теплообмена
одввфазной жидкости; 2 — область пу-
зырькового кипения; 3 — переходная
область; 4 — область пленочного кнпе-
хня.
условиях естественной конвекции зависят
жидкости. Так, например, для воды
при р=0,98-105 Па (1 кгс/см2) дКр~(14-
1,75) -10е Вт/м2— (1 4-1,5) -10е ккал/(м2Х
Хч) и Д/Кр=25,оС; для этилового спирта
в тех же условиях qKP= (0,4654-0,58) X
Х106 Вт/м2~ (0,44-0,5)-106 ккал/(м2-ч) и
Д/кр~20°С; для бензола <7кр=0,407Х
ХЮ6 Вт/м2»0,35 • 106 ккал/(м2«ч) и
д/кр=47°С.
В области развитого пузырчатого ки-
пения жидкости, смачивающей стенку,
расчет теплоотдачи может быть произве-
ден по одной из следующих формул.
При кипении в большом объеме
(в том числе на внешней поверхности
пучков трубок) <в условиях естественной
конвекции [для давлений (0,19—98,0) X
ХЮ5 Па] а определяется по формулам
[Л. 11]:
a=C/?01V'7; (1-37а)
а=С>°'5Д/2-Ч (1-376)
где a = q[M, Вт/(м2-°С); q — плотность теплового потока, Вт/м2; Д^ =
=tc—tw °C; р — давление, Па; С, С' — коэффициенты, зависящие от
свойств жидкости и поверхности нагрева; для воды, кипящей на нор-
мальных технических трубках из цветного металла, можно принять С=
=3 и С'=39. Для других жидкостей С=3<р. Значения коэффициента <р
для ряда исследованных жидкостей даны в табл. 1-7.
Таблица 1-7
Значение коэффициента у для некоторых
жидкостей и растворов
Наименование жидкости или раствора
Значение <р
Вода..................................
9%-ный водный раствор NaCl............
24о/о-иый водный раствор NaCl.........
26°/о-ный водный раствор глицерина . . .
25%-ный водный раствор сахара . • . .
10%-ный водный раствор NaaSO4 . . . .
Керосин ..............................
Газолин ..............................
Бензол ...............................
Этиловый спирт .......................
Метиловый спирт.......................
Гептан ...............................
1,0
0,86
0,62
0,83
0,57
0,91
0,31—0,56
0,27
0,31
0,45
0,36
0,46
Формулу (1-37а) и значения <р для растворов следует рассматривать
хак первое приближение, так как растворам, вообще говоря, свойствен-
ны иные закономерности. Вблизи процесса критической точки кипения,
т. е. при q — qKp, эта формула неприменима.
При пузырчатом кипении в большом объеме коэффициент теплоот-
дачи может быть подсчитан также по формулам [Л. 18]:
при Re^lO-2
Nu*=0,125 Re°’65Pr;
(1-38а)
44
при Re^lO-2
Nu* = 0,0625 Re°’sPr,
(1-386)
где
Re*=g'Z*/(rp"v); Nu.=«Z*A; Pr=
=v!a; l*=cp'оТв/(гр")г, м;
v, с, г, К а и о — кинематическая вязкость, теплоемкость, теплота паро-
образования и коэффициенты теплопроводности, температуропроводно-
сти и поверхностного натяжения жидкости при температуре насыще-
ния /н; р' и р" — плотности жидкости и пара при температуре /и,’ Тп —
температура насыщения, К.
Формулы (1-38а) и (1-386) справедливы при 0,86^ Рг^ 7,6;
10~5^Re*с 104 и давлении р— ('0,04—150) • 105 Па.
Для воды значения Z*, Z*/(rp"v) и 7,/(rp"v) в зависимости от темпе-
ратуры приведены в табл. 1-8.
Значения I*, и для воды
Таблица 1-8
*с м —— 10е. Г p"v м/Вт —-— 10>2, rp"v 1/°С 'И.’С - 10е. м -А— юе, Гр' rv м/Вт V —V 1°’. fp"v 1/«С
30 16 450 277 000 1 040 200 0,296 0,123 27,5
40 5 950 73 300 782 210 0,200 0,0718 23,5
50 2 305 20 900 587 220 0,136 0,0426 20,2
60 960 6 550 450 230 0,0938 0,0254 17,3
70 423 2 200 347 240 0,0646 0,0155 15,1
80 197 797 273 250 0,0451 0,0099 13,6
90 96,0 305 216 260 0,0318 0,0094 П,4
100 38,7 122,4 172 270 0,0224 0,00373 9,80
ПО 25,9 51,7 138 280 0,0158 0,00205 8,80
120 14,2 22,8 ПО 290 0,0114 0,00154 7,47
130 8,05 10,67 96,0 300 0,0080 0,000915 6,16
140 4,70 5,12 75,0 310 0,00565 0,00061 5,64
150 2,82 2,59 60,5 320 0,00398 0,000387 4,93
160 1,73 1,33 52,6 330 0,00278 0,000294 4,34
170 1,08 0,71 44,5 340 0,00192 0,000158 3,77
180 0,715 0,397 37,5 350 0,00126 0,000098 3,36
190 0,450 0,216 32,2
Критическая плотность теплового потока при кипении жидкости
в большом объеме может быть подсчитана по формуле [Л. 18]
Re*KP = 68Ar4-®Pr—1/3,
(1-39)
где
Рр — (?К₽А . Д г (р pf )
Ке*кр—> ^г——г
Обозначения всех величин те же, что и в предыдущих формулах.
Формула применима при 0,86^,Рг^ 13,1 и давлениях р= (0,98-ъ 185) X
ХЮ5 Па.
Формулы (1-37) — (1-39) справедливы для технически гладких не-
окисленных поверхностей. При кипении на окисленных поверхностях не-
обходимо учитывать термическое сопротивление слоя окиси и увеличение
а за счет шероховатости. Приближенная формула для «видимого» коэф-
фициента теплоотдачи (точнее, коэффициента теплопередачи от металли-
45
ческой поверхности через слой окиси к кипящей жидкости) от окислен-
ной поверхности имеет вид:
Ccp/AV,’ + R
(1-40)
Для обычных окисленных стальных труб можно принять С— 6,5 и
R—0,773-10 4 м2-°С/Вт. Значения коэффициента для растворов можно
с известным приближением определить по формуле
L с» \ Р" Ар J М ’
где р, с, р, и К означают плотность, теплоемкость, вязкость и теплопро-
водность; индекс «р» показывает, что эти величины относятся к раствору,
а индекс «в», что они относятся к воде.
При вынужденном движении кипящей жидкости в трубах в услови-
ях, когда она нагрета до температуры насыщения, коэффициент тепло-
отдачи может быть подсчитан по следующим формулам [Л. И и 15]:
a=aw, если а1:/аю<0,5;
ct=ciK, если ак/аш>2;
Z-==fr_+.g»., если 0,5 < — <"2,
(1-41а)
(1-416)
(1-41в)
где а — коэффициент теплоотдачи при кипении в трубах; а1:— коэффи-
циент теплоотдачи при развитом пузырчатом кипении в большом объеме,
определяемый по формуле (1-38а) или (1-386); aw— коэффициент тепло-
отдачи при турбулентном движении однофазной жидкости в трубах,
определяемый по формуле (1-15).
Формулы (1-41а) — (1-41 в) могут применяться только для воды при
давлениях р= (0,98-н 85) • 105 Па, скоростях от 0,2 до 6,7 м/с и объемном
паросодержании меньше 70%.
Граф о-a налитический метод определения коэффи-
циента теплопередачи и поверхности нагрева. В расчете
коэффициента теплоотдачи для конденсирующегося пара (так же как и
для кипящей жидкости) приходится задаваться температурой стенки.
Правильность принятого значения этой температуры проверяется после
расчета, и в случае несовпадения его со значением, полученным в ре-
зультате расчета, задаются другим значением температуры стенки и по-
вторяют расчет до тех пор, пока не достигнут требуемого совпадения.
Описанный метод приближенных вычислений может потребовать значи-
тельного времени. Если расчет коэффициентов теплоотдачи производить
по приближенным формулам, применение графо-аналитического метода
позволяет сократить затрату времени. Графо-аналитический метод осно-
ван на том, что при установившемся тепловом режиме удельное количе-
ство тепла, передаваемого в единицу времени через все слои стенки, есть
величина постоянная и равна количеству тепла, передаваемого от одного
теплоносителя другому, т. е. <71=<72=?з=^4=- •=?, Вт/м2.
Найдем зависимости &t=f(q) для отдельных последовательно распо-
ложенных участков перехода тепла от конденсирующегося водяного па-
ра к нагреваемой воде, проходящей внутри трубок.
1. Теплоотдача от конденсирующегося пара к стенке трубы
<7i= ctiAO,’ A^i = /H ^ci-
Например, для вертикальной стенки по формуле (1-27)
@1=В/(//А/1)0’25, Вт/(м2-°С),
46
где В = l,34(?i3p2v)0’25; Н — активная длина трубок, м; /п— температура
конденсации пара; tc — температура стенки.
Таким образом,
д » В д j ______ В д <0,75
Ql (//Д/^0,25 //0,25
Обозначив постоянную величину В/Н°-25 через А, можно записать:
?1 = ЛД^’75.
2) Передача тепла через стенку
qs = ^-Ms,
° ст
где At2=tcl—^tc2, откуда
q2=BAt2, Вт/(м2'°С).
3. Передача тепла через накипь
qs = ^Ms,
°н
где ДЛз=/с- ^нак, откуда
q3=BM3, Вт/(м2-°С).
4. Передача тепла от накипи к воде
?4 = ССвД^4»
Г де tt= /нак i в-
Взяв для определения ав формулу (1-14), можно записать:
q^r&tt, Вт/(м2’°С).
В рассматриваемом нами случае полная разность температур меж-
ду теплоносителями
A t='Ati+А'^2+А/3+А^4.
Задавшись некоторыми значениями A/i, А/г, At3 и Л/4, строим
(рис. 1-22) четыре линии зависимости А/ от q, из которых в данном слу-
чае одна (для пара) будет кривой, так как это степенная зависимость,
а остальные будут прямыми. Затем строим суммарную кривую зависимо-
сти ДА/ от q. Зная Atfcp для конкретного примера, откладываем значение
его по оси ординат, проводим линию тп, параллельную оси абсцисс, до
пересечения с суммарной кривой в точке п и, опустив перпендикуляр
па на ось абсцисс, находим q — фактическую плотность теплового пото-
ка, т. е. передачу тепла через 1 м2 поверхности нагрева в единицу вре-
мени.
Поскольку Q = qF, Вт, является заданной величиной, поверхность
нагрева аппарата определяем из выражения
F—Qlq, м2.
Коэффициент теплопередачи можно определить из равенства
k = qlAtcv, Вт/(м2-°С).
В случае необходимости можно по графику приближенно найти сц, а2
и tc. На рис. 1-22 показаны отдельные разности температур, а именно
At2=ab— для стенки, At3=ac— для накипи, &tb=ad— от накипи к воде
и A^i = (ze — от пара к стенке. В левой части рис. 1-22 показаны измене-
ния температур по отдельным слоям стенки.
Применение графо-аналитического метода показано на примере 1-3.
47
Рис. 1-22. К определению температурного напора
графо-аналитическим методом.
Пример 1-3. Произвести кон-
структивный тепловой расчет че-
тырехходового вертикального па-
роводяного подогревателя со сво-
бодной нижней решеткой по об-
разцу рис. 1-2,5 при следующих
условиях: производительность ап-
парата Q=25,8-106 Вт=92,7-10е
кДж/ч; параметры греющего пара:
давление р=2,5 • 103 Па; энталь-
пия i=2 723 кДж/кг; температура
/=130 °C при давлении 2,5- 105 Па;
температура насыщенного пара
/Н=127°С и энтальпия жидкости
iH=534 кДж/кг; температура на-
греваемой воды /',=65 °C и /"г=
= 117 °C; поверхность нагрева вы-
полнена из латунных трубок диа-
метром d= 18/20 мм с толщиной
стенки 6=0,001 м; вода проходит
через трубки,
в межтрубное пространство;
бнак=0,0002 м; коэффициент, учи-
сота трубок в одном ходе Н—Л im; толщина накипи
тывающий потери тепла в окружающую среду, т]=0,99.
Решение. Определяем расход пара
О 92,7-10е
(2 723 —534)-0,99 “4300° кг/ч 11,95 кг/с.
D (i — 'н) Ч
Расход воды
у Q_____________________________________________
v- — 4,187 (117 — 65)-965
92,7-10е
а пар поступает
вы-
= 443 м3/ч ^0,123 м’/с,
где с=4,187 кДж/(кг-°C), р=965 кг/м3 — плотность воды при средней температуре
/ср=1/2 (117+65) =91 °C.
Средняя логарифмическая разность температур теплоносителей в подогревателе
62—10
----------------------------------------6^-“28’4 °С-
1п 10
Л“- 1 Д<6
1п дгм
Коэффициент теплопередачи определяем графо-аналитическим методом, для чего
предварительно находим для различных участков перехода тепла зависимость между
плотностью теплового потока q и перепадом температур Д/.
а) Передача тепла от пара к стенке. Коэффициент теплоотдачи определяем по
формуле (1-27)
а, = l,33B'/(/7».23A/f'25);
В’ = 5 700 + 56/н — 0,09/2 = 5 700 _|_ 56.127 _ 0>09.1272;
£'=11 400.
При 77=4 м величина
Н 400
а, = 1,34----------nV- = 10 8ООД/7-0-25
4°.25Д/| 5 1
Для найденного значения щ
91 =аД/1 = 10 8ООД/“0,25; Д/, = 10 800Д/°’75
<7+
Задавшись рядом значений Д/
соответствующие им величины Д/®'7° и
вычисляем
Л/, Л/0.75 <71, Вт/м2
2 1,68 18 150
6 3,85 41 600
10 5,62 60 700
15 7,6 82 400
48
Строим, как это показано на рис. 1-22, кривую Ah=h(<7i)-
б) Передача тепла через стенку. Для латунной стенки Аст = 105 Вт/(м-°С).
При этом
ЛС1 105
= —g—- А/2 = -g Qgj- Ltz — 105 000 Д/2, Вт/м2,
т. е. связь между qz и изображается графически прямой линией. Задавшись любым
значением /2, наносим эту прямую на график.
в) Передача тепла через накипь. Принимаем для накипи Хнак=3,49 Вт/(м-°С),
тогда
Л £1ак 3,49
Qi = Д/з = 0Д002 Д/> = 17 450 Л/з. Вт/м2.
Наносим эту прямую на график.
г) Передача тепла от стенки к воде. Скорость воды в пароводяных подогревате-
лях обычно составляет от 0,6 до 3 м/с, движение воды в трубках турбулентное, по-
этому пользуемся формулой (1-14)
(w)°-8
а4==^-^2—• Вт/(м2-°С).
По табл. 1-4 для средней температуры воды /Ср=91 °C находим величину Л =
=3 100.
Скорость воды в трубках w принимаем равной 1,4 м/с. Подставив соответствую-
щие величины в формулу (1-14), получим:
1,4°.е
а4 = 3 100 -q gig»,2~ =9 200 Вт/(м2-°С) д&7 900 ккал/(м2-ч-®С),
тогда qi—а4Д/4=9 200 Д/4.
Аналогично предыдущему строим зависимость Ati=f(qi), проходящую через на-
чало координат.
Складывая ординаты четырех зависимостей, строим суммарную кривую темпера-
турных перепадов. Из точки т на оси ординат, соответствующей Д/ср = 28,4сС, про-
водим прямую, параллельную оси абсцисс до пересечения ее с суммарной кривой. Из
точки пересечения п опускаем перпендикуляр па на ось абсцисс и находим значение
</==75 600 Бт/м2. При этом коэффициент теплопередачи
k=75 600/28,4 = 2 660 Вт/ (м2 • °C).
Поверхность нагрева теплообменника
<2
Л = = 25,8-106/2 660-28,4 = 342 м2.
Определяем основные конструктивные данные и размеры аппарата. Количество
трубок в одном ходе
4lZ _ 4-447
Л = я^ш-3 600 ~ 3,14-0,0182-1,4-3 600 ~346‘
Общая длина трубок
F 342
L~ Jtdcpn = 3,14-0,019-346 ’“16,6 м-
Число ходов
Z—LIH= 16,6/4^4.
Шаг между трубками принимаем равным 1,5</н, т. е.
s= 1,5 20 = 30 мм.
Для определения диаметра корпуса аппарата необходимо иайти размеры трубной
решетки. Поскольку аппарат четырехходовой, необходимо предусмотреть место для
перегородок и анкерных связей и в каждом ходе разместить по 346 трубок. Принимаем
ромбическое размещение трубок и находим по указанным ранее правилам, что при
данной компоновке трубной решетки диаметр корпуса будет равен 1,8 м.
Размеры водяных и парового штуцеров обычно определяют по скорости для
воды и конденсата, равной 1—2 м/с, и для пара 20—40 м/с; диаметр штуцера подсчи-
тывается по формуле
4—1128 49
где G — расход пара или воды, кг/с; р — плотность пара или воды, кг/м3; ш — скорость
пара или воды в штуцере, м/с.
Пример 1-4. Определить коэффициент теплоотдачи между конденсирующимся па-
ром и стенкой для условий, указанных в примере 1-3, по формулам (1-29а) и (1-30).
Решение, а) По формуле (1-29а) для Z<2 300
Аз
(7/Д/)0.22
14 000
(4-16)0-22
= 5 600 Вт/(м2-°С),
значение As взято из табл. 1-5 при /Н=127°С;
б) по формуле (1-30) для Z>2 300
Re 3 620-Ю3
а= AJiM ~ 8,4-4-16 ~ 6730 Вт/(м2-°С),
где
tz Рг \0,25 -14/3
253 + 0,069 (pp—J Pr°-5(z — 2 300) =
/1,38\°-2’ I4/3
253 + 0,069 (j-go J -1,38°.®(5 100 — 2300) =3620,
Z=A/+H1=16-4- 80=5 100; A4=8,4-10~3 м/Вт.
Значения + и Д4 взяты по табл. 1-5.
Так как для данных условий Z=5 100>2 300, т. е. течение капельно-пленочное, то
выбор неподходящей формулы (1-29а) приводит к занижению коэффициента тепло-
отдачи иа 17%.
Проверочный расчет теплообменных аппаратов.
В практических условиях часто требуется определить конечные темпера-
туры теплоносителей в готовом или запроектированном теплообменном
аппарате при заданных расходах теплоносителей и теплопроизводитель-
ности этого аппарата.
а) Теплопередача без изменения агрегатного состояния теплоноси-
телей. При решении такой задачи известными величинами являются на-
чальные температуры теплоносителей /'4 и t'z, поверхность нагрева F,
приблизительное значение коэффициента теплопередачи k и значения
GiCj и G2c2; искомыми же являются конечные температуры t'\ и Z"2 и
количество переданного тепла Q. Результат расчета зависит от схемы
движения жидкостей.
При прямотоке теплоносителей их конечные температуры /"i и /"2
могут быть определены по формулам из курса теплопередачи [Л. 11]:
Г'1=Л—(fj—Г2)П; (1-42)
+ (1-42а)
и2С2
Таблица 1-9
Значения функции П в уравнениях (1-42) и (1-42а)
GiCi/GaC^ kFIGtC,
0,033 0.10 0,33 0,50 1 2 3 оо
0 0,033 0,10 0,28 0,39 0,63 0,86 0,96 1,00
0,01 0,033 0,10 0,28 0,39 0,63 0,86 0,95 0,99
0,05 0,033 0,10 0,28 0,39 0,62 0,84 0,91 0,95
0,10 0,033 0,10 0,28 0,38 0,61 0,81 0,89 0,91
0,20 0,033 0,10 0,27 0,38 0,58 0,76 0,81 0,83
0,50 0,033 0,10 0,26 0,35 0,52 0,63 0,66 0,67
1,0 0,033 0,09 0,25 0,32 0,43 0,49 0,50 0,50
2,0 0,033 0,09 0.21 0,26 0,32 0,33 0,33 0,33
5,0 0,032 0,08 0,14 0,16 0,17 0,17 0,17 0,17
10,0 0,028 0,06 0,09 0,09 0,09 0,09 0,09 0,09
20,0 0,024 0,04 0,05 0,05 0,05 0,05 0,05 0,05
50,0 0,016 0,02 0,02 0,02 0,02 0,02 0,02 0,02
100,0 0,009 0,01 0,01 0,01 0,01 0,01 0,01 0,01
50
Величины П даны в табл. 1-9 в зависимости от отношений GicJG2C2 и
kFfGiCi.
Для противотока конечные температуры теплоносителей определя-
ются по формулам
(t'i— t'2)Z; (1-43)
= + (l-43a)
U 2^2
Значения Z приведены в табл. 1-10.
Таблица 1-10
Значения функции Z в уравнениях (1-43) и (!-43а)
kF j GiCi
GiCi/GaCa 0,033 0,10 0,33 0,50 i 2 3 CO
0 0,033 0,10 0.28 0,39 0,63 0,86 0,95 1,00
0,01 0,033 0,10 0,28 0,39 0,63 0,86 0,95 1,00
0,05 0,033 0,10 0,28 0,39 0,62 0,86 0,94 1,00
0,10 0,033 0,10 0,28 0,38 0,61 0,85 0,94 1,00
0,20 0,033 0,10 0,28 0,38 0,60 0,83 0,93 1,00
0,50 0,033 0,10 0,26 0,36 0,57 0,78 0,89 1,00
1,00 0,033 0,10 0,25 0,34 0,51 0,68 0,77 1,00
2,0 0,033 0,09 0,23 0,29 0,39 0,46 0,49 0,50
5,0 0,032 0,08 0,16 0,18 0,20 0,20 0,20 0,20
10,0 0,028 0,06 0,10 0,10 0,10 0,10 0,10 0,10
20,0 0,024 0,04 0,05 0,05 0,05 0,05 0 05 0,05
50 0,016 0,02 0,02 0,02 0,02 0,02 0,02 0,02
100,0 0,010 0,01 0,01 0,01 0,01 0,01 0,01 0,01
Расход тепла, если известны конечные температуры, определяется
в обоих случаях из уравнения теплового баланса (1-1).
Формулы (1-42) и (1-43) обладают тем недостатком, что они приме-
нимы лишь к двум наиболее простым схемам движения теплоносителей.
Кроме того, при выводе формул предполагается независимость их пол-
ной теплоемкости от температуры, хотя это далеко не всегда отвечает
действительности. Наконец, строго говоря, точно определить зна-
чение коэффициента теплопередачи, не зная конечных температур тепло-
носителей, нельзя. Поэтому весьма часто не удается использовать приве-
денные выше формулы для проверочного расчета. В таких случаях рас-
чет приходится вести методом последовательных приближений. При этом
следует задаться конечными температурами и производить расчет в по-
рядке изложенного выше конструктивного расчета. Если полученная
в результате этого расчета поверхность нагрева совпадает с действи-
тельной, то расчет на этом заканчивается, так как совпадение свидетель-
ствует о том, что конечные температуры выбраны правильно. В против-
ном случае расчет приходится производить снова, задавшись другими
значениями конечных температур.
б) Теплопередача при изменении агрегатного состояния теплоноси-
телей. Если проходящая через аппарат жидкость нагревается за счет
тепла конденсации пара, то характер зависимости температуры жидко-
сти по длине поверхности нагрева соответствует рис. 1-13. Уравнение
этой кривой в координатах t и F можно составить, исходя из следующих
соображений. При перемещении G кг/с жидкости вдоль элементарной
поверхности нагрева dF температура ее изменяется на величину dt.
Количество тепла, передаваемое от конденсирующегося пара к жидко-
сти через эту элементарную поверхность, может быть выражено уравне-
нием
dQ = G2c2dt=k(ta—t'2)dF.
(1-44а)
4*
51
Разделив переменные и проинтегрировав обе части уравнения в со-
ответствующих пределах, получим:
F t",
f kdF _ f dt
J G2C2 J 2
0 t't
ИЛИ
ft/7 tv t's
G2c2 ~ tK — '
Из этого равенства находим конечную температуру жидкости
_ kF
t"z = ta-(ta-t\)e G‘c'. (1-446)
Для случая кипения жидкости за счет тепла горячего газа или го-
рячей жидкости по аналогии с предыдущим имеем уравнение
dQ = -Glcldt=k(tl—tli)dF. (1-45а)
Знак минус перед членами, содержащими dt, поставлен потому, что
при увеличении F величина t уменьшается, вследствие чего величина dt
является отрицательной. Из уравнения (1-45а) аналогично предыдущему
находим конечную температуру греющей жидкости или газа
kF
. (1-456)
Промежуточные значения температур определяются путем подста-
новки в выражения для конечных температур соответствующих величин F.
Наименьшее давление пара, при конденсации которого возможен на-
грев жидкости или газа до желаемой температуры t"z, определяется ис-
ходя из того соображения, что температура насыщения tn, соответствую-
щая этому давлению, должна быть больше, чем t"z> на некоторую вели-
чину 6/.
Пример 1-5. Определить конечную температуру воздуха на выходе из воздухоох-
ладителя с поверхностью нагрева F=1 ООО м2 при следующих условиях: температура
воздуха, поступающего в воздухоохладитель, Ц = 60сС; объем циркулирующего воздуха
V1=100 000 м3/ч, или 27,8 м3/с; начальная температура охлаждающей воды К2=25°С;
расход воды V2 = 320 м3/ч или 0,089 м3/с; коэффициент теплопередачи й =
=30,5 Bt/(im2 • °С)[26,5 ккал/(м2 - ч • °C)]; схема движения теплоносителей противо-
точная.
Решение. Вычисляем значения Gtct и Огсг:
G1c1=V1p')c1=27,8- 1,025-1,02=
=29,0 кДж/(с • °C) =29000 Вт/°С;
G2c2= V2p'2c2=0,089 • 997 -4,187=
=370 кДж/(с • °C) =370 000 Вт/°С.
Находим отношение
G1c1/G2c2=29 000/370 000 = 0,0785 «0,08;
feF/GiCi=30,5 • 1 000/29 000= 1,05;
для них из табл. 1-10 определяем Z=0,615. Тогда
(/',—f2)Z=60—(60—25) • 0,615=38,5°C.
Количество тепла, передаваемое в воздухоохладителе,
Q=GiCt = 29 000 (60—38,5) = 625 000 Вт.
Конечная температура воды
G с
t”2 = 2 + (Г, — М Z * 1 = 25 + (60 — 25)-0,615-0,08 = 26,7 ”С.
^2С2
52
1-4. КОМПАКТНЫЕ АППАРАТЫ С РЕБРИСТЫМИ
ПОВЕРХНОСТЯМИ НАГРЕВА
Типы и конструкции ребристых теплообменников.
Теплообменники с ребристыми поверхностями нагрева применяются в тех
случаях, когда теплообмен происходит между теплоносителями, из кото-
рых один имеет большой, а другой, наоборот, очень малый коэффициент
теплоотдачи. Увеличивая поверхность теплообмена путем оребрения ее
со стороны теплоносителя с малым коэффициентом теплоотдачи, тем
самым увеличивают количество передаваемого тепла и со стороны не-
оребренной поверхности. В ребристых теплообменниках жидкость или
конденсирующийся пар проходит внутри трубок, а воздух или дымовые
газы, имеющие меньший коэффициент теплоотдачи, — по внешней ребри-
стой поверхности.
Ребристые теплообменники изготовляются самых разнообразных
конструкций. На рис. 1-23 показаны основные типы ребристых теплооб-
менников. Чугунные ребристые трубки по сравнению со стальными или
латунными более громоздки и имеют больший вес, но менее чувствитель-
ны к коррозии.
Ребристые стальные и латунные трубки в небольших количествах
изготовляются напрессовкой на них прямоугольных пластин или круглых
шайб. Для получения надежного контакта между трубкой и ребрами
и предохранения их от коррозии ребристые трубки оцинковывают или лу-
дят. При больших масштабах производства изготовление ребристых тру-
бок и теплообменников механизировано и автоматизировано. Автоматы
навивают на трубки спирали из ленты (рис. 1-23,в) или биспирали из
проволоки (рис. 1-23,ж). Припайка спиралей к трубке припоем произво-
дится электротермически. Качество контакта между трубкой и ребром
оказывает большое влияние на коэффициент теплопередачи. Поэтому на
него следует обращать особое внимание при изготовлении ребристых
трубок. В настоящее время разработана технология изготовления моно-
литных ребристых трубок путём холодной прокатки гладких толсто-
стенных труб (рис. 1-24).
В различных отраслях промышленности, особенно в авиационной,
находят широкое применение различные конструкции компактных ре-
бристых теплообменников (рис. 1-25). Аналогично компактным гофриро-
ванным пластинчатым теплообменникам (см. рис. 1-6) большая поверх-
ность на единицу объема в этих аппаратах достигается за счет примене-
ния тонких ребер, припаянных, приваренных контактной электросваркой
или прикрепленных другим способом и обладающих хорошим термиче-
ским контактом с основной поверхностью *.
Методика расчета и сравнительная оценка компактных теплообмен-
ников даны Кейсом и Лондоном [Л. 13].
Исследования показали, что для каждого типа ребристой поверхно-
сти существует определенная оптимальная высота ребер и межреберных
расстояний, которые при прочих равных условиях определяют его наи-
большую теплопроизводительность и компактность.
Однако выбор типа и конструктивные размеры ребристого теплооб-
менника определяются также и условиями его работы, так, например,
в некоторых случаях возможен занос пылью, обледенение или образова-
ние снежной шубы в межреберных пространствах, что может значи-
тельно снижать их теплопроизводительность.
Расчет ребристых теплообменников. Исходя из выраже-
ния коэффициента теплопередачи для плоской стенки и учитывая раз-
личие поверхностей теплообмена внутри и снаружи грубки, количество
* В компактных гофрированных пластинчатых или щелевых сотовых и т. п. тепло-
обменниках при небольшой длине каналов коэффициент теплоотдачи увеличивается за
счет турбулизации потока газа на входном участке канала.
53
Рис. 1-23. Типы ребристых теплообменников.
а — пластинчатый; б — чугунная трубка с круглыми ребрами; в — трубка со спиральным оребре-
нием; г — чугунная трубка с внутренним оребрением; д — плавниковое оребрение трубок; е—чугун-
ная трубка с двусторонним игольчатым оребрением; ж — проволочное биспиральное оребрение тру-
бок; з — продольное оребрение трубок; и — многоребристая трубка; к — трубка нз цельнокатаных,
разрезанных и изогнутых ребер.
54
тепла, передаваемое за 1 ч через ребристую поверхность трубки, можно
представить в виде
Q = ^p.c^cpi—tcpz)Fv.c, Вт или Дж/с. (1-46)
Коэффициент теплопередачи через ребристую стенку
Вт/(м2-°С),
(1-47)
где щ -— коэффициент теплоотдачи с гладкой стороны; огпр — приведен-
ный коэффициент теплоотдачи со стороны ребристой поверхности; R3ar —
термическое сопротивление загрязнений ребристой поверхности, м2Х
Х°С/Вт; /Ср1 и /СР9 —средние температуры теплоносителей, °C; бс и 7С—
Рис. 1-24 Изготовле-
ние ребристых трубок
путем холодной про-
катки.
они находятся, величиной б/л/ч или
Рис. 1-25. Компактные теплообменники.
а — с плоскими непрерывными ребрами; б — со
сплюснутыми оребренными трубками.
при Огаза=46,5 Вт/(м2-°С) И Оводы =
толшина и коэффициент теплопроводности материала стенки (плоской
стенки или стенки трубки без ребер); Fc— площадь гладкой поверхно-
сти стенки; Fp.c=Fp+Fn — площадь ребристой поверхности стенки, рав-
ная площади ребер Fp и площади стенки в промежутках между реб-
рами Кп.
Термические сопротивления слоев загрязнений учитываются в зави-
симости от того, с какой стороны
Ь"Г/!'Р2 или их суммой, если за-
грязнение имеется с обеих сторон.
При оребрении стремятся к
выполнению условия
c,iF с ~ ОгВ р.с-
Отношение величин оребрен-
ной поверхности Вр.с и гладкой
Fc называют коэффициентом
оребрения и выбирают обычно
в пределах конструктивных воз-
можностей от 4 до 10.
Для тонких чистых поверхно-
стей нагрева, когда можно при-
нять бс~0, в ряде случаев можно
считать, что /г~аГа.-!Э. Например,
= 5 810 Вт/(м2-°С) коэффициент теплопередачи
k = ——-—j—= 46Вт/(м2- °C).
Т8ИГ+ ДбДГ
55
Если в предыдущем примере принять гладкую поверхность трубы,
увеличенную путем оребрения в 10 раз, а коэффициенты теплоотдачи
принять прежними, то коэффициент теплопередачи, определяемый по ве-
личине гладкой внутренней поверхности F, Лс = 370 Вт/(м2-°С), а отне-
сенный к ребристой поверхности (без учета неравномерности распреде-
ления температур по поверхности ребер) &Р.С = 43 Вт/(м2-°С). Поэтому
при оценке эффективности теплообмена ребристых теплообменников сле-
дует знать, к какой поверхности относится коэффициент теплопередачи.
Расчет ребристых поверхностей. По опытам ВТИ для
определения коэффициентов теплопередачи в калориферах системы Гос-
сантехстроя и Госсантехмонтажа (рис. 1-23,а) могут быть рекомендо-
ваны следующие формулы:
а) при < богреве паром
kv.c = a(wcvpcv)b, Вт/(м2-°С), (1-48а)
где «=10,5-5-14 и 6 = 0,5 = 0,7 в зависимости от типа и качества изготов-
ления аппарата; шСррсР— массовая скорость воздуха, кг/(с-м2);
б) при обогреве горячей водой
^p.c = a(wCpPcp)bwc, Вт/(м2-°С), (1-486)
где а= 11,6=23,2, 6 = 0,4 = 0,5; с = 0,1 = 0,15; w —скорость воды в трубках,
м/с.
В формулах (1-48а) и (1-486) 6Р.С отнесен к внешней оребренной по-
верхности калорифера.
Расчет коэффициента теплоотдачи аг в пучках трубок с круглыми я
квадратными ребрами, обтекаемых поперечным потоком газа, в области
значений Re = 3 • 103=2 • 104 и dfb = 3 = 4,3 может быть произведен по фор-
муле ВТИ
Nu = C/?em(t//6)-°-54 (/г/6)-°-14, (1-49)
где Nu —аг&Д; Re = w6/v; b — шаг ребер, м (рис. 1-26); d — наружный
диаметр трубы, м; h — высота ребра, м; К— коэффициент теплопровод-
ности, Вт/(м*°С); v — кинематическая вязкость газа при средней темпе-
ратуре его /г=^с±ДЕч, м2/с; tc — средняя температура стенки трубы; w—
Рис. 1-26. График для определения коэффи-
циента <р в тепловом расчете поверхности
с круглыми ребрами.
скорость газа в узком сечении
пучка /, вычисленная при темпе-
ратуре газа tr, м/с; f=Sib—(db +
+ 2Л'б) —узкое сечение пучка, м2;
Si — поперечный шаг трубок в
пучке, м; 6 — средняя толщина
ребра; С и т — постоянные коэф-
фициенты для коридорных пуч-
ков трубок: с круглыми ребрами
0=0,104, с квадратными ребра-
ми С=0,096; в обоих случаях
т=0,72; для шахматных пучков
трубок с круглыми ребрами С—
= 0,223 и с квадратными С=
= 0,205; в обоих случаях т =
= 0,65.
Расчетный или приведенный
коэффициент теплоотдачи ребри-
стой поверхности (fenp, отнесен-
ный к внешней поверхности на-
грева и учитывающий неравно-
мерность теплообмена по по-
56
верхности ребра, определяют из уравнения
а2ПР — а2 ^Fp o0j + Fp с J ’ С1'50)
в котором аг — коэффициент теплоотдачи к воздуху от поверхности, сво-
бодной от ребер, определяемый по уравнению (1-49); Fp =
= -4—(D2—d2) —поверхность ребер на 1 м длины, м2; п — число ребер
на 1 м; D — диаметр ребер, м; d — наружный диаметр трубы, м; Fn=
=л(/—ndbm— внешняя поверхность трубы, не занятая ребрами, м2; 6 —
толщина ребер, м; Fp.c — полная внешняя поверхность 1 м трубы, со-
стоящая из поверхности ребер и поверхности трубы, не занятой ребрами,
равная Fp+Fn, м2; 01 — разность между температурами основной поверх-
ности трубы и воздуха; 0О— разность между температурами поверхности
ребер и воздуха меньшая, чем 01, вследствие изменения температуры на
поверхности ребер.
Отношение 0o/0i можно найти из равенства
6о _ 4yd
eI ~m(D2 — d2) ’
(1-51)
где <р—m(R—г)] — коэффициент, определяемый по рис. 1-26; г=
=d/2; R=D/2-, m=V 2ajlpb; tkp— коэффициент теплопроводности мате-
риала ребра, Вт/(м-°С); 6 — толщина ребра, м; аг определяется по фор-
муле (1-49).
После определения коэффициента теплоотдачи для внешней ребри-
стой поверхности дальнейший расчет ведется по обычным формулам те-
плопередачи [см. формулу (1-4)].
Коэффициент теплоотдачи для шахматных пучков, состоящих из
трубок с проволочным оребрением, можно определить по формуле ВТИ
(Л. 3]
Nu=2,8 Re0'46 (d/b) ~^6 (l0/h)°-3e, (1-52)
где d — наружный диаметр трубки, м; h — высота оребрения, м; Ь — шаг
оребрения по длине трубки, м; lo=ndlz— шаг витков по окружности
трубки, м; z — число витков по окружности трубки.
Скорость газа определяется в сечении между ребрами.
Формула (1-52) получена на основании обобщения опытов при
Re = 700= 7 ООО; d[b = 1,41 = 2,72; /0/& = 0,1 =0,278; h]b = 0,825= 2,50.
Методика определения расчетного коэффициента теплоотдачи ана-
логична рассмотренной выше для трубок со сплошными круглыми и
квадратными ребрами.
Пример 1-6. Определить коэффициент теплопередачи для ребристого воздухоох-
ладителя при следующих условиях: расположение трубок в пучке шахматное; скорость
воздуха между ребрами ш=6 м/с; диаметр трубки dH/dBH=24/22 мм; материал тру-
бок— латунь с Л= 104,5 Вт/(м-°С); наружный диаметр ребер 0=55 мм; толщина ре-
бер 5р—0,3 мм; теплопроводность ребер ZP=52,4 Вт/(м-°С); шаг ребер fe=4,8 мм;
средняя температура охлаждающей воды /сР2=26сС; средняя температура горячего
воздуха /СР1=50°С.
Решение. Коэффициент теплоотдачи от воздуха к внешней поверхности, сво-
бодной от ребер, определяется из формулы (1-49)
“г— Ь С
wb \т f d h
v J у b J (_ b
При температуре воздуха 50 °C
Л=2,74-10-2 Вт/(м-°С) и
v=18,6- Ю-6 м2/с.
По заданной конструкции аппарата С=0,223; т=0,65 и й=15,5 мм.
57
О 65
15,5\ -о,**
Подставив найденные значения в формулу (1-49), получим:
2 74 IO-2 6-0,0048
“2 — 0,0048 0,22318,6-10-в
= 53,4 Вт/(м2-°С) [48,5 ккал/(№-ч-сС)[.
Расчетный или приведенный коэффициент теплоотдачи определяется по формате
Вт/(м2- °C).
r_Fp___во- ,2
“мр — «2 fp о е> f f
Число ребер на 1 м длины трубки равно:
и= 1000/6= 1 000/4,8=210,
Поверхность ребер
2я/г(Р2 — dE) 2-3,14-210
5-----(0,055й — 0,024г) = 0,81 м2/м.
Поверхность 1 м длины трубы, свободная от ребер,
/глйнб=3,14 0,024—210 3,14 0,024 • 0,0003= 0,07 м2/м
Полная внешняя ребристая поверхность
Кр.с=Кр+Кп=0,81 +0,07=0,88 м2/м.
Поправочный коэффициент
вр _____4yrfH
91 т (D* —
Предварительно находим:
1 Г 2а? । Г 2-53,4
т=У 52,4-0,0003 = 82,4:
0,024
тг — 82,4 —g— 1,0 и
/0,055 0,024
т (Р — г) = 82,4 ( —g-------2—
= 1,4.
По этим значениям из рис. 1-26 находим, что коэффициент <р = 1.21 поэтому
0О _ 4-1,21-0,024 _
9, ~ 82,4 (0,0552С 0,0242) ~ °’578'
/°’81 о —о °’07
огпр —53,4 |^0 88-0,э78 + о,88
Подставив найденные значения в формулу (1-50), получим:
= 32,3 Вт/(м2 °C), или 27,9 ккал/(м2-ч-®С).
Коэффициент теплоотдачи от стенки к воде находим по формуле (1-14)
ш”,8 2°.8
а, = А—оу~= 2 060 ~g~Q22° г ~ 8 000 Вт/(м2-°С), или 6 850 ккал/(мг-ч-°С).
“вн
Коэффициент As взят из табл. 1-4 при средней температуре воды 26 °C.
Определяем коэффициент теплопередачи для чистой ребристой трубки, отнесен-
ный к ребристой поверхности, по формуле (1-47)
1
/1 . ge А Кр.с 1 ’
\ а1 у Fe а2п₽
где Ср.с. — полная внешняя ребристая поверхность, равная (из предыдущих расчетов)
0,88 м2/м, и Kc=ndBE = 3,14 X 0,022=0,0692 м2/м — внутренняя поверхность трубы.
Коэффициент оребрения
Fp.c/fc=0,880/0,692= 12,7;
kt.e = y—j------—Q- -----------j---~=31 Вт/(м2-°С) или 26,4 ккал/(м2-ч-°С).
^ЗОСЮ + 104,5 )' 12>7+Жз“
Коэффициент теплопередачи для чистой ребристой трубки, отнесенный к внутрен-
ней поверхности, будет равен:
kc=kpFp.cIFc=31 • 12,7=394 Вт/(м2-°С), или 338 ккал/(м2-ч-°C).
58
КОНТРОЛЬНЫЕ ВОПРОСЫ
а) По курсу «Теплопередача»1.
1. Назовите три основных вида теплообмена?
2. Какая разница между коэффициентами теплопроводности, теплоотдачи и теп-
лопередачи, какие они имеют размерности?
3. В каких случаях можно применять формулу теплопередачи для плоской стен-
ки к расчету цилиндрических трубок?
4. Какие преимущества по сравнению с прямотоком имеет применение в тепло-
обменниках противотока теплоносителей, не изменяющих агрегатного состояния?
5. Какой случай движения теплоносителей, не изменяющих агрегатного состояния,
дает в большинстве случаев больший температурный напор — противоток или пере-
крестный ток?
6. Имеет ли значение для определения температурного напора направление дви-
жения теплоносителей, если один из них изменяет агрегатное состояние (кипит или
конденсируется) ?
Почему для противотока при GiCi>G2c2 на рис. 1-11 получаются выпуклые кривые,
а при GjCi<G2C2 — вогнутые?
7. В каких случаях расчет температурного напора по формуле для среднеариф-
метической разности температур теплоносителей дает правильные результаты?
8. Имеют ли критерии подобия размерность?
9. Какой критерий является определяемым при определении коэффициента тепло-
отдачи?
Ю. Какие критерии подобия являются определяющими для теплообмена при есте-
ственной и вынужденной конвекции?
II. Какие режимы течения теплоносителя в трубках или каналах возможны при
вынужденной конвекции и какими критериальными уравнениями следует пользоваться?
12. Какой коэффициент теплоотдачи имеет большее значение при движении теп-
лоносителя: в трубках, вдоль или поперек пучка трубок, если температура, давление и
скорость теплоносителя одинаковы?
13. В каком случае будет больший коэффициент теплоотдачи: при капельной или
пленочной конденсации?
14. Какой коэффициент теплоотдачи будет иметь большее значение при конден-
сации пара: на одиночной горизонтальной трубке илн на вертикальной?
15. Для каких условий конденсации пара выведена формула Нуссельта и какие
она дает значения коэффициентов теплоотдачи (против действительных условий тепло-
обмена) : завышенные нли заниженные?
16. В каком случае коэффициент теплоотдачи будет иметь большее значение: при
пузырчатом или пленочном кипении?
.17 . В каких случаях теплообмена целесообразно применять ребристые трубки?
18 . Какой коэффициент теплопередачи имеет большее значение в ребристом теп-
лообменнике: отнесенный к гладкой или ребристой поверхности?
19. Для какого теплоносителя коэффициент теплоотдачи имеет обычно наиболь-
шее значение: воздуха, воды или масла?
б) По теплообменным аппаратам.
1. Дайте сравнительную оценку дымовых газов, водяного пара и воды как тепло-
носителей для теплообменных аппаратов.
2. Какие вещества применяются как холодильные агенты?
3. Какими свойствами должны обладать высокотемпературные теплоносители
и в каких случаях рационально применять их в теплообменниках?
4. Используются ли твердые тела как теплоносители?
5. Дайте определение регенеративного, рекуперативного и смесительного тепло-
обменников.
6. Какие теплообменники более удобны для чистки и компоновки поверхности на-
грева: змеевиковые или кожухотрубчатые?
7. Из каких отдельных элементов состоит трубчатый теплообменник?
8. Перечислите способы компенсации температурных удлинений в трубчатых теп-
лообменниках.
9. В каких случаях могут применяться теплообменники без компенсации разности
температурных удлинений?
10. Какими способами осуществляется крепление трубок в трубной решетке тепло-
обменника?
II. Можно ли сконструировать трубчатый теплообменник с одинаковыми проход-
ными сечениями межтрубного н трубного пространства?
12. Если из теплоносителя при теплообмене выпадает накипь или шлам, куда его
следует направить, исходя из условия удобства чистки теплообменника, в трубки или
межтрубное пространство?
1 В соответствии с методическими указаниями по изучению курса мы предлагаем
первый вопросник для контроля знаний по базовой дисциплине «Теплопередача», изу-
чение которой иредшествует настоящему курсу.
59
13. Какие достоинства и недостатки имеют секционные теплообменники (рис. 1-3)
по сравнению с кожухотрубчатыми?
14. Какие пластинчатые теплообменники можно применять для подогрева воды
газами?
15. Какие достоинства и недостатки имеет спиральный теплообменник по сравне-
нию с кожухотрубчатым?
16. Каким конструктивным элементом достигается пленочное течение воды в кон-
денсаторе (рис. 1-7) и какое это имеет значение для теплообмена?
17. Как осуществляется естественная циркуляция воды в вертикальном испари-
теле (рис. 1-8)?
18. Изложите порядок конструктивного расчета поверхностного теплообменника.
19. Какие вопросы решаются в проверочном расчете теплообменника?
20. Необходимо ли увязывать уравнение теплового баланса с уравнением теп-
лопередачи теплообменника?
21. Что определяют уравнение теплового баланса и уравнение теплопередачи при
конструктивном расчете теплообменника?
22. Следует ли учитывать перегрев пара и переохлаждение конденсата при рас-
чете теплообменника?
23. С чего следует начинать расчет кожухотрубчатого теплообменника: с труб-
ного или межтрубного пространства?
24. Какое расположение трубок в трубной решетке следует предпочесть при боль-
шом числе трубок: по вершинам треугольника или по концентрическим окружностям?
25. Какие преимущества имеет графо-аналитический метод определения коэффи-
циента теплопередачи и когда его рационально применять?
26. Как определяется расчетный (приведенный) коэффициент теплоотдачи для
ребристой поверхности и от каких факторов он зависит?
27. Какие ребристые трубки при одинаковых габаритах и параметрах теплоноси-
телей имеют большие коэффициенты теплоотдачи: с плотно насаженными медными
ребрами на стальную трубку или с монолитными ребрами, образованными холодной
обкаткой медной трубки?
28. Какие чугунные трубки имеют при одинаковых условиях больший коэффи-
циент теплообмена: с иглами или с ребрами?
29. Влияет ли технология изготовления ребристой трубки на коэффициент тепло-
передачи?
30. Калие достоинства и недостатки имеют компактные ребристые теплообменни-
ки по сравнению с обычными?
ГЛАВА ВТОРАЯ
ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА.
ТЕПЛООБМЕННЫЕ АППАРАТЫ СО СМЕШИВАНИЕМ
ТЕПЛОНОСИТЕЛЕЙ
2-1. ФИЗИЧЕСКИЕ СВОЙСТВА ВЛАЖНОГО ВОЗДУХА
Тепло- и массообмен может происходить в условиях однокомпонент-
ных сред (паров, газов или жидкостей), изменяющих свое агрегатное со-
стояние вследствие отвода или подвода тепла. К таким процессам мож-
но отнести конденсацию паров или газов на охлаждающей стенке или
кипение жидкости при непосредственном контакте ее с горячей поверх-
ностью.
Теплообменники с однокомпонентными теплоносителями, изменяю-
щими агрегатное состояние, были рассмотрены нами в гл. 1, где было
указано, что приведенные формулы недействительны для смесей паров,
газов или жидкостей, изменяющих агрегатное состояние.
В данной главе рассматриваются простейшие смесительные тепло-
обменники, в которых происходят тепло- и массообмен между влажным
воздухом (бинарной паровоздушной смесью) и водой при их непосред-
ственном контакте (без разделительной стенки) и показаны особенно-
сти их теплового расчета.
Воздух представляет собой смесь нескольких газов. Его приблизи-
тельный состав у земной поверхности указан в табл. 2-1. Кроме того,
в воздухе содержатся в различных количествах водяной пар и пыль.
60
Энтальпия I, кДж на 1 кг сухого воздуха
Рис. 2-1. /-х-диаграмма для влажного воздуха.
Рп,
61
В тепловых расчетах пользуются энтальпией влажного воздуха, от-
несенной к 1 кг абсолютно сухого воздуха,
I=cCA.t+xia, (2-1)
где t — температура воздуха, °C; tn— энтальпия перегретого водяного
пара, кДж/кг; х— влагосодержание воздуха, т. е. масса водяного пара
в килограммах, приходящаяся на 1 кг сухого воздуха; сс.в— теплоем-
кость сухого воздуха, кДж/(кг-°С).
Таблица 2-1
Объемный и весовой состав воздуха
Вещество Содержание по весу, % Содержание по объему, %
Кислород 23,10 20,90
Азот 75,55 78,13
Аргон 1,30 0,94
Углекислота 0,05 0,03
Большинство процессов тепло- и массообмена при сушке материа-
лов происходит при атмосферном или незначительно отличающемся от
него давлении.
Весовую или массовую теплоемкость сухого воздуха при постоянном
давлении для приближенных расчетов можно принимать равной сс.в =
= 1,0036 кДж/(кг*°С), или 0,24 ккал/(кг-°C). Для точных расчетов
истинные теплоемкости следует определять из таблиц, а по их значениям
находить среднюю расчетную теплоемкость.
Энтальпия влажного воздуха может быть определена по формуле
Л. К- Рамзина
I = 1С в + /п = 0,24/ 4- 0,001 d (595 ф- 0,47/), ккал/кг,
или
/ = /4~ 0,001г/(2 4931,97/) кДж на 1 кг сухого воздуха.
(2-1а)
При определении влажности воздуха пользуются двумя понятиями:
абсолютной и относительной влажностью.
Абсолютная влажность, или влагосодержание воздуха, характери-
зуется массой водяного пара в 1 м3 влажного воздуха.
Относительная влажность воздуха выражается отношением абсо-
лютной влажности воздуха к максимально возможной влажности его
при тех же давлении и температуре или отношением массы водяного
пара, заключенной в 1 м3 влажного воздуха, к массе водяного пара, не-
обходимой для полного насыщения 1 м3 влажного воздуха при тех же
давлении и температуре
ф = Рп/рнас> (2-2)
где р — плотность, кг/м3.
Содержащиеся в воздухе водяные пары при <р< 1 в большинстве
случаев являются перегретыми, поэтому в технических расчетах влаж-
ный воздух рассматривается условно как идеальный газ, следующий за-
конам Бойля—Мариота, Гей-Люссака и закону парциальных давлений
Дальтона, согласно которому давление влажного воздуха слагается из
парциальных давлений сухого воздуха и содержащихся в нем водяных
паров. В этом случае относительная влажность может быть определена
как отношение действительного парциального давления водяных паров
во влажном воздухе к максимально возможному при заданной темпера-
туре
(2-2а)
/’макс ZWc
62
При этом допущении ошибка в расчетах не превосходит 2%. Для
точных расчетов следует руководствоваться соотношением (2-2), так
как для реальных газов относительная влажность зависит от темпера-
туры, т. е.
<P = f (Рп/Рнас, t).
При измерении влагосодержания в граммах на килограмм сухого
воздуха его принято обозначать через d, а при измерении его в кило-
граммах на килограмм сухого воздуха — через х. Числовое значение
влагосодержания можно определить, пользуясь уравнениями состояния
для воздуха и водяных паров
pBV=GB7?B7' и pnV=GnRnT, ,
составленными для одного и того же объема влажного воздуха и одной
и той же температуры. Разделив второе уравнение на первое, получим:
Gn/GB — R.Bpnl RnpB-
Подставив значения газовых постоянных для воздуха RB =
= 288 кДж/(кг-°С), или 29,27 кгс• м/(кг• °C) и для водяных паров 7?п =
=462 кДж/(кг-°С), или 47,1 кгс• м/(кг•°C), получим выражение для
влагосодержания
х = 0,622-^-, кг на 1 кг сухого воздуха, (2-3)
или
d = 622 г на 1 кг сухого воздуха. (2-4а)
Заменив парциальное давление воздуха рв величиной В—рп (где
Рп=фРнас и В — общее давление парогазовой смеси, Па или мм рт. ст.),
получим для влажного воздуха, находящегося под барометрическим
давлением,
d = 622 $ — 622 г на 1 кг сухого воздуха, (2-46)
т. е. при данном барометрическом давлении влагосодержание воздуха
зависит только от парциального давления водяного пара. Максимально
возможное содержание влаги в воздухе при <р= 1
г/макс = Дгас = 622 , Г НЗ 1 КГ СуХОГО ВОЗДуХЭ. (2-4в)
В — Ркъс
Так как давление насыщения растет с температурой, то максималь-
ное количество влаги, которое может содержаться в воздухе, зависит от
его температуры, притом тем больше, чем выше температура,
уравнение (2-46) решить относительно рп, то получится:
Bd
Рп~~ 622-Rd
и аналогично
622В
Рв 622 Ц-d ’
Объем влажного воздуха, отнесенный к 1 кг сухого воздуха,
у — ___________________________-------.=
Квл < (В - ?дЕас)
288 Т . .
= д-------, м влажного воздуха на 1 кг сухого воздуха,
& УРп&е
Если
(2-5)
(2-6)
(2-7)
63
где В — давление парогазовой смеси, Па; ркас—давление насыщения во-
дяного пара при температуре сухого термометра, Па; RB —
= 8314 Дж/(кмоль*°С)—универсальная газовая постоянная; Мв^29—
мольная масса воздуха, кг/кмоль; <р — относительная влажность возду-
ха, доли единицы; Т — рабочая температура, К.
Удельный объем влажного воздуха можно определить, разделив
объем влажного воздуха УВл на массу смеси, приходящуюся на 1 кг су-
хого воздуха, т. е. на 1 + 0,004//.-
1 + o”ooid ’ м’/кг‘ (2’8)
Плотность влажного воздуха
Рвл = Р«-т^-( 1 g—гРиасЬ кг на 1,м влажного воздуха, (2-9)
где р0= 1,293 — плотность сухого воздуха, при нормальных условиях,
кг/м3; 7’о=273К — нормальная температура.
В уравнениях (2-7) и (2-9) давления В, Во и ркас должны выражать-
ся в одних и тех же единицах *.
Первый член уравнения (2-9) представляет плотность сухого воз-
духа. Плотность водяного пара меньше плотности сухого воздуха, по-
этому плотность влажного воздуха всегда меньше плотности сухого воз-
духа.
Приведенными выше формулами можно пользоваться для прибли-
женных расчетов. Для точных расчетов следует пользоваться таблицами
или /-//-диаграммами, построенными по уравнениям для реальных паро-
газовых смесей.
2-2. /-(/-ДИАГРАММА ДЛЯ ВЛАЖНОГО ВОЗДУХА
И ПРИНЦИП ЕЕ ПОСТРОЕНИЯ
/-d-диаграмма влажного воздуха была составлена Л. К. Рамзиным
в 1918 г. Она имела большое значение для развития науки о тепло- и
массообмене и получила широкое 'применение в расчетах: систем ото-
пления, вентиляции, кондиционирования воздуха, сушильных установок
и т. п.
В зависимости от назначения /-//-диаграммы строятся для различ-
ных пределов температур и в различных масштабах энтальпий и вла-
госодержаний. Имеются /—//-диаграммы для расчетов отопления и венти-
ляции с пределами температур от минус 30 до плюс 60 °C. Для расчета
сушилок имеются /-//-диаграммы с температурами от 200 до 1 300 °C и
интервалом влагосодержаний от 80 до 700 г/кг сухого воздуха.
Кроме /-//-диаграмм, имеются /-х-диаграммы Молье, которые по
структуре не имеют принципиального отличия от первых.
/-//-диаграмма строится для влажного воздуха, причем все величи-
ны относятся к 1 кг содержащегося в нем сухого воздуха.
На рис. 2-1 изображена /-х-диаграмма Молье. I-d и /-х-диаграммы
для более удобного расположения линий постоянной относительной
влажности <р=const строятся в косоугольной системе координат. Мас-
штаб для отсчета влагосодержаний сносят на горизонтальную прямую,
проходящую через начало координат. По оси абсцисс диаграммы откла-
дывается влагосодержание, а по оси ординат — энтальпия воздуха.
* Размерности В, рнас и R взаимно связаны так: если давление выражено
в Па (Н/м2), то R=8 314 Дж/(кмоль-°C), если в кгс/м2, то 7?=848 кгс • м/(кмоль • °C),
если давление выражено в мм рт. ст., то /?=62,3 кгс-м/(кмоль-°С).
64
Принцип построения I-d-диаграммы ВТИ для влажного воздуха на
основании приведенных выше упрощенных формул показан на рис. 2-2.
/-d-диаграммы ВТИ строятся для барометрического давления 0,993X
Х105 Па (745 мм рт. ст.). Выбранное давление примерно соответствует
среднему годовому барометрическому давлению в центральных районах
СССР. Использование упрощенных формул для определения параме-
тров влажного воздуха дает небольшие расхождения (3—5%)
с /-d-диаграммой ВТИ, построенной по точным формулам.
Построение /-d-диаграммы начинается с нанесения на лист в вы-
бранном масштабе линий влагосодержаний d= const и линий энтальпий
/=const. Направление изотерм определяется из выражения (2-1а) для
энтальпии влажного воздуха /=/+0,001d(2 493+1,97/% кДж/кг сухого
воздуха, представляющего собой уравнение прямой, причем энтальпия
влажного воздуха равна сумме энтальпий сухого воздуха и водяных па-
ров. Задавшись двумя влагосодержаниями dj=O и d2=d, по формуле
(2-1а) находим две точки (рис. 2-2,а): точка а соответствует энтальпии
сухого воздуха при данной температуре % и влагосодержаний di = 0 и
лежит на оси ординат; точка b на оси ординат соответствует энтальпии
влажного воздуха при той же температуре и влагосодержаний d2=d.
Пересечение линии /1=const, проходящей через точку Ь с линией d2=
= const дает вторую точку изотермы с. Соединив точку а с точкой с
прямой, получим изотерму /i=const.
Так как энтальпия водяных паров при постоянном влагосодержаний
увеличивается с повышением температуры благодаря увеличению в урав-
нении члена 0,001d(2 493+1,97/), то изотермы на /-d-диаграмме рас-
ходятся по мере увеличения влагосодержания (отрезок cd на рис. 2-2,а
растет с ростом температуры).
Согласно формуле (2-5) парциальное давление водяного пара, со-
держащегося в воздухе при постоянном барометрическом давлении, за-
висит только от влагосодержания. Решив уравнение (2-5) для перемен-
ных значений d, получим, что, например, при d=0 р=0; при d=db р=ръ
при d=d2 Р=Р2 и т. д.
Задавшись определенным масштабом для парциальных давлений,
строим кривую парциального давления водяного пара (рис. 2-2,б), ко-
торая обычно располагается в нижней части диаграммы.
После того как на /-d-диаграмме построены изотермы и линии пар-
циального давления, не вызывает трудностей построение линии <р=100%.
При <р = 100°/о воздух полностью насыщен водяными парами и парци-
альное давление их равно давлению насыщенного пара при данной тем-
пературе рп=Рнас- Из таблиц для водяного пара находим давления на-
сыщенного водяного пара, соответствующие некоторым температурам,
например: pHaci при /ъ ркас2 при /& рнас3 при /3 и т. д. Затем находим на
линии парциального давления (рис. 2-2,в) точки а, b и с, соответствую-
щие давлениям рнась Рнасг лРнасз и т. д. Из этих точек проводим прямые,
параллельные оси ординат, до пересечения с соответствующими изотер-
мами /ь t2, ts и т. д. Соединяя точки пересечения, получаем линию <р=
= 100%.
Линия насыщения <р=100%' разделяет I-d-диаграмму на верхнюю
область влажного ненасыщенного воздуха и нижнюю область пересы-
щенного влагой воздуха, в котором лишняя влага может находиться
только в капельном состоянии; линия <р= 100%' также показывает мак-
симально возможное насыщение воздуха влагой при данной темпера-
туре.
Построение линий <р = const<100% производится так же, как и ли-
нии <р= 100%, с той только разницей, что на кривой парциального дав-
ления рп отыскиваются точки, соответствующие не ркас, а <ррНас/Ю0.
Дальнейшее графическое построение линий <p = const<100%‘ аналогично
5—1128 65
описанному для линии <р= 100%. Если, например, строим линию ф=50%,
то рп=0,5рНас- Зная рнас при h. и риас при t2, определяем (рис. 2-2,г)
0,5рнас при tt (точка Ь) и 0,5рНас при /2 (точка а). Из этих точек прово-
дим прямые, параллельные оси ординат, до пересечения с изотермами
ti и /2. Соединяем точки пересечения и получаем линию ф = 50%. Для
построения других значений линии ф= const нужно найти соответствую-
щие им значения рп-
Рис. 2-2. Построение I-d-диаграммы для влажного воздуха.
Необходимо заметить, что на /-(/-диаграммах ВТИ при температу-
рах, больших 100°C (точнее больших 99,4°C), линии ф = const идут вер-
тикально вверх. Последнее объясняется тем, что /-(/-диаграмма ВТИ
построена для барометрического давления. Поэтому при />100 °C в со-
ответствии с формулой (2-2а) относительная влажность (р=рп/рнас (где
66
Рнас=# — барометрическому давлению) и не зависит от температуры.
Для всех точек на вертикали B = const и pn=const.
Поскольку определенному парциальному давлению водяных паров
соответствует определенное влагосодержание, для влажного воздуха
с температурой />100°С и ср = const влагосодержание тоже должно быть
постоянным. В действительности относительная влажность зависит не
только от давления, но и от температуры, поэтому линии <р= const при
температурах, больших 100 °C, не строго вертикальны, а имеют неболь-
шое отклонение от вертикали.
В /-х-диаграммах Молье (рис. 2-1) линии не имеют перегибов при
/=100°С, так как при ее построении для t> 100 °C принимается давление
водяных паров, соответствующее этой температуре.
Определение параметров влажного воздуха на
М-диаграмме. Для определения параметров влажного воздуха t, ср,
I, d, рп, Рв, /р и tM на /-(/-диаграмме должны быть заданы два из них,
по которым легко могут быть найдены все остальные, как это показано
в примере 2-1.
Пример 2-1. Заданы температура (=50 °C и относительная влажность воздуха
<р=30.%. Требуется определить остальные параметры воздуха, если барометрическое
давление В=0,9932- 105 Па (745 мм рт. ст.).
Решение. На диаграмме (рис. 2-1) по заданным параметрам находим точку
А', опускаем из нее перпендикуляр на линию масштаба влагосодержаний, получаем
точку В' и определяем соответствующее влагосодержание d=0,024 кг/кг сухого воз-
духа.
Отрезок В'С' определяет парциальное давление водяных шаров 3,8 кПа (рп=
=27,5 мм рт. ст.).
Точка D' пересечения проведенного перпендикуляра с линией гр =100% соответ-
ствует температуре точки росы (Р=28°С. Если из точки А' провести линию А'Е', па-
раллельную линиям энтальпий, и мысленно продолжить ее до вертикальной линии
масштаба энтальпии, то на ней можно будет прочитать величину энтальпии влажного
воздуха; для рассматриваемого примера она равна 113 кДж/кг (27 ккал на 1 кг сухого
воздуха).
Точка Е' пересечения линии А'Е' с линией <р=100% определяет адиабатную тем-
пературу мокрого термометра (М=33°С. Точное значеие температуры мокрого термо-
метра определяют по т-лпниям, построение которых в /-d-диаграмме рассмотрено ниже.
Согласно закону Дальтона парциальное давление воздуха ps=B—рп=99,324—
-—3,666= 95,658 кПа (717,5 мм рт. ст.).
2-3. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРОЦЕССОВ
НА /d-ДИАГРАММЕ
Многообразные процессы тепло- и массообмена между веществами,
как правило, сопровождаются подогревом, охлаждением, увлажнением
или осушением воздуха. Иногда они возникают в результате смешения
воздуха с различными параметрами. Эти процессы, налагаясь один на
другой, создают весьма сложные закономерности изменения состояния
воздуха.
Процесс нагревания воздуха в рекуперативном те-
плообменнике. Этот процесс в /-(/-диаграмме изображается верти-
кальной линией d=const, так как влагосодержание воздуха при этом
остается без изменения (линия АВ на рис. 2-3,а).
Процесс охлаждения воздуха в рекуперативном те-
плообменнике. Если при охлаждении понижение температуры воз-
духа незначительно и не сопровождается выпадением влаги, то этот про-
цесс протекает также при постоянном влагосодержаний и изображается
линией ВА, обратной по направлению линии АВ (рис. 2-3,а).
Если охлаждение влажного воздуха продолжать, то при достиже-
нии вполне определенной температуры начинается конденсация водяно-
го пара и выпадение его в виде росы, т. е. наступает состояние насыщен-
ного воздуха; эта температура называется точкой росы или температу-
рой насыщения /р. Количество водяного пара в 1 м3 воздуха в состоянии
5* ‘ 67
насыщения будет максимально возможным, предельным содержанием
его в этом объеме при данной температуре. При охлаждении и осуше-
нии влажного воздуха в охладителе поверхностного типа (линия В\С\С2)
процесс конденсации паров идет по линии CiC2 с выпадением влаги.
Количество сконденсировавшейся на 1 кг сухого воздуха влаги опреде-
ляется конечной температурой воздуха (точка С2) и выражается раз-
ностью влагосодержаний.
Рис. 2-3. Изображение основных процессов в /-d-диаграмме.
Процессы тепло- и массообмена между воздухом и
водой. При испарении воды, имеющей температуру О °C, когда тепло,
необходимое для ее испарения, берется только из окружающего воздуха,
не имеющего теплообмена с другими телами, происходит постепенное
увеличение влагосодержания воздуха d и понижение его температуры t.
С увеличением влагосодержания энтальпия воздуха будет оставаться
постоянной, так как на сколько будет уменьшаться первый член t в урав-
нении (2-1а), на столько будет увеличиваться его второй член
0,001/2(2 493+1,97/); на /-//-диаграмме (рис. 2-3,а) этот процесс соот-
ветствует линии /=const (линия В1С3) и носит название процесса адиа-
батного испарения. Пределом охлаждения является адиабатная темпе-
ратура мокрого термометра /ма.
Если в процесс тепло- и массообмена вступает вода, которая имеет
температуру больше нуля или равную температуре мокрого термометра,
то она вносит некоторое дополнительное количество тепла Л. В расчетах
это количество тепла относится к расходу воздуха I, необходимому для
испарения 1 кг влаги. Если учесть это количество тепла и построить
процесс испарения, то он пойдет по линии т (рис. 2-3,а, пунктирная ли-
ния B^Ct). В этом случае /“}>/“.
Построение этих процессов подобно построению процессов сушки
с дополнительным сообщением тепла и подробно рассматривается
в гл. 6.
Адиабатная психометрическая разность tc—/“, не зависящая от по-
сторонних тепловых влияний и скорости потока, характеризует способ-
ность воздуха поглощать влагу и получила название потенциала суш-
ки е.
68
Потенциал сушки выражают также через разность парциальных
давлений и влагосодержаний.
На принципе адиабатного испарения основан психрометр — прибор,
служащий для определения относительной влажности воздуха по пока-
заниям сухого и мокрого термометров, помещенных в потоке исследуемо-
го воздуха. Сухой термометр представляет собой обычный ртутный тер-
мометр, а мокрый отличается от него тем, что его ртутный шарик по-
крывается материей (батистом или марлей), непрерывно увлажняемой
водой. При обдувании шарика мокрого термометра воздухом темпера-
тура воды, находящейся в марле, понижается до tM — предела охлажде-
ния.
Приближенно (без учета скорости) относительную влажность воз-
духа можно определить по показаниям сухого и мокрого термометров
при помощи /-d-диаграммы. Для этого достаточно из точки пересечения
изотермы, соответствующей температуре мокрого термометра, с линией
насыщения <р = 100% (точка Cs на рис. 2-3,а) провести линию /=const
до пересечения ее в точке Bi с изотермой, соответствующей температуре
сухого термометра; точка В4 определяет искомое состояние воздуха (его
энтальпию, относительную влажность, влагосодержание и парциальное
давление).
Более точные результаты определения влажности воздуха по пока-
заниям психрометра можно получить, если из точки Cs провести до пе-
ресечения с заданной tc линию т=const. Принцип построения линии
r=const следующий: из точки С3 откладывается вертикально вверх от-
резок Сз£=0,001/// и из точки Е проводится линия BJE до пересечения
с линией <р=100%' в точке которая и является т-линией для темпера-
туры, соответствующей точке С4.
Следует заметить, что если известны параметры воздуха в точке Bi
(даны /1 и ф) (рис. 2-3,а), то определение адиабатной температуры мо-
крого термометра по линии /=const, проведенной из точки /Ч до пересе-
чения с линией <р= 100% в точке С3, даст значение /“, меньшее истинной
температуры мокрого термометра, полученной по линии т=const про-
ведением прямой из точки Вг до пересечения с линией <р= 100%' в точ-
ке С4. Во всех случаях /“</м.
Линии т=const учитывают неадиабатность процесса вследствие того,
что температура воды, испаряющейся с шарика ртутного термометра,
О=/м>0°С. Точные значения по /с и /м можно получить, пользуясь пси-
хрометрическими таблицами или формулами, в которых учтено влияние
на испарение влаги скорости воздуха, омывающего смоченный ртутный
шарик. Чем выше скорость воздуха, тем меньше отличие табличных дан-
ных от результатов, получаемых по /-d-диаграмме с применением т-ли-
ний.
Процессы смешения воздуха различных состояний
в I-d-л иаграмме. Явления, происходящие при смешении воздуха раз-
личных состояний, представляют большой интерес, так как большинство
установок для кондиционирования воздуха и сушилок работает по прин-
ципу многократной циркуляции, при которой часть отработавшего воз-
духа смешивается с некоторым количеством свежего воздуха и вновь
поступает в аппарат.
Предположим, что требуется смешать Gj кг свежего воздуха, пара-
метры которого Л и di (точка А на рис. 2-3,6), и б2 кг рециркулирующе-
го воздуха с (параметрами /2 и >d2 (точка В), т. е. на GJGi—n кг рецир-
кулирующего воздуха примешивается 1 кг свежего воздуха.
Можно написать равенства
(1 +п)1см> (а)
(1 +n)dcM, (б)
69
где /см и dCM— энтальпия и влагосодержание смеси, отнесенные к 1 кг
сухого воздуха.
Из равенств (а) и (б) имеем:
H = f/a /см9=/см—/1/ (в)
dCM)=dCM—di. (г)
Разделив равенство (в) на равенство (г), получим:
/г /см /см />
CZ2 </см ^СМ </]
т. е. уравнение прямой линии с координатами двух ее точек /ъ di и /2,
J2- Отсюда следует, что точка, определяющая состояние смеси, лежит на
прямой, соединяющей точки, характеризующие компоненты смеси. По-
ложение этой точки на прямой может быть определено заданием либо
dCM, либо /см. В большинстве практических случаев задано dCM и требу-
ется вычислить псм. Из равенства (г) и рис. 2-3,6 имеем:
., _ ^СМ ^1___
z — d2-dCN—CB
Следовательно, точка С, соответствующая dсмл делит отрезок между
точками Л и В на части, отношение которых равно величине п (по пра-
вилу рычага) и лежит тем ближе к точке А, чем меньше п.
Из равенств (а) и (б) величины с/см и /см могут быть найдены анали-
тически:
(24°)
(2-Юа)
Может случиться, что прямая AiBi пересечет кривую <р= 100% и
точка Сь характеризующая состояние смеси, окажется лежащей ни^же
кривой насыщения. Это послужит признаком конденсации части водяных
паров при смешении, т. е. превращения части водяных паров в капель-
ное состояние, в этом случае точка G характеризует не влажный воздух,
а воздух, насыщенный парами и содержащий, кроме того, влагу в ка-
пельном состоянии (пересыщенный воздух).
Без существенной погрешности точку Ct можно перенести по линии
/=const в точку Сг, которая и определит действительные параметры
смеси, так как капельная влага имеет ту же температуру, а ее энталь-
пия ничтожно мала по сравнению с энтальпией влажного воздуха. Раз-
ность влагосодержаний, соответствующих точкам С\ и С2, характеризует
количество влаги, которая находится в воздухе в капельном состоянии.
Пример 2-2. Смешиваются Gi = 1000 кг воздуха с параметрами Л = 20°С и <р1 =
= 60% с, G2=3000 кг воздуха с параметрами /2=50°С и <р2=50%. Определить /см,
^Рсм. de м И /см-
Решение. По /-d-диаграмме находим, что при /1=20 °C и <р±=60% координаты
точки А равны /1=41,87 кДж/кг (10 ккал/кг) и di=0,009 кг на 1 кг сухого воздуха,
а при /а=50 °C и (р2=50.% координаты точки В равны /2=158 кДж/кг (38 ккал/кг) и
</2=0,042 кг на 1 кг сухого воздуха. Находим также
n=G2/Gi = 3 000/1 000=3.
По формулам (2-10) и (2-10а) получаем:
d,+nd2 0,009 + 3-0,042
flCM= —;—j--—-----j—-------=0,0338 кг на 1 кг сухого воздуха
И
/,+п/2 41,87 + 3-158 , „ ,
/см = j । п 1+3 128 кДж/кг.
70
По этим данным находим на / d-диаграмме остальные параметры
/см- 42,5 °C и срсм=60%.
Эту же задачу можно решить графически по /-d-диаграмме, проведя линию АВ
и применив правило рычага (рис. 2-3).
Общее количество смеси равно 3 000 + 1 000=4 000 кг,
СВ/АВ = 1 000/4 000 = 1 /4.
Разделив отрезок АВ на четыре части, найдем точку С, соответствующую пара-
метрам смеси /см = 42,5°С, фсм=60%, dCM=0,0038 кг/кг и /См = 128 кДж/кг.
Пример 2-3. Смешиваются Gf кг воздуха с параметрами ti =—10 °C, <j>i = 100%,
d!=0,002 кг/кг и G2 кг воздуха с параметрами /2=45°С, <р2=80% и d2=0,052 кг/кг,
n=G2/Gi = l.
В этом случае
0,002 + 0,052 Л„
dCM=-------. г-.----= 0,027 кг на 1 кг сухого воздуха.
Поэтому точка, характеризующая смесь, лежит в области пересыщенного воздуха.
Проводим через нее линию Z=const и находим точку пересечения ее с кривой <р= 100%,
соответствующую температуре /=27°С и d=0,023 кг на 1 кг сухого воздуха, которые
можно принять за параметры полученного влажного пересыщенного воздуха.
Рис. 2-4. Процесс тепло- и массообмена между воздухом и во-
дой в скруббере на /-d-дпаграмме.
Процессы тепло- и массообмен а между воздухом и
водой в теплообменниках смешения. При составлении тепло-
вых балансов смесительных теплообменников (скрубберов, камер для кон-
диционирования воздуха ит. п.) необходимо учитывать теплоту испарения
или конденсации влаги, так как в этих аппаратах изменение темпера-
туры воды непропорционально количеству тепла, полученного или от-
данного ей воздухом, и во многих случаях лишь часть этого тепла идет
на нагрев или охлаждение воды, другая же часть идет на испарение или
конденсацию паров воды. В зависимости от условий тепло- и массооб-
мена при этом происходит увлажнение или осушивание воздуха.
Уравнение теплового баланса скруббера согласно схеме, изображен-
ной на рис. 2-4, без учета потерь тепла в окружающую среду можно
представить в виде
Lh+Gct'2=LI2+ (С±АГ)сГг, (2-11)
71
где L — расход воздуха, кг/с; Л и 12— энтальпии влажного воздуха на
входе и выходе из скруббера, кДж на 1кг сухого воздуха (I ккал на
1 кг сухого воздуха); G — количество воды, поступающей в скруб-
бер, кг/с; с — теплоемкость воды, кДж/(кг-°С); /'2 и t"2— температуры
воды на входе и выходе из скруббера, °C; ДЖ=х2—— количество вла-
ги, сконденсировавшейся из воздуха или, наоборот, испарившейся из
воды и увлажнившей воздух, кг/сек.
Если %1>х2, то происходит осушение воздуха и ДЖ в уравнении
(2-11) имеет знак плюс, а если %i<x2, то происходит увлажнение воз-
духа и ДЖ имеет знак минус.
В большинстве практических случаев расчета скрубберов ДЖ по
сравнению с G и L составляет незначительную величину и при построе-
нии процессов тепло- и массообмена на /-d-диаграмме ею пренебре-
гают.
Процесс тепловлагообмена между воздухом и водой на /-d-диа-
грамме можно представить себе как смешение воздуха двух состояний:
воздуха, поступающего в аппарат для тепло- и массообмена, и воздуха,
уже насыщенного влагой в пограничном слое капли воды, поступающей
в аппарат, и имеющего температуру воды и влажность <р= 100%.
Процесс строится по ступеням в следующем порядке. Наносится
точка А (рис. 2-4), соответствующая начальным параметрам воздуха
t'i и Д; далее на линии <р=1000/о отмечаются положения точек С и D,
соответствующих изотермам Д2 и f'2, равным начальной и конечной
температурам воды. Начало процесса смешения воздуха с водой на
/-d-диаграмме изображается прямой, соединяющей точку, характери-
зующую состояние воздуха, с точкой на линии ф=100%, которая соот-
ветствует температуре воды. Затем в зависимости от направления дви-
жения теплоносителей проводится,прямая между точкой А и точкой D,
соответствующей температуре роды t"2 при противотоке, или точкой С
при t'i для прямотока Далее на этой прямой принимается какое-либо
значение /“ (промежуточная энтальпия), немного меньшее или боль-
шее начальной энтальпии Ц в зависимости от условия протекания про-
цесса, но в пределах изменения энтальпий между точками А и D (или
С). Разность этих энтальпий не следует брать значительной, с тем что-
бы на каждом последующем участке изменения температуры воды /“ ,
/*р, и т. д. были настолько незначительными, чтобы направление
линии смешения можно было считать постоянным.
По принятой таким образом величине /“ из уравнения теплового
баланса (2-11) определяется значение промежуточной температуры во-
ды /Пр (величиной ДЖ при этом пренебрегают). Например, для усло-
вий противотока теплоносителей и обозначений, указанных на рис. 2-4,
£^-ZnP) .
пр 2 Gc ’
После определения промежуточной температуры воды между точ-
кой, соответствующей значению Г , и найденной на линии у = 100%
точкой, соответствующей , проводится вторая прямая, на которой вы-
бирается значение /* . Таким образом, вычисляются 'значения /пр и /пр
и строится ряд прямых до тех пор, пока по этим уравнениям не полу-
чится заданное начальное или конечное значение температуры воды Г2
72
или Z"2; энтальпия /"р(/2—209 — на рис 2-4), соответствующая конечной
температуре, определяет конечные равновесные ей параметры воздуха.
При тепло- и массообмене воздуха с большими количествами воды
конечная температура воздуха может значительно изменяться и быть
ниже или выше температуры мокрого термометра. Воздух может при
этом осушаться, если температура охлаждающей воды ниже темпера-
туры росы, или, наоборот, увлажняться, если температура охлаждаю-
щей воды выше температуры росы. В первом случае пределом нагрева-
ния, а во втором случае пределом охлаждения воды является темпера-
тура мокрого термометра.
' При тепло- и массообмене вслед за увлажнением (участок кри-
вой Аа) может следовать процесс осушения воздуха (участок бв на
Рис. 2-5. Процессы тепло- и массообмена между воздухом и водой в скруббере при пря-
мотоке (а) и противотоке (б) теплоносителей.
рис. 2-4) или, наоборот, сначала осушение, а затем увлажнение в за-
висимости от того, имеет ли место противоток или прямоток теплоноси-
телей.
На рис. 2-5 показаны процессы тепло- и массообмена на 7-с?-диа-
грамме для условий прямотока и противотока теплоносителей.
Расчетные уравнения для первых ступеней имеют следующий вид:
для прямотока
е =У.+_Е£--^
пр 2 1 Gc
т <]а _/Ь \
I ъ V пр ' пр/ .
пР пР~ Gc ’
для противотока
е ^(Л-^р).
гр“‘ 2 Gc
1 (fa _Jb 4
____jO. V пр ' пр>
пр пр Gc
73
Определение последующих промежуточных значений Лр , и т. д.
производится аналогичным способом.
Определение средней разности температур между теплоносителями
(температурного напора) в смесительных аппаратах по средней ариф-
метической или средней логарифмической формуле может не дать пра-
вильных результатов, так как эти уравнения не отображают действи-
тельного процесса тепло- и массообмена. Для определения средней раз-
ности температур в смесительных теплообменниках рекомендуется фор-
мула
“=vttz- <212>
где b — отношение изменения температуры воздуха в ступени к полно-
му изменению температуры его в смесительном аппарате; Л/пр— раз-
ность температур теплоносителей для одной ступени, °C.
Ниже дается пример графо-аналитического определения конечных
параметров воздуха и средней разности температур в смесительном
аппарате.
Пример 2-4. Определить температуру воздуха на выходе из скруббера и среднюю
разность температур между теплоносителями при противотоке, если в скруббер посту-
пает воздух в количестве 1=2,78 кг/с при Г1=150°С и Д-418 кДж/кг (100 ккал/кг).
Охлаждающая вода имеет температуру на входе Г2=15°С и на выходе /'Т=55СС.
Решение. Задаемся энтальпией воздуха на выходе из скруббера 209,35 кДж/кг
сухого воздуха ’.
Количество тепла, переданного в скруббере, составит:
Q=L(A—/2) = 2.78(418 -209,35) =582 кДж/кг.
Расход охлаждающей воды
Q _ 582
G~cB(t"2~ t'J 4,187(55—15) 3>47 кг/с. #
Строим ступенчатый процесс на /-d-диаграмме, как это показано на рис. 2-4;
результаты сведены в табл. 2-2.
Таблица 2-2
Определение конечной температуры воздуха
fit 2П₽ Лир Лир Л пр Лпр А = -Д X GC х ^1ПР—^2пр’ Лпр — = *"2ПР-^
ккал/кг кДж/кг ккал/кг кДж/кг ккал/кг кДж/кг
55 100 418,7 100 418,7 0 0 0 55
55 100 418,7 95 397,7 5 21 4 51
51 95 397,7 90 376,7 5 21 4 47
47 90 376,7 85 355,7 5 21 4 43
43 85 355,7 80 334,7 5 21 4 39
39 80 334,7 75 313,7 5 21 4 35
35 75 313,7 70 292,7 5 21 4 31
31 70 292,7 65 271,7 5 21 4 27
27 65 271,7 60 250,7 5 21 4 23
23 60 250,7 55 229,7 5 21 4 19
19 55 229,7 50 207,7 5 21 4 15
При температуре воды Г2=15°С энтальпия воздуха согласно графическому по-
строению тепло- и массообмена между воздухом и водой составляет 209,35 кДж на
1 кг сухого воздуха, а равновесная температура воздуха ГТ=55 °C.
Для определения средней разности температур между теплоносителями определя-
ем температуры, соответствующие разновесным состояниям воздуха и воды, и резуль-
таты расчета сводим в табл. 2-3.
1 Расчет ведется методом последовательных приближений.
74
Т а б л иц а 2-3
*пр. воздуха ^пр. воды 4» Ь Д/пР
150 55 95 0 0
118 51 67 0,335 81 0,00414
104 47 57 0,147 62 0,00238
95 43 52 0,095 54,5 0,00174
83 39 44 0,126 48 0,00262
78 35 43 0,052 43,5 0,00190
73 31 42 0,0525 42,5 0,00122
68 27 41 0,052 41,5 0,00125
63 23 40 0,052 40,5 0,00128
59 19 40 0,042 40 0,0105
55 15 40 0,042 40 0,0105 ь Stt—=0,0186
Сложив приведенные в таблице значения b/Atnp, получим:
откуда
At = 1 /0,0186=54<Л/л = 64 °C,
где ЛСч — средняя логарифмическая разность температур теплоносителей при
= 150 °C, t"i=55 °C, ?2=15°С и Г2=55°С.
2-4. АППАРАТЫ СО СМЕШИВАНИЕМ ТЕПЛОНОСИТЕЛЕЙ
(БЕЗ РАЗДЕЛИТЕЛЬНОЙ СТЕНКИ) И ИХ ТЕПЛОВОЙ РАСЧЕТ
В промышленности нашли широкое применение смесительные теп-
лообменные аппараты, в которых тепло- и массообмен между теплоно-
сителями происходит непосредственно, без теплопроводной стенки меж-
ду ними. В большинстве случаев это аппараты непрерывного действия,
В зависимости от назначения они имеют различные технические назва-
ния. Для осушения или увлажнения воздуха в установках кондициони-
рования применяются кондиционеры; очистка воздуха или газа от пыли,
золы, смолы путем промывки их водой осуществляется в скрубберах;
нагрев жидкости за счет тепла воздуха, газа или пара осуществляется
в смесительных подогревателях или конденсаторах; охлаждение боль-
ших количеств циркуляционной воды от конденсаторов паровых турбин
электрических станций достигается тепло- и массообменом ее с возду-
хом в градирнях и т. д.
По конструктивным признакам различают следующие типы тепло-
обменников смешения:
1. Полые или безнасадочные колонны или камеры (рис. 2-6,а),
в которых жидкость распиливается форсунками в газовую среду; со-
прикосновение между жидкостью и газом происходит на поверхности
образовавшихся при распыливании капель жидкости {Л. 12]. Устройст-
во одной из применяющихся форсунок показано на рис. 2-7.
2. Насадочные колонны (рис. 2-6,е), в которых соприкосновение
газа с жидкостью происходит на смоченной поверхности насадки (коль-
ца Рашига, куски кокса, деревянные доски, рейки и другие устройства,
обеспечивающие пленочное стекание жидкости). Преимуществом наса-
дочных колонн по сравнению с безнасадочными являются меньшие гео-
метрические размеры их. Их недостаток состоит в большом расходе
электроэнергии на вентилятор, который увеличивается по мере забива-
75
ния насадки различными твердыми отложениями, содержащимися в га-
зах или распыляемых растворах.
3. Каскадные аппараты, имеющие внутри горизонтальные либо на-
клонные полки или перегородки, благодаря которым жидкость посте-
пенно перетекает с полки на полку, как это показано на рис. 2-6,6.
4. Струйные смесительные аппараты, в которых происходит нагре-
вание воды эжектируемым или эжектирующим паром (рис. 2-6,г). Раз-
ность между температурой насыщенного эжектирующего пара и темпе-
ратурой нагретой эжектируемой воды в односопловых струйных смеси-
тельных аппаратах составляет 15—20°С, а в двухсопловых около 10°С.
Рис. 2-6. Типы смесительных теплообменников.
а — безна садочный форсуночный; б — каскадный; в — насадочный; г — струйный; д — пленочный
с насадкой нз цилиндров; 1— форсунки; 2 — трубы, распределяющие воду; 3— каскады; 4— насад-
ка; 5 и 6^ сопла первой и второй ступеней струйного смесителя; 7 — насос; 8 и 9 — центробежный
н осевой вентиляторы; 10 — электродвигатель; 11 — концентрические цилиндры; 12 — иллюминаторы-
сепараторы влаги; 13 — подогреватель воздуха.
5. Пленочные смешивающие подогреватели (рис. 2-6,6). Нагрева-
ние воды водяным паром в них происходит почти до температуры на-
сыщения пара [Л. 44]. Преимущество этой конструкции по сравнению
с поверхностными подогревателями заключается в простоте, компакт-
ности, меньшем весе и независимости коэффициента теплообмена от
чистоты поверхности, т. е. от загрязнения ее накипью, маслом и т. п.
Такие аппараты обычно работают с незначительным избыточным дав-
лением (1-г-5)Ю3 Па (0,01—0,05 кг/см2).
Недостатком пленочных подогревателей является коррозия поверх-
ности аппаратов и трубопроводов из-за наличия в воде и частично
в конденсирующемся паре значительного количества кислорода.
6. Пенные аппараты получили применение для улавливания из га-
зов плохо смачиваемой (гидрофобной) пыли. Принципиальная схема
пенных аппаратов приведена на рис. 2-8. Скорость набегающего потока
76
недостаточно. Анализ этих процессов
во всех случаях процессы тепло- и
Рис. 2-7. Форсунка для распиливания жидко-
сти.
газа на решетку обычно принимают 2—2,5 м/с. При большей скорости
усиливается унос воды в виде брызг, а при меньшей скорости умень-
шается пенообразование, и значительная часть жидкости (более 50%)
сливается через отверстия решетки. В нормальных условиях работы
половина жидкости сливается через отверстия в решетке и половина
через сливной порог. Степень очистки газа в пенных аппаратах может
составлять 90—95% [Л. 35].
Теплообмен в аппаратах контактного или смешивающего типа свя-
зан с массообменом и изучен еще
на /-^-диаграмме показывает, что
массообмена подчиняются сле-
дующему правилу. Если пар-
циальное давление паров жид-
кости в газе больше, чем дав-
ление паров над внешней по-
верхностью капелек жидкости
(в пленке Прандтля), то про-
исходит осушение газа, если
же давления пара находятся
в обратном соотношении, то
имеет место увлажнение газа.
Многократные исследова-
ния показали, что при одной
и той же начальной темпера-
туре воздуха коэффициент теплопередачи тепло- и массообмена при
осушении воздуха меньше, чем при увлажнении. Это можно объяснить
тем, что толщина воздушного пограничного слоя над капелькой или по-
верхностью воды больше в условиях конденсации, чем при испарении
влаги. При контактном тепло- и массообмене теплоносителей коэффи-
циент теплоотдачи а и коэффициент
теплопередачи имеют одинаковые
значения (a=k), так как в этом
случае отсутствует теплопроводная
стенка. Расчетные формулы могут
быть выражены как через а, так и
через k.
а)
Отвод
Подвод
жидкости
Вход гаэл
Выход Выход
суспензии I суспензии
Рис. 2-8. Схемы пенных аппаратов.
а — одно полочного; б — трехполочного; 1 —
корпус; 2 — решетки; 3 — гидравлический за-
твор: 4 — порог.
Вследствие трудности определения поверхности теплообмена таких
аппаратов в некоторых случаях расчет их проводят по объемному ко-
эффициенту теплопередачи. При этом уравнение теплопередачи прини-
мает вид:
Q=<kvVAt,
(2-13)
77
где kv — объемный коэффициент теплопередачи, отнесенный к 1 м3
активного объема аппарата, Вт/(м3-°С); V — полезный или активный
объем смесительной камеры, м3; Л/ — средняя разность температур теп-
лоносителей, °C.
Формула (2-13) может быть применена только для условий расче-
та, близких к тем, при которых определялся объемный коэффициент
теплопередачи.
Подробные данные по расчету различных типов смесительных аппа-
ратов для кондиционирования воздуха приведены в [Л. 29].
В процессе тепло- и массообмена коэффициенты переноса тепла и
массы могут изменяться.
В примерах 2-5 и 2-6 дается упрощенная методика таких расчетов
по усредненным значениям коэффициента теплопередачи.
Для определения коэффициента теплоотдачи при тепло- и массопе-
редаче между каплями и газовым потоком в условиях вынужденной
конвекции (Re= 14-200) можно пользоваться формулой А. В. Несте-
ренко
Nu = adKA=Nu0+,l,07(Re)0’48(Pr)0-33(Gu)°-17S, (2-14)
где а — коэффициент теплоотдачи, Вт/(м2-°С); dK— диаметр капель, м;
X — коэффициент теплопроводности воздуха или газа при средней тем-
пературе между поверхностью капель и воздухом, Вт/(м-°С); Nu0 —
критерий Нуссельта при Re—0 (Nu0=2); для значений Nu>80 величи-
ной Nuo можно пренебречь; Re=aM/v— критерий Рейнольдса; здесь
w0 — скорость движения капли относительно газа, м/с; v— коэффициент
кинематической вязкости воздуха при средней его температуре, м2/с;
Pr=v,/a — критерий Прандтля для воздуха (его величина может быть
принята равной 0,72); Gu=(Ec—Тм)/Тс — критерий Гухмана (учиты-
вает влияние массообмена на теплообмен), где Тс и Тм — температуры
воздуха или газа по сухому и мокрому термометрам, К.
Большую трудность представляет определение расчетного диамет-
ра капли, который зависит от типа форсунки п давления жидкости пе-
ред нею. Для приближенных расчетов средний диаметр капли может
быть определен по формуле
, 3105 /О 1
dK=—(2-15)
где р — давление жидкости перед форсункой, Па.
Если принять за форму капель правильный шар, то поверхности ка-
пель в 1 л жидкости может быть получена из следующих соотношений:
/' = пт-d2 , м2,
где п — число капель в единице объема.
Полный объем их
V = and3 /6, л.
К !
Разделив первое выражение на второе, получим удельную, поверх-
ность капель
l=f'/V=6/dK, м2/л. (2-16)
Для определения скорости падения капли воды в скруббере необ-
ходимо определить скорость витания ее. Под скоростью витания капли
понимают такую скорость, при которой наступает равновесие силы тя-
жести капли и сопротивления газовой среды. Это условие равновесия
можно выразить уравнением
“g" (Рк Рг) = £ Рг
ttBHT
(2-17)
78
где dK— диаметр капли, м; рк и рг — плотности капли и газа, кг/м3; g—
коэффициент лобового сопротивления капли в газовом потоке; давит —
скорость витания капли, м/с.
Это уравнение может быть представлено в виде критериальной за-
висимости
Q г --------------
Fe = dK 1/ -g(p«7fa) =lzRe2 В >
У 3v2pr
(2-18)
где Fe— критерий Федорова*; Re — критерий Рейнольдса при скорости,
равной скорости витания частицы; тг — кинематическая вязкость га-
за, М2/с.
Определив при данном диаметре частицы критерий Fe по графику,
представленному на рис. 2-9, находят соответствующее значение ReBIIT,
по которому и определяют скорость
витания частицы:
wBKT = -^7^-- (2-19)
ик
При противотоке теплоносите-
лей действительная скорость паде-
ния капли в скруббере
^ВИТ--
а при прямотоке их
Шд=К>вит + И>г.
Скорость 1падения капли отно-
сительно скорости газа при прети
вотоке
ау0 = аУвит+^г;
при прямотоке
И^0“!Г^вит—’Wr-
Рис. 2-9. График зависимости lgReBH
от 1g Fe.
Скорость витания (осаждения) одиночной частицы, соответствую-
щая равновесной скорости движения среды можно определить также,
используя зависимость
Re3=ArLy, (2-20)
где
. RespK —рг dl (Рк — рг) Prg „ .
Аг = -рр- • =------2------критерии Архимеда;
3 2
Ly = ^T=ReFri^= P.(pK--Mg--------кРитеР™ Лященко;
Fr — ~jBUT —критерий Фруда.
При Аг>3,6 или Ly>0,0022, или Re>0,2 расчет можно осуществить
с помощью номограммы (рис. 2-10).
Оросительные скрубберы с насадками. Для получения
больших активных поверхностей теплообмена между газом и жидкостью
применяют колонны с различными насадками, например: кольцами Ра-
шига, коксом, деревянными рейками в виде хордовых насадок, с метал-
* В работах ЦКТИ этот критерий был назван критерием Кирпичева и обозначен
через Ki.
79
лической стружкой и т. п. На рис. 2-11 показаны различные виды скруб-
берных насадок.
Схема воздухоохладителя с насадкой и принудительным движением
воздуха показана на рис. 2-6,в.
Характеристика скрубберных насадок из колец Рашига, кускового
материала и деревянных решеток (хордовых насадок) дана в табл. 2-4.
Рис. 2-10. Зависимость критериев Ly и Re от критерия Аг для определе-
ния скорости витания или осаждения частицы (при малых скоростях
газовой среды).
1 и 6 — шарообразные частицы; 2 — округленные; 3 — угловатые; 4 — продолго-
ватые; 5 — пластинчатые.
Насадки характеризуются поверхностью единицы объема S, м2/м3;
свободным объемом Усв, м3/м3; проходным сечением f, м2; просветом на
1 м2 поперечного сечения аппарата и периметром U — условным пери-
метром просветов в метрах на 1 м2 поперечного сечения аппарата.
Для правильно уложенной насадки 5 = 67-1 и 17Св=/*1. Для беспо-
рядочно засыпанной насадки величины U и f неопределенны и различ-
ны для каждого сечения, но для средних значений этих величин можно
принять те же соотношения U=S и /=УСв, что и для правильно уло-
женной насадки.
80
В расчетах насадок используется величина гидравлического радиу-
са r=f[U= Vee/S или приведенного диаметра
dr=4r=4I/CB/5. (2-21)
При противоточном движении газа и жидкости в насадочных колон-
нах по мере возрастания скорости наблюдаются четыре характерных ре-
жима движения потоков: пленочный, промежуточный, турбулизации и
эмульгирования.
Рис. 2-11. Насадки для смесительных теплообменников.
а — беспорядочно уложенные кольца; б н в — кольца с перегородками; г — шары; д — пропеллерная
насадка; е — седлообразная насадка; ж — хордовая насадка^
В режиме эмульгирования интенсивность тепло- и массообмена до-
стигает максимального значения, одновременно происходит накаплива-
ние жидкости и, когда вся насадка затапливается жидкостью, проис-
ходит так называемое захлебывание и начинается выброс жидкости из
колонны. При проектировании скрубберов принимают рабочую скорость
куг несколько меньше скорости эмульгирования wa, при которой насту-
пает инверсия (пенообразное перемешивание) фаз:
wr= (0,80-^0,85)даэ, м/с.
Скорость газов, соответствующая оптимальному режиму работы
колонн, определяется из формулы [Л. 48]
Re'=0,045 Ar°'57L/G, (2-22)
где
Re' = Р; Аг==-Э—д2—)g--
В этих формулах даОпт — оптимальная скорость парогазовой сме-
си, м/с; рг — плотность парогазовой смеси при заданной температуре,
кг/м3; рН5 — плотность жидкости при заданной температуре, кг/м3; цг—
вязкость парогазовой смеси, Н-с/м2; с?э=4УСв/5—эквивалентный (гид-
равлический) диаметр насадки, м; L — расход газа, кг/с; G — расход
жидкости, кг/с.
Оптимальная скорость газа
(2-23)
6—1128
81
Характеристика насадок
Таблица 2-4
Вид насадки Размер эле- мента насадки, мм Поверхность в единице объема S, м9/м3 Свободный объем Vn. Объемный вес насадки, кг/м3 Приведенный диаметр, аг = 4VCJS’ м
Кольца Рашига (кера- 15X15X2 330 0,7 690 0,0085
мические, беспоря- 25X25X3 200 0,74 530 0,015
дочно лежащие) 35X35X4 140 0,78 505 0,022
50X50X5 90 0,785 530 0,035
Кольца Рашига кера- 50X50X5 ПО 0,735 650 0,027
мические (правильно 80X80X8 80 0,72 670 0,036
уложенные) 100ХЮ0Х10 60 0,72 670 0,048
Кольца Рашига сталь- 8X8X0,3 630 0,9 780
ные (беспорядочно 10X10X0,5 500 0,88 960 —
лежащие) 15X15X0,5 350 0,92 660 —.
25X25X0,8 220 0,92 640 —
50X50X1 110 0,95 430 —
Кокс 25 120 0,53 600 0,018
40 85 0,55 590 0,026
75 42 0,58 550 0,055
Кварц 25 120 0,37 1 600 0,012
40 85 0,43 1450 0,02
75 42 0,46 1 380 0,044
Хордовая насадка (де- ревянная — СМ. рис. 2-10) юхюо (шаг в све- ту 10) 100 0,55 210 0,022
юхюо (шаг в све- ту 20) 65 0,68 145 0,040
юхюо (шаг в све- ту 30) 48 0,77 110 0,064
Вычисленная по этому методу иуОпт составляет примерно 80% ско-
рости захлебывания.
Определение основных размеров колонны сводится к подсчету по-
лезного или активного объема В, диаметра D и полезной высоты Н.
В насадочных колоннах под полезным или активным объемом и по-
лезной высотой следует понимать объем и высоту насадки.
Полезный или активный объем скруббера определяется по формуле
В = , М\
kb-tStf
(2-24)
где Q — количество тепла, передаваемое в скруббере, Вт;
k — коэффициент теплопередачи насадки, Вт/(м2*°С);
А/ — средняя разность температур теплоносителей, °C;
S — поверхность насадки в единице объема, м2/м3;
Ф — коэффициент смачиваемости.
Коэффициент смачиваемости насадки ф (отношение поверхности
смоченной насадки к полной поверхности ее) можно найти как отно-
шение количества жидкости, удерживаемой 1 м3 насадки, V, к количе-
ству жидкости, удерживаемой 1 м3 насадки при полной ее смачиваемо-
сти, Уо.
•82
Таким образом,
V _
Vo f(H„y
(2-25)
4G
где S— поверхность насадки в единице объема, м2/м3; Hw= —
плотность орошения, м3/(м2-ч).
Таблица 2-5
Значения функции плотности орошения f (Hw)
Hw, м“/(м2-ч) 1 2 4 6 8 10 15 20 30 40 60
f (Яш) 24 15 9,8 7,5 6,6 6,0 5,3 4,8 4,4 4,2 3,8
Значения f(Hw) даны в табл. 2-5. Если <р получается больше едини-
цы, то насадка смачивается полностью и в расчете принимается <р=1.
Для равномерного распределения газа и жидкости по сечению
аппарата отношение высоты насадки к ее диаметру Н/D не должно быть
меньше 1,5—2 и больше 5—7.
Коэффициент теплопередачи при охлаждении воздуха водой
в скрубберах с насадкой можно определить по формуле Тадеуша Хоб-
лера [Л. 54], обобщившего работы Н. М. Жаворонкова и Н. Э. Фурмер:
« = 0,0024— Re°’7Pr°'33 (Реж)°/ =20 «с (1 + еХ),
Hq г г ж
(2-26)
где X — теплопроводность смеси (влажного воздуха), Вт/(м-°С); с?э=
= 41zcb/S — эквивалентный диаметр насадки, м; Rer=ayrf3/vr — критерий
Рейнольдса для парогазовой смеси, в котором шг— скорость газа в на-
садке, м/с; гг — кинематическая вязкость парогазовой смеси, м2/с; Рг =
= Vcm/«cm—критерий Прандтля для парогазовой смеси; Ееж = ЧРДЭ— —
критерий Рейнольдса для жидкости при температуре 20 °C, в котором
4£
—плотность орошения насадки, м3/(м2-ч); L — расход жид-
кости, м3/ч; V» — кинематическая вязкость жидкости при температуре
20°С, м2/с; е= —безразмерный комплекс, учитывающий влия-
ние массообмена; i — энтальпия пара1; г — теплота парообразования;
Ф=а/Р~ср — соотношение Льюиса, где а — коэффициент теплоотдачи;
0— коэффициент массообмена; т = рп/цв — отношение молекулярных
весов пара и воздуха; ср — теплоемкость влажного воздуха на 1 кг су-
хого воздуха; А = 1/427 — тепловой эквивалент единицы работы; R — га-
зовая постоянная влажного воздуха; Т — температура парогазовой
смеси, К-
В большинстве случаев процессы в скрубберах при тепло- и массо-
обмене воздуха с водой протекают при температурах от 20 до 90 °C;
Т. Хоблер предлагает в расчетах принимать среднее значение комплек-
са 8=130; X—средняя концентрация пара в парогазовой смеси:
1 Все величины для определения е имеют размерность в тепловых единицах, осно-
ванных на калории.
6* 83.
где Лц-—концентрация шара в смеси при ее средней температуре, кг/кг;
Х3 — концентрация пара в смеси у зеркала испарения воды при темпе-
ратуре 20 °C, кг/кг.
Пример 2-5. Определить высоту хордовой насадки из досок в скруббере, необхо-
димую для охлаждения при прямотоке /,= 10000 кг/ч воздуха от Г1 = 150 °C до /"t=
=55 °C водой с начальной температурой /'2=15°С и конечной /"2=55°С.
Энтальпия воздуха при входе в скруббер Л=418,7 кДж/кг (100 ккал/кг) сухого воз-
духа; из построения процессов тепло- и массообмена на /-d-диаграмме в примере 2-4
вычислено, что энтальпия воздуха /2 на выходе из скруббера составляет 209,35 кДж/кг
(50 ккал/кг) сухого воздуха. Поверхность насадки в единице объема 5=45 м2/м3; сво-
бодный объем насадки, равный численно ее живому сечению f, VCB=0,5 м3/м3 и экви-
валентный диаметр da=0,045 м.
Решение. Количество тепла, отданное воздухом в скруббере Q=L(/i—/2) =
= 10 000 (418,7—209,35) =2 093 500 кДж/ч, или 581 500 Вт.
Расход охлаждающей воды
_ Q 2 093 500
G — с (t"2 — t's) — 4,187 (50 — 15) “ 14 300 кг/ч’ или 4 л/с'
Для определения оптимальной скорости воздуха по формуле (2-22) находим:
я_ ^Рвл(Рж — Р»и) _ (0,045)3-0,86-(993 — 0,86)-9,8
Аг— ~ (20,6-Ю-6)2 =1,8-10».
Плотность влажного воздуха рвл=0,96 кг/м3 подсчитана по уравнению (2-9) при
его среднем влагосодержании для пятой ступени при dcp=88 г/кг и средней температу-
ре /Ср=102°С (рис. 2-4 и табл. 2-3):
Т„В Д 0,378?Al8C >
Р‘п “ р« ГД, в J
, „„„ 273-745 ! 0,378-0,13-760 \
— 1,293 - 375.750 (1 — 745 )- 0,86.
Плотность воды рж=993 кг/м3 взята при средней температуре 35 °C. Для значе-
ний dcp и /Ср определены значения физических констант и в последующих форму-
лах.
Вязкость влажного воздуха при температуре 102 ГС
1 1-10-6
Н,л— хп хв 0,079 0,921 "-20,6-10-»Н-с/м2.
Р-п +Р« 11,97'*21,90
Весовые концентрации пара и воздуха:
dcy ________________________________ 88
Ха = 1 000 + doP ~ 1 000 + 88 = 0,079;
хв= 1—хи= 1—0,079=0,921.
Критерий Рейнольдса по уравнению (2-22)
G 10 000
Re' = 0,045-Аг»,5’ -т-=0,045 (1,8-10»)».»’ гГопгГ=5 500.
Оптимальная скорость по уравнению (2-23)
Re'[xBJI_5 500-20,6-10~6 _
Юоп1 = d8pM “ 0,045-0,86 2,9 м/с-
Диаметр скруббера
,/ 4Gb if 4-10000-1,16 , „„
D— V адаЗбОО ~ V 1,5-3,14-3 600 ~1,75 м’
где о=1/р=1/0,8б=1,16 м3/кг; w — скорость воздуха в свободном сечении скруббера,
принятая равной 1,5 м/с по проходному сечению насадки 0,5и?Опт=0,5 • 2,9.
84
В этом случае скорость воздуха в живом сечении насадки
G
ю =------------
3 600——рвл/
10 000
3,14-1,52 —2,7 м/с <2,9.
3 600-—~—.0,5-0,86
Определяем коэффициент теплопередачи k.
Критерий Рейнольдса для газа
wdB 2,7-0,045
Re»a== vBn ~23,8-10-«^5100,
где кинематическая вязкость vBл = р/р=20,6• 10_»/0,86=23,8-10~6 м2/с.
Критерий Прандтля
РГви
у.л _ УвлСвлРвл _ 23,8-10-». 1,079-0,86-3 600 _
двл * 117.10-3 U,68,
^вл
117-Ю-3
смеси сВл=сихп'+свхв=1,89-0,079+1,01-0,921 = 1,079 кДж/(кг-°С);
влажного воздуха Хвл = 1,05 (XnSn+lABsB) = 1,05 (88,6-0,1224-
где теплоемкость
теплопроводность
+ 115-0,878)-10-’= 117 кДж/(м • ч-°C), или 32,5-Ю-3 Вт/(м-°С).'
Объемные содержания пара и воздуха в смеси определены по формулам
d 88
Еп== 622 + d
622 + 88
0,122; ев= 1—0,122 = 0,878.
Критерий Рейнольдса для
жидкости
Re,
3 600^1
4G
6,0-0,045
3600-1-10-» ^75,
4-14,3
где плотность орошения Нт — ----з 14-1 752.1 ~
— вязкость воды при 20 °C.
Средняя концентрация пара в смеси по рис. 2-4
6,0 м*/(м2-ч) или 1,65 л/(м2-с);
Х„-Х,_0,088 - 0,0147
*АП 0,088 и,и'30,
1П Хв 1п 0,0147
где Хя и Х3— концентрация пара в смеси при <ср=102оС и у зеркала испарения при
tm=20 °C.
Коэффициент теплопередачи по формуле (2-26)
а=°-0024 ^евл p433r^7 и + w =
32-10“*
=0,0024 0 -045 (5 100)°.’ (0,68)°.33 (75)°-’-(1 + 130-0,035) = 76 Вт/(м»-*С).
Среднюю разность температур для скруббера принимаем равной 54 °C согласно
расчетам, сделанным в примере 2-4.
Коэффициент смачиваемости
1ZS 1^45
Ч = 7,5 =0-48-
Величина f(Hw) определяется по табл. 2-5. Объем насадки скруббера
Q 581500
= kMStf
76-54-45-0,48 — 6>6м’-
Высота насадки
h~~ T.D2
4-6,6
3.14-1.752 2,74 м’
Пример 2-6. Определить для тех же параметров теплоносителей, что и в преды-
дущем примере, объем скруббера без насадки с распыливанием воды форсунками,
обеспечивающими средний диаметр капли dK = l,2 мм. Расход воды 4 л/с, плотность
орошения Яю=2,26 л/(м2-с).
85
Решение. Скорость витания капли определяем по формулам (2-18) и (2-15)
Fe _ d .3= 0 0012 У4-ЩМЗ-0.86) _ 3 5.
I/ 3v~4pBn ’ Г 3 (23,8-10-6)2.0,86
lg Fe= 1,55.
По рис. 2-9 определяем lgReMT=2,35 и Re„HT = 225;
КевиЛл 225-23,8-10-6
да»ит = rfj( — 0,0012 =5=4,4 м/с.
Действительная скорость падения капли для противотока при w=Q м/с
Ид=шВит—ш=4,4—2=2,4 м/с.
Время падения капли в скруббере с высоты 1 м
Т=1/шд= 1/2,4=0,415 с/м.
Поверхность капель, полученных из 1 л, по формуле (2-16)
/=6/d=6/l,2=5 м2/л.
Поверхность капель в 1 м3 объема скруббера
+к = /т//„ = 5 • 0,415 • 2,26=4,7 м2/м3.
Для определения коэффициента теплопередачи по формуле (2-14) находим:
Re = wod/vB„= (2,4+2) - 0,0012/123,8—10“6 = 323,
где сС'и -а.'д + ш; Ren= (323) °-48= 16.
Как и в предыдущем примере,
рг0.зз= (0,68) о-33 = 0,87;
.. 0 1,5 / Л,-У-"5 / (83+ 273)-(53+ 273) \»-”5 „ дг
Gu»”5 = ^~--------j -(----------83+Д/з----------) -°’65’
где /с=83сС и /м=53 °C — температуры сухого и мокрого термометров, взятые из
примера 2-4 по процессу для пятой ступени, изображенному на /-d-диаграмме (соот-
ветственно точкам Е и F).
Подставив полученные величины в формулу (2-14), получим:
Nu=adK/X=Nuo +1,07Re°-48 Рг0-33 X
XGu0-175=2+4,07 • 16 0,87 • 0,65=11,7,
откуда
«= NiA/dK= 11,7- 32 • IO-3/©,0012=312 Вт/(м2-°С).
Активный объем скруббера
Кс = С/(аКкА(ф)=581 500/(312-4,7-54-0,8) =8,7 м3,
где ср — коэффициент, учитывающий несовершенство процессов тепло- и маеевебмена.
Активная высота скруббера
Л=4Пс/(лО2) =4 - 8,7/3,14 • 1,52=5 м.
Активные размеры безнасадочного скруббера получились в 2,5 раза большими,
чем в предыдущем примере для насадочного скруббера.
Большое значение для габаритов аппарата имеет качество распыливания пли
средний расчетный диаметр капли. Например, если принять в расчете dB = 2 мм, то
действительная скорость падения капли составит 10 м/с, а=450 Вт/(м2-°С) и +=
= 0,585 м2; в результате активные размеры скруббера увеличатся более чем в 10 раз
по сравнению со скруббером, имеющим насадку.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. € какой целью /-d-диаграмма влажного воздуха построена в косоугольной
системе координат?
2. Почему изотермы на /-d-диаграмме расходятся веером вверх?
3. Как изменяется атмосферное давление с повышением влажности воздуха?
86
4. Какой воздух, влажный или пересыщенный, при одинаковой температуре име-
ет большую энтальпию?
5. Какой воздух, влажный или сухой, имеет большую плотность?
6. Является ли точным определение относительной влажности воздуха ср по от-
ношению парциального давления паров к давлению насыщения паров при данной тем-
пературе?
7. Почему на /-d-диаграмме ВТИ линии cp=const при температуре, близкой
к 100 DC, идут почти вертикально вверх?
8. При какой влажности воздуха ср температура мокрого термометра равна
температуре сухого термометра?
9. Какая температура мокрого термометра имеет большее числовое значение,
истинная или адиабатная, и как изменяется разность этих температур с увеличением
скорости воздуха, омывающего ртутный шарик термометра?
10. Можно ли организовать процесс нагревания воздуха в помещении по линии
ср=const?
11. Может ли процесс охлаждения воздуха идти по линии cp = consl<l00%?
12 Может ли процесс испарения влаги в воздухе протекать по линии /=const?
Какие условия для этого необходимы?
13. Как определить температуру смеси воздуха в области пересыщенного или
переохлажденного состояния по /-d-диаграмме?
14. Какую воду, холодную или горячую, следует применять для осушения возду-
ха и какую для его увлажнения?
15. Какая температура является пределом нагревания или охлаждения воздуха
в скруббере?
16. Можно ли применять формулу средней логарифмической разности темпера-
тур для определения Л/ при тепло- и массообмене в скрубберах?
17. Может ли при контактном тепло и массообмене у обоих теплоносителей, воз-
духа и воды, снижаться температура?
18. Объясните смысл соотношения Льюиса и область возможного применения
его?
19. Может ли быть одинаковым диаметр капель при распылении жидкости? Как
изменяется средний диаметр капель с повышением давления распиливаемой жидко-
сти?
20. Как изменяются интенсивность испарения жидкости и коэффициент тепло-
отдачи в зависимости от разности температур жидкости и газа и размера капель?
21. Какие значения (большие или меньшие) должна иметь скорость газа по
сравнению со скоростью витания частиц или капель для осаждения и уноса их?
22. Какой физический смысл имеет критерий Gu, учитывающий влияние массо-
обмена на теплообмен?
23. Перечислите достоинства и недостатки скрубберов с насадкой и без нее.
24. Как изменяется гидравлическое сопротивление проходу газа с повышением
плотности орошения насадки водой? Влияет ли плотность орошения насадки на ко-
эффициент теплоотдачи?
25. Как выбирается оптимальная скорость газа в насадке скруббера для устой-
чивой работы его?
26. Какие насадки, из мелких или крупных элементов, имеют большую поверх-
ность в единице объема, больший свободный объем для прохода газа и большее гид-
равлическое сопротивление при одной и той же высоте слоя?
27. Какие преимущества и недостатки имеют смесительные теплообменники ио
сравнению с трубчатыми при нагреве воды водяным паром?
28. В каких смесительных теплообменниках, прямоточных или противоточных,
получается меньший недогрев воды водяным паром?
29. Укажите области применения, преимущества и недостатки пенного аппарата.
ГЛАВА ТРЕТЬЯ
АППАРАТЫ ПЕРИОДИЧЕСКОГО ДЕЙСТВИЯ
И АППАРАТЫ С КИПЯЩИМ СЛОЕМ
8-1. РЕКУПЕРАТИВНЫЕ АППАРАТЫ ПЕРИОДИЧЕСКОГО
ДЕЙСТВИЯ
Рекуперативные аппараты периодического действия широко приме-
няются в различных отраслях промышленности. К таким аппаратам
можно отнести в первую очередь водонагреватели-аккумуляторы, ва-
рочные котлы и реакционные аппараты.
87
Водонагреватели-аккумуляторы (рис. 3-1,п и б) представляют со-
бой сосуды большой емкости с паровым или водяным обогревом и при-
меняются в системах горячего водоснабжения с периодическим расхо-
дом больших количеств воды. Вода в подогревателях нагревается за
4—5 ч и расходуется в течение 20—30 мин (например, в душевых поме-
щениях цехов после очередной смены). Если бы для этой цели исполь-
зовались схемы с теплообменниками непрерывного действия, то пиковый
расход тепла в них был бы в 6—10 раз больше среднечасового расхода
тепла в водонагревателе-аккумуляторе. Такое водоснабжение создавало
бы пиковые нагрузки в котельной или на ТЭЦ.
Рис. 3-1. Типы рекуперативных аппаратов периодического действия.
а и б — водонагреватели-аккумуляторы; в — автоклав с паровой рубашкой; г — варочный котел
с мешалками; d — варочный котел с выносным, подогревателем; 1 — паровая рубашка; 2 —выносной
подогреватель; 3 — циркуляционный насос; 4 — распиливающее сопло; 5 — фильтрующая защитная
сетка; 6 — мешалка.
Варочные котлы (рис. 3-1,г и д), реакционные аппараты периоди-
ческого действия, например автоклавы (рис. 3-1,в), вулканизаторы, за-
парники, конверторы и подобные им теплообменники, нашли широкое
применение в химической и других отраслях промышленности.
В варочных и реакционных аппаратах обрабатываемые материалы
нагреваются до определенной температуры и содержатся в течение не-
которого времени при этой температуре. За определенный промежуток
времени в материале происходят требуемые изменения (большей
частью химического характера), после чего аппарат опорожняется. Вре-
мя обработки материала в аппарате различно в зависимости от техно-
логии производства: иногда ограничиваются только периодом нагрева-
ния, иногда же обрабатываемый материал находится в аппарате при
постоянной температуре весьма продолжительное время.
88
Простейшим варочным аппаратом является открытый чан, в кото-
ром материал обрабатывается жидкостью при атмосферном давлении.
Материал загружается на «ложное дно» (решетку или перекрытие с от-
верстиями), размер ячеек в котором определяется размером кусков
обрабатываемого материала. Решетка устанавливается на некотором
расстоянии от дна чана. Под ложным дном размещается паровой зме-
евик с отверстиями — барботерная трубка. Пар выходит из отверстий
прямо в жидкость, конденсируется и нагревает ее; такой способ нагрева
жидкости паром технологи называют обогревом «острым» паром. Жид-
кость нагревает находящийся в ней материал. Неудобством таких пер-
форированных змеевиков-барботеров является большой шум, который
они создают во время работы. Иногда вместо барботерных змеевиков
устанавливают пароводяные струйные инжекторы, которые лишены это-
го недостатка.
Открытые варочные чаны применяются в том случае, когда обработ-
ка материала происходит при температурах ниже 100 °C и материал не
выделяет вредных паров или газов. При выделении токсичных паров и
газов аппарат закрывают герметичной крышкой с вытяжной трубой,
выведенной за пределы помещения.
Термическую обработку твердых и жидких материалов при высо-
ких температурах и давлениях осуществляют в герметизированных ап-
паратах — автоклавах. Нагревание обрабатываемого материала в этих
аппаратах производится либо «острым» паром через барботерные трубы,
либо «глухим» паром при помощи трубчатых змеевиков или паровых
рубашек (рис. 3-1,в).
Обогрев глухим паром малоэффективен по сравнению с обогревом
острым паром вследствие низкого коэффициента теплопередачи от теп-
лоносителя через стенку к жидкости, а затем к материалу, поскольку
теплообмен происходит только за счет естественной конвекции жидко-
сти. Обогрев острым паром экономичнее глухого обогрева, однако при-
водит ТЭЦ или котельную к большому дефициту конденсата.
С целью сохранения конденсата, увеличения емкости аппарата или
в случае необходимости замены греющего пара горячей водой приме-
няют аппараты с выносными подогревателями (рис. 3-1,д). В аппарате
жидкость прогоняется через выносной подогреватель 1 при помощи цир-
куляционного насоса 2.
Для интенсификации процесса теплообмена, сокращения времени и
экономии пара на процессе прогрева обрабатываемого материала часто
внутри аппарата устанавливают мешалки для перемешивания нагревае-
мого материала в обогревающей жидкости (рис. 3-1,г). Такое усовер-
шенствование ускоряет нагревание, однако требует значительного рас-
хода энергии на вращение мешалки.
Для определения коэффициента теплоотдачи от греющей стенки
к нагреваемой жидкости в аппаратах со змеевиками или рубашками и
лопастными мешалками можно воспользоваться формулой {Л. 48]
:Nu = CRemPr°>33(p/pc)o-i4, (3-1)
где ,
Nu = a£>A; Re=pnrf2/p;
Рг= срД;
a — коэффициент теплоотдачи, Вт/(м2-сС); D — диаметр сосуда, м; X —
коэффициент теплопроводности жидкости, Вт/(м-°С); р — плотность
жидкости, кг/м3; п — число оборотов мешалки в секунду, 1/с; d — диа-
метр лопасти мешалки, м; с — теплоемкость при постоянном давле-
нии, Дж/(кг-°С); рс— вязкость жидкости при температуре стенки; р —
вязкость жидкости при средней температуре /Ср=0,5(/ж+/с), Н-с/м2.
Для аппаратов с рубашками коэффициент С=0,36, показатель сте-
пени т=0,67. Для аппаратов со змеевиками С=0,87; /п=0,62.
89
Значения физических констант надо брать при средней температуре
жидкости в сосуде
Формула (3-1) получена из опытов при d—QfiD, D3M=O,&D, Нам=
= 0,48D и £)<300 мм. Интересную конструкцию представляет собой го-
ризонтальный вращающийся автоклав (рис. 3-2) для обработки твер-
дых материалов. Автоклав имеет полые цапфы и зубчатую передачу. По
одной из цапф с сальниковым уплотнением пропускают греющий пар
Рис. 3-2. Вращающийся автоклав.
в барботер 3. Автоклав может иметь дополнительный (внешний) обо-
грев как в цилиндрической части, так и на торцах; подвод пара для
этой цели и вывод конденсата производятся через другую цапфу (вен-
тили 1 и 2).
Расчет водонагревателя-аккумулятора с паро-
вым обогревом. Нагрев в аппаратах периодического действия про-
Рис. 3-3. График изменения температур
в водонагревателе-аккумуляторе с паро-
вым обогревом.
исходит при переменном тепловом
режиме, поэтому для их расчета не-
применимы ранее приведенные фор-
мулы, относящиеся к аппаратам
непрерывного действия с установив-
шимся тепловым режимом.
Нагревая в аппарате воду, пар
конденсируется при температуре, со-
ответствующей его давлению. Коли-
чество нагреваемой воды G2 в аппа-
рате остается постоянным. Вследст-
вие того что температура конденса-
ции пара постоянна во времени,
а температура воды /2 увеличивает-
ся (рис. 3-3), температурный напор ДГ=/Н—4 с течением времени
уменьшается. В связи с этим уменьшаются расход тепла Q и пара D.
Дифференциальное уравнения теплопередачи и теплового баланса
для элемента времени du, в течение которого температура воды повы-
шается на dt, имеет вид:
dQ=D(i—/н) dr—kF\Ntdx= G2c2dt. (3-2)
Если начальная температура нагреваемой воды равна t'2, а через т
часов будет t"2, то из уравнения (3-2) следует:
-С /"2
J ^2^2 J ^11 ^2
О t'a
90
или после интегрирования
kF
G2c2
= ln
откуда
G2c2 * ?H tr2
(3 3)
Gt — t'z
tg-t"2 ’
Произведение kF называется удельной тепловой производительно-
стью водонагревателя-аккумулятора.
Коэффициент теплопередачи k вычисляют по формуле (1-10) для
плоской стенки, в которой для рассматриваемого случая щ — коэффи-
циент теплоотдачи от конденсирующегося пара к стенке и аг— коэффи-
циент теплоотдачи от стенки к воде при естественной конвекции воды
в аппарате.
Для определения коэффициента теплоотдачи от стенки к нагревае-
мой воде необходимо знать среднюю за время т температуру последней.
Ее можно определить из равенства
/ср2 = Д-Д/ = Д-----(3-4)
1П tg-t'K
При проектировании установки иногда бывает известна поверхность
нагрева аппарата и требуется определить конечную температуру воды.
Чтобы найти ее, можно установить зависимость Д'2 от т из уравне-
ния (3-3)
kFt
= (3-5)
Зависимость расхода пара от времени выражается формулой
kF-г
D=kFt^F^e~~^.
I — 'll
Расчет водонагревателя-аккумулятора с водяным
обогревом. Особенностью режима
ется то обстоятельство, что при по-
стоянных расходе Gt и температуре
воды температура ее на выходе из ап-
парата по мере нагревания воды
в аккумуляторе увеличивается. Изме-
нение температур греющей и нагревае-
мой воды в зависимости от времени
изображено на рис. 3-4. Такой режим
несколько усложняет расчет, так как
необходимо использовать две перемен-
ные во времени: температуру А и t2.
Дифференциальные уравнения теп-
лопередачи и теплового баланса в дан-
ном случае имеют вид:
работы такого аппарата явля-
Рис. 3-4. График изменения темпера-
тур в водонагревателе-аккумуляторе
с водяным обогревом.
dQ=kFA/tdr= GiCift'i—ti) dr— G^oidt, (3-6)
где GiCt и G2C2 — полные теплоемкости теплоносителей; А/— средняя
логарифмическая разность температур:
Д/ =
t't — G
1П
91
t'l, ti и tz — температуры греющей и нагреваемой воды в рассматривае-
мый промежуток времени dr.
Подставив значение Ait в равенство (3-6), получим:
1п 6 —12
и
Cl-jCj tj
откуда
t' -t —
tl —ti ч
kF
Введя обозначение А=-=—, найдем, что температура греющей
OjCj
воды на выходе из аппарата
ti=tz+ (Fi—tz}e~A.
Подставив значение переменной ti, выраженное через t'i и tz, в ра-
венство (3-6) и произведя преобразования, получим:
^-(1 - ё~А) dx = .,dt* .
Gsca ' ' < i + <2
Левую часть уравнения интегрируем в пределах от 0 до т, а пра-
вую— в пределах от начальной температуры t'2 до конечной t"2:
х = щ (3-7)
'J2C2 1 * 2
По уравнению (3-7) можно определить удельную производительность
аппарата:
kF=G^ ----------вА 1 f,-f. >3-8>
1 GjCji: In 1\ — t"a
Зная значение kF и величину коэффициента теплопередачи, опреде-
ляемого по соответствующим формулам, легко определить поверхность
нагрева аппарата F.
Для определения коэффициента теплоотдачи от стенки к нагревае-
мой воде необходимо знать среднюю температуру последней. Она оп-
ределяется приближенно по формуле
f's — t's
t — t’
*2Ср — L :
ln t’i-t’t
1 —
(3-9)
Среднее значение температуры для греющей воды можно найти по
формуле
^Z/ikoh ^Лнач
ft f”
, i 1нач
/7 4ГГ
L 1 L 1К0И
tn —- tr
L icp —L 1
где ^"тач и f'lKoH — температура греющей воды на выходе из аппара-
та в начальный момент и в конце процесса.
S2
Если задана поверхность нагрева аппарата, то конечную темпера-
туру нагреваемой воды Z"2 в зависимости от времени нагрева т можно
определить из уравнения (3-7)
Z"2 = ^i—(i'i—Г2)е-В,
где
D__ f 1_______1 А
еА )
Определение коэффициента теплопередачи для
водонагревателя-аккумулятора. Коэффициенты теплопереда-
чи определяются по формулам для плоской стенки. Коэффициенты теп-
лоотдачи внутри трубок аппаратов с водяным обогревом определяются
по формулам (1-13) и (1-15) для вынужденного движения воды, а для
аппаратов с паровым обогревом, в которых процесс конденсации пара
происходит внутри одиночных горизонтальных труб, — по формуле
(1-34).
Особенностью водонагревателей-аккумуляторов по сравнению с
другими, рассмотренными ранее теплообменниками непрерывного дей-
ствия является то, что теплоотдача к нагреваемой воде в них осуществ-
ляется в большинстве случаев при ее естественной конвекции.
Коэффициент теплоотдачи от вертикальных и горизонтальных труб
при естественной конвекции жидкости и газа в большом объеме может
быть определен по формуле М. А. Михеева
Nur = 4 =C(GrPr)r = С ((3-10)'
Формула применима для жидкостей и газов при Рг^0,7. В ней
обозначено:
AZ=ZC—tr\ +
tc — температура теплоотдающей поверхности стенки; — средняя
температура жидкости; X, v, а, [’>— физические константы жидкости при
температуре граничного слоя /г; /— характерный размер: для горизон-
тально расположенных трубок l—d (d — диаметр трубки), для верти-
кальных трубок Z=/i; h — высота трубки.
Величины Сип зависят от произведения GrPr. В расчетах принимают следующие соотношения: при GrPr<10-3 (пленочный режим) практических
Nu=const=0,5; (3-10a)
при (GrPr) = 1 • 10-3—500 (переходный режим) Nu= 1,18 (GrPr)0,125; (3-106)
при (GrPr) =500-ъ2-107 (ламинарный режим)
Nu = 0,54 (GrPr) °-25; (3-10b)
при (GrPr) >2 107 (вихревой режим)
Nu = 0,135 (GrPr)0’33. (3-1 Or)
Формулы (3-10) для каждого теплоносителя могут быть приведены
к следующему виду:
для труб, сфер, вертикальных плит при 500<(GrPr) <2 -107
а= А, (M/l)1'4 , Вт/(м2-°С); (3-11а)
при (GrPr) >2 • 107
а = ДД?/4 , Вт/(м2 • °)С. (3-116)
В табл. 3-1 приводятся значения коэффициентов Ai и Л2 для воды.
93
Таблица 3-1
Значения коэффициентов Л, и Д для воды в уравнениях (3-11а) и (3-116)
Коэффи- циент Температура tT, °C
0 20 40 60 80 100 150 200
А, 70 112 149 178 205 227 274 304
Аг 102 198 291 363 426 482 607 713
Пример 3-1. Рассчитать водонагреватель аккумулятор с водяным обогревом для
нагревания в течение т=5 ч и 62- 10000 кг воды от 7'2=5°С до 7"2=50°С; расход
греющей воды 64=4 000 кг/ч; температура греющей воды на входе К1=70°С. Грею-
щая вода циркулирует по латунным трубкам диаметром dBH/dH=21/25 мм.
Решение. Расчет начинается с определения удельной производительности
аппарата. Приняв теплоемкости Ci = c2=4,187 кДж/(кг-°С) (1 ккал/(кг • °C)], найдем:
1
kF = GlcI In------tj-------=
U2C2 I 1 — t 2
G1c1t ln t\ — t"2
= 4 000 4,187 In ——ЮООО-4.187 70 — 5 =
1 — 4000-4,187-5~ln 70=50
= 14906 кДж/(ч-°С) = 4 140 Вт/°С.
Средняя температура нагреваемой воды определяется по приближенной формуле
(3-9)
50 — 5
Лер — — 70 • — 7Q-1-5 32 °C.
1п 70 — 50
Средняя температура греющей воды, выходящей из аппарата, будет равна*.
_ kF
/"1Ср = Лер + (/'1 -<ep«) е GlC' = 32 + (70- 32) ё~14 906/ 16 748 = 47,6 °C.
Для вычисления коэффициента теплопередачи задаемся скоростью движения
воды в трубках w=0,4 м/с и определяем режим движения воды в них
ггт/вн 0,4-0,021
Re = —-- = 0-5.10_6- = 16 800 > 10 000.
Коэффициент кинематической вязкости греющей воды v берется при средней тем-
пературе
Коэффициент теплоотдачи сц от греющей воды к стенкам трубки определяем
по формуле (1-14)
w«,8 0 4° 8
а, = A —Q2 = 2 700 ~о 021М = 3 500 Вт/(м2 - °C) [3 000 ккал/(ч • м2 - °C) ].
^ВН ’
Коэффициент теплоотдачи от трубок к нагреваемой воде «2 определяем по фор-
муле для свободной конвекции при горизонтальном расположении труб. Определяем
предварительную температуру стенок
^2Ср + Лер 32-1-58,8
2-------------9-----=45,4 °C.
Средняя температура пограничного слоя нагреваемой воды
Лср + Л 32 4-45,4
tx = = 38,7 °C.
* По этой формуле можно определить конечную температуру греющего теплоноси-
теля в любой момент процесса нагрева.
94
Находим критерий
’ 3,9-10-4-9,81 -0,025s (45,4—32)
Grr— va /павд.1п-6\2 = 1,8-10°;
(0,659-10-6)2
далее по таблице физических констант для воды находим
Ргг = 4,3 и (GrPr)r= 1,8 • 10° • 4,3=7,75 • 10°.
Соответственно этому значению расчет ведем по формуле (3-10в)
Лг-0,54 (GrPr)°’25_ 0,634-0,54-(7,75-10°)°-25
“2 = </н 67625 =
= 720 Вт/(м2-°С) [620 ккал/(ч-м2-°C)]
или по приближенной формуле (3-lla): 4j = 146 по табл. 3-1 при /Г = 38,7°С и
а2 = Д (Д/2/</н)1/4 = 146-13,4°.25-0,025-0.25 = 715 Вт/(м2-°С).
Задавшись толщиной накипи йнак=0,0005 и ее теплопроводностью Хнак =
=2,32 Вт/(м-°С) [2 ккал/(ч • м • °C)], находим коэффициент теплопередачи по формуле
1 _ 1
k = _!_.+ 511ак + 1 - 1 , °-002 O.OOQ5, i
а, "ГХВ8К+аг 3500 ' 64 + 2,32 ’*’715
= 510 Вт/(м2 - °C) [438 ккал,/(ч •м2 - °C) ].
Проверяем принятую температуру стенки
k 510
4 = <2сР + — Д/ = 32+715 (58,8 — 32) = 51,5 °C >45,4 °C.
Из-за несоответствия полученного значения температуры стенки ранее принятому
делаем перерасчет. Задаемся +=51 °C и находим:
4ср + t'e
2
32 + 51
2
41,5 °C;
Д+=+—f2cp=51—32= 19 °C.
Отсюда
а'2 = Л', (ДГ2/</н)1/4 = 151 • 19о.25-0,025~о>25= 780 Вт/(м2-°С) [670 ккал/(ч-м2-°С)].
Коэффициент теплопередачи
# И 0,002 0,0005 Г = 550 Вт/(№- °C).
3 500 ‘ 64 + 2,32 +780
Тогда температура стенки
550
= 32 + тэд-26,8 = 50,8 °C
почти соответствует принятому значению.
Поверхность нагрева аппарата
F = kF'k=i 140/550 = 7,5 м2.
Определяем конструктивные размеры аппарата. Объем аппарата
V=G2/p= 10 000/995= 10,05 м3.
Задаемся диаметром аппарата 1,8 м и определяем его длину
L=4V/nP2=4-10,05/л1,82=3,93 м.
Принимаем £ = 4 м. Количество греющих трубок
4G, _ 4-4 000
П~ ти/^рш-ЗбОО 3,14-0,0212-984-0,4-3600 £
95
Принимаем 8 трубок. Тогда общая длина трубок
£Tp=f/ndcp=7,5/3,14 • 0,023= 10,5 м.
Длина трубки при числе ходов Z=8
l=LfZ= 10,5/8= 1,65 м (меньше диаметра аппарата).
Изменения производительности водонагревателя-аккумулятора и температур теп-
лоносителей во времени приведены в табл. 3-2.
Т а б л и ц а 3-2
Изменения производительности водонагревателя-аккумулятора и температур
теплоносителей во времени
Продолжительность работы т, ч
Наименование показателей
Момент
пуска
Температура нагреваемой воды
= -----, °C
exp[G,(l— е
Конечная температура греющей воды
= °C
е
Производительность (расход тепла)
Q = Gt (f> — 10"3, кДж/ч
21,3 29,5 38
31,7
178
41,3 46,1 51,1
134 115,9 88
57,4 58,2
71,4 54,5
Определение поверхности нагрева реакционного
аппарата. Реакционный аппарат с обогревом глухим1 паром отли-
чается от водонагревателя-аккумулятора в работе тем, что в первом
нужно нагревать не только воду или другую жидкость, в которой про-
исходит обработка материала, но и сам материал.
В расчете водонагревателей-аккумуляторов пренебрегают расходом
тепла на нагрев металлической конструкции самого аппарата и его
внешней изоляции, так как при небольших температурах нагреваемой
воды эти статьи расхода тепла незначительны. В реакционных же ап-
паратах обычно производится за короткое время разогрев до значи-
тельных температур большой по массе металлической конструкции
аппарата и его изоляции. Поэтому в расчете следует учитывать расход
тепла не только на нагрев обрабатываемого материала и жидкости, но
также и на нагрев металлической конструкции аппарата и его изо-
ляции.
Если допустить, что в любой момент времени подогрева аппарата
материал, жидкость, металлическая конструкция и изоляция аппарата
имеют одинаковую температуру, то это значительно упростит тепловой
расчет. И хотя расчет не будет соответствовать действительному про-
цессу, однако он дает относительно небольшую погрешность в сторону
увеличения надежности работы аппарата. Потери тепла аппаратом
в окружающую среду в этих случаях составляют незначительную вели-
чину и в тепловых расчетах их можно не учитывать.
Исходя из перечисленных допущений, расчет реакционного аппа-
рата сводится к следующему. Определяются общий вес аппарата
G = Gi + G2+Сз+ G4
1 Термин «глухим паром» показывает, что теплообмен происходит через теплопро-
водную стенку и пар не смешивается с нагреваемой жидкостью или материалом (в отли-
чие от обогрева острым паром).
96
и средняя удельная теплоемкость аппарата
с =
G,c, Gsc2 + G3cs ~р G4c4
G] + Gs + G3 -j- G4
где G\ — количество материала, загруженного в реакционный аппарат,
кг; G2 — количество жидкости в аппарате, кг; G3— масса (вес) метал-
лической конструкции аппарата, кг; G4 — масса (вес) изоляции, кг;
Ci, с2, Сз, Ci — теплоемкости сухого материала, жидкости, металличе-
ской конструкции и изоляции, кДж/(кг-°С) (ккал/(кг-°С)].
При определении расхода тепла и поверхности нагрева реакцион-
ного аппарата необходимо учитывать теплоту химических реакций. Для
определения теплопередающей поверхности
с обогревом глухим паром можно применять
формулу (3-3), заменяя G2c2 на Gc.
В расчете выносных подогревателей реак-
ционных аппаратов с водяным обогревом мо-
гут быть использованы формулы для водо-
нагревателя-аккумулятора с водяным обогре-
вом. Коэффициент теплопередачи определяет-
ся в зависимости от условий теплообмена.
Графики расхода тепла и пара
для реакционных аппаратов. Время
работы реакционного аппарата складывается
из периода разогрева и периода установивше-
гося режима, в течение которого обрабатывае-
мый материал, нагретый до определенной
температуры, выдерживается в аппарате. Так
как период разогрева бывает значительным
(до 3 ч и более), а емкость аппаратов велика
(до 100 м3 и более), то в начале пуска тре-
буется кратковременный, но очень большой
расход пара, убывающий затем по мере на-
гревания аппарата. После того как материал
достигнет требуемой температуры, пар рас-
ходуется только на покрытие потерь тепла
в окружающую среду. На рис. 3-5,а показан
типовой график расхода тепла для реакцион-
ных аппаратов. Он характерен большой раз-
ницей между максимальным расходом тепла
реакционного аппарата
Температура, °C
Рис. 3-5. Графики расхода
тепла и пара в реакцион-
ных аппаратах.
а — график расхода тепла на
реакционный аппарат; б — гра-
фик потребления пара при по-
следовательном включении в
работу реакционных аппаратов;
qi, <?2, <7з — количества тепла,
затрачиваемые на разогрев ма-
териала, жидкости и конструк-
ции самого агрегата; q$ — поте-
ри тепла в окружающую среду;
2# — суммарный расход тепла.
в начальный момент прогрева аппарата и минимальным расходом его
при установившемся режиме.
На практике избегают одновременного включения большого числа
реакционных аппаратов, так как внезапный рост расхода пара при
включении нескольких аппаратов в работу может вызвать резкое пони-
жение давления в системе паропроводов и в паровых котлах. Для обе-
спечения допустимых колебаний тепловой нагрузки генераторов пара
обычно разрабатывается график последовательного включения в рабо-
ту реакционных аппаратов. Пример суммарного графика потребления
тепла при последовательном включении в работу реакционных аппара-
тов показан на рис. 3-5,6.
3-2. РЕГЕНЕРАТИВНЫЕ АППАРАТЫ
Типы и схемы регенераторов. К числу регенераторов
относится большая группа теплообменных аппаратов, в которых пере-
дача тепла от одного теплоносителя к другому осуществляется посред-
ством неподвижной или перемещающейся насадки. В качестве насадки
7—1128 97
применяют огнеупорный кирпич, металлические листы, пластины, шары,
фольгу и т. п.
В металлургических и стеклоплавильных печах большое распрост-
ранение получили регенераторы с неподвижной насадкой из огнеупор-
ных кирпичей. Для создания в рабочем пространстве таких печей вы-
соких температур (до 2 500°С) требуется предварительный высокий по-
догрев воздуха и горючего газа (до 800—1000°С), который трудно осу-
ществить в металлических рекуператорах, из-за их недостаточной
жаростойкости.
В качестве примера рассмотрим схему работы регенераторов мар-
теновской печи, работающей на мазутном топливе (рис. 3-6,а). В пе-
риод времени, соответствующий положению перекидного шибера 1,
воздух подогревается до необходимой температуры в левой камере; при
этом насадка в ней охлаждается. В этот же период времени насадка
правой камеры нагревается отходящими продуктами сгорания. Через
некоторый промежуток времени перекидной шибер поворачивается, из-
меняет направление движения воздуха и горячих газов, и в следующий
период времени насадка левой камеры нагревается, а правой охлаж-
дается, нагревая воздух. Одновременно с переключением шибера га-
сятся форсунки с левой стороны печи и зажигаются форсунки справа.
В мартеновских печах, работающих на газе, подогревают не только
воздух, но и горючий газ, и поэтому устраивают по две камеры с на-
садкой с каждой стороны.
Типы кирпичных насадок весьма разнообразны, но наиболее рас-
пространены на практике насадки, в которых огнеупорные кирпичи
укладываются в виде сплошных каналов (рис. 3-6,6). Толщина кирпи-
чей, применяемых для регенеративных насадок, составляет 40—50 мм;
форма кирпичей может быть обычной и специальной (для регенерато-
ров Сименса, Каупера и др.).
Недостатками, регенераторов с неподвижной кирпичной насадкой?
является громоздкость, усложнение эксплуатации, связанное с необхо-
димостью периодических переключений регенераторов, и колебание
температуры в рабочем пространстве печи или теплоиспользующего
аппарата, вследствие изменения температуры насадки в процессе теп-
лообмена, поэтому они находят применение только при высоких темпе-
ратурах теплоносителей, не допускающих применения металлических
рекуператоров.
В качестве примера регенераторов с металлической насадкой на
рис. 3-6,в показан регенератор с неподвижной насадкой из алюминие-
вой гофрированной ленты, применяемый в холодильных установках для
глубокого охлаждения азота (до минус 18'5°C).
Достоинство металлической насадки по сравнению с кирпичной?
является большая поверхность теплообмена в небольшом объеме. На-
пример, в 1 м3 объема насадки можно разместить алюминиевую гоф-
рированную ленту с поверхностью теплообмена 2000 м2; при этом раз-
ность температур насадки и теплоносителя может почти по всей длине
насадки составлять только 1—2 °C, а коэффициент использования на-
садки (см. ниже) достигает 99%. Недостатком этого аппарата по срав-
нению с предыдущим является большое гидравлическое сопротивление.
На рис. 3-6,6 изображен регенератор системы Юнгстрема с вра-
щающейся металлической насадкой, получивший применение на элект-
ростанциях в качестве воздухоподогревателя для использования тепла
отходящих газов котельных агрегатов. Вращающаяся насадка аппарата
состоит из профильных металлических листов, которые, двигаясь по
кругу, пересекают поочередно каналы с горячими газами, где они на-
греваются, и (передают тепло воздуху. Скорость вращения ротора
с насадкой невелика и обычно не превышает 3—6 об/мин.
98
Рис. 3-6. Некоторые типы регенераторов.
а — схема мартеновской печи с регенераторами; б
металлической насадкой; г — элемент металлической
регенеративный подогреватель — вентилятор-дымосос;
5 — ротор из пустотелых ребристых лопаток.
- регенеративная насадка из огнеупорного кирпича; в — регенератор с неподвижной
насадки; д — регенеративный аппарат системы Юнгстрема; е — комбинированный
/ - перекидной шибер; 2 — форсунки; 5 —иасадка; 4 — вращающаяся насадка;
Схема теплообменника
Рис. .3-7.
с движущимся твердым промежуточ-
ным теплоносителем.
1 и 2 — камеры охлаждаемого и нагревае-
мого газов; 3 — вращающийся диск, регу-
лирующий подачу твердых частиц; 4 —
электродвигатель; 5 — ковшовый элеватор;
6 и 7 — коллекторы охлажденного и нагре-
того газа; 8— окна коллектора.
Достоинством регенератора Юнгстрема перед регенераторами с не-
подвижной насадкой является практически постоянная средняя темпе-
ратура воздуха на выходе из аппарата, зависящая только от темпера-
туры поступающих в аппарат горячих газов.
По сравнению с рекуперативными воздушными подогревателями
достоинством воздухоподогревателя Юнгстрема является его компакт-
ность, недостатком — сложность конструкции и загрязнение воздуха га-
зами, протекающими через разделительные перегородки.
На рис. 3-6,е показан комбинированный агрегат вентилятор-ды-
мосос с вращающейся поверхностью нагрева в виде ротора, выполнен-
ного из полых герметичных оребренных лопаток, наполовину заполнен-
ных водой. Агрегат разделен по высоте на две части. Через нижнюю
часть агрегата проходят дымовые газы и выпаривают воду, находя-
щуюся в нижней части оребренных лопаток. Через верхнюю часть агре-
гата проходит холодный воздух и нагревается от стенок верхней части
лопаток, заполненных паром; при этом пар в них конденсируется и сте-
кает обратно в нижнюю часть лопаток.
Следует заметить, что комбинированные агрегаты с вращающейся
поверхностью нагрева имеют пока более низкий к. п. д., чем обычные
вентиляторы и дымососы, и поэтому широкого применения не полу-
чили.
В настоящее время в нефтехимической, нефтеперерабатывающей и
других отраслях промышленности, а также в энергетических установках
с высокотемпературными процессами,
когда высоколегированные стали не-
достаточно стойки, получили примене-
ние теплообменники с неподвижным,
кипящим или падающим слоем твер-
дого жаростойкого промежуточного
теплоносителя. В этих теплообменни-
ках перегревают водяной пар, нагре-
вают воздух, газы и пары органиче-
ских жидкостей до температур 1 600—
2 000 °C.
В качестве промежуточных тепло-
носителей применяют твердые частицы
и шарики из каолина, муллита, окиси
алюминия, магния, циркония и т. п.
размером 8—12 м. Материал такого
теплоносителя должен быть жаростой-
ким (не размягчаться и не плавиться
при высокой температуре), обладать
химической стойкостью (не окислять-
ся), не трескаться и не расслаиваться
при резких изменениях температуры,
не истираться и выдерживать ударную
нагрузку, обладать высокой теплоем-
костью, чтобы иметь меньшее весовое
количество при большой тепловой на-
грузке и низкую стоимость.
На практике применяются
обменники с промежуточными
носителями периодического и
рывного действия.
В установках периодического дей-
ствия неподвижный или кипящий слой
твердого промежуточного теплоноси-
тепло-
тепло-
непре-
теля периодически продувается горячими газами и нагреваемым тепло-
носителем. Принцип работы их ничем не отличается от принципа рабо-
ты рассмотренных выше регенераторов промышленных печей.
В установках непрерывного действия твердый теплоноситель все
время перемещается при помощи механических ковшовых элеваторов,
виброподъемников или пневматических устройств. Принципиальная схе-
ма теплообменника с ковшовым элеватором, предложенного А. Д. Али-
фановым и П. Д. Лебедевым, показана на рис. 3-7. В этом теплооб-
меннике загрузочные и разгрузочные штуцера, через которые подаются
и отводятся шарики, должны быть всегда заполнены ими и служить
как бы гидравлическим затвором, исключающим перетекание газа из
камеры охлаждения в камеру нагрева и наоборот.
Поверхность нагрева регенератора Поверхность нагрева регенератора
Рис. 3-8. Изменения температур газов, воздуха и насадки.
а — в идеальном регенераторе; б — в действительном регенераторе.
При проектировании установок с движущимся твердым теплоноси-
телем высокие требования предъявляются к герметизации охлаждае-
мого и нагреваемого газов, а также возникают большие конструктив-
ные трудности, обусловленные высокой температурой частиц и необхо-
димостью регулирования их расхода. Эксплуатация таких установок
усложняется истиранием частиц и быстрым абразивным износом всех
трактов их движения. При пневматической транспортировке частиц осо-
бенно быстро разрушаются трубы из обычной стали и внутренние стен-
ки аппарата, даже облицованные карборундом.
Для улавливания уноса мелких частиц из теплообменника после
выходных патрубков необходима установка обеспыливающего устрой-
ства.
Рассмотренные регенераторы далеко не охватывают разнообразие
существующих типов и конструкций таких аппаратов.
Теплообмен в регенераторах. В регенераторе поверх-
ность насадки попеременно воспринимает и отдает тепло. В течение пе-
риода нагревания или охлаждения изменяются температуры насадки
как по толщине, так и по пути следования, причем после реверсиро-
вания регенератора или соответствующего перемещения подвижной
насадки направление теплового потока в насадке изменяет знак.
Строгое физико-математическое описание и решение задачи не
стационарных процессов теплообмена в регенеративных аппаратах
представляют большие трудности и точных методов расчета регенера-
торов пока не существует. Поэтому здесь эти процессы рассматрива-
ются с упрощающими условиями.
На рис. 3-8,а изображен график изменений усредненных по време-
ни температур поверхности насадки и теплоносителей с одинаковыми
полными теплоемкостями в так называемом идеальном регенераторе,
101
г
4 Перевод клапанд
5 t
Время охлаждения
Время наепеВа
Рис. 3-9. Изменение в течение
цикла локальных температур
поверхности насадки, газов и
воздуха над точкой А поверх-
ности насадки (см. рис. 3-8,6).
Перевод
клапана
в котором Средняя температура насадки за периоды нагревания и ох-
лаждения принимается одинаковой. В этом случае график изменения
средних температур теплоносителей в регенераторе ничем не отлича-
ется от графика изменений температур в рекуператоре.
На рис. 3-8,6 показаны изменения температур газов, воздуха и
насадки в действительном регенераторе по пути следования теплоноси-
телей при условии равенства их водяных эквивалентов. Температура
газов в начале периода нагревания насадки изображается кривой 3,
в конце периода — кривой 1 и средняя за
период нагревания — кривой 2. Темпера-
тура поверхности насадки в конце периода
нагревания и начале периода охлаждения
представляется кривой 4, в начале периода
нагревания и конце периода охлаждения —
кривой 7, средняя за период нагревания —
кривой 5, средняя за период охлаждения—
кривой 6. Температура воздуха в начале пе-
риода охлаждения насадки изображается
кривой 8, в конце периода — кривой 10 и
средняя за период охлаждения — кривой 9.
В рассмотренном графике в зонах на-
чала и конца пути по регенератору не пока-
зано крутое искривление линий, изображаю-
щих температуру насадки (петли гистере-
зиса), возникающее вследствие того, что на-
чальные температуры теплоносителей оста-
ются постоянными. Это явление особенно
заметно в регенераторах с металлической
насадкой небольшой высоты. В действитель-
ных условиях полные теплоемкости тепло-
носителей могут быть различными, что вы-
зывает криволинейность графика измене-
ния температур теплоносителей по длине
насадки. Кроме того, в действительных
условиях температура в любой точке поверхности насадки за период
нагревания изменяется по выпуклой кривой, а за период охлаждения —
по вогнутой, вследствие чего средняя температура насадки за период
нагревания выше, чем за период охлаждения ее. Криволинейно изме-
няются и температуры теплоносителей (рис. 3-9) у рассматриваемой
точки А поверхности насадки на рис. 3-8,6.
В периоды нагрева и охлаждения насадки температура внутрен-
них слоев ее из-за конечной небольшой температуропроводности мате-
риала изменяется меньше, чем на поверхности. Это запаздывание
проявляется в тем большей степени, чем больше толщина материала и
ниже коэффициент температуропроводности. Поэтому в кирпичной на-
садке оно проявляется сильнее, чем в металлической.
Изменение температуры половины толщины элемента насадки во
времени при нагреве и охлаждении показано на рис. 3-10. К началу
периода охлаждения насадки температура поверхности элемента выше,
чем в середине его. Проходящий воздух быстро снижает температуру
поверхностных слоев элемента, и температура кирпича на некоторой
глубине его оказывается более высокой, чем в середине и на поверх-
ности, т. е. отдача тепла в этот момент в разных сечениях элемента
идет в разных направлениях (стрелка а и б). Через некоторое время
температура в середине элемента оказывается более высокой, чем в
других сечениях, и тепловой поток направляется от середины кирпича
наружу.
102
Изменение температуры внутри насадки в период ее прогрева или
охлаждения определяется уравнением теплопроводности
при краевых условиях
т=0 и —Rs^Zx^Z ~i~R, i—to', (3-13а)
т>0 и x = ±R, ±2 (— (3-136)
\ (/X J
которые могут сводиться к критериальной зависимости
tс f г~' n • X \ г ( ОЯ X \ /о 1 л \
6 = -^ = f Т’ ТГ)’ (ЗЛ4)
где а—коэффициент температуропроводности для насадки; К-—коэф-
фициент теплопроводности для насадки; t — температура пластины на
расстоянии х от средней плоскости в момент времени т, считая от на-
чала охлаждения (нагревания); t0 — на-
чальная температура пластины; tr— тем-
пература газа; R — половина толщины
пластины; а — коэффициент теплоотдачи
к насадке.
В учебных пособиях по теплопереда-
че [Л. 11 и 50, т. 1]' даны графики 0 =
=f(Fo, Bi), позволяющие определять
значение температур внутри насадки на
различных расстояниях от ее поверхно-
сти и в различные периоды процесса.
Отношение количества тепла, вос-
принятого элементом насадки, к теплу,
которое могло бы быть им аккумулиро-
вано, если бы температура всей массы
элемента была одинаковой, называется
коэффициентом аккумуляции или исполь-
зования тепла насадкой. В действующих
кирпичных регенераторах этот коэффи-
циент равен т]а=0,5-=-0,7; для металличе-
ских насадок он близок к единице. Тео-
Рис. 3-10. Изменение температуры
по толщине элемента насадки
(кирпича) во времени.
ретические исследования, произведенные
Гребером, показывают, что т]а зависит от
критерия Фурье
Fo = czti//?2,
где a=!klcp — коэффициент температуропроводности
м2/с; Т1 — период нагревания, ч, сек; R—половина
(при двустороннем прогреве), м.
В табл. 3-3 приводится зависимость т]а от Fo.
для насадки, м2/ч,
толщины кирпича
Таблица 3-3
Значения коэффициента аккумуляции тепла т)а в зависимости от критерия Fo
Fo = -jT 0,2 0.4 0.6 0,8 1.0 1.5 2,0 3,0 4,0 5,0
Коэффициент т;а 0,18 0,25 0,31 0,37 0,42 0,54 0,64 0,78 0,86 0,9
103
Тепловой расчет регенераторов. Задачей теплового
расчета регенератора является определение поверхности нагрева и ве-
са насадки.
Тепло, воспринимаемое поверхностью насадки регенератора за пе-
риод нагрева, равняется:
Q — a, (/1Ср — /" ) /\, кДж/период,
где си — коэффициент теплоотдачи от греющих газов (конвекцией и лу-
чеиспусканием) к насадке, кДж/(м2-ч-°C); /1ср и tHK — средние тем-
пературы греющего газа и поверхности насадки за период нагрева-
ния, °C; Ti —период нагрева, ч.
Это количество тепла Q воспринимается насадкой и повышает
температуру ее поверхности на величину Д/н, т. е.
Q=T’(6/2)pcpaA/H, кДж/период,
где 6 — толщина стенки кирпича (вследствие обогрева насадки с двух
сторон в данной форме учитывается половина толщины стенки, обозна-
чаемая через R), м; р —плотность насадки, кг/м3; с — теплоемкость на-
садки, кДж/(кг-°C); Д/н — изменение температуры поверхности насад-
ки за период нагрева, °C; т]а— коэффициент аккумуляции тепла, опре-
деляемый по табл. 3-3.
Для определения изменения температуры поверхности насадки
пользуются следующей эмпирической зависимостью;
м^<-/°н),
где /°—средняя температура поверхности насадки ва период ее охла-
ждения (рис. 3-9); ф — коэффициент, равный 2,2—3,5.
В период охлаждения тепло, аккумулированное насадкой, пере-
дается нагреваемому воздуху;
Q — а2 (Л — /2ср) кДж/период,
где аг — коэффициент теплоотдачи от поверхности насадки к нагревае-
мому воздуху, кДж,/(м2-ч-°C); /2ср— средняя температура воздуха за
период охлаждения, °C; т2— период охлаждения, ч.
Таким образом, получается система следующих трех уравнений:
f. Q 1 .
Чср <-н — F ал >
pi fO __ Q___1 .
н н д Rpc^tf ’
/о / Q 1
н 12CP— p ал '
Сложив левые и правые части этих уравнений, получим;
/ _ # „ Q 1 I 1 л 1 А
юр 2СР р а]Т1 г ^pC7Ja(f । а2т2 J
ИЛИ
0ц=ЛцД(|/1ср—/гср) =^цДА/, кДж/цпкл. (3-15)
В этом уравнении Лц — коэффициент теплопередачи регенератора:
/гц = —j-----4------j—, кДж/ (м2 • цикл °C). (3-16)
«Л ЛрсЧа? “г’а
104
к---- я0,33’
“э
Для более точного расчета вместо среднеарифметических разно-
стей температур /1ср и /г ср можно принимать среднелогарифмическую
разность температур между газом и воздухом.
Тепло от горячих газов (продуктов сгорания) передается насадке
лучеиспусканием и конвекцией. Количество отданного продуктами сго-
рания тепла за одинаковый период времени для одной и той же насад-
ки тем больше, чем выше начальная температура продуктов сгорания,
больше их скорость и содержание в них СО2 и Н2О. В период охлаж-
дения тепло от насадки передается воздуху только конвекцией, так как
воздух является средой лучепрозрачной.
Коэффициенты конвективного теплообмена насадки и горячих га-
зов или воздуха определяются по экспериментальным данным.
Например, для насадки Сименса (рис. 3-6,6)
(3-17)
где К — коэффициент, равный 8,3 при смещенном расположении рядов
и 7,5 при несмещенном расположении их; w0 — скорость при нормаль-
ных условиях для газа в минимальном проходном сечении (плоскость
стыка рядов), обычно wp=0,2 4-0,4 м/с; d3—эквивалентный диаметр
ячейки в плоскости стыка рядов, м.
Величину коэффициента теплообмена лучеиспусканием можно опре-
делить по следующим эмпирическим формулам:
алСОа =0,95 jZpS? [0,0513 (ficp + ) —30,25], Вт/(ма-°С); (3-18)
«лН1о = 0,95p°-8S°’6 [0,107 (ficp +t" ) -46,5], Вт/(м2-°С), (3-19)
где ^1Ср Д'—средние температуры газов и стенки насадки в период
нагрева, °C; р — парциальное давление лучеиспускающего газа в долях
от 105 Па; S3 — эффективная толщина излучающего слоя, м (выбира-
ется по экспериментальным формулам [Л. 11]), м.
Парциальное давление излучающего слоя можно подсчитать по
формулам
2ЕГП Г'., п
Рсо, = г"г + \/"т' Рн2о = у"г ’
где УСОа — объем углекислоты, м3/м3 или м3/кг; VH20 — объем водяных
паров, м3/м3 или м3/кг; V'r и V"r — объемы дымовых газов в начале и
конце периода нагревания, м3/м3 или м3/кг.
Коэффициенты теплопередачи определяют отдельно для горячего
и холодного концов регенератора и при расчете поверхности насадки
пользуются средним арифметическим значением их.
Для кирпичных регенераторов коэффициент теплопередачи
k1}= 18,8 = 31,4 кДж/(м2-цикл*ОС) [4,5—7,5 ккал/(м2-цикл-°C)].
3-3. АППАРАТЫ С КИПЯЩИМ СЛОЕМ
В последние годы для интенсификации нагрева, обжига, горения,
сушки, катализа, адсорбции и некоторых других процессов широкое
применение получили установки с так называемым кипящим слоем.
Перспективными являются регенераторы, котлы-утилизаторы и тепло-
обменники с кипящим слоем.
105
Принцип образования кипящего слоя состоит в следующем. Если
к зернистому материалу, расположенному на решетке, подводить снизу
воздух или газ, постепенно увеличивая его скорость w (рис. 3-11), то
высота слоя материала Н начинает постепенно увеличиваться, как бы
набухать или вспучиваться. При некоторой скорости в слое начи-
нают возникать отдельные фонтаны «кипения» материала, большая же
часть зерен в слое остается почти неподвижной. В этот момент напор
газа достигает максимального значения ДрКр и соответствует весу ма-
териала плюс некоторому перепаду, необходимому для затраты энергии
на отрыв частиц друг от друга {Л. 22, 40 и 49].
Это состояние описывается следующим уравнением:
ДРкр = -J-+ Д₽' = (Р — Рс)(1 — е) + Др' HQg (р — рс)(1 — е0) -ф- Др',
(3-20)
где Дркр — критический перепад
твердых частиц в кипящем слое,
Рис. 3-11. Границы формирования
кипящего слоя.
Др — сопротивление слоя; Юф — скорость
газа в слое (скорость фильтрации); Н —
высота слоя.
давлений в кипящем слое, Па; G — вес
Н; g=9,81 м/с2 — ускорение силы тя-
жести; F — площадь решетки; Н и
Но — высота кипящего и неподвиж-
ного слоев, м; рм и рс — плотности
частиц и среды, удерживающей ки-
пящий слой, кг/м3; е и ео — средние
порозностп кипящего и неподвижно-
го слоев, представляющие собой
отношения величин объемов пустот
и слоя; \р' — перепад давлений, не-
обходимый для отрыва частиц друг
от друга, Па.
С последующим увеличением
скорости газа под решеткой сопро-
тивление слоя Дркр несколько умень-
шается, а скорость воздуха в слое
(скорость фильтрации) Шф увеличи-
вается. При дальнейшем увеличении
скорости газа, подводимого к ре-
шетке, увеличивается высота слоя
Н. Увеличение слоя обеспечивает
стабилизацию проходного сечения
для газа и вследствие этого стабилизируются сопротивление слоя Др
и скорость фильтрации w$, (участок CD).
Повышение скорости газа, подводимого к решетке, ш>и/КИп спо-
собствует возникновению новых очагов кипения. Интенсивность движе-
ния частиц в слое возрастает, кипение выравнивается и устанавлива-
ется цикличное движение частиц в слое. Скорость газов, соответствую-
щую хорошему перемешиванию слоя и незначительному выносу мелких
частиц, обозначают и/'кип-
Скорость набегающего на решетку потока ьукип, соответствующую
началу кипения при бесперебойной засыпке слоя шарообразными моно-
дисперсными частицами средней порозностп е=0,4, можно определить
по формуле Тодеса
R^ кнп
________Аг______
v — 1 400+ 5,22 КАТ ’
(3-21)
Критерий Архимеда
дг —(Рм—Pc)g
vcPc
106
где d — средний расчетный диаметр частичек, м; vc— кинематическая
вязкость среды, м2/с.
Теплообменники и сушилки с кипящим слоем должны работать при
оптимальном значении скорости набегающего потока, которому соот-
ветствует равномерное кипение и перемешивание частичек по всему
объему, а также максимальный коэффициент теплоотдачи. Имеются
формулы для расчета этой скорости. Обычно ее значение в 2—3 раза
больше скорости начала псевдоожижения
Ы'оит ~ (2 "Ъ 3) Ю/кип-
Следует заметить, что если увеличивать скорость газа, подводимо-
го к решетке, выше значения w"wni, то при скорости этих частиц
Ily/"ram=wBIIT начинается их бурный вынос и слой уносится с решетки.
Если создать кипящий слой в вертикальных трубах диаметром
75—100 мм, то при скорости набегающего потока газа на решетку,
Рис. 3-13. Влияние скорости
газа на коэффициент теплоот-
дачи от кипящею слоя зерни-
стого материала к змеевику.
аб — теплоотдача неподвижного
(фильтрующегося) слоя к змеевику;
бв — теплоотдача кипящего слоя
в пределах от се’кр до оптимальной
скорости w 0 п т; вд — теплоотдача
кипящего слоя от oionT ДО скоро-
сти уноса wVH. Линия гд соответ-
ствует теплоотдаче чистого воздуха
(без твердых частиц).
заключающееся в том, что
Рис. 3-12. Изменение структуры кипящего слоя
в трубе с увеличением скорости набегающего по-
тока газа на решетку.
а — неподвижный слой; б — кипящий слой в начальной
фазе; в — пузырчатое кипение слоя: г — поршневое ки-
пение слои.
большей шКр, произойдет прорыв через
кипящий слой крупных пузырей газа
(рис. 3-12,в) и начнется интенсивное вы-
брасывание частиц над поверхностью
слоя. Пузыри могут увеличиваться в
объеме, и таким образом может запол-
ниться все сечение трубы. Начинается
так называемое поршневое кипение слоя,
слой разделяется крупными пузырями и происходит расслоение мате-
риала (рис. 3-12,г).
Явления поршневого кипения наблюдаются в трубах небольшого
диаметра. В установках с большой площадью решетки при вихревом
кипении наблюдаются вертикальное каналообразование в слое и про-
скоки газа, которые увеличиваются с повышением его скорости. Такой
процесс значительно ухудшает тепло- и массообмен слоя с газом.
Для улучшения работы установок с кипящим слоем, имеющих
большой диаметр аппарата, применяют специальные конструкции ре-
шеток и мешалки (специальные устройства для перемешивания слоя),
устраняющие каналообразование при интенсивном кипении.
В теплообменных аппаратах коэффициент теплоотдачи между ки-
пящим слоем и поверхностью теплообмена увеличивается с повыше-
нием скорости движения частиц в фильтрующем газовом потоке до
определенного максимального значения, которому соответствует также
значение оптимальной скорости потока газа, набегающего на решетку
107
(рис. 3-13). При дальнейшем повышении скорости газа увеличивается
порозность слоя и уменьшается объемная концентрация частиц и ко-
эффициент теплоотдачи уменьшается. Для расчета максимального зна-
чения коэффициента теплоотдачи приводятся следующие формулы
[Л. 48].
При ламинарном режиме движения слоя в пределах от wKp до wonT
NuMaKC = 0,0087 Ar°'42Pr°>33(см/сс)0,45• (D/d)°-i6(H0/d)^ (3-22)
При турбулентном режиме в пределах от wKP до щ0Пт
NuMaKc=0,019Ar0-5Pr0"33(cM/Cc)0’1- (D/d)<№(H0/dy>& (3-23)
Формула (3-22) справедлива для
15< Ar< 103; 0,8ссм/сс<1,3;
129<D/d<575; 263<Яо/4<945.
Формула (3-23) справедлива при
2,6- 104<Ar<^8,5-105; 0,8<cM/cc< 1,2;
14<£>/d<67; 17<7/0/d< 120.
Уравнение для определения оптимальной скорости газа, соответст-
вующей максимальному значению коэффициента теплоотдачи, для
частиц неправильной формы с шероховатостью для ламинарной об-
ласти
ReonT=0,2 Аг0-5; (3-24)
для турбулентной области
РеОПт=0,66 Аг0-5. (3-25)
В этих формулах
Аг—d3pIiacg/v2pc; NUmskc = Имакс^/7<с; Pr = vpcCc/Xc; RCoiit ” ^опт^/л?;
см, сс — теплоемкость материала и газа, кДж/(кг-°C); рс, риас — плот-
ность газа и насыпная плотность материала, кг/м3; &с— коэффициент
теплопроводности газа, Вт/(м-°С); v — кинематический коэффициент
вязкости газа, м2/с; аМакс — максимальный коэффициент теплоотдачи
стенки, Вт/(м2-°С); а — коэффициент теплоотдачи стенки (поверхно-
сти), Вт/(м2-°С); Но — высота неподвижного слоя, м; d — средний
эквивалентный диаметр частиц, м; w — скорость газа, рассчитанная по
полному сечению аппарата, м/с; шОпт— оптимальная скорость газа
(при Омаке), рассчитанная по полному сечению аппарата, м/с; D — диа-
метр аппарата, м.
Если технологическим процессом не ограничена скорость газового
потока, то ориентировочно можно принять:
О — 0,8 Омаке-
С. С. Забродский |[Л. 7] предложил следующую формулу для опре-
деления коэффициента теплоотдачи от стенки к кипящему зернистому
слою
«макс = 35,7р°’2с;5С6 d-^e, Вт/(м2• °C), (3-26)
где ZK.c — коэффициент теплопроводности кипящего слоя, Вт/(м-°С).
Коэффициент теплопередачи в теплообменниках с кипящим слоем
получается более высоким, чем в обычных газовых рекуперативных
трубчатых теплообменниках. Его значение возрастает, если кипящий
слой имеет высокую температуру и, кроме конвекции, тепло передается
радиацией.
108
Коэффициент теплоотдачи между поверхностью и кипящим слоем
в общем виде может быть представлен уравнением
С1 = (ХкоВД Иконв + <Хлуч//>, (3-27)
где fo= 1—р/рсв-
Значение аКонд— коэффициента кондуктивной теплоотдачи невели-
ко и его можно не учитывать; алуч также мало при низких температу-
рах. Однако его влияние увеличивается с повышением температуры ки-
пящего слоя и диаметра частичек. Например, в кипящем слое при 900 °C
о..пуч составляет 5% от аМакс для частиц 100 мк (при w = 0,l м/с) и 7%
для 400 мк (при w = 0,4 м/с). С увеличением температуры до 1 500°C
доля лучистого теплообмена возрастает до 15—25%.
Подробнее о теплообмене между зернистым материалом и стенкой
и пучками вертикальных труб — см. [Л. 7, 28, 34, 40].
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие преимущества и недостатки имеют водонагреватели-аккумуляторы
в сравнении с трубчатыми теплообменниками непрерывного действия?
2. Как изменяются во времени теплопроизводительность и расход тепла для во-
донагревателя-аккумулятора?
3. В каком случае выше коэффициент теплопередачи водонагревателя-аккумуля-
тора: при паровом или водяном обогреве греющей поверхности?
4. Какая разность температур больше при нагреве воды в пароводяном водона-
гревателе-аккумуляторе: средняя арифметическая или средняя логарифмическая?
5. Какой обогрев вязких жидкостей в реакционных аппаратах следует предпо-
честь: при помощи змеевика или паровой рубашки?
6, Какое назначение имеют мешалки, устанавливаемые в реакционных аппара-
тах?
7. С какой целью в реакционных аппаратах применяют выносные теплообмен-
ники?
8. Каким паром, острым или глухим, можно быстрее нагреть материал, обрабаты-
ваемый в реакционном аппарате?
9. Какие недостатки имеет обогрев острым паром?
10. Как следует пускать в работу реакционные аппараты, чтобы не вызвать пе-
регрузки котельной установки?
11. Какие преимущества и недостатки имеют регенеративные аппараты по сравне-
нию с рекуперативными?
12. Применяются ли регенеративные аппараты с насадками для теплообмена при
низких температурах?
13. Существуют ли регенеративные аппараты с подвижной насадкой?
14. Могут ли металлические насадки применяться при температурах выше
700—800 °C?
15. Какие насадки обладают большим значением коэффициента аккумуляции теп-
ла: керамические или металлические?
16. От какого критерия зависит коэффициент аккумуляции тепла насадки?
17. Каким параметром отличается критерий Nu от критерия Bi?
18. Где будет больше температура керамической насадки в конце периода охлаж-
дения: в центре или на поверхности?
19. Когда выше средняя температура поверхности насадки в течение цикла:
в период нагревания или в период охлаждения?
20 В каком случае следует учитывать лучистый теплообмен: при передаче тепла
от горячих газов к насадке или при передаче его от насадки к нагреваемому воз-
духу?
21. Какие преимущества и недостатки имеют теплообменные аппараты с кипя-
щим слоем по сравнению с кожухотрубчатыми теплообменниками?
22. Объясните физическую сущность образования кипящего слоя. Как происхо-
дят изменение давления, скорости фильтрации газа и высоты материала с повышением
скорости газа, подаваемого под решетку аппарата?
23. Какие режимы кипения слоя наблюдаются в трубках? Может ли в аппарате
с большим диаметром происходить поршневое кипение?
24. Как изменяется температура газа, уходящего из слоя при появлении пузыр-
чатого кипения?
25. Почему после начала кипения наступает стабилизация давления газа и ско-
рости фильтрации в слое? При какой скорости начинается бурный вынос всего кипя-
щего моя?
109
ГЛАВА ЧЕТВЕРТАЯ
ВЫПАРНЫЕ УСТАНОВКИ
4-1. ОБЩИЕ ПОНЯТИЯ О ПРОЦЕССЕ ВЫПАРИВАНИЯ
ВОДНЫХ РАСТВОРОВ
Выпаривание представляет собой термический процесс кипения
раствора с выделением паров растворителей в практически чистом виде
(если не считаться с уносом жидкости); при этом растворимое нелету-
чее 1 вещество (твердое тело, например соль, или вязкая жидкость, на-
пример вазелин) остается в концентрированном виде в аппарате. По-
лучаемые при выпаривании пары удаляются в атмосферу или в кон-
денсирующее устройство.
Превращаться в пар растворитель может при кипении жидкости
или при поверхностном испарении ее. В выпарных аппаратах применя-
ется более интенсивный из этих способов превращения растворителя
в пар, а именно кипение. Впервые выпаривание получило промышлен-
ное применение в производстве сахара, а в дальнейшем — в химической
промышленности. При концентрировании растворов вода иногда уда-
ляется до 90% первоначального веса.
В технологических процессах в различных отраслях промышленно-
сти выпариваются преимущественно водные растворы различных не-
летучих веществ, поэтому весь последующий материал изложен при-
менительно к водным растворам. В элементарном виде процесс выпа-
ривания можно осуществить в простом открытом или закрытом сосуде,
наполненном раствором, при подводе к нему тепла для кипения и от-
воде образующихся паров в атмосферу или в конденсирующее устрой-
ство.
Выпарные аппараты по принципу работы и конструктивному
оформлению имеют много общего с испарителями, применяющимися на
электрических станциях. Однако процесс выпарки водных растворов
в выпарных аппаратах имеет принципиальное отличие от процесса ки-
пения чистой воды в испарителях.
Предположим, что имеются два открытых сосуда, обогреваемых
паром через паровые рубашки. В первом сосуде находится чистая
вода, а во втором — 70%-ный водный раствор аммиачной селитры
NH4NO3. Пусть давление греющего пара составляет 3,92 • 105 Па
(4 кгс/см2). Вода закипит при температуре около 100 °C; раствор при
том же атмосферном давлении закипит только при температуре 120 °C.
Однако образующиеся из этого раствора водяные пары будут иметь
температуру ту же, что и в случае кипения чистой воды, т. е. около
100 °C* *.
Понижение температуры образующихся из раствора водяных паров
по сравнению с температурой кипения раствора называют физико-хи-
мической температурной депрессией. Обозначив ее через Ai, можем на-
писать:
Ai=tp—
где tp — температура кипения раствора, °C; О — температура образую-
щихся паров воды, °C.
Физико-химическая температурная депрессия различна для разных
растворов. Она больше у растворов веществ с малым молекулярным
1 В действительности абсолютно нелетучих веществ не существует и в парах рас-
творителя может быть незначительное количество (следы) растворимого вещества,
которое в расчетах выпарных установок не учитывают.
* В действительности образуются перегретые водяные пары, содержащие некото-
вое количество уносимой влаги, испарение которой приводит к понижению их темпера-
туры до температуры насыщения.
ПО
весом. Для раствора одного и того же вещества физико-химическая
температурная депрессия увеличивается с повышением его концентра-
ции.
Под концентрацией раствора понимают отношение массы сухого
вещества в растворе к общей массе раствора в процентах 1 *
w ч исух
где b — массовая концентрация раствора, %; № — количество раство-
рителя или воды в растворе, кг; Gcyx — количество растворенного или
сухого вещества в растворе, кг.
Т а б л и ц а 4-1
Величины К в формуле (4-1а)
t, °C К t, "С К /, ”С К t, °C к t, °C К
35 0,6370 55 0,7364 75 0,8643 95 0,9677 135 1,2525
40 0,6609 60 0,7628 80 0,8755 100 1,00 115 1,1025
45 0,6854 65 0,7899 85 0,9057 105 1,0333 120 1,1384
50 0,7106 70 0,8177 90 0,9362 НО 1,0674 125 I,1757
130 1,2135
При выпарке вес сухого вещества в растворе остается постоянным,
а количество растворителя (воды) уменьшается; следовательно, при
этом концентрация раствора увеличивается.
Физико-химическая температурная депрессия для различных рас-
творов может быть определена по справочникам. Справочные данные
обычно относятся к условиям кипения жидкости при атмосферном дав-
лении. На практике выпаривание часто ведут и под вакуумом, и под
давлением. В таких случаях расчетная физико-химическая температур-
ная депрессия может быть вычислена по следующей приближенной
формуле И. А. Тищенко
Д1== 0,01362 ^Д\, (4-1)
где Д1 — искомая физико-химическая температурная депрессия при дав-
лении выпаривания; ДТ — депрессия, взятая из таблиц, при давлении
1,015-105 Па (760 мм рт. ст.); Т — температура кипения чистого рас-
творителя, К; г — скрытая теплота парообразования для воды при дав-
лении выпаривания, кДж/кг.
Если в формуле (4-1) ве-
личину 0,01362 Tz/r заменить
величиной К, то она примет
вид:
Д1=Д'1К. (4-1а)
Величина К—функция Т и
г и, следовательно, зависит от
давления и температуры кипе-
ния чистой воды. В табл. 4-1
даны значения К в зависимо-
сти от температуры кипения
чистой воды.
Концентрация раствора, °/о
Рис. 4-1. Изменение физико-химической темпе-
ратурной депрессии раствора при атмосферном
давлении в зависимости от его концентрации,
меняющейся в процессе кипения.
Значения депрессии A'i для
некоторых наиболее часто
встречающихся растворов в за-
висимости от их концентраций
даны на рис. 4-1.
1 Иногда под концентрацией раствора понимают процентное содержание раство-
ренного вещества в растворителе.
111
Наличие физико-химической температурной депрессии понижает
полезную разность температур между первичным и вторичным паром
в выпарном аппарате. Например, для рассмотренного случая кипения
в открытом сосуде полезная разность температур для чистой воды
д/=,/н_#= 143,6—100=43,6 °C,
где /н= 143,6 °C — температура конденсирующегося греющего пара;
«100 °C— температура кипящей воды, равная температуре вторичного
Рис. 4-2. Изменение плотности раствора
в зависимости от его концентрации.
Рис. 4-3. Изменение относительной вяз-
кости раствора в зависимости от его кон-
центрации.
пара.
Для кипящего раствора ам-
миачной селитры
д/=4—/р= 143,6—120=23,6 °C.
Если в условиях рассматри-
ваемого примера приняты одина-
ковые коэффициенты теплопере-
дачи при кипении чистой воды и
раствора, то для одинаковой
теплопроизводительности Q,
кДж/ч, выпарной аппарат дол-
жен иметь почти вдвое большую
поверхность, чем испаритель или
паропреобразователь (см. рис.
1-8). Действительное увеличение
поверхности нагрева выпарного
аппарата будет еще больше, так
как при выпаривании растворов
по сравнению с кипением чистой
воды не только уменьшается по-
лезная разность температур, но
и в значительной степени сни-
жается коэффициент теплопере-
дачи.
Процесс выпарки характерен
не только наличием физико-хими-
ческой температурной депресии,
но и значительным изменением
физических констант раствора,
связанных с изменением его кон-
центрации. С повышением концентрации раствора увеличиваются его
вязкость, плотность и температурная депрессия и понижаются теплоем-
кость и теплопроводность.
На рис. 4-2 и 4-3 приведены графики зависимости удельного веса
и относительной вязкости некоторых растворов от их концентраций.
Удельную теплоемкость раствора определяют по формуле
Ср = + _Л_, кДж/(кг • °C),
(4-2)
Таблица 4-2
Теплоемкости безводных солей сеух,
кДж/(кг-°С)
Вещество Ссух Вещество Ссух
СаС12 0,687 NH*NOa 1,37
КС1 0,676 NaNOs 1,089
NH4C1 1,52 (NH4)2SO4 1,42
NaCl 0,837 Сахац 1,29
KNOa 0,965 Глицерин 2,41
112
где сСух — удельная теплоемкость безводного нелетучего вещества, рас-
твор которого выпаривается (определяется по справочнику),
кДж/(кг-°C); сЕ — теплоемкость воды, кДж/(кг*°C); b — процентное
содержание вещества в растворе.
Теплоемкости некоторых веществ даны в табл. 4-2.
"Вследствие увеличения вязкости растворов и понижения их тепло-
проводности и теплоемкости уменьшается и коэффициент теплоотдачи
ctp от греющей стенки к кипящему раствору. По опытным данным, на-
пример, в начале выпаривания клеевого раствора с начальной концен-
трацией 2% коэффициент теплопередачи <£ = 3 500 Вт/(м2*°С), а в кон-
це выпаривания при концентрации 50% £=300 Вт/(м2*°С).
4-2. КЛАССИФИКАЦИЯ ВЫПАРНЫХ АППАРАТОВ
И УСТАНОВОК
По принципу работы выпарные установки разделяются на перио-
дически и непрерывно действующие.
В периодически действующих установках жидкость подается
в аппарат, выпаривается до необходимой более высокой концентрации,
затем упаренный раствор удаляется из аппарата. Опорожненный аппа-
рат вновь наполняется неконцентрированным раствором. Периодическое
выпаривание применяется при небольшой производительности установ-
ки или когда сгущенная жидкость не поддается откачке насосом либо
в тех случаях, когда требуется выпарить весь растворитель. В аппара-
тах непрерывного действия неконцентрированный (слабый) раствор
непрерывно подается в аппарат, а упаренный (крепкий) раствор не-
прерывно отводится из него. По сравнению с аппаратами периодически
действующими аппараты непрерывного действия более экономичны
в тепловом отношении, так как в них отсутствуют потери, связанные
с расходом тепла на периодический разогрев аппарата.
В большинстве случаев аппараты непрерывного действия компону-
ются в так называемые многокорпусные выпарные установки, в кото-
рых упариваемый раствор последовательно проходит через ряд отдель-
ных аппаратов. В каждом последующем аппарате устанавливается
большая концентрация раствора, чем в предыдущем.
По давлению внутри аппарата различают выпарные аппараты, ра-
ботающие при избыточном и атмосферном давлениях и вакууме.
Вакуум в выпарных аппаратах применяется в следующих случаях:
а) когда раствор под влиянием высокой температуры разлагается, из-
меняет цвет, запах (например, сахар, молоко); б) когда раствор при
атмосферном давлении имеет высокую температуру кипения, т. е. об-
ладает большой физико-химической температурной депрессией, и тре-
бует высоких параметров греющего пара (например, раствор аммиач-
ной селитры, едкого кали и т. п.); в) когда греющий теплоноситель
имеет низкую температуру и, следовательно, нужно снижать темпера-
туру кипения раствора; г) для увеличения располагаемого температур-
ного перепада в многокорпусной установке.
В тех случаях, когда получаемый в результате выпаривания рас-
твора вторичный пар может быть использован как теплоноситель в дру-
гих теплообменных устройствах и поэтому нет надобности удорожать
выпарную установку подключением вакуум-насоса и конденсатора, мо-
жет оказаться более рациональным выпаривание под давлением.
В качестве греющего теплоносителя наибольшее применение в вы-
парных установках получил водяной пар.
Обогрев дистиллированной водой, высокотемпературными теплоно-
сителями: горячим маслом, дифенильной смесью и др. применяется
только в аппаратах периодического действия небольшой производитель-
ности и требующих высокой температуры обогрева. Система обогрева
8—1128
таких аппаратов состоит обычно из двух соединенных трубопроводами
змеевиков, заполненных одним из указанных теплоносителей; один змее-
вик обогревается в печи, а второй является греющей поверхностью вы-
парного аппарата. Греющий теплоноситель может иметь в змеевиках
естественную или принудительную циркуляцию при помощи насоса.
В случае принудительной циркуляции греющий теплоноситель полно-
стью заполняет систему и находится в ней под давлением, исключаю-
щим вскипание его, что необходимо для нормальной работы циркуля-
ционных насосов. При естественной циркуляции с возможностью паро-
образования система может быть заполнена теплоносителем частично.
Обогрев топочными газами можно встретить в примитивных выпар-
ных установках периодического действия или при концентрировании
растворов в распыленном состоянии, т. е. практически при сушке рас-
творов [Л. 22].
Электрообогрев методами электрического сопротивления или ин-
дукционных токов применяется в основном только в лабораторных вы-
парных аппаратах.
4-3. КОНСТРУКЦИИ НАИБОЛЕЕ РАСПРОСТРАНЕННЫХ
ВЫПАРНЫХ АППАРАТОВ
1. Аппараты с паровым о б о г р е в о м. Наибольшее распро-
странение получили вертикальные выпарные аппараты с трубчатой по-
верхностью нагрева, которые хорошо компонуются и занимают мень-
шую площадь.
Во всех конструкциях выпарных аппаратов для облегчения очист-
ки поверхности нагрева от накипеобразований пар поступает в меж-
трубное пространство, а раствор подогревается и кипит в трубках.
Выпарные аппараты с паровым обогревом можно разбить на три
группы: с естественной циркуляцией раствора, с принудительной цирку-
ляцией раствора и пленочные аппараты.
Аппараты с естественной циркуляцией раствора.
Движущей силой естественной циркуляции раствора является разность
весов столба жидкости в опускных трубах и парожидкостной эмульсии
в подъемных за счет разницы плотностей рж и рэ. Движущий напор
Хр=Н(рж—рэ) расходуется на преодоление трения SApTp, местных со-
противлений ХАрм и на создание динамического напора потока
который определяет скорость циркуляции и>ц, т. е.
&р=Н (рж — рэ) = 2Дртр + 2Дрм + ри>ц /2. (4-3)
В прежних конструкциях этих аппаратов с короткими трубками
естественная циркуляция раствора создавалась за счет устройства
в трубной доске одной центральной или нескольких опускных труб
большого диаметра, чем диаметр трубок (рис. 4-4,а), или же трубный
пучок делался меньше диаметра корпуса аппарата и создавалось пери-
ферийное опускное кольцо (рис. 1-8). В таких аппаратах не удавалось
получить достаточные скорости циркуляции.
В современных конструкциях выпарных аппаратов с более длин-
ными трубками (рис. 4-4,6 и в) при наличии одной или нескольких не-
обогреваемых циркуляционных опускных труб при разности температур
греющего пара и раствора 7—10 °C достигается достаточно высокая
скорость и кратность циркуляции. По опытам А. Ф. Сорокина при вы-
соте кипятильных трубок 5 м и Д/=20°С при естественной циркуляции
можно получить скорости до 2—3 м/с.
1 Конструкции и расчеты выпарных аппаратов приведены в {Л. 4, 6, 15, 20, 34, 53].
114
Кратностью циркуляции К называют отношение количества рас-
твора G, кг/с, циркулирующего в контуре выпарного аппарата, к паро-
производительности аппарата W, кг/с,
K=G/W; (4-4)
G = 0,785 псРыцрр, (4-5)
где d — внутренний диаметр кипятильной трубки; п— число трубок;
и>ц —скорость циркуляции, м/с; рр — плотность раствора, кг/м3.
В выпарных аппаратах с естественной циркуляцией кратность цир-
куляции К=20ч-30.
Рис. 4=4. Вертикальные выпарные аппараты с естественной циркуляцией раствора.
а — с внутренней Центральной опускной трубой; б — с выносной опускной трубой; в — с выносным
расположением сепаратора и опускной трубы; /— греющая камера; 2 —сепаратор; 3—опускная
(циркуляционная) труба; 4 — брызгоуловитель^
При работе выпарного аппарата образующаяся в трубках паро-
жидкостная эмульсия поступает в сепаратор, где происходит сепара-
ция, — пар уходит в паропровод вторичного пара, а жидкость поступает
в циркуляционную трубу и при непрерывной выпарке смешивается
с раствором, поступающим на выпарку, и вновь поступает в греющие
трубки.
Аппарат, представленный на рис. 4-4,в, применяется для упарива-
ния растворов, не образующих осадков на греющей поверхности,
а аппарат 4-4,6— для упаривания растворов, образующих осадок на
греющей поверхности.
Существуют конструкции выпарных аппаратов (рис. 4-5) с вклю-
чением нескольких кипятильников или греющих камер на один сепа-
ратор, с чем чтобы обеспечить бесперебойную работу аппарата и воз-
можность чистки одного из кипятильников во время работы остальных.
Такие аппараты могут применяться как для кристаллизующихся, так
8* 115
а для пенящихся растворов. Для работы с кристаллизующимися рас-
творами устанавливается солеотделитель.
При выпарке кристаллизующихся растворов при осаждении кри-
сталлов на теплопередающих трубках резко снижается производитель-
ность выпарного аппарата. Имеется несколько конструкций аппаратов,
в которых различными методами решается проблема интенсификации
процесса выпаривания кристаллизующихся растворов. На рис. 4-6 по-
казан аппарат со сниженным (низко поставленным) кипятильником,
Рис. 4-5. Выпарной аппарат с выносны-
ми греющими камерами.
I — корпус аппарата; II — выносные кипятиль-
ники; 1 — соединительная труба; 2— сепара-
тор; 3 — разделитель раствора и кристаллов;
4 — опускная труба; 5 — вентиль для греюще-
го пара; 6 — выход конденсата.
Рис. 4-6. Выпарной аппа-
рат со сниженным рас-
положением греющей ка-
меры.
1 — греющая камера; 2 — се-
паратор; 3 — опускная тру-
ба; 4 — отбойный щиток; 5 —
стабилизатор.
в котором выпариваемую жидкость в циркуляционной трубе держат на
высоком уровне (часто на уровне выхода эмульсии в сепаратор). Под
влиянием столба жидкости в кипятильнике возрастает давление и жид-
кость не кипит, а перегревается; поэтому кристаллы из раствора в ки-
пятильнике почти не выделяются. В сепараторе происходит вскипание
жидкости за счет тепла перегрева ее и образование кристаллов, кото-
рые отводятся по опускной трубе через нижний патрубок в солеотделп-
тель или фильтр и осаждаются там.
Для устойчивой работы аппарата на выпускной трубе, подающей
парожидкостиую эмульсию в сепаратор, устанавливают стабилизатор
(трубчатку из полых трубок).
На рис. 4-7,а показан аппарат системы «Рапид» с горизонтальным
расположением греющей камеры, применяемый для выпарки концен-
трированных электролитических щелоков. Он имеет горизонтальный
выносной кипятильник, который на колесах легко откатывается по
рельсам для очистки или ремонта, очень частых при выпарке указан-
ных растворов.
Циркуляция жидкости в аппарате обусловлена разностью гидроста-
тических напоров жидкости на входе в кипятильные трубки и выходе
из них.
.116
Коэффициент теплопередачи в таком аппарате, невелик, в частно-
сти за счет того, что для борьбы с коррозией греющих трубок их дела-
ют из чугуна с присадкой никеля, причем стенки трубок получаются
толстыми. Такие аппараты тяжелы и дороги. Надо полагать, что с уве-
личением производства нержавеющей стали аппараты «Рапид» полу-
чат более совершенную конструкцию.
Для кристаллизующихся растворов применяются также выпарные
аппараты с наклонным выносным кипятильником (рис. 4-7,6), занимаю-
щие как бы промежуточное место между вертикальными и горизонталь-
ными аппаратами. Они несколько удобнее для размещения, чем гори-
Рис. 4-7. Выпарные аппараты с горизонтальным и наклонным расположением греющих
камер и естественней циркуляцией раствора.
а — система «Рапид»; б — система «Беннет»; 1 — греющая камера; 2 — сепаратор; 3 — солеотдели-
тель; 4 — выпускной вентиль; 5 — паровой вентиль: 6 — перфорированное дно: 7 — линия для про-
мывки аппарата паром и водой; 8 — продувочные вентили; 9 — предохранительный клапан.
зонтальные аппараты, так как занимают меньшую площадь, но монтаж
их сложен. Чистка и ремонт этих аппаратов сравнительно удобны; от-
крывается крышка наклонного кипятильника и трубки легко прочища-
ются с помощью «ерша». Вследствие горизонтальности уровня раство-
ра в верхних трубках содержится больше паровых пузырьков, благо-
даря чему усиливается циркуляция раствора.
В аппарате с наклонными кипятильными трубками возможна очи-
стка раствора от осажденной соли на ходу путем отключения солеот-
делителя 3 от сепаратора 1 закрытием вентиля 4. В солеотделителе,
снабженном перфорированным дном, кристаллы осаждаются и периоди-
чески удаляются через герметически закрывающуюся дверцу.
Аппараты с принудительной циркуляцией раство-
р а. Для выпарки вязких растворов, когда получается малая разность
температур греющего пара и раствора (3—4°), получили применение
аппараты, в которых циркуляция жидкости обеспечивается пропеллер-
ным или центробежным насосом, перекачивающим раствор из сепара-
торов в греющую камеру (рис. 4-8). Скорость жидкости в кипятильных
трубках этих аппаратов составляет обычно от 1,5 до 3,5 м/с. Поддер-
жание скорости раствора меньше 1,5 м/с нецелесообразно, так как
117
в этом случае уровень закипания жидкости в трубках располагается
низко и процесс выпаривания происходит примерно так же, как и при
естественной циркуляции. Применение очень высоких скоростей неэко-
номично, так как уже при скоростях 4 м/с увеличение расхода электро-
а)
энергии на привод насоса не оку-
пается незначительным увеличе-
нием тепловой производительно-
сти. Если при упаривании раст-
вора может происходить кристал-
лообразование, то рекомендуется
иметь скорости не менее 2,5 м/с.
Количество прокачиваемого
раствора при вынужденной цир-
куляции во много раз превышает
количество испаряемой воды. По-
этому выходящая из кипятиль-
ных трубок парожидкостная
эмульсия почти целиком состоит
из жидкости. Закипание происхо-
дит только на небольшом участ-
ке верхней части кипятильных
трубок. Отсутствие закипания
внутри трубок уменьшает обра-
зование накипи и в сочетании
с большими скоростями жидкости
Рис. 4-8. Выпарные аппараты
с принудительной циркуляцией
растворов.
а — с соосной греющей камерой;
б — с выносной греющей камерой;
/—греющая камера; 2 — сепара-
тор; 3 — опускная труба; 4 — сепа-
рирующее устройство; 5 — осевой
насос; б — центробежный насос.
118
в трубках обеспечивает более высокий коэффициент теплопередачи, чем
при естественной циркуляции.
Однако на перекачку жидкости тратится значительное количество
электроэнергии, поэтому выбор естественной или вынужденной цирку-
ляции раствора должен решаться технико-экономическим расчетом.
Пленочные аппараты*. Для выпарки чистых некристаллизи-
рующихся растворов и растворов, чувствительных к высоким темпера-
турам, получили применение пленочные выпарные аппараты. На
рис. 4-9,а показан выпарной аппарат с поднимающейся пленкой (при
Рис. 4-9. Выпарные аппараты пленочного типа с длинными
трубками.
а — с поднимающейся пленкой; б—с падающей пленкой; 1 — греющая
камера; 2 — сепарирующее устройство; 3 — сепаратор; 4 — вторичный
пар; 5 — упаренный раствор, б — раствор; 7 — греющий пар.
кипении раствора в трубках). Кипятильные трубки заполняются рас-
твором только на ‘А—Vs их высоты. При достижении температуры кипе-
ния в растворе бурно образуются пузырьки пара, которые, двигаясь
вверх, увлекают за собой раствор, распределяя его тонким слоем по
внутренней поверхности трубки. Иопарение жидкости происходит при
этом в тонком слое, движущемся с большой скоростью (до 20 м/с), что
увеличивает коэффициент теплоотдачи по сравнению с аппаратом, име-
ющим циркуляционную трубку. Парожидкостная эмульсия из трубок
поступает в центробежный сепаратор, где происходит отделение жид-
кости от пара. Вторичный пар поступает в трубопровод, а концентри-
рованный раствор отбирается через патрубок для производственных
целей или отводится в следующий корпус.
В описываемом аппарате циркуляция раствора отсутствует, т. е.
каждая частица раствора однократно омывает греющую поверхность.
В связи с этим эффективность действия таких аппаратов зависит от
уровня раствора: при заполнении аппарата на полную высоту трубок
* Пленочные аппараты неприменимы для выпарки густых и кристаллизирующихся
растворов, так как нижняя и верхняя камеры могут быстро забиться кристаллами.
119
коэффициент теплоотдачи получается наименьшим вследствие незначи-
тельного паросодержания и малой скорости движения жидкой эмуль-
сии внутри трубок; при снижении уровня раствора в трубках ниже до-
пустимого получается недостаточное количество жидкости, она превра-
щается в пар, не достигнув верхних концов трубок. В этом случае
производительность аппарата падает почти до нуля, но не за счет
уменьшения коэффициента теплоотдачи, как в первом случае, а за счет
выключения из работы верхней зоны трубок, т. е. уменьшения активной
поверхности нагрева. Таким образом, существует оптимальная высота
уровня раствора в кипятильных трубках, устанавливаемая опытным
путем. Этой высоте соответствуют и достаточно высокий коэффициент
теплоотдачи, и нужное количество парожидкостной эмульсии, при кото-
ром верхние концы трубок не будут сухими, а в эмульсии будет доста-
точное количество концентрированной жидкости для питания последу-
ющих аппаратов или в качестве готового продукта.
Для получения максимального эффекта от процесса кипения рас-
твора в пленке греющие трубки в аппаратах этой системы имеют дли-
ну 6—8 м. Большой длиной трубок достигаются увеличение скорости
движения парожидкостной эмульсии и уменьшение средней толщины
пленки раствора. Увеличение скорости пара, образующегося при кипе-
нии пленки, происходит вследствие роста его удельного объема с пони-
жением температуры кипения раствора в направлении к верхнему кон-
цу трубок за Счет уменьшения гидростатического давления. В резуль-
тате этих явлений повышается коэффициент теплопередачи через
пленку. Однако температурные деформации длинных трубок часто вы-
зывают их изгиб и нарушение плотности развальцовки в трубных ре-
шетках. Чистка трубок в высоких аппаратах затруднена. При ремонте
приходится вынимать трубки через крышу цеха. Это также ограничи-
вает область применения этих аппаратов.
Пленочные аппараты с поднимающейся пленкой обычно имеют
сепаратор, расположенный соосно, как это показано на рис. 4-9,а.
Для густых чистых некристаллизирующихся растворов применяют-
ся аппараты с падающей пленкой (рис. 4-9,6). В некоторых аппаратах
раствор поступает в нижнюю крышку, имеющую перегородку, и после
подъема парожидкостной эмульсии в первой половине пучка кипя-
тильных труб густой раствор под влиянием силы тяжести опуска-
ется по трубкам второй половины пучка « сепаратору, расположенно-
му внизу.
2. Выпарные аппараты с терморадиационным спосо-
бом подвода тепла. В иоследние годы научно-исследовательские
институты работают над применением лучистого обогрева для выпар-
ных аппаратов. Раствор кипит в жаростойких прозрачных стеклянных
трубках, обогреваемых расположенными внутри корпуса электрически-
ми спиралями. Применение инфракрасных лучей по сравнению с паро-
вым обогревом позволяет передавать большие тепловые потоки через
меньшую поверхность нагрева. При этом могут быть созданы усло-
вия высокой стерильности, которая имеет важное значение для раст-
воров, не допускающих контакта с металлическими поверхностями
нагрева.
До настоящего времени в теплообменниках и выпарных аппаратах
для сильно корродирующих веществ для аппаратов с серной кислотой
применяли свинец, для аппаратов с азотной кислотой — нержавеющую
сталь, для аппаратов с уксусной кислотой — медь; для работы с соля-
ной кислотой применяли керамику и фарфор, отличающиеся плохой
теплопроводностью и малой механической прочностью. В настоящее
время для греющих поверхностей нагрева применяют специальный гра-
фит, отличающийся высокой теплопроводностью £87—128 Вт/(м-°С)] и
хорошей химической и механической стойкостью. Выпаривание в этих
120
аппаратах производится при атмосферном или небольшом давлении.
В качестве защитных средств от коррозии металлов огромные перспек-
тивы открывает применение стеклопластиков и полимерных материалов.
3. Аппараты с погружным горением. В настоящее время
для нагрева и выпаривания до высоких концентраций растворов сер-
ной, соляной, фосфорной и других химически агрессивных кислот, а так-
же растворов мирабилита, хлористого магния, хлористого кальция,
сульфата алюминия, медного и железного купоросов и других солей
получили применение аппараты с погружным горением (Л. 51].
Корпуса аппаратов изготовляют из углеродистой стали, а во избе-
жание коррозии их внутри футеруют кислотоупорными материалами.
Рис. 4-10. Горелки для погружного горения.
а — для сжигания жидкого топлива; б — циклонного типа фирмы Нордак для сжигания газа; в —
для сжигания газа; 1 — форсунка для топлива; 2 — трубка для зажигания; 3 — штуцер для запаль-
ника; 4 — электрическая свеча; 5 — завихритель; 6—смотровая трубка; 7—-смотровое окно; 8 — по-
гружная Футерованная труба (камера горения), 9— колокол для распределения газового потока;
IU — решетчатый распределитель газового потока.
В упариваемый раствор погружаются горелки с барботажными
устройствами, которые также изготовляются из материалов, обладаю-
щих стойкостью к термическим и химическим воздействиям среды (ле-
гированные стали, графит, .пластические массы).
Для погружного горения могут применяться туннельные, диафраг-
мовые и циклонные горелки с трубчатыми, решетчатыми, тарельчатыми
и эрлифтными барботерами, распределяющими продукты сгорания по
объему выпариваемой жидкости. Лучшие результаты в отношении рав-
номерного распределения продуктов сгорания по объему жидкости
дают решетчатые распределители.
121
На рис. 4-10 показаны некоторые типы горелок для погружного
горения. Давление газа перед горелкой должно быть на несколько мил-
лиметров водяного столба больше глубины погружения ее, так как не-
обходимо учитывать гидравлическое сопротивление собственно горелки
с барботажным устройством. Горение в горелке может происходить на
некоторой глубине под уровнем раствора, находящегося в аппарате.
Продукты сгорания выходят из горелки через распределительное
устройство и барботируют через раствор.
Барботаж продуктов сгорания является эффективным способом на-
гревания и выпаривания раствора, так как при этом газы распыляют-
ся в растворе на мелкие пузырьки и образуют большую межфазную
поверхность для тепло- и массообмена. Интенсивное испарение раство-
рителя происходит путем насыщения водяным паром газовых пузырь-
Рис. 4-11. Схема выпарной установки с погружным горением газа.
I — газодувка с ресивером для газа; 2 — компрессор для воздуха с ресивером; 3 — цы-
парной аппарат; 4— погружная горелка; 5 —эрлифтное устройство; б — отстойник; 7 —
шнековый питатель; 8— центрифуга; 9—ленточный транспортер готового концентрата;
10 — взрывная мембрана; II — конденсатор поверхностного типа; 12 — регулирующий
вентиль для подачи раствора; 13 — расходный бачок; 14 — центробежный насос; 15 —
бак для неконцентрированного раствора.
ков, которые всплывают на поверхность раствора, лопаются и таким
образом выносят парогазовую смесь в надрастворное пространство ап-
парата. Температура парогазовой смеси в надрастворном пространстве
превышает температуру жидкости на 2—5 °C.
Коэффициент использования теплоты сгорания топлива при выпари-
вании растворов методом погружного горения достигает 90%.
На рис. 4-11 показана схема установки для погружного горения.
Парогазовая смесь из аппарата уходит в конденсатор, где конденсиру-
ются пары растворителя, а газ удаляется в атмосферу или поступает
в абсорбер. Удаление крепкого раствора из аппарата производят при
помощи эрлифта.
На рис. 4-12 показан аппарат погружного горения эрлифтного типа.
Он состоит из корпуса 4, внутри которого имеется цилиндрический со-
суд, где концентрически располагается погружная горелка 3. Между
корпусом внутреннего сосуда и стенками погружной горелки образова-
на кольцевая щель, по которой эрлифтным путем (за счет разности
плотности газожидкой смеси в кольцевой щели 5 и в корпусе аппарата 4)
выбрасываются продукты 'сгорания и вторичный воздух в виде пу-
зырьков газа, а также некоторого количества жидкости, находящейся
в нижней части аппарата. Для снижения температуры продуктов сгора-
ния по патрубку подается вторичный воздух, а для лучшего распреде-
122
ления газового потока в эрлифтном устройстве в нижней части погруж-
ной горелки размещается смеситель с конусообразным растекателем.
Если при наладочных
работах в сборнике аппа-
рата получают раствор не-
достаточной концентрации,
то путем перепуска через
дозировочное устройство 10
направляют такой раствор
на повторное испарение.
Для обеспечения безопас
ной работы аппарата и осо-
бенно при погасании погруж-
ной горелки предусмотрена
система противоаварийной
защиты с применением фо
тоэлектрического устройства
и автоблокировок.
Достоинствами аппара-
та с погружным горением
являются: высокая корро-
зионная стойкость, простота
устройства, отсутствие грею-
щих поверхностей нагрева и
высокий коэффициент теп-
лоотдачи. Недостатки аппа-
рата: меньшая тепловая
экономичность по сравне-
нию с установками, исполь-
зующими пар от ТЭЦ (ког-
да газ используется для вы-
работки электроэнергии), и
необходимость более строго-
го контроля за его работой
(процессом горения), чтобы
исключить возможность
взрыва газовой смеси в ап-
парате.
Кинетику процесса на-
Рис. 4-12. Аппарат погружного горения эрлифтно-
го типа.
/ — смотровое устройство; 2 — штуцер для электроза-
пальника; 3 — погружная горелка; 4 — корпус аппарата,
состоящий из сепаратора; 5 — внутренний цилиндр для
образования кольцевой щели эрлифта; 6 — крышка аппа-
рата с отбойником; 7 — распределитель газового потока:
8 — спускной штуцер; 9 — запорный кран; 10 — дозиро-
вочное устройство; 11 — предохранительная разрывная
мембрана.
грева и выпаривания жидко-
сти путем барботажа через нее нагретых газов П. Г. Удыма [Л. 51]
предлагает представить упрощенным критериальным уравнением:
П, = 0,01 Re’25 (й/Л)0-25,
(4-6)
где nq = qD2!\tQ^VK — критерий теплового напряжения; Rer=K.'tTD/vr—
критерий Рейнольдса для газового потока в аппарате; h — глубина по-
гружения барботера, м; D — диаметр аппарата, м; q— удельная тепло-
вая нагрузка, отнесенная к единице объема жидкости, находящейся
в аппарате, Вт/м3; Д?Ср — температурный напор, определяемый раз-
ностью температур барботируемого газа и жидкости, °C; лж— коэффи-
циент теплопроводности жидкости при Ц принимается равной 70—
85 °C, Вт/(м-сС); wa — скорость газового потока в аппарате, м/с; тг—
кинематическая вязкость газа при (^г+Ак)/2, м2/с.
Формула применима при Иег=50-ъ7 000 и hJD = 0,454-1,0. Опти-
мальную глубину погружения горелки можно рассчитать по формуле
-^- = 85(^, (4-7)
и -Кеист
123
где RencT = wctZ/v — критерий Рейнольдса, характеризующий режим
истечения газа из сопла барботера в жидкость; d — диаметр сопла, м;
t®c — скорость истечения газа на выходе из сопла барботера; м/с; v —
кинематическая вязкость газа при температуре газа на выходе из соп-
ла, м2/с.
Формула применима при реИст = 1 000-е-100 000.
4-4. СЕПАРАЦИЯ ВТОРИЧНОГО ПАРА В ВЫПАРНЫХ
УСТАНОВКАХ
Чистота вторичного пара паропреобразователей и выпарных аппа-
ратов определяется количеством жидкости (воды), уносимой с паром
в паропровод. Явление уноса состоит в том, что выделяющийся из ки-
пящей жидкости пар захватывает с собой частички жидкости в виде
тумана, отдельных капель или пены и уносит в паропровод, а затем
к потребителям, в конденсатор или во включенный аппарат, для кото-
рого вторичный пар предыдущего контура является греющим. Соли,
содержащиеся в капельках влаги, осаждаются на греющей поверхности
аппарата, снижают коэффициент теплоотдачи, а следовательно, и те-
плопроизводительность аппарата, требуют остановок его для очистки и
ускоряют износ.
Для осаждения влаги во всех сепарирующих устройствах обычно
используют три фактора: действие силы тяжести, под влиянием которой
капельки воды выпадают из потока пара; силу контактного взаимодей-
ствия, т. е. прилипание водяных капель к поверхности сепаратора;
центробежный эффект, в результате которого при движении влажного
пара по кривой траектории капельки жидкости отбрасываются к пери-
ферии, т. е. к стенкам сепаратора, и стекают вниз. В большинстве слу-
чаев эти три способа механического воздействия на влажный пар ис-
пользуются одновременно или сочетаются в разнообразной последова-
тельности и в разной степени
Однако механические способы сепарации пара недостаточно эффек-
тивны при кипении сильно пенящихся растворов, поэтому в настоящее
время для устранения пенообразования и выброса пены из аппарата
в допустимых случаях к раствору добавляют микродозы (1/104—1/106
весовых долей) антипенителей, например КЭ-10-12, АМ-3 и др., кото-
рые обеспечивают нормальную работу выпарных аппаратов даже при
повышенных тепловых нагрузках.
Обычно высоту парового пространства над поверхностью кипящего
раствора принимают не менее 1,5 м, а при выпаривании сильно пеня-
щихся растворов 2,5—3 м.
Необходимый объем парового пространства над поверхностью ки-
пящего раствора определяют по формуле
V=W/Rv, (4-8)
где W—количество выпариваемой воды (вторичного пара), кг/ч; Rv—
допустимое массовое напряжение парового пространства (количество
выпариваемой воды на 1 м3 объема парового пространства в час),
кг/(м3-ч).
Значение Rv приближенно можно определить по формуле
Rv^fJzR3™- (4-9)
Значение Ra™ при р = 0,98-105, Па, принимается для чистой воды
2000 кг/(м3-ч), а для растворов 1 000 кг/(м3-ч). При выпаривании пе-
ПаТМ п
нящихся растворов Rv уменьшают еще в 2 раза.
124
Значение fi зависит от давления в выпарном аппарате
Давление, 105 Па...... 0,393 0,596 0,78 0,98 1,47 1,96 2,45 2,96 3,92
f,.................... 0,85 0,87 0,92 1,0 1,35 1,7 2,05 2,4 3,1
Значение /г зависит от уровня Hw раствора над точкой ввода паро-
жидкостной смеси в паровое пространство (рис. 4-4,а)
Hw............ 0 0,05 0,1 0,15 0,2 0,3 0,4 0,5
f2 ........... 1 0,83 0,69 0,59 0,51 0,4 0,32 0,27
В выпарных аппаратах с уровнем раствора выше кипятильных труб
(рис. 4-4) при вводе парожидкостной смеси над свободной поверхно-
стью раствора R-,: имеет максимальное значение, так как /г=Е С увели-
чением погружения входного штуцера ниже уровня Rv уменьшается
пропорционально значению Hw.
Допустимые напряжения парового пространства в аппаратах с вы-
несенной греющей камерой при вводе парожидкостной смеси над по-
верхностью раствора (парожидкостной эмульсии) в сепараторе при
прочих равных условиях больше, чем в аппаратах с внутренней грею-
щей камерой.
Для уменьшения колебания рабочего давления в выпарных аппа-
ратах целесообразно в сепараторе и в нагревательной камере иметь
минимальные объемы жидкости и вводить парожидкостную смесь в се-
паратор над свободной поверхностью раствора.
Для дополнительного улавливания брызг и пены при колебаниях
тепловой нагрузки в сепараторах и в паровом пространстве аппаратов
с внутренней греющей камерой устанавливаются брызгоуловители.
4-5. ПРИНЦИПИАЛЬНЫЕ СХЕМЫ МНОГОКОРПУСНЫХ
ВЫПАРНЫХ УСТАНОВОК НЕПРЕРЫВНОГО ДЕЙСТВИЯ
Принцип многократного испарения1. Если пар, обра-
зующийся из раствора (вторичный пар одного выпарного аппарата),
направить в греющую камеру другого выпарного аппарата и поддержи-
вать во втором аппарате такое давление, чтобы температура этого па-
ра была больше температуры кипения раствора во втором аппарате, то
в нем тоже может происходить выпаривание, как и в первом аппарате.
Совокупность нескольких выпарных аппаратов, в которых вторичный
пар из каждого предыдущего аппарата направляется в греющую каме-
ру последующего, называется многокорпусной выпарной установкой.
Для возможности кипения раствора в каждом корпусе необходимо
обеспечить соответствующую разность между температурами вторично-
го пара предыдущего корпуса и кипящего раствора следующего за ним
корпуса. Выбор оптимальной температурной разности по корпусам вы-
парной установки будет рассмотрен ниже. Применением выпаривания
в многокорпусных установках достигается значительная экономия па-
ра, а следовательно, и топлива по сравнению с однокорпусным выпа-
риванием при одинаковых производительностях. Если приближенно при-
нять, что с помощью 1 кг греющего пара можно выпарить в однокор-
пусном аппарате 1 кг воды, то в многокорпусной установке благодаря
многократному испарению на 1 кг греющего пара, поступившего в пер-
вый корпус, можно выпарить количество килограммов воды, равное
числу корпусов, т. е. расход пара на выпаривание 1 кг воды в много-
корпусной выпарной установке обратно пропорционален числу последо-
! Установки с многократным испарением правильнее называть многоступенчатыми,
но не многокорпусными, так как в одной ступени может быть несколько корпусов, со-
единенных параллельно. Поскольку в дальнейшем рассматриваются установки только
с одним корпусом в каждой ступени, мы считаем возможным слово «ступень» заменить
словом «корпус», более употребительным на промышленных предприятиях.
125.
вательно включенных корпусов. В этом и заключается смысл примене-
ния многокорпусных выпарных установок.
С учетом потерь тепла расход греющего пара при многокорпусном
выпаривании может быть приближенно подсчитан по формуле
D = W/0,85n, (4-10)
где W— количество выпариваемой воды во всех корпусах, кг/ч; п —
число корпусов; 0,85 — коэффициент, учитывающий увеличение теплоты
фазового перехода с понижением давления, потери тепла с недоисполь-
зованием конденсата, потери в окружающую среду и т. п.
Опытные данные показывают, что в выпарных установках с грею-
щими поверхностями нагрева при переходе от однокорпусного выпари-
вания к двухкорпусному экономия в удельном расходе греющего пара
составляет около 50%, от четырехкорпусного к пятикорпусному—10%,
а от десятикорпусного к одиннадцатикорпусному — меньше 1 %. Поэто-
му наибольшее распространение имеют четырех- и трехкорпусные уста-
новки, однако иногда в промышленности встречаются даже десятикор-
пусные.
Выбор числа корпусов выпарной усгановки является технико-эко-
номической задачей. Оптимальное число корпусов выпарной установки
[Л. 4]
»= / ^та[1’15а+^^(с-одао1',та)]
где k — средний коэффициент теплопередачи, Вт/(м2-°С); /н — темпера-
тура насыщения греющего пара, °C; t'z и t"z— начальная и конечная
температуры охлаждающей воды, °C; /п— температура кипения раство-
ра в последнем корпусе, °C; гп — энтальпия пара, уходящего из послед-
него корпуса, кДж/кг; рк и рп — давление в конденсаторе и парци-
альное давление водяного пара и газовоздушной смеси, отсасываемой
вакуум-насосом, Па; а—стоимость 1 кг греющего пара, руб.; b — стои-
мость эксплуатации 1 м2 поверхности нагрева аппарата (амортизация,
ремонт, обслуживающие здания и т. и.), руб/ч; С—стоимость 1 кг
охлаждающей воды, руб.; d—стоимость 1 квт*ч электроэнергии, руб.
Необходимо отметить, что с увеличением числа корпусов увеличи-
ваются расход металла, начальные затраты на установку и амортиза-
ционные отчисления, расходы на текущие ремонты и, кроме того, услож-
няется эксплуатация, поэтому в большинстве случаев на практике при-
меняют выпарные установки с греющими поверхностями нагрева
с тремя или четырьмя корпусами.
На рис. 4-13 показана четырехкорпусная установка для выпарива-
ния щелоков. Производительность ее 1 000 м3 жидкого щелока в сутки.
Поверхность нагрева каждого аппарата равна 700 м2.
Схемы многокорпусных установок. В схеме прямоточ-
ной выпарной установки (рис. 4-14,а) греющий пар, вторичный пар и
раствор проходят в одном направлении. Раствор переходит из одного
корпуса в другой благодаря разности давлений в корпусах. Прямоточ-
ные выпарные установки по сравнению с противоточными имеют боль-
шее распространение в промышленности вследствие меньшего расхода
пара и электроэнергии, а также незначительных потерь тепла со сгу-
щеннььм раствором, уходящим из установки с наименьшей температу-
рой. Однако для сгущения вязких растворов прямоточная установка
может быть неприменима, или иметь большую поверхность нагрева по
сравнению с рассмотренной ниже противоточной установкой.
В схеме противоточной выпарной установки (рис. 4-14,6) слабый
раствор подается в последний корпус, а в последующие при помощи
126
о *1
IL®
ИЖ
СО№»11
i
Is
Рис. 4-13. Четырехкорпусная выпарная установка.
1 первый корпус; 2 второй корпус; 3 третий корпус; 4 — четвертый корпус; 5 — подогреватель
раствора; 6 у барометрический конденсатор; 7 — вакуум-насос; 8 — подогреватель раствора- Р — цир-
куляционный насос подогревателя: 10 и 11 — плунжерные насосы для подачи раствора; /2 — иасос
для подачи воды в конденсатор; 13 — бак для грязного конденсата; 14 — конденсатоотводчики.
Рис. 4-14. Принципиальные схемы многокор-
пусных выпарных установок.
а — прямоточная; б — противоточная; в — с парал-
лельным питанием; г — со смешанной подачей рас-
твора и отбором экстрапара; 0 — с нуль-корпусом и
двойным первым корпусом; е — с двумя греющими
агентами (паром и маслом).
ров, в 'которых удаление небольших
насосов, установленных между аппаратами, и проходит последователь-
но через все корпуса к первому. Противоточные установки применяют-
ся для выпаривания вязких растворов, которые в условиях прямоточ-
ного выпаривания в последних корпусах (т. е. при низких температу-
рах и высоких концентрациях раствора) становятся настолько вязкими,
что плохо продвигаются по трубопроводам. При этом в последних кор-
пусах неминуемо значительное понижение коэффициентов теплопереда-
чи. Применением противоточ-
ной схемы, при которой с по-
вышением концентрации раст-
вора повышается его темпера-
тура, достигается усиление
теплообмена.
Недостатками противоточ-
ной выпарной установки по
сравнению с прямоточной (при
одинаковом рабочем режиме)
являются: некоторое увеличе-
ние расхода греющего пара (на
5—10%) и несколько больший
расход электроэнергии на пе-
рекачивание раствора из кор-
пуса в корпус в направлении
возрастающих давлений.
Выпарные установки с па-
раллельным питанием раство-
ром (рис. 4-14,в) применяют-
ся при выпарке кристаллизую-
щихся (насыщенных) раство-
количеств воды из раствора
вызывает выпадение кристаллов. Если такие растворы упари-
вать в прямоточной или противоточной по раствору установке, то ин-
тенсивно образующиеся при выпаривании кристаллы неизбежно будут
попадать в трубопроводы и арматуру, забивать их, даже если будут
предусмотрены специальные камеры-солеотделители для осаждения
кристаллов. Вообще же при любой схеме, если возможно хотя бы не-
значительное образование кристаллов, применяются конструкции вы-
парных аппаратов с солеотделителями, имеющими внизу фильтрующую
сетку.
Вторичный пар, отбираемый из какого-либо корпуса для целей по-
догрева раствора или для других технологических целей (но не для
выпаривания), принято называть экстрапаром. Схема выпарной уста-
новки со смешанной подачей раствора и отбором экстрапара показана
на рис. 4-14,г. Экстрапар может быть взят из любого корпуса. Эконо-
мичнее экстрапар отбирать из последних корпусов, однако это не всег-
да возможно, так как от корпуса к корпусу температура экстрапара
снижается.
На рис. 4-14,<9 показана схема выпарной установки с нулевым и
двойным корпусами. Нулевой корпус (нуль-корпус) является как бы
редуктором острого пара, дающим добавочный пар при недостатке мя-
того пара. Системы с нуль-корпусом распространены в сахарной про-
мышленности.
Необходимость двойного корпуса может встретиться в том случае,
когда, например, поверхность нагрева всех корпусов должна быть оди-
наковой, а первый корпус должен использовать как мятый пар, так и
вторичный пар из нуль-корпуса, с тем чтобы обеспечить обогрев второ-
го корпуса и отпуск значительного количества экстрапара, как показа-
но на этой схеме.
.128
Схема двухкорпусной выпарной установки с двумя греющими аген-
тами, например паром и маслом (рис. 4-14,е), применяется в случаях,
когда увеличение концентрации раствора в первом корпусе резко повы-
шает температуру кипения во втором корпусе и температура вторично-
го пара как греющего оказывается недостаточной.
В рассмотренных схемах выпарных установок последние корпуса
могут работать при атмосферном давлении и под вакуумом, а также
с отбором и без отбора экстрапара.
Параллельное включение аппаратов по греющему пару применяют
в том случае, когда располагают греющим паром низкого давления,
однако требуется иметь большую производительность установки. По
питанию раствором аппараты при этом могут соединяться по любой из
рассмотренных схем и работать под давлением или под вакуумом.
Рис. 4-15. Вакуум-испарительная установка для
выпаривания раствора поваренной соли.
а — схема установки; 1 — бак смешения; 2 — циркуля-
ционный насос; 3 — поверхностные конденсаторы; 4 - по-
догреватель раствора; 5 — вакуум-испарители; б — гидро-
затвор; 7 —насос; 8 — отстойник; 9 — центрифуга; 10 —-
эжекторы пароструйные: А — производственная вода;
Б — исходный раствор; В — твердая соль; Г — сброс ча-
сти загрязненного раствора; Д — конденсат; Е — вода
в канализацию; б —• вакуумно-нспарительный аппарат:
1 — подача раствора; 2 — выход раствора; 3 — выход па-
ров: 4 — подача воды.
Многокорпусные в а к у у м - ис-
пари те л ь н ы е установки. При вы-
паривании растворов, у которых при не-
значительном повышении концентрации
начинается выпадение кристаллов, на-
пример при выпарке растворов поварен-
ной соли и т. п., применение многокор-
пусной выпарки в аппаратах поверхност-
ного типа не дает преимуществ, так как
количество тепла на подогрев раствора
(перед или в самом первом корпусе мно-
гокорпусной выпарной установки) иног-
9—1128
129
да превышает количество тепла, затрачиваемого на испарение влаги.
В этих случаях получили применение многокорпусные вакуум-ис-
парительные установки, эффективность которых повышается, если полу-
ченный после выпаривания раствор должен по условиям технологичес-
кого процесса иметь низкую температуру, например 25—30 °C.
На рис. 4-15 представлена девятиступенчатая вакуум-испаритель-
ная установка для выпаривания раствора поваренной сбли. В испари-
тельный аппарат I входит раствор, подогретый выше температуры насы-
щения, соответствующей вакууму, создаваемому эжектором, и в нем
происходит вскипание, благодаря чему концентрация раствора повыша-
ется, далее раствор поступает в корпус II, где поддерживается больший
вакуум по сравнению с I корпусом и т. д., и из корпуса IX сконцентри-
Рис. 4 16. Принципиальная схема опреснительной установки атомной электростанции
с адиабатными испарителями.
1 — реактор; 2 — теплообменники; 3—турбогенератор; 4 — теплообменники регенеративной системы;
5—'Деаэратор; 6 — головной подогреватель опреснительной установки; 7—эжектор; 8 — конденсатор;
У— бак дистиллята; iO — адиабатные испарители; И — морская вода; а, б. в, г — иасосы.
рованный раствор поступает в отстойник и далее на центрифугирова-
ние. Исходный раствор движется противотоком и нагревается последо-
вательно в эжекторных поверхностных конденсаторах и окончательно
догревается до заданной температуры в теплообменнике 4. Преимуще-
ством вакуум-испарительной установки является отсутствие инкруста-
ции или отложения соли на поверхностях нагрева *, которые в вакуум-
испарителях отсутствуют, а также использование физического тепла
раствора на его выпарку и незначительная температура раствора на вы-
ходе из испарителя последней ступени, что повышает экономичность
установки, например расход пара в установке, работающей по схеме,
указанной на рис. 4-15, составляет 0,3 кг на 1 кг выпаренной воды.
Недостатком таких установок является их громоздкость.
Наряду с многоступенчатыми выпарными установками большое
применение для массового опреснения морской воды в настоящее вре-
мя получили стационарные установки большой производительности
с адиабатными опреснителями мгновенного испарения, не отличающие-
ся по принципу работы от аппаратов, рассмотренных на рис. 4-15. Эти
установки имеют от 40 до 50 адиабатных ступеней. Перепад темпера-
тур в каждой ступени составляет 2—3 °C. Производительность таких
* Соль может откладываться на стенках вакуум испарителя, но она не оказывает
никакого влияния на теплообмен или работу испарителя.
130
установок составляет от нескольких десятков до сотен тысяч тонн ди-
стиллята в час.
Принципиальная схема опреснительной установки атомной электро-
станции с адиабатными испарителями и рециркуляцией рассола изо-
бражена на рис. 4-16.
Морская вода насосом а прокачивается через конденсаторы хвосто-
вой группы ступеней испарения, где нагревается конденсирующимся
паром, после чего часть поступает в деаэратор 5, где из питательной
воды выделяется растворенный в ней воздух и добавкой реагентов
уменьшаются ее накипеобразующие свойства. Остальная часть морской
воды сбрасывается из установки. После обработки питательная вода
смешивается с рециркулирующим в установке рассолом и прокачивает-
ся насосом б через конденсаторы основной части установки и подогре-
ватель с внешним подводом тепла. Нагретая соленая вода поступает
в 1-ю ступень испарения, где часть ее испаряется, так как температура
воды выше температуры насыщения, соответствующей давлению в сту-
пени. Неиспарившаяся вода перетекает в следующую ступень испаре-
ния, где часть ее вновь испаряется, и т. д. Полученный пар конденси-
руется на трубках конденсаторов, собирается в лотки под трубками и
каскадом перетекает из ступени в ступень. Из лотка последней ступени
дистиллят откачивается насосом в сборный бак 9. Рассол из последней
ступени испарения откачивается насосом г. Часть его сбрасывается,
а часть поступает на рециркуляцию.
Камеры испарения этих установок выполняются в виде стальных
или железобетонных блоков.
4-6. ТЕПЛОВОЙ РАСЧЕТ ВЫПАРНЫХ УСТАНОВОК
НЕПРЕРЫВНОГО ДЕЙСТВИЯ С ГРЕЮЩИМИ
ПОВЕРХНОСТЯМИ НАГРЕВА
Большое распространение на практике получил .изложенный ниже
метод теплового расчета выпаривания водных растворов, предложен-
ный И. А. Тищенко *.
Материальный баланс процесса выпаривания. Коли-
чество выпаренной воды по корпусам или концентрация раствора опре-
деляется из уравнения материального баланса выпаривания, которое
составлено без учета потерь раствора:
W — СНач GK0H,
где СНач и GEon—начальное и конечное количество раствора, кг/ч; W—
количество воды, выпаренной из раствора, кг/ч.
Обозначив через w количество выпаренной воды на 1 кг раствора
начальной концентрации, кг/кг; Gcyx — масса сухого (безводного) рас-
творенного вещества, кг/ч; 6Нач и йКон — начальную и конечную массо-
вую концентрацию раствора, % общего веса, получим:
G сух = ЬначС нач/100 — 'бкопОкоп/100.
Из этих уравнений определяем:
GEOH=z ЙначСнач/Йрон
И
lF = GHa4
^наА'нач ____( 1 ^нач \
h '-'нач I 1 ь •
"кон V. "кои
* Подробное изложение расчета выпарных установок — см. [Л. 1, 4, 33 и 53].
9* 131
Поскольку обычно расчет ведется на 1 кг раствора начальной кон-
центрации, преобразуем последнее выражение к следующему виду:
w—1——^иач_, кг ВОДЬ1 на । кг раствОра. (4-12)
^кон ''кон
Выражение (4-12) является основным уравнением материального
баланса для определения количества выпаренной воды.
Если заданы количество выпаренной воды, начальная концентра-
ция и начальное количество раствора, то концентрация раствора по
корпусам определяется из следующих соображений. Обозначив иско-
мую концентрацию раствора в первом корпусе через bi, согласно пре-
дыдущему напишем:
IV/ _^иач^иач
w 1 -СГнач fo
И
Л. _ ^нач^нач
бнач-^. ’
где IF, — количество воды, выпаренной в первом корпусе.
Для любого корпуса формула примет вид:
а __ ^нач^нач ______ ^нач^нач (д 1
~Он8Ч-(^, + Г2 + Г3+
Снач- S
1
п
где S IF — количество испаренной воды в /г-корпусах.
1
Изменение весовой концентрации раствора в аппарате неравномер-
но и зависит от количества испаренной воды и начальной концентрации
раствора. Например, для повышения концентрации 1 кг 10%-ного рас-
твора до 50%-ного требуется выпарить 0,8 кг воды, а для дальнейшего
повышения его концентрации от 50 до 100%—только 0,1 кг. Если же
выпаривать 1 кг 30%-ного раствора до концентрации, равной 50%, то
требуется выпарить 0,4 кг воды, а для дальнейшего повышения кон-
центрации от 50 до 100%—0,3 кг. Разница в количествах выпаренной
воды в двух приведенных примерах при одинаковом повышении кон-
центрации раствора с 50 до 100% объясняется тем, что после выпари-
вания в первом случае получаем 0,1 кг сухого остатка, а во втором
0,3 кг.
Определение полной температурной депрессии
в выпарной установке. В выпарной установке потеря темпера-
турного напора вызывается не только одной физико-химической депрес-
сией. В действительных условиях существуют потери температурного
напора также за счет гидростатической и гидравлической температур-
ных депрессий и полная температурная депрессия ib выпарном аппарате
А=Л1+Л2+Дз,
где Аь Аг и Аз — физико-химическая, гидростатическая и гидравличес-
кая температурные депрессии.
В дальнейшем физико-химическая температурная депрессия назы-
вается для краткости температурной депрессией, гидростатическая и
гидравлическая температурные депрессии — гидростатической и гидрав-
лической депрессиями.
Нормальная физико-химическая температурная депрессия, показы-
вающая повышение температуры кипения раствора по сравнению с тем-
132
пературой кипения растворителя при атмосферном давлении, как было
указано ранее, определяется по формуле (4-1).
Гидростатическая депрессия вызывается тем, что во всяком выпар-
ном аппарате нижние слои раствора закипают при более высокой тем-
пературе, чем верхние, вследствие наличия гидростатического давления
верхних слоев жидкости; например, если при атмосферном давлении
подогревать воду до температуры кипения в трубе длиной 10 м, то тео-
ретически верхний слой воды должен закипеть при температуре около
100 °C, нижний же слой, находящийся под давлением 1,96-105 Па
(2 кгс/см2), — при температуре около 120 °C.
Аналогичное явление наблюдается в выпарных аппаратах, но дей-
ствительная гидростатическая депрессия составляет обычно около 20%
теоретической, так как жидкость находится в аппарате не в статиче-
ском состоянии, а в движении, обусловленном конвективными токами
парожидкостной эмульсии, направленными вверх. Строгого аналитичес-
кого метода определения гидростатической депрессии не имеется, так
как она является сложной функцией многих переменных. При расчетах
выпарных установок в зависимости от высоты трубок и степени запол-
нения их раствором ее принимают для каждого аппарата равной от 1
до 3 °C. Для аппаратов, работающих под вакуумом, гидростатическая
депрессия может достигать 5—-8 °C и ее следует подсчитывать хотя бы
приближенно.
Гидравлическая депрессия учитывает снижение температуры, свя-
занное с потерей давления на трение, и местные потери в трубопрово-
дах, соединяющих корпуса выпарной установки; в практических расче-
тах ее принимают равной 1 °C для каждого корпуса или рассчитывают
по соответствующим формулам.
Распределение полезной разности температур по
корпусам выпарной установки. Зная полную температурную
депрессию для каждого аппарата и для всей установки, а также рас-
полагаемую разность температур АГ между греющим и выхлопным па-
ром в установках с противодавлением или между греющим и конденси-
рующимся паром в конденсаторе вакуум-установок, можно определить
полезную разность температур в выпарной установке по формуле
Д^ДГ-ff Д,+ 2 Д2+£ a, j. (4-14)
\ 1 1 1 j
Располагаемая разность температур для выпарных установок, ра-
ботающих с противодавлением, где вторичный пар удаляется в атмо-
сферу,
АГ=</1—100.
Располагаемая разность температур для вакуум-выпарных устано-
вок
А/ ~ti—?к,
где Л—температура греющего пара, °C; tK— температура конденсации
пара в барометрическом или поверхностном конденсаторе, °C.
Полезная разность температур А/, как это следует из рассмотрения
формулы (4-14), всегда ниже располагаемой разности температур АГ
в выпарной установке. Она уменьшается с повышением значений тем-
пературных депрессий.
Вторичный пар при выпаривании концентрированных растворов,
имеющих большую физико-химическую температурную депрессию, мо-
жет иметь значительный перегрев относительно температуры насыще-
ния, соответствующей давлению в надрастворном пространстве. При
распределении полезной разности температур в выпарной установке пе-
133
регрев вторичного пара не 'следует учитывать, так как он не увеличи-
вает температурного напора, который определяется только разностью
температур конденсирующегося пара и кипения раствора. Необходимо
также учесть, что со вторичным паром из аппарата всегда уносится не-
которое количество капельной влаги, на испарение которой и затрачи-
вается теплота перегрева.
При проектировании выпарной установки для заданной производи-
тельности может быть поставлено требование, чтобы поверхности на-
грева всех корпусов были одинаковыми. Соблюдение этого требования
имеет большое значение, так как при этом все аппараты могут быть
выполнены по одним и тем же чертежам, вследствие чего упрощаются
конструирование корпусов и их изготовление; при одинаковых кор-
пусах все детали их получаются соответственно однотипными и взаимо-
заменяемыми.
Иногда при проектировании ставится условие, чтобы суммарная
поверхность нагрева всей установки была минимальной. Этот вариант
рационален в том случае, когда стремление получить аппараты одина-
кового размера требует большого перерасхода ценных материалов.
Наконец, могут быть поставлены оба предыдущих требования, т. е.
чтобы суммарная поверхность нагрева всей установки была минималь-
ной и одновременно поверхности нагрева всех аппаратов были одинако-
выми. Это может быть обеспечено только при особых условиях, кото-
рые рассматриваются ниже.
В зависимости от поставленных требований распределяется и по-
лезная разность температур.
а) Выпаривание при одинаковых поверхностях на-
грева всех корпусов. Количество тепла, передаваемое в каком-
либо корпусе, выражается формулой
Qn=knFn&tn, кДж/ч,
где п — номер корпуса.
Согласно этой формуле отношение тепловой нагрузки произвольно-
го и-го корпуса к тепловой нагрузке первого равно:
Qn
Qi
(4-15)
по условию Fn = Flt следовательно,
_ <2„ ^1
ДС ~~Qi kn'
(4-16)
Итак, при одинаковых поверхностях нагрева отношение полезных
разностей температур прямо пропорционально отношению тепловых на-
грузок и обратно пропорционально отношению коэффициентов тепло-
передачи в аппаратах.
Из равенства (4-16) имеем:
д/ — д/ А.9?.
" /г„ Q,
Так как Д/ = Д/i +|Д/2+1Д^з+ . • • +Atn (где Д/ — полная полезная раз-
ность температур), можно написать равенство
__д/ kj I Qi I <2г I <2з I _l_Qn \
1 Qt\kt 'k2'ks < ••• * knJ’
134
откуда
д. __ A<Qi/fei
К /г2 k3
Q,
д
(4-17)
Если тепловые нагрузки одинаковы, т. е. Q, = Q2 = Qn, то
________д/
fel fel
k2 k3
Д*,=
(4-18)
k,
я
LQ
k
К '
Найдя значение ДД, можно определить:
Qi
(4-19)
или при равенстве тепловых нагрузок
Д tfi —
б) Выпаривание с минимальной общей поверхно-
стью нагрева. Для двух произвольно выбранных корпусов имеем:
Qm = ^тДпДЛтг,
(4-19a)
откуда
Р —
knM,
и
р —.
т k Д/
Обозначим полезную разность температур, приходящуюся на оба
корпуса, через Д/, тогда
ДI' = Мп 4- ДДг
и
p ____ p J p ________________ Qn I Qm
Необходимо найти, при каком значении ДД величина суммарной
поверхности будет минимальной. Для этого достаточно взять первую
производную от F по htn и приравнять ее нулю
dF
d (Д4)
Qm
km (Д/-ДД)2
О,
(4-20)
откуда условие минимума будет:
Q,
Qm
kn^n km^m
(4-20а)
Для доказательства того, что данное равенство
минимума, а не максимума
изводную
функции F, необходимо
является условием
найти вторую про-
d2F
dlfiFy
__ 2 Qn I Qm
I b b
135
Она оказалась положительной при всяком значении Д/„. Поэтому
соотношение (4-20а) соответствует минимуму общей поверхности на-
грева. Из этого соотношения находим зависимость
Qm^n ,
Ы-п ~ V Qnkm
(4-21)
показывающую, что при минимальной общей поверхности нагрева от-
ношение полезных разностей температур прямо пропорционально квад-
ратному корню из произведения отношения тепловых нагрузок на об-
ратное отношение коэффициентов теплопередачи.
При одинаковой тепловой нагрузке обоих корпусов
LtmlLtn^VkJkm. (4-22)
Расчетные формулы при одинаковых тепловых нагрузках корпусов
й любом числе корпусов имеют вид:
1 + УЛ1/£2 + Уkt/кз Уk-Jkn
я
= (4-24)
а при различных тепловых нагрузках корпусов
д/ —__________(4-25)
У Qi -И У Q2A2 Ч~ У Qs/^з + • - - +УQn/^n
и
Ltn^Ltyk^, (4-26)
где Д/— полная полезная разность температур для установки в целом.
в) Выпаривание с минимальной суммарной поверх-
ностью нагрева при одинаковых поверхностях нагре-
ва отдельных корпусов. Чтобы корпуса имели одинаковые по-
верхности нагрева, необходимо соблюдение равенства (4-16)
Ад А.
д/, Q, kn'
Для того чтобы сумма поверхностей нагрева была минимальной,
необходимо соблюдение равенства (4-21)
Ы-п _~.]/Qn
Дй V Q, kn'
Сопоставив оба равенства, найдем:
Д/„/Д^ = VД^/Д/, == 1, (4-27)
т. е. в этом случае
Д Д = Д11.
Таким образом, условие равенства поверхностей нагрева и мини-
мума их суммы может быть соблюдено лишь в том случае, если полез-
ные разности температур по корпусам одинаковы. Но в таком случае
из выражений (4-19) и (4-24) получается, что
_ 1
Q.kn
или
Qn/Qi—knlh.
136
Последнее соотношение, справедливое при любом числе корпусов,
показывает, что тепловые нагрузки должны быть прямо пропорциональ-
ны коэффициентам теплопередачи.
Итак, для возможности одновременного выполнения обоих требо-
ваний необходимо соблюдение следующих условий: полезная разность
температур для всех корпусов должна быть одной и той же, а тепло-
вые нагрузки всех корпусов должны быть прямо пропорциональны ко-
эффициентам теплопередачи. Эти условия могут быть выполнены толь-
ко при определенных отборах экстрапара. И если экстрапар может най-
ти применение, то описанный метод распределения тепловых нагрузок
и температур является наиболее выгодным.
В заключение следует отметить, что величины полезных разностей
температур, вычисленные по указанным выше формулам, могут в неко-
торых случаях требовать пересчета, так как для определения величин
Q и k 'приходится задаваться температурами пара и раствора, которые
могут отличаться от величин, получаемых в конце расчета. Однако осо-
бой точности при проектировании таких установок не требуется и обыч-
но ограничиваются только поверочным расчетом.
Теплоотдача в выпарных аппаратах, а) Коэффициент
теплоотдачи от конденсирующегося пара к трубкам определяется в за-
висимости от типа и конструкции аппарата по формулам, приведенным
в гл. 1; б) коэффициент теплоотдачи при кипении с искусственной цир-
куляцией при тепловой нагрузке <7=30 000-4-46 000 Вт/м2 можно прибли-
женно рассчитать по формуле (1-15) для вынужденного конвективного
теплообмена без изменения агрегатного состояния раствора или по
методике, указанной в гл. 1; в) коэффициент теплоотдачи при пузырь-
ковом кипении раствора в трубах вертикальных выпарных аппаратов
с естественной циркуляцией раствора определяется из формулы [Л. 32]
Nu = 54K°'e/Pr°.3; (4-28)
XVpO.5 0,06 0>e
акип = 780----’ (4-29)
К П а0,5г0,6р0,66со,3р,о,з ' '
где
Nu== K=z= РпгО,078(ро/Рп)М ;
Pr=uc/X; 7— теплопроводность раствора (жидкости), Вт/(м-°С); рж,
рп — плотность жидкости и пара, кг/м3; р0 — плотность пара при р =
= 98 кПа, кг/м3; <т— поверхностное натяжение, Н/м; г — теплота паро-
образования, Дж/кг; с — удельная теплоемкость раствора, Дж/(кг-°С);
и — динамическая вязкость раствора, Н-с/м2; q — плотность теплового
потока, Вт/м2; w — произведение среднего диаметра пузырьков, возни-
кающих при кипении, иа число пузырьков, образующихся в единицу
времени, м/с.
Формулы (4-28) и (4-29) применимы при р=1(0,0984-70,5) • 105 Па
[0,1—72 ат], Рг = 0,84-100, </=9 0004-150 000 Вт/м2.
Формулы (4-28) и (4-29) дают удовлетворительные результаты при
соблюдении оптимального уровня раствора в трубках выпарного аппа-
рата, который определяется приближенно по формуле
Яопт/Я=0,26+0,0014 (рж—рв), (4-30)
где И— высота труб, м; ЛОпт — оптимальный уровень раствора в труб-
ках, м, фиксируемый по водомерному стеклу; рш и рв—плотности рас-
твора и воды, кг/м3.
137
Более точные данные для определения коэффициента теплоотдачи
при кипении растворов сахара дают формулы Кичигина и Тобилевича.
Применение критериальных уравнений для расчета теплоотдачи в вы-
парных аппаратах затрудняется отсутствием значений физических кон-
стант для различных растворов. Некоторые данные можно найти
в (Л. 20].
Пример 2-1. Определить коэффициент теплоотдачи при кипении 40%-кого раство-
ра NaOH под абсолютным давлением 19,6 кПа (0,2 ата). Температура кипения раство-
ра при этом давлении составляет 85 °C. Константы раствора: вязкость ц=
=2,92 • 10“3 Н-с/м2, теплопроводность Z=0,557 Вт/(м-°С); удельная теплоемкость
с=3,44 кДж/(кг-°С); поверхностное натяжение о=0,104 Н/м; плотность рр =
= 1390 кг/м3. Теплота парообразования г = 2 360-103 Дж/кг (563 ккал/кг); плотность
водяного пара составляет: при давлении 19,6 кПа (0,2 ат) рп=0,128 кг/м3; при дав-
лении 98 кПа (1 ат) р0=0,579 кг/м3. Решение по формуле (4-28)
<7
<7
к__________- - ______________2_______________= ? .
рпг0,078 (po/рц)1-1 0,128-2 360-103-0,078 (0,579 0,128)1.1 123000 ’
9;
р-с __ 2,92-10-3 -3 440
= ~Х 0,557
1 /IwT 1 / 1 390-9,81
= Л|/ —— Nu =0,557 у —(ГТ04—’0,0198<7°.6 = 4<7°.6 [при q
= 18400 Вт/м2 а = 4 (18 400)°.« = 1 450 Вт/(м2-°С)= 1 250 ккал/(м2-ч-°С)[.
4-7. ТЕПЛОВЫЕ БАЛАНСЫ И РАСХОД ПАРА ДЛЯ ВЫПАРНЫХ
УСТАНОВОК НЕПРЕРЫВНОГО ДЕЙСТВИЯ
Расчет прямоточной выпарной установки. Рассмо-
трим тепловые расчеты и балансы выпарных установок по методу
И. А. Тищенко. Введем следующие обозначения, в которых индексы 0
соответствуют неконцентрированному раствору, а индексы 1, 2,
3 ... — номерам корпусов:
йо, bh Ьг и Ь3 — концентрации растворов, %;
Со, Сц с2 и с3 — удельные теплоемкости раствора, кДж/(кг • °C);
‘to, ti, и /з — температуры кипения раствора, °C;
i'i, i'z и г'з — энтальпии греющего пара, кДж/кг;
i"i, i"z и /"з — энтальпии вторичного пара, кДж/кг;
&1, йг и -Оз — температуры вторичного пара, °C;
Ti, Т2 и т3—энтальпии конденсата греющего пара, кДж/кг;
di— удельный расход греющего пара, поступающего в аппарат,
кг на 1 кг раствора;
Wt, w2 и — количество выпариваемой воды на 1 кг неконцентри-
рованного раствора, поступающего на выпарку, кг.
На рис. 4-17 показана схема прямоточной многокорпусной выпар-
ной установки. В этой схеме вторичный пар, выходящий из первого
корпуса, служит греющим паром для второго корпуса, из второго —
греющим паром для третьего и т. д.
В этом случае согласно принятым обозначениям получим: i'\=i'z,
и т. д.
В схеме предусмотрено частичное использование теплоты конденса-
та предыдущего корпуса в последующем, осуществляемое обычно при
помощи расширительных сосудов, в которых происходит самовскипание
конденсата с образованием пара; удельное количество последнего про-
порционально разности энтальпий конденсата в двух соседних корпусах.
Такое же количество тепла могло бы быть получено от использования
его при непосредственном перепуске из одного корпуса в другой. Однако
это усложняет эксплуатацию и может ухудшать теплопередачу в аппа-
ратах. При составлении тепловых балансов можно считать, что весь
конденсат каскадно перепускается из одного корпуса в другой.
138
При составлении тепловых балансов не учитываются потери тепла
поверхностью аппаратов в окружающую среду, а также потери тепла,
связанные с откачкой или 'Продувкой из аппаратов паровоздушной смеси
и неконденсирующихся газов. Эти потери приближенно оцениваются
после определения тепловой нагрузки и поверхности нагрева для каж-
дого аппарата в отдельности. Они могут составлять для хорошо изоли-
рованных аппаратов от 3 до 5%, причем большее значение принимается
для первого корпуса.
Рис. 4-17. Схема прямоточной многокорпусной выпар-
ной установки с отбором экстрапара и каскадным пере-
пуском конденсата.
Тепловой баланс первого корпуса выпарной уста-
новки. Тепловой баланс первого корпуса выпарной установки
(рис. 4-17) на 1 кг раствора, поступающего в аппарат, имеет следую-
щий зид:
Приход тепла Расходтепла
С греющим паро?л ..... d,i'i
С растгором...............с0/0
Со вторичным паром . . wti"t
С раствором, уходящим
из аппарата............(1—ш,) с,/
С конденсатом..........JjT,
Составим уравнение теплового баланса
d\i'i-\-\C(,to = wd"i^ (1—Wi) cdi-j-diti. (4-31)
Если в аппарат поступает 1 кг раствора с теплоемкостью с0 и из
него удаляется wt кг воды с теплоемкостью св, то, поскольку при выходе
из аппарата получается (1—ин) кг раствора с теплоемкостью щ, спра-
ведливо равенство
1с0—Ш1СВ= (1—(4-32)
Подставив в уравнение теплового баланса (4-31) вместо (1—Ш1)й
величину (с0—WiCK) и решив его относительно получим:
+ С° i-^ct <4-33)
.Множитель (i'i—Ti)/(i"i—cBfi), равный количеству воды, испаряе-
мому за счет тепла 1 кг греющего пара, называется коэффициентом
испарения а. Он всегда имеет положительное значение.
Выражение (t0——csti) может быть отрицательным, положи-
тельным или равным нулю. Знак его зависит от знака числителя, так
как знаменатель i"i—c^ti всегда положителен. Если температура посту-
пающего в аппарат раствора выше температуры кипящего в аппарате
раствора, т. е. если /о>А, то c0(t0—ti) равно количеству тепла, осво-
бождающемуся из 1 кг раствора за счет понижения его температуры
139
при поступлении в аппарат. Например, если раствор из первого корпуса
прямоточной выпарной установки с температурой ti поступает во второй
корпус, в котором температура раствора i2<Zti, то некоторое количество
воды из поступающего раствора выкипает за счет собственного тепла
перегрева. Испарение жидкости в аппарате за счет тепла поступающего
раствора называется самоиспарением, а величину (t0——cBti) на-
зывают коэффициентом самоиспарения — р.
Таким образом, уравнение (4-33) может быть переписано в следую-
щем упрощенном виде:
кг/кг. (4-ЗЗа)
Расход пара в однокорпусной установке на 1 кг раствора выражает-
ся формулой
dt=^^. (4.34)
Уравнение теплового баланса для второго корпуса согласно схеме
на рис. 4-17 имеет вид:
[Wi—- (si—Л*) (1—Wi) cdiV
+ЙГС1 = W2i"2+ (1 — W1-W2)\t2C2+'
—(ei—R) -|-£fi]T2-
В этом уравнении и на схеме ei, Е2 и т. д. обозначают величины
отбора экстрапара, a R, наоборот, — поступление в выпарную установку
пара из отбора турбины, отработавшего пара из паровой машины, ра-
ботающей с противодавлением, или от какого-либо постороннего паро-
генератора.
Принимая во внимание, как указано выше, что (1—wi)ci = c0—wicB
и соответственно (1—Wi—w2)c2=co—WiCB—w2cB, представляем уравне-
ние в следующем виде:
W'a — (ei — Я) + (Со — WjCb) = W2i"2 -|-
+ (св — w,cB — w2cB) t2 4- w^s — (e, — R) T2 + d^2,
откуда
w = w .//"V 4- (Co — V.) % + dx -----------(e. — R) •
2 2 lf 2-2 2 ^dz 2 2 ^dz 2 2 ^dz
Заменяя
получаем:
w2=Wi«2 +i (co—wicB) p2+
-J-.diO2—(er—R)ct2, (4-35)
где «2 — коэффициент испарения; p2 и ог — коэффициенты самоиспаре-
ния раствора и перепускаемого конденсата для второго корпуса.
Подставив вместо Wi выражение для него согласно формуле
(4-ЗЗа), т. е. №i=.rfioi+c0Pi, получим количество воды, выпаренной во
втором корпусе на 1 кг раствора, поступающего в выпарную установку,
W2=cZi(«ia2—«зргСв + сТг) +
+с0 (a2Pi—Р1Р2СВ+Рг) — (81—R) аг- (4-36)
140
По аналогии можно составить уравнение теплового баланса для
третьего корпуса и после ряда преобразований получить уравнение
И’з=|^1[аз («№—«1р2Св + <г2) —<₽зСв («1 +«i«2—ЩргСв +с2) +
+ сциз + Оз] + Со[из(сг2р1—РгргСв + Рг) —“РзСв (pi + «гр i—рфаСв +
+1Р2) + Р1О3 + Рз]*~ (®i—R) [о2а3-—азрз +<Тз) —Еа«з- (4-37)
Обозначим в этих уравнениях коэффициенты при di через xlt х2
и х3, коэффициенты при со— через у1г у2 и у3, а коэффициенты при
(ei—R) и е2— через z2 и z3; тогда для Wi, w2 и w3 получим следующие
уравнения:
Wi =diXi + c3yi\
w2=diX2+c3y2—' (Ei—R) <z'2;
w3=d1x3+c0ys—(ei—R)iz'3—E2z"3;
Wn—kdtXnСоУп (si R) z n S2^ n £з^ n
Суммируя написанные уравнения по частям, получаем:
wi 4~ w2 4~ ws 4" 4~ wn — (xi 4-А 4~ А”з 4" ••• 4- xn) 4"
H"co G/i 4- У2 4- Уз 4- • • 4- Уп) — (£i — R)(z,2 4~z,3 4~z,4 4~ ••• -}~z'n) —
— s2 (z"s 4"2,,4 4- ••• + z"n) — s3 (Z"'S -hz"'t~l-z"'s 4- ••• + z"'n) —
(4-38)
Приняв для установки с п корпусами следующие обозначения:
W1 + w2 4- w3 4-... 4- wn-,
=Xj 4- x2 4- x3 4~ •.. 4~ xn'>
^71 =У14~^2 4-Уз 4- ••• 4" у™
Zi = zr24-2,s4_2,4 4_--- ~hz'n>
Z2 = z" 3 4~z,,4 4~z,,5 4- ••• -}~z"ni
^3 — z'''i~[~z'"s ~hz"'e 4"--- ~l~z'"n',
уравнение (4-38) можно написать в виде
=diXn + CoYn— (ei—R) Zi—
--62Z2—E3Z3— . . . еп—lZn_i.
Отсюда определяем искомый расход первичного греющего пара,
идущего на обогрев первого корпуса прямоточной многокорпусной вы-
парной установки
J — с<Хп + (е! •— 4- e2Z2-|-...+en 1Z„1 .. OQ\
141
При расходе раствора G, кг/ч, расход пара на первый корпус
D c<XnG ~Ь (ei 4~ ег^г + Ч~ еп-1-^и-1 (4 39а]
Хп
где Wn = G(l—Ь~-'\—количество воды, выпаренной во всех корпусах
кг/ч; R, е,, s2... sn_,—также имеют размерность кг/ч.
Уравнение (4-39) можно представить также в следующем виде:
d, = сЛ (®1ДД + _ ^en-1zn 1, (4_40)
•^п -Л п л п л п
откуда следует, что при отборе экстрапара увеличение расхода греюще-
го пара dt на первый корпус пропорционально отношениям коэффициен-
тов Z/Xn-
Отношения Zi/X-n, Z^Xn и т. д. носят название эквивалентов экстра-
пара. Они показывают, на сколько килограммов увеличивается удель-
ный расход греющего пара на первый корпус при наличии отборов необ-
ходимого количества экстрапара с разными параметрами.
Эквиваленты экстрапара уменьшаются согласно порядку нумерации
корпусов, так как при этом уменьшаются коэффициенты Z. Отсюда сле-
дует, что чем выше номер корпуса, из которого отбирается экстрапар,
тем меньше в первом корпусе расходуется греющего пара на 1 кг отби-
раемого экстрапара.
При наличии потребителей пара низких давлений в целях экономии
общего расхода тепла на теплоиспользующие установки предприятия
в большинстве случаев бывает выгоден максимально возможный отбор
экстрапара из выпарных установок.
Приближенный метод определения расхода пара на
прямоточную выпарную установку.. Изложенный выше метод
определения расхода пара даже для четырехкорпусной установки чрез-
вычайно громоздок. Однако он сильно упрощается, если принять, что
коэффициенты испарения .во всех корпусах равны единице (практически
они составляют 0,92—0,99), а произведения двух или больше коэффи-
циентов самоиспарения равны нулю. Эти допущения дают ошибку не бо-
лее 4—6%’. При этом коэффициенты при di принимают значения:
Xi=|cti = 1;
Х2 = ,ОЦС12—О!1Р2Св + <72= 1—РгСв + Ог/
Х3= 1—РгСв + ог—2р3Св + 2о3-
Коэффициенты при со:
t/l = pl/
У 2 = «2р1-р2 Р1 + Р2 ='Р1 + р2,‘
г/з = Р1 + Рг + Рз и т. д.
Коэффициенты при (e-i—R)’.
z/2=n2= 1;
2Z3 = аз«2-Рз«2 + СГз = 1-Рз + Оз>’
ZZ4=1--Р4+1O3 + 2р4 + 2(74 и т. д.
Коэффициенты при ег’
г//з=о!з=: 1;
2"4 = а4а3—p4a3+G4=l—р4+о4 и т. д.
Коэффициенты при ез-‘
z"'4= 0.4=1 И Т. Д.
142
Таблица 4-За
Коэффициенты X и У в уравнениях (4-39) и (4-39а)
Число корпусов Величина X Величина У
2 Х& -= 2 -— р2св -|~ с2 У2 = 2[i, р2
3 Х3 — 3 —- 2р2св + 2р3св -]- 2с2 —|— 2g3 Уз — 3|?1 2ра 4- р3
4 =4 — 3р2св — 4р3св — 3J4c в 4* + + 4®з -|- Зя4 У4 = 4[3, -I- Зрг 4~ 2f3 + f4
п Хп = п — (л — 1) р2св — 2 (п — 2) р3св— — 3(и — 3) р4св— ... — (л — 1) p„cB4-Son У„ = л₽14-(л-1)₽г + -|-(л — 2) р3 4- (л — 3) р44-... 4-
На основе коэффициентов х, у и z могут быть подсчитаны суммар-
ные коэффициенты X, Y и Z, значения которых приведены в табл. 4-За
и 4-36.
Полученные значения суммарных коэффициентов X, У и Z исполь-
зуются для определения расхода пара по формулам (4-39) и (4-39а).
Таблица 4-36
Коэффициенты Z в уравнениях (4-39) и (4-39а)
Число корпу- сов Величина Z, для Ej — R Величина Zs для s2 Величина Z3 для е3
2 Z, = l
3 = 2 р3 -|- с3 z2 = I
4 Zj = 3 — 2рз — 2|34 2с3 -|- 2с4 Z2 = 2 — р4 -|- а4 Z,= 1
5 Z, = 4 — Зр3 — 4f4 — 3р5 4- Зо3 4" Z2 = зр4 — 2[?5 4- Zj == 2 — ps — я6
4- 4о4 4- 3с5 4-2at4-2os
Если выпарные аппараты работают без перепуска конденсата, то
при определении X, У и Z следует везде принимать о=0. Если отсутст-
вует отбор экстрапара или подача мятого пара, то следует принять /? = 0
И £1 = £г = . . . ==£п = 0.
Расчеты противоточных многокорпусных выпарных установок и уста-
новок с параллельным питанием корпусов, а также других возможных
на практике схем включения выпарных аппаратов рассматриваются
в специальном курсе [Л. 4, 15, 21].
Пример 4-2. Рассчитать двухкорпусную выпарную установку для глицериновой
воды с одинаковыми поверхностями нагрева обоих корпусов. Схема выпарки изобра-
жена на рис. 4-18. Начальная и конечная концентрации глицериновой воды Ьо=2О%
и Ькон = 88%. Производительность GKOH = 643 кг/ч (0,178 кг/с) концентрированного
глицерина. Давление греющего пара ро=4.9-1О5 Па (5 кг/см2) и /Я=158С'С. Давление
во втором корпусе р2=0,144-105 Па (0,147 кгс/см2 абс.) и температура вторичного
пара 0=54 СС. Начальная температура раствора /'i=20°C. Раствор подогревается
в первом подогревателе экстрапаром до /"=80 °C, во втором — острым паром до тем-
пературы кипения раствора в первом корпусе (/о = М; теплоемкость чистого глицерина
с=2,41 кДж/(кг-°С) (0,576 ккал/(кг• СС). Выпарные аппараты имеют принудительную
циркуляцию раствора. Скорость раствора в трубках: в первом аппарате—1,5 м/с, во
втором — 3 м/с. Диаметры нагревательных трубок 38/32 мм. При определении коэф-
фициентов теплопередачи принять толщину накипи в первом аппарате 6Н=1 >мм и во
втором 2 мм; ХСт=58 Вт/(м-°С), Ли=1,163 Вт/(м-°С). Установка работает без пере-
пуска и переохлаждения конденсата.
143
Решение. Определяем количество раствора, поступающего на выпарку,
6кОН 88
Go = G,oh= 643 - go"»2 828 кг/ч.
Количество воды, подлежащее выпарке,
6„он — Ьв 88 — 20
W = GB-^-----= 2 828- —go------= 2 185 кг/ч.
Все дальнейшие расчеты ведем на 1 кг раствора, поступающего на выпарку.
Находим:
w=W'IGB=2 185/2 828=0,7735 кг на 1 кг раствора.
Рис. 4-18. Схема двухкорпусной выпарной установки
к примеру 4-2.
Теплоемкость раствора при начальной концентрации по формуле (4-2)
2,41-20+ (100—20) 4,187
сс=---------------J00--------— = 3,81 кДж/(кг-°С).
Количество тепла для нагревания раствора экстрапаром в первом подогрева-
теле
q=c't( t"—t'i) = 3,81 (80—20) = 228 кДж/кг.
Количество экстрапара, считая предварительно теплоту парообразования г=
=2 220 кДж/кг, получим равным
б[=228/2 220=0,102 кг на 1 кг раствора.
Если принять, что за счет 1 кг вторичного пара во втором корпусе испаряется
такое же количество воды, то количество воды, выпаренной во втором корпусе, бу-
дет:
иГ—в, 0,7735 — 0,102
w2 =-----2---=----------2--------= 0,335 кг на 1 кг раствора.
Количество воды, выпаренной в первом корпусе,
wt=w—ге>2= 0,7735—0,335 = 0,4385 кг на I кг раствора.
Концентрация раствора в первом корпусе
Ьв 20
6’ = 1—Ю1 ~ 1 —0,4385 ~35,6 °/е>
то же во втором корпусе
Ьо 20
6г= 1—ш ~ 1—0,7735 = 88 Уо-
Определяем физические параметры раствора в корпусах. Теплоемкость раствора
в первом корпусе
35,6-2,41 + (100 — 35,6)-4,187
с, = ------------1СЮ-------------=3,56 кДж/(кг-°С),
то же во втором корпусе
88-2,41 + (100 — 88)-4,187
с2 =-------------IPO-------------= 2,62 кДж/(кг-°С).
144
Т а б л и ц а 4-4'
Значение физических констант (к примеру 4-2)
Наименование физических констант Первый корпус Второй корпус
Вода Раствор Вода Раствор
Плотность р, кг/м3 .... 943 1 170 971 1238,0
Теплоемкость с, кДж.'(кг-°С) . 4,25 3,56 4,187 2,62
Вязкость v-10~e, м2/с . 0,226 0,65 0,366 10,2
Теплопроводность А, Вт,'(м-°С) . . 0,686 0,514 0,686 0,326
Физические константы раствора и воды, найденные по справочным материалам,
приведены в табл. 4-4, причем предварительно принято, что температура кипения
раствора в первом корпусе равна 120, а во втором 80 °C.
Физико-химические температурные депрессии определяем по справочным мате-
риалам с соответствующей поправкой на давление; оцениваем гидростатические и гид-
равлические депрессии; все данные сведены в табл. 4-5.
Таблица 4-5
Величины депрессий, °C (к примеру 4-2)
Род депрессии Корпус
I И
Физико-химическая Д, . . . 3,8 23,3
Гидростатическая Д2 . . . . 1 1,0
Гидравлическая Д3 .... 1 0,5
Суммарная ЕД 5,8 24,8
Полная разность температур в установке
,ДГ=/Н—©2= 1,58,1—54= 104,1 °C.
Полезная разность температур
Д/=ДГ—2Д= 104,1—(5,8+24,8) =73,5 °C.
Согласно заданию оба корпуса должны иметь одинаковые поверхности нагрева.
В соответствии с этим согласно формуле (4-16) полезная разность температур рас-
пределяется между корпусами прямо пропорционально их тепловым нагрузкам и обрат-
но пропорционально коэффициентам теплопередачи, т. е.
ДС _____Q2 /г,
Q, k2 '
Тепловые нагрузки корпусов могут быть приняты пропорциональными количествам
выпариваемой в них воды с поправкой в дальнейшем на явление самоиспарения и уве-
личение скрытой теплоты парообразования во втором корпусе. Таким образом,
Q2/Qi=w2lwi =0,335/0,438=0,765.
Отношение коэффициентов теплопередачи по корпусам принимаем предварительно
(по опытным данным) /г1//г2=2. Подставив эти значения, получим:
Д^/Д^=0,765-2/1 = 1,52.
Так как полезная разность температур
Д*=Д*1+Д<2=73,5°С,
то
73,5
= j 152 =29,1 С
и
дгг=73,5—29,1=44,4 °C.
На основе полученных результатов и данных, взятых из таблиц водяного пара,
составляем табл. 4-6 температур и энтальпий пара жидкости.
10—1128 145
Температуры и энтальпии пара и жидкости (к примеру 4-2)
Таблица 4-6
Наименование параметров Первый корпус Второй корпус
Обозначение Величина Обозначение Величина
Температура, °C: греющего пара «н 158,1 S', 123,2
кипения раствора /, 129 /2 78,8
вторичного пара 1), 124,2 «2 54
конденсата Ч 158,1 т2 123,2
Энтальпии пара, кДж кг: греющего 2 750 2 2 710
вторичного 2 720 ^"2 2 590
Теплота парообразования вторич- ного пара, кДж кт Гг 2 170 Гг 2 360
Коэффициент теплоотдачи от конденсирующего пара к стенке для первого корпуса
по формуле (1-24)
ai=l,35B7(A^)°’25= 1,35 12 300/(2,8 • 3)°’25=9 300 Вт/(м2-°С),
где И — высота трубок, принятая равной 3 м;
В' = 5 700 + 56/н — 0,09^ = 5 700 + 56-158,1 — 0,09-158,12= 12 300;
Д/=/н—/ст принимаем равным 2,8 СС, а затем проверим.
Коэффициент теплоотдачи от стенки к кипящей жидкости для первого корпуса
определяем из формулы (1-13) *
Nu =0,023Rel)’8Pr0>4,
a = 0,023 (wrf/v)°.8 (v/<z)°.4;
(a2= *^До,023 (1,5-0,032/0,65-10-e)».8-(0,65-10-6-3,56-1 170-3 600/1,84) °.4 =
= 5 320 Вт/(м2-°С).
Значения физических констант взяты из табл. 4-4, причем значения а рассчитаны
как Х/ср.
Коэффициент теплопередачи для первого корпуса
= П 8^ 8нак 1 = ~ 0,003 0,001 I = 840 Вт/<м2'°С)‘
+ + “2 9300 + 58 +1,163 ‘5320
Проверяем принятую в расчете разность температур
kM, 840-29,1 „ „
Д/=/н— /«= = Q3Q 2,62 °C,
что незначительно отличается от принятого значения 2,8 °C.
Коэффициент теплоотдачи от конденсирующегося пара к стенке для второго кор-
пуса
аг=1,35В7(Д/Я)°-2®=1,35-И 380/(2 - 3)°-25=9 740 Вт/(м2-°С).
Коэффициент теплоотдачи от стенки к кипящей жидкости
0,326 I 3-0,032 \».’ /10,2-10-8-2,620-1 238-3600 \°.4
аг== 07032'0,023( 10,2-Ю-6 ) ( 1,17 ) ~х221° Вт/(мг-°С).
Коэффициент теплопередачи для второго корпуса
= 1 0,003 0,002 1 = 430 Вт/(“2• °с)•
9400 ' 58 +1,163 + 2210
* Пользоваться для -расчета формулами (1-37а)—(1-37в) нельзя, так как нет
данных для о раствора.
146
Проверяем принятую разность температур
Д<=/н—/ст=М^/а2=430 • 44,4/9 400=2,3 °C.
Расход греющего пара в первом корпусе на 1 кг неконценгрированного раствора
определяем по формуле (4 39), а коэффициенты Х2, У2 и Z2 (вычисляем по табл. 4-За и
4-36.
Приняв |3i=0, поскольку t0 = ti и О2=0, найдем:
—/2 129 — 78,8
В2 = —,7^-------= o'-tin---. .7С Q = 0,0223.
п i"2 — с„/2 2 о80— 4,19-78,8
Тогда
Х2=2—р2св=2—0,0223 -4,19 = 1,907,
Уг=2₽1+1₽2=₽,=0,0223.
При этом расход пара в первом корпусе на 1 кг раствора составит:
1Г2 — С„У2-J-61Z2 _ 0,7735 + 3,81-0,0223 + 0,102-1
rfl==‘ Л, 1,907 ~
= 0,403 кг на 1 кг раствора.
Полный расход пара
£>=C0rfi=2 828-0,403=1 150 кг/ч.
Уточняем количество выпаренной воды. Количество воды, выпаренной в первом
корпусе на 1 кг раствора
awi=dia1 + Coi₽i,
так как ai=l и £1=0, то a?i=di=0,403 кг и количество выпаренной воды
«7'1=0,403 - 2 828=1 150 кг/ч.
Количество воды, выпаренной во втором корпусе,
W2=wt—е+ (Со—свда1)|Рг=О,403—0,102+ (3,81—4,1870 • 0,403) 0,0223 = 0,358 кг
на 1 кг раствора, w'2=w2G0=0,358 • 2 828=1 020 кг/ч.
Количество воды, выпаренное во всей установке
И711=И7'1+И7'2=1 150 + 1 020=2 170 кг/ч.
Расхождение с предварительно найденным количеством выпариваемой воды
2 185—2 170=15 кг/ч составляет .всего около 1%. Проверяем количества тепла, передан-
данные в отдельных корпусах.
В первом корпусе
=<71Г0=0 403 • 2085=840 кДж на 1 кг раствора.
Во втором корпусе
qz=(wi—е,)г= (0,403—0,102)2 180= 650 кДж на 1 кг раствора.
Отношение полученных количеств тепла
?2/<7i = 650/840=0,775.
В предварительном расчете это отношение было принято равным 0,765. Таким
образом, расхождение невелико. Проверяем полученные концентрации раствора в пер-
вом корпусе:
Ьо 20
Ь' = 1 —1 — 0,403“33,6 < 35,6 °/о-
Во втором корпусе
Ьо 20
?---у--г——г— т------n , — 84 < 88 %.
2 1—(Wj + w2) 1 — 0,761
Так как расхождение полученных величин с ранее принятыми незначительное, то
пересчета не делаем.
Поверхность нагрева выпарных аппаратов первого корпуса
Q, __ 840-2 828 1 000
F,= k^t, 840-29,1 ’3600 =27 mS*
второго корпуса
Q, _ 650-2 828 1 000
7’2== k2M2 ~ 430-44,4 ‘3 600 = 27 м •
Поверхности нагрева обоих аппаратов согласно условию расчета получились оди-
наковыми.
Ю* 147
4-8. ТЕПЛОВОЙ РАСЧЕТ ВЫПАРНЫХ АППАРАТОВ
ПЕРИОДИЧЕСКОГО ДЕЙСТВИЯ
Рассмотрим два основных варианта периодической выпарки: при пе-
ременном и постоянном уровнях раствора в аппарате.
Выпаривание при переменном уровне раствора
в аппарате. В этом случае температура кипения t, теплоемкость с и
энтальпия I выпариваемого раствора непрерывно изменяются и являют-
ся однозначными функциями концентрации раствора Ь. Энтальпия вто-
ричного пара i не изменяется, так как аппарат обычно работает под
постоянным давлением.
Если пренебречь потерями тепла в окружающую среду Q5, то коли-
чество тепла dQ, отдаваемое теплоносителем за бесконечно малый про-
межуток времени dr, должно расходоваться на образование dW, кг, вто-
ричного пара и изменение энтальпии выпариваемого раствора
dQ=idW+d(GI)=idW+ Gdl+IdG. (а)
Так как количество сухого вещества в растворе при выпаривании
остается постоянным, то
bi Gi=b2G2 =bG=const,
a
d(bG)=bdG+Gdb=O;
тогда
dG!G = —db/b
или
G—'biGilb, (6)
откуда
dG/biGi=—dbfb2, (в)
где Gi и G2 — массовые количества слабого и сгущенного растворов, кг;
bi и &2 — концентрации этих растворов, кг/кг.
С другой стороны, массовое количество раствора в процессе сгу-
щения его непрерывно уменьшается по мере выпаривания воды (dG =
= —dW), поэтому уравнение (в) можно переписать в следующем виде:
dWlbiGi=dblb\ (г)
Подставив из уравнений (б), (в) и (г) значения G, dG и dW
в уравнение (а), получим:
откуда
JL = V-=^-db+{^-dI. (4-41)
bfii J b J b
bi h
Располагая зависимостями температуры кипения и теплоемкости
раствора от его концентрации, можно построить зависимость энтальпии
кипящего раствора I—ct от концентрации, после чего графическим инте-
грированием можно решить уравнение (4-41) относительно искомого
расхода тепла.
Выпаривание при постоянном уровне раствора
в аппарате. Поддержание постоянного уровня раствора в выпар-
ном аппарате периодического действия в эксплуатационных условиях
наиболее удобно. Для этого случая изменение объема раствора про-
порционально изменению его концентрации и плотности, что можно
выразить следующими уравнениями:
blPidV= Vd(bp)
148
или
dV _d (bp)
17 6,р, ’ (a)
а также
Vdp=PidV—dW; dW=PldV + VdV (6)
и
dQ+IoPldV=idW+Vd(Ip), (в)
где pi, bi и Io — плотность, концентрация и энтальпия раствора, пода-
ваемого в аппарат.
Подставив в уравнение (в) значения dW и dV из уравнений (а) и
(б), получим:
откуда после интегрирования получим:
&Р2 - -1 - Р>) + - РЛ)- (4-42)
В этом уравнении индексы 1 и 2 относятся к параметрам кипящего
раствора в начале и конце выпаривания.
Определение поверхности нагрева или продолжи-
тельности процесса выпаривания для выпарных
аппаратов периодического действия. Независимо от ва-
риантов выпаривания теплообмен через поверхность нагрева выпарного
аппарата определяется уравнением
dQ =kF (ti—</р) dr,
где 6T— температура греющего теплоносителя, °C; tp — температура ки-
пящего раствора, °C;
Коэффициент теплопередачи k в процессе выпаривания изменяется.
Для расчета выпарного аппарата необходимо знать зависимость k=f(b),
которую можно представить графически. При заданной поверхности на-
грева аппарата продолжительность выпаривания раствора можно найти
из уравнения
о
Зная зависимость Q, k и от концентрации раствора, можно ре-
шить уравнение (4-43) методом графического интегрирования, как это
показано в примере 4-3. Конечные или промежуточные температуры
раствора в процессе выпаривания можно определить по уравнению (3-5)
или (3-9) в зависимости от вида греющего теплоносителя (пар, масло,
горячая вода и т. п.).
Расчеты показывают, что при периодическом выпаривании раствора
с постоянным уровнем в аппарате расход тепла по сравнению с выпари-
ванием при переменном уровне несколько снижается, но продолжитель-
ность выпаривания увеличивается.
Пример 4-3. В выпарной аппарат периодического действия подано 6(=2000 кг
раствора с начальной концентрацией Ьг=0,05 кг/кг при температуре А>=20°С. Началь-
ная теплоемкость раствора Сг=3,9 кДж/(кг-°С). Аппарат имеет поверхность нагрева
F=40 м2 и работает под вакуумом с рк=0,147• 10® Па (0,15 кг/см2). Начальная темпе-
ратура кипения раствора А=55 °C. Конечная концентрация раствора 62=0,5 кг/кг.
Аппарат обогревается насыщенным водяным паром с температурой ZH=120°C.
149
Требуется определить: продолжительность нагрева раствора 14 от Zo==2() до tt=
=55°C при коэффициенте теплопередачи fe1=350 Вт/(м2-°С); продолжительность вы-
паривания раствора т2 от &4=О,О5 до fe2=0,5 кг/кг; полный расход греющего пара D;
расход тепла на подогрев и выпаривание. Расчет выполнить для варианта постоянного
уровня раствора в аппарате.
Решение. Исходя из условия постоянства объема раствора при выпаривании,
определим количество слабого раствора в начальный момент:
V = const=62/р2= Gi/pi,
откуда С2 = С1р2/р1=2000 • 1 225/1 010=2420 кг, где pi и р2— плотности раствора в на-
чале и в конце выпаривания,
Р= 2 000/1 010=1,98 м3.
Расходы тепла и пара на нагрев раствора до кипения будут равны:
Qi = Gtci(G—to) =2000 • 3,9(55—20) =273 000 кДж;
Q, 273 000
Я1 = Zi — iK~ 2 710 — 502 = 124 кт-
Время нагрева раствора до температуры кипения находим по формуле (3-2)
G,Ci tv— t0 _ 2 ОСО-3,9-1 000 120— 20 _
т* = ktF ]n fH —t, 350-40-3 600 In 120 — 55 ^°’0674 ч-
Расход тепла на выпаривание раствора при постоянном уровне определяем из
уравнения (4-42)
Qz — V | “ // (& 2Р2 — Pi) — (Рг — Pi) + (РгЛ—Р1Л)]
Г 2 600 — 210 _
= 1,98 ------------- (0,5-1 225 —0,05-1 010) — 2600 (1 225— 1 010) +
+ (1 225-322—1 010-210)J = 53-Ю6 кДж.
Расход греющего пара
О, 53-106
£»2 = 2 700 — 500 — 24 000 RT-
Полные расходы тепла и пара на нагрев и выпаривание раствора составят:
0=273 000 + 53-106 ~53,3-106 кДж;
£1 = 124+24 000 = 24 124 кг.
Время выпаривания раствора определится из уравнения (4-43)
Q
_ 1 с dQ
F Jfe8(t„-tp)’
о
для чего составим вспомогательную табл. 4-7,
Таблица 4-7
Величины для определения времени выпаривания раствора
(к п р и’м еру 4-3)
b, кг/кг . . . 0,05 0,1 0 2 0,3 0,4 0,5
1, кДж/кг . . . . ... 210 214 218 230 284 322
р, кг/м3 .... 1 010 1 030 1 080 1 125 1(175 1 225
k, Вт/(м2-еС) . . . . . . .2 150 1 750 1 130 745 490 280
1—/, кДж/кг . . . .... 2 390 2 380 2 370 2 360 2 330 2 270
tp, ®С .... 55 56 60 67 76 95
tH—tp, °C .... 64 60 53 44 25
Q-Ю-6, кДж . . - . . . 0,273 5,10 15 6 27 44,3 53,3
106/fe(tH—tp), м2/ч .... 7,15 8,9 14,75 25,3 46,5 143
Значение физических констант раствора берем по справочнику.
По величинам табл. 4-7 строим на рис. 4-19 зависимость
10е
^2 (t Н ^р)
f(Q)-
150
Умножив полусумму ординат полученной кривой на соответствующий отрезок
абсциссы и последовательно суммируя площадки, построим на рис. 4-19 кривую, харак-
теризующую
53,3
(* dQ
2~ J М*и-М
0,273
имеющую максимальное значение 570 м2 ч.
Пример суммирования:
7,15 + 8,9 1 000,8,9 + 14,75 1 000
------Т---(5-1-°’273)3W + -J2---------(15,6-5,1)от+ .... ^570 м2.ч.
Рис. 4-19. График к примеру 4-2.
Время выпаривания
т2=570/40 =14,25 ч.
Полное время нагревания и выпаривания
т=0,067+14,25—14,3 ч.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое назначение имеет выпаривание растворов?
2. Какой из процессов происходит при выпаривании: кипение или испарение рас-
твора?
3. Чем отличается выпаривание водных растворов от испарения чистой воды?
4. Как изменяются теплоемкость, вязкость, плотность, температурная депрессия
раствора с повышением его концентрации?
5. Как изменяется физико химическая температурная депрессия раствора с повы-
шением и понижением давления в надрастворном пространстве?
6. Для каких растворов больше значение физико-химической температурной де-
прессии: с большим или меньшим молекулярным весом?
7. Как изменяется коэффициент теплоотдачи от стенки к кипящему раствору с по-
вышением концентрации раствора?
8. Можно ли осуществлять выпаривание растворов острым паром, барботирующим
в растворе?
9. Во сколько примерно раз больше расход пара на 1 кг выпаренной воды в одно-
корпусной установке по сравнению с трехкорпусной при одинаковых производительно-
стях их?
10. Для выпаривания каких растворов применяют противоточную многокорпусную
установку?
И. Какой коэффициент теплоотдачи имеет большее значение: от конденсирующе-
гося пара к стенке или от стенки к кипящему концентрированному раствору?
12. Какие выпарные установки имеют больший удельный расход пара на 1 кг
выпаренной воды: периодического или непрерывного действия?
13. Требуется ли установка насоса для подачи раствора, если выпарной аппарат
работает под вакуумом?
14. Имеется ли циркуляция раствора в пленочных выпарных аппаратах (рис. 4-9)?
15. Где парожидкостная эмульсия имеет меньший удельный вес (рис. 4 4): в цир-
куляционной (опускной) трубе или в кипятильных трубках?
16. Какой из выпарных аппаратов в большей степени подвержен отложению наки-
пи на поверхности нагрева: с принудительной циркуляцией или с естественной?
151
17. Какие типы выпарных аппаратов следует применять при выпаривании кристал
лизующихся растворов и какие для пенящихся растворов?
18. Какие три вида температурных депрессий приходится учитывать при расчете
выпарной установки и какая из них имеет наибольшее значение?
19. В какой конструкции выпарного аппарата при прочих равных условиях гидро-
статическая депрессия имеет наибольшее значение?
20. Какие преимущества имеет применение вакуума в выпарной установке?
21. Какие существуют три условия распределения полезной разности температур-
по корпусам выпарной установки?
22. В чем сущность метода, предложенного И. А. Тищенко для теплового расчета
выпарных установок, каким способом удается исключить переменные значения теплоем-
кости растворов?
23. Составьте тепловой баланс для второго корпуса прямоточной выпарной уста
новки и определите значения коэффициентов ct2 и
24. Может ли коэффициент испарения а иметь значение меньше нуля?
25. В чем сущность упрощенного метода расчета выпарной установки?
26. Что такое эквиваленты экстрапара установки, какое они имеют практическое
значение?
27. Из какой ступени четырехкорпусной выпарной установки более экономичен
отбор экстрапара?
28. Какое значение имеет сепарация вторичного пара для нормальной работы вы
парной установки?
29. В каком выпарном аппарате можно допустить большее напряжение объема
парового пространства: работающем под давлением или под вакуумом?
ГЛАВА ПЯТАЯ
ДИСТИЛЛЯЦИОННЫЕ И РЕКТИФИКАЦИОННЫЕ
УСТАНОВКИ
Дистилляция и ректификация, называемые часто перегонкой, пред-
ставляют собой такой термический процесс разделения жидких смесей
на их составные части, в котором из кипящей смеси ‘выделяются пары,
содержащие те же компоненты, но в другой пропорции. Обычно в парах
процент содержания легкокипящих компонентов, имеющих более низкую
температуру кипения при данном давлении, больше, чем в самой жидкой
смеси [Л. 5, 12, 34]. Дистилляцией называют перегонку смеси с полной
конденсацией полученных паров, а ректификацией — перегонку одной и
той же смеси с многократными частичными конденсацией и сепарацией
паров.
Дистилляционные и ректификационные установки получили широ-
кое применение в пищевой, нефтяной, химической и ряде других отрас
лей промышленности.
Путем перегонки смесей выделяют, например, в чистом или концен-
трированном виде следующие продукты: этиловый спирт, бензол, уксус-
ную кислоту, газы при крекинге, продукты переработки нефти — хлоро-
прен, нитротолуол, продукты хлорирования бензола, анилиновую воду,
аммиак и многие другие промежуточные продукты и отходы различных
производств. При перегонке могут разделяться как многокомпонентные,
так и бинарные (состоящие из двух компонентов) смеси. В настоящем
курсе рассматривается перегонка только бинарных смесей.
5-1. ОСНОВНЫЕ ФИЗИКО-ХИМИЧЕСКИЕ СВОЙСТВА БИНАРНЫХ
СМЕСЕЙ
При изучении процессов дистилляции и ректификации бинарные сме-
си можно разделить на три класса: смеси с практически взаимно не-
растворимыми компонентами, смеси с компонентами, полностью раство-
римыми один в другом, и смеси с частично растворимыми компонен-
тами.
Смеси со взаимно нерастворимыми компонентами
(взаимно нерастворимые смеси). Примерами практическивза-
152
имно нерастворимых жидкостей могут служить ртуть и вода или вода и
бензол.
Для кипящей смеси из взаимно нерастворимых компонентов приме-
ним закон Дальтона, согласно которому парциальное давление пара
каждого компонента в паровой смеси равно давлению насыщенного па-
ра чистого компонента при температуре кипящей смеси.
Рассмотрим смесь воды и бензола. Как известно, вода при давлении
1,013-Ю5 Па (760 мм рт. ст.) кипит при 100°С, а бензол — при 80,4°C.
Зависимость температуры кипения воды от давления характеризуется
кривой А на рис. 5-1,с, а температура кипения бензола — кривой В.
‘Складывая ординаты кривых А и В, находим суммарную кривую С.
компонента G живности, %
б)
Рис. 5-1. Графики давлений, температур и процентного состава для взаимно
нерастворимых компонентов бинарной смеси бензола и воды.
Так как согласно закону Дальтона давление паровой или газовой
смеси равно сумме парциальных давлений ее компонентов, то кривая С
показывает зависимость между давлением и температурой кипящей сме-
си бензол — вода. Пересечение кривой С с горизонталью, соответствую-
щей 1,013• 105 Па (760 мм рт. ст.), показывает, что при этом давлении
смесь кипит при температуре около 70 °C, а также что парциальное дав-
ление паров воды в паровой смеси равно 0,3• 105 Па (225 мм рт. ст.),
а паров бензола 0,71 • 105 Па (535 мм рт. ст.) независимо от содержа-
ния воды и бензола в жидкой смеси. Таким образом, смесь из двух вза-
имно нерастворимых жидкостей закипает при температуре более низкой,
чем температура кипения легкокипящей жидкости, входящей в смесь.
Пользуясь этим свойством, в технике применяют дистилляцию не-
которых жидкостей с водяным паром. Как и перегонка под вакуумом,
такой способ особенно пригоден для дистилляции жидкостей, точка ки-
пения которых при атмосферном давлении настолько высока, что они
при температуре кипения разлагаются.
При дистилляции с водяным паром двух- или многокомпонентная
жидкость, подлежащая разгонке, смешивается с водой, смесь кипятится,
а образующиеся пары конденсируются. После конденсации получается
жидкая смесь одного из компонентов и воды, которая в большинстве
случаев разделяется простым расслоением конденсата из-за разных
плотностей компонентов или механическими методами (отстаиванием,
центрифугированием). Часто дистилляция с водяным паром применяется
для отделения высококипящих веществ от нелетучих растворенных при-
месей.
Расход водяного пара при перегонке веществ 'в токе водяного пара
определяется по формуле
D==G кг, (5-1)
Рвйв? ' '
153
где GB — количество перегоняемого вещества, кг; рп и рв — парциальные
давления водяного пара и паров вещества; рп и — молекулярные веса
воды и перегоняемого вещества; <р — коэффициент насыщения, практиче-
ски колеблющийся в пределах от 0,3 до 0,7.
Таблица 5-1 характеризует понижение температуры кипения ряда
веществ при перегонке с водяным паром при атмосферном давлении,
а также содержание перегоняемого вещества в парах.
Таблица 5-1
Понижение температуры кипения жидкостей
при перегонке с водяным паром при
атмосферном давлении
Название вещества Температура кипения, °C Содержание отгоняемого вещества в паре, %
чистого вещества вещества с водяным паром
Анилин 189,9 98,4 23,1
Бензол 80,4 69,2 91,1
Нафталин 128,0 99,3 14,4
Нитробензол .... 208,3 99,3 25,0
Ртуть 356,8 100 0,4
Пользуясь законом Авогадро для идеальных газов, можно считать,
что в одном и том же объеме при одинаковой температуре количество
молей любого газа или пара пропорционально его давлению.
Обозначив |дс, па, Ga и ра молекулярный вес, число молей, количе-
ство и давление лара одного компонента, а через цв, пв, GB и рв — те же
величины для другого компонента, получим следующие соотношения:
отсюда
Ga . „ Gh' па _Са щ_________________________ра
Р-а Р-b П-Ъ P-а Gb Pb
@ а. Ра Р*а
Рь Р-ь ’
(5-2)
что соответствует следующему составу паров в процентах от массы:
-Д 100 =-----------------------100
Ga + Gb Ра^а + PbV-b
и
1 оо=—4^— 1 оо.
Ga + Gb АНа + AHb
(5-3)
(5 За)
Для предыдущего примера смеси бензола с водой находим выход
бензола на единицу выхода воды (для бензола ца=78)
Са РаУ-а 0 , /178 10/1
Сь ~РьУ-ъ-0,30-18— ’
т. е. в парах приблизительно на 10 частей бензола приходится 1 часть
воды.
Температура кипения смеси со взаимно нерастворимыми компонен-
тами постоянна и не зависит от содержания компонентов в жидкой сме-
си. И только в тот момент, когда один компонент выкипит полностью,
она делает скачок и становится равной температуре кипения оставшего-
ся компонента. Содержание компонента в паровой фазе остается посто-
154
янным и то же не зависит от соотношения их в жидкой фазе до того
момента, пока один компонент не выкипит полностью.
На рис. 5-1,6 изображен график для бинарной смеси со взаимно
нерастворимыми компонентами. Зависимость содержания легкокипящего
компонента (бензола) в парах от содержания его в жидкости изобра-
жается прямой Ьс. Пересечение этой прямой в точке а с диагональю Od
соответствует равновесному состоянию, когда содержание по весу легко-
кипящего компонента (бензола) в парах и жидкой фазе одинаково. Точ-
ка а называется азеотропической точкой, а жидкая смесь, соответствую-
щая этому состоянию, — азеотропической смесью.
Температура кипения азеотропической смеси остается постоянной до
полного выкипания смеси.
Азеотропические смеси .характеризуются тем, что ни один компо-
нент их не может быть выделен перегонкой в чистом виде, так как со-
став паров и жидкой смеси совершенно одинаков. Если летучего компо-
нента в первоначальной жидкой смеси больше, чем в азеотропической
смеси (точка А на рис. 5-1,6), то после некоторой перегонки, во время
которой из жидкости удаляются пары с составом азеотропической смеси
(точка А смещается вправо), остается жидкий остаток из чистого лету-
чего компонента (бензола в данном случае). Наоборот, если летучего
компонента в первоначальной жидкой смеси меньше, чем в азеотропиче-
ской смеси (точка В на рис. 5-1,6), то при перегонке точка В смещается
влево и в жидкости остается нелетучий компонент (вода).
Бинарные смеси (растворы) со взаимно раствор им ы-
м и компонентами. Растворы из полностью растворимых друг в дру-
ге жидкостей делятся на подчиняющиеся закону Рауля (идеальные) и
имеющие, как это будет показано ниже, положительное или отрицатель-
ное отклонение от закона Рауля (растворы с минимальной и максималь-
ной температурами кипения).
Закон Рауля гласит, что парциальное давление пара каждого ком-
понента в паровой смеси над кипящей при какой-либо температуре
жидкой смесью равно давлению насыщенного пара этого компонента,
кипящего в чистом виде при той же температуре, умноженному на моле-
кулярную долю этого компонента в жидкой смеси.
Под молекулярной долей компонента подразумевается отношение
числа молей его в смеси к суммарному числу молей обоих компонентов.
Если в бинарной смеси вещество с молекулярным весом находится
в количестве а, %! от массы, а вещество с молекулярным весом ць в ко-
личестве Ь, %', то молекулярные доли компонентов смеси определяются
по формулам:
= (5-4а)
На "Г НЬ
<=-4б>
На + НЬ
причем
Л-а -Р хь = 1 -
Молекулярные доли можно выражать также в процентах. Число
моль-процентов компонента получается умножением формулы (5-4а) или
(5-46) на 100.
•Математически закон Рауля можно выразить в виде
Ра = РаХа, (5-5)
где ра — парциальное давление пара компонента а над кипящей смесью;
ха — молекулярная доля этого компонента в жидкой смеси; Ра — давле-
ние насыщенного пара компонента а при температуре кипения смеси.
155
Аналогичное уравнение для компонента b
рь=Ръ(Д—Ха). (5-5а)
Если Р обозначает суммарное давление, то
Р = ра+Рь = РаХа + Ръ(Д—Ха)- (5-6)
Обозначим через уа молекулярную долю компонента а в парах или
паровой фазе; поскольку в соответствии с уравнениями (5-3) и (5-4) ве-
личина уа равна отношению парциального давления компонента а к сум-
марному давлению, можно написать:
__ Ра _ Ра^а —^.^аХа /С -7\
Уа~ Pa + Pb ~'Ра*а+ Ръ(1-*а)~ Р ’ '
Уравнение (5-7) может быть выражено в виде
^~Pt + ха (Ра + Рь) ' (5’7а>
Если Ра>Рь, т. е. а является летучим компонентом смеси, то
Ра—Рь >ха(Ра—Pb)
ИЛИ
Ра>Pb + Ха(Ра~Ръ).
В этом случае у)х>\ или у>х, т. е. содержание летучего компонен-
та в парах всегда больше содержания его в жидкости.
Если же Ра<Ръ, т. е. а является нелетучим компонентом, то
Ра— Рь<Ха(Ра~Pb) И У<Х,
т. е. содержание нелетучего компонента в парах всегда меньше, чем
в жидкой смеси.
На рис. 5-2,а представлен графически закон Рауля для бинарной
смеси. По оси ординат отложены упругости паров, а по оси абсцисс —
состав смеси в моль-процентах. Начало координат соответствует содер-
Рис. 5-2. Характерные зависимости для бинарных смесей, подчиняющихся закону Рауля,
о — упругость паров над кипящей жидкостью в зависимости от состава; б — диаграмма кипения и
конденсации смеси (фазовая ^-х-диаграмма); в — диаграмма равновесия и~х.
жанию в смеси 100 моль-процентов вещества В (нелетучего компонента)
и, следовательно, нулю моль-процентов вещества А. Конечная точка оси
абсцисс соответствует 100 моль-процентам летучего компонента А.
Из формул (5-5) и (5-5а) следует, что парциальные давления паров
обоих компонентов изображаются прямыми линиями. Суммарное дав-
156
ление тоже изображается прямой, 'проведенной через конечные точки
прямых Л и В.
Таким образом, при смешении двух жидкостей, химически не дей-
ствующих друг на друга и дающих однородный раствор, суммарное дав-
ление паров при изменении состава раствора изменяется монотонно по
прямолинейному закону от величины упругости пара одной жидкости,
кипящей в чистом виде при той же температуре, до величины упругости
пара второй жидкости в тех же условиях.
Графическое изображение связи между температурой кипения
жидкой смеси, составом жидкости и составом получающихся паров при
заданном давлении, называемое диаграммой кипения и конденсации или
фазовой диаграммой, приведено на рис. 5-2,6. По оси ординат этого гра-
фика отложена температура смеси, а по оси абсцисс — молекулярные
доли компонентов в жидкой и паровой фазах. Зависимость между тем-
пературой кипения жидкой смеси и ее составом изображается нижней
линией, называемой кривой кипения или кипящей жидкости. Состав по-
лучающихся паров в зависимости от температуры кипения изображается
верхней пунктирной кривой. Эту кривую называют линией сухого пара.
Так как она является и началом его конденсации, то ее называют также
линией конденсации. Из диаграммы ясно, что содержание легкокипящего
компонента в парах больше, чем в жидкости (у>х). Точки Е и С соот-
ветствуют температурам кипения чистых компонентов при заданном дав-
лении.
Для большинства растворов диаграмма кипения и конденсации, или
фазовая диаграмма, строится по опытным данным. Однако построение
кривых кипения и конденсации сухого пара может быть произведено
на основании закона Рауля, если известна зависимость температуры ки-
пения чистых компонентов от давления. В этом случае для любой про-
межуточной температуры между точками Е и С могут быть найдены
давления ра и ръ паров обоих компонентов, кипящих в чистом виде. Из
уравнения (5-6) следует, что
Ха== Ра-Р^' М
, Определив х для разных температур, можно построить кривую кипе-
ния. Определив по уравнению (5-7) для тех же температур значения
_Рохо_ ЛДР-А)
Уа Р ~~Р(Ра~Рь)
можно построить кривую конденсации сухого пара.
Кривая равновесия для бинарной смеси (рис. 5-2,в) иллюстрирует
зависимость состава пара от состава жидкой смеси. Состав смеси обыч-
но характеризуется содержанием в ней летучего компонента, поэтому
по оси абсцисс откладывается содержание летучего компонента
в жидкости х, а по оси ординат—в парах у. Величины х и у обычно
выражаются или в моль-процентах, или в весовых процентах.
Кривая равновесия может быть построена по кривым кипения и кон-
денсации, если по оси абсцисс откладывать абсциссы кривой кипения,
а по оси ординат — соответствующие той же температуре абсциссы кри-
вой конденсации сухого пара. Эту же диаграмму можно построить, вы-
числив х и у по уравнениям (5-8) и (5-8а).
Согласно уравнению (5-7а) для более летучего компонента у всегда
больше х, поэтому кривая равновесия смеси взаимно растворимых
жидкостей располагается над диагональю квадрата, построенного на сто-
ронах х=100 моль-процентам и у—100 моль-процентам. Отсюда следует,
что для растворов, подчиняющихся закону Рауля, азеотропической точки
не существует.
(5-8а)
157
Пример 5-1. Построить диаграмму кипения и конденсации смеси и диаграмму рав-
новесия для смеси сероуглерода CS2 и четыреххлористого углерода СС14.
Решение. Для построения диаграмм воспользуемся законом Рауля. Упругость
паров чистых компонентов при различных температурах дана в табл. 5-2. При р=
Таблица 5-2
Упругости паров чистых сероуглерода и четырех-
хлористого углерода в интервале температур 40—80°С
Темпера- тура, °C Упругость паров сероугле- рода Упругость паров четырех- хлористого углерода
мм рт. ст. Ю5 Па мм рт. ст. 10® Па
40 617 0,826 215 0,287
45 726 0,969 262 0,350
50 855 1,140 316 0,422
55 1 001 1,333 376 0,502
60 1 169 1,560 449 0,600
65 1 348 1,800 535 0,715
70 1561 2,085 622 0,830
75 1 793 2,398 727 0,970
80 2 033 2,713 843 1,125
= 1,013 • 105 Па (760 мм рт. ст.) точка кипения чистого сероуглерода равна 46 °C, а чи-
стого четыреххлористого углерода 76 °C. Поэтому в таблице приведены значения пар-
циальных давлений для температур от 40 до, 80 °C.
На основании этой таблицы по формулам (5-8) и (5-8а) определяем значения х
и у-молярного содержания низкокипящего CS2 в жидкости и равновесном паре. Резуль-
таты подсчета сведены в табл. 5-3.
Таблица 5-3
Содержание сероуглерода в жидкой и гаровой фазах смеси сероуглерод —
четыреххлористый углерод
Темпера- тура, °C Содержание сероуглерода
в жидкой фазе (ур-ие (5-8)] р-ръ в равновесных парах [ур-ие (5-8а)] Р X у= р
ра~ ръ
40 1,015—0,287 0,826—0,287 — (1,355) 0,826 -1,355 1,015 “ О’101)
45 1,015—0,350 0,969—0,350“ (1,073) 0,969-1,073 1,015 — (1>025)
50 1,015—0,422 1,140—0,422“ 0,823 1,140 • 0,823 1,015 “(°’926)
55 1,015—0,502 1,333—0,502“ 0,614 1,333 0,614 1,015 —°-809
60 1,015—0,600 1,560—0,600“ 0,432 1,560-0,432 „ „ 1,015 “°’664
65 1,015—0,715 1,800—0,715“ 0,277 1,800 • 0,227 1,015 “°-491
70 1,015—0,830 2,085—0,830“ 0,147 2,085 - 0,147 1,015 “ 0,302
75 1,015—0,970 2,398—0,970“ 0,031 2,398 • 0,031 1,015 “0,073
80 1,015—1,125 2,713—1,125 (—0,07) 2,713- (—0,07) 1,015 “< °’187)
Пэ и мечание. Ци[зры в скобках не имеют реального значения, но вычислены для бэлее точного
построения верхних и нижних участков кривых.
По данным табл. 5-3 ниже на рис. 5-18 вычерчены кривые кипения и конденсации
смеси, а на рис. 5-17 — кривая равновесия, которые использованы в примере 5-4 для
определения числа тарелок в ректификационной колонне. Эти кривые можно построить
также по экспериментальным данным.
158
Жидкости, частично растворимые одна в другой.
Для частично взаимно растворимых жидкостей содержание летучего
компонента в парах вычисляется в две стадии. В пределах растворимо-
сти компонентов расчет ведут по закону Рауля или по эксперименталь-
ным таблицам, а во второй фазе (в пределах нерастворимости) — по
закону Дальтона.
Рис. 5-3. График зависимости растворимости и парциальных дав-
лений от состава частично растворимой бинарной смеси фенол—
вода.
Примером частично растворимых жидкостей являются фенол и вода.
При 20°С вода растворяет до 8,4% по весу фенола, а при 50°C раство-
римость его увеличивается до 12,08%. Вода растворяется в феноле при
20°С в количестве до 27,7%, а при 50°С до 37,17% (проценты даны по
отношению ко всей смеси).
Если по оси абсцисс отложить концентрации воды и фенола, а по
оси ординат —температуры, как это представлено на рис. 5-3,6, то ока-
жется, что кривые растворимости одного компонента в другом в дейст-
вительности представляют собой одну кривую, проходящую через мак-
симум в точке, соответствующей составу смеси с 39,9% фенола и 64,1 %
воды при температуре смеси 68,8 °C.
На рис. 5-3,а для иллюстрации
дан график зависимости между со-
ставом жидкой частично раствори-
мой смеси и давлением паровой сме-
си при постоянной температуре.
5-2. ДИСТИЛЛЯЦИОННЫЕ УСТАНОВКИ
Основные процессы в
дистилляционных установ-
ках. Процессы, происходящие в ди-
стилляционных и ректификационных
установках, наиболее ясно можно
представить себе и понять при рас-
смотрении их на 6-х-диаграммах.
Дистилляция может проводить-
ся в установках непрерывного и пе-
риодического действия.
На рис. 5-4 представлена схема
двухступенчатой дистилляционной
установки непрерывного действия.
Бинарная взаимно растворимая
Концентрация летучего компонента
Рис. 5-4. Схема двухступенчатой дистил-
ляционной установки с дефлегмацией и
сепарацией паров во второй ступени и
ее процесс на г-х-диаграмме.
159
смесь'поступает в подогреватель 1 с параметрами, соответствующими точ-
ке Л, и подогревается до состояния кипения, соответствующего точке В.
В дистилляционном аппарате 2 получаются пары смеси, соответствующие
точке С (см. /-х-диаграмму). Далее пары с концентрацией х2 поступают
в конденсатор 3. Конденсация паров бинарной смеси протекает при х2=
= const с понижением температуры ее от Л до t2- Далее Перегнанный ди-
стиллятпоступает во вторую ступень — дистилляционный аттар^т 4, где
получаются еще более концентрированные па ц.хз>х2}7изanna-grinaвто-
рой ступени 4 пары поступают в дефлегматор 5. В дефлегматоре происхо-
дит частичная конденсация паров (линид^^щ цолуча^тся влажный пар,
соответствующий точке F. Он является"таесью сухого пара е+кЙЖентра-
цией, соответствующей точке L, и жидкости с концентрацией, соответст-
вующей точке К. Доля пара в смеси соответствует отрезку FK, а доля
жидкости — отрезку FL. Затем влажный пар поступает в сепаратор 6,
в котором от него отделяется жидкость. Жидкость с концентрацией
х4<х3 поступает в дистилляционный бак 8, а пары с концентрацией х5>
>х3 направляются в конденсатор 7, где превращаются в дистиллят, ко-
торый поступает в бак готового продукта 9. Необходимо отметить, что
при дефлегмации и последующей сепарации смеси паров достигается бо-
лее высокая концентрация, но получается меньшее количество продукта,
чем при простой конденсации.
Пример 5-2. Определить согласно рис. 5-4 концентрацию отсепарированной жидко-
сти х4, если при сепарации 1 кг влажного пара с концентрацией х3=0,6 выделилось
0,5 кг сухого пара с концентрацией х5=0,7 (отрезки FK и FL равны).
Решение. Составляем уравнение материального баланса и находим:
1 кг-0,6=0,5 кг-0,7+0,5*4,
откуда
0,6 — 0,35
= 0,5 =°>5-
Если дистилляция происходит в установке периодического действия,
то содержание летучего компонента в дистилляционном кубе 2 (рис. 5-4)
постепенно уменьшается, причем как в кипящей жидкой смеси, так и
в получаемых из нее парах дальнейшая перегонка идет при переменной,
все увеличивающейся температуре. Содержание легкокипящего компо-
нента в жидкости в начале кипения и в последующие моменты времени
определяется на кривой кипения точками В, В', В" и т. д., соответствен-
но содержание этого компонента в парах определяется точками С, С',
С'' и т. д. на линии конденсации. Все время уменьшаясь, в некоторый
момент содержание летучего компонента в парах становится равным
его первоначальному содержанию в кипящей жидкости, а затем еще
меньше (точка С'"); тогда дальнейшая перегонка смеси становится эко-
номически нецелесообразной.
Перегонка путем многократной дистилляции применяется преиму-
щественно в лабораторных перегонных аппаратах. Если полученные па-
ры (точка С на рис. 5-4) сконденсировать, то получится жидкая смесь
с содержанием легкокипящего компонента х2 (точка D). После вторич-
ной перегонки полученной жидкой смеси равновесное содержание легко-
кипящего компонента в парах соответствует точке Е. Каждая последую-
щая перегонка увеличивает содержание легкокипящего компонента
в конденсате паров, и если жидкая смесь не имеет азеотропической точ-
ки, то методом последовательной дистилляции можно получить летучий
компонент в почти чистом виде. Метод последовательной дистилляции
промышленного значения не имеет вследствие сложности установки, со-
стоящей из большого количества аппаратов.
Простую — однократную — дистилляцию в промышленных условиях
применяют в тех случаях, когда не требуется полное разделение смеси
160
на компоненты или когда точки кипения отдельных компонентов на-
столько далеки друг от друга, что содержание легколетучего компонен-
та в парах очень велико 'по сравнению с содержанием его в жидкости.
Кроме того, простая дистилляция применяется для отделения от жидкой
смеси нелетучих примесей, а также для предварительного глубокого раз-
деления сложных жидких смесей, например нефти или каменноугольной
смолы. .
На рис. 5-5 показана промышленная установка небольшой произво-
дительности для простой дистилляции. Она предназначена для перегон-
ки смелей с высокой температурой
куб 1 обогревается топочными
газами. При низких температурах
кипения куб снабжается паровым
змеевиком.
В установках периодического
действия по мере дистилляции и
удаления летучего компонента
температура перегоняемой смеси
и ее паров повышается. Дистил-
ляцию обычно ведут до опреде-
ленной заданной температуры пе-
регоняемой жидкости. Остаток
смеси выпускают через кран 5 и
вновь заполняют куб первона-
чальной смесью. В тепловом от-
ношении такие установки неэко-
кипения, вследствие чего перегонный
Рис. 5-5. Дистилляционная установка.
1 — перегонный куб; 2 — конденсатор; 3 — бак для
дистиллята; 4— термометр; 5 — кран для спуска
кубового остатка; 6 — топка.
КОМИЧНЫ.
Расчетдистилляционныхустановокпериодическо-
го действия с однократной дистилляцией. Предположим,
что из бинарной смеси, находящейся в кубе в количестве W, с концен-
трацией по легкокипящему компоненту х отогнано бесконечно малое ко-
личество жидкости dW с концентрацией легкокипящего компонента в па-
рах у. Доля легкокипящего компонента в жидкости при этом изменяется
от х до х—dx, а количество жидкости — от W до W—dW. В аппарате
остается (х—dx)(W—dW), кг, компонента и ydW, кг, удаляется из аппа-
рата в виде паров. Уравнение материального баланса для бесконечно
малого промежутка времени имеет следующий вид:
xW= (x—dx) (W.—dW) +ydW
или
xW=xW~Wdx+dWdx—xdW+ydW. (5-9)
Пренебрегая членом dWdx как бесконечно малой величиной второго
порядка, получаем:
dW __ dx
~W~~~y — x ‘
(5-10)
Проинтегрировав это уравнение в пределах от Wi (начальное коли-
чество жидкости) до W2 (конечное) и соответственно от Xi (начальная
концентрация легкокипящего компонента) до х2 (конечная концентра-
ция его), получим:
\ ^я *я
с dW w2 (• dx ,С11Ч
J ~уГ= ln<=J C5'11)
Поскольку величина у является функцией х, причем связь между х
и у дается графиком, выражение dx[(ij—х) можно проинтегрировать
графически при помощи кривой равновесия, выражающей зависимость
между х и у. Методика интегрирования изложена в примере 5-3.
11—1128 161
Пример 5-3. Вычислить состав дистиллята при простой дистилляции смеси, содер-
жащей в начальный момент 43,2 моль-процента сероуглерода и 56,8 моль-процепта че-
тыреххлористого углерода, если в кубовом остатке сероуглерода должно содержаться
14,7 моль-процента.
Решение. Берем зависимость между составами пара в жидкости для этой смеси
табл. 5-3 и определяем значение 1/(г/—х). Результаты расчета сводим в табл. 5-4
Таблица 5-4
К примеру 5-3
из
X, % у. % 1 У—х
43,2 66,4 0,0432
27,7 49,1 0,047
14,7 30,2 0,065
показано на рис. 5-6, кривую. Заштри-
По найденным значениям строим, как это показано на рис. 5-6, кривую. Заштри-
хованная площадь в пределах от *2= 14,7% до Xi=43,2% численно равна значению
xt
Г ТЛ " <
интеграла I ---- Измерение этой площади (планиметрированием или иа милли-
J У — х
ха
метровой бумаге) показывает, что она приблизительно равна 1,36. По уравнению (5-11)
значение интеграла будет 'равно:
1п
Xl
С dx,
I —-----=1,36.
J У — х
Х%
Полагая 11/7=1 кг-моль, находим:
2,3(lg 1—lg IPs) = 1,36.
Й7г~0,25 кг • моль/(кг • моль) первоначальной смеси.
Вес дистиллята 1 — 1Р2=1—0,25=0,75 кг/(кг - моль).
Содержание сероуглерода в остатке
0,25-0,147=0.037 кг-моль.
Содержание сероуглерода в дистилляте
0,432—0,037=0,395 кг моль,
или 0,395 • 100/0,75=53 моль-процента.
дистилляции азеотропных смесей.
Особенности
Большинство жидких полностью растворимых бинарных смесей не сле-
дует закону Рауля; для таких смесей общая упругость пара может
получиться больше или меньше суммы упругостей паров этих компонен-
тов при той же температуре. Смеси определенного состава, имеющие
минимальную упругость паров (рис. 5-7,а), будут кипеть при более вы-
сокой температуре (рис. 5-7,6), а смеси, имею-
щие максимальную упругость паров (рис.
5-7,г), наоборот, будут кипеть при более низ-
кой температуре (рис. 5-7,6), чем смеси с дру-
гим составом этих компонентов. Из рассмотре-
ния рис. 5-7,6 следует, что если в установке
периодического действия осуществлять много-
кратную дистилляцию смесей с концентрация-
ми в точках bi и 62, то эти точки будут пере-
мещаться по кривой кипения до состояния точ-
ки а. В результате перегонки можно в кубо-
вом остатке получить азеотропическую смесь
(состояние точки а); для смеси с начальной
(Концентрацией в точке в погоне (парах)
после его многократной перегонки мож-
но получить в практически чистом виде
Рис.
меру
162
5-6. График к при-
5-3.
компонент В, который будет являться легкокипящим (для левой части
графика), так как концентрация компонента В в парах будет больше,
чем в жидкости ). Для состояния смеси в точке Ьг может
быть выделен в практически (чистом виде компонент А (у^ ^>ха )•
Кривые равновесия на рис. 5-7,в показывают, что компонент А явля-
ется легкокипящим только для концентрации жидкой смеси х>ха, а на
рис. 5-7,е, наоборот, для концентрации х<х0.
Рис. 5-7. График температур и давлений для азеотропных бинарных смесей с макси-
мальной и минимальной температурами кипения.
Если при тех же условиях осуществлять многократную перегонку
для смесей bt и Ьг, имеющих фазовую диаграмму, соответствующую
рис. 5-7,<?, то при многократной перегонке паров в погоне (парах) будет
получаться азеотропическая смесь состава а, а в кубовом остатке для
точки Ьх — в практически чистом виде компонент В и для точки Ь2 —
компонент А.
Чтобы разогнать смесь азеотропического состава, необходимо изме-
нить суммарное давление паров смеси. В этом случае азеотропическая
Таблица 5-5
Азеотропические смеси с максимальной и минимальной температурами кипения.
Давление 0,1013 МПа (760 мм рт. ст.)
.Вид смеси Температура кипения, ®С Содержание первого веще- ства в смеси, %
первого ве- щества второго ве- щества азеотропной смеси
Вода + хлористый водород .... 100 —84 110,0 79,76
Вода бромистый водород .... 100 —67 126,0 52,14
Вода -1- азотная кислота 160 86 120,5 32,0
Ацетон + метиловый спирт .... 56 65 55,95 86,5
Хлороформ + этиловый спирт . . . 61 78,3 59,0 94,0
Пиридин + вода 115 100 92,0 59,0
11
163
точка может передвинуться, так как меняется температура, соответст-
вующая азеотропическому составу смеси. Таким образом, можно под
давлением или под вакуумом разделить азеотропическую смесь, нераз-
делимую при атмосферном давлении.
В табл. 5-5 указаны некоторые азеотропические смеси с максималь-
ной и минимальной температурами кипения.
Существуют также бинарные смеси с переменным знаком отклоне-
ния от закона Рауля. Такие смеси могут иметь на некотором участке
концентраций выпуклую кривую полного давления паров, переходящую
в дальнейшем в вогнутую кривую (например, смесь вода — пиридин).
5-3. РЕКТИФИКАЦИОННЫЕ УСТАНОВКИ
Процессы в ректификационных установках и изо-
бражение их в диаграммах. Практическое осуществление мно-
гократной дистилляции и дефлегмации (частичной конденсации путем
поверхностного охлаждения (см. рис. 5-4) требует большого числа гро-
моздких, неэкономичных аппаратов. Поэтому на практике применяют
принцип многократной частичной конденсации и сепарации путем рек-
тификации, т. е. многократного тепло- и массообмена без ограничитель-
ной стенки, в одном аппарате, ректификационной колонне.
Содержание летучего компонента
£ живности
Рис. 5-8. Принципиальная схема ректификационной колонны и
процесс ректификации на /-x-диаграмме.
На рис. 5-8 показаны схемы и процессы тепло- и массообмена на
/-х-диаграмме в упрощенной ректификационной колонне с тремя тарел-
ками, которые имеют по одному колпачку (в действующих колоннах
иногда устанавливают более 300колпачков на тарелке). Иногда вместо
тарелок колонна имеет сита или заполняется насадкой из колец Рашига.
Рассмотрим по рис. 5-8 совместно принцип работы ректификацион-
ной установки и происходящие в ней процессы тепло- и массообмена.
В перегонном кубе I за счет подвода тепла происходит испарение бинар-
ной смеси. Пары смеси поднимаются в ректификационной колонне,
а навстречу им из дефлегматора III стекает некоторая часть дистиллята,
которая носит название флегмы. Пары на выходе из ректификационной
колонны II с параметрами точки 8 (на Лх-диаграмме) поступают
!64
в дефлегматор III, в котором они частично конденсируются за счет
отдачи тепла подаваемой в него воде (процесс идет по линии 8-Ci).
Парожидкостная эмульсия с параметрами, соответствующими точке Съ
поступает в сепаратор IV-, в нем происходит отделение пара с парамет-
рами точки 10 от жидкости (флегмы), параметры которой определяются
точкой 9. Отсепарированный пар поступает в конденсатор V, где он пол-
ностью конденсируется до состояния точки 11 и в виде готового продук-
та (ректификата) поступает в сборный бак VI.
Процесс тепло- и массообмена на верхней тарелке протекает в сле-
дующем порядке: жидкость (флегма), получающаяся в сепараторе IV,
с параметрами точки 9 вступает в контакт с парами состояния точки 6,
поступающими с предшествующей по ходу пара нижней тарелки; при
этом происходит частичная конденсация паров до состояния с2 и после-
дующая их сепарация, в результате которой образуются пар состояния 8
и флегма состояния 7. Эта флегма по опускной трубе сливается на ниж-
нюю тарелку и вступает в контакт с парами состояния 4. После сепара-
ции образуются флегма состояния 5 и пары состояния 6 и т. д. Надеж-
ное контактирование флегмы с парами осуществляется благодаря
наличию на тарелках колпачков с прорезями в виде зубцов на нижней
кромке, через которые проходят пузырьки пара при движении их с ниж-
ней тарелки на верхнюю.
Таким образом, ректификация представляет собой процессы тепло-
и массообмена при непосредственном смешении жидкой смеси (флегмы)
с парами при их многократной частичной конденсации и сепарации.
В процессе ректификации флегма, опускаясь и вступая в тепло- и массо-
обмен с парами, поднимающимися по колонне, испаряется за счет тепла
конденсации паров и при этом обедняется легкокипящим компонентом,
но обогащается высококипящим компонентом за счет частичной конден-
сации паров; пары же, наоборот, поднимаясь, обогащаются легкокипя-
щим компонентом за счет испарения его из флегмы и обедняются высо-
кокипящим компонентом. В результате такого массообмена возможна
глубокая разгонка бинарных и многокомпонентных смесей.
Количество флегмы в килограммах, приходящееся на 1 кг пара
в любом рассматриваемом сечении колонны, называется флегмовым
числом. В расчетах по всей колонне принимают постоянное флегмовое
число. В действительности оно может изменяться в зависимости от ин-
тенсивности процессов тепло- и массообмена на отдельных тарелках.
Представленные на /-х-диаграмме процессы ректификации возмож-
ны только при переменных для различных тарелок количествах флегмы.
Это следует из рассмотрения диаграммы, представленной на рис. 5-8,
из которой видно, что отношение отрезков, соответствующих количест-
вам флегмы и пара (флегмовые числа), для отдельных ступеней раз-
личны:
Характеристика процессов на отдельных тарелках может изменять-
ся также в зависимости от режима работы колонны.
Классификация и схемы ректификационных уста-
новок. Ректификационные установки разделяются на действующие
периодически и непрерывно. В периодически действующих установках
в перегонный куб заливают смесь с некоторой средней концентрацией
летучего компонента. После отгонки части летучего компонента жид-
кость, содержащую в основном тяжелый компонент, сливают из куба и
заполняют последний вновь первоначальной смесью.
На рис. 5-9,а представлены схемы ректификационной установки
периодического действия; принцип действия ее был рассмотрен на
рис. 5-8. Недостатком таких установок является большой расход тепла,
165
вызванный необходимостью периодического прогрева аппаратов и поте-
рями тепла с удаляемой из перегонного куба нагретой смесью после ее
разгонки. Кроме того, в процессе перегонки жидкая смесь в кубе беднеет
летучим компонентом и для обогащения паров необходимо увеличивать
количество флегмы, вследствие чего увеличиваются расходы тепла и
охлаждающей воды на дефлегматор. Необходимо отметить и большие
трудности автоматизации таких установок. Поэтому ректификационные
установки периодического действия применяются только при малых
Рис. 5-9. Схемы ректификационных установок.
а — для периодической ректификации; б — для непрерывной ректификации; 1 — перегонный куб;
2— колонна с тарелками; 3— дефлегматор; 4— сепаратор; 5 — конденсатор; 6—паровой змеевик;
7 — контрольный фонарь; в — сборный бак для легкокипящего компонента; 9 и 10— укрепляющая
и исчерпывающая части колонны; 11 — сборник кубового остатка; 12 и 13 — теплообменники; 14 —
расходный бак.
масштабах производства, а также в тех случаях, когда требуется почти
полное разделение компонента (например, при разделении смеси бен-
зол— толуол). На рис. 5-10 показан внешний вид установки для перио-
дической ректификации.
В непрерывно действующую ректификационную установку смесь,
подлежащая разгонке, подается без перерыва. Наиболее простыми явля-
ются установки для разгонки бинарных смесей. Схема такой установки
показана на рис. 5-9,6. В этой установке ректификационная колонна
делится на две части: верхнюю — укрепляющую и нижнюю так назы-
ваемую исчерпывающую колонну, в которой во многих случаях летучий
компонент отгоняется почти полностью в верхнюю часть колонны, а ку-
бовый остаток с нелетучим компонентом сливается в перегонный куб.
Устройство и принцип работы установки такие же, как и в установ
ках периодического действия, с той лишь разницей, что в этой установке
из дефлегматора в ректификационную колонну возвращается постоян-
ное количество флегмы и непрерывно отбирается постоянное количество
готового продукта с определенным процентным содержанием летучего
компонента. Правая часть схемы ничем не отличается от рассмотренной
схемы периодически действующей установки. В левой части показано,
что смесь для разгонки поступает в колонну самотеком из бачка 14,
166
который установлен выше, чем исчерпывающая часть колонны (она мо-
жет подаваться и насосом, в этом случае бачок может располагаться
на любом уровне). Перед разгонкой эта смесь подогревается до необ-
ходимой температуры последовательно в двух теплообменниках 12 и 13.
На рис. 5-11 изображена принципиальная схема разгонки тройной
смеси. В первой ступени схемы в остатке получается смесь с большим
Рис. 5-10. Внешний вид установки
для периодической ректификации.
содержанием высококипящего ком-
понента С, а часть дистиллята с бо-
лее летучими компонентами А и В
поступает во вторую ступень. Во вто-
рой ступени в остатке получается
компонент В, а самый летучий из
трех—компонент А—поступает в
конденсатор второй ступени.
В зависимости от температуры
кипения подвергающихся разделе-
нию жидких смесей ректификацион-
ные установки могут работать: а) при
Рис. 5-11. Схема разгонки тройной
смеси.
атмосферном давлении — для жидких смесей с температурами кипения
от 30 до 200°C (этиловый спирт, бензол и др.); б) при вакууме — для
жидких смесей с температурами кипения при атмосферном давлении
выше 200 °C (нитротолуолы, нитрохлорбензолы, некоторые продукты
перегонки нефти и др.); в) под давлением — для жидких смесей с тем-
пературами кипения при атмосферном давлении ниже 30 °C (некоторые
углеводороды, альдегиды и т. п.).
Применение вакуума дает возможность использовать для перегон-
ки высококипящих смесей греющий пар с относительно низкими пара-
метрами, что имеет большое практическое значение.
Таблица 5-6
Зависимость температур кипения некоторых
смесей от давления
Давление Ортонитро- толуол Метаиитро- толуол Паранитро- толуол
МПа мм рт. ст.
0,0040 30 119,2 125,7 130,4
0,0008 50 131,7 138,5 143,8
0,0133 100 150,6 158,4 164
0,0267 200 172,4 180,7 186,5
0,0533 400 196,0 205,5 212,2
0,1018 760 220,4 230,5 237,7
167
a)
6}
Рис. 5-12. Типы ректификационных колони.
а — с туннельными желобчатыми колпачками; б — с капсульными колпачками; в — с ситчатыми
тарелками; г —с насадками из колец Рашига: / — тарелка с туннельными колпачками; 2 — тарелка
с капсульными колпачками; 3— ситчатая тарелка, 4 — насадка; 5—сливные трубки; 6 — тарелки
для равномерного орошения насадки, 7 — люк; 8-- опорная решетка.
31
В табл. 5-6 показана зависимость температур кипения некоторых
смесей от давления. Данные таблицы показывают, что если, наприм-ер,
перегонку паранитротолуола вести при атмосферном давлении с тем-
пературным перепадом 20 °C, то необходимо применять греющий пар
с давлением 34,4-105 Па (35 кгс/см2). При вакууме можно осуществить
перегонку греющим паром с давлением (4,9-и 5,9) • 105 Па.
В большинстве практических случаев нагрев и испарение смеси
в ректификационных установках проводят «глухим» водяным паром, т. е.
паром, поступающим в змеевик. Обогрев «острым» паром (поступаю-
щим непосредственно в жидкость) ведется только в установках для
перегонки высококипящих компонентов в смеси с водяным паром. При-
менение топочных газов для
целей обогрева не нашло ши-
рокого распространения, так
как при этом не удается обе-
спечить точное регулирование
процесса, необходимое для ра-
боты ректификационных уста-
новок.
Другие высокотемпера-
турные теплоносители, а так-
же электрический обогрев, до-
пускающие точную регулиров-
Рис. 5-13. Колпачковые тарелки ректифика-
ционных колонн с капсульными колпачками.
1 — колпачок; 2 — крепление колпачка; 3 — сливная
труба; 4 — диск тарелки.
ку процесса, не нашли приме-
нения вследствие сравнительно
высокой стоимости необходи-
мого для этого оборудования
и большей сложности эксплуатации его.
Типы и конструкции ректификационных колонн1.
Ректификационные колонны, схемы которых представлены на рис. 5-12,
в зависимости от их внутреннего устройства для распределения стекаю-
щей флегмы и восходящих паров разделяются на колпачковые (с кап-
сульными— рис. 5-12,6 и туннельными — рис. 5-42,а колпачками, ситча-
тые— рис. 5-12,в) и насадочные — рис. 5-12,г. Колонна представляет
собой вертикальный цилиндр, изготовленный из стали, чугуна или кера-
мики и состоящий из нескольких царг, соединенных герметично при
помощи разъемных фланцев.
Капсульные колпачки или колпачки с круглым сечением в большин-
стве случаев применяются в колоннах небольших диаметров при диа-
метрально противоположном расположении приточных и сливных тру-
бок на рис. 5-12,а или при периферийном и радиальном сливе флегмы,
когда жидкость течет в плоскости тарелки в одном направлении, а по
высоте колонны — зигзагообразно. Такой перелив флегмы может приме-
няться и для тарелок с другими типами колпачков.
Для больших диаметров колонн применяются тарелки с туннель-
ными колпачками (рис. 5-12,6), так как, например, при диаметре колон-
ны 3 м на одной тарелке вместо- 284—288 капсульных колпачков доста-
точно по условиям тепло- и массообмена разместить только 20 туннель-
ных колпачков.
Исследования последних лет показали, что неравномерность рабо-
ты тарелок и перемешивание жидкости на тарелке более существенны,
чем унос и неравномерность контакта. Особенно ухудшает работу таре-
лок поперечная неравномерность, возникающая на прямоугольных, тун-
нельных и желобчатых тарелках. Поэтому колонны с туннельными
колпачками снимаются с производства.
1 Данные о типоразмерах отечественных ректификационных колонн см. в [Л. 6,
20, 48].
169
В промышленности применяются также ректификационные колонны
с ситчатыми (решетчатыми и дырчатыми) тарелками (рис. 5-12,в и 5-14),
на которых слой жидкости (флегмы) удерживается давлением восходя-
щего потока пара, прорывающегося через отверстия в ситах и барботи-
рующего через слой жидкости. Жидкость, как и в колпачковых тарел-
ках, перетекает с тарелки на тарелку по переточным трубам; предель-
ный уровень жидкости на тарелке регулируется высотой сливной трубки.
В колоннах с тарелками такой конструкции сливные устройства пере-
стают работать при уменьшении количества поднимающегося по колон-
не пара, когда скоростной напор становится недостаточным для поддер-
жания соответствующей высоты слоя жидкости на тарелке. В этом
случае жидкость стекает на нижележащую тарелку через те же отвер-
Рис. 5-14. Ситчатые тарелки ректификационных колонн.
а — решетчатая тарелка; б — дырчатая тарелка; 1 — тарелки; 2 — сливные трубы;
3 — опорное полукольцо.
стия, через которые проходит пар, и работа тарелки происходит по
принципу работы ситчатых тарелок провального типа: в них паровая и
жидкая фазы контактируют при противоточном движении струй без
достаточного барботажа, чем может ухудшать тепло- и массообмен,
поэтому все большее значение приобретают новые типы тарелок — кла-
панные, струйные с отбойниками и др.
При выборе типа контактирующих элементов следует также иметь
в виду, что решетчатые и другие провальные тарелки чувствительны
к инкрустирующим примесям, но не боятся механически взвешенных
в жидкости частиц, если их размеры меньше размеров отверстий в та-
релке.
В насадочных колоннах (рис. 5-12,г) насадка состоит из колец Ра-
шига (металлических, фарфоровых, керамических), пустотелых шаров,
дробленого кокса, кварца и других материалов. Выбор формы насадки
и материала ее диктуется в каждом отдельном случае физико-химиче-
скими свойствами разделяемой жидкости смеси и условиями ректифи-
кации.
Для успешной работы насадочных колонн следует стремиться во
всех случаях к возможно более равномерному распределению стекаю-
щей жидкости по всему сечению колонны. Такому распределению жид-
кости благоприятствуют однородность формы и размеров насадки, мак-
170
Рис. 5-15. Принципиальная схема и царга
ректификационной колонны с вращающи-
мися тарелками.
1 — корпус; 2 — электропривод; 3 — вращающаяся
тарелка; 4 — неподвижная тарелка; 5 — вал; 6 —
подшипник.
симально возможная скорость восходящего потока пара, а также строго
вертикальная установка самой колонны. Опыты показали [Л. 5], что
первоначально достигнутая равномерность распределения жидкости
постепенно нарушается по мере стекания ее, так как пар стремится
счтеснить жидкость к периферии и занять центральную зону слоя насад-
ки. Для борьбы с этим явлением в колоннах с высоким слоем насадки
последний разбивают на несколько слоев меньшей высоты, отделенных
друг от друга свободным, незаполненным пространством, как это пока-
зано на рис. 5-12,г. Кроме того, над каждым слоем насадки устанавли-
вают распределительные тарелки, создающие более равномерное оро-
шение насадки и обеспечивающие равномерное распределение пара по
сечению колонны.
Тарельчатые колонны имеют ряд преимуществ перед насадочными
колоннами. Они допускают большие нагрузки по пару и жидкости, обес-
печивают высокую турбулизацию потоков и хороший контакт между
паром и жидкостью, не имеют застойных зон, позволяют производить
отбор промежуточных продуктов с тарелок и т. д. Однако по сравнению
с насадочными колоннами они имеют большее гидравлическое сопро-
тивление, поэтому они чаще применяются в ректификационных колон-
нах, чем в абсорбционных с вентиляционными установками.
В настоящее время появи-
лись компактные высокопроизво-
дительные ректификационные ко-
лонны с вращающимися тарелка-
ми. На рис. 5-15 показана прин-
ципиальная схема ректификаци-
онной колонны с вращающимися
тарелками, служащей для выде-
ления из воды концентрата тя-
желой воды. Подобная колонна
производительностью 8 л/ч при
флегмовом числе, равном 20, име-
ет диаметр всего 150 мм и число
тарелок 1 250, что совершенно не-
соизмеримо с таковыми для лю-
бой из обычных колонн. Несмо-
тря на это, высота колонны со-
ставляет всего лишь 10,2 м, вклю-
чая соединительные части. Та-
релки представляют собой кони-
ческие воронки с углом наклона
стенок около 40°. Половина таре-
лок по периферии прикрепляется
к неподвижному цилиндрическо-
му корпусу 1, другая половина
прикрепляется у центра к вра-
щающемуся валу 5 и вместе с ним вращается. Вращающиеся тарелки 3
чередуются с неподвижными тарелками 4. Между краями неподвижных
тарелок и валом, с одной стороны, и вращающимися тарелками и кор-
пусом— с другой, оставляются зазоры. Расстояние между двумя сосед-
ними тарелками (неподвижной и вращающейся) составляет всего 8 мм,
чем и объясняется малая высота колонны. Диаметр вала равен 25 мм;
число оборотов его 240 в минуту; мощность привода вала 0,5 кВт. Вал
по высоте охватывается через каждые 1,5 м шариковым подшипником,
работающим без смазки. Для удобства монтажа и разборки весь кор-
пус составляется из отдельных царг длиной 1,5 м, соединяемых флан-
цами; каждая царга содержит опору для шарикового подшипника.
171
Флегма поступает в верхнюю часть колонны, опускается по непо-
движной тарелке и у центра переливается на лежащую ниже вращаю-
щуюся тарелку. Под влиянием центробежного эффекта флегма ползет
по вращающейся тарелке вверх, доходит до ее верхней кромки на пери-
ферии и в виде сплошной кольцевой пленки переливается на лежащую
ниже неподвижную тарелку. Пар все время движется над поверхностью
флегмы противотоком. Дисперсность пленки на вращающихся тарелках
обеспечивает активные тепло- и массообмен, благодаря чему к. п. д.
тарелок доходит до 85% •
В последние годы промышленное применение получил метод пере-
гонки — молекулярная дистилляция высокомолекулярных органических
смесей при вакууме 10-3—10-4 мм рт. ст. При такой перегонке'Свободный
пробег молекул дистиллируемой жидкости по величине равен или боль-
ше расстояния между испаряющей и конденсирующей поверхностями.
Этот способ позволяет выделить из жидкости неустойчивые вещества
без термического разложения их и обеспечивает возможность получе-
ния, например, витаминов А и Е, пенициллина, специальных масел для
диффузионных насосов и т. п.
5-4. ОПРЕДЕЛЕНИЕ ЧИСЛА ТАРЕЛОК1 И РАСХОДА ТЕПЛА
В УСТАНОВКАХ ДЛЯ РЕКТИФИКАЦИИ БИНАРНЫХ СМЕСЕЙ
Определение числа тарелок1. Графо-аналитический рас-
чет теоретического числа тарелок ректификационных колонн осно-
ван на условии существования равновесных состояний пар — жидкость
и по существу сводится только к определению маосопередачи, без учета
теплообмена.
Расчет производится со следующими допущениями. Предполагает-
ся, что разгоняемая смесь вводится в колонну предварительно подогре-
той до температуры кипения ее на данной тарелке (на которую подается
смесь) и за счет тепла, выделяющегося при конденсации 1 моля пара,
испаряется 1 моль жидкости, при этом количество молей пара, подни-
мающегося по колонне, и количество флегмы, стекающей вниз, остаются
постоянными для всех тарелок; изменяется только состав пара и флег-
мы. Далее принимается, что конденсат в дефлегматоре имеет тот же
состав, что и пар, поднимающийся с самой верхней тарелки. Тепло, по-
требное для парообразования перегоняемой смеси, сообщается ей по-
верхностью нагрева, не разжижая жидкость в перегонном кубе.
Для расчета примем следующие обозначения:
хт и хп — содержание летучего компонента в жидкости на т-й и n-й та-
релках колонны в моль-процентах (нумерация тарелок для верхней и
нижней частей колонны устанавливается сверху вниз); уп — моль-про-
цент содержание летучего компонента в паре, поднимающемся с п-та-
релки колонны в моль-процентах.
Считаем заданными:
ха — содержание летучего компонента в дистилляте (готовом продукте),
вытекающем из дефлегматора; xF — то же в начальной смеси; xw — то
же в кубовом остатке; F — число молей начальной смеси, приходящейся
на 1 моль дистиллята (конечного продукта); Д — число молей флегмы,
возвращающейся в верхнюю часть ректификационной камеры, приходя-
щейся на 1 моль готового продукта (флегмовое число); R'— то же для
нижней части колонны; W — количество остатка в молях на 1 моль гото-
вого продукта, выпускаемое из колонны; V — число молей пара на 1 моль
готового продукта, поднимающегося с какой-либо тарелки колонны.
1 Методика и формулы для определения основных конструктивных размеров
ректификационных колонн и отдельных ее деталей (тарелок, колпачков, сливных труб
и т. д.) приведены в [Л. 12, 20, 34, 48].
172
Для упрощения расчета количества ди-
стиллята —тотового продукта, выводимого
из установки в единицу времени, принима-
ем D=1 моль.
На рис. 5-16 изображена схема ректи-
фикационной установки с указанием приня-
тых обозначений. Согласно схеме для пер-
вой (верхней) тарелки без учета потерь ве-
щества имеем следующее уравнение мате-
риального баланса:
Vy2+Rxd= Vyi+Rxi. (5-12)
Принимаем, что в дефлегматоре кон-
центрация смеси не изменяется, т. е. у1=х,г,
кроме того, имеем в виду, что расчет ректи-
фикационной колонны мы ведем на 1 моль
отбираемого дистиллята, т. е. V=R+D=
=7? + 1. Тогда уравнение (5-12) запишется
в виде
(Д + 1)г/2—(5-13)
откуда
Рис. 5-16. Принципиальная схе-
ма к материальному балансу
ректификации.
а для п-й тарелки
Обозначив
R 4- 1 А"’ + R + 1 ’
R+1
Xd
«+1
(5-14)
получим
Уп—Ахп_1 + В.
(5-14а)
Ю0\—
-5d-
90-
80-
*> I
Й 6 7/7
50
§ 1 90
ы|с£ 1
i ™L
!.г
I 0т 10 20 30.90 50 50 70 80 80^100
Состав живности, моль-%
Рис. 5-17. Определение теоретического
числа тарелок по диаграмме равновесия.
{fF=69,3
Выражение (5-14а) —это уравнение прямой линии с тангенсом угла
наклона к оси абсцисс, равным А, отсекающей на оси ординат отрезок В
(рис. 5-17). Его называют уравнением концентрации для верхней
(укрепляющей) части колонны, а прямую, выраженную этим уравне-
нием, — линией концентрации верхней части колонны.
Уравнение концентрации для
нижней части колонны может быть
составлено на основании следую-
щих зависимостей. Согласно схеме
на рис. 5-16 при неизменном 'коли-
честве пара, поднимающегося по ко-
лонне, и отсутствии потерь вещества
уравнение материального баланса
всего потока для нижней тарелки
может быть представлено в виде
Vy + R'Xm-^Vym + R'Xv,. (5-15)
Делаем также допущение, что
пар, поднимающийся из перегонно-
го куба, имеет одинаковый состав
с флегмой, стекающей с последней
тарелки или остатком в перегонном
173
кубе, т е y—xw\ кроме того, согласно схеме на рис. 5-16 R'=R+F,
а У=/?+1.
Подставив эти значения в уравнение (5-15), получим:
(R + 1) Хц;-\- (R 4-Г) Хп,—' = (R +1) ут-\~ (R + F) хгс,
откуда
R + 1 . F — 1 ,г
Хт - 1 R _|_ р Ут д_|_ f Xw (5-1 6)
Введя обозначения
RA- 1 А, F—\ R,
R+~F = A И-^Х^В,
найдем окончательно:
xm-i=A'ym+B'. (5-16а)
Это уравнение прямой с тангенсом угла наклона к оси ординат,
равным А', отсекающей на оси абсцисс отрезок В'; оно называется урав-
нением концентрации для нижней (исчерпывающей) части колонны.
Уравнения (5-14) и (5-16) показывают, что направления линий кон-
центраций зависят только от флегмового числа R, так как величина F,
входящая в выражения для коэффициентов, является величиной по-
стоянной.
Графическое определение теоретического числа тарелок для разгон-
ки бинарной смеси производят на диаграмме равновесия (рис. 5-17).
Для этого проводят диагональ OR и вертикальные прямые x=xw, х—х^
и x=xF, отмечают точки N и W пересечений диагонали соответственной
с первой и второй из этих прямых и точку Ft пересечения третьей пря-
мой с кривой равновесия. Затем по уравнению (5-14) наносят линию
концентрации MR для верхней (укрепляющей) части колонны; чтобы ее
построить, необходимо определить только отрезок ОМ, равный В =
=ха/(7?-г1), так как точка N определяется из условия у\=-х,1 и лежит
на диагонали.
При наличии линии концентрации для верхней части колонны по-
строение линии концентрации нижней (исчерпывающей) части колонны,
удовлетворяющей уравнению (5-16), не требует вычислений, так как
искомой линией концентрации является прямая FW. В самом деле, одной
точкой этой линии должна быть точка F — обязательная общая точка
для обеих рабочих линий, а другой точкой является точка W — соответ-
ствующая концентрации смеси в кубовом остатке.
Определение числа тарелок производят проведением горизонталь-
ных и вертикальных отрезков между кривой равновесия и рабочими ли-
ниями NF и FW. Начиная от точки N, проводят горизонталь 1 до пере-
сечения с кривой равновесия, затем вертикаль до пересечения с рабочей
линией, после чего проводят горизонталь 2 и т. д. До точки F отрезки 1,
2, 3, 4 и 5 проводят от верхней рабочей линии; после точки F процесс
идет уже в нижней части колонны и горизонтальные отрезки 6, 7, 8, 9,
10 и 11 проводят от нижней рабочей линии. Последнюю горизонталь 11
проводят так, чтобы она пересекала прямую xw. Число полученных при
построении ступеней или треугольников соответствует числу теорети-
чески необходимых тарелок ректификационной колонны. Каждый гори-
зонтальный участок ступени соответствует изменению концентрации
флегмы на тарелке, а вертикальный — изменению концентрации паров
над этой тарелкой.
Более простым способом, предложенным П. Д. Лебедевым, теоре-
тическое число тарелок можно определить при помощи фазовой диа-
граммы, как это показано на рис. 5-18. Для этой цели, как и в предыду-
щем случае, проводят прямые xw, xF и хц. Построение процесса начинают
от точки А. Процесс в дефлегматоре при полной конденсации паров
174
соответствует вертикальной линии АВ. Далее из точки В проводят гори-
зонтальную линию ВС, которую делят на отрезки CD и DB так, чтобы
отношение DBICD было равно выбранному флегмовому числу R Из точ-
ки D проводят вертикаль DE, соответствующую процессу ректификации
(частичной конденсации пара) на данной тарелке, затем проводят гори-
зонтальную линию EF, которую делят на два отрезка в прежних соот-
ношениях, и т. д. Определение числа
дает те же результаты (11 тарелок
для примера 5-4), но более просто,
так как оно не требует построения
линий концентраций.
Полученное графическим мето-
дом число тарелок из-за несовер-
шенства аналитического описания
процессов тепло- и массообмена
увеличивают в некоторых случаях
в 2 раза. Опыты многих исследова-
телей показывают, что к. п. д. та-
релки зависит от многих факторов
и ,в первую очередь определяется:
а) величиной поверхности контакта
паровой и жидкой фаз; б) скоростью
прохождения пара и жидкости через
колонну; в) расстоянием между та-
релками; г) высотой слоя жидкости
тарелок по фазовой диаграмме
Рис. 5-18. Определение теоретического
числа тарелок по /-х-диаграммс.
на тарелке, через которую проходят
пары; д) давлением в колонне;
е) физико-химическими свойствами
перегоняемой смеси и т. п.
Зависимость между практически выбираемым и теоретическим чис-
лом тарелок определяется формулой
п=пт/т],
(5-17)
где пт и п — теоретическое и практически выбираемое число тарелок;
— к. п. д. тарелки.
В табл. 5-7 приводятся значения к. п. д. колпачковых колонн
4 = 7/) для смеси этиловый спирт — вода при оптимальных значе-
ниях скорости tiapa в колонне.
Таблица 5-7
Коэффициент полезного действия колпачковых колонн '>} = /(/’, Н)
Рабочее давление р Расстояние между тарелками И, мм
МПа мм рт. ст. 135 200 270 415
0,0066 50 0,62 0,60 0,66 0,68
0,0133 100 0,66 0,68 0,70 0,72
0,0334 250 0,68 0,70 0,72 0,74
0,1013 760 0,70 0,80 0,83 0,88
Как уже было указано выше, направление линии концентрации
зависит только от величины флегмового числа, а рациональный выбор
его определяет капитальные затраты и экономичность работы ректифи-
кационной установки непрерывного действия. Небольшое значение флег-
мового числа вынуждает ставить высокую колонну с большим числом
тарелок, а увеличение его вызывает увеличение расхода греющего пара
на колонну и охлаждающей воды в дефлегматоре.
175
Для приближенных расчетов принимают флегмовое число Д=(1,5-:-
2,5)ДМин, где Дмин—минимально возможное число, которому соответст-
вует бесконечно большое число тарелок, определяемое как
Дыпн
Xd— Ур
Ур Хр
(5-18)
Рис. 5-19. Изменение концентра-
ции пара и движущая сила Лу на
рабочей тарелке при ректифика-
ции.
где Xd —содержание легколетучего компонента в дистилляте; xF — со-
держание летучего компонента в исходной жидкости; yF—содержание
легкокипящего компонента в паре, равновесном с исходной жидкостью.
Координаты ур, xf и Хи показаны на графике 'рис. 5-17.
Более точные значения Дмин определяются и более точными мето-
дами определения числа тарелок и технико-экономическими расчетами.
Существуют более точные методы определения числа действитель-
ных тарелок (Л. 10, 33, 48]*. В настоящее время считается, что выраже-
ние движущейся силы через разности эн-
тальпий более точно, чем через разность
концентраций. Поэтому как в отечествен-
ной, так и зарубежной литературе реко-
мендуется метод определения теоретиче-
ского числа тарелок ректификационных
колонн с применением Д-ху-диаграмм.
Однако, как показывают сравнительные
расчеты, этот метод не дает существен-
ной точности, так как для определения
действительного числа тарелок необходи-
мо вводить в расчет к. п. д. тарелки, что
может вносить большую погрешность.
А. Н. Плановским и А. Г. Касатки-
ным предложен метод расчета ректифи-
кационных тарелочных аппаратов, бази-
рующихся на уравнениях массопередачи
(по численным значениям объемных коэффициентов массопередачи), на
основе которых на r/x-диаграмме строится кинетическая кривая, которая
проводится между линиями равновесия и рабочей линией.
Предлагаемый указанными авторами метод дает возможность опре-
делить реальное число тарелок, не вводя в расчет к. 5п. д. тарелок.
Идея этого метода состоит в том, что в реальных условиях рабочая кон-
центрация пара на тарелке над жидкостью будет всегда меньше равно-
весной z/np и положение точки С согласно рис. 5-19 будет определяться
отношением
____ ^*п Уп+1 emV тар
v У\ — Уп
где ту тар — число единиц переноса.
При условии постоянства состава жидкости на тарелке
т —In У*п — уп+х —kyff-rt _22,4Tpc<fkllf
Утар m Gy збОО^Г.р ’
(5-19)
(5-20)
где ky,f — коэффициент массопередачи, отнесенный к 1 м2 площади та-
релки, кмоль/(м2-с) (Д#=1); Gy—расход пара, кмоль/с; wy — скорость
потока пара, отнесенная к свободному сечению аппарата, м/с; То, р0—
абсолютная температура и давление пара в нормальных условиях,.
* Расчет процессов разделения жидких смесей на ЭВМ рассмотрен в [Л. 12].
176
Т, р — в рабочих условиях; 22,4 — объем 1 кмоля пара при ро. То,
м3/кмоль; <р=/тар/^в — отношение рабочей площади тарелки к свобод-
ному сечению аппарата.
Для каждого значения х определяют величину Су по формуле (5-19)
и затем вычисляют величину отрезка ВС, как это показано на рис. 5-20:
ВС=АС/СУ.
От точек С на кривой равнове-
сия откладывают отрезки СВ и про-
водят кинетическую кривую через
точки В^ В2 и т. д. Между кинетиче-
ской кривой и рабочими линиями
концентрации для верхней и нижней
части колонны строят ступени, об-
щее число которых и определяет не-
обходимое число реальных тарелок
(без учета уноса жидкости с нижних
тарелок на верхние тарелки). Этот
метод позволяет определять также
число реальных тарелок при пере-
менном значении коэффициента мас-
сопередачи с учетом уноса [Л. 34, 48].
Накопление экспериментальных
данных по значениям коэффициен-
тов массопередачи позволяет перей-
ти к более точным методам расчета
ректификационных колонн.
XW XF Xj)
Рис. 5-20. Определение числа реальных
тарелок для процесса ректификации по
кинетической кривой на диаграмме рав-
новесия.
Пример 5-4. Определить число тарелок для разгонки смеси из сероуглерода CS2
и четыреххлористого углерода СС14 от начальной концентрации легкокипящего компо-
нента €S2, равной 30% массы, до конечной концентрации, равной 90%. Дефлегматор
производит полную конденсацию паров. В кубовом остатке содержится 1% CS2. Про-
цесс идет при давлении паров наверху колонны, равном 1,01510s Па (760 мм рт. ст.).
Схема установки соответствует схеме на рис. 5-9,6. Расчет выполнить графо-аналитиче-
ски при помощи диаграммы равновесия у — хи фазовой диаграммы t — х.
Решение. 1. Для смеси сероуглерод — четыреххлористый углерод по данным
табл. 5-3, примера 5-1 на рис. 5-17 вычерчиваем кривую равновесия.
2. Определяем молекулярный процент содержания в начальной смеси летучего
компонента по формуле (5-4); молекулярная масса CS2, цо=76.14; молекулярная масса
СС14, ць = 153,84.
30
100’76,14
Хр =--------------— = 46,5% CS2,
F 30 70
76,14 '153,84
где 30 и 70 — количество процентов массы CS2 и CCU.
Молекулярный процент содержания летучего компонента в дистилляте
90
100 76,14
Xd = -90------IO” =94’8°/oCS2.
76,14+153,84
Молекулярный процент содержания летучего компонента в остатке
__________1____= 1,9o/oCS2
1 99
76,14 ' 153,84
На рис. 5-17 проводим диагональ ОКивертикальныепрямыехю=1,9%; Xd=94,8%
и Хр=46,5%. Отметим точки N и W пересечения диагонали с первыми двумя прямыми
и точку F\ пересечения кривой равновесия с третьей прямой.
12—1128 177
Найденной точке Ft соответствует концентрация CS2 в паре г/г=69,3%, равно-
весном с жидкостью, концентрация CS2 в которой Хг=46,5°/о-
3. Строим линии концентраций. Определяем минимальное значение флегмового
числа по формуле (5-19)
xa — yF 94,8 — 69,3
#мин= ур — Хр —69,3 — 46,5 -1’12-
Принимаем флегмовое число
/?=27?мин=2,24.
Вычисляем отрезок ОМ=В, отсекаемый линией концентрации для верхней части
колонны на оси у, по формуле
94,8
B = R+ 1 “ 2,24+ 1 = 29'3’
В качестве рабочей линии укрепляющей части колонны проводим прямую NM.
Точу пересечения этой прямой с xF соединяем с точкой W, в результате чего получаем
рабочую линию FW исчерпывающей части колонны.
4. Теоретическое число тарелок определяем путем проведения горизонтальных и
вертикальных отрезков между кривой разновесия и линиями концентрации. Левее точ-
ки F процесс идет уже в нижней части колонны. Последнюю горизонталь проведем так,
чтобы она пересекала вертикаль xw. Для условий примера теоретически необходимо
11 тарелок, из них 5 для верхней и 6 для нижней части ректификационной колонны.
Приняв среднее значение к. п. д. тарелки т]=0,5, получим действительное число
тарелок:
«=11/0,5=22.
Для определения числа тарелок в /-x-диаграмме проводим, как это показано на
рис. 6-18, также прямые хю = 1,9%; х₽=46,5% и xd=94,8%. Из точки А проводим вер-
тикальную линию АВ, соответствующую процессу полной конденсации паров в дефлег-
маторе. Далее из точки В проводим горизонтальную линию ВС, которую делим на
отрезки £>В/£>С=2,24 (соответственно выбранному флегмовому числу). Из точки D
проводим вертикаль DB, соответствующую процессу ректификации, и горизонтальную
линию EF, которую делим в прежнем отношении, и т. д. В результате построения по-
лучаются 11 ступеней, или 11 теоретических тарелок, как и в предыдущем случае на
у-х-диаграмме. Приняв тот же к. п. д. тарелки т]=0,5, получим 22 тарелки для действи-
тельной колонны.
Определение расхода пара в ректификационных
установках непрерывного действия.
Для составления тепловых балансов введем следующие обозна-
чения:
Gd — количество получаемого дистиллята, кг/ч; Gw — количество отхода,
выпускаемого из перегонного куба, кг/ч; гА и г и— теплота парообразо-
вания компонентов А и В, кДж/кг (ккал/кг); сА, св и ст — теплоемкости
компонентов Л и В и теплоемкость смеси этих компонентов, кДж/(кг-°C);
tw — температура кубового остатка; Д— количество флегмы, кг/кг или
моль/моль дистиллята; /кип — температура кипения начальной смеси
в кубе, °C; td— температура дистиллята, °C; aF, ad и aw — процентные
весовые содержания компонента А в начальной смеси, дистилляте и от-
ходе; D — расход греющего пара, кг/ч; i — энтальпия греющего пара,
кДж/кг (ккал/кг); гк —энтальпия конденсата, кДж/кг (ккал/кг); Ж
и U/2— расходы охлаждающей воды в дефлегматоре и конденсаторе-
охладителе, кг/кг; t'2 и t"2— начальная и конечная температуры во-
ды, °C.
В непрерывно действующих ректификационных установках началь-
ная смесь обычно поступает в колонну подогретой до температуры кипе-
ния. В этом случае часовой тепловой баланс складывается из следую-
щих частей:
Qi — тепло, вносимое начальной смесью,
Qi= GFcFtF;
Q2 — тепло, вносимое в колонну греющим паром,
Q2—D (i its);
178
Q3— тепло, вносимое флегмой,
__г; I? f г аа । г 1 во аа \ .
\ л ЮО 'св юо j d’
Q4 — тепло, уносимое парами, поднимающимися с верхней тарелки
в дефлегматор.
г< _п /jipi \ ( г I г । в0 Дд \ । ga । ., 100 ад \ f
Q4 — + P. гл 100 "f" 100 / • ,C/ 100 ‘ CB 100 ) d
Q5 — тепло, уносимое с непрерывно выпускаемой жидкостью (отхо-
дом из перегонного куба),
р, _ ( Що | „ ЮО Л:,п \ , .
^5 — 100 ~>Св 100 у1
Qe— потеря тепла в окружающую среду.
Уравнение теплового баланса для колонны имеет вид:
Qi+Qa+Qs^ Qi+Qs+'Cta
откуда расход тепла на колонну определяется равенством
Qz=D(i—iK) = Q4+ Qs + Qe—(Q1 + Q3),
а расход греющего пара
Р Qa + Qs + Qe —(Qi + Qa) (g Qi)
Z lK
Расход воды в дефлегматоре и конденсаторе определяется из урав-
нения теплового баланса дефлегматора
Qd = (t"2 -t'2) = GdR (rA + rB (5-22)
и уравнения теплового баланса конденсатора
Qk = ^2С2 (^”г ^2) = Gd £ ~j 4- гв 100 ) 4"
4“ (^а Ж) 4” св Тост-) ] (5-23)
Температуры t'2 и /"2 в уравнениях (5-22) и (5-23) могут иметь раз-
личные значения.
Уравнение теплового баланса конденсатора-холодильника состав-
лено без учета изменения процентного содержания массы легкокипяще-
го компонента после дефлегматора.
При подсчете количества тепла на испарение смеси теплота раство-
рения не учитывается.
Пример 5-5. Определить расход пара и охлаждающей воды иа разделение смеси
сероуглерод CS2 — четыреххлористый углерод CCI4 в непрерывно действующей ректифи-
кационной установке для условий предыдущего примера при следующих дополнитель-
ных данных: производительность установки 0,139 кг/с (500 кг/ч) готового продукта;
параметры греющего пара: р=3,92-105 Па (4 кгс/см2) (абс.); t=2 740 кДж/кг
(655 ккал/кг); /н = 143°C; параметры воды, охлаждающей дефлегматор и конденсатор:
^2—10 °C и t”t=30 °C; теплота парообразования CS2 гА =350 кДж/кг (84 ккал/кг) и
для CCU гв = 194 кДж/кг (46,4 ккал/кг), теплоемкость CSa Сл = 1,0 кДж/(кг-°С)
[0,24 ккал/(кг • °C)] и для ССЦ св=0,837 кДж/(кг-°С) [0,2 ккал/(кг-°С)]. Потери тепла
в окружающую среду поверхностью колонны оценить в 5% общего расхода тепла. При-
нять, что в дефлегматоре происходит только конденсация флегмы, а в конденсаторе —
конденсация и охлаждение готового продукта до /Ков=20°С.
Решение. Определяем по /-х-диаграмме (рис. 5-18) температуру смеси, посту-
пающей в колонну (подогретой до температуры кипения), /В=59°С (точка я), темпе-
12* 179
ратуру смеси, уходящей из колонны, /Ю = 76°С (точка Ь) и температуру смеси после
дефлегматора td—47 °C (точка А).
1. Количество смеси, поступающей в колонну и уходящей из колонны в виде остат-
ка, определяем из материального 'баланса колонны
GF = Gd+G w и GpCt-p — Gwdw^
где Gr —расход сырой смеси, кг/с; Gd— расход готового продукта, равный 0,139 кг/с;
G.a — расход кубового остатка, кг/с; аг, ad и а„,— весовые процентные содержания
низкокипящего компонента в жидкости.
Из предыдущего примера имеем:
«к=30%, ва=90.% и аю=1°/о.
Подставив цифровые значения, получим:
CF =0,139+G№ и 30Gf=90-0,139+1 Gw,
откуда Gp=0,426 кг/с и Gw =0,288 кг/с.
2. Теплота, вносимая начальной смесью,
Qi=GpCF/p=0,426 • 0,88 • 59= 22,1 кДж/с,
где
aF 100 — aF зо 70
CF = CA wo+ св 100 ~ 1,0 W0 °1837 W0 =0,88 кДж/(кг-°С).
3. Тепло, вносимое в колонну греющим паром,
Q2=D(i—fK) =D(2 740—598).
4. Тепло, вносимое флегмой,
/ ал 100 — ал \
Q* = GaR сАуоб+ ]св jqq j td =
/ 90 , 10 \
=0,139-2,24 I 1,0 j^4==0T337=j^4-47=14I3-Kfl»/c.------
5. Тепло, уносимое парами, поднимающимися с верхней тарелки в дефлегматор,
Q4 = G„(1+R)
«а . ЮО —\ ( ал 100 —ад \
гД100'|'!гв 100 100 f
90 , 10 \ , ( 90 , 10 \
юо+194 woj + ^1’0100+°>837 ЮО }
== 171,5 кДж/с.
6. Тепло, уносимое с непрерывно выпускаемой жидкостью (отходом) из перегон-
ного куба,
Q5 = Gw (са ЮО1св 100 ~~ 0-288 (1,0 jqq +0,837 ।gg^ 76 = 22,8 кДж/с.
7. Расход пара
1,05 [Q4 + Q5—(Q,+ Q3)] __ 1,05 [171,5 + 22,8 —(22,1 + 14,3)]
i — is ' 2 740 — 598
8. Расход охлаждающей воды в дефлегматоре
/ ал , 100 — аа \ „ . „ „ ( „ 90 , 10 \
GiR \ rA WOгв W0 ) 0,139-2,24 ^350 jqq +194-j-ggy
= с, — = 4,187 (30— 10)
0,0755 кг/с.
1,25 кг/с.
9. Расход охлаждающей воды в конденсаторе
г I ( 10° —аа > / аа . 100 —аа > , .1
I V^lOO-1- rB 100 J ^Л100тсВ 100 j(ra—fKoE)j
2 C2(t'r2 - t'z} "I" C2 ((ГГ2- t'i}
„ Г / 90 , 10 \ / 90 . 10 1
°’139 [(35°Тоо + 194Гоо) + (1-°T66+0-837 wo <48 - 2°) j
4> 18 (30 — 10) =0,602 кг/с.
180
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Чем отличается .перегонка жидкой смеси от выпаривания -растворов? Какие
условия необходимы для перегонки жидкой смеси?
2. Для каких бинарных смесей применим закон Дальтона и для каких — закон
Рауля?
3. Какие особенности имеет перегонка взаимно нерастворимых смесей? Что такое
азеотропное состояние смеси и можно ли перегнать азеотропную смесь?
4 Зависит ли состав паров взаимно нерастворимых бинарных смесей от процент-
ного содержания легкокипящего компонента в жидкой фазе?
5. В чем сущность перегонки в водяном паре нерастворимых в воде бинарных
смесей? Какова область применения ее, какие она имеет преимущества и недостатки?
6. Можно ли применением перегонки под вакуумом снизить температуру кипения
высокотемпературной жидкой смеси? Какие это дает преимущества?
7. Чем отличается процесс дефлегмации от процесса конденсации? Изобразите
его в 1-х-диаграмме.
8. В чем сущность процесса ректификации? Изобразите его в /-х-диаграмме.
9 Происходит ли процесс перегонки бинарной смеси в области перегретых паров?
10. Нарисуйте в t х-диаграмме процессы нагрева, испарения, дефлегмации и кон-
денсации и объясните, какие принципиальные отличия имеют эти процессы для двух-
компонентной системы по сравнению с однокомпонентной (для чистой воды).
11. Каковы особенности перегонки бинарных полностью растворимых азеотропных
смесей? В каком случае в погоне и в каком случае в остатке получается азеотропная
смесь?
12. Постройте по диаграмме давлений фазовую /-х-диаграмму и диаграмму рав-
новесия у-х для бинарной азеотропной смеси с максимальной температурой кипения.
13. Напишите уравнение материального баланса для верхней и нижней тарелок
ректификационной колонны непрерывного действия.
14. Определите теоретическое число тарелок по t-x-диаграмме, если флегмовое
число равно 2.
15. Как изменяются: число тарелок ректификационной колонны, расход пара и
охлаждающей воды в дефлегматоре с увеличением флегмового числа?
16. Какое число тарелок потребуется, если точка пересечения линий концентрации
на ^/-x-диаграмме будет лежать на кривой равновесия?
17. Какие ректификационные колонны: с колпачковыми тарелками, ситчатыми та-
релками или насадкой из колец Рашига — более просты в изготовлении?
18. Какие ректификационные аппараты более компактны: с неподвижными или
вращающимися тарелками?
19. Какой теплоноситель (водяной пар, топочные газы или высококипящие ве-
щества) имеет наибольшее применение для нагрева и разгонки смеси в ректификацион-
ных установках?
20. Какие ректификационные установки более экономичны в тепловом отношении:
периодического или непрерывного действия и какие из них проще автоматизировать?
ГЛАВА ШЕСТАЯ
СУШИЛЬНЫЕ УСТАНОВКИ
6-1. ЕСТЕСТВЕННАЯ И ИСКУССТВЕННАЯ СУШКА МАТЕРИАЛОВ
Сушкой называется термический процесс удаления из твердых ма-
териалов или растворов содержащейся в них влаги путем ее испарения.
Этим сушка отличается от других методов удаления влаги, например,
путем поглощения ее химическими реагентами или механического отде-
ления.
Изделия или материалы приходится сушить в зависимости от их
назначений для разных целей. Твердое топливо, например, подсушивают
для повышения теплоты сгорания, улучшения процесса горения, древеси-
ну— для увеличения прочности, предохранения от гниения и плесени,
различные другие изделия — для облегчения обработки, увеличения дол-
говечности, предотвращения сжатия, искривления и растрескивания. Ряд
материалов подвергается сушке для уменьшения их веса и тем самым
удешевления транспортировки, изменения физических свойств (напри-
мер, уменьшения теплопроводности). Перечень материалов, подвергаю-
щихся в процессе их обработки также и сушке, чрезвычайно велик. Глу-
бина обезвоживания материала в каждом отдельном случае определя-
ется многими причинами.
181
В некоторых случаях перед сушкой материалов целесообразно пред-
варительное обезвоживание их механическим или физико-химическим
способом. Механическое обезвоживание (отжатие и отсасывание влаги,
центрифугирование, фильтрование) широко применяется, например,
в текстильной промышленности, для чего в технологический процесс
включаются специальные аппараты — прессы, центрифуги, вакуум-филь-
тры.
Механическое обезвоживание материалов более экономично, чем
тепловая сушка, однако оно применимо только для материалов, допу-
скающих деформацию (торфяная масса, текстиль, шерсть и т. п.). При
этом одно механическое обезвоживание материала в большинстве случа-
ев является недостаточным, так как оно обеспечивает только частичное
удаление свободной влаги (до 40—60%). Поэтому часто комбинируют
различные способы удаления влаги, например в текстильной промыш-
ленности после механического обезвоживания, а в химической после вы-
паривания применяют сушку материалов, достоинством которой являет-
ся возможность получения материала с любой конечной влажностью.
Сушку материалов можно производить естественным и искусствен-
ным путями. Естественная сушка обычно производится на открытом воз-
духе, под навесами или в специальных сараях и представляет собой про-
цесс, при котором сушильный агент (воздух), поглотивший пары влаги,
отводится из зоны сушимого материала без искусственных мероприятий.
Она производится за счет тепла наружного воздуха и применяется при
массовой обработке дешевых влажных материалов, например глины, пе-
ска, торфа, дров, пиломатериалов, сена и т. п., и имеет еще значительное
применение в народном хозяйстве.
Недостатками естественной сушки по сравнению с искусственной
(в сушильных установках) являются большая продолжительность,
зависимость ее от времени года и состояния наружного воздуха,
необходимость большой территории для размещения материала. На
лесозаводах биржи для сушки леса занимают по нескольку квадрат-
ных километров; еще большие площади занимаются штабелями торфа
на торфоразработках и полями разлива при гидравлическом способе до-
бычи его. При естественной сушке материал можно высушить только до
влажности, близкой к равновесной, соответствующей параметрам окру-
жающего воздуха и в ряде случаев недостаточной для последующей тех-
нологической обработки материалов.
Несмотря на кажущуюся простоту и дешевизну, естественная сушка
в производственных масштабах оказывается достаточно дорогой. Напри-
мер, естественная сушка лесоматериалов на биржах иногда незначитель-
но отличается по стоимости от искусственной сушки таких же материа-
лов в сушилках.
Искусственная сушка материалов производится в специальных
устройствах — сушилках, в которых сушильный агент, поглотивший пары
влаги, отводится искусственным способом: при помощи вентиляторов,
инжекторов, вытяжных труб и других устройств. Искусственная сушка
в большинстве случаев осуществляется горячим воздухом.
Изучение естественной сушки материалов, не требующей затраты
тепла от сжигания топлива, не входит в задачу настоящего курса, в ко-
тором рассматриваются основные теоретические и практические вопро-
сы, касающиеся только искусственной сушки материалов, получившей за
последние годы большое развитие во всех отраслях народного хозяйства.
6-2. МЕХАНИЗМ И КИНЕТИКА СУШКИ ВЛАЖНЫХ МАТЕРИАЛОВ
Сушка как технологический процесс обработки материалов приме-
няется с древних времен. Как отрасль науки сушка стала оформляться
в последние два столетия. Уже в 1740—1750 гг. в России изучением про-
182
цессов испарения занимался Г. В. Рихман, соотечественник и друг
М. В. Ломоносова, который сделал ряд важных выводов, предопределив-
ший формулу Дальтона об испарении воды со свободной поверхности.
Механизм сушки влажных материалов определяется в основном
формой связи влаги с материалом и режимом сушки. В основу класси-
фикации формы связи влаги с материалом в настоящее время принята
схема, предложенная П. А. Ребиндером. Ее особенностью является то,
что при рассмотрении форм связи влаги с материалом определяющим
является величина энергии связи, т. е. классификация осуществляется по
свободной энергии обезвоживания. Согласно этой схеме различают:
а) химическую связь (связь в точных количественных соотношениях);
б) физико-химическую связь (связь в различных, не строго определен-
ных соотношениях) и в) физико-механическую связь (удержание воды
в неопределенных соотношениях). Физико-химическая связь делится на
адсорбционную и осмотическую; к последней можно отнести и структур-
ную влагу. Физико-механическая связь может быть разделена на связь
в макрокапиллярах (капилляры с радиусом больше 10-5 см) и связь
в микрокапиллярах (капилляры с радиусом меньше 10~5 см).
При сушке удаляется влага, связанная с материалом физико-меха-
нически и физико-химически. Химически связанная влага обычно не уда-
ляется, так как это привело бы к разрушению материала, а задачей суш-
ки в большинстве случаев яёляется удаление влаги из материала с со-
хранением всех его ценных физико-химических свойств и качеств. В про-
цессе сушки влага 'перемещается из внутренних слоев к поверхности
материала и с нее испаряется в окружающую среду (воздух или другой
сушильный агент).
В первый период сушки влажных материалов испарение влаги с его
поверхности происходит так же, как со свободной поверхности воды, и
подчиняется тем же законам.
Интенсивность испарения жидкости со свободной поверхности при
стационарном режиме приближенно * можно определить по формуле
Дальтона
/='1Е/Ет=рР(рп—Рс), кг/(м2-с), (6-1)
где W— количество испаренной жидкости, кг; F — поверхность испаре-
ния, м2; Рр — коэффициент массоотдачи, отнесенный к разности парци-
альных давлений, кг влаги/(м2-с• Па); рп— парциальное давление диф-
фундирующего вещества над жидкой (твердой поверхностью), Па; рс—
парциальное давление этого же компонента вдали от поверхности раз-
дела фаз, Па; т — время, с.
Для приближенных расчетов пользуются формулой
/=5,7&у°’8(Дп—рс), кг/(м2-ч), (6-2)
где w — скорость воздуха; м/с; и рс — в паскалях.
Количество испаренной жидкости может быть также определено по
уравнению
/=₽с(рп—рс), кг/(м2-с), (6-3)
где рс — коэффициент массоотдачи, отнесенный к разности концентра-
ций диффундирующего вещества, м/с; рп и рс-—концентрации диффунди-
рующего вещества на жидкой (твердой) поверхности раздела фаз и вда-
ли от поверхности раздела фаз, кг/м3.
Коэффициенты массоотдачи |3С и |3У связаны соотношением
₽Р = рс/7?Д (6-4)
* Более точные методы определения интенсивности испарения жидкости со сво-
бодной твердой поверхности рассмотрены в [Л. 29].
183
Между количеством испаренной жидкости и количеством затрачен-
ного тепла имеется следующая зависимость:
q = Ir=a(tc—tE), Дж/(м2- с *°С), (6-5}
где г — удельная теплота испарения, Дж/кг; а — коэффициент теплооб-
мена, Дж/(м2-с • °C), Вт/(м2-°С); tc, tu—температуры окружающей
среды и .поверхности испарения, °C.
Так как при адиабатическом испарении жидкости со свободной по-
верхности температура окружающей среды равняется температуре сухо-
го термометра, а температура поверхности матерала — температуре мо-
крого термометра, то
/ = - Q, кг/(м2 • С). (6-6}
При конвективно-радиационной сушке а равно сумме коэффициен-
тов конвективного и радиационного теплообмена.
В настоящее время для приближенных расчетов массообмена при-
нимается допущение об аналогии между процессами теплообмена и
массообмена, на основе которой уравнения, полученные для условий
теплообмена, используются для расчетов массообмена. Эти допущения
действительны для условий, когда в пограничном слое поля энтальпий
подобны полям концентрации и коэффициент температуропроводности а
равен коэффициенту диффузии D или критерий Льюиса Le = a/D {Л. 24].
Например, уравнение теплообмена для турбулентного течения газа от-
носительно плоской поверхности имеет вид:
Nu = al/к=0,664Re°>5Pr0>33=
=0,664 (w//v)°’5(v/a)0,33; (6-7)
по аналогии для массообмена
Num = $l/Dc = 0,664 Re°-sPr^33 = 0,664 (wZ/v)°-s (v/£>c)”.33, (6-8)
здесь принято am=Dc, Dc — коэффициент концентрационной диффузии
паров жидкости в газовую среду, определяемый из закона Фика®:
кгфг-с), (6-9}
в котором pi — локальная концентрация вещества, равная отношению
массы данного компонента к объему смеси, кг/м3; dpildn— градиент кон-
центрации, направленный в сторону возрастания концентрации.
Для смеси водяного пара и воздуха (т. е. влажного воздуха) коэф-
фициент концентрационной диффузии Dc может быть определен п» фор-
муле
Dc=Do(Т/273)^(pvlp) =2,2.10-s (Т/273)^(р0/р), м2/с, (6-10)
где Do — коэффициент диффузии водяного пара в воздух при О °C, м2/с;
Т — температура смеси, К; р — давление смеси при данной температуре,
Па; р0 — барометрическое давление, Па.
В расчетах используют также коэффициент диффузии Dp, отнесен-
ный к градиенту парциальных давлений:
От=адпДм2/с, (6-11)
г-де 7?п — газовая постоянная пара**.
Пример 6-1. Определить количество воды, испаряющейся в час с 1 м2 горизонталь-
ной поверхности длиной /=0.1 м в направлении движения воздуха, если скорость воз-
духа над поверхностью ш=3 м/с, его температура 20 СС и <р=33%- Давление смеси
740 мм рт. ст., или 0,98- 105 Па. Температура воды 15 °C.
* Более точным выражением закона Фика является его выражение через градиент
химического потенциала.
** Дп=1/?/рп, а значение /? зависит от размерности давления: если р выражено
в Па (Н/м2), то /?=8 314, если р—в кгс/м2, то 7?=848, и если р—® мм рт. ст., тоА=62,3.
184
Определим значение массообменного критерия Num по формуле (6-8)
U / 3-0,1 \о-5 /1,56-10~s\ о.33
NUm=Pc 0,664 (1,56- 10Д ^2,38-10-sJ :=5:80-
Коэффициент концентрационной диффузии определен по формуле (6-10):
/293V.8/ 1-Ю5 \
Dc = 2,2-10-® ^273^ 0,98-105 у~'2’38'10 °. м2/с.
Коэффициент массообмена
Парциальное давление водяного пара над поверхностью воды равно давлению
•насыщения при /=15°С, рп=12,7 мм рт. ст., или 1 700 Па, и в воздухе рс=5,8 мм рт. ст.,
или 775 Па. Количество воды, испаряемой в час с 1 №, по формуле (6-1)
, Вс 11,92-10-2.3 600
/ = (Рп - А) = ’—8314-----700 -775)=0,48 кг/(м2-ч).
“ИГ288
Количество воды, испаряемой в час, по упрощенной формуле (6-2)
/ = 5,7ш°-8 (ри — ре) = 5,7-3°-8 (1 700 — 775) = 0,69 кг/(м2-ч).
В сушильной технике установились два понятия влажности мате-
риала:
влажность на общую массу, применяемая в тепловых расчетах про-
цессов сжигания топлива,
ш.=^1а>=а—— 100»/.; (6-12а)
и влагосодержание материала, кг/кг, или влажность на сухую мас-
су, %, применяемая для исследования и контроля процессов сушки
гис = 1ОО»/о. (6-126)
Для анализа процессов кинетики сушки пользуются понятием кон-
центрации или локальным влагосодержанием материала (кг влаги/кг
сухого материала).
Если при постоянной температуре воздуха t и относительной влаж-
ности его ф вести сушку материала, из которого необходимо удалить не
только свободную, но частично и связанную влагу, то зависимость убы-
ли влаги от времени может быть изображена графиком (рис. 6-1). Ско-
рость сушки dw/dx (излрэнение количества испаряемой влаги во
времени * вначале постоянна, затем наступает уменьшение ее. Период
I — соответствует времени удаления свободной влаги ti, II—-времени
удаления связанной влаги тг- В период постоянной скорости сушки темпе-
ратура на поверхности материала равна температуре мокрого термоме-
тра ,в’=/м. В период падающей скорости сушки температура материала
повышается и стремится к температуре сушильного агента.
В период постоянной скорости сушки происходит адиабатическое
ирпарение жидкости. При влажности материала, большей гигроскопиче-
ской, г. е. при наличии свободной влаги, парциальное давление водяного
пара над материалом равно давлению над чистой водой и не зависит ни
от влажности, ни от характера материала.
Для этого периода могут быть использованы формулы для испаре-
ния жидкости со свободной поверхности.
* Для анализа процессов сушки используются также графики изменения влаго-
содержания W, кг/кг, и интенсивности I, кг/(м2-г), от продолжительности сушки, т.
185
4=const
Рис. 6-1. Кривые сушки и изменения
температуры материала при постоян-
ных параметрах сушильного агента.
Соотношения (6-1)—(6-3) действительны только для периода по-
стоянной скорости сушки. П. Д. Лебедев {Л. 23] предлагает снижение
коэффициента а в периоде падающей скорости сушки учитывать соот-
ветствующим изменением влагосодержаний
а/а0= (wz/wKV)n,
где ао — коэффициент теплоотдачи в периоде постоянной скорости суш-
ки; w2— текущее или конечное влагосодержание материала; щкр— кри-
тическое влагосодержание материала; п — показатель степени, завися-
щий от свойств материала, определяе-
мый экспериментальным путем.
При анализе процессов сушки и
характеристики влажных материалов
пользуются такими понятиями, как
влажность равновесная, гигроскопиче-
ская и критическая.
При длительном пребывании ма-
териала в воздухе с постоянными па-
раметрами с влажностью, достаточной
для того, чтобы процессы сорбции за-
кончились полностью, в материале
устанавливается такая влажность, при
которой давление водяного пара над
материалом находится в равновесии
с парциальным давлением водяного
пара в окружающем воздухе; такая
влажность материала называется рав-
новесной влажностью ьур. Равновесная
влажность материала является функ-
цией относительной влажности и тем-
пературы воздуха.
Давление водяного пара р над
материалом является функцией его
равновесной влажности, и кривая, изображающая эту функцию придан-
ной постоянной температуре, называется изотермой сорбции.
Равновесная влажность, соответствующая р/рНас=1 или ф=100%,
называется гигроскопической влажностью wr; она является границей
между связанной влагой и свободной.
Продолжим рассмотрение кинетики процесса сушки по рис. 6-1.
Точка перехода от постоянной скорости сушки к падающей (точка С
на рис. 6-1) называется критической; она соответствует началу удаления
из материала связанной или гигроскопической влаги. Соответствующая
этой точке влажность называется критической влажностью материа-
ла Шкр.
Критическая влажность больше гигроскопической, так как при суш-
ке материала влажность внутренних слоев больше, чем на его поверхно-
сти. Значение критической влажности тем меньше отличается от значе-
ния гигроскопической влажности, чем меньше разница во влажности на
поверхности и внутри материала. Поэтому критическая влажность зави-
сит от толщины материала и режима сушки (скорости и параметров су-
шильного агента).
При сушке материала его конечная влажность стремится к равно-
весной влажности. Теоретически равновесная влажность может быть
достигнута лишь при бесконечно большой продолжительности сушки;
влажность, близкая к равновесной, достигается по истечении некоторого
промежутка времени.
На рис. 6-2 приведена зависимость равновесной влажности древеси-
ны от температуры и относительной влажности воздуха. По этому гра-
186
фику можно выбрать конечную влажность лесоматериалов в зависимо-
сти от их назначения. Например, при сушке этих материалов для мебе-
ли определяют равновесную влажность по комнатным температуре и
влажности воздуха и принимают ее за конечную влажность материала.
Если материал, высушенный в
сушилке до низкой равновесной
влажности, поместить в условия с
меньшей температурой и большей
относительной влажностью воздуха,
то в силу своих гигроскопических
свойств он может вобрать в себя
влагу до более высокой равновес-
ной влажности, соответствующей
этим новым условиям. Это обстоя-
тельство имеет большое практиче-
ское значение, особенно для таких
сильно гигроскопических материа-
лов, как сахар, текстиль, табак и
т. п. Нецелесообразно сушить ма-
териал до малой равновесной влаж-
ности, если он в дальнейшем при
транспортировке, хранении пли пло-
хой упаковке может вследствие гиг-
роскопических свойств вобрать вла-
гу из окружающего воздуха. Таким
образом, конечная влажность мате-
риала при выходе из сушилки
должна выбираться в зависимости
от его назначения, условий транс-
портировки и хранения. Равновес-
ные влажности для некоторых мате-
риалов приведены в табл. 6-1.
Рис. 6-2. Зависимость равновесной влаж-
ности древесины от температуры и влаж-
ности воздуха.
Таблица 6-1
Равновесные влажности в процентах по весу для некоторых материалов
в зависимости от относительной влажности воздуха при температуре его 25 ®С
Название материала Относительная влажность воздуха. % Примечание
10 20 30 40 53 60 70 80 90
Хлопок 2,6 3,7 4,4 5,2 5,9 6,8 8,1 10,0 14,3 Ткань
Шерсть 4,7 7,0 8,9 10,8 12,8 14,9 17,2 16,9 23,4 Моток
Шелк 3,2 5,5 6,9 8,0 8,9 10,2 11,9 14,3 18,8
Лен 1,9 2,9 3,6 4,3 5,1 6,1 7,0 8,4 10,2 Ткань
Целлюлоза — 4,0 5,8 — 6,3 — 7,8 — 10,5 —
Бумага писчая 3,0 4,2 5,2 6,2 7,2 8,3 9,9 11,9 14,2 Масса с 3»/о золы
Кожа 5,0 8,5 11,2 13,6 16,0 18,3 20,6 24,0 29,2 Дубленая
Резина 0,11 0,21 0,32 0,44 0,54 0,66 0.76 0,88 0,99 Шины
Дерево 3,0 4,4 5,9 7,6 9,3 11,3 14,0 17,5 22,0 —
Мыло 1,9 3,8 5,7 7,7 10,0 12,9 16,1 19,8 23,8 —
Табак 5,4 8,6 11,0 13,3 16,0 19,5 25,0 33,5 50,0 Сигареты
Белый хлеб 0,5 1.7 3,1 4,5 6,2 8,5 11,1 14,5 19,0 —
Мука 2,6 4,1 5,3 6,5 8,0 9,9 12,4 15,4 19,1 —
Зерно — 5,8 7,8 9,7 11,3 13,6 15,6 17,5 •—• По Гофману (пшеница, рожь, овес)
Примечание. Для многих материалов равновесная влажность зависит также и от температуры
воздуха [Л. 24, табл. 1-6].
187
Как следует из рис. 6-1, тангенс угла наклона касательной к кри-
вой сушки в любой точке ее определяет 'скорость сушки в этой точке
tgo=—dwldx^i\,wlAx=N, °/о/ч. (6-13)
Наибольшая скорость сушки будет в первый период — период по-
стоянной скорости испарения. При равновесной влажности аур угол о и
скорость сушки равны нулю.
При анализе процессов сушки пользуются понятиями интенсивно-
сти I и скорости сушки N, между которыми имеется следующая связь.
В период постоянной скорости сушки температура .материала постоянна
dtldx=G, и если тепло, необходимое для испарения влаги, отбирается из
окружающего воздуха путем теплообмена конвекцией, то интенсивность
испарения I прямо пропорциональна плотности потока тепла на поверх-
ности тела
/т = ^_=^_р р/г=(^\ (6-14)
г 100^VP°'r /о 100 г ' ’
где No= (dw/dt) о — скорость сушки в периоде постоянной скорости,
%/ч; Rv=V!F — отношение объема тела к его поверхности, м; ро —
плотность абсолютно сухого материала, кг/м3.
Из уравнений (6-1), (6-6) и (6-14) получаем:
JL(Zc_Q = ?p(pHac-Pc) = ^- (6-15)
Для периода постоянной скорости сушки рп=Рн и /п=/м.а— адиаба-
тической температуре мокрого термометра. Разности (tc—/м.а) и
(рн — Рс) получили название потенциала сушки. Для анализа процессов
тепло- и массообмена на /-«(-диаграмме более удобно пользоваться
разностью (tc—/м.а).
На основании большого количества опытов установлено, что ско-
рость продвижения влаги внутри материала определяется формой свя-
зи влаги с материалом.
Для различных случаев сушки материалов А. В. Лыков насчитывает
шесть возможных форм изменения интенсивности или скорости сушки,
которые показаны на рис. 6-3, и дает им следующее объяснение.
Зависимость 1 (прямая линия) возможна для тонких грубошерст-
ных материалов. Кривая 2 получается при сушке коллоидных тел, со-
держащих адсорбционную и осмотически связанную влагу. Кривая 3
характерна для керамических пористых тел, содержащих капиллярную
влагу. Эти три зависимости не имеют точек перегиба. Кривые 4, 5 и 6
имеют точки перегиба, определяющие вторую критическую влажность.
Точка К2 на кривой 4 указывает на углубление зоны испарения в мате-
риале; эта точка не всегда ясно выражена; иногда она совпадает с точ-
кой Ki, и тогда кривая 4 имеет вид кривой 3. Кривая 5 верхней своей
частью характеризует испарение капиллярной влаги, а нижней частью
Рис. 6-3. Типичные кривые скорости сушки
влажных материалов.
188
(после точки перегиба) харак-
теризует удаление сорбционно
связанной влаги. Кривая 6
встречается редко. Наиболее
часто встречаются типичные
кривые скорости сушки 2, 3 и 5.
На рис. 6-3 в отличие от
графика, представленного на
рис. 6-1, по оси абсцисс отло-
жена влажность материала и
построение кривой dw/dx=
=<р(ш) ведется от начальной и
кончается равновесной влажностью (равновесная влажность является
началом координат).
При сушке влага в материале может перемещаться к его поверхно-
сти под действием разности ее концентрации, под влиянием термовлаго-
проводности и под действием градиента избыточного давления, возни-
кающего в материале при высокотемпературой сушке, когда темпера-
тура материала Ом^НОО °C (фильтрационный перенос). Закон
термовлагопроводности, по которому влага в материале перемещается
по направлению теплового потока, а газ—в противоположную сторо-
ну, был открыт А. В. Лыковым в 1934 г. П. Д. Лебедев из анализа
экспериментальных данных в 1952 г. доказал, что при температуре ма-
териала, близкой или большей 100°C, наблюдается фильтрационный
перенос влаги, когда движущей силой является нерелаксируемый гра-
диент давления *.
В общем виде уравнение переноса массы при сушке материала мо-
жет быть записано следующим образом:
г ди „ dt др
' т- О-т Ро ^7" О^-тпРо <2рРо ’ (6-16)
где qm — количество жидкости, переместившееся внутри тела в единицу
времени через единицу поверхности, названное плотностью .потока жид-
кости или массы, кг/(м2-ч); ат — коэффициент потенциалопроводности,
м2/ч; и — концентрация влаги, кг/кг; х — координата, м; ро — плотность
абсолютно сухого материала, кг/м3; б — термоградиентный коэффи-
циент, 1/°С; Др — коэффициент фильтрационного переноса, м2/ч, Н/м2;
ди/дх, dt/dx и др/дх — частные производные, пропорциональные градиен-
там влажности, температуры и давления (V/7, V/ и Vp), возникающим
в материале при сушке.
Третий член уравнения (6-16) имеет значение как движущая сила
перемещения влаги только при температурах, близких или превышаю-
щих 100°С, в материале, сушимом при атмосферном давлении. В низко-
температурных процессах он равен нулю. Второй член этого уравнения,
наоборот, при температуре около 100°C и выше близок к нулю (б~0).
Поэтому в низкотемпературных процессах сушки при /<100 °C уравне-
ние имеет первые два члена (см. уравнение (6-18)], а при />1'00 °C —
первый и третий члены.
Почти все материалы в процессе сушки изменяют свои размеры, что
называется усадкой материала в процессе сушки. Например, глина имеет
усадку в период постоянной скорости сушки, дерево и уголь — в период
падающей скорости сушки, а торф, кожа и некоторые другие материа-
лы — на всем протяжении процесса сушки.
Некоторые материалы, например древесина, имеют различные
усадки в тангенциальном и радиальном направлениях, различающиеся
иногда в 1,5—2,5 раза, а также различные поперечную и продольную
усадки, что объясняется их физико-химическими свойствами или анато-
мическим строением (древесина и т. п.). Приближенная формула для
определения линейного размера образца после сушки такова:
I — М1 + С (нач—^кон)], (6-17)
где / — начальный линейный размер образца; /0 — длина образца при
конечной равновесной влажности; а —- линейный коэффициент усадки;
ЭДнач и Юкон — начальная и конечная равновесные влажности образ-
ца, %.
* Эти давления в материале были впервые в 1955 г. измерены Г. А. Максимовым.
189-
Таблица 6-2
Коэффициенты усадки
Линейный коэффициент усад-
Название материала
Глина ..................
Подмосковный уголь . . ,
Фрезерный торф...........
Кожа....................
0,007—0,0048
0,0024
0,0012
0,007
ки показывает, на какую долю
первоначального линейного раз-
мера материала сокращается со-
ответствующий размер (длина,
ширина или толщина) материала
при удалении из него 1% влаги.
Если усадка материала про-
исходит только в период по-
стоянной скорости сушки, то под
а
Woh следует понимать ту влаж-
ность, при которой заканчивается
усадка. Под ауНач следует понимать ту влажность, при которой начи-
нается усадка. Формула верна только для образцов с равномерным
распределением влаги. Значения линейного коэффициента усадки при-
ведены в табл. 6-2.
Экспериментально установлено, что чем выше влажность, темпера-
тура или давление внутри материала, тем больше скорость сушки его.
Рис. 6-4. Типичные кривые распределения влажностей и температур в материале при
различных способах подвода тепла.
а — конвективный; б — контактный; в — терморадиационный; г — высокочастотный; д — комбиннро
ванный (радиационный и высокочастотный).
Если температура или влажность в поверхностных слоях материала
больше, чем во внутренних, то перемещение -влаги к поверхности мате-
риала может тормозиться или даже, наоборот, может возникнуть обрат-
ное перемещение влаги во внутренние слои материала. В соответствии
с этим градиенты влажности, температуры и давления могут иметь как
положительный, так и отрицательный знак. Отрицательный знак пока-
зывает, что направление вектора потока влаги не совпадает с направле-
нием градиента и соответствует перемещению влаги из внутренних
слоев материала к его поверхности.
Растрескивание многих материалов вызывается недопустимой вели-
чиной градиента влажности, связанного с напряжениями при усадке
материалов в процессе их сушки. Чем меньше градиент влажности (раз-
ность влажности в центре и на поверхности) в материале при его суш-
ке, тем выше качество высушиваемого материала. Это необходимо всег-
да учитывать при разработке режима сушки.
На рис. 6-4 показаны типичные кривые распределения влажностей
и температур в материале в зависимости от времени при различных
190
способах сушки или подвода тепла (которые описываются ниже). Ана-
лиз этих графиков показывает, что при конвективной (рис. 6-4,а) и
терморадиационной сушке с |двусторонним облучением материала
(рис. 6-4,в) температура материалов в центре ниже, чем на поверхности,
а влажность, наоборот, выше. Перемещение влаги изнутри материала
к его поверхности при этих способах сушки происходит за счет градиен-
та влажности. Градиент температуры оказывает тормозящее действие
на перемещение влаги к поверхности материала. Скорость конвектив-
ной сушки материалов без растрескивания лимитируется градиентом
влажности, а быстрая терморадиационная сушка толстых материалов
без растрескивания невозможна.
При контактной (рис. 6-4,6) и высокочастотной (рис. 6-4,г) сушке
температура внутри материала выше, чем на его поверхности. Переме-
щение влаги внутри материала к его поверхности идет за счет градиен-
та температуры; градиент влажности оказывает тормозящее действие.
Рис. 6-6. Зависимость термо-
градиентного коэффициента 6
от влажности материала.
Рис. 6-5. Зависимость коэффи-
циента потенциалопроводности
ат от влажности материала.
На рис. 6-4,6 показано распределение полей температур и влажно-
сти в функции времени для комбинированной сушки с высокочастотным
и радиационным подводами тепла. Вследствие того что при таком спо-
собе подвода тепла температура материала быстро достигает 100 °C,
сушка (вернее, выпаривание) идет под действием градиента избыточ-
ного давления, возникающего внутри материала. Градиенты тем-
пературы и влажности в этом случае почти не оказывают влияния на
интенсивность сушки.
Из уравнения (6-16) следует, что интенсивность сушки определя-
ется не только значениями V», V/ и Vp; она в значительной степени за-
висит и от коэффициентов потенциалопроводности йт и термоградиент-
ного коэффициента 6, а при высокотемпературной сушке и от ар.
Коэффициенты ат и б зависят от влажности, температуры и струк-
туры 'материала. По изменению значений ат и б в процессе сушки мож-
но судить о формах связи влаги с материалом и механизме перемеще-
ния ее.
На рис. 6-5 показана зависимость коэффициента потенциалопро-
водности ат от влажности материала при постоянной температуре его.
Участок АВ сооответствует перемещению осмотически и капиллярно
связанной влаги в виде жидкости, а участок ВС— перемещению влаги
как в виде пара, так и в виде жидкости. Участок CD —область влаги,
связанной полимолекулярной адсорбцией; перемещение влаги на этом
участке происходит только в виде пара. Участок DE соответствует пере-
мещению наиболее прочно связанной мономолекулярной адсорбцией
влаги.
191
Зависимость термоградиентного коэффициента 6 от влажности ма-
териала (при его постоянной температуре) приведена на рис. 6-6.
Испарение влаги в капиллярах характеризуется увеличением ft
(кривая DB) за счет наличия в них защемленного воздуха.
В капиллярнопористых телах при малых влажностях термогради-
ентный коэффициент б становится отрицательным, так как в этом случае
влага вследствие относительной термодиффузии пара и воздуха пере-
мещается в обратном направлении — от холодных зон к горячим.
На рис. 6-5 и 6-6 пунктирными линиями также показаны кривые
ат и б для температур из рассмотрения которых следует, что
с повышением температуры ат увеличивается, а б уменьшается.
Основными уравнениями для аналитического определения продол-
жительности сушки и прогрева материала являются уравнения влаго-
проводности и теплопроводности. Дифференциальное уравнение термо-
влагопрсводности при температурах материала ниже 100 °C для всех
способов сушки имеет вид:
dtifdt = am\j2u-]-am^st. (6-18)
Дифференциальное уравнение теплопроводности применительно
к изучению процессов сушки в самом общем виде может быть представ-
лено в виде
dt ге ди
1 f cBpo cB dt
(6-19)
где qv — внутренний положительный источник тепла; ро —плотность су-
хого материала; св — теплоемкость влажного материала; г — теплота
парообразования; е-— коэффициент внутреннего испарения влаги; t —
температура материала; а — коэффициент температуропроводности
материала при его средней влажности.
Аналитические решения уравнений (6-18) и (6-19) возможны лишь
при постоянных значениях коэффициентов массопереноса и для некото-
Рис. 6-7. Графический метод определения
приведенной критической влажности.
2, 3 и 5 — типичные кривые скорости сушки (см.
рис. 6-3).
рых упрощенных частных слу-
чаев.
В ряде случаев на основе
дифференциальных уравнений
процессов сушки и соответст-
вующих им граничных условий
методом теории подобия нахо-
дят критериальные соотноше-
ния, которые используются для
обработки экспериментальных
данных
Зная характер изменения
коэффициентов ат и б, можно
с помощью уравнений (6-18) и
(6-19) при соответствующих начальных и граничных условиях дать
качественную характеристику процесса сушки и увязать ее с техноло-
гическим процессом *.
Для количественных расчетов кинетики процесса сушки существу-
ют приближенные уравнения.
А. В. Лыков предлагает кривую скорости сушки во втором пери-
оде заменить прямой линией, как показано на рис. 6-7; при этом из гео-
метрических соотношений получается
dw Ar W-------- 14'р .т . .
— ~N--------------= kN (w — w„),
dt и'к.п—wp F
(6-20)
Такой анализ проведен А. В. Лыковым [Л. 24].
192
где N— постоянная скорость сушки в первом периоде; шк.п — приведен-
ная критическая влажность, которая может быть больше или меньше
действительной критической влажности (рис. 6-7); х=1/(и/к.п—wp)—
относительный коэффициент сушки, зависящий от характеристики мате-
риала и определяемый экспериментально.
Согласно уравнению (6-13)
—dw/dx—N.
Интегрируя уравнения (6-13) и (6-20), получаем общую продолжи-
тельность сушки
1
JV
t^K.n — К>р
ws — Wp
или
1
—“АГ
W. - ^к.п + 2,3 К.п - wp) 1g
(6-21)
где Wi и Wz — начальная и конечная влажность сушимого материала.
Г. К. Филоненко [Л. 52], исследуя кривые сушки для одного и
того же материала при конвективном способе подвода тепла к сушимо-
му материалу, установил, что они совмещаются в общую кривую, если
их перестроить в системе координат dw/dx— скорость сушки и Т —
приведенная скорость
4r_dEj_//dw\ —-Lid?!- (<л
dt {dt I N dt' V ’
I \ J макс I
На основе анализа опытных данных он предлагает следующее
уравнение для приведенной скорости сушки:
ш _ — wp)m
А+ — Wp)m"
(б)
Коэффициенты т, А и р определяются из конкретных условий
опыта.
Из уравнений (а) и (б) была получена формула для определения
общей продолжительности сушки
—dw . 4- р (аук — ЙУ2) ,
(w СУр)т 1 г \ К 2/
(6-22)
где — критическая влажность; N, Wi и йу2 имеют прежние обозначе-
ния.
Продолжительность сушки зависит от рода сушимого материала,
его геометрических размеров, назначения, типа сушилки, способа под-
вода тепла, режима сушки (температуры, влажности и скорости су-
шильного агента) и ряда других причин. Вследствие этого аналитичес-
кое определение продолжительности сушки в ряде случаев представля-
ет непреодолимые трудности. Часто ее определяют экспериментальным
путем.
В различных отраслях промышленности опытным путем установле-
ны оптимальные режимы и продолжительность сушки для многих ма-
териалов. Для определения времени сушки древесины расчетная фор-
мула имеет вид:
т=Тн^1^з-.. knf(w), (6-23)
где тн — продолжительность сушки определенного нормативного пило-
материала при соответствующем режиме; kikzk3...kn — поправочные
коэффициенты, учитывающие отличия от эталона в геометрических раз-
мерах, назначении и других факторах сушки; f(w)—поправка на раз-
личие действительной начальной и нормативной влажностей сушимого
материала.
13—1128 193
6-3. РАСЧЕТ КОНВЕКТИВНЫХ СУШИЛОК С ОДНОКРАТНЫМ
ИСПОЛЬЗОВАНИЕМ ГОРЯЧЕГО ВОЗДУХА
Существует большое количество типов и конструкций сушильных
установок, для которых в следующем параграфе дается классификация
по различным признакам, в том числе и по способу подвода тепла
к сушимому материалу (конвективному, терморадиационному и кон-
тактному) .
Наибольшее распространение получили конвективные сушилки. Им
и будет в дальнейшем уделено наибольшее внимание.
Материальный баланс продукта, подвергающегося
сушке. Количества испаренной из материала влаги и количество су-
хого и сырого продукта связаны уравнением баланса сушки.
Введем следующие обозначения:
Gi — количество материала, поступающего в сушилку, кг/ч; G2—
количество высушенного материала (после удаления части влаги), кг/ч;
Gcyx— количество абсолютно сухого материала, из которого удалена
вся влага (свободная и связанная), кг/ч; w° и wc} —начальные влаж-
ности материала на общую и абсолютно сухую массу, %; Wg и to' —
конечные влажности материала на общую и абсолютно сухую массу, %;
W — количество испаренной влаги, кг/ч.
Пользуясь этими обозначениями, можно написать уравнение мате-
риального баланса продукта, подвергающегося сушке:
Gi = G2+
Количества влаги, поступившей в сушилку с сырым материалом и
выходящей из сушилки с высушенным материалом, равны
Grw?
W1==~To6~’ кг/4’ и
кг/4-
Количество испаренной в сушилке влаги
_ G,w? — G«Wq
W = G1-Gz = W1-Wt = ^2 \ кф (а)
Количество абсолютно сухого вещества
6,(100—1^) Gs(100—®§)
Gcyx= fog - ГОО -» кг/ч,
откуда
G2_ 100- w°
G, ~ (100 —
Разделив члены уравнения (а) на Gi и подставив значение G2/Gi
для влажности на общую массу, получим:
W °2 1 ,0° —“'У О'?—
Gi“ 100 —w" —100 —‘
В результате получим основное уравнение материального баланса
W=Gt -°- -°2- = G2 ---*
100 — ®° 2 100 — w°
(6-24)
194
Аналогично могут быть получены уравнения материального балан-
са для условий, если будет задана влажность материала на сухую
массу:
IF=G,
Wi~ W2 wCl~W2
100 + ^ 2 100+ w='
(6-25)
Формулы пересчета одной влажности в^другую имеют вид:
<6'26>
rfliC Я
ffi’°=TO01^-1OO9/o- (6-27)
Расход воздуха и тепла
для испарения 1 кг влаги. На-
пишем уравнение материального ба-
ланса сушилки согласно обозначениям
на рис. 6-8
/*» | Т ^2 1 I Г
100 *” == ТООJ '
или -Л\ J
ТОо + цббо”=Ga ТОб + ^2i ооо’^6’2^
Принимаем, что присосы и утеч-
ки воздуха в сушильной системе от-
сутствуют, т. е. T.o=L1=£,2=A = const.
Перепишем последнее уравнение
в виде
GjWi G2W2 Г / \ _ г ^2
100 — МЛ2 -М—ь 1 000 -
(6-29)
Поскольку
G,a/, G2k/2 _rw
—loo---------
уравнение7 (6-29) принимает вид:
W = L(x2-xD) = L^^, кг/ч.
Рис. 6-8. Принципиальная схема и
процесс теоретической сушилки на
/-4-диаграмме.
1 — сушилка; 2 и 3 — подогреватели
(основной и дополнительный); 4 — венти-
лятор.
(6-30)
Обозначив расход воздуха на 1 кг испаренной влаги L/W через /,
получим окончательное выражение для определения расхода сухого
воздуха на 1 кг испаренной влаги
/ ~--------=------—, кг на 1 кг испаренной влаги. (6-31)
Теперь определим расход тепла на 1 кг испаренной влаги. Если
каждый килограмм сухого воздуха нагревается от t0 до ti, причем эн-
тальпия его при этом увеличивается от 1о до Ц, а для испарения 1 кг
влаги необходимо затратить I иг сухого воздуха, то расход тепла на
его нагревание
а — 1(1. — Io) = ——= [у — 1? 1 000, кДж на 1 кг влаги. (6-32)
Ха Хо w2 и0
13*
195
В этих формулах влагосодержание воздуха х, кг на 1 кг сухого
воздуха, и d, г на 1 кг сухого воздуха *.
Расчет теоретической сушилки по /-d-диаграмме.
Теоретической сушилкой называют воображаемую сушилку с предва-
рительным подогревом сушильного агента, в которой отсутствуют поте-
ря тепла в окружающую среду, на нагревание транспортных устройств
и высушиваемого материала, а температура материала на входе и вы-
ходе из сушильной камеры равна О °C.
Тепловой баланс теоретической сушилки имеет вид:
LoIo + QK== L2I2, кДж/ч,
где /0— энтальпия влажного воздуха, поступающего в подогреватель,
кДж/кг воздуха; /1— энтальпия влажного воздуха после подогревателя
при входе в сушилку, кДж на 1 кг воздуха; I2 — энтальпия влажного
воздуха за сушилкой, кДж/кг воздуха; QK — количество тепла, сообща-
емое воздуху в подогревателе, кДж/ч.
При Lo=Li = Z.2=const имеем равенство /i=/2=const, показываю-
щее, что в теоретической сушилке процесс сушки идет при постоянной
энтальпии влажного воздуха.
Процесс в теоретической сушилке на /-d-диаграмме построен на
рис. 6-8. Линия АВ соответствует подогреву воздуха в калорифере от
температуры to до температуры /1. Процесс сушки — затрата тепла на
испарение влаги и влагообмен между воздухом и высушиваемым мате-
риалом— идет по линии 1 = const и изображается отрезком ВС.
Расход воздуха в теоретической сушилке согласно уравнению
(6-31)
, 1 1 000 1 000 ,
/ =-------, кг на 1 кг влаги,
х2 — d2 — а0 иСМл
где d2—d0 соответствует отрезку DC, а М&— масштаб по оси влагосо-
держаний.
Если, например, на /-d-диаграмме 1 мм соответствует влагосодер-
жанию 0,2 г на 1 кг сухого воздуха, то
1= 1 000/0,21? С == 5 00Q/DC,
где отрезок DC выражен в миллиметрах.
Согласно уравнению (6-32) расход тепла в калорифере на 1 кг ис-
паренной влаги
5^ДГо1ОООг=Лс д71000> кДж на 1 кг влаги.
Разность Л—/о на диаграмме выражается длиной отрезка АВ (мм),
умноженной на соответствующий масштаб энтальпии, т. е. /1—/о=
=А В • Mi.
Тепловой баланс теоретической сушилки. Основным
условием работы теоретической сушилки является равенство /1 = /2“=
= const. При этом расход тепла на подогрев воздуха
9=/(Л—/о)=/(/2—/о). (6-33)
Далее имеем
/г^Сг/г+хг/а
и
Io=c0to+x0io, кДж на 1 кг воздуха,
где X2=0,001d2 и Xo=O,OOldo—влагосодержания сушильного агента,
кг/кг сухого воздуха; 12 и io — энтальпии водяных паров, содержащихся
в воздухе, кДж/кг.
* В дальнейших размерностях слово испаренный опускается и дается запись
«кг/кг влаги», опускается также и слово сухого и пишется «кг/кг воздуха или г/кг
воздуха».
196
Теплоемкость сухого воздуха считаем не зависящей от температу-
ры, т. е. принимаем, что С2—с0=съ.
Подставив эти величины в уравнение (6-33), получим:
<7 = ^(Св^2 + -£2^2)-/(Св^о + Xot’o) .
Прибавив к правой части этого равенства и вычтя из него величи-
, . ,1
ну lxoi2 и приняв во внимание, что 1 = —--—, после несложных преоб-
Аг — 1
разований получим выражение для удельного расхода тепла, представ-
ляющее собой по существу уравнение теплового баланса теоретической
сушилки:
<7 = /[св(^2—to)+xo(iz—г’о)] + «2, кДж на 1 кг влаги. (6-34)
Из полученного уравнения видно, что в теоретической сушилке
имеются следующие расходы тепла: 1) ?i=/2—расход тепла на испа-
рение влаги из материала; 2) ?2=/Св(^г—to) —потери тепла с сушиль-
ным агентом, входящим в сушилку с температурой to и выходящим из
нее с температурой tz, 3) qo=lxo(iz—io) — потери тепла вследствие уве-
личения энтальпий транзитной влаги, содержащейся в сушильном
агенте при входе в сушилку.
Расчет действительной сушилки. В действительной су-
шилке могут иметь место дополнительные потери и подвод тепла, на-
пример: нагрев воздуха в калориферах, установленных в самой сушиль-
ной камере, тепловыделения при химических реакциях, разморажива-
ние влаги, находящейся в материале в виде льда, нагрев сушильного
агента в вентиляторе и др. В табл. 6-3 приведен тепловой баланс дей-
ствительной сушилки.
Таблица 6-3
Тепловой баланс действительной сушилки для летнего времени
Наименование статьи баланса
Приход
Расход
Тепло, поступающее с воздухом
Тепло, поступающее с материалом
Тепло, поступающее с транспортными уст-
ройствами
Дополнительный нагрев воздуха в подогре-
вателе, установленном в сушильной камере
Потери тепла в окружающую среду
^-0-^0 + Qu.в
с + G^'B,
GjpCtP^'tP
Qbo6
i2/2
G2cm"®2
q5
В табл. 6-3 через -Qn.B обозначено тепло, полученное воздухом пе-
ред сушилкой— в выносном подогревателе.
Составляющие теплового баланса сушилок периодического дейст-
вия относят к отдельным периодам сушки, они имеют размерность
кДж/период, а для сушилок непрерывного действия — к 1 ч работы,
они имеют размерность кДж/ч.
При составлении тепловых балансов сушилок следует учитывать
тепловыделение от вентиляторов, которое необходимо прибавлять в зави-
симости от схемы сушилки к Qn.B или <2ДОб. Тепло на прогрев сушильной
камеры в сушилках непрерывного действия принимают равным нулю.
Уравнение теплового баланса для действительной сушилки непре-
рывного действия имеет вид:
Qn.BЧ-СадТ GzC m'Q’iT'6трСтр,& тр + Qko6 —
= L?I2+с"м Ог'О’г+G ipCip'f/Qp+Qs- (6-35)
197
Отнеся расход тепла к 1 кг испаренной влаги, приняв с/м=с"м=С2
и считая L0—L2=L, получим:
я=%"=4- - ;о) = 4- +-^ (&2 - &х)+
! GTpCTp /О,, О, \ I Qs Сдой Cw^^l / IJ J \ I
I w ' т₽ ’WTflZ ~^Г W—— yoJ-t“
+ <7м + <7п> + '75—<7доб —&А>. (6-36)
где /(/г—/о)—расход тепла для теоретической сушилки; ?м — расход
тепла на нагрев материала; ?Тр — расход тепла на прогрев транспорт-
ных приспособлений; q$— потери тепла в окружающую среду; ?ДОб —
тепло, дополнительно сообщенное в самой сушилке; Cu'fl'i—физическое
тепло влаги, вводимой с сушимым материалом.
Уравнение теплового баланса (6-36) для действительной сушилки
с однократным использованием воздуха в соответствии с введенными
обозначениями можно представить в следующем виде:
q=l(Ii—1о)—1(1г—/о) +^м+^тр+?5—?доб—'Оте™, кДж на 1 кг влаги,
откуда определяем значение
Д=/(/2—Л) =<7доб+с«>&1—(Vm+<7tp+?5), кДж на 1 кг влаги. (6-37)
Это уравнение представляет собой как бы внутренний тепловой ба-
ланс сушилки без учета роли воздуха как теплоносителя.
При работе действительной сушилки могут иметь место следующие
три случая:
а) Д=0; тогда
<7доб + Cw&l = <?м + <7тр + <?5>
т. е. потери тепла компенсируются количеством дополнительно введен-
ного тепла; при этом Д=/(/2—Л)=0; так как /=#0, то /2=/i = const,
т. е. процесс сушки идет при постоянной энтальпии сушильного агента,
как и в теоретической сушилке;
б) Д<0; тогда
foo6 + + фгр + <?5>
т. е. Д=/(/2—71) <0 и, следовательно, Л>/2, или /2=Л—Д/Z;
в) Д>0; тогда
q до б+сj > qM+<7тр+qs,
т. е. Д—/(/2—Л)<0, откуда h<I2 или I2=Ii +Д//.
Таким образом, в случаях «б» и «в» энтальпия воздуха при выхо-
де из сушилки больше или меньше его энтальпии при входе в нее в за-
висимости от знака величины Д.
В зимнее время расход тепла на нагревание материала увеличива-
ется, так как часть влаги в материале находится в замерзшем состоя-
нии. Опытами ВТИ установлено, что в материале замерзает только
свободная влага, а связанная остается в переохлажденной жидкой фа-
зе. Например, в подмосковном угле замерзает влага сверх 22%, в фре-
зерном торфе — 33% и в древесине — выше 28—30% влажности на су-
хую массу.
Размораживание требует дополнительного расхода тепла на подо-
грев льда до 0 °C и таяние (превращение его в воду) при той же тем-
пературе. Поэтому в таких случаях указанное выше значение ?м =
— (,&2—*0'1) следует увеличить на
Д?м +2.1&J, кДж на 1 кг влаги, (6-38)
198
G, [to' — (to')'] c
где W ——-qq —-----------количество замерзшей влаги; (w, )'—влажность
материала, ниже которой влага не замерзает и выше которой вся
влага (вода) находится в состоянии льда.
Потери тепла в окружающую среду ограждениями камеры (стена-
ми, потолками, полом, через дверные проемы) определяются аналити-
чески по формуле теплопередачи
q5=^FkM/W. (6-39)
При определении расхода тепла на сушку необходимо учитывать,
кроме потерь тепла ограждениями, также потери тепла вследствие га-
зопроницаемости стен и неплотности ограждений. Эти потери, назван-
ные нами неорганизованным воздухообменом, не поддаются расчету.
В камерных лесосушилках, где сушка происходит при высокой влажно-
сти сушильного агента, они могут доходить до 20—30% общего расхо-
да тепла на сушку.
Рис. 6-9. Построение действительных процессов сушки на /-d-дия-
грамме.
Расчеты сушилок периодического действия более сложны и гро-
моздки. Рассмотрение их выходит за рамки данного курса.
Построение процесса для действительной сушилки
н а l-d-д и а г р а м м е. Построение процесса для действительной сушилки
н а /-d-диаграмме * при наличии тепловых потерь (А<0, т. е. /г=/1—-Д/Z)
начинается, как это показано на рис. 6-9,а, с построения теоретическо-
го процесса. Затем на изоэнтальпии /i=const теоретического процесса
выбирается произвольная точка Со и вниз от нее откладывается отре-
зок C0E0Mi=A/l.
После замены I его значением для условий данной точки Со полу-
чается
CqEq—ADcjCtjMd/l ООО M.i=DoCoEltn.
Далее из точки В проводится политропа ВЕ0 действительного про-
цесса. На линии ВЕ0 находится конечная точка действительного про-
* На /-d-диаграмме влагосодержание воздуха d, г на 1 кг воздуха. При расчетах
на /-х-диаграммах, где х в кг на 1 кг сухого воздуха в уравнениях вместо 1 000 под-
ставляется единица.
199
цеоса С, определяемая пересечением этой линии с заданной в расчете
линией постоянной влажности <рг или линией температуры t2, соответст-
вующими состоянию уходящего из сушилки воздуха. Определенное по-
ложение политропы действительного процесса при заданном значении
Д/1, не зависящее от выбранного положения точки Со на линии /1 =
«const, проведенной от точки В, объясняется подобием получающихся
при этом треугольников. Из рассмотрения рис. 6-9,а следует, что, на-
пример, треугольник C0E0D0 подобен треугольнику CiEtDi. Для боль-
шей точности построения действительного процесса точку Со на линии
I—const следует выбирать возможно дальше от точки В.
На рис. 6-9,а можно заметить, что конечной точке процесса С на
линии ^2=const соответствует влагосодержание d2 и энтальпия 12 мень-
шие, чем в теоретическом процессе, и вследствие этого больший расход
воздуха на 1 кг испаренной влаги /=1 ООО/D так как DC<DoCo-
Соответственно этому требуется и больший расход тепла на 1 кг испа-
ренной влаги. Таким образом, для действительной сушилки требуются
большая производительность вентиляторов, больший расход электро-
энергии, больший расход тепла и более значительная поверхность на-
грева калориферов, чем для теоретической сушилки.
При построении на Z-rf-диаграмме действительного процесса сушки
с дополнительными выделениями тепла, превосходящего его потери
(Д>0), политропа процесса располагается выше линии теоретического
процесса. Разница в построении этого процесса и процесса при Л<0 со-
стоит только в том, что отрезок CoEo=ACeDoMd/l ООО Mi следует откла-
дывать от точки Со вверх, как показано на рис. 6-9,6. В этом случае
*4>с?т2 и расходы воздуха и тепла в основном калорифере на 1 кг ис-
паренной влаги меньше, чем в теоретической сушилке.
Пример 6-2. Произвести упрощенный тепловой расчет барабанной сушилки при
следующих условиях. Количество продукта, поступающего в сушилку Gi = 2000 кг/ч
(0,55 кг/с); начальная влажность продукта на общую массу ат0 = 18%; конечная влаж-
ность и>20=10%; теплоемкость высушенного продукта сг= 1,255 кДж/(кг-°С), темпера-
тура воздуха, поступающего в калорифер, /ц=20°С; относительная влажность воздуха
Фо=60%; температура воздуха после калорифера /1 = 150 °C, относительная влажность
воздуха, выходящего из сушилки, ф2=80%; температура продукта при входе в сушилку
6'1= 10 °C; температура продукта по выходе из сушилки 02=ЮОСС.
Решение. Определяем количество влаги, испаряющейся в сушилке, по формуле
(6-24)
18 — 10
w== 2 000-w=w=178 кг/4-
Количество материала, выходящего из сушилки,
62=0!—117=2 000—178=1 822 кг/ч. *
Строим теоретический процесс в 7-х-диаграмме (рис. 2-1). Наносим точку А для
параметров воздуха <р0=60% и /о=2О°С и находим /о=42,7 кДж/кг и Хо=О,О1 кг/кг
воздуха.
Проводя линию x0=iconst до пересечения с изотермой Л =150 °C, находим точку В
и определяем параметры воздуха .при входе в сушилку /1=174 кДж/кг; х1=х2=0,01кг
на 1 кг воздуха. Затем проводим изоэнтальпию Л=const до пересечения с линией
<Р2=80% в точке Со.
Определяем Д по формуле (6-37)
Д='[<7доб+с«>,01—(</м + <7тр+<7з)], кДж на 1 кг влаги.
В данном случае
сю0’1=41,87 кДж на 1 кг влаги;
qN - (62 — 6,) = 1 ^lyg25" (10° — Ю) = 1 180 кДж на 1 кг влаги.
Так как сушилка не имеет ни вагонеток, ни транспортеров и добавочные тепловы-
деления, в сушилке отсутствуют, то 9тп=0 и 9дсб=0. Потери тепла q$ для данного
примера оцениваем приближенно в 960 кДж на 1 кг влаги.
200
Подставив найденные величины в формулу (6-37), получим:
A=cw'Oi—(?m+<75) =41,87—(1 180 + 960) «—2 100 кДж на 1 кг влаги,
т. е. в данном случае Д<0.
Строим политропу действительного процесса, для чего на рис. 2-1 определяем
отрезок
С0Е0=Л(х2—%о) =2 100(0,049—0,01) =82 кДж на 1 кг воздуха
и откладываем его от точки Со по вертикали вниз. Из точки В проводим политропу через
точку До. Пересечение политропы с линией <Р2=8О% дает конечную точку Ct действи-
тельного процесса, который соответствует х2=0,034 кг на 1 кг воздуха и /2=428 кДж
на 1 кг воздуха.
Расход воздуха
I — ---------= А ло.1—n~7rr = 41,8 кг на 1 кг влаги и L — IW = 41,8-178 = 7 450 кг/ч.
хг— хо 0,034 — 0,01
Расход тепла
/, —/„ 174 — 42,7
ч= -<=Ь,О34^го,of=5 470 кДж на 1 кг В05луха
и
Q = qW = 5 470-178 = 976 000 кДж/ч.
По величине Q = 976 000 кДж/ч должен быть выбран калорифер, а по величине
£=7 450 кг/ч — вентилятор. Для выбора характеристики вентилятора должно быть
определено гидравлическое сопротивление сушилки и соединительных воздухопроводов.
6-4. ВАРИАНТЫ КОНВЕКТИВНОЙ СУШКИ МАТЕРИАЛОВ
1. Сушка материалов горячим воздухом
Выше были рассмотрены процесс и тепловой расчет при помощи
7-х-диаграммы наиболее простой схемы сушилки с однократным исполь-
зованием сушильного агента. Примером таких сушилок являются кон-
вейерные, пневмотрубы-сушилки и распылительные.
Сушилки с рециркуляцией. Большое применение на прак-
тике имеют сушилки, работающие с рециркуляцией сушильного агента,
т. е. с частичным возвратом отрабо-
тавшего воздуха в сушилку для по-
вторного использования его ('рис. 640).
По выходе из сушилки поток отрабо-
тавшего влажного воздуха с парамет-
рами, соответствующими точке С или
Ci, разветвляется: часть воздуха вы-
пускается в атмосферу, а другая воз-
вращается к вентилятору. Вместо вы-
брошенного отработавшего воздуха
в систему подается такое же количе-
ство свежего воздуха с параметрами,
соответствующими точке А. Свежий
воздух смешивается с отработавшим.
Полученная смесь с параметрами точ-
ки М нагревается в калорифере до
состояния, характеризующегося точкой
Bh и поступает в сушилку. По выходе
из сушильной камеры поток смеси сно-
ва разветвляется и т. д. На 7-Д-диа-
грамме процесс в такой теоретиче-
ской сушилке изображается линией
AMBiCiM. Расходы свежего и выбра-
сываемого из системы отработавшего
воздуха для такой теоретической
Рис. 6-10. Схема сушилки с ре-
циркуляцией воздуха и процесс
сушки на /-d-диаграмме.
201
сушилки одинаковы и выражаются формулой
1 000
DCtMd
1000
4-d„
, кг на 1 кг влаги,
так как всю испаренную влагу уносит только удаляемый отработавший
воздух.
Количество циркулирующего воздуха в сушилке определяется из
условия, что 1 кг смеси увеличивает в сушилке свое влагосодержание
с йсм до d2,
'«=кг на 1 кг маги-
Как видно из последней формулы, возврат отработавшего воздуха
значительно увеличивает количество циркулирующего воздуха, а следо-
вательно, и расход энергии на вентилятор.
Так как ABIDCi=MBilD'Ci, то расход тепла q=l(h—7о), кДж на
1 кг влаги.
Рециркуляция сушильного агента применяется, как правило, при
сушке деформирующихся 'материалов, досок, деревянных и керамиче-
ских изделий и тому подобных материалов, требующих во избежание
их растрескивания значительного содержания влаги в сушильном аген-
те для уменьшения интенсивности испарения влаги с поверхности ма-
териала.
При работе без рециркуляции необходимо было бы увлажнять су-
шильный агент перед вводом в сушильную камеру и затрачивать на это
дополнительно тепло. Применение рециркуляции позволяет вести суш-
ку при высоких влагосодержаниях сушильного агента без расхода теп-
ла на его увлажнение. Кроме того, при рециркуляции возможно регу-
лирование влажности воздуха в сушильной камере, благодаря чему
улучшается качество высушенного материала.
Рециркуляцию воздуха применяют и для недеформируемых мате-
риалов, не требующих обязательной сушки во влажном воздухе.
Применение рециркуляции не дает экономии тепла в теоретическом
процессе (кроме специальных случаев [Л. 52, стр. 106]), так как при
одинаковых начальных и конечных параметрах сушильного агента тре-
угольники ABCi и AfBiCi подобны (см. 7-с?-диаграмму на рис. 6-10),
а следовательно, и расходы тепла в обоих теоретических процессах
одинаковы. Однако при рециркуляции увеличивается скорость воздуха
относительно материала, повышается коэффициент теплообмена и со-
кращается продолжительность сушки материалов, не склонных к рас-
трескиванию, что приводит к уменьшению расхода тепла. При выборе
кратности циркуляции сушильного агента в рециркуляционной сушилке
экономию тепла и сокращение других эксплуатационных расходов на
нее необходимо сравнить с увеличением расхода средств на электри-
ческую энергию для привода вентилятора значительно большей произ-
водительности.
Построение процесса в действительной сушилке с рециркуляцией
сушильного агента на /-^-диаграмме выполняют так же, как и для рас-
смотренного ранее варианта с однократным использованием сушильно-
го агента (рис. 6-10): откладывают по вертикали от произвольной точ-
ки на линии ВС1 соответствующий отрезок eE = efA/m и проводят из
точки Bi политропу действительного процесса BiC до заданного значе-
ния t2 или чзг-
Примером сушилок с рециркуляцией сушильного агента являются
камерная и коридорная сушилки (рис. 6-15 и 6-16).
202
Сушилки с промежуточным подогревом воздуха. Су-
шилка с промежуточным подогревом воздуха состоит из нескольких зон,
в каждой из которых воздух участвует в простом сушильном процессе,
подогреваясь на промежуточных поверхностях нагрева Ft, F2, F3 до тре-
буемых начальных температур t'i, t"i и t"\ или до одной и той же тем-
пературы, как это показано на рис. 6-11. Процесс такой теоретической
сушилки изображается на 7-с?-диаграмме ломаной линией AB'CiB"C2
B"'CS. Расход воздуха одинаков для всех зон сушилки
1 000
. 1UVU 1000 1
1 ~ (С,D, + CsB2+CaDa)Md~DCaMd • кг на 1 кг влаги-
Расход тепла на 1 кг воздуха по ступеням подогрева определяет-
ся отрезками АВ', CiB" и С2В'"\ следовательно, расход тепла на 1 кг
испаренной влаги за весь процесс составляет:
q = I {АВ' + СХВ” + С2В'") =
1 000 {АВ' + С, В" + С2В'") Mj
DC^Md
Как видно из рис. 6-11,
АВ' + СгВ''+С2В'"=АВ,
следовательно,
1 ОООаВЛ^
9 = DCaMd ’
т. е. одноступенчатый процесс АВС3 имеет тот же расход (воздуха и теп-
ла, что и многоступенчатый процесс в пределах тех же параметров на-
ружного воздуха (точка Д) и отработавшего воздуха (точка С3). Одна-
ко максимальная температура воздуха для этого процесса равна ti
вместо t при одноступенчатом процессе, причем Л</. Эти сушилки при-
меняются в тех случаях, когда материал не может подвергаться воз-
действию высоких температур, а также для получения большей равно-
мерности сушки материала.
Построение действительного
процесса выполняется для каждой
ступени отдельно, так же как и
для простой сушилки с однократ-
ным использованием сушильного
агента.
Сушилки с промежуточ-
ным подогревом и рецир-
куляцией воздуха. Схема и
процесс на 7-гЛдиа грамме сушилки
с промежуточным подогревом между
отдельными ступенями и рецирку-
ляцией воздуха между ступенями и
по всей сушилке показаны на
рис. 6-12. Рециркуляция воздуха
осуществляется при помощи осевых
вентиляторов, установленных на об-
щем валу, приводимом в движение
электродвигателем. Эти вентилято-
ры многократно прогоняют воздух
через штабель сушимого материа-
ла, выбрасывают часть этого воздуха
в следующий штабель и взамен
его подсасывают такое же количест-
Рис. 6-11. Схема сушилки с промежу-
точным подогревом воздуха и ее про-
цесс на /-d-диаграмме.
203
Рис. 6-12. Сушилка с промежу-
точным подогревом и рецирку-
ляцией воздуха.
ки С, с наружным воздухом,
во воздуха из предыдущей ступени. Вен-
тилятор (первый по счету от электро-
двигателя) подсасывает смесь из свеже-
го воздуха, характеризующегося пара-
метрами точки А, с рециркулирующим
воздухом после третьего штабеля, харак-
теризующимся параметрами точки С.
Эта смесь с параметрами точки М снова
смешивается с воздухом, возвращающим-
ся из первой ступени, который имеет па-
раметры, соответствующие точке Ci, в
результате чего образуется смесь, имею-
щая параметры точки Mi. Смесь в точ-
ке Mi подогревается в первом калорифе-
ре, энтальпия ее увеличивается (точка
Bi); проходя через первый штабель, она
изменяет параметры по линии /=const.
Конечной точкой процесса в первой сту-
пени является точка Ci, в которой цикл
замыкается. В следующих штабелях про-
исходят аналогичные процессы, которые
также изображены на /-^-диаграмме на
рис. 6-12. Полный процесс в сушилке изо-
бражается тремя элементарными процес-
сами в отдельных ступенях с частичным
возвратом сушильного агента: MMiBiCiM,
С1МгВ2С2М2 и C2MSBSCMS и процессом
смешения рециркулирующего воздуха,
характеризующегося параметрами точ-
параметры которого отвечают точке А,
в результате чего получается смесь, параметры которой соответствуют
точке М. Расход свежего воздуха равен:
1= 1 000/DCMd.
Такое же количество отработавшего воздуха выбрасывается в атмо-
сферу через выхлопную трубу, расположенную за третьим штабелем.
Расход воздуха по отдельным ступеням определяется так:
/i=d 0W/DiCiMd, 12=Л ООО/ДгСгМй и /3=>1 m/D3CMd.
Расход тепла
q=ABM,- 1 000//)CAfd.
Сушилки с промежуточным подогревом и рециркуляцией воздуха
по сравнению с предыдущими требуют еще большего расхода электро-
энергии. Они применяются в случаях, когда требуется получить боль-
шую равномерность сушки материала и осуществить режимы с высоким
насыщением воздуха влагой и невысокой температурой. Примером та-
кой сушилки является ленточная сушилка рис. 6-18.
2. Сушка материалов продуктами сгорания (дымовыми и
топочными газами)
Конвективные сушилки, работающие на смеси продуктов сгорания
с воздухом, получили в настоящее время большое распространение.
Расчет этих сушилок ведут на 1 кг сухих газов с тем, чтобы можно
было для инженерных расчетов1 пользоваться /-//-диаграммой для воз-
духа, построенной для высоких температур.
1 Возможность пользования /-^-диаграммой для инженерных расчетов сушилок на
топочных или дымовых газах показана в [Л. 22, стр. 52].
204
Для построения процесса на /-{/-диаграмме находят значения эн-
тальпии I и влагосодержания d продуктов сгорания.
Влагосодержание
d= \ 000Gn/Gc.r, г на 1 кг сухих газов. (6-40)
Количество сухих газов на 1 кг сжигаемого твердого или жидкого
топлива
Gcr = 1 + “Ьо-------1--[од1--, кг на 1 кг топлива (6-41 а)
где а — коэффициент избытка воздуха; Ар, Н₽ и WP — процентные со-
держания золы, водорода и влаги на рабочую массу топлива.
Для сухого газообразного топлива
Gc г = 1 4- аЦ - СТОН„, (6-416)
где т — знак при Сип — знак при Н, a CmHn — составляющие газооб-
разного топлива, % от массы.
Количество водяных паров при сжигании твердого или жидкого
топлива
Q — 9№-р1^Р_. a£odo . (6-42а1
п~~ 100 '1 000 ^’ (О Д2а;
где W — количество водяного пара, применяемого для дутья или рас-
пыливания топлива.
Для сухого газообразного топлива
<5» = £-®^гс»н"+гаг + 117- <6’426)
Энтальпия смеси продуктов сгорания с воздухом, входящей в су-
шилку
. Qb^t + стА “Р „
1 =-------г-------, кДж на 1 кг сухих газов, (6-43)
ис.г
где Qg —высшая теплота сгорания топлива на рабочую массу,
кДж/кг; т]т — к. п. д. топки; ст и /т — теплоемкость, кДж/(кг-°С), и
температура, °C, топлива; а—коэффициент избытка воздуха в топке;
Lo — теоретическое количество сухого воздуха, необходимое для сжига-
ния топлива, кг/кг топлива; /о — энтальпия воздуха, кДж на 1 кг воз-
духа.
Теоретическое количество абсолютно сухого воздуха, необходимое
для сжигания 1 кг твердого или жидкого топлива,
Le = [0,1150 + 0.345НР — 0,043 (OP — )],
кг на 1 кг топлива, (6-44а)
где величины элементарного состава О, №', ОР и S* должны быть вы-
ражены в процентах на рабочую массу топлива.
Для сухого газообразного топлива
Lo = 1,38 (0,07900 4- 0,248Н2 4- 0,44H2S) 4-
п
мп т + ~
4“ 7 СТОНЭТ—О3, кг на 1 кг газообразного топлива, (6-446)
205
или
Vo = 0,0476 10.5CO + 0,5H2 + 1,5H2S -f-
X CmHn ~ °2] ’ m^m3’
(6-44b)
где CmHn — составляющие газообразного топлива в процентах на об-
щую массу.
Из формулы (6-43) следует, что энтальпия топочных газов, обра-
зующихся в результате сжигания топлива, не зависит от его влажно-
сти и определяется теплотой сгорания топлива, коэффициентом избыт-
ка воздуха а и остальными членами в чис-
лителе уравнения (6-43).
По найденным значениям параметров
топочных газов Ind находят положение
расчетной точки К для последующего рас-
чета сушилки по 1-х или /-tZ-диаграмме
(рис. 6-13) и (6-14).
Сушилки с однократным ис-
пользованием топочных газов.
Сушилки с однократным использованием
топочных газов применяются в большин-
стве случаев, когда сушка материалов про-
изводится при высоких температурах. При-
мером может служить барабанная сушилка
(рис. 6-21). Положение исходной точки К
на /-^-диаграмме (рис. 6-13) определяется
по формулам (6-40) и (6-43). Топочные га-
Рис. 6-13. Схема сушилки
с однократным использованием
топочных газов и ее процесс на
I 4-диаграмме.
зы после топки смешиваются с воздухом
в точке М до заданной начальной темпера-
туры /1 сушильного агента, поступающего
в сушилку. Построение действительного
процесса производится, как и для сушилки»
работающей на горячем воздухе с одно-
кратным использованием сушильного
агента.
Предположим, что в сушилке тепловые
потери преобладают над тепловыделениями
(Д<0). Проводим из точки М линию / =
= const, на ней выбираем точку е и определяем величину отрезка еЕ=
= efE/m (где т= (Mt/Md) -1 000]. Из точки М через точку Е проводим
политропу действительного процесса до пересечения ее с заданной ли-
нией t2 в точке С. Расход смеси топочных тазо-в и воздуха с параметра-
ми, соответствующими точке М, равен.
, 1 000 1 000 ,
lT = j-----, кг на 1 кг влаги.
~~~
Расход тепла на испарение 1 кг влаги (без учета потерь тепла
в топке)
AF АВ
<7 = -^г+Д == кДж на 1 кг влаги;
Zl-O I Q
9= ~DC-m+^-
Влагосодержание сушильного агента в точке К больше влагосодер-
жания его в точке А на величину di—do. Это увеличение происходит за
счет влаги, выделившейся при сжигании топлива.
206
Чтобы в расчете энтальпии газов исключить учет тепла на испаре-
ние влаги из топлива, расчет расхода топлива на сушку материала
следует вести по высшей теплоте сгорания QK В этом случае расчетная
формула для определения расхода топлива будет иметь вид:
B=qW/Q^, кг.
Расход топлива можно определить по формуле
B = /rIF/Gc.r, кг.
(6-45а)
(6-456)
Для одинаковых условий при сушке продуктами сгорания расход теп-
ла на 1 кг испаренной влаги получается всегда больше, чем при сушке
воздухом. Поэтому сравнение двух способов сушки следует вести по
расходу топлива на 1 кг испаренной влаги, который в большинстве слу-
чаев для сушилок, работающих на топочных и дымовых газах, имеет
меньшее значение, чем для суши-
лок с паровым обогревом [Л. 22].
Расход тепла в сушилках на то-
почных газах увеличивается с по-
вышением влажности сжигаемого
топлива.
Сушилки с рециркуля-
цией топочных газов. Если
топочные газы используются для
сушки материалов при низких тем-
пературах, но с высокой влажно-
стью, например в лесосушилках, где
температура смеси не превышает
80—90 °C, а влажность может дохо-
дить при этих температурах до 70%,
то применяют рециркуляцию их.
В этом случае сушилки работа-
ют по схеме, показанной на рис. 6-14.
Правильность графического по-
строения, показанного на рис. 6-14,
проверяют по отношениям:
d2n + dfi _ . . Г2п-\-Г\ _.
„+1 —«см, л+1 — 'см,
Ф 4~ nrd0 _rf, • I1 ~Ь __j,
п' + 1 ’’ п' + 1 ’’
Рис. 6-14. Схема сушилки с рецир-
куляцией топочных газов и ее про-
цесс на /-d-диаграмме.
где п — количество килограммов отработавшей смеси на 1 кг горячей
смеси; п' — количество килограммов холодного воздуха на 1 кг горячих
газов из топки: остальные параметры в этих уравнениях показаны на
рис. 6-14.
Количество выбрасываемых в атмосферу отработавших газов и по-
ступающей взамен их смеси из камеры смешения с параметрами точки
Mi для этой схемы равно:
. 1 000 1 000 .
КГ На 1 КГ ВЛаГИ-
Количество топочных газов с параметрами точки К, которое долж-
но поступать из топки в камеру смешения, чтобы получилась смесь то-
207
печных газов с наружным воздухом с параметрами точки Mlt равно:
lT=lKAMt/AK, кг на 1 кг влаги.
Количество наружного воздуха, поступающего в камеру смешения,
равно:
10—1кКМх!АК, кг на 1 кг влаги.
При этом /м=/т + 4-
Расход тепла для действительного процесса в сушилке без учета
к. п. д. топки
q — CD т, кДж на 1 кг влаги.
Расход топлива в этом случае определяется по тем же уравнениям
(6-44) или (6-45).
6-5. ОСНОВНЫЕ ТИПЫ И КОНСТРУКЦИИ СУШИЛОК
В народном хозяйстве применяется большое количество различных
типов и конструкций сушилок. В табл. 6-4 дана классификация совре-
менных сушилок.
Таблица 6-4
Классификация сушилок
Признак классификации] Типы сушилок
Давление в рабочем пространстве Режим работы Сушильный агент Атмосферные и вакуумные Периодического и непрерывного действия Воздушные, на продуктах сгорания, на смеси воздуха с продуктами сгорания и на перегре- том паре
Направление движения сушильного агента относительно материала Характер циркуляции сушильного агента С прямотоком, противотоком, перекрестным то- ком и реверсивные С естественной и принудительной циркуляцией
Способ нагрева сушильного агента С паровыми воздухоподогревателями, огневыми воздухонагревателями-рекуператорами, путем смешения с продуктами сгорания, с электро- нагревом
Кратность использования сушильного агента Однократные н с рециркуляцией
Схема нагрева сушильного агента С централизованным подогревом, индивидуаль- ными агрегатами и промежуточным подогревом
Способ удаления влаги из сушилки С воздухообменом, конденсационные и с хими- ческим поглощением влаги
Способ подвода тепла к материалу Конвективные, контактные (сушка на горячих поверхностях), с лучистым нагревом (термо- радиационные), с нагревом токами высокой частоты, комбинированные, акустические
Структура сушимого материала Твердый материал, кусковой, ленточный, пыле- видный, паста или жидкий раствор
Конструкция сушилки Коридорная, камерная, шахтная, ленточная, конвейерная, барабанная, трубчатая, вибра- ционная и т. п.
1. Конвективные атмосферные сушилки
В конвективных сушилках, имеющих наибольшее распространение
в промышленности, сушильным агентом является нагретый воздух или
смесь его с дымовыми или топочными газами.
208
а) Сушка крупногабаритных и малогаба-
ритных материалов
Камерные сушилки. Основным элементом камерной конвективной
сушилки (рис. 6-15) является прямоугольная камера, внутри которой
помещается сушимый материал, остающийся неподвижным в течение
всего процесса сушки. Загрузка и выгрузка материала производятся
с одной стороны сушилки. Камерные сушилки являются сушилками пе-
риодического действия и применяются при малых количествах сушимого
материала. В них производят сушку древесины, керамических и силикат-
ных изделий, различных сыпучих и волокнистых материалов, льняной
и конопляной тресты и т. п.
Сушимый материал подается в камерные сушилки на вагонетках,
периодически перемещаемых вручную или при помощи специальных
механизмов.
Туннельные или коридорные вагонеточные сушилки. Туннельная ва-
гонеточная сушилка представляет собой удлиненную камеру, внутри ко-
торой высушиваемый материал перемещается на вагонетках в продоль-
ном направлении; иногда ее называют коридорной. Загрузка и выгрузка
высушиваемого материала происходят в разных концах камеры. По ре-
жиму работы туннельные сушилки — сушилки полунепрерывного дей-
ствия Ч Они применяются для массовой сушки материалов (древесины,
керамических изделий, (различных сыпучих и волокнистых материалов),
которые укладываются для этой цели на вагонетки.
Длина камер туннельных (или коридорных) вагонеточных сушилок
может достигать 60 м, а ширина до 6 м. При проектировании этих су-
шилок и во время их эксплуатации стремятся к тому, чтобы зазор меж-
ду вагонеткой, стеной и потолком не превышал 70—80 мм, а расстоя-
ние между вагонетками 75 мм.
Длина сушильной камеры
L = -р— lB -|-1 = til-в -f- I, M, (6-46)
где П — часовая или суточная производительность сушилки, м3/ч, или
м3/сут; Пп — полезная емкость сушильного штабеля или вагонетки, м3;
/в — габаритная длина штабеля или вагонетки материала, выгружаемо-
го через определенные промежутки времени; т — продолжительность
сушки (определяется по тепловому расчету или берется по норматив-
ным данным), ч; / — дополнительная длина, необходимая для разбега
вагонеток, она может также включать зону предварительного нагрева
или остывания, м; п — число штабелей или вагонеток в сушильной ка-
мере; Vn=&Vr — объем штабеля или вагонетки, занятый материалом
или полезная емкость сушильного штабеля или вагонетки, Ег— габа-
ритный объем штабеля (или вагонетки), м3; <k — коэффициент плотности
или объемного заполнения штабеля (или вагонетки) высушиваемого
материала,
& ='^дл^ш^в = Иц/1,
где /гдл, k-щ, kE— коэффициенты заполнения штабеля по длине, ширине
и высоте.
Емкость сушильной камеры
Ук=77т/24, м3. (6-47)
Коэффициент полезного использования объема камеры
T]=Vrn/VK. (6-48)
1 В этих сушилках имеются периодическая загрузка и одновременная разгрузка
материала с большими интервалами времени.
14—1128 209
о
Рис. 6-15. Камерная сушилка с внутренними осевыми реверсивными вентиляторами.
/-—штабель сушимого материала, 2 — трековые тележки; 3 — ребристые подогревательные трубы, 4 — реверсивный осевой вентилятор; 5 — электродвигатель; 6— при-
точно-вытяжной канал: 7— увлажнительные трубы; 8 — конденсатоотводчик.
Циркуляция сушильного агента осуществляется как за счет естест-
венной, так и вынужденной конвекции (при помощи вентилятора). Прак-
тика эксплуатации показала, что для массовой сушки материалов нера-
ционально применять сушилки с естественной циркуляцией сушильного
агента, так как сушка материалов происходит в них дольше и менее ка-
чественна; удельный расход тепла на сушку в них больше, чем в су-
шилках с принудительной циркуляцией.
Туннельные сушилки могут иметь различные варианты сушильных
процессов, т. е. работать с однократным использованием сушильного
агента, рециркуляцией, промежуточным подогревом и позонной цирку-
Рис. 6-16. Компоновка лесосушильного цеха.
1 — полугазовая топка (см. рис. 6-17); 2 — центробежный вентилятор;
3, 4 и 5 — прямой и обратный туннели для газовоздушной смеси; 6 —
штабель сушимого материала; 7 — выхлопной вентилятор.
ляцией. Наибольшее распространение имеют сушилки с рециркуляцией
сушильного агента. Реверсивность, осуществляемая путем периодиче-
ского изменения направления вращения осевых вентиляторов в зонах,
обеспечивает равномерную сушку материала с той и другой стороны
штабеля. Сушилки с внутренними, обычно осевыми, вентиляторами име-
ют меньший расход электроэнергии, чем с внешними, центробежными,
но менее удобны в эксплуатации.
На рис. 6-16 дана схема компоновки туннельной лесосушки с топоч-
ным отделением, в котором, кроме топки, размещены большой центро-
бежный вентилятор для рециркуляции смеси топочных газов с воздухом
и маленький вентилятор для выброса отработавших газов.
Особенностью топок для лесосушилок является наличие в них спе-
циальных камер и циклонов для очистки топочных газов, которые затем
смешиваются с рециркулирующим сушильным агентом. Кроме того,
в этих топках осуществляется полугенераторный процесс сжигания твер-
дого топлива и дожигания газа подачей вторичного воздуха. Для полу-
чения чистых топочных газов через слой топлива проходит небольшое
количество воздуха (а<1). На рис. 6-17 показана такая топка. Типы то-
пок для сушилок и устройства для сжигания топлива рассмотрены
в [Л. 20, 22].
Ленточные сушилки. Ленточные сушилки работают по принципу не-
прерывного действия и применяются для сушки хлопка, шерсти, пряжи
и других материалов волокнистого строения, фруктов и овощей, нарезан-
ных на мелкие кусочки (ломтики толщиной 5—7 и длиной 20—30 мм),
а также чая, спичек, льняной и конопляной соломки и т. п. Сушилка пред-
ставляет собой камеру, внутри которой высушиваемый материал пере-
Ч* 211
двигается вместе с несущей его лентой. Сушка производится воздухом
или смесью его с топочными газами при температуре смеси 70—170 °C.
Схема ленточной сушилки для спичечной соломки показана на
рис. 6-18. Циркуляция воздуха осуществляется осевыми вентиляторами
ЦАГИ. Воздух пронизывает материал сверху вниз и прижимает суши-
мую соломку к ленточному транспортеру. Высушенный материал сходит
с ленты в ящик или на отводящий транспортер. Такие сушилки строятся
с шириной ленты до 2—2,2 м и длиной 30—40 м. Недостатком их являет-
ся неравномерность сушки по толщине слоя. Лучшие результаты по рав-
номерности сушки имеют многоярусные ленточные сушилки, в которых
материал перемешивается при пересыпке с одной ленты на другую.
Рис. 6-'17. Бесколосниковая полугазовая топка с искроосадительной камерой.
/ — топочная камера; 2 — загрузочная дверца; 3 — гляделка; 4 и 5 — искроосадительные камеры;
6 — шибер; 7— растопочная труба; 8— поддувальная дверца для подачи первичного воздуха; а —
зона горения; б — окошко подачи вторичного воздуха.
Длину рабочей ленты в ленточной сушилке можно определить по фор-
муле (6-46), если вместо Кп подставить объем материала, размещаемый
на 1 м ленты (в этом случае 2=1), а для конвейерной сушилки вместо
Vn подставляют п, или количество изделий, размещаемых на 1 м. В этих
сушилках расход тепла составляет от 5 000 до 7 500 кДж/кг влаги,
а электроэнергии — до 10 кВт-ч на 1 т испаренной влаги.
Конвейерные сушилки. Конвейерные сушилки бывают только непре-
рывного действия и применяются для сушки металлических изделий по-
сле окраски, клееных изделий из шпона и фанеры, в литейных цехах —
для сушки опок и стержней и т. п. Они представляют собой камеры,
внутри которых высушиваемый материал передвигается на несущем
конвейере.
212
to
w
Рис. 6-18. Ленточная сушилка.
1650-
1650
1 — конвейерная лента; 2 — осевой вентилятор; 3 — ребристые паровые подогреватели воздуха; 4—-ворошители; 5 — натяжная звездочка;
6 — редуктор и коробка скоростей; 7 — конденсатоотводчики.
Рис. 6-19. Конвейерная сушилка с подогревом воздуха в газовом рекуператоре для сушки окрашенных автодеталей.
1 — ванна для окраски деталей; 2 — фильтр для очистки свежего воздуха; 3—вентилятор для подачи свежего воздуха; 4— рекуператор;
5 — топка; 6 — дымосос; 7 — вентилятор для удаления отработавшего воздуха.
Конвейерная сушилка для сушки окрашенных автодеталей показа-
на на рис. 6-19. В этой сушилке воздух и высушиваемые детали движут-
ся противотоком. Для сушки некоторых красок и лаков допускается
высокая температура; в этом случае воздух может подогреваться в ре-
куператоре топочными газами из специальной топки. Применение бес-
калориферного подогрева воздуха (смешиванием с газами или в регене-
раторах) в данном случае недопустимо, так как сушильный агент дол-
жен быть совершенно чистым.
Сушилки для сушки красок, растворенных в уайт-спирите, работают
с однократным использованием горячего воздуха, так как повышение
концентрации в воздухе уайт-спирита при рециркуляции недопустимо
из-за опасности взрывов.
б) Сушка сыпучих и измельченных или
диспергированных материалов
Шахтные сушилки. В вертикальной шахте под действием силы тя-
жести высушиваемый сыпучий материал падает и пронизывается дви-
жущимся навстречу ему сушильным агентом. Сушилки могут различать-
ся характером движения материала внутри шахты. Возможны следую-
щие варианты:
а) материал движется внутри шахты со скоростью свободного па-
дения;
б) свободное падение материала искусственно замедляется путем
установки полок различной формы;
в) материал движется в шахте сплошной массой и скорость дви-
жения его определяется периодическим или непрерывным отбором вы-
,2500
Рис. 6-20. Барабанная сушилка.
/ — топка; 2— коллектор для вторичного воздуха; 3 — питатель; 4 — бункер влажно-
го материала; 5 — растопочная труба; 6—барабанная сушилка; 7 — электродвига-
тель; 8— вентилятор; 9— циклон; 10—горелка; 11— ленточный транспортер; 12 — теч-
ка для отделенной пыли.
214
сушиваемого материала в нижней части шахты; шахта всегда заполне-
на сушимым материалом;
г) скорость движения материала в шахте определяется скоростью
транспортирующих механизмов, расположенных внутри нее.
Сушилки первых двух групп применяются для материалов, требую-
щих удаления только поверхностной влаги, например соли, руды и т. п.
Период сушки для сушилок со свободным падением определяется не-
сколькими секундами, а для шахт с замедленным движением — минута-
ми или даже несколькими часами. Шахтные сушилки рационально при-
менять для материалов, которые по технологии производственного про-
цесса необходимо поднимать на значительную высоту (10—20 м).
Шахтные сушилки очень громоздки и в настоящее время вытесня-
ются другими типами сушилок.
Барабанные сушилки |[Л. 22, 28]. Барабанные сушилки (рис. 6-20)
применяются для сушки угля, песка, глины, известняка и других сыпу-
чих материалов. Основным эле-
ментом их является горизон-
тальный или чуть наклоненный
вращающийся со скоростью
2—6 об/мин цилиндрический
барабан, внутри которого пере-
мещается по длине, перемеши-
вается и одновременно сушит-
ся сыпучий материал. Наклон
барабана относительно гори-
зонтальной оси предусмотрен
для постепенного передвиже-
ния материала от одного кон-
ца к другому и составляет
обычно до 6°. Внутри бараба-
на в зависимости от сушимого
материала устанавливают раз-
личные насадки или продоль-
ные лопасти, способствующие
интенсификации процесса
сушки.
Основной характеристикой
барабанных сушилок является
напряжение объема барабана
по влаге, т. е. /1 = U7/Vt— коли-
чество испаряемой влаги в 1 м3
объема барабана в час.
Величина А зависит от
типа, степени заполнения и
числа оборотов барабана, теп-
лофизических свойств и разме-
ров материала, а также от
температуры, влажности и ско-
рости сушильного агента вну-
три барабана и составляет от
50 до 150 кг/(м3-ч). Расход
Рис. 6-21. Схема трубы-сушилки.
1 — мазутная или газовая топка; 2 — вертикальная
труба-сушилка; 3 — компенсатор температурных удли-
нений; 4 — циклон; 5 — шлюзовой затвор; 6 — дымо-
сос; 7 — ударная мельница или вентилятор; 8 — двух-
вальный шнековый смеситель и питатель; а — подача
влажного материала; б — выход сухого материала.
тепла <7=3 340-5-5 000 кДж на 1 кг влаги, а расход электроэнергии на
вращение и вентиляцию барабана равен от 0,005 до 0,007 кВт-ч на 1 кг
испаренной влаги.
Пневматические сушилки [Л. 22, 53]. Пневматические сушилки
в качестве основного агрегата имеют вертикальную камеру или трубу,
в которой сыпучий материал при высушивании находится во взвешен-
ном состоянии. Для поддержания частиц во взвешенном состоянии ско-
215
рость сушильного агента (воздуха или дымовых газов) должна быть
больше скорости витания частиц; в зависимости от размера частиц она
поддерживается от 10 до 40 м/с.
По режиму работы пневматические сушилки — сушилки непрерыв-
ного действия. Они .применяются для сушки дробленого угля, фрезер-
ного торфа, резаной травы, мелкокусковых и кристаллических мате-
риалов. Время пребывания частиц в трубе обычно не превышает 1—2 с,
поэтому удается испарить только свободную влагу и снизить влажность
материала лишь на 4—8%. Расход тепла в этих сушилках составляет
9=4 1804-6 670 кДж на 1 кг влаги. В 1 м3 объема трубы испаряется за
1 ч от 150 до 450 кг влаги. На рис. 6-21 показана пневматическая тру-
ба-сушилка с частичным подмешиванием высушенного материала для
получения сыпучести влажного материала.
Коэффициент теплообмена между газом и частицами приближенно
определяется из уравнения
Nu=ad8/A=0,4 Fe®-9. (6-49)
Критерий Федорова определяется по формуле (2-18).
В пневматических сушильных установках обычно приходится пере-
мещать частицы неправильной формы.
В целях упрощения расчета определение скорости витания таких
частиц производится по уравнениям для шарообразных частиц, но вме-
сто d вводится значение эквивалентного диаметра da. Для таких частиц
неправильной формы эквивалентный диаметр приближенно определяют
как диаметр шара, имеющего объем, равный объему средней частицы,
т. е.
<6-50>
у-, „ g. G • 6 000
где G — масса частиц в средней пробе, кг; п = —§----число частиц
в пробе; р — плотность частиц, кг/м’.
Скорость газа в трубе-сушилке выбирается больше скорости вита-
ния из условия перемещения частиц большего диаметра
wr=( 1,54-2,5) шиит, м/с. (6-51)
Для определения швит пользуются зависимостями Ly=f(ReBIIT) для
частиц неправильной формы (рис, 2-10). Длина трубы /=т(щг—швит).
Дополнительная длина разгонного участка
/доп—0,5 wrdB. (6-52)
Общая длина трубы-сушилки
Ь=1+1лаа. (6-53)
Диаметр трубы-сушилки
B = /-nsr’ (6-54)
где V — объем газа, перемещаемого в трубе-сушилке, м3/с
Время сушки
(6-55)
216
где Q — расход тепла на нагрев частиц и на испарение влаги, кДж/ч;
At — средний температурный напор между газом и частицами сушимого
материала, °C; F — поверхность частиц, проходящих через сушилку в те-
чение часа, определяемая по формуле
F = м2/ч. (6-56)
Сушилки с кипящим слоем [Л. 7, 40, 49]. Они применяются для
сушки различных мелкозернистых материалов. Сушилки сооружаются
в виде цилиндрической или прямоугольной камеры, внутри которой на
одной или нескольких ступенчатых решетках находится в «кипящем»
состоянии высушиваемый материал. На рис. 6-23 показаны схемы су-
Рис. 6-22. Зависимость критерия Лященко Ly от критерия Архимеда Аг при различной
порозности слоя е.
1 — при е—0,4 (начало псевдоожижения); 2 —при 8=1 (для скорости витания); область между ли-
ниями 3-4— ориентировочная область работы сушилок кипящего слоя.
217
шилок с кипящим слоем. Для поддержания равномерного «кипения» ча-
стиц в слое сушильный агент (воздух или топочные газы) подается под
решетку равномерно и с соответствующей скоростью распределяется по
всей ее площади. Подача влажного материала на решетку производится
в верхней части сушильной камеры, а отбор высушенного материала осу-
ществляется на уровне слоя материала в нижней части камеры.
Достоинствами сушки материалов в «кипящем» слое являются вы-
сокая интенсивность сушки, почти одинаковая по всему объему, темпе-
ратура «кипящего» слоя, и возможность регулирования времени пребы-
Рис. 6-23. Одноступенчатая сушилка с кипящим слоем.
/ — рабочая камера сушилки; 2 — подрешеточное пространство; 3 — решетка; 4 — электровентиля-
тор; 5 — люк для чистки; 6 — гидравлический порог; 7 — подача продуктов сгорания (сушильного
агента); 8— подача воздуха для регулирования температуры; 9— отвод отработавших газов-
к циклону; ▼ — уровень кипящего слоя.
вания материала в сушилке (в пределах от нескольких минут до десят-
ков минут); недостатками являются значительный расход электроэнер-
гии для создания давления газа под решеткой 2,94—4,9 кПа (300—
500 мм вод. ст.), обеспечивающего кипение слоя, а также измельчение
частиц материала в кипящем слое.
В настоящее время сушилки с «кипящим» слоем вытесняют бара-
банные сушилки и трубы-сушилки.
Расчет сушилок с кипящим слоем [Л. 20, 40] отличается тем, что
после определения количества испаренной влаги и удельного расхода
газов и тепла вычисляется значение критерия Архимеда по формуле
(2-20), где в качестве определяющего размера подставляется средний
эквивалентный диаметр частиц, а за определяющую температуру при-
нимается температура уходящих газов. Затем, пользуясь графиком Ly =
218
=/(Аг) (рис. 6-22), находят критическое значение LyKp (при 8=0,4) и
«определяют критическую скорость псевдоожижения
, м/с, (6-57)
где рм, рг—плотности частиц и газа, кг/м3; у — кинематическая вязкость
газа, м2/с.
По рис. 6-22 определяют также значение критерия Ly при наиболь-
шей возможной порозности кипящего слоя и находят число псевдоожи-
жения:
k,= /Ly/LyKp: (6-58)
Скорость газа (считая на полное сечение решетки spem)
ш=Л^кр. (6-59)
Скорость газа в отверстиях решетки
wOTO = w-|g^i-fn, (6-60)
где А и t2 — температура газа на входе и на выходе из сушилки, °C; /п—
проходное сечение решетки (принимается от 0,05 до 0,1 величины spem)-
Полная площадь решетки
^реш = A/ppW, (6-61)
где L — секундный расход газа, кг/с.
Диаметр решетки
^реш == V $реш/0,785. (6-62)
Далее рассчитывают сепарационное пространство, высота которого
принимается в 4 раза большей высоты кипящего слоя Нсл, мм, т. е.
Дсеп = 4Дсл, ММ.
Высота кипящего слоя принимается также в 4 раза больше высоты
гидродинамической стабилизации или высоты зоны действия струй
/Усл = 4/1СТ, мм.
Общая высота аппарата над решеткой
Н = Н Сеп + Нс л.
Между высотой гидродинамической стабилизации йст и диаметром
отверстий в решетке d0TB имеется следующая эмпирическая зависимость:
ЙстД?отв = 20. (6-63)
Количество материала, которое должно одновременно находиться
в кипящем слое сушильной камеры,
G = ^-, (6-64)
6аД/п ' '
где рм — плотность частиц, кг/м3; — средний эквивалентный диаметр
частиц, м; Д/л — средняя логарифмическая разность температур между
газом и материалом .в активной зоне сушилки, °C; Q=Qnar+Qncn — коли-
чество тепла, передаваемое от сушильного агента к материалу, находя-
щемуся в кипящем слое, кДж/с; а—коэффициент теплоотдачи, принима-
219
ется по опытным данным или вычисляется по эмпирическим зависимо-
стям, например
Nu = с4А=0,015Refl-8Fe0-53 (H0/dB) (6-65)
В этой формуле Но — высота неподвижного слоя, м.
Сушилки с виброкипящим слоем. В настоящее время разработаны
сушилки с виброкипящим слоем, в которых, например, устанавливается
решетка, вибрирующая с определенной частотой. Благодаря этой вибра-
ции кипящий слой возникает при скоростях фильтрующего газа, в 1,5—
2 раза меньших скоростей соответствующих псевдоожижению. Выбор
этого типа сушилок определяется технико-экономическим расчетом и
технологическими особенностями сушимого материала.
Рис. 6-24. Сушилка с распиливающим диском.
1 — сушильная камера; 2 — вентилятор; 3 электродвигатель с редук-
тором; 4 — распиливающий диск; 5 — скребки; 6 — разгрузочный шиек;
7 — рукавные фильтры; 8 — привод к скребкам и шнеку; 9 — механизм
для встряхивания рукавных фильтров.
Сушилки, работающие по принципу распыливания. Распыливающие
сушилки непрерывного действия применяются для сушки молока, яиц и
различных жидких растворов. Они представляют собой камеру, внутри
которой сушка материала происходит в распыленном состоянии. Рас-
пыливание достигается при помощи механических и пневматических фор-
сунок или быстро вращающегося диска, помещенных внутри сушильной
камеры. На рис. 6-24 показана сушилка с распиливанием сушимого ма-
териала при помощи диска.
Упрощенный расчет этих сушилок ведут по опытным данным на-
пряжения объема сушилки по влаге А, кг влаги/(м3-ч), или по форму-
лам тепло- и массопередачи (Л. 22, 26].
220
2. Терморадиационные сушилки
В последние годы как в нашей стране, так и за границей в различ-
ных отраслях промышленности получил применение новый способ суш-
ки материалов — инфракрасными лучами (лучистой тепловой энергией).
Этот способ применяется для поверхностной сушки лакокрасочных по-
крытий, металлических и деревянных изделий, тонких бумажных, тек-
стильных материалов и измельченных пищевых продуктов, а также при
сушке в тонком слое сыпучих материалов, когда требуется удалить толь-
ко поверхностную влагу или переместить ее внутрь изделия (например,
при сушке литейных форм) [Л. 23].
е
Рис. 6-25. Ламповая терморадиационная сушилка для сушки лакированных электротех-
нических деталей.
/ — лакировальная ванна; 2— наносные лакировальные валики; 3— ленточный транспортер; 4 —
зеркальные лампы; 5 — каркас сушилки; 6 — вытяжной воздуховод; 7 — теплоизоляционные листы;
3—приводная звездочка.
При сушке инфракрасными лучами интенсивность испарения влаги
по сравнению с конвективной или контактной сушкой может увеличи-
ваться в десятки раз. Это объясняется тем, что количество тепла, кото-
рое можно передать материалу при радиационной сушке, значительно
выше, чем при конвективной. Например, в первый период конвективной
сушки при температуре воздуха 100°C, влажности его q? = 5% и скорости
2 м/с и температуре материала, соответствующей температуре мокрого
термометра Ом=7м=40°С, тепловой поток <7=874 Вт/м2, а при сушке
термоизлучением при температуре излучающей поверхности 600 °C и тем-
пературе материала 40 °C тепловой поток </=26 200 Вт/м2, т. е. больше
примерно в 30 раз. Если температуру генераторов излучения увеличить
до 800 °C, то мощность теплового потока может стать в 70 раз больше,
чем при конвективной сушке. Но, как показывают опыты, не всегда мож-
но увеличить скорость сушки пропорционально увеличению теплового
потока, так как она определяется не скоростью передачи тепла, а ско-
ростью перемещения влаги внутри материала и требуемым качеством
готового продукта.
Терморадиационные сушилки бывают как стационарными, так и
переносными.
Переносные терморадиационные сушилки применяются для сушки
объекта на месте, например: влажных обмоток электродвигателей, окра-
шенных после ремонта судов, самолетов, автомобилей, стен помещений
221
и т. п. В качестве излучателя инфракрасных лучей в переносных сушил-
ках обычно применяются специальные электролампы.
По виду генераторов инфракрасного излучения терморадиационные
сушилки можно разделить на ламповые, сушилки с кварцевыми и труб-
чатыми или спиральными электронагревателями и сушилки с металли-
ческими и керамическими излучателями при газовом обогреве. В боль-
шинстве случаев терморадиационные сушилки с газовым обогревом бо-
лее экономичны, чем терморадиационные, использующие электроэнер-
гию.
Рис. 6-26. Терморадиационно-конвективная сушилка для лакокрасочных
покрытий.
а — принципиальная схема; б — общий вид установки; / — сушильная камера: 2—
газопровод; 3 — терморадиационная панель; 4 — вентилятор; 5 — линия подачн отброс-
ного воздуха на горение; 6 — линия забора дымовых газов из панелей; 7 — линия
забора сушильного агента из конвективной зоны; 8 — линия возврата газов на рецир-
куляцию; 9 — воздушная завеса у дверей; 10 — выбросы в атмосферу.
На рис. 6-25 приведена ламповая сушилка, а на рис. 6-26 приведена
принципиальная схема и показан общий вид радиационно-конвективной
сушилки для конвейерной сушки лакокрасочных покрытий на Минском
автозаводе. В радиационной зоне а происходит быстрый нагрев изделия
до 140—150°С, при котором из пленки улетучивается до 90% раствори-
теля. В конвективной зоне б происходит: выравнивание температур по
222
поверхности изделия и полимеризация покрытия. Общая продолжитель-
ность процесса составляет 10 мин. Сжигание газа происходит в щелевых
горелках, установленных в нижней топочной зоне радиационных пане-
лей; продукты сгорания смешиваются газами, циркулирующими в кон-
вективной зоне.
Главной задачей теплового и конструктивного расчета терморадиа-
ционных сушилок является определение количества и размеров генера-
торов лучистой энергии (электроламп, тэнов, излучающих панелей
и т. л.), так как интенсивность термообработки или сушки материалов
определяется плотностью лучистых потоков.
Воздух или его смесь с топочными газами в этих сушилках не явля-
ются сушильным агентом (их роль сводится к вентиляции сушильной
камеры от вредных выделений), поэтому применение для расчета этих
сушилок /-{/-диаграммы теряет смысл.
Уравнение теплового баланса для условий электроламповой сушки
лакокрасочных покрытий (рис. 6-25) можно представить уравнением,
в котором энергия, поглощаемая облучаемым телом за время dr, будет
затрачиваться на его нагрев, потери тепла нагреваемым телом в окру-
жающее пространство конвекцией и излучением, и на испарение из него
влаги:
AEsodz = Gcdt + ак (t — tB) sdt ф- 5,67епр [(Г/100)4 — (То/100)4] sdr ф-
+ qmre~'ld-z, (6-66)
где А — коэффициент поглощения излучения облучаемым телом; Е —
плотность облучения —- плотность лучистого потока по облучаемой по-
верхности, Вт/м2; s0 и s — площадь облучаемой и полной поверхностей
тела, м2; т-—время от начала облучения, с; G— вес облучаемого тела,
кг; с — теплоемкость облучаемого тела, кДж/(кг-°С); t и /в— темпера-
туры тела и окружающего воздуха, °C; ак — коэффициент теплообмена
конвекцией, Вт/(м2’°С); епр — приведенная степень черноты облучаемого
тела и внутренних ограждений сушилки; Т и То — температура тела и
окружающих поверхностей, К; qm — начальная интенсивность или ско-
рость испарения вещества, кг/(м2-с); х—- показатель поглощения излу-
чения телом, 1/м; I — глубина проницаемости вещества лучистым пото-
ком от его наружной поверхности, >м.
Приведенное уравнение действительно и при расчете других типов
терморациационных сушилок, если в правую часть уравнения подста-
вить соответствующее количество тепла, передаваемого от данного из-
лучателя, с учетом обратного отражения лучистого потока [Л. 22].
3. Контактные атмосферные и вакуумные сушилки
В контактных сушилках сушка осуществляется за счет тепла, по-
лученного материалом от соприкосновения с нагретой плоской или ци-
линдрической твердой поверхностью. В большинстве случаев нагрев по-
верхности производится водяным паром, а в некоторых случаях — горя-
чей водой, горячим маслом или высокотемпературными теплоносителями.
Вальцовые сушилки (рис. 6-27). Вальцовые сушилки являются су-
шилками непрерывного действия и предназначаются для сушки текучих
веществ (растворов, коллоидов и суспензий). В качестве основного
узла они имеют один или два полых вращающихся вальца, обогревае-
мых изнутри паром или каким-либо другим теплоносителем. На поверх-
ности вальцев за период менее одного оборота происходит высушива-
ние нанесенного тонким слоем жидкого или пастообразного материала.
Высушенный материал соскабливается с вальца скребком или специ-
альными ножами.
223
9
Вальцо-
Рис. 6-27.
вая вакуум-сушил-
ка непрерывного
действия.
/ — корпус: 2 — валец; 3 — трубка для подачи грею-
щего пара: 4 —трубка для подачи материала; 5 —
высушенный материал; 6 — нож; 7 — труба для отво-
да паров из корпуса; 8 — смотровое стекло; 9 —
змеевик.
ром 100/108 мм для бурых и 119/128 мм
Цилиндрические сушилки
работают по принципу непре-
рывного действия и применя-
ются для сушки ленточных ма-
териалов (тканей, бумаги, цел-
люлозы и т. п.). Основными
элементами сушилки являются
несколько вращающихся по-
лых цилиндров, обогреваемых
изнутри паром, на горячей по-
верхности которых происходит
высушивание ленточного мате-
риала.
Сушилки выполняются с
вертикальным и горизонталь-
ным расположением цилинд-
ров. Материал огибает цилинд-
ры, соприкасаясь с горячей
поверхностью. На рис. 6-28
показана цилиндрическая су-
шилка для сушки хлопчатобу-
мажных тканей.
Трубчатые сушилки (рис.
6-29). Трубчатые сушилки при-
меняются главным образом
для сушки угля и представляют
собой наклонный вращающий-
ся барабан, в днищах которого
завальцованы трубки диамет-
для каменных углей. Они могут
применяться и для других измельченных кусковых материалов.
Влажный материал специальным приспособлением — питателем —
подается в трубки и при вращении барабана передвигается по ним
к выходу для выгрузки. Для лучшего заполнения, перемешивания и
Рис. 6-28. Цилиндрическая сушилка для хлопчатобумажных тканей.
1 — сушильный цилиндр; 2 — направляющий ролик; 3 — станина; 4 — винтовой расправитель; 5 и 6 —
Цилиндрические и конические зубчатые колеса; 7 — конленсатоотводчик.
224
дробления материала с целью увеличения поверхности испарения при
вращении барабана трубки внутри заполнены различными металличес-
кими вставками. В качестве греющего теплоносителя обычно применя-
ется пар из отбора турбины давлением не выше 3,92-Ю5 Па (4кгс/см2).
Интенсивность сушки по материалу составляет от 2 до 4,5 кг/(ч • м2)
поверхности труб, расход тепла </=3 200=3 800 кДж на 1 кг влаги
(750—900 ккал/кг). Расход электроэнергии равен от 5 до 6 кВт-ч на
1 т испаренной влаги.
Рис. 6-29. Трубчатая сушилка.
/ — загрузочное устройство для подачи влажного материала; 2 — передняя цапфа; 3 —
редуктор; 4 — фрикционный привод; 5 —барабан трубчатой сушилки; 6 — трубки; 7 —
винтовые вставки в трубках; 3 —шнек; 9 — камера для выгрузки материала; 10—
трубы от черпаков для отвода конденсата.
Вакуумные контактные сушилки. Вакуумные сушилки вследствие
сложности и дороговизны имеют сравнительно ограниченное примене-
ние и встречаются главным образом в химической промышленности.
В качестве вакуум-сушилок применяются также сушильные шкафы
с установленными по их высоте обогреваемыми полками или плитами,
на которых располагается периодически загружаемый для сушки мате-
риал. Вакуум в сушильных шкафах создается конденсационными
устройствами с конденсаторами поверхностного или смешивающегося
типа.
Преимуществом вакуум-сушилок по сравнению с конвективными
атмосферными сушилками является более интенсивная сушка при низ-
ких температурах, что важно для веществ, не выдерживающих высокой
температуры. Например, при давлении греющего пара 2-Ю5 Па (tH=
= 120 °C) и вакууме в камере 0,867-105 Па (650 мм рт. ст.) температу-
ра материала будет порядка 66°C и разность температур равна 120 —
—54=66 °C против 120—100=20 °C при сушке воздухом в атмосферных
сушилках; испарение с поверхности одинаковой величины при вакуум-
ной сушке теоретически должно происходить в 2—3 раза быстрее, чем
при атмосферной.
Вакуумная сушка требует меньшего расхода тепла вследствие
(почти) отсутствия потерь с уходящим воздухом. Например, на 1 кг
воды, испаряемой при температуре 40 °C, требуется 2 570 кДж тепла
в вакуумной сушилке, а в атмосферной сушилке 3 440 и 3 860 кДж, если
воздух выходит с относительной влажностью соответственно 75 и
15—1128 225
50%. Достоинством вакуум-сушилок является стерильность среды.
Герметичность сушильной камеры дает гарантию против загрязне-
ния продукта пылью из окружающего воздуха и окисления его кис-
лородом воздуха. Имеется также полная возможность исключить выде-
ление из материала вредных паров и газов в окружающую среду, что
особенно важно при сушке ядовитых веществ.
При сушке под вакуумом имеется возможность более полного улав-
ливания ценных или вредных паров. Вместо дорогой абсорбционной
установки, применяющейся для поглощеня таких паров при атмосфер-
ной сушке, в вакуум-сушилке применяется более дешевое и радикаль-
ное средство улавливания паров путем конденсации (до 95% таких
летучих растворителей, как этиловый спирт, ацетон и др.). Наконец,
при вакуумной сушке меньше потери продукта и в виде пыли и меньше
пожарная опасность.
К недостаткам сушки под вакуумом следует отнести высокую сто-
имость сушильного агрегата вследствие сложности его конструкции и
наличия специальной конденсационной установки и трудность надзора
за процессом сушки во время работы сушилки’, так как открывание
люков сушилки нарушает вакуум. Несмотря на ряд преимуществ, ва-
куум-сушилки из-за большой сложности их применяются только в тех
случаях, когда это вызывается технологическими особенностями обра-
ботки высушиваемого материала.
Существуют экспериментальные данные для сушки различных ма-
териалов по напряжению поверхности нагрева контактных сушилок,
B = WIFi — количество испаряемой влаги с 1 м2 поверхности нагрева
в час [Л. 50, т. II]. По этим данным выбирают соответствующий тип и
конструкцию сушилки.
Для теплового расчета контактных сушилок необходимо опреде-
лить 'Коэффициент теплопередачи от греющего теплоносителя через огра-
ничительную стенку к поверхности материала, определение которого
представляет большие трудности.
'•‘‘f 4. Сублимационные сушилки
Сублимация представляет собой процесс испарения твердого тела,
т. е. превращение его непосредственно в газообразное состояние без
промежуточного прохождения через жидкое состояние, и является про-
цессом обезвоживания или сушки материала в замороженном состоянии
[Л. 22, 25, 24]
Сублимационная сушка в зависимости от рода материала произ-
водится при остаточном давлении 0,2—2 мм рт. ст. Процесс сублимаци-
онной сушки материала в замороженном состоянии протекает при не-
прерывном углублении поверхности испарения и может характеризо-
ваться постоянной и падающей скоростью сушки (при удалении связан-
ной влаги). Температура материала в первый период остается постоян-
ной и повышается во второй период сушки.
Тепло на испарение берется из окружающей среды через теплопро-
водные стенки камеры или от специальных термоизлучающих подогре-
вателей, в которых иногда циркулирует вода с температурой 40—60 °C.
Сушка сублимацией применяется в настоящее время для весьма
чувствительных к нагреву материалов, например биологических фарма-
цевтических препаратов (пенициллин, стрептомицин, кровяная плазма,
биопрепараты и т. п.), а также для некоторых пищевых продуктов
(мясо, рыба, ягоды, фрукты и т. п.). Высушенный таким способом мате-
риал имеет пористое губчатое строение, сохраняет полную биологиче-
скую активность, растворимость и допускает длительное хранение.
Принципиальная схема установки для сушки сублимацией, пока-
занная на рис. 6-30, не отличается от схемы вакуум-сушилки. Разница
226
Рис. 6-30. Принципиальная схема сублимационной сушильной установки.
/ — сублиматор с греющими плитами и противнями для продуктов; 2 — кондеисатор-вымораживатель п,зров из сублиматора-испарителя холодильной установки; 3 — ва-
куумный-насос с электродвигателем; 4 — компрессор холодильной установки с электродвигателем 5 — трубчатый элементный кочденсаюр холодильной установки; 6 —
аммиачный ресивер; 7 — бак для горячей воды с электронасосами для оттаивания льда в конденсаторе н сублиматоре; 5 — сепаратор влаги.
состоит в том, что конденсатор охлаждается не водой, а циркулирую-
щим через холодильную установку рассолом, температура которого
поддерживается в пределах от —20 до —40 °C в соответствии с требу-
емым вакуумом. Вследствие того что конструкция непрерывно дейст-
вующих конденсаторов получается очень сложной, из-за необходимости
снятия и удаления образующегося льда, в настоящее время применяют
схемы с двумя конденсаторами, один из которых находится в работе,
а в другом тает лед.
Недостатками сублимационной сушки по сравнению с атмосферной
конвективной или обычной контактной вакуум-сушкой являются высо-
кая стоимость установки, большая сложность ее эксплуатации и значи-
тельный расход электроэнергии на холодильную установку и вакуум-
насос.
5. Сушка материалов в поле токов высокой частоты и
комбинированные способы сушки материалов
В 30-х годах нынешнего столетия получил применение новый спо-
соб интенсивной сушки и термической обработки материалов (электро-
проводников и диэлектриков)—токами высокой частоты [Л. 22,30].
При высокочастотной сушке внутренние, более влажные слои ма-
териала нагреваются быстрее наружных. При этом в средней части ма-
териала устанавливается более высокая температура, чем на его поверх-
ности. Под действием температурного градиента влага интенсивно пе-
Рис. 6-31. Схема двухъярусной ленточной
сушилки для сушки токами высокой часто-
ты порошковых материалов.
ремещается к поверхности,
благодаря чему скорость суш-
ки материалов увеличивается
иногда в десятки раз. Однако
этот способ сушки не получил
широкого промышленного при-
менения вследствие значитель-
ного расхода электроэнергии
(2,5—4 кВт • ч/кг испаренной
влаги) и высокой стоимости
сушки *.
В целях снижения расхо-
да энергии высокочастотную
сушку комбинируют с термора-
диационной или конвектив-
ной1 2. Затрачивая, например,
высокочастотную энергию
только на создание необходи-
мого градиента температур
внутри материала, испарение влаги производят тепловым способом или
же включают в работу высокочастотную установку только в момент
удаления из материала связанной влаги. Применение комбинированных
спосбов подвода тепла позволяет недостатки одного способа подвода
тепла компенсировать преимуществами другого.
Все высокочастотные сушильные установки состоят из двух основ-
ных элементов: высокочастотного генератора и сушильной камеры. Но
так как в сушилках производится сушка разнообразных материалов,
1 Индукционно-контактная сушка и термообработка (древесины, бетона) токами
промышленной частоты требуют меньшего удельного расхода электроэнергии, но также
имеют ряд недостатков и широкого применения не получили.
2 Б. А. Посновым и Н. А. Першановым был предложен комбинированный конвек-
тицно-высокочастотный способ сушки древесины, а П. Д. Лебедевым и А. А. Лисенко-
вьГм — комбинированный терморадиационный и высокочастотный способ сушки мате-
риалов.
228
то они различаются устройством сушильной камеры, конструкцией ге-
нератора, частотой тока и укладкой электродов.
На рис. 6-31 показана принципиальная схема высокочастотной лен-
точной сушильной установки для порошкообразных материалов.
В заключение следует отметить, что в большинстве сушилок кон-
вективных, контактных и терморадиационных происходит сложный теп-
лообмен и их название определяется тем способом подвода тепла, ко-
торый имеет определяющее влияние на интенсивность сушки материа-
ла.
Следует отметить также целесообразность комплексного примене-
ния разных типов сушилок, например, сочетание распылительной су-
шилки с досушкой в кипящем слое, пневмосушилки с сушкой в кипя-
щем слое и т. п.
Весьма перспективно и совмещение в одном агрегате процесса
сушки с другими технологическими процессами, например: сушки и
помола или измельчения материала, сушки и обжига, сушки и
полимеризации и т. п.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Укажите области рационального применения естественной и искусственной суш-
ки материалов.
2. Чем отличается процесс испарения от процесса кипения или выпаривания? Ка-
кая влага имеет наибольшую и какая наименьшую энергию связи с материалом?
3. Как называются периоды сушки материала? Объясните, как изменяются влаж-
ность и температура материала в эти периоды.
4. Что такое критическая влажность материала? Какую конечную влажность дол-
жен иметь материал: а) чтобы отсутствовал период падающей скорости сушки;
б) чтобы отсутствовал период постоянной скорости сушки?
5. Что такое гигроскопическая влажность и какое она имеет практическое значе-
ние? Какая влажность имеет большее численное значение при сушке материалов: кри-
тическая или гигроскопическая? Для каких материалов эта разница больше: толстых
или тонких и как она изменяется с повышением скорости сушки?
6. Что такое равновесная влажность и как она изменяется с повышением и по-
нижением температуры и относительной влажности сушильного агента?
7. Что такое градиент влажности в материале? В каких случаях происходит
растрескивание материала и какие меры принимают для его устранения?
8. От каких параметров зависит интенсивность испарения влаги с поверхности
материала?
9. Напишите уравнение переноса влаги в материале при температуре его до 100 °C
и выше (при высокотемпературной сушке). Какими градиентами определяется перенос
влаги из материала при его низкотемпературной и высокотемпературной сушке?
10. Чем отличается локальная влажность и, используемая в дифференциальных
уравнениях, от средней влажности материала ш?
11. Укажите, какой градиент определяет перенос влаги в материале при конвектив-
ной, контактной и терморадиационной сушке и при сушке материала в поле токов
высокой частоты и какой градиент задерживает или тормозит перемещение влаги из
центра .материала к его поверхности? Как изменяются t и и в средней части и на по-
верхности материала при этих способах сушки?
12. Как изменяются коэффициенты термовлагопроводности б и потенциалопровбд-
ности ат в зависимости от температуры материала и его средней влажности?
13. Напишите дифференциальное уравнение термовлагопроводности для низкотем-
пературной и высокотемпературной сушки. Какую основную задачу они решают и при
каких граничных условиях?
14. Напишите формулы для определения расходов сухого воздуха и тепла на 1 кг
испаренной влаги.
15. Имеются ли потери тепла в теоретической сушилке? Изобразите на /-d-диа-
грамме процесс в теоретической сушилке с однократным использованием сушильного
агента. Почему процесс в теоретической сушилке протекает при /=const?
16. Чем отличается действительная сушилка от теоретической? Что означает ве-
личина Д в действительной сушилке? Какие она может иметь значения и как в зависи-
мости от ее значения изменяются удельные расходы воздуха и тепла на 1 кг испарен-
ной влаги?
17. Какая влажность материала, на общую или сухую массу, используется в тепло-
вых расчетах и какая — при анализе кинетики процессов сушки?
18. Какая влага, содержащаяся в материале, не замерзает при низких темпера-
турах?
229
19. Объясните, что такое потенциал сушки, какое он имеет значение и какая из
трех разностей: рн—р, tc—tM или d2—dt получила большее распространение в качестве
потенциала сушки?
20. Изобразите на /-d-диаграмме процесс в действительной сушилке с однократным
использованием сушильного агента при Л<0 и Д>0.
21. Изобразите на /-d-диаграмме теоретические процессы для вариантов сушки
горячим воздухом: а) с 'рециркуляцией сушильного агента и б) с промежуточным по-
догревом. Как построить для этих вариантов действительные процессы при А<0 и
Д>0?
22. Какие преимущества и недостатки имеют сушилки на горячем воздухе с ре-
циркуляцией и промежуточным подогревом по сравнению с сушилкой с однократным
использованием сушильного агента и в каких случая они применяются?
23. Изобразите на /-d-диаграмме теоретические процессы для сушки материала
топочными газами для вариантов с однократным использованием и рециркуляцией су-
шильного агента. Укажите, как определяются расходы тепла и газов на 1 кг испарен-
ной влаги. Зависит ли расход тепла от влажности топлива?
24. Какие преимущества и недостатки имеет сушка материала топочными газами
по сравнению с сушкой горячим воздухом? Каким образом снижается пожарная опас-
ность сушилок на топочных газах? Укажите области применения сушилок, работающих
на топочных газах.
25. Какие вентиляторы, центробежные или осевые, целесообразно применять в су-
шилках с рециркуляцией сушильного агента?
26. Какие сушилки более экономичны в отношении расхода тепла: непрерывного
или периодического действия, большой или малой производительности?
27. Какие конвективные камерные и коридорные сушилки имеют большие перспек-
тивы применения: с вынужденной или естественной циркуляцией сушильного агента?
28. Укажите, какие материалы целесообразно сушить в барабанных, пневмосушил-
ках, сушилках с «кипящим» слоем и распылительных сушилках. Приведите сравнение
этих типов сушилок.
29. Укажите достоинство и недостатки вакуумных и сублимационных сушилок.
30. Укажите область применения сушки в поле токов высокой частоты, сушки
методом сублимации.
31. Какие преимущества дают комбинированные способы подвода тепла, комбини-
рованные методы сушки, а также комбинирование процесса сушки с другими техноло-
гическими процессами? Приведите соответствующие примеры.
ГЛАВА СЕДЬМАЯ
ГИДРАВЛИЧЕСКИЙ И МЕХАНИЧЕСКИЙ РАСЧЕТЫ
ТЕПЛООБМЕННЫЕ АППАРАТОВ
7-1. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТЕПЛООБМЕННЫХ
АППАРАТОВ
Гидравлический расчет устанавливает затрату энергии на движе-
ние теплоносителей через аппарат. Полный напор Др, необходимый для
движения жидкости или газа (при скорости газа, не превышающей 0,2
скорости звука) через теплообменник, определяется по формуле
Др = 2Дрт,р+2Дрм+ЕЛру+ДРг, Па (кгс/см2), (7-1)
где 2ЛрТр — сумма гидравлических потерь на трение; 22Лрм — сумма
потерь напора в местных сопротивлениях; 2Дру — сумма потерь напо-
ра, обусловленных ускорением потока; Дрг — перепад давления для пре-
одоления гидростатического столба жидкости.
Гидравлические потери на трение в трубах, каналах и при продоль-
ном омывании пучка труб теплообменного аппарата определяются по
формуле
ДАр = Я^--^, Па, (7-2)
где I — длина трубы, м; da — эквивалентный (гидравлический) диаметр,
м; w — средняя скорость теплоносителя на данном участке, м/с; р—
плотность теплоносителя, кг/м3; X — коэффициент сопротивления трения
(величина безразмерная).
230
При изотермическом движении жидкости1 в гладких трубах и ка-'
налах X=f(Re), а в шероховатых A.=/(Re, 6/г) (где 6— средняя высо-
та выступов шероховатости, а г — радиус трубы). Значения X и р бе-
рутся при средней температуре теплоносителя (значения 7. даны
в [Л. 48 и 50]).
Коэффициенты сопротивления для пучка труб при поперечном омы-
вании (перпендикулярно оси труб):
а) для шахматных пучков при sdd<s2]d
"к= (4 + 6,6 т) Re"41'28;
б) для шахматных пучков при si/d>s2/d
Х= (5,4+ 3,4 m)Re-°’29
в) для коридорных пучков
X=(6 + 9m) (s1/d)~°’33Re.
Здесь + — расстояние между осями труб поперек движения пото-
ка (по ширине пучка); s2 — расстояние между осями труб вдоль дви-
жения потока (по глубине пучка); d — наружный диаметр трубы; т—
число рядов в пучке в направлении движения.
Гидравлические потери да.вления в местных сопротивлениях: в па-
трубках, крышках, трубных решетках, перегородках, диффузорах, на-
садках, задвижках, вентилях и других элементах теплообменника опре-
деляются по формуле
ДРм = ^>ау2/2, Па, (7-3)
где g — коэффициент местного сопротивления; его находят отдельно для
каждого элемента теплообменника, затем подсчитывают все Дрм, зна-
чения которых суммируют.
Потери давления, обусловленные ускорением потока вследствие
изменения объема теплоносителя при постоянном сечении канала,
А/+ = p2w2 — p,w2, Па, (7-4)
где Wj, pi и w2, р2 — скорости, м/с, и плотности газа, кг/м3, во входном
и выходном сечениях потока; для капельных жидкостей Ару ничтожно
мало и не принимается в расчет.
Если газовая полость айпарата сообщается с окружающей сре-
дой, то
Apr—hg (pt—р2), Па, (7-5)
где h— расстояние по вертикали между входом и выходом теплоноси-
теля, м; pi и р2 — плотности газа в аппарате и окружающей среде.
Величина Арг в случае движения газа называется сопротивлением
самотяги. Если теплообменник не сообщается с окружающим воздухом
(включен в замкнутую систему), то Арг=0.
Формула (7-1) включает все возможные виды сопротивлений и
является обобщенной. Применение ее для расчета гидравлических со-
противлений различных теплообменников требует пояснений. Например,
при расчете потерь напора для скруббера 2Артр = 0, так как он не име-
ет поверхностей нагрева. Определение Арг невозможно без знания ме-
ста включения теплообменного аппарата в схеме и т. д.
1 Данные для расчета гидравлических сопротивлений в трубах и каналах при не-
изотермическом движении жидкости приведены в [Л. 11, 32].
231
Рассмотрим некоторые простейшие схемы включения теплообмен
ника. В схеме на рис. 7-\,а теплообменник подключен к тепловой сети
Горячая вода поступает из прямого трубопровода (отмечен плюсом),
проходит по аппарату в качестве греющего теплоносителя и, охладив-
шись, уходит из него в обра-
В этом случае бывает задано
мой и обратной линиях сети).
Рис. 7-1. Схемы подключения теплообмен-
ников.
с " к теплосети; б — к топке с естественной цир-
куляцией теплоносителя; в — с разрывом струи;
г — с сифоном; д — последовательное включение
двух теплообменников; е — параллельное включе-
ние двух теплообменников; / — теплообменники;
2 — насосы; 3 — топка; 4 — баки или колодцы; 5 —
трубы теплосети; 6 — вентили или задвижки.
трубопровод (отмечен минусом).
Apc = pi—рг (разность давлений в пря-
Необходимо так спроектировать тепло-
обменник, чтобы Арс=Ар+Арт
(где Ар и Арт— гидравлические
сопротивления теплообменника и
трубопроводов, соединяющих его
с тепловой сетью).
Если Ар+Арт>Арс, то вслед-
ствие меньшего расхода теплоно-
сителя теплообменник будет
иметь теплопроизводительность
меньше расчетной; если Ар +
+Дрт<Арс, то будет больший
расход теплоносителя, (чем тре-
буется), т. е. окажется бесполез-
но завышенной поверхность на-
грева теплообменника. Следует
также заметить, что при расчете
полного гидравлического сопро-
тивления теплообменника Ар по
формуле (7-1) принимают 2Ару=
= 0 и Арг=0.
На рис. 7-1,6 представлена
схема подвода тепла в теплооб-
менник от змеевика, расположен-
ного в топке. Циркуляция грею-
щего теплоносителя происходит
здесь за счет гравитационного
напора, поэтому для гидравличе-
ского расчета в этом случае ис-
пользуется другая формула
Apr=ftg(pi—рг) =2Артр +
+2Арм+1Арт+1Ар зм>
(7-6)
где h — высота между уровнями верхней и нижней отметок схемы, м;
pi и рг — плотности опускающегося и поднимающегося теплоносителя,
циркулирующего в системе, кг/м3; 2АрТр и 2Дрм— потери на трение и
местные сопротивления в теплообменнике, Па; Арт— гидравлические
потери в подводящих трубопроводах, Па; Дрзм— потери в змеевике, Па.
Если в схему включен насос и теплообменник может быть установ-
лен на одном уровне с топкой, то расчет Ар ведется по формуле (7-1)
при Арг=0.
На рис. 7-1,6 показана схема, в которой теплообменник располо-
жен на некоторой высоте относительно насоса и теплоноситель слива-
ется в верхний бак с разрывом струи. В этом случае для определения
Ар теплообменника действительна формула (7-1). При определении
мощности насоса необходимо учесть сопротивление подающих трубо-
проводов (Alpi=/igp).
На рис. 7-1,г представлена схема включения теплообменника с си-
фоном, при которой приемный и выходной патрубки трубопроводов
погружены в резервуары с той же жидкостью, находящейся при одина-
232
ксвом давлении. В этом случае при определении Ар по формуле (7-1)
принимают Арг=0. По такой схеме включаются конденсаторы паровых
турбин электростанций.
В схеме с теплообменниками, включенными последовательно
(рис. 7-1,д), их гидравлические сопротивления суммируются. При опре-
делении гидравлического сопротивления в этой замкнутой схеме Дрг=0.
В случае параллельного включения теплообменников, имеющих
одинаковое сопротивление (рис. 7-1,е), расчет потери напора ведется
для более удаленного от насоса теплообменника.
Если два калорифера с пластинчатыми ребрами (см. рис. 1-23,а),
имеющие каждый гидравлическое сопротивление Api = ga>2ip/2, вклю-
чить последовательно по воздуху при p = const и том же расходе воз-
духа, тогда то же количество воздуха должно пройти через вдвое
меньшее проходное сечение, т. е. его скорость должна удвоиться (w2=
— 2w1), а гидравлическое сопротивление одного калорифера учетве-
риться:
Ap2=b(2r«i)2p/2.
Гидравлическое сопротивление двух калориферов, включенных по-
следовательно, при станет большим в 8 раз:
2 А р2 = 2 (2w i) 2р/2
или
ЕДА _ 8w? , _ R
В 8 раз увеличится и расход электроэнергии на вентиляцию. При
числе переключаемых с параллельной на последовательную работу сек-
ции, равном п, общее сопротивление их возрастает в 2Apn/Api=nn2=
= п3 раз.
Это сравнение является приближенным, так как в нем не выдержа-
но важное условие — постоянство теплопроизводительности сравнивае-
мых вариантов. Тем не менее оно показывает, что при переключении
калориферов с параллельного соединения по воздуху на последователь-
ное может резко возрасти сопротивление, снизиться производительность
вентилятора и резко уменьшиться теплопроизводительность теплообмен-
ника.
Гидравлическое сопротивление теплообменника зависит от квадра-
та скорости теплоносителя wz. С повышением скорости, с одной сторо-
ны, растет коэффициент теплоотдачи, т. е. уменьшается поверхность на-
грева, уменьшаются размеры и соответственно стоимость теплообмен-
ника, а с другой — увеличиваются расход электроэнергии и ее стои-
мость. Поэтому выбор оптимальной скорости теплоносителя
в теплообменнике должен решаться на основании технико-экономиче-
ских соображений. Однако в большинстве случаев последовательное
соединение по воздуху ребристых калориферов и других теплообменных
аппаратов нерентабельно и может быть оправдано только конструктив-
ными условиями компоновки агрегата.
Во многих случаях определяется не гидравлическое сопротивление
отдельного теплообменника, а сопротивление всей системы, в которую
включен аппарат. Например, для системы барабанной сушилки
(рис. 6-21) гидравлическое сопротивление складывается из сопротивле-
ния топки, барабанной сушилки, разгрузочной камеры и циклона. Гид- '
равлическое сопротивление спирального теплообменника (рис. 1-5)
можно определить по формуле (7-1), принимая
Я = 0,02 + , (7-7)
^Wdg
233
где d3 — эквивалентный диаметр канала, м; w — скорость теплоносите-
ля, м/с.
Гидравлическое сопротивление сухих насадок в скруббере или рек-
тификационной колонне1
2
. , Н ои'д , На а?2рг , , о.
АРсух — "д о — з о > Па. (7’8)
св
Эквивалентный диаметр в формуле (7-8) определяется как
d-э — 4Rr—4Гсв/о, м.
Действительная скорость
WR = w/Vc-B, м/с.
Здесь Н— высота слоя насадки, м; л — коэффициент сопротивле-
ния насадки; рг — плотность газа, кг/м3; дад — действительная скорость
газа между телами насадки, м/с; w — скорость потока на входе в на-
садку (в сечении незаполненного скруббера), м/с; о — удельная по-
верхность насадки, м2/м3; Гсв— свободный объем насадки, м3/м3; RT —
гидравлический радиус насадки, м.
Характеристика различных насадок дана в табл. 2-6.
Коэффициент сопротивления X является функцией критерия Rer
De __ _ fe'Pr
Г Н-r Рт® ’
где цг — динамическая вязкость газа, Н • с/м2; остальные величины имеют
обозначения, указанные в формуле (7-8).
По данным Кафарова и Бляхмана [Л. 48]:
z=400/Re"’85 (при Re<80), (7-9а)
z = 70/Re°’45 (при 80 < Re < 400), (7-96)
Z= 16,5/Re°’2 (при Re ^>400). (7-9в)
Определение X для правильно уложенных насадок дано в [Л. 34].
В случае орошения насадок их гидравлическое сопротивление уве-
личивается. Гидравлическое сопротивление орошаемой водой насадки
Дрсм = (1 »2+0,04 Hw) Лрсух, (7-10)
где Hw— плотность орошения, м3/(м2-ч).
Мощность, необходимая для перемещения жидкости или газа через
аппарат, т. е. мощность на валу насоса или вентилятора, определяется
по формуле
N V (Др + Дрт) _ G (&р -р Дрт) Вт
7) 7)р ’ ’ ' '
где V — объемный расход жидкости или газа, м3/с; G — массовый рас-
ход, кг/с; р — плотность теплоносителя перед насосом (вентилятором),
кг/м3; Арт— гидравлический напор, затрачиваемый в подводящих тру-
бопроводах, Па; Ар — сопротивление теплообменника, Па; ц— к. п. д.
насоса или вентилятора.
7-2. РАСЧЕТ ТЕПЛООБМЕННЫХ АППАРАТОВ НА ПРОЧНОСТЬ2
Многие теплообменные аппараты работают при избыточном внут-
реннем давлении или под вакуумом. Вследствие этого в них возникают
напряжения, обусловленные разностью давления в сосуде и окружаю-
щей среде. На эти напряжения накладываются термические напряже-
1 Гидравлическое сопротивление, тарельчатых ректификационных колонн рассмот-
рено в {Л. 12, 48).
2 Более подробные данные о расчетах на прочность — см. (Л. 8, 42].
234
ния, напряжения от собственной массы сосуда, находящихся в нем
теплоносителей и пр. Необходимо, чтобы в этих условиях теплообмен-
ный аппарат был достаточно прочным.
Неисправность или недостаточная надежность теплообменных ап-
паратов, работающих под давлением,
риям. Поэтому если теплообменный
аппарат емкостью больше 25 л ра-
ботает под избыточным давлением
более 0,69-105 Па (0,7 кгс/см2) и
произведение его емкости в литрах
на избыточное давление в атмосфе-
рах составляет величину больше
500, то он подлежит контролю ин-
спекции Госгортехнадзора [Л. 37] и
должен отвечать строго определен-
ным требованиям. Ни один тепло-
обменный аппарат, изготовленный
с нарушением этих правил, не мо-
жет быть пущен в эксплуатацию.
За нарушение правил виновные под-
лежат наказанию, как за уголовное
преступление.
1. Расчет толщины стен-
ки цилиндрического кор-
пуса. Сосуды, работающие под
давлением, делятся на тонкостенные
и толстостенные. Тонкостенными
считают такие сосуды, у которых
может привести к серьезным ава-
Рис. 7-2. Схемы распределения уси-
лий к расчету толщины цилиндриче-
ского корпуса теплообменника.
а — радиальные усилия; б — осевые уси-
лия; зигзагообразная линия показывает
место возможного разрыва аппарата под
действием этих усилий.
отношение наружного диаметра к внутреннему равно или меньше 1,1.
Определим упрощенным методом толщину цилиндрического тонко-
стенного корпуса из условия действия радиальных сил. В этом случае
согласно рис. 7-2,а можно составить уравнение равновесия
— 2£бк(Тдоп,
откуда толщина стенки корпуса
8
К
= ТГ—М'
-сдоп
(7-12а)
Если вертикальный аппарат имеет относительно тонкий корпус, на
стенку которого передается нагрузка от собственной массы сосуда и
массы находящихся в нем теплоносителей или обрабатываемого матери-
ала, то необходимо проверить сосуд на прочность в поперечнохМ сече-
нии, т. е. на действие аксиальных сил. Согласно рис. 7-2, б в этом слу-
чае можно составить следующее уравнение:
G +
4
,г^вн®кадоп>
откуда толщина стенки
+ м(см)1,
^°доп ''^-увн°доп
(7-126)
где р — максимальное избыточное давление, МПа (кгс/см2); £)вн—
внутренний диаметр цилиндра, м(см); L — длина цилиндра, м (см);
1 Для уравнения (7-12) приведены размерности в СИ и в технической системе:
МПа=106 Н/м2 — величина, близкая к значению 10 кгс/см2, точное значение ее соответ-
ствует 9,81 кгс/см2.
235
одоп=,г]о*доп — допустимое напряжение, МПа (кгс/см1 2); G — нагрузка
на стенки цилиндра от собственной массы и массы находящегося в нем
теплоносителя или материала, Н, кг; о*Доп— нормативное допустимое
по запасу прочности (по пределу прочности или текучести) напряжение
при расчетной температуре; т] — поправочный коэффициент, учитываю-
щий условия эксплуатации сосуда или аппарата.
Расчет сосудов и аппаратов следует производить на основе норм
и методов расчета на прочность сосудов и аппаратов [Л. 42]. Толщина
корпуса сосуда или аппарата, работающего под 'внутренним давлением,
._________РрРвН______
>к~’ 2a*Mn-rjf —Др
•ф- С, м,
(7-13)
где рр — расчетное или рабочее давление, равное избыточному давле-
нию \ возникающему при нормальном пр