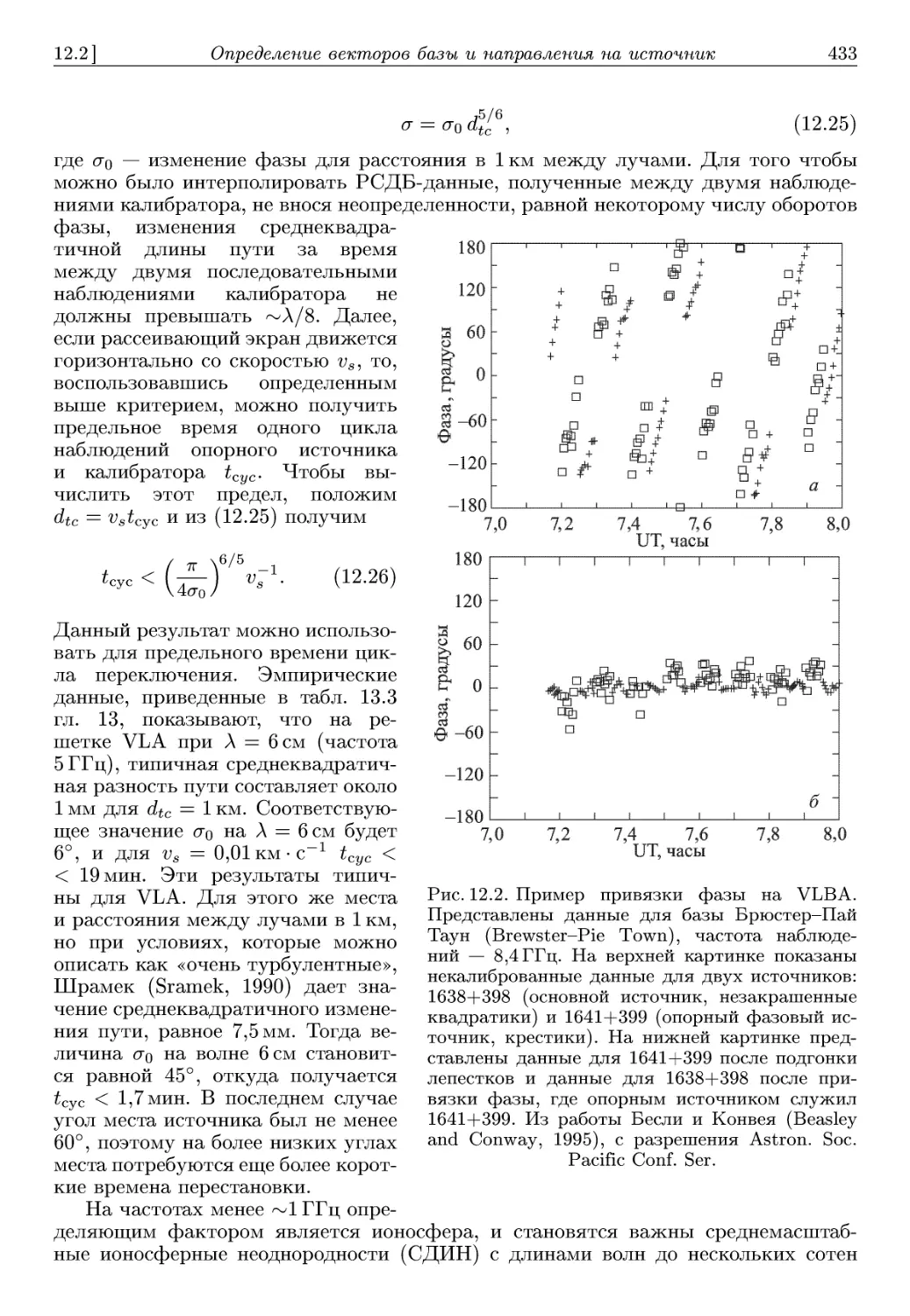
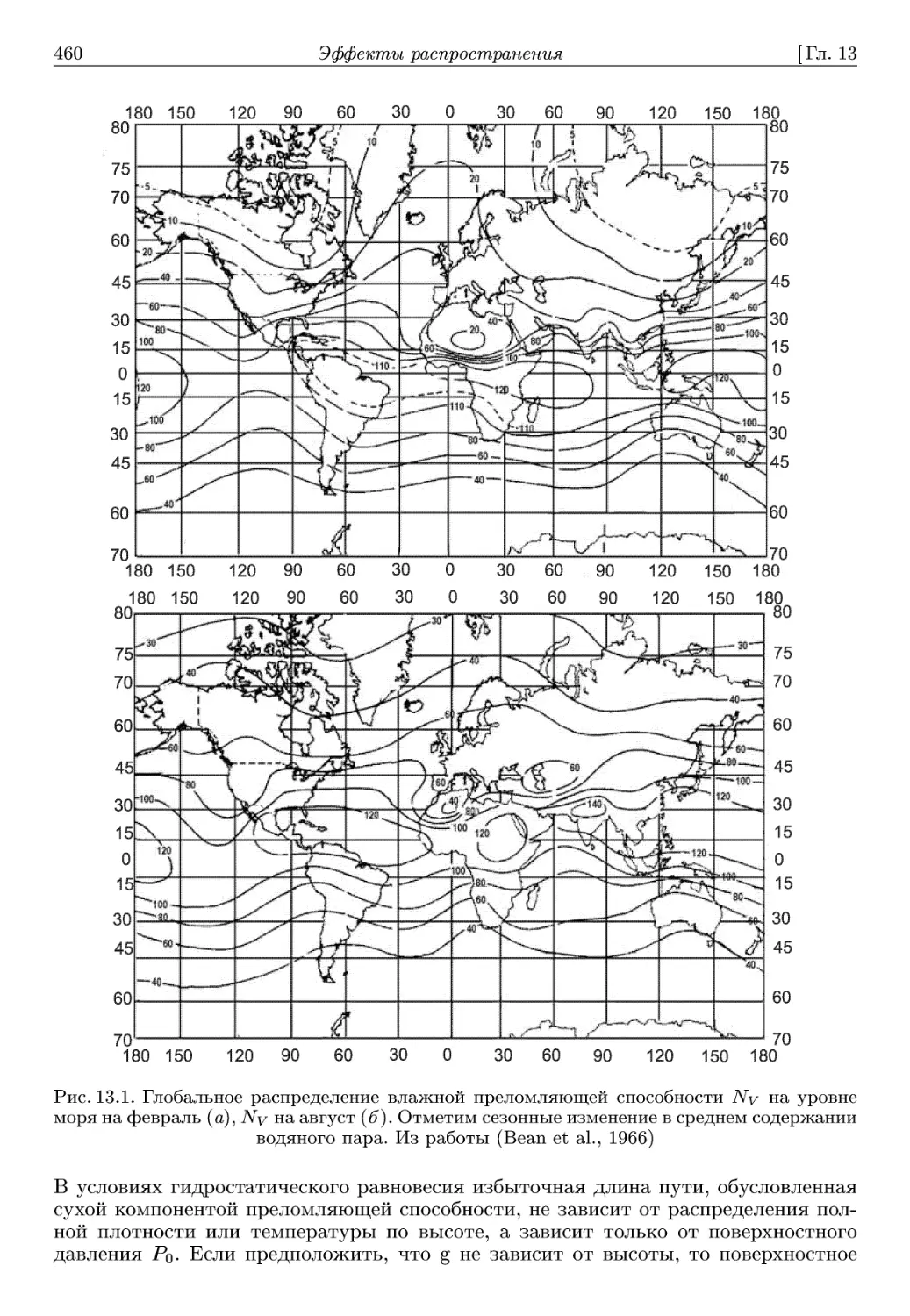
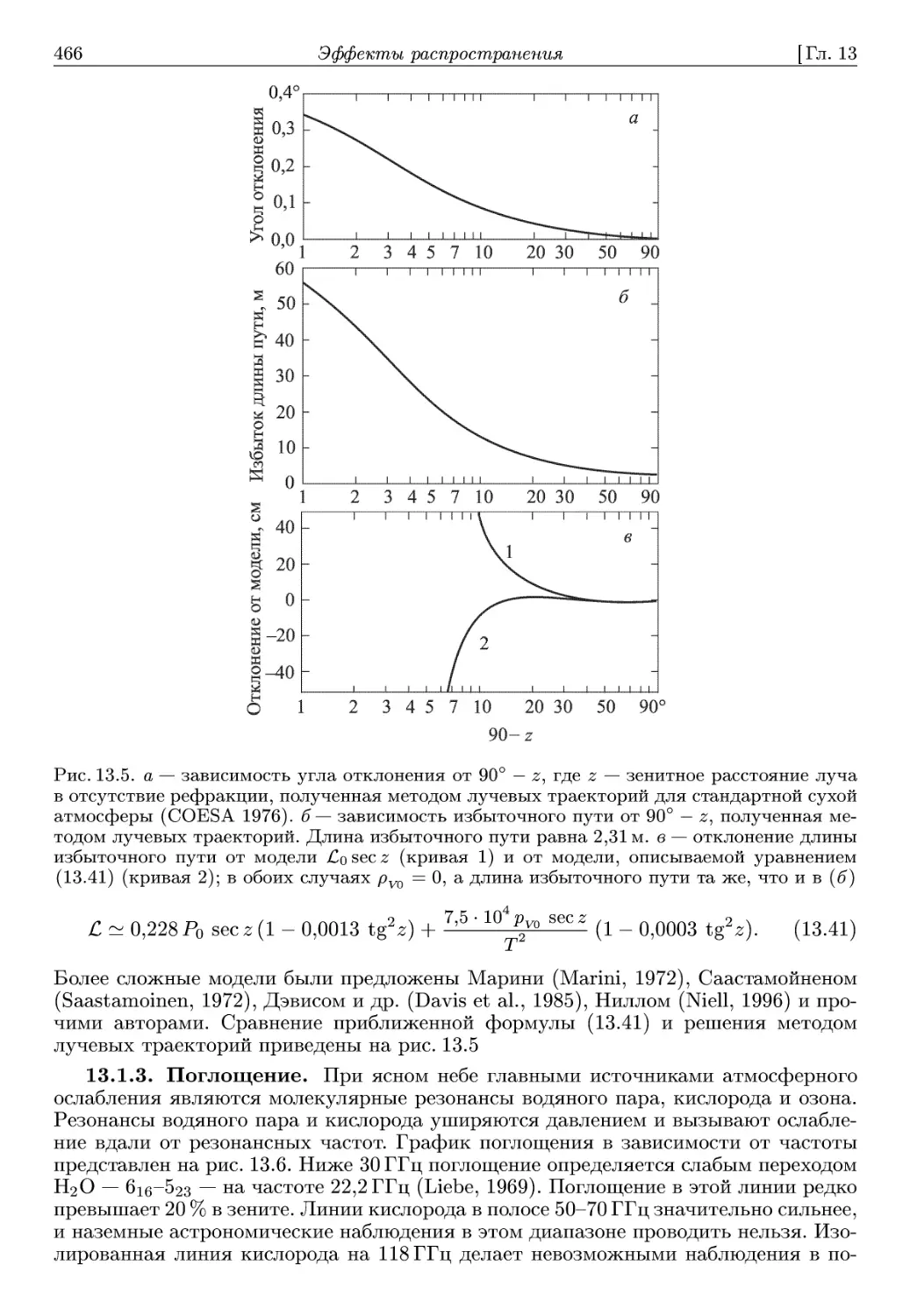
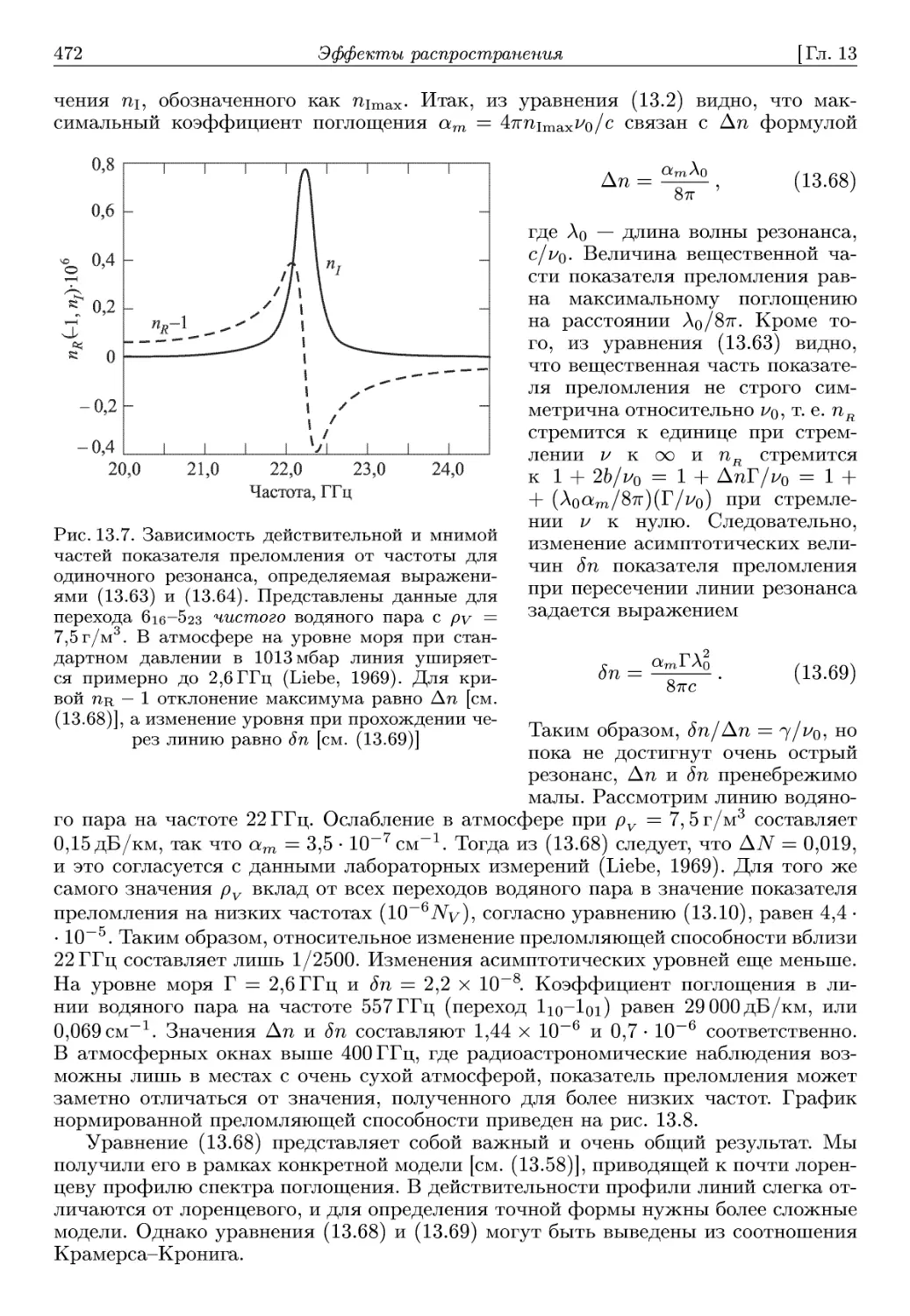
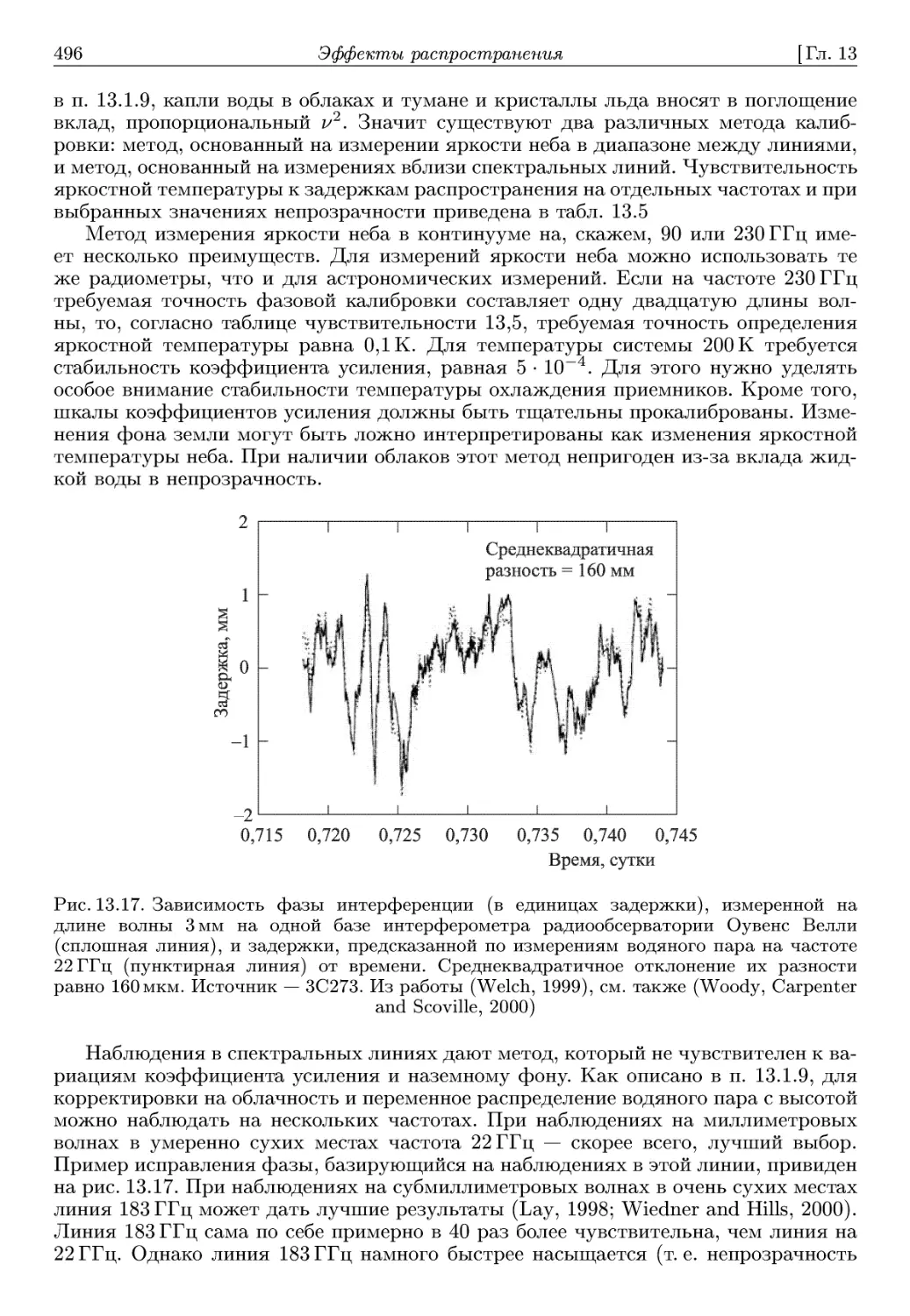
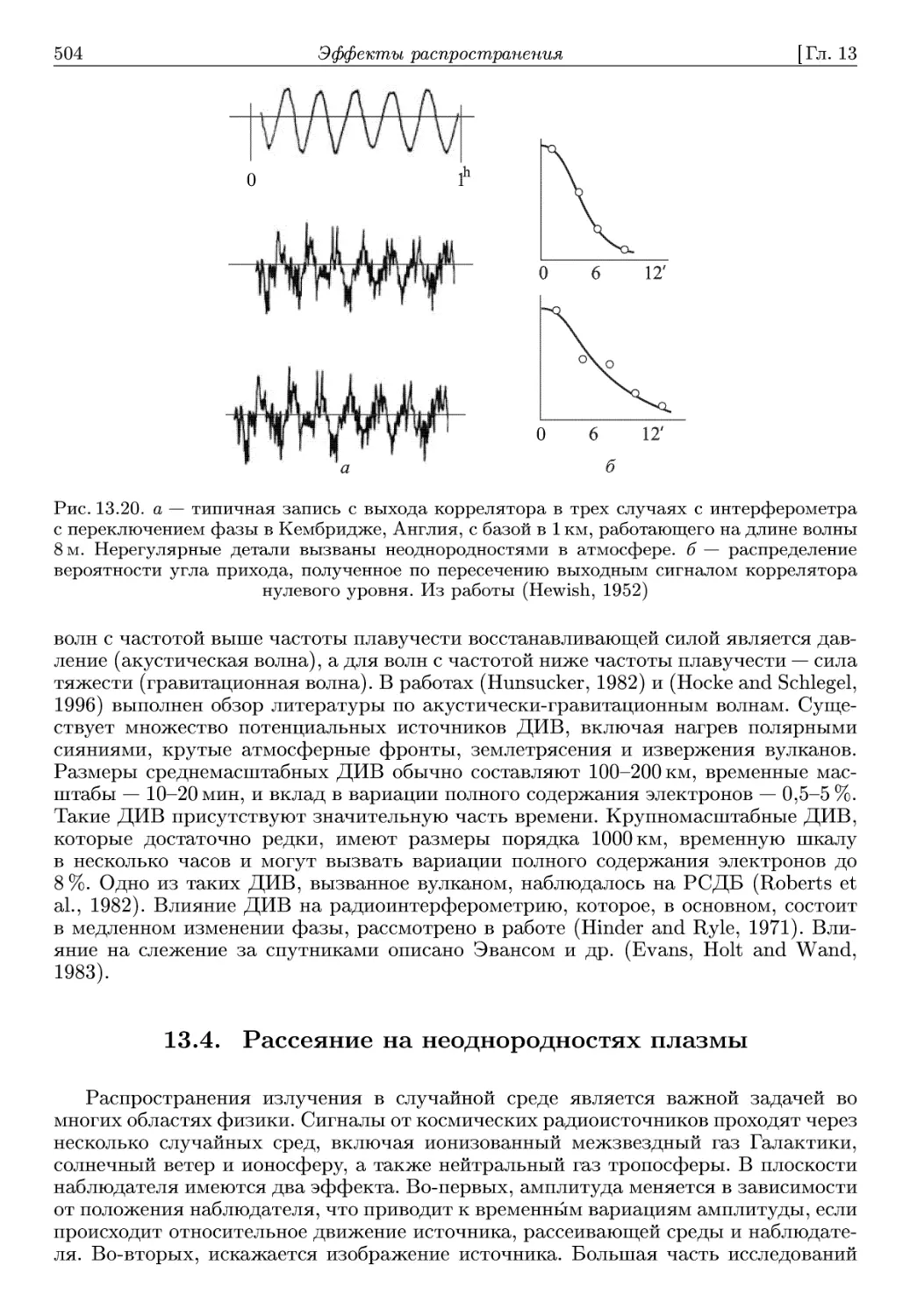
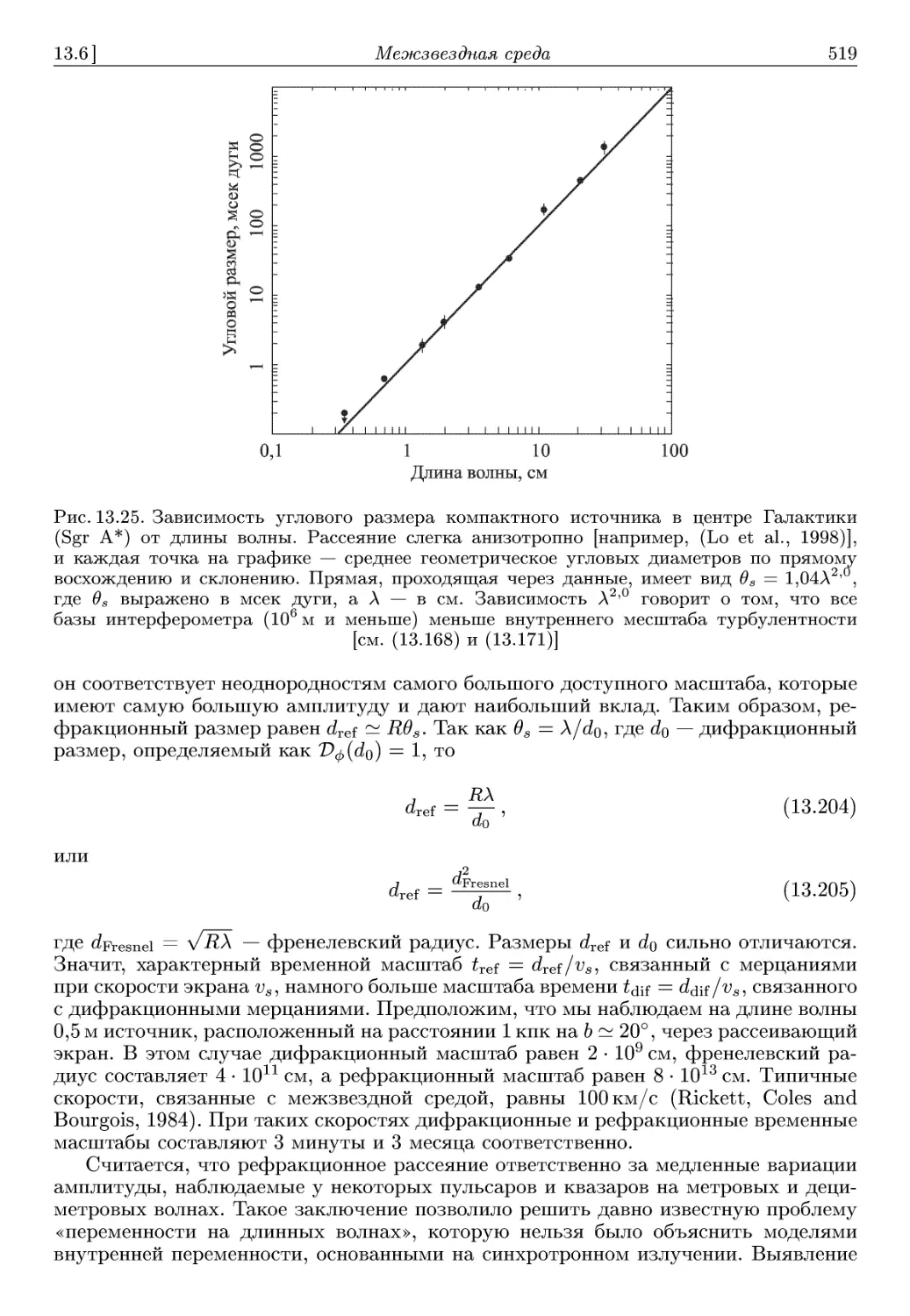
Автор: Томпсон А.Р. Моран А.Р. Свенсон Д.М.
Теги: инструменты, приборы и методы астрономических наблюдений, измерений и анализа радиоастрономия астрономия
ISBN: 5-9221-0015-7
Год: 2003
Текст
УДК 520.27
ББК 22.64
Т56
Томпсон А. Р., Моран Д. М., Свенсон Д. У. Интерферометрия и син-
синтез в радиоастрономии / Перевод с англ. под ред. Л.И. Матвеенко. — 2-е изд. — М.:
ФИЗМАТЛИТ, 2003. - 624 с. - ISBN 5-9221-0015-7.
В монографии видных американских радиоастрономов рассмотрен широкий спектр
проблем, связанных с применением радиоинтерферометрии для получения изображений
астрономических объектов, решения задач астрометрии, геодезии, геодинамики и косми-
космической навигации. Затронуты и другие методы исследований с высоким угловым разреше-
разрешением: интерферометр интенсивностей, метод лунных покрытий, спекл-интерферометрия.
Большое внимание уделяется обработке данных наблюдений.
Настоящее второе издание книги A-е изд. — 1986 г.) является переработанным и допол-
дополненным в соответствии с современными достижениями в радиоастрономии.
Книга предназначена для научных работников и инженеров, работающих в области ра-
радиоастрономии, астрометрии, геодезии, астрофизики и радиофизики, а также для студентов
старших курсов и аспирантов соответствующих специальностей.
Научное издание
ТОМПСОН А.Ричард
МОРАН Джеймс М.
СВЕНСОН Джордж У.
ИНТЕРФЕРОМЕТРИЯ И СИНТЕЗ В РАДИОАСТРОНОМИИ
Перевод под редакцией Л. И. Матвеенко
Редактор О. В. Салецкая
Оригинал-макет: Н.Ю. Савченко
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 20.06.03. Формат 70x100/16. Бумага офсетная.
Печать офсетная. Усл. печ. л. 49,71. Уч.-изд. л. 54,6. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
ISBN 5-9221-0015-7
9 785922 100151
ISBN 0-471-25492-4 (англ.)
ISBN 5-9221-0015-7 (русск.)
© John Wiley & Sons, Inc., 2001 (англ.)
© ФИЗМАТЛИТ, 2003 (русск.)
Предисловие ко второму изданию
Посвящается
Шейле, Барбаре, Джейнис,
Саре, Сьюзен и Майклу
Предисловие ко второму изданию
Выдающиеся научные достижения в астрономии за прошедшее полстолетия
стали возможны благодаря использованию методов радиоинтерферометрии. По-
После 1986 г. — года первой публикации этой книги, была создана система VLB A
(сверхбольшая антенная решетка), предназначенная для сверхдлинной интерферо-
интерферометрии (РСДБ), проведена глобализация сетей РСДБ с использованием орбиталь-
орбитальных антенн, что сильно повысило значение спектральных наблюдений и улучшило
инструментальные возможности как в высокочастотном, так и в низкочастотном
диапазонах радиоспектра. На высоких частотах были значительно расширены воз-
возможности решеток миллиметровых волн ассоциации Беркли-Иллинойс-Мериленд
(BIMA), радиообсерватории в Нобейяма (NRO) и радиообсерватории в Оуэнс-
Велли (OVRO), находившиеся на стадии ввода в действие в 1986 г. Разрабаты-
Разрабатываются Субмиллиметровая решетка (SMA) и Большая миллиметровая решетка
в Атакама (ALMA), представляющие собой основные международные проекты
миллиметровых и субмиллиметровых волн. На низких частотах, где существуют
специфические трудности, связанные с влиянием ионосферы и реализацией широ-
широкого поля зрения при картографировании, частотный диапазон Большой антенной
решетки (VLA) был расширен до 75 МГц, и был сдан в эксплуатацию Гигант-
Гигантский радиотелескоп метровых волн (GMRT), действующий вплоть до частоты 38
МГц. Австралийский телескоп и протяженная Многоэлементная радиосвязанная
интерферометрическая сеть (MERLIN) расширили возможности на сантиметровых
волнах.
Этот прогресс послужил причиной появления данного переработанного издания,
цель которого не только привести материал в соответствие с современным состоя-
состоянием дел, но также расширить его границы, сделать более глубоким и полезным.
В нескольких случаях символы, используемые в первом издании, были изменены в
соответствии с общепринятым их использованием в современной радиоастрономии.
В каждой главе содержится новый материал, появились новые рисунки и много
новых ссылок. Материал, вошедший в 1-м издании в гл. 3, бывший вспомогатель-
вспомогательным для основного обсуждения, сжат и перенесен в гл. 14. Глава 3 теперь содержит
основной анализ отклика интерферометра. Раздел поляризации в гл. 4 значительно
расширен, и краткое введение в теорию антенн добавлено в гл. 5. В гл. 6 содержится
обсуждение чувствительности для широкого круга конфигураций инструментов.
Обсуждение наблюдений спектральных линий добавлено в гл. 10. Глава 13 расши-
расширена для того, чтобы учесть новые методы коррекции атмосферной фазы, проверку
данных месторасположений и методы на миллиметровых длинах волн. Добавлена
гл. 14 — в нее включены материалы, частично перешедшие из первоначальной гл. 3,
проведен анализ теоремы Ван Циттерта-Цернике, обсуждается пространственная
когерентность и рассеяние.
За рецензии и другую помощь во время подготовки переиздания особую
благодарность заслуживают многие наши коллеги. Среди них Д. С. Бейкер,
Дж. У. Бенсон, М. Беркиншоу, Г. А. Блейк, Р. Н. Брейсуэлл, Б. Ф. Берк, Б. Батлер,
С. Л. Кэрилл, Б. Г. Кларк, Дж. М. Кордес, Т. Дж. Корнуэлли, Л. Р. Д'Аддарио,
Т.М.Дж. Дэйм, Дж. Дэйвис, Дж. Л. Дэйвис, Д. Т. Эмерсон, Р. П. Эскоффер,
Е. Б. Фомалонт, Л.Дж. Гринхилл, М. А. Гарвелл, СР. Гвинн, К. И. Келлерманн,
6 Предисловие к первому изданию
А. Р. Керр, Е. Р. Кито, СР. Кулхарни, С. Мацушита, Д. Моррис, Р. Нарайан,
С. К. Пан, С.Дж.Е. Рэдфорд, Р. Рао, М.Дж. Рейд, А. Ричичи, А. Е. Е. Роджерс,
Дж. Е. Сейлах, Ф. Р. Шваб, С. Р. Спанглер, Е. С. Саттон, Б. Е. Тернер, Р. Ф. С. Вес-
сот, У. Дж. Уэлч, М. С. Уайднер, и Дж. X. Жао. За помощь в подготовке текста и
рисунков мы благодарим Дж. Хейденрича, Г. Л. Кесслера, П. Смайли, С. Уоткинса,
и П. Винна. Мы особенно признательны П. Л. Симмонсу за большую помощь в
подготовке этой монографии. Мы благодарны П. А. Ванден Боуту — директору
Национальной астрономической обсерватории, и И. И. Шапиро — директору
Гарвардского Смитсонианского центра астрофизики за ободрение и поддержку.
Национальная радиоастрономическая обсерватория работает под управлением
Ассоциации университетов по контракту с Национальным научным фондом, а
Гарвардский Смитсонианский центр астрофизики действует под управлением
Гарвардского университета и Смитсонианского института.
А. Ричард Томпсон
Джеймс М. Моран
Джордж У. Свенсон-мл.
Шарлоттсвилл, Вирджиния
Кембридж, Массачусетс
Урбана, Иллинойс
ноябрь, 2000 г.
... вполне уверен, что все результаты, кои получены или, возможно, еще будут
получены посредством столь благородного инструмента как астролябия, доселе
не были известны ни одному смертному ...
Джеффри Чосер
«Трактат об астролябии»
1391 г.
Предисловие к первому изданию
За прошедшие четыре десятилетия техника радиоинтерферометрии в области
астрофизики и астрометрии развивалась бурными темпами, что привело к улуч-
улучшению углового разрешения инструментов от градусов до миллисекунд, т. е. более
чем на шесть порядков. С разработкой антенных решеток для получения радиокарт
методами апертурного синтеза 1), радиометоды превзошли оптические методы в
области определения тончайшей структуры изображений астрономических объек-
объектов. Прогресс в этом направлении обеспечил новые возможности в астрометрии,
измерении движения полюсов Земли и подвижек геоплатформ. Теория и методы,
лежащие в основе этих успехов, продолжают совершенствоваться. В настоящее
время они достигли достаточно высокого уровня развития и могут быть система-
систематически изложены.
Эта книга предназначена главным образом для студентов старших курсов уни-
университетов и специалистов в области астрономии, радиотехники, физики и смеж-
смежных наук, которые захотят использовать методы интерферометрии или апертурного
синтеза, применяемые в астрономии, астрометрии или геодезии. Она написана с
х) Мы определяем синтезированное картографирование как восстановление изображения
по измерениям фурье-образов распределений радиояркости. Термины «карта», «изобра-
«изображение» и «распределение радиояркости» в значительной степени взаимозаменяемы в этой
книге.
Предисловие к первому изданию
учетом мнения (опыта) радиоинженеров-комплексников и включает рассмотрение
важных параметров и особенностей инструментов разных типов. Мы поставили
перед собой цель объяснить принципы, лежащие в основе соответствующей интер-
ферометрической техники, не останавливаясь подробно на деталях ее реализации.
Такие аспекты, как программное и аппаратное обеспечение, в значительной степени
специфичны для каждого инструмента и существенно изменяются с развитием
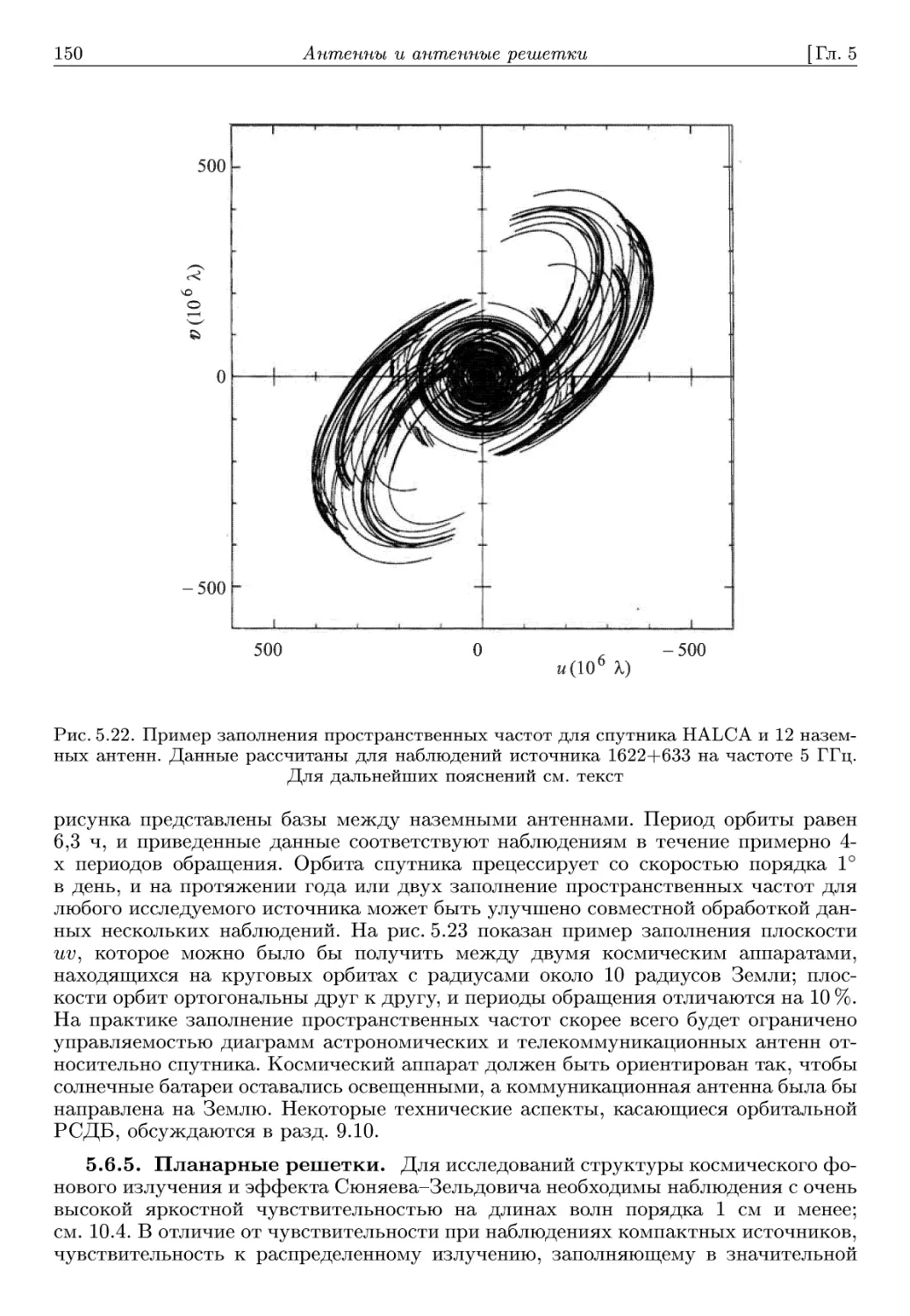
электроники и вычислительной техники. Изучив рассматриваемые принципы, чи-
читатель легко разберется в инструкциях и технических описаниях, имеющихся в
большинстве обсерваторий.
В основе книги не лежит какой-либо курс лекций, но включенные в нее мате-
материалы могут быть использованы в специальных курсах. Преподаватель, имеющий
опыт в области описываемых методов, сможет при необходимости легко дополнить
их различными пособиями, чтобы подчеркнуть астрономические, технические или
любые другие аспекты.
В первых двух главах дан краткий обзор основных понятий радиоастрономии и
истории развития радиоинтерферометрии и рассмотрены основные принципы рабо-
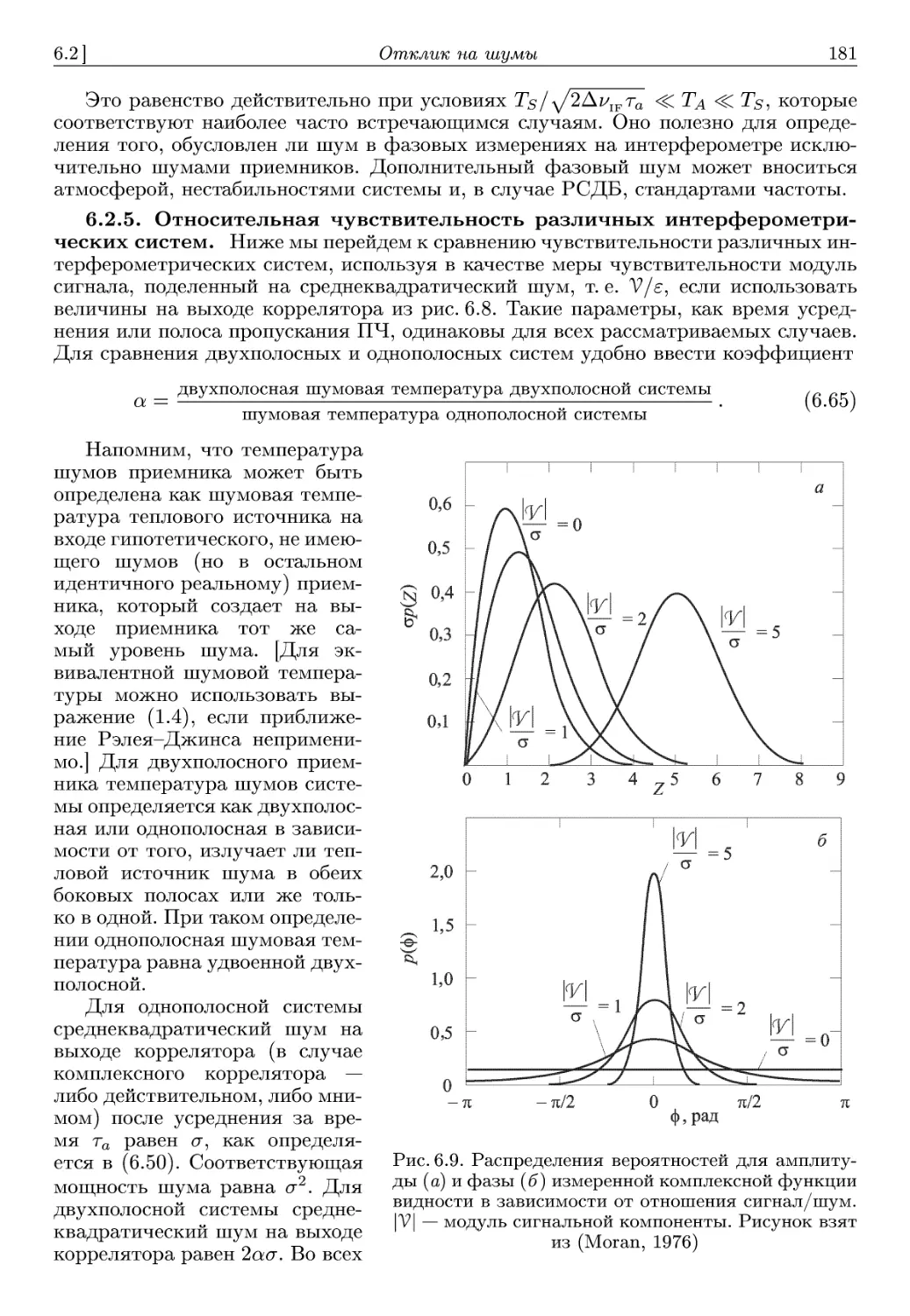
работы интерферометра. В гл. 3 обсуждаются основные соотношения интерферометрии
с точки зрения теории частичной когерентности, и при первом чтении она может
быть пропущена. В гл. 4 вводятся системы координат и параметры, необходимые
для описания картографирования методами апертурного синтеза. На основе этого
материала в гл. 5 исследуются различные конфигурации многоэлементных синтези-
синтезируемых решеток. Главы 6-8 связаны с различными аспектами разработки приемных
систем и анализа их откликов, включая эффекты квантования уровней в цифровых
корреляторах. Специфические особенности интерферометрии со сверхдлинными
базами (РСДБ) рассматриваются в гл. 9. Далее подробно описывается измерение
комплексной функции видности, что непосредственно связано с получением ра-
радиокарт, рассматриваемым в главах 10 и 11. В первой из них представлен метод
преобразования Фурье, а в следующей — более мощные алгоритмы, объединяю-
объединяющие и калибровку, и преобразование. Прецессионные наблюдения в астрометрии
и геодезии составляют предмет гл. 12. Далее рассматриваются факторы, кото-
которые могут ухудшать возможности системы в целом: эффекты распространения
радиоволн в атмосфере, межпланетной и межзвездной среде рассматриваются в
гл. 13, а влияние радиопомех — в гл. 14. Распространение радиоволн обсуждается
более подробно, так как этот вопрос охватывает широкий спектр сложных явлений,
налагающих принципиальные ограничения на точность измерений. В последней
главе описываются близкие методы, в том числе интерферометрия интенсивности,
спекл-интерферометрия и наблюдения лунных покрытий.
В книге приводятся ссылки на основополагающие работы и другие публикации
и обзоры, имеющие отношение к ее разделам. Для иллюстрации приводятся мно-
многочисленные описания инструментов и наблюдений. Подробности первоначально
использовавшихся методов приводятся во всех случаях, когда это помогает разъяс-
разъяснению принципов или исходных положений современных методов или же когда они
сами по себе интересны. Из-за разнообразия описываемых явлений в некоторых слу-
случаях пришлось для различных математических величин использовать одинаковые
обозначения. Вслед за последней главой приводится список основных обозначений.
Материалы для этой книги лишь частично взяты из опубликованных источни-
источников, и большая их часть накапливалась в течение многих лет из научных дискуссий,
семинаров, опубликованных отчетов, памятных записок различных обсерваторий.
Поэтому мы считаем своим долгом выразить признательность нашим коллегам,
слишком многочисленным для упоминания каждого в отдельности. Среди тех, кого
мы особенно благодарим за критический анализ отдельных частей книги и заме-
Предисловие к первому русскому изданию
чания — Д. С. Бейкер, Д. С. Багри, Р. X. Т. Бейтс, М. Биркиншоу, Р. Н. Брейсуэлл,
Б. Г. Кларк, Дж. М. Коридес, Т. Дж. Корнуэлл, Л. Р. Д'Аддарио, Дж. Л. Дейвис,
Р. Д. Икерс, Дж. В. Эванс, М. Фочерри, С. Дж. Фрэнк, Дж. Грэнланд, Л. Дж. Грин-
хилл, СР. Гвинн, Т. А. Херринг, Р. Дж. Хилл, У. А. Джеффри, К. И. Келлер-
манн, Дж. А. Клоубахр, Р. С. Лоренс, Дж. М. Маркэйд, Н. С. Матур, Л. А. Молнар,
П. С. Майерс, П.Дж. Нейпирью, П. Найсенсон, Х.В. Пур, М.Дж. Рейд, Дж. Т. Ро-
Роберте, Л. Ф. Родригес, А.Е. Е. Роджерс, А. X. Роте, Дж. Е. Сейлах, Ф.Р. Шваб,
И. И. Шапиро, Р. А. Шрамек, Р. Стачник, Дж. Л. Тернер, Р. Ф. С. Вессот, Н. Уокс
и У. Дж. Уэлч. Приведенные рисунки из других публикаций имеют ссылки в со-
соответствующих подписях, и мы благодарим их авторов и издателей за согласие
на использование этих материалов. Большой вклад в подготовку издания внесли
С. С. Баррет, С. Ф. Берджесс, Н.Дж. Даймонд, Дж. М. Джиллберг, Дж. Г. Хэмуй,
Э.Л. Хейнс, Г. Л. Кесслер, К. И. Молдонис, А. Патрик, В.Дж. Петерсон, С. К. Ро-
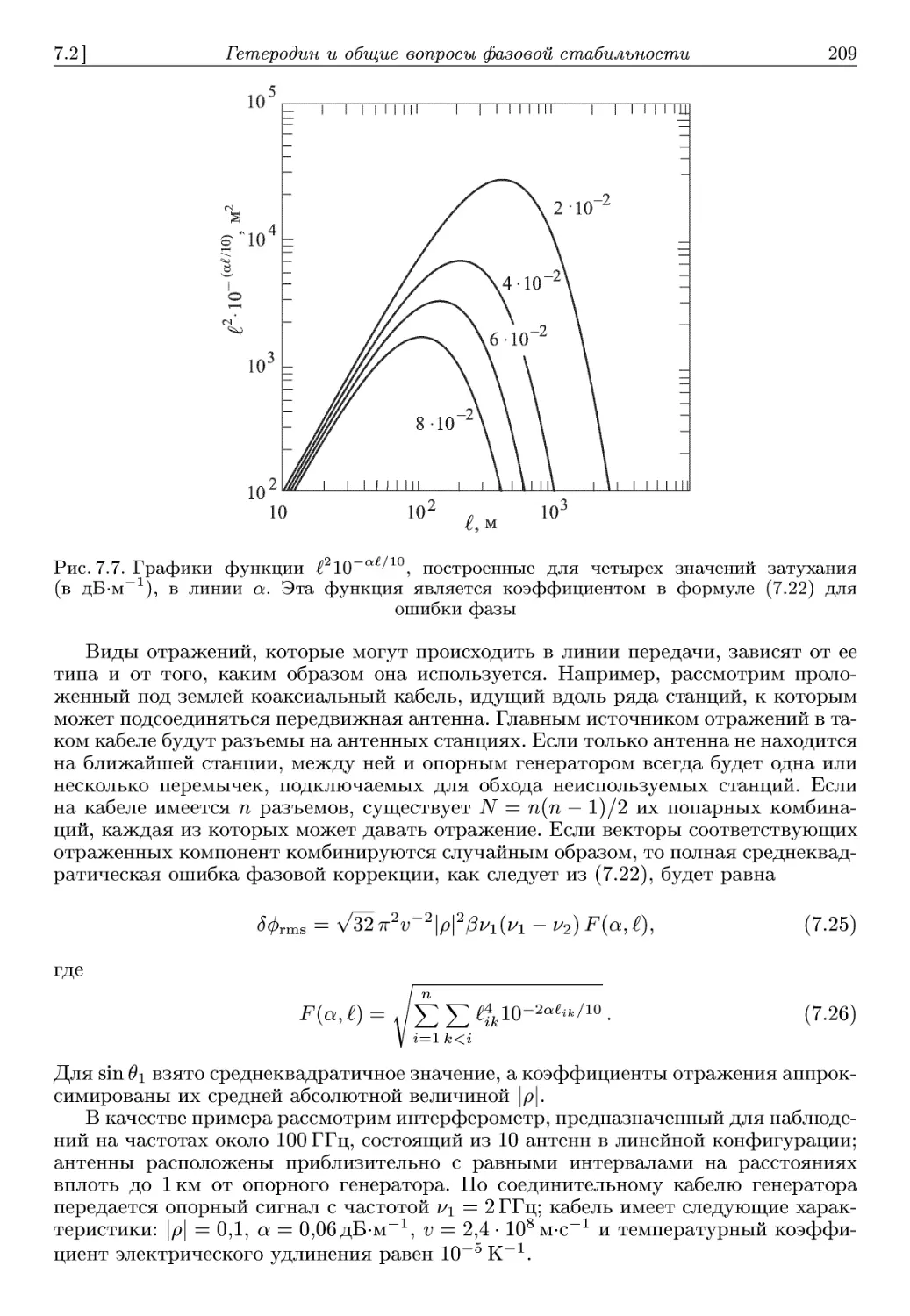
зенталь, А. У. Шеферд, Дж. Ф. Сингарелл, М. Б. Уимс и С. X. Уильяме. Мы хотим
выразить им благодарность. Мы признательны М. С. Робертсу и П.Дж:. Ванден
Боуту — бывшему и нынешнему директорам Национальной радиоастрономической
обсерватории, а также Г. Б. Филду и И. И. Шапиро — бывшему и нынешнему ди-
директорам Гарвардского Смитсонианского центра астрофизических исследований, за
ободрение и поддержку. Значительная часть книги была написана Дж. М. Мораном
в свободное от лекций время в радиоастрономической лаборатории Калифорний-
Калифорнийского университета в Беркли, и он выражает признательность У. Дж. Уэлчу за
гостеприимство. Дж. У. Свенсон-мл. благодарит Гагенхеймский фонд за финансо-
финансовую поддержку в 1984-1985 гг. В заключение мы благодарим за поддержку наши
организации: Национальную радиоастрономическую обсерваторию, действующую
под управлением Ассоциации университетов по контракту с Национальным науч-
научным фондом; Гарвардский Смитсонианский центр астрофизических исследований,
действующий под управлением Гарвардского университета и Смитсонианского ин-
института, и университет штата Иллинойс.
А. Ричард Томпсон
Джеймс М. Моран
Джордж У.Свенсон-мл.
Шарлоттсвилл, Вирджиния
Кембридж, Массачусетс
Урбана, Иллинойс
январь, 1986 г.
Предисловие к первому русскому изданию
Эта книга впервые была опубликована в Нью-Йорке в 1986 г. В течение времени,
прошедшего до ее перевода на русский язык, во всем мире продолжались усилия
по развитию радиоинтерферометрии и методов синтезирования изображений. В
Австралии и Индии создаются новые антенные решетки со связанными элементами,
во многих странах антенны модернизируются для выполнения астрономических
или геодезических программ, использующих методы радиоинтерферометрии со
сверхдлинными базами (РСДБ). Базы интерферометров уже превышают размеры
Земли. В эксперименте, проведенном в 1986 г., были получены радиоинтерферен-
радиоинтерференционные лепестки с использованием наземных антенн и антенны, установленной на
геостационарном спутнике. Однако возможности исследования тонкой структуры
источников, связанные с переменными базами между антеннами на поверхности
Земли и на негеостационарном спутнике, пока еще не использовались. В настоящее
время существуют проекты, в которых предполагается реализовать эту возмож-
Предисловие редактора перевода 9
ность, в том числе советский проект «Радиоастрон» и европейский «Quasat» —
оба спутника могут быть выведены на орбиту в будущем десятилетии. Базы в
проекте «Радиоастрон» превысят 75 000 км, что на частоте 22 ГГц соответствует
разрешению лучше 40 микросекунд дуги.
«Радиоастрон» обещает стать следующим замечательным шагом в ряду успе-
успехов советских ученых в области радиоастрономии. Среди них молено упомянуть
теоретические исследования, такие, как астрономическая интерпретация синхро-
тронного механизма излучения, обзоры радиоисточников и измерения с высоким
угловым разрешением. В 1965 г. в статье Матвеенко, Кардашева и Шоломицкого
был впервые опубликован анализ возможностей РСДБ — за два года до первой
демонстрации этого метода. Впоследствии во многих РСДБ-наблюдениях с наивыс-
наивысшим угловым разрешением использовались радиотелескопы в СССР, работающие
совместно с антеннами, расположенными в Европе, Австралии и Северной Америке.
Очень удачно, что д-р Л. И. Матвеенко, один из пионеров в области ГСДБ, смог
взять на себя задачу согласования вопросов перевода и редактирование издания
этой книги на русском языке. Мы выражаем благодарность всем тем, кто прини-
принимал участие в подготовке этого издания и надеемся, что эта книга будет нашим
вкладом не только в углубление понимания принципов радиоинтерферометрии и
ее приложений, но и в развитие между народного сотрудничества как в наземных,
так и в наземно-космических экспериментах.
Ричард Томпсон
Джеймс Моран
Джордж Свенсон-мл.
Шарлоттсвилл, Виргиния,
Кембридж, Массачусетс
Урбана, Иллинойс
март, 1988 г.
Предисловие редактора перевода
Первое издание книги Р. Томпсона, Дж. Морана и Дж. Свенсона: «Интерфе-
«Интерферометрия и синтез в радиоастрономии» на русском языке, вышедшее в 1989 г.
в издательстве «Мир», вызвало большой интерес у широкого круга специалистов
как за рубежом, так и у нас в стране. Она посвящена технике и методам радио-
радиоастрономических исследований и стала настольной книгой радиоастрономов мира.
Выдающиеся успехи современной астрофизики во многом определены успехами
радиоастрономии. И это не случайно: угловое разрешение, чувствительность, ча-
частотное разрешение, точность поляризационных измерений открыли широчайшие
возможности для исследований астрономических объектов. Были открыты ней-
нейтронные звезды — пульсары, исследованы ядра радиогалактик и квазаров, мазерное
излучение в активных областях газопылевых комплексов.
Современные радиоастрономические инструменты широко используют методы
интерферометрии. Это, как правило, сложные антенно-вычислительные комплексы,
обладающие широким полем зрения и высоким разрешением. Они работают во всем
спектре радиоволн от миллиметровых до метровых включительно. Ограничение
углового разрешения на радиоволнах было преодолено благодаря предложению (в
СССР) и реализации (учеными США и независимо Канады) в 60-х гг. метода сверх-
сверхдальней радиоинтерферометрии. Практически было снято техническое ограничение
на угловое разрешение. В настоящее время все крупные радиотелескопы мира объ-
объединены в единую глобальную сеть. Ее угловое разрешение на несколько порядков
превосходит разрешающую силу оптических телескопов и достигает долей милли-
10 Предисловие редактора перевода
секунд дуги. Исторически это эквивалентно созданию Галилеем первого телескопа.
Столь высокое угловое разрешение открыло необычайно широкие возможности для
исследований тонкой структуры таких компактных астрономических объектов как
квазары, ядра галактик, областей звездообразования.
Принципиально новая основа заложена для таких традиционных направлений
как геодезия, геодинамика, астрометрия, астронавигация. Передвижение астронав-
астронавтов на Луне контролировалось с точностью в несколько десятков сантиметров,
а траектории движения аэростатов в атмосфере Венеры — Проект ВЕГА — с
точностью до нескольких сот метров. За время, прошедшее с момента первого
издания книги, техника и методы радиоинтерферометрии получили дальнейшее
существенное развитие. Выведен на орбиту вокруг Земли и успешно работает с
глобальной сетью космический элемент интерферометра — VSOP. Разрабатывается
космический радиотелескоп — проект Радиоастрон. Созданы специализированные
центры обработки данных радиоинтерферометрических наблюдений. Разработаны
широкополосные системы регистрации сигналов, что существенно повысило чув-
чувствительность измерений, стали возможны исследования в поляризованном излуче-
излучении и миллиметровых волнах. Начато объединение элементов сети оптоволоконны-
оптоволоконными системами связи с центрами обработки, что обеспечит получение изображений
объектов в реальном времени.
Авторы книги являются крупными специалистами в области теории, методики
и техники радиоинтерферометрических исследований. Под их руководством и при
их непосредственном участии создавались и вводились в действие такие системы
как VLA и VLB А. Этот богатый опыт нашел свое отражение в рассматриваемой
монографии. Ими детально проанализированы требования как к системам в целом,
так и отдельным их частям и элементам, рассмотрены ограничения, связанные с
распространением радиоволн в межзвездной, межпланетной и околоземных сре-
средах, влияние помех на точность измеряемых величин. Уделено большое внимание
математическому обеспечению построения изображений объектов, калибровке дан-
данных радиоинтерферометрических наблюдений. Приведены конкретные результаты
исследований структуры астрофизических объектов. Авторами рассмотрены и со-
современные оптические интерферометры, спекл-интерферометрия. В книге широко
представлена библиография по рассматриваемым вопросам.
Перевод монографии выполнен Ю.Ю. Ковалевым, (главы 10, 11, 16), К. В. Се-
менковым (главы 12, 13), В. В. Тимофеевым (главы 6—8) и А. В. Шевченко (Преди-
(Предисловия, главы 1—5, 9, 14 и 15). Данная монография является обобщением большого
опыта, накопленного в современной радиоинтерферометрии. Это прекрасное посо-
пособие для широкого круга специалистов, работающих в области как астрофизических,
так и прикладных исследований. В ней удачно сочетаются строгость теоретических
изложений основ интерферометрии с практическим отражением реального подхода
к созданию современного радиотелескопостроения, математического обеспечения
обработки данных и методики исследований. Книга будет полезна как научным
сотрудникам, так и инженерам и по стилю изложения доступна широкому кругу
специалистов, студентов старших курсов и аспирантов.
Профессор Л. И. Матвеенко
Глава 1
ВВЕДЕНИЕ И ИСТОРИЧЕСКИЙ ОБЗОР
Задачей этой книги является изложение основ радиоинтерферометрии примени-
применительно к измерению естественных радиосигналов от космических радиоисточников.
Такие измерения используются главным образом в астрономии, астрометрии и гео-
геодезии. Во введении мы рассмотрим применение техники радиоинтерферометрии,
некоторые основные понятия и соотношения, а также историю развития инстру-
инструментов и их использования.
1.1. Применение радиоинтерферометрии
Радиоинтерферометры и решетки апертурного синтеза (по существу представ-
представляющие собой наборы двухэлементных интерферометров) используются для из-
измерения тонких угловых деталей в радиоизлучении неба. Угловое разрешение
одиночных радиоантенн для многих астрономических задач недостаточно. Прак-
Практически их разрешающая способность ограничена несколькими десятками секунд
дуги. Например, ширина диаграммы направленности антенны диаметром 100 м на
длине волны 7 мм равна приблизительно 17/;. В оптике дифракционный предел
больших телескопов (диаметр ~8 м) составляет около 15 мсек дуги, но из-за атмо-
атмосферной турбулентности их угловое разрешение, достигаемое с помощью обычных
методов на поверхности Земли, ограничено примерно одной угловой секундой. Для
прогресса астрономии в частности важны измерения положений радиоисточников
с точностью, обеспечивающей их отождествление с объектами, обнаруженными
в оптическом и других диапазонах электромагнитного спектра. Особенно важны из-
измерения с сопоставимым угловым разрешением в радиодиапазоне и в оптике таких
параметров, как яркость, поляризация и частотный спектр. Радиоинтерферометрия
позволяет проводить такие исследования.
Задачей астрометрии является точное измерение угловых положений звезд
и других космических объектов, в том числе — изучение малых изменений небесных
координат вследствие параллакса, обусловленного орбитальным движением Зем-
Земли, а также изменений координат в результате собственных движений объектов.
Такие измерения существенны для определения шкалы расстояний во Вселенной.
Астрометрические измерения являются также средством проверки общей теории
относительности и определения динамических параметров Солнечной системы. При
проведении астрометрических измерений важно определить систему опорных коор-
координат. Система координат, в которой в качестве опорных используются положения
чрезвычайно удаленных сверхмассивных источников, почти идеальна. Радиоизме-
Радиоизмерения далеких компактных внегалактических источников в настоящее время наи-
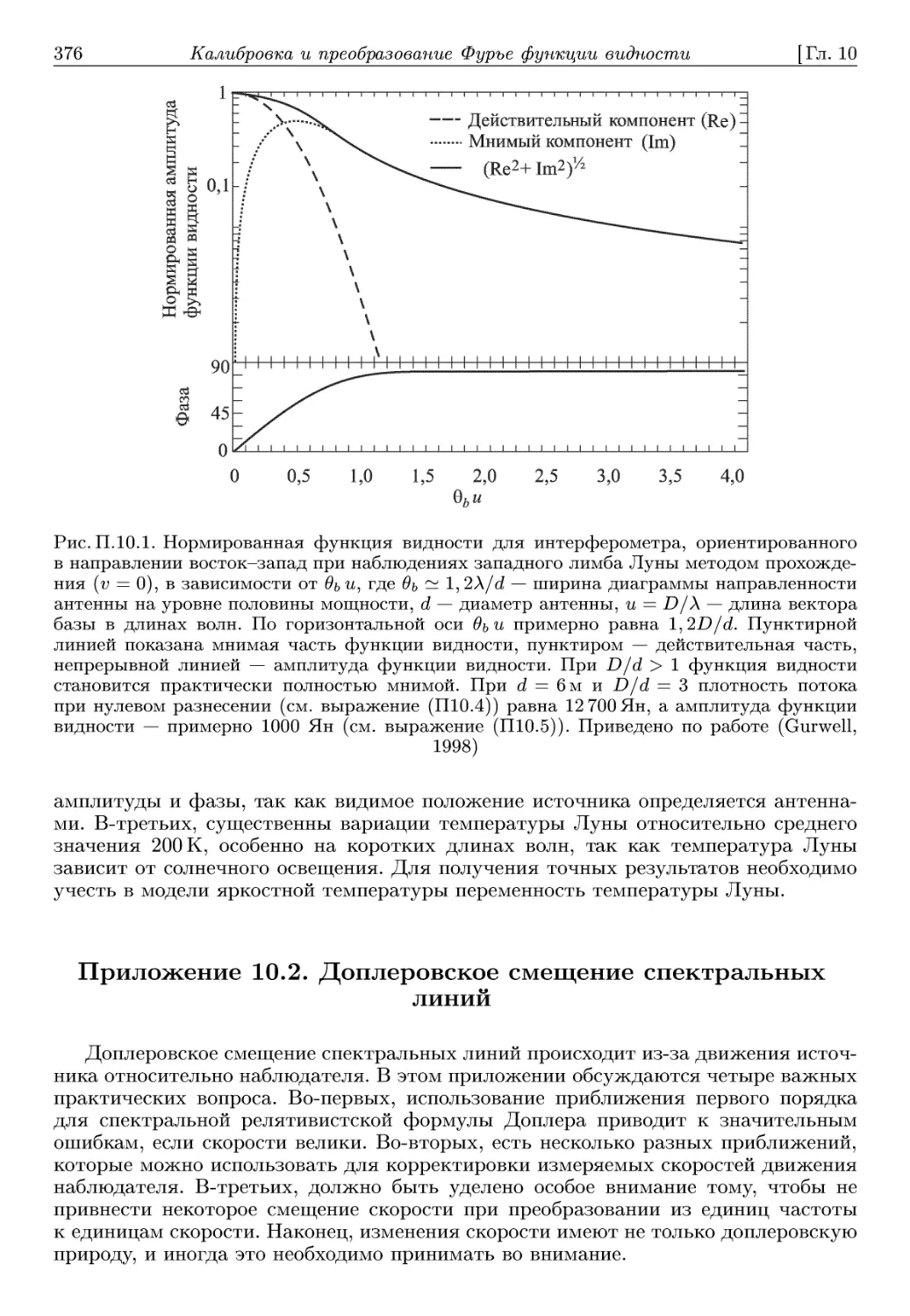
наиболее перспективны для определения такой системы. Радиотехнические средства
обеспечивают точность порядка 1 мсек для абсолютных и 10 мксек дуги и лучше
для относительных положений объектов, разделенных небольшим угловым рассто-
расстоянием. Оптические измерения изображений звезд при наблюдениях сквозь земную
атмосферу позволяют определять координаты с точностью около 50 мсек дуги.
Однако спутником Hipparcos положения звезд измерялись с точностью ~1 мсек
12 Введение и исторический обзор [Гл. 1
дуги, а оптические измерения с запуском проекта «Космический интерферометр»
(SIM) Национального управления по аэронавтике и космическим исследованиям
(NASA) обещают точность до ~4 мксек дуги.
Частью процесса астрометрических измерений является определение ориента-
ориентации инструмента относительно небесной опорной системы координат. Таким обра-
образом, наземные наблюдения дают возможность измерять вариации кинематических
параметров Земли. Помимо хорошо известных эффектов прецессии и нутации оси
вращения существуют нерегулярные смещения земной оси относительно поверх-
поверхности. Эти смещения, называемые движением полюсов, являются следствием гра-
гравитационных воздействий Солнца и Луны на экваториальную выпуклость Земли
и динамических процессов в земной мантии, коре, океанах и атмосфере. Эти же
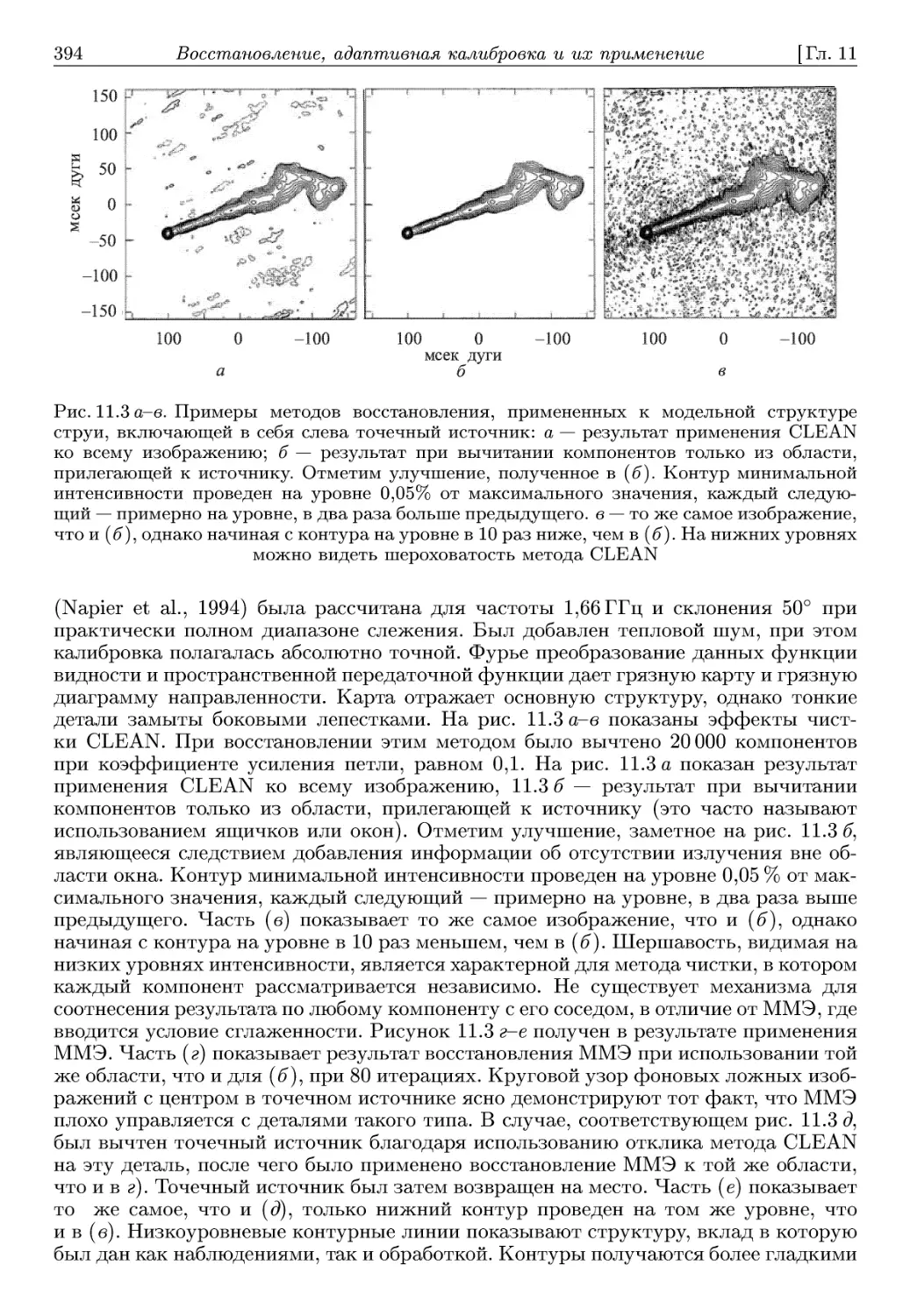
причины вызывают изменения угловой скорости вращения Земли, которые прояв-
проявляются в необходимости внесения поправок в систему Всемирного времени. Измере-
Измерения кинематических параметров важны для изучения динамики Земли. В течение
1970-х годов стало ясно, что радиоастрономические методы обеспечивают точные
измерения этих эффектов, и в конце 1970-х годов первые программы радиона-
радионаблюдений, посвященные контролю Всемирного времени и слежению за движением
полюсов, были начаты совместно Военно-морской обсерваторией и Военно-морской
исследовательской лабораторией США, а также NASA и Национальной геодези-
геодезической службой США. Полярные движения могут быть также исследованы по
наблюдениям спутников, в частности Глобальной Позиционной Системы (GPS), но
удаленные радиоисточники являются лучшим стандартом для измерения вращения
Земли.
Помимо обнаружения изменений в движении и ориентации Земли точные интер-
ферометрические измерения обеспечивают астрономическое определение вектора
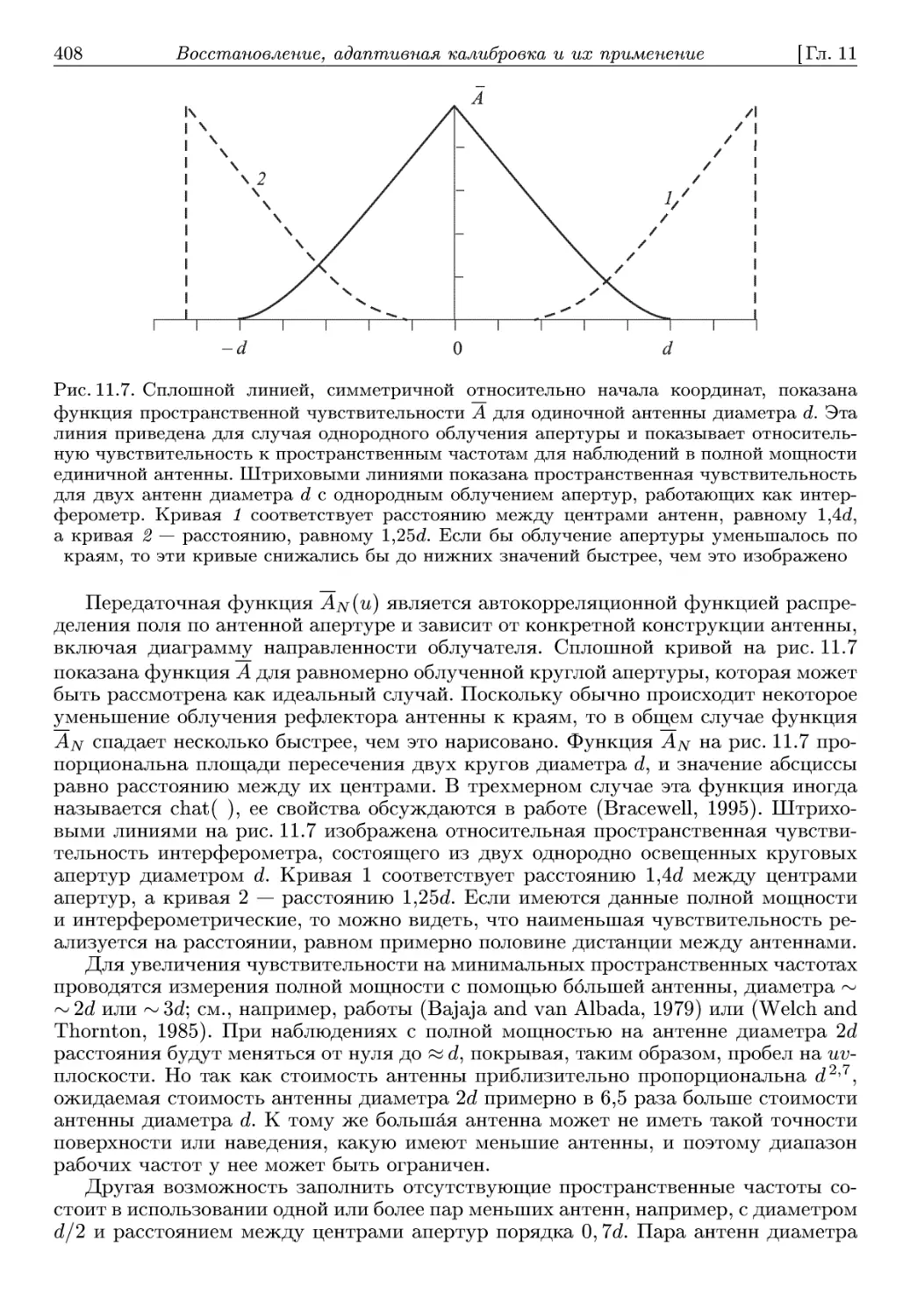
базы между антеннами, которое для расстояний ~100 км и более, как правило,
точнее получаемого обычными геодезическими методами. В интерферометрии со
сверхдлинными базами (РСДБ) расстояния между антеннами составляют сотни
или тысячи километров, а ошибки определения этих расстояний уменьшились от
нескольких метров в 1967 г., когда такие измерения были сделаны впервые, до
нескольких миллиметров. Средние относительные движения удаленных друг от
друга объектов, находящихся на разных тектонических плитах, составляют 1—10 см
в год и интенсивно отслеживаются с помощью РСДБ сетей. Интерферометрические
методы также были использованы для слежения за аппаратами на поверхности
Луны и для определения положений космических станций. В этой книге, однако,
мы ограничимся главным образам рассмотрением измерений естественных сигна-
сигналов от астрономических объектов. Достижение сверхвысокого углового разрешения
в радиодиапазоне электромагнитного спектра частично обусловлено простотой пре-
преобразования радиочастотных сигналов. Кроме того, фазовые искажения, вносимые
земной нейтральной атмосферой, в радиодиапазоне меньше, чем на более коротких
длинах волн. Будущая техника позволит достигнуть даже более высокого углового
разрешения в инфракрасном и оптическом диапазонах на обсерваториях, выне-
вынесенных за пределы земной атмосферы. Однако радиоволны останутся существенно
важными для астрономии, поскольку они способны проходить сквозь галактические
пылевые облака, непрозрачные для оптического излучения, и позволяют обнаружи-
обнаруживать объекты, не излучающие в других областях спектра.
1.2]
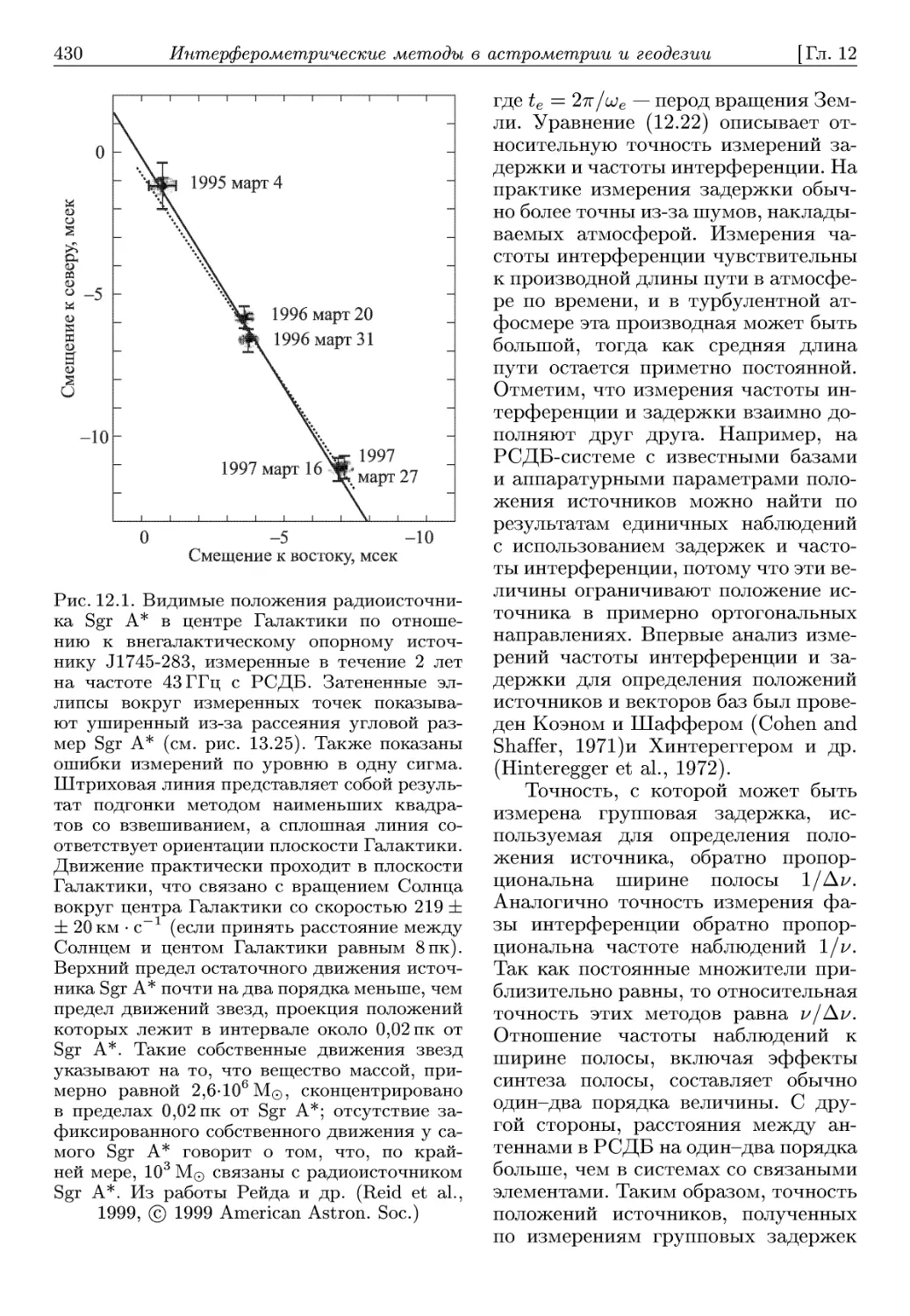
Основные определения и соотношения,
13
1.2. Основные определения и соотношения
Этот раздел написан для читателей, не знакомых с основами радиоастрономии,
и представляет собой краткий обзор некоторых основных сведений, полезных при
рассмотрении предмета радиоинтерферометрии.
1.2.1. Космические сигналы. О напряжениях, индуцированных излучением
космических источников, обычно говорят как о сигналах, хотя они не содержат
информации в обычном техническом смысле. Такие сигналы генерируются есте-
естественными процессами и почти всегда имеют форму гауссового случайного шума.
Другими словами, напряжение на выходе приемной антенны в зависимости от
времени может быть описано в виде ряда очень коротких случайных импульсов,
представляющего собой суперпозицию монохроматических волн с гауссовым рас-
распределением амплитуд. В полосе частот Az/ огибающая радиочастотных колебаний
выглядит как набор случайных флуктуации длительностью порядка 1/Az/. Для
большинства радиоисточников характеристики сигналов не зависят от времени, по
крайней мере, на интервалах в несколько минут или часов, типичных для продол-
продолжительности радиоастрономических наблюдений. Полагается, что колебания этого
типа идентичны шумовым напряжениям, генерируемым в резисторах и усилителях.
Такие процессы обычно считают стационарными и эргодическими, т. е. их усредне-
усреднение по времени и по множеству наблюдений приводит к одинаковым результатам.
Большая часть энергии находится в виде непрерывного излучения,
спектр мощности которого изменяется незначительно с изменением часто-
частоты. Поэтому это излучение и может быть принято постоянным в преде-
пределах принимаемой полосы частот большинства радиоастрономических ин-
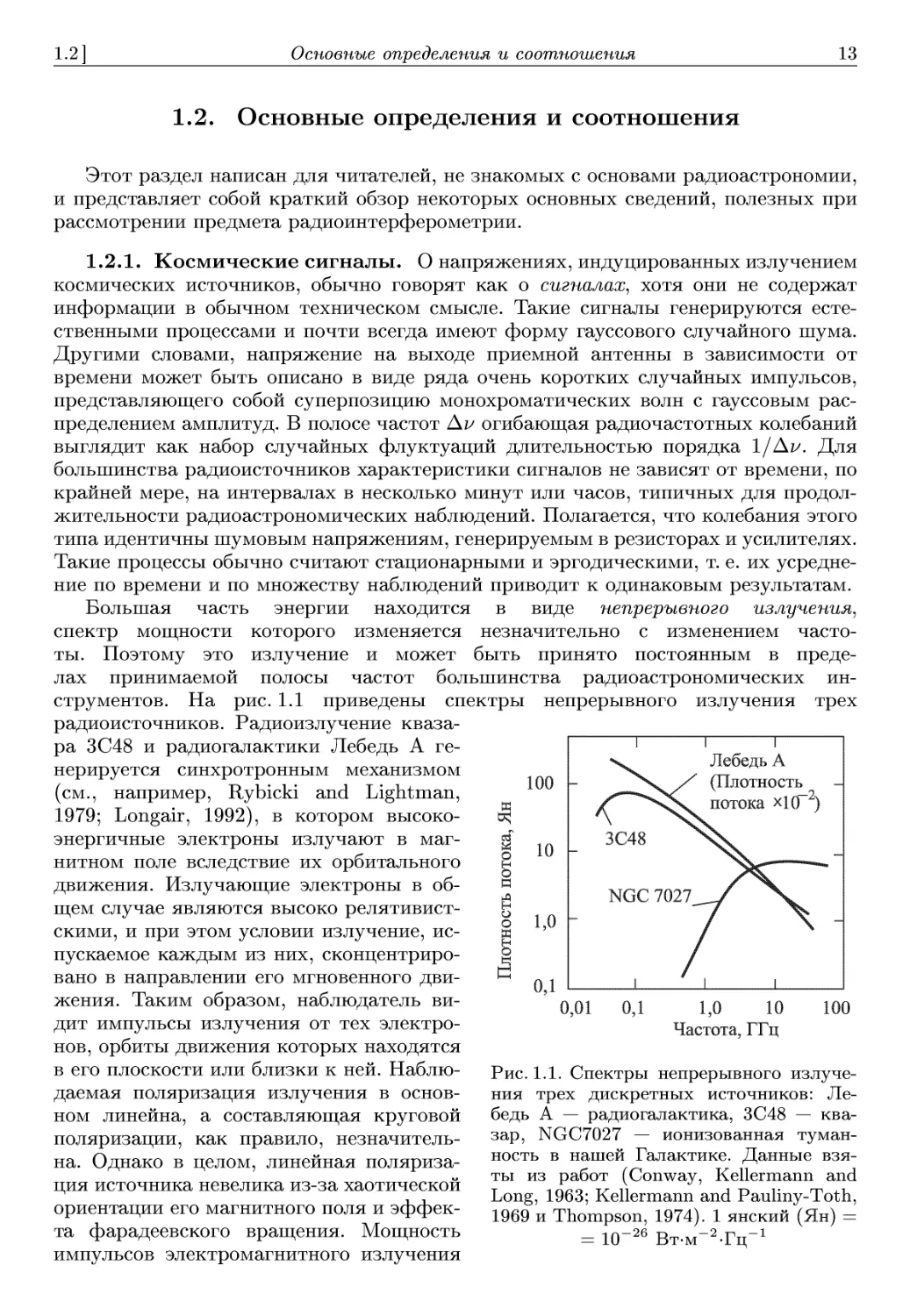
инструментов. На рис. 1.1 приведены спектры непрерывного излучения трех
радиоисточников. Радиоизлучение кваза-
квазара ЗС48 и радиогалактики Лебедь А ге-
генерируется синхротронным механизмом
(см., например, Rybicki and Lightman,
1979; Longair, 1992), в котором высоко-
высокоэнергичные электроны излучают в маг-
магнитном поле вследствие их орбитального
движения. Излучающие электроны в об-
общем случае являются высоко релятивист-
релятивистскими, и при этом условии излучение, ис-
испускаемое каждым из них, сконцентриро-
сконцентрировано в направлении его мгновенного дви-
движения. Таким образом, наблюдатель ви-
видит импульсы излучения от тех электро-
электронов, орбиты движения которых находятся
в его плоскости или близки к ней. Наблю-
Наблюдаемая поляризация излучения в основ-
основном линейна, а составляющая круговой
поляризации, как правило, незначитель-
незначительна. Однако в целом, линейная поляриза-
поляризация источника невелика из-за хаотической
ориентации его магнитного поля и эффек-
эффекта фарадеевского вращения. Мощность
импульсов электромагнитного излучения
о
i
100
10
1,0
0 1
ЗС48
NGC 7027
j
/
i i
Лебедь А
(Плотность
потока хЮ~
V
I I
2)"
0,01 0,1
1,0 10
Частота, ГГц
100
Рис. 1.1. Спектры непрерывного излуче-
излучения трех дискретных источников: Ле-
Лебедь А — радиогалактика, ЗС48 — ква-
квазар, NGC7027 — ионизованная туман-
туманность в нашей Галактике. Данные взя-
взяты из работ (Conway, Kellermann and
Long, 1963; Kellermann and Pauliny-Toth,
1969 и Thompson, 1974). 1 янский (Ян) =
= Ю-26 Вт-м-^Гц-1
14 Введение и исторический обзор [Гл. 1
электронов сконцентрирована на гармониках орбитальных частот, и непрерывное
распределение электронов по энергии приводит к непрерывному радиоспектру. Ко-
Количество импульсов излучения электронов слишком велико, чтобы их можно было
отделить друг от друга, и поэтому электромагнитное поле представляет собой слу-
случайный непрерывный процесс с нулевым средним значением. Наклон спектральной
кривой соответствует функции энергетического распределения электронов. Квазар,
спектр которого показан на рис. 1.1, представляет собой существенно более ком-
компактный объект, чем радиогалактика, поэтому плотность электронов и напряжен-
напряженность магнитного поля в нем достаточно высоки, что вызывает самопоглогцение
излучения на низких частотах.
Планетарная туманность NGC7027, спектр которой также приведен на рис. 1.1,
находится в нашей Галактике и состоит из газа, ионизованного излучением цен-
центральной звезды. Радиоизлучение имеет тепловую природу и является результатом
свободно-свободных переходов при столкновениях между несвязанными электрона-
электронами и ионами в плазме. На низкочастотном конце спектральной кривой туманность
непрозрачна для собственного излучения и излучает чернотельный спектр, хорошо
аппроксимируемый законом Релея—Джинса. С увеличением частоты способность
к поглощению и, следовательно, излучению уменьшается пропорционально v
(см. Rybicki and Lightman, 1979), где v — частота. Это соответствует обратной
зависимости v2 в законе Релея-Джинса. Следовательно, на высоких частотах, где
туманность непрозрачна для излучения, спектр ее — плоский. Излучение этого типа
неполяризовано.
В отличие от непрерывного излучения спектральное излучение генерируется на
определенных частотах атомными и молекулярными процессами. Фундаментальное
значение имеет линия нейтрального атомарного водорода на частоте 1420,405 МГц,
соответствующая переходу между двумя энергетическими уровнями атома, опре-
определяемыми ориентацией вектора спина электрона в магнитном поле ядра. Соб-
Собственная ширина водородной линии пренебрежимо мала, но доплеровские сдвиги
частоты вследствие теплового движения атомов и крупномасштабного движения
облаков газа приводят к уширению этой линии излучения. Полное доплеровское
уширение в нашей Галактике составляет несколько сотен килогерц. Сравнение
наблюдаемых скоростей газа со скоростями из моделей галактического вращения
дает информацию о галактической структуре.
В нашей и других подобных ей галактиках находятся большие молекулярные
облака с температурами 10—100 К, в которых идет непрерывный процесс звездо-
звездообразования. В этих облаках создаются условия для многих атомарных и моле-
молекулярных переходов в далеком инфракрасном и радио диапазонах. Обнаружено
более 4500 молекулярных линий примерно от 80 молекулярных образований (Lo-
vas, Snyder and Johnson, 1979; Lovas, 1992). Перечень атомарных и молекулярных
линий приведен в работе (Rohlfs and Wilson, 1996). Некоторые из наиболее важных
линий перечислены в табл. 1.1. Отметим, что в этой таблице содержится менее
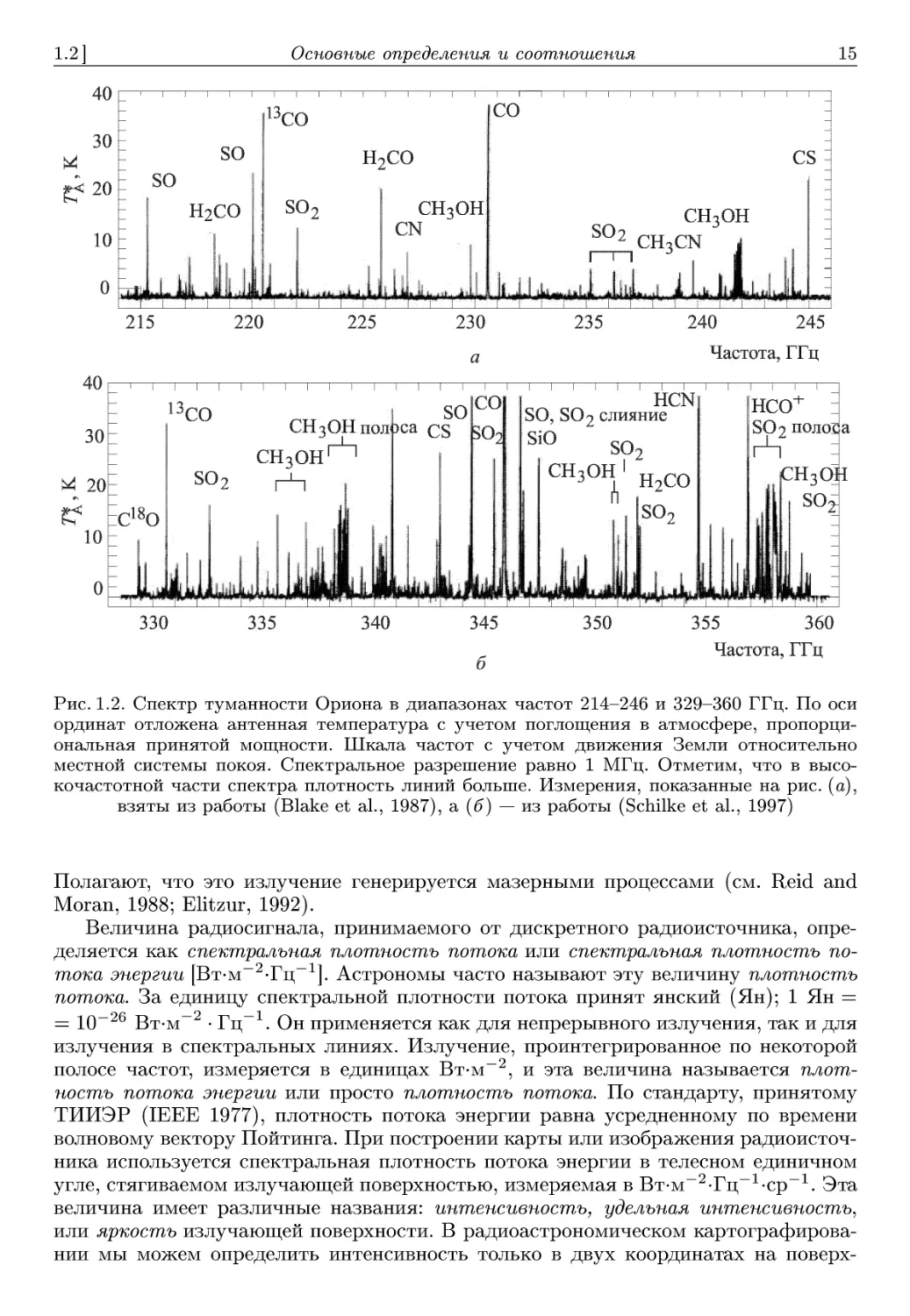
1 % известных линий в частотном диапазоне до 1 ТГц. На рис. 1.2 показан спектр
излучения многих молекулярных линий туманности Ориона в диапазонах частот
214-246 и 329-360 ГГц. Хотя радиопрозрачность земной атмосферы заканчивается
за ~1 ТГц, чувствительные субмиллиметровые и миллиметровые интерферомет-
интерферометры могли бы обнаружить такие линии, как 2Рз/2 —^ 2Р\/2 линия СН на частоте
1,90054 ТГц A58 мкм), которая смещается в радиодиапазон вследствие эффекта
Доплера для красных смещений (z) больше ~2. Некоторые источники очень малого
углового размера излучают очень интенсивные линии ОН, Н2О, SiO и СНзОН.
1.2]
Основные определения и соотношения,
15
40
30
20
10
о
so
so
н2со
Jco
Н2СО
CN
СН3ОН
hi iL
со
CS =
so2
СН3ОН
CH3CN
215
220
225
230
235
240 245
Частота, ГГц
HCN
SO, SO2 слияние
SIO
355 360
Частота, ГГц
Рис. 1.2. Спектр туманности Ориона в диапазонах частот 214-246 и 329-360 ГГц. По оси
ординат отложена антенная температура с учетом поглощения в атмосфере, пропорци-
пропорциональная принятой мощности. Шкала частот с учетом движения Земли относительно
местной системы покоя. Спектральное разрешение равно 1 МГц. Отметим, что в высо-
высокочастотной части спектра плотность линий больше. Измерения, показанные на рис. (а),
взяты из работы (Blake et al., 1987), а (б) — из работы (Schilke et al., 1997)
Полагают, что это излучение генерируется мазерными процессами (см. Reid and
Moran, 1988; Elitzur, 1992).
Величина радиосигнала, принимаемого от дискретного радиоисточника, опре-
определяется как спектральная плотность потока или спектральная плотность по-
потока энергии [Вт-м~2-Гц~1]. Астрономы часто называют эту величину плотность
потока. За единицу спектральной плотности потока принят янский (Ян); 1 Ян =
_ ю~26 Вт-м~ • Гц~ . Он применяется как для непрерывного излучения, так и для
излучения в спектральных линиях. Излучение, проинтегрированное по некоторой
полосе частот, измеряется в единицах Вт-м~2, и эта величина называется плот-
плотность потока энергии или просто плотность потока. По стандарту, принятому
ТИИЭР (IEEE 1977), плотность потока энергии равна усредненному по времени
волновому вектору Пойтинга. При построении карты или изображения радиоисточ-
радиоисточника используется спектральная плотность потока энергии в телесном единичном
угле, стягиваемом излучающей поверхностью, измеряемая в Вт-м~2-Гц~1-ср~1. Эта
величина имеет различные названия: интенсивность, удельная интенсивность,
или яркость излучающей поверхности. В радиоастрономическом картографирова-
картографировании мы можем определить интенсивность только в двух координатах на поверх-
16
Введение и исторический обзор
[Гл. 1
Таблица 1.1. Некоторые важные радиолинии
Химическое название
Химическая
формула
Переход
Частота
(ГГц)
Дейтерий
Водород
Радикал гидроксила
Радикал гидроксила
Радикал гидроксила
Радикал гидроксила
Метиладин
Радикал гидроксила
Формальдегид
Радикал гидроксила
Метанол
Гелий
Метанол
Формальдегид
Циклопропенилиден
Вода
Аммиак
Аммиак
Аммиак
Метанол
Окись кремния
Окись кремния
Сульфид углерода
Окись кремния
Цианистый водород
Формил
Диазенил
Сульфид углерода
Окись углерода
Окись углерода
Окись углерода
Окись углерода
Сульфид углерода
Вода
Окись углерода
Сульфид углерода
Сульфид углерода
Окись углерода
Вода
Окись углерода
Тяжелая вода
Углерод
Вода
Аммиак
Окись углерода
Окись углерода
Углерод
D
HI
OH
OH
OH
OH
CH
OH
H2CO
OH
СНзОН
3He+
CH3OH
H2CO
C3H2
H2O
NH3
NH3
NH3
CH3OH
SiO
SiO
CS
SiO
HCN
HCO+
N2H+
CS
12C18q
13C16q
12C17q
12C16O
CS
H2O
12C16O
CS
CS
12C16O
H2O
12C16O
HDO
Cl
H2O
NH3
12C16O
12C16O
Cl
2sl,
2Пз
2Пз
2Пз
2m
2Ш
2m
lio2-
2n§
5i -
25i,
2
2o-
2n -
lio-
616 -
1, 1
2, 2
3, 3
62-
v =
v =
J =
V =
J =
J =
J =
J =
J =
J =
J =
J =
J =
З13-
J =
J =
J =
J =
4l4"
J =
loi -
3P1
lio -
lo-
J =
J =
3P2-
. F =
. F =
, J =
, «/ =
, J =
, ^ =
, J =
, J =
-In,
, ^ =
> 60 ^4
, F =
> 3-i .
-+2i2,
-^ loi
-^ 52з,
^1,
^2,
^3,
^ 61, J
2, J
1, J
1, J
: 1 ->>
1 ->>
: 1 -)>
: 2 —>>
1 ^
1 ->>
: 1 -)>
1 —>>
3^
-^ 22o
: 2 —>>
: 5^
: 7^
3^
"^321
: 4^
-^ Ooo
-^ 3Po
-> loi
^ Oo
6^
: 7^
-)> 3Pl
. ± v ±
: 1 ^0
3 77 _ 1 __v 9
: |, F = 1-^ 1
: |, F = 2^2
: |, F = 2^ 1
: f, F = 1-^ 1
- |, F = 1 —>> 0
# F-nepexodoe
5 771 Q v Q
2, Г — 6 —> 6
+
1^0
E
4 F-nepexoda
5 F-nepexodoe
1, 18 F-nepexodoe
2, 7 F-nepexodoe
3, 7 F-nepexodoe
= l->0
= l->0
0
= 2 —>> 1
0, 5 F-nepexoda
0
0, 7 F-nepexodoe
1
0
0
0, 5 F-nepexoda
0
2
1
4
6
2
3
5
6
0,327
1,420
1,612"
1,665"
1,667"
1,721"
3,335
4,766"
4,830
6,035"
6,668"
8,665
12,179"
14,488
18,343
22,235"
23,694
23,723
23,870
25,018
42,821"
43,122"
48,991
86,243"
88,632
89,189
93,174
97,981
109,782
110,201
112,359
115,271
146,969
183,310"
230,538
244,936
342,883
345,796
380,197
461,041
464,925
492,162
556,936
572,498
691,473
806,652
809,340
aСильное мазерное излучение.
1.2]
Основные определения и соотношения,
17
ности небесной сферы, и измеренное излучение представляет собой компоненту,
ортогональную к этой поверхности по отношению к наблюдателю.
В теории излучения интенсивность или удельная интенсивность, часто
обозначаемая Iv, — поток энергии, излучаемой с единичной поверхности
в единицу времени в единичной полосе частот и единичном телесном угле.
Как показано на рис. 1.3, поток энергии в направлении s в пределах телесного
угла d?l, полосы частот dv и площадки dA равен /^(s) d?ldvdA. Это определение
применимо к излучению с поверхности объекта, к излучению, проходящему
через некоторую площадку в пространстве, или к при-
принимаемому излучению на поверхности преобразователя
или детектора. Последний случай соответствует приему
антенной, и тогда телесным углом определяется область
небесной сферы, из которой приходит излучение. Отсюда
и далее мы используем / для обозначения Iv. Отметим, что
в оптической астрономии удельная интенсивность обычно
определяется как интенсивность на единичную длину вол-
волны I\ (Rybicki and Lightman, 1979).
Для чернотельного теплового излучения связь интен-
интенсивности и физической температуры Т излучающего ве-
вещества описывается формулой Планка:
I =
2kTv
hv
кТ
ehv/kT _
(l.i)
Рис. 1.3. Элементы те-
телесного угла и площад-
площадки поверхности, иллю-
иллюстрирующие определе-
определение интенсивности. dA
перпендикулярна s
где к — постоянная Больцмана, с — скорость света и h —
постоянная Планка. При условии, что hv <C кТ, молено
использовать приближение Ре лея-Джинса. В этом слу-
случае выражение в квадратных скобках приравнивается
к единице. Для применения аппроксимации Ре лея-Джинса необходимо условие
v (ГГц) <С 20 Т (К), справедливое на высоких частотах и при низких температурах
для многих астрономических объектов. Однако яркостную температуру Тв можно
определить для любого механизма излучения:
С21
A.2)
В области действия приближения Релея-Джинса яркостная температура Тв соот-
соответствует физической температуре абсолютно черного тела: Т = Тв- В примерах
на рис. 1.1 для NGC7027 значение Тв составляет порядка 104 К и соответствует
температуре электронов. Для источников Лебедь А и ЗС48 величина Тв достигает
108 К и более и является мерой плотности энергии электронов и магнитного поля,
а не физической температуры. Как пример для спектральных измерений, Тв линий
окиси углерода в молекулярных облаках обычно находится в пределах 10-100 К.
В этом случае Тв пропорциональна температуре возбуждения, связанной с энерге-
энергетическими уровнями перехода, и соответствует как температуре и плотности газа,
так и температуре поля излучения.
1.2.2. Координаты и обозначения радиоисточников. Положения радио-
радиоисточников измеряются в небесных координатах прямое восхождение и склонение.
На небесной сфере эти величины аналогичны соответственно долготе и широте на
Земле. Началом отсчета прямого восхождения произвольно выбрана точка, в кото-
которой Солнце пересекает небесный экватор; на данную эпоху она находится в начале
18 Введение и исторический обзор [Гл. 1
созвездия Овна. По международной системе обозначений (IAU 1974) названия ра-
радиоисточников записываются следующим образом. Первые четыре знака дают часы
и минуты прямого восхождения (RA), пятый знак — знак склонения, а оставшиеся
три знака — градусы и округленные десятые доли градуса склонения (Dec.) для
среднего экватора и равноденствия 1950 г. Например, источник с координатами
RA 01h34m49,83s, Dec. 32° 54' 20, 5" обозначается как 0134 + 329. В ряде случаев
применяются старые обозначения источников. Так, на рис. 1.1, Лебедь А — силь-
сильнейший радиоисточник в созвездии Лебедя, а ЗС48 обозначает источник номер
48 в Третьем кембриджском каталоге (Edge et al., 1959). NGC7027 — оптическое
обозначение и относится к Новому общему каталогу незвездных объектов Дрейера
(Dreyer, 1888), в котором главным образом перечислены галактики.
Положения объектов в небесных координатах изменяются вследствие прецессии
и нутации земной оси вращения, аберрации и собственного движения. Положения
источников обычно приводятся на стандартные эпохи 1950 или 2000. Процедуры
для редукции этих координат к нужной дате и времени даны в (Seidelmann, 1992).
В обзорном каталоге Большой антенной решетки (VLA, 1,4 ГГц) содержится при-
приблизительно 2х106 источников (Condon et al., 1998). Полагают, что большинство
обнаруженных радиоисточников представляют собой радиогалактики или квазары,
находящиеся далеко за пределами нашей Галактики. Другой замечательный список
источников содержит 212 внегалактических объектов с точностью положений луч-
лучше 1 мсек дуги, использовавшихся при создании каталога Между народной небесной
опорной системы координат (ICRF) MAC, и 396 источников с точностью координат
в пределах нескольких угловых миллисекунд (Ma et al., 1998).
1.2.3. Прием космических сигналов. Большинство радиоастрономических
антенн представляют собой рефлекторы, смонтированные таким образом, чтобы
обеспечить возможность наблюдения большей части небосвода. Исключение состав-
составляют в основном инструменты, созданные для наблюдений на метровых и декамет-
ровых длинах волн. Собирающая поверхность А рефлекторной антенны для излуче-
излучения, приходящего в центр главного лепестка диаграммы направленности, равна гео-
геометрической площади, умноженной на коэффициент эффективности апертуры 1),
типичные значения которого находятся в пределах 0,3—0,8. Для неполяризованного,
с плотностью потока S источника, малого по сравнению с шириной диаграммы
направленности, мощность Ра, выделяемая антенной на согласованной нагрузке
в полосе частот Az/, определяется формулой
PA = ^ASAv. A.3)
Отметим, что S равна интенсивности /, проинтегрированной по телесному углу
источника. Коэффициентом 1/2 учитывается тот факт, что антенна принимает
только половину мощности неполяризованного излучения. Часто удобно выражать
мощность случайного шума Р через эффективную температуру Т = P/k Az/, где к —
постоянная Больцмана. В приближении Ре лея-Джинса Р соответствует мощности
шума, выделяемой резистором с физической температурой Т на согласованной
нагрузке (Nyquist, 1928). В общем случае, если мы пользуемся формулой Планка,
можно записать Р = &TpianckAz/, где Tpianck — эффективная температура излуче-
излучения, или температура шума нагрузки с физической температурой Т, определяемая
х) Также применяется термин коэффициент использования поверхности (КИП). —
Прим. перев.
1.2] Основные определения и соотношения, 19
формулой
L Planck
= Т
кТ
ehu/kT _
A.4)
Мощность шума приемной системы 1) можно выразить через температуру шу-
шума системы Т^, связанную с согласованной активной нагрузкой, дающей равный
уровень мощности при подключении к эквивалентному, не имеющему собственного
шума приемнику. Т$ определяется как мощность, выделяемая на такой нагрузке,
деленная на к Аи. Применяя формулу Планка, соотношение между Т$ и физической
температурой Т нагрузки получается заменой Tpianck в формуле A.4) на Т#.
Температура системы состоит из двух частей: температуры приемника Tr,
соответствующей собственным шумам усилителей приемника, и температуры ан-
антенны TfA, представляющей собой нежелательный шум антенны, создаваемый окру-
окружающим излучением, поглощением в атмосфере, омическими потерями и другими
источниками.
Важно отметить, что термин антенная температура также применяется для
обозначения части мощности на антенном выходе, создаваемой исследуемым источ-
источником, и чаще всего именно в этом смысле используется в данной книге. В этом
случае мощность, принятая антенной от источника, равна
РА = кТААи, A.5)
и Тд связана с плотностью потока формулами A.3) и A.5). Полезно представить это
отношение как Тд [К] = S [Ян\хА [м2]/2800. Астрономы иногда характеризуют эф-
эффективность антенны величиной, измеряемой в единицах янский/келъвин, которая
представляет собой плотность потока (в единицах 10~26 Вт-м~2-Гц~1) точечного
источника, увеличивающего Тд на один кельвин. Таким образом, эта величина
в Ян/К равна 2800/А [м2].
Еще один встречающийся термин, эквивалентная плотность потока систе-
системы Se, характеризует одновременно чувствительность антенны и приемной систе-
системы. Эта величина равна плотности потока точечного источника, расположенного
в главном лепестке диаграммы направленности антенны, и создающего двойную
мощность шума в приемнике по сравнению с шумами системы в его отсутствие.
Подставляя в формулу A.3) Ра — kT$Av, получим
SE = —д- • A.6)
Отношение мощности сигнала источника к мощности шума в приемном усилителе
равно Та/Т$. Вследствие случайной природы сигнала и шума, измерения уровней
мощности, выполненные с интервалами времени BАг/)~\ могут рассматриваться
как независимые. Измерения с усреднением величины сигнала за время т содержат
примерно 2Аит независимых отсчетов. Отношение сигнал/шум 7Zsn на выходе под-
подключенного к приемнику измерителя мощности увеличивается пропорционально
квадратному корню из числа независимых отсчетов и представляется в виде
A.7)
х) Термины приемник и приемная система, широко используемые в радиоастрономии,
обозначают подключаемую к выходу антенны (или антенн) электронную систему. В эти
понятия могут включаться (или не включаться) один или несколько детекторов или
корреляторов (о которых речь пойдет позднее) и аппаратура обработки и записи.
20 Введение и исторический обзор [Гл. 1
где С — постоянная величина. Этот результат, по-видимому, впервые был по-
получен Дикке (Dicke, 1946). Более детальное исследование (см. Tiuri, 1964; Tiuri
and Raisanen, 1986) показывает, что С = 1 в случае приемника с квадратичным
детектором и прямоугольной полосой пропускания и достигает ~2 в случае более
сложных систем. При обычных значениях Аг/ иг, равных соответственно 50 МГц
и 5 ч, радиометрический выигрыш (Az/rI/2 имеет порядок 106. Таким образом,
можно обнаружить сигнал, уровень мощности которого составляет немногим более
10~6 шума системы. В качестве примера особенно эффективного использования
большого времени накопления можно привести наблюдения космического фонового
излучения спутником СОВЕ, во время которых можно было измерить детали на
уровне яркостной температуры менее 10~7 от температуры шума системы (Smoot
et al., 1990, 1992). Насколько малы значения энергии в радиоастрономии, помогут
проиллюстрировать следующие вычисления. Рассмотрим большой радиотелескоп
с полной собирающей поверхностью 104 м2, принимающий сигнал в полосе частот
50 МГц, и направленный на источник с плотностью потока 1 мЯн A0~3 Ян). За
103 лет полная принятая энергия составит около 10~7 Дж A эрг), что сравнимо
с несколькими процентами кинетической энергии одной падающей снежинки. Что-
Чтобы обнаружить такой источник с помощью рассматриваемого телескопа и темпера-
температурой шума системы 50 К, потребовалось бы наблюдательное время около 5 мин,
в течение которого была бы принята энергия 10~15 Дж.
1.3. Развитие радиоинтерферометрии
1.3.1. Эволюция техники синтеза. В этой части кратко описывается исто-
история интерферометрии в радиоастрономии. Следующий список в качестве введения
показывает наиболее важные этапы прогресса — от интерферометра Майкельсона
до создания многоэлементных решеток апертурного синтеза и РСДБ:
1. Звездный интерферометр Майкельсона. Этим инструментом положено нача-
начало технике применения двух раздельных приемных апертур для измерения
амплитуды интерференционных лепестков и определения угловых размеров
объектов A890-1921).
2. Первые астрономические наблюдения на двухэлементном радиоинтерферо-
радиоинтерферометре. Наблюдения Солнца (Ryle and Vonberg, 1946).
3. Интерферометр с модуляцией фазы. Первая реализация функции перемно-
перемножения напряжений в корреляторе — устройстве для совместной обработки
сигналов, принятых с двух антенн A952 г.).
4. Калибровочные радиоисточники. Накопление в течение 1950-1960-х гг. ком-
компактных радиоисточников с точными координатами путем отождествления
с оптическими объектами и другими методами.
5. Первые измерения угловых размеров источников. Применение интерферомет-
интерферометров с переменной базой (примерно с 1952 г.).
6. Солнечные антенные решетки. Создание многоэлементных решеток с исполь-
использованием следящих антенн сантиметрового диапазона позволило получить
подробные карты и профили солнечного диска (с середины 1950-х гг.).
7. Антенные решетки с сопровождающими элементами. Общая тенденция пе-
перехода от неподвижных антенн метрового диапазона к следящим антеннам
1.3] Развитие радиоинтерферометрии 21
сантиметрового диапазона длин волн. Создание многоэлементных решеток
с отдельным коррелятором для каждой базы A960-е гг.).
8. Синтез с использованием вращения Земли. Предложен Райлом (были преце-
прецеденты при картографировании Солнца). Существенной составляющей было
создание компьютеров для управления приемными системами и выполне-
выполнения быстрого преобразования Фурье, необходимого при картографировании
A962).
9. Спектральные исследования. В радиоинтерферометрии начаты примерно
в 1962 г.
10. Развитие методов построения изображений. В основе используются про-
процедуры замыкания фазы, нелинейной свертки и другие методы, описанные
в главах 10 и 11 (примерно с 1974 г.).
11. Интерферометрия со сверхдлинными базами {РСДБ). Первые наблюдения
проведены в 1967 г. Метод предложен в 1962 г., опубликован в работе (Мат-
веенко, Кардашев, Шоломицкий, 1965).
12. Инструменты миллиметровых волн (~100-300 ГГц). Основное развитие с се-
середины 1980-х.
13. Орбитальная РСДБ (ОРСДБ). Эксперимент со спутниковой системой слеже-
слежения и ретрансляции данных США (TDRSS, 1986-88). Спутник HALCA A997).
14. Инструменты субмиллиметровых волн C00 ГГц - 1 ТГц). JCMT-CSO ин-
интерферометр A992-1996). Субмиллиметровая антенная решетка Смитсониан-
ской астрофизической обсерватории (SAO) и Китайской Академии наук Тай-
Тайваня B001). Большая миллиметровая решетка в Атакама (ALMA) — первое
десятилетие двадцать первого века.
1.3.2. Интерферометр Майкельсона. Начало применению методов интер-
интерферометрии в астрономии было положено работами Майкельсона (Michelson, 1890,
1920) и Майкельсона и Пиза (Michelson and Pease, 1921) в оптике, которые смогли
получить достаточно высокое угловое разрешение, чтобы измерить диаметры неко-
некоторых ближайших звезд наибольших размеров, таких, как Арктур и Бетельгейзе.
Радиоастрономы сразу заметили, что теории поля оптического и радиоизлучения
в основном похожи, и опыт, накопленный в оптике, явился ценным вкладом в тео-
теорию радиоинтерферометрии.
Как показано на рис. 1.4, лучи света от звезды проходят через две апертуры
и собираются телескопом. Получающееся в результате изображение звезды имеет
конечный размер и зависит от атмосферной турбулентности, дифракции на зер-
зеркалах и принимаемой полосы частот излучения. Максимумы интенсивности света,
получающиеся в результате интерференции, образуются на углах #, для которых
разность хода лучей А от звезды до точки сложения световых волн равна целому
числу длин волн, соответствующих эффективному центру оптической полосы. Если
угловые размеры звезды малы по сравнению с расстоянием в между соседни-
соседними максимумами, то изображение звезды пересекается чередующимися темными
и светлыми полосами, известными как интерференционные полосы. В случае если
размеры звезды сравнимы с расстоянием между максимумами, то получающееся
в результате изображение может быть представлено как суперпозиция изображе-
изображений ряда точечных источников, формирующих звезду. Максимумы и минимумы
22
Введение и исторический обзор
[Гл. 1
ага2
т2
тъ
ч Телескоп
Яркость
изображения
Расстояние
б
Рис. 1.4. а — схема звездного интерферометра Майкельсона—Пиза. Приходящие лучи пе-
переотражаются в апертуру телескопа зеркалами т\-т±. Две апертуры интерферометра
определяются крайней парой зеркал. Лучи а\ и Ь\ проходят равные пути до окуляра,
в котором создается изображение, а приходящие под углом в к инструментальной оси
лучи CL2 и &2 проходят расстояния, отличающиеся на величину А. б — интенсивность
изображения в зависимости от позиционного угла в направлении, параллельном разнесе-
разнесению апертур интерферометра. Сплошной линией показаны интерференционные профили
неразрешенной звезды (Vm = 1,0), а штриховой — частично разрешенной, когда Vm = 0,5
интерференционных полос для различных точек не совпадают, и их контрастность
смягчается, как показано на рис. 1.4 & Для измерения относительной амплитуды
интерференционных полос Майкельсон ввел понятие интерференционной видно-
сти Vm-
яркость в максимуме — яркость в минимуме
яркость в максимуме + яркость в минимуме
A.8)
Отметим, что в этом определении видность нормирована к единице при условии,
что интенсивность минимумов равна нулю, т. е. размер звезды мал по сравнению
с расстоянием меду интерференционными полосами. Если видность интерферен-
интерференционных полос заметно меньше единицы, то говорят, что источник разрешен ин-
интерферометром. Пусть /(/,7тг) — двумерная интенсивность звезды или, в случае
радиоинтерферометра, источника. (/,га) — координаты на небесной сфере, причем
/ измеряется параллельно вектору расстояния между апертурами, а т — перпенди-
перпендикулярно. Интерференционными полосами измеряется разрешение только в направ-
направлении, параллельном разнесению апертур. В ортогональном направлении отклик
просто пропорционален интенсивности, проинтегрированной по телесному углу.
Таким образом, интерферометр измеряет проекцию интенсивности на направление
1.3]
Развитие радиоинтерферометрии
23
1,0
Г\
а 12
1,0; ^а/2
0; ?<^
hit)
= sin лам
паи
?>а12 о
1,0
3,0
и, в единицах На
-а 12 а 12 ?
0; ?<-а/2, ?> а 12 0
1Д)
м, в единицах На
-а 12 а 12
а=
2,0 3,0
и, в единицах На
Рис. 1.5. Одномерные профили интенсивности 1\{1) для трех простых моделей распреде-
распределения интенсивности: однородный прямоугольный источник — (а, слева), однородный
круглый источник — E, слева), круговое гауссово распределение — (в, слева). Соответ-
Соответствующие функции видности Майкельсона Vm показаны справа. / — переменный угол на
небесной сфере, и — расстояние между приемными апертурами, измеренное в длинах волн,
а — угловой размер модели. Сплошными линиями на графиках Vm представлены модули
преобразования Фурье Ii(l), а штриховыми — отрицательные значения преобразования.
См. для дальнейших пояснений текст
/, т. е. одномерный профиль
= f
A.9)
Как будет показано в этой главе позлее, видность интерференционных полос про-
пропорциональна модулю преобразования Фурье /i(Z) в зависимости от расстояния
24 Введение и исторический обзор [Гл. 1
между апертурами, выраженного в длинах волн. На рис. 1.5 показаны интегральные
профили /i для трех простых моделей звезды или радиоисточника и соответствую-
соответствующие им функции видности в зависимости от и — расстояния между апертура-
апертурами, измеряемого в длинах волн. В верхней части рисунка показано равномерное
прямоугольное распределение, в средней — равномерное круговое, в нижней ча-
части рисунка — круговое гауссово распределение. Прямоугольным распределением
представлен равномерно яркий прямоугольник на небесной сфере со сторонами,
параллельными осям / и т, и шириной, равной а в направлении I. Равномерным кру-
круговым распределением представлен равномерно яркий круглый диск диаметра а.
В проекции на ось / профиль одномерной функции интенсивности 1\ представляет
собой полукруг. Гауссова модель соответствует источнику с круговой симметри-
симметрией и гауссовым профилем интенсивности с максимумом в центре. Интенсивность
пропорциональна функции ехр [—4 In 2 (Z2 + т2)/а2} и образует круговые контуры
с диаметром, равным а на уровне половины максимума. Любые сечения модели,
перпендикулярные плоскости /т, образуют гауссов профиль с одинаковой полуши-
полушириной а.
Майкельсон и Пиз для интерпретации наблюдений использовали главным об-
образом модель круглого диска и определяли диаметр звезды по положению первого
минимума функции видности, для определения которого изменяли расстояние меж-
между апертурами. Юстировка такого инструмента и визуальная оценка Vm требовали
большой аккуратности, поскольку полосы были нестабильны и хаотически переме-
перемещались по изображению вследствие атмосферных флуктуации. Опубликованные
результаты измерений диаметров звезд этим методом так и не вышли за пределы
списка Пиза (Pease, 1931), содержащего семь ярких звезд; подробнее см. обзор (Han-
bury BrownHanbury Brown, 1968). Тем не менее, применение электронно-оптических
технологий в настоящее время значительно повысило возможности инструментов
в оптической интерферометрии, что обсуждается в разд. 16.4 гл. 16.
1.3.3. Первые двухэлементные радиоинтерферометры. В 1946 г. Райл
и Вонберг сконструировали радиоинтерферометр для исследования космического
радиоизлучения, открытого и подтвержденного ранее (Jansky, 1933; Reber, 1940;
Appleton, 1945; Southworth, 1945). В радиоинтерферометре использовались ди-
польные антенные решетки на частоте 175 МГц с базой (т. е. расстоянием между
антеннами), изменяемой от 10 до 140 длин волн (от 17 до 240 м). Схема такого
инструмента и типичная запись полученных данных показаны на рис. 1.6. В этом
и в большинстве других интерферометров, построенных в 1950—1960-х годах для
метрового диапазона длин волн, диаграммы антенн были направлены по меридиану,
и сканирование по прямому восхождению обеспечивалось вращением Земли.
Приемник, показанный на рис. 1.6, чувствителен в узкой полосе частот и упро-
упрощенный анализ отклика интерферометра может быть сделан в приближении мо-
монохроматических сигналов с центральной частотой щ. Мы рассматриваем сигнал
от радиоисточника очень малых угловых размеров, находящегося на достаточно
большом расстоянии, так что приходящий волновой фронт можно считать плоским.
Представим напряжение сигнала правой антенны на рис. 1.6 в виде V sin Bttz/o^)-
Более длинный путь сигнала до левой антенны приводит к появлению временной
задержки г = (D/c) sin #, где D — расстояние между антеннами, в — угол направ-
направления на источник и с — скорость света. Таким образом, сигнал от левой антенны
равен V sin [2тп/о(? — т)\- Выход детектора приемника представляет собой квадрат
суммы напряжений сигналов:
{V sin BttzV) + V sin [2тп/0(г - г)]}2 A.10)
1.3]
Развитие радиоинтерферометрии
25
На выходе детектора находится низкочастотный фильтр, не пропускающий частоты
свыше нескольких герц или десятков герц, так что, раскрывая выражение A.10),
мы можем отбросить члены с гармониками 2тп/о?? соответствующие радиочастотам.
Отсюда для выхода детектора получаем
F = V [1 + cos Bтг1/ог)]- A.11)
Поскольку г изменяется медленно при вращении Земли, частотная гармоника
cos Bтп/от) не отфильтровывается. В зависимости от положения источника #, полу-
F =
лг2\
= V
L
1 + cos
smO\
J
A.12)
Таким образом, при движении ис-
источника по небесной сфере отклик
интерферометра F изменяется от
0 до V2, как видно для источников
на рис. 1.6 5. Отклик модулиру-
модулируется диаграммой направленности
антенн, и его максимум направлен
по меридиану. Косинусная функ-
функция в уравнении A.12) представ-
представляет собой Фурье-компоненту яр-
яркости источника, на которую от-
откликается интерферометр. Угло-
Угловая ширина интерференционных
лепестков меньше угловой шири-
ширины диаграммы направленности ан-
антенны во столько же раз (при-
(приблизительно), во сколько раз раз-
размер антенн меньше длины базы D,
т. е. для нашего случая, прибли-
приблизительно в 10 раз. Использование
интерферометра вместо одиноч-
одиночной антенны приводит к соответ-
соответствующему увеличению в точно-
точности измерения времени прохожде-
прохождения источника. Интерференцион-
Интерференционная диаграмма, заданная урав-
уравДипольные антенные
Приемник
с квадратичным
детектором
±
| Самописец |
о g
х Б
PQ
16,00 17,00 18,00
19,00 20,00
Время, часы
Рис. 1.6. Простой интерферометр с суммировани-
суммированием сигналов (а); запись, полученная на таком ин-
интерферометре с антеннами, разнесенными в на-
направлении восток-запад {б). Ось ординат — пол-
полная принятая мощность, ось абсцисс — время.
Источник слева — Лебедь А, справа — Кассио-
Кассиопея А. Уровень сигнала вблизи Лебедя А возрас-
возрастает из-за галактического фонового излучения,
нением A.12), также применима сконцентрированного в плоскости Галактики, но
полностью разрешенного интерферометром. Ри-
Рисунок взят из работы (Ryle, 1952)
и для интерферометра Майкельсо-
на, действующего по схеме, пред-
представленной на рис. 1.4.
1.3.4. Морской интерферометр. Другую реализацию принципа интерфе-
интерферометрии, известную как морской интерферометр, или зеркальный интерферометр
Ллойда (Bolton and Slee, 1953), представляли направленные на горизонт антенны
около Сиднея в Австралии. Они были установлены в нескольких местах на побере-
побережье на высоте 60-120 м над уровнем моря в качестве радаров во время Второй миро-
мировой войны. Как показано на рис. 1.7, принимается одновременно прямое и отражен-
отраженное от поверхности моря излучение от восходящего источника. Частоты наблюдений
находились в пределах 40-400 МГц. Неровности морской поверхности на высоких
частотах и ионосферное влияние на низких частотах определили оптимальную
26
Введение и исторический обзор
[Гл. 1
среднюю часть диапазона. Эффект внезапного появления восходящих источников
использовался для их различия. Благодаря отраженной волне, принятая в макси-
максимуме интерференции мощность была в четыре раза больше по сравнению с прямым
приемом одиночной антенной, и в два раза больше по сравнению с суммирующим
интерферометром (см. рис. 1.6 а) из двух аналогичных антенн. Первая опублико-
опубликованная запись интерференционных лепестков в радиоастрономии была получена
по наблюдениям Солнца с применением такой системы (McCready, Pawsey and
Payne-Scott, 1947). Наблюдения источника Лебедь А Болтоном и Стэнли (Bolton
and Stanley, 1948) показали возможность существования дискретных несолнечных
источников. Таким образом, морской интерферометр сыграл важную роль в ран-
ранней радиоастрономии, но эффекты больших задержек при прохождении сигналов
через атмосферу и неровности морской поверхности помешали его дальнейшему
развитию.
Прямой луч
Антенна
Отраженный луч
Поверхность моря
Зеркальное ^
отражение ^
антенны
Рис. 1.7. Схематическое изображение морского интерферометра (а); Интерференционная
картина похожа на ту, которая получилась бы с двумя реальными приемными антеннами,
одна из которых находилась бы на месте своего зеркального отражения в море. Отражен-
Отраженный луч проходит до приемной антенны дополнительное расстояние А, а его фаза при
отражении изменяется на 180°. б— запись излучения источника Лебедь А, полученная
с помощью морского интерферометра на частоте 100 МГц Болтоном и Стэнли (Bolton
and Stanley 1948). Источник взошел над горизонтом примерно в 23.17. Штриховой лини-
линией показано, что запись могла интерпретироваться, исходя из постоянной и переменной
компонент; позднее было показано, что переменность имела ионосферное происхождение.
Ширина интерференционного лепестка составляла около 1,0° и источник не был разрешен,
т. е. его угловые размеры малы по сравнению с интерференционными лепестками. Часть
б перепечатывается с разрешения Nature, Vol. 161, No. 4087, p. 313; copyright ©1948
Macmillan Journals Limited
1.3]
Развитие радиоинтерферометрии
27
1.3.5. Интерферометр с модуляцией фазы. Проблема с интерферометри-
ческими системами, показанными на рисунках 1.6 и 1.7, состоит в том, что кроме
сигнала от источника на выходе приемника присутствуют шумы от других источ-
источников, таких, как галактическое фоновое излучение, тепловое излучение земной
поверхности, принятое боковыми лепестками антенны, и собственные шумы усили-
усилителей приемника. Суммарная мощность шума приемника на несколько порядков
превышает сигнал любого космического источника, за исключением нескольких
наиболее ярких. Это большое отклонение шума было компенсировано на записях,
показанных на рисунках 1.6 б и 1.7 б. Уровень смещения пропорционален усилению
приемника, изменение которого трудно учесть полностью. Из-за появляющегося
по этой причине дрейфа уровня выходного сигнала снижается точность измерения
интерференционных лепестков и трудно обнаруживать слабые источники. По мето-
методике 1950-х годов выходной сигнал приемника обычно записывали на диаграммную
ленту и сигнал мог теряться, если уровень смещения выводил перо самописца за
пределы шкалы.
Применение Райлом (Ryle, 1952) модуляции фазы, которая устраняла нежела-
нежелательные компоненты на выходе приемника и оставляла только интерференционные
колебания, явилось наиболее важным техническим усовершенствованием в ран-ней
радиоинтерферометрии. Если V\ и V^ — напряжения поступающих с антенн сиг-
сигналов, то выход простого суммирующего интерферометра пропорционален (Vi +
+ V2J. В системе с фазовой модуляцией, показанной на рис. 1.8, фаза одного из
Приемник
с квадратичным
детектором
Синхронный
детектор
Генератор
частоты
модуляции
На самописец
Рис. 1.8. Интерферометр с модуляцией фазы. Фаза сигнала с одной из антенн периодиче-
периодически изменяется, что осуществляется здесь переключением дополнительной полу волновой
секции в линии передачи
сигналов периодически переключается на 180°, так что выходной сигнал детектора
принимает значения (Vi + V2J или (Vi — V2J. Частота переключений составляет
несколько десятков герц и разностный сигнал двух выходных уровней, пропор-
пропорциональный V1V2, выделяется синхронным детектором. Таким образом, выходной
сигнал интерферометра с модуляцией фазы представляет собой усредненное по
времени произведение напряжений входных сигналов, т. е. пропорционален их крос-
скорреляции. Элемент, в котором происходит перемножение и усреднение сигналов,
в современном интерферометре называется коррелятором', общее определение кор-
коррелятора будет дано позже. Сравнение с выходным сигналом системы, представлен-
представленной на рис. 1.6, видно, что если поступающие с антенн сигналы перемножать вместо
28 Введение и исторический обзор [Гл. 1
11
I
Sr^
09,30 10,00 10,30 11,00
Время, часы
Рис. 1.9. Выходной сигнал интерферометра с модуляцией фазы в зависимости от времени,
показывающий отклик для нескольких источников (Ryle, 1952)
того, чтобы суммировать и возводить в квадрат, то постоянная составляющая
в квадратных скобках в уравненииA.12) пропадает и остается только косинусный
член. Как показано на рис. 1.9, на выходе остаются только интерференционные
колебания. С уменьшением влияния нестабильности усиления инструмента, для
компенсации потерь в линиях передачи стала практиковаться установка усилителей
на антеннах. Прогресс выразился в увеличении размеров антенных решеток и рас-
расстояний между антеннами. В начале 1950-х гг. в большинстве интерферометров
начали применять фазовую модуляцию, которая впервые реализовала действие
коррелятора. В настоящее время нет необходимости использовать модуляцию фазы
для перемножения напряжений, но она часто применяется как вспомогательное
средство для устранения различных инструментальных дефектов, как описано
в разд. 7.5.
1.3.6. Оптическое отождествление и калибровочные источники. Ин-
терферометрические наблюдения (Bolton and Stanley, 1948; Ryle and Smith, 1948;
Ryle, Smith and Elsmore, 1950 и др.) доказали существование многочисленных дис-
дискретных источников. Для их отождествления с оптически видимыми объектами
требовалось точное измерение радиокоординат. Основной метод, применявшийся
тогда для измерения координат с помощью интерферометров с базой восток-запад
заключался в определении времени прохождения центрального лепестка и часто-
частоты интерференционных колебаний, которая пропорциональна косинусу склонения.
Измерение координат точно настолько, насколько известно положение диаграммы
направленности интерферометра, определяемое относительным положением элек-
электрических центров антенн. Кроме того, любое неравенство путей распространения
сигналов в кабелях и усилителях от антенн до точки их суммирования приводит
к появлению инструментальной составляющей фазы, которая смещает интерфе-
интерференционную диаграмму направленности. Смит (Smith, 1952a) получил координаты
четырех источников со среднеквадратичными погрешностями ±20" по прямому вос-
восхождению и ±40" по склонению и привел детальный расчет достигнутой точности.
Оптическое отождествление Лебедя А и Кассиопеи А Бааде и Минковским (Baade
and Minkowski, 1954a,b) было прямым следствием уточнения Смитом (Smith, 1951)
и Миллсом (Mills, 1952) координат в радиодиапазоне. Лебедь А оказался удаленной
галактикой, а Кассиопея А — остатком сверхновой, но интерпретация оптических
наблюдений в то время была понята не полностью.
Необходимость в абсолютной калибровке антенн и приемных систем быстро
отпала после того, как большое количество компактных радиоисточников было
отождествлено с оптическими объектами. Оптические координаты с точностью ~ 1"
теперь могли быть использованы и наблюдения таких источников обеспечивали
калибровку параметров базы и фазы интерференционной диаграммы. Хотя нельзя
было предположить, что координаты источника в оптике и радиодиапазоне совпада-
1.3] Развитие радиоинтерферометрии 29
ют точно, но их разности для различных источников были ориентированы случай-
случайным образом. Таким образом, ошибки уменьшались по мере того, как становились
доступны новые калибровочные объекты. Другим важным методом в определении
точных координат радиоисточников в 1960—1970-х гг. было наблюдение их лунных
покрытий, которые описываются в разд. 16.2.
1.3.7. Первые измерения угловых размеров. Сравнение угловых разме-
размеров радиоисточников с соответствующими размерами их оптических аналогов по-
помогало в ряде случаев подтвердить отождествление, а также получить необходимые
данные для физических моделей процессов излучения. В простейшем приближении,
измерения амплитуды интерференционного сигнала интерпретируются в рамкам
моделей интенсивности, таких как показанные на рис. 1.5. Пиковая амплитуда ин-
интерференции для данного расстояния между антеннами, нормированная к той же
величине для случая неразрешенного источника, дает величину интерференцион-
интерференционной видности, эквивалентную определенной в A.8).
Одни из первых измерений были выполнены Миллсом (Mills, 1953), использо-
использовавшим на частоте 101 МГц интерферометр, в котором небольшая перемещаемая
решетка, состоящая из элементов Уда-Яги, могла быть удалена от большой ан-
антенны на расстояние до 10 км. Сигнал от этой подвижной антенны передавался
обратно по радиолинии для формирования интерференционных лепестков. Смит
(Smith, 1952b,с) в Кембридже (Англия), также измерял изменение амплитуды ин-
интерференционных лепестков в зависимости от расстояния между антеннами, но
использовал более короткие длины баз по сравнению с Миллсом, и сосредоточился
на точных измерениях малых изменений амплитуды интерференционного сигнала.
В результате оба исследователя смогли определить угловые размеры ряда наиболее
сильных источников: Кассиопеи А, Крабовидной туманности, NGC4486 (Дева А)
и NGC5128 (Центавр А).
Третья группа исследовала угловые размеры радиоисточников на эксперимен-
экспериментальной станции в Джодрелл-Бэнк *) (Англия), используя другую методику —
интерферометрию интенсивности (Jennison and Das Gupta, 1953, 1956; Jennison,
1994). Ханбери Браун и Твис (Hanbury Brown and Twiss, 1954) показали, что
флуктуации интенсивности сигналов от двух удаленных антенн после прохождения
квадратичных детекторов, являются результатом гауссовых флуктуации напряжен-
напряженности полей и коррелируют друг с другом. Степень корреляции меняется пропорци-
пропорционально квадрату видности, которая была бы получена в обычном интерферометре
при сложении сигналов до детектирования. Интерферометр интенсивности имеет
то преимущество, что отсутствует необходимость сохранения фазы радиочастотных
сигналов до места их обработки. Это упрощает использование длинных баз, размер
которых в данном случае достигал 10 км. Для измерения корреляции продетектиро-
ванных сигналов от удаленных антенн использовалась СВЧ-радиосвязь. Недоста-
Недостаток интерферометра интенсивности состоит в необходимости высокого отношения
сигнал/шум, и даже для Лебедя А и Кассиопеи А — двух космических источников
с наибольшими потоками, приходилось конструировать большие дипольные решет-
решетки, работавшие на частоте 125 МГц. Интерферометр интенсивности обсуждается
далее в разд. 16.1. Недостаточная чувствительность ограничила его применение
в радиоастрономии.
х) Позже известную как радиоастрономическая лаборатория в Наффилде, а с 1999 г. —
как обсерватория в Джодрелл-Бэнк.
30
Введение и исторический обзор
[Гл. 1
Наиболее важным результатом измерений с интерферометром интенсивности
было открытие того, что для Лебедя А интерференционная видность профиля
интенсивности в направлении восток—запад уменьшалась, приближаясь к нулю,
а затем возрастала до вторичного максимума по мере увеличения расстояния меж-
между антеннами. Две симметричные модели источника соответствовали полученным
значениям видности. Это была двухкомпонентная модель, в которой фаза интерфе-
интерференционных лепестков изменялась на 180° при прохождении через минимум, и трех-
компонентная модель, в которой фаза не изменялась. Интерферометр интенсивно-
интенсивности не дает информации о фазе интерференционного сигнала, потому в последую-
последующем эксперименте, выполненном Дженнисоном и Латхэмом (Jennison and Latham,
1959), использовался обычный интерферометр. Поскольку инструментальная фаза
была не достаточно стабильной, чтобы обеспечить калибровку, использовались три
антенны и три набора интерференционных откликов для трех пар комбинаций,
записываемых одновременно. Если фшп — фаза интерференционного отклика для
антенн т и п, то легко показать, что в любой момент времени комбинация
0123 = 012 + 023 + 031
A.13)
независима от инструментальных и атмосферных фазовых эффектов и измеряет
соответствующую фазовую комбинацию интерференционных сигналов. При пере-
перемещении одной из антенн было обнаружено, что фаза действительно изменяется
примерно на 180° в минимуме видности, что соответствует двухкомпонентной мо-
модели, показанной на рис. 1.10. Применение комбинаций одновременных измерений
видности в соответствии с уравнением 1.13, называемых замыканием фазы, стало
существенно через 20 лет в методике обработки изображений. Замыкание фазы
и условия его применимости обсуждаются в разд. 10.3.
Результаты, полученные по Лебе-
Лебедю А, показали, что простые модели,
представленные на рис. 1.5, в общем
случае не подходят для описания ра-
радиоисточников. Даже для определения
общей структуры, чтобы выделить не-
несколько компонент, необходимо прово-
проводить измерения далеко за пределами
первого минимума функции видности
в нескольких позиционных углах по ис-
источнику.
Первые наблюдения, целью кото-
которых было получение высокого углового
разрешения и высокой чувствительно-
чувствительности, проведены Ханбери Брауном, Пал-
мером, и Томпсоном (Hanbury Brown,
N
30"
1'28'
Рис. 1.10. Двухкомпонентная модель Лебе-
Лебедя А, полученная Дженнисоном и Дас Гуп-
том (Jennison and Das Gupta, 1953), ис-
использовавшими интерферометр интенсив-
интенсивности. Перепечатано с разрешения Nature,
Vol. 172, No. 4387, p. 996; copyright ©1953
Macmillan Journals Limited
Palmer and Thompson, 1955) на экспери-
экспериментальной станции в Джодрелл-Бэнк,
Англия. В этом интерферометре была
применена техника гетеродинирования, заменившая модуляцию фазы, и также поз-
позволившая замедлить частоту интерференционных лепестков до пределов времени
отклика диаграммного самописца, использовавшегося для записи выходных сигна-
сигналов. Сигнал от удаленной антенны передавался по радиолинии. Используя рассто-
расстояния между антеннами до 20 км на частоте 158 МГц, было обнаружено, что три
источника имеют угловые размеры менее 12" (Morris, Palmer and Thompson, 1957).
1.3]
Развитие радиоинтерферометрии
31
В течение 1960-х годов этот инструмент был доработан для достижения разрешения
лучше 1" и более высокой чувствительности (Elgaroy, Morris and Rowson, 1962).
Эта программа позднее привела к разработке многоэлементного ретрансляционного
интерферометра, известного как решетка MERLIN (Thomasson, 1986).
1.3.8. Обзорные интерферометры и крест Миллса. В середине 1950-х
годов основная работа была направлена на создание каталогов большого числа
источников с точностью координат достаточной для оптического отождествления.
Инструменты работали в основном на метровых длинах волн, где спектр был менее
зашумлен промышленными помехами. Большой интерферометр в Кембридже был
образован четырьмя антеннами, расположенными в углах прямоугольника со сто-
сторонами 580 м в направлении восток-запад и 49 м в направлении север-юг (Ryle
and Hewish, 1955). Такая конфигурация обеспечивала одновременное получение
интерференционных диаграмм в соответствующих направлениях для измерения
прямого восхождения и склонения.
Другой тип обзорного инструмента, разработанный Миллсом и др. (Mills et al.,
1958) во Фларсе, вблизи Сиднея, представлял собой две длинные узкие антенные
решетки, расположенные крестообразно, как показано на рис. 1.11. Каждая решетка
имела веерную диаграмму, т. е. диаграмму, узкую в плоскости, проходящей через
продольную ось решетки, и широкую — в ортогональном направлении. Сигналы
двух решеток поступали на приемник с фазовым модулятором, и перемножение на-
напряжений давало диаграмму направленности по мощности, равную произведению
диаграмм двух решеток по напряжению. Синтезированный отклик имел форму
узкой карандашной диаграммы направленности. У решеток был общий электриче-
электрический центр, так что интерференционных лепестков не было. Решетки имели в длину
457 м, и крест формировал луч ширины 49' и почти круглого сечения на частоте
85,5 МГц. Луч был ориентирован по меридиану и его угол места мог изменяться
коррекцией фазы диполей направления север-
юг. В результате обзора неба, выполненного на
этом инструменте, был получен список, состоя-
состоящий более чем из 2200 источников.
Сравнение каталогов источников, получен-
полученных на кресте Миллса и на кембриджском ин-
интерферометре, первоначально работавшем на
частоте 81,5 МГц (Shakeshaft et al., 1955), по-
показало плохое совпадение между списками ис-
источников в общих участках неба (Mills and Slee,
1957). Как выяснилось, расхождение в основном
было следствием путаницы источников в кем-
кембриджских наблюдениях. Когда два или более
источника одновременно находятся в диаграм-
диаграммах антенн, они создают интерференционные
лепестки, частоты которых слегка отличаются
из-за разницы их склонений. Максимумы ам-
амплитуды интерференции, появляющиеся при случайном совпадении фаз интерфе-
интерференционных компонент, могут маскировать отклики источников. Это была серьез-
серьезная проблема, поскольку диаграммы направленности антенн интерферометра были
слишком широки. Но эта проблема не возникает в кресте Миллса, сконструиро-
сконструированном так, чтобы обеспечить разрешение, необходимое для измерения координат
в одиночном карандашном луче. Частота кембриджского интерферометра была
позднее увеличена до 159 МГц, тем самым, телесные углы диаграмм были умень-
L
L
J
Фазово-
модуляционный
приемник
Рис. 1.11. Упрощенная схема кре-
крестообразного радиотелескопа Мил-
Миллса. Перекрещивающиеся площад-
площадки представляют собой апертуры
двух антенн
32
Введение и исторический обзор
[Гл. 1
шены в четыре раза, и новый список из 471 источника был быстро составлен (Edge
et al., 1959). Это был обзор ЗС (имена источников, начинающиеся с ЗС, указывают
на Третий кембриджский каталог), обновленная версия которого (Bennett, 1962)
стала краеугольным камнем радиоастрономии следующего десятилетия. Чтобы из-
избежать проблемы путаницы на инструментах такого типа, некоторые астрономы
рекомендовали впоследствии, чтобы плотность источников каталога не превыша-
превышала в среднем одной двадцатой телесного угла диаграмм направленности антенн
(Pawsey, 1958; Hazard and Walsh, 1959).
В 1960-х годах начало появляться новое и более многочисленное поколение
обзорных инструментов. Два таких инструмента, разработанных в Кембридже, по-
показаны на рис. 1.12. Первый инструмент представлял собой интерферометр с одной
антенной, вытянутой в направлении восток-запад, а другой — в направлении север-
юг. Второй инструмент был большой Т-образной решеткой, по своим характеристи-
характеристикам подобной крестообразному телескопу, как показано в разд. 5.3. В каждом из
этих инструментов элемент, вытянутый в направлении север—юг, был неполным,
Ж
И
Рис. 1.12. Схемы двух инструментов, в каждом из которых малая антенна перемещается
в новое положение между последовательными наблюдениями для синтеза отклика, кото-
который получился бы с полной апертурой, соответствующей прямоугольнику, показанному
штриховой линией. Конфигурация двух перемножающих сигналы корреляторов с дей-
действительным (R) и мнимым (/) выходами объясняется в п. 6.1.7. Инструменты обоих
типов — Т-решетка (а) и двухэлементный интерферометр (б) — были сконструированы
в Маллардской радиоастрономической обсерватории, Кембридж:, Англия
но заполненная апертура синтезировалась с помощью малой антенны, перемещав-
перемещавшейся дискретно, чтобы обеспечить требуемое заполнение; причем каждое новое
положение использовалось для 24-часового скана по прямому восхождению (Ryle,
Hewish and Shakeshaft, 1959; Ryle and Hewish, 1960). Записи, полученные при
различных конфигурациях, обрабатывались компьютером, чтобы синтезировать
отклик с заполненной апертурой север-юг. Анализ этих инструментов приводится
в (Blythe, 1957). На большом интерферометре был получен каталог 4С (Четвер-
(Четвертый кембриджский), содержащий свыше 4800 источников (Gower, Scott and Wills,
1967). В Молонгло (Австралия) был создан большой крест Миллса (Mills et al.,
1963) с решетками длиной в 1 милю каждая, что обеспечило ширину диаграммы
направленности в 2,8' на частоте 408 МГц. Развитие креста Миллса описывается
в статьях (Mills and Little, 1953; Mills, 1963; и Mills et al., 1958, 1963). В северном
полушарии расположены крестообразные телескопы сравнимых размеров в Боло-
Болонье (Италия) (Braccesi et al., 1969) и вблизи Серпухова (Российская федерация)
(Виткевич и Калачев, 1966).
1.3.9. Картографирование Солнца на сантиметровых волнах. Ряд ин-
инструментов был разработан специально для картографирования Солнца. Антенны
обычно представляли собой параболические зеркала, смонтированные для сопро-
1.3] Развитие радиоинтерферометрии 33
84
и*
Рис. 1.13. а — линейная решетка из восьми расположенных на одинаковом расстоянии
друг от друга антенн, соединенных так, что сигналы от антенн до входа приемника
проходят одинаковое расстояние. Такая конфигурация иногда называется дифракционной
решеткой, и на практике обычно состоит из 16 или более антенн, б — восьмиэлементная
дифракционная решетка, соединенная с двухэлементной для улучшения углового разреше-
разрешения. Приемник с фазовой модуляцией, обозначенный символом умножения, используется
для того, чтобы получить произведение напряжений сигналов, поступающих с двух ре-
решеток. В выходном сигнале приемника присутствуют одновременно отклики пар антенн
с 16 различными расстояниями между ними. Системы этого общего типа называются
компаунд-интерферометрами
вождения Солнца. Но, поскольку Солнце — сильный радиоисточник, апертуры не
должны быть слишком большими. На рис. 1.13 а показана решетка антенн, сигналы
от которых синфазны на входе приемника, когда угол в между направлением на
источник и плоскостью, нормальной к линии решетки, таков, что ?\ sin# — целое,
где ?\ — расстояние между соседними антеннами, измеренное в длинах волн. Этот
тип антенных решеток иногда называют дифракционными, так как ими формиру-
формируется диаграмма направленности в виде ряда узких в направлении в веерных лучей,
похожая на отклик оптической дифракционной решетки. Христиансен и Варбартон
(Christiansen and Warburton, 1955) получили двумерную карту спокойного Солнца
на длине волны 21 см, используя комбинацию дифракционных решеток восток-
запад и север—юг. Решетки состояли из 32 параболических антенн, расположенных
на равном расстоянии друг от друга в направлении восток-запад, и 16 — в на-
направлении север-юг. Солнце при перемещении по небесной сфере сканировалось на
различных углах разными лучами, и двумерная карта могла быть синтезирована
посредством Фурье-анализа профилей сканов. Наблюдения продолжались более
8 месяцев для того, чтобы получить подходящий диапазон углов сканирования.
В последующих инструментах, предназначенных для картографирования Солнца,
в общем случае требовалось получение полной карты в течение одного дня для
исследования изменений повышенного солнечного излучения, связанного с актив-
активными областями. В нескольких инструментах использовались дифракционные ре-
решетки, состоящие обычно из 16 или 32 антенн и пересекающиеся наподобие кре-
креста Миллса. Крестообразными дифракционными решетками формировалась диа-
диаграмма направленности в виде прямоугольной матрицы лучей на небесной сфере,
и возможность получить достаточно сканов для ежедневного картографирования
активных областей и других особенностей обеспечивалась вращением Земли. Среди
инструментов этого типа — кресты во Флёрсе (Австралия) на длине волны 21 см
(Christiansen and Mullaly, 1963) и в Стэнфорде (Калифорния) на длине волны 10 см
2 Томсон
34 Введение и исторический обзор [Гл. 1
(Bracewell and Swamp, 1961), а также Т-решетка на длине волны 1,9 м в Нансе
(Франция) (Blum, Boischot and Ginat, 1957; Blum, 1961). Это были первые решетки,
предназначенные для картографирования, с большим числом A6 и более) антенн.
На рис. 1.13 6 показан принцип конфигурации, известный как компаунд-
интерферометр (Covington and Broten, 1957), который использовался для
расширения возможностей дифракционной решетки или другой антенны для
высокого одномерного углового разрешения. Показанная система образована
комбинацией дифракционной и двухэлементной решеток. При внимательном
рассмотрении рис. 1.13 6 видно, что пары антенн, образуемые одной антенной из
дифракционной решетки и другой — из двухэлементной, могут быть найдены
для всех баз — от одного до шестнадцатикратного единичного расстояния ?\. В
то время как одной дифракционной решеткой образуются базы только от одного
до семикратного единичного расстояния, при добавлении двух антенн число
различных баз, одновременно формирующих отклик, увеличивается более чем
в 2 раза добавлением двух антенн. Конфигурации такого типа использовались
для улучшения углового разрешения при одномерном сканировании сильных
источников (Picken and Swarup, 1964; Thompson and Krishnan, 1965). В комбинации
дифракционной решетки с большой дополнительной антенной может быть также
уменьшено количество дифракционных откликов на небесной сфере (Labrum et
al., 1963). Как в крестообразных дифракционных решетках, так и в компаунд-
интерферометрах, для приема выходных сигналов субрешеток первоначально
использовались приемники с модуляцией фазы. В настоящее время сигнал каждой
антенны преобразуется к промежуточной частоте (ПЧ), и для каждой базы
используется свой перемножающий коррелятор. Таким образом, обеспечиваются
дополнительные возможности конфигурации антенн, позволяющие получить
максимальное число различных баз, как обсуждается в разд. 5.5.
1.3.10. Измерения профилей интенсивности. Систематические измере-
измерения структуры источников показали, что, в общем случае, профили интенсивности
не симметричны, и поэтому их преобразования Фурье и, следовательно, функции
видности — комплексные. Это будет объяснено подробно в последующих главах,
а здесь мы отметим, что фаза интерференционного отклика, так же как и амплиту-
амплитуда, изменяется с изменением расстояния между антеннами, и должна быть измере-
измерена для восстановления профилей интенсивности. Функция видности представляется
как комплексная для того, чтобы учесть и амплитуду, и фазу. Измерения фазы
интерференционного сигнала стали возможны в 1960-1970-х гг. К этому времени
большое количество компактных источников с достаточно точными координата-
координатами стало доступно для калибровки интерференционной фазы. Также улучшилась
фазовая стабильность аппаратуры, а для записи и обработки получаемых данных
стали применять компьютеры. Усовершенствование антенн и приемников сделало
возможными измерения в сантиметровом диапазоне длин волн (на частотах выше
~1 ГГц) с использованием следящих антенн.
Интерферометр радиообсерватории в Оуэне Вэлли, Калифорния (Read, 1961),
является хорошим примером первых инструментов, эффективно использовавшихся
для определения структуры радиоисточников. Он образован двумя параболически-
параболическими антеннами диаметра 27,5 м на экваториальной монтировке с системой пере-
перемещения по железнодорожным путям, позволяющей изменять расстояние между
антеннами до 490 м как в направлении восток—запад, так и в направлении север-
юг. Интерферометр использовался главным образом на частотах от 960 МГц до
нескольких гигагерц. Применение этого инструмента для измерения распределений
1.3]
Развитие радиоинтерферометрии
35
е «
1,0
0,8
0,6
0,4
0,2
0,0
0,8
0,6
0,4
0,2
0,0
-0,2
Функция вещности ЗС33.1
[3 2 -
1 ™
-
/
А
А
Интерпретация 3 СЗ 3.1
Модельное решение
v/Л
1 1 1 ^^^ 1
о
500
1000 1500 2000 2500
Расстояние, в длинах волн
4 2 0 2 4
Восток тт Запад
Положение, угл. мин
Главное решение
0
500 1000 1500 2000 2500
Расстояние, в длинах волн
4 2
Восток Запад
Положение, угл. мин
Рис. 1.14. Пример интерферометрических измерений одномерного распределения интен-
интенсивности (яркости) — профиль источника ЗС33.1 в направлении восток-запад, измеренный
на интерферометре радиообсерватории в Оуэне Вэлли на частоте 1425 МГц (Fomalont,
1968): а, в — точками показаны измеренные амплитуда и фаза видности; б— профиль,
полученный вписыванием гауссовых компонент в данные видности, показанный кривой,
проведенной через измеренные точки видности; г — профиль, полученный преобразова-
преобразованием Фурье наблюдаемых значений видности. Единица фазы видности равна 2тг радиан
интенсивности, пример которых показан на рис. 1.14, иллюстрируется исследовани-
исследованиями (Maltby and Moffet, 1962 и Fomalont, 1968).
1.3.11. Интерферометрия спектральных линий. В начале 1960-х гг. ин-
интерферометр в Оуэне Вэлли и некоторые другие был оборудован спектральными
приемными системами. Полоса пропускания каждой приемной системы разделя-
разделялась на ряд каналов набором фильтров, обычно по ПЧ (промежуточной частоте),
и для каждого канала сигналы двух антенн поступали на отдельный коррелятор.
В другом методе сигналы ПЧ оцифровывались и использовалась цифровая филь-
фильтрация, как описывается в разд. 8.7. В идеале ширина каналов должна быть мень-
меньше ширины наблюдаемой линии для исследования ее профиля. Интерферометрия
спектральных линий позволяет получать распределение спектрального излучения
по источнику. В работе (Roger et al., 1973) описывается решетка в Канаде, постро-
построенная специально для наблюдений на частоте 1420 МГц (длина волны 21 см) линии
нейтрального водорода.
Спектральные линии могут также наблюдаться в поглощении, особенно в случае
линии нейтрального водорода. На частоте линии газ поглощает непрерывное излу-
излучение от любого, наблюдаемого сквозь него, более удаленного источника. Сравнение
спектров излучения и поглощения нейтрального водорода дает информацию о его
температуре и плотности. Измерения спектров поглощения источников могут быть
выполнены на одиночных антеннах, но в этом случае антенной регистрируется
широко распределенное излучение газа в пределах ее диаграммы направленности.
36
Введение и исторический обзор
[Гл. 1
Северный полюс
Спектры поглощения для слабых ис-
источников трудно отделить от линии
излучения. С помощью интерферо-
интерферометра широкие эмиссионные детали
на небесной сфере почти полностью
разрешаются, и спектр поглощения
можно наблюдать непосредственно.
В качестве примеров линии погло-
поглощения водорода см. (Clark, Radhakr-
ishnan and Wilson, 1962 и Hughes,
Thompson and Colvin, 1971), а для
4,8 МГц линии поглощения формаль-
формальдегида — (Marscher, 1995).
1.3.12. Картографирование и
синтез вращением Земли. Очень
важным шагом в развитии синтеза
изображений было использование из-
изменения проекции базы между ан-
антеннами вследствие вращения Зем-
Земли. На рис. 1.15 проиллюстрирован
этот принцип так, как он был описан
Райлом (Ryle, 1962). Для источника
с высоким склонением позиционный
угол вектора базы, спроецированно-
спроецированного на плоскость, перпендикулярную
направлению на источник, изменя-
изменяется за 12 ч на 180°. Таким обра-
образом, если источник сопровождается
на небесной сфере в течение несколь-
нескольких 12-часовых интервалов, причем
в каждом интервале — с другой ба-
базой, то требуемые двумерные функ-
функции видности могут быть получены изменением расположения антенн только в од-
одном направлении.
Кембриджский одномильный радиотелескоп был первым инструментом, раз-
разработанным специально для использования метода вращения Земли и применен-
примененный к большому числу радиоисточников. Использование вращения Земли не было
неожиданным поворотом в радиоастрономии и применялось ранее в исследовани-
исследованиях Солнца в течение многих лет. Как отмечено ранее, Христиансен и Варбартон
(Christiansen and Warburton, 1955) получили двумерную карту Солнца, исполь-
используя следящие антенны и две дифракционные решетки. В Джодрелл-Бэнк Роусон
(Rowson, 1963) использовал двухэлементный интерферометр с сопровождающими
антеннами для картографирования сильных источников. Райл и Невилл (Ryle and
Neville, 1962) также получили карту района северного полюса, используя вращение
Земли, для демонстрации этого метода. Однако, первые карты, опубликованные по
наблюдениям на Кембриджском одномильном телескопе сильных источников Кас-
Кассиопея А и Лебедь A (Ryle, Elsmore and Neville, 1965), показали тонкую структуру
с недоступным ранее разрешением, и это определило развитие картографирования
методом апертурного синтеза. Карта Лебедя А показана на рис. 1.16.
Рис. 1.15. Использование вращения Земли в
синтезировании изображений по описанию
Райла (Ryle, 1962). Антенны А и В находят-
находятся на линии восток-запад. Изменяя каждый
день расстояние между антеннами и проводя
наблюдения для каждой конфигурации в тече-
течение 12 ч, можно получить все базы от центра до
границы эллиптической области, показанной
в нижней части рисунка. 12-часовых наблюде-
наблюдений достаточно, ибо базы, полученные в тече-
течение следующих 12 ч, будут такими же, но толь-
только с переставленными антеннами. Печатается
с разрешения Nature, Vol. 194, No. 4828, p. 517;
copyright ©1962 Macmillan Journals Limited
1.3]
Развитие радиоинтерферометрии
37
-40° 38'
- 40° 34'
19h57m50s 19h57m45s 19h 57m40s A950,0)
Прямое восхождение
Рис. 1.16. Карта источника Лебедь А — один из первых результатов (Ryle, Elsmore and
Neville, 1965), полученных на Кембриджском одномильном телескопе с использованием
принципа вращения Земли, показанного на рис. 1.15. Частота — 1,4 ГГц. Масштаб карты по
склонению выбран таким образом, чтобы сечение диаграммы направленности по уровню
половины мощности было круглым, как показано заштрихованной областью в нижнем
правом углу. Эллипсом, обозначенным точками, отмечена внешняя граница оптического
источника; здесь же показана его центральная структура. Печатается с разрешения Na-
Nature, Vol. 205, No. 4978, p. 1260; copyright ©1965 Macmillan Journals Limited
1.3.13. Развитие решеток апертурного синтеза. Вслед за успехами Кем-
Кембриджского одномильного телескопа многие интерферометры, такие, как инстру-
инструмент NRAO (Hogg et al., 1969) в Грин Бэнке (Западная Вирджиния), были быстро
доработаны, чтобы обеспечить возможность картографирования методом апертур-
апертурного синтеза. Несколько больших решеток, сконструированных с целью увеличе-
увеличения скорости картографирования, повышения чувствительности и углового раз-
разрешения, были введены в действие в течение 1970-х годов. Среди них следует
отметить Пятикилометровый радиотелескоп в Кембридже (Англия) (Ryle, 1972),
Вестерборкский радиотелескоп апертурного синтеза в Нидерландах (Baars et al.,
1973) и Большую антенную решетку (VLA) в Нью-Мексико (Thompson et al., 1980;
Napier, Thompson and Ekers, 1983). Эти инструменты позволяют получать карты
источников с угловым разрешением лучше 1" на сантиметровых длинах волн. Ис-
Используя па антенн, достигающих 27 в упомянутых решетках, можно одновременно
получить па (па — 1)/2 баз. Если решетка разрабатывается с минимизацией избы-
избыточности (см. гл. 5), то скорость измерения функции видности пропорциональна
примерно Vba. Карты Лебедя А, полученные на двух из упомянутых выше решет-
решетках, показаны на рисунках 1.17 и 1.18. Обзор развития инструментов апертурного
синтеза в Кембридже дан Райлом в его Нобелевской лекции (Ryle, 1975). В Индии
38
Введение и исторический обзор
[Гл. 1
24^
12"
g Зб'ОО'
I 48'
° 36'
24"
J
До
_ ^
J(|P -
г
f л,
j
J
i i
¦'в
'»If6/
ft
J
\
—-^w
^1
1
ОН
0
50s 49 48 47 46 45 44s 43 42 41
Прямое восхождение
40 39s
19h57m
Рис. 1.17. Карта источника Лебедь А, полученная на Кембриджском пятикилометровом
телескопе на частоте 5 ГГц (Hargrave and Ryle, 1974). На карте показаны впервые обнару-
обнаруженное радиоядро, связываемое с центральной галактикой, и области с высокой яркостью
на внешних краях «радиоушей». Печатается с разрешения Королевского астрономического
общества
вблизи Пуна (Pune) в 1998 г. было закончено строительство решетки с большой
эффективной площадью — Гигантского радиотелескопа метровых волн (GMRT),
действующего на частотах от 38 до 1420 МГц (Swamp et al., 1991). Современный
прогресс в технологии широкополосных антенн и высокоуровневые интегральные
схемы должны обеспечить дальнейшее значительное увеличение эффективной пло-
площади в будущем, какое дает, например, решетка SKA с площадью, равной 1 квад-
квадратному километру (Hopkins et al., 1999; Smolders and van Harlem, 1999).
В течение 1980—1990-х годов были созданы решетки апертурного синтеза, дей-
действующие на коротких миллиметровых длинах волн (частоты от 100 ГГц и выше).
Спектральные линии особенно многочисленны на этих частотах. Отдельные аспек-
аспекты существеннее на миллиметровых волнах, чем на сантиметровых. Поскольку дли-
длина волн намного короче, любая неоднородность на пути распространения сигнала
через атмосферу оказывает пропорционально большее влияние на его фазу. Погло-
Поглощение в нейтральной атмосфере гораздо больше на миллиметровых волнах. Кроме
того, диаграммы направленности отдельных антенн на коротких волнах становятся
уже, и необходимость сохранения достаточно широкого поля зрения является одной
из причин тенденции уменьшения диаметров антенн с увеличением частоты. Таким
образом, чтобы получить необходимую чувствительность, требуется большее коли-
количество антенн по сравнению с сантиметровыми волнами. Решетки, действующие
на миллиметровых волнах, находятся в Хэт Крик, Калифорния (Welch, 1994),
Оуэне Вэлли, Калифорния (Scoville et al., 1994), Нобейяме, Япония (Morita et al.,
1994), Плато де Бю, Франция (Guilloteau, 1994), Мэн Ки, Гавайи (Могап, 1998а),
и Чайнанторе, Чили (Brown, 1998).
1.3.14. Интерферометрия со сверхдлинными базами. Исследование уг-
угловых размеров квазаров и других объектов, вероятно имеющих почти точечную
структуру, представляло важное направление в первые годы радиоастрономии.
Шагом вперед, приведшим к немедленному увеличению углового разрешения на
порядок, а в дальнейшем — еще на несколько порядков, стало применение неза-
независимых гетеродинов и систем регистрации сигналов. Используя на каждой ан-
1.3] Развитие радиоинтерферометрии 39
Рис. 1.18. Радиоизображение Лебедя А, полученное на VLA на частоте 4,9 ГГц (Perley,
Dreher and Cowan, 1984). Использовались наблюдения с четырьмя конфигурациями ре-
решетки, разрешение составляет 0,4". Чтобы получить изображение, показанное здесь, для
повышения контрастности тонкой структуры применялись нелинейные методы. Тем са-
самым удалось выделить джет, направленный от центральной галактики к северо-западному
«уху» (вверху справа), и волокнистую структуру в главных «ушах». Сравнение различных
изображений Лебедя А в этой главе иллюстрирует технический прогресс в течение трех
десятилетий. Печатается с разрешения NRAO/AUI
тенне гетеродины, управляемые высокоточными стандартами частоты, можно со-
сохранить когерентность сигналов на интервалах времени, достаточно длительных
для измерения интерференционных лепестков. Принятые сигналы преобразуются
к промежуточной частоте, достаточно низкой, чтобы они могли быть записаны
непосредственно на магнитную ленту, а ленты впоследствии собраны вместе и вос-
воспроизведены в корреляторе. Этот метод получил название интерферометрии со
сверхдлинными базами (РСДБ), и ранняя история его развития рассматривается
в работе (Moran, 1998b). Технические требования для РСДБ широко обсуждались
в начале 1960-х гг. (см., например, Матвеенко, Кардашев и Шоломицкий, 1965).
Один из первых успешных экспериментов был проведен в январе 1967 г. группой
университета штата Флорида, получившей интерференционные лепестки на частоте
18 МГц от вспышки излучения на Юпитере (Brown, Carr and Block, 1968). Посколь-
Поскольку принимались сильные сигналы, и использовалась низкая частота, полоса записи
шириной 2 кГц была достаточной, и стандартами частоты служили кварцевые
генераторы. Много более чувствительные и точные системы РСДБ, использовавшие
более широкие полосы и атомные стандарты частоты, были разработаны другими
тремя группами. В Канаде была создана аналоговая система записи с полосой
регистрации сигнала 1 МГц, основанная на применении телевизионных видеомагни-
видеомагнитофонов (Broten et al., 1967). Лепестки были получены в апреле 1967 г. на частоте
448 МГц с базами 183 и 3074 км для нескольких квазаров. Другая группа в Со-
Соединенных Штатах из Национальной радиоастрономической обсерватории (NRAO)
и Корнельского университета разработала совместимую с ЭВМ цифровую систему
регистрации с полосой 360 кГц (Bare et al., 1967). Они получили интерференцион-
интерференционные лепестки для нескольких квазаров в мае 1967 г. на частоте 610 МГц с базой
220 км. Третья группа из Массачусетского технологического института MIT стала
участвовать в развитии системы NRAO и Корнельского университета в начале
1967 г. и в июне 1967 г. получила интерференционные лепестки на частоте 1665 МГц
40
Введение и исторический обзор
[Гл. 1
- ЗС273
О
10,65 ГГц™
1977,56 -
1978,24 -
с базой 845 км для нескольких ОН-мазеров со спектральной обработкой (Moran et
al., 1967).
В первых экспериментах использовались полосы регистрации шириной менее
1 МГц, но в 1980-х гг. были созданы системы регистрации с полосами записи
сигналов шириной свыше 100 МГц, что привело
к соответствующему улучшению чувствительно-
чувствительности. Была продемонстрирована передача через гео-
геостационарный спутник на коррелятор в реальном
времени сигналов, принимаемых на удаленных те-
телескопах (Yen et al., 1977). Были выполнены так-
также эксперименты по передаче через спутник сиг-
сигнала гетеродина (Knowles et al., 1982). Этот про-
прогресс уменьшил различие между РСДБ и обыч-
обычной интерферометрией. Тем не менее, в методе
РСДБ есть много технических особенностей, кото-
которые описываются в гл. 9.
Сверхвысокое угловое разрешение, достижимое
методом РСДБ, хорошо иллюстрируется измерени-
измерениями (Burke et al., 1972), в которых на длине волны
1,3 см, используя антенны в Вестфорде (Массачу-
(Массачусетс) и в Симеизе (Крым), получено угловое разре-
разрешение 0,2 мсек дуги. Первые результаты, получен-
полученные с использованием малого числа баз, обычно
интерпретировались, исходя из простых моделей,
представленных на рис. 1.5. В середине 1970-х гг.
несколько групп астрономов начали объединять
свои усилия с целью получить измерения с десятью
и более базами одновременно. В состав объеди-
объединенной сети пользователей Соединенных Штатов
входили Хайстекская обсерватория в Массачусет-
Массачусетсе (NEROC), Грин Бэнк в Западной Вирджинии
(NRAO), обсерватория Вермильон Риве в Илли-
Иллинойсе (университет штата Иллинойс), Норе Ли-
Либерти в Айове (университет штата Айова), Форт
Дейвис в Техасе (обсерватория Гарвардского кол-
колледжа), обсерватория в Хэт Крике в Калифорнии
(университет штата Калифорния), радиообсерва-
радиообсерватория в Оуэне Вэлли в Калифорнии (Калтек), Ме-
1978,92-
1979,44 -
1980,52 -
Рис. 1.19. Карты квазара ЗС273, полученные методом
РСДБ в пять различных эпох, показывающие относи-
относительные положения двух компонент. Исходя из рассто-
расстояния до объекта, установленного по величине оптиче-
оптического красного смещения, видимая скорость разлета
компонент превосходит скорость света, но это может
быть объяснено релятивистскими и геометрическими
эффектами. Частота наблюдений 10,65 ГГц. Угловой
масштаб 0,002" показан в правом нижнем углу рисунка
(Pearson et al., 1981). Печатается с разрешения Nature,
Vol. 290, No. 5805, p. 366; copyright ©1981 Macmillan
Journals Limited
1.3]
Развитие радиоинтерферометрии
41
риленд Пойнт в Мериленде (Военно-морская обсерватория США) и Голдстоун
в Калифорнии (лаборатория реактивного движения JPL). Наблюдения этих групп
привели к более сложным структурам (см., например, Cohen et al., 1975). Важными
результатами стали открытие и исследование сверхсветовых (с видимой скоростью
больше скорости света) движений в квазарах (Whitney et al., 1971; Cohen et al., 1971;
Кларк и др., 1972; Батчелор и др., 1976), как показано на рис. 1.19, и измерение
собственных движений Б^О-мазеров (Genzel et al., 1981). В 1994 г. в Националь-
Национальной радиоастрономической обсерватории США была введена в действие первая
антенная решетка, созданная специально для астрономических измерений методом
РСДБ — Антенная решетка со сверхдлинными базами (VLBА). Она состоит из
десяти 25-метровых антенн, одна из которых расположена на островах Вирджин
США, восемь — на континентальной территории Соединенных Штатов и одна —
на Гавайях (Napier et al., 1994). VLB А часто используется с дополнительными
антеннами для образования решеток еще больших размеров.
Одна из проблем наблюдений методом РСДБ состоит в том, что при исполь-
использовании несинхронизованных гетеродинов калибровка фазы интерференционных
лепестков усложняется. Для разрешения этой проблемы Роджерс и др. (Rogers et
al., 1974) впервые применили уравнение замыкания фаз A.13) для данных РСДБ.
Метод был вскоре развит в процедуру построения
изображений, известную как гибридное картографи-
картографирование. Эта и подобные ей процедуры используются
также для картографирования в решетках со свя-
связанными элементами 1) и рассматриваются в гл. 11.
Примеры гибридного картографирования приводят-
приводятся на рисунках 1.19 и 1.20. В некоторых спектраль-
спектральных наблюдениях, когда источник состоит из про-
пространственно разнесенных мазеров, сигналы кото-
которых разделяются индивидуальными доплеровскими
смещениями, можно получить карты мазеров, ис-
используя метод опорной фазы (Reid et al., 1980).
Большой потенциал РСДБ для астрометрии
и геодезии был немедленно признан (см., например,
Gold, 1967)). Его использование в этих направлени-
направлениях развивалось быстрыми темпами в течение 1970—
1980-х гг. (см., например, Whitney et al., 1976 и Clark
et al., 1985). В Соединенных Штатах в начале 1980-х
гг. NASA и некоторые другие федеральные аген-
ства приняли совместную программу геодезических
измерений. Развитию работ отчасти способствова-
способствовало использование комплексов дальней космической
связи DSN для наблюдений методом РСДБ. Про-
Программой предусматривается применение транспор-
транспортируемых антенн для периодического мониторинга
координат многих мест. Астрометрия с субмиллисе-
кундной точностью открыла новые возможности для
астрономии; например, измерение движения Солнца
вокруг центра Галактики по собственному движению
Суд А 1979,44
Рис. 1.20. Карта малой цен-
центральной детали Лебедя А
(Linfield, 1981), полученная
методом РСДБ на частоте
10,65 ГГц с использованием
четырех антенн. Синтезиро-
Синтезированный луч диаграммы на-
направленности по уровню по-
половины мощности показан за-
заштрихованной областью, его
угловые размеры составля-
составляют 0,5x1 мсек2. Изофоты да-
даны в яркостных температу-
температурах с интервалом 8-Ю8 К. На-
Направление главной оси источ-
источника совпадает с направле-
направлением джета, показанного на
рис. 1.17
х) Понятие элементно-соединенная или элементно-связанная используют для описания
решеток обычного типа, в которых сигналы поступают в коррелятор в реальном времени,
обычно по фидерным или радиолиниям, в отличие от систем, в которых сигналы ПЧ
записываются для последующей корреляционной обработки.
42 Введение и исторический обзор [Гл. 1
Стрельца A (Reid et al., 1999; Backer and Sramek, 1999). Международная опорная
система координат, принятая Международным астрономическим союзом, основана
на измерениях 212 внегалактических источников (Ma et al., 1998).
Комбинация РСДБ и обработки спектральных линий особенно эффективна при
решении совместных задач астрометрии и динамического анализа астрономических
систем. В галактике NGC4528, с активным ядром, были обнаружены малые обла-
области, излучающие сильные мазерные линии водяного пара на частоте 22,235 ГГц.
Наблюдения методом РСДБ с разрешением 0,2 мсек дуги обеспечили точность из-
измерений относительных положений мазеров в несколько микроксекунд дуги, а точ-
точность измерений радиальной скорости доплеровского смещения составила 0,1 км/с.
NGC4528 удачно расположена таким образом, что ее диск виден с Земли почти
с ребра. Орбитальные скорости мазеров точно известны как функции радиусов от
центра вращения, поскольку описываются законом Кеплера. Таким образом, срав-
сравнивая линейные и угловые движения, можно найти расстояние. Величина угловой
скорости составляет около 30 в год. Эти результаты позволили определить величину
центральной массы в 3,9-107 солнечных масс (Miyoshi et al., 1995) и расстояние
7,2±0,3 Мпк (Herrnstein et al., 1999). Величину центральной массы невозможно
объяснить в рамках модели плотного скопления звезд, но это является сильным
Рис. 1.21. Искривленный кольцеобразный диск, окружающий центральную массу
NGC4258, смоделированный по положениям мазеров, их скоростям и ускорениям,
полученным методом РСДБ со спектральной обработкой данных. Черной точкой
в середине отмечен динамический центр диска. Диаметр диска составляет 0,6 пк A пк =
3,1 • 1016 м). Излучение в непрерывном спектре на длине волны 1,3 см показано серым
цветом в виде структуры вблизи центра. Положение источника непрерывного излучения
по отношению к мазерам получено с точностью несколько угловых микросекунд. Из
работы (Moran et al., 1999), J. Astrophys. Astr., опубликованной Академией Наук Индии,
Бангалор
доказательством существования черной дыры в центре NGC4258. Анализ орбит
мазерных источников свидетельствует, что диск, окружающий черную дыру, имеет
слегка искривленный профиль, как показано на рис. 1.21. Расстояние до внега-
внегалактического объекта, измеренно непосредственно с беспрецедентной точностью в
4%, которая вряд ли будет улучшена дальнейшими исследованиями этой и других
подобных галактик.
1.3.15. РСДБ с антеннами на орбите. Применение спутниковых антенн
в РСДБ-наблюдениях называется методом ОРСДБ (орбитальная РСДБ). Первые
наблюдения этим методом были проведены в 1986 г. с использованием спутника
системы слежения и передачи данных (TDRSS) Соединенных Штатов. Спутники
находятся на геостационарных орбитах на высоте примерно 36000 км и использу-
используются для ретрансляции данных низкоорбитальных спутников на Землю. На них
устанавлены две антенны диаметра 4,9 м для связи с другими спутниками на
частотах 2,3 и 15 ГГц, и антенна меньшего диаметра для связи с землей. В этом
эксперименте одна из 4,9 м антенн была использована для наблюдений радиоисточ-
радиоисточника, а другая — для приема опорного сигнала водородного стандарта частоты, на-
1.4] Квантовый эффект 43
ходящегося на земле (Levy et al., 1989). Принятые сигналы передавались на Землю
и записывались на магнитную ленту системой регистрации РСДБ для последующей
корреляционной обработки с сигналами наземных антенн. Было зарегистрировано
23 и 11 источников на частотах 2,3 и 15 ГГц соответственно (Linfield et al., 1989,
1990). На частоте 15 ГГц ширина интерференционного лепестка была порядка
0,3 мсек дуги. Интерпретация полученных результатов в рамках кругового гаус-
сового распределения показала, что яркостные температуры достигают 2-Ю12 К.
РСДБ-наблюдения с использованием спутника, находящегося на негеостацио-
негеостационарной орбите, были впервые проведены в 1997 г. после запуска японского спутника
HALCA (Hirabayashi et al., 1998), созданного специально для наблюдений методом
ОРСДБ. На нем была установлена антенна диаметра 8 м, и наблюдения проводи-
проводились на частотах 1,6 и 5 ГГц. Период обращения был примерно 6,6 ч, а апогей —
21000 км. Быстрое перемещение спутника обеспечивает большее изменение векто-
векторов баз, образованных с наземными антеннами, по сравнению с геостационарным
спутником, и, следовательно, более эффективное измерение структуры источников.
Однако, для коррекции изменения фазы данных вследствие перемещения спутника
требовалось очень точное моделирование орбиты.
В работе (Hagfors, Phillips and Belcora, 1990) обсуждалось достижение очень
больших баз посредством отражения поверхностью Луны — естественного спутника
Земли. Отражение от поверхности Луны может обеспечить длины баз, приближаю-
приближающиеся к радиусу лунной орбиты. Для слежения за Луной и приема отраженного
сигнала от исследуемого источника могла бы использоваться антенна диаметра
100 м или больше, а для приема прямого сигнала могла бы использоваться малая
антенна. Оценки показали, что чувствительность была бы примерно на три по-
порядка меньше по сравнению с прямым наблюдением источника обеими антеннами.
Дополнительные трудности возникают вследствие неровности лунной поверхности
и из-за либрации. Этот метод мог бы быть полезным при проведении специальных
наблюдений, требующих сверхвысокого углового разрешения сильных источников,
например, вспышек излучения на Юпитере. Также в будущем возможно прове-
проведение наблюдений методом РСДБ с использованием лунной станции. Создание
лунной РСДБ-станции рассматривалось Н. С. Кардашевым в рамках Советско-
французского Проекта в 1969 г.
1.4. Квантовый эффект
Развитие РСДБ внесло новый аспект в кажущийся парадокс квантово-
механического описания интерферометрии (Burke, 1969). Радиоинтерферометр
является аналогом двухщелевого интерферометра в эксперименте Янга. Хо-
Хорошо известно (Louden, 1973), что один фотон создает интерференционную
картину, но любая попытка определить, в какую из щелей он попал, приведет
к исчезновению интерференции; в противном случае нарушался бы принцип
неопределенности. Методика РСДБ предполагает, что определить, на какую из
антенн прибыл данный фотон возможно, поскольку его след остается на магнитной
ленте, а также присутствует в интерференционной картине, генерируемой при
корреляции. Однако, в радиочастотном диапазоне входные каскады приемников,
используемых в качестве измерительных приборов, состоят из усилителей или
смесителей, сохраняющих фазу принятого сигнала на выходе. Этим обеспечивается
формирование интерференции на последующих стадиях. Отклик таких приборов
должен удовлетворять принципу неопределенности: АЕ At ~ /г/2тг, где АЕ и At —
неопределенности энергии сигнала и времени измерений. Этот принцип может быть
44 Введение и исторический обзор [Гл. 1
выражен через неопределенности числа фотонов AN и фазы Аф в виде
ANAф~l, A.14)
где АЕ = hvAN и Аф = 2тп/Д?. Чтобы сохранить фазу, Аф должно быть мало,
a AN — соответственно, велико, и, следовательно, должна быть неопределенность,
по крайней мере, в один фотон на единицу полосы частот в единицу времени на
выходе усилителя приемника. Таким образом, отношение сигнал/шум для предель-
предельного случая одного фотона оказывается меньше единицы, и определить, на какую
из антенн он прибыл, невозможно. Альтернативное, но эквивалентное утверждение
заключается в том, что на выходе любой приемной системы должна присутствовать
шумовая составляющая не меньше эквивалентной принятой мощности, примерно
равной hv на единичной полосе частот.
Отдельные фотоны, из которых состоит сигнал, попадают на антенну в случай-
случайное время, но со средней скоростью, пропорциональной величине сигнала. В яв-
явлениях такого типа, число событий, происходящих в течение данного промежутка
времени т, варьируется статистически в соответствии с распределением Пуассона.
Для сигнала мощности Psig среднее количество фотонов, пришедших в течение
времени т, равно N = Ps[gr/hv. Среднеквадратичное отклонение этой величины
в течение серии интервалов г по статистике Пуассона определяется как AN = V TV .
Неопределенность фазы, получающаяся в результате из уравнения 1.14,
Мы можем также выразить неопределенность измерений фазы сигнала через шум,
присутствующий в приемной системе. Минимальная мощность шума Pnoise при-
примерно равна тепловому шуму согласованной активной нагрузки, находящейся при
температуре hv /k\ т. е. Pnoise = hvAv. В этом случае неопределенность фазы, изме-
измеренная за время усреднения т, равна
Отметим, что Аф — погрешность, с которой может быть измерена фаза сигнала,
усиленного и принятого одной антенной, например, при доплеровском слежении за
спутником (Cannon, 1990). Здесь не должно быть путаницы с погрешностью изме-
измерений фазы сигнала интерферометра. На частоте v = 1 ГГц эффективная шумовая
температура hv /к равна 0,048 К. Таким образом, для частот вплоть до нескольких
десятков гигагерц, шум вследствие квантового эффекта дает лишь малую состав-
составляющую в шуме приемника. На частоте 900 ГГц, обычно рассматриваемой как
верхний предел частоты для наземной радиоастрономии, hv /к = 43 К, и этот вклад
в температуру шума системы становится важен. В оптическом диапазоне частот
v ж 500 ТГц, hv /к & 30000 К, и гетеродинные системы вряд ли реальны, что об-
обсуждается в разд. 16.4. Однако, в оптическом диапазоне можно создать устройства
«прямого детектирования», регистрирующие мощность без сохранения фазы, так
что Аф в уравнении 1.16 эффективно стремится к бесконечности и, следователь-
следовательно, нет необходимости рассматривать точность измерения числа фотонов. Так, во
многих оптических интерферометрах интерференционные лепестки формируются
принятым светом непосредственно, и параметры интерференции определяются из-
измерением получающихся в результате распределений интенсивности.
Для дальнейшего изучения общих вопросов, связанных с тепловым и квантовым
шумом, см., например, (Oliver, 1965 и Kerr, Feldman and Pan, 1997). В работе
1.4] Основная литература 45
(Nityananda, 1994) сравниваются квантовые эффекты в радио и в оптическом диа-
диапазонах, а в (Radhakrishnan, 1999) обсуждаются основные концепции.
Основная литература
Alder В., Fernbach S. and Rotenberg M., Eds., Methods in Computational Physics, Vol. 14,
Academic Press, New York, 1975.
Berkner L. V., Ed., IRE Trans. Antennas Propag., Special Issue on Radio Astronomy, AP-9,
No. 1, 1961.
Biraud F., Ed., Very Long Baseline Interferometry Techniques, Cepadues, Toulouse, France,
1983.
Bracewell R. Ж, Ed., Paris Symposium on Radio Astronomy, IAU Symp. No. 9, Stanford Univ.
Press, Stanford, С A, 1959. (Имеется перевод: Р. Брейсуэлл, ред., Радиоастрономия. — М.:
ИЛ, 1961.)
Bracewell R. Ж, Radio Astronomy Techniques, in Handbuch Der Physik, Vol. 54, S. Flugge,
Ed., Springer-Verlag, Berlin, 1962.
Burke B. F. and Graham-Smith F., An Introduction to Radio Astronomy, Cambridge Univ.
Press, Cambridge, UK, 1997.
Christiansen W. N. and Hogbom J. A., Radiotelescopes, Cambridge Univ. Press, Cambridge,
UK, 1969 Bnd ed. 1985). (Имеется перевод: У. Христиансен, И. Хегбом. Радиотелескопы. —
М.: Мир, 1972; 2-е изд., 1988.)
Cornwell Т. J. and Perley R. A., Eds., Radio Interferometry: Theory, Techniques and Appli-
Applications, Astron. Soc. Pacific Conf. Ser., 19, 1991.
Findlay J. W., Ed., Proc. IEEE, Special Issue on Radio and Radar Astronomy, 61, No. 9,
1973. (Имеется перевод: ТИИЭР, 61, 9, 1973.)
Frater R. H. and Brooks J. W., Eds.,Proc. IREE Australia, Special Issue on the Australia
Telescope, 12, No. 2, 1992.
Goldsmith P. F., Ed., Instrumentation and Techniques for Radio Astronomy, IEEE Press, New
York, 1988.
Haddock F. Т., Ed., Proc. IRE, Special Issue on Radio Astronomy, 46, No. 1, 1958.
Ishiguro M. and Welch W. J., Eds., Astronomy with Millimeter and Submillimeter Wave
Interferometry, IAU Colloquium 140, Astron. Soc. Pacific. Conf. Ser., 59, 1994.
Kraus J. D., Ed., IEEE Trans. Mil. Electron., Special Issue on Radio and Radar Astronomy,
Mil-8, Nos. 3 and 4, 1964, также издан IEEE Trans. Antennas Propag., AP-12, No. 7, 1964.
Kraus J. D., Radio Astronomy, McGraw-Hill, New York, 1966, 2nd. ed., Cygnus-Quasar,
Powell, OH, 1986. (Имеется перевод: Джон Д. Краус. Радиоастрономия. — М.: Сов. радио,
1973.)
Lovell В. and Clegg J. A., Radio Astronomy, Chapman and Hall, London, 1952.
Meeks M. L., Ed., Methods of Experimental Physics, Vol. 12, Parts В and C, Academic Press,
New York, 1976.
Pawsey J. L., Ed., Proc. IRE Aust., Special Issue on Radio Astronomy, 24, No. 2, 1963.
Pawsey J. L. and Bracewell R. N., Radio Astronomy, Oxford Univ. Press, Oxford, UK, 1955.
(Имеется перевод: Жд. Л. Пози, Р. Брейсуэлл. Радиоастрономия. — М.: ИЛ, 1958.)
Perley R. A., Schwab F. R. and Bridle A. H., Ed., Synthesis Imaging in Radio Astronomy,
Astron. Soc. Pacific Conf. Ser., 6, 1989.
Raimond E. and Genee R., Eds., The Westerbork Observatory, Continuing Adventure in
Radio Astronomy, Kluwer, Dordrecht, 1996.
Rohlfs K. and Wilson T. L., Tools of Radio Astronomy, Springer-Verlag, Berlin, 1986, 1996.
46 Введение и исторический обзор [Гл. 1
Sullivan W. Т., Ill, Ed., The Early Years of Radio Astronomy, Cambridge Univ. Press,
Cambridge, UK, 1984.
Taylor G. В., Carilli C. L. and R. A. Perley, Eds., Synthesis Imaging in Radio Astronomy II,
Astron. Soc. Pacific Conf. Ser., 180, 1999.
Wild J. P., Ed., Proc. IREE Aust., Special Issue on the Culgoora Radioheliograph, 28, No. 9,
1967.
Wohlleben R., Mattes H. and Krichbaum Т., Interferometry in Radioastronomy and Radar
Techniques, Kluwer, Dordrecht, 1991.
Yen J. L., Image Reconstruction in Synthesis Radio Telescope Arrays, in Array Signal Pro-
Processing, S. Haykin Ed., Prentice Hall, Englewood Cliffs, NJ, 1985, p. 293-350.
Есепкина Н. А., Корольков Д. В., Парийский Ю. Н. Радиотелескопы и радиометры.— М.:
Наука, 1972.
Кузьмин А. Д., Соломонович А. Е. Радиоастрономические методы измерений параметров
антенн.— М.: Сов. радио, 1964;
Шкловский И. С, Космическое радиоизлучение, — М.: ГИТТЛ, 1956.
Цитированная литература
Appleton E. V., Departure of Long-Wave Solar Radiation from Black-Body Intensity, Nature,
156, 534-535, 1945.
Baade W. and Minkowski R., Indentification of the Radio Sources in Cassiopeia, Cygnus A and
Puppis A, Astrophys. J., 119, 206-214, 1954a.
Baade W. and Minkowski R., On the Indentification of Radio Sources, Astrophys. J., 119,
215-231, 1954b.
Baars J. W. M., van der Brugge J. F., Casse J. L., Hamaker J. P., Sondaar L. H., Visser
J. J. and Wellington K. J., The Synthesis Radio Telescope at Westerbork, Proc. IEEE, 61,
1258-1266, 1973. (Имеется перевод: ТИИЭР, 61, 9, с. 115-128, 1973.)
Backer D. С. and Sramek R. A., Proper Motion of the Compact, Nonthermal Radio Source in
the Galactic Center, Sagittarius A*, Astrophys. J., 524, 805-815, 1999.
Bare C, Clark B. C, Kellermann K. L, Cohen M. H. and Jauncey D. L., Interferometer
Experiment with Independent Local Oscillators, Science, 157, 189-191, 1967.
Bennett A. S., The Revised 3C Catalog of Radio Sources, Mem. R. Astron. Soc, 68, 163-172,
1962.
Blake G. A., Sutton E. C, Masson С R. and Phillips T. G., Molecular Abundances in OMC-1:
The Chemical Composition of Interstellar Molecular Clouds and the Influence of Massive Star
Formation, Astrophys. J., 315, 621-645, 1987.
Blum E. J., Le Reseau Nord-Sud a Multiples, Ann. Astrophys., 24, 359-366, 1961.
Blum E. J., Boischot A. and Ginat M., Le Grand Interferometre de Nancay, Ann. Astrophys.,
20, 155-164, 1957.
Blythe J. H., A New Type of Pencil Beam Aerial for Radio Astronomy, Mon. Not. R. Astron.
Soc, 117, 644-651, 1957.
Bolton J. G. and Slee О. В., Galactic Radiation at Radio Frequencies, V. The Sea Interferom-
Interferometer, Aust. J. Phys., 6, 420-433, 1953.
Bolton J. G. and Stanley G. J., Variable Source of Radio Frequency Radiation in the Constel-
Constellation of Cygnus, Nature, 161, 312-313, 1948.
Braccesi A., Ceccarelli M., Colla G., Fanti R., Ficarra A., Gelato G., Greuff G. and Sinigaglia
G., The Italian Cross Radio Telescope, III. Operation of the Telescope, Nuovo Cimento B, 62,
13-19, 1969.
1.4] Цитированная литература 47
Bracewell R. N. and Swarup G., The Stanford Microwave Spectroheliograph Antenna, a Mi-
crosteradian Pencil Beam Interferometer, IRE Trans. Antennas Propag., AP-9, 22-30, 1961.
Broten N. W., Legg T. H., Locke J. L., McLeish С W., Richards С W., Chisholm R. M.,
Gush H. P., Yen J. L. and Gait J. A., Observations of Quasars Using Interferometer Baselines
up to 3,074 km, Nature, 215, 38, 1967.
Brown G. W.j CarrT. D. and Block W. F., Long Baseline Interferometry of S-Bursts from
Jupiter, Astrophys. Lett., 1, 89-94, 1968.
Brown R. L., Technical Specification of the Millimeter Array, in SPIE Conf. Advanced
Technology MMW, Radio and Terahertz Telescopes, Kona, Hawaii, March 1998, T. G. Phillips,
Ed., Proc. SPIE 3357, 231-237, 1998.
Burke B. F., Quantum Interference Paradox, Nature, 223, 389-390, 1969.
Берк Б. Ф., Доюонстон К. Д., Ефанов В. А., Кларк Б. Д., Коган Л. Р., Костенко В.
И., Ло К. У., Матвеенко Л. И., Моисеев И. Г., Моран Д. М., Хоулс С. X., Папа Д.
К., Пападополус Г. Д., Роджерс А. И., Шварц П. Р., Наблюдения источников мазерного
радиоизлучения с угловым разрешением 0,0002", Астрон. ж., 49, 3, с. 465-469, 1972.
Cannon W. H., Quantum Mechanical Uncertainty Limitations on Deep Space Navigation by
Doppler Tracking and Very Long Baseline Interferometry, Radio Sci., 25, 97-100, 1990.
Christiansen W. N. and Mullaly R. F., Solar Observations at a Wavelength of 20 cm with a
Cross-Grating Interferometer, Proc. IRE Aust., 24, 165-173, 1963.
Christiansen W. N. and Warburton J. A., The Distribution of Radio Brightness over the Solar
Disk at a Wavelength of 21 cm, III. The Quiet Sun—Two Dimensional Observations, Aust. J.
Phys., 8, 474-486, 1955.
Clark B. G., Radhakrishnan V. and Wilson R. W., The Hydrogen Line in Absorption, Astro-
Astrophys. J., 135, 151-174, 1962.
Clark T. A. and Twenty Coauthors, Precision Geodesy Using the Mark-Ill Very-Long-Baseline
Interferometer System, IEEE Trans. Geosci. Remote Sens., GE-23, 438-449, 1985.
Cohen M. H., Moffet А. Т., Romney J. D., Schilizzi R. Т., Shaffer D. В., Kellermann K. I.,
Purcell G. H., Grove G., Swenson Jr. G. W., Yen J. L., Pauliny-Toth I. I. K., Preuss E.,
Witzel A. and Graham D., Observations with a VLBI Array, I. Introduction and Procedures,
Astrophys. J., 201, 249-255, 1975.
Cohen M. H., Cannon W., Purcell G. H., Shaffer D. В., Broderick J. J., Kellermann K. I.
and Jauncy D. L., The Small-Scale Structure of Radio Galaxies and Quasi-Stellar Sources, at
3.8 Centimeters, Astrophys. J., 170, 202-217, 1971.
Condon J. J., Cotton W. D., Greisen E. W., Yin Q. F., Perley R. A., Taylor G. B. and
Broderick J. J., The NRAO VLA Sky Survey, Astron. J., 115, 1693-1716, 1998.
Conway R. G., Kellermann K. I. and Long R. J., The Radio Frequency Spectra of Discrete
Radio Sources, Mon. Not. R. Astron. Soc, 125, 261-284, 1963.
Covington A. E. and Broten N. W., An Interferometer for Radio Astronomy with a Single-
Lobed Radiation Pattern, Proc. IRE Trans. Antennas Propag., AP-5, 247-255, 1957.
Dicke R. H., The Measurement of Thermal Radiation at Microwave Frequencies, Rev. Sci.
Instrum., 17, 268-275, 1946.
Dreyer J. L. E., New General Catalog of Nebulae and Clusters of Stars, Mem. R. Astron. Soc,
49, Part 1, 1888 (rep. R. Astron. Soc. London, 1962).
Edge D. O., Shakeshaft J. R., Me Adam W. В., Baldwin J. E., and Archer 5., A Survey of
Radio Sources at a Frequency of 159 Mc/s, Mem. R. Astron. Soc, 68, 37-60, 1959.
Elgaroy O., Morris D. and Rowson В., A Radio Interferometer for Use with Very Long
Baselines, Mon. Not. R. Astron. Soc, 124, 395-403, 1962.
Elitzur M., Astronomical Masers, Kluwer, Dordrecht, 1992.
Fomalont E. В., The East-West Structure of Radio Source at 1425 MHz, Astrophys. J. Suppl.,
15, 203-274, 1968.
48 Введение и исторический обзор [Гл. 1
Genzel R., Reid М. J., Мог an J. М. and Downes D., Proper Motions and Distances of H2O
Maser Sources, I. The Outflow in Orion-KL, Astrophys. J., 244, 884-902, 1981.
Gold Г., Radio Method for the Precise Measurement of the Rotation Period of the Earth,
Science, 157, 302-304, 1967.
Gower J. F. R., Scott P. F. and Wills D., A Survey of Radio Sources in the Declination Ranges
-07° to 20° and 40° to 80°, Mem. R. Astron. Soc, 71, 49-144, 1967.
Guilloteau 5., The IRAM Interferometer on Plateau de Bure, in Astronomy with Millimeter
and Submillimeter Wave Interferometry, M. Ishiguro and W. J. Welch, Eds., Astron. Soc.
Pacific. Conf. Ser., 59, 27-34, 1994.
Hagfors Т., Phillips J. A. and Belcora L., Radio Interferometry by Lunar Reflections, Astro-
Astrophys. J., 362, 308-317, 1990.
Hanbury Brown R., Measurement of Stellar Diameters, Ann. Rev. Astron. Astrophys., 6, 13-
38, 1968.
Hanbury Brown R., Palmer H. P. and Thompson A. R., A Rotating-Lobe Interferometer and
its Application to Radio Astronomy, Philos. Mag., Ser. 7, 46, 857-866, 1955.
Hanbury Brown R. and Twiss R. (J., A New Type of Interferometer for Use in Radio Astronomy,
Philos. Mag., Ser. 7, 45, 663-682, 1954.
Hargrave P. J. and Ryle M., Observations of Cygnus A with the 5-km Radio Telescope, Mon.
Not. R. Astron. Soc, 166, 305-327, 1974.
Hazard C. and Walsh D., A Comparison of an Interferometer and Total-Power Survey of
Discrete Sources of Radio Frequency Radiation, in The Paris Symposium on Radio Astronomy,
R. N. Bracewell, Ed., Stanford Univ. Press, Stanford, С A, 1959, p. 477-486. (Имеется перевод:
P. H. Брейсуэлл, ред., Радиоастрономия, — M.: ИЛ, с. 468-477, 1961.)
Herrnstein J. R., Мог an J. M., Greenhill L. J., Diamond P. J., Inoue M., Nakai N., Miyoshi
M., Henkel C. and Riess A., A Geometric Distance to the Galaxy NGC4258 from Orbital
Motions in a Nuclear Gas Disk, Nature, 400, 539-841, 1999.
Hirabayashi H. and 52 coauthors, Overview and Initial Results of the Very Long Baseline
Interferometry Space Observatory Programme, Science, 281, 1825-1829, 1998.
Hogg D. E., Macdonald G. H., Conway R. G. and Wade С. М., Synthesis of Brightness
Distribution in Radio Sources, Astron. J., 74, 1206-1213, 1969.
Hopkins A., Ekers R., Jackson G, Cram L., Green A., Manchester D., Staveley-Smith L. and
Norris R., Summary of the "Sub-microjansky Radio Sky" Workshop, Pub. Astron. Soc. Aust.,
16, 152-159, 1999.
Hughes M. P., Thompson A. R. and Colvin R. S., An Absorption-line Study of Galactic Neutral
Hydrogen at 21 cm Wavelength, Astrophys. J. Suppl., 23, 232-367, 1971.
IAU, Trans. Int. Astron. Union, 15B, 142, 1974.
IEEE, Standard Definitions of Terms for Radio Wave Propagation, Std. 211-1977, The Institute
of Electrical and Electronics Engineers, New York, 1977.
Jansky K. G., Electrical Disturbances Apparently of Extraterrestrial Origin, Proc. IRE, 21,
1387-1398, 1933.
Jennison R. C, A Phase Sensitive Interferometer Technique for the Measurement of the Fourier
Transforms of Spatial Brightness Distributions of Small Angular Extent, Mon. Not. R. Astron.
Soc, 118, 276-284, 1958.
Jennison R. C, High Resolution Imaging Forty Years Ago, in Very High Angular Resolution
Imaging, IAU Symp. 158, J. G. Robertson and W. J. Tango, Eds., Kluwer, Dordrecht, 1994,
p. 337-341.
Jennison R. C. and Das Gupta M. K., Fine Structure in the Extra-terrestrial Radio Source
Cygnus 1, Nature, 172, 996-997, 1953.
Jennison R. C. and Das Gupta M. K., The Measurement of the Angular Diameter of Two
Intense Radio Sources, Parts I and II, Philos. Mag., ser. 8, 1, 55-75, 1956.
1.4] Цитированная литература 49
Jennison R. С. and Latham V., The Brightness Distribution Within the Radio Sources Cygnus
A A9N4A) and Cassiopeia B3N5A), Mon. Not. R. Astron. Soc, 119, 174-183, 1959.
Kellermann K. I. and Pauliny-Toth I. I. K., The Spectra of Opaque Radio Sources, Astrophys.
J., 155, L71-L78, 1969.
Kerr A. R., Feldman M. J. and Pan S.-K., Receiver Noise Temperature, the Quantum Noise
Limit and the Role of Zero-Point Fluctuations, Proc. 8th Int. Symp. Space Terahertz Tech-
Technology., March 25-27, 1997, also available as MMA Memorandum 161, NRAO, Socorro, NM
1997.
Knowles S. H., Waltman W. В., Yen J. L., Gait J., Fort D. N., Cannon W. H., Davidson D.,
Petrachenko W. and Popelar J., A Phase-Coherent Link via Synchronous Satellite Developed
for Very Long Baseline Radio Interferometry, Radio Sci., 17, 1661-1670, 1982.
Labrum N. R., Harting E., Krishnan T. and Pay ten W. J., A Compound Interferometer with
a 1.5 Minute of Arc Fan Beam, Proc. IRE Aust., 24, 148-155, 1963.
Levy G. S. and 31 coauthors, VLBI Using a Telescope in Earth Orbit. II. The Observations,
Astrophys. J., 336, 1089-1104, 1989.
Linfield R., VLBI Observations of Jets in Double Radio Galaxies, Astrophys. J., 244, 436-446,
1981.
Linfield R. P. and Ц coauthors, VLBI Using a Telescope in Earth Orbit. II. Brightness
Temperatures Exceeding the Inverse Compton Limit, Astrophys. J., 336, 1105-1112, 1989.
Linfield R. P. and 27 coauthors, 15 GHz Space VLBI Observations Using an Antenna on a
TDRSS Satellite, Astrophys J., 358, 350-358, 1990.
Longair M. S., High Energy Astrophysics, B vols.), Cambridge Univ. Press, Cambridge, UK,
1992.
Loudon R., The Quantum Theory of Light, Oxford Univ. Press, London, 1973, p. 229.
Lovas F. J., Recommended Rest Frequencies for Observed Interstellar Molecular Microwave
Transitions—1991 Revision, J. Phys. and Chem. Ref. Data, 21, 181-272, 1992.
Lovas F. J., Snyder L. E. and Johnson D. R., Recommended Rest Frequencies for Observed
Interstellar Molecular Transitions, Astrophys. J. Suppl., 41, 451-480, 1979.
Ma G, Arias E. F., Eubanks T. M., Fey A. L., Gontier A.-M., Jacobs C. S., Sovers O. J.,
Archinal B. A. and Chariot P., The International Celestial Reference Frame as Realized by
Very Long Baseline Interferometry, Astron. J., 116, 516-546, 1998.
McCready L. L., Pawsey J. L. and Payne-Scott R., Solar Radiation at Radio Frequencies and
its Relation to Sunspots, Proc. R. Soc. A, 190, 357-375, 1947.
Maltby P. and Moffet А. Т., Brightness Distribution in Discrete Radio Sources, Astrophys. J.
Suppl., 7, 93-163, 1962.
Michelson A. A., On the Application of Interference Methods to Astronomical Measurements,
Philos. Mag., ser. 5, 30, 1-21, 1890.
Michelson A. A., On the Application of Interference Methods to Astronomical Measurements,
Astrophys. J., 51, 257-262, 1920.
Michelson A. A. and Pease F. G., Measurement of the Diameter of a Orionis with the
Interferometer, Astrophys. J., 53, 249-259, 1921.
Mills B. Y., The Positions of the Six Discrete Sources of Cosmic Radio Radiation, Aust. J.
Sci. Res., A5, 456-463, 1952.
Mills B. Y., The Radio Brightness Distribution Over Four Discrete Sources of Cosmic Noise,
Aust. J. Phys., 6, 452-470, 1953.
Mills B. Y., Cross-Type Radio Telescopes, Proc. IRE Aust., 24, 132-140, 1963.
Mills B. Y.j Aitchison R. E., Little A. G. and McAdam W. В., The Sydney University Cross-
Type Radio Telescope, Proc. IRE Aust., 24, 156-165, 1963.
Mills B. Y. and Little A. G., A High Resolution Aerial System of a New Type, Aust. J. Phys.,
6, 272-278, 1953.
50 Введение и исторический обзор [Гл. 1
Mills В. Y., Little A. G., Sheridan К. V. and Slee О. В., A High-Resolution Radio Telescope
for Use at 3.5 m, Proc. IRE, 46, 67-84, 1958.
Mills B. Y. and Slee О. В., A Preliminary Survey of Radio Sources in a Limited Region of the
Sky at a Wavelength of 3.5 m, Aust. J. Phys., 10, 162-194, 1957.
Miyoshi M.j Мог an J., Herrnstein J., Greenhill L., Nakal N., Diamond P. and Inoue M.,
Evidence for a Black Hole from High Rotation Velocities in a Sub-parsec Region of NGC4258,
Nature, 373, 127-129, 1995.
Moore E. M. and Marscher A. P., Observational Probes of the Small-Scale Structure of
Molecular Clouds, Astrophys. J., 452, 671-679, 1995.
Moran J. M., The Submillimeter Array, in SPIE Conf. Advanced Technology MMW, Radio
and Terahertz Telescopes, Kona, Hawaii, March 1998, T. G. Phillips, Ed., Proc. SPIE 3357,
208-219, 1998a.
Moran J. M., Thirty Years of VLBI: Early Days, Successes, and Future, in Radio Emission
from Galactic and Extragalactic Compact Sources, Astron Soc. Pacific Conf. Ser., 144, J. A.
Zensus, G. B. Taylor and J. M. Wrobel, Eds., 1-10, 1998b.
Moran J. M., Crowther P. P., Burke B. F., Barrett A. H., Rogers A. E. E., Ball J. A., Carter J.
С and Bare С. С, Spectral Line Interferometer with Independent Time Standards at Stations
Separated by 845 Kilometers, Science, 157, 676-677, 1967.
Moran, J. M., L. J. Greenhill and J. R. Herrnstein, Observational Evidence for Massive Black
Holes in the Centers of Active Galaxies, J. Astrophys. Astr. (Indian Acad. Sci.), 20, 165-185,
1999.
Morita K.-L, The Nobeyama Millimeter Array, in Astronomy with Millimeter and Submil-
Submillimeter Wave Interferometry, M. Ishiguro and W. J. Welch, Eds., Astron. Soc. Pacific. Conf.
Ser., 59, 18-26, 1994.
Morris D., Palmer H. P. and Thompson A. R., Five Radio Sources of Small Angular Diameter,
Observatory, 77, 103-106, 1957.
Napier P. J., Thompson A. R. and Ekers R. D., The Very Large Array: Design and Performance
of a Modern Synthesis Radio Telescope, Proc. IEEE, 71, 1295-1322, 1983. (Имеется перевод:
ТИИЭР, 71, 11, с. 78-111, 1983.)
Napier P. J., Bagri D. S., Clark B. G., Rogers A. E. E., Romney J. D., Thompson A. R. and
Walker R. C, The Very Long Baseline Array, Proc. IEEE, 82, 658-672, 1994.
Nityananda R., Comparing Optical and Radio Quantum Issues, in Very High Resolution
Imaging, IAU Symp. 158, J. G. Robertson and W. J. Tango, Eds., Kluwer, Dordrecht, 1994,
p. 11-18.
Nyquist H., Thermal Agitation of Electric Charge in Conductors, Phys. Rev., 32, 110-113,
1928.
Oliver В. М., Thermal and Quantum Noise, Proc. IEEE, 53, 436-454, 1965.
Pawsey J. L., Sydney Investigations and Very Distant Radio Sources, Pub. Astron. Soc. Рас,
70, 133-140, 1958.
Pearson T. J., Unwin S. C, Cohen M. H., Linfield R. P., Readhead A. C. S., Seielstad G.
A., Simon R. S. and Walker R. C, Superluminal Expansion of Quasar 3C273, Nature, 290,
365-368, 1981.
Pease F. G., Interferometer Methods in Astronomy, Ergeb. Exakten Naturwiss., 10, 84-96,
1931.
Perley R. A., Dreher J. W. and Cowan J. J., The Jet and Filaments in Cygnus, Astrophys.
J., 285, L35-L38, 1984.
Picken J. S. and Swarup G., The Stanford Compound-Grating Interferometer, Astron. J., 69,
353-356, 1964.
Radhakrishnan V., Noise and Interferometry, in Synthesis Imaging in Radio Astronomy II, G.
B. Taylor, С L. Carilli and R. A. Perley, Eds., Astron. Soc. Pacific Conf. Ser., 180, 671-688,
1999.
1.4] Цитированная литература 51
Read R. В., Two-Element Interferometer for Accurate Position Determinations at 960 Me,
IRE Trans. Antennas Propag., AP-9, 31-35, 1961.
Reber G., Cosmic Static, Astrophys. J., 91, 621-624, 1940.
Reid M. J., Haschick A. D., Burke B. F., Мог an J. M., Johnston K. J. and Swenson G. W.,
Jr., The Structure of Interstellar Hydroxyl Masers: VLBI Synthesis Observations of W3@H),
Astrophys. J., 239, 89-111, 1980.
Reid M. J. and Мог an J. M., Astronomical Masers, in Galactic and Extragalactic Radio
Astronomy, 2nd ed., G. L. Verschuur and K. I. Kellermann, Eds., Springer-Verlag, Berlin,
1988, p. 255-294.
Reid M. J., Readhead A. C. S., Vermuelen R. С and Treuhaft R. N., The Proper Motion of
Sagittarius A*. I. First VLBA Results, Astrophys. J., 524, 816-823, 1999.
Roger R. S., Costain C. H., Lacey J. D., Landaker T. L. and Bowers F. K., A Supersynthesis
Radio Telescope for Neutral Hydrogen Spectroscopy at the Dominion Radio Astrophysical
Observatory, Proc. IEEE, 61, 1270-1276, 1973. (Имеется перевод: ТИИЭР, 61, 9, с. 134-141,
1973.)
Rogers A. E. E., Hinteregger Н. F., Whitney A. R., Counselman С. С, Shapiro I. L, Wittels J.
J., Klemperer W. K., Warnock W. W., Clark T. A., Button L. K., Marandino G. E., Ronnang
B. O., Rydbeck O. E. H. and Niell A. E., The Structure of Radio Sources 3C273B and 3C84
Deduced from the Closure Phases and Visibility Amplitudes Observed with Three-Element
Interferometers, Astrophys. J., 193, 293-301, 1974.
Rowson В., High Resolution Observations with a Tracking Radio Interferometer, Mon. Not. R.
Astron. Soc, 125, 177-188, 1963.
Rybicki G. B. and Lightman A. P., Radiative Processes in Astrophysics, Wiley-Interscience,
New York, 1979 (repr. 1985).
Ryle M., A New Radio Interferometer and its Application to the Observation of Weak Radio
Stars, Proc. R. Soc. A, 211, 351-375, 1952.
Ryle M., The New Cambridge Radio Telescope, Nature, 194, 517-518, 1962.
Ryle M., The 5-km Radio Telescope at Cambridge, Nature, 239, 435-438, 1972.
Ryle M., Radio Telescopes of Large Resolving Power, Science, 188, 1071-1079, 1975.
Ryle M.j Elsmore B. and Neville A. C, High Resolution Observations of Radio Sources in
Cygnus and Cassiopeia, Nature, 205, 1259-1262, 1965.
Ryle M. and Hewish A., The Cambridge Radio Telescope, Mem. R. Astron. Soc, 67, 97-105,
1955.
Ryle M. and Hewish A., The Synthesis of Large Radio Telescopes, Mon. Not. R. Astron. Soc,
120, 220-230, 1960.
Ryle M.j Hewish A. and Shakeshaft J. R., The Synthesis of Large Radio Telescopes by the Use
of Radio Interferometers, IRE Trans. Antennas Propag., 7, S120-S124, 1959.
Ryle M. and Neville A. C, A Radio Survey of the North Polar Region with a 4.5 Minute of
Arc Pencil-Beam System, Mon. Not. R. Astron. Soc, 125, 39-56, 1962.
Ryle M. and Smith F. G., A New Intense Source of Radio Frequency Radiation in the Constel-
Constellation of Cassiopeia, Nature, 162, 462-463, 1948.
Ryle M.j Smith F. G. and Elsmore Б., A Preliminary Survey of the Radio Stars in the Northern
Hemisphere, Mon. Not. R. Astron. Soc, 110, 508-523, 1950.
Ryle M. and Vonberg D. ?>., Solar Radiation at 175 Mc/s, Nature, 158, 339-340, 1946.
Scoville N.j Carlstrom J., Padin S., Sargent A., Scott S., and Woody D., The Owens Valley
Millimeter Array, in Astronomy with Millimeter and Submillimeter Wave Interferometry, M.
Ishiguro and W. J. Welch, Eds., Astron. Soc. Pacific. Conf. Ser., 59, 10-17, 1994.
Schilke P., Groesbeck Т., Blake G. A. and Phillips T. G., A 325 to 360 GHz Emission Line
Survey of the Orion KL Region, Astrophys. J. Suppl., 108, 301-337, 1997.
Seidelmann P. K., Ed., Explanatory Supplement to the Astronomical Almanac, University
Science Books, Mill Valley, CA, 1992.
52 Введение и исторический обзор [Гл. 1
Shakeshaft J. R., Ryle М., Baldwin J. Е., Elsmore В. and Thomson J. H., A Survey of Radio
Sources Between Declinations -38° and +83°, Mem. R. Astron. Soc, 67, 106-154, 1955.
Smith F. G., An Accurate Determination of the Positions of Four Radio Stars, Nature, 168,
555, 1951.
Smith F. G., The Determination of the Position of a Radio Star, Mon. Not. R. Astron. Soc,
112, 497-513, 1952a.
Smith F. G., The Measurement of the Angular Diameter of Radio Stars, Proc. Phys. Soc. В.,
65, 971-980, 1952b.
Smith F. G., Apparent Angular Sizes of Discrete Radio Sources-Observations at Cambridge,
Nature, 170, 1065, 1952c.
Smolders A. B. and van Haarlem M. P., Eds., Perspectives on Radio Astronomy: Technologies
for Large Antenna Arrays, ASTRON, Dwingeloo, Netherlands, 1999.
Smoot G. and 27 coauthors, СОВЕ Differential Microwave Radiometers: Instrument Design
and Implementation, Astrophys. J.,360, 685-695, 1990.
Smoot G. F. and 27 coauthors, Structure in the СОВЕ Differential Microwave Radiometer
First-Year Maps, Astrophys. J., 396, L1-L5, 1992.
Southworth G. C, Microwave Radiation from the Sun, J. Franklin Inst., 239, 285-297, 1945.
Swarup G., Ananthakrishnan S., Kapahi V. K., Rao A. P., Subrahmanya C. R. and Kulkarni
V. K., The Giant Meter-wave Radio Telescope, Current Sci., 60, 95-105, 1991.
Thomasson P., MERLIN, Quat. J. R. Astron. Soc, 27, 413-431, 1986.
Thompson A. R., The Planetary Nebulae as Radio Sources, in Vistas in Astronomy, Vol. 16,
A. Beer, Ed., Pergamon Press, Oxford, 1974, p. 309-328.
Thompson A. R., Clark B. G., Wade С. М. and Napier P. J., The Very Large Array, Astrophys.
J. Suppl., 44, 151-167, 1980.
Thompson A. R. and Krishnan Т., Observations of the Six Most Intense Radio Sources with a
1,0' Fan Beam, Astrophys. J., 141, 19-33, 1965.
Tiuri M. E., Radio Astronomy Receivers, IEEE Trans. Antennas Propag., AP-12, 930-938,
1964.
Tiuri M. E. and Raisanen A. V., Radio-Telescope Receivers, in Radio Astronomy, 2nd ed., J.
D. Kraus, Cygnus-Quasar Books, Powell, OH, 1986, Ch.7.
Welch W. J., The Berkeley-Illinois-Maryland Association Millimeter Array, in Astronomy with
Millimeter and Submillimeter Wave Interferometry, M. Ishiguro and W. J. Welch, Eds., Astron.
Soc. Pacific. Conf. Ser., 59, 1-9, 1994.
Whitney A. R., Rogers A. E. E., Hinteregger H. F., Knight C. A., Levine J. I., Lippincott S.,
Clark T. A., Shapiro I. L, and Robertson D. 5., A Very Long Baseline Interferometer System
for Geodetic Applications, Radio Sci., 11, 421-432, 1976.
Whitney A. R., Shapiro I. I., Rogers A. E. E., Robertson D. S., Knight С A., Clark T. A.,
Goldstein R. M., Marandino G. E. and Vandenberg N. R., Quasars Revisited: Rapid Time
Variations Observed via Very Long Baseline Interferometry, Science, 173, 225-230, 1971.
Yen J. L., Kellermann K. L, Rayher В., Broten N. W., Fort D. N., Knowles S. H., Walt-
man W. B. and Swenson G. W., Jr., Real-Time, Very Long Baseline Interferometry Based on
the Use of a Communications Satellite, Science, 198, 289-291, 1977.
Виткевич В. В., Калачев П. Д. Радиотелескопы. Труды ФИАН, — М.: Наука, т. 28, 1966.
Кларк Б. Д., Бродери Д. Д., Ефанов В. А., Келлерманн К. И., Коуэн М. Н., Коган Л.
Р., Костенко В. И., Матвеенко Л. И., Моисеев И. Г., Мухина М., Штейншлейгер В.
Б. Наблюдения компактных объектов космического радиоизлучения на волне 3,35 см с
предельным угловым разрешением. Астрон. Ж., 4, 700-703, 1972.
Матвеенко Л. И., Кардашев Н. С, Шоломицкий Г. Б. О радиоинтерферометре с большой
базой. — Изв. ВУЗов. Радиофизика, т. 8, 4, с. 651-654, 1965.
Глава 2
ВВЕДЕНИЕ В ТЕОРИЮ ИНТЕРФЕРОМЕТРИИ
И СИНТЕЗА ИЗОБРАЖЕНИЙ
По мере обзора в первой главе истории развития интерферометрии мы ввели
в рассмотрение некоторые из ее основополагающих принципов. В этой главе при-
приводится упрощенный анализ интерферометрии и вводятся некоторые соотношения,
связанные с преобразованием Фурье, а также другие основные понятия. Тем самым
дается широкое введение в основы синтеза изображений с целью облегчить пони-
понимание более подробного развития этого вопроса в последующих главах.
2.1. Анализ в плоскости база-источник
Мгновенный отклик интерферометра для точечного источника может быть про-
проанализирован в простейшем случае распространения сигналов в плоскости рас-
расположения фазовых центров антенн интерферометра и наблюдаемого источника.
При продолжительных наблюдениях необходимо учитывать вращение Земли и рас-
рассматривать трехмерную геометрическую конфигурацию как показано на рис. 1.15.
Тем не менее, плоская геометрия служит хорошим приближением в случае крат-
кратковременных наблюдений, и упрощенное рассмотрение способствует визуализации
картины отклика.
Рассмотрим геометрическую ситуацию, показанную на рис. 2.1, когда антенны
расположены в направлении восток—запад. Две антенны разделены расстоянием
D — базой. Наблюдается один и тот же космический источник, находящийся
в дальней зоне интерферометра, т. е. на достаточно большом расстоянии, что-
чтобы приходящий волновой фронт мог считаться плоским на всем расстоянии D.
+ D >
Рис. 2.1. Геометрия простого интерферометра. D — база интерферометра
Временно предположим, что источник имеет бесконечно малые угловые размеры.
Предположим также, что приемники снабжены узкополосными фильтрами, про-
пропускающими только очень близкие по частоте v компоненты сигнала.
Как показано в гл. 1, в интерферометре с модуляцией фазы напряжения сигна-
сигналов перемножаются и затем усредняются по времени, что дает эффект фильтрации
54 Введение в теорию интерферометрии и синтеза изображений [Гл. 2
высоких частот. Волновой фронт излучения от источника, находящегося в направ-
направлении #, достигает сначала правой антенны, а затем левой с разницей по времени
rg = (D/c) sin#, где тд называется геометрической задержкой, а с — скорость света.
Тогда для частоты v выход умножителя пропорционален
F = 2 sin Bтп/?) sin 2тп/ (t - rg) =
= cos 2-KVTg — cos (Ani/i) cos {2-куТд) — sin (Ani/i) sin Bтп/тд). B.1)
Центральная частота приемников, в общем случае, может быть в диапазоне от де-
десятков мегагерц до сотен гигагерц. Так как Земля вращается, наибольшая скорость
изменения в равна угловой скорости земного вращения, порядок величины которой
составляет 10~4 рад/с. Кроме того, поскольку для наземных интерферометров D не
может быть больше, скажем 107 м, скорость изменения vrg меньше vt по крайней
мере на шесть порядков. Наиболее быстро переменные члены в выражении B.1)
легко отфильтровываются, оставляя интерференционную функцию
F = cos 2тпутд = cos f^l) , B.2)
где / = sin#; определение переменной I рассматривается далее в разд. 2.4. Для
небесных источников при изменении в со временем вследствие земного враще-
вращении в корреляторе генерируется квазисинусоидальный интерференционный сигнал,
представляющий собой выходной сигнал интерферометра. На рис. 2.2 показан при-
пример этой функции, которая может быть представлена как приемная диаграмма
направленности интерферометра по мощности для случая, когда антенны либо
Рис. 2.2. График интерференционной функции F = cos [BttD/\) sin#] в полярной системе
координат. Радиальная составляющая равна \F\ и в отсчитывается от вертикальной оси.
Противоположные лепестки, соответствующие положительным и отрицательным полу пе-
периодам квазисинусоидальной интерференционной диаграммы, отмечены знаками «плюс»
и «минус». Чтобы упростить картину, используется очень малое значение D/X, равное 3.
Хорошо видно уширение интерференционных лепестков вследствие уменьшения длины
базы с увеличением |0|. Максимум в горизонтальном направлении является следствием
произвольно выбранного целого значения D/X
сопровождают источник, либо имеют изотропные отклики и не оказывают влияния
на ее форму.
Альтернативный и эквивалентный способ представить формирование синусои-
синусоидальных интерференционных лепестков заключается в рассмотрении того факта,
2.2] Влияние полосы пропускания 55
что вследствие вращения Земли антенны имеют различные проекции скорости
в направлении на источник. Поэтому сигналы, приходящие на антенны, испыты-
испытывают различные доплеровские смещения. При перемножении сигналов, сдвинутых
вследствие эффекта Доплера, возникают биения, соответствующие синусоидально-
синусоидальному выходному сигналу.
Этот простой анализ может быть развит далее, если мы рассмотрим две фурье-
компоненты принятого сигнала на частотах z/i и 1/2- Частотные компоненты стати-
статистически независимы, так что выходной сигнал интерферометра представляет собой
линейную сумму откликов двух частот. Следовательно, на выходе присутствуют
компоненты F\ и i^, определенные формулой B.2). Для частоты V2 коэффициент
2ttD/X = 2ttD V2Iс будет иметь другое значение, чем для частоты z/i, так что период
Fi будет отличаться от периода F\ для любого заданного угла в. Это различие в пе-
периодах приведет к интерференции между F\ и Fi, так что интерференционные мак-
максимумы будут модулированы функцией, также зависящей от в. Подобный эффект
возникает и в случае непрерывной полосы частот. Например, если на коррелятор
поступают сигналы с однородной спектральной плотностью по мощности в полосе
частот Az/ и центральной частотой v$, to выходной сигнал будет равен
/
г/7ч 1 Г BirDlv\ BkDIvo\ sin (ttDZAiz/c) ,o o^
Fit) = -— cos dv = cos ^———y-^ . B.3)
w Аг/ J \ с J \ с J ttDIAv/c v ;
V0—A1//2
Таким образом, интерференционная диаграмма имеет огибающую вида sine-
функции: sine (ж) = ^ттгх/тгх. Этот результат является примером более общего
вывода, обсуждаемого в следующем разделе: в случае однородной спектральной
плотности по мощности принимаемых антеннами сигналов огибающая интерферен-
интерференционной диаграммы представляет собой преобразование Фурье инструментальной
частотной характеристики.
2.2. Влияние полосы пропускания
На рис. 2.3 показан интерферометр того же общего типа, что и на рис. 2.1, но
с выделенными усилителями Hi и Н2, умножителем и интегратором (по времени).
В одно из плеч интерферометра вводится аппаратная временная задержка Т{. Пред-
пол ожим, что для точечного источника с обеих антенн на коррелятор поступают
сигналы с одинаковыми напряжениями V(t), и один из сигналов запаздывает отно-
относительно другого на время задержки т = тд — Ti, определяемое базой D и направле-
направлением на источник в. Постоянная времени интегратора в корреляторе равна 2Т, т. е.
выходной сигнал умножителя накапливается в течение 2Т секунд, регистрируется
и затем обнуляется. Выходной сигнал интегратора может быть в виде напряжения,
тока или кодированной последовательности логических уровней, но в любом случае
он представляет физическую величину, соответствующую квадрату напряжения.
Для точечного источника выходной сигнал коррелятора равен
т
т = h \ v{t) v{t"r) dt B-4)
-T
Мы не учли шум системы и предположили, что частотные характеристики двух
усилителей идентичны, включая конечные полосы пропускания Ai/, за предела-
пределами которых сигнал не принимается. Обычно время интегрирования 2Т находится
56
Введение в теорию интерферометрии и синтеза изображений
[Гл.2
в диапазоне от миллисекунд до секунд, т. е. его величина много больше 1/Ai/. Таким
образом, выражение B.4) можно переписать как
1
r(r) = lim J- \ V(t) V(t - t) dt,
Т-ЮО 21 J
-T
B.5)
что соответствует (ненормированной) автокорреляционной функции 1). Условие
Т —> оо удовлетворяется, если за время 2Т происходит очень большое число измене-
изменений амплитуды сигнала с интервалом
r^l/Ai/. В действительности время
усреднения конечно и должно быть
много меньше периода интерферен-
интерференционного сигнала.
Как показано в гл. 1, сигнал от
естественного космического источни-
источника может быть представлен в виде
случайного непрерывного процесса,
откуда следует, что в широком спек-
спектре фаза представляет собой случай-
случайную функцию частоты. Для нашей
непосредственной цели предположим,
что усредненная по времени ампли-
амплитуда космического сигнала постоянна
во всей полосе пропускания приемни-
приемника для любого конечного интервала
частот.
Квадрат амплитуды частотного
спектра известен как спектральная
плотность мощности или энергетиче-
энергетический спектр. Энергетический спектр
' | —' J Коррелятор
Выход
Рис. 2.3. Схема простого интерферометра, на
которой показаны полосовые усилители Hi
и Н2, геометрическая временная задержка т9
и аппаратная временная задержка т», а также
коррелятор, состоящий из умножителя и ин-
интегратора
сигнала представляет собой образ Фу-
Фурье его автокорреляционной функ-
функции. Это соотношение известно как
соотношение Винера-Хинчина и бу-
будет рассматриваться в разд. 3.2. Оно
применимо к сигналам либо детерми-
детерминированным, либо статистическим по своей природе, и может быть записано в виде
Я(г/)|2= | г{т) e-j2*VT dr
B.6)
(r)= J \H{v)\2 e>2*VT dv,
B.7)
x) Для простоты мы рассматриваем только сигналы, принимаемые от точечного источ-
источника, которые идентичны во всем, за исключением временной задержки. В реальных
системах сигналы, поступающие на коррелятор, могут содержать частично коррелиро-
коррелированные сигналы от частично разрешенного источника, также как и аппаратурный шум.
Эти особенности могут быть приняты во внимание при рассмотрении кросскорреляционной
функции.
2.2]
Влияние полосы пропускания
57
где Н(и) — амплитудная характеристика (по напряжению) и, следовательно,
\Н(у)\2 — энергетический спектр сигнала на входе коррелятора. В этом случае,
поскольку предполагается, что у космического сигнала должен быть спектр с по-
постоянной амплитудой, спектр Н(у) определяется только характеристиками полосы
пропускания (амплитудно-частотными характеристиками) усилителей. Таким обра-
образом, выход интерферометра как функция временной задержки т представляет собой
преобразование Фурье энергетического спектра космического сигнала, ограничен-
ограниченного полосой пропускания усилителей. В качестве простого примера предположим,
что полоса пропускания описывается функцией Гаусса с центральной частотой щ:
\H{v)
exp
2<т2
exp
(у +
2<т2
B.8)
где а — характерная полоса частот (полная ширина полосы пропускания на уровне
половины максимума равна л/8 In2 а).
Отметим, что для выполнения преобразований Фурье в выражениях B.6) и B.7)
мы добавили отрицательную амплитудно-частотную характеристику с центральной
частотой — z/q. В этом случае спектр становится симметричным относительно нуле-
нулевой частоты, и это согласуется с тем фактом, что автокорреляционная функция
действительна. Отрицательные частоты не имеют физического смысла и появля-
появляются математически вследствие применения экспоненциальной формы ядра преоб-
преобразования. Таким образом, отклик интерферометра равен
r(r) = e
cos Bтп/()т)
B.9)
что проиллюстрировано на рис. 2.4 а. Отметим, что г(т) — косинусная функция,
умноженная на функцию огибающей, имеющей в данном случае гауссову форму,
Рис. 2.4. Отклик интерферометра на точечный источник для полосы пропускания в виде
функции Гаусса (а) и прямоугольной формы (б). По оси абсцисс отложена геометрическая
задержка тд. Огибающая интерференционного сигнала определяется откликом по полосе
пропускания
ширина которой зависит от полосы пропускания усилителей. Эта огибающая функ-
функция часто называется откликом по задержкам, откликом по полосе пропускания,
или функцией замывания лепестков.
58 Введение в теорию интерферометрии и синтеза изображений [Гл. 2
Приравнивая аппаратную задержку Т{ к нулю и подставляя в B.9) выражение
для геометрической задержки тд = (D/c) sin#, получим отклик
B.10)
= ехр —2 ( sin64 cos ( sm#J .
Период интерференционных лепестков изменяется обратно пропорционально вели-
величине vqD/c = D/X и не зависит от характерной полосы частот а. Однако отклик
по полосе пропускания является функцией как а, так и D: широким полосам
пропускания и большим базам соответствуют узкие огибающие интерференционных
лепестков. Этот результат имеет вполне общее значение. Например, для усилите-
усилителя с полосой пропускания прямоугольной формы шириной Ai/ форма огибающей
функции соответствует [sin (тгДг/т^ДтгДг/т), что следует из уравнения B.3) и пока-
показано на рис. 2.4 б.
При картографировании огибающая интерференционных лепестков является
ограничением, хотя в некоторых случаях, особенно в интерферометрии со сверх-
сверхдлинными базами, огибающая функция полезна. В большинстве случаев жела-
желательно наблюдать интерференционные лепестки вблизи максимума диаграммы,
где амплитуда интерференции наибольшая. Это условие может быть достигнуто
подбором задержки т\ таким образом, чтобы разностная задержка г = тд — т\ была
достаточно малой. Если т\ изменяется с шагом, равным обратной величине цен-
центральной частоты щ 1) 1 т0 отклик остается косинусной функцией от тд. Отметим,
что по мере приближения Аи к v ширина огибающей функции становится настолько
узкой, что остается только центральный интерференционный лепесток. Эта ситуа-
ситуация встречается главным образом в оптике, где центральный лепесток такого типа
часто называют интерференцией «белого света».
2.3. Одномерный синтез источников
За исключением нескольких низкочастотных инструментов, большинство радио-
радиоастрономических антенн действуют на частотах выше ~ 1 ГГц, для реализации
широкой полосы пропускания, улучшающей чувствительность, и увеличивающей
угловое разрешение. Сопровождение источника при его движении по небесной
сфере становится важным, так как диаграммы направленности антенн сужаются
с увеличением частоты, и поскольку вращение Земли используется в двумерном
картографировании, как показано на рис. 1.15. При рассмотрении интерферометра,
в котором антенны и аппаратная задержка сопровождают источник, удобно опре-
определять углы диаграмм направленности антенн и другие переменные относительно
опорной точки на небесной сфере: как правило, по центральному или номинальному
положению наблюдаемого источника. Эта точка обычно называется положением
опорной фазы. Поскольку диапазон углов относительно этой точки, необходимый
для определения распределения интенсивности источника, обычно не превышает
несколько градусов, можно воспользоваться преимуществом малых приближений.
Аппаратная задержка постоянно изменяется для уравнивания ее с геометрической
задержкой излучения относительно опорного положения. Если мы обозначим это
направление как 6q, то т = тд\в=во — Т{ = 0 и тд\в=во = (D/c) sin#0- Для излучения
из направления (#0 — Д#M гДе Д# — малый угол, функция интерференционного
х) Этот метод подстройки полезно рассмотреть здесь, но обычно используемые методы
рассматриваются в п. 7.3.4.
2.3] Одномерный синтез источников 59
отклика равна
cos Bтп/от) = cos < 2тг!/о — sin (во — АО) — тА > ~
~ cos[2ttz/0 р/с) sin Д(9 cos0o]. B.11)
Для источника с произвольным положением на небесной сфере угловое разреше-
разрешение интерференционных лепестков определяется длиной базы, спроецированной на
плоскость, ортогональную направлению на источник. На рис. 2.1, например, это
расстояние обозначено D cosO. Таким образом, мы вводим величину и, равную про-
проекции расстояния между антеннами на направление, перпендикулярное опорному
положению #о- Она измеряется в длинах волн Л на центральной частоте vo, т. е.
_ D cos 0о _ voD cos 0o ,Q 1 оч
u-^—- - . B.12)
Так как АО мало, мы можем предположить, что отклик по полосе пропускания
близок к максимуму (единице) в направлении во — АО. Тогда из B.11) и B.12)
отклик для излучения из этого направления равен
F(l) = cos Bтг1/от) = cos Bтт/), B.13)
где / = sinA0. Это выражение представляет собой отклик интерферометра с ре-
результирующей задержкой тд — т^, равной нулю при 0 = Oq для случая точечного
источника, находящегося в направлении 0 = Oq — АО. Как мы покажем далее,
параметр и интерпретируется как пространственная частота. Она может быть
выражена в периодах на радиан, так как пространственная переменная /, будучи
мала, может быть выражена в радианах.
2.3.1. Отклик интерферометра как свертка. Отклик одиночной антенны
или интерферометра может быть выражен через свертку. Рассмотрим для нача-
начала отклик одиночной антенны и приемник, измеряющий принятую мощность. На
рис. 2.5 показана приемная диаграмма направленности антенны по мощности А(в)
в виде графика в полярных координатах эффективной площади антенны как функ-
функции углового расстояния относительно оси главного лепестка. На рисунке также
показан одномерный профиль интенсивности источника 1\(в'), определяемый фор-
формулой A.9), где в' измеряется относительно центра или номинального положения
источника. Выходная мощность в полосе частот Av элемента dO1 источника, равна
A/2) Av А@' — 0) I\@') dO1', где коэффициент 1/2 учитывает способность антенны
принимать только одну из компонент не поляризованного излучения. Опуская по-
постоянный сомножитель Az//2, получим, что полная мощность на выходе антенны
пропорциональна
[ А@'- 0) h@') dO'. B.14)
source
Этот интеграл равен кросс-корреляции приемной диаграммы направленности ан-
антенны и распределения интенсивности источника. Удобно определить Л(в) = А(—в),
где Л — зеркальное отражение А относительно 0. Тогда выражение B.14) сводится
к виду
[ Л(в - в') h(e') d9'. B.15)
60
Введение в теорию интерферометрии и синтеза изображений
[Гл.2
А(В)
Интеграл в выражении B.15) представляет собой интеграл свертки; см., например,
(Bracewell, 2000) или (Champeney, 1973). Мы можем сказать, что выходная мощ-
мощность антенны представляет собой свертку источника с зеркальным отображением
приемной диаграммы направленности антенны по мощности. Зеркальную диаграм-
диаграмму направленности можно представить как отклик антенны на точечный источник.
В случае интерферометра мы можем выразить его отклик через свертку, заме-
заменив диаграмму направленности антенны по мощности B.15) суммарной диаграм-
диаграммой направленности интерферометра. Как следует из результатов, представленных
ранее, отклик интерферометра определяет-
определяется тремя функциями:
• приемной диаграммой направленно-
направленности антенн, которую мы представили
как АA);
• интерференционной диаграммой F(l),
определенной уравнением B.13) и по-
показанной на рис. 2.2. Отметим, что
интерференционный член в выраже-
выражении для выходного сигнала интерфе-
интерферометра, будучи произведением двух
напряжений, пропорционален мощно-
мощности;
• откликом по полосе пропускания,
например, sine-функцией в форму-
формуле B.3). В общем случае мы можем
представить ее как FbA).
Отметим, что все эти функции идеально
симметричны, и, следовательно, мы можем
пренебречь различием между диаграммой
направленности интерферометра по мощ-
мощности и ее зеркальным отображением, ис-
используемым в соотношении свертки.
Теперь рассмотрим интерферометр со
следящими антеннами и аппаратной за-
задержкой, регулируемой таким образом, что источник при его движении по небесной
сфере также сопровождается откликом по полосе пропускания. В действительно-
действительности, диаграммы направленности антенн и отклики по полосе пропускания изменя-
изменяют распределение интенсивности. Мы можем, следовательно, представить выход
интерферометра в виде свертки интерференционной диаграммы (ее зеркального
отображения) с модифицированной интенсивностью. Используя интеграл свертки,
отклик можно записать как
О
Рис. 2.5. Диаграмма направленности
антенны А{в) по мощности и профиль
интенсивности источника Ii@f), исполь-
используемые для иллюстрации соотношения
свертки. Угол в измеряется относитель-
относительно оси диаграммы направленности ОС,
и в' измеряется относительно направле-
направления на номинальное положение источ-
источника О В
R{1) = cos [2тги (I - /')] А{1') FB{lf) h{lf) dlf.
B.16)
Обычно удобно использовать символ «звездочка» (*) для сокращенного обозначе-
обозначения свертки, и тогда формула B.16) приводится к виду
R(l) = cos {2-kuI) * [A(l) FB(l)
B.17)
2.3] Одномерный синтез источников 61
(Отметим, что свертка обладает свойством коммутативности, т. е., /*# = #*/•)
Измеренное интерферометром распределение интенсивности модифицировано А{1)
и FbA), но поскольку это измеряемые инструментальные характеристики, то Ii(l)
может быть восстановлено в общем случае. Часто угловой размер источника мал
по сравнению с размерами диаграмм направленности антенн и отклика по полосе
пропускания, так что эти две функции дают лишь постоянное смещение в отклике
интерферометра. Чтобы упростить обсуждение, мы далее рассмотрим именно этот
случай и, опуская постоянные слагаемые, запишем собственно отклик интерферо-
интерферометра в виде
R(l) =cosB7m/)* Ji(Z). B.18)
В первых интерферометрах, таких как показанный на рис. 1.6, в которых антенны
фиксировались по меридиану и отсутствовало сопровождение источников, задерж-
задержки сигналов между антеннами до точки их перемножения были равны, и перемен-
переменная аппаратная задержка отсутствовала. Таким образом, все три функции, опре-
определяющие диаграмму направленности интерферометра по мощности, фиксированы
по отношению к базе интерферометра. Диаграмма направленности интерферометра
по мощности сводится к виду A(l) cos Bтга/) FbA) А. Следовательно, отклик интер-
интерферометра на источник равен [A(l) cos Bтга/) FbA)] * Ii(l)-
Как обсуждалось выше, интерферометры с фиксированными антеннами в об-
общем случае ограничены по частоте максимум несколькими сотнями мегагерц. На
таких больших длинах волн можно использовать антенны с большой собирающей
поверхностью и при этом иметь достаточно широкие диаграммы направленности,
обеспечивающие несколько минут наблюдательного времени при их прохождении
источником. Обычно полоса пропускания таких низкочастотных инструментов ма-
мала, так что Fb{1) широка и может не учитываться. Кроме того, диаграммы направ-
направленности антенн обычно шире источника и достаточно велики, так что несколько
периодов интерференционного отклика могут быть измерены при прохождении
источника через диаграмму. Таким образом, и при отсутствии сопровождения,
значительная часть отклика представляется формулой B.18). За исключением
нескольких инструментов, построенных специально для низкочастотных наблюде-
наблюдений, фиксированные антенны большей частью являются особенностью ранних лет
радиоастрономии.
2.3.2. Теорема свертки и пространственные частоты. Теперь мы рас-
рассмотрим отклик интерферометра, представленный формулой B.18), используя тео-
теорему свертки фурье-образов. Этой теоремой утверждается, что фурье-образ сверт-
свертки двух функций равен произведению их фурье-образов:
f*g-FG, B.19)
где f ^± J7, g ^± Q, и ^ обозначает преобразование Фурье. Доказательство теоремы
свертки может быть найдено почти в любом учебнике по преобразованиям Фурье.
Рассмотрим преобразования Фурье трех функций в уравнении B.18) относительно
/ ли. Для отклика интерферометра мы имеем г (и) ^ R(l). В частном случае и = щ
и преобразование Фурье интерференционного члена выглядит как
cos Bтгио1) ^ \ [6(и + щ) + 6(и - щ)], B.20)
62 Введение в теорию интерферометрии и синтеза изображений [Гл. 2
где 5 — дельта-функция. Образ Фурье от /]_(/) представляет собой функцию видно-
сти V(u). Таким образом, из формул B.18), B.19) и B.20) получаем
г(и) = - [5(и + и0) + 5(и - щ)] V(u) =
\ [ + uo) + V(uo) S{u - щ)]. B.21)
Этот результат показывает, что мгновенный отклик интерферометра как функция
пространственной частоты состоит из двух дельта-функций, расположенных в точ-
точках плюс/минус щ на оси и. Теперь V(u) — образ Фурье от Д(/), представляет собой
амплитуду и фазу синусоидальной компоненты профиля интенсивности с простран-
пространственной частотой и, измеряемой в периодах на радиан. Интерферометр действует
как фильтр, пропускающий только пространственные частоты zbi^o- Отрицательная
пространственная частота — щ, подобно отрицательной частоте в формуле B.8),
не имеет физического смысла. Она появляется в связи с использованием для ма-
математического удобства экспоненциальной формы преобразования Фурье вместо
синусного и косинусного преобразований, что лучше отражает физику явления.
В результате спектр пространственных частот симметричен относительно начала
координат в эрмитовом смысле, т. е. с четной действительной и нечетной мнимой
частями, и соответствует реальности, поскольку интенсивность является веществен-
вещественной, а не комплексной величиной.
Интерференционная видность по оригинальному определению Майкельсона
\Ум — см- Ф°РМУЛУ A-8-)] представляет собой действительную величину, норми-
нормированную к единице для неразрешенного источника. Для того чтобы обеспечить
картографирование источников с асимметричной и сложной структурой, вводит-
вводится определение комплексной видности (Bracewell, 1958), используемой для уче-
учета фазы функции видности, измеряемой как фаза интерференционного сигнала.
Нормировка удобна при сравнении измерений с простыми моделями, такими как
показанные на рис. 1.5. Однако в картах или изображениях желательно указывать
величину интенсивности или яркостную температуру, так что общепринято на
практике оставлять измеренное значение видности без нормировки, поскольку в нем
содержится необходимая информация. Таким образом, видность V, используемая
здесь, представляет собой ненормированную комплексную величину, измеряемую
в единицах [Вт-м~2-Гц-1]. Величина и, введенная как проекция базы, выраженная
в длинах волн, как было показано, представляет собой также пространственную
частоту фурье-компонент интенсивности. Концепция пространственной частоты
и спектра пространственных частот является фундаментальной в синтезе астро-
астрономических изображений с использованием преобразований Фурье; этот общий
подход рассмотрен в основополагающей статье Брейсуэлла и Робертса (Bracewell
and Roberts, 1954).
2.3.3. Пример одномерного синтеза. Чтобы проиллюстрировать наблюда-
наблюдательный процесс, показанный в этой главе, мы представим простейшее моделиро-
моделирование измерений комплексной видности источника с использованием произвольных
параметров. Источник состоит из двух компонент, расположенных на расстоянии
0,34° друг от друга, плотность потока которых находится в соотношении 2:1. Из-
Измерения проводятся с расстояниями между антеннами, кратными 30 длинам волн.
Измеряются все базы от единичной до 23-х кратной. Эти результаты могут быть
получены при использовании двух антенн и одного коррелятора в наблюдениях
источника при его прохождении через меридиан в течение 23 дней с ежедневным
перемещением антенны для создания новой базы. С другой стороны, можно про-
провести 23 одновременных измерения, используя 23 коррелятора и 8 антенн, если
их расположить по принципу минимальной избыточности баз, как обсуждается
2.3]
Одномерный синтез источников
63
1,0
°'8
0,6
0,4
0,2
\
1 /
\
11
/
\
\
\
и
п \ \п м/
'¦\ш
11 1 1 \|/|
Ы1 1 UI
МММ
4 8 12 16 20 24
Длина базы решетки, усл. ед.
0 4 8 12 16 20 24
Длина базы решетки, усл. ед.
0,6
0,2
-0.2
АД
Л Л 1
щ
А I I
Ш Ал,
1
Л
1
дд
Дд/
к Л Л
0,6
0,2
-0,2
-1,0 -0,6 -0,2 0,2 0,6
Угловое положение, град
1,0
-1,0 -0,6 -0,2 0,2 0,6 1,0
Угловое положение, град
Рис. 2.6. Модельные измерения видности двойного источника: амплитуда (а) и фаза вид-
ности (б) представлены как функции расстояния между антеннами кратного единице; в —
профиль, полученный из измерений; г — отклик для точечного источника
в разделе 5.5. Угловые размеры двух компонент источника слишком малы для
того, чтобы их можно было разрешить интерферометром, так что рассматриваются
точечные излучатели. Обе компоненты излучают шумовые некоррелированные сиг-
сигналы. Источник находится на значительном расстоянии и волновой фронт может
считаться плоским для всех измеряемых баз.
На рисунках 2.6 а и 2.6 6^ показаны, соответственно, амплитуда 1) и фаза, кото-
которые были бы измерены. Поскольку данные получены в модельном приближении,
ошибки измерений отсутствуют и точками указаны значения преобразования Фу-
Фурье распределения интенсивности источника, которое можно представить как две
дельта-функции с отношением величин 1:2. Применяя обратное преобразование
Фурье к видности, получим синтезированное изображение источника, показанное
на рис. 2.6 в. Явно представлены две компоненты источника. Дополнительные ос-
осцилляции возникают как следствие конечной протяженности измерений функции
видности, равномерно взвешенных и ограниченных 23-кратным единичным рас-
расстоянием. Этот эффект также виден на рис. 2.6 г, где показан отклик, полученный
описанной процедурой измерений для точечного источника, или, что эквивалентно,
синтезированная диаграмма направленности. Профиль отклика представляет собой
х) Нужно отметить, что модуль комплексной видности следует называть не амплиту-
амплитудой, а скорее величиной, поскольку размерность видности соответствует мощности, а не
напряжению. Тем не менее, термин амплитуда видности широко используется в радио-
радиоастрономии, вероятно как следствие ранней практики регистрации интерференционных
лепестков в виде квазисинусоидальных сигналов с последующим анализом амплитуды
и фазы колебаний.
64 Введение в теорию интерферометрии и синтеза изображений [Гл. 2
sine-функцию, т. е. преобразование Фурье прямоугольной функции, вследствие от-
отсечки измерений на больших базах. В пространстве изображения двухкомпонент-
ный профиль источника может быть представлен в виде свертки источника и откли-
отклика на источник точечной структуры. Величина боковых лепестков максимальна из-
за точечных размеров компонент модели, и они могли бы быть частично сглажены,
если бы размеры компонент были сравнимы с размерами боковых лепестков.
Как следует из соотношения свертки, информация о структуре источника содер-
содержится во всем отклике, показанном на рис. 2.6 в, т. е. как в главном, так и боковых
лепестках. Можно было бы извлечь максимум информации о структуре источника
вписыванием с соответствующим масштабом отклика, показанного на рис. 2.6 г,
в два пика на рис. 2.6 в с последующим вычитанием их из профиля. В реальных
наблюдениях при этом остались бы шум и любая структура, которая могла бы
присутствовать дополнительно к точечным источникам, но боковые лепестки при
этом были бы удалены полностью или почти полностью. Процесс вписывания от-
отклика точечного источника можно было бы регулировать для минимизации какой-
нибудь меры остаточных флуктуации, и следующие компоненты можно было бы
вписать в любые остающиеся пики и вычесть. Этот метод, очевидно, был бы хо-
хорошим способом оценки величины и положения двух компонент, а также проверки
наличия какой-нибудь низкоуровневой структуры, возможно спрятанной боковы-
боковыми лепестками, показанными на рис. 2.6 в. В алгоритме CLEAN, рассматриваемом
в гл. 11, этот принцип используется, но также замещаются и сами компоненты,
которые убираются модельным откликом в виде центрального лепестка, свободного
от боковиков. Устранение боковых лепестков позволяет проводить исследование
низкоуровневой структуры вплоть до уровня шума. Большинство синтезирован-
синтезированных изображений получается нелинейными алгоритмами такого типа, и диапазон
уровней интенсивности, достигаемый в некоторых двумерных изображениях, пре-
превосходит 105.
2.4. Двумерный синтез
Для того чтобы синтезировать карту или изображение источника по двум коор-
координатам на небесной сфере, необходимы измерения двумерного спектра простран-
пространственных частот на гш-плоскости, где v — координата в направлении север-юг,
как показано на рис. 2.7 а. Подобным образом необходимо определить двумерную
систему координат (/,га) на небесной сфере. Начало (/,т)-координат определяется
опорным положением или фазовым центром (опорной фазой), которые были вве-
введены в предыдущем разделе. Ранее в этой главе при рассмотрении одномерных
функций можно было определить / в формуле B.2) через синус угла. В двумерном
анализе I u m определяются как косинусы углов между направлением (/, т) и осями
и ж v соответственно, как показано на рис. 2.7 в. Если угол между направлением
(/,777,) и осью w мал, то / и 777, могут рассматриваться как компоненты этого угла,
измеряемые в радианах, в направлениях восток—запад и север—юг соответственно.
Чтобы измерить видность как функцию и и v для источника вблизи небесного
экватора, необходимы наблюдения с двумерной решеткой интерферометров, т. е.
с решеткой, в которой базы между парами антенн образуют проекции как в на-
направлении север-юг, так и в направлении восток-запад. И, хотя мы рассматри-
рассматривали только базы восток-запад, результаты, полученные для углов, измеряемых
относительно плоскости, ортогональной линии базы, справедливы для баз любого
направления.
Источник с высоким склонением (находящийся вблизи полюса небесной сферы)
может быть картографирован в двух измерениях как двумерной, так и одномерной
2.4]
Двумерный синтез
65
v периодов на рад.
q периодов
на рад.
периодов
на рад.
Рис. 2.7. а — плоскость uv, на которой стрелкой показана пространственная частота д,
измеряемая в периодах на радиан, для одной фурье-компоненты карты (или изображения)
интенсивности радиоисточника. Компоненты ил v пространственной частоты измеряются
вдоль осей восток—запад и север—юг, соответственно, б — плоскость 1т, в которой един-
единственная компонента пространственной частоты в области определения интенсивности
имеет форму синусоидальных изменений на небесной сфере. Показанные на рисунке
волны соответствуют одной такой компоненте. Диагональными линиями показаны гребни
максимальной интенсивности. Точками показаны положения этих максимумов вдоль ли-
линий в трех направлениях. В направлении, перпендикулярном гребням, частота колебаний
равна q периодов на радиан, а в направлениях, параллельных и и v осям — и и v периодам
на радиан соответственно, в — координаты (и, г>), определяющие плоскость, и перпендику-
перпендикулярная ей координата w. Координаты (Z,ra) используются для определения направления
на небесной сфере в двух измерениях и определяются как косинусы углов, образованных
с осями и ж v соответственно
решетками, как показано на рис. 1.15 и далее объясняется в гл. 4. При вращении
Земли проекция базы на небесную сферу также вращается и укорачивается. График
изменения длины и направления проекции базы представляет собой эллипс на uv-
плоскости. Параметры эллипса зависят от склонения источника, длины, ориентации
и широты центра базы. При разработке решеток апертурного синтеза относитель-
относительные положения антенн выбираются таким образом, чтобы обеспечить распределе-
распределение измерений в и и г>, согласующееся с заданным угловым разрешением, полем
зрения, диапазоном склонений и уровнем боковых лепестков, как обсуждается
в гл. 5. Затем двумерное распределение интенсивности получается посредством
двумерного преобразования Фурье полученной из наблюдений видности V(u,v).
2.4.1. Теорема проекции—сечения. Некоторые важные соотношения меж-
между одномерными и двумерными функциями интенсивности и видности обобщены
на рис. 2.8, которым иллюстрируется теорема «проекции—сечения» преобразований
Фурье (Bracewell, 1956, 1995, 2000). В верхней левой части рисунка показано дву-
двумерное распределение интенсивности источника /(/, т), а в нижнем правом углу —
соответствующая функция видности V(u, v). Эти две функции связаны двумерным
преобразованием Фурье, как отмечено на указателях между ними. Отметим общее
свойство преобразований Фурье: размер в одной области определения соотносится
инверсно с размером в другой области определения. В левой нижней части рисунка
показана проекция /(/, т) на ось / — одномерное распределение интенсивности /].(/).
Эта проекция получается линейным интегрированием вдоль линий, параллельных
оси т, как определяется формулой A.9). 1\ связано одномерным преобразованием
Фурье с видностью, измеренной вдоль оси и и показанной в нижней правой части
3 Томсон
66
Введение в теорию интерферометрии и синтеза изображений
[Гл.2
рисунка: т.е. профилем сечения V(u,0) функции видности V(u,v), показанным
заштрихованной областью на графике. V(u, 0) может быть измерена, например, по
наблюдениям источника при его прохождении через меридиан с набором баз интер-
интерферометров в направлении восток-запад. Это соотношение встречалось в гл. 1 при
описании интерферометра Майкельсона, и пример такой пары функций показан
на рис. 1.5. В правой верхней части рисунка показана проекция V(u,v) на ось и —
Vi(u) = JV(u,v) dv. Она связана одномерным преобразованием Фурье с профилем
сечения интенсивности источника /(/,0) вдоль оси /, показанным в правой верхней
части рисунка заштрихованной областью. Соотношение между проекциями и се-
сечениями не ограничивается осями и и /, но применимо к любому набору осей,
Ш,т)
1A,0)
Пи)
Направление
интегрирования
Направление
интегрирования
О
Рис. 2.8. Иллюстрация теоремы «проекции—сечения», объясняющая соотношение между
одномерными проекциями и поперечными сечениями функций интенсивности и видности.
Одномерные преобразования Фурье расположены горизонтально, а проекции — верти-
вертикально. Символами F и 2F обозначены одномерное и двумерное преобразования Фурье
соответственно. См. для дальнейших пояснений текст. С разрешения журнала из статьи
(Bracewell, Strip Integration in Radio Astronomy, Aust. J. Phys. Vol. 9, p. 208, 1956)
параллельных в двух областях определений. Например, интегрирование 1A, т)
вдоль линий, параллельных ОР, даст в результате кривую, преобразование Фурье
которой будет профилем сечения V(u,v) вдоль линии QR.
Соотношения, представленные на рис. 2.8, применимы к преобразованиям Фурье
в целом и нашли применение в радиоастрономии на начальном этапе развития
этой науки. Например, определяя двумерную интенсивность источника из серий
веерного сканирования при различных углах, можно получить значения V вдоль
ряда линий, проходящих через начало координат гш-плоскости, получив тем самым
двумерную видность V(u, v). В этом случае /(/, т) может быть получено двумерным
преобразованием Фурье. В годы становления радиоастрономии, до того как стали
широко использоваться компьютеры, такие вычисления были очень трудоемкой
задачей, поэтому были разработаны различные альтернативные процедуры получе-
получения изображений для веерного сканирования (Bracewell, 1956; Bracewell and Riddle,
1967).
2.4] Цитированная литература 67
Цитированная литература
Bracewell R. TV., Radio Interferometry of Discrete Sources, Proc. IRE, 46, 97-105, 1958.
Bracewell R. TV., Strip Integration in Radio Astronomy, Aust. J. Phys., 9, 198-217, 1956.
Bracewell R. TV., The Fourier Transform and Its Applications, McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Bracewell R. TV., Two-Dimensional Imaging, Prentice-Hall, Englewood Cliffs, NJ, 1995.
Bracewell R. N. and Riddle A. C, Inversion of Fan Beam Scans in Radio Astronomy, Astro-
phys. J., 150, 427-434, 1967.
Bracewell R. N. and Roberts J. A., Aerial Smoothing in Radio Astronomy, Aust. J. Phys., 7,
615-640, 1954.
Champeney D. C, Fourier Transforms and Their Physical Applications, Academic Press,
London, 1973.
Глава 3
АНАЛИЗ ОТКЛИКА ИНТЕРФЕРОМЕТРА
В этой главе мы проведем полный двумерный анализ отклика интерферометра
без аппроксимации малых углов и затем рассмотрим приближение малого поля
зрения, обычно применяемое в преобразовании измерений видности в распреде-
распределении интенсивности. Затем мы обсудим соотношение между кросскорреляцией
принятых сигналов и кроскорреляционным энергетическим спектром, следующее
из соотношения Винера—Хинчина и являющееся основой интерферометрии спек-
спектральных линий. В этой главе также дан анализ отклика приемной системы в целом.
В приложении рассмотрены некоторые подходы к представлению сигналов шумовой
природы, включая аналитический сигнал.
3.1. Связь интенсивности и видности преобразованием
Фурье
Источник
Для начала мы выведем соотношение между интенсивностью и вид-
ностью в независимом от системы отсчета виде, а затем покажем, какое
влияние выбор системы координат оказывает на знакомую форму преоб-
преобразования Фурье. Предположим, что наблюдаемый источник сопровожда-
сопровождается антеннами, что является наиболее общим случаем, и пусть введенное
в разд. 2.3 направление опорной фазы
задано единичным вектором So, показан-
показанным на рис. 3.1. Это направление, ко-
которое иногда называется фазовым цен-
центром сопровождения, определяет центр
картографируемого поля. Мощность из-
излучения, принимаемая каждой из двух
антенн от элемента источника, заклю-
заключенного в пределах телесного угла dQ
и находящегося в направлении s = Sq +
+ о-, равна A/2) А(сг) I(а) Аи du, где
А (<т) — эффективная площадь каждой
антенны, 1(<т) — распределение интен-
интенсивности источника, наблюдаемого на
разнесенных антеннах, и Аи — полоса
пропускания приемной системы. Легко
видеть, что это выражение имеет раз-
размерность мощности, поскольку / изме-
измеряется в единицах Вт-м~2-Гц~1-ср~1. Из
соображений, отмеченных при выводе выражений B.1) и B.2) с учетом условия
нахождения источника в дальней зоне, следует, что соответствующий сигнал на
выходе коррелятора пропорционален принимаемой мощности излучения и интерфе-
интерференционному члену cos Bттитд), где тд — геометрическая задержка. Если вектором
Da обозначить базу, измеряемую в длинах волн, то итд = Da -s = Da • (sq + <т).
Таким образом, выходной сигнал коррелятора может быть представлен как
Рис. 3.1. Векторы базы и направлений,
определяющие интерферометр и источник.
Источник показан замкнутой линией на
небесной сфере
3.1] Связь интенсивности и видности преобразованием Фурье 69
r(DA, s0) = Av Г А(сг) 1{сг) cos [2ttDa • (s0 + <r)] du =
= Av cos BttDa • s0) [ A(cr) I (a) cos BttDa • <r) du-
4тг
- Av sin BttDa • s0) [ A(<r) I (a) sin BttDa • cr) du. C.1)
4тг
Отметим, что для интегрирования по dQ отклика на источник в формуле C.1)
необходимо выполнение условия пространственной некогерентности, т. е. излуча-
излучаемые различными элементами источника dQ волновые сигналы должны быть
некоррелированны. Это предположение справедливо по существу для всех кос-
космических радиоисточников. Пространственная когерентность рассматривается да-
далее в разд. 14.2. Пусть А о — эффективная площадь антенны в направлении
Sq центрального лепестка. Введем нормированную диаграмму направленности
An(ct) = A(ct)/Aq и рассмотрим модифицированное распределение интенсивности
An((t)I((t). Определим на этот раз комплексную функцию видности 1) как
V = | V| ej^ = J AN(cr) I (a) e~j2^x'" du. C.2)
4тг
Далее, разделяя действительную и мнимую части, получим
j AN(cr) I (a) cos BttDa- a) du = \V\ cos фу, C.3)
4тг
An((t)I((t) sinB7rDA-<r)dft = -|V| sin0v C.4)
4тг
и из выражения 3.1
r(DA, s0) = A0Av |V| cos BttDa- s0 - </>v). C.5)
Таким образом, выходной сигнал коррелятора может быть представлен в виде ин-
интерференционной диаграммы направленности, соответствующей гипотетическому
точечному источнику в направлении опорной фазы Sq. Как отмечено ранее, обыч-
обычно это центр или номинальное положение картографируемого источника. Модуль
и фаза V равны амплитуде и фазе интерференционных лепестков, причем фаза из-
измеряется относительно интерференционной фазы гипотетического источника. Как
было определено выше, V имеет размерность плотности потока [Вт-м~2-Гц~1], что
соответствует ее связи с / преобразованием Фурье. Некоторые авторы определяют
видность как нормированную безразмерную величину; в этом случае необходимо
восстановление шкалы интенсивности получаемого изображения. Отметим, что при
х) Формулируя фундаментальное в картографировании методом апертурного синтеза
соотношение преобразований Фурье, следующее из выражения C.2), мы используем отри-
отрицательный аргумент экспоненты для вывода комплексной функции видности (или функ-
функции взаимной когерентности) из распределения интенсивности и положительный — для
обратной операции. С физической точки зрения выбор чисто произволен, и в литературе
встречаются примеры как такого, так и противоположного подхода. Мы следуем подходу
Борна и Вольфа (Born and Wolf, 1999), и Брейсуэлла (Bracewell, 1958).
70
Анализ отклика интерферометра
[Гл. 3
Полюс
выводе формулы C.5) предполага-
предполагалось, что ширина полосы частот
мала по сравнению с центральной
частотой.
Для определения системы ко-
координат рассмотрим геометриче-
геометрическую ситуацию, показанную на
рис. 3.2. Центр картографируемо-
картографируемого поля сопровождается двумя
антеннами. Они предполагаются
идентичными; в противном слу-
случае, An (а) — среднее геометри-
геометрическое их диаграмм направленно-
направленности. Величина вектора базы из-
измеряется в длинах волн на цен-
центральной частоте полосы наблю-
наблюдений, и база имеет проекции
u,v,w в правой системе коорди-
координат, где и и v находятся в плоско-
плоскости, ортогональной направлению
на опорную фазу. Проекция ба-
базы v измеряется к северу на плос-
плоскости, проходящей через начало
координат, источник и полюс ми-
мира, а и — к востоку. Проекция
w измеряется в направлении So,
т. е. в направлении опорной фа-
фазы. В преобразовании Фурье поло-
положение опорной фазы становится
началом системы отсчета получа-
получаемого распределения интенсивно-
интенсивности /(/,?77,), где / и т — направ-
направляющие косинусы относительно осей и и v. Применяя эти координаты, получим
Рис. 3.2. Геометрическое соотношение между на-
наблюдаемым источником /(/, га) и интерферомет-
интерферометром, или парой антенн решетки. Вектор базы, вы-
выраженный в длинах волн, имеет длину D\ и про-
проекции и, v, w
DA-s0 = w,
• s = (ul + vm + wyl — I2 — m2 ),
ло _ dldm
~ y/l-l2 - m2 '
C.6)
где коэффициент \/l — I2 — m2 равен третьему направляющему косинусу п отно-
относительно оси w *). Отметим также, что DA- <х = T)\- s — DA- Sq. Таким образом, из
) Выражение для dQ получается из рассмотрения сферы единичного радиуса с центром
в начале системы отсчета u,v,w. Точка Р на сфере с координатами (u,v,w) проецируется
на плоскость uv при и = l,v = т и приращениями dl, dm определяется луч квадратно-
квадратного сечения, проходящий через (u,v,0) параллельно оси w. Луч образует угол arccosn
с нормалью к поверхности сферы в точке Р, и dQ соответствует площадке отсекаемого
лучом участка поверхности, равной dldm/n или dl dm/y/l — I2 — га2 . С другой стороны,
телесный угол может быть представлен в полярных координатах как сЮ = sin в dO d(f), где
3.1]
Связь интенсивности и видности преобразованием Фурье
71
выражения C.2) получим
оо оо
(u,v,w) =
— оо —оо
х ехр \-j2n \ul + vm + wUl-l2 - т2 - 1I ) / dldm -. C.7)
^ L ^J д/l _ /2 _ Ш2
Сомножитель е-7'271"™ в правой части уравнения C.7) появляется в результате изме-
измерения углового положения относительно оси w. Для источника на оси w аргумент
экспоненты в выражении C.7) равен нулю, так как / = т = 0. Для любого другого
источника фаза интерференции измеряется относительно фазы источника на оси
гу, совпадающей с направлением опорной фазы so- Функция Ajyl в уравнении C.7)
равна нулю при I2 + т2 ^ 1и практически уменьшается до очень малых значений
в направлениях за пределами поля картографирования в результате влияния диа-
диаграмм направленности антенн, отклика по полосе пропускания, или как следствие
конечных размеров источника. Таким обра-
образом, мы можем расширить пределы инте-
интегрирования до =Ь оо. Отметим однако, что
в уравнении C.7) не требуется предполо-
предположение малости углов. Причина, по которой
мы в теории интерферометра пользуемся
направляющими косинусами, а не линейны-
линейными мерами углов, состоит в том, что они по-
появляются в экспоненциальном члене этого
соотношения.
Система координат (/, т), определенная
выше, удобна для представления распре-
распределения интенсивности. Она соответству-
соответствует проекции небесной сферы на плоскость,
касательную к центру картографируемого
поля, как показано на рис. 3.3. Расстояние
от начала координат (/,т) до любой точ-
точки на карте пропорционально синусу со-
соответствующего угла на небесной сфере,
так что для малых областей картографиро-
картографирования расстояния почти пропорциональны
соответствующим углам. Это же соотноше-
соотношение обычно применяется к полю зрения оптического телескопа. Для подробного
анализа соотношений на небесной сфере и касательных плоскостях см. (Konig,
1962).
Если бы все измерения могли быть выполнены с антеннами, расположенными на
плоскости, ортогональной к направлению w, так что w = 0, то выражение C.7) све-
свелось бы к точному двумерному преобразованию Фурье. В общем случае это не так,
и теперь мы рассмотрим способы, позволяющие применять преобразование. Для
начала напомним, что основой синтеза радиокарт является измерение V в широком
диапазоне значений и л v. Для наземных решеток этого можно достичь изменением
длины и направления базы, а также сопровождением центра наблюдаемой области
Рис. 3.3. Картографирование небесной
сферы на плоскость, показанное в одном
измерении. Положение точки Р опреде-
определяется направляющим косинусом га от-
относительно оси v. При проецировании
на плоскую поверхность с масштабом,
линейным по га, точке Р будет соответ-
соответствовать точка Р1, находящаяся на рас-
расстоянии от центра поля С, пропорцио-
пропорциональном sin ф
0 и ф — полярный и азимутальный углы в пространстве uvw, т.е. в = arcsin \/l2 + га2
и ф = arctg (m/l). Вычисление якобиана перехода от координат (в, ф) к координатам (/, га)
дает в результате сЮ = dl dm/у/1 — Р — га2 (Apostol, 1962).
72
Анализ отклика интерферометра
[Гл. 3
при вращении Земли. Суточное вращение приводит к изменению проекции Бд на
плоскость uv. Таким образом, продолжительность наблюдений часто составляет 6-
12 ч. При движении антенн в пространстве вследствие вращения Земли вектор базы
находится в одной плоскости только при условии, что проекция Da на ось вращения
равна нулю, т. е. база должна быть ориентирована в направлении восток-запад на
поверхности Земли. В общем случае мы имеем дело с трехмерным распределением
измерений V. Простейшая форма соотношения преобразований, которую можно
использовать, основана на приближении, верном до тех пор, пока размеры синте-
синтезируемого поля не слишком велики. Если / и т достаточно малы, то слагаемым
--! (I2 +
m2) w
C.8)
можно пренебречь и уравнение C.7) сводится к виду
оо оо
V(u v w)~V(u v 0)- [ I AN(l,m)I(l,ml j27T (ul+vm) d[ d /3 g)
J J VI - I2 - m2
— оо —оо
Таким образом, для ограниченного диапазона значений /ит, V(u, v,w) приближен-
приближенно можно считать не зависящей от ги, и для обратного преобразования получаем
AN(l,m) 1A,т)
оо оо
= [ [ V(u,v)ej2*{ul+vmUudv. C.10)
— оо —оо
В этом приближении зависимость от w обычно не учитывается, и видность запи-
записывается как двумерная функция V(u,v). Отметим, что знаменатель \/1 — I2 — т2
в выражениях C.9) и C.10) может быть при желании учтен в функции АнA,гп).
Уравнение C.10) представляет собой форму используемой в оптике теоремы Ван
Циттерта-Цернике, которая рассматривается в разделе 14.1.
Вследствие аппроксимации в выражении C.9) появляется фазовая ошибка,
равная умноженной на 2тг величине отброшенного слагаемого, т. е. равная тг(/2 +
+ m2)w. Размеры синтезируемого поля ограничиваются необходимостью сведения
этой ошибки к некоторому приемлемому
значению, что можно грубо оценить сле-
следующим образом. Если наблюдаемый источ-
источник сопровождается антеннами до низких
углов места, то величина w может прибли-
приблизиться к максимальному расстоянию между
антеннами решетки (Da)max, как показано
на рис. 3.4. Кроме того, если измеренные
пространственные частоты равномерно рас-
распределены вплоть до максимальных баз, то
ширина синтезированного лепестка въ при-
примерно равна (?>А)тах- Таким образом, мак-
максимальная фазовая ошибка равна приблизи-
приблизительно
Рис. 3.4. При наблюдениях с азимута-
азимутами, близкими к азимуту базы и с малы-
малыми высотами, пространственная компо-
компонента w становится сравнимой с дли-
длиной базы D\, выраженной в длинах
волн
C.11)
3.1]
Связь интенсивности и видности преобразованием Фурье
73
где Of — размер синтезируемого поля. Условие, что фазовые ошибки не могут быть,
скажем, больше 0,1 рад, в этом случае записывается как
ef<\V6b, C.12)
где углы измеряются в радианах. Например, если въ = 1", то Of < 2,5'. Многие
синтезированные карты в астрономии получают в пределах этого ограничения, но
позже мы обсудим способы картографирования более протяженных областей.
Вернемся теперь к случаю решеток, элементы которых расположены только
в направлении восток-запад, и рассмотрим условия, при которых можно принять
w = 0, и возникающие при этом эффекты. Пусть система координат (u,v,w) пово-
поворачивается относительно оси и до тех пор, пока ось w не совпадет с направлением
на полюс мира, как показано на рис. 3.5. Величины, измеренные в этой системе,
обозначим штрихами. Оси и'', v' находятся в плоскости, параллельной экватору
Экваториальная
плоскость
Рис. 3.5. Система координат (V, г/, w') для решетки восток-запад. Плоскость и v является
плоскостью экватора, и векторы баз описывают дуги концентрических окружностей при
вращении Земли. Отметим, что направления осей и' и г/ выбраны таким образом, что ось
v находится в плоскости, проходящей через точки полюса мира, наблюдателя и точку
наблюдений (ао,6о). Карта небесной полусферы получается как проекция на касательную
плоскость в точке полюса мира преобразованием Фурье между плоскостями u'v' и I'm!.
Также показаны координаты (u,v,w) при наблюдениях в направлении (ао,5о)
Земли. Базы восток-запад содержат компоненты только в этой плоскости (т. е. w' =
= 0), и их векторы описывают концентрические окружности относительно начала
координат (г/, г/) при вращении Земли. Используя формулу C.7), можно записать
V(u>
оо оо
', m'
/', m')
l' dm
. - Vz - т'<
C.13)
— oo — oo
где Г, т! — направляющие косинусы относительно и'', г/. Уравнение C.13) справед-
справедливо для всей полусферы над плоскостью экватора. Обратным преобразованием
получим
AN(l',m')I(
л/i -1'2 -
оо оо
1',т') = Г Г
m/2 J J
(зл4)
— oo —oo
74 Анализ отклика интерферометра [Гл. 3
В картографировании этим методом полусфера проецируется на касательную плос-
плоскость к полюсу мира, как показано на рис. 3.5. На практике, однако, карта обыч-
обычно строится для малой области в пределах главных лепестков диаграмм направ-
направленности антенн. В окрестности такой площадки с центром (ao,So) п0 прямому
восхождению и склонению угловые расстояния на карте сжимаются в sinJ0 раз
в направлении т!. Кроме того, при картографировании окрестности («о? ^о) УД°бн°>
если точка отсчета позиционных угловых переменных совмещается с точкой (ао,5о).
Изменение масштаба и сдвиг начала отсчета могут быть выполнены преобразова-
преобразованием координат
/ = /'? т" = {т! — cos Jo) cosec So- C.15)
Если мы запишем левую часть уравнения C.14) как F(l',m'), то
F(l',m')?±V{ur,v') C.16)
F[lf,(m' -cos 60) cosec Jo] ^ |sin 60\V(uf, v' sin 50) e-j27rv'cos6°, C.17)
где ^ обозначает преобразование Фурье. При выводе соотношения C.17) мы ис-
использовали замену переменных в паре Фурье и применили теоремы подобия и сдви-
сдвига (см., например, Bracewell, 2000). Координатами (uf, v' sin So) в правой части
соотношения C.17) определяется проекция экваториальной плоскости на перпен-
перпендикулярную направлению (ао,#о) плоскость uv. В системе координат (u,v,w) и =
= и' и v = vf smSo- Координата w, показанная на рис. 3.5, равна —vf cosSo- Таким
образом, e~i27TV cosS° в соотношении C.17) — тот же коэффициент, что и в уравне-
уравнении C.7), поскольку фаза видности измеряется относительно точечного источника
в направлении w. Уравнение C.14) теперь принимает вид
АмA,гп") 1A,т")
т"
л/l - I2 - m
оо
= [ [ V(ul,v'sm50)\sm5o\e-j2™'cosSoej2*iu'l'+v'm'Uu'dv'=
J J
oo oo
= I" I" V(u,v)ej2*{ul+vm")dudv. C.18)
— оо —оо
— ОО —ОО
Подобный анализ приводится в работе (Brouw, 1971).
При выводе уравнения C.18) из C.14) мы переопределили координату т, но не
делали никаких аппроксимаций. Уравнение C.18) имеет ту же форму, что и C.10),
где был отброшен сомножитель, представленный формулой C.8). Следовательно,
если мы используем основанную на пренебрежении этим членом схему картографи-
картографирования C.10) в наблюдениях с решеткой восток-запад, то карта будет искажена
фазовыми ошибками в точном соответствии с переопределением переменной т
на тп. Поскольку тп получена из направляющего косинуса относительно оси v'
в экваториальной плоскости, то наблюдается прогрессирующее изменение углового
масштаба карты в направлении север-юг. Множитель cosec So в уравнении C.15)
дает правильный угловой масштаб в центре карты, но эта простая коррекция при-
применима только для малых областей. Здесь важно отметить, что если измеренные
3.2] Кросс-корреляция и соотношение Винера-Хинчина 75
в плоскости значения видности представлены в (и, г>, w)-координатах, то kj — ли-
линейная функция от и и и (и линейная функция только от v для баз восток-запад).
Следовательно, фазовая ошибка тт (/2 + m2)w линейна относительно и л v. Фазовые
ошибки такого типа вносят в итоговую карту эффект позиционных смещений, но
однозначное соответствие точек на карте и небесной сфере сохраняется. Эффект,
таким образом, заключается в образовании предсказуемой и, следовательно, ис-
исправляемой дисторсии координат.
Как ясно из рис. 3.5, если все измерения выполнены в плоскости u'v1', то значения
v на плоскости uv значительно сокращаются для направлений, близких небесному
экватору. Чтобы получить двумерное разрешение в этих направлениях, необходимы
базы с проекциями, параллельными земной оси. Конструкции таких решеток рас-
рассматриваются в гл. 5. Влияние вращения Земли, следовательно, состоит в том, что
измерения в пространстве uvw распределены таким образом, что не находятся более
в одной плоскости, если только наблюдения не кратковременны. Во многих случаях
ограничение на размер синтезируемого поля, представленное соотношением C.12),
приемлемо. Однако, на низких частотах (~100 МГц и менее) антенны имеют широ-
широкие главные лепестки, и часто необходимо картографирование по всему лепестку,
чтобы избежать эффекта путаницы источников. При таких обстоятельствах воз-
возможно применение нескольких методов, основанных на следующих подходах.
1. Уравнение C.7) может быть представлено в форме трехмерного преобразова-
преобразования Фурье. Итоговое распределение интенсивности в этом случае определяет-
определяется на поверхности единичной сферы в пространстве 1тп.
2. Большие карты могут быть составлены из карт меньших размеров, каждая из
которых соответствует ограниченному полю зрения двумерного преобразова-
преобразования. Центры отдельных карт должны быть взяты в точках касания с той же
единичной сферой, что и в предыдущем пункте.
3. Поскольку в большинстве наземных решеток антенны расположены на при-
приблизительно плоской поверхности, то измерения, выполненные на коротких
интервалах времени, оказываются близкими к плоскости в гшги-пространстве.
Таким образом, при обработке наблюдений продолжительностью несколько
часов можно синтезировать ряд карт короткой длительности, соединяемых
последовательно после соответствующей коррекции масштаба координат.
Практическая реализация трех описанных выше подходов требует применения тех-
техники нелинейной свертки, описываемой в гл. 11. Более подробный анализ исполь-
используемых таким образом методов дан в разд. 11.8.
3.2. Кросс-корреляция и соотношение Винера—Хинчина
Соотношение преобразований Фурье между энергетическим спектром волново-
волнового сигнала и автокорреляционной функцией, представленное выражениями B.6)
и B.7), известно как соотношение Винера-Хинчина. Полезно также рассмотреть
соответствующее соотношение для кросс-корреляционной функции двух различных
волновых сигналов. Отклик коррелятора, применяемого в радиоинтерферометре,
можно записать как
т
г(т) = Hm J- [ Vi(t) V2*(t - т) dt. C.19)
Т—)-оо ?1 J
-Т
76 Анализ отклика интерферометра [Гл. 3
Практически корреляция измеряется на конечных интервалах времени 2Т, как
правило, длительностью несколько секунд или минут, но больших по сравнению
как с периодом, так и с обратной величиной полосы частот волновых сигналов.
Коэффициент 1/BТ) иногда опускается, но для рассматриваемых здесь процессов,
он необходим, чтобы обеспечить сходимость. Кросс-корреляция обозначается сим-
символом пентаграммы (•):
т
V1(t)*V2(t)= lim J- [ Vi(*)y2*(*-r)d*. C.20)
Т-юо 21 J
-т
Этот интеграл можно представить в виде свертки следующим образом:
V1(t)*V2{t) = lim ±= \ V1(t)V2*_(T-t)dt = V1(t)*V2*_(t), C.21)
— оо
где V2-(i) = V2(—i). Преобразования Фурье по z/, t, обозначаемые ^, выглядят
как: Vi(t) ^ V\(v), V2{t) ^ V2(v) и V2*_(t) ^ V2 {у) "О • Тогда по теореме свертки
получим
V1(t)*V2(t) ^ ViHVfiv). C.22)
Правая часть соотношения C.22) известна как кросс-корреляционный спектр мощ-
мощности Vi(t) и V2(t). Кросс-корреляционный спектр мощности является функцией ча-
частоты, и мы видим, что он соответствует преобразованию Фурье кросскорреляции,
являющейся функцией т. Это полезный результат, и при V\ = V2 он переходит в со-
соотношение Винера—Хинчина. Соотношение C.22) — основа кросс-корреляционной
спектроскопии, описываемой в 8.7.2.
3.3. Основы отклика приемной системы
С математической точки зрения, основными составляющими приемной систе-
системы интерферометра являются следующие устройства: антенны, преобразующие
принимаемые электромагнитные поля в высокочастотные напряжения; фильтры,
выделяющие полосы частот для обработки; коррелятор, образующий усредненное
произведение сигналов. Эти элементы показаны на рис. 3.6. Большая часть других
эффектов может быть представлена в виде мультипликативных коэффициентов
усиления, которыми мы здесь пренебрежем, или как в случае изменений в полосе
пропускания, они могут быть учтены в выражениях для фильтров. Таким образом,
мы предполагаем амплитудно-частотные характеристики антенн и величину при-
принимаемого сигнала фактически постоянными по полосе пропускания фильтров, что
вполне реально в большинстве наблюдений непрерывного излучения.
3.3.1. Антенны. Для независимого анализа откликов двух антенн мы долж-
должны определить их диаграммы направленности по напряжению, поскольку отклик
коррелятора представляет собой произведение напряжений сигналов. Диаграмма
направленности антенны по напряжению Уа{1,гп) имеет размерность длины и яв-
является откликом на напряженность электрического поля, измеряемую в вольтах на
х) Мы используем знак циркумфлекса (крышечка) для обозначения функций частоты
в случаях, когда одной и той же буквой обозначены функции и частоты, и времени.
3.3]
Основы отклика приемной системы
77
метр. УдG,т) — преобразование Фурье распределения поля ?(X,Y) по апертуре,
как показано в 14.1. X и Y — позиционные координаты в пределах апертуры
антенны. Опуская постоянные коэффициенты, мы можем записать
C.23)
Фильтр
Hi(v)
Фильтр
H2(v)
Коррелятор
где Л — длина волны. В выражении C.23) X и Y измеряются относительно центра
апертуры каждой антенны. Диаграмма направленности по мощности пропорцио-
пропорциональна квадратам модулей диаграмм направленности по напряжению. Уд(/,ттг) —
комплексная величина и в ней представлены
и фаза, и амплитуда напряжений высокоча-
высокочастотных сигналов на выходах антенн. Отклик
интерферометра (антенны которого обозначе-
обозначены индексами 1 и 2) пропорционален свертке
VaiV^-) которая действительна в случае иден-
идентичных антенн. Эффективная площадь каж-
каждой антенны А{1,т) — также действительная
величина. На практике отклики антенн обыч-
обычно определяют как АA,т), и Уа{1,гп) заменя-
заменяют на величину у/АA,т), пропорциональную
модулю Уа(гп,п). Фаза, появляющаяся вслед-
вследствие различия антенн, исключена из рассмот-
рассмотрения, но фактически учитывается в фазовых
откликах усилителей, фильтров, линий пере-
передачи и других элементов на пути сигнала до
входа коррелятора. Полный инструментальный
отклик интерферометра как по фазе, так и по
амплитуде калибруется наблюдениями неразре-
неразрешенного источника с известными координатами
и плотностью потока.
В случае, когда источник сопровождается
антеннами, оси диаграмм направленности ан-
антенн и центр источника находятся в начале
(/, 777,)-координат. Если ЕA,т) — принимаемое поле, то напряжение на выходе ан-
антенны может быть записано (без учета постоянных коэффициентов усиления) как
Выход, г
Рис. 3.6. Основные составляющие
приемной системы двухэлементно-
двухэлементного интерферометра
V =
C.24)
Если антенны не сопровождают источник, применяется соотношение свертки в фор-
форме, приведенной в выражении B.15).
3.3.2. Фильтры. Фильтры на рис. 3.6 рассматриваются как суммарное воз-
воздействие элементов, определяющих амплитудно-частотную характеристику при-
приемных каналов, включая усилители, кабели и другие компоненты, в том числе
и собственно фильтры. Амплитудно-частотная характеристика фильтра обозначена
H(v). Сигнал на выходе фильтра Vc(y) связывается с сигналом на его входе V{v)
следующим образом:
= Н{у) V{y).
C.25)
78 Анализ отклика интерферометра [Гл. 3
Преобразование Фурье Н(у) по частоте дает импульсную характеристику фильтра
h(t), которая представляет собой отклик на импульс напряжения S(i) на его входе.
Таким образом, в области времени уравнению C.25) соответствует
Vc(t)= [ h(t')V(t-t')dt' = h(t)*V(t). C.26)
Для описания фильтров обычно применяют амплитудно-частотную, а не импульс-
импульсную характеристику, поскольку первая более непосредственно связана с представ-
представляющими интерес свойствами приемной системы и легче измеряется.
3.3.3. Коррелятор. Коррелятором г) обеспечивается кросс-корреляция двух
подаваемых на него напряжений. Если V±(t) и V^(^) — напряжения сигналов на
входе коррелятора, то сигнал на его выходе равен
т
r(r)= lim -5- [ Vi(*)V2*(*-<r)d*. C.27)
Т-Юо 21 J
-Т
Время т, на которое напряжение V2 задерживается относительно напряжения Vi,
при наблюдениях непрерывного излучения поддерживается равным нулю или ма-
малой величине. Функции V\ и У2, соответствующие сигналам в формуле C.27),
могут быть комплексными. Выходом одного перемножающего устройства является
действительное напряжение или число. Для того чтобы получить комплексную
кросс-корреляцию, представляющую как амплитуду, так и фазу видности, можно
записать интерференционные колебания и измерить их фазу, или использовать ком-
комплексный коррелятор, состоящий из двух перемножающих модулей, как описано
в 6.1.7. Как следует из уравнений C.20) и C.22), преобразование Фурье г (г) соответ-
соответствует кросс-корреляционному спектру мощности, используемому в наблюдениях
спектральных линий. Его обычно получают введением в сигнал ряда аппаратных
задержек, чтобы определить кросс-корреляцию как функцию т, как описано в 8.7.3.
3.3.4. Отклик на принимаемое излучение. Мы используем индексы 1 и 2
для обозначения двух антенн и приемных каналов, как показано на рис. 3.6. Отклик
антенны 1 на поле сигнала Е{1,т), определяемый формулой C.24), представляет
собой спектр по напряжению V(v). Умножим его на H{v), чтобы получить сигнал
на выходе фильтра, и затем выполним преобразование Фурье, чтобы перейти из
области частот в область времени. Тогда
оо оо оо
Vcl(t) = [ [ [ E(l,m) y/Aifam) Ях{у) ej2lTUt dldmdv. C.28)
—00 —00 —00
Подобное выражение может быть записано и для сигнала VC2(t) антенны 2, а вы-
выходной сигнал коррелятора соответствует формуле C.27). Отметим также, что если
х) Термином коррелятор, как правило, называют устройство, измеряющее комплексную
кросс-корреляционную функцию г(т), определяемую формулой C.27). Этот термин также
применяется для обозначения простых систем, в которых временная задержка т равна
нулю или оба сигнала представлены действительными функциями. В больших системах,
осуществляющих кросс-корреляцию пар сигналов в многоэлементных решетках, могут
использоваться 10 и более корреляционных модулей для обработки сигналов большого
числа антенн и большим числом спектральных каналов. Комплексы такого типа также
обычно называют корреляторами.
3.3] Основы отклика приемной системы 79
излучение обладает некоторой степенью пространственной когерентности, то мы
должны выполнить интегрирование по / и т независимо для каждой антенны
(Swenson and Mathur, 1968), но здесь мы пользуемся обычным предположением
некогерентности. Таким образом, выходной сигнал коррелятора равен
оо оо оо оо
г(т)= lim -^ [ [ [ [ E(l,m)E*(l,m)y/A1(l,m)A2(l,m) x
Т—)-оо Zl J J J J
— оо —оо —оо —оо
) H*2(v) e^vt e-^v(t-^ dldmdtdv =
= [ [ [ 1A,m) y/Aiil,™,) A2(l,m) H^v) Щ(ь>) ej2™T dldmdv. C.29)
oo oo oo
— oo —oo —oo
Здесь мы заменили квадрат амплитуды поля на интенсивность /. Результат получен
в общей форме, поскольку применение раздельных функций отклика А\ и А2
для двух антенн позволяет учесть их различные конструктивные особенности, или
различные систематические ошибки наведения, или и то, и другое одновременно.
Также используются различные амплитудно-частотные характеристики Н\ и Н2.
В случае, когда антенны и фильтры идентичны, уравнение C.29) сводится к виду
оо оо оо
г{т) =
— оо —оо —оо
ии ии ии
т)= [ [ [ 1A, m) A(l,m) \H(v)\2 ej2nvT dldmdv. C.30)
Результат является функцией задержки г сигнала VC2(t) относительно Vci(i). Гео-
Геометрическая составляющая задержки обычно компенсируется регулируемой аппа-
аппаратной задержкой (что обсуждается в главах 6 и 7), так что г = 0 для излучения,
приходящего из направления начала координат /,т. В случае спектральных на-
наблюдений, в корреляционную систему могут включаться дополнительные элемен-
элементы задержки так, чтобы корреляция измерялась как функция т. Для волнового
фронта направления (/,га) разница времен прихода двух сигналов на коррелятор
определяется разницей их путей распространения в (ul + vm) длин волн при выпол-
выполнении условий, определямых формулами C.8) и C.9). Соответствующее различие
по времени равно (ul + vm)/v. Если мы предположим, что сигнал V\ приходит
с антенны, для которой путь распространения больше (при положительных / и т),
то из формулы C.30) получим на выходе коррелятора
оо оо оо
|2 „-?
г= [ [ [ 1A,m) A(l,m) \H(v)\2 e-j2lT(lu+rnv) dldmdv. C.31)
— оо —оо —оо
Формула C.31) показывает, что на выходе коррелятора измеряется преобразование
Фурье распределения интенсивности, модифицированного диаграммой направлен-
направленности антенны. Предположим распространенный случай, когда интенсивность и
диаграмма направленности антенны постоянна в пределах полосы пропускания
фильтров и размеры источника малы по сравнению с лучем антенны. Тогда вы-
выходной сигнал коррелятора равен
= \ \ I(l,m)A(l,m)e-j27r{lu+mv) dldm j \H(v)\2 dv =
— OO —OO
80 Анализ отклика интерферометра [Гл. 3
= A0V{u,v) | \H{v)\2dv, C.32)
где Aq — эффективная площадь антенн в направлении максимального отклика глав-
главных лепестков и V — видность. Амплитудно-частотная характеристика фильтра
является безразмерной величиной (усилением). Если амплитудно-частотные харак-
характеристики фильтров фактически постоянны в полосе частот Az/, то уравнение C.32)
сводится к виду
r = A0V(u,v)Av. C.33)
Размерность V(u,v) равна [Вт-м^-Гц], Ао [м2] и Az/ [Гц]. Это соответствует раз-
размерности выходного сигнала коррелятора г, пропорционального коррелированной
компоненте принятой мощности.
Приложение 3.1. Математическое представление сигналов
шумовой природы
Электромагнитное поле и высокочастотные сигналы с размерностью напря-
напряжения, создаваемые излучением астрономических объектов, в общем случае ха-
характеризуются изменениями случайной природы. Принимаемый волновой сигнал
обычно описывается как эргодический (усредненный по времени и по множеству
наблюдений, имеющий равные значения), что удовлетворяет определению стаци-
стационарности. Для подробного анализа см., например, (Goodman, 1985). Хотя такие
поля и напряжения действительны, часто удобно представлять их математически
как комплексные функции. Эти комплексные функции могут использоваться в экс-
экспоненциальной форме, и тогда на последнем этапе вычислений необходимо брать
их действительную часть.
Аналитический сигнал. Для представления сигналов как функций време-
времени при их анализе в оптике или радио используется определение аналитический
сигнал (см., например, Born and Wolf, 1999; Bracewell, 2000 или Goodman, 1985),
введенный Табором (Gabor, 1946). Пусть Vr(€) — действительная функция, спектр
Фурье (по напряжению) которой равен
V{v)= J VR(t) e-'2™* dt, (П3.1)
— оо
где мы воспользовались циркумфлексом для обозначения функции частоты. Обрат-
Обратное преобразование Фурье равно
оо
VR(t) = | V(v) ej2™f dv. (П3.2)
Чтобы сформировать аналитический сигнал, образуется комплексная функция,
мнимая часть которой является преобразованием Гильберта Vr(?) (см., например,
Bracewell, 2000). Один из способов получить преобразование Гильберта состоит
в умножении спектра Фурье оригинальной функции на j sgn (у) г). В преобразова-
преобразовании Гильберта какой-либо функции амплитуда ее спектральной компоненты Фурье
х) Функция sgn (у) равна +1 при v ^ 0 и — 1 при v < 0. Преобразование Фурье sgn (у)
равно —j/irt.
3.3] Приложение 3.1. Математическое представление сигналов шумовой природы 81
не изменяется, а фаза сдвигается на тг/2, причем знаки сдвига противоположны для
отрицательных и положительных частот. Преобразование Гильберта Vr(?), которое
становится мнимой частью Vj(?), получается как обратное преобразование Фурье
модифицированного спектра следующим образом:
оо 0 оо
Vi(t) = -j [ sgn (v) V(v) ej2vut dv = j [ V(v) ej2vut dv - j [ V{v) ej2vut dv.
— OO —OO 0
(ПЗ.З)
Аналитический сигнал, представляющий Vr(?), является комплексной функцией
и равен
V(t) = VR(t) + j У/(*) = | A + j2) V(v) e^vt dv + | A - f) V(v) e^vt dv =
-оо О
OO
= 2 J V(v) ej27TUt dv. (П3.4)
о
Можно заметить, что в аналитическом сигнале отрицательные частотные ком-
компоненты отсутствуют. Из формулы (П3.4) следует, что другой способ получить
аналитический сигнал действительной функции Vr(?) заключается в подавлении
отрицательных частотных компонент в спектре и увеличении амплитуды положи-
положительных частотных компонент в два раза. Можно также показать (см., например,
Born and Wolf, 1999), что
{[VR{t)f) = (iVjit)}2) = \ (V(t) V*(t)), (П3.5)
где угловыми скобками ( ) обозначено математическое ожидание. Аналитический
сигнал называется так потому, что как функция комплексной переменной он явля-
является аналитическим в нижней комплексной полуплоскости.
Из уравнений (ИЗ.2) и (ИЗ.4) получим
оо оо -,
[ V(v) ej2nvt dt = 2 Re [ V(v) ej27TUt dt . (П3.6)
-оо Ц J
Это важное равенство может использоваться для любой эрмитовой функции и со-
сопряженной ей переменной.
В большинстве случаев, представляющих интерес для радиоастрономии и оп-
оптики, полоса частот сигнала мала по сравнению со средней частотой z/q, которая
во многих инструментах является центральной частотой фильтра. Такой волновой
сигнал представляет собой синусоиду, амплитуда и фаза которой изменяются со
временем медленно по сравнению с периодом l/i^o- Аналитический сигнал в этом
случае может быть записан как
V(t) = C(t) ej [2™°*-ф(*)], (П3.7)
где С и Ф — действительные переменные. Спектральные компоненты рассматрива-
рассматриваемой функции существенны только при малых значениях \г/ — vq\. Следовательно,
82 Анализ отклика интерферометра [Гл. 3
C(t) и Ф(?) образуются низкочастотными компонентами, и характерный период из-
изменений СиФсо временем равен обратной величине полосы частот. Действительная
и мнимая части аналитического сигнала могут быть представлены как
VR(t) = C(t) cos [2тг1/0* - Ф(*)], (П3.8)
Уг(*) = C(i) sin [2тг1/0* - Ф(*)]. (П3.9)
В комплексном аналитическом сигнале модуль C(i) молено рассматривать как моду-
модуляционную огибающую, а Ф(?) — как фазу. Очевидно, что в случаях, когда ширина
полосы частот сигнала и модуляция не имеют значения, С и Ф могут считаться по-
постоянными, т. е. сигнал может быть представлен как монохроматическое колебание
с частотой z/q, что и было сделано во введении. Случай, когда полоса частот мала
по сравнению с центральной частотой, представлен формулой (П3.7) и называется
квазимонохроматическим.
Простой пример: e^27Tut — аналитический сигнал, соответствующий действи-
действительной функции от времени cosBttz/?). В спектре Фурье e^27Tut находится только
одна компонента на частоте г/, а в спектре Фурье cos Bтгг/?) — две компоненты
на частотах ±z/. Отрицательные частотные компоненты необходимо принимать во
внимание в общем случае при анализе волновых сигналов, если только они не
определены в соответствии с формализмом аналитического сигнала, когда отрица-
отрицательные частотные компоненты равны нулю. Например, отрицательные частотные
компоненты учитываются в формуле B.8). Если бы мы исключили отрицательные
частоты и удвоили амплитуду положительных, то косинусный член в формуле B.9)
следовало бы заменить на eJ °Т. Затем мы взяли бы действительную часть, чтобы
получить корректный результат. В подходе, примененном в гл. 2, отрицательные
частоты учитывать было необходимо, так как автокорреляционная функция дей-
действительна и, следовательно, ее преобразование Фурье эрмитово; т. е. действитель-
действительная и мнимая части обладают соответственно четной и нечетной симметрией на
оси частот. В этой книге мы как правило рассматриваем отрицательные частоты,
а не пользуемся аналитическим сигналом, и применяем представленное форму-
формулой (П3.6) соотношение только в случаях, когда это дает преимущества.
Интересно отметить другое свойство функций, в которых действительная и мни-
мнимая части связаны преобразованием Гильберта. Если действительная и мнимая
части волнового сигнала (т. е. функции времени) образуют пару преобразований
Гильберта, то их спектральные компоненты равны нулю на отрицательных ча-
частотах. Рассматривая обратное преобразование Фурье, можно увидеть, что если
амплитуда волнового сигнала равна нулю на отрицательных частотах при t < 0, то
действительная и мнимая части спектра образуют пару преобразований Гильберта.
Отклик любой радиотехнической системы на импульсную функцию, приложенную
в момент времени t = 0, равен нулю при t < 0, поскольку следствие не может быть
раньше причины. Функция, представляющая такой отклик, называется причинной
функцией, и к ее спектру применимо соотношение преобразований Гильберта.
Ограниченная функция. Другой вопрос в представлении волновых сигналов
связан с существованием преобразования Фурье. Условием существования преобра-
преобразования является конечное значение интеграла Фурье в пределах ±оо. И хотя это
условие выполняется не всегда, можно образовать функцию, для которой суще-
существовал бы интеграл Фурье и которая приближалась бы к исходной функции при
стремлении некоторого параметра к предельному значению. Например, исходная
функция может быть умножена на функцию Гаусса таким образом, чтобы значение
произведения стремилось к нулю при переменной интегрирования, стремящейся
к бесконечности, и интеграл Фурье существовал. Преобразование Фурье произве-
произведения приближается к преобразованию Фурье исходной функции при увеличении
3.3] Цитированная литература 83
ширины функции Гаусса до бесконечности. Такие ограниченные преобразования
подходят для периодических функций вида cosBttz/?), как показано Брейсуэллом
(Bracewell, 2000). В случае волновых сигналов шумовой природы, частотный спектр
временной функции всегда может быть получен с необходимой точностью анализом
на достаточно длительном (но не бесконечном) интервале времени. Практически
длительность временного интервала должна быть большой по сравнению со связан-
связанными с волновыми сигналами физически значимыми масштабами времени, такими
как обратные величины средней частоты и полосы частот. Таким образом, если
функция V{t) ограничена на интервале ±Т, то преобразование Фурье по частоте
может быть записано как
т
V(u) = lim ±= \ V{t) e~^vt dt. (П3.10)
-Т
Иногда полезно определить ограниченную функцию Vr(t) в виде
VT(t) = V(t), \t\^T,
(П3.11)
vT(t) = о, \t\ > т,
и записывать преобразование Фурье как
о
\т{1) e~i2™*dt (ПЗЛ2)
В случае аналитического сигнала, ограничение действительной части не обяза-
обязательно следует из ограничения преобразования Гильберта. Следовательно, может
потребоваться, чтобы пределы интегрирования по времени были не dz T, а =Ьос как
в формуле (П3.12).
Цитированная литература
Apostol Т. М., Calculus, Vol. II, Blaisdel, Waltham, MA, 1962, p. 82.
Born M. and Wolf E., Principles of Optics, 7th ed., Cambridge Univ. Press, Cambridge, UK,
1999. (Имеется перевод: Борн М., Вольф Э.. Основы оптики. — М.: Наука, 1973.)
Bracewell R. TV., Radio Interferometry of Discrete Sources, Proc. IRE, 46, 97-105, 1958.
Bracewell R. N., The Fourier Transform and Its Applications, McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Brouw W. N., Data Processing for the Westbrook Synthesis Radio Telescope, Univ. Leiden,
1971.
Gabor D., Theory of Communication, J. Inst. Elect. Eng., 93, Part III, 429-457, 1946.
Goodman J. W., Statistical Optics, Wiley, New York, 1985.
Konig A., Astrometry with Astrographs, in Astronomical Techniques, Stars and Stellar Sys-
Systems, Vol. 2, W. A. Hiltner, Ed., Univ. Chicago Press, Chicago, 1962, p. 461-486.
Swenson G. W.j Mathur Jr. and N. C, The Interferometer in Radio Astronomy, Proc. IEEE,
56, 2114-2130, 1968. (Имеется перевод: ТИИЭР, 56, 12, с. 20-36, 1968.)
Глава 4
ГЕОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ
И ПОЛЯРИМЕТРИЯ
В этой главе мы рассмотрим некоторые практические аспекты интерферомет-
интерферометрии, в том числе: базы, монтировки антенн, формы диаграмм направленности
и отклик на поляризованное излучение. Все эти аспекты связаны с системами коор-
координат и геометрическими соотношениями. Основное внимание мы сосредоточим на
наземных решетках с полноповоротными антеннами, которые хорошо иллюстриру-
иллюстрируют рассматриваемые понятия, хотя эти же подходы могут применяться и к другим
системам, например с одной или несколькими антеннами на околоземной орбите.
4.1. Координаты антенн и траектории на плоскости uv
Для описания относительных положений антенн в решетке используются раз-
различные системы координат, и одна из них, наиболее подходящая для наземных
систем, представлена на рис. 4.1. Используется правая декартова система коорди-
координат, в которой оси X и Y находятся в плоскости, параллельной экватору Земли:
ось X совпадает с плоскостью меридиана (которая определяется как плоскость,
проходящая через полюса Земли и опорную точку антенной решетки), ось Y от-
считывается в восточном направлении, и ось Z направлена к северному полюсу
мира. В координатах часового угла Н и склонения 5, оси X, У, Z соответствуют
направлениям (Н = О, 5 = 0), (Н = —6h, 5 = 0) и E =
Z = 90°). Если проекции вектора базы Т)\ в системе ко-
ко(8=90°)
Рис. 4.1. Система координат
(X, Y, Z) для определения
относительных положений
антенн. Направления осей
представлены в экватори-
экваториальных координатах часо-
часовым углом Н и склонени-
склонением 6
)
ординат (X, У, Z) равны
(u,v,w) определяются:
то его проекции
sin H cos H
— sin 5 cos H sin 5 sin H
cos 5 cos H - cos 5 sin H
0 "
cos 5
sin 5
'Xx
Yx
Zx
D.1)
Здесь (Н,5), как обычно, — часовой угол и склоне-
склонение точки фазового центра. (В наблюдениях РСДБ
принято направлять ось X по Гринвичскому мериди-
меридиану и в этом случае Н отсчитывается относительно
Гринвичского, а не местного меридиана.) Элементы
вышеприведенной матрицы преобразования представ-
представляют собой направляющие косинусы осей u,v,w отно-
относительно осей X, У, Z и могут быть легко получены из
соотношений, показанных на рис. 4.2. Вектор базы мо-
может быть также выражен через его длину D, часовой
угол h и склонение d точки пересечения направления
базы и северной небесной полусферы. В этом случае
его координаты в системе (X, У, Z) находятся как
4.1]
Координаты антенн и траектории на плоскости uv
85
Полюс мира
Местный
меридиан
Рис. 4.2. Соотношения между системами координат (X,Y,Z) и (u,v,w). Координаты
(u,v,w) определены для наблюдений в направлении точки S с часовым углом Н и скло-
склонением S. На рисунке точка S показана в восточной области небесной полусферы и по-
поэтому часовой угол Н отрицателен. Направляющие косинусы в матрице преобразования
в уравнении D.1) определяются из представленных на рисунке соотношений. Можно также
перейти к уравнению D.2), если принять, что точкой S обозначено направление базы,
и заменить координаты (Н, 5) на координаты базы (h, d)
X'
Y
Z
= D
' cos d cos h
— cos d sin h
sine/
D.2)
Из уравнений D.1) и D.2) получим координаты в системе (u,v,w):
"cos d sin (H — h)
sin d cos 5 — cos d sin 5 cos {H — h)
sin d sin 5 + cos d cos 5 cos (H — h)
D.3)
Система координат (Z), /г, d) широко использовалась в ранних публикациях, в част-
частности, для образованных только двумя антеннами инструментов (см., например,
Rowson, 1963).
Для определения проекций (X, У, Z) новой базы обычно используются геоде-
геодезические методы, позволяющие определить высоту 8, азимут Л и длину базы.
Соотношения между системой координат (?, Л) и другими системами представлены
на рис. 4.3, см. также приложение 4.1. Для наблюдателя, находящегося на широте
?, используя уравнения D.2) и (А4.2), получим
= D
"cos С sin S — sin С cos S cos Л
cos? sin Л
sin С sin S + cos С cos 8 cos Л
D.4)
Из уравнений D.1) и D.3) следует, что геометрическим местом точек проекций
пространственных компонент базы и и v является эллипс с переменным часовым
углом. Пусть (Но, So) — координаты точки опорной фазы. Тогда из уравнения D.1)
получим
Геометрические соотношения и поляриметрия
[Гл.4
Горизонт
Рис. 4.3. Соотношение экваториальных (Н,5) и горизонтальных (?,Л) координат точки
S для наблюдателя на широте С. Здесь Р — полюс мира и Z — точка зенита в месте
наблюдений. Параллактический угол фр — позиционный угол вертикала наблюдаемого
источника, отсчитываемый от точки севера к востоку. Длины дуг, стягивающих цен-
центральные углы сферы с центром в точке О, определяются следующим образом: ZP =
= 90° -C,PQ = С, SR = SRQ = Л, SZ = 90° -S, SP = 90° - S, SQ = cos (cos S cos Л).
Необходимые соотношения могут быть получены, применяя формулы синусов и косинусов
к сферическим треугольникам ZPS и PQS, и приведены в приложении 4.1. Отметим, что
для точки наблюдений S, находящейся как показано на рисунке к востоку от наблюдателя,
углы Н и фр отрицательны
Рис. 4.4. Годограф на плоскости uv, определяемый уравнением D.5) (а); годограф на плос-
плоскости u'v', определяемый уравнением D.8) {б). Нижние дуги на графиках соответствуют
сопряженным значениям функций видности. Если источник не находится вблизи полюса,
то длины дуг ограничиваются периодом видимости источника над горизонтом
2 . / v - Z\ cos So
D.5)
Уравнением D.5) определяется эллипс на плоскости uv, большая полуось которого
4.2]
Плоскость u'v'
87
qj/=90°, 8 = 70°
Рис. 4.5. Примеры изменения дуг эллипсов на гш-плоскости в зависимости от азимута базы
Л и склонения наблюдаемого источника 5 (высота базы 8 равна нулю). Длина базы во
всех случаях равна длине оси, измеренной относительно начала координат. Длительность
интервала наблюдений составляет от —4 до +4 ч при S = —30°, и — от —6 до +6 ч — во всех
остальных случаях. Штрихами на эллипсах показаны 1-часовые интервалы наблюдений.
Отметим изменение эллиптичности для базы восток—запад (*Д = 90°) при S = 30° и 6 =
70°. Расчет выполнен для широты 40°
равна л/Х^ + Y^ , а малая полуось — sin Jo уХд + Уд , как показано на рис. 4.4 а.
Центр эллипса находится на оси v в точке (u,v) = @,Z\ cos Jo)- Дуга эллипса,
описываемая за время наблюдений, определяется азимутом, высотой и широтой
базы, склонением источника и интервалом часовых углов наблюдений, как показано
на рис. 4.5. Поскольку V(—u, —v) = V*(u,v), то для любых наблюдений измерения
одновременно выполняются на двух дугах, являющихся частями одного и того же
эллипса, лишь при Z\ = 0.
4.2. Плоскость u'v1
Плоскость u'v', введенная в разд. 3.1 при рассмотрении отклика решетки с ба-
базами восток—запад, полезна также при обсуждении определенных аспектов общих
характеристик решеток. Эта плоскость перпендикулярна направлению на полюс
мира и может рассматриваться как экваториальная плоскость Земли. Для баз,
не совпадающих с направлением восток-запад, мы также можем рассматривать
проекции пространственных векторов на плоскость u'v'. Все векторы спроециро-
ванны таким образом, что при вращении Земли описывают круговые траектории.
Проекции на плоскости u'v' связываются с проекциями на плоскости uv простыми
преобразованиями и' = и и v' = v cosec So. Используя проекции базы двух антенн
(X\,Y\,Z\), из уравнения D.1) получим
и' = Х\ sin Hq + Уд cos Hq ,
D.6)
88 Геометрические соотношения и поляриметрия [Гл. 4
v = -Хх cosНо + Yx sinНо + Zx ctg50. D.7)
Траектории представляют собой окружности с центрами в точках (О, Z\
и радиусами д', заданными уравнением
^ = м'2 + („' _ Zx ctg 5oJ = X2 + уД
как показано на рис. АЛ б. Проекции векторов баз, образующие треки, вращаются
с постоянной угловой скоростью uje — скоростью суточного вращения Земли, кото-
которое легче себе представить, чем движение по эллипсу на плоскости uv. В частно-
частности, связанные с временными параметрами задачи, такие как усреднение значений
видности, удобно рассматривать на плоскости u'v'. Примеры ее использования
приводятся в разделах 4.4, 6.4 и 15.2. В преобразовании Фурье сопряженными пере-
переменными и1', v1 являются переменные /', ттт/, где V = I u т' = т sin #о, т. е. плоскость
карты сжимается в sin 8о раз в направлении т.
4.3. Частота интерференции
Компонентой w базы представлена разница в пути распространения плоской
волны, принимаемой двумя антеннами из направления опорного источника. Со-
Соответствующая временная задержка равна w/vq, гДе Щ — центральная частота
в полосе наблюдений. Относительная фаза сигналов двух антенн изменяется на 2тг
радиан при изменении w на единицу. Таким образом, частота колебаний на выходе
коррелятора равна
— = —77 —г- = —ше [Х\ cos 5 sinH + Y\ cos 5 cosH\ = — uoeu cos 5, D-9)
Cll CL±i Cll
где uje = dH/dt = 7,29115-10~5 рад-с — угловая скорость суточного вращения
Земли; для большей точности см. (Seidelmann, 1992). Знак dw/dt указывает на
возрастание или убывание фазы со временем. Полученный результат применим
к случаю, когда фазы сигналов между антеннами и входами коррелятора не пре-
претерпевают аппаратурных изменений во времени. В решетках с сопровождающи-
сопровождающими источник антеннами временные задержки, компенсирующие разность w путей
распространения сигналов для обеспечения их корреляции, вводятся ЭВМ. Если
бы точная компенсирующая задержка осуществлялась в высокочастотной части
приемников, то относительная фаза сигналов на входе коррелятора оставалась бы
постоянной, и на его выходе лепестки бы отсутствовали. Однако компенсирующие
задержки обычно вводятся на промежуточной частоте, центральная частота ко-
которой щ обычно много меньше частоты i/q радиосигнала. Регулировкой компен-
компенсирующей задержки вводится скорость изменения фазы, равная 2tti/^ (dw/'di)/'uq =
= —ujeu (cos 5) Vd/vo- Получающаяся в результате частота интерференции на выходе
коррелятора равна
*. / м = cos6 / щ Dло)
J dt \ щ/ \ щ/
где отрицательный знак соответствует приему сигнала в верхней боковой полосе
частот, а положительный — в нижней; эти различия и случай двухполосного приема
рассматриваются в разд. 6.1. Из уравнения D.3) следует, что правая часть выра-
выражения D.10) равна —uoeD cosd cos 5 sin (H — h) (i/q =p vd)/c- Отметим, что величина
(i/qT^) обычно определяется частотами одного или нескольких гетеродинов.
4.4]
Частоты видности
89
4.4. Частоты видности
Как показано в разд. 3.1, фаза комплексной функции видности измеряется
относительно фазы видности гипотетического опорного точечного источника. Из-
Изменения частоты интерференции не оказывают влияния на функцию видности,
но в ней присутствуют более медленные изменения, определяемые положением
излучающих источников в пределах картографируемого поля. Найдем максималь-
максимальную частоту изменений видности со временем. Для этого рассмотрим точечный
источник, представленный дельта-функцией 8(li,mi). Функция видности является
преобразованием Фурье ?(/i,mi) и равна
e~j27V Hi+^i) = cos 2тг (uh + vrrn) - j sin 2тг (uh +vrrn). D.11)
Это выражение представляет два ряда синусоидальных волновых поверхностей —
действительной и мнимой. Волновая поверхность, представленная действительной
частью уравнения D.11), по-
показана в координатах (uf,vf)
на рис. 4.6, где аргументы
тригонометрических функ-
функций в D.11) преобразованы
к виду 2тг (u'h + v'mi sin^o).
Частота волны, выраженная
в периодах на единичный
интервал на плоскости u'v'',
равна /i в направлении г/,
mi sin 5q — в направлении v'
и
+ т\ sin2Jo D.12)
в направлении наиболее бы-
быстрых изменений. Выраже-
Выражение D.12) достигает максиму-
максимума в точке полюса мира и при
этом принимает значение ri,
равное угловому расстоянию
источника от начала коорди-
координат (/,777,). Для любой пары
антенн траектории простран-
пространственных частот на плоско-
плоскости u'v' представляют собой
окружности радиуса q', об-
образуемые вектором, вращаю-
вращающимся с угловой скоростью
Рис. 4.6. Синусоидальные волновые поверхности на
u'v'-плоскости, представляющие функцию видности
для точечного источника. Чтобы не усложнять ри-
рисунок, показана только действительная часть функ-
функции. Наиболее быстрые изменения видности проис-
происходят в точке Р, в которой годограф вектора базы
перпендикулярен направлению максимумов функции
видности. ие — угловая скорость суточного вращения
Земли
о;е, при этом q определяется
выражением D.8). Из рис. 4.6
очевидно, что временные вариации измеренной видности максимальны в точке Р
и равны uJer^q'. Это важный результат, который показывает, что если г\ соответ-
соответствует точке на краю картографируемого поля, то считывание наиболее быстрых
изменений видности должно выполняться на интервалах времени достаточно малых
по сравнению с (ujer'1q')~1. Кроме того, может возникнуть необходимость переклю-
переключения во время наблюдений между двумя частотами или поляризациями, и эти
90 Геометрические соотношения и поляриметрия [Гл. 4
переключения должны выполняться за такие лее малые интервалы времени. Отме-
Отметим, что это требование также учитывается теоремой выборок, рассматриваемой
в разд. 5.2.
4.5. Калибровка базы
Позиционные параметры (X, У, Z) каждой антенны по отношению к общему
реперу, как правило, могут быть определены обычными геодезическими методами
с точностью до нескольких сантиметров или миллиметров. За исключением длин-
длинных волн, требуется более высокая точность. Фаза для опорного точечного источни-
источника должна быть рассчитана при любых часовых углах с точностью, скажем, порядка
1°, и вычтена из измеренных значений. Опорная фаза представлена сомножителем
ej27rw B уравнении C.7) и, следовательно, w необходимо рассчитывать с точностью
до 1/360 длины волны наблюдений. Параметры базы могут быть измерены с необхо-
необходимой точностью по наблюдениям калибровочных источников с точно известными
координатами. Фаза такого источника, расположенного в фазовом центре (Hq, Jo),
в идеальном случае должна быть равна нулю. Однако, если принять во внимание
реальные ошибки, то измеренная фаза определяется в соответствии с уравнени-
уравнением D.1) как
2nAw + ф[п = 2тг (cos 50 cos Но АХХ - cos 50 sin Яо АУЛ + sin 50 AZX) + Фт, D.13)
где префиксом А обозначены неопределенности соответствующих величин, а ф[п —
аппаратурная фаза двух антенн, участвующих в наблюдениях. Если калибровочный
источник наблюдается в широком интервале часовых углов, то АХХ и АУХ могут
быть получены соответственно из четной и нечетной компонент изменения фазы
в зависимости от Щ. Для измерения AZX необходимо использование калибровоч-
калибровочных источников с разными склонениями. Процедура измерений может состоять из
повторяющихся в течение нескольких часов наблюдений ряда таких источников.
Для k-го наблюдения, используя уравнение D.13), мы можем записать
akAXx + bkAYx + ckAZx + ф[п = фк, D.14)
где а&, Ък и ск — известные параметры источника, а фк — измеряемая фаза. Точные
координаты калибровочного источника знать необязательно, поскольку фазовые
измерения могут использоваться для определения как координат баз, так и источ-
источника. Методика этих вычислений рассматривается в разд. 12.2. Практически аппа-
аппаратурная фаза ф-1П с течением времени изменяется очень медленно; стабильность
аппаратуры рассматривается в гл. 7. Необходимо учитывать также атмосферные
фазовые флуктуации, рассматриваемые в гл. 13. Этими эффектами определяются
окончательные ограничения достижимой точности наблюдений как калибровочных,
так и исследуемых источников.
Для измерений параметров базы с точностью порядка 1 : 107 (например, 3 мм
на 30 км) требуется точность хранения времени порядка Ю^ ~ 1 мс. Хранение
времени рассматривается в подразделах 9.5.8 и 12.4.3.
4.6. Монтировки антенн
При обсуждении зависимости измеряемой фазы от точности знания параметров
базы эффекты, связанные с антеннами, нами не рассматривались, что было рав-
равносильно предположению идентичности антенн и исключению их воздействия на
4.6]
Монтировки антенн
91
Полярная ось Ось высот
У///////////////////Л
У////////////////////,
Рис. 4.7. Схемы антенн с экваториальной (полярной) (а) и азимутальной (б) монтировкой.
В показанных положениях инструментов оси склонений и высот ортогональны к плоскости
рисунка. В экваториальной монтировке ось склонений смещена относительно полярной оси
на расстояние Da, а в азимутальной монтировке оси вращения обычно пересекаются, как
показано на рисунке
сигналы. Однако это предположение верно лишь в первом приближении. Эффек-
Эффективные площади большинства антенн в апертурных решетках должны составлять
десятки и сотни квадратных метров для обеспечения необходимой чувствительно-
чувствительности. Причем эти большие конструкции должны точно сопровождать радиоисточник
на небесной сфере. Полноповоротные антенны обычно имеют экваториальную (так-
(также называемую полярной) или азимутальную монтировку, как показано на рис. 4.7.
Полярная ось экваториальной монтировки параллельна оси вращения Земли, и для
сопровождения источника достаточно, чтобы антенна поворачивалась вокруг по-
полярной оси со скоростью вращения небесной сферы. Экваториальные монтировки
механически более сложны в изготовлении по сравнению с азимутальными, и ими
оборудованы антенны, построенные как правило до внедрения компьютеров для
управления и преобразования координат.
Антенны большинства следящих решеток, используемых в радиоастрономии,
представляют собой осесимметричные рефлекторы. Желательно, чтобы ось сим-
симметрии отражающей поверхности пересекала обе оси вращения монтировки. Если
это условие не выполняется, то при сопровождении источника в движении антенны
появляется составляющая, вдоль оси диаграммы направленности. В этом случае
необходимо учитывать фазовые изменения, связанные с небольшими поправками
наведения, которые могут отличаться для разных антенн. Однако в большинстве
как экваториальных, так и азимутальных монтировок ось зеркала пересекается
с осями вращения с достаточной степенью точности, и фазовыми ошибками этого
типа можно пренебречь.
Удобно, но не обязательно, чтобы оси вращения монтировки пересекались. Тогда
точка пересечения образует хороший репер для определения базы между антен-
антеннами, так как независимо от направления антенны плоскость ее апертуры всегда
находится на одинаковом расстоянии от этой точки вдоль оси диаграммы направ-
направленности. Часто в больших антеннах с экваториальными монтировками полярная
ось и ось склонений не пересекаются. Во многих случаях смещение между осями
достигает нескольких метров. Уэйд (Wade, 1970) рассмотрел влияние этого сме-
смещения на точность фазовых измерений и показал необходимость учета изменений
его величины и точности ориентации полярной оси. Эти результаты могут быть
92 Геометрические соотношения и поляриметрия [Гл. 4
получены следующим образом. Пусть ins — единичные векторы в направлении
полярной оси и наблюдаемого источника соответственно, и Da — вектор смещения
между двумя осями в направлении, перпендикулярном i (см. рис. 4.7 а). Величина,
которую необходимо вычислить, равна проекции Do на направление наблюдений,
т.е. — Dos. Поскольку направление вектора Do перпендикулярно i, то косинус
угла между Do и s равен у/1 — (i • sJ . Таким образом,
Da s = Da л/1 - (i' sJ , D.15)
где Da — модуль Do. В системе координат X, У, Z, в которой измеряются проекции
базы, вектор i задан направляющими косинусами (гх, iY и iz), а направляющие
косинусы вектора s определяются матрицей преобразования в правой части урав-
уравнения D.2), если переменные h и d заменить переменными Н и 5, представляющими
направление наблюдений. Если точность ориентации полярной оси не хуже 1', то
порядок значений гх и iY равен 10~3, и iz ~ 1. Таким образом, подставляя в урав-
уравнение D.15) направляющие косинусы и опуская члены второго порядка малости по
гх и zv, получим
Da-s = Da (cos S - ix sinS cosH + iY sin 5 sin if). D.16)
Если Da выражается в длинах волн, то при расчете опорной фазы в центре поля
зрения разность значений Da- s для двух антенн следует добавить к проекции базы
w, определяемой уравнением D.1). Для этого необходимо в первую очередь найти
неизвестные константы в D.16), что можно выполнить, добавив в правую часть
уравнения D.13) слагаемое вида 2тг (a cos 5q + /3 sin So cos Hq + 7 sin So sin Hq) и рас-
расширив тем самым его решение параметрами а, C и 7- Тогда в результате получим
разницу соответствующих механических параметров двух антенн. Отметим, что
члены гх и iY в уравнении D.16) существенны только для больших Da. Если Da
меньше одной длины волны, то ими можно пренебречь.
Полученный результат можно применить к случаю азимутальных монтировок,
полагая, что i соответствует направлению азимутальной оси, как показано на
рис. 4.7 б. Тогда гх = cos (С, + е), iY = sin^ и iz = sin (С + е), где С — широта, а е
и е' — соответственно ошибки наклона азимутальной оси монтировки в плоскости
XZ и в плоскости оси Y и местного вертикала. Значения ошибок как и ранее долж-
должны быть порядка 10~3. Часто азимутальные монтировки конструируются таким
образом, чтобы их оси пересекались, и в этом случае величиной Da представлены
только конструктивные допуски. Таким образом, мы предполагаем, что значение
Da достаточно мало, чтобы членами iYDa и sDa можно было пренебречь, и тогда
уравнение D.15) приводится к виду
Da- s = Da I — (sin? sin 5 + cos? cos 5 cos ifJ = Da cos ?, D-17)
где S — высота точки наблюдений в направлении s: см. формулы (А4.1) в приложе-
приложении 4.1. Поправочные члены такого вида могут быть добавлены в выражения для
калибровки базы и для w.
4.7. Влияние ширины и формы диаграммы направленности
Интерпретация данных, полученных на решетках, образованных антеннами
с различными диаграммами направленности, — далеко не всегда легко выполнимая
задача. Отклик каждой пары антенн определяется эффективным распределением
4.8 ] Поляриметрия 93
интенсивности, которое равно произведению среднего геометрического нормирован-
нормированных диаграмм направленности и реального распределения интенсивности излуче-
излучения на небесной сфере. Если отклики различных пар антенн определяются различ-
различными эффективными распределениями, то в принципе /(/, т) и V(w, v) не могут свя-
связываться преобразованием Фурье для всей совокупности наблюдений. Решетки сме-
смешанного типа часто применяются в РСДБ, когда приходится использовать антенны
с различными конструкциями. Однако в таких наблюдениях размеры исследуемой
структуры источников много меньше ширины диаграмм направленности антенн,
различия которых могут не учитываться в данном случае. При использовании
различных диаграмм, ширина которых сравнима с размерами источника, область
измерений может быть ограничена размерами самой узкой диаграммы посредством
применения свертки функции видности с подходящей функцией переменных (и, v).
Аналогичная задача возникает в случае антенн с азимутальными монтировками,
если профили диаграммы направленности в плоскости, ортогональной ее номиналь-
номинальной оси, не обладают центральной симметрией. При сопровождении наблюдаемо-
наблюдаемого источника антенной с азимутальной монтировкой ее диаграмма направленно-
направленности поворачивается на небесной сфере вокруг номинальной оси. Этот эффект не
проявляется для экваториальных монтировок. Угол между вертикалом источника
и направлением на северный полюс мира в точке наблюдений (это направление
определяется по большому кругу, проходящему через источник и северный полюс
мира) — параллактический угол фр, показанный на рис. 4.3. Применяя формулу
синусов к сферическому треугольнику ZPS, получим
— sin фр _ — sin Н _ sin Л
cos? cos? cos 6
D.18)
откуда, используя формулы (А.4.1) или (А.4.2), угол фр можно выразить в виде
функции (Д, S) или (Н, 5). Если диаграмма направленности имеет вытянутую фор-
форму и ширину, сравнимую с размерами наблюдаемого источника, то вращение луча
на небесной сфере приводит к изменению эффективного распределения интенсив-
интенсивности в зависимости от часового угла. Однако в большинстве следящих решеток
эта проблема вряд ли существенна, поскольку диаграммы направленности антенн
осесимметричны с достаточной степенью точности.
4.8. Поляриметрия
4.8.1. Параметры определения поляризации. Поляризационные измере-
измерения занимают важное место в радиоастрономии. Например, для большей части
синхротронного излучения отмечается малая степень поляризации, указывающая
на распределение магнитного поля в источнике. Как отмечалось в гл. 1, эта по-
поляризация как правило линейная (планарная), и ее степень и позиционный угол
могут меняться по источнику. При увеличении частоты степень поляризации излу-
излучения часто возрастает, поскольку уменьшается деполяризация, вызванная фараде-
евским вращением. Поляризация радиоизлучения может быть также обусловлена
эффектом Зеемана в атомах и молекулах, циклотронным механизмом излучения
и плазменными колебаниями в солнечной атмосфере, а также отражением под
углом Брюстера от поверхности планет. В качестве меры поляризации в астрономии
почти повсеместно применяется набор четырех параметров, предложенных в 1852
году сэром Георгом Стоксом. Предполагается, что читатели знакомы с концепцией
параметров Стокса или могут навести справки в одном из многочисленных пособий,
их описывающих (см., например, Born and Wolf, 1999; Kraus and Carver, 1973; Rohlfs
and Wilson, 1996; Есепкина и др., 1973).
94 Геометрические соотношения и поляриметрия [Гл. 4
Параметры Стокса связаны с амплитудами компонент Ех и Еу электрическо-
электрического поля, разложенного на два взаимно ортогональных направления, перпендику-
перпендикулярных направлению распространения излучения. Таким образом, если Ех и Еу
представить соответственно как ?x(i) cos [2тп/? + Sx(i)] и ?y(i) cos [2тп/? + Sy(i)], то
параметры Стокса определяются как
D.19)
U = 2(Sx(t) ?y(t) cos [6x(t) ~ Sy(tj\),
V = 2(?x(t) ?y(t) sin [Sx(t) - 8y(t)]),
где угловыми скобками обозначено математическое ожидание или усреднение по
времени. Усреднение необходимо в связи с тем, что в радиоастрономии мы имеем
дело с полями, изменяющимися во времени случайным образом. Четыре параметра
Стокса представляют собой следующие величины: / — полная интенсивность вол-
волнового сигнала, Q и U — линейно поляризованные компоненты, л V — компонента
круговой поляризации. Параметры Стокса могут быть представлены в виде, имею-
имеющем непосредственный физический смысл:
те = V47U . D-20)
тс = j , D.21)
D.22)
(К^тг, D.23)
где 7?г^, тс и mt — степени линейной, круговой и полной поляризации соответствен-
соответственно, а в — позиционный угол плоскости линейной поляризации. Для монохромати-
монохроматических сигналов mt = 1, и поляризация может быть полностью определена только
тремя параметрами. Для случайных сигналов, соответствующих излучению косми-
космического происхождения, mt ^ 1 и требуются все четыре параметра. Все параметры
Стокса имеют размерность плотности потока или интенсивности и распространя-
распространяются также как и электромагнитное поле. Поэтому они могут быть измерены или
рассчитаны для любой точки вдоль направления распространения волнового сиг-
сигнала, и их относительной величиной определяется состояние поляризации в данной
точке измерений. Для независимых волн параметры Стокса складываются адди-
аддитивно. Когда они используются для определения полного излучения в некоторой
точке источника, то параметр /, представляющий полную интенсивность, всегда
положителен, но Q, U и V могут принимать как положительные, так и отрица-
отрицательные значения в зависимости от позиционного угла или направления вращения
поляризации. Соответствующие значения видности, измеряемые интерферометром,
будут комплексные, как мы обсудим позже.
До сих пор, рассматривая отклики интерферометров и решеток, мы не учитыва-
учитывали поляризацию. Это упрощение было основано на предположении, что мы имеем
4.8 ] Поляриметрия 95
дело с полностью неполяризованным излучением, для которого / — единственный
не равный нулю параметр. В этом случае отклик интерферометра с одинаковыми
поляризациями антенн пропорционален полной плотности потока излучения. Как
будет показано ниже, в общем случае отклик интерферометра пропорционален
линейной комбинации двух или более параметров Стокса в зависимости от по-
поляризации антенн. Проводя наблюдения на антеннах с различной поляризацией,
можно разделить отклики для четырех параметров и определить соответствующие
компоненты видности. Таким образом, могут быть получены карты распределения
каждого параметра по источнику и определена поляризация излучения в любой
его точке. Поляризация волны может быть описана и другими методами, возможно
наиболее важный из которых — матрица когерентности (Ко, 1967а, Ь). Тем не менее,
классический подход с использованием параметров Стокса остается практически
универсальным при использовании в астрономии, и поэтому мы будем следовать
здесь этому подходу.
4.8.2. Эллипс поляризации антенны. Поляризацию антенны как в случае
передачи, так и в случае приема можно представить в виде вектора электрического
поля, описывающего эллипс в плоскости волнового фронта. Большинство антенн
сконструировано таким образом, что эллипс в центральной части диаграммы на-
направленности принимает форму линии или окружности соответственно для линей-
линейной или круговой поляризации. Однако практически отклики с точной линейной
или круговой поляризацией не получаются. Как показано на рис. 4.8 а, эллипс
поляризации можно определить двумя параметрами: позиционным углом большой
оси ф и отношением его осей, которое удобно представить как тангенс угла %, где
-тг/4 ^ х ^ тг/4.
Антенна с произвольной поляризацией может быть представлена в виде двух
идеальных диполей, как показано на рис. 4.8 б. Рассмотрим излучение такой антен-
антенны, подавая на вход синусоидальный сигнал. Напряжения сигналов поступающих
на диполи через элементы цепи соответствуют cos% и sm%. Сигнал на диполь у'
проходит дополнительно через цепочку, вносящую фазовую задержку тг/2. Таким
образом, антенной создаются компоненты поля с амплитудами Ех> ж 8у> в направ-
направлениях большой и малой осей эллипса со сдвигом по фазе 90° друг относительно
друга. Если на вход антенны подается высокочастотный синусоидальный сигнал
Vo cos 2тп/?, то компоненты поля записываются как
?xi cos2irvt ос Vo cosx cosBttz/?),
D.24)
i iB?)
?у> sm27rist ос
В этих выражениях компонента у' запаздывает на тг/2 относительно компоненты х'.
Если х = тг/4, то вектором напряженности излучаемого электрического поля описы-
описывается окружность с направлением вращения от оси х' к оси у' (т. е. против часовой
стрелки на рис. 4.8 а). Это соответствует четвертьволновой задержке сигнала в ди-
диполе у'. В этом случае поляризация волны, распространяющейся в положительном
направлении z' в правой системе координат (т. е. на рис. 4.8 а — к читателю), будет
правой круговой по определению ТИИЭР (IEEE, 1977). (Это определение широко
используется в настоящее время, но в некоторых более ранних работах поляризация
такой волны была бы определена как левая круговая.) Международный Астроно-
Астрономический Союз (IAU, 1973) принял определение ТИИЭР, а также установил, что
позиционный угол вектора напряженности электрического поля на небесной сфере
следует отсчитывать от севера к востоку в системе экваториальных координат.
MAC также установил, что «поляризация принимаемого излучения, для которого
при измерении вектора напряженности электрического поля в фиксированной точке
пространства позиционный угол в увеличивается со временем, характеризуется как
96
Геометрические соотношения и поляриметрия
[Гл.4
Север
Восток
Рис. 4.8. а — общий случай поляризации антенны в виде эллипса, описываемого вектором
напряженности электрического поля при излучении синусоидального сигнала. Позицион-
Позиционный угол ф большой оси эллипса измеряется относительно оси ж, направленной к северу на
небесной сфере. Принимаемый сигнал направлен на читателя, что соответствует положи-
положительному направлению оси z. Для такой волны стрелкой на эллипсе указано направление
правой поляризации, б — схема антенны, излучающей сигнал, представленный эллипсом
в части (а) рисунка, при подаче напряжений на вход A. cos% и sin% соответствуют
амплитудам сигналов в приведенных элементах схемы; тг/2 — фазовая задержка
правая и положительная». Отметим, что параметрами Стокса в формулах D.19)
поле определяется только в плоскости ху, и для того, чтобы определить, имеет
волна правую или левую круговую поляризацию, необходимо задать направление
его распространения. Из выражения D.19) и предшествующих ему определений Ех
и Еу следует, что поляризация волны, распространяющейся в направлении z в пра-
правой системе координат, будет правой круговой при положительном значении V.
При работе на прием вектор напряженности электрического поля вращается по
часовой стрелке (рис. 4.8) и возбуждает в диполе у' напряжение, упреждающее по
фазе напряжение в диполе х' на тг/2, поэтому два сигнала складываются синфазно
в точке А. При вращении против часовой стрелки сигналы в точке А складываются
в противофазе и гасят друг друга. Таким образом, показанная на рис. 4.8 антенна
принимает излучение с правой поляризацией, приходящее из положительного на-
направления z (т. е. распространяющееся в направлении отрицательных z), и передает
сигнал с правой поляризацией в пол ожите льном направлении z. Для приема волны
с правой поляризацией (распространяющейся в положительном направлении z)
полярность одного из диполей должна быть заменена на противоположную, при
этом х должно быть равно — тг/4.
Чтобы получить отклик интерферометра, рассмотрим выходной сигнал антен-
антенны, схема которой показана на рис. 4.8 б. Представим компоненты поля в комплекс-
комплексной форме:
Ex{t) = Sx(t) ej Рт^
Ey(t) = ?y(t) e
j P
D.25)
Напряжение сигнала, принятого в точке А на рис. 4.8 б, записывается в комплекс-
комплексном виде как
V = Ех, cos х ~ jEy, sin x, D.26)
где коэффициентом —j учитывается фазовая задержка тг/2, введенная в сигнал
у', для определенного формулами D.25) поля. Далее нам необходимо выразить
4.8 ] Поляриметрия 97
поляризацию принимаемого волнового излучения через параметры Стокса. В со-
соответствии с определением MAC (IAU, 1973) используются оси, направленные к се-
северу и востоку на небесной сфере, и обозначенные х и у на рис. 4.8 а. Компоненты
поля в направлениях ж и у связаны с компонентами поля в направлениях х' и у'
следующим образом:
Ex'(i) = \Sx(t) ej6*^ со$ф + Sy(i) ejSy^ sin^l ej2niy\
D.27)
Ey,(i) = [Sx(i) e^*W втф + Sy(t) e^«W cosф] e^vt.
Чтобы получить отклик на выходе коррелятора для т-й и n-й антенн решетки, тре-
требуется выполнить последовательные преобразования некоторых довольно громозд-
громоздких выражений, которые мы здесь не будем воспроизводить. Последовательность
этапов следующая:
1. Подставляем выражения D.27) для Ех> и Еу> в D.26), чтобы получить выход-
выходной сигнал для каждой антенны.
2. Отмечаем значения ф, х и V Для ДВУХ антенн индексами шипи получаем
сигнал на выходе коррелятора в виде Яшп = Cmn(l/^^n*)> гДе Gmn — коэф-
коэффициент усиления аппаратуры.
3. Заменяем переменные ?х, ?у, 5Х, 5у параметрами Стокса, используя форму-
формулы D.19), следующим образом:
((ехе>'')(?хе>*')*) = {El) = \{I + Q),
{{?ye>s*){?ye>svY) = (el) = Ul-Q),
1 D.28)
{{?хе>6'){?уе>*у)*) = (?х?уе№--Ы) = \ (U + jV),
((?хе>*'У(?уе>*у)) = (?х?уе-^-^) = \ (U - JV).
В результате получим
Rmn= ^ Grnn{lv [COS (фт-фп) COS (Xm ~ Xn) + j sin (фт ~ фп) Sm(xm+Xn)] +
+ Qv [cos (фт + фп) cos (xrn + Xn) + j sin (^m + фп) sin (xm - Xn)] +
+ Uv [sin (фш + ^n) COS (Xm + Xn) - j COS (фш + ^n) Sm (^m ~ Xn)] ~
- Vv [cos (фт - фп) sin (xm + Xn) + j sin (^m - ^n) cos (x
В этом уравнении индекс v был добавлен к символам параметров Стокса, чтобы
подчеркнуть соответствие этих переменных комплексной видности распределения
соответствующего параметра по источнику, а не просто интенсивности или яркости
излучения. Уравнение D.29) — общая и весьма полезная формула, применимая во
всех случаях. Этот результат первоначально был получен (Morris, Radhakrishnan
and Seielstad, 1964) и позднее — (Weiler, 1973). В первой публикации знак Vv
противоположен по сравнению со второй и уравнением D.29). Эта разница следует
из соглашения о направлении вращения круговой поляризации. В нашем подходе,
в соответствии с рис. 4.8, параметры двух одинаковых антенн, настроенных на
прием излучения в правой круговой поляризации, были бы следующие: фш = фп
4 Томсон
X)]
Xn)] }• D.29)
98 Геометрические соотношения и поляриметрия [Гл. 4
и Хт = Хп = ~~тг/4. В уравнении D.29) эти параметры представлены положитель-
положительным значением Т^,. Таким образом, положительное значение Vv в уравнении D.29)
соответствует правой круговой поляризации излучения, приходящего с небесной
сферы, что согласуется с определением MAC. В публикации (Morris et al., 1964),
выполненной до принятия MAC этого решения, использовалось предыдущее согла-
соглашение.
Отметим, что дополнительные сомножители к коэффициенту 1/2 в уравне-
уравнении D.29) не приводятся, поскольку предполагается, что они входят в общий коэф-
коэффициент усиления.
4.8.3. Видность в параметрах Стокса. Как отмечено выше, символами Iv,
Qv, Uv и Vv в уравнении D.29) представлены измеряемые разнесенными антеннами
соответствующие значения видности. Поэтому мы далее будем называть эти вели-
величины видностями Стокса, следуя определению (Hamaker, Bregman and Sault, 1996).
Видности Стокса представляют собой величины, необходимые при построении карт
поляризованного излучения, и могут быть получены из выходного сигнала корреля-
коррелятора при использовании уравнения D.29). Это выражение существенно упрощается
при подстановке поляризационных характеристик реальных антенн. Для начала
рассмотрим случай, когда состояния поляризации обеих антенны идентичны. Тогда
Хт = Хп, Фт = Фи, и выражение D.29) приводится к виду
Rrnn = Gmn [Iv + Qv cos2^m cos2xm + Uv sin 2фш cos2xm - Vv sin2xm]. D.30)
Если антенны настроены на прием линейно поляризованного излучения, то удобно
пользоваться индексами хну для обозначения двух ортогональных плоскостей
поляризации. Например, переменной Rxy описывается выходной сигнал корреля-
коррелятора для антенн типе состояниями поляризации хну соответственно. Для
антенн с линейной поляризацией Хт = Хп = 0. Рассмотрим две антенны с от-
отдельными выходами для линейных поляризаций х л у в каждой антенне. Тогда
для параллельных поляризаций, опуская постоянные коэффициенты усиления, из
уравнения D.30) получим
Rxx = Iv + Qv cos2^m + Uv sin2^m. D-31)
Здесь фш — позиционный угол поляризации антенны, который отсчитывается от
точки севера на небесной сфере к востоку. Угол плоскости поляризации у равен углу
плоскости поляризации х плюс тг/2. Для значений фт, равных 0°, 45°, 90° и 135°,
выходной сигнал Rxx коррелятора пропорционален соответственно {Iv + Qv), (Iv +
+ Uv), (Iv — Qv) и (Iv — Uv). Используя антенны с этими углами поляризации,
можно измерять /v, Qv и GV, но не 14- В большинстве случаев степень круговой
поляризации пренебрежимо мала, и невозможность измерения Vv не является се-
серьезной проблемой. Однако Qv и Uv часто лишь на несколько процентов отличаются
от /v, и при попытке измерений с помощью одинаковых облучателей возникает
обычная проблема измерения малой разности двух больших величин. С теми же
трудностями приходиться сталкиваться при попытке измерения Vv одинаковыми
облучателями с круговой поляризацией, для которых % = ± тг/4 и отклик пропор-
пропорционален (Iv =р V^,). Эти проблемы частично снимаются при измерениях Qv, Uv
или Vv облучателями с противоположными поляризациями. В качестве примера
измерений Vv см. (Weiler and Raimond, 1976).
Для облучателей с противоположными поляризациями подставим в уравне-
уравнение D.29) фп = фт + тг/2 и Хт — ~Хп- В случае линейной поляризации члены с х
равны нулю и плоскости поляризации ортогональны. Тогда антенны называются
4.8 ] Поляриметрия 99
кросс-поляризованными по аналогии с пересекающимися диполям. Отбрасывая по-
постоянные коэффициенты усиления и используя индексы жиг/, определенные выше,
получим следующие выходные сигналы коррелятора:
Rxy = ~Qv sin2^m + Uv cos2^m +jVv,
D.32)
Ryx = -Qv sm2^m + Uv cos2^m - jVv,
где фт соответствует углу плоскости поляризации (х или у), обозначенному первым
индексом переменной R в том же уравнении. Тогда при значениях фт, равных 0°
и 45°, отклик Rxy пропорционален (Uv + jVv) и (—Qv -\-jVv). Если величина Vv
предполагается равной нулю, то этого достаточно для измерения поляризованной
компоненты. Если обе антенны способны принимать кросс-поляризованное излуче-
излучение и их выходные сигналы разделяются на два приемных канала, то для каждой
пары антенн могут быть использованы четыре коррелятора. Тогда могут быть
получены отклики одновременно для ортогональных и параллельных поляризаций:
Позиционные углы Измеряемые видности
Стокса
jv _j_ Qv Позиционный угол I
Uv+jVv
Uv - jVv " D33)
I -О
Iv + Uv Позиционный угол II
-Qv+jVv
-Qv-jVv
Iv - Uv
Таким образом, если плоскости поляризации можно периодически поворачивать на
45°, как отмечено позиционными углами I и II, например, поворачивая облучатели
антенн, то величины Qv, Uv и Vv могут быть измерены без привлечения разности
откликов с Iv. Применение поворачиваемых облучателей, тем не менее, оказалось
ограниченным на практике. Поворот облучателя относительно главного зеркала
оказывает малое, но значительное влияние на форму диаграммы направленности
и поляризационные свойства антенны. Это происходит вследствие того, что вра-
вращение вызывает отклонения от центральной симметрии диаграмм облучателей,
различным образом связанными с эффектами затенения фокальной конструкци-
конструкцией и любыми отклонениями от осевой симметрии главного зеркала. Более того,
в радиоастрономических системах для достижения наивысшей чувствительности,
облучатели вместе с малошумящими охлаждаемыми усилителями устанавливаются
в едином модуле, вращение которого проблематично. Но при сопровождении ис-
источника антенной с азимутальной монтировкой параллактический угол изменяется
т
0°
0°
90°
90°
45°
45°
135°
135°
п
0°
90°
0°
90°
45°
135'
45°
135'
100 Геометрические соотношения и поляриметрия [Гл. 4
в зависимости от часового угла, что приводит к вращению диаграммы направ-
направленности антенны на небесной сфере. В публикации (Conway and Kronberg, 1969)
отмечено это преимущество азимутальных монтировок, позволяющее отделить ап-
аппаратурные эффекты от истинной поляризации источника при продолжительности
наблюдений несколько часов.
В Вестерборкском радиотелескопе апертурного синтеза антенны установлены
на экваториальных монтировках, и параллактический угол поляризации остается
фиксированным при сопровождении источника. Уэйлером (Weiler, 1973) описано
применение облучателей с ортогональными состояниями линейной поляризации.
В этой решетке выходные сигналы ряда перемещаемых антенн коррелируют с сиг-
сигналами стационарных антенн. Позиционные углы плоскостей поляризации переме-
перемещаемых антенн равны 45° и 135°, а позиционные углы стационарных — 0° и 90°.
В результате получаются следующие отклики:
Позиционные углы Измеряемые видности Стокса
т п
0° 45° (Iv + Qv + Uv + jVv)/V2 , ч
D.34)
0° 135° (-Iv - Qv + Uv + jVv)/y/2
90° 45° (Iv - Qv + Uv - jVv)/y/2
90° 135° (Iv - Qv - Uv + jVv)/y/2
Несмотря на то, что по сравнению с D.33) величина откликов уменьшается в у2
раз, потери в чувствительности отсутствуют, поскольку каждая видность Стокса
находится во всех четырех выходах коррелятора. Тем не менее, отметим, что эта
схема не позволяет использовать все возможные антенные пары вследствие того,
что коррелируют только сигналы антенн с различными поляризациями.
Облучатели с противоположными круговыми поляризациями имеют опреде-
определенные преимущества при измерениях линейной поляризации. При определении
откликов мы будем считать позиционный угол фш произвольным для антенны
т, чтобы выделить эффект вращения, обусловленного, например, азимутальной
монтировкой. Если на выходах антенн одновременно представлены сигналы, соот-
соответствующие противоположным направлениям круговой поляризации (обозначен-
(обозначенным г и ?), и для каждой антенной пары используется четыре коррелятора, то их
выходные сигналы пропорциональны следующим величинам:
Круговая поляризация Измеряемые видности Стокса
т п
ТУ J -I- У
П О Т Т/"
Здесь мы учли, что i/j? = фг + тг/2 и то, что % = —тг/4 для правой круговой по-
поляризации, и % = тг/4 — для левой. Необходимости во вращении облучателей при
4.8] Поляриметрия 101
проведении наблюдений нет, и отклики Qv и Uv получаются отдельно от отклика Iv.
Выражения D.35) молено упростить, выбирая значения фг равными тг/2, тг/4 или
0. Например, если фг = 0, то сумма откликов г? и ?г позволяет измерить видность
Стокса Uv. Напомним, что в случае азимутальных монтировок следует принимать
во внимание изменение позиционного угла. Коунвей и Кронберг (Conway and Kro-
nberg, 1969), по всей видимости, были первыми, кто применил интерферометр с ан-
антеннами, принимающими круговую поляризацию для измерений слабой линейной
поляризации источников. С тех пор антенны с круговой поляризацией стали широко
использоваться в радиоастрономии.
4.8.4. Инструментальная поляризация. Отклики антенн с различными
комбинациями линейных и круговых поляризаций, рассмотренные выше, получены
в предположении, что поляризации строго линейные или круговые, и что пози-
позиционные углы линейно поляризованных облучателей точно известны. В действи-
действительности это не так, и эллипс поляризации никогда не может быть представлен
идеальной окружностью или прямой линией. Неидентичные характеристики антенн
служат причиной того, что неполяризованный источник кажется поляризованным.
Этот эффект называется инструментальной или паразитной поляризацией. Если
отклонения от идеальных характеристик известны, то их влияние можно опреде-
определить из уравнения D.29). Приведенные в выражениях D.33), D.34) и D.35) отклики
представляют собой лишь главные члены, и в общем случае, с учетом аппаратурных
факторов, в них включаются все четыре видности Стокса. Рассмотрим, например,
случай облучателей с ортогональными линейными поляризациями и номинальными
позиционными углами, равными 0° и 90°. Пусть реальные значения ф и х таковы,
что (фх + фу) = тг/2 + А^+, (фх - фу) = -тг/2 + Аф~, Хх + Ху = Дх+, Хх ~ Ху =
= Дх~. Тогда из уравнения D.29) получим
Rxy ~ 1ь(Аф- - JAX+) - Qv(Aip+ - JAX~) + Uv+jVv. D.36)
Как правило, антенны могут быть настроены так, чтобы Д-члены не превышали
~1°. Мы предположим, что они достаточно малы, чтобы их косинусы можно было
представить единицами, синусы — углами, а произведения двух синусов — нулями.
Часто паразитная поляризация различна даже для аналогичных антенн и необхо-
необходимо введение поправок в измеренные значения видности до построения карты.
Хотя мы вывели выражения для отклонений от идеальной поляризации антенн,
используя параметры эллиптичности и ориентации эллипса поляризации в уравне-
уравнении D.29), знание этих параметров антенн не обязательно в случае, когда возможно
устранить аппаратурные эффекты из измерений так, чтобы они не проявлялись
в окончательной карте или изображении. При калибровке откликов антенн широко
используется подход определения паразитной поляризации через отклик антенны
на волновой сигнал, поляризация которого ортогональна или противоположно на-
направлена по сравнению с номинальным откликом. В этом случае для линейно
поляризованных антенн, следуя анализу (Sault, Killeen and Kesteven, 1991), мы
можем записать
vx = vx + Dxvy и v'y = vy-\- Dyvx, D.37)
где индексами х и у обозначаются две ортогональные плоскости поляризации; v' —
принятый сигнал; v — сигнал, который был бы принят с идеально поляризованными
антеннами; слагаемыми с коэффициентом D представлен отклик реальной антенны
на поляризацию, ортогональную номинальной. Эти слагаемые часто описываются
как просачивание ортогональной поляризации в антенне (Bignell, 1982) и соот-
соответствуют паразитной поляризации. Для каждого типа поляризации паразитная
составляющая определяется одним комплексным числом, т. е. используется столько
же параметров, сколько необходимо для определения эллиптичности и ориентации
102 Геометрические соотношения и поляриметрия [Гл. 4
эллипса поляризации, представленных двумя действительными числами. В прило-
приложении 4.2 выражения для Dx и Dy выведены через параметры эллипса поляриза-
поляризации:
Вх~фх- jXx и Dy ~ -фу + jxy, D.38)
где приближение верно в случае малых значений параметров \ и Ф- Отметим,
что в выражениях D.38) фу измеряется относительно направления у. Для ан-
антенны с идеальной линейной поляризацией оба параметра Хх и Ху равны нулю,
и плоскости поляризации точно совпадают с направлениями х и у относительно
антенны. Таким образом, для идеальной антенны параметры фх и фу также равны
нулю. Ограничения точности аппаратуры в реальной антенне представлены выра-
выражениями D.38), и мы видим, что действительная и мнимая части коэффициентов
паразитной поляризации могут быть связаны соответственно с несовпадением осей
и эллиптичностью поляризации.
Для пары антенн тип применение коэффициентов паразитной поляризации
дает возможность связать измеряемые сигналы на выходах коррелятора R'xx, Ryy,
R' и R' с истинными параметрами, представляющими соответствующие корре-
корреляционные коэффициенты, которые были бы измерены идеально поляризованными
антеннами:
тУ
rLxx тэ _|_ Г) Р _|_ Г)* Р _|_ п г)* р
* — ?Xjxx \ -LSxm-Lbyx ~г 1Ухп±ьху ~т ихшихп±ъуу,
УхтУхп
IXjxy ту _|_ Г) ГУ _|_ 7~)* ГУ _|_ Г) 7~)* 7Э
* — rtxy \ J-^xm-r^yy ~г J-^yn-r^xx ~г ^жт^р-^уж)
Рт,Руп D.39)
-—^^ = ^уж + DymRxx + D*nRyy + DymD*nRxy,
УутУхп
/У
у у р i 7~) P -U D* Р
\ 1Jyn?Xjyx
у у
* УУ ym
УутУуп
Коэффициентами д представлено усиление по напряжению в соответствующих сиг-
сигнальных каналах. Это комплексные величины, представляющие амплитуду и фазу,
и уравнения могут быть нормированы таким образом, чтобы значения коэффициен-
коэффициентов д были близки к единице. Отметим, что в уравнениях D.39) не использовалось
приближение малых величин. Тем не менее, как правило, величины коэффициентов
паразитной поляризации не превышают нескольких процентов, и их произведения-
произведениями можно пренебречь. Тогда, как следует из уравнений D.31) и D.32), отклики
могут быть выражены через видности Стокса следующим образом:
-^Цг- =h + Qv [cos 2фш - (Dxrn + D*xn) sin 2фт] +
QxmQxn
+ Uv [sin2^m + (Dxm + D*xn) cos2^m] - jVv (Dxm - ?>*„),
* — J-v \-LJxm ~r -lJyn) Ц/v [Sin Z 1рш ~г \J-Jxm yn) COS А1рш\ +
QxmQyn
+ Uv [cos 2фт - {Dxm - D* ) sin 2фт] + jVv, D.40)
V = /„ (Dym + D*xn) - Qv [зт2фт - (Dym - D*xn) соз2фт]
9
9ym9xn
+ Uv [cos2^m + (Dym - D*xn) sin2^m] - jVv,
4.8 ] Поляриметрия 103
Вуу „г | / П I Г1* Л • О / 1
^г- = Iv — Qv [cos2^m + yJJyrn + J^yn) sm2^mJ -
9ym9yn
- Uv [sin 2фт - (Dym + D*yn) cos 2фт] + jVv (Dym - D*yn).
Отметим, что фт относится к поляризации (х или у), обозначенной первым из
двух индексов В' в том же уравнении. В публикации (Sault, Killeen and Kesteven,
1991) описывается применение уравнений D.40) для случая сильной поляризации.
В их выводе величина видностей Стокса не ограничивается, но коэффициенты
паразитной поляризации предполагаются малыми. В случае слабо поляризованного
излучения произведениями Qv, Uv и Vv с коэффициентами паразитной поляризации
можно пренебречь. Уравнения D.40) в этом случае приводятся к виду
Вг
ж^г- = Iv + Qv cos 2фт + Uv sin2^m,
9xm9xn
V = Iv iDxm + D*) - Qv sin 2фш + Uv cos 2фт + jVv,
9xrn9yn (±Al)
^V = Iv (Dym + D*xn) - Qv sin 2фт + Uv cos 2^TO - j'K,
Л,|7| _ T _ Q 9 / _ Г Г - 9 /
9ym9yn
Можно ож:идать, что при использовании антенн на частотах, не превышающих
предельные значения, поляризационные коэффициенты будут оставаться практиче-
практически постоянными со временем, так как гравитационные отклонения, изменяющиеся
в зависимости от направления на источник, должны быть малы. Аппаратурные
коэффициенты усиления могут учитывать атмосферные эффекты с характерным
масштабом времени порядка секунд или минут, а также эффекты, связанные с элек-
электроникой.
Аналогичным образом могут быть определены коэффициенты паразитной по-
поляризации для антенн с круговой поляризацией и получены подобные выражения
для аппаратурного отклика. Эти коэффициенты паразитной поляризации опреде-
определяются следующими уравнениями:
v'r=vr + Drv?, v'? = v? + D?vr, D.42)
где, как и прежде, v' — измеряемые напряжения сигналов, v — сигналы в случае
антенн с идеальной поляризацией, D — коэффициенты паразитной поляризации.
Индексами г и ? обозначены правое и левое направления вращения. Соотношение
между коэффициентами паразитной поляризации, ориентацией и эллиптичностью
откликов антенн также выведено в приложении D.2). Получаем следующий резуль-
результат, не пользуясь в данном случае приближением малых углов:
Dr = ej2** tg AXr, D? = e-j2*< tg AX?, D.43)
где Axr и ^xi определяются уравнениями Xr = —45° + A%r и xi — 45° + Axf • Что-
Чтобы выразить выходной сигнал интерферометра через паразитные коэффициенты
поляризации и видности Стокса, обозначим четыре выходных сигнала коррелятора
как В'гг, В!ш Bfri и В'?г. Они связаны с исходными величинами, которые были бы
104
Геометрические соотношения и поляриметрия
[Гл. 4
получены при наблюдениях с идеально поляризованными антеннами, следующим
образом:
в!
= Rr
D*nRr?
9lm9rn
D.44)
Далее, используя выражения D.35), получим выходные сигналы через видности
Стокса:
9гт9г
Г) П* ) _ ;Л
UrrnUrn) JLJV
_ Г)* р-з2фт\ I у (Л _ Г)
9rm9ln
П* \ — п
Uv
Г) Г)*
™ - DrmD*en e^~) - Vv (Drm - D*ln), D.45)
i
I
Vm _ D?mD*rn
Vv (Dlm - D*rn),
=IVA + DtmD*tn) - jQv {Dim
Uv (Di
D\
\n
- Vv A - DtmD*ln)
Здесь, так же как и в предыдущем случае, фш относится к направлению поля-
поляризации (г или ?), обозначенному первым из двух индексов переменной R' в том
же уравнении. Угол фт равен параллактическому углу плюс любые паразитные
отклонения. Мы не делали никаких упрощений при выводе уравнений D.45) [в
подобных уравнениях D.40) слагаемые с произведениями двух коэффициентов D
были опущены]. Если коэффициенты паразитной поляризации малы, то любыми
произведениями этих двух коэффициентов можно пренебречь, как и в случае силь-
сильной поляризации для линейно поляризованных антенн в уравнениях D.40). В случае
слабой поляризации соответствующие уравнения могут быть получены из случая
сильной поляризации исключением сомножителей Qv, Uv и Vv с коэффициентами
4.8 ] Поляриметрия 105
паразитной поляризации:
Rrr _ т _|_ у
-"-t-I — Т (Л -4- П* "I (id TJ \ p-32^m
9rm9ln ^щ
-%- = Iv (Dim + D*rn) - (jQv + Uv) e^-
Подобные уравнения 1) приводятся в публикации (Fomalont and Perley, 1989). Для
применения формул, полученных для отклика с использованием коэффициентов
паразитной поляризации и усиления, следует рассмотреть калибровку этих вели-
величин, что мы сделаем позднее.
4.8.5. Представление в матричном виде. Приведенное выше описание по-
ляриметрии с использованием параметров эллипса поляризации дано на основе
физической модели антенны и электромагнитного излучения. Исторически ис-
исследования оптической поляризации развивались более продолжительное время.
Описание поляриметрии в радиодиапазоне соответствует подходу, первоначально
разработанному в оптике (Hamaker, Bregman and Sault, 1996; Sault, Hamaker and
Bregman, 1996; Hamaker and Bregman, 1996; Hamaker 2000; Hamaker, 1996). Матема-
Математический анализ дан в основном в терминах матричной алгебры, что, помимо всего
прочего, дает возможность независимо представить различные составляющие пути
сигнала, такие как — атмосфера, антенны, электронная аппаратура и объединить
их в окончательном решении.
В матричной формулировке электрическое поле поляризованной волны пред-
представляется двухэлементным вектором-столбцом. Воздействие любой линейной си-
системы на волну или напряжение волнового сигнала может быть представлено мат-
матрицей размера 2x2 следующим образом:
Щ _ [ai а2] \Ер
Е>\ ~ [а3 а4\ [Ед
где Ер и Eq описывают состояние поляризации на входе (ортогонально линейное или
противоположно круговое), а Е'р и E'q — на выходе. Матрица 2 х 2 в уравнении D.47)
называется матрицей Джонса (Jones, 1941) и ей могут быть представлены любые
простые линейные преобразования волнового сигнала. Матрицей Джонса можно
описать вращение волны относительно антенны, отклик антенны с учетом эффек-
эффектов паразитной поляризации или усиление сигналов в приемной системе до входа
коррелятора. Суммарное воздействие этих операций представляется произведением
соответствующих матриц Джонса точно так же, как воздействие на скалярное
напряжение может быть представлено произведением коэффициентов усиления
и откликов различных модулей приемной системы. Для волнового сигнала, описы-
описываемого двумя противоположными компонентами круговой поляризации, матрицы
х) Отметим, что при сравнении выражений, описывающих поляризационные измерения
полученных разными авторами, различия в знаках коэффициентов j могут быть следстви-
следствием различных определений параллактического угла по отношению к антенне и подобных
произвольных факторов.
106
Геометрические соотношения и поляриметрия
[Гл.4
Джонса вышеперечисленных операций можно записать в следующем виде:
9 вращение
просачивание
9 усиление
0
0 exp(-j0)
Gr 0
0 G/
D.48)
D.49)
D.50)
Здесь переменной в представлено вращение, а коэффициентами паразитной поляри-
поляризации Dr и Di — кросс-поляризованные сигналы антенны. В случае неидентичных
антенн диагональные коэффициенты могут слегка отличаться от единицы, но в дан-
данном случае это различие учитывается в матрице коэффициентов усиления двух
каналов. Коэффициенты усиления антенн и электронной аппаратуры могут быть
представлены единственной матрицей, и поскольку любые кросс-поляризованные
сигналы могут быть подавлены в усилителях, только диагональные коэффициенты
отличны от нуля в матрице усиления.
Допустим Jm соответствует произведению матриц Джонса, необходимому для
описания воздействий на сигнал, принимаемой антенной т, вплоть до точки входа
коррелятора. Допустим Jn — подобная матрица для антенны п. Поступающие на
вход коррелятора сигналы равны JmEm и JnEn, где векторы Ет и Еп — сигналы,
принимаемые антеннами. Сигнал на выходе коррелятора может быть представлен
внешним произведением (которое также называется произведением Кронекера, или
тензорным произведением) сигналов на его входе:
Е^ ® Е^ = (JmEn) ® (J*E*), D-51)
где (g) обозначает внешнее произведение. Внешнее произведение А 0 В получается
заменой каждого элемента а^ матрицы А на произведение а^В. Таким образом,
внешнее произведение двух матриц размера п х п будет матрицей размера п2 х п2.
Внешнее произведение обладает также следующим свойством:
(AiBi) О (А^В/с) = (Ai 0 Ak) (В; 0 Bfc).
Таким образом, мы можем переписать уравнение D.51) в виде
D.52)
D.53)
Усреднение по времени уравнения D.53) соответствует выходному сигналу корре-
коррелятора
Е* \ —
« ) —
Bpq
f>qp
Rqq
D.54)
где р и q обозначают противоположные состояния поляризации. Вектор-столбец
в уравнении D.54) называется вектором когерентности и соответствует четырем
взаимным произведениям выходных сигналов коррелятора для антенн тип. Из
4.8]
Поляриметрия
107
уравнения D.53) очевидно, что измеряемый, учитывающий аппаратурные эффек-
эффекты, и истинный, свободный от них, векторы когерентности R^n и Rmn связываются
внешним произведением матриц Джонса, которым эти эффекты представлены:
™„ = (J
D.55)
Чтобы определить отклик интерферометра на принимаемое излучение через вид-
ности Стокса, представленные комплексными величинами, мы введем вектор вид-
ности Стокса:
uv
KJ
D.56)
Видности Стокса могут рассматриваться как альтернативная система координат
для вектора когерентности. Пусть S — матрица размера 4x4 преобразования
параметров Стокса в поляризационных координатах антенн. Тогда получим
Для идеальных антенн с линейной кросс-поляризацией (ортогональной поляри-
поляризацией), отклик, выраженный через видности Стокса, определяется выражения-
выражениями D.33). Мы можем представить этот результат в матричном виде:
¦Rxx
&ху
1
0
0
1
1
0
0
-1
0
1
1
0
0"
j
-j
0
ГЛЛ
Qv
uv
yv_
D.58)
где индексы х и у в данном случае относятся к позиционным углам 0° и 90°
соответственно. Так же для противоположных круговых поляризаций мы можем
переписать выражения D.35) в виде
Rrr
0
0
O
0
il
0
о
-U
Qv
uv
D.59)
Матрицы 4 x 4 в уравнениях D.58) и D.59) представляют собой матрицы пре-
преобразования видностей Стокса к вектору когерентности для случаев линейного
кросс-поляризованного излучения и излучения с противоположными круговыми
поляризациями соответственно. Отметим, что эти матрицы зависят в частности от
принятых нами определений углов ф и х и ДРУГИХ факторов, представленных на
рис. 4.8, которые могут не совпадать с соответствующими параметрами, использу-
используемыми другими авторами.
Выражение 8-1(Лт(ЭЛ^)8 представляет собой матрицу, связывающую векторы
когерентности на входе и выходе системы, в которой эти величины определены
в координатах Стокса. В оптике подобная матрица называется матрицей Мюллера
(Mueller, 1948). Более подробное исследование матриц Джонса и Мюллера можно
найти в некоторых учебниках по оптике (например, O'Neill, 1963).
108
Геометрические соотношения и поляриметрия
[Гл.4
В качестве примера использования матриц, получим матрицу коэффициентов
паразитной поляризации и усиления для случая противоположных круговых по-
поляризаций. Для антенны т матрица Джонса Jm — следующее произведение двух
матриц Джонса паразитной поляризации и усиления:
0
0
Dr
дГгп
D.60)
Здесь элементами д представлено усиление по напряжению, элементами D описы-
описывается паразитная поляризация, а индексами г и ? обозначено направление поля-
поляризации. Для антенны п требуется соответствующая матрица Jn. Тогда, если мы
обозначим штрихами компоненты вектора когерентности (т. е. выходные сигналы
коррелятора) для антенн шип, можно записать:
Кг
Rir
= 3r
0
0
O
0
1 ¦
0
0
-1
Qv
uv
v
D.61)
где матрица 4 x 4 — та же матрица, что и в уравнении D.59), связывающая видности
Стокса с вектором когерентности. Также получим
D.62)
Подстановка уравнения D.62) в уравнение D.61) и вычисление произведения мат-
матриц приводит к уравнению D.45) для отклика системы с облучателями, поляризо-
поляризованными по кругу.
4.8.6. Калибровка аппаратурной поляризации г) . Порядок величины от-
относительной поляризации почти всех астрономических источников сравним с вели-
величиной коэффициентов паразитной поляризации и усиления, введенных ранее в этой
главе. Следовательно, для того чтобы обеспечить точное измерение поляризации ис-
источника, необходима точная калибровка этих параметров. Как правило, необходимо
проводить независимую калибровку для каждого сеанса наблюдений, поскольку
коэффициенты усиления прежде всего зависят от температуры и настроек электро-
электроники и не могут оставаться неизменными между сеансами наблюдений. Очевидный
способ определения коэффициентов паразитной поляризации и усиления состоит
в проведении наблюдений (например, измерений вектора когерентности) источ-
источников, для которых параметры поляризации уже известны. Число неизвестных
калибровочных параметров пропорционально числу антенн по, но число измерений
пропорционально числу баз па(па — 1)/2. Таким образом, неизвестные параметры
обычно определяются с избыточностью, и для обработки применяется метод наи-
наименьших квадратов.
х) Общее описание калибровки приводится в гл. 10, в частности, в разд. 10.1, который
полезно было бы прочитать, прежде чем приступать к более сложному рассмотрению
калибровки поляризации. Калибровка поляризацационных измерений обсуждается в этой
главе в связи с рассматриваемым здесь развитием поляриметрии.
4.8]
Поляриметрия
109
Для любой антенны с ортогонально поляризованными приемными каналами
существует семь степеней свободы, т. е. семь неизвестных, которые должны быть
прокалиброваны, чтобы полностью интерпретировать измеренные видности Стокса.
Это относится к общему случаю, и число неизвестных может быть уменьшено при
рассмотрении приближений слабой поляризации источника или малой паразитной
поляризации. Выраженные через параметры эллипса поляризации, эти неизвест-
неизвестные могут рассматриваться как ориентация и эллиптичность поляризации двух
ортогональных облучателей и комплексные коэффициенты усиления (амплитуда
и фаза) двух приемных каналов. После объединения выходных сигналов двух ан-
антенн используется только разность фаз, и, таким образом, остается только семь
степеней свободы для каждой антенны. Солт, Хамейкер и Брегман (Sault, Hamaker
and Bregman, 1996), применяя матрицы Джонса с четырьмя комплексными элемен-
элементами для каждой антенны, пришли к этому же выводу. Они также вывели общее
решение, показывающее семь степеней свободы или неизвестных коэффициентов.
В этом уравнении неисправленные (измеренные) видности Стокса (обозначенные
штрихами) связываются с истинными значениями через семь 7 и 5 коэффициентов:
к
Q'v
и1,.
-Iv'
-Qv
-и„
1
7++
- -JS-
Л—
Qv
Uv
vv
D.63)
V — V
Семь 7 и 5 коэффициентов определены следующим образом:
7++= (Адхт + Адут) + (Ад*хп + Ад*уп),
7+_= (Адхт - Адут) + (Ад*хп - Ад*уп),
7—= (Адхт - Адут) - (Ад*хп - Ад*уп),
S++= (Dxm + Dym) + (D*xn + D*yn), D.64)
<5+_= (Dxm - Dyn) + (D*xn - D*yn),
6-+= (Dxm + Dym) - (?>*„ + D*yn),
5__= (Dxm - Dym) - (D*xn - D*yn).
Здесь предполагается, что уравнение D.39) нормировано так, чтобы коэффициенты
усиления были близки к единице и коэффициенты Ад определяются как д^ = 1 +
+ Agik. Коэффициенты D (паразитной поляризации) и коэффициенты Ад доста-
достаточно малы, чтобы произведением двух таких величин можно было пренебречь.
Результат, как показано уравнениями D.63) и D.64), применим к антеннам, линейно
поляризованным в направлениях х и у. Тот же результат получается и в случае
антенн с круговой поляризацией, если индексы х и у заменить соответственно
индексами г и ?, а в правом столбце уравнения D.63) Qv, Uv и Vv заменить
соответственно на Vv, Qv и Uv. Подобный результат приводится в работе (Sault,
Killeen and Kesteven, 1991). Семь введенных выше коэффициентов 7 и 8 опреде-
определяются ошибками процесса калибровки, так что существует семь степеней свободы
в механизме образования этих ошибок.
Наблюдения одного калибровочного источника, для которого известны четыре
параметра Стокса, позволяют определить четыре степени свободы. Однако по-
поскольку измеряемые величины взаимосвязаны, необходимы, по крайней мере, три
110 Геометрические соотношения и поляриметрия [Гл. 4
калибровочных наблюдения, чтобы определить все семь неизвестных параметров
(Sault, Hamaker and Bregman, 1996). Для калибровки желательно пронаблюдать
один неполяризованный источник, но наблюдения второго такого же источника
решений не добавят. Необходимы наблюдения по крайней мере одного линейно
поляризованного источника, чтобы определить относительную фазу двух каналов
с противоположными поляризациями, т. е. относительную фазу комплексных ко-
коэффициентов усиления дхшдуП и дутд*хп, или дТшд\п и д?шд*п. Отметим, что с ан-
антеннами с азимутальными монтировками наблюдения калибровочного источника
с линейной поляризацией, выполненные с интервалом времени, в течение которого
позиционный угол значительно изменяется, могут в сущности рассматриваться
как наблюдения независимых калибровочных источников. При этом условии три
наблюдения одного и того же калибровочного источника достаточны для полного
решения. Более того, поляризация калибровочного источника не обязательно долж-
должна быть известна заранее, но может быть определена из наблюдений.
В случаях, когда возможны наблюдения только неполяризованного источника,
можно дополнительно определить две степени свободы, принимая во внимание,
что сумма коэффициентов паразитной поляризации для всех антенн должна быть
равна нулю. Как видно из выражений, полученных для коэффициентов паразитной
поляризации в приложении 4.2, это естественное предположение для одинаковой
конструкции. Однако разность фаз сигналов от облучателей до коррелятора для
двух ортогональных поляризаций в каждой из антенн остается неизвестной. Для
ее определения необходимы наблюдения источника с линейной поляризацией или
метод измерения инструментальной фазы. Например, в компактной решетке Ав-
Австралийского телескопа (Frater and Brooks, 1992) на каждой антенне установле-
установлены источники шума, генерирующие общий сигнал в оба поляризационных канала
(Sault, Hamaker and Bregman, 1996). Для таких систем требуется установка допол-
дополнительного коррелятора на каждой антенне, или переключение корреляционных
входов, чтобы измерить относительную фазу калибровочных сигналов для двух
поляризаций.
В приближении слабой поляризации, из уравнений D.41) и D.46) видно, что
если коэффициенты усиления известны, то коэффициенты паразитной поляриза-
поляризации могут быть определены по наблюдениям неполяризованного источника. Для
противоположных круговых поляризаций из уравнения D.46) следует, что если Vv
мало, то решения для коэффициентов усиления могут быть получены только из
комбинаций Ы и г г выходных сигналов при условии, что число баз в несколько раз
больше числа антенн. Коэффициенты паразитной поляризации тогда могут быть
найдены отдельно. Из уравнения D.41) следует, что это возможно только в случае,
когда линейная поляризация (параметры Qv и Uv) калибровочного источника опре-
определена из независимых измерений.
Выбор оптимальной стратегии калибровки поляризационных наблюдений яв-
является задачей, требующей детального изучения ряда вопросов: характеристик
используемых решеток апертурного синтеза, диапазона часовых углов наблюдений,
доступности калибровочных источников (что может зависеть от частоты наблюде-
наблюдений) и других факторов, особенно, если находятся решения для случая сильной
поляризации. Описания таких наблюдений могут быть найдены в работах (Conway
and Kronberg, 1969; Weiler, 1973; Bignell, 1982; Sault, Killeen and Kesteven, 1991;
Sault, Hamaker and Bregman, 1996; и Smegal et al., 1997). При поляризационных
измерениях в РСДБ существуют некоторые особенности (см., например, Roberts,
Brown and Wardle, 1991; Cotton, 1993; Roberts, Wardle, and Brown, 1994; Kemball,
Diamond and Cotton, 1995).
Для значительной части больших решеток апертурного синтеза разработана
эффективная методика калибровки, а также соответствующее программное обеспе-
4.8] Поляриметрия 111
чение. Поэтому наблюдатель не должен быть обескуражен кажущейся сложностью
необходимых калибровочных процедур. Ниже перечислены общие заключения, от-
относящиеся к поляризационным наблюдениям.
• Поскольку поляризация многих источников изменяется на масштабах времени
порядка месяцев, желательно рассматривать поляризацию калибровочного ис-
источника как одну из переменных, для которой должно быть найдено решение.
• ЗС286 и ЗС138 — два источника с относительно сильной линейной поляризаци-
поляризацией, позиционные углы которой, по всей видимости, не изменяются. Они могут
быть полезны для контроля разностной фазы для каналов с противоположной
поляризацией.
• Для большинства источников параметр круговой поляризации Vv очень мал —
~0,2 % или меньше, и может не учитываться. Следовательно, измерения на
антеннах с круговыми поляризациями позволяют точно измерить Iv. Однако
круговая поляризация важна при измерениях магнитного поля по Зееманов-
скому расщеплению. В качестве примера успешных измерений чрезвычай-
чрезвычайно малой степени круговой поляризации в работе (Fiebig and Glisten, 1989)
описаны измерения, для которых V/I — 5-10~5. Расщепление Зеемана для
нескольких компонент линии Н2О на частоте 22,235 ГГц наблюдалось на оди-
одиночной антенне — 100-м параболоиде Института радиоастрономии им. Мак-
Макса Планка, с приемной системой, переключаемой между противоположными
круговыми поляризациями с частотой 10 Гц. Для определения паразитных
откликов линейно поляризованного излучения использовался вращающийся
модуль облучатель-приемник. При этом требовалась калибровка относитель-
относительного положения двух диаграмм направленности с точностью 1".
• Хотя степень поляризации излучения большей части источников мала, воз-
возможны случаи, когда видности Стокса Qv и Uv сравнимы с величиной /v,
когда протяженный неполяризованный источник почти разрешен, а компакт-
компактная поляризованная компонента, не разрешена. В таких случаях могут возни-
возникать ошибки при использовании приближений слабой поляризации (уравне-
(уравнения D.41) и D.46)) при обработке данных.
• Для большинства антенн величина паразитной поляризация изменяетмя
в пределах главного луча диаграммы направленности, возрастая на его краях.
Кросс-поляризационные боковые лепестки расположены на краях главного
луча. По этой причине такие поляризационные измерения обычно проводятся
для источников, угловые размеры которых малы по сравнению с размерами
главного луча. В таких измерениях электрическая ось диаграммы направлен-
направленности должна совпадать с направлением на источник.
• Вызываемое ионосферой фарадеевское вращение плоскости поляризации при-
принимаемого излучения становится существенным на частотах ниже нескольких
гигагерц (см. табл. 13.6 в гл. 13). Периодические наблюдения сильно поля-
поляризованного источника полезны во время поляризационных измерений для
мониторинга изменений вращения плоскости поляризации, связанных с из-
изменением плотности электронов на луче зрения в ионосфере. Игнорирование
фарадеевского вращения может привести к ошибкам в калибровке, см., на-
например, (Sakurai and Spangler, 1994).
• В некоторых антеннах облучатели смещены относительно оси главного зер-
зеркала, например, при использовании системы облучения Кассегрена, когда об-
облучатели для различных длин волн размещены по окружности относительно
112 Геометрические соотношения и поляриметрия [Гл. 4
номинального фокуса. Для облучателей с круговой поляризацией это осевое
смещение приводит к различным ошибкам наведения для двух противополож-
противоположных поляризаций. Обычно различие направлений центральных лучей состав-
составляет ~0,1 от их ширины, что затрудняет измерения круговой поляризации
или делает их непрактичными, поскольку Vv пропорционально (Rrr — Яц).
Для линейно поляризованных облучателей соответствующий эффект состоит
в увеличении амплитуды кросс-поляризованных боковых лепестков по краям
центрального луча (см. также разд. 5.1).
• В РСДБ-наблюдениях необходимо принимать во внимание различие парал-
параллактических углов для различных антенн при больших расстояниях между
ними.
• Величины гп? и mt в уравнениях D.20) и D.22) характеризуются распределе-
распределением Раиса, представленным уравнением F.63а), а соответствующие распре-
распределения позиционных углов представлены формулой F.63Ь). Оценки степени
поляризации могут быть завышены и необходимо ввести поправки (Wardle
and Kronberg, 1974). Эта проблема обсуждается в конце п. 9.3.3.
Следующие выводы относятся к конструктивным особенностям антенных решеток,
предназначенных для поляризационных измерений.
• Вращение антенны с азимутально-угломестной монтировкой относительно
небесной сферы в большинстве случаев дает дополнительные преимущества
в поляризационных измерениях. Вращение может быть нежелательно при по-
попытке получить карту в поляризованном излучении в пределах значительной
части антенного лепестка. Исправление изменений паразитной поляризации
в пределах главного луча может быть затруднено при его вращении относи-
относительно небесной сферы.
• В случае антенн с линейной поляризацией ошибки калибровки, чаще всего
связанные с /v, приводят к искажению линейных параметров Qv и Uv, так
что измерения линейной поляризации с помощью антенн, поляризованных
по кругу, имеют преимущества. Подобным образом, ошибки калибровки, как
правило, связанные с /v, приводят к искажениям Vv, так что для измерений
круговой поляризации предпочтительнее линейно поляризованные антенны.
• Относительная полоса пропускания облучателей с линейной поляризацией для
зеркальных антенн может быть не менее 2 : 1, в то время как для облучате-
облучателей с круговой поляризацией максимальная относительная полоса пропуска-
пропускания обычно составляет 1,4 : 1. Во многих конструкциях таких облучателей
ортогональные линейные компоненты поля складываются с относительным
фазовым сдвигом ±90° и полоса пропускания ограничивается элементом фа-
фазового сдвига. По этой причине линейная поляризация предпочтительнее для
некоторых решеток апертурного синтеза, таких как Австралийский телескоп
(James, 1992), в котором хорошие поляризационные возможности обеспечива-
обеспечиваются тщательной калибровкой.
• Стабильность инструментальной (аппаратурной) поляризации, значительно
облегчает точную калибровку в широком диапазоне часовых углов и, пожа-
пожалуй, является наиболее важной конструктивной особенностью антенн. Поэто-
Поэтому необходим особый подход в случае использования поворачиваемых облуча-
облучателей относительно главного зеркала или если антенны используются вблизи
верхней границы их частотного диапазона.
4.8] Приложение 4-2. Определение коэффициентов паразитной поляризации 113
Приложение 4.1. Связь экваториальных и горизонтальных
координат
Хотя положения космических источников почти всегда определяются в эквато-
экваториальных координатах (часовой угол и склонение), для целей наблюдений обычно
требуется их преобразование в высоту и азимут. Формулы перехода от часового
угла и склонения (Н,5) к высоте и азимуту (?, Л) и обратно могут быть получены
применением формул косинусов и синусов к сферическим треугольникам, показан-
показанным на рис. 4.3. Для наблюдателя, находящегося на широте ?, формулы перехода
от (Н, 5) к (Д, S) следующие:
sin S = sin С sin 5 + cos С cos 5 cos H,
cos S cos Л = cos С sin 5 — sin С cos 5 cos H, (П4.1)
cos S sin Л = — cos 5 sin i7.
Подобным лее образом для перехода от (Д, 8) к (i7, J) получим
sin 5 = sin С sin ? + cos С cos ? cos Л,
cos S cos Я = cos? sin? - sin? cos? cos Л, (П4.2)
cos S sin H = — cos ? sin Л.
Азимуты здесь отсчитываются от точки севера к востоку.
Приложение 4.2. Определение коэффициентов паразитной
поляризации через параметры эллипса поляризации
Ниже рассмотрены коэффициенты паразитной поляризации, выраженные через
эллиптичность и ориентацию эллипса поляризации каждой из антенн.
Линейная поляризация. Рассмотрим антенну, показанную на рис. 4.8 и пред-
пол ожим, что ее номинальная поляризация линейная в направлении х. В этом
случае, х и Ф ~ малые углы, которыми представлены конструктивные допуски.
Вектор поля Е, направленный вдоль оси ж, как показано на рис. 4.8 а, представля-
представляется проекциями Ех> и Еу> вдоль осей х' и у' направления диполей, показанных на
рис. 4.8 б. Тогда, из уравнения D.26) получим, что напряжение выходного сигнала
антенны (в точке А на рис. 4.8 б") равно
V'x = E(cosip cosx + J sin^; sinx)- (П4.3)
Отклик для того же поля излучения, но направленного вдоль оси у, равен
Vy = ^(sin^ cos% — j cos^ sinx)- (П4.4)
Переменной V'x представлен ожидаемый отклик поля вдоль оси ж, а переменной Vy —
паразитный отклик для кроссполяризованной компоненты. Коэффициент паразит-
паразитной поляризации равен отношению кросс-поляризованного отклика к ожидаемому
отклику на ж-поляризации, т. е.
г) _ YL -
х ~
V'x cos^ cosx* +3
114 Геометрические соотношения и поляриметрия [Гл. 4
где индексом х обозначено ж-поляризованное излучение. Соответствующий ко-
коэффициент Dy для условий, при которых на рис. 4.8 показана номинальная
у-поляризация антенны, получается как Vx/Vy путем инвертирования уравне-
уравнения (П4.5) и замены фх на фу + тг/2 и \х на Ху Тогда угол фу, отсчитываемый от оси
у так лее, как угол фх отсчитывается относительно оси ж, т. е. углы увеличиваются
в направлении против часовой стрелки как показано на рис. 4.8. Таким образом,
мы получим
[cos (Фу + тг/2) cos Ху + 3 sin (фу + тг/2) sin хУ] _
[sin (фу + тг/2) cos Ху ~ 3 cos (Фу + V2) sin Ху]
(cos фу cos Xy+J sin фу
, .
— yv * JXy
Подобные выралсения для Dx и Dy также были получены в работе (Sault, Killeen and
Kesteven, 1991). Отметим, что Dx и Dy имеют сравнимые величины и противопо-
противоположные знаки, поэтому можно ожидать, что среднее значение всех коэффициентов
D для решетки из антенн должно быть очень малым. Как и ранее в этой главе,
индексы тип добавлены к коэффициентам D для обозначения отдельных антенн.
Круговая поляризация. Для приема излучения с правой круговой поляри-
поляризацией антенна, показанная на рис. 4.8 б, должна быть согласована с направлением
вращения вектора напряженности электрического поля против часовой стрелки
в плоскости рисунка, как показано ранее. Для этого угол х должен быть равен
—45°. Исходя из компонент поля в направлениях жиг/, для вращения против
часовой стрелки требуется, чтобы Ех опережало Еу по фазе на тт/2, тогда Ех = jEy
для компонент поля, определенных уравнением D.25). Определим для компонент
поля Ех и Еу соответствующие компоненты в направлениях х' и у', затем получим
выражения для выходных сигналов антенны для обоих видов поляризации прини-
принимаемого поля излучения. Для вращения против часовой стрелки
Е'х = Ех со^ф + Еу йтф = Ех (со^ф — j sin^), (П4.7)
Е'у = —Ех йтф + Еу со^ф = —Ех (ътф + j со^ф). (П4.8)
Для номинальной правой поляризации Хг = —тг/4 + АхГ5 гДе ^Хг является мерой
отклонения поляризации от круговой. Тогда из уравнения D.26) получим
V; = Ех е-М' (cosxr ~ sinxr) = V2 Ех e~j^ cos AXr- (П4.9)
Следующий шаг заключается в повторении вышеописанной процедуры для случая
приема левой круговой поляризации излучения, для которого вращение вектора
электрического поля будет по часовой стрелке и Еу = jEx. В результате получим
VI = Ех eiVv (cosxr + sinxr) = л/2 Ех ej2pr sin AXr. (П4.10)
Относительная величина отклика с противоположной поляризацией для номиналь-
номинальной круговой правой поляризации представляет коэффициент паразитной поляри-
поляризации
Dr = Ц = е>2** tg ДХг =~ е^Ьхг- (П4.11)
Vr
Соответствующий коэффициент паразитной поляризации, с использованием в дан-
данном случае полного выражения, равен
f * \ Р** 2Дг ^ ё"*' АХг. (П4.12)
f 2/ \
VI + tg2 Дхг 2
4.8] Цитированная литература 115
Для левой круговой номинальной поляризации относительная величина отклика
противоположной поляризации получается инвертированием правой части уравне-
уравнения (П4.11) и подстановкой А\г + тг/2 для А%г и фе — тг/2 для фг. Для соответ-
соответствующего коэффициента паразитной поляризации Д^, представляющего правую
паразитную поляризацию для левой номинальной круговой поляризации антенны,
получим
D? = e~j2^ tgAxi ~ e-j2*lAxi. (П4.13)
Поскольку —тг/4 ^ х ^ ^/4, А%г и Лх^ имеют противоположные знаки. Следова-
Следовательно, так же как и в случае линейной поляризации, Dr и Dg имеют сравнимые
величины и противоположные знаки.
Цитированная литература
Bignell R. С, Polarization, in Synthesis Mapping, Proceedings of NRAO Workshop No. 5,
Socorro, NM, June 21-25, 1982, A. R. Thompson and L. R. D'Addario, Eds., National Radio
Astronomy Observatory, Green Bank, WV, 1982.
Born M. and Wolf E., Principles of Optics, 7th ed., Cambridge Univ. Press, Cambridge, UK,
1999. (Имеется перевод: Борн M., Вольф Э.. Основы оптики. — М.: Наука, 1973.)
Conway R. G. and Kronberg P. P., Interferometer Measurement of Polarization Distribution
in Radio Sources, Mon. Not. R. Astron. Soc, 142, 11-32, 1969.
Cotton W. D., Calibration and Imaging of Polarization Sensitive Very Long Baseline Interfer-
Interferometer Observations, Astron. J., 106, 1241-1248, 1993.
Fiebig D. and Gu'sten R., Strong Magnetic Fields in Interstellar Maser Clumps, Astron. Astro-
phys., 214, 333-338, 1989.
Fomalont E. B. and Perley R. A., Calibration and Editing, in Synthesis Imaging in Radio
Astronomy, R. A. Perley, F. R. Schwab, and A. H. Bridle, Eds., Astron. Soc. Pacific, Conf.
Ser., 6, 83-115, 1989.
Frater R. H. and Brooks J. W., Eds., J. Electric. Electron. Eng. Australia, Special Issue on the
Australia Telescope, 12, No. 2, 1992.
Hamaker J. P., A New Theory of Radio Polarimetry with an Application to the Westerbork
Synthesis Radio Telescope (WSRT), in Workshop on Large Antennas in Radio Astronomy,
ESTEC, Noordwijk, The Netherlands, 1996
Hamaker J. P., Inderstanding Radio Polarimetry. IV. The Full-Coherency Analogue of Scalar
Self-Calibration: Self-alignment, Dynamic Range and Polarimetric Fidelity, Astron. Astrophys.
Suppl., 143, 515-543, 2000.
Hamaker J. P., Bregman J. D. and Sault R. J., Understanding Radio Polarimetry. I. Mathe-
Mathematical Foundations, Astron. Astrophys. Suppl., 117, 137-147, 1996.
Hamaker J. P. and Bregman J. D., Understanding Radio Polarimetry. III. Interpreting the
IAU/IEEE Definitions of the Stokes Parameters, Astron. Astrophys. Suppl., 117, 161-165,
1996.
IAU, Trans. Int. Astron. Union, 15B, 166, 1973.
IEEE, Standard Definitions of Terms for Radio Wave Propagation, Std. 211-1977, Institute of
Electrical and Electronics Engineers, Inc., New York, 1977.
James G. L., The Feed System, J. Electric. Electron. Eng. Australia, Special Issue on the
Australia Telescope, 12, No. 2, 137-145, 1992.
Jones R. C, A New Calculus for the Treatment of Optical Systems. I Description and Discus-
Discussion of the Calculus, J. Opt. Soc. Am., 31, 488-493, 1941.
Kemball A. J., Diamond P. J. and Cotton W. D., Data Reduction Techniques for Spectral Line
Polarization VLBI Observations Astron. Astrophys. Suppl., 110, 383-394, 1995.
116 Геометрические соотношения и поляриметрия [Гл. 4
Ко Н. С, Coherence Theory of Radio-Astronomical Measurements, IEEE Trans. Antennas
Propag., AP-15, 10-20, 1967a.
Ко H. C, Theory of Tensor Aperture Synthesis, IEEE Trans. Antennas Propag., AP-15, 188-
190, 1967b.
Kraus J. D. and Carver K. R., Electromagnetics, 2nd ed., McGraw-Hill, New York, 1973, p.
435.
Morris D., Radhakrishnan V. and Seielstad G. A., On the Measurement of Polarization Dis-
Distributions over Radio Sources, Astrophys. J., 139, 551-559, 1964.
Mueller #., The Foundations of Optics (abstract only), J. Opt. Soc. Am., 38, 661, 1948.
O'Neill E. L. Introduction to Statistical Optics, Addison-Wesley, Reading, MA, 1963. (Имеется
перевод: О'Нейл Э.. Статистическая оптика. — М.: Мир, 1966.)
Roberts D. H., Brown L. F. and War die J. F. C, Linear Polarization Sensitive VLBI, in Radio
Interferometry: Theory, Techniques and Applications, T. J. Cornwell and R. A. Perley, Eds.,
Astron. Soc. Pacific Conf. Ser., 19, 281-288, 1991.
Roberts D. H., Wardle J. F. C. and Brown L. F., Linear Polarization Radio Imaging at
Milliarcsecond Resolution, Astrophys. J., 427, 718-744, 1994.
Rohlfs K. and Wilson T. L., Tools of Radio Astronomy, 2nd ed., Springer-Verlag, Berlin, 1996.
Rowson В., High Resolution Observations with a Tracking Interferometer, Mon. Not. R. Astron.
Soc, 125, 177-188, 1963.
Sakurai T. and Spangler S. R., Use of the Very Large Array for Measurement of Time Variable
Faraday Rotation, Radio Science, 29, 635-662, 1994.
Sault R. J., Hamaker J. P. and Bregman J. D., Understanding Radio Polarimetry. III. Instru-
Instrumental Calibration of an Interferometer Array, Astron. Astrophys. Suppl., 117, 149-159, 1996.
Sault R. J., Killeen N. E. B. and Kesteven M. J., AT Polarization Calibration, Aust. Tel.
Tech. Doc. Ser. 39.3/015, CSIRO, Epping, NSW, 1991.
Seidelmann P. K., Ed., Explanatory Supplement to the Astronomical Almanac, University
Science Books, Mill Valley, CA, 1992.
Smegal R. J., Landecker T. L., Vaneldik J. F., Routledge D. and Dewdney P. E., Aperture
Synthesis Polarimetry: Application to the Dominion Astrophysical Observatory Synthesis Tele-
Telescope, Radio Sci., 32, 643-656, 1997.
Wade C. M., Precise Positions of Radio Sources, I. Radio Measurements, Astron. J., 162, 381-
390, 1970.
Wardle J. F. C. and Kronberg P. P., Linear Polarization of Quasi-Stellar Radio Sources at
3.71 and 11.1 Centimeters, Astrophys. J., 194, 249-255, 1974.
Weiler K. W., The Synthesis Radio Telescope at Westerbork, Methods of Polarization Mea-
Measurement, Astron. Astrophys., 26, 403-407, 1973.
Weiler K. W. and Raimond E., Aperture Synthesis Observations of Circular Polarization,
Astron. Astrophys., 52, 397-402, 1976.
Есепкина Н. А., Корольков Д. В., Парийский Ю. М. Радиотелескопы и радиометры. — М.:
Наука, 1973.
Глава 5
АНТЕННЫ И АНТЕННЫЕ РЕШЕТКИ
Эта глава начинается с краткого обзора основных типов антенн. В основной
части главы рассматриваются конфигурации антенн в интерферометрах и решетках
апертурного синтеза. Удобно классифицировать типы антенных решеток следую-
следующим образом.
1. Решетки с пассажными антеннами.
2. Интерферометры и решетки с антеннами, сопровождающими источник при
его перемещении по небесной сфере:
• одномерные решетки,
• решетки в форме открытых конфигураций (крестообразные, Т- и Y-
решетки),
• решетки в форме замкнутых конфигураций (окружности, эллипсы и тре-
треугольники Руло),
• решетки РСДБ,
• планарные решетки.
В главе описываются примеры решеток указанных типов, и сравниваются их про-
пространственные передаточные функции (или пространственные чувствительности).
Среди других вопросов обсуждаются необходимые размеры и количество антенн,
образующих решетку.
5.1. Антенны
Различные аспекты, связанные с антеннами, хорошо исследованы в многочис-
многочисленных публикациях: см. библиографию в конце главы. Здесь мы вкратце рас-
рассмотрим лишь некоторые детали, касающиеся особых требований, предъявляемых
к антеннам в радиоастрономии. В гл. 1 приведены примеры первых радиоастроно-
радиоастрономических антенн, работавших в основном на метровых длинах волн и часто пред-
представлявших собой дипольные решетки или рефлекторы в форме параболических
цилиндров. Их эффективные площади были велики, но поскольку использовались
достаточно большие длины волн, то обычная ширина лепестка диаграммы направ-
направленности составляла 1° и более. Для обнаружения источников и создания катало-
каталогов достаточно было наблюдений при прохождении источников через неподвиж-
неподвижную диаграмму направленности. Таким образом, в общем случае для этих антенн
слежение за источниками не требовалось. Более современный пример пассажной
дипольной решетки см. (Koles, Frehlich and Kojima, 1994). Из-за сужения диаграм-
диаграммы на сантиметровых и миллиметровых длинах волн необходимо сопровождение.
За исключением нескольких инструментов, созданных специально для работы на
метровых волнах, в большинстве решеток апертурного синтеза используются следя-
следящие антенны, установленные на экваториальных или азимутальных монтировках,
описанных в разд. 4.6.
118
Антенны и антенные решетки
[Гл.5
Требование высокой чувствительности и высокого разрешения в астрономиче-
астрономических изображениях послужило причиной создания больших антенных решеток.
В целях более эффективного использования этих инструментов обычно они кон-
конструируются с перекрытием большого диапазона частот. Инструменты сантиметро-
сантиметровых волн как правило охватывают спектр от нескольких сотен мегагерц до десятков
гигагерц. Антенны чаще всего имеют форму параболических или подобных типов
рефлекторов с отдельными облучателями для разных частотных диапазонов. Поми-
Помимо широкополосности следующим преимуществом параболических зеркал является
то, что вся, собранная ими энергия, практически без потерь попадает в фокус. Это
позволяет в полной мере реализовать преимущества облучателей с низкими поте-
потерями и охлажденных входных каскадов усилителей для обеспечения максимальной
чувствительности.
На рис. 5.1. показано несколько фокальных систем, из которых наиболее часто
применяется система Кассегрена. Фокус Кассегрена имеет ряд преимуществ. Вы-
Выпуклое гиперболическое зеркало переотражает излучение и направляет его в фокус
Кассегрена, находящийся недалеко от основания главного рефлектора. Боковые
лепестки облучателя, выходящие за пределы вторичного зеркала напралены в небо,
температура шума которого невелика. Если облучатель расположен в первичном
У \
Рис. 5.1. Системы облучения зеркальных антенн: а — первичный фокус; б— фокус Кассе-
Кассегрена; в — фокус Нейсмита; г — смещенный фокус Кассегрена. При использовании фокуса
Нейсмита рупорный облучатель устанавливается на алидадной конструкции, располо-
расположенной ниже показанной штриховой линией оси высот, и для линейно поляризованного
сигнала угол плоскости поляризации изменяется относительно облучателя в зависимости
от угла места. В некоторых других системах, например в лучеводных антеннах (не пока-
показанных на рисунке), используются несколько зеркал, в том числе зеркало на азимутальной
оси, позволяющее устанавливать рупорный облучатель неподвижно относительно Земли.
В этом случае угол поляризации изменяется при изменении как азимута так и угла места
фокусе, то боковые лепестки при переоблучении главного зеркала направлены на
землю, что создает дополнительный уровень нежелательного шума. Преимуще-
Преимуществом фокуса Кассегрена также является возможность установить сразу за главным
зеркалом в любой антенне, за исключением самых маленьких, закрытую кабину
для размещения малошумящих входных каскадов электронной аппаратуры. Однако
располагаемые в первичном фокусе облучатели имеют меньшие апертуры, чем
расположенные в фокусе Кассегрена, и по этой причине первичный фокус часто
используется для более длинных волн.
Система Кассегрена также позволяет повысить эффективность апертуры изме-
изменением формы двух зеркал антенны (Williams, 1965). Этот подход может быть луч-
лучше всего продемонстрирован на примере передающей антенны. Если использовать
главное и вторичные зеркала общепринятой параболической и гиперболической
формы, то излучение облучателя концентрируется к центру апертуры антенны,
в то время как для достижения максимальной эффективности электрическое поле
5.1] Антенны 119
должно быть распределено равномерно. Если слегка изменить форму вторичного
зеркала, то к внешней части главного зеркала молено направить больше энергии,
улучшая тем самым однородность распределения. Далее следует изменить форму
параболоида главного зеркала так, чтобы восстановить равномерность фазы волно-
волнового фронта излучения антенны. Такая «шепированная» форма зеркал использует-
используется, например, на антеннах VLA в Нью-Мексико с диаметром главного зеркала 25 м.
В случае VLA среднеквадратичное отклонение поверхности зеркала от наиболее
близкого к его форме параболоида составляет ~1 см. Таким образом, антенны
могут быть использованы с облучателями в первичном фокусе на длинах волн более
~ 16 см. Шепирование не всегда оказывается предпочтительным, поскольку при
этом несколько ограничиваются внеосевые возможности антенн, что нежелательно
в случае многочастотного облучения.
Большая часть антенн в решетках апертурного синтеза представляет собой
полноповоротные параболические зеркала, однако существуют их многочисленные
конструктивные различия. Например, если требуется установить несколько облу-
облучателей для различных частотных диапазонов во вторичном фокусе, то они иногда
размещаются на поворотном устройстве так, чтобы используемый облучатель нахо-
находился на оси главного зеркала. С другой стороны, облучатели можно расположить
неподвижно по окружности, сцентрированной на ось параболоида, и использовать
слегка асимметричную конструкцию для фокусировки излучения на нужном облу-
облучателе простым поворотом вторичного зеркала.
В параболических зеркальных антеннах с несимметричным расположением об-
облучателей могут проявляться нежелательные эффекты паразитной поляризации,
исключаемые большей частью в осесимметричных конфигурациях. Это может
происходить в конструкциях антенн с незатененным раскрывом, как показано на
рис. 5.1 г, или в конструкциях, в которых набор облучателей используется для
наблюдений в нескольких частотных диапазонах, когда облучатели расположены
близко к оси параболоида, но не точно с ней совмещены. Если используются облуча-
облучатели с ортогональными линейными поляризациями, то в результате асимметрии по-
появляются большие кросс-поляризованные боковые лепестки в пределах центрально-
центрального лепестка диаграммы направленности. В случае облучателей с противоположны-
противоположными круговыми поляризациями плоскость, в которой две диаграммы направленности
смещены в противоположных направлениях, ортогональна плоскости, содержащей
ось симметрии рефлектора и центр облучателя. Это смещение является серьезной
проблемой при измерениях круговой поляризации, поскольку результат получается
из разности измерений на антеннах с противоположными круговыми поляриза-
поляризациями (см. выражения D.35)). Для измерений линейной поляризации смещение
не так существенно, поскольку при этом используются произведения выходных
сигналов с противоположными направлениями вращения и получающийся в ре-
результате отклик симметричен относительно оси параболоида. Эти эффекты можно
почти полностью исключить компенсирующим смещением вторичного зеркала. Для
дальнейших пояснений см. (Chu and Turrin, 1973 и Rudge and Adatia, 1978).
Рассморим требование к точности изготовления поверхности зеркал. Откло-
Отклонения поверхности от заданной формы приводят к изменениям фазы электро-
электромагнитного поля в фокусе антенны. Мы можем представить поверхность зеркала
состоящей из многочисленных площадок, смещенных от идеальной поверхности на
расстояние е — случайную переменную величину с распределением вероятностей
Гаусса:
E.1)
120 Антенны и антенные решетки [Гл. 5
где (б) = 0, (б2) = а2 и ( ) обозначено математическое ожидание. Используя урав-
уравнение E.1), молено получить следующее важное соотношение:
(eje) = (cos б) + (j sin б) = (cos б) = Г cos (б) р(е) de = е'^/2. E.2)
— оо
Отклонение от заданной поверхности на величину е приводит к отклонению в длине
пути отраженного луча примерно на 2е, причем точность приближения возрастает
с увеличением относительного фокусного расстояния. Таким образом, отклонение
на величину е вызывает смещение фазы равное ф ~ 4тгб/Л, где Л — длина волны.
В результате электрическое поле компонент в фокусе антенны имеет фазовое рас-
распределение типа Гаусса с <7ф = 4тгсг/Л. Для N независимых площадок поверхности
величина собирающей площади пропорциональна квадрату электрического поля:
-У
рЗФг \ — t^L. \ " /рЗ {Фг~Фк\ г^ Агл/рЭФЛ'2 (^ Ч\
е ' — 7V2 2^\е /-ло\е ;, [0.6)
где А о — площадь идеальной собирающей поверхности. Для достаточно большого
N членами с г = к можно пренебречь. Тогда из уравнений E.2) и E.3) получим
А = Ао e-D™AJ. E.4)
Это соотношение в радиотехнике называется формулой Руза (Ruze, 1966), а в неко-
некоторых других разделах астрономии — критерием Штреля. Например, если а/Х =
= 1/20, то эффективность апертуры A/Aq равна 0,67. Если в антенне исполь-
используются несколько отражающих поверхностей, то суммарное среднеквадратичное
отклонение определяется из суммы соответствующих нормальных распределений.
Вторичные зеркала, такие как зеркало Кассегрена, меньше главного рефлектора,
и их среднеквадратичные отклонения как правило соответственно меньше.
Несколько принципов были разработаны для улучшения параметров параболи-
параболических антенн, например, компенсации ошибок главного зеркала корректировкой
формы вторичного рефлектора (Ingalls et al., 1994; Mayer, Emerson and Davis, 1994).
Другие улучшения относятся к фокальной несущей конструкции, обеспечивающей
минимальное затенение апертуры и уменьшающей величину боковых лепестков
(рассеяния) в направлении земной поверхности (Lawrence, Herbig and Readhead
1994; Welch et al., 1996). Обычно фокальная аппаратурная кабина устанавливается
на трех или четырех опорах. Если опоры закрепляются на краях главного зеркала,
а не в пределах его апертуры, то они взаимодействуют только с плоским волновым
фронтом принимаемого излучения, и сферический волновой фронт в направлении
главного фокуса не искажается. Использование отражателя со смещенным облу-
облучателем позволяет полностью избежать затенения волнового фронта принимаемого
излучения вплоть до точки фокуса. Однако применение обоих методов уменьшения
затенения усложняет обеспечение механической жесткости конструкции. В резуль-
результате эти методы, как правило, используются для антенн малого диаметра, таких
как антенны, разрабатываемые для миллиметрового диапазона длин волн.
5.2. Выборка значений функции видности
5.2.1. Теорема выборки. Выбор конфигурации решетки апертурного синте-
синтеза основан на оптимизации, представляющей в некотором роде выборку значений
Выборка значений функции видности
121
Рис. 5.2. Иллюстрация теоремы выборки: а — функция видности V(u), показана только
действительная часть; б — функция выборки, в которой стрелками показаны дельта-
функции; в — выборочные значения функции видности; г — функция распределения
интенсивности /i(Z); д — функция повтора; е — восстановленная функция распределения
интенсивности. Функции г, д и е представляют собой преобразования Фурье функций а, б
и в соответственно, сне — восстановленное распределение интенсивности, иллюстрирующее
эффект путаницы, показанный заштрихованными областями, вследствие слишком боль-
большого интервала выборки
функции видности на плоскости uv. Поэтому, рассматривая структуру решетки,
логично начать с исследования требований к выборкам. Эти требования опреде-
определяются теоремой выборки в преобразованиях Фурье (Bracewell, 1958). Рассмотрим
для начала измерения одномерного распределения интенсивности источника Ii(l).
Необходимо измерить комплексную видность V в соответствующем направлении на
земной поверхности для ряда значений проекций антенных баз. Например, одним
из способов измерения профиля восток—запад является проведение наблюдений
источника вблизи его прохождения через меридиан с использованием базы восток-
запад и изменением ее длины день ото дня.
На рис. 5.2 а—в показана выборка одномерной функции видности V(u). Операция
выборки может быть представлена как умножение V(u) на ряд дельта-функций:
lAul
Ш
5 (и — г Аи),
E.5)
где левая часть уравнения может быть выражена через shah-функцию III, введен-
введенную в работе (Bracewell and Roberts, 1954). Ряд бесконечен в обоих направлениях,
и дельта-функции распределяются равномерно с шагом Аи. Преобразование Фурье
выражения E.5) представляет собой ряд дельта-функций, показанных на рис. 5.2 е:
Аи
Аи)
E.6)
р= — оо
122 Антенны и антенные решетки [Гл. 5
В /-области преобразование Фурье выборки видности равно свертке выраже-
выражения E.6) и преобразования Фурье V(iz), представляющего собой одномерную интен-
интенсивность Ii(l)- В результате /i(/) повторяется с интервалом (Аи)~1, как показано
на рис. 5.2 е. Если Ii(l) соответствует источнику конечных размеров, то повторяю-
повторяющиеся функции Ii(l) не будут накладываться друг на друга до тех пор, пока они
отличаются от нуля только в пределах такого интервала /, который не превышает
(Аи)~1. Пример перекрывающихся функций показан на рис. 5.2 сне. Информация,
возникающая вследствие такого наложения, обычно называется ложной, так как
при этом значения функции в пределах перекрывающейся области перестают од-
однозначно соответствовать краевым точкам исходной функции, которым они при-
принадлежат на самом деле. Чтобы избежать ложной информации, необходимо, чтобы
интервал выборки Аи не превышал обратной величины интервала по переменной
/, в пределах которого функция /]_(/) отлична от нуля. Говоря более точно, следу-
следует рассматривать размеры источника, расширенные конечным пространственным
разрешением наблюдений, а не его истинные размеры; но это, как правило, эффект
второго порядка — см. обсуждение просачивания 1] в работе (Bracewell, 2000).
Требования к восстановлению функции по набору отсчетов, например, пред-
представленной на рис. 5.2 а по отсчетам, показанным на рис. 5.2 в, легко понять, рас-
рассматривая преобразования Фурье на рис. 5.2 г и 5.2 е. Интерполяция в области
значений и соответствует исключению повторов в области значений /, что может
быть выполнено умножением функции, показанной на рис 5.2,е, и прямоугольной
функции, показанной штриховой линией. В области и это умножение будет соот-
соответствовать свертке значений выборки с преобразованием Фурье прямоугольной
функции, представляющем собой sine-функцию единичной площади:
sin пи/Аи ,_ 7^
. E.7)
7TU
Если путаница не возникает, то свертка с E.7) дает точную интерполяцию
исходной функции по выборочным значениям. Таким образом, мы можем сфор-
сформулировать как теорему выборки для функции видности следующее утверждение:
если распределение интенсивности отлично от нуля только внутри интервала
шириной lw, то 1\{1) полностью определяется выборкой значений функции вид-
видности в точках с шагом Аи = l/lw no координате и. В двумерном случае нужно
просто применить эту теорему последовательно к источнику по координатам / и т.
Дальнейшее обсуждение теоремы выборки см., например, в (Unser, 2000).
5.2.2. Дискретное двумерное преобразование Фурье. Получение карты
или изображения из измеренных значений видности составляет предмет гл. 10, но
для данного изложения важно понять форму представления данных в этом преоб-
преобразовании. Дискретная форма преобразования Фурье очень широко используется
в картографировании методом апертурного синтеза по причине больших вычис-
вычислительных преимуществ алгоритма быстрого преобразования Фурье (БПФ); см.,
например (Brigham, 1988). Также может использоваться быстрое преобразование
Хартли (Bracewell, 1984). В дискретном преобразовании функции V(u,v) и 1A,т)
представляются в виде прямоугольных матриц выборочных значений с равномер-
равномерными приращениями двух принятых переменных. Прямоугольная сетка точек, на
которой получена интенсивность, представляет удобную форму для дальнейшей
обработки данных.
х) Здесь термин просачивание используется в другом смысле по сравнению с поляримет-
рией.
5.2]
Выборка значений функции видности
123
Двумерная форма дискретного преобразования пар Фурье / и g определяется
M-1N-1
как
г=0 fe=0
и соответствующее обратное преобразование выглядит следующим образом:
М-1 N-1
jlirkq/N
E.8)
E.9)
См., например, (Oppenheim and Schafer, 1975). Функции являются периодическими
и их периоды равны М отсчетам по переменным г, рж N отсчетам по переменным к,
q. Для прямого вычисления выражений E.8) и E.9) требуется выполнить примерно
(MNJ комплексных перемножений. С другой стороны, если числа М и N взяты
в квадрат, то в алгоритме БПФ необходимо выполнить всего A/2) M7Vlog2(M7V)
комплексных перемножений.
Преобразования между V(u,v) и 1A, т), где / — двумерная интенсивность
излучения источника, получаются подстановкой д(г,к) = 1(гА1,кАт) и f(p,q) =
= V(pAu, qAv) в уравнения E.8) и E.9). Соотношение между интегральной и дис-
дискретной формами преобразования Фурье приведено в нескольких публикациях: см.,
например, (Rabiner and Gold, 1975 или Papoulis, 1977). Размеры области с данными
на плоскости uv равны МАи х NAv. На плоскости 1т интервал между точками
равен А/ по переменной / и — Am по
переменной т, и размеры карты рав-
равны МА1 х NAm. Приращения в двух
областях определений взаимосвязаны
следующим образом:
Аи = {МЫ)
-1
Av = (NAm)
-i
Al = (MAu)~\ Am = (NAv)~\
E.10)
Расстояние между точками в одной
области определения равно обрат-
обратной величине всего интервала изме-
измерений в другой области. Следователь-
Следовательно, если полный размер сетки данных
в области измерений интенсивности
выбран достаточно большим, чтобы
функция интенсивности была не рав-
равна нулю только в пределах площадки
МА1 х NAm, то величина прираще-
приращений Аи и Av в формулах E.10) удо-
удовлетворяет теореме выборки.
Чтобы применить дискретное пре-
преобразование к задаче синтеза изоб-
изображения, необходимо получить значе-
значения V(u,v) в точках с шагом Аи по и
Аи
Рис. 5.3. Точки прямоугольной сетки на плос-
плоскости uv, в которых выбираются значения
видности для использования в дискретном
преобразовании Фурье. Показаны равные ин-
интервалы Аи и Av. Также показано разбиение
плоскости на ячейки размера Аи х А г;
и Av по г>, как показано на рис. 5.3. Однако точки измерений в общем случае не
совпадают с (u,v) точками сетки, поскольку для сопровождающих интерферомет-
интерферометров измерения выполняются на участках эллипса плоскости uv, как объяснялось
124 Антенны и антенные решетки [Гл. 5
в разд. 4.1. Поэтому необходимо получить величины в точках сетки интерполяцией
или подобными процедурами. На рис. 5.3 плоскость разделена на ячейки разме-
размеров Аи х Дг>, центры которых совпадают с узлами сетки. Очень простой метод
определения значений видности, назначаемых каждой точке сетки, заключается
в вычислении среднего значения всех измерений, попадающих в данную ячейку. Эта
процедура была названа усреднением по ячейкам (Thompson and Bracewell, 1974).
Как правило, применяются более совершенные процедуры — см. 10.2.2. Однако
концепция усреднения по ячейкам помогает представить требуемое распределение
измерений: в идеальном случае минимум одно или несколько измерений следует вы-
выполнить в пределах каждой ячейки. Поэтому базы нужно выбирать таким образом,
чтобы расстояния между треками на плоскости uv были не больше размера ячейки,
чтобы получить максимальное количество пересекаемых треками ячеек. Пустые
ячейки интерпретируются как дыры на плоскости uv и минимизация количества
таких дыр представляет важный критерий при проектировании антенной решетки.
5.3. Вступление к антенным решеткам
5.3.1. Синфазные и корреляционные антенные решетки. Антенны ре-
решетки могут быть соединены для работы как в синфазной так и в корреляционной
решетках. Синфазные решетки применялись в ранних солнечных наблюдениях,
например, решетка, показанная на рис. 1.13 а, синфазные решетки из малых антенн
могут входить в состав больших корреляционных решеток как одиночные элементы.
На рис. 5.4 а показана простая схема синфазной антенной решетки с квадратичным
детектором на выходе, число антенн па в которой равно четырем. Если напряжения
на выходах антенн равны V\, V2, V3 и т.д., то выходной сигнал квадратичного
детектора пропорционален величине
(V1+V2 + V3 + --- + VnaJ. E.11)
Отметим, что число перекрестных произведений вида VmVn для различных антенн
тип равно па(па — 1), где па — общее количество антенн, а число автопроиз-
автопроизведений вида V^ равно па. Если пути сигналов от каждой антенны до детектора
имеют одинаковую электрическую длину (с учетом смещений фазы), то сигналы
складываются синфазно для направления принимаемого излучения
• -i (N
)•
где N — любое целое число, включая ноль, и ?\ — расстояние между соседними
антеннами, измеряемое в длинах волн. Направления максимумов, представляющих
диаграмму направленности антенной решетки, могут изменяться регулировкой фа-
фазового смещения на выходах антенн, что делает диаграмму управляемой и, напри-
например, позволяет сканировать определенную область небесной сферы для получения
изображения.
На рис. 5.4 ?Г показана корреляционная решетка, выходы корреляторов которой
для каждой пары антенн VmVn соответствуют произведениям напряжений. Выход-
Выходные сигналы корреляторов равны кросс-произведениям синфазной решетки. Вы-
Выходы корреляторов могут быть просуммированы так, чтобы получить максимумы,
подобные максимумам синфазной решетки. Если фазовый сдвиг вводится на выходе
одной из антенн корреляционной решетки, то это приводит к соответствующему из-
изменению фазы интерференционных лепестков, измеряемых коррелятором, подклю-
подключенным к данной антенне. С другой стороны, эффект фазового смещения на выходе
5.3]
Вступление к антенным решеткам
125
антенны может быть имитирован изме-
изменением измеренных фаз в процессе сум-
суммирования коррелированных выходов.
Таким образом, сканирующий луч мо-
может быть получен в процессе суммирова-
суммирования измеряемых кросс-корреляционных
сигналов соответствующими сдвигами
фазы компьютером. Это как раз тот слу-
случай, что и в вычислении преобразования
Фурье функции видности, т. е. преобра-
преобразование Фурье коррелированных сигна-
сигналов как функции пространственных ча-
частот. Потеря авто-корреляционных чле-
членов приводит к ухудшению мгновенной
чувствительности по мощности в (па —
— 1)/па раз, что близко к единице при
условии, что па велико. Однако для лю-
любого момента времени в отклике кор-
корреляционной решетки представлено все
поле отдельных антенн, в то время как
отклик, сформированный синфазной ре-
решеткой, представляет собой узкий луч,
если только не используется более слож-
сложная схема согласования сигналов, позво-
позволяющая получить несколько лучей одно-
одновременно. Таким образом, картографи-
картографирование с корреляционной решеткой бо-
более эффективно чем с синфазной.
Отклики корреляционной и синфаз-
синфазной антенных решеток на точечный
источник одинаковы, за исключением
авто-корреляционных членов. Отклик
фазированной решетки состоит из од-
одного или нескольких лучей, направле-
направления которых соответствуют синфазно-
синфазному суммированию откликов антенн. Эти
главные лучи окружены боковыми ле-
лепестками, форма и величина которых
определяются количеством и расположе-
расположением используемых антенн. Сигнал меж-
между боковыми лепестками может умень-
уменьшаться до низкого уровня — вплоть
до нулевого, но не может быть отрица-
отрицательным, поскольку не может быть от-
отрицательным выходной сигнал квадра-
квадратичного детектора. Теперь посмотрим,
что произойдет в результате вычитания
авто-корреляционных членов для ими-
имитации сигнала корреляционной решет-
решетки. В пределах поля зрения, малого по
сравнению с размером диаграммы на-
направленности отдельной антенны, каж-
Квадратичный
детектор
Рис. 5.4. Простая четырехэлементная ли-
линейная антенная решетка. ?\ — единичное
расстояние между антеннами, выраженное
в длинах волн, 0 — угол, определяющий на-
направление принимаемого сигнала, а — кон-
конфигурация фазированной решетки с регу-
регулируемым фазовым смещением на выхо-
выходе каждой антенны и суммарным сигна-
сигналом, подаваемым на вход квадратичного
детектора. Сумматор представляет собой
согласованный элемент, выходной сигнал
которого пропорционален сумме напряже-
напряжений высокочастотных сигналов, поданных
на его входы, б— те же антенны, соединен-
соединенные как корреляционная решетка, в — по
оси ординат представлен отклик антенной
решетки: левая ось соответствует синфаз-
синфазной решетке, правая — корреляционной.
Отсчеты на оси абсцисс пропорциональ-
пропорциональны в в единицах l^1 рад. Вследствие рав-
равного расстояния между антеннами в этой
простой дифракционной решетке появля-
появляются боковые лучи, повторяющие форму
главного
126 Антенны и антенные решетки [Гл. 5
дый авто-корреляционный член может быть представлен постоянным уровнем сиг-
сигнала, а каждый кросс-корреляционный член — как интерференционные колеба-
колебания. В случае отклика на точечный источник величина всех этих членов будет
одинаковой. Вычитание авто-корреляционных членов из отклика фазированной
решетки приведет к смещению нулевого уровня в положительном направлении на
величину, равную 1/па от максимального уровня, как показано штриховой линией
на рис. 5.4 в. Точки, представляющие нули в отклике синфазной решетки, станут
минимумами отрицательных лепестков. Таким образом, в отклике корреляционной
решетки положительные значения становятся в (па — 1)/па раз меньше значений
отклика синфазной решетки. В отрицательном направлении отклик достигает уров-
уровня — 1/{па — 1) от величины максимума, но не может быть меньше, поскольку
этот уровень соответствует нулевому уровню синфазной решетки. Ограничение
на величину отрицательных лепестков корреляционной решетки было получено
Коганом (Kogan, 1999), который также отметил, что эта предельная величина опре-
определяется только количеством антенн в решетке и не зависит от их расположения.
Ни одно из этих заключений не применимо к положительным лепесткам. Этот
результат полностью справедлив только для кратковременных наблюдений (т. е.
наблюдений, за время которых покрытие плоскости uv не успевает существенно
измениться вследствие вращения Земли) и при равных весовых коэффициентах
выходных сигналов корреляторов.
В заключение рассмотрим некоторые характеристики синфазной решетки, по-
показанной на рис. 5.4 а. Сумматор представляет собой элемент пассивного типа, при-
примером которого является разветвленная линия передачи, показанная на рис. 1.13 а.
Если на каждый вход сумматора подать коррелированный (когерентный) сигнал
мощности Р, то мощность сигнала на выходе сумматора будет равна паР. Приме-
Применительно к напряжениям V сигналов на каждом входе это означает, что линейно
суммируются части каждого из напряжений на входе, равные 1/у/п^,, и напряже-
напряжение выходного сигнала равно у/п^ V, или мощность — паР. Теперь, если на вход
подаются некоррелированные (некогерентные) сигналы, то опять доля напряжения
каждого сигнала составляет V/^/n^, но линейно суммируются мощности (как сум-
сумма квадратов напряжений), так что в этом случае мощность сигнала на выходе
равна мощности сигнала Р на одном из входов. Таким образом, вклад в выходной
сигнал составляет только часть мощности каждого из входных сигналов, равный
1/по, а остаток рассеивается на оконечных согласованных входах сумматора (т. е.
излучается антеннами в случае, если они соединены с сумматором напрямую). Если
источник не разрешается главным лучом антенной решетки, то сигналы полностью
коррелированы, а шумовые составляющие, вносимые антеннами и усилителями, —
не коррелированы. Таким образом, в случае, если потери в линиях передачи или
сумматоре отсутствуют, то одинаковое отношение сигнал/шум на детекторе полу-
получится при установке усилителей на выходе каждой антенны, или при установке
единственного усилителя на выходе сумматора. Однако эти потери часто значи-
значительны, и выгоднее использовать усилители на антеннах. Отметим также, что если
одна половина антенн решетки направлена на источник, а другая — на пустой
участок небесной сферы, то мощность сигнала на выходе сумматора равна четверти
мощности по сравнению со случаем, когда все антенны направлены на источник.
5.3.2. Пространственная чувствительность и пространственная пере-
передаточная функция. Рассмотрим чувствительность антенны или решетки к про-
пространственным частотам на небесной сфере. Диаграмма направленности антенны
одна и та же при передаче или приеме, и в данном случае удобнее рассмотреть
антенну на передачу. Тогда поле в апертуре антенны формируется подаваемой на ее
вход мощностью. Функция W(u,v) определяется как автокорреляционная функция
распределения электрического поля ?(х\, у\) в апертуре, где х\ и у\ — координаты
5.3] Вступление к антенным решеткам 127
в плоскости апертуры антенны, выраженные в длинах волн. Таким образом,
оо оо
W(u,v) = ?(х\,у\)**?*(хх,у\) = J J S(x\,y\)?*(x\-u,y\-v)dx\dy\.
— оо —оо
E.13)
Символ ** обозначает двумерную автокорреляцию. Интеграл в уравнении E.13)
пропорционален числу путей, соответствующим образом взвешенных интенсивно-
интенсивностью поля, в которых пространственный вектор (u,v) может быть расположен
в апертуре антенны. В случае работы на прием W(u,v) измеряется чувствительно-
чувствительностью антенны к различным пространственным частотам. В сущности, антенна или
решетка работают как фильтры пространственных частот, и W(u,v) общепринято
называть передаточной функцией по аналогии с использованием этого термина
в теории фильтров. Также W(u,v) называют функцией спектральной чувствитель-
чувствительности (Bracewell, 1961, 1962) аналогично спектру пространственных частот (а не
спектру радиоизлучения) в отклике антенной решетки. При обсуждении W(u, v) мы
используем термины пространственная передаточная функция и пространствен-
пространственная чувствительность. Площадка плоскости uv, в которой могут выполняться
измерения (т. е. ограниченная область определения W(u, г>), в которой эта функция
не равна нулю) называется заполнением пространственных частот или (и, v)-
заполнением.
Рассмотрим отклик антенны или решетки на точечный источник. Поскольку
видность точечного источника постоянна на плоскости uv, измерения в области про-
пространственных частот пропорциональны W(u,v). Таким образом, отклик на точеч-
точечный источник АA,т) получается преобразованием Фурье W(u,v). Этот результат
был формально выведен Брейсуэллом и Робертсом (Bracewell and Roberts, 1954).
[Напомним, что как следует из выражения B.15), отклик на точечный источник
равен зеркальному отображению диаграммы направленности антенны, АA,т) =
= А(—1, —яг), но это различие практически несущественно, поскольку рассматри-
рассматриваемые функции обычно симметричны.] Пространственная передаточная функция
W(iz, v) занимает важное место в этой главе, и ее взаимосвязь с функциями, исполь-
используемыми при построении радиоизображений, дополнительно показана на рис. 5.5.
На рис. 5.6 а показан интерферометр с неуправляемыми антеннами, представ-
представленными двумя прямоугольниками. Допустим, что распределение ?(х\, у\) по апер-
апертуре равномерно, как в случае решетки диполей с однородным возбуждением.
Для начала предположим, что выходные сигналы с двух апертур суммируются
по напряжению и поступают на измеряющий мощность приемник, как в некоторых
первых инструментах. Три прямоугольных площадки на рис. 5.6 в представляют
собой автокорреляционную функцию распределения поля в апертурах, т. е. про-
пространственную передаточную функцию. Отметим, что автокорреляция для двух
апертур состоит из автокорреляций отдельных апертур (прямоугольник в центре
рис. 5.6 б) плюс их кросскорреляционная функция (заштрихованные прямоуголь-
прямоугольники). Если антенны соединяются коррелятором, а не приемником мощности, то
пространственная чувствительность будет представлена только заштрихованными
областями, поскольку коррелятор формирует только кросс-произведение сигналов
двух апертур. Таким образом, пространственная передаточная функция W(u,v)
может не включать все составляющие автокорреляционной функции апертуры,
в зависимости от соединения корреляторами и (или) детекторами.
Интерпретация пространственной передаточной функции как преобразования
Фурье отклика на точечный источник может применяться как при суммировании,
так и при корреляции сигналов. Например, при использовании интерферометра, по-
показанного на рис. 5.6 а, в комбинации с коррелятором отклик на точечный источник
получается преобразованием Фурье функции, представленной заштрихованными
128
Антенны и антенные решетки
[Гл.5
Функция облучения
апертуры &(хх,ух)
Приемная диаграмма
направленности
по напряжению 12A, да)
Автокорреляция
Умножение на комплексную
V сопряженную
-de
Передаточная функция
(пространственная
чувствительность) W(u, и)
»яже
Приемная диаграмма
направленности
по мощности АA,т)
Функция
видности <У"(и, v)
Распределение
интенсивности 1A, т)
Рис. 5.5. Взаимосвязь функций, используемых в процессе получения изображения источ-
источника. Начиная сверху слева, автокорреляция распределения электрического поля ?(х\, у\)
по апертуре антенны определяет пространственную передаточную функцию W(u,v). Из-
Измеряемая видность наблюдаемого источника — произведение видности V(u,v) и простран-
пространственной передаточной функции. Вверху справа — произведение диаграммы направленно-
направленности по напряжению VaA, тп) с ее комплексно сопряженным отображением равно диаграмме
направленности по мощности A(l,m). Карта источника с распределением интенсивности
/(/, га) получается сверткой этой функции с диаграммой направленности по мощности.
Эти функции, определенные в областях (х\,у\), (u,v), а также (/,га), связываются преоб-
преобразованиями Фурье, как показано на рисунке. Если пространственная чувствительность
синтезирована вращением Земли, например, при сопровождении антенной решеткой ис-
источника, то в общем случае она не может быть представлена автокорреляцией какого-либо
распределения поля. Тогда используется только часть диаграммы ниже штриховой линии
областями. Это преобразование Фурье равно
L 7ГЖЛ1/
7ТУХ1ГП J
E.14)
где x\i и у\i — координаты в плоскости апертуры, и D\ — расстояние между
апертурами, выраженное в длинах волн. Квадратами sine-функций представлена
диаграмма направленности равномерно облучаемых апертур прямоугольной фор-
формы, а косинусный член соответствует интерференционной диаграмме. В первых
инструментах относительная величина пространственной чувствительности контро-
контролировалась только распределением поля по антеннам, но применение компьютеров
для обработки изображений позволяет корректировать эту величину после прове-
проведения наблюдений.
Некоторые наиболее часто встречающиеся конфигурации антенных решеток
и границы их автокорреляционных функций показаны на рис. 5.7. Автокорреля-
Автокорреляционной функцией отображается мгновенная пространственная чувствительность
заполненной апертуры, форма которой приведена в соответствующей части ри-
рисунка. Из уравнения E.13) видно, что автокорреляционная функция представляет
собой интеграл произведения распределения поля и его комплексно сопряженной
5.3]
Вступление к антенным решеткам
129
D,
ХХ1
8*3*
(ххьУ%\)
Рис. 5.6. Две апертуры в части (а) рисунка представляют двухэлементный интерферометр,
пространственная передаточная функция которого показана в части (б). Заштрихован-
Заштрихованными прямоугольниками показаны составляющие пространственной чувствительности,
соответствующие кросскорреляции сигналов двух антенн. При равномерном распределе-
распределении поля по апертурам величина пространственной чувствительности линейно спадает.
Это показанно треугольниками с и <i, которые представляют ортогональные профили
пространственной передаточной функции
функции, смещаемой по и и v. Рассматривая значения и и г>, для которых изобра-
изображения двух апертур пересекаются, легко определить границу области, в которой
пространственная передаточная функция отлична от нуля, используя описанные
Брейсуэллом графические процедуры (Bracewell, 1961, 1995). Можно также опреде-
определить гребни высокой автокорреляции, возникающие при смещении пространствен-
пространственных частот в направлениях плеч таких конфигураций, как показанные на рисун-
рисунках 5.7 а, 5.7 б"или 5.7 в. В случае кольцевой конфигурации, показанной на рис. 5.7 г,
автокорреляционная функция пропорциональна площади пересечения кольца и его
смещенного изображения в двух точках. Эта площадь приблизительно пропорци-
пропорциональна обратной величине синуса угла между касательными к кольцам в точке
их пересечения и представлена графиком на рис. 5.7 тс, где ось абсцисс направлена
от центра к краю круга автокорреляции. Когда угол между касательными равен
тг/2, образуется широкий минимум пространственной чувствительности, определя-
определяемый для кольца единичного радиуса уравнением \/и2 + v2 = y2. Если апертура
заполнена не полностью, т. е. конфигурация на рисунке представлена дискретной
решеткой из отдельных антенн, то функция пространственной чувствительности
представлена рядом автокорреляционных функций. Например, в случае крестооб-
крестообразной конфигурации антенн, расположенных на равном расстоянии друг от друга,
квадрат на рис. 5.7 6" будет преобразован в матричную форму, ограниченную его
размерами. Далее конфигурации, представленные на рис. 5.7, будут рассмотрены
более подробно.
5.3.3. Крестообразные и Т-решетки для метровых длин волн. Кресто-
Крестообразный телескоп и его автокорреляционная функция показаны на рисунках 5.7 а
и 5.7 б. Предполагается, что ширина плеч решетки мала по сравнению с их длиной,
но имеет конечное значение. В случае креста Миллса (Mills, 1963), кратко описанно-
описанного в гл. 1, выходные сигналы двух плеч поступают на один кросс-корреляционный
приемник, так что пространственная чувствительность решетки представлена квад-
квадратом на рис. 5.7 б. Перпендикулярные линии, проведенные от центров сторон квад-
квадрата, соответствуют автокорреляционным функциям отдельных плеч и не образу-
5 Томсон
130
Антенны и антенные решетки
[Гл.5
Рис. 5.7. Конфигурации апертур антенных решеток и границы областей, в пределах ко-
которых соответствующие автокорреляционные функции не равны нулю. Конфигурации
показаны в плоскости апертуры (х\,у\), а автокорреляционные функции — в плоскости
пространственных частот uv: а — крест; б— границы его автокорреляции; в — Т-решетка;
г — границы ее автокорреляции; д — равноугольная Y-конфигурация; е — границы ее
автокорреляции. Штриховыми линиями на изображениях б, г и е показаны гребни авто-
автокорреляционных максимумов, ж — кольцо из — границы его автокорреляции. Автокорре-
Автокорреляционная функция кольца центрально симметрична, и на графике к показан радиальный
профиль функции, представленной кругом в части з рисунка, в направлении от центра
круга к его краю, и — треугольник Руло. Штриховыми линиями показан равносторонний
треугольник; в его вершинах находятся центры окружностей, дуги которых и образуют
треугольник Руло. Область автокорреляции треугольника Руло ограничивается той же
окружностью, что и в части з рисунка
ются при кросс-корреляции. Однако они формируются в случае, когда крест состо-
состоит из двух линий отдельных антенн, так как при этом в кросс-корреляции линеек
появляются дополнительные составляющие, образованные парными комбинациями
антенн в плечах решетки. Случай Т-решетки похож: на предыдущий и представлен
5.4] Пространственная передаточная функция следящей решетки 131
на рисунках 5.7 в и 5.7 г. Опять же, если только кросс-корреляция формируется
для плеч восток-запад и север-юг, причем второе плечо в два раза короче первого,
то заполнение пространственных частот представлено только квадратом в области
автокорреляции. Эквивалентность пространственных передаточных функций кре-
крестообразной и Т-решетки может быть однозначно интерпретирована следующим
образом: для любой пары точек в апертуре креста, например для одной точки
в восточном плече и другой — в северном, найдется соответствующая пара точек
в западном и восточном плечах, пространственные векторы которых будут иден-
идентичны. Следовательно, любое из четырех плеч половинной длины можно удалить,
не ухудшая при этом гш-заполнение пространственной передаточной функции.
Если чувствительность (т. е. эффективная площадь на единицу длины) равно-
равномерна вдоль плеч креста или соответствующей Т-решетки, то весовые коэффи-
коэффициенты пространственной чувствительности одинаковы в пределах квадрата на
плоскости uv; отметим, что при этом эффект линейного спада в направлении от
центра, показанный на рис. 5.6, отсутствует. На границе прямоугольной площадки
пространственная чувствительность падает до нуля на расстоянии, равном ширине
плеч. Такой резкий скачок вследствие равномерной чувствительности приводит
к образованию больших боковых лепестков. Поэтому при проектировании креста
Миллса было введено снижение по закону Гаусса чувствительности элементов вдоль
плеч решетки до 10 % на их краях. Это значительно снизило величину вторичных
максимумов в отклике от боковых лепестков вне главного луча за счет некоторого
уширения центрального луча.
На рис. 1.12 а показана реализация Т-решетки, являющаяся примером пассажно-
пассажного корреляционного интерферометра, в котором малая антенна перемещается шаг
за шагом, постепенно увеличивая заполнение плоскости uv и имитируя тем самым
апертуру больших размеров; см. (Blythe, 1957; Ryle, Hewish, and Shakeshaft, 1959;
Ryle and Hewish, 1960). Заполнение пространственных частот получается таким же,
как и в случае разовых наблюдений с антенной, размеры апертуры которой были
бы равны апертуре, имитируемой перемещениями малой антенны, хотя величина
пространственной чувствительности при этом не точно такая же. Термин апертур-
ный синтез был введен для описания таких наблюдений.
5.4. Пространственная передаточная функция следящей
решетки
Диапазон пространственных частот выходного сигнала интерферометра с со-
сопровождающими антеннами показан на рис. 5.8 б. Двумя заштрихованными обла-
областями показана кросскорреляция двух апертур интерферометра восток-запад для
источника, проходящего через меридиан. Изменение гш-заполнения в зависимости
от часового угла источника показано полосой, центрированной относительно трека
на плоскости uv для двух антенн. Вспомним из разд. 4.1, что для наземного интер-
интерферометра эти треки представляют собой дуги эллипса, и, поскольку V(—u, —v) =
= V*(u, г>), любой парой антенн измеряется видность вдоль двух дуг, симметричных
относительно начала (и, v)-координат, причем обе дуги включаются в простран-
пространственную передаточную функцию.
Так как источник сопровождается антеннами, оси диаграмм направленности
антенн остаются неподвижными относительно некоторой точки исследуемого ис-
источника и антенная решетка измеряет произведение распределения интенсивности
источника и диаграммы направленности антенны. Другой подход к этой задаче
заключается в рассмотрении приема излучения малыми участками апертур двух
антенн, центры которых отмечены точками А\ и А<± на рис. 5.9. Апертурами антенн
132
Антенны и антенные решетки
[Гл.5
О
о
Рис. 5.8. а — апертура двухэлементного интерферометра восток-запад; б— соответствую-
соответствующее заполнение пространственных частот, показанное заштрихованными областями. Если
источник сопровождается антеннами, то вектором базы описывается эллипс (показанный
сплошной линией) на плоскости uv. Область пространственных частот, в которой измеря-
измеряются значения функции видности, выделена штриховыми линиями в части б рисунка. Рас-
Расстояние между штриховыми линиями определяется кросскорреляцией антенных апертур
заполняется диапазон пространственных частот от и — d\ до и + d\ длин волн, где
d\ — диаметр антенны в длинах волн. Если диаграммы направленности антенн оста-
остаются неподвижными при прохождении через них источника, то в выходном сигнале
коррелятора присутствуют комбинации интерференционных компонент с частота-
частотами от оое(и — d\) cos5 до ше(и + d\) cos 5, где иое — угловая скорость вращения Земли
и S — склонение источника. Чтобы выяснить эффект слежения за источником,
рассмотрим точку В антенны, которая в этом случае перемещается в направлении
источника со скоростью ujeAu cos 5 длин волн в секунду. Вследствие этого про-
происходит доплеровское смещение сигнала, принимаемого в точке В. Чтобы опре-
определить частоту интерференции сигналов, принимаемых в точках А\ и В, вычтем
из частоты интерференции для случая неподвижных антенн частоту доплеровского
сдвига, и в результате получим [сое(и + Аи) cos 5] — (ujeAu cos 5) = (иоеи cos 5). Таким
образом, частота интерференции при сопровождении источника получается та же,
что и для точек А\ и^ в центрах апертур. (Этот результат верен для любой пары
точек; при выборе одной точки в центре апертуры в приведенном примере обсу-
обсуждение становится немного проще.) Следовательно, в случае сопровождения ис-
источника антеннами частоты интерференции всех пар точек в апертурах одинаковы
на выходе коррелятора. По этой причине составляющие синусоидального сигнала
на выходе коррелятора не могут быть разделены анализом Фурье, и информация
об изменениях видности в интервале от и — d\ до и + d\ теряется. Тем не менее,
если движение антенн не совпадает с идеальным сопровождением источника, то
эта информация, в принципе, может быть восстановлена. При картографировании
источника, размеры которого превышают размеры антенных лучей, в сопровожде-
сопровождение антенн добавляют сканирование, что позволяет перекрыть область источника
полностью. В результате сканирования измерения видности по и и v выполняются
с интервалами, достаточно малыми для источника протяженных размеров. Этот
метод, называемый мозаикой, рассматривается в разд. 11.6.
Чтобы учесть эффекты, связанные с сопровождением источника антеннами, ис-
используется модификация распределения интенсивности с помощью нормированной
диаграммы направленности. При этом распределение интенсивности принимает вид
Лдг(/, т) 1A,777,), как показано в разд. 3.1. Пространственная передаточная функция
W(u, v) двух антенн, сопровождающих источник, в любой момент времени может
быть представлена парой двумерных дельта-функций 25(и, v) и 25(—щ—v). Для
антенной решетки результирующая пространственная передаточная функция по-
5.4]
Пространственная передаточная функция следящей решетки
133
77777/7777/77777777777777777777777777777^
Рис. 5.9. Иллюстрация влияния сопровождения на частоту интерференции выходного сиг-
сигнала коррелятора. Показана только проекция базы и, поскольку частота интерференции
не зависит от проекции v. Направление вращения антенн показано стрелкой в центре
рисунка
лучается в виде ряда дельта-функций с весовыми коэффициентами, пропорциональ-
пропорциональными величине инструментального отклика. При вращении Земли дельта-функции
образуют набор эллиптических треков в плоскости пространственных частот. Эти
треки и представляют пространственную передаточную функцию следящей антен-
антенной решетки.
Рассмотрим наблюдения источника 1A, т) с функцией видности V(u,v) и нор-
нормированной диаграммой направленности Адг(/, т). Тогда, если W(u, v) — простран-
пространственная передаточная функция, то измеряемая видность равна
[V(u, v) * * AN(u, v)] W(u, v),
E.15)
где символом ** обозначена двумерная свертка, а надчеркиванием — преобра-
преобразование Фурье. Преобразованием Фурье выражения E.15) получим измеряемую
интенсивность
[l(l,m) AN(l,m)] **Щ/,т). E.16)
Если наблюдается точечный источник, положение которого совпадает с началом
(/, 777,)-координат, где А^ = 1, то выражение E.16) сводится к отклику на точечный
источник bo(l,m). В этом случае получим
ЬоA, т) = [25{l, m) AN(l, т)] * * W(l, т) = W(l, m),
E.17)
где точечный источник представлен функцией 5A, т). Как и ранее, отклик на
точечный источник равен преобразованию Фурье пространственной передаточной
функции. При сопровождении источника пространственные частоты, на которых
выполняются измерения, определяются выражением W(u,v) * *An(u,v). Отметим,
что А^ (и, v) в два раза шире по сравнению с размерами соответствующей антенной
апертуры в координатах (ж, у).
Термин апертурный синтез иногда распространяется на наблюдения с сопро-
сопровождением по часовому углу. Однако для следящей антенной решетки определить
точную эквивалентную апертуру невозможно. Например, рассмотрим случай со-
сопровождения источника двумя антеннами с базой восток-запад в течение 12 часов.
Пространственная передаточная функция принимает вид эллипса на плоскости uv
134 Антенны и антенные решетки [Гл. 5
с центром в начале координат, причем чувствительность внутри эллипса равна
нулю (за исключением точки в начале координат, которая может быть сопоставлена
с измерением полной мощности, принимаемой антенной). Эквивалентная апертура
описывалась бы в этом случае функцией, автокорреляция которой представляла бы
тот же эллипс, что и пространственная передаточная функция. Такой апертурной
функции не существует, — следовательно, использование термина апертурный син-
синтез для описания большей части наблюдений с сопровождением по часовому углу
весьма условно.
5.4.1. Требуемые характеристики пространственной передаточной
функции. В качестве первого шага при определении конфигурации антенн
полезно рассмотреть требуемое заполнение пространственных частот (г/, г>); см.,
например, (Keto, 1997). Для любых конкретных наблюдений оптимальное uv-
заполнение, очевидно, определяется ожидаемым распределением интенсивности
исследуемого источника, поскольку предпочтительнее сконцентрировать воз-
возможности инструмента на участках плоскости uv, где видность не равна нулю.
Однако большинство антенных решеток используется для наблюдений различных
типов астрономических объектов, так что требуется некоторый компромиссный
подход. Поскольку в общем случае ориентация астрономических объектов на
небесной сфере случайна, то предпочтительное направление высокого разрешения
отсутствует. Поэтому логично выбрать для измерений видности круглую область
на плоскости uv с центром в начале координат.
Как описано в разд. 5.2, данные измерений видности обычно интерполируются
на прямоугольной сетке для удобства выполнения преобразования Фурье, и если
для каждого узла сетки используется примерно равное количество измерений, то
в процессе преобразования им могут быть назначены одинаковые весовые коэффи-
коэффициенты. Неравномерное взвешивание приводит к потерям в чувствительности, так
как при этом шумовые составляющие в одних отсчетах оказываются больше, чем
в других. С этой точки зрения желательно, чтобы естественное взвешивание (т. е.
назначение весовых коэффициентов, определяемое только конфигурацией антенной
решетки, без дополнительных коррекций) было настолько равномерным, насколько
это возможно в пределах круглой площадки.
Для антенных решеток общего назначения дальнейшая оптимизация в пределах
круглой измеряемой площадки затруднительна. Однако существуют исключения из
правила для равномерных измерений в пределах круга. Как упоминалось выше, в
кресте Миллса с идентично связанными излучающими элементами в плечах про-
пространственная чувствительность равномерна. Для уменьшения боковых лепестков
введена спадающая гауссова связь, что приводит к подобному спаду пространствен-
пространственной чувствительности. Это было особенно важно, поскольку как отмечено в гл. 1, на
рабочих частотах таких инструментов, обычно в диапазоне 85-408 МГц, путаница
источников представляла серьезную проблему. Отклики боковых лепестков могли
быть ошибочно приняты за источники, и могли блендировать истинный источник.
В случае равномерной пространственной передаточной функции прямоугольного
вида форма диаграммы направленности описывается sine-функцией (вттгж/тгж),
относительная величина первого бокового лепестка которой равна 0,217. При рав-
равномерной круговой пространственной передаточной функции форма диаграммы
направленности описывается функцией ^(тгж)/тгж, и в этом случае относительная
величина первого бокового лепестка равна 0,132. Боковые лепестки при равномерно
круговом (и, v)-заполнении меньше, чем при прямоугольном, но все же представ-
представляют проблему в условиях путаницы источников. По этой причине однородное
взвешивание может быть не оптимальным вариантом при такой высокой плотности
источников, как та что обнаружена на низких частотах.
5.5] Одномерные следящие решетки 135
Б.4.2. «Дыры» в заполнении пространственных частот. Рассмотрим
круг на плоскости uv диаметра а\ длин волн, в котором дыры в данных отсут-
отсутствуют, т. е. данные измерений видности, интерполированные на прямоугольную
сетку для преобразования Фурье, не имеют пропусков. Тогда при равных весовых
коэффициентах синтезированная диаграмма направленности, которая получается
преобразованием Фурье выбранной в точках сетки передаточной функции, описы-
описывается функцией JiGra\6)/Gra\6)i где угол 0 отсчитывается от оси диаграммы. Если
использовать центрально симметричные весовые коэффициенты, увеличивающиеся
к центру, то диаграмма направленности примет вид этой сглаженной функции.
Определим (гл, г>)-область, описанную выше, как полное покрытие плоскости uv,
а соответствующую диаграмму направленности — как полный отклик. Теперь,
если часть данных пропущена, истинное заполнение плоскости uv равно полному
покрытию минус (и, v)-распределение пропущенных значений. Вследствие свойства
аддитивности преобразований Фурье соответствующий синтезированный луч равен
полному отклику минус образ Фурье распределения дыр. Дыры добавляют нежела-
нежелательную составляющую в полном отклике, проявляющуюся в виде дополнительных
боковых лепестков в синтезированной диаграмме направленности. По теореме Пар-
севаля среднеквадратичная амплитуда боковых лепестков дыр пропорциональна
среднеквадратичной величине недостающей пространственной чувствительности,
представленной дырами. Другие боковые лепестки появляются в результате осцил-
осцилляции функции JiGra\6)/Gra\6)i описывающей профиль полного отклика, но вклад
дыр очевиден.
5.5. Одномерные следящие решетки
В этом разделе мы рассмотрим интерферометры или решетки, конфигурация
антенн которых представляет прямую линию. Мы видели, что для пары антенн,
расположенных в направлении восток—запад, треки на плоскости uv образуют на-
набор эллипсов с центрами в начале координат. Чтобы получить полные эллипсы,
необходимо перекрыть часовые углы в пределах 12 часов. Если разнесение антенн
решетки восток—запад увеличивается с одинаковым шагом, то пространственная
чувствительность выглядит как ряд концентрических эллипсов с равномерно воз-
возрастающей длиной осей. Получаемое угловое разрешение обратно пропорционально
ширине заполнения плоскости uv в соответствующем направлении, причем ширина
в направлении v равна ширине в направлении и, умноженной на синус склонения
5. Решетки восток-запад с расстоянием между антеннами, кратным единичному
интервалу, получили широкое распространение в радиоастрономии, особенно для
наблюдений с \5\ больше ~30°.
В простейшем типе одномерной решетки антенны расположены на равных рас-
расстояниях ?\ друг от друга (см. рис. 1.13 а). Такие решетки, по аналогии с оптикой,
иногда называются дифракционными. Если в решетке па антенн, то на ее выходе
представлены (па — 1) комбинаций единичных баз, (па — 2) — двойных и т. д.
Таким образом, короткие базы высоко избыточны и приходится искать другие
способы расположения антенн, чтобы получить больше различных баз при данном
па. Отметим, однако, что избыточные наблюдения могут использоваться в целях
калибровки аппаратурного отклика и эффектов, связанных с атмосферой, так что
некоторая степень избыточности определенно выгодна (Hamaker, O'Sullivan and
Noordam, 1977).
Конфигурация антенн, не содержащая избыточных баз, была применена Арса-
ком (Arsac, 1955) и показана на рис. 5.10 а. Все шесть возможных комбинаций пар
образуют базы разной длины. При использовании более четырех антенн всегда су-
136 Антенны и антенные решетки [Гл. 5
• • | | • 1 • ществует некоторая избыточность
а или потеря баз. Пятиэлементная
конфигурация минимальной избы-
т . . I • I I • точности, полученная Брейсуэл-
лом (Bracewell, 1966), показана на
6 рис. 5.10 6 Моффет (Moffet, 1968)
т-» г 1л тт 1 « привел примеры решеток с мини-
Рис. 5.10. Две конфигурации одномерной ре- « ^
г—* ^ j г ^ ^ г г мальнои избыточностью, число эле-
шетки, антенны которой показаны точками: ' Л л
а - не избыточная конфигурация Арсака (Аг- ментов которых достигает 11, и ре-
sac, 1955), в которой представлены все ба- шения для решеток больших разме-
зы вплоть до шестикратной базы единич- Ров обсуждаются в работе (Ishiguro,
ной длины; б — конфигурация Брейсуэлла 1980). Моффет определил два клас-
(Bracewell, 1966), в которой представлены все са. Это ограниченные решетки, в ко-
базы вплоть до девятикратной базы единичной торых представлены все базы вплоть
длины, и дважды — единичная база д0 максимальной длины nmax?A (т. е.
полной длины решетки), и решетки
общего типа, в которых полностью представлены длины баз лишь до некоторой
определенной величины и частично — базы большего размера. Примеры для восьми
элементов приведены на рис. 5.11. Мера избыточности одномерной решетки опре-
определяется как
п°(п"-1), E.18)
т. е. число антенных пар, деленное на число единичных баз, определяющих базу
максимальной длины. Для конфигураций, показанных на рис. 5.10 а и 5.10 6, ме-
меры избыточности равны 1,0 и 1,11 соответственно. Исследования в теории чисел
(Leech, 1956) показали, что при большом числе элементов значение коэффициента
избыточности приближается к 4/3. Пример одномерной решетки с минимальной
избыточностью, показанный на рис. 5.10 6, описан в работе (Bracewell et al., 1973).
11 9 4 3 3 2
• • • • • • •
13 6 6 2 3 2 а
8 10 1 3 2 7 8
• • •••• • =|7
Рис. 5.11. Восьмиэлементные одномерные антенные решетки минимальной избыточности;
числами указаны длины баз, кратные единичному интервалу, а — две решетки с рав-
равномерным распределением длин баз от 1 до 23 единичных интервалов, б — решетка
с равномерным распределением длин баз от 1 до 24 единичных интервалов, но при этом ее
длина составляет 39 единичных интервалов. Длины избыточных баз кратны 8,31 (двойная
избыточность) и 39 единичным интервалам. (Moffet, 1968), ©1968 IEEE
Перемещение малого числа элементов существенно расширяет возможности ре-
решетки. На рис. 5.12 показано расположение трех элементов Кембриджского од-
одномильного телескопа (Ryle, 1962). Антенны 1 и 2 неподвижны, и их выходные
сигналы коррелируют с выходом 3-й антенны, которая может перемещаться по
железнодорожному полотну. В каждом положении 3-й антенны наблюдаемый ис-
источник сопровождается в течение 12 часов, и видность измеряется на двух дугах
эллипса плоскости uv. Наблюдения повторяются при последовательных перемеще-
перемещениях 3-й антенны, и расстояние между эллиптическими треками на плоскости uv
определяется величиной этого перемещения. По теореме выборки (разд. 5.2) тре-
требуемое расстояние между эллипсами обратно пропорционально угловому размеру
5.5] Одномерные следящие решетки 137
^77777777777777777777777777777/ _
~* Рельсовый >
путь
Рис. 5.12. Кембриджский одномильный радиотелескоп. Антенны 1 и 2 — стационарные,
принятые ими сигналы попарно коррелируют с сигналом антенны 3, которая может уста-
устанавливаться в различных положениях вдоль железнодорожного полотна. Стационарные
антенны находятся друг от друга на расстоянии 762 м, а железнодорожное полотно тянется
дальше еще на 762 м. Минимальная длина базы равна шагу перемещения антенны 3
и могут быть получены все базы, кратные единичной, вплоть до 1524 м
наблюдаемого источника в радианах. При возможности изменения шага перемеще-
перемещения гибкость использования антенной решетки увеличивается и сокращается необ-
необходимое количество антенн. Конфигурация большего инструмента такого типа —
Вестерборкского радиотелескопа апертурного синтеза (Baars and Hooghoudt, 1974;
Hogbom and Brouw, 1974; Raimond and Genee, 1996), показана на рис. 5.13. В этом
инструменте используются десять пассажных антенн в комбинации с четырьмя
подвижными, и скорость накопления данных примерно в 20 раз выше по сравнению
с трехэлементной решеткой.
Запад Восток
Рельсовый путь
Рис. 5.13. Антенная конфигурация Вестерборкского радиотелескопа апертурного синтеза.
Десять черных кружочков обозначают стационарные антенны, а четыре белых — антенны,
перемещаемые по железнодорожным путям. Для корреляции сигнала каждой из стаци-
стационарных антенн с сигналом каждой из подвижных используются сорок корреляторов.
Диаметр антенн равен 25 м, и интервал между фиксированными антеннами составляет
144 м. Первоначально в состав решетки входили только 12 западных антенн, и позднее,
чтобы удвоить возможную длину баз, были добавлены еще две восточные антенны
Выборка значений функции видности в точках концентрических эллипсов, раз-
размеры которых увеличиваются с одинаковым шагом, приводит к появлению в от-
отклике кольцевых лепестков. Этот эффект связан с тем фактом, что мгновенные
пространственные частоты одномерной антенной решетки в каждом направлении
представлены рядом дельта-функций, как показано на рис. 5.14 а. Если решетка
содержит все базы, кратные единичной до N?\ включительно, и если соответствую-
соответствующие измерения видности обрабатываются с одинаковыми весовыми коэффициента-
коэффициентами, то мгновенный отклик принимает форму веерных лепестков, профиль каждого
из которых описывается sine-функцией, как показано на рис. 5.14 а. Это следует из
соотношения преобразований Фурье для ограниченного ряда дельта-функций:
N оо
i= — N k= — oo
где ^ обозначает преобразование Фурье, а дельта-функциями в левой части соотно-
соотношения представлены пространственные частоты в области и. Ряд слева ограничен,
что может быть представлено как выборка из бесконечного ряда умножением на
прямоугольную функцию окна. Правой частью соотношения представлена диаграм-
диаграмма направленности, в которой преобразование Фурье функции окна определяется
сверткой с дельта-функциями. Вращение Земли приводит к тому, что векторы
138
Антенны и антенные решетки
[Гл.5
I I I i
б 1
, r\ /Л /
ч/ V/ \ /
2/х -/х 0
\ /Л/л/\/\/\/¦'''
у. >^ w w v^
v y^*v/^
21)
/1
1 А /
w V .
\
\
-1 \
А
/г
Рис. 5.14. а — ограниченный ряд дельта-функций, представляющий мгновенное распреде-
распределение пространственных частот одномерной антенной решетки с равномерным распределе-
распределением длин баз и равными весовыми коэффициентами для каждой базы; б— ограниченный
ряд соответствующих веерных лучей, составляющих мгновенный отклик решетки. Рядами
а и <э представлены соответственно левая и правая части соотношения E.19)
баз описывают эллипсы на плоскости ш;, и молено визуально представить, что
соответствующее вращение решетки относительно небесной сферы приводит к скру-
скручиванию веерной диаграммы в узкий карандашный луч, в то время как соседние
лепестки образуют низкоуровневые кольцевые отклики вокруг центрального луча,
как показано на рис. 5.15. Эти общие рассуждения дают правильное представление
о расположении боковых лепестков, профиль которых соответствует модифициро-
модифицированной sine-функции.
Рис. 5.15. Пример кольцевых лепестков. Отклик антенной решетки, пространственная пе-
передаточная функция которой представлена рядом из девяти концентрических окружно-
окружностей с центрами в начале координат (u,v), получается, например, в результате 12-часовых
наблюдений с одномерной решеткой восток-запад в направлении высокого склонения.
Радиусы окружности представляют последовательность целых чисел, кратных длине еди-
единичной антенной базы. Весовая функция соответствует основному отклику, рассматрива-
рассматриваемому в 10.2.2 (Bracewell and Thompson, 1973)
Если пространственная чувствительность на плоскости uv представлена рядом
окружностей, образуемых дельта-функциями с радиусами g, 2g,..., TVg, то форма
k-ro кольцевого лепестка описывается как
sine
1/2
-к)],
E.20)
5.5]
Одномерные следящие решетки
139
где г = Vl2 + т2 • Функция sinc1/2(x) показана на рис. 5.16 и представляет собой
дробную производную порядка 1/2 функции smTrx/тгх. Ее молено вычислить с по-
помощью интегралов Френеля (Bracewell and Thompson, 1973).
Рис. 5.16. Поперечное сечение кольцевого лепестка основного отклика на точечный ис-
источник для решетки восток—запад с равномерным шагом приращения расстояния между
антеннами. Левая часть графика соответствует внутренней стороне кольца, а правая —
внешней. Точками показано отрицательное среднее значение осцилляции с внутренней
стороны кольца (Bracewell and Thompson, 1973)
Согласно теореме выборки (разд. 5.2) шаг приращения базы, выраженный в дли-
длинах волн, не должен быть больше обратной величины размера источника. Приме-
Применительно к кольцевым лепесткам это требование означает, что минимальное рас-
расстояние между ними не должно быть меньше размеров источника. Таким образом,
если следовать теореме выборки, то отклик на источник по центральному лучу
диаграммы направленности не перекрывается откликами для того же источника,
образующими кольцевые лепестки. В решетках, таких как на рисунках 5.12 и 5.13,
кольцевые лепестки могут быть эффективно подавлены, если шаг перемещения
подвижных антенн чуть меньше их диаметра, поскольку в этом случае кольцевые
лепестки оказываются вне главного луча диаграммы направленности антенны. Тем
не менее отметим, что первая база не может быть меньше диаметра антенны,
и пропущенные измерения с низкими пространственными частотами, возможно,
следует получить другими способами (см. обсуждение метода мозаики в разд. 11.6).
Кольцевые лепестки могут также значительно подавляться методами обработки
изображений, такими как алгоритм CLEAN, рассматриваемый в разд. 11.2.
Хотя эллиптические треки плоскости uv находятся на равных интервалах друг
от друга, естественное взвешивание данных одномерной решетки восток—запад ока-
оказывается неравномерным, поскольку расстояния, на которые перемещаются век-
векторы базы за какой-либо интервал времени, пропорциональны их длине. При ис-
использовании проекции плоскости uv на экваториальную плоскость Земли, которая
рассматривалось в разд. 4.2 как векторы u'v', пространственных частот вращаются
с постоянной угловой скоростью, и плотность точек измерений пропорциональна
Я.
= ^ + V ) = (iZ +
г; cosec
E.21)
Усредненная по площадке, размеры которой сравнимы с величиной минимальной
базы, выраженной в длинах волн, плотность измерений на плоскости uv обратно
пропорциональна величине \/и2 + v2 cosec25. Вдоль прямой линии, проходящей
140 Антенны и антенные решетки [Гл. 5
через начало координат (u,v), плотность измерений обратно пропорциональна ве-
величине \/и2 + v2 .
5.6. Двумерные следящие решетки
Как отмечено ранее, заполнение пространственных частот для одномерной ан-
антенной решетки восток—запад сокращается в направлении v при наблюдении источ-
источников вблизи небесного экватора. Для таких наблюдений требуются конфигурации
антенн, в которых проекции антенных баз на ось Z, определенную в разд. 4.1,
сравнимы с величиной проекций X и Y. Это достигается добавлением баз с азиму-
азимутами, отличающимися от направления восток—запад. Таким образом конфигурация
становится двумерной. Если решетка расположена на средней широте и оптимизи-
оптимизирована для работы с низкими склонениями, то на ней можно проводить наблюдения
источников от полюса до склонений порядка 30° противоположной полусферы. Этот
диапазон охватывает около 70 % небесной сферы, что почти в три раза превышает
возможности решетки восток-запад. Поскольку проекция Z не равна нулю, эллипсы
на плоскости uv разделяются на две части, как показано на рис. 4.4. В результате
(щ v)-заполнение становится более сложным по сравнению с одномерной решеткой
восток-запад, а также усложняется структура боковых лепестков по сравнению
с кольцевыми лепестками при равномерно расположенных треках. В двумерном
случае выбор конфигурации минимальной избыточности не такой простой, как
для одномерной решетки. Прежде всего, необходимо определить оптимальную про-
пространственную передаточную функцию W(u,v). Аналитического метода перехода
от W(u,v) к конфигурации антенн не существует, но можно воспользоваться ме-
методами последовательных приближений для нахождения оптимального или почти
оптимального решения.
Для начала рассмотрим, что происходит при слежении за источником на небес-
небесной сфере, и предположим, что для источника вблизи зенита мгновенное запол-
заполнение пространственных частот представлено почти равномерной выборкой точек
в пределах окружности с центром в начале (и, v)-координат. При сопровождении
источника (щ v)-заполнение в любой момент времени получается проецированием
зенитного заполнения на плоскость небесной сферы и его некоторым вращением,
зависящим от часового угла и склонения источника. В результате проецирования
круговая форма заполнения сжимается в эллиптическую, центр которой также
остается в начале (и, v)-координат, и эта величина сжатия минимальна при про-
прохождении источника через меридиан. Эффект наблюдения в некотором интервале
часовых углов может быть представлен как усредненный набор эллиптических
площадок на плоскости uv, главная ось которых претерпевает некоторое вращение.
Область в центре плоскости uv находится внутри сжимаемого заполнения в течение
всего времени наблюдений, и, если мгновенное заполнение было однородным, то
в пределах этой области оно однородным и остается. Во внешней области сжатие
будет приводить к сглаживанию заполнения. Эти эффекты зависят от склонения
источника и интервала сопровождения по часовому углу. Практически некоторое
сглаживание измеряемых значений видности редко составляет серьезную проблему.
Таким образом, двумерные решетки, число антенн в которых достаточно велико для
обеспечения хорошего мгновенного заполнения плоскости uv, также имеют хорошие
возможности при сопровождении источников по часовому углу.
5.6.1. Открытые конфигурации. Заполнение пространственных частот для
открытых конфигураций таких, как крест, Т и Y показано на рис. 5.7. Заполнение
пространственных частот крестообразной и Т-решетки имеет четырехстороннюю
симметрию в обоих случаях; мы игнорируем эффект отсутствия малых продол-
5.6]
Двумерные следящие решетки
141
жений на верхней и нижней сторонах квадрата для Т-конфигурации. Заполнение
пространственных частот Y-решетки (углы между плечами которой равны 120°)
характеризуется шестисторонней симметрией. (Фигура с n-сторонней симметрией
не изменяется при ее повороте с шагом 2тг/п. В случае окружности п бесконечно,
и симметрия фигур приближается к центральной с увеличением п.) Автокорреля-
Автокорреляционная функция равноугольной Y-решетки ближе к центральной симметрии по
сравнению с крестообразной и Т-решеткой. В этом плане решетка с пятью лучами,
предложенная Хелмингом (Hjellming, 1989), была бы еще лучше, но дороже.
В качестве примера открытой конфигурации рассмотрим более подробно идео-
идеологию VLA (Thompson et al., 1980; Napier, Thompson and Ekers, 1983). Этот ин-
инструмент находится в Нью-Мексико на широте 34° к северу от экватора и способен
сопровождать объекты со склонениями до —30° к югу в течение почти 7 часов
при высотах больше 10°. Технические требования предусматривали возможность
картографирования с максимальным угловым разрешением по крайней мере до
—20° по склонению и получение карт не более чем за 8 часов наблюдений без
передвижения антенн на новые площадки. При разработке решетки, для сравнения
возможностей различных конфигураций антенн, вычислялась пространственная
передаточная функция, имитирующая сопровождения источников с различными
склонениями в интервале ±4 ч. При обсуждении достоинств какой-либо конфигу-
конфигурации главным критерием была минимизация боковых лепестков синтезированной
диаграммы направленности. Оказалось, что процент дыр в заполнении плоскости
uv — хороший индикатор уровня боковых лепестков, и таким образом, вычислять
детальную структуру отклика требовалось не всегда (NRAO, 1967, 1969). Как
выяснилось, при данном количестве антенн равноугольная Y-конфигурация более
предпочтительна по сравнению с крестообразной и Т-конфигурацией; см. рис. 5.17.
Рис. 5.17. а — предполагаемая конфигурация антенн для VLA, полученная на ЭВМ Мату-
ром (Mathur, 1969) в результате оптимизации параметров; б — степенная конфигурация
(Chow, 1972), принятая для VLA (Napier, Thompson and Ekers, 1983), ©1983 IEEE
Инвертирование Y-решетки не оказывает влияния на диаграмму направленно-
направленности, но при одинаковых радиальных распределениях антенн возможности системы
для склонений, близких к экватору, улучшаются при таком ее повороте, когда
номинальное северное или южное плечо образует с направлением север-юг угол,
примерно равный 5°. Без этого поворота базы между соответствующими антеннами
двух других лучей точно совпадали бы с направлением восток-запад, и при 5 = 0°
эллипсы пространственных частот вырождались бы в прямые линии, совпадающие
142
Антенны и антенные решетки
[Гл.5
с осью и с высокой избыточностью. Общее число антенн 27 выбрано исходя из
анализа заполнения плоскости uv и величины боковых лепестков; в результате мак-
максимальный уровень боковых лепестков по крайней мере на 16 дБ меньше отклика
главного луча, исключая 5 = 0°, где использование вращения Земли не эффективно.
27 антенн образуют 351 пару.
8 = 45°
8 = 0°
iMMvi
S = 30°
Зенит
Рис. 5.18. Заполнение пространственных частот для VLA со степенной конфигурацией,
показанной на рис. 5.17 б: а — S = 45°; б— S = 30°; в — 5 = 0°; г — мгновенное заполнение
в направлении зенита. Интервал часовых углов равен ±4 ч или ограничен минимальным
углом места 9°; для «мгновенного заполнения» интервал наблюдений равен ±5 мин. Длина
осей и, v от начала координат соответствует величине максимального удаления антенны от
центра решетки, что составляет 21 км для максимальной конфигурации (Napier, Thompson
and Ekers, 1983), ©1983 IEEE
Положения антенн вдоль плеч решетки представляют еще один набор перемен-
переменных, которые должны быть определены для оптимизации пространственной переда-
передаточной функции. На рис. 5.17 показаны два возможных решения задачи. Конфигу-
Конфигурация а была получена с использованием псевдодинамического метода вычислений
(Mathur, 1969), в котором произвольно выбранные начальные условия изменяются
компьютером до достижения почти оптимального заполнения плоскости uv. В части
б рисунка представлена степенная конфигурация, полученная Чоу (Chow, 1972).
Его расчеты привели к заключению, что конфигурация, в которой n-я антенна пле-
плеча решетки находится на расстоянии, пропорциональном па от ее центра, должна
обеспечить хорошее (и, v)-заполнение. Сравнение эмпирически оптимизированной
5.6] Двумерные следящие решетки 143
конфигурации и степенного расположения антенн при а ~ 1, 7 показало, что воз-
возможности обеих конфигураций почти одинаковы. Степенное расположение антенн
было выбрано в основном по экономическим причинам. В техническом задании
требовалось, чтобы четыре конфигурации расположения антенн осуществлялись
изменением масштаба разнесения в 4 шага для обеспечения разрешения и поля
зрения для разных астрономических объектов. Если а выбрать равным логарифму
с основанием 2 коэффициента изменения масштаба, то положение п-й площадки
в одной конфигурации совпадает с положением 2п-й площадки в следующей кон-
конфигурации меньшего размера. Общее количество необходимых антенных площадок
таким образом уменьшается со 108 до 72. «Моментальный снимок» на рис. 5.18 г
показывает мгновенное заполнение плоскости uv, достаточное для получения изоб-
изображений простой структуры сильных источников.
5.6.2. Замкнутые конфигурации. По большей части мы будем следовать
здесь анализу, приведенному в работе (Keto, 1997). Возвращаясь к предложенному
критерию равномерного распределения измерений внутри окружности на плоско-
плоскости uv, отметим, что конфигурация расположенных по окружности антенн (коль-
(кольцевая решетка) является хорошим начальным приближением, поскольку распреде-
распределение длин баз резко обрывается вдоль всех направлений диаметра окружности.
Это показано на рисунках 5.7 ж и 5.7 з. Для начала рассмотрим мгновенное (u,v)-
заполнение для источника в направлении зенита. Оно показано на рис. 5.19 а для
21 антенны, где их положения отмечены треугольниками, и антенны находятся на
одинаковом расстоянии друг от друга. Образуется 21 база минимальной длины,
причем распределение направлений баз по азимуту равномерно и каждая база пред-
представлена двумя точками на плоскости uv. To же самое относится к любым базам
кратной длины вдоль окружности. В результате пространственная передаточная
функция представлена точками, расположенными вдоль ряда окружностей и ради-
радиальных линий. Отметим также, что когда длины баз приближаются к диаметру
окружности, их приращения становятся весьма малыми. Например, расстояние
между антеннами, разнесенными на 10 интервалов по кругу, будет не намного
больше, чем расстояние между антеннами на 9 интервалах. Таким образом, плот-
плотность измерений увеличивается на максимальных базах (расстояние между точка-
точками вдоль любой из радиальных линий сокращается), так же как — в направлении
центра. Отметим, что распределение плотности похоже на радиальный профиль
автокорреляционной функции, показанный на рис. 5.7 к, за исключением области
вблизи начала координат, поскольку на рис. 5.19 показана только кросскорреляция
антенных пар.
Один из способов получить более однородное распределение заключается в слу-
случайном расположении антенн вдоль окружности. В этом случае точки на плоскости
uv не находятся более на сетке радиальных линий и окружностей, и на рис. 5.19 б
показан пример, в котором частичная оптимизация была выполнена с использова-
использованием вычислений по алгоритму нейронных сетей. Различные алгоритмы, оптимизи-
оптимизирующие однородность пространственной чувствительности, рассмотрены в статье
(Keto, 1997). Хорошая равномерность заполнения круговой области на плоскости
uv была получена также в результате более раннего исследования кольцевых ре-
решеток (Cornwell, 1988). В этом случае была использована программа, основанная
на методе имитации отжига, и расположение антенн относительно окружности
проявляло некоторую степень симметрии, вследствие чего заполнение плоскости
uv было похоже на кристаллическую структуру.
Оптимизация антенных конфигураций может также рассматриваться более ши-
широко, и в работе (Keto, 1997) отмечено, что ограниченное некоторым значением
по всем направлениям заполнение плоскости uv не является уникальным свойст-
свойством кольцевой конфигурации. Существуют другие фигуры, например треугольник
144
Антенны и антенные решетки
[Гл.5
л
.•. *'л.
-I \-
-1
О
1
о
1
Рис. 5.19. а — кольцевая решетка, образованная 21 равномерно разнесенными антеннами,
показанными треугольниками, и мгновенное заполнение пространственных частот, пока-
показанное точками. Масштаб координат одинаков для положений антенн и пространственных
частот и и v. б — решетка и заполнение пространственных частот те же, что и в части
а рисунка, но с измененным расположением антенн вдоль окружности для улучшения
однородности заполнения, в — решетка из 24 антенн, равномерно расположенных по
сторонам треугольника Руло, и соответствующее заполнение пространственных частот.
г — решетка и пространственная чувствительность те же, что и в части в рисунка, после
изменения расстояний между антеннами для оптимизации (и, v)-заполнения (Keto, 1997),
©1997 American Astron. Soc.
Руло, ширина которого одинакова во всех направлениях. Треугольник Руло, пока-
показанный на рис. 5.7 и, образован тремя равными дугами окружностей, прочерченны-
прочерченными сплошной линией. Периметр треугольника равен длине окружности, диаметр
которой в свою очередь равен одной из сторон равностороннего треугольника,
показанного штриховой линией. Подобные фигуры могут быть образованы для
любого правильного многоугольника с нечетным количеством сторон, и окруж-
окружность — предельный случай, когда количество сторон стремится к бесконечности.
Треугольник Руло наименее симметричен из всего семейства. С другими свойствами
треугольника Руло и подобных фигур можно ознакомиться в работе (Rademacher
and Toeplitz, 1957).
Поскольку оптимизация кольцевой решетки, показанной на рис. 5.7 и сводит-
сводится к уменьшению симметрии, то можно предположить, что решетка на основе
треугольника Руло должна обеспечить более равномерное заполнение простран-
пространственных частот по сравнению с кольцевой решеткой. Это действительно так, что
5.6]
Двумерные следящие решетки
145
можно видеть, сравнивая рисунки 5.19 а и 5.19 в, когда в обоих случаях расположе-
расположение антенны равномерно. Неравномерное расположение антенн кольцевой решетки,
показанное на рис. 5.19 6, получено исходя из начального приближения кольцевой
конфигурации с изменениями положений антенн в пределах малого интервала. Это
ограничение не позволило программе получить полностью оптимизированное ре-
решение. Если не ограничивать программу оптимизации и разрешить ей достичь схо-
сходимости, то в результате антенны будут расположены близко к треугольнику Руло
на неравных расстояниях друг от друга, как показано на рис. 5.19 г. Этот результат
не зависит от начальной конфигурации. Сравнение рисунков 5.19 а и 5.19 б показы-
показывает, что различие между кольцевой конфигурацией и треугольником Руло почти
незаметно, если в обоих случаях положения антенн слегка изменены случайным
образом относительно образующих фигур; хотя при внимательном рассмотрении
видно, что однородность на рис. 5.19 а чуть лучше по сравнению с рис. 5.19 б.
1,0
0,5
0,0
-0,5
-1,0
-1,0 -0,5 0,0 0,5 1,0
-1,0 [
L__ -
-1,0 -0,5 0,0 0,5 1,0
1,0 I
0,5 •¦
-0,5 \
-1,0 -0,5 0,0 0,5 1,0
Рис. 5.20. Заполнение пространственных частот замкнутой конфигураций из 24 антенн,
оптимизированной для однородных измерений в режиме мгновенных наблюдений: а —
мгновенные наблюдения в направлении зенита; б— 5 = +30°; в — 6 = 0°] г — 5 = —28°. Тре-
Треугольниками в части а рисунка показаны положения антенн. Чтобы упростить сравнение
с VLA (рис. 5.18), треки рассчитаны для широты решетки 34°. Диапазон сопровождения
для каждого склонения определяется интервалом часовых углов, при котором угол места
источника не менее 25° (Keto, 1997), ©1997 American Astron. Soc.
На рис. 5.20 показано заполнение пространственных частот для решетки с оп-
оптимизированной конфигурацией треугольника Руло. Интервал сопровождения по
146 Антенны и антенные решетки [Гл. 5
часовому углу составляет ~ ±3 ч, а широта равна широте VLA. Сравнение рисунка
с соответствующими рисунками 5.18 для VLA показывает, что заполнение простран-
пространственных частот треугольником Руло ближе к круговой однородной выборке по
сравнению с равноугольной Y-конфигурацией. Как показано на рис. 5.7, автокорре-
автокорреляционная функция лучевой конфигурации достигает больших значений в направ-
направлениях совпадения плеч решетки и осей симметрии соответствующей передаточной
функции. Этот эффект приводит к недостаточно однородной пространственной
чувствительности Y-решетки. Закругление лучей или псевдослучайное поперечное
смещение антенн относительно осей симметрии способствует размытию структуры
пространственной передаточной функции и делает ее менее отчетливой. Такие
высокие значения вдоль радиальных линий отсутствуют в автокорреляционной
функции окружности или подобной замкнутой фигуры, и это одна из причин,
по которой конфигурации этого типа обеспечивают более равномерное заполнение
пространственных частот.
Несмотря на не совсем идеальные характеристики равносторонней Y-
конфигурации, качество изображений астрономических объектов, получаемых
на VLA, очень высокое. Круговая форма и равномерность заполнения простран-
пространственных частот — полезные критерии, однако они не являются определяющими.
В том случае, когда наблюдения охватывают диапазон по и и г>, в котором значения
видности достаточны для измерений, и если потери чувствительности вследствие
неравномерного взвешивания находятся в допустимых пределах, могут быть полу-
получены превосходные результаты. Y-решетка дает ряд практических преимуществ по
сравнению с замкнутой конфигурацией. Если для увеличения диапазона углового
разрешения требуется использование нескольких масштабируемых конфигураций,
то альтернативные положения антенн оказываются вдоль тех же лучей решетки,
в то время как в случае окружности или треугольника Руло необходимо создание
новых конфигураций с соответствующими масштабами. Трансформируемость Y-
решетки особенно полезна при наблюдениях VLA южной области небесной сферы,
для которых проекции баз значительно сокращаются в направлении север-юг. Для
проведения таких наблюдений антенны северного луча могут быть передвинуты
в следующую конфигурацию большего масштаба, чем в значительной степени
компенсируется сокращение длины проекций.
Ниже перечислены некоторые другие интересные примеры важных конфигура-
конфигураций.
• Компактная решетка Австралийского телескопа — одномерная решетка
восток—запад, состоящая из шести антенн, перемещаемых по железнодорож-
железнодорожным путям. (Frater, Brooks and Whiteoak, 1992)
• UTR-2 — Т-решетка с широкополосными диполями большого диаметра, по-
построенная Академией наук Украины вблизи Граково (Braude et al., 1978).
Диапазон частот наблюдений равен 10-25 МГц. Создано несколько подобных
антенн меньшего размера, расположенных на расстояниях до 900 км от Гра-
Граково и используемых в РСДБ-наблюдениях.
• Решетка из 720 конических спиральных антенн в Т-конфигурации, действую-
действующая в диапазоне частот 15—125 МГц, была создана в Боррего Спрингс, Кали-
Калифорния (Erickson, Mahoney and Erb, 1982).
• Радиотелескоп на Маврикии, вблизи Брас д'О (Bras d'eau) — Т-решетка из
спиральных антенн, действующая на частотах до 150 МГц. Протяженность
плеча восток-запад — 2 км. Длина южного плеча равна 880 м и синтезируется
5.6] Двумерные следящие решетки 147
перемещением группы антенн на специальных тележках. Конструкция решет-
решетки в основном похожа на показанную на рис. 1.12 а. Создана для наблюдений
большей части южной полусферы.
• GMRT, Гигантский радиотелескоп метровых волн вблизи Пуна, Индия, со-
состоит из 30 антенн, 16 из которых расположены в форме Y-решетки с искрив-
искривленными лучами примерно 15 км длины. Остальные 14 антенн расположены
псевдослучайным образом в 2 км от центральной части (Swamp et al., 1991).
Антенны стационарны, их диаметр равен 45 м. Максимальная частота наблю-
наблюдений равна ~ 1,6 ГГц.
• Кольцевая решетка с равномерно расположенными 96 антеннами создана
в Калгуре, Австралия, для наблюдений Солнца (Wild, 1967). Эта мульти-
лепестковая сканирующая фазовая, а не корреляционная, решетка состояла
из 96 антенн, равномерно расположенных по окружности диаметра 3 км,
и работала на частотах 80 и 160 МГц. Для подавления нежелательных бо-
боковых лепестков Уайлд (Wild, 1965) разработал оригинальную схему фазовой
модуляции, названную J-синтезом. Пространственная чувствительность этой
решетки исследована в работе (Swenson and Mathur, 1967).
• Субмиллиметровая решетка (SMA) Смитсонианской астрофизической обсер-
обсерватории и Китайской академии наук (Тайвань) расположена в Маунт Ки, Га-
Гавайи, и представляет собой первую решетку, которая должна быть построена
с использованием конфигурации треугольника Руло (Могап, 1998).
5.6.3. Конфигурации РСДБ. В конфигурациях РСДБ расположение ан-
антенн определяется как заполнением плоскости uv, так и возможностью практи-
практической реализации. Важными факторами являются близость к действующим об-
обсерваториям для технической поддержки и возможность быстрой отправки лент
в центр обработки данных. Также следует рассматривать диапазон часовых углов
и склонений, наблюдаемых одновременно находящимися на большом расстоянии
друг от друга обсерваториями. Хотя расположение значительно удаленных друг от
друга антенн в решетке РСДБ существенно не плоское, угловые размеры наблю-
наблюдаемых источников обычно достаточно малы, что позволяет использовать прибли-
приближение малых размеров картографируемого поля при восстановлении изображений
радиоисточников, как обсуждалось в разд 3.1. Подобные же факторы относятся
к решеткам с длинными базами и связанными элементами, в которых для пере-
передачи опорных сигналов и сигналов ПЧ применяется радиосвязь. Примером такой
решетки является Многоэлементная радиосвязанная интерферометрическая сеть
(MERLIN) обсерватории в Джодрелл Бэнк, Англия, образованная из шести антенн,
максимальная длина базы между которыми достигает 233 км (Thomasson, 1986).
Любой подходящий радиотелескоп, оборудованный атомным стандартом часто-
частоты, системой гетеродинов с синхронизацией фазы и соответствующими приемной
и записывающей системами, может быть использован в эксперименте РСДБ. Не-
Несколько сетей было организовано для координации совместных экспериментов меж-
между различными обсерваториями. Наблюдения в течение первых двух десятилетий
после обоснования методики РСДБ проводились, в основном, по соглашению меж-
между различными организациями. Решетки, полностью предназначенные для РСДБ-
наблюдений, рассматривались еще в 1975 г. (Swenson and Kellermann, 1975), но
работы по их созданию не начинались целое десятилетие. Расположение антенн
в решетке РСДБ проанализировано в работе (Seielstad, Swenson and Webber, 1979).
Для сравнения возможностей различных конфигураций пространственная переда-
передаточная функция вычислялась для разных склонений. Часть ячеек сетки на плоско-
плоскости uv определенного размера, содержащая данные измерений, затем взвешивалась
148
Антенны и антенные решетки
[Гл.5
пропорционально площади небесной сферы для каждого склонения и усреднялась.
При увеличении индекса, в действительности, минимизировалось количество дыр
(незаполненных ячеек). В других исследованиях рассчитывался отклик для предпо-
предполагаемого источника, синтезировалась карта, и полученный результат сравнивался
с моделью.
Рис. 5.21. Антенная решетка со сверхдлинными базами (VLBА) в США: а — расположе-
расположение 10 антенн, и 5 — заполнение пространственных частот (в тысячах километров) для
склонений 64°, 30°, 6° и —18°, где время наблюдений для каждой антенны ограничено
предельным значением угла места 10° (Walker, 1984)
Конструкция решетки, предназначенной для РСДБ, — Антенной решетки со
сверхдлинными базами (VLBА) в США, описана в работе (Napier et al., 1994).
Местоположения антенн перечислены в табл. 5.1 и показаны на рис. 5.21 а. Выбор
месторасположений проанализирован Уолкером (Walker, 1984). Антенны, располо-
расположенные на Гавайях и С ант Круа, обеспечиваются длинные базы восток-запад. Нью
5.6]
Двумерные следящие решетки
149
Таблица 5.1. Расположение антенн VLB A
Местонахождение
Ст. Круа, VI
Ханкок, NH
Норе Либерти, IA
Форт Дейвис, ТХ
Лос Аламос, NM
Пай Таун, NM
Кит Пик, AZ
Оуэне Велли, СА
Брюстер, WA
Мауна Kea, HI
Северная
]
о
17
42
41
30
35
34
31
37
48
19
лирота
45
56
46
38
46
18
57
13
07
48
и
30,57
00,96
17,03
05,63
30,33
03,61
22,39
54,19
52,80
15,85
Западная
долгота
о
64
71
91
103
106
108
111
118
119
155
i
35
59
34
56
14
07
36
16
40
27
и
02,61
11,69
26,35
39,13
42,01
07,24
42,26
33,98
55,34
28,95
Высота над
уровнем
моря (м)
16
309
241
1615
1967
2371
1916
1207
255
3720
Данные из (Napier et al., 1994), ©1994 IEEE.
Гемпшир—С ант Круа — самая длинная база в направлении север—юг. Антенна на
Аляске находилась бы еще севернее, но выигрыш был бы ограничен для источников
южной полусферы. Для источников с южными склонениями заполнение простран-
пространственных частот было бы улучшено дополнительной антенной в южном полуша-
полушарии. Из-за высокого содержания паров воды в атмосфере юго-восточные районы
Соединенных Штатов не рассматривались. Промежуточные базы в направлении
север-юг получены расположением антенн в более сухих районах западного побе-
побережья. Размещением антенны в Айова заполнен пропуск между Нью Гемпширом
и юго-западными антеннами. Короткие базы расположены в районе VLA для того,
чтобы использовать возможность связи с этой решеткой в реальном времени, и как
следствие этого, в заполнении пространственных частот наблюдается концентрация
к центру плоскости uv. Такое расположение антенн позволяет выполнять измерения
для более широкого диапазона размеров источников по сравнению с однородной
конфигурацией при том же количестве антенн. Однако это достигается ценой неко-
некоторого ухудшения возможностей картографирования источников сложной струк-
структуры.
5.6.4. Антенны РСДБ на орбите. Использование дополнительных антенн
в космосе является логическим шагом в развитии наземных решеток РСДБ (Ко-
стенко, Матвеенко, 1982; Preston et al., 1983; Burke, 1984). Комбинация орбитальной
РСДБ (ОРСДБ) и наземных антенн дает ряд очевидных преимуществ. Может быть
достигнуто более высокое угловое разрешение, которое ограничивалось бы только
межзвездными мерцаниями; см. разд. 13.6. Орбитальное движение космического
аппарата способствует заполнению плоскости uv, и таким образом улучшается
структурный и динамический диапазоны получаемых изображений.
На рис. 5.22 показан пример заполнения плоскости uv для наблюдений с кос-
космическим аппаратом HALCA (Hirabayashi et al., 1998) и рядом наземных антенн:
одной антенной в Усуду, Япония, одной антенной VLA и 10 антеннами VLB А.
Наклонение орбиты спутника к земному экватору составляет 31°, высота спутника
над поверхностью Земли равна 21400 км в апогее и 560 км в перигее. Заполнение
плоскости uv показано для частоты 5 ГГц, частоты и и v даны в единицах 106
длин волн, и максимальная база достигает 5-Ю8 длин волн, что соответствует
размеру лепестка 0,4 мсек дуги. Треками приблизительно круговой формы в центре
150
Антенны и антенные решетки
[Гл.5
^500 -
иA0° X)
Рис. 5.22. Пример заполнения пространственных частот для спутника HALCA и 12 назем-
наземных антенн. Данные рассчитаны для наблюдений источника 1622+633 на частоте 5 ГГц.
Для дальнейших пояснений см. текст
рисунка представлены базы между наземными антеннами. Период орбиты равен
6,3 ч, и приведенные данные соответствуют наблюдениям в течение примерно 4-
х периодов обращения. Орбита спутника прецессирует со скоростью порядка 1°
в день, и на протяжении года или двух заполнение пространственных частот для
любого исследуемого источника может быть улучшено совместной обработкой дан-
данных нескольких наблюдений. На рис. 5.23 показан пример заполнения плоскости
uv, которое можно было бы получить между двумя космическим аппаратами,
находящихся на круговых орбитах с радиусами около 10 радиусов Земли; плос-
плоскости орбит ортогональны друг к другу, и периоды обращения отличаются на 10 %.
На практике заполнение пространственных частот скорее всего будет ограничено
управляемостью диаграмм астрономических и телекоммуникационных антенн от-
относительно спутника. Космический аппарат должен быть ориентирован так, чтобы
солнечные батареи оставались освещенными, а коммуникационная антенна была бы
направлена на Землю. Некоторые технические аспекты, касающиеся орбитальной
РСДБ, обсуждаются в разд. 9.10.
5.6.5. Планарные решетки. Для исследований структуры космического фо-
фонового излучения и эффекта Сюняева-Зельдовича необходимы наблюдения с очень
высокой яркостной чувствительностью на длинах волн порядка 1 см и менее;
см. 10.4. В отличие от чувствительности при наблюдениях компактных источников,
чувствительность к распределенному излучению, заполняющему в значительной
5.6]
Двумерные следящие решетки
151
21R
-21R
0 21RE-21RE 0 21% -21RE О 21%
а б в
Рис. 5.23. Заполнение пространственных частот для антенн, установленных на двух спут-
спутниках с круговыми орбитами, радиус которых примерно равен десяти радиусам Земли Re'
а — положение источника совпадает с осью Х\ 6— положение источника совпадает с осью
Y или Z\ в — источник находится в среднем положении относительно осей X , Y и Z.
Плоскости орбиты совпадают с плоскостями XY л XZ декартовой системы координат.
Периоды обращения спутников отличаются на 10%, и продолжительность наблюдений
составляет около 20 дней (Preston et al., in Very Long Baseline Interferometry Techniques,
F. Biraud, Ed., Cepadues, France, 1983)
степени центральный лепесток диаграммы направленности, не улучитается с увели-
увеличением эффективной площади антенны. Поэтому для измерений космического фона
не требуется использование больших антенн. Для того чтобы получить значимые
результаты измерений на уровне в несколько десятков микрокельвинов на луч, т. е.
порядка 10~6 янских на квадратную угловую минуту, необходима чрезвычайно вы-
высокая стабильность аппаратуры. С этой целью были сконструированы специальные
антенные решетки. Ряд антенн размещается на платформе, причем их апертуры
находятся в одной плоскости. Вся конструкция затем устанавливается на азиму-
азимутальной монтировке, так что антенны могут быть направлены для сопровождения
любого участка небесной сферы. Например такой инструмент — Телескоп космиче-
космического фона (CBI), был разработан А. К. С. Ридхедом и его коллегами в Калтехе
(Padin et al., 2001). Он образован из тринадцати параболоидов диаметра 90 см
с фокусами Кассегрена, и действует на частотах 26—36 ГГц. В этом инструменте
основание антенн имеет форму неравностороннего шестиугольника с тремя осями
симметрии и максимальным размером около 6,5 м, как показано на рис. 5.24. Для
специфических измерений планарная антенная решетка имеет ряд замечательных
особенностей по сравнению с одиночной антенной или антеннами, установленными
на отдельных монтировках. Эти особенности перечислены далее.
• Использование набора антенн позволяет измерять выходной сигнал в виде
кросс-корреляции антенных пар. Вследствие этого результаты измерений чув-
чувствительны не к полной мощности шума приемной системы, а только к кор-
корреляции принимаемых антеннами сигналов. Влияние изменений усиления су-
существенно меньше, чем в случае регистрации полной мощности. Тепловое из-
излучение земной поверхности через боковые лепестки, в значительной степени
разрешается.
• Антенны могут быть расположены максимально близко друг к другу, на-
насколько это возможно физически. Таким образом, существенные пропуски
в измеряемых пространственных частотах отсутствуют, и исследуемая струк-
структура может быть картографирована вплоть до размеров диаграммы антенны.
Апертуры не перекрывают друг друга, что происходит в случае близко рас-
расположенных антенн в тесных решетках.
152
Антенны и антенные решетки
[Гл.5
Рис. 5.24. Вид сверху на антенную платформу Телескопа космического фона, показываю-
показывающий одну из возможных конфигураций из 13 антенн (а); соответствующие проекции
антенных баз в координатах (u,v) для длины волны 1 см (б)
• В решетке, показанной на рис. 5.24, антенны могут поворачиваться как одно
целое относительно оси, перпендикулярной апертурной плоскости. Благодаря
этому, вращение баз управляемо в соответствии с решаемой задачей и не зави-
зависит от вращения Земли. Если направление наблюдений фиксировано и плат-
платформа поворачивается относительно нормали, то вид заполнения плоскости
uv не изменяется при сопровождении источника. Принимаемое боковыми ле-
лепестками излучение Земли может изменять сигнал на выходе коррелятора
в соответствии с изменениями азимута и угла места сопровождаемого источ-
источника. Эти изменения могут помочь отделить паразитный отклик системы.
• Некоторое взаимное влияние антенн друг на друга вследствие малого рас-
расстояния между ними приводит к появлению ложного коррелированного шума
в приемных системах соседних антенн. Однако поскольку антенны жестко
закреплены на платформе, ложная кросс-корреляция остается постоянной
величиной и не зависит от времени как в случае отдельных антенн. Поэтому
она может быть легко учтена. В конструкции CBI взаимное влияние антенн
уменьшается до —110 -=—120 дБ с помощью экранов цилиндрической формы
вокруг каждой антенны и специальной конструкции опор субрефлекторов,
уменьшающей рассеяние до минимума.
На частоте 30 ГГц ошибка наведения, равная 1", приводит к ошибке фазы функ-
функции видности, равной 1°. Точность наведения становится критичной, и антенны
CBI устанавливаются в раскрываемых куполах, которые защищают их от ветра,
достигающего большой силы в месте расположения решетки на высоте 5000 м над
уровнем моря в Лиано де Чайнанторе, Чили.
5.7. Заключительные замечания
относительно конфигураций антенн
Наиболее точные прогнозы возможностей решеток получаются при расчете от-
откликов заданной конфигурации антенн для моделей источников в предполагаемых
5.7] Заключительные замечания относительно конфигураций антенн 153
наблюдениях. Однако в этой книге мы более нацелены на широкое сравнение воз-
возможностей различных конфигураций, чтобы показать общие принципы конструи-
конструирования решеток. Ниже суммированы некоторые заключительные замечания.
• Окружность с центром в начале (г/, г>)-координат может рассматриваться как
оптимальная граница распределения данных измерений видности. Следую-
Следующим во многих случаях полезным критерием является равномерность распре-
распределения точек измерений внутри окружности. Этот критерий не годится, если
боковые лепестки синтезированной диаграммы направленности представляют
серьезную проблему, например в случае низкочастотных решеток, действую-
действующих в условиях путаницы источников, как упоминалось в гл. 1. Если масштаб
конфигурации решетки не может быть изменен для адаптации широкого ин-
интервала угловых размеров источников, то распределение, сконцентрированное
к центру, позволяет измерять больший диапазон угловых размеров при огра-
ограниченном количестве антенн. Если важна чувствительность к протяженным
объектам малой яркости, то предпочтительнее использовать большее коли-
количество антенных пар с короткими базами, на которых такие источники не
сильно разрешаются. Отметим, что в каждой из двух наибольших решеток
со стационарными антеннами, CMRT и VLBA, помимо антенн, находящихся
на больших расстояниях друг от друга, есть группа антенн с относительно
короткими базами, обеспечивающих широкий диапазон измеряемых размеров
источников.
• Хотя влияние боковых лепестков в синтезированной диаграмме направлен-
направленности может быть в значительной степени уменьшено на стадии обработки
изображений алгоритмами CLEAN и ему подобными, которые будут описаны
в гл. 11, для получения максимального динамического диапазона (т. е. диапа-
диапазона относительных измерений интенсивности порядка 106 и более) хорошее
заполнение пространственных частот и эффективная обработка изображе-
изображений требуются одновременно. Минимизация количества дыр (пустых ячеек)
в заполнении плоскости uv, которое, как было показано, хороший показатель
уровня боковых лепестков, — основная задача при конструировании решетки.
• Одномерные решетки использовались в больших и малых инструментах для
двумерного заполнения, требовались наблюдения в пределах ±6 ч. Такие
решетки наиболее полезны для наблюдений области неба в пределах примерно
60° от северного полюса мира и представляют собой наиболее экономичные
конфигурации с точки зрения использования земли для дороги или желез-
железнодорожного полотна. Значительное количество малых решеток, изначально
построенных как одномерные, позднее было преобразовано в крестообразные
или Т-конфигурации.
• Равноугольной Y-решеткой обеспечивается наилучшее заполнение простран-
пространственных частот по сравнению с существующими открытыми лучевыми кон-
конфигурациями. В автокорреляционной функции для решеток с нечетным чис-
числом лучей проявляется более высокая степень центральной симметрии по
сравнению с четными конфигурациями с совпадающими направлениями про-
противоположных лучей. Линейные гребни в заполнении плоскости uv (например,
в мгновенном изображении, показанном на рис. 5.18) сглаживаются с помо-
помощью искривления лучей или случайным смещением антенн. Эти особенности
также сглаживаются во время слежения за источником, и наиболее существен-
существенны для кратковременных наблюдений.
154 Антенны и антенные решетки [Гл. 5
• Наиболее однородное распределение измерений создается кольцевой конфи-
конфигурацией или треугольником Руло. При равномерном расположении антенн
треугольником Руло обеспечивается более однородное заполнение плоскости
uv по сравнению с кольцевой конфигурацией, но изменение расстояний между
антеннами квазислучайным образом улучшает обе конфигурации и уменьша-
уменьшает различие между ними, см. рис. 5.19.
• Кольцевая конфигурация может быть вытянута в направлении север-юг
и преобразована в эллиптическую для компенсации сокращений в направ-
направлениях заполнения пространственных частот для предельных склонений; по-
подобным же образом могут быть растянуты и другие конфигурации.
5.8. Другие конструктивные особенности
В предыдущем разделе мы основное внимание уделили конфигурациям антенн.
При конструировании решеток учитываются возможности проведения наблюдений
источников, размеры которых больше размеров антенного луча, а также чувстви-
чувствительность и влияние атмосферы. Более подробно возможности антенных решеток,
определяемые конфигурацией, обсуждаются в последующих главах, а для общего
представления см. (Hjellming, 1989). В этом разделе мы вкратце опишем некоторые
из наиболее важных факторов.
5.8.1. Чувствительность. Чувствительность в случае точечного источника
пропорциональна эффективной площади антенны, умноженной на число антенн,
т. е. пропорциональна пос/2, где па — количество антенн и d — размер аперту-
апертуры. В случае, когда размеры источника превосходят ширину диаграммы отдель-
отдельной антенны, что характерно для миллиметровых наблюдений, источник может
быть исследован методом мозаики, в котором используются несколько направлений
наведения, как обсуждается в разд. 11.6. Необходимое число наведений обратно
пропорционально величине телесного угла диаграммы, т. е. пропорционально d2.
Чувствительность для каждого выбранного направления пропорциональна корню
квадратному из времени накопления данных в этом направлении, так что пол-
полная чувствительность, в случае протяженного источника, пропорциональна nad.
Чтобы получить максимальную чувствительность при наблюдениях компактных
источников следует максимизировать nad , но для наблюдений объектов протя-
протяженной яркости требуется максимизация nad, а также использование компактной
конфигурации. Другие аспекты чувствительности, в том числе и шум системы,
рассматриваются в разд. 6.2.
По общепринятой эмпирической оценке, стоимость антенны пропорциональна
сР, где а « 2,7 для значений d от нескольких метров до десятков метров. Таким
образом, чтобы получить большую эффективную площадь, дешевле использовать
много малых антенн, по крайней мере до тех пор, пока стоимость электронного обо-
оборудования, по большей части пропорциональная количеству антенн, относительно
невелика. В частности, стоимость корреляционной системы пропорциональна числу
антенных пар, т. е. п2, и в случае использования широкополосного многоканального
коррелятора для наблюдений спектральных линий, может стать существенной со-
составляющей в суммарных расходах. Так что выбор размера антенн и их количества
определяется оптимизируемыми параметрами решетки, а также соображениями
стоимости.
5.8.2. Длинные волны. На низких частотах, под которыми мы подразумева-
подразумеваем частоты ниже нескольких сотен мегагерц (длины волн ~1 м и более), ионосфера
вносит значительные фазовые флуктуации в проходящих через нее сигналах, как
5.8] Цитированная литература 155
обсуждается далее в разд. 13.3. Калибровка этого эффекта особенно затрудни-
затруднительна, если дополнительная длина пути распространения сигнала значительно
изменяется в пределах диаграммы направленности антенны, что происходит при
ширине луча большей, чем размеры ионосферных неоднородностей. Таким образом,
при наблюдениях на низких частотах целесообразно использовать большие антенны
с узкими диаграммами направленности. Например, в решетке GMRT, действующей
на частотах 75-1600 МГц, используются антенны диаметром 45 м (Swamp et al.,
1991).
5.8.3. Миллиметровые волны. Для работы на частотах 100 ГГц и выше
размеры антенн не превышают 10-20 м, чтобы обеспечить требуемую точность
поверхности. Тем не менее, обычно размеры диаграмм весьма малы, например, 25"
в случае 10—метровой антенны на частоте 300 ГГц. Для наблюдений в этих условиях
протяженных источников, таких как туманности или молекулярные облака, важной
становится техника мозаики, упоминаемая ранее; см. разд. 11.6. Поскольку чувстви-
чувствительность при этом пропорциональна no<i, то оптимизация чувствительности даже
сильнее направлена на сокращение d и увеличение па по сравнению с наблюдениями
источников, размеры которых меньше ширины луча. Если используется большое
количество антенн, то можно получить удовлетворительное заполнение плоскости
uv за меньшее время наблюдений. В этом случае также уменьшается необходимость
наблюдений при низких углах места, на которых влияние атмосферы наиболее
критично.
Важным требованием мозаики является измерение видности при значениях и
и г>, меньших диаметра антенны. Это возможно, но необходимы наблюдения с крат-
кратчайшими базами. Наименьшее расстояние обычно определяется условиями, при ко-
которых соседние антенны могут быть ориентированы в различных направлениях без
опасности столкновения. При конструировании решеток миллиметрового диапазона
рассматривается минимизация этого расстояния, зависящая от фокального отноше-
отношения и конструкции монтировок антенн. Минимальное расстояние между антеннами,
расположенными на отдельных монтировках, примерно равно 1,25б/ (Welch et al.,
1996). Некоторые требования мозаики к конструкции антенных решеток рассмат-
рассматриваются в работе (Cornwell, Holdaway and Uson, 1993).
Основная литература
Balanis С. A., Antenna Theory Analysis and Design, Wiley, New York, 1982, 1997.
Collin R. E., Antennas and Radiowave Propagation, McGraw-Hill, New York, 1985.
Imbriale W. A. and M. Thorburn, Eds., Proc. IEEE, Special Issue on Radio Telescopes, 82,
633-823, 1994.
Johnson R. C. and H. Jasik, Eds., Antenna Engineering Handbook, McGraw-Hill, New York,
1984.
Love A. W., Ed., Reflector Antennas, IEEE Press, The Institute of Electrical and Electronics
Engineers, New York, 1978.
Milligan T. A., Modern Antenna Design, McGraw-Hill, New York, 1985.
Stutzman W. L. and G. A. Thiele, Antenna Theory and Design, 2nd ed., Wiley, New York,
1998.
Цитированная литература
Arsac J., Nouveau Reseau Pour l'Observation Radioastronomique de la Brillance sur le Soleil
a 9530 Mc/s, C. R. Acad. Sci., 240, 942-945, 1955.
156 Антенны и антенные решетки [Гл. 5
Baars J. W. M. and В. G. Hooghoudt, The Synthesis Radio Telescope at Westerbork, General
Layout and Mechanical Aspects, Astron. Astrophys., 31, 323-331, 1974.
Blythe J. H., A New Type of Pencil Beam Aerial for Radio Astronomy, Mon. Not. R. Astron.
Soc, 117, 644-651, 1957.
Bracewell R. TV., Interferometry of Discrete Sources, Proc. IRE, 46, 97-105, 1958.
Bracewell R. TV., Interferometry and the Spectral Sensitivity Island Diagram, IRE Trans.
Antennas Propag., AP-9, 59-67, 1961.
Bracewell R. TV., Radio Astronomy Techniques, in Handbuch der Physik, Vol. 14, S. Flugge,
Ed., Springer-Verlag, Berlin, 1962, p. 42-129.
Bracewell R. TV., The Fourier Transform and Its Applications, McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Bracewell R. TV., Optimum Spacings for Radio Telescopes with Unfilled Apertures, in Progress
in Scientific Radio, Report on the 15th General Assembly of URSI, Publication 1468 of the
National Academy of Sciences, Washington, DC, 1966, p. 243-244.
Bracewell R. TV., The Fast Hartley Transform, Proc. IEEE, 72, 1010-1018, 1984. (Имеется
перевод: ТИИЭР, 72, 8, с. 19-27, 1984.)
Bracewell R. TV., Two-Dimensional Imaging, Prentice-Hall, Englewood Cliffs, NJ, 1995.
Bracewell R. N., R. S. Colvin, L. R. D'Addario, C. J. Grebenkemper, К. М. Price and A.
R. Thompson, The Stanford Five-Element Radio Telescope, Proc. IEEE, 61, 1249-1257, 1973.
(Имеется перевод: ТИИЭР, 61, 9, с. 103-114, 1973.)
Bracewell R. TV. and J. A. Roberts, Aerial Smoothing in Radio Astronomy, Aust. J. Phys., 7,
615-640, 1954.
Bracewell R. TV. and A. R. Thompson, The Main Beam and Ringlobes of an East-West Rotation-
Synthesis Array, Astrophys. J., 182, 77-94, 1973.
Braude S. Ya., A. V. Megn, B. P. Ryabov, TV. K. Sharykin and I. TV. Zhouck, Decametric
Survey of Discrete Sources in the Northern Sky, Astrophys. Space Sci., 54, 3-36, 1978.
Brigham E. O., The Fast Fourier Transform and Its Applications, Prentice Hall, Englewood
Cliffs, NJ, 1988.
Burke B. F., Orbiting VLBI: A Survey, in VLBI and Compact Radio Sources, R. Fanti, K.
Kellermann and G. Setti, Eds., Reidel, Dordrecht, Holland, 1984.
Chow Y. L., On Designing a Supersynthesis Antenna Array, IEEE Trans. Antennas Propag.,
AP-20, 30-35, 1972.
Chu T.-S. and R. H. Turrin, Depolarization Effects of Offset Reflector Antennas, IEEE Trans.
Antennas Propag., AP-21, 339-345, 1973.
Cornwell T. J., A Novel Principle for Optimization of the Instantaneous Fourier Plane Coverage
of Correlation Arrays, IEEE Trans. Antennas Propag., 36, 1165-1167, 1988.
Cornwell T. J.; M. A. Holdaway and J. M. Uson, Radio-Interferometric Imaging of Very Large
Objects: Implications for Array Design, Astron. Astrophys., 271, 697-713, 1993.
Erickson W. C, M. J. Mahoney and K. Erb, Astrophys. J. Suppl., 50, 403-420, 1982.
Frater R. H., J. W. Brooks and J. B. Whiteoak, The Australia Telescope-Overview, Proc.
IREE, Aust., 12, 102-112, 1992.
Hamaker J. P., J. D. О'Sullivan and J. E. Noordam, Image Sharpness, Fourier Optics and
Redundant Spacing Interferometry, J. Opt. Soc. Am., 67, 1122-1123, 1977.
Hirabayashi H. and 52 coauthors, Overview and Initial Results of the Very Long Baseline
Interferometry Space Observatory Program, Science, 281, 1825-1829, 1998.
Hjellming R. M., The Design of Aperture Synthesis Arrays, Synthesis Imaging in Radio
Astronomy,R. A, Perley, F. R. Schwab, and A. H. Bridle, Eds., Astron. Soc. Pacific. Conf.
Ser., 6, 477-500, 1989.
Hogbom J. A. and W. TV. Brouw, The Synthesis Radio Telescope at Westerbork, Principles of
Operation, Performance and Data Reduction, Astron. Astrophys., 33, 289-301, 1974.
5.8] Цитированная литература 157
Ing alls R. P., J. Antebi, J. A. Ball, R. Barvainis, J. F. Cannon, J. C. Carter, P. J. Charpentier,
B. E. Corey, J. W. Crowley, K. A. Dudevoir, M. J. Gregory, F. W. Kan, S. M. Milner, A. E.
E. Rogers, J. E. Salah and M. S. Zarghamee, Upgrading of the Haystack Radio Telescope for
Operation at 115 GHz, Proc. IEEE, 82, 742-755, 1994.
Ishiguro M., Minimum Redundancy Linear Arrays for a Large Number of Antennas, Radio
Sci., 15, 1163-1170, 1980.
Keto E., The Shapes of Cross-Correlation Interferometers, Astrophys. J., 475, 843-852, 1997.
Kogan L., Level of Negative Sidelobes in an Array Beam, Pub. Astron. Soc. Pacific, 111, 510-
511, 1999.
Koles W. A., R. G. Frehlich and M. Kojima, Design of a 74-MHz Antenna for Radio Astronomy,
Proc. IEEE, 82, 697-704, 1994.
Lawrence C. R., T. Herbig and A. C. S. Readhead, Reduction of Ground Spillover in the Owens
Valley 5.5-m Telescope, Proc. IEEE, 82, 763-767, 1994.
Leech J., On Representation of 1, 2..., n by Differences, J. London Math. Soc, 31, 160-169,
1956.
Mathur N. C, A Pseudodynamic Programming Technique for the Design of Correlator Super-
synthesis Arrays, Radio Sci., 4, 235-244, 1969.
Mayer С E., D. T. Emerson and J. H. Davis, Design and Implementation of an Error-
Compensating Subreflector for the NRAO 12-m Radio Telescope, Proc. IEEE, 82, 756-762,
1994
Mills B. Y., Cross-Type Radio Telescopes, Proc. IRE Aust., 24, 132-140, 1963.
Moffet А. Т., Minimum-Redundancy Linear Arrays, IEEE Trans. Antennas Propag., AP-16,
172-175, 1968.
Moran J. M., The Submillimeter Array, in Advanced Technology MMW, Radio and Terahertz
Telescopes, T. G. Phillips, Ed., Proc. SPIE, 3357, 208-219, 1998.
Napier P. J., D. S. Bagri, B. G. Clark, A. E. E. Rogers, J. D. Romney, A. R. Thompson and
R. С Walker, The Very long Baseline Array, Proc. IEEE, 82, 658-672, 1994.
Napier P. J., A. R. Thompson and R. D. Ekers, The Very Large Array: Design and Performance
of a Modern Synthesis Radio Telescope, Proc. IEEE, 71, 1295-1320, 1983. (Имеется перевод:
ТИИЭР, 71, 11, с. 78-111, 1983.)
National Radio Astronomy Observatory (NRAO), A Proposal for a Very Large Array Radio
Telescope, National Radio Astronomy Observatory, Green Bank, WV, Vol. 1, Jan. 1967; Vol.
3, Jan. 1969.
Oppenheim A. V. and R. W. Schafer, Digital Signal Processing, Prentice-Hall, Englewood
Cliffs, NJ, 1975, Ch. 3.
Padin S., J. K. Cartwright, B. S. Mason, T. J. Pearson, A. C. S. Readhead, M. С Shepherd,
J. Sievers, P. S. Udomprasert, W. L. Holzapfel, S. T. Myers, J. E. Carlstrom, E. M. Leitch,
M. Joy, L. Bronfman and J. May, First Intrinsic Anisotropy Observations with the Cosmic
Background Imager, Astrophys. J. Letters, 549, L1-L5, 2001.
Papoulis A., Signal Analysis, McGraw-Hill, New York, 1977, p. 74.
Preston R. A., B. F. Burke, R. Doxsey, J. F. Jordan, S. H. Morgan, D. H. Roberts, I. I.
Shapiro, The Future of VLBI Observations in Space, in Very Long Baseline Interferometry
Techniques, F. Biraud, Ed., Cepadues, Toulouse, France, 1983, p. 417-431.
Rabiner L. R. and B. Gold, Theory and Application of Digital Signal Processing, Prentice-Hall,
Englewood Cliffs, NJ, 1975, p. 50.
Rademacher H. and O. Toeplitz, The Enjoyment of Mathematics, Princeton Univ. Press,
Princeton, NJ, 1957.
Raimond E. and R. Genee, Eds., The Westerbork Observatory, Continuing Adventure in Radio
Astronomy, Kluwer, Dordrecht, 1996.
Rudge A. W. and N. A. Adatia, Offset-Parabolic-Reflector Antennas: A Review, Proc. IEEE,
66, 1592-1618, 1978. (Имеется перевод: ТИИЭР, 66, 12, с. 5-36, 1978.)
158 Антенны и антенные решетки [Гл. 5
Ruze J., Antenna Tolerance Theory — A Review, Proc. IEEE, 54, 633-640, 1966.
Ryle M., The New Cambridge Radio Telescope, Nature, 194, 517-518, 1962.
Ryle M. and A. Hewish, The Synthesis of Large Radio Telescopes, Mon. Not. R. Astron. Soc,
120, 220-230, 1960.
Ryle M.j A. Hewish and J. R. Shakeshaft, The Synthesis of Large Radio Telescopes by the Use
of Radio Interferometers, IRE Trans. Antennas Propag., 7, S120-S1204, 1959.
Seielstad G. A., G. W. Swenson Jr. and J. C. Webber, A New Method of Array Evaluation
Applied to Very Long Baseline Interferometry, Radio Sci., 14, 509-517, 1979.
Swarup G., S. Ananthakrishnan, V. K. Kapahi, A. P. Rao, C. R. Subrahmanya and V. K.
Kulkarni, The Giant Metre-Wave Radio Telescope, Current Science, (Current Science Associ-
Association and Indian Academy of Sciences), 60, 95-105, 1991.
Swenson G. W.j Jr. and K. I. Kellermann, An Intercontinental Array — A Next-Generation
Radio Telescope, Science, 188, 1263-1268, 1975.
Swenson G. W., Jr. and N. C. Mathur, The Circular Array in the Correlator Mode, Proc. IREE
Aust., 28, 370-374, 1967.
Thomasson P., MERLIN, Quat. J. Royal Astron. Soc, 27, 413-431, 1986.
Thompson A. R. and R. N. Bracewell, Interpolation and Fourier Transformation of Fringe
Visibilities, Astron. J., 79, 11-24, 1974.
Thompson A. R., B. G. Clark, C. M. Wade and P. J. Napier, The Very Large Array, Astrophys.
J. Suppl., 44, 151-167, 1980.
Unser M., Sampling — 50 Years After Shannon, Proc. IEEE, 88, 569-587, 2000.
Walker R. C, VLBI Array Design, in Indirect Imaging, J. A. Roberts, Ed., Cambridge Univ.
Press, Cambridge, UK, 1984, p. 53-65.
Welch W. J. and 36 coauthors, The Berkeley-Illinois-Maryland Association Millimeter Array,
Pub. Astron. Soc. Pacific, 108, 93-103, 1996.
Wild J. P., A New Method of Image Formation with Annular Apertures and an Application
in Radio Astronomy, Proc. R. Soc. A, 286, 499-509, 1965.
Wild J. P., Ed., Proc. IRE Aust., Special Issue on the Culgoora Radioheliograph, Vol. 28, No.
9, 1967.
Williams W. F., High Efficiency Antenna Reflector, Microwave J., 8, 79-82, 1965, (reprinted
in Love A978); see Bibliography).
Костенко В. И., Матвеенко Л. И. Прецизионная антенна космического радиотелескопа//
Космические исследования. XX.1, 1982, с. 149-151.
Глава 6
ОТКЛИК ПРИЕМНОЙ СИСТЕМЫ
Эта глава посвящена отклику приемной системы, на которую поступают сиг-
сигналы от антенн, которая их усиливает и фильтрует, а также измеряет кросс-
корреляцию для различных антенных пар. Мы рассмотрим, как зависят получае-
получаемые результаты от основных параметров системы. На некоторые из этих эффектов
мы обратили внимание в предыдущих главах, но здесь они рассмотрены более
подробно, что позволит нам перейти в главах 7 и 8 к вопросам проектирования
приемных систем.
6.1. Преобразование частоты,
вращение интерференционных лепестков
и комплексные корреляторы
6.1.1. Преобразование частоты. Практически во всех приемных системах
в радиоастрономии частота принимаемого антенной сигнала изменяется путем сме-
смешивания его с сигналом гетеродина. Эта операция, называемая преобразованием
частоты [гетеродинированием), позволяет производить основную обработку сиг-
сигнала на промежуточных частотах, наиболее подходящих для усиления, передачи,
фильтрации, задержки, регистрации и других подобных операций.
Преобразование частоты происходит в смесителе, в котором преобразуемый
сигнал совместно с сигналом гетеродина подается на элемент с нелинейной вольт-
амперной характеристикой. Таким элементом может быть диод, как показано на
рис. 6.1 а. Ток через диод г может быть представлен в виде степенного ряда от
приложенного напряжения V:
i = ao + a1V + a2V2 + a3V3 + ... F.1)
Предположим теперь, что V является суммой напряжений гетеродина
Ъ\ cosB7rz/LO? + въо) и сигнала, одна из Фурье-компонент которого равна
Ъ2 cos BтплД + ф8). Член второго порядка по V приведет в этом случае к появлению
на выходе смесителя произведения вида
bi cos Bttz/lo? + въо) b2 cos Bтп/в? + ф8) = - М2 cos [27Г (у8 + i/LO) t + ф8 + 6>LO] +
+ i W>2 cos [2тг (i/e - z/LO) t + ф3 - 0ЪО]. F.2)
Таким образом, ток через диод будет содержать компоненты с частотами, рав-
равными сумме и разности i/s и z/LO. Другие члены разложения F.1) дадут другие
комбинации частот, например, 3z/LO ± z/s, однако показанный на рис. 6.1 фильтр Н
пропускает только ограниченную часть спектра, и при правильном расчете можно
исключить прохождение нежелательных компонент через его полосу пропускания.
Обычно напряжение сигнала значительно меньше напряжения гетеродина, поэтому
гармоники и интермодуляционные компоненты (т. е. ложные сигналы, получающи-
получающиеся в результате комбинаций различных частот в пределах полосы спектра входного
160
Отклик приемной системы
[Гл. 6
Н
ПЧ
>
v
Гетеродин
Отклик
Полоса
промежуточной
частоты
Боковые полосы
нижняя верхняя
T
) ^o (vLO+v0)
Частота
Рис. 6.1. Преобразование частоты в приемной системе: а — упрощенная схема смесителя
и фильтра Н, определяющего полосу промежуточной частоты (ПЧ). В качестве нелинейно-
нелинейного элемента показан диод; б— спектр, показывающий верхнюю и нижнюю боковые полосы
сигнала, преобразуемые к промежуточной частоте. Частота щ соответствует центру по-
полосы ПЧ
сигнала) будут малы по сравнению с интересующими нас членами, содержащими
В большинстве случаев при преобразовании частота сигнала понижается, поэто-
поэтому для нас важен второй член в правой части F.2). Тогда фильтр Н определяет
полосу сигнала промежуточной частоты (ПЧ) с центром в точке щ, показанную на
рис. 6.1 б. Сигналы преобразуются и пропускаются фильтром в диапазонах z/LO — щ
и z/LO + щ. Эти диапазоны называются соответственно нижней и верхней боковыми
полосами (они также показаны на рисунке), и если требуется принимать только одну
из них, то нежелательную полосу можно устранить с помощью дополнительного
фильтра, размещаемого перед смесителем. В некоторых случаях принимаются обе
полосы, что дает на выходе отклик на двухполосный сигнал.
6.1.2. Отклик однополосной системы. На рис. 6.2 показана приемная си-
система для двух антенн тип, входящих в синтезируемую решетку. Здесь нас инте-
интересуют особенности преобразования частоты, которые мы пока не рассматривали.
Разница во времени rg между моментами прихода на антенны сигнала от радио-
радиоисточника непрерывно меняется из-за того, что антенны отслеживают его переме-
перемещение по небу, связанное с вращением Земли. Аппаратная задержка Т{ непрерывно
подстраивается таким образом, чтобы компенсировать геометрическую задержку
rg и сигналы поступали на коррелятор одновременно. Приемные тракты, через
которые проходят сигналы, содержат усилители и фильтры, суммарные частотные
(амплитудные) характеристики которых для антенн тип равны соответственно
Нш{у) и Нп{у). Здесь v обозначает частоту на входе коррелятора; на входе антенны
ей соответствует частота г/ъо ± v. Сигналы, обрабатываемые приемной системой,
складываются из космических шумов и шумов системы; мы рассматриваем ти-
типичный случай, когда их спектры не меняются в пределах полосы пропускания
приемника. Спектры на входах коррелятора, таким образом, будут определяться
в основном характеристиками отклика приемной системы. Пусть фш — набег фазы
сигнала при его прохождении через приемный тракт антенны т, обусловленный
задержкой rg и фазой гетеродина, а фп — соответственно набег фазы в тракте
антенны п, включая Т{. Величины фш и фп, в совокупности с инструменталь-
инструментальным фазовым сдвигом (обусловленным характеристиками усилителей и фильтров),
представляют фазу сигнала от источника на входах коррелятора; отрицательные
их значения соответствуют запаздыванию по фазе (задержке сигнала). Отклик для
источника, функция видности которого V(u,v) = |V|e-^u, проще всего получить,
воспользовавшись выражением C.5), заменив в нем разность фаз 2ttDa • Sq на более
общую фп — фш. Тогда отклик на выходе коррелятора для интервала частот dv
6.1] Преобразование частоты, вращение интерференционных лепестков 161
можно записать в виде
dr = Re [A0\V\Hm{v) Я» еР^-Фт-Ф.) dl/J ? F.3)
а отклик для всей полосы частот приемной системы
\ F.4)
Мы включили в интер-
интервал интегрирования как по-
положительные, так и отрица-
отрицательные частоты. Предпола-
Предполагается, что V в наблюдае-
наблюдаемой полосе частот существен-
существенно не меняется. Выражение
F.4) представляет действи-
действительную часть комплексной
кросс-корреляции; позже мы
покажем, как получить обе ее
составляющие (действитель-
(действительную и мнимую).
6.1.3. Прием верхней
боковой полосы. При при-
приеме верхней боковой поло-
полосы фильтр или усилитель
на входе приемника выделя-
выделяет частоты в полосе, опре-
определяемой входным спектром
коррелятора (частота г/), сло-
сложенным с частотой гетероди-
гетеродина г/ъо. Выразим теперь фа-
фазы фт и фп с точки зре-
зрения тех воздействий, кото-
которым подвергаются сигналы
на рис. 6.2. Сигнал на часто-
частоте г/ьо + z/, поступающий на
антенну т, имеет геометри-
геометрическую задержку rg и, таким образом, сдвигается по фазе на 2tt(z/lo + i/)rg. Кроме
того, в смесителе его фаза уменьшается на величину фазы гетеродина вт. В ре-
результате мы получаем
Рис. 6.2. Упрощенная схема приемной системы для
двух антенн, входящих в антенную решетку. Задержка
Тг постоянно подстраивается компьютером таким обра-
образом, чтобы компенсировать геометрическую разность
хода сигналов rg. Функции Hm(i/) и Нп(у) представля-
представляют суммарные частотные характеристики усилителей
и фильтров в сигнальных каналах
= -2tt(i/l
F.5)
Фаза сигнала, поступающего на антенну п, уменьшается на величину фазы
гетеродина вп\ затем сигнал на частоте v подвергается аппаратурной задержке т^,
что соответствует фазовому сдвигу 2тпу^. Общий фазовый сдвиг для антенны п
составляет
0п. F.6)
6 Томсон
162 Отклик приемной системы [Гл. 6
Из F.4)—F.6) получаем отклик на выходе коррелятора
Г °г 1
ги=Ке\А0\У\е:>^^о^+(ОгП-вп)-Ф,] Hn(y)H*n{v)el'lvvAT dv\. F.7)
Действительная часть интеграла F.7) равна половине фурье-образа эрмитова
кросс-корреляционного спектра мощности Нш(у) Н^(у) относительно ошибки ком-
компенсации задержки Ат = rg — т^, которая вызывает линейное изменение фазы в по-
полосе спектра *). Мы предполагаем, что V в наблюдаемой полосе частот существенно
не изменяется. Например, если полосы пропускания ПЧ имеют прямоугольную фор-
форму с центром на частоте z/q, шириной Az/IF и идентичные фазовые характеристики,
то для положительных частот
Нт{у)\ = \Нп(и)\ =
" О,
Воспользовавшись формулой (A3.6) приложения 3.1 для эрмитовой функции
НтНп, можно написать
j Hm{v) Я*(i/) ej27TiyAr dv = 2 Re I J Я02 ej2™Ar dv \ =
Li/0-(Ai/ip/2)
™ ~ " ~ г. F.9)
В общем случае мы можем определить аппаратурный коэффициент усиления
Сшп = \Gmn\e^G следующим образом:
Л) j Hm(v) H^(v) ej27TuAr dv = Gmn(Ar)ej2w°Ar = |Сшп(Дт)| е^B7Г1/°Аг+^).
— oo
F.10)
Изменение Gmn в зависимости от Аг приводит к эффекту распределения по
задержкам, рассмотренному в предыдущих главах. Фаза фа обусловлена различи-
различием фазовых характеристик усилителей и фильтров. Фазы гетеродина 0ш и 0п не
включаются в суммарную аппаратную фазу фо, поскольку они входят в верхнюю
и нижнюю полосы с разными знаками.
Подставляя F.10) в F.7), получаем для приема в верхней боковой полосе
ru = |V||Gmn(Ar)| cos [2тг (^LOrg + щАт) + (вт - 9п) - фь + фв]. F.11)
Член 27ri/LOrg в аргументе косинуса приводит к «синусоидальным» осцилляциям
при движении источника по интерференционной диаграмме. Фаза этих осцилляции
определяется ошибкой задержки Аг, относительной фазой сигналов гетеродинов,
) Мы считаем здесь, что источник находится достаточно близко к центру картографи-
картографируемой области, так что условие Аг = 0 означает нулевую ошибку компенсации. Эффект
вариации ошибки по задержке в более широком поле зрения рассматривается в разд. 6.3.
6.1] Преобразование частоты, вращение интерференционных лепестков 163
фазовыми характеристиками сигнальных каналов и фазой функции видности. Ча-
Частоту осцилляции на выходе v^odrz/dt часто называют естественной частотой
интерференции. Осцилляции возникают потому, что задержки сигнала на rg и Т{
происходят на разных частотах — rg на входной и Т{ на промежуточной частоте,
а эти две частоты отличаются на ръо . Таким образом, даже если эти две задержки
равны, они приводят к различным сдвигам по фазе, и они растут либо убывают по
мере вращения Земли.
6.1.4. Прием нижней боковой полосы. Рассмотрим теперь случай, когда
частоты, поступающие от антенн, относятся к нижней боковой полосе, т. е. меньше
частоты уъо на частоту входных сигналов коррелятора. Соответствующие фазы
равны
^m = 27r(i/LO-i/)rg + (9m) F.12)
И
фп = -2тпуп + 0п. F.13)
Их знаки и знак фи отличаются от случая приема в верхней полосе, поскольку уве-
увеличение фазы сигнала на антенне соответствует уменьшению фазы на корреляторе.
Выражение для выходного сигнала коррелятора будет иметь вид
ej27rAr dv \. F.14)
Действуя далее аналогично случаю верхней боковой полосы, получаем
n(Ar)| cos[2^(z/LOrg - i/оДт) + Fm - 6n) - фу - фо]. F.15)
6.1.5. Многократное преобразование частоты. В реальных системах
между антеннами и корреляторами сигналы могут подвергаться нескольким
частотным преобразованиям. Системы с многократными преобразованиями
работают в сущности так же, как и рассмотренно выше. Преобразование частоты,
в результате которого получается нижняя боковая полоса (т. е. частота гетеродина
минус частота входного сигнала), приводит к обращению спектра сигнала, при
котором частоты на верхнем конце входного диапазона оказываются в нижней
части выходного, и наоборот. Если производится четное число преобразований
нижней полосы, результирующий спектр не будет обращен и можно применить
формулу F.11), заменив z/LO комбинацией частот гетеродинов, которую иногда
называют алгебраической суммой, так как некоторые частоты входят в нее
с прямым, а другие — с обратным знаком. Аналогичным образом фазы гетеродинов
0ш и вп заменяются комбинациями фаз отдельных гетеродинов. Если имеет место
обращение частотного диапазона, подойдет выражение F.15) с аналогичными
модификациями.
6.1.6. Отслеживание задержки и вращение интерференционных ле-
лепестков. Ввод компенсирующей задержки (т^ на рис. 6.2) производится и рассчи-
рассчитывается, исходя из положения антенн фазового центра наблюдаемого поля. Одну
из антенн решетки можно принять в качестве опорной и устанавливать задержки
для других антенн таким образом, чтобы для волнового фронта, исходящего из
фазового центра, сигналы, регистрируемые различными антеннами, приходили на
коррелятор одновременно.
Чтобы контролировать частоту синусоидальных изменений на выходе корреля-
коррелятора, в один из сигналов гетеродина можно ввести непрерывное изменение фазы.
Выражения F.11) и F.15) показывают, что частота интерференции может быть
164
Отклик приемной системы
[Гл.6
сведена к нулю, если заставить От — Оп меняться с такой скоростью, чтобы поддер-
поддерживать постоянным (с точностью до 2тг) член [27ri/LOrg + (вш — вп)]. Этого можно
достигнуть прибавлением частоты 2тгvbO(drg/dt) к 0п или вычитанием ее из вш.
Обратите внимание, что drg/dt можно оценить из D.9), где w — третья компонента
базы интерферометра, равная crg (в длинах волн). Например, для антенн, разне-
разнесенных в направлении восток-запад на 1 км, максимальным значением для drg/dt
является 2,42 • 10 ~10, так что частота интерференции обычно мала по сравнению
с принимаемыми радиочастотами. Снижение выходной частоты уменьшает коли-
количество данных, требующих обработки, так как, чтобы не потерять информацию,
каждый из выходов коррелятора нужно опрашивать по крайней мере дважды за
период выходной частоты (критерий Найквиста, обсуждаемый в разд. 8.2). При
разнесении антенн, обеспечивающем угловое разрешение порядка миллисекунды
дуги (как это случается в РСДБ), естественная частота интерференции vl^odrgjdt
может превышать 10 кГц. В случае решетки с несколькими парами антенн можно
снизить каждую из выходных частот до одной и той же доли ее естественной
величины либо до нуля. Сведение к нулевой частоте — так называемая остановка
интерференционных лепестков — обычно оказывается предпочтительнее. После
этого, чтобы получить выходную амплитуду и фазу, примененяются некоторые
специальные средства, например, описанный в следующем параграфе комплексный
коррелятор.
6.1.7. Простые и комплексные корреляторы. Рис. 6.3 иллюстрирует ме-
метод измерения амплитуды и фазы выходного сигнала коррелятора в случае, когда
частота интерференции на выходе коррелятора сведена к нулю. Используются два
коррелятора: один перемножает сигналы рассмотренным ранее, а другой имеет на
Усиленные
входные ^ *
сигналы ^
с двух антенн
\ »•
- Фазовращатель
Умножитель
Умножитель
Интегратор
Действ,
(cos) часть
Интегратор
Мнимая
(sin) часть
Рис. 6.3. Использование двух корреляторов для измерения действительной и мнимой ча-
частей функции видности. Такое устройство молено назвать комплексным коррелятором
одном из входов квадратурную фазосдвигающую цепочку. Эта цепочка сдвигает
фазу каждой из частотных компонент входного диапазона на тг/2, и ее выходной
сигнал является, таким образом, гильбертовым преобразованием входного. Для
сигналов с конечной шириной спектра фазовый сдвиг не эквивалентен задержке.
Этот фазовый сдвиг можно также осуществить, подав сигнал на два отдельных
смесителя, перемножающих его с двумя гетеродинами, фазы которых сдвинуты
на тг/2. Выходной сигнал второго коррелятора можно получить, заменив Нш{р)
на Нш(у) е~^12. В соответствии с F.10) результатом будет сдвиг фо на —тг/2 и,
таким образом, в F.11) и F.15) функция косинуса превратится в ± синус. Для
двух корреляторов на рис. 6.3 можно также заметить, что выход действительного
коррелятора, если опустить постоянные множители, равен
rreal
=Re|v
=Re{V} | Hm{v)H*n(y)dv,
F.16)
6.1] Преобразование частоты, вращение интерференционных лепестков 165
где интеграл действителен в силу того, что Hm(u) и Н^(и) эрмитовы (действитель-
(действительная часть четна, мнимая нечетна), и, следовательно, произведение Нш(и) H^{v)
также эрмитово. Выход мнимого коррелятора пропорционален выражению
J Hm(v)H*n(v)e-^l2dA=Im{V} J Hm{v)Я» dp. F.17)
— oo —oo
Таким образом, два выхода соответствуют откликам на действительную и мни-
мнимую части функции видности V.
Комбинацию двух корреляторов с квадратурной цепочкой называют обычно
комплексным коррелятором, а два его выхода — косинусным и синусным (или
действительным и мнимым) выходами. (Если необходимо подчеркнуть различие,
мы будем иногда называть одиночный перемножитель с интегратором простым пе-
перемножителем или коррелятором с одним перемножителем.) При наблюдениях
источников с непрерывным спектром компенсирующая задержка устанавливается
так, чтобы Ат равнялось 0, а вращение лепестков поддерживало равным нулю
значение 2тгу^оТ{ + (вш — вп). Таким образом, косинусный и синусный выходы
представляют собой действительную и мнимую части GmnV(i?, г>). При использо-
использовании комплексного коррелятора вращение Земли, «сканирующее» источник ин-
интерференционной диаграммой, не является более необходимым элементом измере-
измерения функции видности. Важной особенностью комплексного коррелятора является
независимость шумовых флуктуации на косинусном и синусном выходах, что мы
покажем в разд. 6.2.
Спектральные корреляционные системы, в которых для измерения корреля-
корреляции как функции временного смещения или «канала задержки», обозначенного
г в C.27), используется несколько корреляторов, рассматриваются в разд. 8.7.
Корреляция как функция т, измеренная с помощью корреляторов с квадратурным
сдвигом фаз на одном из входов, является гильбертовым преобразованием той
же самой величины, измеренной без квадратурных фазовых сдвигов (Lo et al.,
1984). Таким образом, в противоположность случаю, когда корреляция измеряется
только для г = 0, здесь достаточно использовать простые корреляторы, так как
синусные выходы не давали бы никакой добавочной информации. См. также 8-й
пункт в пояснениях к табл. 6.1.
6.1.8. Отклик двухполосной системы. Двухполосной называется такая
приемная система, которая дает на выходе отклик как на верхнюю, так и на
нижнюю боковые полосы. Из F.11) и F.15) получаем для отклика системы
rd = ги + п = 2|V||Gmn(Ar)| cos Bтп/0Дт + фо) cos [2тп/ьот6 + @Ш - вп) - фу].
F.18)
Здесь имеется существенное отличие от случаев приема единственной боковой
полосы. Фаза сомножителя, соответствующего частоте интерференции, т. е. функ-
функции косинуса, содержащей выражение 27rz/LOrg, не зависит более от Аг или фо,
однако последние появляются в сомножителе, определяющем амплитуду интерфе-
интерференционных лепестков:
\Gmn(Ar)\ cosB7ti/oAt + 0g). F.19)
Если зафиксировать задержку т^, то Аг будет непрерывно изменяться, что
приведет к косинусоидальной модуляции интерференционных лепестков из-за
сомножителя-косинуса в F.19). Кроме того, как показывает рис. 6.4, благодаря
этому сомножителю кросс-корреляция (амплитуда интерференционного сигнала)
спадает быстрее, чем в однополосном случае, где она зависит только от Gmn(Ar).
166
Отклик приемной системы
[Гл.6
Ат
Рис. 6.4. Пример изменений амплитуды лепестков как функции Ат в двухполосной систе-
системе (сплошная линия). В данном случае центры двух боковых полос отстоят друг от друга
на три ширины полосы ПЧ, т.е. щ = 1,5 A^IF, а частотная характеристика тракта ПЧ
прямоугольна. Штриховой линией показана эквивалентная функция для однополосной
системы с той же частотной характеристикой ПЧ
Соответственно повышаются требования к точности аппаратной компенсации гео-
геометрической задержки. Отсутствие зависимости фазы лепестков от фазовой харак-
характеристики сигнального канала обусловлено тем, что последняя влияет на боковые
полосы одинаковым, но с обратным знаком.
Отклик двухполосной системы с комплексным коррелятором для косинусного
выхода дается выражением F.18); для синусного выхода фа нужно заменить на
/
d)sine = 2|V||Gmn(Ar)| sinB7rz/0Ar
cos [2ttz/l
(От —
F.20)
Если регулировать 2тгг/оДт + фс так, чтобы на действительном F.18) или мни-
мнимом F.20) выходе получался максимальный сигнал, то на другом выходе сигнал
будет нулевым. Это означает, что при наблюдениях в континууме, где сигнал
в обеих полосах имеет равную мощность, комплексный коррелятор не дает никакого
выигрыша в чувствительности.
Чтобы наглядно представить разницу между интерферометрическими система-
системами с одной и двумя боковыми полосами, на рис. 6.5 показаны выходы коррелятора
в комплексной плоскости. Однополосный случай иллюстрируется рис. 6.5 а. Вектор
г представляет выход комплексного коррелятора. Если лепестки не остановлены,
вектор г поворачивается на 2тг всякий раз, когда rg изменяется на длину волны.
Длину волны на частоте гетеродина, если аппаратурная задержка отслеживает гео-
геометрическую. Проекции вектора на действительную и мнимую оси соответствуют
действительному и мнимому выходам коррелятора, которые представляют собой
синусоиды с частотой, равной частоте интерференции, сдвинутые относительно
друг друга на тг/2. Если же лепестки остановлены, позиционный угол вектора г
остается постоянным. Рисунок 6.Б б иллюстрирует двухполосный случай. Векторы
ги и Г? представляют компоненты выхода от верхней и нижней полос. В этом
случае изменение rg приводит к вращению ги и Г? в противоположных направле-
направлениях. Чтобы в этом убедиться, вспомним, что действительные компоненты выхода
коррелятора выражаются F.11) и F.15), а соответствующие мнимые компоненты
получаются заменой фо на фо — тг/2. Затем, приняв (вш — вп) = 0 (нет вращения
лепестков), нужно рассмотреть эффект небольшого изменения rg.
Вращающиеся в противоположных направлениях векторы, соответствующие
двум боковым полосам на выходе коррелятора, совпадают с угловым положением
(определяемом аппаратурной фазой), которое мы обозначили на рис. 6.5 б" линией
6.1]
Преобразование частоты, вращение интерференционных лепестков
167
Im
Im
Re
Re
Рис. 6.5. Представление на комплексной плоскости выходов коррелятора в (а) однополос-
однополосной и (б) двухполосной приемных системах. Точка С в случае (б) соответствует сумме
верхней и нижней боковых компонент на выходе коррелятора
АВ. Вектор их суммы, таким образом, движется вдоль этой линии, и фазы интер-
интерференционных синусоид на действительном и мнимом выходах совпадают. Предпо-
Предположим теперь, что мы регулируем фазу (ЯтпуоАт + фо) в F.18) так, чтобы получить
максимальную амплитуду лепестков не действительном выходе. Тогда линия А В
развернется и совпадет с действительной осью, и мнимый выход комплексного
коррелятора не будет содержать никакого сигнала, а только шум. Из F.18) можно
видеть, что фаза функции видности фу представлена фазой вектора, амплитуда
которого осциллирует вдоль вещественной оси. Эту фазу можно восстановить, осво-
освободив интерференционные лепестки и вписав синусоиду в сигнал на действительном
выходе. Если лепестки остановлены, можно определить их амплитуду и фазу путем
переключения на тг/2 фазы гетеродина на одной из антенн. В выражении F.18)
это переключение может быть представлено как 0ш —>> @т — тг/2), что приведет
к замене второй функции косинуса на синус; это позволит определить аргумент
в квадратных скобках. Однако в этом случае значения косинусной и синусной
компонент выхода измеряются не одновременно, так что эффективное время усред-
усреднения составляет всего половину от того, что имеет место в случае однополосного
комплексного коррелятора. На рис. 6.5 ?Г видно, что переключение фазы гетеродина
на тг/2 приводит к повороту ru и г^ на тг/2 в противоположных направлениях, так
что вектор суммы двух боковых полос остается на линии А В. Относительная чув-
чувствительность различных систем обсуждается в разд. 6.2; см. табл. 6.1 и пояснения
к ней.
6.1.9. Двухполосная система с многократным преобразованием ча-
частоты. При многократном преобразовании частоты отклик для двухполосного
интерферометра имеет более сложный вид, чем для однополосного; мы проиллю-
проиллюстрируем его на примере системы, показанной на рис. 6.6. Заметим, что в случае,
когда после первого смесителя сигнал ПЧ подвергается нескольким однополосным
преобразованиям, второй смеситель каждой из антенн на рис. 6.6 можно считать
представлением нескольких последовательных смесителей, a у<± — суммой частот
гетеродинов с соответствующими знаками, учитывающими то, какая — верхняя
или нижняя — полоса преобразуется. Члены для фаз сигналов определяются из
соображений, аналогичных описанным при выводе выражений F.5) и F.6). Таким
образом, мы получаем
± у)
; T "ml "" '
F.21)
fin = -27Г (l/2 + V) Гц - 2тГ1/Т»2 T 0п1 - 6п2,
F.22)
168
Отклик приемной системы
[Гл. 6
где верхние знаки соответствуют преобразованиям верхней боковой полосы на обо-
обоих смесителях каждой из антенн, а нижние — преобразованию нижней боковой
полосы на первом и верхней боковой на втором смесителе. Далее мы действуем,
как в предыдущих примерах, т. е. подставляем выражения F.21) и F.22) для фт
и фп в F.4), выделяем интеграл по частоте (г/) от НШН^, как в F.7), и подставляем
выражение для интеграла из F.10). В результате получаем
ги = |V||Gmn(Ar)| cos
2тп/2 (rg - тц
2тп/0Дт +
вп1) + {ош2
еп2)
F.23)
= |V||Gmn(Ar)| cos
- 2тп/2 (rg -
- 0nl) - @m2 - 0n2) -фу- фо]. F.24)
Двухполосный отклик будет равен
г а = г и
= 2|V||Gmn(Ar)| cos
- rg) -
x cos
6>mi
F.25)
где Ar = rg — r^i — Ti2. Обратите внимание, что фаза выходной интерференцион-
интерференционной картины, определяемая вторым косинусом, зависит только от фазы первого
гетеродина. Таким образом, при реализации вращения лепестков фазовый сдвиг
должен вводиться в этот гетеродин. Первый косинус в F.25) влияет на амплитуду
лепестков; здесь нужно рассмотреть два случая:
1. В качестве компенсирующей задержки используется тц (на промежуточной
частоте сразу после двухполосного смесителя), при этом т^2 = 0. Тогда, если частот-
частотные характеристики двух каналов близки, тц — rg ~ 0 и фаза фо в первой функции
косинуса в F.25) должна быть мала. Для получения максимальной амплитуды
интерференционного сомножителя необходимо только уравнять #т2 и #п2. Это
аналогично случаю однократного преобразования F.18).
2. В качестве компенсирующей задержки используется т^2, которая вводится
после последнего смесителя; при этом тц = 0. (Это имеет место в любых антенных
решетках, где компенсирующие задержки реализуются цифровыми методами, что
типично для больших решеток.) Тогда, чтобы при изменении rg значение функ-
функции косинуса поддерживалось близким к единице, необходимо в F.25) вводить
непрерывно фазовый сдвиг в #т2 или #п2. Этот фазовый сдвиг не влияет на фазу
выходных интерференционных лепестков, а только на их амплитуду; см., например,
(Wright et al., 1973).
6.1.10. Остановка лепестков в двухполосной системе. Возьмем две ан-
антенны, показанные на рис. 6.6, и рассмотрим случай, когда rg компенсируется
аппаратной задержкой, вводимой непосредственно перед коррелятором, так что
тц = 0. Можно представить себе интерференционные лепестки как эффект, обу-
обусловленный доплеровским сдвигом сигнала на одной из антенн, который приводит
к частотным биениям сигналов при перемножении их в корреляторе. Предполо-
Предположим, что геометрическая задержка rg на пути сигнала к антенне m (слева на
рисунке) увеличивается со временем, т. е. антенна m удаляется от источника (по
отношению к антенне п). Тогда волновой фронт сигнала от источника с частотой
z/RF будет принят антенной m на частоте ^RFA — drg/dt). Если сигнал принима-
принимается в верхней боковой полосе, его частота на входе коррелятора будет равна
6.1]
Преобразование частоты, вращение интерференционных лепестков
169
drs\
F.26)
Чтобы остановить лепестки, нам нуж-
нужно соответствующим образом снизить ча-
частоту сигнала от антенны п, чтобы оба
сигнала поступали на коррелятор с одной
и той лее частотой. Для этого мы умно-
умножаем частоты обоих гетеродинов антен-
антенны п на коэффициент A + drg/dt). Заме-
Заметим, что это эквивалентно прибавлению
27r(drg/dt)ui к 6ni и 2n(dTg/dt)v2 K #п2 5
эти приращения представляют собой ско-
скорости изменения фаз гетеродинов, обес-
обеспечивающие постоянное значение обеих
функций косинуса в F.25). Соответствую-
Соответствующий сигнал от антенны п подвергается за-
задержке Tii на частоте z/RF — {у\ + ^)A +
+ drg/dt), и так как задержка непрерывно
подстраивается под значение rg, сигнал
редуцируется по частоте на коэффициент
A — drg/dt). Таким образом, на входе кор-
коррелятора частота сигнала антенны п бу-
будет
_|_
F.27)
что эквивалентно F.26), если пренебречь
членами drg/dt второго порядка малости.
(Вспомните, что, например, для километ-
километровой базы максимально возможное зна-
значение drg/dt равно 2,42 • 10~10.) Для ниж-
Рис. 6.6. Приемная система для двух ан-
антенн с двойным преобразованием часто-
частоты, первое из которых — двухполосное,
а второе — в верхней боковой полосе. Вво-
Вводятся две компенсирующие задержки, тц
и Тг2, чтобы при выводе отклика двухпо-
двухполосной системы можно было определить,
в какой точке относительно первого сме-
смесителя вводится задержка. На практике
требуется только одна компенсирующая
задержка. Полные частотные характери-
характеристики Нт и Нп определяются как функ-
функции частоты v на входе коррелятора
ней боковой полосы также применимы
выражения F.26) и F.27), если поменять знаки частот z/RF и v\\ и в этом случае
частоты на входе коррелятора окажутся одинаковыми. Таким образом, в результате
лепестки будут остановлены в обеих боковых полосах.
6.1.11. Сравнительная характеристика двухполосных и однополосных
систем. Главная причина, по которой в интерферометрии используется двухпо-
двухполосный прием, заключается в том, что в некоторых случаях минимальные шумовые
температуры приемника достигаются применением входных каскадов, являющихся
по сути своей двухполосными устройствами. Для миллиметровых и более корот-
коротких волн (частот, больших ~100 ГГц) малошумящие усилители создать трудно,
и в приемных системах в качестве входного каскада часто используют смеситель
типа сверхпроводник—изолятор—сверхпроводник (SIS) с последующим малошумя-
щим усилителем ПЧ; см., например, (Tucker and Feldman, 1985). Как смеситель,
так и усилитель ПЧ охлаждают до низких температур, обеспечивающих сверх-
сверхпроводимость смесителя и минимальный уровень шумов усилителя. Если между
антенной и смесителем поместить фильтр, отсекающий одну из боковых полос, то
мощность принимаемого сигнала уменьшится вдвое, но никакого снижения шумов
от смесителя и каскадов ПЧ не произойдет. Отношение сигнал/шум уменьшится, и,
следовательно, в данном случае наилучшей чувствительности в континууме можно
170 Отклик приемной системы [Гл. 6
достичь, сохранив обе боковые полосы. В качестве исторической справки заметим,
что двухполосные системы использовались на сантиметровых волнах в 60-70-х гг.;
см., например, (Read, 1961), иногда с вырожденным параметрическим усилителем
в качестве входного каскада. Эти усилители были принципиально двухполосными
устройствами; их применение в интерферометрии обсуждается в (Vander Vorst and
Colvin, 1966).
Двухполосные системы имеют ряд недостатков. Требуется повышенная точность
установки задержки и, вероятно, подстройка частоты и фазы двух или большего
числа гетеродинов; усложняется интерпретация спектральных данных в случае,
когда в обеих боковых полосах имеются спектральные линии; удваиваются требова-
требования к ширине свободного от помех радиодиапазона. Наконец, усиливается эффект
«размывания», обусловленный конечной шириной полосы; он будет обсуждаться
в разд. 6.3. Эти проблемы стимулировали разработку схем, обеспечивающих раз-
разделение откликов от верхней и нижней боковых полос.
6.1.12. Разделение боковых полос. Чтобы проиллюстрировать метод, с по-
помощью которого отклики от двух боковых полос на выходе коррелятора приемной
системы могут быть разделены, мы исследуем сумму откликов от верхней и нижней
полос из F.11) и F.15). Она равна
rd = ru + г? = |V||Gmn(Ar)|{cos [2тг (i/LOrg + i/оДт) + вшп - фу + фа] +
+ cos [2тг (i/LOrg - 1У0Аг) + вшп -фу- фа]}, (8.28)
где Отп = От — вп. Выражение F.28) определяет сигнал на действительном выходе
комплексного коррелятора. Мы перепишем его в виде
rd = |V||Gmn| (сояФп + сояФ^), F.29)
где Фп и Ф^ представляют соответствующие выражения в квадратных скобках из
F.28). Рассмотренные выше отклики соответствуют нормальному выходу интер-
интерферометра, который мы назовем «состоянием 1». Выражение для мнимого выхода
получается заменой фо на фо — тг/2. Назовем «состоянием 2» случай, когда в сигнал
первого гетеродина антенны т вводится фазовый сдвиг на тг/2, так что 0шп перехо-
переходит в 0тп — тг/2. Сигналы на выходах коррелятора для двух состояний получаются
из F.28) и F.29):
> состояние 1, F.30)
? {Опт -^ 0шп ~ к/2) состояние 2, F.31)
где ri и гз обозначают действительные выходы коррелятора, а Г2 и г^ — мнимые.
Тогда отклик от верхней полосы, выраженный в комплексной форме, будет равен
|V||Gmn| (cos*u + jsin*u) = | [(п - r4) + j(r2 +r3)}. F.32)
Аналогичным образом отклик от нижней полосы будет иметь вид
|V||Gmn| (cos-Jv + jsin*/) = \ [(п + n)-j(r2 - r3)]. F.33)
6.1] Преобразование частоты, вращение интерференционных лепестков 171
Если периодически менять фазовый сдвиг гетеродина на тг/2, то из F.32) и F.33)
можно будет получить значения откликов для верхней и нижней боковых полос.
Сходная реализация разделения боковых полос, авторство которой принадле-
принадлежит Б. Г. Кларку (В. G. Clark), основана на идее, использующей частоты интерфе-
интерференционных лепестков. Этот метод исходит из того факта, что малый сдвиг частоты
первого гетеродина увеличивает на ту же самую величину частоту интерференции
в корреляторе для обеих боковых полос, но тот же самый сдвиг частоты последую-
последующего гетеродина увеличивает частоту интерференции для одной боковой полосы
и уменьшает ее для другой. Пусть имеются две антенны, интерференционные ле-
лепестки от которых остановлены, как было описано при обсуждении выражений
F.26) и F.27). Предположим теперь, что мы увеличиваем чистоту первого гетеро-
гетеродина антенны п на величину 8v и уменьшаем на ту же самую величину частоту
второго гетеродина. Частота интерференции для сигнала в верхней боковой поло-
полосе не изменится; другими словами, интерференционные лепестки останутся непо-
движномы. В нижней боковой полосе частоты сигналов после второго смесителя
окажутся уменьшенными на 25 v. Для нижней полосы на выходе появятся интер-
интерференционные лепестки с частотой 25v{l — drg/dt) « 2Jz/, которые при усреднении
дадут малый остаточный сигнал, если их период B5v)~1 либо мал по сравнению
с интервалом интегрирования на выходе коррелятора, либо он целое число раз
укладывается в этот интервал. Если частота второго гетеродина не уменьшается,
а увеличивается на Jz/, то будет остановлена нижняя боковая полоса, а в верхней
останется только малый усредненный сигнал. Чтобы применить такую схему на
решетке из па антенн, смещение частоты на всех антеннах должно быть различным;
этого можно достигнуть, используя на антенне п смещение n5is, где п меняется
от 0 до па — 1. Преимуществом этой схемы разделения полос является то, что ее
реализация не требует никакой специальной аппаратуры помимо тех же управля-
управляемых гетеродинов, которые используются для остановки лепестков. В отличие от
схемы с переключением фазы гетеродина на тг/2, в данном методе одна из боковых
полос исключается. Однако, как уже отмечалось, схемы разделения полос такого
типа разделяют только коррелированную компоненту сигнала, но не шумы. Чтобы
разделить шумы, SIS-смесители на входе приемника могут быть смонтированы по
схеме разделения полос, описанной в приложении 7.1. В таких системах достигаемая
в цепи смесителя развязка полос может составлять ~15 дБ, что вполне достаточно
для того, чтобы удалить большую часть шума, вносимого нежелательной полосой,
но недостаточно для подавления сильных спектральных линий. Описанная выше
методика Кларка очень хорошо подходит для дополнительного подавления неже-
нежелательной боковой полосы, которая уже была частично ограничена в смесителе.
Эффекты частоты интерференции могут также использоваться для разделения
полос в РСДБ-наблюдениях. В системах РСДБ вращение интерференционных ле-
лепестков производится обычно во время воспроизведения сигнала с помощью гете-
гетеродина, более удаленного от входа приемного тракта, чем первый гетеродин. В этом
случае вращение лепестков приводит к снижению их частоты в одной из боковых
полос и повышению ее в другой полосе. Если вращение осуществляется так, чтобы
в одной из полос лепестки остановились, то лепестки, порождаемые другой полосой,
будут, как правило, иметь достаточно высокую частоту (учитывая огромную длину
баз) и будут сведены к пренебрежимо малому уровню при усреднении по времени на
выходе коррелятора. Данные воспроизводятся и проходят через коррелятор дваж-
дважды, по одному разу для каждой из боковых полос, с соответствующим вращением
лепестков.
172 Отклик приемной системы [Гл. 6
6.2. Отклик на шумы
Реальная чувствительность приемной системы определяется главным образом
ее шумами. В данном разделе мы рассматриваем отклик на шумы и определяемый
ими порог чувствительности; мы начнем с влияния шумов на выходной сигнал кор-
коррелятора и той неопределенности, которую они вносят в действительную и мнимую
части функции видности V. Это приведет нас к вычислению среднеквадратического
уровня шума в синтезированном изображении (карте) в его связи с максимумом от-
отклика на источник с заданной плотностью потока. Наконец, мы исследуем шумовые
эффекты с точки зрения среднеквадратических флуктуации амплитуды и фазы
функции видности V.
6.2.1. Обработка сигнала и шума в корреляторе. Рассмотрим наблюде-
наблюдения, в которых картографируемая область содержит только точечный источник,
расположенный в ее опорном фазовом центре. Пусть Vm(t) и Vn(t) — напряжения
на входе коррелятора, создаваемые сигналами от антенн тип. На выходе мы
получим
r=(Vm(t)Vn(t)), F.34)
где все три функции действительны, а математическое ожидание, обозначенное
угловыми скобками, аппроксимируется на практике усреднением за конечный от-
отрезок времени г). Чтобы получить относительные уровни мощности сигнальной
и шумовой компонент г, мы определим спектры их мощности, вычислив сначала
автокорреляционные функции. Автокорреляция произведения сигналов в F.34)
равна
Pr(t) = {Vm(t) Vn(t) Vm(t -T)Vn(t-r)). F.35)
Это выражение можно оценить, воспользовавшись следующим соотношением
для моментов четвертого порядка 2):
(z1z2z3z4) = (z1z2)(z3z4) + (z1z3)(z2z4) + (z1Z4)(z2z3), F.36)
где z\, z2, Z3 и z4 — взаимосвязанные гауссовы случайные величины с нулевым
средним. Таким образом,
Рт(т) = (Vm(t) Vn(t))(Vm(t - т) Vn(t - г)) +
+ (Vm(t) Vm(t - T))(Vn(t) Vn(t - т)) + (Vm(t) Vn(t - T))(Vm(t - t) Vn(t)) =
= Pmn(O) + Pm(r) Рп(т) + Ртп(т) pmn(-T), F.37)
где рш и рп — ненормализованные функции автокорреляции двух сигналов, соот-
соответственно Vm и Fn, а Ршп — функция их взаимной корреляции. Каждый член
V является суммой сигнальной компоненты s и шумовой п, и чтобы исследовать,
какой вклад эти компоненты вносят в выходной сигнал коррелятора, мы подставим
их в F.37). Произведения некоррелированных компонент, т. е. напряжений сигнала
х) Результат A.7) для системы (с одной антенной), измеряющей полную мощность, может
быть выведен из F.34), если положить в данном случае Vm = Vn и провести анализ как
сделано ниже.
2) Это соотношение является частным случаем более общего выражения для математиче-
математического ожидания произведения N переменных, которое равно нулю, если N нечетно, и сумме
попарных произведений, если N четно. Соотношение F.36) можно найти в (Lawson and
Uhlenbeck, 1950), (Middleton, 1960) и (Wozencraft and Jacobs, 1965).
6.2] Отклик на шумы 173
и шума или шумовых напряжений от разных антенн, имеют нулевое математиче-
математическое ожидание, и опуская их, мы получаем
рг(т) = (Sm(t) 8n(t))(sm(t - т) 8n(t - т)) +
+ (Sm(t) Sm{t - т) + nm(t) nm{t - T))(sn(t) Sn(t - t) + 7ln{t) Tln(t - r)) +
+ (Sm(t) Sn(t ~ T))(sm(t - Г) Sn(t)), F.38)
где три строки в правой части соответствуют трем членам последней строки F.37).
Чтобы определить влияние частотной характеристики приемной системы на раз-
различные составляющие р(т), нам нужно преобразовать их в спектры мощности.
Затем, воспользовавшись соотношением Винера-Хинчина, мы должны рассмотреть
Фурье-образы каждой из составляющих в правой части равенств F.37) и F.38).
Первый член в F.37), р^п@), является константой, и преобразование Фурье
от него дает дельта-функцию в нулевой точке частотной области, умноженную на
Pmnity- -И-3 F.38) мы видим, что в р^тт(О) входят только сигнальные компоненты,
которые удобно представить в виде антенных температур. Согласно интегральной
теореме фурье-преобразования, ртп@) равняется интегралу (по всей частотной оси)
фурье-образа ртп(т) и, таким образом, фурье-образ р^п@) равен
[ос
I
k2TAmTAn\ Hm{v)H*n(v)dv\ S(v), F.39)
где k — постоянная Больцмана, Тдт и Тдп — компоненты антенных температур,
обусловленные сигналом от источника [см. A.5)], а Нш(у) и Нп(у) — частотные
характеристики приемных трактов.
Результат фурье-преобразования второго слагаемого в F.37), рш(т)рп(т), равен
свертке фурье-образов рш и рп, т. е.
k2(TSm+TAm)(TSn+TAn) | Hm{v)H*m{p)Hn{v'-p)H*n{v'-p)dp, F.40)
где Tsm и Tsn — шумовые температуры систем. Заметим, что величина этого сла-
слагаемого пропорциональна произведению суммарных шумовых температур.
Фурье-преобразование третьего слагаемого в F.37), Ртп{т)ршп(—т), эквивалент-
эквивалентно свертке образов ршп{т) и ршп{—т), причем второй из них является комплексно
сопряженным первому, поскольку величина ршп действительна. Таким образом,
фурье-преобразование рШп{т)рШп{-т) дает
оо
k2TAmTAn | Hm{v)Hl{V)H*m{v' -i/) #„(!/' -v)dv. F.41)
В выражение F.39), как и в F.37), входят только антенные температуры, так как
шумы приемников разных антенн не вносят вклада в кросс-корреляцию.
Выражение F.39) определяет мощность сигнала на выходе коррелятора, а F.40)
и F.41) соответствуют шумам. Эффект усреднения по времени на выходе корре-
коррелятора можно моделировать как фильтр, пропускающий частоты от 0 до A^LF.
Выходная полоса пропускания A^LF на много порядков меньше входной полосы
коррелятора. Следовательно, спектральную плотность шума на выходе можно при-
принять равной ее значению на нулевой частоте, т. е. положить в F.40) и F.41) z/ =
= 0. Приняв во внимание эти соображения и то, что Нш(ту) и Нп(у) — эрмитовы,
174
Отклик приемной системы
[Гл.6
после усреднения на выходе коррелятора мы получаем, что отношение напряжении
сигнала и среднеквадратического шума имеет вид
I dv
\
F.42)
где 2Ai/LF — эквивалентная ширина полосы после усреднения, включая отрица-
отрицательные частоты. Обычно нет необходимости знать отношение сигнал/шум lZsn
простого коррелятора с точностью лучше пяти процентов. На самом деле, обычно
трудно вообще определить Ts со сколько-нибудь лучшей точностью, так как влия-
влияние на Ts излучения земли и поглощения в атмосфере меняется по мере сопровож-
сопровождения антенной источника. Поэтому вполне удовлетворительной будет представле-
представление Нш(у) и Нп(у) в виде идентичных прямоугольных функций с шириной Ai/IF.
Кроме того, при расчетах чувствительности чаще всего интересуются источниками,
находящимися на пороге обнаружения, когда Тд <С Ts. С учетом этих упрощений
F.42) принимает вид
/ m m I Л _
F.43)
На рис. 6.7 показаны спектры сигнала и шума в предположении, что полоса
пропускания имеет прямоугольную форму. Отметим, что входные спектры |i7m(i/)|2
Спектральная
плотность
кТА
Частота
Спектральная
плотность
8@)
г Н*к2ТА2АУш
- Av 0 Av.
IF
2v0
Частота
Рис. 6.7. Спектры входного (а) и выходного (б) сигналов коррелятора. Входные полосы
имеют прямоугольную форму с шириной AuIF. Нижний спектр (б) является полным
спектром перемножаемых сигналов, включая шумовые составляющие на частотах, вдвое
превышающих входную. Через усредняющую цепочку проходят только частоты, очень
близкие к нулю. Сюда входит и полезный сигнал, спектр которого имеет вид дельта-
функции (представлен на рисунке стрелкой). Предполагается, что Та ^ Ts
и \Hn{v)\2 содержат как положительные, так и отрицательные частоты и сим-
симметричны относительно нуля оси v. Выходной спектр шума можно представить
функцией, пропорциональной свертке либо кросс-корреляции \Нш{р)\2 и \Hn{v)\2.
6.2] Отклик на шумы 175
Ширина выходной полосы пропускания связана с временем усреднения данных
та, так как усреднение можно рассматривать как свертку по времени с прямоуголь-
прямоугольной функцией, имеющей единичную площадь и ширину то. Отклик усредняющей
цепи по мощности в зависимости от частоты будет квадратом фурье-образа этой
прямоугольной функции, т.е. sin2 (тг Tai;) / (тгта1уJ. Эквивалентная ширина полосы
пропускания, включая положительные и отрицательные частоты, равна
оо
= [
J
[ ^^l dv= 1. F.44)
— оо
Затем из F.43) мы получаем
F.45)
Заметим, что 2Az/IFro равняется числу независимых выборок сигнала за мремя
та, как упоминалось в разд. 1.2 (п. 1.2.3).
Если излучение источника не поляризовано, то каждая из антенн принимает
половину полной плотности потока ?, и плотность принятой мощности равна
кТА = i AS, F.46)
где А — эффективная площадь антенны. Для одинаковых антенн и шумовых тем-
температур приемных систем мы получаем из F.45) и F.46)
nsn =
Аналогичным образом это соотношение выводится в работах (Blum, 1959),
(Colvin, 1961) и (Tiuri, 1964). Обычно выражение F.47), при выводе которого мы
предположили, что Ts ^> Тд, и является искомым результатом. В другом пре-
предельном случае, с которым можно столкнуться при наблюдениях очень сильных
не разрешенных источников, для которых Тд ^> Tg, мы имеем 7Zsn = <\JAv1FTa .
Отношение сигнал/шум определяется флуктуациями уровня сигнала и не зависит
от площади антенн. Анализ уровней шума при наблюдении очень интенсивных
источников можно найти в (Anantharamaiah et al., 1989).
На рис. 6.7 можно видеть, откуда в F.47) появляется множитель ^ Av1Fra ,
позволяющий достигать в радиоастрономии очень высокой чувствительности. Шум
в корреляторе возникает в результате биений между компонентами двух входных
полос и, следовательно, простирается по частоте вплоть до AvlF. Треугольный
спектр шума на рис. 6.7 прямо пропорционален числу биений на единичный интер-
интервал частоты. Однако только очень малая доля этого шума, попадающая в выходную
полосу пропускания, остается после усреднения сигнала. Заметим, что ширина
полосы сигнала Az/IF, с которой мы имеем здесь дело, — это полоса частот на входе
коррелятора. В двухполосной системе она составляет только половину от полной
полосы частот, принимаемых антенной.
Здесь следует ввести еще один фактор, влияющий на отношение сигнал /шум.
Если перед вводом в корреляторы сигналы квантуются и оцифровываются, воз-
возникает дополнительный множитель rjQ, характеризующий качество квантования,
и F.47) принимает вид
ГК*"а F.48)
176 Отклик приемной системы [Гл. 6
или, в выражении через антенную температуру,
F.49)
Значение tjq может меняться от 0,637 до 1, что рассматривается в гл. 8; см.
табл. 8.1. В РСДБ на отношение сигнал/шум влияют еще и другие потери, поэтому
tjq заменяется общим коэффициентом потерь 7/, рассматриваемым в разд. 9.7; см.
(9.156).
6.2.2. Шумы при измерении комплексной функции видности. Чтобы
понять, что же собой представляет 7?sn, следует обратить внимание на то, что при
выводе F.48) и F.49) не предполагалось никакой задержки между компонентами
сигнала в корреляторе, а фазовые характеристики сигнальных каналов полагались
идентичными. Это означает, что источник находится в центральном лепестке интер-
интерференционной картины, и в этом частном случае отклик соответствует максимуму
лепестка, который представляет собой абсолютное значение функции видности.
Чтобы представить среднеквадратический уровень шума на выходе коррелятора
как эквивалентную плотность потока а от точечного источника, для которого на
вершине лепестка получается тот же отклик, мы положим в F.48) 7ZSn = 1 и заме-
заменим S на а:
F.50)
где а выражено в единицах Вт-м~2-Гц -1. Рассмотрим случай инструмента с ком-
комплексным коррелятором, на выходе которого флуктуации замедлены до нулевой
частоты, как описывалось выше. Шумовые флуктуации действительного и мнимого
выходов, как мы сейчас покажем, не коррелируют между собой. Предположим,
антенны направлены в область неба, свободную от источников, так что на корреля-
корреляторы (рис. 6.3) поступают только шумовые сигналы nm, nn и п^, причем последний
является гильбертовым преобразованием от nm, полученным в результате квад-
квадратурного фазового сдвига. Математическим ожиданием произведения действи-
действительного и мнимого выходов будет (nmnnn^nn); воспользовавшись соотношением
F.36), легко показать, что оно равно нулю, если учесть, что все математические
ожидания (птпп), (nmn^) и (n^nn) должны быть равны нулю. Следовательно,
шумы на действительном и мнимом выходах не коррелируют 1).
На рис. 6.8 сигнальная и шумовая компоненты при измерении комплексной
функции видности показаны в виде векторов на комплексной плоскости. Здесь
V — функция видности, какой она была бы в отсутствие шумов, a Z является
представлением суммы функции видности и шума V + е. Мы рассматриваем Z и ?
как векторы, компоненты которых представляют действительную и мнимую части
соответствующих величин. Шум в обеих компонентах Z имеет среднеквадратиче-
ское значение а. На практике для измерения функции видности мы должны объ-
объединить действительный и мнимый отклики коррелятора, так что окончательная
погрешность измерения
х) Шум на выходах коррелятора представлен ансамблем частотных компонент \vm — vn
где Vm и vn являются частотными компонентами шумов пт и пп на входах коррелятора.
Мнимые выходные компоненты сдвинуты по частоте на ±тг/2 относительно соответствую-
соответствующих действительных компонент. Отметим, что для любой пары входных компонент знак
сдвига на мнимом выходе принимает противоположные значения в зависимости от вы-
выполнения условий vm > vn или vm < vn. Как следствие, шумовые сигналы на выходах
коррелятора не связаны преобразованием Гильберта и не могут быть выведены друг из
друга.
6.2]
Отклик на шумы
177
srms = V/(Z-Z)-(ZJ =
так как (е - е) = (si) + {г2у) = 2сг2, где
= V2a,
F.51)
= D) + (Ф =
компоненты е. Если измерения производятся
с помощью коррелятора с одним перемножите-
перемножителем, можно периодически применять к одному
из входов квадратурный сдвиг фазы, получая
таким образом действительный и мнимый от-
отклики, на каждый из которых будет приходить-
приходиться половина времени наблюдения. Тогда коли-
количество данных будет вдвое меньше того, кото-
которое можно было бы получить с помощью ком-
комплексного коррелятора, и, следовательно, шум
в измеренной функции видности будет больше
Действительная
часть (х)
Рис. 6.8. Комплексная величина Z,
являющаяся суммой абсолютного
значения истинной функции видно-
видности |V| и шума е. Шум имеет дей-
действительную и мнимую компонен-
компоненты со среднеквадратическим зна-
значением <т; ф является отклонени-
в у/2 раз. Тот же результат можно получить, ем фазы, обусловленным наличием
записав выходной сигнал с ненулевой частотой шума
интерференции и вписав в него затем синусо-
синусоидальную кривую. Если положение неразрешенного источника известно, можно
остановить лепестки на максимуме выходного сигнала и, таким образом, измерить
амплитуду функции видности с той же точностью, что и при использовании ком-
комплексного коррелятора. Однако при этом не будет измерена комплексная функция
видности, и потому этот метод редко бывает полезен.
6.2.3. Отношение сигнал/шум в синтезированном изображении.
Определив погрешность, вносимую шумом в функцию видности, перейдем
к рассмотрению отношения сигнал/шум в изображении, или карте. Рассмотрим
решетку с пр антенными парами и предположим, что данные для функции
видности усредняются за время то и что весь сеанс наблюдения охватывает
временной интервал tq. Тогда общее число независимых точек данных на (u,v)-
плоскости
F.52)
то
= пр — .
Та
При картографировании неразрешенного источника, расположенного в центре
поля зрения, где данные для функции видности складываются в фазе, мы вправе
ожидать, что отношение сигнал/шум в изображении будет больше полученного из
F.48) и F.49) в -\/прто/та раз. Это простое соображение оказывается справедливым
в случае, когда данные комбинируются с одинаковыми весами. Теперь мы получим
более общий результат для случая произвольно взвешенных данных.
Совокупность измеренных данных может быть представлена в виде
F.53)
где 25 обозначает двумерную дельта-функцию, a Si — комплексный вклад шума
в г-е измерение. Каждое значение данных появляется в двух точках гш-плоскости,
центрально-симметричных относительно ее начала координат. Перед выполнением
фурье-преобразования данных в F.53), каждой точке присваивается вес W{ (выбор
весовых множителей обсуждается в разд. 10.2, в параграфе «Взвешивание данных
функции видности»). Для упрощения вычислений предположим, что источник то-
точечный и расположен в фазовом центре карты; таким образом, он имеет постоянную
178 Отклик приемной системы [Гл. 6
действительную функцию видности V, равную его плотности потока S. Тогда яр-
яркость в центре карты
F.54)
где em — действительная часть в{. Отметим, что в центре карты мнимая часть
Е{ при суммировании комплексно-сопряженных компонент исчезает. Для соседних
точек карты один и тот лее среднеквадратический уровень шума распределяется
между действительной и мнимой компонентами е. Математическое ожидание для
/о равно
(Jo) =V = S, F.55)
поскольку (е-тн) = 0. Квадратичное отклонение оценки яркости, а^, равно
V 2/ 2 \
^ = (/о2) - W2 = ^%^ • F.56)
Соотношение F.56) выводится непосредственно из F.54), если учесть тот факт,
что шумовые вклады от различных точек гш-плоскости не коррелируют друг с дру-
другом, т. е. {s<Ki?nj) = 0 при г ф j. Средний весовой коэффициент wmean и среднеквад-
среднеквадратический вес wrms мы определим как
F.58)
lljd
Вклад шума [см. F.51)] одинаков для каждой точки гш-плоскости и равен
(е^) = а2, где а дается выражением F.50). Таким образом, с учетом F.55)—F.58)
можно получить отношение сигнал/шум в виде
(/о) _ S^fUd Wmean /- rg\
<Jm (J Wrms
Для решетки антенн с комплексными корреляторами из F.50) следует
(/о) = ASriQy/ndAi/IFTa Wmean
&т \[2 kTS ^rms
Если используются все попарные комбинации антенн, то пр = \па(па — 1), где
па — число антенн. Так как п^ = пртъ/та, мы получаем
2kTS
^ ' '
Чтобы выразить среднеквадратический уровень шума через плотность потока,
положим в F.61) 1о/ат = 1. Тогда S будет соответствовать плотности потока от
6.2] Отклик на шумы 179
точечного источника, для которого максимум отклика равен среднеквадратическо-
му уровню шума, и мы можем написать
q Лгь-L S ^rms (n /?г>\
^ = • (O.OZJ
^rms 1
A7)Q у/Па (Па ~
Если все весовые коэффициенты Wi равны, то и)теап/и)гтз = 1, что соответствует
естественному взвешиванию. В этом случае отношение сигнал/шум, определяемое
F.61), будет таким лее, как при использовании приемника полной мощности с ан-
антенной, апертура которой равна у/па(па — 1) А и с ростом числа антенн стремится
к паА. Анализ чувствительности систем с одной антенной молено найти, например,
в (Tiuri, 1964), (Tiuri and Raisanen, 1986).
Выражение F.62) определяет чувствительность точечного источника систе-
системы. В случае источника, видимый размер которого больше ширины синтезиро-
синтезированной диаграммы направленности, важно знать яркостную чувствительность.
Плотность потока (в Вт-м~2-Гц~1), принимаемого от протяженного источника со
средней яркостью / (Вт-м~2-Гц~1-рад~2) в пределах диаграммы направленности,
равна 7Т7, где Q — эффективный телесный угол синтезированной диаграммы на-
направленности. Таким образом, уровень яркости, эквивалентный среднеквадратиче-
скому шуму, равен SrYns/Q. Отметим, что яркостная чувствительность падает при
сужении диаграммы направленности, поэтому для обнаружения слабых протяжен-
протяженных источников лучше всего подходят компактные антенные решетки. Однако для
измерения яркости однородного фона требуется измерение полной мощности, при-
принимаемой антенной, поскольку корреляционный интерферометр не дает отклика на
такой фон.
Отношение wmean/u>rms всегда меньше единицы за исключением случая, когда
взвешивание однородно. Хотя отношение сигнал/шум зависит от метода взвеши-
взвешивания, на практике эта зависимость не особенно критична. Использование есте-
естественного взвешивания дает лучшую чувствительность для обнаружения точечного
источника в протяженной области, но может также существенно расширить син-
синтезированную диаграмму направленности. Выигрыш в чувствительности обычно
мал. Например, если плотность точек данных обратно пропорциональна расстоя-
расстоянию от начала координат гш-плоскости, как в случае решетки восток—запад с рав-
равномерным увеличением расстояния между антеннами, то при весовых множите-
множителях, обеспечивающих равномерное эффективное распределение данных, получается
^mean/^rms = 2\/2/3 = 0,94. Естественное взвешивание в данном случае приводит
к нежелательному профилю диаграммы направленности, в которой отклик на боль-
больших угловых расстояниях от оси диаграммы остается положительным и затухает
медленно.
В гл. 10 дается обзор различных методов фурье-преобразования данных функ-
функции видности, и к ним можно применить результаты, выражаемые соотношениями
F.61) и F.62), если использовать соответствующие значения wmean и wrms. Обыч-
Обычной операцией является свертка данных на гш-плоскости для получения значений
функции видности в узлах прямоугольной сетки. В общем случае данные в соседних
узлах сетки не будут независимыми, что приведет к спаду огибающей сигнала
и шума при удалении от центра изображения. Появление ложных изображений
также может привести к неоднородности отношения сигнал/шум в полученном
изображении. (Эти эффекты объясняются при обсуждении рис. 10.5.) В подобных
случаях полученные здесь результаты применимы вблизи центра изображения, где
влияние спада огибающей и неоднозначности изображений несущественно. Сред-
неквадратический уровень шума в изображении может быть получен применением
равенства Парсеваля к шумам в функции видности.
180 Отклик приемной системы [Гл. 6
На практике ряд факторов, влияющих на отношение сигнал/шум, трудно учесть
с достаточной точностью. Например, Т$ несколько изменяется в зависимости от
угла места антенны. Существуют также эффекты, которые могут уменьшать от-
отклик на источник, не снижая при этом шумов, однако они имеют значение только
для источников, достаточно удаленных от начала координат картинной плоскости
(/,777,). Сюда входит размывание изображения из-за конечной ширины полосы прие-
приема и из-за усреднения функции видности, обсуждаемое далее в этой главе, и эффект
некомпланарных баз, описанный в разделах 3.1 и 11.8.
Отметим также, что во многих инструментах принимаются и обрабатываются
сразу два противоположно поляризованных сигнала (с ортогональными линейны-
линейными или противоположными круговыми поляризациями); при этом используются
отдельные усилители ПЧ и корреляторы. В этом случае для неполяризованных
источников общее отношение сигнал/шум будет в у2 раз больше значений, полу-
полученных выше, в которых учитывается только один сигнал от каждой антенны.
6.2.4. Амплитудные и фазовые шумы функции видности. При постро-
построении изображений мы обычно имеем дело с данными в форме действительной
и мнимой частей функции видности V, но иногда приходится работать с ее ампли-
амплитудой и фазой. Каким будет распределение вероятностей для амплитуды и фазы
в предположении, что к действительной и мнимой частям V добавляется гауссов
шум со стандартным отклонением а? Ответ хорошо известен, поэтому мы не будем
заниматься здесь его выводом. Сумма функции видности и шума представляется
в виде Z = Ze-7^, причем действительную ось мы выберем таким образом, чтобы
фаза ф измерялась относительно фазы V, как на рис. 6.8. Тогда при Тд <С Ts
распределения вероятности для результирующих амплитуды и фазы будут иметь
вид
*(^)(Ш), Z>0, F.63a)
|V|cos<
2 ^ ex4^^7 i1 + erf { Vf7
F.636)
где /q — модифицированная функция Бесселя нулевого порядка, erf — функция
ошибок, а а определяется соотношением F.50). Распределение амплитуд анало-
аналогично случаю зашумленной синусоиды; вывод этого утверждения имеется в (Rice,
1944, 1954), (Vinokur, 1965) и (Papoulis, 1965), причем в последних двух работах
выводится и результат для фазы. Функцию p(Z) иногда называют распределением
Раиса, и при V = 0 оно сводится к распределению Рэлея. Графики p(Z) и р{ф) при-
приведены на рис. 6.9. Сравнение кривых для случаев |V|/ct = 0h|V|/ct = 1 показывает,
что присутствие слабого сигнала легче обнаружить, исследуя не амплитуду, а фазу
функции видности.
Приближения p(Z) кр(ф) для случаев \V\/a <С 1 и \V\/a ^> 1 приведены в п. 9.3.3.
Там же даются выражения для моментов Z и ф и их среднеквадратических отклоне-
отклонений. Чрезвычайно полезной величиной, особенно для астрометрии и диагностики,
является среднеквадратическое отклонение фазы сгф. В случае, когда |V|/a ^> 1,
для <7ф справедливо выражение аф ~ 0"/|V|; см. выражение (9.60). Этот результат
интуитивно ясен из рис. 6.8. Подставляя F.50) в выражение для аф, считая |V| рав-
равным плотности потока от источника S (что допустимо, если источник не разрешен)
и используя F.46), чтобы связать плотность потока с антенной температурой, мы
получаем
<тФ = TS ¦ F.64)
6.2]
Отклик на шумы
181
Это равенство действительно при условиях T(sr/y/2Az/IFra <C Тд <С Х^, которые
соответствуют наиболее часто встречающимся случаям. Оно полезно для опреде-
определения того, обусловлен ли шум в фазовых измерениях на интерферометре исклю-
исключительно шумами приемников. Дополнительный фазовый шум может вноситься
атмосферой, нестабильностями системы и, в случае РСДБ, стандартами частоты.
6.2.5. Относительная чувствительность различных интерферометри-
ческих систем. Ниже мы перейдем к сравнению чувствительности различных ин-
терферометрических систем, используя в качестве меры чувствительности модуль
сигнала, поделенный на среднеквадратический шум, т. е. V/e, если использовать
величины на выходе коррелятора из рис. 6.8. Такие параметры, как время усред-
усреднения или полоса пропускания ПЧ, одинаковы для всех рассматриваемых случаев.
Для сравнения двухполосных и однополосных систем удобно ввести коэффициент
а =
двухполосная шумовая температура двухполосной системы
шумовая температура однополосной системы
F.65)
Напомним, что температура
шумов приемника может быть
определена как шумовая темпе-
температура теплового источника на
входе гипотетического, не имею-
имеющего шумов (но в остальном
идентичного реальному) прием-
приемника, который создает на вы-
выходе приемника тот же са-
самый уровень шума. [Для эк-
эквивалентной шумовой темпера-
температуры можно использовать вы-
выражение A-4), если приближе-
приближение Рэлея-Джинса непримени-
неприменимо.] Для двухполосного прием-
приемника температура шумов систе-
системы определяется как двухполос-
двухполосная или однополосная в зависи-
зависимости от того, излучает ли теп-
тепловой источник шума в обеих
боковых полосах или же толь-
только в одной. При таком определе-
определении однополосная шумовая тем-
температура равна удвоенной двух-
двухполосной.
Для однополосной системы
среднеквадратический шум на
выходе коррелятора (в случае
комплексного коррелятора —
либо действительном, либо мни-
мнимом) после усреднения за вре-
время га равен а, как определя-
определяется в F.50). Соответствующая
мощность шума равна а2. Для
двухполосной системы средне-
среднеквадратический шум на выходе
коррелятора равен 2аа. Во всех
-ж/2
0 л/2
ф,рад
Рис. 6.9. Распределения вероятностей для амплиту-
амплитуды (а) и фазы (б) измеренной комплексной функции
видности в зависимости от отношения сигнал/шум.
|V| — модуль сигнальной компоненты. Рисунок взят
из (Могап, 1976)
182 Отклик приемной системы [Гл. 6
случаях сигнал приходит от неразрешенного источника. Для однополосной системы
мы принимаем напряжение сигнала на выходе коррелятора равным V, как на
рис. 6.8. Для двухполосной системы со входным сигналом только в одной из боковых
полос сигнал на выходе коррелятора равен V, а при наличии сигнала в обеих
входных полосах выход коррелятора равен 2V.
Значения относительной чувствительности обсуждаются ниже и сведены
в табл. 6.1. Аналогичные результаты приводятся в (Rogers, 1976).
1. Однополосная система с комплексным коррелятором. Выходной сигнал ра-
равен V, а среднеквадратический шум от каждого из выходов коррелятора равен а.
Как можно видеть из рис. 6.8 и соотношения F.51), отношение амплитуды сигнала
к среднеквадратическому шуму равно V/(v2а). Мы примем это в качестве эталона,
относительно которого будет определяться чувствительность других систем.
2. Однополосная система и простой коррелятор со вписыванием лепестков.
Чтобы измерить как действительную, так и мнимую части комплексной функции
видности, остановка лепестков не производится и они появляются на выходе в виде
синусоиды с амплитудой V и частотой интерференции Vf. Сигналу сопутствует
шум со среднеквадратической амплитудой а. Амплитуда и фаза измеряются по-
посредством «вписывания лепестков», т. е. в выходной сигнал коррелятора методом
наименьших квадратов вписывается синусоида. Эта процедура включает в себя
умножение выходного сигнала коррелятора cos Bтп//?) и sin Bтп//?) с последующим
интегрированием за период времени то. Результаты представляют собой соответ-
соответственно действительную и мнимую части кросс-корреляции. Мы рассчитываем
влияние вписывания лепестков на сигнал и на шум по отдельности и предпо-
предполагаем, без потери общности, что при вписывании лепестки совпадают по фазе
с косинусной компонентой; в этом случае синусная компонента сигналя равна нулю.
Выход коррелятора имеет полосу пропускания Дг/С, достаточную для прохождения
сигнала с частотой интерференции, и опрашивается через интервалы времени rs =
= l/Bz/c) с последующей оцифровкой. За период времени то производится N =
= 2Аисга опросов. Таким образом, для косинусной компоненты сигнала амплитуда
равна
± Y, Vcos\2i:wsts) = | + ^ ]Г cos DwiufTe). F.66)
г=1 г=1
Второе слагаемое в правой части равенства соответствует граничным эффектам
и приблизительно равно нулю, если в интервал интегрирования то укладывается
целое число полу периодов частоты интерференции. Оно также становится срав-
сравнительно малым с увеличением ^/то, и мы предполагаем здесь, что в интервал
та попадает достаточное число интерференционных периодов (скажем, десять или
больше), чтобы граничными эффектами можно было пренебречь. Чтобы опреде-
определить влияние вписывания лепестков на шум, мы представляем опрошенный шум
функцией n(irs), умножаем на функцию косинуса и определяем стандартное откло-
отклонение (среднеквадратическое значение). При усреднении за время то получаем
1
TV
N
cos {2nivfTs)
г=1
2 л N N
cos [2-kivfTs) n{krs) cos {2nkvfTs).
N f=LK_L
F.67)
Нам нужно определить для этого выражения математическое ожидание, кото-
которое мы обозначаем угловыми скобками. В математическое ожидание вносят вклад
только члены, для которых г = к. Таким образом, среднеквадратический шум при-
6.2] Отклик на шумы 183
нимает вид
( ^ Е n4irs) [1 + cos (ШиГв)] \ = у . F.68)
Данный результат показывает, что в косинусную компоненту вписанных ле-
лепестков входит половина всей шумовой мощности, а , присутствующей на выходе
коррелятора. Другая половина попадает в синусную компоненту. Общий средне-
квадратический шум от двух компонент равен а, а отношение сигнала к шуму
после вписывания лепестков равно V/Ba). Относительная чувствительность равна
3. Однополосная система с простым коррелятором и переключением фазы
гетеродина на тг/2. В этом случае лепестки остановлены, и для определения ком-
комплексной функции видности в один из гетеродинов периодически вводится фазовый
сдвиг на тг/2 [т. е. производится замена 0п —>> 0п + тг/2 в F.11) или F.15)], так что
коррелятор фактически работает в режиме разделения времени между действи-
действительной и мнимой частями кросс-корреляционной функции, которые усредняются
по отдельности. Следовательно, может быть определена фаза функции видности.
Сигнал в двух фазовых состояниях равен V cos (фу) и V sin (фу), а среднеквадрати-
ческий шум, связанный с каждой из этих компонент, равен \[2 а (коэффициент \/2
появляется потому, что шум в каждом из выходных сигналов усредняется только
за время т/2). Таким образом, модуль сигнала равен V, а среднеквадратический
шум от двух компонент 2а. Отношение сигнал/шум равно V/Bcr), а относительная
чувствительность 1/у2-
4. Двухполосная система с простым коррелятором и вписыванием лепестков.
Мы рассмотрим случай сигнала в обеих боковых полосах от источника с непрерыв-
непрерывным спектром в предположении, что аппаратная задержка подстраивается таким
образом, что весь сигнал проходит на (действительный) выход простого коррелято-
коррелятора, как косинусоидальная волна амплитуды V с частотой интерференции. В плане
соотношения F.18) сомножитель cos Bтп/оДт0 + фо) равен единице. Тогда для двух-
двухполосной системы амплитуда сигнала равна 2V, а среднеквадратический шум 2аа.
Процедура вписывания лепестков проводится как в случае 2, но теперь амплитуда
сигнала вдвое больше и равна V. Среднеквадратический шум увеличивается в 2а
раз. Таким образом, отношение сигнал/шум равно V/Baa) и относительная чув-
чувствительность 1/(л/2 а).
5. Двухполосная система с простым коррелятором и переключением фазы
гетеродина на тг/2. Здесь лепестки остановлены, и для определения фазы функции
видности необходимо производить переключение фазы на тг/2, как в описанном
выше случае 3. (В двухполосной системе переключение фазы должно выполняться
на первом гетеродине.) Амплитуда сигнала равна 2V, так как система имеет двой-
двойную полосу пропускания, а среднеквадратический уровень шума увеличивается до
2у2 аа, поскольку время усреднения для каждой из компонент сокращается до
та/2 из-за разделения времени коррелятора между двумя фазовыми состояниями.
Указанный уровень шума относится и к косинусной, и к синусной компонентам
сигнала, поэтому отношение сигнал/шум равно V/Baa). Относительная чувстви-
чувствительность равна 1/(\/2 а).
6. Одна боковая полоса двухполосной системы с переключением фазы гетероди-
гетеродина на тг/2 и разделением боковых полос после корреляции. Используется комплекс-
комплексный коррелятор и производится процедура, соответствующая формулам F.30)-
F.33). Мы рассмотрим верхнюю боковую полосу и пренебрежем членами, отно-
относящимися к сигналу в нижней полосе. Компоненты 7*1,7*2,7*3,7*4 имеют амплитуду,
равную V, умноженной на косинус либо синус Фп. Таким образом, из F.30) и F.31),
184 Отклик приемной системы [Гл. 6
пренебрежем членами для нижней полосы, мы получаем для правой части F.32)
выражение 0,5BV cos\I/n + j2V sin\I/n), модуль которого равен V. Среднеквадрати-
ческий шум, связанный с каждым из членов ri, Г2, ^з и Г4 равен 2у2 аа, поскольку
система имеет две полосы и, кроме того, из-за переключения гетеродина эффек-
эффективное время усреднения составляет та/2. Следовательно, общий среднеквадрати-
ческий шум, связанный с правой частью F.32), равен 2\/2 аа, как в случае 5. От-
Отношение сигнал/шум равно V/B\/2 aa) и относительная чувствительность 1/Bа).
Данный результат применим к сигналу, присутствующему только в одной из полос,
такому, как спектральная линия. В случае источника с непрерывным спектром
кросс-корреляция может быть измерена для каждой из боковых полос, и если затем
результаты усредняются, то относительная чувствительность становится равной
1/(\/2 а). Члены г 2 и г 4 при усреднении правых частей F.32) и F.33) сокращаются,
и результат оказывается таким же, как в случае простого коррелятора с переклю-
переключением фазы гетеродина, описанном выше в п. 5.
7. РСДБ-наблюдения с двухполосной системой и комплексным коррелятором.
В РСДБ-наблюдениях иногда используется двухполосная система, а вращение
лепестков осуществляется уже по воспроизведении записанного сигнала, о чем
упоминалось в разд. 6.1. В одной из боковых полос лепестки останавливаются,
однако в другой они теряются при усреднении на выходе коррелятора, так как
частоты интерференции высоки. Таким образом, при однократном воспроизведе-
воспроизведении мы имеем сигнал однополосной системы и шум двухполосной на каждом из
двух (действительном и мнимом) выходов коррелятора, т. е. отношение сигнал/шум
V/B\/2 aa) и относительную чувствительность 1/{2а) для каждой из боковых полос
по отдельности.
8. Измерение кросс-корреляции как функции временной задержки. Цифровые
спектральные корреляторы, измеряющие кросс-корреляцию как функцию задерж-
задержки по времени, описываются в разд. 8.7. В корреляторе с задержками кросс-
корреляция измеряется как функция временного смещения, которое реализует-
реализуется с помощью аппаратных линий задержки. Преобразование Фурье от кросс-
корреляции как функции относительной задержки между сигналами дает кросс-
корреляцию как функцию частоты, которая требуется при спектральных изме-
измерениях. Как упоминалось в разд. 6.1 (параграф «Простые и комплексные кор-
корреляторы»), для таких измерений достаточно иметь простой коррелятор. Диа-
Диапазон временного смещения двух сигналов охватывает как положительные, так
и отрицательные значения, а измеренная кросс-корреляция содержит и четную,
и нечетную компоненты. Следовательно, фурье-преобразование даст в результате
как действительную, так и мнимую компоненты кросс-корреляции как функции ча-
частоты. Полная чувствительность сохраняется до тех пор, пока диапазон временного
смещения сравним с обратной шириной полосы сигнала или больше нее; см. Потери
подавления боковой полосы при сдвиге частоты интерференции в табл. 9.6 из
гл. 9. В табл. 6.1 мы не включили потери квантования, обсуждаемые в разд. 8.3.
Демонстрация чувствительности при использовании простого коррелятора, когда
измеряемая корреляция является функцией задержки, проводится в (Mickelson and
Swenson, 1991).
Из всех случаев, включенных в табл. 6.1, чаще всего используется система
с одной боковой полосой и комплексным коррелятором, благодаря ее чувствитель-
чувствительности и отсутствию сложностей, с которыми сопряжена двухполосная обработка
сигнала. Пункты 2 и 3 включены в таблицу главным образом ради полноты охвата
обсуждаемого вопроса. На высоких частотах, для которых не существует мало-
шумящих усилителей (как правило, выше ~100 GHz), наиболее чувствительным
типом входного устройства приемника является SIS-смеситель. Последний имеет
6.2]
Таблица 6.1.
Тип системы
Относительная
Отклик на шумы
чувствительность
для
185
различных типов систем
Чувствительность
1. Одна полоса с комплексным коррелятором 1
1
2. Одна полоса с простым коррелятором —,=
3. Одна полоса, простой коррелятор, остановка лепестков, 1
переключение фазы на тг/2 у/2
4. Две полосы, простой коррелятор*, вписывание лепестков, -*-
непрерывный спектр сигнала у/2 а
5. Две полосы, простой коррелятор, остановка лепестков, -*-
переключение фазы на тг/2, сигнал в континууме у/2 а
ба. Две полосы, остановка лепестков, разделение полос J_
[(б.ЗО)-(б.ЗЗ)], сигнал в одной полосе 2а
бб. То же, что и 6а, но для непрерывного спектра и объеди- -*-
нения функций видности от обеих полос у/2 а
7а. РСДБ, две полосы, комплексный коррелятор, одна поло- J_
са удалена усреднением быстрых лепестков 2а
76. То же, что и 7а, для непрерывного спектра, коррели- 1
руемого по отдельности в каждой из полос с объединением пг
результатов
8. Одна полоса, цифровой спектральный коррелятор с про-
простыми элементами и измерением корреляции как функции 1
смещения по времени (см. разд. 8.7)
*Для двух полос и комплексного коррелятора см. текст, относящийся к рис. 6.5.
принципиально двухполосный отклик, и хотя нежелательная полоса может быть
удалена фильтрацией или с помощью соответствующей схематики разделения полос
(приложение 7.1), предпочтение может все же быть отдано двухполосной систе-
системе, позволяющей избежать потерь чувствительности или уменьшения гибкости
настройки, которое связано со сложностью удаления одной боковой полосы. Из
двухполосных схем важнейшими являются те, что представлены пунктами таблицы
6а и 66. Случай, когда нежелательная боковая полоса подавляется лишь частично,
обсуждается в приложении 6.1.
6.2.6. Параметр температуры системы а. Как уже отмечалось, двухпо-
двухполосные системы используются гласным образом на миллиметровых и субмилли-
субмиллиметровых волнах, где входным каскадом обычно является SIS-смеситель. Такую
систему можно переделать в однополосную, если применить фильтр, отсекающий
нежелательную полосу, и поставить на соответствующий вход холодную нагрузку.
Если потери в атмосфере велики, а шумовая температура приемника низка, боль-
большая часть шумов системы будет приходить от антенны, а применение холодной
нагрузки в качестве заглушки для одной из полос снизит уровень шума в приемнике
примерно вдвое. Шумовая температура такой однополосной системы примерно
равна двухполосной температуре двухполосной системы, а значение параметра а
[определенного в F.65)] приближается к 1. С другой стороны, если потери в ат-
атмосфере и на антенне невелики и шум системы обусловлен в основном смесителем
и каскадами ПЧ, то холодная нагрузка вместо холодного неба на одном из входов
мало влияет на уровень шума приемника. Шумовая температура системы будет
в этом случае близка к однополосной температуре двухполосной системы, которая
186 Отклик приемной системы [Гл. 6
вдвое больше двухполосной температуры. Значение а в этом случае приближается
к 1/2. Подытожим сказанное. Если атмосферные шумы преобладают над шумами
приемника, то а приближается к 1, но если превалируют шумы приемника, то а
будет близким к 1/2. Однако следует заметить, что значение а не ограничивается
диапазоном 1/2 < а < 1. Например, если шум от антенны низок, а заглушка зер-
зеркальной полосы в однополосной системе не охлаждается и вносит высокий уровень
шума, то а может быть < 1/2. Если вход приемника настроен на частоту, близкую
к линии атмосферного поглощения, и зеркальная полоса попадает как раз в диапа-
диапазон частот повышенного атмосферного шума, то а может быть > 1.
6.3. Эффекты полосы пропускания
Как было показано в предыдущем разделе, чувствительность приемной системы
к широкополосным космическим сигналам увеличивается с расширением ее полосы
пропускания. Теперь мы исследуем влияние полосы пропускания на угловой ин-
интервал, в пределах которого обнаруживаются лепестки, и на амплитуду лепестков.
Эти эффекты обусловлены вариацией частоты лепестков (в периодах на радиан
в картинной плоскости) в зависимости от принимаемой частоты сигнала. Если
монохроматический отклик интегрируется по полосе пропускания, то в направле-
направлениях, близких к тем, для которых задержки распространения сигнала от источника
до входов коррелятора равны, лепестки усиливаются, в то время как для других
направлений фаза лепестков изменяется по полосе пропускания. Этот эффект, изме-
измеренный в плоскости, на которой расположена база интерферометра, приводит к спа-
спаду амплитуды интерференционных лепестков с увеличением угла подобно тому, как
это происходит из-за влияния диаграммы направленности антенны (Swenson and
Mathur, 1969); это иногда называют эффектом диаграммы задержки. Его можно
использовать в целях ограничения оклика интерферометра определенной областью
неба, уменьшая тем самым возможность смешивания источников, которое может
происходить, когда одновременно регистрируются интерференционные лепестки от
двух или более источников. Примеры такого использования можно найти в некото-
некоторых ранних интерферометрах, работавших на частотах ниже 100 МГц (Goldstein,
1959), (Douglas et al., 1973). Эта методика менее полезна для инструментов, в кото-
которых антенны отслеживают часовой угол, поскольку ширина диаграммы задержки
увеличивается с уменьшением проекции базы.
6.3.1. Построение изображений в режиме континуума. Влияние полосы
пропускания на амплитуду интерференционных лепестков обсуждался в разд. 2.2.
Выражение B.3) описывает лепестки, наблюдаемые от точечного источника на базе
восток-запад длины D при прямоугольной полосе пропускания сигнала шириной
Az/. Амплитуда лепестков пропорциональна
, sin (irDlAv/c)
Рассмотрим решетку, в которой D является длиной базы для наиболее разнесен-
разнесенных антенн. Ширина синтезированной диаграммы въ равняется примерно Xo/D =
= c/vqD, где щ — наблюдаемая частота, а Ао — соответствующая ей длина волны.
(Заметим, что в этом разделе uq обозначает центральную частоту полосы входного
сигнала, а не ПЧ.) Таким образом, F.69) принимает вид
F.70)
6.3] Эффекты полосы пропускания 187
Параметр Az//i/z/q^6 равен относительной ширине полосы, умноженной на уг-
угловое расстояние до источника от начала координат плоскости 1т, выраженное
в ширинах диаграммы. Если этот параметр равен единице, В!ь = 0 и измеренная
функция видности обращается в нуль. Чтобы значение R'b было близким к единице,
требуется, чтобы Az///z/0#b <С 1. Таким образом, чтобы избежать недооценки функ-
функции видности на длинных базах, нужно учитывать существование предела угловых
размеров изображения, обратно пропорционального относительной полосе.
Теперь мы исследуем данный эффект более подробно, рассмотрев искажения,
вносимые им в синтезированное изображение. Прежде всего вспомним, что отклик
антенной решетки может быть записан в виде
V(u,v)W(u,v) ^ 1A,т)**Ъ0A,т), F-71)
где значок ^ обозначает преобразование Фурье. Функция видности лепестков
умножается на W(u,v) — пространственную функцию чувствительности решетки
для конкретного наблюдения. Фурье-преобразование левой части F.71) соответ-
соответствует распределению яркости /(/,га), свернутого с функцией синтезированной
диаграммы Ьо(^ т)- Для простоты мы пренебрегаем влиянием антенной диаграммы
и другими второстепенными эффектами, связанными с особенностями дискретного
преобразования Фурье. Синтезированная диаграмма направленности определена
здесь как фурье-образ W(u,v).
При работе в режиме континуума данные для функции видности, полученные
в полосе сигнала Az/, интерпретируются так, как если бы они были измерены
монохроматической приемной системой, настроенной на центральную частоту щ.
Таким образом, для всех частот в пределах полосы сигнала значения и ж v соответ-
соответствуют частоте щ. На другой частоте v в пределах полосы пропускания истинные
пространственные частоты uv и vv связаны со значениями и vl v соотношением
F.72)
Вклад в измеренную функцию видности от узкого диапазона частот с центром
на частоте v равен
, v) =VU( , ^ — /( — , . F.73)
Здесь мы воспользовались теоремой подобия фурье-образов [см., например,
(Bracewell, 2000)]. Таким образом, вклад в измеряемую яркость равен истинной
функции распределения яркости, масштабированной по координатам (/,га) с ко-
коэффициентом z//z/q и по яркости в (z//z/q) раз. Полученное распределение ярко-
яркости свертывается с Ъ$A, т), синтезированной диаграммой направленности, соответ-
соответствующей частоте щ. Диаграмма не меняется с частотой, так как для представления
всего частотного диапазона используется одна и та же пространственная функция
чувствительности W(u,v). Полный отклик получается интегрированием по всей
полосе частот с соответствующим взвешиванием:
• ЬоA,т). F.74)
188
Отклик приемной системы
[Гл.6
т
Отклик
главного
лепестка
Источник
Отклик
кольцевого
лепестка
Рис. 6.10. Радиальное размывание,
являющееся эффектом полосы про-
пропускания, для точечного источника
с координатами (Zi,rai). Рисунок
демонстрирует влияние размывания
на главный лепесток и кольцевой
боковой лепесток (т. е. боковой
лепесток, аналогичный показанному
на рис. 5.15)
Отметим, что интегралы нужно брать по
всей полосе частот входного сигнала, обозна-
обозначенного индексом RF, включая обе боковые
полосы в случае двухполосной системы. Мы
предполагаем, что функция полосы пропуска-
пропускания i^Rp(^) одинакова для всех антенн. Значе-
Значения / и т в функции яркости из F.74) умно-
умножаются на коэффициент z//z/q, который изме-
изменяется в процессе интегрирования по полосе
и равен единице в ее центре. Таким образом,
можно рассматривать интегрирование в квад-
квадратных скобках в F.74) как процесс усредне-
усреднения большого количества изображений, каж-
каждое из которых имеет собственный масштаб.
Масштабные множители равны z//z/0, а диа-
диапазон значений v определяется наблюдаемой
полосой частот. Изображения выровнены в на-
начале координат, и, следовательно, интегриро-
интегрирование по частоте приводит к радиальному раз-
размыванию распределения яркости до того, как
будет выполнена свертка с диаграммой. От-
Отклик на точечный источник с координатами
(/, 777,) вытягивается в радиальном направлении
в \Jl2 -\- m2 Az//i/q раз. На больших расстояниях от начала координат, где вытягива-
вытягивание велико по сравнению с шириной синтезированной диаграммы, детали источника
сглаживаются за счет размывания, так что оно фактически налагает ограничение
на ширину поля зрения. Измеренная яркость равна размытому распределению,
свернутому с синтезированной диаграммой направленности.
Свойства полученного распределения яркости можно вывести из F.74). Напри-
Например, предположим, что диаграмма направленности содержит кольцевой боковой
лепесток на большом расстоянии от оси диаграммы, и что на карте отклик от
удаленного источника приводит к попаданию кольцевого лепестка в окрестность
начала координат. Расширяется ли боковой лепесток около начала координат? Так
как удаленный источник вытянут, боковой лепесток будет размыт в направлении,
параллельном линии, соединяющей источник с началом координат, как показано на
рис. 6.10. Он будет расширяться вблизи начала координат, но не в точке, отстоящей
от него на 90°, если отсчитывать угол относительно источника.
Чтобы оценить степень подавления удаленных источников, полезно определить
Rb, максимум отклика от точечного источника на расстоянии г\ от начала ко-
координат плоскости (/,777,), как долю отклика на тот же источник, помещенный
в начало координат. Поскольку мы рассматриваем радиальное размывание, нам
нужна только яркость вдоль радиуса, проходящего через точку (/, т), как показано
на рис. 6.11 а. Мы будем рассматривать идеальную модель. Полоса пропускания
представлена прямоугольной функцией шириной Az/, а синтезированная диаграмма
является функцией Гаусса от модуля радиус-вектора со стандартным отклонением
сгъ = #fr/\/81n2, где въ — ширина на уровне половинной мощности. Для простоты
множитель (zz/z/qJ в верхнем интеграле F.74) опущен, что допустимо, поскольку
относительная полоса редко превышает 5 %. Свертка становится одномерной (ради-
(радиальной) операцией, как видно из рис. 6.11 б. Радиально вытянутый источник пред-
представлен прямоугольной функцией от г\A — Az//2z/q) до г\A + Ai//2z/q) с единичной
площадью. Диаграмма направленности представлена функцией е~г '2(Тъ, которая
равна единице на оси диаграммы. Когда последняя направлена на источник, как
6.3]
Эффекты полосы пропускания
189
показано на рис. 6.11, Rb определяется выражением
= 1,0645
График Rb как функции парамет-
параметра r\Av/6ъЩ, являющегося расстоя-
расстоянием до источника от начала коор-
координат, выраженным в ширинах диа-
диаграммы и умноженным на относи-
относительную полосу, показан на рис. 6.12.
Значения этого параметра 0,2 и 0,5
снижают отклик соответственно на
0,9 и 5,5%.
Если полоса пропускания прием-
приемника является функцией Гаусса экви-
эквивалентной ширины Аи (т. е. со стан-
стандартным отклонением Дг//2,5066),
поправочный множитель принимает
вид
. F.76)
VI + @,939п
График этой функции также по-
показан на рис. 6.12. Сравнение двух
кривых дает представление о зави-
зависимости отклика от формы полосы
пропускания.
6.3.2. Картографирование в
широком поле зрения с приме-
применением многоканальной систе-
системы. Широкополосные карты могут
быть получены и при наблюдени-
наблюдениях с многоканальной системой (т. е.
спектральной приемной системой,
erf fo,8326
F.75)
7-(r-r{J/2a2
ш
/>уу
0
Рис. 6.11. Отклик решетки с широкополосной
приемной системой от точечного источника на
расстоянии п от начала координат плоско-
плоскости (l,m). a — точечный источник (дельта-
функция) на расстоянии п от центра растяги-
растягивается в радиальном направлении и становится
прямоугольной функцией единичной площади
(показан жирной линией), б — сечение рас-
распределения яркости в направлении г. Синте-
Синтезированная диаграмма представлена функцией
Гаусса. Максимум яркости в отклике на источ-
источник пропорционален заштрихованной площади
описанной в разд. 8.7). В этом слу-
случае полоса пропускания делится на ряд каналов, либо с помощью набора узко-
узкополосных фильтров, либо в спектральном цифровом корреляторе. В каждом из
каналов функция видности измеряется независимо, поэтому значения и и v можно
корректно масштабировать и построить для каждого канала независимую кар-
карту. Масштабирование приводит к изменению пространственной функции чувстви-
чувствительности в пределах полосы, и на частоте v синтезированная диаграмма равна
(у/щJЬоAг//щ, гпту/щ), где bo(l, тп) — монохроматическая диаграмма на частоте щ.
Карты можно суммировать, и при условии равных весов результат для N каналов
может быть представлен в виде
1{1,т)
N
1 X^fvi\ 7 Aщ тщ\
N ^-^ \щ/ \1У0 щ J
1
г=1
F.77)
190
Отклик приемной системы
[Гл.6
1,0
0,8
0,2
ОД
Прямоугольная полоса
{пропускания или
\ функция усреднения
г Гауссова полоса
пропускания
(только для Rfr)
2 4 6
Av/9^Vq или
8
, In I
10
Рис. 6.12. Относительная амплиту-
амплитуда максимального отклика на то-
точечный источник как функция рас-
расстояния от центра поля, а также
относительной полосы или времени
усреднения
В этом случае никакого размывания распре-
распределения яркости не происходит, но имеет место
радиальное размывание диаграммы направлен-
направленности, которое производит полезный эффект
подавления удаленных боковых лепестков. Та-
Таким образом, этот режим наблюдений хорошо
подходит для картографирования широких об-
областей поля зрения. Улучшение диаграммы на-
направленности обусловлено увеличением числа
измеренных точек гш-плоскости; этот эффект
используется также в многочастотном синтезе,
обсуждаемом в разд. 11.7.
6.4. Эффекты
усреднения функции видности
6.4.1. Усреднение функции видности.
В большинстве синтезирующих антенных реше-
решеток выход каждого из каналов усредняется за
последовательные интервалы времени га и, та-
таким образом, состоит из действительных и комплексных значений, распределенных
во времени с промежутками та. Целесообразно делать та достаточно большим,
чтобы снизить темп считывания данных коррелятора. Однако для та существует
ограничение, которое обусловлено соображениями, вытекающими из обсуждавшей-
обсуждавшейся в разд. 5.2 теоремы выборки и которое мы вкратце объясним следующим обра-
образом. При дискретном фурье-преобразовании функции видности яркости исходные
данные распределены с интервалами Аи и Дг>, как показано на рис. 5.3. Если размер
картографируемой области в направлениях / и m равен 0/, то Аи = Av = 1/0/.
Перемещение вектора базы на (щ г>)-плоскости за время то не должно превышать
Ащ в противном случае данные функции видности не будут являться независи-
независимыми измерениями, что означает потерю информации. Рассмотрим случай, когда
самая длинная база ориентирована в направлении восток—запад, а наблюдаемый
источник имеет высокое склонение, что даст наивысшую скорость перемещения
вектора базы. Если длина базы составляет D\ длин волн, вектор описывает на uv-
плоскости приблизительно круговую траекторию, двигаясь со скоростью 0JeD\ длин
волн за единицу времени, где сое — угловая скорость вращения. Мы требуем, следо-
следовательно, чтобы выполнялось условие raujeD\ < 1/0/, которое на практике сводится
ктай С /(ujeD\0f), где коэффициент С с большой вероятностью лежит в диапазоне
0,1-0,5. Отметим, что D\6f приблизительно равно числу синтезированных диа-
диаграмм, укладывающихся в поле зрения, и, таким образом, то должно быть несколько
меньше времени, за которое Земля поворачивается на один радиан, поделенного на
это число. Хотя для более коротких баз усреднение могло бы производиться за более
длинные интервалы времени, в большинстве синтезирующих решеток все выходы
корреляторов опрашиваются одновременно, с периодом, допустимым для наибо-
наиболее длинных баз. Другое соображение относительно времени усреднения состоит
в том, что спорадические помехи и неисправности аппаратуры можно исключить
из данных с минимальными потерями информации, если то невелико. Для больших
решеток та, как правило, лежит в диапазоне от десятков миллисекунд до десятков
секунд. Определение функции видности в узлах сетки с шагом (Агх, Av) по данным,
измеренным на траекториях решетки в гш-плоскости, обсуждается в п. 10.2.3, и эта
операция также может повлиять на выбор та.
6.4]
Эффекты усреднения функции видности
191
6.4.2. Эффекты усреднения по времени. Теперь мы исследуем влияние
усреднения на синтезируемое распределение яркости более подробно. При усредне-
усреднении данных все значения функции видности в пределах каждого интервала времени
та рассматриваются как относящиеся к моменту времени в середине интервала
усреднения. Таким образом, измерения, например, в начале каждого периода интер-
интервала усреднения входят в данные функции видности для значений и и г>, которые
относятся к моментам времени на та/2 позже истинных. Фактически полученная
карта будет результатом усреднения большого количества карт с собственными
временными смещениями, распределенными вдоль диапазона от —та/2 до та/2. Эти
временные смещения относятся только к присваиванию (и, v)-значениям и не соот-
соответствуют ошибкам часов, которые влияют на всю приемную систему. Рассмотрим
точечный источник, представленный дельта-функцией. Чтобы упростить ситуацию,
мы возьмем наблюдения с базами восток—запад и исследуем данный эффект на
плоскости u'v' и соответствующей ей картинной плоскости I'm' (см. разд. 4.2). Тра-
Траектории решетки представляют собой дуги окружностей, порождаемых векторами,
вращающимися с угловой скоростью с<;е, как показано на рис. 6.13 а. Рассмотрим
сначала линейную решетку восток-запад; в этом случае из компонент разнесения
антенн (X, У, Z), определенных на рис. 4.1, не равна нулю только Y. Центры дуг
траекторий решетки совпадают с началом координат (г/, г/), как на рис. 6.13 6,
и временное смещение St эквивалентно повороту осей u',v' на угол иое St. Функция
видности источника является суммой двух частей — действительной и мнимой —
синусоидальной формы:
Рис. 6.13. Траектории на ?/?/-плоскости для общего случая (а) и для базы восток-
запад (б). Угол (jJeTa, на котором происходит усреднение, для наглядности увеличен;
например, для времени усреднения 30 секунд этот угол будет составлять 7,5'
^ cos2tt(u'1'1 +vrm'1) - j sm27r(u'l'1
F.78)
Направление гребней связано с позиционным углом ф' = arctg (m^/^) точеч-
точечного источника, как показывает рис. 6.14. Изменение ф' вызывает эквивалентный
поворот гребней, и наоборот. Для решетки восток-запад временные смещения, та-
таким образом, соответствуют пропорциональным поворотам распределения яркости
в плоскости I'm'. Отсюда следует, что эффект усреднения по времени состоит в кру-
круговом размывании, аналогичном тому, что обусловлен шириной полосы приема, но
ортогональном последнему. Если мы выразим положение точек на /'т'-плоскости
в полярных координатах (г',т//), показанных на рис. 6.14 а, то изображение, полу-
полученное из усредненных данных, можно связать с истинным распределением яркости
192
Отклик приемной системы
[Гл.6
1{г'\ф') соотношением
ы
F.79)
-ojera/2
где bo — синтезированная диаграмма направленности.
Рис. 6.14. Точечный источник, расположенный в плоскости /^mi (а), и действительная
часть соответствующей функции видности (б). Гребни синусоидальных волн, представ-
представляющих функцию видности на и v -плоскости, ортогональны радиус-вектору г[ положения
источника на плоскости I'm
Относительное снижение максимума отклика на точечный источник проще всего
рассматривать на плоскости I'm!. Для базы восток-запад контуры синтезированной
диаграммы имеют на /'т'-плоскости приблизительно круговую форму, если время
наблюдений приближается к 12 часам, что дает полные круговые траектории на
и'^'-плоскости. Если предположить, что синтезированная диаграмма может быть
представлена функцией Гаусса, как в расчетах эффекта полосы пропускания, гра-
график для прямоугольной полосы на рис. 6.12 будет применим и к эффекту усредне-
усреднения. В одном случае функция расширения является «радиальной» и имеет ширину
7*i Az//z/q, а в другом она «круговая», с шириной г[сиета. Таким образом, для эффекта
усреднения можно заменить г\ Аи/Оь^о в выражении F.75) и на рис. 6.12 (сплошная
линия) на г^ШеТа/О'ъ, учитывая, что г[ = Jl\ + m\ sin250 и что в'ь, ширина синтези-
синтезированной диаграммы на плоскости I'm', равна ширине диаграммы в направлении
восток—запад на плоскости lm. Следовательно, уменьшение отклика на точечный
источник, обусловленное усреднением, может быть записано в виде
Ra = 1,0645
erf @,
8326
F.80)
Как правило, то выбирают так, чтобы Ra в любой точке изображения было лишь
немного меньшим единицы, и в этом случае мы можем аппроксимировать функцию
ошибок интегралом от двух первых членов степенного ряда для функции Гаусса:
1 / 0,8326 иеТа
sin2
F.81)
6.4]
Приложение 6.1. Частичное подавление боковой полосы
193
Это полезная формула для проверки того, что то не является слишком боль-
большой. Следует отметить два аспекта усреднения, на которые указывает соотношение
F.81). Во-первых, если источник расположен вблизи оси т' и имеет низкое склоне-
склонение, эффект усреднения очень мал. Это объясняется тем, что в этом случае гребни
синусоидальных волн функции видности идут примерно параллельно оси uf, и в
результате преобразования и' = и cosec 5o период колебаний вдоль оси v увеличива-
увеличивается во много раз. В сравнении с этим дуга, которую вектор базы проходит за время
та, мала и, следовательно, усреднение будет мало влиять на амплитуду функции
видности. Во-вторых, для источника на оси /' значение Ra не зависит от 5о. В этом
случае гребни волн идут параллельно оси г>, и увеличение масштаба в направлении
этой оси не влияет на период синусоиды.
Для решеток с базами, отличными от направления восток—запад, центры со-
соответствующих траекторий на г/?/-плоскости смещены относительно начала ко-
координат, как на рис. 6.13 а, и временное смещение уже не эквивалентно простому
повороту осей. Однако это не может увеличить размывание функции видности, так
что результат вряд ли будет хуже того, что имеет место в случае решетки восток-
запад с базами примерно той же длины.
Приложение 6.1. Частичное подавление боковой полосы
В однополосной системе со смесителем в качестве входного каскада нежелатель-
нежелательная (зеркальная) полоса может быть подавлена с помощью различных средств. В их
число входит волноводный фильтр, интерферометр Мартина-Паплетта [(Martin and
Puplett, 1969), (Payne, 1989)], настроенная волноводная закороченная секция или
разделяющая полосы конфигурация из двух смесителей (как в приложении 7.1).
Практические соображения, особенно в случае миллиметровых волн, иногда за-
заставляют ограничиться частичным подавлением зеркальной полосы. Пусть отклик
на зеркальную полосу, в смысле усиления приемника по мощности, равен отклику
на нужную (сигнальную) полосу, умноженному на р, где 0 < р < 1. На практике р
могло бы быть ~ 1/10.
В случае спектральных наблюдений, когда нужная линия присутствует только
в сигнальной полосе, шум, вносимый зеркальной полосой, приведет к увеличению
среднеквадратического шума на выходе коррелятора в A + р) раз. Таким образом,
коэффициент снижения чувствительности будет равен A + р).
При наблюдениях в континууме зеркаль-
зеркальная полоса тоже несет сигнальную компоненту.
Предположим, что функция видности в обе-
обеих полосах одинакова, лепестки остановлены,
а переключение фазы первого гетеродина на
тг/2 позволяет измерять комплексную функ-
функцию видности. Используется комплексный кор-
коррелятор, и для простоты мы считаем, что аппа-
аппаратурная фаза подстраивается таким образом,
что линия АВ на рис. 6.5 ^совпадает с действи-
действительной осью. Комплексный выходной сигнал
коррелятора для нулевого сдвига гетеродина
можно представить в виде
-JW*
Im
Re
а для сдвига фазы гетеродина на тг/2
(П6.2)
Рис. П.6.1. Векторы на комплекс-
комплексной плоскости, соответствующие
параметрам в (П6.1) и (П6.2). По-
Постоянный коэффициент усиления
Gmn опущен. Если р известно, а из-
измеряются Со и CV/2, соотношение
(П6.3) дает оптимальную оценку V
7 Томсон
194 Отклик приемной системы [Гл. 6
Здесь Gmn — усиление в сигнальной полосе, поэтому усиление в зеркальной
полосе равно pGmn. Заметим, что в выражении для С^/2 множители j для двух
боковых полос имеют разные знаки, так как фазовый сдвиг на тг/2 поворачивает
соответствующие векторы на комплексной плоскости на тг/2 в противоположных
направлениях, как показано на рис. П6.1. Оптимальной оценкой функции видности
в данном случае будет
hi (Со jC*^ + TIT* (С
+ р 1 + Р
Первый член в квадратных скобках соответствует отклику сигнальной полосы,
а второй — зеркальной. Полная мощность шума, подаваемая на вход коррелятора,
пропорциональна A + р), поэтому среднеквадратический шум, соответствующий
первому члену в квадратных скобках, пропорционален A + р)/A + р2), а для вто-
второго — эквивалентен выражению рA + р)/A + р2)- Таким образом, среднеквадра-
среднеквадратический шум V из (П6.3) пропорционален A + р)/у/A + р2) . Чувствительность
пропорциональна y^l + р2) /A + р). Для р « 1/10 или меньших, р2 очень мал и ко-
коэффициент ухудшения чувствительности равен приблизительно A + р) (Thomp-
(Thompson and D'Addario, 2000).
Цитированная литература
Anantharamaiah К. R., R. D. Ekers, V. Radhakrishnan, Т. J. Cornwell and W. M. Goss. Noise
in Images of Very Bright Sources. Synthesis Imaging in Radio Astronomy, R. A. Perley, F. R.
Schwab and A. H. Bridle. Eds., Pub. Astron. Soc. Pacific Conf. Ser., 6, 431-442, 1989.
Blum E. J. Sensibilite des Radiotelescopes et Recepteurs a Correlation. Ann. d'Astrophys. 22,
140-163, 1959.
Bracewell R. N. The Fourier Transform and Its Applications. McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Colvin R. S. A Study of Radio Astronomy Receivers. Ph. D. thesis, Stanford Univ. Stanford,
CA, 1961.
Douglas J. N., F. N. Bash, F. D. Ghigo, G. F. Moseley and G. W. Torrence. First Results
from the Texas Interferometer: Positions of 605 Discrete Sources. Astron. J. 78, 1-17, 1973.
Goldstein S. J. Jr. The Angular Size of Short-Lived Solar Radio Disturbances. Astron. J. 130,
393-399, 1959.
Lawson J. L. and G. E. Uhlenbeck. Threshold Signals. Radiation Laboratory Series, Vol. 24,
McGraw-Hill, New York, 1950, p. 68.
Lo W. F., P. E. Dewdney, T. L. Landecker, D. Routledge and J. F. Vaneldik. A Cross-
Correlation Receiver for Radio Astronomy Employing Quadrature Channel Generation by
Computed Hilbert Transform. Radio Sci. 19, 1413-421, 1984.
Martin D. H. and E. Puplett. Polarized Interferometric Spectrometry for the Millimeter and
Submillimeter Spectrum. Infrared Phys. 10, 105-109, 1969.
Mickelson R. L. and Swenson G. W. Jr. A Comparison of Two CorrelationSchemes. IEEE
Trans. Instrum. Meas. IM-40, 816-819, 1991.
Middleton D. An Introduction to Statistical Communication Theory. McGraw-Hill, New York,
1960, p. 343.
Moran J. M. Very Long Baseline Interferometric Observations and Data Reduction. Methods
of Experimental Physics. Vol. 12C, M. L. Meeks, Ed., Academic Press, New York, 1976, p.
228-260.
6.4] Цитированная литература 195
Papoulis A. Probability, Random Variables and Stochastic Processes. McGraw-Hill, New York,
1965.
Payne J. M. Millimeter and Submillimeter Wavelength Radio Astronomy. Proc. IEEE. 77,
993-1017, 1989.
Read R. B. Two-Element Interferometer for Accurate Position Determinations at 960 Me. IRE
Trans. Antennas Propag. AP-9, 31-35, 1961.
Rice S. O. Mathematical Analysis of Random Noise. Bell Syst. Tech. J. 23, 282-332, 1944; 24,
46-156, 1945; repr. in Noise and Stochastic Processes. N. Wax, Ed., Dover, New York, 1954.
Rogers A. E. E. Theory of Two-Element Interferometers. Methods of Experimental Physics.
Vol. 12C, M. L. Meeks Ed., Academic Press, 1976, p. 139-157 (seeTable 1).
Swenson G. W. Jr. and N. C. Mathur. On the Space-Frequency Equivalence of a Correlator
Interferometer. Radio Sci. 4, 69-71, 1969.
Thompson A. R. and L. R. D'Addario. Relative Sensitivity of Double- and Single-Sideband
Systems for both Total Power and Interferometry. ALMA Memo. 304, National Radio Astron-
Astronomy Observatory, Socorro, NM, 2000.
Tiuri M. E. Radio Astronomy Receivers. IEEE Trans. Antennas Propag. AP-12, 930-938,
1964.
Tiuri M. E. and A. V. Rdisdnen. Radio-Telescope Receivers. Radio Astronomy. J. D. Kraus,
2nd ed., Cygnus-Quasar Books, Powell, OH, 1986, Ch. 7.
Tucker J. R. and M. J. Feldman. Quantum Detection at Millimeter Wavelengths. Rev. Mod.
Phys. 57, 1055-1113, 1985.
Vander Vorst A. S. and R. S. Colvin. The Use of Degenerate Parametric Amplifiers in
Interferometry. IEEE Trans. Antennas Propag. AP-14, 667-668, 1966.
Vinokur M. Optimisation dans la Recherche d'une Sinusoide de Periode Connue en Presence
de Bruit. Ann. d'Astrophys. 28, 412-445, 1965.
Wright M. C. H., B. G. Clark, C. H. Moore and J. Сое. Hydrogen-Line Aperture Synthesis
at the National Radio Astronomy Observatory: Techniques and Data Reduction. Radio Sci. 8,
763-773, 1973.
Wozencraft J. M. and I. M. Jacobs. Principles of Communication Engineering. Wiley, New
York, 1965, p. 205.
Глава 7
ПРОЕКТИРОВАНИЕ АНАЛОГОВОЙ ПРИЕМНОЙ
СИСТЕМЫ
Основные функции приемной системы были очерчены в предыдущих главах.
Теперь мы рассмотрим некоторые аспекты проектирования приемных систем более
подробно. Это касается в основном аппаратуры, расположенной между антенна-
антеннами и корреляторами и, в частности, ее характеристик, критичных в отношении
чувствительности и точности измерения функции видности. К этим характеристи-
характеристикам относятся шумовая температура, фазовая стабильность, частотные характери-
характеристики, паразитные сигналы и автоматическая регулировка уровня. Проведенный
анализ позволит сформулировать требования к параметрам системы, которые поз-
позволяют достичь заданных характеристик чувствительности и точности. Здесь мы
рассматриваем только аналоговую часть приемных систем, а вопросы оцифровки,
задержки и коррелирования сигналов будут рассмотрены в гл. 8.
7.1. Основные составляющие приемной аппаратуры
Мы дадим только краткое описание основных элементов приемной системы. Оп-
Оптимальная технология и компоненты, применяемые в электронном оборудовании,
постоянно изменяются с развитием техники, и в литературе можно найти примеры
разработок, относящихся к различным периодам времени; см., например, (Read,
1961), (Elsmore, Kenderdine and Ryle, 1966), (Baars et al., 1973), (Bracewell et al.,
1973), (Wright et al., 1973), (Welch et al., 1977, 1996), (Thompson et al., 1980), (Batty
et al., 1982), (Erickson, Mahoney and Erb, 1982), (Napier, Thompson and Ekers, 1983),
(Sinclair et al., 1992), (Young et al., 1992) и (Napier et al., 1994). Более ранние работы
в этом списке интересны в основном с исторической точки зрения.
На рис. 7.1 показана упрощенная блок-схема приемной системы большой решет-
решетки со связанными элементами. При проектировании удобно разбить всю систему на
ряд подсистем, к рассмотрению которых мы теперь переходим.
7.1.1. Малошумящие входные устройства. В целях минимизации шумо-
шумовой температуры радиоастрономических приемников обычно применяется крио-
криогенное охлаждение усилительных или смесительных каскадов от входа и до той
точки, где вкладом шумов от последующих каскадов молено пренебречь. Входные
малошумящие каскады объединяются с охлаждающей системой, а иногда еще и с
облучающим рупором, в единый блок, который называют приемником или вход-
входным устройством. Активным элементом является обычно транзисторный усили-
усилитель или, на субмиллиметровых волнах, SIS-смеситель (сверхпроводник-изолятор-
сверхпроводник), за которым следуют транзисторные усилители. Описание подоб-
подобных систем можно найти, например, в (Reid et al., 1973), (Weinreb et al., 1977a),
(Weinreb, Fenstermacher and Harris, 1982), (Casse, Woestenburg and Visser, 1982),
(Phillips and Woody, 1982), (Tiuri and Raisanen, 1986), (Payne, 1989), (Phillips, 1994),
(Payne et al., 1994), (Pospieszalski et al., 1997) и (Webber et al., 1998).
7.1]
Основные составляющие приемной аппаратуры
197
Аппаратура, установ-
установленная на антенне —J
Аппаратура,
установленная
L в аппаратном зале .
Входное
малошумящее
устройство
Система
ПЧ
Управляемый
гетеродин
К остальным устройствам
till
Устройство
управления
и контроля
Линия
передачи
сигналов
Система ПЧ
и видеокон-
вертер
Устройство
дискретизации
К осталь яым
Задающий
гетеродин
[ устройствам I
IY Г1 1
Линия
переменной
задержки
Устройство
управления
и контроля
От других
антенн!
Корреляторы
Управляющий
компьютер
К накопителю
данных
Рис. 7.1. Упрощенная блок-схема типичной синтезируемой решетки. Каждый из блоков со-
соответствует одной из описанных далее подсистем, кроме устройств управления и контроля,
которые относятся к цифровой системе обмена данными, при посредстве которой компью-
компьютер контролирует состояние аппаратуры, устанавливает частоты гетеродинов и т. п. За
исключением опорного генератора и компьютера, для каждой антенны требуется по одно-
одному блоку каждого типа. ^Жирными линиями показаны сигнальные тракты. В некоторых
случаях блоки преобразования ПЧ и оцифровки расположены на антеннах, а сигналы
передаются в цифровом виде
Анализ шумов, вносимых приемником, мы начнем с рассмотрения случая, когда
приближение Рэлея—Джинса является удовлетворительным. Это область Нту /кТ <С
<С 1, где h — константа Планка, а Т — температура источника теплового глума. Это
условие, как отмечается при рассматрении выражения A.1), может быть записано
в виде v (ГГц) <С 20 Т (К). Удобно определять мощность шума в единицах темпера-
температуры согласованной нагрузки, подключенной ко входу приемника. В приближении
Рэлея-Джинса мощность шума на выводе нагрузки, имеющей температуру Т, равна
кТ Ату, где к — константа Больцмана, а Ату — полоса частот, в которой измеряется
шум (Nyquist, 1928). Один градус Кельвина соответствует спектральной мощности
A/к) Вт-Гц~ . Шумовая температура приемника Тц является мерой полной шу-
шумовой мощности системы и равна температуре нагрузки, подключенной ко входу
гипотетического, не имеющего шумов (но в остальном идентичного реальному) при-
приемника, на выходе которого получается шум эквивалентной мощности. Температура
системы Ts является мерой общего уровня шума, в который, помимо Т#, входит
шум от антенны и шумы, связанные с потерями в компонентах, расположенных
между антенной и приемником:
где Т'А представляет антенную температуру, создаваемую атмосферой и другими
нежелательными источниками шума, L — коэффициент потерь мощности в линии
передачи между антенной и приемником (определяемый как отношение мощности
на входе к мощности на выходе), а Т^ — температуру этой линии передачи.
198 Проектирование аналоговой приемной системы [Гл. 7
Определяя шумовую температуру приемника, следует отметить, что на практике
вход приемника всегда подключается к некоторой нагрузке, которая сама по себе
является источником шума. Шум на выходе приемника, таким образом, состоит
из двух компонент, — шума от источника на входе, который соответствует в G.1)
антенне и линии передачи, и шума, производимого самим приемником.
7.1.2. Измерение шумовой температуры. Шумовую температуру прием-
приемника часто измеряют методом У-фактора. Используемый при таких измерениях
источник теплового шума обычно представляет собой согласованную резистивную
нагрузку, подключаемую ко входу приемника посредством волновода или коак-
коаксиального кабеля. Вход приемника поочередно подключается к двум нагрузкам
с температурами Thot (горячая) и Tcoid (холодная). Фактор Y определяется как
отношение мощностей шума, измеренных в этих условиях:
Y = Tr + "^
и, таким образом,
rp -^hot ¦* -^cold /ij q\
Типичными значениями являются Thot = 290 К (комнатная температура) и Тсо\^ =
= 77 К (температура жидкого азота).
Температура приемника может быть выражена через шумовые температуры
последовательных каскадов на пути прохождения сигнала [см., например, (Kraus,
1966)]:
TR = TR1 + TR2G^ + TR3(G1G2)-1 + • • • G.4)
Здесь TRi — шумовая температура г-го каскада приемника, a Gi — его усиление по
мощности. Если первым каскадом является не усилитель, а смеситель, то G\ может
быть меньше единицы, и очень важной становится шумовая температура второго
каскада.
Для криогенно охлаждаемых приемников миллиметровых и субмиллиметровых
волн приближение Рэлея-Джинса может давать значительную ошибку. Спектраль-
Спектральная мощность (мощность на единицу полосы частот) уже не будет линейной функ-
функцией температуры излучателя или нагрузки. Отношение h/k равняется 0,048 К на
гигагерц, так что, например, если Т = 4К (температура жидкого гелия), то для
у = 83 ГГц hv jkT = 1. Таким образом, при росте частоты и снижении температуры
нельзя пренебрегать квантовыми эффектами. При этих условиях в вычислениях
шума вместо физической температуры можно использовать эффективную темпера-
температуру, равную мощности шума на единицу частотной полосы, поделенной на к. Для
определения эффективной шумовой температуры теплового источника в случае,
когда нужно учитывать квантовые эффекты, используются две формулы. Одна
из них — это формула Планка, другая — формула Каллена-Вельтона (Callen and
Welton, 1951). Для эффективных шумовых температур одномодового волновода
с согласованной тепловой нагрузкой или кабеля с резистивной нагрузкой эти две
формулы дают следующие результаты:
Г 7 /7 m ~\
G.5)
7.1]
Основные составляющие приемной аппаратуры
199
где Т — физическая температура. Из G.5) и G.6) получаем
= ^Planck + -jV •
G.7)
20
15
10
230 ГГц
T(C&W)/
/T(C&W)
"rfohys)"-
F(C&W)
/F(Plank)
-Г(Р1апк)
Г(Р1апк)
- r(phys)
О 5 10 15 20
Физическая температура, К
Рис. 7.2. Зависимость температуры шума от физической температуры для абсолютно чер-
черного тела, излучающего на частоте 230 ГГц, в соответствии с формулами Рэлея—Джинса,
Планка и Каллена-Вельтона. Штриховыми линиями показаны разности между тремя
кривыми излучения. Кривая Рэлея-Джинса при высоких температурах сходится с кривой
Каллена-Вельтона, в то время как кривая Планка остается на hv/2k ниже последней. По
данным (Kerr et al., 1997)
Формула Каллена—Вельтона отличается от формулы Планка добавочным чле-
членом hv/2k, который соответствует дополнительной половине фотона. Эта половина
фотона является уровнем шума от тела при температуре абсолютного нуля и на-
называется шумом нулевых флуктуации. На рис. 7.2 показаны соотношения физи-
физической и шумовой температур для частоты 230 ГГц, соответствующие формулам
Рэлея—Джинса, Планка и Каллена—Вельтона. Заметим, что в случае hv/kT <C 1 мы
можем положить exp (hv/kt) — 1 ~ (hv/kt) + (hv/ktJ/2, так что формула Каллена-
Вельтона сведется к соотношению Рэлея-Джинса, в то время как формула Планка
дает результат, меньший на hv/2к.
При вычислении шумовой температуры приемника по формуле G.1) в качестве
Thot и ^coid нужно использовать не физическую температуру, а шумовые темпе-
температуры, полученные по формуле Планка или Каллена-Вельтона (если только мы
не находимся в области Рэлея-Джинса). Соответственно для формулы Планка мы
можем написать
_ ^hot(Planck) ~~ ^"cold(Planck)
~ У- 1
G.8)
Аналогичное выражение можно написать для формулы Каллена—Вельтона. Из
G.4), G.5) и G.6) мы получаем
hi/
G.9)
200 Проектирование аналоговой приемной системы [Гл. 7
При использовании результатов любых измерений шумовой температуры прием-
приемника валено знать, каким образом они получены,— соответствуют ли они формуле
Планка, формуле Каллена-Вельтона или лее физической температуре (т. е. при-
приближению Рэлея-Джинса). Если шумовые температуры отдельных компонентов
выводились из физических температур по формуле Каллена-Вельтона, суммарная
температура будет на hv/2k больше, чем для формулы Планка; см. G.7). Однако ес-
если формулу Каллена-Вельтона применить для вычисления шумовой температуры
приемника, то мы получим результат на h/2k меньший, чем при использовании фор-
формулы Планка; см. G.9). Таким образом, температура системы, являющаяся суммой
входной температуры и температуры приемника, окажется той же самой, какой бы
формулой мы ни пользовались. Тем не менее во избежание недоразумений следует
единообразно применять ту или иную формулу во всех вычислениях, связанных
с шумовыми температурами.
Относительно того, какова природа шума нулевых флуктуации, нужно ли его
рассматривать как исходящий от нагрузки, присоединенной ко входу приемника,
или же как генерируемый в его входных каскадах, высказывались различные мне-
мнения; см., например, (Tucker and Feldman, 1985), (Zorin, 1985) и (Wengler and Woody,
1987). На высоких частотах, когда существенны квантовые эффекты, обычным
типом входного устройства является SIS-смеситель, квантовая теория которого
была дана Таккером (Tucker, 1979). Обзор некоторых выводов, к которым приходят
различные авторы относительно вопросов шумовой температуры, можно найти
в (Kerr, Feldman and Pan, 1997) и (Kerr, 1999).
Подытожим сказанное. Уровень излучения, который дает формула Каллена—
Вельтона, равен уровню излучения по Планку плюс уровень нулевых флуктуации
hv/2. Последнюю компоненту можно рассматривать как мощность, исходящую от
абсолютно черного тела или резистивной нагрузки при температуре абсолютно-
абсолютного нуля. Шумовая температура приемника, если при интерпретации измеренно-
измеренного У-фактора использовалась формула Каллена-Вельтона, оказывается на hv/2к
меньше, чем при использовании формулы Планка. Однако антенная температура,
полученная по формуле Каллена-Вельтона, на hv/2к больше соответствующего
значения по Планку. Температура системы, являющаяся суммой температуры шу-
шумов и антенной температуры, оказывается в обоих случаях одинаковой. Поскольку
чувствительность радиотелескопа определяется полной шумовой температурой си-
системы, эти детали могут показаться маловажными. Тем не менее, выбирая для
входного каскада усилитель или смеситель, важно знать, как определялась его
шумовая температура.
В дополнение к шуму, порождаемому электроникой, шум приемной системы
содержит компоненты, поступающие от антенны. Эти компоненты происходят от
космических источников, земной атмосферы, земной поверхности и других объек-
объектов в боковых лепестках антенны. Поглощение в атмосфере, которым обусловлен
ее вклад в шумы системы, обсуждается в гл. 13.
7.1.3. Гетеродин. Как уже говорилось в предыдущей главе, на антеннах и,
возможно, в каких-то других точках на пути сигнала к корреляторам необходимы
сигналы гетеродинов. Чтобы когерентность сигналов сохранялась, частоты соответ-
соответствующих гетеродинов различных антенн должны быть синхронизированы по фазе.
Фазы гетеродинов на антеннах могут и не совпадать, но их разность должна быть
достаточно стабильной и допускать калибровку. Для поддержания синхронности ге-
гетеродинов на антеннах необходимо передавать одну или несколько опорных частот
от центрального задающего генератора, которые можно было бы использовать для
7.1] Основные составляющие приемной аппаратуры 201
фазового захвата местных генераторов. Затем можно синтезировать гетеродинные
частоты, нужные для смесителей.
Для некоторых смесителей требуются специальные дополнительные сдвиги фаз,
реализующие вращение (остановку) интерференционных лепестков, о чем говори-
говорилось в п. 6.1.6 и переключение фазы, описанное в разд. 7.5. Часто эти сдвиги
проще всего осуществляются методами цифрового синтеза, например, применением
микросхем так называемых генераторов с числовым управлением. Они могут вы-
выдавать сигнал с частотой порядка нескольких мегагерц, несущий все необходимые
частотные и фазовые коррекции. Изменения фазы могут быть введены в цепь захва-
захвата фазы гетеродина, использующего синтезированный сигнал в качестве опорного.
7.1.4. ПЧ и линии передачи сигналов. Прежде чем достичь корреляторов,
сигналы после усиления во входных малошумящих каскадах должны пройти через
различные усилители ПЧ и подсистему линий передачи. Передача сигналов между
антеннами и аппаратной может осуществляться посредством коаксиальных или
двухпроводных линий, волноводов, световодов или микроволновой радиосвязи. На
небольших расстояниях часто используются кабели, но с увеличением расстояния
может потребоваться большое число промежуточных усилителей, компенсирующих
затухание сигнала, и в этих условиях обычно предпочтительнее оказываются опто-
оптоволоконные линии. При создании VLA, за несколько лет до освоения оптоволокон-
оптоволоконной связи, применялись волноводы типа TEqi (Weinreb et al., 1977b); (Archer, Caloc-
cia and Serna, 1980). Чтобы уменьшить влияние колебаний температуры, кабельные
или оптоволоконные линии могут прокладываться на глубине 1—2 м. Полоса пе-
передаваемых по кабелю сигналов обычно ограничивается затуханием и составляет
несколько десятков мегагерц; ограничения того же порядка на полосу высокочастот-
высокочастотной радиосвязи определяются числом доступных каналов. Наилучшие возможности
для передачи широкополосных сигналов имеют оптоволоконные линии связи.
После прихода на коррелятор сигналы обычно преобразуются к последней про-
промежуточной частоте, на которой формируется полоса пропускания и вводятся
компенсирующие временные задержки. Фазовые ошибки, возникающие из-за тем-
температурной нестабильности фильтров, и ошибки установки задержек могут быть
сведены в данной точке к минимуму, если выбрать эту промежуточную часто-
частоту возможно более низкой. Поэтому оконечные усилители ПЧ часто работают
в видеополосе, задаваемой фильтром нижних частот. Частота нижней границы
полосы пропускания составляет всего несколько процентов от частоты верхнего
среза фильтра. В инструментах, где для спектральных наблюдений используется
цифровой коррелятор, обычно имеется ряд фильтров, каждый из которых имеет
полосу в два раза шире предыдущего; они подключаются непосредственно перед
устройством оцифровки сигналов. Полосы пропускания выбираются в соответствии
с характеристиками цифрового коррелятора, как описано в разд. 8.7. В некоторых
случаях для преобразования к видеополосе используется однополосный смеситель
(см. приложение 7.1), но достигаемое при этом подавление зеркального канала не
превышает, как правило, 20—ЗОдБ.
7.1.5. Передача по оптоволоконному кабелю. Появление оптоволоконных
линий связи позволило сделать огромный шаг вперед в области передачи
широкополосных сигналов на большие расстояния. Сигнал модулирует оптическую
несущую с длиной волны, лежащей обычно в диапазоне 1300-1550 нм, и передается
по стеклянному световоду. Затухание в световоде минимально на длине волны
около 1550 нм и составляет приблизительно 0,2дБ-км-1, а на 1300 нм примерно
О^дБ-км. Эти значения гораздо ниже тех, что могут быть достигнуты для ра-
радиочастотных линий передачи. Стеклянный сердечник оптического волокна покрыт
202 Проектирование аналоговой приемной системы [Гл. 7
оболочкой из стекла с меньшим показателем преломления, поэтому пучок световых
волн, направленный в сердечник под достаточно малым углом к его оси, будет
распространяться в условиях полного внутреннего отражения. Если внутренний
сердечник имеет диаметр около 50 мкм, в нем могут возбуждаться несколько раз-
различных мод. Эти моды имеют слегка различающиеся скорости распространения,
что ограничивает эффективность многомодовых световодов. Если диаметр сердеч-
сердечника уменьшить примерно до 10 мкм, распространяется только мода НЕц. При-
Применение световодов такого типа необходимо на самых больших расстояниях и/или
самых больших частотах и широких полосах. На 1550 нм интервал длин волн в 1 нм
соответствует полосе частот шириной приблизительно 125 ГГц. Малое затухание
и высокая пропускная способность упрощают реализацию связанных широкополос-
широкополосных решеток с длинными базами. Сигналы могут передаваться в аналоговой форме
или оцифровываться (как описывается в гл. 8) и передаваться в виде импульсных
пакетов. Так как в оптической передаче сигнала участвует не только световод,
но также лазеры, генерирующие оптическую несущую, и детекторы, восстанавли-
восстанавливающие сигнал, проектирование оптических линий передачи гораздо сложнее, чем
проектирование кабельных систем. Здесь мы дадим лишь краткий обзор некоторых
основных особенностей оптической передачи сигналов. Более подробные сведения
можно найти, например, в (Agrawal, 1992) или (Borella et al., 1997).
На практике ширина полосы и дальность передачи сигналов ограничиваются
шумами лазера, генерирующего оптический сигнал на передающем конце линии,
и шумами диодного демодулятора и усилителя на приемном конце. Чтобы избежать
ухудшения чувствительности при аналоговой передаче, в большинстве радиоастро-
радиоастрономических приложений спектральная мощность сигнала (измеренная в Вт-Гц)
должна на ~20дБ превышать спектральную мощность шума, генерируемого в си-
системе передачи. Однако полная мощность сигнала ограничивается диапазоном ли-
линейности характеристик модулятора и демодулятора. В результате ширина полосы
передаваемого сигнала имеет свой предел, так как мощность сигналов с плоским
спектром пропорциональна их полосе. На практике предельная ширина полосы для
одной пары передатчик/приемник составляет 10-20 ГГц при передаче сигнала на
расстояние в несколько десятков километров.
В процессе модуляции мощность несущей изменяется пропорционально напря-
напряжению сигнала. Благодаря этому в оптоволоконных системах передачи влияние
слабых нежелательных компонент сигнала значительно снижается. Рассмотрим,
например, слабую компоненту оптического сигнала, возникающую из-за отражений
внутри световода. Если оптическая мощность отраженной компоненты на х дВ
меньше мощности основной, то после демодуляции на фотодетекторе вклад в мощ-
мощность сигнала от отраженной компоненты окажется на 2х дВ меньше вклада глав-
главной компоненты. То же самое относится к нежелательным эффектам, возникающим
из-за ограниченной эффективности ответвителей, вентилей и других элементов.
Гораздо меньшими, чем у кабеля, оказываются неравномерности частотной ха-
характеристики, обусловленные стоячими волнами, возникающими в микроволновых
линиях передачи.
При проектировании систем с оптоволоконными линиями связи нужно прини-
принимать в расчет фактор дисперсии скорости света ?>, обычно измеряемой в пс-(нм-
•км). Разность во времени распространения по световоду длины ? двух световых
волн, длины которых отличаются на АЛ, составляет VAXi. На рис. 7.3 показана
дисперсия для световодов двух различных типов. Кривая 1 представляет светово-
световоды, использовавшиеся в ранних разработках, а кривая 2 соответствует световоду,
у которого точка нулевой дисперсии смещена таким образом, что она примерно
совпадает с длиной волны наименьшего затухания 1550 нм. Такая оптимизация для
7.1]
Основные составляющие приемной аппаратуры
203
I
10
0
10
/
/
/
/
/
У
У
i
уУ
У
2
1,1
1,2 1,3
1,4 1,5 1,6
Длина волны, мкм
1,7
волны 1550 нм достигнута благо-
благодаря тому, что дисперсия цилин-
цилиндрического волновода, образуемо-
образуемого сердечником оптического во-
волокна, компенсирует собственную
дисперсию стекла на этой длине
волны.
Рассмотрим спектральную ко-
компоненту с частотой vm широко-
широкополосного сигнала, который мо-
модулирует оптическую несущую.
Амплитудная модуляция приво-
приводит к появлению боковых состав-
составляющих, отстоящих по частоте от
несущей на ±z/m. Из-за дисперсии
скорости света обе боковых состав-
составляющих и несущая распространяются по волокну каждая со своей, отличной от
других, скоростью и, следовательно, достигают приемного конца с относительным
расхождением во времени. Это расхождение приводит к ослаблению высокочастот-
высокочастотных компонент аналоговых сигналов и расширению импульсов, которыми обычно
представляются цифровые данные. Таким образом, и при аналоговой, и при цифро-
цифровой передаче сигналов величина произведения полоса х расстояние лимитируется не
только наличием шума, но и дисперсией. Анализ влияния дисперсии на аналоговые
сигналы дается в приложении 7.2.
Рис. 7.3. Дисперсия V для двух одномодовых оп-
оптических волокон различного типа как функция
длины волны света
7.1.6. Линии задерлеки и корреляторы. Компенсации задержки и кор-
корреляторы могут быть реализованы на основе как аналоговых, так и цифровых
технологий. Аналоговая система компенсации задержки может быть выполнена
в виде ряда переключаемых линий задержки с временными номиналами, обра-
образующими двоичную последовательность, в которой п-й элемент равен 2п~1то; то
соответствует линии с минимальной задержкой. Такая схема, состоящая из N
элементов, обеспечивает изменение задержки в диапазоне от нуля до B^ — 1)то
с шагом го- Для задержек, не превышающих ~ 1 мке, могут использоваться отрезки
коаксиального кабеля или световоды. Кабели для больших задержек становятся
слишком громоздкими; такие задержки можно получить с помощью устройств на
поверхностных акустических волнах. Системы с аналоговыми задержками обычно
имеют и аналоговые корреляторы. Проектирование аналоговых перемножающих
цепей обсуждалось Алленом и Фратером (Allen and Frater, 1970). Пример широ-
широкополосного аналогового коррелятора приводится в (Padin, 1994). В спектральных
корреляционных системах аналогового типа оконечный усилитель ПЧ имеет линей-
линейку фильтров, центральные частоты которых отстоят друг от друга на интервал,
равный ширине их полосы пропускания. Каждый фильтр определяет отдельный
сигнальный канал, и для каждого канала каждой пары антенн требуется отдельный
коррелятор.
Разработка цифровых схем, способных работать на высоких тактовых частотах,
привела к тому, что теперь сигнал последней ПЧ обычно оцифровывают, чтобы
затем можно было производить задержку и корреляцию сигналов цифровыми
методами. Такие цифровые системы обсуждаются в гл. 8. Их преимущество перед
аналоговыми системами заключается в большей точности измерения функции
видности, так как при аналоговой задержке сигнала, когда в сигнальных каналах
непрерывно включаются и выключаются различные элементы, очень трудно
204 Проектирование аналоговой приемной системы [Гл. 7
обеспечить постоянство частотной характеристики. Так лее трудно осуществить
и точную калибровку больших задержек, если только температура линий задержки
не поддерживается постоянной.
7.2. Гетеродин и общие вопросы фазовой стабильности
7.2.1. Схемы измерения фазы методом отражения. Синхронизация ге-
гетеродинов на антеннах может быть достигнута путем их «фазового захвата» сиг-
сигналом опорной частоты, передаваемым от центрального задающего генератора.
Наивысшую стабильность линий передачи обеспечивают кабели или световоды,
проложенные под землей. На глубине 1—2 м практически полностью устраняются
суточные колебания температуры, однако годовые колебания понижаются всего
лишь в 2—10 раз. Обсуждение температурных колебаний в грунте в зависимости от
глубины можно найти в (USAF, 1965). В качестве примера возьмем проложенный
под землей десятикилометровый кабель с коэффициентом температурного удлине-
удлинения 10~5 К. Такой кабель может подвергаться суточным колебаниям температуры
порядка 0,1 К, которые приведут к изменениям его электрической длины в пределах
1 см. Для проходящего по кабелю сигнала частотой 1 ГГц это будет соответствовать
изменению фазы на 12°. Такие же по величине фазовые сдвиги возникнут в кабеле
длиной 50 м, идущем от основания антенны в приемную кабину, который испыты-
испытывает температурные колебания в 20 К. Свой вклад в изменения фазы вносят также
вращающиеся соединения и гибкие кабели.
Изменения длины кабельного тракта могут быть определены с помощью пилот-
сигнала известной частоты. Необходимо, чтобы сигнал прошел по кабелю в обоих
направлениях, т. е. от задающего генератора к антенне и обратно, так как именно
задающий генератор представляет собой ту опорную точку, относительно которой
должна измеряться фаза. Такой способ называют методом отражения. Коррекция
измеренного отклонения фазы может выполняться как аппаратно, с использовани-
использованием фазовращателя, которым управляет измерительная система, так и программно,
путем введения коррекций в данные от коррелятора — либо в реальном времени,
либо на последующих этапах анализа данных. Наконец, можно скомбинировать два
сигнала, идущих в противоположных направлениях, и получить сигнал, в котором
фазовые отклонения будут значительно уменьшены. В качестве иллюстрации такой
процедуры рассмотрим сигнал, поданный на ближний конец свободной от потерь
линии передачи, который на дальнем ее конце даст напряжение Vb cosBttz/?). На
расстоянии ?, отсчитываемом от дальнего конца назад, исходящий сигнал равен
Vi = Vb cos2ttz/(? + ?/v), где v — фазовая скорость сигнала в линии. Предположим,
сигнал отражается от дальнего конца линии без изменения фазы. В той же точке на
расстоянии ? от дальнего конца отраженный сигнал будет равен V2 = Vq cos 2ttz/(? —
— ?/v), а сумма двух сигналов
Vi + V2 = 2V0 cos B7rz/t) cos (^) • G.10)
Первая функция косинуса в G.10) соответствует радиочастотному сигналу, фаза ко-
которого (с точностью до тг) не зависит от ? и изменений длины линии. Вторая функ-
функция косинуса является амплитудой стоячей волны. Однако на практике подобную
систему реализовать непросто из-за затухания сигнала и паразитных отражений;
поэтому появились более сложные схемы. Далее мы будем рассматривать кабельные
линии, хотя основные принципы приложимы и к другим системам передачи сиг-
7.2]
Гетеродин и общие вопросы фазовой стабильности
205
налов. Некоторые общие соображения, касающиеся, в частности, микроволновых
каналов связи, приведены в работе (Thompson et al., 1968).
7.2.2. Система С вару па и Янга. По мере развития экспериментальной тех-
техники были разработаны различные схемы отраженных измерений, и одной из пер-
первых была схема Сварупа и Янга (Swamp and Yang, 1961). Система, основанная
на ней, показана на рис. 7.4. Часть исходящего сигнала отражается на антенне
в известной точке, и изменения длины пути до отражателя контролируются путем
измерения относительной фазы сигналов на детекторе. Фаза отраженного сигнала
сравнивается с фазой опорного сигнала. Последняя может изменяться посредством
подвижного зонда, введенного в тракт исходящего сигнала. Поскольку в линии
передачи происходит много других отражений, требуемую компоненту необходимо
идентифицировать. Для этого применяется модулируемый отражатель, например,
слабо связанный с линией диод. Его состояние переключается сигналом прямо-
прямоугольной формы; для выделения модулированной компоненты отраженного сигна-
сигнала используется синхронный детектор.
Генератор
прямоугольных
импульсов
напряжения
Синхронный
детектор
К выходному
индикатору
Опорный
Резонансный
усилитель
Детектор
Модулируемый
отражатель
Генератор
частота у)
Вентиль
Модулированный
х отраженный сигнал
Направленный Направленный
отвствитель ответвитель
Длинная линия
Нагрузка
(синхронизируемый
генератор частоты v)
Подвижный
зонд
Центральная i
аппаратная '
Аппаратная
антенны
Рис. 7.4. Система для контроля изменений электрической длины линии передачи, осно-
основанная на схеме Сварупа и Янга (Swarup and Yang, 1961). Сигнал на выходе синхронно-
синхронного детектора является синусоидальной функцией разности фаз опорного (излучаемого)
и отраженного сигналов на детекторе. Выходной сигнал будет нулевым, если эти фазы
находятся в квадратурном соотношении, и положение зонда, при котором это достигается,
является мерой фазы отраженного сигнала. Благодаря вентилю зонд воспринимает только
излученную компоненту сигнала
Увеличение длины линии передачи на А? обнаруживается как соответствую-
соответствующее смещение положения зонда для нулевого отклика, равное 2А?. Оно приводит
к увеличению на антенне фазы сигнала с частотой ui на 2ttA^z/i/i7, где v — фазовая
скорость сигнала в линии. Соответствующие изменения фаз гетеродинов и сигналов
ПЧ, передаваемых по той же трассе, могут быть вычислены и использованы в ка-
качестве корректирующих значений для фаз функции видности. Другим решением
может быть введение коррекции непосредственно в сигналы с помощью фазовраща-
фазовращателя или линии переменной длины. В первоначальной разработке Сварупа и Янга
линия передачи была частью разветвленной кабельной системы антенной решетки.
206
Проектирование аналоговой приемной системы
[Гл.7
7.2.3. Система отражения со сдвигом частоты. Во второй схеме, показан-
показанной на рис. 7.5, фаза отраженного сигнала измеряется непосредственно. Сигналы,
идущие в противоположных направлениях, имеют частоты z/i и z^ отличающиеся
лишь на небольшую величину, однако достаточную, чтобы их можно было легко
разделить. Системы такого типа широко используются, и мы разберем детали этой
схемы более подробно. Заметим, что хотя направленные ответвите ли или цирку-
ляторы позволяют разделять сигналы одной частоты, если они идут в противо-
противоположных направлениях, достигаемое с их помощью подавление нежелательного
сигнала составляет всего лишь 20—ЗОдБ. Нежелательная компонента с уровнем
—30 дБ может привести к фазовой ошибке в 1,8°. Смещение частоты позволяет
разделить сигналы гораздо более уверенно.
Центральная
аппаратная
Передающая линия
-L-
Аппаратная
антенны
Управляющее
напряжение
1 Набег фазы отраженного сигнала
к компьютеру
Циркулятор
Усилитель
Смеситель
.— Направленный
I ответвитель
Рис. 7.5. Схема фазового захвата генератора частоты v^ на антенне. На аппаратуру антен-
антенны передаются частоты v\ и v\ — 1/2, используемые для получения опорной фазы. Частоты
v\ и ь>2 почти равны, поэтому разность v\ — v^ мала. Сигнал с частотой ь>2 передается на
центральную аппаратную для измерения фазы отраженного сигнала
Генератор частоты v^ на антенне захвачен по фазе разностным сигналом частот
v\ n i/i — i/2, приходящих на антенну по линии передачи. Разностная частота {ъ>\ —
— V2) мала по сравнению v\ и^. Частота v^ возвращается к месту расположения
опорного генератора для сравнения фаз.
На антенне фазы сигналов с v\ и v\ — z/2, по отношению к их фазам на цен-
центральной станции, равны 2tti/iL/v и 2tt(z/i — i/2)L/v, где L — длина кабеля. Фаза
генератора г/2 на антенне регулируется схемой захвата и равна разности этих фаз,
т. е. 2kv2L/v. Набег фазы сигнала V2 на обратном пути к центральной аппаратной
равен 2kv2L/v и, следовательно, измеренное значение фазы отраженного сигнала
(с точностью до 2тг) будет равно Att^L/v. Предположим теперь, что длина линии
изменилась на небольшую [3. Фаза генератора частоты v2 на антенне относительно
опорного генератора станет равна 2ttzv2Z/A + /3)/v. Требуемая коррекция генератора
г/2 равна половине измеренного изменения фазы. Возникающая здесь проблема со-
состоит в том, что различные эффекты, в том числе отражения и дисперсия скорости
в линии передачи, могут вносить ошибку в измеренное значение фазы. Эта ошибка
приводит к отклонению фазы генератора на антенне, которое не имеет значения до
тех пор, пока оно остается постоянным. Однако на практике оно подвержено в ли-
7.2]
Гетеродин и общие вопросы фазовой стабильности
207
янию температуры окружающей среды. Наибольшая ошибка обычно обусловлена
отражениями, и именно она определяет верхнюю границу разности частот v\ — v2.
Исследуем это ограничение.
Посмотрим, что произойдет, если в точках А и В, расположенных на линии
на расстоянии ? друг от друга, происходят отражения (см. рис. 7.5). Пусть ком-
комплексные коэффициенты отражения в этих точках равны рА и ps, и их значения
для частот v\ и v2 одинаковы. После прохождения по кабелю сигналы v\ и v2
будут содержать компоненты, которые отразились по одному разу в обоих точках
А ж В. Коэффициенты рА и рв достаточно малы, так что компонентами, которые
испытали большее число отражений, можно пренебречь. Для частоты v\ амплитуда
(напряжение) принтедшей на антенну отраженной компоненты, по отношению к не
испытавшей отражений, равна
Л= |pA||pJl(T^/10, G.11)
где а является коэффициентом затухания в кабеле в децибелах на единицу длины.
Заметим, что затухание по напряжению равно квадратному корню из затухания
по мощности. Фаза отраженной компоненты
относительно неотраженной равна, с точно- ! л
стью до 2тг,
G.12)
где фА и фв являются фазовыми углами ко-
коэффициентов рА и рв (т.е. рА = \рА\&^А
и т.д.), a v — фазовая скорость сигнала в
линии. На рис. 7.6 показано векторное пред-
представление отраженной и неотраженной ком-
компонент и их относительная фаза 0\. Отра-
Отраженная компонента приводит к отклонению
фазы сигнала на угол 0i, определяемый вы-
выражением
Падающая
компонента
единичной
амплитуды
Отраженная
компонента
амплитуды Л
Результирующий
сигнал
01 - tg0i =
Л sin#i
1 + Л cos 0i
G.13)
Рис. 7.6. Векторная диаграмма пере-
передаваемых по кабелю компонент с ча-
частотой V\
Аналогичным образом фаза сигнала с часто-
частотой v2 отклоняется на угол 02, который да-
дается выражениями, совпадающими с G.12) и G.13), если заменить индекс 1 на 2.
С учетом эффектов отражений, которые проявляются в отклонениях фаз ф\
и 02, возвратная фаза для линии длиной L оказывается равной
-1
ф\
G.14)
Если линия равномерно удлиняется до L(l + /3), углы
от ?, становятся равными соответственно ф\ + 5ф\ и
сигнала равна теперь
-1A+^) +01+501+1
\ и 02, нелинейно зависящие
02 + 5ф2- Фаза отраженного
G.15)
(Мы пренебрегаем влиянием отражения на фазу сигнала с частотой v\ — z/2, так
как v\ — v2 значительно меньше v\ или z/2, и отражения на сравнительно низкой
частоте могут быть очень малы. Кроме того, коэффициент изменения фазы v\ — v2
208 Проектирование аналоговой приемной системы [Гл. 7
в зависимости от длины линии соответственно тоже мал.) Коррекция на удлинение
линии равна половине измеренного изменения возвратной фазы:
2ttz/2/3L^-1 + i (бфг + 5ф2). G.16)
Но точное значение коррекции должно быть равно изменению на антенне фазы z/2,
т. е.
2тпу2(ЗЬу-1 + 5ф2. G.17)
Таким образом, фазовая коррекция отличается от правильного значения на вели-
величину
| Fфг + 5ф2) -5ф2 = \ {5фх - 6ф2). G.18)
Если i>\ и v2 равны, ошибка равняется нулю. Мы можем, таким образом, определить
предельное значение разности частот, исходя из допустимой величины фазовой
ошибки.
Как следует из G.13), разность фазовых углов ф\ и ф2 равна
1Л cos(9i(l + A cos6>i) + 4tt^A2 sin26>i , л
O1/1 A + Acos#i)
G.19)
Чтобы фазовые ошибки лежали в допустимых пределах, амплитуда отраженного
сигнала Л должна быть много меньше единицы, поэтому в числителе выражения
G.19) можно опустить члены с Л2, а знаменатель приблизительно равен единице.
Следовательно,
01 - ф2 ~ 4тгЬЛA/1 - i/2) cos 01. G.20)
Изменение ф\ — ф2 в зависимости от длины линии дается выражением
5ф1-6ф2=C?^(ф1-ф2) =
= Атту~гА [cos 0i - 0,lia(lnl0) cos#i - 4тгг;~1?г/1 sin6>i] (i/x - i/2))Sl G.21)
Максимальное значение выражения в квадратных скобках G.21) определяется тре-
третьим слагаемым, которое имеет порядок числа длин волн в линии. Если пренебречь
двумя другими слагаемыми, то мы получаем величину фазовой ошибки в следую-
следующем виде:
i {5ф1 - 5ф2) ~ 8ir2v-2\pA\\pB\p?210-ae/10v1 (Vl - v2) sin^. G.22)
Множ:итель ?2 • lQ-ai/10 достигает максимального значения при
? = 20(aln 10)-1. G.23)
Этот максимум возникает потому, что при малых значениях ? изменение угла
в с частотой или удлинением кабеля также мало, а для больших ? отраженная
компонента сильно затухает. Максимальное значение равно
[?21(Г^/10]тах = 10,21а-2. G.24)
Графики ?210~а?/10 для различных значений а (они соответствуют кабелям хо-
хорошего качества) приведены на рис. 7.7. Очевидно, что снижение затухания в кабеле
приводит к увеличению ошибки фазовой коррекции в G.22).
7.2]
Гетеродин и общие вопросы фазовой стабильности
209
10"
2-10'
,-2
10J
Рис. 7.7. Графики функции ^210 а?/105 построенные для четырех значений затухания
(в дБ-м), в линии а. Эта функция является коэффициентом в формуле G.22) для
ошибки фазы
Виды отражений, которые могут происходить в линии передачи, зависят от ее
типа и от того, каким образом она используется. Например, рассмотрим проло-
проложенный под землей коаксиальный кабель, идущий вдоль ряда станций, к которым
может подсоединяться передвижная антенна. Главным источником отражений в та-
таком кабеле будут разъемы на антенных станциях. Если только антенна не находится
на ближайшей станции, между ней и опорным генератором всегда будет одна или
несколько перемычек, подключаемых для обхода неиспользуемых станций. Если
на кабеле имеется п разъемов, существует N = п(п — 1)/2 их попарных комбина-
комбинаций, каждая из которых может давать отражение. Если векторы соответствующих
отраженных компонент комбинируются случайным образом, то полная среднеквад-
ратическая ошибка фазовой коррекции, как следует из G.22), будет равна
- v2)F(a,t),
G.25)
где
F(a,e) =
G.26)
Для sin вi взято среднеквадратичное значение, а коэффициенты отражения аппрок-
аппроксимированы их средней абсолютной величиной \р\.
В качестве примера рассмотрим интерферометр, предназначенный для наблюде-
наблюдений на частотах около 100 ГГц, состоящий из 10 антенн в линейной конфигурации;
антенны расположены приблизительно с равными интервалами на расстояниях
вплоть до 1 км от опорного генератора. По соединительному кабелю генератора
передается опорный сигнал с частотой v\ = 2 ГГц; кабель имеет следующие харак-
характеристики: \р\ = 0,1, а = 0,06 дБ-м, v = 2,4 • 108м-с~1 и температурный коэффи-
коэффициент электрического удлинения равен 10~5К~1.
210
Проектирование аналоговой приемной системы
[Гл.7
Из выражения G.26) находим, что F(a,?) = 1,1 • 104. При колебаниях темпера-
температуры 0,1 К относительное удлинение C = 10~6. Если фазовые ошибки на частоте
100 ГГц не должны превышать 1°, то значение 5фгтз не должно превосходить 0,02°,
и, как следует из G.25), v\ и v2 должны отличаться не более чем на 1,6 МГц.
7.2.4. Система с автоматической коррекцией. Интересный вариант схе-
схемы с отражением, показанный на рис. 7.8, был предложен Дж. Гранлундом (NRAO,
1967). Он особенно подходит для передачи стабильного опорного сигнала в ряд
пунктов, расположенных вдоль линейной антенной решетки. Стабильные генерато-
генераторы вырабатывают частоты v\ и z/2, которые подаются на противоположные концы
линии передачи. Как и ранее, разность частот v\ — v2 очень мала. На промежуточ-
промежуточной станции оба сигнала снимаются с линии с помощью направленных ответвителей
и перемножаются, давая в результате суммарную частоту. Фаза этой суммы частот
на антенной станции (рис. 7.8) равна
-1 + 2tti/2 (L -
-1 -2тгA/1 -;
¦ — 1л )V
G.27)
Для двух точек на линии в положениях 1\ и ?2 разность фаз суммарной частоты
Антенная станция
Центральный пост
Оконечная станция
Рис. 7.8. Схема, предложенная Дж. Гранлундом (NRAO, 1967) для подачи сигнала с ча-
частотой v\ + v<2 на несколько станций, расположенных вдоль линии передачи. Показана
только одна станция
равна
, -1
G.28)
Эта разность равнялась бы нулю, если бы ui и v2 были равны, но необходимо
сохранять некоторую конечную разницу частот, так как степень подавления про-
противоположного сигнала в направленных ответвителях обычно недостаточна для
адекватного разделения сигналов. В данной схеме эффект удлинения линии не
измеряется явным образом; коррекция происходит автоматически, если не считать
малого члена в G.28). Как было показано выше, свою ошибку вносят отражения
в кабеле, и они могут стать определяющим фактором при выборе разнесения частот.
Практическая реализация схемы на рис. 7.8 описана в (Little, 1969).
7.2] Гетеродин и общие вопросы фазовой стабильности 211
7.2.5. Оптоволоконная передача сигналов гетеродина. В большинстве
описанных систем гетеродинов кабельные линии передачи сигнала можно заменить
на оптоволоконные (световоды). Однако при этом нужно принимать в расчет неко-
некоторые особенности, которые перечислены ниже.
• Чтобы упростить разделение сигналов в системе с отражением, можно ис-
использовать для противоположных направлений различные длины волн. На
антенне частота лазерного сигнала от опорного гетеродина может быть сме-
смещена на несколько десятков мегагерц с помощью специального модулятора
и подана в линию в обратном направлении. Другим вариантом является ис-
использование для обратного сигнала отдельного лазера. Следует принимать
в расчет дисперсионные эффекты в оптическом волокне и температурные
изменения длины волны лазерного излучения, особенно в случае использо-
использования двух лазеров. Однако получающиеся при этом ошибки можно свести
к минимуму, если выбрать длины волн лазеров достаточно близко к точке
нулевой дисперсии световода.
• Как упоминалось в разд. 7.1, оптические компоненты, такие, как вентили
и направленные ответвители, гораздо эффективнее соответствующих микро-
микроволновых устройств. При продуманной разработке с помощью этих компонен-
компонентов вполне возможно разделение лазерных сигналов одной и той же длины
волны, распространяющихся по оптоволоконной линии в противоположных
направлениях. Известны системы, в которых радиочастотный сигнал переда-
передавался на оптической несущей, а на приемном конце ставилось полупрозрачное
зеркало, направляющее часть сигнала обратно в линию для измерения фазы
отраженного сигнала. На передающем конце, возможно, потребуется устано-
установить вентиль, чтобы достигающий лазера отраженный сигнал был как можно
слабее. Отражение сигнала лазера на его выход может нарушить его работу.
• Как правило, при изгибе многоволоконного кабеля эффективные длины
отдельных волокон изменяются незначительно и остаются согласованными
в гораздо большей степени, чем это имеет место в случае пучка коаксиальных
кабелей. С учетом требований к точности, в схеме с фазой отраженного сигна-
сигнала возможно использование двух отдельных световодов для противоположных
направлений.
• Установлено, что скручивание прямого световода, когда прочие механиче-
механические напряжения постоянны, приводит к меньшему изменению его электри-
электрической длины, чем изгиб. Скручивание, однако, может давать небольшие из-
изменения в амплитуде переданного сигнала из-за остаточной чувствительности
оптического приемника к углу линейной поляризации света.
• Для стабилизации длины оптического пути в световоде можно применить
схему с фазой отраженного сигнала, работающую на оптической длине волны.
На практике для этого потребуется автоматическая цепь коррекции, в которой
фаза обратного сигнала управляет устройством регулировки длины, так как
изменения оптического пути, сравнимые с длиной волны, могут происходить
за время гораздо меньшее секунды.
• Частота гетеродина может передаваться как разность частот двух лазерных
сигналов, передаваемых по одному световоду. Радиочастота генерируется пу-
путем суммирования оптических сигналов на фотооптическом диоде. При этом
212 Проектирование аналоговой приемной системы [Гл. 7
молено получить электрическую мощность порядка нескольких микроватт, что
достаточно для использования сигнала в качестве гетеродина SIS-смесителя.
Такая схема особенно привлекательна для приемников миллиметровых и суб-
субмиллиметровых волн (Payne et al., 1998).
• Для стандартного оптического волокна температурный коэффициент удли-
удлинения составляет приблизительно 7- 10~6К~1. Высокостабильное волокно,
разработанное Сумимото для специальных применений, имеет температурный
коэффициент примерно на порядок меньший.
7.2.6. Фазовая автоподстройка и опорные частоты. Следует упомянуть
о нескольких моментах, касающихся практической реализации систем гетеродинов.
В двух описанных выше схемах генераторы на антенне управляются системой
фазовой автоподстройки частоты (ФАПЧ). Детали разработки таких систем можно
найти, например, в работе (Gardner, 1979); здесь мы коснемся только вопроса о вы-
выборе собственной частоты схемы ФАПЧ. Как правило, эта частота должна быть
по крайней мере на порядок ниже частоты на входах фазового детектора, иначе
цепь обратной связи может оказаться слишком быстродействующей и будет вно-
вносить нежелательную фазовую модуляцию на рабочей частоте детектора. В системе
на рис. 7.5 частота входных сигналов фазового детектора равна разности ui — v<ii
верхний предел для которой был установлен исходя из рассмотрения отражений
в линии. Кроме того, полоса шумов, пропускаемых схемой ФАПЧ, пропорциональна
ее собственной частоте. Эти соображения определяют верхний предел для собствен-
собственной частоты цепи регулировки, что, в свою очередь, налагает ограничения на выбор
управляемого генератора. Для генератора с плохой стабильностью (в отсутствие
регулировки) требуется схема автоподстройки с более высокой собственной часто-
частотой, чем для высокостабильного. Для кварцевых генераторов, обладающих весьма
высокой стабильностью, требуется схема фазовой автоподстройки с собственной ча-
частотой всего в несколько герц. Они особенно подходят для длинных линий передачи,
потому что полоса шума, пропускаемого схемой ФАПЧ, соответственно также узка.
При использовании на антеннах кварцевых генераторов опорную частоту можно пе-
передавать не непрерывно, а пакетами. Сигналы, идущие в противоположных направ-
направлениях, могут в этом случае быть разделены мультиплексированием по времени
и разнесения частот не потребуется. Однако точность измерения возвратной фазы
может ограничиваться изменением импеданса на концах кабеля в моменты обраще-
обращения направления сигнала. Системы такого типа были разработаны для нескольких
больших решеток (Thompson et al., 1980); (Davies, Anderson and Morison, 1980).
Помимо установки на каждой антенне генератора, охваченного цепью фазовой
автоподстройки на опорной частоте (равной v на рис. 7.4, V2 на рис. 7.5 и v\ +
+ 1/2 на рис. 7.8), необходимо также генерировать гармоники или субгармоники этой
частоты, необходимые для частотных преобразований принимаемого сигнала. При
умножении частоты отклонения фазы возрастают пропорционально коэффициенту
умножения. Какая из частот в цепочке умножений от стандарта частоты до пер-
первого гетеродина будет выбрана для передачи с центральной станции на антенну,
обычно не имеет особого значения. Однако в случае, если передача сигнала вносит
значительные шумы, желательно передавать более высокую частоту, чтобы свести
к минимуму эффект умножения фазовых ошибок, связанных с увеличением уровня
шума.
Минимизация фазовых отклонений в цепи умножения частоты сводится глав-
главным образом к вопросу снижения температурных влияний, и в этой связи заслужи-
заслуживает внимания схема, представленная на рис. 7.9. Она может быть полезна для гене-
7.2]
Гетеродин и общие вопросы фазовой стабильности
213
рации «гребенки» частот, содержащей ряд гармоник, которые молено использовать,
например, для перестройки с дискретным шагом по частоте. Такую гребенку можно
получить, подавая ее основную частоту на варакторный диод, но напряжение, при
котором варактор переходит в проводящее состояние, изменяется в зависимости
от температуры. Соответственно изменяется фазовый угол опорного сигнала, при
котором на каждом периоде включается варактор. Это приводит к изменению фаз
генерируемых гармоник. В схеме на рис. 7.9 эффект этих изменений устраняется.
Опорный сигнал основной частоты v не подается непосредственно на генератор
гармоник, а используется для захвата фазы управляемого генератора, работающего
на той же частоте; он, в свою очередь, питает генератор гармоник. Сигнал на
основной частоте, сравниваемый с опорным, получается из сигнала от варактора
путем выделения двух соседних гармоник и суммирования их на смесительном
диоде. Фазовая цепь обратной связи поддерживает постоянной фазу этого сигна-
сигнала относительно опоры z/, подстраивая фазу управляемого генератора так, чтобы
компенсировать временное смещение точки включения варактора.
Входная
частота v
Генератор
(v)
т
f
Схема фазовой
подстройки
Фазовый
детектор
Генератор
гармоник
^*
к». =
Фильтр
1
?
Смесительный
ДИОД
Выход
гармоник
частоты v
Рис. 7.9. Схема для генерации гребенчатого спектра гармоник частоты г/, в которой фа-
фазовые изменения в генераторе гармоник компенсируются включением его в цепь фазовой
автоподстройки. Фильтр пропускает две гармоники, которые суммируются на смеситель-
смесительном диоде, давая сигнал с частотой v
В случае решетки со связанными элементами низкочастотные компоненты фа-
фазового шума центрального опорного генератора вызывают одинаковые изменения
фазы гетеродина на каждой антенне и, следовательно, их вклады в относительные
фазы сигналов, поступающих на коррелятор, должны взаимно компенсировать-
компенсироваться. Однако частотные компоненты фазового шума испытывают фазовые сдвиги
из-за временной задержки на пути распространения опорного сигнала от центра
к каждой из антенн, а также из-за задержки распространения сигнала ПЧ от со-
соответствующего смесителя до входа коррелятора (включая переменную задержку,
которая компенсирует геометрическую). Поэтому компенсация эффективна только
для компонент фазового шума с частотой настолько низкой, что эти фазовые
сдвиги мало различаются от антенны к антенне. Ширина полосы цепей фазовой
автоподстройки гетеродинов также ограничивает частотный диапазон, в котором
фазовый шум центрального генератора компенсируется. На практике подавление
фазового шума опорного генератора, как правило, эффективно вплоть до частоты,
лежащей в диапазоне от нескольких сотен герц до сотни килогерц в зависимости
от характеристик конкретной системы.
7.2.7. Фазовая стабильность фильтров. Резонансные фильтры, использу-
используемые для выделения нужных частот гетеродинов, также являются источником
температурных изменений фазы. Фазовый отклик ф фильтра в пределах его полосы
пропускания Аг/ (по уровню ЗдБ) меняется приблизительно на шг/2, где п —
порядок фильтра (число его звеньев). Соответственно скорость изменения фазы
214 Проектирование аналоговой приемной системы [Гл. 7
с частотой, измеренная на центральной частоте isq, равна
дф _ птгкг ( ,
где к\ является константой порядка единицы, зависящей от конструкции фильтра.
Центральная частота меняется в зависимости от физической температуры Т в со-
соответствии с уравнением
^ = к2и0, G.30)
где &2 — константа, определяемая коэффициентами теплового расширения и из-
изменением диэлектрической проницаемости материалов фильтра. Таким образом,
скорость изменения фазы с температурой дается выражением
дф _ дф
df ~ ~д^
дщ
Коэффициент щ/Аи есть добротность (Q-фактор) фильтра. Комбинация констант
&1&2 может быть определена экспериментально и для трубчатых полосовых филь-
фильтров с центральной частотой в диапазоне от 1 МГц до 1 ГГц имеет значение порядка
10~5 К. Если, например, для такого фильтра допускаются колебания температу-
температуры в пределах 1 К и его вклад в изменение фазы не должен превышать 0,1°, то отно-
относительная полоса пропускания должна быть не уже п/110, т. е. 5,4% для фильтра
шестого порядка. Фильтры с узкой относительной полосой должны применяться
с осторожностью. Чтобы выделить определенную частоту из ряда близко располо-
расположенных гармоник, целесообразнее иногда вместо фильтра использовать генератор
с фазовой автоподстройкой.
7.2.8. Эффекты фазовых ошибок. Быстро меняющиеся фазовые ошибки,
например, обусловленные шумом в цепях гетеродинов, приводят к потерям в ам-
амплитуде сигнала и, следовательно, в чувствительности. Они могут также приво-
приводить к ошибкам в фазе функции видности, но этот эффект незначителен, так как
быстрые вариации фазы функции видности сильно сглаживаются в результате ее
усреднения. Чтобы определить потери в чувствительности, представим сигналы от
двух антенн как напряжения V^e^71^ и Vne^n^ на входе коррелятора, где через ф
обозначены фазовые ошибки для антенн тип. На выходе коррелятора получим
r=(Vme+™Mv*e+»(-% G.32)
где угловые скобки обозначают математическое ожидание. Тогда, если Аф =
= \Фт{$) ~ Фп($)\ — фазовая ошибка, мы имеем
г = VXV* [(cos Аф) + j(sin Аф)]. G.33)
Если распределение вероятности для Аф является четной функцией с нулевым сред-
средним, что обычно и имеет место, среднее значение (по времени) слагаемого с синусом
имеет нулевое математическое ожидание. Тогда, взяв первые два члена в степенном
разложении косинуса, мы можем выразить результат через среднеквадратическую
ошибку фазы Афгтз:
[i2J G.34)
Для значений A0rms, меньших ~ 37°, точность аппроксимации косинуса не хуже
1 %. Ухудшение чувствительности на 1 % наступает при АфГШ8 = 8,1°.
7.3] Частотные характеристики сигнальных каналов 215
7.3. Частотные характеристики сигнальных каналов
7.3.1. Оптимальная частотная характеристика. Сигналы в синтезирую-
синтезирующей решетке на своем пути от выходов антенн до входов коррелятора обычно
проходят через ряд усилителей, фильтров, смесителей и линий передачи. Харак-
Характеристики всех этих устройств накладывают на сигналы свой отпечаток, и поэтому
мы должны рассмотреть их влияние на чувствительность и точность измерения
функции видности. Для учета этого влияния в принципе достаточно знать сквозную
частотную характеристику приемного канала. Важнейшими вопросами являются
определение оптимальной частотной характеристики и формулировка допустимых
отклонений от нее для каналов различных антенн. Следующее ниже обсуждение
опирается на анализ, проведенный в работе (Thompson and D'Addario, 1982).
Мы предполагаем, что радиоастрономический сигнал и шум приемника имеют
плоский спектр в пределах полосы ПЧ или спектрального канала. Тогда спектр
сигнала, поступающего на корреляторы от данной антенны, определяется ча-
частотной характеристикой соответствующей приемной аппаратуры. Если H(v) =
= \Н(у)\е^^ — функция комплексной частотной характеристики, то сигнал на
выходе коррелятора для антенн шип, обусловленный космическими сигналами,
будет пропорционален интегралу
\Hm(y)H*n{v)dv
Lo
[со "I
dv , G.35)
где мы воспользовались соотношением из (П3.6), учитывая, что произведение
НШН^ эрмитово; индексы обозначают соответствующие антенны. Нас интересует
зависимость отношения сигнал/шум от частотных характеристик сигнальных ка-
каналов. На практике частотные характеристики отличны от нуля только в пределах
ограниченного диапазона частот шириной Az/. Исходя из F.42), мы можем опре-
определить коэффициент ?>, равный относительному значению фактора сигнал/шум
в сравнении со случаем идентичных прямоугольных характеристик шириной Az/:
Re j Hm{y)H^{y)dv\
V = Lo ^ . G.36)
Ai/J|tfm(i/)|2|tfn(i/)|2di/
\ о
Это выражение достигает максимального значения, если \Нт(и)\ и |i?n(z/)| по-
постоянны в пределах полосы Az/, т. е. если амплитудная характеристика является
прямоугольной функцией. Если, кроме того, ф{у) для обеих антенн совпадают, V ра-
равен единице. Таким образом, прямоугольная полоса пропускания дает наивысшую
чувствительность в пределах ограниченной полосы частот. Заметим, что интеграл
от НШН^ равно приложим к обоим — и действительному, и мнимому — каналам
комплексного коррелятора, а следовательно, и к абсолютному значению функции
видности.
216 Проектирование аналоговой приемной системы [Гл. 7
Среди других эффектов воздействия полосы пропускания на отклик синтези-
синтезирующей решетки наиболее важным является размывание деталей синтезированного
отклика, которое ограничивает полезное поле зрения в картографируемой области.
Этот эффект был описан в разд. 6.3. При заданной чувствительности прямоуголь-
прямоугольная частотная характеристика дает наименьшее размывание, поскольку является
наиболее компактной в частотном измерении.
В точности прямоугольная полоса пропускания — это, разумеется, только иде-
идеальная модель. На практике крутизна склонов частотной характеристики определя-
определяется конкретной конструкцией и числом полюсов в комплексном отклике фильтров.
С увеличением числа полюсов форма характеристики может быть сделана более
близкой к прямоугольнику, при этом соответственно возрастает дф/дТ, как видно
из G.31). При определении допустимых отклонений действительной частотной ха-
характеристики нужно учитывать два момента: 1) ухудшение отношения сигнал/шум
и 2) появление ошибок при определении коэффициентов усиления для отдельных
антенн; эти эффекты обсуждаются ниже.
7.3.2. Допустимые отклонения частотной характеристики: ухудшение
чувствительности. Рассмотрим сначала влияние частотной характеристики на
чувствительность. Равенство G.36) определяет коэффициент ухудшения ?>, являю-
являющийся фактором сигнал/шум для частотных характеристик Нш{у) и Hn(v), взятым
по отношению к соответствующему фактору для гипотетических прямоугольных
характеристик шириной A(i/). При конструировании приемной системы обычно ста-
ставится целью получение плоской характеристики с крутыми склонами, но на практи-
практике такие эффекты, как неравномерное затухание и отражения в кабелях приводят
к появлению наклонов и осцилляции частотной характеристики, меняющихся от
антенны к антенне. Чтобы изучить эти эффекты, можно вычислить значение Т> для
исходно прямоугольной полосы, на которую накладываются различные искажения.
Рассматриваемые искажения таковы:
1. Наклон амплитудно-частотной характеристики в полосе пропускания с линей-
линейной зависимостью логарифма амплитуды от частоты.
2. Волнообразные осцилляции частотной характеристики; могут возникать из-за
отражения в линии передачи.
3. Смещение центральной частоты полосы пропускания.
4. Изменение фазовой характеристики в зависимости от частоты.
5. Ошибка компенсирующей задержки, которая приводит к появлению фазовой
компоненты, линейно зависящей от частоты.
Выражения для частотных характеристик, соответствующих перечисленным эф-
эффектам, приведены в первом столбце табл. 7.1. Во втором столбце даются выраже-
выражения для коэффициента ухудшения чувствительности Т)\ индексами тип обозначе-
обозначены параметры для конкретных антенн. Выражения из табл. 7.1 использовались для
определения предельно допустимых искажений полосы пропускания для каждого из
эффектов, при которых потери чувствительности не превышают 2,5 % (V = 0,975).
Полученные значения для допустимых отклонений показаны в табл. 7.2.
7.3]
Частотные характеристики сигнальных каналов
217
I
1*2
II
Он
ф
b
b
e
ь
ь
b
+
CD
CM
-4-
в С
о w w
C"~ <M CO -^ Ю CD
218
Проектирование аналоговой приемной системы
[Гл.7
Таблица 7.2. Примеры допустимых отклонений частотной характеристики
Тип отклонения
Критерий
Ухудшение отношения сиг- Ошибка коэфффициента
нал/шум на 2,5 % усиления в 1 %
Наклон характеристи- тт о г ^ и о т г?
^ ^ На 3,5 дБ в пределах полосы На 2,7 дБ в пределах полосы
Размах 2,0 дБ
ки
Осцилляции Размах 2,9 дБ
Смещение центральной „_.
частоты '
Отклонение фазовой фтП = 12,8° (среднеквадра- фтп = 9,1° (среднеквадра-
характеристики тичное) тичное)
Ошибка задержки
0,12/Az/
0,05/Az/
7.3.3. Допустимые отклонения частотной характеристики: погрешно-
погрешности измерения усиления. Второй эффект, накладывающий ограничение на до-
допустимые искажения частотной характеристики, связан с ошибками, возникающи-
возникающими в ходе калибровки. Если опустить шумовые составляющие, сигнал на выходе
коррелятора для пары антенн можно представить в виде
п — ^тп *тгп
G.37)
где Vmn — зависящая от источника комплексная функция видности, исходя из
которой можно построить распределение радиояркости, a Gmn — коэффициент
усиления, связанный с частотными характеристиками сигнальных каналов. Мы
предполагаем, что эти характеристики включают в себя частотные характеристики
антенн и электронной аппаратуры, так что Gmn пропорционален выходному сиг-
сигналу коррелятора для антенной пары (т, п) при наблюдении точечного источника
с единичной плотностью потока, расположенного в центре поля зрения. На практике
значения Сшп можно определить путем наблюдения калибровочных источников
с известными функциями видности. Измеренные значения усиления для антенных
пар можно непосредственно использовать для коррекции выходных данных корре-
коррелятора, однако в силу определенных соображений выгоднее определить коэффици-
коэффициенты усиления (по напряжению) для отдельных антенн д = |д|ег(^; при этом
Gmn = gmg*n- G.38)
Поскольку в большой решетке число коррелируемых пар антенн гораздо больше,
чем самих антенн (до па{па — 1)/2 пар для па антенн), не требуется использовать
все калибровочные данные. Тем самым обеспечивается значительная гибкость ка-
калибровочной процедуры; например, источник, разрешаемый на наиболее длинных
базах решетки, может использоваться для определения усиления антенн исходя из
измерений, выполненных только на менее разнесенных антенных парах. Тот же
принцип лежит в основе адаптивной калибровки, описанной в разд. 11.4.
Вообще говоря, разбиение на сомножители в G.38) предполагает, что частотные
характеристики всех антенн одинаковы или отличаются только постоянными мно-
множителями. Если это требование выполнено, мы можем представить коэффициенты
7.3] Частотные характеристики сигнальных каналов 219
усиления в виде
9= , \\H{v)\>dv . G.39)
N °
В реальных условиях частотные характеристики различаются, поэтому можно по-
получить только приблизительное решение для системы уравнений G.38), определив
оптимальные д, которые минимизируют сумму
J2\Gmn - дтд*п\2, G.40)
где суммирование производится по всем антенным парам (га, п), для которых зна-
значение Gmn может быть измерено исходя из наблюдений калибровочного источника.
При калибровке последующих наблюдений неизвестных источников вместо Gmn
в G.37) используются произведения дтдп для всех антенных пар вне зависимости
от того, прокалиброваны они непосредственно или нет. Чтобы такая методика не
вносила заметных ошибок, разности
Smn = Gmn ~ 9rn9n GЛ1)
должны быть малы, что, в свою очередь, должно обеспечиваться малым отклонени-
отклонением частотных характеристик. Таким образом, здесь мы имеем дело с отклонениями
частотных характеристик антенн не от идеальной характеристики, а друг от друга.
Используя модельные частотные характеристики для группы антенн, можно
вычислить коэффициенты усиления для их пар, оптимальные коэффициенты для
отдельных антенн и остаточные разности, что позволит определить предельно до-
допустимые отклонения частотных характеристик. Парные коэффициенты усиления
для различных типов искажений приведены в третьем столбце табл. 7.1.
В табл. 7.2 приведены примерные значения допустимых отклонений. Результаты
в определенной степени зависят от распределения искажений в модельных харак-
характеристиках, которое в случае показанных результатов были выбраны так, чтобы
максимизировать остаточные разности. Критерии, указанные в табл. 7.2 — потери
чувствительности в 2,5 % и максимальная ошибка усиления в 1 %,— использовались
при ранних наблюдениях на VLA (Thompson and D'Addario, 1982) и не обязательно
окажутся подходящими во всех случаях. В зависимости от требований к чувстви-
чувствительности и динамическому диапазону системы могут быть уместны более строгие
критерии. Для многих инструментов приемлемый уровень ошибки усиления может
быть определен путем вычисления отклика для моделей источника с различными
уровнями ошибок, введенных в модельные данные видности. В работе (Bagri and
Thompson, 1991) проводится обсуждение причин и эффектов ошибок коэффициен-
коэффициентов усиления в решетке VLA.
7.3.4. Допустимые погрешности установки задержки. Неточность
установки компенсирующих временных задержек в решетке может иметь место по
двум причинам. Неточность может быть обусловлена ошибками при калибровке
положения антенн или устройств задержки сигнала. Такие ошибки могут быть
уменьшены выбором калибровочного источника, находящегося недалеко от наблю-
наблюдаемого. Допустимые пределы ошибок определяются эффектами, перечисленными
в табл. 7.2. Существуют также ошибки, обусловленные дискретным характером
компенсирующих задержек. В аналоговых системах в тракте сигналов осуществля-
осуществляется подключение и отключение элементов с задержками, образующими двоичный
ряд значений. В цифровых системах задержка может регулироваться с шагом,
определяемым частотой тактовых импульсов, как описано в разд. 8.5. В любом
220 Проектирование аналоговой приемной системы [Гл. 7
случае имеется некоторое минимальное приращение задержки то- Если задержка
для каждой антенны переустанавливается в момент, когда величина ошибки до-
достигает го/2, вероятностное распределение ошибок является равномерным в ин-
интервале от —го/2 до го/2. Среднеквадратичная ошибка задержки для отдельной
антенны составляет, следовательно, то/2\/3- Обычно предполагается, что у любой
пары антенн их индивидуальные ошибки изменяются независимо. Следовательно,
вероятностное распределение разностной ошибки для любой пары антенн равняется
свертке распределений их индивидуальных ошибок. Это распределение является
треугольной функцией с максимальными значениями ошибки ±то и среднеквадра-
среднеквадратичным ее значением то/уб . Для однополосной приемной системы ошибки задерж-
задержки приводят к ошибке в фазе функции видности, среднеквадратическое значение
которой равняется произведению среднеквадратичной ошибки задержки на 2тп/гт8,
где г/гт8 — среднеквадратическая частота диапазона промежуточной частоты, на
которой вводится компенсирующая задержка.
Одним из методов устранения фазовой ошибки от ступенчатого изменения за-
задержки является выбор то равным обратному значению средней частоты, на кото-
которой вводится задержка. Тогда приращения задержки приводят к изменениям фазы
на целое число периодов. При такой методике требуется, чтобы полоса ПЧ была
мала по сравнению со средней частотой, чтобы значение то составляло небольшую
часть от обратной полосы. Методика успешно применялась в некоторых ранних
конструкциях решеток с узкой полосой принимаемых сигналов. Для инструментов
с широкими полосами пропускания можно свести фазовые ошибки к приемлемому
уровню, если реализовать достаточно малый шаг задержки то и выбрать достаточно
низкой промежу точную частоту, на которой задержка вводится в сигнал. Если
используется видеополоса, т. е. полоса пропускания ПЧ формируется фильтром
нижних частот, то ^rms равна Дг//уЗ. Такая схема хорошо подходит для систем
с цифровой задержкой. Она используется, например, в решетке VLA, где т$ =
= 1/C2Дг/); взяв в качестве среднеквадратичной ошибки задержки то/л/б , получим
для фазовой ошибки тг/D8\/2) рад = 2,65°. В соответствии с G.34) потери чувстви-
чувствительности составят 0,11 %.
Помимо ухудшения чувствительности, связанные с задержкой фазовые ошибки
вносят вклад в фазу измеренной функции видности. В этом плане критическими
являются значения ошибок после усреднения, а не мгновенные значения. В про-
простом методе усреднения по ячейкам, описанном в разд. 5.2, эффективное время
усреднения имеет порядок времени, за которое вектор базы пересекает ячейку.
В синтезирующей решетке компенсирующая задержка для каждой антенны регули-
регулируется таким образом, чтобы при перемещении источника по небу задержка сигнала
оставалась постоянной относительно некоторой опорной точки. Если расстояния
между антеннами велики, задержка при пересечении большинства ячеек будет из-
изменяться несколько раз, и в результате усреднения данных фазовые ошибки будут
уменьшаться. Однако для любой пары антенн скорость изменения геометрической
задержки, пропорциональная и, проходит через нуль, когда вектор базы пересекает
ось v (см. разд. 4.3). Скорость изменения аппаратных задержек в этот момент зави-
зависит от положения антенн по отношению к выбранной опорной точке задержки, но
для некоторых антенн решетки может оказаться малой. В зависимости от деталей
конфигурации решетки можно ожидать, что для некоторой (возможно, небольшой)
части данных функции видности фазовые ошибки будут сглажены усреднением
лишь незначительно.
7.3.5. Реализация требований к полосе пропускания. Требования, сум-
суммированные в табл. 7.2, относятся ко всей системе, от антенн до входов коррелятора.
На практике частотная характеристика определяется главным образом фильтра-
7.4] Ошибки рассогласования поляризаций 221
ми в оконечных каскадах сигнального тракта, непосредственно предшествующих
корреляторам или устройствам оцифровки. Спецификации этих фильтров должны
предусматривать требования к допустимым рассогласованиям частотных характе-
характеристик и учитывать температурные эффекты, о которых говорилось в разд. 7.2
(параграф «Фазовая стабильность фильтров»). Частотная избирательность эле-
элементов первых каскадов может быть тогда сведена к минимуму, необходимому
для подавления помех, и не будет оказывать заметного влияния на общую частот-
частотную характеристику. Фильтрация может быть также реализована не аналоговыми,
а цифровыми методами, уже после дискретизации сигналов. В этом случае оциф-
оцифровка осуществляется во всей полосе ПЧ. В общих чертах цифровая фильтрация
обсуждается в разд. 8.7; она имеет то преимущество, что получаемая полоса пропус-
пропускания не зависит от настройки отдельных фильтров сравнительно нечувствительна
к изменениям температуры.
7.4. Ошибки рассогласования поляризаций
Отклик двух антенн на неполяризованный источник максимален при одинако-
одинаковой их поляризации. Небольшие отклонения поляризации одной антенны относи-
относительно другой могут быть результатом механических неточностей. Эти отклонения
ведут к ошибкам в определении коэффициентов усиления антенн, подобным тем,
что возникают из-за расхождения частотных характеристик. Чтобы исследовать
данный эффект, рассчитаем отклик двух произвольно поляризованных антенн на
источник с хаотичной поляризацией, которая определяется сомножителем при па-
параметре Стокса Iv в выражении D.29). Обозначения углов относятся к эллипсу
поляризации; см. рис. 4.8 и пояснительный текст. Позиционной угол большой оси
равен ф, отношение осей равно tg%, а индексы тип соответствуют двум антеннам
решетки. В качестве примера рассмотрим две антенны с одинаковой круговой поля-
поляризацией, для которых Хт = тг/4 + А%т и Хп = тг/4 + А%п, где А-члены обозначают
отклонения соответствующих параметров от идеального значения. Искомый отклик
имеет вид
Gmn = Go [cos (фт - фп) cos {Axrn ~ A%n) + j sin (фт - фп) cos (Axm + A%n)].
G.42)
Разность фт — фп и А-члены определяются конструктивными погрешностями и ма-
малы по величине. Поэтому можно ограничиться членами первого и второго порядка
в разложении тригонометрических функций. В результате получим
Gmn = Go {l - \ [(фт - ф„J + (АХт - АХпJ] +3 (Фт -Фп)}- G.43)
Задавая модельные характеристики поляризации для группы антенн и вычислив
парные коэффициенты усиления, оптимальные коэффициенты для антенн и оста-
остаточные разности, можно провести анализ, аналогичный проделанному в разд. 7.3
для частотных характеристик. Для простоты предположим, что разброс значений
параметров х и Ф примерно одинаков. Тогда максимальная остаточная разность
усиления в 1% получится при разбросе % и ^, равном ±3,6°. Значение А% = 3,6°
соответствует отношению осей эллипса поляризации, равному 1,13. Разработка об-
облучателей с отклонениями от круговой поляризации, не превышающей этого зна-
значения вблизи оси диаграммы направленности, не представляет особых трудностей.
Аналогичный анализ для антенн с линейной поляризацией дает для допустимых
отклонений значения того же порядка (Thompson, 1984).
222 Проектирование аналоговой приемной системы [Гл. 7
7.5. Модуляция фазы
7.5.1. Снижение отклика на ложные сигналы. Метод модуляции фазы
для двухэлементного интерферометра был описан в гл. 1, где он рассматривался
в качестве одного из первых способов получения произведения аналоговых сигна-
сигналов. Его принцип ясен из рис. 1.8. Однако позднее квадратичный детектор был
заменен коррелятором. Хотя сейчас применяются более простые методы перемно-
перемножения сигналов, модуляция фазы может оказаться полезной для устранения малых
смещений на выходе коллерятора, возникающих из-за несовершенства сигнальных
трактов или из-за паразитных сигналов. Избавиться от последних довольно трудно,
так как в сложной приемной системе в тракт сигнала всегда могут просочиться
комбинации гармоник гетеродинов, попадающие в полосу пропускания системы
или полосу любой из ПЧ. Такие сигналы, слишком слабые для обнаружения при
обычном тестировании, могут быть все же достаточно сильны для того, чтобы дать
нежелательные компоненты на выходе коррелятора. Для решетки из па антенн
с полосой приема Az/, при времени наблюдения г порог обнаружения сигнала будет
находиться на уровне порядка (пау/~Кпт )~г по отношению к мощности шума;
например, — 75 дБ от уровня мощности шума для па = 27, Az/ = 50 МГц и т =
= 8 ч. Похожие эффекты могут возникать и в результате взаимодействия небольших
шумовых сигналов, проникающих из одного канала ПЧ в другой.
Поскольку паразитные сигналы вызывают появление в функции видности ком-
компонент, медленно меняющихся во времени, они проявляются в виде ложных деталей
вблизи начала координат изображения. Если такой сигнал попадает в приемный
тракт в точке, находящейся после модулятора фазы, то на синхронном детекторе
он даст компоненту, не изменяющуюся с частотой модуляции; модуляция фазы
в этом случае позволяет ослабить паразитную компоненту на несколько порядков.
7.5.2. Реализация фазовой модуляции. Рассмотрим задачу модуляции
фазы в многоэлементной решетке, где формируются произведения сигналов для
всех возможных пар антенн. Модуляцию фазы можно представить как умножение
принимаемых сигналов на периодические функции, значениями которых могут
быть +1 и — 1. Пусть для антенн тип этими функциями являются fm(t) и fn(i).
Для синхронного детектирования на выходе коррелятора этих двух антенн требует-
требуется опорный сигнал fm (i) fn (i), при этом любая неменяющаяся и немодулированная
компонента будет ослаблена на множитель
n{t)fn{t)dt, G.44)
при усреднении за время т. Для модулирующих функций, которые нас интересу-
интересуют, этот коэффициент будет равен нулю, если г кратно минимальному периоду
ортогональности тог функций fm(i) и fn(t). В действительности нежелательные
компоненты на выходе могут и не быть в точности постоянными, поскольку от-
отслеживание компенсирующих задержек приводит к медленным изменениям отно-
относительной фазы комбинирующихся паразитных сигналов. Однако нежелательные
выходные сигналы могут быть сильно ослаблены синхронным детектированием,
если их изменения за время тог будут малы. Если ортогональность модулирующих
функций зависит от их относительного сдвига, функции должны быть установлены
таким образом, чтобы они были ортогональны на входах коррелятора. Таким обра-
образом, может потребоваться регулировка фазы модулирующих функций на антеннах,
чтобы компенсировать изменение аппаратных задержек при движении источника
по небу.
7.5] Модуляция фазы 223
Реализация модуляции фазы в решетке из па антенн требует па взаимно ортого-
ортогональных двухуровневых функций. Наборы прямоугольных функций с частотами,
пропорциональными целым степеням двойки (функции Радемахера), ортогональны
при гог, равном периоду наименьшей ненулевой частоты набора. При модуляции
фазы тог равняется времени усреднения данных, которое в типичных случаях со-
составляет единицы секунд, но иногда может быть весьма малым (вплоть до Юме).
Кратчайший интервал времени между переходами модулирующих функций rsw ра-
равен половине периода самой высокочастотной функции. С аппаратной точки зрения
целесообразно, чтобы отношение ror/rsw не превышало примерно двух порядков
величины. Если на одной из антенн модуляция не производится, то ror/rsw = 2Па~1.
Прямоугольные функции одной частоты будут ортогональны, если их фазы сдвину-
сдвинуты по времени на четверть периода. Если включить в набор функции со сдвигами,
то Тог/tsw = 2n+1, где п — наименьшее целое, большее или равное (па — 3)/2.
Отношение ror/rsw уменьшается, однако ортогональность функций будет зависеть
от их относительного сдвига на входах коррелятора; в случае функций различных
частот их ортогональность от сдвига не зависит. В любом случае отношение ror/rsw
оказывается для больших решеток слишком велико; например, при па = 27 оно
имеет порядок 108 в первом случае и 104 во втором.
Полезно отметить, что условием сохранения ортогональности двух функций
разной частоты при произвольном относительном сдвиге является отсутствие у них
фурье-гармоник одной частоты. Прямоугольные функции обладают тем свойством,
что все их фурье-компоненты с четным номером (т. е. четные гармоники основной
частоты) имеют нулевую амплитуду. Таким образом, хотя синусоиды с частотами,
пропорциональными 1, 2, 3,... взаимно ортогональны, прямоугольные функции
с теми же частотами ортогональными не будут. Например, прямоугольные функции
с частотами 1, 2 и 4 не имеют общих гармоник и взаимно ортогональны, но функции
с частотами 1, 3 и 5 имеют общие гармоники и не являются ортогональными.
Д'Аддарио (D'Addario, 2001), обобщая этот анализ, показывает, что минимальный
по частотам набор N взаимно ортогональных прямоугольных функций состоит из
функций с частотами, пропорциональными 2П, где п = 0, 1,..., (N — 1), т. е. это
обсуждавшиеся выше наборы Радемахера. Поскольку различные функции из набо-
набора Радемахера не имеют общих фурье-гармоник, их ортогональность сохраняется
вне зависимости от относительного временного сдвига. Заметим также, что при
модуляции фазы строгая ортогональность не обязательна. Нежелательные отклики
могут быть ослаблены до относительной величины 10~4 и менее, если использовать
модулирующие сигналы с к периодами на время усреднения, где к являются про-
простыми числами, большими 100.
Результатов, аналогичных получаемым при модуляции фазы, можно также
достигнуть посредством синусоидальной частотной модуляции сигналов, т. е. вве-
введением в сигналы на антеннах набора ортогональных синусоид в качестве сме-
смещений частоты гетеродинов. Полезные выходные сигналы коррелятора при этом
оказываются смещенными по частоте относительно паразитных откликов, которые
не подвергаются смещению. Если при этом вращение лепестков производится не
в корреляторе, устранение частотного сдвига нужных компонент будет более слож-
сложным, чем эквивалентная схема модуляции фазы. В случае РСДБ частотные смеще-
смещения на антеннах, которые получаются естественным образом благодаря суточному
движению источника по небу, оказываются обычно настолько велики, что делают
модуляцию фазы ненужной.
224
Проектирование аналоговой приемной системы
[Гл.7
Альтернативным набором двухуровневых ортогональных функций, которые
можно использовать для реализации модуляции фазы, являются функции Уол-
ша. Это прямоугольные функции, у которых интервалы между переходами из +1
в —1 и обратно изменяются, но должны целое число раз укладываться в базовом
интервале времени, как на рис. 7.10. Описание функций Уолша (Walsh, 1923) см.,
например, в (Harmuth, 1969, 1972) или (Beauchamp, 1975). Используются различные
системы обозначения и упорядочения функций Уолша. В одной из них (Harmuth,
sal(l,t)
calC, t)
sal(9, t)
calA2, t)
Рис. 7.10. Четыре примера функций Уолша, каждая из которых показана на интервале,
соответствующем одному базовому интервалу времени. В пределах этого интервала sal-
функции нечетны, а cal-функции четны. Каждая функция принимает значения 1 и —1.
Первое число в скобках является обозначением последовательности и равно половине
числа переходов через нуль в пределах базового интервала. Время t измеряется в долях
базового интервала
1972) функции с четной симметрией обозначаются как cal (&, ?), а функции с нечет-
нечетной симметрией — как sal (&,?). Здесь t — время, выраженное в долях базового
времени Т, являющегося периодом повторения функции, а к обозначает ее по-
последовательность и равняется половине числа переходов через нуль в пределах
базового интервала времени. Функции Уолша с различными последовательностями
ортогональны, a cal- и sal-функции одной последовательности ортогональны, но
отличаются только смещением по времени. Требование ортогональности означает,
что базовые интервалы отдельных функций должны быть выровнены, поэтому
смещение по времени не допускается. Функции Уолша с последовательностями,
равными целой степени двойки, являются прямоугольными волнами. Если одна
из антенн не модулируется и используются только cal- или только sal-функции,
то наибольшей требуемой последовательностью будет (па — 1). Тогда ror/rsw = 2п,
где п является наименьшей степенью двойки, большей или равной (па — 1). Если
используются оба вида функций — cal и sal,— то п равно наименьшей степени
двойки, большей или равной (па — 1)/2. Например, для па = 64 отношение ror/rsw
равно 128 в первом случае и 64 во втором.
Другим обозначением функций Уолша является wal (n, ?), которое единообразно
представляет cal- и sal-функции, причем cal (n, t) = wal Bn, t) и sal (n, t) = wal Bn —
— 1, i). Один из методов порождения функций Уолша использует матрицы Адамара;
матрица наименьшего порядка имеет вид
1 1
1 -1
G.45)
Матрицы более высокого порядка получаются заменой каждого из элементов Н2
матрицей К^ умноженной на заменяемый элемент [что эквивалентно внешнему
7.5]
Модуляция фазы
225
произведению матриц; см. D.51)]. Если, например, произвести эту операцию два-
дважды, мы получим
11111111] cal@,0, pal @,0
1-1 1-1 1-1 1-1
1 1-1-1 1 1-1-1
1-1-1 1 1-1-1 1
1 1 1 1-1-1-1-1
1-1 1-1-1 1-1 1
1 1-1-1-1-1 1 1
1-1-1 1-1 1 1-1
sal D,0, pal D,0
sal B,0, pal B,0
calB,0, pal F,0
sal A,0, pal A,0
cai lo, v), pai iо, v)
cal(l,O, pal C,0
sal C,0, pal G,0-
G.46)
Строки матрицы соответствуют показанным функциям Уолша, причем в данном
конкретном процессе знаки нечетных последовательностей должны быть изменены.
Сигнал, необходимый для фазового детектора, является произведением двух моду-
модулирующих функций антенн. Произведение двух функций Уолша является также
функцией с последовательностью, большей или равной разности двух исходных
функций.
Функции Уолша могут также генерироваться как произведения функций Ра-
демахера. Функции Радемахера обозначаются выражениями вида R(n, 0? гДе п —
целое, а полупериод функции равен Т/2П; другими словами, в базовый период Т
укладывается 2п~1 полных циклов. Функция R@,0 имеет постоянное единичное
значение. В примерах рис. 7.10 функция sal A,0 совпадает с функцией Радемахера,
a cal C,0 и sal (9,0 являются произведениями sal A,0 и ДРУГОИ функции Радемахе-
Радемахера. Рассматривая функции Уолша как произведения функций Радемахера, удобно
использовать обозначения Пэли pal(n, 0 (Paley, 1932). Целое п называется нату-
натуральным порядком функции Уолша. Функция pal (n, 0? являющаяся произведением
функций Радемахера R(z,0? Щ.7>0? • • •? Щ^?0? имеет натуральный порядок п =
= 2г~1 + 2-7 + ... + 2Ш~1. Произведение двух функций Уолша (также функция
Уолша) имеет натуральный порядок, равный сумме по модулю 2 (сложение без
переноса) двоичных натуральных порядков двух своих компонент.
Табл. 7.3 показывает взаимосвязь между натуральными порядками ряда функ-
функций Уолша и компонентами Радемахера, из которых они образуются. Произведение
двух функций Уолша можно представить в виде произведения их компонент Раде-
Радемахера, например,
pal G,0 х pal A0,0 = [R(l,0 х RB,0 x RC,0] x [RB,0 x RD,0] =
= R(l,0 x RB,0 x RB,0 x RC,0 x RD,0 =
= R(l, 0 x RC,0 x RD,0 = pal A3,0, G.47)
где мы воспользовались тем фактом, что умножение функции Уолша или Радемахе-
Радемахера на саму себя дает тождественную единицу. Натуральные порядки двух функций
Уолша в этом примере равны 7 и 10, или в двоичной форме 0111 и 1010. Сложение
их по модулю 2 дает 1101, или 13 в десятичной форме; это и есть натуральный
порядок проиизведения.
Исследуя функции Уолша как произведения функций Радемахера, можно по-
понять, как они работают в схеме модуляции фазы, эффективно устраняя нежела-
нежелательные компоненты сигнала (Emerson, 1983). Пусть U(t) — паразитная компонента
отклика, обусловленная просачиванием сигналов ПЧ или ошибками в устройстве
оцифровки сигнала. Компонента U(t) возникает уже после первоначальной моду-
модуляции сигнала, поэтому на позднем этапе синхронного детектирования с помощью
8 Томсон
226 Проектирование аналоговой приемной системы [Гл. 7
Таблица 7.3.
Натуральные
порядки
pal @,*)
pal(l,*)
pal B,*)
pal C,*)
pal D,*)
pal E,*)
pal F,*)
pal G,*)
pal (8,*)
pal (9,*)
pal A0,*)
pal A1,*)
pal A2,*)
pal A3,*)
pal A4,*)
pal A5,*)
Компоненты
Радемахера некоторых функций Уолша
Компоненты
R@,*) R(l,*
1
1
1
1
1
1
1
1
1
) RB
1
1
1
1
1
1
1
1
Радемахера
,*) RC,*)
1
1
1
1
1
1
1
1
RD,*)
1
1
1
1
1
1
1
1
Последовательные
порядки
cal @,*)
sal(l,*)
sal B,*)
cal(l,*)
sal D,*)
cal C,*)
cal B,*)
sal C,*)
sal (8,*)
cal G,*)
cal F,*)
sal G,*)
cal D,*)
sal E,*)
sal F,*)
cal E,*)
модулирующего сигнала W(?) становится равной W(t) pal (n, t), и получившееся про-
произведение эффективно сглаживается последующим усреднением. Предположим,
что pal (n, t) является произведением т функций Радемахера R(z,t), R(j, i), ...,
R(?, t). Мы можем рассматривать умножение U(i) на pal(n, t) как эквивалентное
последовательным умножениям на функции Радемахера из соответствующего на-
набора компонент. Предположим, кроме того, что период функций Радемахера мал по
сравнению с характерным временем вариаций U(i). Тогда после первого умножения
и усреднения среднее остаточное напряжение паразитного сигнала будет равно
(t) = l - ¦ Mi _st ш _ т ш
2 2 dt 2*+1 dt '
где St равняется половине периода функции Радемахера Т/2г. Значение Ui вычисля-
вычисляется для одного периода R(i, *), но в предположении, что U(i) изменяется медленно,
Ui молено принять равным среднему значению за базовое время Уолша Т. Умно-
Умножение на вторую функцию Радемахера соответствует замене U в выраженииG.48)
на Ui, что дает
А
7.5] Модуляция фазы 227
Для т компонент Радемахера мы получаем
UU^=2iiJ...+t+m)d-Jr, G.50)
где остаются только высшие производные Ы.
Функции Уолша pal(n,?), у которых п равняется целой степени двойки, наи-
наименее эффективны в плане устранения паразитных откликов, так они являются
просто отдельными функциями Радемахера. Как показывает изучение табл. 7.3,
наибольшее число компонентов Радемахера содержат те функции, для которых
п = 2к — 1, где к — целое. Для решеток с небольшим числом антенн, где не тре-
требуется большое число различных модулирующих функций, молено выбрать функ-
функции Уолша, наиболее эффективные в плане подавления нежелательных компонент.
Аналогичным образом, функции Уолша могут быть эффективнее прямоугольных
волн в некоторых приложениях с одиночной антенной, таких, как переключение
диаграммы с источника на калибровочную точку неба (Emerson, 1983). Одно из
первых приложений функций Уолша в линиях передачи описано в (Fowle, 1904).
Другой набор возможных функций, модулирующих фазу — т-последователь-
ности — рассматривается в (Keto, 2000) для случаев, где требуется переключать
фазу как на 90°, так и на 180°.
7.5.3. Связь модуляции фазы с вращением лепестков и компенсацией
задержек. Эффективность модуляции фазы в плане подавления откликов на па-
паразитные сигналы зависит от того, в какой точке эти паразитные сигналы попадают
в сигнальный тракт. Ниже приведены три наиболее важных случая.
1. Нежелательный сигнал появляется на входе антенн или в некоторой точке
сигнальных трактов, предшествующей модуляции фазы, вращению лепестков
и компенсации задержки. В этом случае нежелательный сигнал подвергает-
подвергается модуляции фазы наравне с полезным и не подавляется при синхронном
детектировании (хотя он может ослабляться благодаря вращению лепестков,
если частота интерференции высока, как это имеет место в РСДБ). Таким же
образом ведут себя внешние помехи, влияние которых обсуждается в гл. 15.
2. Нежелательный сигнал появляется после модуляции фазы, но до вращения
лепестков и компенсации задержки. Фазовые сдвиги при вращении лепестков,
которые должны сводить к нулю частоту интерференции полезных сигналов
на выходе коррелятора, воздействуют на паразитный сигнал таким обра-
образом, что на выходе коррелятора он выглядит как компонента с естественной
частотой интерференции, соответствующая точечному источнику в позиции
фазового центра. Затем эта компонента подвергается синхронному детектиро-
детектированию посредством функции Уолша. Если естественная частота интерферен-
интерференции случайно совпадет с фурье-гармоникой этой функции, может возникнуть
паразитный отклик.
3. Паразитный сигнал появляется после модуляции фазы и вращения ле-
лепестков, но до компенсации задержек. Затем сигнал в результате изменения
компенсирующей задержки испытывает фазовые сдвиги. Соответствующая
компонента на выходе коррелятора имеет частоту, равную естественной ча-
частоте интерференции в случае, если бы наблюдения велись на частоте ПЧ,
на которой вводятся компенсирующие задержки. В результате осцилляции
имеют частоту на один — три порядка более низкую, чем естественная частота
интерференции, и, следовательно, в этом случае проще избежать совпадения
с частотой одной из компонент функции Уолша.
228
Проектирование аналоговой приемной системы
[Гл.7
Из сказанного ясно, что модуляцию фазы и вращение лепестков выгоднее про-
производить на возможно более ранних стадиях прохождения сигнала через прием-
приемный тракт. В качестве примера на рис. 7.11 показана схема, используемая на VLA
(Granhmd, Thompson and Clark, 1978). Модуляция фазы на антенне производится
в гетеродине, а не в тракте сигнала, поэтому не требуется широкополосный фа-
фазовый модулятор. Сигналы оцифровываются на выходе оконечного усилителя ПЧ
и, соответственно, подвергаются задержке и перемножению уже в цифровом виде.
Поскольку цифровые схемы не подвержены, в отличие от аналоговых, нежелатель-
нежелательным дрейфам и сдвигам, нет смысла включать их в тракт между модулятором фазы
и синхронным детектором. Поэтому синхронное детектирование может выполнять-
выполняться просто путем обращения знакового бита в цифровом представлении сигнала,
и производится оно лишь в па сигнальных каналах, а не на па (па — 1)/2 выходах
коррелятора.
Входное
устройство
смеситель и ПЧ
Полноводная
передающая
система
Оконечный
усилитель ПЧ
Устройство
дискретизации
±
Компенсирующая
задержки
Переключатель
фазы
Гетеродин
Буферный
регистр
Компьютер
Буферный
регистр
К цифровым
корреляторам
Рис. 7.11. Упрощенная схема приемного канала одной из антенн VLA. Значения функ-
функции Уолша, генерируемые компьютером, периодически загружаются в цифровые буферы,
откуда они подаются на переключатель фазы и схему обращения знака в устройстве
дискретизации. Рисунок взят из (Granhmd, Thompson and Clark, 1978). ©1978 IEEE
7.6. Автоматическая регулировка уровня и калибровка
усиления
В большинстве синтезирующих антенных решеток имеются схемы авто-
автоматической регулировки усиления (АРУ), которые служат для поддержания
в определенных критических точках постоянного уровня общего сигнала, т. е. сум-
7.6] Приложение 7.1. Смеситель с разделением полос 229
марного уровня космического сигнала и системного шума. Часть сигнала детекти-
детектируется и полученное напряжение сравнивается с известным значением; получаемый
в результате управляющий сигнал подается на тот или иной элемент сигнально-
сигнального тракта с переменным усилением. К точкам, критичным в отношении уровня
сигнала, относятся модуляторы для передачи сигналов ПЧ по оптоволоконным
или микроволновым линиям связи, входы аналоговых корреляторов или устройств
дискретизации. Обсуждение допустимых уровней сигнала проводится в разд. 8.4.
Действие цепи АРУ сводится к поддержанию постоянного значения \д\2 (Т$ +
+ Та) Д^Л гДе 9 — усиление по напряжению от входа антенны до контрольной
точки, Ts — температура системы, а Та — составляющая антенной температуры,
обусловленная наблюдаемым источником. Таким образом, \д\ необходимо изменять
в направлении, обратном сумме (Ts + Та), которая может существенно зависеть
от угла места антенны, как следствие изменений уровня излучения почвы, захва-
захватываемого боковыми лепестками диаграммы, и атмосферного поглощения. Чтобы
контролировать эти изменения усиления, на вход приемной системы может пода-
подаваться сигнал от широкополосного источника шума. Этот источник модулируется
обычно с частотой от единиц до сотен герц; соответствующая компонента сигнала
выделяется и контролируется с помощью синхронного детектора. Источник шума
добавляет к общей шумовой температуре системы Тс калибровочную компоненту,
которая не должна превышать нескольких процентов от Ts, чтобы не ухудшить
чувствительность. Амплитуда переключаемой компоненты прямо пропорциональна
усилению системы, и при Ts ^> Та отношение уровней сигнала при подключенном
и отключенном источнике шума равно 1 + Тс /Ts, что дает возможность постоянно
контролировать Ts. Такая схема учитывает изменение коэффициента усиления ан-
антенны из-за механических деформаций, поэтому он должен калиброваться отдельно
посредством периодического наблюдения радиоисточника.
Приложение 7.1. Смеситель с разделением полос
Принцип работы смесителя с разделением полос (с подавлением зеркальной по-
полосы) показан на рис. П7.1. Члены cos B-Kvut) и cos Bтп^?) представляют частотные
компоненты входного сигнала соответственно в верхней и нижней боковых полосах
частот. Входной сигнал подается на два смесителя, сигналы гетеродинов которых,
с частотой г/ъо, имеют квадратурное соотношение фаз. Смесители выдают произве-
произведения входных сигналов с сигналами гетеродинов, а фильтры пропускают только
составляющие с частотой, равной разности г/ъо и одной из частот г/и или щ. Сигнал
с нижнего смесителя проходит также через фазосдвигающую цепь, задерживающую
его на тг/2. Складывая сигналы в точках А ж В, получаем отклик для сигнала
верхней боковой полосы. Точно также, подавая те же сигналы на вычитающую
схему, можно получить отклик нижней полосы. В любом случае степень подавления
отклика от нежелательной боковой полосы определяется точностью реализации
фазовых квадратур, точностью соответствия частотных характеристик смесителей
и фильтров, а также потерями, вносимыми фазосдвигающей цепочкой. На практике
при преобразовании сигнала видимого диапазона до нескольких гигагерц, нетруд-
нетрудно получить уровень подавления — 20 дБ. При тщательной настройке достижимы
уровни подавления, приближающиеся к —30 дБ (Archer, Granlund and Mauzy, 1981).
При преобразовании сигналов миллиметрового диапазона подавление зеркальной
полосы может быть менее эффективным.
230
Проектирование аналоговой приемной системы
[Гл.7
Вход
о—
cos 2tivm t +
+ cos
Фильтр ПЧ
или
видеофильтр
i
cos 2nvL01
cos BhvLq f - я/2)
Фильтр ПЧ
или
видеофильтр
cos2n(vL0- Vp )t
- Vj )t]
Схема
задержек
по фазе на те/2
Рис. П.7.1. Схематическая иллюстрация принципа работы смесителя с разделением полос
(с подавлением зеркальной полосы). Отклик от верхней полосы получается как сумма
сигналов с выходов А и В, а отклик от нижней полосы — как разность этих сигналов
Приложение 7.2. Дисперсия в оптическом волокне
Для частотной компоненты vm сигнала, модулирующего оптическую несущую
A sin B7Ti/opt + 0), которая передается по оптоволоконной линии, сигнал на выходе
последней может быть представлен в виде
А2 [1 + т cos Bтп/ш?)] sin2B7rz/optt + ф) =
= A2 sin2B7rz/opt? + ф) + ^-^ sin [2тг (i/opt + i/m)(t + At) + 0] sin B7n/opt? + 0) +
A2m
sin [2тг (i/opt -
+ 0] sin B7ri/optt + ф), (П7.1)
где 777, — коэффициент модуляции. Эта формула напоминает обычное выражение
для амплитудной модуляции, за исключением того, что здесь модулирующим сигна-
сигналом линейно варьируется мощность несущей. Поэтому в левой части стоит квадрат
выражения для несущей. Временное смещение ±At в членах для частоты i/opt ± г/т
выражает зависимость скорости распространения от частоты. Величина At может
принимать как положительные, так и отрицательные значения в зависимости от
знака дисперсии V, показанной на рис. 7.3. Каждое из слагаемых в (П7.1) пропорци-
пропорционально оптической мощности и, таким образом, амплитуде модуляции. Применяя
выражение для произведения синусов к каждому из слагаемых в правой части
(П7.1) и отбрасывая члены для радиочастоты и постоянного тока, мы получаем
для амплитуды сигнала на выходе оптического приемника
{cos [27rz/m(t + At) - 27ri/optAt] + cos [2тп/т(* - At) - 27ri/optAt]} =
= ^p~ {cos [2тг (vmt - i/opt At)] cos B7ri/mAt)}. (П7.2)
Световая длина волны в вакууме, соответствующая частоте ^opt? равна Aopt, а раз-
разность длин волн для частот z/opt и z/opt + z/m равна Л2р1.1/т/с. Если Т> — дисперсия,
а ? — длина световода, то At = V?\2ptvm/c и z/optAt = V?Xopt. Таким образом,
восстановленный сигнал может быть записан в виде
А2тп
{cos [2тп/т(* - V?Xopt)] cos B
(П7.3)
7.6] Цитированная литература 231
Изменение фазы, вносимое At на частоте несущей ^opt, проявляется в фазе частоты
модуляции в первой функции косинуса правой части (П7.2). На частоте vm этот фа-
фазовый член эквивалентен временной задержке V?\ovt, как молено видеть из (П7.3).
Эта задержка существенно больше, чем At, и соответствует разнице между фазовой
и групповой скоростями света в оптическом волокне. Второй косинус модифицирует
амплитуду компоненты г/т модулирующего сигнала. Например, при дисперсии V =
= 2пс (нм-км) (заметим, что это эквивалентно 2-10~6 с-м~2), ? = 50км, Aopt =
= 1550 нм и уш = 10 ГГц, получаем At = 8пс, X>?Aopt = 155 нс, и отклик на частоте
vm уменьшается на 1,1 дБ по сравнению с низкочастотной границей спектра моду-
модулирующего сигнала. Отметим, что выше мы предположили, что ширина спектра
лазерного луча определяется исключительно частотной полосой модуляции, что
вполне оправдано в случае высококачественного лазера с внешним модулятором.
Модуляция диодного лазера посредством изменения питающего напряжения мо-
может приводить к нежелательной частотной модуляции, еще более расширяющей
оптический спектр.
Цитированная литература
Agrawal G. P. Fiber-Optic Communication Systems. Wiley, New York, 1992.
Allen L. R. and R. H. Frater. Wideband Multiplier Correlator. Proc. IEEE, 117, 1603-1608,
1970.
Archer J. W.j E. M. Caloccia and R. Serna. An Evaluation of the Performance of the VLA
Circular Waveguide System. IEEE Trans. Microwave Theory Tech., MTT-28, 786-791, 1980.
Archer J. W., J. Granlund and R. E. Mauzy. A Broadband UHF Mixer Exhibiting High Image
Rejection over a Multidecade Baseband Frequency Range. IEEE J. Solid-State Circuits, SC-
16, 385-392, 1981.
Baars J. W. M., J. F. van der Brugge, J. L. Casse, J. P. Hamaker, L. H. Sondaar, J. J.
Visser and K. J. Wellington. The Synthesis Radio Telescope at Westerbork. Proc. IEEE, 61,
1258-1266, 1973.
Bagri D. S. and A. R. Thompson. Hardware Considerations for High Dynamic Range Imaging.
Radio Interferometry: Theory, Techniques and Applications, T. J. Cornwell and R. A. Perley,
Eds., Pub. Astron. Soc. Pacific Conf. Ser., 19, 47-54, 1991.
Batty M. J., D. L. Jauncey, P. T. Rayner and S. Gulkis. Tidbinbilla Two-Element Interfer-
Interferometer. Astron. J., 87, 938-944, 1982.
Beauchamp K. G. Walsh Functions and Their Applications. Academic Press, London, 1975.
Borella M. S., J. P. Jue, D. Banergee, B. Ramamurthy and B. Mukherjee. Optical Components
for WDM Lightwave Networks. Proc. IEEE, 85, 1274-1307, 1997.
Bracewell R. N., R. S. Colvin, L. R. D'Addario, C. J. Grebenkemper, К. М. Price and A. R.
Thompson. The Stanford Five-Element Radio Telescope. Proc. IEEE, 61, 1249-1257, 1973.
Callen H. B. and Welton T. A. Irreversibility and Generalized Noise. Phys. Rev., 83, 34-40,
1951.
Casse J. L., E. E. M. Woestenburg and J. J. Visser. Multifrequency Cryogenically Cooled
Front-End Receivers for the Westerbork Synthesis Radio Telescope. IEEE Trans. Microwave
Theory Tech., MTT-30, 201-209, 1982.
D'Addario L. R. Orthogonal Functions for Phase Switching and a Correction to ALMA Memo.
287. ALMA Memo. 385, National Radio Astronomy Observatory, Socorro, NM, 2001.
Davies J. G., B. Anderson and I. Morison. The Jodrell Bank Radio-Linked Interferometer
Network. Nature, 288, 64-66, 1980.
Elsmore В., S. Render dine and M. Ryle. Operation of the Cambridge One-Mile Diameter Radio
Telescope. Mon. Not. R. Astron. Soc, 134, 87-95, 1966.
232 Проектирование аналоговой приемной системы [Гл. 7
Emerson D. Т. The Optimum Choice of Walsh Functions to Minimize Drift and Cross-Talk.
Working Report 127 IRAM, Grenoble, July 18, 1983.
Erickson W. C, M. J. Mahoney and K. Erb. The Clark Lake Teepee-Tee Telescope. Astrophys.
J. Suppl., 50, 403-420, 1982.
Fowle F. F. The Transposition of Electrical Conductors. Trans. Am. Inst. Elect. Eng., 23,
659-689, 1904.
Gardner F. M. Phaselock Techniques. 2nd ed., Wiley, New York, A979).
Granlund J., A. R. Thompson and B. G. Clark. An Application of Walsh Functions in Radio
Astronomy Instrumentation. IEEE Trans. Electromagn. Compat., EMC-20, 451-453, 1978.
Harmuth H. F. Applications of Walsh Functions in Communications. IEEE Spectrum, 6, No.
11, 82-91, 1969.
Harmuth H. F. Transmission of Information by Orthogonal Functions. 2nd ed., Springer-Verlag,
Berlin 1972.
К err A. R. Suggestions for Revised Defintions of Noise Quantities, Including Quantum Effects.
IEEE Trans. MTT, 1999.
Kerr A. R., M. J. Feldman and S.-K. Pan. Receiver Noise Temperature, the Quantum Noise
Limit and the Role of Zero-Point Fluctuations. Proc. 8th Int. Symp. Space Terahertz Technol-
Technology, March 25-27, p. 101-111, 1997; also MMA Memo. 161, NRAO, Charlottesville, VA, 1997.
Keto E. Three-Phase Switching with m-Sequences for Sideband Separation in Radio Interfer-
ometry. Pub. Astron. Soc. Pacific, 112, 711-715, 2000.
Kraus J. D. Radio Astronomy. McGraw-Hill, New York, 1966, p. 261-263; 2nd ed., Cygnus-
Quasar Books, Powell, OH, 1986.
Little A. G. A Phase-Measuring Scheme for a Large Radiotelescope. IEEE Trans. Antennas
Propag., AP-17, 547-550, 1969.
Napier P. J., D. S. Bagri, B. G. Clark, A. E. E. Rogers, J. D. Romney, A. R. Thompson and
R. С Walker. The Very Long Baseline Array. Proc. IEEE, 82, 658-672, 1994.
Napier P. J., A. R. Thompson and R. D. Ekers. The Very Large Array: Design and Performance
of a Modern Synthesis Radio Telescope. Proc. IEEE, 71, 1295-1320, 1983.
NRAO. A Proposal for a Very Large Array Radio Telescope. Vol. II, National Radio Astronomy
Observatory, Green Bank, WV, 1967, Ch. 14.
Nyquist H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev., 32, 110-113, 1928.
Padin S. A Wideband Analog Continuum Correlator for Radio Astronomy. IEEE Trans.
Instrum. Meas., IM-43, 782-784, 1994.
Paley R. E. A Remarlable Set of Orthogonal Functions. Proc. London Math. Soc, 34, 241-279,
1932.
Payne J. M. Millimeter and Submillimeter Wavelength Radio Astronomy. Proc. IEEE, 77,
993-1071, 1989.
Payne J. M.j L. D'Addario, D. T. Emerson, A. R. Kerr and B. Shillue. Photonic Local Oscil-
Oscillator for the Millimeter Array. Advanced Technology MMW, Radio and Terahertz Telescopes,
T. G. Phillips, Ed., Proc. SPIE, 3357, 143-151, 1998.
Payne J. M.j J. W. Lamb, J. G. Cochran and N. J. Bailey. A New Generation of SIS Recievers
for Millimeter-Wave Radio Astronomy. Proc. IEEE, 82, 811-823, 1994.
Phillips T. G. Millimeter and Submillimeterwave Receivers. Astronomy with Millimeter and
Submillimeter Wave Interferometry, M. Ishiguro and W. J. Welch, Eds., Astron. Soc. Pacific
Conf. Ser., 59, 68-77, 1994.
Phillips T. G. and D. P. Woody. Millimeter- and Submillimeter-Wave Receivers. Ann. Rev.
Astron. Astrophys., 20, 285-321, 1982.
Pospieszalski M. W., W. J. Lakatosh, E. Wollack, Loi D. Nguyen, M. Le, M. Lui, T. Liu.
Millimeter-Wave Waveguide-Bandwidth Cryogenically-Coolable InP HEMPT Amplifiers. 1997
IEEE MTT-S International Microwave Symposium Digest, Denver, CO, 1285-1288, 1997.
7.6] Цитированная литература 233
Read R. В. Two-Element Interferometer for Accurate Position Determinations at 960 Me. IRE
Trans. Antennas Propag., AP-9, 31-35, 1961.
Reid M. S.j R. С Clauss, D. A. Bathker and С. T. Stelzried. Low Noise Microwave Receiving
Systems in a Worldwide Network of Large Antennas. Proc. IEEE, 61, 1330-1335, 1973.
Sinclair M. W., G. R. Graves, R. G. Gough and G. G. Moorey. The Receiver System. Proc.
IREE Aust., 12, 147-160, 1992.
Swarup G. and K. S. Yang. Phase Adjustment of Large Antennas. IRE Trans. Antennas
Propag., AP-9, 75-81, 1961.
Thompson A. R. Tolerances on Polarization Mismatch. VLB Array Memo. 346, National Radio
Astron. Obs. Charlottesville, VA, March 1984.
Thompson A. R., B. G. Clark, C. M. Wade and P. J. Napier. The Very Large Array. Astrophys.
J. Suppl., 44, 151-167, 1980.
Thompson A. R. and L. R. D'Addario. Frequency Response of a Synthesis Array: Performance
Limitations and Design Tolerances. Radio Sci., 17, 357-369, 1982.
Thompson M. C., L. E. Wood, D. Smith and W. B. Grant. Phase Stabilization of Widely
Separated Oscillators. IEEE Trans. Antennas Propag., AP-16, 683-688, 1968.
Tiuri M. E. and A. V. Rdisdnen. Radio-Telescope Receivers. Radio Astronomy, 2nd ed., J. D.
Kraus, Cygnus-Quasar Books, Powell, OH, 1986, Ch. 7.
Tucker J. R. Quantum Limited Detection in Tunnel Junction Mixers. IEEE J. Quantum Elect.,
QE-15, 1234-1258, 1979.
Tucker J. R. and Feldman M. J. Quantum Detection at Millimeter Wavelengths. Rev. Mod.
Phys., 57, 1055-1113, 1985.
USAF. Handbook of Geophysics and Space Environments. S. L. Valley, Ed., U.S. Air Force
Cambridge Research Laboratories, Bedford, MA, 1965, p. 3-20-3-22.
Walsh J. L. A Closed Set of Orthogonal Functions. Ann. J. Math, 55, 5-24, 1923.
Webber J. C., A. R. К err, S.-K. Pan and M. W. Pospieszalski. Receivers for the Millimeter
Array. Advanced Technology MMW, Radio and Terahertz Telescopes. T. G. Phillips, Ed.,
Proc. SPIE, 3357, 122-131, 1998.
Weinreb S., M. Balister, S. Maas and P. J. Napier. Multiband Low-Noise Receivers for a Very
Large Array. IEEE Trans. Microwave Theory Tech., MTT-25, 243-248, 1977a.
Weinreb S., D. L. Fenstermacher and R. W. Harris. Ultra-Low-Noise 1.2- to 1.7-GHz Cooled
GaSaFET Amplifiers. IEEE Trans. Microwave Theory Tech., MTT-30, 849-853, 1982.
Weinreb S., R. Predmore, M. Ogai and A. Parrish. Waveguide System for a Very Large
Antenna Array. Microwave J., 20, March, 49-52, 1977b.
Welch W. J., J. R. Forster, J. Dreher, W. Hoffman, D. D. Thornton and M. С. Н. Wright.
An Interferometer for Millimeter Wavelengths. Astron. Astrophys., 59, 379-385, 1977.
Welch W. J. and 36 coauthors. The Berkeley-Illinois-Maryland-Association Millimeter Array.
Pub. Astron. Soc. Pacific, 108, 93-103, 1996.
Wengler M. J. and Woody D. P. Quantum Noise in Heterodyne Detection. IEEE J. Quantum
Electron., QE-23, 613-622, 1987.
Wright M. C. H., B. G. Clark, C. H. Moore and J. Сое. Hydrogen-Line Aperture Synthesis at
the National Radio Astronomy Observatory: Techniques and Data Reduction. Radio Sci., 8,
763-773, 1973.
Young A. C, M. G. McCulloch, S. T. Abies, M. J. Anderson and Т. М. Percival. the Local
Oscillator System. Proc. IREE Aust., 12, 161-172, 1992.
Zorin A. B. Quantum Noise in SIS Mixers. IEEE Trans. Magn., MAG-21, 939-942, 1985.
Глава 8
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
Применение цифровой техники вместо аналоговой имеет важные практические
преимущества в плане реализации компенсирующих задержек и вычисления кор-
корреляции сигналов. В цифровых схемах задержки ее точность определяется точно-
точностью тактовых импульсов системы, и точность порядка десятков или сотен пико-
секунд для больших задержек гораздо проще достигается цифровыми средствами,
чем с помощью аналоговых линий задержки. Более того, цифровые устройства
не вносят в сигнал никаких искажений, не считая заранее известных эффектов
квантования. С другой стороны, в аналоговой системе трудно сохранять в допу-
допустимых пределах форму частотной характеристики, когда в сигнальных каналах
происходит постоянное подключение и отключение элементов задержки. Корреля-
Корреляторы *) с широким динамическим диапазоном также проще реализуются цифро-
цифровыми средствами, в том числе корреляторы с многоканальным выходом, требуе-
требуемые для спектральных наблюдений. Для аналоговой реализации многоканальных
корреляторов требуются блоки фильтров, разбивающих полосу сигнала на много
узких каналов. Такие фильтры при изменениях температуры окружающей среды
могут быть источником фазовой нестабильности. Наконец, если не брать в расчет
случаи предельных тактовых частот (полос сигнала), цифровые схемы требуют
гораздо меньших настроек, чем аналоговые, и более подходят для тиражирования
в больших количествах (для больших антенных решеток).
Преобразование сигнала в цифровую форму требует периодической выборки
значений напряжения с последующим их квантованием, которое позволяет пред-
представить каждое из значений сигнала конечным числом бит. Число бит на одно
значение обычно мало, иногда это всего один бит. В результате поток цифровых
данных не становится чрезмерно большим. Однако грубое квантование приводит
к потере чувствительности, поскольку приведение уровня сигнала к квантованным
значениям по сути эквивалентно введению в сигнал дополнительной компонен-
компоненты «шума квантования». В большинстве случаев многочисленные преимущества
перевешивают эти потери. При разработке цифровых корреляторов приходится
идти на компромисс между чувствительностью и сложностью системы, и в этой
главе серьезное внимание уделяется вопросу о выборе числа уровней квантова-
квантования. Цифровая обработка радиоастрономических сигналов впервые была приме-
применена при создании автокорреляторов, вычисляющих автокорреляцию сигнала от
одной антенны как функцию смещения по времени. Затем, как результат фурье-
преобразования, определялся спектр мощности, который использовался в изучении
спектральных линий и в других приложениях. Первая такая система в радиоастро-
радиоастрономии была построена Вайнребом (Weinreb, 1963). Другой ранний автокоррелятор
использовался Гольдштейном (Goldstein, 1962) для детектирования эхо-сигналов
при радиолокации Венеры.
х) Определение термина «Коррелятор» (как мы его здесь используем) см. в разд. 3.3,
параграф Коррелятор.
8.2] Периодическая выборка 235
8.1. Двумерное гауссово распределение вероятностей
Прежде чем двигаться дальше, целесообразно ввести здесь понятие двумерной
гауссовой функции вероятностей [см., например, (Abramowitz and Stegun, 1964, p.
936)], которая будет постоянно использоваться в дальнейшем. Если хну являются
совместными гауссовыми случайными переменными с нулевым средним и диспер-
дисперсией а2, то вероятность того, что одна переменная окажется в интервале от х до
х + dx, и одновременно другая — в интервале от у до у + dy, равна р(х,у) dx dy, где
~\ /О1\
2сг A — р ) \
Вид этой функции показан на рис. 8.1. Здесь р является коэффициентом корреля-
корреляции, равным (ху)I\/(х2)(у2), где ( ) обозначает математическое ожидание, которое,
в обычном предположении об эргодичности, аппроксимируется средним значением
за большое число испытаний. Заметим, что — 1 ^ р ^ 1. При р <С 1 экспоненту можно
раскрыть, что дает
ехр (=4)] [-?= ехр (=4)] (l + \ ш
\22J\[V2^ \2сг2 j \ \ а2)
При /9 = 0 выражение переходит в простое произведение двух гауссовых функций.
Выражение (8.1) можно также записать в виде
р(х, у) = —р= ехр
г A - р
Если данное выражение проинтегрировать по у в интервале от — оо до +оо, то
получится гауссова функция от х. При приближении р к единице выражение (8.3)
становится произведением гауссовых функций для х и у — х\ последняя имеет стан-
стандартное отклонение cry 1 — р2 , стремящееся к нулю. Равенства (8.1) и (8.2) будут
использоваться при изучении отклика различных корреляторов и устройств кванто-
квантования. Для автокорреляторов, работающих с одиночными антеннами, измеряемой
величиной является функция автокорреляции (v(t) v(t — г)), где v — принимаемый
сигнал. В этом случае следует положить х = v(t) и у = v(t — г).
8.2. Периодическая выборка
Сначала мы рассмотрим процесс выборки без квантования, когда полностью
сохраняется точность амплитуды сигнала.
8.2.1. Частота Найквиста. Если полоса частот сигнала ограничена,
т. е. спектр мощности сигнала отличен от нуля только в пределах конечного
диапазона частот, в процессе выборки не происходит никакой потери инфор-
информации, при условии, что частота выборки достаточно высока. Это следует из
теоремы выборки, обсуждавшейся в разд. 5.2. Здесь мы производим выборку
функции, зависящей от времени, и должны избежать наложений в частотной
области. Для видеоспектра прямоугольной формы с верхней частотой среза
Az/ ширина спектрального диапазона, включая отрицательные частоты, равна
236
Цифровая обработка сигналов
[Гл.8
2Az/. Функция с таким спектром полностью
определяется значениями, отстоящими друг
от друга по времени на интервал, не боль-
больший l/BAz/), т. е. отсчетами с частотой 2Av
или выше. Эта критическая частота выбор-
выборки, 2Az/, называется частотой Найквиста г)
для данного сигнала (еще говорят о крите-
критерии Найквиста). Более подробные сведения
можно найти, например, в (Bracewell, 2000)
или (Oppenheim and Schafer, 1975). Во многих
цифровых радиоастрономических системах сиг-
сигнал последней ПЧ имеет спектр в видеополо-
видеополосе и опрашивается с частотой Найквиста. Для
прямоугольной полосы пропускания такого ви-
Рис. 8.1. Линии равной плотности да автокорреляционная функция, которая, со-
вероятности для двумерного гаус- гласно соотношению Винера-Хинчина, являет-
сова распределения из (8.1). Кри- ся фурье-преобразованием спектра мощности,
вые определяются уравнением х2 + равна
+ у2 — 2рху = const. При р = 0 они <
становятся окружностями, а при -Roo(r) = ~
р = — 1 сливаются с прямой х = — у
где индекс оо обозначает отсутствие квантова-
квантования по уровню (т. е. точность не ограничена конечным числом уровней квантова-
квантования). Выборка Найквиста может также применяться к полосовому спектру, и если
спектр отличен от нуля только в диапазоне от nAv до (п + l)Az/, где п целое, ча-
частота Найквиста также будет равна 2Ai/. Таким образом, чтобы выборка с частотой
Найквиста была возможна, нижняя и верхняя границы спектрального диапазона
должны быть кратны его ширине. Автокорреляционная функция сигнала, имею-
имеющего плоский спектр в таком диапазоне, равна
/ ч sinGrAzyr)
ЛТ) = —4 cos
(8.5)
Эта функция обращается в ноль при значениях т, кратных 1/BАг/). Следовательно,
в случае спектра прямоугольной формы последовательные отсчеты с частотой Най-
Найквиста не коррелируют между собой. Выборки с частотой, большей или меньшей
частоты Найквиста, называют соответственно избыточными или недостаточными.
Для любого сигнала выбор центральной частоты спектра, удовлетворяющей
описанному выше условию для полосовой выборки, минимизирует частоту выборки,
при которой не происходит наложений. Если спектр не соответствует этому усло-
условию, необходимо определить более широкий частотный диапазон, который будет
удовлетворять требованиям выборки и одновременно охватывать весь наличный
спектр сигнала. После этого можно опрашивать сигнал с частотой Найквиста,
соответствующей новому, более широкому, спектральному диапазону.
8.2.2. Корреляция выборки неквантованных сигналов. Исследуем те-
теперь отклик гипотетического коррелятора, входные сигналы которого опрошены
в соответствии с критерием Найквиста, не подвергаясь при этом квантованию.
Достаточно рассмотреть только корреляторы с одним перемножителем, поскольку
комплексные корреляторы можно реализовать посредством комбинации простых,
как показано на рис. 6.3. Обсуждаемую систему можно представить себе как такую,
х) Шеннон (Shannon, 1949) цитирует различные источники, имеющие отношение к фор-
формулировке данного результата, из которых самым ранним является (Nyquist, 1928).
8.2] Периодическая выборка 237
в которой выборки либо остаются в виде аналоговых напряжений, либо кодиру-
кодируются таким большим числом бит, что ошибками квантования молено пренебречь.
Поскольку ни при квантовании, ни при выборке не происходит никаких потерь
информации, отношение сигнал/шум в измеренной корреляции должно быть, по-
видимому, таким же, какое получилось бы при подаче сигналов на аналоговый
коррелятор без выборки. Вероятно, нет практических причин, которые потребовали
бы создания коррелятора с неквантованной выборкой. Тем не менее, сравнивая
результаты с теми, что получаются в случае квантованного опроса, который мы
рассмотрим позднее, проще понять эффекты квантования как такового.
Два ограниченных по полосе сигнала, x(t) и y(t), опрашиваются с частотой
Найквиста, и для каждой пары выборок перемножитель в корреляторе выдает
результат, пропорциональный произведению входных амплитуд. Интегратор поз-
позволяет усреднять эти результаты за любой требуемый интервал времени. Далее,
(нормализованный) коэффициент корреляции сигналов x(i) и y(t) при нулевой
задержке по времени между ними равен
р = <*(«>У<*» . (8.6)
(Не следует путать коэффициент корреляции р с функцией автокорреляции для х
или т/, Rqq.) Поскольку х и у имеют одинаковую дисперсию а2, то
{x(t)y(t)) = pa2. (8.7)
Левая часть выражения представляет собой усредненное произведение двух сигна-
сигналов и, таким образом, соответствует выходным данным коррелятора. Значение на
выходе цифрового коррелятора после обработки NN выборок равно
где индекс TV обозначает частоту Найквиста. Так как выборки Х{ и yi подчиняются
той же самой гауссовой статистике, что и непрерывные сигналы, мы, очевидно,
можем написать:
(гте> = ра2. (8.9)
Итак, значение на выходе коррелятора линейно зависит от корреляции р. Дисперсия
его равна
<4 = (rl) - <гоо>2, (8.Ю)
N
гJ + N-2 f ^(хжхкук), (8.11)
г=1 кфг
где мы разделили слагаемые, для которых г = к и те, для которых г ф к. Первая
сумма в правой части (8.11) имеет значение а4A + 2р2) N~lm. исходя из (8.3) можно
показать, что
оо оо
x2y2p{x,y)dxdy = a\l + 2p2). (8.12)
NN NN
= N~2 У^ У^ (xiyiX
i=lk=l
NN
wk)=n-2 y:
i=l
— ОО —ОО
238 Цифровая обработка сигналов [Гл. 8
Вторую сумму в (8.11) легко вычислить, используя соотношение для моментов
четвертого порядка из F.36). Так как последовательные выборки каждого сигнала
не коррелируют (в предположении прямоугольной полосы сигнала), {xiyiXkyk) =
= (xiyi)(xkyk) и указанное суммирование дает значение A — N^1) р2а4. Возвраща-
Возвращаясь к (8.10), можно написать:
*1 = A + 2р2) a'N-1 + A - N-1) р2а4 - р2о4 = tr'N-^l + р2). (8.13)
Отношение сигнал/шум при неквантованной выборке равно
(8.14)
где приблизительное равенство справедливо при р <С 1. Заметим, что в большинстве
практических задач условие р<1 вполне приемлемо. [Вычисляемое отношение сиг-
сигнал/шум на выходе коррелятора представляет интерес главным образом для слабых
сигналов. Для времени наблюдения т число отсчетов Njy = 2Аит обычно составляет
106-1012. Порог обнаружения сигнала в соответствии с (8.14) равен py/N^ — 1, т. е.
р ~ 10~3—10~6.] Отношение сигнал/шум, выраженное через ширину полосы сигнала
и время измерения, равно lZsnoo = pVZAiTr . При наблюдениях точечного источника
с использованием идентичных антенн и приемников р равняется отношению антен-
антенной и системной температур, Та/Т$. Этот результат совпадает с выражением F.45)
для аналогового коррелятора с недискретизированными входными сигналами при
ТА < Ts.
Прежде чем закончить обсуждение неквантованной выборки, мы должны рас-
рассмотреть вопрос о выборках с частотой, отличной от частоты Найквиста. Значения
последовательных выборок любого одиночного сигнала в этом случае уже не будут
независимы. Возьмем частоту выборки, в /3 раз большую частоты Найквиста, и чис-
число выборок N = /3NN. Период выборок rs = B/ЗАи)~1. Выборки, отстоящие друг
от друга на интервал grs, где q целое, имеют, в соответствии с (8.4), коэффициент
корреляции, равный
Roo{qTs) ^ i^hlM (8.15)
irq
в случае прямоугольной видеополосы. Поскольку выборки не являются независи-
независимыми, мы должны заново оценить вторую сумму в правой части (8.11). Слагаемые,
у которых q = \г — к\ настолько мало, что значением Roo{qTs) пренебречь нельзя,
дадут дополнительный вклад, равный
[<72Доо(дтв)]2. (8.16)
Таким образом, величина Щ^ очень мала для всех кроме малой части N(N —
— 1) слагаемых второй суммы в (8.11). Из (8.15) следует, что R^ не превышает
(/3/тгдJ и при q = 103 имеет порядок 10~6. Однако, как отмечалось выше, N
может достигать значений 106-1012. Итак, во второй сумме из (8.11) вклад от
слагаемых, у которых выборки г и к практически независимы, остается по существу
неизменным. Произведения, для которых R^ имеет заметную величину, вносят
дополнительный вклад, равный
N—1 оо
2a4N~2 J2(N-q) Д^(дгв) ~ 2<r4N~1 ? RUqrs). (8.17)
8.3] Выборки с квантованием 239
Дисперсия значений на выходе коррелятора равна теперь
3.18)
q=l
а отношение сигнал/шум корреляционных измерений равно
\
q=l
Сравним этот результат с выражением (8.14) для выборки Найквиста. Для значений
/3, равных 1/2, 1/3, 1/4 и т.д., которые соответствуют недостаточным выборкам,
Rvq = 0 и знаменатель в (8.19) равен единице. Чувствительность падает, как и сле-
следовало ожидать в случае уменьшения ансамбля данных. При избыточной выборке
C > 1 и ^2 R^o(qrs) = (f3 — 1)/2, как показано в приложении 8.1. Знаменатель
9=1
в (8.19) равен в этом случае \ffi , и чувствительность остается той же, что и в случае
выборки с частотой Найквиста. Этого и следовало ожидать, так как при выборке
Найквиста не происходит никаких потерь информации. Ситуация меняется в случае
квантованной выборки, как будет показано в следующем разделе.
8.3. Выборки с квантованием
В некоторых схемах дискретизации сначала производится квантование, затем
опрос (выборка) сигнала; в других — сначала производится опрос, затем кванто-
квантование. Теоретически в обоих случаях результат один и тот же, и в целях анализа
мы можем выбрать более удобный для нас порядок операций. Предположим, что
сигнал с ограниченной полосой частот сначала квантуется, а затем опрашивается.
Квантование порождает новые частотные компоненты сигнала, так что он уже
не будет ограничен прежней полосой частот. Если он опрашивается с частотой
Найквиста, соответствующей неквантованному сигналу (что обычно и делается),
некоторая часть информации будет потеряна и чувствительность окажется хуже,
чем в случае неквантованной выборки. Кроме того, поскольку квантование являет-
является нелинейной операцией, мы не можем предполагать, что измеренная корреляция
квантованных сигналов будет линейной функцией коэффициента корреляции р,
который мы хотим измерить. Итак, прежде чем использовать цифровую обработку
сигналов, необходимо прояснить следующие три пункта: A) как соотносятся между
собой р и измеренное значение корреляции, B) каково ухудшение чувствительности
и C) в какой мере избыточная выборка может восстановить утерянную чувствитель-
чувствительность. Исследование этих вопросов можно найти в работах (Weinreb, 1963), (Cole,
1968), (Burns and Yao, 1969), (Cooper, 1970), (Hagen and Farley, 1973), (Bowers and
Klingler, 1974) и (Jenet and Anderson, 1998). Изложение этого раздела ближе всего
к подходу Хэйгена и Фарли.
Заметим, что при обсуждении выборок с квантованием часто говорят о «выборке
Найквиста», подразумевая под этим квантованную выборку с частотой Найквиста,
соответствующей неквантованному сигналу. Мы также будем придерживаться этой
терминологии.
240
Цифровая обработка сигналов
[Гл.8
8.3.1. Двухуровневое квантование. Эпюра двухуровневой (однобитовой)
выборки показана на рис. 8.2. Операция квантования сохраняет только знак мгно-
мгновенного значения напряжения. Это достигается многократным усилением сигнала
и ограничением. Переходы через нуль при этом резко выделяются и, таким образом,
сводятся к минимуму ошибки, которые могут происходить при совпадении момента
выборки со сменой знака сигнала.
Коррелятор для двухуровневых сигналов состоит из схемы перемножения, за
которой следует счетчик, усредняющий произведения входных выборок. Входным
сигналам приписываются значения +1 или —1 в зависимости от положительного
или отрицательного напряжения сигнала, и произве-
произведения на выходе перемножителя принимают значение
^^_^^_ +1 или —1 соответственно для совпадающих или несов-
несовпадающих входных значений. Мы рассмотрим выбор-
выборку как на частоте Найквиста, так и на кратных ей
частотах; при этом N будет означать число отсчетов,
х прошедших через коррелятор. Средний коэффициент
двухуровневой корреляции равен
1-
п _
n
(8.20)
Рис. 8.2. Эпюра двухуров-
двухуровневого квантования. По оси
абсцисс отложено входное
напряжение, а по оси ор-
ординат — квантованный вы-
выходной сигнал х
где TVii — среднее число произведений, в которых обе
выборки имеют значение +1, TV-q — среднее число про-
произведений, в которых выборка х имеет значение +1,
а выборка у — значение — 1 и т. д. Знаменатель в выра-
выражении (8.20) равен выходному значению, которое по-
получилось бы в случае, когда значения во всех парах
входных выборок совпадают. Коэффициент р2 можно
связать с коэффициентом корреляции р неквантованных сигналов через двумерное
распределение вероятностей (8.1), из которого следует
= NP1± =
N
ехр
о о
— 2рху)
dxdy, (8.21)
где Рц — вероятность того, что оба неквантованных входных сигнала одновременно
больше нуля. Другие необходимые вероятности получаются изменением пределов
интегрирования в (8.21): J0^ J0^ для Ртт; J0^ J^° для PTl; $™ f^ для PlT.
Заметим, что Рц = Pjj и P-^j = -Pyi- Таким образом,
Р2 = 2(РП-Р1Т). (8.22)
Интеграл из (8.21) вычисляется в приложении 8.2, откуда мы получаем
Рц = -Л + — arcsinp. (8.23)
4 2тг
Аналогично
и, следовательно,
1 1
4 2тг
= — arcsmp.
7Г
(8.24)
(8.25)
8.3] Выборки с квантованием 241
Равенство (8.25), известное как соотношение ван Флека 1), позволяющее по изме-
измеренной корреляции р2 восстановить р. Для малых значений р пропорционально р2.
Чтобы определить для измеренной корреляции отношение сигнал/шум, вычис-
вычислим дисперсию о\ значений на выходе коррелятора
где
г=1
(8.26)
(8-27)
Отметим, что в этой главе для обозначения квантованных сигналов используется
диакритический значок^. Поскольку р2 = (ху), то из (8.27) следует (г2) = р2- Таким
образом, г2 является несмещенной оценкой р2. Выражение для (г|) эквивалентно
(8.11) для неквантованных сигналов:
(r22) = N-2 ?<????> + N-2 Y, J2(xtmxkyk). (8.28)
Первая сумма в правой части (8.28) равна JV, так как произведения х^щ для
двухуровневой выборки принимают значения ±1. При вычислении второй суммы
ситуация аналогична той, что имела место в случае неквантованной выборки.
Сомножитель а4 в (8.17) заменяется теперь на квадрат дисперсии квантованного
сигнала, который для двухуровневого квантования равен единице. Для всех членов,
кроме малой их части, q = \г — к\ достаточно велико, так что выборки г и к одного
и того же сигнала не коррелируют. Эти члены дают суммарный вклад, близкий
к р\. Те члены, у которых выборки ink коррелируют, вносят дополнительный
вклад, равный приблизительно ^
2^Е^Ы, (8.29)
9=1
где i^C?") — коэффициент автокорреляции для сигнала после двухуровневого кван-
квантования. Таким образом,
су\ = N'1 + A - N'1) р\ + 27V-1 ? Rl{qrs) - р\ ~ N~
q=l
, (8.30)
q=l
где мы предположили, что p<i <С 1 и пренебрегли членом — N 1р2. Отнопгение
сигнал /шум равно t
(r2) 2pVN
/vSn2 = = 1 • {O.6L)
\
q=l
Сравнивая это отношение с отношением сигнал/шум для неквантованной выборки
(8.14), можно определить коэффициент эффективности процесса квантованной
х) Этот результат был впервые получен ван Флеком во время второй мировой войны
при изучении спектра мощности сильно ограниченного шума, использовавшегося при
постановке электромагнитных помех. Работа была засекречена и опубликована много лет
спустя (Van Vleck and Middleton, 1966).
242
Цифровая обработка сигналов
[Гл.8
корреляции:
\
(8.32)
Здесь мы принимаем N = /3NN, т. е. рассматриваем то же время наблюдения, что
и в случае выборки Найквиста, но опрашиваем сигнал в /3 раз чаще.
Равенство (8.25) дает соотношение для коэффициентов корреляции двух сигна-
сигналов до и после двухуровневого квантования. Этот результат справедлив и в случае
автокорреляции, когда два сигнала отличаются только вследствие задержки. Таким
образом, можно написать
(8.33)
Равенство (8.15) дает значение Roo(qTs) для прямоугольного спектра сигнала, опра-
опрашиваемого с частотой в Р раз выше частоты Найквиста, и (8.33) принимает вид
- arcsin
тг
irq
J
(8.34)
Функция R2(qrs), таким образом, обращается в ноль при тех же значениях grs, что
и Roo{qTs) (для арксинуса берется главное значение), и при /3 = 1, 1/2, 1/3 и т.д.
мы получаем
оо
= 0. (8.35)
S
В этих случаях отношение сигнал/шум отличается от значения для неквантован-
ной выборки с той же частотой на коэффициент 2/тг (=0,637). Для избыточной
выборки с/3 = 2л/3 = 3 этот коэффи-
коэффициент, согласно (8.32) и (8.34), имеет зна-
значение соответственно 0,744 и 0,773. Ана-
Аналогичные результаты приводятся в (Burns
and Yao, 1969) и других работах. Заметим,
что во всех проводившихся выше вычис-
вычислениях присутствует неявная зависимость
от формы полосы сигнала, выражающаяся
в предположении, что для выборок в (8.28),
у которых г не равно /с, р2 <С 1. Для /3^2
имеет место дальнейший рост зависимости
от формы полосы из-за влияния автокор-
автокорреляционной функции R2{qTs).
Уже отмечалось, что квантование
порождает дополнительные спектральные
компоненты. Теперь мы можем сравнить
спектры мощности сигнала до и после
квантования, так как эти спектры являют-
являются Фурье-образами автокорреляционных
функций, которые связаны соотношени-
соотношением (8.25). На рис. 8.3 показан спектр,
полученный после двухуровневого кванто-
0
Частота
Рис. 8.3. Спектр шума ограниченного
прямоугольной полосой до и после
двухуровневого квантования. Первона-
Первоначальный спектр соответствует харак-
характеристике фильтра нижних частот и
показан штриховой линией. Спектр по-
после квантования показан сплошной ли-
линией. Уровни мощности (т. е. площадь
под кривыми) обоих сигналов совпада-
совпадают, а их преобразования Фурье связаны
соотношением (8.25)
8.3]
Выборки с квантованием
243
вания шума, имевшего исходно прямоугольный спектр. Часть первоначально огра-
ограниченного полосой спектра превратилась в длинный низкоуровневый шлейф, очень
медленно спадающий с частотой.
8.3.2. Четырехуровневое квантование. Представление амплитуды каждой
выборки двумя битами приводит к меньшему ухудшению отношения сигнал /шум,
чем однобитовое квантование. Возможность двухбитового представления сигнала
естественным образом ведет к четырехуровневому квантованию, которое было ис-
исследовано различными авторами; следует отметить работы (Cooper, 1970) и (Hagen
and Farley, 1973). Эпюра такого квантования показана на рис. 8.4, где порогами
квантования являются —г>о, 0 и v$. Четырем состояниям квантования присвоены
значения —п, —1, +1 и +п, где п, не обязательно целое, может быть выбрано
так, чтобы достигалась оптимальная эффективность. Произведение двух выборок
может принимать значения ±1, =Ьп или ±п2. Коэффициент четырехуровневой кор-
корреляции р4 может быть представлен выражением, аналогичным (8.20) для двух-
двухуровневого случая, т. е.
Р4 =
2n2Nnn - 2
- 2NlT
(8.36)
где черточка над индексом обозначает отрицательное значение. Числитель пропор-
пропорционален значению на выходе коррелятора и совпадает со знаменателем при р = 1,
т. е. когда входные сигналы идентичны. Числа для различных комбинаций уровней
могут быть вычислены исходя из соответствующих совместных вероятностей. Так,
например,
лг _ т\гр _
N
2тпт
у2 -
2G A-р
dx dy,
(8.37)
и, как в и случае двух уровней, остальные вероят-
вероятности вычисляются заданием соответствующих пре-
пределов интегрирования. В случае р С 1 вычисления
упрощаются, если применить приблизительное вы-
выражение (8.2) для распределения вероятностей.
Хотя /94 может быть вычислено согласно (8.36)
так, как описано выше, мы воспользуемся другим
подходом, который позволит быстрее получить тре-
требуемый результат. Этот подход следует работе (Ha-
(Hagen and Farley, 1973) и основан на теореме Прайса
(Price, 1958). Мы применим эту теорему в форме
dp
дх ду
дх ду
(8.38)
где г4 — ненормализованный выход коррелятора, а х
и у обозначают, как и прежде, квантованные формы
входных сигналов. Для четырехуровневой выборки
-1
Рис. 8.4. Эпюра четырехуров-
четырехуровневого квантования. По оси
абсцисс отложено некван-
тованное напряжение ж, по
оси ординат — квантован-
квантованные уровни х. Точка vo
соответствует пороговому на-
напряжению
^ = (n - 1) 5(х + v0) + 2 ?(ж) + (п - 1) 5(ж - v0),
(8.39)
где 5 обозначает дельта-функцию; аналогичное выражение может быть написа-
написано для ду/ду. Выражение (8.39) представляет собой производную функции на
244 Цифровая обработка сигналов [Гл. 8
рис. 8.4. Чтобы определить математическое ожидание произведения двух произ-
производных в правой части (8.38), величину каждого из девяти членов произведения
нужно умножить на вероятность его появления. Так, например, член (п — 1J5(х +
+ vq) 5(у + г>о) имеет величину (п — IJ и вероятность
(8.40)
Объединяя члены правой части с равными вероятностями, получаем
d(r*) ! it 1Ч2 Г ( "«о V f -«о М ^
\ (8-41)
Р
f ^ {{ - IJ [ехр (^—] + ехр
+ 4 (n - 1) ехр B(т2A^2)) + 2} de, (8.42)
где ^ — переменная интегрирования. Чтобы получить коэффициент корреляции р^
нужно поделить (г4) на математическое ожидание значений на выходе коррелятора
в случае, когда входные сигналы идентичны, как в (8.36):
4(8-43)
Р4 = 4тг'
Ф + п A - Ф)
где Ф обозначает вероятность того, что уровень неквантованного сигнала лежит
в пределах ±г>о, т. е.
Ф
=—^ f expf^-)^ = erff-^V (8.44)
aV2^ J V2G2/ \aV2J V ;
Выражения (8.42)-(8.44) формулируют соотношение между р^ и р, аналогичное
соотношению ван Флека для двухуровневого квантования.
Выбор значений для п и vq делается обычно из соображений оптимизации
отношения сигнал /шум, к рассмотрению которого мы теперь переходим. Для р <С 1
выражения (8.42) и (8.43) сводятся к
( \ 2[(nl)? + l]2
(Р4Wl = Р
7Г[Ф + П A-Ф)]
где Е = ехр (—г>о/2сг2). Дисперсия измерения г4 равна
о\ = (г24) - <г4>2 = (г2) - р\ [Ф + п2A - Ф)]2 . (8.46)
8.3]
Выборки с квантованием
245
Сомножитель [Ф + п2A — Ф)]2 является дисперсией квантованного сигнала и зани-
занимает здесь место а2 в соответствующих выражениях для неквантованной выборки.
Как и прежде, мы следуем процедуре, описанной для неквантованного случая,
и пишем
(rf) = N-2 J2i^yf) + N-2 ? J2(xiyixkyk). (8.47)
Вычисляя первую сумму, заметим, что {xiyiJ может принимать значения 1, п2 или
п4, и сумма этих значений, умноженных на их вероятности, равна [Ф + п2{1 — Ф)]2.
Вклад второй суммы равен
A - N-1) р\ [Ф + п2A - Ф)] +
+ п2A - Ф)]2
(8.48)
q=l
где второе слагаемое соответствует эффекту избыточной выборки и аналогично
(8.17), а Д4 обозначает автокорреляционную функцию после четырехуровневого
квантования. Из (8.46) получаем
j=
(8.49)
q=l
Так как мы предполагаем, что р <С 1, членом р\ можно пренебречь, и отношение
сигнал/шум при четырехуровневом измерении корреляции получается равным
2p[(n-l)E+l]2VN
СГ4
- Ф)
\
(8.50)
q=l
Значение фактора сигнал/шум, взятого по отноптению к его значению для некван-
неквантованной выборки Найквиста, получается из (8.14) при N = /3NN, и равно
щ =
V
'^sno
(8.51)
q=l
При выборке с частотой Найквиста /3 = 1 и
щ =
= 2[(n-l)E+lf
7Г[Ф + П2A-Ф)]
^.52)
Значения 774, очень близкие к оптимальной чувствительности, достигаются при п =
= 3 и vq = 0,996а, и при п = 4 и г>о = 0,942сг; см. табл. 8.5 в приложении 8.3. Заметим,
что выбор целого значения для п упрощает коррелятор. Для двух этих случаев щ
(значение фактора сигнал/шум по отношению к неквантованной выборки) равно
соответственно 0,881 и 0,880. Кривые относительной чувствительности как функции
vo/a для п = 2, 3 и 4 представлены на рис. 8.5. Аналогичные выводы получены
в работах (Hagen and Farley, 1973) и (Bowers and Klingler, 1974).
Выбрав значения для лиио, мы можем вернуться к выражениям (8.42) и (8.43),
чтобы исследовать связь р и р4- Кривая 1 на рис. 8.6 показывает связь р и р4-
246
Цифровая обработка сигналов
[Гл.8
0,9
0,7
1,4а
0,0 0,2 0,4 0,6 0,8 1,0
Корреляция квантованных сигналов
Рис. 8.6. Коэффициент корреляции
р для неквантованныых сигналов
как функция корреляции, которая
была бы измерена после квантова-
квантования. Кривыми представлены: 1 —
полная сп = 3иг>о=сг или п = 4
и vo = 0,95сг; 2 — четырехуровневая
система с отбрасыванием произве-
произведений низшего уровня, п = 4 и vq =
= 0,9сг; 3 — трехуровневая система
с v0 = 0,6сг. (Cooper, 1970)
Рис. 8.5. Отношение сигнал/шум для четырех-
четырехуровневой системы и некоторых ее модифи-
модификаций по сравнению с корреляцией некван-
тованных сигналов. По оси абсцисс отложе-
отложено пороговое напряжение г>о, взятое в едини-
единицах среднеквадратичного значения входного
сигнала. По оси ординат отложена чувстви-
чувствительность (фактор сигнал/шум) по отношению
к случаю коррелятора без квантования. Кри-
Кривыми представлены: 1 — полная четырехуров-
четырехуровневая система с п = 2; 2 — полная четырех-
четырехуровневая система с п = 3; 3 — полная четы-
четырехуровневая система с п = 4; 4 — четырех-
четырехуровневая система с п = 3 и отбрасыванием
произведений низшего уровня; 5 трехуровне-
трехуровневая система. (Cooper, 1970)
Экстраполяция линейной зависимостью с наклоном, соответствующим малым зна-
значениям р, приводит к ошибке в 1 % при р = 0,5, 2 % при р = 0,7 и 2,8 % при р =
= 0,8; процентное значение ошибки взято по отношению к истинному значению р.
Таким образом, линейное приближение вполне пригодно для большинства случаев,
если р не превосходит ~ 0,6. Линейное приближение упрощает последний момент
нашего обсуждения четырехуровневого квантования, а именно, вычисление повы-
повышения чувствительности благодаря избыточной выборке.
Соотношение между автокорреляционной функцией для неквантованного шума
Roq и автокорреляцией того же сигнала после четырехуровневого квантования
такое же, как между соответствующими функциями взаимной корреляции в (8.45),
поэтому можно написать
= 2[(n-l)E+lfRo
fi . 2 /-i ячМ
(8.53)
при условии, что Roq < rsj 0,6. Значение ii^, даваемое (8.15), удовлетворяет этому
условию при q = 1 и коэффициенте избыточности /3 = 2. При п = 3, соответствующе-
соответствующему оптимальному значению г>о, получаем Е = 0,6091, Ф = 0,6806 и R^ = 0,881Доо.
Для C = 2 мы используем выражения (8.15), (8.53) и (А8.5) из приложения 8.1,
чтобы вычислить сумму в знаменателе (8.51), и получаем щ = 0,935; это в 1,06
раза больше того, что получается при /3 = 1. В работе (Bowers and Klingler, 1974)
отмечается, что оптимальное значение порога квантования г>о несколько меняется
8.3]
Выборки с квантованием
247
1
с изменением коэффициента избыточности. Однако диапазон оптимальных значе-
значений довольно широк (см. рис.8.5) и влияние упомянутых изменений на чувстви-
чувствительность очень мало.
В работе (Cooper, 1970), посвященной двухбитовым корреляторам, рассматрива-
рассматривается, как влияет на корреляцию отбрасывание в процессе перемножения некоторых
произведений. Например, если все произведения младших битов считать вместо
±1 нулями, то потери в отношении сигнал/шум составят приблизительно 1 %, как
показывает кривая 4 на рис. 8.5. В этом случае накапливать нужно только произ-
произведения, которые в полной четырехуровневой системе, описанной выше, подсчиты-
ваются как zbn и ±п ; в модифицированной системе им можно приписать значения
соответственно =Ы и ±п, что упрощает схематику интегрирующих счетчиков. Еще
большего упрощения можно достичь, опустив также произведения промежуточного
уровня и приписав значения ±1 наибольшим произведениям. Такая модификация
реализует 92 % чувствительности полного четырех-
четырехуровневого коррелятора. Мы не будем рассмат-
рассматривать случай, когда отбрасываются только про-
произведения низшего уровня, но отметим, что при
выводе коэффициента корреляции как функции
р можно описать работу коррелятора, используя
две различные характеристики квантования (На-
gen and Farley, 1973), или вернуться к выражению
(8.36) и опустить в нем соответствующие члены.
Если же отбрасываются произведения как низшего,
так и промежуточного уровня, работу коррелятора
можно описать более просто, без произвольного от-
отбрасывания членов произведения, введя новую ха-
характеристику квантования, называемую трехуров-
трехуровневым квантованием.
8.3.3. Трехуровневое квантование. Трех-
Трехуровневое квантование приобрело значительное
практическое значение; эпюра показана на рис. 8.7.
В данном случае следует также воспользоваться
подходом, основанном на теореме Принса.
Выражения для функциональных свойств трех-
трехуровневого коррелятора можно получить из выве-
выведенных в предыдущем параграфе, опустив члены,
относящиеся к произведениям низшего и промежу-
промежуточного уровней и установив соответствующим об-
образом весовые коэффиценты. Таким образом, эквивалентом производной, необхо-
необходимой для теоремы Принса, является
-1
Рис. 8.7. Эпюра трехуровнево-
трехуровневого квантования. По оси абсцисс
отложено неквантованное на-
напряжение ж, а по оси ординат —
квантованный выходной сиг-
сигнал х. Точка vo соответствует
пороговому напряжению. По-
Поскольку абсолютная величина
х принимает только одно нену-
ненулевое значение, ее без потери
общности можно принять рав-
равной единице
дх
~дх~
= 6(х -
(8.54)
и, согласно упомянутой теореме, математическое ожидание на выходе коррелятора
равно
ехр
2
<72(i + 0
+ ехр
3.55)
где ? — переменная интегрирования. Нормализованный коэффициент корреляции
равен
Рз = PL , (8.56)
248 Цифровая обработка сигналов [Гл. 8
где Ф дается выражением (8.44). При р< 1 выражения (8.55) и (8.56) дают
ЫР«1 = р (Л ф) , (8.57)
где Е определяется в соответствии с (8.45). Дисперсия гз равна
Y^rI(qts)-pI > (8-58)
g=l
где R% обозначает коэффициент автокорреляции после трехуровневого квантова-
квантования. Если величиной р\ в (8.58) можно пренебречь, то значение фактора сиг-
сигнал/шум, по отношению к случаю без квантования, равно
(8.59)
тг8Пз (г3>
7^-snoo СГЗ^-snoo
7гA
-Ф)
2
\
V/3 Е2
оо
l + 2^2Rl(qrs)
q=l
Для выборки Найквиста максимальная чувствительность, по отношению к некван-
тованному случаю, получается при vq = 0,6120а, для которого 773 равно 0,810 (см.
кривую 5 на рис. 8.5). При этом оптимизированном пороговом значении Ф = 0,4595,
Е = 0,8292 и мы можем написать Rs(qrs) = 0,810Roo(qrs), полагая, что р является
приблизительно линейной функцией г%. Тогда из (8.15), (8.59) и (П8.5) мы находим,
что для прямоугольного видеоспектра при коэффициенте избыточности /3 = 2 зна-
значение ?7з становится равным 0,890, что в 1,10 больше значения при C = 1. В табл.
8.1 дается сводка результатов для двух-, трех- и четырехуровневого квантования.
Таблица 8.1. Коэффициент эффективности tjq для различных уровней
квантования
Число уровней Чувствительность по отношению к неквантованному случаю
квантования (Q) /3 = 1 /3 = 2
2 0,637 0,744
3 0,810 0,890
4 0,881а 0,935
аСм. также табл. П8.1 (приложение 8.3)
8.3.4. Квантование с восемью и более уровнями. При восьми или боль-
большем количестве уровней квантования потери чувствительности из-за квантования
малы, и можно воспользоваться более простым, приближенным методом вычис-
вычисления потерь (Thompson, 1998). В основе его лежит вычисление частичного при-
приращения дисперсии сигнала, которое является результатом квантования. Отноше-
Отношение сигнал/шум на выходе коррелятора обратно пропорционально этой дисперсии.
Такой подход особенно интересен потому, что он показывает, как связана потеря
чувствительности с ошибками, вносимыми процессом квантования.
На рис. 8.8 показана кусочно-линейная аппроксимация гаусового распределения
вероятностей сигнала от одной антенны. Такая аппроксимация упрощает анализ.
8.3]
Выборки с квантованием
249
/
I
/
I
I
\
I
\
1
\
1
Is
-3,5 -2,5 -1,5 -0,5 0,5 1,5 2,5 3,5
Рис. 8.8. Кусочно-линейная аппроксимация гауссового распределения вероятностей ампли-
амплитуды сигнала ПЧ. Пересечения кривой с вертикальными линиями соответствуют точным
значениям гауссова распределения. По оси абсцисс отложена амплитуда (напряжение)
сигнала в единицах ?сг, а числа обозначают значения, приписываемые уровням после
квантования. Для восьмиуровневой выборки пороги квантования показаны семью вер-
вертикальными линиями, лежащими между — 3,5гсг и 3,5есг по оси абсцисс. Уровням сигнала
вне диапазона ±4есг, показанным заштрихованными участками, присваивается значение
Пересечения кривой с вертикальными линиями соответствуют точным значениям
гауссова распределения. Для восьмиуровневой выборки пороги квантования пока-
показаны семью вертикальным линиям, лежащими между —3,5sа и 3,5sа по оси абсцисс.
Расстояние между уровнями по напряжению равны sa, т. е. s в единицах а, где а2 —
дисперсия неквантованного сигнала. Сначала мы рассмотрим случай, когда число
уровней четно, как на рис. 8.8. Вероятность того, что единичная выборка попадет
между двумя смежными порогами в точках msa и (m + l)sa, где т целое, равна
;. (8.60)
л/2тг a
Любой выборке, попавшей в данный интервал, была бы присвоена величина (т +
+ sa/2). Например, любое напряжение в интервале от 2 до 3 кодируется как имею-
имеющее амплитуду 2,5 в единицах sa. Среднее приращение дисперсии в результате
такого представления сигнала равно
есг/2
(
3 V 2
(8.61)
Это выражение является точным для кусочно-линейной кривой вероятности, пока-
показанной на рис. 8.8. То же увеличение дисперсии в результате квантования относится
к диапазону уровней сигнала от —4sа до 4sа на рис. 8.8. Доля площади под гауссо-
гауссовой кривой вероятности, лежащей между этими уровнями, составляет
dx = ^ (**
V2
(8.62)
Отсюда дисперсия, обусловленная квантованием выборок сигнала с амплитудами
в диапазоне ±4sa, равна
(8.63)
1 fecr\2 г ( 4е\
з (т) erf Ы •
Мы будем полагать, что ошибка квантования не существенно коррелирует с некван-
тованным сигналом. В предельном случае двухуровневой выборки ошибка кван-
квантования сильно коррелирована с неквантованным сигналом, поэтому проводимый
250 Цифровая обработка сигналов [Гл. 8
здесь анализ для этого случая не подходит. Рассмотрим, однако, случай восьми-
уровневого квантования, представленный на рис. 8.8. Если напряжение сигнала по-
постоянно увеличивается, ошибка квантования уменьшается от максимума на каждом
пороге квантования до нуля, когда напряжение равняется среднему значению двух
порогов. На каждом из порогов ошибка меняет знак, и цикл повторяется. Такое
поведение ошибки квантования сильно снижает ее зависимость от сигнала.
Необходимо также учесть влияние того, что всем уровням сигнала ниже — 4еа
приписывается значение — 3,5б:сг, а уровням выше -\-4scr значение +3,5?сг. Чтобы
приблизительно оценить это влияние, разделим диапазон уровней сигнала за пре-
пределами ±4?сг на интервалы шириной еа. Рассмотрим, например, интервал с центром
в 6,5^0". Вероятность того, что сигнал попадет в этот интервал, равняется соответ-
соответствующей площади под кривой, которая в случае кусочно-линейной аппроксимации
равна
? Г -FеJ/2 , -GеJ/2] (Я RA\
Квадрат средней ошибки, возникающей от квантования сигнала внутри этого ин-
интервала, примерно оценивается значением [F,5 — 3,5)?сг] ; таким образом, суммар-
суммарная дисперсия от квантования сигналов вне диапазона ±4^сг равна
20 Г 2 2 2 2 I
га=4
Верхний предел суммирования в (8.65) выбран достаточно большим для того, чтобы
его дальнейшее увеличение не меняло существенно результата. Ошибка квантова-
квантования от усечения значений вне интервала ±4^сг, очевидно, до определенной степе-
степени коррелирует с уровнем неквантованного сигнала. Однако это малый эффект,
поскольку доля выборок, соответствующая уровням сигнала вне =Ь4?сг, при вось-
миуровневом квантовании меньше 1,6%, если е оптимизировано для получения
максимальной чувствительности. Этот процент снижается при увеличении числа
уровней квантования. В силу вышесказанного мы будем рассматривать ошибку
квантования, связанную с усечением пиков сигнала, как не коррелирующую с сиг-
сигналом, но не будем забывать, что это предположение может внести в вычисления
некоторую неопределенность.
Дисперсия квантованного сигнала равна дисперсии неквантованного сигнала
(с2) плюс дисперсия ошибок квантования из (8.63) и (8.65), т. е.
f (m - ЗJ [в"™2*2/2 + е-(™+1Jе2/2] . (8.66)
Если дисперсия обоих сигналов на входе коррелятора одинакова, а корреляция мала
(т. е. р <С 1, как предполагалось для случаев двух, трех и четырех уровней), то от-
отношение сигнал/шум на выходе коррелятора обратно пропорционально дисперсии.
Таким образом, эффективность квантования равна
(m -
8.3] Выборки с квантованием 251
Это выражение обобщено для случаев с 2Л/" уровнями. Для нечетного числа уров-
уровней, 2Л/"+ 1, один из которых совпадает с нулем, эквивалентным выражением для
эффективности квантования является
7Г т=Л/+1
Результаты из (8.67) и (8.68) подытожены в табл. 8.2.
Во второй колонке табл. 8.2 приведены значения Л/", а в третьей е. Значения
е были выбраны так, чтобы получить значения 7/q, близкие к максимальным,
и не являются критическими, поскольку максимум достаточно широк. В четвертой
колонке приведены значения Р, т. е. доля выборок, у которых амплитуда сигнала
лежит вне диапазона =ЬЛ/*?сг для четного числа уровней и ±(Л/* + 1/2) ест для нечет-
нечетного. При восьми уровнях Р является долей выборок сигнала, вносящих вклад
в дисперсию в (8.65).
Таблица 8.2. Эффективность квантования и другие параметры для восьми
или большего числа уровней
Число уровней (Q)
8
9
16
32
Я
4
4
8
16
е
0,60
0,55
0,34
0,19
Р
0,016
0,013
0,006
0,002
VQ
0,960
0,968
0,988
0,996
Результаты для девятиуровневого квантования можно сравнить с соответствую-
соответствующими результатами, полученными Ф. Р. Швабом (F. R. Schwab), использовавшим
более точные методы, описанные здесь для трех и четырех уровней. Шваб получил
щ = 0,969 при е = 0,534. Эффективность квантования с изменением е меняется
медленно, и значение щ из (8.68) согласуется со значением, полученным Швабом,
с точностью не хуже ~ 0,1 %, или ~ 3% в коэффициенте ухудшения A — 779). Это
согласие подтверждает пригодность представленного здесь метода в пределах такой
точности. Шваб также нашел, что эффективность квантования можно несколько
улучшить, задав весовые коэффициенты и ширину уровней, увеличивающиеся с ам-
амплитудой сигнала. Проведя такую оптимизацию, он получил для эффективности
значение 0,9655 при восьми уровнях квантования, что примерно на 0,5 % выше
значения из табл. 8.2. Значения tjq в табл. 8.2 примерно с той же точностью
согласуются и с работой (Jenet and Anderson, 1998), где проводятся детальные
вычисления для квантования с разрядностью от двух до восьми бит, как при
равномерном, так и неравномерном распределении пороговых уровней. Для случаев
более, чем с четырьмя уровнями применяется метод Монте-Карло. При значениях
эффективности, приближающихся к единице, роль ограничивающих факторов на-
начинают играть другие эффекты, такие, как отклонение частотных характеристик
от идеально прямоугольной формы.
252 Цифровая обработка сигналов [Гл. 8
8.3.5. Коррекция квантования. В результате квантования выходные значе-
значения коррелятора лишь приблизительно линейно зависят от корреляции р. В част-
частности, при двухуровневом квантовании корреляция пропорциональна синусу вы-
выходного значения коррелятора, как показывает выражение (8.25). При слабых
сигналах, для которых р <С 1, нелинейностью можно пренебречь, но при некото-
некоторых наблюдениях требуется коррекция, которую иногда называют коррекцией ван
Флека. Соответствующее точное соотношение для четырехуровневого квантования
может быть получено из равенств (8.42)—(8.44), а линейное приближение для случая
р <С 1 дается выражением (8.45). Аналогично, для трехуровневого квантования
точное соотношение между корреляцией и значениями от коррелятора получается
из равенств (8.44), (8.55) и (8.56), а линейное приближение дается выражением
(8.57). Как показывает рис. 8.6, зависимости для трех и четырех уровней кванто-
квантования по существу линейны вплоть до значений р ~ 0,6. Линейное приближение,
следовательно, будет вполне удовлетворительным при корреляции сигналов от двух
антенн, где некоррелированное зашумление сигналов и, возможно, разрешение ис-
источника ограничивают величину корреляции. Для очень сильных источников или
при измерении автокорреляции сигнала от одной антенны необходима коррекция
квантования. Для каждого выхода коррелятора коррекция должна производиться
один раз за период усреднения, длительность которого обычно лежит в пределах
от Юме до 10с. Для простоты вычислений корреляция может быть представле-
представлена в виде рациональной функции (или другого подобного приближения) от зна-
значений на выходе коррелятора; относительно четырехуровневого квантования см.
приложение 8.3. Процедуры определения р по значениям на выходе коррелятора
в случае трехуровневого квантования даются в работах (Kulkarni and Heiles, 1980)
и (D'Addario et al., 1984).
8.3.6. Сравнение схем квантования. На данном этапе полезно подвести
итог тому, что было сказано о характеристиках схем квантования, которые мы
перечислили в таблицах 8.1 и 8.2. Не следует забывать, что эти значения были
получены в предположении, что р <С 1. Рассматривая сравнительные преимущества
различных схем, мы прежде всего замечаем, что и коэффициент эффективности
?7q, и полоса принимаемых частот могут ограничиваться размером и быстродей-
быстродействием системы коррелятора. Полная чувствительность пропорциональна tjq\/Ais .
Рассмотрим две ситуации. Во-первых, полоса наблюдаемых частот может быть
ограничена не возможностями цифровой системы, а какими-то другими фактора-
факторами. Это может происходить при спектральных наблюдениях или в случаях, когда
полоса наблюдений ограничена шириной свободного от помех диапазона. Ограни-
Ограничения на чувствительность, налагаемые коррелятором, обусловлены в этом случае
только коэффициентом эффективности tjq из табл. 8.1, и выбор схемы квантова-
квантования сводится к выбору между чувствительностью и простотой. Во-вторых, полоса
наблюдаемых частот может определяться максимальной скоростью поступающих
битов, которые способна обработать цифровая система, что может иметь место
при наблюдениях в континууме на высоких частотах. При фиксированной частоте
поступающих битов щ частота выборки равна щ/Nb, где Nb — число бит на одну
выборку, и максимальная полоса сигнала Аи равна щ/BCNb). Таким образом,
чувствительность пропорциональна tjq/'^/3Nb , и этот коэффициент для различных
систем приведен в табл. 8.3, TVj, = 1 для Q = 2 и Nb = 2 для Q = 3 или 4. Заметим, что
в данных обстоятельствах избыточная выборка всегда ухудшает работу системы.
В ситуациях, когда объем обрабатываемых данных определяется возможностями
коррелятора, двухуровневая выборка Найквиста со значением эффективности 0,64
дает наилучшие общие показатели.
8.4] Точность цифровой выборки 253
Таблица 8.3. Коэффициент чувствительности tjq/^/Щ^ъ ? определяемый
коррелятором
Число уровней
квантования (Q)
2
3
4
Wv
/3 = 1
0,64
0,57
0,62
0 = 2
0,52
0,45
0,47
Четырехуровневая выборка почти столь же хороша; четыре или большее число
уровней будут предпочтительнее в случаях, когда полоса имеет ограниченную
ширину, как при спектральных наблюдениях. Интерес представляют также схемы
кодирования с нецелыми значениями TVj,, например, при записи данных на магнит-
магнитную ленту. В этом случае главным предметом рассмотрения становится количество
информации на один бит данных, что обсуждается в разд. 9.6.
В работе (Bowers et al., 1973) описана конструкция коррелятора 3x5 уровней
с эффективностью квантования tjq, равной 0,86, предназначенного для построе-
построения изображений в линиях на двухэлементном интерферометре. Использование на
входах коррелятора различного числа бит дает возможность несколько упростить
систему для двух антенн, если аппаратная задержка применяется к сигналу с мень-
меньшим числом уровней.
8.3.7. Чувствительность системы. Относительная чувствительность раз-
различных интерферометрических схем, определяемая характеристиками аналоговой
обработки сигнала, обсуждалась в разд. 6.2 (см. табл. 6.1). В системах с цифровой
обработкой дополнительным вопросом для рассмотрения является шум квантова-
квантования. Например, в аналоговом корреляторе произведения синус х синус и косинус х
х косинус для сигналов от двух антенн несут, в принципе, совершенно одинаковую
информацию. Однако в цифровом корреляторе шум квантования для синусной
и косинусной компонент сигнала является практически независимым, поэтому по-
потери квантования можно снизить, вычисляя оба произведения и затем усредняя их.
8.4. Точность цифровой выборки
8.4.1. Основные причины погрешностей. Отклонения от идеала в реаль-
реальных устройствах выборки приводят к ошибкам, которые, если их не корректиро-
корректировать, могут ограничить точность изображений, синтезируемых на основе корре-
корреляционных данных. Однако, как только сигнал преобразован в цифровую форму,
доля ошибок, вносимых дальнейшей обработкой, становится обычно пренебрежимо
малой.
Двухуровневые устройства выборки, воспринимающие только знак напряжения
сигналов, являются простейшими по конструкции. Наиболее серьезные ошибки, ко-
которые могут в них возникать, связаны с определением нулевого уровня напряжения,
который может иметь небольшое смещение. Результатом смещения в устройствах
выборки является небольшое положительное или отрицательное смещение на выхо-
выходах коррелятора, которое в значительной мере может быть устранено модуляцией
фазы, как описано в разд. 7.5. В качестве альтернативы можно измерять смещения
на входе корреляторов, применяя счетчики, сравнивающие количество поступаю-
поступающих положительных и отрицательных выборок. Соответствующая коррекция мо-
может применяться к выходным данным коррелятора [см., например, (Davis, 1974)].
254 Цифровая обработка сигналов [Гл. 8
В устройствах выборки с тремя или большим числом уровней квантования
эффективность зависит от значения уровней по отношению к среднеквадратическо-
му уровню сигнала а. Поэтому на входе устройства выборки иногда применяется
автоматическая регулировка уровня (АРУ). Ошибки, возникающие в результате
неправильной амплитуды сигнала, с ростом числа уровней квантования становятся
менее значимы; при большом числе уровней амплитуда сигнала становится просто
линейным коэффициентом в выходных данных коррелятора. В системах с ком-
комплексными корреляторами для сигнала обычно требуются два устройства выборки,
по одному на каждый из выходов квадратурной цепи. Точность квадратурной цепи
и возможное рассогласование тактовых импульсов выборки также могут вносить
ошибки в данные.
8.4.2. Допустимые погрешности при трехуровневом квантовании. Ре-
Результаты этого параграфа основаны главным образом на изучении требований
к точности при трехуровневом квантовании, изложенном в работе (D'Addario et
al., 1984). Мы начнем с исследования диаграммы на рис. 8.9, на которой показаны
пороги квантования выборок двух коррелируемых сигналов. Пороги v\ и —v2 отно-
относятся к сигналу x(t), а г^з и — г>4 к сигналу y(t). Распределение вероятностей х и у
дается выражением (8.1), а отклик коррелятора пропорционален интегралу этой
вероятности по плоскости ху с весовыми коэффициентами, равными ±1 и нулю,
как показано на рисунке. Такой подход позволяет исследовать влияние отклонений
порогов устройства выборки от оптимума г>о = 0,612а. При трехуровневом кванто-
квантовании оклик коррелятора может быть записан в виде
(гз(ск, р)) = [L(ai, с^з, р) + L(a2, ol^-, р) — L(a±, ol^ —p) — L(a2, ol^-, ~рУ\-> (8.69)
где щ = Vi/a и
оо оо
Г Г 1 Г / -17-2 , т/>-2 ^ w-\ "I
(8.70)
Здесь X = ж/а, Y = у/а, а интегрируемое выражение в (8.70) соответствует правой
части (8.1), где переменные измерены в единицах а.
В (D'Addario et al., 1984) подчеркивается, что поскольку при отклонении по-
порогов от оптимума на ±40 % потери в отношении сигнал/шум составляют менее
5 %, требуемая точность установки порогов на практике зависит в основном от
применяемого алгоритма коррекции. Предположим, положение порогов поддержи-
поддерживается близким, но не равным, оптимальному. Для устройства выборки х на рис. 8.9
отклонения от идеального порогового значения а$ могут быть выражены через
четную
и нечетную часть
Аож = \ (ai -a2). (8-72)
Для устройства выборки у точно так же определяются Agy и Аоу. Члены Ag при-
приводят к ошибкам в коэффициенте усиления. Они эквивалентны ошибкам в уровне
сигнала на устройстве выборки и дают мультипликативную ошибку в измеренной
корреляции. Члены Ао приводят к ошибкам смещения на выходе коррелятора
8.4]
Точность цифровой выборки
255
и потенциально более опасны, поскольку такие
ошибки могут быть велики по сравнению с низки-
низкими уровнями корреляции сигналов от слабых ис-
источников. Ошибки смещения, однако, могут быть
существенно уменьшены посредством модуляции
фазы. Компенсация смещения происходит за счет
обращения либо знака выборок, либо значений на
выходе коррелятора, как описано в разд. 7.5. От-
Отклик коррелятора с модуляцией фазы имеет вид
r3s(a,p) = i [r3(a,p)-r3(a,-p)]. (8.73)
-«г—
v4—
Рис. 8.9. Пороговая диаграмма
коррелятора, на входы
которого поданы трехуровневые
квантованные сигналы, х и у
обозначают неквантованные
сигналы, а заштрихованные об-
области показывают комбинации
входных сигналов, дающие на
выходе ненулевой отклик
Если все значения а лежат в пределах ±10 % от о^,
отклик коррелятора будет отличаться не более чем
на 10~3 (относительная ошибка) от отклика корре-
коррелятора с теми же ошибками усиления, но без сме-
смещений в устройствах выборки. Заметим также, что
согласно рис. 8.5 ошибки на 10 % в установке поро-
порогов приводят к потерям в отношении сигнал/шум
не более 1 %. Таким образом, при модуляции фазы
допустимы ошибки пороговых уровней величиной
в 10%, а влияние ошибок усиления можно скорректировать, если действительные
положения порогов известны. Поскольку плотность распределения вероятности ам-
амплитуд сигналов можно считать гауссовой, уровни порогов можно определить путем
подсчета относительного числа значений +1, 0 и —1 на выходе каждого устройства
выборки. Когда р мало (несколько процентов), можно выполнить простую коррек-
коррекцию ошибок усиления, поделив отклик коррелятора на арифметическое среднее
чисел выборок высокого уровня (=Ы) двух сигналов. Тогда ошибки уровня порогов
в 10 % приведут к ошибкам менее 1 % в р.
Другим аспектом неидеального поведения устройств квантования и опроса яв-
является то, что уровень порога может быть фиксирован не точно и меняться в зависи-
зависимости направления и скорости изменений сигнала, значения предыдущей выборки
(гистерезис) и других причин. Результат может быть смоделирован, включая эф-
эффекты неопределенности отклика устройства выборки в зонах от а*. — А до aj~ + A.
Предполагается, что сигнал, попадающий в эту зону, с равной вероятностью дает
на выходе одно из двух значений, ассоциированных с данным порогом. Пороговая
диаграмма с зонами неопределенности показана на рис. 8.10.
Весовые коэффициенты в зонах неопределенности зависят от вероятности слу-
случайных значений выборок и равны 1/4, когда оба сигнала попадают в зону неопре-
неопределенности, и 1/2, если в зону неопределенности попадает только один из сигна-
сигналов, а другой дает ненулевой отклик. Как и прежде, отклик коррелятора можно
получить интегрированием взвешенной вероятности значений сигналов по плос-
плоскости XY. На рис. 8.11 показано снижение отклика коррелятора как функция от
А для нескольких значений р, вычисленное разложением в ряд Маклорена по А
(D'Addario et al. 1984). Для всех случаев кроме тех, где р приближается к едини-
единице, снижение отклика сравнительно невелико в силу того факта, что когда один
входной сигнал попадает в зону неопределенности, другой обычно не попадает.
В специальном случае р = 1 входные сигналы идентичны и попадают в эти зоны
одновременно. Снижение отклика тогда пропорционально А, как показано пунк-
пунктирной линией на рис. 8.11; однако этот случай не имеет особого практического
значения. Для максимальной ошибки в 1 % значение А не должно превосходить
0,Пег, так что ширина зоны неопределенности может достигать ±18 % от порогового
256
Цифровая обработка сигналов
[Гл.8
0,96 -
0,94
\l,0 ^
\
- \
\
\
\
\
\
\
\
\
\
\
\
\
I
v °'!
V
\
\
i
—
0,8
у
Л
\\
\\\
\\\
WV
\\\
0,0 ОД 0,2 А 0,3
А
Рис. 8.10. Пороговая диаграмма трехуровневого
коррелятора с выделенными зонами неопреде-
неопределенности; заштрихованы те их области, которые
дают ненулевой отклик коррелятора. Значение
отклика указывают цифры ±1, ±1/2 и ±1/4.
Значения сигналов на плоскости XY нормали-
нормализованы их среднеквадратическим значением а
значения. Для ошибки 0,1% указанные пределы нужно разделить на у10- Итак,
зоны неопределенности имеют достаточно большие допуски и их влиянием часто
можно пренебречь.
Рис. 8.11. Влияние зон неопределенно-
неопределенности на отклик трехуровневого корре-
коррелятора. Предполагается, что пороги
имеют оптимальное значение 0,612<т
и ширина зон неопределенности равна
2сгА. Значения отклика взяты по отно-
отношению к его значению при А = 0
8.5. Цифровые схемы задержки
Задержки битового потока, кратные периоду выборки сигнала, можно легко
получить, пропустив биты данных через регистры сдвига, тактируемые частотой
выборки. Регистры сдвига различной разрядности обеспечивают формирование
различных фиксированных задержек. В работе (Napier, Thompson and Ekers, 1983)
описан метод использования двух регистров для получения задержки, изменяемой
с шагом тактовых импульсов. Однако самый экономный способ реализации боль-
больших задержек обеспечивают микросхемы памяти с произвольным доступом (RAM),
разработанные для компьютерных применений.
Другой полезной методикой является преобразование из последовательной в па-
параллельную форму, т. е. разделение битового потока с частотой v на п параллель-
параллельных потоков с частотой v/п, где п является целой степенью двойки. Это позволяет
использовать для задержки, корреляции и других процессов более медленные и эко-
экономичные цифровые схемы.
Необходимая точность установки задержки обсуждалась в п. 7.3.4, и она обычно
равна некоторой доле обратной аналоговой полосы сигнала. В любой схеме задерж-
задержки, тактируемой с частотой выборки, элементарное приращение задержки равно
обратной частоте выборки. Более мелкий шаг задержек можно получить, варьируя
момент импульса выборки в промежутке между элементарными тактами с шагом,
в несколько раз, например 16, меньшим их периода. Таким образом, если требуется
8.7] Цифровые корреляторы 257
дополнительная задержка, например, в 5/16 тактового интервала, устройство вы-
выборки запускается через 11/16 интервала после предыдущего тактового импульса,
и данные задерживаются на 5/16 тактового интервала перед тем, как они будут
синхронизированы с основными тактовыми импульсами. Коррекция дискретности
задержки может быть также произведена после корреляции сигналов, если приме-
применить фазовую коррекцию к коррелированному спектру, как описано в п. 9.7.3.
8.6. Квадратурный фазовый сдвиг цифрового сигнала
Мы упоминали, что комплексные корреляторы для цифровых сигналов мо-
могут быть реализованы введением квадратурного фазового сдвига в аналоговый
сигнал, как на рис. 6.3, после чего используются раздельные устройства выборки
для исходного и сдвинутого сигналов. Преобразование Гильберта, каким является
фазовый сдвиг, может быть произведено и над цифровым сигналом, что позво-
позволяет исключить фазосдвигающую цепочку, дополнительные устройство выборки
и линию задержки, но достигаемая точность при этом ограничена. Математически
преобразование Гильберта эквивалентно свертке с функцией (—тгт), простираю-
простирающейся от минус до плюс бесконечности [см., например, (Bracewell, 2000), р. 364].
Соответствующая усеченная последовательность, например, 1/3, 0, 1, 0, —1, 0,
— 1/3, позволяет выполнить свертку цифровых данных, реализующую требуемый
фазовый сдвиг. Однако усечение приводит к тому, что спектр полученного сигнала
оказывается свернутым с фурье-образом функции усечения, т. е. sine-функцией. Это
вызывает появление осцилляции и на несколько процентов ухудшает соотношение
сигнал/шум. Кроме того, суммирование увеличивает число бит в выборках, но
младшие биты могут быть отброшены, чтобы избежать чрезмерного усложнения
коррелятора. Результатом являются дополнительные потери квантования. Все это
приводит к тому, что мнимый выход коррелятора подвергается спектральным иска-
искажениям и имеет несколько худшее отношение сигнал/шум, чем действительный вы-
выход. Эти проблемы носят наиболее серьезный характер в широкополосных системах,
где высокая скорость потока данных позволяет выполнять только весьма простую
обработку. В работе (Lo et al., 1984) описана система, в которой действительная
часть корреляции измеряется как функция временного смещения, как описано
ниже для спектральных корреляторов, а мнимая часть затем вычисляется через
преобразование Гильберта.
8.7. Цифровые корреляторы
8.7.1. Корреляторы для наблюдений в континууме. При наблюдениях
в континууме измеряется средняя корреляция по полосе сигнала, а более подробная
спектральная информация может и не требоваться. В таких случаях корреляция
сигналов измеряется только для нулевого смещения задержки. Цифровые корреля-
корреляторы могут быть сконструированы для работы на частоте выборки сигналов или на
меньшей частоте, соответствующей разделению данных от устройства выборки на
ряд параллельных потоков. В последнем случае пропорционально возрастает число
блоков коррелятора, а их выходы затем аддитивно комбинируются. Наиболее
просто реализуются двухуровневые и трехуровневые корреляторы, в которых
произведения представляются значениями —1, 0 и +1. Корреляторы, у которых
один из входов является двухуровневым или трехуровневым, а другой имеет более
высокую разрядность, также не слишком сложны. В этом случае коррелятор по
существу является накопительным регистром, в который вводятся значения канала
9 Томсон
258 Цифровая обработка сигналов [Гл. 8
с большей разрядностью. Двухуровневое или трехуровневое значение определяет,
должно ли другое число складываться, вычитаться или лее игнорироваться. В кор-
корреляторах, у которых оба входа имеют более трех уровней квантования, выход
перемножителя для каждого отдельного произведения представляет собой число
из некоторого диапазона. Одним из методов реализации такого перемножителя
является использование постоянного запоминающего устройства (ПЗУ) в качестве
таблицы, содержащей все возможные произведения. Перемножаемые входные биты
определяют адрес требуемого произведения в памяти.
Выходное значение перемножителя может принимать как положительные, так
и отрицательные значения, и для интегратора идеально подошел бы реверсивный
счетчик. Поскольку такие счетчики обычно медленнее обычных суммирующих, ино-
иногда применяют два обычных счетчика, которые независимо аккумулируют положи-
положительные и отрицательные значения. Другим возможным методом является подсчет
значений, например, —1, 0 и +1 как 0, 1 и 2 с вычитанием, в ходе последующей
обработки, избыточного значения, равного в данном случае числу произведений.
Для наблюдений в континууме часто используют и спектральные корреляторы.
Это имеет некоторые преимущества, например, возможность подавления узкопо-
узкополосных помех или разделения всей полосы частот на более узкие поддиапазоны,
что позволяет уменьшить эффект размывания из-за широкой полосы сигнала, опи-
описанный в разд. 6.3.
8.7.2. Принципы спектральных цифровых измерений. При спектраль-
спектральных наблюдениях требуется выполнять измерения для различных частот в полосе
сигнала. Цифровыми методами такие измерения можно осуществить с помощью
спектральной корреляционной системы, которая чаще всего реализуется измере-
измерением корреляции сигналов как функции их временного смещения (относительного
запаздывания). Фурье-преобразование этой величины дает спектр коррелированной
мощности, который можно рассматривать как комплексную функцию видности, яв-
являющуюся также функцией частоты. Эта фурье-взаимосвязь, называемая обычно
соотношением Винера-Хинчина, обсуждалась в разд. 3.2. В случае автокоррелятора
(используемого с одной антенной) два входных сигнала идентичны с точностью
до сдвига по времени. Поэтому функция автокорреляции симметрична, а спектр
мощности действителен и четный. Однако коррелированный спектр сигналов от
двух различных антенн является комплексным, а функция корреляции имеет как
четную, так и нечетную части.
Выход спектрального коррелятора представляет собой совокупность значений
функции видности в N частотных интервалах полосы сигнала. Эти интервалы
называют иногда частотными каналами, а их разнесение — полосой канала, как
в случае с аналоговым спектральным коррелятором, где полоса сигнала разбивается
на отдельные каналы с помощью набора из N аналоговых фильтров с отдельным
коррелятором для каждого канала. Чтобы понять принцип работы спектрально-
спектрального цифрового коррелятора, рассмотрим коррелированный спектр мощности S(y)
сигналов от двух антенн, в идеализированной форме показанный на рис. 8.12.
Здесь предполагается, что наблюдаемый источник имеет плоский спектр без от-
отдельных линий, а оконечный усилитель ПЧ (перед устройством выборки) имеет
прямоугольную частотную характеристику в видеополосе. В график на рис. 8.12
включены также и отрицательные частоты, поскольку они являются необходимой
частью в соотношениях комплексного преобразования Фурье. Для — Az/ ^ v $С Az/
действительная и мнимая части S{y) имеют величину соответственно а и 6, а фаза
функции равна arctg (b/a). Функция корреляции р(т) является Фурье-образом <S(z/),
где т обозначает смещение по времени:
8.7]
Цифровые корреляторы
259
р(т) = (а - jb) I ej2™T dv+(a + jb) [ ej27ri/T di/ =
-Аи
sin BтгДг^т) , 1 - cos BnAv r) ]
.74)
У)
Таким образом, р(т) имеет четную составляю-
составляющую вида sin ж/ж, которая соотносится с дей-
действительной частью <S(z/), и нечетную состав-
составляющую вида A — cos x)/ж, соответствующую
мнимой части. Спектральный коррелятор из-
измеряет р(т) для задержек, кратных интервалу
выборки т8. Мы рассмотрим случай выборки
Найквиста, для которой rs = l/BAz/). Изме-
Измеренная корреляция относится к квантованным
сигналам; результаты, полученные в разд. 8.3,
показывают, каким образом измеренная вели-
величина связана с корреляцией неквантованных
сигналов. Для не слишком больших уровней
корреляции эти две величины примерно про-
пропорциональны друг другу, поэтому для про-
простоты будем считать, что выражение (8.74) от-
относится к измеренной корреляции. Измерения
производятся для 27V смещений по времени
между сигналами от —Nrs до (N — 1)т5, а пре-
преобразование Фурье от этих дискретных значе-
значений дает коррелированный спектр мощности
в частотных интервалах шириной BNrs)~1 =
= Av/N (при выборке Найквиста). Требуется
получить N комплексных значений спектра по-
положительных частот. Их мнимые части определяются нечетной составляющей г(т).
Итак, при измерении корреляции достаточно использовать корреляторы с одним
перемножителем, определяющие 27V действительных значений г (г) как для поло-
положительных, так и отрицательных значений задержки т одной антенны по отно-
отношению к другой. Альтернативой измерению только действительной части является
использование комплексных корреляторов для измерения действительной и мнимой
частей корреляции, как на рис. 6.3, для диапазона смещений по времени от нуля
до (JV — 1)ts. С практической точки зрения обычно предпочтительнее использовать
корреляторы с одним перемножителем, где не требуются широкополосные квадра-
квадратурные цепи, необходимые в большинстве комплексных корреляторов. Неравномер-
Неравномерность частотных характеристик таких цепей может стать фактором, ограничиваю-
ограничивающим возможности антенной решетки.
Измерение корреляции в ограниченном диапазоне задержек эквивалентно из-
измерению г(т), умноженной на прямоугольную функцию ширины 2Nrs. Спектр
коррелированной мощности, получающийся из ограниченных измерений, равняется
истинному спектру, свернутому с фурье-образом прямоугольной функции, т. е. sine-
функцией
-Av
Рис. 8.12. Спектр коррелированной
мощности S(u) двух сигналов, спек-
спектры мощности которых имеют пря-
прямоугольную форму с шириной по
частоте от нуля до Аи. В спектр
включаются отрицательные часто-
частоты. Сплошной линией показана дей-
действительная часть S(v), а штрихо-
штриховой — мнимая. Соответствующая
функция корреляции выводится из
(8.74)
sin GrisN/Av)
3.75)
260 Цифровая обработка сигналов [Гл. 8
нормированной к единичной площади по отношению к v. Каждая деталь спектра
будет уширяться в соответствии с (8.75) и, в зависимости от своего профиля,
может приобретать характерные осциллирующие шлейфы. Ширина sine-функции
на половине высоты (полуширина) равна 1,2 Аи/N, т. е. в 1,2 раза шире расстояния
между каналами; эта ширина определяет эффективное частотное разрешение.
Таблица 8.4. Применяемые функции сглаживания
Взвешивающая Полуширина Максимальный
функция w(t) [w(t) = 0, \т\ > п = Nr8] (в ед. Av/N) боковой лепесток
Равномерная
Бартлетта
Ханнинга
Хемминга
Блэкмана
w(t) = 1
w(t) = 1-(\t\/t1)
w(t) = 0,5 + 0,5 cos (тгг/п)
w(t) = 0,54 + 0,46 cos (тгг/п)
w(r) = 0,42 + 0,50 cos (тгг/п) +
+ 0,08 cosB7tt/ti)
1,21
1,77
2,00
1,82
2,30
0,22
0,047
0,027
0,0073
0,0012
Осцилляции sine-функции придают частотному спектру структуру, напоминаю-
напоминающую лепестки в диаграмме направленности антенны. Они возникают из-за крутых
спадов прямоугольной функции, на которую умножается функция корреляции.
Такие лепестки нежелательны и могут быть уменьшены применением определен-
определенных взвешивающих функций, отличных от прямоугольной, но которые вне изме-
измеряемого диапазона также равны нулю. Взвешивающие функции обычно плавно
спадают до нуля при \т\ = Nts, уменьшая в результате нежелательные осцилля-
осцилляции сглаживающей функции (функции свертки), но имеют как можно большую
ширину, чтобы сглаживающая функция была как можно уже. Эти требования,
вообще говоря, мало совместимы, поэтому взвешивающие функции, дающие очень
низкие боковые лепестки, сильно ухудшают частотное разрешение. Некоторые ши-
широко применяемые функции взвешивания представлены в табл. 8.4. Взвешивание
Ханнинга, называемое также «поднятым косинусом», уменьшает первый боковой
лепесток в 9 раз, но ухудшает разрешение в 1,67 раза по сравнению с равномерным
взвешиванием. Фурье-образ взвешивающей функции Ханнинга является суммой
трех sine-функций с относительными амплитудами 0,25, 0,5 и 0,25. В спектральной
области взвешиванию Ханнинга соответствует сглаживающая функция, показанная
на рис. 8.13. В обычном случае, когда число дискретных точек в спектре соответ-
соответствует числу точек в функции корреляции (т. е. нет заполняющих нулей; см. «FX-
коррелятор»), сглаживание (или свертка) может быть реализовано как скользящее
трехточечное среднее с относительными весами 0,25, 0,5 и 0,25. Другими словами,
сглаженное значение спектра коррелированной мощности в частотном канале п
дается выражением
nAv\ _ 1 [(n-l)Ai/] I . (nAv\ I
Взвешивающая функция Хемминга очень похожа на функцию Ханнинга и могла бы
показаться более совершенной, так как обеспечивает лучшее разрешение и меньшую
амплитуду первого лепестка. Однако лепестки функции сглаживания Хемминга
8.7]
Цифровые корреляторы
261
0,0
Рис. 8.13. а — sine-функция sin (jrvN/ Ais) / (ttvN/ Ais), соответствующая частотному откли-
отклику спектрального коррелятора с каналами ширины Au/N на узкую линию в точке v = 0.
По оси абсцисс отложена частота v относительно центра полосы принимаемого сигнала.
б— та же кривая после применения сглаживания Ханнинга согласно (8.76)
падают по амплитуде не так быстро, как у функции Ханнинга. Взвешивающие
функции детально рассматриваются в (Blackman and Tukey, 1959) и (Harris, 1978).
Другой эффект конечности интервала смещений по времени усложняет ка-
калибровку аппаратной частотной характеристики и состоит в следующем (Willis
and Bregman, 1981). Частотные характеристики усилителей на различных ан-
антеннах редко совпадают, что рассматривалось в разд. 7.3. Чтобы прокалибро-
прокалибровать по спектральным каналам отклик для каждой пары антенн, обычно изме-
измеряют спектр коррелированной мощности неразрешенного источника, о котором
известно, что он излучает плоский спектр в пределах наблюдаемой полосы ча-
частот. Мы можем рассмотреть получаемый результат с точки зрения идеализи-
идеализированных спектров мощности на рис. 8.12. Если не используется никакой спе-
специальной функции взвешивания, действительная и мнимая части свертываются
с одной и той же sine-функцией (8.75). Когда
с последней свертывается функция, имеющая
крутой срез, результатом является появление
осцилляции (феномен Гиббса), показанных на
рис. 8.14. Но дело в том, что действительная
часть S[y) на рис. 8.12 плавно проходит через
нуль частот, в то время как мнимая часть де-
демонстрирует резкое изменение знака. Поэтому
вблизи нулевой частоты наблюдаемая мнимая
часть S(y) будет испытывать осцилляции,
относительная амплитуда которых может
достигать 18 %, в то время как действительная
часть будет осциллировать в этой точке
сравнительно слабо (см. также рис. 10.6 и по-
пояснительный текст). Как следствие, величина
-Ь-Ь
-5
0
5 х
Рис. 8.14. Свертка ступенчатой
функции (штриховая линия) с sine-
функцией sin (тгх)/ттх. Здесь х =
= uN/Av, а пол у период осцилляции
приблизительно равен ширине
спектрального канала
262 Цифровая обработка сигналов [Гл. 8
и фаза, измеренные для <S(z/), будут демонстрировать осцилляции, амплитуда кото-
которых зависит от относительной величины действительной и мнимой частей, т. е. от
фазы некалиброванной функции видности. Некалиброванная фаза, измеренная для
любого источника, зависит как от аппаратных факторов, например, длины кабелей,
так и от положения источника, которое может быть неизвестно. Вообще говоря,
фаза для наблюдаемого и для калибровочного источников будет не одной и той
же. Поэтому вблизи нулевой частоты применять калибровку нужно с некоторыми
предосторожностями. Возможны следующие решения данной проблемы: 1) калиб-
калибровать действительную и мнимую части по отдельности, 2) наблюдать источник
в достаточно широкой полосе частот и затем отбросить крайние спектральные
каналы, в которых осцилляции проявляются наиболее сильно, или 3) применить
сглаживание по частоте, чтобы уменьшить осцилляции.
Еще одна проблема, с которой приходится сталкиваться при наблюдении спек-
спектральных линий, имеющих фон с непрерывным спектром, возникает из-за отраже-
отражений в антенной конструкции. Эти отражения приводят к синусоидальным изме-
изменениям усиления в полосе пропускания, период которых равен обратной задержке
сигнала, возникшего в результате отражений. В корреляционном интерферометре
величина осцилляции на выходе является почти постоянной долей коррелированной
плотности потока в континууме, и осцилляции устраняются, когда спектр наблю-
наблюдаемого источника делится на спектр калибровочного.
8.7.3. Коррелятор с задержками (XF-коррелятор). На рис. 8.15
показана упрощенная блок-схема коррелятора с задержками, измеряющего
корреляцию двух сигналов. Реальные системы часто бывают значительно
сложнее и проектируются так, чтобы в полной мере использовать гибкость
цифровых методов обработки сигналов. Требуемые для спектральных исследований
полосы каналов варьируются в широчайших пределах, от нескольких сотен
герц до десятков мегагерц. Такая гибкость необходима потому, что на ширину
спектральных деталей влияют доплеровские сдвиги, которые пропорциональны
частоте покоя и скоростям излучающих атомов и молекул. Такие эффекты,
как, например, компрессионное уширение, также имеют немаловажное значение.
По этой причине многие цифровые спектральные системы имеют в тракте ПЧ
ряд фильтров, позволяющих сузить полосу пропускания до 1/2, 1/3, 1/4 и т.д.
максимальной ширины. Когда полоса сигнала сужается вдвое, уменьшается
вдвое частота Найквиста и устройства выборки могут работать на частоте вдвое
меньше максимальной (либо можно отбрасывать каждый второй отсчет). Однако
если корреляторы продолжают работать на частоте, используемой для макси-
максимальной полосы сигнала, то они могут обрабатывать выборку данных дважды,
так что диапазон смещений по времени может быть удвоен. Соответственно
удваивается число спектральных каналов, а полоса одного канала сужается в 4
раза. Использование такого приема позволяет и далее сужать полосу сигнала
и увеличивать число спектральных каналов по мере необходимости. Обычно число
каналов является целой степенью двойки, и полоса пропускания также сужается
по степеням двойки, чтобы поддерживалась совместимость с техникой цифровой
обработки. Для реализации описанной схемы необходимы устройства рециркуляции
данных, которые являются в своей основе устройствами памяти, которые хранят
блоки входных выборок и позволяют считывать их с тактовой частотой входа
коррелятора. Эти устройства памяти должны работать парами: пока одно из них
заполняется данными в темпе выборки Найквиста, соответствующей установленной
полосе сигнала, второе считывается с максимальной тактовой частотой. К тому
моменту, когда первое устройство памяти будет заполнено, второе будет считано
требуемое число раз, и устройства поменяются местами. Корреляторы, реализую-
8.7]
Цифровые корреляторы
263
щие описанные принципы работы, на-
зывают рециркулирующими (Ball, 1973).
Пример рециркулирующего коррелятора
задержек для решетки миллиметровых
волн описан в (Okumura et al., 2000).
Входные сигналы
8.7.4. FX-коррелятор. Аббревиа-
Аббревиатура FX обозначает коррелятор, в кото-
котором преобразование Фурье к частотной
области производится до перемножения
данных от различных антенн. В таком
корреляторе входной битовый поток от
каждой антенны преобразуется в частот-
частотный спектр посредством БПФ (быстрого
преобразования Фурье), выполняемого
в реальном времени, после чего для
каждой пары антенн производится
перемножение комплексных амплитуд
в частотных каналах, в результате чего
получается спектр коррелированной
мощности. Основной объем вычислений
выполняется при фурье-преобразовании
и пропорционален числу антенн. Для
сравнения отметим, что в корреляторе
задержек (который иногда называют
XF-коррелятором) объем вычислений
в основном пропорционален числу
антенных пар. Таким образом, схема FX
оказывается несколько экономнее в плане
объема аппаратуры, особенно если число
антенн велико. Принцип FX-коррелятора,
в основе которого лежит применение спе-
специального БПФ-процессора, обсуждался
в работе (Yen, 1974), а первая практическая его реализация в большой системе
описана в (Chikada et al., 1984, 1987). Описание системы, спроектированной для
РСДБ, приводится в (Benson, 1995). Использовались две несколько отличающихся
реализации FX-коррелятора. В одной из них производится выборка компонент
с исходной фазой и с квадратурным сдвигом, что дает последовательность
из N комплексных отсчетов; затем она подвергается фурье-преобразованию,
в результате чего получаются N значений комплексной амплитуды в частотной
области. В другой системе преобразуются 2N действительных отсчетов, давая
N значений комплексной амплитуды. В обоих случаях число частотных каналов
(или точек спектра) равно N. Выкладки почти идентичны, и в следующем ниже
обсуждении мы ориентируемся на вторую схему.
На рис. 8.16 показана блок-схема основных операций в FX-корреляторе. Входной
поток выборок от антенны подвергается фурье-преобразованию отдельными
последовательностями длиной по 27V отсчетов каждая, идущими друг за другом;
N обычно выбирается равным целой степени двойки, чтобы алгоритм БПФ работал
эффективно. Результатом каждого преобразования является последовательность
из N комплексных амплитуд сигнала как функции частоты. Расстояние по частоте
между преобразованными элементами данных равно l/B7Vrs), где rs — временной
Последующие задержки
и корреляторы
Рис. 8.15. Блок-схема спектрального кор-
коррелятора с задержками (XF) для двух
сигнальных выборок. rs обозначает за-
задержку на время, равное интервалу вы-
выборки; С — корреляторы. Корреляция из-
измеряется для нулевой задержки, для сиг-
сигнала ж, задержанного относительно у (ле-
(левый блок корреляторов), и для сигнала
у, задержанного относительно х (правый
блок корреляторов). Задержки кратны rs
264
Цифровая обработка сигналов
[Гл.8
Оцифрованный
сигнал —>—
от антенны 1
Регистр сдвига, 2N каскадов
V V
БПФ, 2N действительных входов
N комплексных выходов
Оцифрованный
сигнал —>—
от антенны 2
Сг^ N значений спектра
'-г' коррелированной
А МОЩНОСТИ
БПФ, 2N действительных входов
N комплексных выходов
I
I
Регистр сдвига, 2N каскадов
Рис. 8.16. Блок-схема FX-коррелятора для двух антенн. Оцифрованные сигналы вводятся
в регистры сдвига, и через каждые 27V периодов выборки выполняется БПФ. Элементы
коррелятора (С) формируют произведения одного сигнала с комплексно сопряженным
значением для второго сигнала. В решетке с па антеннами выходы каждого БПФ-
процессора разветвляются по (па — 1) направлениям для перемножения с комплексными
амплитудами от всех остальных антенн
интервал выборки сигналов. В процессе перемножения, который следует за этапом
БПФ, комплексная амплитуда от одной из антенн каждой пары умножается на
значение, комплексно сопряженное амплитуде от другой антенны. Эти перемноже-
перемножения происходят в элементах коррелятора, показанных на рис. 8.16. Заметим, что
данные любой входной последовательности комбинируются только с данными от
других антенн, относящимися к последовательностям того же самого интервала
времени, и такое ограничение ведет к некоторым потерям информации. Эти потери
лучше всего можно проиллюстрировать, рассмотрев измерения корреляции (как
они выполнялись бы на корреляторе задержек), производимые над одной после-
последовательностью из 27V отсчетов для двух антенн. Измерение корреляции для наи-
наибольших задержек, равных ±B7V — l)rs, происходит лишь однажды, для задержек
±B7V — 2)ts дважды и т.д. вплоть до единичной задержки, для которой имеется
27V — 1 измерений. Как видим, имеет место треугольное взвешивание измеренной
корреляции как функции задержки, показанное на рис. 8.17. Данные для длинных
задержек представлены беднее. Положение можно улучшить, разрешив смежным
последовательностям перекрываться. При перекрытии в 50%, часто реализуемом
на практике, данные в центре одной последовательности становятся крайними
в соседней. Может также проводиться взвешивание данных вдоль каждой последо-
последовательности с целью уменьшения боковых лепестков в частотном отклике, причем
перекрытие позволяет данным, имеющим низкий вес в одной последовательности,
получить больший вес в следующей. Подобная процедура, называемая взвешенным
усреднением перекрытий, была впервые описана в (Welch, 1967) в качестве мето-
методики общего спектрального анализа; детальный разбор см. в (Percival and Walden,
1993).
8.7]
Цифровые корреляторы
265
^ 2N Число измерений
корреляции
Задержка
\в единицах
-2N
О
+ 2N
Рис. 8.17. Число эффективных корреляций в FX-корреляторе как функция задержки меж-
между отсчетами. N равно числу частотных каналов (точек спектра) в полосе сигнала. Для
иллюстрации мы взяли N = 8, но на практике более типичны значения в диапазоне от 128
до 1024
Интересно показать, каким образом с помощью FX- и XF-методов можно по-
получить одну и ту же корреляцию в случае дискретных сигналов (Могап, 1976).
В FX-корреляторе преобразования Фурье сигналов х{г) и у (г), состоящих из 27V
отсчетов, равны
Y M =
г=0
к=0
где диакритический значок ^ обозначает квантованную переменную. Пусть ti =
= г/BДг/) n tk = /c/BAi/), где Ai/ — частотная полоса, и пусть у = ?Ay/N. Тогда
спектр коррелированной мощности, S(y) = X(y)Y*(y), равен
2N-12N-1
Функция корреляции
2N-1
р(п) = J2 *m ^tn'N
1=0
Подставляя (8.78) в (8.79), меняя порядок суммирования и замечая, что
jir? (i-k-n)/N _ J u при i-k-пфО,
1=0
получим
2N-1
i=o
2N при г — к — п = 0,
0< (i + n) < B7V -1),
5.78)
3.79)
(8.80)
(8.81)
для гг в интервале между — B7V — 1) и B7V — 1). Итак, из отклика FX-коррелятора
мы получили корреляцию в том виде, как она измеряется коррелятором с за-
задержками, если не считать треугольного взвешивания FX-системы, обсуждавшегося
в связи с рис. 8.17.
Треугольное взвешивание данных корреляции проявляется в свертке коррели-
коррелированного спектра мощности с функцией sinc2B7Vrsi/). Для сравнения отметим,
266 Цифровая обработка сигналов [Гл. 8
что в корреляторе задержек измерения корреляции взвешены по задержке равно-
равномерно, и спектр коррелированной мощности свертывается с sine-функцией (8.75).
Диапазон задержек, в котором измеряется корреляция, составляет 47Vrs, что со-
соответствует основанию треугольника на рис. (8.17), поэтому по теореме выборки
спектр коррелированной мощности должен быть представлен отсчетами с шагом по
частоте l/DiWs). Спектр, полученный в соответствии со сказанным выше об FX-
корреляторе, согласно данному критерию представлен с двукратной недостаточ-
недостаточностью. Таким образом, если попытаться получить функцию корреляции посред-
посредством фурье-преобразования значений коррелированного спектра, недостаточность
выборки приведет к наложению и, следовательно, ошибочным результатам. Такой
ситуации можно избежать, применяя к входным последовательностям длины 27V
фурье-преобразование по 4N точкам, причем данные размещаются в позициях с О
по 27V, а в позициях с B7V + 1) по 47V размещаются нули (O'Sullivan, 1982; Granhmd,
1986). Такую методику называют нулевым заполнением.
При БПФ длиной 27V, равной длине входной последовательности данных,
отклик на узкую спектральную линию, попадающую в середину интервала
между двумя частотами выходного спектра, падает до относительного значения
sine2 A/2) = 0,41. При БПФ длиной 47V с заполнением половины входной последо-
последовательности нулями линия, попадающая между двумя точками выходного спектра,
понижается до sine2 A/4) = 0,81. Если потеря в амплитуде из-за более разреженного
по частоте опроса приемлема, и если нет необходимости выполнять обратное
преобразование к корреляционной функции для коррекции квантования, то БПФ
длиной 27V будет удовлетворительным. В противном случае предпочтительнее
применить БПФ длиной 47V с нулевым заполнением половины входного диапазона.
8.7.5. Сравнение коррелятора с задержками и FX-коррелятора. Число
операций. В корреляторе с задержками число операций в секунду при вычислении
корреляции равно произведению частоты выборки 2Az/, числа различных задержек
на одну базу 27V и числа попарных комбинаций антенн па{па — 1)/2, где N — число
точек спектра в полосе сигнала ПЧ Az/, а па —число антенн. Преобразование Фурье
в частотную область происходит после интегрирования корреляционных данных
за большое число циклов (как правило, > 104), поэтому его вкладом в общий
объем вычислений можно пренебречь. Таким образом, число операций в секунду,
выполняемых в корреляторе задержек, можно оценить как
nLAG » 2NAvna (na - 1), (8.82)
где каждая операция включает в себя одно умножение действительных чисел и одно
сложение. В FX-корреляторе фурье-преобразование производится по одному разу
для каждой антенны через каждые 27V отсчетов, поэтому общее число преобразова-
преобразований в секунду равно Avna/N. Каждое преобразование требует N log2 N комплекс-
комплексных умножений. Кроме того, в FX-корреляторе через каждые 27V отсчетов произво-
производится Nna(na — l)/2 перемножений комплексных амплитуд. Каждую комплексную
операцию мы подсчитываем как четыре операции над действительными числами,
поэтому общее число эквивалентных действительных операций оценивается как
nFX « 2Az/na B log2 N + па - 1). (8.83)
Равенства (8.82) и (8.83) следует рассматривать только в качестве приблизи-
приблизительных, поскольку на практике параметры системы могут меняться в зави-
зависимости от деталей реализации тех или иных операций. Однако отношение
nLAo/nFx ~ Nna/B log2 N + па) отражает основные тенденции, в которых
преобладающую роль играет обычно фактор N. Например, если N = 1000 и па =
= 10, ^LAG/^FX ~ 330. Следует также заметить, что в корреляторе с задержками
8.7] Цифровые корреляторы 267
в основном производятся операции над теми числами, которые генерируются
устройством выборки, т. е. состоящими обычно из одного или двух бит. В FX-
корреляторе числа практически сразу преобразуются в БПФ к значениям, для
представления которых требуется гораздо большее количество бит, например, 16 (по
шесть для действительной и мнимой частей и четыре для их двоичного порядка).
Поэтому преимущество FX-коррелятора существенно меньше, чем показывает
отношение nbAG/nF^.
Разработка интегральных микросхем. Большие корреляторы, т. е. те, у которых
число антенн и число спектральных каналов велики, весьма практичны, потому что
для них могут быть специально разработаны микросхемы сверхбольшой степени
интеграции (СБИС), приспособленные к особенностям конструкции коррелятора.
Такие микросхемы позволяют параллельно выполнять большие объемы операций.
Например, были разработаны схемы СБИС, реализующие 1024 задержки одного
входа относительно другого. Для постройки системы вроде показанной на рис. 8.15
потребовалось бы всего две таких микросхемы, по одной на каждый из двух
блоков коррелятора слева и справа на схеме. Архитектура коррелятора задержек
несколько лучше подходит для реализации ее на основе сверхбольших микросхем,
чем архитектура FX-коррелятора. В частности, в корреляторе задержек число
бит на одну точку данных мало по сравнению с многоразрядным представлением,
которое требуется для FX-коррелятора, о чем говорилось в предыдущем пункте.
Малая разрядность чрезвычайно упрощает ввод данных в микросхему и внутренние
ее взаимосвязи.
Цифровое вращение интерференционных лепестков. Хотя вращение лепестков
часто выполняется в ходе аналоговой обработки сигнала, в некоторых случаях
выгоднее реализовать его после оцифровки сигнала. Например, в наблюдениях
РСДБ, когда данные записываются в виде цифровых отсчетов, полезно иметь
возможность повторить их обработку с другими частотами интерференции, если
положение источника не известно до наблюдений с достаточной точностью.
Цифровое вращение лепестков применяется к оцифрованному сигналу ПЧ
непосредственно перед его поступлением на коррелятор и осуществляется
умножением на цифровой сигнал смещения частоты интерференции, как описано
в п. 9.7.1. Желательно использовать несколько бит для представления вращаемых
данных, чтобы сохранить требуемую точность, поэтому при этой операции число
бит во входном потоке данных коррелятора увеличивается. Как отмечалось
выше, увеличение числа бит на отсчет в корреляторе задержек приводит
к пропорциональному росту сложности и связано с определенными трудностями.
Поэтому может оказаться необходимым усечение данных перед их поступлением
на коррелятор, что приводит к повторным потерям квантования. Напротив, в FX-
схеме многоразрядное представление данных необходимо для выполнения БПФ,
поэтому увеличение разрядности в результате вращения лепестков не приводит
к принципиальным усложнениям схемы.
Коррекция дробной задержки отсчета. При цифровой реализации компенси-
компенсирующих задержек одним из способов регулировки задержки с шагом, меньшим
интервала выборки, является регулировка импульсов, управляющих выборкой
сигнала, как описано в разд. 8.5. Другой способ введения дробных задержек
реализуется после преобразования к частотной области; он состоит в приращении
значений фазы на величину, меняющуюся по полосе ПЧ пропорционально
частоте. В FX-корреляторе это сделать просто, поскольку в каждом цикле БПФ
сигналы преобразуются в форму спектра амплитуд, и требуемая коррекция
может применяться к каждой из антенн по отдельности, до того, как данные
будут комбинироваться по парам антенн. В случае коррелятора задержек здесь
возникают две проблемы. Во-первых, преобразование к спектру производится
268 Цифровая обработка сигналов [Гл. 8
после того, как данные скомбинированы по парам антенн, поэтому корректировать
приходится гораздо больший объем данных. Во-вторых, для длинных баз требуемые
коррекции могут происходить чаще той частоты, с которой в иной ситуации было бы
необходимо выполнять преобразование значений корреляции в спектры мощности.
В результате может оказаться, что возможна лишь статистическая, но не точная
коррекция. См. также п. 9.7.3.
Коррекция квантования. Нелинейность амплитуды корреляции, измеренной
при грубом квантовании выборок, очевидна из соотношения ван Флека (8.25)
и кривых на рис. 8.6. Пользуясь соотношениями, подобными (8.25), можно по
измеренным значениям получить истинное значение корреляции. В корреляторе
задержек это прямолинейный процесс, так как значения корреляции вычисляются
непосредственно. Чтобы получить значения корреляции в FX-корреляторе, данные
спектра коррелированной мощности нужно перевести посредством преобразования
Фурье из области частот в область задержек. После применения коррекции
данные преобразовывают обратно в частотный спектр. Заметим, что коррекция
необходима только в том случае, если для любой пары антенн корреляция полных
сигналов (сигнал плюс шум) велика. Это условие подразумевает наблюдение
источника, практически неразрешенного и настолько сильного, что мощность
сигнала в приемнике сравнима с шумом или превышает его. В случае спектральных
наблюдений важна средняя мощность в полосе пропускания приемника.
Исключение ошибочных данных. Отбрасывание данных с целью исключения
помех или других кратковременных ошибок может стать в FX-корреляторе
серьезной проблемой, поскольку недействительные или отсутствующие выборки
в последовательности длиной 2N отсчетов могут сделать недействительной
всю эту последовательность. Проблема не столь серьезна в случае коррелятора
с задержками, так как там нет какой-то определенной длины последовательности,
которая должна быть свободна от ошибок.
Адаптируемость. Схема FX допускает более простое применение или
адаптируется к специфическим требованиям, так как система ориентирована
скорее на антенну, а не базу, как это имеет место в корреляторе с задержками.
Добавление к FX-коррелятору еще одной антенны не требует столь радикальной
перестройки, как в корреляторе с задержками.
Наблюдения пульсаров. Для наблюдения пульсаров выход коррелятора
должен быть снабжен схемой затвора, отделяющего данные, полученные
в период излучения пульсара, чтобы чувствительность не ухудшалась из-за
шума, принимаемого в то время, пока пульсар не излучает. Для большинства
пульсаров, периоды которых ^ 0,1с, для адекватной работы затвора требуется
разрешение по времени порядка 1 мс *). В первоначальном корреляторе задержек
на VLA, например, основной цикл синхронизации требует, чтобы считывание
данных из коррелятора происходило с интервалами времени 92,8 мкс, к которым
должна быть адаптирована и схема затвора (Hankins, 1999). Это может стать
ограничивающим фактором при наблюдениях очень быстрых пульсаров. Для FX-
коррелятора необходимо собирать данные законченными последовательностями из
27V отсчетов, поэтому пульсарная схема должна воспринимать данные, приходящие
с интервалами ~ 2Nrs. Например, при N = 1000 и полной ширине полосы
х) Многие решетки могут также использоваться в фазируемом режиме, когда имеется по
одному выходу на поляризацию. Специально разработанный пульсарный процессор может
в этом случае обеспечить измерения с высоким разрешением по времени для изучения
профиля и временных характеристик импульса. В таких случаях решетка используется
только для формирования большой эффективной площади, обеспечивающей высокую
чувствительность; см. разд. 9.9
8.7] Цифровые корреляторы 269
пропускания 10 МГц интервал 2Nrs = 100 мкс. Такое разрешение по времени, как
уже было сказано, может ограничить возможности наблюдения самых быстрых
пульсаров. Привлекательной особенностью FX-коррелятора является то, что
для каждого интервала длительностью 2Nrs получается полный спектр. При
дальнейшем усреднении по времени можно обрабатывать частотные каналы по
отдельности и варьировать для каждого из них время срабатывания затвора, чтобы
оно соответствовало смещению импульса из-за дисперсии межзвездной среды.
Выбор схемы коррелятора. Поскольку сравнительные достоинства FX-схемы
и коррелятора задержек, обсуждавшиеся выше, включают в себя несколько
различных моментов, выбор наилучшей архитектуры для любого конкретного
приложения может и не быть очевидным. Обычно требуется детальное изучение
различных подходов к проблеме, формулировка точных спецификаций и проек-
проектирование схем СБИС. Более подробное исследование корреляторов задержек
и FX-корреляторов см. в (D'Addario, 1989) и (Romney, 1995).
8.7.6. Гибридный коррелятор. При разработке широкополосного корреля-
коррелятора может оказаться выгодным разделить аналоговый сигнал от каждой антенны
на п смежных узких поддиапазонов; в типичном случае п — число порядка 10.
Для каждого поддиапазона используется отдельное устройство цифровой выборки,
а коррелятор имеет п модулей, работающих параллельно и охватывающих всю
полосу частот исходного сигнала. Система подобного типа, включающая как ана-
аналоговую фильтрацию, так и цифровой частотный анализ, называется гибридным
коррелятором. Если в цифровой части используется схема коррелятора с задерж-
задержками, то необходимое быстродействие уменьшается в п раз по сравнению с кор-
коррелятором, обрабатывающим всю полосу сигнала без разбиения на поддиапазоны.
Это можно видеть из (8.82), где для одного поддиапазона ширина полосы равна
Аг//п, требуемое число каналов N/n, но требуется п таких модулей цифровой обра-
обработки. Гибридный коррелятор такого типа описывается в (Weinreb, 1984). Однако,
если в цифровой части используется коррелятор типа FX, гибридная схема дает
очень малый выигрыш в числе операций, так как в (8.83) N входит как логарифм.
Общим недостатком гибридных корреляторов являются повышенные требования
к калибровке частотных характеристик поддиапазонов, поскольку нужно избегать
разрывов коэффициента усиления на их краях. В антенных решетках миллиметро-
миллиметровых волн полоса пропускания ПЧ часто имеет ширину порядка 10 ГГц и более, и та
или иная аналоговая фильтрация все равно необходима, чтобы сузить такой диа-
диапазон частот до значений, делающих возможной выборку Найквиста. Как правило,
выгоднее использовать возможно более быстрые устройства выборки, чтобы свести
к минимуму необходимую аналоговую фильтрацию.
8.7.7. Демультиплексирование в широкополосных корреляторах.
Скорость битовых потоков в сверхбольших (СБИС) интегральных микросхемах,
используемых в больших системах корреляторов, обычно составляет несколько
сотен Мбит/с, что по крайней мере на порядок меньше, чем у устройств цифровой
выборки широкополосных корреляторов. Преобразование выхода устройства
выборки из последовательной в параллельную форму, т. е. демультиплексирование
во временной области, позволяет получить оптимальные скорости поступления
данных на коррелятор. Рассмотрим систему, в которой выход каждого устройства
выборки демультиплексируется на п потоков, и предположим для простоты, что
каждая выборка представлена одним битом; параллельная архитектура обеспечи-
обеспечивает обработку нескольких бит. Любые п смежных выборок попадают в разные
потоки. Чтобы получить все произведения для пары сигналов ПЧ, необходимые
270 Цифровая обработка сигналов [Гл. 8
в корреляторе с задержками, потребовалось бы производить корреляцию каждого
из потоков одного сигнала со всеми потоками другого. Для упрощения системы
Эскофьер разработал схему (Escoffier, 1997), в которой п демультиплексированных
потоков бит от каждого сигнала записываются в оперативную память большого
объема (RAM) и считываются из нее в переупорядоченном виде. Каждый демуль-
демультиплексированный поток теперь состоит из последовательности не смежных по
времени блоков из ~ 105 отсчетов. Каждый блок содержит смежные по времени
данные в таком порядке, как они появлялись на выходе устройства выборки. Та-
Таким образом, для любой пары входных сигналов и каждого значения задержки
требуется п корреляторов, работающих с демультиплексированной тактовой часто-
частотой. Кроме того, для каждого сигнала нужно иметь два блока памяти, один из
которых заполняется, а другой считывается. В системе Эскофьера частота выборки
равна 4Гбит/с, п = 32, а длина блока демультиплексированных данных составляет
примерно 1 мс. Так как корреляция не выходит за пределы отдельно взятого блока,
потери в эффективности очень малы и составляют в данном случае приблизительно
0,2%. Другой возможный подход основан на демультиплексировании в частотной
области, как в гибридном корреляторе. После этого остается только прокоррелиро-
вать соответствующие частотные каналы между всеми антеннами, так что число
корреляторов на одну задержку также равно п. В работе (Carlson and Dewdney,
2000) описана чисто цифровая реализация принципа демультиплексирования ча-
частот, на котором основан гибридный коррелятор. Широкополосные сигналы оциф-
оцифровываются в полной полосе частот, разделяются на частотные каналы с помощью
цифровых фильтров, и перед коррелированием производится повторная выборка
с пониженной частотой. Такая схема позволяет избежать трудностей, связанных
с разбросом частотных характеристик аналоговых фильтров. Как схема Эскофьера
с переупорядочением битов, так и частотное демультиплексирование открывают
подходы к разработке больших широкополосных корреляторов. Для последней
схемы требуется меньше задержек, поскольку частичное спектральное разрешение
обеспечивается цифровыми фильтрами.
Для фильтрации оцифрованных сигналов могут быть использованы фильтры
с ограниченным импульсным откликом (FIR, Finite Impulse Response), в которых
входной поток цифровых отсчетов свертывается с заданным рядом чисел; фурье-
образ этого ряда дает частотную характеристику фильтра (Escoffier et al., 2000).
Заданные веса могут храниться в памяти с произвольным доступом и при необходи-
необходимости изменяться. Преимуществом цифровых фильтров является высокая стабиль-
стабильность. Однако может потребоваться усечение выходных отсчетов до разрядности,
которая может обрабатываться коррелятором, вследствие чего могут возникать
повторные потери квантования.
Приложение 8.1. Вычисление суммы ^ R^
q=l
Периодическая функция f(t) может быть представлена в виде ряда Фурье:
q=l L
8.7] Приложение 8.2. Интеграл вероятности для двухуровневого квантования 271
где /3 — период функции и
cos, , *<jL\dt. (П8.2)
0
Теорема Парсеваля для (П8.1) принимает вид
(П8.3)
q=l
Пусть теперь f(t) является суммой прямоугольных функций единичной высоты
и ширины, центр одной из которых совпадает с t = 0, а центры других отстоят от
него на расстояния, кратные ±/3. Тогда получаем
2 sm(nq/P) и _ n f *2лл л+ _ -, (П8.4)
(П8.5)
Из (П8.3) и (П8.4) следует
I2_
J 2 '
что и является суммой, необходимой для оценки выражения (8.19).
Приложение 8.2. Интеграл вероятности для двухуровневого
квантования
Интегрирование вероятности в (8.21) молено выполнить следующим образом.
Искомая вероятность выражается интегралом
оо оо
п 1 Г Г \~(х2 + У2 — 2РХУ)\ j j /тто г\
Рц = —. ехр —^ т^- о ахау. (П8.6)
0 0
Восстановим круговую симметрию интеграла, положив
z = У рХ2 , dj/ = л/l- р2 dz. (П8.7)
Тогда
оо оо
iz. (П8.8)
Теперь подставим ж = г cos 0 и z = r sin 6. Нижний предел интегрирования по
z в (П8.8) представляет собой прямую z = —px/^/l — р2 , составляющую с осью
х угол 0,0 = — arcsinp. Интеграл охватывает область плоскости (ж, z) между данной
272 Цифровая обработка сигналов [Гл. 8
прямой и осью z @ = тг/2). Таким образом,
оо тг/2
I
О — arcsin р
Наконец, подставим и = г2 /2а2:
Pn = J_ [ du \ e~ud0. (П8.10)
2тг J J
О — arcsin р
Выражение (П8.10) может быть проинтегрировано непосредственно и дает
Рг1 = -Л + ^- arcsin р. (П8.11)
4 2тг
Приложение 8.3. Коррекция для четырехуровневого
квантования
В работе (Schwab, 1986) были исследованы различные аспекты оптимизации
корреляторов с четырехуровневым квантованием. В их число входят точные зна-
значения оптимальных пороговых уровней и эффективности квантования, а также
выражения для вычисления корреляции как функции значений на выходе корре-
коррелятора. Пороговые значения и соответствующие эффективности приведены в табл.
П8.1.
Таблица П.8.1. Оптимальные пороги и эффективность четырехуровневого
квантования
Ур/сг Щ
3
3,3358750
4
0,99568668
0,98159883
0,94232840
0,8811539496
0,8825181522
0,8795104597
Значения эффективности квантования щ для п = 3 и 4 находятся в пределах 0,3 %
от наивысшего значения и представляют интерес потому, что нецелые значения
весового коэффициента п потребовали бы, в случае коррелятора задержек, суще-
существенного усложнения его схемы.
Рациональные приближения для корреляции р являются «минимаксными» ре-
решениями; другими словами, они минимизируют максимальную относительную
ошибку. Переменная rN является нормализованным выходным значением корреля-
коррелятора, т. е. измеренным значением, поделенным на соответствующий результат при
р = 1. Первые три приближения, приведенные ниже, пригодны для всех \rN\ ^ 1.
8.7] Цитированная литература 273
Для п = 3 и соответствующего значения vq/<j из табл. П8.1 следующее прибли-
приближение дает максимальную относительную ошибку 1,51 • 10~4:
_ ч 1,1347043 - 3,09713127^ + 2,9163894ri - 0,89047693r^ /TTO Л оЧ
О\Т ) = 7* (Но 1^)
1 - 2,6892104г^ + 2,4736683г^ - 0,72098190r^ N' '
Для n ~ 3,3359 и соответствующего значения г>о/сг из табл. П8.1 следующее при-
приближение дает максимальную относительную ошибку 1,46 • 10~4:
~( \ - М329552 - 3,1056902г^ + 2,9296994г^ - 0,90122460г^
~ 1 - 2,7056559г^ + 2,5012473г^ - 0,73985978r^ ^
Для п = 4 и соответствующего значения г>о/сг из табл. 8.5 следующее приближе-
приближение дает максимальную относительную ошибку 1,50 • 10~4:
_ ч 1,1368256 - 3,0533973r2^ + 2,8171512ri - 0,85148929г^ /тто 1 Л.
р\т ) = — — — т (По 14)
1 - 2,6529114r^ + 2,4027335r^ - 0,70073934r^ N'
Следующее приближ:ение такж:е относится к случаю п = 4и соответствующему
значению vq/<j из табл. 8.5, но применимо только для \rN\ ^ 0,95. Оно дает макси-
максимальную относительную ошибку 2,77 • 10~5:
_ 1Д369813 - 1,2487891г^ + 4,5380174 • 10~2r4N - 9,1448344 • lO~3r6N
~ 1 - 1,0617975г^ Г^'
Цитированная литература
Abramowitz M. and I. A. Stegun. Handbook of Mathematical Functions. National Bureau of
Standards, Washington, DC, 1964, rep. by Dover, New York, 1965.
Ball J. A. The Harvard Minicorrelator. IEEE Trans. Instrum. Meas. IM-22, 193, 1973.
Benson J. M. The VLBA Correlator. Very Long Baseline Interferometry and the VLA, J. A.
Zensus, P. J. Diamond and P. J. Napier, Eds., Astron. Soc. Pacific Conf. Ser., 82, 117-131,
1995.
Blackman R. B. and J. W. Tukey. The Measurement of Power Spectra. Dover, New York,
1959.
Bowers F. K. and R. J. Klingler. Quantization Noise of Correlation Spectrometers. Astron.
Astrophys. Suppl. 15, 373-380, 1974.
Bowers F. K., D. A. Whyte, T. L. Landecker and R. J. Klingler. A Digital Correlation
Spectrometer Employing Multiple-Level Quantization. Proc. IEEE, 61, 1339-1343, 1973.
Bracewell R. N. The Fourier Tramsform and Its Applications. McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Burns W. R. and S. S. Yao. Clipping Noise Loss in the One-Bit Autocorrelation Spectral Line
Receiver. Radio Sci., 4, 431-436, 1969.
Carlson B. R. and P. E. Dewdney. Efficient Wideband Digital Correlation. Electronics Letters,
36, 987-988, 2000.
Chikada Y., M. Ishiguro, H. Hirabayashi, M. Morimoto, K. Morita, K. Miyazawa, K. Nagane,
K. Murata, A. Tojo, S. Inoue, T. Kanzawa and H. Iwashita. A Digital FFT Spectro-Correlator
for Radio Astronomy. Indirect Imaging, J. A. Roberts, Ed., Cambridge Univ. Press, Cambridge,
UK, 1984, p. 387-404.
274 Цифровая обработка сигналов [Гл. 8
Chikada Y., М. Ishiguru, Н. Hirabayashi, М. Morimoto, К. I. Morita, Т. Kanzawa, Н. Iwashita,
К. Nakazimi, S. I. Ishiwaka, Т. Takashi, К. Handa, Т. Kasuga, S. Okumura, Т. Miyazawa,
Т. Nakazuru, К. Miura and S. Nagasawa. A 6 x 320-MHz 1024-Channel FFT Cross Spectrum
Analyzer for Radio Astronomy. Proc. IEEE, 75, 1203-1210, 1987.
Cole T. Finite sample Correlations of Quantized Gaussians. Aust. J. Phys., 21, 273-282, 1968.
Cooper B. F. C. Correlators with Two-Bit Quantization. Aust. J. Phys., 23, 521-527, 1970.
D'Addario L. R. Cross Correlators. Synthesis Imaging in Radio Astronomy. R. A. Perley, F.
R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser., 6, 59-82, 1989.
D'Addario L. R., A. R. Thompson, F. R. Schwab and J. Granlund. Complex Cross Correlators
with Three-Level Quantization: Design Tolerances. Radio Sci., 19, 931-945, 1984.
Davis W. F. Real-Time Compensation for Autocorrelation Clipper Bias. Astron. Astrophys.
Suppl. 15, 381-382, 1974.
Escoffier R. P. The MMA Correlator. MMA Memo. 166, National Radio Astronomy Observa-
Observatory, Socorro, NM, 1997.
Escoffier R. P., J. С Webber, L. R. D'Addario and С M. Broadwell. A Wideband Digital
Filter using FPGAs. Proc. SPIE, 4015, 106-113, 2000.
Goldstein R. M. A Technique for the Measurement of the Power Spectra of Very Weak Signals.
IRE Trans. Space Electron. Telem., 8, 170-173, 1962.
Granlund J. O'Sullivan's Zero-Padding. VLBA Correlator Memo. 66, National Radio Astron-
Astronomy Observatory, Charlottesville, VA, 1986.
Hagen J. B. and D. T. Farley. Digital Correlation Techniques in Radio Science. Radio Sci., 8,
775-784, 1973.
Hankins Т. H. Pulsar Observations at the VLA. Synthesis Imaging in Radio Astronomy II, G.
B. Taylor, С L. Carilli and R. A. Perley. Eds., Astron. Soc. Pacific Conf. Ser., 180, 613-624,
1999.
Harris F. J. The Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.
Proc. IEEE, 66, 51-83, 1978.
Jenet F. A. and S. B. Anderson. The Effects of Digitization on Nonstationary Stochastic Signals
with Applications to Pulsar Signal Baseband Recording. Pub. Astron. Soc. Pacific, 110, 1467-
1478, 1998.
Kulkarni S. R. and C. Heiles. How to Obtain the True Correlation from a Three-Level Digital
Correlator. Astron. J., 85, 1413-1420, 1980.
Lo W. F., P. E. Dewdney, T. L. Landecker, D. Routledge and J. F. Vaneldik. A Cross-
Correlation Receiver for Radio Astronomy Employing Quadrature Channel Generation by
Computed Hilbert Transform. Radio Sci., 19, 1413-421, 1984.
Мог an J. M. Very Long Baseline Interferometer Systems. Methods of Experimental Physics,
Vol. 12C, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 174-197.
Napier P. J., A. R. Thompson and R. D. Ekers. The Very Large Array; Design and Performance
of a Modern Synthesis Radio Telescope. Proc. IEEE, 71, 1295-1320, 1983.
Nyquist H. Certain Topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng.,
47, 617-644, 1928.
Okumura S. K., M. Momose, N. Kawaguchi, T. Kanzawa, T. Tsutsumi, A. Tanaka, T.
Ichikawa, T. Suzuki, K. Ozeki, K. Natori and T. Hashimoto. 1-GHz Bandwidth Digital Spectro-
Correlator System for the Nobeyama Millimeter Array. Publ. Astron. Soc. Japan, 52, 393-400,
2000.
Oppenheim A. V. and R. W. Schafer. Digital Signal Processing. Prentice-Hall, Englewood
Cliffs, NJ, 1975.
О'Sullivan J. D. Efficient Digital Spectrometers - A Survey of Possibilities. Note 375 Nether-
Netherlands Foundation for Radio Astronomy, Dwingeloo, 1982.
Percival B. D. and A. T. Walden. Spectral Analysis for Physical Applications. Cambridge
Univ. Press, 1993, p. 289.
8.7] Цитированная литература 275
Price R. A Useful Theorem for Nonlinear Devices Having Gaussian Inputs. IRE Trans. Inf.
Theory, IT-4, 69-72, 1958.
Romney J. D. Theory of Correlation in VLBI. Very Long Baseline Interferometry and the VLA,
J. A. Zensus, P. J. Diamond and P. J. Napier. Eds., Astron. Soc. Pacific Conf. Ser., 82, 17-37,
1995.
Schwab F. Two-Bit Correlators: Miscellaneous Results. VLBA Correlator Memo. 75, Nat. Radio
Astron. Obs., Charlotesville, VA, 1986.
Shannon С. Е. Communication in the Presence of Noise. Proc. IRE, 37, 10-21, 1949.
Thompson A. R. Quantization Efficiency for Eight or More Sampling Levels. MMA Memo.
220, National Radio Astronomy Observatory, Socorro, NM, 1998.
Van Vleck J. H. and D. Middleton. The Spectrum of Clipped Noise. Proc. IEEE, 54, 2-19,
1966.
Weinreb S. A Digital Spectral Analysis Technique and Its Application to Radio Astronomy.
Technical Report 412, Research Lab. for Electronics, MIT, Cambridge, MA, 1963.
Weinreb S. Analog-Filter Digital-Correlator Hybrid Spectrometer. IEEE Trans. Inst. Meas.,
IM34, 670-675, 1984.
Welch P. D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A
Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio
Electroacoust., AU-15, 70-73, 1967.
Willis A. G. and J. D. Bregman. Effects in Fourier Transformed Spectra. User's Manual
for Westerbork Synthesis Radio Telescope, Netherlands Foundation for Radio Astronomy,
Westerbork, Netherlands, 1981, Ch. 2, App. 2.
Yen J. L. The Role of Fast Fourier Transform Computers in Astronony. Astron. Astrophys.
Suppl., 15, 483-484, 1974.
Глава 9
ИНТЕРФЕРОМЕТРИЯ СО СВЕРХДЛИННЫМИ БАЗАМИ
В 1967 г. был разработан новый интерферометрический метод с приемными
элементами, разнесенными на большие расстояния друг от друга, с независимой
регистрацией сигналов без передачи данных в реальном времени. При этом резуль-
результаты измерений записываются на магнитные ленты для последующей кросскорре-
ляционной обработки на специализированном вычислительном центре. Этот метод
назвали радиоинтерферометрией со сверхдлинными базами (РСДБ); термин напо-
напоминает самые первые длиннобазовые интерферометры в Джодрелл Бэнк, в кото-
которых элементы соединялись линиями С ВЧ-связи, длина которых достигала 127 км.
Принципы, используемые в РСДБ, в основном те же, что и в интерферометрии со
связанными элементами. Магнитофон может рассматриваться как линия задержки
ПЧ не ограниченной величины — недели вместо микросекунд. Применение магни-
магнитофонов объясняется экономическими соображениями, что накладывает на систему
определенные ограничения. Практически были продемонстрированы спутниковые
линии связи (Yen et al., 1977), но их стоимость высока.
9.1. Первые эксперименты
Стимулом развития РСДБ явилось то, что во многих радиоисточниках были
обнаружены компоненты, которые не разрешаются на интерферометрах с базами
в несколько сотен километров. К середине 1960-х годов было хорошо известно,
что мерцания (эффект мерцаний рассматривается в гл. 13) и временная пере-
переменность излучения квазаров свидетельствуют об угловых размерах менее 0,01//.
Области мазерного излучения молекул ОН на длине волны 18 см не разрешались
на уровне ОД". Низкочастотные вспышки излучения Юпитера, по-видимому, про-
происходили в районах с малыми угловыми размерами. Целью первых РСДБ экс-
экспериментов было измерение угловых размеров этих радиоисточников (Шоломиц-
кий и др., 1965; Matveenko, Kostenko, 1979). Целесообразно рассмотреть первые
РСДБ-эксперименты в их наиболее простом виде. Рассмотрим два радиотелескопа
с температурами шума системы Tsi и Т52, которые при наведении на компактный
источник дают антенные температуры Та\ и Тд2- На каждой станции за время
когерентности, т. е. в течение интервала времени, при котором независимые ге-
генераторы остаются достаточно стабильными для усреднения лепестков, записы-
записывается по N дискретных отсчетов. При последующей обработке потоки данных
выравнивают, коррелируют друг с другом и после сдвига квазисинусоидальных
интерференционных лепестков усредняют по времени. Для точечного источника
расчетный коэффициент корреляции равен
„ ~„ / ТА1ТА2
Ро ~VV (Tsi+TA1)(TS2+TA2) '
9.1] Первые эксперименты 277
где rj rsj 0,5 — коэффициент, учитывающий потери квантования сигналов и их
обработки (см. разд. 9.7). Здесь удобно ввести нормированную функцию видности
у Р Р
VN = — = -
где р — измеренный коэффициент корреляции в предположении Тд <С Т#. Средне-
Среднеквадратичный уровень шума равен
(9.3)
где Az/ — полоса сигнала ПЧ и тс — время когерентного накопления. Таким образом,
из (9.1)-(9.3) получаем отношение сигнал/шум:
Если принять, что минимальное отношение сигнал /шум равно 4, то из A.3), A-5)
и (9.4) минимальная обнаружимая плотность потока равна
где к — постоянная Больцмана, а А\ и А2 — эффективные площади антенн. В 1967 г.
типичными параметрами были А ~ 250 м2 (телескоп с диаметром зеркала 25 м),
Ts — 100 К, г) ~ 0,5 и N = 1,4-Ю8 бит (один бит на отсчет); в системе Mark I
NRAO использовался накопитель на магнитных лентах со стандартной плотностью
записи 800 бит на дюйм. Для неразрешенного источника б^т ~ 2 Ян. Прогресс за
последующие три десятилетия характеризуют следующие значения параметров:
А ~ 1600 м (телескоп диаметром 64 м), Ts — 30 К и N = 5 • 1012 бит — емкость
специализированного накопителя на магнитных лентах с полосой записи 64 МГц.
Для Vn = 1 из (9.5) получим Бш[п ~ 0,6 мЯн. В обоих примерах предполагается,
что время когерентности больше времени записи ленты. Размер источника можно
оценить по единичному измерению Vдг, сравнением полученного результата с функ-
функцией видности, рассчитанной для симметричной гауссовой модели. При этом, как
показано на рис. 1.5, полная ширина источника а по уровню половины максимума
равна
2л/1п2
а=
тги
где и — проекция базы (в длинах волн).
РСДБ может использоваться только для изучения объектов с очень высокой
интенсивностью излучения. Поэтому исследуются процессы обычно нетепловой
природы. Чтобы источник был зарегистрирован на базе длиной Z), его размеры
должны быть меньше расстояния между интерференционными лепестками. По-
Поскольку плотность потока S равна 2/гТвГ?/А2, где Тв — яркостная температура,
А — длина волны и ?} — телесный угол источника, то минимально обнаружимая
яркостная температура равна
{TB)min~^-D2Smin, (9.7)
278 Интерферометрия со сверхдлинными базами [Гл. 9
поскольку п ~ тг(А/2?>J. Если D = 103 км и Smin = 2мЯн, то (TB)min ~ 106 К.
Поэтому наблюдения явлений тепловой природы, происходящих в молекулярных
облаках, компактных областях НИ и в большинстве звезд, невозможны. С другой
стороны, без особых трудностей могут быть изучены источники синхротронного
излучения, такие как остатки вспышек сверхновых, радиогалактики и квазары, яр-
костная температура которых ограничивается 1012 К из-за потерь на комптоновское
рассеяние, а также мазеры, в которых Тв — 1015К, и пульсары.
Первые РСДБ-измерения дали результаты в трех направлениях:
1) простые распределения яркости, полученные сравнением измеренных функ-
функций видности с моделями источников;
2) карты мазеров по сопоставлению частот интерференции для различных спек-
спектральных деталей;
3) координаты источников измерены с точностью порядка ~ 1", а длины баз —
с точностью до нескольких метров.
Обзор первых методов наблюдений дан в (Klemperer, 1972). С тех пор техника
интерферометрии непрерывно совершенствовалась с целью получения достоверных
изображений радиоисточников, имеющих сложную структуру. В основном при этом
используется метод замыкания фазы (см. разд. 10.3), обеспечивающий наиболее
полную фазовую информацию, когда сеть РСДБ образована достаточным количе-
количеством антенн.
9.2. Различие РСДБ и обычной интерферометрии
В этом разделе мы кратко рассмотрим различия между РСДБ и интерферомет-
интерферометрией со связанными элементами. Более подробно они рассматриваются в последую-
последующих разделах главы. Прежде всего подчеркнем единство теории интерферометрии.
Основная цель любого интерферометрического эксперимента — измерение свойств
когерентности электромагнитного поля. Поэтому принципы интерферометрии со
связанными элементами и РСДБ в сущности одинаковы. Однако в РСДБ требу-
требуется применение особой техники из-за специфических наблюдательных ограниче-
ограничений. Можно представить, что в будущем, когда гш-плоскость будет непрерывно
заполняться в пределах от нескольких метров до более чем 105 км и наибольшие
базы будут обеспечиваться размещением элементов на удаленных спутниках; будут
использоваться оптоволоконные или другие современные коммуникационные систе-
системы, делающие ненужной запись сигналов, определение РСДБ как особого метода
станет предметом истории. А пока нам приходится иметь дело с определенными
ограничениями, по причине которых РСДБ на практике несколько отличается от
интерферометрии со связанными элементами.
Первые РСДБ-эксперименты организовывались различными группами обсер-
обсерваторий для фундаментальных радиоастрономических исследований. У каждого
телескопа были свои ограничения, калибровки и руководство. Для стандартизации
методики и автоматизации проведения экспериментов был создан ряд сетей РСДБ.
Такие локальные сети работают на периодической основе, и связь между их элемен-
элементами с целью проверки согласования действия во время наблюдений ограничена.
Небольшая часть данных по сильным источникам может быть передана с антенн
на коррелятор по телефонным линиям и прокоррелирована для подтверждения
работоспособности аппаратуры и определения аппаратурных задержек. Позднее
были созданы решетки, специально предназначенные для РСДБ (см., например,
Napier et al., 1994).
9.2] Различие РСДБ и обычной интерферометрии 279
В РСДБ стабильность системы в целом хуже контролируема вследствие ис-
использования на каждом элементе независимых стандартов частоты. Отклонение
частот стандартов от номинала приводит к ошибкам времени. Они, как правило,
включают в себя систематическую ошибку, величина которой составляет пример-
примерно несколько микросекунд, и плавный дрейф со скоростью нескольких десятых
долей микросекунды в сутки (разд. 9.5). Поэтому для определения и контроля
аппаратурной задержки необходимо измерение корреляционной функции приня-
принятых сигналов [относительной временной задержки т, как определено формулой
C.27)]. Напротив, ошибки задержки в интерферометрах со связанными элементами,
являющиеся следствием главным образом ошибок определения базы и задержек
сигнала в атмосфере, обычно менее 30 пс, что соответствует расстоянию 1см. Та-
Такие ошибки несущественны для полос пропускания меньше 1 ГГц. Таким образом,
отклик интерферометров со связанными элементами всегда центрирован к интер-
интерференционной полосе «белого света». Задержка становится значимой только при
слишком большом поле зрения по сравнению с полосой частот (см. разделы 2.2 и 6.3)
или когда спектральные измерения выполняются с использованием сдвига сигналов
по времени. В РСДБ, чтобы найти правильное соотношение времени и получить
максимальный коэффициент корреляции, необходимо провести поиск в некото-
некотором интервале значений задержек. Обычно коэффициенты корреляции для ряда
сдвигов по задержке рассчитываются одновременно, так что РСДБ-коррелятор
имеет близкое сходство с цифровым спектральным коррелятором, хотя количество
спектральных каналов может быть меньше обычно используемого в спектральных
наблюдениях. Отклонения частоты стандартов от номинала, вызывающие плавное
изменение аппаратурной задержки с течением времени, также приводят к смеще-
смещению частоты интерференции. Поэтому РСДБ-эксперимент начинают с двумерного
поиска по задержке и по частоте интерференции (скорости изменения задержки),
чтобы найти максимум корреляционной функции. Этот процесс называется поис-
поиском интерференционных лепестков (fringe fitting).
Концепция когерентности в РСДБ и интерферометрии со связанными элемента-
элементами понимается по-разному. В интерферометрии со связанными элементами в преде-
пределах нескольких градусов от исследуемого источника обычно находится калибровоч-
калибровочный, который наблюдается через каждые несколько минут. Таким образом, время
накопления, в принципе, не ограничено даже при изменении аппаратурной фазы,
и его понятие заменяет интервал между калибровками. В РСДБ кратковременная
фазовая стабильность (t < 103 с) хуже. Атмосферные флуктуации над станция-
станциями, вообще говоря, полностью некоррелированны, и вносят в интерференционные
лепестки фазовый шум, так же как стандарты частоты и умножители. Однако
основное различие между интерферометрией со связанными элементами и РСДБ
следует из того факта, что при существующих уровнях чувствительности лишь
малая часть неразрешенных источников может использоваться в качестве калиб-
калибровочных. Не всегда возможно найти калибровочный источник, расположенный
достаточно близко к наблюдаемому для его использования в качестве точки опорной
фазы. Время, необходимое для перестановки антенн, также как и декорреляция
сигналов в атмосфере, возрастает с увеличением углового расстояния между источ-
источниками. Таким образом, время когерентности в РСДБ — один из главных факторов
ограничения чувствительности. При усреднении сигнала за время больше времени
когерентности усредняется амплитуда интерференционных лепестков. В этом слу-
случае чувствительность улучшается лишь как корень четвертой степени из времени
накопления (см. п. 9.3.5). Калибровка фазы в РСДБ-системах также сложнее, хотя
ситуация улучшилась к концу 90-х, так как увеличение чувствительности приве-
привело к увеличению количества доступных калибровочных источников. Улучшение
фазовой стабильности аппаратуры и более точное моделирование баз, атмосферы
280 Интерферометрия со сверхдлинными базами [Гл. 9
и других подобных параметров позволяют выполнять фазовую привязку для калиб-
калибровочных источников в пределах до нескольких градусов. Этот метод опорной фазы
рассматривается в разд. 12.2, и приведен на рис. 12.2. Фазовая информация также
может использоваться в методе замыкания фазы. При определении координат в ка-
качестве измеряемых величин полезны частота интерференции и групповая задержка
(влияние отклика, определяемого задержкой, рассматривается в разделах 2.2 и 6.3).
Хранение не детектированных сигналов до корреляции порождает несколько
проблем в РСДБ. Средняя полоса сигнала ПЧ ограничивается записывающей ап-
аппаратурой и, следовательно, ограничивает чувствительность. Для сохранения дан-
данных с максимально возможной эффективностью сигнал представляется в простой,
квантованной форме, с выборкой на частоте Найквиста. При таком представлении
сигнала основные операции сдвига интерференционных лепестков и отслеживания
задержки, применяемые к записанным данным, оказывают значительное влия-
влияние на результат, что необходимо учитывать при определении функции видности
(разд. 9.7).
9.3. Основные характеристики системы РСДБ
9.3.1. Ошибки времени и частоты. Блок-схема с основными элементами
системы РСДБ и возможной конфигурацией процессора показана на рис. 9.1. Фазы
гетеродинов и последовательности временных импульсов для магнитофонов «при-
«привязаны» к атомным стандартам частоты. Во многих прикладных направлениях
РСДБ, таких, как спектральные наблюдения или астрометрические программы,
должны точно учитываться эффекты, зависящие от частоты. Для спектрального
анализа системы рассмотрим изменение фазы одной спектральной компоненты.
В приближении плоского волнового фронта сигнал, принимаемый антенной 1,
относительно которой мы будем определять временные параметры, равен ei27Tut,
и сигнал, принимаемый антенной 2 равен е^2п1У^~Т9\ где rg — геометрическая
задержка. Фазы гетеродинов равны 2тпуьог + в\ и 2тп/ьо? + #2, где г/ъо — частота
гетеродина, а в\ и #2 — медленно изменяющиеся переменные, представляющие
фазовый шум, вносимый стандартами частоты. Для начала, рассмотрим отклик для
верхней полосы частот, когда частота гетеродина ниже частоты сигнала, в системе,
показанной на рис. 9.1. В этом случае фазы на выходах смесителей равны
ф^ 2n{vvbo)teu
(9.8)
21] = 2тг (г/ - i/LO) t - 2тп;тд - в2.
В обоих записываемых сигналах содержатся ошибки часов т\ и т2, с учетом которых
-ръо)(г-т1)-61,
(9.9)
42) = 2тг (i/ - i/LO) (t - т2) - 2-KVTg - 02.
При обработке временные последовательности дискретных отсчетов, полученных
на антенне 2, сдвигаются на время т' расчетного значения задержки тэ, так что
43) =2ж{у- ръо) (t-r2+ т'д) - 2жут9 - 02. (9.10)
Выход коррелятора с набором задержек и процессора, выполняющего преобразова-
9.3]
Основные характеристики системы РСДБ
281
Стандарт
частоты
Гетеродин
с системой
фазовой
автоподстройки
(ФАП)
Генератор
кода
времени
Усилитель
Усилитель
Смеситель
Видеопре-
Видеопреобразователь
Форматор
Смеситель
Видеопре-
Видеопреобразователь
Форматор
Гетеродин
с системой
фазовой
автоподстройки
(ФАП)
Генератор
кода
Стандарт
частоты
Магнитофон Магнитофон
Процессор
_L
Магнитофон
(воспроизведение)
Генератор
временных
импульсов
Буфер
данных
Магнитофон
(воспроизведение)
Буфер
данных
ЭВМ
Т
А.
Буфер
задержек
Коррелятор
Рис. 9.1. Блок-схема основных элементов системы РСДБ, включая получение и обработку
данных. На входы смесителей могут поступать сигналы в верхней и нижней или в обеих бо-
боковых полосах частот в зависимости от полосы пропускания усилителей. При проведении
миллиметровых наблюдений в качестве входного каскада приемника часто используется
SIS-смеситель, что позволяет принимать обе боковые полосы частот. Квантование и выбор-
выборка сигналов осуществляется в блоках форматора. В показанной системе обработки данных
иллюстрируется подход, описанный аналитически выражениями (9.16)-(9.21). Процессоры
в основном отличаются положением модуля смещения частоты интерференции (СЧИ),
который может находиться перед коррелятором (см. рис. 9.17)
ние Фурье, представляет кросскорреляционный энергетический спектр. На выходе
процессора фаза компоненты сигнала на частоте v равна
= 27г(гу-гуьо)(т2--
¦021, (9.11)
282 Интерферометрия со сверхдлинными базами [Гл. 9
где Arg = тд — т'д — ошибка задержки, те = т2 — т\ — ошибка часов, и д2\ =
= в2 — 01- Уравнение (9.11) получено для преобразования частоты верхней полосы
пропускания в смесителях (рис. 9.1), когда промежуточная частота (ПЧ), равная
[у — г/ьо), положительна. Для общности мы приводим также отклик для нижней
полосы частот, когда ПЧ равна [уъо — v). В этом случае
12 2 (i/
= 2тг (i/LO - v) (re + Атд) - 2мьотд - 021. (9.12)
Отметим, что в идеальном приближении, когда т\ = т2, в\ = в2 ж тд = т'д, уравне-
уравнения (9.11) и (9.12) сводятся к виду ф\2 = 2тпУьотд — Для верхней полосы частот,
и 012 = ~^уъот9 ~ Для нижней.
Корреляционная функция на выходе коррелятора действительна, но нечетна,
поэтому кросскорреляционный энергетический спектр S\2 сигнала источника непре-
непрерывного излучения обладает свойством
512И = 5Г2(-1/'), (9-13)
где v1 — промежуточная частота, равная (у — ^LO). Предполагается, что частотные
характеристики фильтров в электронных схемах одинаковы и поэтому не вносят
никаких смещений фазы. Таким образом, частотные характеристики аппаратурных
фильтров по мощности действительны и, используя частотные характеристики по
напряжению H{v) фильтров двух антенн, получим S(v') = Hi{v') = Hi(i/f)H?(i/f).
Объединяя фазу из выражения (9.11) с частотной характеристикой по мощности,
кросскорреляционный энергетический спектр для верхней полосы частот можно
записать в виде
S12(v') = <S(z/) exp {j [2тг1/'(те + ArJ + 2мъотд + 021] } . (9.14)
Соответствующее уравнение для нижней боковой полосы частот можно получить
из выражения (9.12). Кросскорреляционную функцию для верхней боковой полосы
пропускания можно получить из выражений (9.13) и (9.14):
Pi2(r)= f S12{v')ei2™'Tdv'. (9.15)
Для обеих полос интегрирование выполняется как по положительным, так и по
отрицательным частотам, и, так как S\2 — эрмитова функция, a S — полностью
действительная, получаем
Pl2(r) = 2F1(t') cosB7rz/LOr^ + <92i) - 2F2(rf) sin Bтпуьотд + 02i), (9.16)
где r; = г + re + Д7-3 и
Fi(r) = [ S(v') cosBttz/t) dv1,
So (9.17)
F2(t) = j S{v') sinB7ri/V) di/.
0
Если S(vf) — низкочастотный спектр прямоугольной формы с шириной полосы
пропускания Дг/, то
sin 2тгДг/т т-, / \ л sin2 тгАит
(9.18)
9.3]
Основные характеристики системы РСДБ
283
Эти функции показаны на рис. 9.2. Подставляя (9.18) в (9.16), кросскорреляцион-
ную функцию можно записать в виде
р12(т) = 2Az/ cos B7П/]
lo ' g
ttAz/t')
бшттАтут'
ttAvt'
(9.19)
Подобный анализ приводится Роджерсом (Rogers, 1976).
Изменение rg в зависимости от времени приводит к появлению интерферен-
интерференционных лепестков на выходе коррелятора. Частота интерференции (/)/
остается постоянной в преде-
пределах полосы пропускания при-
приемника, поскольку вносимые
геометрической задержкой из-
изменения фазы по полосе ча-
частот устраняются изменением
аппаратурной задержки. Для
верхней и нижней полос про-
пропускания знаки скорости из-
изменения фазы противополож-
противоположны — обратите внимание на
слагаемое 2тгиъотд в уравнени-
уравнениях (9.11) и (9.12). См. также
рис. 6.5 для дальнейших пояс-
пояснений. В РСДБ естественная
частота интерференции доста-
достаточно велика, и сигнал может
быть потерян после усреднения
корреляционных данных, по-
поэтому интерференционные ле-
лепестки на выходе коррелятора,
показанного на рис. 9.1, оста-
останавливают вращением фазы.
Если в двухполосной системе
лепестки остановить в одной
полосе частот, то в другой ча-
частота интерференции удвоится.
Однако данные каждой полосы
частот могут быть обработаны
раздельно с соответствующим
Рис. 9.2. Функции Fi(t) и
Avx
определены форму-
формулой (9.18), величина амплитуды y/F? (т) + F| (т)
сдвигом частоты интерференции в каждом случае. В РСДБ положение источника
и другие параметры не всегда известны с достаточной точностью по окончании на-
наблюдений, поэтому на рис. 9.1 лепестки останавливаются после считывания данных,
путем перебора различных частот вращения интерференции. Для этого исполь-
используется смещение фазы квантованных сигналов на входе или выходе коррелятора
(см. п. 9.7.1). Преобразование кросскорреляционной функции или кросскорреляци-
онного энергетического спектра может быть описано как домножение сигнала на
е~з KvbOTg ^B верХней полосе частот) и его фильтрация для выделения низкочастот-
низкочастотной составляющей. В результате получается комплексная корреляционная функция
вида
^^ (9.20)
р'12(т) = Av exp [jB^bOArg + в21 +
Отметим, что слагаемое 2тп/ъотд, которым представлена основная частота интерфе-
интерференции, исключено, но остаточная частота интерференции может присутствовать
284
Интерферометрия со сверхдлинными базами
[Гл.9
в коррелированном сигнале из-за слагаемых с Дт3 и Аи. В результате для крос-
скорреляционного энергетического спектра получаем
= S(v') exp {j [2тг1/(те + Атэ)
2ttz/loAt5
в21] } .
(9.21)
V/WVWW
wwww
Время
Рис. 9.3. Восемь синусоид представляют кор-
корреляционную функцию [действительную часть
выражения (9.20)], изменяющуюся в зависимо-
зависимости от времени, для отдельных сдвигов по за-
задержке (сверху вниз: 7/2, 5/2, 3/2, 1/2, -1/2,
—3/2, —5/2, —7/2 интервалов Найквиста). Ко-
Колебания наблюдаются на остаточной частоте
интерференции, в которую включаются любые
отклонения от номинала стандартов частоты
двух антенн. Отметим возрастающий сдвиг фа-
фазы на 90° между значениями корреляционной
функции для последовательных сдвигов по за-
задержке
Этот результат применим для верх-
верхней боковой полосы частот, в кото-
которой остановлены лепестки, при этом
сигнал второй полосы частот на вы-
выходе коррелятора в среднем равен
нулю.
Пример р[2(т) Для восьми зна-
значений т показан на рис. 9.3. Си-
Синусоидальные сигналы представля-
представляют выходной сигнал коррелятора
как функцию времени для вось-
восьми различных сдвигов по задержке
(lgs), последовательно отличающих-
отличающихся на один интервал, соответствую-
соответствующий частоте Найквиста. Отметим
наличие фазового сдвига тг/2 меж-
между соседними шагами по задерж-
задержке. Фаза интерференционных ле-
лепестков может быть восстановле-
восстановлена соответствующей интерполяцией
(см. п. 9.7.3) к максимуму корреля-
корреляционной функции или по фазе крос-
скорреляционного энергетического
спектра при у1 = 0. Групповую за-
задержку можно определить по поло-
положению корреляционного максимума
или по наклону фазы кросскорреля-
ционного энергетического спектра.
Отметим, что измеренная задержка
равна A/2тг) Aф\2/ dv и, следователь-
следовательно, представляет собой групповую, а не фазовую задержку.
Частоты реальных гетеродинов могут отличаться от номинального значения уъо
из-за намеренного смещения относительно номинальной частоты или вследствие
ошибки установки частоты стандарта. Мы можем расширить смысл фазовых членов
01 и #2, включив в них смещения частоты Ау\ и Ау2 и фазовые компоненты 0[ и 02
с нулевыми средними значениями:
01 = 2ttAz/i? + 0i, в2 =
Тогда из (9.21) для фазы интерференционных лепестков получим:
ф12{у') = 2тг [у'{те + Атд
Атд
(9.22)
(9.23)
где Ауъо = Ау2 — Ayi — разность частот гетеродинов и в21 = в2 — 0[. Эта разность
частот гетеродинов входит в частоту интерференции A/2тг) йф^/йг. Если смещение
частоты А У\ является следствием отклонения частоты стандарта от номинала и не
равно нулю, то измеренная фаза интерференционных лепестков в действительности
9.3] Основные характеристики системы РСДБ 285
будет иметь более сложный вид, чем показано выражением (9.23). Ошибка часов
изменяется с течением времени из-за ошибки частоты стандарта и равна
(9.24)
Восстановленное в процессоре время, основанное на времени станции 1, связано
с «истинным» временем t как
h = Gi)t=0 + A + —) t, (9.25)
так что все измеренные значения частоты и фазы оказываются несколько сме-
смещенными. Следовательно, существует принципиальная асимметрия между опорной
станцией, относительно которой определено время, и остальными станциями (Whit-
(Whitney et al., 1976).
При спектральных наблюдениях функция S(v') в (9.21) представляет собой
спектр (временно-частотный) функции видности источника, умноженный на от-
отклик интерферометра, определяемый полосой принимаемых частот. Этот отклик
может быть получен при наблюдениях источника непрерывного излучения с плос-
плоским спектром. С другой стороны, если фазовые характеристики элементов интерфе-
интерферометра одинаковы, то отклик, определяемый полосой принимаемых частот, может
быть найден из среднего геометрического спектров мощности отдельных элементов.
Эти спектры получаются при наблюдениях источника непрерывного излучения
или участка неба, не содержащего источников, и измерением автокорреляционных
функций сигналов, принятых на каждой антенне. Частотный спектр нормирован-
нормированной функции видности можно получить, разделив спектр измеренной функции
видности на среднее геометрическое спектров мощности источника, измеренных
на каждой из антенн. Более подробно калибровочные процедуры в спектральных
наблюдениях РСДБ рассмотрены в публикациях (Могап, 1973; Reid et al., 1980;
Moran and Dhawan, 1995; и Reid, 1995, 1999).
9.3.2. Запаздывающие базы. Оценка задержки rg должна быть достаточно
точно рассчитана чтобы сигнал гарантированно попадал в диапазон переборов по
задержке и частоте интерференции процессора. В простейшем приближении
rg = ^, (9.26)
где D = 1*1 — Г2, 1*1 и Г2 — векторы, направленные к станциям из центра Земли,
и So — единичный вектор в направлении центра области наблюдений. Следует
учитывать тот факт, что Земля в течение интервала времени между прибытием
волнового фронта на одну и другую станцию перемещается, поскольку не является
инерциальной системой отсчета. Поэтому при расчете задержки следует использо-
использовать не мгновенные базы, а «запаздывающие» (Cohen and Shaffer, 1971). Плоская
волна достигает первой и второй станции в моменты времени t\ и^, удовлетворяю-
удовлетворяющие уравнению
к • n(ti) - 2тп/*1 = к • r2(t2) - 2тп/г2, (9.27)
где к = Btt/A)so. Поскольку t<i — t\ = тд, то
2тпутд = к • [r2(*i + тд) - ri(*i)]. (9.28)
Разлагая г2 в ряд Тейлора, получим
г2(*1 + тд) ~ r2(*i) + Ы*1)т9 + ... (9.29)
286 Интерферометрия со сверхдлинными базами [Гл. 9
и
~ к • [D(*i) + f2(ti) тд]. (9.30)
Отсюда решение для тд получается в виде:
so D
где все величины вычисляются относительно t\. Поскольку г = u;exr, где ше —
вектор угловой скорости Земли и х обозначено векторное произведение, мы можем
переписать (9.31) как
? [^^)! (9.32)
ИЛИ
тд ~ т3о A + А), (9.33)
где 1 + А соответствует выражению в квадратных скобках в правой части уравне-
уравнения (9.32). Используя определения w в D.3), получим
Тдо = — [sin d sin S + cos d cos S cos (H — h)]. (9.34)
Здесь (i7, 5) и (/i, d) — часовой угол и склонение источника и вектора базы соот-
соответственно; на практике РСДБ часовой угол обычно определяется относительно
Гринвичского меридиана. Также имеем
д = ^1 C0S?2 cos5 sin(/z2 -Я), (9.35)
где ?2^2 и Г2 — соответственно широта, часовой угол и модуль вектора Г2- Мак-
Максимальное значение функции А порядка 1,5 • 10~6, и тд может отличаться от тдо на
величину, не превышающую примерно 0,05 мкс. Отметим, что используемые в (9.34)
координаты не учитывают рефракцию или суточную аберрацию. Эквивалентный
способ учета запаздывания базы заключается в использовании для задержки вы-
выражения (9.26), но с h и 5, исправленными соответствующим образом за суточную
аберрацию для удаленного пункта.
Существуют и другие способы представления параметров измерений в РСДБ.
Одна из систем, которая может быть названа станционной, основана на измерениях
относительно центра Земли. Если при этом ленты, записанные на двух антеннах,
обработать один раз, а затем поменять местами и обработать повторно, то фаза
во втором случае будет обратной по сравнению с первым. В этом методе предпо-
предполагается использование модели Земли, поскольку радиусы-векторы должны быть
известны. Для целей астрометрии и геодезии обычно предпочтительнее базовая
система, в которой параметры измерений не зависят априори от параметров модели
Земли. Более точное обсуждение параметров измерений в РСДБ, можно найти
в (Shapiro, 1976) и (Cannon, 1978). Для полной барицентрической формулировки
см. (Sovers, Fanselow, and Jacobs, 1998).
9.3.3. Шумы в РСДБ-наблюдениях. Мы начнем анализ шума с обзора
статистических свойств амплитуды и фазы интерференционных лепестков, рас-
рассмотренных в разд. 6.2; см. также (Могап, 1976). Измеренная функция видности
может быть представлена вектором Z = V + в, где V и е соответствуют истинной
функции видности (сигналу) и шумовой компоненте. Выберем систему координат
с осями х (действительной) и у (мнимой) таким образом, чтобы вектор V лежал
9.3] Основные характеристики системы РСДБ 287
вдоль оси ж, как показано на рис. 6.8. Вследствие шума фаза измеренной функции
видности представляет собой случайную переменную, обозначенную ф. Проекции
вектора е имеют независимые вероятностные распределения Гаусса с нулевыми
средними значениями в координатах х и у со среднеквадратичным отклонением
а, определяемым выражением F.50). В полярных координатах модуль е имеет
рэлеевское вероятностное распределение, а фаза е — равномерное, см., например,
(Papoulis, 1965). Следовательно, Z — случайная переменная, вероятностное распре-
распределение проекций Zx и Zy которой на оси х и у равно
p(Zx,Zy) = -L_ eXp pS.-Py + gg] . (9.36)
Часто приходится иметь дело с абсолютным значением и фазой функции видности,
обозначенными Z и ф соответственно, вероятностные распределения которых равны
[соотношения F.63а) и F.636)]:
21±П?)(^), Z>0, (9.37)
где Z = ^Zl + Z2y и
(9.38)
где /о — модифицированная функция Бесселя нулевого порядка, erf — функция
ошибок, a p(Z) известно как распределение Раиса. Отметим, что (ф) = 0, как
и ожидалось, поскольку значение фазы V было положено равным нулю. Графики
распределений вероятности приведены на рис. 6.9. Математические ожидания Z,
Z2 и Z4 равны соответственно
(Z2) = \V\2 + 2а2 (9.40)
(Z4) = |V|4 + 8a2|V|2 + 8a4, (9.41)
где 1\ — модифицированная функция Бесселя первого порядка. Высшие четные мо-
моменты Z можно легко вычислить, используя теорему моментов для распределения
вероятностей Гаусса. В отсутствие сигнала /о@) = 1, и распределения вероятностей
Z и ф — суть шумовые распределения, т. е. рэлеевское и равномерное соответствен-
соответственно:
p(Z) = ^eXp^-?^j, Z>0 (9.42)
Р(Ф) = ^' 0 ^ </»< 2тг. (9.43)
В случае отсутствия сигнала (Z) = у7г/2 a, az = у/\Z2) — (ZJ = <Jy/2 — тг/2
и Оф = тг/л/З.
288 Интерферометрия со сверхдлинными базами [Гл. 9
Для случая слабого сигнала, определенного как |V| <C <т, вероятностные распре-
распределения Z и ф равны
Р(Ф) - ^~ + ~^= — С0*Ф (9-45)
2тг V8 сг
/8тг
с точностью до слагаемых с первого порядка по |V|/a. Тогда
>|2 N
(9.46)
(9.47)
(9.48)
В случае сильного сигнала, когда |V| ^> а, функции вероятностных распределений
Z и ф приблизительно соответствуют распределению Гаусса и находятся как
(9.49)
В этом случае
(9.51)
(Tz~all- -?—г (9.52)
°Ф*щ. (9-53)
Следовательно, для сильных сигналов статистика Z приблизительно гауссова (см.
рис. 6.9) и (Z) стремится к |V|. При этом если усредняется N записей Z, то от-
отношение сигнал/шум улучшается как \/N. В случае слабых сигналов искажение
рэлеевского шумового распределения сигналом мало и, как будет далее показано
в этом разделе, отношение сигнал/шум трудно улучшить при усреднении за преде-
пределами времени когерентности системы.
Выражения (9.46) и (9.51) показывают, что (Z) представляет собой смещенную
оценку |V|. При единственном возможном измерении Z наиболее вероятное значение
|V| то, при котором p(Z), определенное выражением (9.37), максимально. Этот мак-
максимум близко аппроксимируется как ^max = \/|V|2 + а2 с точностью приближения
для всех значений |V| лучше 8 %, а при \V\/a > 2 — лучше 1 %. Следовательно, если
возможно лишь одно измерение Z, то наиболее вероятное значение |V| примерно
равно л/Z2 — а2 .
9.3]
Основные характеристики системы РСДБ
289
9.3.4. Вероятность ошибки при поиске сигнала. Обработка новой се-
серии наблюдений РСДБ на произвольной решетке, начинается с задачи поиска
лепестков. Это требуется из-за погрешностей станционных часов, их хода времени
и означает, что необходимо найти
значения аппаратурной задержки
и частоты интерференции. Дан-
Данный этап часто не нужен для спе-
специализированных решеток РСДБ,
в которых значения поправок час-
частоты интерференции и задержки
постоянно обновляются из после-
последовательных наблюдений. Поиск
может быть проведен на боль-
большой двумерной сетке значений,
как показано на рис. 9.4. В каче-
качестве примера, рассмотрим экспе-
эксперимент, в котором Az/ = 50 МГц
при частоте наблюдений 1011 Гц.
Шаг по задержке равен интервалу
выборки 0,01 мкс. При неопреде-
неопределенности задержки ±1 мкс необ-
необходим перебор 200 интервалов.
Если время когерентного накопле-
накопления составляет 200 с и относитель-
относительная точность стандартов частоты
всего лишь около 10~п, то тре-
требуется просмотреть диапазон ±
±1Гц, который при шаге 0,005 Гц
представляет собой 400 дискрет-
дискретных частот. Общее число ячеек,
которые необходимо просмотреть,
равно 80000. Если сигнала нет,
Частота
Рис. 9.4. Амплитуда интерференционного сигна-
сигнала как функция остаточной частоты интерфе-
интерференции и задержки. Одномерные графики пред-
представляют собой пиковую амплитуду интерферен-
интерференционного сигнала в зависимости от задержки и
частоты интерференции. Вероятностное распре-
распределение шума в этих графиках задано выраже-
выражением (9.57), а уровень смещения — выражени-
выражением (9.58)
то p(Z) определяется выражени-
выражением (9.42). Интегральное распределение вероятности, т. е. вероятность того, что Z
меньше Zq, в этом случае находится интегрированием (9.42) от нуля до Zq:
(9.54)
Интегральное распределение вероятности максимальной величины п независимых
отсчетов Zm = max {Zi, Z2,..., Zn} равно
P(Zm)= 1-
7 2 \ 1 n
(9.55)
Таким образом, вероятность того, что один или несколько отсчетов превысят вели-
величину Zm, что мы назовем вероятностью ошибки ре, равна
(9.56)
10 Томсон
290
Интерферометрия со сверхдлинными базами
[Гл.9
zmi(J
Рис. 9.5. Вероятность [по определению (9.56)] того, что при отсутствии сигнала один или
несколько отсчетов амплитуды интерференционных лепестков превысят величину Zm/cr.
На графиках указано число измерений в выборке
Эта функция показана на рис. 9.5. Вероятностное распределение Zm получается
дифференцированием (9.55):
/ Г7 \
п-1
(9.57)
При больших п это распределение почти гауссово, со средним значением и стан-
стандартным отклонением, заданными как
(9.58)
(9.59)
Примеры p(Zrn) для различных значений п приведены на рис. 9.6. Часто оказывает-
оказывается полезным преобразование двумерной функции, такой, как показанная на рис. 9.4
амплитуда интерференционных лепестков в зависимости от частоты интерферен-
интерференции и задержки, в одномерную, используя поиск максимального значения функции
по одной переменной. Такой поиск приводит к смещению одномерной функции,
равному (Zm). Смещение возрастает с увеличением числа отсчетов и затрудняет
обнаружение слабых сигналов.
Мы можем также вычислить вероятность ошибочного определения сигнала.
Предположим, что мы располагаем измерениями амплитуды интерференционных
лепестков для двух значений задержки или частоты интерференции, из которых
сигнал присутствует только в одном случае. Вероятность того, что амплитуда
в канале (Z\) с сигналом больше амплитуды в канале (Z2) с одним шумом, равна
>Z2)=
L о
(9.60)
9.3]
Основные характеристики системы РСДБ
291
Рис. 9.6. Вероятностное распределение максимума п случайных переменных с рэлеевским
распределением, определяемое выражением (9.57)
Величина p(Zi) задана выражением (9.37), a p(Z2) — выражением (9.42). Этот
результат может быть обобщен для поиска по п каналам при амплитуде сигнала
в канале, равной Zs. Вероятность того, что Zs больше Z в других каналах, из (9.54)
и (9.60) равна
p(Zs
Zn) = | p(Z) [l - exP (-
1
(9.61)
где p(Z) задано выражением (9.37). Таким образом, вероятность того, что один или
несколько отсчетов превысят амплитуду сигнала, находится как
п-1
dZ.
(9.62)
Графики р'е показаны на рис. 9.7. Например, если просматривается более 100 кана-
каналов, то для того, чтобы вероятность ошибочного определения сигнала была менее
0,1%, необходимо отношение \V\/a > 6,5.
9.3.5. Когерентное и некогерентное усреднение. Оценим величину пре-
предельно обнаружимого сигнала. Рассмотрим временную последовательность значе-
значений выходного сигнала коррелятора, в котором (j)(t) — фаза, вносимая шумами
приемников, флуктуациями в стандартах частоты или атмосфере. Пример изме-
изменения фазы в зависимости от времени в эксперименте РСДБ показан на рис. 9.8.
Выходной сигнал коррелятора равен
r(t) = Z(t) e
(9.63)
Каким образом оценить |V|, если временной диапазон данных превышает вре-
время когерентности? Возможны две полезные процедуры. Во-первых, заметим, что
преобразование Фурье r(t) на временном интервале г равно R(y). Используя
ю*
292
Интерферометрия со сверхдлинными базами
[Гл.9
теорему Парсеваля
г оо
\r(t)r*(t)dt= J R{v)R*{v)dv (9.64)
и выражение (9.40), получим оценку ам-
амплитуды |V|e:
2 4 6 8 10
Амплитуда сигнала Ы /ст
Рис. 9.7. Вероятность (в зависимости от
амплитуды сигнала |V|) того, что одно
или несколько значений амплитуды ин-
интерференции среди отсчетов без сигнала
превысят значение амплитуды интерфе-
интерференции в отсчете с сигналом, определяе-
определяемая выражением (9.62). Графики отме-
отмечены в соответствии с полным числом
отсчетов п. Асимптотическое значение
р'е при |V|/cr, стремящемся к нулю, рав-
равно 1 — 1/п
оо
= i J \R{
\2dv-2a2.
(9.65)
Несмещенная оценка амплитуды равна
Выражение (9.65) показывает, что по спек-
спектру частоты интерференции |i^(z/)|2 мож-
можно оценить амплитуду функции видности
для временной последовательности дан-
данных, длительность которой превышает тс.
Эта процедура представляет собой фор-
форму некогерентного усреднения, посколь-
поскольку квадраты спектральных составляющих
в области частоты интерференции склады-
складываются.
В другом методе некогерентного
усреднения вычисляется среднее квадратов
последовательных по времени отсчетов.
где
ti+rc
pi = — \ Z(t) em) dt.
и
(9.66)
(9.67)
Из (9.40), (9.41) и (9.66) следует, что <|Л7||> = |V|2 и {\V\fj = |V|4 + 4a2(|V|2 + a2)/N,
откуда для отношения сигнал/шум получаем
2а2
|V|2
(9.68)
Отноптение |V|/a равно отношению сигнал/птум на выходе одноканального корре-
коррелятора в соответствии с формулами F.48) и F.49). В наблюдениях РСДБ вместо
коэффициента rjQ, описанного в разд. 8.3 и представляющего потери квантования,
используется общий коэффициент потерь 7/, рассматриваемый в разд. 9.7; из F.64)
получаем \V\/a = (ТаТ]/Тз)л/2А1утс . Тогда выражение (9.68) принимает вид
Av2ttc
A
Ai/rc/Tj)
(9.69)
9.3]
Основные характеристики системы РСДБ
293
180°
90
0
-
-
-
10 20 30 40
50 60 70
Время, с
80 90 100 ПО 120
Рис. 9.8. Фаза интерференционного сигнала в зависимости от времени, полученная по
наблюдениям сильного источника [мазерный источник линии водяного пара в W3(OH)]
в эксперименте РСДБ с тремя базами на частоте 22 ГГц. Две станции — обсерватория
в Хайстеке и Военно-морская исследовательская лаборатория (обсерватория в Мериленд
Пойнт) были оборудованы водородными стандартами частоты, тогда как в Националь-
Национальной радиоастрономической обсерватории использовался рубидиевый стандарт частоты.
Фазовый шум на верхнем графике определяется в основном приемниками и атмосферой,
а на двух нижних — фазовым шумом рубидиевого стандарта частоты. Данные получены
в 1971 г. с системой РСДБ Mark I
где г = Ntc — полное время накопления. В двух предельных случаях (9.69) примет
вид
Та » Jf , (9.70)
(9.71)
Отметим, что в случае сильного сигнала в некогерентном усреднении нет необходи-
необходимости. При использовании некогерентного усреднения время когерентного накоп-
накопления должно быть настолько большим, насколько это возможно без уменьшения
амплитуды интерференционных лепестков. Если мы предположим, что для обна-
обнаружения сигнала lZsn = 4, и вспомним, что т = Ntc, to в случае слабого сигнала
минимальная обнаружимая антенная температура может быть получена из выра-
выражения (9.71):
(TA)min = ^vf^__ . (9.72)
Таким образом, вследствие зависимости 7V1/4 в (9.72) некогерентное усреднение эф-
эффективно лишь при не слишком больших значениях N. Если время когерентности
294
Интерферометрия со сверхдлинными базами
[Гл. 9
по порядку величины равно 1/Ai/, то система наблюдений сводится к некогерентной
интерферометрии или интерферометрии интенсивностей; см. разд. 16.1 и (Clark,
1968). Тогда в случае слабого сигнала выражение (9.71) преобразуется к виду
(9.73)
9.4. Поиск лепестков для многоэлементной решетки
9.4.1. Обобщенный поиск интерференционных лепестков. В разде-
разделе 9.3 мы рассмотрели задачу поиска интерференционных лепестков для одной
базы. Основное требование РСДБ к поиску интерференционных лепестков заклю-
заключается в определении фазы интерференционного сигнала (т. е. фазы функции вид-
ности) и скорости ее изменения в зависимости от времени и частоты или задержки.
Частота интерференции изменяется в результате ошибок в координатах источни-
источника или антенн, а также вследствие относительных эффектов, таких как отличие
частоты гетеродинов. Большинство этих эффектов могут быть определены как
факторы, относящиеся к отдельным антеннам, а не к базам, ими образованными.
По этой причине для определения параметров частоты интерференции одновре-
одновременно могут использоваться данные всех баз. Одновременно, используя все данные
многоэлементной РСДБ-решетки, можно найти лепестки, слишком слабые, чтобы
быть обнаруженными на одной базе. Это представляет практическую ценность
для решеток РСДБ с однотипными антеннами и приемниками; для произвольных
решеток возможной альтернативой является поиск интерференционных лепестков
по данным двух наиболее чувствительных антенн и использование полученного
результата для нахождения решений на других базах.
Метод анализа, основанный на одновременном использовании полного набора
данных наблюдений с большим количеством антенн, был разработан Швабом и Кот-
тоном (Schwab and Cotton, 1983) и называется обобщенным поиском интерференци-
интерференционных лепестков. Пусть Zmn(t) — выходной сигнал коррелятора, т. е. измеряемая
видность для базы, образованной антеннами тип. Комплексное усиление (по
напряжению) антенны п и соответствующей приемной системы равно gn(tk?^)?
где tk представлена (когерентно) интегрированная по времени выборка данных на
выходе частотного канала vg коррелятора. Тогда
Zmn{tk, щ) = gm(tk, щ) g*(tk,
n(tk
(9.74)
где Vmn — истинная видность для базы тп, а ?тпы описывает ошибки наблюдений,
главным образом шумовой природы. Следует помнить, что шумовые составляющие
присутствуют во всех измерениях, но далее они как правило не будут включаться
в уравнения. Коэффициенты усиления могут быть представлены в виде
gn(tk,«//) = |gn|ei^(tb'"A (9.75)
Чтобы упростить формулу (9.75), мы предположим, что коэффициенты усиления
и амплитуда видности постоянны в области пространства (?, v\ охваченной наблю-
наблюдениями. Тогда, учитывая только члены первого порядка малости, можно записать
exp
: exp \j
dt
'¦к ~ to) +
dv
{у\ -
(9.76)
9.4] Поиск лепестков для многоэлементной решетки 295
где фтп — фаза истинной видности Vmn. Степень изменения фазы измеряемой
видности в зависимости от времени и частоты является частотой интерференции
_ д(фщ ~фп+ Фтг
Г run ~ т
(9-77)
и задержкой
Тшп ~
dv
(9.78)
для базы ran, времени to и частоты щ. Используя эти величины, мы можем свя-
связать измеряемую видность (выходной сигнал коррелятора) с истинной видностью
следующим образом:
Zmn{tk,V?) = |gm||gn|Vmn(tk,^) вхр {j [(^m - фп) \t=tQ +
+ (rm - rn)(tk - t0) + (rm - тп){щ - i/q)] }. (9.79)
Для каждой антенны получается четыре неизвестных параметра: модуль усиле-
усиления, фаза усиления, частота интерференции и задержка. Поскольку все данные
получены в виде разностной фазы для двух антенн, необходимо определить одну
из антенн в качестве опорной. Для этой антенны фаза, частота интерференции
и задержка обычно принимаются равными нулю, и таким образом остается Апа — 3
параметров для определения. Однако, возможно еще больше упростить процедуру
и рассматривать только фазовые члены при поиске интерференционных лепест-
лепестков. Соответственно, амплитуда усиления антенн калибруется отдельно. Число
определяемых параметров таким образом уменьшается до 3(по — 1). Далее, что-
чтобы получить обобщенное решение интерференционных лепестков, видность Vmn
представляется моделью источника, параметры которого вписываются в уравнение
(9.79) методом наименьших квадратов относительно измеренных данных. Детали
применения метода наименьших квадратов см. в (Schwab and Cotton, 1983). Модель
источника, используемая как «начальное приближение» его структуры, в некото-
некоторых случаях может быть упрощена до точечного источника.
Другой метод одновременного использования данных, полученных на несколь-
нескольких базах, для поиска интерференционных лепестков представляет собой расши-
расширение метода, описанного выше для одной базы. Требуется выразить измерен-
измеренные данные видности через частоту интерференции и задержку, что можно сде-
сделать, например, посредством временно-частотного преобразования Фурье данных
по задержкам каналов коррелятора. Тогда для каждой пары антенн существует
матрица значений отклика интерферометра с последовательными приращениями
по задержке и частоте интерференции. Решение для этих величин находится как
максимальная амплитуда на данной базе, что показано на рис. 9.4. Однако этот
метод можно расширить и включить отклики, полученные на нескольких базах,
используя принцип замыкания фазы, обсуждаемый более подробно в разд. 10.3.
Поскольку мы рассматриваем поиск лепестков только по фазовым данным, изме-
измеряемые переменные представляются как фшп. Так как аппаратурная фаза фтп для
базы тп равна разности измеренной и истинной фазы функции видности, то можно
записать
Фгпп =Фгп-фп= Фгпп - Фтп, (9.80)
296 Интерферометрия со сверхдлинными базами [Гл. 9
где i/ьчленами представлена аппаратурная фаза и ^-членами — фаза видности,
а тильдой ~ обозначена измеренная фаза видности. Теперь рассмотрим, что про-
произойдет, если подключить третью антенну, обозначенную р. Для такой комбинации
мы можем записать
Фтрп = Фтр + Фрп = (Фт ~ Фр) + (Фр ~ Фп) =Фт- Фп- (9.81)
Таким образом, фшрп предусматривает другую измеряемую величину фшп, равную
Фтр + Фрп = (Фтр - Фтр) + (Фрп ~ Фрп)• (9.82)
Подобным образом для четырех антенн получим
Фгпрдп = Фтп ~ Фп = (Фтр + Фрд + Фдп) ~ (Фтр + Фрд + Фдп)- (9.83)
Таким образом, оценки величины фтп могут быть найдены по измерениям на коль-
кольце антенных пар, начиная с антенны т и заканчивая антенной п. Комбинации более
чем трех баз (четырех антенн) могут быть представлены комбинациями меньшего
числа антенн, и шумы в этом случае не будут независимыми. Кольца из трех или
четырех антенн позволяют получить дополнительную информацию, улучитающую
чувствительность и точность поиска интерференционных лепестков для антенн т
и п. Отметим, что в данном методе также необходимо использование модельной
видности.
Из этих двух методов вписывание методом наименьших квадратов лучше с точ-
точки зрения однородности комбинации данных, но при этом требуется хорошая на-
начальная оценка для его эффективной сходимости. Шваб и Коттон (Schwab and
Cotton, 1983) использовали второй метод, чтобы получить начальное приближение
для решения методом наименьших квадратов. Эта процедура в дальнейшем стала
основой стандартных программ обработки данных РСДБ (Walker, 1989a,b).
Несмотря на то, что обобщенным подбором лепестков обеспечивается большая
чувствительность по сравнению с поиском на отдельных базах, на практике требу-
требуется некоторый опыт для определения, в каких случаях применение обобщенного
метода предпочтительнее. Если изучаемый источник имеет сложную структуру
с большими изменениями амплитуды видности, то он, возможно, не будет хорошо
представлен модельной видностью, необходимой в обобщенном методе. В таком
случае может быть лучше начать поиск интерференционных лепестков с неболь-
небольшого количества антенн или, если источник достаточно сильный, рассматривать
базы по отдельности. С другой стороны, если в источнике присутствует сильная
неразрешенная компонента, то может быть достаточно отдельно использовать ма-
малые группы антенн для уменьшения суммарной загрузки компьютера.
9.4.2. Сравнение методов обнаружения интерференционных лепест-
лепестков. В случае, когда чувствительность ограничена фазовым шумом, тщательное
исследование методов обнаружения гарантирует получение результата. Наиболее
важные из этих методов были исследованы (Rogers, Doeleman and Moran, 1995) для
определения их сравнительных возможностей. Мы предполагаем во всех случаях,
что данные видности на выходе коррелятора усредняются за время, равное вре-
времени когерентности тс, рассмотренное выше. Мы видели из уравнения (9.72), что
некогерентное усреднение по времени N сегментов данных приводит к уменьшению
уровня регистрируемого сигнала на величину, пропорциональную TV/4. Роджер-
Роджерсом и др. показано, что в случае, когда порог обнаружения таков, что вероятность
ложного обнаружения составляет < 0,01% при переборе 106 значений, пороговый
сигнал оказывается меньше по сравнению со случаем когерентного усреднения (при
9.4] Поиск лепестков для многоэлементной решетки 297
котором N = 1) в 0,537V/4 раз. Этот результат точен только при больших 7V,
и эмпирически установлено, что при меньших значениях N величина порога об-
обнаружения уменьшается пропорционально 7V~0'36; говоря другими словами, улуч-
улучшение с увеличением N для малых значений N больше. Коэффициент выигрыша
0,537V/4 приводится в табл. 9.1 вместе с другими результатами, рассматриваемы-
рассматриваемыми ниже. В четвертой колонке табл. 9.1 приведены численные расчеты относитель-
относительной чувствительности для N = 200 временных отрезков и па = 10 антенн. Отметим,
что для строк 1—5 табл. 9.1 в качестве критерия обнаружения принята вероятность
ошибки менее 1 % при переборе 106 значений задержки и частоты интерференции
для каждого из па — 1 элементов решетки; для опорной антенны эти величины были
приняты равными нулю. Для 6-й строки поиск выполняется в двух измерениях по
прямому восхождению и склонению.
Таблица 9.1. а Пороговые уровни различных методов обнаружения6
№ Метод Порог (Относит, плотность потока)
.. Одна база, когерентное усред- i i
нение
2 Одна база, некогерентное о,53ЛГ1/4 0,14 GV=200)
усреднение
о Три базы, тройное произведе- f ^_\ 0,52 (N = 200)
ние \N/
. Решетка из па элементов, ко- ( — ) 0 45 (па = 10)
герентный обобщенный поиск \ па )
/ , \ 1/4
5 Обобщенный поиск с некоге- 0,53 ( —Ц- I 0,05 (N = 200, па = 10)
рентным усреднением \Nna )
6 Некогерентное усреднение по 0,53 ( ) 0,05 (N = 200, па = 10)
временным сегментам и базам \Nna(na — 1)/
аИз работы (Rogers, Doeleman and Moran, 1995).
6См. текст для критериев обнаружения.
9.4.3. Тройное произведение или биспектр. Выходной сигнал многоэле-
многоэлементной решетки может быть также представлен как тройное произведение или
биспектр, т. е. произведение комплексных выходных сигналов, полученных для трех
баз, образующих треугольник. Тройное произведение получается перемножением
измеренных видностей:
Рг = \Z12\\Z23\\Z31\ езп"+Ф*>+**1) = \Z12\\Z23\\Z31\ej^, (9.84)
где фс представлена замкнутая фаза (раздел 10.3), равная нулю для неразрешенного
источника. Мы предполагаем здесь, что амплитуда измеряемой видности Z калиб-
калибруется отдельно, так что модули коэффициентов gm и gn в уравнении (9.74) равны
единице. В каждом из сомножителей, представляющих измеренную видность, при-
присутствует мощность шума, равная 2сг2, т. е. мощность шума на выходе комплексного
коррелятора. Для случая малого сигнала дисперсия тройного произведения опре-
определяется шумом и равна
298 Интерферометрия со сверхдлинными базами [Гл. 9
(|Р3|2) = (\Z12\2\Z23\2\Z31\2) = 8а6 (9.85)
В случае точечного источника сигнал представляет собой действительную величину
и равен (A1еРзJ) = (|^з|2)/2, где Re обозначает действительную часть. Отношение
сигнальной составляющей тройного произведения к шуму в действительном выходе
коррелятора равно V3/2сг3. В работе (Rogers, Doeleman and Moran, 1995) также при-
приводится выражение для отношения сигнал/шум, не ограниченное приближением
малой величины сигнала, а в работе (Kulkarni, 1989) дано обобщенное выражение
и приводится детальный анализ.
Теперь рассмотрим некогерентное усреднение N значений тройного произве-
произведения для трех антенн, причем каждым из значений представлено усреднение
сигнала на выходе коррелятора по интервалу когерентности тс. Мы представим
некогерентное усреднение тройного произведения как
F3 = -^?|Z12||Z23||Z3i|e^. (9-86)
N
Если амплитуды сигналов одинаковы, то математическое ожидание действительной
части Рз равно
(ReP3)=V3 (9.87)
и второй момент Re P3 равен
((КеРзJ) = ^(|РзГ)(со820с). (9.88)
В случае малого сигнала, при котором величина (|Рз|2) определяется главным обра-
образом шумом, из уравнения (9.85) математическое ожидание второго момента равно
4сг6 /N. Отношение сигнал/шум равно математическому ожиданию Рз> деленному
на корень квадратный из математического ожидания второго момента:
^ , (9.89)
Zo~
откуда следует
V = B7г8ПI/3сг7У-1/б (9>90)
Величина сигнала в строке 3 табл. 9.1 приведена для значения 7?sn, позволяющего
обнаружить сигнал на уровне, соответствующем указанному критерию ошибки.
9.4.4. Поиск лепестков для многоэлементной решетки. Количество ин-
информации, собираемой РСДБ-решеткой из па антенн за данное время больше по
сравнению с единственной парой антенн в па(па — 1)/2 раз. Следовательно, мож-
можно ожидать, что улучшение чувствительности при использовании такой решетки
~ [па(па — 1)/2]1/2. Однако с увеличением количества антенн также существенно
увеличивается исследуемое пространство параметров. Таким образом, вероятность
получить шумовой отсчет большой амплитуды внутри этого пространства соответ-
соответственно возрастает. Поэтому требуется увеличение уровня сигнала, используемого
в качестве порога обнаружения с целью избежать повышения вероятности ложного
обнаружения.
Рассмотрим двухэлементную решетку, для которой число точек данных, пере-
перебираемых в пространстве параметров (частота х задержка), равно П&. Если ввести
третью антенну и измерять корреляцию на всех базах, то количество точек перебора
9.5] Фазовая стабильность и атомные стандарты частоты 299
возрастет до n2d. В случае па антенн оно равно п^а~ К Распределение вероятности
максимального значения для п величин, представляющих сигнал плюс шум, Zm,
и распределенных по закону Рэлея, дано формулой (9.57), и при больших п характе-
ризуется средним значением сгB Inn) ; см. уравнение (9.58). Таким образом, при
данной вероятности случайной ошибки, с увеличением числа исследуемых точек от
rid ДО П(ра~ уровень Zm возрастает от сгB lnn^I/2 до а[2 (па — 1) mnj1/2, т.е.
/ Л\1/2 Г7 г (па — 1)
вероятность найти отклонение на уровне [па — 1) Zm при переборе nd точек
та лее, что и найти отклонение на уровне Zrn при переборе п^ точек. При увеличении
числа антенн от 2 до па суммарная среднеквадратичная неопределенность уровня
сигнала уменьшается в [па(па — 1)/2]1/2 раз, но поскольку уровень обнаружения
увеличивается в {па — II'2 раз, эффективное улучшение чувствительности обна-
обнаружения источников составляет лишь (па/2I/2. В работах (Rogers, 1991) и (Rogers,
Doeleman and Moran, 1995) рассмотрены также другие факторы, влияющие на
полученный результат, и показано, что для получения суммарного коэффициента
улучшения чувствительности величину (ria/2I'2 следует умножить на коэффици-
коэффициент, значение которого находится в пределах от 0,94 до 1. Этот дополнительный
коэффициент не учитывается в табл. 9.1.
9.4.5. Многоэлементная решетка с некогерентным усреднением. По-
Последние две строки табл. 9.1 относятся к некогерентному усреднению данных, по-
полученных многоэлементной решеткой. В 5-й строке характеризуется метод, который
состоит в первоначальном усреднении данных в пределах времени когерентности
и последующем некогерентном усреднении перед применением процедуры обобщен-
обобщенного поиска лепестков. Величина относительного уровня обнаружения получается
как произведение этих значений из 4-й строки для многоэлементного обобщенного
поиска лепестков и из строки 2 для некогерентного усреднения с одной базой.
Метод, характеризуемый 6-й строкой, заключается в некогерентном усреднении как
по временным сегментам (с интервалом времени равным времени когерентности),
так и по базам. Относительная величина уровня обнаружения получается из зна-
значения, приведенного во 2-й строке с увеличением числа точек данных от N (число
временных сегментов для одной базы) до величины JV, умноженной на число баз.
9.5. Фазовая стабильность и атомные стандарты частоты
Высокостабильные генераторы непрерывно совершенствовались, начиная
с 1920-х годов, когда изобретение управляемого кварцем (кварцевого) генератора
нашло немедленное применение в задаче хранения времени. В начале 1950-х годов
часы, созданные на пучке атомов цезия, обеспечили возможность лучшего хранения
времени, чем можно было получить из астрономических наблюдений. Этот
прогресс привел к вводу атомного времени, отличающегося от астрономического,
и к определению секунды времени, основанной на частоте определенного перехода
атома цезия.
Математическая теория интерпретации измерений фазы генерируемых сигналов
была систематизирована комитетом ТИИЭР (Barnes et al., 1971). Эта публикация
помогла определить стандартный подход к трактовке низкочастотного нарастания
шума в генераторах. Физическая теория шума в генераторах была создана Эдсо-
ном (Edson, 1960). В этом разделе развиваются соответствующие аспекты теории
и описываются принципы действия атомных стандартов частоты, причем особое
внимание уделяется активному водородному стандарту. Более подробно теория
и анализ фазовых флуктуации рассматриваются в (Blair, 1974) и (Rutman, 1978).
300 Интерферометрия со сверхдлинными базами [Гл. 9
9.5.1. Анализ флуктуации фазы. Требуемый сигнал генератора представ-
представляет собой чисто синусоидальное колебание вида
V(t) = Vo cos2ttzV. (9.91)
Однако это недостижимо, поскольку все электронные устройства обладают некото-
некоторым фазовым шумом. Более реалистичная модель представлена выражением
V(t) = Vo cos [27riy0t + <t>{t)\, (9.92)
где (j)(i) — случайный процесс, характеризующий фазовое отклонение от чисто
синусоидального колебания. Нами не рассматриваются флуктуации амплитуды, как
не оказывающие прямого влияния на задачи РСДБ. Мгновенная частота i/(t) равна
производной аргумента в выражении (9.92), деленной на 2тг, т. е.
v(t) = i/0+ &/(*)> (9-93)
где
Mf) = i«U. @.94)
Мгновенное относительное отклонение частоты определяется следующим образом:
Это определение позволяет сравнивать характеристики генераторов на различных
частотах.
Предположим, что случайные процессы <fi(t) и y(t) статистически стационарны,
так что могут быть определены корреляционные функции. Это предположение не
всегда выполняется и может приводить к затруднениям (Rutman, 1978). Автокор-
Автокорреляционная функция y(t) равна
Ry{T) = {y(t)y(t + T)). (9.96)
Поскольку Ry(r) — действительная и четная функция, то S'y(f) — энергетиче-
энергетический спектр y(i), представляет собой действительную четную функцию частоты
/. Чтобы предотвратить путаницу между v{t) и ее частотными составляющими,
мы в последующем спектральном анализе используем для частотной переменной
символ /. Следуя не совсем стандартному определению, применяемому в большей
части литературы по фазовой стабильности (Barnes et al., 1971), мы используем
вместо двустороннего спектра S'y(f) односторонний спектр Sy(f), где Sy(f) = 2Sy(f)
при /H и Sy(f) = 0 ПРИ / < 0- Поскольку S'y(f) — четная функция, потерь
информация при этом не происходит. Таким образом, соотношение преобразования
Фурье Ry(r) ^ Sy(f) может быть также записано в виде
Sy(f) = 4 { Ry(T) cos B7Г/Г) <*
о
Д„(т)= |5у(/)со8Bтг/тLГ.
° (9-97)
9.5] Фазовая стабильность и атомные стандарты частоты 301
Аналогично определяется автокорреляционная функция фазы:
т)). (9.98)
Величина 5^(/) — энергетический спектр 0, и Яф(т) связаны друг с другом преоб-
преобразованием Фурье. Применяя свойство производных преобразований Фурье, можно
показать, что Sy(f) и 5^(/) связываются друг с другом следующим образом:
Величины Sy(f) и 5^(/) представляют собой первичные меры стабильности часто-
частоты. Размерность обеих величин равна [1/Гц]. Другая общепринятая характеристика
возможностей генератора ?(/) определяется как мощность в интервале частот 1 Гц
на частоте / в одной из полос двухстороннего спектра, выраженная в долях полной
мощности генератора. При фазовых отклонениях, малых по сравнению с величиной
1 радиан, ?(/)~5Д/)/2.
Второй подход к стабильности частоты основан на измерениях во временной
области. Среднее относительное отклонение частоты представляется выражением
tk+r
= \ \ y(t)dt, (9.100)
которое с учетом (9.78) может быть представлено в виде
ф(Ь+т)-ф(Ь)
где измерения ук повторяются с периодом Т (Т ^ г) таким, что tk+i = ?& + Т (см.
рис. 9.9 а). Измерения ук получают непосредственно с помощью обычных частото-
частотомеров. Мерой стабильности частоты служит выборочная дисперсия ук, определяе-
определяемая как
\п=1 \ к =
где N — число отсчетов для одной оценки сг^. В предельном случае при N —>•
—>- оо эта величина равна истинной дисперсии, которую мы представим как 12(т).
Однако во многих случаях выражение (9.102) не сходится из-за низкочастотных
свойств Sy(f), и тогда /2(т) не определено. Для того чтобы устранить некоторые
из проблем сходимости, в частности в уравнении (9.102), широко примененяется
двухточечная дисперсия, или дисперсия Аллана сГу(т) (Allan, 1966). Дисперсия
Аллана, для которой Т = т (без потери времени между измерениями) и N = 2,
определяется следующим образом:
или, из (9.102),
302
Интерферометрия со сверхдлинными базами
[Гл.9
e3
щ
i.
_L
h
t5 t1
Время
Рис. 9.9. a — интервалы времени при измерении ук в соответствии с выражением (9.101).
б— показан ряд фазовых измерений в зависимости от времени. Дисперсия Аллана, опреде-
определенная в (9.103), равна среднему значению квадрата отклонения EфJ каждого измерения
относительно среднего двух смежных с ним измерений
Процедуру оценки дисперсии Аллана можно понять следующим образом. Возьмем
ряд фазовых измерений с периодом Т, как показано на рис. 9.9 б. Для каждого
набора из трех независимых точек между внешними точками проводится прямая
линия и измеряется отклонение центральной точки относительно этой линии. При
т отсчетах среднее квадратов отклонений у, деленное на Bтп/отJ, представляет
собой оценку (Ту(г), которая обозначается как сг^е(г), где
га — 1
- УкJ-
(9.105)
Точность оценки определяется формулой (Lesage and Audoin, 1979)
( \ К
(9.106)
где К — постоянный коэффициент порядка единицы, точное значение которого
зависит от энергетического спектра у.
Мы можем теперь связать истинную дисперсию и дисперсию Аллана с энергети-
энергетическим спектром у или ф. Из (9.101) следует, что истинная дисперсия /2(т) = {у?}
задается выражением
г)) -
которое в соответствии с (9.98) можно переписать в виде
(9.107)
(9.108)
9.5] Фазовая стабильность и атомные стандарты частоты 303
Поскольку Лф{т) равно преобразованию Фурье 5^(/), применяя (9.99), получим из
(9.108)
\(^} df. (9.109)
О
Аналогично, из (9.104),
1 - Шф(т) + Яф{2т)] (9.110)
Bтп/от)
и, следовательно,
/2(г) и с^(т) — безразмерные величины, измеряемые в рад2, но мы можем предста-
представить их как мощность, полученную после прохождения сигнала y(t) через фильтры
с двумя различными частотными характеристиками Hj(f) и i^(/), соответственно
заданными выражениями
(^J (9.И2)
Функции Hj(f) и iir|(/), а также соответствующие импульсные характеристики
hj(t) и На(?) показаны на рис. 9.10. Отметим, что 12(т) можно оценить по ряду
измерений ук как среднее квадрата величины hi(tk) *У&, где звездочкой обозна-
обозначена свертка. Аналогично можно оценить сТу{т) как среднее квадрата величины
h>A{tk) * У к- Могли быть выбраны и другие передаточные функции. При измерениях
во временной области может выполняться дополнительная фильтрация с отсечками
по высокой и низкой частоте. Например, исключение долговременных изменений из
частотных данных представляет собой форму фильтрации (пропускания) высоких
частот. Очевидно, что измерения Sy(f) предпочтительнее измерений <Jy(r), так как
а у можно вычислить из Sy, применяя выражение (9.111), но Sy из а2 вычислить
невозможно. Однако во многих случаях, представляющих практический интерес,
например в степенных спектрах, рассматриваемых ниже, вид а2 указывает на
свойства Sy. Традиционно легче было выполнять измерения во временной области,
и большая часть опубликованных результатов приводится, исходя из дисперсии
Аллана а2.
Влияние шума гетеродинов на измеряемую когерентность сигналов, принима-
принимаемых двумя антеннами, описывается уравнением G.34), исходя из среднеквадра-
среднеквадратичного отклонения фазы сигнала гетеродина одной антенны относительно дру-
другой. В РСДБ это среднеквадратичное отклонение равно корню квадратному из
суммы истинных дисперсий сигналов гетеродинов двух антенн. В случае решет-
решетки со связанными элементами низкочастотные составляющие фазового шума за-
задающего генератора оказывают подобное влияние на фазу гетеродинов каждой
антенны, и, следовательно, их суммарный вклад в разностную фазу различных
антенн стремится к нулю. Для полного обнуления временные задержки в пути
распространения опорного сигнала от задающего генератора до каждой антенны
304
Интерферометрия со сверхдлинными базами
[Гл.9
-г/2
hj(t)
1/т
т/2 t
1/2т
ш
т f
Рис. 9.10. Вверху — импульсная функция hi(t) и квадрат ее преобразования Фурье
Hi(f)\2, заданный выражением (9.112), которое используется для связи степенного спек-
спектра Sy(f) с истинной дисперсией / (т), как определяется в выражении (9.109). Внизу —
импульсная характеристика /ia(?) и квадрат ее преобразования Фурье \На(/)\2, заданный
выражением (9.113), которое используется для связи степенного спектра <Sy(f) с дисперси-
дисперсией Аллана (Ту(т), как определяется выражением (9.111). Отметим, что чувствительность
дисперсии Аллана быстро возрастает с уменьшением частоты при / < 0,3/т
плюс временные задержки в сигнале ПЧ от соответствующих смесителей до входа
коррелятора (с учетом переменной задержки, компенсирующей геометрическую)
должны быть равны для каждой из антенн. Поддержание этого равенства часто
оказывается нецелесообразно. Диапазон частот, в пределах которого фазовый шум
задающего генератора исключается, также ограничен конечной величиной поло-
полосы пропускания схем фазовой автоподстройки сигналов гетеродинов. На практике
устранение фазового шума, вносимого задающим генератором, как правило должно
быть эффективно вплоть до частоты /, значение которой находится в пределах от
нескольких сотен герц до нескольких сотен килогерц, в зависимости от параметров
конкретной системы.
Лабораторные измерения показывают, что Sy(f) часто представляет собой ком-
комбинацию степенных компонент. Полезным приближением, показанным на рис. 9.11,
является формула
ЗД) = Е
о < / <
(9.114)
а = -2
где а — показатель степени, принимающий целые значения от —2 до +2, и Д — ча-
частота отсечки фильтра нижних частот. Формулу, подобную (9.114), можно получить
и для <ЯД/), используя выражение (9.99). Каждое слагаемое в (9.114) или в соот-
соответствующем выражении для 5<^(/) имеет название, основанное на традиционной
терминологии (см. табл. 9.2). Шум со степенной зависимостью /°, не зависящий
от частоты, называется «белым шумом», /-1 — «фликкер-шум», а /~2 называют
«шумом случайных блужданий». Природа некоторых из этих процессов, которые
мы рассмотрим вкратце (см. также Vessot, 1976), хорошо известна. Частотные
зависимости, данные ниже в скобках, приводятся для Sy.
9.5]
Фазовая стабильность и атомные стандарты частоты
305
Рис. 9.11. а — идеализированный степенной спектр Sy(f) относительного отклонения ча-
частоты y(t) [см (9.114)]; б—двухточечное среднеквадратичное отклонение, или стандартное
отклонение Аллана, в зависимости от интервала времени между измерениями. Различные
участки поведения спектров отмечены римскими цифрами и в круглых скобках даны
показатели степени. Участки соответствуют следующим режимам: I — белый фазовый
шум, II — фазовый фликкер-шум, III — белый частотный шум, IV — частотный фликкер-
шум и V — частотный шум случайных блужданий. Спектральные режимы отмечаются
римскими цифрами и в круглых скобках даны показатели степени
1. Белый фазовый шум (/2) обычно обусловлен аддитивным шумом вне генера-
генератора, например усилителями. Этот процесс доминирует при больших значе-
значениях /, соответствующих малым интервалам усреднения.
2. Фазовый фликкер-шум (f1) наблюдается в транзисторах и может быть обу-
обусловлен явлением диффузии через барьер.
3. Белый частотный шум или фазовый шум случайных блужданий (/°) обу-
обусловлен внутренним аддитивным шумом в генераторах, таким, как тепловой
шум в камере резонатора. Дробовой шум имеет такую лее спектральную ха-
характеристику.
4. Частотный фликкер-шум (f~1) и частотный шум случайных блужданий
(/~2) — процессы, ограничивающие долговременную стабильность генера-
генераторов. Они обусловлены случайными изменениями температуры, давления
и магнитного поля в окружающей генераторы среде. Эти шумы связаны с дол-
гопериодическими плавными изменениями. Частотный фликкер-шум встре-
встречается во многих случаях и ему посвящено большое количество литературы:
см. (Keshner, 1982) для общего рассмотрения, (Dutta and Horn, 1981) — для
приложений физики твердого тела, и (Press, 1978) — для астрофизики.
306 Интерферометрия со сверхдлинными базами [Гл. 9
Для различных типов шума, описанных выше, могут быть вычислены дисперсии
/2(т) и (Ту(г). В случаях а = 1 и а = 2 дисперсии сходятся только при условии,
что определена высокочастотная отсечка Д. В пределах этого ограничения а у
сходится во всех случаях, а /2(т) сходится лишь при а ^ 0. Эти функции приводят-
приводятся в табл. 9.2. За исключением логарифмической зависимости в случае фазового
фликкер-шума, каждая шумовая компонента соответствует компоненте дисперсии
Аллана вида т^. Из табл. 9.2 полную дисперсию Аллана молено записать как
сг2(г) = \К\ + К\ In BтгДт)]т-2 + Kir'1 + К\ + К2 2т, (9.115)
где К — постоянные величины. Нижние индексы соответствуют индексам h (см.
табл. 9.2). Белый фазовый и фазовый фликкер-шум оба дают /i ~ —2, но для этих
двух процессов могут различаться Д. Отметим, что для белого фазового и белого
частотного шума справедливы следующие соотношения [см. (9.109) и (9.111)]:
^0") = §/2(т), а = 2, (9.116)
^(т) = /2(т), а = 0. (9.117)
В общем случае, если определено /2(т), из выражений (9.108) и (9.110) следует, что
а2у(т) = 2[12(т)-12Bг)]. (9.118)
Таблица 9.2. Характеристики шумов в генераторах*1
Тип шума «\W Ьф\1) ^уКТ) М 7 VTJ
Белый фазовыйв ^/ ^0^2 2 2 —2 2 2
^ 4тг т 2тг т
Фликкер фазовый ^i/ ^0^1/ 4 2 2 ^П №7rfhT' ~ ~^ ~
Белый частотный, или слу- ^ v2hof~2 — —1 —
чайные блуж:дания фазы 2т 2т
Фликкер частотный ^-i/ ^0^-1/ B1n2)/i_i 0 -
Случайные блуж:дания ча- h_2f~2 v2h-2f~4 27Г T/^_2 1 -
стоты 3
аПо данным (Barnes et al., 1971).
бПоказатель степени дисперсии Аллана: сгу(т) ос тм.
вДлясг2(т), 2тгДт» 1.
9.5.2. Время когерентности генератора. Время когерентности — величи-
величина, представляющая особый интерес в РСДБ. Время когерентности приблизительно
равно времени тс, за которое среднеквадратичная ошибка фазы достигает значения
1 радиан:
2жиотсау{тс) ~ 1. (9.119)
9.5] Фазовая стабильность и атомные стандарты частоты 307
Выведено более точное выражение для времени когерентности (Rogers and Moran,
1981), определенное через функцию когерентности:
С(Т) =
(9.120)
где Ф{г) — составляющая фазы интерференционного сигнала аппаратурного про-
происхождения, а Т — произвольное время накопления. В ф{г) учитываются явления,
такие как атмосферные неоднородности и шум в стандартах частоты, вызывающие
блуждания интерференционной фазы. Среднеквадратичное значение С(Т) явля-
является монотонно убывающей функцией времени, изменяющейся от 1 до 0. Время
когерентности определяется как значение Т, при котором (С2(Т)) уменьшается до
некоторого заданного значения, скажем 0,5. Среднеквадратичное значение С равно
тт
?p{j [ф{€) - ф(Ь')] }) dtdt'. (9.121)
о о
Если ф — гауссова случайная переменная, то
тт Г 2 ' 1
(С2(Т)) = \ J J ехр -а У ) dtdt', (9.122)
оо ^ ^
где <j2(t,tf) — дисперсия ([</>(?) — ф(г')}2), которая, как мы полагаем, зависит только
от г = t' — t. Тогда из (9.98) получим
a2(tf,t) = сг2(г) = {[ф(Ъ) - ф{Ь')]2) = 2[Д^@) - Яф(т)}. (9.123)
Отметим, что сг2(т) — структурная функция фазы, связанная с 12(т) выражени-
выражением (9.108):
а2(т)=4тг2т21/2/2(т). (9.124)
Интеграл в (9.122) можно упростить, учитывая тот факт, что подынтегральное
выражение равно постоянной величине вдоль диагональных линий в пространстве
(?, ?'), для которых t' — t = г. Длина этих линий равна \/2 (Т — г), поэтому
т
(С2(Т)} = | } (l - ?) ехр [-^Ii] dr. (9.125)
о
Таким образом, из (9.109) и (9.124),
Т оо
'2СО> = 11 (l - fj ехр \-2(тгщтJ | Sy(f) H2(f) df\ dr, (9.126)
о о
{С2
где H2(f) определяется формулой (9.112). Поскольку Sy(f) часто неизвестно, по-
полезно связать между собой величины (С2(Т)) и а2(г). Уравнение (9.118) можно
решить относительно /2(г), используя разложение в ряд
2/2(т) = аЦт) + а2уBт) + а2Dт) + а2у(8т) + ..., (9.127)
308 Интерферометрия со сверхдлинными базами [Гл. 9
при условии, что ряд сходится. Следовательно, из (9.124), (9.125) и (9.127) получаем
т
{С2{Т)) = ! J (l - 1) ехр {-А02т2 Уу{т) + <т2Bт) + ...}} dr. (9.128)
о
Этот интеграл легко вычисляется в случаях, когда 1 (т) определено.
Далее мы рассмотрим белый фазовый шум и белый частотный шум, которые
играют важную роль в стандартах частоты на коротких масштабах времени. Для
случая белого фазового шума а2 = К\т~2, где К\ = З/^Л^тг2 — дисперсия Аллана
за 1 с (см. табл. 9.2), и функцию когерентности можно получить из выражений
(9.126) или (9.128):
= ехр j^Z^oM^ = exp {-h2fhvl). (9.129)
Для белого частотного шума а у = К^т~1, где К$ = /io/2, и таким образом,
(С2(Т)) = "^"^-^ ¦ (9.130)
а Т
Здесь а = 2тг2г/2К2 = тг2/го^о- В предельных случаях для белого частотного шума
получим
Ч^2
^ 0
{С2(Т)) = { 3 (9.131)
Приближ:енное выражение (9.119) для времени когерентности соответствует средне-
среднеквадратичным значениям функции когерентности 0,85 и 0,92 для белого фазового
шума и белого частотного шума соответственно. Эти расчеты предполагают, что на
одной из станций установлен идеальный стандарт частоты. На практике результи-
результирующая дисперсия Аллана равна сумме дисперсий Аллана двух генераторов:
<72.=G2.1+G2.2. (9.132)
Таким образом, если на обеих станциях используются подобные стандарты частоты,
то потери когерентности удваиваются, если они малы. Если кратковременная ста-
стабильность определяется главным образом белым фазовым шумом, что обычно име-
имеет место для водородных стандартов частоты, то функция когерентности не зависит
от времени. Это означает, что существует максимальная частота, за пределами
которой данный стандарт не может использоваться в целях РСДБ, независимо от
времени накопления. Эта частота примерно равна 1/Bтг.К2) Гц, что для водородного
стандарта частоты соответствует значению около 1000 ГГц.
Фактически когерентность С(Т) измеряется по максимуму амплитуды выходно-
выходного сигнала коррелятора, который изменяется как функция частоты интерференции.
Эта операция эквивалентна исключению из фазовых данных постоянного дрейфа
частоты и может рассматриваться как высокочастотная фильтрация (пропускание)
данных с частотой отсечки 1/Т. Моделированием этой операции в виде отклика
однополюсного фильтра высоких частот можно показать, что сходимость (9.128)
гарантируется для всех процессов, для которых показатель степени дисперсии
Аллана /i < 1. Для сравнения различных представлений стабильности частоты
9.5]
Фазовая стабильность и атомные стандарты частоты
309
10'
-24
с*
i-25 .r-
10'
,-26 _
10'
«o10-20
-14
10
,-26
10
-5
10"
10
-3
10"
r-2
10 10° 101
Рис. 9.12. а — степенной спектр относительного отклонения частоты Sy(f) для водород-
водородного стандарта частоты; б— нормированный степенной спектр фазового шума ^o<S</>(/).
Величины Sy(f) и «S^(/) связаны друг с другом выражением (9.99). Для частот выше 10 Гц
S(p(f) приближается к спектру кварцевого генератора, который управляется по фазе; этот
спектр спадет как /~3. Использованы данные измерений Вессота (Vessot, 1979)
на рисунках 9.12 и 9.13 показан пример характеристик водородного генератора,
определенных по функциям сг^, Sy(f) и (Cf2(T)I/2.
9.5.3. Прецизионные стандарты частоты. В число прецизионных стандар-
стандартов частоты, представляющих интерес для РСДБ, входят кварцевые генераторы
и атомные стандарты частоты, такие, как ячейки на парах рубидия, резонаторы
на пучках атомов цезия и водородные мазеры (Lewis, 1991). Кварцевые генераторы
входят в состав атомных стандартов частоты и захватываются по фазе или частоте
атомными процессами с помощью петли обратной связи с постоянными времени 0,1—
1 с, так что кратковременная стабильность определяется стабильностью кварцевого
генератора. Практическое осуществление цепи обратной связи подробно рассмат-
рассматривается в (Vanier, Tetu and Bernier, 1979). Характеристики кварцевого генератора
очень валены, так как в случае, если он не обеспечивает высокой спектральной
чистоты сигнала, цепь обратной связи, используемая при формировании сигнала
гетеродина от сигнала частоты стандарта, не работает надлежащим образом (Ves-
(Vessot, 1976).
Для начала рассмотрим стандарт частоты в виде «черного ящика», выдающего
стабильный синусоидальный сигнал подходящей частоты, например 5 МГц или
более высокой, охваченный цепью обратной связи. Характеристики различных
устройств показаны на рис. 9.14. Из этих несколько идеализированных графиков
видно, что дисперсия Аллана для стандартов имеет три области: область корот-
копериодического шума, где преобладает белый фазовый или белый частотный
шум; область частотного фликкер-шума, называемое «фликкер-уровнем», так как
в этой области дисперсия Аллана принимает наименьшее значение; и наконец, при
больших интервалах времени — область частотного шума случайных блужданий.
Могут быть введены еще два параметра — скорость дрейфа и точность. Скорость
дрейфа определяется как линейное изменение частоты за единичный интервал
времени. Отметим, что если стандарт связан с часами, то постоянная скорость
дрейфа приводит к ошибке часов, накапливающейся пропорционально квадрату
310
Интерферометрия со сверхдлинными базами
[Гл.9
100 -
10 -
о
а ,
i
—
I
i
i
i i
I i
i i
i ilOOOrf*
1 1
^**^^ 1000
1 1
1
1
1
\лоо\з
1
mTs
i
—
1
100"
300
л-
10
-1
101 102 К
Время, с
104
ю5
Рис. 9.13. а — стандартное отклонение Аллана для водородного стандарта частоты по
данным Вессота (Vessot, 1979); б— когерентность у/(С2(Т)) в зависимости от частоты,
определенная выражением (9.125), для двух стандартов, дисперсия Аллана которых пока-
показана в части а рисунка; в — отношение сигнал/шум измеренной функции видности, норми-
нормированное на единицу для односекундного интервала, в зависимости от времени накопления
на различных частотах. В системе РСДБ когерентность и отношение сигнал/шум будут
уменьшаться из-за атмосферных флуктуации
времени. Точность показывает, насколько хорошо может быть выставлена номи-
номинальная частота стандарта. Технические параметры приведены в табл. 9.3.
Атомные стандарты частоты основаны на эффекте атомного или молекулярного
резонанса. Для любого стандарта частоты могут быть выделены три этапа (см.,
например, Kartashoff and Barnes, 1972): 1) подготовка частиц, 2) удержание частиц
и 3) опрос частиц. В подготовку частиц включается увеличение разницы в населен-
населенности используемых уровней. Это требуется для переходов в газе с температурой Т9,
для которого hv/кТд <С 1, так что населенности уровней почти равны. Подготовка
обычно осуществляется отбором квантовых состояний при прохождении пучка че-
через магнитное или электрическое поле, или оптической накачкой. Удержание частиц
дает возможность получить в результате большого времени взаимодействия узкие
резонансные линии, поскольку в соответствии с принципом неопределенности Гей-
зенберга ширина линии обратно пропорциональна времени взаимодействия. Части-
Частицы могут удерживаться в пучках или в накопительных ячейках. В накопительных
ячейках либо содержится буферный газ, либо на стенки наносится специальное
покрытие, так что столкновения частиц не приводят к изменениям фазы. Наконец,
опрос частиц представляет собой процесс измерения взаимодействия частиц с полем
излучения. Стандарты частоты могут быть либо активными, либо пассивными.
Мазерный генератор представляет собой пример активного стандарта частоты. Для
пассивных стандартов требуется внешнее поле излучения, и переходы наблюдают
9.5]
Фазовая стабильность и атомные стандарты частоты
311
стандартов частоты
1СГ
10"
15
101
10z
Время, с
ю-
ю-
10е
10'
Рис. 9.14. Идеализированные характеристики различных стандартов частоты и других
систем. Пульсарные данные взяты из (Davis et al., 1985). Данные РСДБ, показывающие
влияние стабильности пути распространения сигнала в атмосфере в примерно средних
условиях, взяты из (Могап, 1981)
Таблица 9.3. Средние характеристики*1 применяемых стандартов частоты6
Тип
Н (активный)
Cs
Csr
Rb
Crystal
A0-12s)
0,1
-
-
-
1
Ко
(lO-^s1/2
0,03
50
7
7
-
) (ю-15)
0,4
100
40
500
500
K-2
0,1
3
3
300
300
Скорость
<1
1
1
102
103
Относительная
точность A0~12)
1
5
2
102
-
aДвухточечное стандартное отклонение Аллана; коэффициент определяется из (9.115).
бПо данным (Hellwig, 1979) с дополнениями.
вОтносительное изменение частоты за сутки.
гЦезиевый стандарт высокого качества.
методами поглощения, переизлучения, обнаружения перешедших на новый уровень
частиц и косвенно, посредством измерения таких величин, как изменение интен-
интенсивности оптической накачки. Чтобы показать, как некоторые принципы осуще-
312 Интерферометрия со сверхдлинными базами [Гл. 9
ствляются на практике, приведем краткие описания нескольких типов стандартов.
Другие типы стандартов частоты находятся в стадии разработки (Drullinger, Rol-
ston and Itano, 1996; Berkland et al., 1998).
9.5.4. Рубидиевый и цезиевый стандарты. Рубидий — щелочной металл
с единственным валентным электроном и потому имеет водородоподобный спектр.
Основное электронное состояние атома расщепляется на два уровня с частотой пе-
перехода между ними 6835 МГц. Эти уровни соответствуют двум ориентациям спина
неспаренного электрона — совпадающей с ориентацией вектора спина ядра и проти-
противоположной. Упрощенная схема генератора показана на рис. 9.15. Высокочастотный
плазменный разряд в трубке с 87Rb возбуждает газ до электронного уровня при-
примерно 0,8 мкм над основным состоянием. Свет от разряда проходит через фильтр,
не пропускающий компоненты, соответствующие уровню F = 2, и прозрачный для
света с длиной волны 0,7948 мкм. Фильтр состоит из ячейки с атомами 85Rb, уровни
энергии которых слегка смещены по сравнению с уровнями атомов 87Rb, так что оба
газа имеют переходы вблизи 0,7800 мкм. Отфильтрованный свет пропускается через
другую ячейку с газом 87Rb, расположенную в резонаторе с резонансной частотой,
соответствующей частоте перехода между уровнями F = 2 и F = 1. Когда сигнал
на резонатор не подан, газ прозрачен и на фотодетектор попадает не ослабленный
пучок света. Включение сигнала с частотой 6835 МГц индуцирует переход с уровня
F = 2 на уровень F = 1. Атомы, попадающие на нижний уровень, затем переводятся
в возбужденное состояние отфильтрованным светом лампы на 87Rb. Следователь-
Следовательно, свет 87Rb испытывает поглощение. Буферный газ, состоящий из инертных
атомов, упруго сталкивающихся в ячейке резонатора с атомами 87Rb, позволяет
увеличить время взаимодействия до 10~2 с — среднего периода столкновений со
стенками ячейки и дает резонансное поглощение с шириной линии около 102 Гц.
Чтобы свести к минимуму влияние внешних магнитных полей, резонатор окружен
магнитным экраном. К резонатору прикладывается слабое однородное магнитное
поле, такое, что возможны лишь переходы с АМр = 0, для которых сдвиг частоты
вследствие эффекта Доплера первого порядка равен нулю. Ширина резонансного
поглощения равна 102—103 Гц. Белый частотный шум обусловливается дробовым
шумом, создаваемым отдельными фотонами.
Сигнал модулируется по частоте или по фазе, так что резонансная линия непре-
непрерывно сканируется. Управляющее напряжение формируется сравнением сигналов
модулятора и детектора и подается обратно на вспомогательный генератор, пере-
перестраивая его резонатор для совмещения частоты СВЧ-сигнала с вершиной резо-
резонансной кривой.
Преимуществами рубидиевых стандартов являются их небольшие размеры,
невысокая стоимость и простота транспортировки. Они иногда применяются
в РСДБ на частотах ниже 1 ГГц, где стабильность системы определяется
ионосферой. На более высоких частотах применение рубидиевых стандартов
приводит к ухудшению стабильности. Они полезны для хранения времени в период
профилактики первичного стандарта и также могут использоваться на космических
аппаратах ОРСДБ для уменьшения неопределенности времени при разрыве
радиосвязи с наземной станцией.
Цезий, как и рубидий,— щелочной металл с единственным валентным электро-
электроном. Цезий служит для определения стандарта атомного времени. Частота перехода
с изменением ориентации спина между уровнями сверхтонкой структуры основного
состояния, которая равна точно 9192, 631770 МГц, служит для определения секунды
атомного времени. Пучок атомов цезия проходит через магнитный селектор
9.5]
Фазовая стабильность и атомные стандарты частоты
313
87Rb
Лампа
о
Резонатор Фотодетектор
а ВЧ-вход
Цепь
управления ВЧ
0,7800 мкм
0,7948 мкм
«34,582605 МГц
D,4 см)
6835 Мгц
Магнитное поле
в
Частота
г
Рис. 9.15. а — упрощенная схема стандарта частоты на ячейке с парами рубидия; б —
накачка и переходы СВЧ; в — расщепление уровней тонкой структуры в зависимости от
величины магнитного поля; г — поглощение излучения 87Rb в зависимости от частоты
(Vessot, 1976)
состояний, пропускающий в резонатор атомы с уровнем F = 3. Цезиевые стандарты
частоты больше по размерам и существенно дороже рубидиевых стандартов. Из-за
низкого отношения сигнал/шум они имеют плохую кратковременную стабильность.
По этой причине цезиевые стандарты не применяются в РСДБ для управления
частотами гетеродинов. Тем не менее они обладают хорошей долговременной ста-
стабильностью и используются для контроля времени. Цезиевые стандарты также
использовались для подтверждения возможности синхронизации времени с помо-
помощью РСДБ (Clark et al., 1979). История развития резонаторов на цезиевом пучке
описывается в (Forman, 1985).
9.5.5. Активный водородный стандарт частоты. В РСДБ обычно исполь-
используются водородные стандарты частоты, и мы рассмотрим принципы их действия
более подробно. Квантовомеханический анализ активного водородного стандарта
представлен в классической статье (Kleppner, Goldenberg and Ramsey, 1962). Фун-
Фундаментальные основы теории мазеров даны в работе (Shimoda, Wang and Townes,
1956), а их конструкция подробно описывается в работах (Kleppner et al., 1965)
и (Vessot et al., 1976).
В генераторе на водородном мазере используется переход между уровня-
уровнями сверхтонкой структуры основного состояния атома водорода с частотой
1420,405 МГц, соответствующий хорошо известной в радиоастрономии линии
21см. Упрощенная схема генератора показана на рис. 9.16. Водород в мазер
поступает из резервуара молекулярного водородного газа, который диссоциирует
в высокочастотном разряде. Диссоциированный газ ионизован и при рекомбина-
рекомбинации атомов водорода каскадом переходов к основному состоянию излучается
красноватое свечение, соответствующее бальмеровской серии линий. Пучок
атомарного газа из диссоциатора проходит через шестиполюсный магнитный
селектор состояний. Однородное магнитное поле отделяет два верхних состояния
F = 1, Мр = 1 и F = 1, Мр = 0 от двух нижних состояний F = 1, Мр = — 1 и F = 0,
Мр = 0. Пучок атомов, находящихся в двух верхних состояниях, направляется
314
Интерферометрия со сверхдлинными базами
[Гл.9
v= 1420,405751768 МГц
' 'К приемнику Магнитный
Накопительная
колба
;f=i
f=o
Область
дрейфа
Ш
ВЧ диссоциатор
Источник
атомарного
водорода
F=l,MF=0
F=0, MF= -1
Шестиполюсный
магнитный
селектор
состояний
Магнитное поле
б
Частота резонатора (ус)
Рис. 9.16. а — упрощенная схема водородного мазерного стандарта частоты. Показанная
частота линии соответствует частоте перехода в свободном пространстве (Hellwig et al.,
1970). Действительное значение частоты будет отличаться на ~0,1Гц из-за затягивания
резонатором эффекта Доплера второго порядка и отражения от стенок, б — энергии
уровней сверхтонкой структуры в магнитном поле для перехода на волне 21см (Vessot
et al., 1976). в — резонансные частоты щ в зависимости от частоты резонатора vc для
двух значений ширины линии [см. формулу (9.138)]. Точка пересечения, которая может
быть найдена опытным путем, соответствует наилучшему значению рабочей частоты
в накопительную колбу, размещенную внутри СВЧ-резонатора с резонансной ча-
частотой 1420,405 МГц в режиме ТЕон или ТЕщ. Атомы испытывают около 105
соударений со стенками колбы, прежде чем выйти через ее входное отверстие. От-
Отработанные атомы удаляются из системы ионным насосом, работающим при низком
давлении. Резонатор окружен несколькими слоями материала с высокой магнитной
проницаемостью, который экранирует его от окружающих магнитных полей. Вну-
Внутри экрана находится соленоид, создающий слабое однородное поле. Это поле дает
возможность получить излучение, соответствующее переходу (F = 1,Мр = 0) —>¦
—>> (F = 0, Мр = 0), и свести к минимуму переход с уровня F = 1, Мр = 1. Эффект
Зеемана первого порядка для перехода с АМр = 0 не наблюдается (см. рис. 9.16).
Генерация в мазере возникает при условии, что резонатор будет настроен близко
к частоте перехода, а потери будут достаточно малы. В активном мазере сигнал
с частотой 1420 МГц отбирается витком связи из резонатора и используется для
захвата по фазе кварцевого генератора, из сигнала которого синтезирован сигнал
на частоте линии водорода.
9.5] Фазовая стабильность и атомные стандарты частоты 315
Продолжительность времени жизни атома в колбе может быть описана экспо-
экспоненциальной вероятностной функцией
/(*) = 7е*, (9.133)
где 7 ~~ суммарная скорость релаксации. Профиль линии имеет приблизительно
лоренцевскую форму с шириной (полной шириной на уровне половины максималь-
максимального значения) Ai/0 на уровне 7/71"- Наибольший вклад в 7 вносит скорость утечки
атомов через входное отверстие, равная
7е = ^ , (9.134)
где г>о = л/SkT^Jm — средняя скорость частиц, Тд — температура газа, m — масса
атома водорода, Ah — площадь входного отверстия, V — объем колбы. Величина
7е примерно равна 1с. После многих столкновений со стенками атомы утрачи-
утрачивают когерентность, что приводит к потерям jw ~ 10~4 с. Столкновения между
атомами водорода вызывают спин—обменную релаксацию 7se? пропорциональную
плотности газа и vq. Полный коэффициент релаксации примерно равен сумме трех
наиболее существенных компонент:
7 = 7е + lw + Ise = 7ГД1/О. (9.135)
Все три члена пропорциональны vq и, следовательно, пропорциональны л/Т^ • От-
Отметим, что случайные тепловые движения атомов не приводят к уширению линий
из-за эффекта Доплера первого порядка, поскольку взаимодействие между атомами
и высокочастотным полем осуществляется в объеме резонатора (Kleppner, Golden-
berg and Ramsey, 1962).
В мазерном генераторе имеются две резонансные частоты — частота линии
vL и резонансная частота резонатора z/c, определяемая его размерами. Частота
классических генераторов равна среднему значению этих двух частот, взвешенных
в соответствии с коэффициентами добротности Q линии Ql и резонатора Qc-> T- е-
Коэффициент добротности Q определяется как увеличенная в тг раз величина,
обратная относительным потерям энергии за период резонансной частоты. Сле-
Следовательно, из (9.133) получаем для Ql (см., например, Siegman, 1971)
™« (9.137)
7 Az^o
Типичное значение Ql имеет порядок 109. Фактическое значение Qc для резона-
резонатора с серебряным покрытием достигает 5 • 104. Поскольку Ql ^> Qc> резонансная
частота примерно равна
VQ~vL + 9°{yc-VL). (9.138)
Выражение (9.138) описывает эффект «затягивания резонатором» резонансной
частоты. Изменения температуры приводят к изменению размера резонатора и,
следовательно, резонансной частоты. Таким образом, для относительной стабиль-
стабильности частоты мазера 10 ~15 необходима относительная механическая стабильность
резонатора порядка 5-10~10. Размеры резонатора, следовательно, должны быть
316 Интерферометрия со сверхдлинными базами [Гл. 9
стабильны на уровне 10~8 см. Резонатор должен быть сделан из материала с ма-
малым температурным коэффициентом расширения или его температура должна
тщательно контролироваться. Очень высокая механическая стабильность требуется
также для того, чтобы изменения атмосферного давления не влияли на частоту.
Резонатор типа ТЕОц, представляет собой цилиндр около 27 см длиной и такого
же диаметра, что заметно больше длины волны в свободном пространстве из-за
влияния накопительной колбы. Грубая настройка осуществляется перемещением
нижней пластины резонатора, а плавная — параметрическим диодом. Из (9.138)
очевидно, что мазерная частота наиболее стабильна в случае, когда vc совмещается
с vL, так что vq равно vL независимо от значений Qc и Ql- Оптимальную точку
настройки мазера можно найти по графику изменения vq в зависимости от z/c,
который в соответствии с (9.138) представляет собой прямую линию с наклоном
Qc/Ql- Варьируя Ql-> например, изменяя давление газа и тем самым изменяя 7?
можно получить семейство прямых линий, пересекающихся на требуемой частоте
у0 = уь = ус (см. рис. 9.16 в). В некоторых конструкциях для того, чтобы резона-
резонатор мазерного стандарта частоты оставался постоянно настроенным, используются
сервосистемы.
Характеристики водородных стандартов частоты показаны на рисунках 9.13
и 9.14. При интервалах времени короче 103 с они ограничиваются двумя фунда-
фундаментальными процессами: 1) белым частотным шумом, обусловленным тепловым
шумом в резонаторе, и 2) белым фазовым шумом, обусловленным тепловым шумом
во внешнем усилителе. Тепловой шум, создаваемый внутри резонатора, характери-
характеризуется относительной частотной дисперсией (дисперсией Аллана)
о 1 кТ
Vf Ql P0T '
где Pq — мощность, выделенная атомами (Edson, 1960; Kleppner, Goldenberg and
Ramsey, 1962). Кроме того, в резонаторе наблюдается дробовой шум, обуслов-
обусловленный дискретным излучением фотонов. Однако дисперсия Аллана c^s, которой
описывается этот процесс меньше а * в hv/kTg раз, что для комнатной температуры
равно 2-10~4. Спонтанное излучение также вносит небольшой шум, эквивалентный
повышению Тд на hv /к ~ 0,07 К. Наконец, мощность шума, вносимого приемником
в отбираемый из резонатора сигнал, равна kT^Av, где Т# — шумовая температура
приемника, a Av — его полоса частот. Дисперсия Аллана для этого шума равна
(Cutler and Searle, 1966)
°k=(dbj*^- (9-140)
Оба рассмотренных процесса независимы, так что полная дисперсия Аллана равна
<j2 = <j2 \ 0-2 . Эффект этих процессов хорошо виден в данных, представленных
на рис. 9.14. Отметим, что фликкер-уровень не достигнут из-за долгопериодиче-
ских изменений частоты. Кратковременные характеристики могут быть улучшены
увеличением потока атомов и соответственно Pq. Однако с увеличением потока
увеличивается скорость спин-обменных взаимодействий, уменьшающих Qhi и в ре-
результате генератор становится более восприимчивым к долговременным эффектам,
связанным с затягиванием частоты резонатором.
Частота мазера не равна точно частоте атомного перехода из-за нескольких
эффектов. Этими эффектами ограничивается точность, с которой может быть
установлена частота. Большинство из них зависит от температуры, поэтому они,
вероятно, вносят вклад в частотный фликкер-шум и в частотный шум случайных
блужданий. Большое значение имеет эффект затягивания частоты резонатором,
9.5] Фазовая стабильность и атомные стандарты частоты 317
отмеченный выше; для его минимизации резонатор следует тщательно настраи-
настраивать. Происходящие при столкновениях атомов спин-обменные процессы приводят
к смещению частоты, зависящему от Q^, как и при затягивании резонатором. Таким
образом, этот эффект тоже устраняется его настройкой. Столкновения атомов со
стенками накопительной колбы дают эффект, получивший название «стеночного
сдвига», который с трудом предсказывается и может быть единственным ограни-
ограничивающим фактором в достижении абсолютной точности частоты мазерного стан-
стандарта (Vessot and Levine, 1970). Этот сдвиг зависит от температуры и материала,
покрывающего внутреннюю поверхность колбы. Относительная величина сдвига
порядка 1СР11. Эффект Доплера первого порядка не имеет значения в отличие от
эффекта Доплера второго порядка, пропорционального v2/с2 (Kleppner, Goldenberg
and Ramsey, 1962). Относительное смещение частоты в этом случае примерно равно
-1,4 • 10~13Т9. Наконец, эффект Зеемана первого порядка в переходе (F = 1, MF =
= 0) —> (F = 0, Мр = 0) отсутствует. Однако эффект Зеемана второго порядка
приводит к относительному смещению частоты 2,0 • 10 В , где В — величина маг-
магнитного поля в теслах.
9.5.6. Стабильность гетеродинов. Сигналы гетеродинов формируются по-
посредством умножения сигнала генератора, управляемого стандартом частоты. Как
упоминалось в разд. 7.2, умножители должны обладать исключительно высокой
стабильностью, чтобы исключить дополнительные шумы и дрейф сигнала. Несовер-
Несовершенные умножители чувствительны к вибрациям и температуре и могут модулиро-
модулировать сигнал на гармониках частоты электрической сети. В идеальном умножителе
сигнал вида (9.92) преобразуется к виду
V(t) = cos [2тг Mvot + Мф(Ь)], (9.141)
где М — коэффициент умножения, щ — основная частота, и ф — случайный фазо-
фазовый шум стандарта частоты. Если фазовый шум мал (Мф(г) <С 1), то односторонний
энергетический спектр V(t) записывается в виде
Sv{v) = 6{v - Mi/0) + М2БФ{1У - Mi/0), (9.142)
где 5 — дельта-функция, соответствующая рассматриваемому сигналу, и Бф — энер-
энергетический спектр фазового шума. Таким образом, мощность шума увеличивается
пропорционально квадрату коэффициента умножения. В общем случае Sv можно
записать как (Lindsey and Chie, 1978)
00 м2п
Sv{v) = 5{v - Мщ) + Y^ ^~r №ф(" ~ Ml/°) * S<t>(" ~ Ml/°) *'••]' (9-143)
n=l
где в квадратных скобках находится п последовательных сверток одной и той
же функции. Если остается только главный член в сумме, то уравнение (9.143)
сводится к виду (9.142). Члены высшего порядка в (9.143) образуют ряд, ком-
компоненты которого вследствие повторяющейся операции свертки имеют примерно
гауссово распределение. Среднеквадратичное отклонение фазы выходной частоты
Мщ умножителя пропорционально среднеквадратичному напряжению шума по
полосе пропускания выходного сигнала, т. е. среднеквадратичные флуктуации фазы
пропорциональны М.
9.5.7. Система калибровки фазы. Один из способов проверки работоспо-
работоспособности всей системы РСДБ заключается в подаче на вход приемника высокоча-
высокочастотного сигнала, сформированного из сигнала стандарта частоты независимым
318 Интерферометрия со сверхдлинными базами [Гл. 9
образом. Высокочастотный тестовый сигнал молено получить с помощью диода
с накоплением заряда, управляемого, скажем, частотой стандарта 1 МГц, и, таким
образом, генерирующего последовательность импульсов с периодом 1 мкс. Такой
сигнал имеет высокочастотные гармоники с шагом 1 МГц, фазы которых одинаковы
на сравниваемых интервалах. При преобразовании полосы ВЧ к видеополосе можно
сделать так, чтобы одна из введенных гармоник оказалась на подходящей частоте
порядка 10 кГц. Затем она сравнивается с опорным сигналом стандарта частоты. Во
время записи эксперимента РСДБ-сигнал калибровки фазы можно подавать непре-
непрерывно, если установить достаточно низкий его уровень, обнаруживаемый лишь при
очень узкой полосе фильтрации в процессоре (~10Гц). Калибровка позволяет ком-
компенсировать отклонения фазы, вызванные, например, тепловыми эффектами в ка-
кабелях (Whitney et al., 1976; Thompson and Bagri, 1991; Thompson, 1995). Подобные
методы применяются в некоторых интерферометрах со связанными элементами.
9.5.8. Синхронизация времени. Часы на станциях РСДБ должны быть
синхронизованы достаточно точно, чтобы избежать больших затрат времени при
поиске интерференционных лепестков. Для контроля времени на станциях РСДБ
примерно до середины 80-х годов широко использовалась система Loran С. Система
Loran — сокращение от Long Range Navigation (Навигационная система большого
радиуса действия), первоначально была разработана для целей морской навигации
во время Второй мировой войны (Pierce, McKenzie and Woodward, 1948). Сигналы
передавались на частоте 100 кГц. Положение наблюдателя на поверхности Земли
определяется по времени относительного запаздывания сигналов, принимаемых
от трех станций. Подробное описание Loran С дано в (Frank, 1983). Достигаемая
точность синхронизации составляла от нескольких сот наносекунд до микросекунд
в зависимости от точности оценки времени распространения сигнала.
Глобальной навигационной системой (GPS) обеспечивается более высокая точ-
точность по сравнению с Loran С, и с начала 80-х годов она используется почти во
всех системах РСДБ. Пользователи GPS принимают сигналы на частотах 1,23
или 1,57 ГГц от ряда спутников с известными координатами, часы которых син-
синхронизованы с Всемирным координированным временем (UTC, см. разд. 12.3).
Если измеряется время прихода сигналов, принимаемых от четырех спутников,
и учитываются эффекты распространения радиоволн в атмосфере, то пользователи
могут определить свое положение по трем координатам, а также ошибки часов.
Точность времени, доступная для гражданских пользователей улучшилась за деся-
десятилетие от 100 не (Parkinson and Gilbert, 1983; Lewandowski and Thomas, 1991) до
~7 не и ожидается ее дальнейшее улучшение (Lewandowski, Azoubib and Klepczyn-
ski, 1999). Анализ проблемы синхронизации времени с учетом эффектов теории
относительности дан в работе (Ashby and Allan, 1979). Для общей информации
о пользовании GPS см., например, (Leick, 1995).
Относительная точность контроля времени по наблюдениям пульсаров на мас-
масштабах времени около года приближается к 10~14 (Davis et al., 1985). В конечном
счете, наилучшая синхронизация часов может быть получена из обработанных
данных РСДБ (Clark et al., 1979).
9.6. Системы регистрации
Форма представления сигнала и метод регистрации информации находятся
в основе анализа любой записывающей системы. Запись может быть цифровой либо
аналоговой, и возможны различные методы накопления данных. Здесь рассматри-
рассматривается только цифровая запись на магнитные ленты, так как эта технология хорошо
подходит для РСДБ и широко используется.
9.6] Системы регистрации 319
Основным параметром системы регистрации является скорость записи данных,
щ (бит/с). Этим параметром ограничивается число бит, которые молено записать
в заданное время, и, следовательно, чувствительность наблюдений источников
с непрерывными спектрами, в которых возможная полоса ПЧ превышает величину
Vb/2Nb, где Щ — число бит на один отсчет. Сигнал представляется в виде дис-
дискретных значений с Q уровнями квантования, получаемых с частотой Найквиста,
увеличенной в /3 раз. Для N дискретных отсчетов возможны QN конфигураций
данных, что требует как минимум 7Vlog2 Q бит. Поэтому, как отмечалось в п. 8.3.6,
максимальная ширина полосы ВЧ равна
А"= = й (
Отношение сигнал/шум, получающееся за время т, пропорционально rjQ \/Avt , где
rjQ — коэффициент эффективности квантования, введенный в разд. 8.3. Из (9.144)
получаем
Щ (9-145)
Если г — время записи всей ленты, то число записанных бит равно щт. Таким
образом, величиной rjQ/'\fj3Nb характеризуется эффективность системы в расчете
на один бит, которая должна быть, конечно, максимальной. При двух и четырех-
четырехуровневой выборке данных очевидны схемы кодирования один бит на отсчет и два
бита на отсчет соответственно. При трехуровневой выборке мы сталкиваемся с труд-
трудностями, поскольку кодирование одного дискретного отсчета (находящегося в одном
из трех возможных состояний) в два бита данных (представляющих собой четыре
возможных состояния) неэффективно. Преобразование трех дискретных отсчетов
в пять бит или пяти отсчетов в восемь бит дает скорости потока данных 1,67 и 1,60
бит на отсчет в сравнении с теоретически оптимальным значением log2 3 = 1,585.
Значения величины г]я/у//ЗЩ для различных значений Q и /3 и нескольких схем
кодирования приводятся в табл. 9.4. Наилучшее отношение сигнал/шум достигается
при трехуровневой выборке с частотой Найквиста, хотя двух и четырехуровневое
квантование дают почти такие же значения.
В дополнение к рассмотренным выше схемам кодирования, в которых число
бит, необходимое для данного числа дискретных отсчетов, постоянно, может быть
рассмотрена также схема, в которой число бит зависит от значений отсчетов,
т. е. код переменной длины. Например, Д'Аддарио (D'Addario, 1984) предложил
кодирование значений +1, 0 и —1 при трехуровневом квантовании в виде двоичных
чисел 11, 0, и 10 соответственно. Такой поток данных может быть восстановлен
единственным образом, так как все однобитные представления начинаются с 0, а все
двухбитные — с 1. Среднее число бит на отсчет зависит от вероятностного распре-
распределения амплитуды сигнала и установленных уровней ограничения. Для данного
числа бит уровни ограничения, при которых достигается максимальное отношение
сигнал/шум, вообще говоря, отличаются от полученных в разд. 8.3 и оптимальных
для данного числа бит на отсчет. В схеме кодирования Д'Аддарио наилучшие
характеристики достигаются при установлении порогов ограничения, таких, что
tjq = 0,769 и Nb = 1,370 бит/отсчет; при этом значение характеристического
коэффициента tjq/'л/Щ^ь равно 0,657. Таким образом может быть достигнуто улуч-
улучшение чувствительности около 3 % по сравнению с применением схемы с записью
1,6 бит/отсчет. Тем не менее, влияние ошибок в битах данных или сигналов помех,
изменяющих амплитудное распределение, может быть более значительно. Наконец,
320 Интерферометрия со сверхдлинными базами [Гл. 9
Таблица 9.4. Характеристики различных способов представления сигналов
в зависимости от числа уровней квантования, частоты выборки и формата
кодирования21
Представление сигнала
Выборка с частотой Найквиста (/3 = 1)
Два уровня
Три уровня
Четыре уровня
Выборка с двойной
Два уровня
Три уровня
Четыре уровня
«Идеальное» кодирование6
5 отсчетов/8 бит
3 отсчета/5 бит
1 отсчет/2 бита
Все произведения
Кроме нижнего уровня
1 частотой Найквиста (/3 = 2)
«Идеальное» кодирование6
5 отсчетов/8 бит
3 отсчета/5 бит
1 отсчет/2 бита
Все произведения
0,637
0,810
0,810
0,810
0,810
0,881
0,87
0,74
0,89
0,89
0,89
0,89
0,94
Nb
1,0
1,585
1,60
1,667
2,0
2,0
2,0
1,0
1,585
1,60
1,667
2,0
2,0
0,637
0,643
0,640
0,627
0,573
0,623
0,61
0,52
0,50
0,50
0,49
0,45
0,47
а r\Q — коэффициент эффективности квантования, Nb — число бит на отсчет,
/3 — коэффициент избыточности выборки.
6 N отсчетов кодируется в 7Vlog23 6HT.
данные могут кодироваться статистически в большие блоки, что позволило бы
получить теоретически оптимальное значение TVj,, равное 1,317 бит/отсчет, что при
tjq = 0,769 дало бы значение характеристического коэффициента 0,670 (D'Addario,
1984).
На практике желательность простой схемы кодирования и другие конструктив-
конструктивные соображения обычно приводят к выбору двухуровневого квантования. Во всех
пяти системах РСДБ, разработанных в США в течение 1968-1997 годов (Mark I,
Mark II, Mark III, VLB А и Mark IV), применяется двухуровневая выборка. В слу-
случае спектральных наблюдений, когда ширина полосы сигнала мала по сравнению
с шириной полосы системы записи, многоуровневое квантование предпочтительнее.
Отметим, что при многоуровневом квантовании емкость устройств записи исполь-
используется более эффективно по сравнению с выборкой выше частоты Найквиста (см.
табл. 9.4).
В каждом отсчете данных явно либо неявно должна присутствовать метка
времени. Хотя величина ошибки частоты декодирования данных около 10~3 при-
приемлема, сдвиг по оси времени на один бит недопустим. Фактически во всех систе-
системах регистрации данные записываются блоками. Каждая новая запись начинает-
начинается в точный момент времени, так что время регистрации потока данных может
9.6]
Системы регистрации
321
11 Томсон
322 Интерферометрия со сверхдлинными базами [Гл. 9
быть восстановлено в случае его потери в предыдущей записи. Эти длины записей
следующие: Mark I — 0,2с A44000бит), Mark II — 16,7мс F6600бит) и Mark III
5мс B0000бит). В системе Mark I, где использовался стандартный компьютерный
формат магнитных лент, точность регистрации была очень высока, и время для
любого бита данных получалось подсчетом числа бит от начала записи и числа
записей от начала ленты. В системе Mark II, в которой используются видеомагни-
видеомагнитофоны, данные записываются параллельно с кодом времени, тогда как в системе
Mark III, где применяются специализированные магнитофоны, переходы данных
сами по себе служат часами. Характеристики нескольких систем даны в табл. 9.5.
Во всех этих случаях используется цифровая запись данных, за исключением ка-
канадской системы, применяемой в течение 1971-1983 годов. В работе (Wietfeldt and
D'Addario, 1991) рассмотрена совместимость некоторых из этих систем.
9.7. Системы обработки данных
Процессор в РСДБ выполняет две основные функции: 1) восстановление непре-
непрерывных потоков данных и 2) кросскорреляционный анализ этих потоков. Можно
ожидать, что в потоке данных, поступающих с магнитофона, имеются неравно-
неравномерности шкалы времени до 100 мкс, возникающие вследствие ошибок механики
системы воспроизведения, и что часть данных теряется из-за дефектов ленты.
В процессоре должна восстанавливаться истинная шкала времени либо по импуль-
импульсам времени, в случае записи временного кода, либо по переходам данных, если
используется синхронизатор бит. Необходимо достаточное буферное накопление
для того, чтобы отслеживались механические смещения, по крайней мере. Геомет-
Геометрическая задержка может корректироваться с использованием минимума буферной
памяти посредством изменения времени воспроизведения, в этом случае данные
остаются на ленте до тех пор, пока не понадобятся в корреляторе. Если ленты
читаются синхронно, то для компенсации геометрической задержки необходима
емкость памяти буфера данных, примерно в 5 • 104 раз превышающая частоту кода
времени в мегагерцах.
Основное различие между разработкой корреляционной части процессора для
РСДБ и обычного интерферометра связано с тем фактом, что сдвиг интерференци-
интерференционных лепестков и компенсация задержки в процессоре РСДБ обычно выполняется
с дискретным и квантованным сигналом. Это приводит к особым проблемам, ко-
которые рассматриваются в этом разделе. Ухудшение отношения сигнал/шум вслед-
вследствие представления сигналов в цифровой форме описывается несколькими коэф-
коэффициентами: tjq — коэффициент потерь, связанный с амплитудным квантованием
записанных сигналов, рассматривавшийся в разд. 8.3; tjr — коэффициент потерь,
вызванный квантованием фазы функции смещения частоты интерференции (сдвига
интерференционных лепестков); rjs — коэффициент потерь вследствие неполного
подавления боковой полосы из-за ограниченного числа задержек в корреляторе;
r\D — потери, вызванные дискретностью компенсации геометрической задержки.
Сдвиг частоты интерференции и компенсацию задержки можно выполнить для
аналоговых сигналов непосредственно на телескопе до записи. Например, смещение
частоты интерференции может быть выполнено на телескопах изменением частоты
гетеродинов, как описывалось в п. 6.1.6 для решеток со связанными элементами.
Преимущество этого подхода заключается в том, что требуется вычисление только
действительной корреляционной функции (как с положительными, так и с отрица-
отрицательными задержками); см. разделы 8.7 и 9.1. Следовательно, достаточно лишь по-
половины корреляционных каналов. Кроме того, отсутствуют потери чувствительно-
чувствительности, вносимые цифровым вращением интерференционных лепестков. Недостатком
9.7] Системы обработки данных 323
является то, что приходится усреднять выходной сигнал коррелятора на достаточно
коротких интервалах времени, чтобы получить остаточную частоту интерференции
для некоторого источника везде в пределах главных лепестков диаграмм направ-
направленности антенн. Максимальная остаточная частота интерференции источника на
уровне половины максимума главного лепестка равна Ai/f ~ Duoe/d [см. выраже-
выражение A2.21)], где D — длина базы, d — диаметр антенны, и иое — угловая скорость
вращения Земли в рад/с. Следовательно, время усреднения сигнала коррелятора
должно быть менее l/BAz/^); например, оно не должно превосходить 30 мс для баз,
равных диаметру Земли, и d = 25 м. Корреляционные функции могут быть усредне-
усреднены далее после прохождения устройства остановки интерференционных лепестков,
понижающего остаточную частоту интерференции. Кроме того, устройство на теле-
телескопе, непрерывно изменяющее частоту гетеродина, должно быть сконструировано
достаточно точно, чтобы обеспечивалось полное фазовое соответствие для астро-
метрических программ. Дальнейшая информация по РСДБ системам и алгоритмам
обработки данных может быть найдена в работах (Thomas, 1981) и (Herring, 1983).
9.7.1. Потери при вращении интерференционных лепестков (rjR).
Вращение интерференционных лепестков (смещение частоты интерференции)
применяется для того, чтобы свести к нулю частоту интерференционной состав-
составляющей коррелированных сигналов (см. п. 6.1.6). Здесь частота интерференции
рассматривается с учетом влияния отклонений частоты стандартов от номинала.
Сдвиг частоты интерференции может быть осуществлен в процессоре несколькими
способами, как показано на рис. 9.17. Если смещение лепестков выполняется
после коррелятора (рис. 9.17а), то усреднение корреляционной функции должно
выполняться на коротких интервалах времени по сравнению с периодом
интерференционного сигнала. Такое короткое время усреднения неизбежно
приводит к высокой плотности потока данных на выходе коррелятора, что делает
непривлекательной эту конфигурацию. С другой стороны, до поступления на
коррелятор один из потоков данных может быть пропущен через цифровой
однополосный смеситель, сдвигающий фурье-компоненты сигнала на подходящую
частоту интерференции, как показано на рис. 9.17 6. Фазовый сдвиг в смесителе
на 90° без внесения при этом спектральных искажений осуществить трудно,
поэтому такой способ вращения лепестков применяется редко (см. также разд. 8.7).
Обычно используется схема, показанная на рис. 9.17 в, но применение вращения
интерференционных лепестков к квантованным сигналам сталкивается с двумя
трудностями. Во-первых, интерференционная функция, на которую умножается
сигнал, должна быть грубо квантована, чтобы не увеличивать число бит на отсчет
на входе коррелятора; это также относится к схеме на рис. 9.17 6. Во-вторых,
в результате умножения образуется нежелательная боковая шумовая полоса, что
описывается ниже в п. 9.7.2. Здесь мы рассмотрим первую из этих проблем.
Поток данных умножается на комплексную функцию Т, действительная
Tr и мнимая J-j части которой представляют собой аппроксимированные cos ф
и sin ф, где ф — требуемая функция изменения фазы. В простейшем случае
эти функции представляются сигналами прямоугольной формы с подходящей
частотой и фазами. Таким образом, как показано на рис. 9.18, квантованный сигнал
умножается на функцию смещения частоты интерференции, амплитуда которой
постоянна, а фаза меняется не непрерывно, а на 90° каждую четверть периода. По-
Получающаяся в результате функция видности имеет фазовую составляющую с 90°-й
пилообразной модуляцией на частоте интерференции. Это похоже на фазовый
шум, в котором фаза равномерно распределена в пределах ±45°. Следовательно,
11*
324
Интерферометрия со сверхдлинными базами
[Гл.9
амплитуда усредненного сигнала
уменьшается в sin (тг/4)/(тг/4) =
= 0,900 раз. Другой подход, позволяю-
позволяющий вычислить потери в отношении
сигнал/шум, заключается в расчете
гармоник функции смещения частоты
интерференции. Амплитуда первой
гармоники Tr или Ti, равна 4/тг =
= 1,273. На выходе процессора остает-
остается только сигнал, смешанный с первой
гармоникой, так как остальные гармо-
гармоники исключаются в процессе усред-
усреднения по времени. Таким образом,
часть сигнала теряется вне полосы
пропускания интерференционных
лепестков. Оставшаяся часть равна
корню квадратному из отношения
мощности первой гармоники к полной
мощности функции смещения и равна
у^/тг = 0,900. Эта величина пред-
представляет собой потери в отношении
сигнал/шум. Кроме того, изменяется
масштабный множитель, так как
при сдвиге частоты интерференции
амплитуда интерференционного
сигнала увеличивается. Поэтому
амплитуду сигнала следует разделить
на 4/тг — относительную амплитуду
первой гармоники Tr.
Функция смещения частоты ин-
интерференции, представленная трех-
трехуровневой аппроксимацией синуса,
лучше (Clark, Weimer and Weinreb,
1972) и показана на рис. 9.18 б. Когда
эта функция равна нулю коррелятор
«запирается». Так как действительная
и мнимая части Т никогда не равны
нулю одновременно, все биты данных
используются по крайней мере один раз. Такую функцию смещения частоты ин-
интерференции молено представить вектором на фазовой плоскости, описывающим
квадрат такой, что фаза изменяется скачками по 45°, а амплитуда принимает
поочередно значения \[2 и 1. Получающееся в результате дрожание фазы рав-
равномерно распределено в пределах ±22,5° и приводит к уменьшению амплитуды
сигнала до (sin7r/8)/Gr/8) = 0,974. Кроме того, изменение длины фазового вектора
приводит к неоднородному взвешиванию дискретных значений сигналов. Допол-
Дополнительный коэффициент уменьшения отношения сигнал/шум равен A + у/2)/\//6
= 0,986. Суммарный коэффициент потерь в отношении сигнал/шум равен 0,960.
Ухудшение отношения сигнал/шум также равно корню квадратному из отношения
мощности первой гармоники к полной мощности, заключенной в Tr. Величина
первой гармоники Tr равна D/тг) cos (тг/8) = 1,18, что представляет собой попра-
поправочный масштабный множитель для функции видности. Трехуровневая функция
смещения, рассмотренная здесь, применяется во многих процессорах РСДБ. Для
Рис. 9.17. Различные конфигурации процес-
процессора, показывающие возможные положения
системы изменения частоты интерференции.
Tr и Ti — косинусное и синусное представ-
представления интерференционной функции. См. для
дальнейших пояснений текст
9.7]
Системы обработки данных
325
Время
Время
Время
2ж
ей
jo
Время
I [ Время
1 1
©
яялл
Время
Время
Рис. 9.18. а — математическая модель двухуровневой схемы вращения интерференцион-
интерференционных лепестков, где показаны функции Tr и Ti, аппроксимирующие cos ф и sin</> (слева),
амплитудное и фазовое представления Т (в середине) и график Т на фазовой плоскости
(справа) .6 — те же графики для случая трехуровневой схемы вращения интерференци-
интерференционных лепестков
того чтобы сформировать Т, период интерференционных лепестков делится на 16
частей. Переходы в Т, происходящие в моменты времени, кратные 1/16 периода
интерференционных лепестков, при этом располагаются не оптимальным образом,
но это приближение дает в результате не более 0,1 % дополнительных потерь. От-
Отметим, что молено создать FX-коррелятор, с которым проще обрабатывать данные,
представленные более чем одним или двумя битами на отсчет, по сравнению с кор-
коррелятором задержек. Чем больше бит в одном отсчете сигнала, тем более точная
аппроксимация синусной и косинусной функций может использоваться.
9.7.2. Потери подавления боковой полосы интерференции (rjs)' Схема
смещения частоты интерференции, показанная на рис. 9.17 в, не является совер-
совершенным однополосным смесителем. По этой причине одновременно с полезным
сигналом, смещенным по частоте на величину частоты интерференции, появляет-
появляется нежелательная шумовая составляющая, соответствующая зеркальному отклику
смесителя. Чтобы понять этот эффект, рассмотрим кросскорреляционный энер-
энергетический спектр на выходе коррелятора. Вспомним, что z/ — промежуточная
частота, определенная в соответствии с формулой (9.13), и отметим, что выходы
спектрального коррелятора z/ > 0 и z/ < 0 относятся к верхней и нижней боковой
полосе частот соответственно. Для верхней полосы частот кросскорреляционный
326 Интерферометрия со сверхдлинными базами [Гл. 9
спектр сигнала определяется выражением (9.21), которое отличается от нуля только
в этой полосе. Однако шумы будут присутствовать как на положительных, так и на
отрицательных частотах. Таким образом, кросскорреляционный энергетический
спектр на выходе коррелятора имеет вид
>0,
(9.146)
< О,
где S(v') — аппаратурный отклик, определенный в (9.21), j<&(y') — показатель
степени в формуле (9.21), а пи и щ — шумовые спектры для откликов в верх-
верхней и нижней полосе частот соответственно. При наблюдениях с использованием
спектрального коррелятора величина S'^iy1} может быть рассчитана и шумы в об-
области v' < 0 просто проигнорированы. В наблюдениях источников с непрерывными
спектрами шумы при v1 < 0 приводят к дополнительным шумам в корреляционной
функции, и их необходимо исключить. Прямой способ устранения шумов в области
у1 < 0 заключается в расчете спектра S'12{y') и его умножении на фильтрующую
функцию вида
A, 0<z/<Az/,
HF(y') = { (9.147)
[О в остальных случаях.
Затем корреляционная функция может быть восстановлена обратным преобразова-
преобразованием Фурье результирующей функции 8'12{у')Нр(у'). С другой стороны, фильтра-
фильтрацию можно осуществить сверткой корреляционной функции на выходе коррелятора
с преобразованием Фурье Hf(v'), которое равно
hF(r) = Ave*AvT (SJ^1) (9.148)
V 7Г1Л1УТ )
ИЛИ
hF(T) = F^t) + j F2(t), (9.149)
где Fi и F2 определены в (9.18). Свертка оставляет полезный сигнал без измене-
изменений, но устраняет шум в отрицательной (нижней) боковой полосе частот. Таким
образом, корреляционная функция по-прежнему имеет форму (9.20), плюс шумы
в положительной (верхней) боковой полосе частот, которые устранить невозможно.
Роль Нр(т) можно представить другим способом. Корреляционная функция
на выходе коррелятора рассчитывается для дискретных задержек с интер-
интервалами BAi/)-1. Следовательно, полная ширина корреляционной функции
в выражении (9.20) на уровне половины максимума составляет около трех
интервалов по задержке. Для оценки амплитуды и фазы корреляционной функции
желательно сделать больше, чем просто взять эти значения из максимума
Pi2(r)- Предпочтительнее было бы использовать всю информацию, которую
дает корреляционная функция на различных задержках. Нр(т) представляет собой
удобную интерполяционную функцию, должным образом взвешивающую функцию
корреляции, суммируя при этом мощность на различных задержках и обеспечивая
тем самым оптимальную оценку амплитуды, фазы и задержки интерференционных
лепестков. Отметим, что Нр(т) и р[2{т) имеют идентичную форму, за исключением
неизвестной амплитуды, фазы и задержки. Эти неизвестные величины могут быть
оценены обычной процедурой согласованной фильтрации, или, что эквивалентно,
9.7] Системы обработки данных 327
методом наименьших квадратов, в котором корреляционная функция свертывается
с Нр{т). Однако р[2{т) измеряется лишь для конечного числа шагов по задержке,
вследствие чего часть информации теряется и ухудшается отношение сигнал/шум.
Предположим, что характеристика нижней полосы пропускания системы имеет пря-
прямоугольную форму и что ошибки задержек Arg и те равны нулю, вследствие чего
корреляционная функция центрирована относительно диапазона задержек корре-
коррелятора. Допустим, что число шагов (переборов) по задержке в корреляторе равно
М. Коэффициент потерь rjs находится делением величины отношения сигнал /шум
при М возможных значениях корреляционной функции на величину отношения
сигнал /шум, когда корреляционная функция известна полностью:
\
м'
Е 1
т , (9.150)
Е i
где Tk = fc/BAz/), M' = (М — 1)/2 и М — нечетное целое. Знаменатель в (9.150)
равен 2Ai/2 [см., например, (А8.5)], так что
\
Л/Г I
k=l
При М = 1 rjs = 1/л/2 , что соответствует не подавленной зеркальной полосе частот.
Для того чтобы можно было с уверенностью определить максимум корреляционной
функции, М должно быть равно по крайней мере 3; значение М ~ 7, для которого
rjs = 0,975, подходит для большинства задач. Отметим, что поскольку мы предпо-
предположили, что корреляционная функция точно центрирована, то ее значения равны
нулю на 2, 4, 6, 8, ... и т.д. шагах по задержке. Это предполагает, например, что
коррелятор с 9 задержками (М'=4) ничем не лучше коррелятора с 7 задержками
(М'=3). В действительности коррелятор с 9 задержками будет лучше, поскольку
корреляционная функция вряд ли идеально выравнивается. Вообще говоря, если
корреляционная функция в корреляторе не идеально центрирована, то значение rjs
будет несколько меньше, чем дано выражением (9.151) (Herring, 1983).
9.7.3. Потери дискретного изменения задержки (tjd)- Задержка, вво-
вводимая для выравнивания потоков бит данных, квантуется на частоте выборки,
которую мы предположим равной частоте Найквиста. Таким образом появляется
периодическая пилообразная ошибка задержки с размахом амплитуды, равным
интервалу выборки. Этот эффект также называют ошибкой дискретного смещения
бит. Из-за ошибки задержки возникает периодическое смещение фазы, представ-
представляющее собой функцию видеочастоты, как показано на рис. 9.19. Полный размах
ошибки фазы равен
</>рр = 5^ (9-152)
а частота «пилы» пропорциональна частоте интерференции и имеет максимальное
значение
z/ds(max) = ( переключении задержки в секунду), (9.15о)
328
Интерферометрия со сверхдлинными базами
[Гл.9
0
Частота Av
ж/2
О
-ж/2
1,0
0,5
0,0
Рис. 9.19. Эффект дискретного изменения задержки: а — случай смещения частоты интер-
интерференции к нулевой частоте видеополосы; б — случай смещения частоты интерференции
с фазовым сдвигом тг/2 при изменении задержки на один отсчет Найквиста. Вверху — фаза
в зависимости от времени на частоте z/. В середине — изменения фазы по видеополосе для
трех различных моментов времени, обозначенных 1, 2 и 3. Внизу — средняя амплитуда
в зависимости от видеочастоты
где D — длина базы, а иое — угловая скорость вращения Земли в рад/с. Если
этот эффект не исправляется и время усреднения амплитуды интерференционных
лепестков многократно превышает l/z^ds? T0 фаза на любой частоте z/ равномерно
распределена в области фрр. Потери амплитуды как функция видеочастоты равны
I cos@Pp/2)<
Фрр/2
I
(9.154)
и из (9.152) и (9.154) для суммарного ухудшения отношения сигнал/шум в видео-
видеополосе Аи получим
Г 8ШGГ»//2А»/) , =
J 7ri//2Ai/
(9.155)
Если амплитуда интерференционных лепестков усредняется не для целого числа
периодов интерференционного сигнала, то появляется остаточная фазовая ошибка,
величина которой уменьшается с увеличением числа периодов. Когда частота ин-
интерференции близка нулю, эта ошибка может быть значительной.
Влияние дискретного перебора задержек можно компенсировать без каких-либо
потерь в чувствительности. Величина ошибки задержки вследствие ее квантования
9.7] Системы обработки данных 329
известна и приводит к наклону фазы в кросскорреляционном энергетическом спек-
спектре. Следовательно, если кросскорреляционный энергетический спектр рассчиты-
рассчитывается для интервала, малого по сравнению с величиной 1/z/ds? которая может быть
порядка 20мс при длине базы 5000км и Az/ = 20МГц [см. выражение (9.153)], то
эффект дискретного перебора задержек можно исключить исправлением наклона
фазы кросскорреляционного спектра. Коррекция легко выполнима в спектральных
наблюдениях, где спектры вычисляются в любом случае. Отметим, что без этой
коррекции коэффициент потерь в чувствительности на высокочастотном конце по-
полосы, в соответствии с (9.154), равен 0,64. В этом случае амплитудная характеристи-
характеристика должна исправляться делением кросскорреляционного энергетического спектра
на L{v'). При наблюдениях в непрерывном спектре коррекция иногда опускается,
так как требуется выполнять преобразование Фурье в частотную область, а затем
обратно к кросскорреляции.
Способ частичной компенсации влияния дискретного перебора задержек состоит
в смещении частоты, на которой фаза не искажается, с нулевой частоты к Az//2.
Фаза в схеме вращения интерференционных лепестков увеличивается на ttAz/Ats,
где Ars — ошибка задержки. Таким образом при изменении задержки на один
интервал выборки в схеме вращения вводится скачок фазы тг/2. В результате коэф-
коэффициент потерь на концах полосы равен всего лишь 0,90. Средние потери по всей
полосе частот определяются выражением, подобным (9.155), но с заменой верхнего
предела интегрирования на Ai//2, и равны 0,966. Кроме того, при симметричной
частотной характеристике остаточная фазовая ошибка равна нулю, так как сум-
суммарный фазовый сдвиг по всей полосе в любой момент времени равен нулю.
9.7.4. Суммарные потери обработки данных. Рассмотренные коэффици-
коэффициенты потерь представляют собой мультипликативные величины, так что полная
величина потерь определяется как
V = VqVrVsVd, (9.156)
где tjq — потери квантования, t]r — потери вращения интерференционных ле-
лепестков, rjs — потери подавления боковой полосы интерференции и t\d — потери
дискретного перебора задержки.
Если схема вращения интерференционных лепестков используется для обоих
сигналов, поступающих на коррелятор, то потери смещения частоты интерферен-
интерференции будут равны ?7^, так как фазы схем вращения не должны быть коррелированы.
Коэффициенты потерь суммируются в табл. 9.6. Например, процессор может иметь
двухуровневое квантование (tjq = 0,637), трехуровневые схемы вращения интер-
интерференционных лепестков в двух сигнальных каналах {t]r = 0,922), 11-канальную
корреляционную функцию (rjs = 0,983) и компенсацию задержки к центру полосы
(tjd = 0,966), что дает для коэффициента суммарных потерь значение 0,558. Таким
образом, чувствительность по сравнению с идеальной аналоговой системой с той
же полосой частот, оказывается хуже почти в 2 раза.
Существуют и другие, не рассмотренные здесь потери. Частотная характери-
характеристика в действительности не идеально плоская, либо отклик на частотах выше
половины частоты выборки Найквиста не равен нулю. Эти отклонения приводят
к потерям, достигающим для идеального 9-полюсного фильтра Баттерворса 2 %
(Rogers, 1980). Частотные характеристики различных антенных систем не идентич-
идентичны (см. разд. 7.3). Значения фазы схемы вращения интерференционных лепестков
могут вычисляться точно в соответствующие интервалы времени и экстраполиро-
экстраполироваться разложением в ряд Тейлора, при этом приближении вносятся периодические
скачки фазы. Сигналы гетеродинов могут иметь гармоники по питанию и шумы
в боковой полосе, размывающие часть мощности интерференционного сигнала за
330 Интерферометрия со сверхдлинными базами [Гл. 9
Таблица 9.6. Потери в отношении сигнал/шум
1. Потери квантования
(а) Двухуровневое 0,637
(б) Трехуровневое 0,810
(в) Четырехуровневое, все произведения 0,881
2. Потери вращения частоты интерференции (tir)
(а) Двухуровневое, один сигнальный канал 0,900
(б) Трехуровневое, один канал 0,960
(в) Двухуровневое, два канала 0,810
(г) Трехуровневое, два канала 0,922
3. Потери подавления боковой полосы интерференции (rjs)
(а) 1 канал 0,707
(б) 3 канала 0,952
(в) 7 каналов 0,975
(г) 11 каналов 0,983
4. Потери квантования задержки (tjd)
(а) Спектральная коррекция 1,000
(б) Коррекция к центральной видеочастоте 0,966
(в) Без коррекции 0,873
а Рассматриваются в разд. 8.3.
пределы полосы пропускания обычного интерференционного фильтра. Эмпириче-
Эмпирические значения 77, типичные для первого десятилетия развития РСДБ, составляли
примерно 0,4 (Cohen, 1973).
Таблица 9.7. Нормировочные коэффициенты*1
1. Квантование сигналов6
(а) Двух уровневое 1,57
(б) Трех уровневое 1,23
(в) Четырех уровневое 1,13
2. Вращение интерференционных лепестков
(а) Двух уровневое, один сигнальный канал 0,786
(б) Трех уровневое, один канал 0,850
(в) Двух уровневое, два канала 0,617
(г) Трех уровневое, два канала 0,723
а Чтобы получить нормированную корреляционную функцию, сигнал
коррелятора умножается на приведенный в таблице коэффициент.
6 См. разд. 8.3.
9.8] Синтез полосы частот 331
Значения rj характеризуют потери в отношении сигнал/шум. Амплитуда интер-
интерференционных лепестков также должна быть исправлена, поскольку ее масштаб
изменяется вследствие квантования сигнала и смещения частоты интерференции.
Мультипликативные нормировочные коэффициенты, необходимые для коррекции
амплитуды интерференционных лепестков, приведены в табл. 9.7.
9.8. Синтез полосы частот
Для целей геодезии и астрометрии полезно измерение геометрической групповой
задержки
с максимально возможной точностью. Для однополосного ВЧ-сигнала задержка
может быть найдена вписыванием прямой линии в зависимость фазы от частоты
в кросскорреляционном энергетическом спектре. Неопределенность этой задержки
при использовании обычного метода наименьших квадратов равна
где <7ф — среднеквадратичный фазовый шум в полосе Az/ и Az/rms — среднеквад-
среднеквадратичная ширина полосы частот, которая для единственной полосы Az/ равна
Az//B\/3) (см. приложение 12.1). Выражение для аф можно получить из F.64),
и если не учитывать потери при обработке данных, то формула (9.158) преобразу-
преобразуется к виду
T (9.159)
где ? — постоянная величина, равная тг^бЗI'4 ~ 16,5 [см. вывод (А12.33)], a Ts
и Та — средние геометрические температур шума системы и антенн соответственно.
Много большее значение Ai/rms может быть получено при наблюдениях на несколь-
нескольких различных радиочастотах. Это можно осуществить, переключая частоту ге-
гетеродина однополосной системы последовательно во времени по N частотам, или
разделением записанного сигнала на N одновременных полос (каналов) ВЧ, рас-
расположенных в широком интервале частот. Метод последовательного переключения
имеет тот недостаток, что в результате изменений фазы в цикле переключений
частоты оценка задержки теряет точность или смещается. Эти методы принято
называть синтезом полосы частот (Rogers, 1970, 1976).
В реальной системе записываются сигналы небольшого количества ВЧ-полос
(~ 10). Задача определения оптимального расположения полос по частотам подобна
задаче нахождения в линейной решетке распределения антенных баз с минималь-
минимальной избыточностью, как рассматривалось в разд. 5.5. Однако здесь не требуются
все значения вплоть до некоторого максимального, кратного единичному (частот-
(частотному) интервалу, и некоторые пропуски не обязательно являются недостатком. Со
спектральной точки зрения желательно расположить полосы в некоторой геомет-
геометрической прогрессии таким образом, чтобы фазу можно было экстраполировать
от одной полосы к последующей без неопределенности 2тг в процессе связывания
значений фазы друг с другом, как показано на рис. 9.20. Среднеквадратичная
ширина полосы зависит критичным образом от величины единичного интервала,
332
Интерферометрия со сверхдлинными базами
[Гл.9
е
20
15
10
5
о
5
Неопределенность
привязки фазы ; „
Экстраполяция
фазы
1
v/v.
Рис. 9.20. Фаза интерференционного сигнала в зависимости от частоты для системы син-
синтеза полосы частот. Фаза измеряется в пределах дискретных частотных полос (заштрихо-
(заштрихованы), находящихся друг от друга на расстояниях, кратных основной частоте разделения
полос vs. Набор неопределенностей приводят к появлению боковых лепестков в функции
разрешения по задержке, определенной выражением (9.161) и показанной на рис. 9.21
который зависит в свою очередь от минимального отношения сигнал/шум. Точ-
Точность задержки для многополосной системы получается из выражения (9.158) так
же, как и (9.159), но без условия Az/rms = Дг//B\/3)- Таким образом,
Стт =
TS
(9.160)
где A^rms для типичной системы синтеза полосы составляет примерно 40% от пере-
перекрываемого диапазона частот, Az/ — полная ширина полосы и г — время накопления
сигнала в каждой полосе частот. Исключим подробности рассмотрения привязки
фазы и введем эквивалентную функцию задержки из энергетических кросскорре-
ляционных спектров [см. соотношение (9.21)] различных полос наблюдений:
N Аи
(9.161)
*=i о
где щ — частоты гетеродинов относительно их наименьшей частоты и v — щ —
видеочастота. Максимум |Дя(т)| дает максимальную вероятностную оценку ин-
терферометрической задержки (Rogers, 1970). Априори нормированная функция
разрешения по задержке, получается из (9.161) приравниванием переменной S\2
к единице на частотах ее измерений и к нулю — во всех остальных случаях:
\Dr(t)\ =
ttAvt
N
(9.162)
Огибающая в виде sine-функции представляет собой функцию разрешения по за-
задержке одного канала. Частоты щ следует выбирать таким образом, чтобы ширина
Dr{t) была минимальной, при этом не допуская появления дополнительного макси-
максимума на таком уровне, чтобы его можно было спутать с основным пиком. В случае
низкого отношения сигнал/шум минимальный единичный интервал должен быть
примерно в четыре раза больше ширины полосы частот одного канала. Функция
разрешения по задержке для пятиканальной системы показана на рис. 9.21.
9.9]
С фазированные решетки как элементы РСДБ
333
0,0
0,3
Avx
Рис. 9.21. Функция разрешения по задержке для пятиканальной системы с единичным
интервалом vs = 4Az^ и разделением полос, кратным 0, 1, 3, 7 и 15 vs-, как показано
на рис. 9.20. Чтобы избежать неопределенности задержки, необходимо лишь ограничить
«дифракционный» лепесток на rAv = 0,25 до уровня, достаточно меньшего единицы
9.8.1. Наблюдения в импульсном режиме. Для определенных наблюде-
наблюдений наблюдательное время целесообразно ограничивать длительностью коротких
всплесков, при которых частота бит может быть много больше средней частоты
считывания данных, ограниченной устройством записи на магнитную ленту (см.,
например, Wietfeldt and Frail, 1991). В наблюдениях пульсаров длительность им-
импульсного излучения обычно составляет около ~3 % всего времени, так что при
записи только в момент импульса пульсара полоса регистрации может быть увели-
увеличена в ~33 раза по сравнению с максимальной полосой непрерывных наблюдений.
Для этого метода требуется использование высокоскоростных форматоров данных,
высокоскоростной памяти, и схем импульсного срабатывания на каждой антенне.
Во время импульса данные накапливаются в памяти с большой скоростью, а за-
затем непрерывно считываются с относительно малой. Если отношение скоростей
равно w, то полоса регистрации может быть увеличена примерно во столько же
раз относительно наблюдений с неизменной скоростью потока данных. В случае
пульсарных наблюдений это приводит к улучшению чувствительности в w раз,
причем выигрыш в y/w связан с увеличением полосы частот и еще в y/w — с тем,
что во время отсутствия импульсов не регистрируются шумы. Второй из двух
коэффициентов улучшения чувствительности в y/w раз может быть получен без
увеличения скорости потока данных, простым их стиранием в период отсутствия
импульсного излучения. Наблюдения в импульсном режиме также полезны для
астрометрии и геодезии, поскольку они улучшают точность измерений геомет-
геометрической задержки и используются в наблюдениях источников с непрерывными
спектрами на миллиметровых волнах.
9.9. Сфазированные решетки как элементы РСДБ
Сфазированная решетка представляет собой набор антенн, сигналы которых
объединяются по схеме, показанной на рис. 5.4. Фазу и задержку сигнала каждой
антенны можно откорректировать так, чтобы сигналы, принимаемые из определен-
334 Интерферометрия со сверхдлинными базами [Гл. 9
ного направления небесной сферы, суммировались синфазно, обеспечивая тем са-
самым максимальную чувствительность. Применение синфазных решеток в качестве
элементов РСДБ важно рассмотреть по двум причинам. Во-первых, антенны решет-
решетки со связанными элементами могут быть объединены в сфазированную решетку,
при этом улучшается отношение сигнал/шум сверхдлиннобазового интерферомет-
интерферометра, в состав которого они входят как единая станция. Во-вторых, в случаях, когда
требуются элементы с очень большой эффективной площадью для достижения
высокого отношения сигнал/шум, на каждой базе создание сфазированных решеток
может оказаться выгоднее чем антенны с заполненными апертурами, поскольку
стоимость антенны с параболическим зеркалом увеличивается примерно пропорци-
пропорционально его диаметру в степени 2,7 (Meinel, 1979).
Решетки апертурного синтеза, такие как Вестерборкская антенная решетка,
VLA и некоторые другие, также используются как фазированные для достижения
большой эффективной площади одного из элементов системы РСДБ. Синфазность
решетки обеспечивается коррекцией фазы и задержки сигналов каждой антенны
таким образом, чтобы различие в геометрическом пути распространения волнового
фронта компенсировалось для нужного направления. Коррекция легко выполняет-
выполняется с помощью использования систем смещения задержки и частоты интерференции,
применяемых при синтезе изображений. Затем сигналы суммируются и поступают
на устройство записи данных РСДБ.
Мы можем проанализировать возможности фазированной решетки, использу-
используемой в качестве одной большой антенны. Рассмотрим решетку, состоящую из па
одинаковых элементов, каждый из которых характеризуется температурой шума
системы Ts и антенной температурой Тд для данного источника, не разрешенного
на самой длинной базе решетки. На выходе суммирующего разъема получим
+ ?i)' (9-163)
где переменными Si и е% представлены соответственно случайный сигнал и случай-
случайное напряжение шума г-ж антенны. Поскольку (si) = (б{) = 0, то, опуская постоян-
постоянные коэффициенты усиления, мы можем записать (s?) = Та и (е?) = Ts- Уровень
мощности суммарного сигнала определяется как среднеквадратичное значение V^um
из уравнения (9.163):
(Kum) = ?[<««**> + (SiSj) + (SjSi) + (SiSj)]. (9.164)
Для точно сфазированной решетки S{ = Sj. Кроме того, поскольку нами рассматри-
рассматривается неразрешенный источник, то (siSj) = Тд. Если бы решетка была полностью
расфазирована, т. е. фаза сигналов в точке суммирования была бы случайна, то
(siSj) = Та только при г = j и (siSj) = 0 при г ф j. В любом случае, (siSi) = О
и (siSj) = 0. Таким образом, уравнение (9.164) можно привести к виду
(^sum) = na^A + naTs (сфазированная решетка), (9.165)
(Kmm) = паТл + TiaTs (не сфазированная решетка), (9.166)
где первыми слагаемыми в уравнениях представлен сигнал, а вторыми — шум.
Для сфазированной решетки отношение сигнал/шум (по мощности) равно
паТА/Т$1 для не сфазированной — Та/Т$. Таким образом, эффективная площадь
сфазированной решетки равна сумме эффективных площадей отдельных антенн,
а для не сфазированной, в среднем, равна эффективной площади одной антенны.
9.9] С фазированные решетки как элементы РСДБ 335
Интерес представляет случай, когда чувствительность антенн различается
вследствие их разной эффективной площади и (или) температуры шума системы.
Это практически валено далее для однородных решеток, поскольку программы
поддержки или модернизации могут привести к различиям в чувствительности.
Рассмотрим фазированную решетку, в которой температуры шума системы
и антенные температуры отдельных элементов представлены соответственно как
Tsi и Та%- Здесь Таг определяется как сигнал точечного источника с плотностью
потока равной единице *), так что величина Та% характеризует только антенну
и пропорциональна ее эффективной площади. Мы рассматриваем случай малого
сигнала, когда Тд <С Т$- Для источника с плотностью потока S напряжение
выходного сигнала г-ж антенны Vi = S{ + 6{, и мы можем записать (s?) = STai
и {е}) = Т3г.
Удобно представить выходной сигнал каждой антенны как меру плотности по-
потока источника, равную V?/Таг- Математическое ожидание измеренного значения
S должно быть одинаково для всех антенн. Соответствующие напряжения равны
y/S = Vil\JTai для сигнала и si/^Tai — для шума. При кросскорреляции выходно-
выходного сигнала антенной решетки с другой антенной РСДБ отношение сигнал/шум на
выходе коррелятора пропорционально отношению сигнал/шум на выходе решетки
по напряжению. Таким образом, при объединении напряжений сигналов антенной
решетки, в действительности, основной задачей является достижение максималь-
максимальной величины отношения сигнал/шум оценки y/S. Поскольку антенны в решетке
не идентичны, при объединении их сигналов следует использовать весовые коэф-
коэффициенты W{. Веса должны быть назначены так, чтобы получить в суммарном
выходном сигнале решетки максимальное отношение сигнал/шум, которое равно
(по напряжению)
Отметим, что мы суммируем напряжения сигналов и квадраты среднеквадра-
среднеквадратичных напряжений шума. Выбор весовых коэффициентов, обеспечивающих наи-
наилучшее отношение сигнал/шум для Уъ/у/Таъ , математически эквивалентен задаче
получения наилучшей оценки измеренной величины из ряда измерений, средне-
среднеквадратичные уровни ошибок которых отличаются, но известны. Оптимальная
процедура состоит в нахождении среднего значения, в котором вес каждого измере-
измерения обратно пропорционален дисперсии ошибки измерений [см. уравнение (А12.6)].
Дисперсия Vi пропорциональна Tsi, и, следовательно, дисперсия У%1у/Та% равна
Tsi/TAi- Таким образом, подстановкой Wi = TAi/Tsi в уравнение (9.167) получим
(9.168)
Отметим, что Vi в числителе умножается на отношение y/TAi jTgi-, которое, сле-
следовательно, представляет собой весовой коэффициент (напряжения) суммируемого
сигнала, обеспечивающий оптимальную чувствительность. Этот вывод согласуется
с анализом, данным в работе (Dewey, 1994). (Отметим, что весовые коэффициенты
напряжений сигналов в точке их суммирования представлены г^, а не Wi/'y/TAi •)
) Поскольку важны только относительные значения весовых коэффициентов, то Та%
можно определить для любого источника, общего для всех антенн, но использование
плотности потока равной единице делает объяснение проще.
336 Интерферометрия со сверхдлинными базами [Гл. 9
Соответствующие весовые коэффициенты мощности сигналов в точке их сумми-
суммирования пропорциональны Tai/T^.
В решетках апертурного синтеза, таких как VLA, каждый из сигналов ПЧ
антенн поступает на цифровой преобразователь с одинаковым уровнем мощности
(сигнала вместе с шумом), и суммирование выполняется после оцифровки, так что
может использоваться цифровой ввод необходимых временных задержек. Таким
образом, для того чтобы обойтись без модификации приемных систем (предназна-
(предназначенных для синтеза изображений), сигналы суммируются с равной мощностью,
когда решетка используется в качестве фазированной. В рассматриваемом нами
случае Та <С Ts, соответствующие весовые коэффициенты равны Wi = 1/y/Tsi,
и отношение сигнал/шум записывается как
/ / —
(9.169)
Равномерным по мощности взвешиванием обычно обеспечивается чувствитель-
чувствительность, совпадающая с оптимальным взвешиванием в пределах нескольких процен-
процентов.
При оптимальном взвешивании суммируемых сигналов вклад всех антенн в уве-
увеличение отношения сигнал /шум одинаков. В другом виде взвешивания суммарная
чувствительность может быть улучшена исключением антенн с плохими параметра-
параметрами. Этот метод при равномерных по мощности весовых коэффициентах исследован
Мораном (Могап, 1989). Чтобы упростить анализ, Та предполагалось равным для
всех антенн и варьировалось только Ts- Рассмотрим решетку с модернизируемыми
входными каскадами приемников, часть из которых, равная ni/na, оснащена новы-
новыми входными каскадами, уменьшающими температуру шума системы от Т$ до Т$/?.
После переоборудования определенной части антенн, чувствительность решетки
улучшается исключением не модернизированных антенн, поскольку их входные
каскады усиления более шумные. Если Та не изменяется, то мы можем представить
напряжения сигналов, принятых каждой антенной, как V, и уравнение (9.169) при
равномерном по мощности взвешивании принимает вид
(9Л70)
Таким образом, мы можем записать
7^sn2(ni улучшенных) _ 1 {п!л/?\ I 1 (nx\J~j
I . (9.171)
n2 (все па антенн) fn{ \ /т^ ) / Jn~ \ fT^ ' /Т^ ) '
Не модернизированные антенны должны быть исключены, если значение вышепри-
вышеприведенного выражения больше единицы, что происходит при
(9-172)
На рис. 9.22 показан график n\jna как функции ?. Так, например, если в результате
модернизации Ts улучшается в шесть раз, то после завершения работ на поло-
половине антенн, остальные антенны должны быть исключены. Однако до тех пор,
пока ? $J 4, следует использовать все антенны. Практически улучшение в 4 раза
проблематично, поэтому исключение антенн вряд ли полезно. Подобный анализ
9.10]
Орбитальная РСДБ (ОРСДБ)
337
18 20
Рис. 9.22. Доля антенн ni/na сфазированной решетки с равномерным по мощности взве-
взвешиванием, температура шума которых должна быть уменьшена в ? раз для того, чтобы
исключить остальные антенны. Из работы (Могап, 1989). Воспроизводится с разрешения
©1989 by Kluwer Academic Publishers
с использованием уравнения (9.168) показывает, что при оптимальном взвешивании
чувствительность никогда не улучшается исключением антенн.
Перед записью на магнитную ленту в эксперименте РСДБ выходной сигнал
фазированной решетки обычно квантуется заново для уменьшения количества бит.
Квантованием до суммирования сигналов вносится шум, распределение вероятно-
вероятности которого после суммирования стремится к гауссовому распределению с увели-
увеличением числа антенн. Следовательно, для таких решеток величина дополнительных
потерь вследствие второго квантования сигналов близка к значению t]q, получен-
полученному в гл. 8, где предполагалось гауссово распределение шума. Для других случаев
см. (Kokkeler, Fridman and van Ardenne, 2001).
9.10. Орбитальная РСДБ (ОРСДБ)
Основные требования к станции РСДБ (орбитальной или наземной) включают
систему времени, способную сопоставить каждому дискретному отсчету принимае-
принимаемого сигнала определенный момент времени, который может быть впоследствии
восстановлен, а также знание координат антенны с достаточной точностью для
определения частоты интерференции (но не обязательно фазы). Система времени
должна быть стабильна до долей периода принимаемого сигнала на интервалах
времени когерентности, составляющих десятки и сотни секунд. Прецизионный стан-
стандарт частоты не может быть установлен на спутнике, поэтому необходима передача
на его борт сигналов времени соответствующей стабильности. Обеспечение такой
системы времени, питающей гетеродины и часы форматора на спутнике, является
главной технической задачей ОРСДБ. Радиальным движением спутника вносит-
вносится доплеровское смещение, а тангенциальное перемещение приводит к тому, что
линия связи смещается относительно неоднородностей атмосферы. На спутник по
радиосвязи передаются одна или несколько опорных частот. Положение спутника
в любой момент времени определяется стандартными методами измерений парамет-
параметров орбиты с точностью порядка нескольких десятков метров. Этого достаточно
338
Интерферометрия со сверхдлинными базами
[Гл.9
для определения (г/, v)-координат базы, но недостаточно для требуемой точности
времени. Для решения задачи времени требуется применение в радиосвязи фазо-
фазовой системы «туда-обратно». Этот метод в принципе идентичен системам «туда-
обратно» для фидерных линий, рассмотренных в разд. 7.2. Основные требования
системы времени обсуждаются (D'Addario, 1991).
Антенна
у радиотелескопа
мшу Фильтр
Форматор
Линия передачи времени Линия передачи данных
Наземная станция
Коррелятор Устройство ,г
Ат записи
Стандарт частоты
Счетчик
Н- П
Рис. 9.23. Упрощенная блок-схема основных этапов передачи и обработки сигналов, необ-
необходимых для спутника ОРСДБ и наземной станции слежения. Для дальнейших пояснений
см. текст. (D'Addario, 1991), ©1991 IEEE
На рис. 9.23 показан упрощенный пример системы спутник-наземная станция,
иллюстрирующий основные ее функции. В данном случае в состав спутника не
входит стандарт частоты. Опорная частота синтезатора 5Х, сигнал которого пере-
передается на спутник, поступает со стандарта частоты наземной станции. Этот сигнал
служит опорным для синтезаторов Sy, 5L и Ss, сигналы которых используются соот-
соответственно в фазовых измерениях «туда-обратно», гетеродине (LO) радиоастроно-
радиоастрономического приемника и часах форматора. Сигнал гетеродина Sy передается на на-
наземную станцию, где его фаза сравнивается в корреляторе с сигналом станционного
гетеродина той же частоты. На выходе коррелятора измеряется Ат — изменение
задержки времени в суммарной линии передачи. Сигнал радиотелескопа на борту
спутника поступает на малошумящий усилитель (МШУ), фильтр и смеситель,
в котором преобразуется к промежуточной частоте (ПЧ) сигналом LO гетеродина
Бъ. Сигнал ПЧ затем поступает на усилитель ПЧ, модуль выборки, показанный
переключателем, и схему квантования — Q(x). Счетчик п управляется сигналом
часов форматора, получаемым в синтезаторе Ss, и генерирует сигналы времени.
Эти сигналы обеспечивают запись моментов времени каждой точки полученных
данных, информацию для их форматирования и другие необходимые на спутнике
функции времени. Счетчиком ng обеспечивается время наземной станции. Некото-
Некоторые проблемы при использовании показанной схемы перечислены ниже.
9.10] Орбитальная РСДБ (ОРСДБ) 339
1. Схема измерения фазы суммарного распространения сигнала в линии переда-
передачи методом «туда-обратно» приводит к неопределенности фазы, равной цело-
целому числу длин волн. Ею обеспечивается непрерывное относительное измерение
длины линии передачи.
2. Частоты, генерируемые тремя синтезаторами на спутнике, должны быть гар-
гармониками одной или нескольких подаваемых опорных частот (в этом случае
не требуется деление частоты в синтезаторах), иначе фазы частот не будут
однозначно определены.
3. Время распространения сигналов опорной частоты и данных может разли-
различаться из-за дисперсии в линии передачи или различий электронного обору-
оборудования.
Эти ограничения приводят к проблемам в случаях прерываний радиосвязи между
спутником и станцией слежения. Если связь во время наблюдений непрерывна, то
после обнаружения лепестков суммарная неопределенность может быть найдена.
Непрерывное отслеживание изменений в пути распространения сигналов позволяет
найти решение для всего периода наблюдений. Однако, если связь со спутником
теряется вследствие помех, атмосферных эффектов или проблем с оборудованием,
то в кольцевых схемах фазового захвата синтезаторов происходит разрыв и после
его восстановления появляется дополнительная неопределенность фазы. При дол-
долговременном разрыве связи «туда-обратно» может потребоваться еще один поиск
интерференционных лепестков.
Первым космическим аппаратом, специально предназначенным для использо-
использования в качестве орбитального элемента решетки РСДБ, был японский спутник
HALCA, запущенный в 1997 году (Hirabayashi et al., 1998). В качестве примера
ниже перечислены несколько частот, выбранных для этого спутника.
1. Частоты наблюдений: 1,7; 5; 22 ГГц.
2. Суммарная ширина полосы частот регистрации: 64 МГц (максимальное зна-
значение) .
3. Опорная частота радиосвязи Земля—космос: 15,3 ГГц.
4. Опорная частота радиосвязи космос-Земля: 14,2 ГГц.
5. Частота несущей сигнала данных РСДБ: 142 ГГц.
6. Частота следования бит данных: 128Мбит/с (максимальное значение).
7. Схема модуляции данных: QPSK (кодирование с квадратичным сдвигом фа-
фазы).
В схеме QPSK модуляции данных частота несущей принимает одно из четырех
различных значений, кратных 90°, что соответствует 2 битам. Фаза переключается
последовательно с частотой 64 МГц или, при использовании более узкой полосы,
с частотой 32 или 16 МГц. Поскольку значения данных по существу случайны,
амплитуда вектора на фазовой плоскости усредняется до нуля в течение многих
периодов. На станции слежения генератор опорной частоты замыкается по фазе
принятым видеосигналом, и таким образом восстанавливается цифровой поток
данных, а также несущая частота. В спутнике HALCA восстановленная несущая
используется как опорная частота передачи данных. Для замыкания фазы несущей
видеосигналом применяется четырех-фазовая петля Костаса или подобная ей схема
340 Интерферометрия со сверхдлинными базами [Гл. 9
(см., например, Gardner, 1979). В фазе несущей, восстановленной по модулиро-
модулированному QPSK-сигналу, появляется 90°-я неопределенность. Это не представляет
серьезной проблемы в проекте HALCA, но использование отдельной опоры для
передаваемых на Землю данных позволило бы исключить один из источников
разрыва фазы во время прерываний радиосвязи. Поскольку частоты сигналов пе-
передаваемых и принимаемых данных отличаются, нельзя предположить, что дли-
длина пути распространения сигнала в одном из направлений точно равна 1/2 пути
распространения, измеренного методом «туда—обратно». Для коррекции различий
пути распространения на двух частотах обычно используют модель ионосферы.
Д'Аддарио (D'Addario, 1991) показал, что существуют способы создания систе-
системы, в которой неопределенность была бы исключена. Параметрами орбиты спутни-
спутника обеспечивается оценка задержки «туда—обратно» в пределах неопределенности
5т порядка 10~7 с, и если использовать этот метод на частоте, не превышающей
5т~1 Гц, то неопределенность может быть разрешена. Измерения методом «туда-
обратно» на более высоких частотах все же необходимы для того, чтобы получить
требуемую точность фазы гетеродина на борту спутника, частота которого должна
быть близкой к частоте радиоастрономического сигнала, т. е. может достигать зна-
значений в десятки гигагерц и более. Для такой системы, исключающей неопределен-
неопределенность, требуются измерения «туда-обратно» на двух или более частотах. При лю-
любых измерениях методом «туда-обратно» использование одинаковых частот в обоих
направлениях должно упростить определение времени распространения сигнала
в одном из направлений, поскольку влияние дисперсии в значительной степени
исключается. Это может быть технически осуществимо с помощью разделения
времени или небольшого смещения частоты, что позволило бы разделить сигналы,
передаваемые в двух направлениях. Однако в международных соглашениях по
радиочастотам обычно устанавливаются различные полосы для этих двух направле-
направлений передачи. Измерения пути распространения «туда—обратно» на двух частотах,
следовательно, существенны для определения относительного вклада нейтральной
и ионизованной сред в измеренное время распространения сигналов. Если на борту
спутника установлен стандарт частоты, обладающий высокой стабильностью, то
он может использоваться в качестве основных часов или для хранения сигналов
времени, передаваемых по радиосвязи, в случае ее сбоев. Использование бортовых
часов усложняется релятивистскими эффектами, которые приводят к изменениям
времени на спутнике относительно часов наземных станций при его перемещении
в пространстве изменяющегося гравитационного поля Земли (Ashby and Allan, 1979;
Vessot, 1991).
В измерениях ОРСДБ используется, в принципе, такой же коррелятор, как
и в обычной РСДБ, но требуется, чтобы он был способен обрабатывать большие
доплеровские смещения, временные задержки и скорости изменений этих вели-
величин относительно наземных станций. Описание коррелятора задержек, специально
предназначенного для ОРСДБ станций, дано в работе (Carlson et al., 1999).
9.10] Цитированная литература 341
Основная литература
Biraud F. Ed. Very Long Baseline Interferometry Techniques., Cepadues, Toulouse, France,
1983.
Chi A. R. Ed. Proc. IEEE, Special Issue on Frequency Stability, 54, No. 2, 1966.
Enge P. and P. Misra. Eds. Proc. IEEE, Special Issue on Global Positioning System, 87, No.
1, 16-172, 1999.
Felli M. and R. E. Spencer. Eds. Very Long Baseline Interferometry, Techniques and Applica-
Applications, NATO ASI Series, Kluwer, Dordrecht, 1989.
Hirabayashi H., M. Inoue and H. Kobayashi. Eds. Frontiers of VLBI, Universal Academy Press,
Tokyo, 1991.
Jespersen J. and D. W. Hanson. Eds. Proc. IEEE, Special Issue on Time and Frequency, 79,
No. 7, 1991.
Kroupa V. F. Ed. Frequency Stability: Fundamentals and Measurement, IEEE Press, New
York, 1983.
Morris D. Ed. Radio Sci., Special Issue Devoted to the Open Symposium on Time and
Frequency, 14, No. 4, 1979.
Zensus J. A., P. J. Diamond and P. J. Napier. Eds. Very Long Baseline Interferometry and
the VLBA, Astron. Soc. Pacific Conf. Ser., 82, 1995.
Цитированная литература
Allan D. W. Statistics of Atomic Frequency Standards. Proc. IEEE, 54, 221-230, 1966.
Ashby N. and D. W. Allan. Practical Implications of Relativity for a Global Coordinate Time
Scale. Radio Sci., 14, 649-669, 1979.
Bare C, B. G. Clark, K. I. Kellermann, M. H. Cohen and D. L. Jauncey. Interferometer
Experiments with Independent Local Oscillators. Science, 157, 189-191, 1967.
Barnes J. A., A. R. Chi, L. S. Cutler, D. J. Healey, D. B. Leeson, Т. Е. McGunigal, J. A.
Mullen, W. L. Smith, R. L. Sydnor, R. F. C. Vessot and G. M. R. Winkler. Characterization
of Frequency Stability. IEEE Trans. Instrum. Meas., IM-20, 105-120, 1971.
Berkeland D. J., J. D. Miller, J. C. Bergquist, W. M. Itano and D. J. Wineland. Laser-Cooled
Mercury Ion Frequency Standard. Phys. Rev. Lett., 80, 2089-2092, 1998.
Blair В. Е. Time and Frequency: Theory and Fundamentals. NBS Monograph 140, U.S.
Government Printing Office, Washington, DC, 1974, p. 223-313.
Broten N. W., T. H. Legg, J. L. Locke, С W. McLeish, R. S. Richards, R. M. Chisholm, H.
P. Gush, J. L. Yen and J. A. Gait. Long Baseline Interferometry: A New Technique. Science,
156, 1592-1593, 1967.
Cannon W. H. The Classical Analysis of the Response of a Long Baseline Radio Interferometer.
Geophys. J. R. Astron. Soc, 53, 503-530, 1978.
Cannon W. H., D Baer, G. Feil, B. Feir, P. Newby, A. Novikov, P. Dewdney, B. Carlson,
W. P. Petrachenko, J. Popelar, P. Mathieu, R. D. Wietfeldt. The S2 VLBI System. Vistas in
Astronomy, 41, 297-302, 1997.
Carlson B. R., P. E. Dewdney, T. A. Burgess, R. V. Casoro, W. T. Petrachenko and W. H.
Cannon. The S2 VLBI Correlator: A Correlator for Space VLBI and Geodetic Signal Processing.
Pub. Astron. Soc. Pacific, 111, 1025-1047, 1999.
Clark B. G. Radio Interferometers of Intermediate Type. IEEE Trans. Antennas Propag., AP-
16, 143-144, 1968.
Clark B. G. The NRAO Tape-Recorder Interferometer System. Proc. IEEE, 61, 1242-1248,
1973. (Имеется перевод: ТИИЭР, 61, 9, с. 94-103, 1973.)
342 Интерферометрия со сверхдлинными базами [Гл. 9
Clark В. G., R. Weimer and S. Weinreb. The Mark II VLB System. NRAO Electronics Division
Internal Report 118, National Radio Astronomy Observatory, Green Bank, WV, 1972.
Clark T. A. , B. E. Corey, J. L. Davis, G. Elgered, T. A. Herring, H. F. Hinteregger, С А.
Knight, J. I. Levine, G. Lundqvist, C. Ma, E. F. Nesman, R. B. Phillips, A. E. E. Rogers,
B. O. Ronnang, J. W. Ryan, B. R. Schupler, D. B. Shaffer, I. I. Shapiro, N. R. Vandenberg,
J. C. Webber and A. R. Whitney. Precision Geodesy Using the Mark III Very Long Baseline
Interferometry System. IEEE Trans. Geodesy Remote Sens., GE-23, 438-449, 1985.
Clark Т. А., С С. Counselman, P. G. Ford, L. B. Hanson, H. F. Hinteregger, W. J.
Klepczynski, C. A. Knight, D. S. Robertson, A. E. E. Rogers, J. W. Ryan, I. I. Shapiro and
A. R. Whitney. Synchronization of Clocks by Very Long Baseline Interferometry. IEEE Trans.
Instrum. Meas., IM-28, 184-187, 1979.
Cohen M. H. Introduction to Very-Long-Baseline Interferometry. Proc. IEEE, 61, 1192-1197,
1973. (Имеется перевод: ТИИЭР, 61, 9, с. 30-36, 1973.)
Cohen M. H. and D. В. Shaffer. Positions of Radio Sources from Long-Baseline Interferometry.
Astron. J., 76, 91-100, 1971.
Cutler L. S. and С L. Searle. Some Aspects of the Theory and Measurement of Frequency
Fluctuations in Frequency Standards. Proc. IEEE, 54, 136-154, 1966.
D'Addario L. R. Minimizing Storage Requirements for Quantized Noise. VLBA Memo. 332,
National Radio Astronomy Observatory, Charlottesville, VA, 1984.
D'Addario L. R. Time Synchronization in Orbiting VLBI. IEEE Trans. Instrum. Meas., IM-
40, 584-590, 1991.
Davis M. M.j J. H. Taylor, J. M. Weisberg and D. C. Backer. High Precision Timing of the
Millisecond Pulsar PSR 1937 + 21, Nature, 315, 547-550, 1985.
Dewey R. J. The Effects of Correlated Noise in Phased-Array Observations of Radio Sources.
Astron. J., 108, 337-345, 1994.
Drullinger R. E., S. L. Rolston and W. M. Itano. Primary Atomic Frequency Standards: New
Developments. Review of Radio Science 1993-1996, W. R. Stone Ed., Oxford Univ. Press,
Oxford, UK, 1996, p. 11-41.
Dutta P. and P. M. Horn. Low-Frequency Fluctuations in Solids: 1// Noise. Rev. Mod. Phys.,
53, 497-516, 1981.
Edson W. A. Noise in Oscillators. Proc. IRE, 48, 1454-1466, 1960.
Forman P. Atomichron: The Atomic Clock from Concept to Commercial Product. Proc. IEEE,
73, 1181-1204, 1985. (Имеется перевод: ТИИЭР, 73, 7, с. 31-57, 1985.)
Frank R. L. Current Developments in Loran-C. Proc. IEEE, 71, 1127-1139, 1983. (Имеется
перевод: ТИИЭР, 71, 10, с. 8-23, 1983.)
Gardner F. M. Phaselock Techniques. 2nd ed., Wiley, New York, 1979.
Hellwig H. Microwave Time and Frequency Standards. Radio Sci., 14, 561-572, 1979.
Hellwig H., R. F. С Vessot, M. W. Levine, P. W. Zitzewitz, D. W. Allen and D. J. Glaze.
Measurement of the Unperturbed Hydrogen Hyperfine Transition Frequency. IEEE Trans.
Instrum. Meas., IM-19, 200-209, 1970.
Herring T. A. Precision and Accuracy of Intercontinental Distance Determinations Using
Radio Interferometry. Air Force Geophysics Laboratory, Hanscom Field, MA, AFGL-TR-84-
0182, 1983.
Hinteregger H. F., A. E. E. Rogers, R. J. Capallo, J. С Webber, W. T. Petrachenko and H.
Allen. A High Data Rate Recorder for Astronomy. IEEE Trans. Magn., MAG-27, 3455-3465,
1991.
Hirabayashi H. and 52 coauthors. Overview and Initial Results of the Very Long Baseline
Interferometry Space Observatory Program. Science, 281, 1825-1829, 1998.
Kartashoff P. and J. A. Barnes. Standard Time and Frequency Generation. Proc. IEEE, 60,
493-501, 1972. (Имеется перевод: ТИИЭР, 60, 5, с. 27-36, 1972.)
9.10] Цитированная литература 343
Kawaguchi N. VLBI Recording System in Japan. Frontiers of VLBI, H. Hirabayashi, M. Inoue
and H. Kobayashi, Eds.,Universal Academy Press, Tokyo, 1991, p. 75-77.
Keshner M. S. 1// Noise. Proc. IEEE, 70, 212-218, 1982. (Имеется перевод: ТИИЭР, 70, 2,
с. 60-67, 1982.)
Klemperer W. К. Long Baseline Radio Interferometry with Independent Frequency Standards.
Proc. IEEE, 60, 602-609, 1972. (Имеется перевод: ТИИЭР, 60, 5, с. 171-180, 1972.)
Kleppner D., H. С. Berg, S. В. Crampton, N. F. Ramsey, R. F. C. Vessot, H. E. Peters and
J. Vanier. Hydrogen-Maser Principles and Techniques. Phys. Rev. A, 138, 972-983, 1965.
Kleppner D., H. M. Goldenberg and N. F. Ramsey. Theory of the Hydrogen Maser Phys. Rev.,
126, 603-615, 1962.
Kokkeler A. B. J., P. Fridman and A. van Ardenne. Degradation due to Quantization Noise
in Radio Astronomy Phased Arrays. Experimental Astronomy, 11, 33-56, 2001.
Kulkarni S. R. Self Noise in Inteferometers: Radio and Infrared. Astron. J., 98, 1112-1130,
1989.
Leick A. GPS Satellite Surveying. 2nd ed., Wiley, New York, 1995.
Lesage P. and C. Audoin. Characterization and Measurement of Time and Frequency Stability.
Radio Sci., 14, 521-539, 1979.
Lewandowski W., J. Azoubib and W. J. Klepczynski. GPS: Primary Tool for Time Transfer.
Proc. IEEE, Special Issue on Global Positioning System, 87, No. 1, 163-172, 1999.
Lewandowski W. and С Thomas. GPS Time Transfer. Proc. IEEE, 79, 991-1000, 1991.
Lewis L. L. An Introduction to Frequency Standards. Proc. IEEE, 79, 927-935, 1991.
Lindsey W. C. and С. М. Chie. Frequency Multiplication Effects on Oscillator Instability.
IEEE Trans. Instrum. Meas., IM-27, 26-28. 1978.
Matveyenko L. I., Kostenko V. I. On the Structure of the Crab Nebula, Austral. J. Phys., No.
1-2, 105-111, 1979.
Meinel A. B. Multiple Mirror Telescopes of the Future. MMT and the Future of Ground-
Based Astronomy, Т. С Weeks, Ed., SAO Special Report, Vol. 385, Harvard-Smithsonian
Astrophysical Obs., Cambridge, MA, 1979, p. 9-22.
Moran J. M. Spectral-Line Analysis of Very-Long-Baseline Interferometric Data. Proc. IEEE,
61, 1236-1242, 1973. (Имеется перевод: ТИИЭР, 61, 9, с. 86-93, 1973.)
Moran J. M. Very Long Baseline Interferometric Observations and Data Reduction. Methods
of Experimental Physics, Vol. 12C, M. L.Meeks, Ed., Academic Press, New York, 1976, p.
228-260.
Moran J. M. Introduction to VLBI. Very Long Baseline Interferometry, Techniques and
Applications, M. Felli and R. E. Spencer, Eds., Kluwer, Dordrecht, 1989, p. 27-45.
Moran J. M. and V. Dhawan. An Introduction to Calibration Techniques for VLBI. Very
Long Baseline Interferometry and the VLB A, J. A. Zensus, P. J. Diamond and P. J. Napier
Eds. Astron. Soc. Pacific Conf. Ser., 82, 161-188, 1995.
Napier P. J., D. S. Bagri, B. G. Clark, A. E. E. Rogers, J. D. Romney, A. R. Thompson and
R. С Walker. The Very Long Baseline Array Proc. IEEE, 82, 658-672, 1994.
Papoulis A. Probability, Random Variables and Stochastic Processes. McGraw-Hill, New York,
1965.
Parkinson B. W. and S. W. Gilbert. NAVSTAR: Global Positioning System - Ten Years Later.
Proc. IEEE, 71, 1177-1186, 1983. (Имеется перевод: ТИИЭР, 71, 10, с. 75-86, 1983.)
Pierce J. A., A. A. McKenzie and R. H. Woodward. Loran. Radiation Laboratory Series, Vol.
4, McGraw-Hill, New York, 1948.
Press W. H. Flicker Noises in Astronomy and Elsewhere. Comments Astrophys., 7, 103-119,
1978.
Reid M. J. Spectral-Line VLBI. Very Long baseline Interferometry and the VLB A, J. A.
Zensus, P. J. Diamond and P. J. Napier. Eds. Astron Soc. Pacific Conf. Ser., 82, 209-225,
1995.
344 Интерферометрия со сверхдлинными базами [Гл. 9
Reid М. J. Spectral-Line VLBL Synthesis Imaging in Radio Astronomy II, G. B. Taylor, C.
L. Carilli and R. A. Perley. Eds. Astron Soc. Pacific Conf. Ser., 180, 481-497, 1999.
Reid M. J., A. D. Haschick, B. F. Burke, J. M. Мог an, K. J. Johnston and G. W. Swenson.
Jr. The Structure of Interstellar Hydroxyl Masers: VLBI Synthesis Observations of W3@H).
Astrophys. J., 239, 89-111, 1980.
Rogers A. E. E. Very Long Baseline Interferometry with Large Effective Bandwidth for Phase
Delay Measurements. Radio Sci., 5, 1239-1247, 1970.
Rogers A. E. E. Theory of Two-Element Interferometers. Methods of Experimental Physics,
Vol. 12C, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 139-157.
Rogers A. E. E. The Sensitivity of a Very Long Baseline Interferometer. Radio Interferometry
Techniques for Geodesy, NASA Conf. Pub. 2115, National Aeronautics and Space Administra-
Administration, Washington, DC, 1980, p. 275-281.
Rogers A. E. E. Very Long Baseline Fringe Detection Thresholds for Single Baselines and
Arrays. Frontiers of VLBI, H. Hirabayashi, M. Inoue and H. Kobayashi, Eds., Universal
Academy Press, Tokyo, 1991, p. 341-349.
Rogers A. E. E. VLB A Data Flow: Formatter to Tape. Very Long Baseline Interferometry
and the VLB A, J. A. Zensus, P. J. Diamond and P. J. Napier. Eds. Astron. Soc. Pacific Conf.
Ser., 82, 93-115, 1995.
Rogers A. E. E., R. J. Cappallo, H. F. Hinteregger, J. I. Levine, E. F. Nesman, J. C. Webber,
A. R. Whitney, T. A. Clark, C. Ma, J. Ryan, B. E. Corey, С С. Counselman, Т. A. Herring, I.
I. Shapiro, C. A. Knight, D. B. Shaffer, N. R. Vandenberg, R. Lacasse, R. Mauzy, B. Rayhrer,
B. R. Schupler and J. C. Pigg. Very-Long-Baseline Interferometry: The Mark III System for
Geodesy, Astrometry and Aperture Synthesis. Science, 219, 51-54, 1983.
Rogers A. E. E., S. S. Doeleman and J. M. Moran. Fringe Detection Methods for Very Long
Baseline Arrays. Astron. J., 109, 1391-1401, 1995.
Rogers A. E. E. and J. M. Moran. Coherence Limits for Very-Long-Baseline Interferometry.
IEEE Trans. Instrum. Meas., IM-30, 283-286, 1981.
Rutman J. Characterization of Phase and Frequency Instability in Precision Frequency Sources:
Fifteen Years of Progress. Proc. IEEE, 66, 1048-1075, 1978. (Имеется перевод: ТИИЭР, 66,
9, с. 70-102, 1978.)
Schwab F. R. and W. D. Cotton. Global Fringe Search Techniques for VLBI. Astron. J., 88,
688-694, 1983.
Shapiro I. I. Estimation of Astrometric and Geodetic Parameters. Methods of Experimental
Physics, Vol. 12C, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 261-276.
Shimoda К., Т. С Wang and С. Н. Townes. Further Aspects of the Theory of the Maser.
Phys. Rev., 102, 1308-1321, 1956.
Siegman A. E. An Introduction to Lasers and Masers. McGraw-Hill, New York, 1971, p. 404
Sovers O. J., J. L. Fanselow and C. S. Jacobs. Astrometry and Geodesy with Radio Interfer-
Interferometry: Experiments, Models, Results. Rev. Mod. Phys., 70, 1393-1454, 1998.
Thomas J. B. An Analysis of Radio Interferometry with the Block О System. JPL Pub. 81-49,
Jet Propulsion Laboratory, Pasadena, С A, 1981.
Thompson A. R. The VLB A Receiving System: Antenna to Data Formatter. Very Long
Baseline Interferometry and the VLB A, J. A. Zensus, P. J. Diamond and P. J. Napier. Eds.
Astron. Soc. Pacific Conf. Ser., 82, 73-92, 1995.
Thompson A. R. and D. S. Bagri. A Pulse Calibration System for the VLB A. Radio Interfer-
Interferometry: Theory, Techniques and Applications, T. J. Cornwell and R. A. Perley. Eds. Astron.
Soc. Pacific Conf. Ser., 19, 55-59, 1991.
Vanier J., M. Tetu and L. G. Bernier. Transfer of Frequency Stability from an Atomic
Frequency Reference to a Quartz-Crystal Oscillator. IEEE Trans. Instrum. Meas., IM-28,
188-193, 1979.
Vessot R. F. C. Frequency and Time Standards. Methods of Experimental Physics, Vol. 12C,
M. L. Meeks, Ed., Academic Press, New York, 1976, p. 198-227.
9.10] Цитированная литература 345
Vessot R. F. С. Relativity Experiments with Clocks. Radio Sci., 14, 629-647, 1979.
Vessot R. F. C. Applications of Highly Stable Oscillators to Scientific Measurements. Proc.
IEEE, 79, 1040-1053, 1991.
Vessot R. F. С and M. W. Levine. A Method for Eliminating the Wall Shift in the Atomic
Hydrogen Maser. Metrologia, 6, 116-117, 1970.
Vessot R. F. C, M. W. Levine, E. M. Mattison, T. E. Hoffman, E. A. Imbier, M. Tetu, G.
Nystrom, J. J. Kelt, H. F. Trucks and J. L. Vaniman. Space-Borne Hydrogen Maser Design.
Proc. 8th Annual Precise Time and Interval Meeting, U.S. Naval Research Laboratory, X-814-
77-149, 1976, p. 227-333.
Walker R. C. Very Long Baseline Interferometry I: Principles and Practice. Synthesis Imaging
in Radio Astronomy, R. A. Perley, F. R. Schwab and A. H. Bridle. Eds. Astron Soc. Pacific
Conf. Ser., 6, 355-378, 1989a.
Walker R. C. Calibration Methods. Very Long Baseline Interferometry, Techniques and
Applications, M. Felli and R. E. Spencer, Eds., Kluwer, Dordrecht, 1989b, p. 141-162.
Whitney A. R. The Mark IV Data-Acquisition and Correlation System. Developments in
Astrometry and Their Impact on Astrophysics and Geodynamics, IAU Symp. 156, I. I. Mueller
and B. Kolaczek, Eds., Kluwer, Dordrecht, 1993, 151-157.
Whitney A. R., A. E. E. Rogers, H. F. Hinteregger, C. A. Knight, J. I. Levine, S. Lippincott,
T. A. Clark, I. I. Shapiro and D. S. Robertson. A Very Long Baseline Interferometer System
for Geodetic Applications. Radio Sci., 11, 421-432, 1976.
Wietfeldt R. D. and L. R. D'Addario. Compatibility Issues in VLBI. Radio Interferometry:
Theory, Techniques and Applications, T. J. Cornwell and R. A. Perley. Eds. Astron. Soc.
Pacific Conf. Ser., 19, 98-101, 1991.
Wietfeldt R. D., D. Baer, W. H. Cannon, G. Feil, R. Jakovina, P. Leone, P. S. Newby and H.
Tan. The S2 Very Long Baseline Interferometry Tape Recorder. IEEE Trans. Instrum. Meas.,
IM-45, 923-929, 1996.
Wietfeldt R. D. and D. A. Frail. Burst Mode VLBI and Pulsar Applications. Radio Interfer-
Interferometry: Theory, Techniques, and Applications, T. J. Cornwell and R. A. Perley. Eds. Astron.
Soc. Pacific Conf. Ser., 19, 76-80, 1991.
Yen J. L., K. I. Kellermann, B. Rayhrer, N. W. Broten, D. N. Fort, S.H. Knowles, W. B.
Waltman and G. W. Swenson. Jr. Real-Time, Very-Long-Baseline Interferometry Based on the
Use of a Communcations Satellite. Science, 198, 289-291, 1977.
Коган Л. Р., Чесалин Л. С. Программно-математическое обеспечение экспериментов на
интерферометре со сверхдлинной базой на основе ЭВМ единой серии. Астрон. Ж., 58, 4,
с.898-903, 1981.
Матвеенко Л. И., Сагдеев Р. 3., Балебанов В. М., Шевченко В. И., Костенко В. И.,
Гришмановский В. А., Велихов В. Е., Игнатов С. П., Каневский Б. 3., Коган Л. Р.,
Козлов А. Н., Копелянский Г. Д., Молодяну А. П., Молотов Е. П., Папаценко А. X.,
Романов A. M.j Струков И. А., Тимофеев В. В., Шевченко А. В., Северный А. В., Моисеев
И. Г., Сороченко Р. Л., Цивилев А. П., Мартиросян Р. М., Асланян А. М., Гулян А. Г.,
Яцкив Я. С, Головня М. В. Сверхдальняя радиоинтерференционная сеть на волне 18 см.
Письма в АЖ. т. 12, № 1, 59-65, 1986.
Шоломицкий Г. В., Слепцова Н. Ф., Матвеенко Л. И. Спектры компонент ЗС 273. Астрон.
Ж., 6, 1136, 1965.
Глава 10
КАЛИБРОВКА И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
ФУНКЦИИ ВИДНОСТИ
В этой главе мы детально обсудим калибровку и фурье-преобразование функции
видности, главным образом, в применении к синтезу, основанному на вращении Зем-
Земли. Будут рассмотрены использование быстрого алгоритма дискретного преобразо-
преобразования Фурье (БПФ) и методы оценки функции видности в узлах прямоугольной
сетки. Специально рассмотрены некоторые типы наблюдений, включая наблюде-
наблюдения спектральных линий. Приведены также некоторые практические советы по
выявлению и исключению ошибок на картах радиоизображений и планированию
наблюдений. Эта глава посвящена исключительно линейным методам, нелинейная
обработка изображений обсуждается в гл. 11.
10.1. Калибровка функции видности
Цель калибровки функции видности состоит в устранении, насколько это воз-
возможно, результатов воздействия на измерения инструментальных факторов. Эти
факторы в значительной степени зависят от отдельных антенн или антенных пар
и их общей электроники, поэтому поправки должны быть внесены в значения функ-
функции видности до того, как они будут объединены при построении карты. Редакти-
Редактирование данных функции видности с целью устранения помех и инструментальных
ошибок обычно осуществляется перед самой калибровкой. Сюда входит анализ вы-
выборок данных с целью выявления неправдоподобных уровней или дисперсий уровня
и фазы сигнала. Особенно полезны здесь данные наблюдений опорных источников,
поскольку отклик на такой источник предсказуем и должен медленно и плавно
меняться во времени.
В начале процедуры калибровки учитываются инструментальные параметры,
которые стабильны в течение периода времени в несколько недель и более. К ним
относятся следующие:
1) координаты антенн, которые определяют базы между ними;
2) поправки наведения антенн, учитывающие погрешности электрической оси
или другие возможные механические отклонения;
3) нуль-пункты инструментальных задержек, т. е. поправки, для которых за-
задержки от антенн ко входам коррелятора равны.
Перечисленные выше параметры меняются только в результате существенных
изменений, таких, как изменение положения антенны. Они могут быть прокалиб-
прокалиброваны посредством наблюдений неразрешенных источников с известными коорди-
координатами. Мы предполагаем здесь, что они определены заранее перед наблюдениями.
Мы предполагаем также, что поправка за нелинейность при квантовании сигнала,
обсуждавшаяся в п. 3.8.5, вводится автоматически при необходимости.
10.1] Калибровка функции видности 347
10.1.1. Поправки на предсказуемые или непосредственно измеряемые
эффекты. Калибровка измерений функции видности с целью учета эффектов,
которые изменяются в течение периода наблюдения, состоит, главным образом,
в поправке комплексных коэффициентов усиления антенных пар. Различают эф-
эффекты, поведение которых может быть предсказано или непосредственно измерено,
и другие, для которых это должно быть определено при наблюдении опорного
источника в течение данного эксперимента. Путем расчета могут быть учтены
следующие эффекты:
1. Постоянная составляющая атмосферного поглощения излучения, являющаяся
функцией зенитного расстояния (см. п. 13.1.3).
2. Изменение коэффициента усиления антенны в зависимости от угла места,
обусловленное упругими деформациями ее конструкции под действием гра-
гравитации.
3. Затенение одной антенны другой при малых базах и низких углах места.
Учет затенения, когда одна антенна частично закрывает апертуру другой, яв-
является, как правило, трудной задачей. Влияние геометрического перекрытия усу-
усугубляется дифракцией. При этом искажается форма главного лепестка диаграммы
направленности, а также сдвигается положение фазового центра апертуры, изме-
изменяя, таким образом, и базу интерферометра. Данные, полученные на затененных
антеннах, часто отбрасываются.
К эффектам, внутренним или внешним по отношению к приемному комплексу,
которые могут непрерывно измеряться в течение наблюдений, относят:
1. Изменение шумовой температуры системы, которое может происходить из-
за изменения вклада излучения Земли через боковые лепестки во время
слежения антенны за источниками. Этот эффект может также приводить
к изменениям коэффициента усиления в результате действия системы АКУ
(автоматический контроль уровня), которая используется на некоторых ин-
инструментах для регулировки уровней сигнала дискретизатора или корреля-
коррелятора (см. разд. 7.6). Измерение шумовой температуры может проводиться
путем ввода малого модулируемого шумового сигнала на входе приемника
и его выделения в системе позднее.
2. Уход фазы в системе местного гетеродина, контролируемый измерениями
фазы при прохождении сигнала в прямом и обратном направлениях (см.
разд. 7.2).
3. Переменная компонента запаздывания сигнала в атмосфере, контролируемая
с помощью радиометров, установленных на антеннах и измеряющих содержа-
содержание водяного пара в атмосфере Земли (см. п. 13.1.9).
Учет поправок на вышеперечисленные эффекты происходит обычно во время
первой стадии процедуры калибровки.
10.1.2. Использование опорных источников. Дальнейшие шаги в методи-
методике калибровки касаются параметров, которые могут меняться на временных мас-
масштабах порядка минут или часов и требуют наблюдения одного или более опорных
источников. Будем называть картографируемым источником объект, являющийся
предметом астрономического исследования, отличая его от опорного источника или
348 Калибровка и преобразование Фурье функции видности [Гл. 10
калибратора. Исходя из соотношения C.9), мы можем записать выражение для
отклика интерферометра в следующем виде:
^)]uncal = Gmn(i) [ f AN{l,
J J л/1
— oo — oo
л/i -12 -'
где [V(i?, f)]uncai является некалиброванной функцией видности, а 1A, т) — яркость
источника.
Комплексный коэффициент усиления Gmn (t) является функцией антенной пары
(т, п) и в результате нежелательных эффектов может зависеть от времени. Через
Адг(/,7тг) обозначается диаграмма направленности антенны, нормированная к еди-
единице в направлении главного лепестка. Ее влияние на получаемое изображение ис-
источника может быть устранено на последнем этапе обработки изображения. Коэф-
Коэффициент Адг(/, m)/\/l — I2 — т2 в соотношении яркость-функция видности близок
к единице и далее опускается везде, кроме случая картографирования в широком
поле, который обсуждается в разд. 11.8. Для калибровки Gmn(t) можно наблюдать
неразрешенный опорный источник, измеряемый отклик на который равен
Vc(u,v) = Gmn(t)Sc, A0.2)
где нижний индекс «с» указывает на опорный источник с плотностью потока Sc.
При калибровке коэффициента усиления лучше всего рассматривать амплитуду
и фазу раздельно, так как ошибки этих двух величин возникают по разным причи-
причинам. Например, на коротких сантиметровых длинах волн атмосферные флуктуации
приводят к флуктуациям фазы, однако мало влияют на амплитуду. Для калибровки
функции видности картографируемого источника мы можем записать
,V) — — j-t — [V[U, ^JJuncal hrr
1
- •
J
При наблюдениях опорного источника он помещается в фазовый центр поля.
Тогда, полагая, что калибратор неразрешен, фаза сигнала непосредственно равна
измеряемой инструментальной фазе. Таким образом, для фазовой калибровки кар-
картографируемого источника требуется лишь вычесть фазу калибратора из наблюдае-
наблюдаемой. Амплитуда функции видности может быть прокалибрована при использовании
модуля членов выражения A0.3), содержащих функцию видности. Отклик на опор-
опорный источник должен быть исправлен за рассчитываемые и/или непосредственно
измеряемые эффекты перед проведением калибровки коэффициента усиления. При
наличии отдельных приемных каналов для двух противоположных поляризаций на
каждой антенне, калибровка должна быть проведена отдельно для каждого кана-
канала. Для измерения поляризации источника необходима дополнительная процедура
калибровки, которая описана в п. 4.8.6.
Калибровочные наблюдения требуют периодического прерывания наблюдений
картографируемого источника. На сантиметровых длинах волн интервал между
калибровочными наблюдениями зависит от стабильности инструмента и обычно
составляет от 15 минут до одного часа. На метровых и миллиметровых длинах
волн влияние ионосферы и нейтральной атмосферы сказывается на фазе и коэф-
коэффициенте усиления, учет чего может потребовать наблюдений опорного источника
на таких коротких временных интервалах, как две минуты.
Как видно из уравнения G.38), Cmn = дшд^ т.е. измеряемые коэффициенты
усиления для антенных пар могут быть использованы для определения коэффици-
коэффициентов усиления индивидуальных антенн. Использование коэффициентов усиления
10.1] Калибровка функции видности 349
антенн вместо коэффициентов усиления для антенных пар сокращает объем калиб-
калибровочных данных, который необходимо сохранить, и помогает в мониторинге харак-
характеристик индивидуальных антенн. Этот метод позволяет также опустить некоторые
базы во время калибровочных наблюдений, поскольку в калибровку включается
каждая из антенн. На практике таблицы коэффициентов усиления для антенн,
включающие и амплитуду, и фазу, генерируются как функции времени и интерпо-
интерполируются на моменты наблюдения картографируемого источника. Интерполяция
должна проводится отдельно для амплитуды и фазы, а не для действительной
и мнимой частей коэффициента усиления. В противном случае ошибки фазы могут
уменьшить амплитуду и наоборот. Ниже перечисляются желательные характери-
характеристики опорного источника.
Плотность потока. Опорный источник должен быть достаточно сильным, что-
чтобы за короткое время можно было получить хорошее отношение сигнал/шум
с целью сведения к минимуму зон покрытия (гл, г>), потерянных у картогра-
картографируемого источника. Потери в покрытии (г/, v) более серьезны в случае
линейной решетки, когда теряются целые сектора, чем в случае двумерной
решетки, для которой мгновенное покрытие более широко распределено по и
и v.
Угловой размер. Опорный источник должен быть, по возможности, неразрешен-
неразрешенным, чтобы не привлекать информацию о его функции видности.
Координаты. Опорный источник должен располагаться близко к картографи-
картографируемому источнику. При этом лучше учитываются изменения коэффициента
усиления, вызванные эффектами в атмосфере или антеннами, в зависимости
от угла наведения, и потери времени на перемещение антенн между опорным
и картографируемым источниками сравнительно невелики. При наблюдениях
на миллиметровых волнах, когда в первую очередь должна калиброваться
фазовая задержка в атмосфере, расстояние между картографируемым и опор-
опорным источниками не должно превышать характерного углового размера атмо-
атмосферных неоднородностей. Обычно, он составляет величину не более несколь-
нескольких градусов на небесной сфере.
Не всегда оказывается возможным найти опорный источник, удовлетворяющий
всем перечисленным выше требованиям. В таких случаях бывает необходимо най-
найти источник, в достаточной мере неразрешенный, близкий к картографируемому,
и затем прокалибровать его по одному из более широко используемых источников,
опорных по плотности потока, таких как ЗС48, ЗС147, ЗС286иЗС295. Последний ис-
источник является постоянным с наибольшей достоверностью. Тепловые источники,
такие, как планетарная туманность NGC 7027, могут быть полезны как калибраторы
по амплитуде для коротких баз. На миллиметровых волнах особенно сложно найти
сильный калиброванный источник. Планеты становятся разрешенными на довольно
коротких базах, однако может оказаться полезным использование лимбов Луны или
планет (см. Приложение 10.1).
Для РСДБ-наблюдений с миллисекундным угловым разрешением есть лишь
малое количество подходящих опорных источников. Иногда угловая структура на
этих масштабах меняется за несколько месяцев, поэтому следует быть вниматель-
внимательным при использовании в качестве опорного ранее измеренного частично разрешен-
разрешенного источника. Альтернативный подход к амплитудной калибровке РСДБ-данных
состоит в точном определении эффективных площадей и температур систем, как
описано ниже. Вначале результат кросс-корреляции должен быть отнормирован
к единице для случая, когда два входных потока данных полностью коррелируют.
350 Калибровка и преобразование Фурье функции видности [Гл. 10
Для проведения такой нормировки данные делятся на произведение среднеквадра-
среднеквадратичных величин потоков данных на двух входах коррелятора. (Для двухуровневых
сигналов это среднеквадратичное значение равно единице, а для других типов выбо-
выборок оно зависит от установленного порога выборки относительно уровня аналогово
сигнала.) Далее, для преобразования нормированного коэффициента корреляции
в функцию видности V в единицах плотности потока (Ян) амплитуда умножается
на среднее геометрическое величин системной эквивалентной плотности потока для
двух антенн интерферометра. Системная эквивалентная плотность потока Se =
= 2kTs/А, определяется выражением A.6). Для определения температуры системы
Ts и эффективной площади А обычно требуются измерения в режиме полной мощ-
мощности на обеих антеннах. Если величина Т$ соответствует сигналу над атмосферой,
получаемые величины функции видности будут поправлены за потери в атмосфе-
атмосфере. Соотношения замыкания из разд. 10.3 позволяют построить карты по РСДБ-
данным с некалиброванной фазой, если не требуется информация об абсолютных
координатах.
10.2. Получение распределения видимой яркости
из функции видности
10.2.1. Построение изображения посредством прямого преобразова-
преобразования Фурье. Прямым методом получения распределения яркости из измеряемой
функции видности является преобразование Фурье, т. е. осуществление преобразо-
преобразования без придания функции видности какой-либо специальной формы, как, напри-
например, для БПФ, описанного в разд. 5.2. Измеренная функция видности Vmeas(?i, v)
может быть записана в виде
Vmeas(^, v) = W(щ v) w(u, v) V(u, v), A0.4)
где W(u, v) — передаточная функция, или функция пространственной чувствитель-
чувствительности, введенная в разд. 5.3, a w{u,v) представляет собой любую используемую
функцию взвешивания. Преобразование Фурье уравнения A0.4) представляет собой
видимое распределение интенсивности
1теаяA, Гп) = /(/, Гп) * * Ь0(*, Гп). A0.5)
Здесь двойная звездочка означает двумерную свертку, а Ьо — синтезированная
диаграмма направленности, являющаяся преобразованием Фурье взвешенной пе-
передаточной функции:
) — W(u, v) w(u, v), A0.6)
где знак ^ обозначает операцию фурье-преобразования. Такие эффекты, как
некомпланарность баз, конечность ширины полосы пропускания сигнала и усред-
усреднение функции видности, пренебрежимо малы во многих экспериментах и здесь не
рассматриваются.
Функция видности измеряется на ансамбле пар точек тт^, симметричных по
отношению к началу координат плоскости uv, а прямое преобразование Фурье этих
данных представляется в виде
nd r
У^ Wi Vmeas(^ Vi) eJ27T(uil+virn) + Vmeas( — Ui —vA e-J27T(uil+vim)
10.2]
Получение распределения видимой яркости из функции видности
351
Весовой коэффициент W{ введен для контроля формы синтезированной диаграммы
направленности. Поскольку функция видности в точке (—щ,—У{) является ком-
комплексным сопряжением функции видности в точке (г^,г^), полученная яркость яв-
является действительной величиной. Мы предполагаем, что антенны имеют идентич-
идентичную поляризацию; для рассмотрения других случаев см. разд. 4.8. При проведении
фурье-преобразования функции видности интенсивность обычно рассчитывается
в узлах прямоугольной сетки с однородными приращениями по / и т, так как такая
форма представления очень удобна для дальнейшей обработки.
10.2.2. Взвешивание данных функции видности. Для получения лучше-
лучшего отношения сигнал/шум при суммировании измерений с гауссовым шумом каждое
измерение должно быть взвешено обратно пропорционально своим дисперсиям. То
же самое справедливо и для набора синусоидальных компонент карты источника,
амплитуды которых пропорциональны соответствующим точкам функции видно-
видности. Таким образом, для получения наилучшего отношения сигнал/шум необходи-
необходимо, чтобы веса Wi, введенные в выражение A0.7), были обратно пропорциональны
дисперсиям. Если данные получены на однородной сетке идентичных антенн и при-
приемников, а также одинаково время усреднения для всех данных, тогда дисперсии
должны быть одинаковыми и наибольшее отношение сигнал/шум будет получено
при использовании всех данных с одинаковым весом. Это называется естествен-
естественным взвешиванием. Естественное взве-
взвешивание для большинства сеток при-
приводит к плохой форме диаграммы на-
направленности с широким пьедесталом
по той причине, что излишне выде-
выделяются малые базы. Таким образом,
обычный подход заключается в том,
чтобы включить во взвешивание неко-
некоторый коэффициент, который обратно
пропорционален плотности данных на
единицу площади плоскости uv. По-
Поверхностная плотность ра(и, v) опреде-
ляется числом точек в пределах и ±
=Ь du/2, v ± dv/2 и равна pa(u,v) dudv
(Thompson and Bracewell, 1974). Хотя
Per в любой точке зависит от прираще-
приращений du и dv, обычно не представляет
труда определить с достаточной точ-
точностью изменение относительной плот-
плотности и ввести соответствующую по-
поправку на него. В качестве простого
примера достаточно взять наблюде-
наблюдения источника с высоким склонени-
склонением с помощью многоэлементной антен-
антенной решетки, ориентированной по ли-
линии восток—запад, расстояния между
элементами которой являются безиз-
быточными целыми множителями еди-
единичной величины. При этом точки
функции видности лежат на концен-
концентрических окружностях, как показано
на рис. 10.1. Тогда, если функция вид-
видности измеряется через равные интер-
Радиус = ип
Рис. 10.1. Передаточная функция (годогра-
(годографы баз) в плоскости uv в случае наблюде-
наблюдений источника с высоким склонением при
использовании многоэлементной решетки в
направлении восток-запад с равными прира-
приращениями расстояний между антеннами. Точ-
Точки указывают на измерения функции видно-
видности и их положение на плоскости uv, отра-
отраженные относительно начала координат, че-
через одинаковые промежутки времени. Угол
ф указывает данные для определенного часо-
часового угла. Если значения функции видности
взвесить пропорционально радиусам точек,
то плотность данных функции видности бу-
будет эффективно однородной вплоть до ра-
радиуса ?imax
352 Калибровка и преобразование Фурье функции видности [Гл. 10
валы часового угла, то поверхностная плотность на любой окружности будет обрат-
обратно пропорциональна ее радиусу. Если величина w(u, v) пропорциональна 1/ра(и, г>),
то эффективная плотность данных однородна в пределах окружности радиуса г^тах,
определяемого максимальным расстоянием между антеннами. Тогда диаграмма
направленности достаточно точно представляется фурье-преобразованием функции
круглого диска, которая, будучи нормированной в максимуме к единице, определя-
определяется в виде
7 1 \\\j.o)
7Гь'итах
где J\ — функция Бесселя первого рода и первого порядка. Полная ширина диа-
диаграммы направленности на уровне половины максимума равна 0,705 г?~ах, а от-
отклик первого бокового лепестка находится на уровне 13,2 % от величины главного
лепестка 1). Аналогично, если эффективная плотность постоянна в пределах пря-
прямоугольника с размерами 2i?max x 2г>тах, то диаграмма достаточно хорошо аппрок-
аппроксимируется выражением
sin B7mmaxZ) sin Bтг^тахгп) , ,
2тттах/ 2тг?;тахт
Эта диаграмма не обладает круговой симметрией, и первый боковой лепесток имеет
максимум на уровне 22 % в направлениях восток—запад и север—юг, проходящих
через ее центр.
При однородном взвешивании большие боковые лепестки малых порядков (близ-
(близкие к главному лепестку) на рис. 10.2 блендируют слабые детали изображения
и уменьшают, таким образом, интервал значений видимой интенсивности, который
может быть надежно измерен. Боковые лепестки малых порядков в функциях,
выражающих диаграмму направленности в выражениях A0.8) и A0.9), могут быть
уменьшены за счет некоторого увеличения ширины синтезированного главного
лепестка путем введения в весовую функцию плавного спада гауссового или ана-
аналогичного типа. Эффект от применения такого спада к функции видности показан
на рис. 10.2. Плавный спад может быть определен через амплитуду спадающей
функции на расстоянии i?max от начала координат (u,v)\ обычно используется
уровень спада ~—13 дБ от центрального значения. Тогда весовая функция w(u,v)
представляет собой произведение двух функций: wu(u, v) — весовой функции, необ-
необходимой для получения равномерной эффективной плотности, и wt(u,v) — плавно
спадающей функции. Таким образом, синтезированная диаграмма является преоб-
преобразованием Фурье от W(u, v) wu(u, v) wt(u, v):
bo(l,m) = W(l,m) * *wu(l,m) * *wt(l,m), A0.10)
где черта над буквой обозначает преобразование Фурье. Преобразование Фурье от
W(u, v) wu(u, v) представляет собой просто диаграмму направленности для случая
равномерного распределения эффективной плотности; см., например, выражение
A0.8) или A0.9). Если величина Wt(u,v) является двумерной гауссовой функцией, то
ее преобразование Фурье тоже имеет гауссову форму. Поэтому уменьшение уровня
боковых лепестков является результатом свертки с гауссовой функцией в области
х) Этот результат не следует путать с коэффициентом усиления равномерно облученной
параболической антенны с круговой апертурой и радиусом г. В этом случае коэффици-
коэффициент усиления пропорционален [JiB7rrZ/A)/GrrZ/A)]2, а диаграмма имеет полную ширину
0,514А/г по уровню половины максимума, первый нуль при 0,610А/г и первый боковой
лепесток на 1,7%. Усиление антенны пропорционально преобразованию Фурье функции
автокорреляции однородной круговой апертуры.
10.2]
Получение распределения видимой яркости из функции видности
353
Рис. 10.2. Примеры профилей синтезированной диаграммы. Кривые без плавного спада
соответствуют распределению функции видности, которое постоянно в пределах прямо-
прямоугольной области шириной 2г^тах (а) и круга диаметром 2итах (б). Эти кривые описыва-
описываются выражением A0.9) для (а) и A0.8) — для (б). Показано также воздействие гауссова
ослабления, которое уменьшает функцию видности на краях распределения до 30 % и до
10%. Обратите внимание на разные масштабы по оси ординат
(/,777,). Дисперсии функций аддитивны при свертке (см., например, Bracewell, 2000),
так что диаграмма, полученная сверткой с Wt, шире диаграммы без спадающей
функции, как это очевидно из рис. 10.2.
Однородное взвешивание проявляет интересное свойство. Если положить, что
неизмеренные значения функции видности равны нулю, однородное взвешивание
минимизирует среднеквадратичное отклонение получаемого распределения види-
видимой интенсивности от истинной интенсивности. Это молено понять следующим
образом. Истинное распределение интенсивности 1A, т) и истинная функция вид-
видности V(u, г>), как и полученное распределение интенсивности /0(/, т) и взвешенная
измеренная функция видности, являются фурье-парой. Следовательно, разности
этих величин, находящиеся в двух плоскостях, также являются фурье-парой, к ко-
которой может быть применена теорема Парсеваля. Вспомним, что W{u, v) является
передаточной функцией, wu(u,v) — это взвешивание, необходимое для получения
эффективной однородной плотности данных в плоскости гш, a Wt(u,v) — применя-
применяемый плавный спад. Таким образом, можно записать
V(u,v)—V(u,v)W(u,v)wu(u,v)wt(u,v)\ dudv-\- \V(u,v) dudv =
unmeas
oo oo
= [ [ \l(l,m)-I0(l,m)\2dldm. A0.11)
— oo —oo
Два слагаемых в левой части A0.11) выражают измеренную и неизмеренную об-
области на плоскости uv, соответственно. В измеренной области W(u,v) wu(u,v) = 1.
В случае однородного взвешивания wt = 1, так что первый интеграл в левой части
12 Томсон
354 Калибровка и преобразование Фурье функции видности [Гл. 10
равен нулю. Это обстоятельство минимизирует квадратичную разницу между ис-
истинным и наблюдаемым распределением интенсивности, приведенную в последней
строке. Если /(/, т) — распределение интенсивности для неразрешенного точечного
источника, то 1оA,т) равно синтезированной диаграмме направленности. Одно-
Однородное взвешивание минимизирует квадратичную разность, проинтегрированную
по 4тг стерадиан, между синтезированной диаграммой направленности и откли-
откликом на точечный источник, как это наблюдалось бы при неограничном покрытии
плоскости uv. В этом смысле иногда говорится, что однородное взвешивание мини-
минимизирует боковые лепестки синтезированной диаграммы направленности. Однако,
как показано на рис. 10.2, гауссовый плавный спад уменьшает боковые лепестки
ценой уширения диаграммы направленности. Возникает кажущееся противоречие
утверждений о «минимизации боковых лепестков», если четко не оговаривается,
что под ними подразумевается. Карты, полученные из данных функции видности,
которые однородно взвешены в области измерений на плоскости uv, называются
главным решением или главным откликом (Bracewell and Roberts, 1954).
Бриггс (Briggs, 1995) разработал методику, известную как робастное взвеши-
взвешивание, для снятия проблем, которые возникают при использовании однородного
взвешивания. Некоторые измерения функции видности могут оказаться изолиро-
изолированными на плоскости uv от других, например, из-за потери соседних точек по
причине неисправности аппаратуры или случайных помех. Однородное взвешива-
взвешивание придаст этим данным большие веса. Если они окажутся на тех координатах
и, v, где функция видности имеет малые значения, такие данные могут, главным
образом, содержать шум. Фурье-преобразования ложных точек плоскости uv и их
сопряжений внесет в фон на карте интенсивности компоненту в виде косинусо-
идальной волнистости, которая ограничит динамический диапазон изображения.
Робастное взвешивание предлагает алгоритм, который учитывает отношение сиг-
сигнал/шум отдельных точек в соответствии с их весами (дисперсиями) и ослабляет
вес точек с большим шумом. В более общем смысле, робастное взвешивание может
быть рассмотрено как оптимизирующее совокупное влияние шума и протяженных
боковых лепестков. Это достигается варьированием веса точек между крайними
значениями, полученными при естественном взвешивании, которое оптимизирует
чувствительность, и при однородном взвешивании, которое улучшает плохую фор-
форму диаграммы направленности, полученную при естественном взвешивании (Briggs,
Sramek and Schwab, 1999). Аналогичный подход полезен в случае сетки с антеннами
разного размера или при разной чувствительности приемников, так как необходи-
необходимо взвешивать данные обратно пропорционально их дисперсиям для получения
максимального отношения сигнал/шум. Соответствующая методика уменьшения
отклика боковых лепестков в оптическом картографировании называется аподиза-
цией. Имеется обширная литература по этой методике (см., например, Jacquinot
and Roizen-Dossier, 1964; Slepian, 1965).
10.2.3. Построение изображения при помощи дискретного преобразо-
преобразования Фурье. Скорость быстрого алгоритма дискретного преобразования Фурье
(БПФ), вкратце описанного в разд. 5.2, является основным преимуществом при по-
построении больших карт с помощью компьютера. Однако использование БПФ вносит
два осложнения в дополнение к уже отмеченным в случае прямого преобразования:
1) необходимость вычисления функции видности в точках прямоугольной сетки
и 2) возможность появления ложных деталей изображения вне синтезированного
поля. Расчет значений функции видности в узлах сетки часто называется гридиро-
ванием. Результат этой процедуры может быть представлен с помощью следующего
выражения:
w{u,v) 2т
AuAv
Ш (^, ?j) {С(щ v) * * [W(u, v)V(u, v)} }. A0.12)
10.2] Получение распределения видимой яркости из функции видности 355
Здесь функция видности V(u,v), измеренная в точках, определяемых функцией
преобразования W(u,v), свертывается с функцией C(u,v) для создания непрерыв-
непрерывного распределения функции видности. Последнее затем повторно дискретизуется
в точках прямоугольной сетки с шагами Аи и Av. Такая процедура часто называ-
называется конволюционным гридированием. Повторная дискретизация здесь представля-
представляется с помощью двумерной шаховой функции 2Ш (Bracewell, 1956a), определяемой
в виде
4ll(^^-)=AuAv jr jr 25{u-iAu,v-kAv), A0.13)
i= — oo k = — oo
где 8 — двумерная дельта-функция. К повторно дискретизованным данным приме-
применяется взвешивание с целью оптимизации диаграммы направленности. Хотя этот
процесс описывается математически с помощью свертки и последующей дискре-
дискретизации сигнала, на практике свертка вычисляется только в узлах сетки. Фурье-
преобразование выражения A0.12) представляет собой измеренную интенсивность:
/measG, ™) = 2Щ1Ащ TTlAv) * * ШA, ш) * *{С(/, ш) [W(l, ш) * * /(/, ш)] }. A0.14)
В результате фурье-преобразования функция интенсивности 1A, т) свертывается
с фурье-образом передаточной функции, умножается на функцию СA,т), являю-
являющуюся фурье-образом свертывающей функции, а затем свертывается с фурье-
образами взвешивающей и дискретизирующей функций. Последняя свертка при-
приводит к дублированию всей карты через интервалы Аи-1 по / и Аг>-1 по т.
Эти интервалы соответствуют размерам карты в плоскости 1т, т. е. Аи-1 = МА1
и Av~x = TV Am, для решетки из М х TV точек. С(/, га) представляет собой спадаю-
спадающую функцию, используемую при обработке карты, и если эта функция не очень
сильно меняется в масштабе ширины гп(/,га), что обычно выполняется в случае
больших карт, то w(l, т) в уравнении A0.14) может быть свернута непосредственно
с W(l,m) * */(/,га). Тогда соотношение A0.14) приобретает вид
/measG, Гп) ~ 2Ш(/ Ащ ГП Av) * *{C(Z, m) [/(/, m) * * Ь0(/, Гп)] }, A0.15)
где синтезированная диаграмма направленности bo(l,m) определяется соотноше-
соотношением A0.6). Сравнение с выражением A0.5) показывает, что эффект вычисления
в точках сетки (гридирования) и восстановления дискретизации сводится к умно-
умножению карты на СA,т) и ее дублированию. Это дублирование вносит ложный
сигнал.
Возвращаясь к вычислению функции видности в узлах сетки, можно ожидать,
что наилучшей методикой могла бы быть одна из форм точной интерполяции,
при которой результирующие значения были бы равны тем, которые получаются
путем измерения в узлах сетки. Метод такого типа был описан в работе (Thompson
and Bracewell, 1974). Однако проблема появления ложного изображения остается,
и наиболее эффективный способ борьбы с ней состоит в свертке данных в плоскости
uv с фурье-преобразованием такой функции, которая в плоскости 1т слабо меняется
по всей карте, а затем резко падает на ее краях. Соответственно, мы ищем такую
свертывающую функцию С (и, г>), для которой фурье-образ С(/, т) обладает указан-
указанными свойствами. Идеальная функция с бесконечно резким обрезанием на краях
карты могла бы полностью исключить появление ложных изображений, поскольку
при этом отсутствовало бы наложение дублируемых карт. К сожалению, этот идеал
не достигается на практике, так как необходимая свертывающая функция не огра-
ограничена в плоскости uv. Тем не менее, можно существенно подавить ложные изоб-
изображения при аккуратном выборе функций. Совмещение в одну операцию гридиро-
гридирования и свертки широко используется в качестве одного из методов минимизации
12*
356 Калибровка и преобразование Фурье функции видности [Гл. 10
ложных изображений. Заметим, однако, что в тех точках плоскости uv, в которых
проводятся измерения, в общем случае функция С (и, v) * * [W(w, v) V(u, v)] не равна
измеряемой функции видности V(u,v). Таким образом, процедура сетчатой выбор-
выборки данных не может быть описана как интерполяция. Аналогично, в результате
свертки дискретизованные в узлах сетки данные являются средними от значе-
значений функции видности в локальной окрестности каждого узла, а не значениями
функции видности в самих узлах. Отметим также в заключение, что, хоть свертка
и эффективна при подавлении различных артефактов, появляющихся в результате
сетчатой выборки данных, она не уменьшает отклики от боковых или кольцевых
лепестков на источники, расположенные вне поля карты.
10.2.4. Функции свертки и эффект ложного изображения. Из предыду-
предыдущего обсуждения мы можем сделать вывод, что принципиальным моментом исполь-
использования БПФ является выбор свертывающей функции. Подробное рассмотрение
свертывающих функций приводится в работе (Schwab, 1984). Удобно использовать
такие функции, которые разделяются на одномерные функции одного и того же
вида от переменных и и г>, т. е.
C(u,v) = C1{u)C1{v). A0.16)
Рассмотрим далее некоторые примеры функции С\.
Прямоугольная функция. Эта функция использовалась в разд. 5.2 при усредне-
усреднении по ячейкам. Она записывается в виде
A0.17)
где П — единичная прямоугольная функция, определяемая как
х\ ^ о
Щх) = I * A0.18)
[о, N>-.
Фурье-преобразование функции С\(и) имеет вид
A0.19)
(ЛЬ
На краях синтезированного поля / = BАи)~1, a Ci(l/BAu)) = 2/тг. Сужение карты
осуществляется с помощью профиля sine-функции в направлениях / и т и профи-
профиля sine-квадратной функции вдоль диагоналей. Функция A0.19) представлена на
рис. 10.3; значение первого максимума за краем карты составляет 0,22 от значе-
значения в центре карты. Эффект ложного изображения показан более наглядно на
рис. 10.4 а, представляющем собой график Ci(/)/Ci[/(/)], где /(/) — значение /
в пределах карты (т. е. |/(/)| < BАи)~1), при котором появляется ложное изображе-
изображение детали при /. Эта величина дает относительный отклик на ложное изображение
детали на карте, которое корректируется спадающей функцией С±A). Ясно, что
простое усреднение данных по прямоугольным ячейкам слабо подавляет эффект
ложного изображения.
Функция Гаусса. Здесь мы рассматриваем
Ci(«) =
10.2]
Получение распределения видимой яркости из функции видности
357
1
I
1 III
—
-
-
\
\ \
\ \
\
\
ii'l
—
X
!\
| \
/ \ / ~
1 1
j
1
и 1,0
Ci(l) = e K ' . A0.zl)
Выбор желаемой ширины про- До
филя функции осуществляется с по- ^
мощью постоянной а. Если а слиш- w
ком мала, то профиль С\{и) будет ^
слишком узким, и при картографи-
картографировании эффективно будут исполь-
использоваться лишь измерения, близкие
к узлам сетки. Если а слишком ве-
велика, то С\(и) будет охватывать
большое число измеряемых точек
и проводимые вычисления будут из-
избыточными. Свертывающая функ-
функция Гаусса широко использовалась
в первые годы работы Вестерборг-
ской антенной решетки при а =
= 2лЛп4/тг = 0,750 (Brouw, 1971).
При этом значение коэффициен-
коэффициента e-(V«A^J в d(u) равно 0,41
для точки, лежащей на диагонали
между двумя точками сетки, распо-
расположенной в плоскости uv. Следова-
Следовательно, все измеренные точки появ-
появляются на карте со значительными
весами, а на краю карты спадаю-
спадающая функция Ci(u) = 1/4. Кривая
для этой функции Гаусса дана на
рис. 10.3.
Sine-гауссова функция. Идеальным видом спадающей функции С\{1) могла бы
быть прямоугольная функция, соответствующая свертке с sine-функцией (см. выра-
выражение A0.19)). Однако при возрастании аргумента огибающая sine-функции стре-
стремится к нулю очень медленно, и поэтому вычисления, необходимые для свертки,
будут слишком громоздкими. Усечение sine-функции нежелательно, потому что
в области значений / искомая прямоугольная функция свертывается с преобразо-
преобразованием Фурье усеченной функции, а это нарушает резкое обрезание поля на краях
карты. Более приемлемая процедура заключается в перемножении sine-функции
с гауссовой функцией:
1(Г2 =
1(Г3 =
10"
Рис. 10.3. Три примера спадающей функции
Ci(Z), являющейся образом Фурье свертываю-
свертывающей функции Сг(и). Для свертывающей функ-
функции Гаусса а = 0,75. Для sine-гауссовой свер-
свертывающей функции аг = 1,55, «2 = 2,52, далее
четвертого второстепенного максимума показа-
показана лишь огибающая максимумов. Центр карты
по оси абсцисс имеет координату 0, а край при
1,0. Данные для sine-гауссовой функции были
вычислены Ф.Р. Швабом
(u/a2AuJ
и тогда
СгA) = ЩагАи1) * [v^F
A0.22)
A0.23)
Хорошие результаты получаются с а± = 1,55 и а2 = 2,52, если свертка производится
на области шириной 6Аи. Соответствующие кривые для С\{1) и результирующие
ложные сигналы приведены на рисунках 10.3 и ЮЛ б. Эта свертывающая функция
намного лучше рассмотренных в двух предыдущих примерах.
358
Калибровка и преобразование Фурье функции видности
[Гл. 10
0
-1
О
-1
123456789
[ к
Мл пл
пЛаА V
11W»
' 1 111 1
i 1
лад
1
1
1
А
/ \
i \
у \
"* X ^
1 I
1
/\
/ \
/ \
I 1
1
/
/
/
123456789
Рис. 10.4. Логарифмический график коэффициента, на который умножаются амплитуды
структур за пределами карты при их попадании на карту за счет эффекта ложного
изображения. На шкале абсцисс 1 соответствует краю карты, а 2, 4, 6 — центрам сосед-
соседних дублей, а — коэффициент ложного изображения для прямоугольной свертывающей
функции с шириной, равной Аи (усреднение по ячейкам); б — коэффициент ложного
изображения для sine-гауссовой свертывающей функции с оптимизированными парамет-
параметрами, приведенными в тексте. Штриховая линия показывает огибающую максимумов.
Вычисления проведены Ф.Р. Швабом
Сферические функции. Молено использовать другие функции, обладающие необ-
необходимыми для свертки свойствами. В качестве меры оценки эффективности по-
подавления эффекта ложного сигнала Брау (Brouw, 1975) предложил следующую
величину:
f [ [C(/,rn)]2 dldm
A0.24)
и
dldm
равную доле интеграла от квадрата амплитуды спадающей функции, которая по-
попадает внутрь карты. Критерий выбора свертывающей функции состоит в поиске
максимума выражения A0.24). Такой подход привел к рассмотрению продольных
сферических волновых функций (см., например, Slepian and Pollack, 1961) и сфе-
сферических функций (Rhodes, 1970). Шваб (Schwab, 1984) обнаружил, что среди
функций, которые он исследовал, сферические являются наилучшим приближе-
приближением к оптимальной свертывающей функции. Сферические функции являются
решениями специальных дифференциальных уравнений и не выражаются в про-
простой аналитической форме. При использовании таких функций для свертки данных
функции видности они вычисляются заранее и представляются в виде справочной
таблицы. Сравнение некоторых функций этого типа с sine-гауссовой функцией по-
показывает, что коэффициент ложного сигнала С\{1)/ С\ [/(/)] падает так же быстро
от центра к краям карты, но по мере возрастания / вне карты его значения ста-
становятся на порядок или более ниже, чем у sine-гауссовой функции (Briggs, Sramek
and Schwab, 1999). Вычислительные возможности усложняют выбор оптимальной
10.2] Получение распределения видимой яркости из функции видности 359
функции, поскольку они ограничивают площадь плоскости гш, на которой может
быть осуществлена свертка. Обычно размер этой области составляет от шести до
восьми ячеек сетки с центром в точке интерполяции. Ошибки округления при пре-
преобразовании Фурье усиливаются при удалении спадающей функции, и это может
ограничить допустимый спад на краях карты.
10.2.5. Ложное изображение и отношение сигнал /шум. Ложные де-
детали, внесенные на карту под влиянием сигналов вне ее границ, включают не
только изображения деталей неба, но также и случайные вариации, возникающие
в результате шумов системы. Если мы рассмотрим прямое преобразование Фурье
шумовой компоненты функции видности, то, как следует из соотношения A0.7),
для любой точки (/,777,) данные функции видности взвешиваются комплексными
экспоненциальными коэффициентами, имеющими один и тот же модуль. Поскольку
шумы независимы для каждой точки в плоскости гш, дисперсия шумов в плоско-
плоскости 1т статистически постоянна по всей карте. Однако, если используется БПФ,
среднеквадратичный по всей карте уровень шума умножается на функцию СA,т),
и на карту извне попадают ложные детали. Отметим, что вклады от шумовых
составляющих входят в дисперсию аддитивно. Поэтому в одном случае дисперсия
шума как функция / пропорциональна
III(ZAiz)*|Ci(Z)|2. A0.25)
Дублирование в результате БПФ также может быть представлено в виде сум-
суммирования, тогда дисперсия шума в какой-либо точке / в пределах карты будет
пропорциональна
J2 \C1(l-\-iAu~1)\2. A0.26)
г= —оо
Обычно С\{1) убывает достаточно быстро с изменением /, поэтому лишь шум сосед-
соседнего дубля карты вносит существенный вклад через эффект ложного изображения.
Этот вклад наиболее значителен вблизи края карты, как показано на рис. 10.5
(Crane and Napier, 1989).
Если свертывающая функция имеет тип sine-гауссовой, то, как показано на
рис. 10.4 б, всюду, за исключением интервала значений 2Aul между 1,0 и 1,1,
ложные сигналы уменьшаются по амплитуде более чем в 10 раз, а по квадрату
амплитуды — более чем в 100 раз. Таким образом, увеличение уровня шума из-за
эффекта ложного изображения несущественно, за исключением узкой зоны вблизи
края карты.
В другом крайнем случае эффект ложного изображения наиболее значителен
при усреднении по ячейкам, когда С\(и) является sine-функцией, определяемой
уравнением A0.19). Соотношение A0.26) тогда приобретает вид
^> sin2 [тг(Аи1 + г)] _
- г)]2
откуда видно, что эффект ложного изображения полностью гасит спад, а дисперсия
шума не меняется по / даже до того, как к изображению применяется какая-
либо коррекция на спад. (Полученный результат также может быть выведен из
того, что при усреднении по ячейкам каждое измерение функции видности вносит
вклад только в один узел сетки, и, следовательно, шумовые компоненты функции
видности в узлах сетки являются независимыми.) Однако распределение яркости
360
Калибровка и преобразование Фурье функции видности
[Гл. 10
1,0
к
Q
&
1,0
о
1,0
1
2,0
1,0
Рис. 10.5. Воздействие эффекта ложного изображе-
изображения на дисперсию шума вдоль карты. По оси аб-
абсцисс в каждом случае отложены величины I в еди-
единицах половины ширины карты; центр карты соот-
соответствует 0, край — 1,0, а центр соседнего дубля —
2,0. а — сплошная кривая показывает спад для слу-
случая свертывающей функции Гаусса Ci, а штрихо-
штриховые кривые иллюстрируют эффект ложного изоб-
изображения; б — дисперсия шума, включающая ком-
компоненту, появившуюся из-за эффекта ложного изоб-
изображения, после коррекции на спадающую функцию
С\. Приведено по работе (Napier и Crane, 1982)
точника в этой точке определяется факторами,
неба в пределах картографиру-
картографируемого поля плавно убывает за
счет функции Ci(Z), коррекция
лее на этот спад ведет к воз-
возрастанию шума в направлении
краев карты. При выборе спа-
спада в виде sine-функции шум воз-
возрастает в тг/2 раз на краях кар-
карты по осям / и т и в (тг/2)
раз — в углах. В центре кар-
карты вклад из-за эффекта ложно-
ложного изображения возникает в уз-
узлах, для которых величина 2Aul
является четным целым числом
на графиках рис. 10.4, и в обо-
обоих изображенных случаях коэф-
коэффициент ложного изображения
Ci(l)/Ci [/(/)] падает до очень
малой величины. При использо-
использовании любой из рассмотренных
нами свертывающих функций не
наблюдается существенного уве-
увеличения шума в центре карты,
и отношение сигнал/шум для не-
нерассмотренными в разд. 6.2.
10.3. Соотношения замыкания
Эффекты замыкания представляют собой соотношения между значениями
функции видности для баз, формирующих замкнутую картину, например, треуголь-
треугольник или четырехугольник с антеннами в вершинах. Как было показано в выраже-
выражениях G.37) и G.38), выход коррелятора для антенной пары (га, п) может быть
записан в виде
Гтп = GmnVmn = #m#* Vmn, A0.28)
где Gmn — комплексный коэффициент усиления антенной пары, gm и дп — коэффи-
коэффициенты усиления индивидуальных антенн. Мы пренебрегаем теми членами коэффи-
коэффициента усиления, которые отсутствуют в выражениях для индивидуальных антенн
(см. п. 7.3.3). Рассматривая вначале фазовые соотношения, обозначим аргументы
комплексных величин rmn, gm, дпж Vmn как
Таким образом, можно записать
гтп, фдт, фдп
соответственно.
Фгтпп = Фдтп ~ Фдп + Фушп- A0.29)
Тогда соотношение фазового замыкания для трех антенн га, п и р имеет вид
¦ + Фгютп = Футпп +Фупю + Фургп- A0.30)
гпр
^vnp
Коэффициенты усиления антенны дш и дп, включают эффекты влияния пути,
пройденного в атмосфере, инструментальные эффекты, а поскольку эти члены
отсутствуют в уравнении A0.30), то, очевидно, что комбинация трех фаз выходов
коррелятора определяет наблюдаемую величину, которая зависит только от фазы
10.3] Соотношения замыкания 361
функции видности. Это свойство соотношения фазового замыкания было впервые
отмечено и использовано Дженнисоном (Jennison, 1958) в экспериментах, упомяну-
упомянутых в п. 1.3.7.
Если имеется па антенн и измеряется корреляция всех пар, то число независи-
независимых соотношений фазового замыкания равно числу выходных фаз коррелятора за
вычетом числа неизвестных инструментальных фаз, одна из которых может быть
произвольно выбрана. Если не имеется избыточного разнесения, каждое соотно-
соотношение замыкания дает разную информацию о структуре источника. Количество
соотношений замыкания равно
\ па К - 1) - К - 1) = i (па - 1) К - 2). A0.31)
Это число может быть также получено, если мы возьмем одну антенну и рассмотрим
количество разных групп из трех антенн, включающих данную. Каждая из этих
групп должна включать одну базу, не содержащуюся в любой другой группе так,
чтобы соотношения были независимыми.
В соотношение замыкания амплитуд входят четыре антенные пары, для фор-
формирования которых необходимы четыре антенны m, n, р и q:
\rpq\ | Утп 11 Урд | /-.q qo\
nP\\rnq\ \Vmp\\Vnq\ '
Доказательство соотношения A0.32) проводится подстановкой членов выражения
drndn^rnn B левую часть уравнения A0.32), с учетом выражения A0.28). Далее
сокращаются модули членов д. Имеются два независимых соотношения замыкания
для четырех антенн; второе может быть получено заменой индексов в числителе
(или знаменателе) уравнения A0.32) на mq и пр. Число независимых соотноше-
соотношений замыкания амплитуд для па антенн без избыточных баз равно количеству
измеренных амплитуд па (па — 1)/2 минус количество неизвестных коэффициентов
усиления антенн па, т. е.
2 Па (па ~ 1) - Па = - Па (Па - 3). A0.33)
На начальном этапе этот принцип использования отношений амплитуд наблюдае-
наблюдаемой функции видности применялся для исключения инструментальных коэффици-
коэффициентов усиления (Smith, 1952; Twiss, Carter and Little, 1960).
Отметим, что фундаментальные требования на обоснованность соотношений
замыкания заключаются в возможности представления пути от источника до корре-
коррелятора в виде одного члена комплексного коэффициента усиления в любой момент.
Поэтому атмосферные эффекты должны быть постоянны для наблюдаемого источ-
источника, т. е. угловой размер источника не должен превышать величины изопланарного
участка атмосферы. Изопланарным участком называется площадка на небе, внутри
которой падающие волны проходят в атмосфере одинаковый путь с точностью
до малой доли длины волны (см. также п. 11.9.2). Размер изопланарного участ-
участка меняется с частотой. На нескольких сотнях мегагерц или ниже в диаграмму
направленности антенны нередко попадает более одного источника, разнесенные
на угловое расстояние, достаточно большое для того, чтобы ионосферные условия
различались для этих источников. В этом случае использование принципов замы-
замыкания становится значительно более сложным, чем в рассмотренном выше случае
одиночного источника.
Оказывается, что соотношения замыкания очень важны для синтезного карто-
картографирования. В случае точечного источника замкнутая фаза должна равняться
362 Калибровка и преобразование Фурье функции видности [Гл. 10
нулю, а замкнутая амплитуда — единице. Таким образом, эти соотношения могут
быть использованы для проверки точности калибровки и контроля инструменталь-
инструментальных эффектов. В случае разрешенного источника они валены в ситуациях, когда
прямая калибровка по наблюдениям калибровочного источника не осуществима, что
происходит иногда в РСДБ-экспериментах. Что самое важное, они могут быть ис-
использованы для улучшения точности калибровки наблюдений, в которых требуется
получить высокий динамический диапазон, что обсуждается в разд. 11.5. Соотно-
Соотношения замыкания для амплитуд используются менее часто в силу того, что обычно
калибровка амплитуд функции видности проводится проще, чем калибровка фаз.
Тем не менее, они оказываются полезными, предоставляя возможность проверки
калибровки, когда требуется особо высокая точность измерений амплитуды.
10.4. Модельная аппроксимация
Согласование моделей распределения яркости с данными функции видности
очень широко практиковалось на ранних этапах развития интерферометрии, осо-
особенно в отсутствие хорошей калибровки фазы функции видности или достаточных
данных для осуществления преобразования Фурье. Примеры моделей показаны на
рисунках 1.5, 1.10 и 1.14. В отсутствие фазовой информации имеется неопреде-
неопределенность в 180° в определении позиционного угла модели. Однако при некоторых
обстоятельствах модельная аппроксимация обеспечивает преимущество при интер-
интерпретации интерферометрических данных, это происходит в следующих случаях:
• Интерпретация РСДБ-наблюдений с экстремальным угловым разрешением,
например, наблюдений с базой между Землей и космосом, когда гш-покрытие
может оказаться довольно бедным.
• Для определенных типов источников радиоизлучение может быть описано
с достаточной точностью в рамках физической модели, привлекающей только
небольшое количество параметров. В этих случаях, когда источник разрешен
только частично, параметры физической модели могут быть определены наи-
наилучшим образом при аппроксимации наблюдаемых величин непосредствен-
непосредственно моделью функции видности. Соответствующим случаем представляется
излучение протяженной звездной оболочки, связанное со звездным ветром.
Хорошим примером являются измерения Уайта и Бэккера (White and Becker,
1982) Р Cygni, для которых относительная амплитуда функции видности
составляла величину не менее ~0,35 на наибольших базах в эксперименте.
• Определение изменения параметров источника, когда наблюдения, разнесен-
разнесенные во времени, имеют разные покрытия плоскости uv. Результаты подгонки
одной и той же модели (при варьировании интересующих нас параметров)
к обоим наборам данных могут быть наилучшим свидетельством возможных
изменений. Интересный пример можно найти в работе (Masson, 1986), кото-
который измерял угловое расширение компактной планетарной туманности. Автор
имел несколько эпох наблюдений. Изображение, полученное в одну эпоху,
с наилучшим гш-покрытием использовалось как модель при подгонке данных
в остальные эпохи. Поэтому автор избежал прямого сравнения изображений,
полученных с разными синтезированными диаграммами направленности.
• Определение возможных ошибок измеренных параметров. Обработка нели-
нелинейными алгоритмами, в частности CLEAN (см. разд. 11.2), которые обычно
необходимы для максимального увеличения динамического диапазона, может
10.4] Модельная аппроксимация 363
привести к шуму в плоскости распределения интенсивности, характеристики
которого достаточно сложны. С другой стороны, при моделировании в плос-
плоскости uv шум обычно имеет гауссовую природу.
• Выбор начальных данных для восстановления изображения методом макси-
максимума энтропии и самокалибровки, описанным в гл. 11. Упрощенная модель —
обычно все, что нужно в данном случае.
10.4.1. Основные соотношения для модельной аппроксимации. Гаус-
Гауссовы функции весьма удобны в качестве составляющих модели распределения яр-
яркости источника. Они всегда положительны и плавно меняются в зависимости от
угла, что характерно для структур многих туманностей и радиогалактик. Функция
Гаусса с круговой симметрией, шириной на уровне половинной амплитуды \/81n2 a
и центром Gi, ?77,i) имеет вид
т п \ т \—(l — h) — (m — mi)\ /1ПО.ч
IG(l, m) = /о ехр -ь U А LL . A0.34)
L 2сг J
Соответствующая функция видности представляется выражением
VG(u,v) = \/2^сг/0 exp{-[27r2cr2(^2 + ?;2)+j27r(^/i+?;mi)]}. A0.35)
Функция видности имеет действительную и мнимую составляющие, подобные
гофрированной поверхности синусоидальной формы, гребни которой нормальны
к радиусу-вектору в точке (Zi,mi) в области распределения интенсивности. Эти
компоненты функции видности модулированы по амплитуде функцией Гаусса,
центр которой соответствует началу координат (u,v), а ширина обратно пропорци-
пропорциональна а. Изучение распределения функции видности позволяет, таким образом,
определить форму и положение основных компонент распределения интенсивности.
Обсуждение и примеры модельной аппроксимации такого типа приведены, напри-
например, в работах (Maltby and Moffet, 1962; Fomalont, 1968; Fomalont and Wright, 1974).
Рассмотрение связи между функцией видности и моментами распределения
интенсивности позволяет прояснить процедуру аппроксимации модели. В простом
одномерном случае функция видности может быть представлена в виде ряда Тей-
Тейлора
v(u) = v(o) + uV(o) + |у v"(o) + • • • + ^г v(n)(o) + • • • (ю.36)
Производные функции видности связаны с моментами распределения яркости сле-
следующим образом:
оо
[ nh{l)dl. A0.37)
Уравнение A0.37) следует из общего соотношения между производными функции
в начале координат и моментами ее фурье-образа (см., например, Bracewell, 2000).
Момент нулевого порядка равен плотности потока 5, моменты нечетных
порядков дают вклад в мнимые компоненты функции видности, а моменты четных
порядков — в ее действительную часть. Если источник симметричен по координате
/, нечетные члены равны нулю. Если, кроме того, источник разрешен лишь слабо,
уменьшение V происходит, в основном, из-за второго момента. Тогда источник
может быть представлен любой симметричной моделью с подходящим вторым
364 Калибровка и преобразование Фурье функции видности [Гл. 10
моментом (Moffet, 1962). Изучение функций видности для простых симметричных
моделей, показанных на рис. 1.5, указывает на то, что, практически, можно ис-
использовать любую из моделей, если функция видности не измерена от 1 до ~ 0,25.
Лучше всего различия обнаруживаются при исследовании темпа падения функции
с увеличением длины базы и амплитуды осцилляции, если таковая присутствует.
Обзор методов модельной аппроксимации дан в работе (Pearson, 1999). Сле-
Следующий шаг после выбора модели заключается в выборе функции, которая будет
оценивать качество подгонки. В предположении гауссовости ошибок (шума) в плос-
плоскости ш;, выразим правдоподобие модели через гауссовы члены:
П{ехр [-1 (%.^)-%.».;«ь..,»Р)|2| у A038)
1=1
где rid — количество независимых данных функции видности, М — фурье-образ
модели, имеющий р параметров с а± по ар, G{ — стандартное отклонение V(ui,Vi).
Максимизация правдоподобия эквивалента минимизации отрицательного логариф-
логарифма от A0.38), а именно минимизации
2 _ \^{V(ui,Vj) - M(ui,Vi]ai,..., ар)
х -2Д -
il
Здесь х2 имеет обычное статистическое определение (см., например, Taylor, 1982).
Так, для гауссовых ошибок, метод становится методом наименьших квадратов.
Отметим, что он может быть не применим в случае присутствия помех. Методы
расчета для наименьших квадратов обсуждаются в Приложении 12.1, также они мо-
могут быть найдены, например, в работе (Bevington and Robinson, 1992). Ожидаемый
минимум х2 равен п^ — р, а стандартное отклонение %2, соответственно, л/Щп^—р).
Если измеренная функция видности прокалибрована недостаточно хорошо, вместо
индивидуальных значений при моделировании функции видности могут быть ис-
использованы замкнутые величины фазы и/или амплитуды.
10.4.2. Анизотропия космического фона. При исследовании анизотропии
реликтового излучения, например, при помощи решетки типа представленной на
рис. 5.24, задача состоит в определении статистических свойств угловых вариаций
яркостной температуры. Это может быть получено напрямую из данных функции
видности без создания карт распределения яркости по небу. Требования на привле-
привлекаемую статистику полностью определяются амплитудами сферических гармоник,
в которых могут быть представлены вариации реликтового фона. Для сферических
гармоник порядка ? амплитуда пропорциональна функции видности V(u,v), где
? = 2тг\/и2 + v2 . Поэтому покрытие плоскости uv определяет интервал значений
?, который может быть изучен. Расширение измерений по нескольким областям,
смежным первичной диаграмме направленности, как при мозаичных наблюдениях
(см. разд. 11.6), увеличивает пространственное разрешение по и и v и, следователь-
следовательно, также разрешение гармонических амплитуд по ?. Основная проблема связана
с удалением компонент яркости, присутствующих из-за объектов «переднего пла-
плана», таких как Галактика и дискретные радиоисточники (см., например, White et
al., 1999).
10.5] Наблюдения спектральных линий 365
10.5. Наблюдения спектральных линий
10.5.1. Общие соображения. Коррелятор радиоспректроскопических на-
наблюдений проводит измерения во многих точках полосы пропускания приемни-
приемника, и для каждой из этих точек могут быть получены различные распределения
интенсивности. Обработка радиоспректроскопических данных принципиально не
отличается от процедуры получения изображения в континууме, но на практике
имеются некоторые различия. Число каналов, по которым делится полученный
сигнал, обычно равно 100-1000. Содержание данного раздела основано, главным
образом, на работах (Ekers and van Gorkom, 1984; van Gorkom and Ekers, 1989).
Калибровка отклика инструментальной полосы пропускания, возможно, — са-
самый важный шаг в получении точных радиоспектроскопических данных. Обычно
различия между каналами относительно стабильны во времени и не требуют та-
такой частой калибровки, как переменные во времени эффекты полного усиления
приемника. Изменения коэффициента полного усиления требуют периодических
наблюдений опорного источника, как это описано для наблюдений в континууме.
Для этого часто используется суммарный отклик отдельных каналов, так как для
получения достаточного уровня отношения сигнала к шуму в каждом узком канале
понадобилось бы много больше наблюдательного времени. Для калибровки полосы
пропускания можно провести более длительное наблюдение опорного источника,
чтобы определить относительные коэффициенты усиления спектральных каналов.
Поскольку относительные коэффициенты усиления разных каналов, на которые
делится полоса пропускания, очень слабо меняются со временем, провести калиб-
калибровку полосы пропускания нужно лишь один или два раза в течение, например,
восьмичасовых наблюдений. Опорный источник, используемый для калибровки
полосы пропускания, должен быть неразрешенным, достаточно сильным для хоро-
хорошего отношения сигнал/шум в спектральных каналах и должен иметь достаточно
плоский спектр. Однако, нет необходимости в том, чтобы он был расположен на
небе близко к картографируемому источнику.
Осцилляции полосы пропускания, возникающие из-за наличия стоячих волн
между облучателем и отражателем антенны и являющиеся серьезной проблемой
для систем одиночных антенн полной мощности, значительно менее важны
для интерферометров. Это происходит потому, что инструментальный шум,
включая собранный боковыми лепестками тепловой шум, не коррелирован
между антеннами. С другой стороны, для цифровых корреляторов осцилляции
в полосе пропускания, возникающие из-за явления Гиббса в преобразовании
Фурье от задержек к частотам, представляют проблему, отсутствующую
в автокорреляторах. Поскольку кросс-корреляция сигналов от двух антенн
является действительной, но не симметричной функцией задержки, кросс-
корреляционный спектр мощности является комплексной функцией частоты.
(Автокорреляционная функция сигнала от одиночной антенны — действительная
и симметричная, и автокорреляционный спектр мощности — действительная
функция.) Как объясняется в разд. 8.7 (см. рис. 8.12), мнимая часть кросс-
корреляционного спектра мощности меняет знак в начале координат, а действи-
действительная часть — нет. Из-за этого значительного разрыва по частоте в начале
координат, осцилляции мнимой части спектра по частоте имеют большую
относительную амплитуду, чем осцилляции действительной части. Максимальный
провал мнимой части составляет 18% (9% от полного размера ступеньки); см.
также (Bos, 1954, 1955). На рис. 10.6 показан рассчитанный пример. Отношение
действительной к мнимой части зависит от инструментальной фазы (которая не
366
Калибровка и преобразование Фурье функции видности
[Гл. 10
прокалибрована на данной стадии анализа) и от положения источника излучения
по отношению к фазовому центру поля.
Re
Re
Ьп
Ьп
Рис. 10.6. а — кросс-корреляционный спектр мощности, получающийся от протяженного
источника непрерывного излучения, в котором фаза выбрана произвольно так, чтобы
амплитуды действительной и мнимой частей были равны, б — рассчитанный отклик на
спектр а кросс-коррелятора с 16 каналами. Заметьте разницу осциляций по амплитуде
у мнимой и действительной частей. Приведено здесь из работы (D'Addario, 1989) с разре-
разрешения Astron. Soc. Pacific Conf. Ser.
Увеличение числа задержек запаздывающего коррелятора, или размера БПФ
в FX-корреляторе, улучшает спектральное разрешение и ограничивает появле-
появление осцилляции, возникающих из-за явления Гиббса, областями, более близкими
к краям полосы пропускания. Данные, поступающие из каналов на краях полосы,
часто отбрасываются из-за осцилляции и спада частотного отклика. Эффективным
способом уменьшения амплитуды осциляций является введение плавного спада
для кросс-корреляционной функции, из-за чего происходит сглаживание кросс-
корреляционного спектра мощности. Для этого сглаживания часто используется
функция Ханнинга (см. табл. 8.4). Ван Горком и Экере (Van Gorkom and Ekers,
1989) обратили внимание на следующие примеры.
1. Если поле содержит источник радиолинии без континуума и эта радиолиния
находится в центральной части полосы пропускания, то у спектра нет разры-
разрывов на краях полосы пропускания. Это единственный случай, когда для карто-
картографируемого и опорного источников с непрерывным спектром целесообраз-
целесообразно использовать разные функции плавного спада для кросс-корреляционной
функции.
2. Если вместе с источником радиолинии поле содержит один точечный источник
непрерывного спектра, и если этот точечный источник и опорный источник
с непрерывным спектром находятся в центрах своих полей, тогда возможна
точная калибровка пульсаций полосы пропускания.
3. В более сложных случаях, например, когда поле содержит источник радиоли-
радиолинии и протяженный источник непрерывного спектра, пульсации будут разны-
разными для этих двух источников, и точная калибровка невозможна. Тогда реко-
рекомендуется применять сглаживание Ханнинга для спектров обоих источников,
картографируемого и опорного.
10.5] Наблюдения спектральных линий 367
10.5.2. РСДБ-наблюдения спектральных линий. Поскольку РСДБ-наб-
людения ограничены источниками с очень высокой яркостной температурой, радио-
радиоспектроскопия линий в РСДБ проводится, в основном, для исследования мазеров
и поглощения молекулярными облаками излучения от ярких внегалактических
источников. Наблюдаемыми мазерными радиолиниями часто являются линии мо-
молекул ОН, Н2О, СНзОН и SiO. Для исследования поглощения может наблюдаться
много типов атомов и молекул, так как выполнение условия на величину яркост-
яркостной температуры обеспечивается фоновым источником. Техника обработки сигнала
радиолинии описана в разд. 9.3. В разд. 12.5 особо рассмотрены астрометрические
измерения. В настоящем разделе мы обсудим несколько проблем практического тол-
толка, связанных с обработкой спектральных данных в радиодиапазоне. Использование
на антеннах независимых стандартов частоты приводит к зависящим от времени
ошибкам синхронизации, из-за которых происходит наклон фазы внутри полосы.
Разница между доплеровскими сдвигами разных антенн может быть значительна,
и, следовательно, остаточная частота интерференции также может быть велика, что
неизбежно повлечет за собой короткие времена интегрирования для калибровки.
Для мазеров фазовая калибровка может быть проведена по отдельной спектральной
детали в качестве опорной. Амплитудная калибровка может быть получена из изме-
измерений спектров на индивидуальных антеннах. Дальнейшие подробности процедуры
обработки данных радиоспектроскопии можно найти в (Reid, 1995, 1999).
В спектральном РСДБ-эксперименте опорный компактный источник непрерыв-
непрерывного спектра наблюдается, обычно, несколько раз в час, источник выбирается
предпочтительно достаточно сильным для точного измерения интерференционных
лепестков за одну или две минуты интегрирования. Если для кросс-корреляции сиг-
сигналов используется коррелятор с задержками, на выходе имеем функцию времени
и задержки. Уравнение (9.16), в котором Arg и #21 — функции времени, дает кросс-
корреляцию как функцию времени и задержки. В результате преобразования Фурье
аргументы t и т могут быть заменены на соответствующие сопряженные перемен-
переменные, — частоту интерференции Vj и частоту спектральной детали v. Таким образом,
выход коррелятора может быть выражен в виде функций от (?, г), (z//, r), (?, у) или
(z/f,z/), которые взаимозаменяются в разных плоскостях переменных посредством
преобразования Фурье. Это важно, так как некоторые этапы калибровки выполня-
выполняются наилучшим образом для особых переменных. Заметим, что частота интерфе-
интерференции в РСДБ-наблюдениях получается, в основном, из разницы между истинной
частотой интерференции и модельной, используемой для остановки интерференци-
интерференционных лепестков. Рассмотрим сначала данные, полученные от опорного источника
с непрерывным спектром. При подгонке лепестков для источника с непрерывным
спектром выгодно использовать данные функции видности в виде функции от ча-
частоты интерференции Vj и задержки т, как показано на рис. 9.4. В этих переменных
данные функции видности наиболее компактно сосредоточены и поэтому наиболее
простым образом отождествляются в присутствии шума. При отсутствии ошибок
функция видности будет сконцентрирована на начале координат в плоскости VfT.
Сдвиг от начала координат по координате г означает наличие ошибок синхрони-
синхронизации из-за расхождения часов или из-за ошибок, связанных с базами. Сдвиг Ат
представляет собой разницу ошибок для двух антенн. Величины Ат, определенные
из наблюдений опорного источника, используются для поправок к спектральным
данным. Изменение величин Аг со временем ведет к необходимости интерполяции
на время наблюдения радиоспектроскопии. Данные континуума также могут быть
использованы для калибровки полосы пропускания, для определения относитель-
относительных амплитудной и фазовой характеристик спектральных каналов.
368 Калибровка и преобразование Фурье функции видности [Гл. 10
Для подгонки интерференционных лепестков спектральных данных выгодно
перейти к переменным (?, г/), так как, в отличие от данных с непрерывным спектром,
спектральные данные имеют узкополосные детали. Поэтому кросс-корреляционная
функция соответствующим образом расширена по координате задержки и, в общем
случае, более сжата по частоте. Заметим, что в преобразовании от г к v переменная
v — это не частота излучения, принимаемая антенной, потому что частота гетеро-
гетеродина (или комбинации гетеродинов) г/ьо была вычтена. Таким образом, здесь v
представляет собой частоту внутри ПЧ-полосы, которая собрана и записана для
передачи на коррелятор. Плоскость переменных tv тоже подходит для внесения
поправок на ошибки синхронизации Дт, оцениваемые из данных с непрерывным
спектром. Эти поправки производятся путем введения фазовых сдвигов, которые
пропорциональны частоте. Поэтому данные в виде функции переменных (?, v) до-
множаются на exp (j 2тг Дтг/) 1). Если изменение величин At со временем проис-
происходит из-за ошибок хода часов на одной или на обеих антеннах, то должна быть
внесена поправка на соответствующую ошибку в частоте г/ьо на антеннах. Резуль-
Результирующая ошибка в фазе исправляется путем перемножения выходных данных
коррелятора на exp (j 2тг Дтг/ьо).
Поскольку поправки на доплеровское смещение (см. Приложение 10.2) редко
вводятся в виде сдвигов локальных осцилляторов на антеннах, то эти поправки
должны быть внесены на корреляторе или после обработки анализа полученных
данных. Суточный Доплеровский сдвиг обычно устраняется на станции докор-
реляционным вращением лепестков, когда сигналы запаздывают и сдвинуты по
частоте по отношению к центру Земли. Поправки на доплеровское смещение из-за
орбитального движения Земли и местного стандартного покоя, так же, как любой
другой частотный сдвиг, могут быть внесены подходящим образом после прове-
проведения корреляции. При этом используется теорема сдвига, т. е. корреляционная
функция домножается на exp (j 2тг Дг/т), где Av — величина необходимого полного
смещения по частоте.
Спектры функции видности могут быть прокалиброваны в единицах плотности
потока путем перемножения нормированных спектров функции видности и средне-
среднего геометрического от эквивалентных плотностей потока системы (SEFD) двух рас-
рассматриваемых антенн, как это обсуждается в п. 10.1.2. SEFD определен в уравнении
A.6). Он может быть получен из случающихся время от времени дополнительных
измерений на антеннах, а результаты могут быть проинтерполированы во времени.
Для сильных источников лучшим методом является расчет автокорреляционного
спектра мощности источника с использованием автокорреляционных функций для
данных, полученных на каждой антенне. Эти данные должны быть исправлены
с учетом отклика полосы пропускания, который может быть получен из авто-
автокорреляционных функций отклика на калибратор интерференционных лепестков
(источник непрерывного спектра). Амплитуда отдельной спектральной особенности
обратно пропорциональна величине SEFD. Если необходима большая чувствитель-
чувствительность, тогда каждый измеренный спектр может быть сопоставлен со спектральным
шаблоном, полученным из общего усреднения всех данных одиночных антенн или
из спектра, полученного на наиболее чувствительной антенне решетки. Неудобство
данного метода состоит в том, что только в редких экспериментах оказывается
возможным измерять характеристики полосы пропускания настолько часто, чтобы
гарантировать достаточную точность вычитания подложки для слабых источников.
) Отметим, что необходимый знак в экспоненте в этом и аналогичных выражениях, ис-
используемых в данном подразделе книги, может быть положительным или отрицательным
в зависимости от других принятых соглашений по поводу знаков.
10.5] Наблюдения спектральных линий 369
Если полная ширина полосы при измерениях набирается с помошью двух или
более ПЧ-полос приемной системы, тогда необходимо ввести поправку на разницу
в их инструментальных фазовых откликах. Это может быть сделано с привлечением
измерений опорного источника с непрерывным спектром, усредняя величины фаз
для разных каналов в каждой ПЧ-полосе, и вычитая эти средние величины из
соответствующих спектральных данных функции видности.
В заключение необходимо внести поправку на оставшиеся инструментальные
фазы и на различные атмосферные и ионосферные сдвиги фазы, которые могут
быть значительны для далеко разнесенных пунктов. При картографировании силь-
сильных источников с непрерывным спектром на этом этапе могут быть использованы
фазовые замыкания, как это описано в разд. 10.3. Аналогичный подход может быть
применен при картографировании распределения точечных мазерных источников
путем выбора сильного спектрального компонента, видимого со всех баз, пред-
предполагая, что он представляет собой одиночный точечный источник. Тогда, если
положить равной нулю фазу этого компонента на одной произвольно выбранной
антенне, относительные фазы для других антенн могут быть вычислены из фазы
интерференции. Поскольку эти фазы относятся на счет атмосферы над каждой
антенной, поправки могут быть внесены для каждого частотного компонента вну-
внутри измеренного спектра. Этот метод использования одного мазерного компонента
как фазового репера более подробно обсуждается в разд. 12.5, где рассматривается
картографирование методом частоты интерференции для определения положений
основных компонент на большом поле мазеров.
10.5.3. Изменение пространственной частоты по ширине полосы. Вли-
Влияние использования центральной частоты полосы пропускания приемника при
расчете величин и и v для всех частот внутри полосы обсуждается в разд. 6.3.
Рассмотрим, например, одиночный дискретный источник, для которого функция
видности имеет максимум в начале координат плоскости uv и монотонно убывает
в области увеличивающихся значений и и v. Если мы используем величину z/q
(частота в центре полосы) для расчета и и v па, верхнем краю полосы г/, т. е. v > z/q,
тогда величины и и v будут недооценены. Измеренная функция видности будет
спадать слишком быстро по и и v и центральный пик функции видности будет
слишком узким. Поэтому ширина изображения по / и т будет слишком большая.
Таким образом, если источник излучает радиолинию на голубом крыле полосы, его
угловые размеры могут быть переоценены, и наоборот, недооценены на красном
краю полосы. Этот эффект называется хроматической аберрацией.
Как сказано в разд. 6.3, при наблюдениях с радиоспектрометрическим (мно-
(многоканальным) коррелятором функция видности, измеренная для каждого канала,
может быть представлена как функция величин (u,v) соответственно частоте дан-
данного канала. Это исправляет хроматическую аберрацию, но приводит к увеличению
(щ v)-диапазона, внутри которого измеряется функция видности, пропорционально
частоте. Таким образом, ширина синтезированной диаграммы направленности (т. е.
угловое разрешение) и характерная ширина боковых лепестков меняются внутри
полосы. При необходимости можно скорректировать вариацию разрешения обреза-
обрезанием или введением плавного спада функции видности для уменьшения разреше-
разрешения до величины, соответствующей самой низкой частоте в полосе пропускания.
10.5.4. Точность наблюдений спектральных линий. Спектральный ди-
динамический диапазон карты после окончательной калибровки — это оценка точ-
точности наблюдений спектральных деталей, выраженная в долях амплитуды макси-
максимального сигнала. Она может быть определена как изменение отклика различных
370 Калибровка и преобразование Фурье функции видности [Гл. 10
каналов на сигнал с непрерывным спектром, деленное на величину максималь-
максимального отклика. Вариация отклика отдельного канала является результатом шума
и инструментальных ошибок. Когда амплитуда спектральной линии составляет
лишь несколько процентов от амплитуды имеющегося непрерывного спектра, как
в случае рекомбинационных линий или слабых линий поглощения, точность из-
измерения особенностей спектральной линии зависит от точности, с которой отклик
на непрерывный спектр может быть отделен от отклика на линию. В таком случае
для измерения профиля линии с точностью 10 % необходим динамический диапазон
порядка 103. Этим определяется важность точной калибровки полосы пропускания
и поправок на хроматическую аберрацию.
Для вычитания из карты отклика на излучение в непрерывном спектре использо-
использовались различные методики. Необходимо выбрать такую ширину полосы приемни-
приемника, чтобы она содержала несколько каналов, регистрирующих только непрерывный
спектр, с частотами, лежащими с любой стороны от спектральной детали. Прямой
метод заключается в использовании среднего канала без спектральных линий для
построения карты излучения в непрерывном излучении и вычитания этой карты
из карт, полученных в каждом канале, регистрирующем излучение спектральной
линии. Если ширина полосы приемника не достаточно мала по сравнению с цен-
центральной частотой, то, вероятно, при получении карты излучения о непрерывном
излучении должна быть внесена поправка на хроматическую аберрацию. Если
непрерывное излучение исходит от точечных источников, то оно моделируется поло-
положениями и плотностями потоков этих источников. Для наиболее точного вычитания
отклик на непрерывное излучение должен рассчитываться отдельно для каждого
канала при использовании частот индивидуальных каналов для определения ве-
величин (u,v). Вычитание должно производиться для данных функции видности.
Использование восстанавливающих алгоритмов для вычитания континуума кратко
описано в п. 11.9.1.
10.5.5. Представление и анализ наблюдений спектральных линий.
Спектральные данные могут быть представлены как трехмерные распределения
пикселей в пространстве Imv. Доплеровское смещение часто переводится из раз-
размерности частоты в размерность радиальной скорости vr по отношению к частоте
линии покоя для физической интерпретации. Связь между частотой и скоростью
приведена в Приложении 10.2. Модель такого трехмерного распределения показана
на рис. 10.7. Источники с непрерывным спектром представлены в виде цилиндри-
цилиндрических функций с сечениями по / и т.
Куб трехмерных данных, содержащий карты для индивидуальных каналов, мо-
может рассматриваться как демонстрация профилей линий каждого элемента в дву-
двумерном пространстве 1т. Чтобы упростить набор карт, часто бывает полезно по-
построить одну карту в плоскости 1т для какой-то характерной детали профиля
линии. Это может быть сделано также и для интегральной интенсивности
A0.40)
где г — номера спектральных каналов, которые разнесены по частоте интервалами
Az/. Для оптически тонкой излучающей среды, такой как нейтральный водород,
величина A0.40) пропорциональна лучевой концентрации излучающих атомов или
молекул. Взвешенная по интенсивности средняя скорость является мерой макро-
макроскопических движений,
10.5]
Наблюдения спектральных линий
371
A0.41)
Взвешенная по интенсивности дисперсия скорости
A0.42)
О
является мерой случайных движений
внутри источника. Суммирование по
скоростям проводится раздельно для
каждого элемента (Z,m) карты. В каж-
каждой из трех величин A0.40)-A0.42) ин-
интенсивность соответствует конкретной
рассматриваемой линии, после вычита-
вычитания непрерывного спектра. Для полу-
получении наилучшей оценки этих трех ве-
величин необходимо помнить следующее.
Включение в окончательный резуль-
результат данных для тех диапазонов значе-
значений (/, т, г>г), которые не содержат раз-
различаемого излучения, только добавит
шум.
Изучение зависимостей между
трехмерными изображениями в про-
пространстве lmvr и трехмерным рас-
распределением излучающего вещества
имеет астрономическое значение. В
качестве простого примера рассмотрим
сферическую оболочку излучающего
вещества. Если вещество находится в
состоянии покоя, в пространстве lmvr
появится круглый диск в плоскости
с нулевым значением скорости, с
уярчением на внешнем крае. Если
оболочка расширяется во все стороны с
одинаковой скоростью, в пространстве
lmvr получится полая эллиптическая
или, при подходящей подгонке шкалы
скоростей, сферическая оболочка. Ин-
Интерпретация наблюдений вращаю-
вращающихся спиральных галактик является
более сложной задачей. Пример модели галактики дан в работе (Roelfsema, 1989),
более широкое обсуждение приводится в (Burton, 1988).
Прямое
восхождение /(RA)
Рис. 10.7. Трехмерное представление дан-
данных наблюдений спектральных линий
по прямому восхождению, склонению
и частоте. Ось частоты проградуирована
значениями скорости, соответствующей
доплеровскому смещению частоты линии
покоя. Плотность потока или интенсивность
излучения не показана, но может быть
изображена цветом или штриховкой.
Указанная скорость не имеет физического
смысла для источников с непрерывным
спектром, которые показаны цилиндрами
с сечениями перпендикулярно оси скорости.
Излучение в спектральных линиях показано
изменением положения или интенсивности
со скоростью. Приведено по работе
(Roelfsema, 1989) с разрешения Astron.
Soc. Pacific Conf. Ser.
372 Калибровка и преобразование Фурье функции видности [Гл. 10
10.6. Другие соображения
10.6.1. Интерпретация видимой интенсивности. Величиной, измеряемой
на синтезированной карте, является радиоинтенсивность, но обычно V калибрует-
калибруется в единицах эквивалентной плотности потока точечного источника, а единицей
интенсивности результирующей карты является плотность потока в телесном угле
главного лепестка диаграммы направленности Г^о:
П0= [[ У'"*)*<*" A0.43)
V 1 — Р — т2
главный
лепесток
Отклик на протяженный источник представляет собой свертку яркости неба /(/, т)
с синтезированной диаграммой направленности bo(l,m). Отметим, что, поскольку
измеренное значение функции видности в начале координат (u,v) обычно отсут-
отсутствует, интеграл Ъ${1,т) по всем углам равен нулю, т. е. отсутствует отклик на од-
однородный уровень яркости. В любой точке протяженного источника, где его яркость
меняется медленно по сравнению с шириной синтезированной диаграммы, свертка
ЬоA,т) дает плотность потока, приблизительно равную 10,$. Таким образом, вели-
величина, приведенная на карте, по своей размерности также может интерпретировать-
интерпретироваться как интенсивность, измеренная в единицах плотности потока на телесный угол
главного лепестка диаграммы направленности Г?о • Картографирование источников
большого углового размера и измерения интенсивности излучения протяженных
компонент на низких пространственных частотах обсуждаются в разд. 11.6.
10.6.2. Ошибки на картах. Очень полезная методика исследования сомни-
сомнительных или необычных деталей любого синтезированного изображения, получен-
полученного как для непрерывного спектра, так и для спектральной линии, заключается
в проведении обратного преобразования Фурье (т. е. переходе от распределения
интенсивности к функции видности) только данной детали. На инструментальные
эффекты может указывать получение зависимости, при которой данные сосредото-
сосредоточены в плоскости uv только одной одиночной базы или наборе баз с одной общей
антенной. Распределение остаточных (только для данной детали) данных функции
видности, соответствующее определенному интервалу часовых углов источника,
может указывать на наличие случайной помехи.
Информация о поведении фурье-образов весьма существенна для распознавания
ложных деталей (см., например, (Bracewell, 2000) и обсуждение в работе (Ekers,
1999)). Постоянная ошибка, возникающая в одной антенной паре, расположенной по
линии восток—запад, будет распределена по эллипсу с центром в начале координат
(u,v), а в плоскости 1т она приведет к появлению эллиптической детали с ради-
радиальным профилем в виде функции Бесселя нулевого порядка. Кратковременная
ошибка, произошедшая на одной базе, проявляется как две дельта-функции, пред-
представляющие собой результат измерения и сопряженную ему величину. На карте
это проявляется как синусоидальный гофр в плоскости 1т. Амплитуда ошибки
в плоскости карты мала, поскольку в матрице функции видности, состоящей из
М х N точек, влияние двух ошибочных точек ослабляется в 2(M7V)~1 раз, что
обычно соответствует множителю порядка 10 ~3 — 10~6. Таким образом, единичной
кратковременной ошибкой можно полностью пренебречь, если она мала по сравне-
сравнению с шумом карты.
Аддитивные ошибки складываются со значениями истинной функции видности.
На карте фурье-образ распределения ошибок ?add(^> v) складывается с распределе-
распределением интенсивности, и мы получаем
V(u, v) + sadd{u, v) ^ /(/, m) + eadd(/, m)- A0.44)
10.6] Другие соображения 373
Аддитивные ошибки других типов возникают из-за помех, перекрестной связи
шумов системы между антеннами и ошибки задержки в корреляторе. Солнце по
яркости на много порядков превосходит другие радиоисточники и в силу своего
суточного движения создает помехи, отличающиеся по своим характеристикам от
помех, создаваемых земными источниками. Отклик на Солнце определяется в ос-
основном боковыми лепестками диаграммы направленности, различием частот ин-
интерференции для Солнца и источника, шириной полосы пропускания и эффектами
усреднения функции видности. Наиболее неприятные помехи от Солнца возника-
возникают на решетках с низким разрешением и небольшой шириной полосы. Взаимные
помехи (перекрестные наводки) возникают лишь между близко расположенными
антеннами и особенно значительны при низких углах места, когда происходит
взаимное затенение антенн.
Ко второму типу ошибок относятся те, которые комбинируются с функцией
видности путем перемножения:
V(u, v) emui(u, v) ^ /(/, га) * * emui(/, ra). A0.45)
Фурье-преобразование распределения ошибок свертывается с распределением ин-
интенсивности, и в результате искажений создается ложная структура, связанная
с основными деталями карты. В противоположность этому случаю распределе-
распределение ошибок аддитивного типа не связано с истинным распределением яркости.
Мультипликативные ошибки, в основном, свойственны постоянным коэффициентам
усиления антенн и появляются в результате ошибок калибровки, включая ошибки
наведения, и помех в случае РСДБ систем (см. разд. 15.3).
Искажения, растущие с расстоянием от центра карты, относятся к ошибкам
третьего типа. Сюда входят эффекты, связанные с некомпланарностью баз (см.
разделы 3.1 и 11.8), шириной полосы пропускания (см. разд. 6.3) и усреднением
функции видности (см. разд. 6.4). Эти эффекты предсказуемы и, следовательно,
по своей природе несколько отличаются от других искажений, упомянутых выше.
10.6.3. Некоторые замечания по планированию и обработке данных
наблюдений. Наилучшее использование синтезированных решеток и аналогич-
аналогичных инструментов требует эмпирического подхода в некоторых областях, и выбор
оптимальной методики анализа данных часто исходит из опыта. Много полезной
информации можно найти в руководствах по конкретным инструментам, трудах
конференций и т.д. (см., например, Bridle, 1989). Несколько примеров рассматри-
рассматриваются ниже.
При выборе ширины полосы пропускания для наблюдений непрерывного излуче-
излучения нужно рассмотреть радиальное размытие, так как отношение сигнал/шум для
точечного источника вблизи края поля не обязательно становится максимальным
при увеличении ширины полосы. Далее, при выборе времени усреднения данных
результирующее размытие по окружности может быть примерно равным ради-
радиальному эффекту. Необходимое условие получается из соотношений F.75) и F.80)
и для больших склонений имеет вид
— с* шета. A0.46)
Здесь щ — центральная частота наблюдаемой полосы пропускания, Дг/ — ширина
полосы, иое — скорость вращения Земли, а та — время усреднения. Когда пред-
предпринимаются попытки обнаружить слабый источник с поддающимся измерению
угловым диаметром или найти излучение протяженного фона, то важно наблюдать
с не слишком высоким угловым разрешением. Как уже отмечалось в предыду-
предыдущем разделе, отношение сигнал/шум для протяженного источника приблизительно
374 Калибровка и преобразование Фурье функции видности [Гл. 10
пропорционально IQq. Время наблюдения, необходимое для получения заданного
0^
д
отношения сигнал /шум, пропорционально Qq или 0^ , где въ — ширина синтези-
синтезированной диаграммы.
Если в диаграмму направленности антенны попадает источник, намного более
сильный, чем изучаемые детали, то отклик на этот источник можно либо вычесть,
если источник точечный, либо точно смоделировать. Это лучше всего осуществля-
осуществляется путем вычитания рассчитанной функции видности перед оценкой значений из-
измеренной величины в узлах сетки в методе БПФ. Тогда эффект боковых лепестков
синтезированной диаграммы будет корректно исключен из отклика. Тем не менее,
точность снизится, если отклик на источник испытывает значительное воздействие
эффектов ширины полосы пропускания, усреднения функции видности и аналогич-
аналогичных эффектов. Возможно, лучшим выходом будет поместить вычитаемый источник
в центр поля.
При наблюдении очень слабого источника может оказаться целесообразным
сдвинуть его от начала координат G, т) на расстояние, равное нескольким ширинам
диаграммы, чтобы избежать путаницы с остаточными ошибками из-за коррелятор-
ных сдвигов. Опыт работы с конкретными инструментами покажет, есть ли в этом
необходимость.
Полезным шагом в процедуре получения любой карты также оказывается по-
построение карты с низким разрешением, покрывающей всю область главного ле-
лепестка диаграммы направленности антенны. Для построения такой карты дан-
данные могут быть существенно исправлены плавным спадом в плоскости uv с це-
целью уменьшения разрешения и, следовательно, объема вычислений. Такая карта
позволит обнаружить любые источники вне поля окончательной карты, которые
могут вносить искажения за счет эффекта ложного изображения в методе БПФ.
Эффект ложного изображения от таких источников может быть подавлен путем
вычитания их функции видности или использования подходящей свертывающей
функции. Отклики боковых или кольцевых лепестков на такие источники также
исключаются путем вычитания этих источников, но не за счет свертки в плоскости
uv. Карта с низким разрешением будет также подчеркивать любые протяженные
детали малой яркости, которые иначе могли бы быть пропущены.
Приложение 10.1. Использование края Луны в качестве
опорного источника
При проведении тестовых сеансов на интерферометре, который вводится в экс-
эксплуатацию, полезно наблюдать источники, дающие лепестки с большим отношени-
отношением сигнал/шум. На частотах более ~100ГГц таких источников немного. Солнце,
Луна и планеты, диски которых разрешаются лепестками интерферометра, тем не
менее, имеют значительную коррелированную плотность потока благодаря их рез-
резким краям. Рассмотрим лимб Луны и случай, когда главный лепесток диаграммы
направленности элементов интерферометра имеет размер значительно меньше 3(У
(лунный диаметр). Когда антенна следит за лимбом Луны, видимое распределение
интенсивности по источнику равно диаграмме направленности антенны, помножен-
помноженной на ступенчатую функцию; мы принимаем здесь, что яркостная температура
Луны не меняется в пределах главного луча диаграммы. Аппроксимируя диа-
диаграмму направленности антенны гауссовой функцией, предположим, что антенна
направлена на западный лимб Луны, а также опустим кривизну лунного лимба.
Тогда эффективное распределение интенсивности по источнику можно выразить
10.6] Приложение 10.1. Использование края Луны в качестве опорного источника 375
в виде
О, х < О,
где х и у — угловые координаты с началом координат на оси диаграммы направ-
направленности, 0ъ — полная ширина диаграммы направленности на уровне половинной
мощности, а /о = 2кТт/Х2 (приближение Рэлея-Джинса), где Тш — температура
Луны. Функция видности тогда будет иметь вид
о
2 2 1
Ы2)х2/в* (cos2ttux - j sm27rux) dx\ x
J
1
-4 (in 2)y*/el CQS 2wvy dy _ (niO.2)
x I j e
о
Интеграл с косинусом берется просто, а интеграл с синусом может быть записан че-
через вырожденную гипергеометрическую функцию \F\ (см. Gradshteyn and Ryzhik,
1994, уравнение 3.896.3). Тогда получим
V(u, v) = I0S0 e-*-W+v)/4 «h j^_^_ (9ъи) iFi I t, 1, ^_ 1 , (ПЮ.З)
где величина
= ккттвъ (П10.4)
4A2ln2 V J
является плотностью потока излучения Луны, попадающей в половину диаграммы
направленности гауссовой формы.
В пределе (и, v) ^> @,0), мнимая часть функции видности равна нулю,
a V(u, v) = So, как и ожидалось. Для Тш = 200 К и 0ъ = 1,2А/с/, где d —
диаметр антенн интерферометра в метрах, So — 460 ООО/сР Ян. Интеграл по х
в выражении (П10.2) может быть также записан с помощью функции ошибок.
В пределе, когда и ^> d/А, асимптотическое поведение функции ошибок приводит
к удобной аппроксимации:
V(u, v = 0) = jJj^r- — - j 0,41 ^^ , (П10.5)
где D — длина вектора базы.
Мы наблюдаем интересную особенность: функция видности для данной величи-
величины базы увеличивается при уменьшении диаметра антенны, пока 0ъ <С 30'. Аппрок-
Аппроксимация в выражении (П10.5) имеет точность до 2 % при D > 2d. Полная функция
видности показана на рис. П. 10.1 в зависимости от величины проекции базы. Заме-
Заметим, что функция видности, измеренная на интерферометре, ориентированном по
направлению восток-запад, при слежении за северным или южным лимбом Луны
будет обязательно равна нулю. В общем случае максимальное значение видности
будет получено при слежении за лимбом Луны, перпендикулярным направлению
вектора базы.
Хотя Луна и может дать сильные лепестки, она не является идеальным опорным
источником. Во-первых, либрация может затруднить процесс слежения за нуж-
нужным краем Луны. Во-вторых, ошибки слежения могут привести к флуктуациям
376
Калибровка и преобразование Фурье функции видности
[Гл. 10
ей
К
1г
0,1-
/ \
¦/ \
/ \
j \
i \
i у
i 1 1 1 1 1 1 1 1 1
i i i i i X
\
\
\
\
1^ I
— Действительный компонент
........ Мнимый компонент (Im)
^— (Re2+ Im2I/2
11111111111111111
—¦
Ч—1—1—1—1—h
(Re) =
ИМ 1 1
-
1 1 1
1 1 1 1 1 1 _
90
е 45
о
О 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0
%и
Рис. П.10.1. Нормированная функция видности для интерферометра, ориентированного
в направлении восток-запад при наблюдениях западного лимба Луны методом прохожде-
прохождения (г> = 0), в зависимости от въ и, где въ — 1, 2X/d — ширина диаграммы направленности
антенны на уровне половины мощности, d — диаметр антенны, и = D/X — длина вектора
базы в длинах волн. По горизонтальной оси въ и примерно равна l,2D/d. Пунктирной
линией показана мнимая часть функции видности, пунктиром — действительная часть,
непрерывной линией — амплитуда функции видности. При D/d > 1 функция видности
становится практически полностью мнимой. При d = 6 м и D/d = 3 плотность потока
при нулевом разнесении (см. выражение (П10.4)) равна 12 700 Ян, а амплитуда функции
видности — примерно 1000 Ян (см. выражение (П10.5)). Приведено по работе (Gurwell,
1998)
амплитуды и фазы, так как видимое положение источника определяется антенна-
антеннами. В-третьих, существенны вариации температуры Луны относительно среднего
значения 200 К, особенно на коротких длинах волн, так как температура Луны
зависит от солнечного освещения. Для получения точных результатов необходимо
учесть в модели яркостной температуры переменность температуры Луны.
Приложение 10.2. Доплеровское смещение спектральных
линий
Доплеровское смещение спектральных линий происходит из-за движения источ-
источника относительно наблюдателя. В этом приложении обсуждаются четыре важных
практических вопроса. Во-первых, использование приближения первого порядка
для спектральной релятивистской формулы Доплера приводит к значительным
ошибкам, если скорости велики. Во-вторых, есть несколько разных приближений,
которые можно использовать для корректировки измеряемых скоростей движения
наблюдателя. В-третьих, должно быть уделено особое внимание тому, чтобы не
привнести некоторое смещение скорости при преобразовании из единиц частоты
к единицам скорости. Наконец, изменения скорости имеют не только доплеровскую
природу, и иногда это необходимо принимать во внимание.
10.6]
Приложение 10.2. Доплеровское смещение спектральных линий
377
Доплеровское смещение (см., например, Rybicki and Lightman, 1979) выражается
следующим соотношением:
__
Ло
1 + - cos в
с
1- -
(П10.6)
где Ло и z/0 — длина волны и собственная частота, измеренные в системе отсчета ис-
источника. Соответствующие переменные без индекса 0 являются длиной волны и ча-
частотой в системе отсчета наблюдателя, v — величина скорости движения источника
относительно наблюдателя, а в — угол между вектором скорости и лучем зрения
в системе отсчета наблюдателя. Для удаляющегося источника в < 90°. Числитель
в выражении (П10.6) является классическим доплеровским смещением в результате
изменения расстояния между источником и наблюдателем. Знаменатель — это ре-
релятивистский коэффициент временного запаздывания, который учитывает разницу
между периодом излученной волны в системах покоя источника и наблюдателя.
Из-за эффекта запаздывания времени возникает доплеровское смещение вто-
второго порядка, даже если движение перпендикулярно лучу зрения. Далее мы будем
рассматривать только радиальные скорости, т. е. полагаем в = 0° или 180°. В случае
в = 0° уравнение доплеровского смещения имеет вид
(П10.7)
где vr — радиальная скорость, положительная для удаляющегося источника. По-
Получаем выражение для скорости:
А
Ао
V
\
1 +
1-
Vr
с
Vr
С,
(П10.8)
или
А2-А2,
Разложение правых частей уравнений (П10.8) и (П10.9) по Тейлору дает
vr Av 1 Аи
— 1" о —Г
С Uq Z ]уп
(П10.9)
(П10.10)
АХ
Ао
(П10.11)
где Ai/ = v — щ и А А = А — Aq. Для отрицательных значений Av скорость положи-
положительна или «сдвинута в красную область». Так как Ais/i/q ~ — AA/Aq, члены второго
порядка в уравнениях (П10.10) и (П10.11) имеют примерно одинаковую величину,
но обратный знак.
Спектральные приборы в радио- и оптическом диапазонах имеют однородное
распределение по частоте и длине волны. Следовательно, в первом приближении,
скорость может быть рассчитана как линейное преобразование частоты или длины
378 Калибровка и преобразование Фурье функции видности [Гл. 10
волны. К сожалению, это приводит к двум различным приближениям для оценки
скорости:
^rradio =_А^ (П10.12)
с щ
и
tVoptical^AA (П10.13)
с Ло
Разницу между этими двумя приближениями можно оценить, обратив внимание на
то, что vrradioIе = —АЛ/Л. Использование каждой шкалы скоростей приводит к по-
появлению ошибок второго порядка при оценке истинной скорости. Таким образом,
в радиодиапазоне происходит недооценка скорости, а в оптическом — переоценка ее
на ту же величину. Разность между скоростями, определенными в разных шкалах,
есть функция скорости:
2
5vr = vroptical - vrradio ~ ^ . (П10.14)
Следовательно, отождествление используемой шкалы скоростей очень важно
для внегалактических источников. Например, если vr = 10 000 км/с, тогда
5vr ~ 330 км/с. Разница между существующими соглашениями по используемым
шкалам скоростей может привести к значительным проблемам, когда проводятся
наблюдения в узкой полосе пропускания.
Для интерпретации скоростей спектральных линий необходимо отнести их
к подходящей инерциальной системе отсчета. Скорость вращения наблюдателя на
экваторе вокруг центра Земли равна ^0,5 км/с, скорость вращения Земли вокруг
Солнца — ж 30 км/с, скорость движения Солнца относительно ближайших звезд —
^20 км/с (это определяет понятие местного стандарта покоя — МСП или LSR);
скорость вращение МСП вокруг центра Галактики равна ж 220 км/с, скорость дви-
движения нашей Галактики относительно местной группы — ~ 310 км/с, а скорость
движения местной группы относительно реликтового излучения реликтового фона
~ 630 км/с. Наиболее точная система отсчета вне солнечной системы определяется
относительно реликтового излучения. Скорость Солнца относительно реликтово-
реликтового фона определена по измерениям дипольной анизотропии реликтового излуче-
излучения, что дало необыкновенно точную оценку 370,6 ± 0,4 км/с в направлении ? =
= 264,31° ± 0,17° и Ъ = 48,05° ± 0,10° (Lineweaver et al., 1996). Сведения о разно-
разнообразных системах отсчета представлены в табл. П10.1. Результаты большинства
современных наблюдений приводятся либо к барицентру солнечной системы, либо
к местному стандарту покоя. Скорости движения звезд и галактик даются обычно
в первой системе, а наблюдения незвездных объектов Галактики (например, мо-
молекулярных облаков) — во второй. Коррекция скорости во многих радиоастроно-
радиоастрономических экспериментах проводятся с помощью программы DOP (Ball, 1969; см.
также Gordon, 1976), которая дает точность ~ 0,01 км/с, так как не учитывает
планетарные возмущения. Такие программы, как CVEL в пакете AIPS, основаны на
этом коде. Значительно более высокая точность может быть получена при исполь-
использовании более сложных программ, таких как Planetary Ephemeris Program (Ash,
1972) или JPL Ephemeris (Standish and Newhall, 1995). Интерпретация наблюдений
пульсарного тайминга также требует точной корректировки скорости.
Иногда происходит путаница при пересчете частоты в приемной системе к ис-
истинной наблюдаемой частоте. Когда рассчитывается спектр в наблюдаемой полосе
фурье-преобразованием потока данных или функции корреляции быстрого преоб-
преобразования Фурье, первый канал соответствует нулевой частоте, его приращение
равно — Ai/IF/7V, где AvIF — ширина полосы (половина частоты выборки Най-
квиста), а N — полное количество частотных каналов. JV-й канал соответствует
10.6] Приложение 10.2. Доплеровское смещение спектральных линий 379
Таблица П.10.1. Системы отсчета для спектральных наблюдений
Скорость Направление"
Название Вид движения (км/с) ? ( ) о ( )
Топоцентрическая Вращение Земли вокруг своей оси и, 5 — —
^ Вращение Земли вокруг барицен- п П1Ч - -
Геоцентрическая ^ о ,KJ ^ u,uio
^ тра системы Земля/Луна
Гелиоцентрическая Вращение Земли вокруг Солнца
30
Вращение Солнца вокруг бари-
Барицентрическая центра солнечной системы (пла- 0,012 - -
нетарные возмущения)
Местный стандарт Движение Солнца относительно 20 57 23
покоя6 близких звезд
Галактоцентри- Движение МСП вокруг центра 220 90 0
ческаяс Галактики
Местный галакти- Движение центра Галактики
ческий стандарт относительно галактик местной 310 146 —23
покоя6 группы
т-ч Движение местной группы галак-
Реликтовое ^ ^J коп п^а qo
ь тик относительно реликтового из- оои z' ° ои
излучение ^
J лучения
аГалактическая широта и долгота.
6Стандарт, принятый MAC в 1985 г. (Kerr and Lynden-Bell, 1986).
с(Сох, 2000).
частоте Ai/IFA — 1/АГ). Если N — четная (N обычно равно степени двойки), канал
N/2 соответствует центральной частоте полосы. Для системы с преобразованием
в верхней боковой полосе, истинная частота первого канала (нулевая частота по-
полосы) является суммой частот местного генератора. Заметим, что оси скоростей
направлены в разные стороны (v ос — v и v ос ту) для систем с преобразованием
в верхней и нижней боковых полосах соответственно.
Существует несколько эффектов недоплеровской природы, приводящих к сдви-
сдвигу скорости, которые следует принимать во внимание. Для спектральных линий,
образующихся в глубокой потенциальной яме, например, близко к черным дырам,
существует дополнительный член, учитывающий замедление времени, записывае-
записываемый при г ^> rs как
^ (Ш0Л5)
где г — расстояние от центра черной дыры, a rs — Шварцшильдовский радиус (rs =
= 2GM/с ). Полный частотный сдвиг, полученный обобщением уравнения (П10.6),
имеет вид
^( ^)b7o, (П10.16)
где 7Ь = 1/д/1 ~~ vr /с2 — так называемый лорентц-фактор. Например, излучение
водяного мазера в NGC4258 (см. рис. 1.21), который обращается вокруг черной
380
Калибровка и преобразование Фурье функции видности
[Гл. 10
дыры на расстоянии 40 000rs, испытывает сдвиг по скорости, примерно равный
4 км/с.
Наиболее важное частотное смещение недоплеровской природы для источников,
находящихся на космологических расстояниях, происходит из-за расширения Все-
Вселенной. Для относительно близких объектов это составляет
А
Ао
Нр <
(П10.17)
где Но — постоянная Хаббла, a d — расстояние до источника. Сегодня предпола-
предполагается, что Hq ж 70км/(с-Мпк) (Mould et a., 2000). Для больших расстояний (z >
> 1), связь между расстоянием и временем зависит от выбранной космологической
модели (см., например, Peebles, 1993). Однако, при известном z истинное значение
частоты всегда будет связано с ней соотношением
v =
(П10.18)
Другие вопросы, связанные с наблюдениями источников спектральных линий
на космологических расстояниях обсуждаются в работе (Gordon, Baars and Cocke,
1992). Пример спектральных интерферометрических наблюдений молекулярного
облака на космологическом расстоянии (z = 3,9) может быть найден в работе
(Downes et al., 1999).
Приложение 10.3. Исторические замечания
Получение карт с помощью одномерных профилей. Первые карты
Солнца и нескольких других сильных источников были получены при помо-
помощи линейных решеток (см., напри-
например, решетку и компаунд-интерферо-
компаунд-интерферометр на рис. 1.13). Результаты были
получены при помощи сканирования
диаграммой направленности веерной
формы. Для таких инструментов дан-
данные функции видности в любой мо-
момент времени располагаются на пря-
прямой линии, проходящей через нача-
начало координат в плоскости uv (см.
рис. 10.1). Фурье-преобразование дан-
данных, полученных при таких одномер-
одномерных наблюдениях, приводит к форме
гофрированной поверхности с профи-
профилем, определяемым сканированием ве-
веерной диаграммой, как показано на
рис. П. 10.2. Это можно рассматривать
как одну компоненту двумерной карты
Солнца. Так как Земля вращается, ме-
меняется позиционный угол диаграммы
на небе, добавляются компоненты и та-
Рис. П. 10.2. Поверхность для переменных
A,т), являющаяся фурье-образом данных
функции видности переменных (u,v), изме-
измеренных вдоль линии, образующей угол ф +
+ тг/2 с осью и, как показано с помощью
штриховой линии на рис. 10.1
ким образом формируется двумерная
карта Солнца. Однако при сканирова-
сканировании такими решетками с веерной диаграммой вклад каждой пары антенн в ре-
результирующий профиль имеет одинаковый вес. Это приводит к построению карты
10.6] Цитированная литература 381
с нежелательным естественным взвешиванием. В пятидесятые годы, когда ЭВМ
были недоступны, преобразование данных в двумерные карты с заданным взвеши-
взвешиванием представляло собой весьма трудоемкий процесс. Христиансен и Уорбертон
(Christiansen and Warburton, 1955) провели преобразование Фурье, взвешивание
и повторное преобразование данных с помощью ручных вычислений при постро-
построении солнечной карты. Позднее Брейсуэлл и Риддл (Bracewell and Riddle, 1967)
предложили метод обработки данных веерного сканирования без преобразования
Фурье, с использованием свертки для взвешивания функции видности. Некоторые
основные соотношения между одномерным и двумерным откликами (Bracewell,
1956b) рассматриваются в разд. 2.4. Те же самые идеи применимы для обработ-
обработки изображений в других областях науки, например, томографии (Bracewell and
Wernecke, 1975).
Аналоговое преобразование Фурье. Оптическая линза может быть исполь-
использована в качестве аналогово устройства для проведения преобразования Фурье.
Проводились исследования аналоговых систем обработки данных, основанных на
оптическом, акустическом или электронно-лучевом процессах, однако их свойства
обычно оказывались неудовлетворительными для применения в синтезном карто-
картографирования. Им не хватает гибкости, кроме того, возникает проблема ограни-
ограничения динамического диапазона, представляющего собой отношение максимально-
максимального уровня яркости к шуму карты. Для сохранения высокого качества изображе-
изображения любой итеративный процесс требует последовательного фурье-преобразования
и повторного преобразования некоторых данных, как это происходит в некоторых
методиках восстановления (см. гл. 11), в которых необходима высокая точность.
Обзор возможностей аналоговых средств обработки данных проведен в работе
(Cole, 1979).
Основная литература
Perley R. A., F. R. Schwab and A. Н. Bridle. Eds., Synthesis Imaging in Radio Astronomy.
Astron. Soc. Pacific Conf. Ser., 6, 1989.
Taylor G. В., С. L. Carilli and R. A. Perley. Eds., Synthesis Imaging in Radio Astronomy II.
Astron. Soc. Pacific Conf. Ser., 180, 1999.
Thompson A. R. and L. R. D'Addario. Eds., Synthesis Mapping, Proc. NRAO Workshop No.
5 (Socorro, NM, June 21-25, 1982), National Radio Astronomy Observatory, Green Bank, WV,
1982.
Цитированная литература
Ash M. E. Determination of Earth Satellite Orbits. MIT Lincoln Laboratory Technical Note,
1972-5, 1972.
Ball J. A. Some Fortran Subprograms Used in Astronomy. MIT Lincoln Laboratory Technical
Note, 1969-42, 1969.
Bevington P. R. and D. K. Robinson. Data Reduction and Error Analysis for the Physical
Sciences. 2nd ed., McGraw-Hill, New York, 1992.
Bos A. On Ghost Source Mechanisms in Spectral Line Synthesis Observations with Digital
Spectrometers. Indirect Imaging, J. A. Roberts. Ed., Cambridge Univ. Press, 1984, p. 239-243.
Bos A. On Instrumental Effects in Spectral Line Synthesis Observations. Ph. D. Thesis, Univ.
of Groningen, 1985, see section 10.
Bracewell R. N. Two-dimensional Aerial Smoothing in Radio Astronomy. Aust. J. Phys., 9,
297-314, 1956a.
Bracewell R. N. Strip Integration in Radio Astronomy. Aust. J. Phys., 9, 198-217, 1956b.
382 Калибровка и преобразование Фурье функции видности [Гл. 10
Bracewell R. N. The Fourier Transform and Its Applications. McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Bracewell R. N. and A. C. Riddle. Inversion of Fan-Beam Scans in Radio Astronomy. Astro-
phys. J., 150, 427-434, 1967.
Bracewell R. N. and J. A. Roberts. Aerial Smoothing in Radio Astronomy. Aust. J. Phys.,7,
615-640, 1954.
Bracewell R. N. and S. J. Wernecke. Image Reconstruction over a Finite Field of View. J.
Opt. Soc. Am. 65, 1342-1346, 1975.
Bridle A. H. Synthesis Observing Strategies. Synthesis Imaging in Radio Astronomy, R. A.
Perley, F. R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser., 6, 443-476, 1989.
Briggs D. S. High Fidelity Deconvolution of Moderately Resolved Sources. Ph.D. thesis, New
Mexico Institute of Mining and Technology, Socorro, NM, 1995.
Briggs D. S., R. A. Sramek and F. R. Schwab. Imaging. Synthesis Imaging in Radio Astronomy
II, G. B. Taylor, С L. Carilli and R. A. Perley. Eds., Astron Soc. Pacific Conf. Ser., 180, 127-
149, 1999.
Brouw W. N. Data Processing for the Westerbork Synthesis Radio Telesscope. Univ. Leiden,
1971.
Brouw W. N. Aperture Synthesis. Methods in Computational Physics, Vol. 14, B. Alder, S.
Fernbach and M. Rotenberg. Eds., Academic Press, New York, 1975, p. 131-175.
Burton W. B. The Structure of Our Galaxy Derived from Observations of Neutral Hydrogen.
Galactic and Extragalactic Radio Astronomy, G. L. Verschuur amd K. I. Kellermann. Eds.,
Springer-Verlag, Berlin, p. 295-358, 1988.
Christiansen W. N. and J. A. Warburton. The Distribution of Radio Brightness over the Solar
Disk at a Wavelength of 21 cm. III. The Quiet Sun-Two-Dimensional Observations. Aust. J.
Phys., 8, 474-486, 1955.
Cole T. W. Analog Processing Methods for Synthesis Observations. Image Formation from
Coherence Functions in Astronomy, C. van Schooneveld, Ed., Reidel, Dordrecht, 1979, p. 123-
141.
Cox A. N. Ed. Allen's Astrophysical Quantities. 4th ed., AIP Press, Springer, New York, 2000.
Crane P. C. and P. J. Napier. Sensitivity. Synthesis Imaging in Radio Astronomy, R. A.
Perley, F. R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser., 6, 139-165 1989.
D'Addario L. R. Cross Correlators. Synthesis Imaging in Radio Astronomy, R. A. Perley, F.
R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser. 6, 59-82, 1989.
Downes D., R. Neri, T. Wiklind, D. J. Wilner and P. A. Shaver. Detection of COD-3), CO(9-
8) and Dust Emission in the Broad Absorption Line Quasar АРМ 08279+5255 at a Redshift
of 3.9. Astrophys. J. Lett., 513, L1-L4, 1999.
Ekers R. D. Error Recognition. Synthesis Imaging in Radio Astronomy II, G. B. Taylor, C. L.
Carilli and R. A. Perley. Eds., Astron, Soc. Pacific Conf. Ser., 180, 321-334, 1999.
Ekers R. D. and J. H. van Gorkom. Spectral Line Imaging with Aperture Synthesis Radio
Telescopes. Indirect Imaging, J. A. Roberts. Ed., Cambridge Univ. Press, Cambridge, UK,
1984, p. 21-32.
Fomalont E. B. The East-West Structure of Radio Sources at 1425 MHz. Astrophys. J. Suppl.,
15, 203-274, 1968.
Fomalont E. B. and M. С. Н. Wright. Interferometry and Aperture Synthesis. Galactic and
Extragalactic Radio Astronomy, G. L. Verschuur and K. I. Kellermann. Eds., Springer-Verlag,
New York, 1974, p. 256-290.
Gordon M. A. Computer Programs for Radio Astronomy. Methods of Experimental Physics,
Vol. 12C, M. L. Meeks. Ed., Academic Press, New York, 1976.
Gordon M. A., J. W. M. Baars and W. J. Cocke. Observations of Radio Lines from Unre-
Unresolved Sources: Telescope Coupling, Doppler Effects and Cosmological Corrections. Astron.
Astrophys., 264, 337-344, 1992.
10.6] Цитированная литература 383
Gradshteyn I. S. and I. M. Ryzhik. Table of Integrals, Series and Products. Academic Press,
New York, 5th ed. 1994.
Gurwell M. Lunar and Planetary Fluxes at 230 GHz: Models for the Haystack 15-m Baseline.
SMA Technical Memo. 127, Smithsonian Astrophysical Observatory, 1998.
Jacquinot P. and B. Roizen-Dossier. Apodisation. Progress in Optics, Vol. 3, p. 29-186, E.
Wolf, Ed., North Holland, Amsterdam, 1964.
Jennison R. C. A Phase Sensitive Interferometer Technique for the Measurement of the Fourier
Transforms of Spatial Brightness Distributions of Small Angular Extent. Mon. Not. R. Astron.
Soc, 118, 276-284, 1958.
Kerr F. J. and D. Lynden-Bell. Review of Galactic Constants. Mon. Not. Roy. Ast. Soc, 221,
1023-1038, 1986.
Lineweaver C. H., L. Tenorio, G. F. Smoot, P. Keegstra, A. J. Banday, and P. Lubin. The
Dipole Observed in the СОВЕ DMR 4 Year Data. Atrophys. J., 470, 38-42, 1996.
Maltby P. and A. T. Moffet. Brightness Distribution in Discrete Radio Sources, III. The
Structure of the Sources. Astrophys. J. Suppl., 7, 141-163, 1962.
Masson C. R. Angular Expansion and Measurement with the VLA: The Distance to NGC 7027.
Astrophys. J., 302, L27-L30, 1986.
Moffet A. T. Brightness Distribution in Discrete Radio Sources, I. Observations with an East-
West Interferometer. Astrophys. J. Suppl., 7, 93-123, 1962.
Mould J. R. and 16 coauthors. The Hubble Space Telescope Key Project on the Extragalactic
Distance Scale. XXVIII. Combining the Constraints on the Hubble Constant. Astrophys. J.,
529, 786-794, 2000.
Napier P. J. and P. C. Crane. Signal-to-Noise Ratios. Synthesis Mapping, Proc. NRAO
Workshop No. 5 (Socorro, NM, June 21-25, 1982), A. R. Thompson and L. R. D'Addario.
Eds., National Radio Astronomy Observatory, Green Bank, WV, 1982.
Pearson T. J. Non-Imaging Data Analysis. Synthesis Imaging in Radio Astronomy II, G. B.
Taylor, C. L. Carilli and R. A. Perley. Eds., Astron Soc. Pacific Conf. Ser., 180, 335-355,
1999.
Peebles P. J. E. Principles of Physical Cosmology. Princeton Univ. Press, Princeton, NJ, 1993.
Reid M. J. Spectral-Line VLBI. Very Long baseline Interferometry and the VLB A, J. A. Zensus,
P. J. Diamond and P. J. Napier. Eds., Astron Soc. Pacific Conf. Ser., 82, 209-225, 1995.
Reid M. J. Spectral-Line VLBI. Synthesis Imaging in Radio Astronomy II, G. B. Taylor, C.
L. Carilli and R. A. Perley. Eds., Astron Soc. Pacific Conf. Ser., 180, 481-497, 1999.
Rhodes D. R. On the Spheriodal Functions. J. Res. Natl. Bur. Stand. (U.S.) B, 74, 187-209,
1970.
Roelfsema P. Spectral Line Imaging I: Introduction. Synthesis Imaging in Radio Astronomy,
R. A. Perley, F. R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific conf. Ser., 6, 315-339,
1989.
Rybicki G. B. and A. P. Lightman. Radiative Processes in Astrophysics. Wiley, New York,
1979 (reprinted 1985).
Schwab F. R. Optimal Gridding of Visibility Data in Radio Interferometry. Indirect Imaging,
J. A. Roberts. Ed., Cambridge Univ. Press, Cambridge, UK 1984, p. 333-346.
Slepian D. Analytic Solution of Two Apodization Problems. J. Opt. Soc. Am., 55, 1110-1115,
1965.
Slepian D. and H. O. Pollak. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncer-
Uncertainty. I. Bell Syst. Tech. J., 40, 43-63, 1961.
Smith F. G. The Measurement of the Angular Diameter of Radio Stars. Proc. Phys. Soc. B,
65, 971-980, 1952.
Standish E. M. and X. X. Newhall. New Accuracy Levels for Solar System Ephemerides. Proc.
IAU Symp. 172, Dynamics, Ephemerides and Astrometry of Solar System Bodies, Kluwer,
Dordrecht, 1995, p. 29-36.
384 Калибровка и преобразование Фурье функции видности [Гл. 10
Taylor J. R. An Introduction to Error Analysis. University Science Books, Mill Valley, CA,
1982.
Thompson A. R. and R. N. Bracewell. Interpolation and Fourier Transformation of Fringe
Visibilities. Astron. J., 79, 11-24, 1974.
Twiss R. Q., A. W. L. Carter and A. G. Little. Brightness Distribution Over Some Strong
Radio Sources at 1427 Mc/s. Observatory, 80, 153-159, 1960.
van Gorkom J. H. and R. D. Ekers. Spectral Line Imaging II: Calibration and Analysis.
Synthesis Imaging In Radio Astronomy, R. A. Perley, F. R. Schwab and A. H. Bridle. Eds.,
Astron. Soc. Pacific Conf. Ser., 6, 341-353, 1989.
White R. L. and R. H. Becker. The Resolution of P Cygni's Stellar Wind. Astrophys. J., 262,
657-662, 1982.
White M.j J. E. Carlstrom, M. Dragovan and W. L. Holzapfel. Interferometric Observations
of Cosmic Microwave Background Anisotropies. Astrophys. J., 514, 12-24, 1999.
Глава 11
ВОССТАНОВЛЕНИЕ, АДАПТИВНАЯ КАЛИБРОВКА
И ИХ ПРИМЕНЕНИЕ
В этой главе речь пойдет о методах обработки, являющихся в значительной
степени нелинейными. Они позволяют осуществлять дальнейшее улучшение каче-
качества карты, построенной методами, описанными в гл. 10. Данные функции видно-
сти имеют два основных недостатка, ограничивающих точность синтезированных
изображений: 1) ограниченность перекрытия пространственных частот по и и v
и 2) ошибки измерений. Ограничение перекрытия пространственных частот может
быть уменьшено при проведении процедур восстановления, которые позволяют
отсутствующим значениям функции видности придать ненулевые значения в пре-
пределах некоторых общих ограничений на изображение. Качество калибровки может
быть улучшено с помощью адаптивных методов, при которых коэффициенты уси-
усиления антенн, как и необходимое изображение, определяются по данным функции
видности. Также в этой главе будут обсуждаться картографирование в большом
поле, многочастотное картографирование и некоторые другие специальные прило-
приложения.
11.1. Ограничение покрытия области пространственных
частот
Распределение интенсивности (или, что то же самое, видимой яркости) /о(/,га),
получаемое при синтезном картографировании, может рассматриваться как ис-
истинная интенсивность (яркость) /(/,т), свернутая с синтезированной диаграммой
направленности ЪоA,т):
/0(/, га) = /(/, га) * * Ь0(г, га). A1.1)
Зная /q(/,777,) и ЪоA,т), можем ли мы найти 1A, т)? Аналитическая процедура по
обращению свертки двух функций состоит в фурье-преобразовании свертки, кото-
которое равно произведению фурье-преобразований компонент, деленному на фурье-
преобразование известной функции, и завершается обратным преобразованием. Из
соотношения A1.1) следует, что
/(/, га) * * bo(l, га) ^ V(u, v) [W(u, v)wu(u, v)wt(u, v)], A1.2)
где ^ обозначает преобразование Фурье, V(u, v) — функция видности, W(u, v) —
пространственная передаточная функция, wu(u,v) — вес, необходимый для полу-
получения эффективно однородной плотности данных на гш-плоскости, a wt(u,v) опре-
определяет плавный спад. Однако передаточная функция содержит области нулевых
значений, поэтому мы не можем делить на нее, чтобы получить V(u, v). Неизмерен-
Неизмеренные значения функции видности представляют собой одну из основных проблем,
и любая процедура, не считая взвешивания функции видности, улучшающая по-
полученную интенсивность, должна оперировать ненулевыми значениями функции
видности в неизмеренных областях гш-плоскости.
13 Томсон
386 Восстановление, адаптивная калибровка и их применение [Гл. 11
Брейсуэлл и Роберте (Bracewell and Roberts, 1954) указали, что существует
бесконечное число решений уравнения свертки A1.1), поскольку в непокрытых
областях плоскости uv молено добавлять любые произвольные значения функции
видности. Преобразование Фурье этих добавленных значений формирует невиди-
невидимое распределение, которое нельзя обнаружить с помощью инструмента с соответ-
соответствующими областями нулевых значений передаточной функции. Можно было бы
утверждать, что при интерпретации наблюдений в неизмеренных на радиотелеско-
радиотелескопах областях спектральной чувствительности следует помещать только нули, чтобы
не вносить произвольную информацию. С другой стороны, сами нули являются
произвольными величинами, причем некоторые из них определенно неверны. Что
необходимо, так это такая процедура, которая позволяла бы функции видности
в неизмеренных точках принимать значения, соответствующие наиболее разумным
или правдоподобным распределениям интенсивности, и которая минимизировала
бы в то же время добавление произвольных деталей. Мы имеем априорную инфор-
информацию о том, что видимая интенсивность должна быть больше нуля, а угловая
структура источника — ограничена; эта информация может быть учтена при по-
построении карты. Отрицательные значения интенсивности и протяженная синусои-
синусоидальная структура — примеры инструментальных ложных деталей, которые необ-
необходимо удалить. Как предполагается в обсуждении рис. 2.6, должны существовать
методики устранения эффектов боковых лепестков. Обзор алгоритмов обработки
дан в работе (Sault and Oosterloo, 1996).
11.2. Алгоритм восстановления «чистка» (CLEAN)
11.2.1. Алгоритм чистки. Одним из наиболее успешных методов восстанов-
восстановления является алгоритм чистки (CLEAN), разработанный Хегбомом (Hogbom,
1974). В своей основе он представляет собой процесс численного обращения свертки
в области (/,?77,). Процедура состоит в разбиении распределения яркости на отклики
от точечных источников, а затем замену каждого из них на отклик «чистой» диа-
диаграммы направленности, т. е. диаграммы без боковых лепестков. Основные этапы
заключаются в следующем.
1. Вычисление карты и отклика на точечный источник с помощью преобразо-
преобразования Фурье функции видности и взвешенной передаточной функции. Эти
функции — синтезированная яркость и синтезированная диаграмма — на-
называются часто «грязной картой» и «грязной диаграммой» соответственно.
Расстояния между точками выборки на плоскости 1т не должны превышать
одной трети ширины синтезированной диаграммы.
2. Нахождение на карте точки с максимальной интенсивностью и вычитание
отклика на точечный источник, включая полную (с боковыми лепестками)
диаграмму направленности с центром в выбранной точке. Максимальная ам-
амплитуда вычитаемого точечного источника равна коэффициенту 7, умножен-
умноженному на соответствующую амплитуду точки на карте. Величина 7 называ-
называется коэффициентом усиления петли по аналогии с отрицательной обратной
связью в электрических системах и обычно имеет значение, равное несколь-
нескольким десятым. Запоминание координат и амплитуды вычтенного компонента,
добавляя компонент в виде 5-функции в модель, последняя версия которой
потом будет использована для построения чистой карты.
11.2] Алгоритм восстановления «чистка» (CLEAN) 387
3. Возврат к пункту 2 и осуществление итераций до тех пор, пока все значимые
элементы структуры источника не будут удалены из карты. Существует не-
несколько возможных индикаторов выполнения этого условия. Например, мож-
можно сравнивать максимальный пик со среднеквадратичным уровнем интенсив-
интенсивности на остаточной карте, определять момент, когда среднеквадратичный
уровень не убывает при вычитании, либо когда наряду с положительными
начинает вычитаться значительное число отрицательных компонентов.
4. Свертка S-функций «чистой» модели с откликом «чистой» диаграммы на-
направленности, т. е. замена каждой S-функции функцией чистой диаграммы
с соответствующей амплитудой. Чистая диаграмма чаще всего выбирается
гауссовой формы с шириной на уровне половины амплитуды, равной пер-
первоначальной ширине синтезированной (грязной) диаграммы, или какой-то
аналогичной положительной функцией.
5. Добавление остаточной карты (остаточных значений интенсивности из пунк-
пункта 3) к чистой карте, что дает результирующую карту метода.
Предполагается, что каждый вычитаемый профиль грязной диаграммы направ-
направленности представляет собой отклик на точечный источник. Как уже отмечалось
в разд. 4.4, функция видности точечного источника состоит из действительной
и мнимой синусоид, простирающихся до бесконечности на плоскости uv. Любая
деталь распределения интенсивности, для которой функция видности одна и та же
в пределах области (г/, г>), определяемой передаточной функцией, дает отклик на
карте, идентичный отклику на точечный источник. Хегбом (Hogbom, 1974) отметил,
что большая часть неба представляет собой случайное распределение точечных ис-
источников при отсутствии фонового излучения, и алгоритм чистки CLEAN первона-
первоначально был разработан именно для такой ситуации. Тем не менее опыт показывает,
что алгоритм чистки также хорошо работает в случае протяженных и сложных
источников.
Результат первых трех из отмеченных выше шагов процедуры чистки можно
представить в виде модельного распределения интенсивности, состоящего из ряда 5-
функций, величины и положения которых соответствуют вычтенным компонентам.
Поскольку модуль преобразования Фурье от каждой 5-функции монотонно прости-
простирается в бесконечность в плоскости (u,v), то функция видности экстраполируется,
насколько это необходимо, за пределы обрезания передаточной функции.
Набор J-функций не может являться удовлетворительной моделью для астро-
астрономических целей. Но на самом деле группы из J-функций, разнесенных не более
чем на ширину диаграммы, могут описывать протяженную структуру. Свертка
модели из S-функций с чистой диаграммой направленности, описанная в пункте 4,
устраняет опасность неправильной интерпретации. Таким образом, алгоритм
чистки по своей сути выполняет интерполяцию в плоскости uv. Желательно,
чтобы чистая диаграмма не имела боковых лепестков, особенно отрицательных,
и чтобы ее преобразование Фурье было постоянным в пределах измеренной области
плоскости uv, а вне ее — резко падало. По существу эти требования несовместимы,
поскольку резкое обрезание в плоскости uv приводит к колебаниям в плоскости 1т.
Обычно в качестве компромисса выбирается диаграмма в виде функции Гаусса,
которая вызывает гауссов спад в плоскости uv. Так как эта функция вносит плавное
монотонное ослабление в данные измерений и в неизмеренные данные, генериру-
генерируемые алгоритмом чистки, результирующее распределение интенсивности более не
согласуется с измеренной функцией видности. Однако, отсутствие сильных боковых
лепестков малых порядков улучшает динамический диапазон изображения, т. е.
13*
388
Восстановление, адаптивная калибровка и их применение
[Гл. 11
Рис. 11.1. Пример применения алгоритма чистки CLEAN к наблюдениям объекта ЗС224.1,
проведенным на частоте 2695 МГц на интерферометре в Грин Бэнк при довольно бедном
покрытии гш-плоскости: а — синтезированная «грязная» карта; б — карта после одной
итерации при величине коэффициента усиления петли 7—1; 6 — после двух итераций; г —
после шести итераций. На каждой карте вычтенные компоненты восстановлены сверткой
с чистой диаграммой направленности. Контуры равной интенсивности проведены на уров-
уровнях 5, 10, 15, 20, 30 и т. д. % от максимального значения. Приведено из работы (Hogbom,
1974), с любезного согласия Astron. Astrophys. Suppl
увеличивает интервал значений интенсивности, в котором структура может быть
надежно измерена.
Как обсуждалось ранее, мы не можем непосредственно выделить весовую пе-
передаточную функцию в правой части уравнения A1.2), так как она обрезается до
нуля вне областей измерения. В алгоритме чистки CLEAN эта проблема решается
путем разложения измеренной функции видности на синусоидальные компоненты
с последующим устранением обрезания таким образом, чтобы эти компоненты
простирались на всю гш-плоскость. Выбор максимальной амплитуды в области
(/,777,) эквивалентен выбору комплексной синусоиды с самой большой амплитудой
в плоскости uv.
11.2] Алгоритм восстановления «чистка» (CLEAN) 389
Обычно предполагается, что в точке, где прекращается процесс вычитания ком-
компонент, остаточное распределение интенсивности состоит, в основном, из шума. Со-
Сохранение остаточного распределения внутри карты является, как и свертка с чистой
диаграммой, неидеальной процедурой, которая необходима для предотвращения
ошибок в интерпретации окончательного результата. Без остаточного фона, кото-
который добавляется на пятом шаге, произошло бы обрезание амплитуды у структуры,
соответствующей самой меньшей из вычитаемых компонент. Наличие флуктуации
уровня фона дает также сведения об уровне неопределенности значений интенсив-
интенсивности. Пример обработки данных с помощью алгоритма чистки CLEAN показан на
рис. 11.1.
11.2.2. Реализация и характеристики алгоритма чистки. Идея алго-
алгоритма чистки, предназначенного для уменьшения влияния боковых лепестков,
проста для понимания. Будучи в значительной степени нелинейным, этот алго-
алгоритм, однако, не поддается полному математическому анализу. Ряд важных ре-
результатов получен Шварцем (Schwarz, 1978, 1979), который показал, что условие
сходимости алгоритма чистки состоит в том, чтобы синтезированная диаграмма
была симметричной, а ее образ Фурье, т. е. взвешенная передаточная функция,
был неотрицательным. Эти условия выполняются при обычной процедуре синтеза.
Анализ Шварца показывает также, что если число компонент в виде 5-функций
в CLEAN-модели не превышает числа независимых данных функции видности, то
этот алгоритм обеспечивает сходимость к решению. Решение представляет собой
приближение по методу наименьших квадратов фурье-образов компонент в виде
J-функций к измеренной функции видности. При перечислении данных функции
видности ведется независимый подсчет либо действительной и мнимой частей, либо
сопряженных величин (но не тех и других одновременно). В картах, построенных
с использованием БПФ, имеется одинаковое количество точек сетки в плоскостях
uv и /т, но не все точки сетки uv содержат измерения функции видности. Для
поддержания условия сходимости алгоритм чистки применяют лишь в пределах
ограниченной области или «окна» первоначальной карты.
Чтобы очистить карту заданного размера, необходимо иметь диаграмму на-
направленности размером в два раза больше размеров карты, с тем чтобы точечный
источник можно было вычесть из любой точки карты. Однако на практике часто
бывает удобно, чтобы карта и диаграмма имели один и тот же размер. В этом слу-
случае должным образом может быть обработана лишь центральная четверть карты.
Поэтому обычно рекомендуется, чтобы карта, полученная путем первоначального
преобразования Фурье, была по размерам в два раза больше окончательной карты.
Как было отмечено выше, использование такого «окна» гарантирует, что число уда-
удаленных компонент не превышает числа данных функции видности, и в отсутствие
шума остаточный фон внутри окна приближался к нулю.
На результат чистки влияет произвольный выбор нескольких параметров. К ним
относятся параметр 7? площадь окна и условие для окончания чистки. Коэффици-
Коэффициент усиления петли 7 обычно принимает значения между 0,1 и 0,5, и, согласно
общему опыту, для протяженной структуры алгоритм работает лучше, если этот
коэффициент находится в нижней части указанного диапазона. Время вычисления
быстро растет по мере уменьшения 7, так как увеличивается необходимое число
итераций вычитания. Если отношение сигнал/шум обозначить 7?sn, то тогда необ-
необходимое число циклов для одного точечного источника равно — Iog7?sn/log(l — 7)-
Например, при 7Zsn = 100 и 7 = 0,2 для обработки точечного источника требуется
21 цикл.
390
Восстановление, адаптивная калибровка и их применение
[Гл. 11
Хорошо известна проблема алгоритма чистки, связанная с генерацией ложной
структуры в виде пятен или гребней, модулирующих протяженные структуры.
Эвристическое объяснение этого эффекта дано Кларком (Clark, 1982). Алгоритм
находит максимум в протяженной
детали и устраняет компонент то-
точечного источника, как показано на
рис. 11.2. Отрицательные боковые
лепестки диаграммы добавляют но-
новые максимумы, которые обнару-
обнаруживаются в последующих циклах.
Таким образом, появляется тен-
Рис. 11.2. Вычитание отклика на точечный ис-
точник (штриховая линия) в максимуме широ-
кой детали при использовании алгоритма чист-
ки CLEAN (Clark, 1982)
денция расположения вычитаемых
компонент через интервалы, рав-
ные удалению первого бокового ле-
лепестка от главного первоначально
синтезированной (грязной) диаграммы направленности. Результирующая карта
содержит гребни, внесенные алгоритмом чистки, но она согласована с данными
измерений функции видности. В работе (Cornwell, 1983) была предложена модифи-
модификация алгоритма чистки, призванная уменьшить эту нежелательную модуляцию.
Оригинальный алгоритм чистки минимизирует выражение
]T^|v™eas-vrdeT, A1-3)
где V™eas — измеренная функция видности в точке (г^,г^), W{ — используемая
функция взвешивания, V™odel — соответствующая функция видности в модели, по-
полученной методом чистки. Суммирование проводится по всем точкам с ненулевыми
значениями на карте до начала чистки. Модифицированный алгоритм Корнуэлла
(Cornwell) минимизирует выражение
-Ks, A1.4)
где s — мера сглаживания, а к — подбираемый параметр. Корнуэлл обнаружил,
что среднеквадратичная интенсивность модели, взятая с отрицательным знаком,
является эффективной реализацией значения s.
Эффекты применения плавного спада к функции видности проявляются как
на первоначальной карте, так и в диаграмме направленности, и поэтому величины
и положения вычитаемых компонент в процессе чистки должны быть существенно
независимыми от вида спадающей функции. Однако, поскольку спадание уменьша-
уменьшает разрешение, обычно на практике при проведении процедуры чистки карт исполь-
используют однородное взвешивание. С другой стороны, в ряде сложных случаев, таких
как при наличии протяженной гладкой структуры, уменьшение боковых лепестков
за счет применения спадающей функции может улучшить действие алгоритма
чистки.
Существенное уменьшение объема вычислений, необходимого для алгоритма
чистки, было достигнуто Кларком (Clark, 1980). Оно основано на вычитании
откликов на точечный источник в плоскости uv и использовании БПФ для обмена
данными между областями uv и 1т. Процедура включает в себя два цикла, малый
и основной. Последовательность малых циклов используется для определения ком-
компонент, удаляемых путем приближенных вычитаний с использованием лишь глав-
главного и первых боковых лепестков синтезированной диаграммы. Затем в основном
11.3] Метод максимума энтропии (ММЭ) 391
цикле без применения приближения (с использованием всей диаграммы) вычита-
вычитаются идентифицированные отклики на точечные источники в плоскости uv. Таким
образом, свертка ^-функций с грязной диаграммой направленности производится
путем перемножения их фурье-образов. Последовательность малых и основных
циклов повторяется до тех пор, пока не будет выполнено требуемое условие на
окончание итерационного процесса. Кларк использовал этот метод для обработки
данных, полученных на VLA, и обнаружил, что время вычислений уменьшается
в 2—10 раз по сравнению с первоначальным алгоритмом чистки.
Были предложены также и другие модификации процедуры чистки; одним
из наиболее широко используемых является алгоритм Коттона-Шваба (Cotton-
Schwab, Schwab, 1984; см. раздел IV). Вычитания в основном цикле производятся
с данными функции видности, не разбитыми на ячейки, что исключает, таким об-
образом, появление ложного изображения на данном этапе. Этот алгоритм также был
разработан для того, чтобы сделать возможной обработку смежных полей, которые
рассматривались отдельно во время малого цикла, однако во время основного цикла
компоненты удалялись одновременно со всех полей.
Суммируя характеристики процедуры чистки, отметим, что этот алгоритм
прост для понимания с качественной точки зрения, легко реализуем, и его по-
полезность доказана широким использованием. С другой стороны, трудно провести
полный анализ его действия. Результат применения алгоритма чистки не являет-
является единственным, и он может создавать ложные образы. Иногда этот алгоритм
используется в сочетании с методами модельной подгонки: например, дисковая мо-
модель может быть вычтена из изображения планеты, а остаточная интенсивность —
обработана с помощью алгоритма чистки. Также чистка применяется как часть
более сложных методов построения изображений, которые описаны ниже в этом
разделе. Для более подробного рассмотрения, включающего советы по применению,
рекомендуем обратиться к работе (Cornwell, Braun and Briggs, 1999).
11.3. Метод максимума энтропии (ММЭ)
11.3.1. Алгоритм ММЭ. Принцип работы важного класса алгоритмов вос-
восстановления изображения состоит в построении карты, согласующейся в пределах
уровня шума с измеренной функцией видности, а выбор результата осуществляется
путем максимизации какой-либо меры качества изображения. Из всех таких мето-
методов метод максимальной энтропии получил особое признание в радиоастрономии.
Пусть /'(/, 777,) — распределение интенсивности, полученное по методу максимальной
энтропии, F{I') — определяемая функция, которая называется энтропией распре-
распределения. F(I') полностью определяется распределением V как функция телесного
угла без какого-либо учета структурных форм в пределах карты. При построении
карты F(If) максимизируется с учетом того ограничения, что образ Фурье от V
должно соответствовать наблюдаемым значениям функции видности. В области
формирования астрономических изображений метод максимальной энтропии впер-
впервые был применен к оптическим изображениям (Frieden, 1972). В радиоастрономии
этот метод впервые обсуждался в работах (Abies, 1974) и (Ponsonby, 1973). Цель
этого метода, согласно (Abies, 1974), состоит в получении распределения интенсив-
интенсивности, которое согласуется со всеми рассматриваемыми данными и имеет мини-
минимальную зависимость от опущенных данных. Таким образом, F{I') должна быть
выбрана таким образом, чтобы максимизация позволяла обоснованно использовать
априорную информацию, а функции видности в неизмеренных областях присваи-
присваивались значения, которые сводили бы к минимуму вводимую деталь изображения.
392 Восстановление, адаптивная калибровка и их применение [Гл. 11
Используются несколько видов функции F(If), в частности,
(n-5a)
A1.5b)
где I[ = If(k, rrii),Ifs = J^ /г-, M^ — некоторая априорная модель, а суммы берутся по
всем дискретным ячейкам карты. F% может быть охарактеризована как относитель-
относительная энтропия, так как определяемые значения интенсивности модельно зависимы.
В ряде работ обсуждается вывод выражений для энтропии, исходя из теоре-
теоретических и философских соображений. В ряде случаев привлекается байесовская
статистика (см. Jaynes, 1968, 1982). В работе (Gull and Daniell, 1979) рассматрива-
рассматривались распределения квантов интенсивности, случайно рассеянных по небу, и было
получено выражение в виде i*\, которое также использовалось в работе (Frieden,
1972). Энтропия в виде F<i была получена в работах (Abies, 1974) и (Wernecke and
D'Addario, 1977). Другие исследователи подходят к методу максимума энтропии
с прагматической точки зрения (Hogbom, 1979; Subrahmanya, 1979; Nityananda and
Narayan, 1982). Они рассматривают этот метод как эффективный алгоритм, при
этом даже допуская отсутствие фундаментальной физической или информационно-
теоретической основы для выбора параметров метода. Согласно (Hogbom, 1979),
оба вида функции F\ и F^ обладают необходимыми математическими характери-
характеристиками: первые производные стремятся к бесконечности по мере приближения
V к нулю, поэтому максимизация F\ или F<i приводит к появлению положител-
тьных значений на изображении. Вторые производные везде отрицательны, что
способствует однородности распределения интенсивности. В работе (Narayan and
Nityananda, 1984) исследовался общий класс функций F, обладающих свойствами
d2F/dl'2 < 0 и d3F/dIf3 > 0. Рассмотренные выше функции F\ and F^ являются
членами этого класса.
При максимизации выражения F(I') для энтропии, условие согласованности ре-
результирующей модели распределения интенсивности и данных измерений функции
видности проверяется при помощи статистики у2. Величина у2 является мерой
среднеквадратичной разности между измеренными величинами функции видности
V™eas = V(uk,Vk) и соответствующими величинами в модели V™odel:
где <у\ — дисперсия шума в V™eas, а суммирование проводится по всем данным
функции видности. Получение решения осуществляется с применением итератив-
итеративной процедуры (см. Wernecke and D'Addario, 1977; Wernecke, 1977; Gull and Daniell,
1978; Skilling and Bryan, 1984), а также обзор (Narayan and Nityananda, 1984).
Например, в работе (Cornwell and Evans, 1985) максимизировался параметр J,
имеющий вид
J = F3-aX2~ /3Smodeh A1.7)
где F3 определяется выражением A1.5c). 5modei ~~ полная плотность потока модели.
Она присутствует в этом выражении, потому что (для сходимости процесса к удо-
11.3] Метод максимума энтропии (ММЭ) 393
влетворительному результату) оказалось необходимым добавить условие равенства
полной плотности потока модели и измеренной плотности потока. Подгоночными
параметрами являются коэффициенты Лагранжа а и /3. Они выбираются в процессе
подгонки модели такими, чтобы х2 и 5modei оказались равны ожидаемым вели-
величинам. Благодаря использованию F3 в окончательную карту может быть внесена
априорная информация. Различные алгоритмы, разработанные для применения
в ММЭ, обычно используют градиенты энтропии и параметра %2 для корректи-
корректировки модели в каждом итерационном цикле.
Особенность карт, полученных с помощью метода максимальной энтропии, со-
состоит в том, что в общем случае отклик на точечный источник меняется в зависимо-
зависимости от положения, и угловое разрешение по всей карте оказывается не постоянным.
Сравнение карт, полученных с помощью метода максимальной энтропии и прямого
преобразования Фурье, показывает более высокое угловое разрешение первых. Экс-
Экстраполяция значений функции видности может обеспечить некоторое увеличение
разрешения по сравнению с традиционными методиками построения изображений.
11.3.2. Сравнение метода чистки CLEAN и ММЭ. Метод CLEAN опре-
определяется как последовательность действий, и поэтому он прост в применении,
однако анализ шумов результата крайне затруднен из-за нелинейности обработ-
обработки. ММЭ, напротив, использует понятие изображения, удовлетворяющего данным
наблюдений с точностью до шумов при максимизации некоторого параметра карты.
Шум в ММЭ учитывается благодаря применению критерия %2, и результирующее
влияние на шум анализируется более просто, чем при использовании CLEAN (см.,
например, (Bryan and Skilling, 1980)). Вот некоторые дополнительные сравнитель-
сравнительные характеристики этих методов:
• Для применения ММЭ требуется начальная модель источника, что не явля-
является необходимым для CLEAN.
• В применении к небольшим картам CLEAN обычно быстрее, чем ММЭ, однако
ММЭ быстрее работает с очень большими избражениями. Авторы работы
(Cornwell, Braun and Briggs, 1999) оценили, что их скорости соизмеримы для
106 ячеек в случае типичного VLA-изображения.
• CLEAN-карты имеют тенденцию к мелкомасштабным шероховатостям, что
является следствием основного принципа CLEAN, который моделирует все
изображения в виде ансамблей точечных источников. Существующее в ММЭ
ограничение на решение подчеркивает сглаженность карты.
• Протяженные, гладкие структуры лучше восстанавливаются при использова-
использовании ММЭ, тогда как CLEAN может привнести полоски и другие ошибочные
детали. ММЭ плохо работает с точечными источниками, особенно если они
накладываются на протяженный фон, который предотвращает появление от-
отрицательных боковых лепестков в виде областей с отрицательной величиной
интенсивности на грязной карте.
Для иллюстрации характеристик метода чистки и ММЭ приведем на рис. 11.3
примеры обработки модельной структуры струи из работ (Cornwell, 1995)
и (Cornwell, Braun and Briggs, 1999), используя модельные расчеты Бриггса (Briggs).
Модель струи основана на похожей структуре в М87 и, в сущности, идентична
контурам равной интенсивности, показанным на рис. 11.3 е. Левый край струи яв-
является точечным источником, сглаженным до углового разрешения моделируемых
наблюдений. Модельная функция видности, соответствующая гш-покрытию VLBA
394
Восстановление, адаптивная калибровка и их применение
[Гл. 11
150
\МЩ?1ШГЩШЩ
Рис. 11.3 а-в. Примеры методов восстановления, примененных к модельной структуре
струи, включающей в себя слева точечный источник: а — результат применения CLEAN
ко всему изображению; б — результат при вычитании компонентов только из области,
прилегающей к источнику. Отметим улучшение, полученное в (б). Контур минимальной
интенсивности проведен на уровне 0,05% от максимального значения, каждый следую-
следующий — примерно на уровне, в два раза больше предыдущего, в — то же самое изображение,
что и (б"), однако начиная с контура на уровне в 10 раз ниже, чем в (б). На нижних уровнях
можно видеть шероховатость метода CLEAN
(Napier et al., 1994) была рассчитана для частоты 1,66 ГГц и склонения 50° при
практически полном диапазоне слежения. Был добавлен тепловой шум, при этом
калибровка полагалась абсолютно точной. Фурье преобразование данных функции
видности и пространственной передаточной функции дает грязную карту и грязную
диаграмму направленности. Карта отражает основную структуру, однако тонкие
детали замыты боковыми лепестками. На рис. 11.3 а— в показаны эффекты чист-
чистки CLEAN. При восстановлении этим методом было вычтено 20 000 компонентов
при коэффициенте усиления петли, равном 0,1. На рис. 11.3 а показан результат
применения CLEAN ко всему изображению, 11.3 б — результат при вычитании
компонентов только из области, прилегающей к источнику (это часто называют
использованием ящичков или окон). Отметим улучшение, заметное на рис. 11.3 6,
являющееся следствием добавления информации об отсутствии излучения вне об-
области окна. Контур минимальной интенсивности проведен на уровне 0,05 % от мак-
максимального значения, каждый следующий — примерно на уровне, в два раза выше
предыдущего. Часть (в) показывает то же самое изображение, что и F), однако
начиная с контура на уровне в 10 раз меньшем, чем в F). Шершавость, видимая на
низких уровнях интенсивности, является характерной для метода чистки, в котором
каждый компонент рассматривается независимо. Не существует механизма для
соотнесения результата по любому компоненту с его соседом, в отличие от ММЭ, где
вводится условие сглаженности. Рисунок 11.3 г— е получен в результате применения
ММЭ. Часть (г) показывает результат восстановления ММЭ при использовании той
же области, что и для F), при 80 итерациях. Круговой узор фоновых ложных изоб-
изображений с центром в точечном источнике ясно демонстрируют тот факт, что ММЭ
плохо управляется с деталями такого типа. В случае, соответствующем рис. 11.3 д,
был вычтен точечный источник благодаря использованию отклика метода CLEAN
на эту деталь, после чего было применено восстановление ММЭ к той же области,
что и в г). Точечный источник был затем возвращен на место. Часть (е) показывает
то же самое, что и (д), только нижний контур проведен на том же уровне, что
ив (в). Низкоуровневые контурные линии показывают структуру, вклад в которую
был дан как наблюдениями, так и обработкой. Контуры получаются более гладкими
11.3]
Метод максимума энтропии (ММЭ)
395
150 ^^:-^:^шжж \
Шт
Рис. 11.3 2-е. г — показывает результат восстановления ММЭ при использовании той же
области, что и для (б), при 80 итерациях. Круговой узор фоновых ложных изображений
с центром в точечном источнике ясно демонстрируют тот факт, что ММЭ не справляется
с такими контрастными деталями, д— был вычтен точечный источник благодаря использо-
использованию отклика от метода CLEAN на эту деталь, после чего было применено восстановление
ММЭ к той же области, что и (г). Точечный источник был затем возвращен на место, е — то
же самое, что и (д), только нижний контур проведен на том же уровне, что ив (в). Заметим,
что в случае ММЭ контуры получаются более гладкими, чем в методе чистки. Карты
(в) и (е) имеют сравнимую точность воспроизведения начальной модели. Все шесть карт
приведены из работы (Cornwell, 1995) с любезного согласия Astron. Soc. Pacific Conf. Ser.
в случае ММЭ. Карты (в) и (е) имеют сравнимую точность воспроизведения началь-
начальной модели. Комбинация методов, такая как использование CLEAN для вычитания
отклика на точечный источник из карты и последующее использование ММЭ для
обработки более протяженых деталей подложки может иногда, как показано выше,
эффективно применяться при обработке сложных изображений.
11.3.3. Другие методы восстановления. Бриггс (Briggs, 1995) применил
для восстановления так называемый неотрицательный алгоритм наименьших
квадратов (НОНК). Развитый в работе (Lawson and Hanson, 1974) алгоритм
НОНК дает решение матричного уравнения вида АХ=В, где, применительно
к радиоастрономии, А — грязная диаграмма направленности, В — грязная
карта. Этот алгоритм дает для интенсивности X решение, характеризуемое
наименьшим среднеквадратичным отклонением, при условии отсутствия отри-
отрицательных значений. Однако, в отличие от случая ММЭ, не вводится критерия
гладкости. Решение методом НОНК требует большей вычислительной мощности,
чем CLEAN или ММЭ, но исследование Бриггса указывает на то, что НОНК
работает более совершенно, особенно для компактных объектов с размером,
равным лишь нескольким ширинам синтезированной диаграммы направленности.
Было обнаружено, что НОНК уменьшает остаточные значения до уровня,
близкого к наблюдательным шумам системы. В определенных случаях было
найдено, что данный алгоритм работает эффективнее CLEAN при гибридном
картографировании и самокалибровке (рассмотренными ниже) и позволяет
достичь большего динамического диапазона. В алгоритме ММЭ остаточные
значения могут быть не абсолютно случайными, а коррелированными в плоскости
изображения, что может привести к смещению (и, г>)-данных, а это, в свою
очередь, ограничит достижимый динамический диапазон. В некоторой степени
аналогично ведет себя, CLEAN, если ограничивать его продвижение на уровне
396 Восстановление, адаптивная калибровка и их применение [Гл. 11
шумов. Дальнейшее обсуждение можно найти в работах (Briggs, 1995) и (Cornwell,
Braun and Briggs, 1999).
11.4. Адаптивная калибровка и картографирование при
наличии только амплитудных данных
Калибровка амплитуды функции видности часто осуществляется с точностью
до нескольких процентов, фазовые же ошибки, выражаемые в долях радиана, могут
быть много больше вследствие ионосферных или тропосферных вариаций. Тем не
менее, относительные значения некалиброванной функции видности, измеренные
одновременно на ряде баз, содержат информацию о распределении интенсивности,
которая может быть выделена с помощью соотношений замыкания A0.30) и A0.32)
из гл. 10. Мы называем адаптивной калибровкой оба метода, использующие эти
данные: гибридное картографирование и самокалибровку, как это было предло-
предложено в работе (Schwab, 1980). Мы также кратко опишем картографирование при
использовании только данных об амплитуде функции видности.
11.4.1. Гибридное картографирование. Возрождение интереса к методам
замыкания в 70-е годы началось вместе с их повторным открытием Роджерсом и др.
(Rogers et al., 1974), использовавшими замкнутые фазы для получения модельных
параметров РСДБ-данных. В работе (Fort and Yee, 1976) и позднее в других работах
метод замыкания был объединен с методикой итерационного картографирования.
Мы опишем данную процедуру в соответствии с работой (Readhead et al., 1980).
1. Получение первоначальной пробной карты на основе анализа амплитуд функ-
функции видности и любых априорных данных, например, карты на другой длине
волны или эпохи. Если пробная карта ошибочна, сходимость будет медленной,
но обычно вполне достаточно выбрать произвольную пробную карту, такую
как изображение одиночного точечного источника.
2. Определение полного набора независимых уравнений замыкания амплитуды
и/или фазы для каждого интервала интегрирования функции видности. Для
каждого такого набора вычисляется такое число модельных значений функ-
функции видности, при добавлении которого к соотношениям замыкания общее
число независимых уравнений будет равно количеству баз.
3. Нахождение комплексной функции видности, соответствующей каждой базе,
и построение карты по данным функции видности с помощью преобразования
Фурье.
4. Применение метода чистки CLEAN к карте, полученной на 3-м шаге, но
пренебрегая остатком.
5. Отбор компонент с положительной амплитудой в пределах ограниченной
области (удаление компонент, имеющих отрицательную интенсивность или
лежащих за пределами области источника).
6. Проверка на сходимость и, если необходимо, возврат к шагу 2, используя карту
из шага 5 в качестве новой модели.
Отметим, что решение улучшается при итерации в связи с ограничением области
и положительностью значений интенсивности, введенных на пятом шаге. Эти
11.4]
Адаптивная калибровка и картографирование
397
нелинейные процессы можно представить как размытие ошибок модельных значе-
значений видности по данным видности так, чтобы они были ослаблены при комбиниро-
комбинировании с наблюдаемыми значениями в следующем итеративном цикле.
Описанный процесс и большинство его вариантов формируют карту с использо-
использованием данных модели и прямых измерений. Термин гибридное картографирование,
впервые введенный в работе (Baldwin and Warner, 1978), стал широко использо-
использоваться как общее понятие. Использование фазового замыкания не позволяет из-
измерять абсолютные координаты, однако исключает неоднозначность позиционного
угла изображения. При использовании замыкания амплитуд определяются лишь
относительные уровни интенсивности, но обычно бывает нетрудно прокалибровать
данные, чтобы установить шкалу интенсивности. Во многих случаях результаты
наблюдений амплитудных данных достаточно точны и возникает необходимость
использовать только соотношения фазового замыкания; в работе (Readhead and
Wilkinson, 1978) описан вариант рассмотренного выше алгоритма с использованием
лишь замыкания по фазе. Другие варианты этого метода, отличающиеся от опи-
описанного в основном в деталях реализации, были развиты в работах (Cotton, 1979)
и (Rogers, 1980). Если имеется некоторая избыточность баз, то уменьшается число
свободных параметров (Rogers, 1980).
Очевидно, что количество антенн па является важным фактором при карто-
картографировании с использованием соотношений замыкания, поскольку оно влияет на
эффективность использования данных. Можно количественно оценить эту эффек-
эффективность как функцию от па, рассматривая количество данных замыкания как долю
тех данных, которые можно было бы использовать при возможности полной ка-
калибровки. Количество независимых данных замыкания определяется выражениями
A0.31) и A0.33). Количество полностью калиброванных данных равно количеству
баз, которое, при отсутствии избытка,
равно ^па(па — 1). Для фазовых дан-
данных эта доля равна
\{па -
[Па ~ 2)
- Па (Па -
A1.6
Для амплитудных данных она состав-
составляет
- Па (Па - 3)
- Па (па — 1)
Па - 3
Па ~ 1
12
A1.9)
16 20 24 28
Число антенн
Рис. 11.4. Данные функции видности, кото-
которые могут быть получены с помощью ме-
методов адаптивной калибровки, выраженные
в виде части тех данных, которые получа-
получаются от полностью прокалиброванной решет-
решетки. Кривые соответствуют уравнениям A1.8)
и A1.9)
Эти доли также равны отношениям
количества полученных данных к ко-
количеству полученных плюс модельных
данных в каждой итерации процедуры
гибридного картографирования. Гра-
Графики уравнений A1.8) и A1.9) приве-
приведены на рис. 11.4. При па = 4 соотно-
соотношения замыкания дают лишь 50 % возможных фазовых данных и только 33 %
амплитудных данных, однако при па = 10 соответствующие значения составля-
составляют 80% и 78%. Таким образом, в любой решетке, в которой атмосферные или
инструментальные эффекты могут ограничить точность калибровки по опорному
источнику, желательно иметь по крайней мере десять, а лучше более, антенн. Число
398 Восстановление, адаптивная калибровка и их применение [Гл. 11
итераций, необходимых для получения решения с помощью гибридного метода,
зависит от сложности источника, числа антенн, точности первоначальной модели
и других факторов, включая особенности используемого алгоритма.
11.4.2. Самокалибровка. Другая группа программ построения изображе-
изображения, которые в основном выполняют ту же функцию, что и метод гибридного
картографирования, но другим способом, обычно называется самокалибровкой.
В данном случае комплексные коэффициенты усиления антенн рассматриваются
как свободные параметры, получаемые явным образом наряду с интенсивностью.
В некоторых случаях суть процесса легко описать. Например, при картографирова-
картографировании протяженного источника, содержащего компактный компонент (что характерно
для многих радиогалактик), протяженная структура разрешается с помощью более
длинных баз, а компактный источник не затрагивается. Он может быть использован
в качестве опорного источника, позволяющего найти для антенных пар с большими
базами относительные фазы, но не абсолютную фазу, поскольку его положение не
известно. Далее, если в решетке имеется достаточное количество длинных баз, то
с их помощью могут быть получены коэффициенты усиления антенн. Такая осо-
особенность распределения интенсивности, однако, не принципиальна для метода, и с
помощью итерационного подхода практически любой источник можно использовать
в качестве опорного для самого себя. Программы такого типа были разработаны
(Schwab, 1980) и (Cornwell and Wilkinson, 1981). Обзоры соответствующих методик
даны в (Pearson and Readhead, 1984) и (Cornwell, 1989).
Процедура самокалибровки предусматривает использование метода наимень-
наименьших квадратов для минимизации квадрата модуля разности между наблюдаемой
функцией видности V™^as и соответствующими значениями V™^ для рассчитыва-
рассчитываемой модели. Минимизируется выражение
ЕГ ?/, |T?meas _ n *r?model 2 /-.-. -. q\
/ „ wmn\vmn УтУпутп ? ^±±.±UJ
time m<n
где весовой коэффициент wmn обычно выбирается обратно пропорциональным дис-
дисперсии функции V™^as, а все приведенные величины являются функциями времени
в пределах интервала наблюдений. Выражение A1.10) может быть записано в виде
z2 z2 w
time m<n
где
^meas
A1.12)
Если модель является точной, то отношение Хтп некалиброванной измеренной
функции видности к функции видности, предсказанной моделью, не зависит от
и и г>, но пропорционально коэффициентам усиления антенн. Таким образом, ве-
величина Хшп моделирует отклик на опорный источник и позволяет определить ко-
коэффициенты усиления. Однако, поскольку первоначальная модель является лишь
приближенной, желаемый результат достигается путем итераций.
Процедура самокалибровки включает следующие этапы.
1. Составление пробной карты, как в методе гибридного картографирования.
2. Вычисление коэффициентов Хшп для каждого интервала интегрирования
функции видности в пределах времени наблюдения.
пп
х7
|<-\omodel
1 тп
2\х
¦yrneas
* тп
- УшУп
11.4]
Адаптивная калибровка и картографирование
399
3. Определение коэффициентов усиления антенн для каждого интервала инте-
интегрирования.
4. Использование коэффициентов усиления для калибровки измеренных значе-
значений функции видности и построение карты.
5. Использование алгоритма чистки CLEAN и выбор компонент модели с уче-
учетом их положительности и пределов изображения. В работе (Cornwell, 1982)
рекомендуется исключить все детали, для которых |/(/,т)| меньше модуля
наиболее отрицательной детали.
6. Проверка на сходимость и возврат к шагу 2, если это необходимо.
Количество независимых измерений, используемых в вышеописанной проце-
процедуре, равно, как и в случае гибридного картографирования, числу независимых
соотношений замыкания (выражения 10.31 и 10.33), т. е. па (па — 3)/2 для амплитуд
и (па — 1) (па — 2)/2 для фаз. Таким образом, оба метода, гибридное картографи-
картографирование и самокалибровка, в основном эквивалентны друг другу и отличаются
лишь в деталях и реализации. Эффективность как функция числа антенн (рис. 11.4)
применима к обоим методам. Примеры использования методики самокалибровки
показаны на рисунках 11.5 и 11.6.
15h48m24s 23s 22
21s 20s 19s
Прямое восхождение A950.0)
21s
б
20s
19s
Рис. 11.5. Эффект применения самокалибровки при построении радиоизображения ква-
квазара 1548+115, полученного на VLA: а — изображение, полученное с помощью обычных
методов калибровки, которое имеет ложные детали на уровне 1% от максимальной ин-
интенсивности; б — изображение, полученное методом самокалибровки, на котором уровень
ложных деталей ниже уровня 0,2 радиоизофот составляет 0,6%. Заимствовано из работы
(Napier, Thompson and Ekers, 1983); ©1983 IEEE
Использование коэффициентов усиления, являющихся основными неизвестны-
неизвестными величинами, в качестве свободных параметров в методе самокалибровки яв-
является более прямым подходом по сравнению с применяемым в методе гибрид-
гибридного картографирования. Общая оценка инструментальных факторов получается
при использовании полного набора данных. В работе (Cornwell, 1982) отмечалось,
что гораздо проще проводить корректную обработку шума, если рассматривать
400
Восстановление, адаптивная калибровка и их применение
[Гл. 11
Рис. 11.6. Три стадии обработки наблюде-
наблюдений источника Лебедь А, показанного на
рис. 1.18 (Perley, Dreher and Cowan, 1984).
Верхнее изображение является резуль-
результатом преобразования прокалиброванных
данных функции видности с помощью
алгоритма БПФ. Опорный источник на-
находится приблизительно в 3° от Лебе-
Лебедя А. Центральное изображение пока-
показывает результат обработки с помощью
метода максимальной энтропии. Он ком-
компенсирует главным образом недостаток
пространственных частот и тем самым
устраняет боковые лепестки из синтези-
синтезированной диаграммы направленности. Ре-
Результат аналогичен получаемому с помо-
помощью алгоритма чистки CLEAN. Нижний
рисунок показывает эффект применения
метода самокалибровки при условии, что
в качестве первоначальной модели было
взято изображение, полученное по методу
максимальной энтропии. Эта последняя
стадия улучшает динамический диапазон
в три раза. Если первоначальная калиб-
калибровка не так хороша, как в данном слу-
случае, самокалибровка обычно обеспечивает
еще более значительное улучшение. Поле
наблюдения имеет протяженность 2,1 ми-
минут дуги вдоль большей оси и содержит
приблизительно 1000 ячеек. Рисунок вос-
воспроизводится с разрешения НРАО/МАС
комплексную функцию видности в век-
векторной форме, как при самокалибровке,
а не рассматривать амплитуду и фазу
раздельно, как в случае гибридного ме-
метода построения карты. Шум добавляет-
добавляется аддитивно в векторную компоненту,
что приводит к гауссовому распределе-
распределению, в то время как в случае раздель-
раздельной обработки модуля и фазы возникают
более сложные распределения вероятно-
вероятности Раиса (уравнение F.63)). В рабо-
работе (Cornwell and Wilkinson, 1981) был
разработан метод адаптивной калибров-
калибровки, учитывающий различные распреде-
распределения вероятности флуктуации амплиту-
амплитуды и фазы, включая шумы системы, для
различных антенн. Метод использовался
на решетке MERLIN, которая состоит из
антенн разных размеров и конструкций
(Thomasson, 1986). Распределения веро-
вероятностей ошибок, связанных с антенна-
антеннами, — это вполне достоверная априорная
информация, которая может быть эмпи-
эмпирически получена для любой решетки.
Опыт показывает, что методы адап-
адаптивной калибровки во многих случаях
обеспечивают приближение к удовлетво-
удовлетворительному результату при использо-
использовании одиночного точечного источника
в качестве первоначальной модели, хотя
ее неточность увеличивает число необ-
необходимых итеративных циклов. Точечный
источник является хорошей моделью для
фазы симметричного распределения ин-
интенсивности, однако может быть плохой
моделью для амплитуды. Также следу-
следует помнить, что точность соотношений
замыкания зависит от точности согласо-
согласования частотных характеристик и поля-
поляризационных параметров антенн (см. об-
обсуждение в разделах 7.3 и 7.4). Вообще
любой эффект, который не может быть
представлен одним коэффициентом уси-
усиления для каждой антенны, например,
аномальное поведение коррелятора, ухуд-
ухудшает точность замыкания.
При использовании методов адаптив-
адаптивной калибровки интервал интегрирова-
интегрирования данных не должен быть больше ко-
когерентного времени фазовых изменений,
поскольку в противном случае амплиту-
амплитуда функции видности может уменьшится.
11.5] Картографирование с высоким динамическим диапазоном 401
Время когерентности может определяться атмосферой, временная шкала для кото-
которой составляет величину порядка минут. Чтобы работала процедура картографи-
картографирования, поле наблюдений должно содержать достаточно компактную структуру,
обеспечивающую опорную фазу, и достаточно яркую для ее регистрации при высо-
высоком отношении сигнал/шум в пределах времени когерентности. Итак, адаптивная
калибровка не позволяет решить все проблемы и не может быть использована для
обнаружения очень слабого источника в поле, свободном от других деталей.
11.4.3. Картографирование с помошью данных только об амплитуде
функции видности. Некоторые исследования были посвящены вопросу о воз-
возможности построения изображений при использовании только данных об ампли-
амплитуде функции видности. Образ Фурье квадрата модуля функции видности равен
функции автокорреляции распределения интенсивности 1**1:
\V(u,v)\2 = V(u,v)V*(u,v) ^ I(l,m)**I(l,m). A1.13)
Правая часть этого выражения может быть также записана в виде свертки
1A, т) * */(—/,—га). Проблема картографирования при наличии только данных
|V| связана, в основном, с интерпретацией карты автокорреляции /. В отсутствие
сведений о фазе положение центра поля не может быть определено, и существует
неопределенность в 180° в определении ориентации позиционного угла карты. Од-
Однако часто эти ограничения оказываются приемлимыми.
Примеры исследований, относящихся к картографированию без фазовых дан-
данных, можно найти в работах (Bates, 1969, 1984), (Napier, 1972) и (Fienup, 1978).
В (Napier and Bates, 1974) приведен обзор некоторых результатов. Требование
положительности обычно оказывается недостаточным для того, чтобы обеспечить
единственное решение для одномерного профиля, однако в случае двумерных карт
в некоторых случаях удалось добиться однозначности (Bruck and Sodin, 1979).
В работе (Baldwin and Warner, 1978; 1979) рассмотрен случай двумерного распре-
распределения точечных источников и с некоторым успехом получена карта источника
из функции автокорреляции. Хотя эти подходы предвещали продвижение вперед
в интерпретации данных радиоинтерферометров, они не оказались особенно важны
для радиоастрономии. Не был найден простой, достоверный метод интерпретации
данных только об амплитуде функции видности, и, что более важно, разработка
методик, использующих соотношения замыкания, позволила получать полезную
информацию из данных о фазе функции видности даже при отсутствии хорошей
калибровки.
11.5. Картографирование с высоким динамическим
диапазоном
Динамический диапазон изображения обычно определяется как отношение мак-
максимального значения интенсивности к среднеквадратичному уровню фона карты.
Предполагается, что этот среднеквадратичный уровень определяет минимальную
интенсивность, которую можно измерить. Термин точность изображения исполь-
используется для обозначения степени того, насколько точно полученная карта отражает
истинное изображение источника на небе. Точность воспроизведения карты невоз-
невозможно измерить напрямую для конкретного источника, однако численное модели-
моделирование наблюдений модельного источника и обработка данных функции видности
позволяет сравнить полученное изображение с моделью. Таков путь исследования
402 Восстановление, адаптивная калибровка и их применение [Гл. 11
конфигураций антенн, методов обработки и др. вопросов. Соответствующие требо-
требования и методики подробно обсуждаются в работах (Perley, 1989; 1999а).
Высокий динамический диапазон требует высокой точности калибровки, исклю-
исключения всех ошибочных данных и аккуратного восстановления изображения, т. е. он
требует высокой точности измерений функции видности и очень хорошего запол-
заполнения гш-плоскости. Фазовая ошибка Аф может рассматриваться как привносящая
в данные функции видности ошибочную компоненту с относительной амплитудой
sin Аф в квадратуре фазы к истинной функции видности. Амплитудная ошибка
величиной еа % может рассматриваться как ошибочная компонента с относительной
амплитудой еа %, привносимая в функцию видности. Таким образом, например,
фазовая ошибка в 10° приводит к ошибочной компоненте, соответствующей ам-
амплитудной ошибке в 17%. Амплитудная ошибка в 17% будет считаться необычно
большой в большинстве случаев, исключая условия сильного поглощения в атмо-
атмосфере. Однако, фазовая ошибка в 10° будет значительно чаще наблюдаться на
частотах, где важную роль играют ионосферные или тропосферные неоднородно-
неоднородности. Фазовая ошибка Аф (рад) на выходе коррелятора вносит в результирующую
карту ошибочную компоненту со среднеквадратичной относительной амплитудой
Аф/^/2 . При наличии аналогичных ошибок на па(па — 1)/2 базах динамический
диапазон мгновенного изображения, ограничен величиной ~па/Аф.
Проведение самокалибровки является существенным шагом в минимизации
ошибок коэффициентов усиления. Однако, после калибровки коэффициентов усиле-
усиления антенн, остаются небольшие члены (связанные с базами), которые также необ-
необходимо откалибровать. Эти добавочные члены появляются из-за вариаций полос
пропускания и поляризационных характеристик антенн (см. обсуждение в разде-
разделах 7.3 и 7.4) и других аналогичных эффектов. Заметим, что в решетках, имеющих
очень высокую чувствительность на более длинных волнах, необходимость наблю-
наблюдений вплоть до предела, определяемого шумами системы в присутствии источ-
источников фона, устанавливает нижний предел на требуемый динамический диапазон.
В таких случаях выгодно иметь большое число элементов решетки (Lonsdale et al.,
2000).
Желание получить максимально возможный динамический диапазон приводит
к необходимости обращать внимание на детали, специфичные для конкретного
инструмента. В случае VLA в качестве примерных характеристик наблюдения
хорошего качества даются следующие числа. Основная калибровка приводит к ди-
динамическому диапазону порядка 1000 : 1. После самокалибровки можно получить
динамический диапазон вплоть до ~20 000 : 1. После аккуратного исправления оши-
ошибок, связанных с базами, диапазон может стать ~80 000 : 1. В случае использования
спектрального коррелятора, который свободен от ошибок, свойственных квадра-
квадратурной схеме широкополосного коррелятора, и имеет пониженные требования на
точность задержки, достижима величина ~ 200 000 : 1 при достаточном отношении
сигнал/шум.
11.6. Мозаика
Мозаикой называется техника, позволяющая произвести картографирование об-
области неба с размерами больше, чем диаграмма направленности элементов решетки.
Это становится особенно важным на миллимитровых волнах, где диаграммы на-
направленности антенн относительно узки. Радиоастрономические антенны, работаю-
работающие в миллиметровом диапазоне длин волн, обычно меньше антенн сантиметрового
диапазона, но из-за разницы длин волн ширины диаграмм направленности первых
часто уже.
11.6] Мозаика 403
Рассмотрим картографирование квадратного поля, сторона которого в п раз
больше ширины главного лепестка диаграммы направленности антенны. Можно
разделить данную площадь на п2 площадок размером с диаграмму направленно-
направленности, и картографировать отдельно каждую такую площадку. Далее эти п2 карт
подгоняются друг к другу как кусочки мозаики и образуют требуемое полное поле.
Можно ожидать, что для получения однородной чувствительности встретятся опре-
определенные трудности, особенно вблизи границ элементов мозаики, но несомненно,
что эта идея осуществима. Из теоремы выборки, описанной в разд. 5.2, следует, что
число точек выборки функции видности по координатам и и г>, необходимое для
карты, покрывающей площадь, равную п2 площадям диаграммы напрвленности,
в п2 раз больше того числа, которое требуется для карты, покрывающей площадь
только одной диаграммой направленности. При мозаике увеличенный объем дан-
данных получается путем использования п2 различных направлений наведения антенн.
В результате выборка значений функции видности по и и v должна производиться
с интервалом в п раз меньшим, чем тот, который используется для поля размером
с диаграмму направленности. Этот интервал обычно меньше диаметра апертуры
антенны. Однако мы покажем далее, что можно определить, как меняется функция
видности на масштабах меньших, чем диаметр антенны.
На рис. 5.9 изображены две антенны, следящие за некоторым источником. Про-
Проекция расстояния между антеннами на направление на источник равна и, а диаметр
каждой антенны равен d\ (обе величины измерены в длинах волн). В направлении и
интерферометр регистрирует пространственные частоты в диапазоне от (и — d\) до
(и + d\), так как соответствующие расстояния могут быть найдены в пределах апер-
апертур антенн. Измерения функции видности в этом диапазоне баз позволяют полу-
получить хорошую выборку данных, необходимых для мозаики. Разница длин путей от
источника до апертур двух антенн равна w длин волн, и по мере того, как антенны
сопровождают источник, из-за изменения w на выходе коррелятора формируются
интерференционные лепестки. Поскольку апертуры антенн остаются перепендику-
лярны к направлению на источник, разность длин путей w и скорость ее изменения
одинаковы для любой пары точек, каждая из которых принадлежит плоскости
апертуры, независимо от расстояния между ними. Таким образом, при слежении
принимаемые сигналы от любых двух таких точек на выходе коррелятора име-
имеют одинаковые частоты интерференции. Поэтому эти компоненты не могут быть
разделены путем фурье-анализа, и внутри диапазона пространственных частот от
(и — d\) до (и + d\) информация об изменении функции видности теряется. Однако
при построении мозаик антенны сканируют поле, т. е. периодически переставляют
точки наведения, либо непрерывно сканируют, образуя растр. Скнирование являет-
является дополнительным движением по отношению к обычному слежению за источником
по небу. Из рис. 5.9 можно видеть, что если антенны вдруг повернутся на небольшой
угол Д0, то положение точки В сместится на расстояние, равное Аи АО длин волн
в направлении, параллельном направлению на источник. В результате фаза ин-
интерференционного компонента, соответствующего расстоянию (и + Аи) (например,
между точками А\ и В), изменится примерно на 2т:Аи АО. Так как это изменение
фазы пропорционально Ащ изменение функции видности для диапазона от (и — d\)
до (и + d\) может быть получено путем фурье-преобразования сигнала на выходе
коррелятора соответствующего сдвигу наведения АО. Таким образом, изменения
в наведении приводят к изменениям фазы интерференции, которые зависят от
расстояния между приходящими лучами в пределах апертур антенн. Этот эффект
позволяет сохранить информацию об изменениях функции видности.
Приведенный выше вывод о том, что сканирование антеннами позволяет полу-
получить информацию о величинах функции видности, был впервые сделан в работе
404 Восстановление, адаптивная калибровка и их применение [Гл. 11
(Ekers and Rots, 1979). Авторы провели следующий математический анализ. Рас-
Рассмотрим пару антенн, разделенных вектором (щ,Уо) и направленных по вектору
Aр,тр). Так как угол наведения меняется, эффективное распределение интенсив-
интенсивности по интерисующему нас полю представляет собой функцию 1A, т), сверну-
свернутую с нормированной диаграммой направленности антенны Адг(/, т). Наблюдаемая
функция видности является образом Фурье 1A, т) по и и у, помноженным на
отклик антенны для данного наведения:
V(uo,yo,lp,mp) = \ \AN(l-lp,m-mp)I(l,m)e-j2^Uol+Vom) dldm. (П.14)
Предполагая, что диаграмма направленности антенны симметрична, мы можем
переписать уравнение A1.14) в виде
V(uo,yo,lp,mp) = [ \ AN(lp - 1,тр - т) I(l,m) e-j27r{u°l+Vorn) dl dm, A1.15)
который является двумерной сверткой
V(u0, vo, lP, mp) = [l(l, m) e-^W^m>] * * AN(l, m). A1.16)
Теперь проведем фурье-преобразование V по и и у, что даст информацию
о функции видности полного поля, полученной в результате использования ансамб-
ансамбля углов наведения:
V(u, V)=\\ [
= [V(u, у) * *25(и0 -u,v0- v)] AN(u,v). A1.17)
Здесь функция А(и, v) — это образ Фурье от А^A, т), т. е. функция автокорреляции
распределения поля по апертуре одиночной антенны. Она называется передаточной
функцией или функцией пространственной чувствительности антенны. Двумерная
J-функция 25(щ — и, vq — v) является фурье-образом e-J2K(uoi+vom) ^ Наконец, урав-
уравнение A1.17) приобретает вид:
V(u, v) = V[(u0 - и), {v0 - у)} AN{u, у). A1.18)
Из уравнения A1.18) можно сделать вывод, что если отнаблюдать поле разме-
размером в несколько ширин диаграммы направленности, получить функцию видности
для ряда направлений наведения, а затем провести для каждой антенной пары
фурье-преобразование функции видности относительно данных направлений, то
в результате будут получены значения функции видности в области (и, у), где
определена функция An (и, у). Для антенны с круглым рефлектором диаметра d
функция An (и, у) является ненулевой внутри окружности диаметра 2с/. Таким
образом, если функция An (и, у) известна с достаточной точностью, т.е. форма
диаграммы направленности достаточно хорошо определена, то функция видности
может быть получена в промежуточных точках, что необходимо для построения
карты полного поля.
На практике, при обработке данных функции видности, используемых для моза-
мозаики, преобразование Фурье по отношению к наведению обычно явно не проводится.
Важность рассуждений, приведенных выше, состоит в демонстрации того, что
в данных присутствует информация с необходимым разрешением, если проводится
сканирование источника антенной, либо в процессе непрерывного движения, либо
как последовательность дискретных наведений. Процесс получения распределения
11.6] Мозаика 405
интенсивности обычно основан на использовании нелинейных алгоритомов восста-
восстановления.
Корнуэлл (Cornwell, 1988) указал на то, что необходимое угловое расстояние
между центрами наведения на небе может быть выведено из теоремы выборки
преобразований Фурье (разд. 5.2). В более общем виде эта теорема может быть
сформулирована так: если некоторая функция f{x) ненулевая только внутри ин-
интервала шириной А по координате ж, то она полностью определена, если ее фурье-
образ F(s) известен в точках, расстояние между которыми не превышает А
по координате s. При более разреженной выборке появляются ложные детали,
и воспроизвести исходную функцию будет невозможно. Здесь мы рассматриваем
диаграмму антенны, направленную на источник, достаточно широкий, чтобы по-
покрыть большую часть диаграммы направленности, т. е. главный лепесток и первые
боковые лепестки. По мере движения диаграммы направленности антенны с раз-
различными углами наведения для охвата всего источника, производится эффективное
накопление данных о свертке объекта и диаграммы. Диаграмма направленности
получается преобразованием Фурье автокорреляционной функции распределения
поля по апертуре антенны. Поле обрезается по краям апертуры, ширина которой
равна d\ длин волн. Следовательно, автокорреляционная функция обрезается на
ширине 2d\. Вспомним, что ранее, при использовании функции выборки (разд. 5.2),
именно размер источника определял наличие резкого спада. В настоящем же слу-
случае теорема указывает на то, что интервал А1р между наведениями не должен
превышать l/Bd\) для того, чтобы обеспечить полную выборку данных о свертке
источника и диаграммы направленности. На практике функция облучения антенны
постепенно убывет на краю, и поэтому автокорреляционная функция значительно
спадает еще до того, как она достигнет ширины обрезания 2d\. Таким образом,
если Alp немного превышает 1/Bб/д), привносимая ошибка может быть небольшой.
11.6.1. Методы получения мозаичной карты. Основные шаги метода мо-
мозаики заключаются в следующем:
1. Наблюдение функции видности для принятой последовательности центров
наведения.
2. Независимая обработка данных для каждой точки наведения и получение
ряда карт, каждая из которых покрывает приблизительно площадь одной
диаграммы направленности антенны.
3. Объединение карт с площадью одной диаграммы направленности в необходи-
необходимую карту полного поля.
На шаге 2 для каждой карты с площадью, соответствующей одной диаграмме
направленности, желательно также удалить эффекты, вносимые синтезированной
диаграммой направленности для того, чтобы избавиться от влияния боковых
лепестков в отклике. Это может быть сделано, например, с помощью алгоритмов
CLEAN или ММЭ. Использование этих нелинейных алгоритмов может дать инфор-
информацию о некоторых частотных компонентах интенсивности, которые были упущены
при данном покрытии антенной решетки. В работах (Cornwell, 1988) и (Cornwell,
Holdaway and Uson, 1993) описаны две процедуры мозаичного картографирования.
Первый метод, называемый авторами линейной мозаикой, по существу состоит из
трех перечисленных выше этапов, с использованием метода наименьших квадратов
при комбинировании отдельных карт на третьем этапе. Хотя нелинейное восста-
восстановление производится отдельно для каждой карты с площадью одной диаграммы
406 Восстановление, адаптивная калибровка и их применение [Гл. 11
направленности, комбинирование карт является линейным процессом. Второй ме-
метод, отличие которого состоит в том, что восстановление проводится совместно,
называется нелинейной мозаикой и включает в себя такой нелинейный алгоритм
как ММЭ. В ходе восстановления неизмеренные данные функции видности можно
оценить точнее, если при этом использовать сразу полное поле ансамбля углов
наведения, а не обрабатывать по отдельности каждую карту размера с отдельный
лепесток диаграммы направленности. Можно показать преимущество совместного
восстановления комбинированной полной карты, если рассмотреть неразрешенный
компонент распределения интенсивности, который в двух или более случаях распо-
расположен на краю отдельных карт с площадью, равной одной диагармме направлен-
направленности.
Амплитуда компоненты, расположенной на краю диаграммы направленности
(где отклик меняется быстро), с большой вероятностью будет определена неточно,
но такие ошибки будут иметь тенденцию усредняться и исчезать из комбинииро-
ванных данных. Наибольшая энтропия в случае мозаики соответствует построению
карты, которая согласуется со всеми данными функции видности для различных
направлений наведения с неопределенностью, обусловленной шумом.
Корнуэлл (Cornwell, 1988) обсуждает применение алгоритма максимума энтро-
энтропии, предложенного в (Cornwell and Evans, 1985) для мозаики. Этот алгоритм
кратко описан в разд. 11.3 (см. уравнение 11.7). По сути эта процедура аналогична
той, что используется при картографировании единичным наведением, за исключе-
исключением нескольких дополнительных шагов при определении %2 и его градиента. Как
и в уравнении A1.6), %2 является статистичекой характеристикой, показывающей
отклонение модели от измеренной функции видности и здесь может быть выражена
в следующем виде:
2 = v^v^ I Vras ^model |2
где индексы гир указывают на г-ю величину функции видности при р-м наведении,
a cr2ip — это дисперсия функции видности. Необходимо задать начальную модель
и далее осуществить следующие шаги, описанные в работе (Cornwell, 1988):
1. Для первой точки наведения умножить текущую пробную модель на диа-
диаграмму направленности антенны при данном наблюдении и произвести пре-
преобразование Фурье по отношении к (/,т), чтобы получить предсказанные
(модельные) величины функции видности.
2. Вычесть измеренные величины функции видности из модельных для получе-
получения набора остаточных значений. Подставить остаточные значения в накап-
накапливающую функцию х2 уравнения A1.19).
3. С помощью преобразования Фурье перевести остаточные значения функции
видности, взвешенные обратно пропорционально их дисперсиям, в распре-
распределение интенсивности. Это распределение сглаживается путем домножения
на диаграмму направленности антенны и записывается как массив данных
с размерностью полной модели, построенной ММЭ.
4. Повторить шаги 1-3 для каждого наведения. На 2-м шаге добавить величину
X2 к величинам %2, полученными для других наведений в этом цикле. На
3-м шаге добавить остаточные значения функции видности в массив данных.
Значения, собранные в этом массиве, используются для получения градиента
X2 по изображению, построенному ММЭ.
11.6] Мозаика 407
Причина, по которой на 3-м шаге остаточное распределение необходимо допол-
дополнительно умножить на диаграмму направленности, сосотоит в том, что это умень-
уменьшает нежелательные отклики от боковых лепестков, которые попадают на смежные
площадки наведения. Это также взвешивает данные в соответствии с отношением
сигнал/шум. Завершение процедуры ММЭ может потребовать несколько десятков
циклов описанных выше шагов, чтобы получить сходимость к окончательному
изображению. В завершение всего процесса, чтобы уменьшить влияние перемен-
переменного разрешения внутри карты, рекомендуется провести сглаживание при помощи
двумерной гауссовой диаграммы направленности с шириной, равной разрешению
решетки.
Несколько другая процедура нелинейной мозаики описана в работе (Sault,
Stavely-Smith and Brouw, 1996). В данном случае карты с площадью, соответствую-
соответствующей одной диаграмме направленности, линейно объединяются без индивидульного
восстановления, затем восстанавливается комбинированная карта. При линейном
объединении каждый элемент изображения на полной карте представляет собой
взвешенную сумму соответствующих элементов отдельных карт площадью одной
диаграммы направленности. В качестве примера Солт (Sault) и др. приводят ре-
результаты мозаики Малого Магелланового Облака, проведенной на австралийской
решетке АТСА с 320 точками наведениями. Они показывают, что совместное вос-
восстановление, используемое при нелинейной мозаике, лучше линейной комбинации
карт отдельнах полей, даже если к каждой из них была применена индивидуальная
процедрура восстановления. Авторы также проводят восстановление при помощи
двух методов, разработанных ими (Cornwell, 1988), и делают вывод, что результаты
имеют сравнимое качество.
11.6.2. Некоторые требования к антенным решеткам при мозаике.
При картографировании источников, размер которых больше диаграммы направ-
направленности антенны, важно получить величины функции видности в точках, рассто-
расстояния между которыми по и и v меньше диаметра антенны. Данные, практически
равнозначные непрерывному покрытию по и и г>, могут быть получены при наблю-
наблюдениях в различных направлениях, как это описано выше. Минимальное расстояние
между двумя антеннами ограничено по механическим причинам, в результате обра-
образуется пробел или область с низкой чувствительностью, соответствующая расстоя-
расстоянию, равному приблизительно половине минимального расстояния между центрами
апертур антенн. Это минимальное расстояние зависит от конструкции антенны, но
в общем, если интервал зенитных расстояний не ограничен, две антенны диаметра
d не могут быть расположены ближе, чем на расстоянии 1,4с/, или, возможно, 1,25с/
при специальной конструкции. В противном случае существует опасность меха-
механического столкновения антенн, особенно, если не исключена возможность того,
что они могут быть иногда наведены в разных направлениях. При наблюдениях
в режиме полной мощностью на одиночной антенне, в принципе, расстояние может
меняться от нуля до d/А, но некоторые наблюдения на пространственных частотах
больше, чем ~0,5с//Л, являются ненадежными, потому что функция пространствен-
пространственной чувствительности антенны падает до низких значений в результате уменьшения
освещенности рефлектора по краям. Потеря данных на малых значениях (u,v) при-
приводит к появлению широких отрицательных боковых лепестков у синтезированной
диаграммы направленности, таких, что кажется, будто диаграмма направленности
помещена в неглубокую чашеобразную впадину. Этот эффект наиболее заметен,
когда картографируемое поле настолько широко, что в его центральную часть
попадает несколько пустых (и, г>)-ячеек.
408
Восстановление, адаптивная калибровка и их применение
[Гл. 11
-d
Рис. 11.7. Сплошной линией, симметричной относительно начала координат, показана
функция пространственной чувствительности А для одиночной антенны диаметра d. Эта
линия приведена для случая однородного облучения апертуры и показывает относитель-
относительную чувствительность к пространственным частотам для наблюдений в полной мощности
единичной антенны. Штриховыми линиями показана пространственная чувствительность
для двух антенн диаметра d с однородным облучением апертур, работающих как интер-
интерферометр. Кривая 1 соответствует расстоянию между центрами антенн, равному l,4<i,
а кривая 2 — расстоянию, равному l,25<i. Если бы облучение апертуры уменьшалось по
краям, то эти кривые снижались бы до нижних значений быстрее, чем это изображено
Передаточная функция An (и) является автокорреляционной функцией распре-
распределения поля по антенной апертуре и зависит от конкретной конструкции антенны,
включая диаграмму направленности облучателя. Сплошной кривой на рис. 11.7
показана функция А для равномерно облученной круглой апертуры, которая может
быть рассмотрена как идеальный случай. Поскольку обычно происходит некоторое
уменьшение облучения рефлектора антенны к краям, то в общем случае функция
Ajq спадает несколько быстрее, чем это нарисовано. Функция An на рис. 11.7 про-
пропорциональна площади пересечения двух кругов диаметра с/, и значение абсциссы
равно расстоянию между их центрами. В трехмерном случае эта функция иногда
называется chat( ), ее свойства обсуждаются в работе (Bracewell, 1995). Штрихо-
Штриховыми линиями на рис. 11.7 изображена относительная пространственная чувстви-
чувствительность интерферометра, состоящего из двух однородно освещенных круговых
апертур диаметром d. Кривая 1 соответствует расстоянию 1,4б/ между центрами
апертур, а кривая 2 — расстоянию 1,25с/. Если имеются данные полной мощности
и интерферометрические, то можно видеть, что наименьшая чувствительность ре-
реализуется на расстоянии, равном примерно половине дистанции между антеннами.
Для увеличения чувствительности на минимальных пространственных частотах
проводятся измерения полной мощности с помощью большей антенны, диаметра ~
~ 2d или rsj 3d; см., например, работы (Bajaja and van Albada, 1979) или (Welch and
Thornton, 1985). При наблюдениях с полной мощностью на антенне диаметра 2d
расстояния будут меняться от нуля до ~ б/, покрывая, таким образом, пробел на uv-
плоскости. Но так как стоимость антенны приблизительно пропорциональна б/2'7,
ожидаемая стоимость антенны диаметра 2d примерно в 6,5 раза больше стоимости
антенны диаметра d. К тому же большая антенна может не иметь такой точности
поверхности или наведения, какую имеют меньшие антенны, и поэтому диапазон
рабочих частот у нее может быть ограничен.
Другая возможность заполнить отсутствующие пространственные частоты со-
состоит в использовании одной или более пар меньших антенн, например, с диаметром
d/2 и расстоянием между центрами апертур порядка 0, 7d. Пара антенн диаметра
11.6] Мозаика 409
d/2 имеет в 4 раза меньшую площадь, и, следовательно, в 4 раза меньшую чувстви-
чувствительность по тонкой структуре, чем пара антенн диаметра d. Так как диаграмма на-
направленности меньшей антенны характеризуется телесным углом в 4 раза меньшим,
чем у антенны диаметра с/, то потребуется в 4 раза меньше наблюдений в разных
направлениях, и время итегрирования для каждого из них может быть в 4 раза
больше. Корнвел и др. (Cornwell, Holdaway and Uson, 1993) продемонстрировали,
что можно удовлетворительно провести процедуру мозаики с однородной решеткой,
а именно, с решеткой, состоящей из антенн одинакового размера. При этом необ-
необходимо выполнить наблюдения полной мощности и интерферометрические наблю-
наблюдения с некоторыми антеннами, расположенными как можно ближе друг у другу.
Итерации восстановления при обработке данных помогут заполнить остающиеся
пробелы в покрытии гш-плоскости.
На частотах в несколько сотен ГГц, когда диаграммы направленности антенн
имеют ширину порядка минуты дуги, построение карт объектов размера порядка
одного градуса требует большого числа наблюдений разных точек поля: от 102 до
104. Так как нельзя быстро повторить любую заданную конфигурацию наведения,
то может оказаться непрактичным использовать вращение Земли для заполнения
небольших пробелов в покрытии гш-плоскости. Таким образом, решетки, сконстру-
сконструированные для мозаики больших объектов, должны давать хорошее мгновенное
покрытие гш-плоскости. На таких высоких частотах также желательно избегать
больших зенитных расстояний, чтобы минимизировать влияние атмосферы.
Альтернативой слежению за дискретными центрами наведения является про-
прочесывание диаграммами направленности исследуемой площадки неба в режиме
растрового сканирования. Эта методика названа мозаикой «на лету». Она имеет
несколько следующих преимуществ:
• Покрытие гш-плоскости для всех точек поля становится максимально одно-
однородным, что приводит к однородности синтезированной диаграммы направ-
направленности результирующей карты и таким образом упрощает обработку изоб-
изображений.
Каждая точка поля наблюдается много раз подряд настолько долго, насколько
это возможно, и поэтому для заполнения гш-плоскости можно воспользоваться
вращением Земли.
Если проводятся измерения полной мощности, сканирующее движение диа-
диаграммы направленности может быть использовано для исключения атмосфер-
атмосферных эффектов, аналогично тому, как используется переключение диаграммы
направленности в больших одиночных телескопах.
• Устраняются потери времени при перестановке антенн от одного центра наве-
наведения к другому.
Неудобство наблюдений «на лету» состоит в том, что время интегрирования
на выходе коррелятора должно быть несколько меньше того времени, за которое
диаграмма направленности сканирует любую точку поля, в результате генерируется
большое количество данных функции видности, где каждое значение получено для
отдельного направления наблюдения.
410 Восстановление, адаптивная калибровка и их применение [Гл. 11
11.7. Многочастотный синтез
Наблюдения на нескольких различных радиочастотах являются эффективным
способом улучшения выборки функции видности в гш-плоскости. Эта методика на-
называется многочастотным синтезом или синтезом в полосе. Обычно диапазон частот
состовляет примерно ±15% от центральной частоты. Использование такого диапа-
диапазона может быть эффективным для заполнения дырок в покрытии, и, поскольку
он не слишком широк, не должно приводить к большим изменениям структуры
источника с частотой (см., например, (Conway, Cornwell and Wilkinson, 1990)). Од-
Однако такие изменения могут быть достаточно значительными, и необходимо сужать
динамический диапазон, если не предпринять некоторые шаги, описанные ниже.
Основные механизмы формирования космического радиоизлучения соответствуют
радиоспектрам, плавно меняющиеся с частотой, а интенсивность обычно имеет
степенную зависимость от частоты:
@", (п.20)
где а — спектральный индекс, зависящий от (/,га). Если спектр не описывается
степенным законом, тогда, в действительности, мы можем записать
«¦15- <1L21)
Если бы спектральный индекс был постоянным по всему источнику, можно было
бы исключить спектральные эффекты. Но на самом деле это не так: спектральные
эффекты ослабляются первоначальным испралением данных с учетом «среднего»
или «характерного» спектрального индекса всей картографируемой структуры.
Тогда с этого момента а будет представлять собой спектральный индекс отклонения
распределения интенсивности источника от этого приближения первого порядка.
Рассмотрим случай, когда это изменение интенсивности может быть приближенно
описано линейной зависимостью:
1A/) = 1Ы + д? (i/ - i/o) = 1Ы + alM^pl - J(i/0) + alM ^^ ,
V A1.22)
где опорная частота щ находится вблизи центра используемого диапазона частот.
Выражение A1.22) представляет собой сумму члена, зависящего от одиночной
частоты, и спектрального члена. Для расчета синтезированной диаграммы на-
направленности решетки, работающей в многочастотной моде, рассмотрим отклик
на точечный источник со спектром A1.22). Отклик на член, зависящий от одной
частоты, может быть рассчитан путем преобразования Фурье пространственной
передаточной функции. Передаточная функция представляет собой J-функцию от
и и v для каждого измерения функции видности. Каждой используемой частоте
соответствует свой набор J-функций. Отклик на спектральный член получается
путем умножения передаточной функции на (у — щ)/щ и проведения преобразова-
преобразования Фурье. Если обозначить одночастотный член через Ь'о, а спектральный член —
через 6^, то синтезированная диаграмма направленности будет равна
Ьо(/, т) = Ъ'оA, т) + a(/, m)bi(/, га). A1.23)
Первая компонента представляет собой условную диаграмму направленности, а вто-
вторая — нежелательный артефакт. Измеренное распределение интенсивности, полу-
11.8] Некомпланарные базы 411
ченное путем преобразования Фурье измеренной функции видности, равно
10A,т) = 1A, т) * *br0(l,m) + a(l,m)I(l,m) * *Ь[A,т), A1.24)
где 1A, т) — истинная интенсивность на небе. В работах (Conway, Cornwell and
Wilkinson, 1990) и (Sault and Wieringa, 1994) разработаны алгоритмы восстановле-
восстановления, основанные на методе чистки CLEAN, которые восстанавливают и bf0, и Ь[.
В методе, разработанном в первой работе, компоненты, содержащие в себе каждую
из двух диаграмм направленности, исключаются поочередно. В методе, предложен-
предложенном во второй работе, каждый исключенный компонент представлял обе диаграммы
направленности. Эти методы дают распределения интенсивности источника и спек-
спектрального индекса как функции частоты. Конвей (Conway et al.) также рассмотрели
логарифмический, а не линейный закон изменения частоты относительно щ. Дан-
Данные анализа показали, что для разброса частот порядка ±15 % типичная величина
отклика на компоненту Ь[ составляет 1 % и иногда может быть проигнорирована.
Удаление компоненты Ь[ уменьшает спектральные эффекты до ~0,1 %.
11.8. Некомпланарные базы
В разд. 3.1 было показано, что, за исключением случая линейных решеток
Восток-Запад, базы синтезирующей решетки не остаются в одной плоскости по
мере вращения Земли. Было также показано, что для полей зрения малого углового
размера (приближенно определяемого уравнением 3.12) связь преобразования Фу-
Фурье между функцией видности и интенсивностью может быть удовлетворительно
выражена в двумерном виде. Этот факт является основой большой части всего син-
тезного картографирования. Однако, на практике для частот меньше нескольких
сотен МГц предположение о малом угловом размере поля не всегда применимо.
На метровых длинах волн главный лепесток диаграммы направленности антенн
широкий, например, для 25-метровой антенны на длине волны 2 м его размер
составляет ~ 6°. К тому же, ввиду высокой плотности сильных источников на небес-
небесной сфере на метровых длинах волн, необходимо во избежание путаницы проводить
картографирование всей диаграммы направленности. Рассмотрим случай, когда
условие C.12) не выполняется, и двумерное решение не может быть использовано.
Следующая обработка предложена в работах (Sramek and Schwab, 1989; Cornwell
and Perley, 1992); Perley, 1999b). Используем точный результат уравнения C.7):
оо оо
V(u,v,w) =
An (I, га) 1A, га)
—^— x
VI - I2 - m2
— oo —oo
X
exp {-j2tt [ul + vm + w(y/l-l2 -га2 - l)] } dl dm. A1.25)
Здесь V(u, v, w) — функция видности в зависимости от трехмерной пространствен-
пространственной частоты, А^A, га) — нормированный главный лепесток диаграммы направлен-
направленности антенны и 1A, т) — картографируемое двумерное распределение интенсив-
интенсивности.
Далее перепишем уравнение A1.25) в виде трехмерного преобразо-
преобразования Фурье, куда входит третий направляющий косинус п, опреде-
определяемый по отношению к оси w. Фаза видности V(u, v, w) измеряет-
измеряется относительно функции видности некоего (гипотетического) источни-
источника, расположенного в точке фазового репера наблюдения. В результате
в экспоненциальном члене в правой части уравнения A1.25) появляется
412 Восстановление, адаптивная калибровка и их применение [Гл. 11
коэффициент e^27VW, как это было отмечено в тексте после уравнения C.7). Из-за
вращения лепестков, обсуждаемом в п. 6.1.6, появляется соответствующий сдвиг
фазы. Этот коэффициент позволяет использовать величину п' = п — 1 в качестве
сопряженной к переменной w для того, чтобы получить трехмерное преобразование
Фурье. Функции от п' будут обозначаться штрихом. Таким образом перепишем
уравнение A1.25)в следующем виде:
оо оо оо
Г Г Г АмA m)I(l m) / /
r\r\ / \ III -*4v \Ь5 III) J- U) III) r- / /^ jr\ r\ I
v(u, v,w) = — =^-о yy 1 — lz — mz —n —
J J J л/1 - P - m2
— oo —oo —oo
x exp {— j2tt (?x/ + vm + г^п7)} с// б/ттг б/тт/. A1.26)
Дельта-функция 8{у\ — I2 — m2 — n' — 1) введена, чтобы выполнялось условие п =
= v 1 — Р — т2 и величина п' могла быть использована в преобразовании Фурье
как независимая переменная. На практике V измеряется только в точках, в кото-
которых дискретизирующая функция W(u, v, w) не равна нулю. Преобразование Фурье
полученной функции видности определяет трехмерную функцию интенсивности 1%
следующим образом:
оо оо оо
Г3A,т,п') = [ [ [ W(u,v,w)V(u,v,w)ej2^ul+v™+wn/) dudvdw. A1.27)
— оо —оо —оо
Данное выражение представляет собой фурье-преобразование произведения двух
функций, W(u, v, w) и V(i?, г;, к;), и, с учетом теоремы свертки, равно свертке фурье-
преобразований двух функций. Таким образом,
/з(/, ш, п) = < — v = > * * * W (/, m, n ). A1.28)
I V1 - P - m2 )
Здесь W (/, 7тг, п') — преобразование Фурье трехмерной дискретезирующей функции
W(u, v, w), а тройная звездочка обозначает трехмерную свертку. Зная результат
преобразования Фурье, мы теперь можем заменить п' на (п — 1), и уравнение A1.28)
примет вид
Г AN(l, m)I(l, m) S(y/l -P-m2 -n)\ —
/3(/, Ш, П) = < ^^ V = > * * * VF(/, 771, П). A1.29)
I V1 — P — m2 )
Выражение в скобках в правой части уравнения A1.29) определено только на по-
поверхности единичной сферы п = \/1 — I2 — т2 , поскольку 5-функция не равна нулю
только на этой сфере. Функция W, с которой она свернута, — это преобразование
Фурье дискретизирующей функции, являющейся по сути трехмерной грязной диа-
диаграммой направленности. Свертка привносит эффект растяжения (см. последнее
выражение), в результате чего /з имеет конечную протяженность в радиальном
направлении сферы. На рис. 11.8 а изображена единичная сфера с центром в начале
координат (/, ттг, п) — точке R. Плоскость /ттг, в которой лежат решения стандартного
двумерного анализа, касается единичной сферы в точке О, в которой п = 1 и п' =
= 0. Заметим, что, поскольку /, ттг и п являются направляющими косинусами, то
единичная сфера в координатах (/, ттг, п) — это математическое понятие, а не сфера
в реальном пространстве.
Можно использовать следующие несколько способов получения неискаженной
карты широкого поля зрения (Cornwell and Perley, 1992).
11.8]
Некомпланарные базы
413
Рис. 11.8. а — единичная полусфера в координатах A,т,п). Точка R — начало коорди-
координат A,т,п). Точка О — начало координат (l,m,nf) и точка отсчета фазы, б— сечение
единичной сферы плоскостью (га, п). Затененная область представляет собой протяжение
функции /з. Источник в точке А не появится или будет в значительной степени ослаблен
при двумерном анализе в плоскости 1т. Ширина трехмерной «диаграммы направленно-
направленности» в направлении п должна быть сравнима с шириной по I и га, так как диапазон
функции дискретизации по w сравним с диапазоном по и и г>, если наблюдения занимают
большой интервал часовых углов. (В похожей, на первый взгляд, ситуации, изображен-
изображенной на рис. 3.5, функция интенсивности не ограничена поверхностью сферы, так как все
измерения сделаны в плоскости w' = 0.)
1. Трехмерное преобразование. Функция /з(/,га, п) может быть восстановлена
с помощью трехмерного расширения алгоритма чистки CLEAN. Этот способ ослож-
осложняется тем, что на практике функция видности не настолько хорошо считана по
гу, как по и и v. Из рис. 3.4 видно, что большие значения w реализуются для
больших зенитных расстояний картографирумого источника. На рис. 11.8 б' шири-
ширина поля обозначена как Of. Преобразование должно быть рассчитано в некото-
некотором диапазоне значений (/,т) внутри этого поля и в интервале PQ значений п.
Корнуэлл и Перлей (Cornwell and Perley) предложили использовать прямое (а не
дискретное) преобразование Фурье от п к w, поскольку иначе ограниченная вы-
выборка может привести к появлению опасных боковых лепестков и ложных деталей.
Таким образом, двумерные БПФ проводятся для последовательности плоскостей,
перпендикулярных оси п. Число необходимых плоскостей равно PQ, деленному на
необходимый интервал выборки в направлении п. Ширина диапазона измеренных
величин функции видности в направлении w равна 2|u>|max, поэтому, по теореме
выборки, функция интенсивности полностью определена по координате п, если она
известна через интервалы, равные B|гу|тах)~1. Расстояние PQ приблизительно рав-
равно 0I% « (|/2 + ш2|тах)/2 (заметим, что угол POQ = 0//4 и F>//2J = \12 + ш2|тах).
Следовательно, число плоскостей, для которых должна быть рассчитана двумерная
интенсивность, равно \l2 + m2|max |ги|тах. Этот результат может быть также получен
при рассмотрении фазового члена в уравнении C.8), опущенного при переходе от
трех к двум измерениям, и получении его значений через интервалы Найквиста,
равные половине оборота фазы. Наибольшая возможная величина w равна Dmax/A,
где ?)тах — самая длинная база решетки. Если ширина Of ограничена шириной
диаграммы направленности антенн диаметром б/, для которых угловое расстояние
от центра диаграммы направленности до первого нуля равно ~ А/б/, необходимое
число плоскостей равно ~ (А/с/J х Dmax/A = А?)тах/б/2. Примеры карт, построен-
построенных данным методом, приведены в работе (Cornwell and Perley, 1992).
414 Восстановление, адаптивная калибровка и их применение [Гл. 11
2. Картографирование многогранников. Поверхность единичной сферы, для ко-
которой требуется построить карту, может быть разделена на некоторое количество
площадок, которые можно картографировать отдельно, используя приближение
малого поля. Для всех них строятся двумерные карты на плоскостях, касающихся
единичной сферы в разных точках. Эти точки касания являются фазовыми цен-
центрами отдельных площадок. Для каждой отдельной карты необходимо устанавли-
устанавливать и фазы функции видности, и координаты (u,v,w) всей базы данных отно-
относительно своего фазового центра. Отдельные площадки могут быть объединены
с использованием методов, аналогичных тем, которые применяются при мозаике,
включая совместное восстановление. Этот подход назывался картографирование
многогранников, потому что различные плоскости карт образуют часть поверхности
многогранника. Опять же, примеры этого метода даны в (Cornwell and Perley, 1992).
3. Объединение мгновенных изображений. В большинстве синтезных решеток
антенны установлены примерно на уровне поверхности земли и, таким образом,
находятся приблизительно в одной плоскости в любой момент времени. При этом
долговременные наблюдения могут быть поделены на последовательности мгновен-
мгновенных «снимков», для каждого из которых условие планарности баз применяется от-
отдельно. Следовательно, можно построить карту путем объединения последователь-
последовательности откликов снимков. Каждый снимок представляет собой истинное распределе-
распределение интенсивности, свернутое с разными грязными диаграммами направленности,
так как покрытие гш-плоскости меняется постепенно по мере движения источника
по небу. В идеальном случае, для восстановления потребовалась бы оптимизация
распределения интенсивности с совместным, а не по отдельности, использованием
снимков. Необходимо заметить, что в общем случае плоскость, в которой лежат
базы снимка не перпендикулярна направлению на картографируемый источник.
В результате перпендикуляры, опущенные из точек на поверхности единичной сфе-
сферы на плоскость 1т на рис. 11.8 а, не параллельны оси п и двигаются при изменении
положения источника на небе. Положения источников на картах снимков имеют
сдвиг в плоскости 1т, нулевой в фазовом центре, но увеличивающийся с расстоя-
расстоянием от него. Карты еще до объединения должны быть исправлены с учетом этого
эффекта. Поскольку необходимая поправка зависит от часового угла источника, при
долгих наблюдениях этот эффект может приводить к загрязнению изображений
источника во внешней части карты. Перлей (Perley, 19996) обсуждает этот эффект
и его исправление. Метод, аналогичный описанному выше объединению снимков,
был рассмотрен в работе (Bracewell, 1984).
4. Восстановление с переменным откликом точечного источника. В случаях,
когда основным эффектом двумерного преобразования Фурье является искажение
отклика точечного источника во внешних частях поля без серьезного ослабления
отклика, можно предпринять восстановление с использованием отклика точечного
источника (грязной диаграммы направленности), варьируемого по полю для согла-
согласования с рассчитанным откликом (McClean, 1984). Этот подход был использован
в работе (Waldram and McGilchrist, 1990) при анализе обзора данных, полученных
на Кэмбриджском низкочастотном синтезном телескопе на частоте 151 МГц с ис-
использованием вращения Земли и с базами, повернутыми относительно направления
восток-запад на 3°. Отклики точечного источника были рассчитаны для сетки
положений внутри поля, и впоследствии отклик с любым положением мог быть
получен интерполяцией. Главное требование заключалось в определении точных
положений и плотностей потока для источников, идентифицированных на картах,
полученных двумерным преобразованием. Подбор подходящего отклика теорети-
теоретической диаграммы направленности для каждого положения источника позволял
11.9] Другие случаи анализа изображений 415
учесть искажение диаграммы направленности, включая любой сдвиг положения.
Этот метод относительно недорог по затратам компьютерного времени.
11.9. Другие случаи анализа изображений
11.9.1. Применение CLEAN и самокалибровки к даным спектральных
линий. Процедура, позволяющая тщательно отделить непрерывный спектр от
линий, использует алгоритм восстановления CLEAN (van Gorkom and Ekers, 1989).
Однако, если CLEAN применяется к картам отдельно для разных каналов, то ошиб-
ошибки, появляющиеся в процессе чистки CLEAN, проявляются как различия между
каналами и могут быть спутаны с истинными спектральными особенностями. Этих
ошибок можно избежать, если вычесть континуум до применения алгоритма чистки
CLEAN к данным в линиях. Сначала CLEAN применяется к среднему из каналов,
получающих только излучение непрерывного спектра, и компоненты функции вид-
ности, удаленные из этих каналов, также удаляются из данных функции видности
в каналах, содержащих излучение линий. Когда процесс чистки завершается, оста-
остаточные значения также удаляются из данных по линиям. Результирующие карты
для каналов с линиями (в которых, согласно предыдущему процессу, должны при-
присутствовать только данные по линиям), могут быть восстановлены по отдельности.
Заметим, что, поскольку поглощение непрерывного спектра может происходить и в
каналах с линиями, то карты излучения линии-минус-континнум могут содержать
как положительные, так и отрицательные детали интенсивности. Следовательно,
в подобных случаях применение алгоритмов, зависящих от знака интенсивности,
например, метода максимальной энтропии, может быть затруднено.
Применяя самокалибровку для исключения фазовых ошибок в спектральных
данных, обычно можно принять, что разница в фазе и амплитуде между каналами
меняется со временем очень незначительно и устраняется в процесссе калибровки
полосы пропускания. Это верно в отношении и атмосферных, и инструментальных
эффектов. Таким образом, самые сильные спектральные особенности в исследуемом
поле могут быть использованы при нахождении решения для калибровки фазы,
которое затем может быть применено ко всем каналам. Эта деталь может быть
излучением с непрерывным спектром, полученным как среднее от каналов без
линий, или излучением сильной мазерной линии в одном канале.
11.9.2. Картографирование на низких частотах. Синтезное картографи-
картографирование на длинах волн более двух метров, т. е., на частотах ниже 150 МГц, обычно
предполагает наличие широких полей зрения вследствие широких главных лепест-
лепестков диаграмм направленности антенн. Синхротронное излучение радиоисточников
обычно становится сильнее при уменьшении частоты, поэтому плотность сильных
источников на небе возрастает с уменьшением частоты. В результате на низких
частотах часто оказывается важным построение карты для всей диаграммы направ-
направленности антенны, чтобы избежать путаницы источников из-за появления ложных
изображений. К тому же коэффициент усиления главного лепестка диаграммы
направленности зеркальной антенны уменьшается с уменьшением частоты, а если
используются фазированные решетки диполей, то они должны быть очень боль-
большими для получения высокого коэффициента усиления. В результате, источники,
попадающие в боковые лепестки, подавляются не так эффективно по сравнению
с источником в главном лепестке, как это происходит на более высоких частотах.
При анализе данных можно вычесть нежелательные отклики от сильных источ-
источников с известными положениями, но на практике вычислительные возможности
416 Восстановление, адаптивная калибровка и их применение [Гл. 11
могут ограничить количество источников, которые можно исключить таким обра-
образом.
Непременное усложнение процесса построения карты для широкого поля зрения
обусловлено проблемой некомпланарных баз, рассмотренной в разд. 11.8. Другая
проблема заключается в переменности ионосферных эффектов (Baldwin, 1990).
Дополнительная длина пути в ионосфере пропорциональна v~2 (см. разд. 13.3,
уравнение A3.138)), а соответствующее изменение фазы пропорционально is~1.
Область неба, в которой изменение длины пути падающей волны мало по срав-
сравнению с длиной волны наблюдения, называется изопланатическим участком. На
сантиметровых и более коротких длинах волн угловые размеры диаграммы на-
направленности рефлекторных антенн в составе синтезных решеток обычно меньше
изопланатического участка. Таким образом, эффект неоднородности ионосферы
(или тропосферы) постоянен для диаграммы направленности и может быть учтен
для каждой антенны с помощью одной коррекции фазы, например, при самока-
самокалибровке. Однако на метровых длинах волн размер диаграммы направленности
антенны может быть в несколько раз больше ионосферного изопланатического
участка. Например, при наблюдениях на VLA в Нью-Мехико Эриксон (Erickson,
1999) оценил, что размер изопланатического участка на 74 МГц равен ~3°-4°,
в то время как ширина диаграммы направленности 25-метровой антенны на той
же частоте равна ~13°.
Кассим и др. (Kassim et al., 1993) описывают одновременные измерения ряда
сильных источников на 74 и 330 МГц с использованием процедуры фазовой привяз-
привязки для калибровки фаз на низкой частоте. На 74 МГц флуктуации фазы, в основ-
основном, обусловлены ионосферой, и было обнаружено, что скорость изменения фазы
достигает величины одного градуса за секунду. Это ограничивает обычные методы
калибровки. Однако на частоте 330 МГц скорость изменения фазы невелика, чтобы
можно было построить карты сильных источников. Далее результрующие фазы на
330 МГц были пересчитаны к частоте 74 МГц и использовались для удаления ионо-
ионосферного компонента из данных на 74 МГц, записанных одновременно с 330 МГц.
Процедура получения карт на 74 МГц состояла в следующем:
1. Были проведены одновременные наблюдения сильного источника на 74 и
330 МГц, а также периодические наблюдения опорного источника на 330 МГц.
2. Была построена карта исследуемого источника на 330 МГц с использованием
стандартных методик (т. е. с использованием калибратора, как на сантиметро-
сантиметровых волнах). Эта карта стала начальной моделью для самокалибровки данных
на 330 МГц.
3. Самокалибровка позволила откалибровать фазу для каждой антенны на
330 МГц. Затем эти значения были приведены к частоте 74 МГц (с учетом того,
что ионосферные изменения фазы обратно пропорциональны частоте), и с их
помощью были исключены ионосферные вариации из данных на 74 МГц.
4. Инструментальные фазы на 330 и 74 МГц различаются на каждой антенне из-
за различных длин кабелей и т.д. Для калибровки этих различий был измерен
неразрешенный калибратор на 330 и 74 МГц. Ионосферные флуктуации могут
быть исключены из фаз калибратора на 74 МГц по схеме фазовой привязки,
описанной в пункте 3. Таким путем были получены инструментальные разни-
разницы фаз.
11.9] Другие случаи анализа изображений 417
5. Была построена карта исследуемого источника на 74 МГц по калиброванным
фазовым данным. Для удаления остаточных фазовых дрейфов была проведе-
проведена самокалибровка данных на 74 МГц; для этого в качестве начальной модели
служила карта на 330 МГц.
Дла самых сильных источников с высоким отношением сигнал/шум за вре-
время усреднения не более 10 с, в большинстве случаев было достаточно самокалиб-
самокалибровки на 74 МГц. Хотя только восемь антенн VLA были оборудованы для рабо-
работы на частоте 74 МГц, для нескольких источников были получены изображения
с динамическим диапазоном лучше 20 дб. В этих измерениях не было пробле-
проблемы некомпланарных баз, так как источники были достаточно компактными для
удовлетворительного двумерного картографирования. Также эти источники были
достаточно сильными для того, чтобы могли быть проигнорированы другие источ-
источники в главном и боковых лепестках диаграммы направленности. Для наблюдения
более слабых источников, когда в диаграмму направленности попадает несколько
источников с близкими плотностями потока, необходима более сложная процедура
корректировки, чтобы суметь разобраться с более чем одним изопланатическим
участком.
11.9.3. Чистка линз. Известны случаи, когда изображение квазара или ра-
радиогалактики искажено гравитационным полем другой галактики. Это явление
было открыто Уолшем и др. (Walsh, Carswell and Weymann, 1979). Луч от линзи-
руемого источника пересекает или проходит очень близко от некоторой галактики.
В некоторых случаях гравитационное линзирование приводит к множественным
изображениям одиночного точечного квазара, а в других случаях появляется про-
протяженная структура (см., например, работу (Narayan and Wallington, 1992)). В ис-
исследованиях гравитационного линзирования структура гравитационного поля име-
имеет огромное астрофизическое значение. Термином чистка линз называется метод
анализа, включая несколько вариациий оригинального алгоритма, позволяющего
определить линзирующее поле при синтезном построении изображений. Основа
этих методов аналогична самокалибровке, при которой изображение настолько
сильно переопределено в ходе измерений функции видности, что можно также
определить комплексные коэффициенты усиления антенн. А при чистке линз опре-
определяется структура гравитационного поля. Дополнительное ограничение состоит
в том, что каждая точка источника может давать вклад в более чем одну точку
синтезированного изображения.
Оригинальная процедура чистки линз (Kochanek and Narayan, 1992) основана
на адаптации алгоритма чистки CLEAN. Главный принцип может быть сформу-
сформулирован следующим образом. Рассмотрим случай, когда линзируемый источник
содержит протяженную структуру. Выбирается начальная модель линзы. В иде-
идеальном случае интенсивность должна иметь одну и ту же величину во всех тех
точках изображения, в которые попадает в результате линзирования данная точка
источника, так как линзирование подразумевает только геометрическое искривле-
искривление хода лучей от источника, как в оптической системе. Предположим, что j-й
элемент источника соответсвует на карте rij элементам изображения. На практике
интенсивности этих элементов изображения не одинаковы из-за несовершенства
модели линзы и шума изображения. Лучшей оценкой интенсивности элемента ис-
источника является средняя интенсивность соответсвующих элементов изображения.
Таким образом, из изображения, как в методе чистки CLEAN, можно вычесть
компоненты и построить карту источника. Для каждого элемента источника, для
которого rij > 1, рассчитывается среднеквадратичная дисперсия интенсивности со-
соответствующего элемента изображения от средней интенсивности rij > 1 элементов
изображения, <т|. Для хорошей модели линзы средняя величина а? по элементам
14 Томсон
418 Восстановление, адаптивная калибровка и их применение [Гл. 11
на карте источника не должна превышать дисперсии шума в изображении cruise-
Если количество степеней свободы на карте источника равно числу элементов,
тогда статистической мерой качества модели линзы является х2 = ХХ0"!/anoise)' гДе
суммирование проводится по j элементам источника. Таким образом, можно варьи-
варьировать параметры линзы для минимизации х2 • На практике эта процедура более
сложна, чем описано выше. Она модифицируется с учетом конечного разрешения
изображения, которое проявляется в растяжении каждого элемента источника на
некоторое количество элементов изображения на карте. Кроме этого, для любой
неразрешенной структуры в источнике интенсивность соответствующей структуры
на изображении зависит от усиления линзы.
В работе (Ellithorpe, Kochanek and Hewitt, 1996) была предложена процеду-
процедура чистки линз в функции видности, когда компоненты CLEAN удаляются из
функции видности, не разбитых на ячейки сетки, при ограничениях, наложенных
некой моделью линзы. Квадратичные отклонения измеренной функциии видности
от модельной используются для расчета статистики х2 • Качество подгонки оцени-
оценивается по дисперсии измеренной функции видности, количество степеней свободы
равно 27Vvis — 37Vsrc — Aliens, где 7Vvis — число измерений функции видности (каж-
(каждое из которых имеет две степени свободы), 7Vsrc — число независимых CLEAN-
компонентов в модели источника (с тремя степенями свободы: координаты и ам-
амплитуда), a Aliens — число параметров в модели линзы. Эллиторп (Ellithorpe et
al.) сравнили результаты оригинальной чистки линз с результатами чистки линз
в функции видности и обнаружили превосходство второго метода, а также возмож-
возможность дополнительного улучшения, если добавлен этап самокалибровки. Также ис-
исследовалась возможность использования алгоритма ММЭ в качестве альтернативы
CLEAN (Wallington, Narayan and Kochanek, 1994).
Основная литература
Roberts J. A. Ed., Indirect Imaging. Cambridge Univ. Press, Cambridge, UK, 1984.
van Schooneveld C. Ed., Image Formation from Coherence Functions in Astronomy. Reidel,
Dordrecht, 1979.
Цитированная литература
Ash M. E. Determination of Earth Satellite Orbits. MIT Lincoln Laboratory Technical Note,
1972-5, 1972.
Abies J. G. Maximum Entropy Spectral Analysis. Astron. Astrophys. Suppl., 15, 383-393,
1974.
Bajaja E. and G. D. van Albada. Complementing Aperture Synthesis Radio Data by Short
Spacing Components from Single Dish Observation. Astron. Astrophys., 75, 251-254, 1979.
Baldwin J. E. The Design of Large Arrays at Meter Wavelengths. Radio Astronomical Seeing,
J. E. Baldwin and Wang S. Eds., International Academic Pubublishers and Pergamon Press.
Oxford, 1990.
Baldwin J. E. and P. J. Warner. Phaseless Aperture Synthesis. Mon. Not. R. Astron. Soc,
182, 411-422, 1978.
Baldwin J. E. and P. J. Warner. Fundamental Aspects of Aperture Synthesis with Limited
or No Phase Information. Image Formation from Coherence Functions in Astronomy, C. van
Schooneveld. Ed., Reidel, Dordrecht, 1979, p. 67-82.
Bates R. H. T. Contributions to the Theory of Intensity Interferometry Mon. Not. R. Astron.
Soc, 142, 413-428, 1969.
11.9] Цитированная литература 419
Bates R. Н. Т. Uniqueness of Solutions to Two-Dimensional Fourier Phase Problems for
Localized and Positive Images. Сотр. Vision, Graphics Image Process., 25, 205-217, 1984.
Bracewell R. N. Inversion of Nonplanar Visibilities. Indirect Imaging, J. A. Roberts. Ed.,
Cambridge Univ. Press, 1984, p. 177-183.
Bracewell R. N. Two-Dimensional Imaging. Prentice-Hall, Englewood Cliffs, NJ, 1995.
Bracewell R. N. and J. A. Roberts. Aerial Smoothing in Radio Astronomy. Aust. J. Phys., 7,
615-640, 1954.
Briggs D. S. High Fidelity Deconvolution of Moderately Resolved Sources. Ph.D. thesis, New
Mexico Institute of Mining and Technology, 1995.
Bruck Y. M. and L. G. Sodin. On the Ambiguity of the Image Reconstruction Problem. Opt.
Commun., 30, 304-308, 1979.
Bryan R. K. and J. Shilling. Deconvolution by Maximum Entropy, as Illustrated by Application
to the Jet of M87. Mon. Not. R. Astron. Soc, 191, 69-79, 1980.
Clark B. G. An Efficient Implementation of the Algorithm «CLEAN». Astron. Astrophys., 89,
377-378, 1980.
Clark B. G. Large Field Mapping. Synthesis Mapping, Proc. NRAO Workshop No. 5 (Socorro,
New Mexico, June 21-25, 1982), A. R. Thompson and L. R. D'Addario. Eds., National Radio
Astronomy Observatory, Green Bank, WV, 1982.
Conway J. E., T. J. Cornwell and P. N. Wilkinson. Multi-Frequency Synthesis: a New Tech-
Technique in Radio Interferometric Imaging Mon. Not. R. Astr. Soc, 246, 490-509, 1990.
Cornwell T. J. Self Calibration. Synthesis Mapping, Proceedings of NRAO Workshop No. 5
(Socorro, New Mexico, June 21-25, 1982), A. R. Thompson and L. R. D'Addario. Eds., National
Radio Astronomy Observatory, Green Bank, WV, 1982.
Cornwell T. J. A Method of Stabilizing the Clean Algorithm. Astron. Astrophys., 121, 281-
285, 1983.
Cornwell T. J. Radio-interferometric Imaging of Very Large Objects Astron. Astrophys., 202,
316-321, 1988.
Cornwell T. J. The Applications of Closure Phase to Astronomical Imaging. Science, 245, 263-
269, 1989.
Cornwell T. J. Imaging Concepts. Very Long Baseline Interferometry and the VLB A, J. A.
Zensus, P. J. Diamond and P. J. Napier. Eds., Astron. Soc. Pacific Conf. Ser. 82, 39-56, 1995.
Cornwell T. J., R. Braun and D. S. Briggs. Deconvolution. Synthesis Imaging in Radio
Astronomy II, G. B. Taylor, C. L. Carilli and R. A. Perley. Eds., Astron. Soc. Pacific Conf.
Ser., 180, 151-170, 1999.
Cornwell T. J. and K. F. Evans. A Simple Maximum Entropy Deconvolution Algorithm.
Astron. Astrophys., 143, 77-83, 1985.
Cornwell T. J., M. A. Holdaway and J. M. Uson. Radio-interferometric Imaging of Very Large
Objects: Implications for Array Design. Astron. Astrophys., 271, 697-713, 1993.
Cornwell T. J. and R. A. Perley. Radio-interferometric Imaging of Very Large Fields. Astron.
Astrophys., 261, 353-364, 1992.
Cornwell T. J. and P. N. Wilkinson. A New Method for Making Maps with Unstable Radio
Interferometers Mon. Not. R. Astron. Soc, 196, 1067-1086, 1981.
Cotton W. D. A Method Of Mapping Compact Structure in Radio Sources Using VLBI
Observations. Astron. J., 84, 1122-1128, 1979.
Ekers R. D. and Rots, A. H. Short Spacing Synthesis from a Primary Beam Scanned Inter-
Interferometer. Image formation from Coherence Functions in Astronomy, C. van Schoonveld, Ed.,
Reidel, Dordrecht, 1979, p. 61-63.
Ellithorpe J. D., C. S. Kochanek and J. N. Hewitt. Visibility Lensclean and the Reliability of
Deconvolved Radio Images. Astrophys. J., 464, 556-567, 1996.
Erickson W. C. Long Wavelength Interferometry. Synthesis Imaging in Radio Astronomy II, G.
B. Taylor, С L. Carilli and R. A. Perley. Eds., Astron. Soc. Pacific Conf. Ser., 180, 601-612,
1999.
14*
420 Восстановление, адаптивная калибровка и их применение [Гл. 11
Fienup J. R. Reconstruction of an Object from the Modulus of its Fourier Transform. Opt.
Lett., 3, 27-29, 1978.
Fort D. N. and H. К. C. Yee. A Method of Obtaining Brightness Distributions from Long
Baseline Interferometry. Astron. Astrophys., 50, 19-22, 1976.
Frieden B. R., Restoring. With Maximum Likelihood and Maximum Entropy. J. Opt. Soc.
Am., 62, 511-518, 1972.
Gull S. F. and G. J. Daniell. Image Reconstruction from Incomplete and Noisy Data. Nature,
272, 686-690, 1978.
Gull S. F. and G. J. Daniell. The Maximum Entropy Method. Image Formation from Coherence
Functions in Astronomy, С van Schooneveld, Ed., Reidel, Dordrecht, 1979, p. 219-225.
Hogbom J. A. Aperture Synthesis with a Non-Regular Distribution of Interferometer Baselines.
Astron. Astrophys. Suppl., 15, 417-426, 1974.
Hogbom J. A. The Introduction of A Priori Knowledge in Certain Processing Algorithms.
Image Formation from Coherence Functions in Astronomy, C. van Schooneveld, Ed., Reidel,
Dordrecht, 1979, p. 237-239.
Jaynes E. T. Prior Probabilities. IEEE Trans. Syst. Sci. Cyb., SSC-4, 227-241, 1968.
Jaynes E. T. On the Rationale of Maximum-Entropy Methods. Proc. IEEE, 70, 939-952, 1982.
Kassim N. E., R. A. Perley, W. C. Erickson and K. S. Dwarakanath. Subarcminute Resolution
Imaging of Radio Sources at 74 MHZ with the Very Large Array. Astron. J., 106, 2218-2228,
1993.
Kochanek C. S. and R. Narayan. Lensclean: An Algorithm for Inverting Extended, Gravita-
tionally Lensed Images with Application to the Radio Ring Lens PKS 1830-211. Astrophys. J.,
401, 461-473, 1992.
Lawson C. L. and R. J. Hanson. Solving Least Squares Problems. Prentice-Hall, Englewood
Cliffs, NJ, 1974.
Lonsdale C. J., S. S. Doelman, R. J. Capallo, J. N. Hewitt and A. R. Whitney. Exploring the
Performance of Large-N Radio Astronomical Arrays. Radio Telescopes, H. R. Butcher. Ed.,
Proc. SPIE, 4015, 126-134, 2000.
McClean D. J. A Simple Expansion Method for Wide-Field Mapping. Indirect Imaging, J. A.
Roberts. Ed., Cambridge Univ. Press, Cambridge, UK, 1984, p. 185-191.
Napier P. J. The Brightness Temperature Distributions Defined by a Measured Intensity
Interferogram. NZ J. Sci., 15, 342-355, 1972.
Napier P. J. and R. H. T. Bates. Inferring Phase Information from Modulus Information in
Two-Dimensional Aperture Synthesis. Astron. Astrophys. Suppl., 15, 427-430, 1974.
Napier P. J., A. R. Thompson and R. D. Ekers. The Very Large Array: Design and Performance
of a Modern Synthesis Radio Telescope. Proc. IEEE, 71, 1295-1320, 1983.
Napier P. J., D. S. Bagri, B. G. Clark, A. E. E. Rogers, J. D. Romney, A. R. Thompson and
R. C. Walker. The Very Long Baseline Array. Proc. IEEE, 82, 658-672, 1994.
Narayan R. and R. Nityananda. Maximum Entropy - Flexibility Versus Fundamentalism.
Indirect Imaging, J. A. Roberts. Ed., Cambridge Univ. Press, Cambridge, UK, 1984, p. 281-
290.
Narayan R. and S. Wallington. Introduction to Basic Concepts of Gravitational Lensing.
Gravitational Lenses, R. Kayser, T. Schramm and L. Nieser. Eds., Springer-Verlag, Berlin,
1992, p. 12-26.
Nityananda R. and R. Narayan. Maximum Entropy Image Reconstruction - A Practical Non-
Information-Theoretic Approach. J. Astrophys. Astron., 3, 419-450, 1982.
Pearson T. J. and A. C. S. Readhead. Image Formation by Self Calibration in Radio Astron-
Astronomy. Ann. Rev. Astron. Astrophys., 22, 97-130, 1984.
Perley R. A. High Dynamic Range Imaging. Synthesis Imaging in Radio Astronomy, R. A.
Perley, F. R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser., 6, 287-313, 1989.
11.9] Цитированная литература 421
Perley R. A. High Dynamic Range Imaging. Synthesis Imaging in Radio Astronomy II, G. B.
Taylor, С L. Carilli and R. A. Perley. Eds., Astron. Soc. Pacific Conf. Ser., 180, 275-299,
1999a.
refPerley R. A. Imaging with Non-Coplanar Arrays. Synthesis Imaging in Radio Astronomy
II, G. B. Taylor, С L. Carilli and R. A. Perley. Eds., Astron. Soc. Pacific Conf. Ser., 180,
383-400, 1999b.
Perley R. A., J. W. Dreher and J. J. Cowan. The Jet and Filaments in Cygnus A. Astrophys.
J., 285, L35-L38, 1984.
Ponsonby J. E. B. An Entropy Measure for Partially Polarized Radiation and its Application to
Estimating Radio Sky Polarization Distributions from Incomplete «Aperture Synthesis» Data
by the Maximum Entropy Method. Mon. Not. R. Astron. Soc, 163, 369-380, 1973.
Readhead A. C. S., R. C. Walker, T. J. Pearson, M. H. Cohen. Mapping Radio Sources with
Uncalibrated Visibility Data Nature, 285, 137-140, 1980.
Readhead A. C. S. and P. N. Wilkinson. The Mapping of Compact Radio Sources from VLBI
Data. Astrophys. J., 223, 25-36, 1978.
Rogers A. E. E. Methods of Using Closure Phases in Radio Aperture Synthesis. Soc. Photo-
Opt. Inst. Eng., 231, 10-17, 1980.
Rogers A. E. E., H. F. Hinteregger, A. R. Whitney, С. С Counselman, I. I. Shapiro, J. J.
Wittels, W. K. Klemperer, W. W. Warnock, T. A. Clark, L. K. Button, G. E. Marandino,
B. O. Ronndng, O. E. H. Rydbeck and A. E. Niell. The Structure of Radio Sources 3C273B
and 3C84 Deduced from the «Closure» Phases and Visibility Amplitudes Observed with Three-
Element Interferometers. Astrophys. J., 193, 293-301, 1974.
Sault R. J. and T. A. Oosterloo. Imaging Algorithms in Radio Interferometry. Review of Radio
Science 1993-1996, W. R. Stone. Ed., Oxford Univ. Press, Oxford, 1996, p. 883-912.
Sault R. J., L. Stavely-Smith and W. N. Brouw. An Approach to Interferometric Mosaicing.
Astron. Astrophys. Supp., 120, 375-384, 1996.
Sault R. J. and M. H. Wieringa. Multi-Frequency Synthesis Techniques in Radio Interferomet-
Interferometric Imaging. Astron. Astrophys. Suppl. Ser., 108, 585-594, 1994.
Schwab F. R. Adaptive Calibration of Radio Interferometer Data. Soc. Photo-Opt. Inst. Eng.,
231, 18-24, 1980.
Schwab F. R. Relaxing the Isoplanatism Assumption in Self Calibration: Applications to Low-
Frequency Radio Astronomy. Astron. J., 89, 1076-1081, 1984.
Schwarz U. J. Mathematical-Statistical Description of the Iterative Beam Removing Technique
(Method CLEAN). Astron. Astrophys., 65, 345-356, 1978.
Schwarz U. J. The Method «CLEAN» - Use, Misuse and Variations. Image Formation from
Coherence Functions in Astronomy, C. van Schooneveld, Ed., Reidel, Dordrecht, 1979, p. 261-
275.
Skilling J. and R. K. Bryan. Maximum Entropy Image Reconstruction: General Algorithm.
Mon. Not. R. Astron. Soc, 211, 111-124, 1984.
Sramek R. A. and F. R. Schwab. Imaging. Synthesis Imaging in Radio Astronomy, R. A.
Perley, F. R. Schwab and A. H. Bridle. Eds., Astron. Soc. Pacific Conf. Ser., 6, 117-138, 1989.
Subrahmanya C. R. An Optimum Deconvolution Method. Image Formation from Coherence
Functions in Astronomy, C. van Schooneveld, Ed., Reidel, Dordrecht, 1979, p. 287-290.
Thomasson P. MERLIN. Q. J. Royal Astron. Soc, 27, 413-431, 1986.
van Gorkom J. H. and R. D. Ekers. Spectral Line Imaging II: Calibration and Analysis.
Synthesis Imaging in Radio Astronomy, R. A. Perley, F. R. Schwab and A. H. Bridle. Eds.,
Astron. Soc. Pacific Conf. Ser. 6, 341-353, 1989.
Waldram E. M. and M. M. McGilchrist. Beam-Sets - A New Approach to the Problem of
Wide-Field Mapping with Non-Coplanar Baselines. Mon. Not. Royal Astron. Soc, 245, 532-
541, 1990.
Wallington S., R. Narayan and C. S. Kochanek. Gravitational Lens Inversion Using the
Maximum Entropy Method. Astrophys. J., 426, 60-73, 1994.
422 Восстановление, адаптивная калибровка и их применение [Гл. 11
Walsh D., R. F. Carswell and R. J. Weymann. 0957+561A,B: Twin Quasistellar Objects or
Gravitational Lens? Nature, 279, 381-384, 1979.
Welch W. J. and D. D. Thornton. An Introduction to Millimeter and Submillimeter Interfer-
ometry and a Summary of the Hat Creek System. Int. Symp. Millimeter and Submillimeter
Wave Radio Astronomy, International Scientific Radio Union, Institut de Radio Astronomie
Millimetrique, Granada, Spain, 1985, p. 53-64.
Wernecke S. J. Two-Dimensional Maximum Entropy Reconstruction of Radio Brightness.
Radio Sci., 12, 831-844, 1977.
Wernecke S. J. and L. R. D'Addario. Maximum Entropy Image Reconstruction. IEEE Trans.
Comput., C-26, 351-364, 1977.
Глава 12
ИНТЕРФЕРОМЕТРИЧЕСКИЕ МЕТОДЫ
В АСТРОМЕТРИИ И ГЕОДЕЗИИ
Интерференционная диаграмма позволяет измерить скалярное произведение
векторов базы и положения источника: D • s. До сих пор мы предполагали, что эти
факторы описываются константой, которую можно определить с высокой точно-
точностью. Однако, для измерения положений источников с точностью до миллисекунд
дуги требуется учитывать вариации вектора вращения Земли. Необходимая точ-
точность определения вектора базы сравнима с той, когда можно зарегистрировать
изменения в положении антенн, вызванные движениями земной коры. Калибровку
базы и измерение положений источников можно произвести за несколько дней в хо-
ходе одного цикла наблюдений. Геодезические 1) данные получаются при повторении
этой процедуры в течение месяцев или лет, что позволяет выявить вариации базы
и параметров вращения Земли.
В этой главе описаны методы, с помощью которых можно измерить угловые
положения с максимально достижимой точностью, а также интерферометры, пред-
предназначенные для оптимального определения положения источника, базы и геодези-
геодезических параметров.
Новое определение метра оказало определенное влияние на единицы измерения
базы, получаемой по интерферометрическим данным. Интерферометр измеряет
относительное время прихода волнового фронта сигнала между двумя антеннами,
т. е. геометрическую задержку. Следовательно, базы, определяемые по интерферо-
интерферометрическим данным, получаются в единицах времени прохождения света. Перевод
в метры прежде зависел от значения, принятого для с. Однако в 1983 г. Генераль-
Генеральная конференция по мерам и весам приняла новое определение метра: «метр —
это длина пути, проходимого светом в вакууме за промежуток времени, равный
1/299792458 с». В настоящее время секунда и скорость света являются первичными
величинами, а метр — производной величиной. Таким образом, длины баз мож-
можно однозначно выразить в метрах. Исследования, посвященные фундаментальным
единицам измерения, обсуждаются в работе Петли (Petley, 1983).
12.1. Требования астрометрии
Измерения положений радиоисточников с точностью, не превышающей несколь-
нескольких десятых угловой секунды представляют главным образом исторический инте-
интерес, и о них упомянуто в гл. 1. В самых ранних исследованиях подобного рода век-
вектор базы часто получали на основании геодезических измерений положений антенн,
аппаратурную фазу оценивали путем калибровки линий передач, и таким образом
определяли положения максимумов лепестков на небе. Содержательный обзор этих
методик, включающий различные процедуры минимизации аппаратурных ошибок,
выполнен Смитом (Smith, 1952). В данной главе мы рассмотрим более современные
методики, точность которых — порядка одной миллисекунды дуги или лучше. Мы
х) Для простоты мы используем понятие геодезический для геодинамических и статиче-
статических явлений, имеющих отношение к форме и ориентации Земли.
424 Интерферометрические методы в астрометрии и геодезии [Гл. 12
начнем с эвристического обсуждения того, как молено определить параметры базы
и положения источника. Строгое исследование проведено в разд. 12.2.
При измерении склонения источника сопровождающим интерферометром мож-
можно независимо определить как положение источника, так и параметры базы. Это
можно просто проиллюстрировать путем следующих рассуждений. Фаза лепест-
лепестков интерферометра — 2тгк;, где w — пространственная компонента, определяемая
уравнением D.3). Фазу можно записать следующим образом:
ф = 2ttD\ [sin d sin 5 + cos d cos 5 cos (H — h)] + ф-ш, A2.1)
где D\ — база, выраженная в длинах волн, Н и 5 — часовой угол и склонение
источника, h и d — часовой угол и склонение вектора базы, а ф[п — аппаратурный
фазовый член. Для базы с ориентацией «восток-запад» h = — тг/2, если вести отсчет
от местного меридиана, d = 0, и фаза сводится к
ф = -2ttDx cos 5 sinH + ф[п. A2.2)
Таким образом, ф пропорциональна cos 5 и, наблюдая источник вблизи небесного
экватора, где зависимость от 5 мала, можно определить D\ с высокой точностью
(например, (Ryle and Elsmore, 1973)). Затем можно определить положения источни-
источников с более высокими склонениями, и использовать их для калибровки базы «север-
юг» и более точного измерения источников с низкими склонениями.
При определении прямых восхождений интерферометрические наблюдения
обеспечивают относительные измерения, т. е., разность прямых восхождений
различных источников. Нуль прямых восхождений определяется как большой круг,
проходящий через полюс и место пересечения небесного экватора и эклиптики
в точке весеннего равноденствия. Точка весеннего равноденствия — это место,
где видимое Солнце переходит из южного небесного полушария в северное.
Это направление можно точно установить на основании движения планет,
которые являются удобными объектами для оптических наблюдений. Оно связано
с положениями ярких звезд, которые образуют систему координат для оптических
измерений положения на небесной сфере. Привязать радиоизмерения к нулю
прямых восхождений сложно, потому что радиоизлучение объектов Солнечной
системы, как правило, мало или они не содержат достаточно компактных деталей.
В 1970-х отдельные результаты были получены по наблюдениям покрытий Луной
источника ЗС247В (Hazard et al., 1971) и слабого радиоизлучения от близких звезд,
таких как Алголь (/3 Persei) (Ryle and Elsmore 1973; Elsmore and Ryle, 1976).
Чтобы определить направление на точку весеннего равноденствия с помощью
пассивных радионаблюдений, предлагались различные методики. Например, радио-
интерферометрические наблюдения малых планет можно использовать для опреде-
определения их положений в системе отсчета, связанной с внегалактическими источника-
источниками (Johnston, Seidelmann and Wade, 1982). Другой метод основан на сравнении поло-
положений пульсаров, полученных посредством измерения времени прихода импульсов,
с положениями, полученными с помощью радиоинтерферометрии с использованием
внегалактических источников в качестве опорных объектов (Fomalont et al., 1992;
Taylor et al., 1984; Bartel et al., 1985). Так как в результате измерения времени при-
прихода импульсов получаются положения в системе координат, связанной с орбитой
Земли, а интерферометрические наблюдения привязаны к системе, опирающейся
на внегалактические источники, можно привязать положение точки весеннего рав-
равноденствия и другие динамические параметры земной орбиты к внегалактической
системе.
12.1] Требования астрометрии 425
В астрометрии при обработке интерферометрических измерений функцию вид-
ности интерпретируют, исходя из предположения, что источники точечные. В це-
целом, обработка данных эквивалентна модельной подгонке с использованием ком-
компонент с интенсивностью, описываемой дельта-функцией. Функция видности таких
компонент рассматривалась в разд. 4.4. Необходимую информацию о положении
получают из прокалиброванной фазы функции видности или, как во многих РСДБ-
наблюдениях, из геометрической задержки, которую измеряют путем определения
максимума кросс-корреляции сигналов (т. е. используется частотная характеристи-
характеристика), и по частоте лепестков. Так как информация о положении содержится в фазе
функции видности, то измерения замкнутых фаз, рассмотренные в разд. 10.3,
пригодны для целей астрометрии и геодезии частично, как средство коррекции
эффектов, связанных со структурой источника. Равномерность гш-покрытия менее
важна, чем в задачах построения изображений, поскольку, как правило, не тре-
требуется высокий динамический диапазон. Определение положения неразрешенного
источника зависит от точности калибровки фазы интерферометра и достаточного
числа баз, исключающего неоднозначность в определении положения.
Системы отсчета. Можно ожидать, что система отсчета, привязанная к поло-
положениям удаленных внегалактических объектов, будет иметь большую временную
стабильность, чем система отсчета, привязанная к положениям звезд, и которая
ближе инерциальной системе. Инерциальная система отсчета — это такая система
отсчета, которая находится в состоянии покоя или равномерного прямолинейного
движения по отношению к абсолютному пространству и не находится в состоянии
ускорения или вращения (см. например, (Mueller, 1981)). В такой системе отсчета
выполняется первый закон Ньютона. Подробное описание астрономических систем
отсчета выполнено Джонстоном и де Вегтом (Johnston, de Vegt, 1999). Междуна-
Международная небесная опорная система (ICRS), принятая MAC, определяет точки отсче-
отсчета и направления осей системы координат, используемой для задания положений
небесных объектов. Измеренные положения ряда опорных объектов в координатах
опорной системы определяют Международную небесную систему отсчета (ICRF).
Таким образом, эта система отсчета дает опорные точки, относительно которых
измеряются положения других объектов.
Наиболее точными измерениями положений небесных тел являются измерения
положений выбранных внегалактических источников, наблюдаемых методами
РСДБ. Как итог измерений, проведенных для целей астрометрии и геодезии,
существуют большие базы данных таких наблюдений с высоким разрешением. Эти
измерения, в основном, проводились с 1979 г. с использованием РСДБ-системы
Mark III на двух частотах — 2,3 и 8,4 ГГц — для исправления атмосферных
эффектов. Положения определены, главным образом, по данным на 8,4 ГГц.
Анализировались (Ma et al., 1998) измерения на Mark III, полученные до 1995 г.,
и состоящие из 1,6 хЮ6 значений групповой задержки и фазовой задержки.
Были рассмотрены данные для каждого из 618 источников. Критерии для
отбраковки источника включали в себя несовместимость измерений положений,
признаки собственного движения или наличия протяженной структуры. В ходе
исследования выяснилось, что 212 источников удовлетворяют всем тестам,
294 не удовлетворили одному из критериев, а еще 102 источника, включая
ЗС273 — нескольким. Эти 212 источников из лучшей группы были использованы
для установления системы отсчета. Только 27% из них находятся в Южном
полушарии. Глобальное решение дало положения источников вместе с положениями
антенн и различными геодезическими и атмосферными параметрами. Ошибки
положений 212 опорных источников, в основном, не превышают 0,5 мсек
дуги как по прямому восхождению, так и по склонению и почти во всех
426 Интерферометрические методы в астрометрии и геодезии [Гл. 12
случаях меньше 1 мсек дуги. Результаты этих измерений были приняты Между на-
народным астрономическим союзом (MAC) в 1998 г. в качестве ICRF. Более ранние
системы отсчета целиком основывались на оптических положениях звезд, самыми
современными являются положения из каталога FK5.
Около 50% источников из ICRF имеют красные смещения больше 1. Исполь-
Использование таких удаленных объектов для определения системы отсчета обеспечивает
уровень астрометрической недостоверности, по крайней мере, на порядок лучший,
чем при оптических измерениях звезд. Степень недостоверности при объединении
радио- и оптических систем отсчета, главным образом, определяется ошибками
оптических положений, которые будут существенно улучшены в будущем при ис-
использовании оптической интерферометрии в космических программах. Радиоизме-
Радиоизмерения положений некоторых близких звезд дадут возможность сравнения радио-
и оптических систем отсчета. Лестрейд и др. (Lestrade et al., 1990, 1995) измерили
положения примерно 10 звезд с помощью РСДБ, достигнув точности, находящейся
в пределах 0,5-1,5 мсек дуги. Эти результаты устанавливают связь между ICRF
и положениями звезд из каталога Гиппаркоса. Видимые звездные величины опти-
оптических объектов, отождествленных с опорными источниками системы отсчета, в ос-
основном, лежат в пределах от 15 до 21 величины; точные положения объектов слабее
18 звездной величины очень трудно получить. Необходимо уточнить понимание
пределов точности положений, полученных по радиоизмерениям. Фей и Шарло (Fey
and Chariot, 1997) исследовали поправки к положениям для источников, у которых,
как у ЗС273, разрешается структура, и ввели индекс структурности, чтобы оценить
качество этих объектов как источников для астрометрических измерений.
12.2. Определение векторов базы и направления на источник
При определении базы интерферометра необходимо использовать опорные ис-
источники, угловое положение которых известно с требуемой точностью. Однако, это
не существенно, и часто параметры источника и базы опрелеляются одновременно.
12.2.1. Системы со связанными элементами. Рассмотрим наблюдения,
проводящиеся на сопровождающем интерферометре с произвольной базой, когда
источник не разрешен. Пусть Т>\ — предполагаемый вектор базы, измеренный
в единицах длины волны, a (Da — AD a) ~~ истинный вектор. Пусть также s —
единичный вектор, указывающий на предполагаемое положение источника, a (s —
— As) соответствует истинному положению. Отметим, что в данном случае А-
член равен разности между предполагаемым и истинным значением. Ожидаемая
фаза интерференционной картины для предполагаемых положений равна 2ttDa • s.
Наблюдаемая фаза, измеренная относительно ожидаемой, является функцией ча-
часового угла источника и равна
Аф(Н) = 2тг [Бд • s - (DA - ADA) • (s - As)] + ф-т = 2тг (ADA • s + DA • As) + ф-т.
A2.3)
Мы пренебрегли членами второго порядка, включающими ADA • As, так как под-
подразумеваем, что относительные ошибки DA и s малы.
Вектор базы можно записать в системе координат, введенной в разд. 4.1, сле-
следующим образом:
АУА
A2.4)
12.2] Определение векторов базы и направления на источник 427
где X, Y и Z образуют правую систему координат, в которой ось Z параллельна
оси вращения Земли, а X лежит в меридиональной плоскости интерферометра.
Вектор положения источника можно выразить в системе XYZ через часовой угол Н
и склонение источника 5 по формуле D.2):
s = [sx sY sz] = [cos5 cosH — cosS s'mH sinS]. A2.5)
Взяв производную от уравнения A2.5), мы можем записать
As ~ [— sin S cos H AS + cos 5 sin H Aa sin S sin H A5 + cos 5 cos H Aa cos S AS],
A2.6)
где Ааи А<5 — угловые ошибки по прямому восхождению и склонению, а знак Аа
противоположен знаку соответвующей ошибки часового угла. После подстановки
уравнений A2.4)-A2.6) в A2.3) выражение для измеренной фазы можно записать
в следующем виде:
Аф(Н) = 0О + 4>\sx — ф2SY =0o + 0i cos 8 cos H -\- ф2 cos 5 sinH, A2.7)
где
фо = 2tt(AZx sm5-\-Zx cos 5 А5) + ф{п, A2.8)
0i = 2тг (АХЛ + Yx Aa - Хх tanJAJ), A2.9)
02 = 2тг (-АУЛ + Хх Aa + Yx tanJAJ). A2.10)
Из уравнения A2.7) видно, что Аф(Н) представляет собой синусоиду от Н со
смещением на 0о- Таким образом, все три параметра: амплитуду, фазу и смещение —
можно измерить для любого источника, наблюдая его периодически или непрерыв-
непрерывно в течение примерно 12 часов. Если наблюдается ns источников, то получается
3ns величин. Число неизвестных параметров, требующихся для определения ns
положений, вектора базы и аппаратурной фазы (которая считается постоянной)
равно 2ns + 3; прямое восхождение одного из источников выбирается произвольным
образом. Итак, если ns ^ 3, то все необходимые величины можно определить. Отме-
Отметим, что источники должны располагаться в как можно более широком интервале
склонений, чтобы в уравнении A2.8) можно было отличить AZX от 0^п. Метод наи-
наименьших квадратов дает одновременные решения для инструментальных парамет-
параметров и положений источника. Обычно наблюдают намного больше трех источников,
поэтому имеется избыточная информация, и можно включить в решение вариации
аппаратурной фазы со временем и другие параметры. Обсуждение анализа методом
наименьших квадратов приведено в приложении к этой главе.
12.2.2. Измерения на РСДБ-системах. Использование на антеннах РСДБ-
систем независимых гетеродинов не дает, за исключением особых случаев, возмож-
возможности легко откалибровать фазу лепестков. Ранее в РСДБ использовался анализ
частоты интерференци. Частота интерференции — это изменение фазы интерфе-
интерференционного сигнала от времени. Таким образом, из формулы A2.1) частота ин-
интерференции выражается как
Vf = f- = -ujeDx cos d cos 5 sin (H — h) + ^m, A2.11)
2тг at
где oog — угловая скорость вращения Земли (dH/dt), a i/[n — инструментальный
член, равный dфiп/dt. Компонента г/[п обусловлена, главным образом, остаточной
разностью частот водородных мазеров, которые синхронизируют опорную частоту
локальных гетеродинов.
428 Интерферометрические методы в астрометрии и геодезии [Гл. 12
Величина Dx cos <i, обозначенная De , — это проекция вектора базы на эквато-
экваториальную плоскость.
i/f = -uoeDE cos 5 sin (Я - К) + i/B. A2.12)
Полярная компонента вектора базы (проекция вектора базы на ось мира) в урав-
уравнении для частоты интерференции отсутствует. Линии постоянной фазы интерфе-
интерферометра, база которого параллельна оси вращения Земли, параллельны небесно-
небесному экватору, и фаза интерферометра не меняется при изменении часового угла.
Следовательно, полярную компоненту вектора базы нельзя определить из анализа
частоты интерференции.
В РСДБ принято отсчитывать часовые углы от Гринвичского меридиана. Мы
будем придерживаться этих правил и использовать правую систему координат, где
ось X проходит через Гринвичский меридиан, a Z направлена на Северный полюс
мира. Тогда формула A2.12) запишется в виде
Vf = -иое cos 5 (Х\ sin Я + Y\ cos Я) + i/in. A2.13)
Остаточную частоту интерференции А^/, т. е. разность между наблюдаемой и ожи-
ожидаемой частотами интерференции, можно расчитать, продифференцировав уравне-
уравнение A2.13) по 5, Я, Х\, и Уд и включив также неизвестную величину z/in. Тогда
получим:
z/in + a\ cos Я + a2 sin Я, A2.14)
где
ai =ue(Yx sm5A5 + Xx cos5 Aa - cos5 AYX) A2.15)
и
a2 = ooe (Xx sin5 A5 - Yx cos5 Aa - cos5AXx). A2.16)
Отметим, что Ai/f — синусоида с периодом в одни сутки и среднее значение
Ai/f равно инструментальной компоненте частоты интерференции г/[п. Информация
о положении источников и базах содержится в двух параметрах: а\ и а2. Следова-
Следовательно, в отличие от фазового метода [уравнение A2.7)], где каждому источнику
соответствуют три параметра, получить одновременное решение для источника
и вектора базы по данным о частоте интерференции невозможно. Например, из
наблюдений ns источников получается 2ns + 1 величин. Полное число неизвестных
(два параметра вектора базы, 2ns параметров источников и щп) равно 2ns + 3. Если
известно положение одного из источников, то оставшиеся положения источников
и Xx, Yx и z/;n определить можно. Заметим, что точность измерений склонений
уменьшается для источников, близких небесному экватору, из-за члена sin 5 в урав-
уравнении A2.15) и A2.16).
Для иллюстрации порядка величин, наблюдаемых частот интерференции, пред-
пол ожим, что имеются две антенны с экваториальной проекцией базы, равной
1000км, а наблюдения проводятся на волне Зсм. Тогда De — 3-Ю7 длин волн,
а частота интерференции для источника с низким склонением составит примерно
2 кГц. Предположим, что время когерентности у независимых стандартов частоты
примерно равно 10'. На этот период приходится 106 периодов сигнала. Если предпо-
предположить, что фазу можно измерить с точностью до 0,1 оборота, то Vf будет получена
с точностью 1 • 10~7. Ошибки De и углового положения составляют 10 см и 0,02"
соответственно.
Чтобы преодолеть ограничения метода частоты интерференции, были разрабо-
разработаны методики точного измерения относительной групповой задержки приходящих
12.2] Определение векторов базы и направления на источник 429
на антенны сигналов. Использование синтеза ширины полосы для улучшения точ-
точности измерения задержек обсуждалось в разд. 9.8. Групповая задержка равна
геометрической rg, за исключением того, что она содержит нежелательную компо-
компоненту, связанную с отличием синхронизации часов на антеннах и атмосферными
условиями на путях прохождения сигналов. Фаза интерференции, измеренная на
интерферометре со связанными элементами, работающем на частоте i/, равна 2тп/тд
с точностью до 2тг. Следовательно, за исключением эффектов дисперсии в ионосфе-
ионосфере, групповая задержка содержит ту же информацию, что и фаза интерференции,
но без неоднозначности в 2тг. Таким образом, измерения групповой задержки поз-
позволяют получить решения для баз и положений источников, подобные описанным
выше для интерферометра со связанными элементами, за тем исключением, что
нужно также учитывать разность показаний часов.
В большинстве астрометрических экспериментов измерения групповой задерж-
задержки и частоты интерферениции (или, что эквивалентно, изменению фазовой за-
задержки) анализируются совместно. Оценки точности измерения каждой из этих
величин приводятся в Приложении 12.1 [уравнения (П12.27) и (П12.34)], и их можно
записать в виде
A2.18)
где <jf и ат — среднеквадратичные ошибки частоты интерференции и задержки, Т$
и Та — шумовая температура системы и антенная температура, Аи — ширина поло-
полосы ПЧ, г — время интегрирования, a Ai/rms — среднеквадратичная ширина полосы,
введенная в разд. 9.8 [см. также (П12.32) и соответствущее описание в Приложении
12.1]. Обычно, Ai/rms составляет 40% от ширины полосы. Для прямоугольной поло-
полосы радиочастот Az/rms = Ai//\/l2 . Чтобы выразить ошибки измерения в угловых
единицах, заметим, что геометрическая задержка равна
тд = — sin (9, A2.19)
где в — угол между вектором, направленным на источник, и плоскостью, перпен-
перпендикулярной вектору базы. Таким образом, чувствительность задержки к угловым
изменениям равна
^- = — cos#, A2.20)
где Авт — приращение #, соответствующее приращению Атд в тд. Аналогично,
чувствительность частоты интерференции к угловым изменениям [так как vj =
= u(drg/dt)] выражается (для баз с ориентацией восток—запад) как
$?-= Dxwe ажв, A2.21)
L\Uf
где А#^ — приращение 0, соответствующее приращению Ai/f в Vj. Таким образом,
положив Ai/f = (if и Атд = ат и пренебрегая геометрическими факторами, получим
следующее уравнение:
^^f, A2.22)
430
Интерферометрические методы в астрометрии и геодезии
[Гл. 12
1995 март 4
1996 март 20
1996 март 31
1997
>арт27
-5
Смещение к востоку, мсек
Рис. 12.1. Видимые положения радиоисточни-
радиоисточника Sgr А* в центре Галактики по отноше-
отношению к внегалактическому опорному источ-
источнику Л745-283, измеренные в течение 2 лет
на частоте 43 ГГц с РСДБ. Затененные эл-
эллипсы вокруг измеренных точек показыва-
показывают уширенный из-за рассеяния угловой раз-
размер Sgr А* (см. рис. 13.25). Также показаны
ошибки измерений по уровню в одну сигма.
Штриховая линия представляет собой резуль-
результат подгонки методом наименьших квадра-
квадратов со взвешиванием, а сплошная линия со-
соответствует ориентации плоскости Галактики.
Движение практически проходит в плоскости
Галактики, что связано с вращением Солнца
вокруг центра Галактики со скоростью 219 =Ь
± 20 км • с~ (если принять расстояние между
Солнцем и центом Галактики равным 8 пк).
Верхний предел остаточного движения источ-
источника Sgr А* почти на два порядка меньше, чем
предел движений звезд, проекция положений
которых лежит в интервале около 0,02 пк от
Sgr А*. Такие собственные движения звезд
указывают на то, что вещество массой, при-
примерно равной 2,6-1О6М0, сконцентрировано
в пределах 0,02 пк от Sgr А*; отсутствие за-
зафиксированного собственного движения у са-
самого Sgr А* говорит о том, что, по край-
крайней мере, 10 М0 связаны с радиоисточником
Sgr А*. Из работы Рейда и др. (Reid et al.,
1999, © 1999 American Astron. Soc.)
где te = 2тг/сие — перод вращения Зем-
Земли. Уравнение A2.22) описывает от-
относительную точность измерений за-
задержки и частоты интерференции. На
практике измерения задержки обыч-
обычно более точны из-за шумов, наклады-
накладываемых атмосферой. Измерения ча-
частоты интерференции чувствительны
к производной длины пути в атмосфе-
атмосфере по времени, и в турбулентной ат-
фосмере эта производная может быть
большой, тогда как средняя длина
пути остается приметно постоянной.
Отметим, что измерения частоты ин-
интерференции и задержки взаимно до-
дополняют друг друга. Например, на
РСДБ-системе с известными базами
и аппаратурными параметрами поло-
положения источников можно найти по
результатам единичных наблюдений
с использованием задержек и часто-
частоты интерференции, потому что эти ве-
величины ограничивают положение ис-
источника в примерно ортогональных
направлениях. Впервые анализ изме-
измерений частоты интерференции и за-
задержки для определения положений
источников и векторов баз был прове-
проведен Коэном и Шаффером (Cohen and
Shaffer, 1971)и Хинтереггером и др.
(Hinteregger et al., 1972).
Точность, с которой может быть
измерена групповая задержка, ис-
используемая для определения поло-
положения источника, обратно пропор-
пропорциональна ширине полосы 1/Az/.
Аналогично точность измерения фа-
фазы интерференции обратно пропор-
пропорциональна частоте наблюдений 1/z/.
Так как постоянные множители при-
приблизительно равны, то относительная
точность этих методов равна z//Az/.
Отношение частоты наблюдений к
ширине полосы, включая эффекты
синтеза полосы, составляет обычно
один-два порядка величины. С дру-
другой стороны, расстояния между ан-
антеннами в РСДБ на один—два порядка
больше, чем в системах со связаными
элементами. Таким образом, точность
положений источников, полученных
по измерениям групповых задержек
12.2] Определение векторов базы и направления на источник 431
на РСДБ-системах, сравнима в точностью измерений, полученных по фазовым
измерениям на системах со связанными элементами, где базы намного короче.
Измерения положений на РСДБ с использованием привязки фаз, как это будет
описано ниже, являются наиболее точным радиоизмерением.
Основные ограничения на наземную интерферометрию накладывает атмосфера.
Измерения на двух частотах практически исключают ионосферные фазовые шумы
(см. п. 13.3.3). Среднеквадратичный фазовый шум тропосферы растет примерно
как с/5/6, где d — проекция вектора базы, для баз короче нескольких километров
[см. формулу A3.101) и табл. 13.3]. В этом режиме точности измерений углов
медленно растут с увеличением длины базы. Для баз, превышающих ~100км,
эффекты, связанные с тропосферой над элементами интерферометра, не корре-
коррелируют, и можно ожидать, что точность измерений будет расти с увеличением
длины базы быстрее. Однако, у далеко разнесенных элементов могут существенно
различаться зенитные углы, и модель атмосферы очень важна. Угловая точность,
достижимая на системах со связанными элементами, достигает 10~2 с дуги (Kaplan
et al., 1982; Perley, 1982), а на РСДБ-системах — превышает 10~3 с дуги (Fanselow et
al., 1984; Herring, Gwinn and Shapiro, 1985; Lestrade, 1991; Ma et al., 1998). Например,
движение источника Sgr А* в центре Галактики измерялось в течение 16 лет на VLA
(система со связанными элементами) (Backer and Sramek, 1999) и в течение 2 лет
на VLBA (РСДБ-решетка) (Reid et al., 1999). Изменения положений, измеренные
на VLB А, представлены на рис. 12.1.
12.2.3. Привязка фазы в РСДБ. В РСДБ-измерениях относительных по-
положений близких источников можно измерить относительную фазу интерференции
и таким образом реализовать точность, достигаемую на длинных базах и соот-
соответствующую очень высокому угловому разрешению. Наиболее точные измерения
можно провести для таких близких источников, которые вместе попадают в диа-
диаграммы направленности антенн (см. например, (Marcaide and Shapiro, 1983)), или
если они разнесены лишь на несколько градусов, и, следовательно, влияние тропо-
тропосферы и ионосферы практически одинаково (Shapiro et al., 1979; Bartel et al., 1984;
Ros et al., 1999). Тогда один из источников можно использовать в качестве опорного
(калибратора) по методике, подобной калибровке фазы в системах со связанными
элементами. В РСДБ такая процедура называется привязкой фазы. Она позволяет
получать изображения источников, плотности потоков которых слишком малы,
чтобы можно было надежно провести самокалибровку. Данное изложение следует
обзорам привязки фазы Алефа (Alef, 1989) и Бесли и Конвея (Beasley and Conway,
1995).
При наблюдениях с привязкой фазы проводятся попеременные измерения
основного источника и близкого калибратора с интервалами по несколько минут.
(Отметим, что калибратор часто называют опорным фазовым источником). Во
время измерения величина изменения фазы должна быть достаточно мала, чтобы
от одного наблюдения калибратора до другого можно было провести интерполяцию
фазы исключая неоднозначности порядка 2тг. Необходимо использовать и тщатель-
тщательно разработанные модели, чтобы устранить геодезические и атмосферные эффекты,
включая тектонические движения плит, движение полюсов, земные приливы и оке-
океаническую нагрузку и провести точную коррекцию с учетом прецессии и нутации
положений источников. Может оказаться, что нужно учитывать и более тонкие
эффекты: например, гравитационные деформации антенн, которые практически
компенсируются в решетках со связанными элементами, но могут повлиять на базы
в РСДБ из-за различия углов места на далеко разнесенных станциях. Наблюдения
с привязкой фазы становятся все более важными по мере того как разрабатываются
432 Интерферометрические методы в астрометрии и геодезии [Гл. 12
улучшенные модели для более точного учета этих эффектов, а также повышается
чувствительность и фазовая стабильность приемных систем.
Рассмотрим случай, когда в момент времени t\ мы наблюдаем калибратор,
в момент ^2 — основной источник, и в момент ts — опять калибратор. Для любого
из этих наблюдений измеренная фаза выражается как
</>meas = </>vis + </>inst + </>pos + phiant + (/>atmos + </>ionos, A2.23)
где слагаемые в правой части — это, соответственно, компоненты фазы, связанные
с видностью источника, аппаратурными эффектами (кабели, ошибки часов и т.д.),
ошибками предполагаемого положения источника, антенн, эффектами нейтральной
атмосферы, ионосферными эффектами. Чтобы исправить фазу основного источни-
источника, нам нужно проинтерполировать измерения калибратора в моменты времени t\
и t%, чтобы оценить, какова была бы его фаза при измерении в момент t^, а затем
вычесть проинтерполированную величину из измеренной фазы основного источни-
источника. Если положения основного источника и калибратора достаточно близки на небе
(не более нескольких градусов друг от друга), то лучи зрения на любой антенне
от этих источников проходят через одну и ту же изопланатическую часть, поэтому,
разностью атмосферных и ионосферных членов можно пренебречь. Можно предпо-
предположить, что аппаратурные члены при малых изменениях положения значительно
не меняются, а если калибратор не разрешен, то фаза его функции видности равна
нулю. Если калибратор частично разрешен, он должен быть достаточно сильным,
чтобы можно было построить его изображение методом самокалибровки, и в его
фазу внести поправки. Таким образом, скорректированная фаза основного источ-
источника сводится к
ф* - фс = 0tis + @pos - ^os). A2-24)
где верхние индексы t и с относятся к основному источнику и калибратору со-
соответственно, а тильда указывает на интерполированные значения. Правая часть
уравнения A2.24) зависит только от структуры и положения основного источника
и положения калибратора. На рис. 12.2 приведен пример привязки фазы, где под-
подгонка лепестков проводилась по опороному источнику (т. е. с учетом ошибок базы,
разности стандартов времени на пунктах и аппаратурных фаз). Результаты для
опорного источника (калибратора) показаны крестиками, а полученные поправки
для фазы и ее изменения были проинтерполированы на моменты времени, где
имеются данные для основного источника, отмеченные незакрашенными квадра-
квадратиками. Исправленная фаза опорного источника представлена на нижнем рисунке.
При подгонке лепестков желательно иметь сильный неразрешенный источник, по-
поэтому опорный фазовый источник должен выбираться из этих соображений, если
основной источник слаб или разрешается.
Из всех эффектов, содержащихся в A2.23) и устраняемых методом привязки
фазы, атмосферные эффекты меняются со временем быстрее всего и на часто-
частотах выше нескольких гигагерц они определяются не ионосферой, а тропосферой.
Таким образом, на сантиметровых волнах тропосферные вариации ограничивают
время каждого цикла наблюдений основного и калибровочного источников. Ва-
Вариации, описываемые моделью движущегося экрана, рассматриваются в п. 13.1.6;
характеристики экрана основываются на теории турбулентности (Tartarski, 1961).
Относительное среднеквадратичное изменение фазы основного и калибровочного
источника, чьи лучи распространяются в атмосфере на расстоянии dtc друг от
друга, пропорционально dt'c :
12.2]
Определение векторов базы и направления на источник
433
где ctq — изменение фазы для расстояния в 1 км между лучами. Для того чтобы
можно было интерполировать РСДБ-данные, полученные между двумя наблюде-
наблюдениями калибратора, не внося неопределенности, равной некоторому числу оборотов
фазы, изменения среднеквадра-
среднеквадратичной длины пути за время 180
между двумя последовательными
наблюдениями калибратора не
должны превышать ~А/8. Далее,
если рассеивающий экран движется
горизонтально со скоростью vs, то,
воспользовавшись определенным
выше критерием, можно получить
предельное время одного цикла
наблюдений опорного источника
и калибратора tcyc. Чтобы вы-
вычислить этот предел, положим
dtc = vstcyc и из A2.25) получим
v6/5
-1
A2.26)
Данный результат можно использо-
использовать для предельного времени цик-
цикла переключения. Эмпирические
данные, приведенные в табл. 13.3
гл. 13, показывают, что на ре-
решетке VLА при Л = 6 см (частота
5 ГГц), типичная среднеквадратич-
среднеквадратичная разность пути составляет около
1 мм для dtc = 1км- Соответствую-
Соответствующее значение его на Л = 6 см будет
6°, и для vs = 0,01 км-с tcyc <
< 19 мин. Эти результаты типич-
типичны для VLA. Для этого же места
и расстояния между лучами в 1 км,
но при условиях, которые можно
описать как «очень турбулентные»,
Шрамек (Sramek, 1990) дает зна-
значение среднеквадратичного измене-
изменения пути, равное 7,5 мм. Тогда ве-
величина erg на волне 6 см становит-
становится равной 45°, откуда получается
tcyc < 1,7 мин. В последнем случае
-180
7,2
7,4 7,6
UT, часы
7,8
8,0
Рис. 12.2. Пример привязки фазы на VLBA.
Представлены данные для базы Брюстер-Пай
Таун (Brewster-Pie Town), частота наблюде-
наблюдений — 8,4 ГГц. На верхней картинке показаны
некалиброванные данные для двух источников:
1638+398 (основной источник, незакрашенные
квадратики) и 1641+399 (опорный фазовый ис-
источник, крестики). На нижней картинке пред-
представлены данные для 1641+399 после подгонки
лепестков и данные для 1638+398 после при-
привязки фазы, где опорным источником служил
1641+399. Из работы Бесли и Конвея (Beasley
and Conway, 1995), с разрешения Astron. Soc.
Pacific Conf. Ser.
угол места источника был не менее
60°, поэтому на более низких углах
места потребуются еще более корот-
короткие времена перестановки.
На частотах менее ~1 ГГц опре-
определяющим фактором является ионосфера, и становятся валены среднемасштаб-
ные ионосферные неоднородности (СДИН) с длинами волн до нескольких сотен
434 Интерферометрические методы в астрометрии и геодезии [Гл. 12
километров, движущиеся со скоростями 100-300м-с (Носке and Schlegel, 1996).
Флуктуации фазы, обусловленные ионосферой или тропосферой, минимизируются
в диапазоне 5-15 ГГц, где с помощью методов привязки фазы можно получить
хорошую точность.
Имеются также ограничения на пределы углов, которые могут быть использо-
использованы при переводе на опорный фазовый источник, так как даже при статичной
атмосфере вносятся фазовые ошибки, которые увеличиваются с ростом угла пере-
перевода. Рос и др. (Ros et al., 1999) показали возможность привязки фазы с точно-
точностью 0,1 мсек на углах превышающих 7°. Интересное применение метода привязки
фазы для измерения гравитационного отклонения излучения источника ЗС273В
Солнцем описано в работе Каунсельмана и др. (Counselman et al., 1974). В этом
случае выбранный для сравнения источник ЗС279 располагался примерно в 10°
от ЗС273В, чтобы он был относительно свободен от воздействия Солнца. На каж-
каждой из двух станций РСДБ использовались две антенны, работающих от одного
стандарта частоты; каждая из антенн наблюдала свой источник, чтобы обеспечить
непрерывное сравнение фазы и дать возможность точного устранения эффектов,
связанных с несинхронностью часов. На частоте 8,1 ГГц была достигнута точность
определения положений порядка Змеек. Использовались также измерения поло-
положения относительно внегалактических источников, чтобы определить параллакс
и собственное движение пульсара PSR B2021+51 (Campbell et al., 1996). Умень-
Уменьшение интенсивности пульсара с ростом частоты привело к тому, что наблюдения
проводились на одной частоте, равной 2,218 ГГц, но использование двух опорных
источников в пределах 2,5° позволило достичь точности определения положений,
примерно равной 0,3 мсек. Преобразование Фурье и обращение свертки позволяют
строить изображения, а для привязки фазы использовать большие времена усред-
усреднения для достаточно слабых источников. Для малых потоков можно использовать
самокалибровку. Списки источников — калибраторов фазы, можно найти, напри-
например, в работах Патнаика и др. (Patnaik et al., 1992), Джонстона и др. (Johnston et
al., 1995) и Ma и др. (Ma et al., 1998).
12.3. Время и движение Земли
Рассмотрим теперь влияние на интерферометрические измерения изменений
величины и направления вектора угловой скорости вращения Земли. Эти изме-
изменения приводят к вариациям видимых небесных координат источников, векторов
баз и всемирного времени. Изменения вращения Земли можно разделить на три
составляющие.
1. К первой относятся изменения направления оси вращения, главным образом,
из-за прецессии и нутации вращающегося тела. Поскольку направление оси
определяет положение полюса системы небесных координат, появляются ва-
вариации прямого восхождения и склонения небесных объектов.
2. Ось вращения слегка смещается относительно Земли, т. е. точка, где ось
пересекается с земной поверхностью, перемещается. Этот эффект известен
как движение полюсов. Поскольку в системе координат (X, Y,Z), введенной
в разд. 4.1 для определения базы, в качестве оси Z выбрано направление
земной оси, то движение полюсов приводит к вариациям измеренных векторов
баз (но, конечно, не длин баз). Оно также вызывает изменение всемирного
времени.
12.3] Время и движение Земли 435
3. Скорость вращения Земли меняется из-за процессов в земной атмосфере и ко-
коре, что, в свою очередь, приводит к изменениям всемирного времени.
Мы кратко рассмотрели эти эффекты. Более детальное изложение с геофизической
точки зрения можно найти в работе Ламбека (Lambeck, 1980).
12.3.1. Прецессия и нутация. Гравитационные воздействия Солнца, Луны
и планет на несферическую Землю вызывают ряд возмущений ее орбитального
и вращательного движений. Чтобы учесть эти эффекты, необходимо знать возни-
возникающие изменения эклиптики, которая определяется плоскостью земной орбиты,
а также изменения небесного экватора, определяемого вращательным движением
Земли. Гравитационное влияние Солнца и Луны на экваториальную выпуклость
(квадрупольный момент) Земли проявляются в прецессии земной оси вокруг полюса
эклиптики.
Вектор вращения Земли наклонен примерно на 23,5° к полюсу ее орбитальной
плоскости — эклиптики. Период возникающей прецессии равен приблизительно
26 000 лет, что соответствует движению вектора угловой скорости Земли, пример-
примерно равному 20" в год [2тг sin B3,5°)/26 000 радиан в год]. Наклонение эклиптики
к экватору B3,5°) не является постоянным и убывает со скоростью 47" за сто
лет из-за воздействия планет, которое также вносит вклад в прецессию. Лунно-
солнечные и планетарные прецессионные эффекты вместе с меньшей по величине
релятивистской прецессией известны как общая прецессия. Прецессия приводит
к движению линии пересечения плоскостей эклиптики и небесного экватора. Эта
линия называется линией узлов, она определяет точки равноденствий и нуль пря-
прямых восхождений, который прецессирует со скоростью 50" в год. Кроме того,
меняющиеся во времени лунно-солнечные гравитационные эффекты вызывают ну-
нутацию оси вращения Земли с периодами до 18,6 лет и полной амплитудой порядка
9". Помимо только что описанных основных изменений эклиптики и экватора
существуют и другие, меньшие по величине эффекты. Общая точность, в преде-
пределах которой можно вычислить изменения положения источника, составляет менее
1 мсек (Herring, Gwinn and Shapiro, 1985). Выражения для прецессии можно найти
в работе Лиске и др. (Lieske et al., 1977), а для нутации — у Вара (Wahr, 1981).
Необходимые процедуры рассмотрены в учебниках по сферической астрономии,
например, (Woolard and Clemence, 1966; Taff, 1981; Seidelmann, 1992).
Так как прецессия и нутация проявляются в вариациях небесных координат,
которые могут достигать 50" в год для объектов с низкими склонениями, эти
эффекты нужно учитывать не только в астрометрических, но вообще почти во
всех наблюдениях. Поэтому положения объектов в астрономических каталогах при-
приводятся к координатам стандартных эпох В 1900.0, В 1950.0 или J2000.0. Эти даты
означают начало бесселева или юлианского года, на что указывают буквы В или J.
Положения соответствуют среднему экватору и средней точке весеннего равноден-
равноденствия на определенную эпоху. «Среднее» означает, что положения экватора и точки
равноденствия получают из общей прецессии без учета нутации. Дополнительные
разъяснения и обсуждение методов пересчета между стандартными эпохами содер-
содержатся в работе Зейдельманна (Seidelmann, 1992). Необходима также поправка на
аберрацию, т. е. видимое изменение положения, обусловленное конечной скоростью
света и движением наблюдателя. Аберрация содержит две компоненты: годовую
аберрацию из-за орбитального движения Земли с максимальным значением око-
около 20" и суточную аберрацию из-за вращения Земли с максимальным значением
0,3". Понятие запаздывающей базы (разд. 9.3), используемое при обработке РСДБ-
данных, учитывает суточную аберрацию. Для ближайших звезд необходимо вно-
вносить поправки на собственное движение (т. е. истинное движение звезды в простран-
пространстве), а в некоторых случаях и на параллакс из-за изменения положения Земли на
436
Интерферометрические методы в астрометрии и геодезии
[Гл. 12
орбите. Применение радиометодов, особенно РСДБ, позволяет уточнить классиче-
классические соотношения и параметры. Такие эффекты, как отклонение электромагнитных
волн в гравитационном поле Солнца, также должны учитываться при определении
положений с высшей степенью точности (см. п. 13.5.1).
12.3.2. Движение полюсов. Термин движение полюсов обозначает пере-
перемещение полюсов вращения Земли (географических полюсов) относительно зем-
земной коры. Оно дает составляющую, отличную от прецессионного и иных дви-
движений, в движение небесных полюсов. Движение полюсов имеет в основном, но
не полностью, геофизическую природу. Движение географического полюса во-
вокруг полюса фигуры Земли нерегулярно, и в течение последнего столетия рас-
расстояние между этими двумя полюсами менялось в пределах до 0,5", или 15 м,
на поверхности Земли. Характерная величина годового перемещения оси фи-
фигуры составляет 6 м или меньше. Движение полюсов может быть представле-
представлено в виде нескольких компонент, имеющих регулярный и нерегулярный харак-
характер, и в настоящее время еще не ясно, с какими факторами связаны некото-
некоторые из них. Две основные компоненты имеют периоды 12 и 14 месяцев. Двена-
Двенадцатимесячная компонента представляет собой вынужденное движение, обуслов-
обусловленное годичным перераспределением воды и атмосферного углового момента,
она находится далеко от какого-либо ре-
резонанса. Компонента с периодом в 14
месяцев, известная как чандлеровский
период (Chandler, 1891),— это движение
с резонансной частотой, вынуждающая
сила которого неизвестна. Более деталь-
детальное описание см. в работе Вара (Wahr,
1996).
Движение полюса вращения измеря-
измеряется угловым или линейным расстояни-
расстоянием в направлениях х и у , как показано
на рис. 12.3. Начало координат (х,у) —
это средний полюс на период 1900—
1905 гг., который называется условным
международным началом (СЮ), а ось
х расположена в плоскости Гринвичско-
Гринвичского меридиана (Markowitz and Guinot,
1968). Поскольку движение полюсов
вносит сравнительно небольшой угловой
вклад, его часто не учитывают при кар-
картографических наблюдениях, особенно
если функция видности измеряется по
отношению к калибратору, расположен-
расположенному всего в нескольких градусах от
центра картографируемого поля.
Рис. 12.3. Система координат, используе-
используемая при измерении движения полюсов. Ко-
Координата х находится в плоскости Гринвич-
Гринвичского меридиана, а ось у повернута на 90°
к западу. СЮ — условное международное
начало
12.3.3. Всемирное время. Как и само вращательное движение Земли, осно-
основанная на нем система измерения времени является сложной темой; ее детальное
обсуждение можно найти в работе Смита (Smith, 1972) или в работах, упомянутых
выше при рассмотрении прецессии и нутации. Мы кратко изложим некоторые
основные вопросы. Солнечное время определяется вращением Земли вокруг
Солнца. На практике звезды представляют собой более удобные объекты для изме-
измерения, поэтому солнечное время получается измерением сидерического вращения.
12.3]
Время и движение Земли
437
В положения звезд или радиоисточников, использующихся для таких измерений,
вносятся поправки на прецессию, нутацию и т. д. Таким образом, итоговые измере-
измерения времени зависят только от угловой скорости Земли и движения полюсов. При
переходе на шкалу солнечного времени эти измерения дают всемирное время (UT),
известное как UT0; оно в действительности не является «всемирным», поскольку
эффекты движения полюсов, которые могут достигать 35 мс, зависят от положения
обсерватории. Если исправить UT0 с учетом влияния движения земных полюсов, то
получим время UT1. Поскольку UT1 является мерой вращения Земли относительно
фиксированных небесных объектов, то эта форма всемирного времени необходима
для астрономических наблюдений, включая интерферометрию, навигацию и топо-
топографию. Однако в UT1 содержатся эффекты небольших изменений в скорости вра-
вращения Земли, обусловленные, в основном, геофизическими явлениями, такими как
сезонные вариации распределения воды между поверхностью и атмосферой. Флук-
Флуктуации длительности суток в течение года составляют обычно около 1 мс. Чтобы
обеспечить более однородную меру времени, определяют время UT2, вводя в UT1
поправку на сезонную неравномерность вращения Земли. Шкала UT2 используется
редко. В UT1 и UT2 входят эффекты постепенного уменьшения скорости враще-
вращения Земли, что приводит к небольшому увеличению длительности суток в шкале
UT1/UT2 по сравнению с международным атомным временем IAT, основанным
на частоте линии цезия (см. п. 9.5.4). IAT лежит в основе основой другой формы
UT — координированного всемирного времени UTC, сдвиг которого по отношению
к IAT таков, что |UT1—UTC| < 1 с. Это соотношение поддерживается введением
1 секунды (секундных скачков) в UTC в определенные дни года. Большинство
служб времени, таких, как Loran С, и GPS (см. п. 9.5.8), передают UTC.
Практика работы многих обсерваторий состоит в поддержании UTC или IAT
с помощью атомных стандартов частоты, а затем в получении UT1 по опубли-
опубликованным значениям AUT1. Поскольку AUT1 измеряется, а не вычисляется, то,
в принципе, его можно определить только после измерения. Однако его можно
предсказать с достаточно высокой степенью точности за одну-две недели путем
экстраполяции и тем самым реализовать UT1 в реальном времени. Значения UT1
можно получить в Международном бюро времени (ВШ), основанном в 1912 г.
в Парижской обсерватории для координации хранения времени во всем мире, и в
Морской обсерватории, США. В этих организациях можно получить оперативные
данные для экстраполяции.
12.3.4. Измерения движений полюсов и UT1. Классический метод опти-
оптических измерений движения полюсов и UT1 состоит в измерении времени прохожде-
прохождения меридиана звездами с известными положениями. Для определения всех трех
параметров (ж, у, AUT1) необходимо проводить на различных долготах наблюдения
звезд с разными склонениями. В 70-х годах стало ясно, что эти астрометрические
задачи можно решить и с помощью радиоинтерферометрии (McCarthy and Pilking-
ton, 1979)
Для данных измерений определим компоненты базы интерферометра, в системе
XYZ, введенную в разд. 4.1, с осью X, направленной вдоль Гринвичского мери-
меридиана. Пусть АХ, AY и AZ — изменения компонент базы в результате движения
полюса (х,у) (в радианах) и вариаций времени (UT1—UTC), соответствующих В
рад. Тогда можно записать:
A2.27)
АХ-
АУ
AZ
=
0
в
—х
-е
0
У
) X
-у
0
'X
Y
Z
438 Интерферометрические методы в астрометрии и геодезии [Гл. 12
где квадратная матрица — трехмерная матрица вращения для малых углов пово-
поворота. В, х и у — углы вращения вокруг осей Z, У, и X соответственно. Из A2.27)
получим
АХ = -SY + xZ, AY = вХ - yZ, AZ = -хХ + yY. A2.28)
Таким образом, если периодически наблюдаются несколько источников и опре-
определяются изменения параметров базы, то уравнение A2.28) молено использовать
для определения UT1 и движения полюсов. Для интерферометра с базой восток-
запад (Z = 0) можно определить В, но нельзя разделить эффекты по ж и у.
Интерферометр с базой восток-запад, расположенный на Гринвичском меридиане
[X = Z = 0), позволил бы измерить В и у, но не х. Если бы он имел компоненту
базы север-юг (Z ф 0), то можно было бы по-прежнему измерить т/, но нельзя было
бы разделить эффекты по ж и В. Вообще, все три величины на одной базе измерить
нельзя, поскольку одно направление определяется лишь двумя параметрами. Для
получения полного решения подходят, например, системы из двух интерферометров
восток—запад, разнесенных примерно на 90° по долготе или трехэлементный некол-
линеарный интерферометр. Пример интерферометрических измерений положений
полюса можно найти в работе (Carter, Robertson and MacKay, 1985). Развитие Гло-
Глобальной Позиционной Системы также дает способы измерений положения полюса
(см. например, (Herring, 1999)).
Описанные методы применимы, как к наблюдениям, проводимым на интерфе-
интерферометрах со связанными элементами, в которых можно откалибровать фазу, так и к
РСДБ-наблюдениям, где полоса достаточна для осуществления точных измерений
групповой задержки. Если измеряется только частота интерференции, как в случае
РСДБ-систем с узкой полосой, то результат будет нечувствителен к Z-компоненте
базы. Тогда в уравнении A2.28) мы получим измерения только АХ и AY и, вообще
говоря, не сможем разделить эффекты движения полюсов и вариации UT1. Однако,
если Z = 0 (база восток—запад), то можно найти UT1. Сравнение определений
UT1 и движения полюсов методами РСДБ, лазерной локации спутников и анализ
Международным бюро времени стандартных астрометрических данных выполнен
Робертсоном и др. (Robertson et al., 1983) и Картером и др. (Carter et al., 1984).
12.4. Геодезические измерения
Определенные геофизические явления, например земные приливы (Melchior,
1978), движения литосферных плит могут приводить к вариациям вектора базы
системы РСДБ. Вариации длины вектора базы обусловлены именно такими явле-
явлениями, в то время как вариации направления могут быть вызваны также движением
полюсов и флуктуациями вращательного движения. Эти эффекты имеют величины
порядка 1—10 см в год для движения плит и 30 см (суточные) для земных приливов
и, следовательно, доступны для измерений с помощью наиболее точных методов
РСДБ. Земные приливы впервые были обнаружены Шапиро и др. (Shapiro et
al., 1974); Герринг и др. (Herring et al., 1983) провели более тонкие измерения.
Помимо приливов упруго деформируемой Земли, видимо, поддаются измерениям
и движения континентальных масс, вызванные приливными смещениями водных
масс (океанической нагрузкой). Первые свидетельства движения литосферных плит
в нашу эпоху приведены Геррингом и др. (Herring et al., 1986). Обзоры геодезиче-
геодезических приложений РСДБ сделаны в работах Шапиро (Shapiro, 1976), Коунсельмана
(Counselman, 1976), Кларка и др. (Clark et al., 1985), Картера и Робертсона (Carter
and Robertson, 1993) и Соверса, Фанселоу и Джекобса (Sovers, Fanselow and Jacobs,
1998).
12.5] Картографирование космических мазеров 439
12.5. Картографирование космических мазеров
В оболочках многих молодых либо сильно проэволюционировавших звезд ра-
радиоизлучение молекул типа Н2О и ОН имеет мазерную природу. Частотный спектр
такого излучения зачастую сложен, содержит много спектральных деталей или
компонент, вызванных наличием облаков газа, движущихся с различными луче-
лучевыми скоростями. На картах сильных мазерных источников наблюдаются сотни
компактных компонент с яркостными температурами, близкими к 1015 К, угловыми
размерами порядка ОДмсек и плотностями потоков до 106 Ян. Эти компоненты
обычно распределены в области диаметром в несколько угловых секунд, а диапазон
доплеровских скоростей составляет 10-300 км/с (от 0,7-20 МГц для Н2О-мазерного
перехода на частоте 22ГГц). Отдельные детали имеют ширины около 1км/с или
меньше G4 кГц на 22 ГГц). Физика и феноменология мазеров рассмотрена в работах
Рейда и Морана (Reid and Moran, 1988) и Элицура (Elitzur, 1992). Для обработки
и анализа мазерных данных необходимы большие системы корреляции, поскольку
отношение требуемой полосы к спектральному разрешению велико A02-104), а так-
также громадный объем работы по восстановлению изображений из-за большого A02—
104) отношения поля зрения к пространственному разрешению. Экстремальным
примером может служить Н2О-мазер в W49, у которого имеются сотни деталей,
распределенных в области размером в 3" (Gwinn, Moran and Reid, 1992). Полное
картографирование источника при разрешении 1 мсек с тремя элементами изобра-
изображения на интервал разрешения потребовало бы создания 600 карт, содержащих по
меньшей мере 108 пикселов каждая. Однако большинство ячеек карт не содержит
сигнал. Поэтому обычная процедура состоит в приближенном измерении положе-
положений компонент с помощью анализа частоты интерференции, а затем в картографи-
картографировании областей в этих местах с помощью фурье-синтеза. Примеры построения
карт на основе анализа частоты интерференции приведены в работе (Walker, Mat-
sakis and Garcia-Barreto, 1982; Shevchenko et al., 1995), анализа фазы — в (Genzel
et al., 1981; Norris and Booth, 1981; Matveenko, 1981), фурье-синтеза — в (Reid et
al., 1980; Norris, Booth and Diamond, 1982; Matveenko, Graham and Diamond, 1988;
Boboltz, Diamond and Kemball, 1997; Matveenko, Diamond and Graham, 2000). Далее
мы вкратце обсудим некоторые методы, использующиеся при картографировании
мазеров, и их точность. Отметим, что геометрическую (групповую) задержку точно
измерить нельзя из-за малой ширины мазерных линий.
При картографировании мазеров необходимо подробно рассмотреть частотную
зависимость функции видности интерферометра. Предположим, что мазерный ис-
источник состоит из ряда точечных компонент. Измерения выполняются с помощью
РСДБ-системы, и частотная полоса преобразуется в полосу одного канала. Приме-
Применяя (9.23), можно представить остаточную фазу интерференции какой-либо одной
мазерной компоненты на частоте v в виде
Аф(и) = 2тг [vArg(v) + A/ - иъо) те + i/Tat] + фы + 2тга, A2.29)
где те — относительная ошибка задержки, вызванная рассинхронизацией часов;
Tat — дифференциальная атмосферная задержка; /\тд(у) — разность между истин-
истинной геометрической задержкой источника тд(у) и ожидаемой (опорной) задержкой;
уъо — частота местного гетеродина; ф[п — аппаратурная фаза, которая включает
разность частот гетеродинов и может быть быстро меняющейся функцией вре-
времени; 2тгп — неоднозначность определения фазы. Обычно можно найти часто-
частоту, на которой имеется только одна неразрешенная мазерная компонента, и эту
компоненту можно взять в качестве опорного фазового источника. Использование
опорной детали служит основой для всех процедур анализа мазеров и позволяет
440 Интерферометрические методы в астрометрии и геодезии [Гл. 12
строить с высокой степенью точности карты относительных положений мазерных
компонент. Отличие остаточной фазы интерференции между мазерной деталью на
частоте v и опорной деталью на частоте vR равно
А2ф(и) = Аф(и) - А0Ю, A2.30)
а, воспользовавшись уравнением A2.29), получим:
А2ф(») = 2тг {v \тд{у) - rg{yR)} + [у - i/J [rg{yR) - rfg(uR)] + (i/ - i/J [re + rat] },
A2.31)
где Tfg(vR) — ожидаемая задержка опорной детали, a rg{vR) — истинная задержка.
Члены ф-1П и 2тгп, не зависящие от частоты, отсутствуют в уравнении A2.31). Однако
в этом уравнении имеются остаточные члены, пропорциональные разности частот
между анализируемой и опорной деталями. Эти члены возникают, потому что
фазы на разных частотах в уравнении A2.30) отличаются. Следуя обозначениям
формулы A2.3), мы можем записать A2.31) в виде
0() ^ D • Д8„н - ^ AD • Дз„д -
" ^ [(" " "Я)(ДП • sR + D • Двя)] + 2тг (!/ - 1/я)(ге + rat), A2.32)
где D — база, AD — ошибка базы, sR — предполагаемое положение опорной де-
детали, a AsR — соответствующая ошибка определения положения, AsuR — вектор
расстояния между опорной и исследуемой деталью на частоте i/, и, следовательно,
истинное положение детали на частоте v равно sR — AsR + AsuR.
Первый член в правой части уравнения A2.32) представляет собой искомую
величину, из которой можно получить положение исследуемой компоненты относи-
относительно опорной детали, а остальные члены описывают фазовые ошибки, связанные
с ошибками базы, положения источника, синхронизации часов, атмосферной за-
задержки. Эти фазовые члены можно приближенно преобразовать в угловые ошиб-
ошибки, разделив их на c/2-kvD. Так, например, ошибка базовой компоненты, равная
0,3 м, порождает ошибку задержки порядка 1нс в члене AD • sR уравнения A2.32)
и фазовую ошибку в 10~3 периода для деталей, разнесенных на 1 МГц. Эта фа-
фазовая ошибка соответствует номинальной ошибке 1 мксек дуги для базы 2500 км
на 22 ГГц, что дает погрешность фазы интерференции, равную 1 мсек. Аналогично
ошибка синхронизации или атмосферная ошибка величиной в 1 не приведет к такой
же ошибке в определении положения. Та же по величине ошибка базы приведет
к дополнительным ошибкам в члене AD • AsuR около 0,1 мксек дуги для деталей
разнесенных на 1". Подробный анализ ошибок картографирования в этом методе
калибровки можно найти в статье (Genzel et al., 1981).
Другой метод калибровки фазы интерференционных лепестков состоит в пере-
переносе фазы опорной детали к частоте калибруемой компоненты, т. е.:
А2ф(и) = Аф(и) - Аф(ин) —. A2.33)
Этот метод калибровки более точен, чем метод, где используется уравнение A2.30),
так как здесь не появляются члены, пропорциональные v — vR. Однако имеются
другие дополнительные члены, включающие неоднозначность фазы и аппаратур-
аппаратурную фазу. Поэтому такой метод калибровки применим только в случае, если фаза
интерференции достаточно точно прослеживается, и неоднозначности фазы отсут-
отсутствуют.
12.5] Картографирование космических мазеров 441
Карты с меньшей точностью и чувствительностью, чем те, что получаются при
обработке фазовых данных, могут быть построены на основе данных о частоте
интерференции. Предположим, что интерферометр хорошо прокалиброван. Диф-
Дифференциальная частота интерференции, т. е. разность частот интерференции между
деталью на частоте v и опорной деталью, может быть представлена в виде [с учетом
уравнения A2.14)]
Д2^ {у) ~ uAa'{v) + vAS(y), A2.34)
где й u v — производные по времени компонент проекции базы, Аа'(г/) и AS (г/) —
координаты относительно опорной детали, а Аа'(у) = Aa(y)cos8. Относительное
положение мазерной компоненты можно определить путем подгонки уравнения
A2.34) к наборам измерений частоты интерференции на различных часовых углах.
Этот метод был впервые применен Мораном и др. (Moran et al., 1968)) для картогра-
картографирования ОН-мазера. Ошибки при измерениях частоты интерференции убывают,
как г3/2 [см (П12.27)], где г — продолжительность наблюдений, но для больших зна-
значений т дифференциальная частота интерференции A2vf не является постоянной
величиной, так как и и v не равны нулю. Таким образом, имеется ограниченное поле
зрения для точных измерений. Его можно оценить, приравняв среднеквадратичную
ошибку измерения частоты интерференции в уравнении (П12.27) к величине т,
умноженной на производную по времени от дифференциальной частоты интерфе-
интерференции. Следовательно, для базы восток-запад
A2.35)
где АО — поле зрения. Если у/2тг2/3 cos О ~ 1, то поле зрения становится
Ав ~ f* , , A2.36)
или
М ^ * а 2 , A2.37)
lZsn-O\UJer
где 7Zsn — отношение сигнал/шум. Предположим, что 7Zsn = 10ит = 100с. Тогда
поле зрения составит около 2000 размеров интерференционных лепестков. Это огра-
ограничение часто оказывается важным. Обычно, когда деталь найдена, фазовый центр
поля перемещают в точку с координатами, равными полученным координатам де-
детали, и затем положение детали определяют вновь. С помощью метода частоты
интерференции только те компоненты, которые обнаруживаются при отдельных
наблюдений на каждой из баз, могут быть картографированы. Таким образом,
метод картографирования с помощью частоты интерференции менее чувствителен,
чем синтезное картографирование, при котором достигается полная когерентная
чувствительность.
Процедура анализа частоты интерференции может быть распространена на
случай, когда в одном частотном канале имеется много точечных компонент. По
данным каждого наблюдения (т. е. измерения на одной базе в течение нескольких
минут) вычисляется спектр частоты интерференции. Появляется многокомпонент-
многокомпонентный профиль с деталями на разных частотах интерференции, как это показано на
рис. 12.4. Частота интерференции каждой детали определяет линию в пространстве
(Да',Д?), на которой расположен мазерный источник. Наклон этой линии равен
arctg (г;/й). По мере изменения проекции базы изменяется и наклон линий. Точки
пересечения линий определяют положения источников (см. рис. 12.4). Чтобы метод
442
Интерферометрические методы в астрометрии и геодезии
[Гл. 12
-1,0
1,0
10 0 10
Частота, мГц
20
Рис. 12.4. б — спектр частоты интерференции для одной из спектральных линий Н2О-
мазера в W49N для определенного часового угла. По ординате отложена плотность потока.
Имеются 4 пика, каждый из которых соответствует отдельной детали на небе, а — прямые,
соответствующие многим сканам. Пики на нижнем графике и соответствующие прямые
на верхнем обозначены A-D. На этой частоте имеются, по крайней мере, четыре отдель-
отдельных детали. Их положения сответствуют точкам пересечения многих прямых. Деталь,
соответствующая прямой D, расположена достаточно далеко от фазового центра, поэтому
ее частота интерференции значительно изменяется за время интегрирования 20 мин, что
существенно ухудшает оценку положения. Окно, в котором точное определение положений
возможно, имеет размеры 0,5" по прямому восхождению и 2" по склонению. Его можно
перемещать, сдвигая фазовый центр данных, (Walker, 1981), с разрешения The Astronom-
Astronomical Journal
работал, разнос компонент должен быть достаточным для создания отдельных пи-
пиков в спектре частоты интерференции. Разрешение метода частоты интерференции
составляет г , что определяет эффективную ширину диаграммы
A6f =
D\ujeT cos в
A2.38)
Картографирование методом частоты интерференции подробно рассматривает-
рассматривается, например, в работе (Walker, 1981).
Приложение 12.1. Анализ методом наименьших квадратов
Принципы анализа методом наименьших квадратов играют фундаментальную
роль в астрометрии, где целью является выделение ряда параметров из измерений
при наличии шумов. Мы кратко рассмотрим их на элементарном уровне, опуская
математические тонкости и применим его к задачам, встречающимся в интерфе-
интерферометрии. Детальное обсуждение статистического анализа данных можно найти,
например, книгах (Bevington and Robinson, 1992) и (Hamilton, 1964). Предположим,
что мы хотим измерить величину га. Мы выполняем серию измерений г/^, которые
представляют собой сумму искомой величины га и шумового вклада щ:
?/. — т _|_ 71. (П12 11
где щ — гауссова случайная величина с нулевым средним значением и дисперсией
af. Вероятность того, что г-е измерение даст значение
вероятности
J p-(yi-rnJ/2a2i
задается плотностью
рШ =
(П12.2)
12.5] Приложение 12.1. Анализ методом наименьших квадратов 443
Если измерения независимы, то вероятность того, что эксперимент даст серию из
N измерений у\, у2,..., yN, равна
N
L = Y[p(yi), (П12.3)
г=1
где YI означает произведение членов р(у{). Величина L, рассматриваемая как функ-
функция га, называется функцией правдоподобия. Метод максимального правдоподобия
основан на предположении, что лучшей оценкой га будет та, которая максимизирует
L. Максимизация L эквивалентна максимизации lnL, где
/y*~2m) . (П12.4)
Поскольку первый член в правой части соотношения (П12.4) является константой,
а второй умножается на —1/2, то максимизация L эквивалентна минимизации
второй суммы в уравнении (П12.4) по га. Таким образом, мы хотим минимизировать
величину %2, определяемую соотношением
N 2
X2 = Y1 ~2 • (П12.5)
i=i г
В более общей задаче, рассматриваемой ниже в данном приложении, га заменя-
заменяется функцией с одним или более параметрами, описывающими модель системы.
С учетом этого обобщения выражение (П12.5) становится основным уравнением
метода взвешенных наименьших квадратов. В этом методе параметры модели опре-
определяются посредством минимизации суммы квадратов разностей между измерен-
измеренными и модельными значениями, взвешенных дисперсиями измерений. Величина
X2 свидетельствует о качестве модели — это случайная переменная, среднее зна-
значение которой равно разности измеренных и расчетных точек модели адекватно
описывающей измерения. Метод наименьших квадратов, применяемый, когда шум
представляет собой гауссов случайный процесс, является частным случаем более
общего метода максимального правдоподобия. Гаусс предложил метод наименьших
квадратов, вероятно, в 1795 г., используя рассуждения, аналогичные приведенным
выше для оценки орбитальных параметров планет и комет (Gauss, 1809). Метод
был независимо развит Лежандром в 1806 г. (Hall, 1970).
Возвращаясь к уравнению (П12.5), мы можем оценить га, полагая производную
от х2 п0 т равной нулю. Полученная оценка га, обозначаемая как гае, равна
гае = ^- , (П12.6)
где суммирование производится от г = 1 до N. Из уравнения (П12.2), следует,
что (у{) = га и (у2) = га2 + а2. Следовательно, если вычислить математическое
ожидание (П12.6), то (гае) = (yi) = га, и легко показать, что:
\ (П12.7)
444 Интерферометрические методы в астрометрии и геодезии [Гл. 12
Отсюда дисперсия оценки те равна
-1
(П12.8)
Как показывает уравнение (П12.8), когда данные с шумами или низкого качества
добавляются к данным высокого качества, величина ат уменьшается несуществен-
несущественно. Если статистические ошибки всех измерений одинаковы, то уравнение (П12.8)
сводится к хорошо известному результату
(П12.9)
и те является средним значением измерений. Во многих случаях а неизвестна.
Оценка а получается из соотношения
(П12.10)
Однако т неизвестна, известна лишь ее оценка те. Если использовать те вместо т
в уравнении (П12.10), то значение а2 будет недооценивать а2 из-за способа, которым
было определено те при минимизации %2. Несмещенная оценка а2 равна
Подставив (П12.6) в уравнение (П12.11), легко показать, что (а2) = а2. В уравнении
(П12.11) появляется коэффициент N — 1, который называется степенью свободы,
потому что имеется N точек данных и один свободный параметр.
Рассмотрим модель, описываемую функцией /(ж;рь • • • ,рп)? гДе х ~ независи-
независимая переменная, которая принимает значения х^ г = 1, 2,..., N в точках выборки,
a pi,... ,рп — набор параметров. Предположим, что точные значения независимой
переменной известны. Если функция / корректно моделирует систему измерений,
то серия измерений задается выражением
Vi = f{xi]pi, • • • ,pn) + Щ, (П12.12)
где щ — ошибки измерений. Основная проблема состоит в отыскании значений
параметров, при которых функция %2, задаваемая обобщением уравнения (П12.5)
х2^[г/»-/Ы]2; (Ш2ЛЗ)
достигает минимума.
Простым примером этой задачи является вписывание прямой линии в набор
данных. Пусть
f{x-a,h) = а + Ъх, (П12.14)
где а и Ъ — искомые параметры. Минимизация %2 достигается решением уравнений
2(у<-a-bxj)
? = _ j^ 2(yi-a-bxi)xi =
(П12.15а)
= Q (П12.15Ь)
12.5] Приложение 12.1. Анализ методом наименьших квадратов 445
В матричных обозначениях имеем:
Уг ^ ХгУг] _ IV^ I V^ Xi V^ Xi V^ хЦ г } ( ,
где истинные значения параметров и их оценки различаются индексом е. Решение
имеет вид:
где А — определитель квадратной матрицы в уравнении (П12.16), который равен
Оценки опЕибок параметров ае и Ъе могут быть получены из (П12.17) и (П12.18)
и выражаются следующим соотношением:
]4 (Ш2.20)
al = {bl)-{bef = ^Y,^- (Ш2-21)
Отметим, что ае и Ъе являются случайными переменными и в общем случае величи-
величина (aebe) не равна нулю, следовательно оценки параметров коррелированы. Оцен-
Оценки ошибок в уравнениях (П12.20) и (П 12.21) включают нежелательные эффекты
корреляции между параметрами. В данном примере корреляцию можно сведести
к нулю выбором начала оси ж, так чтобы ^2(xi/crf) = 0.
Приведенный выше анализ можно использовать для оценки точности измерений
частоты интерференции и задержки. Частоту интерференции — изменение интер-
интерференционной фазы от времени
можно оценить путем вписывания прямой линии в данные измерений фаз, равно-
равномерно разнесенных по времени. Частота интерференции пропорциональна наклону
этой линии. Предположим, что выполнено N измерений фазы ф{ с одинаковыми
среднеквадратичными ошибками аф в моменты времени ^, с интервалом Т рас-
пол оженные в интервале от —NT/2 до NT/2 так, что общее время наблюдений
составляет т = NT. Из (П 12.21) и приведенных выше определений, включая урав-
уравнение (П12.22), ошибка оценки частоты интерференции равна
°*f=,n JL.2> (П12.23)
446 Интерферометрические методы в астрометрии и геодезии [Гл. 12
так как ^2ti = 0. Член ^2 Щ приближенно выражается формулой
r2 '2*=^S=ir- (ni2-24)
-т/2
Здесь т/\/12 может рассматриваться как среднеквадратичный разброс данных во
времени. Таким образом, выражение (П12.23) приобретает вид
а) = 12°ф . (П12.25)
Если источник неразрешен и потери при обработке отсутствуют, то выражение для
Оф F.57) записывается в виде
(Уф = ^ , (П12.26)
Tav2Az/T
где Ts — пгумовая температура системы, Тд — антенная температура, обусловлен-
обусловленная источником, а Аи — ширина полосы. Подставляя (П12.26) в (П12.25), получим
[(Гц)]. (П12.27)
Отметим, что этот результат не зависит от особенностей процедуры анализа, напри-
например, от выбора N. Аналогично можно оценить частоту интерференции, определив
максимум интерференционно-частотного спектра, т. е. максимум преобразования
Фурье ej(j)i.
Задержка соответствует изменению фазы от частоты:
"??• <Ш2-28>
Следовательно, задержку можно оценить по наклону прямой линии, аппроксими-
аппроксимирующей последовательность измерений фазы как функции частоты. Для одиночной
полосы такие данные могут быть получены из кросс-спектра мощности, фурье-
преобразования кросс-корреляционной функции. Предположим, что сделано N из-
измерений фазы на частотах щ и каждое измерение имеет ширину полосы Ais/N
с ошибкой <7ф. В этом расчете важны лишь относительные частоты. Для удобства
анализа полагаем центральную частоту, равной нулю, так что ^^щ = 0. Ошибка
задержки [из (П12.19), (П12.21) и (П12.28)] равна:
/ 2 • (П12.29)
Bтг) 22 ч
Вычисляя ^2 уГ{ аналогично соотношению (П12.24), можно записать (П12.29) в виде
Ют2
2 и°Ф (П12.30)
Следовательно, подстановка (П12.26) (со временем интегрирования т и полосой
Ai//N) в (П12.30) приводит к
(). (П12.31)
2тг2 \ТА) VA^7
12.5] Приложение 12.1. Анализ методом наименьших квадратов 447
Мы можем определить среднеквадратичную ширину полосы как
(П12.32)
и получить из (П12.26) и (П12.29) результат, приведенный в разд. 9.8 [уравнение
(9.159)]:
1 ГТяЛ г (П12.33)
где ? = тг^бЗI/4. (Отметим, что в разд. 9.8 <Уф относится к полной полосе Дг/).
Выражения для ат в (П12.30), (П 12.31) и (П12.33) включают в себя условие A^rms =
= Az//v±2 и применяется к непрерывной полосе пропускания шириной Дгл
При синтезе полосы, описанном в разд. 9.8, измерительная система состоит из
N каналов шириной Ai//7V, которые в общем случае не прилегают друг к другу.
Среднеквадратичную ошибку задержки получим, подставив (П12.26) и (П12.32)
в (П12.29):
^ = ^ Ш "^ ' (П12'34)
где A^rms определяется формулой (П12.32), а Аи — полная ширина полосы. A^rms
обычно составляет примерно 40% полного диапазона.
Общая формулировка линейного решения методом наименьших квадратов мо-
может быть найдена, когда функция модели / является линейной функцией парамет-
параметров р/с, т. е. когда
f(X;Pl,...,pn) = J2^Lpk, (П12.35)
k=l
где п — число параметров. Например, модель может быть кубическим многочленом
/(ж;ро5РъР2,Рз) =Ро +Pix+p2x2 +р3ж3, (П12.36)
и в этом случае df/dpk = хк при к = 0,1, 2 и 3. Если параметры представлены в виде
линейных коэффициентов, минимизация (П12.13) приводит к системе п уравнений
вида
^-=0, А; = 1,2,..., п. (П12.37)
орк
Подставляя (П12.13) в (П12.37) и используя (П12.35), получаем систему п уравне-
уравнений
п
Dk = J2TkjPj, fc = l,2,...,n, (П12.38)
где
TV
JJk = у — —— (lllz.oyj
г=1 г
И
N
TJk = УЛ Цг^ df{xi)dpk , (П12.40)
448 Интерферометрические методы в астрометрии и геодезии [Гл. 12
и суммирование проводится по серии из N независимых измерений. В матричной
форме система уравнений (П12.38) имеет вид
[D] = [Т][Ре], (П12.41)
где [D] — матрица-столбец с элементами D&, [Ре] — матрица-столбец, содержащая
оценки параметров реи, а [Т] — симметричная квадратная матрица с элементами
Tjk. По очевидным причинам [Т] иногда называют матрицей нормальных уравне-
уравнений. Заметим, что уравнение (П12.41) является обобщением уравнения (П12.16).
Матрицы [Т] и [D] иногда записывают в виде произведения других матриц (Hamil-
(Hamilton, 1964, гл. 4). Пусть [М] — матрица дисперсий (размером N х 7V), диагональные
элементы которой равны af, а недиагональные — нулю и [F] — матрица-столбец,
содержащая данные у^ и [А] — матрица частных производных (размером п х JV),
элементы которой равны df{xi)/dpk- Тогда можно записать [Т] = [А]Т[М]-1[Л]
и [D] = [Л]т[М]-1[^], где [А]т — результат транспонирования [А], а [М] —
матрица, обратная [М]. Анализ можно обобщить на случай, когда ошибки между
измерениями коррелированы. Тогда [М] должна включать в себя не диагональные
элементы сг^сг^р^-, где р1- — коэффициент корреляции между г-м и j-м измерениями.
Решение уравнения (П12.41) записывается в виде
[Ре] = РГЧ-DL (П12.42)
где [Т]~г — матрица, обратная [Т], а [Ре] — матрица-столбец, содержащая оцен-
оценки параметров. Элементы матрицы [Т]~г обозначаются Т'-к. С помощью прямых
вычислений можно показать, что оценки ошибок параметров <т^к являются диаго-
диагональными элементами матрицы [Т], которая называется матрицей ковариации.
Следовательно,
<4 = Т'кк. (П12.43)
Вероятность того, что параметр р^ будет находиться в пределах ±<т& от своего
истинного значения, составляет 0,68, что равно интегралу от одномерного гауссова
распределения вероятности в пределах ±<Т?. Вероятность того, что все п параметров
будут лежать в пределах ±сг от своих истинных значений (т. е. внутри куба ошибок
в n-мерном пространстве), составляет приблизительно 0,68п при умеренных корре-
корреляциях.
Нормированные коэффициенты корреляции между параметрами пропорцио-
пропорциональны недиагональным элементам матрицы [Т]:
Рзк = «Р***)(*•**»» = Ъ . (П12.44)
GkGj /rrf T1'
Для любых двух параметров существует совместное гауссово распределение веро-
вероятности, которое описывает распределение ошибок
4^11 (П12.45)
где ek = Рек — Рк и ?j = Pej — Pj- Контур р(б&, €j) = р@, 0)е~1^2 определяет эллипс,
изображенный на рис. П12.1 и известный как эллипс ошибок. Вероятность того,
что оба параметра будут лежать внутри эллипса ошибок, определяется интегралом
от (П12.45) по площади эллипса ошибок, которая равна 0,46. Ориентация эллипса
12.5]
Приложение 12.1. Анализ методом наименьших квадратов
449
ошибок определяется выражением
^ = \ arctg (Щ^Ч) ¦ (П12.46)
Ошибки в параметрах рк полностью опреде-
определяются матрицей [Т] по формулам (П12.43)-
(П12.45). Элементы [Т] зависят лишь от част-
частных производных модельной функции и вели-
величин ошибок измерений, которые обычно можно
предсказать заранее на основании характеристик
измерительной аппаратуры. Следовательно, при
планировании эксперимента можно предсказать
ошибки из [Т] безотносительно данных. Поэто-
Поэтому матрицу [Т] иногда называют матрицей кон-
конструкции. Исследуя матрицу конструкции какого-
либо отдельного эксперимента, можно получить
очень высокую корреляцию между двумя пара-
параметрами, приводящую к большим ошибкам оцени-
оцениваемых значений. Зачастую можно видоизменить
эксперимент, чтобы получить больше данных, что
уменьшит корреляцию. После анализа данных
можно вычислить х • Если модель хорошо согла-
согласуется с данными, то %2 должен приблизительно
равняться N — п — числу измерений минус число
параметров. Если это не так, то трудность часто
состоит в том, что значения G{ оценены неверно
или модель неадекватно описывает измеритель-
измерительную систему, т. е. в модели слишком мало параметров или она неверна. Даже если
X2 — N — п, полученные в (П12.43) ошибки могут не иметь связи с реальными,
и их называют «формальные ошибки». Формальные ошибки описывают качество
оценки параметров. Точность измерения параметров — это отличие оценки от
истинного значения параметра. Часто бывает трудно определить точность изме-
измерения. Например, в данных эксперимента может иметь место неизвестный эффект,
который «маскируется» под функциональную зависимость одного из параметров
модели. Модель может выглядеть хорошей, но точность какого-либо отдельного
рассматриваемого параметра может оказаться намного хуже ожидаемой из-за си-
систематических ошибок, вносимых не учтенным в модели эффектом.
Линейный анализ методом наименьших квадратов может быть обобщен непо-
непосредственно на случай нелинейных функций. Предположим, что f(x;p) имеет один
нелинейный параметр рп. Для рассмотрения мы можем разделить / на линейную
и нелинейную части, /ь(ж;рь • • • ,pn-i) и fNL(x:>Pn) и аппроксимировать нелиней-
нелинейную функцию первыми двумя членами разложения в ряд Тейлора:
fNL(x;pn) ~ fNL(x,pOn) + Ц^ Арп, (П12.47)
Рис. П.12.1. Эллипс ошибок, или
контур ошибок, по уровню е~г
совместной функции распреде-
распределения вероятности [уравнение
(П12.45)] для оценок парамет-
параметров pk и pj. Величины pek — Рк
и pej — pj — разности оценок па-
параметров и их истинных значе-
значений. Угол г/jjk определяется из
уравнения (П12.46)
где роп первоначальная оценка параметра рп, а Арп = рп — рОп. Предположим, что
первоначальные оценки параметров, достаточно точны для того, чтобы выполня-
выполнялось уравнение (П12.47). Заменим данные значениями у^ — fNL{xi;pon), а затем
вычислим элементы матриц [D] и [Т] по частным производным, включая dfNL/dpn.
п-й параметр матрицы [Ре] в (П12.42) будет дифференциальным параметром Арп,
определенным в (П12.47). Затем решение уточняется посредством итераций с новым
15 Томсон
450 Интерферометрические методы в астрометрии и геодезии [Гл. 12
рядом Тейлора, центрированным на параметре роп + Арп. Таким образом, нелиней-
нелинейные функции можно включить в анализ посредством линеаризации, но при этом
требуются первоначальные предположения о нелинейных параметрах и поиск ре-
решения методом итераций. В некоторых случаях вопросы, связанные с нелинейными
оценками, могут вызвать трудности (см., например, (Lampton, Margon and Bowyer,
1976; Press et al., 1992)).
Представим, как принципы анализа методом наименьших квадратов исполь-
используются в большом астрометрическом эксперименте. Рассмотрим гипотетический
РСДБ-эксперимент, проведенный на решетке из трех станций. Предположим, что
за один день (эпоху) получается 10 записей по 20 источников в каждой. Наблюдения
повторяются 6 раз в год в течение 5 лет. Набор данных составит 18000 измерений B0
источников х 10 наблюдений х 3 базы х 30 эпох) задержек и частот интерферен-
интерференции, всего 36 000 измерений. При анализе можно объединить измерения задержки
и частоты интерференции, поскольку в методе наименьших квадратов рассматрива-
рассматриваются квадраты измеренных значений, деленные на их дисперсии, а они безразмерны
[уравнение (П12.13)]. Теперь подсчитаем число параметров анализируемой модели:
39 координат источников (одно прямое восхождение фиксировано); 9 координат
станций; 90 атмосферных параметров (избыточная длина пути в зените для каждой
станции на каждую эпоху); 120 параметров синхронизации (ошибка синхронизации
и ошибка частоты синхронизации на двух станциях на каждую эпоху) и 90 парамет-
параметров движения полюсов и UT1-UTC, а также ряд других параметров моделирования
прецессии, нутации, приливов в теле Земли, гравитационного отклонение Солнцем,
движения станций и других эффектов, таких как смещения антенных осей (см. разд.
4.6). Общее число параметров примерно равно 360. Параметры в пределах одной
эпохи связаны из-за общей синхронизации и атмосферных параметров. Параметры
между эпохами связаны параметрами баз, прецессии и нутации. Естественно, до
того как пытаться найти общее глобальное решение, следует получить частные ре-
решения на основе подмножеств данных. Имеются процедуры получения глобальных
решений, не требующие обращения матриц с размерами, равными общему числу
параметров (Morrison, 1969). Эксперименты такого масштаба уже были проведены
(Fanselow et al., 1984; Herring, Gwinn and Shapiro, 1985; Ma et al., 1998).
Последний вопрос касается оценки координат радиоисточника с помощью хоро-
хорошо прокалиброванного интерферометра, у которого точно известны базы и аппа-
аппаратурные фазы. В этом случае, на основании уравнения A2.1), дифференциальная
фаза интерферометра записывается как
Аф = 2ttD\ { [sind cos 5 — cos d sin5 cos (H — h)] AS + cos d cos S sin (H —
(П12.48)
Выражая геометрические величины через компоненты проекций баз, можно
представить (П12.48) следующим образом:
Аф = 2тг (uAaf + vAS), (П12.49)
где Aaf = Аа cos 5. Чтобы определить Аа' и А5, можно проанализировать методом
наименьших квадратов измерения фазы на одной или более базах. Частные про-
производные равны df/dpi = 2тги и df/dp2 = 2тгг>, где р\ = Аа' ир2 = AS. С учетом
(П12.40) и (П12.49) матрица нормального уравнения принимает вид
(Ш2.50)
12.5] Приложение 12.1. Анализ методом наименьших квадратов 451
где предполагается, что все измерения имеют одинаковую ошибку сгф, определяе-
определяемую выражением (П12.26). Матрица, обратная [Т], равна:
где А — определитель матрицы из формулы (П12.50):
A— Y^7/2\^??2 IX^iiи- 1 (ТТ19 ^9"!
Коэффициент корреляции, определяемый соотношением (П12.44), равен
Дисперсии оценок параметров задаются диагональными элементами (П 12.51):
оЬ = 2^^Л^ ^т. (Ш2-54)
4тг > Vi > щ -
^ • (П12.55)
Если геометрические места точек гш-плоскости далеко разнесены по времени (т. е.
наблюдения охватывают значительную часть суток), то ^2 ЩУ{ будет мала по срав-
сравнению с ^]^2, так что
аа. ~ %= , (П12.56)
(П12.57)
Более того, если для источника с большим склонением используется только одна
база, то щ — vi — D\ и обе ошибки сводятся к интуитивно понятному результату:
(П12.58)
2ttVNDx
Полож:ение источника также можно найти с помощью фурье-преобразования
функции видности. Эту процедуру можно рассматривать как картографирование
или как умножение данных функции видности на экспоненциальные коэффициенты
ехр[2тт(щАа' + ViAS)] с последующим суммированием по всем данным. Результи-
Результирующая «функция» максимизируется по Аа' и AS. Отсюда легко понять, что основа
картографирования (т. е. без монотонного ограничения или сетки данных) — это
процедура максимального правдоподобия для поиска положения точечного источ-
источника и, следовательно, формально эквивалентна методу наименьших квадратов.
Синтезированная диаграмма bo для N измерений равна
bo(Aaf, AS) = — J2 cos [27Г (гцДс/ + ViAS)]. (П12.59)
15*
452 Интерферометрические методы в астрометрии и геодезии [Гл. 12
Форму диаграммы bo вблизи максимума можно найти, разложив соотношение
(П12.59) в ряд Тейлора до членов второго порядка:
) (П12.60)
Из (П12.60) легко видеть, что контуры синтезированной диаграммы пропорцио-
пропорциональны эллипсу ошибок, определенному формулами (П12.45), (П12.46) и (П12.53)-
(П12.55). Отметим, что метод наименьших квадратов применим лишь при доста-
достаточно большом отношении сигнал/шум, позволяющем разрешить неоднозначности
фазы. Однако метод фурье-синтеза можно применять в любом случае.
Основная литература
Calame, О. Ed., High-Precision Earth Rotation and Earth-Moon Dynamics, Reidel, Dordrecht,
1982.
Davis R. J. and R. S. Booth. Eds., Sub-arcsecond Radio Astronomy, Cambridge Univ. Press,
Cambridge, UK, 1993.
Enge P. and P. Misra. Eds., Proc. IEEE, Special Issue on Global Positioning System, 87, No.
1, Jan. 1999.
Jespersen J. and D. W. Hanson. Eds., Proc. IEEE, Special Issue on Time and Frequency, 79,
No. 7, July 1991.
Johnston K. J. and C. de Vegt. Reference Frames in Astronomy, Ann. Rev. Astron. Astrophys.,
37, 97-125, 1999.
McCarthy D. D. and J. D. H. Pilkington. Eds., Time and the Earth's Rotation, IAU Symp. 82,
Reidel, Dordrecht, 1979.
NASA, Radio Interferometry Techniques for Geodesy, NASA Conf. Pub. 2115, National Aero-
Aeronautics and Space Administration, Washington, DC, 1980.
Reid M. J. and J. M. Moran. Eds., The Impact of VLBI on Astrophysics and Geophysics, IAU
Symp. 129, Kluwer, Dordrecht, 1988.
Цитированная литература
Alef W. Introduction to Phase-Reference Mapping, Very Long Baseline Interferometry. Tech-
Techniques and Applications, M. Felli and R. E. Spencer. Eds., Kluwer, Dordrecht, 1989, p. 261-274.
Backer D. C. and R. A. Sramek. Proper Motion of the Compact, Nonthermal Radio Source in
the Galactic Center, Sagittarius A*, Astrophys. J., 524, 805-815, 1999.
Bartel N., M. I. Ratner, I. I. Shapiro, R. J. Cappallo, A. E. E. Rogers and A. R. Whitney.
Pulsar Astrometry via VLBI, Astron. J., 90, 318-325, 1985.
Bartel N., M. I. Ratner, I. I. Shapiro, T. A. Herring and В. Е. Corey. Proper Motion of
Components of the Quasar 3C345. VLBI and Compact Radio Sources, R. Fanti, K. Kellermann
and G. Setti. Eds., IAU Symp. 110, Reidel, Dordrecht, 1984, p. 113-116.
Beasley A. J. and J. E. Conway. VLBI Phase-Referencing, Very Long Baseline Interferometry
and the VLB A, J. A. Zensus, P. J. Diamond and P. J. Napier. Eds., Astron. Soc. Pacific Conf.
Ser., 82, 327-343, 1995.
Bevington P. R. and D. K. Robinson. Data Reduction and Error Analysis for the Physical
Sciences, 2nd ed., McGraw-Hill, New York, 1992.
Boboltz D. A., P. J. Diamond and A. J. Kemball. R Aquarri: First Detection of Circumstellar
SiO Maser Proper Motions, Astrophys. J., 487, L147-L150, 1997.
12.5] Цитированная литература 453
Campbell R. М., N. Bartel, I. I. Shapiro, M. I. Ratner, R. J. Capallo, A. R. Whitney and
N. Putnam. VLBI-Derived Trigonometric Parallax and Proper Motion of PSR B2021+51,
Astrophys. J., 461, L95-L98, 1996.
Carter W. E. and D. S. Robertson. Very-Long-Baseline Interferometry Applied to Geophysics.
Developments in Astrometry and Their Impact on Astrophysics and Geodynamics, /. /. Mueller
and B. Kolaczek. Eds., Kluwer, Dordrecht, 1993, p. 133-144.
Carter W. E., D. S. Robertson and J. R. MacKay. Geodetic Radio Interferometric Surveying:
Applications and Results, J. Geophys. Res., 90, 4577-4587, 1985.
Carter W. E., D. S. Robertson, J. E. Pettey, B. D. Tapley, B. E. Schutz, R. J. Eanes and M.
Lufeng. Variations in the Rotation of the Earth, Science, 224, 957-961, 1984.
Chandler S. С On the Variation of Latitude, Astron. J., 11, 65-70, 1891.
Clark T. A., B. E. Corey, J. L. Davis, G. Elgered, T. A. Herring, H. F. Hinteregger, С. А.
Knight, J. I. Levine, G. Lundqvist, C. Ma, E. F. Nesman, R. B. Phillips, A. E. E. Rogers,
B. O. Ronndng, J. W. Ryan, B. R. Schupler, D. B. Shaffer, I. I. Shapiro, N. R. Vandenberg,
J. C. Webber and A. R. Whitney. Precise Geodesy Using the Mark-III Very-Long-Baseline
Interferometer System, IEEE Trans. Geosci. Remote Sensing, GE-23, 438-449, 1985.
Cohen M. H. and D. B. Shaffer. Positions of Radio Sources from Long-Baseline Interferometry,
Astron. J., 76, 91-100, 1971.
Counselman С. С. Ill, Radio Astrometry, Ann. Rev. Astron. Astrophys., 14, 197-214, 1976.
Counselman C. C, III, S. M. Kent, С A. Knight, I. I. Shapiro, T. A. Clark, H. F. Hinteregger,
A. E. E. Rogers and A. R. Whitney. Solar Gravitational Deflection of Radio Waves Measured
by Very Long Baseline Interferometry, Phys. Rev. Lett., 33, 1621-1623, 1974.
Elitzur M. Astronomical Masers, Kluwer, Dordrecht, 1992.
Elsmore B. and M. Ryle. Further Astrometric Observations with the 5-km Radio Telescope,
Mon. Not. R. Astron. Soc, 174, 411-423, 1976.
Fanselow J. L., O. J. Sovers, J. B. Thomas, G. H. Purcell, Jr., E. J. Cohen, D. H. Rogstad,
L. J. Skjerve and D. J. Spitzmesser. Radio Interferometric Determination of Source Positions
Utilizing Deep Space Network Antennas - 1971 to 1980, Astron. J., 89, 987-998, 1984.
Fey A. L. and P. Chariot. VLB A Observations of Radio Reference Frame Structures. II
Astrometric Suitability Based on Observed Structure, Astrophys. J. Suppl., Ill, 95-142, 1997.
Fomalont E. В., W. M. Goss, A. G. Lyne, R. N. Manchester and K. Justtanont. Positions and
Proper Motions of Pulsars, Mon. Not. R. Astron. Soc, 258, 479-510, 1992.
Gauss K. F. Theoria Motus, 1809; repr. in transl. as Theory of the Motion of the Heavenly
Bodies Moving about the Sun in Conic Sections, Dover, New York, 1963, p. 249.
Genzel R., M. J. Reid, J. M. Moran and D. Downes. Proper Motions and Distances of H2O
Maser Sources. I. The Outflow in Orion-KL, Astrophys. J., 244, 884-902, 1981.
Gwinn C. R., J. M. Moran and M. J. Reid. Distance and Kinematics of the W49N H2O Maser
Outflow, Astrophys. J., 393, 149-164, 1992.
Hall T. Karl Friedrich Gauss, MIT Press, Cambridge, MA, 1970, p. 74.
Hamilton W. C. Statistics in Physical Science, Ronald, New York, 1964.
Hazard C, J. Sutton, A. N. Argue, C. M. Kenworthy, L. V. Morrison, and С A. Murray.
Accurate Radio and Optical Positions of 3C273B, Nature Phys. Sci., 233, 89-91, 1971.
Herring T. A. Geodetic Applications of GPS, Proc. IEEE, Special Issue on Global Positioning
System, 87, No. 1, 92-110, 1999.
Herring Т. А., В. Е. Corey, С. С Counselman III, I. I. Shapiro, A. E. E. Rogers, A. R.
Whitney, T. A. Clark, С A. Knight, С Ma, J. W. Ryan, B. R. Schupler, N. R. Vandenberg,
G. Elgered, G. Lundqvist, B. O. Ronndng, J. Campbell and P. Richards. Determination of
Tidal Parameters from VLBI Observations. Proc. 9th Int. Symp. Earth Tides, J. Kuo. Ed., E.
Schweizerbart'sche Verlagsbuchhandlung, Stuttgart, 1983, p. 205-211.
Herring Т. А., С R. Gwinn and I. I. Shapiro. Geodesy by Radio Interferometry: Corrections
to the IAU 1980 Nutation Series. Proc. MERIT/COTES Symp., /. /. Mueller. Ed., Ohio State
Univ. Press, Columbus, OH, 1985.
454 Интерферометрические методы в астрометрии и геодезии [Гл. 12
Herring Т. A., I. I. Shapiro, Т. A. Clark, С. Ma, J. W. Ryan, В. R. Schupler, С. A. Knight,
G. Lundqvist, D. В. Shaffer, N. R. Vandenberg, H. F. Hinteregger, R. B. Phillips, A. E. E.
Rogers, J. C. Webber, A. R. Whitney, G. Elgered, B. O. Ronnang, B. E. Corey and J. L. Davis.
Geodesy by Radio Interferometry: Evidence for Contemporary Plate Motion, J. Geophys. Res.,
91, 8344-8347, 1986.
Hinteregger H. F., I. I. Shapiro, D. S. Robertson, C. A. Knight, R. A. Ergas, A. R. Whitney,
A. E. E. Rogers, J. M. Moran, T. A. Clark and B. F. Burke. Precision Geodesy Via Radio
Interferometry, Science, 178, 396-398, 1972.
Hocke K. and K. Schlegel. A Review of Atmospheric Gravity Waves and Travelling Ionospheric
Disturbances 1982-1995, Ann. Geophysicae, 14, 917-940, 1996.
Johnston K. J., A. L. Fey, N. Zacharias, J. L. Russell, С Ma, С de Vegt, J. E. Reynolds, D.
L. Jauncey, B. A. Archinal, M. S. Carter, T. E. Corbin, T. M. Eubanks, D. R. Florkowski,
D. M. Hall, D. D. McCarthy, P. M. McCulloch, E. A. King, G. Nicolson and D. B. Shaffer. A
Radio Reference Frame, Astron. J., 110, 880-915, 1995.
Johnston K. J., P. K. Seidelmann and C. M. Wade. Observations of 1 Ceres and 2 Pallas at
Centimeter Wavelengths, Astron. J., 87, 1593-1599, 1982.
Kaplan G. H., F. J. Josties, P. E. Angerhofer, K. J. Johnston and J. H. Spencer. Precise
Radio Source Positions from Interferometric Observations, Astron. J., 87, 570-576, 1982.
Lambeck K. The Earth's Variable Rotation: Geophysical Causes and Consequences, Cambridge
Univ. Press, Cambridge, UK, 1980.
Lampton M., B. Margon and S. Bowyer. Parameter Estimation in X-Ray Astronomy, Astro-
phys. J., 208, 177-190, 1976.
Lestrade J. F. VLBI Phase-Referencing for Observations of Weak Radio Sources, Radio In-
Interferometry: Theory, Techniques and Applications, T. J. Cornwell and R. A. Perley. Eds.,
Astron. Soc. Pacific Conf. Ser., 19, 289-297, 1991.
Lestrade J.-F., D. L. Jones, R. A. Preston, R. B. Phillips, M. A. Titus, J. Kovalevsky, L.
Lindegren, R. Hering, M. Froeschle, J.-L. Falin, F. Mignard, С S. Jacobs, O. J. Sovers, M.
Eubanks and D. Gabuzda. Preliminary Link of the Hipparcos and VLBI Reference Frames,
Astron. Astrophys, 304, 182-188, 1995.
Lestrade J.-F., A. E. E. Rogers, A. R. Whitney, A. E. Niell, R. B. Phillips and R. A. Preston.
Phase-Referenced VLBI Observations of Weak Radio Sources. Milliarcsecond Position of Algol,
Astron. J., 99, 1663-1673, 1990.
Lieske J. H., T. Lederle, W. Fricke and B. Morando. Expressions for the Precession Quantities
Based upon the IAU A976) System of Astronomical Constants, Astron. Astrophys., 58, 1-16,
1977.
Ma C, E. F. Arias, T. M. Eubanks, A. L. Fey, A.-M. Gontier, С S. Jacobs, O. J. Sovers, B.
A. Archinal and P. Chariot. The International Celestial Reference Frame as Realized by Very
Long Baseline Interferometry, Astron. J., 116, 516-546, 1998.
MacCarthy D. D. and J. D. H. Pilkington. Eds., Time and the Earth's Rotation, IAU Symp.
82, Reidel, Dordrecht, 1979 (see papers on radio interferometry).
Marcaide J. M. and I. I. Shapiro. High Precision Astrometry via Very-Long-Baseline Radio
Interferometry: Estimate of the Angular Separation between the Quasars 1038 + 528A and B,
Astron. J., 88, 1133-1137, 1983.
Markowitz W. and B. Guinot. Eds., Continental Drift, Secular Motion of the Pole and Rotation
of the Earth, IAU Symp. 32, Reidel, Dordrecht, 1968, p. 13-14.
Matveenko L. I. The bright H2O Maser Source in Orion A, Astron. Lett., 7A), 54-57, 1981.
Matveenko L. I., D. A. Graham and P. J. Diamond. The H2O Maser Flare Region in the
Orion-KL Nebula, Sov. Astron. Lett., 14(8), 468-477, 1988.
Matveenko L. I., P. J. Diamond, D. A. Graham. Ring Structure in Orion-KL, Astron. Reports
44, 9, 592-610, 2000.
Melchior P. The Tides of the Planet Earth, Pergamon Press, Oxford, 1978.
12.5] Цитированная литература 455
Moran J. М., В. F. Burke, A. Н. Barrett, A. E. E. Rogers, J. A. Ball, J. С. Carter and D. D.
Cudaback. The Structure of the OH Source in W3. Astrophys. J. (Lett.), 152, L97-L101, 1968.
Morrison N. Introduction to Sequential Smoothing and Prediction, McGraw-Hill, New York,
1969, p. 645.
Mueller I. I. Reference Coordinate Systems for Earth Dynamics: A Preview, in Reference
Coordinate Systems for Earth Dynamics, E. M. Gaposchkin and B. Kolaczek. Eds., Reidel,
Dordrecht, 1981, p. 1-22.
Norris R. P. and R. S. Booth. Observations of OH Masers in W30H, Mon. Not. R. Astron.
Soc, 195, 213-226, 1981.
Norris R. P., R. S. Booth and P. J. Diamond. MERLIN Spectral Line Observations of W30H,
Mon. Not. R. Astron. Soc, 201, 209-222, 1982.
Patnaik A. R., I. W. A. Browne, P. N. Wilkinson and J. M. Wrobel. Interferometer Phase
Calibration Sources-I. The Region 35° ^ 5 ^ 75°, Mon. Not. R. Astron. Soc, 254, 655-676,
1992.
Perley R. A.. The Positions, Structures and Polarizations of 404 Compact Radio Sources,
Astron. J., 87, 859-880, 1982.
Petley B. W. New Definition of the Metre, Nature, 303, 373-376, 1983.
Press W. H., S. A. Teukolsky, W. T. Vetterling and B. P. Flannery. Numerical Recipes, 2nd
ed., Cambridge Univ. Press, Cambridge, UK, 1992.
Reid M. J., A. D. Haschick, B. F. Burke, J. M. Moran, K. J. Johnston, and G. W. Swenson.
Jr., The Structure of Interstellar Hydroxyl Masers: VLBI Synthesis Observations of W3@H),
Astrophys. J., 239, 89-111, 1980.
Reid M. J. and J. M. Moran. Astronomical Masers. Galactic and Extragalactic Radio Astron-
Astronomy, G. L. Verschuur and K. I. Kellermann. Eds., Kluwer, Dordrecht, 1988.
Reid M. J., A. C. S. Readhead, R. C. Vermeulen and R. N. Treuhaft. The Proper Motion of
Sagittarius A*. I. First VLBA Results, Astrophys. J., 524, 816-823, 1999.
Robertson D. S., W. E. Carter, R. J. Eanes, B. E. Schutz, B. D. Tapley, R. W. King, R. B.
Langley, P. J. Morgan and I. I. Shapiro. Comparison of Earth Rotation as Inferred from Radio
Interferometric, Laser Ranging and Astrometric Observations, Nature, 302, 509-511, 1983.
Ros E., J. M. Marcaide, J. C. Guirado, M. I. Ratner, I. I. Shapiro, T. P. Krichbaum, A.
Witzel and R. A. Preston. High Precision Difference Astrometry Applied to the Triplet of S5
Radio Sources B1803+784/Q1928+738/B2007+777, Astron. Astrophys., 348, 381-393, 1999.
Ryle M. and B. Elsmore. Astrometry with 5-km Telescope, Mon. Not. R. Astron. Soc, 164
223-242, 1973.
Seidelmann P. K. Ed., Explanatory Supplement to the Astronomical Almanac, University
Science Books, Mill Valley, CA, 1992.
Shapiro I. I. Estimation of Astrometric and Geodetic Parameters, in Methods of Experimental
Physics, Vol. 12C, M. L. Meeks. Ed., Academic Press, New York, 1976, p. 261-276.
Shapiro I. I., D. S. Robertson, C. A. Knight, С. С Counselman III, A. E. E. Rogers, H. F.
Hinteregger, S. Lippincott, A. R. Whitney, T. A. Clark, A. E. Niell and D. J. Spitzmesser.
Transcontinental Baselines and the Rotation of the Earth Measured by Radio Interferometry,
Science, 186, 920-922, 1974.
Shapiro I. I., J. J. Wittels, С. С. Counselman III, D. S. Robertson, A. R. Whitney, H. F.
Hinteregger, С A. Knight, A. E. E. Rogers T. A. Clark, L. K. Button and A. E. Niell.
Submilliarcsecond Astrometry via VLBI. I. Relative Position of the Radio Sources 3C345 and
NRAO512, Astron. J., 84, 1459-1469, 1979.
Shevchenko A. V., Matveenko L. I., Kopelyanskii G. D., Graham D. A., Nesterov N. S. and
Yu. N. Gorshenkov. Studies of the W51 Object structure in the Hydroxyl Line, Sov. Astron.
Lett., 21, 2, 114-118, 1995.
Smith F. G. The Determination of the Position of a Radio Star, Mon. Not. R. Astron. Soc,
112, 497-513, 1952.
456 Интерферометрические методы в астрометрии и геодезии [Гл. 12
Smith H. М. International Time and Frequency Coordination, Proc. IEEE, 60, 479-487, 1972.
Sovers O. J., J. L. Fanselow and C. S. Jacobs. Astrometry and Geodesy with Radio Interfer-
ometry: Experiments, Models, Results, Rev. Mod. Phys., 70, 1393-1454, 1998.
Sramek R. A. Atmospheric Phase Stability at the VLA. Radio Astonomical Seeing, J. E.
Baldwin and Wang Shouguan. Eds., International Academic Publishers and Pergamon Press,
Oxford, 1990, p. 21-30.
Taff L. G. Computational Spherical Astronomy, Wiley, New York, 1981.
Tatarski V. I. Wave Propagation in a Turbulent Medium, transl. by R. A. Silverman, McGraw-
Hill, New York, 1961.
Taylor J. H., C. R. Gwinn, J. M. Weisberg and L. A. Rawley. Pulsar Astrometry. VLBI and
Compact Radio Sources, R. Fanti, K. Kellermann and G. Setti. Eds., IAU Symposium 110,
Reidel, Dordrecht, 1984, p. 347-353.
Wahr J. M. The Forced Nutations of an Elliptical, Rotating, Elastic and Oceanless Earth,
Geophys. J. R. Astron. Soc, 64, 705-727, 1981.
Wahr J. M. Geodesy and Gravity, Samezdot Press, Golden, CO, 1996.
Walker R. C. The Multiple-Point Fringe-Rate Method of Mapping Spectral-Line VLBI Sources
with Application to H2O Masers in W3-IRS5 and W3@H), Astron. J., 86, 1323-1331, 1981.
Walker R. G, D. N. Matsakis and J. A. G arcia-Barret о. H2O Masers in W49N. I. Maps.
Astrophys. J., 255, 128-142, 1982.
Woolard E. W. and G. M. Clemence. Spherical Astronomy, Academic Press, New York, 1966.
Глава 13
ЭФФЕКТЫ РАСПРОСТРАНЕНИЯ
Нейтральная и ионизованная среды между радиоисточником и поверхностью
Земли часто оказывают сильное влияние на распространяющееся через нее поле
излучения. Наиболее важными из этих сред являются нейтральная нижняя атмо-
атмосфера, или тропосфера, ионосфера, ионизованная межпланетная и межзвездная
среда. Мы рассмотрим три типа эффектов, вызванных этими средами. Во-первых,
присутствие в средах крупномасштабных структур вызывает эффекты рефракции.
Эти эффекты, которые можно изучать на основе геометрической оптики и принци-
принципа Ферма, являются отклонение радиоволн, изменение их скорости распростране-
распространения и поворот плоскости поляризации. Во-вторых, излучение может поглощаться.
Наконец, излучение может рассеиваться на турбулентных структурах, имеющихся
в среде. Явление рассеяния приводит к мерцаниям, или размытию изображения.
В тропосфере важную роль в распространении радиоволн играет водяной пар.
Преломляющая способность водяного пара в радиодиапазоне примерно в 20 раз
больше, чем в ближнем инфракрасном или оптическом диапазонах. Флуктуации
фазы в радиоинтерферометрах на сантиметровых, миллиметровых и субмилли-
субмиллиметровых волнах, в основном, вызваны флуктуациями распределения водяного
пара. Водяной пар слабо перемешан в атмосфере, и его полную плотность на
луче зрения нельзя точно измерить, основываясь на наземных метеорологических
данных. Неопределенность содержания водяного пара — основное ограничение на
точность РСДБ-измерений. Мелкомасштабные (<1км) флуктуации распределения
водяного пара ограничивают угловое разрешение интерферометров со связанными
элементами. Кроме того, спектральные линии водяного пара являются причиной
значительного поглощения на частотах выше 100 ГГц, и обычно тропосфера ста-
становится полностью непрозрачной на частотах между 1 и ЮТГц C00 и ЗОмкм).
Итак, при любом рассмотрении нейтральной атмосферы нужно, в первую очередь,
учитывать влияние водяного пара. Эффекты распространения в нейтральной атмо-
атмосфере с точки зрения радиосвязи обсуждаются в работах (Crane, 1981) и (Bohlander,
McMillan and Gallagher, 1985).
Выше нейтральной атмосферы излучение проходит через три морфологически
различных слоя плазмы: ионосферу, межпланетную и межзвездную среды. Боль-
Большинство плазменных эффектов пропорциональны v~2. Следовательно, нежелатель-
нежелательное воздействие можно ослабить, проводя наблюдения на наиболее высокой из
возможных частот. Однако влияние ионосферы на РСДБ-измерения легко просле-
прослеживается на частотах, по меньшей мере, вплоть до 10 ГГц. Однако астрофизические
требования таковы, что многие наблюдения нужно проводить на таких частотах,
где плазменные эффекты вызывают проблемы.
Наш интерес к средам распространения радиоволн обусловлен тем, что эти
среды затрудняют интерферометрические измерения радиоисточников. С другой
стороны, наблюдения радиоисточников можно использовать для исследования ха-
характеристик среды распространения. Для этой цели широко используются радио-
интерферометрические измерения.
458 Эффекты распространения [Гл.13
13.1. Нейтральная атмосфера
В самой нижней части атмосферы температура убывает от поверхности земли
монотонно со скоростью 6,5 К/км, за исключением небольшой случайной инверсии,
пока не достигает значения 218 К на высоте примерно 11км. Этот самый нижний
слой называется тропосферой. Выше 11км температура постоянна на протяжении
примерно 10 км в области, называемой тропопаузой. Выше тропопаузы температура
в стратосфере начинает расти с высотой. Наибольшее влияние на распространение
радиоволн в нейтральной атмосфере оказывает тропосфера. Прежде чем подробно
обсуждать рефракцию, поглощение и рассеяние радиоволн в тропосфере, рассмот-
рассмотрим некоторые основные физические представления.
13.1.1. Физические основы. Рассмотрим уравнение для плоской волны, рас-
распространяющейся вдоль направления у в однородной диссипативной диэлектриче-
диэлектрической среде,
) = E0e^kny-27TUt\ A3.1)
где к — волновое число в вакууме, равное 2тгг//с, с — скорость света a Eg — ампли-
амплитуда электрического поля. Величина п — комплексный показатель преломления,
равный nR -\- jnl. Если мнимая часть показателя преломления положительна, то
волна экспоненциально затухает. Коэффициент поглощения мощности определяет-
определяется выражением
_ 4тг^ (лъоЛ
Волновое число в атмосфере равно значению /с, умноженному на действительную
часть показателя преломления, что может быть записано в виде
A3.3)
с Up
где п = nR — показатель преломления в отсутствие поглощения, a vp — фазовая
скорость. В нижней атмосфере фазовая скорость волны с/п меньше примерно на
0,03 %. Дополнительное время, необходимое на прохождение среды с показателем
преломления п(у) по сравнению с временем прохождения того же расстояния в ва-
вакууме, равно
Д* = - \(п - 1) dy, A3.4)
С J
Здесь мы пренебрегаем различием между длиной истинного пути луча и расстоя-
расстоянием по прямой. Избыточная длина пути с At определяется выражением
A3.5)
Мы ввели преломляющую способность N как N = 106(п — 1). Заметим, что понятие
избыточной длины пути, широко используемое в этой главе, не представляет собой
истинную траекторию.
Преломляющая способность влажного воздуха в радиодиапазоне определяется
эмпирической формулой (см. ниже п. 13.1.5)
N = 77,6 ^ + 64,8^+ 3,776 • Ю5^ , A3.6)
13.1] Нейтральная атмосфера 459
где Т — температура в Кельвинах, pD — парциальное давление сухого воздуха,
a pv — парциальное давление водяного пара в миллибарах Aмбар = 100 Н/м =
= 100Па; 1 атм = 1013мбар). Первые два члена в A3.6) возникают из-за поля-
поляризационного смещения газовых составляющих воздуха. Третий член обусловлен
постоянным дипольным моментом водяного пара. Уравнение A3.6) справедливо
с точностью лучше 1 % на частотах ниже 100 ГГц. Вклад дисперсионных состав-
составляющих преломляющей способности, связанный с резонансами, очень мал (см.
п. 13.1.4).
Преломляющую способность можно выразить через плотность газа, используя
уравнение состояния идеального газа
где pup — парциональное давление и плотность любой газовой составляющей, R —
универсальная газовая постоянная, равная 8,314 Дж/(моль-К), Л4 — молекулярный
вес, который для сухого воздуха в тропосфере равен A4d = 28,96 г/моль, а для во-
водяного пара Mv = 18,02г/моль. Таким образом, pD = pdRT/Md Pv = pvRT/Mv,
где pD и pv — плотности сухого воздуха и водяного пара соответственно. Поскольку
полное давление Р есть сумма парциальных давлений, а полная плотность рт —
сумма плотностей составляющих, то уравнение A3.7) можно записать в виде Р =
= РтКГ/Мт, где
(L^ L^y1. A3.8)
Рт Mv рт
Подставляя соответствующее уравнение A3.7) и выражение pD = рт — pv
в A3.6), получаем
N = 0,2228рт + 0,076pv + 1742 Ц-, A3.9)
где рт и pv измеряются в г/м3. Так как второй член в правой части A3.9) мал по
сравнению с третьим членом, их можно объединить, и для Т = 280 К
N ~ 0,2228рт + 1763 Ц- = ND + Nv. A3.10)
Уравнение A3.10) определяет сухую и влажную преломляющие способности, Nd
и Ny соответственно. Этим определениям не всегда следуют в литературе. От-
Отметим, что Nd пропорциональна полной плотности и поэтому содержит вклад,
обусловленный индуцированным дипольным моментом водяного пара. Картина
глобального распределения средних значений Ny показана на рис. 13.1.
Атмосфера с высокой степенью точности описывается уравнением гидростатиче-
гидростатического равновесия (Humphreys, 1940). Масса газа при статическом равновесии между
давлением и силой тяжести определяется уравнением
где g — гравитационное ускорение, приблизительно равное 980см/с2, a h — высота
над поверхностью Земли. Используя уравнение состояния идеального газа A3.7),
можно проинтегрировать уравнение A3.11) для профилей температуры и соотно-
соотношений концентраций компонент определенного вида. В предположении изотерми-
изотермической атмосферы и постоянного соотношения концентраций рт является экспо-
экспоненциальной функцией со шкалой высот RT/ЛЛд ~ 8,5 на 290 К, что близко к на-
наблюдаемой шкале высот атмосферы. Другие модели описаны Гессом (Hess, 1959).
460
Эффекты распространения
[Гл. 13
180 150 120 90
30 0
30 60 90 120 150 180
180 150 120 90 60 30 0 30 60 90 120 150 180
180 150 120 90 60 30 0 30 60 90 120 150 180
180 150 120 90
60
60
70
30 0 30 60 90 120 150 180
Рис. 13.1. Глобальное распределение влажной преломляющей способности Ny на уровне
моря на февраль (a), Ny на август (б). Отметим сезонные изменение в среднем содержании
водяного пара. Из работы (Bean et al., 1966)
В условиях гидростатического равновесия избыточная длина пути, обусловленная
сухой компонентой преломляющей способности, не зависит от распределения пол-
полной плотности или температуры по высоте, а зависит только от поверхностного
давления Pq. Если предположить, что g не зависит от высоты, то поверхностное
13.1] Нейтральная атмосфера 461
давление можно получить интегрированием уравнения A3.11):
оо
Po = g\ PT(h)dh. A3.12)
Из A3.5), A3.10) и A3.12) получим, что избыточная длина пути в направлении на
зенит, обусловленная сухой компонентой, равна
оо
CD = ИГ6 [ ND dh = АР0, A3.13)
о
где А = 77foR/gM.D = 0,228 см/мбар. При стандартных условиях, когда Pq =
= 1013 мбар, значение Со = 231см.
Водяной пар не очень хорошо перемешан в атмосфере, и поэтому его рас-
распределение не очень хорошо коррелирует с измеренными на поверхности земли
метеорологическими параметрами (Reber and Swope, 1972). В среднем плотность
водяного пара имеет экспоненциальное распределение до высоты 2 км. Парциальное
давление и плотность водяного пара, согласно A3.7), связаны соотношением
^ [г/м3]. A3.14)
Парциальное давление водяного пара для насыщенного воздуха pvs при темпе-
температуре Т, полученное из уравнения Клаузиуса-Клапейрона (Hess, 1959), можно
выразить с точностью лучше 1% в диапазоне температур 240-310 К с помощью
следующей формулы (Crane, 1976):
Pvs = 6,11 (^)~5'3 е25'2 <т73>/т [мбар]. A3.15)
Относительная влажность равна pv/pvs. Составляющая длины пути, в основном,
обусловленная постоянным дипольным моментом водяного пара, пропорциональна
интегралу от Ny из A3.10), который равен
Су = 1763 • Ю-6 [ ^l dh, A3.16)
J TW
где единицы измерения Су те же самые, что и для h. Если предположить, что
атмосфера изотермична и pv убывает экспоненциально до высот 2 км, то из A3.14)
и A3.16) следует
?y = 7,6-104^f [см], A3.17)
где pvo — парциальное давление водяного пара на поверхности Земли. Следова-
Следовательно, если Т = 273К, ?у, выраженная в сантиметрах, приблизительно равнаpVQ,
выраженному в миллибарах. Для экспоненциального распределения плотности до
высот 2км и температурой 280К длина пути задается выражением Су = 1,26pVQ,
где pvo — плотность водяного пара на земле.
Полная плотность водяного пара, или высота сконденсированного из атмосферы
столба воды, определяется выражением
оо
= — \pv(h)dh, A3.18)
Pw J
W
Pw
0
462
Эффекты распространения
[Гл. 13
где pw = 106 г/м3 — плотность воды. В изотермической атмосфере при 280 К
Су -6,3 к;.
A3.19)
Эта широко используемая в литературе формула является хорошим приближением
на частотах меньше 100 ГГц. В окнах на частоте выше 100 ГГц отношение Cy/w
может меняться в пределах от 6,3 до примерно 8 (см. рис. 13.8 и пояснения).
Значения Су в экстремальных условиях для среднего местоположения на уровне
моря можно вычислить по приведенным выше формулам. При Т = 303 К C0°С)
и относительной влажности = 0,8 получим pvo = 34мбар, pvo = 24г/м3, w = 4,9 см,
а Су = 28 см. При Т = 258 К (—15°С) и относительной влажности 0,5, получаем
pvo = 1,0мбар, pvo = 0,8 г/м3, w = 0,15 см, а Су = 1,1 см. Полная избыточная длина
пути в атмосфере в зените С — Cd + Су из уравнений A3.13) и A3.19) равна
С ~ 0,228Р0 + 6,3к; [см],
A3.20)
где Pq выражено в миллибарах, a w — в сантиметрах. Уравнение A3.20) является
достаточно точным для оценок, так как относительные колебания температуры
в нижней атмосфере и шкалы высот водяного пара обычно не превышают 10 %.
Однако оно не достаточно корректно, чтобы предсказывать длину пути с точностью
до малых долей длины волны на миллиметровых длинах волн.
13.1.2. Рефракция и задержка распространения. Если вертикальные
распределения температуры и давления водяного пара известны, то точные оценки
угла прихода и избыточного времени распространения для луча, падающего на
атмосферу под произвольным уг-
х # К источнику лом, можно получить, иссле-
исследуя траектории лучей. Ниже
мы рассмотрим несколько эле-
элементарных случаев, чтобы полу-
получить простые аналитические вы-
выражения. Простейшим случаем
является интерферометр в од-
однородной или плоскопараллель-
плоскопараллельной атмосфере, изображенный
на рис. 13.2. Преломление луча
подчиняется закону Снеллиуса:
Рис. 13.2. Двухэлементный интерферометр, атмо-
атмосфера моделируется однородным плоским слоем.
Геометрическая задержка такая же, как если бы ин-
интерферометр находился в свободном пространстве
sin Zq = sin;
A3.21)
где z — зенитное расстояние на
входе в атмосферу (где п = 1), а
zq — зенитное расстояние у поверхности (где п = щ). Геометрическая задержка
в интерферометре, определенная в гл. 2, равна
n0D
D .
= — smz.
с
A3.22)
Величину rg можно вычислить по углу прихода zq и скорости света на поверхности
Земли с/по или по z и скорости света в свободном пространстве. Таким образом,
если атмосфера однородна и кривизной Земли можно пренебречь, то получающаяся
геометрическая задержка такая же, как и в свободном пространстве. Необходимо
лишь вычислить угол рефракции для обеспечения правильного сопровождения ис-
источника антеннами. Угол рефракции, Az = z — zq, с учетом A3.21) можно записать
в виде
13.1]
Нейтральная атмосфера
463
z = z — sin x I — sin z ) .
\Пг> J
A3.23)
Это уравнение можно разложить в ряд Тейлора по щ — 1, и, учитывая члены
первого порядка, получим
Az~(no-l)tgz. A3.24)
Поскольку на поверхности Земли по — 1 — 3 • 10~4, то A3.24) можно записать в виде
Az [мин дуги] ~tgz.
A3.25)
Угол рефракции можно рассчитать и для более реальных случаев. Предполо-
Предположим, что кривизна Земли отсутствует и атмосфера состоит из большого числа
плоскопараллельных слоев, пронумерованных от 0 до га, как показано на рис. 13.3.
Пусть показатель преломления на
поверхности равен по, а показа-
показатель преломления верхнего слоя —
пш = 1. Применяя закон Снеллиуса
к этим слоям, получим следующую
систему уравнений:
no sinzo = n I sinzi,
П\ SmZi = 77,2 SmZ2,
A3.26)
nm_i sinzm_i = sinz,
где z = zm. Из этих уравнений вид-
видно, что no sinzo = sinz. Этот ре-
результат идентичен результату, по-
полученному для случая однородной
среды. Таким образом, независимо
от вертикального распределения ко-
коэффициента преломления, угол ре-
рефракции определяется уравнением
A3.21), где по — значение показате-
показателя преломления на поверхности Зем-
Земли. Этот результат можно также по-
получить, просто применив принцип
Ферма. Интересное применение это-
этого результата состоит в том, что если по = 1 (измерительный прибор помещен
в вакуумную камеру на поверхности Земли), то чистая рефракция отсутствует, т. е.
z0 = z.
Для атмосферы, состоящей из сферических слоев, угол рефракции определяется
следующей формулой (Smart, 1977):
Поверхность
Рис. 13.3. Модель атмосферы в виде набора
тонких однородных слоев. Угол падения на
верхний слой Zm равен зенитному расстоянию
в свободном пространстве z, а угол падения
на поверхности Земли равен zq. Полный угол
преломления равен Az = z — zq
Az = r0п0 sin z0
dn
^ ny
rznz — \
sin
2zq
A3.27)
где г — расстояние от центра Земли до слоя с показателем преломления п, г о —
радиус Земли. Этот результат получен из закона Снеллиуса, записанного в сфериче-
сферических координатах: nr sinz = const (Smart, 1977). При малых зенитных расстояниях
разложение A3.27) дает
464
Эффекты распространения
[Гл. 13
Az ~ (п0 - 1) tgz0 - а2 tgz0 sec2z0,
где п2 = const. Выражение A3.28) также можно записать в виде
Az ~ оц tgz0 -a2 tg3z0,
A3.28)
A3.29)
где ai ~ 56", a a2 — 0,07" для сухой атмосферы при стандартных условиях (COESA
1976). Рефракция на горизонте составляет примерно 0,46° (см. рис. 13.5). Более
детальный анализ проведен в работе Саастамойнена (Saastamoinen, 1972).
Дифференциальная задержка, вносимая в интерферометр тропосферой с го-
горизонтальной слоистостью, является следствием разности зенитных расстояний
источника на антеннах. Рассмотрим две близко расположенные антенны. Если
избыточный путь в направлении на зенит составляет Со, то в других направлениях
он будет приблизительно равен Со sec z. При больших зенитных расстояниях это
приближение становится неточным. Разность избыточных путей АС составит
AC ~ C0Az
A3.30)
где Az — разность зенитных расстояний на двух антеннах.
Если антенны находятся на экваторе и источник имеет нулевое склонение, то Az
равна разности долгот D/го, где D — расстояние между антеннами. В этом случае
Зенит
К источнику
Рис. 13.4. Геометрия задержки рас-
распространения с учетом сферичности
Земли. Предполагается, что луч рас-
распространяется вдоль координаты у.
Угол Zi — зенитное расстояние лу-
луча на высоте h. Этот угол необхо-
необходим в расчетах длины избыточного
пути через ионосферу [см. уравнения
A3.129) и A3.130)]
CoD sinz
ro cos2z
A3.31)
Если D = 10 км, Co = 230 см, r0 = 6370 км
и z = 80°, то AC = 12 см. Вычисление раз-
разности избыточных путей можно легко обоб-
обобщить следующим образом. Пусть i*i и г2 —
векторы, направленные из центра Земли к
каждой антенне. Геометрическая задержка
равна (ri • s — г2 • s)/c, где s — единичный век-
вектор в направлении на источник. Поскольку
coszi = (i*i -s)/ro и cosz2 = (r2 •s)/ro, где z\
и Z2 — зенитные расстояния на двух антеннах,
то геометрическую задержку можно записать
как
rg = — (cos zi - cos z2) ~ — Az sin z. A3.32)
Подставляя Az из A3.32) в A3.30), получаем
выражение для разности избыточных путей,
справедливое для интерферометров с малы-
малыми базами и умеренных зенитных расстояний:
АС ~
го
sec2z.
A3.33)
Для интерферометров со сверхдлинными
базами выражение A3.30) не выполняется.
Разность избыточных путей приблизительно
равна АС = ?iseczi — ^2secz2, где ?i, ?2,
13.1] Нейтральная атмосфера 465
zi, и Z2 — значения избыточных путей в зените и зенитные расстояния для двух
антенн. Теперь получим более точное выражение для длины избыточного пути для
каждой антенны. Предположим, что коэффициент преломления распределен экспо-
экспоненциально, и шкала высот равна ho. Геометрия показана на рис. 13.4. Избыточная
длина пути составит
С = 1(T67VO { ехр (-A) dy, A3.34)
о
где Щ — преломляющая способность на поверхности Земли, h — высота над по-
поверхностью Земли, a dy — дифференциальная длина вдоль траектории луча. Ис-
Искривлением траектории луча пренебрегаем. Исходя из геометрии рис. 13.4, можно
показать, что
2
h ~ у cos z + — sin2z. A3.35)
2vq
Следовательно,
С ~ 10~67V0 ехр (-/¦ cosz ) ехр --^ sin2z dy. A3.36)
V До / V Irnhn J
о
Аргумент самой правой экспоненты в формуле A3.36) мал, поэтому экспоненту
можно разложить в ряд Тейлора и
оо
— ^- cosz ) х ( 1 У— sin2z ... J dy. A3.37)
До / \ 2roho J
о
Проинтегрировав A3.37), получим
п л (Л — 6 д г 7 A ho , 2 ^ /-iooo\
С ~ 10 Noho sec z 1 tg z . A3.38)
V го /
Уравнение A3.38) можно также записать в следующем виде:
/io\ „л„„ ^о _ з,
С ~ lO-6N0h0 |Yl + —) secz - ^ sec3zl . A3.39)
L V го J го J
Таким образом, С является функцией нечетных степеней sec z, в то время
как угол рефракции в A3.29) является функцией нечетных степеней tgz. Оба
выражения — A3.38) и A3.39) — расходятся при стремлении z к 90°. При z =
= 90° из выражения A3.35) следует h ~ у2/2г0. Таким образом, согласно A3.34),
избыточный путь на горизонте равен
С ~ 1(Г6АЦ/^^ ~ 70?0 ^ 14А^о [см], A3.40)
при го = 6370 км и ho = 2 км. Модель, включающую и сухую атмосферу с высотой
hD = 8 км, и влажную атмосферу с высотой hv = 2 км, можно получить, применив
соотношения A3.38) к сухой и влажной компонентам и воспользовавшись A3.13)
и A3.17). В результате имеем
466
Эффекты распространения
[Гл. 13
0,4*
10
20 30 50 90
1 1 1 1 1 1
-
Ill 1 1
Y
\l
[ 1 1 1 1 1
в
I 20
g-20 -
CD
1-40
О 1 2 3 4 5 7 10 20 30 50 90°
90™ z
Рис. 13.5. а — зависимость угла отклонения от 90° — z, где z — зенитное расстояние луча
в отсутствие рефракции, полученная методом лучевых траекторий для стандартной сухой
атмосферы (COESA 1976). б— зависимость избыточного пути от 90° — z, полученная ме-
методом лучевых траекторий. Длина избыточного пути равна 2,31 м. в — отклонение длины
избыточного пути от модели Со sec z (кривая 1) и от модели, описываемой уравнением
A3.41) (кривая 2); в обоих случаях pvo = 0, а длина избыточного пути та же, что ив E)
С ~ 0,228 Ро sec z A - 0,0013 tg2z)
7'5 '10
Более сложные модели были предложены Марини (Marini, 1972), Саастамойненом
(Saastamoinen, 1972), Дэвисом и др. (Davis et al., 1985), Ниллом (Niell, 1996) и про-
прочими авторами. Сравнение приближенной формулы A3.41) и решения методом
лучевых траекторий приведены на рис. 13.5
13.1.3. Поглощение. При ясном небе главными источниками атмосферного
ослабления являются молекулярные резонансы водяного пара, кислорода и озона.
Резонансы водяного пара и кислорода уширяются давлением и вызывают ослабле-
ослабление вдали от резонансных частот. График поглощения в зависимости от частоты
представлен на рис. 13.6. Ниже 30 ГГц поглощение определяется слабым переходом
Н2О — 616-623 — на частоте 22,2 ГГц (Liebe, 1969). Поглощение в этой линии редко
превышает 20 % в зените. Линии кислорода в полосе 50-70 ГГц значительно сильнее,
и наземные астрономические наблюдения в этом диапазоне проводить нельзя. Изо-
Изолированная линия кислорода на 118 ГГц делает невозможными наблюдения в по-
13.1]
Нейтральная атмосфера
467
лосе 116—120 ГГц. На более высоких частотах имеется ряд сильных линий водяного
пара на 183, 325, 380, 448, 475, 557, 621, 752, 988, и 1097ГГц и выше (Liebe, 1981).
Наблюдения молено проводить в окнах между этими линиями в местах с низкой
влажностью, обычно расположенных на больших высотах. Физика атмосферного
поглощения детально обсуждается в работе Вотерса (Waters, 1976), а модель по-
поглощения на частотах ниже 100ГГц разработана Либе (Liebe, 1981, 1985, 1989).
Здесь мы рассмотрим только феноменологию поглощения и его калибровку.
Коэффициент поглощения зависит от температуры, плотности газа и полного
давления. Например, коэффициент поглощения в линии Н2О на частоте 22 ГГц
можно записать в виде (Staelin, 1966):
а = C,24 • 10-4е-644/т) ^f (l + 0,
0147
/ L(zy-22,235J+,
(у + 22,235J +
+ 2,55- 10- spvv
V тЗ/2
см), A3.42)
где Ai/ приблизительно равна полуширине линии, отсчитываемой на уровне поло-
половины максимума в гигагерцах, и определяется уравнением
Ai/ = 2,58 • КГ3 (l
0147^) ?-
'Ui47 P ) (Т/318H'625 '
A3.43)
где v — частота в гигагерцах, Т — темпе-
температура в кельвинах, Р — полное давление
в миллибарах, ару — плотность водяно-
водяного пара в граммах на кубический метр.
Оказывается, что форма линии, опреде-
определяемая выражением A3.42) — профиль
ван Флека-Вайскопфа — лучше соответ-
соответствует эмпирическим данным, чем дру-
другие теоретические профили (Hill, 1986).
Возможны и другие параметрические
представления профиля линии, см., на-
например, (Pol, Ruf and Keihm, 1998).
Интенсивность луча, проходящего че-
через поглощающую среду, подчиняет-
подчиняется уравнению переноса излучения. Мы
предполагаем, что среда находится в со-
состоянии локального термодинамическо-
термодинамического равновесия при температуре Т, и что
рассеяние пренебрежимо мало. В об-
области, где справедливо приближение
Рэлея-Джинса функции Планка, т. е. где
интенсивность пропорциональна яркост-
ной температуре, уравнение переноса излучения может быть записано в виде (Ry-
bicki and Lightman, 1979)
^- = -а(Тв-Т), A3.44)
где Тв — яркостная температура, а а — коэффициент поглощения, определенный
в A3.2) и A3.42). Решение уравнения A3.44) для излучения, распространяющегося
50 100 150 200 250 300
Частота, ГГц
Рис. 13.6. Непрозрачность атмосферы в зе-
зените. Поглощение в узких линиях озона
не учитывалось. Из работы (Waters, 1976).
Непрозрачность в зените на частотах выше
300 ГГц рассматривается в работах (Liebe,
1981, 1989). Отметим, что 2г/см2 Н2О со-
соответствуют w = 2 см
468 Эффекты распространения [Гл.13
вдоль оси у, принимает вид
оо
ТвП = Тво(и) е~т» + J a(u,y) Т{у) e~< dy, A3.45)
о
где Тво — яркостная температура при отсутствии поглощения, включая компоненту
космического фона,
У
^(v,y')dy', A3.46)
= \a(v,y')dy'. A3.47)
Здесь у — расстояние, измеряемое от наблюдателя, ти называется оптической тол-
толщей, или непрозрачностью. Первый член правой части уравнения A3.45) описывает
поглощение сигнала, а второй — вклад излучения атмосферы. Уравнение A3.45) ил-
иллюстрирует фундаментальный закон: поглощающая среда должна излучать. Если
Т(у) постоянна в данной среде, то выражение A3.45) можно записать в виде
Тв(и) = ТвоИ е"т- + ТA - е~т»). A3.48)
Наличие поглощения может оказать существенное влияние на работоспособность
системы. Если температура приемника равна Tr, to температура системы, являю-
являющаяся суммой Tr и яркостной температуры атмосферы (в пренебрежении эффек-
эффектами излучения Земли), равна
Ts = Tfi + Tat(l-e-T-), A3.49)
где Tat — температура атмосферы. Предполагается, что в отсутствие космического
источника антенная температура равна яркостной температуре неба. Кроме того,
если шкала яркостной температуры привязывается к точке вне атмосферы путем
умножения данных измерений яркостной температуры [см A3.48)] на еТи, то эф-
эффективная температура системы равна Т$еТи или
T's = TReT» + Tat (er- - 1). A3.50)
В целом, атмосферные потери моделируются эквивалентным аттенюатором на
входе приемника. Предположим, что Тц = 30 К, Tat = 290 К, а ти = 0,2; тогда
эффективная температура системы будет равна 100 К. В этом случае атмосфера
ухудшит чувствительность системы более чем в 3 раза. Отметим, что потери в чув-
чувствительности возникают, в основном, из-за увеличения температуры системы, а не
из-за ослабления сигнала, которое составляет лишь 20 %. Излучение атмосферы
вызывает в разнесенных антеннах некоррелированные сигналы и тем самым вносит
вклад лишь в шумы на выходе интерферометра.
Поглощение можно оценить непосредственно из измерений, выполненных на ра-
радиотелескопе. При использовании одного из методов, который называется методом
разреза атмосферы, непрозрачность определяется по излучению атмосферы. Если
антенна сканирует небо от зенита до горизонта, то наблюдаемая яркостная темпе-
температура в отсутствие источников фонового излучения будет зависеть от зенитного
угла, поскольку непрозрачность пропорциональна длине пути через атмосферу,
13.1] Нейтральная атмосфера 469
которая меняется приблизительно как sec z. Таким образом, яркостная температура
атмосферы равна
TB=Tat(l-e-T°secz), A3.51)
где го — непрозрачность в зените. Величина tq это коэффициент наклона кривой
In (Tat —Тв) как функции secz, взятый с обратным знаком, так как
-rosecz. A3.52)
Точность этого метода ограничена излучением Земли через боковые лепестки,
которое меняется в зависимости от зенитного расстояния. Непрозрачность можно
оценить и по измерениям поглощения излучения радиоисточника в определенном
интервале зенитных углов. На одном и том же зенитном расстоянии наблюдаемая
разность температур антенны, наведенной на источник и на область рядом с источ-
источником, равна
-r°secz, A3.53)
где Tso — вклад источника в антенную температуру в отсутствие атмосферы. Из
A3.53) получим
In АТВ - inTso = -т0 secz. A3.54)
Итак, го можно определить, не зная Tsoi если перекрыть достаточный диапазон по
sec z. Этот метод зависит от изменений коэффициента усиления антенны в зависи-
зависимости от зенитного расстояния.
Другой метод, называемый методом дискового модулятора, обычно использу-
используют на миллиметровых волнах. Диск, состоящий из попеременно расположенных
открытых и поглощающих секций, устанавливается перед рупорным облучателем
антенны. При вращении диска радиометр попеременно смотрит на небо или по-
поглощающие секции и синхронно измеряет разность температур неба и дискового
модулятора при температуре Tq. Таким образом, температуры при наведении и от-
отводе антенны от источника выражаются как
ЛТОП = Tso e~r» + Tat A - е"т") - То A3.55)
AToff = Tat(l-e-^)-T0. A3.56)
Измерения можно объединить, чтобы получить Tso и тем самым исключить влия-
влияние атмосферного поглощения. В случае, когда Tq = Tat,
гр /AToff —
Tso={
{ лго„
Когда важна чувствительность, дисковый модулятор используется только для ка-
калибровки выходного сигнала антенны, отведенной от источника. При этом AToff —
— АТОП в числителе выражения A3.57) заменяется на Toff — Топ. Измерение Tso
дает плотность потока источника, которая определяет функцию видности в начале
координат гш-плоскости.
Непрозрачность можно оценить и по наземных метеорологическим измерениям,
когда другие данные недоступны. Этот метод не так точен, как описанные выше
методы прямых радиометрических измерений, но имеет то преимущество, что не
расходует наблюдательное время. Вотерс (Waters, 1976) провел анализ данных по-
поглощения в зависимости от плотности водяного пара на уровне моря для различных
частот, пытаясь описать их зависимостью вида tq = «о + aiPV0- Коэффициенты а0
и«1, приведены в табл. 13.1.
470 Эффекты распространения [Гл.13
Таблица 13.1. Эмпирические коэффициенты для оценки непрозрачности,
исходя из относительной влажности на поверхности61
V
(ГГц)
15
22,2
35
90
а0
(непер)
0,013
0,026
0,039
0,039
аг
(непер м3/г)
0,0009
0,011
0,0030
0,0090
Источник: (Waters, 1976).
аАппроксимировались из уравнения то = с*о +
данными по непрозрачности, полученными из наблю-
наблюдений радиозондов, и измерениями абсолютной влаж-
влажности на поверхности pvo, г/м3.
13.1.4. Возникновение рефракции. Исходя из практических соображений,
мы раздельно рассматривали эффекты задержки распространения и поглощения
радиоволн в нейтральной атмосфере. Однако задержка и поглощение тесно связа-
связаны, поскольку они получены из действительной и мнимой частей диэлектрической
проницаемости газа в атмосфере. Эти части не являются независимыми, а связаны
соотношением Крамерса—Кронига, которое аналогично преобразованию Гильберта
(Van Vleck, Purcell and Goldstein, 1951). Теперь рассмотрим эту взаимосвязь с фи-
физической точки зрения на основе классической теории дисперсии. Из анализа станет
ясно, почему задержка, обусловленная атмосферой, слабо зависит от частоты даже
вблизи спектральных линий, вызывающих сильное поглощение.
Разреженный газ, состоящий из молекул, можно представить в виде связанных
осцилляторов. В каждой молекуле электрон с массой т и зарядом — е гармонически
связан с ядром, а движение электрона характеризуется резонансной частотой z/q
и постоянной затухания 2тгГ. Уравнение движения при наличии внешней гармо-
гармонической силы —eE$e~jt, создаваемой электрическим полем электромагнитной
волны, имеет вид
тх + 2тгшГж + 4тг2т^х = -еЕ0 e~j27TU\ A3.58)
где х — смещение связанного электрона, Eq и ту — амплитуда и частота приложенно-
приложенного электрического поля, а точки означают производные по времени. Стационарное
решение имеет вид х = хо e~i27Tut, где
_ еЕ0/Dтг2т) A4^
у -щ +j^r
Величина дипольного момента на единицу объема Р равна —птехо, где пт —
концентрация молекул газа. Относительная диэлектрическая проницаемость 1) е
х) В этом разделе и разд. 13.2 мы используем международную систему единиц СИ.
В ней основное соотношение между вектором индукции D, вектором напряженности
электрического поля Е и вектором поляризации Р записывается в виде D = боЕ + Р = еЕ,
где бо — диэлектрическая проницаемость вакуума, а б — диэлектрическая проницаемость
среды. Относительная диэлектрическая проницаемость е равна е/бо. Сравнение различных
систем единиц и уравнений в электричестве и магнетизме можно найти в работе Джексона
(Jackson, 1999).
13.1] Нейтральная атмосфера 471
равна 1 + Р/(боЕ), так что
_ -, птв2/Dтг2гпб0) ( v
^ - ^о + J^r
Эта классическая модель не предсказывает ни резонансной частоты, ни абсолютной
амплитуды колебания. Полное рассмотрение задачи требует применения квантовой
механики. Корректный квантовомеханический расчет системы со многими резонан-
сами дает результат, близкий к выражению A3.60) [см., например, (Loudon, 1983)]:
^рA3.61)
4тг тео ^ v - vO
где fi — так называемая сила осциллятора г-го резонанса. Все /^, подчиняются
правилу сумм: J2 fi = 1.
Относительная диэлектрическая проницаемость (г = ?r + jsi) и показатель пре-
преломления (п = nR + jni) связаны соотношением Максвелла
п2 = е. A3.62)
Таким образом, sR = п2^ — п2 и е\ = 2ni?7,R. Поскольку для разреженного газа
77,r ~ 1 и щ <С 1, то получим ?7,R ~ y^R и щ ~ б\/2. Следовательно, для случая
газа с одиночным резонансом
1
(^-^ + ^ A3-64)
Резонанс обычно бывает узким, т. е. Г <С щ, и выражения для nR и п1 мож:но
упростить, рассматривая их поведение вблизи резонансной частоты z/0, и тогда
v2 — ъ>1 = {у + ^о)(^ - ^о) — 2^о (^ - щ)- A3.65)
Таким образом,
(у- щ) +Г /4
где 6 = пте2/C2тг2шбО^о)-
Уравнение A3.67) определяет ненормированный лоренцев профиль ni, который
симметричен относительно частоты i/0 и имеет полную ширину на уровне
половины максимума Г и максимальную амплитуду 46/Г. Функция 71r — 1
антисимметрична относительно частоты щ и имеет экстремальные значения
±26/Г на частотах z/0 =Ь Г/2 соответственно. Графики функций ?t,r и ni приведены
на рис. 13.7. Заметим, что максимальное отклонение от единицы действитель-
действительной части показателя преломления An равно половине максимального зна-
472
Эффекты распространения
[Гл. 13
чения 7ii, обозначенного как nimax. Итак, из уравнения A3.2) видно, что мак-
максимальный коэффициент поглощения аш = 47rnimaxz/o/c связан с An формулой
An =
8тг
A3.68)
22,0 23,0
Частота, ГГц
24,0
Рис. 13.7. Зависимость действительной и мнимой
частей показателя преломления от частоты для
одиночного резонанса, определяемая выражени-
выражениями A3.63) и A3.64). Представлены данные для
перехода 616-623 чистого водяного пара с pv =
7,5г/м3. В атмосфере на уровне моря при стан-
стандартном давлении в 1013 мбар линия уширяет-
уширяется примерно до 2,6ГГц (Liebe, 1969). Для кри-
кривой riR — 1 отклонение максимума равно An [см.
A3.68)], а изменение уровня при прохождении че-
через линию равно 5п [см. A3.69)]
где Ао — длина волны резонанса,
c/uq. Величина вещественной ча-
части показателя преломления рав-
равна максимальному поглощению
на расстоянии Ло/8тг. Кроме то-
того, из уравнения A3.63) видно,
что вещественная часть показате-
показателя преломления не строго сим-
симметрична относительно v$, т. е. nR
стремится к единице при стрем-
стремлении v к ос и nR стремится
к 1 + 2b/v0 = 1 + АпГ/i/q = 1 +
+ (Aoam/87r)(r/z/o) при стремле-
стремлении v к нулю. Следовательно,
изменение асимптотических вели-
величин 5п показателя преломления
при пересечении линии резонанса
задается выражением
A3.69)
8тгс
Таким образом, Sn/An = 7/^0 •> н0
пока не достигнут очень острый
резонанс, An и 5п пренебрежимо
малы. Рассмотрим линию водяно-
водяного пара на частоте 22 ГГц. Ослабление в атмосфере при pv = 7, 5 г/м3 составляет
0,15дБ/км, так что ат = 3,5 • 10~7см~1. Тогда из A3.68) следует, что AN = 0,019,
и это согласуется с данными лабораторных измерений (Liebe, 1969). Для того же
самого значения pv вклад от всех переходов водяного пара в значение показателя
преломления на низких частотах A0~6 Ny), согласно уравнению A3.10), равен 4,4 •
• 10~5. Таким образом, относительное изменение преломляющей способности вблизи
22 ГГц составляет лишь 1/2500. Изменения асимптотических уровней еще меньше.
На уровне моря Г = 2,6 ГГц и 5п = 2,2 х 10~8. Коэффициент поглощения в ли-
линии водяного пара на частоте 557 ГГц (переход lio~loi) равен 29 000дБ/км, или
0,069 см. Значения An и 5п составляют 1,44 х 10~6 и 0,7- 10~6 соответственно.
В атмосферных окнах выше 400 ГГц, где радиоастрономические наблюдения воз-
возможны лишь в местах с очень сухой атмосферой, показатель преломления может
заметно отличаться от значения, полученного для более низких частот. График
нормированной преломляющей способности приведен на рис. 13.8.
Уравнение A3.68) представляет собой важный и очень общий результат. Мы
получили его в рамках конкретной модели [см. A3.58)], приводящей к почти лорен-
цеву профилю спектра поглощения. В действительности профили линий слегка от-
отличаются от лоренцевого, и для определения точной формы нужны более сложные
модели. Однако уравнения A3.68) и A3.69) могут быть выведены из соотношения
Крамерса-Кронига.
13.1]
Нейтральная атмосфера
473
200
400 600
Частота, ГГц
800
1000
Рис. 13.8. Зависимость предсказанной и вызванной наличием водяного пара избыточной
длины пути на единицу плотности в столбе от частоты. Формулы взяты из работы (Liebe,
1989). Рисунок из работы (Sutton and Hueckstaedt, 1996), с разрешения Astron. Astrophys.
Suppl
Уравнение Смита-Вайнтрауба A3.9) показывает, что значение показателя пре-
преломления на низких частотах состоит из вкладов всех переходов на более высоких
частотах. Суммируя эти вклады [см. формулу A3.69)] для многих линий, каждая
из которых характеризуется параметрами Ani,I\,ami, и i/Qb получаем следующее
значение показателя преломления на низких частотах.
nq =
&г<
8ттс
A3.70)
Молекула водяного пара имеет большое число сильных вращательных переходов
в диапазоне от ЗОмкм до 0,3 мм (ЮТГц-ЮООГГц). Из-за наличия этих линий
атмосфера непрозрачна в большей части данного диапазона, и их вклад в пре-
преломляющую способность на низких частотах составляет примерно 98 %. Остаток
дает линия на 557 ГГц. Преломляющая способность, обусловленная водяным па-
паром, мала в оптике, но в радиодиапазоне она в 22 раза больше. Поэтому влияние
водяного пара очень незначительно в оптическом диапазоне, но очень существенно
в радиодиапазоне. Преломляющая способность сухого воздуха, связанная, в ос-
основном, с резонансами кислорода и азота в ультрафиолете, примерно одинакова
в оптическом и радиодиапазонах.
13.1.5. Уравнение Смита—Вайнтрауба. Детальное рассмотрение уравне-
уравнения для преломляющей способности в радиодиапазоне молено найти в работах (Bean
and Dutton, 1966; Thayer, 1974; Hill, Lawrence and Priestley, 1982). Основываясь
на классической работе Дебая (Debye, 1929), молено показать, что преломляющая
способность молекул с индуцированными дипольными переходами меняется про-
пропорционально давлению иТ, а молекул с постоянными дипольными моментами —
пропорционально давлению и Т~2. Так как основные составляющие атмосферы,
молекулы кислорода О 2 и азота N2, представляют собой молекулы с равноправными
474 Эффекты распространения [Гл.13
ядрами, то у них нет постоянных электрических дипольных моментов. Однако
такие молекулы, как Н2О и другие малые составляющие, имеют постоянные диполь-
ные моменты. Таким образом, общая форма уравнения преломляющей способности
имеет вид
где рп и pv — парциальные давления сухого воздуха и водяного пара; К\, K<i,
и Кз — константы, Z& и Zy — коэффициенты сжимаемости газов сухого воздуха
и водяного пара, которые обеспечивают поправку за неидеальность газа и в усло-
условиях атмосферы отклоняются от единицы менее чем на 10~3. Эти коэффициенты
сжимаемости определяются уравнениями (Owens, 1967)
Ю-8 (l + ^) - 9,4611 • Ю~4(Г~2273I A3.72а)
Z'1 = 1 + 1650^- [1 - 0,01317 (Т - 273) + 1,75 • ПГ4(Т - 273J +
+ 1,44 • 10~6(T - 273K], A3.72b)
где pd и ру выражены в миллибарах. Первый и второй члены уравнения A3.71)
связаны с индуцированными дипольными электронными переходами в ультрафио-
ультрафиолете для молекул сухого воздуха и водяного пара соответственно, а третий член
обусловлен постоянными дипольными вращательными ИК-переходами водяного
пара. Если мы пренебрежем всеми членами, отличными от 1, в коэффициентах
Z, то уравнение A3.71) примет вид
N = 77,6 ^ + 64,8^ + 3,776 • 105^ . A3.73)
Уравнение A3.73) можно переписать с учетом полного давления в виде
N = 77,6 ^ - 12,8 Ц- + 3,776 • 105^ . A3.74)
При температурах около 280 К последние два члена в правой части A3.74) можно
объединить и получить
^( ^) A3.75)
Уравнение A3.75) — хорошо известное уравнение Смита-Вайнтрауба (Smith and
Weintraub, 1953). Точность этого уравнения порядка 1 % или около ±7V на частотах
ниже 100 ГГц. Точность выражений A3.74) и A3.75) можно повысить, добавив
малый член, монотонно возрастающий с частотой и учитывающий влияние крыльев
ИК-переходов (см. рис. 13.8). Хилл и Клиффорд (Hill and Clifford, 1981) показали,
что из-за этого эффекта преломляющая способность влажной атмосферы возрас-
возрастает примерно на 0,5 % на 100 ГГц и на 2 % на 200 ГГц по сравнению со значением
на низких частотах.
Чтобы получить оптическую преломляющую способность, опустим член с по-
постоянным дипольным моментом в уравнении A3.73) и получим
7Vopt~ 77,6 ^+64,8^. A3.76)
13.1] Нейтральная атмосфера 475
Лучи зрения V^r < —
Антенны
Рис. 13.9. Двухэлементный интерферометр и тропосферный экран из неоднородностей
концентрации водяного пара различных размеров. Экран движется над интерферометром,
и составляющая скорости, параллельная вектору базы, равна vs. Распределение неодно-
неоднородностей становится важным при разработке схем компенсации фазы, которые обсужда-
обсуждаются в разд. 13.2. Отметим, что флуктуации с масштабом, превышающим длину базы,
закрывают обе антенны и влияют на фазу интерферометра незначительно. Из работы
(Masson, 1994), с разрешения Astron. Soc. Pacific Conf. Ser.
В случае повышенных требований к точности имеются (Сох, 2000) более точные
значения iVopt, включающие малые члены, которые зависят от длины волны и опи-
описывают влияние крыльев УФ-переходов. Отношение преломляющих способностей
влажной атмосферы в радио- и оптической областях спектра получено исключе-
исключением из выражений A3.73) и A3.76) членов, описывающих вклад сухого воздуха;
JVyrad/AVopt — 1 + 5830/Т. Для Т ~ 280 К это отношение примерно равно 22, как
уже упоминалось раньше при обсуждении соотношения A3.70).
13.1.6. Фазовые флуктуации. Для радиодиапазона наиболее важной неод-
неоднородно распределенной в тропосфере величиной является плотность водяного
пара. Изменения распределения водяного пара в тропосфере, которая движется
над интерферометром, приводят к фазовым флуктуациям, ухудшающим качество
измерений. В оптике основным источником фазовых флуктуации являются флук-
флуктуации температуры, а не содержания водяного пара. Эта ситуация схематически
изображена на рис. 13.9. Критическим размером является размер первой зоны
Френеля y\h, где h — расстояние от экрана до наблюдателя. При Л = 1 см и h =
= 1 км френелевский размер примерно равен 3 м. На таких масштабах флуктуации
фазы, обусловленные атмосферой, очень малы (<С 1рад). В таком случае флук-
флуктуации могут привести к искажению изображения, но не к вариациям амплитуды
(т. е. мерцаниям). Этот режим называется режимом слабого рассеяния. Рассеяние
на плазме в межзвездной среде относится к сильному рассеянию, где эффекты
значительно более сложны.
Флуктуации вдоль первоначально плоского волнового фронта, пересекающего
атмосферу, можно охарактеризовать так называемой структурной функцией фазы.
Эта функция определяется выражением
V,/,^) = ([Ф(х) - Ф(х - d)]2), A3.77)
где Ф(х) — фаза в точке ж, Ф(х — d) — фаза в точке х — с/, а угловые скобки означают
усреднение по ансамблю. Мы предполагаем, что Т>ф зависит только от величины
разнесения точек измерений, т. е. от длины проекции базы интерферометра d.
476
Эффекты распространения
[Гл. 13
Среднеквадратичное изменение фазы интерферометра равно
<тф = y/V4,(d). A3.78)
Для иллюстрации предположим, что Оф имеет простую функциональную форму:
d sC dm A3.79а)
>
A3.79b)
где а — постоянная, а аш = 2тгас/^/Л. Вид зависимости A3.79) показан на
рис. 13.10а. Такая зависимость может быть в случае разномасштабной степенной
модели спектра фазовых флуктуации. При этом должно существовать предельное
расстояние <im, выше которого флуктуации заметно не возрастают; иначе метод
РСДБ не будет работать. Этот предел, называемый внешней шкалой флуктуации,
1,5
Рис. 13.10. а — простая модель среднеквадратичных флуктуации, вносимых тропосферой,
согласно уравнению A3.79), в интерферометре с длиной базы d. б — функция отклика
на точечный источник Ша@) для различных моделей степенной зависимости, получаемой
фурье-преобразованием функции видности при d < dm- Значения 0s полной ширины на
уровне половины максимума wa@) для разных моделей: гауссова модель (/3 = 1), л/81п2 а;
модифицированная лоренцева модель (/3 = 1/2), 1,537га а2; модель Колмогорова (/3 =
= 5/6), 2,75А~1//5а6/5. Здесь А - длина волны, а — константа, определенная в A3.79а)
возможно, составляет несколько километров. На расстояниях выше этого предела
флуктуации длин путей становятся некоррелированными.
Рассмотрим сначала интерферометр, работающий на базах короче dm. Измерен-
Измеренная функция видности Vm связана с истинной функцией видности соотношением
Vm = Vei0, A3.80)
где ф = Ф(ж) — Ф(х — d) — случайная переменная, описывающая фазовые флуктуа-
флуктуации, вносимые атмосферой. Предполагая, что ф — гауссова случайная переменная
13.1] Нейтральная атмосфера 477
с нулевым средним значением, получим для математического ожидания функции
видности
(Vm) = V(e^) = Ve-^/2 = Ve~v^2. A3.81)
Рассмотрим в целом полезный случай, когда /3 = 1. Это соответствует атмосфере,
состоящей из неоднородных линз с масштабом, превышающим длину базы. Тогда
<7ф пропорциональна d и константа а безразмерна. Подставляя соотношение A3.79а)
в A3.81), получаем
(Vm)=Ve-27r2°V, A3.82)
где q = \/и2 + v2 = d/X. Следовательно, в среднем, измеренная функция видности
равна истинной функции видности, умноженной на атмосферную весовую функцию
wa(q), определяемую выражением
Wa(q) = e-2^a2q\ A3.83)
В плоскости изображения получаемая карта представляет собой свертку истинного
распределения источника и преобразования Фурье от wa(q), которое равно
wa@) ос е-02'2, A3.84)
где в — переменная, сопряженная с q. Полная ширина на половинном уровне Ша@)
равна
в8 = л/81п2 а. A3.85)
Таким образом, разрешение ухудшилось, поскольку полученная карта свернута
с гауссовым лучом ширины 6S (дополнительно к воздействию других весовых функ-
функций, описанных в п. 10.2.2). Величина 0s — это угол видности. Изображения с разре-
разрешением лучше 0s иногда можно получить при использовании процедур адаптивной
калибровки, описанных в разд. 11.4. Теперь из A3.79а) получаем
а = ^ = Ц , A3.86)
2nd d ' у J
где <Jd = аф\/2тг — среднеквадратичная неопределенность длины пути. Таким об-
образом,
0в = 2,35^ [рад]. A3.87)
Поскольку dd/d — константа, то 0s не зависит от длины волны. Эта независимость
вытекает из условия C = 1 в A3.79а). В радиодиапазоне ad примерно равна 1 мм
на базах в 1км, следовательно а ~ 10~6 и 0s ~ 0,5". Пусть do — длина базы, для
которой <7ф = 1рад. Как следует из A3.86), выражение A3.85) можно записать
в виде
Для случая, когда /3 имеет произвольное значение, находим wa@), подставляя
A3.79а) в A3.81) и записывая двумерное преобразование Фурье в виде преобра-
преобразования Ханкеля (Bracewell, 2000). Тогда
юа(в) ос | ехр [-2тг2а2\2^-^д213] JoBTrq0) q dq, A3.89)
478 Эффекты распространения [Гл.13
где Jo — функция Бесселя нулевого порядка, а имеет размерность см'1"^. В общем
виде wa@) получить аналитически невозможно. Однако с помощью соответствую-
соответствующих подстановок в выражении A3.88) легко показать, что 6S ос a1^X^~1^f3. Ана-
Аналитически можно рассмотреть случай, когда C = 1/2. Тогда получаем (Bracewell,
2000, с. 338):
которое представляет собой лоренцев профиль в степени 3/2 с широкими крыльями.
Полная ширина на половинном уровне Ш(в) равна
A3.91)
А
или
0s = 2ZI А ~ 0,12 А A3.92)
2тг do do
турбулентности Колмог
Численное интегрировг
результату:
Для случая турбулентности Колмогорова, который будет обсуждаться в этом разде-
разделе, C = 5/6. Численное интегрирование выражения A3.88) приводит к следующему
везультату:
в8 ~ 2,75 a6/5A~1/5 ~ 0,30 А . A3.93)
Графики waF) для различных степенных моделей флуктуации фазы представлены
на рис. 13.10 б.
Теперь рассмотрим случай интерферометра с базами, превышающими <im, когда
Оф — константа, равная ат. Этот случай лучше всего подходит к РСДБ-решеткам
или к большим решеткам со связанными элементами. Если временная шкала флук-
флуктуации мала по сравнению с временем измерений, то в среднем все измерения функ-
функции видности уменьшаются в е"*7™/2 раз. Таким образом, этот тип атмосферных
флуктуации не уменьшает разрешения. Однако в среднем измеряемая плотность
потока уменьшается по сравнению с истинным значением в е~агп'2 раз. Если времен-
временная шкала флуктуации велика по сравнению со временем наблюдений, то каждое
измерение функции видности содержит фазувую ошибку е-7^. Предположим, что
произведено К измерений видности точечного источника с плотностью потока S.
Если рассматривать для простоты только одномерный случай, то карта источника
имеет вид
q к .
wa\v) = jt 2_^e eJ . A3.94)
Математическое ожидание wa@) при в = 0 равно
<гПа(О)> = 5е-(Т-/2 A3.95)
Измеренная плотность потока меньше S. Утерянная плотность потока рассеяна по
карте. Это непосредственно следует из теоремы Парсеваля
?К№)|2= ^ ?1^Ы|2= s2. A3.96)
i г
Таким образом, полная плотность потока может быть получена интегрировани-
интегрированием квадрата отклика в плоскости изображения. Среднеквадратичное отклонение
плотности потока, измеренное при максимальном отклике на источник при в = 0,
13.1] Нейтральная атмосфера 479
равно величине \/{w2a{6)) — (wa@)J , которую мы обозначим через as- Ее можно
вычислить по формуле A3.92):
as = -|= \Л - е-°2т , A3.97)
что приводит к G5 — Sarflj\[K при сгт <С 1.
13.1.7. Колмогоровская турбулентность. Теория распространения излу-
излучения через турбулентную нейтральную атмосферу детально рассмотрена в пуб-
публикациях Татарского (Tatarski, 1961, 1971). Она была развита и широко исполь-
использовалась в задачах повышения качества оптических изображений (см., например,
Roddier, 1981; Woolf, 1982; Coulman, 1985) и ИК-интерферометрии (Sutton, Subra-
manian and Townes, 1982). Мы ограничимся обсуждением некоторых центральных
вопросов, касающихся структурной функции фазы, и покажем, как она связана
с другими функциями, которые используются для описания атмосферной турбу-
турбулентности.
Когда число Рейнольдса — безразмерный параметр, включающий вязкость, ха-
характерный масштаб и скорость потока,— превышает критическое значение, поток
становится турбулентным. В атмосфере число Рейнольдса почти всегда достаточно
высоко, так что мы имеем дело с развитой турбулентностью. В колмогоровской
модели турбулентности кинетическая энергия, связанная с крупномасштабными
турбулентными движениями, передается более мелким масштабам турбулентности,
пока окончательно не рассеется, преобразуясь в тепло вследствие вязкого трения.
Если турбулентность полностью развита и изотропна, то двумерный степенной
спектр флуктуации фазы (или показателя преломления) меняется как qs ' , где
qs [Мм] — пространственная частота, сопряженная б/, аналогична д, сопряженной
в. Структурная функция показателя преломления Vn(d) определяется аналогично
структурной функция фазы в уравнении A3.77), т. е. Vn(d) — среднеквадратичное
уклонение разности показателей преломления в двух точках, которые разнесены на
расстояние с/, или Vn(d) = ([п(х) — п(х — d)}2). Можно показать, что для вышеука-
вышеуказанных условий Т>п определяется соотношением
Vn{d) = eld2'5, Linner < d < Louter, A3.98)
где Linner и Louter называются внутренним и внешним масштабами турбулентности,
и могут достигать сантиметра и нескольких километров соответственно. Параметр
С^ характеризует силу турбулентности. Заметим, что водяной пар, являющийся
основным источником флуктуации показателя преломления, в тропосфере пере-
перемешан слабо, и поэтому он может служить лишь приближенным индикатором
динамической турбулентности.
Структурная функция фазы для атмосферы, где С\ меняется с высотой от
поверхности Земли до предельной высоты L, приведена в уравнении F.65) работы
(Tatarski, 1961):
2 L
(^) \2n{h)dh, A3.99)
которое справедливо в диапазоне \/ТЛ < d < Louter. Заметим, что коэффициент 2,91
является безразмерной константой, а С^ имеет размерность (длина)/3. Нижний
предел d эквивалентен пренебрежению эффектами дифракции. Если С2 не меняется
480 Эффекты распространения [Гл.13
с высотой, то выражение A3.99) сводится к виду
= 2,91 (Щ)* C2nLdb'z. A3.100)
V А /
Таким образом, с учетом A3.78) среднеквадратичное изменение фазы молено запи-
записать в виде
аф = 1,71 (^) у/Щь d5/6 A3.101)
Длину базы с/о, для которой аф = 1рад, молено вычислить, полагая Т>ф в A3.100)
равной 1рад2. Тогда выражение для do сведется к виду:
d0 = 0,058 A6/5(C^L)-3/5. A3.102)
Другим масштабом, пропорциональным do, является длина Фрида г о j (Fried,
1966). Этот масштаб особенно полезен при рассмотрении эффектов турбулент-
турбулентности в телескопах с круговой апертурой и широко используется в литературе,
посвященной оптическим наблюдениям. Структурная функция фазы может быть
записана в виде 1)ф = 6,88 (<i/roM'3, где множитель 6,88 — приближенное значение
2 [B4/5) ГF/5)]5/6 (Fried, 1967). Отсюда, из A3.100) и A3.102), получим г0 = 3,18 do-
Длина Фрида вводится таким образом, что эффективная площадь телескопа с боль-
большой круговой апертурой при равномерном освещении и наличии колмогоровской
турбулентности равна тгг^/4. Значит при диаметре апертуры меньше г о разрешение
ограничено дифракцией на апертуре. На апертуре, большей го, разрешение огра-
ограничено турбулентностью и примерно равно А/го- Точное значение для разрешения
в этом случае можно получить из A3.93), и результат равен 6S = 0,97А/го- До-
Дополнительно скажем, что среднеквадратичная ошибка фазы на апертуре диаметра
Го равна 1,01 рад. Причина, по которой г о больше do, связана с понижением веса
больших баз в двумерных апертурах [см. выражение A4.13) и его обсуждение]. На
апертуре диаметра г о отношение эффективной площади к геометрической площади,
которое в оптической литературе называется отношением Стреля, равно 0,45 (Fried,
1965).
Как показывает выражение A3.102), do пропорционально А6/5, и, следователь-
следовательно, угловое разрешение или предел видности (^A/cfo) пропорционально А/5 [см.
рис. 13.10 и уравнение A3.93)]. Это соотношение может выполняться в широком
диапазоне длин волн, пока С^ остается константой. В оптическом диапазоне пара-
параметр С^ связан с температурными флуктуациями, а в радиодиапазоне С^ определя-
определяется турбулентностью водяного пара. Интересным совпадением является тот факт,
что предел видности примерно равен 1" ив оптике, и в радиодиапазоне для иде-
идеальных антенн. Основное различие состоит во временных масштабах флуктуации,
тс. Если принять критический уровень флуктуации равным 1 радиан, то тс ~ do/vs,
где vs — скорость экрана, параллельная вектору базы. Все схемы компенсации
в адаптивной оптике должны работать на временных масштабах меньше тс. Из
A3.93) тс выражается в виде
Гс-0,3-^-. A3.103)
vsVs
При vs = Юм-с и 6S = 1", тс = Змс на 0,5мкм и 60с на 1см.
х) В этом пункте данный символ означает длину Фрида. Во всей остальной части главы
он означает радиус Земли.
13.1] Нейтральная атмосфера 481
Двумерный энергетический спектр фазы, S2(qx-)Qy)^ является фурье-образом
двумерной автокорреляционной функции фазы В,ф(с1х,с1у). Если Лф является функ-
функцией только аргумента б/, где d2 = d^ -\- d2, то S2 — функция gs, где q2 = q2 +
+ q2,, и S2(gs) и Яф((Г) образуют пару преобразования Ханкеля. Поскольку Т>ф((Г) =
], то
= 4тг j [1 - Jo Bтг^)] <S2(gs) qs dqs, A3.104)
о
где Jo — функция Бесселя нулевого порядка. Если Т*ф(в) определяется уравнением
A3.100), то S2(qs) равно
52(ge) = 0,0097 (^ff C2nLq^3 A3.105)
Зачастую полезно изучить временные изменения, вызванные турбулентностью
в атмосфере. Для того чтобы связать пространственные и временные вариации, ис-
используем гипотезу о вмороженном экране, иногда приписываемую Тейлору (Taylor,
1938). В этом приближении предполагается, что турбулентные вихри не меняются
за время, пока они пересекают линию базы d. Одномерный временной спектр
флуктуации фазы S^(f) (двусторонний спектр) может быть вычислен из S2(qs)
следующим образом:
оо
f (qx = t, qy) dqy, A3.106)
где vs измеряется в м/с. Подставляя A3.105) в A3.106), получим
A3.Ю7)
Примеры временных спектров флуктуации водяного пара можно найти в работах
(Hogg, Guiraud and Sweezy, 1981; Masson, 1994a) (см. рис. 13.15). Временная струк-
структурная функция VT(r) = ([(j)(i) — (j)(t — т)]2) связана с пространственной соотноше-
соотношением Т)ф{<1 = vsr). Значит для случая колмогоровской турбулентности из A3.100)
следует
ZV(r) = 2,91 (^J (%Lv6e'3T6/3. A3.108)
Величины Т>т(т) и S^(f) связаны преобразованием Фурье. Возможность исполь-
использования временных структурных функций для оценки влияния флуктуации на
интерферометры обсуждается в работах (Treuhaft and Lanyi, 1987; Lay, 1997a).
Дисперсия Аллана сг^(т), или относительная стабильность частоты за время
г, связанная с 5^(/), была определена в разд. 9.4. Она может быть вычислена
подстановкой (9.99) в (9.111), что дает
} ;(/) sin4Grr/) df. A3.109)
16 Томсон
482
Эффекты распространения
[Гл. 13
Подставляя A3.107) в A3.109) и учитывая, что [sin (тгж)]/ж8/3 dx = 4,61, получим
а2у(г) =
Ю
-17
A3.110)
Армстронг и Шрамек (Armstrong and Sramek, 1982) дали общие выражения для
соотношения между 52,5^,^, и ау для произвольных показателей степени. Если
с>2 ос д~а, то Т>ф{в) ос cP~2,<S^ ос /1-а, и а2 ос та~4. Эти соотношения приведены
в табл. 13.2.
Таблица 13.2. Энергетические соотношения для турбулентности
Показатель степени
Величина
ЗБ-турбулент-
ность (а=11/3)
2Б-турбулент-
ность (а=8/3)
2D-, ЗБ-спектр мощности
Структурная функция CD)
Временной фазовый спектр
Дисперсия Аллана
Временная структурная функ-
функция
<S2(gs),<S(<?s)
—а
а -
1-
а -
а -
-2
- а
-4
-2
-11/3
5/3
-8/3
-1/3
5/3
-8/3
2/3
-5/3
-4/3
2/3
Из работы (Wright, 1996, с. 526), публикуется с разрешения Astronomical Society of the
Pacific.
Достоверную модель тропосферной турбулентности можно построить следую-
следующим образом. На базах меньше некоторого значения Gorans турбулентность трех-
трехмерна и Т>ф ~ с/5/3, б/trans мала по отношению к ~2км шкале водяного пара. Для
d > ^trans турбулентность двумерна и Т)ф ~ с/2/3. При достижении некоторой базы
^outer атмосферные флуктуации перестают коррелировать и Т)ф ~ с/0, другими сло-
словами, Т>ф перестает зависеть от длины базы. Значение c/outer по порядку величины
равно размеру облаков в несколько километров (Hamaker, 1978). Эти три области
ясно различаются на рис. 13.11. Для изображенных на нем данных c/trans = 1,2 км,
^outer = 6 км, а наклон кривой близок к наклону при колмогоровской турбулент-
турбулентности. В табл. 13.3 собраны данные по структурным функциям многих источни-
источников. Эти данные получены по множеству наблюдений при разных атмосферных
условиях и не дают возможности точно сравнить качество разных обсерваторий.
Тем не менее, они показывают, что, как и ожидалось, флуктуации задержки не
зависят от частоты и, в целом, уменьшаются при увеличении высоты расположения
обсерватории. Для обсерватории в Мауна Кеа приведены значения на уровне 50 %
разброса день—ночь, изображенного на графике в левом нижнем углу рис. 13.13
разд. 13. В данных для обсерватории Чахнантор присутствует похожий суточный
разброс. Роджерс и Моран (Rogers and Moran, 1981) и Роджерс и др. (Rogers et al.,
1984) обсуждают воздействие тропосферы на РСДБ-измерения, и полученный ими
график дисперсии Аллана в атмосфере показан на рис. 9.14 в качестве кривой для
данных РСДБ. Общее сравнение данных измерений и теоретических результатов
выполнено в работе (Coulman, 1990). Сравнения других обсерваторий можно найти
в работе (Masson, 1994b).
13.1]
Нейтральная атмосфера
483
Расположение
Кембридж:
Грин Бэнк
Хэт Крик
Хэт Крик
Хэт Крик
Хэт Крик
NRO
NRO
VLA
VLA
VLA
VLA
Плато де Бюр
Мауна Kead
Чахнантор^
Таблица
База,
км
1,6
2,5
0,006-0,1
0,006-0,85
0,01-0,15
1-1200
0,035
0,03-0,54
0,1-3
0,1-35
1-35
0,05-35
0,02-0,3
0,1
0,3
13.3. Измерения структурной функции
Высота,
м
17
840
1043
1043
1043
1043
1350
1350
2124
2124
2124
2124
2552
4070
5000
Частота,
ГГц
5
2,7
86
86
86
100
19
22
22
22
5
5/15
86
12
11
а
ММ
0,7-2,6
0,4-4
0,7-1,0
0,8-2,2
1,2
0,7
1,9
0,5-0,9
0,6
0,65
1,0
0,6-1,6
0,3-0,7
0,4-2,7
0,3-1,5
Р\
1,3
—
1,1-1,4
0,8-1,3
1-2
0,3-0,6
1,2
1,6
0,72
0,85
1,4
0,6-0,8
1,1-1,9
0,75
—
13-50
7-70
13-18
15-41
22
13
35
9-17
11
12
18
11-30
6-13
7-49
5-29
Л-рас
1
2
3
4
5
3
6
7
8
9
10
11
12
13
14
Лит. источник: (Wright, 1996, р. 524), с разрешения Astronomical Society of the Pacific.
ao~do — среднеквадратичное отклонение длины пути на базе в 1000 м. Следовательно
<jd = a do (d/1000 м)^. Если измерения на d = 1000 м не проводились, то предполагалось,
что /3 = 5/6.
Показатель степени в зависимости a do от базы. Для двумерной и трехмерной
колмогоровской турбулентсности C = 0,33 и 0,83 соответственно.
сЛит. источники: A) Hinder A970), Hinder and Ryle A971), B) Baars A967),
C) Wright and Welch A990), D) Wright A996), E) Bieging et al. A984), F) Ishiguro,
Kanzawa and Kasuga A990), G) Kasuga, Ishiguro and Kawabe A986), (8) Sramek A983),
(9) Carilli and Holdaway A999), A0) Armstrong and Sramek A982), A1) Sramek A990),
A2) Olmi and Downes A992), A3) Masson A994a), A4) NRAO A998).
Минимальные и максимальные значения представляют собой средний уровень фазо-
фазовых флуктуации в течение всего года в ночное (~6 ч местного времени) и дневное (~15 ч
местного времени) соответсвенно. (См. рис. 13.13, где изображены суточные и сезонные
вариациии для Мауна Кеа.)
Величину фазовых флуктуации, характеризуемую параметром а^ (введенным
в A3.86)), или C^L, предсказать трудно. Измерения на VLA показали, что нет доста-
достаточно хорошей корреляции между C^L и абсолютной влажностью на поверхности
земли. Преобладающая корреляция, возможно, связана с конвекцией, вызванной
Солнцем. Сильная зависимость от времени суток описана в разд. 13.2 (рис. 13.13).
Давно известна высокая стабильность интерферометров, работающих на метровых
волнах при облачном небе (см., например, Hinder, 1972).
13.1.8. Аномальная рефракция. Ширина диаграммы направленности мно-
многих миллиметровых телескопов достаточно мала для того, чтобы можно было заре-
зарегистрировать эффекты атмосферных фазовых флуктуации. Обычно наблюдается,
что при определенных погодных условиях видимые положения неразрешенных ис-
источников меняются в пределах примерно Ъ" на временных интервалах в несколько
16*
484
Эффекты распространения
[Гл. 13
1,5
0,5
i i i i i i i i i i
Толстый экран
(трехмерный)
Ptheory U»5J
- Фе1ес =1° de§
°/
° /¦
/
/
у
/"
-
/
-
¦
I 1 1 1 I 1 1 I 1 1
1 1 1 1 1 1 1
Тонкий экран
(двумерный)
pobs = 0,41±0,03
1 I 1 1 I I I
1 1 1 1 1 1 1
fle a в» в
Внешняя
область
;
¦ i 1 i i 1 i
2,0
2,5
3.0
3,5
lg базы, м
4,0
4,5
Рис. 13.11. Корень из фазовой структурной функции (среднеквадратичное отклонение
фазы) по данным наблюдений на VLA на 22 ГГц. Незакрашенные кружки — зависимость
среднеквадратичного изменения фазы от длины базы для источника 0748+240 в течение
90 минут. Закрашенные квадраты — эти же данные после устранения постоянного вклада
шумов приемника со среднеквадратичной амплитудой 10°. Все три режима в структурной
функции фазы отмечены вертикальными линиями (на 1,2 и 6 км). Из работы (Carilli and
Holdaway, 1999), ©1999 by the American Geophys. Union
секунд (см. например, Altenhoff et al., 1987; Downes and Altenhoff, 1990). Вели-
Величины эффектов, как и предполагалось, практически не зависят от длины волны,
если эффекты эти обусловлены неоднородностями водяного пара в атмосфере. Эти
неоднородности, возможно, являются частью или тесно связаны с неоднородностя-
неоднородностями, возникшими в результате колмогоровской турбулентности, которая влияет на
интерферометрические наблюдения (см. рис. 13.11). Следовательно термин «ано-
«аномальная рефракция» не очень удачен. Если предположить, что эти неоднородности
имеют клиновидную форму, то их основным проявлением был бы поворот волнового
фронта (линейное изменение фазы в зависимости от положения) в течение времени
их прохождения через диаграмму направленности антенны. Дифференциальная
дополнительная длина пути в 0,5 мм на масштабе 300 м дает отклонение волнового
фронта на 6" и временную шкалу в 30 с при скорости ветра в 10 м/с. Видимое
изменение положения источника не зависит от длины волны. Никакого влияния
на амплитуду сигнала не оказывается, потому что рассеяние слабое (фазовые
флуктуации на френелевском масштабе, который обычно равен нескольким метрам,
малы), равно как и на видимый угловой размер источника, потому что основным
изменением волнового фронта является наклон.
13.1.9. Радиометрия водяного пара. Избыточная длина пути распростра-
распространения в определенном направлении, связанная с наличием водяного пара, может
быть получена из измерений яркостной температуры в том же направлении на
частотах вблизи резонансов водяного пара или в окнах между ними. Этот метод
был впервые предложен в работах (Westwater, 1967) и (Schaper, Staelin and Waters,
1970). Чтобы оценить степень корреляции между длиной пути во влажной атмо-
13.1] Нейтральная атмосфера 485
сфере и яркостной температурой, необходимо изучить зависимость этих величин от
давления, плотности водяного пара и температуры. Ниже мы рассмотрим интер-
интерпретацию измерений вблизи резонанса на 22,2 ГГц. Соотношения A3.42) и A3.43)
для коэффициента поглощения довольно сложны, но вблизи центра линии он может
быть приближенно представлено в виде
гу ~ О Ч(\ Pv г-644/Г ПЧ11П
ат — и,зо 1?875 е •> ^la.iiij
где Т — температура в Кельвинах; мы пренебрегли всеми членами выражения
A3.42) кроме первого. Предполагается, что непрозрачность, заданная соотноше-
соотношением A3.47), мала, так что яркостная температура, заданная уравнением A3.45),
может быть записана в виде
с 17,8 | -^^ e-^Tdh, A3.112)
где мы пренебрегаем температурой фона Тво и вкладами от облаков. С учетом
A3.16) получим
Су ~ 0,001763 Г Цг dh. A3.113)
о
Итак, если бы Р и Т не менялись с высотой и равнялись 1013 мбар и 280 К соот-
соответственно, мы могли бы воспользоваться выражением A3.19) Су — 6,Згу, чтобы из
A3.112) получить соотношение Тв — 12,7гу, где гу — высота столба водяного пара
[см. A3.18)]. В описанном выше приближении получаем для 22,2ГГц
ТВ[К] -2,1 Су [см]. A3.114)
Отметим, что данное приближение справедливо на уровне моря. Так как из-за
уширения давлением яркостная температура меняется обратно пропорционально
полному давлению [см A3.112)], то коэффициент в A3.114) для антенны, находя-
находящейся на высоте 5000 м, где давление примерно равно 540 мбар, увеличивается
до 3,9. Измерения яркостной температуры и длины пути, оцениваемой по
профилям радиозондов, показывают, что выражение A3.114) является хорошей
аппроксимацией (см, например, (Moran and Rosen, 1981)). Вспомним теперь, что
pv имеет приблизительно экспоненциальное распределение со шкалой высот
2 км. Температура в среднем уменьшается примерно на 2 % на километр.
Это изменение влияет на пропорциональность между Тв и Су только через
показатель экспоненты в уравнении A3.112) и небольшое отличие в степенной
зависимости для температуры. Таким образом, температура оказывает малое
влияние. Давление снижается на 10 % на километр, так что водяной пар
на больших высотах вносит более сильный вклад в Те, чем это следовало
бы для оценки с помощью радиометрии. Чувствительность Те к давлению
уменьшается при смещении резонансной частоты к частоте вблизи точки
половинной мощности перехода. Смысл этого смещения состоит в том, что по мере
возрастания давления профиль линии уширяется, а интегральный профиль линии
остается постоянным. Поэтому поглощение в центре линии падает, а в крыльях
возрастает. В работе Вествотера (Westwater, 1967) показано, что поглощение на
частоте 20,6 ГГц почти инвариантно по отношению к давлению. Эта выделенная
частота называется центральной. Непрозрачность на этой частоте меньше, чем
486 Эффекты распространения [Гл.13
в центре линии, поэтому нелинейная связь между Тв и непрозрачностью менее
существенна.
Выше мы предполагали, что измерения Тв проводятся в условиях чистого неба.
Наличие водяных капель в облаках или тумана приводит к значительному погло-
поглощению, но лишь к небольшому изменению показателя преломления по сравнению
с показателем преломления водяного пара. К счастью, молено исключить влияние
облаков, объединяя измерения на двух частотах. В облаках, не дающих осадков,
размеры водяных капель обычно не превышают 100 мкм, и на длинах волн больше
нескольких миллиметров рассеяние мало, а ослабление обусловлено, в основном,
поглощением. Коэффициент поглощения определяется эмпирической формулой
(Staelin, 1966)
1^0,0122 B91-Т)
«clouds ^ Pb л2 [м], A3.115)
Л
где рь — плотность жидких водяных капель в граммах на кубический метр, Л —
длина волны в метрах, Т — температура в Кельвинах. Эта формула верна при Л
больше ~ Змм, где размеры капель далеки от Л/Bтг). На более коротких волнах
поглощение меньше предсказанного формулой A3.115) (Freeman, 1987; Ray, 1972).
Очень влажное кучевое облако с плотностью воды 1 г/м3 и размером 1 км будет
иметь коэффициент поглощения 7-10~5м~1 и, следовательно, яркостную темпе-
температуру около 20 К на 22 ГГц. Коэффициент преломления жидкой воды при Т =
= 280 К на 22 ГГц составляет около 5 (Goldstein, 1951). Реальная длина избыточного
пути распространения через облако, связанная с наличием жидкой воды, равна
примерно 4 мм, а предсказанное на основе уравнения A3.114) значение составляет
10 см. Значит яркостную температуру на одной частоте нельзя использовать для
достоверной оценки длины избыточного пути в присутствии облаков. Чтобы исклю-
исключить вклад в яркостную температуру от облаков, следует проводить измерения на
двух частотах v\ и z/2, одна из которых близка, а другая, соответственно, достаточно
удалена от линии воды. Яркостная температура выражается как
TBi=TBVi + TBCi, A3.116)
где Tbvi и Тва ~~ соответственно яркостные температуры, обусловленные нали-
наличием водяного пара и облаков на частоте г. Здесь не учитывается влияние атмо-
атмосферного О2. Поскольку из уравнения A3.115) следует, что Твс °с z^2, то можно
выразить наблюдаемую величину
2 2
- ТВ2 — = TBvi — TBv2 — , A3.117)
которая исключает влияние облаков. Корреляцию между Tbvi ~ yH^)
и Cv можно оценить из модельных расчетов, основанных на соотношениях A3.45)
и A3.16). Внерезонансная частота обычно выбирается близкой к 31 ГГц. Задача
отыскания двух оптимальных частот и соответствующих коэффициентов корреля-
корреляции для предсказания Cv широко обсуждалась в работах (Westwater, 1978; Wu,
1979; Westwater and Guiraud, 1980). Жидкая составляющая облаков может быть
также измерена с помощью двухчастотного метода [см., например, (Snider, Burdick
and Hogg, 1980)].
Применение многочастотной микроволновой радиометрии для калибровки дли-
длины пути во влажной атмосфере описано в работах (Guiraud, Howard and Hogg, 1979;
Elgered, Ronnang and Askne, 1982; Resch, 1984; Elgered et al., 1991; Tahmoush and
Rogers, 2000). Результаты показывают, что величину Cv можно оценить с точно-
точностью выше нескольких миллиметров. Такая точность достаточна для калибровки
13.2] Влияние атмосферы на миллиметровых и субмиллиметровых волнах 487
РСДБ-измерений задержки и увеличения времени когерентности. Измерения Тв
на антеннах короткобазовых интерферометров могут быть полезными при коррек-
корректировке фазы интерферометра (см. разд. 13.2). Более точные предсказания Су или
фазы интерферометра молено получить с использованием измерений в других ча-
частотных полосах. Например, измерения в крыльях линии атмосферного кислорода
вблизи 50 ГГц могут применяться для зондирования вертикального температурного
профиля тропосферы [см., например, (Miner, Thornton and Welch, 1972; Snider,
1972)]. Точность этих методов была проанализирована в работе (Solheim et al., 1998).
13.2. Влияние атмосферы на миллиметровых
и субмиллиметровых волнах
13.2.1. Тестирование телескопов методом измерения непрозрачности.
На миллиметровых и субмиллиметровых волнах поглощение и флуктуации длины
пути в атмосфере ограничивают качество синтезированных изображений. Данный
раздел посвящен исследованиям параметров атмосферы для выбора оптимального
расположения обсерваторий и методам атмосферной калибровки для устранения
фазовых ошибок. Этой теме уделялось много внимания в ходе разработки несколь-
нескольких крупных инструментов, работающих на миллиметровых и субмиллиметровых
длинах волн.
Таблица 13.4. Непрозрачность в зените как функция высоты столба
водяного пара
V
(ГГц)
15
22,2
35
90
225
225
225
225
493
Местонахождение"
Уровень моря
Уровень моря
Уровень моря
Уровень моря
Южный полюс
Мауна Кеа
Чахнантор
Чахнантор
Южный полюс
Высота
(м)
0
0
0
0
2835
4070
5000
5000
2835
Аи
(непер)
0,013
0,026
0,039
0,039
0,030
0,01
0,006
0,007
0,33
Bv
(непер мм)
0,002
0,02
0,006
0,018
0,069
0,04
0,033
0,041
1,49
Метод6
1
1
1
1
2
2
2
2
2
Литература0
1
1
1
1
2
3
4
5
6
аПоложения: Южный полюс — станция Амундсен—Скотт; Мауна Кеа — располо-
расположение субмиллиметровых телескопов Мауна Кеа; Чахнантор — Льяно де Чахнан-
Чахнантор, пустыня Атакама, Чили.
ъМетоды: A) непрозрачность получена по данным радиозондов, оценки для водя-
водяного пара получены на основании влажности на поверхности при шкале высот
в 2 км; B) непрозрачность получена по данным разрезов атмосферы, высота
столба водяного пара получена по данным радиозондов.
сЛит. источники: A) Waters A976); B) Chamberlin and Bally A995); C) Masson
A994a); D) Holdaway et al. A996); E) Delgado et al. A998); F) Chamberlin, Lane
and Stark A997).
Для заданных параметров атмосферы непрозрачность в зените (оптическая
толща) го может быть рассчитана как функция частоты с использованием модели
Эффекты распространения
[Гл. 13
200 400 600 800 1000
3
200 400
600 800 1000
Частота, ГГц
Рис. 13.12. а — коэффициент пропускания атмосферы в зените на высоте 5000 м при уровне
осадков 1 мм, расчитанный в модели Либе (Liebe, 1989) в диапазоне частот 0-1000 ГГц.
Существуют дополнительные окна с коэффициентом пропускания порядка 0,10 примерно
на 1100, 1300 и 1500 ГГц. б— коэффициент пропускания на высоте 2124 м при уровне
осадков 4 мм. Отметим, что пропускание атмосферы зависит от высоты из-за уширения
линий поглощения давлением. В целом пропускание атмосферы на любой частоте будет
хуже на телескопах, расположенных ниже при том же количестве осадков. Из работы
(Carilli and Holdaway, 1999), ©1999 the American Geophys. Union
распространения Либе (Liebe, 1989). На рис. 13.12 представлены кривые пропус-
пропускания exp (—го), для уровней осадков в 4мм на высоте 2124м и 1мм на 5000м,
что соответствует антеннам VLA и ALMA. Для выбора подходящего места для
обсерватории необходим тщательный мониторинг атмосферы, покрывающий и су-
суточные, и годичные вариации. Предположим, что непрозрачность в зените можно
представить в виде
= Av
A3.118)
где Ajy и Bv — эмпирические константы, зависящие от частоты, высоты обсерва-
обсерватории и погодных условий. Отдельные результаты измерений этих констант пред-
представлены в табл. 13.4.
Непрозрачность можно исследовать, измеряя полную мощность шумов, приня-
принятых небольшой антенной, как функцию зенитного расстояния (т. е. методом сколь-
скользящего сканирования, описанным в п. 13.1.3). Для мониторинга непрозрачности
13.2] Влияние атмосферы на миллиметровых и субмиллиметровых волнах 489
О 5 10 15 20 2 4 6 8 10 12
Часы (местное время) а Месяцы
5 10 15 20
Часы (местное время)
6 8 10 12
Месяцы
Рис. 13.13. а — суточная и сезонная непрозрачность в зените на 225 ГГЦ, измерявшаяся
на антенне CSO в Мауна Кеа (высота 4070 м) в течение Злет (август 1989-июль 1992),
построенная по данным 14900 измерений. Показаны минимальные значения на уровнях
25, 50 и 75%. Увеличение непрозрачности в течение дня обусловлено инверсным слоем,
который поднимается над горой днем, б — суточные и сезонные вариации среднеквадра-
среднеквадратичной длины пути на Мауна Кеа при базе в 100м, полученные по наблюдениям геоста-
геостационарного спутника на 11 ГГц. Из работы (Masson, 1994a), с разрешения the Astron. Soc.
Pacific Conf. Ser.
обычно используют частоту 225 ГГц, лежащую в атмосферном окне 200—310 ГГц
(см. рисунки 13.6 и 13.12) вблизи важной линии СО.
Типичный радиометр для измерения непрозрачности использует небольшой пер-
первичный параболический рефлектор с шириной диаграммы направленности ~3° на
225 ГГц. Диск с лопастями, действующий как плоский отражатель, расположен
в узкой части луча между первичным и вторичным зеркалами и поочередно на-
направляет сигнал на вход приемника с выхода антенны, опорного сигнала с нагрузки
при 45°С и калибровочной нагрузки при 65°С. Усиленные сигналы поступают на
линейный детектор мощности, а потом на синхронный детектор, который выделяет
напряжения, пропорциональные разности между антенной температуры и 45° С —
искомый сигнал — и разности между 45 и 65° С — калибровочный сигнал. Измерения
антенной температуры проводятся в некотором интервале зенитных расстояний.
Когда система присоединена к антенне, то измеренная антенная температура со-
490 Эффекты распространения [Гл.13
стоит из трех компонент:
Tmeas = Tconst + Tat A - e"r°secz) + Tcb e~T°secz. A3.119)
Здесь Tconst представляет собой сумму шумовых компонент, которые не меняют-
меняются при изменении угла места, т. е. шумы приемника, тепловые шумы, вызванные
потерями между антенной и входом приемника, смещения шкалы детектора в ра-
радиометре и т. д. Второй член в A3.119) — шумовая составляющая от атмосферы:
Tat — температура атмосферы, z — зенитное расстояние. Тсъ — 2,7 К — температура
реликтового излучения. Мы предположим, что Tat и Тсь являются яркостными
температурами и связаны с физическими температурами формулой Планка или
Каллена и Велтона (см. п. 7.1.2). Если Tat известна, то по Tmeas можно определить
го как функцию z. Предположим, что температура атмосферы отклоняется от
температуры воздуха на поверхности земли Тать, и предположим, что скорость
падения температуры с высотой / постоянна. Тогда на высоте h температура равна
Тать — lh. Мы вводим условие, что средняя температура взвешена в соответствии
с содержанием водяного пара, который распределен экспоненциально со шкалой
высот h$:
оо
I lheh/h°dh
§= Tamb - lh0. A3.120)
J
eh/ho dh
Скорость падения температуры 9,8 К/км, обусловленного адиабатическим расшире-
расширением поднимающегося воздуха, можно использовать как приближенное значение,
но, как отмечалось ранее, типичный результат соответствует ~6,5 К/км. Шкала
высоты водяного пара примерно равна 2 км. Таким образом, Tat систематически
меньше, чем Tamb на ~13-20К.
На рис. 13.13 приведен пример данных, полученных на Мауна Кеа, где прояв-
проявляются суточные и сезонные эффекты. Суммарное распределение непрозрачночти
в зените на 225 ГГц, измеренное на Льяно де Чахнантор в Чили, Мауна Кеа и на
Южном полюсе, представлено на рис. 13.14. Измерения средней непрозрачности
обеспечивают основу для расчетов потерь чувствительности, вызванных поглоще-
поглощением сигнала и добавочными шумами в атмосфере [см. A3.50)]. Непрозрачность
меняется в течение суток и в течение года, поэтому для надежного сравнения
различных обсерваторий требуются измерения с часовым интервалом в течение
года или более. Долгопериодическая переменность, обусловленная климатическими
эффектами, например, эль Ниньо, может стать существенной. В табл. 13.4 показано
влияние высоты обсерватории на непрозрачность. Сравнение измерений Av и Ви
показывает, что оба параметра убывают с высотой из-за эффекта уширения дав-
давлением. Сравнение непрозрачностей на различных частотах может быть проведено
с помощью широкополосных фурье-спектрометров (Hills et al., 1978; Matsushita et
al., 1999; Paine et al., 2000; Pardo, Serabyn and Cernicharo, 2001).
13.2.2. Тестирование площадок путем прямого измерения фазовой
стабильности. Интерферометрические наблюдения предоставляют собой прямой
метод измерения атмосферных флуктуации фазы. Обычно используют сигналы
с геостационарного спутника, потому что сильные сигналы можно принимать на
небольших неподвижных антеннах. Этот подход был развит в работах (Ishiguro,
Kanzawa and Kasuga, 1990; Masson, 1994a; Radford, Reiland and Shillue, 1996). Он
использовался при выборе места субмиллиметровой решетки SAO на Мауна Кеа
13.2] Влияние атмосферы на миллиметровых и субмиллиметровых волнах 491
1,0 -
0,5 -
- 0
У / Начало
/ * Конец
/ / 75 %
/// 50%
- у/ 25%
Чахнантор
95-04
99-04
0,126
0,067
0,040
SCO
97-01
99-07
0,141
0,085
0,054
;
Юж. полюс
92-01
92-12
0,066
0,053
0,043
0,0
0,0 ОД 0,2 0,3
Оптическая толщина в зените на частоте 225 Ггц (Т225)
Рис. 13.14. Суммарное распределение оптической толщи в зените на 225 ГГц на Льяно
де Чахнантор, Чили (высота 5000м, сплошная линия), площадке CSO на Мауна Кеа,
Гавайи (высота 4070 м, штриховая линия), и на Южном полюсе (высота 2835 м, пунктирная
линия) за периоды с апреля 1995 г. по апрель 1999 г., с января 1997 г. по июль 1999 г. и с
января 1992 г. по декабрь 1992 г. соответственно. Заметим, что средняя непрозрачность
на площадке VLBA на Мауна Кеа (высота 3720 м) на том же интервале времени, что
и для площадки CSO была равна 0,13. Средняя непрозрачность для VLA (высота 2124 м)
за период с 1990 г. по 1998 г. равнялась 0,3 (Butler, 1998). Условия на нижележащих
обсерваториях, соответственно, хуже. Например, на площадке, расположенной на уровне
моря в Кембридже, штат Массачусетс, США, непрозрачность на 225 ГГц, проэкстраполи-
рованная по результатам наблюдений на 115 ГГц равнялась 0,5 для 6-месячных зимних
сезонов на протяжении с 1994 по 1997 гг. См. также (Radford and Chamberlin, 2001)
на Гавайях и Большой миллиметровой решетки в Атакаме на Льано де Чахнан-
Чахнантор. Несколько подходящих геостационарных спутников работают на частотах,
выделенных для стационарных широковещательных служб в области 11 ГГц. Две
коммерческие спутниковые телевизионные антенны диаметром 1,8 м обеспечива-
обеспечивают близкое к 60 дБ отношение сигнал/шум. Для измерения атмосферной фазы
использовались базы 100-300 м. Остаточное движение спутника, а также темпе-
температурные вариации могут стать причиной нежелательных фазовых сдвигов. Они,
как правило, медленнее атмосферных эффектов, и их можно удалить, вычитая
из данных среднее значение и тренды. Дисперсию флуктуации, обусловленных
шумами системы, тоже можно распознать и вычесть из дисперсии измеренных
фаз. Тестовый интерферометр обеспечивает измерение структурной функции фазы
Т>ф((Г) для одного значения проекции вектора базы d (см. рис. 13.13 б).
В приближении вмороженного экрана, показатель в степенном законе может
быть определен по излому в спектре мощности флуктуации. Пример показан на
рис. 13.15. Таким образом, экстраполируя значения Т>ф(с1), полученные в результате
одиночных измерений, можно не опираться на теоретические значения показателя
с/, а использовать измерения Т>ф{т\ чтобы определить его диапазоны и вариации
[см. A3.108) и табл. 13.2]. Для примера, приведенного на рис. 13.15, наклон пока-
показателя степени на частотах выше 0,01 Гц равен 2,5, что чуть ниже значения 2,67
для колмогоровской турбулентности. Спектр уплощается на частотах ниже 0,01 Гц
из-за эффектов фильтрации в интерферометре. В этом случае флуктуации, превы-
превышающие длину базы, в данном случае 100 м, почти не влияют на фазу (см. рис.
492
Эффекты распространения
[Гл. 13
10
icr2
Частота, Гц
10"
Рис. 13.15. Квадратный корень из временного спектра мощности [т. е. A3.107)], измерен-
измеренный на 100 м базе на Мауна Кеа (площадка CSO). Скорость тропосферного ветра вдоль
вектора базы молено рассчитать по излому в спектре. Из работы (Masson, 1994a), с разре-
разрешения Astron. Soc. Pacific Conf. Ser.
13.9). Значит частота излома fc равна vs/d. Тогда оцениваемое значение скорости
ветра вдоль направления вектора базы примерно равно 1 м/с.
При расчетах ожидаемых флуктуации фазы необходимо помнить, что вариации
величин с изменением зенитного расстояния зависят от длины базы. Для баз, кото-
которые намного короче толщины слоя водяного пара, среднеквадратичные вариации
фазы пропорциональны >/secz , а для длинных баз они пропорциональны sec z. Этот
результат молено понять, если учесть, что на коротких базах влияние крупномас-
крупномасштабных неоднородностей на двух антеннах компенсируется, и вариации вызваны
мелкими неоднородностями, количество которых примерно пропорционально длине
пути. На длинных же базах доминирует влияние самых крупных неоднородностей,
размер которых сравним с толщиной слоя.
Атмосферные фазовые ошибки при анализе их влияния на карту или изображе-
изображение можно рассматривать как фазовые ошибки антенн. В разд. 11.5 показано, что
динамический диапазон мгновенного изображения примерно равен
A3.121)
где фГШ8 — среднеквадратичная ошибка фазы, измеренная на парах антенн, выра-
выраженная в радианах, а па — число антенн. Например, если фгт8 = 1 рад, а па = 30,
то динамический диапазон ~30. Для ориентира скажем, что значения фгтз от 0,5
до 1 рад соответствуют качеству решетки от хорошего до предельно допустимого.
Возможность улучшить изображение при увеличении времени накопления зависит
от спектра фазовых флуктуации.
13.2.3. Устранение атмосферных фазовых ошибок калибровкой. На
сантиметровых волнах для калибровки фазы обычно наблюдают опорные источни-
источники с интервалами в ~20-30 минут. На миллиметровых волнах этого, как правило,
недостаточно, потому что флуктуации фазы в атмосфере намного больше. Методы,
13.2] Влияние атмосферы на миллиметровых и субмиллиметровых волнах 493
которые могут применяться на миллиметровых и субмиллиметровых длинах волн
для устранения эффектов флуктуации фазы в атмосфере описаны ниже.
Самокалибровка. Самым простым способом устранения эффектов флуктуации
фазы в атмосфере является использование самокалибровки, которая описана в раз-
разделах 10.3 и 11.4. Этот метод зависит от соотношений замыкания фазы в группах
из трех и более антенн. Применяя данный метод, необходимо усреднить данные
коррелятора за время, достаточное для обнаружения источника, т. е. измеренные
фазы функции видности должны, в основном, определяться источником, а не аппа-
аппаратурными шумами. Однако время накопления ограничено частотой флуктуации,
поэтому применение самокалибровки для источников, детектирование которых тре-
требует больших времен накопления, бесполезно.
Частая калибровка (быстрое переключение). Частая калибровка фазы с ис-
использованием неразрешенных источников, близких к опорному (исследуемому) ис-
источнику, может значительно снизить атмосферные фазовые ошибки (Holdaway et
al., 1995; Lay, 1997b). Чтобы атмосферные фазы, измеренные для калибратора,
были близки к фазам основного источника, угловое расстояние между двумя этими
источниками не должно превышать нескольких градусов. Временное разнесение
должно быть меньше ~1 мин, поэтому требуется быстрый перевод антенны между
основным источником и калибратором. В слое, содержащем большую часть водя-
водяного пара прямые, направленные от антенны на основной источник и калибратор,
проходят на расстоянии dfC друг от друга. При номинальной толщине экрана в 1 км,
dtc — 170, где в — угловое расстояние, выраженное в градусах, a dtc измеряется
в метрах. Для одиночной антенны среднеквадратичная разность между двумя пу-
путями в любой момент времени равна yD^{dtc) • Если tcyc — время, затрачиваемое на
один цикл наблюдений источника и калибратора, то средняя разность времен меж-
между наблюдениями двух этих источников составляет to^/2. За время tcyc/2 атмосфера
сместится на vsto^/2. Таким образом, разность фаз между измерениями на двух
путях прохождения эффективно равна ТУф^^ + vsto§/2). Это оценка для самого
плохого случая, поскольку мы суммировали векторные величины, соответствующие
dtc и г>5, как скаляры. Для разности длины путей, измеряемых интерферометром,
среднеквадратичное значение будет в \/2 раз больше, чем для одной антенны,
поэтому остаточные атмосферные фазовые ошибки измеренной функции видности
составляют
A3.122)
Отметим, что фггпз не зависит от базы, поэтому фазовые ошибки не должны
расти с увеличением длины базы. Время одного полного цикла наблюдений двух
источников — это сумма времен наблюдений основного и опорного источников,
удвоенного временем перевода антенны между источниками и удвоенного временем
между окончанием перевода антенны и началом записи данных. Время наблюдений,
требующееся для каждого источника, зависит от плотности потоков и чувствитель-
чувствительности инструмента. Для калибратора иногда существует выбор между близким
слабым источником и более сильным и требующим меньше наблюдательного време-
времени, но больше времени на перевод антенны. Чтобы использование калибровочных
источников стало общепринятым решением проблемы атмосферных фаз, подходя-
подходящие калибраторы должны находиться на расстоянии нескольких градусов от любой
точки неба. Так как плотности потоков калибраторов обычно падают с увеличением
частоты, может возникнуть необходимость наблюдать опорные источники на более
низких частотах, чем наблюдаются основные. Тогда измеренную фазу калибратора
494
Эффекты распространения
[Гл. 13
перед вычитанием из фазы основного источника надо умножить на ^source/^cai (так
как в тропосфере практически нет дисперсии), поэтому требования к точности для
фазы калибратора возрастают. Таким образом, частота наблюдений калибратора
не должна быть слишком низкой; частота в районе 90 ГГц может быть выбрана
из практических соображений при наблюдениях опорного источника на частотах
до нескольких сотен мегагерц. Эффективность метода быстрого переключения
продемонстрирована на рис. 13.16. Заметим, что излом кривой при 300-секундном
усреднении при разнесении антенн на 1500 м указывает на то, что скорость ветра
была примерно равна 2 • 1500/300 = Юм-с (Carilli and Holdaway, 1999).
'60
1 40
о
20
о о
"I Г
I I
I I
"I Г
540 с
¦¦¦¦¦
300 с
°сР°о°о
э°о °°соо<Р0 о о о°
"о
¦Ъ
¦о
20 с
°о ооооО_
•••••••.•«
1,5-104
2-104
Рис. 13.16. Зависимость квадратного корня из структурной функции фазы, которая равна
среднеквадратичному отклонению фазы, от длины базы для данных, полученных на VLA
на частоте 22 ГГц при разных временах усреднения. Эти данные показывают эффектив-
эффективность метода быстрого переключения фазы. В этих измерениях основной и опорный источ-
источники совпадали @748+240). Закрашенные квадратики (время накопления 540 с) показыва-
показывают среднеквадратичные флуктуации фазы без переключения (эти же данные изображены
на рис. 13.11). Кружками и звездочками показаны среднеквадратичные отклонения фазы
для циклов переключения в 300 с и 20 с соответственно. Из работы (Carilli and Holdaway,
1999), ©1999 the American Geophys. Union
Пары или группы антенн. Альтернативой быстрому перемещению между основ-
основным и опорным источниками является размещение антенн близко расположенными
парами. Одна антенна из каждой пары непрерывно наблюдает основной источник,
а другая — калибратор. При такой схеме tcyc в A3.122) равно нулю, но необходи-
необходимо учесть расстояние между антеннами dp. Тогда среднеквадратичная остаточная
атмосферная ошибка фазы функции видности равна
Фгтз = у 22?ф (dtc + dp).
Как и в A3.122), фгт8 — это оценка для худшего случая,
сложили векторные величины, соответствующие dtc d.
A3.123)
поскольку мы скалярно
При расстоянии между
основным источником и калибратором в 2° и эффективной высоте водяного пара
13.2] Влияние атмосферы на миллиметровых и субмиллиметровых волнах 495
в 1км dfC = 35 м. При диаметре антенны, равном ~10м (что типично для антенн,
работающих на частотах до 300ГГц), dp должно быть около 15м, чтобы избежать
значительного затенения одной антенны другой. Это меньше, чем vstcyc/2 в методе
быстрого переключения, так как vs обычно составляет 6-12 м/с, a tcyc обычно
равно 10 или более секундам. Итак, фазовые ошибки тесных пар антенн несколько
меньше, чем при быстром переключении. Более того, не тратится наблюдательное
время на перевод антенны и переключение аппаратуры. Однако при быстром пере-
переключении на основной источник отводится примерно половина времени, а в тесных
парах антенн половина антенн наблюдает основной источник, поэтому в последнем
случае чувствительность уменьшается в ~у2 раз. Если антенны сгруппированы не
в пары, а тройки или четверки, где одна антенна из группы наблюдает калибратор,
то потери чувствительности уменьшаются.
Таблица 13.5. Изменения яркостной температурыа, обусловленные
изменением длины пути на 1мм (Aw = 0,16 мм) для площадки,
расположенной на высоте 5000 м и w = 1 мм
у АТВ
(ГГц) Источник непрозрачности (К)
22,2 Центр линии F16-623) 0,5
90 Континуум 0,3
183,3 Центр линии Ci3-22o) Юь
185,5 Крыло линии 16
230 Континуум 2,0
аРассчитано на основании данных работы (Carilli and Holdaway, 1999).
bЛиния насыщена при w = 1 мм.
Прямые измерения водяного пара. Практический метод калибровки фазовых
флуктуации состоит в измерении полного содержания водяного пара в пределах
диаграммы направленности каждой антенны. Для этого обычно требуется
дополнительный радиометр для измерения воды на каждой антенне, чтобы
определить яркостную температуру неба, как описано в п. 13.1.9. Различные
методики рассматривались в работе Уелча (Welch, 1999). Для корректировки
задержки в РСДБ-системах для радиометра водяного пара обычно достаточно
использовать дополнительную антенну. При исправлении фазы на миллиметровых
и субмиллиметровых интерферометрах важно, чтобы диаграммы направленности
системы радиометра водяного пара и элементов интерферометра совпадали.
Так как тропосфера находится в ближней зоне диаграмм направленности, то
их можно сориентировать так, чтобы они проходили практически через один
и тот же объем тропосферы. Водяной пар — основной источник непрозрачности
на радиочастотах (за исключением полос кислорода на 50—70 и 118 ГГц) даже
на частотах, весьма далеких от центров линий водяного пара, как показано на
рис. 13.6. Вдали от центров спектральных линий непрозрачность обусловлена
широкими крыльями линий инфракрасных переходов. Имеется и значительная
контпину умная составляющая поглощения, вызванная водяным паром, которая
меняется пропорционально v2 (Rosenkranz, 1998). Она включает в себя различные
квантовомеханические эффекты, связанные с молекулами воды, например, обра-
образование димеров (Chylek and Geldart, 1997). Эту компоненту обычно приходится
моделировать, используя эмпирический коэффициент. Вдобавок как описано
496
Эффекты распространения
[Гл. 13
в п. 13.1.9, капли воды в облаках и тумане и кристаллы льда вносят в поглощение
вклад, пропорциональный v2. Значит существуют два различных метода калиб-
калибровки: метод, основанный на измерении яркости неба в диапазоне между линиями,
и метод, основанный на измерениях вблизи спектральных линий. Чувствительность
яркостной температуры к задержкам распространения на отдельных частотах и при
выбранных значениях непрозрачности приведена в табл. 13.5
Метод измерения яркости неба в континууме на, скажем, 90 или 230 ГГц име-
имеет несколько преимуществ. Для измерений яркости неба можно использовать те
же радиометры, что и для астрономических измерений. Если на частоте 230 ГГц
требуемая точность фазовой калибровки составляет одну двадцатую длины вол-
волны, то, согласно таблице чувствительности 13,5, требуемая точность определения
яркостной температуры равна 0,1 К. Для температуры системы 200 К требуется
стабильность коэффициента усиления, равная 5 • 10~4. Для этого нужно уделять
особое внимание стабильности температуры охлаждения приемников. Кроме того,
шкалы коэффициентов усиления должны быть тщательны прокалиброваны. Изме-
Изменения фона земли могут быть ложно интерпретированы как изменения яркостной
температуры неба. При наличии облаков этот метод непригоден из-за вклада жид-
жидкой воды в непрозрачность.
1°
-1
I I I
Среднеквадратичная
разность =160 мм
0,715 0,720 0,725 0,730
0,735 0,740 0,745
Время, сутки
Рис. 13.17. Зависимость фазы интерференции (в единицах задержки), измеренной на
длине волны Змм на одной базе интерферометра радиообсерватории Оувенс Велли
(сплошная линия), и задержки, предсказанной по измерениям водяного пара на частоте
22 ГГц (пунктирная линия) от времени. Среднеквадратичное отклонение их разности
равно 160 мкм. Источник — ЗС273. Из работы (Welch, 1999), см. также (Woody, Carpenter
and Scoville, 2000)
Наблюдения в спектральных линиях дают метод, который не чувствителен к ва-
вариациям коэффициента усиления и наземному фону. Как описано в п. 13.1.9, для
корректировки на облачность и переменное распределение водяного пара с высотой
можно наблюдать на нескольких частотах. При наблюдениях на миллиметровых
волнах в умеренно сухих местах частота 22 ГГц — скорее всего, лучший выбор.
Пример исправления фазы, базирующийся на наблюдениях в этой линии, привиден
на рис. 13.17. При наблюдениях на субмиллиметровых волнах в очень сухих местах
линия 183 ГГц может дать лучшие результаты (Lay, 1998; Wiedner and Hills, 2000).
Линия 183 ГГц сама по себе примерно в 40 раз более чувствительна, чем линия на
22 ГГц. Однако линия 183 ГГц намного быстрее насыщается (т. е. непрозрачность
13.3]
Ионосфера
497
превышает единицу), чем линия 22ГГц, что существенно снижает эффективность
измерений. Чтобы избежать этой проблемы, можно наблюдать линию 183 ГГц
в крыльях, где непрозрачность меньше единицы. Более того, поглощение, пропор-
пропорциональное i/2, на 183 ГГц будет в 79 раз больше, чем на 22 ГГц, что может стать
недостатком коррекции фазы, основанной на более высокочастотных наблюдениях
из-за вклада компонент, не связанных с водяным паром.
13.3. Ионосфера
Ионосфера активно исследуется, начиная с первых экспериментов Эплтона
и Барнетта (Appleton and Barnett, 1925), Брайта и Туве (Breit and Tuve, 1926).
Литература по этой теме огромна. Магнитоионная теория распространения радио-
радиоволн в применении к ионосфере глубоко развита Рэтклиффом (Ratcliffe, 1962) и
Бадденом (Budden, 1961), морфология ионосферы описана Ровером (Rawer, 1956),
а прекрасное общее исследование распространения в ионосфере выполнено Дэвисом
(Davies, 1965). Обзоры, имеющие особое, значение для радиоастрономии, можно
найти в работах (Evans and Hagfors, 1968) и (Hagfors, 1976). Бейнон (Beynon,
1975) привел интересные исторические эпизоды ранних ионосферных исследований.
В этом разделе мы рассмотрим лишь те особенности ионосферы, которые оказыва-
оказывают отрицательное воздействие на интерферометрические наблюдения. В табл. 13.6
Таблица 13.6. Наиболее вероятные величины ионосферных эффектов на
частоте 100 МГц на зенитном расстоянии 60°
Эффект
Фарадеевское вращение
Групповая задержка
Избыточная длина пути
Изменение фазы
Стабильность фазы
(от пика до пика)
Стабильность частоты (среднеквадр.)
Поглощение
(в диапазонах D и F)
Рефракция (ambient)
Изопланатическая область
Максимум6
(день)
15 оборотов
12 мкс
3500 м
7500 рад
±150 рад
±0,04 Гц
ОД дБ^
0,05°
—
Минимум0
(ночь)
1,5 оборота
1,2 мкс
350 м
750 рад
±15 рад
±0,004 Гц
0,01 дБ
0,005°
-5°
Частотная
зависимость
v~2
v~2
v~2
V-1
I/-1
v-1
v-2
v-2
V
Из работы (Evans and Hagfors, 1968).
аЧтобы получить значения в зените, надо разделить числа (кроме рефракции)
на значение sec^, которое примерно равно 1,7 [см. A3.140)]. Чтобы получить типич-
типичные, а не максимальные параметры, разделите числа на 2.
Полное содержание электронов = 5-10 м~ .
сПолное содержание электронов = 5 • 1016 м~2.
dl дБ = 0,230 непера.
498
Эффекты распространения
[Гл. 13
приведены величины различных эффектов распространения для дневной и ночной
ионосферы. Большинство из них зависит от частоты как z/~2, и их можно свести
к минимуму, наблюдая на более высоких частотах. Длина избыточного ионосфер-
ионосферного пути обычно равна длине избыточного пути в нейтральной атмосфере на
частоте около 2 ГГц, однако частота, на которой выполняется это равенство, может
варьироваться от 1 до 5 ГГц. На частоте 20 ГГц длина избыточного ионосферного
пути обычно составляет только 1 % от соответствующей избыточной длины тропо-
тропосферного пути.
13.3.1. Физические основы. Ионизация верхней атмосферы вызвана уль-
ультрафиолетовым излучением Солнца. Характерные дневные и ночные вертикаль-
вертикальные профили электронной концентрации показаны на рис. 13.18. Распределение
электронов и полное содержание электронов меняются также в зависимости от
геомагнитной широты, времени года и цикла солнечной активности. Имеются так-
также значительные ветры, движущиеся ионосферные возмущения и неоднородности.
Ионосфера пронизана квазидиполь-
1000г "inщи 'inщи ^ч>1 "пч. " i 11щи п ным магнитным полем Земли. Рас-
800 - X. ^v " пространение излучения описывает-
600 f- ^v ^v H ся теорией электромагнитных волн
в замагниченной плазме с учетом
столкновений.
Для выяснения некоторых фун-
фундаментальных свойств ионосферы,
связанных с распространением элек-
электромагнитных волн, рассмотрим про-
простейшие случаи. Сначала рассмот-
рассмотрим плоскую монохроматическую
волну с линейной поляризацией, рас-
распространяющуюся через однородную
плазму с электронной концентраци-
концентрацией пе, в отсутствии магнитного по-
поля и столкновений между части-
частицами. Электроны колеблются под
действием электрического поля, од-
однако протоны из-за их большой мас-
массы остаются относительно невозму-
невозмущенными. Показатель преломления
можно найти, вычислив либо инду-
индуцированный ток, либо дипольный мо-
момент. Любой из этих методов дает
один и тот же результат. Используем
Концентрация электронов,
Рис. 13.18. Идеализированное распределение
электронной концентрации в ионосфере Зем-
Земли. Кривые относятся к ожидаемым концен-
концентрациям в максимуме солнечной активности
на умеренных широтах. Максимумы солнечной
активности повторяются с периодом 11 лет,
в последний раз они были в 1989 и 2000. Из
работы (Evans and Hagfors, 1968)
последний метод, как это уже дела-
делалось при рассмотрении показателя преломления водяного пара с использованием
модели связанного осциллятора в п. 13.1.4. Уравнение движения свободного элек-
электрона, в плазме имеет вид
: -eE0e"i2^, A3.124)
где т, е и х — соответственно масса, величина заряда и смещение электрона, a Eq
hz/ — амплитуда и частота электрического поля Е падающей волны. Магнитное поле
плоской волны пренебрежимо слабо влияет на электроны, пока их скорость мала
по сравнению со скоростью света с, а электрическое поле оказывает пренебрежимо
малое влияние на движение протонов. Стационарное решение уравнения A3.124)
13.3] Ионосфера 499
имеет вид
Отметим, что плотность индуцированного тока i = пеех, а скорость частицы х
отличается по фазе на 90° от возбуждающего электрического поля. Таким об-
образом, работа, проделанная волной над частицами (i • Е), равна нулю, и волна
распространяется без потерь, как и следовало ожидать, поскольку в A3.124) нет
диссипативных членов. Дипольный момент единицы объема Р равен пеехо, где xq —
амплитуда колебаний. Диэлектрическая проницаемость е равна 1 + (Р/Ео)/бо, где
бо — диэлектрическая проницаемость вакуума, а значит
г = 1 A
4тт v вот
Диэлектрическая постоянная вещественна и меньше единицы, потому что индуци-
индуцированный диполь сдвинут по фазе на 180° по отношению к возбуждающему полю.
Показатель преломления п равен квадратному корню из е и в данном случае
является действительной величиной:
A3.127)
V V
где
v> = -k^*»^ (Гц)' A3-128)
а пе выражена в м~3. Величина vp называется плазменной частотой и является
также частотой свободных механических колебаний в плазме [см., например, (Holt
and Haskell, 1965)]. Плазменная частота ионосферы (см. рис. 13.18) обычно меньше
12 МГц. Волны с частотой ниже z/p, падающие по нормали на плазму, полностью
отражаются. Фазовая скорость волны с v > vv в плазме больше с и равна с/п,
а групповая скорость волнового пакета равна сп, т. е. меньше с.
Рассмотрим теперь плазму со статическим магнитным полем В, ориентирован-
ориентированным в направлении распространения плоской волны. Уравнение движения электро-
электрона записывается в виде
mv = -е [Е + v x В]. A3.129)
Допустим, падающее поле представляет собой волну с круговой поляризацией.
Если В = 0, то частица будет следовать за концом вектора электрического поля,
двигаясь по круговой орбите. Если В отлично от нуля, то сила v x В, действующая
в радиальном направлении, и электрическая сила должны быть уравновешены цен-
центростремительным ускорением. Таким образом, плазме свойственна анизотропия,
зависящая от того, по правому или по левому кругу поляризована волна, поскольку
знак члена v x В в этих двух случаях меняется. Радиус Re круговой орбиты
электрона можно получить из уравнения баланса сил еЕ$ dz evB = mv2 /Re, где
v = 2тгг//?е, В — величина магнитного поля, верхний и нижний знаки относятся
к левой и правой круговой поляризациям соответственно. Таким образом, получаем
Re = ^ . A3.130)
4тг2ггш2 =F 2irveB V J
500 Эффекты распространения [Гл.13
Следуя той же самой процедуре, что описана после уравнения A3.125), получим,
что коэффициент преломления определяется соотношением
П2 = 1_^р A3.131)
где vB — гирочастота или циклотронная частота, определяемая выражением
Гирочастота — это частота, с которой электрон будет обращаться по спирали вокруг
силовой линии магнитного поля в отсутствие электромагнитного излучения. При
отсутствии затухания Re будет стремиться к бесконечности, если частота прило-
приложенного электрического поля будет равна vB. Гирочастота (магнитное поле Земли
в ионосфере ~ 0,5 • 10~4 Тл) равна примерно 1,4 МГц.
Уравнение A3.121) определяет показатель преломления для случая продольного
магнитного поля, т. е. когда поле параллельно направлению распространения вол-
волны. Решение для случая поперечного поля имеет другой вид. Решение для квазипро-
квазипродольного случая получается заменой В на В cos #, где 0 — угол между направлением
распространения волны и направлением магнитного поля. Квазипродольное реше-
решение применимо, когда угол 0 меньше угла, определяемого неравенством (Ratcliffe,
1962):
2 2
i sin (9 tg0 < V ~vV* • A3.133)
Если v > 100 МГц, г/р ~ 10 МГц, a vB ~ 1,4 МГц, квазипродольное решение верно при
\Q\ < 89°, или почти во всех рассматриваемых случаях. Следовательно, с высокой
точностью, когда i/>(i/phj/b), мы можем разложить A3.131) и получить
^^^ A3.134)
где мы пренебрегли членами порядка i/4 и выше. При распространении в направ-
направлении В показатель преломления волны с левой круговой поляризацией ниже, чем
у волны с правой круговой поляризацией.
Различие показателей преломления для волны с правой и левой круговой поля-
поляризациями приводит к важному явлению — фарадеевскому вращению, в результате
которого плоскость поляризации линейно поляризованной волны вращается при
распространении этой волны в плазме. Линейно поляризованную волну с позици-
позиционным углом ф можно разложить на лево- и правополяризованные волны равной
амплитуды, фазы которых отличаются на 2ф. Фазы этих двух волн с круговой
поляризацией при распространении через плазму в направлении у равны 2itvnry / с
и 2тпуп?у/с, где пг и пц — показатели преломления право- и левополяризованной
мод соответственно. Разность фаз между этими волнами равна 2тп/ (пг — щ)у/с. Из
A3.134) следует, что пг — ni = b'pisBb'~3 cos#, следовательно, плоскость поляризации
поворачивается на угол
Аф = Д, [ vlvB cos 0 dy, A3.135)
cv J y
где vv,vB, и 0 могут быть функциями у.
При постоянных магнитном поле и электронной плотности A3.135) можно за-
записать в виде
А^ = 2,6 • 103 neBX2L cos (9, A3.136)
13.3] Ионосфера 501
где Аф измеряется в радианах, пе — в м~3, В — в тесла и положительно, если поле
направлено к наблюдателю, Л — длина волны в метрах, a L — длина пути в метрах.
Магнитное поле, направленное к наблюдателю, увеличивает позиционный угол, т. е.
плоскость поляризации падающего излучения вращается против часовой стрелки
(если смотреть с поверхности Земли).
13.3.2. Рефракция и задержка распространения. Рефракция в ионосфе-
ионосфере уменьшает зенитное расстояние вне атмосферных сигналов. Это отклонение
вызвано кривизной ионосферы. Если бы ионосфера являлась структурой, состоя-
состоящей из плоско-параллельных слоев, то, в соответствии с A3.26), угол наклона
был бы равен нулю. В известном приближении (Bailey, 1948) предполагалось, что
атмосфера состоит из слоя толщины А/г, внутри которого концентрация элетронов
распределена по параболическому закону с максимумом на высоте hi. В этом случае
угол отклонения равен
—) (cos2z + —) , A3.137)
то / V то /
л _ 2Ah sinz
Z ~ Sr~o
где г/р — плазменная частота на hi. Если константа Ahvz выбрана удачно, то
точность Az лучше 5 % для всех значений z.
Избыточную длину пути в зените можно рассчитать по формулам A3.5),
A3.128), и A3.134), если предположить, что v ^> (ур и г/в). Тогда получим
оо 2 оо
?0 ~ _1 Г \МЩ dh _ _j®$ f п^ dh^ A3.138)
2 J L v J ^ J
о о
где v измеряется в герцах, a ne(h) и vp(h) — распределение электронов (в м~3)
и плазменная частота в зависимости от высоты. Интеграл электронной концен-
концентрации по высоте в A3.138) называется полным содержанием электронов или
плотностью в столбе. Избыточная длина пути соответствует фазовой задержке
и в ионосфере отрицательна. Если мы аппроксимируем ионосферу тонким слоем
на высоте /г^, то избыточная длина пути будет меняться по секансу зенитного
расстояния луча, проходящего через этот слой. Таким образом,
С = Со seczi, A3.139)
где Zi (см рис. 13.4) задается выражением
= Sin
Если z = 90° и sec Zi ~ 3 для hi = 400 км. Закон секанса представляет достоверную
модель для оценок избыточной длины пути в ионосфере. Более подробную модель
можно найти в работе (Spoelstra, 1983). Графики Az и ?, полученные по формулам
A3.137) и A3.139) и по расчетам распространения лучей, приведены на рис. 13.19.
Иногда необходимо корректировать измерения частоты интерференции на ионо-
ионосферную задержку. Вызванный ионосферой сдвиг частоты на антенне равен
(ту/с) dC/dt. Изменение избыточной длины пути dC/dt имеет две составляющие:
одна dz/dt обусловлена изменением зенитного расстояния, а вторая dC^/dt — изме-
изменением jCq по времени. Во многих случаях, особенно на восходе и заходе Солнца,
последний член может преобладать (Mathur, Grossi and Pearlman, 1970).
502
Эффекты распространения
[Гл. 13
20 40 60 80
z0, град, дуги
40 60 80
z0, град, дуги
Рис. 13.19. а — зависимость угла отклонения в ионосфере от зенитного угла на частоте
1000 МГц, полученная по расчетам прохождения лучей при дневном профиле плотности
из рис. 13.12. Отклонение, предсказанное уравнением A3.137), с параметрами vv = 12 МГц,
hi = 350 км, A/i = 225 км и го = 6370 км отличается от этой кривой не более, чем на 5 %. б —
зависимость нормированной избыточной длины пути в ионосфере от зенитного расстояния
для того же самого профиля электронной концентрации, полученная по расчетам прохо-
прохождения лучей (сплошная кривая), и из уравнения A3.139) (штриховая кривая). Полное
содержание электронов равно 6,03 • 1017м~2, а избыточная длина пути в зените — 24,3 м.
Отклонение и длина пути пропорциональны v~
13.3.3. Калибровка ионосферной задержки. Длина избыточного пути
в ионосфере должна быть прокалибрована максимально возможно, при проведе-
проведении экспериментов по точному определению положений источников или баз. Здесь
возможны три подхода. Можно построить модели ионосферы, зависящие от таких
параметров, как геомагнитная широта, солнечное время, время года, солнечная ак-
активность. Существуют две такие модели: Международная стандартная ионосфера
(International Reference Ionosphere, IRI) (Bilitza, 1997) и Параметрическая модель
ионосферы (Parameterized Ionospheric Model, PIM) (Daniell et al., 1995). При другом
подходе оценка полного числа электронов может быть получена по двухчастотному
зондированию на Системе глобального положения (GPS) (Но et al., 1997; Mannucci
et al., 1998). GPS быстро вытесняет более традиционные методы, такие как ионо-
ионосферные зонды, измерения фарадеевского вращения сигналов спутников, оценки
некогерентного обратного рассеяния (Evans, 1969). Наконец, эффекты дифферен-
дифференциальной длины пути можно практически исключить для неразрешенных источни-
источников посредством астрономических наблюдений, проводимых одновременно на двух
достаточно широко разнесенных частотах v\ и V2- Если фазы интерферометра на
этих частотах равны ф\ и ф2, то величина
A3.141)
содержит информацию о положении источника и в значительной степени свобод-
свободна от влияния ионосферной задержки. Малая остаточная ошибка остается из-за
присутствия в показателе преломления частотных членов более высокого порядка
и из-за того, что траектории на двух частотах несколько различны. Двухчастот-
ные наблюдения широко используются в астрометрической радиоинтерферомет-
радиоинтерферометрии, когда можно пренебречь структурой источника (см., например, (Fomalont and
Sramek, 1975; Kaplan et al., 1982; Shapiro, 1976)). Отметим, что различие в полном
электронном содержании вдоль лучевых траекторий к элементам интерферометра
можно оценить из измерений ф^ — {у21у\)Ф\- Подобные двухчастотные системы
можно применять для передачи частоты локального гетеродина на РСДБ-станцию,
находящуюся в космосе (см., например, (Могап, 1989) и разд. 9.10).
13.3] Ионосфера 503
13.3.4. Поглощение. Поглощение в ионосфере вызвано столкновениями
электронов с ионами и нейтральными частицами. На частотах, много больших z/p,
коэффициент поглощения мощности равен
а = 2,68 • 1(Г7^ (м-1), A3.142)
v
где vc — частота соударений, а пе выражается в м~3. Частота соударений в герцах
приблизительно равна
/ Т \—3/2 / rri \ 1/2
1/с~6,Ы0-9(—J щ + 1,8- Ю4( —J пп, A3.143)
где щ — концентрация ионов, а пп — концентрация нейтральных частиц; обе вели-
величины измеряются в м~3 (Evans and Hagfors, 1968). Численные значения поглощения
приведены в табл. 13.3.
13.3.5. Мелкомасштабные и крупномасштабные неоднородности.
Мелкомасштабные неоднородности распределения электронной концентрации
вносят случайные изменения в волновой фронт проходящей электромагнитной
волны. Вследствие этого с помощью интерферометра молено легко наблюдать
флуктуации амплитуды и фазы интерференции на частотах ниже нескольких
сотен мегагерц. На заре радиоастрономии были обнаружены флуктуации
сигналов Лебедя А и других компактных источников с временным масштабом
0,1-1 мин. Вначале считалось, что эти флуктуации связаны непосредственно
с самими источниками (Hey, Parsons and Phillips, 1946), но позднее наблюдения
с разнесенными приемниками показали, что флуктуации перестают коррелировать
при удалении приемников на несколько километров (Smith, Little and Lovell, 1950).
Этот результат привел к заключению, что неоднородности ионосферы искажают
космические сигналы. Было обнаружено, что основной масштаб неоднородностей
равен нескольким километрам. Временной масштаб флуктуации указывает на
то, что скорость ионосферных ветров лежит в диапазоне 50—300 м/с. Эффекты
этих флуктуации интенсивно исследовались на частотах между 20 и 200 МГц
и наблюдались на частотах до 7 ГГц (Aarons et al., 1983). Один из первых
примеров флуктуации, наблюдавшихся при интерферометрических измерениях,
показан на рис. 13.20. В работах Хьюиша (Hewish, 1952), Букера (Booker, 1958),
и Лоренса и др. (Lawrence, Little and Chivers, 1964) приведен обзор ранних
результатов и методов. Исчерпывающий обзор теории и наблюдений ионосферных
флуктуации содержится в работах (Crane, 1977; Fejer and Kelley, 1980; Yeh and
Liu, 1982), а сводка глобальной морфологии — в работах (Aarons, 1982; Aarons et
al., 1999). Измерения на GPS могут оказаться очень полезными при мониторинге
ионосферных флуктуации [например, (Но et al., 1996; Pi et al., 1997)]. Влияние
ионосферных мерцаний на синтезируемый телескоп было описано Споельстрой
и Келдером (Spoelstra and Kelder, 1984). В разд. 13.4 мы рассмотрим теорию
мерцаний, которая применима к ионосфере и межпланетной и межзвездной среде.
Крупномасштабные вариации электронной концентрации, проинтегрированные
по лучу зрения, вызваны движущимися ионосферными возмущениями (ДИВ). ДИВ
являются проявлениями гравитационно-акустических волн в верхней атмосфере, —
это квазипериодические крупномасштабные возмущения электронной концентра-
концентрации. Атмосфера обладает естественной плавучестью, так что объем газа, который
сместили в вертикальном направлении и отпустили, будет колебаться с частотой,
известной под названием частоты Брюнта-Вейселе, или частоты плавучести. Эта
частота равна примерно 0,5-2 мГц (периоды 10-20 мин) на высотах ионосферы. Для
504
Эффекты распространения
[Гл. 13
12#
0 6 12#
б
Рис. 13.20. а — типичная запись с выхода коррелятора в трех случаях с интерферометра
с переключением фазы в Кембридже, Англия, с базой в 1 км, работающего на длине волны
8 м. Нерегулярные детали вызваны неоднородностями в атмосфере, б — распределение
вероятности угла прихода, полученное по пересечению выходным сигналом коррелятора
нулевого уровня. Из работы (Hewish, 1952)
волн с частотой выше частоты плавучести восстанавливающей силой является дав-
давление (акустическая волна), а для волн с частотой ниже частоты плавучести — сила
тяжести (гравитационная волна). В работах (Hunsucker, 1982) и (Носке and Schlegel,
1996) выполнен обзор литературы по акустически-гравитационным волнам. Суще-
Существует множество потенциальных источников ДИВ, включая нагрев полярными
сияниями, крутые атмосферные фронты, землетрясения и извержения вулканов.
Размеры среднемасштабных ДИВ обычно составляют 100—200 км, временные мас-
масштабы — 10-20 мин, и вклад в вариации полного содержания электронов — 0,5-5 %.
Такие ДИВ присутствуют значительную часть времени. Крупномасштабные ДИВ,
которые достаточно редки, имеют размеры порядка 1000 км, временную шкалу
в несколько часов и могут вызвать вариации полного содержания электронов до
8 %. Одно из таких ДИВ, вызванное вулканом, наблюдалось на РСДБ (Roberts et
al., 1982). Влияние ДИВ на радиоинтерферометрию, которое, в основном, состоит
в медленном изменении фазы, рассмотрено в работе (Hinder and Ryle, 1971). Вли-
Влияние на слежение за спутниками описано Эвансом и др. (Evans, Holt and Wand,
1983).
13.4. Рассеяние на неоднородностях плазмы
Распространения излучения в случайной среде является важной задачей во
многих областях физики. Сигналы от космических радиоисточников проходят через
несколько случайных сред, включая ионизованный межзвездный газ Галактики,
солнечный ветер и ионосферу, а также нейтральный газ тропосферы. В плоскости
наблюдателя имеются два эффекта. Во-первых, амплитуда меняется в зависимости
от положения наблюдателя, что приводит к временным вариациям амплитуды, если
происходит относительное движение источника, рассеивающей среды и наблюдате-
наблюдателя. Во-вторых, искажается изображение источника. Большая часть исследований
13.4]
Рассеяние на неоднородностях плазмы
505
в этой области инициирована попытками понять наблюдаемые характеристики
пульсаров [см., например, (Gupta, 2000)].
13.4.1. Модель гауссова экрана. Начнем наше рассмотрение с простой мо-
модели, которая служит для иллюстрации многих особенностей нашей задачи. Эта
модель была впервые предложена Букером, Рэтклиффом и Шинном (Booker, Rat-
cliffe and Shinn, 1950) для объяснения ионосферных мерцаний и модифицирована
Рэтклиффом (Ratcliffe, 1956). Шойер (Scheuer, 1968) применил их к наблюдениям
пульсаров. В данной модели предполагается, что неоднородная среда ограничена
тонким экраном и что неоднородности (сгустки) имеют один характерный масштаб
а. Эффектами дифракции внутри неоднородной среды пренебрегают; принимается
во внимание только изменение фазы, вызванное
средой. Дифракция учитывается в свободном про- ^^^^^^^~^^^^^^^~ **" а
странстве между неоднородной средой и приемни-
приемниками.
Геометрия показана на рис. 13.21. Предполо-
Предположение о тонком экране не является особо огра-
ограничивающим. Однако предположение о том, что
экран заполнен сгустками плазмы с одним ха-
характерным размером, накладывает ограничения
и отличает данную модель от степенной модели,
имеющей широкий диапазон масштабов неодно-
родностей. Из A3.128) и A3.134) получим, что
коэффициент преломления плазмы может быть
записан в виде
гепе\
2тг
A3.144)
где ге — классический радиус электрона, равный
е2/Dтгбогас2), или 2,82 • 10~15 м, а членом с vB мы
пренебрегли. Таким образом, избыточный сдвиг
фазы при прохождении волны через один сгусток
равен
Аф\ = ге\а Апе
A3.145)
где Апе — избыточная электронная концентрация
в сгустке по сравнению с окружающей средой.
Если толщина слоя равна L, то волна встретит на
пути L/а сгустков и среднеквадратичное отклоне-
отклонение фазы Аф составит Аф-y^jLja , или
Аф = ге\Апе
A3.146)
Рис. 13.21. Геометрия мерцаний
в модели тонкого экрана. Ис-
Исходный плоский фронт волны
(а) падает на тонкий фазовый
экран (б). Выходящий волно-
волновой фронт (в) становится нере-
нерегулярным. По мере распростра-
распространения волны к наблюдателю
развиваются флуктуации ампли-
амплитуды, обусловленные пересече-
пересечением лучей. Ниже антенн при-
приведен график интенсивности в
зависимости от положения вдоль
волнового фронта. Если экран
движется к наблюдателю, то бу-
будут наблюдаться пространствен-
пространственные флуктуации в виде вре-
временных флуктуации принимае-
принимаемой мощности или функции вид-
ности
Волновой фронт, проходя экран, теряет прямоли-
прямолинейность, т. е. амплитуда волны не изменяется, но
фаза не остается постоянной и приобретает случайные отклонения со среднеквад-
среднеквадратичным значением Аф. Следовательно, эту волну можно разложить в угловой
спектр волн, распространяющихся под различными углами. Полную ширину угло-
углового спектра, 0S, можно оценить, если предположить, что случайная среда состоит
из преломляющих клиньев, вызывающих отклонение волнового фронта на величину
±А0А/2тг на расстоянии а. Таким образом,
506 Эффекты распространения [Гл.13
1 Л2л IL
Os = -re\2AneA - . A3.147)
7Г V а
Если источник не является бесконечно удаленным, то падающий фронт волны не
будет плоским. В этом случае видимый угол рассеяния 6's зависит от положения
экрана относительно источника и наблюдателя. Поскольку 6S и 6's являются малыми
углами, из геометрии рис. 13.16 следует
jOs, A3.148)
где R и R' определены на рис. 13.6. Следовательно, эффективность рассеивающего
экрана снижается, если экран расположен ближе к источнику. Этот эффект рычага
очень важен в астрофизических ситуациях. Им можно воспользоваться, чтобы раз-
разделить галактические и внегалактические источники, излучение которых проходит
через один и тот же рассеивающий экран (Lazio and Cordes, 1998).
Амплитудные флуктуации нарастают по мере того, как волна уходит от экрана.
Если фазовые флуктуации велики, Аф > 1, то при пересечении лучей возникают
значительные амплитудные флуктуации (см. рис. 13.21). Критическое расстояние,
за пределами которого наблюдаются флуктуации с большими амплитудами, равно
Rf - у ¦ A3-149)
Отметим, что если Аф = 2тг, то Rf — расстояние, для которого размер сгустка равен
размеру первой зоны Френеля. Распределение случайного электрического поля на
Земле в плоскости, перпендикулярной направлению распространения, называется
дифракционной картиной. Она имеет характерный радиус корреляции dc:
dc^^r. A3.150)
Если экран движется с относительной скоростью vs в направлении, перпендику-
перпендикулярном направлению распространения, так что дифракционная картина проходит
перед наблюдателем, то временная шкала переменности равна
Сигнал, достигающий наблюдателя, при распространении вдоль пути рассеянного
луча запаздывает на величину
' - A3.152)
по сравнению с нерассеянным сигналом. Фаза рассеянной волны равна 2тп/тс по
отношению к прямой (нерассеянной) волне, и интерференция между этими двумя
волнами вызывает мерцания. Ширина полосы Д^с, в пределах которой относитель-
относительная фаза меняется на 2тг, называется шириной полосы корреляции. Ширина полосы
корреляции является величиной, обратной тс, и для случая R = R' равна
Avc ~ -^ , A3.153)
13.4]
Рассеяние на неоднородностях плазмы
507
где Rs — расстояние между источником и наблюдателем. Если в наблюдениях
используется приемник с шириной полосы больше Дг/С, то амплитудные флукту-
флуктуации заметно снизятся. Отметим, что, согласно уравнениям A3.153) и A3.147), Avc
меняется пропорционально А~4.
Наконец, если источник имеет две равные компоненты, отстоящие друг от друга
на расстояние ?, то каждая компонента будет создавать одну и ту же дифракцион-
дифракционную картину, однако эти картины будут смещены на Земле на расстояние ?R/R'.
Если это расстояние больше с/с, то дифракционная картина будет сглажена и ам-
амплитудные флуктуации уменьшены. Таким образом, если размер источника больше
критического размера #с, то
амплитудные флуктуации бу-
будут сильно уменьшены, так как
дифракционные картины ком-
компонент будут накладываться
и сглаживать друг друга. Со-
Согласно A3.148) и A3.150), 0с Источник
можно записать в виде
R0.
= -=?-. A3.154)
Следовательно, мерцают толь-
только источники малого углово-
углового размера. Аналогичное оп-
оптическое явление заключается
Экран
Рис. 13.22. Путь преломленного луча в модели тон-
тонкого фазового экрана, среднеквадратичный угол
рассеяния 0s задан уравнением A3.137)
в том, что звезды мерцают,
а планеты нет. Элегантное применение уравнению A3.257) было найдено Фрайлем
и др. (Frail et al., 1997) при определении углового размера расширяющегося радиои-
радиоисточника, связанного с 7-всплеском. Они определили, что амплитудные флуктуации
радиоизлучения (если предположить, что они вызваны межзвездным рассеянием),
прекратились в течение первой недели после всплеска. Это указывает на то, что
диаметр источника в этот момент превысил критический размер 3 мксек дуги.
Полезной величиной является среднее по ансамблю значение функции видности
Vm, измеренное интерферометром при наличии мерцаний. Предположим, что фазы
01 и 02 в двух точках вдоль фазового экрана, разнесенных на расстояние d —
случайные переменные, характеризуемые совместным гауссовым распределением
с дисперсией Аф2 и нормированной корреляцией p(d). Величина p(d) является
корреляционной функцией фазы или переменной компоненты показателя прелом-
преломления. Совместная плотность вероятности для фазы вдоль волнового фронта равна
1
2тгАф2Л/1-
ехр
ф1 - 2 p(d) фгф2
A3.155)
где p(d) = (Ф1Ф2}/Аф2. Математическое ожидание величины
равно
A3.156)
что можно получить непосредственно из A3.155), в итоге
A3.157)
508 Эффекты распространения [Гл.13
Для точечного источника с плотностью потока S усреднение функции видности по
ансамблю дает
(Vm) = S(ej(fIe~j<tJ), A3.158)
или
(Vm) = Se~A<t) ^~рЩ A3.159)
Если собственная функция видности источника равна Vq, to усреднение по ансам-
ансамблю приводит к
\Vm/ — ^0 е • ^lo.lDUJ
Этот результат был впервые получен Рэтклиффом (Ratcliffe, 1956) и Мерсье
(Mercier, 1962). В большинстве ранних радиоастрономических работ предполага-
предполагалось, что p(d) — Гауссова функция:
p{d) = e~d2/2a\ A3.161)
где характерный масштаб а соответствует размеру облака плазмы в вышеприведен-
вышеприведенном рассмотрении. Эта модель, называемая моделью гауссова экрана, по-видимому,
содержит нереалистичные ограничения, поскольку вне всякого сомнения имеется
много масштабов. В случае когда Аф ^> 1, Vm быстро убывает с ростом d и необходи-
необходимо рассмотреть лишь случай d <C а. Тогда, подставляя A3.161) в A3.160), получим
\УШ) — Vq е ^ ' . (Io.Idzj
Таким образом, распределение яркости точечного источника, наблюдаемое через
гауссов экран, является гауссовым с диаметром (полной шириной на уровне поло-
половины максимума), равным
Л 1 Л I' С\ Л ~С\ I Т
A3.163)
Эта формула для 0s в значительной степени эквивалентна выражению A3.137).
В случае когда Аф <С 1, нормированная функция видности падает от единицы
до е~Аф при d ^> а. Следовательно, результирующее распределение яркости то-
точечного источника имеет вид неразрешенного ядра, окруженного гало. Отношение
плотности потока в гало к плотности потока в ядре равно еАф — 1.
13.4.2. Степенная модель. Спектр флуктуации электронной концентрации
ионизованной астрофизической плазмы обычно моделируется степенным законом
Рпе = C2eq~a, A3.164)
где q — трехмерная пространственная частота, q2 = q2 + q2 + q2 и С^е характеризует
силу турбулентности. Величина С^е определена в литературе по-разному в зависи-
зависимости от того, предполагается ли ее постоянство в спектре структурной функции.
Двумерный спектр мощности фазы [см. соотношение между ф и пе в A3.145)]
выражается как
Рф{ц) = 2тгг2еХ2ЬРпе. A3.165)
Значит, согласно A3.104), структурная функция фазы равна
= 8тг2г2е\2Ь [ [1 - J0(qd)} Pne(q)qdq. A3.166)
13.4] Рассеяние на неоднородностях плазмы 509
Для степенного спектра вида A3.164) структурная функция запишется в виде
Vф{d) = 8ж2г2Х2С2пеЬ Да) da~2, A3.167)
где f(ot) — величина порядка единицы. Показатель степени а часто полагают
равным 11/3, т. е. значению для колмогоровской турбулентности, когда f(ot) =
= 1,45 [другие значения f(a) см. в работе (Cordes, Pidwerbetsky and Lovelace, 1986)
Интерферометрическая функция видности, усредненная по ансамблю [см. A3.81)
равна
(V) = Vo e-v*l2, A3.168)
(V)=Voe-47r2^A2c"eb/(«)^-2. A3.169)
Наблюдаемое распределение интенсивности, фурье-преобразование от A3.169),
немного отличается от гауссова распределения, как показано на рис. 13.10 5. Угол
рассеяния (полная ширина на уровне половины максимума), полученный из шири-
ширины распределения интенсивности, равен
0s~4,l-lO-13(C2eLK/5An/5 (сек дуги), A3.170)
где Л измеряется в метрах, a C^eL — в м~17/3. Таким образом, различие между
степенной и гауссовой моделями состоит в том, что угол в 0S, измеренный по-
посредством преобразования Фурье данных функции видности с различными базами,
пропорционален А2'2 для степенной и Л2 для гауссовой модели. Заметим, что если бы
функция видности (V) измерялась на единственной базе, т. е. при фиксированном
с/, и если бы оценка 0s получалась из сравнения измеренной функции видности
с функцией видности, ожидаемой для гауссова распределения яркости, то тогда
в обеих моделях 6S изменялась бы как Л2.
Для того чтобы получить усреднение по ансамблю в A3.168), A3.169), A3.170),
измерения функции видности должны проводится со значительными временами
усреднения (Cohen and Cronyn, 1974). Подробное рассмотрение времени усреднения,
которое требуется, чтобы получить усреднение по ансамблю, выполнено Нарайяном
(Narayan, 1992).
Можно ожидать, что в плазме степенной закон будет выполняться на интервале
от внутреннего масштаба до Д° внешнего масштаба q\\ т. е. флуктуации меньше 1/gi
или больше I/go отсутствуют. В случае, если qd <C 1, т. е. база меньше внутреннего
масштаба, функция Бесселя в A3.166) превращается в 1 — q2г2/4 и интеграл берется
аналитически:
о 2 2л2гл2
Т> (J\ Z7r 'еЛ ^ипе / 4 —а 4 — а\ ?2 (л о л пл \
ф( ' = 4^ (Ql ~% ' A3.171)
Этот результат имеет два интересных следствия. Во-первых, структурная функция
меняется пропорционально d независимо от а. Во-вторых, при а < 4 в структурной
функции преобладает влияние мелких неоднородностей, а при а > 4 — крупных.
Он также дает возможности разграничить плазму с а < 4 и а > 4. Случай, когда
а < 4, называется Тип А (плоский спектр), а когда а > 4 — Тип В (крутой спектр)
(Narayan, 1988).
Рассмотрим ситуацию, в которой спектр состоит из трех частей:
Рпе = Спе<?0~" Я. < <?0,
= C2neq-«, qo<q<qu A3-172)
= 0, q>qi-
510
Эффекты распространения
[Гл. 13
da~
d2
Inlq,
Рис. 13.23. a — модельный спектр флуктуации электронной концентрации с внутренним
и внешним масштабами на пространственных частотах qo и q\. б — соответствующая
структурная функция фазы: см. A3.172) и A3.173). Из работы (Могап, 1989), ©1989
Kluwer Academic Publishers
Подстановка A3.172) в A3.166) дает
=(^-X d2, d<2ir/qu
\qido J
(—)
\qodo I
A3.173)
ol-2
d > 2тг/д0,
где мы ввели такой нормировочный множитель б/0> что ДДс/о) = 1? как и в обсулс-
дениях тропосферы в п. 13.1.7. Мы предположили также, что 2тг/^1 < do < 2тг/до-
Этот спектр и структурная функция для данной модели представлены на рис. 13.23.
13.5. Межпланетная среда
13.5.1. Рефракция. Радиоволны, проходящие вблизи Солнца, отклоняются
под действием ионизованной среды солнечной короны и солнечного ветра. Общие
характеристики солнечной короны и солнечного ветра можно найти в работе (Win-
terhalter et al., 1996). Расчет рефракции в протяженной солнечной атмосфере важен
для понимания особенностей солнечного радиоизлучения на низких частотах, где
углы отклонения велики (Kundu, 1965), а также для проверки релятивистского
отклонения электромагнитного излучения, проходящего вблизи Солнца (Shapiro,
1967; Fomalont and Sramek, 1977). Точность измерения релятивистского отклонения
в радиодиапазоне ограничена точностью, с которой может быть учтено отклонение,
обусловленное ионизованной средой. Ниже рассматривается рефракция в случае,
имеющем отношение к экспериментам по определению релятивистского отклоне-
отклонения, т. е. в микроволновом диапазоне, когда отклонение под действием ионизован-
ионизованной среды мало.
Электронную концентрацию как функцию расстояния от Солнца можно изме-
измерить различными методами. Анализ данных оптических наблюдений томсоновского
рассеяния во время солнечных затмений позволяет построить модели распределе-
распределения электронной плотности:
п(
= A,55г~6 + 2,99г~16) • 10
14
A3.174)
13.5] Межпланетная среда 511
где г, радиальное расстояние от Солнца в единицах солнечного радиуса, не превы-
превышает ~4. Уравнение A3.174) известно как формула Аллена-Баумбаха (Allen, 1947).
Данные по затмениям тоже интерпретируются в виде модели вида
пе = п1 г~6 + а2 г~2'33, A3.175)
для г > 3 (см. ссылки в (Muhleman, Ekers and Fomalont, 1970)). Коэффициенты а\
и п2 зависят от уровня солнечной активности и могут изменяться примерно в 5 раз
в течение 11-летнего цикла. Измерения мерцания во время покрытия Крабовидной
туманности на частоте 26 МГц достаточно хорошо представляются моделью
пе = 5-10пг-2 (м~3) A3.176)
для 4 < г < 20 (Erickson, 1964; Evans and Hagfors, 1968). Дисперсионные измерения
пульсаров во время их покрытий Солнцем дают примерно такой же результат,
что и уравнение A3.176) (Counselman and Rankin, 1972; Counselman et al., 1974).
Угол преломления луча, проходящего вблизи Солнца, довольно просто вычисляется
для случая, когда этот угол мал. Траектория луча подчиняется закону Снеллиуса
в сферических координатах, nr sinz = const (Smart, 1977), где п — показатель
преломления, a z — угол между лучом и прямой, проходящей через центр Солнца,
как показано на рис. 13.24. Из этого соотношения угол отклонения равен
A3.177)
где гш — наименьшее расстояние между траекторией луча и Солнцем, ар — при-
прицельное расстояние (см. рис. 13.24). Предположим, что электронная концентрация
распределена по степенному закону
пе = пеОг"/3, A3.178)
где пео — электронная плотность в (м~3) на расстоянии одного солнечного радиуса,
а /3 — постоянная. Для полностью ионизованного солнечного ветра, характеризуе-
характеризуемого постоянной скоростью движения и постоянной скоростью истечения, /3 равно
2. Этот случай применим при г ^ 10.
Показатель преломления получается подстановкой A3.178) и A3.128) в A3.134)
и пренебрежении членом с г/в. Графическое решение уравнения A3.177) для боль-
больших углов отклонения дано в работе (Jaeger and Westfold, 1950). Для небольших
углов отклонения приближенное решение уравнения A3.177) можно получить по-
посредством подстановки nr/p = sec в [см. также дискуссию после уравнения A3.185)]:
въ ~ 80,6 yft ^f V ^J p-P, A3.179)
где р измеряется в единицах солнечного радиуса, а Г — гамма-функция. Заметим,
что лучи отклоняются наружу от Солнца. Угол отклонения в модели, представлен-
представленной уравнением A3.176), равен
въ ~ 2,4 \2р~2 (мин дуги), A3.180)
512 Эффекты распространения [Гл.13
.Солнце
Рис. 13.24. Путь луча через ионизованный газ, окружающий Солнце. Параметр р — при-
прицельный параметр, а — угол элонгации Солнца, т. е. между Солнцем и источником в от-
отсутствие отклонения Солнцем
где Л — длина волны в метрах. Для составной степенной модели распределения
электронной концентрации, соответствующей уравнениям C.174) и A3.175), углы
отклонения для каждой составляющей могут суммироваться, если они малы.
Релятивистское отклонение. Общее релятивистское отклонение можно описать
в рамках классического подхода с помощью эффективного коэффициента прелом-
преломления 1 + 2GMq/tcг, где G — гравитационная постоянная, Mq — масса Солнца.
Угол отклонения при небольших значениях р равен (Weinberg, 1972):
6GR ~ -1,75^ (сек дуги). A3.181)
Знак минус означает, что релятивистское отклонение лучей направлено к Солнцу.
Эффект гравитационного релятивистского отклонения лучей был проверен РСДБ-
наблюдениями с точностью не хуже 1/1000 (Lebach et al., 1995). В экспериментах
по измерению релятивистского отклонения модель фазы интерферометра устанав-
устанавливается с использованием уравнения A3.179), а солнечная модель — с помощью
степенных составляющих, определяемых уравнением A3.178) с коэффициентом
пеоь для каждой. Релятивистское отклонение и коэффициенты можно оценить
одновременно на основе интерферометрических данных. Однако если распределе-
распределение электронной концентрации имеет составляющую с C = 1, то релятивистский
эффект будет маскироваться, если измерения выполняются только на одной ча-
частоте. Солнечному ветру свойственна сильная переменность, и попытки описать
его посредством степенной модели с постоянными коэффициентами могут быть
недостаточными для прецизионных экспериментов.
Для больших угловых расстояний от Солнца лучше подходит приближение
(Misner, Thorne and Wheeler, 1973)
0GR ~ -0.00407W ;^^ (сек дуги), A3.182)
где а — солнечная элонгация, т. е. угол между Солнцем и источником. Такое от-
отклонение, составляющее около 4,1 мсек дуги для а = 90°, можно обнаружить почти
при всех значениях солнечной элонгации с помощью РСДБ-измерений (Robertson,
Carter and Dillinger, 1991). Во многих интерферометрических измерениях необхо-
необходимо вносить поправку на эффект релятивистского отклонения траектории лучей.
Уравнение A3.182) получено для бесконечно удаленного источника. Его нужно
модифицировать, если исследуемый источник находится в пределах Солнечной
системы (Shapiro, 1967).
13.5] Межпланетная среда 513
Избыточный фазовый путь луча, проходящего через корону в случае, когда
эффектом отклонения луча можно пренебречь, согласно A3.138) выражается со-
соотношением
оо
?- -Щг \ nedy, A3.183)
— оо
где у измеряется вдоль траектории луча, как показано на рис. 13.24. Для степенной
модели, определяемой уравнением A3.178), избыточный путь равен
оо
?^_40^ne0 | _^__. A3.184)
— оо
Проинтегрировав, получим
г,'*-1
A3.185)
Отметим, что изменение зависимости С от р описывает наклон волнового фронта
и является углом отклонения; следовательно, въ — dC/dp (Bracewell, Eshleman and
Hollweg, 1969). Дифференцирование A3.185) по р дает A3.179).
13.5.2. Межпланетные мерцания. Мерцания внегалактических источни-
источников, вызванные неоднородностями солнечного ветра, были обнаружены Кларком
(Clarke, 1964) и Хьюишем и др. (Hewish, Scott and Wills, 1964). Межпланетные
мерцания легко отличаются от ионосферных, поскольку характерное время [урав-
[уравнение A3.151)] и критический размер источника [уравнение A3.154)] составляют
соответственно приблизительно 1с и 0,5" для межпланетных мерцаний и 30 с и 1(У
для ионосферных. Дальнейшие наблюдения межпланетных мерцаний (Cohen et al.,
1967) показали, что при использовании A3.154) угловой размер радиоисточника
ЗС273В оказывается меньше 0,02". Этот результат, как и данные интерферомет-
интерферометрии с длинными базами стимулировали развитие РСДБ. Подробное рассмотрение
и интерпретацию межпланетных мерцаний можно найти в работах (Salpeter, 1967;
Young, 1971; Scott, Coles and Bourgois, 1983). Для грубых расчетов угол рассеяния,
обусловленный влиянием межпланетной среды, может быть приближенно выражен
(Erickson, 1964)
0s ~ 50 (-) (мин дуги), A3.186)
где Л выражена в метрах, р — прицельный параметр (в солнечных радиусах). Это
соотношение основано на измерениях, проведенных в 1960—61 гг. на длине волны
11м для прицельных параметров, лежащих в интервале между 5 и 50 радиуса-
радиусами Солнца. Анализ РСДБ-наблюдений на 3,6 и 6 см, проведенный в 1991г. для
ряда прицельных параметров в интервале от 5 до 50 солнечных радиусов приве-
привели к модели для С\е вида С\е = l,5-1014(r/i2©)~3'7 (Spangler and Sakurai, 1995).
Отметим, что ожидаемый показатель степени должен быть равен примерно —4.
Этот вывод базируется на элементарных рассуждениях, что С^е пропорционален
дисперсии электронной плотности, которая пропорциональна квадрату плотности.
При постоянной скорости ветра плотность пропорциональна г~2, а, следовательно,
С^е пропорционален г~4. Отклонения от 4 вызваны радиальной зависимостью маг-
магнитного поля, которое влияет на турбулентность. Проинтегрировав С^е вдоль луча
17 Томсон
514 Эффекты распространения [Гл.13
зрения и используя A3.170), получаем оценку угла рассеяния 6S = 3100(р/А)~2'2 сек
дуги, что сопоставимо с результатами, приведенными в A3.186).
Представление о том, что протяженные источники не столь сильно мерцают, как
точечные [см. A3.154)], можно обобщить, чтобы получить информации о струк-
структуре источника. Предположим, что мерцания вызваны экраном, расположенным
на расстоянии R от Земли, как показано на рис. 13.22, где R <C Rs, и интенсив-
интенсивность у поверхности Земли равна /(ж, г/), где х и у — координаты в плоскости,
параллельной экрану (см. рис. 13.21). Функция Д/(ж, у) равна /(ж,у) — (/(ж,у)),
где (/(ж,у)} — средняя интенсивность. Ее энергетический спектр равен Sio(qx,qy)
для точечного источника и Si(qx,qy) для протяженного источника, где qx и qy —
пространственные частоты. Если V(qxR,qyR) — функция видности источника, то
можно показать (Cohen, 1969), что
Sj(g.,O = SI0(q.,qv) \V(qmR,qvR)\2, A3.187)
где qxR и qyR соответствуют координатам проекции вектора базы и и v. Индекс
мерцания источника ms определяется выражением
SiiQxiQ )dqxdq . A3.188)
В принципе, Si(qx,qy) можно вычислить из одновременных измерений Д/(ж,у)
с помощью большого числа разнесенных приемников. На практике из-за движения
солнечного ветра дифракционная картина пробегает через один телескоп таким
образом, что из измерений Д/(?) может быть вычислен временной спектр мощности
S(f). Если дифракционная картина движется со скоростью vs в направлении ж, то
S(f) можно связать с пространственным спектром, поскольку qx = f/vs:
оо
S(f) = - f sAqx = -L,qu) dqy. A3.189)
В принципе, величину |V|2 можно получить по формуле A3.187), наблюдая источ-
источник при различных положениях относительно солнечного ветра. Здесь ситуация
полностью аналогична той, которая возникает при наблюдении покрытия источ-
источника Луной (разд. 16.2), за исключением того, что при лунном покрытии можно
получить и фазу функции видности. Оценку диаметра источника можно получить
из ширины временного спектра мощности (Cohen, Gundermann and Harris, 1967)
или из индекса мерцаний [уравнение A3.188] (Little and Hewish, 1966).
Межпланетные мерцания в целом являются слабыми, за исключением направ-
направлений, близких к Солнцу. Эффекты рефракционных мерцаний (обсуждаемые в сле-
следующем разделе и в разд. 14.3), которые могут стать важными в случае сильного
рассеяния, исследовались Нарайяном, Анантарамайяхом и Корнвеллом (Narayan,
Anantharamaiah and Cornwell, 1989).
13.6. Межзвездная среда
В табл. 13.7 приведены характерные величины и масштабы различных эффек-
эффектов, обусловленных межзвездной средой. Они обсуждаются ниже.
13.6]
Межзвездная среда
515
Таблица 13.7. Характерные значения61 влияния межзвездной среды на
излучение на частоте 100 МГц
Номер Зависимость от
Эффект уравнения Величина частоты
Угловое уширение
Уширение импульса6
Полоса мерцаний6
Спектральное уширение6
Время мерцаний6
Время мерцаний0
Оптическая толща свободно-свободных пе-
переходов
Фарадеевское вращение
13,163
13,152
13,153
—
13,151
—
13,142
13,193
0,3"
1(Г4 с
104 Гц
1Гц
Юс
106с
0,01
10 рад
V
,.-1
V
,-1
Из работы (Cordes, 2000).
а Для источника в галактической плоскости на расстоянии в 1 кик. Реальные значения
могут отличаться на порядок.
6 Дифракционное рассеяние.
° Рефракционное рассеяние.
13.6.1. Дисперсия и фарадеевское вращение. Однородная ионизованная
компонента межзвездной среды наглей Галактики оказывает влияние на распро-
распространение излучения в виде задержки и фарадеевского вращения. Время прихода
импульса излучения, например от пульсара, определяется выражением
A3.190)
где L — путь распространения, vg = сп — групповая скорость, а п приведено
в A3.127). Дифференцирование A3.190) дает
J ne dy.
dtp
dv
Интеграл от пе вдоль пути называется мерой дисперсии
= J ne dy,
A3.191)
A3.192)
которая соответствует полному числу электронов на луче зрения. Величину dtp/'dv
можно измерить по времени прихода импульсов пульсара на различных частотах,
а меру дисперсии затем можно рассчитать по формуле A3.191). Если известно
расстояние до пульсара, то можно вычислить среднюю электронную концентра-
концентрацию. Типичное значение (пе) в плоскости нашей Галактики составляет 0,03 см~3
(Weisberg, Rankin and Boriakoff, 1980). И наоборот, если расстояние до пульсара
неизвестно, то его можно оценить по формуле A3.191), используя принятое среднее
значение пе.
17*
516 Эффекты распространения [Гл.13
Магнитное поле Галактики вызывает фарадеевское вращение плоскости поля-
поляризации излучения внегалактических радиоисточников. Уравнение A3.135) можно
переписать в виде
Аф = \2Rm, A3.193)
где Rm — мера вращения, определяемая выражением
еБц^. A3.194)
Здесь Яш измеряется в рад/м2, А — в м, Бц — продольная компонента маг-
магнитного поля — в Гс AГс = 10~4 тесла), пе — в см~3, а у — в пк Aпк = 3,1 х
х 1016 м). Величину межзвездного магнитного поля можно оценить, разделив меру
вращения на меру дисперсии. Типичные значения напряженности магнитного поля,
полученные таким способом, составляют 2мкГс (Heiles, 1976). Такая процедура
дает заниженную оценку магнитного поля, если оно меняет направление по лучу
зрения. Формула для грубой оценки меры вращения, обусловленной магнитным
полем Галактики, имеет вид (Spitzer, 1978)
Rm = -18 | cot b\ cos (I - 94°), A3.195)
где ? и b — галактическая долгота и широта. Обзор измерений меры вращения в за-
зависимости от направления можно найти в работе (Simard-Normandin and Kronberg,
1980).
Фарадеевское вращение внутри радиоисточника деполяризует его излучение.
Эта деполяризация происходит из-за того, что излучение от областей внутри источ-
источника, находящихся на различных глубинах, испытывает неодинаковое фарадеевское
вращение. Таким источником может быть, например, релятивистский газ, излучаю-
излучающий поляризованное синхротронное излучение, погруженный в тепловую плазму,
которая вызывает фарадеевское вращение. Степень поляризации наблюдаемого
излучения можно описать через соотношения преобразований Фурье, пренебрегая
самопоглощением. Введем сначала функцию М — комплексную степень линейной
поляризации:
M = meej2^ = Q±iE, A3.196)
где гп? — степень линейной поляризации, ф — позиционный угол электрического
поля, Q, U и / — параметры Стокса, введенные в разд. 4.8. Если у — линейное рас-
расстояние до источника, ф(у) — внутренний позиционный угол излучения на глубине
1/iJviy) ~ объемная излучательная способность источника и \2{3(у) — фарадеевское
вращение, испытываемое излучением, идущим с глубины т/, то степень поляризации
наблюдаемого излучения можно записать как
М(А2) = * . A3.197)
J ju
Знаменатель в соотношении A3.197) представляет собой полную интенсивность.
Фарадеевская глубина f3(y) монотонно возрастает в источнике, пока не изменится
13.6] Межзвездная среда 517
знак направления продольного магнитного поля. В любом случае можно проинте-
проинтегрировать все излучение, приходящее с одной фарадеевской глубины, и записать
интегралы в A3.197) как функцию от /3 вместо у, в результате чего получим
М(Л2) = | F(/3) ej2x2P d/3, A3.198)
где
п'МШ6*2*™ . A3.199)
Таким образом, М(Л2) и F(/3) образуют пару преобразования Фурье. F(/3) иногда
называется фарадеевской функцией дисперсии. К сожалению, F(/3) в общем случае
нельзя найти, так как М невозможно измерить для отрицательных значений Л2. Из-
за этой трудности F(/3) обычно оценивают с помощью модельного согласования.
Однако если ф(у) — константа, то М(—Л2) = М*(Л2), и F(/3) можно получить
с помощью преобразования Фурье.
Обсудим результат для простой модели источника, в которой rri?, ф и jv посто-
постоянны. Из A3.198) следует
М(Л2) = М@) [81п2ДДт1 ejx2R™, A3.200)
|_ A Rm J
где Rm — мера фарадеевского вращения вдоль всего источника. Если фарадеевское
вращение возникает перед источником излучения, то комплексная степень поляри-
поляризации равна
М(Л2) = М@) ei2x2Rm. A3.201)
В этом случае деполяризация отсутствует и фарадеевское вращение в два раза
сильнее, чем в случае A3.200), когда излучающая среда однородно распределена по
всей вращающей среде. Детальное описание внутреннего фарадеевского вращения
см. в работах (Burn, 1966) и (Gardner and Whiteoak, 1966).
13.6.2. Дифракционное рассеяние. Дифракционное межзвездное рассея-
рассеяние подробно исследовалось при наблюдениях пульсаров и компактных внегалак-
внегалактических радиоисточников. У пульсаров можно измерить временное уширение
импульсов A3.152), ширину полосы декорреляции A3.153) и угловое уширение
A3.147). Интерпретация измерений в рамках модели тонкого экрана позволяет
предположить, что Апе/пе ~ 10~3 и что масштаб, ответственный за мерцания —
величина порядка 1011 см. Временные вариации, или мерцания сигнала пульса-
пульсара, вызваны движением наблюдателя и пульсара относительно квазистационарной
межзвездной среды. Измерение ширины полосы декорреляции можно использовать
для оценки угла рассеяния A3.153). Такую оценку угла рассеяния и измерение
характерного времени мерцаний A02—103) с на 408 МГц можно использовать для
оценки относительной скорости рассеивающего экрана по формуле A3.141). Зная
относительную скорость экрана, можно найти поперечную скорость пульсара. Ско-
Скорости и, следовательно, собственные движения пульсаров, оцененные таким мето-
методом (Lyne and Smith, 1982), согласуются со значениями, непосредственно измерен-
измеренными с помощью интерферометров [см., например, (Campbell et al., 1996)]. Была
также измерена поперечная компонента орбитальной скорости двойного пульсара
(Lyne, 1984).
518 Эффекты распространения [Гл.13
Наблюдения показывают, что флуктуации электронной плотности молено опи-
описать степенным спектром с показателем степени 3,7 ± 0,3, что близко к значению
11/3 для колмогоровской турбулентности (Rickett, 1990; Cordes, Pidwerbetsky and
Lovelace, 1986). Степенной спектр простирается в пределах размеров от менее чем
1010 см до более чем 1015 см. Внутренний размер может устанавливаться гирочасто-
той протонов (~107см), а внешний — шкалой высот Галактики (~1020 см). Наблю-
Наблюдательные потдверждения наличия внутреннего характерного размера приведены
в работе (Spangler and Gwinn, 1990).
Многочисленные измерения угловых размеров внегалактических радиоисточни-
радиоисточников были использованы для получения приближенной формулы для 0s в рамках
модели гауссового экрана [см. (Harris, Zeissig and Lovelace, 1970; Readhead and
Hewish, 1972; Cohen and Cronyn, 1974; Duffett-Smith and Readhead, 1976) и др.].
(мсек дуги), \b\ > 15° A3.202)
где b — галактическая широта, а Л — длина волны в метрах. Пульсарные данные
интерпретировались Кордесом (Cordes, 1984) в рамках степенной модели для полу-
получения приближенных формул для 6S.
6S ~ 7,5 Л11/5 (сек дуги), \Ь\ ^ 0°,6,
~ 0,5 | sin6|-3/5 Лп/5 (Сек дуги), 0°,6 < \Ь\ < 3° - 5°, A3.203)
~ 13 | sin6|-3/5 Лп/5 (Мсек дуги), \Ь\ ^ 3° - 5°.
Точность выражений A3.203) падает с уменьшением \Ь\. В частности, угол рассея-
рассеяния на низких широтах \Ь\ < 1°, может иметь большой разброс (Cordes, Ananthakr-
ishnan and Dennison, 1984). Намного более подробная модель с 23 параметрами,
характеризующими распределение электронов в Галактике, была разработана Тей-
Тейлором и Кордесом (Taylor and Cordes, 1993). На основании этой модели можно
получить более точные оценки 0s.
Примером компактного радиоисточника, испытывающего сильное межзвездное
рассеяние, является Sagittarius А*, находящийся в центре нашей Галактики. Этот
источник имеет угловой размер около 15 мсек дуги на длине волны волне 3,6 см [по
сравнению с значением 7,7мсек, следующим из A3.203)]. Угловой размер меняется
приблизительно как квадрат длины волны во всем диапазоне измерений от 1,3 до
30 см, как показано на рис. 13.25. Данные на Л = 0,7 и 0,3 см позволяют предполо-
предположить, что структуру источника можно увидеть на Л < 0,7мм (Lo et al., 1998).
Межзвездное рассеяние, возможно, налагает физический предел на измерения
угловых размеров, которые могут быть выполнены с помощью интерферометра.
Видимые размеры межзвездных мазеров, которые обнаружены в Галактике, в ос-
основном, на низких галактических широтах, иногда подвержены влиянию межзвезд-
межзвездного рассеяния (Gwinn et al., 1988).
13.6.3. Рефракционное рассеяние. Вывод Зибера (Sieber, 1982), что ха-
характерный период амплитудных мерцаний пульсаров на протяжений дней и ме-
месяцев коррелирует с их мерами дисперсий привела Риккетта, Коулса и Бургуа
(Rickett, Coles and Bourgois, 1984) к отождествлению другого важного размера
в турбулентной межзвездной среде — рефракционного масштаба dTef. Рефракцион-
Рефракционный масштаб — это размер дифракционного кружка рассеяния, который является
проекцией конуса расеянного излучения на рассеивающий экран, расположенный
на расстоянии R от наблюдателя. Размер дифракционного диска равен R0s. Кружок
рассеяния представляет собой максимальную область на экране, излучение из кото-
которой может прийти к наблюдателю. При степенном распределении неоднородностей
13.6]
Межзвездная среда
519
1 10
Длина волны, см
100
Рис. 13.25. Зависимость углового размера компактного источника в центре Галактики
(Sgr А*) от длины волны. Рассеяние слегка анизотропно [например, (Lo et al., 1998)],
и каждая точка на графике — среднее геометрическое угловых диаметров по прямому
восхождению и склонению. Прямая, проходящая через данные, имеет вид 0s = 1,04А2'0,
где 6S выражено в мсек дуги, а Л — в см. Зависимость Л2'0 говорит о том, что все
базы интерферометра A0 ми меньше) меньше внутреннего месштаба турбулентности
[см. A3.168) и A3.171)]
он соответствует неоднородностям самого большого доступного масштаба, которые
имеют самую большую амплитуду и дают наибольший вклад. Таким образом, ре-
рефракционный размер равен dre{ ~ R6S. Так как 6S = A/<io, где do — дифракционный
размер, определяемый как Т>ф^о) = 1? т0
ДА
do
или
dFri
esnel
do
A3.204)
A3.205)
где dpresnei = VRX — френелевский радиус. Размеры dTef и do сильно отличаются.
Значит, характерный временной масштаб tref = dref/vs, связанный с мерцаниями
при скорости экрана г>5, намного больше масштаба времени ^if = d^/vs, связанного
с дифракционными мерцаниями. Предположим, что мы наблюдаем на длине волны
0,5 м источник, расположенный на расстоянии 1 кпк на Ъ ~ 20°, через рассеивающий
экран. В этом случае дифракционный масштаб равен 2 • 109 см, френелевский ра-
радиус составляет 4 • 1011 см, а рефракционный масштаб равен 8 • 1013 см. Типичные
скорости, связанные с межзвездной средой, равны 100 км/с (Rickett, Coles and
Bourgois, 1984). При таких скоростях дифракционные и рефракционные временные
масштабы составляют 3 минуты и 3 месяца соответственно.
Считается, что рефракционное рассеяние ответственно за медленные вариации
амплитуды, наблюдаемые у некоторых пульсаров и квазаров на метровых и деци-
дециметровых волнах. Такое заключение позволило решить давно известную проблему
«переменности на длинных волнах», которую нельзя было объяснить моделями
внутренней переменности, основанными на синхротронном излучении. Выявление
520 Эффекты распространения [Гл.13
двух масштабов в межзвездной среде дает сильные аргументы в пользу степенной
модели. Эти два масштаба дают возможность оценить показатель степени, так как
относительный вклад рефракционного рассеяния возрастает с ростом крутизны
спектра. Интересно, что эти два масштаба проявляются у явления со степенным
законом, где нет собственного размера. Размеры связаны с распространением и за-
зависят от длины волны и расстояния до экрана.
Кроме амплитудных мерцаний, рефракционное рассеяние является причиной
видимых блужданий углового положения источника во времени. Амплитуда и вре-
временной масштаб примерно равны 0s и ?ref соответственно. Характер этих блужда-
блужданий зависит от показателя степени флуктуации. Предел показателя степени был
получен из предела амплитуды блужданий относительных положений скоплений
мазеров (Gwinn et al., 1988).
Редкие неожиданные изменения интенсивности нескольких внегалактических
источников, которые называются событиями Фидлера, или случаями предельного
рассеяния (Fiedler et al., 1987), вероятно, вызваны рефракционным рассеянием
в межзвездной среде. В классическом примере плотность потока внегалактического
источника 0954+658 увеличилась на 30%, а затем упала на 50% в течение месяца,
после чего симметричным образом восстановилась. Скорее всего, между источни-
источником и Землей перемещалось большое облако плазмы, вызывая изменения плотности
потока из-за фокусировки и преломления.
Так как имеется два временных масштаба, связанных с сильным рассеянием,
то при построении изображений на основе интерферометрических данных, полу-
полученных за время ^nt, выделяются три режима усреднения, а именно: t-int > tref
(изображение, усредненное по ансамблю), ?ref > tint > ?<ш (среднее изображение),
и ^int < ^dif (мгновенное изображение). Характеристики этих режимов построения
изображения описаны в работах (Narayan, 1992; Narayan and Goodman, 1989; Good-
Goodman and Narayan, 1989). При усреднении по ансамблю [см A3.168)—A3.170)] изоб-
изображение представляет собой свертку с соответствующей функцией пропускания.
Режим мгновенных изображений открывает захватывающие возможности восста-
восстановления изображений. В этом режиме возможно получить изображение источника
с разрешением X/dref, что может намного превосходить разрешение, достижимое на
наземных интерферометрах. В этом случае рассеивающий экран служит апертурой
интерферометра. Так как рефракционное рассеяние обеспечивает многолучевое
распространение, когда к наблюдателю приходит излучение от далеко разнесенных
участков рассеивающего экрана, то эффективные базы могут быть очень большими.
См. разд. 14.3 для дальнейшей дискуссии, включающей результаты наблюдений
Вольжана и Кордеса (Wolszczan and Cordes, 1987).
Основная литература
Baldwin J. E. and Wang Shougun. Eds., Radio Astronomical Seeing, International Academic
Publishers and Pergamon Press, Oxford, 1990.
Cordes J. M., B. J. Rickett and D. C. Backer. Radio Wave Scattering in the Interstellar
Medium, American Institute of Physics Conference Proceedings 174, New York, 1988.
Janssen M. A. Atmospheric Remote Sensing by Microwave Radiometry, Wiley, New York,
1993.
Narayan R. The Physics of Pulsar Scintillation, Phil. Tran. R. Soc. Lond. A, 341, 151-165,
1992.
Tatarski V. I. Wave Propagation in a Turbulent Medium, Dover, New York, 1961.
Westwater R. Ed., Specialist Meeting on Microwave Radiometry and Remote Sensing Appli-
Applications, National Oceanic and Atmospheric Administration, U. S. Dept. Commerce, 1992.
13.6] Цитированная литература 521
Цитированная литература
Aarons J. Global Morphology of Ionospheric Scintillations, Proc. IEEE, 70, 360-378, 1982.
Aarons J., J. A. Klobuchar, H. E. Whitney, J. Austen, A. L. Johnson, and C. L. Rino.
Gigahertz Scintillations Associated with Equatorial Patches, Radio Sci., 18, 421-434, 1983.
Aarons J., M. Mendillo, B. Lin, M. Colerico, T. Beach, P. Kintner, J. Scali, B. Reinisch,
G. Sales and E. Kudeki. Equatorial F-Region Irregularity Morphology during an Equinoctial
Month at Solar Minimum, Space Science Reviews, 87, 357-386, 1999.
Allen C. W. Interpretation of Electron Densities from Corona Brightness, Mon. Not. R. Astron.
Soc, 107, 426-432, 1947.
Altenhoff W. J., J. W. M. Baars, D. Downes and J. E. Wink. Observations of Anomalous
Refraction at Radio Wavelengths, Astron. Astrophys., 184, 381-385, 1987.
Appleton E. V. and M. A. F. Barnett. On Some Direct Evidence for Downward Atmospheric
Reflection of Electric Rays, Proc. R. Soc. Lond. A, 109, 621-641, 1925.
Armstrong J. W. and R. A. Sramek. Observations of Tropospheric Phase Scintillations at 5
GHz on Vertical Paths, Radio Sci., 17, 1579-1586, 1982.
Baars J. W. M. Meteorological Influences on Radio Interferometer Phase Fluctuations, IEEE
Trans. Antennas Propag., AP-15, 582-584, 1967.
Bailey D. K. On a New Method of Exploring the Upper Atmosphere, J. Terr. Mag. Atmos.
Elec, 53, 41-50, 1948.
Bean B. R., B. A. Cahoon, C. A. Samson and G. D. Thayer. A World Atlas of Atmospheric
Refractivity, U.S. Government Printing Office, Washington, DC, 1966.
Bean B. R. and E. J. Button. Radio Meteorology, National Bureau of Standards Monograph
92, U.S. Government Printing Office, Washington, DC, 1966.
Beynon W. J. G. Marconi, Radio Waves and the Ionosphere, Radio Sci., 10, 657-664, 1975.
Bieging J. H., J. Morgan, J. H., J. Morgan, W. J. Welch, S. N. Vogel, and M. С. Н. Wright.
Interferometer Measurements of Atmospheric Phase Noise at 86 GHz, Radio Sci., 19, 1505-
1509, 1984.
Bilitza D. International Reference Ionosphere - Status 1995/96, Adv. Space Res., 20, 1751-
1754, 1997.
Bohlander R. A., R. W. McMillan and J. J. Gallagher. Atmospheric Effects on Near-Millimeter-
Wave Propagation, Proc. IEEE, 73, 49-60, 1985.
Booker H. G. The Use of Radio Stars to Study Irregular Refraction of Radio Waves in the
Ionosphere, Proc. IRE, 46, 298-314, 1958.
Booker H. G., J. A. Ratcliffe and D. H. Shinn. Diffraction from an Irregular Screen with
Applications to Ionospheric Problems, Philos. Tran. R. Soc. Lond. A, 242, 579-607, 1950.
Bracewell R. N. The Fourier Transform and Its Applications, 3rd ed., McGraw-Hill, New York,
2000.
Bracewell R. N., V. R. Eshleman and J. V. Hollweg. The Occulting Disk of the Sun at Radio
Wavelengths, Astrophys. J., 155, 367-368, 1969.
Breit G. and M. A. Tuve. A Test of the Existence of the Conducting Layer, Phys. Rev., 28,
554-575, 1926.
Budden K. G. Radio Waves in the Ionosphere, Cambridge Univ. Press, Cambridge, UK, 1961.
Burn B. J. On the Depolarization of Discrete Radio Sources by Faraday Dispersion, Mon. Not.
R. Astron. Soc, 133, 67-83, 1966.
Butler B. Precipitable Water at the VLA - 1990-1998, MMA Memo. 237, Nat. Radio Astron.
Obs., Socorro, NM, 1998.
Campbell R. M., N. Bartel, I. I. Shapiro, M. I. Ratner, R. J. Cappallo, A. R. Whitney and
N. Putnam. VLBI-Derived Trigonometric Parallax and Proper Motion of PSR B2021+51,
Astrophys. J., 461, L95-L98, 1996.
522 Эффекты распространения [Гл.13
Carilli С. L. and М. A. Holdaway. Tropospheric Phase Calibration in Millimeter Interferometry,
Radio Science, 34, 817-840, 1999.
Chamberlin R. A. and J. Bally. The Observed Relationship Between the South Pole 225-GHz
Atmospheric Opacity and the Water Vapor Column Density, Int. J. Infrared and Millimeter
Waves, 16, 907-920, 1995.
Chamberlin R. A., A. P. Lane and A. A. Stark. The 492 GHz Atmospheric Opacity at the
Geographic South Pole, Astrophys. J., 476, 428-433, 1997.
Chylek P. and D. J. W. Geldart. Water Vapor Dimers and Atmospheric Absorption of Elec-
Electromagnetic Radiation, Geophys. Res. Lett., 24, 2015-2018, 1997.
Clarke M. Two Topics in Radiophysics, Ph.D. thesis, Cambridge Univ., 1964 (see App. II).
COESA, U.S. Standard Astmosphere, 1976, NOAA-S/T 76-1562, U.S. Government Printing
Office, Washington, DC, 1976.
Cohen M. H. High-Resolution Observations of Radio Sources, Ann. Rev. Astron, Astrophys.,
7, 619-664, 1969.
Cohen M. H. and W. M. Cronyn. Scintillation and Apparent Angular Diameter, Astrophys.
J., 192, 193-197, 1974.
Cohen M. H., E. J. Gundermann, H. E. Hardebeck and L. E. Sharp. Interplanetary Scintilla-
Scintillations. II Observations, Astrophys. J., 147, 449-466, 1967.
Cohen M. H., E. J. Gundermann and D. E. Harris. New Limits on the Diameters of Radio
Sources, Astrophys. J., 150, 767-782, 1967.
Cordes J. M. Interstellar Scattering. VLBI and Compact Radio Sources, IAU Symp. 110, R.
Fanti, K. Kellermann and G. Setti, Eds., Reidel, Dordrecht, 1984, p. 303-307.
Cordes J. M. Interstellar Scattering: Radio Sensing of Deep Space through the Turbulent
Interstellar Medium. Radio Astronomy at Long Wavelengths, R. G. Stone, K. W. Weiler, M.
L. Goldstein and J.-L. Bougeret, Eds., Geophysical Monograph 119, Am. Geophys. Union, p.
105-114, 2000.
Cordes J. M.j S. Ananthakrishnan and B. Dennison. Radio Wave Scattering in the Galactic
Disk, Nature, 309, 689-691, 1984.
Cordes J. M.j A. Pidwerbetsky and R. V. E. Lovelace. Refractive and Diffractive Scattering in
the Interstellar Medium, Astrophys. J., 310, 737-767, 1986.
Coulman С. Е. Fundamental and Applied Aspects of Astronomical "Seeing", Ann. Rev. Astron.
Astrophys., 23, 19-57, 1985.
Coulman С. Е. Atmospheric Structure, Turbulence and Radioastronomical "Seeing". Radio
Astronomical Seeing, J. E. Baldwin and Wang Shouguan, Eds., International Academic Pub-
Publishers and Pergamon Press, Oxford, 1990, p. 11-20
Counselman C. C, III., S. M. Kent, C. A. Knight, I. I. Shapiro, T. A. Clark, H. F. Hinteregger,
A. E. E. Rogers and A. R. Whitney. Solar Gravitational Deflection of Radio Waves Measured
by Very-Long-Baseline Interferometry, Phys. Rev. Lett., 33, 1621-1623, 1974.
Counselman C. C, III and J. M. Rankin. Density of the Solar Corona from Occupations of
NP0532, Astrophys. J., 175, 843-856, 1972.
Cox A. N. Ed., Allen's Astrophysical Quantities, 4th ed., AIP Press, New York, Springer,
2000, Sec. 11.20, p. 262.
Crane R. K. Refraction Effects in the Neutral Atmosphere, in Methods of Experimental
Physics, Vol. 12B, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 186-200.
Crane R. K. Ionospheric Scintillation, Proc. IEEE, 65, 180-199, 1977.
Crane R. K. Fundamental Limitations Caused by RF Propagation, Proc. IEEE, 69, 196-209,
1981.
Daniell R. E., L. D. Brown, D. N. Anderson, M. W. Fox, P. H. Doherty, D. T. Decker, J. J.
Sojka and R. W. Schunk. Parameterized Ionospheric Model: A Global Ionospheric Parameter-
Parameterization Based on First Principles Models, Radio Sci., 30, 1499-1510, 1995.
13.6] Цитированная литература 523
Davies К. Ionospheric Radio Propagation, National Bureau of Standards Monograph 80, U.S.
Government Printing Office, Washington, DC, 1965.
Davis J. L., T. A. Herring, I. I. Shapiro, A. E. E. Rogers and G. Elgered. Geodesy by Radio
Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length, Radio
Sci., 20, 1593-1607, 1985.
Debye P. Polar Molecules, Dover, New York, 1929.
Delgado G., A. Otdrola, V. Belitsky and D. Urbain. The Determination of Precipitable Water
Vapour at Llano de Chajnantor from Observations of the 183 GHz Water Line, ALMA Memo
271, National Radio Astronomy Observatory, Socorro, NM, 1998
Downes D. and W. J. Altenhoff. Anomalous Refraction at Radio Wavelengths, in Radio Astro-
Astronomical Seeing, J. E. Baldwin and Wang Shouguan, Eds., International Academic Publishers
and Pergamon Press, Oxford, 1990, p. 31-40.
Duffett-Smith P. J. and A. C. S. Readhead. The Angular Broadening of Radio Sources by
Scattering in the Interstellar Medium, Mon. Not. R. Astron. Soc, 174, 7-17, 1976.
Elgered G., J. L. Davis, T. A. Herring and I. I. Shapiro. Geodesy by Radio Interferometry:
Water Vapor Radiometry for Estimation of the Wet Delay, J. Geophys. Res., 96, 6541-6555,
1991.
Elgered G., B. O. Ronnang and J. I. H. Askne. Measurements of Atmospheric Water Vapor
with Microwave Radiometry, Radio Sci., 17, 1258-1264, 1982.
Erickson W. C. The Radio-Wave Scattering Properties of the Solar Corona, Astrophys. J.,
139, 1290-1311, 1964.
Evans J. V. Theory and Practice of Ionospheric Study by Thomson Scatter Radar, Proc. IEEE,
57, 496-530, 1969.
Evans J. V. and T. Hagfors. Radar Astronomy, McGraw-Hill, New York, 1968.
Evans J. V., J. M. Holt and R. H. Wand. A Differential-Doppler Study of Traveling Ionospheric
Disturbances from Millstone Hill, Radio Sci., 18, 435-451, 1983.
Fejer B. G. and M. C. Kelley. Ionospheric Irregularities, Rev. Geophys. Space Sci., 18, 401-
454, 1980.
Fiedler R. L., B. Dennison, K. J. Johnston and A. Hewish. Extreme Scattering Events Caused
by Compact Structures in the Interstellar Medium, Nature, 326, 675-678, 1987.
Fomalont E. B. and R. A. Sramek. A Confirmation of Einstein's General Theory of Relativity
by Measuring the Bending of Microwave Radiation in the Gravitational Field of the Sun,
Astrophys. J., 199, 749-755, 1975.
Fomalont E. B. and R. A. Sramek. The Deflection of Radio Waves by the Sun, Comments
Astrophys., 7, 19-33, 1977.
Frail D. A., S. R. Kulkarni, L. Nicastro, M. Ferocl and G. B. Taylor. The Radio Afterglow
from the 7-ray Burst of 8 May 1997, Nature,389, 261-263, 1997.
Freeman R. L. Radio System Design for Telecommunications A-100 GHz), Wiley, New York,
1987.
Fried D. L. Optical Resolution Through a Randomly Inhomogeneous Medium for Very Long
and Very Short Exposures, J. Opt. Soc. Am., 56, 1372-1379, 1966.
Fried D. L. Optical Heterodyne Detection of an Atmospherically Distorted Signal Wave Front,
Proc. IEEE, 55, 57-67, 1967.
Gardner F. F. and J. B. Whiteoak. The Polarization of Cosmic Radio Waves, Ann. Rev.
Astron. Astrophys., 4, 245-292, 1966.
Goldstein H. Attenuation by Condensed Water, in Propagation of Short Radio Waves, MIT
Radiation Laboratory Series, Vol. 13, D. E. Kerr, Ed., McGraw-Hill, New York, 1951, p. 671.
Goodman J. and R. Narayan. The Shape of a Scatter-Broadened Image: II. Interferometric
Visibilities, Mon. Not. R. Astron. Soc, 238, 995-1028, 1989.
Guiraud F. O., J. Howard and D. C. Hogg. A Dual-Channel Microwave Radiometer for
Measurement of Preciptable Water Vapor and Liquid, IEEE Trans. Geosci, Electron., GE-17,
129-136, 1979.
524 Эффекты распространения [Гл.13
Gupta Y. Pulsars and Interstellar Scintillations. Pulsar Astrometry - 2000 and Beyond, M.
Kramer, N. Wex and R. Wielebinski. Eds., Astron. Soc. Pacific Conf. Ser., 202, 539-544, 2000.
Gwinn C. R., J. M. Moran, M. J. Reid and M. H. Schneps. Limits on Refractive Interstellar
Scattering Toward Saggitarius B2, Astrophys. J., 330, 817-827, 1988.
Hagfors T. The Ionosphere. Methods of Experimental Physics, Vol. 12B, M. L. Meeks, Ed.,
Academic Press, New York, 1976, p. 119-135.
Hamaker J. P. Atmospheric Delay Fluctuations with Scale Sizes Greater than One Kilometer,
Observed with a Radio Interferometer Array, Radio Sci., 13, 873-891, 1978.
Harris D. E.j G. A. Zeissig and R. V. Lovelace. The Minimum Observable Diameter of Radio
Sources, Astron. Astrophys., 8, 98-104, 1970.
Heiles C. The Interstellar Magnetic Field, Ann. Rev. Astron. Astrophys., 14, 1-22, 1976.
Hess S. L. Introduction to Theoretical Meteorology, Holt, Rinehart, Winston, New York, 1959.
Hewish A. The Diffraction of Galactic Radio Waves as a Method of Investigating the Irregular
Structure of the Ionosphere, Proc. R. Soc. Lond. A, 214, 494-514, 1952.
Hewish A., P. F. Scott and D. Wills. Interplanetary Scintillation of Small Diameter Radio
Sources, Nature, 203, 1214-1217, 1964.
Hey J. S., S. J. Parsons and J. W. Phillips. Fluctuations in Cosmic Radiation at Radio
Frequencies, Nature, 158, 234, 1946.
Hill R. J. Water Vapor-Absorption Line Shape Comparison Using the 22-GHz Line: the Van
Vleck-Weisskopf Shape Affirmed, Radio Sci., 21, 447-451, 1986.
Hill R. J. and S. F. Clifford. Contribution of Water Vapor Monomer Resonances to Fluctuations
of Refraction and Absorption for Submillimeter through Centimeter Wavelengths, Radio
Sci.,16, 77-82, 1981.
Hill R. J., R. S. Lawrence and J. T. Priestly. Theoretical and Calculational Aspects of the
Radio Refractive Index of Water Vapor, Radio Sci., 17, 1251-1257, 1982.
Hills R. E., A. S. Webster, D. A. Alston, P. L. R. Morse, C. C. Zammit, D. H. Martin, D. P.
Rice and E. I. Robson. Absolute Measurements of Atmospheric Emission and Absorption in
the Range 100-1000 GHz, Infrared Phys., 18, 819-825, 1978.
Hinder R. A. Observations of Atmospheric Turbulence with a Radio Telescope at 5 GHz,
Nature, 225, 614-617, 1970.
Hinder R. A. Fluctuations of Water Vapour Content in the Troposphere as Derived from
Interferometric Observations of Celestial Radio Sources, J. Atmos. Terr. Phys., 34, 1171-
1186, 1972.
Hinder R. A. and M. Ryle. Atmospheric Limitations to the Angular Resolution of Aperture
Synthesis Radio Telescopes, Mon. Not. R. Astron. Soc, 154, 229-253, 1971.
Ho C. M., A. J. Mannucci, U. J. Lindqwister, X. Pi and В. Т. Tsurutani. Global Ionospheric
Perturbations Monitored by the Worldwide GPS Network, Geophys. Res. Lett., 23, 3219-
3222, 1996.
Ho C. M.j B. D. Wilson, A. J. Mannucci, U. J. Lindqwister and D. N. Yuan. A Comparative
Study of Ionospheric Total Electron Content Measurements Using Global Ionospheric Maps of
GPS, TOPEX Radar and the Bent Model, Radio Sci., 32, 1499-1512, 1997.
Hocke K. and K. Schlegel. A Review of Atmospheric Gravity Waves and Travelling Ionospheric
Disturbances: 1982-1995, Ann. Geophysicae, 14, 917-940, 1996.
Hogg D. G, F. O. Guiraud and W. B. Sweezy. The Short-Term Temporal Spectrum of
Precipitable Water Vapor, Science, 213, 1112-1113, 1981.
Holdaway M. A., M. Ishiguro, S. M. Foster, R. Kawabe, K. Kohno, F. N. Owen, S. J. E.
Radford and M. Saito. Comparison of Rio Frio and Chajnantor Site Testing Data, MMA
Memo 152, National Radio Astronomy Observatory, Socorro, NM, 1996.
Holdaway M. A., S. J. E. Radford, F. N. Owen and S. M. Foster. Fast Switching Phase
Calibration: Effectiveness at Mauna Kea and Chajnantor, MMA Memo 139, National Radio
Astronomy Observatory, Socorro, NM, 1995.
13.6] Цитированная литература 525
Holt Е. Н. and R. Е. Haskell. Foundations of Plasma Dynamics, Macmillan, New York, 1965,
p. 254.
Humphreys W. J. Physics of the Air, 3rd ed., McGraw-Hill, New York, 1940.
Hunsucker R. D. Atmospheric Gravity Waves Generated in the High-Latitude Ionosphere: A
Review, Rev. Geophys. Space Phys., 20, 293-315, 1982.
Ishiguro M., T. Kanzawa and T. Kasuga. Monitoring of Atmospheric Phase Fluctuations
Using Geostationary Satellite Signals, in Radio Astronomical Seeing, J. E. Baldwin and Wang
Shouguan, Eds., International Academic Publishers and Pergamon Press, Oxford, 1990, p. 60-
63.
Jackson J. D. Classical Electrodynamics, 3rd ed., Wiley, New York, 1999, p. 775-784.
Jaeger J. C. and К. C. Westfold. Equivalent Path and Absorption for Electromagnetic Radi-
Radiation in the Solar Corona, Aust. J. Phys., 3, 376-386, 1950.
Kaplan G. H., F. J. Josties, P. E. Angerhofer, K. J. Johnston and J. H. Spencer. Precise
Radio Source Positions from Interferometric Observations, Astron. J., 87, 570-576, 1982.
Kasuga Т., M. Ishiguro and R. Kawabe. Interferometric Measurement of Tropospheric Phase
Fluctuations at 22 GHz on Antenna Spacings of 27 to 540 m, IEEE Trans. Antennas Propag.,
AP-34, 797-803, 1986.
Kundu M. R. Solar Radio Astronomy, Wiley-Interscience, New York, 1965, p. 104.
Lawrence R. S., C. G. Little and H. J. A. Chivers. A Survey of Ionospheric Effects upon Earth-
Space Radio Propagation, Proc. IEEE, 52, 4-27, 1964.
Lay O. P. The Temporal Power Spectrum of Atmospheric Fluctuations Due to Water Vapor,
Astron. Astrophys. Suppl., 122, 535-545, 1997a.
Lay O. P. Phase Calibration and Water Vapor Radiometry for Millimeter-Wave Arrays,
Astron. Astrophys. Suppl., 122, 547-557, 1997b.
Lay O. P. 183 GHz Radiometric Phase Correction for the Millimeter Array, MMA Memo. 209,
National Radio Astronomy Observatory, Socorro, NM, 1998.
Lazio T. J. W. and J. M. Cordes. Hyperstrong Radio-Wave Scattering in the Galactic Center.
I. A Survey for Extragalactic Sources Seen through the Galactic Center, Astrophys. J. Suppl.,
118, 201-216, 1998.
Lebach D. E., B. E. Corey, I. I. Shapiro, M. I. Ratner, J. C. Webber, A. E. E. Rogers, J. L.
Davis and T. A. Herring. Measurements of the Solar Deflection of Radio Waves Using Very
Long Baseline Interferometry, Phys. Rev. Lett., 75, 1439-1442, 1995.
Liebe H. J. Calculated Tropospheric Dispersion and Absorption Due to the 22-GHz Water
Vapor Line, IEEE Trans. Antennas Propag., AP-17, 621-627, 1969.
Liebe H. J. Modeling Attenuation and Phase of Radio Waves in Air at Frequencies below 1000
GHz, Radio Sci., 16, 1183-1199, 1981.
Liebe H. J. An Updated Model for Millimeter Wave Propagation in Moist Air, Radio Sci., 20,
1069-1089, 1985.
Liebe H. J. MPM-An Atmospheric Millimeter-Wave Propagation Model, Int. J. Infrared and
MM Waves, 10, 631-650, 1989.
Little L. T. and A. Hewish. Interplanetary Scintillation and Relation to the Angular Structure
of Radio Souces, Mon. Not. R. Astron. Soc, 134, 221-237, 1966.
Lo K. Y., Z.-Q. Shen, J. H. Zhao and P. Т. Р. Но. Instrinsic Size of Sagittarius A*: 72
Schwarzschild Radii, Astrophys. J., 508, L61-L64, 1998.
Loudon R. The Quantum Theory of Light, 2nd ed., Oxford Univ. Press, London, 1983.
Lyne A. G. Orbital Inclination and Mass of the Binary Pulsar PSR0655+64, Nature, 310,
300-302, 1984.
Lyne A. G. and F. G. Smith. Interstellar Scintillation and Pulsar Velocities, Nature, 298,
825-827, 1982.
526 Эффекты распространения [Гл.13
Mannucci A. J., В. D. Wilson, D. N. Yuan, С. Н. Но, U. J. Lindqwister and Т. F. Runge.
A Global Mapping Technique for GPS-Derived Ionospheric Total Electron Content Measure-
Measurements, Radio Sci., 33, 565-582, 1998.
Marini J. W. Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile,
Radio Sci., 7, 223-231, 1972.
Masson C. R. Atmospheric Effects and Calibrations. Astronomy with Millimeter and Submil-
limeter Wave Interferometry, M. Ishiguro and W. J. Welch. Eds., Astron. Soc. Pacific Conf.
Series 59, 87-95, 1994a.
Masson C. R. Seeing. Very High Angular Resolution Imaging, J. G. Robertson and W. J.
Tango. Eds., IAU Symposium 158, Kluwer, Dordrecht, 1994b, p. 1-10.
Mathur N. G, M. D. Grossi and M. R. Pearlman. Atmospheric Effects in Very Long Baseline
Interferometry, Radio Sci., 5, 1253-1261, 1970.
Matsushita S., H. Matsuo, J. R. Par do and S. J. E. Radford. FTS Measurements of
Submillimeter-Wave Atmospheric Opacity at Pampa la Bola II: Supra-Terahertz Windows
and Model Fitting, Pub. Ast. Soc. Japan, 51, 603-610, 1999.
Mercier R. P. Diffraction by a Screen Causing Large Random Phase Fluctuations, Proc. R.
Soc. Lond. A, 58, 382-400, 1962.
Miner G. F., D. D. Thornton and W. J. Welch. The Inference of Atmospheric Temperature
Profiles from Ground-Based Measurements of Microwave Emission from Atmospheric Oxygen.
J. Geophys. Res., 77, 975-991, 1972.
Misner C. W.j K. S. Thome and J. A. Wheeler. Gravitation, Freedman, San Francisco, 1973,
Sec. 40.3.
Мог an J. M. The Effects of Propagation on VLBI Observations. Very Long Baseline Inter-
Interferometry: Techniques and Applications, M. Felli and R. E. Spencer, Eds., Kluwer, Dordrecht,
1989, p. 47-59.
Moran J. M. and B. R. Rosen. Estimation of the Propagation Delay through the Troposphere
from Microwave Radiometer Data, Radio Sci., 16, 235-244, 1981.
Muhleman D. O., R. D. Ekers and E. B. Fomalont. Radio Interferometric Test of the General
Relavistic Light Bending Near the Sun, Phys. Rev. Lett., 24, L1377-L1380, 1970.
Narayan R. From Scintillation Observations to a Model of the ISM-The Inverse Problem.
Radio Wave Scattering in the Interstellar Medium, J. M. Cordes, B. J. Rickett and D. C.
Backer. Eds., American Institute of Physics Conf. Proc. 174, New York, 1988, p. 17-31.
Narayan R. The Physics of Pulsar Scintillation, Phil. Tran. R. Soc. Lond. A, 341, 151-165,
1992.
Narayan R., K. R. Anantharamaiah and T. J. Cornwell. Refractive Radio Scintillation in the
Solar Wind, Mon. Not. R. Astron. Soc, 241, 403-413, 1989.
Narayan R. and J. Goodman. The Shape of a Scatter-Broadened Image: I. Numerical Simula-
Simulations and Physical Principles, Mon. Not. R. Astron. Soc, 238, 963-994, 1989.
Niell A. E. Global Mapping Functions for the Atmospheric Delay at Radio Wavelengths, J.
Geophys Res., 101, 3227-3246, 1996.
NRAO, Recommended Site for the Millimeter Array, National Radio Astronomy Observatory,
Charlottesville, VA, May 1998.
Olmi L. and D. Downes. Interferometric Measurement of Tropospheric Phase Fluctuations at
86 GHz on Antenna Spacings of 24 m to 288 m, Astron. Astrophys., 262, 634-643, 1992.
Owens J. C. Optical Refractive Index of Air: Dependence on Pressure, Temperature and
Composition, Appl. Opt., 6, 51-58, 1967.
Paine S., R. Blundell, D. C. Papa, J. W. Barrett and S. J. E. Radford. A Fourier Transform
Spectrometer for Measurement of Atmospheric Transmission at Submillimeter Wavelengths,
Pub. Astron. Soc. Pacific, 112, 108-118, 2000.
Pardo J. R., E. Serabyn and J. Cernicharo. Submillimeter Atmospheric Transmission Mea-
Measurements on Mauna Kea During extremely Dry El Nino conditions, J. Quant. Spect. and
Rad. Trans., 68, 419-433, 2001.
13.6] Цитированная литература 527
Pi X., A. J. Mannucci, U. J. Lindqwister and С. M. Ho. Monitoring of Global Ionospheric
Irregularities Using the Worldwide GPS Network, Geophys. Res. Lett., 24, 2283-2286, 1997.
Pol S. L. С, С S. Ruf and S. J. Keihm. Improved 20- to 32-GHz Atmospheric Absorption
Model, Radio Sci., 33, 1319-1333, 1998.
Radford S. J. E. and R. A. Chamberlin. Atmospheric Transparency at 225 GHz over Cha-
jnantor, Mauna Kea and the South Pole, ALMA Memo. 334, National Radio Astronomy
Observatory, Socorro, New Mexico, 2000.
Radford S. J. E., G. Reiland and B. Shillue. Site Test Interferometer, Pub. Astron. Soc.
Pacific, 108, 441-445, 1996.
Ratcliffe J. A. Some Aspects of Diffraction Theory and Their Application to the Ionosphere,
Rep. Prog. Phys., 19, 188-267, 1956.
Ratcliffe J. A. The Magneto-Ionic Theory and Its Application to the Ionosphere, Cambridge
Univ. Press, Cambridge, UK, 1962.
Rawer K. The Ionosphere. Ungar, New York, 1956.
Ray P. S. Broadband Complex Refractive Indices of Ice and Water, Applied Optics, 11, 1836-
1843, 1972.
Readhead A. C. S. and A. Hewish. Galactic Structure and the Apparent Size of Radio Sources,
Nature, 236, 440-443, 1972.
Reber E. E. and J. R. Swope. On the Correlation of Total Precipitable Water in a Vertical
Column and Absolute Humidity, J. Appl. Meteorol., 11, 1322-1325, 1972.
Resch G. M. Water Vapor Radiometry in Geodetic Applications, in Geodetic Aspects of
Electromagnetic Wave Propagation through the Atmosphere, F. K. Brunner, Ed., Springer-
Verlag, Berlin, 1984.
Rickett B. J. Radio Propagation through the Turbulent Interstellar Medium, Ann. Rev. Astron.
Astrophys., 28, 561-605, 1990.
Rickett B. J., W. A. Coles and G. Bourgois. Slow Scintillation in the Interstellar Medium,
Astron. Astrophys., 134, 390-395, 1984.
Roberts D. H., A. E. E. Rogers, B. R. Allen, С L. Bennet, B. F. Burke, P. E. Greenfield,
C. R. Lawerence and T. A. Clark. Radio Interferometric Detection of a Traveling Ionospheric
Disturbance Excited by the Explosion of Mt. St. Helens, J. Geophys. Res., 87, 6302-6306,
1982.
Robertson D. S., W. E. Carter and W. H. Dillinger. New Measurement of Solar Gravitational
Deflection of Radio signals using VLBI, Nature, 349, 768-770, 1991.
Roddier F. The Effects of Atmospheric Turbulence in Optical Astronomy, in Progress in Optics
XIX, E. Wolf, Ed., North-Holland, Amsterdam, 1981, p. 281-376.
Rogers A. E. E., A. T. Moffet, D. C. Backer and J. M. Moran. Coherence Limits in VLBI
Observations at 3-Millimeter Wavelength, Radio Sci., 19, 1552-1560, 1984.
Rogers A. E. E. and J. M. Moran. Coherence Limits for Very Long Baseline Interferometry,
IEEE Trans. Instrum. Meas., IM-30, 283-286, 1981.
Rosenkranz P. W. Water Vapor Microwave Continuum Absorption: A Comparison of Mea-
Measurements and Models, Radio Sci., 33, 919-928, 1998.
Rybicki G. B. and A. P. Lightman. Radiative Processes in Astrophysics, Wiley-Interscience,
New York, 1979 (reprinted 1985).
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction, Bull.
Geodesique, 106, 383-397, 1972a.
Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio
Ranging of Satellites. The Use of Artificial Satellites for Geodesy, Geophysical Monograph
15, American Geophysical Union, Washington, DC, 1972b, p. 247-251.
Salpeter E. E. Interplanetary Scintillations. I. Theory, Astrophys. J. 147, 433-448, 1967.
Schaper L. W., Jr., D. H. Staelin and J. W. Waters. The Estimation of Tropospheric Electrical
Path Length by Microwave Radiometry, Proc. IEEE, 58, 272-273, 1970.
528 Эффекты распространения [Гл.13
Scheuer P. A. G. Amplitude Variations in Pulsed Radio Sources, Nature, 218, 920-922, 1968.
Scott S. L., W. A. Coles and G. Bourgois. Solar Wind Observations Near the Sun Using
Interplanetary Scintillation, Astron. Astrophys., 123, 207-215, 1983.
Shapiro I. I. New Method for the Detection of Light Deflection by Solar Gravity, Science, 157,
806-808, 1967.
Shapiro I. I. Estimation of Astrometric and Geodetic Parameters, in Methods of Experimental
Physics, Vol. 12C, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 261-276.
Sieber W. Causal Relationship Between Pulsar Long-Term Intensity Variations and the Inter-
Interstellar Medium, Astron. Astrophys., 113, 311-313, 1982.
Simard-Normandin M. and P. P. Kronberg. Rotation Measures and the Galactic Magnetic
Field, Astrophys. J., 242, 74-94, 1980.
Smart W. M. Textbook on Spherical Astronomy, 6th ed., rev. R. M. Green, Cambridge Univ.
Press, Cambridge, UK, 1977.
Smith E. K., Jr. and S. Weintraub. The Constants in the Equation for Atmospheric Refractive
Index at Radio Frequencies, Proc. IRE, 41, 1035-1037, 1953.
Smith F. G., C. G. Little and А. С. В. Lovell. Origin of the Fluctuations in the Intensity of
Radio Waves from Galactic Sources, Nature, 165, 422-424, 1950.
Snider J. B. Ground-Based Sensing of Temperature Profiles from Angular and Multi-Spectral
Microwave Emission Measurements, J. Appl. Meteorol., 11, 958-967, 1972.
Snider J. В., H. M. Bur dick and D. C. Hogg. Cloud Liquid Measurement with a Ground-Based
Microwave Instrument, Radio Sci., 15, 683-693, 1980.
Solheim F., Godwin, J. R., Westwater, E. R., Han, Yong, Keihm, S. J., Marsh, K. and Ware
R. Radiometric Profiling of Temperature,, Water Vapor and Cloud Liquid Water Using Various
Inversion Methods, Radio Sci., 33, 393-404, 1998.
Spangler S. R. and C. R. Gwinn. Evidence for an Inner Scale to the Density Turbulence in the
Interstellar Medium, Astrophys. J., 353, L29-L32, 1990.
Spangler S. R. and T. Sakurai. Radio Interferometry of Solar Wind Turbulence from the Orbit
of Helios to the Solar Corona, Astrophys. J., 445, 999-1061, 1995.
Spitzer L. Physical Processes in the Interstellar Medium, Wiley-Interscience, New York, 1978,
p. 65.
Spoelstra Т. А. Т. The Influence of Ionospheric Refraction on Radio Astronomy Interferometry,
Astron. Astrophys., 120, 313-321, 1983.
Spoelstra Т. А. Т. and H. Kelder. Effects Produced by the Ionosphere on Radio Interferometry,
Radio Sci., 19, 779-788, 1984.
Sramek R. VLA Phase Stability at 22 GHz on Baselines of 100 m to 3 km, VLA Test Memo.
143, National Radio Astronomy Observatory, Socorro, NM, 1983.
Sramek R. A. Atmospheric Phase Stability at the VLA. Radio Astronomical Seeing, J. E.
Baldwin and Wang Shouguan, Eds., International Academic Publishers and Pergamon Press,
Oxford, 1990, p. 21-30.
Staelin D. H. Measurements and Interpretation of the Microwave Spectrum of the Terrestrial
Atmosphere near 1-Centimeter Wavelength, J. Geophys. Res., 71, 2875-2881, 1966.
Sutton E. C. and R. M. Hueckstaedt. Radiometric Monitoring of Atmospheric Water Vapor
as It Pertains to Phase Correction in Millimeter Interferometry, Astron. Astrophysics Suppl.,
119, 559-567, 1996.
Sutton E. C., S. Subramanian and С. Н. Townes. Interferometric Measurements of Stellar
Positions in the Infrared, Astron. Astrophys. 110, 324-331, 1982.
Tahmoush D. A. and A. E. E. Rogers. Correcting Atmospheric Variations in Millimeter
Wavelengh Very Long Baseline Interferometry Using a Scanning Water Vapor Radiometer,
Radio Science, 35, 1241-1251, 2000.
Tatarski V. I. Wave Propagation in a Turbulent Medium, Dover, New York, 1961.
13.6] Цитированная литература 529
Tatarski V. I. The Effects of the Turbulent Atmosphere on Wave Propagation, National
Technical Information Service, Springfield, VA, 1971.
Taylor G. I. Spectrum of Turbulence, Proc. Roy. Soc, 164A, 476-490, 1938.
Taylor J. H. and J. M. Cordes. Pulsar Distances and the Galactic Distribution of Free
Electrons, Astrophys. J., 411, 674-684, 1993.
Thayer G. D. An Improved Equation for the Radio Refractive Index of Air, Radio Sci., 9,
803-807, 1974.
Treuhaft R. N. and G. E. Lanyi. The Effect of the Dynamic Wet Troposphere on Radio
Interferometric Measurements, Radio Sci., 22, 251-265, 1987.
Van Vleck J. H., E. M. Purcell and H. Goldstein. Atmospheric Attenuation, in Propagation of
Short Radio Waves, MIT Radiation Laboratory Series, Vol. 13, D. E. Kerr, Ed., McGraw-Hill,
New York, 1951, p. 641-692.
Waters J. W. Absorption and Emission by Atmospheric Gases, in Methods of Experimental
Physics, Vol. 12B, M. L. Meeks, Ed., Academic Press, New York, 1976, p. 142-176.
Weinberg S. Gravitation and Cosmology: Principles and Applications of the General Theory
of Relativity, Wiley, New York, 1972, p. 188.
Weisberg J. M., J. Rankin and V. Boriakoff. HI Absorption Measurements of Seven Low
Latitude Pulsars, Astron. Astrophys., 88, 84-93, 1980.
Welch W. J. Correcting Atmospheric Phase Fluctuations by Means of Water-Vapor Radiome-
try. Review of Radio Science, 1996-1999, W. R. Stone. Ed., Oxford Univ. Press, Oxford, 1999,
p. 787-808.
Westwater E. R. An Analysis of the Correction of Range Errors Due to Atmospheric Refraction
by Microwave Radiometric Techniques, ESSA Technical Report IER 30-ITSA 30, Institute for
Telecommunication Sciences and Aeronomy, Boulder, CO, 1967.
Westwater E. R. The Accuracy of Water Vapor and Cloud Liquid Determination by Dual-
Frequency Ground-Based Microwave Radiometry, Radio Sci., 13, 677-685, 1978.
Westwater E. R. and F. O. Guiraud. Ground-Based Microwave Radiometric Retrieval of
Precipitable Water Vapor in the Presence of Clouds with High Liquid Content, Radio Sci.,
15, 947-957, 1980.
Wiedner M. C. and R. E. Hills. Phase Correction on Mauna Kea Using 183 GHz Water Vapor
Monitors, in Imaging at Radio through Submillimeter Wavelengths, J. G. Mangum and S. J.
E. Radford, Eds., Astron. Soc. Pacific Conf. Ser., 217, 327-335, 2000.
Winterhalter D., J. T. Gosling, S. R. Habbal, W. S. Kurth and M. Neugebauer. Solar Wind
Eight, Proc. 8th Int. Solar Wind Conf., AIP Conference Proceedings, Vol. 382, American
Institute of Physics, New York, 1996.
Wolszczan A. and J. M. Cordes. Interstellar Interferometry of the Pulsar PSR 1237+25,
Astrophys. J., 320, L35-L39, 1987.
Woody D., J. Carpenter and N. Scoville. Phase Correction at OVRO Using 22 GHz Water
Line, in Imaging at Radio through Submillimeter Wavelengths, J. G. Mangum and S. J. E.
Radford. Eds., Astron. Soc. Pacific Conf. Ser., 217, 317-326, 2000.
Wool/ N. J. High Resolution Imaging from the Ground, Ann. Rev. Astron. Astrophys. 20,
367-398, 1982.
Wright M. С. Н. Atmospheric Phase Noise and Aperture-Synthesis Imaging at Millimeter
Wavelengths, Pub. Astron. Soc. Pacific, 108, 520-534, 1996.
Wright M. C. H. and Welch W. J. Interferometer Measurements of Atmospheric Phase Noise
at 3 mm. Radio Astronomical Seeing, J. E. Baldwin and Wang Shouguan. Eds., International
Academic Publishers and Pergamon Press, Oxford, 1990, p. 71-74.
Wu S. C. Optimum Frequencies of a Passive Microwave Radiometer for Tropospheric Path-
Length Correction, IEEE Trans. Antennas Propag., AP-27, 233-239, 1979.
Yeh К. С and С. Н. Liu. Radio Wave Scintillations in the Ionosphere, Proc. IEEE, 70, 324-
360, 1982.
Young A. T. Interpretation of Interplanetary Scintillations, Astrophys. J., 168, 543-562, 1971.
Глава 14
ТЕОРЕМА ВАН ЦИТТЕРТА-ЦЕРНИКЕ,
ПРОСТРАНСТВЕННАЯ КОГЕРЕНТНОСТЬ
И РАССЕЯНИЕ
В этой главе рассмотрена теорема Ван Циттерта—Цернике, предположения, сде-
сделанные при выводе теоремы, требование пространственной некогерентности источ-
источника и отклик интерферометра на когерентный источник. Кратко обсуждаются
некоторые подходы к рассеянию в неоднородной среде. Развитие теории когерент-
когерентности и аналогичные концепции электромагнитного излучения большей частью из-
излагаются в литературе по оптике. Терминология иногда отличается от используемой
в радиоинтерферометрии, но многие физические подходы похожи или идентичны.
Мы частично используем терминологию из оптики и вводим понятие взаимной
когерентности, включающее комплексную видность.
14.1. Теорема Ван Циттерта—Цернике
Мы показали в главах 2 и 3, что кросс-корреляция сигналов, принятых простран-
пространственно разнесенными антеннами может быть использована для картографирова-
картографирования распределения интенсивности далеких космических источников посредством
преобразования Фурье. Этот результат представляет собой одну из форм теоремы
Ван Циттерта—Цернике, полученной в оптике. Теорема основана на исследовании,
опубликованном в 1934 г. Ван Циттертом, и на полученном через несколько лет
Цернике более простом ее выводе. Результат, полученный Ван Циттертом и Цер-
Цернике, изложен в (Born and Wolf, 1999, гл. 10). Из оригинального представления
теоремы не следовало непосредственно существование преобразования Фурье меж-
между интенсивностью и взаимной когерентностью, но по существу это было так.
Рассмотрим протяженный квазимонохроматический источник, и предположим,
что взаимная когерентность излучения измеряется в двух точках Pi и Р2 на плоско-
плоскости, перпендикулярной направлению на источник, как показано на рис. 14.1. Пред-
пол ожим далее, что источник заменили апертурой идентичной формы и размера,
облученной извне пространственно когерентным волновым фронтом. Распределе-
Распределение амплитуды электрического поля по апертуре пропорционально распределению
интенсивности по источнику. Картина фраунгоферовой дифракции на апертуре на-
наблюдается на плоскости, содержащей точки Р\ и Р2. Относительное положение Р\ и
Р2 одинаково в обоих случаях, но в случае апертуры геометрическая конфигурация
такова, что точка Р<2 совпадает с максимумом дифракционной картины. Тогда вза-
взаимная когерентность, измеряемая для некогерентного источника и нормированная
к единице для нулевого расстояния между Р\ и Р2, равна комплексной амплитуде
созданного дифракцией на апертуре поля в точке Pi, нормированной к максимуму
в точке Р2.
Такая форма представления теоремы следует из того факта, что свойства вза-
взаимной когерентности и дифракции Фраунгофера могут быть описаны подобными
соотношениями преобразований Фурье. Вывод теоремы дает возможность проверки
14.1]
Теорема Ван Циттерта-Цернике
531
Источник
Апертура
Рис. 14.1. а — относительное расположение далекого пространственно некогерентного ис-
источника и точек Pi и Рг, в которых измеряется взаимная когерентность излучения.
Плоскости источника 17 и измерений ху параллельны, но находятся на большом рас-
расстоянии друг от друга, б — подобная геометрическая конфигурация при измерении поля
излучения апертуры, расположенной на плоскости XY и облучаемой извне когерентным
волновым фронтом. Поле излучения максимально в точке Рг. Направляющие косинусы I
и т определены относительно координатных осей ж, у плоскости измерений, а V и т —
относительно осей X, Y плоскости апертуры
сделанных предположений и приводится далее. Анализ подобен данному Борном
и Вольфом, но несколько изменен для использования преимуществ более простой
геометрии, когда источник находится на астрономическом расстоянии. Заметим
вначале, что функция взаимной когерентности поля E(t), измеряемая в точках
1 и 2, в оптике представлена следующим образом:
T12{u,v,t)= lim ±=
Т—)-оо ?1
E*{t - т) dt,
A4.1)
-т
где и и v — проекции расстояния между точками измерений, выраженные в длинах
волн. Функция Ti2(u, v, 0) при равном нулю сдвиге времени эквивалентна комплекс-
комплексной видности V(u,v), используемой в радиоастрономии.
14.1.1. Взаимная когерентность некогерентного источника. Геометри-
Геометрическая конфигурация для случая некогерентного источника показана на рис. 14.1 а.
Рассмотрим источник, находящийся на удаленной плоскости, обозначенной XY.
Поле излучения измеряется в двух точках Pi и P<i в плоскости ху, параллельной
плоскости источника. В случае радионаблюдений этими точками представлены
антенны интерферометра. Удобно определять положение точки на плоскости XY
через направляющие косинусы /ига, измеряемые относительно осей хну. Источник
находится достаточно далеко, чтобы направления к любой его точке, измеряемые
из Pi и Р2, были одинаковы. Поля в точках Pi и Р2, создаваемые одним и тем
же элементом источника, расположенным в точке (Z,ra), определяются следующим
образом:
К ехР [— 7'2тп/ (t — Ri/c)]
P[ J „ ^± , 14.2
Hi
532 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
ехр Г— j2ttu (t — iWc)l
P[ J _/ ^-^ , 14.3
где ?(l,m,t) — фазовое представление комплексной амплитуды электрического
поля элемента источника в точке G, m). R\ и R2 — расстояния от этого элемента до
точек Р± и Р2 соответственно, и с — скорость света. Экспоненциальными членами
в формулах A4.2) и A4.3) описывается изменение фазы вдоль поля от источника
до Pi и Р2.
Комплексная кросскорреляционная функция напряжений поля излучения, со-
создаваемых элементом (/,га) в точках Pi и Р2, при нулевом сдвиге времени равна
exp [-j2kv (t - Ri/c)] exp \j2in/ (t - Д2/с)] _
R1R2
= (S(l,m,t)r(l,m,t- g^i)) eXP E2™^- ^ , A4.4)
где звездочкой обозначено комплексная сопряженная, а угловыми скобками ( ) —
усреднение по времени. Напомним, что источник предполагается пространственно
некогерентным, и это означает, что члены вида (Ei(lp,mp,t)E%(lq,mq,i)} равны
нулю, где индексы р и q соответствуют различным элементам источника. Если
сомножитель (R2 — R\)/c мал относительно обратной величины полосы пропуска-
пропускания приемника, то им можно пренебречь в амплитудном члене уравнения A4.4),
представленном угловыми скобками. Тогда A4.4) принимает вид
n, t) S* (I, m, t)) exp [j2ttu (Д1 - R2)/c]
Величина (?(l,m,t) ?*(l,m,t)) представляет собой меру усредненной по времени
интенсивности 1A, т) источника. Для того чтобы получить функцию взаимной
когерентности для поля в точках Pi и Р2, возьмем интеграл по источнику, где ds —
элемент площади на плоскости XY:
г12(«,«,о)= [ ^W^^-^/c]^
J R1R2
Здесь и и v — проекции расстояния между точками Pi и Р2 на оси ж, у, выра-
выраженные в длинах волн. Заметим, что (Ri — R2) представляет собой разность пути
распространения от точки (/,га) источника до Pi и Р2. Координаты Pi и Р2 равны
(xi,yi) и (ж2,г/2) соответственно, так что и = (х\ — ж2)г//с и v = (у\ — г/2)г//с, где
с/г/ — длина волны. Таким образом, получим (i?2 — Ri) = (ul + vm)c/v. Поскольку
расстояние до источника намного больше расстояния между точками Pi и Р2, то
для остальных Д-членов мы можем принять R\ ~ R2 — R, где R — расстояние межу
точками отсчета координат (X, Y) и (ж, у). Тогда ds = R2dl dm, и из формулы A4.6)
получим
[ [ I(l,m)e-j2*{ul+vm)dldm. A4.7)
ИСТОЧНИК
Так как подынтегральное выражение в A4.7) равно нулю вне источника, то мо-
могут быть взяты бесконечные пределы интегрирования, и взаимная когерентность
14.1] Теорема Ван Циттерта-Цернике 533
1^12(^,^,0), эквивалентная комплексной видности V(u,v), представляет собой пре-
преобразование Фурье распределения интенсивности /(/,т) по источнику. Этот ре-
результат общепринято называть теоремой Ван Циттерта-Цернике. Однако интересно
рассмотреть формулировку теоремы, исходя из описанной в начале этого раздела
дифракции на апертуре.
14.1.2. Дифракция на апертуре и отклик антенны. Чтобы проанализи-
проанализировать поле дифракции Фраунгофера на апертуре как функцию угла, восполь-
воспользуемся геометрической конфигурацией, показанной на рис. 14.1 б. В этом случае
апертура облучается электромагнитным полем ?(/,т,?), и мы снова используем
направляющие косинусы относительно осей хну для обозначения точек апер-
апертуры в соответствии с тем, как они видны из Р\ и Р2. Плоскость ху находится
в дальней зоне для волнового фронта, создаваемого любой точкой апертуры, так
что на расстоянии Р\Р2 он может считаться плоским. Апертура с центром в точке
О перпендикулярна направлению ОР2. Распределение фазы в пределах апертуры
предполагается однородным, и компоненты поля, следовательно, суммируются син-
фазно в точке Р2. Таким образом, на плоскости ху максимум напряженности поля
наблюдается в точке Р2. Теперь рассмотрим поле в точке Р\ с координатами (ж, у).
Созданная излучением элемента апертуры (Z,m) составляющая поля в точке Р\
находится по формуле A4.2). Расстояния от точки (/,га) источника до точек Р\ и
Р2 равны соответственно R\ и R2, и R2 — R\ = lx + ту. Таким образом, используя
A4.2), можно записать
-j2iru(t-R2/c) , р \
Ег (/, m, t) = ? (Z, m,t - — ) e~j2™ (*'+*™)/c. A4.8)
Как и ранее, для остальных Д-членов мы принимаем Ri ~ R2 — R. Далее интегри-
интегрированием по всей апертуре находим полную величину поля в точке Р\\
(f)Ua, A4.9)
апертура
где Л — длина волны, и элемент площади ds пропорционален dl dm. Член перед
знаком интеграла в правой части уравнения A4.9) представляет собой коэффициент
распространения, характеризующий изменения амплитуды и фазы между источ-
источником и точкой Р2 (рис. 14.1 б). Применяя полученный результат к излучению,
формируемому апертурой, заменим функции Е и ?, зависящие от времени, соот-
соответствующими среднеквадратичными амплитудами поля, которые мы обозначим
как Е и 8:
Щх, у) ос Г [ ?(l, m) e~j27T K*/A) /+(*/А>т^ dl dm, A4.10)
апертура
где опущен коэффициент распространения из уравнения A4.9). Сравнивая A4.7)
и A4.10), получим толкование теоремы Ван Циттерта—Цернике, соответствующее
данному в начале раздела. Из найденной пропорциональности между некогерент-
некогерентной интенсивностью и когерентной амплитудой поля следует, что
/14Ш
Г12@,0,0) ?7@,0) '
Подынтегральные выражения A4.7) и A4.10) вне апертуры равны нулю. Поэтому в
обоих случаях пределы интегрирования могут быть расширены до =Ьос, и уравнения
534 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
принимают форму преобразований Фурье. При вычислении взаимной когерентно-
когерентности для источника и апертуры получаются аналогичные результаты, поскольку гео-
геометрия и математические приближения одинаковы. Следует подчеркнуть однако,
что эти подходы различны с физической точки зрения. В первом случае излучение
на поверхности рассматриваемого источника пространственно некогерентно, тогда
как во втором случае поле в апертуре полностью когерентно.
Полученное в результате выражение A4.10) также описывает угловое распре-
распределение излучения антенны, представляющей собой возбуждаемую апертуру. Для
антенны больше подходит определение диаграммы излучения через угловые пара-
параметры (I', ттт/) в направлении излучения из апертуры антенны, а не относительно
положения точки Pi, и определение распределения поля излучения по апертуре
через линейные, а не угловые единицы. Пусть V,т' — направляющие косинусы
относительно осей X, Y. Поскольку рассматриваемые углы малы, мы можем под-
подставить в выражение A4.10) х = RV', у = Rm!', / = X/R, т = Y/R, dl = dX/R,
dm = dY/R, и в результате получим
#'(/', т') ос J J ?XY(X,Y) e-J2n[(x/x)i'^(Y/x)rn'] dxdY A4Л2)
апертура
Этим выражением представлено распределение поля вследствие фраунгоферовой
дифракции на апертуре (см., например, Silver, 1949). Им учитывается случай пе-
передающей антенны, когда апертура параболического рефлектора облучается из-
излучателем, расположенным в фокальной точке. Если такая антенна используется
на прием, то принимаемое напряжение от источника, находящегося в направлении
(/', ттт/), пропорционально правой части выражения D.12). Таким образом, приемная
диаграмма направленности по напряжению Уд^^ттт/), введенная в п. 3.3.1, пропор-
пропорциональна правой части выражения A4.12).
Чтобы найти диаграмму направленности антенны по мощности, требуется полу-
получить отклик в виде \Е (V,т')\2. Из автокорреляционной теоремы преобразований
Фурье следует, что квадрат амплитуды Е {I', ттт/) равен автокорреляции преобра-
преобразования Фурье Е (I1, ттт/) (см., например, (Bracewell, 2000); заметим также, что это
соотношение является обобщением соотношения Винера-Хиничина, выведенного в
разд. 3.2). Таким образом, мощность излучения, как функция угла, определяется
следующим образом:
'Ux dY,
апертура
A4.13)
где S(X,Y) ** S(X,Y) — двумерная автокорреляционная функция распределения
поля по апертуре. Требуемый коэффициент пропорциональности для определения
абсолютной величины поля излучения может быть найден интегрированием вы-
выражения D.13) по 4тг ср, что даст полную мощность излучения, и последующим
приравниванием полученного результата к мощности, поданной на вход антенны.
Мощность, собираемая антенной при работе на прием, пропорциональна мощности,
излучаемой при передаче, так что форма диаграммы одинакова в обоих случаях.
Чтобы проиллюстрировать физическую интерпретацию выражения D.13), рассмот-
рассмотрим простой случай прямоугольной апертуры с равномерным возбуждением элек-
электрического поля. Функция ?xy(X,Y) при этом представляет собой произведение
двух одномерных функций по X и Y. Если ширина апертуры равна d в направлении
X, то автокорреляционная функция представляет собой треугольник с основанием
14.1] Теорема Ван Циттерта-Цернике 535
2б/, и после преобразования Фурье получим
A4.14)
Полная ширина лепестка такой диаграммы по переменной /' на уровне половины
мощности равна 0,886A/d; например, 1° для d/X = 50,8 длин волн. Для равномерно
облучаемой круглой апертуры диаметра d диаграмма направленности центрально
симметрична и представлена выражением
y^l2, A4.15)
где индексом г обозначено радиальное сечение, в котором l'r измеряется от центра
диаграммы. Полная ширина лепестка диаграммы на уровне половины мощности
равна l,03A/d.
Диаграмма фраунгоферового излучения апертуры антенны может быть получе-
получена прямым способом, если напряженность поля волнового фронта излучения сразу
рассматривать как функцию направления, а не анализировать напряженность поля
в некоторой точке Pi, как описано выше. Однако примененный метод был выбран
по той причине, что позволяет получить прямую аналогию с откликом интерфе-
интерферометра для пространственно некогерентного источника. Более подробный анализ
отклика антенны приводится, например, в (Booker and Clemmow, 1950; Bracewell,
1962), или в учебных пособиях по антеннам, перечисленных в списке основной
литературы гл. 5.
14.1.3. Предположения при выводе теоремы Ван Циттерта—Цернике
и ее применение. Перечислим предположения и ограничения, применяемые в
теории интерферометрического отклика, и дать их общий обзор.
1. Поляризация электрического поля. Хотя электрическое поле является век-
векторной величиной, направление которой зависит от поляризации излучения,
его компоненты, принимаемые антенной от различных элементов источника,
могут быть объединены так же, как скалярные величины. Поля измеряются
антеннами в точках Р1? Р2> и каждая антенна откликается на компоненту
излучения, поляризация которой согласована с поляризацией антенны. Если
поля поляризованы случайным образом, а поляризация антенн идентична,
то произведением сигналов в выражении A4.4) представлена половина всей
мощности на каждой антенне. Однако поляризации антенн не должны быть
идентичны, поскольку, в общем случае, интерферометрическая система от-
откликается на некоторую комбинацию компонент интенсивности источника,
определяемую поляризациями антенн. Способы, которыми могут быть вы-
выбраны поляризации антенн для исследования всех поляризаций принимаемого
излучения, описаны в п. 4.8.3. Таким образом, скалярное приближение поля
не приводит к потере общности результата.
2. Пространственная некогерентностъ источника. Излучение от любой точки
источника статистически независимо от излучения любой другой его точки.
Это применимо почти повсеместно к астрономическим источникам и дает воз-
возможность интегрирования выражения A4.6) без учета перекрестных произ-
произведений, представляющих различные элементы источника. Для соотношения
536 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
преобразований Фурье, полученного из теоремы Ван Циттерта—Цернике тре-
требуется, чтобы источник был пространственно некогерентен. Пространствен-
Пространственная когерентность и некогерентность рассматриваются в разд. 14.2. Заме-
Заметим, что некогерентным источником образуется когерентный или частично
когерентный волновой фронт при распространении излучения в космическом
пространстве. Если бы это было не так, то взаимная когерентность (или вид-
ность) некогерентного источника, измеряемая разнесенными антеннами была
бы всегда равна нулю.
3. Отклик по полосе частот. Предположение, что величина (Д2 — R\)/c мень-
меньше величины обратной полосы частот (Az/), необходимое для того, чтобы
перейти от уравнения A4.4) к A4.5), можно записать следующим образом:
^^ ^^ A4.16)
где 1^ и md — максимальные угловые размеры источника. Это означает тре-
требование, что источник должен удовлетворять ограничениям в соответствии с
откликом по полосе пропускания интерферометра, который рассматривался в
разд. 2.2. Или напротив, максимально возможная полоса частот ограничена
необходимым полем зрения. Дисторсия, вызванная эффектом полосы частот
и рассматриваемая далее в разд. 6.3, если и не всегда, то часто может быть
исправлена.
4. Расстояние до источника. Для решетки с максимальной длиной базы D
отклонение волнового фронта от плоскости для источника, находящегося на
расстоянии Д, примерно равно ~D2/R. Таким образом, требование дальней
зоны Rff, определенной как расстояние, при котором отклонение мало по
сравнению с длиной волны Л, задано соотношением
Щ/ > d2А- A4-!7)
Условие дальней зоны означает, что антенны видны под малым углом со
стороны источника, и дает возможность аппроксимации дифракции Фраун-
гофера. Если источник находится на известном расстоянии, которое меньше
расстояния дальней зоны, то фазовый член может быть компенсирован. Это
иногда необходимо при исследованиях Солнечной системы. Например, для
антенн, расположенных на расстоянии 35 км друг от друга, при длине волны
1 см, расстояние дальней зоны превышает 1,2-1011 м, что примерно равно рас-
расстоянию до Солнца. Отметим, что в дальней зоне информацию о продольной
структуре источника получить невозможно, и наблюдается только проекция
распределения интенсивности на картинную плоскость небесной сферы.
5. Применение направляющих косинусов. При переходе от формулы A4.6) к
A4.7) разность пути распространения R<i — R\ выражается через координаты
базы (u,v) и полярные координаты (/,7?г). Выражение для разности пути
распространения точно, когда / и т заданы в виде направляющих косинусов.
При интегрировании по источнику элемент площади, ограниченный прираще-
приращениями dl и dm, равен dl dm/n, где п — третий направляющий косинус, равный
\/1 — I2 — т2 . В оптике, при выводе теоремы Ван Циттерта-Цернике, обычно
используется предположение, что источником стягиваются только малые углы
в плоскости измерений. Тогда / и т могут быть аппроксимированы малыми
углами и п можно принять равным единице. В результате соотношение между
14.2] Пространственная когерентность 537
V и / принимает форму двумерного преобразования Фурье, как и в приближе-
приближении ограниченного поля зрения, рассмотренном в разд. 3.1. В радиоастроно-
радиоастрономии требуется менее жесткое приближение, представленное формулой C.7) —
см. разделы 3.1 и 11.8.
6. Трехмерное распределение измерений видности. При сопровождении антенна-
антеннами источника векторы антенных баз, обозначенные выше проекциями (гл, г>),
могут не находиться в одной плоскости, и в этом случае для их определения
необходимы три координаты (u,v,w). При этом преобразование Фурье стано-
становится более сложным, но при условии, что подлежащее картографированию
поле зрения мало, можно воспользоваться упрощающим приближением. Эти
эффекты рассматриваются в разделах 3.1 и 11.8.
7. Космическая рефракция. В приведенном выше анализе неявно предполага-
предполагалось, что между антеннами и источником пространство свободное, или, как
минимум, что любая среда в нем характеризуется одинаковым показателем
преломления, так что искажения в приходящем от источника волновом фрон-
фронте отсутствуют. На практике, межзвездная и межпланетная среда, а также
земная атмосфера и ионосфера могут вызывать эффекты, включающие вра-
вращение позиционного угла линейно поляризованной компоненты излучения,
рассмотренные в разд. 13.3 [см. формулу A3.135)].
14.2. Пространственная когерентность
При выводе интерферометрического отклика в главах 2 и 3, а также урав-
уравнения A4.5), предполагалось, что рассматриваемый источник пространственно
некогерентен. Это означает, что волновые сигналы, принимаемые от различных
пространственных элементов источника не коррелированы, что дает возможность
сложения выходных сигналов коррелятора при различных угловых приращениях,
выполняя интегрирование по источнику. Здесь мы рассмотрим это требование бо-
более подробно. Для иллюстрации применяемого подхода достаточно рассмотрения
одного измерения на небесной сфере, позиционная координата которого определена
как направляющий косинус /.
14.2.1. Принимаемое поле. Рассмотрим электрическое поле E(l,t) на
поверхности Земли, соответствующее волновому фронту в направлении / и моменту
времени t. На рис. 14.2 показана геометрическая конфигурация, когда / = О
для направления OS центрального или номинального положения наблюдаемого
источника. Направляющий косинус / измеряется относительно направления ОВ,
перпендикулярного OS. Лучом OS' показано направление для другой части источ-
источника. Излучением из направления OS' создается волновой фронт, параллельный
О В'. Волновые фронты от точек источника плоские, поскольку рассматриваемый
источник находится в дальней зоне интерферометра. Линией О А показана проекция
базы, перпендикулярная направлению на источник, и расстояние О А, выраженное
в длинах волн, равно и. Рассмотрим волновые фронты из направлений S и S1',
приходящие в один и тот же момент времени в точку О. Чтобы достичь точки Л,
волновой фронт из S' должен пройти дополнительное расстояние А А'. Используя,
как обычно, приближение малых углов, получим, что расстояние А А' равно
ulc/v, т. е. ul длин волн. Таким образом, волна из направления S' запаздывает
в А на интервал времени г = ul/v относительно волны из направления S. Если
мы представим волну из направления S' как E(l,t) в точке О, то в точке А она будет
538
Теорема Ван Циттерта-Цернике, когерентность и рассеяние
[Гл. 14
представлена как E(l,t — т). По-
Поскольку приходящие волновые
фронты плоские, то амплитуда
волны не изменяется на отрезке
А А1'. Фаза при этом изменяется
на г/т = ul, так что для волны из
S' в А получим
)
A4.18)
Если е(и, t) — суммарное поле в
точке А, созданное излучением
всего источника, то
Рис. 14.2. Схема, иллюстрирующая изменение фа-
фазы вдоль линии ОВ, перпендикулярной направ-
направлению на источник OS, где I — направляющий
косинус, которым задано направление OS' и опре-
определенный относительно ОВ. Угол SOS' мал и по-
поэтому примерно равен /, как показано. Линия OS'
направлена к другой части источника, а ОВ' ей
перпендикулярна
e(u,t)=
A4.19)
Далее предположим, что угло-
угловые размеры источника не вели-
велики, так что
E(l,t) = 0, |/| ^ 1. A4.20)
Условие, определенное выражением A4.20), дает нам возможность использования
пределов интегрирования ±оо в A4.19). Отметим, что выражение A4.19) имеет
форму преобразования Фурье, и обратное преобразование e(u,t) равно E(l,t). Вы-
Выражение A4.19) потребуется нам в следующем разделе.
14.2.2. Когерентность источника. Здесь мы вернемся к пространственной
когерентности источника и последуем более углубленному анализу (Swenson and
Mathur, 1968). В качестве меры пространственной когерентности введем функцию
когерентности источника 7- Она определяется как кросскорреляция сигналов,
принятых из двух различных направлений 1\ и /2 в два различных момента времени:
lim -j- \
-Т
A4.21)
Для обеспечения сходимости в интеграле используются конечные пределы инте-
интегрирования. Функция 7(^ъ^2?т) подобна функции когерентности источника или
объекта, рассматриваемой в работах (Drane and Parrent, 1962; Beran and Parrent,
1964).
Нормированная функция когерентности источника называется комплексной
степенью когерентности протяженного источника:
A4.22)
где 7^ъТ) определяется подстановкой 1г = 12 в формуле A4.21), так что
7(^ъг) = 7^ъ^ът)- Используя неравенство Шварца, можно показать, что
0 ^ \1n{W^2^)\ ^ 1- Предельные значения 0 и 1 соответствуют случаям полной
некогерентности и полной когерентности соответственно. Если рассматривается
14.2] Пространственная когерентность 539
протяженный источник произвольного спектрального диапазона, то возможна
ситуация, когда для данной пары точек /i и /2 величина \jN(h,h,T)\ для одного
значении т равна нулю, а для другого — нет. Следовательно, требуется более
строгое определение полной когерентности и некогерентности. Используются
следующие определения, предложенные (Parrent, 1959).
1. Излучение из направлений 1\ и 1^ полностью когерентно (некогерентно), если
|7лг(^ъ h,T)\ = 1 @) при всех значениях т.
2. Протяженный источник когерентен (некогерентен), если излучение из всех
пар направлений /i,/2 в пределах источника когерентно (некогерентно).
Во всех остальных случаях протяженный источник считается частично когерент-
когерентным.
Рассмотрим теперь функцию когерентности поля e(x\,t) далекого источника,
измеряемую, скажем, на земной поверхности, причем х\ — линейная координата,
выраженная в длинах волн, в направлении, перпендикулярном / = 0:
т
Г(жл1,яА2,т) = lim ^ e(x\1,t)e*{x\2it-T)dt = {e{x\1,t)e*{x\2it-r)).
Т-Юо 21 J
-Т
A4.23)
Это выражение представляет собой форму функции взаимной когерентности Г12 из
формулы A4.1), в которой используются абсолютные координаты точек измерений,
определенные как х\\ и х\2, вместо относительных координат, заданных проекци-
проекциями базы. Применяя соотношение преобразований Фурье между E(l,t) и e(u,t),
выведенное в формуле A4.19), и заменяя и на х\, получим
Т(хХ1,хХ2,т) = J J l(li,h,r) e-J2^(x^tl-xMia) dh ^ A424)
— оо —оо
а также обратное преобразование:
^^hhU A4.25)
Соотношения, представленные формулами A4.24) и A4.25) не дают средства из-
измерения распределения интенсивности источника, за исключением случая полной
некогерентности. В этом случае функция когерентности может быть представлена
как
-r(h,h,T)='r(h,T)8(h-h), A4.26)
где 5 — дельта-функция. Используя A4.26) совместно с формулами A4.24) и A4.25),
получим, что функция самокогерентности полностью некогерентного источника и
ее спектр пространственных частот являются преобразованиями Фурье друг друга:
Г(и,г)= | -y(l,r)e-j2wuldl, A4.27)
— ОО
ОО
7A, т)= | T{u,T)ej2wuldu, A4.28)
540 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
где и = x\i — х\2- Очевидно, что Т(и, т) не зависит от х\\ и х\2, а зависит лишь от
их разности. Как показано в п. 2.3.2, переменная и может быть интерпретирована
как расстояние между двумя выбранными точками, в которых измеряется когерент-
когерентность поля, а также как пространственная частота функции видности, измеренной
на той же базе. При г = 0 из уравнений A4.21) и A4.22) получим
7(/,0) = (|?@|2), A4.29)
что представляет собой одномерное распределение интенсивности Д источника,
введенное формулой A.9). Тогда из A4.21) и A4.29) следует, что
оо
Г(и,0)= [ (\E(l)\2) e~j2™1 dl. A4.30)
— оо
Функция Г(г?, 0) измеряется между точками вдоль линии, перпендикулярной на-
направлению / = 0. В интерферометрических измерениях это также комплексная
видность V. Уравнение A4.30) представляет собой соотношение преобразований
Фурье между взаимной когерентностью (видностью) и интенсивностью.
При подстановке условия некогерентности A4.26) в уравнения A4.24) и A4.25)
получаются два результата: соотношение Ван Циттерта-Цернике между взаимной
когерентностью и интенсивностью, и стационарность взаимной когерентности по и.
Физическое основание этих результатов ясно из рассмотрения рис. 14.2. Когда при-
приходящие волновые фронты объединяются в какой-либо точке, относительные фазы
их частотных (Фурье) компонент изменяются линейно в зависимости от координат
этой точки (например, положение А на линии О В на рис. 14.2), и при малых / они
изменяются также линейно в зависимости от угла на небесной сфере. В результате
фазовые разности фурье-компонент в двух точках зависят только от относительных
координат этих точек, а не от их абсолютных значений. Интерферометрические
измерения взаимной когерентности включают в себя измерения фазовых разностей
в диапазоне углов падения, который определяется угловыми размерами источника
и шириной диаграмм направленности антенн. Линейное соотношение между фазой
и позиционным углом дает возможность восстановления углового распределения
интенсивности принимаемого волнового излучения по изменению взаимной коге-
когерентности как функции и посредством анализа Фурье. Если угловые размеры
источника достаточно малы, чтобы расстояние А А' на рис. 14.2 всегда было много
меньше длины волны, то форма электрического поля не изменяется вдоль линии
О А и источник остается неразрешенным.
14.2.3. Полностью когерентный источник. Паррентом (Parrent, 1959) по-
показано, что протяженный источник может быть полностью когерентным только в
том случае, если он монохроматический. В качестве примера такого источника мож-
можно представить апертуру удаленной большой антенны или ансамбль излучающих
элементов, управляемых одним и тем же монохроматическим сигналом. Апертура,
рассмотренная в п. 14.1.2, концептуально является примером когерентного источни-
источника. Разницу между откликами интерферометра на полностью когерентный и полно-
полностью некогерентный источники можно объяснить следующей физической картиной.
Источник может быть представлен как ансамбль излучателей, распределенных
внутри некоторого телесного угла на небесной сфере. В случае когерентного источ-
источника сигналы излучателей монохроматические и когерентные. Излучением в любом
направлении образуется единственный монохроматический волновой фронт, и на
каждую антенну интерферометра поступает монохроматический сигнал. Выходной
сигнал коррелятора прямо пропорционален произведению двух (комплексных) ам-
амплитуд сигналов антенн. Таким образом, если когерентный источник наблюдается
14.3] Рассеяние и распространение когерентности 541
на па антеннах, то па(па — 1)/2 измеренных кросскорреляционных сигналов могут
быть разложены на па значений комплексной сигнальной амплитуды.
С другой стороны, для некогерентного источника, сигналы излучающих элемен-
элементов не коррелированы и должны рассматриваться независимо. Каждый сигнал дает
свой вклад в интерференционную картину на выходе коррелятора. Но поскольку
фазы этих интерференционных составляющих определяются положением излуча-
излучателей в источнике, то суммарный отклик пропорционален не только амплитудам
сигналов антенн, но также и коэффициенту, который зависит от углового распре-
распределения излучателей. Этот коэффициент, величина которого ^ 1, равен модулю
видности, нормированному к единице для неразрешенного (точечного) источника
с плотностью потока той же, что и у наблюдаемого. Если источник не являет-
является неразрешенным, то разложить измеренную кросс-корреляцию по величине ам-
амплитуд сигналов антенн невозможно. Так как сигналы излучающих элементов не
коррелированы, то информация об их распределении по источнику содержится в
ансамбле волновых фронтов, поступающих на антенны.
Как показано при выводе угловой зависимости излучения когерентно облуча-
облучаемой апертуры [формула A4.12)] и по аналогии с большой антенной, излучение
когерентного источника имеет высокую степень направленности. Поэтому величина
наблюдаемого сигнала зависит от абсолютных координат антенн интерферометра,
как в формулах A4.24) и A4.25), а не только от их относительных координат как
в случае некогерентного источника. Возможность разложения сигналов на выходе
коррелятора, измеренных на различных базах, и нестационарность этих измерений
в зависимости от абсолютных координат антенн — две характеристики, позво-
позволяющие отличить когерентный источник (МасРЫе, 1964). Из анализа в разд. 14.1
очевидно, что для разрешения некогерентного источника и для исследования диа-
диаграммы излучения когерентного источника тех же угловых размеров требуются
аналогичные диапазоны расстояний между антеннами.
14.3. Рассеяние и распространение когерентности
Хорошо известно, что изображения одиночных звезд, полученные на оптическом
телескопе с временами экспозиции короткими по сравнению с характерным вре-
временем атмосферных флуктуации, представляют собой суперпозицию изображений
(см. п. 16.4.4). Эти изображения получаются в результате рассеяния света звезды
неоднородностями земной атмосферы. Иногда практически аналогичные эффекты
наблюдаются при получении изображений неразрешенных радиоисточников, на-
наблюдаемых сквозь среду с сильным неоднородным рассеянием, такую как межпла-
межпланетная среда в пределах нескольких градусов от Солнца, что описано в п. 13.5.2.
Поскольку каждое рассеянное изображение создается излучением одного и того же
источника, следует ожидать, что в такой ситуации имитируется эффект распре-
распределения точечных когерентных источников. В этом разделе мы проанализируем
эффекты рассеяния, рассматривая при этом распространение когерентности в про-
пространстве и частично следуя изложению (Cornwell, Anantharamaiah, and Narayan,
1989). Такой формализм предполагает методы восстановления нерассеянного изоб-
изображения по картине, полученной из наблюдений.
Для данной излучающей поверхности мы хотим найти функцию взаимной ко-
когерентности на другой (возможно, виртуальной) поверхности в пространстве. В
типичной радиоастрономической ситуации относительно геометрии задачи могут
быть сделаны многочисленные упрощающие предположения. Рассмотрим конфи-
конфигурацию, показанную на рис. 14.3, когда узкополосные радиосигналы распростра-
542
Теорема Ван Циттерта-Цернике, когерентность и рассеяние
[Гл. 14
Рис. 14.3. Упрощенная геометрическая
конфигурация, используемая при анализе
распространения когерентности. S —
протяженный источник, Q — положение
рассеивающего экрана и В — плоскость
измерений. Поверхности S, Q и В —
плоские и параллельные, и п, гг, d\
и с?2 много больше длины волны. Все
лучи почти (но не обязательно точно)
перпендикулярны поверхностям
няются от поверхности S к поверхно-
поверхности Q. Взаимная когерентность двух то-
точек в пространстве представляет собой
математическое ожидание произведения
электрических полей (одинаково поля-
поляризованных) в этих точках. Для сигна-
сигналов, коррелированных с произвольной
задержкой времени, взаимная когерент-
когерентность равна
r(Qi, Q2, т) = {E(Q1} t) E*(Q2, t - r)>.
A4.31)
Функция взаимной когерентности Г
представляет собой функцию поля в
двух точках и временной задержки
т. Мы рассматриваем распространение
взаимной интенсивности, т. е. взаим-
взаимной когерентности, рассчитанной при
т = 0. Следуя общепринятой прак-
практике, представим взаимную интенсив-
интенсивность как J(QUQ2) = r(QbQ2,0). Эта
функция будет отмечаться индексами
5, Q или В для обозначения плос-
плоскости (рис. 14.3), соответствующей ве-
величине взаимной интенсивности. Мы
предполагаем излучающую поверхность
полностью некогерентной, что обычно
для астрономических объектов, и что наблюдаемое излучение ограничено узкой
полосой частот, как диктуется характеристиками приемных систем. Из форму-
формулы A4.31) и формулировки излучения по Гюйгенсу-Френелю можно показать (Born
and Wolf, 1999; Goodman, 1985) расчетами, подобными сделанным при выводе фор-
формулы A4.6), что взаимная интенсивность для точек Qi и Q2 равна
Jq(Qi,Q2) = А
dSldS2,
A4.32)
где dS± и dS2 — элементы поверхности S, и Л — длина волны в центре полосы частот
наблюдений.
Условие некогерентности может быть сформулировано с использованием дельта-
функции (Beran and Parrent, 1964), как в A4.26). И поскольку в данном случае вза-
взаимная интенсивность представлена дельта-функцией, распределение интенсивности
на поверхности Q находится посредством сближения точек Qi и Q2:
Т (С п \ \^ Г/'С ^ Jif С п \ (Л Л сХеХ\
где коэффициент Л2 добавлен для сохранения физической размерности интенсив-
интенсивности. Уравнение A4.32) тогда приводиться к виду
dS.
A4.34)
14.3] Рассеяние и распространение когерентности 543
Если угловые размеры источника бесконечно малы, т. е. источник неразрешен, то
интегрирование по источнику становится тривиальным, и взаимная интенсивность
может быть разложена на сомножители, зависящие, соответственно, от г\ и г2:
Jq{QuQ2) = До) I — I I — I , A4.35)
где ri и г2 отсчитываются от одной и той же точки S. В общем случае, когда
источник разрешен, интегральное выражение A4.34) разложено быть не может.
Формулами A4.34) и A4.35), для их соответствующих случаев, описывается рас-
распространение взаимной когерентности в ситуации, показанной на рис. 14.3, и таким
образом они могут использоваться для определения взаимной интенсивности на
поверхности Q в результате некогерентного облучения с поверхности S. Анализ
уравнения A4.31) показывает, что для протяженного источника S взаимная интен-
интенсивность на Q зависит как от ri, так и от т2 для всех пар точек на Q. Таким образом,
поле на Q, по крайней мере частично, когерентно для всех источников, включая
источники конечных размеров. Это интуитивно ясно, поскольку все точки Q облу-
облучаются всеми точками S. На самом деле, можно строго показать, что некогерентное
поле в свободном пространстве существовать не может (Parrent, 1959).
Предположим, что в действительности поверхность Q представляет собой экран,
образованный неоднородной средой такой как плазма или пыль, рассеивающей
излучение от S. Взаимная интенсивность на экране модифицируется комплексным
коэффициентом передачи T(Q), что в результате дает взаимную интенсивность
излучения
jQt(Qi,Q2)=T(Q1)T*(Q2)JQi(Qi,Q2), A4.36)
где индексами г и t обозначены интенсивность освещения и интенсивность излу-
излучения соответственно. Из уравнения A4.32) выведем «функцию распространения»
(Cornwell, Anantharamaiah and Narayan, 1989) взаимной интенсивности:
= Г T(Q)eM-J2n(r + d)/X]
J rd
где г и d показаны на рис. 14.3. Отсюда получим взаимную интенсивность на
поверхности В как функцию взаимной интенсивности протяженного источника S:
W*(S2,B2)dS1dS2. A4.38)
s
Для протяженного некогерентного источника
,B1)W*(S,B2)dS, A4.39)
а в случае точечного источника с плотностью потока F взаимная интенсивность на
поверхности В равна
В2) = F\~2 W(S, Bi) W*(S, B2). A4.40)
Как и ранее, в случае неразрешенного источника, взаимная интенсивность на
поверхности В представлена двумя сомножителями, каждый из которых зависит
от положения одной точки на В. Однако в случае некогерентного распределения
544 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
источников на ?, взаимная интенсивность зависит от разности положений и следо-
следовательно, не может быть разложена.
Наличие рассеивающего экрана между источником и наблюдателем, имеющим
в распоряжении инструмент ограниченной апертуры, дает возможность значитель-
значительного улучшения углового разрешения, поскольку протяженность рассеивающего
экрана намного больше. Из-за частичной когерентности излучения экрана ин-
интенсивность должна измеряться во всех точках плоскости В, расстояние между
которыми обусловлено критерием Найквиста, а не во всех точках спектра простран-
пространственных частот, как допускается по теореме Ван Циттерта—Цернике. Первый тип
наблюдений дает гораздо больше данных, чем второй. Это приводит к их большой
избыточности в двух пространственных измерениях, так что в принципе могут быть
получены не только характеристики рассеивающего экрана, но также и источника.
В этом отношении данная задача подобна задаче автокалибровки (разд. 11.4). К
сожалению, в случае рассеивающего экрана практические трудности велики, но
несколько важных попыток использования описанного подхода были сделаны. Воз-
Возможности статистического синтеза изображений с использованием рассеивающего
экрана для получения сверхвысокого разрешения методом, похожим на спекл-
интерферометрию (см. разд. 16.4) рассмотрены в работе (Cornwell and Narayan,
1993).
Излучение радиоисточника, претерпевшее сильное рассеяние при распростра-
распространении в пространстве, было исследовано в работах (Anantharamaiah, Cornwell,
and Narayan, 1989; Cornwell, Anantharamaiah, and Narayan, 1989). Чтобы проде-
продемонстрировать отклик радиотелескопа для такого пространственно когерентного
распределения интенсивности, авторами были проведены наблюдения сильного и
почти точечного источника ЗС279, каждый год проходящего вблизи Солнца. При
таких условиях рассеяние достаточно велико, чтобы вызвать амплитудные мер-
мерцания принимаемых сигналов. Авторы использовали VLA в ее наиболее протя-
протяженной конфигурации, для которой максимальная длина базы равна примерно
35 км. Неоднородности перемещались вдоль решетки примерно за ~100мс вслед-
вследствие солнечного ветра, скорость которого порядка 100-400 км/с, и потребовались
«мгновенные» наблюдения продолжительностью 10-40 мс, чтобы исключить сма-
смазывание изображений из-за движения рассеивающего экрана. Наблюдения были
проведены на длинах волн 20, 6 и 2 см, когда источник находился на расстоянии
от 0,9° до 5° от Солнца. Было обнаружено, что выходной сигнал коррелятора
можно разложить на сомножители, как и ожидалось для когерентного источника.
После усреднения коррелированных сигналов в течение примерно 6 с было получено
увеличенное изображение источника, при этом увеличение возрастало с уменьше-
уменьшением расстояния между Солнцем и источником. Также была продемонстрирована
возможность определения характеристик рассеивающего экрана по измерениям
функции взаимной интенсивности на поверхности Земли, доказывая тем самым, что
эта функция полностью измерима в двумерной области пространственных частот.
Различить протяженный пространственно когерентный источник и рассеивающий
экран, облучаемый точечным источником, невозможно.
Важные наблюдения были проведены Вольжаном и Кордесом (Wolszczan and
Cordes, 1987), в результате которых оказалось возможным сделать предположение
о размерах структуры в пульсаре PSR 1237+25, используя случай межзвездного
рассеяния. Пульсар наблюдался на одиночной 308-м антенне в Аресибо, на частоте
430 МГц. Динамические спектры принятого сигнала (принятая мощность, представ-
представленная как функция времени и частоты) показали четкую полосовую структуру с
максимальным разделением по частоте ~300—700 кГц. Это было интерпретировано
в рамках модели тонкого экрана межзвездной среды при рефракции лучей пульсара
в двух отдельных его точках. Анализ такой модели затруднен, поскольку вместе с
14.3] Цитированная литература 545
рефракцией наблюдалось дифракционное рассеяние на структурах, соответственно
больше и меньше масштаба Френеля (Cordes, Pidwerbetsky, and Lovelace, 1986).
Вследствие рефракции на радиотелескопе образуются два изображения источника,
что приводит к интерференционным полосам интенсивности принятого сигнала.
Расстояние до пульсара @,33 кпк) и поперечная скорость A78 км/с) были известны
из других наблюдений, а расстояние до экрана было принято равным половине
расстояния до пульсара. Был сделан вывод, что угол между изображениями равен
~ 3,3 мсек дуги, что соответствует линейной шкале ~1 а. е. между преломляющими
структурами. В сущности, преломляющими структурами был образован двухэле-
двухэлементный интерферометр с расстоянием между лепестками ~1 мксек дуги. Для
сравнения, угловое разрешение с равной диаметру Земли базой на частоте 430 МГц
составило бы 44 мсек дуги. Особые условия, благодаря которым стали возможны эти
наблюдения, продолжались не менее 19 дней и в течение этого времени наблюдения
других пульсаров не показали такого рассеяния. Этим в значительной степени
подтверждается, что причиной наблюдаемого явления была удачная конфигурация
межзвездной среды в направлении на пульсар.
За исключением таких случаев рассеяния как вышеописанные, практически
других событий с пространственно когерентными астрономическими источниками
не было, хотя механизм когерентности может существовать в пульсарах и мазерных
источниках (Verschuur and Kellermann, 1988). Полностью когерентные источни-
источники не подходят для синтезного картографирования с использованием принципа
Ван Циттерта—Цернике, и по этой причине не соответствуют концепции этой кни-
книги. Материал по когерентности и частичной когерентности может быть найден,
например, в (Beran and Parrent, 1964; Born and Wolf, 1999; Drane and Parrent, 1962;
Mandel and Wolf, 1965, 1995; MacPhie, 1964; Goodman, 1985).
Цитированная литература
Anantharamaiah К. R., Т. J. Cornwell and R. Narayan. Synthesis Imaging of Spatially Co-
Coherent Objects. Synthesis Imaging in Radio Astronomy, R. A. Perley, F. R. Schwab, and A.
H. Bridle, Eds., Astron. Soc. Рас. Conf. Ser., 6, 415-430, 1989.
Beran M. J. and G. B. Parrent. Jr., Theory of Partial Coherence, Prentice-Hall, Englewood
Cliffs, NJ, 1964; repr. by Society of Photo-Optical Instrumentation Engineers, Bellingham, WA,
1974.
Booker H. G. and P. C. Clemmow. The Concept of an Angular Spectrum of Plane Waves, and
Its Relation to that of Polar Diagram and Aperture Distribution, Proc. IEE, 97, 11-17, 1950.
Born M. and E. Wolf. Principles of Optics, 7th ed., Cambridge Univ. Press, Cambridge, MA,
1999. (Имеется перевод: М. Борн, Э. Вольф. Основы оптики. — М.: Наука, 1973.)
Bracewell R. N. Radio Astronomy Techniques, in Handbuch der Physik, Vol. 54, S. Flugge,
Ed., Springer-Verlag, Berlin, 1962, p. 42-129.
Bracewell R. N. The Fourier Transform and Its Applications, McGraw-Hill, New York, 2000
(earlier eds. 1965, 1978).
Cordes J. M.j A. Pidwerbetsky, and R. V. E. Lovelace. Refractive and Diffractive Scattering
in the Interstellar Medium, Astrophys. J., 310, 737-767, 1986.
Cornwell T. J., K. R. Anantharamaiah and R. Narayan. Propagation of Coherence in Scatter-
Scattering: An Experiment Using Interplanetary Scintillation, J. Opt. Soc. Am., 6A, 977-986, 1989.
Cornwell T. J., and R. Narayan. Imaging with Ultra-Resolution in the Presence of Strong
Scattering, Astrophys. J., 408, L69-L72, 1993.
Drane C. J. and G. B. Parrent. Jr., On the Mapping of Extended Sources with Nonlinear
Correlation Antennas, IRE Trans. Antennas Propag., AP-10, 126-130, 1962.
Goodman J. W. Statistical Optics, Wiley, New York, 1985.
18 Томсон
546 Теорема Ван Циттерта-Цернике, когерентность и рассеяние [Гл. 14
MacPhie R. Н. On the Mapping by a Cross Correlation Antenna System of Partially Coherent
Radio Sources, IEEE Trans. Antennas Propag., AP-12, 118-124, 1964.
Mandel L. and E. Wolf. Coherence Properties of Optical Fields, Rev. Mod. Phys., 37, 231-287,
1965.
Mandel L. and E. Wolf. Optical Coherence and Quantum Optics, Cambridge Univ. Press,
Cambridge, UK, 1995.
Parrent G. B. Jr., Studies in the Theory of Partial Coherence, Opt. Acta, 6, 285-296, 1959.
Silver S. Microwave Antenna Theory and Design, Radiation Laboratory Series Vol. 12,
McGraw-Hill, New York, 1949, p. 174.
Swenson G. W.j Jr. and N. C. Mathur. The Interferometer in Radio Astronomy, Proc. IEEE,
56, 2114-2130, 1968. (Имеется перевод: ТИИЭР, 56, 12, с. 20-36, 1968.)
Verschuur G. L. and K. I. Kellermann. Eds., Galactic and Extragalactic Astronomy, Springer-
Verlag, New York, 1988.
Wolszczan A. and J. M. Cordes. Interstellar Interferometry of the Pulsar PSR 1237+25,
Astrophys. J., 320, L35-39, 1987.
Глава 15
РАДИОПОМЕХИ
По мере освоения радиочастот для связи, навигации и в других целях, исклю-
исключение мешающих сигналов становится все более и более сложной задачей в радио-
радиоастрономии. Помехи создают особую проблему для радиоастрономов, поскольку
уровни сигналов космических источников намного меньше уровня активных (пере-
(передающих) средств радиосвязи, а для обеспечения требуемой чувствительности необ-
необходимы широкие полосы. Хотя определенные диапазоны частот на метровых и сан-
сантиметровых волнах выделены исключительно для радиоастрономии и пассивного
приема сигналов, эти полосы зачастую слишком узки, чтобы обеспечить нужную
чувствительность. Кроме того, частоты многих космических спектральных линий
находятся вне пределов радиоастрономических диапазонов. Поэтому радиоастроно-
радиоастрономам иногда бывает необходимо проводить наблюдения в диапазонах, выделенных
другим службам. При таких условиях наилучший способ избежать помех — раз-
размещение радиотелескопов в местах, удаленных от промышленных и подобных им
центров человеческой деятельности, а также использование рельефа местности для
экранирования излучения передатчиков. Основным параметром при выборе места
и согласования с другими пользователями диапазонов частот служит предельный
уровень помех, т. е. плотность потока мешающего сигнала в полосе частот радиоте-
радиотелескопа, превышение величины которой приводит к ухудшению астрономических
наблюдений. Величина этого порога зависит от типа и рабочих параметров радиоте-
радиотелескопа. Именно эта зависимость является предметом рассмотрения данной главы.
В Приложении 15.1 кратко описывается Международная система стандартизации
радиочастотного спектра.
15.1. Основные положения
Предельная чувствительность радиотелескопа определяется шумами системы,
и сигнал помехи может быть допустимым, если его вклад мал по сравнению с шу-
шумовыми флуктуациями на выходе. Отклик на помеху, равный одной десятой средне-
среднеквадратичного уровня глума измерений, служит удобным критерием при вычисле-
вычислении порога помех. Соответствующая плотность потока такого сигнала может быть
рассчитана, если известна эффективная площадь антенны. Диаграммы направлен-
направленности радиоастрономических антенн обычно узки, и вероятность приема помехи
в главном луче или ближайших к нему боковых лепестках невелика, особенно если
источник помехи находится на Земле. Таким образом, можно полагать, что обычно
помехи принимаются дальними боковыми лепестками антенны. На рис. 15.1 показа-
показана эмпирическая функциональная зависимость величины максимального усиления
боковых лепестков от углового расстояния, отсчитываемого от оси главного луча.
Зависимость получена по измерениям диаграмм ряда больших зеркальных антенн.
Для настоящих расчетов удобно использовать величину усиления, равную ОдБ
(т. е. ОдБи по отношению к изотропному излучателю), что соответствует угловому
расстоянию 19° относительно главного луча. Значение 0 дБи также соответствует
среднему усилению антенны по пространственному углу 4тг ср, и эффективная
площадь при таком усилении равна А2/4тг, где А — длина волны. Если F^ [Вт/м2] —
18*
548
Радиопомехи
[Гл. 15
40
ей
3-20
-20
^G=32-251gcp
дБи
=—10д
плотность потока сигнала помехи в
принимаемой полосе частот, то отно-
отношение мощности помехи к мощности
шума приемника равно
FhX2
12 5 10 20 50 100 180°
Угол ф (град) между электрической осью
главного луча и рассматриваемым направлением
Рис. 15.1. Эмпирическая модель боковых ле-
лепестков для зеркальных антенн с диаметром,
превышающим 100 длин волн. Измерения на
действующих антеннах показывают, что 90 %
максимумов боковых лепестков находятся ни-
ниже представленной функциональной зависимо-
зависимости. Уровень боковых лепестков может быть
снижен на ЗдБ и более в системах с от-
отсутствующим или минимальным затенением
апертуры элементами облучения. Приведенная
модель относится к большим антеннам с тре-
треугольной либо четырехугольной несущей кон-
конструкцией облучателя, обычно применяемой в
радиоастрономии (ITU-R, 1997а)
A5.1)
где к — постоянная Больцмана,
Ts — шумовая температура систе-
системы и Az/ — ширина полосы пропус-
пропускания приемника. В этой формуле
подразумевается, что поляризация
сигнала помехи соответствует поля-
поляризации антенны. Поскольку радио-
радиоастрономическими антеннами обыч-
обычно принимаются две поляризации,
ортогональные линейные или про-
противоположные круговые, выбор по-
поляризации мало помогает в борьбе
с помехами. На практике уровень
принятого сигнала помехи изменя-
изменяется с течением времени вследствие
эффектов, связанных с распростра-
распространением радиоволн, и сопровождаю-
сопровождающего движения радиотелескопа, при
котором боковыми лепестками пересекается направление на передатчик.
Для сравнения с корреляционными системами рассмотрим сначала более про-
простой пример приемника, измеряющего полную мощность на выходе одиночной
антенны. Отношение сигнал/глум на выходе квадратичного детектора после усред-
усреднения за время та дано выражением A5.1), умноженным на \/Аита . Этот результат
следует из рассмотрения, приведенного в п. 6.2.1. Если в качестве порогового кри-
критерия сигнала помехи использовать отношение помеха/шум, равное 0,1, то получим
A5.2)
Заметим, что пороговый уровень помехи возрастает с увеличением частоты про-
пропорционально v , что определяется зависимостью эффективной площади боковых
лепестков от Л. С увеличением частоты обычно также возрастает шумовая темпе-
температура системы и используемая полоса частот. Выраженный через спектральную
плотность потока, соответствующий пороговый уровень Sh [Вт-м~2-Гц~1] равен
Fh
A5.3)
Если наблюдения проводятся в непрерывном спектре с полосой частот, находящейся
в выделенном для радиоастрономии диапазоне, то при определении критического
уровня помехи Az/ обычно принимается равной всему выделенному спектрально-
спектральному диапазону. Наиболее чувствительны к помехам радиотелескопы, измеряющие
полную мощность. Таким образом, результаты, представленные формулами A5.2)
и A5.3), дают определение порогового уровня помехи для наихудшего случая в ра-
радиоастрономических наблюдениях. Значения F^ и 6^, рассчитанные для систем пол-
полной мощности с типичными параметрами, приводятся (ITU-R, 1995; ITU-R, 1997b)
15.1]
Основные положения
549
для различных радиоастрономических диапазонов. Для Sh эти данные показаны на
нижнем графике рис. 15.2. Поскольку причиной большей части радиоастрономиче-
радиоастрономических помех является широкополосное побочное излучение, величина Sh особенно
полезна.
1000
Рис. 15.2. Графики, показывающие пороговые уровни помех Sh в единицах децибел спек-
спектральной плотности потока [дБ-Вт-м~2-Гц~1] для наблюдений в непрерывном спектре.
Расчеты выполнены с использованием типичных аппаратурных характеристик для каждо-
каждого частотного диапазона и типа инструментов. График для радиометров полной мощности
построен по формуле A5.3) на основе данных (ITU-R, 1997b). Антенные решетки со
связанными элементами представлены MERLIN и VLA, для которой графики рассчитаны
для самой компактной и самой протяженной конфигураций. Графики для решеток со
связанными элементами построены по формуле A5.15). График для систем РСДБ основан
на формуле A5.25). Обратите внимание, что для решеток апертурного синтеза величина
Sh увеличивается при уменьшении ширины лепестка синтезированной диаграммы направ-
направленности на любой данной частоте
Помехи низкого уровня, амплитуда которых сравнима с шумами на выходе
приемника, приводят к ухудшению чувствительности, тем самым препятствуя обна-
обнаружению слабых источников. При наблюдениях сильных источников такие помехи
ухудшают точность измерений, вследствие чего уменьшается возможность обнару-
обнаружения тонких деталей или изменений в структуре или интенсивности, которые час-
часто оказываются ключевыми для новых открытий в астрономии. По этой причине,
если в наблюдениях произошла помеха, то следует удалить все данные, которые
могли быть искажены.
В последующем анализе рассматривается отклик на помехи для стандартных ме-
методов наблюдений и обработки данных, и не рассматриваются методы, специально
предназначенные для уменьшения влияния помех. Среди последних — адаптивная
компенсация сигналов помех в приемнике и адаптивное гашение отклика решетки
в направлении регистрации помехи [см., например, (Barnbaum and Bradley, 1998)].
550 Радиопомехи [Гл. 15
15.2. Решетки с короткими и промежуточными базами
Рассмотрим теперь чувствительность к помехам корреляционной решетки, рас-
расстояние между антеннами которой достигает нескольких десятков километров,
что типично для антенных решеток со связанными элементами. Чувствительность
такой решетки к помехам меньше по сравнению с системой измерения полной
мощности благодаря двум эффектам. Во-первых, источник помех не перемещается
по небесной сфере, в отличие от наблюдаемого объекта, испытывающего суточное
движение; по этой причине частота интерференции помехи отличается от частоты
интерференции полезного сигнала. Во-вторых, аппаратурные задержки подбирают-
подбираются таким образом, чтобы уравнять пути сигналов для излучения, принимаемого из
направления наблюдений, и корреляция сигналов из других направлений, если они
широкополосные, должна быть до некоторой степени уменьшена. При рассмотрении
этих эффектов, мы следуем анализу Томпсона (Thompson, 1982).
15.2.1. Усреднение на частоте интерференции. Рассмотрим сначала эф-
эффект частоты интерференции. Предположим, что для уменьшения частоты интер-
интерференции полезного сигнала до нуля используется аппаратурное фазовое смещение,
как описано в п. 6.1.6. Исключенные из космических сигналов фазовые изменения
добавляются в сигналы помех. Если источник помехи неподвижен относительно ан-
антенн, то на выходе коррелятора помехи представлены колебаниями с естественной
частотой интерференции наблюдаемого источника, которая, согласно формуле D.9)
(знак dw/dt опускается), равна
Vj = uoeu cos 5, A5.4)
где иое — угловая скорость вращения Земли, и — проекция антенной базы и 5 —
склонение наблюдаемого источника. Усреднение такого интерференционного сиг-
сигнала в интервале времени та эквивалентно свертке с прямоугольной функцией
шириной то. Таким образом, коэффициент уменьшения амплитуды находится как
преобразование Фурье функции свертки и равен
8Ш (М,Та) ^ ( }
Чтобы определить пороговую величину помехи, найдем отношение ее среднеквад-
среднеквадратичного уровня к среднеквадратичному уровню шума на радиокарте, и затем как
и ранее, приравняем полученный результат к 0,1. Первый шаг состоит в определе-
определении среднеквадратичной величины модуля компоненты помехи в данных функции
видности. Из спектра выходного сигнала коррелятора, показанного на рис. 6.7 б,
видно, что компонента коррелированного сигнала, в данном случае помеха, на вы-
выходе коррелятора представлена дельта-функцией. Предполагая, как и раньше, что
помеха принимается через боковые лепестки с усилением ОдБи и поляризация со-
согласована, подставим в качестве амплитуды дельта-функции кТд Az/ = F^c2/Dтг^2).
Таким образом, сумма квадратов модулей помехи в пг точках сетки выборки на
плоскости uv равна
Здесь Г{ — отклик коррелятора на помеху, Hq — коэффициент усиления по
напряжению, и (f2) — среднеквадратичное значение коэффициента Д из
формулы A5.5), представляющее собой результат усреднения видности на частоте
15.2]
Решетки с короткими и промежуточными базами
551
интерференции. Для определения среднеквадратичного значения /i используем
простое приближение, суть которого состоит в рассмотрении изменения этой ве-
величины на плоскости u'v1', когда вектор базы вращается с постоянной скоро-
скоростью uje и им описывается окружность, как показано в разд. 4.2. Предполо-
Предположим также, что при интерполяции значений видности на прямоугольной сет-
сетке точек плоскости uv измеренные значения усредняются с равными весовыми
коэффициентами в прямоугольных ячейках, центры которых совпадают с точ-
точками сетки (см. описание усреднения по ячейкам в п. 5.2.2). Тогда эффектив-
эффективное время усреднения г для помехи равно времени, за которое ячейка пере-
пересекается вектором базы, как показано на рис. 15.3. Заметим, что как следует
из формулы A5.4), величина частоты интерфе-
интерференции равна нулю на оси г/, и в этом случае
/i равно единице. При малых значениях угла ф,
показанного на рис. 15.3, длина пути через ячейку
почти равна Аи и время пересечения ячейки со-
составляет г = Au/ujeqf, где q' = \/и'2 + v'2 . Кроме
того, i/fT = Аи 8тф cos5. Далее, Аи равно обрат-
обратной величине размера синтезированного поля, ко-
который во всех диапазонах частот, за исключени-
исключением наблюдений на длинных волнах, обычно не
превышает 0,5°. Предположим, что величина Аи
порядка 100 или больше, что позволяет сделать
следующее упрощение. Если Аи = 100 и 5 < 70°,
то f2 изменяется от 1 до 10~3 при изменении ф
от 0 до < 17°. Таким образом, наибольший вклад
в f2 вносится при малых ф, и в формуле A5.5)
можно произвести подстановку VjT
откуда получим
At/sin \|/+
+ At/cos \|/
тг/2
^u cos S)
1
cos 8)
тгАи cos 5
Рис. 15.3. Определение среднего
времени пересечения ячейки на
участке годографа простран-
пространственных частот, показанного
штриховой линией. Скорость
вектора базы на плоскости
u'v' равна ueq'. Средняя длина
пути через ячейку в направлении
штриховой линии равна площади
ячейки Аи' Av', деленной на ее
ширину, спроецированную на
нормаль к этому направлению
A5.7)
Поскольку Аи велико, то при вычислении инте-
интеграла мы заменили верхний предел интегрирова-
интегрирования на оо.
Для определения величины шума обратимся снова к рис. 6.7 6. Спектральная
плотность мощности шума вблизи нулевой частоты равна Н^к2Т^Аи^ и эквивалент-
эквивалентная ширина полосы г, включая отрицательные частоты, определяется процессом
усреднения; см. уравнение F.44). Таким образом, среднеквадратичная компонента
шума для пг точек сетки равна
A5.8)
где (г г) — среднее значение г 1. Как показано на рис. 15.3, среднее время пересе-
пересечения ячейки равно
Аи |cosec?|
т =
'c^e (| sin ^| 4- |cosec <5| | cos V7!)
A5.9)
552 Радиопомехи [Гл. 15
о
и после усреднения по пг точкам на плоскости uv получим
(г-1)
где q' = у Хд + У^ , и Хд, Уд — проекции антенной базы на экваториальную плос-
плоскость, определенные в разд. 4.1. Мы предположили, что Аи' = Av' sin 5 (т. е. Аи =
= Av) и что во всех ячейках, за исключением небольшого их количества, участок
годографа пространственных частот может быть аппроксимирован прямой линией.
Среднее значение г в окрестности окружности на плоскости u'v' (см. разд. 4.2),
как следует из формулы A5.9), равно
тг/2
1 f rd^ = ^-A + | sm*|), A5.10)
7Г J 7Tl\u
A5.11)
(M)cp.KB. _ f^ х Qg 22)
I п|;ср.кв.
По теореме Парсеваля отношение среднеквадратичных величин помехи и шума на
карте равно отношению этих величин в области определения функции видности из
уравнения A5.12). Для расчета порогового уровня помех Fh приравняем правую
часть уравнения к 0,1, что дает в результате
Fh = и'""87Ш"е 4 - Е Я' ¦ A5-13)
Из уравнений A5.6)—A5.8) и A5.11) получаем отношение помеха/шум
Коэффициент у cos 5A + | sin <5|) был принят равным единице, и при этом сум-
суммарная ошибка должна быть менее 1дБ для 0<|5|<71°и менее 2,3 дБ для 5 =
= 80°. Заметим, что при фиксированных положениях антенн q' пропорционально
z/, и соответственно, Fh пропорционально i/2'5. Число точек на плоскости u'v',
которые относятся к соответствующей паре антенн, пропорционально q1', поэтому
для расчетов по формуле A5.13) удобно записать
где пр —число коррелированных антенных пар в решетке.
Пороговый уровень помех Sh в единицах [дБ-Вт-м~2-Гц~1] равен
Значения Sh для VLA и MERLIN показаны на рис. 15.2. Из двух графиков, по-
показанных для VLA, нижний и верхний рассчитаны для конфигураций, в которых
15.2] Решетки с короткими и промежуточными базами 553
максимальные расстояния между антеннами вдоль рукавов решетки составляют
соответственно 0,59 и 21км (см. рис. 5.17 6).
Поскольку усреднение неэффективно для снижения помех при величине и близ-
близкой к нулю, значения видности с наибольшим вкладом помех концентрируются
вдоль оси v. Следует ожидать некоторую долю случайности в появлении боль-
больших отсчетов, поскольку уровень боковых лепестков, через которые принимаются
помехи, не постоянен. В соответствии с (и, v)-распределением, помехи в области
переменных (/,т) представляют квазислучайную структуру, вытянутую в направ-
направлении восток—запад; см., например, (Thompson, 1982). Такая концентрация дает
возможность уменьшения отклика на помехи с помощью удаления каких-либо по-
подозрительных значений измеренной видности, находящихся близко к оси v. Вслед-
Вследствие ухудшающегося при этом заполнения плоскости uv, боковые лепестки в син-
синтезированной диаграмме направленности могут увеличиваться. Эффект боковых
лепестков может быть до некоторой степени подавлен при использовании процедур
восстановления изображений, описываемых в гл. 11.
Рассмотренные выше случаи имеют отношение к наблюдениям достаточной про-
продолжительности, когда плоскость uv хорошо заполнена и уровень помехи остается
приблизительно постоянным во время наблюдений. Если лишь часть а годографов
на плоскости uv пересекает ось г>, то знаменатели в формулах A5.13) и A5.15)
должны быть умножены на коэффициент у/а. Сильные спорадические помехи,
конечно, могут дать отклики, отличающиеся от вышеописанного.
15.2.2. Декорреляция широкополосных сигналов. Поскольку помехи
и полезные сигналы обычно принимаются с разных направлений, их временные
задержки на входе коррелятора в общем случае не одинаковы. Корреляция
широкополосных сигналов помех по этой причине уменьшается, что приводит к
дальнейшему уменьшению их отклика. Величина уменьшения не может быть
рассчитана в общем случае аналогично, например, усреднению на частоте
интерференции, но может быть определена в каждом конкретном случае антенной
конфигурацией и положением источника помех. По этой причине, а также потому,
что декорреляции подвержены только широкополосные сигналы, рассматриваемый
эффект не учитывался в формулах A5.13) и A5.15), определяющих пороговый
уровень помех.
Пусть для любого времени наблюдений 0s — угол между плоскостью, нормаль-
нормальной к линии базы, образованной парой антенн, и направлением на наблюдаемый
источник. Переменной 0s определяется круг равных задержек на небесной сфере.
Аналогично предположим, что 0i — соответствующий угол для источника помех.
Разность задержек интерферирующих сигналов в корреляторе равна
где D — длина базы. Выражения для 0s и 6i могут быть получены из уравне-
уравнения D.3), поскольку sin 0s = w\/D, где w — третья пространственная координа-
координата, как показано на рис. 3.2, и Л — длина волны. Предположим, что принятый
сигнал помехи имеет прямоугольный спектр ширины Аи и центральной частотой
z/q, определяемый либо самим сигналом, либо полосой пропускания приемника.
Автокорреляционная функция такого сигнала по соотношению Винера-Хинчина
записывается в виде
sinfrAi/r,) A5л7)
Выражением A5.17) представлена действительная часть комплексного сигнала на
выходе коррелятора как функция разностной задержки Т&. Мнимая часть выход-
выходного сигнала описывается подобным выражением, в котором используется синус
554 Радиопомехи [Гл. 15
вместо косинуса. Таким образом, декорреляция модулей комплексного выходного
сигнала в зависимости от задержки т^ представлена коэффициентом
sin(.A,rd)_
тгАг/Td
При фиксированном положении передатчика величина Oi остается постоянной, а
6S изменяется в соответствии с направлением антенн. Таким образом, величина т^
может быть равна нулю, и в этом случае величина /2 максимальна, но в отличие
от /i, максимум /2 может быть получен в любой точке на плоскости uv. Пары
антенн, для которых максимумы Д и /2 накладываются друг на друга, вносят
наибольший вклад в помехи при построении изображения, а парами, для которых
расстояние между максимумами достаточно велико, вносится наименьший вклад.
Таким образом, для широкополосных сигналов эффекты частоты интерференции
и декорреляции должны рассматриваться совместно. Например, при расчете от-
отклика VLA на геостационарный спутник, находящийся в меридиане, был получен
следующий коэффициент дополнительного уменьшения среднеквадратичной поме-
помехи вследствие декорреляции (Thompson, 1982):
\
<«.»>
Суммирование в выражении A5.19) было выполнено по всем парам антенн при
равных приращениях часового угла, а множители q' были введены для компенсации
неравномерности распределения точек на плоскости гш, появляющейся в результате
данного метода выборки. Рассматривалось расположение антенн VLA как в ком-
компактной, так и в наиболее протяженной конфигурациях для частот наблюдений
от 1,4 до 23 ГГц и полос пропускания от 25 до 50 МГц. Результаты расчетов по-
показывают, что подавление широкополосных помех вследствие декорреляции может
изменяться от 4 до 34 дБ и сильно зависит от склонения наблюдаемого источника.
Распределение помехи предполагалось равномерным по полосе частот, следствием
чего должна быть сделана переоценка уровня подавления в реальных наблюдениях.
15.3. Системы со сверхдлинными базами
В решетках РСДБ, когда расстояние между антеннами достигает сотен и тысяч
километров, корреляция компонент сигнала помехи, поступающих на вход корреля-
коррелятора, обычно оказывается пренебрежимо малой величиной. Это происходит потому,
что здесь естественная частота интерференции больше по сравнению с решетками
антенн, базы которых не превышают нескольких десятков километров, а также
вследствие большего отклонения задержек сигналов, направления которых не сов-
совпадают с направлением наблюдений. Кроме того, если только сигналы помех не
созданы космическим аппаратом или спутником, то маловероятно, чтобы они могли
присутствовать в двух значительно удаленных друг от друга пунктах наблюдений.
Рассмотрим сигнал помехи, поступающий на одну из антенн коррелированной
пары. Измеренная величина корреляции снижается помехой, и суммарный эффект
аналогичен увеличению шума системы на этой антенне. На рис. 15.4 x(t) и y(t)
представлены сигналы плюс шумы систем двух антенн при отсутствии помех,
a z(t) соответствует сигналу помехи на одной из антенн. Средние значения трех
15.3]
Системы со сверхдлинными базами
555
x(t)
а
z(t)
ст
(
э
Коррелятор
Рис. 15.4. Компоненты сигналов на входе коррелятора, используемые при рассмотрении
влияния помех на РСДБ-наблюдения
указанных сигналов равны нулю, и стандартные отклонения равны а для ж, у и U{
для z. В отсутствие помехи измеренный коэффициент корреляции равен
Pi =
а при ее наличии равен
Р2 =
¦{xz
A5.20)
A5.21)
Помеха не коррелирует с ж и у, поэтому (xz) = (yz) = 0. Кроме того, при пороговом
уровне помехи a2 <C сг2. Таким образом, из уравнений A5.20) и A5.21) следует
A5.22)
Помехи уменьшают измеренную корреляцию. В системах с автоматической ком-
компенсацией уровня (АКУ) уменьшение корреляции может интерпретироваться как
результат уменьшения коэффициента усиления системы, вызванного увеличением
мощности при поступлении помехи. Ошибка, вносимая в корреляционные измере-
измерения, следовательно, скорее мультипликативная, чем аддитивная. Помеха является
причиной аддитивных ошибок при наблюдениях на одиночных антеннах или ре-
решетках с достаточно короткими базами, когда отклик детектора или коррелятора
напрямую зависит от сигнала помехи. Различные последствия двух типов ошибок
были рассмотрены в п. 10.6.2. В принципе, изменения эффективного усиления могут
отслеживаться при использовании калибровочного сигнала, что рассматривалось
в разд. 7.6. Однако калибровка может быть затруднена при помехе с быстро ме-
меняющимся уровнем. Поэтому пороговый уровень помехи должен быть определен
достаточно малым, чтобы внесенные ошибки не приводили к существенному ухуд-
ухудшению точности измерений. В общем случае в качестве такого уровня целесообразно
выбрать величину изменений амплитуды функции видности, вызванных помехой,
равную 1 %. Если учесть возможность появления одновременных, но не коррелиро-
коррелированных помех на обеих антеннах, то в результате получим
^ 0,01.
A5.23)
556 Радиопомехи [Гл. 15
Из теоремы Парсеваля следует, что среднеквадратичная ошибка измерений функ-
функции видности, равная 1 %, приводит к величине среднеквадратичной ошибки в рас-
распределении интенсивности на карте, равной 1 % от соответствующего среднеквад-
среднеквадратичного значения интенсивности истинного распределения. Изменение динами-
динамического диапазона интенсивности на карте зависит от формы распределения интен-
интенсивности и распределения ошибок. Для карты с единственным точечным источни-
источником среднеквадратичная ошибка интенсивности составила бы примерно 10~2у///пг
от величины максимальной интенсивности, где / — доля данных, искаженных поме-
помехой при выборке из пг значений функции видности на сетке измерений. Здесь пред-
предполагается, что флуктуации принимаемого сигнала помехи достаточно быстрые,
чтобы уровни помех в каждой точке выборки были по существу независимыми.
Если это не так, то результирующая ошибка будет больше.
В соответствии с критерием A5.23), отношение мощности помехи к шуму систе-
системы, представленное формулой A5.1), не должно превышать 0,01. Таким образом,
для порогового уровня помехи получим
Fh = *^kTfAV ¦ A5-24)
С
Пороговый уровень помехи, выраженный в единицах [Вт-м~2-Гц~1], равен
Fh 2
S = =
Отметим, что здесь отношение помеха/шум, равное 0,01, получено для уровней на
входе коррелятора. В случае систем полной мощности (одиночных антенн) и реше-
решеток, рассмотренных в разд. 15.2, когда ошибки аддитивны, критерий помеха/шум,
равный 0,1, применяется к усредненному по времени выходу коррелятора или де-
детектора. Соответственно, при этом пороговый уровень меньше (т. е. критерий более
строгий) по сравнению с его определением в формулах A5.24) и A5.25) для РСДБ.
В графике для РСДБ, данном на рис. 15.2, использованы типичные значения Т^.
Пороговые уровни помех в среднем на 40 дБ менее строгие по сравнению с систе-
системами полной мощности.
15.4. Помехи от авиационных и космических передатчиков
Используя величины Fh и Sh, выведенные ранее, следует помнить, что они
относятся лишь к помехам от стационарных наземных передатчиков. Часто оказы-
оказывается возможным проведение наблюдений при достаточно больших углах места, не
менее 19° в стороне от любого такого передатчика; при таком угловом расстоянии
относительно главного луча уровень большинства боковых лепестков становится
ниже изотропного уровня модели на рис. 15.1. Передатчики на самолетах и спутни-
спутниках представляют особую проблему. В радиоастрономии не могут использоваться
полосы частот совместно со спутниковыми передатчиками «космос—земля» (линия-
(линиями телеметрик). Однако под давлением необходимости расширения спектрального
диапазона коммуникационным службам были выделены полосы частот соседние
или достаточно близкие к радиоастрономическим диапазонам. Побочное излучение
спутниковых передатчиков, за пределами выделенного для спутников диапазона ча-
частот, вне всяких сомнений, представляет наиболее серьезную проблему проведению
радиоастрономических наблюдений. Движение спутника по небесной сфере чаще
всего приводит к увеличению частоты интерференции на корреляционных выходах
15.4] Помехи от авиационных и космических передатчиков 557
решеток апертурного синтеза, что является причиной уменьшения интерференци-
интерференционного отклика. Кроме того, такие сигналы могут приниматься боковыми лепест-
лепестками более высокого уровня вблизи главного луча. Передатчики спутников на гео-
геостационарных орбитах (ГЕО) наносят особый ущерб радиоастрономии, поскольку
их положения фиксированы на высоких углах места вблизи небесного экватора.
Сигналы помех от ряда таких спутников, расположенных вдоль геостационарной
орбиты, могут в результате привести к тому, что в полосе небесной сферы вблизи
орбиты высокочувствительные наблюдения значительно ограничены.
Примеры побочного излучения, выходящего далеко за пределы разрешенного
диапазона для спутниковых систем, приводятся в работах (Gait, 1990; Combrinck,
West, and Gaylord, 1994). В этих случаях паразитное излучение чаще всего является
следствием применения модуляции с простым переключением фазы, и более со-
современной техникой [например, Гауссовой модуляцией с минимальным частотным
сдвигом (GSMK)] обеспечивается гораздо более резкое ограничение спектральных
полос (Murota and Hirade, 1981; Otter, 1994). Однако гармоники перекрестной моду-
модуляции, появляющиеся вследствие нелинейности усилителей, несущих большие число
коммуникационных каналов, остаются проблемой.
В некоторых случаях действующие требования и ограничения, связанные с кос-
космосом, создают дополнительные трудности для уменьшения побочного излучения.
Иногда в спутниковых системах для покрытия зоны их действия используется боль-
большое число узких лучей, так что одни и те же частотные каналы могут использовать-
использоваться соответствующее количество раз для охвата большого числа потребителей. Для
этого необходимы фазированные антенные решетки с большим числом (порядка
сотни и более) малых излучающих элементов, каждый со своим усилителем (см.,
например, Schuss et al., 1999). Поскольку энергопотребление ограничено солнечны-
солнечными батареями, эти усилители работают в режиме максимальной эффективности по
мощности и с компромиссной линейностью, что приводит в результате к побочному
излучению гармоник взаимной модуляции. Фильтрация каждого отдельного сиг-
сигнала, подаваемого на излучатели, может быть непрактичной из-за ограниченности
веса.
Рекомендованные предельные уровни побочного излучения (ITU-R 1997с) тре-
требуют от космических служб, чтобы мощность паразитного сигнала, измеренная
в полосе частот 4 кГц на выходе передатчика в действительности не превышала
—43дБВт. Так например, для низкоорбитального спутника на высоте 800 км, излу-
излучающего паразитный сигнал такого уровня боковым лепестком с усилением ОдБи,
на поверхности Земли была бы зарегистрирована спектральная плотность потока
побочного излучения равная — 208 дБ-Вт-м~2-Гц~1. Этот результат можно сравнить
с пороговыми уровнями помех в радиоастрономии, которые составляют —239 и
—255дБ-Вт-м~2-Гц~1 соответственно для спектральных измерений и измерений
в непрерывном спектре на частоте 1,4 ГГц. Хотя в этом простом расчете рассмат-
рассматривается наихудшая ситуация, разница в несколько десятков децибел показывает,
что предложенные ограничения не достаточны для защиты радиоастрономии. По
этой причине радиоастрономические требования должны рассматриваться особо на
поэтапной основе по мере выделения новых спектральных диапазонов и создания
новых систем. Ответственность, гарантирующая такую координацию, лежит на
радиоастрономах.
558 Радиопомехи [Гл. 15
Приложение 15.1. Регулирование радиочастотного спектра
Для стандартизации использования радиочастотного спектра был создан Меж-
Международный союз электросвязи (ITU), базирующийся в Женеве и являющийся
специализированным агентством Организации Объединенных Наций. Радиоастро-
Радиоастрономия была официально признана ITU службой радиосвязи в 1959 г. Сектор ра-
радиосвязи ITU (ITU-R) был создан в марте 1993 г. и заменил собой Междуна-
Международный радиоконсультативный комитет (МРКК), бывший ранее подразделением
ITU. Система исследовательских групп в ITU—R отвечает за технические вопросы.
Исследовательская группа 7 или Научная группа отвечает за такие направления как
радиоастрономия, стандарты времени и частоты, различные аспекты космических
исследований. В состав исследовательских групп входят рабочие группы, которые
связаны с конкретными направлениями. Их главной задачей является изучение
проблем, важных в данное время для координации частот, например, определенные
случаи совместного использования спектральных диапазонов различными служба-
службами, а также выпуск документированных рекомендаций по их решению. В результате
обсуждений в ITU чаще всего находятся взаимоприемлемые решения. Рекоменда-
Рекомендации должны быть приняты всеми исследовательскими группами и после этого, как
правило, становятся частью стандартов радиосвязи ITU. Рекомендации, имеющие
отношение к радиоастрономии см. в (ITU-R, 1997b) и других публикациях серии
RA.
ITU-R организует совещания исследовательских групп, рабочие встречи, а так-
также новые группы, необходимость в которых возникает время от времени для изу-
изучения отдельных проблем. Всемирные конференции по радиосвязи (WRC) устраи-
устраиваются с периодичностью два или три года, и на них распределяются новые спек-
спектральные диапазоны и, при необходимости, пересматриваются стандарты радио-
радиосвязи ITU. Руководства многих стран присылают делегации на WRC, и результаты
этих конференций имеют статус соглашений. Участвующие страны могут делать
исключения из международных стандартов до тех пор, пока это не оказывает
влияние на использование спектра в других странах. По этой причине во многих
странах разработаны свои собственные системы стандартов радиосвязи, по большей
части основанные на стандартах радиосвязи ITU, но с некоторыми исключениями,
учитывающими их особые требования. Для дальнейшей информации см., например,
(Pankonin and Price, 1981; Thompson, Gergely, and Vanden Bout, 1991; ITU-R, 1995).
Основная литература
Crawford D. L. Ed., Light Pollution, Radio Interference, and Space Debris, Astron. Soc. Pacific
Conf. Series, 17, ASP, San Francisco, CA, 1991.
ITU-R. Handbook on Radio Astronomy, International Telecommunication Union, Geneva,
1995 (или следующие издания).
Kahlmann H. С. Interference: The Limits of radio Astronomy, in Review of Radio Science
1996-1999, W. R. Stone, Ed., Oxford Univ. Press, Oxford, 1999, p. 751-785.
Swenson G. W. Jr., and A. R. Thompson. Radio Noise and Interference, in Reference Data
for Engineers: Radio, Electronics, Computer, and Communications, Sams, Indianapolis, 1993.
15.4] Цитированная литература 559
Цитированная литература
ВагпЬаит С. and R. F. Bradley. A New Approach to Interference Excision in Radio Astron-
Astronomy: Real-Time Adaptive Cancellation, Astron. J., 116, 2598-2614, 1998.
Combrinck W. L., M. E. West, and M. J. Gaylord. Coexisting with Glonass: Observing the
1612 MHz Hydroxyl Line, Pub. Astron. Soc. Pacific, 106, 807-812, 1994.
Gait J. Contamination from Satellites, Nature, 345, 483, 1990.
ITU-R Handbook on Radio Astronomy, International Telecommunication Union, Geneva, 1995
(или следующие издания).
ITU-R Recommendation SA.509-1, Generalized Space Research Earth Station Antenna Radi-
Radiation Pattern for Use in Interference Calculations, Including Coordination Procedures, ITU-R
Recommendations, SA Series, International Telecommunication Union, Geneva, 1997a (или
следующие издания).
ITU-R Recommendation RA.769-1, Protection Criteria for Radioastronomical Measurements,
ITU-R Recommendations, RA Series, International Telecommunication Union, Geneva, 1997b
(или следующие издания).
ITU-R Recommendation SA.329-7, Spurious Emissions, ITU-R Recommendations, SA Series,
International Telecommunication Union, Geneva, 1997c (или следующие издания).
Murota К. and К. Hirade. GMSK Modulation for Digital Mobile Radio Telephony, IEEE
Trans. Commun, COM-29, 1044-1050, 1981.
Otter M. A Comparison of QPSK, OQPSK, BPSK and GMSK Modulation Schemes, Report of
the European Space Agency, European Space Operations Center, Darmstadt, Germany, June
1994.
Pankonin V. and R. M. Price. Radio Astronomy and Spectrum Management: The Impact of
WARC-79, IEEE Trans. Electromagn. Compat., EMC-23, 308-317, 1981.
Schuss J. J., J. Upton, B. Myers, T. Sikina, A. Rohwer, P. Makridakas, R. Francois, L.
Wardle, and R. Smith. The IRIDIUM Main Mission Antenna Concept, IEEE Trans. Antennas
Propag., AP-47, 416-424, 1999.
Thompson A. R. The Response of a Radio-Astronomy Synthesis Array to Interfering Signals,
IEEE Trans. Antennas Propag., AP-30, 450-456, 1982.
Thompson A. R., T. E. Gergely, and P. Vanden Bout. Interference and Radioastronomy,
Physics Today, 41-49, November 1991.
Глава 16
СМЕЖНАЯ ТЕХНИКА
В различных областях астрономии молено встретить идеи и методы, подобные
тем, которые используются в радиоинтерферометрии и при синтезировании радио-
радиокарт. Здесь рассматриваются некоторые из них, включая оптические методы, что
позволит читателю получить более широкое представление о затронутых в книге
проблемах. Все эти темы детально разобраны в литературе, поэтому наша основная
цель состоит лишь в общем описании основополагающих принципов и связи между
ними и материалом, подробно рассмотренным в предыдущих разделах.
16.1. Интерферометр интенсивностей
В интерферометрии с большими базами использование интерферометра интен-
интенсивностей приводит к некоторым техническим упрощениям, которые в основном
имели значение на ранней стадии развития радиоастрономии.
Как уже упоминалось в п. 1.3.7, практическое применение интерферометра
интенсивностей в радиоастрономии ограничено (Jennison and Das Gupta, 1956; Carr
et al., 1970; Dulk, 1970), так как по сравнению с обычным интерферометром он тре-
требует для приемной системы намного более высокого отношения сигнал/шум и при
этом измеряется лишь модуль функции видности. Интерферометр интенсивностей
был разработан Ханбери Брауном, который описал его устройство и применение
(Hanbury, Brown, 1974).
Усилитель
и
фильтр
Квадратичный
детектор
После-
детекторный
фильтр
Компенсирую-
Компенсирующая задержка
Коррелятор
Усилитель
и
фильтр
Квадратичный
детектор
После-
детекторный
фильтр
Ретранслятор
J
7
Рис. 16.1. Интерферометр интенсивностей. Блок усилителя и фильтра может также вклю-
включать в себя гетеродин и смеситель. Компенсирующая задержка выравнивает временные
задержки сигналов от источника на входах коррелятора. Последетекторные фильтры
устраняют постоянную и ВЧ-составляющие сигналов
16.1] Интерферометр интенсивностей 561
В интерферометре интенсивностей сигналы, поступающие от антенн, усилива-
усиливаются, а затем пропускаются через квадратичные (линейные по мощности) детек-
детекторы прежде, чем они поступают на коррелятор, как это показано на рис. 16.1.
В результате среднеквадратичные напряжения сигналов на входах коррелятора
пропорциональны мощности (интенсивности) принимаемых антеннами сигналов.
Интерференционные лепестки не возникают, так как фаза радиочастотных сиг-
сигналов теряется при детектировании, но выход коррелятора соответствует степени
корреляции продетектированных сигналов. Пусть V\ и V2 — напряжения на входах
детекторов. На выходах детекторов имеем V^ и V^2, каждый из которых состоит из
постоянной составляющей, устраняемой фильтром, и переменной, которая поступа-
поступает на вход коррелятора. Из соотношения для момента четвертого порядка гауссовых
процессов F.36) получим выражение для выхода коррелятора в виде
((V? - №))№ - (V22))) = (V?V?) - (V?){V22) = 2{Уг V2J. A6.1)
Выходной сигнал коррелятора пропорционален квадрату выходного сигнала корре-
коррелятора обычного интерферометра и пропорционален квадрату модуля комплексной
функции видности исследуемого источника.
Теперь мы приведем другой вывод отклика, дающий физическое представление
о том, каким образом сигналы от различных областей источника объединяются
внутри инструмента. Источник представлен в виде одномерного распределения
яркости на рис. 16.2. Предположим, что его можно рассматривать как линейное
распределение многих небольших областей, каждая из которых достаточно велика,
чтобы излучать сигнал с характеристиками стационарного случайного шума, но
с угловой шириной, которая мала по сравнению с величиной 1/гл, определяющей
угловое разрешение интерферометра. Источник считается пространственно некоге-
некогерентным, так что сигналы от различных его областей некоррелированы. Рассмот-
Рассмотрим две области источника к и ?, с координатами в к и вц и угловыми размерами dOk
и dOi, как показано на рис. 16.2. Каждая из областей излучает широкий спектр, но
мы сначала рассмотрим только выходной сигнал, связанный с фурье-составляющей
на частоте vk от области к и на частоте щ — от области ?. Пусть Ai@) — приемная
диаграмма направленности по мощности двух антенн и 1\(в) — распределение
интенсивности источника, причем обе функции одномерны. Тогда выходной сигнал
детектора первого приемника будет равен
[Vk cos 2тп/кг + Vt cos Btti/^ + фх)]2, A6.2)
где ф\ — фазовый член, появляющийся из-за разности путей, а напряжения сигна-
сигналов Vk и Уц определяются выражениями:
V% = Ax{eh)Ix{eh)d0hdvh, A6.3)
V? = Ai(^)/i(^) deedve. A6.4)
Разлагая выражение A5.2) в ряд и опуская постоянные и высокочастотные члены,
получаем выход детектора приемника 1 в виде
VkVe cos [2тг К ~vi)t- Ф1] • A6.5)
Аналогично выход детектора приемника 2 имеет вид
VkVt cos [2тг [ук -vt)t- ф2] • A6.6)
562
Смежная техника
[Гл. 16
Выход коррелятора пропорционален усредненному по времени произведению вы-
выражений A5.5) и A5.6), т. е.
со*
-ф2)).
A6.7)
Источник
Пока ширина полосы много меньше от-
отношения разрешения к полю зрения (см.
выражение F.69) и соответствующее обсу-
обсуждение), изменение фазового члена по ча-
частоте мало. При таком ограничении выра-
выражение A6.7) не зависит от частот vk и z/?,
поэтому, если проинтегрировать его отно-
относительно vk и уц по прямоугольной полосе
приемника шириной Az/, то dvk dvg заме-
заменится на Av2.
Фазы ф\ и 02 появляются из-за раз-
разностей путей kk! и it!, показанных на
рис. 16.3. Заметим, что ф\ и 02 имеют про-
противоположные знаки, поскольку длина до-
дополнительного пути к антенне 1 отсчиты-
вается от точки 1,ак антенне 2 — от точки
к. Если источник отстоит от антенн на рас-
расстояние Rs, то расстояние Ы в самом ис-
источнике приблизительно равно RsFk — 6i).
Угол ак + оц приблизительно равен u\/Rs,
поскольку и представляет собой проекцию
базы на нормаль к источнику, измеренную
в длинах волн. Рассмотренные выше приближения справедливы, если ак, осц и угол,
под которым наблюдается источник, малы. Таким образом, разность фаз составляет
1
Рис. 16.2. Расстояния и углы, используе-
используемые при рассмотрении интерферометра
интенсивностей
1 - 02 = 27rRs{Uk -
~ Z7TU (вк -
A6.8)
Используя выражение A6.7), можно записать выход коррелятора в виде
(Ai@fe) А^вг) hFk) /i(^) Av2 cos [2тги (вк - 0?)] d6k dOg). A6.9)
Проинтегрировав выражение A6.9) относительно вк и 6g по всему источнику в пред-
пол ожении пространственной некогерентности, получим выход от всех пар областей
в пределах источника
J Аг{в?) h@?) cos
, A6.10)
где предполагается, что отклик антенны Ai@) имеет постоянное значение Ао по
всему источнику, а нижние индексы R и I означают соответственно действительную
и мнимую части функции видности. Полученный результат следует из определения
функции видности, которое дано для двумерного источника в разд. 3.1. Таким
образом, выход коррелятора пропорционален квадрату модуля комплексной функ-
функции видности. Более подробное рассмотрение этого подхода можно найти в статье
16.2] Метод лунных покрытий 563
(Hanbury, Brown and Twiss, 1954). Анализ, основанный на взаимной когерентности
излучаемого поля, приведен в работе (Bracewell, 1958).
В некотором отношении интерферометр интенсивностей имеет преимущество
перед обычным интерферометром. Интерферометр интенсивностей намного менее
чувствителен к атмосферным фазовым флуктуациям, так как каждая компонен-
компонента сигнала на выходе коррелятора представляет собой разность между двумя
высокочастотными компонентами, про-
прошедшими почти один и тот же путь через k ?
атмосферу. Фазовые флуктуации компо- mzzzzzzzz^z^^zzzzzz^^/^///////M Источник
нент разностных частот в детекторах во
столько раз меньше фазовых флуктуации
ВЧ-сигналов, во сколько раз разностная
частота меньше ВЧ-частоты, а это отно-
отношение достигает порядка 10~5. В обычном
интерферометре такие фазовые флуктуа-
флуктуации могут значительно затруднить изме-
измерение как амплитуды, так и фазы функ- Рис. 16.3. Относительные задержки пу-
ции видности. Аналогично флуктуации тей кк' и ??' от областей источника к
фаз местных гетеродинов двух приемни- и ? для лучей, распространяющихся в на-
ков не вносят вклад в фазы компонент правлениях антенн 1 и 2
разностных частот. Поэтому нет необхо-
необходимости в синхронизации местных гетеродинов или даже в использовании высо-
высокостабильных стандартов частоты, как в случае РСДБ. Эти преимущества были
полезными, хотя и не существенными, на ранних этапах внедрения радиоинтерфе-
радиоинтерферометра интенсивностей. Если бы диаметры исследуемых источников были порядка
секунд, а не минут дуги, тогда эти особенности интерферометра интенсивностей
играли бы более существенную роль.
Серьезным недостатком интерферометра интенсивностей является его относи-
относительно небольшая чувствительность. В силу наличия детекторов в приемниках
отношение мощности сигнала к мощности шума на входах коррелятора пропорци-
пропорционально квадрату соответствующего отношения по ВЧ (см. соотношение (9.73)),
причем точное значение зависит от ширин полос ВЧ и последующих каскадов
(Hanbury, Brown and Twiss, 1954). В обычном интерферометре имеется возмож-
возможность обнаруживать сигналы, которые примерно на 60 дБ ниже уровня шума на
входах коррелятора. В интерферометре интенсивностей аналогичное отношение
сигнал/шум на входе коррелятора потребует увеличения отношения сигнал/шум
в ВЧ-каскадах на ~30дБ. Это обстоятельство, наряду с отсутствием чувствитель-
чувствительности к фазе функции видности, значительно ограничивает использование ин-
интерферометра интенсивностей в радиоастрономии. Интерферометр интенсивностей
играл аналогичную роль в первые годы развития оптической интерферометрии (см.
п. 16.4.3), пока не был разработан современный интерферометр Майкельсона.
16.2. Метод лунных покрытий
Измерения интенсивности излучения звезд при их покрытии Луной были пред-
предложены Мак Маоном (MacMahon, 1909) для определения их размеров и координат.
Его анализ, основанный на простых соображениях геометрической оптики, был
подвергнут Эддингтоном (Eddington, 1909) критике. Эддингтон утверждал, что ди-
дифракционные эффекты будут скрывать детали на угловых масштабах порядка раз-
размеров звезд. Статья Эддингтона, наверное, охладила на некоторое время интерес
к наблюдениям лунных покрытий. О первых измерениях лунных покрытий было
564
Смежная техника
[Гл. 16
Луна ^-
V Источник
Rn
сообщено только 30 лет спустя Витфордом (Whitford, 1939). Он провел наблюдения
звезд Р Capricorni и v Aquarii и получил четкую дифракционную картину.
В начале XX века у Эддингтона и других ученых не было понимания того,
что, хотя переменный отклик на покрытие и не является простой ступенчатой
функцией, как это должно быть для случая геометрической оптики и точечного
источника, преобразование Фурье отклика на точечный источник, которое
характеризует чувствительность к пространственной частоте на небе, имеет
ту же самую амплитуду, что и ступенчатая функция, и отличается только
фазой. Следовательно, затмения чувствительны ко всем фурье-компонентам
и не существует внутреннего предела на реализуемое разрешение, за исключением
налагаемого ограниченного отношения сигнал/шум. Эта эквивалентность амплитуд
была впервые замечена Шоером (Scheuer, 1962), который предложил метод
получения одномерного распределения интенсивности 1\ из кривой покрытия.
К тому времени понятие пространственной частоты стало повсеместно воспри-
воспринято благодаря применению радиоинтерферометрии. Поскольку при лунных
покрытиях дифракция происходит вне атмосферы Земли, высокое угловое
разрешение не снижается значительно из-за атмосферных эффектов, как это
происходит при наземной интерферомет-
интерферометрии. Более того, только отношение сиг-
сигнал/шум определяет получаемое разреше-
разрешение, зависящее исключительно от размера
телескопа. Впервые с помощью этой методи-
методики в радиоастрономии были измерены коор-
координаты и размеры ЗС273 в работе (Hazard,
Mackey and Shimmins, 1963; Шоломицкий и
др., 1965), что привело к отождествлению
квазаров. Как отмечено в разд. 12.1, такое
измерение координат использовалось много
лет в качестве опорного по прямому восхо-
восхождению для РСДБ-каталога координат. Ра-
Радиоизмерения лунных покрытий наиболее
важны на метровых волнах, так как на более
коротких волнах сильное тепловое излуче-
излучение Луны затрудняет наблюдения (Артюх
и др., 1966; Матвеенко, 1969). Радионаблю-
Радионаблюдения затменным методом в значительной
степени вытеснены сегодня интерферомет-
рическими, однако покрытия Луной исполь-
используются до сих пор в оптике и ИК-области.
На рис. 16.4 показана геометрия и вид
кривой затмения. Отклонение лимба Луны
от прямой линии из-за кривизны и шеро-
шероховатости мало по сравнению с размером
первой зоны Френеля на радиочастотах. Та-
Таким образом, отклик на точечный источ-
источник представляет собой хорошо известную
картину дифракции на краю экрана, приве-
приведенную во многих учебниках по физической
оптике. Основное изменение принимаемой
мощности на рис. 16Л б соответствует по-
покрытию или открытию Луной первой зоны
Френеля, а колебания обусловлены зонами
у/////////////////////////////////////////.
Принятая
мощность
Рис. 16.4. Покрытие радиоисточника
Луной: а — геометрическая схема, угол
0 измеряется по часовой стрелке от
направления на источник, в данном
случае он отрицателен; б — кривая
покрытия для точечного источника,
амплитуда которой пропорциональна
V(9). По абсциссе отложен угол в
в единицах ^X/2Rm , где Л — длина
волны, Rm — расстояние до Луны
16.2] Метод лунных покрытий 565
более высоких порядков. Характерным расстоянием является размер первой зоны
Френеля, y/(XRm/2), где 1{ш ~ 3,84 • 105 км — расстояние от Земли до Луны. Это
дает 4400 м на длине волны 10 см и 10 м на 0,5 мкм, или величину угла, видимого
с Земли, равную 2,3 сек дуги и 5 мсек дуги соответственно. Максимальная скорость
затеняющего края Луны равна примерно 1 км/с, однако эффективная скорость
зависит от положения объекта на лимбе Луны. Обычно используется величина
0,6 км/с. Таким образом, время покрытия первой зоны Френеля, которое определя-
определяет характерное время спада и период колебаний, составляет обычно приблизительно
7 с на 10 см и 16 мс на 0,5 мкм.
В гипотетическом случае покрытия в рамках геометрической оптики наблюдае-
наблюдаемая кривая была бы интегралом от Д как функции угла 9 между источником и лим-
лимбом Луны, измеренным, как показано на рис. 15.4 а. Распределение интенсивности
Д тогда можно было бы получить путем дифференцирования. В действительности
наблюдаемая кривая покрытия QF) представляет собой свертку Д@) с дифракци-
дифракционной картиной точечного источника на лимбе Луны VF), т. е. равна Д@) * V@).
Ее дифференцирование по в дает
д\в) = 11(в)*г'(в), (i6.il)
где штрихи обозначают производные. Преобразование Фурье обеих частей уравне-
уравнения A6.11) дает
O'(«)=71(u)P/(u), A6.12)
где черта указывает на преобразование Фурье, штрих — на производную по #, а и
является сопряженной переменной 9.
В случае геометрической оптики Т{9) была бы ступенчатой функцией, соот-
соответственно V'{9) — дельта-функцией, для которой преобразование Фурье является
константой. Для дифракционно-ограниченного случая функция V(u), взятая из
работы (Cohen, 1969), определяется выражением
V(u) = J- exp [j2tt92fu2 sgnu], A6.13)
и
где вр — угловой размер первой зоны Френеля, который равен ^/\/2Rm , sgn —
знаковая функция, которая принимает значения ±1 для учета знака и. Из теоремы
о производной преобразования Фурье следует, что V (и) = j2ttV(u) имеет посто-
постоянную амплитуду без нулей и ее можно выделить из уравнения A6.12). Из этого
следует, что Д @) равно <?'(#), свернутой с функцией, преобразование Фурье которой
равно 1/V (и). Шоер (Scheuer, 1962) показал, что эта последняя функция пропор-
пропорциональна V'{—в) и может быть использована как восстанавливающая функция
следующим образом:
1^6) = д'(в) * т'(-в) = д(в) * Т"(-в). A6.14)
Вторая форма более удобна практически, поскольку она позволяет избежать
трудностей дифференцирования зашумленной кривой покрытия. В принципе, в от-
отличие от случая решетки, это обеспечивает восстановление Д без ограничения
на угловое разрешение. Однако следует помнить, что амплитуда чувствитель-
чувствительности к пространственным частотам кривой покрытия, приведенная в форму-
формуле A6.13), пропорциональна 1/и. Таким образом, восстанавливаемые амплитуды
фурье-компонент в выражениях A6.14), включающие и шумы, возрастают пропор-
пропорционально и. Возрастание шума налагает предел на полезное разрешение. Этот
предел удобно представить заменой V"{9) в A6.14) на V"(9), свернутую с гауссовой
566 Смежная техника [Гл. 16
функцией от в с разрешением АО. Тогда получаем распределение /i, как если бы
оно наблюдалось с диаграммой той лее гауссовой формы. На практике введение
гауссовой функции существенно для метода, поскольку это обеспечивает сходи-
сходимость интеграла свертки в выражении A6.14). Оптимальный выбор АО зависит
от отношения сигнал/шум. Примеры восстанавливающих функций для различных
разрешений молено найти в работе (von Hoerner, 1964).
Приведенное рассмотрение соответствует классическому подходу к обработке
наблюдений покрытия радиоисточника Луной, который был разработан по ана-
аналогии с геометрической оптикой. Молено предложить более компактную процедуру
обработки, включающую преобразование Фурье кривой покрытия, деление на V(u)
(с подходящим весом для контроля возрастания шума) и повторное преобразование
к области 0. Этот процесс математически эквивалентен уравнению A6.14).
Оценка предела, налагаемого шумами на угловое разрешение, может быть по-
получена в приближении геометрической оптики, так как отношения сигнал /шум
для фурье-компонентов такие же, как для действительного отклика на точечный
источник. Рассмотрим участок кривой покрытия (см. рис. 15.4^), на котором про-
происходит основное изменение принимаемой мощности, и пусть г — интервал времени,
за который произошедшее изменение уровня записи равно среднеквадратичному
уровню шума. Тогда, если vm — угловая скорость движения лимба Луны по радио-
радиоисточнику, то достигаемое угловое разрешение приблизительно равно
АО = vmr. A6.15)
За время г плотность потока на входе антенны изменится на AS. Пусть 0s —
ширина основной детали источника в направлении, перпендикулярном лимбу Лу-
Луны, a, S — полная плотность потока источника. Тогда для источников с простой
структурой средняя яркость приблизительно равна S/б^, и изменение телесного
угла покрываемой части источника за время т составляет 6SA6. Таким образом,
— ^—. A6.16)
Отношение сигнал/шум на выходе приемника для составляющей плотности потока
AS составит
П™ 2kTs ' A6Л7)
где А — эффективная площадь антенны, Ai/ и Ts — соответственно ширина по-
полосы и шумовая температура системы, к — постоянная Больцмана. Заметим, что
тепловая составляющая излучения Луны может давать значительный вклад в Т^.
Рассматриваемые условия соответствуют lZsn ^ 1, и из соотношений A6.15)—A6.17)
получаем
Заметим, что частота (или длина волны) не входит непосредственно в уравнение
A6.18), однако величины некоторых параметров, например, 5, Av и Ts, зависят
от частоты наблюдений. В качестве примера рассмотрим наблюдение на частоте
в диапазоне 100-300 МГц, с параметрами А = 2000 м2, Ts = 200 К и Av = 2 МГц.
Для довольно слабого радиоисточника примем S = 10~26 Вт/м2/Гц A Jy) и 0s = Ъ".
Угловая скорость vm обычно равна 0,3" в секунду. При этих значениях уравнение
A6.18) дает Д# = 0,7". Хотя соотношение A6.18) получено в приближении
16.3] Измерения параметров антенн 567
геометрической оптики, это не ограничивает его применимость. Для наблюдаемой
кривой покрытия эквивалентная кривая для случая геометрической оптики может
быть получена подбором фаз фурье-компонент, который не оказывает влияния на
отношение сигнал/шум.
Ширина полосы приемной системы влияет на размытие угловых деталей при
наблюдениях покрытий в такой же степени, как и при наблюдениях с помощью
антенной решетки. Поскольку отношение сигнал/шум возрастает с шириной поло-
полосы, для любого наблюдения существует такая ширина полосы, для которой чув-
чувствительность к тонкой угловой структуре источника максимальна. Она примерно
равна v АО Rm/c. Эту оценку молено получить исходя из требования того, что
фазовый член в выражении A6.13) незначительно меняется по полосе пропускания.
Этот результат можно сравнить с ограничением на полосу, полученным для антен-
антенной решетки (выражение F.70)), если заметить, что наблюдение лунного покрытия
с разрешением АО подразумевает исследование волнового фронта на расстоянии
Луны на линейных масштабах Х/Ав. Такой масштаб виден с Земли под углом
X/(A0Rm). Дальнейшее обсуждение подобных деталей и практического осуще-
осуществления методики восстановления Шоера дано в работах (von Hoerner, 1964; Cohen,
1969; Hazard, 1976). Заметим, что источник может испытывать несколько покрытий
в течение нескольких месяцев, при этом лимб Луны будет пересекать источник
под различными позиционными углами. Если были проведены наблюдения для
достаточного диапазона позиционных углов, одномерные распределения яркости
могут быть объединены с целью получения двумерного изображения источника
[см., например, (Taylor and DeJong, 1968)].
Метод лунных покрытий широко использовался в оптической и ИК-астрономии
для измерения размеров и затемнений лимбов звезд, а также расстояния между
компонентами тесных двойных систем. Согласованность полученных результатов
и результатов оптической интерферометрии доказывает, что метод лунных покры-
покрытий не подвержен искажениям из-за лунной топографии, как это могло ожидаться
при величине отклонений сравнимых со шкалой Френеля. Типичными являются
измерения угловых размеров вплоть до 1 мсек дуги. Анализ кривых покрытий звезд
обычно выполняется путем подгонки параметризованных моделей, а не метода-
методами восстановления, используемыми в радионаблюдениях, описанных выше. Обзор
специальных соображений для наблюдений лунных покрытий в оптическом и ИК
диапазонах дан в работе (Richichi, 1994). Проведены обширные измерения звездных
диаметров [см., например, (White and Feierman, 1987)] и расстояний между компо-
компонентами двойных систем [см., например, (Evans et al., 1985)]. Одним из прочих
приложений является измерение пылевых оболочек с размерами до секунды дуги,
окружающих звезды Вольфа-Райе [см., например, (Ragland and Richichi, 1999)].
16.3. Измерения параметров антенн
Измерение распределения электрического поля по апертуре антенны является
важным шагом в оптимизации ее работы, особенно в случае больших зеркальных
антенн, для которых эти данные указывают на точность изготовления поверхности.
Преобразование Фурье, представляющее собой связь между диаграммой отклика
напряжения антенны и распределением поля в апертуре, было выведено в п. 14.1.2.
Если х и у — координатные оси в плоскости апертуры, то распределение поля
?(х\,у\) представляет собой преобразование Фурье диаграммы направленности
излучения (приема) по напряжению в дальней зоне Уд(/,т) (см. разд. 3.3), где
/ и т — направляющие косинусы, измеренные по отношению к осям ж и у, а индекс
568 Смежная техника [Гл. 16
Л показывает, что измерение выполнено в длинах волн. Таким образом,
VA(l,m) ос | J ?(хх,ух) е^Ш+у^) dxx dyx. A6.19)
Прямые измерения ? сложны, поскольку они связаны с задачей введения в апертуру
зонда без возмущения поля. Такая методика полезна для получения характеристик
рупорных антенн в миллиметровом диапазоне длин волн (Chen et al., 1998). Однако
во многих случаях, особенно для больших полноповоротных антенн, проще изме-
измерить Уд. Чтобы осуществить преобразование Фурье для ?(х\, у\), необходимо изме-
измерить как амплитуду, так и фазу Уд(/, т). Для выполнения этих измерений диаграм-
диаграмма испытываемой антенны может сканировать удаленный передатчик, а вторая
неподвижная антенна используется для приема сигнала с опорной фазой. Функция
Уд(/,7?г) может быть получена из произведения сигналов двух антенн. Этот метод
напоминает использование опорного пучка в оптической голографии, поэтому ан-
антенные измерения такого типа описываются как голографические (Napier and Bates,
1973; Bennett et al., 1976).
Тот же самый принцип применяется к наблюдениям с использованием интерфе-
интерферометров и антенных решеток апертурного синтеза. Если параметры инструмента
(базы и т.д.) и положение источника точно известны, а изменения фазы из-за
атмосферы незначительны, тогда для неразрешенного источника значения калиб-
калиброванной функции видности будут иметь действительную часть, соответствующую
плотности потока источника и мнимую часть, равную нулю (за исключением шума).
Тогда, если одна из антенн коррелированной пары сканирует источник, в то время
как другая продолжает сопровождать его, соответствующие значения функции
видности будут пропорциональны амплитуде и фазе Уд(/,га) для сканирующей ан-
антенны. Рассмотренное выше измерение параметров антенных решеток апертурного
синтеза было впервые описано в статье (Scott and Ryle, 1977), этому анализу, наряду
с результатами (D'Addario, 1982; Костенко, Матвеенко, 1982), мы в значительной
степени придерживаемся далее.
Удобным является представить наглядно данные в плоскости апертуры ?(х\, у\)
и в плоскости неба Уд(/,7тг) как дискретные наблюдения в точках сетки, образую-
образующие два массива размера N х 7V, которые будут использоваться для дискретного
преобразования Фурье. Для простоты рассмотрим квадратную апертуру антенны
с размерами d\ x d\. Поскольку ?(х\,у\) равно нулю вне интервала ±б2д/2, то из
теоремы выборки для преобразований Фурье следует, что сканирование должно
осуществляться с угловым шагом по (/, т) не более l/d\. (Этот шаг в два раза боль-
больше шага сканирования при диаграмме направленности полной мощности, так как
она является преобразованием Фурье от автокорреляционной функции ?(х\,у\).)
Если данные сканирования VaA, га) разделены интервалами 1/с/д, данные апертуры
заполняют массив ?(х\,у\). Шаг сканирования по апертуре равен d\/N. В силу
этого обычно N выбирается так, чтобы шаг сканирования позволял проводить не-
несколько измерений на каждой панели поверхности. В плоскости 1т диапазон углов,
по которому проводится сканирование, в N раз больше чем интервал наведения,
т. е. равен N/d\. Величина этого сканируемого интервала составляет примерно N
ширин диаграммы направленности. Процедура состоит в сканировании тестируе-
тестируемой антенной за N2 дискретных направляющих шагов и получении таким путем
данных Уд(/,777,) для заполнения массива, соответствующего плоскости неба.
Рассмотрим отношение сигнал/шум 7?sn, полученное за время то с диаграммами
направленности обоих антенн, направленными прямо на источник. Теперь предпо-
предположим, что плоскость апертуры (жд,т/д) разделена на квадратные ячейки (как на
16.3] Измерения параметров антенн 569
рис. 5.3) со сторонами d\/N, центрами которых являются измеряемые точки. Рас-
Рассмотрим для исследуемой антенны вклад в сигнал на выходе коррелятора от одной
такой ячейки апертуры площадью (d\/NJ. Эффективная ширина диаграммы на-
направленности такой ячейки апертуры в N раз больше ширины диаграммы направ-
направленности антенны, т. е. приблизительно равна полной необходимой ширине сканиро-
сканирования. Такая площадка дает 1/7У2-ю часть сигнала на выходе коррелятора. Поэтому
связанная с шумом доля от одной апертурной ячейки на выходе коррелятора равна
1Zsn/N2 за время та, или 7Zsn/N за время N2ra, которое является полным временем
измерения. Точность измерений фазы части сигнала от одной апертурной ячейки,
5ф в у2 раз отличается от соответствующего отношения сигнал/шум, а именно,
равна 7V/(v2 7?sn). Коэффициент у2 появляется в результате того, что только
компонент шума системы, нормальный по отношению к вектору сигнала (функции
видности), дает ошибку в измерение фазы (см. рис. 6.8). Теперь смещение е по
поверхности апертурной ячейки приводит к изменению фазы 4тг?/А отраженного
сигнала. Таким образом, неопределенность по фазе 5ф этой составляющей сигнала
приводит к неопределенности 5е = Хбф/(Атг) = XN/ D:\/2 7rlZsn). Задавая желаемую
точность измерения поверхности Ss, мы определяем, что апертура должна быть
такова, чтобы отношение сигнал/шум за время то составило
?*— A6.20)
б
при том, что обе диаграммы направлены на источник. Определив 7?sn, мы можем
воспользоваться соотношениями F.48) и F.49), чтобы получить величины антенных
температур или плотности потока сигнала в единицах Вт-м~2-Гц~1. Если две эти
антенны разного размера, тогда в уравнениях F.48) и F.49) Л, Тд и Ts заменяются
геометрическими средними от соответствующих величин. Выше было использовано
несколько упрощающих приближений. Утверждение, что одна апертурная ячейка
дает 1/N -ю долю на выходе антенны, подразумевает, что напряженность поля
постоянна по апертуре. Если облучение апертуры спадает, то для сохранения точ-
точности на внешних краях потребуется большая величина 7Zsn. Рассмотрение квад-
квадратной антенны ведет к переоценке 7Zsn в 4/тг раза относительно круговой апертуры
диаметра d\. Ситуация может значительно отличаться в случае, когда сигнал,
используемый в голографических измерениях, является постоянным (непрерывный
сигнал), часто поступающим от ИСЗ. Получаемая мощность сигнала Р может
быть велика по сравнению с шумом приемника кТцАи (D'Addario, 1982). В этом
случае шум на выходе коррелятора подавляется кросс-произведениями напряжений
сигнала и шума приемника. Результирующее отношение сигнал/шум за время т
равно -y/PAi/ тj(кТцАи) и не зависит от ширины полосы пропускания приемника.
Пример голографических измерений антенны решетки апертурного синтеза на
субмиллиметровых длинах волн показан на рис. 16.5. Некоторые практические мо-
моменты перечислены ниже.
• Источник, используемый в голографических измерениях, должен быть в иде-
идеале достаточно сильным, чтобы получить высокое отношение сигнал/шум.
Обычно используется либо сигнал передатчика ИСЗ, либо космический
мазерный источник. Моррис и др. (Morris et al., 1988) описывают наблюдения
на 30-м антенне в Пико де Велета, когда была достигнута точность измерений
(повторяемость) в 25мкм при использовании 22,235 ГГц водяного мазера
570 Смежная техника [Гл. 16
10 20 30 40 50 60 ю 20 30 40 50 60
200 100 0 100 200
Рис. 16.5. а— отклонения поверхности 6-метрового SMA рефлектора, измеренные гологра-
фически на 92 ГГц с помощью маяка, расположенного на расстоянии 250 м. Изображение
имеет 64x64 пикселей и разрешение порядка 9 см. Пиксели снаружи зеркала, а также под
квадрупольными опорами и вторичным зеркалом, скрыты. Среднеквадратичное откло-
отклонение равно 73мкм. 64 панели расположены в четыре ряда. Можно видеть систематиче-
систематическую ошибку установки в радиальном направлении, б — результат после одной итерации
установки панелей. Среднеквадратичное отклонение поверхности равно ЗОмкм. Данные
измерений Тирупати (S. К. Tirupati)
в Орионе. При голографии с элементами интерферометра могут быть исполь-
использованы частично разрешенные источники (Serabyn, Phillips and Masson, 1991).
• Если исследуемая антенна имеет азимутальную монтировку, то во время на-
наблюдений диаграмма направленности будет вращаться вокруг своей оси отно-
относительно неба (паралакс). При определении направления наведения оси 1т на
плоскости неба должны быть привязаны к местному горизонтальному и вер-
вертикальному направлению. Если антенна имеет экваториальную монтировку,
то оси 1т должны совпадать с направлениями на восток и север в плоскости
неба (это соответствует обычному определению 1т).
• Если источник имеет сильную линейную поляризацию и антенны имеют ази-
азимутальные монтировки, может возникнуть необходимость скомпенсировать
поворот диаграммы направленности. Это необходимо, если антенны наблюда-
наблюдают в двух ортогональных поляризациях.
• При использовании двух отдельных антенн разницы путей сигналов из-за
тропосферных неоднородностей могут привести к ошибкам по фазе. Для
определения величины такого эффекта необходимо периодически записывать
сигнал с обеими диаграммами направленности, выставленными на источник.
В случае наблюдений на одной большой антенне для получения опорного сиг-
сигнала от источника иногда используется небольшая дополнительная антенна,
установленная на ее конструкции, и направленная в том же направлении. При
этом исключаются фазовые ошибки из-за тропосферных эффектов.
• Антенна может быть повернута (внутри ограниченного углового интервала)
вокруг любой оси, проходящей через ее фазовый центр, при этом, фаза
принимаемого сигнала остается неизменной. Фазовый центр параболического
16.3] Измерения параметров антенн 571
рефлектора лежит на оси параболоида и расположен приблизительно посе-
посередине между фокальной точкой и плоскостью апертуры 1). При сканирова-
сканировании максимальный угол, на который антенна отклоняется от направления на
источник, равен N/Bd\). Если ось, вокруг которой поворачивается антенна,
находится на расстоянии г от фазового центра, длина фазового пути до ан-
антенны будет увеличена на г [1 — cos (N/2d\)]. Если это расстояние составляет
значительную величину в единицах длин волн, должна быть применена фа-
фазовая коррекция сигнала на выходе коррелятора.
• Необходимо применять коррекцию в случае антенны, находящейся под защит-
защитным куполом, элементы которого могут приводить к рассеянию падающего
излучения. Рогерс и др. (Rogers et al., 1993) описали такие коррекции для
измерений на 37-м антенне в Хайстеке.
• При проведении измерений на антеннах корреляционной решетки в случае,
когда количество антенн па велико, можно пользоваться следующей методи-
методикой. Одна антенна следит за источником и дает опорный сигнал, при этом все
остальные элементы решетки сканируют источник. Однако лучшая методика
заключается в использовании па/2 антенн для слежения за источником в то
время, когда другие па/2 антенны проводят сканирование. Время усреднения
будет в два раза меньше, чем при использовании первой методики, для того,
чтобы антенны могли поменяться ролями посередине наблюдений. Однако
для каждой антенны мы будем иметь па/2 разных измерений, что даст нам
в ^/па/4 раз большую чувствительность, чем в первом методе. Также кросс-
корреляция сигналов от сопровождающих антенн даст информацию о фазовой
стабильности атмосферы, что будет полезно при интерпретации измерений.
Моррисом (Morris, 1985) был разработан метод, который требует измерения
только амплитуды диаграммы направленности в дальней зоне. В этой методике
не требуется опорная антенна. Метод основан на алгоритме Миселла (Misell, 1973)
и заключается в следующем. Сначала необходимо принять в качестве первого
приближения некоторую начальную модель амплитуды и фазы распределения поля
по апертуре антенны. Затем надо провести два измерения амплитуды диаграммы
направленности в дальней зоне: одно с правильно сфокусированной антенной,
и другое с антенной, расфокусированной так, чтобы дать фазовые ошибки величи-
величиной в несколько радиан на краю зеркала. Далее модельное распределение апертуры
используется для расчета амплитуды и фазы диаграммы направленности в дальней
зоне и рассчитанная амплитуда заменяется на измеренную при сфокусированной
антенне. Измеренная на сфокусированной антенне амплитуда и рассчитанная фаза
затем используются для расчета соответствующих амплитуды и фазы апертуры, по-
последние используются в дальнейшем как новая модель апертуры. Эта новая модель
х) Рассмотрим передачу от антенны, у которой параболическая поверхность образована
вращением параболы х = ау2 вокруг оси х. Излучение кольцеобразного элемента поверх-
поверхности между плоскостями х = х и х = х + dx имеет эффективный фазовый центр на оси
х в точке х . Площадь такого элемента, спроектированного на плоскость апертуры (т.е.
перпендикулярно оси ж), не зависит от х . Если облучение апертуры однородно, каждый
ее элемент между плоскостями, перпендикулярными оси х и разделенными одинаковым
расстоянием, дает одинаковый вклад в электрический вектор поля в дальней зоне. Таким
образом, эффективный фазовый центр полного излучения должен находится на оси х,
где-то на полпути между фокальной точкой и плоскостью апертуры. Заметим, что мы
провели здесь только приблизительный анализ (в приближении геометрической оптики).
572 Смежная техника [Гл. 16
используется затем для расчета диаграммы направленности расфокусированной
антенны в дальней зоне. При этом полагается, что расфокусировка затрагивает
только фазу апертуры и потому она вносит компоненту, которая меняется по
апертуре как квадрат радиуса. Рассчитанная амплитуда расфокусированной диа-
диаграммы направленности затем заменяется на измеренную и рассчитывается соот-
соответствующее распределение сфокусированной апертуры, которое становится новой
моделью. В последующих итерациях попеременно рассчитываются амплитуды при
сфокусированной и расфокусированной антенне. После каждого расчета амплитуда
диаграммы заменяется на соответствующее измерение, и результат используется
для улучшения модели. Необходимое решение, к которому процесс должен сойтись,
представляет собой модель, которая пригодна для сфокусированного и расфокуси-
расфокусированного откликов. Эта методика требует более высокого отношения сигнал /шум,
чем при проведении измерений фазы. При измерениях в области нулей диаграммы
направленности, требуемое отношение сигнал/шум примерно равно квадрату того,
которое необходимо при фазовых измерениях (Morris, 1985).
Голографический метод с участием только одного телескопа, пригодный для
больших субмиллиметровых антенн, описан в (Serabyn, Phillips and Masson, 1991).
Измерения проводятся в фокальной плоскости с помощью подвижного элемента
интерферометра, что является адаптацией методики, используемой для оптических
инструментов.
16.4. Оптическая интерферометрия
Основные принципы оптической интерферометрии в значительной степени
идентичны радиоинтерферометрическим, но выполнение точных измерений пред-
представляет собой более сложную задачу. Одна из трудностей связана с атмосферными
неоднородностями, которые меняют эффективную длину пути. Эти изменения ве-
велики по сравнению с длиной волны и приводят к многократному нерегулярному из-
изменению фазы. Достижение механической стабильности инструмента, необходимой
для получения интерференционных полос на длинах волн порядка 500 нм, пред-
представляет собой задачу огромной сложности. Поэтому очень трудно прокалибровать
отклик инструмента по фазе, и во многих случаях измеряется только амплитуда
функции видности. Однако реальность практического использования синтезного
картографирования в оптическом диапазоне была продемонстрирована в работах
(Haniff et al., 1987; Baldwin et al., 1996), в которых использовался метод замкнутых
фаз (см. разд. 10.3). В отсутствие фазы функции видности данные по амплитуде
могут быть интерпретированы в рамках моделей или автокорреляционной функ-
функции распределения яркости, как рассмотрено в п. 11.4.3. Можно применять также
и методы двумерного восстановления без фазовых данных [см., например, (Bates,
1984)]. Оптическая интерферометрия является активно развивающейся областью,
и здесь мы приводим лишь обзор некоторых основных принципов. Общий обзор
дан в работе (Shao and Colavita, 1992), а подробное описание теории в (Tango and
Twiss, 1980). Очень полезное собрание некоторых наиболее важных публикаций
по оптической интерферометрии было составлено в работе (Lawson, 1997) — см.
библиографию.
Прежде чем рассмотреть инструменты, кратко остановимся на некоторых атмо-
атмосферных параметрах. Неоднородности атмосферы вызывают случайные изменения
показателя преломления в широком диапазоне линейных масштабов. Для любой
заданной длины волны существует масштаб, в пределах которого участки волно-
волнового фронта остаются достаточно плоскими по сравнению с длиной волны, т. е.
фазовые изменения, вызванные атмосферными эффектами, малы по сравнению
16.4] Оптическая интерферометрия 573
с 2тг. Этот масштаб описывается параметром го, называемым длиной Фрида (Fried,
1966) [см. обсуждение после соотношения A3.102)]. Длина Фрида равна 3,2<i0, где
do — расстояние между путями в атмосфере, для которых среднеквадратичная
разность фаз равна одному радиану, [см. выражение A2.102)]. Области, в которых
неоднородности фазы не превосходят этого предела, называются ячейками вид-
ности. Масштаб го и высота, на которой возникают доминирующие неоднородно-
неоднородности, определяют изопланатический угол (или размер изопланатического участка),
т. е. интервал углов, в пределах которого волновые фронты, идущие от различ-
различных точек небесной сферы, испытывают одинаковые фазовые сдвиги. В пределах
изопланатического участка функция разброса точек остается постоянной, поэтому
остается справедливым соотношение свертки между источником и изображением.
Типичные значения для 50-процентильной величины го, которая ведет себя как
Л6/5 (см. соотношение A3.102)), и изопланатического угла даны в табл. 16.1. Для
сравнения в таблице приведены также соответствующие значения дифракционного
предела разрешения телескопа с апертурой 1 м. Оптические интерферометры дают
мощный инструментарий для изучения структурных функций атмосферы в ИК
и оптическом диапазонах длин волн [см., например, (Bester et al., 1992; Davis et al.,
1995)]. Заметим, что методика, использующая коррекцию атмосферного искажения
волнового фронта с помощью приборов, установленных на телескопах, называется
адаптивной оптикой [см., например, (Roggemann, Welch and Fugate, 1997; Milonni,
1999)].
Таблица 16.1. Атмосферные и инструментальные параметры в видимом
и ИК-диапазоне длин волн (Woolf, 1982)
Длина
волны,
мкм
0,5 (видимый)
2,2 (ИК)
20 (ИК)
Го, М
0,14
0,83
11,7
Изопланатический
угол
в зените
5,5"
33"
8'
Разрешение
апертуры
диаметра 1 м
0,13"
0,55"
5,0"
Атмосферное
разрешение,
Л/го
0,70"
0,55"
0,35"
16.4.1. Современный интерферометр Майкельсона. Первоначальный
инструмент Майкельсона был кратко рассмотрен в разд. 1.3, где указывалось, что
дрожание интерференционных полос является ограничивающим фактором в оценке
функции видности. Характерное время атмосферных флуктуации составляет вели-
величину порядка Юме, что требует применения электронной системы для управления
и измерения интерференционных полос. Упрощенная схема, иллюстрирующая
основные особенности современного интерферометра Майкельсона, показана на
рис. 16.6. Два зеркала S установлены как сидеростаты и сопровождают объект
исследования. Уголковые зеркала R непрерывно подстраиваются так, чтобы
уравнивать длины оптических путей от источника до точки суммирования В.
Компенсация задержки обычно производится в вакуумных трубках, так как
геометрическая задержка интерферометра происходит в основном над атмосферой.
Если применялись воздушные линии, то необходимо было устройство для
компенсации дисперсии задержки, что сложно сделать для широкополосных систем
[см., например, (Benson et al., 1997)]. Сидеростаты установлены на стабильных
платформах, а остальная часть системы обычно монтируется на системе оптических
стоек в контролируемом модуле. Апертуры интерферометра, определяемые
574
Смежная техника
[Гл. 16
Q
т
--к
V
D2
Рис. 16.6. Основные элементы современного интерферометра Майкельсона с прямым де-
детектированием. Штриховая линия показывает траекторию пути света от звезды, из работы
(Davis and Tango, Proc. Astron. Soc. Australia, 6, 34-38, 1985)
зеркалами S, размеры которых не превышают масштаб vq. Поэтому фронт вол-
волны в пределах зеркала практически остается плоским, а эффект неоднородностей
выражается в изменении угла приходящего волнового фронта. Такие вариации
недопустимы, так как лучи в точке суммирования В должны быть в пределах 1".
Для ослабления этого эффекта применяется поляризационный отклонитель луча —
куб Р, отражающий свет на квадратный детектор Q, который выдает напряжение,
пропорциональное отклонению светового луча. Эти напряжения управляют углами
наклона зеркал Т, компенсируют изменения фронта волны. Серво-система обратной
связи с шириной полосы ~ 1 кГц компенсирует наиболее быстрые атмосферные
эффекты. Фильтры F определяют рабочую длину волны. Два детектора D\ ж F)^
реагируют на точки интерференционной картины, разнесенные на одну четверть
ширины интерференционной полосы, и выдают мгновенно измеренные амплитуды
и фазы интерференционных полос. Этот метод описан Рогстадом (Rogstad, 1968),
который также отметил, что в многоэлементной системе фазовая информация мо-
может быть использована с помощью соотношений замыкания, как это обсуждалось
в разд. 10.3.
Оптические интерферометры могут обладать очень широкими полосами про-
пропускания, а именно А А/ А ~ 0,1 или даже больше, так что центральная, или белая,
интерференционная полоса легко различима. Если такая система работает с дву-
двумя широкими полосами одновременно, то тогда атмосферные эффекты, имеющие
небольшую дисперсию, могут быть устранены. Наземная оптическая астрометрия
с двухволновыми фазосопровождающими интерферометрами позволяет получить
точные положения звезд (Colavita, Shao and Staelin, 1987). В качестве примера
первых интерферометрических экспериментов, приведем работу (Currie, Knapp and
Liewer, 1974), в которой авторы проводили измерения с двумя апертурами на одном
большом телескопе, а в работе (Labeyrie, 1975) были проведены первые успешные
измерения при помощи двух телескопов. Для описания последующих, более слож-
сложных, инструментов см., например, (Davis and Tango, 1985; Shao et al., 1988; Baldwin
et al., 1994; Mourard et al., 1994; Armstrong et al., 1998; Davis et al., 1999a,b). Большие
надежды связываются с идеей оптической интерферометрии в космосе, где нет
влияния земной атмосферы. Космическая Интерферометрическая Миссия (Shao,
1998; Allen and Boker, 1998; Boker and Allen, 1999) представляет собой космический
интерферометр для диапазона длин волн 0,4-1,0 мкм с переменной базой до 10 м.
16.4] Оптическая интерферометрия 575
Планируется, что она будет получать синтезированные изображения с разрешением
в 10 мсек и измерять интерференционные фазы с точностью, необходимой для
определения координат звезд с ошибкой не хуже 4мксек. Возможность использо-
использования космической интерферометрии для обнаружения планет вокруг удаленных
звезд обсуждалась в (Bracewell and MacPhie, 1979). Отношение сигнала от планеты
к сигналу от звезды максимизируется, если выбрать длину волны в длинноволновой
части ИК-диапазона равной 20мкм, а также поместить нуль интерференционной
картины в направлении на звезду. Описание зануляющей методики на наземном
телескопе дано в (Hinz et al., 1998).
В описанных выше системах интерференционные полосы формируются путем
объединения приходящего излучения на той же длине волны, на которой оно
было принято, как в классическом звездном интерферометре Майкельсона. Они
также называются системами прямого детектирования. Альтернативой оптиче-
оптической системе прямого детектирования является гетеродинная система, в которой
свет от каждой апертуры смешивается с когерентным светом центрального лазера
для перехода на промежуточную частоту (ПЧ). Сигналы ПЧ затем усиливаются
и коррелируются в электронной системе, такой же, как в радиоинтерферометрии.
По сравнению с системой прямого детектирования чувствительность гетеродинной
системы сильно ограничена квантовыми эффектами, упомянутыми в разд. 1.4. Она
также ограничивается шириной полосы, которую могут пропустить электронные
усилители, если выходы смесителей не разделены на несколько частотных каналов,
каждый из которых преобразуется параллельно. Широкие полосы затем могут
обрабатываться с помощью соответствующего числа усилителей и корреляторов.
Разделение полосы частот также приводит к увеличению разницы длин путей,
в пределах которой сигналы остаются когерентными. Гетеродинный метод был
использован в ИК-интерферометрии [см., например, (Johnson, Betz and Townes,
1974; Assus et al., 1979; Bester, Danchi and Townes, 1990). Возможности его приме-
применения к большим многоэлементным телескопам с многополосной обработкой в ИК
и видимом диапазонах обсуждались в (Swenson, Gardner and Bates, 1986).
Разница между субмиллиметровым и оптическим диапазонами длин волн со-
составляет величину порядка ~103 и еще ~103 — с рентгеновским диапазоном. Рент-
Рентгеновская астрономия может иметь чрезвычайное преимущество, обладая потен-
потенциально более высоким угловым разрешением при использовании методов интер-
интерферометрии. Возможность рентгеновской интерферометрии, пригодной для астро-
астрономического картографирования, была показана в лабораторных условиях Кэшем
и др. (Cash et al., 2000). Она имеет перспективу получения чрезвычайно высокого
углового разрешения при наблюдениях над атмосферой. На длине волны 2 нм,
база в 1 м дает интерференционные лепестки 0,4 мсек. В лабораторных услови-
условиях апертуры инструмента выполнены в виде плоских отражающих поверхностей,
которые реагируют на касательное попадание фотонов, что снижает требования
на точность поверхности. Доступен только метод прямого детектирования, и, если
интерференционные лепестки получаются простым схождением отраженных лучей
на поверхности детектора, то необходимы большие расстояния для получения до-
достаточного разнесения лепестков. При разнесении лепестков на 0,4 мсек, соседний
максимум будет отстоять только на 1 мкм на расстоянии 500 м. Таким образом,
вероятно, необходимы более сложные системы для применения интерферометрии
в практической астрономии.
16.4.2. Чувствительность систем прямого детектирования и гетеро-
гетеродинных систем. Факторы, определяющие чувствительность оптических систем,
такие, как потери за счет рассеяния, частичного отражения и поглощения, отли-
отличаются от соответствующих эффектов в радиодиапазоне. Однако в гетеродинных
системах наиболее важное отличие заключается в роли квантовых эффектов. Энер-
576 Смежная техника [Гл. 16
гия оптических фотонов более чем на пять порядков превышает энергию радиофо-
радиофотонов, соответственно, квантовые эффекты пренебрежимо малы в радиодиапазоне
на частотах меньше ~ 100 МГц. В оптическом диапазоне (длина волны ~ 500 мкм)
частота порядка 600 ТГц, и полоса может иметь ширину 100 ТГц. В обычной гетеро-
гетеродинной системе ИК-диапазона длина волны 10 мкм соответствует 30 ТГц, а ширина
полосы ~ЗГГц [см., например, (Townes et al., 1998)].
В системах прямого детектирования детектор или счетчик фотонов не сохраняет
информацию о фазе сигнала, и, таким образом, шум не возникает из-за принципа
неопределенности, обсуждавшийся в разд. 1.4. Главным образом, шум является
дробовым — происходящим из-за случайности времен прихода фотонов. Число
фотонов, принимаемых от источника интенсивности /, составляет
N = Юз^А1/ [фотоны/с], A6.21)
где Qs — телесный угол источника (в отсутствие атмосферного размытия), А —
собирающая площадь телескопа, Аи — ширина полосы, v — частота, h — постоянная
Планка. Если источник является черным телом с температурой Т, то по формуле
Планка
2/ш3 1
1
—
Заметим, что мы рассматриваем сигнал в обеих поляризациях для системы прямого
детектирования. Тогда
2Jh^_l__ [фотоны/с]. A6.23)
Принимаемая мощность равна
Р = hvN. A6.24)
Флуктуации мощности APd обусловлены фотонным дробовым шумом и, следова-
следовательно, пропорциональны yN. Поэтому
APD = hv\fN. A6.25)
Величина АРр известна как эквивалентная мощность шума (ЭМШ). Отношение
сигнал/шум за одну секунду равно Р/АРр = л/iV, а за время интегрирования та
отношение сигнал/шум составит
2ОЖ А- iV2
где индекс D означает прямое детектирование. Заметим, что 7?snD пропорционален
л/А из-за дробового шума, а не А, как в случае радиоволн.
В гетеродинной системе шум определяется принципом неопределенности,
поскольку смеситель является линейным устройством, который сохраняет фазу.
Минимальный шум равен одному фотону на моду (один фотон на Гц/с), как отме-
отмечено в обсуждении после формулы A.14). Это эквивалентно температуре системы,
равной hv/к [см., например, (Heffner, 1962; Caves, 1982)]. Следовательно, за период
16.4] Оптическая интерферометрия 577
в одну секунду неопределенность по мощности составит
APH = huVA^. A6.27)
Детектор гетеродина откликается только на компонент излучения, с которым со-
согласована его поляризация, поэтому полная принимаемая мощность равна половине
той, которая определяется соотношением A6.24). Таким образом, отношение сиг-
сигнал/шум для гетеродинной системы (обозначенной индексом Н) за одну секунду
равно Р/BДРн)? а за время то:
Заметим, что выражение A6.28) сводится к обычному выражению для радиоволн
A.7), если hv /kT <С 1. В этом случае Тд = T?lsA/\2, и можно использовать мини-
минимальное значение hi/ /к для температуры системы. Коэффициент между отноше-
отношениями сигнал/шум для двух рассмотренных систем (с прямым детектированием
и гетеродинной), если все параметры, за исключением ширины полосы, равны,
имеет вид
nD ~ у I 2A2 )
TlsnD ~ у I 2A2 ) eh»<kT
Как было отмечено ранее, д/Дг/н / Ai/D может быть очень мало, вплоть до ~ 4 • 10~3.
Однако при прямом детектировании задержки распространения через разные си-
сидеростаты к точке формирования интерференционных полос должны поддержи-
поддерживаться постоянными с точностью до ~1/10 эквивалентной полосы. Это требование
ограничивает ширины полос, которые можно использовать на практике, особенно
при длинах баз в сотни метров. Гетеродинная система нуждается в более простом
оборудовании, которое дает требуемую точность на Юмкм и, возможно, в соседнем
атмосферном окне на 5мкм. Она также позволяет разделять усиленные ПЧ сиг-
сигналы без потери чувствительности для многократных одновременных корреляций
в многоэлементной решетке. Сравнительные преимущества гетеродинной системы
и системы прямого детектирования обсуждаются в (Townes and Sutton, 1981; de
Graauw and van de Stadt, 1981).
16.4.3. Оптический интерферометр интенсивностей. Использование ин-
интерферометра интенсивностей для оптических измерений звезд было продемонстри-
продемонстрировано Ханбери Брауном и Твиссом (Hanbury Brown and Twiss, 1956a) вскоре после
успеха радиоинтерферометра интенсивностей, описанного в п. 1.3.7 и разд. 16.1.
В то время возможность существования когерентности между фотонами в разных
лучах, идущих от одного и того же источника, находилась под вопросом. Физи-
Физическая база и согласованность с квантовой механикой были разъяснены в работах
(Hanbury Brown and Twiss, 1956c) и (Purcell, 1956). Лабораторная демонстрация
корреляции флуктуации интенсивности света Ханбери Брауном и Твиссом (Han-
(Hanbury Brown and Twiss, 1956b) привела к широким исследованиям в области кванто-
квантовой статистики и ее применения к пучкам частиц и электромагнитному излучению
(Henny et al., 1999).
В оптическом интерферометре интенсивностей фотоумножитель, размещенный
в фокусе зеркала каждого телескопа, заменили ВЧ-, ПЧ-каскады и приемники ра-
радиоинтерферометра. Выходы фотоумножителей усиливаются и подаются на входы
коррелятора. Оптический интерферометр интенсивностей в значительной степени
нечувствителен к атмосферным фазовым флуктуациям по причинам, которые были
19 Томсон
578 Смежная техника [Гл. 16
рассмотрены в разд. 16.1. Следовательно, размер собирающих апертур не ограничен
масштабом неоднородностей. Также нет необходимости в том, чтобы отражающие
зеркала создавали дифракционное изображение, и их точность должна быть лишь
достаточной для передачи всего света к катодам фотоумножителей. Это является
очень благоприятным фактором, поскольку ранее упомянутая для случая радио-
радиодиапазона низкая чувствительность требует использования больших собирающих
площадей. Ханбери Браун (Hanbury Brown, 1974) провел анализ отклика оптиче-
оптического интерферометра и показал, что он пропорционален квадрату модуля функ-
функции видности, как и в случае радиоинтерферометра. Для объединения выходов
фотоумножителей могут быть использованы коррелятор, либо счетчик совпадений
фотонов.
В интерферометре интенсивностей, сооруженном в Наррабри (Австралия) (Han-
(Hanbury Brown, Davis and Allen, 1967; Hanbury Brown, 1974), использованы два рефлек-
рефлектора диаметром 6,5 м и ширина полосы 60 МГц для сигналов на входах коррелятора.
В результате предельная звездная величина +2,5 позволила провести измерения 32
звезд. В работе (Davis, 1976) рассмотрены сравнительные достоинства интерфе-
интерферометра интенсивностей и современных вариантов интерферометра Майкельсона
с целью разработки более чувствительного инструмента.
16.4.4. Спекл-интерферометрия. Изображение неразрешенного точечного
источника, наблюдаемого телескопом с большой апертурой, размеры которой ве-
велики по сравнению с длиной Фрида го, зависит от времени экспозиции, в пре-
пределах которого усредняется изображение. При экспозиции не более 10 мс возни-
возникает группа ярких спеклов, каждый из которых имеет размер пятна Эйри (т. е.
дифракционное изображение точечного источника) телескопа. Если экспозиция
намного больше, то картина замывается в пятно (пятно рассеяния) с типичным
диаметром 1", определяемым атмосферой. Характерное время флуктуации Юме
в оптическом диапазоне соответствует времени прохождения элемента размером
го — 0,14 м через любую точку апертуры телескопа с типичной скоростью ветра 10—
20 м/с. Использование последовательности изображений с короткими экспозициями
для получения информации на дифракционном пределе большого телескопа извест-
известно как спекл-интерферометрия (или спекл-картографирование). Спекл-структуры
отражают случайное распределение атмосферных неоднородностей по апертуре
и различаются от одного экспонирования к другому на 10-мс временном интер-
интервале. Необходимо обработать много экспозиций для наблюдений слабых объектов
с помощью этого метода.
Теория спекл-отклика изложена, например, в работах (Dainty, 1973; Bates, 1982)
или (Goodman, 1985). Здесь отметим, что структуру изображения с высоким раз-
разрешением, даваемого одним спекл ом, можно понять, если рассматривать каждый
спекл как результат, получаемый от нескольких ячеек рассеяния волнового фронта,
расположенных в точках, распределенных по апертуре телескопа. Эти ячейки дают
приблизительно равные фазовые сдвиги от волнового фронта до спекл-изображения
(Worden, 1977). Тогда, по аналогии с антенной решеткой, разрешение соответствует
максимальному разнесению ячеек, т. е. оно составляет величину порядка А/б/, где
d — апертура телескопа. Аберрации рефлектора не ухудшают существенно спекл-
структуру до тех пор, пока доминируют неоднородности фазы, обусловленные
атмосферой. Площадь изображения, в пределах которой разбросаны спеклы,
соответствует на небе А/го, и она превращается в пятно рассеяния при большом вре-
времени экспонирования. Ячейки рассеяния могут рассматриваться как субапертуры
в пределах основной апертуры телескопа, отклики которых объединяются в изоб-
изображении со случайными фазами. Количество спеклов по порядку величины равно
16.4] Оптическая интерферометрия 579
числу субапертур, (d/roJ. Для большого телескопа (d ~1м) это число порядка 50
для оптических длин волн. Размер ячеек также возрастает с длиной волны, и в
ИК-диапазоне в изображении появляются лишь несколько спеклов.
Достаточно простая методика восстановления изображения, названная алго-
алгоритмом «сдвинь-сложи» («shift-and-add») может быть применена к спекл-картам
(Christou, 1991). Она работает наилучшим образом в случае, когда в поле попадает
точечный источник, и в ИК диапазоне, когда в кадр попадает относительно немного
спеклов и изопланатический участок относительно велик (см. табл. 16.1). Короткие
спекл-экспозиции выравниваются друг относительно друга по своим наиболее яр-
ярким спеклам и суммируются. Функция расплывания точки («грязная диаграмма
направленности»), которая может быть получена из изображения точечного источ-
источника поля, будет иметь дифракционный компонент и более широкий компонент,
состоящий из более слабых спеклов. Этот шаг может сопровождаться другими
восстанавливающими алгоритмами, такими как CLEAN (см. разд. 11.2), для даль-
дальнейшего улучшения качества изображения [см., например, (Eckart et al., 1994)].
Когда алгоритм «сдвинь-еложи» не применим, модуль функции видности мо-
может быть получен методом спекл-интерферометрии, берущим начало с работы
(Labeyrie, 1970). Эта процедура может быть понята на основе следующего упрощен-
упрощенного рассмотрения. На одном изображении с короткой экспозицией появляется ряд
приблизительно дифракционно ограниченных спеклов в случайно расположенных
точках в пределах диска рассеяния. Спекл-изображение /s(/, m) может быть описа-
описано как свертка действительного распределения интенсивности 1A, т) с функцией
рассеяния спеклов ТA,т)\
/8(/, т) = /(/, т) * * Р{1, т). A6.30)
Величина V(l,m) — это случайная функция, не поддающаяся точному определе-
определению. В качестве первого приближения предположим, что V{1, m) является откликом
функции &о(^ т) размытия точки в телескопе в отсутствие атмосферных эффектов
на положение каждого спекла. Поэтому можно записать
-k,m-mi), A6.31)
где li и rrii — положения спеклов. Предполагается, что все спеклы имеют одинако-
одинаковую интенсивность. Из A6.30) и A6.31) получим
/8(/,ш) = ^/(/,га) **Ъ0A -li,m-mi). A6.32)
Если преобразование Фурье от bo(l,m) равно bo(u,v), то преобразование Фурье от
bo(l ~^i-lTn ~ mi) есть bo(u,v) exp [j27r(uli + vrrii)]. Следовательно, преобразование
Фурье уравнения A5.32) можно записать как
7s(u,v) = ?V(u,t7)bo(«,«)ei2'r(u'<+'m4 A6-33)
где V и / — соответственно преобразования Фурье / и Is. Спекл-преобразования
Is нельзя непосредственно суммировать из-за случайных фазовых коэффициентов
в уравнении A6.33). Чтобы исключить эти фазовые коэффициенты, вычислим 11s\
~I8{u,v)\2 =
i k
jy _|_ у^ eJ2Tr[u(li-lk)+v(mi-mk)]
, A6.34)
19*
580 Смежная техника [Гл. 16
где N — число спеклов. Поскольку математическое ожидание суммирующего члена
во второй строке соотношения A6.34) равно нулю, математическое ожидание A6.34)
<|7e(u,«)|2> = No\V(u,v)\2\bo(u,v)\2, A6.35)
где Nq — среднее число спеклов. Следовательно, средняя величина из серии из-
измерений \Is(u, v)\2 с короткими экспозициями пропорциональна квадрату модуля
V(u, г>), умноженному на квадрат модуля bo(u, v). Поскольку bo(u, v) не равна нулю
для \и\, \v\ < -D/A, то функция \V(u, v)\2 может быть определена в той же самой
области и и v, если известна bo(u,v). На практике спеклы не могут быть точно
смоделированы с помощью уравнения A6.31). Однако мы можем записать
(\7s(u,v)\2) = \V(u,v)\2(\V(u,v)\2), A6.36)
где V(u,v) — преобразование Фурье от V(l,m). Из уравнений A6.35) и A6.36)
следует, что (| 7^(г^,, г;)|2) должна быть примерно пропорциональна \Ъо(и, г>)|2. Она
может быть оценена путем наблюдения точечного источника в тех же условиях,
что и исследуемого.
Фазовая информация может быть получена в рамках метода спекл-
интерферометрии, однако путем значительно больших расчетных усилий.
Большинство алгоритмов исправления фазы являются вариациями двух основных
методов: Нокс-Томпсона (Knox-Thompson), или кросс-спектрального (Knox and
Thompson, 1974; Knox, 1976), и дву-спектрального (Lohmann, Weigelt and Wirnitzer,
1983). Эти методы подробно описаны в работе (Roggeman, Welch and Fugate, 1997).
Основная литература
Lawson P. R. Ed., Selected Papers on Long Baseline Stellar Interferometry, SPIE Milestone
Ser. MS139, SPIE, Bellingham, WA, 1997.
Lawson P. R. Ed., Principles of Long Baseline Stellar Interferometry, Course Notes from the
1999 Michelson Summer School, Jet Propulsion Laboratory, Pasadena, CA, 2000.
Lena P. J. and A. Quirrenbach. Eds., Interferometry in Optical Astronomy, Proc, SPIE, 4006,
SPIE, Bellingham, WA, 2000.
Reasenberg R. D. Ed, Astronomical Interferometry, Proc. SPIE, 3350, SPIE, Bellingham,
WA, 1998.
Robertson J. G. and W. J. Tango. Eds., Very High Angular Resolution Imaging, IAU Symp.
158, Kluwer, Dordrecht, 1994.
Цитированная литература
Allen R. J. and T. Boker. Optical Interferometry and Aperture Synthesis in Space with the
Space Interferometry Mission. Astronomical Interferometry, R. D. Reasenberg. Ed., Proc.
SPIE, 3350, 561-570, 1998.
Armstrong J. Т., D. Mozurkewich, L. J. Rickard, D. J. Butter, J. A. Benson, P. F. Bowers,
N. M. Elias II, С A. Hummel, K. J. Johnston, D. F, Buscher, J. H. Clark III, L. Ha, L.-C.
Ling, N. M. White, R. S. Simon. The Navy Prototype Optical Interferometer, Astrophys. J.,
496, 550-571, 1998.
Assus P., H. Choplin, J. P. Corteggiani, E. Cuot, J. Gay, A. Journet, G. Merlin and Y. Rabbia.
L'lnterferometre Infrarouge du C.E.R.G.A., J. Opt. (Paris), 10, 345-350, 1979.
16.4] Цитированная литература 581
Baldwin J. Е., М. G. Beckett, R. С. Boysen, D. Burns, D. F. Buscher, G. С. Сох, С A. Haniff,
C. D. Mackay, N. S. Nightingale, J. Rogers, P. A. G. Scheuer, T. R. Scott, P. G. Tuthill, P.
J. Warner, D. M. A. Wilson and R. W. Wilson. The First Images from an Optical Aperture
Synthesis Array: Mapping of Capella with COAST at Two Epochs, Astron. Astrophys., 306,
L13-L16, 1996.
Baldwin J. E., R. C, Boysen, G. С. Сох, С A. Haniff, J. Rogers, P. J. Warner, D. M. A.
Wilson and C. D. Mackay. Design and Performance of COAST, Amplitude and Intensity
Spatial Interferometry II, J. B. Breckinridge. Ed., Proc. SPIE, 2200, 118-128, 1994.
Bates R. H. T. Astronomical Speckle Imaging, Phys. Rep., 90, 203-297, 1982.
Bates R. H. T. Uniqueness of Solutions to Two-Dimensional Fourier Phase Problems for
Localized and Positive Images, Сотр. Vision, Graphics Image Process., 25, 205-217, 1984.
Bennett J. C, A. P. Anderson and P. A. Mclnnes. Microwave Holographic Metrology of Large
Reflector Antennas, IEEE Trans. Antennas Propag., AP-24, 295-303, 1976.
Benson J. A., D. J. Hutter, N. M. Elias, P. F. Bowers, K. J. Johnston, A. R. Haijian, J.
T. Armstrong, D. Mozurkewich, T. A. Pauls, L. J. Rickard, C. A. Hummel, N. A. White, D.
Black and C. S. Denison. Multichannel Optical Aperture Synthesis Imaging of Eta 1 Ursae
Majoris with the Navy Optical Prototype Interferometer, Astron. J., 114, 1221-1226, 1997.
Bester M.j W. C. Danchi, C. G. Degiacomi, L. J. Greenhill and С. Н. Townes. Atmospheric
Fluctuations: Empirical Structure Functions and Projected Performance of Future Instruments,
Astrophys. J., 392, 357-374, 1992.
Bester M.j W. C. Danchi and С. Н. Townes. Long Baseline Interferometer for the Mid-Infrared,
Amplitude and Intensity Spatial Interferometry, J. B. Breckinridge. Ed., Proc. SPIE, 1237,
40-48, 1990.
Boker T. and R. J. Allen. Imaging and Nulling with the Space Interferometer Mission, Astro-
Astrophys. J. Suppl., 125, 123-142, 1999.
Bracewell R. N. Radio Interferometry of Discrete Sources, Proc. IRE, 46, 97-105, 1958.
Bracewell R. N. and R. H. MacPhie. Searching for Nonsolar Planets, Icarus, 38, 136-147,
1979.
Carr T. D., M. A. Lynch, M. P. Paul, G. W. Brown, J. May, N. F. Six, V. M. Robinson
and W. F. Block. Very Long Baseline Interferometry of Jupiter at 18 MHz, Radio Sci., 5,
1223-1226, 1970.
Cash W., A. Shipley, S. Osterman and M. Joy. Laboratory Detection of X-ray Fringes with a
Grazing-Incidence Interferometer, Nature, 147, 160-162, 2000.
Caves С. М. Quantum Limits on Noise in Linear Amplifiers, Phys. Rev., 26D, 1817-1839,
1982.
Chen M. Т., C.-Y. E. Tong, R. Blundell, D. С Papa and S. Paine. Receiver Beam Char-
Characterization for the SMA. SPIE Conf. Advanced Technology MMW, Radio and Terahertz
Telescopes, Kona, Hawaii, March 1998, T. G. Phillips, Ed., Proc. SPIE 3357, 106-113, 1998.
Christou J. C. Infrared Speckle Imaging: Data Reduction with Application to Binary Stars,
Experimental Astronomy, 2 27-56, 1991.
Cohen M. H. High Resolution Observations of Radio Sources, Ann. Rev. Astron. Astrophys.,
7, 619-664, 1969.
Colavita M. M., M. Shao and D. H. Staelin. Two-color Method for Optical Astrometry: Theory
and Preliminary Measurements with the Mark III Stellar Interferometer, Appl. Opt., 26, 4113-
4122, 1987.
Currie D. G., S. L. Knapp and К. М. Liewer. Four Stellar-Diameter Measurements by a New
Technique: Amplitude Interferometry, Astrophys. J., 187, 131-134, 1974.
D'Addario L. R. Holographic Antenna Measurements: Further Technical Considerations,
12 Meter Millimeter Wave Telescope Memo. 202, National Radio Astronomy Observatory,
Charlottesville, VA, 1982.
Dainty J. C. Diffraction-Limited Imaging of Stellar Objects using Telescopes of Low Optical
Quality, Opt. Commun., 7, 129-134, 1973.
582 Смежная техника [Гл. 16
Davis J. High Angular Resolution Stellar Interferometry, Proc. Astron. Soc. Aust., 3, 26-32,
1976.
Davis J., P. R. Lawson, A. J. Booth, W. J. Tango and E. D. Thorvaldson. Atmospheric path
Variations for Baselines up to 80 m Measured with the Sydney University Stellar Interferometer,
Mon. Not. R. Astron. Soc, 273, L53-L58, 1995.
Davis J. and W. J. Tango. The Sydney University 11.4 m Prototype Stellar Interferometer,
Proc. Astron. Soc. Aust., 6, 34-38, 1985.
Davis J., W. J. Tango, A. J. Booth, T. A. ten Brummelaar, R. A. Minard and S. M. Owens.
The Sydney University Stellar Interferometer - I. The Instrument, Mon. Not. R. Astron. Soc,
303, 773-782, 1999a.
Davis J., W. J. Tango, A. J. Booth, E. D. Thorvaldson and J. Giovannis. The Sydney
University Stellar Interferometer - II. Commissioning Observations and Results, Mon. Not. R.
Astron. Soc, 303, 783-791, 1999b.
de Graauw T. and H. van de Stadt. Coherent Versus Incoherent Detection for Interferometry
at Infrared Wavelengths, Proc. ESO Conf. Scientific Importance of High Angular Resolution
at Infrared and Optical Wavelengths, M. H. Ulrich and K. Kjar, Eds., European Southern
Observatory, Garching, 1981.
Dulk G. A. Characteristics of Jupiter's Decametric Radio Source Measured with Arc-Second
Resolution, Astrophys. J., 159, 671-684, 1970.
Eckart A., R. Genzel, R. Hofmann, B. J. Sams, L. E. Tacconi-Garman and P. Cruzalebes.
Diffraction Limited Near-Infrared Imaging of the Galactic Center. The Nuclei of Normal
Galaxies, R. Genzel and A. Harris. Eds., Kluwer, Dordrecht, 1994, p. 305-315.
Eddington A. S. Note on Major MacMahon's paper «On the Determination of the Apparent
Diameter of a fixed Star», Mon. Not. R. Astron. Soc, 69, 178-180, 1909.
Evans D. S., D. A. Edwards, M. Frueh, A. McWilliam and W. Sandmann. Photoelectric
Observations of Lunar Occultations. XV, Astron. J., 90, 2360-2371, 1985.
Fried D. L. Optical Resolution through a Randomly Inhomogenious Medium for Very Long
and Very Short Exposures, J. Opt. Soc. Am., 56, 1372-1379, 1966.
Goodman J. W. Statistical Optics, Wiley, New York, 1985, p. 441-459.
Hanbury Brown R. and R. Q. Twiss. A New Type of Interferometer for Use in Radio Astronomy,
Philos. Mag., ser. 7, 45, 663-682, 1954.
Hanbury Brown R. and R. Q. Twiss. A Test of a New Type of Stellar Interferometer on Sirius,
Nature, 178, 1046-1048, 1956a.
Hanbury Brown R. and R. Q. Twiss. Correlation Between Photons in Two Coherent Light
Beams, Nature, 177, 27-29, 1956b.
Hanbury Brown R. and R. Q. Twiss. A Question of Correlation Between Photons in Coherent
Light Rays, Nature, 178, 1447-1448, 1956c
Hanbury Brown R., J. Davis and L. R. Allen. The Stellar Interferometer at Narrabri
Observatory-I, Mon. Not. R. Astron. Soc, 137, 375-392, 1967.
Haniff C. A., C. D. Mackay, D. J. Titterington, D. Sivia, J. E. Baldwin and P. J, Warner.
The First Images from Optical Aperture Synthesis, Nature, 328, 694-696, 1987.
Hazard C. Lunar Occultation Measurements. Methods of Experimental Physics, Vol. 12C, M.
L. Meeks, Ed., Academic Press, New York, 1976.
Hazard C., M. B. Mackey and A. J. Shimmins. Investigation of the Radio Source 3C273 by
the Method of Lunar Occultations, Nature, 197, 1037-1039, 1963.
Heffner H. The Fundamental Noise Limit of Linear Amplifiers, Proc. IRE, 50, 1604-1608,
1962.
Henny M., S. Oberholzer, C. Strunk, T. Heinzel, K. Esslin, M. Holland and C. Schonenberger.
The Fermionic Hanbury Brown and Twiss Experiment, Science, 284, 296-298, 1999.
Hinz P. M., J. R. P. Angel, W. F. Hoffmann, D. W. McCarthy Jr., P. С McGuire, M.
Cheselka, J. L. Hora and N. J. Woolf. Imaging Circumstellar Environments with a Nulling
Interferometer, Nature, 395, 251-253, 1998.
16.4] Цитированная литература 583
Jennison R. С. and М. К. Das Gupta. The Measurement of the Angular Diameter of Two
Intense Radio Sources, Philos. Mag., Ser. 8, 1, 55-75, 1956.
Johnson M. A., A. L. Betz and С. H. Townes. 10-fim Heterodyne Stellar Interferometer, Phys.
Rev. Lett., 33, 1617-1620, 1974.
Knox К. T. Image Retrieval from Astronomical Speckle Patterns, J. Opt. Soc. Am., 66, 1236-
1239, 1976.
Knox K. T. and B. J. Thompson. Recovery of Images from Atmospherically Degraded Short-
Exposure Photographs, Astrophys. J., 193, L45-L48, 1974.
Labeyrie A. Attainment of Diffraction Limited Resolution in Large Telescopes by Fourier
Analysing Speckle Patterns in Star Images, Astron. Astrophys., 6, 85-87, 1970.
Labeyrie A. Interference Fringes Obtained on Vega with Two Optical Telescopes, Astrophys.
J., 196, L71-L75, 1975.
Lohmann A. W., G. Weigelt and B. Wirnitzer. Speckle Masking in Astronomy: Triple Corre-
Correlation Theory and Applications, Applied Optics, 22, 4028-4037, 1983.
MacMahon P. A. On the Determination of the Apparent Diameter of a fixed Star, Mon. Not.
R. Astron. Soc, 69, 126-127, 1909.
Milonni P. W. Resource Letter: AOA-1: Adaptive Optics in Astronomy, Am. J. Phys., 67,
476-485, 1999.
Misell D. L. A Method for the Solution of the Phase Problem in Electron Microscopy, J. Phys.
D., 6, L6-L9, 1973.
Morris D. Phase Retrieval in the Radio Holography of Reflector Antennas and Radio Tele-
Telescopes, IEEE Trans. Antennas Propag., AP-33, 749-755, 1985.
Morris D., J. W. M. Baars, H. Hein, H. Steppe, C. Thum and R. Wohlleben. Radio-Holographic
Reflector Measurements on the 30-m millimeter Radio Telescope at 22 GHz with a Cosmic
Signal Source, Astron. Astrophys., 203, 399-406, 1988.
Mourard D., I. Tallon-Bosc, A. Blazit, D. Bonneau, G. Merlin, F. Morand, F. Vakili and A.
Labeyrie. The G12T Interferometer on Plateau de Calern, Astron. Astrophys., 283, 705-713,
1994.
Napier P. J. and R. H. T. Bates. Antenna-Aperture Distributions from Holographic Type of
Radiation-Pattern Measurements, Proc. IEEE, 120, 30-34, 1973.
Purcell E. M. A Question of Correlation between Photons in Coherent Light Rays, Nature,
178, 1449-1450, 1956.
Ragland S. and A. Richichi. Detection of a Sub-Arcsecond Dust Shell around the Wolf-Rayet
Star WR112, Mon. Not. R. Astron. Soc, 302, L13-L16, 1999.
Richichi A. Lunar Occultations. Proc. Very High Angular Resolution Imaging, IAU Symp.
158, J. G. Robertson and W. J. Tango. Eds., Kluwer, Dordrecht, 1994, p. 71-81.
Rogers A. E. E., R. Barvainis, P. J. Charpentier and В. Е. Corey. Corrections for the Effect of
a Radome on Antenna Surface Measurements Made by Microwave Holography, IEEE Trans.
Antennas. Propag., AP-41, 77-84, 1993.
Roggemann M. С., В. М. Welch and R. Q. Fugate. Improving the Resolution of Ground-Based
Telescopes, Rev. Mod. Phys., 69, 437-505, 1997.
Rogstad D. H. A Technique for Measuring Visibility Phase with an Optical Interferometer in
the Presence of Atmospheric Seeing, Appl. Opt., 7, 585-588, 1968.
Scheuer P. A. G. On the Use of Lunar Occultations for Investigating the Angular Structure of
Radio Sources, Aust. J. Phys., 15, 333-343, 1962.
Scott P. F. and M. Ryle. A Rapid Method for Measuring the Figure of a Radio Telescope
Reflector, Mon. Not. R. Astron. Soc, 178, 539-545, 1977.
Serabyn E., T. G. Phillips and C. R. Masson. Surface Figure Measurements of Radio Telescopes
with a Shearing Interferometer, Applied Optics, 30, 1227-1241, 1991.
Shao M. SIM the Space Interferometry Mission. Astronomical Interferometry, R. D. Reasen-
berg. Ed., Proc. SPIE, 3350, 536-540, 1998.
584 Смежная техника [Гл. 16
Shao М. and Colavita М. М. Long-Baseline Optical and Stellar Interferometry, Ann. Rev.
Astron. Astrophys., 30, 457-498, 1992.
Shao M., M. Colavita, B. E. Hines, D. H. Staelin, H. J. Hutter, K. J. Johnston, D.
Mozurkewich, R. S. Simon, J. L. Hershey, J. A. Hughes and G. H. Kaplan. The Mark III
Stellar Interferometer, Astron. Astrophys., 193, 357-371, 1988.
Swenson G. W.j Jr., C. S. Gardner and R. H. T. Bates. Optical Synthesis Telescopes, Proc.
SPIE, 643, 129-140, 1986.
Taylor J. H. and M. L. De Jong. Models of Nine Radio Sources from Lunar Occultation
Observations, Astrophys. J., 151, 33-42, 1968.
Tango W. J and R. Q. Twiss. Michelson Stellar Interferometry, in Prog. Opt., 17, 239-277,
1980.
Townes С H., M. Bester, W. С Danchi, D. D. S. Hale, J. D. Monnier, E. A. Lipman, P.
G. Tuthill, M. A. Johnson and D. Walters. Infrared Spatial Interferometer. Astronomical
Interferometry, R. D. Reasonberg. Ed., Proc. SPIE, Vol. 3350, 908-932, 1998.
Townes C. H. and E. C. Sutton. Multiple Telescope Infrared Interferometry, Proc. ESO Conf.
on Scientific Importance of High Angular Resolution at Infrared and Optical Wavelengths, M.
H. Ulrich and K. Kjar. Eds., European Southern Observatory, Garching, 1981, p. 199-223.
von Hoerner S. Lunar Occupations of Radio Sources, Astrophys. J., 140, 65-79, 1964.
White N. M. and В. Н. Feierman. A Catalog of Stellar Angular Diameters Measured by Lunar
Occultation, Astrophys. J., 94, 751-770, 1987.
Whitford A. E. Photoelectric Observation of Diffraction at the Moon's Limb, Astrophys. J.,
89, 472-481, 1939.
Woolf N. J. High Resolution Imaging from the Ground, Ann. Rev. Astron. Astrophys., 20,
367-398, 1982.
Worden S. P. Astronomical Image Reconstruction, Vistas in Astron., 20, 301-318, 1977.
Артюх В. С, Виткевич В. В., Власов В. И., Кафаров Г. А., Матвеенко Л. И. О рас-
распределении радиояркости Крабовидной туманности на метровых волнах по наблюдениям
покрытия Луной 4 августа 1964 г. Астрон. Ж., 1, 13-19, 1966.
Костенко В. И., Матвеенко Л. И. Измерение фазовой характеристики диаграммы на-
направленности антенны на интерферометре со сверхдлинной базой. XIV Всесоюзная радио-
радиоастрономическая конференция по аппаратуре, антеннам и методам. 28-30 октября 1982,
Ереван.
Матвеенко Л. И. Распределение радиояркости Крабовидной туманности на волне 32,5 см.
Астрон. Ж., 2, 250-259, 1969.
Шоломицкий Г. В., Слепцова Н. Ф., Матвеенко Л. И. Спектры компонент ЗС 273.
Астрон. Ж., 6, 1136, 1965.
Основные обозначения 585
Основные обозначения
Ниже приводятся основные символы, используемые в книге. Символы, имеющие огра-
ограниченное применение, включены выборочно.
а модельный размер, характерный размер, постоянная модели атмосфе-
атмосферы (разд. 13.1), характерный размер неоднородностей в ионосфере
(разд. 13.4)
А эффективная площадь антенны (приемная диаграмма направленности)
А поляризационная матрица антенны (гл. 4)
А\ одномерная диаграмма направленности
Ао эффективная площадь антенны в направлении оси
An нормированная диаграмма направленности
Л зеркальное отражение диаграммы направленности, азимут
Ъ галактическая широта (разд. 13.6)
bo синтезированная диаграмма направленности, отклик на точечный источ-
источник
Ьм нормированная синтезированная диаграмма направленности
В величина магнитной индукции
В вектор магнитной индукции
с скорость света
С функция когерентности (гл. 9), функция свертки (гл. 10)
Сп? Спе параметры величины турбулентности для индекса рефракции, плотности
электронов (гл.13)
С амплитуда комплексного сигнала (прил. 3.1)
d расстояние, диаметр антенны, склонение вектора базы, проекция вектора
базы (гл. 13)
dtc разница пути лучей между исследуемым и калибровочным источниками
в области турбулентности
do расстояние, при котором ср. кв. отклонение фазы = 1 рад (гл. 13)
D база (расстояние между антеннами), развязка поляризации (гл. 4)
D вектор базы
D\, Da база, выраженная в длинах волн
Da, -Da, расстояние между осями монтировки антенны (гл. 4)
De экваториальная проекция базы
Dm мера дисперсии (гл. 13)
Dr функция разрешения по задержке (ур. 9.161)
V дисперсия в оптическом волокне (разд. 7.1, прил. 7.2), коэффициент ухуд-
ухудшения чувствительности (разд. 7.3)
Т>т структурная функция фазы (временная) (гл. 13)
Т>ф структурная функция фазы (пространственная) (гл. 12, 13)
Т>п структурная функция показателя преломления (пространственная)
(гл. 13)
е заряд электрона = — е (гл. 13))
Е, Е напряженность электрического поля (обычно в плоскости измерений),
спектральные компоненты электрического поля, энергия
586 Смежная техника [Гл. 16
Ех, Еу проекции вектора напряженности электрического поля
8 напряженности электрического поля в источнике или апертуре (гл. 3,
14, 16), угол места
/ частота фурье-компонент энергетического спектра (гл. 9, 13)
fi сила осциллятора в точке резонанса г (гл. 13)
/т, /п сигналы переключения фазы (гл. 7)
F плотность потока мощности [Вт-м~2], интерференционная функция
Fh пороговый уровень помех [Вт-м~2] (гл. 15)
F(/3) функция фарадеевской дисперсии (гл. 13)
Fi, F2 см. ур. (9.17)
Fi, i*2, ^з меры энтропии (гл. 11)
Fb отклик по полосе пропускания (гл. 2)
J~r, J~i дискретные значения функции вращения частоты интерференции
(гл. 9)
д коэффициент усиления антенны по напряжению, гравитационное уско-
ускорение (гл. 13)
G гравитационная постоянная
Gi коэффициент усиления приемника г-й антенны (гл. 7)
Gran коэффициент усиления коррелированной антенной пары
Go коэффициент усиления (гл. 7)
Q функция покрытия (гл. 16)
h постоянная Планка, импульсная характеристика фильтра (разд. 3.3),
часовой угол, высота
ho эффективная толща атмосферы (гл. 13)
Н часовой угол, амплитудно-частотная характеристика по напряжению,
матрица Адамара (разд. 7.5)
Но эффективное усиление
г электрический ток
i единичный вектор в направлении полярной или азимутальной оси
(гл. 4), вектор тока (гл. 13)
/ интенсивность, параметр Стокса
I2 дисперсия относительного отклонения частоты (гл. 9)
Is интенсивность спеклов (гл. 16)
Iv видность параметра Стокса
/о максимальная интенсивность на карте точечного источника, измерен-
измеренное (синтезированное) распределение интенсивности, модифицирован-
модифицированная функция Бесселя нулевого порядка (гл. 6, 9)
/i функция одномерного распределения интенсивности, модифицирован-
модифицированная функция Бесселя первого порядка (гл. 9)
Хт мнимая часть
з
J матрица Джонса (гл. 4)
ju объемная излучательная способность (гл. 13)
J взаимно-коррелированная интенсивность (гл. 14)
Jo функция Бесселя первого рода и нулевого порядка
Основные обозначения 587
Ji функция Бесселя первого рода и первого порядка
к постоянная Больцмана, волновое число 2тг/А (гл. 13)
к волновой вектор с абсолютным значением 2тг/А (гл. 9)
I направляющий косинус относительно г^-проекции базы, вертикальный
градиент температуры (гл. 13)
L длина линии передачи, коэффициент потерь в линии передачи (гл. 7),
интеграл вероятности (ур. 8.70), длина пути, функция правдоподобия
(гл. 12), толща атмосферного турбулентного слоя или экрана (гл. 13)
-dinner, Pouter характерные размеры турбулентности (гл. 13)
? длина, галактическая долгота (гл. 13)
?\ база единичной длины (в длинах волн) в дифракционной антенной
решетке (гл. 1, 5)
С долгота, избыточная длина пути (гл. 13)
Cd,?>v избыточная длина пути для сухого воздуха, водяного пара
т направляющий косинус относительно ^-проекции базы, коэффициент
модуляции (пр. 7.2), измеренная величина (пр. 12.1), масса электрона
(гл. 13)
mi, mc, mt степень линейной, круговой и полной поляризации
М коэффициент умножения частоты (гл. 9), модельная функция (гл.10),
масса, комплексная степень линейной поляризации (гл. 13)
M,Md,Mv молекулярный вес: суммарный, сухого воздуха, водяного пара (гл. 13)
п направляющий косинус относительно и>-проекции базы, весовой коэф-
коэффициент при квантовании (гл. 8), шумовая компонента, показатель
преломления (гл. 13)
п = nR + jrtj комплексный показатель преломления
па число антенн
rid число точек данных
пе,Пг,пп,пт плотность электронов, ионов, нейтральных частиц и молекул (гл. 13)
пр число антенных пар
ns число источников
пг число точек в прямоугольной антенной решетке (точек сетки)
По показатель преломления у поверхности Земли (гл. 13)
N число отсчетов (гл. 8), полная преломляющая способность (гл. 13)
Nb число бит на отсчет (гл. 8)
Nd,Nv преломляющая способность: сухого воздуха, водяного пара (гл. 13)
Nn число отсчетов на частоте Найквиста (гл. 8)
J\f 2J\f и BЛ/* +1) — четные и нечетные номера уровней квантования
(гл. 8)
р плотность вероятности или распределение вероятности [т.е., р(х) dx —
вероятность нахождения случайной переменной в интервале от х до
х + dx], двумерная функция нормального распределения вероятно-
вероятности (гл. 8), число параметров модели (гл. 10), парциальное давление
(разд. 13.1), параметр столкновения (разд. 13.5)
рв парциальное давление сухого воздуха (гл. 13)
pv парциальное давление водяного пара (гл. 13)
588 Смежная техника [Гл. 16
Р мощность, интегральная вероятность, полное атмосферное давление (гл. 13)
Ро давление атмосферы на поверхности Земли (гл. 13)
Р дипольный момент на единицу объема
Рз тройное произведение (биспектр)
Ртпр коэффициент инструментальной (паразитной) поляризации
Рпе спектр флуктуации плотности электронов
*Р отклик на точечный источник на краю лунного лимба (разд. 16.2), функция
рассеяния спеклов (разд. 16.4)
q расстояние на гш-плоскости
q' расстояние на u'v1 -плоскости
qx, qy проекции в плоскости пространственных частот (в периодах на метр) (гл. 13)
Q параметр Стокса, добротность линии или резонатора (разд. 9.5), число уров-
уровней квантования (разд. 9.6)
Qv видность параметра Стокса
г коррелированный сигнал, расстояние на 1т-плоскости, радиальное расстоя-
расстояние
г геоцентрический позиционный вектор антенны
ге классический радиус электрона (гл. 13)
Г? коррелированный сигнал для нижней боковой полосы частот
го радиус Земли (гл. 13), длина Фрида (гл. 16)
г и выходной сигнал коррелятора для верхней полосы частот
R автокорреляционная функция, выходной сигнал коррелятора, функция Раде-
махера (разд. 7.5), расстояние, газовая постоянная (гл. 13)
R корреляционная матрица (гл. 4)
Ra усредненный отклик видности (гл. 6)
Rb отклик в определенной полосе пропускания (гл. 6)
Re радиус орбиты электрона (гл. 13)
Rff радиус дальней зоны
Rm мера вращения (гл. 13), расстояние до лунного лимба (гл. 16)
Rn автокорреляция при n-уровневом квантовании (гл. 8)
Ry автокорреляционная функция относительного отклонения частоты (гл. 9)
Rep автокорреляционная функция фазы (гл. 9, 13)
IZe действительная часть
IZsn отношение сигнал/шум
s сигнал, параметр сглаживания (гл. 11)
s единичный позиционный вектор (гл. 3)
50 единичный позиционный вектор в направлении центра площадки (гл. 3)
S плотность потока (спектральная) [Вт м~2 Гц]
Sc плотность потока калибровочного источника
Se эквивалентная плотность потока системы
Sh пороговый уровень помех [Вт м~ Гц~ ] (гл. 15)
S кросскорреляционный спектр мощности (гл. 9)
51 спектр мощности флуктуации интенсивности (гл. 13)
Основные обозначения 589
Sy, S'y однополосный и двухполосный спектры мощности относительного откло-
отклонения частоты (однополосный спектр мощности используется только в
разд. 9.4)
<S</>, Б'ф однополосный и двухполосный спектры мощности фазовых флуктуации
(однополосный спектр мощности используется только в разд. 9.4)
е>2 двумерный энергетический спектр фазы (гл. 13)
t время
te период вращения Земли вокруг своей оси (гл. 12)
tcyc период обращения исследуемого и калибровочного источников
Т температура, интервал времени, коэффициент передачи (гл. 14)
Tat температура атмосферы (гл. 13)
Та составляющая антенной температуры, приходящаяся на полезный сигнал
ТА полная антенная температура
Тв яркостная температура
Тс температура шума калибровочного сигнала
Тд температура газа (гл. 9)
Tr температура шума приемника
Ts температура шума системы
Т интервал времени
и координата базы в единицах длин волн (пространственная частота)
и проекция координаты и на экваториальную плоскость
U параметр Стокса
Uv видность параметра Стокса
U паразитный отклик (разд. 7.5)
v координата базы в единицах длин волн (пространственная частота), фа-
фазовая скорость в линии передачи (гл. 8)
v проекция координаты v на экваториальную плоскость
vg групповая скорость (гл. 13)
vm скорость углового перемещения лунного лимба (гл. 16)
vp фазовая скорость (гл. 13)
vr радиальная скорость
vs скорость рассеивающего экрана (если необходимо, то параллельно вектору
базы) (гл. 12, 13)
vo уровень квантования (гл. 8), скорость частицы (гл. 9)
V напряжение, параметр Стокса
Va отклик антенны по напряжению
Vv видность параметра Стокса (гл. 4)
V, V комплексная видность, вектор видности
Vm измеренная комплексная видность
Vm видность интерференционных полос Майкельсона
Vn нормированная комплексная видность
w координата антенной базы в единицах длин волн (пространственная ча-
частота), функция взвешивания, высота столба осажденной воды (гл. 13)
w' проекция w на направление полюса мира
590 Смежная техника [Гл. 16
wa атмосферная функция взвешивания (гл. 13)
wmean среднее весовых коэффициентов (гл. 6)
UJrms среднеквадратичное значение весовых коэффициентов (гл. 6)
Wt функция сглаживания видности (гл. 10)
wu функция коррекции амплитуды видности для эффективного однородного
взвешивания (гл. 10)
W функция спектральной чувствительности (пространственная передаточ-
передаточная функция); функция распространения (гл. 14)
х пространственная координата, координата в антенной апертуре, напряже-
напряжение сигнала
х\ координата ж, выраженная в длинах волн
X координата базы (см. ур. 4.1), монохроматический сигнал, измеренный в
единицах ср. кв. амплитуды (гл. 8), координата точки в пределах источ-
источника или апертуры (гл. 3, 14), спектр сигнала (разд. 8.7)
Х\ координата X, выраженная в длинах волн
у пространственная координата, координата в антенной апертуре, напряже-
напряжение сигнала, расстояние вдоль луча (гл. 13)
yk относительное отклонение частоты (гл. 9)
ух координата у, выраженная в длинах волн
Y координата базы (ур. 4.1), У-фактор (гл. 7), координата точки в пределах
источника или апертуры (гл. 3, 14), монохроматический сигнал, измерен-
измеренный в единицах ср. кв. амплитуды (разд. 8.4), спектр сигнала (разд. 8.7)
Y\ координата У, выраженная в длинах волн
z позиционная координата, напряжение сигнала, зенитное расстояние
(гл. 13)
z\ координата z, выраженная в длинах волн
Z координата базы (ур. 4.1), видность плюс шум на выходе коррелятора
(гл. 6, 9)
Zd,?v коэффициенты сжимаемости для сухого воздуха и водяного пара (гл. 13)
Z векторная сумма видности и шума (гл. 6, 9)
Z\ координата Z, измеренная в длинах волн
ol прямое восхождение, коэффициент ослабления мощности, порог кванто-
квантования в единицах а (гл. 8), спектральный индекс (гл. 11), коэффициент
поглощения и показатель степени (табл. 13.2 и текст, разд. 13.1), показа-
показатель степенного закона флуктуации электронной плотности (ур. 13.164,
разд. 13.4), солнечная элонгация (разд. 13.5)
C относительное изменение длины линии передачи (гл. 7), коэффициент
избыточности дискретизации (гл. 8), показатель степени длины базы в
степенной зависимости ср. кв. флуктуации фазы (ур. 13.79а, разд. 12.2,
13.1), показатель степенного закона плотности солнечных электронов
(ур. 13.178, разд. 13.5), фарадеевская толща (разд. 13.6)
7 коэффициент инструментальной (паразитной) поляризации (разд. 4.8),
частота релаксации в мазере (гл. 9), усиление в цикле CLEAN (гл. 11),
функция когерентности источника (гл. 14)
Г постоянная затухания (гл. 13), функция взаимной когерентности (гл. 14),
гамма-функция
Г12 функция взаимной когерентности (гл. 14)
Основные обозначения 591
6 склонение, префикс приращения, дельта-функция (Дирака), коэффициент
инструментальной (паразитной) поляризации (разд. 4.8)
2 S двумерная дельта-функция
А малый интервал, префикс приращения
Av полоса частот, доплеровское смещение (прил. 10.2)
AvIF ширина полосы промежуточных частот
A^LF ширина полосы низких частот
Аиъо разность частот гетеродинов
Ат ошибка задержки
Аи, Av приращения на г^г>-плоскости
A/, Am приращения на 1т-плоскости
б ширина уровня квантования в единицах а (гл. 8), шумовая составляющая
в сигнале ПЧ (гл. 9), диэлектрическая проницаемость (гл. 13)
еа амплитудная ошибка (гл. 11)
во диэлектрическая проницаемость вакуума (гл. 13)
s шумовая компонента на выходе коррелятора (гл. 6, 9), остаток, вклад
ошибок, относительная диэлектрическая проницаемость (гл. 13)
е вектор шума
rj коэффициент потерь
tjd коэффициент потерь при квантовании задержки
rjQ коэффициент эффективности (потерь) Q-уровневого квантования
rjR коэффициент потерь при вращении интерференционных лепестков
rjs коэффициент потерь при ограничении полосы частоты интерференции
в угол; угол, измеряемый относительно плоскости, перпендикулярной век-
вектору базы; аппаратурная фаза
во угловое положение центра источника или площадки
въ ширина синтезированной диаграммы направленности, угол отклонения
(гл. 13)
Of размер синтезированной площадки
Of ширина первой зоны Френеля
0ЪО фаза гетеродина
6т, 0п фаза гетеродинов на антеннах тип (гл. 6)
6S эффективная ширина диаграммы направленности с учетом атмосферных
флуктуации (гл. 13), размер источника (гл. 16)
Gs изменение суточного вращения Земли (UT1—UTC) (гл. 12)
Л длина волны
Aopt длина несущей волны в оптическом волокне (пр. 7.2)
Л амплитуда отражения в линии передачи (гл. 7)
fi показатель степенного закона дисперсии Аллана (гл. 9)
v частота
v частота, измеренная относительно центральной частоты или частоты ге-
гетеродина (гл. 9)
щ частота бит
ь>в гирочастота (гл. 13)
592 Смежная техника [Гл. 16
vc частота соударений (гл. 13)
vc частота резонатора (гл. 9)
Vd промежуточная частота, на которой вводится задержка
Vds частота изменения задержки (гл. 9)
Vf частота интерференции
z^in инструментальная компонента частоты интерференции (гл. 12)
vIF промежуточная частота
уъо частота гетеродина
vi частота корреляционного канала (гл. 9)
vm частота модуляции несущего сигнала в оптическом волокне (гл. 7)
vnF радиочастота
vopt частота несущего сигнала в оптическом волкне (пр. 7.2)
vp плазменная частота (гл. 13)
ь>о центральная частота полосы ПЧ или ВЧ, частота максимального погло-
поглощения (гл. 13)
р автокорреляционная функция, кросс-корреляционный коэффициент, ко-
коэффициент отражения (гл. 7), плотность газа (гл. 13)
Pd,Pv,Pt плотность сухого воздуха, водяного пара, суммарная (гл. 13)
РтП кросс-корреляция
Ра плотность заполнения гш-плоскости (гл. 10)
Рт, рп коэффициент отражения в линии передачи (гл. 7)
pw плотность воды (гл. 13)
а стандартное отклонение, ср. кв. уровень шума
<т вектор направления на сфере единичного радиуса
(Ту стандартное отклонение Аллана (cry2 — дисперсия Аллана)
аТ ср. кв. неопределенность задержки (гл. 9)
<7ф ср. кв. отклонение фазы
г интервал времени
та время усреднения (интегрирования)
rat ошибка задержки в атмосфере (гл. 12)
тс время когерентного накопления (гл. 9)
те ошибка часов
тд геометрическая задержка
Тг аппаратурная задержка
го шаг аппаратурной задержки, продолжительность наблюдений (гл. 6),
оптическая толща (непрозрачность) атмосферы в направлении зенита
(гл. 13)
т8 интервал выборки по времени
Тог минимальный период ортогональности (гл. 7)
rsw интервал переключений (гл. 7)
tv оптическая толща (непрозрачность) (гл.13)
ф фазовый угол
фт фаза сигнала, принятого га-й антенной
фу фаза видности
Прочие символы 593
Фс ф'т аппаратурная фаза коррелированной пары антенн
фрр размах фазовой ошибки (гл. 9)
Ф фаза комплексного сигнала (пр. 3.1), интеграл вероятности (ур. (8.44),
гл. 8), фаза сигнала (разд. 13.1)
X арктангенс отношения осей эллипса поляризации
\2 статистический критерий
ф позиционный угол, фаза
фр параллактический угол
иое угловая скорость вращения Земли
Q телесный угол
?ls телесный угол, стягиваемый источником
Qo телесный угол главного лепестка синтезированной диаграммы направлен-
направленности
Часто используемые индексы
1, 2 обозначения антенн
2, 3, 4, оо уровни квантования (гл. 8)
А антенна
d задержка, двойная боковая полоса частот
D сухая компонента (гл. 13)
/ мнимая часть
ПЧ промежуточная частота
? левая круговая поляризация, нижняя боковая полоса частот
LO гетеродин
О центр полосы частот или площадки на небесной сфере, поверхность Земли
(гл. 13)
m, n обозначения антенн
N нормированная величина, частота Найквиста (разд. 8.2, 8.3)
г правая круговая поляризация
R действительная часть
S система
и верхняя боковая полоса частот
V водяной пар (гл. 13)
Л величина, измеренная в длинах волн
Прочие символы
П единичная прямоугольная функция
Y[ символ произведения
III одномерная шах-функция
2III двумерная шах-функция
^ преобразование Фурье
* одномерная свертка
594
Смежная техника
[Гл. 16
точка (')
две точки (")
надчеркивание (~), ( )
циркумфлекс (^)
циркумфлекс ( )
двумерная свертка
одномерная кросс-корреляция
двумерная кросс-корреляция
математическое ожидание (или его аппроксимация на конеч-
конечном интервале)
первая производная по времени
вторая производная по времени
усреднение (гл 1, 9, разд. 14.1), преобразование Фурье функ-
функции (гл. 3, 5, 8, 10, 11, 13, разд. 14.2)
квантованная переменная (гл. 8)
функция частоты (гл. 3)
Функции
Для определений см. Abramowitz M., and I. A. Stegun, Handbook of Mathematical
Functions, National Bureau of Standards, Washington, D. C, 1964, reprinted by Dover, New
York, 1965.
erf функция ошибок
Jo функция Бесселя первого рода и нулевого порядка
J\ функция Бесселя первого рода и первого порядка
/о модифицированная функция Бесселя нулевого порядка
/i модифицированная функция Бесселя первого порядка
Г гамма-функция, отметим, что Г(ж + 1) = xY{x)
6 дельта-функция Дирака
Предметный указатель
595
Предметный указатель
Cl 479
С2пе 508
J2 синтез (J-квадрат синтез) 147
ЗС-источники, см. Радиоисточники
SKA (Антенна с эффективной площадью 1 кв.
км) 38
SMA (Субмиллиметровая решетка) 21, 147, 570
Sine-функция 55
ALMA 21, 488. См. также Чайнантор, Чили
CCIR 558
CLEAN-алгоритм (чистка) 64, 139, 362, 386-389
—, автокалибровка 398
—, алгоритм Кларка 390
—, гибридное картографирование 397
—, коэффициент обратной связи 386, 389
—, применение 389-391
—, протяженные источники 390, 393-395
—, спекл-изображение 579
—, спектральные данные 415
—, сравнение с MEM 393-395
СМВ, см. Космическое микроволновое фоновое
излучение
COESA (Комитет по стандартной атмосфере)
464, 466
Cosmic Background Explorer 20
Cosmic Background Imager 151
FX-спектральный процессор 263
GMRT 38, 147
GPS (Глобальная навигационная система) 12,
318, 437, 438, 502, 503
HALCA спутник 21, 43, 149-150, 339-340
Hipparcos, спутник 11
—, каталог звезд 426
ICRF 18, 425
ICRS 425
ITU 557-558
LO, см. Гетеродин
Lensclean (алгоритм) 417
MERLIN 31, 147, 400, 549. 552
MKSA единицы 470
NAVSTAR, см. GPS
NRAO, см. Национальная радиоастрономиче-
радиоастрономическая обсерватория
QPSK-модуляция 339
TDRSS-эксперимент 42
UTR-2 146
VLA, см. Большая антенная решетка
VLB А, см. Антенная решетка со сверхдлинны-
сверхдлинными базами
Аберрация 18
— суточная 286, 435
— хроматическая 369
Австралийский телескоп 110, 112, 146
Автокалибровка 398-401
Автокоррелятор 234
Автокорреляционная функция 56, 127-130, 172
, определение 56, 127
, распределения интенсивности (на карте)
401, 572
Автоматическая коррекция фазы 208
Автоматическая регулировка уровня
(АРУJ28, 254, 347, 555
Адаптивная калибровка 396-400. См. также
Гибридное картографирование, Автокалибров-
Автокалибровка
, оптика 573
, ограничения 400
, сравнение методов 399-400
Азимут 86, 113
Азимутальная монтировка (угломестная) 91—
92, 110, 112
Академия Наук Китая (Тайвань) 21, 147
Алголь 424
Алгоритм неотрицательных наименьших квад-
квадратов 395
Алгоритм суммирования-сдвига 579
Аналоговая обработка данных
, преобразование Фурье 382
, сравнение с цифровой обработкой 234
Аномальная рефракция 483-484
Антенна (антенны) 76, 117-120, 534
—, годографы пространственных частот 86-87
—, голографические измерения 567-572
—, , алгоритм Майзеля 571
—, , практические вопросы 569-571
—, , требуемая чувствительность 569
—, изменение формы зеркала 118
—, изменение частоты интерференции при со-
сопровождении источника 117—118
—, измерения поверхности 567-572
596
Предметный указатель
—, конструкция 117-119
— космическая 42-43, 149-150
—, коэффициент использования поверхности
(коэффициент апертуры) 18, 120
—, миллиметровые длины волн 155
—, минимальное количество 397
—, модель боковых лепестков 548
—, монтировки 90—92
—, мощность принятого сигнала 18, 59
—, незатененная апертура 118
—, несимметричное расположение облучателей
119
—, облучение апертуры 128, 408, 567
—, отклонение осей 91, 92, 450
—, полоса пропускания облучателей 112
—, поляризация
кросс- 99
круговая 97-98
модель 95-98
одинаковая 98
противоположная, см. кросс
—, приемная диаграмма направленности 60, 127
—, приемная диаграмма направленности по на-
напряжению 77, 128, 534, 540
—, смещение облучателя 111, 112
—, стоимости 154
—, температура 18
—, точность поверхности 119-120
—, угловое разрешение (ширина луча) 5, 534
—, фокус Кассегрена 118-120
—, смещенный 118
—, фокус Нейсмита 118
—, фокус первичный 118
—, эффективная поверхность 18, 77, 120
Антенная решетка со сверхдлинными базами
(VLBA) 41, 148-149, 321
, опорная фаза 432-433
Антенные усилители 126
Апертура, диаграмма направленности излуче-
излучения 352, 534-535
Апертурный синтез 131, 133
Аподизация (взвешивание) 354
Аппаратурная (компенсирующая) задержка,
см. Задержка, аппаратурная
Аресибо, Пуэрто-Рико 544
Астрометрия 11, 286, 423-452, 502
— РСДБ 427-431
—, движение полюсов 436-438
—, координатные измерения 426-427
—, нутация 435
—, опорные системы отсчета 425-426
—, прецессия 435
—, точность 430
Атмосфера нейтральная 457-501
, водяной пар, см. Водяной пар
, избыточная длина пути 464-465
, калибровка, см. Калибровка, атмосфер-
атмосферная
, кислород 466, 486
, непрозрачность 487-489. См. такэюе по-
поглощение
— —, параметр Фрида (радиус когерентно-
стиL80, 573
, поглощение 466-473
, рефракция (преломление) 462-465
, учет эффектов РСДБ 478-483
, в астрометрии 430-431
, в облаках 492
, функции видности 475-483
, частоты интерференции и задержки
430-431
, фазовые флуктуации 475-484
, яркостная температура 485-487
База
— восток-запад 53, 74, 191
—, задержка 285
—, калибровка 70, 426-427, 450
—, координаты 84-86
— обзора 12, 85-86, 423-424
—, определение 53-54
—, точка отсчета 91
—, экваториальная проекция 428
Базы некомпланарные 75
Бартлета взвешивание (сглаживание) 260
Бесселев год 435
Биспектр (двумерный спектр) 297-298
Блуждающие ионосферные возмущения (TIDs)
503-504
Блэкмана взвешивание (сглаживание) 260
Боковая полоса (полосы) частот 160
двойная 165-171, 183-184
, зависимость частоты интерференции 88
, неравенство откликов 193-194
одиночная (верхняя, нижняя) 160, 161-
163
— — —, относительные преимущества одно и
двухполосной регистрации 169-170
, разделение 170-171
, смеситель с разделением полос (с по-
подавлением зеркального канала) 229
, частичное подавление 193-194
Болонья, Италия 32
Большая антенная решетка (VLA) 37, 39, 201,
219, 416, 431, 494, 544
, автокалибровка 399
— — —, атмосферный фазовый шум 432-433,
483-484
, динамический диапазон 402
, заполнение ш;-плоскости 142, 143
, изображения источников 39, 399, 400
, конфигурация антенн 140-142
, непрозрачность 487-488
, пороговый уровень помех 549, 553
, приращения задержки 220
, режим сфазированной решетки (РСДБ)
334
, фазовая модуляция 228
Предметный указатель
597
Большая миллиметровая решетка в Атакама,
см. ALMA
Боррего Спрингс, Калифорния 146
Быстрое преобразование Фурье (БПФ) 122—
124, 354-355
Быстрое преобразование Хартли 122
Ван Флека-Вайскопфа профиль 467
Варакторный диод 213, 316
Веерный луч 31, 138
Величина видности 63
Вермильон Ривер, обсерватория, Иллинойс 40
Вероятность
— ложного обнаружения 290
— ошибки 289-291
Вестерборкский радиотелескоп апертурного
синтеза 37, 100, 137, 334, 357
Вестфорд, Массачусетс, см. Хайстекская обсер-
обсерватория
Взвешивание
— видности 177-178, 351-354
— возбуждения антенны 131, 407-409
— натуральное 179, 351, 354
—, функция
—, — атмосферная 477
—, — спектральная 259-262, 367
Видимость 457. См. также Мерцания
—, диск 578
—, ячейка 573
Видность
—, lensclean (алгоритм) 418
—, вписывание модели 362-364
— интерференционных полос (Майкельсона) 22
— комплексная 33-34, 62
определение 69
— на малых пространственных частотах 402-
405,407-409
—, наиболее вероятная величина 289
—, разложение в ряд Тейлора 363
—, уменьшение вследствие фазового шума 214,
475-478, 507-509
—, усреднение 190-193
—, частоты 89
Видность в параметрах Стокса 98-101
Видность-интенсивность соотношение 68-71,
530-537
Винера-Хинчина соотношение 56, 76, 173, 236,
258, 553
Внешнее произведение 106, 225
Водяной пар
, воздействие на фазу 475-479
, глобальное распределение 460
, коэффициент сжимаемости 474
, линия 22 ГГц 472
, мазер 293, 439-442
, поглощение 466-469
, преломляющая способность 458-460, 473-
474
, резонансная модель 470-473
, турбулентность 479-483
Военно-морская исследовательская лаборато-
лаборатория (NRL) 12, 293
Военно-морская обсерватория США
(USNOL37
Волновод 201-202
Волоконная оптика, см. Оптический волновод
Восстановление по выборке, см. Теорема вы-
выборки
Вращение Земли, см. таксисе Всемирное время
синтез 36
сканирование 25
Время
— Всемирное 318, 436-437
— когерентности 276,280,293, 306-310, 428
— Международное атомное (IAT) 312-313, 437
— восстановление 269-270
— кодирование 212
— методы передачи 318
— определение секунды 312
— синхронизация 318
— солнечное 436-437
— точность 90, 318
— усреднение видности 190-193
— цикла 433, 493
Вспышечное излучение Юпитера 37, 276
Входной каскад. См. таксисе Приемник 196
Выборка 235-253. См. таксисе Квантование
— спектра полосы пропускания 235—236
— цифровая, точность 253-256
Гамма-функция 511
Гауссов случайный шум 13
Гауссова sine-функция 357
Гауссова случайная переменная 13, 172, 287-
288, 307. См. таксисе Двумерное распределение
вероятности Гаусса
Гауссова функция свертки 356-357
Гауссово ослабление 131, 134, 352-353, 387
Генератор, время когерентности 306-308
—, интенсивность 471
— с синхронизацией фазы 206, 212-213, 223
, собственная частота петли обратной
связи 212-213
Геодезические измерения 41, 423, 438
Геометрическая задержка 54, 68, 162, 281-282,
322-323, 462, 573
Гетеродин, см. таксисе Стандарты частоты 160,
200-201
— лазерный 575
— независимый 38—39, см. таксисе РСДБ
— несинхронизованный 563
—, синхронизация 204-213
—, суммирование частот с учетом знака 163
—, умножение частоты, стабильность 317
—, фазовая модуляция 228
Гетеродинное преобразование, см. Частотное
преобразование
Гибридное картографирование 41, 396-297
598
Предметный указатель
Гибридный коррелятор 269
Гидростатическое равновесие 459
Гирочастота 500
Главное решение, см. Главный отклик
Главный отклик 354
Голдстоун, Калифорния 40
Голография, см. Антенные измерения, гологра-
голография
Гравитационное отклонение, см. Относитель-
Относительность
Гребенчатый спектр 211
Грин Бэнк, Западная Вирджиния 37, 40, 388,
483
Гринвичский меридиан 84, 286, 428, 436, 437
Группа пользователей сети (США) 40, 41
Групповая задержка 280, 284, 331, 354-356, 428,
438, 497
Групповая скорость 499, 515
Грязная карта 386
Грязный луч, см. Луч синтезированный
Дальняя зона, приближение 53, 68, 536
Данные радиозондов 469-470, 485, 487
Движение полюсов 12, 436
, измерение
Двумерное (совместное) распределение вероят-
вероятности Гаусса 321, 322
Двумерные решетки 64-65, 140-149
Двумерный синтез 64-65
Двухполосная система регистрации 165-171,
182-184
Двухщелевой интерферометр Янга 43
Дельта-функция
—, выборка видности 62, 177-178
—, компоненты CLEAN 332-387
—, преобразование Фурье набора дельта-
функций 138
—, теорема Прайса 243, 247
— точечного источника 89, 133, 191, 425
— частоты гетеродина 317
—, шах-функция 121, 355
Деполяризация 517
Детектор
— линейный по мощности (квадратичный) 27,
548, 561
— синхронный 27, 205, 222, 469
Дефекты изображения, см. такэюе Фазовый
шум
дисторсия 373
, корреляционный сдвиг 373
, ошибки в данных видности 372-373
Джодрелл Бэнк обсерватория, Англия 29, 30,
36, 147
Диаграмма направленности, эффекты формы
93, 351-352
Диаграмма направленности, эффекты ширины
93, 351-352
Диаметр звезды 21-24, 578
Динамический диапазон 381, 401-403, 556
Диод 159-160, 205, 213, 316, 317
Диод с накоплением заряда 317
Дискретное преобразование Фурье 122-124,
354-356
Дисперсия
— Аллана 301-302, 310
для атмосферы 481-482
для стандартов частоты 301-311, 316
—, классическая теория 470-473
— в оптическом волноводе 202-203, 230
—, мера 515
Дифракционная картина
, лунное покрытие 564, 567
, мерцания 506, 514
Дифракционная решетка 33-34, 380-381
Дифракция на апертуре 533
Диэлектрическая проницаемость 471
Длиннобазовый интерферометр 30, 276
Длинноволновые решетки 155
Добротность (Q-фактор)
— резонатора 315-316
— фильтра 214
Дополнение нулями 266
Дополнительная секунда 237
Допустимые отклонения
полосы пропускания (отклика по частоте)
218-220
поляризации 221
трехуровневой выборки 254—256
установки задержки 219-220
Допустимые погрешности установки 165-166,
219-220
Дробовой шум фотонов 312, 314, 576
Единичная прямоугольная функция 217, 356
Задающий генератор 500
Задержка
— аналоговая 203
— аппаратурная 55, 88, 161, 219-220, 322-323
— геометрическая 54, 68, 161, 322-323, 462, 573-
574
— групповая 280, 284, 331, 428
—, компенсация, см. Задержка, аппаратурная
— опорная 163, 220
—, отклик по задержке, см. Полоса частот, от-
отклик,
— относительная выборочная коррекция 267
—, ошибки измерений 331-332
— подсистемы (компоненты системы) 203, 256-
257
—, регулировка 57-58, 219-220
—, сопровождение 163
—, схемы, цифровая 256-257
—, ошибки 219-220
Закон Шнеля 463
в сферических координатах 463, 511
Замыкание амплитуды 361. См. такэюе Адап-
Адаптивная калибровка
Предметный указатель
599
Замыкание фазы 29-30, 41, 278, 350, 360-362
Запаздывание базы 285-286
Запись на магнитную ленту 39-40, 318-321
Затенение 347
Затухание в кабеле 209
Затухание в оптическом волокне 201-202
Затягивание резонатором 315, 316
Звездное время (вращение Земли) 88
Звезды
-, наблюдения 21-24, 424, 563, 567, 574, 577-
578
—, модели видности 363
—, собственное движение 436
Земля, см. такэюе Геодезические измерения,
Движение полюсов
—, атмосфера 457-462
—, движение тектонических плит 12, 438
—, ионосфера 497-504
—, магнитное поле 499
—, приливы 438
—, радиус-вектор 285, 464
—, экваториальная выпуклость 435
Зенит, непрозрачность 467, 487-490
Зеркало Ллойда 25
Зеркальное отображение приемной диаграммы
направленности 60
Зона
— ближняя, проведение наблюдений 536
— дальняя, требование 536
Зона Френеля 506, 564
Избыточная выборка 236, 238, 239, 241-242,
246, 248, 252
Избыточная длина пути 459
, ионосфера 498, 501
, межпланетная среда 513
, тропосфера 464-465, 485-487
Излучение в непрерывном спектре 13
Изображение 16
Изопланарный
— угол, нейтральная атмосфера 573
— участок, ионосфера 361, 416, 497
— участок, нейтральная атмосфера 573
Импульсная калибровка (РСДБK17-318
Импульсный режим в РСДБ 332-333
Инерциальная система координат 425
Интенсивность 16, 372
—, измерение 350-360
—, интерпретация 372
—, масштаб 371, 397
Интерполяция 122, 354-356. См. таксисе Раз-
Разделение по ячейкам
Интерференции частота, см. Частота интерфе-
интерференции
Интерференционные лепестки
, белый свет 58, 279, 574
, видность 22
, вращение (остановка) 163-164, 168-169,
201, 227-228
, вращение цифровое 267, 323-325
, огибающая 54, 58
, первые радионаблюдения 26
, подбор параметров 182
, подбор параметров, обобщенный 294-299
, поиск, см. Поиск сигнала
, функция (диаграмма) 25, 54, 60
, функция замывания 57
Интерференция белого света 58, 279, 574-575
Интерферометр Майкельсона 20, 21-24
Интерферометр интенсивности 29, 560-563
Майкельсона 21-24
инфракрасный, см. Инфракрасный интер-
интерферометр
компаунд 34
корреляционный 27
морской 25-26
— — оптический (современный Майкельсона)
572-578
, основные элементы 76-78
спектральный 35
суммирующий (простой) 24-28
, чувствительность 294, 563
Интерферометрия со сверхдлинными базами,
см. РСДБ
Инфракрасная интерферометрия
, обнаружение гетеродинов 577
, обнаружение планет 575
Иона Ки, Гавайи 37, 147, 483, 487, 489-492
Ионосфера
—, ВЧ-разряд 312, 313
—, акусто-гравитационные волны 503
—, влияние неоднородностей 503-504
—, задержка распространения 501-508
—, колебания 93
—, коэффициент преломления 499-501
—, мерцания 503-504
—, модель гауссового экрана 505-509
—, перемещающиеся возмущения (TIDs) 503,
504
—, поглощение 497-503
—, полное число электронов 497, 501, 504
—, распределение плотности электронов 498
—, распространение 497-520
—, рефракция 501
—, степенная модель 508-600
—, турбулентность 508-509
—, фазовая стабильность 497
—, фарадеевское вращение 497, 500
—, частота 499
Исправление данных 269, 346
, исключение помех 548-549
Исследования Солнечной системы 33-34, 512,
536
Исследуемый источник 347
История развития 20-43
РСДБ 39-41, 276-280
аналогового преобразования Фурье 381
картографирования по одномерным про-
профилям 380-381
600
Предметный указатель
приемников 169-170, 196
Источник, см. Радиоисточник
—, вычитание. См. также CLEAN алгоритм
—, калибровка 279, 346-350
—, когерентность 538-541
—, модель, см. Модель
—, полная когерентность 540-541
— протяженный, см. Протяженные источники
—, радиоизлучение, см. Радиоисточник
—, требование некогерентности 69, 531-532
—, условие дальней зоны 53, 68, 536
Кабель
—, дисперсия скорости 206
—, затухание 209
—, отражение 207, 209, 217
Калгура, решетка (Австралия) 147
Калибровка 346-349
— адаптивная 396-401
— атмосферная
задержки 502-503
фазы быстрой модуляцией 493-495
фазы в РСДБ 318
фазы измерением водяного пара 495-497
фазы парой антенн 494-495
— базы, см. База, калибровка
— кабелей 77, 416
—, калибровочные источники 28, 279-280, 347-
349
—, полоса пропускания 365—366, 369
— поляризации 108-111
— спектральная 365-369
— усиления 347
Калибровочный источник. См. таксисе Калиб-
Калибровка, калибровочный источник
Каллена-Велтона формула 198-200
Канадская сеть РСДБ 39, 321
Карандашный луч (диаграмма) 31, 138
Карта 16
Картографирование
— двумерное 64-65
— по амплитуде видности только 401
—, синтез, определение 6
— Солнца 33-34, 380-381
— широкоугольное 73-76, 189-190, 403-407,
411-415
Кассегрена фокус 118
Квадратура
-, сеть 164, 254, 259
—, фазовый сдвиг (тг/2) 170-171, 176, 227, 257
Квазар 13, 40-41, 278, 399. См. таксисе Радио-
Радиоисточник
Квантование
— в системах РСДБ 320, 329
— восьмиуровневое 245-251
— двухуровневое 240-242
—, исправление 252
—, коэффициент эффективности 175, 249, 251,
322, 330
—, области отсутствия решения 255—256
— повторное (переквантование) 270, 337
—, пороги 243, 247, 249
—, сравнение схем 252-253
— трехуровневое 247-248
— четырехуровневое 243-247
—, шум 234, 248-251
Квантовый парадокс 43
Квантовый шум 43-44, 576
Кварцевый генератор 212, 299, 309, 314
Кембридж (Англия) 31, 136, 283
—, Низкочастотный телескоп апертурного син-
синтеза 414
—, Одномильный радиотелескоп 36-37, 136
—, Пятикилометровый радиотелескоп 37
—, Третий Кембриджский каталог 17-18, 32
—, Четвертый Кембриджский каталог 32
Классический радиус электрона 505
Клаузиуса-Клапейрона уравнение 461
Ковариационная матрица 448
Когерентность
— взаимная 530-531, 563
— водородного стандарта 310
—, время, см. Время когерентности
— генератора 307-310
—, комплексная степень 538
—, матрица, см. Матрица когерентности
— пульсаров и мазеров 545
— распространения 541-545
—, функция источника 69, 535, 538-541
—, временная 307-308. См. таксисе Авто-
Автокорреляционная функция
— частичная 538
Когерентный источник 540-541
Кольцевые лепестки 137-139
Компаунд-интерферометр 34
Компенсирующая задержка, см. Задержка, ап-
аппаратная
Комплексная видность 34, 62, 69
Комплексная степень когерентности 537
Комплексный коррелятор, см. Коррелятор
комплексный
Комптоновские потери 278
Координатные измерения
, методы, см. Астрометрия
первые 28
Координаты
—, преобразование 113
— разнесенных антенн 84-87
—, системы 64, 65, 70, 84-88
Корнелльский университет 39
Короткие (точечные) наблюдения 142, 145
Коррелятор 78
— FX 166
— аналоговый 213
— гибридный 269
— задержек (XF) 262
— комплексный 164-165
—, объединение каналов, разделение каналов
269-270
Предметный указатель
601
—, представление выходного сигнала на ком-
комплексной плоскости 167, 176-177
— простой (с одним перемножением) 164-165,
184
—, система 78
—, смещение напряжения 222, 253, 373-374
—, сравнение XF- и FX-корреляторов 266-269
— циркулярный 262-253
— цифровой 257
Космический интерферометр, проект (SIM,
NASA) 12, 574
Космическое микроволновое фоновое излуче-
излучение (СМВ) 151, 364, 378, 468
, анизотропия 151, 364, 468
Коэффициент (мера) избыточности 136
— преломления, см. Рефракция, коэффициент
преломления
Крамерса-Кронига соотношение 470, 472
Крест Миллса 31, 32, 129, 134
Криогенное охлаждение 169, 196
Кросс-корреляция 76-78
—, коэффициент 237
Кросс-спектр мощности 76, 258-261, 326, 446.
См. таксисе Спектральная линия
Круговая поляризация 111
, определение ТИИЭР (IEEE) 95
, степень 94
Круговая решетка 143
Линейные решетки 135-139
Линии связи, см. Кабели; Гетеродины, синхро-
синхронизация
Линия водорода 16, 35, 313-315
Лоренц-фактор 380
Лоренцев профиль 471, 472, 476, 478
Луна как калибровочный источник 374-376
Луна, см. Лунное покрытие, Прецессия
Лунное покрытие (оптика) 563, 567
(радио) 424, 514, 563-567, 29
Луч. См.таксисе Диаграмма направленности
— веерный 31-32
— карандашный 31, 138
— синтезированный (грязный) 141, 188-189,
372, 451, 578
—, частота интерференции 442
—, чистка 386-389
MAC
—, обозначения радиоисточников 18
—, стандарт поляризации 95-96
Маврикий, радиотелескоп 146
Магнитные поля
в стандартах частоты 313-314, 315, 316-
317
земного происхождения 500
межзвездные 516
Мазерные радиоисточники 14-15, 39-40, 276,
278, 293, 518
, пространственная когерентность 545
, процедуры картографирования 439-443
Мазерный стандарт частоты (водородный)
405-407
Маллард, радиоастрономическая обсервато-
обсерватория, см. Кембридж: (Англия)
Малое Магелланово облако 407
Малошумящий входной каскад 169, 196-197
Малые пространственные частоты 139, 155, 408
Матрица Джонса 105
Матрица Мюллера 108
Матрица дисперсий 448
Матрица когерентности (поляризационная) 95-
96
Матрицы Адамара 224
Международная небесная система опорных ко-
координат
Международное атомное время (IAT) 437
Международное бюро времени (ВШ) 437
Международный астрономический союз, см.
MAC
Межзвездная среда 514-520
, воздействие на сигналы пульсаров 515
, мера дисперсии 515
, плотность электронов 515
, рассеяние
, — Фидлера 520
, — дифракционное 517-518
рефракционное 518-520
, фарадеевское вращение 515-517
Межпланетная среда 510-513
, избыточная длина пути 513
, мерцания 513-514
, плотность электронов 511
, рефракция 510-513
Мера вращения 516, 517
Меридиан 84
— Гринвичский 84, 286, 428, 436, 437
— местный 85, 86, 424, 437
— плоскость 84, 427
—, прохождение (пересечение) 437
Мериленд Пойнт обсерватория, Мериленд 40,
293
Мерцания
— амплитудные 540
—, длина корреляции 506
—, индекс 514
— ионосферные 503-504
—, критический размер источника 507
— межзвездные 149, 517-520
— межпланетные 513-514
—, модель гауссового экрана 505-508
— нейтральной атмосферы 479-483
—, полоса частот корреляции 506
—, спектр углового распределения 505, 509
—, степенная модель 508-510
—, тонкий экран 505-508
—, угол рассеяния 505, 509
Метод максимального правдоподобия 332, 443,
451
— максимальной энтропии (MEM) 391-393
602
Предметный указатель
— модуляции отражением 469
— наименьших квадратов 442-452
, CLEAN (чистка) 389
, автокалибровка 398
взвешенный 443
, коррелированные измерения 448
, матрица дисперсий 448
, матрица ковариации 448
— — —, матрица нормальных уравнений 448,
451
, матрица плана 449
, матрица частных производных 448
, матричная формулировка 448
, нелинейный случай 449
, обработка больших баз данных 449-450
, оценка задержки 446
, оценка частоты интерференции 445
, ошибки координат источника 450-452
, синусоидальное решение 182
, точность (абсолютная) 449
, точность 449
, функция правдоподобия 443
, эллипс ошибок 449, 452
Метод последовательного сканирования 468
Метр, определение 423
Миллибар 459
Минимальная избыточность, см. Решетки ми-
минимальной избыточности, Полоса частот, син-
синтез
Многочастотный синтез 410-411
Модель
— Аллена-Баумбаха 511
—, Лебедь А 29-30
—, адаптивная калибровка 398
— без фазовых данных 362
— гауссова 23, 35, 363
—, дельта-функция (CLEANK89
—, звездная оболочка 362
—, круглый диск 23, 391
—, моменты 363
—, подбор 362-364
— прямоугольная 23
Мозаика (мозаичное картографирование) 402-
409
— линейная 405
— нелинейная 406
—, специализированные решетки 407-409
Молонгло, Австралия 32
Морской интерферометр 25-26
Наблюдения в ближней зоне 536
Наблюдения, планирование и обработка 373-
374
— покрытий, см. Лунное покрытие
Найквиста критерий (частота). См. также Те-
Теорема выборки 235-236
Нансе, Франция 34
Направленный ответвитель 205
Направляющий косинус 65, 70, 536
Наррабри, Австралия 578
Натуральное взвешивание 179, 351, 354
Наффилд, радиоастрономические лаборато-
лаборатории, см. Джодрелл Бэнк обсерватория
Национальная геодезическая служба (NGSI2
Национальная радиоастрономическая обсерва-
обсерватория (NRAOK7, 39, 141, 277, 321, 400. См.
такэюе ALMA, Грин Бэнк, Большая антенная
решетка (VLA), Антенная решетка со сверх-
сверхдлинными базами (VLBA)
Национальное управление по аэронавтике и
космическим исследованиям (NASA) 12, 41, 321
Небесная сфера 68, 85
Небесные координаты 86, 113
Небесный экватор 85-86, 140
Нейтральная атмосфера
—, непрозрачность 487-490
—, фазовая стабильность 490-492
Некогерентное усреднение 291-294, 299
Некогерентный источник, отклик 538-540
Некомпланарные базы 75, 411-414
, трехмерное преобразование Фурье 413
, комбинация коротких наблюдений 414
, многогранное картографирование 414
, переменный отклик на точечный источ-
источник 414-415
Неоднозначность 179, 235, 374, 415. См. таксисе
Кольцевые лепестки
—, исправление на картах 356—360
—, определение 121
Непрозрачность 466-468
—, измерение 468-470
Низкочастотное картографирование 415-417
Нобейяма радиообсерватория (NRO), Япония
38, 483
Нобелевская лекция Райла 37
Норе Либерти, Айова 40
Нутация 12, 18, 435
ОРСДБ 41-43, 150, 337-339
—, телеметрия времени 338-339
—, телеметрия данных 339-340
—, фаза «туда-обратно» 338-339
Обзор интерферометров 31-32
Облака атмосферные
, поглощение 486
, показатель преломления 486
Область определения функции 127
Облучатели, полоса пропускания 112
Облучение, апертура, см. Антенна, облучение
апертуры
Обозначения радиоисточников 18
Обратная свертка 385-395
, сравнение CLEAN и MEM 393-395
Огибающая интерференции, зона корреляции
201, 235, 328
Ограничение (шумового сигнала) 240, 241. См.
такэюе Квантование
Предметный указатель
603
Однополосный смеситель, см. Смеситель с раз-
разделением полос
Опорная фаза
РСДБ 431-434
, атмосферные эффекты 492-494
, мазеры 439
, положение точки отсчета 58, 68, 84
, преимущества 440
Оптическая интерферометрия 44, 572-577
, прямая и гетеродинная регистрация
Оптическая толща, см. Непрозрачность
Оптическое волокно 201-203, 211
, высокая стабильность 212
, дисперсия 203, 230-231
Орбитальная РСДБ, см. ОРСДБ
Ослабление, см. Гауссово ослабление, Взвеши-
Взвешивание
Относительная диэлектрическая проницае-
проницаемость 471
плазмы 499
Относительная чувствительность систем 181—
186
Относительное отклонение частоты 300
Отражатель модулированный 205
Отражения
— в кабеле 206-207, 208, 217
— в оптическом волокне 202
Отрицательные частоты 57, 62, 81-82
Оуэне Белли радиообсерватория, Калифорния
35, 36, 39, 40, 496
Ошибки
— аддитивные 372-373, 555
— координат A,т) 374
— мультипликативные 373, 555
— на картах 372-373
— наведения 346, 373
— фазовые 214, 402
— часов (РСДБ) 282, 285
ПЧ, см. Промежуточная частота
Параболическое зеркало 118
Паразитная поляризация 101-104, 108-112
степени свободы
Параллакс 436
Параллактический угол 86, 93, 100, 110, 112
Параметрический усилитель, вырожденный
169
Параметры Стокса 94
Парсеваля теорема 179, 271, 292, 353, 478, 552,
556
Передаточная функция 126-127, 131-134, 350,
385-386. См. таксисе Пространственная чув-
чувствительность
VLA 142
VLBA 148
ОРСДБ 149-150
Перекрестная связь 152, 225, 373
Перенос излучения, уравнение 467
Пико де Велета, Испания 569
Плазма, см. таксисе Межпланетная среда,
Межзвездная среда,
Планарные решетки 150-152
Планетарная туманность 15, 349, 363
Планеты 391, 424, 435. См таксисе Вспышечное
излучение Юпитера
— как калибровочные источники 374—375
Плато де Бю, Франция 38, 483
Плоскость uv (плоскость пространственных ча-
частот) 64, 69-70
в алгоритме CLEAN 382
, восприимчивость к помехам 550
, годографы 86-87, 142, 145, 148-151
, заполнение, см. Пространственные часто-
частоты, заполнение
, интерполяция 122-124, 355-359
, координаты 64, 69
, пропуски заполнения 135
— u'v' 73-75, 87-88
Плотность потока энергии 15
Поверхностная плотность 351
Поглощение
— в ионосфере 497, 503
— в облаках (водойL86
— в тропосфере 466-472
— водяным паром 466, 484-487
—, калибровка сканированием 493
—, коэффициент 471-472, 458, 466
—, модуляционная калибровка вращением 469
— предельное для осцилляторной модели 470-
472
—, спектр 35
Подбор параметров интерференции обобщен-
обобщенный 294-296
Поиск сигнала (РСДБ) 289-294
Пойтинга вектор 16
Поле зрения
, влияние полосы частот 185-190
, картографирование по частоте интерфе-
интерференции 441
, ограничения 186-190, 536
, эффект усреднения видности 190-193
Полное число электронов, см. Ионосфера, пол-
полное число электронов
Полоса пропускания
гауссова 57, 190
, допустимые отклонения 216-219
прямоугольная 58, 188, 215
Полоса частот
, влияние на карты 186-190
выходного сигнала (коррелятора) 173
гауссова профиля 57
, корреляция 506
, отклик 57, 536
прямоугольная 57-58, 215
синтезированная 331-332. 428
среднеквадратичная 331, 429, 447
Поляризация
—, допустимое рассогласование 221
—, зависимость от параллактического угла 100
604
Предметный указатель
—, калибровка 108-112
—, комплексная степень 516-517
—, конструкции 111-112
— круговая 94, 95, 100, 102, 111
— линейная 94, 99-100, 112
—, матричная формулировка 105-108
— паразитная 101-104, 221
—, позиционный угол 94, 96. См. такэюе Фара-
деевское вращение
—, процессы излучения 13, 93
—, степень 94
— эллиптическая 95-96
Поляриметрия 93-115
Помехи в радиодиапазоне 547—558
ITU 558
РСДБ 554-556
в решетках со связанными элементами
550-554
, одиночная антенна 550
, пороговый уровень 548-549
, распределение на ш;-плоскости 551-552
солнечные 373
, спутники 556-557
, усреднение по частоте интерференции
550-552
, эффект декорреляции 553-554
Поправки наведения 346
Последовательно-параллельное преобразова-
преобразование 256
Последовательность 224
Постоянная Хаббла 380
Потери дискретного смещения бит , см. РСДБ,
потери дискретного изменения задержки
Правило Максвелла 471
Предположение некогерентности (простран-
(пространственной) 69, 535-536
Преобразование
— Гильберта 80, 82, 164, 176, 257
— последовательно-параллельное 256
— Фурье
, аналоговая техника 381
быстрое 123, 263-264
дискретное 122-124, 354-356
, знак в экспоненте 69
, интегральная теорема 173
прямое 350-351
, свойство производной 301, 363, 565-566
, соотношения, картографирование 128
, теорема подобия 187
, теорема проекции-сечения 65-66
, теорема сдвига 368
трехмерное 75, 411-413
— Ханкеля 477
— Хартли 122
— частоты, см. Частота, преобразование
Прецессия 11, 18, 435
Приближение замороженного экрана 481, 491
Приемная диаграмма направленности по мощ-
мощности, см. Антенна, приемная диаграмма
Приемная диаграмма направленности по на-
напряжению (отклик) 76-77, 128, 534,567-568
Приемник
—, температура 19, 198-200
—, фазовая модуляция 27-28, 31, 33, 222-228.
См. такэюе Фазовая модуляция
—,электроника 196-203
—, — каскадов 198
Принцип неопределенности 44, 310, 576
Причинная функция 82
Проекции на г^игс-пространство 69-70, 72, 411-
414
при усреднении видности (по времени)
191-193
при усреднении по частоте интерферен-
интерференции 550-551
Проекция на ось w 70, 72, 88, 411-414, 424
Производная дробного порядка 139
Промежуточная частота (ПЧ) 160
, модуль 201
, усилитель 201
Пропуски в заполнении пространственных ча-
частот 135
Просачивание (выборки) 122
Просачивание (поляризации) 102, 113-115
Пространственная некогерентность, см. Источ-
Источник, требование некогерентности
Пространственная передаточная функция, см.
Передаточная функция
Пространственная чувствительность
, антенны с заполненной апертурой 407-409
корреляционной решетки 126-129
, область определения 127
Пространственно-когерентный источник 540-
542
Пространственные частоты 59, 62, 126-127, 350
, заполнение 126-129, 385-386
, фильтр 127
Протяженные источники
, мозаика 402-409
, обращение свертки 287, 390, 393-394
, отклик 372
, отношение сигнал/шум 178
Прямое восхождение 17
, измерение 424, 426-428, 450
, точка отсчета 424
Прямое детектирование, в оптике 44, 575
Пульсар 333 см. такэюе Радиоисточник
—, астрометрия 424
—, измерение дисперсии 511, 515-516
—, мерцания 518
—, определение весеннего равноденствия 424
—, пространственная когерентность 545
—, собственные движения 517
—, стробирование коррелятором 268
—, точность времени 311, 318
Путаница (смешение) радиоисточников 31, 134,
411, 415
Пятно Эйри (дифракция на круглой апертуре)
352, 578
Предметный указатель
605
РСДБ
—, TID, наблюдения 503-504
—, антенны
—, — в космосе 149-150, 337-340
—, — неидентичные 93
—, астрометрия 427-434, 449-450
—, атмосферные ограничения 430-431, 478
— в геодезии 41, 438
—, групповая задержка 285, 331
—, вращение интерференционных лепестков
322-325, 330
—, время когерентности 277, 306-308
—, гибридное картографирование 396-397
—, двухполосная система 171, 185
—, замыкание фазы 41, 296, 396-400
—, запаздывание базы 285-286
—, измерения релятивистского искривления
512-513
—, импульсная система калибровки 317-318
—, импульсный режим 332-333
—, когерентное и некогерентное усреднение
291-294, 297-299
—, кодировка данных 319-322
—, мазеры, картографирование 439-442
—, наблюдения движения полюсов 437-438
—, обнаружение интерференционных лепестков
296-297
—, опорная фаза 431-435
— орбитальная, см. ОРСДБ
—, отношение сигнал/шум 277-278, 292-294,
323-331
—, ошибки часов 282-285
—, подбор параметров интерференции
обобщенный (мультибазовый) 294-299
одна база (один элемент) 289-294
—, потери вращения интерференционных ле-
лепестков 323-325
—, потери дискретного изменения задержки
327-329
—, потери дискретного смещения бит, см. поте-
потери дискретного изменения шага задержки
—, потери квантования 277, 329-330
—, потери подавления зеркальной полосы ча-
частот 325-327
—, радиометрия водяного пара 484-487
—, развитие 38-41, 276-278, 513
—, разделение полос регистрации 171, 185
—, распределения вероятностей 286-291
—, решетки 39-41
— сети 40
—, синтез полосы частот 331-332
—, синхронизация времени 318
—, система К-4 321
-, система Mark-I 277, 293, 320-321
—, система S2 321
—, системы Mark-II, III и IV 320-321
—, системы регистрации 318-321
—, системы фазовой калибровки 317-318
—, спектральная линия 284-285, 328, 367-369
—, спутниковая телеметрия 40
—, стабильность гетеродинов 316-317
—, стандарты частоты высокоточные 309—317
—, сфазированные (синфазные) решетки как
элементы РСДБ 333-337
—, тройное произведение 299
—, угол (параллактический) антенной поляри-
поляризации 112
—, фазовая стабильность, генераторы 299-308
—, фазовый глум. См. также атмосферные
ограничения 180-181
—, чувствительность к помехам 554-556
—, шумы 286-289
Равноденствие 424, 435
Равномерное взвешивание 353-354
Радиальное размытие, см. Полоса частот, вли-
влияние на карты
Радиоисточник
- 0134+329 18
- 0748+240 484
- 1548+115 399
- 1622+633 150
- 1638+398 433
- 1641+399 433
- ЗС138 111
- ЗС147 349
- ЗС224 5, 388
- ЗС273 40, 424, 434, 513
- ЗС279 434, 544
- ЗС286 111, 349
- ЗС295 349
- ЗСЗЗ 36
- ЗС48 13, 14, 18, 349
- J1745-283 430
- М87, см. NGC5128
- NGC4258 42
- NGC4486 29
- NGC5128 29
- NGC7027 15, 18, 349
- P-Cygni 362
- PSR 1237+25 544
- PSR B2021+51 434
- W3(OH) 293
- W49 439
- Венера 234
- Дева А, см. NGC4486
- Кассиопея А 25, 28, 29, 36
- Крабовидная туманность 29, 511
- Лебедь А 18, 26, 28, 29, 503
, интерференционная диаграмма 25, 26
, карта или изображение 30, 36, 37, 39,
400
, центральное ядро (РСДБ) 41
- Солнце 33-34, 147, 380-381, см. таксисе
Солнце
- Стрелец A* (Sgr A*) 41, 431, 518
- Телец А, см. Крабовидная туманность
- туманность Ориона 14, 15
- Центавр А, см. NGC5128
- Юпитер 39, 276
—, мазер линии водяного пара в Орионе 569
606
Предметный указатель
Радиолинии, см. Спектральные линии
Радиометрия водяного пара 484-487, 495-497
Радиопомехи
—, декорреляция 553-554
— передатчиков самолетов и спутников 556-557
—, пороги pfd и spfd
—, усреднение по частоте интерференции 550-
553
-, РСДБ 554-556
—, короткие и промежуточные базы 550-554
—, системы полной мощности 547-549
Радиосвязь 29-30, 31, 41, 201, 339
Радиус Шварцшильда
Развитие техники синтеза 20—21
Разделение каналов 169-270. См. таксисе Ко-
релятор
Разделение по ячейкам (в процедуре свертки)
354-356, 428, 437, 497. См. также
Размытие
— кольцевое, см. Видность, усреднение
— радиальное, см. Полоса частот, влияние на
карты
Разрешение
— MEM 393
—, ограничение атмосферой 475-484
Распределение вероятности
Гаусса 119, 172, 235-236, 248-249, 287, 288,
443, 476
Раиса 180, 287
Релея 180, 287, 288, 291
двумерное Гаусса 235-236, 448, 507
, ошибки установки задержки 219-220
угла падения 504
— Пуассона 44
— Раиса 180, 287
— Релея 180, 287
— частот 558
Распространение электромагнитных волн
в ионосфере 497-504
в межзвездной среде 514-520
в межпланетной среде 510—514
в нейтральной атмосфере 458-486
, постоянная 285, 458
Рассеяние 514, 517-520, 544. См. также Мер-
Мерцания
Релятивистские эффекты
, Лоренц-фактор 380
, влияние на сигналы времени 318
, гравитация 379
, искривление пространства-времени 512-
513
Рентгеновская интерферометрия 575
Рефракция (преломление)
— аномальная 483-484
— в нейтральной атмосфере 458, 462-465
— в плоско-параллельной атмосфере 462-463
— ионосферная 499, 501
— межпланетная 510—513
— оптическая 457, 473
—, природа 470-473
— сферически симметричная 463-464, 510-513
Преломляющая способность 458. См. также Ре-
Рефракция, коэффициент преломления
в оптике 475
, уравнение Смита-Вейнтрауба 473-474
Решетка восток-запад 73, 136-139, 381-352
Решетка со связанными элементами 41
Решетки
— Т-формы 32, 141, 129-130
— Y-формы 141-142
— Арсак 135
— Брейсуэлл 136
— РСДБ 147-150
— двумерные 140-152
— дифракционные 33-34
—, замкнутые конфигурации 143-146
— корреляционные 124-126
— крестообразные 129, 141, 31-32. См. таксисе
Крест Миллса
— круговые (кольцевые) 144-145
— линейные 135-139
— миллиметровых волн 38, 155, 169, 407-408
— минимальной избыточности 135—136
—, мозаика 407-409
— одномерные, см. линейные
—, открытые конфигурации 140-143
— пассажные 117
— планарные 150-152
— следящие, передаточные функции 131-132
— смешанные 92
— со связанными элементами (определение) 41
— сфазированные, см. Сфазированные решет-
решетки
—, треугольник Руло 117, 143-144, 147
—, чувствительность 154
СВЧ-связь, см. радиосвязь
Самопоглощение 15
Свертка 60
—, теорема 61
Сверхсветовое движение 40-41
Секунда, определение 312-313, 423. См. так-
таксисе Время
Серпухов, Российская Федерация 32
Сигнал
— аналитический 80—82
Сигнал/шум, отношение
—, — в оптике 576-577
—, — в приемных системах 181-186 Передача
сигналов 201-203
—, — для лунных покрытий 566
—, — для сфазированных решеток 333-337
—, —, интерферометр интенсивности 294, 563
—, —, картографирование по частоте интерфе-
интерференции 441
—, —, квантовый эффект 576
—, —, когерентное усреднение 291-294
—, —, коэффициенты потерь, РСДБ 322-331
—, — на картах 177-180
Предметный указатель
607
—, —, некогерентное усреднение 291-294
—, —, общий анализ 172-185
—, —, отклик по частоте, зависимость 215-216
—, — при вычислении уровня помехи 547-556
—, —, эффект квантования 239-253
—, —, эффект путаницы 359-360
—, —, стандарта частоты 309-312
Сигналы
— космические 13-17
— ложные 222, 227, см. таксисе Ошибки
— эргодические 13, 80
Симеиз, Украина 40
Симметрия п-кратная 141
Синтезированный (грязный) луч
, модель огибающей 547-548
, размытие полосой пропускания 188
Синтезное картографирование 6-7
, развитие методов 20-21
Синфазно-квадратурная петля 340
Синхронный детектор 27, 205, 222, 469
Синхротронное излучение 13, 93, 278, 516
Система Сварупа-Янга 205
Систематическое отклонение
MEM 395
в поляризационных измерениях (распре-
(распределение Раиса) 112
дисперсии среднего 444
измеренной видности 288? 289? 291
Системы опорных координат, см. ICRF, ICRS
Системы регистрации (РСДБ) 318-321
Склонение 17, 18
—, измерение 423-424, 426-428, 449
—, преобразование координат 111
Скорости стандарт, см. Спектральные линии
Скорость света 54, 423
Скрытое распределение 386
Смеситель 159. См. таксисе Частота, преобра-
преобразование
—, разделение полос (подавление зеркального
канала) 22900230
Смещенное косинусное взвешивание, см. Хан-
нинга взвешивание
Смитсонианская астрофизическая обсервато-
обсерватория (SAO) 21, 147
Собственное движение 18, 435
Современный интерферометр Майкельсона
573-575
Солнечный ветер 512
Солнце
—, гравитационные эффекты 435
—, ионосфера 497-498
—, корональная рефракция 510-511
—, наблюдения 26, 33-34, 380-381
—, помехи 373
—, релятивистское отклонение 511
—, солнечное время 436
—, солнечный ветер 510-512
Соотношения замыкания 30, 360-362, 397
амплитуды 361
фазы 30, 298, 360
Спекл-изображение 578-580
, суммирование-сдвиг 579
, фазовая информация 580
Спектральная линия (линии)
Н2СО 16
Н2О 16, 41, 293, 439, 442, 496-497
СО 489
ОН 16, 276, 439
SiO 16
, адаптивная калибровка 415
, аналоговый коррелятор 203
водорода 15, 16, 35, 313
, двухполосные наблюдения 169—170
, доплеровское смещение 377-380
системы отсчета 380-379
, калибровка полосы пропускания 365-366
, неоднородность баз 261-262
— —, неравномерность полосы пропускания
258-262, 365-366
, поглощение в атмосфере 466-469, 488
, поглощения 35
, представление 370-371
, процедуры CLEAN 415
, процедуры РСДБ 41, 285, 367-369, 438-
442
, процедуры калибровки 365-369
, системы 35-36, 203, 257-269
, системы отсчета скорости 379
, таблицы наиболее важных 16
, точность 369-370
, хроматическая аберрация 369
, цифровые корреляторы 257-270
Спектральная плотность потока 15
энергии 15
Спектральный коррелятор 257—270
Спутник
—, передача сигналов времени 318
—, помехи 554, 556-557
—, сигналы, фарадеевское вращение 502
—, телеметрия данных 40, 338-339
Среднеквадратичная полоса частот 331, 429,
447
Стандарт частоты 299-313
водородный 313-317
кварцевый 213-214, 309, 311
рубидиевый 312, 313
, фазовые шумы 314-316
цезиевый 312
Стенфорд, Калифорния 33
Степенная антенная конфигурация 141-142
Степенные зависимости турбулентности 482
Структурная функция
, измерения 483
— — коэффициента преломления (простран-
(пространственная) 479
фазовая (временная) 307, 481
фазовая (пространственная) 475, 479-482,
508-509
Субмиллиметровая решетка (SMA) 21, 147, 570
Сумматор мощности 124-126
608
Предметный указатель
Сфазированная решетка 124-126, 147, 268, 333-
337
, случайная фазировка 334
— —, сравнение с корреляционной решеткой
124-126
, элемент РСДБ 333-337
Сферические волновые функции 358
Схема Гренланда 210
ТИИЭР (IEEE)
—, комитет по стабильности частот 399
—, плотность потока энергии 15
—, стандарт поляризации 95
Тангенциальная плоскость 71, 73, 412
Тектонические плиты 84, 438
Телефонная передача сигнала 278
Температура
— антенны 19
— земной поверхности 204
— приемника 19, 198-200
— системы 19, 173-176, 185-186, 347
, измерение 229
, учет поглощения в атмосфере 468
Температурный коэффициент линейного рас-
расширения 204
Теорема Ван Циттерта-Цернике 72, 530-537
, вывод 530-532
, приближения 535—537
Теорема Прайса 243, 247
Теорема выборки 120-122, 137, 139, 236, 405,
568
Теорема квадрупольных моментов, см. Форму-
Формула моментов четвертого порядка
Теорема проекции-сечения 65-66
Тестирование станции наблюдений
, непрозрачность 487-490
, фазовая стабильность 490-492
Томография 381
Томсоновское рассеяние (некогерентное обрат-
обратное рассеяние) 510-511
Точечный источник, отклик 57, 127, 133, 386,
476. См. таксисе Луч, синтезированный (гряз-
(грязный)
Точка поворота 485
Треугольник Руло 144-145, 147
Трехопорная конструкция 120
Тройное произведение 297-298
Тропосфера, см. Атмосфера, нейтральная
Турбулентность
— Колмогорова 476, 478-483, 509-510, 519
— в нейтральной атмосфере 479-483
— внутренний и внешний масштабы 479-480
— дисперсия Аллана 481
— спектр флуктуации фазы 481
— степенные зависимости 482
— структурная функция фазы 479-482
Уалша функции 224-227
нулевого порядка
, ортогональность, период
, последовательность
Угол Брюстера 93
Угол места 86, 113
Удельная интенсивность, см. Интенсивность
Умножитель (напряжения) 27, 160-161. См.
такэюе Коррелятор
Уравнение Смита-Вейнтрауба 473-474
Усеченная функция 82-83
Усиление
—, калибровка 229
—, коэффициент 162
—, ошибки 218-219, 254
Условная международная точка отсчета (нача-
(начало координат) (СЮL36. См. такэюе
Устойчивое взвешивание 354
Усуда, Япония 149
Фаза
— ошибки, влияние на чувствительность 214
— «туда-обратно» 214-209
—, шум
—, — в приемниках 180-181, 286-288
—, — в стандартах частоты 293, 300-306
—, — в умножителях частоты 317
—, — ионосферный 503-504
—, — нейтральной атмосферы 475-483, 563
—, —, эффекты на картах 401, 440
Фазовая модуляция 222-228, 253, 255
в кресте Миллса 31
в первых решетках 32-33
в простом интерферометре 27-28
, использование для вращения лепестков и
задержки 227
Фазовая стабильность
, анализ 299-308
в опорном распределении 204-212
гетеродинов 317
стандартов частоты 309-317
фильтров 300-301
Фазовые данные
, изображение без фазовых данных
некалиброванные 396-400
Фазовый центр сопровождения 68. См. такэюе
Опорная фаза, положение точки отсчета
Фарадеевская толща 516
Фарадеевская функция дисперсии 517
Фарадеевское вращение 13, 93, 111, 500
в ионосфере 497, 500
в межзвездной среде 515-517
функция дисперсии 517
Феномен Гиббса 261, 365
Фидлера события 520
Фильтры 80, 160
— Баттерворса 329
— видео 201
—, влияние на отношение сигнал/шум 216
—, генератор с фазовой автоподстройкой 214
—, добротность 214, 315-316
Предметный указатель
609
— спектральных линий 204-270
— узкополосные 214
—, фазовая стабильность 214
— цифровые 269
—, число полюсов 214
Флере, Австралия 31, 33
Формула Ван Флека 241, 244
— моментов четвертого порядка 172, 238, 561
— Планка 17, 18, 199-200, 576
— Релея-Джинса 17, 18, 197, 198. См. таксисе
Формула Планка
— Руза 120
Форт Дейвис, Техас 40, 149
Фраунгоферова дифракция, см. Зона дальняя,
требования
Фрида параметр (радиус когерентности) 480,
573
Функция взаимной когерентности 531-532
— ошибок (erf) 180, 244, 250
— правдоподобия 443
— Радемахера 223, 225-227
— разрешения по задержке. См. таксисе Поло-
Полоса частот, синтез
— рассеяния точки (аппаратная функция) 579.
См. таксисе Точечный источник, отклик
— свертки 355-358. См. таксисе Функции сгла-
сглаживания
Гаусса 357
Гаусса sine 357
прямоугольная 356
сферическая 358
— сглаживания 260
Хайстекская обсерватория, Вестфорд, Масса-
Массачусетс 40, 293, 571
Хамминга взвешивание (сглаживание) 260
Ханнинга взвешивание (сглаживание) 260
Хат Крик обсерватория, Калифорния 38, 40,
483
Хи-квадрат параметр (х2) 364, 443-445
Циклотронная частота 500
Циклотронное излучение 93
Цилиндрический параболоид 117
Циркулятор 206
Цифровая обработка сигналов 234-273
, выборка 235-256
, погрешность 255-256
, спектральные измерения 258-269
, умножение 259
Чайнантор, Чили 38, 483, 487, 491
Чандлеровское колебание 436
Часовой угол 84-86, 113
Частичная когерентность 539
Частота Брунта-Вайсала 503
— интерференции 88, 163
, базовое решение 428
в РСДБ 289
в астрометрии 427-429
, влияние ионосферы 502
естественная 163
, использование в картографировании 441—
442
, лепесток эффективный 442
, определение 88
, спектр 292, 442, 445-446
, точность измерения 445-446
, усреднение 550
, эффект подавления помехи 550-553
, эффект сопровождения 88-89, 131-132
—, каналы 258
—, отклик 215-220
—, преобразование 159-160
—, разделение каналов 270
—, регулирование 558
—, умножение 212, 317
—, —, допустимые отклонения 216-220
—, — кратное 163, 167
—, — оптимальное 215
—б — оптическое 577
Черное тело, см. Формула Планка
Четырехопорная конструкция 120, 570
Число Рейнольдса 479
Шах-функция 121
— двумерная 266
Широкоугольное картографирование 73-75,
189-190, 302-409, 410-114
Штреля отношение 120
Шум, см. таксисе Сигнал/шум отношение
— амплитудный и фазовый 180
— в РСДБ 286-288
— в генераторах
белый фазовый 304-306
белый частотный 304-306
фликкер-фазовый 304-306
фликкер-частотный 304-306
частоты случайных блужданий 304-306
— в данных комплексной видности 176-177
— гауссов 13
— дробовой фотонов 312
—, измерение температуры 198-200
—, квантовый эффект 43-44
—, мощность 19, 197
— на карте 177-180
—, отклик 172-177
—, эквивалентная мощность (NEP) 576
Экваториальная монтировка 91—92
Эквивалентная плотность потока системы
(SEFD) 19, 350, 368
Эклиптика 435
Электроника
— модули 196-198, 200-203
— прогресс 196
Электронная плотность
20 Томсон
610
Предметный указатель
галактическая 515-516
ионосферы 498
межзвездной среды 515
мелейланетной среды 511
Эллиптические волновые функции 359
Энергетический спектр (мощностиM6, 76
атмосферной фазы 479-481
выходного сигнала коррелятора 174
межпланетных мерцаний 513—514
флуктуации фазы и частоты 299-3-8
Энтропия 391
Эргодический сигнал 13, 80
Эффект Доплера 55, 132, 262, 312, 314, 317, 439
, анализ и формулы 376-380
, системы отсчета 378-379
Эффект Зеемана 93, 111, 314, 317
Эффективная площадь 18
Эффективность
— апертуры 120, 567-568
— квантования 175, 248, 252, 329-330
Южный полюс 487, 489, 491
Юлианский год 435
Юпитер 39, 276
.Янский (единица) 15
Яркость 16. См. таксисе Интенсивность
—, температура 17
Ячейка
—, время пересечения 551
—, усреднение по ячейкам 123, 220, 359, 550
Именной указатель
Aarons J., 502
Abies J. С, 391, 392
Abramowitz M., 235
Adatia N.A., 119
Agrawal G. P., 202
Alef W., 430
Allan D. W., 301, 318, 340
Allen C. W., 511
Allen L. R, 203, 578
Allen R. J., 574
Altenhoff W. J., 484
Ananthakrishnan S., 518
Anantharamaiah K. R., 175, 514, 541, 543, 544
Anderson В., 212
Anderson S. В., 239, 251
Apostol Т. М., 71
Appleton E. V., 24, 497
Archer J. W., 201, 229
Armstrong J. Т., 483, 574
Arsac J., 135
Ash M. E., 378
Ashby N., 318, 340
Askne J. I. H., 486
Assus P., 575
Audoin C, 302
Azoubib J., 318
Baade W., 28
Baars J. w. M., 37, 137, 196, 380, 483
Backer D. C, 42, 431
Bagri D. S., 219, 318
Bailey D. K., 501
Bajaja E., 408
Baldwin J. E., 397, 401, 416, 572, 574
Ball J. A., 263, 378
Bally J., 487
Bare C, 39, 321
Barnbaum C, 549
Barnes J. A., 299, 300, 306, 310
Barnett M. A. F., 497
Bartel N., 423, 430
Bates R. H. Т., 401, 568, 572, 575, 578
Batty M. J., 196
Bean B. R., 460, 473
Beasley A. J., 430, 432
Beauchamp K. G., 224
Becker R. H., 362
Belcora L., 43
Bennett A. S., 32, 568
Benson J. A., 263, 573
Beran M. J., 538, 542, 545
Berkland D. J., 312
Bernier L. G., 309
Bester M., 573, 575
Betz A. L., 575
Bevington P. R., 364, 442
Bieging J. H., 483
Bignell R. C, 101, 110
Bilitza D., 502
Blackman R. В., 261
Blair В. Е., 299
Blake G. A. , 15
Block W. F., 39
Blum E. J., 34, 175
Blythe J. H., 32, 131
Boboltz D. A. , 439
Bohlander R. A., 457
Boischot A., 34
Boker Т., 574
Bolton J. G., 25, 26, 28
Booker H. G., 503, 505, 535
Booth R. S., 439
Borella M. S., 202
Boriakoff V., 515
Born M., 69, 80, 81, 93, 530, 542, 545
Bos A., 365
Bourgois G., 513, 518, 519
Bowers F. K., 239, 245, 246, 253
Bowyer S., 450
Braccesi A., 32
Bracewell R. N., 34, 60, 62, 65, 66, 69, 74, 80,
83, 121, 122, 124, 127, 129, 136, 138, 139, 187,
196, 236, 257, 351, 353-355, 363, 372, 381, 386,
408, 414, 477, 478, 513, 534, 535, 563, 575
Bradley R. F., 549
Braude S. Ya., 146
Braun R., 391, 393, 396
Bregman J. D., 98, 105, 109, 110, 261
Breit G., 497
Bridle A. H., 373
Briggs D. S., 354, 358, 391, 393, 395, 396
Brigham E. O., 122
Brooks J. W., 110, 146
Broten N. W., 34, 39, 321
Brouw W. N., 74, 137, 357, 407
Brown G. W., 38, 39, 110, 560, 563
Bruck Y. M., 401
Bryan R. K., 392, 393
Budden K. G., 497
Burdick H. M., 486
Burke B. F., 40, 43, 149
Burn B. J., 517
Burns W. R., 239, 242
Burton W. В., 371
Butler В., 491
Callen H. В., 198
Caloccia E. M., 201
Campbell R. M., 434, 517
Cannon W. H., 286, 321
Carilli C. L., 483, 484, 488, 494, 495
Carlson B. R., 270, 340
Carpenter J., 496
Carr T. D., 39, 560
20*
612
Именной указатель
Carswell R. F., 417
Carter A. W. L., 361
Carter W. E., 438, 512
Carver K. R., 93
Cash W., 575
Casse J. L., 196
Caves С. М., 576
Cernicharo J., 490
Chamberlin R. A., 487, 491
Champeney D. C, 60
Chandler S. C, 436
Chariot P., 426
Chen M. Т., 568
Chie С. М., 317
Chikada Y., 263
Chivers H. J. A., 503
Chow Y. L., 141, 142
Christiansen W. N., 33, 36, 381
Christou J. C, 579
Chu T.-S., 119
Chylek P., 495
Clark B. G., 36, 171, 228, 294, 313, 321, 390,
Clark T. A., 41, 318, 321, 438
Clarke M., 509
Clegg J. A., 45
Clemence G. M., 435
Clemmow P. C, 535
Clifford S. F., 474
Соске W. J., 380
Cohen M. H., 41, 285, 330, 430, 509, 513, 514, 518,
567
Colavita M. M., 572, 574
Cole Т., 239, 382
Coles W. A., 513, 518, 519
Colvin R. S., 36, 170, 175
Combrinck W. L., 557
Condon J. J., 18
Conway J. E., 13, 100, 101, 110, 410, 411, 431, 433
Cooper B. F. C., 239, 243, 246, 247
Cordes J. M., 506, 509, 515, 518, 520, 544, 545
Cornwell T. J., 143, 155, 390-393, 395, 396, 398-
400, 405-407, 409-414, 514, 541, 543, 544
Cotton W. D., 110, 294-296, 391, 397
Coulman С. Е., 479, 482
Counselman С. С, 434, 438, 511
Covington A. E., 34
Cowan J. J., 39, 400
Cox A. N., 379
Crane P. C, 359, 360, 457, 461, 503
Crawford D. L., 558
Cronyn W. M., 509, 518
Currie D. G., 574
Cutler L. S., 316
D'Addario L. R., 194, 215, 219, 223, 252, 254, 255,
269, 319, 320, 322, 338, 340, 366, 392, 569
Dainty J. C., 578
Danchi W. C, 575
Daniell G. J., 392
Daniell R. E., 502
Das Gupta M. K., 29, 30, 560
Davies J. G., 212, 497
Davis J., 573, 574, 578
Davis J. L., 466
Davis M. M., 311, 318
Davis R. J., 452
Davis W. F., 253
de Graauw Т., 577
de Vegt C, 425
Debye P., 473
DeJong M. L., 567
Delgado G., 487
Dennison, 518
Dewdney P. E., 270
Dewey R. J., 335
Dhawan V., 285
Diamond P. J., 110, 439
Dicke R. H., 20
Dillinger W. H., 512
Doeleman S. S., 296-299
Douglas J. N., 186
Downes D., 380, 483, 484
Drane C. J., 538, 545
Dreher J. W., 39, 400
Dreyer J. L. E., 18
Drullinger R. E., 312
Duffett-Smith P. J., 518
Dulk G. A., 560
Dutta P., 305
Dutton E. J., 473
Eckart A., 579
Eddington A. S., 563
Edge D. O., 18, 32
Edson W. A., 299
Ekers R. D., 37, 141, 142, 196, 256, 365, 366, 372,
399, 404, 415, 511
Elgaroy O., 31
Elgered G., 486
Elitzur M., 15, 439
Ellithorpe J. D., 418
Elsmore В., 28, 36, 37, 196, 424
Emerson D. Т., 120, 225, 227
Erb K., 146, 196
Erickson W. C, 146, 196, 416, 511, 513
Escoffier R. P., 270
Eshleman V. R., 513
Evans D. S., 567
Evans J. V., 497, 498, 502-504, 511,
Evans K. F., 392, 406,
Fanselow J. L., 286, 431, 438, 450
Farley D. Т., 239, 243, 245, 247
Feierman В. Н., 567
Fejer B. G., 503
Feldman M. J., 44, 169, 200
Fenstermacher D. L., 196
Fey A. L., 425
Fiebig D., Ill
Fiedler R. L., 520
Fienup J. R., 401
Fomalont E. В., 35, 105, 363, 424, 502, 510, 511
Именной указатель
613
Forman P., 313
Fort D. N., 396
Fowle F. F., 227
Frail D. A., 333, 507
Frank R. L., 318
Frater R. H., 110, 146, 203
Freeman R. H., 486
Frehlich R. G., 117
Fridman P., 337
Fried D. L., 480, 573
Frieden B. R., 391, 392
Fugate R. Q., 573, 580
Gabor D., 80
Gallagher J. J., 457
Gait J., 557
Garcia-Barreto J. A., 439
Gardner C. S., 575
Gardner F. F., 517
Gardner F. M., 212, 340,
Gauss K. F., 443
Gaylord M. J., 557
Geldart D. J. W., 495
Genee R., 137
Genzel R., 41, 439, 440
Gergely Т. Е., 558
Gilbert S. W., 318
Ginat M., 34
Gold В., 123
Gold Т., 41
Goldenberg H. M., 313, 315, 317
Goldstein H., 470, 486
Goldstein R. M., 234
Goldstein S. J., Jr., 186
Goodman J. W., 80, 520, 542, 545, 578
Gordon M. A., 378, 380
Gower J. F. R., 32
Gradshteyn I. S., 375
Graham-Smith F., 45
Granhmd J., 228, 229, 266
Grossi M. D., 501
Guilloteau S., 38
Guinot В., 436
Guiraud F. O., 481, 486
Gull S. F., 392
Gundermann E. J., 514
Gupta Y., 505
Gurwell M., 376
Gusten R., Ill
Gwinn C. R., 431, 435, 439, 450, 518, 520
Haddock F. Т., 45
Hagen J. В., 239, 243, 245, 247
Hagfors Т., 43, 497, 498, 503, 511
Hall Т., 443
Hamaker J. P., 98, 105, 109, 110, 135, 482
Hamilton W. C, 442
Hanbury Brown R., 29, 30, 560, 563, 577, 578
Haniff C. A., 572
Hankins Т. Н., 268
Hanson D. W., 341, 452
Hanson R. J., 395
Hargrave P. J., 38
Harmuth H. F., 224
Harris D. E., 514, 518
Harris F. J., 261
Harris R. W., 196
Haskell R. E., 499
Hazard C, 32, 424, 564, 567
Heffner H., 576
Heiles C, 252, 516
Hellwig H., 311, 314
Henny M., 577
Herbig Т., 120
Herring T. A., 323, 327, 431, 435, 438, 450
Herrnstein J. R., 42
Hess S. L., 459, 461
Hewish A., 31, 32, 131, 503, 504, 513, 514, 518
Hewitt J. N., 418
Hey J. S., 503
Hill R. J., 467, 473, 474
Hills R. E., 490, 496
Hinder R. A., 483, 504
Hinteregger H. F., 321, 430
Hinz P. M., 575
Hirabayashi H., 43, 149, 339
Hirade K., 557
Hjellming R. M., 141, 154
Но С. М., 502, 503
Носке К., 434, 504
Hogbom J. A., 45, 137, 386, 387, 392
Hogg D. C, 481, 486
Hogg D. E., 37
Holdaway M. A., 155, 405, 409, 483, 484, 487, 488,
493-495
Hollweg J. V., 513
Holt J. M., 499, 504
Hooghoudt B. G., 137
Hopkins A., 38
Horn P. M., 305
Howard J., 486
Hueckstaedt R. M., 473
Hughes M. P., 36
Humphreys W. J., 459
Hunsucker R. D., 504
Imbriale W. A., 155
Ingalls R. P., 120
Ishiguro M., 136, 483, 490
Itano W. M., 312
Jackson J. D., 470
Jacobs C. S., 286, 438
Jacobs I. M., 172
Jacquinot P., 354
Jaeger J. C., 511
James G. L., 112
Jansky K. G., 24
Jaynes E. Т., 391
Jenet F. A., 239, 251
Jennison, 29, 30, 361, 560
Johnson R. C., 14, 575
614
Именной указатель
Johnston К. J., 424, 425, 434
Jones R. С, 105
Kahlmann H. С, 558
Kanzawa Т., 483, 490
Kaplan G. H., 431, 502
Kartashoff P., 310
Kassim N. E., 416
Kasuga Т., 483, 490
Kawabe R., 483
Kawaguchi N., 321
Keihm S. J., 467
Kelder H., 503
Kellermann K. L, 13, 147, 545
Kelley M. C, 503
Kemball A. J., 110, 439
Kenderdine S., 196
Kerr A. R., 44, 199, 200
Kerr F. J., 379
Keshner M. S., 305
Kesteven M. J. L., 101, 103, 109, 110, 114
Keto E., 134, 143-145, 227
Killeen E. В., 101, 103, 109, 110, 114
Klemperer W. K., 278
Klepczynski W. J., 318
Kleppner D., 313, 315, 317
Klingler R. J., 239, 245, 246
Knapp S. L., 574
Knowles S. H., 40
Knox К. Т., 580
Ко Н. С, 95
Kochanek С. S., 417, 418
Kogan L. R., 126
Kojima M., 117
Kokkeler A. B. J., 337
Koles W. A., 117
Konig, 71
Kostenko V. L, 276
Kraus J. D., 93, 198
Krishnan Т., 34
Kronberg P. P., 100, 101, 110, 112, 516
Kulkarni S. R., 252, 298
Kundu M. R., 510
Labeyrie A., 574, 579
Labrum N. R., 34
Lambeck K., 435
Lampton M., 450
Lane A. P., 487
Lanyi G. E., 481
Latham V., 30
Lawrence C. R., 120
Lawrence R. S., 473, 503
Lawson C. L., 395
Lawson J. L., 172
Lawson P. R., 572
Lay O. P., 481, 493, 496
Lazio T. J. W., 506
Lebach D. E., 512
Leech J., 136
Leick A., 318
Lestrade J.-F., 426, 431
Levine M. W., 317
Levy G. S., 43
Lewandowski W., 318
Lewis L. L., 309
Liebe H. J., 466, 467, 472, 473, 488
Lieske J. H., 435
Liewer К. М., 574
Lightman A. P., 13, 14, 17, 376, 467
Lindsey W. C., 317
Linfield R., 41, 43
Little A. G., 32, 210, 361, 503, 514
Liu С. Н., 503
Lo K. Y., 518, 519
Lo W. F., 165, 257
Lohmann A. W., 580
Long R. J., 13
Longair M. S., 13
Lonsdale C. J., 401
Louden R., 43, 471
Lovas F. J., 14
Lovelace R. V., 509, 518, 545
Lovell А. С. В., 503
Lynden-Bell D., 379
Lyne A. G., 517
Ma C., 18, 42, 425, 431, 434, 450
MacKay J. R., 438
Mackey M. В., 564
MacMahon P. A., 563
MacPhie R. H., 541, 545, 575
Mahoney M. J., 146, 196
Maltby P., 35, 363
Mandel L., 545
Mannucci A. J., 502
Marcaide J. M., 431
Margon В., 450
Marini J. W., 466
Markowitz W., 436
Marscher A. P., 36
Martin D. H., 193
Masson C. R., 362, 475, 481-483, 487, 489, 490,
492, 570, 572
Mathur N. C, 79, 141, 142, 147, 186, 501, 538
Matsakis D. N., 439
Matsushita S., 490
Matveenko L. I., 438
Matveyenko, 21, 276, 439
Mauzy R. E., 229
Mayer С. Е., 120
McCarthy D. D., 437
McClean D. J., 414
McCready L. L., 26
McGilchrist M. M., 414
McKenzie A. A., 318
McMillan R. W., 457
Meinel А. В., 334
Mercier P., 508
Michelson A. A., 21
Mickelson R. L., 184
Middleton D., 172, 241
Именной указатель
615
Mills В. Y., 28, 29, 31, 32, 129
Milonni P. W., 573
Miner G. F., 487
Minkowski R., 28
Misell D. L., 571
Misner C. W., 512
Miyoshi M., 42
Moffet А. Т., 35, 136, 363, 364
Moran, 15, 38-40, 42, 147, 181, 265, 285, 286, 296-
299, 307, 311, 321, 336, 337, 439, 441, 482, 485,
502, 510
Morison L, 212
Morita K.-L, 38
Morris D., 30, 31, 97, 98, 569, 571, 572
Morrison N., 450
Mould J. R., 379
Mourard D., 574
Mueller H., 107
Mueller I. L, 425
Muhleman D. O., 511
Mullaly R. F., 33
Murota K., 557
Napier P. J., 37, 41, 141, 142, 148, 196, 256, 278,
359, 360, 394, 399, 401, 568
Narayan R., 391, 417, 418, 509, 514, 520, 541, 543,
544
Neville A. C, 36, 37
Newhall X. X., 378
Niell A. E., 466
Nityananda R., 45, 392
Noordam, 135
Norris R. P., 439
Nyquist H., 18, 197, 236
O'Neill E. L., 107
O'Sullivan J. D., 135, 266
Okumura S. K., 263
Oliver В. М., 44
Olmi L., 483
Oosterloo T. A., 386
Oppenheim A. V., 123, 236
Otter M., 557
Owens J. C., 474
Padin S., 151, 203
Paine S., 490
Paley R. E., 225
Palmer H. P., 30
Pan S.-K., 44, 200
Pankonin V., 558
Papoulis A., 123, 180, 287
Parkinson B. W., 318
Parrent G. В., Jr., 538-540, 542, 543, 545
Parsons S. J., 503
Patnaik A.R., 434
Pauliny-Toth I. L, 13
Pawsey J. L., 26, 32
Payne J. M., 193, 196, 212
Payne-Scott R., 26
Pearlman M. R., 501
Pearson T. J., 40, 364, 398
Pease F. G., 21, 24
Peebles P. J. E., 380
Percival B. D., 264
Perley R. A., 39, 105, 400, 402, 411-414, 431
Petley B. W., 423
Phillips J. A., 43,
Phillips J. W., 503
Phillips T. G., 196, 570, 572
Pi X., 503
Picken J. S., 34
Pidwerbetsky A., 509, 518, 545
Pierce J. A., 318
Pilkington J. D. H., 437
Pol S. L. C., 467
Pollack H. O., 358
Ponsonby J. E. В., 391
Pospieszalski M. W., 196
Prado J. R., 490
Press W. H., 305, 450
Preston R. A., 149, 151
Price R., 243
Price R. W., 558
Priestley J. Т., 473
Puplett E., 193
Purcell E. M., 470, 577
Rabiner L. R., 123
Rademacher H., 144
Radford S. J. E., 490, 491
Radhakrishnan V., 36, 45, 97
Ragland S., 567
Raimond E., 98, 137
Raisanen A. V., 20, 179, 196
Ramsey N. F., 313, 315, 317
Rankin J. M., 511, 515
Ratcliffe J. A., 497, 500, 505, 508
Rawer K., 497
Ray P. S. , 486
Read R. В., 34, 170, 196
Readhead A. C. S., 120, 396-398, 518
Reber E. E., 461
Reber G., 24
Reid M. J., 15, 41, 42, 196, 285, 367, 430, 431, 439
Reiland G., 490
Resch G. M., 486
Rice S. O., 180
Richichi A., 567
Rickett B. J., 518, 519
Riddle A. C., 66, 380
Roberts D. H., 110, 504
Roberts J. A., 62, 121, 127, 354, 386,
Robertson D. S., 438, 512
Robertson J. G., 580
Robinson D. K., 364, 442
Roddier F., 479
Roelfsema P., 371
Roger R. S., 35
Rogers A. E. E., 41, 182, 283, 296-299, 307, 321,
329, 331, 332, 396, 397, 482, 486, 571
Roggeman M. C., 573, 580
616
Именной указатель
Rogstad D. H., 574
Rohlfs К., 14, 93
Roizen-Dossier В., 354
Rolston S. L., 312
Romney J. D., 269
Ronnang В. О., 486
Ros E., 431, 434
Rosen B. R., 485
Rosenkranz P. W., 495
Rots A. H., 404
Rowson В., 31, 36, 85
Rudge A. W., 119
Ruf C. S., 467
Rutman J., 299, 300
Ruze J., 120
Rybicki G. В., 13, 14, 17, 376, 467
Ryle M., 20, 25, 27, 28, 31, 32, 36-38, 131, 136,
196, 424, 483, 504, 568
Ryzhik I. M., 375
Saastamoinen J., 464, 466
Sakurai Т., Ill, 513
Salpeter E. E., 513
Sault R. J., 98, 101, 103, 105, 109, 110, 114, 385,
407, 411
Schafer R. W., 123, 236
Schaper L. W., 484
Scheuer P. A. G., 505, 564, 565
Schilke P., 15
Schlegel K., 434, 504
Schuss J. J., 557
Schwab F. R., 251, 272, 294-296, 354, 356-358,
391, 396, 398, 411
Schwarz U. J., 389
Scott P. F., 32, 513, 568
Scott S. L., 513
Scoville N. J., 38, 496
Searle C. L., 316
Seidelmann P. K., 18, 88, 424, 435
Seielstad G. A., 97, 147
Serabyn E., 490, 570, 572
Serna R., 201
Shaffer D. В., 285, 430
Shakeshaft J. R., 31, 32, 131
Shannon С. Е., 236
Shao M., 572, 574
Shapiro I. L, 286, 431, 435, 438, 450, 502, 510, 512
Shevchenko, 439
Shillue В., 490
Shimmins A. J., 564
Shimoda K., 313
Shinn D. H., 505
Sholomitsky G. В., 21
Sieber W., 518
Silver S., 534
Simard-Normandin M., 516
Sinclair M. W., 196
Skilling J., 392, 393
Slee О. В., 25, 31
Slepian D., 354, 358
Smart W. M., 463, 511
Smegal R. J., 110
Smith E. K., Jr., 474,
Smith F. G., 28, 29, 361, 423, 503, 517
Smith H. M., 436
Smolders А. В., 38
Smoot G. F., 20
Snider J. В., 486, 487
Snyder L. E., 14
Sodin L. G., 401
Solheim F., 487
Southworth G. C., 24
Sovers O. J., 286, 438
Spangler S. R., Ill, 513, 518
Spitzer L., 518
Spoelstra Т. А. Т., 501, 503
Sramek R. A., 42, 354, 358, 411, 431, 433, 483,
502, 510
Staelin D. H., 467, 484, 486, 574
Standish E. M., 378
Stanley G. J., 26, 28
Stark A. A., 487
Stavely-Smith L., 407
Stegun I. A., 235
Subrahmanya C. R., 392
Subramanian S., 479
Sutton E. C., 473, 479, 577
Swamp G., 34, 38, 147, 155, 205
Sweezy W. В., 481
Swenson G. W., Jr., 79, 147, 184, 186, 538, 575
Swope J. R., 461
Taff L. G., 435
Tahmoush D. A., 486
Tango W. J., 572, 574
Tatarski V. I., 432, 479
Taylor G. В., 381
Taylor G. I., 481,
Taylor J. H., 424, 518, 567
Taylor J. R., 364
Tetu M., 309
Thayer G. D., 473
Thomas C., 318
Thomas J. В., 323
Thomasson P., 31, 147, 400
Thompson P., 13, 30, 34, 36, 37, 124, 138, 139,
141, 142, 194, 196, 212, 215, 219, 221, 228,
248, 256, 318, 351, 355, 399, 550, 553, 554,
558
Thompson B. J., 580
Thompson M. C., 205
Thorne K. S., 512
Thornton D. D., 408, 487
Tirupati S. K., 570
Tiuri M. E., 20, 175, 179, 196
Toeplitz O., 144
Townes С. Н., 313, 479, 575-577
Treuhaft R. N., 481
Tucker J. R., 169, 200
Tukey J. W., 261
Turrin R. H., 119
Tuve M. A., 497
Именной указатель
617
Twiss R. Q., 29, 361, 563, 572, 577
Uhlenbeck G. E., 172
Unser M., 122
Uson J. M., 155, 405, 409
Van Albada G. D., 408
Van Ardenne A., 337
Van de Stadt H., 577
Van Gorkom J. H., 365, 366, 415
van Harlem M. P., 38
Van Vleck J. H., 241, 470
Vanden Bout P., 558
Vander Vorst A. S., 170
Vanier J., 309
Verschuur G. L., 545
Vessot R. F. C, 304, 309, 310, 313, 314, 317, 340
Vinokur M., 180
Visser J. J., 196
Von Hoerner S., 566, 567
Vonberg D. D., 20
Wade С. М., 91, 424
Wahr J. M., 435, 436
Walden А. Т., 264
Waldram E. M., 414
Walker R. C, 148, 296, 439, 442
Wallington S., 417, 418
Walsh D., 32, 417
Walsh J. L., 224
Wand R. H., 504
Wang Т. С, 313
Warburton J. A., 33, 36, 381
Wardle J. F. C, 110, 112
Warner P. J., 397, 401
Waters J. W., 467, 469, 470, 484, 487
Webber J. C, 147, 196
Weigelt G., 580
Weiler K. W., 97, 98, 100, 110
Weinberg S., 512
Weinreb S., 196, 201, 234, 239, 269
Weintraub S., 474
Weisberg J. M., 515
Welch В. М., 573, 580
Welch P. D., 264
Welch W. J., 38, 120, 155, 196, 408, 483, 487, 495,
496,
Welton T. A., 198
Wengler M. J., 200
Wernecke S. J., 381, 392
West M. E., 557
Westfold К. С., 511
Westwater E. R., 484-486
Weymann R. J., 417
Wheeler J. A., 512
White M., 364
White N. M., 567
White R. L.,362
Whiteoak J. В., 146, 517
Whitford A. E., 564
Whitney A. R., 41, 285, 318, 321
Wiedner M. C., 496
Wieringa M. H., 411
Wietfeldt R. D., 321, 322, 333
Wild J. P., 147
Wilkinson P. N., 397, 398, 400, 410, 411
Williams W. F., 118
Willis A. G., 261
Wills D., 32, 513
Wilson R. W., 36
Wilson T. L., 14, 93
Winterhalter D., 510
Wirnitzer В., 580
Woestenburg E. E. M., 196
Wolf E., 69, 80, 81, 93, 530, 542, 545
Wolszczan A., 520, 544
Woodward R. H., 318
Woody D. P., 196, 200, 496
Woolard E. W., 435
Woolf N. J., 479, 573
Worden S. P., 578
Wozencraft J. M., 172
Wright M. С. Н., 168, 196, 363, 482, 483
Wu S. C., 486
Yang K. S., 205
Yao S. S., 239, 242
Yee H. К. С, 396
Yeh К. С., 503
Yen J. L., 40, 263, 276
Young A. C, 196
Young А. Т., 513
Zeissig G. A., 518
Zensus J. A., 341
Zorin А. В., 200
Артюх В. С., 564
Балебанов В. М., 321
Виткевич В. В., 32
Есепкина Н. А., 93
Калачев П. Д., 32
Кардашев Н. С., 21, 39, 43
Коган Л. Р., 321
Костенко В. И., 149, 568
Матвеенко Л. И., 21, 39, 149, 321, 564, 568
Сагдеев Р. 3., 321
Чесалин Л. С., 321
Шоломицкий Г. В., 21, 39, 276, 564
618 Оглавление
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 5
Предисловие к первому изданию 6
Предисловие к первому русскому изданию 8
Предисловие редактора перевода 9
Глава 1. Введение и исторический обзор 11
1.1. Применение радиоинтерферометрии 11
1.2. Основные определения и соотношения 13
1.2.1. Космические сигналы A3). 1.2.2. Координаты и обозначения радиоис-
радиоисточников A7). 1.2.3. Прием космических сигналов A8).
1.3. Развитие радиоинтерферометрии 20
1.3.1. Эволюция техники синтеза B0). 1.3.2. Интерферометр Майкель-
сона B1). 1.3.3. Первые двухэлементные радиоинтерферометры B4).
1.3.4. Морской интерферометр B5). 1.3.5. Интерферометр с модуляцией
фазы B7). 1.3.6. Оптическое отождествление и калибровочные источни-
источники B8). 1.3.7. Первые измерения угловых размеров B9). 1.3.8. Обзорные
интерферометры и крест Миллса C1). 1.3.9. Картографирование Солнца на
сантиметровых волнах C2). 1.3.10. Измерения профилей интенсивности C4).
1.3.11. Интерферометрия спектральных линий C5). 1.3.12. Картографирова-
Картографирование и синтез вращением Земли C6). 1.3.13. Развитие решеток апертурного
синтеза C6). 1.3.14. Интерферометрия со сверхдлинными базами C8).
1.3.15. РСДБ с антеннами на орбите D2).
1.4. Квантовый эффект 43
Основная литература 45
Цитированная литература 46
Глава 2. Введение в теорию интерферометрии и синтеза изобра-
изображений 53
2.1. Анализ в плоскости база—источник 53
2.2. Влияние полосы пропускания 55
2.3. Одномерный синтез источников 58
2.3.1. Отклик интерферометра как свертка E9). 2.3.2. Теорема свертки и
пространственные частоты F1). 2.3.3. Пример одномерного синтеза F2).
2.4. Двумерный синтез 64
2.4.1. Теорема проекции-сечения F5).
Цитированная литература 67
Глава 3. Анализ отклика интерферометра 68
3.1. Связь интенсивности и видности преобразованием Фурье 68
3.2. Кросс-корреляция и соотношение Винера-Хинчина 75
3.3. Основы отклика приемной системы 76
3.3.1. Антенны G6). 3.3.2. Фильтры G7). 3.3.3. Коррелятор G8). 3.3.4. От-
Отклик на принимаемое излучение G8).
Приложение 3.1. Математическое представление сигналов шумовой приро-
природы 80
Цитированная литература 83
Оглавление 619
Глава 4. Геометрические соотношения и поляриметрия 84
4.1. Координаты антенн и траектории на плоскости uv 84
4.2. Плоскость u'v' 87
4.3. Частота интерференции 88
4.4. Частоты видности 89
4.5. Калибровка базы 90
4.6. Монтировки антенн 90
4.7. Влияние ширины и формы диаграммы направленности 92
4.8. Поляриметрия 93
4.8.1. Параметры определения поляризации (93). 4.8.2. Эллипс поляризации
антенны (95). 4.8.3. Видность в параметрах Стокса (98). 4.8.4. Инструмен-
Инструментальная поляризация A01). 4.8.5. Представление в матричном виде A05).
4.8.6. Калибровка аппаратурной поляризации A08).
Приложение 4.1. Связь экваториальных и горизонтальных координат .... 113
Приложение 4.2. Определение коэффициентов паразитной поляризации че-
через параметры эллипса поляризации 113
Цитированная литература 115
Глава 5. Антенны и антенные решетки 117
5.1. Антенны 117
5.2. Выборка значений функции видности 120
5.2.1. Теорема выборки A20). 5.2.2. Дискретное двумерное преобразование
Фурье A22).
5.3. Вступление к антенным решеткам 124
5.3.1. Синфазные и корреляционные антенные решетки A24). 5.3.2. Простран-
Пространственная чувствительность и пространственная передаточная функция A26).
5.3.3. Крестообразные и Т-решетки для метровых длин волн A29).
5.4. Пространственная передаточная функция следящей решетки 131
5.4.1. Требуемые характеристики пространственной передаточной функ-
функции A34). 5.4.2. «Дыры» в заполнении пространственных частот A34).
5.5. Одномерные следящие решетки 135
5.6. Двумерные следящие решетки 140
5.6.1. Открытые конфигурации A40). 5.6.2. Замкнутые конфигурации A43).
5.6.3. Конфигурации РСДБ A47). 5.6.4. Антенны РСДБ на орбите A49).
5.6.5. Планарные решетки A50).
5.7. Заключительные замечания относительно конфигураций антенн . 152
5.8. Другие конструктивные особенности 154
5.8.1. Чувствительность A54). 5.8.2. Длинные волны A54). 5.8.3. Миллимет-
Миллиметровые волны A55).
Основная литература 155
Цитированная литература 155
Глава 6. Отклик приемной системы 159
6.1. Преобразование частоты, вращение интерференционных лепестков и
комплексные корреляторы 159
6.1.1. Преобразование частоты A59). 6.1.2. Отклик однополосной систе-
системы A60). 6.1.3. Прием верхней боковой полосы A61). 6.1.4. Прием нижней
боковой полосы A63). 6.1.5. Многократное преобразование частоты A63).
6.1.6. Отслеживание задержки и вращение интерференционных лепест-
лепестков A63). 6.1.7. Простые и комплексные корреляторы A64). 6.1.8. Отклик
620 Оглавление
двухполосной системы A65). 6.1.9. Двухполосная система с многократным
преобразованием частоты A67). 6.1.10. Остановка лепестков в двухполосной
системе A68). 6.1.11. Сравнительная характеристика двухполосных и
однополосных систем A69). 6.1.12. Разделение боковых полос A70).
6.2. Отклик на шумы 172
6.2.1. Обработка сигнала и шума в корреляторе A72). 6.2.2. Шумы при из-
измерении комплексной функции видности A76). 6.2.3. Отношение сигнал/шум
в синтезированном изображении A77). 6.2.4. Амплитудные и фазовые шумы
функции видности A80). 6.2.5. Относительная чувствительность различных
интерферометрических систем A81). 6.2.6. Параметр температуры системы
а A85).
6.3. Эффекты полосы пропускания 186
6.3.1. Построение изображений в режиме континуума A86). 6.3.2. Карто-
Картографирование в широком поле зрения с применением многоканальной систе-
системы A89).
6.4. Эффекты усреднения функции видности 190
6.4.1. Усреднение функции видности A90). 6.4.2. Эффекты усреднения по
времени A90).
Приложение 6.1. Частичное подавление боковой полосы 193
Цитированная литература 194
Глава 7. Проектирование аналоговой приемной системы 196
7.1. Основные составляющие приемной аппаратуры 196
7.1.1. Малошумящие входные устройства A96). 7.1.2. Измерение шумовой
температуры A98). 7.1.3. Гетеродин B00). 7.1.4. ПЧ и линии передачи сиг-
сигналов B01). 7.1.5. Передача по оптоволоконному кабелю B01). 7.1.6. Линии
задержки и корреляторы B03).
7.2. Гетеродин и общие вопросы фазовой стабильности 204
7.2.1. Схемы измерения фазы методом отражения B04). 7.2.2. Система Сва-
рупа и Янга B05). 7.2.3. Система отражения со сдвигом частоты B05).
7.2.4. Система с автоматической коррекцией B10). 7.2.5. Оптоволоконная пе-
передача сигналов гетеродина B11). 7.2.6. Фазовая автоподстройка и опорные
частоты B12). 7.2.7. Фазовая стабильность фильтров B13). 7.2.8. Эффекты
фазовых ошибок B14).
7.3. Частотные характеристики сигнальных каналов 215
7.3.1. Оптимальная частотная характеристика B15). 7.3.2. Допустимые
отклонения частотной характеристики: ухудшение чувствительности B16).
7.3.3. Допустимые отклонения частотной характеристики: погрешности
измерения усиления B18). 7.3.4. Допустимые погрешности установки
задержки B19). 7.3.5. Реализация требований к полосе пропускания B20).
7.4. Ошибки рассогласования поляризаций 221
7.5. Модуляция фазы 222
7.5.1. Снижение отклика на ложные сигналы B22). 7.5.2. Реализация фазовой
модуляции B22). 7.5.3. Связь модуляции фазы с вращением лепестков и
компенсацией задержек B27).
7.6. Автоматическая регулировка уровня и калибровка усиления 228
Приложение 7.1. Смеситель с разделением полос 229
Приложение 7.2. Дисперсия в оптическом волокне 230
Цитированная литература 231
Глава 8. Цифровая обработка сигналов 234
8.1. Двумерное гауссово распределение вероятностей 235
8.2. Периодическая выборка 235
Оглавление 621
8.2.1. Частота Найквиста B35). 8.2.2. Корреляция выборки неквантованных
сигналов B36).
3.3. Выборки с квантованием 239
8.3.1. Двухуровневое квантование B40). 8.3.2. Четырехуровневое квантова-
квантование B43). 8.3.3. Трехуровневое квантование B47). 8.3.4. Квантование с восе-
восемью и более уровнями B48). 8.3.5. Коррекция квантования B51). 8.3.6. Срав-
Сравнение схем квантования B52). 8.3.7. Чувствительность системы B53).
8.4. Точность цифровой выборки 253
8.4.1. Основные причины погрешностей B53). 8.4.2. Допустимые погрешности
при трехуровневом квантовании B54).
8.5. Цифровые схемы задержки 256
8.6. Квадратурный фазовый сдвиг цифрового сигнала 257
8.7. Цифровые корреляторы 257
8.7.1. Корреляторы для наблюдений в континууме B57). 8.7.2. Принципы
спектральных цифровых измерений B58). 8.7.3. Коррелятор с задержками
(XF-коррелятор) B62). 8.7.4. FX-коррелятор B63). 8.7.5. Сравнение кор-
коррелятора с задержками и FX-коррелятора B66). 8.7.6. Гибридный корре-
коррелятор B69). 8.7.7. Демультиплексирование в широкополосных коррелято-
корреляторах B69).
Приложение 8.1. Вычисление суммы ^ it^(grs) 270
9=1
Приложение 8.2. Интеграл вероятности для двухуровневого квантования . 271
Приложение 8.3. Коррекция для четырехуровневого квантования 272
Цитированная литература 273
Глава 9. Интерферометрия со сверхдлинными базами 276
9.1. Первые эксперименты 276
9.2. Различие РСДБ и обычной интерферометрии 278
9.3. Основные характеристики системы РСДБ 280
9.3.1. Ошибки времени и частоты B80). 9.3.2. Запаздывающие базы B85).
9.3.3. Шумы в РСДБ-наблюдениях B86). 9.3.4. Вероятность ошибки при по-
поиске сигнала B89). 9.3.5. Когерентное и некогерентное усреднение B91).
9.4. Поиск лепестков для многоэлементной решетки 294
9.4.1. Обобщенный поиск интерференционных лепестков B94). 9.4.2. Сравне-
Сравнение методов обнаружения интерференционных лепестков B96). 9.4.3. Тройное
произведение или биспектр B97). 9.4.4. Поиск лепестков для многоэлементной
решетки B98). 9.4.5. Многоэлементная решетка с некогерентным усреднени-
усреднением B99).
9.5. Фазовая стабильность и атомные стандарты частоты 299
9.5.1. Анализ флуктуации фазы B99). 9.5.2. Время когерентности генерато-
генератора C06). 9.5.3. Прецизионные стандарты частоты C09). 9.5.4. Рубидиевый
и цезиевый стандарты C12). 9.5.5. Активный водородный стандарт часто-
частоты C13). 9.5.6. Стабильность гетеродинов C17). 9.5.7. Система калибровки
фазы C17). 9.5.8. Синхронизация времени C18).
9.6. Системы регистрации 318
9.7. Системы обработки данных 322
9.7.1. Потери при вращении интерференционных лепестков (f]R) C23).
9.7.2. Потери подавления боковой полосы интерференции (vs) C25).
9.7.3. Потери дискретного изменения задержки (tjd) C27). 9.7.4. Суммарные
потери обработки данных C29).
9.8. Синтез полосы частот 331
9.8.1. Наблюдения в импульсном режиме C33).
622 Оглавление
9.9. Сфазированные решетки как элементы РСДБ 333
9.10. Орбитальная РСДБ (ОРСДБ) 337
Основная литература 341
Цитированная литература 341
Глава 10. Калибровка и преобразование Фурье функции видности 346
10.1. Калибровка функции видности 346
10.1.1. Поправки на предсказуемые или непосредственно измеряемые эффек-
эффекты C47). 10.1.2. Использование опорных источников C47).
10.2. Получение распределения видимой яркости из функции видности 350
10.2.1. Построение изображения посредством прямого преобразования Фу-
Фурье C50). 10.2.2. Взвешивание данных функции видности C51). 10.2.3. По-
Построение изображения при помощи дискретного преобразования Фурье C54).
10.2.4. Функции свертки и эффект ложного изображения C56). 10.2.5. Лож-
Ложное изображение и отношение сигнал/шум C59).
10.3. Соотношения замыкания 360
10.4. Модельная аппроксимация 362
10.4.1. Основные соотношения для модельной аппроксимации C63).
10.4.2. Анизотропия космического фона C64).
10.5. Наблюдения спектральных линий 365
10.5.1. Общие соображения C65). 10.5.2. РСДБ-наблюдения спектральных
линий C67). 10.5.3. Изменение пространственной частоты по ширине
полосы C69). 10.5.4. Точность наблюдений спектральных линий C69).
10.5.5. Представление и анализ наблюдений спектральных линий C70).
10.6. Другие соображения 372
10.6.1. Интерпретация видимой интенсивности C72). 10.6.2. Ошибки на кар-
картах C72). 10.6.3. Некоторые замечания по планированию и обработке данных
наблюдений C73).
Приложение 10.1. Использование края Луны в качестве опорного источника 374
Приложение 10.2. Доплеровское смещение спектральных линий 376
Приложение 10.3. Исторические замечания 380
Основная литература 381
Цитированная литература 381
Глава 11. Восстановление, адаптивная калибровка и их примене-
применение 385
11.1. Ограничение покрытия области пространственных частот 385
11.2. Алгоритм восстановления «чистка» (CLEAN) 386
11.2.1. Алгоритм чистки C86). 11.2.2. Реализация и характеристики алгорит-
алгоритма чистки C89).
11.3. Метод максимума энтропии (ММЭ) 391
11.3.1. Алгоритм ММЭ C91). 11.3.2. Сравнение метода чистки CLEAN и
ММЭ C93). 11.3.3. Другие методы восстановления C95).
11.4. Адаптивная калибровка и картографирование при наличии только ам-
амплитудных данных 396
11.4.1. Гибридное картографирование C96). 11.4.2. Самокалибровка C98).
11.4.3. Картографирование с помошью данных только об амплитуде функции
видности D01).
11.5. Картографирование с высоким динамическим диапазоном 401
11.6. Мозаика 402
Оглавление 623
11.6.1. Методы получения мозаичной карты D05). 11.6.2. Некоторые требова-
требования к антенным решеткам при мозаике D07).
11.7. Многочастотный синтез 410
11.8. Некомпланарные базы 411
11.9. Другие случаи анализа изображений 415
11.9.1. Применение CLEAN и самокалибровки к даным спектральных ли-
линий D15). 11.9.2. Картографирование на низких частотах D15). 11.9.3. Чист-
Чистка линз D17).
Основная литература 418
Цитированная литература 418
Глава 12. Интерферометрические методы в астрометрии и геоде-
геодезии 423
12.1. Требования астрометрии 423
Системы отсчета D25).
12.2. Определение векторов базы и направления на источник 426
12.2.1. Системы со связанными элементами D26). 12.2.2. Измерения на РСДБ-
системах D27). 12.2.3. Привязка фазы в PCДБ D31).
12.3. Время и движение Земли 434
12.3.1. Прецессия и нутация D35). 12.3.2. Движение полюсов D36).
12.3.3. Всемирное время D36). 12.3.4. Измерения движений полюсов и
UT1 D37).
12.4. Геодезические измерения 438
12.5. Картографирование космических мазеров 439
Приложение 12.1. Анализ методом наименьших квадратов 442
Основная литература 452
Цитированная литература 452
Глава 13. Эффекты распространения 457
13.1. Нейтральная атмосфера 458
13.1.1. Физические основы D58). 13.1.2. Рефракция и задержка распро-
распространения D62). 13.1.3. Поглощение D66). 13.1.4. Возникновение рефрак-
рефракции D70). 13.1.5. Уравнение Смита-Вайнтрауба D73). 13.1.6. Фазовые флук-
флуктуации D75). 13.1.7. Колмогоровская турбулентность D79). 13.1.8. Аномаль-
Аномальная рефракция D83). 13.1.9. Радиометрия водяного пара D84).
13.2. Влияние атмосферы на миллиметровых и субмиллиметровых волнах . . 487
13.2.1. Тестирование телескопов методом измерения непрозрачности D87).
13.2.2. Тестирование площадок путем прямого измерения фазовой стабиль-
стабильности D90). 13.2.3. Устранение атмосферных фазовых ошибок калибров-
калибровкой D92).
13.3. Ионосфера 497
13.3.1. Физические основы D98). 13.3.2. Рефракция и задержка распростра-
распространения E01). 13.3.3. Калибровка ионосферной задержки E02). 13.3.4. По-
Поглощение E02). 13.3.5. Мелкомасштабные и крупномасштабные неоднород-
неоднородности E03).
13.4. Рассеяние на неоднородностях плазмы 504
13.4.1. Модель гауссова экрана E05). 13.4.2. Степенная модель E08).
13.5. Межпланетная среда 510
13.5.1. Рефракция E10). 13.5.2. Межпланетные мерцания E13).
13.6. Межзвездная среда 514
13.6.1. Дисперсия и фарадеевское вращение E15). 13.6.2. Дифракционное рас-
рассеяние E17). 13.6.3. Рефракционное рассеяние E18).
624 Оглавление
Основная литература 520
Цитированная литература 521
Глава 14. Теорема Ван Циттерта—Цернике, пространственная ко-
когерентность и рассеяние 530
14.1. Теорема Ван Циттерта-Цернике 530
14.1.1. Взаимная когерентность некогерентного источника E31). 14.1.2. Ди-
Дифракция на апертуре и отклик антенны E33). 14.1.3. Предположения при
выводе теоремы Ван Циттерта—Цернике и ее применение E35).
14.2. Пространственная когерентность 537
14.2.1. Принимаемое поле E37). 14.2.2. Когерентность источника E38).
14.2.3. Полностью когерентный источник E40).
14.3. Рассеяние и распространение когерентности 541
Цитированная литература 545
Глава 15. Радиопомехи 547
15.1. Основные положения 547
15.2. Решетки с короткими и промежуточными базами 550
15.2.1. Усреднение на частоте интерференции E50). 15.2.2. Декорреляция ши-
широкополосных сигналов E53).
15.3. Системы со сверхдлинными базами 554
15.4. Помехи от авиационных и космических передатчиков 556
Приложение 15.1. Регулирование радиочастотного спектра 558
Основная литература 558
Цитированная литература 559
Глава 16. Смежная техника 560
16.1. Интерферометр интенсивностей 560
16.2. Метод лунных покрытий 563
16.3. Измерения параметров антенн 567
16.4. Оптическая интерферометрия 572
16.4.1. Современный интерферометр Майкельсона E73). 16.4.2. Чувстви-
Чувствительность систем прямого детектирования и гетеродинных систем E75).
16.4.3. Оптический интерферометр интенсивностей E77). 16.4.4. Спекл-
интерферометрия E78).
Основная литература 580
Цитированная литература 580
Основные обозначения 585
Предметный указатель 595
Именной указатель 611