Автор: Штейнгауз Г.
Теги: управление предприятиями, организация производства, торговли и транспорта математика
Год: 1976
Текст
Г.ШТЕИНГАУЗ
СТО ЗАДАЧ
Г. ШТЕЙНГАУЗ
СТО ЗАДАЧ
Перевод с польского
Г. Ф. БОЯРСКОЙ и Б. В. БОЯРСКОГО
Издание второе^ исправленное
и дополненное
ИЗДАТЕЛЬСТВО «НАУКА»
\\/?т главная редакция
ФИ ЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕ
Москва 1976
51
Ш 88
УДК 651/512/513
HUGO STEINHAUS
STO ZADAN
PANSTWOWB WYDAWNICTWO
NAUKOWE
Warszawa 1 958
Ш
20202-071
053 @2)-76
•83-76
i Перевод на р
Главная реда]
физико-мате]
издательства
с изменениям!
ОГЛАВЛЕНИЕ
От редактора ««,,•,•»»••»..»• 7
Из предисловия к английскому изданию 9
Из предисловия автора к польскому изданию , • * . 10
Глава I
ЧИСЛА, РАВЕНСТВА И НЕРАВЕНСТВА
1. Упражнение по таблице умно-
умножения » . .
2. Интересное свойство чисел • . *
3. Делимость на И
4. Делимость чисел
5. Облегченная теорема Ферма . .
6. Расстановка чисел
7. Обобщение » » . •
7а. Перестановка букв ••»»•••
8. Пропорция
8а. Симметрические выражения . . .
9. Иррациональность корня . . . *
10. Неравенство * . •
11. Числовые последовательности . .
Глава II
ТОЧКИ, МНОГОУГОЛЬНИКИ, ОКРУЖНОСТИ, ЭЛЛИПСЫ
12. Точки на плоскости .,»..». 15 64
13. Исследование угла ..*.»»*. 15 65
14. Площадь треугольника . * * . . 15 65
15. Деление периметра треугольника 16
на равные части 66
15а. Центр тяжести * • » * 16 70
16. Деление треугольника ...»»* 16 70
17. Треугольники 16 71
18. Треугольная сеть (I) *...»« 16 71
19. Треугольная сеть (II) 17 72
20. Что останется от прямоугольни-
прямоугольника? , .... t .... 17 73
дачи
11
11
12
12
12
12
12
13
13
13
14
14
14
Решения
53
53
56
56
57
58
58
61
62
62
62
62
63
дачи
17
17
18
18
18
18
19
19
19
Решения
74
74
76
77
78
78
78
79
80
20а. Четырехугольники ••••»• • •
21. Разбиение квадрата .»¦••¦•
22. Сеть квадратов
23. Решетка точек
24. Точки решетки, заключенные
внутри круга
25. 14 = 15
26. Многоугольник
27. Точки и окружность
28. Геометрическая задача
Глава III
ПРОСТРАНСТВО, МНОГОГРАННИКИ, ШАРЫ
29. Деление пространства 20 80
30. Две проекции 20 81
31. Куб 20 81
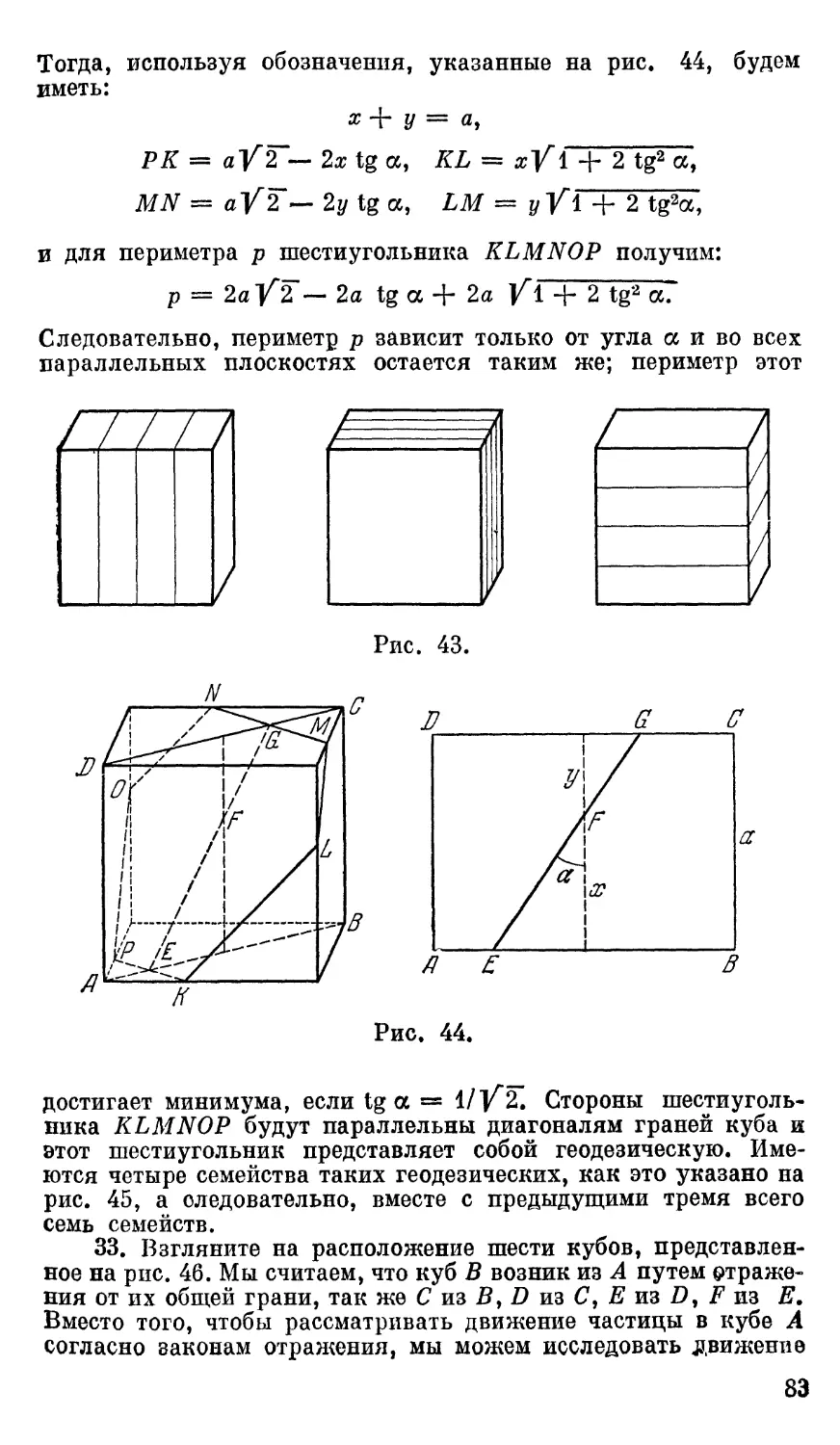
32. Геодезические 21 82
33. Движение молекулы 21 83
34. Развертка куба 21 84
35. Кубы 21 85
36. Гексаэдр ..»>,» 22 86
37. Тетраэдр 22 87
38. Тетраэдр с конгруэнтными гра-
гранями ....... . 22 88
39. Октаэдр 22 90
40. Расстояние на поверхности • » • 22 91
41. Путешествие мухи ..*.»•»• 22 92
42. Правильный додекаэдр ...... 23 93
42а. Вписанный многогранник • , . , 23 94
43. Многогранник » . * 23 100
44. Невыпуклый многогранник . . • 23 101
44а, Модели правильных многогран- ЮЗ
ников 23
45. Задача из Страны чудес ¦ . . . » 24 114
46. Три сферы и прямая ...».» 25 114
47. Одно свойство сферы ...... 25 115
47а. Укладывание шаров (I) . . . • « 25 116
476, Укладывание шаров (!!)....# 25 117
Глава IV
ЗАДАЧИ ПРАКТИЧНЫЕ И ..« НЕПРАКТИЧНЫЕ
47в. Опечатка в учебнике »•»••• 26 119
4S. Игрушка , • 26 119
4\). Праздничный окорок .•»,.,, 26 120
50. Раздел лепешки • » 27 120
51. Раздел треугольного торта • • • 27 121
52. Взвешивания 28 122
52а. Когда его день рождения? ... 28 123
53. Сколько лет Софье Сергеевне? , 28 123
54. Сколько рыб в пруду?
55. Калибровка валиков
56. Сто двадцать шариков
57. Лента на трубке
58. Часы с одинаковыми стрелками
59. Великаны и карлики
60. Ученики классов А и В
61. Статистика
62. Группы крови
63. Снова о группах крови . . . » •
бза. Кассовая задача
бзб. Сады
64. Излишек труда
65. Диагональ прямоугольного па-
параллелепипеда
66. Перевязывание коробок
66а. Другое перевязывание
67. Безмен . .
68. Минимум длины
69. Деление на части прямоуголь-
прямоугольников и квадратов
70. Практическая задача
71. Соседние города
72. Железнодорожная сеть (I) ...
73. Железнодорожная сеть (II) ....
74. Пробный полет
75. Солнце и Луна . # . #
76. Космография
Глава V
ШАХМАТЫ, ВОЛЕЙБОЛ, ПОГОНЯ
77. Шахматная доска
78. Еще раз о шахматной доске .
79. Ладья на шахматной доске •
80. Эллиптический бильярд ....
81. Спортивная задача (I) ...»
82. Спортивная задача (II) ....
83. Теория спортивных розыгрышей
84. Объединение волейбольных ко-
манд
85. Турниры
86. Велосипедист и пешеходы , • ¦ .
87. Четыре собаки .
88. Погоня (I)
89. Погоня (II)
90. Действительно ли условия задачи
неполные?
91. Моторная лодка (I)
92. Моторная лодка (II) , , . , • •
Задачи
28
28
29
30
30
30
30
31
32
33
33
34
34
34
35
35
35
35
36
36
37
37
37
37
37
37
Решения
124
124
124
125
125
127
128
128
130
130
131
131
132
134
134
135
136
137
137
143
144
144
145
147
148
148
38
38
38
39
39
39
39
40
40
41
41
41
41
42
42
42
149
149
153
156
156
156
157
157
158
159
159
159
160
160
161
161
Задачи Решения
Глава VI
МАТЕМАТИЧЕСКИЕ ПРИКЛЮЧЕНИЯ
ДОКТОРА ШАР АДЕНА
93. Удивительное число , 43 162
94. «Сантиметр» . # 43 162
95. Игра в слова 43 163
96. Студенческие долги 44 163
96а. «Криптоним № 2» 44 164
966. Кубики 45 165
97. Странное общество • 45 165
98. Счеты * 46 166
99. Поливание улиц »»#¦.,.. 46 167
100. Французские города ¦„,,,.• 47 167
Глава VII
ЗАДАЧИ БЕЗ РЕШЕНИЯ
Плюсы и минусы . . » . ¦ 48
Треугольник в треугольнике » . . * • 49
Части квадрата » . * 49
Деление окружности .».»*•».. 49
Лучи в пространстве • • » « 50
Неограниченная шахматная доска . . 50
Еще раз счеты *•»»»»••*..« 50
Сравнивание весов 50
Банки в ящике . . . 51
Бактерии , 51
Подъезжает цирк! »..»...... 51
Три ковбоя ............. 52
Допрос 52
Стрелки на додекаэдре 52
ОТ РЕДАКТОРА
Автор настоящей книги Гуго Штейнгауз A887—
1972) — видный польский ученый, один из основопо-
основоположников всемирно известной польской математиче-
математической школы *). Наряду с разносторонними чисто
научными интересами в жизни Штейнгауза большое
место занимали и педагогические увлечения. Блестя-
Блестящий преподаватель и популяризатор науки Г. Штейн-
Штейнгауз сыграл видную роль в становлении польского
математического университетского преподавания.
Статьи и книги, обращенные к учащимся средних
школ, были для него отнюдь также не редкостью.
В 1938 г., накануне войны, появился уникальный
«Математический калейдоскоп» Г. Штейнгауза —
книга с картинками, которую сам автор характеризует
как своеобразный «математический зоопарк», знаком-
знакомство с которым бесспорно доставит читателю удоволь-
удовольствие, а кое-кого серьезно приохотит к математике.
Эта замечательная книга и по сей день пользуется ши-
широкой известностью во всем мире: первый ее англий-
английский перевод был издан в США в год выхода польского
оригинала книги; после войны появилось весьма богато
изданное русское издание (М.~ Л., Гостехиздат, 1949),
а вслед за тем — английское издание в Англии; вен-
венгерское издание; чешское издание и т. д. **). Почти
*) На русский язык переведена, например, обстоятельная
монография С. Качмаж и Г. Штейнгауз, Теория ор-
ортогональных рядов (М., Физматгиз, 1958), давно уж причисляе-
причисляемая чуть ли не к «математической классике».
**) В 1954 г. в Польше появилось 2-е значительно расши-
расширенное издание «Математического калейдоскопа», вскоре вслед
за тем также переведенное на многие языки (например, на не-
немецкий и на английский).
таким же успехом пользуется и книга «Сто задач»,
вышедшая в свет в польском оригинале в 1958 г.
и уже в следующем году изданная и по-русски (М.,
Физматгиз, 1959). Наконец, недавно в нашей стране
была посмертно издана книга Г. Штейнгауза «Задачи
и размышления» (М., «Мир», 1974), объединившая ряд
журнальных публикаций выдающегося польского педа-
педагога и популяризатора; этой книге предпослан перевод
обширной статьи о Штейнгаузе польского математика
Э. Марчевского.
В 1963 г. в Польше книга «Сто задач» была переиз-
переиздана на английском языке. В подготовке этого издания
активное участие принял автор книги: он расширил
или переработал решения некоторых задач и пополнил
книгу рядом новых тем; при этом, стремясь во что бы
то ни стало оправдать заголовок книги, он пошел на
исключение из ее текста некоторых задач с тем, чтобы
общее их число по-прежнему равнялось ста. В основу
настоящего издания положено именно это английское
издание книги; мы, однако, не сочли нужным исключать
из ее состава некоторые из входящих в первое издание
задач, что было сделано, явно, лишь из чисто формаль-
формальных соображений (из любви к «круглому» числу сто);
эти исключенные из английского издания книги задачи
помечаются буквами а, б и т. д. после их номера.
Все входящие в первое русское издание задачи и их
решения даны в переводе Г. Ф. Боярской и Б. В. Бо-
Боярского, который публиковался ранее; этот перевод,
однако, был для настоящего издания заново пересмот-
пересмотрен и кое-где исправлен. Новые задачи и их решения
перевели с английского Е. О. Головина и Ю. О. Го-
Головин. В некоторых местах редактор снабдил текст
книги подстрочными примечаниями, указывающими на
иную относящуюся к разбираемым темам литературу;
эти весьма немногочисленные примечания помечены
звездочками в отличие от нумерованных сносок автора.
ИЗ ПРЕДИСЛОВИЯ
К АНГЛИЙСКОМУ ИЗДАНИЮ
Эта небольшая книга возникла как отклик на то
неблагополучие в математической подготовке школь-
школьников, которое вскоре после войны ощутили многие
работники университетов и технических институтов.
Стала очевидной необходимость более тесного сотруд-
сотрудничества между преподавателями средних школ и твор-
творчески работающими математиками. Некоторые ученые
начали публиковать в общеобразовательных журналах
задачи для учащихся средних школ, стремясь стимули-
стимулировать таким путем интерес школьников к математике.
В этой книге читатель найдет 100 элементарных задач
и решения всех этих задач. Некоторые из задач могут
оказаться известными учащимся старших классов, но
в основном я старался избегать дублирования тех уп-
упражнений, которые имеются в распространенных посо-
пособиях для средних школ. Не стремясь к исчерпывающей
классификации задач, я отдавал предпочтение в первую
очередь тем из них, которые естественным образом воз-
возникают из геометрических рассмотрений. Не предпо-
предполагая знакомства читателя с высшей математикой,
я был ограничен в возможном выборе задач. Этим и
объясняется небольшой размер настоящего сборника.
Решения, одпако, изложены достаточно подробно для
того, чтобы быть понятными как учителям средних
школ, так и тем из их учеников, которые любят или,
во всяком случае, не боятся самостоятельно думать.
Последнюю главу книги составляют задачи, решения
которых здесь не указаны, причем во многих случаях
у меня была весьма уважительная причина эти решения
опустить: дело в том, что я их не знаю. Я надеюсь,
9
что читатели постараются решить некоторые из этих
задач, причем хорошо, если они будут считать, что
решения задач известны: это заблуждение может при-
придать им силы и позволит достичь цели там, где автору
это не удалось.
«Сто задач» могут помочь и некоторым студентам-
первокурсникам, обескураженным трудностями выс-
высшей математики. Демонстрируя им элементарную ма-
математику с новой для них стороны, «Сто задач» могут
помочь перекинуть мост через кажущуюся пропасть
между «элементарной» и «высшей» математикой.
Эта книга первоначально была опубликована по-
польски; английский ее вариант был дополнен, а ре-
решения старых задач иногда отредактированы заново.
Существует также русский перевод «Ста задач», опуб-
опубликованный тиражом в 100 000 экземпляров.
Г. Штейпгауз
ИЗ ПРЕДИСЛОВИЯ АВТОРА
К ПОЛЬСКОМУ ИЗДАНИЮ
Настоящий сборник элементарных задач должен
ввести читателей в практику универсального метода
трактовки явлений, которому греки дали название
математика, облегчить им переход от практики средней
школы к настоящей математике и показать им эту науку
на доступном материале. В связи с этим предлагаемый
сборник предназначен, прежде всего, для учителей и
более способных учеников.
Большинство задач оригинальны, но не все: неко-
некоторые из них общеизвестны, некоторые принадлежат
другим авторам; в тех случаях, когда автор известен,
я называю его имя.
Несмотря на помощь многих лиц, я должен все-
таки сослаться на латинскую поговорку, которая хва-
хвалит уже само желание, если даже исполнение отстало
от намерений. Но главная цель будет достигнута,
если читатели увидят на примере ста задач смысл
и дух настоящей математики.
Г. Штейнгауз
ЗАДАЧИ
ГЛАВА I
ЧИСЛА, РАВЕНСТВА И НЕРАВЕНСТВА
1, Упражнение по таблице умножения. Строим сле-
следующую последовательность цифр.
Пусть первой цифрой будет 2, следующей 3,
2-3 - 6,
третьей цифрой последовательности будет 6;
3-6 = 18,
четвертой цифрой будет 1, а пятой 8;
6.1 = 6, 1-8 = 8,
шестой цифрой является 6, затем следует цифра 8
и т. д.
Вот последовательность цифр, которую мы получим»
Дужки внизу между цифрами означают выполнен-
выполненные умножения, результаты которых мы уже вписали
как очередные цифры последовательности; например,
теперь следовало бы умножить 8 на 6 и вписать цифры
результата: 4, 8. Недостатка в множимых цифрах у
нас никогда не будет, так как при каждом умножении
дужки передвигаются на один шаг, а полученный ре-
результат по меньшей мере однозначен, а часто и дву-
двузначен, и поэтому прибавляется по меньшей мере
одна цифра.
Доказать, что цифры 5, 7, 9 никогда не появятся
в этой последовательности.
2. Интересное свойство чисач. Напишем произволь-
произвольное натуральное число в десятичной системе счисления
11
(например, 2583) и вычислим сумму квадратов цифр
этого числа B2 + 5а + 82 + З2 = 102). С полученным
числом проделаем то же самое (I2 + 0а + 22 = 5) и
будем поступать таким же образом и далее
E2 = 25, 22 + 52 = 29, 22 + 92 =* 85,. . . ).
Доказать, что если этот процесс не приведет нас
к единице (ясно, что после этого единица будет повто-
повторяться бесконечное число раз), то наверняка приведет
к числу 145, после чего появится цикл
145, 42, 20, 4, 16, 37, 58, 89,
который далее будет все время повторяться.
3. Делимость на 11. Доказать, что при любом на-
натуральном к число
55fc+1 л. 4б&+2 -4- 35fc
делится на 11.
4. Делимость чисел, Число
3*05 -f 4105
делится на 13, 49, 181 и 379, но не делится на 5
и 11.
Как это проверить?
5. Облегченная теорема Ферма. Если х, у, z, n —
натуральные числа, причем п% z, то равенство хп +
+ уп = zn невозможно.
6. Расстановка чисел. Найти 10 таких чисел хи
#2> #3» ^4»' • - > #10» ЧТОбы
число хг находилось внутри интервала [0, l]f
числа хг и х2 по одному находились в первой и вто-
второй половине этого интервала,
числа хи х21 х3 по одному находились в каждой
из трех равных частей интервала,
числа xlf x2, xS9 я4 по одному находились в каждой
четверти этого интервала и т. д.,
наконец, чтобы
числа х19 х2, . . . , х10 по одному находились в каж-
каждой из частей интервала [0,1], полученных путем его
деления на 10 равных отрезков.
7. Обобщение. Разрешима ли предыдущая задача,
если вместо 10 искать п чисел (п — произвольное на-
12
яуральное число), удовлетворяющих п аналогичным
условиям?
7а. Перестановка букв. Из комплекса букв ааЪЪсс
можно получить 90 различных перестановок. Из пере-
перестановки ааЪсЪс можно получить перестановку aacbcb,
записывая букву с вместо буквы Ъ и букву Ъ вместо
буквы с; из перестановки aacbcb можно получить пере-
перестановку bcbcaa, если прочесть ее в обратном порядке,
а из этой последней перестановки путем замены букв
можно получить перестановку acacbb, и т. д.
Бее такие перестановки, как aabebe, aacbcb, bcbcaa9
acaebb, мы считаем несущественно различными. Пере-
Перестановки же, как, например, aabebe и abebca, мы
считаем существенно различными, так как ни замена
букв, ни прочитывание их в обратном порядке, ни
многократное применение этих операций не могут пре-
преобразовать один комплекс в другой.
Вопрос: сколько имеется существенно раз-
различных перестановок букв aabbec?
8. Пропорция. Числа А, В, С, р, q, r связаны
между собой соотношениями
А : В = р, В : С = q, С : А = г.
Записать пропорции
в таком виде, чтобы на пустых местах появились вы-
выражения, состоящие из р, q, г, и чтобы эти выражения
получались одно из другого путем циклической пере-
перестановки букв р, д, г. (Мы понимаем это следующим
образом: если вместо р напишем q, вместо q напишем г,
а вместо г напишем р, то первое выражение преобра-
преобразуется во второе, второе — в третье, а третье — в
первое).
8а. Симметрические выражения. Такие выражения,
как х + у + z или xyz, являются симметрическими.
Под этим мы понимаем, что их значение не меняется
при перестановке в них переменных х, у, z каким
угодно образом. Приведенные выше примеры очевид-
очевидны; но существуют симметрические выражения, сим-
симметричность которых не является очевидной, например:
II х-у\ + х+ y-2z \ + \x-y\ + x+ y+2z.
13
Докажите симметричность этого выражения и оп-
определите его значение таким образом, чтобы симметрич-
симметричность стала очевидной.
9. Иррациональность корня. Докажите элементар-
элементарным путем, что положительный корень уравнения
хь + z ~ 10
является иррациональным.
10. Неравенство. Доказать неравенство
+с ^
¦Ъ + С + с
в котором все буквы обозначают положитедьные числа.
11. Числовые последовательности. Найти последо-
последовательность а0, а1} O2f ... положительных чисел та-
такую, что а0 =з 1 и ап — ап+1 = ап+2 при п = 0, 1, 2, . . .
Показать, что существует только одна такая последо-
последовательность.
ГЛАВА II
ТОЧКИ, МНОГОУГОЛЬНИКИ, ОКРУЖНОСТИ,
эллипсы
12. Точки на плоскости. На плоскости дано несколь-
несколько (или несколько десятков) точек. Каждую из них
соединяем отрезком прямой с ближайшей точкой; при
этом не возникает сомнения, какая из точек явля-
является ближайшей, ибо предполагается, что все рас-
расстояния различны.
Доказать, что полученная фигура не содержит зам-
замкнутого многоугольника или пересекающих отрезков.
13. Исследование угла. Пусть х19 х29 . . . , хп —- по-
положительные числа. Выберем на плоскости луч ОХ,
отсечем на нем ОРг = х19 затем перпендикулярно к
ОРг отсечем РХР2 = #2» затем перпендикулярно к ОР2
отсекаем Р2РЪ = хз и т- Д- вплоть до Рп.гРп = хп.
При этом прямые углы ориентированы так, что их
левые стороны проходят через точку О. Можно
считать, что луч ОХ вращается вокруг точки О (от
первоначального положения, проходя через точки Р19
Р2, . . . ) до конечного положения ОРП9 описывая не-
некоторый угол.
Доказать, что при данных числах xt угол этот будет
наименьшим, если они пронумерованы в убывающем
порядке, хг > х2 >. . . > хп, и будет наибольшим, ес-
если они пронумерованы в возрастающем порядке.
14. Площадь треугольника. Доказать без помощи
тригонометрии, что если в треугольнике 2/тА= 60°,
то площадь S треугольника определяется формулой
Я = ^[аа-(&-сЛ, A)
15
а если /_ A = 120°, то
S=?.[a?-(b-cT\. B)
15. Деление периметра треугольника на равные
части. Возьмем произвольный треугольник. Мы, конеч-
конечно, можем пересечь его прямой так, чтобы разделить
его периметр пополам. Мы даже можем заранее задать
направление пересекающей прямой. Если мы это про-
проделаем дважды, в двух различных направлениях, то
прямые пересекутся в некоторой точке Q. Тогда через
точку Q пройдут две прямые, делящие периметр по-
пополам.
Существует ли точка, черев которую могут пройти
три такие прямые? Если существует, то как ее найти?
15а, Центр тяжести. Пусть Р — центр тяжести
трех точек А, В, С (говоря о центре тяжести каких-
либо трех точек, будем подразумевать, что массы,
размещенные в этих точках, одинаковы). Пусть
Аи Ви Сх — соответственно центры тяжести следую-
следующих троек точек: В, С, Р; С, А, Р; А, В, Р.
Доказать, что центром тяжести тройки Аг, Вх, Сх
снова является точка Р.
16. Деление треугольника. Разделить треугольник
на 19 треугольников так, чтобы в каждой вершине по-
полученной фигуры (а также в вершинах большого тре-
треугольника) сходилось одинаковое число сторон.
В этой задаче число 19 нельзя заменить большим
числом, но можно заменить меньшими числами. Каки-
Какими же?
17. Треугольники. В этой задаче п обозначает на-
натуральное число. На плоскости заданы ~3/г точек,
никакие три из которых не лежат на одной прямой.
Можно ли образовать из этих точек (приняв их за вер-
вершины) п треугольников, не пересекающихся и не со-
содержащих друг друга?
Подобную задачу при An точках можно поставить
для четырехугольников, при Ъп точках — для пяти-
пятиугольников и т. д. Все ли эти, задачи решаются поло-
положительно?
18. Треугольная сеть (I). Как известно, всю пло-
плоскость можно покрыть сетью равносторонних треуголь-
треугольников.
16
Можно ли в каждом узле этой сети поместить один
из знаков плюс или минус так, чтобы для каждого
из треугольников, составляющих сеть, имело место
следующее правило: если в двух вершинах треуголь-
треугольника имеется одинаковый знак, то в третьей вершине
будет плюс, а если наоборот — то в третьей будет
минус.
Конечно, можно всюду расставить плюсы, но это
тривиальное решение мы исключаем.
19, Треугольная сеть (II). Доказать, что нельзя
покрыть всю плоскость сетью треугольников так, что-
чтобы в каждой вершине сходилось пять треугольников.
20, Что останется от прямоугольника? Золотой
прямоугольник — это такой прямоугольник, стороны
а и Ъ которого находятся в пропорции золотого сечения,
т. с. удовлетворяют равенству
а : Ъ = Ъ : (а — Ъ).
Вообразим, что прямоугольник этот вырезан из бу-
бумаги и лежит на столе, обращенный к нам своей более
длинной стороной. Отсечем по левую сторону прямо-
прямоугольника наибольший квадрат, который можно из
©его вырезать; остаток снова будет золотым прямо-
прямоугольником. Становимся по левую сторону стола, чтобы
снова иметь перед собой более длинную сторону пря-
прямоугольника, и поступаем с новым прямоугольником
так же, как и с предыдущим. Таким образом обходим
стол вокруг по направлению хода часовой стрелки
и по очереди отсекаем квадраты. Каждая точка пря-
прямоугольника, за исключением одной, будет раньше
или позже отречена. Определить положение этой исклю-
исключительной точки.
20а. Четырехугольники. Соединяем поочередно се-
середины сторон выпуклого четырехугольника. Мы полу-
получим меньший четырехугольник. Доказать, что он яв-
является параллелограммом, площадь которого равна
половине площади большого четырехугольника. Сох-
Сохранит ли силу эта теорема без предположения о вы-
выпуклости?
21, Разбиение квадрата. Квадрат площади 1 км*
разбит на три части А, 3d, $. Каким бы это разбиение
ни было, обязательно найдется по крайней мере одна
Шфа точек Р и (), принадлежащих одной части и таких,
17
что расстояние между ними не меньше |^65/64«
да 1,00778 (км).
Как это доказать?
22. Сеть квадратов. Плоскость можно покрыть рав-
равными квадратами; узлы этой сети в математике назы-
называют целочисленной решеткой.
Можно ли эти узлы обозначить буквами я, Ь, с, d
так, чтобы каждый составной квадрат имел в своих
вершинах все четыре буквы и чтобы в каждом столбце
и « каждой строке решетки тоже фигурировали все
четыре буквы?
23. Решетка точек. Определение целочислен-
целочисленной решетки дано в условии задачи 22. Ясно,
что выбирая подходящий радиус, всегда можно добить-
добиться, чтобы окружность этого радиуса с центром в точке
A^2, уЗ) проходила через заданную точку решетки.
Требуется доказать, что, однако, на каждой такой
окружности лежит не более одной точки решетки.
24. Точки решетки, заключенные внутри круга,
В этой задаче мы имеем дело с решеткой, расположенной
внутри круга К, точнее, с теми точками целочисленной
решетки, которые заключены внутри этого круга (но
не на его окружности).
Доказать, что для любого целого неотрицательного
числа п существует круг, содержащий ровно п точек
решетки.
25. 14 =г 15. На съезде участников математической
олимпиады во Вроцлаве в 1952 году проф. Я. Мику-
синский указал такое деление всей плоскости на семи-
семиугольники, в каждой вершине которого сходятся три
семиугольника. Исходя из этого, я покажу, что 14 =а
= 15. Обозначим через Р угол в 180°. Сумма углов
в семиугольнике равна 5Р, поэтому средняя величина
угла в семиугольнике равна у Р. Так как вся плоскость
покрыта семиугольниками, то средняя величина угла
в паркетажеравнауР. Но в каждой вершине сходятся
три таких угла, следовательно, средняя величина угла
2
при каждой вершине равна -^Р* Отсюда вытекает, что
средняя величина угла в паркетаже равна -д- "у так
18
как каждый угол принадлежит какой-нибудь вершине.
Следовательно,
3 7' Т ~~ 7 » д "" 1Jf
что и требовалось доказать.
Найти ошибку в приведенном выше рассуждении.
26. Многоугольник, На плоскости даны п точек;
никакие три из них не лежат на одной прямой. Всегда
ли можно найти замкнутый и-угольник с непересекаю-
непересекающимися сторонами, вершинами которого являются эти
точки?
27. Точки и окружность. На плоскости даны четыре
точки, через которые нельзя провести ни окружность,
ни прямую. Можно ли эти точки так обозначить бук-
буквами -4,5, С, Z), чтобы точка D лежала внутри окруж-
окружности, проходящей через точки А, В, С?
28. Геометрическая задача. Дан эллипс, длина боль-
большой оси которого равна 2а, а длина малой оси равна
26. Нарисовать замкнутую кривую той же длины, что
и длина эллипса, ограничивающую площадь, большую
площади эллипса на (а — ЬJ.
ГЛАВА III
ПРОСТРАНСТВО, МНОГОГРАННИКИ, ШАРЫ
29. Деление пространства. Через фиксированную
точку пространства проводим плоскости так, чтобы
разделить пространство на возможно большее число
частей. Одна плоскость разделит пространство на две
части, две пересекающиеся плоскости — на четыре час-
части, три пересекающиеся в некоторой точке плоскости
и не имеющие другой общей точки делят пространство
на восемь частей. Какое максимальное число частей
можно получить при четырех плоскостях? А какое —
при п плоскостях?
30. Две проекции. Представим себе плоскость Пи
касательную к земному шару в Северном полюсе N,
и плоскость Пъ касательную к земному шару в Юж-
Южном полюсе S. Можно начертить одну карту, про-
проектируя каждую точку на поверхности земли из N
на ЛГ2, и другую карту, проектируя каждую точку из
S на Пх\ это — так называемая стереографическая
проекция. Теперь мы можем сложить обе плоскости
так, чтобы меридианы сошлись. Каждой точке одной
карты отвечает определенная точка другой карты, сле-
следовательно, мы определили некоторое отображение пло-
плоскости на себя. Как непосредственно определить это
отображение?
31. Куб. Держа в руке модель куба так, чтобы
он мог вращаться вокруг своей самой длинной оси
(т. е. вокруг прямой, соединяющей противоположные
вершины), можно намотать на него без просветов чер-
черную пряжу. Пряжа заштрихует только половину куба
(почему?). То же самое можно проделать с другой
осью; их всего четыре, и каждый раз мы используем
другой цвет пряжи (черный, красный* голубой и
20
желтый). Вся модель будет покрыта разными цветами,
а из их смешения возникнут смешанные цвета (модель
куба белая и этого цвета мы не учитываем). Сколько
будет цветовых оттенков на кубе и каких?
32. Геодезические. Эта задача не требует знания
математики. Наложим на неподвижный куб резинку
(так называемую «рецептную», используемую в аптеках
для упаковки лекарств) таким образом, чтобы она дер-
держалась на кубе и не пересекала сама себя.
Линию, по которой уложится эта резинка, мы назы-
называем геодезической линией,
1. Сколько раз все геодезические линии покроют
поверхность куба (т. е. сколько геодезических линий
нройдет через каждую точку поверхности куба)?
2. Сколько имеется различных семейств геодези-
геодезических линий, покрывающих поверхность куба?
33. Движение молекулы. Внутри кубической короб-
коробки движется без воздействия внешних сил материаль-
материальная частица, которая отражается от стен коробки,
согласно классическому закону (угол падения равен
углу отражения, т. е. перпендикуляр к грани в точке
отражения есть биссектриса угла, образованного пря-
прямой, по которой молекула прибывает, и прямой, по
которой она удаляется). Возможно ли, чтобы молекула
беспрестанно двигалась по замкнутому шестиугольнику,
поочередно ударяясь при каждом обходе обо все сто-
стороны коробки? Определить точки отражений и прове-
проверить, заузлен ли полученный шестиугольник или нет.
34. Развертка куба. Модели многогранников де-
делаются из плоских разверток. В развертке грани при-
прилегают друг к другу ребрами, а модель строится путем
загибания картонной развертки вдоль ребер. Таких
различных разверток правильный тетраэдр имеет две.
Сколько их имеет куб?
35. Кубы. Как известно, все пространство можно
заполнить равными кубами. В каждой вершине будет
сходиться восемь кубов. Поэтому можно — путем соот-
соответствующего отсечения вершин у кубов и склейки
смежных отсеченных частей в одно тело — заполнить
пространство правильными октаэдрами (восьмигранни-
(восьмигранниками) и телами, оставшимися от кубов. Какие это
будут тела? Если мы максимально возможно увеличим
октаэдры, то какую часть пространства они займут?
21
36. Гексаэдр. Существует ли отличный от куба
гексаэдр (шестигранник), все грани которого являются
конгруэнтными ромбами?
37. Тетраэдр. Имеются 6 стержней различной дли-
длины, причем известно, что при любом их упорядочении
из них можно составить тетраэдр (треугольную пира-
пирамиду). Сколько различных тетраэдров при этом может
получиться?
38. Тетраэдр с конгруэнтными гранями. Можно
ли построить треугольную пирамиду (тетраэдр), все
грани которой являются конгруэнтными треуголь-
треугольниками с произвольно заданными длинами а, Ь, о
сторон?
Если это возможно, то каков объем этого тетраэдра?
39. Октаэдр. Можно ли построить восьмигранник
(октаэдр), все грани которого являются конгруэнтны-
конгруэнтными четырехугольниками? Можно ли построить деся-
десятигранник (декаэдр) и, общее, 2гс-гранник (где п ]> 3 —
произвольное целое число), обладающий тем же свой-
свойством?
40. Расстояние на поверхности. Сопоставим каждой
паре точек замкнутой выпуклой поверхности кратчай-
кратчайшую из соединяющих их дуг (не исключено, что та-
такая дуга не единственная, например, для любой пары
диаметрально противоположных точек сферы сущест-
существует бесконечно много кратчайших дуг). Расстоянием
между точками А и В на поверхности назовем длину
кратчайшей дуги АВ. Теперь мы можем говорить про
расстояние РХ между Р и произвольной точкой X
нашей поверхности. Для каждой точки Р можно найти
самую дальнюю от нее точку Q поверхности
(конечно, такая точка также может быть не единствен-
единственной). Пример со сферой может создать впечатлетшот
что для подобпой пары точек. PQ всегда имеются по
крайней мере две соединяющие пх кратчайшие дуги.
Показать, что для некоторого тетраэдра это утвержде-
утверждение неверно.
41. Путешествие мухи. Муха села на вершину мо-
модели правильного додекаэдра (двенадцатигранника) и
решила обойти его, двигаясь по ребрам додекаэдра;
при этом ей удалось посетить все вершины, не побывав
ни в одной из них дважды и вернувшись в конце путе-
путешествия в исходную вершину. После этого она иопро-
22
бовала обойти тем же способом все вершины ромби-
ромбического додекаэдра, ограниченного 12 ромбами (рис. 1).
Удалось ли ей это?
42. Правильный додекаэдр. Грани правильного
додекаэдра (двенадцатигранника) можно раскрасить в
четыре цвета так, чтобы каждые
две смежные грани были разных
цветов. Доказать, что существуют
всего четыре способа решения этой
задачи, если условиться считать
одним решением две раскраски,
которые можно получить одну из
другой вращением додекаэдра.
42а. Вписанный многогранник.
В правильный додекаэдр можно рИСв ^
вписать куб так, чтобы ребра куба
являлись диагоналями правильных пятиугольников,
служащих гранями додекаэдра. Это можно сделать не-
несколькими способами; сколькими же? Все такие кубы
образуют звездчатый многогранник; каков объем этого
полученного в объединении всех кубов многогранника,
если объем додекаэдра равен 1?
Какое тело образует общая часть (пересечение) всех
кубов?
43. Многогранник. Все грани выпуклого много-
многогранника обязательно выпуклы. А обратно, обязательно
ли является многогранник выпуклым, если все его
грани — выпуклые многоугольники? В частности, су-
существуют ли два многогранника (например, два три-
дцатигранника), ограниченных одинаковым числом по-
попарно конгруэнтных граней (грани одного и того же
тела'не обязательно должны быть конгруэнтными между
собой), из которых одно является выпуклым, а второе
не является?
44. Невыпуклый многогранник. Может ли невы-
невыпуклый многогранник быть ограничен конгруэнтными
четырехугольниками?
44а. Модели правильных многогранников. Из ше-
шести ребер правильного тетраэдра можно выбрать че-
четыре ребра, образующих замкнутый косой, т. е. неплос-
неплоский четырехугольник. Этот четырехугольник можно
считать моделью тетраэдра, ибо он содержит все вер-
вершины тетраэдра. То же самое легко проделать с кубом;
23
тогда мы получим (неплоский) восьмиугольник, содер-
содержащий все вершины куба. Можно ли этот прием рас-
распространить на другие правильные многогранники,
т. е. на октаэдр, додекаэдр и икосаэдр? Сколько реше-
решений имеет задача?
45. Задача из Страны чудес. Люде Кэррол, мате-
математик и знаменитый детский писатель, был автором за-
забавных нелепиц. Он советовал, например, пользоваться
картой с масштабом 1:1, ибо достаточно разложить
ее на земле, чтобы в любой момент знать, где нахо-
находишься: надо просто прочитать надпись, на которой
стоишь*
Представим себе, что, последовав этому совету, мы
проведем на земном шаре прочной краской по суше
и по морю меридианы и параллели и повсюду поместим
каллиграфические названия городов, портов и стран.
Компас станет излишним, но одна трудность все-таки
останется: как отыскать кратчайший путь
к избранной точке. Известно, что ортодромы, т. е.
кратчайшие пути, не являются па этой карте Алисы
из Страны чудес локсодромами, т. е. линиями, пересе-
пересекающими меридианы (и параллели) под постоянным
углом. Хуже всего то, что никакая перестройка коор-
координатных линий нам не поможет, ибо все системы ко-
координат будут обладать этим недостатком. Виноват
в этом, конечно, земной шар, который так непрактично
устроен.
Чтобы исправить пашу планету, лучше всего, ко-
конечно, начать с ее карты. Можно, например, начертить
прямоугольную сеть параллелей и меридианов и свер-
свернуть карту в цилиндр так, чтобы параллели преврати-
превратились в окружности. На такой цилиндрической планете
кратчайший путь от однсй точки к другой точке всегда
пересекает меридианы под постоянным углом. Можно
также разрезать карту вдоль параллели, обозначив
на ней точку N9 и свернуть ее в конус с вершиной в
точке N. У конической планеты в точке N будет Се-
Северный полюс, параллели не будут пересекаться, ис-
исходящие из N меридианы тоже не будут, но каждая па-
параллель пересечет каждый меридиан в двух точках,
точно так же как и па земном шаре. И так же, как и
раньше, кратчайший путь вновь будет иметь постоян-
постоянное направление.
24
Но можно найти еще более интересную модель.
На карте будет прямоугольная сеть координатных ли-
линий, но на планете появится только одно семейство ли-
линий: каждая линия пересечет любую другую в двух
точках, а также и себя в одной точке. Принцип посто-
постоянного направления будет сохранен. Что это за модель?
Магистр Р. Новаковский, когда я ему рассказал
об этих двух моделях, немедленно определил третью:
прямоугольная сеть состоит из меридианов, паралле-
параллелей и «посредников».
46. Три сферы и прямая. Три сферы имеют общую
точку jP, причем известно, что никакая прямая, прохо-
проходящая через точку Р, не касается сразу всех сфер. По-
Показать, что эти сферы имеют еще одну общую точку.
47. Одно свойство сферы. Пусть известно, что все
плоские сечения некоторой поверхности являются ок-
окружностями (точка рассматривается как окружность
нулевого радиуса). Доказать, что эта поверхность яв-
является сферой.
47а. Укладывание шаров (I). У нас имеется неогра-
неограниченный запас одинаковых шаров. Уложим три из
них так, чтобы все они соприкасались между собой,
и затем присоединим четвертый шар так, чтобы он сопри-
соприкасался с тремя первыми. У нас получатся четыре гнез-
гнезда, и в каждое из них можно вложить по одному шару.
Теперь у нас уже восемь шаров. Сколько гнезд они об-
образуют? Сколько теперь можно уложить шаров новым
слоем?
Можно ли продолжать этот процесс?
476. Укладывание шаров (II). У нас имеется неогра-
неограниченный запас одинаковых шаров. Берем один из них
и обкладываем его двенадцатью шарами, соприкаса-
соприкасающимися с ним. Сколько будет теперь гнезд для после-
последующих шаров? Можно ли в каждое гнездо уложить
шар? Из скольких шаров будет состоять третий слой
(первый состоит из одного, второй из 12 шаров)? Всегда
ли мы сможем в последующих слоях заполнить все
гнезда?
ГЛАВА IV
ЗАДАЧИ ПРАКТИЧНЫЕ И... НЕПРАКТИЧНЫЕ
47в. Опечатка в учебнике. Некий автор, читая
свой учебник, заметил, что в предложении: «Отсечь
9 см на левой стороне угла в 60°, а на правой... и вы-
вычислить расстояние между полученными таким образом
точками» — на месте проставленных нами точек имеет-
имеется опечатка: наборщик увеличил число сантиметров,
указанное в рукописи, на 1. Конечно, наборщик и не
подумал изменить ответ, напечатанный в конце учеб-
учебника. Несмотря на это, опечатка не привела к ошибке.
Какое число набрал наборщик в задаче?
48. Игрушка. На картонном кружке нарисован
концентрический меньший кружок, разделенный на
восемь секторов равной величины: четыре белых и че-
четыре черных. Оставшееся кольцо разделено на 10 рав-
равных секторов, белых и черных вперемежку, по пять
секторов каждого цвета. Кружок надеваем на гвоздь
и приводим в быстрое вращательное движение. Внача-
Вначале секторы сливаются в однообразный серый цвет, но
через минуту появляется кольцо, вращающееся в од-
одну сторону, и кружок, вращающийся в обратную сто-
сторону, хотя все сделано из одного куска картона.
Эта игрушка действует только при электрическом
освещении, но не в каждом городе. Почему?
49. Праздничный окорок. Три соседки сложились
по 15 рублей и купили окорок (без кожи, сала и костей).
Одна из них разделила его на три части, уверяя, что
части по весу равны. Другая заявила, что доверяет
только весам в магазине на углу; там оказалось, что
якобы равные части после пересчета стоимости соответ-
соответствуют 14, 15 и 16 рублям. Третья участница проверила
26
вес на домашних весах, которые также дали иной ре-
результат. Возник спор, ибо первая настаивала, что она
разделила окорок на равные части, другая признавала
только магазинные весы, а третья — свои. Как можно
успокоить спорящих и разделить куски (не разрезая
их больше) так, чтобы каждая женщина признала, что
получила окорок стоимостью по крайней мере в 15 руб-
рублей при пересчете его стоимости по тем весам, которым
она доверяет?
50. Раздел лепешки. Каждую лепешку независимо
от ее формы можно разделить па четыре равные части
двумя взаимно перпендикулярными сечениями. Други-
Другими словами, для каждой плоской области с площадью
Р можно найти такие две взаимно перпендикулярные
прямые, что в каждой из четырех образуемых ими
четвертей лежит часть этой области, имеющая пло-
площадь Р/4.
(Доказать эту теорему значительно легче, чем факти-
фактически разделить на четыре равные части, скажем, тре-
треугольник со сторонами 3, 4, 5.)
51. Раздел треугольного торта. Павел и Гавел долж-
должны разделить между собой треугольный торт. Гавел
поставил условие, что он прямолинейным разрезом от-
отрежет свою часть, а Павел согласился на это с тем ус-
условием, что он заранее обозначит точку Р, через ко-
которую должен пройти этот разрез. Так как торт имеет
одинаковую толщину в любом месте, а также однороден
по вкусу, то задача имеет планиметрический характер.
Вопрос ставится следующим образом: как Павел дол-
должен выбрать точку Р, чтобы лучше защитить себя от
чревоугодия Гавла? Второй вопрос: какой величины
излишек перепадет Гавлу, если Павел удачно решит
первую задачу, а Гавел потом отрежет себе возможно
большую часть торта?
Если бы форма торта зависела от Павла, то он мог бы
выбрать фигуру, имеющую центр симметрии (т. е.
круг, квадрат, эллипс и т. д.), и поместить Р в этом
центре. Тогда у Гавла не оказалось бы никаких преиму-
преимуществ. Однако интересен вопрос, какая форма торта
(при сохранении указанных вначале условий раздела)
будет самой удобной для Гавла и какой наибольший
излишек он сможет себе обеспечит^ удачно выбрав
форму торта?
27
52. Взвешивания. Имеется 5 предметов различного
веса, которые нужно упорядочить по убыванию весов,
пользуясь чашечными весами без гирь, с помощью
которых можно сравнить веса любых двух предметов. Как
нужно действовать, чтобы решить задачу, используя
наименьшее возможное число взвешиваний? Чему равно
это число?
52а. Когда его день рождения? День рождения
Невядомского отмечали в многочисленном кругу. Кро-
Кроме сестры хозяина Екатерины и его брата Иоахима,
присутствовал известный путешественник Педанткевич
и много других друзей Невядомского, которые ценили
его варшавское гостеприимство.
Кто-то спросил Педанткевича, что он делал год
тому назад. Тот взял блокнот и с присущей ему педан-
педантичностью ответил: «Точно год тому назад я вышел на
восходе солнца из палатки, прошел прямо на юг милю
или немного больше, свернул на запад и через несколько
часов, ничего не подстрелив, свернул на север. Своих
собственных следов я уже не пересекал и, идя все время
на север, вышел к палатке». Когда день рождения Не-
Невядомского?
53. Сколько лет Софье Сергеевне? Наша знакомая
Софья Сергеевна еще не стара, ибо родилась после
цервой мировой войны, но она не любит прямо отве-
отвечать на вопрос — сколько ей лет.
Когда ее спросили 27 июля 1950 г., сколько ей лет,
она ответила: мне всего один год, так как я отмечаю день
своего рождения только тогда, когда он совпадает
с днем недели, в который я родилась, а такой день рож-
рождения я отмечала всего лишь один раз.
Сколько лет Софье Сергеевне?
54. Сколько рыб в пруду? Некий ихтиолог хотел
определить, сколько в пруду рыб, годных для улова.
Для этого он забросил сеть с заранее выбранным раз-
размером ячеек и, вытащив ее, обнаружил 30 рыб, отметил
каждую из них меткой и бросил обратно в пруд. На дру-
другой день забросил ту же самую сеть и поймал 40 рыб,
на двух из которых были его метки. Как по этим данным
он приблизительно вычислил количество рыб в пруду?
55. Калибровка валиков. Одна из составных частей
бензинового двигателя имеет форму валика. Для из-
измерения толщины валика служит стальная плита, в
28
которой в ряд высверлены 15 отверстий с точно уста-
установленными размерами. Первое отверстие имеет ди-
диаметр 10 мм, каждое последующее имеет диаметр, на
0,04 мм больший предыдущего. Калибровка валика
заключается во вкладывании его в отверстие; если он
не помещается, то его диаметр считают больше диаметра
отверстия, а если помещается, то считают его меньше.
Таким образом, в конце концов диаметр валика опре-
определяется с погрешностью менее чем 0,04 мм (валики
с диаметром меньше, чем 10 мм, или больше, чем
10,56 мм, не принимаются во внимание; остальные же
идут на дальнейшую обработку).
Рабочие, которым поручена калибровка, пробуют
каждый валик на одном и том же числе отверстий, но,
конечно, на разных отверстиях. Сколько проб изме-
измерения необходимо для каждого валика? Какова долж-
должна быть очередность проб?
56. Сто двадцать шариков. Мастерская точной ме-
механики заказала 120 стальных шариков диаметром
в 6,1 мм. Им прислали действительно 120 шариков,
однако измерения выявили, что диаметры не отвечают
требованиям точности. В результате этих измерений
было обнаружено:
10 шариков диаметром в 6,01, мм 6 шариков диаметром в 6,11 мм,
6 » » »6,02 мм, 8 » » »6,12 мм,
4 » » »6,03 мм, 10 » » »6,14мм,
10 » » » 6,05 мм, 17 » » »6,16 мм,
19 » » »6,07 мм, 6 » » »6,17 мм,
11 » » »6,08 мм, 7 » » »6,18 мм.
6 » » »6,10 мм,
К счастью, другая мастерская согласилась принять
шарики при условии, что их доставят в двух ящиках,
отдельно большие и отдельно меньшие, и что на каждом
ящике будет указан общий диаметр для всего ящика,
В задаче требуется определить предельный диаметр,
ниже которого шарики войдут в ящик А (а следовательно,
в ящике В окажутся шарики диаметром больше пре-
предельного), а также отыскать числа а и Ь, которые следует
выписать на ящиках. Эти три числа должны быть та-
таковы, чтобы сумма абсолютных погрешностей была
наименьшей. Абсолютной погрешностью мы здесь на-
называем абсолютную разность между диаметром шара
и надписью на ящикел в который его вложили.
29
57. Лента на трубке. 25 м ленты толщиной в 0,1 мм
намотали плотно на картонную трубку — получился
валик диаметром в 1 дм. Каков диаметр трубки?
58. Часы с одинаковыми стрелками. Известно, что,
определяя время без часов, никто не ошибается более
чем на шесть часов.
Часовой мастер вставил в часы две одинаковые
стрелки, так что невозможно отличить малую от боль-
большой. Какова будет наибольшая ошибка, которая гро-
грозит владельцу часов?
59. Великаны и карлики. На уроке физкультуры
в классе, в котором все ученики были разного роста,
учитель, построив класс прямоугольным строем, ска-
сказал: «Сейчас мы увидим, кто среди вас самый высокий
карлик». Отыскал в каждом ряду самого низкого, а
когда эти «карлики» выступили из строя и создали пе-
переднюю шеренгу, он выбрал самого высокого из них:
«Вот самый высокий карлик».
Мальчики вернулись на старые места, и тогда учи-
учитель сказал: «Сейчас я вам покажу самого низкого ве-
великана». Указал в каждой шеренге на самых высоких,
а когда «великаны» выступили вперед, нашел самого
низкого среди них: «Вот самый низкий великан».
Могло ли случиться, что один и тот же мальчик
мог оказаться самым низким «великаном» и самым вы-
высоким «карликом»? Существуют ли такие классы, в ко-
которых самый низкий «великан» меньше самого высокого
«карлика»? А как обстояло бы дело, если бы учитель
при определении «великанов» искал бы их в рядах,
а не в шеренгах, т. е. точно как же, как искал «кар-
«карликов»?
60. Ученики классов А и J5. В школе есть два клас-
класса: А и В. Ученики класса А хвастаются, что они выше
ростом, чем ученики класса В, а ученики класса В
считаются лучшими математиками. Когда однажды
один из учеников класса А свысока посмотрел на уче-
ученика класса В, тот спросил: что, собственно, означает,
что вы выше нас ростом? Значит ли это, что:
1) любой из вас выше любого из нас?
2) самый высокий из вас выше самого высокого из
нас?
3) для любого из учеников класса А найдется уче-
ученик класса В ниже ростом?
30
4) каждый из учеников класса В ниже хотя бы од-
одного из учеников класса А?
5) для каждого ученика класса А можно указать
ученика класса В ниже ростом, причем разным ученикам
класса А соответствуют разные ученики класса В?
6) Для каждого из учеников класса В можно ука-
указать ученика класса А выше ростом, причем разным
ученикам класса В соответствуют разные ученики клас-
класса А?
7) самый низкий ученик класса В ниже самого низ-
низкого из учеников класса А?
8) число учеников класса В, меньших ростом самого
маленького из учеников класса А, больше числа уче-
учеников класса А, меньших ростом самого высокого из
учеников класса В?
9) суммарный рост учеников класса А больше сум-
суммарного роста учеников класса В?
10) средний рост учеников класса А больше среднего
роста учеников класса 5?
И) среди вас больше таких, которые выше кого-либо
из нас, чем у нас таких, которые выше кого-либо из вас?
12) среди вас больше учеников выше нашего сред-
среднего роста, чем среди нас учеников выше вашего среднего
роста?
13) серединный по росту из вас выше серединного
по росту из нас (в том случае, если учеников в классе
четное число, серединным ростом считается среднее
арифметическое от роста серединной пары учеников)?
Ошеломленный потоком вопросов ученик класса А
стал как будто ниже. Мы спрашиваем читателей: за-
зависят ли эти вопросы друг от друга, а если зависят, то
укажите, какие именно? Другими словами, нужно
найти такие пары вопросов, для которых положитель-
положительный ответ на один из них предопределяет положитель-
положительный ответ и на второй. Существуют ли эквивалентные
вопросы, т. е. существуют ли такие пары, для которых
ответы на оба вопроса обязательно должны быть одина-
одинаковы? Существуют ли пары вопросов зависимых, но
не эквивалентных?
61. Статистика. Некий статистик решил исследовать,
как используются купе для некурящих на железных
дорогах в различных странах. Он выделил следующие
возможности:
31
a) курящие чаще всего едут в купе для курящих,
а') не а («не а» обозпачает отрицание предложе-
предложения а),
b) некурящие чаще ьсего едут в купе для курящих,
V) не Ь,
c) в купе для курящих большей частью едут курящие,
с') не с,
d) в купе для некурящих чаще всего едут курящие,
dr) не d.
Каждую страну можно охарактеризовать с помощью
четырех букв а, &, с, d со штрихами или без; конечно,
ни одна буква не может появиться в символе одновре-
одновременно со штрихом и без, ибо каждый штрих обозначает
предложение, противоречащее предложению без штри-
штриха. Поэтому всех возможных символов имеется 16.
Можно ли в 16 поездах разместить путешественни-
путешественников так, чтобы каждому поезду соответствовал иной
символ?
62. Группы крови. Как хорошо известно (Ланд-
штейн, Янский, Мосс и др.), У людей бывает 4 группы
крови: О, А, В, АВ (терминология Дангерна и Хирш-
фельда; эта классификация дает возможность выяснить,
может ли данный человек служить донором для опре-
определенного другого человека). Обозначим символом X ->
->- У утверждение: «индивидуум с группой крови X
может дать свою кровь индивидууму с группой кроки
У без опасности для последнего». Тогда законы, откры-
открытые названными выше учеными, могут быть сформули-
сформулированы так:
I. X ->- X для любого X.
II. О ->- X для любого X.
III. X -> АВ для любого X.
IV. Любое отношение X -»- У, не сводимое к I, II
и III, является ложным.
Доказать, что
1° Система законов I—IV невротиворечива.
2° Из законов I—IV следует, что при любых X,
У, Z из X г->- У и У -> Z вытекает, что X -»- Z.
3° Из I—IV следует, что отношение А -> В ложно.
Пояснение. Выражение «для любого X» в
I, II, III означает, что импликация -> справедлива
для X, совпадающего с О, Л, В или АВ» Аналогичное
замечание относится и к 2°.
32
63. Снова о группах крови. Феликс Бернштейн (чье
имя ассоциируется у нас обычно с теорией множеств*))
первым сформулировал законы наследования групп
крови О, А, В, АВ. Предположим, например, чтр отец
имеет группу крови А, а мать — группу АВ> Припи-
Припишем к однобуквенному символу А букву О, т. е. мы
обозначим группу, к которой относится отец, через АО.
Группы обоих родителей будут, следовательно, АО и
АВ. Для составления символа группы крови их по-
потомства мы должны взять одну букву символа крови
матери и одну букву символа крови отца. Мы полу-
получим, таким образом, следующие возможные символы
группы крови ребенка: А А, АВ, О А иОВ. Затем эти сим-
символы упрощаются: вместо двух букв АА можно писать
просто А и можно отбросить букву О, где бы она ни
встретилась в двубуквенном символе. Итак, мы получи-
получили группы крови А, АВЬ А, В, т. е. ребенок может иметь
любую из трех групп крови А, В, АВ и не может иметь
группы О.
Указанные правила приписывания буквы О, ком-
бинщювания букв родителей, сокращения двубуквен-
ных символов из одинаковых букв и отбрасывания буквы
О полностью определяют (причем не только в приве-
приведенном выше примере) так называемую фенотипическую
теорию наследования групп крови. Правила допустимых
переливаний крови мы перечислили в задаче 62.
Два брата знают законы переливания крови и знают,
что никто из них не может дать свою кровь другому, но
каждый из них может получить кровь от матери.
Может ли их сестра заменить мать?
63а. Кассовая задача. Если у кого-либо имеется сум-
сумма денег в 5 злотых 27 грошей, то среди них обязательно
найдется сумма в 2 гроша **), в то время как сумма в
*) Еще в бытность Ф. Бернштейна студентом Гёттингенского
университета он доказал знаменитое утверждение Г. Кантора
(ныне известное как теорема Кантора—-Вернште й-
н а), лежащее в основе всей канторовской теории множеств
(если существуют взаимно-однозначные' отображения множества
А на подмножество множества В и множества В на подмножество
множества А, то между А и В можно установить взаимно одно-
однозначное соответствие).
**) В Польекой Народной Республике находятся в обращении
монеты достоинством в 1 грош, 2 гроша, 5 грошей, затем в 10
грошей, 20 грошей, 50 грошей, 1 злотый (=100 грошей) и денеж-
33
17 грошей может и не найтись. Мы понимаем под этим
следующее: без монеты в 2 гроша, либо двух монет по
1 грошу нельзя составить сумму в 5 злотых 27 грошей,
однако указанную сумму можно составить при наличии
купюры в 5 злотых и монет в 20 грошей, 5 грошей и
2 гроша^ в последнем случае мы никак не составим сум-
суммы в 17 грошей. После этого пояснения становится яс-
ясным смысл предложения* «Некоторая денежная сумма
обязательно содержит другие суммы».
Какая из денежных сумм от 1 гроша до 999 грошей
наверняка содержит наибольшее число различных
сумм?
636. Сады. На Бискупине во Вроцлаве имеются
сады, а в них различные сорта фруктовых деревьев.
Не зная точного числа, предположим, что существует
т садов и п сортов деревьев. Имеется $г таких садов,
в которых растет только по одному сорту деревьев
(не обязательно один и тот же во всех), имеется s2
таких садов, в которых растет только по два разных
сорта деревьев, и т. д. ..., имеется sn таких садов, в
которых растет по п сортов (следовательно, все сорта).
Имеется gx таких сортов деревьев, каждый из которых
растет тойько в одном саду, имеется g2 таких сортов,
каждый из которых растет в двух (и только в двух)
садах, и т. д. ..., имеется gm сортов, которые растут
в т садах (следовательно, во всех садах). Какие соот-
соотношения существуют между числами su s2, . . м sni gl9
64. Излишек труда. Если мы хотим вбить по гвоз-
гвоздю в каждый из нескольких десятков столбов, расстав-
расставленных на равных расстояниях вдоль дороги, то лучше
всего начать с первого, а закончить последним. Но как
сделать то же самое хуже всего, т. е. так, чтобы проде-
проделанный нами путь был самым длинным?
65. Диагональ прямоугольного параллелепипеда*
При помощи масштабной линейки измерьте диагональ
кирпича, имеющего форму прямоугольного параллеле-
параллелепипеда, т. е. расстояние между самыми отдаленными
его вершинами
ные купюры в 2 злотых, 5 злотых и т. д. В обращении отсутст-
отсутствуют монеты в 3 гроша, 15 грошей и денежные купюры в 3
8лотых и 25 злотых, (Прим, переев
34
Укажите практический способ, пригодный для ра-
работы в мастерских (а не школьный пример на приме-
йение теоремы Пифагора).
66. Перевязывание коробок. В кондитерских для
перевязывания коробок конфет цоступают так: лента
идет наискось и ббразует один замкнутый косой (не-
цлоский) восьмиугольник; на покрышке видны два
параллельных отрезка ленты, а внизу лента проходит
подобным же образом. Зная все измерения коробки,
можно вычислить длину ленты, а также под какими
углами она пересекает ребра коробки. И, наконец, мож-
можно доказать, что лента может быть смещена не только
вдоль самой себя, но также и по коробке.
66а. Другое перевязывание. Коробка, имеющая фор-
яу прямоугольного параллелепипеда, обычно перевя-
перевязывается накрест: шнурки пересекаются под прямым
углом в центре покрышки 1Уив центре основания Р.
Доказать, что прочное склеивание шнурков в N
и Р делает невозможным всякое их смещение.
67. Безмен. Безмен — это деревянный (или металли-
металлический) тонкий стержень (постоянной толщины), сде-
сделанный из однородного материала. На одном конце
к нему приделан довольно тяжелый груз, а на другом —
крючок, поддерживающий взвешиваемые предметы.
На стержне с помощью зарубок нанесена шкала, по
которой мы прочитываем (например, в килограммах)
вес подвешенного на крючке предмета. Для этого на
безмене нужно найти точку, в которой он, подпираемый
пальцем (или острием ножа), уравновешивается: соот-
соответствующее э;гой точке деление шкалы укажет искомый
вес. Шкалу легко сделать экспериментально, если
есть гири,—чем богаче их комплект, тем точнее будет
шкала.
Как составить шкалу геометрическим способом, если
у нас есть только одна гиря, например только кило-
килограммовая гиря?
68. Минимум длины. Линейка L прибита к столу,
а подвижная линейка R углом В скользит вдоль края
линейки L (см. рис. 134 на стр. 137), постоянно опираясь
своим краем о гвоздь О, вбитый в стол; этот край окан-
оканчивается углом А. При таком движении расстояние АО
при некотором положении линейки R достигнет мини-
минимума. Найти это положение и вычислить минимальное
35
расстояние АО, зная расстояние гвоздя от неподвиж-
неподвижной линейки и ширину подвижной линейки.
69. Деление на части прямоугольников и квадратов,
Если прямоугольник разделен на два прямоугольника, то
совершенно очевидно, что эта конфигурация возникла
в результате одного деления и не могла возникнуть ина-
иначе. Однако если мы разделим данный прямоугольник
на три прямоугольника, то никто не сможет угадать,
возникла ли эта конфигурация сразу же в результате
деления на три части или же поочередно в результате
деления первоначального прямоугольника на два,
а затем последующего деления одного из полученных
двух прямоугольников на два меньших. Будем говорить,
что деление прямоугольника на две части является пер-
первичным, а деление его на три части не явлется первич-
первичным. Точнее, мы называем первичным такое деление,
которое не может возникнуть в результате последова-
последовательного деления (совершенно безразлично, как оно
возникло в действительности). Это определение дал проф.
Лось, который заметил, что существуют первичные де-
деления на 2, б, 7, 8, ... частей и в то же время не бывает
первичных делений на 3, 4 и 6 частей. (Пусть читатель
сам докажет, что не существует первичных делений
на 3 и 4 части, и найдет первичное деление на 5 и:
7 частей; проф. Ч. Рылл-Нардзевский доказал, что
не существует первичного деления на 6 частей.)
1°. Указать пример первичного деления квадрата
на 5 равных частей.
2°. Указать пример первичного деления квадрата на
7 равных частей.
3°. Указать пример первичного деления квадрата
на 8 равных частей.
70. Практическая задача. Фабричная территория —
плоская, но отлогая. У нас имеются нивелировочный
инструмент, состоящий из горизонтальной люнетки,
вращающейся вокруг вертикальной оси (причем углы
поворота мы прочитываем по шкале горизонтального
круга), и веха, на которую мы наводим, чтобы прочесть
разность уровней, а также расстояние, на котором
установлена веха (благодаря двум горизонтальным
ниткам в люнетке и шкале на вехе). Как проще всего
определить наклон земельного участка и направление
наклона?
36
71. Соседние города. На карте Европы соединяем
каждый город с ближайшим к нему, предполагая при
этом, что расстояния между любыми двумя парами го-
городов не равны.
Доказать, что ни один город не будет соединен бо-
более чем с пятью соседними городами.
72. Железнодорожная сеть (I). Имеется пять горо-
городов; из них никакие три не лежат на одной прямой. Эти
города нужно соединить железнодорожной сетыр, со-
состоящей из четырех прямых дорог; при этом можно
провести железнодорожную линию одну йад другой
по виадукам.
Сколько существует таких различных железнодо-
железнодорожных сетей?
73. Железнодорожная сеть (И). Города А> В, С, D
лежат в вершинах квадрата со стороной в 100 км.
Нужно наметить железнодорожную сеть так, чтобы
каждый город был соединен с любым из остальных трех
городов (причем допустимо образование узловых стан-
станций в местах, отличных от А, В, С, D) и чтобы общая
длина линий была по возможности наименьшей. Какова
искомая сеть и какова ее длина?
74. Пробный полет. Самолет нового типа вылетел
из Осло, направляясь по кратчайшему пути к аэро-
аэродрому X, находящемуся в Южной Америке, на самом
экваторе. Свидетели отлета из Осло видят, как самолет
исчезает на горизонте в точке, лежащей точно на запад.
Какова длина трассы полета? В какой точке гори-
горизонта должны ждать самолета зрители, встречающие
его на аэродроме в X?
75. Солнце и Луна. Расстояние Солнца от Земли
в 387 раз больше, чем расстояние Луны от Земли. Во
сколько раз объем Солнца превышает объем Луны?
76. Космография. Вычислить длину самого коротко-
короткого дня во Вроцлаве. Решение требует знания двух уг-
углов. Каких?
ГЛАВА V
ШАХМАТЫ, ВОЛЕЙБОЛ, ПОГОНЯ
77. Шахматная доска. Пусть квадратная или пря-
прямоугольная шахматная доска имеет нечетное число кле-
клеток (например, 49 или 63). Клетки с общей стороной
будем называть смежными.
На каждой клетке шахматной доски расставляем
по одной пешке, затем собираем пешки и снова расстав-
расставляем на клетках шахматной доски.
Возможно ли, чтобы каждая пешка оказалась в
клетке, смежной с той, которую она занимала перво-
первоначально?
78. Еще раз о шахматной доске. На каждой клетке
шахматной доски ставим по пешке. Пешки собираем и
расставляем заново, но так, чтобы пешки, стоявшие
в левых углах, заняли свои прежние места и чтобы
дешки, которые были соседними (т. е. занимали смеж-
смежные клетки), снова стояли по соседству.
Возможно ли, чтобы какая-нибудь пешка оказалась
на другом месте, чем первоначально?
79. Ладья на шахматной доске. Шахматная доска,
которой мы воспользуемся, имеет столько же строк,
сколько и столбцов, но отличается от обычной шахмат-
шахматной доски тем, что расположение белых и черных клеток
может быть произвольным, лишь бы в каждом столбце
была до крайней мере одна белая клетка и лишь бы
по крайней мере один столбец был целиком белый.
Будем говорить, что нам удалось расположить ладьи
(а у нас их достаточный запас, так что недостатка в
них не будет) на шахматной доске, если мы удовлетворим
следующим условиям: 1) ладьи стоят только на белых
Хд 2) на шахматной доске стоит хотя бы одна
38
ладья, 3) ладьи не атакуют друг друга (т. е. они стоят
так, что не могут бить друг друга), 4) каждая белая
клетка, не занятая ладьей, но находящаяся по горизон-
горизонтали под угрозой ладьи, находится также под угрозой
некоторой ладьи и по вертикали.
Доказать, что всегда можно расставить ладьи со-
согласно требованиям 1), 2), 3) и 4).
80. Эллиптический бильярд. На эллиптическом
бильярде шар А лежит у края, а шар В — на отрезке s,
соединяющем фокусы эллипса. Нужно ударить шар А
так, чтобы, оттолкнувшись от края, он столкнулся с
шаром В\ однако запрещается пересечение отрезка s
шаром А перед ударом о край.
Доказать, что задача неразрешима.
81. Спортивная задача (I). В классе 25 учеников.
Из них 17 умеют ездить на велосипеде, 13 умеют пла-
плавать, а 8 — ходить на лыжах. Ни один из учеников не
владеет всеми тремя видами спорта, но как велосипе-
велосипедисты, так и пловцы и лыжники имеют хорошие или
удовлетворительные оценки по математике, что тем бо-
более знаменательно, так как шесть учеников имеют не-
неудовлетворительные оценки по этому предмету.
Сколько учеников имеют отличные оценки по ма-
математике? Сколько пловцов умеют ходить на лыжах?
82. Спортивная задача (II). 3 бегуна Л, В и С си-
систематически состязались в беге на 200 метров, замечая
после каждого пробега порядок, в котором они достига-
достигали финиша. Подводя итоги, они обнаружили, что в
большинстве состязаний А обгонял В и что в большин-
большинстве случаев В бежал быстрее С, а также, что в боль-
большинстве случаев С приходил к финишу раньше А.
Как это могло случиться?
83. Теория спортивных розыгрышей. Шахматный
клуб доктора Сильвестра Шарадека насчитывает 10 чле-
членов. Ежегодно происходят розыгрыши с целью раз-
разделения игроков на классы. Каждый играет с каждым
до первой результативной партии (ничьи не принимают-
принимаются в расчет). Будем говорить, что «А выигрывает у В»,
если А выиграл у В в классификационном розыгрыше
нынешнего года. Таких результатов после окончания
турнира будет 45, а игроки разделятся на классы, на-
например: на игроков, выигравших у восьмерых, вы-
выигравших у семерых, и т. д. (Заметим, что система
39
45 розыгрышей допускает возможность, что А выигры-
выигрывает у В, В выигрывает у С и С выигрывает у А.)
Вопрос касается возможных результатов класси-
классификаций. В частности, возможно ли, чтобы клуб был
разделен на три класса?
84. Объединение волейбольных команд. Лучшие
команды по волейболу образуют объединение, которое
устраивает сезонные встречи; каждая команда играет
один раз с любой другой. Может случиться, что одна
из команд победит все другие, но это не обязательно.
Поэтому согласимся называть чемпионом такую коман-
команду, которая победила любую другую либо обычным
путем, либо косвенно, т. е. через третью. Другими
словами, будем считать, что команда А победила ко-
команду 5, если существует команда С, проигравшая
команде А, но победившая в матче с В, Не будем, од-
однако, считать косвенной победой команды А над В,
если А побеждает С, С побеждает D, a D побеж-
побеждает В,
Доказать, что 1) розыгрыши в объединениях всегда
позволяют выявить одного или более чемпионов; 2) ко-
команда, которая непосредственно выиграла наибольшее
число встреч, всегда является чемпионом.
85. Турниры. Так называемая кубковая система
определения победителя из 8-ми спортсменов состоит
в разбиении игроков на пары с помощью жеребьевки.
4 матча определяют четырех победителей, которые уча-
участвуют во втором туре; третий тур соревнований яв-
является финалом. Победитель финального матча полу-
получает первый приз, а его соперник получает второй
приз. Будем считать, что каждый игрок имеет опре-
определенную силу (подобно тому, как каждый предмет
имеет определенный вес) и что более сильный игрок
всегда выигрывает у более слабого (подобно тому,
как более тяжелый предмет всегда перевешивает более
легкий, если они помещены на разные чаши весов).
В таких предположениях описанный выше процесс
годен для определения чемпиона, так как победитель
действительно будет сильнее всех своих соперников;
однако второе место вовсе не всегда будет занято вто-
вторым по силе игроком.
Какова вероятность того, что второй участник фи-
финального матча в самом деле достоин второго приза?
40
86. Велосипедист и пешеходы. Директор совхоза
отправил двух пеших посыльных: одного с письмом
на почту в город, другого — на четверть часа позд-
позднее — в противоположном направлении, в соседний сель-
сельсовет. Но вдруг сообразил, что перепутал письма и
выслал велосипедиста с поручением догнать обоих,
исправить ошибку и вернуться. Велосипедист пред-
предполагает, что оба посыльных идут с одинаковой ско-
скоростью и колеблется, догнать ли сначала того, который
вышел раньше, или того, который вышел позже. А так
как он едет быстро, то в обоих случаях исполнит по-
поручение.
Кто решит эту задачу, пусть скажет, каково было
бы решение, если бы директор не перепутал писем,
а только забыл бы дать посланцам деньгиги хотел бы
это исправить.
87. Четыре собаки. Четыре собаки Л, 5, С и D
стоят в углах квадратного луга и вдруг начинают го-
гоняться друг за другом, как указы-
указывают стрелки на рис. 2.
Каждая собака бежит прямо к
соседней: А к В, В к С, С к D, D
к А. Сторона луга равна 100 м, а ско-
скорость бега собак равна 10 м/с.
Через какой промежуток времени
собаки встретятся? Пересекутся ли
их пути и где? Какова длина каждо- с*
го пути?
88. Погоня (I). Корабль Р заметил корабль (?,
который плывет в направлении, перпендикулярном
к PQ, сохраняя свой курс. Корабль Р гонится за <?,
постоянно направляясь к Q; скорость обоих кораблей
в каждый момент одинакова (но может изменяться со
временем). Без вычислений видно, что Р плывет по
кривой линии; если погоня длится достаточно долго,
то траектория догоняющего корабля и траектория
убегающего корабля в конце концов становятся почти
идентичными. Каково будет тогда расстояние PQ,
если в начале оно было равно 10 морским милям?
89. Погоня (II). Корабль Ог замечает другой ко-
корабль О2, плывущий в момент наблюдения перпенди-
перпендикулярно к прямой ОгО2. Корабль О2 не замечает сигна-
сигналов Ог и сохраняет свой первоначальный курс и свою
41
скороть i?2. Корабль Ог хочет обратить на себя внимание,
так как ему необходима помощь, и с максимальной
скоростью vlf на которую он только способен, шщвет
в таком направлении, чтобы как можно ближе подойти
к 02. Какой он должен взять курс? Каково будет рас-
расстояние между обоими кораблями в момент наиболь-
наибольшего сближения, если начальное расстояние било рав-
равно d, а отношение скоростей vxlv2 равно к и меньше 1?
90. Действительно ли условия задачи неполные?
Кто-то, не очень внимательно прочитав предыдущую
задачу, рассказал ее доктору Шарадеку и спросил,
как определить курс, исходя из условий задачи. К со-
сожалению, он забыл, какой из кораблей имеет большую
скорость, а какой — меньшую, но помнил, что отно-
отношение скоростей к известно и меньше 1. Однако он не
знал, означает ли к отношение скорости сигнализирую-
сигнализирующего корабля к скорости замеченного корабля или на-
наоборот. И велико же было его изумление, когда мастер
тотчас же определил курс на основе неполных данных!
Каким образом доктор Шарадек сделал это?
91. Моторная лодка (I). Моторная лодка контра-
контрабандистов имеет втрое большую скорость, чем сторо-
сторожевой корабль, находящийся на расстоянии половины
пути от лодки к тому месту побережья, до которого лод-
лодка хочет добраться. Капитан лодки решает плыть к
цели вдоль двух сторон квадрата. Какая часть этого
пути будет опасной?
92. Моторная лодка (II). В предыдущей задаче
капитан лодки решил плыть так, чтобы по пути один
раз изменить курс на 90°. Какой он должен выбрать
рейс, чтобы наверняка обойти сторожевой карабль и
как можно быстрее достигнуть цели?
ГЛАВА VI
МАТЕМАТИЧЕСКИЕ ПРИКЛЮЧЕНИЯ ДОКТОРА
ШАРАДЕКА
93. Удивительное число. Доктор Шарадек решил
в корйе изменить математическую запись.. Он считает
большим недоразумением то, что существует число,
известное детям, начинающим учиться в школе, ко-
которое наряду с обычной записью имеет еще другую
запись, о которой эти дети узнают лишь несколько
лет спустя, а также еще и третью, очень сложную,
о которой (к сожалению!) они узнают в более зрелом
возрасте, причем никто им не говорит, что это — то
же самое число. Только доктор Шарадек и его друзья
знают этот секрет. Какое же это число?
94. «Сантиметр». Портные называют «сантиметром»
ленту с нанесенными на ней сантиметровыми делениями.
Доктор Сильвестр Шарадек имеет (разумеется) иной
«сантиметр», чем обычные смертные. Он выглядит так,
как показано на рис. 3 (нарисована только часть лен-
ленты), т. е. в начале ленты он имеет оковку в полсан-
полсантиметра. Доктор Шарадек утверждает, что его «санти-
«сантиметр» лучше обычного. Почему?
Рис. 3.
95. Игра в слова. Доктор Сильвестр Шарадек объя-
объявил, что он всегда может отгадать загаданное слово,
если ему будет разрешено задать 20 вопросов,, отвечать
43
на которые следует лишь словами «да» или «нет»,
и если загаданное слово имеется в словаре. Как вы ду-
думаете, не хвастает ли он?
96. Студенческие долги. Семь студентов живут в
одной квартире. В течение всего года они взаимно одал-
одалживают друг другу мелкие суммы денег. Доктор Силь-
Сильвестр Шарадек посоветовал им, чтобы каждый отмечал
у себя, сколько денег он взял взаймы и сколько дал
взаймы, но не записывал, у кого или кому одолжил
деньги. Перед отъездом на каникулы студенты решили
рассчитаться друг с другом, однако они не знали, как
это сделать. Достаточна ли такая бухгалтерия Шара-
дека для того, чтобы студенты могли расплатиться друг
с другом? Сколько в худшем случае необходимо сделать
выплат? {Выплатой мы называем вручение одному че-
человеку какой-либо суммы денег другим человеком.)
96а. «Криптоним № 2». Доктор Сильвестр Шарадек
решает любые задачи. Его друг, который хотел его ис-
испытать, принес ему 12 однозлотовых монет, на вид
одинаковых, и сказал: «Что касается одиннадцати,
то я уверен, что они не фальшивые, но двенадцатая
может быть фальшивой, однако я не знаю, легче она
или тяжелее обычной». Говоря это, он высыпал монеты
на стол и воскликнул: «Теперь я уже не знаю, которая
из них подозрительная, но ты Сильвестр, наверное,
обнаружишь это в результате трех взвешиваний,
причем без разновесок, на обычных весах с двумя
чашками». Мастер ответил: «Я сейчас же это сделаю
благодаря моему безошибочному методу, называемому
„криптоним № 2"». Сказав это, он сложил монеты в
ряд и написал на них мелом буквы К, i?, Yy P, Г,
О, N, I, M, J9, W, А9 так что каждую монету обозначил
одной буквой. Затем он проделал три взвешивания,
каждый раз укладывая на весы сразу по четыре монеты
на каждую чашку. Его приятель с удивлением заметил*
что буквы сложились в слова:
Левая чашка Правая чашка
I взвешивание MYTO RAKI
II взвешивание MOD A WJNT
III взвешивание WYKA PION
Но через минуту приятное лицо мастера потемнело
от гнева. «Бесчестный обманщик! —воскликнул он,—
ты хотел меня обмануть, MeHflt Сильвестра Шарадека,
44
доктора всех математических наук! Но это тебе не
удалось, ибо мой «криптоним № 2» разоблачил тебя!
среди твоих монет по крайней мере две фальшивые!»
Его друг с раскаянием сознался, что он виновен.
Исследуйте, смог бы мастер, если бы не подвох,
найти фальшивую монету и узнать, тяжелее она или
легче настоящей монеты, а если бы все монеты были
настоящими, сумел ли бы он обнаружить и это. Ска-
Скажите, каковы были результаты взвешиваний, которые
позволили мастеру заметить подвох. И, наконец, оп-
определите, мог ли приятель Шарадека так изменить вес
двух монет (оставляя остальным монетам их настоящий
вес), чтобы провести мастера вместе с его чудесным
«криптонимом № 2».
966. Кубики. Доктор С. Шарадек сообщил мне,
что сто лет тому назад на царских именинах появилась
делегация в 25 офицеров, по пять из пяти разных пол-
полков, причем каждый полк был представлен полковни-
полковником, подполковником, майором, капитаном и поручи-
поручиком, и генерал, возглавляющий делегацию, расставил
ее квадратным строем так, чтобы в каждом ряду стояли
представители всех рангов и всех полков и так же в
каждой колонне. Я спросил его, имели ли офицеры
ордена, причем ордена пяти разных наименований так,
чтобы каждый полк имел их все и каждый ранг имел
их все, но каждый офицер — только один? Не сбитый
с толку доктор Шарадек уверил меня, что именно так
и было, что в каждой колонне и в каждом ряду были
все ордена!
Перещеголяем фантазию знаменитого ученого и
составим 125 кубиков в большой куб, обозначив предва-
предварительно каждый кубик цветом (белым, голубым, зе-
зеленым, красным и желтым), буквой (А, В, С, Z>, E)
и номером A, 2, 3, 4, 5) так, чтобы было по 25 кубиков
каждого цвета, по 25 — каждой буквы и по 25 — каж-
каждого номера, а кроме того, так, чтобы каждый горизон-
горизонтальный слой кубиков был моделью строя, аналогич-
аналогичного описанному выше, причем даже тогда, когда мы
примем за горизонтальную плоскость любую грань
большого куба.
97. Странное общество. Один человек рассказал,
что однажды он оказался в обществе, состоящем (вместе
с ним самим) из двенадцати человек^ причем
45
а) каждый из них не был знаком с шестью другими
людьми, но знал всех остальных;
б) каждый принадлежал некоторой тройке знако-
знакомых между собой людей;
б) среди собравшихся нельзя было выбрать четырех
попарно знакомых людей;
г) среди собравшихся нельзя было выбрать также
ш четырех попарно незнакомых лиц;
д) каждый из собравшихся входил в тройку попарно
незнакомых лиц;
е) каждый мог найти среди незнакомых ему людей
человека, с которым он не имеет в этой компании общих
знакомых.
Услышав этот рассказ, доктор Шарадек заявил,
что однажды он был в обществе, в котором условия
б), в), г), д) выполнялись, но каждый знал ровно 6 че-
человек и имел знакомого, который мог познакомить
его со всеми остальными.
Поясните эти ситуации.
98. Счеты. Представьте себе счеты, состоящие из
10 горизонтальных проволок, а на каждой проволоке
по одной костяшке. Пусть эти костяшки передвигаются
с постоянной скоростью, одинаковой для всех, туда и
обратно по проволокам, поворачивая при ударе о сто-
сторону счетов. Начальное положение костяшек неизвестно.
Вертикальная ось симметрии
делит счеты на левую и пра-
правую половину. Пусть движе-
движение происходит так, что одно-
одновременно никогда не окажется
более семи костяшек в правой
половине счетов. Доктор
Сильвестр Шарадек утверж-
утверждает, что там никогда не ока-
окажется менее трех костяшек.
Прав ли он?
99. Поливание улиц. Род-
Родной город доктора Шараде-
ка имеет автоцистерну для
поливания улиц, но не
имеет подходящего гаража. Доктора попросили обо-
обозначить на плане города (который мы помещаем на рис. 4)
самое лучшее место для гаража, т. е. такова которое
4G
Рис. 4.
позволит кратчайшим путем объехать все улицы города
и вернуться в гараж. Доктор Шарадек выбрал свой
дом (на карте он обозначен темным квадратиком).
Поступил ли он правильно?
100. Французские города. Доктор Шарадек, знаю-
знающий хорошо стратегию, интересовался последней вой-
войной и в 1940 году познакомился с картой француз-
французского театра военных действий. Отсюда, вероятно,
и возникла следующая задача. Расстояние (по воздуху,
как и все расстояния в этой задаче) от Шалона до
Витри равно 30 км, от Витри до Шомона 80 км, от Шо-
мона до Сэн-Кантэна 236 км, от Сен-Кантэна до Реймса
86 км, от Реймса до Шалона 40 км. Вычислить в этом
замкнутом многоугольнике расстояние от Реймса до
Шомона. Без карты это умеет сделать только Сильвестр
Шарадек!
ГЛАВА VII
ЗАДАЧИ БЕЗ РЕШЕНИЯ
Решение некоторых приведенных здесь задач известны, ре-
решения же других задач до сих пор еще не найдены. В этом
разделе есть и легкие, и трудные зада-
Н—Ь h~H—Ь чи, однако решение какой-либо из них
_| -^ может свидетельствовать об умении само-
_ л- 4- 4- — стоятельно мыслить.
f_ -| Плюсы и минусы. Приведенная
I , слева фигура состоит из 14 знаков
«+» и из 14 знаков «—». Они рас-
i ставлены таким образом, что под
двумя одинаковыми знаками всегда
стоит знак «+», а под двумя различными знаками —
знак «—».
Если бы в первой строке было п знаков, то в ана-
4—— 4- + + ** логичной фигуре было
_ + _ + ~ (- + + — бы всего ^ л (л + 1)
1 - 4- ~» знаков (наш пример от-
4- 4- И— Ь + — --* вечает числу п, равно-
+ + ^ +^ + -+ мУ7).Таккак4-Аг(л+1)
L л- 4- 4- 4- есть ч^тное число при
JV+ + + л - 3, 4, 7, 8, И, 12
i I ^ и т. д., то можно спро-
, . сить, возможно ли для
, любого из этих п по-
_ строить фигуру, анало-
аналогичную нарисованной
и начинающуюся с п знаков в самой верхней строке.
В частности, мы спрашиваем о случае п = 12.
Общее решение до сих пор неизвестно. Приводим
решения ддя п = 12 (на стр. 48) и п = 20 (на стр. 49),
из которых путем отбрасывания первой строки полу-
получаем также решения для п = 11 и п = 19.
- ¦+- + - + + + +
+ + л +
Треугольник в треугольнике. Один треугольник
имеет стороны а, Ь, с, а другой — стороны а\ Ъ\ с'.
Какие условия, связывающие числа а, Ь, с, а', Ь', с',
необходимы и достаточны для того, чтобы первый тре-
треугольник можно было поместить внутри другого?
Части квадрата. Единичный квадрат разделен на
3 произвольные части. Пусть г — некоторое положи-
положительное число, меньшее 4
Всегда ли будет верно утверждение, что найдется
часть, содержащая по крайней мере 2 точки Р, Q с
PQ «г?
Деление окружности. На окружности длины 1 мы
отмечаем точку Р и откладываем от нее поочередно
дуги иррациональной длины v. Таким образом полу-
получаем точки Pl9 Р2, . . ., Рп> • • •> причем длина любой
дуги РцРц+х всегда равна v. Точки Р9 Plf . . ., Рп_х
делят окружность на п дуг. Доказать что точка Рп
окажется в наибольшей из них.
49
Лучи в пространстве. Три луча в пространстве ис-
исходят из общей вершины и образуют плоские углы
А9 Вг С. Какие из неравенств:
1) А + В > С,
2) sin A + sin В > sin С,
3) sin у Л + sin 1-В > sin i С,
4) sin2 A -f sin2 В > sin2 С,
5) sin2i^ + sin2
всегда верны, а какие — не всегда?
Неограниченная шахматная доска. На неограничен-
неограниченной шахматной доске ограничить фигуру, состоящую
из 100 квадратов, т. е. из 100 клеток шахматной доски,
таким образом, чтобы диаметр этой фигуры был по воз-
возможности наименьшим (диаметром называется наи-
наибольшее расстояние между точками фигуры).
Найти этот диаметр. Найти радиус наименьшего
круга, охватывающего 100 клеток шахматной доски.
Еще раз счеты. Пусть костяшки, о которых говорит-
говорится в задаче 98, занумерованы от 1 до 10. В любом поло-
положении их проекции на основание счетов дают одну
из возможных перестановок чисел 1, 2, 3, . . ., 10.
Пусть костяшки передвигаются по проволоке, как
и в задаче 98, каждая с постоянной, но отличной от
других скоростью, причем каждая скорость выража-
выражается целым числом см/с. Можно ли так подобрать эти
скорости, чтобы — независимо от начального положе-
положения — счеты дали во время движения костяшек все
возможные их перестановки (т. е. перестановки из
чисел 1, 2% 3, . . ., 10). Доктор Шарадек уверяет, что
он знает такое распределение скоростей, при котором
ни одна перестановка чисел не повторится, прежде
чем не появятся все другие!
Сравнивание весов. Имеется четыре предмета раз-
разного веса, а также весы без гирь. На весах можно
сравнивать вес любых двух предметов. Легко указать
способ, который дает возможность установить поря-
порядок весов данных предметов самое большее после пяти
взвешиваний. Доказать, что не существует такого спо-
способа, который бы гарантировал установление порядка
весов предметов после четырех взвешиваний,
50
Известно, что для 10 предметов существует способ
устанавливания порядка весов, требующий 24 взве-
взвешиваний; можно ли это число взвешиваний уменьшить?
Банки в ящике. В ящике формы прямоугольного
параллелепипеда, дно которого имеет размеры 186 мм
на 286 мм, можно плотно уместить 16 одинаковых же-
жестяных цилиндрических банок, имеющих высоту, рав-
равную высоте ящика, и стоящих основанием на дне его.
Однако какое-либо увеличение диаметра банок уже не
позволит их поместить в ящике. Каков диаметр банки?
Бактерии. Доктор Шарадек открыл вид бактерий,
которые размножаются удивительным образом. От пер-
первичной бактерии отрывается часть и становится само-
самостоятельной бактерией; обычно она короче оставшейся?
таким образом, появляются две бактерии различной
длины. От длиннейшей из них снова отрывается часть,
тоже короче оставшейся, и этот процесс длится до тех
пор, пока не приведет к остатку более короткому»
чем какая-нибудь ранее оторванная часть. Тогда
от длиннейшей из оставшихся отрывается часть, равная
по длине кратчайшей из оставшихся. Это единственное
правило (одновременно с неравным начальным разде-
разделением) достаточно для описания всего процесса раз-
размножения, однако нужно помнить, что в каждый мо-
момент самое большее одна бактерия делится на две.
Доказать, что в колонии бактерий никогда не бы-
бывает более трех различных длин, и если первое деление
было иррациональным, то постоянно будут повторяться
моменты, при которых окажутся всего только две раз-
личные длины, а также моменты, когда различных длин
будет три, и, наконец, возможно такое первоначальное
деление, при котором отношение длин сохранится при
всех дальнейших делениях на части.
Подъезжает цирк! Дети играют на лугу рядом с
шоссе. Вдруг замечают в том месте, где шоссе выбегает
из леса, шута на коне — это подъезжает цирк... Дети
хотят подбежать к шоссе, чтобы увидеть шута; стоящие
дальше уже не добегут, но хотят по крайней мере уви-
увидеть его как можно ближе. Все дети бегут с одинаковой
скоростью, но шут едет быстрее.
Нужно: а) начертить линию, отделяющую ту часть
луга, с которой можно добежать до шута, от остальной;
б) определить путь бегущих детей, находившихся на
51
этой линии; в) определить путь для детей, которые не
добегут вовремя; г) найти путь детей, которые успеют
добежать к шоссе прежде, чем шут их минует.
Тем, кто будет решать эту задачу, мы советуем
познакомиться с задачей 89.
Три ковбоя. Три ковбоя охраняют стадо на большом
квадратном пастбище. Ковбои хотят так разделить па-
пастбище, чтобы: 1) каждый из них отвечал за х/3 поля,
2) самая дальняя точка пастбища, за которую отвечает
ковбой А, находилась на таком же расстоянии от его
поста, как и самая дальняя точка пастбища, охраняе-
охраняемого ковбоем В, от поста ковбоя В и самая дальняя точ-
точка пастбища, охраняемого ковбоем С, от поста ковбоя С.
Кроме того ковбои хотели бы, чтобы: 3) это максималь-
максимальное расстояние было по возможности наименьшим и
4) чтобы в случае какого-либо происшествия к месту про-
происшествия всегда подъезжал ближайший из них.
Доказать, что задача неразрешима, и привести
решение, которое можно получить, отбросив одно или
же два условия.
Допрос. Судья: Итак, свидетель видел пожар?
А что свидетель делал непосредственно перед пожаром?
Свидетель: Я ходил по межам.
Судья: Как проходят межи в вашей деревне?
Свидетель: Параллельно и перпендикулярно
к шоссе.
Судья: Вы гуляли без цели?
Свидетел ь: Нет, идя от шоссе межами, я рас-
рассматривал поля соседей, ни разу не возвращался той
же межой и снова вышел на шоссе.
Судья: А пересекали ли вы свою дорогу?
Свидетель: Нет. Но помню, что около рапса
я проходил дважды, причем первый раз он был у меня
по правую руку, так что я мог видеть дом, а когда про-
проходил мимо него во второй раз, то он оказался по ле-
левую руку. Вот тогда я и услышал, что кричат «Горит!».
Судья велел арестовать свидетеля, как подозреваемо-
подозреваемого. Почему?
Стрелки на додекаэдре. Представим себе модель
правильного додекаэдра, на каждой из его граней на-
нарисуем стрелку ->; доказать, что найдутся две сосед-
соседние стрелки, т. е. помещенные на смежных гранях,
которые образуют уголл больший 90°.
РЕШЕНИЯ ЗАДАЧ
1. Прежде всего заметим, что в данной последовательности
каждая нечетная цифра может появиться только между двумя
четными цифрами.
Действительно, предположим, что два последовательных чле-
члена с, d рассматриваемой последовательности — нечетные. Тог-
Тогда могут иметь место два случая:
или число cd является произведением двух членов а, Ь дан-
данной последовательности, предшествующих членам с, d и не-
нечетных,
или же цифра с является последней цифрой произведений
двух членов а, Ъ данной последовательности, предшествующих
членам с, d и нечетных.
Таким образом, из предпосылки, что два последовательных
члена с, d рассматриваемой последовательности являются нечет-
нечетными, следовало бы, что два других члена этой последователь-
последовательности, предшествующие членам с, d, являются нечетными. По-
Поэтому из предпосылки, что два последовательных члена с, d
рассматриваемой последовательности являются нечетными,
следовало бы, что среди трех начальных цифр данной последо-
последовательности имеются две нечетные, что в действительности не
имеет места.
Из приведенного замечания, что в рассматриваемой последо-
последовательности никогда не выступают два соседних нечетных члена,
следует, что цифра 9 в данной последовательности не появится.
Действительно, цифра 9 могла бы появиться только в произведе-
произведении двух чисел не меньшем, чем 90, а произведение двух одно-
однозначных чисел всегда меньше 90.
Не может также появиться и цифра 7, так как единственным
двузначным произведением однозначных чисел разной четности,
в котором появляется цифра 7, является произведение 8-9 =
= 72, но цифры 9 в данной последовательности нет.
Мы не встретим также в этой последовательности и цифры 5,
ибо только два произведения однозначных чисел разной четности
содержат цифру 5, а именно, 54 = 6»9 и 56 = 7»8, но оба они
содержат такие цифры, которые не появляются в данной после-
последовательности.
2. Обозначим произвольное натуральное n-значное число
через
53
а сумму квадратов его цифр через
Li = «I + а\_х + . . . + а\ + а\ + о\.
Имеем:
L-Lt = A0»-» - ап) ап + A0»-» - «„-О ап_, + . . .
. . . + A03 - Ч)Ч + A02 - а3) а3 + (Ю - <h) Ч - («1 - *) «1-
Заметим, что
К - 1) <ц < 72.
Таким образом, если мы предположим, что гс J> 3, то (так
как ап =^= 0) будем иметь:
A0"-1 - nn) an > 99,
вместе с тем
(К)* — ai) яг > 0 для г = 2, 3,. . ., п — 1,
поэтому
Из последнего неравенства вытекает, что, исходя из данного
по меньшей мере трехзначного числа L и образуя описанным в за-
задаче способом последовательность
Ьг, L2, L3,. . . A)
сумм квадратов цифр, мы получим убывающую последователь-
последовательность, прка члены этой последовательности будут по меньшей
мере трехзначными; а так как они могут быть только натуральны-
натуральными числами, то, исходя из произвольного числа L, в котором
не менее трех цифр, после некоторого числа шагов описанного
в задаче процесса наверняка придем к не более чем трехзначному
числу. Отсюда следует, что достаточно проверить, верно ли
утверждение задачи для чисел самое большее трехзначных.
Предположим, следовательно, что дано трехзначное число
L, т. е. что п = 3. Тогда а3 ф 0 и получаем:
L — Lx = A00 — я3) а3 + A0 — а2) <% — {аг - 1) аг >
> 99—72 = 27,
или
Lt < L — 27.
Из последнего неравенства вытекает, что некоторый член пос-
последовательности A) является самое большее двузначным числом.
Пусть этим членом будет
Lq = 10/ + к.
Так как члены последовательности
не изменятся, если число Lq заменим числом 10& + /, то наше
предположение достаточно доказать для чисел Lq при условиях
54
Если Lq = 10/ + fc, а также / > к > 0 и / > 1» то Lq+1
является одним из чисел следующей таблицы значений выраже-
выражения f + к2:
\
1
2
3
4
5
6
7
8
9
0
1
4
9
16
25
36
49
64
81
1
2
5
10
17
26
37
50
65
82
2
8
13
20
29
40
53
68
85
3
18
25
34
45
53
73
ео
4
32
41
52
65
80
97
5
50
61
74
89
106
6
72
85
100
117
7
98
ИЗ
130
8
128
145
9
162
Из этой таблицы мы можем отбросить числа
1, 10, 100,
а также названные в условии задачи числа
145,20,4,16,37,58,89,
так как для них теорема верна. Кроме того, мы можем отбросить
числа
2, 40, 50, 52, 61, 73, 80, 81, 85, 90, 98, 130,
которые отличаются от предшествующих чисел или же от других
чисел таблицы перестановкой цифр или же приписыванием
цифры 0. Тогда останется 28 чисел, а именно,
5, 8, 9, 13, 17, 18, 25, 26, 29, 32, 34, 36, 41, 45, 49, 53, 64, 65, 68,
72, 74, 82, 97, 106, 113, 117, 128, 162,
для которых нужно проверить достоверность теоремы.
Результаты прокерки запишем в таблицу. В первом столбце
запишем число, для которого проверяем теорему, а во втором
столбце запишем поочередно члены последовательности A),
образованной именно для этого числа. Проверку прервем, если
дойдем до одного из чисел, для которых теорема верна.
5
8
9
18
32
36
49
25, 29,
64, 52
81
65, 61
13, 10
45, 41,
97, 130
85
17, 50
72
74
82
106
ИЗ
128
162
53,
65
68,
37
и,
69,
41
34,25
100
2
117, 51, 26, 40
55
Так как в каждом случае в конце концов приходим к числу 1
или же к одному из чисел
145, 42, 20, 4, 16, 37, 58, 89,
которые периодически повторяются, то указанная в задаче тео-
теорема доказана.
3. При делении степеней 5а, 4^, 3Y на 11 (где а, р, у обозна-
обозначают целые неотрицательные числа, не превышающие 5) полу-
получаем следующие остатки:
Число
50
51
52
5з
5*
5»
Остаток
1
5
3
4
9
1
Число
4°
41
42
4з
4*
4б
Остаток
1
4
5
9
3
1
Число
30
31
З2
З3
3*
Зб
Остаток
1
3
9
5
4
1
Обозначим соответственно через R Ea), R D^), R CY) ос-
остатки, полученные от деления чисел 5а, 4*\ 3V на 11. Остатки
эти можно прочесть по приведенной выше таблице. Обозначим,
далее, через к, т, п три произвольных неотрицательных целых
числа. Числа 56fe, 4б?п, 38П при делении на И дают в остатке еди-
единицу. Поэтому числа 55fc+flt, 45m+^, 35n+Y при делении на И дают
соответственно остатки R Ea), R D^), R CY). В таком случае
выражение
только тогда делится на 11, когда сумма R Ea) + R D^) +
+ R CY) делится на 11. Это имеет место при
к = т = nt а = 1, р = 2, v = 0.
Можно привести 14 других выражений типа A), делящихся
на 11. Их находят, выбврая из трех столбцов приведенной выше
таблицы по одному числу так, чтобы в сумме получить число, де-
делящееся на 11.
4. Выражение ап + Ъп делится на а + Ь, если п — нечет-
нечетное число. Поэтому число
делится на З3 +
7-13. Аналогично из равенств
Зю5
§ = C1L + D?)
следует, что данное число делится на 35 + 45 = 7'181 и на 3?
+ 42 в 49-379.
56
Заметим, далее, что
43 = _ 1 (mod 5)
(эта формула обозначает, что число 43 при делении на 5 дает
остаток — 1). Отсюда вытекает, что
4Ю5 = (_1)зв (mod 5),
следовательно,
4Ю5 = _ 1 (mod 5).
Подобным же образом З2 = — 1 (mod 5), отсюда следует, что
Зш == (_!)б2 (mod 5),
следовательно,
Зш = 1 (mod 5)
и
$Щ = 3 (mod 5)*
Так как
4Юб == _ 1 (mod 5) и зг°5 = 3 (mod 5),
то
Зю5 + 4105 = 2 (mod 5);
это означает, что число З105. + 4105- при делении на б дает в ос-
остатке 2.
Подобным же образом
43 = — 2 (mod li), откуда 41* = — 32 (mod 11),
а так как —32 ~ 1 (mod И), то
4^=1 (mod 11)
и, в конечном счете,
№ = 1 (mod И),
Точно так же убеждаемся в том, что
35 == 1 (mod 11), откуда 3*°§ == 1 (mod 11),
Поэтому
ЗЮ5 + 410§ == 2 (mod 11);
вто означает, что число 310& + 4105 при делении йа И дает в ос-
остатке 2.
5. Пусть существуют натуральные числа а?, у, г, п такие,
что п > z и хп + уп = Л Нетрудно заметить что х < л, у < *
и а; =? #; ввиду симметрии можно предположить, что х < у,
тогда
_ уп
57
вопреки нашему предположению, что хп + уп = zn. Отсюда сле-
следует справедливость сформулированного в задаче утвержде-
утверждения.
6. Можно привести много последовательностей чисел х1У
#2»» • •> #ю> удовлетворяющих условиям задачи* Вот две из них:
0,95 0,05 0,34 0,74 0,58 0,17 0,45 0,87 0,26 0,66
0,06 0,55 0,77 0,39 0,96 0,28 0,64 0,13 0,88 0,48.
Числа первой из этих последовательностей располагаются сле-
следующим образом в частях интервала [0,1]:
0,95
0,05
0,34
0,74
0,58
0,17
0,45
0,87
0,26
0,66
2
2
1
3
3
1
2
4
4
1
2
3
5
5
1
2
4
3
6
6
1
3
5
4
2
7
7
1
3
6
5
2
4
8
8
1
3
6
5
2
4
7
9
9
1
4
7
6
2
5
8
3
10
10
1
4
8
6
2
5
9
3
7
Эта таблица имеет следующий смысл. В столбце, помеченном
сверху числом 2, в первой строке выписано число 2, а во второй—
1; эю указывает на то, что 0,05 принадлежит первой половине
интервала [0,1], а 0,95—второй половине этого интервала.
Сказанное переносится, разумеется, на любой столбец таблицы.
Так, например, 6 в столбце, помеченном сверху числом 8, принад-
принадлежит строке, в левом столбике которой стоит дробь 0,74; это
указывает на то, что 0,74 принадлежит 6-й из тех частей интер-
интервала [0, 1], которые мы получаем при делении его на 8 равных ча-
частей /т. е. что — < 0,74 < — \ . Нетрудно проверить справедлив
\ 8 8 /
вость всех просуммированных в этой таблице данных. Поскольку
в каждом столбце мы имеем ровно столько чисел, сколько указы-
указывает число вверху этого столбца, причем все стоящие в одном
столбце числа различны, то условия задачи выполнены.
7. Система 14 чисел (п = 14), удовлетворяющих условиям,
аналогичным приведенным в предыдущей задаче, существует:
0,06 0,55 0,77 0,39 0,96 0,28 0,64
0,13 0,88 0,48 0,19 0,71 0,35 0,82
(она возникает путем дописывания чисел 0,49, 0,71, 0,35, 0,82
ко второй системе, приведенной в предыдущей задаче).
58
Расположение чисел этой системы в интервале [О, 1J сле-
следующее:
2 3 4 5 6 7 8 9 10 И 12 13 14
0,06
0,55
0,77
0,39
0,96
0,28
0,64
0,13
0,88
0,48
0,19
0,71
0,35
0,82
1 1 1
2 2 3
3 4
2
1
3
4
2
5
1
4
5
3
6
2
1
4
6
3
7
2
5
1
5
7
4
8
3
6
2
1
5
7
4
9
3
6
2
8
1
6
8
4
10
3
7
2
9
5
1
7
9
5
И
4
8
2
10
6
3
1
7
10
5
12
4
8
2
И
6
3
9
1
8
И
6
13
4
9
2
12
7
3
10
5
1
8
11
6
14
4
9
2
13
7
3
10
5
12
Так как числа 0,35 и 0,39 находятся между 5/15 = 0,33...
и 6/15 -- 0,4, то приведенную выше систему уже нельзя допол-
дополнить пятнадцатым числом с сохранением условия задачи.
Любопытно, что числа системы можно переставить таким
образом, чтобы условие задачи по-прежнему было выполнено,
например:
0,19 0,96 0,55 0,39 0,77 0,06 0,64
0,28 0,88 0,48 0,13 0,71 0,35 0,82.
А. Шинцель показал, что в общем случае ответ на вопрос
вадачи — отрицательный, следующим образом установив нераз-
неразрешимость ее для случая п = 75*).
Предположим, что числа х1ч х2,. • ., хъ удовлетворяют тре-
требуемым условиям. Тогда для некоторых натуральных i <; ^ 35
имеем
7 8 9 ^ ^ 10 (л\
Следовательно,
1 _l * < 1 а- 1 — 4П B')
хг-Х} ^ х{ ^9/35-8/з5 ^ 7/з5
и
/у» ____ /у» лп I 7/ А С\ К
3 * ! ~ ^ /35 /35 , 1U О /9Ч
х) М. Вармус (М. Warmus) совсем недавно доказал, что пос-
последним значением п, для которого задача разрешима, является
п = 17,
59
Пусть
егда, обозначается целая часть
и,
85 (»,-*,)-?<*<35 (*,-*,) + .?, C)
Через [х] здесь, как всегда, обозначается целая часть
числа х\ другими словами,
D)
-L<m<_L + i. E)
Из (З) и D) следует, что
а сопоставив E) и B'), мы получим
35<т<35+ —* + J_ + 1<76,
xj ~~ xi xi
ИЛИ
36 < т < 75. F)
Из неравенства E), кроме того, следует, что (т — 1) xt <
< I ^ тХ}, откуда
[{т — 1) х^ < [тх\]. G)
С другой стороны, в силу E), D) и A),
Аналогично, в силу B)
Комбинируя полученные неравенства, мы найдем, что
I + к < (т - i)xj <mxj<l+k+l,
60
откуда
[{т - 1) xjl = [mxjl (8)
Из G) и (8) следует, что
Nm-i = К» - 1) xj] - [(т - 1) xt] > [mxj] - [mxt] = Nm. (9)
Однако из условия задачи и из неравенства F) следует,
что последовательность чисел [(т — 1) х±], [(т — 1) #а],« . ¦
. . ., [(т — 1) a^^] получается из последовательности
0,1, .. м тл. — 2 простой перестановкой входящих в нее чисел
и, аналогично, последовательность [mzj, [тпа:2],. . ., Ima?m]
получается перестановкой из последовательности 0, 1,» # .
...? яг — 1.
Так как *, / < 35 < т — 1, то Nm_x — это число решений
неравенства xt < a?f < a?j в натуральных числах ? ^ m «-* 1 и
,ЛГт — число решений этого неравенства в натуральных чис-
числах t ^ тп. Следовательно, Nm_1 ^ l^m, что противоречит не-
неравенству (9). Это противоречие и завершает доказательство.
7а. Существует 90 перестановок. Однако если мы будем
считать перестановки, полученные путем замены букв, отли-
отличающимися несущественно, то получим только 90 : в = 15
различных групп перестановок, ибо существует в == 3! переста-
перестановок букв а, 6, с:
аЪс асЬ Ъас Ъса cab сЪа.
Выпишем из каждой из этих 15 различных групп переста-
перестановок одну перестановку, именно ту, в которой первой буквой
является а, второй, отличной от а, буквой является b, a третьей,
отличной от предыдущей буквы, является буква с:
1) ааЬЬсс (aabbcc — 1) 9) аЬЬсса (аЬЬсса — 9)
2) ааЬсЪс (ababcc •- 4) 10) аЬсаЬс (abcabc —- 10)
3) ааЪссЪ (аЪЬасс *— 7) 11) аЪсасЬ (аЬсЪас — 12)
4) ababcc (ааЪсЪс — 2)* 12) аЪсЪас (аЪсасЪ — 11)*
5) аЬасЬс (аЪасЬс — 5) 13) аЬсЪса (abcbca *— 13)
6) аЪассЪ (dbbcac — 8) 14) аЪссаЪ (аЪссаЪ —« 14)
7) аЬЪасс (ааЪссЪ — 3)* 15) аЪсбЪа (аЬссЬа — 15)
8) аЪЬсас (аЪассЪ — 6)*
Рядом с каждой перестановкой мы выписали в скобках пред-
представителя и номер той группы перестановок, которую мы полу-
получаем из перестановок данной группы, прочитывая их с конца.
В качестве представителя мы подбираем такую перестановку,
в которой первой буквой является а, второй, отличной от нее,
буквой будет &, а третьей, отличной от предыдущих, будет
буква с.
Совершенно очевидно, что группы 4, 7, 8 и 12 (отмеченные
бвездочками) не отличаются существенно соответственно от групп
2, 3, 6 и 11, если прочитывать их с конца. Поэтому групп пере-
перестановок, отличающихся существенно, всего И. Из них 7 групп
содержат по 6 перестановок, а 4 группы — по 12 перестановок.
61
8. Можно принять
Действительно, в силу легко доказываемого равенства
pqr = 1
имеем:
rp
Используя вторично равенство pqr = 1, мы можем из при-
приведенной выше пропорции получить другую, также обладаю-
обладающую требуемыми свойствами:
А:В:С =
8а. Обозначим выражение, симметричность которого сле-
следует доказать, буквой w. Легко заметить, что
для \x — i
для | а? — 1
Рассматривая еще случаи ж —- г/ !> О и я — i/^O, заклю-
заключаем, что
{4# для х — 2^0 и х — у^О,
4у для 2/ — а?>0 и y — z^O,
4г для z—у^О и z — 5
т. е. w = 4 max {ж, г/, г}, откуда непосредственно следует сим-
симметричность этого выражения.
9. Для х > 0 левая часть уравнения возрастает с возраста-
возрастанием х, и легко заметить, что при х = 1,5 она меньше 10, а при
я = 1,6 — больше 10. Поэтому корень уравнения лежит внутри
интервала A,5, 1,6). Запишем его как неприводимую дробь р/а.
Тогда уравнение примет следующий вид: р5 + рФ ~ 10^ ,
откуда следует, что р — делитель числа 10, следовательно, р
равно одному из чисел 1, 2, 5, 10. Однако выписывая дроби
с числителями 1, 2, 5, 10, сразу же замечаем, что ни одна из них
не попадает внутрь интервала A,5, 1,6).
10. Заметим сначала, что имеет место следующая лемма:
если р, q, х, у — положительные числа, то неравенства
влекут за собой неравенство
X ^
62
Действительно, по условию
1>1>0 и *
поэтому
следовательно,
В таком случае
X
следовательно,
X
+7'
X
X + р
У #
или 0
> у
У + Я
Таким образом, лемма доказана.
Так как А, В, С, а, Ъ, с, г — положительные числа, то
поэтому, согласно доказанной лемме,
А+а + В+Ъ ^ А + а ...
^ "Т с "Г
Подобным же образом получаем:
J_> L^ и В+Ь+С+с>С+с,
а следовательно, в силу доказанной леммы,
• С -\- с ^^ С + с /q\
- с + а +Т ^ С + с+ А + a + b+r ' *
Складывая неравенства A) и B), получим неравенство, правиль
ность которого мы и должны были доказать.
11. Уравнение 1 — z = z2 имеет один и только один положи-
тельный корень z = S—-—i . Следовательно, это z удовлетворя
ет уравнениям
Л ^ - -2 т ^ »2 73 7П —_ 7W+1 — 71+2
» • 4 1
Обозначив число zn через ал (тг = 0, 1, 2,. . . ) мы получим
нужную нам последовательность. Так как 0 < z < 1, предел
этой последовательности (геометрической прогрессии) равен 0.
Пусть теперь Ъо, &?,. . . — другая последовательность, удов-
удовлетворяющая условиям задачи, тв е, такая, что Ьо = 1 и
63
?n—bn+1 s= Ьп+2 при n = 0, 1,. . . Если эта последовательность
отлична от построенной выше геометрической прогрессии, то най-
найдется некоторый ее элемент bh, отличный от zte, т. е. такой, что
bit *= zli + <*» гДе ^ #= 0. Пусть Л — первый номер такой, что
bfr =? $\ так как &0 = 1 == z°, то & > 1 и, значит, существует
элемент Ък_г второй последовательности, совпадающий с эле-
элементом z^ первой последовательности: Ък_± = гк~г. Таким об-
образом, мы имеем
:«**.
Поскольку 2К+Р стремится к 0 при р -» oo, то для достаточно
больших р знак элемента Ь^+р определяется знаком выражения
± Cpd, абсолютная величина которого заведомо не меньше d.
Но целые числа ±Ср (коэффициенты при d) попеременно положи-
положительны и отрицательны, а значит, в последовательности {Ьп}
встретятся как положительные, так и отрицательные числа,
что противоречит условию задачи. Таким образом, предположе-
предположение о несовпадении последовательностей {Ьп} и {zn} приводит
к противоречию и, следовательно, последовательность {zn} до-
доставляет единственное решение задачи.
12. I. Предположим, что полученная фигура содержит
замкнутый многоугольник ABCDE. . .MN.
Предположим, кроме того, что AN < Л В, т. е. что точка
А соединена с точкой N, как с самой ближайшей. Тогда А В <
< ВС. Но точки В л С соединены отрезком, следовательно,
ВС < CD. Рассуждая подобным же образом, получим, далее,
что CD < D?"<...< MN <NA, т. е. что АВ < NA, а это
противоречит нашему предположению, что AN <АВ.
Так как при условии, что AN > АВЛ можно рассуждать
подобным же образом, то сделанное нами предположение ведет
к противоречию. Отсюда следует, что наша фигура не может со-
содержать замкнутого многоугольника.
II. Предположим, что образованная фигура содержит два
пересекающихся отрезка А В и CD (рис. 5).
Допустим, что точки А и В потому были соединены отрез-
отрезками, что точка В ближе всего расположена к точке А и что точ-
64
ка D ближе всего расположена к точке С Тогда
АВ < AD, CD < СВ, откуда АВ + CD < AD + СВ,
что противоречит утверждению, что в выпуклом четырехуголь-
четырехугольнике сумма диагоналей больше суммы его двух
противоположных сторон.
Таким образом, мы доказали и вторую
часть теоремы.
13. Для упрощения введем следующие
обозначения:
Докажем, что если а <С Ъ, то порядок
угол, чем
Рис. 5.
первоначальный порядок
дает меньший
#i, х2,. . ., xk_v а, Ъ, х
С этой целью достаточно сравнить углы Р^ОР^ в обоих по-
порядках. На рис. 6 угол Рк+1ОРк_х отвечает первоначальному
Рис. 7.
порядку, а угол Р'^ОР^— измененному порядку. Так как
ОР'к+1*= ОР"к+1(=: V г2+а2+&2), то следует доказать неравен-
неравенство Рк-nR" < Pk+1R'9 т. е. неравенство
аЬ ^ аЬ
которое вытекает из предположения, что а «< Ь.
14. Если в треугольнике ABC со сторонами а, 6, с дан
/_А = 60°, то ^ Я + Z С = 12°°» и шесть таких треуго-
треугольников можно уложить венком (рис, 7), ограниченным
65
извне правильным шестиугольником со стороной а, а изнутри
правильным шестиугольником со стороной Ъ — с. Вычисляя
площади обоих шестиугольников, получим формулу A), данную
в условии задачи.
В случае, когда в треугольнике дан /_А = 120°, то
/5 + /С = 60°; три таких треугольника укладываются
в треугольный венок (рис. 8). Рассуждение, подобное предыду-
предыдущему, дает формулу B).
15. Проведем прямую, которая пересечет стороны АХА2 и
А3А$ треугольника АгА2А% и разделит его периметр, равный 2р,
пополам (рис. 9). Примем прямые АгА2 и АгА3 за координатные
оси и пусть прямая CSC2 пройдет через точки С3(?+А, 0) и
С2@* д — X), где q = J~p, а К — произвольное число. Прямая
С3С2, конечно, делит пополам периметр треугольника А±А2АВщ
Рис. 8«
Рис. 9.
Из условия, что прямая С$С2 пересекает стороны АЛА2 и
f, а не их продолжения, получаем:
0 < q + Я < du9
— q, Л
<q. J
откуда
Совершенно очевидно, что из неравенства di < d2 + d$
следует неравенство 2dt < 2p, или dt < p, и что подобным же
образом d2 < p, d3 < р. Видно также, что из неравенства
р > rfg следует неравенство q^> ds — q и что подобным же об-
образом из неравенства р > йъ получаем неравенство q — d% > — q.
{Тоэтому систему неравенств A) мы можем заменить двойным не-
неравенством
q - d2 < % < d9 - q, B)
определяющим допустимые значения параметра X. Уравнение
прямой CSC2 имеет вид
_ I) х
0.
C)
Если, начертив треугольник АгА2Ав, мы измерили бы его
периметр 2р, а затем, поочередно подставляя различные число-
66
вые зпачения вместо параметра А,, определили для каждого зна-
значения Я точки С3, С2 и начертили прямую С3С2, то мы бы убеди-
убедились (рис. 10), что все прямые С3С2 касательны к одной и той же
кривой, которая является огибающей семейства прямых C),
Рис. 10.
Нетрудно подсчитать, что уравнением этой кривой будет
Аху = (р — х — уJ, D)
Кривая D) — парабола, ибо это — кривая второго порядка,
которая с каждой прямой, определенной уравнением у = х +
4- к имеет, независимо от значения параметра кг только одну
Рис. 11.
общую точку. Поэтому ось параболы D) параллельна прямой
у =?= х, т. е. биссектрисе угла А±. Подставляя в уравнение D)
вместо х и у поочередно значения у = 0 и х — 0, мы убедимся,
что парабола D) касается сторон угла Л1 в точках Т3 (/?, 0) и
^г@» P)t как показано на рис, 11* А так как треугольник ЛХТ2Т9
67
равнобедренный, то биссектриса угла At перпендикулярна к
T2Tg и делит этот отрезок пополам, т. е. является осью пара-
параболы D).
Подставляя теперь поочередно крайние значения параметра
к, определенные неравенствами B), получим при к = q — d2
прямую 48#з, касательную к параболе D) в точке Р3, с коорди-
координатами
=
а при X = d3 — q прямую А2В2, касательную к параболе D)
в точке Р2, с координатами
y = -
) — dzV
причем AiBa = р — d2, В3А2 = р —i di9 А±В2 г= р — d3i B2A3 =
= р — d\. Если через В\ обозначить точку, делящую сторону
Рис. 12.
А2А§ на отрезки р — ^ир — d29 то нетрудно проверить, что
точки Г2, Bit ^2» а также точки Г§, Bi, P§ расположены на одной
прямой. Видно также, что прямые Т2Вг и TBBi соответственно
параллельны биссектрисам углов А$ и А2. И, наконец, можно за-
заметить, что окружность, проходящая через точки Z?i, T21 Тв,
касается в них прямых Л2Л§, А3Т2> А2Т3.
Итак, каждая прямая, делящая периметр треугольника
AiA2A3 пополам и пересекающая стороны треугольника А\А2
и AsAi, касательна к дуге параболы D), и наоборот.
То же рассуждение можно применить к каждому из трех
углов треугольника. Таким образом, получим три дуги парабо-
параболы, которые вместе с отрезками общих касательных составляют
криволинейный треугольник Т (рис. 12).
Теперь мы можем сформулировать следующие выводы.
1Q Через каждую точку Р, лежащую внутри треугольника
AiA2A$, но вне треугольника Т, проходит одна и только одна
прямая, делящая периметр данного треугольника пополам.
Это — касательная, которую из точки Р можно провести к од-
одной из трех дуг параболы, указанных на рис. 12.
2Q Через каждую точку Р, лежащую внутри треугольника Г,
проходят три и только три прямые, делящие периметр данного
треугольника АiA2A3 пополам. Это — три касательные, которые
из точки Р можно провести к дугам парабол, указанных на
рис. 11.
3° Если на плоскости дано направление, то всегда можно
провести параллельную ему прямую, делящую периметр тре-
треугольника пополам. С этой целью достаточно провести по данному
направлению касательную к одной из дуг данной параболы.
4° Если даны два направления, то можно всегда провести
две параллельные этим направлениям прямые, каждая из кото-
которых делит периметр треугольника пополам. Общая точка Q
этих прямых лежит внутри кри-
криволинейного треугольника Т,
вследствие чего всегда, когда да-
даны две прямые, делящие пери-
периметр данного треугольника попо-
пополам, через их точку пересечения
Q можно провести третью прямую,
делящую периметр данного тре-
треугольника пополам.
5° Если дана система трех
прямых Zi, Z2, l3 (рис. 13), жестко
связанных между собой (напри- р *о
мер, начерченных тушью па цел- *
лофане), то всегда можно так рас-
расположить эту систему на плоскости, чтобы каждая из прямых
h, l2, h делила периметр треугольника А\А2А$ пополам.
Решение задачи дало довольно неожиданный результат:
точку, обладающую требуемым свойством, совсем не нужно
искать, так как каждая точка Q, о которой говорится в задаче,
обладает этим свойством.
Если бы мы треугольник заменили другой фигурой, напри-
например четырехугольником, то задача решалась бы подобным же
образом. Правда, вместо криволинейного треугольника Т полу-
получилась бы область, ограниченная четырьмя дугами парабол, но,
как и прежде, через каждую точку, лежащую внутри четырех-
четырехугольника, можно было бы — так же как и в треугольнике —
провести одну или три прямые, делящие периметр пополам. Если
же фигура имеет центр симметрии, то область, состоящая из
точек, через которые можно провести три прямые, делящие
69
периметр пополам, сводится к одной точке, и каждая пря-
прямая, проходящая через эту точку, делит периметр пополам.
15а. Сначала напомним, что центр тяжести трех произволь-
произвольных точек одновременно является и центром тяжести треуголь-
треугольника, вершинами которого служат эти точки. Воспользуемся
этим свойством и раздел ям тре-
треугольник ABC на треугольни-
треугольники ВСР, САРшАВР(^псЛА),
и массы каждого из них
поместим в их центрах тяжести
Aiy Bib C\. Эти массы равны,
так как равны площади тре-
треугольников ВСР, САР и АВР
(почему?), следовательно, Р
есть центр тяжести трех точек
Ai, #i, Си
16. Чтобы разделить тре-
рис# 14. угольник па некоторое число
треугольников так, чтобы
в каждой вершине образован-
образованной фигуры сходилось одинаковое число сторон, воспользуемся
правильными многогранниками, грани которых являются тре-
треугольниками. Это могут быть следующие многограппики: пра-
правильные тетраэдр, октаэдр и икосаэдр, и только они.
Если внутри тетраэдра мы выберем точку, лежащую близко
от центра одной из граней, и из этой точки спроектируем ребра
тетраэдра на плоскость, то получим фигуру, изображенную на
рис. 15. Она состоит из трех треугольников, соответствующих гра-
граням тетраэдра; четвертая грань при проектировании перешла в
Рис, 15.
Рис. 16.
Рис. 17.
большой треугольник ABC. В каждой вершине фигуры сходятся
три стороны, так как в каждой вершине тетраэдра сходятся три
ребра.
Подобным же образом, при помощи центральной проекции,
получим из правильного октаэдра фигуру, состоящую из семи
треугольников, в каждой вершине которой сходится четыре
стороны (рис. 16), а из правильного икосаэдра — фигуру, со-
состоящую из 19 треугольников, в каждой вершине которой схо-
сходится пять сторон (рис. 17).
Не существует фигуры, отвечающей условиям задачи и от-
отличающейся от изображенных на рис. 15—17, так как ей соот-
70
ветствовал бы правильный многогранник, отличающийся от трех
приведенных выше, а такого не существует — ср. со сказанным
в темах 70—80 (стр. 80—91) книги «Математический калейдо-
калейдоскоп»*) о так называемых Платоновых телах (или «правильных
многогранниках»): правильные многогранники с треугольными
гранями бывают только трех типов, отвечающих рис. 14—16;
соответствующие значения числа F частей плоскости (= числу
граней многогранника) суть 4, 8 и 20**).
17. Ответ на поставленный в задаче вопрос положителен.
Так как имеется только конечное число прямых, каждая из ко-
которых проходит через какие-нибудь две точки из данных 3/г
точек, то мы можем выбрать прямую, не проходящую ни через
одну из данных Зд точек так, чтобы все эти точки лежали по одну
сторону от нее. Если будем передвигать эту прямую по плоско-
плоскости, не изменяя ее направления, то все точки сначала будут ле-
лежать по одну сторону прямой, потом она поочередно минует точ-
точки первую, вторую, третью,. . ., Згс-ю. Положения прямой,
после того как она минует 3, 6,. . ., 3/г — 3 точек, делят плос-
плоскость на полосы, а в каждой из этих полос лежит только один
треугольник.
Точно таким же образом можно построить не пересекающие-
пересекающиеся и не вмещающие друг друга четырехугольники, пятиуголь-
пятиугольники и т. д.
18. Ответ на поставленный в задаче вопрос положителен:
в узлах сети можно поместить зна-
знаки плюс, минус так, чтобы усло-
условие задачи было выполнено.
Начнем с замечания, что если
решение задачи существует, то
могут иметь место только два
случая: Рис. 18. Рис. 19.
1) в трех вершинах каждого
равностороннего треугольника находятся только знаки плюс
(рис. 18),
2) в двух вершинах каждого треугольника находятся знаки
минус, а в одной вершине —• знак плюс (рис. 19).
Первый случай исключается.
Присоединяя к треугольникам как на рис. 19 отрезки, от-
отмеченные одинаковыми знаками, и соответствующие треуголь-
треугольники, мы можем построить бесконечную полосу (рис. 20).
*) См. ссылку на эту книгу на стр. 7.
**) Относительно доказательства этого (оно имеется во 2-м
польском издании «Математического калейдоскопа»), см.,
например, Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в,
И. М. Я г л о м, Избранные задачи и теоремы элементарной
математики, ч. 3, Геометрия (стереометрия), М., Гостех-
издат, 1954, цикл задач 3; Б. Н. Д е л о н е, О. К. Ж и т о-
м и р с к и й, Задачник по геометрии, М., Физматгиз, 1959,
задача 436 и след.; Г. Радемахер, О. Теплиц, Числа
и фигуры, М., «Наука», 1966, тема 14; Г. С. М. К о к с т е р,
Введение в геометрию, М., «Наука», 1966, гл, 10f
71
Мы видим, что по краям этой полосы в вершинах треуголь-
треугольников поочередно выступают: знак плюс, затем два энака ми-
минус — и дальше в том же порядке.
Отсюда следует, что, складывая соответственным образом
такие же полосы (рис. 20), мы можем всю плоскость покрыть
Рис. 20.
сетью равносторонних треугольников, удовлетворяющей усло-
условию задачи (рис. 21). Из построения сети, отвечающей условию
задачи, следует, что размещение знаков плюс и минус в узлах
этой сети единственно.
Рис. 21.
19. Предположим обратное, т. е. что можно покрыть плос-
плоскость сетью треугольников так, чтобы в каждом узле W сходи-
сходилось пять треугольников (рис. 22). Тогда сумма углов при вер-
вершине W четырех произвольных из этих
пяти треугольников должна была бы
быть больше 180°.
Возьмем произвольный треугольник
Ту принадлежащий сети (рис. 23). Тогда
треугольники сети, которые имеют с тре-
треугольником Т по крайней мере одну об-
общую точку, образовали бы шестиуголь-
шестиугольник S (рис. 24), в трех вершинах кото-
которого А19 А2, Л§ сходилось бы по три
треугольника, а в трех остальных вер-
вершинах Вг, В2, В3 — по два треуголь-
треугольника. К шестиугольнику S в вершинах
Av A2J $з прилегало бы по два тре-
треугольника (рис. 25), а в вершинах Bt,
В2, 2?3, прилегало бы, кроме упомянутых выше треугольников,
еще по одному треугольнику (рис. 26). Вся эта фигура, со-
состоящая из шестиугольника S и пояса прилегающих треуголь-
треугольников, была бы треугольником СгС2Съ (рис. 26). В каждой вер-.
72
Рис. 22.
шине этого треугольника сходилось бы по четыре треугольника
сети, сумма углов которых при этой вершине была бы меньше
180°, что противоречит сделанному в начале замечанию.
Противоречие приводит к выводу, что сети, описанной в за-
задаче, не существует.
20. Пусть ОА0= а, ОВ0=
= Ъ (рис. 27). По условию зада-
чи Ъ = ад, где
Сторона первого из отсеченных
квадратов равна aq, сторона
второго равна яд2, сторона
третьего равна яд3, и т. д. Рис. 23. Рис. 24.
Пусть ОАп = хп, АпВп =
~Уп (п = 1» 2,. . .)• Отрезки
ОА1 = xt, ОА3 = х3, ОАЪ = лгб, * . * образуют возрастающую
последовательность, а отрезки ОА2 = я2, ОА± == ж4, ОАъ —
= же, . . . образуют убывающую последовательность; обе эти
Рис. 25.
Рис. 26.
последовательности сходятся к одному и тому же пределу, яв-
являющемуся абсциссой х некоторой точки А. Так как О А х =
^ Б ЛЛ яд9, . .. , то
. = . ад .
1 — д
lim х2п+1 = а
Аналогично отрезки уг = ЛхВ^ у3 = Л3^3> 2/s ^ <^б^5»* • •
образуют убывающую последовательность, а отрезки у% ==
= А2В21 1/4 — ^4-^4» 2/6 = АъВв, . . . образуют возрастающую
последовательность; обе эти последовательности сходятся
73
к одному и тому же пределу, являющемуся ординатой у точки
А* Мы имеем:
у = lim г/„„ = ад* + ags -f ад12 + .. . = ag .
1 — (/*
Из прямоугольника останется точка ^4 с координатами
Она лежит на пересечении взаимно-перпендикулярных прямых
Ло?о и ЛхС.
п
С
о
^4
Рис. 27.
20а. Меньший четырехугольник (рис. 28) является паралле-
параллелограммом, так как его стороны попарно параллельны диагона-
диагоналям первоначального четырехугольника. Эти диагонали делят
большой четырехугольник на
четыре треугольника, а ма-
малый — на четыре параллело-
параллелограмма. Каждый из этих парал-
параллелограммов имеет площадь
вполовину меньшую площади
соответствующего треугольни-
треугольника, следовательно, площадь
меньшего четырехугольника
равна половине площади боль-
большого четырехугольника. Это
же. имеет место и в невыпук-
невыпуклом четырехугольнике(рис.29),
однако доказательство в этом случае отличается тем, что сложе-
сложение площадей соответствующих треугольников или параллело-
параллелограммов заменится вычитанием площадей.
21. Начертим квадрат S со стороной 1. Если два противо-
противоположных угла принадлежат одной и той же части, то это раз-
74
Рис. 28.
Рис. 29.
биение, очевидно, обладает нужным свойством, так как диаго-
диагональ S равна У 2, т. е. больше чем У65/64.
Пусть теперь каждые две противоположные вершины квад-
квадрата принадлежат разным его частям. Рассмотрим 2 случая:
1° существует часть, не содер-
содержащая вершин S;
2° каждый кусок квадрата со-
содержит одну или 2 его вершины.
Рис. 30 относится к случаю
1°, с рассмотрения которого мы и
начнем. Обозначим кусок, содер-
содержащий вершины А1 и А2, через
^-, а кусок, содержащий вершины
Bt и 2?2,— через W; последняя
часть квадрата, вовсе не содержа-
содержащая его вершин, пусть будет Чо,
Вертикальные отрезки Агк, А2М
имеют длины 1/4 и 1/2 соответ-
соответственно. Если М принадлежит части с& (если М ЕЕ ^), то мы бе-
берем Р = М, <?»= Аг и получаем PQ = У5/4 > Уб5/64, т. е.
снова получаем подтверждение требуемого свойства разбие-
разбиений квадрата. Если М 6Е сЗ?, то мы полагаем Р = М, Q — Вх
и получаем PQ = 1^5/4 > У65/64, как и выше. Если N
мы полагаем Р = N, Q = А2, в резуль-
результате чего имеем PQ = У" 17/16 > Уб5/64;
если Л" ЕЕ *$, мы берем Р = N, Q = B2
и получаем Р() = 5/4 > Уб5/64. Если
же ни М, ни JV не принадлежат частям
с^, «^, то обе эти точки обязательно при-
принадлежат части ^; но тогда мы можем
принять Р — Мл Q = iV, что дает
Р<? = /Шб > У65/64-
Перейдем теперь ко второму слу-
случаю — ему соответствует рис. 31. Обо-
Обозначим часть квадрата, содержащую
вершины Аг и А2, через «??, часть, со-
содержащую вершину В, — через &
и часть, содержащую вершину С, — через *??. Середина М ос-
основания J561 квадрата S может принадлежать «^, «^ или *??. Если
М лежит в «^, мы берем Р = ЛТ, (? = Аг и получаем Р<2 = У 5/4.
Если М G «^, то рассмотрим точку iV, лежащую на левой сторо-
стороне квадрата S на расстоянии 1/3 от Av Могут иметь место три
возможности:
Рис. 30.
(О
N е
{Hi) N (Е<8.
Мы полагаем Р — N вне зависимости от того, в какой части
находится N, но
выбираем Q = Аъ в случае (г) и получаем PQ = 1^65/64,
выбираем Q = М в случае (ii) и получаем PQ — У 65/64,
выбираем Q = С в случае (г и) и получаем P(J = 1^113/64 >
75
Если, наконец, М е %, то мы выберем на правой стороне
квадрата S на расстоянии 1/8 от правой верхней вершины точку
N' и дальше поступим, как и в случае ikf ЕЕ «35*; наклонные линии
на рис. 31 могут быть заменены други-
другими такими линиями, выходящими не из
N, а из N'.
Рассуждения здесь, по существу,
не будут отличаться от использован-
использованных выше, только части & и ^ квадра-
квадрата поменяются ролями.
Этим самым мы полностью доказали
требуемое утверждение. Исследуем те-
теперь вопрос о том, можно ли уси-
усилить утверждение задачи, заменив чи-
число У 65/64 « 1,008 на большее (напри-
(например, на 1,01). Ответ на этот вопрос яв-
является отрицательным, что можно доказать следующим при-
примером. Разобьем единичный квадрат на 3 равновеликие части
^, i?, %, как показано на рис. 32. Трапеции «Я? и ^ конгруэнтны
и их общие стороны имеют длину 11/24. Длина каждого верти-
вертикального отрезка, являющегося стороной 5-угольника, равна 1/8.
Рис. 32 нужно понимать следующим образом:
внутренняя часть 5-угольника принадлежит «^, внутренняя
часть левой трапеции принадлежит <^?, правой трапеции — ^.
Все точки сторон 5-угольника, за
исключением Сг Ez ^, целиком при-
принадлежат <?#. Стороны левой трапе-
трапеции принадлежат «^, кроме стороны
АЪА±, которая, по условию, принад-
принадлежит ^. Стороны правой трапеции
принадлежат <&, кроме А^Сг и корот
кой вертикальной стороны Л4#2дли-
ны 11/24,которая вся (за исключени-
исключением точки А± 6Е Jk) принадлежит ЗВ.
Легко видеть, что большая диа-
диагональ всех рассматриваемых мпо-
Рис' 32# гоугольников равна 1^65/64. Отсю-
Отсюда следует, что невозможно найти
пару точек Р, (), принадлежащих одной части разбиения, рас-
расстояние между которыми превышало бы 1^65/64. Отмеченный
пунктиром отрезок Л3^42имеет длину, равную У65/64, его кон-
цы принадлежат
б
2 Ду, ру 1,
Заметим, что это — единственная пара
й *)
ц рд , дая пар
точек, обладающая свойством, указанным в условии задачи *).
22. Обозначение узлов сети способом, указанным в условии
задачи, невозможно.
Для доказательства предположим обратное, т. е. что узлы
сети можно обозначить так, как этого требует условие задачи,
*) Относительно намеченной в этой задаче проблематики
см., например, Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в,
И. М. Я г л о м, Геометрические оценки и задачи из комбинатор-
комбинаторной геометрии, М., «Наука», 1974, цикл задач 5,
76
и рассмотрим произвольную строку сети. В этой строке обяза-
обязательно имеются три следующих друг за другом узла, в которых
выступят три различные буквы, например буквы а, Ъ, с (в против-
противном случае строка могла бы содержать самое большее две разные
буквы, что противоречит условию задачи).
В последующей строке (см. середину рис. 33), ниже узлов,
обозначенных буквами я, Ъ, с, должны находиться узлы, соот-
соответственно обозначенные буквами с, d, а, если обозначение узлов
отвечает условию задачи. Тогда узлы следующей строки должны
быть соответственно отмечены буквами а, Ь, с (правая часть,
рис. 33).
Продолжая это рассуждение, мы видим, что в каждом из
трех столбцов рассматриваемого участка сети выступают только
—{#) Ф) ф—
Рис. 33.
две различные буквы: в первом выступают только буквы а, с,
во втором —- буквы b, d, в третьем — буквы с, а.
Итак, в узлах каждой строки и каждого столбца не могут
выступать четыре различные буквы, и следовательно, не сущест-
существует такого обозначения сети, о котором идет речь в задаче.
23. Если на окружности радиуса г с центром в точке
2, /з~)расположены две точки (#, у) и (u,v) нашей решетки, то
(х - УJ + (у -
(и - /2J + (и
(= г2)
откуда
с V2 + d /3 = и2 + у2 —
= п,
и п — целые числа*
где с = 2 (и — х), d = 2 (и — у)
Следовательно,
2с2 + Ъд? + led УЪ = п\
Но поскольку У% — иррациональное число, а с, d — целые чис-
числа, то предположение о том, что cd-=t= 0, приводит к противоре-
противоречию (в этом случае /б = п ~~ с — рационально), поэтому
слССь
cd ±= 0. Если .с = 0, то d /3 =и, что может иметь место лишь при
d = п = 0; аналогично, d = 0 дает с = 0. Следовательно,
с = d = 0, т. е. х = ut у = vt что и означает совпадение точек
(я, ^) и (и, у).
77
24. Определение целочисленной решетки дано в условии
вадачи 22.
Для любого г обозначим через / (г) число точек решетки,
находящихся внутри (не на границе!) круга радиуса г с центром
в точке A^2, V13). Из предыдущей задачи следует, что при воз-
возрастании г число / (г) увеличивается единичными скачками,
%1и покажем, что для достаточно малых г имеем / (г) = 0, а для
больших г величина / (г) принимает произвольно большие зна-
значения. Очевидно, что для г = 0,1 имеем / (г) = 0. Любой квад-
квадрат со сторонами, параллельными осям координат, длина кото-
которых больше натурального числа п, содержит по крайней мере
п2 точек решетки, потому что между прямыми х = а их = а + п
имеется по крайней мере п перпендикулярных рядов точек решет-
решетки и между прямыми у = buy = Ъ + п тоже заключено по край-
крайней мере п горизонтальных рядов точек решетки. Но круг радиуса
г > п содержит квадрат со сторонами, большими п (и параллель-
параллельными осям координат), и, следовательно, он содержит по крайней
мере п2 точек решетки, т. е. / (г) > п2 при г = п + 1. Таким
образом, мы выяснили, что / (г) — неограниченная функция,
звозрастающая от значения 0 единичными скачками, а следова-
следовательно, она принимает все целые положительные значения.
25. Ошибка заключается в том, что среднее арифметическое
элементов бесконечной последовательности зависит от
порядка рассматриваемых чисел (например, среднее чисел после-
последовательности 1, 0,1, 0, 1, 0, ... равно 1/2, а среднее тех же чи-
чисел, но упорядоченных следующим образом:
1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,
равно 0). Ложное равенство 14=15 вытекает именно из исполь-
вования различных способов упорядочения бесконечной последо-
последовательности, элементами которой являются углы семиугольни-
семиугольников, заполняющих плоскость.
26. Предположим, что для п точек, из которых никакие три
не лежат на одной прямой, можно найти замкнутый л-угольник,
вершинами которого являются эти точки; пусть п + 1 точек
расположено так, что никакие три из них не лежат на одной пря-
прямой. Среди этих точек есть одна, например, точка Р, которую
можно отделить прямой от остальных точек. Пусть Wn — много-
многоугольник, который согласно принятому предположению удовлет-
удовлетворяет условиям задачи и вершинами которого являются точки,
отделенные от точки Р.
Ответ на поставленный в задаче вопрос будет утвердитель-
утвердительным, если мы покажем, что по крайней мере одна из сторон мно-
многоугольника Wn целиком видна из точки Р, ибо тогда, заменяя
эту сторону двумя отрезками, соединяющими точку Р с концами
этой стороны, мы получим многоугольник Wn+V отвечающий
условиям задачи. Выберем какую-либо из сторон многоугольника
Wni например сторону AtAin (рис. 34). Если эта сторона пол-
полностью не видна из точки Р, т. е. если ее полностью или частично
васлойяет другая сторона многоугольника Wn, то через сторону
Л^$+1 проведем прямую и удалим все те стороны многоуголь-
многоугольника, которые эта прямая полностью отделяет от точки Р# После
этой операции число неудаленных сторон уменьшится по край-
ней мере на 1 (а именно на сторону AtAi+1). Эту же операцию
проделаем с остальными сторонами многоугольника, снова вы-
выбирая одну сторону произвольно.
Самое большее после тг-кратпого повторения такой опера-
операции на последней прямой будет лежать сторона, целиком види-
видимая из точки Р. Устраняя эту
сторону и соединяя ее концы
с точкой Р, мы получим иско-
искомый (п + 1)-угольпик.
Так как утверждение зада-
задачи является очевидным для
случая п = 3, то положитель-
положительный ответ на вопрос, постав-
поставленный в задаче, можно счи-
считать доказанным.
27. Проведем окружности /?о=
соответственно через точки 1,
2, За 1,2,4. Если точка 4 ле-
лежит внутри окружности 12 3
или точка 3 лежит внутри ок-
окружности 1 2 4, то ответ на
поставленный в задаче вопрос
будет положительным. Допу- Рис. 34.
стим поэтому, что ни одна из
этих возможностей не имеет места. Легко заметить, что тогда
дуга окружности 12 3, лежащая вне окружности 12 4 делит-
делится на три части 13', З'З" и 3" 2 (рис. 35) такие, что если точка
3 лежит на 13', то точка 1 лежит внутри окружности 2 3 4,
Рис. 35.
если 3 лежит на 3" 2, то 2 лежит внутри 1 3 4, и если 3 лежит
на З'З", то имеют место оба эти явления.
Заметим еще, что одна (рис. 36) или две из трех названных
выше частей дуги 1 2, могут исчезнуть. Однако всегда ответ аа
поставленный в задаче вопрос будет положительным.
79
28. Искомую кривую получаем, рассекая эллипс на четыре
части и складывая их так, как показано на рис. 37.
А вот еще другое решение, не требующее «переворачивания»
частей, т. е. выхода из плоскости эллипса. Соединяя поочередно
вершины эллипса хордами (рис. 38), получаем ромб, окружен-
окруженный четырьмя сегментами эллипса. Заменяем этот ромб, пло-
площадь которого равна 2а&, квадратом, площадь которого равна
Рис. 37.
с2 = а2 + Ь2, так, чтобы четыре сегмента эллипса по-прежнему
прилегали к сторонам квадрата. Площадь, ограниченная кривой,
увеличивается на разность площадей квадрата и ромба, т. е. на
с2 — lab = а2 + Ь2 — 1аЪ = (а — Ъ)\
29. Вместо всего пространства будем делить шар, через
центр которого проводим плоскости. На поверхности шара (на
Рис. 38.
ограничивающей его сфере) возникнут взаимно пересекающиеся
большие окружности. Примем одну из них за экватор и все эти
окружности спроектируем из центра щара на плоскость, каса-
касательную к шару в полюсе. Проекциями наших окружностей
(за исключением одной, являющейся экватором и вовсе ни во что
не проектирующейся) будут прямые. Следовательно, нужно вы-
вычислить максимальное число областей плоскости, разделенной
п — 1 прямыми. Методом индукции легко получить, что оно равно
1 + 1 -j- 2 + 3 + ... + {п «1) = 1 + J п (п » !Ь ибо при к «1
80
существующих прямых к-я прямая может увеличить число обла-
областей самое большее на к. Так как на сфере имеется вдвое больше
областей, чем на ее плоской проекции, то искомое число будет
вдвое больше вычисленного нами выше, следовательно, оно равно
п (п — 1) + 2. В частности, при п = 4 искомым числом явля-
является 14.
30. Легко проверить, что преобразование, о котором идет
речь в задаче, есть инверсия *). Действительно, пусть Пг и #2 —•
касательные плоскости к земному шару соответственно в точках
JV" и S (рис. 39). Пусть, согласно определенному в задаче пре-
преобразованию, точка Рг на плоскости Пг и точка Р2 на плоскости
Рис. 39.
П2 соответствуют друг другу. Рассмотрим сечение земного шара
и плоскостей Пг и #2 плоскостью, проведенной через ось NS
(рис. 40). Обозначив NPt = rlt SP2 = r2, NS = 2г, мы из по-
подобия прямоугольных треугольников NT Pi, STN, P2TS получим
равенство rfr2 = 4га, определяющее инверсию: если «поднять»
плоскость #2, совместив ее с П19 то точки Р^ и Р2 будут лежать
на одной прямой с центром N = S инверсии и NP1*NP2 = 4г2 =
= const.
31. Пряжа, наматываемая на куб, вращающийся вокруг
одной из осей (рис. 41), удержится только на тех ребрах, которые
не имеют общих точек с осью вращения; пряжа закрасит поло-
половину каждой грани куба, т. е. половину поверхности куба.
Теперь станем поочередно вращать куб вокруг каждой из
четырех осей, каждый раз наматывая пряжу иного цвета.
Так, при вращении вокруг оси АС используем пряжу цвета
а (черного), при вращении вокруг оси DB' — пряжу цвета Ъ
*) См., например, И. М. Я г л о м, Геометрические пре-
преобразования II, Мм Гостехиздат, 1956, §§ 1 и 4 гл. II; Г. С. М.
К о к с т е р, Введение в геометрию, гл. 6; Г. Р а д в м а х е р,
О. Теплиц, Числа и фигуры, тема 18; Д. Г и л ь б е р т,
С. Кон-Фоссен, Наглядная геометрия, М., Гостехиздат,
1951, § 36,
81
(красного), при вращении вокруг оси BD' — пряжу цвета с
(желтого) и, наконец, при вращении вокруг оси С А1 используем
пряжу цвета d (голубого).
Куб окажется закрашенным так, как это показано на рис.
42, на котором каждая грань разделена на четыре треугольника;
буквы, размещенные в соответ-
соответствующих треугольниках, обозна-
обозначают цвета пряжи, покрывающей
этот треугольник.
Легко заметить, что:
1° на поверхности куба вы-
выступит шесть оттенков, т. е. столь-
столько, сколько существует комбина-
комбинаций из четырех элементов по два,
а именно: аЬ, ас, ad, be, bd и cd\
2е на каждой грани будет че-
четыре разных оттенка;
3° поверхность куба будет по-
покрыта двумя слоями пряжи;
4Q противоположные грани
куба будут окрашены в те же
самые оттенки, расположенные
в обратном циклическом по-
порядке.
32. Докажем, что через каж-
каждую точку поверхности куба про-
проходят четыре различные геодезические, всего же мы имеем семь
семейств геодезических линий.
Если предположим, что куб гладкий, то резинка, обвитая
вокруг него, уложится таким образом, что периметр созданного
ею многоугольника достигнет минимума.
JJ
В
Рио. 41.
Три рода таких положений, а следовательно, три семейства
таких геодезических, приведены на рис. 43- они лежат на плоско-
плоскостях, параллельных граням куба. Чтобы убедиться, что возмож-
возможны еще другие семейства геодезических, рассечем куб плоскостью,
параллельной диагонали основания (рис. 44),
82
Тогда, используя обозначения, указанные на рис. 44, будем
иметь:
* + У = «>
= а
— 2х tg a, KL = я/
— 2у tg а, LM = у
+ 2 tg2 а,
+ 2 tg2a,
и для периметра р шестиугольника KLMNOP получим:
р = 2aV2 — 2a tg a + 2a /1 + 2 tg2 a."
Следовательно, периметр р зависит только от угла а и во всех
параллельных плоскостях остается таким же; периметр этот
Рис. 43.
У
/
/а
\ /
\/
\/
г
i
i
t
i
В
Рис, 44.
достигает минимума, если tg a = 1/1^2. Стороны шестиуголь-
шестиугольника KLMNOP будут параллельны диагоналям граней куба и
этот шестиугольник представляет собой геодезическую. Име-
Имеются четыре семейства таких геодезических, как это указано на
рис. 45, а следовательно, вместе с предыдущими тремя всего
семь семейств.
33. Взгляните на расположение шести кубов, представлен-
представленное на рис. 46. Мы считаем, что куб В возник из А путем отраже-
отражения от их общей грани, так же С из В, D из С, Е из Dt F из Е.
Вместо того, чтобы рассматривать движение частицы в кубе А
согласно законам отражения, мы можем исследовать движение
83
частицы в системе кубов А, , . ., F по прямой линии. Если дви-
движение должно проходить по замкнутому шестиугольнику, то
точка на передней грани А, с которой частица начала свой путь,
в результате названных выше отражений должна совпасть с точкой
Рис. 45.
на задней грани F, Если отрезок проведен так, как показано
на рис. 47, то он пройдет все кубы Л, . . ., F и не выйдет из них.
«Стягивая» кубы в один, т. е. отражая куб F в грани, отделяющей
G
6
Рис. 46.
Рис. 47.
F от Е, куб Е в грани, отделяющей Е от D, и т. д., мы получим
в качестве пути движения шестиугольник, показанный на рис. 48.
34. Все существующие развертки (которых всего И) мы при-
приводим на рис. 49. Шесть первых решений дают те развертки,
84
в которых четыре грани куба расположены в одной полосе раз-
развертки. Других решений этого типа не существует. Последующие
четыре развертки — это те, в которых есть три грани в одной
Рис. 48.
а
в
и
Рис. 49.
полосе, но нет четырех граней. И, наконец, в последнем реше-
решении ни в одной полосе нет трех граней.
35. Тела, образованные путем отсечения восьми углов куба,
имеют 14 граней (количество граней куба + количество вершин
85
куба). Восемь из них — это треугольники, шесть — восьмиуголь-
восьмиугольники (рис. 50).
Рис. 50.
При наибольших возможных октаэдрах грани четырнад-
цатигранника будут треугольниками и квадратами (рис. 51).
Так как октаэдр возникает
из куба путем отсечения
восьми тетраэдров (тре-
(треугольных пирамид) с осно-
основанием, равным 1/8 сторо-
стороны куба, и высотой, рав-
равной половине стороны ку-
куба, то тетраэдры займут
8444=4-частьпро-
странства. В каждой вер-
вершине сходятся шесть тел:
четыре четырпадцатигран-
ника и два октаэдра (вось-
(восьмигранника).
рис 51. 36. Нетрудно заметить,
что ответ на вопрос, постав-
поставленный в задаче, будет положительным: гексаэдром, отве-
отвечающим условию задачи, является параллелепипед, у кото-
которого равны ребра и равны три плоских угла при одной из
вершин,
86
Предположим, что дан ромб с острым углом а и диагоналями
2а и 2Ь. Складывая три таких ромба вершинами острых углов,
получим трехгранный угол. Как этот угол, так и его ортогональ-
ортогональная проекция на плоскость (вид с вершины) показаны на рис. 52.
Два сложенных вместе угла образуют
гексаэдр, о котором говорится в за-
задаче.
Заметим, что если а < 60°, т. е.
а г
если Ъ — a ctg^jr >а У 3, то гексаэдр
можно построить только описанным
выше способом. Если же а > 60°, т. е.
если а < Ь < а 1^3 или а > b/ У"з^
то из трех ромбов можно соста-
составить трехгранный угол не толькр
складывая их вершинами острых уг-
углов, но также вершинами тупых уг-
углов 180° — а (рис. 53). В этом случае,
кроме гексаэдра рис. 52, мы получим
удовлетворяющий условию задачи
гексаэдр, изображенный на рис. 53.
Если а = 90°, то а = Ъ и оба
гексаэдра являются одинаковыми те-
телами, а именно кубами.
На рис. 54 мы видим развертки
обоих гексаэдров, рассмотренных в
задаче.
Стоит еще заметить, что гексаэдры, изображенные на рис. 52
и 53, представляют собой пример двух различных выпуклых
многогранников с одинаковым числом попарно конгруэнтных
граней.
37. Ответ зависит от того, считаем ли мы различными или
нет два тетраэдра, получающихся друг из друга зеркальным отра-
Рис. 52.
Рис. 53.
жением. Мы покажем, что в первом случае существует 60 различ-
различных тетраэдров; во втором случае число их, очевидно, сокра-
сократится до 30.
Рассмотрим рис. 55, на котором изображен тетраэдр с реб-
ребрами, обозначенными буквами а, Ь, с, d, e, /. Пронумеруем стерж-
стержни, из которых мы собрали тетраэдр, числами от 1 до 6;
87
стержень может использоваться в качестве каждого из ребер
я, Ь, с, d, г, /. Следовательно, можно составить 6! = 720 тетра-
тетраэдров, правда, некоторые из них будут отличаться друг от друга
лишь положением в пространстве.
Временно предположим, что изображенный на рис. 55 тет-
тетраэдр является правильным. Выясним, сколькими способами
Рис. 54.
этот тетраэдр можно совместить сам с собою, перемещая его в про-
пространстве. Ясно, что расположение тетраэдра вполне определено
тек, 1Q какая из четырех граней тетраэдра переходит в основание
и 2° какое из трех ребер этой грани сов-
совмещается с одним фиксированным реб-
ребром основания, например, с ребром а.
Следовательно, существуют всего 3*4 =»
=^12 различных положений тетраэдра.
Поэтому 720 возможных перестано-
перестановок наших стержней, взятых в каче-
качестве ребер а — /, образуют каждый
тетраэдр 12 раз, и, значит, существуют
720 : 12 == 60 различных тетраэдров,
которые могут быть собраны из шести
различных стержней. Если отожде-
отождествить тетраэдры, получающиеся друг
отражением, то различных тетраэдров
е. 60 : 2 = 30.
Рис.
из друга зеркальным
будет вдвое меньше, т.
38. Возьмем два треугольника со сторонами а, &, с и нало-
наложим один на другой так, чтобы с была их общей стороной (рис. 56).
Рис. 56.
Рис. 57.
Рис. 58.
Раздвигая плоскости этих треугольников (рис. 57), мы увеличи-
увеличиваем расстояние между вершинами Сг и С2 (рис. 57) вплоть до
максимального расстояния при треугольниках, снова лежащих
в одной плоскости, но с противоположных сторон от А В (рис. 58) f
88
Обозначим расстояние СхСй на рис. 55 через dXi то же самое
расстояние на рис. 58 через d2. Условием существования тетра-
тетраэдра, отвечающего условию задачи, является, следовательно, не-
неравенство
dt<c< d2.
Для того чтобы имело место неравенство d, < с, необходимо
и достаточно, чтобы каждый из углов А и В был острый, а для
того чтобы выполнялось неравенство с < d2, необходимо и
достаточно, чтобы угол С был острый. Поэтому для существо-
существования тетраэдра необходимо
и достаточно, чтобы тре-
треугольник ABC был остро-
остроугольным.
Предположим, что так
и есть. На рис. 59 мы имеем
развертку тетраэдра, отве-
отвечающего условию задачи,
причем
АхВг || АВ, ЯЛ || ВС,
СХАХ\\СА.
Пусть
ВС = а, С А = Ь, АВ = с, а < Ъ < с, 2р = а + Ъ + с,
Сохраняя обозначения, используемые на рис. 59 и 60, заме-
замечаем, что высоту h— SO тетраэдра мы можем вычислить из пря-
прямоугольного треугольника SHxO, снчала вычислив SHX = AxHi
и НгО. Действительно,
е
= НгИа - ОНа, НхНа =
89
a 0Ha мы можем вычислить из пропорции
СгНа
вытекающей из подобия треугольников СгОНа и С
вычисление дает:
пп — (а2 + &2--с2) (д2 + с2 — б2)
Простое
4а у /> (/> — а) (р — 6) (/> — с)
Мы имеем теперь:
__ (а2 + б2 —
а - она)
с2 — Ь2)
+ с2 — а2)
И, наконец, обозначая объем тетраэдра через F, получаем:
v = A
= L- /(а2 + б2 _ С2)
6 У2
— 62)
39. 2п-гранник, отвечающий условиям задачи, существует,
и нетрудно указать способ его построения. С этой целью пред-
представим себе два параллельных круг-
круглых диска Тг и 7*2 одинаковых радиу-
радиусов, центры которых Ог и О2 лежат на
общем перпендикуляре к плоскостям
дисков Тг и Т2 (рис. 61). Разделим ок-
окружность каждого диска на п^З оди-
одинаковых частей, пусть точки Pi,P2,...,
Рп и точки Qi, Q2» • • •» Qn обозначают
соответственно точки деления окруж-
окружностей дисков Tf и Т2> Повернем диск
7*1 в его плоскости так, чтобы орто-
ортогональная проекция точки Р% на
плоскость диска Т2 совпала с цент-
центром дуги QkQk+i (проекция точки
Рп — с центром дуги <?„<?!).
На продолжениях отрезка ОХО2
отложим отрезки OtSi и O2S2 одина-
одинаковой длины h (рис. 61).
Затем соединим отрезком точ-
точку Si с каждой из точек Р^
а также точку S2 с каждой из
точек Qk. Подобным же образом
соединим каждую точку Р^ с точками Q^, Q^+r Таким образом
возникает остов 4/г-гранника, часть которого представлена на
рис. 61»
Рис. 61,
90
Докажем, что размеры этого многогранника можно подоб-
подобрать таким образом, чтобы он представлял собой 2п-гранник
с конгруэнтными друг другу гранями.
Действительно, пусть длина отрезка Ofi* равна g. Рассмот-
Рассмотрим четырехугольник S1P1Q2P2, Пусть М обозначает середину
отрезка Р\Р^ Для того чтобы названный выше многогранник был
2/г-гранником с конгруэнтными гранями, необходимо и доста-
достаточно, чтобы отрезок SiQ2 пересекал отрезок РХР2 в точке М*
Это условие будет выполнено, если будет иметь место равенство
откуда
ft: OXM = (Л + g)
(J\M
При п = 4 получим октаэдр, требуемый в задаче.
Можно доказать, что гранями 2п-гранника, отвечающего
условию задачи, являются конгруэнтные дельтоиды, которые
будут ромбами только при п = 3 (см. задачу 36).
40. В качестве требуемого тетраэдра рассмотрим пирамиду,
основанием которой служит равносторонний треугольник АВС9
а боковые грани являются равнобедренными треугольниками
А ВТ, ВСТ и CAT с углами при вершинах Т в 30°. Изобразим
на плоскости развертку пирамиды, получаемую, если разрезать
пирамиду по ребру СТ (рис. 62). Рассмотрим точку М — сере-
середину ребра А В и вершину пирамиды 7\ Среди всех линий, соеди-
соединяющих точки М и 7\ отрезок МТ имеет наименьшую длину —
это непосредственно следует из того, что МТ есть отрезок пря-
прямой не только на нашей развертке, но и в пространстве, а все
91
остальные соединяющие М и Т линии будут отличны от отрезка
прямой. Поскольку этот отрезок лежит на поверхности пирами-
пирамиды, то измеренное по поверхности расстояние между точками М
и Т равно длине этого отрезка. Однако мы еще должны показать,
что точка Т — самая дальняя от М точка поверхности пирамиды.
На рис. 62 АТС В — равносторонний и, следовательно, /_ТС'В
равен 60°, а /_ТС'М>Ь0°. Так как Z.CTM = 45°, то он меньше
/_ТС'М и, следовательно, ТМ>С'М. Отсюда следует, что если
точка S движется вдоль ребра С Г, то длина отрезка MS при ею
изменении от отрезка МС' до отрезка МТ все время увеличи-
увеличивается. Это показывает, что любая точка S ребра С Т находится
на меньшем расстоянии от точки М, чем вершина Т. Если теперь
q — произвольная точка треугольника С ТМ, то длина отрезка
MQ меньше длины отрезка MS, где S — точка пересечения
прямой MQ с ребром пирамиды СТ. Следовательно, расстояние
от М до Q по поверхности пирамиды тем более меньше длины М Т.
Очевидно, что в треугольнике СМА точка С дальше всего
удалена от точки М, а в треугольнике МА С такой точкой является
С\ остается заметить, что длины отрезков С'М ж МС меньше дли-
длины МТ. Так как, кроме того, развертка симметрична относи-
относительно прямой ТС, то доказано, что точка Т дальше всех осталь-
остальных точек пирамиды отстоит от точки М.
Мы предлагаем читателю, который хочет понять эту задачу
до конца, подумать, почему мы не взяли в качестве примера пра-
правильный тетраэдр.
41. Многогранник образует пространственную сеть, сторо
нами которой являются ребра, узлами — вершины, а ячейками-
Рис. 63.
Рис. 64.
грани многогранника. Дорога мухи должна образовать замкну-
замкнутую ломаную линию, без кратных точек, принадлежащую ука-
указанной выше сети. Возможность выделения такой дороги сохра-
сохранится, если мы деформируем сеть так, чтобы уместить ее на
плоскости.
На рис. 63 мы видим растянутую на плоскости сеть ребер
правильного додекаэдра. Жирной линией обозначен путь мухи,
отвечающий условию задачи.
Теперь подобным же образом растянем на плоскости сеть
ромбического додекаэдра (рисг 64). Узлы сети можно разделить
92
на два класса: на такие, в которых сходятся три ребра, и на
такие, в которых сходятся четыре ребра (на рисунке последние
обозначены черными точками).
Каждый узел первого класса соединен отрезком только с уз-
узлами второго класса, и наоборот. Поэтому муха во время своего
путешествия должна была проходить поочередно через узлы пер-
первого класса и узлы второго класса. Так как узлов первого класса
восемь, а узлов второго класса шесть, то муха не может посе-
посетить всех вершин ромбического додекаэдра, передвигаясь по
ребрам так, чтобы не пройти через одну вершину дважды и вер-
вернуться к исходной точке.
42. Расположим правильный додекаэдр так, чтобы иметь
одну его грань Р прямо перед собой; будем ее называть передней
гранью. Параллельную ей грань (невидимую нами) будем назы-~
вать задней гранью. Совокупность пяти видимых граней, окру-
окружающих переднюю грань, назовем кольцом /, а совокупность
пяти невидимых граней, окружающих заднюю грань, назовем
кольцом //.
Так как в задаче речь идет об определении числа способов
окраски граней додекаэдра, то мы можем додекаэдр заменить
Рис. 65.
Рис. 66.
плоским его изображением, как показано на рис. 65 (задней гра-
грани Т соответствует часть плоскости, лежащая вне большого пя-
пятиугольника), или еще более простым плоским изображением,
воспроизведенным на рис. 66.
Правильный додекаэдр нельзя выкрасить в три цвета так,
чтобы смежные грани всегда отличались окраской. В самом деле,
если бы, например, передняя грань была цвета А, то пять гра-
граней кольца /, смежных с передней гранью, следовало бы выкра-
выкрасить двумя цветами — В и С, что невозможно.
Предположим теперь, что грани додекаэдра можно выкра-
выкрасить в четыре цвета А, В, С, D требуемым в задаче способом.
Легко заметить, что тогда каждый из этих цветов выступал бы
три раза. Чтобы это обосновать, предположим обратное: что
какой-то цвет, например Л, выступает менее чем 3 раза, тогда
иной цвет, например В, выступал бы более чем 3 раза. Предпо-
Предположим, например, что передняя грань выкрашена в цвет В. Тогда
в кольце / цвет В не мог бы выступить, вследствие чего из шести
93
невидимых граней по крайней мере три должны были бы быть
цвета В. Однако это невозможно, ибо если бы задняя грань была
цвета В, то в кольце 77 цвет В вообще не мог бы выступить,
а если бы задняя стена не была цвета В, то в кольце // цвет В
мог бы выступить самое большее два раза.
Из приведенного выше рассуждения следует также, что
задняя грань не может быть такого же цвета, как передняя, но
должна быть такого цвета, который в коль-
кольце / выступает два раза.
Наконец, заметим, что, устанавливая
цвета кольца /, очередность, в которой
эти цвета выступают, а также цвет задней
грани, мы одновременно однозначно уста-
устанавливаем способ окраски всего двенадца-
двенадцатигранника. Действительно, например,
в случае, представленном на рис. 67, пе-
Рис 67 редняя грань должна быть цвета А. Что
же касается граней кольца //, то грань 1
не может быть иного цвета, кроме А ;в этом
случае грань 2 будет цвета D, грань 5 —- цвета В, вследствие
чего грани 3 и 4 будут соответственно цвета В и А. Рассмотрен-
Рассмотренный вами пример подтверждает, что окраска додекаэдра в че-
четыре цвета возможна.
Предположим, что передняя грань додекаэдра, раскрашен-
раскрашенного в четыре цвета, будет цвета А. Тогда в кольце / могут вы-
выступить шесть различных расположений цветов, так как при
каждом расположении цветов задняя грань может быть выкра-
выкрашена двумя различными способами; всего существует 12 воз-
возможных размещений цветов, как это видно из рис. 68. Но так как
в додекаэдре, выкрашенном в четыре цвета, грань цвета А вы-
выступает только 3 раза, то при выборе какого-либо способа окрас-
окраски из числа показанных на рис. 68 мы можем путем вращения
додекаэдра исчерпать самое большее еще два способа окраски,
т. е. всего три способа. Из этого следует, что способов окраски
додекаэдра существует самое меньшее четыре.
Легко можно убедиться, что существуют в точности четыре
способа окраски.
Действительно, при каждом из способов окраски, показан-
показанных в первой строке рис. 68, будут исчерпаны те способы, кото-
которые изображены в том же самом столбце.
42а. На рис. 69 представлена фотография модели додека-
додекаэдра с вписанным кубом; рис. 70 представляет параллельную
проекцию этого додекаэдра с вписанным кубом.
Куб можно вписать в додекаэдр пятью различными спосо-
способами *). На рис. 71 изображен один и тот же куб (тот, который
*) С существованием этих пяти кубов тесно связана невоз*
можность решения в радикалах общего уравнения 5-й степени,
на чем мы, однако, никак не можем здесь остановиться. (По
поводу связи учения о разрешимости в радикалах алгебраиче-
алгебраических уравнений с теорией правильных многогранников см., на-
например, Ф. К л е й н, Элементарная математика с точки зрения
высшей, те I, М4— Л., ОНТИ, 1935, стр» 190-237.)
94
Рис. 68.
I'nc. 69»
Рис, 70,
Рис. 71.
Рис. 72,
Рис. 73.
изображен и на рис. 70) и четыре других, пронизывающих его
куба, вписанных в додекаэдр.
Рис. 72 представляет осевое сечение додекаэдра с вписанны-
вписанными в него кубами; сечение тела, образованного всеми кубами,
доказано на рисунке жирной линией. Исходя из этого рисунка,
можно легко составить развертку или рисунок тела, образован-
образованного всеми кубами; им будет ввездчатый Ъ&О-гранник. Основным
элементом этого тела является пятилучевая звезда, образованная
из ребер кубов (рис. 73). Такая звезда соответствует каждой
Рис. 74.
грани додекаэдра; следовательно: всего их будет 12. Каждая из
них имеет в центре пятигранное углубление, окруженное пятью
трехгранными углублениями. Каждая звезда окружена пятью
четырехгранными углублениями, посредством которых она со-
соединяется с пятью соседними звездами (на рис. 73 показано толь-
только по две грани каждого из четырехгранных углублений).
Рис. 74 изображает прямоугольную проекцию тела, образо-
образованного всеми кубами со стороны граней описанного додекаэдра.
На нем видна центральная звезда, окруженная венцом пяти
соседних звезд, воспроизведенных на рисунке в искаженном
виде. Острия звезд по три сходятся в вершинах описанного до-
додекаэдра и образуют 30 двенадцатигранных башенок. Башенки
эти окружены равносторонними треугольниками, образованными
ребрами кубов. На рис. 75 показано тело в прямоугольной про-
проекции, видимое со стороны башенки, т. е. со стороны вершины
описанного додекаэдра. На рисунке видны три звезды, сходящие-
сходящиеся у данной башенки. Видны также три дальнейшие звезды,
прилегающие к предыдущим звездочкам.
97
Наконец, на рис. 76 изображена прямоугольная проекция
тела, видного со стороны грани одного из кубов, т. е. со стороны
Рис.. 75.
Рис. 76.
четырехгранного углубления, соединяющего соседние звезды
тела, или со стороны ребра додекаэдра.
Чтобы вычислить объем тела, легче всего начать с вычисле-
вычисления площадей всех частей, на которые делит грань додекаэдра
звезда, изображенная на рис. 73, а затем, используя рис. 72,
вычислить расстояния от грани додекаэдра до вершин углубле-
углублений звезды рис. 73. Это даст возможность вычислить объемы
пирамид, которые необходимо вычесть из объема додекаэдра,
чтобы получить объем звездчатого тела.
Если через а обозначим ребро додекаэдра, а через
Я = 2а
*— радиус описанной вокруг его грани окружности, то подсчет
даст нам следующие значения соответственно для площадей ос-
оснований и высот пирамид:
для каждого из трехгранных углублений
* = ПгG^5-15)
lb
для пятигранного углубления
Si = ^ G - 3 У 5) VlO + 2 VI,, *.== Л.C- V),
lb 4
для половины каждого из четырехгранных углублений
Поэтому, чтобы вычислить объем V1 звездчатого тела, сле-
следует из объема додекаэдра
4
вычесть двенадцатикратную сумму объемов перечисленных выше
пирамид, т. е.
12- -1
о
откуда, наконец, следует, что
? = 1.G9 У5"-175).
Остается установить, какое тело образует общая часть всех
кубов. Снова воспользовавшись осевым сечением додекаэдра
с вписанными кубами (рис. 77, на котором жирной линией обо-
обозначено сечение рассматриваемого нами сейчас тела), приходим
к выводу, что общая часть всех кубов является ромбоидальным
тридцатигранником, изображенным в параллельной проекции на
ряс, 78. А В является длиной большей диагонали, а АС — дли-
длиной меньшей диагонали ромба. На рис. 79—81 изображен тот
же тридцатигранник в прямоугольной проекции: со стороны
пятигранного угла (ось аа! на рис. 77), со стороны трехгранного
угла (ось bb' на рис. 77) и со стороны грани (ось ее' на рис. 77).
43. Возьмем произвольный выпуклый многогранник. Одну
из его граней примем за основание пирамиды с настолько
малыми двугранными углами при основании, чтобы многогран-
Рис. 78.
Рис.
ник, полученный из выпуклого многогранника путем пристройки
к нему этой пирамиды, был выпуклым и чтобы можно было в пер-
первоначальном многограннике сделать углубление, симметричное
этой пирамиде относительно избранной грани. Таким образом
получим два многогранника: выпуклый и невыпуклый, с гранями
выпуклыми и попарно конгруэнтными. На рис. 82 показаны два
100
многогранника ABODE и ABCDE'', полученных описанным выше
способом из тетраэдра ABCD.
Два тридцатигранника: выпуклый и невыпуклый, с выпук-
выпуклыми попарно конгруэнтными гранями изображены на рис. 83
и 84.
44. Примеры многогранников, удовлетворяющих условиям
задачи, мы видим на рис. 85 и 86. Многогранник, изображенный
Рис. 80.
Рис. 81.
на рис. 86, состоит из двух параллелепипедов с ромбоидальными
гранями, прилегающих друг к другу одной гранью.
Существует также невыпуклый ромбический додекаэдр.
Мы можем его получить из выпуклого ромбического додекаэдра,
Л
Рис. 82.
если удалим передний трехгранный угол (см. рис. 87, а) и заме-
заменим его задним трехгранным углом, передвигая его параллельно
по ребрам, образованным шестью остальными гранями (см. рис.
87, б).
Видно, что возникшее тело состоит из трех параллелепипе-
параллелепипедов. Если мы удалим один из них, то у нас останется тело, изо-
изображенное на рис, 86,
101
Рис. 83.
Рис. 84.
Рис. 85.
Рис. 86.
44а. Отыскание всех многоугольников, образованных реб-
ребрами правильного многогранника, способом, описанным в зада-
задаче, а особенно отыскание тех из многоугольников, которые отли-
отличаются только положением, а не формой,— особенно затрудни-
затруднительно в случае икосаэдра. Поэтому установим некоторый метод
решения, замепяя многогранники плоскими схематическими
изображениями их разверток (рис. 88). Это даст нам возможность
рассматривать данную задачу как задачу плоскую.
Рис. 87.
Соответствующее плоское изображение развертки мы можем
получить, если представим себе, что ребра многогранника —
растягивающиеся, и станем растягивать многогранник, начав,
например, с «задней» грани, так, чтобы все вершины многогран-
многогранника оказались в одной плоскости. Вершинам многогранника
Рис. 88.
соответствуют узлы плоской сети, ребрам соответствуют отрезки
или дуги, соединяющие узлы, а каждой грани многогранника
соответствует либо отдельная ячейка сети, либо внешняя область.
Обходу по ребрам многогранника соответствует обход по сторо-
сторонам и дугам плоской сети, а замкнутому косому (неплоскому)
многоугольнику, соединяющему все вершины правильного
многогранника, соответствует замкнутая ломаная, не имеющая
узлов и проходящая через все узлы плоской сети. Эта ломаная
имеет столько сторон, сколько вершин у данного правильного
многогранника, причем «сторонами» мы считаем также дуги
103
(впрочем, это зависит лить от рисунка, ибо плоские изображения
можно нарисовать так, чтобы они состояли из одних отрезков).
Чтобы можно было различать косые многоугольники, обра-
образованные способом, описанным в задаче, установим некоторую
систему их обозначения, приписывая им некоторые символы.
А именно: представим себе пловца, который плывет по ребру
А В многогранника лицом к многограннику. Доплыв до вершины
В, пловец имеет возможность выбрать количество дорог, равное
уменьшенному на единицу числу ребер, выходящих из одной
вершины данного много-
многогранника. Будем обозначать
эти дороги в той последова-
последовательности, в которой они
следуют одна за другой по
направлению вращения ча-
часовой стрелки, соответствен-
соответственно цифрами 0, 1 для пра-
правильного тетраэдра, куба
и додекаэдра, цифрами О,
1, 2 — для правильного
Рис. 89. октаэдра и цифрами 0,1, 2,
3— для правильного икоса-
икосаэдра.Таким образом, каждо-
каждому замкнутому косому многоугольнику проходящему через все
вершины многогранника, будет соответствовать символ, состав-
составленный из такого числа цифр, сколько вершин имеет многогран-
многогранник. Так, например, многоугольники рис. 89 соответственно
будут обозначаться символами 00110011 и 11001100, е.сли обход
их начнем от вершины А по направлению, обозначенному
стрелкой.
Заметим, что совершенно безразлично, с которой цифры мы
начнем прочитывание символа многоугольника, лишь бы мы после
последней цифры прочли еще пропущенные начальные циф-
цифры. Действительно, началу прочитывания символа многоуголь-
многоугольника с другой цифры соответствует начало обхода многогранника
с иной вершины. Поэтому два многоугольника рис. 89 иден-
идентичны, хотя и по-разному расположены.
Заметим, далее, что если дан символ многоугольника, то
легко можно написать символ многоугольника, полученного из
данного путем зеркального отражения (т. е. путем симметрии
относительно плоскости). Для этого достаточно заменить цифры
0,1 соответственно цифрами 1, 0, если символ составлен из цифр
0, 1, или заменить цифры 0, 2 соответственно цифрами 2, 0
(оставляя цифру 1 без изменения), если символ составлен из цифр
0, 1, 2, или же заменить цифры 0, 1 , 2, 3 соответственно цифра-
цифрами 3, 2, 1, 0, если символ составлен из цифр 0, 1, 2, 3. Так, на-
например, из двух многоугольников, представленных на рис* 89,
каждый возникает из другого путем симметричного отражения,
что следует из сравнения их символов.
Наконец, заметим, что каждый многоугольник можно обой-
обойти в двух противоположных направлениях. Обходя многоуголь-
многоугольник рис. 90, начиная с вершины Л, по направлению АВ% а за-
затем, начиная с вершины В, по направлению В А, мы соответст-
ственно получим символы 201201 и 12Q120. Второй из этих сим-
104
Рис. 90.
волов мы можем получить из первого, прочитывая его в обратном
порядке, при такой замене цифр, которая соответствует симмет-
симметричному отражению.
В случае, представленном на рис. 90, оба символа, которые
обозначают ту же самую замкнутую ломаную, проходимую в
двух противоположных направлениях, в сущ-
сущности, являются идентичными, ибо второй
символ, прочитываемый со второй цифры,
дает то же самое, что и первый. Однако не всег-
всегда так бывает. Например, замкнутая ломаная
рис. 91, обегаемая от Л к В, имеет символ
102302301132, а та же самая ломаная, про-
проходимая от В к А, имеет символ 102230130132.
Эти символы не являются идентичными, хотя
линии, представленные ими, отличаются лишь
направлением обхода.
Нетрудно объяснить этот факт. Если пловец плывет лицом
к додекаэдру вдоль ломаной (см. рис. 91) в направлении АВу то
по правую руку он будет иметь те грани додекаэдра, которые
на рис. 91 находятся внутри замкнутой ломаной. Плывя же вдоль
этой ломаной (см. рис. 91) в противоположном направлении, оп
будет иметь по правую руку то,
что останется от додекаэдра после
удаления из него тех граней, ко-
которые составляют внутренность
ломаной, изображенной на рис. 91.
Итак, введенный нами символ ха-
характеризует не только саму лома-
ломаную, но и часть многогранника,
принимаемую за ее внутренность.
Поэтому, если данная ломаная
делит поверхность многогранни-
многогранника на две одинаковые части (как
в примере, показанном на рис. 90),
то символ ломаной не меняется
при изменении направления об-
обхода. В противном же случае (как
на рис. 91) изменение направле-
направления обхода вызывает изменение
символа ломаной.Таким образом,при отождествлении многоуголь-
многоугольников необходимо помнить, что один и тот же многоугольник
может иметь два разных символа.
После этих предварительных замечаний, которые облегчат
нам перечисление и идентификацию многоугольников, отличаю-
отличающихся только положением, а не формой, мы можем перейти к
решению задачи, поочередно рассматривая различные правиль-
правильные многогранники.
Начнем с правильного тетраэдра, имеющего четыре грани.
Многоугольник, о котором идет речь в задаче, имеет, следова-
следовательно, четыре стороны. Такому многоугольнику соответствует
четырехзначный символ, записанный при помощи цифр 0 и 1.
В этом символе, однако, не могут выступать подряд ни две циф-
цифры 0, ни две цифры 1, так как они вызывают замыкание треуголь-
треугольника (рис. 92). Ввиду этого в символе многоугольника должны
105
Рис. 91.
выступать попеременно цифры 0 и 1. Единственным многоуголь-
многоугольником с таким символом является многоугольник 0101, так как
символ 1010 обозначает тот же самый многоугольник.
Следовательно, в случае тетраэдра задача имеет только одно
решение (рис. 93); при этом можно проверить, что, симметрично
Рис. 92.
Рис. 93.
преобразовывая многоугольник 0101 или обегая его в противо-
противоположном направлении, мы всегда получаем тот же самый много-
многоугольник.
В случае куба (восемь вершин) многоугольником, отвечаю-
отвечающим условию задачи, будет восьмиугольник с восьмизначным
символом. В этом символе не могут выступать подряд на три
цифры 0, ни три цифры 1 (ибо это вызывает замыкание четырех-
четырехугольника, см. рис. 94). В связи с этим в символе многоуголь-
многоугольника, отвечающего условию задачи, должны выступать как циф-
цифры 0, так и цифры 1. А так как многоугольник 01010101 не реа-
реализует условия задачи (рис. 95), то в символе каждого много-
многоугольника, отвечающего условию задачи, должны выступать
Рис. 94.
Рис. 96.
подряд или две цифры 0, или две цифры 1. Заменяя в этом послед-
последнем случае многоугольник симметричным ему многоугольником,
мы можем ограничиться перечислением многоугольников, про-
проходящих через ребро А В, символы которых начинаются двумя
цифрами 0. Остальные многоугольники (если они существуют)
мы получим путем симметричного отражения.
Однако существует только один многоугольник, отвечаю-
отвечающий этим условиям, а именно многоугольник 00110011 (рис. 96).
А так как зеркальное отражение даст нам тот же самый много-
106
Рис. 97.
угольник 11001100, то и в этом случае задача имеет только одно
решение (рис. 97). Нетрудно проверить, что, обегая многоуголь-
многоугольник 00110011 в противоположном направлении, мы получим тот
же самый многоугольник, т. е. замкнутая ломаная рис. 97 делит
поверхность куба на конгруэнтные части.
Перейдем теперь к правильному ок-
октаэдру (рис. 98). Замкнутая ломаная, от-
отвечающая условиям задачи, состоит из шес-
шести сторон, т. е. она имеет шестизначный
символ, составленный из цифр 0, 1,2. Так
как в таком символе не могут выступать
подряд три цифры 1 (ибо это вызывает за-
замыкание четырехугольника), то каждый
символ шестиугольника, отвечающего ус-
условию задачи, содержит по крайней мере
одну из цифр: 0 или 2. Заменяя в по-
последнем случае шестиугольник симметричным шестиугольником,
мы видим, что для решения задачи достаточно перечислить шести-
шестиугольники, проходящие, например, через ребро Л В, символы
которых начинаются с цифры 0. Существует три таких шести-
шестиугольника (рис. 99) с символами
[1] 012012, [2] 020202, [3] 021021.
Преобразовывая их симметрично, получим
шестиугольники
210210, 202020, 201201,
совпадающие соответственно с шестиугольни-
шестиугольниками [3], [2] и [1]. Отсюда следует, что при
преобразовании симметрии первый шести-
шестиугольник переходит в третий, третий — в первый,
рой переходит сам в себя.
Поэтому для правильного октаэдра задача имеет три реше-
решения: одно симметричное 020202 и два асимметричных: 012012,
021021 (рис 100).
Обегая каждую из полученных замкнутых ломаных в об-
обратном направлении, получим те же самые символы; это
Рис. 98.
а вто-
Рис. 99.
означает,что каждая из указанных замкнутых ломаных делит по-
поверхность октаэдра на конгруэнтные числа.
Для правильного додекаэдра (рис. 101) многоугольник, от-
отвечающий условию задачи, состоит из двадцати сторон и имеет
107
двадцатизначный символ, составленный из цифр 0 и 1. Так как
многоугольник
01010101010101010101
не отвечает условию задачи (рис. 102), то в символе каждого
многоугольника, отвечающего условию задачи, выступают под-
подряд по крайней мере две цифры 0 или две цифры 1. Заменяя в
Рис. 100.
последнем случае многоугольник симметрично отраженным много-
многоугольником, мы ограничимся перечислением многоугольников,
проходящих через ребро АВ,
символы которых вначале имеют
две цифры 0. Остальные много-
многоугольники (если они существуют)
мы получим путем симметрично-
симметричного отражения.
Исследуя поочередно все воз-
возможные случаи, мы можем легко
убедиться, что существуют четыре
многоугольника, проходящих че-
через ребро А В, символы которых
начинаются двумя цифрами 0 (рис. 103). Это многоугольники
Рис. 102.
[1] 00010101110001010111, [2] 00011101010001110101,
[3] 00101011100010101110, [4] 00111010100011101010.
Многоугольники [1], [3] идентичны; кроме того, идентичны
многоугольники [2] Л4], а многоугольник [2] получается из много-
многоугольника [1] в результате зеркального отражения. Каждый из
многоугольников [1], [2], обегаемый в обратном направлении,
дает тот же самый символ. Отсюда следует, что для правильного
додэкаэдра задача имеет два асимметричных и взаимно симмет-
симметричных решения; каждая из полученных замкнутых ломаных де-
делит поверхность додекаэдра на две конгруэнтные части (рис. 104).
Самым трудным является случай правильного икосаэдра
(рис. 105). В этом случае многоугольник, отвечающий условию
задачи, должен быть двенадцатиугольником, символ которого
построен из двенадцати цифр 0,1, 2,3. Пусть дан многоугольник
W с символом, например,
102123102123,
(W)
108
удовлетворяющий условиям задачи. Обозначим буквой S много-
многоугольник, образованный из многоугольника W путем симметрич-
симметричного отражения. Символ многоугольника S получаем, заменяя
цифры 0, 1, 2, 3 соответственно цифрами 3, 2, 1, 0:
231210231210. (S)
Затем обозначим буквой (S') символ многоугольника 5,
обегаемого в противоположном направлении; символ («S')
Рис. 103.
Рис. 104.
получаем, прочитывая в обратном порядке символ (W):
321201321201. (S')
Обозначим, наконец, буквой (W) символ многоугольника Wb
обегаемого в противоположном направлении; символ (W) по-
получаем, прочитывая в обратном порядке символ (S):
012132012132. (W)
109
Можно легко убедиться, что в символе произвольного
многоугольника, удовлетворяющего условию задачи, не могут
подряд выступать ни две цифры 0, ни две цифры 3 (ибо это вызы-
вызывает замыкание треугольника). А так как многоугольник
030303030303 не отвечает условиям задачи (см. рис. 105), то,
следовательно, в символе каждого многоугольника, отвечающего
условиям задачи, выступает по
крайней мере один раз цифра 1
или же цифра 2. Заменяя во вто-
втором случае многоугольник W
симметричным многоугольником
5, мы можем ограничиться пере-
перечислением таких многоугольни-
многоугольников, символы которых содержат
цифру 1. Остальные многоуголь-
многоугольники (если они существуют) по-
получаем путем симметричного от-
отражения. Докажем теперь, что
если символ многоугольника, от-
отвечающего условиям задачи, со-
содержит цифру 1, то он содержит
также и группу (комплекс) цифр
10 или 01, или же комплекс цифр
23 или 32 (а тогда символ симмет-
симметричного многоугольника содер-
содержит комплекс цифр 10 или же 01).
Действительно, если цифра 1 не выступает в комплексе
цифр 10 или 01, то обязательно выступит в одном из комплексов
И1, 112, ИЗ, 212, 213, 313 или в одном из комплексов, получен-
Рис. 105.
Рис. 106.
Рис. 107.
ных из предшеств ующих путем прочтения их в обратном поряд-
порядке. Заменяя в последнем случае многоугольник W многоуголь-
многоугольником S', мы можем ограничиться исследованием первого
случая.
Комплекс 111 не может выступить, если многоугольник W
отвечает условию задачи, ибо вершина е не могла бы тогда при-
принадлежать многоугольнику W (рис, 106),
110
В том случае, когда выступит комплекс 112 (или 113),
должно существовать соединение fej (рис. 107), которому соот-
соответствовала бы цифра 0 в вершине / и цифра 1 в вершине а,
т. е. комплекс цифр 01 в символе многоугольника.
В случае, когда выступит комплекс 212 (или 213), должно
существовать соединение cbe (рис. 108). Если бы вершина е
соединялась с вершиной /, то ломаной febc в символе многоуголь-
многоугольника соответствовал бы комплекс 10. А если бы вершина е со-
соединялась с вершиной/, то ломаной beja в символе многоуголь-
многоугольника соответствовал бы комплекс цифр 10.
И, наконец, если бы выступил комплекс 313, та должно
было бы выступить также соединение bid (рис. 109). Вершины
Рис. 108.
Рис. 109,
7, к не могут соединяться ни непосредственно между собой, ни
с вершиной /, вследствие чего должно выступить соединение
je или kg. Ограничиваясь из-за симметрии рассмотрением первого
случая, мы видим, что тогда возможны три следующих соеди-
соединения вершин е, Ъ: или еЪ, или ecb, или efcb. В случае соедине-
соединения еЪ ломаной beja в символе многоугольника W соответствует
комплекс цифр 10, а в случае соединения есЪ или efcb лома-
ломаной dibc в символе многоугольника соответствует комплекс
цифр 32.
Таким образом, мы констатируем, что если только в
символе многоугольника выступает цифра 1, то выступает так-
также и комплекс цифр 10 либо 01, или 23 либо 32. Поэтому заменяя
в случае надобности многоугольник W многоугольником S
и беря соответственно вместо символов (W) и (S) символы (Sf)
и (W), мы можем ограничиться перечислением таких многоуголь-
многоугольников, которые проходят через определенное произвольно вы-
выбранное ребро и символы которых начинаются с комплекса
цифр 10. Остальные многоугольники (если они существуют)
получим путем симметричного отражения.
Существуют два метода перечисления описанных выше много-
многоугольников. Один, аналогичный тому, который мы применяли
для додекаэдра, основан на исследовании всех возможных
рисунков. Другой состоит в комбинировании сначала трех,
111
а потом шести вершин, через которые могут проходить рассматри-
рассматриваемые многоугольники. Каждый из этих методов (детали опус-
опускаем) ведет к следующим многоугольникам:
1]
2]
3]
18]
19
0:
21
22;
23
24
25
26
27
102123102123 1
41
102132013023 [5]
102132020313 [6]
ь\
103022301123
103023030123
103023103023
103023110313
103030320123
[28
29
30
31
103031301132 [32
103032030132
103032102303
103032103032
103032110322
102230130132
102230202303
102230203032
102230210322
103103220123
103123011231
103130301231
103131030231
103131103131
[8]
[9
10
И
12
13
14
15
16
17
33
34
35
36
37
38
39
40
41
1023013.20123
102302301132
102303030132
102303102303
102303103032
102303110322
102310231023
102310320132
102312013203
102312102312
103201321023
103203201231
103213011321
103220123103
103220301321
103221023031
103221022302
103221030321
103221103221
Теперь остается отбросить из числа приведенных выше
многоугольников те, которые идентичны другим, и дописать
многоугольники, полученные путем симметричного отражения
и отличные от предыдущих.
(W)
2
3^
4:
5
6
7
[8
[10
И]
12
13
14
26
27
[32
[41]
(S)
[17]
[42] 231201313020
431
44
45
46
34]
21]
30]
29]
15]
221
20
19
18
14
230301230301
230301223011
230202230202
230112230122
(W) ((S) в
обратном
направлении)
in
[9]
[23]
[351
18]
[10]
[24]
[37]
[26]
127]
[41]
(S)((W) в
обратном
направлении)
[16]
[42]
[28]
[15]
[22]
[43]
144]
[46]
112
Сразу видно, что многоугольник [25] идентичен многоуголь-
[12],
[28],
л>азу
112],
нику 112], что обозначим символически равенством [25]
и подобным же образом: [31] = [21], [33] =±= [15], [36]
[38] = [13], [39] = 17], [40] = [27].
Отбросив многоугольники [25], [31],
[33], [36], [38], [39], [40], мы займемся
остальными, которых всего 34. Их симво-
символы выписаны в таблицу на стр. 112.
Из этой таблицы видно, что много-
многоугольники [9], [28], Г23], [35], [24], [37]
соответственно идентичны многоугольни-
многоугольникам [4], [34], [6], [7], [12], [13], и что, сим-
симметрично преобразуя многоугольники [3],
[26], [27], [32], [41], получаем новые много-
многоугольники, отличные от рассмотренных
выше.
В результате, для икосаэдра задача имеет 33 решения,
а именно: один симметричный многоугольник [14] и 16 много-
Рис. 110,
Рис.. 111,
ИЗ
угольников [1], [2], [3], [4], [5], [6], [7], [8], [10], [И], [12], [13],
[26], [27], [32], [41], симметричных 16 многоугольникам: [17],
[16], [42], [34], [21], [30], [29], [15], [22], [20], [19], [18], [43],
[44], [45], [46].
Из них многоугольники [2], [16], [3], [42], [8], [15], [10],
[22], [26], [43], [27], [44], [41], [46] делят поверхность икосаэдра
на конгруэнтные части.
На рис. 110 показано решение [14], и на рис. 111 приведены
16 остальных решений из столбца (W) предыдущей таблицы;
симметричных решений мы не помещаем.
Обход мы начинаем с нижней вершины,
а поочередные решения на рис. 111 рас-
расположены вдоль строк.
45. Три модели конусообразных пла-
планет, о которых шла речь в условии зада-
задачи, мы получаем из прямоугольной сети
меридианов и параллелей (рис. 112), рас-
рассекая ее одним из трех способов, указан-
указанных на рис. 113, и сворачивая затем
остальную часть в конус с вершиной
Рис 112 в точке ^#
На рис. 114 дан вид этого конуса
«сверху», т. е. со стороны вершины. Мы
ясно различаем два семейства кривых: «меридианы» и «парал-
«параллели». Меридианы не пересекают друг друга, параллели тоже, но
каждый меридиан пересекает каждую параллель в двух точках,
/1
/
f
lv
\
\
V
ч.
\
\\
]
/
/
Рис. 113.
как и на земном шаре. Кратчайшие пути имеют постоянное на-
направление, т. е. пересекают параллели и меридианы под посто-
постоянным углом.
На рис. 115 и 116 дан вид «сверху» второго и третьего конуса,
или проекции семейств кривых на плоскости, перпендикуляр-
перпендикулярные к оси конуса. На первом конусе имеется одно семейство кри-
кривых, на другом — три.
Стоит заметить, что приведенные решения не единственны.
46. Среди трех данных сфер нет двух, касающихся друг дру-
друга. В самом деле, в противном случае общая касательная плос-
плоскость этих двух сфер, проходящая через точку Р, пересечет
третью сферу по окружности. Касательная к этой окружности
114
в точке Р будет, очевидно, касательной ко всем трем сферам,
что противоречит условию задачи.
Итак, две сферы должны пересекаться по окружности, про-
проходящей, очевидно, через точку Р. Эта окружность не может иметь
Рис. 114.
Рис. 115.
с третьей сферой только одну общую точку, так как иначе каса-
касательная к окружности в точке Р была бы общей касательной
к трем сферам. Точка пересечения этой окружности с третьей
сферой, отличная от точки Р, при-
принадлежит всем трем сферам.
47. Пусть окружность К яв-
является сечением нашей поверхно-
поверхности S, и пусть L — ось окружно-
окружности К, т. е. прямая, проходящая
через центр К перпендикулярно
ее плоскости. Рассмотрим плос-
плоскость Р, проходящую через L\ она
высекает на S окружность, кото-
которую мы обозначим через С (Р).
Очевидно, С(Р) пересекает К
в двух диаметрально противопо-
противоположных точках А и В, Ясно, что
Л В является хордой окружности
С(Р), а ось L будет осью сим-
симметрии этой хорды. Как извест-
известно, ось симметрии хорды ок-
окружности проходит через центр этой окружности; поэтому L
проводит через центр С(Р) и пересекает эту окружность в диа-
диаметрально противоположных ее точках М ж N (которые, разу-
разумеется,суть точки пересечения ?и?).Следовательно,любая окруж-
окружность С(Р), получающаяся в сечении поверхности S произволь-
произвольной плоскостью Р, проходящей через прямую L, содержит одни и
те же точки М и N. Очевидно, не существует других точек ?,
принадлежащих S, так как если Q — такая точка, то сечение S
плоскостью Р будет отлично от окружности. Отсюда мы заклю-
заключаем, что отрезок МN прямой L является общим диаметром всех
115
Рис. 116#
окружностей С(Р). Поэтому все эти окружности могут быть по-
получены вращением вокруг MN любой из них. Таким образом,
множество всех сечений S плоскостями, проходящими через
L, дает нам сферу 2, являющуюся частью поверхности S. Но S
не может содержать никаких точек, отличных от точек 2, пото-
потому что если некоторая точка Т поверхности S не принадлежит Е>
то пересечение S плоскостью, проходящей через Т и L, будет от-
отлично от окружности. Следовательно, поверхность S — это
сфера 2.
47а. Если уложить вместе четыре шара радиуса г, то их
центры образуют правильный тетраэдр с ребром 2г (левая часть
В
Рис. 117.
рис. 117), в котором двугранный угол а ^ 70°32', что нетрудно
1
папти из равенства cos а = —.
«3
Если мы и дальше будем строить многогранники, образо-
образованные из центров шаров, то вкладыванию нового шара в какое-
нибудь из оставшихся гнезд будет соответствовать достройка
к ранее построенному тетраэдру нового тетраэдра, симметричного
предыдущему относительно одной из его граней. Так как гнезд
было всего четыре, то докладыванию четырех шаров соответст-
соответствует достройка к тетраэдру четырех тетраэдров. В результате
мы получим звездчатый многогранник, изображенный на пра-
правой части рис. 117. Он имеет двенадцать граней, а следовательно,
фигура, состоящая из шаров, имеет 12 гнезд.
Если бы мы теперь хотели в каждое из образованных гнезд
вложить по одному шару, то оказалось бы, что не все шары вме-
вмещаются. Действительно, если, например, при грани А'ВС мы
достроим тетраэдр A'BCD", а при грани BCD' — тетраэдр
A"BCD'tio действительно, это построение может быть выполнено,
ибо 5а < 360°, но расстояние A"D" между вершинами достроен-
достроенных тетраэдров будет равно 2r }^3 sin 1180°—___ а\
т. е. _ г,
116
а следовательно, будет меньше 2г. Поэтому точки А" и D*
одновременно не могут быть центрами шаров с радиусом г.
Таким образом, из каждой пары гнезд дри каждом из внут-
внутренних ребер звездчатого многогранника можно только в одно
гнездо вложить новый шар, т. е. в качестве третьего слоя всего
можно доложить только шесть шаров. Этот один шар можно дей-
действительно поместить, так как, например,
Постоянно говоря дальше «грань» вместо «гнездо» и «вер-
«вершина» вместо «центр шара», предположим, что «активными»
гранями являются грани A'BD, B'CD, CAD, ABD\ BCD',
A CD', а остальные пусть будут «мертвыми» (неактивными).
Тогда к данному многограннику можно будет достроить
тетраэдры A'BDG, B'CDE, AC'DF, ABC'D', A"BCD\ ABnCb\
имеющие всего 18 граней. Три последних тетраэдра будут иметь
только по одной активной грани. Подобным же образом каждый
из трех начальных тетраэдров будет иметь только по одной
активной грани, т. е. всего в четвертом слое будет шесть шаров.
Этот процесс, конечно, можно продолжить. После присое-
присоединения каждого последующего слоя шаров некоторые грани
многогранников, образованные центрами шаров, будут «отми-
«отмирать», но остальные активные грани будут порождать новые
тетраэдры.
476. Пусть г обозначает радиус данных шаров.
Прежде всего, заметим, что один шар мы можем обложить
венцом из шести шаров так, чтобы каждый из них касался пер-
первого шара (который мы будем счи-
считать первым слоем) и двух сосед-
соседних шаров и чтобы центры всех
шаров лежали в одной плоскости
(рис. 118). Углубления, образо-
образованные каждыми тремя взаимно
касающимися шарами, из числа
этих семи шаров, образуют 12
гнезд для последующих шаров;
принимая плоскость, изображен-
изображенную на рис. 118, за плоскость,
проходящую через центры наз-
названных семи шаров, в гнездах,
находящихся выше этой плоско-
ети, мы можем поместить толь- р *.~
ко три шара касательно к шару с' •
первого слоя. Шары эти, обозна-
обозначенные на рис. 118 пунктиром, действительно можно уместить,
так как легко убедиться в том, что расстояния между их цент-
центрами будут равны 2г. В гнездах, находящихся ниже плоско-
плоскости, можно уместить тоже только три шара, причем двумя спо-
способами: непосредственно ниже шаров, находящихся в верхних
гнездах, или же между ними.
Итак, один шар можно двумя способами обложить 12 шара-
шарами, составляющими второй слой, Центры этих 12 шаров
117
представляют собой вершины двух четырнадцатигранников Wx и
W2 (рис. 119 и 120), шесть граней которых являются квад-
квадратами, а восемь граней — равносторонними треугольни-
треугольниками; стороны квадратов и треугольников равны 2г. Так как
центры шаров второго слоя находятся на одинаковом расстоя-
расстоянии 2г от центра шара первого слоя, то и вершины четырнадцати-
четырнадцатигранников Wx и W2 тоже находятся на одинаковом расстоянии
от центра шара первого слоя. Расстояние это равно 2г. Основы-
Основываясь на этом, можно вычислить, двугранные углы многогран-
многогранников Wx и W2. В самом деле, соединяя вершины многогранни-
многогранников с центром шара первого слоя, мы можем выделить в обоих
Ряс. 119.
Рис. 120.
многогранниках шесть пирамид с квадратными основаниями и
одинаковыми ребрами, равными 2г, а также восемь правильных
тетраэдров с ребрами длиной в 2г. Обозначая двугранный угол
у основания пирамиды через а, а двугранный угол тетраэдра
через р, легко найдем, что
cos a =
1
cos р = _
откуда
а = 54°44\ р = 70°32\
Двугранные углы многогранника W^ поэтому равны а + C;
двугранные углы многогранника W2 соответственно равны:
между двумя треугольными гранями 2р, между двумя квадрат-
квадратными гранями 2а, а между треугольной и квадратной гранью
сс+ Р.
Обе системы шаров, центры которых являются вершинами
четырнадцатигранников Wx и W2 содержат по 14 гнезд; восемь
гнезд, образованных тремя шарами, шесть — четырьмя шарами.
Легко убедиться, что в каждое гнездо можно уместить шары
(как это доказать?). Следовательно, третий слой будет состоять
из 14 шаров. Так как звездчатый многогранник Wf ргтс. 121
имеет 48 граней, то шары третьего слоя, центры которых состав-
118
ляют этот многогранник, образуют 48 гнезд. Ни в одно из них не
возможно уже вместить шар (почему?).
Рассмотрим еще систему шаров, центрами которых являют-
являются вершинычетырнадцатигранника W2, и звездчатый многогран-
многогранник W\t построенный на многограннике W2. В этом случае в
гнездах третьего слоя системы шаров можно поместить три шара
образующие четвертый слой, но на этом окончится, так же как
Рис. 121.
Рис. 122.
и раньше, укладывание шаров в гнезда. Мы уже не сможем по-
поместить пятого слоя шаров *).
47в. Решение иллюстрирует рис. 122. Наборщик набрал
5 см вместо указанных автором учебника 4 см.
48. Электрическое освещение в большинстве городов питает-
питается переменным током с периодом, равным —сек.; в течение
50
секунды электрический свет 100 раз загорается и гаснет, а между
двумя очередными моментами наивысшего напряжения всегда
проходит 0,01 сек.
Если диск вращается по направлению вращения часовой
стрелки со скоростью 25 оборотов в секунду, то в течение 0,01 сек.
каждый из участков внутреннего диска выполнит 0,25 оборота
и займет такое положение, какое раньше занимал участок того же
самого цвета. В результате нам будет казаться, чго внутренний
*) По поводу затронутой задачами 47а и 476 тематики см.,
например, Л. ФейешТот, Расположения на плоскости, на
сфере н в пространстве, М., Физматгиз, 1958, гл. VII, или § 7
названной на стр. 81 книги Л. Гильберта и С. Кон-
Ф о с с е п а.
119
диск не вращается. При скорости вращения, несколько превы-
превышающей 25 оборотов в секунду, нам будет казаться,, что диск
соответственно вращается в направлении движения часовой стрел-
стрелки, а при скорости вращения немного менее 25 оборотов в се-
секунду нам будет казаться, что диск вращается в направлении,
противоположном движению часовой стрелки.
Для внешнего кольца будет то же самое, однако критиче-
критическая скорость будет равна 20 оборотам в секунду.
Предположим теперь, что мы станем вращать диск с очень
большой скоростью. Если скорость, уменьшаясь, дойдет до 25
оборотов в секунду, то нам будет казаться, что внутренний диск
неподвижен, а внешнее кольцо вращается по направлению дви-
движения часовой .стрелки. При скорости диска менее 25, но более
20 оборотов в секунду нам будет казаться, что внутренний диск
врашается в направлении, противоположном вращению внешне-
внешнего кольца. При 20 оборотах в секунду внешнее кольцо задер-
задержится, после чего как внутренний диск, так и внешнее кольцо
будут вращаться в направлении, противоположном направлению
движения часовой стрелки.
Игрушка лучше всего действует при свете ионной лампы,
а совсем плохо при свете обыкновенных электрических лампочек
большой мощности, нить накала которых обладает большой
тепловой инерцией, весьма сильно снижающей эффекты, свя-
связанные с характером переменного тока.
49. Спор можно разрешить следующим образом.
Право первенства выбора куска ветчины предоставим третьей
участнице покупки. Она, конечно, выберет тот кусок, который
на домашних весах весил не менее каждого из двух остальных
кусков, а следовательно, тот, который, по ее мнению, по своей
стоимости соответствует не менее чем 15 рублям. Такой кусок
должен существовать, так как при разделе целого на три части
одна из этих частей должна быть не менее 1/3 целого.
Затем выбирает свой кусок вторая участница покупки. И
эта тоже должна быть довольна, так как после того, как выбрала
себе кусок третья участница, остался по крайней мере один ку-
кусок, который, по показанию весов в магазине на углу, соответ-
соответствует по своей стоимости не менее чем 15 рублям.
Первая участница покупки получит оставшийся кусок;
она тоже должна быть довольна, ибо она считала все куски рав-
равными по весу.
50. Систему двух произвольных взаимно-перпендикуляр-
взаимно-перпендикулярных прямых назовем кратко крестом. Отметим на этом кресте
один луч, т. е. одну полупрямую (на рис. 123 он обозначен
стрелкой). Крест, расположенный произвольно относительно
плоской области, можно всегда параллельно сдвинуть так, что-
чтобы четверти области, прилегающие к выделенному нами лучу,
имели площади, равные Р/4 (на рис. 123 крест обозначен пункти-
пунктиром; верхние четверти, имеющие площади Р/4, тоже заштрихо-
заштрихованы пунктиром). Если и нижние четверти имеют те же самые
площади, то теорема доказана.
Предположим, что это не так, т. е. что левая нижняя чет-
четверть имеет площадь больше Р/4 (и больше правой нижней чет-
четверти). Будем теперь вращать крест по часовой стрелке так,
чтобы четверти, прилегающие к его отмеченному лучу, всегда
120
имели площади, равные Р/4. После того как мы повернем крест
на 90°, он займет положение, обозначенное на рис. 123 сплош-
сплошной линией. Для того чтобы четверти, заштрихованные сплош-
сплошной линией, имели площади, равные Р/4, вертикальный луч
должен переместиться влево, а горизонтальный — ввврх. При
новом положении креста нижняя левая четверть (по отношению
к выделенному лучу) имеет
площадь меньше Р/4, так как
является частью заштрихован-
заштрихованной пунктиром четверти, имею-
имеющей площадь Р/4, а поэтому
правая нижняя четверть имеет
площадь больше Р/4. Следова-
Следовательно, мы получили обратное
тому, что было при первона-
первоначальном положении креста;
поэтому при вращении креста
обязательно найдется такое его
положение, при котором все
четверти будут иметь одина-
одинаковые площади, равные Р/4.
(Представленное нами до-
доказательство возможности раз-
раздела лепешки на четыре рав-
равные части обошлось без всяких
вычислений. Но они были бы
необходимы — причем достаточно сложны *— при фактическом
разделе на четыре части данного треугольника, например, со
сторонами 3, 4, 5.)
51. Сначала заметим, что если Павел выберет точку Р в
центре тяжести треугольника (рис. 124), то наилучшим для
?ис. 123.
Рис. 124.
Рис. 125.
Гавла будет такой раздел торта, при котором сечение парал-
параллельно какой-либо из сторон треугольника. Для доказательства
этого факта достаточно показать, что треугольник, заштрихо-
заштрихованный один раз на рис. 124, имеет площадь меньшую, чем тре-
треугольник, заштрихованный дважды. Площадь части Л BCD
торта равна 5/9 площади целого торта, следовательно, торт бу-
будет поделен между Гавлом и Павлом в отношении 5 : 4.
121
Легко проверить, что выбор центра тяжести является для
Павла наилучшим, ибо при каждом ином положении точки Р,
Гавел мог бы себе отрезать не только трапецию ABCD, но еще,
сверх того, кусок торта (рис. 125).
Ответить на остальные вопросы мы предлагаем читателям.
Во всяком случае легко доказать, что если торт имеет причудли-
причудливую форму, представленную
на рис. 126, то при любом выборе
точки Р Гавел может отсечь по
меньшей мере 2/3 торта. И нако-
наконец, мы предлагаем читателям-
доказать, используя результат
задачи 50, что при любой форме
торта Гавел не отрежет более чем
3/4 торта *).
52. Сравним вначале по весу
первую пару предметов, затем
вторую пару, и, наконец,— пред-
предмет, который оказался более тя-
р |9А желым в первой паре, с более тя-
тяжелым предметом второй пары.
Мы можем записать результаты этих взвешиваний как
А<В <С
V
А
где М < N означает, что М легче N.
5-й предмет Е может быть включен в ряд А — В — С, для
чего надо сравнить его сперва с В\ если он окажется тяжелее,
чем В, мы сравним его с С, а если Е легче, чем В, мы сравним его
с А. Таким способом, с помощью двух взвешиваний мы включим
Е в последовательность А —В — Си придем к одной из следую-
следующих четырех конфигураций:
t 2°
V V
D D
3° #<Л<#<С, 4° Л <?<#<?.
V V
D D
Мы сделали пока всего 5 взвешиваний. Если в результате
мы пришли к 1°, сравним далее D с А, если окажется, что D <
< Л, то задача решена; если же окажется, что А < D, мы срав-
сравним D с В — это седьмое взвешивание завершит процесс, и мы
получим A <D <В <С <Е или Л<?<1><С<?Г.
Если первые 5 взвешиваний дадут 2°, то мы можем включить D в
*) По поводу связанной с этой задачей проблематики, см.,
например, первую часть книги Б. Грюнбаум, Этюды по
комбинаторной геометрии и теории выпуклых тел, М., «Нау-
«Наука», 1971.
122
ряд с помощью двух взвешиваний, начиная со сравнения D о
В — всего мы используем опять 7 взвешиваний. Конфигурации
3° и 4° отличаются от 2° только обозначениями, так что здесь рас-
рассуждения, по существу, не отличаются от относящихся к слу-
случаю 2°.
Следовательно, семи взвешиваний всегда достаточно для
упорядочения пяти предметов.
52а. Из описания дороги путешественника следует, что его
палатка стояла на Северном полюсе. В этом месте земного шара
восход солнца бывает только раз в году — в день весеннего рав-
равноденствия, т. е. 21 марта. Это и есть день рождения Невядом-
ского.
53. Обозначим поочередно дни недели через I, II, . . ., VII
и составим таблицу, условившись, что день недели, который
выпал на некоторую определенную дату 1911 года, обозначен
числом I.
А
1911
1912
1913
1914
1915
1916
1917
1918
1919
1920
1921
1922
1923
1924
1925
1926
1927
1928
1929
1930
в
I
II
IV
V
щ
VII
II
III
IV
V
VII
I
II
III
V
VI
VII
I
III
IV
с
I
III
IV
V
VI
I
II
III
IV
VI
VII
I
II
IV
V
VI
VII
II
III
IV
D
I
VI
IV
II
VII
А
1931
1932
1933
1934
1935
1936
1937
1938
1939
1940
1941
1942
1943
1944
1945
1946
1947
1948
1949
1950
В
V
VI
I
II
III
IV
VI
VII
I
II
IV
V
VI
VII
II
III
IV
V
VII
I
с
V
VII
I
II
III
V
VI
VII
I
III
IV
V
VI
I
II
III
IV
VI
VII
I
D
V
III
I
VI
IV
В столбце А приведены годы (високосные годы напечатаны
жирным шрифтом). В столбце В приведены дни недели, выпадаю-
выпадающие в разные годы на ту же самую дату, что и в 1911 году, если
эта дата находится в пределах между 1 января и 28 февраля.
В столбце С приведены дни недели, выпадающие в различные
годы на ту же самую дату, если эта дата находится в пределах
между 1 марта и 31 декабря. В столбце D приведены дни недели,
выпадающие в отдельные високосные годы на 29 февраля.
Из этой таблицы видно, что день недели, выпадающий на
определенную дату до 1 марта, перемещается после обычного
123
года на 1, а после високосного года на 2; день же недели, выпадаю-
выпадающий на определенную дату после 1 марта, перемещается перед
обычным годом на 1, а перед високосным годом на 2.
Из этой таблицы также видно, что если определенная дата
(отличная от 29 февраля) выпадает в некотором году, например,
в понедельник, то во второй раз в этот же самый день недели,
она выпадет или через 5 лет, или через 6 лет, или же через 11 лет
(если в рассматриваемый период не было года, номер которого
является числом, делящимся на 100, но не делящимся на 400).
Если бы Софья Сергеевна родилась в какой-либо день, от-
отличный от 29 февраля, а до 27 июля 1950 г. отмечала день своего
рождения только один раз, то в этот день она была бы еще несо-
несовершеннолетней, следовательно, не было бы повода называть ее
Софьей Сергеевной, а также говорить, что она еще не стара.
Предположим, следовательно, что Софья Сергеевна роди-
родилась 29 февраля. День недели, выпадающий на эту дату, переме-
перемещается через каждые четыре года на 5, вследствие чего 29 февра-
февраля выпадает в тот же самый день недели, через каждые 7*4 = 28
лет (если в этот период не было года, номер которого делится
на 100, но не делится на 400). Так как Софье Сергеевне «всего
один год», то первый день своего рождения она отмечала самое
раннее в 1924 году, а самое позднее в 1948 году.
Но так как известно, что Софья Сергеевна родилась после
первой мировой войны, то впервые день своего рождения она
отмечала в 1948 году, а родилась 29 февраля 1920 года.
54. Пусть п обозначает число рыб в пруду, годных для уло-
улова. Тогда отношение числа рыб, помеченных меткой, к числу всех
рыб равно 30/тг.
Во второй раз ихтиолог поймал 40 рыб, среди которых две
рыбы были помечены. Отношение числа рыб помеченных к чис-
числу всех выловленных рыб равно 1/20.
Если предпояожить, что помеченные рыбы в пруду равно-
равномерно распределены среди всех рыб, то оба отношения должны
быть одинаковы, т. е.
Ё2 = ±
п 20'
откуда п = 600.
Следовательно, число рыб в пруду, годных для улова данной
сетью, приблизительно равно 600.
55. В любом случае достаточно четырех цроб, если принять
следующий метод: будем сравнивать валик со средним отверсти-
отверстием, т„ е. восьмым по счету, потом — в зависимости от результа-
результата — с четвертым или двенадцатым и т. д. Результатом каждой
пробы будет ответ «да» (если валик поместится в отверстии) или
«нет» (если валик не поместится в отверстии). Четыре пробы да-
дадут 16 возможностей, т. е. столько, сколько существует типов ва-
валиков, различаемых данным прибором.
56. Если 2п чисел хг, х21 . . ., х2П расположены в возрастаю-
возрастающем порядке и если хт < аГ< vm+v то сумма абсолютных по-
погрешностей при замене чисел xv х2, . . ., х2П числом х равна
<«-*!)+<*-*,)+... +>-*«>+ . ...
+(*т+1 — х) + • • • + (Х2п — *)« (!)
124
Легко проверить, что самым меньшим из чисел вида A) является
число
. + (у — хп) +
(у — #i) + (у — х2) +
+(#«+1 - у) + . . . + fen -
л (сле-
(слегде хп < у < xn+v Действительно, если, например,
довательно, х > у), то разность чисел A) и B) равна
п (х — у) + ((я — #п+1) +.««+(# — ят)) —
> п (х — у) + 0 — (т — га)(а; — i/) + Bи — т)\у — я) = 0.
Подобным же образом можно проверить, что если систему
An чисел xv х2, . . ., хт разделим на две части:
числа первой части заменим числом х', причем таким, что хт <^
<С х' <С #т+1, числа второй части заменим числом х", причем
таким, что х2п+т < х" < #2м+т+1» Т0 сУмма абсолютных погреш-
погрешностей будет наименьшей при т — п.
Отсюда следует, что предельный диаметр для 120 шариков
равен 6,09 мм (имеется 60 шариков диаметром менее чем 6,09 мм
и столько же шариков диаметром
более чем 6,09 мм), а надписи на ко-
коробках следующие: а = 6,06 мм,
Ъ = 6,15 мм.
57. Площадь поперечного сече-
сечения валика равна 25я см2, лента
заполняет площадь 25 см2, следова-
следовательно, сердцевина имеет площадь
25(я — 1) см2. Обозначим через d
диаметр трубки (без ленты); тогда
из уравнения
я — = 25 (я -
4
¦1)
8
следует, что
d = 10
Рис. 127.
см ж 8,26 см.
58. Как известно, время, которое показывают часы, пол-
полностью определено координатой малой стрелки на шкале часов
(рис. 127); большая стрелка имеет всего лишь вспомогательное
значение, а именно, она создает на диске часов что-то вроде но-
нониуса, что позволяет двенадцатикратно увеличить точность оп-
определения координаты малой стрелки.
Если координату малой стрелки на диске часов обозначим
через 5» а координату большой стрелки через г), то получим:
т| - 12 {1} = 0, 0 < I < 12, 0 < ц < 12,
где {^} обозначает дробную часть числа ?•
125
Предположим, что обе стрелки часов одинаковы. Обозна-
Обозначим через х координату одной стрелки, а через у — координату
другой.
Могут иметь место три случая.
I. Если
х-12{у}фО,
то обязательно
и часы показывают время х.
II. Если
то обязательно
и часы показывают время у.
III. Если одновременно имеют место равенства
У _ 12 {х) = 0 и х —
= О,
то при помощи часов с одинаковыми стрелками мы не можем
прочесть время, ибо каждую из стрелок можно принять за ма-
малую стрелку, а следовательно,
одинаково возможно время х и
время у\ таких исключительных
положений стрелок существует
всего 143.
Отвечающие им числа хну
являются координатами 143 точек
пересечения графиков функций
У = 12 {а:} и х = 12 {у} (рис. 128).
Точки эти лежат на 23 прямых,
определенных уравнениями
»=*+"* A)
Рис. 128.
(Л = 0, ±1,. ..,±11).
Если теперь обозначим через
г = | х — у |
ошибку, которую мы допустим, приняв вместо одного из двух
показаний часов (х и у) другое, то согласно равенству A) будем
иметь:
r = g|ft| (fc = 0, ±1 ±11).
Отбрасывая, согласно условию задачи, ошибку более чем
в б часов, мы получаем наибольшее значение ошибки для к =
72 7 6
= ±6. Она равна г==г5==:^то' т. е. 5 часам 32 минутам 18 -^
13 1о 1о
секундам. (В какое время грозит нам эта ошибка?) Конечно,
в этом рассуждении мы предположили, что хозяин часов без-
безошибочно прочитывает координаты стрелок.
126
59. 1) Могло случиться, что один и тот же мальчик оказался
самым низким великаном и самым высоким карликом. Более то-
того, класс, состоящий из km учеников разного роста (кит — на-
натуральные числа, большие 1; к обозначает число рядов, т обоз-
обозначает число шеренг), можно расставить в прямоугольном строю
таким образом, чтобы произвольно выбранный ученик гг, кото-
который имеет по меньшей мере к — 1 товарищей ниже себя и по
меньшей мере т — 1 товарищей выше себя, оказался одновре-
одновременно самым низким великаном и самым высоким карликом:
12 3
1
2
3
. меньше . . . и
I
т
2) Нет таких классов, в которых самый низкий великан
меньше самого высокого карлика.
Чтобы это доказать обозначим через и самого высокого кар-
карлика, а через U — самого низкого великана. Предположим,
что U < м. Ученики и и U не могут стоять ни в одном и том же
ряду (так как тогда и не был бы самым низким в своем ряду),
ни в одной и той же шеренге (так как тогда U не был бы самым
большим в своей шеренге). Обозначим через щ^ ученика, стоя-
стоящего в точке пересечения ряда и шеренги, в которых, соот-
соответственно, стоят ученики и и U. Получим тогда
и < wife, им < Ut
вследствие чего и < U, вопреки сделанному предположению,
что U <С и. Предположение, что U < и привело, следовательно,
к противоречию и поэтому оно не верно.
3) Если бы учитель при определении великанов искал их
так же, как и карликов, т. е. в рядах, а не в шеренгах, то один
и тот же ученик не мог бы быть, что совершенно очевидно, самым
низким великаном и самым высоким карликом, так как тогда в
своем ряду он должен был бы быть одновременно самым низким
и самым высоким учеником, что невозможно.
Однако в этом случае самый низкий великан может быть
или больше или меньше самого высокого карлика.
Действительно, из класса, насчитывающего km учеников
разного роста, выберем совершенно произвольно 2к + т — 2
учеников и расставим их вдоль трех сторон прямоугольника по
росту в убывающем порядке
Mi, и21 . . .} UzH+m-z
127
следующим образом:
ик последняя шеренга
и*+т-1 пеРвая
Оставшихся учеников расставим прямоугольным строем
совершенно произвольно.
Ученик щ является самым низким великаном, ученик щ+тт_х
является самым высоким карликом, а так как щ > мк+ти-1» то
самый низкий великан будет больше самого высокого карлика.
Если же к -{- 2т — 2 учеников uv и2, . . •, w/c+2m_2 расста-
расставим в убывающем порядке по росту так:
wfe+2m_2 первая шеренга и\
а остальных учеников расставим в прямоугольном строю совер-
совершенно произвольно, то ученик ик+т_х будет самым низким вели-
великаном, а ученик ит будет самым высоким карликом и вследствие
неравенства un+m-i < ит самый низкий великан будет ниже
самого высокого карлика.
60. Вопросы, поставленные в задаче, обозначим соответст-
соответственно теми номерами, под которыми они выступают, и исполь-
используем символ р —> q (импликация) для обозначения того, что из
ответа «да» на вопрос р следует ответ «да» на вопрос q. Тогда
верны следующие импликации:
2,1
10,
6
-з.
1 _»
-2,
8-
11, 1 -
2-» 4,
3-7,
4-2,
5-7,
6-4,
7-3,
-3, 8-
1 _»
-12.
6-
-7.
7,1
1 -¦
¦9,
Q
13,
Итак, одинаковыми являются ответы на вопросы 2 и 4, а
также 3 и 7.
61. Символы, о которых идет речь в задаче, следующие:
1° abed, 5° a'bed, 9° ab'cd\ 13° a'be'd',
2° abed', 6° abe'd', 10° a'be'd, 14° a'b'cd',
3° abe'd, 7° ab'c'd, 11° a'bed', 15° a'b'c'd,
4° ab'cd, 8° a'b'cd, 12° ab'c'd', lb°a'b'c'd'.
128
Докажем, что среди этих 16 символов есть два, а именно
db'c'd и a'bed', которыми нельзя обозначить поезда.
Пусть символ Рр обозначает число курящих путешествен-
путешественников в купе для курящих, Рп — число курящих путешествен-
путешественников в купе для некурящих, Np — число некурящих путешест-
путешественников в купе для курящих, a Nn — чиело некурящих путе-
путешественников в купе для некурящих.
Рассмотрим теперь символ db'c'd* Соответственно смыслу
букв а, Ъ', с', d должны быть выполнены следующие неравенства:
Рр > Рп, NP < Nn, Рр < NPt Pn > Nn. A)
Из трех первых неравенств получаем:
Nn>Np>Pp> Pn,
следовательно, Nn > Рп, что противоречит четвертому из нера-
неравенств A).
Символ db'c'd — как противоречивый — не может служить
для обозначения поезда.
Противоречивым является также символ a'bed', так как сре-
среди определяющих его неравенств
Pv
Nn, Pp > Np, Pn <
три первые противоречат четвертому.
Остальными четырнадцатью символами можно обозначить
поезда, как это следует из приведенной ниже наглядной схемы:
Номер
поезда
1
2
3
4
5
6
8
9
10
12
13
14
15
16
Символ
abed
abed'
abe'd
ab'cd
a'bed
abe'd'
a'b'cd
ab'cd'
a'be'd
ab'c'd'
a'be'd'
a'b'cd'
a'b'c'd
a'b'c'd'
Размещение путешественников в
для курящих
РРР
РРРР
РРР
РРРР
РРР
РР
РР
РР
Р
РР
Р
РР
Р
Р
NN
NNN
NNNN
N
NN
NNN
N
N
NN
NNN
NNNN
N
NN
NN
купе
для некурящих
РР
Р
РР
РРР
РРРР
Р
РРР
Р
РР
Р
РР
РРР
РРРР
РР
N
NN
N
NN
N
NN
NN
NN
N
NNNN
NNN
NNNN
NNN
NNN
129
62. Расположим символы, обозначающие группы крови, в
одну строку и в один столбец: доноров поместим в столбец, а
реципиентов — в строку, и полученную таблицу заполним зна-
знаками «+» и «—» следующим образом:
Реципиенты
О А В АВ
О + + + +
Л - + - +
Доноры в __ _ + +
АВ — — — +
Эту таблицу нужно понимать так: выберем произвольную стро-
строку (например, 2-ю) и произвольный столбец (например, 3-й);
если в их пересечении стоит знак +, то донор выбранной строки
может дать свою кровь для переливания реципиенту, указанно-
указанному в выбранном столбце; он не может этого сделать, если в пере-
пересечении строки и столбца стоит знак —. Так, в случае второй
строки и третьего столбца мы получаем, что донор с группой кро-
крови А не может давать свою кровь человеку с группой крови В.
Таким образом, таблица указывает, кто кому может и кто кому
не может дать свою кровь.
Легко проверить, что это определение удовлетворяет закону
I. Действительно, этот закон сводится к тому, что на диагонали
должны стоять только знаки +, что, очевидно, выполнено. За-
Закон II требует, чтобы в строке донора О стояли только знаки
+ , это требование также удовлетворено. Закон III требует, что-
чтобы в столбце реципиента АВ стояли только знаки +; но это, оче-
очевидно, тоже верно. Если в отношениях I, II, III мы заменим X
на символы О, А, В, АВ, то получим ровно 9 отнршений, а имен-
именно те, которые обозначены в нашей таблице знаком + . Так как
все остальные места в таблице (их число равно 7) заполнены зна-
знаками —, то, очевидно, закон IV тоже выполнен.
Итак, наша таблица эквивалентна законам I—IV, что и
доказывает утверждение 1°. Утверждение 2° также может быть
проверено с помощью таблицы. Например, О —* А и А —» АВ,
но также и О —» АВ, что и подтверждается нашей таблицей. Для
всех остальных случаев утверждение 2° может быть проверено
таким же образом. Утверждение 3° вытекает из наличия знака —
в соответствующей клетке таблицы.
63. Условимся обозначать через X также и человека с груп-
группой крови X. В частности, этих братьев мы обозначим символами
X и Y. Так как X не может дать свою кровь У, то в таблице,
построенной в решении предыдущей задачи, на пересечении стро-
строки X со столбцом Y стоит знак —. Так как Y не может дать свою
кровь X, то на пересечении строки Y со столбцом X также сто-
стоит знак —. (Эти два минуса симметричны относительно диагонали
таблицы, состоящей из одних лишь знаков +.) Но легко усмот-
усмотреть, что пара симметрично расположенных относительно диаго-
диагонали минусов находится только на пересечении строки А со столб-
столбцом В и строки В со столбцом А. Поэтому один из братьев имеет
группу крови А, а другой — группу крови В. Таблица показы-
показывает, что А может получать кровь только от О и от А, В — толь-
130
ко от О и от В. Так как оба брата могут получить кровь от своей
матери, то она должна иметь группу крови О. Законы наследова-
наследования групп крови требуют приписывания О к однобуквенным сим-
символам родителей, в соответствии с этим обозначим мать симво-
символом 00.
Закон комбинирования букв, заимствованных из символов
крови обоих родителей, показывает, что братья получили свои
символы А и В от отца, так как их мать не обладает ими. Следо-
Следовательно, их отец есть АВ. Родители с символами АВ и 00 мо-
могут иметь детей лишь с символами АО и ВО, т. е. А и В (в соот-
соответствии с законом вычеркивания О); следовательно, сестра этих
братьев тоже относится к группе А или В. Значит, как показы-
показывает таблица, она может дать свою кровь одному и только одному
из братьев. (Никто в этой семье не может брать кровь у отца,
но каждый может взять кровь у матери.)
63а. Находящиеся в обращении монетные единицы для гро-
грошей, десятков грошей и злотых одинаковы и равны 1, 2 и 5. Та-
Таким образом, для решения задачи достаточно исследовать, сколь-
сколько различных сумм наверняка содержит каждая сумма от 1 до 9
грошей. Результаты иллюстрирует следующая таблица:
Сумма грошей
Наверняка содер-
содержит суммы гро-
грошей
1
1
2
2
1,
3
2,
3
4
2,4
5
5
6
6
2,
7
5,
7
8
2,6,8
2,
9
4,
V,
5,
9
Пользуясь этой таблицей, мы можем вычислить, сколько
различных сумм содержит наверняка данная сумма. Например,
имея 527 грошей, можно выплатить любую сумму, которая на
месте сотен будет иметь одну из цифр 0 или 5, на месте десятков
будет иметь одну из цифр 0 или 2, на месте единиц будет иметь
одну из цифр 0, 2, 5, 7. Всего различных сумм будет 2«2«4 = 16,
а если мы не станем принимать в расчет сумму 000, то их
будет 15.
Больше всего сумм наверняка содержит сумма в 999 грошей,
а именно б3—1 = 215 различных сумм.
Стоит заметить, что интересным свойством обладает число 6.
Сумма в 6 грошей может быть составлена либо из монеты в 5 гро-
грошей и монеты в 1 грош, либо из трех монет по 2 гроша каждая.
В первом случае мы не могли бы выплатить сумм в 2, 3, 4 гроша,
а во втором случае не могли бы выплатить сумм ни в 1, ни в 5
грошей. Таким образом, имея 6 грошей, мы можем выплатить
наверняка (в смысле, определенном в задаче) всего лишь одну
сумму, а именно 6 грошей. Однако же, имея 6 грошей, мы безус-
безусловно можем выплатить по меньшей мере три различные суммы!
636. Из условий задачи легко получить соотношения
?i
= w.
131
Так как один и тот же сорт деревьев может расти в несколь-
нескольких садах, а также в одном и том же саду может расти несколько
сортов деревьев, то справедливы следующие соотношения:
I-*! + 2-s2 + . . . + rc-sn> п,
1-#! + 2-g2 + . . . + m-gm > т.
64. Если столб М расположен между столбами L и N, то
путь
ЛВС . . . LMN . . . Т
короче пути
ABC.. . LN . .. ТМ
на отрезок ТМ. Отсюда вывод: чтобы путь
ABC . . . LMN . . . Т
был самым длинным путем, необходимо, чтобы всегда два сосед-
соседних отрезка этого пути имели противоположные направления.
Тогда длина пути выразится следующей формулой:
d = IS — Ж + ~CD — Ш + .. .,
причем, если число столбов нечетное, то
d' = АВ — Ш + CD — Ш+ ... + 755- ST,
а если число столбов четное, то
d*-= АВ — Ш+СБ — Ш + ... —RS + lST.
Обозначим через
#0» #1» #2» • • •» ХП A)
координаты столбов А, В, С, . > ., Т,
Вследствие сказанного выше, будет
#о ^ xv xi ^ х2у Х2 ^ хз* хз ^ хь • • •
Так как по условию задачи столбы расставлены на равных
расстояниях, то можно считать, что последовательность A) яв-
является некоторой перестановкой чисел 0, 1, 2, . . ., п.
Тогда из равенств
АВ = хг — хо, ВС = Х2 — #ь CD = хз — Х2, .. .;
получаем:
d' = п (п + 1) - 4 (х2 + *4 + *в + , . . + *п_2) - 3 (х0 +
или
<f = п (п + 1) — 4 (*2 + а:4 + ж + • * . + *n-i) - (За:0 + а
в зависимости от того, является ли п четным числом или нет,
132
I. Если число столбов нечетно (п — четное), то разделим
множество п + 1 чисел
О, 1, 2 п
на три части:
множество С1? охватывающее~ — 1 чисел: 0,1, 2,..., п "~".. ,
4 2
„л
множество Сй, охватывающее 2 числа: —--— , -L
множество С3, охватывающее i чисел:
'
и обозначим:
произвольную перестановку чисел множества Сх через
произвольную перестановку чисел множества Сг через
Тогда
произвольную перестановку чисел множества С3 через
^и ^з» жб> • • •» xn-v
равно длине максимального пути, который можно пройти, вби-
вбивая гвозди. Дорогу эту, начиная от одного из столбов множеотва
С2, проходим, поочередно переходя от столбов множества С\ к
столбам множества Съ и наоборот, а закончим на втором из стол-
столбов множества С2. При этом длина пути не зависит от того, в ка-
какой очередности мы исчерпываем столбы множества Сг и столбы
множества С3.
II. Если число столбов четное (п — нечетное), то обозначим
произвольную перестановку чисел
0,l,2t....IlzJ
через
произвольную перестановку чисел
п + 3 п+Ъ п + 1
133
через
и примем
Тогда
тг —1
—4
n-'3 (!:
2. \
2
равно длине максимального пути, который можно пройти, вби-
вбивая гвозди. Эту дорогу мы также можем пройти по-разному.
65. Поставим кирпич на стол так, как показано пунктиром
на рис. 129, а, и проведем карандашом риску на ребре стола в
том месте, где заканчивается реб-
ребро кирпича. Затем будем пере-
передвигать кирпич вдоль этого ребра
стола до тех пор, пока вершина
кирпича не совпадет с риской (но-
(новое положение кирпича показано
С
у
! /
W
\ 1
\ !
\!
7]
б)
Рис. 129.
на рисунке сплошной линией), и после этого измерим линей-
линейкой расстояние от вершины А стола до вершины С сдвинутого
кирпича.
Укажем еще одно решение. Совместим ребро дощечки с дву-
двумя противоположными вершинами верхнего основания кирпича
так, чтобы дощечка краем упиралась в одну из вершин, и отме-
отметим на дощечке риской отрезок, равный длине диагонали верх-
верхнего основания кирпича. После этого сдвинем дощечку на расстоя-
расстояние, равное длине этой диагонали (рис. 129, б), и измерим расстоя-
расстояние AM.
66. Если на коробке, имеющей форму прямоугольного па-
параллелепипеда, мы нарисуем след ленточки, то на развертке ко-
коробки этот след образует прямую линию (см. рис. 131, на кото-
134
ром две грани коробки повторены). Из рисунка легко заметить,
что:
1° длина ленточки равна 2 Y{a + сJ + (Ь + сJ",
b
ъ
а
с
с
/
Ь
/
с
с
/
а
Рис. 130.
равен
2° тангенс угла, под которым ленточка пересекает ребра,
а -А- с Ь Л- с
~ > или Т
или
+ с а-\- с
3° ленточку можно перемещать по коробке, не растягивая
ее (на рис. 130 показаны параллельные перемещения),
4° длина ленточки будет тогда наименьшей, когда с < а и
с <С Ь, т. е. когда по два отрезка ленточки проходят по самым
большим граням коробки.
N
-J—~
У
Рис. 131.
66а. Совершенно очевидно, что шнурки нельзя перемещать,
не растягивая их, так, чтобы какой-либо из их отрезков пере-
перестал быть параллельным соответствующему ребру коробки.
Нельзя также изменить только положение точек скрещивания
шнурков на покрышке и основании, ибо и в этом случае один из
кусков шнурка, соединяющих эти точки, должен был бы удли-
удлиниться (рис. 131).
135
67. Ограничимся случаем, когда мы располагаем гирей в
1 кг.
Пусть АС ^ I (рис. 132) обозначает расстояние между цент-
центром тяжести С незагруженного безмена и точкой А подвеса гру-
груза. Пусть Q •— вес безмена. Центр тяжести безмена определяем
экспериментальным путем.
Предположим, что при нагрузке безмена в точке А гирей в
1 кг безмен, подпираемый в точке В, окажется в равновесии.
Длину отрезка А В обозначим через а.
Рис. 132.
Пусть D обозначает точку опоры безмена, находящегося в
состояний равновесия при нагрузке его в точке А произвольным
грузом в р кг. Длину отрезка AD обозначим через х.
Из условия равновесия для обоих приведенных выше слу-
случаев следует равенство моментов
откуда
рх I — х
а I — а
A)
Для нанесения шкалы на стержень безмена начертим на бу-
бумаге отрезок А С, обозначим на нем точку В и из концов А и С
этого отрезка проведем два
параллельных луча Am и
Сп, как показано на рис 133.
Затем на луче Сп, начи-
начиная от точки С, отложим
равные отрезки произволь-
произвольной длины С1, 12, 23, ...
и через точку L этого луча,
соответствующую единице,
а также через точку В от-
отрезка А С проведем прямую,
которая пересечет луч Am
в точке К.
Из подобия треуголь-
треугольников A KB и CLB получим
Рис. 133.
для отрезка
ношение
АК — к соот-
B)
при этом всегда I > а.
Шкалу на луче Сп спроектируем теперь на прямую АС, при-
принимая точку К за центр проекции. Пусть S — проекция точки
Р. Из подобия треугольников AKS и CPS, учитывая равенство
136
B), получим:
В
I — a
Сравнивая полученный результат с равенством A), мы за-
мечаем^ что AS *= я, а следовательно, S является той точкой, в
которой необходимо подпереть безмен, нагруженный грузом
в р кг.
Итак, путем проектирования равномерной шкалы описан-
описанным выше способом мы можем нанести на безмен шкалу, учиты-
учитывающую не только целое число
килограммов.
Из приведенных выше рассуж-
рассуждений следует, что требование по-
постоянной толщины и однородно-
однородности стержня безмена было в усло-
условии задачи излишним.
68. Как видно из рис. 134,
мы имеем АО = VOB2 — А В2.
Так как А В равно ширине s под-
подвижной линейки, а наименьшее
ОВ равно расстоянию h гвоздя от
неподвижной линейки, то мини-
минимальное АО равно Vh2 — Д
69. Первичное деление прямо-
прямоугольника на две части является очевидным (рис. 135).
Заметим теперь, что если прямоугольник первичным обра-
образом разделен более чем на две части, то каждая из его сторон
должна пересекать по крайней мере одну из делящих линий.
Другими словами, не определяет, например, первичного деления
О
Рис. 134.
Рис. 135.
Рис. 436.
такая конфигурация, как на рис. 136, при которой вертикаль-
вертикальная линия деления отсекает от целого прямоугольника левый
прямоугольник, внутри которого мы уже не имеем дальнейших
линий деления, а в правом заштрихованном прямоугольнике мы
имеем произвольное расположение делящих линий.
Из сделанного замечания следует, что не существует пер-
первичного деления на три части (рис. 137), ибо при каждом
делении прямоугольника на три части по крайней мере одну
из сторон прямоугольника не пересекала бы ни одна из линий
деления и поэтому деление не было бы первичным. Из этого за-
замечания также следует, что не существует первичного деления
прямоугольника на четыре части.
137
Рис. 137.
Рис. 138.
Рис. 139.
Рис, 140,
Первичное деление прямоугольника на пять частей, конеч-
конечно, возможно (рис. 138). Подобным же образом возможно пер-
первичное деление прямоугольника на семь и более частей, причем
вопрос усложняется потому, что можно привести различные спо-
способы деления прямоугольника на то же самое число частей.
Например, на рис. 139 показаны два различных первичных де-
деления на семь частей, а на рис. 140 — че-
четыре различных первичных деления на
восемь частей.
Перейдем теперь к решению задачи,
т. е. к первичным делениям квадрата на
некоторое число равных частей.
Деление на пять равных
частей. Пусть дан квадрат со сто-
стороной 1. Предположим, что квадрат
этот разделен первичным образом на
пять равных частей (рис. 141).
Ограничимся исследованием симме-
симметричного деления. Обозначая через х
сторону центрального квадратика, _по-
лучим, что х1 — 1/5, откуда % = У 5/5.
Рис. 141.
Поэтому размеры четырех оставшихся прямоугольников
следующие: __
Ъ-УЪ в 5 + УЪ
будут
10
10
Деление на семь равных частей. Снова
возьмем квадрат со стороной 1, предполагая, что он разделен на
Р* рз
ги.
Рв
Pf р*
Рис. 142.
семь равных частей по схеме, приведенной на рис. 142. Обозна-
Обозначим стороны прямоугольников, на которые разделен квадрат,
так, как указано на рис. 142.
139
Пусть w1 = х. Тогда рх = l/7#, и далее последовательно по-
получаем:
1 _ 6— 7a? w ^ 1— x
7A— x) 7A—a?) ' 3 6—7a?
__i_ 1 _7a? — 1 w _ x
Ix Ix ' m 7a? — 1 '
x x(lx— 2)
- tt?4 = a? — = —1 - ,
7a; — 1 7 a? — 1
7a:— 1
. — — = 7x "~ * — 7a:—1 __ Ga?—1) Ga? --- 3)
> — /?4 Рь 7^, 7X Ga:— 2) 7ж Gа? —2) '
Ga? —1) Ga: —3)
Так как w3 + ш4 + w$ = 1, то
1 — a: , a? , a? Ga: — 2) __,
6—7a: 7a: — 1 Ga? — 1) Ga?"—3)
откуда после простых преобразований получаем уравнение
196а:3 — 294а;2 + 128а: - 15 = 0.
Одним из корней этого уравнения является х — 1/2. Корень
этот не дает решения задачи, так как при х = 1/2 получаем
Wl = w21 следовательно, рг = р2 — и деление квадрата не будет
первичным. Остальными корнями полученного уравнения явля-
являются
7+ /19 7— /19
14 И 14
^ 3 _ 6
Так как, согласно условию задачи, должно быть х ^ ~у — тт
(ибо в противном случае было бырв < 0), то в качестве решения
7 J- /19
подходит только число Л • Ему соответствует решение
задачи, представленное на рис. 143. Оно указано проф. Я. Ми-
Минусинским.
Можно доказать, что не существует первичного деления
на семь равных частей такого типа, как изображено на рис. 139
справа. Однако может быть и существует первичное деление на
семь равных частей какого-либо иного типа.
Деление на восемь равных частей. Пе-
Перейдем теперь к первичному делению квадрата на восемь равных
частей.
Предположим, что возможно деление квадрата со стороной
1 по симметричной схеме, изображенное на рис. 144; каждый из
частичных прямоугольников имеет тогда площадь, равную 1/8.
140
A
5
±G-Щ
Рис. 143.
Рг Р,
р*
Pi Рг
Рис. 144,
Принимая во внимание симметрию, мы имеем и?2 == 1/2 и,
следовательно, р2 = 1/4. Пусть тг = х. Тогда
_
2 '
а так как /?4 = р3 — рх, то в конечном счете
1 _ 1 _ 1
8 A — х) 8а? *
8
(-¦И
откуда ж A — я?) = ж ^— ~\ — (х— L\ A —я?), и
после некоторых преобразовании,
6я2 — Ъх + 1 = 0.
наконец,
з ч V3
Из последнего уравнения получаем а?1,г~ — — , причем,
3 4- 1/^3
так как должно быть х > 1/2, то только корень Х2 = —^g
удовлетворяет условиям задачи.
3+1/3
8
т
6
г
1
2
Ж
F
1
2
V3
В"
Рис. 145.
На рис. 145 изображено первичное деление квадрата на во-
восемь равных частей, причем указаны размеры отдельных прямо-
прямоугольников,
142
Кроме рассмотренного выше способа деления, возможго
еще иное первичное деление квадрата на восемь равных частей,
представленное на рис. 146; мы получаем его подобным же обра-
образом, как и предыдущее.
70. Задача решается следующим образом: устанавливаем
люнетку в точке О данного участка (рис. 147) и измеряем наклон
участка в произвольно выбранном направлении OCV С этой
целью устанавливаем в точке Аг в том же направлении веху и
6-Ув
20
4+W
70
6-Л/6
20
72
72
ж
70
8
24-
W
72
72
20
Рис. 147.
измеряем расстояние dt и разность уровней hx между точками О
и Av Наклон участка определяем как частное tr = hjd^ Затем
поворачиваем люнетку на 90° и в направлении OC2J перпендику-
перпендикулярном к ОСг, измеряем наклон участка, выражающийся числом
t2 — h2fd2 •
Принимая луч ОСг за ось Ох, ОС2 за ось Оу, находим вектор
с компонентами ?17 ?2 на этих осях; направление этого вектора
143
является направлением наклона участка, а его длина, т. е. чис-
число У t\ + t\, равна наклону участка.
А вот обоснование этого метода. Пусть р — линия уровня,
проходящая через точку О, q — линия наклона, q' — проекция
линии наклона на горизонтальную плоскость П, J3 — угол нак-
наклона, а а — пусть будет неизвестным углом, который образуют
направление ОС2 с направлением q'.
Имеем:
tgp-*! = *• ,
Xl X2
откуда
Х2 Ь,2
?i = sina, xl = cos се,
Кроме того, имеем:
поэтому
следовательно, приведенный выше метод отыскания направле-
направления наклона, правильный.
Наконец, вычисляем наклон участка:
__ xidz h\d2 _ h .
Х2 di cos a d2 l *
71. Предположим, что город М соединен отрезками МА,
MB, MC, MD, ... с городами А, В, С, D, . . . (рис. 148).
Соединим отрезком точки А и В. Имеем AM <С А В и ВМ <
< АВ> так как в противном случае вместо по крайней мере од-
одного из соединений АМшВМ имело
¦гВ бы место соединение А В.
Из неравенств
AM <AB и ВМ <АВ
следуют неравенства
у > а и у > Р;
складывая эти неравенства и еще
равенство у = у, получаем
Зу > a + р + у или Зу > 180°,
следовательно, у > 60°.
Рис 148 Коль скоро, однако, имеет место
* неравенство у > 60°, то в точке М
могут сходиться вершины самое боль-
большее пяти треугольников, что и требовалось доказать.
72. Могут существовать три рода железнодорожных сетей,
изображенные на рис. 149.
1) В первом случае каждый из городов может быть узлом, в
котором сходятся четыре пути, следовательно, различных сетей
подобного рода будет пять.
144
2) Во втором случае город, который будет узлом и в кото-
котором сходятся три линии, можно соединить с тремя другими го-
городами четырьмя способами (число сочетаний из четырех эле-
элементов по три),, а пятый город в каждом из этих случаев можно
соединить с каждым из этих трех городов, следовательно, всего
возможных соединений существует 4-3 = 12. А так как каждый
из пяти городов может быть узлом, то различных сетей рассмат-
рассматриваемого нами рода будет всего 5-12 = 60.
3) В третьем случае в сети, соединяющей города, можно
произвольно изменять очередность городов, а следовательно,
получим всего столько сетей, сколько существует перестановок
из пяти элементов, т. е. 5! = 120. Но каждая перестановка и
Рис. 149.
обратная перестановка определяют ту же самую сеть, поэтому
различных сетей будет 120 : 2 — 60.
Всего сетей существует 5 + 60 + 60 = 125.
73. 1) Из всех треугольников с постоянным основанием и
постоянной высотой наименьший периметр имеет равнобедрен-
равнобедренный треугольник. Для доказательства достаточно заметить
Рис. 150.
(рис. 150), что точка Р, лежащая на касательной к эллипсу, про-
проходящей через точку М, лежит вне этого эллипса, вследствие чего
КР + PL > КМ + ML,
2) Из приведенного выше рассуждения следует, что если точ-
точки К, L, М являются вершинами равнобедренного треугольника
с основанием KL — 2р и высотой МО = h (рис. 151), то сеть
KS + LS + MS короче сети КР + LP + МР.
3) Введем обозначения (рис. 151):
OS = х, KS + LS + MS
m)
145
тогда получим:
откуда
— x t==: m,
Зя2 — 2 (т — Л)* + 4р2 — (т — /*J = 0;
вследствие этого (из условия действительности корней) полу-
получаем:
{т — hf — Зр2 > 0.
Это условие ведет к следующему ограничению для т\
причем т получает наименьшее значение при
тогда /OKS = 30°.
4) В случае соединения городов А, В, С, D железнодорож-
железнодорожной сетью без узлов кратчайшим был бы путь, представленный
на рис. 152 (или же один из трех иных путей, который можно по-
получить из этого, поворачивая его на 90°, 180° или 270° вокруг
центра квадрата). Длина такого соединения равна 300 км.
JD
Л В
Рис. 152.
В Л
Рис. 153.
5) Предположим, что города Л, В, С, D соединены железно-
железнодорожной сетью с одним узлом S. Узел этот должен быть соеди-
соединен по крайней мере с тремя из городов А, В, C,D, ибо в против-
противном случае, выпрямляя дорогу, ведущую через узел, мы полу-
получили бы более короткую сеть. Пусть узел ? будет соединен
с городами А у В, С (рис. 153). Тогда город D может быть сое-
соединен или с одним из городов Л и С, или же с узлом S.
В первом случае согласно тому, что доказано в пунктах 2 и
Ь (р = h = 50)^2 км), длина кратчайшей сети была бы равна
100 + 50УГA + VT) « 293,2 км.
Во втором случае согласно доказанному в пункте 1 сеть будет
кратчайшей, если точка S будет лежать на оси симметрии сторо-
стороны А В квадрата и на оси симметрии стороны ВС квадрата, т. е.
если она будет лежать в центре квадрата; тогда длина сети будет
равна
2-100 УТ« 282,8 км,
146
6) Предположим, что города А, 2?, С, D соединены железно-
железнодорожной сетью, содержащей два узла Sx и S2. Узел ?х должен
быть соединен по крайней мере с тремя из точек Л, В, С, D, Szt
в противном случае выпрямление дороги, ведущей через узел,
дало бы более короткую сеть.
Пусть узел S1 соединен с городами А и В и с узлом S2. Тог-
Тогда узел S2 будет соединен с городами С и D и сеть будет иметь
конфигурацию, представленную на рис. 154.
Если точки Sx и S2 не лежат на оси
симметрии стороны квадрата А В, то, как
это следует из рассуждений пункта 1, сеть
с узлами Si и S2 длиннее сети с узлами Рг
и Р2, Следовательно, эта сеть будет крат-
кратчайшей тогда, когда точки Рг и В2 распо-
расположены симметрично относительно центра
квадрата, так что /_ РХАВ = /__ P2CD =
= 30°. Длина сети равна (см. пункт 3, где
принимаем, что р = h = 50):
100 A +
273,2 км.
Рис. 154.
Рис. 155.
7) Увеличение числа узлов более чем на 2 вызывает удлине-
удлинение сети. Поэтому длина кратчайшей сети, которая можег соеди-
соединить города А, В, С, D, со-
согласно условию задачи,
равна
100 A + УТ) ж 273,2 км.
Она может быть реализова-
реализована двояко, как это иллю-
иллюстрирует рис. 155.
74. Кратчайшим путем
на шаре (земном) является
дуга большого круга, т. е.
круга, образованного пере-
пересечением шара с плоскостью, проходящей через центр шара.
Так как самолет, вылетающий из Осло, исчез из глаз зри-
зрителей, находящихся на аэродроме, в точке горизонта, лежащей
точно на запад, то самолет летел по большому кругу, пересекаю-
пересекающему меридиан в Осло (а = 10° 43' восточной долготы) под пря-
прямым углом.
Пусть на рис. 156 S и О соответственно обозначают центр
земного шара и точку, в которой лежит Осло, и пусть Q, G, О'
соответственно обозначают точки пересечения с экватором?
большого круга, по которому летел самолет, нулевого меридиапа,
а также меридиана, проходящего через Осло.
Легко заметить, что угол QSO' — прямой; отсюда имеем?
Z. GSQ = 90° — Z. GS0' = 90° — 10°43/ = 79°17\
следовательно, точка, в которой должен приземлиться самолет,
лежит на экваторе на 79°17' западной долготы (точка с такими
147
координатами лежит в провинции Пихинха в 120 км на запад от
Кито, столицы Эквадора), а так как дуга OQ равна 1/4 большого
круга, то трасса полета приблизительно равна 10 000 км.
Плоскость OSQ наклонена к плоскости экватора под углом
р = 59°55'; под этим углом относительно восточного направле-
направления должны ожидать само-
самолета зрители, находящиеся
на аэродроме в Эквадоре,
75. При полном затме-
затмении Солнца размеры Солн-
Солнца и Луны кажутся нам
приблизительно одинаковы-
одинаковыми. Отсюда следует, что
диаметр Солнца в 387 раз
больше диаметра Луны, а
отношение их объемов рав-
равно 3873»58.106.
76. Самый короткий
день во Вроцлаве (т. е. вре-
время,, которое протекает меж-
междувосходом и заходом Солн-
Солнца в один и тот же день)
наступит, конечно, тогда,
когда Солнце окажется в
зените на тропике Козерога
(ежегодно приблизительно
23 декабря).
Для определения длины этого дня мы должны знать географи-
географическую широту Вроцлава ф = 51°07' и угол, который образует
плоскость экватора земного шара с плоскостью эклиптики, 6 =»
= 23°27' (значения обоих углов даны приближенно).
Пусть на рис. 157 буквы О и М соответственно обозначают
центр земного шара и положение Вроцлава на этом шаре, и пусть
прямая NS обозначает ось вращения земного шара. Пусть пло-
плоскостью эклиптики будет плоскость Оху\ плоскость экватора,
проходящая через точку Л, образует с ней угол 6. Плоскость
OWZ, перпендикулярная к плоскости эклиптики и к направлению
Ох падения лучей Солнца, отделяет на земном шаре освещенную
часть от неосвещенной. Вроцлав на восходе Солнца проходит
через точку Z, идет по дуге ZMW и на заходе Солнца оказы-
оказывается в точке W. Длина дня во Вроцлаве пропорциональна
углу ZOtW.
Длина самого короткого дня во Вроцлаве, конечно, пропор-
пропорциональна длине дуги ZMW параллели, проходящей через Вроц-
Вроцлав, или же, короче, величине угла 20 = ZOXW.
На основании рис. 157 из прямоугольных треугольников
ООХМ% ООХР и OXPW мы легко получаем:
Рис. 156.
откуда
148
57°27'35\
Для длины t самого короткого дня во Вроцлаве получаем
пропорцию
t: Т = р : 180° (Т = 24 час),
откуда
t — 1 час. 39 мин. 40 сек.
Стоит еще заметить, что истинная длина самого короткого
дня во Вроцлаве больше вычисленной нами приблизительно на
четверть часа. На это влияет так называемая астрономическая
рефракция, возникающая из-за преломления солнечных лучей
в слоях атмосферы, окружающей земной шар.
77. Клеткой, смежной с белой клеткой, является черная,
и наоборот. На шахматной доске с нечетным числом клеток число
белых клеток не равно числу черных, поэтому требуемое в задаче
перемещение пешек невозможно.
78. Ответ на поставленный в задаче вопрос отрицателен:
ни одна из пешек не изменит своего положения. При этом безраз-
безразлично, считаем ли мы соседними только такие две клетки, которые
прилегают друг к другу сторонами, или также и клетки, сопри-
соприкасающиеся в вершипах. Во втором случае следует, однако, пред-
предположить, что шахматная доска (квадратная) состоит более чем
из четырех клеток.
Доказательство для обоих случаев можно вести совместно
следующим образом.
Обозначим через (?, к) клетку, расположенную в i-й «строке»
и в к-м «столбце» шахматной доски с числом клеток п2 (причем
п > 2), а через F (i, к) обозначим клетку, на которой установим
пешку, стоявшую раньше в клетке (i, к).
Предполагая, что F A, 1) = A, 1), F (п, 1) = (тг, 1) и что
преобразование F (i, к) сохраняет соседство клеток, нужно
149
доказать, что
F(i, &) = (*, &)для* = 1,2,. . .,»;*= 1, 2,. . м п.
Сразу видно, что число клеток, соседних с некоторой опре-
определенной клеткой шахматной доски, меньше для угловых клеток,
чем для остальных крайних клеток шахматной доски, а для пос-
последних меньше, чем для внутренних клеток шахматной доски.
Так как при новой расстановке ни одна из пешек не может иметь
меньше соседних пешек, чем имела прежде, то если клетка (t, к) —
внутренняя, то клетка F (t, к) также является внутренней, или
обе они являются угловыми, или, наконец, обе расположены по
краям и не являются угловыми.
Последовательность A, 1), B, 1), . . ., (п, 1) является после-
последовательностью очередных смежных клеток, расположенных
вдоль края шахматной доски. Тем же самым свойством должны
обладать клетки последовательности F A, 1), F B, 1), ...
. . ., F (п, 1). Но F A, 1) = A, 1), а с клеткой A, 1) будут смеж-
смежными (при условии, что п > 2) только две клетки края: A, 2)
и B, 1); функция F B, 1) может принимать, следовательно, толь-
только одно из этих двух значений. Рассмотрим эти два случая.
а) F B, 1) = A, 2). В этом случае клетка F C, 1), как край-
крайняя, смежная с клеткой F B, 1), т. е. с клеткой A, 2), и отличная
от A, 1), должна была бы совпасть с клеткой A, 3); подобным
те образом получилось бы F D, 1) = A, 4) и т. д. Наконец, уг-
угловая клетка F (п, 1) была бы клеткой A, п), вопреки условию,
что F (п, 1) = (и, 1). Случай а), следовательно, не может иметь
места, поэтому будет иметь место следующий случай.
б) F B, 1) = B, 1). Тогда, рассуждая так же, как и в случав
а), поочередно получаем:
F C, 1) = C, 1), F D, 1) = D, 1), . . ., F (и, 1) - (и, 1),
w. е. окажется, что пешки первого столбца останутся на месте.
Равенства F (t, 1) = (t, 1), где i = 1, 2, . . ., п, в свою оче-
очередь влекут за собой равенства F (i, 2) = (?, 2) для i = 1, 2, ...
. * ., п. Действительно, клетка F A, 2) является крайней клеткой,
смежной с клеткой A,1) и отличной от клетки B, 1), следова-
следовательно, F A, 2) = A, 2); клетка F B, 2) является смежной
с клетками F B, 1) и F A, 2), или с клетками B, 1) и A, 2) и от-
отличной от A, 1), следовательно, F B, 2) = B, 2), и т. д.
Таким же образом проверяем равенство F (t, к) = (t, к)
для следующих столбцов шахматной доски.
Обобщение. Полученный результат позволяет нам сде-
сделать некоторый общий вывод.
Рассматриваем функцию F, которая каждой клетке шахмат-
шахматной доски ставит в соответствие некоторую определенную клетку
той же шахматной доски таким образом, что двум различным
клеткам соответствуют различные клетки и что смежным клеткам
соответствуют тоже смежные клетки.
Такими функциями (преобразованиями) являются, например,
тождественное преобразование (или преобразование, при котором
каждая клетка остается на месте), симметрия относительно каж-
каждой из четырех осей симметрии квадрата шахматной доски, а так-
также повороты на 90°, 180° и 270° вокруг центра шахматной доски,
150
Докажем, что каждое преобразование F рассматриваемого
г^ами типа должно быть одним из восьми названных выше преобра-
вований.
Действительно, пусть F будет таким преобразованием. Как
мы знаем, угловым клеткам соответствуют угловые клетки, сле-
следовательно, могут иметь место только следующие случаи:
I. Преобразование F оставляет клетку A, 1) на месте. В этом
случае имеет место одна из двух возможностей:
1) Клетка (и, 1) тоже остается на месте. Тогда преобразова-
преобразование, как мы это доказали выше, является тождественным.
2) Клетка (и, 1) совпадает с другой угловой клеткой. Это
может быть только клетка A, я), в чем убеждаемся, рассуждая
так же, как и раньше, т. е. рассматривая последовательность
F A, 1), F B, 1), . . ., F (п, 1). Выполним, после преобразования
F, еще преобразование симметрии S± относительно главной диа-
диагонали шахматной доски, т.. е. диагонали, проходящей через
A, 1) и (и, и).
Произведение х) F-Si является преобразованием рассматри-
рассматриваемого типа, которое каждую из клеток A, 1) и (и, 1) оставляет
на месте, следовательно, это тождественное преобразование J
F-S1 = /.
Умножая обе части этого равенства на St, получаем (F'S^*
*St = I'Si, т. e. F'S\ = S^ а так как S\ = /, то F = St, т. е<
преобразование F в данном случае является симметрией относи-
относительно главной диагонали шахматной доски.
II. Клетка A,1) переходит при преобразовании F в клетку
(и, п). Пусть S2 обозначает симметрию относительно другой диа-
диагонали шахматной доски; она преобразует клетку (п, п) в клетку
A, 1). Следовательно, преобразование F*S2 оставляет клетку
D. 1) на месте, вследствие чего согласно 1) имеют место две воз-
возможности: произведение F*S2 является единичным преобразова-
преобразованием или же симметрией.
3) Произведение F'S2 есть единичное преобразование, т. е«
F-S9 = /.
х) Пусть А г В обозначают отображения (преобразования) не-
некоторого множества на себя. Произведением А «Б называется
преобразование, получаемое в результате выполнения сначала
преобразования А, а затем преобразования В. Если, например,
А является осевой симметрией на плоскости, то А-А, т. е. А2, яв-
является тождественным преобразованием; если А и В — преобра-
преобразования симметрии относительно пересекающихся осей а и Ь,
то А-В есть вращение вокруг точки пересечения осей а и Ъ на
угол, вдвое больший угла, образованного осями. Если /
является тождественным преобразованием, а А — произвольным
преобразованием, тоА'1 — 1*А=А. Произведение преобразо-
преобразований подчиняется ассоциативному закону, т. е. (А-В)»С =
= А (В*С). [Иногда результат последовательного выполнения
преобразований А и В (сначала Л, затем В) обозначают через
В-А или БЛ.— Ред.]
151
Умножая это равенство справа на ?2, получаем:
F ~ ?2,
т. е. F есть преобразование симметрии относительно диагонали
шахматной доски, проходящей через клетки A, л) и (л, 1).
4) Произведение F*S2 является симметрией 5Х:
F*S2 = Sv
Умножая это равенство справа на 52, получаем:
F = SVSV
Преобразование F является, следовательно, в этом случае
поворотом на 180° вокруг центра шахматной доски, или централь-
центральной симметрией относительно этой точки.
III. Клетка A,1) переходит при преобразовании F в клетку
(п, 1). Тогда преобразование F*Ss, где S3 обозначает симметрию
относительно горизонтальной оси симметрии шахматной доски,
оставляет клетку A, 1) на месте, и мы снова имеем две возмож-
возможности:
5) F-$,= /, откуда F = S9,
или
6) F'S3 = StJ откуда после умножения этого равенства спра-
справа на S3 получаем:
F=St-S9,
а тогда преобразование F является поворотом на 90° вокруг цен-
центра шахматной доски.
IV. Клетка A,1) переходит при преобразовании F в клетку
A, п). Обозначая через ?4 симметрию относительно вертикальной
оси симметрии шахматной доски, получаем, так же как в случае
III, две возможности:
7) F = St
ИЛИ
8) F = S^Sfr т. е. преобразование является вращением на
270° вокруг центра шахматной доски.
Мы доказали, что каждое преобразование множества клеток
шахматной доски на себя, сохраняющее смежность клеток, яв-
является одним из восьми преобразований:
h Sfi S2, S3, «S4, S1*S2y Si'Sbi Si'S*»
Преобразования эти образуют так называемую группу *).
Возвращаясь к задаче о пешках, на основе этой теоремы мы
сможем сформулировать следующий более общий вывод.
Если при новой расстановке пешек мы должны оставить на
Старом месте хотя бы одну пешку, не стоящую ни на одной из осей
симметрии, или две пешки, не находящиеся на одной и той же
оси симметрии шахматной доски, то каждая пешка должна
остаться на своем месте.
*) См., например, П. С. Александров, Введение в те-
теорию групп, М., Учпедгиз, 1938,
152
79. Задача будет решена, если мы укажем способ расположе-
расположения ладей на шахматной доске, удовлетворяющий условиям
1), 2), 3), 4). Для простоты введем некоторые термины. Столбец
доски назовем свободным, если на нем не стоит ни одна ладья и
если он содержит по крайней мере одну белую клетку, не атако-
атакованную по горизонтали. Напротив, столбец назовем занятым, если
хотя бы одна белая его клетка занята ладьей, не атакованной по
горизонтали никакой другой ладьей. Строку мы назовем свобод-
свободной, если она свободна от ладей.
На пустой шахматной доске число свободных столбцов сов-
совпадает с числом свободных строк. Выпишем сначала над каждым
столбцом число белых клеток этого
столбца и будем последовательно рас- 42338 425
ставлять ладей. А именно, очередную
ладью ставим в тот столбец, над ко-
которым стоит число, не превосходящее
все остальные числа, стоящие над
незанятыми столбцами. Если мы до-
добьемся успеха на этом пути, то зада-
задача будет решена, так как условия 1),
2), 3), 4) будут удовлетворены. При-
Пример такого расположения ладей изоб-
изображен на рис. 158. Маленькие круж-
кружки на белых клетках обозначают ла-
ладей, а числа в кружках указывают
на последовательность их расстанов-
расстановки на доске. Очевидно, что это рас-
расположение не единственно
©
©
®
®
Рис. 158.
Однако описанный выше процесс может натолкнуться на
определенные трудности.
а) При расположении очередной ладьи все белые поля нуж-
нужного столбца могут быть уже атакованы, т. е. в этот столбец ста-
ставить ладьи согласно условию 3) нельзя, а в силу условия 4) ладью
туда поставить необходимо.
В этой ситуации мы пытаемся сдвинуть вертикально одну из
уже поставленных ладей на другое белое поле. Если это нам
удается, то можно искать место для следующей ладьи. Пример
такого рода иллюстрирует рис. 159.
Здесь после выставления первых четырех ладей (см. первую
доску) все белые поля столбцов d и е окажутся атакованными
по горизонтали. Поэтому мы ищем среди занятых столбцов
такой, где есть белые поля, не атакованные по горизонтали
(в нашем примере — это столбец g). Сдвигая 2-ю ладью на поле g5
(см. вторую доску), получаем возможность поставить 5-ю
ладью на поле d4 в столбце d. Аналогично, сдвигая 3-ю ладью
на поле Ь8, освобождаем место для 6-й ладьи, которую теперь
можно поставить на поле е2. Таким способом мы иногда можем
преодолеть возникшие трудности и расставить ладьи в соответ-
соответствии с условиями 1), 2), 3), 4) (как это удалось в нашем приме-
примере — см. последнюю доску на рис. 159).
б) Может случиться, однако, что в одном или в нескольких
столбцах все белые поля атакованы по горизонтали или, более
того, в столбцах, в которых мы уже расставили ладьи, не осталось
свободных белых клеток, куда ладьи можно переместить. Мы
153
будем говорить тогда, что соответствующий столбец блокирован*
В блокированный столбец мы не можем поставить ладью, не на-
нарушив условие 3), а также не можем сдвинуть ладьи в уже заня-
занятых столбцах.
Мы покажем на примере, как преодолеть подобную труд-
трудность. На первой доске рис. 160 столбец е блокирован: все белые
поля этого столбца атакованы B-й, 4-й и 5-й ладьями), и притом
мы не имеем возможности сдвинуть угрожающие нам ладьи.
В этом случае мы снимаем все эти ладьи и вообще отказываемся
ставить ладьи как на блокированный до этого столбец, так и на
столбцы и строки, в которых стояли снятые ладьи. В нашем при-
примере это: столбцы Ь, с, d и е и строки 2, 3 и 4. Заметим, что при
этом всегда число строк, в которые мы запрещаем ставить ладьи,
меньше числа таких же столбцов, а также, что на пересечении
«вычеркнутых» столбцов и свободных от ладей строк стоят чер-
черные поля. Поэтому нет опасности, что при расстановке новых
ладей они будут атаковать по горизонтали белые поля в «вычерк-
«вычеркнутых» столбцах.
Может случиться так, что в «вычеркнутых» столбцах оста-
остались белые поля, атакованные по горизонтали ладьями, постав-
поставленными раньше, но не убранными при «снятии блокады». В со-
соответствии с условием 4), эти поля должны быть атакованы по
вертикали. Однако эти столбцы вычеркнуты, т. е. мы не можем
ставить в них ладьи. Такую ситуацию мы назовем вторичной
блокировкой. В нашем примере поле Ы (вторая доска рис. 160)
в вычеркнутом столбце b атакована по горизонтали ладьей 1.
Имеются два пути снятия вторичной блокады.
Сначала мы проверяем, не осталось ли свободное невычерк-
нутое белое поле в столбце, где расположена ладья, участвую-
участвующая во вторичной блокировке. Если такое поле имеется, мы пе-
переставляем на него эту ладью, после чего продолжаем ставить
новые ладьи. Если же поля, о котором говорилось выше,
не имеется, то мы вычеркиваем строку и столбец, где расположе-
расположена ладья, саму ладью мы при этом, конечно, снимаем. В нашем
примере (рис. 160) ладья 3 может быть сдвинута на поле а8, чем
вторичная блокада снимается. А если бы поле а8 было черным,
то нам пришлось бы снять эту ладью и зачеркнуть столбец а
и строку 1. В обоих случаях при дальнейшей расстановке
в нашем примере ладей мы не встретимся ни с какими труд-
трудностями.
Уничтожая вторичную блокировку и вычеркивая при этом
определенные столбцы и строки, мы получаем возможность про-
продолжать расстановку ладей.
В случае повторного возникновения блокады, первичной или
вторичной, мы применяем тактику, описанную выше.
Можно показать, что в результате этих операций минимум
одна ладья останется на доске, так что мы не нарушим соответ-
соответствующего условия. Заметим сперва, что, ставя ладьи в свобод-
свободные столбцы, в которых белых клеток не больше чем в других!
свободных столбцах, мы последнюю ладью поставим в столбец,
целиком состоящий из белых полей. Мы всегда сможем поставить
ладью в этот столбец, независимо от того, встречались ли мы
в процессе расстановки ладей с блокировками одного или обоих
одпов, или нет,
154
<ч
Nh
ч
i
i
i
i
©
p
H
P
H
P
©
Ш
Щ
Ш
©
p
p
©
is
p
1
®
©
p
©
ч
1
©
о
1
Ш
i
©
i
©
р
d
1
Ш
1
Ш
Ш
d
1
1
®
p
©
Ш
©
i
©
p
©
I
Рч
1
1
Ш
Ш
i
ш
©
i
i
i
i
i
H
i
i
Щ
i
-h
1
' 1
i
i
i
1
r
i
I*
-h
i
i
—
©
о
CO
Ш
1
1
1
1
p
1
p
p
1
©
1
1
Ш
Ш
1
1
©
p
1
1
©
©
Ш
1
1
1
Щ
i
i
i
i
©
i
©
P
Ш
1
©
p
©
4
Рис. 161.
Пусть, поставив п — 1 ладью, мы ни разу не пришли к си-
ситуации блокировки. Все расставленные ладьи стоят в разных
столбцах и строках; следовательно, останется только одна сво-
свободная строка и один свободный столбец, который, очевидно,
целиком состоит из белых полей. Поэтому ладью можно поставить
на клетку, имеющуюся в пересечении этого столбца со свободной
строкой, в результате чего мы получим нужную расстановку
ладей.
Если же у нас появлялись блокировки, то, «вычеркивая»
указанные строки и столбцы и сдвигая оставшиеся, мы получим
прямоугольную доску, у ко-
которой число строк больше
числа столбцов. Последняя
ладья снова ставится в стол-
столбец, состоящий из белых по-
полей; поскольку до этого по-
поставлено было не больше
п — 1 ладей, то это не со-
составляет затруднений.
Легко видеть, что при-
приведенное решение годится
не только для квадратных,
но также и для прямоуголь-
прямоугольных досок, число строк
у которых больше числа
столбцов.
80. Воспользуемся следующим свойством: касательная
к эллипсу в произвольной точке образует одинаковые углы с от-
отрезками, соединяющими эту точку с фокусами эллипса. Это оз-
означает, что бильярдный шар, посланный из фокуса Fv должен
оттолкнувшись от края, попасть в фокус F2 (на рис. 161
путь бильярдного шара обозначен пунктиром). Поэтому предпо-
предположение, что задача имеет решение, как показывает этот же ри-
рисунок, противоречит законам отражения, ибо требует, чтобы угол
падения был больше угла отражения.
81. Всего учеников в классе 25. Так как 6 учеников имеют
неудовлетворительные оценки по математике, то учеников
с оценками по крайней мере удовлетворительными всего 19;
спортсменов в классе не более 19. «Спортсменоучеников» (если
считать за единицу один вид спорта, которым занимается один
ученик) в классе всего 17+ 13+ 8 = 38, а так как ни один уче-
ученик не занимается сразу всеми тремя видами спорта, то, следо-
следовательно, учеников, занимающихся спортом — ввиду предыду-
предыдущего замечания — всего 19 и каждый из них занимается одновре-
одновременно двумя видами спорта.
Теперь уже легко ответить на вопрос,поставленный в задаче.
а) Ни один ученик в классе не имеет отличной оценки по ма-
математике.
б) Из 19 спортсменов 17 умеют ездить на велосипеде; по-
поэтому только двое учеников умеют одновременно плавать и хо-
ходить на лыжах, а следовательно, двое пловцов умеют ходить на
лыжах.
82. В первый день бегуны завершили пробег в порядке А, В
С. На второй день порядок был В, С, Л, а на третий — С, Л, В.
156
Результаты этих состязаний таковы, что А обогнал В в двух
случаях из трех возможных; аналогично, в двух из трех случаев
В обогнал Сив двух из трех случаев С обогнал Л.
Возможно ли, чтобы аналогичные результаты имели место
в трех из четырех забегов, т. е. в 75% (или более) всех забегов?
83.. Невозможно, чтобы все члены клуба образовали один
класс, т. е. чтобы они все имели одинаковое число побед, ибо число
розыгрышей D5) не делится на 10.
Невозможно также разделить спортсменов на девять клас-
классов. Действительно, если бы было девять классов, то в одном
классе было бы два игрока, а в остальных восьми — по одному
игроку. Это противоречит условию задачи. Действительно, за-
засчитаем каждому игроку по одному очку за каждый выигрыш.
Девять игроков, представляющих девять классов, не могли бы
иметь ни 0 + 1 + 2 + . . . +8 = 36, ни 1 + 2 + 3 + . . . +
+ 9 = 45 очков, ибо тогда десятый игрок имел бы 9 или 0 очков
и было бы десять классов. Те же самые девять игроков, однако,
не могут иметь 0+1+.. .+ *+(*+2)+.., + 9 =
= 36+8 — i очков, ибо тогда девятый игрок должен был бы
иметь i + 1 очков и снова было бы десять классов.
Однако спортсменов можно разделить на 10, 8, 7, 6, 5, 4, 3
и 2 класса.
Приведем примеры разбиения на 7 и на 3 класса. Игроки обоз*
начены буквами: Цифрой 1 на пересечении строки к и столбца i
обозначен выигрыш игрока, находящегося в строке &, над игро-
игроком, находящимся в столбце ?, а цифрой 0 обозначен проигрыш.
Разбиение на 7 классов
А
В
С
D
Е
F
G
Н
I
J
А
0
0
0
0
0
0
0
0
0
в
1
0
0
0
0
0
0
0
0
с
1
1
0
0
0
0
0
0
0
D
1
1
1
0
0
0
0
0
0
Е
1
1
1
1
1
0
0
0
0
F
1
1
1
1
0
1
0
1
0
G
1
1
1
1
1
0
1
0
1
н
1
1
1
1
1
1
0
1
0
J
1
1
1
1
1
0
1
0
1
J
1
1
1
1
1
1
0
1
0
Какие можно привести примеры разбиения игроков на 10,
8, б, 5, 4 и 2 класса?
84. Сначала докажем с помощью математической индукции,
что всегда какая-нибудь команда является чемпионом. Пусть
в спортивном объединении будет п команд. Соберем в одной ком-
комнате капитанов этих команд, а одного из них (назовем его К)
попросим покинуть комнату вместе с капитанами всех команд,
непосредственно побежденных командой К. В комнате останется,
157
Разбиение на 3 класса
А
В
С
D
Е
F
G
Н
I
J
А
0
1
0
0
0
0
0
0
1
в
1
0
0
0
0
0
0
0
1
с
0
1
1
0
0
0
0
0
0
D
1
1
0
0
0
0
0
0
0
Е
1
1
1
1
0
1
1
0
0
F
1
1
1
1
1
1
0
0
0
G
1
1
1
1
0
0
1
1
0
н
1
1
1
1
0
1
0
1
0
I
1
1
1
1
1
1
0
0
0
J
0
0
1
1
1
1
1
1
1
следовательно, п' капитанов; имеем п' < п. Если теорема верна
для всех п\ меньших п, то в комнате находится капитан — чем-
чемпион по отношению ко всем остальным, оставшимся в комнате.
Так как он остался в комнате, следовательно, он является не-
непосредственным победителем над К, а косвенным над иными, ко-
которые покинули комнату,— следовательно, он является чемпио-
чемпионом спортивного объединения всех п команд, что мы и хотели
доказать.
Доказательство 2) является таким же легким. Обозначим все
команды через Dx, Z>2, . . ., Dn. Пусть команда Dx непосредствен-
непосредственно побеждает наибольшее число команд, например команды />2,
D3y . . ., Dm (и не побеждает непосредственно остальные коман-
команды). Следует доказать, что команда Dx косвенно побеждает ко-
команды Dm+U . . ., Dn. Предположим обратное, что, например,
команда Dm+l не побеждена ни командой /J, ни командой #з, . ...
ни командой Z>m, т. е. непосредственно побеждает все эти
команды. Так как Dx ее побеждает (непосредственно) Dm+V сле-
следовательно, Dm+l побеждает Dly или Dm+l непосредственно по-
побеждает больше команд, чем Z),, вопреки предположению о D±.
Полученное противоречие доказывает 2).
85. Вопрос нужно понимать так: в кубковой системе может
случиться, что игрок, который заслуживает второй приз, потому
что он сильнее, чем все остальные игроки, за исключением чем-
чемпиона, встретился с чемпионом до финиша, т. е. в случае восьми
игроков, в первом или во втором туре; в таком случае, второй приз
будет выдан несправедливо. Это может случиться тогда и только
тогда, когда при жеребьевке для определения партнеров игрок,
который заслуживает серебряной медали, т. е. второго места,
попадает в ту же подгруппу из четырех игроков, что и чемпион.
Обозначим чемпиона через Ч, а «истинного» серебряного при-
призера — через С; так как в группе, в которую попал Ч, кроме
него имеется всего 3 места, на каждое из которых может попасть
С, то из семи возможных для С мест 4 благоприятны для него^
158
a 3 — нет. Вероятность того, что С получит второй приз равна,
следовательно, 4/7 = 0,5714 ..., т. е. чуть больше 57%.
86. На рис. 162 на горизонтальной оси откладываем дорогу:
влево — на почту, вправо — к сельсовету. На вертикальной оси
откладываем время. Линии ОРг и ОО'Р2 обозначают дорогу по-
посыльных. Если велосипедист сначала будет догонять посыльного,
вышедшего раньше, то его дорогу определит линия KArBxC-J)^
- /(почте
/f сельсовет!/—>
Рис. 162.
если же он будет сначала догонять посыльного, вышедшего поз-
позже,—- то линия KA2B2C2D2. Из рисунка видно, что велосипедист
должен выбрать вторую возможность,— и даже тогда, когда он
должен будет передать посланцам только деньги, т. е. тогда, когда
его дорога закончится в точке Ег или Е2.
87. Так как каждая собака бежит под прямым углом к нап-
направлению движения собаки, которая ее догоняет, а та, которая
догоняет, бежит прямо к убегающей, то догоняющая прибли-
приближается к соседней собаке со скоростью 10 м/с и поймает ее по про-
прошествии 10 сек. Вследствие этого путь каждой собаки равен 100 м.
В каждый момент четыре собаки образуют квадрат. Этот квадрат
вращается и уменьшается: его стороны уменьшаются равномерно
со скоростью 10 м/с. Пути пересекутся в центре S первоначаль-
первоначального квадрата. Это будут кривые линии (логарифмические спи-
спирали). Они не пересекутся раньше, ибо если бы какая-нибудь
собака пересекла след другой, это означало бы, что она была бы
в этом месте раньше, а это невозможно ввиду равенства в каждый
момент расстояния всех собак от S.
88. Пусть а обозначает мгновенный угол между направле-
направлением PQ и дорогой корабля Q (рис. 163), a v — скорость кораб-
кораблей Р и Q в этот же момент. На взаимное сближение кораблей
влияет скорость v корабля Р, направленная на Q, а также ком-
компонента v cos а скорости корабля Q, обе одинакового направле-
направления. Поэтому скорость сближения кораблей равна v A — cos a).
Проекция S точки Р на путь корабля Q перемещается по это-
этому пути со скоростью ycosa, а корабль Q уходит со ско-
скоростью и, следовательно, расстояние SQ возрастает со скоростью
159
v A — cos а). Так как расстояние PQ уменьшается, как мы
заметили раньше, с той же скоростью, то сумма PQ + SQ постоян-
постоянна, а следовательно, равна 10 милям, как и в начальный момент.
После бесконечно долгого
времени Р совместится с S и
будет равно PQ + SQ =
= 2PQ = 10 милям и Р<?=5
милям.
89. Пусть Ръ Р2 и <91?
О2 соответственно обознача-
обозначают положения обоих кора-
кораблей в начальный момент
(когда второй из кораблей
замечен первым), а также в
момент, когда их расстояние
наименьшее. Если так, то
первый корабль плыл из
рис 163
р
точки Рг к Ох по прямой
линии РгО2 (рис. 164). Кро-
Кроме того, в конечный момент
компоненты скоростей обоих кораблей вдоль ОХО2 должны быть
равны, т. е.
vt = v2 sin a, sin a = k.
Угол a определяет курс первого корабля. Так как корабли
дошли до точек О1? О2 в одно время, то
Р2О2
Так как
d
cos a
то искомое наименьшее расстояние кораблей равно
р7 О\Оч = ^ — ^ s*n2 a —
cos a cos a
= d cos a = d УЧ — к2.
90. Если к имеет такое же
значение, как и в предыдущей
задаче, то курс сигнализирую-
сигнализирующего корабля определяется
через угол а (рис. 164) сле-
следующим образом:
sin a = к = v±.
Рис. 164. Если же, наоборот, к обозна-
обозначает отношение скорости за-
замеченного корабля к скорости сигнализирующего корабля,
то при курсе, снова определяемом равенством sin a = к, ко-
корабли встретятся в точке О2 (рис*. 164), ибо
РгОг __
VI
160
или
1 __tga ^
#1 COS Ot i?2
sina = ?i = /c.
Следовательно, во втором случае курс определяется таким же
способом, как и в первом.
91. В момент, о котором идет речь в задаче, сторожевой ко-
корабль находится в точке Sy а моторная лодка — в точке М
(рис. 165). Лодка движется по
сторонам квадрата MN, NW.
Сторожевой корабль не догонит
лодку на отрезке MN, ибо его
скороеть для этого слишком мала.
Обозначим через а длину сторо-
стороны квадрата, а через v — скорость
корабля (следовательно, скорость
лодки равна Ъи). Точка Р, лежа-
лежащая на отрезке NW, опасна для
лодки, если сторожевой корабль
может до нее добраться не позд-
позднее лодки, т. е. если
или
Так как
а + NP
Рис. 165.
>, (a + iVPJ > 9 (SP)\
(SP)* = (NP)* + 2l — a -iVP,
2»
то приведенное выше неравенство эквивалентно следующему
квадратному неравенству относительно NP:
16 (NPJ — 22a-NP + 7а2 < О,
Неравенство это выполняется для
следовательно, опасная часть дороги равна 8/ie целого и начи-
начинается по прохождении 3/4 дороги, а кончается по прохождении
ябАб дороги.
92. В начальный момент лодка находится в точке М, сторо-
сторожевой корабль в точке S; лодка должна прибыть к побережью
в точке W (рис. 166). Точки М, 5, W лежат на одной прямой
MS = SW. Из текста задачи следует, что лодка должна плыть по
сторонам прямого угла MNW, вписанного в окружность диамет-
диаметра MW.
Путь лодки должен быть по возможности кратчайшим, по-
поэтому первый его отрезок (MN) должен образовать возможно
161
меньший угол с направлением МW. Кроме того, лодка должна
наверняка избежать сторожевого корабля. Поэтому ее путь не
должен пересекать аполлониевой окружности TUV, которая
является геометрическим местом точек, в которых встречаются
корабль и лодка, плывущие со-
соответственно из точек S и М со
своими максимальными скоростя-
скоростями по прямым линиям. Центром
аполлониевой окружности являет-
является точка О, положение которой на
отрезке М W определяем из соот-
соотношений
МТ = 3S7\
MV = 3SF,
ОТ = OF.
Из этих равенств следует, что
Рис. 166.
16
о
а радиус аполлониевой окружности равен — MW. Если бы
16
отреаюк MN касался окружности TUV, то путь лодки равнялся бы
2 l/ -4- 1
,— о MWt а если MN не имеет общих точек с этой окруж-
окружностью, то путь будет длиннее, чем
1^2 + 1
MW. Следует еще
только проверить, что если отрезок MN проходит достаточно
близко к окружности TUV, то сторожевой корабль не настигнет
лодку и на отрезке NW. Оставим это читателям.
Итак, курс лодки, отвечающий условию задачи, определен
полностью.
93. Таким удивительным числом является число один, ко-
которое можно записать тремя способами:
1, 100% и 57°17'44",8. . . A радиан).
94. Новый «сантиметр» при измерении может дать ошибку
в V2 см, так же как и старый, и не в этом следует искать его
ff В
j1
1
/
2
3
4
N
N+1
Рис. 167.
преимущество. При измерении некоторого отрезка АВ конец В,
вообще говоря, окажется между штрихами шкалы. Используя
новую ленту (рис.. 167), мы, без сомнения, припишем этому от-
162
резку длину в N см, если N является надписью между штрихами.
При использовании же обычной ленты мы должны еще устано-
установить, лежит ли В ближе к левому или к правому штриху. В исклю-
исключительном же случае, когда при использовании новой ленты
конец В совпадает со штрихом, лежащим между числами N и
N + 1, записываем:
AB = N+±- см.
95. Не существует словарей, содержащих более миллиона
слов. Если, например, словарь содержит 500 страниц, то мы от-
откроем его посредине и найдем самое последнее слово на странице
250, предположим, «нарцисс». Первый вопрос должен быть таким:
находится ли отгадываемое слово в словаре после слова «нар-
«нарцисс»? Если ответ будет гласить «да», то мы открываем словарь
на странице 375, а если «нет», мы откроем его на странице 125 и
опять спросим о расположении загаданного слова jno отношению
к последнему слову на открытой странице, и т. д. Если в какой-
то момент мы получим дробное число страниц (например, 62,5),
то мы округлим его до ближайшего большего целого числа. Пос-
После девяти таких вопросов поиски слова ограничатся одной стра-
страницей. Если на этой странице 2 столбца, то с помощью 10-го
вопроса мы определим столбец. В столбце самое большее 64 сло-
слова и, следовательно, 16-й вопрос приведет нас к одному слову,
которое, если мы еще раньше не отгадали нужное слово, мы
и укажем загадавшему его.
Словарь, который мы указали в качестве примера, содержит
не более 128-500 = 64 000 слов. Так как число слов в словаре
ограничено миллионом, то в нем может быть не более чем в 16 раз
больше слов, чем в словаре, рассмотренном выше F4 000-16 =
= 1 024 000). Для словаря с максимальным количеством слов
потребуются 4 дополнительных вопроса B4 = 16), т. е. всего
20 вопросов.
Мы видим, таким образом, что доктор Шарадек говорит
правду.
96. Каждый студент, одалживающий кому-либо деньги,
записывает соответствующую сумму как положительное число,
а одалживая у кого-либо деньги, записывает эту сумму как от-
отрицательное число. Сумма всех записанных чисел дает в конце
года положительное или отрицательное сальдо данного студента,
причем сумма всех сальдо дает нуль.
Бухгалтерии Шарадека достаточно для выравнивания дол-
долгов, а необходимо для этого самое большее шесть выплат. Дей-
Действительно, предположим, что «наименьший» должник выплачи-
выплачивает всю сумму «наибольшему» кредитору. Тогда, после первой
выплаты, общее число должников и кредиторов будет равно самое
большее шести, а после пятой выплаты, произведенной по тому же
самому принципу, число должников и кредиторов будет равно
самое большее двум, вследствие чего самое большее после шестой
выплаты все долги будут выравнены. Конечно, может случиться,
что после какой-либо очередной выплаты один из кредиторов ста-
станет должником, но этот факт не изменит числа кредиторов и
должников,
163
96а. Обозначая буквой р правую чашку весов, а буквой / —
левую чашку, получим следующее расположение монет после
трех взвешиваний:
I взвешивание
II взвешивание
III взвешивание
к
Р
1
R
Р
У
1
1
Р
Р
т
1
р
О
1
1
р
N
Р
Р
1
Р
Р
Р
м
1
1
D
1
W
Р
1
А
Р
1
1
Предположим теперь, что одна монета тяжелее остальных»
Тогда, обозначая знаком «О» равновесие чашек, знаком «+» пе-
перевес правой чашки весов, а знаком «—» перевес левой чашки ве-
весов, будем иметь следующие возможности, в зависимости от того»
какая монета (с названием, указанным в соответственном столбце)
тяжелее:
I взвешивание
II взвешивание
III взвешивание
к
+
0
—
R
+
0
0
У
¦
0
—
р
0
0
+
г
_
+
0
О
—
+
N
0
+
+
+
м
___
0
D
0
—
0
w
0
+
А
+
—
Если бы одна монета была легче остальных, то имели бы
место следующие возможности:
I взвешивание
II взвешивание
III взвешивание
к
_
0
+
R
_
0
0
У
+
0
+
р
0
0
—
г
+
0
О
+
+
N
0
-—
I
_
—
—
м
+
+
0
D
0
+
0
w
0
—
+
А
_
+
+
Так как все расстановки трех знаков в двух приведенных
выше таблицах различные, то, преддолагая, что только одна
монета фальшивая, можно из наличия соответственной расстанов-
расстановки знаков заключить, какая из монет фальшивая, а также тя-
тяжелее она или легче остальных.
Из трех элементов можно образовать всего З3 = 27 сочета-
сочетаний с повторениями, поэтому две приведенные выше таблицы
не охватывают еще трех случаев, а именно:
0_+, 0+-, 0- +
164
Первый случай — при условии, что по крайней мере 11
взвешенных монет являются одинаковыми,— вызывает равен-
равенство всех монет. Следовательно, мастер мог прийти к выводу,
что все монеты настоящие, предполагая лишь, что самое большее
одна монета фальшивая.
Два остальных случая не могут иметь места, если только
одна монета фальшивая.
Поэтому, если выступает один из этих случаев, то можно
заключить, что по крайней мере две монеты фальшивые. Если
же, однако, имеет место один из этих случаев, то фальшивыми
могут быть пары У7\ У W, TW или тройки KTY, RPD и т. д.
Обман был обнаружен потому, что мастер обозначил фальшивые
монеты двумя из трех букв 7\ У, W; если бы случилось иначе,
обман не был бы открыт. Действительно, если бы, например,
фальшивыми (и, более тяжелыми) оказались монеты Z?, P, то
результат взвешиваний, представленный символически, был бы
следующим:
MYTO < RAK1, MODA = WINT, WYKA = PION,
а тогда мастер считал бы, что фальшивой (и более тяжелой) мо-
монетой является 7?, что не соответствует истине.
Постараемся ответить еще на последний вопрос: мог ли
приятель Шарадека так изменить вес тщ и тп2 двух монет (остав-
(оставляя остальным монетам их вес иг), чтобы сделать невозможным
обнаружение обмана. Если
т1 ф m, т2 Ф т и тх ^ т2
(что можно предположить), то возможен один из трех случаев:
I. т < т1 ^ т2, II. т1 < т < т2, III. т1 ^ т2 < т.
Теперь достаточно соответственно обозначить монеты с весом
т1 и т2 через W и У, или же через D и У, или же через W и
У, чтобы результат взвешивания был следующий: —|— или
Н [-. Приятель Шарадека, следовательно, не мог так изменить
вес монет, чтобы быть полностью уверенным в том, что проведет
мастера, хотя обнаружение подвоха зависит от того, обозначил
ли мастер монеты буквами именно так, как следует, в чем мастер
также не может быть уверен.
966. Нижний слой показан на рис. 168. Каждый другой слой
получаем, перемещая в предыдущем слое первый столбец на
правый край. Условие задачи, очевидно, выполняется.
97. Требуемое общество будет сконструировано, если мы
посадим каждого из 12 не знакомых друг с другом лиц, на
«свою» грань правильного додекаэдра и потребуем, чтобы каж-
каждый познакомился со своими «соседями», т. е. с обитателями
смежных граней.
Условие е) здесь соблюдается, так как двое лиц,, занимаю-
занимающих противоположные грани додекаэдра, не имеют общих
соседей.
Общество, описанное доктором Шарадеком, также населяет
грани правильного додекаэдра, но в этом случае нужно посту-
поступить обратным образом, а именно, познакомить каждого чело-
человека со всеми лицами, не являющимися его соседями.
165
98. Доктор Шарадек прав. Действительно, предположим
обратное, т. е, что в определенный момент в правой половине
находятся только две костяшки или еще меньше (рис. 169).
А
белый
ЛГ
Красный Голубой
ДЗ
ГолуШ
Желтый Зеленый
32
белый
Зеленый Красный Голубой
из
Красный Голубой
Зелый
Я4-
Шелтш Зеленый
Шелтьш Звленьш Красный Голубой
Мел/льш
Яелый
?3
G2
Зеленый Красный
Л2
Желтый
Л4- ;
Рис. 168.
А
А
Рис. 169.
Рис. 170.
После промежутка времени, который необходим каждой кос-
костяшке для перемещения по всей проволоке, расположение костя-
костяшек будет симметричным предыдущему (рис. 170): в левой по-
лорине счетов будут находиться две костяшки (или меньше),
а в правой — восемь костяшек (или больше), чта противоречит
условию задачи,
166
99. Решение доктора Шарадека является удачным, незави-
независимо от того, где он живет. Действительно, рис. 171 показывает,
как можно объехать все улицы города и вернуться к произволь-
произвольно выбранной точке выезда. Длина кратчайшего объезда превы-
превышает на 16,7% длину всех улиц города.
Рис. 171.
100. Пять городов Шал он, Витри, Шомон, Сэн-Кантэн и
Реймс образуют замкнутый пятиугольник; одна из его сторон
(сторона Шомон — Сэн-Кантэн) является суммой четырех ос-
остальных, ибо 236 = 86 + 40 + 30 + 80. Это возможно только
тогда, когда вершины пятиугольника лежат на одной прямои.
Города расположены на прямой в следующем порядке: Сэн-
Какгэн, Реймс, Шалон, Витри и Шомон. Расстояние между Рейм-
Реймсом и Шомоном, следовательно, равно 40+ о0 + ви = юикм.
Г. Штейнгауз
СТО ЗАДАЧ
М., 1976 г., 168 стр. с илл.
Редактор И. М. Я г л о м
Техн. редактор А. П. Колесникова
Корректор М. Л. Медведская
Сдано в набор 19/П 1976 г.
Подписано к печати 06.10.1976.
Бумага 84хЮ87з2. Физ. печ. л. 5,25.
Условн. печ. л. 8,82. Уч.-изд. л. 9,14.
Допечатка тиража 200 000 s
Цена книги 44 коп. Заказ №
Издательство «Наука»
Главная редакция
физико-математической лите]
117071, Москва, В-71, Ленинский
2-я типография издательства «На
Москва, Г-99, Шубинский пер.,