СИНТЕЗ ИЗОБРАЖЕНИЙ
Базовые
алгоритмы

synthese d'image:
algorithmes
elementaires
par
Gerard HEGRON
IRISA/INRIA-Rennes
Preface de Michel LUCAS
Professeur a l'Universite de Nantes
яшшвшцтщцш
DUNOD
TnfonnatTque

Ж. Эгрон
СИНТЕЗ ИЗОБРАЖЕНИЙ
Базовые
алгоритмы
Перевод
с французского
канд. техн. наук А.В. Серединского
МОСКВА
«РАДИОИ СВЯЗЬ»
1993

ББК 32.97
Э17
УДК 681.327.82
Федеральная целевая программа книгоиздания России
Редакция литературы по информатике и вычислительной технике
ЭгронЖ.
Э17 Синтез изображений. Базовые алгоритмы: Пер. с франц. — М.:
Радио и связь, 1993. — 216 с: ил.
ISBN 5-256-00431-Х.
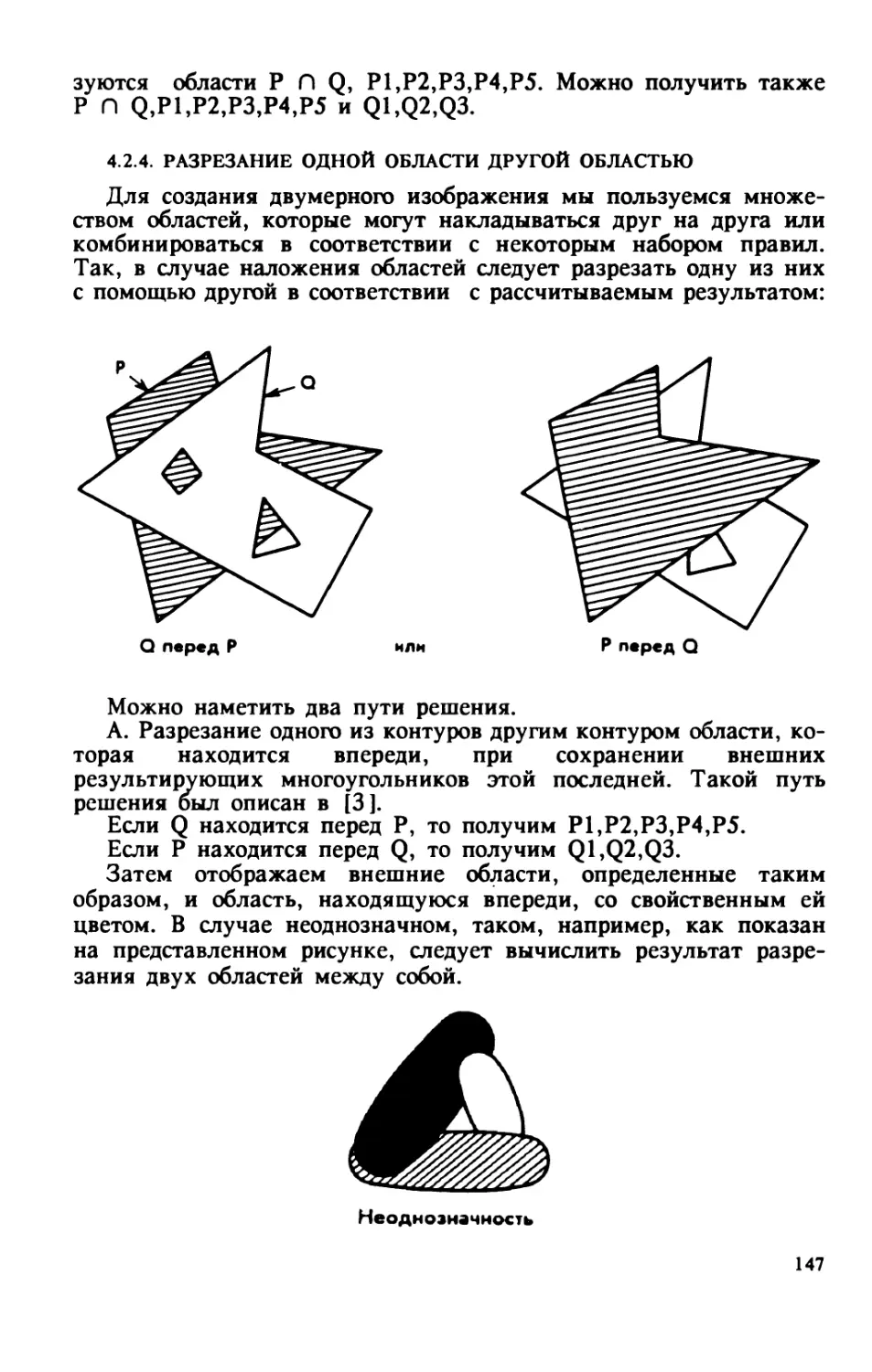
В книге французского специалиста собраны и систематизированы основные
алгоритмы машинной графики, используемые при синтезе изображений с
помощью ЭВМ. Описываются операции генерирования кривых, заполнения
областей и взаимодействия геометрических объектов. Приведено около 50
программ, составленных на языке высокого уровня, что позволяет читателю
воспользоваться готовой программой для конкретных условий. Автор
ограничивается простейшим математическим аппаратом.
Для специалистов, использующих графические системы.
2404010000—061
Э 046(01)Ч>3 "-" ББК3297
Производственное издание
ЭГРОН ЖЕРАР
СИНТЕЗ ИЗОБРАЖЕНИЙ. БАЗОВЫЕ АЛГОРИТМЫ
Заведующий редакцией Ю.Г.Ивашов. Редактор И.И.Рюжина. Обложка художника
Н.И.Казакова. Художественный и технический редактор Л.А.Горшкова.
Компьютерная верстка О.В.Сергеева. Корректор Н.Л.Жукова
ИБ№2075
ЛР № 010164 от 04.01.92.
Подписано в печать с оригинал-макета 26.10.93. Формат 60x90/16. Бумага газетная.
Гарнитура Тайме. Печать офсетная. Усл. печ. л. 13,5. Усл. кр.-отт. 13,75.
Уч.-изд. л. 10,17. Тираж 5000 экз. Изд. №23091. Заказ №1342. С-061.
Издательство „Радио и связь", 101000, Москва, Почтамт, а/я 693.
Московская типография № 6 Министерства печати и информации РФ, 109088,
Москва, Ж-88, Южнопортовая ул., 24.
ISBN 5-256-00431-Х (рус) QBORDAS, Paris, 1985
ISBN 2-04-016427-8 (франц.) © Перевод на русский язык,
примечания. Серединский А. В., 1993

ПРЕДИСЛОВИЕ
Сегодня, когда каждый желающий может восхищаться изобра-
жениями, созданными с помощью ЭВМ, особо отмечая их
реалистичность и совершенство отделки, возникает вполне резон-
ный вопрос: имеет ли смысл посвящать целую книгу изучению
элементарных операций, используемых в процессе синтеза изобра-
жений? Но ведь тысячи пользователей персональных компьютеров,
появившихся благодаря настоящему взрыву в информатике, вы-
нуждены каждый раз заново открывать для себя базовые ал-
горитмы. Нельзя забывать и об инженерах, занятых разработкой
и созданием генераторов синтезированных изображений, которым
хотелось бы иметь возможность выбрать наилучшие алгоритмы для
своих синтезаторов.
И вот в чем заключается явный парадокс: даже самые совер-
шенные из ежедневно появляющихся изображений создаются с
помощью алгоритмов, не освоенных в должной мере и к тому же
настолько многочисленных, что неизвестно, какой из них и почему
следует выбрать.
Достоинством данной книги является то, что в ней систе-
матизирован отбор некоторых более или менее известных ал-
горитмов и описаны достоинства и недостатки каждого из них. В
результате этой тщательнейшим образом выполненной кро-
потливой работы оказались собранными под одной обложкой мето-
ды, обычно разбросанные по многочисленным и не всегда легкодо-
ступным публикациям.
Второе достоинство книги заключается в том, что читатель по-
лучит здесь знания не только из области элементарных базовых
алгоритмов, но и из области основ синтеза изображений в целом,
поскольку в книге содержатся сведения о трех основных задачах
синтеза: генерировании кривых, заполнении площадей и обработке
геометрических объектов.
И наконец, несмотря на широкое многообразие алгоритмов, ав-
тору удалось свести их воедино и выделить два метода, связыва-
ющие между собой некоторые алгоритмы, которые могут составить
основу программного пакета: генерирование кривых методом Бре-
зенхема и различные виды обработки, базирующиеся на прос-
5

леживании контуров. Этот аспект книги представляется наиболее
важным и интересным.
Я нисколько не сомневаюсь в том, что книга сослужит немалую
пользу и окажет заметное влияние на разработку программного
обеспечения компьютерной графики. Я предсказываю книге дол-
гую жизнь.
Мишель Люка,
профессор
Нантского университета,
Франция

ВВЕДЕНИЕ
С тех пор как в качестве видеотерминалов современных ЭВМ
начали использоваться устройства с разверткой телевизионного
типа, появилось новое направление в исключительно важной
области интерактивной машинной графики — синтез изображений.
В дальнейшем будем пользоваться термином "изображение", в
отличие от термина "рисунок", полагая, что последний содержит
в качестве единственного базового элемента только черно-белые
линии. В то же время изображение позволит использовать все вы-
разительные возможности графики, сочетая в себе элементы,
состоящие как из отрезков линий, так и из окрашенных участков
поверхности (областей).
В многочисленных литературных источниках описываются раз-
нообразные методы, используемые при создании изображений. Ча-
сто предлагаемые решения не согласуются между собой. Данная
книга посвящена нижнему уровню проблемы синтеза изображений,
т.е. той базе, на которой основаны практически все методы,
применяемые в процессе управления информационным содер-
жанием экрана.
В книге рассматриваются три основных класса задач:
генерирование кривых (гл. 2);
заполнение площадей (гл. 3);
алгоритмы разрезания и элементарной обработки гео-
метрических объектов (гл. 4).
Для каждого класса задач выбор представленных здесь ал-
горитмов явился результатом проведенного автором "сравнитель-
ного анализа базовых алгоритмов синтеза изображений" (см.
[19]). Тем самым оказалось возможным достичь сразу нескольких
целей:
собрать и классифицировать многочисленные публикации в
этой области (о чем красноречиво свидетельствует список литера-
туры);
отобрать и представить библиотеку отлаженных алгоритмов;
выделить набор методологических приемов, позволяющих
решать наибольшее число задач, начиная с частных и кончая са-
мыми общими.
Эта книга дает в руки пользователю графической системы эле-
менты для их практической реализации (элементарные алгоритмы
визуализации). Попутно можно отметить, что, хотя разработанные
алгоритмы предназначены главным образом для синтеза изобра-
7

жений, большинство из них применимы и для создания рисунков
(генерирование кривых, штриховка, разрезание контуров и обра-
ботка геометрических объектов). Алгоритмы намеренно представ-
лены в описательной форме, чтобы пользователь мог составить по
ним программу на любом языке по своему выбору.
Другая цель данной книги состоит в четкой классификации
множества различных применяемых алгоритмов с их особенно-
стями, методическими приемами, оригинальными решениями при
единой методологической форме.
Для этого мы выделяем два наиболее общих метода. Первый из
них — метод Брезенхема — предназначен для инкрементного ге-
нерирования отрезков прямых линий и кривых второго порядка.
Второй — метод прослеживания контуров — позволяет выполнять
большинство элементарных операций, связанных с обработкой
областей.
ВЫРАЖЕНИЕ ПРИЗНАТЕЛЬНОСТИ
Появление этой книги явилось результатом диссертационной работы автора по
информатике [19], выполненной им под руководством профессора Нантского
университета M. Люка, являющегося руководителем группы "Графическая обработ-
ка и САПР". Написание ее стало отчасти возможным благодаря тому, что Институт
информатики и системных исследований Реннского университета 1 продлил на два
месяца ассигнования на наши исследовательские работы.
Автор считает приятным долгом выразить глубокую признательность профессору
Люка, своевременно подавшему мысль о создании книги и написавшему к ней
столь теплое предисловие. Благодарю также Мари-Анн Руа и Жака Андрэ,
прочитавших первоначальный вариант книги и сделавших немало полезных заме-
чаний, что позволило автору существенно улучшить ее окончательный вариант.
Особенно благодарю Маризу Фуше, весьма квалифицированно и терпеливо вы-
полнившую машинописную работу.

ГЛАВА 1
ОБЩИЕ ПРЕДСТАВЛЕНИЯ О БАЗОВЫХ АЛГОРИТМАХ
СИНТЕЗА ИЗОБРАЖЕНИЙ
Чтобы яснее очертить круг понятий, определяемых термином
"элементарные алгоритмы синтеза изображений", уточним, что мы
будем понимать под теми видами обработки, которые называются
"элементарными" или "базовыми", а также уточним, что такое
изображение как предмет применения этих видов обработки.
1.1. АЛГОРИТМЫ И ЭЛЕМЕНТАРНАЯ ОБРАБОТКА
Наиболее общая структурная схема последовательности прог-
рамм, необходимых для разработки программного обеспечения
интерактивной графической системы, состоит из следующих эле-
ментов (рис. 1.1):
средства описания, позволяющие кодировать сцену на основе
информации, поставляемой прикладной программой;
Алгоритмы
подготовки
визуализации
Алгоритмы
обработки
рисунков
|*| Средства f*j Элементар-
но д готовки
визуализации U
Рис. 1.1 Обобщенная схема программных средств интерактивной графики [23]

средства подготовки визуализации в форме графического
файла, в котором двумерная сцена описана на основе исходного
кода;
элементарные средства, позволяющие получать рисунок или
результирующее изображение на основе указаний, поступающих
от программ подготовки визуализации. Элементарные, или базо-
вые, средства предназначены для составления списка визуализации
и обеспечения управления экраном.
Набор алгоритмов элементарной обработки относится к базовым
программным средствам. Представляемая и отображаемая структу-
ра выражается в виде двумерной сцены.
1.2. ИНФОРМАЦИОННОЕ СОДЕРЖАНИЕ ИЗОБРАЖЕНИЙ
Изображение представляет собой структурированный массив
информации, который, будучи отображенным на экране, осмыс-
ленно воспринимается глазом человека.
В соответствии с этим определением отчетливо разделяются два
пространства, связанные с изображением: первое — пространство
пользователя, в котором находятся структуры отображаемого
объекта (или сцены), и второе — пространство экрана, где распо-
лагаются дискретные графические структуры сцены и непосредст-
венное представление (в прямом смысле слова) изображения на
экране (рис. 1.2).
Поверхность визуализации представляет собой мозаичный эк-
ран, имеющий вид регулярной прямоугольной сетки, в декартовой
системе координат, где любой паре чисел (X,Y) соответствует эле-
ментарная квадратная площадка, называемая "пикселом"
(рис. 1.3).
Каждая точка этой поверхности характеризуется яркостью и
цветом. Таким образом, можно сказать, что изображения состоят
из точек и областей, образованных совокупностью точек. В
отличие от рисунков, образованных отрезками линий и точками,
будем говорить об изображениях (этот же технический термин
используется в телевидении, где применяется иной метод восп-
роизведения, более совершенный, чем поточечный).
В процессе воспроизведения изображения используются оба ме-
тода: представление на основе кривых и на основе окрашенных
поверхностей, или областей. Наиболее важным параметром, ха-
рактеризующим некоторую область, является контур, или линия
ограничивающего ее силуэта. Действительно, отображение множе-
ства точек, образующих область, выполняется на основе описания
ее контура.
Поясним, что мы будем в дальнейшем понимать под описанием
контура или области в процессе их отображения с помощью
графических примитивов (отрезков прямых, дуг окружностей и
т.п.).
Ю

Восприятие
Пространство
пользователя
Прообразов амия
Пространство экрана
т
Рис. 1.2. Пространства, связанные
с изображением
Рис. 1.3. Поверхность для поэлементного
отображения
Определим контур как непрерывную и замкнутую последова-
тельность примитивов, представляющих собой линии границ меж-
ду областями. Такая последовательность имеет структуру кольца.
В общем случае будем предполагать, что примитивы одного кон-
тура, как и примитивы различных контуров, могут пересекаться
между собой или накладываться друг на друга. Будем говорить,
что контур многоугольный, если он задан множеством отрезков
прямых или упорядоченной последовательностью своих вершин. В
дальнейшем с целью упрощения терминологии будем иноща назы-
вать "контуром" не обязательно всю замкнутую линию, но и ее
отдельные части.
Метод генерирования областей, или, в более общем случае,
изображений, составленных из совокупности областей, зависит от
исходного кодирования контуров или ограниченных ими участков
поверхности.
1.3. КОДИРОВАНИЕ ИЗОБРАЖЕНИЯ
Выбор кода, описывающего изображение, определяется нес-
колькими критериями:
объемом памяти,
временем регенерации содержимого на экране,
и

скоростью передачи изображения,
скоростью генерирования изображения.
Разнообразие кодов для представления изображений
практически бесконечно. Однако следует различать коды, описы-
вающие изображение на нижнем уровне, поскольку изображение
уже дискретизировано (пространство экрана), и коды, описыва-
ющие изображение независимо от способа визуализации (прост-
ранство пользователя) (см. рис. 1.2).
Кодирование в пространстве экрана
•ПОВЕРХНОСТИ:
бинарная матрица — область кодируется точка за точкой ("О"
- не высвечивается, "1" — высвечивается) в бинарной матрице;
кодирование по участкам — для каждой строки развертки за-
поминаются точки пересечения контура со строкой; таким обра-
зом, отрезки определяются как некоторые зоны или участки.
•КОНТУРА:
кодирование разностей по участкам — измеряют значения раз-
ностей положений концов участка в одной строке по отношении
к другой;
инкрементный код — код области определяется исходной точ
кой и последовательностью элементарных перемещений, что поз
воляет переходить от точки к точке (код Фримена, рис. 1.4).
1 1 МЧ
1 hi I l<
LkIJH
И И у
if И
2\ \2\2\ У
Л \ А 1 1*
N'lN
и N
Кит
irm
г ГМ
1 I6 I I6 I
•NlN
J Ni
v\ И
И4Г
i41 j i v
*И4К
1 |б 1 1 1
"1—W—l 1 h
5 n * Г?
Принцип
кодирования
P - исходная точка
этот элемент рисунка будат
иметь код: 2232221121
Кодирование элемента рисунка
Рис. 1.4. Код Фримена
12

Кодирование в пространстве пользователя
•СИНТАКСИЧЕСКИЕ КОДЫ:
рисунки рассматриваются как графы R .
• КОДИРОВАНИЕ КОНТУРА:
контур описывается совокупностью примитивов, таких, как
отрезки прямых, кривых второго порядка или сплайнами, записан-
ными в аналитическом виде.
•КОДИРОВАНИЕ СТРУКТУРЫ:
примитивами — область описывается как совокупность глобаль-
ных примитивов (прямых, кривых и т.д.), на которых можно вы-
полнять некоторые операции (наклона, симметрии и др.),
скелетными линиями — область кодируется своей скелетной
линией и функцией, определяющей толщину этой линии в каждой
точке.
Одним из важных критериев для выбора кода является его спо-
собность адаптации к методу генерирования используемых изобра-
жений. Например, инкрементное кодирование контура может быть
(после некоторой доработки) использовано в терминалах с развер-
ткой телевизионного типа [26]. Франклин [14], сравнив одиннад-
цать алгоритмов построчного отображения рисунков, сделал сле-
дующий вывод: оптимальный метод состоит в разделении экрана
на горизонтальные полосы, каждая из которых целиком записыва-
ется в память, а затем в выделении по полосам отрезков прямых
и кривых, пересекающих границы, и в воспроизведении каждой
кривой для каждой полосы, точки за точкой, после чего в их отоб-
ражении.
Нас будут интересовать два метода генерирования рисунков или
изображений на дискретизированной поверхности.
1. Первый метод родствен тому, который используется при вос-
произведении векторных рисунков на поверхности (например, при
проведении кривых): точка за точкой отображаются инкрементным
методом (код Фримена, рис. 1.4). Этот метод хорошо подходит для
генерирования элементарных объектов (кривых, отрезков прямой
и др.).
2. Второй метод получил свое развитие с появлением видео-
терминалов телевизионного типа (с последовательной разверткой),
где отображение происходит построчно, строка за строкой
(рис. 1.5).
Последовательная развертка обладает следующими до-
стоинствами:
она хорошо приспособлена для генерирования и получения век-
торных рисунков и изображений;
Ее иногда называют прогрессивная. — Прим. перев.
13

Видимая часть строки
Обратный ход по строк*
Обратный ход
по кадру
Рис. 1.5. Последовательная развертка
она также хорошо приспособлена для отображения и передачи
изображений телевизионного типа, поскольку нет необходимости в
преобразовании кода, в отличие, например, от инкрементного ме-
тода.
В следующей главе будет показано, что имеется немало методов
создания изображений, в которых сочетаются оба способа ге-
нерирования.
1.4. ВИДЫ ОБРАБОТКИ ПРИ СИНТЕЗЕ ИЗОБРАЖЕНИЙ
Для выполнения различных видов обработки существует не-
сколько методов, зависящих от кодированной структуры изобра-
жения.
Рассмотрим несколько вариантов, определяя область либо в
пространстве пользователя, либо в пространстве экрана (рис. 1.6):
пространство пользователя — область задана математическим
описанием контура;
пространство экрана — будем определять область множеством
составляющих ее точек (будем обрабатывать матрицы точек); мно-
жеством горизонтальных интервалов, представляющих собой
отрезки строк развертки, попадающих внутрь рассматриваемой
области (будем обрабатывать структуры, состоящие из интервалов,
называемых также участками или зонами); поточечной записью
контура в матрице изображения; множеством отрезков линий
штриховки, если область заштрихована ( будем обрабатывать мно-
жество отрезков прямых).
Чтобы генерировать область на экране, необходимо выполнить
последовательно следующие операции (рис. 1.6):
записать контур области, точку за точкой. В этом состоит
основная задача процесса генерирования кривых;
окрасить внутреннюю часть области одним цветом (в прямом
смысле слова "заполнение") или заштриховать ее.
Как видно из рис. 1.6, существуют различные переходы из про-
странства пользователя в пространство экрана (штриховые линии
со стрелками).
ч ' Л—--■*
14

ПРОСТРАНСТВО ПОЛЬЗОВАТЕЛЯ
Множество примитивов
отображения: отрезки прямыж,
дуг окружностей и т.д.
(• аналитической форме) ^i^J
ПРОСТРАНСТВО ЭКРАНА
Множество
^ горизонтальны!
интервалов
, -* (или участков)
* •
J I Заполнение (строке
11м строкой или
. построчное )
•••
••••
••••••
••••••••••••• Множество
••••••••
•г
л
Окрашивание
Множество
отрезков прямых
J .*• Контур, заданный!
• # # • • последовательностью!
•»• точек
Рис. 1.6. Представление области и виды обработки
Процесс создания изображения можно представить также в
форме соединения множества областей. При этом придется иссле-
довать случаи взаимного пересечения областей и их контуров. В
дальнейшем будет показано, что элементарные геометрические за-
дачи, возникающие в процессе взаимодействия геометрических
объектов, существенно зависят от того, как будут представлены
области (контурами, наборами точек, горизонтальными интерва-
лами и т.д.).
Среди различных процессов, используемых для создания изоб-
ражений, особое внимание будет уделено одному из них, называ-
емому "прослеживание контура". С его помощью можно решать
большинство задач, основываясь на структурированном описании
контура в пространстве пользователя без обращения к описанию
области в пространстве экрана.
Мы не будем касаться здесь таких проблем, как анализ изоб-
ражений и их распознавание, относящихся скорее к принципам
"обработки изображений", чем к "синтезу изображений". В свою
очередь, и обработку, и синтез следует рассматривать как своего
рода дополнения к процессам создания изображения с помощью
ЭВМ.
15

ГЛАВА 2
ГЕНЕРИРОВАНИЕ КРИВЫХ НА ДИСКРЕТНОЙ
ПОВЕРХНОСТИ
2.1. ВВЕДЕНИЕ
В процессе синтеза изображений встречаются несколько ситу-
аций, требующих применения алгоритма генерирования кривой на
дискретной поверхности:
генерирование рисунка (множества кривых) в поэлементном
режиме (точка за точкой);
генерирование контуров областей, заданных набором
примитивов (отрезками прямых, дугами кривых второго порядка и
т.п.);
заполнение площадей — построчное генерирование контура при
методе слежения по нему или кодирование контура при методе
построчной развертки (см. гл. 3).
Постановка задачи. Записать кривую на дискретной поверх-
ности означает найти такую ее аппроксимацию, по которой глаз
человека смог бы восстановить исходную кривую. При этом вы-
полняется переход от непрерывного представления кривой к
дискретному (квантованному) .
Пусть, например, отрезок прямой определен своими начальной
и конечной точками (рис.2.1а). Задача состоит в том, чтобы по-
лучить последовательность точек, расположенных на дискретной
сетке экрана, наилучшим образом приближающую исходный отре-
зок (рис.2.16).
Изучение методов решения этой задачи позволяет выделить два
больших класса алгоритмов:
численные,
инкрементные.
■ ■
а б
Рис. 2.1 Генерирование отрезка прямой:
а — сетка и точки на концах отрезка; б — дискретное описание отрезка
1 Здесь под квантованием понимается пространственная дискретизация на
плоскости. — Прильперев.
16

2.2. ОБЩАЯ КЛАССИФИКАЦИЯ
Рассмотрим вкратце некоторые характеристики этих двух клас-
сов алгоритмов.
2.2.1. ЧИСЛЕННЫЕ МЕТОДЫ
Для этих методов расчеты основаны на численном анализе
кривой с использованием ее уравнения и частных производных.
Обычно исследуются точки пересечения кривой с горизонтальными
линиями (у-п). Для этого используется циклическая структура
вычислений y(t) для t-mAt, вде m-mo, то + 1,..., и для каждого
т, такого, что y(mAt) < n < y(mAt + t), находится x(mAt). Если
шаг изменения переменной t фиксирован, то вычисления у(тДО
и x(mAt) выполняются рекуррентно.
Использование данного метода сопряжено с двумя затруд-
нениями. Во-первых, часто бывает невозможно зафиксировать At
без риска пересечь на каждом шаге более одной горизонтальной
линии. Во-вторых, точность связана с рекуррентными вычис-
лениями, влияющими на ухудшение вида кривой. Для уменьшения
последнего эффекта Максвелл и Бейкер [24 ] предложили исследо-
вать и учесть все вероятные источники погрешности.
Реализация численных методов осуществляется, главным обра-
зом, двумя путями:
программированием параметрического представления кривой,
заданной парой уравнений: x-x(t) и y-y(t);
использованием цифровых дифференциальных анализаторов,
представляющих собой гибридные вычислительные устройства,
в которых одновременно реализуются аналоговые и цифровые опе-
рации.
Численные методы основаны на арифметических операциях над
вещественными числами, и здесь почти никогда не удается
избавиться от операций умножения и деления.
2.2.2. ИНКРЕМЕНТНЫЕ МЕТОДЫ
Основной принцип инкрементных методов состоит в следую-
щем: кривую описывают на всем ее протяжении, от начальной
точки до конечной, вычисляя на каждом шаге направление эле-
ментарного движения от текущей точки к следующей за ней.
В каждой точке можно задать либо 4 возможных направления
движения (рис.2.2а), либо 8 направлений (рис.2.26) .В результате
обхода всей кривой получают так называемый "код Фримена".
На каждом шаге направление элементарного движения
вычисляется с помощью структурных свойств и неявных методов,
поскольку кривая представлена в этом случае в непараметричес-
кой форме уравнением вида f (х,у)-0, ще x,y Е R. Здесь одновре-
17

У+1
У
y-i
У+1
y-i
3.
4
51
,2
• I
0
7
Д-1
ж + 1
1-1
X
6
x+1
Рис. 2.2 Код Фримена:
a — 4 направления; 6 — 8 направлений; текущая точка имеет координаты (х,у)
менно используются неявное представление кривой, ее гео-
метрияеские свойства и свойства поверхности визуализации.
В инкрементных методах применяются арифметические опе-
рации над целыми числами и во многих случаях удается избежать
необходимости пользоваться операциями умножения и деления.
2.2.3. ВЫВОДЫ
В этой книге будем интересоваться в основном инкрементными
методами, поскольку перед численными методами они обладают
следующими преимуществами:
использование арифметических операций над целыми числами;
как правило, отсутствие операции умножения и деления;
программная реализация методов, делающая их независимыми
от аппаратных средств (что не исключает, впрочем, возможности
использования устройств на жесткой логике);
с другой стороны, инкрементные методы тесно примыкают к
методам "прослеживания контуров", поскольку в процессе ге-
нерирования кривой приходится "двигаться" вдоль идеальной
линии от одного ее конца до другого. В дальнейшем будет пока-
зано, каким образом эти методы включаются в алгоритмы запол-
нения областей.
2.3. ИНКРЕМЕНТНЫЕ МЕТОДЫ
2.3.1. ВВЕДЕНИЕ
Среди трех классов алгоритмов, образующих множество инкре-
ментных методов (неявные, арифметические и структурные), вы-
делим два семейства алгоритмов:
в первое включим общие инкрементные методы, основанные на
представлении кривых уравнениями в неявной форме (методы
Даниельсена, Жордана и Коэна);
18

к второму будем относить множество более или менее
специализированных алгоритмов, предназначенных для ге-
нерирования кривых того или иного типа (например, отрезков пря-
мых или дуг кривых второго порядка).
2.3.2. ОБЩИЕ ИНКРБМЕНТНЫЕ МЕТОДЫ
132.1. ОБЩИЕ ПОЛОЖЕНИЯ
w Общие инкрементные методы применяются к функциям класса
С , заданным уравнениями в неявной форме (f(x,y)-0, где
х,у е R}.
Вычисление кривых основано на формуле Тейлора:
00
f(x+h,y+k)-f(x,y)+^(h^+k^)nf(x,y).
п=1
Переменные h и к принимают здесь значения ±1 или 0 и вы-
ражают элементарный шаг в направлении х или у. Даниельсен и
Коэн ограничиваются четырьмя направлениями движения точки из
заданного положения вдоль координатных осей, а Жордан вклю-
чает еще четыре диагональных направления.
Зная, что начальная точка принадлежит кривой, и в соот-
ветствии с гипотезой об элементарных движениях вдоль кривой,
вычисляют каждую следующую точку, исходя из значения и зна-
ка функции и ее первых производных в текущей точке.
Вычисления выполняются на основе разложения Тейлора.
Несколько замечаний. Изучение перечисленных алгоритмов
позволяет [15] дать некоторые оценки.
•Теоретические предпосылки, из которых получены алгоритмы
Даниельсена, Жордана и Коэна, обеспечивают применение их
для широкого класса кривых.
•С точки зрения практики эти общие методы во многих случа-
ях позволяют ограничиться только простейшими арифмети-
ческими операциями — сложением и вычитанием — применитель-
но к целым числам (в частности, это относится к полиномам
второй степени и меньших степеней). Однако Рамо и Бельзер
подчеркивают необходимость осторожного подхода к этим ал-
горитмам, несмотря на их простоту, из-за возможного появления
значительной погрешности. Некоторые функции, перед тем как к
ним будут применены эти алгоритмы, целесообразно исследовать,
чтобы выяснить, не изменяется ли угол наклона касательной
слишком сильно на интервале, равном шагу сетки.
•С другой стороны, алгоритм Жордана обеспечивает получение
более "гладких" кривых, чем обеспечивают алгоритмы Даниельсе-
на и Коэна, поскольку использование в нем восьми элементарных
направлений движения уменьшает "эффект ступенек" . По той же
причине приближение результирующей кривой к идеальной полу-
B литературе этот эффект часто называют термином "алиайзинг*: — Прим.
перев.
19

чается более точным. Кроме того, уменьшается и число требу-
ющихся шагов, так как количество вычисляемых точек получается
меньшим, чем в случае четырех направлений. Поэтому далее оста-
новимся на методе Жордана более подробно.
23.22. МЕТОД ЖОРДАНА И ДР.
Пусть плоская кривая задана уравнением в неявной форме:
f(x,y)-0, (2.1)
а ее производные непрерывны:
* df * df
fх ' д х • fу " д7 '
fx
af
, f:
a2f
ax' lxy aydx' lyy
» fyy "
a2f
ay2'
(2.2)
Предположим также, что начальная точка принадлежит
кривой, а шаг равен 1.
Метод заключается в том, чтобы "следовать" вдоль кривой с
максимально возможной точностью.
Пусть мы находимся в данный момент в точке Р-(х,у)
(рис.2.3). Тоща для нее имеем восемь соседних точек с координа-
тами соответственно: (х±1,у), (х,у±1), (х±1, у±1).
V А
У*1
У-1
♦ V ж
Иу. ♦.)
X
X
-L
1-1 К Х4>1
Рис. 2.3. Участок кривой, точка Р и восемь возможных шагов
Возможны два направления движения вдоль кривой: +v~(-fy,fx)
или -v:
ЛХ будет иметь знак, противоположный знаку fy,
AY будет иметь тот же знак, что и знак fx.
20

Выбирая в качестве направлений движения +у*или -v\ умень-
шаем число возможных шагов из текущей точки с восьми до трех.
Г1, если выбрано направление +vt
Пусть D
Тоща
[О, если выбрано направление -v;
(2.3)
ZQ
m
ш
ДХ-и-1;
ДХ~1;
ДУ=+1;
(2.4)
(2.5)
если (fy>0 и D-0) иди (fy<0 и D-1),
ШШ (fy<0 и ЕЮ) иди (fy^O и D-1)
если (fx<0 и D-0) ИЛИ (fx^O и D-1)
если (fx£0 и D-0) ИДИ (fx<0 и D-1), iq AY—1
Теперь выбираем такую ближайшую точку, для которой зна-
чение | f | минимально:
f - f (x+ AX,y), (2.6)
F - f (x,y+ Ay), (2.7)
f** - f (x+ АХ, у+Ду). (2.8)
Таким образом,
ШШ <|f*|<l^l) и (I^Mf^l), m Y:-0; {шаг по X},
ШШ (\Р \*\г[) H(|fy]<|ryJ) ,mX-0; {шаг по Y}, (2.9)
ШИ (\&\ * |f*|) и (|^|< |F|), m {шаг по X и по Y}.
Частные производные определяются в соответствии с выра-
жениями
fx-fx+fxxAx+fxyAy+2(fx3(Ax)2+2fx2y(Ax Ay)+fxy2(Ay)2)+..
fy-fy+fyyAy+fyXAx+i(fyx2(Ax)2+2fy2x(AxAy)+fy3(Ay)2)+.<
(2.10)
Поскольку переменные Ах и Ау могут принимать только зна-
чения +1, -1 или 0, вычисление производных по выражениям
(2.10) выполняется только с помощью операций сложения и
вычитания. Кроме того, вычисления еще более упрощаются для
полиномов второй степени относительно переменных х и у.
Новые значения величин f^, fy, f*y зависят от выполненного
шага. Пусть а - х для шага по X, а - у для шага по Y и а - ху
для шага по X и по Y. Тоща имеем
f* - f* + fx Ax + ^ fxx Ax2 + ...,
^ - f* + fy Ay + ^ fyy Ay2 + ..., (2.11)
f*y - f + fxAx + fyAy + ^ (fxxAx2 +2fxyAxAy + fyyAy2) + ...
21

Общий алгоритм можно представить в следующем виде.
АЛГОРИТМ ЖОРДАНА
Начало
получить первую точку;
отобразить первую точку;
инициализировать: f a - 0, частные производные;
направление D (-0 или 1);
Пока текущая точка не конечная выполнять
Начало
Вычислять Ахи Ау по выражениям (2.4) и (2.5);
Вычислять f*, P и f* по выражению (2.11);
Определить шаг и уточнить f по выражению (2.9);
Следующая точка: ■■ текущая точка + шаг;
Отобразить следующую точку;
Уточнить частные производные по выражениям (2.10)
конец
Конец
Если последняя точка на кривой не обязательно вычисляется с
помощью этого алгоритма, то можно предложить другой критерий
окончания.
Пусть (xr, yf) — координаты последней точки на кривой.
Любая точка кривой, порождаемая в результате действия ал-
горитма Жордана, расположена на расстояниях ±1 по теоретиче-
ской кривой в направлениях х и у, а следовательно, от последней
точки (xf, yf), которая, по определению, принадлежит исходной
кривой. Следовательно, логично было бы использовать в качестве
критерия окончания работы алгоритма такое условие
(|х - xf|S 1 и |у - уг|£ 1). (2.12)
Однако этому критерию удовлетворяют девять точек. Упростить
ситуацию можно, анализируя угол наклона касательной к кривой
в ее конечной точке. Если касательная расположена в 1, 4, 5 и
8-м "октантах" , то по х будет больше шагов, чем по у, т.е.
достаточно выполнения равенства по х и неравенства по у.
Тоща критерием окончания будет
(x-xf) и (|у - yf|«s 1). (2.13)
Для "октанте»" 2, 3, 6 и 7 критерий окончания основывается
на равенстве по у:
Здесь и далее на протяжении всей книги автор использует термин "октант",
понимая под этим "половину квадранта". Поскольку в русском языке понятие
"полуквадрант" не используется, для того, чтобы у читателя не возникало
естественной связи этого термина с общепринятым понятием октанта как одной
восьмой части пространства, разделенного тремя плоскостями, будем брать это
слово в кавычки. — Прим. перее.
22

(|x - xf|<; 1) и (у - yf). (2.14)
Этому критерию удовлетворяют всего 3 точки. Кроме того, та-
кая проверка проще проверки в соответствии с выражением (2.12),
однако чтобы решать, какой из критериев (2.13) или (2.14) сле-
дует использовать, необходимо заранее определить "октант", в ко-
тором находится последняя точка.
2323. ВЫВОДЫ
В работе [19] нами было показано, что для генерирования
отрезков прямых и кривых второго порядка алгоритмы
Даниельсена, Жордана и Коэна не могут конкурировать с ал-
горитмами, специально разработанными для этих целей, поскольку
приходится выполнять значительно больше вычислений для опре-
деления функций f (x,y) и ее производных и для сравнения полу-
чаемых значений, а особенно из-за большого числа образующихся
точек. Вообще можно сказать, что в этих обобщенных методах не
учитываются особенности каждой кривой.
2.3.3. СПЕЦИАЛЬНЫЕ ИНКРЕМЕНТНЫЕ МЕТОДЫ
233.1. ОБЩИЕ ПОЛОЖЕНИЯ
В табл. 2.1 приведено большинство специальных инкремент-
ных алгоритмов, предназначенных для генерирования отрезков,
прямых и кривых второго порядка. Приведенное нами сравнитель-
ное исследование [19] этих алгоритмов показало, что принцип
Брезенхема характеризуется следующим:
Таблица 1. Сравнение специальных инкрементных алгоритмов
для генерирования отрезков прямых и кривых второго порядка
Методы
Неявные
Арифмети-
ческие
Структурные
Примечай»
алгоритмов. 2.
логических цег
Отрезки прямых
Люка
Хорл -*
Брезенхем -*
Стоктон
Ирншоу
Сюэнага
и др. -*
Седерберг
Окружности
Хорн
Дорош
Брезенхем -»
Сюэнага
и др.
Эллипсы
Питтуэй
Руа ■*
Параболы
Руа -в-
Гиперболы 1
Эгрон
!я: 1. Стрелками обозначена логическая связь (преемственность)!
Подчеркнуты имена авторов, алгоритмы которых лежат в основе!
ючек следующих за ними алгоритмов. 1
23

<r*l.q*0
(г.У,)
возможно обобщение на широкий класс кривых;
наилучшие графические свойства генерируемых кривых (точ-
ность, симметричность);
последовательность точек образуется в результате действия
операций сложения и вычитания над целыми числами;
наибольшей практической полнотой полученных алгоритмов
(по оценке числа элементарных операций).
2332. ОБОБЩЕНИЕ ПРИНЦИПА БРЕЗЕНХЕМА
Предположим, что мы рассматриваем точку с целочисленными
координатами (r,q), наиболее близко расположенную к идеальной
кривой (рис.2.4). Для вычисления следующей точки ограничимся
либо двумя элементарными направлениями движения (если прост-
ранство разбито на восемь
октантов относительно теку-
щей точки), либо тремя (если
пространство разбито на
четыре квадранта). Последние
определяются углом наклона и
направлением касательной в
данной точке.
Отметим, что разбиение на
октанты (два направления
движения) было бы пред-
почтительнее, чем разделение
плоскости на квадранты (три
направления движения). В
дальнейшем будем анализи-
ровать случаи разбиения на
октанты, останавливаясь в
основном на первом "октанте",
так как все рассуждения оста-
ются справедливыми и для семи остальных.
Предположим, что перемещение происходит в границах первого
"октанта" (рис.2.4).
Пусть Pi(r,yi) — точка на идеальной кривой, имеющая
абсциссу г и ординату yiG [q - 1/2 , q + 1/2 [. Пусть D(r,q ) —
арифметическое выражение, позволяющее оценить отклонение
yi - q. Пусть Рг(г+1,у2) — следующая точка на кривой, подле-
жащая отображению. Если наклон касательной к кривой
принадлежит интервалу [0,1 [, то имеем
q + 3/2 > у2 > q - 1/2 .
Тогда на следующем этапе будем иметь две возможных точки
выбора (см.рис.2.4):
либо точку (г+1, q+1), соответствующую перемещению по
диагонали,
либо Точку (г+1, q), соответствующую движению вдоль оси.
Рис. 2.4. Расположение точек выбора
относительно идеальной кривой
(первый "октант")
24

Точка Р2 может соответствовать одному из следующих четырех
случаев:
а) q + 3/2 > у2 2 q + 1,
б) q + 1 > уг £ q + 1/2, J
в) q + 1/2 > уг > q,
г) q > уг ^ q - 1/2,
перемещение по диагонали,
перемещение вдоль оси.
Следующее перемещение определится выражениями D(r+1, q)
и D(r+1, q+1), оценивающими разности соответственно (y2~q) и
(уг - (q+Ш, в результате чего идентифицируется на экране такая
точка, которая ближе всего расположена к идеальной кривой.
Для любой исследуемой криьой задача состоит в том, чтобы по-
лучить выражение D(r,q) из ее неявного уравнения, а через него
найти выражение для Е, позволяющее вычислить следующую
величину элементарного перемещения, используя арифметические
операции над целыми числами, и только простейшие из них (сло-
жения и вычитания).
В общем виде выражение для Е выглядит как
Е - D(r + 1, q) + D(r + 1, q + 1).
Следующая точка выбирается исходя из удовлетворения одному
из условий: если Е<0, то выполняется движение вдоль оси, в
противном случае — по диагонали.
2333. ВЫВОДЫ
В следующих разделах мы вновь вернемся к алгоритмам, пред-
ложенным Брезенхемом для генерирования отрезков прямых, а за-
тем обобщим его метод на генерирование эллипсов, парабол и
гипербол. Для этих кривых второго порядка будем рассматривать
отдельно "простые" случаи, когда ось симметрии кривой парал-
лельна координатной оси, и отдельно случаи более общие, когда
ось симметрии повернута относительно оси координат.
2.4. ГЕНЕРИРОВАНИЕ ОТРЕЗКОВ ПРЯМОЙ
Отрезок прямой представляет собой наиболее часто встреча-
ющийся графический примитив, используемый для построения
векторных рисунков. Отрезок задается координатами двух точек
начала (xd, yd) и конца (xf, yf).
Особый интерес представляют два алгоритма генерирования
отрезка прямой — Люка и Брезенхема.
25

2.4.1. АЛГОРИТМ ЛЮКА
Для генерирования отрезка прямой Люка [23] обращается к
первому "октанту". Поскольку на каждом шаге выполняется
систематическое перемещение вдоль оси х, оценивается возникаю-
щая ошибка по ординате у, которая, естественно, накапливается.
Чтобы минимизировать ее, достаточно модифицировать у (доба-
вить 1), когда ошибка достигнет или превысит единицу.
В общем виде алгоритм записывается так:
Генерирование ОТРЕЗКА- вариант! (х& yd, Xf, у г. целые)
Начало {метод Люка}
целые: АХ, AY, XI NCR, YINCR, CUMUL, X, Y;
х := Xd, У := yd!
отобразить точку (х,у);
XINCR :« если Xd < Xf то +1 иначе -1;
YINCR :« если yd < yf то +1 иначе -1;
ДХ: = abs (Xd-Xf), AY :» abs (yd-yf);
если АХ > AY (отображается максимум точек}
то. CUMUL :=* Х/2;
Аля I :- 1 до АХ выполнят
X := X + XINCR
CUMUL :* CUMUL + AY;
если CUMUL > АХ
10 CUMUL :* CUMUL - AX;
Y :» Y + YINCR;
конец если
отобразить точку (х,у);
конец для
иначе CUMUL :» AY/2;
Аля I := 1 до. AY выполнять
Y := Y + YINCR;
CUMUL :» CUMUL + АХ;
Если CUMUL > AY
то CUMUL :« CUMUL - AY;
X :» X + XINCR ;
конец если
отобразить точку (х, у)
конец для
конец если
Конец
26

2.4.2. АЛГОРИТМ БРЕЗЕНХЕМА
Для генерирования отрезков прямых Брезенхем [6 ] на каждом
шаге находит точку, наиболее близко расположенную к идеально-
му отрезку (рис.2.5). С этой целью он рекуррентно оценивает раз-
ность Si — S2 (для первого октанта). Если Si — S2 < 0, то вы-
полняется движение по оси, в противном случае — по диагонали.
дооивмиа по дмдгомали
(г+1, я+»
Рис. 2.5.
Движение
к ближайшей л§
точке (алгоритм <*р#ави , _ ^
Бреэенхема) (,#q) (r*l.q) **•£•"••• по o«*
В общем виде алгоритм записывается как
Генерирование ОТРЕЗКА-вариант2( Xd, у<ь Xf, yr. целые)
Начало (метол Бреэенхема}
целые: DX, DY, XINC, YINC, S, DX2, DY2, DXY, X, Y;
DX2 :« DX + DX; DY2 :« DY + DY;
XINC :» если Xd<Xf jo_ +1 иначе -1; DX:«
abs (Xd - Xf);
YINC :« если y<Kyf 10 +1 иначе -1; DY:«
abs (yd - yf);
X :- Xd; Y :« yd; отобразить точку (х,у);
если DX > DY
то fx изменяется быстрее» чем у}
~S :- DY2- DX ; DXY : - DY2- DX2;
Аля I :« 1 до DX выполнять
если S^O
"То Y :« Y+YINC;
— S :« S+(DXY);
иначе S :- S+(DY2);
конец если
X :« X+XINC
отобразить точку (х, у);
конец для
иначе (у изменяется быстрее, чем х }
—3~:- DX2- DY; DXY :« DX2- DY2;
Аля I :« 1 до DY выполнять
если S^O
~то X :« X + XINC;
27

S := S + (DXY);
иначе S := S + (DX2);
конец если
Y := Y + YINC;
отобразить точку (х,у);
конец для
конец если
Конец
2.4.3. ГЕНЕРИРОВАНИЕ СЕМЕЙСТВА ОТРЕЗКОВ ПРЯМЫХ
Чтобы в процессе генерирования семейства отрезков прямых
сэкономить машинное время или объем памяти, можно использо-
вать различные методы:
алгоритм Люка предпочтительнее алгоритма Брезенхема, если
в семействе прямолинейных отрезков большинство составляют
горизонтальные или вертикальные;
полезно применять также методы сжатия и повторения.
2*43.1. СЖАТИЕ
В приведенных выше алгоритмах генерирования прямолиней-
ных отрезков никак не учитывался тот факт, что последователь-
ности элементарных перемещений, вычисленных в соответствии с
этими алгоритмами, могут содержать участки с неизменным на-
правлением движения, т.е. вдоль горизонтали, вертикали или
диагонали.
Сжатие информации о таких однородных участках позволяет
экономить объем памяти ЭВМ, но выигрыш существенно зависит
от характера сцены. Та минимальная длина 'однородных" участ-
ков, начиная с которой уже имеет смысл использовать принцип
сжатия, зависит от характера представления чисел при конкретной
аппаратной реализации.
Наконец, необходимо следить за тем, чтобы время, затрачива-
емое на осуществление процедуры сжатия в процессе ге-
нерирования и на восстановление в процессе отображения, не было
бы слишком большим. В противном случае это может ухудшить
общие характеристики системы в целом.
2А32. ПОВТОРЕНИЕ
В процессе генерирования прямолинейных отрезков могут
встречаться такие случаи, когда вычисленная последовательность
отрезков содержит участки, повторяющиеся фиксированное число
раз.
Для примера рассмотрим вариант расположения отрезка в пер-
вом квадранте (описываемый прием непосредственно обобщается и
на другие квадранты).
Пусть АХ и AY — приращения соответственно по осям X и Y.
Тоща возможны следующие случаи.
С л у ч а й 1:
отрезок вертикальный или горизонтальный,
28

т.е. ЛХ - 0 или AY - О.
Тогда имеем повторение движения вдоль оси.
С л у ч а й 2:
диагональный отрезок,
т.е. АХ - AY.
Тоща имеем повторение движения по диагонали.
С л у ч а й 3:
АХ - 1 или AY - 1.
Пусть, например, AY « 1.
Тогда будем иметь движение по диагонали в средней части
отрезка. Пусть N1 — целая часть ((AX-D/2);
Тогда:
если (AX-D/2 — целое число,
то выполняются N1 перемещений вдоль оси,
1 перемещение по диагонали,
N1 перемещений вдоль оси,
иначе выполняются N1 движений вдоль оси,
1 движение по диагонали,
N1+1 движений вдоль оси,
или выполняются N+1 движений вдоль оси,
1 движение по диагонали,
N1 движений вдоль оси.
С л v ч а й 4*
AY>1 и АХ/AY — целое число (*1) .
Вновь возвращаемся к предыдущему случаю, но с той только
разницей, что основная последовательность повторяется AY раз.
С л у ч а й 5:
AY>1 и АХ/AY — не целое число.
Вычисляется наибольший общий делитель чисел АХ и AY,
являющийся коэффициентом повторения. Базовая последователь-
ность будет вычисляться по одному из алгоритмов генерирования
отрезков.
Выигрыш от применения метода повторений тем больше, чем
длиннее генерируемый отрезок и чем больше коэффициент повто-
рений.
С точки зрения целесообразности наибольший интерес пред-
ставляет использование первых четырех случаев, так как среди
всех генерируемых отрезков достаточно быстро можно найти
минимально необходимое количество подходящих вариантов, чего
нельзя сказать о случае 5. Кроме того, следует иметь в виду, что
в случаях 4 и 5 требуется выполнение неприятной операции де-
ления. Д,/^7/ ,,.МШМъ .-с И(& ht Мли«(А **}*+**„*, /лиг^
2.5. ГЕНЕРИРОВАНИЕ ОКРУЖНОСТЕЙ
Любая окружность характеризуется координатами своего центра
и величиной радиуса R.
2.5.1. АЛГОРИТМ БРЕЗЕНХБМА
Идея, использованная Брезенхемом для алгоритма ге-
нерирования окружностей [7], подобна той, на основе которой им
29

был построен алгоритм генерирования отрезков прямой: вычислять
точки, наиболее близко расположенные к исходной окружности,
используя только операции сложения и вычитания для целых
чисел.
Анализ будем проводить в квадранте 1 от точки с координатами
(0,R) до точки (R,0), полагая, что центр окружности совпадает с
началом координат. Из данной точки возможны три направления
элементарных движений: mi, шг и тз. Каждая из них определя-
ется рекуррентным методом по минимальному расстоянию от иде-
альной окружности до той, которая проходила бы через точку вы-
бора, находящуюся на соответствующем направлении (рис.2.6).
|(Ж>*1. у, 4 1)
Pi
(2).
tf^^l
■>(«в*1.У|)
О) (5) I
1 4-1-V-4
Рис. 2.6. Положение точек
выбора относительно
идеальной окружности
(метод Брезенхема)
Приводимый ниже алгоритм Брезенхема вычисляет точки, ле-
жащие на окружности радиуса R с центром (хс, ус).
Генерирование ОКРУЖНОСТИ (хс, ус, R: целые)
Начало" {метод Брезенхема}
М3:«1;
XI:— R+Xc,Yl:«yc {текущая точка}
Повторять
X: «I, Y:=R+R-1;
A:=*Y-1;
М1:=МЗ,М2:=М1+1,МЗ:=М2+1;
если М3*9 Tio M3: =1 конец если
пока Y^O выполнять
Начало
ЭГ-й+Д;
если д<0
то ft«d+X;
"если д<0 то Y:»Y-2, A:=A+Y;
— MOVE <-МЗ;
иначе X:=X+2,Y:=Y-2;
ЗГ^З+Y-X;
M0VE<-M2;
конец если
иначе ft«a-Y;
зо

если Э>0 то. Х:=Х+2, Д:=Д-Х;
M0VE<-M1;
иначе X:=X+2,Y:=Y-2;
Д:=Д+У-Х;
M0VE<-M2;
конец если
конец если
конец
AO~W=l
Конец
В этом алгоритме используется обход по часовой стрелке
(рис.2.7а), начиная с точки (-R,0). Нумерация направлений
движений показана на рис.2.76.
(-R. О )
уг j
5 \J
Рис. 2.7. Условные обозначения:
а - направление обхода окружности; б - нумерация направлений движения
Примеры окружностей,
генерированных
по методу Брезенхема
2.5.2. ГЕНЕРИРОВАНИЕ ДУГ ОКРУЖНОСТИ
23.2.1. ПОСТАНОВКА ЗАДАЧИ
•Задача состоит в том, чтобы создать дугу окружности
радиусом R и с центром в точке (хс ,ус), причем при задании на-
чальной и конечной точек дуги. Рассмотрим рис. 2.8. Здесь есть
два варианта движения от начальной точки дуги (хо, уо) до ко-
нечной (xi, yi): либо по часовой стрелке (Ь-0), либо против
(D-1).
•Практически дугу окружности можно определить двумя раз-
личными способами: или тремя точками, или двумя точками и по-
ложением касательных в этих точках. Но в любом случае требу-
ется вычислить радиус R и положение центра окружности (хс, ус).
Для окружности, проходящей через три точки. Исходя из
уравнения окружности (х-хс) + (у-ус) - R ■ 0 и принимая точ-
31

<«*Vt>
Рис. 2.8. Генерирование
дуги окружности
<Ч. П)
ку (xi, yi) за начало новой системы координат, получаем систему
из двух уравнений с двумя неизвестными:
2Х|ХС - 2Y|YC - 0, i - 2, 3,
Xi - xi - xi; Yi - yi - yi; i - 2, 3;
(Xi2 + Yi2)
где
Xc - xc - xi; Yc - yc - yi;
R2 - Xc2 + Yc2.
Для окружности, заданной точками А, В и касательными в
этих точках, соответственно Та и ТЬ. Координаты центра легко
получить как точку пересечения двух нормалей к заданным каса-
тельным:
нормаль в точке A: Y- -(1/Ta) X+Ya, где Ya- YA + (1/Та)*ХА;
нормаль в точке В: Y- -(l/Tb)X+YD, где Yb- YB+(l/Tb)*YB.
Центр окружности имеет координаты
Xc - (Yb-Ya) (Ta*Tb) / (Ta-Tb), Yc - (Ya • Ta-Yb • Tb) / (Ta-Tb).
\ \ A =r (XA.YA)
\ J^ B=(XBVB)
1SZ2. АЛГОРИТМ БРЕЗЕНХЕМА
Брезенхем [7] приспособил свой алгоритм генерирования
окружностей для получения дуг таких окружностей, координаты
центра которых и радиус задаются нецелыми числами. 2
Пусть окружность задана уравнением (х-а) +(у-Ь) - R , а на-
чальной и конечной точками дуги этой окружности соответственно
являются (xs, ys) и (xt, yt). Направление обхода можно выбрать
либо по часовой стрелке (D-1), либо противоположное (D*—1).
Введем следующие обозначения:
xi — значение абсциссы, отнесенное к i-му шагу, в первом
квадранте, при обходе в направлении по часовой стрелке (D-1);
yi — то же для ординаты;
32

Mi
Ji — число квадрантов, которые предстоит пересечь;
ц, Мг, Мз — направления движения в квадранте 1 под углами
соответственно 0, 315 и 270°; 2 2
Ai — величина разности {[(xi + 1) +(yi - 1) ] - R }, ее знак
определяет, находится ли точка (xi + 1, yi - 1) внутри или вне
ИСХОДНОЙ ОКРУЖНОСТИ; 2 2 2
д — величина суммы {[(xi + 1) + у ] - R } + Ai, ее знак опре-
деляет, какая из двух точек, (xi + 1, yi) или (xi + 1, yi - 1), рас-
положена ближе к окружности* 2 2
д' — величина суммы {[(хг + (yi - 1) ] - R } + Ai; ее знак
определяет, какая из двух точек, (xi, yi - 1) или (xi + 1, yi - 1),
расположена ближе к окружности.
Таблица 2. Преобразование
Квад- Направление
рант ' обхода
III CCW]
II CCW^ D—1
IV CCW|
I CCWj
III CW ]
II CW [D-l
IV CW j
|l CW J
X
<0
<0
£0
£0
<0
<0
£0
*0
параметров
Y
<0
£0
<0
;>0
<0
£0
<0
;>0
Индекс
0
1
2
3
4
5
6
7
x
i*i
i*i
i*i
i^i
i*i
i*i
i*i
i*i
Y
1*1
1*1
1*1
1*1
1*1
1*1
1*1
1*1
q
3
2
0
1
2
3
1
0
Ml
0,-1
-1.0
1.0
0,1
-1,0
0,1
0,-1
1.0
M2
l.-l
-l.-l
1.1
-1.1
-1,1
1.1
-l.-l
l.-l
M3 1
1,0
0,-1
0,1
-1,0
0,1
1,0
-1.0
o.-i |
Если координаты (xs, ys) и (xt, ^t), а также радиус R — целые
числа, то инициализация значении (x's, y's) и (x't, y't) сводится
к следующему:
(x's, y's)-(xs, ys), a (x't, y't)-(xt, yt).
Дуги окружностей, генерированные
по методу Брезенхема
Генерирование
^вещественные,
Начало {метод
(Инициализация)
ДУГИ ОКРУЖНОСТИ
D: целое)
Брезенхема)
(xs,ys,xt,y =
2 - Ж. Эгрон
33

1 - Определить точки начала и конца -
целые (x's, y's) и (x't, y't),
наиболее близко расположенные к теоретической
окружности, начиная с (xs, ys) и (xt, yth
находя соответствующие "единичные квадраты"
для cs и ct, окружающие их в соответствии с
выражениями: с( х', /) =
{(Ш> ШЫ W. Гу1).( М, [У1)>> (М, Ш) и
находя точку, принадлежащую Cs
(соответственно Ct), которая минимизирует
величину | [(х' -а) Ч(у2-Ь) *]-Rz \.
2 j Перенос центра _окружности в точку (0,0)
x^s •= х s - a, y_s i = у s - d,
xt : - х' t - a, yt : = y't _- _Ь.
3 -_ Нормализация на основе (xs, ys) и
(*t>yt) ' перемещение в первый квадрант,
направление обхода D=l для определения с
помощью табл. 2.2 величин
Xs ж Xq, Ys = Yq, qs>
Mls * MIq, M2S = M2q» M3S = M3q,
Xt> Yt, qt.
4 - Вычисление количества пересекаемых
квадрантов:
Q :■ *4(qt - qs) (сложение по модулю 4)
Если Q = 0 и Xt < Ys и Yt > Ys,
IP. Qo - 3 л
иначе Qo =Q - 1;
5 - Вычисление начального значения А0:
Ао - (Xs+D2 + (Ye-ir - (х,-а)2 + (Ус-Ь)2=
=(x's-a)2 + (/s-b)f - (х8-аГ + (У.-Ь)г +
+ 2(XS - Ys + 1);
6 - Направление обхода:
D=l или -1.
7 - Первая точка
л * = X Sy Y ♦ — У si
8 - Получаем
Xi := Х0; Yi := Y0; Ai : - А0; Qj :- Q0;
(генерирование точек)
Конец : = ложно
Пока не (конец) выполнять
34

Начало
Если Yi >0
т£ {вычисление движения}
Если Ai<0
10. д :=2Д, + 2Yi - 1;
если 3 <0 то движение
в направлении Ml;
Иначе движение
в направлении М2 конец если
иначе Э':= 2Ai - 2Xi - 1;
если д'<0 т£ движение
в направлении М2;
иначе движение
в направлении МЗ конец если
конец если
если направление движения = Ml
то. Xi+i: =Xi+l, Yi+i: =Yi; Ai+i: =Ai+2Xi+i+l;
иначе если = M2
10 Xi+n-Xi+ь Yi+i:- Yi-1;
Ai+i :- Ai+2Xi+i-2Yi+i+2;
иначе Xi+i:=Xi, Yi+i:-Yrl,
Ai+i := Ai-2Yi+i+l
(МЗ) конец если
конец если
иначе (повторная инициализация)
Хо •= * Y i; Yo * = Xi;
Ао : = Ai - 4Xi';
Qj+i :- Qj - 1;
Mlj+i := M3j; M2j+i := D(M2(2) j'-M2(l) j);
M3j+i := D(M3(2)j' - N3(1) j).
конец если
{Проверка переменной Конец}
если Qj < О
то если (Xt > Xi) и (Yt > Yi)
то. Конец : = истинно;
конец если
конец пока
Конец

2.6. ГЕНЕРИРОВАНИЕ ЭЛЛИПСОВ
2.6.1. ПРОСТОЙ ЭЛЛИПС (АЛГОРИТМ РУА)
Пусть простой эллипс (рис.2.9) с центром в точке с(Хс, Yc) за-
дан уравнением
[(X - Хс)2/а2] + [(Y - Yc)2/b2] = 1,
где a,b G N*: XC) Yc G Z.
у
уС«-Ь
(ХС. YC)
(ХС ♦ */{J ♦ b*)"1) t(XC*«) X
Рис. 2.9. Генерирование простого эллипса в первом квадранте
по методу Руа
Алгоритм генерирования простого эллипса, разработанный Руа,
имеет вид
Генерирование простого эллипса (ХС,YC,В; целые)
Начало {метод Руа}
целые: А2, В2, DS, DT, DXT
Xinc,Yinc,X,Y
Т, S, E, CA, CD
А2 := А * А
В2 :- В * В
DS := 4 * А2
DT := 4 * В2
DXT := ОКРУГЛИТЬ (A2/SQR( A2+B2))
Xi nc:= +1
Yinc:= -1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
Yi nc:= +1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
36

Xinc:= -1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
Yinc:= -1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
Конец
Процедура ПРОВЕДЕНИЯ ДУГИ В КВАДРАНТЕ
Т
S
Е
СА
CD
=0
= -4 -
= -S/2
:= -6
:= СА
А2
- 2
В2
4
В
В2
А2
А2
X := ХС
Y := YC - yinc * В
Отобразить (X, Y)
Для I : = 1 шаг. 1 до DXT выполнять
Начало
X := X -
f Xinc
Если Е>0
то начало
Е := Е + Т + СА
Т := Т - DT
конец
иначе начало
Y
Е :
Т :
S :
= Y + Yinc
= E + T - S + CD
= T - DT
= S + DS
конец
отобразить точку (X, Y)
конец
DYT := ABS (Y-YC)
Е := E-T/2-S/2-B2-A2 {Т и S-четные}
СА := -б * А2
CD := СА - 4 * В2
Для I : = 1 шаг_ 1 до^ DYT выполнять
Начало

Y := Y + Yinc
если Е <0
то начало
E := E -
S := S +
KOH
иначе
E
S
T
X
KOH
отобрази
конец
Конец проце/
начало
:- Е -
:- S +
:- Т -
:= X +
ВЦ.
ть (X,Y)
1УРЫ
S +
DS
S +
DS
DT
Xinc
CA
CD
2.6.2. ПРОИЗВОЛЬНЫЙ ЭЛЛИПС (АЛГОРИТМ РУА)
Если оси эллипса параллельны координатным осям, то его
уравнение имеет вид
Ь2(Х0 - Хс)2 + a2(Y0 - Yc)2 - a2b2,
где
a,b 6 N*; Xc, Yc G Z.
Поворот фигуры на угол в е ] - я/2, я/2[ изменяет вид урав-
нения
(р2Ь2 + ш2а2)(Х - Хс)2 +(b2m2 + a2p2HY - Yc)2 +
+ 2(b2 - а^рпКХ - XC)(Y - Yc) - aV(p2 + m2), (2.15)
ще tg в - m/p, m G Z, p E Z .
Введем обозначения:
a - p2b2 + a2m2; 0 - b2m2 + a2p2;
yo - (b2 - a2)pm; y-2yo; k - a2b2(p2 + m2).
Тоща уравнение (2.15) можно записать в виде
а (X - Хс)2 + р (Y - Yc)2 + у (X - Xc)(Y - Yc) - k. (2.16)
Ниже приводится алгоритм, результатом действия которого
является произвольный эллипс, описываемый уравнением (2.16).
Часть этого эллипса, ось которого повернута на угол в относитель-
но оси X, показана на рис. 2.10.
38

♦ l/
[ / -Dxt2
Yi
DyO
Dyoo
С
i
Xe
с
I
/%
■ / • -^l
DxO Dxtl/ Dx» XH
/ I
Рис. 2.10. Генерирование произвольного эллипса (метод Руа)
Генерирование ПРОИЗВОЛЬНОГО ЭЛЛИПСА (ЦЕЛЫЕ:
ХС, YC, А, В, М, Р)
Начало (метод Руа)
ЦЕЛЫЕ а, А уо, у. к, Е, Т, S ,D
ЦЕЛЫЕ Ca, Cd, Dsa, Dsd, Dta, Dsd
ЦЕЛЫЕ Dxtl, Dxt2, DXO, DYO, DY».
ВЕЩЕСТВЕННЫЕ U
{Инициализация}
A2
B2
M2
P2
a
I
Dxtl
Dxt2
= A*A
= B*B
= M*M
= P*P
P2*B2+M2*A2
M2*B2+P2*A2
(B2-A2)*P*M
2*yo
A2*B2*(P2+M2)
= a*p-y0*yo
-ОКРУГЛЕНИЕ (SQR (k+(/3+y0) l/lla+в+у)*!)))
«ОКРУГЛЕНИЕ (SQR (k+(/J-y0) 2A(a+p-y)*l)))
39

U := y0*SQR(k/(a*Z))
DxO : ОКРУГЛЕНИЕ (U)
Если у0 = О то Dy0 : = В
иначе Dy0 := ОКРУГЛЕНИЕ (a*U/y0)
Dy« := ОКРУГЛЕНИЕ (yo/0)*SQR(k*0/Z))
D := 2*( k-^ar*DX02-/3*DY02*DXO*DYO)
Т := 4*a*DXO - 2*y*DY0
S := 4*0*DYO - 2*y*DX0
(Первый квадрант}
X :=XC-Dx0
Y :=YC+Dy0
Dxt : * Dxt2
Xi nc : =+1
Yinc :=-l
Sg := 1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
(Второй квадрант}
X := Xc+Dx0
Y :- Yc-Dy„
Yi nc : =+1
Dxt :=Dxtl
Sg :=-l
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
(Третий квадрант}
X : =ХС +Dx0
Y :=YC -Dy0
Xinc :=-l
Dxt : =DXt2
Sg : =+1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
(Четвертый квадрант}
X := Xc-Dx0
Y := Yc-Dy0
Yinc := -1
40

Dxt : = Dxtl
Sg := -1
ПРОВЕДЕНИЕ ДУГИ В КВАДРАНТЕ
ПРОЦЕДУРА ПРОВЕДЕНИЯ ДУГИ В КВАДРАНТЕ
Е := D+T+S/2-2*a-0+Sg*y
Т := Sg.T
S := S
Са:= -6*a+Sg*y
Cd:= Ca-4*(0-Sg*y)
Dta:=-4*a
Dsa:=2*Sg*y
Dtd: =Dta+Dsa
Dsd:=Dsa-4*£
Отобразить (X, Y)
Bt := ABS(X-Xc-Xinodxt)
Аля I : = 1 до Bt выполнять
Начало
X :« X+Xinc
Если E >0
TO He
E
T
S
KOH
иначе
Y
E
T
S
KOH
Отобрази
конец
E := E-T/2
Ca := -6*/J+
Cd :- Ca-4*|
Dta := Dsa
тало
:= E+T+Ca
:= T+Dta
:= S+Dsa
ец.
начало
:= Y+Yi nc
:= E+T+S+Cd
:= T+Dtd
:= S+Dsd
ть (X,Y)
+S/Z+a-p
Sg*y
[«-Sg*y)
41

Dsa:= -4*0
Dyt:= ABS (Y-Yc +Xinc*Dy»)
Аля I : - 1 до Dyt выполнять
Начало
у := Y + Yinc
Если E <0
то начало
E := E+S+Ca
T := T+Dta
S : = X+Dsa
KOHI
иначе
X
E
T
S
KOH
Отобрази
конец
КОНЕЦ ПРОВЕ/
Конец
начало
: = X+Xi nc
: = E+T+S+Cd
:= T+Dtd
:= S+Dsd
ть (X,Y)
£НИЕ ДУГИ В
КВАДРАНТЕ
2.7. ГЕНЕРИРОВАНИЕ ПАРАБОЛ
2.7.1. ДУГА ПРОСТОЙ ПАРАБОЛЫ (АЛГОРИТМ РУА)
Простая парабола описывается уравнением у - а(х - хс) + Ь,
где (хс, Ь) — координаты вершины параболы (рис. 2.11).
Пусть требуется провести простую параболу через две точки:
начальную с координатами (ХА, YA) и конечную (ХВ, YB) так,
(ХВ, YB)
Рис. 2.11. Генерирование
дуги параболы (метод Руа)
42

чтобы ее вершина находилась в точке (Хс, Ь),т.е. чтобы осью
симметрии параболы была бы прямая х - хс. Тогда
a-(YB - YA)/((XB - ХА) * (ХВ + ХА - 2»ХС)),
(ХВ - XC)2*YA - (XA-XC)2»YB
b- .
(ХВ - XAWXB + ХА - 2*ХС)
Алгоритм генерирования дуги параболы, разработанный Руа,
имеет следующий вид:
Генерирование ДУГИ ПАРАБОЛЬК Целые: ХА, YA, ХВ, YB, ХС)
Начало {метод Руа}
Целые : YC, DSX0, СВО
Если (ХА<ХС и ХС<ХВ) или (ХВ<ХС и ХС<ХА)
то начало
если ABS(XA-XC)=ABS(XB-XC) то читать YC
иначе DSX0 := (ХВ-ХА)* (ХВ+ХА-2*ХС)
СВО :« (XB-XC)2*YA-(XA-XCK*YB
YC := ОКРУГЛЕНИЕ (CB0/DSX0)
конец если
ПРОВЕСТИ (ХС, YC, ХА, YA)
ПРОВЕСТИ (ХС,YC,ХВ, YB)
конец t,
иначе начало
если (ХС <ХА и ХА<ХВ) или
(ХС>ХА и ХА>ХВ)
тр_ ПРОВЕСТИ (ХА, YA, ХВ, YB)
иначе ПРОВЕСТИ (ХВ, YB, XA, YA)
конец
Конец
Процедура ПРОВЕСТИ (Целые: XD,YD,XF,YF)
Начало
Целые: DX, DY, DELTAY, DT, DSX, DXT,
X, Y, XINC, YINC, T, T, CA, CD
DX := XF-XD
DY := YF-YD
DELTAY := ABS(DY)
DT := 4*DELTAY
DSX := DX*(XF+XD-2*XC)
DXT := ОКРУГЛЕНИЕ (2*DSX/DT)
Если DX>0
43

10. XINC :» +1
иначе XINC := -1
Если DY>0
то YINC := +1
иначе YINC := -1
X := XD
Y := YD
Отобразить (X, Y)
T := DT*ABS(X-XC)
E := T+DT/2-DSX {DT четные)
Если ABS (X-XC)<DXT
то начало {тангенс угла наклона
касательной Е [0,1]}
СА := 6*DELTAY
CD := CA-2*DSX
ВТ := MIN(ABS(DX),-ABS(X-XC)+DXT)
Для I : = 1 до ВТ выполнять
начало
X := X + XINC
Если Е<0
то (движение вдоль
Е := Е+СА+Т
иначе (движение по
Y := Y+YINC
Е := E+CD+T
Т :« T+DT
Отобразить (X, Y)
конец
конец
DYT := ABS (YF-Y)
Если DYT * 0
оси}
диагонали}
то начало(тангенс угла наклона G]l,+«[}
С А := 2*DSX
CD := СА - 4*DELTAY
Т := -Т
Е := -E-T/2+DELTAY+DSX
Аля I := 1 шаг. 1 до.
начало
Y := Y+YINC
Если Е<0
(Т - четные}
DYT выполнять
то. (движение вдоль оси)
44

E := E+CA
иначе (движение по диагонали}
X := X+XINC
Е := E+CD+T
Т := T-DT
Отобразить (X, Y)
конец
конец
ПРОЕПГГИ.
Конец
Примечание: В случае, коща IXA -XCI-IXB-XCI,
величина b выбирается произвольно и алгоритм применяется пос-
ледовательно сначала для точек I (Xc, Yc), (ХА, YA) I, а затем для
точек 1(Хс, Yc), (XB, YB)I.
2.7.2. ДУГА ПРОИЗВОЛЬНОЙ ПАРАБОЛЫ
Пусть Y - Yc - а(Х-Хс) — уравнение параболы с центром
симметрии (Xc, Yc). Если повернуть ее на угол в G]-n/2y л/2[,
то получим
a tg2 в (Y-Yc)2 + 2а tgg (X-Xc)(Y-Yc) + a(X-Xc)2 -
- (Y-Yc) Vl+ft% + (X-Xc) tg0 Vl+^e - 0.
В этом случае невозможно применить тот прием, который мы
уже использовали при генерировании эллипса. Действительно, в
приведенном здесь уравнении появляются новые члены — пере-
менные X и Y в первой степени с коэффициентом
Наличие этого коэффициента препятствует использованию
арифметических операций над целыми числами, которые приме-
нялись для построения эллипса. Здесь приращения, вычисляемые
на каждом шаге, не были бы целыми величинами, что привело бы
к накоплению ошибок. В то же время главным достоинством всех
методов, рассматриваемых нами до сих пор, было использование
только операций над целыми числами.
2.8. ГЕНЕРИРОВАНИЕ ГИПЕРБОЛ
В качестве примера рассмотрим обобщение метода Брезенхема,
(см.п.2.3.2.2) на генерирование гипербол.
2.8.1. ОБОБЩЕНИЕ МЕТОДА БРЕЗЕНХЕМА НА СЛУЧАЙ "ПРОСТЫХ"
ГИПЕРБОЛ
Пусть дана гипербола, центр которой совпадает с началом ко-
ординат:
(X2/a2)-(Y2/b2) - 1, где a,b e N*.
45

Обобщение на случай гиперболы, центр которой находится в
произвольной точке (Xc,Yc), осуществляется простым сдвигом
вдоль соответствующих координатных осей.
У гиперболы имеются две асимптоты — прямые с тангенсами
угла наклона соответственно а/b и -b/а. Будем рассматривать
только первый квадрант (Х>0, Y>0), поскольку другие дуги
гиперболы могут быть легко получены исходя из свойства
симметрии. В этом квадранте касательные к кривой имеют наклон,
находящийся в пределах ]Ь/а, +оо [. Можно сделать два предполо-
жения:
если Ь/а>1, то кривая находится внутри октанта (рис.2.12а);
если Ь/а<1, то кривая выходит за пределы одного октанта
(рис.2.126).
/ /
/ /
/ /
/ /
/
i
i
L
а
Рис.2.12. Генерирование гиперболы (первый квадрант):
а — b£a; б — Ь<а
Рассматриваемый квадрант может быть разделен на две части.
А. Наклон касательных к кривой принадлежит интервалу
[1,+оо[. Это соответствует точкам (х,у), таким, что
х G [а,+<»[, если Ь>а,
или
х Е [а, а2/ ^а2-Ь2 [, если Ь<а.
Выполняется приращение по Y.
Б. Наклон касательных к кривой принадлежит интервалу
]Ь/а, 1[. Это соответствует точкам (х,у), таким, что
х G ]a2/Va2-b2,+oo[, если Ь<а.
Выполняется приращение по X.
А. Наклон касательной Е [1, + »[.
Предположим, что мы рассматриваем точку с координатами (r,q).
46

•Пусть Pi (xi, q) — точка отображаемой кривой, а точка
(r,q) — наиболее близко расположенная к кривой точка с
целочисленными координатами. Тогда имеем
г - 1/2 < xi< г + 1/2.
2 2 2 2 2 2
Положим D(r, q) - a q + a b - b r . Тогда D(r, q) — целое
число, имеющее тот же знак, что (xi - г).
Пусть Рг(х2, q+1) - следующая точка отображаемой гиперболы.
Поскольку наклон G [1, +<»[, то будем иметь
г - 1/2 < Х2 < г + 3/2.
Покажем, что величина EeD(r, q+1) + D(r+1, q+1) определяет
выбор между направлением движения вдоль оси и вдоль диаго-
нали:
если Е<0 (случай (а) и (Ь)), то движение происходит вдоль оси;
если Е>0 (случай (с) и (d)), то движение диагональное.
Имеем
Е - 2D (г, q) + 2*S(q) + Т(г) + 2а2 - Ь2.
В случае осевого движения переходим в точку (г, q+1).
Следующим значением величины Е, подлежащим рассмот-
рению, будет
Ег, q + 2*S(q) + 6а2.
В случае диагонального движения переходим к точке (г+1, q+1).
Тогда следующим значением величины Е, подлежащим рассмот-
рению, будет:
Ег, q + 2*S(q) + 2*T(r) + 6а2 - 4b2,
где
T(r) = d D(r,q)/d г = - 2b2r;
S(q) = d D(r,q)/d q= + 2a2q;
T(r+1) = T(r) - 2b2;
S(q+1) - S(q) + 2a2.
47

Вывод: точка кривой, следующая за точкой (r,q), определяется
таким образом:
£СДИ Е <0,
XQ движение осевое (по Y)
Е:- Е + 2*S + 6а2;
S:« S + 2а2;
иначе диагональное движение
Е:« Е + 2«S + 2»Т + 6а2 - 4Ь2;
S:« S + 2а2;
Т- Т - 2Ь2;
Б. Наклон касательной € ]+Ь/а, +1[. Предположим, что рас-
смотрение начинается с точки, имеющей координаты (r,q).
1
('*♦')
(r.q>
1
(d)_
/£) —
i <•> —
(г*1.Я*'2>
L 1
(г* 1, Я*
^♦!.Я)
|(г*1.Я-1
|
Г
1)-
'
1
•Пусть Pi (г, yi) — точка отображаемой кривой, a (r,q) —
точка с целочисленными координатами, наиболее близко располо-
женная к кривой. Тогда
q - 1/2 < yi < q + 1/2.
Величина D(r,q) - b2r2 - a2b2 - a2q2 имеет тот же знак, что
•Пусть Рг(г+1, у2) — следующая точка отображаемой гипербо-
лы. Поскольку наклон G ]а/Ь, 1 [, будем иметь
q - 1/2 < у2 < q + 3/2.
Покажем, что величина E«D(r+l, q) + D(r+1, q+1) определяет
выбор между направлением движения вдоль оси и вдоль диаго-
нали:
если Е<0 (случай (а) и (Ь)), то движение происходит вдоль
оси;
если Е>0 (случай (с) и (d)), то движение диагональное.
Имеем
Е - 2D(r,q) + 2Т(г) + S(q) + 2b2 - a2.
В случае аксиального движения переходим в точку (r+l,q).

Следующим значением величины Е, подлежащим рассмот-
рению, будет
Е(г, q) + 2»T(r) + 6Ь2.
В случае диагонального движения переходим к точке (г+1, q+1).
Следующее значение величины Е будет
Er,q + 2*Т(г) + 2»S(q) + 6b2 - 4а2,
где
Т(г) - dD(r, q)/dr - + 2b2r;
S(q) - dD(r, q)/dq - - 2a2q;
T(r+1) - T(r) + 2b2;
S(q+1) - S(q) - 2a2.
Вывод: следующая точка, наиболее близко расположенная к
кривой, определяется согласно алгоритму
если Е S О,
XQ {новое значение (по X)} .
Е : - Е + 2Т + 6Ь2;
Т : - Т + 2Ь2;
днане {диагональное движение}
Е: - Е + 2«Т + 2*S + 6b2 - 4а2;
S: - S - 2а2;
Т: - Т + 2Ь2.
Алгоритм
♦Инициализация
А — случай наклона е [1, + »[
Исходная точка задается координатами:
XD - ХС + а,
YD - YC,
где (XC.YC) — центр симметрии.
Эта точка принадлежит гиперболе, следовательно, D(XD,YD)4).
Тогда имеем
T(XD)- -2b2(XD-XC) - -2b2»a,
S(YD)- 2a2(YD-YC) - 0.
Следующая инициализация:
T: - -2a*b2,
S: - 0, , ,
E: - T + 2a2 - b2
Б — случай наклона Е ]b/a, +1[ (т.е. Ь<а)
В случае перемещения по Y имеем
Dy(r, q) - a2(q-Yc) + а2Ь2 - b2(r-Xc)2,
Ту (г) - -2b2(r-Xc),
Sy(q) - 2a2(q-Yc),
49

Ey(r,q) - 2Dy(r,q)2 + 2«Sy(q) + Ty(r) + 2a2 - b2.
В случае перемещения по X
Dx(r,q) - -Dy(r,q),
Тх(г) - -Ty(г),
Sx(q) - -Sy(q),
Ex(r,q) - -(E + Ty(r) - Sy(q) - b2 - a2).
Тогда следующая инициализация дает
Е: « -Е - Т + S + b2 + а2,
Т: - -Т,
S: - -S.
Последняя точка может быть определена установлением
граничных значений для X или Y, или фиксацией точки (XF,YF),
принадлежащей гиперболе.
•Следующий алгоритм порождает гиперболу, оси которой
параллельны координатным осям (рис. 2.13):
(х-хс)2/а2 - (у-ус)2/Ь2-1.
Получаем алгоритм (при условии, что XF — максимальное зна-
чение абсциссы для ветви кривой, стремящейся к асимптоте):
О • Dxf
50
Рис. 2.13. Генерирование гиперболы в первом квадранте
при Ь<а и (Xc,Yc)-(0, 0) (обобщение метода Брезенхема)

Генерирование ГИПЕРБОЛЫ (Хс, Yc, H, В, XF: целые)
Начало (генерирование в первом квадранте)
целые: А2, В2, DS, DT, СА, CD, S, Т, Е, X, Y, DXT
(инициализация)
А2
В2
DS
DT
если
=А*А;
=В*В;
=+2*А2 ;
В<А ™ DXT := ОКРУГЛЕНИЕ (A2/SQR(A2-B2));
иначе DXT := XF-XC (наклон £l,Vx)
X : = ХС+А;
Y : = YC;
Отобразить точку
Т
S
Е
СА
CD
-2*А*В2;
0;
Т+2*А2-В2;
б*А2;
СА-4*В2;
(X,Y)
(перемещение на координатную ось)
Пока X<DXT выполнять
начало
Y := Y+1;
если Е<0
тр_ (осевое перемещение)
Е := E+2*S+CA;
S : = S+DS;
иначе (диагональное перемещение)
Х+1;
E+2*S+2*T+CD:
S+DS;
X
Е
S
Т
= T+DT;
конец если
Отобразить
конец
если Ь<а
то. DS : =
DT : =
Е : =
точку (X,Y);
-DS;
DT;
■E-T+S+B2+A2;
51

T := -T; S := -S;
СА:= 6*В2; CD := СА-4*А2;
(перемещение вдоль оси абсцисс}
Пока X<XF выполнять
Начало
X := Х+1;
если Е<0,
то (осевое перемещение}
Е := Е+2*Т+СА;
Т := T+DT;
иначе (диагональное перемещение}
Y := Y+1;
Е := E+2*T+2*S+CD;
S : = S+DS;
Т := T+DT;
конец если
Отобразить точку (X, Y)
конец
конец если
конец
В первом квадранте приращения по X и Y равны (1,1). Для
второго, третьего и четвертого квадрантов они равны соответствен-
но (1,-1), (-1,-1), (-1,1).
2.8.2. ГИПЕРБОЛА, ПОВЕРНУТАЯ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ
ОСЕЙ
Если оси симметрии гиперболы параллельны осям координат,
то ее уравнение будет
b2Xo2 - a2Yo2 - a2b2.
Выполнив поворот на угол GTE]- jt/2, + я/2[, получим другое
уравнение:
(p2b2-a2m2)X2+(b2m2-a2p2)Y2-2(a2+b2)p.m.XY=a2b2(p2+m2), (2.17)
где
tg в - m/p; m G Z, p G Z*.
Введем обозначения
2* 2 2 2
а» р b - am;
52

P - b2m - a2p2;
yo - (a2 + b2)pm;
У - 2 yo;
к - a2b2(p2+m2).
Тоща уравнение (2.17) можно переписать в виде
аХ2 + /3 .Y2 + y.XY - к. (2.18)
•Изменение квадранта. Как и в случае эллипса, переход в
другой квадрант происходит в точках, ще тангенс угла наклона
касательной равен либо нулю, либо бесконечности.
Покажем, что бесконечный наклон возникает тоща и только
тоща, коща m/p<a/b. В этом случае координаты точек, в которых
наклон равен бесконечности, определяется координатами
(DXoo, DYoo) и (-DXoo, -DYoo), ще
DXoe. VHT
a/S-yfl
DYoo — Ш DXoo .
Аналогично касательная с нулевым наклоном существует тогда
и только тогда, когда m/p>b/a. В этом случае координаты точек
определяются числами (DXo,DYo) и (-DXo,-DYo), где
DXo- yoV ok 2 ,
DYo -~jDXo.
•Изменение направления движения (октант). Изменение
происходит в точках, в которых тангенс угла наклона касательной
к кривой равен +1 или -1.
Касательная, наклон которой равен +1, существует тогда и
только тоща, коща b/a<l (m-p)/(m+p) I. В этом случае координаты
точек определяются величинами (DXi, DYi) и (-DXi, -DYi), где
DXl . УШ^+УО)2
(a+0-2yo)(a/S-y8) '
Аналогично касательная с наклоном -1 существует тогда и
только тогда, коща b/a< I (m+p) / (т-р) I, а координаты точек опре-
деляются величинами (DX-i, DY-i) и (-DX-i, -DY-i), где
53

DX l ■ \d W-YO?
(a+/3-2yo)(a/3-y3) '
•Асимптоты гиперболы имеют наклон
Pi » (am + bp)/(ap - bm),
P2 - (am - bp)/(ap - bm).
Условия существования касательных с соответствующим накло-
ном таковы:
если Pi>0, то существует касательная с бесконечным наклоном,
если Р2>0, то существует касательная с нулевым наклоном,
если 0<Р<1, то существует касательная с наклоном +1,
если -oo<Pi<-l, то существует касательная с наклоном -1,
если 1<Р2<+°°, то существует касательная с наклоном +1,
если -1<Р2<0, то существует касательная с наклоном -1.
Условия 0<Pi<l и 1<Р2<+«> , как 4 условия -<»<Pi<l и -1<Рг<0,
являются исключительными.
Поскольку квадранты и изменения направлений движения, как
и условия их существования, определены, то, как и в случае
эллипса, для каждого квадранта с учетом асимптотических ветвей
и симметрии можно определить последовательности, по которым
вычисляются точки, наиболее близко лежащие к кривой.
2.9. УЛУЧШЕНИЕ КАЧЕСТВА ВЕКТОРНЫХ РИСУНКОВ
2.9.1. ВВЕДЕНИЕ
В результате квантования на изображении возникает эффект
лестничных ступенек, который мешает эстетическому
восприятию .
Для уменьшения мешающего влияния этого эффекта было
предложено несколько методов. В частности, идея Брезенхема со-
стояла в том, чтобы распределить яркость между двумя точками
(одна точка — основная, выбранная в соответствии с ранее
описанными алгоритмами, а вторая — вспомогательная, выбранная
в зависимости от их относительного расстояния до кривой). Руа
[35] обобщил эту идею для улучшения качества линий окружно-
стей, эллипсов и парабол (рис. 2.14), исходя из алгоритмов ге-
нерирования кривых второго порядка на основе базового метода
Брезенхема. Кроме того, было показано, что этот метод проще и
эффективнее других, в частности использующих цифровые
фильтры.
Этот эффект получил в литературе название "алиайзинг", а методы борьбы с ним
— "антиалиайзинг". — Прим.перев.
54

wo
wo
Рис. 2.14. Улучшение качества векторных рисунков (различные степени
зачернения получены с использованием матрицы размером 3><3) [35]:
а - отрезок прямой; 6 - дуга параболы; в - окружность; г • эллипсы
2.9.2. МЕТОД БРЕЗЕНХЕМА
2.9.2.1. ПРИНЦИП ДЕЙСТВИЯ
Метод уменьшения мешающего влияния эффекта лестничных
ступенек вытекает непосредственно из алгоритма генерирования
отрезков прямых, предложенного Брезенхемом. В соответствии с
этим методом находят две точки - основную и вспомогательную,
причем вспомогательную выбирают исходя из условий, чтобы
отрезок проходил между нею и основной точкой. Обе эти точки
являются расположенными наиболее близко к теоретическому
отрезку. Яркость, присваиваемая каждой точке, зависит от ее рас-
стояния до отрезка. Сумма яркостей основной и вспомогательной
точек равна максимальной яркости (Imax), которая может быть
присвоена пикселу.
Описываемый метод улучшения качества линий не содержит
существенных отличий от алгоритма Брезенхема. В нем использу-
ется только та информация, которая содержится в исходных дан-
ных. Действительно, различные варианты направлений движения
при воспроизведении фигур разделяются на две группы: осевое и
диагональное. Этих двух направлений достаточно для получения
любой фигуры.
Выполняемые действия сводятся к арифметическим операциям
над целыми числами (сложение и вычитание) и логической опе-
рации сравнения. К вещественным числам относится только ко-
эффициент, определяющий распределение яркости между основной
55

и вспомогательной точками. Сам этот коэффициент представляет
собой результат деления двух целых чисел.
Существенным достоинством описываемого метода является то,
что эти два целых числа уже были найдены в процессе выпол-
нения исходного алгоритма, и, следовательно, их не надо находить
специально для установления значений яркости точек.
2.9.2Д. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЯ ОТРЕЗКОВ ПРЯМЫХ
Обратимся снова к работе [75], ще прямолинейный отрезок
определяется координатами своих концов (XD,YD), (XF,YF).
Обозначим через Imax максимальную яркость, а через 1р и Is
яркости основной и вспомогательной точек соответственно.
Генерирование ОТРЕЗКА с улучшением
(XD,YD,XF,YF,Imax . целые)
Начало (метод Руа}
DX := XF-XD
DY := YF-YD
DELTAX := ABS(DX)
DELTAY := ABS(DY)
Если DX>0
то_ Xi nc : = +1
иначе Xinc := -1
Если DY>0
то_ Yi nc : = +1
иначе Yinc := -1
X := XD ; Y := YD
Отобразить точку (X, Y, Imax)
В соответствии с вариантом выполнять
DELTAX >DELTAY
Начало
D :=0
Аля I := 1 шац 1 до DELTAX выполнять
Начало
X := X + Xinc
D := D + DELTAY
Если D>0
jo Ys := Y-Yinc
иначе начало
если D-DELTAX<0
то начало
56

если 2*D-DELTAX<0
10. Ys := Y+Yinc
иначе начало
Ys:= Y
Y :- Y+Yinc
D := D-DELTAX
конец
конец
иначе начало
Y : = Y+Yi nc
Ys := Y+Yinc
D := D-DELTAX
конец
конец
Cp
Is
IP
= ABS(D/DELTAX)
= ОКРУГЛЕНИЕ (Cp*Imax)
= I max-Is
Отобразить точку (X, Y, Ip)
Отобразить точку (X,Ys,Is)
конец
конец
DELTAY>DELTAX
Начало
D := О
Аля I : = 1 шаг. 1 до DELTAY выполнять
Начало
Y := Y+Yi nc
D := D+DELTAX
Если DsO
то. Xs : = X- Xi nc
иначе начало
Если D-DELTAY<0
то начало
Если 2 *D-DELTAY <0
12 Xs : = X+Xi nc
иначе начало
Xs := X
X := X+Xinc
D := D-DELTAY
конец
57

конец
иначе начало
X := X+Xinc
Xs := X+Xi nc
D := D-DELTAY
конец
конец
Ср := ABS(D/DELTAY)
Is := ОКРУГЛИТЬ (Cp*Imax) (Яркость,
присваиваемая вспомогательной точке}
Ip := Imax -Is (Яркость, присваиваемая
основной точке}
Отобразить точку (X, Y, 1р)
Отобразить точку (Xs,Y,Is)
конец
конец
Конец вариантов
Конец
2.9.3. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ КРИВЫХ ВТОРОГО ПОРЯДКА
2.93.1. МЕТОД РУА
Используя принцип, предложенный Брезенхемом для пря-
молинейных отрезков, Руа разработал алгоритм подавления эф-
фекта алиайзинга в процессе генерирования эллипсов и дуг пара-
бол.
2.93.2. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ ЭЛЛИПСОВ
•Простые эллипсы. Рассмотрим эллипс с центром в точке
C(XC,YC), описываемый уравнением
(Х-ХС)2/А2 + (Y-YC)2/B2 - 1.
Алгоритм Руа имеет следующий вид:
Улучшенное генерирование ПРОСТОГО ЭЛЛИПСА
(ХС, YC, А, В, I max: целые)
Начало (метод Руа}
А2 : = А*А
В2 := В*В
DS := 2*А2
DT := 2*В2
58

DXT := ОКРУГЛЕНИЕ (A2/SQR(A2+B2))
Xinc := +1 (1-й квадрант }
Yinc := -1
ПРОВЕДЕНИЕ ПРОСТОГО ЭЛЛИПСА В КВАДРАНТЕ
Yinc := +1 {2-й квадрант }
ПРОВЕДЕНИЕ ПРОСТОГО ЭЛЛИПСА В КВАДРАНТЕ
Xinc := -1 {3-й квадрант }
ПРОВЕДЕНИЕ ПРОСТОГО ЭЛЛИПСА В КВАДРАНТЕ
Yinc i= ~1 f4~fi kb<iad<iht1
ПРОВЕДЕНИЕ ПРОСТОГО ЭЛЛИПСА В КВАДРАНТЕ
Процедура ПРОВЕДЕНИЯ ПРОСТОГО ЭЛЛИПСА В
КВАДРАНТЕ
Начало
Т := О
S := -2*А2*В
D :=0
X : = ХС
Y := YC-YincB
Отобразить (X, Y, Imax)
Аля I : =1 шаг 1 до. DXT выполнять
Начало
X := X+Xinc
D := D+T-B2
Если D>0
10. YS := Y-Yinc
иначе начало
Если D-S-A2>0
то начало
если 2*D-S-A2>0
10. YS := Y+Yinc
иначе начало
YS := Y
59

Y
D
S
Y+Yinc
D-S-A2
S+DS
конец
T
Cp
Is
IP
конец
иначе начало
Y := Y+Yi nc
YS := Y+Yinc
D := D-S-A2
S := S+DS
конец
конец
= T-DT
= ABS (D/S)
- Cp*Imax
= I max-Is
Отобразить точку (X,Y,Ip)
конец
DYT : =
Аля I
Начало
Y
D
ABS (Y-YC)
: =1 шаг. 1 до DYT выполнять
= Y+Yinc
= D-S-A2
Если D^O
тр_ XS : = X- Xi nc
иначе начало
Если D+T-B2<0
то начало
Если 2*D+T-B2<0
IP_ XS :=X+Xinc
иначе начало
XS
X
D
T
конец
: =
: =
: =
X
X+Xi nc
T-B2+D
T-OT
конец
иначе начало

X : = X+Xi nc
XS := X+Xi nc
D := D+T-B2
T := T-DT
конец
конец
S := S+DS
Cp := ABS {D/J)
Is := Cp*Imax
Ip := I max-Is
Отобразить точку (X, Y, Ip)
Отобразить точку (XS, Y, Is)
конец
Конец ПРОВЕДЕНИЯ ПРОСТОГО ЭЛЛИПСА В КВАДРАНТЕ
Этот алгоритм может быть использован также для улучшения
линий окружности радиусом R при A-B-R.
•Произвольный эллипс. В приводимом ниже алгоритме Руа рас-
сматривается простой эллипс, оси которого повернуты на угол
0G ]-jt/2, + jt/2[, определяемый соотношением
tg в «М/Р, где М G Z ; Р 6 Z*.
Улучшенное генерирование ПРОИЗВОЛЬНОГО ЭЛЛИПСА
(XC,YC,A,B,M,P: целые)
Начало {метод Руа)
ЦЕЛЫЕ a,Ayo,y,k,D,Dl,T,S
ЦЕЛЫЕ Dsa, Dsd, Dta, Dtd
ЦЕЛЫЕ Dxtl, Dxt2, Dxo, Dyo, Dy oo.
ВЕЩЕСТВЕННЫЕ U
(Инициализация)
A2
B2
M2
P2
a
/5
Уо :
: =
: =
:«
:-
: =
: =
s
A*A
B*B
M*M
P*P
P2*B2+M2*A2
M2*B2+P2*A2
(B2-A2)*P*M
61

у := 2*у0
к := А2*В2*(Р2+М2)
Dxtl: =ОКРУГЛЕНИЕ( SQR( k*(£+у0) 2/( (аф2*у0) *( а*р- у02)))
Dxt2: =ОКРУГЛЕНИЕ( SQR( к*(в-у0) 2/( («+/5-2*уо) *( «*£-у02)))
U : =y0*SQR( k/( /3*а2- а*у0?))
DXO := ОКРУГЛЕНИЕ (U)
Если уо=0 Т£ Dyo : =)3
иначе Dyo := ОКРУГЛЕНИЕ (a*U/y0)
Dyoo := OKPyr/OHE((yo//S)*SQR(k*£/(£*a-y02)))
Dl := k-a*DX02-)3*DY04y*DXO*DYO
TO := 2*a*DXO-y*DYO
SO := 2*y3*DYO-y*DXO
(1-й квадрант)
X :=Xc-DXO
Y :=Yc+DYO
Dxt : = Dxt2
Xi nc : = +1
Yinc := -1
Sg := 1
ПРОВЕДЕНИЕ
ПРОИЗВОЛЬНОГО
ЭЛЛИПСА В КВАДРАНТЕ
(3-й квадрант)
X
Y : =
Xinc
Dxt
Xc+DXO
Yc-DYO
:= -1
= Dxt2
Sg := 1
ПРОВЕДЕНИЕ
ПРОИЗВОЛЬНОГО
ЭЛЛИПСА В КВАДРАНТЕ
(2-й кваадрант)
X := Xc+DXO
Y := Yc-DYO
Yi nc : = +1
(4-й квадрант)
X := Xc-DXO
Y := Yc+DYO
Yinc := -1
Dxt : = Dxtl
Dxt := Dxtl Sg := -1
Sg := -1 ПРОВЕДЕНИЕ
ПРОВЕДЕНИЕ ПРОИЗВОЛЬНОГО
ПРОИЗВОЛЬНОГО ЭЛЛИПСА В КВАДРАНТЕ
ЭЛЛИПСА В КВАДРАНТЕ
Конец
62

Процедура ПРОВЕДЕНИЯ ПРОИЗВОЛЬНОГО ЭЛЛИПСА В
КВАДРАНТЕ
D : =
Dta
Dsa
Dtd
Dsd
СП —1
II II
Если
Cp :
Is :
Ip :
Dl
= -l*a
= Sg.y
= Sg*y
= -2ф
TO.Sg
SO
D>0 то Ys
иначе
= ABS(D/S)
= Cp*Imax
= I max-Is
:= Y-Yinc
Ys := Y+Yinc
Отобразить точку (X, Y, I p)
Отобразить точку (X,Ys,Is)
Bt := ABS(X-Xc-XinoDxt)
Аля I : = • 1 до Bt выполнять
Начало
X : = X+Xi nc
D : = D+T-a
Если D>0
10. Ys := Y-Yinc
иначе начало
Если D+S-£+Dsa>0
то начало
Если 2*D+S-£+Dsa>0
тр_ Ys :=Y+Yinc
иначе начало
Ys := Y
Y := Y+Yi nc
D : = D+S-/3+Dtd
T := Dtd+T
63

S := Dsd+S
конец
конец
иначе начало
Y :=Y+Yinc
Ys : = Y+Yi nc
D : = D+S-0+Dtd
T : = Dtd+T
S : = Dsd+S
конец
конец
S := S+Dsa
T := T+Dta
Cp : = ABS( D/S)
Is := Cp*Imax
Ip := I max-Is
Отобразить (X, Y, Ip)
Отобразить (X,Ys,Is)
конец
Dta := Sg*y
Dsa
Dtd
Dsd
:= -2*/3
:= -2*a
:= Sg*y
Dyt := ABS(Y-Yc+Xinc*Dyoo)
Аля I : =1 до Dyt выполнять
Начало
Y := Y+Yinc
D := D+S-/5
Если D<0
то. Xs :=X-Xinc
иначе начало
Если D+T- a+Dta<0
10. начало
Если 2*D+T-a+Dta<0
64

то Xs :* X+Xinc
иначе начало
Xs :- X
X :» X+Xi nc
D
T
s
* D+T- a+Dta
- T+Dtd
= S+Dsd
конец
конец
иначе начало
X :« X+Xinc
Xs :« X+Xi nc
D
T
s
конец
конец
T := T+Dta
S := S+Dsa
D+T-a+Dta
T+Dtd
S+Dsd
Cp
Is
IP
= ABS(DA)
= Cp*Imax
= I max-Is
Отобразить точку (X, Y, Ip); Отобразить точку
(Xs,Y,Is)
конец
КОНЕЦ ПРОВЕДЕНИЯ ПРОИЗВОЛЬНОГО ЭЛЛИПСА В
КВАДРАНТЕ
Примечание: Случай больших значений кривизны.
Такие случаи имеют место, либо когда величина Dxtl или Dxt2
близка к значению Dxo или Dxoo, иначе говоря, когда А«В или
В«А, либо когда численные значения величин А и В относительно
малы.
Можно заметить, что в этих случаях для точек с резко выра-
женной кривизной величины 1р и Is вычисляются неверно.
Действительно, значения яркости здесь получаются как бы
противоположными (т. е. величина 1р связана с S, a Is — с Р).
Причина этого заключается в том, что величины Т или S быстро
3 - Ж. Эгрон
65

уменьшаются (в некоторых случаях они даже становятся равными
нулю). Такое быстрое их уменьшение не сказывается в тех слу-
чаях, коща рассматриваются "ступенчатые" варианты.
Избавиться от подобного недостатка можно, изменив способ
вычисления величин 1р и Is следующим образом:
Если Т=0 (соответственно S=0)
то. Ср := О
иначе начало
Ср := |ОД ((соответственно |D/S|)
Если Ср > 1/2 то. Ср : = 1-Ср
конец
Is := Cp*Imax
Ip :* I max-Is
2233. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ ДУГ ПАРАБОЛЫ
Дуга параболы задается уравнением Y-A(X-XC) +B и двумя
концевыми точками и координатами (XA,YA), (XB,YB), где (ХС,
В) — координаты кривой (см. рис. 2.11 в разд. 2.7).
Алгоритм, разработанный Руа, имеет вид
Улучшенное генерирование ДУГИ ПАРАБОЛЫ
(ХА, YA, XB, YB, ХС: целые)
Начало (метод Руа}
Если (ХА<ХС и ХС<ХВ) или (ХВ<ХС и ХС<ХА)
то начало
Если ABS(XA-XC)=ABS(XB-XC)
то. читать YC
иначе DSX0 := (ХВ-ХА)*(ХВ+ХА-2*ХС)
СВО: = (ХВ- ХС) 2*YA- (XA*XC) 2*YB
YC : «ОКРУГЛЕНИЕ (CB0/DSX0)
ПРОВЕСТИ (ХС, YC, ХА, YA) ~
ПРОВЕСТИ (ХС, YC, XB, YB)
конец
иначе начало
Если (ХС<ХА и ХА<ХВ) или (ХС>ХА и ХА>ХВ)
10. ПРОВЕСТИ (ХА, YA, XB, YB)
иначе ПРОВЕСТИ (XB, YB, XA, YA)
конец
Конец
ПРОВЕСТИ (XD, YD.XF. YF)
DX :« XF-XD
66

DY := YF-YD
DELTAY := ABS(DY)
DT := 2*DELTAY
DSX := DX*(XF+XD-2*XC)
DXT := ОКРУГЛЕНИЕ (DSX/DT)
Если DX>0
10. XINC := +1
иначе XINC := -1
Если DY>0
10. YINC := +1
иначе YINC := -1
X := XD
Y := YD
Отобразить точку (X, Y, I max)
T := DT*ABS(X-XC)
D := 0
Если ABS (X-XC)<DXT
то начало {случай тангенса угла наклонаG[ 0,1]}
ВТ := MIN(ABS(DX),-ABS(X-XC)+DXT)
Для I : = 1 шаг. 1 до ВТ выполнять
Начало
X := X+XINC
D := D+T+DELTAY
Если D<0
IP_ YS := Y-YINC
иначе начало
Если D-DSX<0
то начало
Если 2*D-DSX<0
то YS := Y+YINC
иначе
начало
YS := Y
Y := Y+YINC
D := D-DSX
конец
3*
67

конец
иначе начало
Y : =
YS :
D : =
конец
конец
Т := T+DT
Y+YINC
= Y+YINC
■■ D-DSX
Ср :« ABS(D/DSX)
Is := Cp*I
Ip := I max
Отобразить
Отобразить
конец
конец
DYT
Если
:- ABS(YF-Y)
DYT * 0
max
-Is
точку (X,
точку (X,
Y,Ip)
Ys,Is)
то начало (случай тангенса угла наклона
е]1,+°°[}
Т := -Т
D := -D
Для i
Начало
Y :-
D : =
Если
то
:= 1 шаг_ 1
Y+YINC
D+DSX
D<0
Xs := X-XINC
до DYT выполнять
иначе начало
Если D+T-DELTAY<0
то начало
Если 2*D+T-DELTAY<0
то Xs := X+XINC
иначе
начало
Xs : =
X : =
D :-
Т :«
конец
X
X+XINC
D+T-DELTAY
T-DT
68

конец
иначе начало
X :- X+XINC
XS :- X+XINC
D :« D+T-DELTAY
Т := T-DT
конец
конец
Ср := ABS(DA)
Is := Cp*Imax
Ip := I max-Is
Отобразить точку (X, Y, Ip)
Отобразить точку (XS,Y,Is)
конец
конец
КОНЕЦ ПРОВЕСТИ
2.9.4. МОДЕЛИРОВАНИЕ УРОВНЕЙ ЯРКОСТИ
2.94.1. ВВЕДЕНИЕ
Алгоритмы, устраняющие эффект ступенек, предназначены для
использования их в аппаратуре, на экране дисплея которой
яркость отдельных элементов может изменяться. Если же аппарат-
ные средства такого изменения не допускают, приходится прибе-
гать к моделированию.
Среди многочисленных методов (таких, например, как метод
"случайных порогов" Флойда и Стернберга [7,20,29]) особое
внимание обратим на метод предварительно определенных (пре-
допределенных) ячеек, который наиболее прост в использовании и
наилучшим образом приспособлен для векторных рисунков.
2.9.4.2. ИСПОЛЬЗОВАНИЕ ПРЕДОПРЕДЕЛЕННЫХ ЯЧЕЕК
•Принцип действия. Основная идея метода заключается в том,
что один элемент изображения заменяется квадратной матрицей
смежных элементов размером n x п. Побочным нежелательным
эффектом такого метода является ухудшение разрешающей спо-
собности экрана.
Реализация метода состоит в выполнении следующих опе-
раций:
69

каждой отображаемой точке с координатами (r,q) присваивается
значение яркости In;
отображение п соответствующих точек экрана происходит в
результате сравнения яркости In со значением, определяемым
опорной матрицей Ln:
Есди In>Ln(i,j),
m точка экрана (3*r+i, 3»q+2-j)
высвечивается,
иначе данная точка не высвечивается.
Пусть, например, имеется изображение, в котором значения
яркости изменяются в пределах 0...9 и которое необходимо пред-
ставить с помощью ячеек размером 3*3. Матрица L3 может иметь,
например, вид
Гб 8 4]
10 3.
[5 2 71
На рис. 2.15 показано, какая ячейка соответствует каждому
значению яркости.
ав вв щ щ
гГп ГГп Щ ГП
1111
Рис. 2.15. Моделирование девяти уровней яркостей
Одна из проблем, возникающих при использовании подобных
матриц, заключаются в появлении паразитных фигур.
Действительно, некоторые конфигурации точек ячейки могут соз-
давать нежелательную штриховку или другие вторичные меша-
ющие эффекты. Метод, известный под названием "упорядоченные
колебания" (ordered dither — англ.) [20], позволяет получать
матрицы L2, L4, L8, ..., уменьшающие эти явления. Матрицу Ln
можно записать следующим образом:
Ln
[4Lm
" [4Lm +
3Um
4 Lm + 2 Urn
4Lm + Urn
]•
ще m« n/2, a Um — квадратная матрица размером m*m, все эле-
менты которой равны 1.
70

Положив L1-0, получим матрицы L2 и L4:
0 8 2 101
12 4 14 6 I
3 11 1 9 Г
15 7 13 5\
•Устранение вторичных эффектов. Использование только
одной матрицы приводит к тому, что генерируемая кривая ста-
новится похожей на витой шнурок и нарушается симметрия
кривой (особенно это заметно на эллипсе). На рис. 2.16 показаны
некоторые результаты, полученные при применении матрицы.
Рис. 2.16. Устранение вторичных эффектов [35]:
а - вторичные эффекты, полученные при использовании единственной опорной матрицы; б - мо-
делирование уровня яркости после устранения вторичных эффектов
Чтобы сгладить такой неблагоприятный эффект, Руа предложил
учитывать "ориентацию" отображаемой кривой, используя вместо
одной матрицы четыре опорных матрицы, каждая из которых со-
ответствовала бы одной из четырех возможных "ориентации"
кривой:
71
L2 -
0 2
3 1
L4

Ll-Ь-
L2-
L3-
L4-
Го
5
8
'2
4
7
"8
б
2
'7
3
0
3
1
б
б
1
3
5
1
4
4
1
5
71
4
2
8]
5
О
°1
31
7
21
б|
8|
связана с полу квадрантами 3 и 4;
связана с полуквадрантами 7 и 8;
— связана с полу квадрантами 1 и 2;
— связана с полуквадрантами 5 и 6;
Однако данный метод не в состоянии сохранить симметрию
кривой. Воспользуемся тем, что применяемые алгоритмы прове-
дения кривых показывают положение вторичных точек
относительно главных точек. В работе Руа [35] предложена сле-
дующая "стратегия":
главной точке Р присваивается индекс опорной матрицы, соот-
ветствующий тому полуквадранту, которому она принадлежит
(индекс обозначается lib),
второй точке присваивается индекс одной из четырех опорных
матриц в зависимости от положения точки S относительно точки
Р и индекса lib.
Присваивание выполняется следующим образом:
1 lib
индекс, присвоенный
точке Р
111с
S расположена
над Р
Не
S расположена
под Р
lid
S расположена
справа от Р
S расположена
слева от Р
Полу квадранты
3 и 4
1
2
1
1
2
Полу квадранты
2
2
1
1
2
Полуквадранты
1 и 2
3
3
4
3
4
Полуквадранты 1
5 и 6 1
4
3
4
3
4
72

Присваивание значений lib, lie, lie, lid и Ilg выполняется
одновременно с определением значений переменных, характеризу-
ющих приращение координат: Xinc и Yinc.
Отображение точек происходит в соответствии со следующим
алгоритмом:
ЯРКОСТЬ (ЦЕЛЫЕ ТАВ(*,4), NBP,
L2(3,3), L3(3,3), L4(3,3))
Начало
ЦЕЛЫЕ Хе, Ye, Xo, Yo
ЦЕЛЫЕ Lx(3,3), In, II
Ll(3,3),
Для
I : =
Начало
Хо : =
Yo : =
In : =
11 : =
Соответ
Начало
П =
11 =
11 =
11 =
конец
Ye : =
Для к
Начало
Хе :
Для
1 до
ТАВ(1
ТАВ(1
ТАВ(1
ТАВ(1
NBP i
,1)*3
, 2)*3+2
,3)
,4)
выполнять
{TAB содержит
наты, яркости и
опорных матриц
коорди-
индексы
отображаемых точек}
ственно варианту выполнять
1
2
3
4
Yo
:= 1
= Хо
J : =
Начало
Если In
Хе
конец
Ye :
конец
конец
Конец
ЯРКОСТЬ
L
= Ye
: Lx
: Lx
: Lx
: Lx
AP_ ■
1 АО
>Lx(K,J
Хе +
- 1
:= L1
:= L2
:= L3
:= L4
1 выполнять
3 выполнять
) то отобразить
1
(Xe,Ye)
73

В результате устранения вторичных эффектов моделирование
дает верное представление о том, каким было бы изображение на
экране с изменяемой яркостью. На рис. 2.16 показаны примеры
кривых, отображение которых улучшено путем использования
предложенного решения.
2.10. ЗАКЛЮЧЕНИЕ
Для рассмотренного только что семейства кривых можно сделать
вывод о том, что инкрементный метод Брезенхема представляется
наиболее удачным по следующим причинам:
вычисленные точки наиболее близко расположены к теоретиче-
ской кривой;
используются только арифметические операции над целыми
числами и операции сложения-вычитания для вычисления точек;
наибольшая простота в использовании и минимальные
вычислительные затраты.
Таким образом, по всем параметрам метод Брезенхема является
наиболее предпочтительным. В то же время следует подчеркнуть,
что, хотя метод Брезенхема и не может быть обобщен на любые
типы произвольных кривых, они могут быть, как известно, ап-
проксимированы отрезками прямых, дугами окружностей или
эллипсами.
Попутно отметим, что многие авторы исследовали вопросы ап-
проксимации произвольных линий отрезками прямых и отрезками
кривых второго порядка (например, [34]).
ГЛАВА 3
ЗАПОЛНЕНИЕ ОБЛАСТЕЙ
3.1. ВВЕДЕНИЕ
Термином "заполнение областей" будем обозначать три вида
обработки изображений:
окрашивание,
заполнение (в собственном смысле слова),
штрихование.
•Как только некоторая область на экране отделена от других
замкнутой линией контура, то первая мысль, возникающая у
пользователя, — окрасить ее в какой-нибудь цвет, начиная с
исходной "затравочной" точки, находящейся внутри данной
области (в английской литературе используется термин seed —
ядро, зародыш).
Такую операцию будем называть окрашиванием.
•Заполнение области представляет собою операцию, заключа-
ющуюся в том, чтобы заполнить некоторую часть области, либо
74

• e
Рис. З.1. Представления контура:
a • контур, описанный замкнутым многоугольником:
б • контур, описанный поэлементно (точка за точкой)
ограниченную многоугольным (или каким-то иным) контуром в
пространстве пользователя (рис. 3.1а), либо описанную точка за
точкой в памяти изображений и отображенную на экране
(рис. 3.16).
В общем случае алгоритм заполнения состоит из двух фаз:
1) подготовка контура, т. е. составление списка его ребер, если
контур рассматривается в пространстве пользователя, или зане-
сение кодированных значений элементов контура в матрицу изоб-
ражения, представленного на визуализированной поверхности;
2) собственно заполнение области внутри контура требуемым
цветом.
• Задача штрихования весьма близка по характеру решения к
задаче заполнения области внутри контура последовательностью
линий, в частности, алгоритму "прослеживания контура". Далее
будет рассмотрен метод наклонной штриховки без поворота.
При изучении алгоритмов в дальнейшем будем пользоваться
понятием "контекста", связанного с каждой строкой развертки,
под которым будем понимать некоторое множество логических
переменных, позволяющих описывать определенную информацию
на каждой строке. Характер этой информации будем уточнять для
каждого конкретного алгоритма.
3.2. ОКРАШИВАНИЕ
3.2.1. ОСНОВНОЙ ПРИНЦИП
Во многих прикладных задачах контур области, подлежащей
заполнению, описан в памяти путем перечисления всех своих то-
чек. Основной принцип в таком варианте состоит в следующем:
необходимо отнести все внутренние точки связной области,
начиная с некоторой исходной "затравочной" точки, к данной
области, охватывая все точки, "связанные" с исходной (рис. 3.2).
Базовый алгоритм разработан Смитом [41]. После того как
определена исходная точка (seed) с координатами seedx и seedy,
75

I |_Д11 |_JU I
Рис. 3.2. Контур, описанный поэлементно, и его внутренняя точка.
* • исходная "затравочная точка с координатами х,у
находящаяся внутри замкнутой области, вначале заполняется
весь горизонтальный отрезок, которому принадлежит данная точка
(т. е. всем точкам, находящимся на данной строке развертки и
расположенным между исходной точкой и контуром, присваивает-
ся заданный цвет). Затем находятся отрезки, принадлежащие со-
седним строкам выше и ниже текущей строки, такие, которые со-
держат по крайней мере один пиксел, имеющий общую сторону
хотя бы с одним пикселом данной текущей строки (свойство
связности). Эта точка, (пиксел) становится новым источником но-
вого отрезка, и описанный выше процесс повторяется до тех пор,
пока вся область оказывается заполненной. Для запоминания и
повторного использования исходных точек применяется стековая
память.
На рис. 3.3 показаны различные этапы описанной процедуры:
черные квадратики — элементы контура, звездочка — исходный
"затравочный" пиксел, а черные точки внутри белых квад-
ратиков — новые исходные пикселы.
НпДщЯс oBHiHtj ЯНИ^Нп
ЕПСшИЕН шСшС] сЛСгПИи!
Рис. 3.3. Заполнение области внутри контура (иллюстрация процесса
окрашивания)
76

В процессе окрашивания могут встретиться два типа случаев,
приводящих к специфическим искажениям.
•Если контур представлен незамкнутой линией, т. е. когда в
процессе генерирования контура в нем возникают изолированные
точки, заполнение области внутри контура происходит с
ошибками, значение которых зависит от числа этих точек
(рис. 3.4).
Изолированные точки Неокрашенные
/точки области
Рис. 3.4. Пример особенности, встречающейся при окрашивании
(несвязная область):
а -исходный контур; б • контур после окрашивания
•Окрашиваемая область может примыкать к краю экрана, что
приводит для некоторых алгоритмов (например, алгоритма
Павлидиса и др.) к выходу за пределы области.
Для предотвращения этого используют два способа: либо на
каждом шаге осуществляют проверку, не превзойдены ли пределы
поля памяти, либо увеличивают объем памяти на краях, чтобы за-
ранее исключить возможность появления ошибки. Хотя второй
способ ведет к некоторому увеличению объема памяти, для него
не требуется никаких дополнительных вычислений.
Для уменьшения вычислительных затрат при реализации базо-
вого алгоритма были использованы две идеи:
избавиться от повторного сканирования смежных горизон-
тальных отрезков (алгоритм Смита [41], Либермана [21]);
представить контур в виде графа (алгоритм Шани [38 ] и
Павлидиса [32]).
Вычислительные затраты. Если NBI — число внутренних то-
чек области, a NBC — число точек контура, то затраты для ал-
горитма Павлидиса пропорциональны NBI+3NBC. Для ал-
горитмов же Смита, Либермана и Шани затраты пропорциональны
3NBI. Таким образом, при NBC«NBI алгоритм Павлидиса
априори представляется более предпочтительным.
Рассмотрим вначале базовый алгоритм Смита, а затем алгоритм
Павлидиса.
77

3.2.2. АЛГОРИТМ СМИТА
Чтобы избавиться от необходимости систематического обследо-
вания каждого горизонтального отрезка, примыкающего к данному
и расположенному выше и ниже него, Смит предложил следующее
решение:
Если текущий горизонтальный отрезок Sc примыкает к уже
обработанному отрезку Sp и если концы отрезка Sc находятся
внутри отрезка Sp, то не существует других отрезков над Sc, и
связанных с ним, если Sc расположен под Sp (соответственно,
под Sc, если расположен над Sp). Варианты взаимного располо-
жения отрезков показаны на рис. 3.5.
Sc , ,
Spl I I I Sp
a » i Sc
Рис. 3.5. Варианты расположения примыкающих отрезков Sc и Sp:
а — Sc над Sp; б — Sc под Sp
Алгоритм Смита имеет следующий вид:
Алгоритм СМИТА (seedx, seedy, newpv)
Наыадо.
х : = seedx, у : = seedy
new := newpv; old := pvaleur(x, y)
eCAU old = new то коней:
yref : = у, 1 xref : = x, rxref =x;
Занести в стек (х, у) ;
QOKi (стек не пустой) выполнять:
Начало
Взять из стека (х, у) ;
Если pvaleur (x, у)* new
Ш FILLINE
если HIV0ISIN
Ш SCANHI;
иначе если L0V0ISIN
Ш SCANL0;
иначе SCANHI; SCANL0;
конец если
конец если
конец если
yref :=y, lxref =1; rxref :=r;
конец
Конец
78

Обозначения:
newpv — новое значение точек области;
old — старое значение точек области;
(seedx, seedy) — координаты внутренней точки;
1х и гх — соответственно левый и правый концы
горизонтального отрезка;
Xmin, Xmax, Ymin, Ymax — граничные значения поля памяти
изображения.
Функция pvaleux (x,y) принимает значения точки (х,у).
FILLINE (заполнение горизонтального отрезка}
Начало
FILLRIGHT; (заполнение вправо}
FILLLEFT; (заполнение влево}
Конец ;
FILLRIGHT
Начало
хранить х ;
Пока (pvaleur (х, y)=old ^ х<хтах),
выполнять
Начало
pvaleur (х, у) := new ;
х : = х+1 ;
конец
гх := х-1
восстановить х ;
конец
FILLLEFT
Начало
хранить х ;
х : * х-1 ;
Пока (pvaleur (х, у) = old и_
x>xmi n), выполнять
Начало
pvaleur (x, у) := new
х : = х-1 ;
конец
1 х : = х+1 ;
восстановить х ;
конец
79

SCANHI
Начало
если у+1 > ymax то конец ;
Хранить х и у ;
х : = 1 х ; у : - у+1 ;
Пока х<гх, выполнять
Начало
Пока pvaleur (x, у) Ф old и
х<гх выполнять
Начало х : = х+1 конец ;
Если х>гх то конец ;
Занести в стек (х, у);
Пока pvaleur (х, у) = old и_
х<гх выполнять;
Начало х : = х+1 конец ;
конец
Восстановить х, у ;
конец ;
SCANL0
Начало
если у-1 < ymin то конец конец если
Хранить х, у ;
х := 1Х ; У :- У-1 ;
(1) из SCANHI ;
Восстановить х и у ;
конец ;
Логическая функция HIVOISIN (LOVOISIN) проверяет, явля-
ется ли текущий горизонтальный отрезок примыкающим к преды-
дущему, расположен ли он над ним или под ним, а также
определяет, имеется ли какой-либо иной отрезок, связанный с
ним и находящийся выше или ниже.
Подпрограмма HIVOISIN
Начало
если (y=yref+l и lx^lxref-l и rx<rxref+l)
то истинно ;
иначе ложно ;
конец ;
80

Для вычисления LOVOISIN заменяют yref+1 на угеМ.
Можно заметить, что данный алгоритм заполнения обес-
печивает окрашивание уже существующей монохромной
области новым цветом (newpv) или окрашивание в новый цвет
области, заданной предварительно описанным контуром, если его
внутренняя часть монохромна. Если же внутренняя область кон-
тура содержит несколько цветов, этот алгоритм также может быть
использован после некоторой модификации испытаний значений
точек.
3.2.3. АЛГОРИТМ ПАВЛИДИСА
3.23.1. ПРИНЦИП
Для моделирования области Павлидис использует два графа,
элементами которых служат горизонтальные отрезки, составлен-
ные из пикселов одного цвета, и пары примыкающих друг к другу
одноцветных отрезков. Этими графами являются графы смежности:
строк контура (contour-line adjacency graph — C-LAG),
строк внутренней части области (interieur-line adjacency
graph — I-IAG).
Будем считать, что два отрезка внутренней области примыка-
ют друг к другу, если содержат хотя бы две точки с одной общей
стороной, а отрезки контура считаем примыкающими, даже если
его две точки имеют всего лишь одну общую вершину или общий
угол (рис. 3.6).
Рис. 3.6. Определение C-LAG и I-LAG
Основная идея алгоритма заполнения состоит в использовании
графа смежности строк контура вместо графа смежности внутрен-
ней части области. Целесообразность такой замены объясняется
возможностью применения алоритмов, идентичных алгоритмам
контроля четности, и возможностью ускорения процесса запол-
нения.
Процесс исследования начинается с узла (горизонтального
отрезка), которому принадлежит внутренняя точка. Затем опреде-
ляются затравочные точки примыкающих к нему узлов путем рас-
смотрения контура на обоих его концах, а далее последовательно
81

для всех остальных отрезков (информация о затравочных точках
находится в стековой памяти).
Число узлов контура (порядок), связанных с тем узлом, кото-
рый расположен на одном из концов горизонтального отрезка
(узел графа смежности строк внутренней части области), позволя-
ет определить, достигнут ли экстремум, и вычислить исходные
точки отрезков того же графа, примыкающих к текущему отрезку.
3.23.2. ДЕЙСТВИЕ АЛГОРИТМА
Перед тем как перейти к изложению основной части алгоритма,
рассмотрим некоторые вспомогательные процедуры.
•Вспомогательные процедуры. Пусть, например, величина р
определяет адрес некоторой точки экрана, имеющей координаты
х, у. Тогда р-1 означает адрес точки, находящейся слева от р
на той. же горизонтальной строке, а р+1 — адрес точки, распо-
ложенной справа от нее (рис. 3.7а). Процедура LEFT(p) находит
самую левую точку того монохромного интервала, в котором со-
держится точка р (аналогично процедура RIGHT (р) находит са-
мую правую), как показано на рис. 3.76.
Процедура LRIGHT(p)-LEFT(LEFT(p)-l)-l находит край-
нюю правую точку отрезка, имеющего тот же цвет, что и те-
кущий отрезок, и находящегося слева от текущего на той же стро-
ке , причем оба отрезка разделены по крайней мере одним пиксе-
лом другого цвета (рис. 3.7в).
Р-1 р*1
т
LEFT(p)
■ шин I II
Г Т
LRIGHT(p) *
Рис. 3.7. Определения
Порядок вершины (интервала) графа, содержащего точку р,
вычисляется процедурой LINK(p,v) путем определения вектора
v*(a, b, pi, p2, el, е2), где а и b — порядки вершин, нахо-
дящихся выше и ниже того, где содержится р, a pi, р2, е2 —
точки, положение которых ясно из рис. 3.8 (если эти точки не
определяются, то переходят к значению NIL).
82

ш*
V/.
Рис. 3.8. Определение величин pi, р2, el, e2:
точка р принадлежит интервалу д>2, pl[
Обозначения:
pnext — точка, принимаемая за начальную при заполнении
следующего интервала;
Pother — точка, которая может принимать значения pabove (p
верхняя) или pbelow (p нижняя); расположена непосредст-
венно над текущей точкой или под ней;
empiler (S, р) — поместить в стек; означает направить точку р
в стек S, при этом точка р окажется верхней в стеке;
pi — внутренняя точка, цвет которой соответствует
цвету, присвоенному области.
Алгоритм ПавлиАиса
Издало,
(инициализация стеков}
если pi above G контур
LQ. LINK (piabove) ;
аСАИ. (a,b) * (0,2)
Ш LINK (LEFT(pi));
занести в ctck(S, el);
Занести в CTeK(Sd, up);
конец если
иначе Занести в стек (S,LEFT(pi above);
Занести в стек (Sd,up);
конец если
Занести в стек (S,LEFT(pi); занести в
стек (Sd, down)
(Заполнение)
QOKi стек S не пустой выполнять
Напало.
р next := взять из стека (S);
направление : = взять из стека
Sd, Pright=X-max
(RIGHT(P)}
если направление = down
10. u:=2, other: = below,
иначе u:=l, other=above
83

Повторять
если. (pnext=nil паи. заполнен)
LQ_ выйти из цикла
конец если
р:=pnext; {pnext становится
текущей затравкой}
LINK(p-l); {контур слева}
(1) если (направление=(1оот и. а>1) или
(направлением и. Ь>1)
И. р справа от pright lq. выйти из
цикла конец если
(2) елли. (а>0 и Ь>0)
то pnext : = ей;
иначе {экстремум} если, р
не заполнен ю_
занести в стек( S, LEFT( LRI 6НТ( р))),
занести в стек (Sd, - направление);
асди. (а=0 и. Ь*0 и. направление
=down) иди (а *0 ц Ь=0
и направление = up)
ISL pnext : = eu;
иначе если pother не заполнен
La pnext: =LEFT(pother);
иначе pnext:-nil;
коней если
конец если
конец если
Заполнить линию от р до pright
цветом C0ULEUR;
LINK (pright+1) ; {контур справа}
(3) Если (а=0 или b=0) n (pi не
заполнен)
Ш. занести в стек (S, pi)
если. а>0 ia занести в
стек (Sd, up)
иначе занести в стек
(Sd, down)
конец если
конец если
до. конец цикла

Примечания. В алгоритме Павлидиса при движении
в направлении развертки проверка (1) устанавливает, достигнут
ли внутренний край области. Если развертка направлялась вниз и
если а>1, то, следовательно, достигнут либо "нижний край"
(рис. 3.9а), либо одна из двух конфигураций, показанных на
рис. 3.9 — аа и ab. Первый вариант характеризуется тем, что те-
кущая точка р находится справа от точки pright, а следовательно,
и вне контура (в противном случае р находится внутри).
pright
wf'
Ш
pright
pright
Рис. 3.9. Конфигурации, обнаруживаемые при проверке (1)
Проверка (2) устанавливает необходимость в процессе обра-
ботки отметить экстремум слева от затравочной точки р. Пример
подобного рода показан на следующем рисунке при а=0:
i
ш
и
LRIGHT(P)
ЦЯ LEFT(LRIGHT(P))
Находите* в стеке S
Ниже приведены два варианта расположения следующей точки
pnext:
Направление
Р\ Pnext
Ys
а = 0
pnext s e2
Точка в стеке (направление: верх)
челе
ш
ч
pnext
Ь = 0
pnext r LEFT (pother)
Проверка (3) обнаруживает экстремум справа от только что за-
полненного отрезка.
В процедуре LINK для исследуемого горизонтального отрезка
используется цвет С, задаваемый выражением v(p)= цвет точки р.
85

LINK (p,(a,b,el,e2,pl))
Начало
с := v(p);
a : =b : =0;
el :=e2 :=pl :«nil;
p : =LEFT( p), pa : «pabove; pb : «pbel ow;
если v(pa-l)=c то a := a+1 конец если
если v(pb-l)=c то b := b+1 конец если
Пока v(p)=c выполнять
Начало
если (v(pa)=c и. v(pa-l)^c) то а := а+1
конец если
если (v(pb)=c и. v(pb-l)^c) то b := b+1
конец если
если (v(pa)^c и. v(pa-l)=c) tjo, el := pa
конец если
если (v(pb)^c и. v(pb-l)=c) тр. е2 := pb
конец если
конец
если (v(pa)=c и. v(pa-l)*c то. а :- а+1
конец если
если (v(pb)=c и. v(pb-l)*c то b := b+1
конец если
если v(pa)*c то. el :» RIGHT(pa)+l;
иначе если v(pa-l)=c то el :*ра;
конец если
если v(pb)=c tjo e2 := RI6HT(pb)+l;
иначе если v(pb-l)=c ™ e2 :*pb;
конец если
pl := р;
конец
3.2.4. ЗАКЛЮЧЕНИЕ
Резюмируя изложенное, отметим, что с помощью алгоритмов
окрашивания заполняются только связанные области. Затравочная
точка, с которой начинается заполнение, часто оказывается трудно
определяемой автоматически, поэтому алгоритмы подобного рода
чаще используются в интерактивном режиме. С другой стороны,
сравнение методов позволяет утверждать, что алгоритм Павлидиса
86

обладает преимуществами в большинстве случаев, поскольку он
основывается, главным образом на точках контура, а не на внут-
ренних точках области.
3.3. ЗАПОЛНЕНИЕ ОБЛАСТЕЙ
3.3.1. ВВЕДЕНИЕ
Заполнение одноцветных областей представляет собой опе-
рацию, состоящую в заполнении плоской фигуры, заданной сово-
купностью контуров. Для правильного выполнения алгоритма не-
обходимо знать, находится ли текущая точка в каждый данный
момент внутри или снаружи заполняемой области. Такая инфор-
мация легко получается с помощью "контроля четности", т. е.
подсчета числа пересечений линий контура строкой, на которой
находится точка, что показывает, находится ли она внутри или
снаружи (рис. 3.10).
• внутренняя точка; число
пересечений нечетное
О наружная точка; число
пересечений четное
-О
Рис. 3.10. Контроль четности
Однако может встретиться немало случаев, когда алгоритм бу-
дет давать ошибочные результаты, если не учитывать некоторые
особенности контуров (рис. 3.11):
а) - горизонтальные участки,
б) - вершины,
в) - перекрытия ребер,
г) - сдвоенные точки и т. д.
Особенности Ошибки заполнения, Правильное
контура вызванные "контролем заполнение
четности"
Рис. 3.11. Особенности контуров, встречающиеся в процессе заполнения
87

Для устранения указанных недостатков алгоритма были предло-
жены различные методы, которые можно разделить на две группы:
"построчной развертки", основанные на кодировании контура в
матрице, представляющей поверхность визуализации; в этих слу-
чаях операции выполняются в пространстве изображения;
"прослеживания контуров", при которых области заполняются
на основе структурированного описания контура; здесь
вычисления производятся в пространстве пользователя.
3.3.2. ПОСТРОЧНАЯ РАЗВЕРТКА
33.2.1. ВВЕДЕНИЕ
Во всех алгоритмах такого типа используется память изобра-
жения, в которой выполняются кодирование и заполнение.
Постановка задачи. Во многих случаях при использовании ал-
горитма контроля четности можно получать ошибочные результа-
ты, вызванные тем, что встреча текущей точки с контуром не
изменяет контекста (следует знать, находится ли текущая точка
в данный момент внутри заполняемой области или вне ее):
в результате квантования часто возникает несколько последо-
вательных точек на одной строке (1);
тесно примыкающие друг к другу после квантования участки
близко расположенных ребер (2);
некоторые вершины, сохраняющие контекст (3).
°» « ■ О)
Рассмотрим несколько методов, направленных на устранения
этих недостатков применительно к многоугольным контурам, а за-
тем обобщим их на области произвольной формы.
33^2. ЗАПОЛНЕНИЕ МНОГОУГОЛЬНИКОВ
Классификация методов. Известные к настоящему времени ал-
горитмы можно сгруппировать в три класса:
1. Кодирование точек контура в про-
цессе квантования. Каждое ребро в матрице
изображения порождается точка за точкой, а потеря информации
компенсируется путем кодирования, означающего изменения кон-
текста. Затем используется алгоритм контроля четности.
В этом классе можно выделить два алгоритма:
•Люка [23], в котором алгоритм генерирования отрезков пря-
мых использован для создания и кодирования ребер в зависимости
от встречающихся особенностей;
•Эк ланд а и Уэста [1], в котором для квантования ребер
используется только одна точка на строке развертки, что позволя-
ет легко деформировать контур.
88

2. Последовательные инверсии изо-
бражения. В этом варианте, разработанном Мартинесом
[25], квантование ребра сопровождается инверсией точек, распо-
ложенных справа от него. Поскольку квантование происходит в
процессе заполнения, информация не теряется (рис. 3.12).
Рис. 3.12. Заполнение треугольника путем последовательной инверсии
содержимого памяти
3. Построчное заполнение контура,
описанного поточечно. Для каждой строки,
пересекающей контур, анализ контекста выполняется с учетом
информации, получаемой от выше и ниже расположенных точек
контура. Естественно, при этом необходимо знать, находится ли
текущая точка на входе внутри области или на выходе из нее.
Павлидис [31 ] разработал три алгоритма такого типа, основанные
на переходах через сдвоенные, строенные и т. д. точки. Здесь мы
не будем останавливаться на этих методах, так как они относятся
не столько к задаче синтеза изображений, сколько к задачам обра-
ботки изображений (в частности, к распознаванию контуров).
Сравнение алгори т_м о в. Сопоставление двух
алгоритмов: с одной стороны, Люка, а с другой, Экланда и Уэс-
та — показывает, что хотя они и достаточно близки между собой,
все же метод Экланда и Уэста предпочтительнее как менее слож-
ный. Действительно, использование только одного кода (1) вместо
двух (1 и 2) требует меньшего числа операций (в частности,
испытаний и обращений к таблице). В то же время, хотя такое
кодирование контура увеличивает скорость выполнения операций,
при этом ухудшается самоизображение контура и появляются не-
желательные паразитные эффекты, такие, например, как непре-
дусмотренные взаимные соприкосновения заполняемых областей.
Главный недостаток алгоритма Мартинеса состоит в том, что
много точек обрабатывается бесполезно. В работе [25] автор
показывает, что этот недостаток устраняется в аппаратуре на же-
сткой логике, поскольку операция инверсии выполняется в этом
случае почти мгновенно.
Алгоритм Люка. Упомянутые в п. 3.3.21 трудности преодоле-
ваются следующими приемами:
89

А. Горизонтальные участки: используется такой код, под
действием которого отрезок окрашивается, но не изменяется кон-
текст (код 2);
Б. Вершина, общая для двух ребер, находящихся по одну сто-
рону от горизонтального отрезка, проходящего через эту вершину:
код ведет к окрашиванию, но без изменения контекста (код 2);
I 2 I
В. Перекрытия: могут быть вызваны либо пересечением двух
ребер, либо недостаточно высокой разрешающей способностью в
процессе дискретизации. Если число перекрытий четное, то кон-
текст изменяется, если нечетное - не изменяется.
Г. Горизонтальный отрезок, образовавшийся в результате ап-
проксимации : можно отметить только изменение порядка в пос-
ледовательности (код 1);
Представляемый ниже алгоритм Люка учитывает эти труд-
ности.
ОБЛАСТЬ (целые XMIN, XMAX, YMIN, УМАХ; целочисленная
таблица X, Y, Z( *); целые C0ULEUR)
начало (заполнение области, вписанной в
прямоугольник XMI N, YMI N, XMAX, YMAX; координаты
вершин контура находятся в таблице X,Y,Z;
функция SOMMETSUIVANT (следующая вершина)
обеспечивает индекс точки контура во
время прослеживания края области}
логические UPL,UPM,POINTE; целые L,LP,M;
логические INTERIEUR; логические ILYAS0MMET;
(назначение цвета фона}
90

Аля I : =XMI N ш§£ 1 до ХМАХ выполнять
для J :=YMIN шаг_ 1 до YMAX выполнять
i mage (I,J) : =0;
{запись периметра}
LP: «PREMIER SOMMET; L :- SOMMETSUI VANT;
пока Y(LP)=Y(L) выполнять
(пропуск горизонтальных ребер}
начало
LP : - L;
L := SOMMETSUIVANT
конец;
(обход контура области}
UPL :« Y(LP)<Y(L); LP : «L; (начальная вершина}
ILYASOMMET :» истинно;
пока ILYASOMMET выполнять
начало
М :- SOMMETSUIVANT;
если Y(L)=Y(M)
то начало (горизонтальный отрезок}
РА := если X(L)<X(M) то +1 иначе -1;
Аля I :=X(L) шаг. РА до, Х(М) выполнять
IMAGE (I,Y(L)):=2
конец
иначе начало
UPM: *Y( L) <Y( M); POINTE: =( UPM-UPL);
SEGMENT( X( L), Y( L), X( M), Y( M), POI NTE)
конец
L :=M; ILYASOMMET :=(M=LP)
(описание области)
ма J :=YMIN mac l до. YMAX выполнять
иаыада
INTERIEUR := ложно;
Аля I :»XMIN шаг_ 1 до ХМАХ выполнять
91

начало
если IMAGE (I,J)=1 {точка контура)
то начало
INTERIEUR :--• INTERIEUR;
IMAGE (I,J):- COULEUR
конец
иначе если INTERIEUR или (IMAGE (I,J)=2)
то. IMAGE(I,J) := COULEUR
конец
конец
конец ОБЛАСТЬ;
ОТРЕЗОК (целые XA,YA,XB,YB; логическое P0INTE);
иаыадо. (проведение отрезка при подготовке к
заполнению области)
целые DELTAX, DELTAY, XI NCR, YI NCR, CUMUL, X, Y, YPREC;
X :»XA; Y: = YA; (X, Y) текущая точка
если. POINTE (обработка случая b)
I0_ IMAGE(X,Y):=(g£AJi IMAGE(X,Y)*1 ip_ 2
инаые. 1)
иыане. IMAGE(X,Y):=(fi£AH IMAGE(X,Y)=1 id. 2
плане. 1);
XINCR:= если ХА<ХВ тр_ +1 иначе -1;
YINCR:= если YA<YB тр_ +1 иначе -1;
DELTAX: =ABC( XA- XB); DELTAY: =ABS( YA- YB); YPREC: =Y;
если DELTAX>DELTAY
тр_ начало (обработка случая d)
CUMUL: «DELTAX/2;
для I:-l шаг. 1 д£ DELTAX-1 выполнять
(точка не последняя)
начало
X: =X+XINCR; CUMUL: =CUMUL+DELTAY;
если CUMUL >DELTAX
то начало
CUMUL: =CUMUL-DELTAX;
Y:=Y+YINCR
конец
если (YPREC=Y) или (Y-YB)
то начало (тот же Y)
92

если. IMAGE(X,Y)*1 ш IMAGE(X,Y):=2;
конец
иначе начало {новый Y}
IMAGE(X,Y):=(££AH I MAGE( X, Y) =1 ш 2
инаае. 1);
YPREC: =Y
кдыед
Ш1£Ц.
иначе начало {безразлично, есть ли
перемещение по Y}
CUMUL: =DELTAY/2;
АЛЯ 1:=1 шал 1 да DELTAY выполнять
Y: =Y+YINCR; CUMUL: -CUMUL+DELTAX;
е£дц CUMUL >DELTAY
то начало
CUMUL: -CUMUL-DELTAY;
X:«X+XINCR
К£Н£Ц.
IMAGE(X,Y):=(eCAn IMAGE(X,Y)=1
lq. 2 нндне. 1)
Kjuieii.
коней ОТРЕЗОК
3323. ЗАПОЛНЕНИЕ ОБЛАСТЕЙ ПРОИЗВОЛЬНОЙ ФОРМЫ
Предположим, что заполняемая область состоит из набора кон-
туров, не являющихся многоугольниками. Каждый контур может
быть описан одним из двух методов: либо упорядоченным списком
примитивов отображения, таких как отрезки прямых, дуги
окружностей, либо упорядоченным списком составляющих его то-
чек. Иначе говоря, в обоих случаях имеем структуру кольца.
Обобщим алгоритмы Люка и Экланда — Уэста, кодируя точки,
порождаемые контуром, а затем применяя к ним операцию конт-
роля четности.
Особенности, которые следует при этом учитывать :
горизонтальные отрезки;
точки экстремумов;
перекрытия и т. д.
Общая идея. Кодирование выполняется шаг за шагом для каж-
дого контура путем анализа положения текущей точки относитель-
но предыдущей, только что вычисленной.
93

Пусть хс, ус — координаты текущей точки, хр, ур — ко-
ординаты предыдущей. Пусть также IMAGE (*,*) — матрица
изображения, начальное значение всех элементов которой равно
нулю. По изменению координат можно обнаруживать горизонталь-
ные отрезки и отмечать их концы.
Будем использовать два типа кодов:
1 — для кодирования изменения контекста,
2 — для кодирования точек контура, в которых не происходит
изменения контекста. Можно было бы обойтись и одним кодом, но
в алгоритме Экланда — Уэста получающаяся область несколько
деформируется, вследствие чего возникает задача сопряжения.
Установим следующие правила кодирования.
Обозначим символом ф операцию ИЗОБРАЖЕНИЕ (х, у)
ф КОД, определяемую таблицей:
1 ИЗОБРАЖЕНИЕ
(IMAGE)
0
2
код |
Ф 1
2
1
е 2 I
2
1
2 1
1 —
3 -
IMAGE (хс, ус):- IMAGE (хс, ус)Ф 2;
ур<ус (возрастающая кривая)
IMAGE (хс, ус):- IMAGE (хс, ус) Ф 1;
ур>ус (убывающая кривая)
IMAGE (хр, ур):
IMAGE (хр, ур) ф 1;
IMAGE (хс, ус):- IMAGE (хс, ус) Ф 2;
Обратное кодирование предыдущей точки на убывающей
кривой, как и операция ф , позволяет решить задачу поиска экс-
тремума. Операция ф подавляет также ошибки, вызванные пере-
сечениями и перекрытиями (рис. 3.13)
fflffiS
111 21 |
ш
1
[J_
1
1
2
5J
1
[1
1
1
1
1j
111
£
1
1
1
1
2
2
1
'?
1
1
2
2
1
ll
[!_
1
1
1
2
1
1
1
71
Рис. 3.13. Кодирование контура:
а • экстремум; б - горизонтальные отрезки; в • перекрытия (пересечения)
94

Примечание. Под правильным действием алгоритма
подразумевается, что для каждого контура последовательность
описывающих его точек должна быть замкнута, т. е. должна иметь
структуру кольца. Если это условие не выполняется, т. е. первая
и последняя точка не совпадают, то контур необходимо кодировать
как отрезок (точка первая, точка последняя).
Собственно заполнение состоит в обходе матрицы изображения
IMAGE последовательно, строка за строкой, с использованием кон-
троля четности (см. алгоритм Люка).
Пример заполнения площади произвольной формы по алгоритму
кодирования контура:
а - контур и его особые точки; 6 - правильное заполнение
33.2.4. ЗАКЛЮЧЕНИЕ
Главный вывод, который можно сделать после рассмотрения
приведенных алгоритмов построчного заполнения, состоит в том,
что необходимо иметь в распоряжении булеву память изобра-
жения. Уточним сказанное. С одной стороны, если обрабатываемые
области не накладываются друг на друга, то можно работать не-
посредственно в памяти синтезатора на жесткой логике. С другой
стороны, себестоимость компонентов непрерывно уменьшается.
Методы прослеживания контуров, которые будут рассмотрены в
следующей главе, позволят избавиться от этих трудностей.
3.3.3. ПРОСЛЕЖИВАНИЕ КОНТУРА
333.1. ПРИНЦИП ДЕЙСТВИЯ
Действие алгоритма основывается на использовании струк-
турированного описания контура, позволяющего отделять левый
95

край от правого. Область заполняется отрезками прямой, уклады-
ваемыми между краями контура, в результате чего внутренняя
область оказывается окрашенной (рис. 3.14).
-^Направление развертки
Рис. 3.14. Отображение путем прослеживания контура
Вся работа проходит в пространстве пользователя, и в процессе
заполнения не приходится выходить за пределы области.
2332. ЗАПОЛНЕНИЕ МНОГОУГОЛЬНИКОВ
Существуют два варианта алгоритмов такого рода. Первый из
них состоит в вычислении и упорядочении всех точек пересечения
линий контура со строками развертки до заполнения (это алгоритм
YX, разработанный Ньюменом и Спруллом [29]). Второй, разра-
ботанный автором данной книги, позволит вычислить и найти
пересечения, а также отобразить результат последовательно, стро-
ка за строкой.
Алгоритм YX
1. Для каждой стороны многоугольника вычислить все точки
пересечения ее со строками развертки, а координаты х, у каждой
точки пересечения занести в список.
2. Упорядочить список таким образом, чтобы точка с координа-
тами xl, yl предшествовала бы точке (х2, у2) тогда и только тог-
да, когда yl>y2 и xl<x2.
3. Произвести заполнение строка за строкой, отображая для
каждой строки развертки у отрезки, ограниченные точками (х2к-ь у)
и (х2к, у) (здесь для всего списка величина к равна половине числа
пересечений).
Во избежание ошибок, вызванных особенностями фигуры
(горизонтальные отрезки и др.), Ньюмен и Спрулл предлагают
сдвинуть ординаты всех вершин на расстояние, равное половине
расстояния между соседними строками, как показано на следую-
щем рисунке.
96

Сложность. Пусть nbl — число строк развертки, пере-
секающих контур; nbam — среднее число ребер, которые пересе-
каются каждой строкой (для выпуклого контура nbam - 2);
nba — число ребер. Тогда объем памяти, требующейся для
реализации алгоритма, пропорционален (nba + nbl * nbam), a
сложность перебора составляет величину О ((nbl*nbam)
log(nbbnbam) + nbl (nbam log nbam)).
Следует иметь в виду, что для больших заполняемых областей
память, необходимая для хранения списка пересечений, и время,
требующееся для его упорядочения, достаточно велики и процеду-
ра становится весьма дорогостоящей. Поэтому предпочтительнее
в этих случаях применять другие алгоритмы.
Алгоритм прослеживания контура. Легко заметить, что при
работе с алгоритмом YX в каждый данный момент необходимо
знать только точки пересечения ребер с текущей строкой. Поэтому
возникает мысль о целесообразности сохранения в памяти инфор-
мации о контуре не в виде списка пересечений, а в виде списка
его ребер (сторон). Стороны квантуются построчно по мере запол-
нения.
Алгоритм для каждой строки выглядит следующим образом:
1. Определить множества ребер, которые пересекают строку.
2. Вычислить координаты точек пересечения.
3. Упорядочить точки пересечения.
4. Отобразить горизонтальные отрезки.
•Чтобы избавиться от необходимости повторять все вычисления
полностью заново для каждой строки, воспользуемся корреляцией,
которая существует между двумя соседними строками в каждой
многоугольной фигуре. Если Ei — число ребер контура, пересека-
ющих строку i, то Ei+i - Ei — {ребра, которые заканчиваются на
строке i} + {ребра, которые начинаются на строке i+1}.
Если xi — абсцисса точки пересечения ребра с i-й строкой, то
xj+i -xi +Dxy, где DXy — приращение абсцисс ребра между двумя
строками (i и i+1).
Чтобы задействовать алгоритм, будем использовать две струк-
туры данных. Образуем список ребер, ориентированных вниз и
начинающихся на текущей строке развертки, пересекающей кон-
тур. Это будет структура контура. В процессе заполнения создадим
4 - Ж. Эгрон
97

список Ei тех ребер, которые пересекают текущую строку, упоря-
дочив их по признаку возрастания абсцисс точек пересечения.
•Но здесь снова возникает проблема учета особенностей линий
контура в те моменты, когда на строке развертки могут на-
ходиться:
точки соединения двух ребер (строка ii на рис. 3.15);
горизонтальные отрезки (строки \2 и i3 на рис. 3.15).
в * —— »з : Э пересеченна ?
i, : 3 пересечения?
ij : 4 пересечения?
Рис. 3.15. Особые случаи, встречающиеся в процессе
выполнения алгоритма прослеживания контура
Для устранения нежелательных эффектов предлагается удалить
горизонтальные ребра в списке ребер, а из списка Ei удалить
отрезки, заканчивающиеся на текущей строке. Тоща изображение,
показанное на следующем рисунке слева, преобразуется в такое,
которое изображено справа.
±
i-1 1 i-i
превращается в
i+1
ш превращается ■ , «■
Л— i+' т
Если никакие ребра контура не пересекаются, то можно
удалить выборку из списка Ei, упорядочив ребра в структуре кон-
тура в порядке возрастания абсцисс их первых концов, а для
одинаковых абсцисс — в порядке возрастания Dxy. Добавление
одного ребра в список Е\ станет тоща вставкой, которая не на-
рушит этого порядка.
•Действие. Для задействования алгоритма слежения за
контуром используем две структуры данных.
•Контур заполняемой области образован множеством
произвольных многоугольников, описанных упорядоченными пос-
ледовательностями своих вершин. В нашем распоряжении имеется
таблица Т(*) целочисленных значений, содержащих координаты
вершин, где список вершин для каждого многоугольника за-
канчивается величиной NIL. Переменная N представляет число
элементов, содержащихся в таблице Т(*).
98

•Список ребер. Каждое ребро Ак будет определяться
абсциссой своей начальной точки Axd(k), ординатой конечной
точки Ayf (к) и приращением абсцисс по отношению к приращению
ординат Dxy(k).
Для каждой строки развертки у мы располагаем списком
начинающихся на ней ребер:
Строка у
БЕ
kl
ki
кЗ|
к4
»
пг
J
3
TLISTE (у) = 0: список пустой,
иначе список ребер,
начинающихся на строке у,
есть { к,,к2|...,кт}
•Список ребер, пересекающих текущую строку
развертки. Номера Nbai ребер, пересекающих строку у, будут
содержаться в таблице целых чисел Ei(*), а абсциссы точек пере-
сечения запоминаться в таблице вещественных чисел INTER (*).
Алгоритм можно записать в следующем виде:
Заполнение riPOCAFXMBAHMFM КОНТУРА (N, Т( *): целые)
Цаымо.
Создание списка ребер;
Заполнение;
Шш
Создание списка ребер
Найма.
Me каждого ребра ак выполнять
Начало
если ак горизонтальное
14. не учитывать ребро;
иначе ориентировать ребро вниз и
занести его в список ребер;
конем если
коней
Заполнение
4*
99

Панам,
строка i:= первая строка развертки,
пересекающая контур ;
Создать списки (INTER, Ei);
Повторять
сортировать (INTER,Ei ), INTER основная;
Провести горизонтальные отрезки
(от INTER(2k-l) до INTER (2k));
Следующая строка развертки: i= i+1;
если, строка i ** последняя строка развертки
10. пропустить, начиная с
(Ei , INTER) ребра,
заканчивающиеся на строке i;
вычисление пересечений строки i с реб-
рами Е Ei;
добавить к (Ei,INTER) ребра, начинаю-
щиеся на строке i;
иначе конец
конец если
до конец
Конец
Теперь раскроем более подробно каждый модуль общего ал-
горитма:
Создание списка ребер
Начало
Инициализировать Ymin и Ymax;
{использовать соответственно
наибольшее и наименьшее целое}
к := 0 ; {счетчик негоризонтальных ребер}
i := 1 ; {текущий индекс Т(*)}
Пока i<N выполнять
Начало
i0 := i; {первая вершина многоугольника}
Xd := T(i); Yd := T(i+1);
i := i+2 ; X := T(i);
Конец : = ложно
Повторять
если X*NIL то Xf: =Х; Yf:=T(i+l);

иначе Xf:=T(i0); Yf:=T(i0+l);
f i ni =истинно* i i =i +1 *
{обработка ребра ((Xd, Yd),(Xf, Yf))}
ЁШ1 Yd*Yf
Ifl. k:=k+l; {ребро не горизонтальное}
есдц Yd>Yf {направление ребра вниз}
Ш Axd{k):=Xd; Ayf(k):=Yf;
l:=Yd;
Dxy(k):=(Xf-Xd)/(Yd-Yf);
иначе Axd(k):=Xf; Ayf(k):=Yd;
l:=Yf;
Dxy(k):=(Xd-Yf)/(Yf-Yd),
конец если
{занести ребро в TLISTE}
j:= TLISTE(l);
если j:=o
Ш TLISTE(l):=k;
иыаые. qoju. LlSTE(j)* о выполнять
j:=LISTE(j) выполнено
LISTE(j):=k
коней если
есдц YtnaxYf isl Ymax: =Yf коней если
если Ynri nYf m. Ymi n: =Yf коней если
коней если
{следующее ребро}
асдц не {Конец) lq. Xd: =Xf; Yd: =Yf;
I: =1+2; X:=T(I);
До. Конец {конец многоугольника}
коней пока
Конец.
Пробегаем по строкам развертки в последовательности убы-
вания ординат. Другие модули записываются следующим образом:
•первая строка развертки: у := Ymax;
•следующая строка развертки у :» у-1;
•последняя строка развертки: y<Ymin.
СозАание списков (Ei, INTER)
Nbai:=0; {число ребер, пересекающих строку
развертки}
j:=TLISTE (у);
Qqka j*0 выполнять
101

Иаыам.
Nbai: =Nbai+l;
Ei(Nbai):=j;
INTER(Nbai):=Axd(j);
j:=LISTE(j);
Коней создания
Проведение горизонтальных отрезков
Цаыадо.
kl:-l;
Ожа. kKNbai выполнять
Начало
k2* =kl+l;
отобразить отрезок ((INTER(kl),Y),(INTER(k2),Y));
kl := k2+l;
щщц.
Конец Проведение;
Отбрасывание ребер, заканчивающихся на строке v
ЦздАдо.
ki := 1;
Шжа. ki <Nbai выполнять
Иаыадо.
k := Ei(ki);
есди. Ayf(к): =у
1Д. j :=ki+l;
Qqkjl j ^Nbai выполнять
Ц&ч£до.
Ei(j-l) := Ei(j);
INTER(j-l) := INTER (j);
j :- j+l;
Ш1£Ц.
Nbai := Nbai-1; ki := ki-1;
конец если
ki : = ki +1;
КШ£Ц.
Kiuieji
Вычисление точек пересечения
Ыаыадо.
Мя. к :=1 до. Nbai выполнять
I NTER( к): =1 NTER( к) +Dxy( Ei (к));
Конец;
102

Добавление лат", начинающихся на строке Y
Начало
j := TLISTE(y);
Пока j*0 выполнять
Начало
Nbai := Nbai+1;
Ei(Nbai) : =j;
INTER(Nbai):=Axd(j);
j:-LISTE(j);
конец
Конец добавления;
Вот пример заполнения площади по алгоритму слежения за
контуром:
Сравнение алгоритмов. Пусть nbl — число строк развертки,
пересекающих многоугольный контур; nbam — среднее число
ребер, пересекающих каждую строку развертки (nbam-2, если
контур выпуклый); nba — число ребер.
Объем памяти, необходимой для реализации алгоритма YX,
пропорционален (nba+nbl*nbam), а для предложенного автором —
(nba+nbl+nbam). Сложность выборки пересечений составляет
величину О ((nbl*nbam) log (nbl*nbam)+nbl (nbam log (nbam))) для
алгоритма YX и О (nbl (nbam log (nbam))) для нашего варианта.
Однако сложность алгоритма YX может быть уменьшена за счет
гого, что для каждой строки развертки перебор и отображение вы-
полняются параллельно. С другой стороны, практическая слож-
ность выполненного перебора в нашем варианте меньше теоретиче-
ской сложности. Действительно, список Ei не упорядочивается
голько в те моменты, когда добавляется одно ребро или когда
цва ребра пересекаются. Поскольку значение nbam не очень
велико и используется простой алгоритм перебора (типа "сортиров-
ка шаров"), сложность перебора будет О (Nbam) для всех строк
развертки, где такое изменение не происходит.
103

3333. ЗАПОЛНЕНИЕ МНОЖЕНСТВА МНОГОУГОЛЬНИКОВ
Постановка задачи. Здесь речь идет о заполнении совокуп-
ности областей в форме многоугольников таким образом, чтобы
конечный результат соответствовал последовательности приорите-
тов, заранее присвоенных каждой области (рис. 3.16).
Приоритеты:
А:1
В:2
С:3
D:4
А
]А
у
, С
/ X,
/ч
s
с
>
j~i
N
^
£|
Рис. 3.16. Совокупность областей и присвоенных им приоритетов
Первое решение заключается в том, чтобы заполнять каждую
область, одну за другой, в той последовательности, в какой уста-
новлены приоритеты.
Во DoD[i53
(i)
(2)
(3)
(4)
Второе решение дает возможность заполнять все области однов-
ременно, строка за строкой, соблюдая соответствующие
приоритеты.
XNO
П х^Ч
0)
(2)
гх>
(3)
(6)
Алгоритм прослеживания контура. Используя те же структуры
данных, что и в предыдущем случае (см. п, 3.3.3.2), создадим для
каждой строки развертки упорядоченный список ребер.всех мно-
гоугольных областей, пересекаемых этой строкой, в порядке
абсцисс точек пересечения, а затем, исходя из этих списков,
отобразим горизонтальные отрезки, соблюдая приоритеты отобра-
104

жения областей. Для этого каждому ребру необходимо присвоить
номер, соответствующий своему приоритету.
Сешер [36] показал, что в частном случае, когда одновремен-
но заполняются соприкасающиеся (смежные) области (даже с со-
ответствующими приоритетами), получающаяся сложность пред-
почтительнее той, которая получилась бы при последовательном
заполнении каждой области по алгоритму слежения за контуром.
ЗЗЗА. ЗАПОЛНЕНИЕ ОБЛАСТЕЙ ПРОИЗВОЛЬНОЙ ФОРМЫ
Предположим, что контуры заполняемой области образованы
множеством примитивов отображения (отрезки прямых, дуги
окружностей и т. д.).
Генерирование области должно выполняться за один проход в
последовательности убывания ординат. Для этого разрезаем кон-
туры на множество прямолинейных и криволинейных участков
(называем их "звеньями") . Каждое звено представляет собой
часть контура, монотонную относительно координаты Y, и заклю-
чено между локальным максимумом, или точкой рождения, и ло-
кальным минимумом, или точкой гибели (рис. 3.17).
4fr - точка рождения
+ - точка гибели;
AB,AD,CB,CD . звенья
Рис. 3.17. Разделение контуров на звенья
Как и для алгоритма прослеживания контура, разработанного
для многоугольных областей (см. п. 3.3.3.2), заполнение
происходит последовательно, строка за строкой, с учетом
взаимовлияния двух соседних строк развертки для вычисления то-
чек пересечения и составления списка звеньев, пересекающих
строку. Трудности, вызываемые особыми точками, преодолеваются
уже известными способами.
В то же время можно предложить два метода структурирования
контура:
подобный описанному в п. 3.3.3.2; составляется последователь-
но, строка за строкой, список примитивов, направленных вниз
(рис.3.18а);
В оригинале автор использует термин parol, что переводится как "перегородка",
истенка" — Прим. перев.
105

# начала примитивов
направление обжода
Описание кольца
* А? t В? * СР t DA
t ,4dt
I - обратное звено
D - прямое звено
Ч
Четный
указатель 1
Четный
указатель 2
I
Рис. 3.18. Структуры контура:
а • список звеньев, направленных вниз; б • структуры кольца и дерева
106

описанный в работе [10]; представляет контур с помощью
груктуры кольца и дерева. Каждое кольцо есть описание одной
гязанной составляющей, разрезанной па последовательность пря-
олинейных участков и дуг окружностей. Для каждого кольца де-
гво адресует (для всех точек рождения с одной и той же
хциссой в кольце) множество звеньев, которые здесь начинаются
шс. 3.186).
^
Рис. 3.19. Разделение дуги окружности по квадрантам
В каждой из обеих общих структур звенья разделяются на под-
зенья, т. е. на элементарные примитивы отображения. Для
тисания большинства контуров достаточно иметь только отрезки
рямых и дуги окружностей (см. "методологию декомпозиции
южных кривых" в работе [40]).
Точки пересечения примитивов с каждой строкой развертки
ячисляются сверху вниз. Это может быть выполнено с помощью
тгоритма Брезенхема для генерирования кривых при сохранении
>лько одной значащей точки на строке. Контекст, который необ-
здимо запоминать на каждом шаге, различен в зависимости от
римитива (контекст: возрастание по X в соответствии с полу-
задрантом, рекуррентные выражения). Дуги окружностей будут
доделены по квадрантам для того, чтобы избежать переобозна-
гний в процессе генерирования кривой, при котором уменьшается
азмер контекста. Во время этого разделения получающиеся дуги
рдут направлены вниз подобно отрезкам прямых (рис.3.19).
333.5. ПРИЛОЖЕНИЕ: ВКЛЮЧЕНИЕ ТЕКСТА В ПРОИЗВОЛЬНЫЙ МНОГОУГОЛЬНИК [18]
Постановка задачи. Хотелось бы записать некоторый текст в
роизвольный многоугольник. С проблемами такого рода встреча-
йся, например, когда надо сделать надпись в штампе, в рисунке
зрговой марки, на ленте и т. п. Например:
107

Текст
2
•лисам • произвольный
ь
многоугольник
Текст\ / алисан ■
произУ вольный
много/ \ угольник
Внутренний контур
Пересекающиеся ребра
Разъединенные
контуры
Определения. Записываем текст на строку, ограниченную
нижней и верхней линиями. Расстояние между линиями определя-
ется размером выбранного шрифта (рис. 3.20).
Верх
Низ
Высота
ПРОГРАММЫ
\ Строка шрифга
ф Пробел между строками илифг
/ Строка шрифта
Рис. 3.20. Определение строки шрифта
Множество левых и правых границ, образованных много-
угольниками, образуют строки развертки, содержащие между вер-
хней и нижней линиями полосы надписи, множество горизонталь-
ных интервалов (рис. 3.21). На каждой строке многоугольник
порождает также интервалы записи, в которые можно было бы
Верх _
Низ _
V
Tv.
\v\
i/i
■ 11
Ч ! '
i5i:
1 с
—Ц
V
. I^._
. .iV
11 \
a2! !
J—[ I
■I6!
~ » 1
no
3
3
7
11
*
у
11
1
V
\8
i V
1 iK
1 1 1
14 1 1
с iei
Е,и—■— J 1
112
С 3
Рис. 3.21. Определение горизонтальных интервалов
108

вставлять текст (рис. 3.22). Можно выдвинуть две гипотезы: либо
символы точно вписываются в многоугольник (рис. 3.22а), либо
символы могут пересекать многоугольник (рис. 3.226). Вторая
гипотеза интересна в тех случаях, когда мы хотим, чтобы текст
принял форму многоугольника без отображения последнего.
Полоса шрифт * >J \ Полос, шрифта ,
Имтераал для ыписи
Интервал для записи 5
а
Рис. 3.22. Определение интервалов записи:
а — буквы четко вписываются в многоугольник; б — буквы могут пересекать контур
Идея и алгоритм. Для записи каждой текстовой строки мно-
жество интервалов получаются либо путем реализации пересе-
чений списков горизонтальных интервалов, образованных много-
угольным контуром на строке, заключенной между верхней и
нижней линиями текстовой строки (если верна первая гипотеза),
либо соединением тех же горизонтальных интервалов между каж-
дой линией развертки (если верна вторая гипотеза).
Для вычисления горизонтальных интервалов будем использо-
вать алгоритм прослеживания контура, уже применявшийся для
заполнения (те же структуры данных и та же логика). Интервалы
для записи, принадлежащие каждой текстовой строке, будут полу-
чены путем вычисления пересечений или объединений горизон-
тальных интервалов последовательных строк развертки, взятых
попарно.
Для внесения текста в предназначенные для него интервалы
могут быть предложены различные стратегии.
•Записывать текст по мере того, как вычислятся текстовые
строки, и остановиться, когда весь текст отображен. Если в диало-
говом режиме весь текст не вписывается, то следует стереть текст,
начав процесс заново, затем снова переназначить новый размер
шрифта и новое расстояние между текстовыми строками и
предпринять новую попытку записи.
•Отобразить текст, если все интервалы для записи вычислены
и текст может туда войти полностью. В противном случае назна-
чают новый размер символов и новый пробел между строками и
процесс повторяют заново.
109

Первое решение предпочтительнее, если априори известно, что
весь текст может поместиться. Общий алгоритм, приведенный
ниже, реализует именно этот метод.
Запись текста в многоугольник
Начало
получить первую строку записи (верх, низ);
Цока, (строка записи не последняя и запись
текста не закончена)
выполнять
Обрабатывать строку текста;
Е£АИ запись не закончена ю_ строка
текста следующая
выполнено
Обработка строки текста
Начало
текущая строка : = верхняя;
вычисление точек пересечения текущей строки
с контуром (список L1);
список интервалов записи (список Li):=Ll;
Пока текущая строка * нижняя ВЫПОЛНЯТЬ
Начало
текущая строка := следующая строка;
вычисление пересечений (список L1);
Li := Li П Li (или Li U Li )
{интервалы текста}
коней
Если Li* 0 iq_ записать текст в Li
конец если
Установить "Запись текста не закончена";
Коыш
Алгоритмы объединения и пересечения двух списков интервалов
разрабатываются в гл. 4.
Приведем версию программы по этому алгоритму, написанную
на языке Бейсик для компьютера НР9354, позволяющую вписы-
110

вать текст точно внутрь контура произвольной формы. Структуры
данных, использованных для описания многоугольного контура,
список ребер и список точек пересечения на строке развертки
обозначены так же, как это было уже сделано в алгоритме запол-
нения методом "прослеживания контура" (п. 3.3.3.2(2)).
10 SUB Текст многоугольник (INTEGER N,Т(*),
20 Высота, Ширина, Сдвиг, Td, Tf, Текст$)
ЗАПИСЬ ТЕКСТА В МНОГОУГОЛЬНУЮ ОБЛАСТЬ
МЕТОДОМ ПРОСЛЕЖИВАНИЯ КОНТУРА
Текст: определен первым (Td) и последним
(Tf) символами непрерывной последователь-
ности из Текст$(*), шириной и высотой
символов, сдвигом между строками записи;
Многоугольная область: определена множест-
вом многоугольных контуров, описанных
упорядоченной последовательностью их вершин
NIL в (N,T(*))
30
40
50
60
70
80
90
100
ПО
ПО
120
130
140 ! Пояснения
150 OPTION BASE l
160 ! структуры данных многоугольника
170 INTEGER Axd(40), Ayd(40), Ayf(40), Nba, Ymax, Ymin
180 REAL Dxy(40)
190 INTEGER Tliste(454),Liste(40)
200 INTEGER Ei(20), Nbai
210 REAL Inter(20)
220 !
230 ! структуры данных записей
240 INTEGER Y, Yp, Ys, Yb, Md, Mf, Nbc ar,
Длинаслова, Конецтекста, Хро,Ypo
250 REAL Интервал!20), XI, X2
260 INTEGER Nbint, Длина
270 !
280 ! divers
290 INTEGER 1,10, J, K, Kl, K2, Ki, Конец
in

300
310
320
330
340
350
360
370
380
390
400
410
420
430
440
450
460
470
480
490
500
510
520
530
540
550
560
570
580
590
600
610
620
630
640
650
INTEGER
X,Xd,Yd,Xf,Yf,Nil,
REAL Dx, Dy
! СОЗДАНИЕ СПИСКА РЕБЕР, ОРИЕНТИРОВАННЫХ ВНИЗ
Ni1=9999
Ymin=Nil
Ymax=-Ni1
Nba=0 !
1=1
! ПОКА
IF I>N
10=1
Xd=T(I]
1
число ребер
I<N выполнять
THEN 1000
1
Yd=T(I+l)
1=1+2
X=T(I)
Конец
=0
! ПОВТОРЯТЬ
IF
PEN
MOVE
DRAW
i
X=Ni1 THEN 550
Xf=X
Yf=T(I+l)
GOTO 590
! последнее ребро текущего контура
Xf=T(I0)
Yf=T(I0+l)
Конец =1
1=1+1
КОНЕЦ IF
Обрабатывать ребро (Xd,Yd),(Xf, Yf)
Отобразить ребро
1
Xd,Yd
Xf, Yf
112

660
670
680
690
700
710
720
730
740
750
760
770
780
790
800
810
820
830
840
850
860
870
880
890
900
910
920
930
940
950
960
970
980
990
1000
1010
1020
1030
1040
IF Yd<Yf THEN 750
Nba=Nba+l
Axd(Nba)=Xd
Ayd(Nba)=Yd
Ayf(Nba)=Yf
Dx=Xf-Xd
Dy=Yd-Yf
Dxy(Nba)=Dx/Dy
GOTO 860
IF Yd=Yf THEN 840
Nba=Nba+l
Axd(Nba)=Xf
Ayd(Nba)=Yf
Ayf(Nba)=Yd
Dx=Xd-Xf
Dy=Yf-Yd
Dxy( Nba) =Dx/tiy
GOTO 850
! удаленный горизонтальный
! Конец IF
! Конец IF
IF YmaxYf THEN Ymax=Yf
IF YminYf THEH Ymin-Yf
! Конец обработки ребра
! Следующее ребро
IF Конец=1 THEN 980
Xd=Xf
Yd=Yf
1=1+2
X-T(I)
GOTO 490
! До КОНЕЦ контура
GOTO 420
КОНЕЦ ПОКА
Создание списка ребер
[=0 ! индекс Tliste
отрезок
113

1050 J=0 • ! индекс Tliste
1060 K=0 ! индекс ребер
1070 MAT Tliste = ZER
1080 MAT Liste = ZER
1090 FOR K=l TO Nba
1100 I=Ayd(K)
1110 IF Tliste(I)<>0 THEN 1150
1120 ! Tliste(I)=0
1130 Tliste(I)=K
1140 GOTO 1230
1150 ! Tliste(I)#0
1160 J= Tliste(I)
1170 ! Пока Liste(J)#0 выполнять
1180 IF Liste(J)=0 THEN 1210
1190 J= Liste(J)
1200 GOTO 1170
1210 ! Конец пока
1220 Liste(J)=K
1230 ! Конец IF
1240 NEXT К
1250
1260
1270
1280
1290
1300 ! Получить первую строку записи
1310 Yp=Ymax ! Первая строка развертки
1320 Ys=Yp-Сдвиг ! Верх строки записи
1330 Yb=Ys-Высота ! Низ строки записи
1340 Конец_текста=0
1360 ! Получить первое слово
1370 Md=Td ! Первый символ слова
1380 I=Md
1390 IF Текст$[1,1]<>" THEN 1420
1400 1=1+1 ! Пропустить белые участки
1410 GOTO 1390
1420 ! Конец IF
1430 IF (I>Tf) OR (Текст$[1,1]=н ) THEN 1460
1440 1=1+1 ! Пропустить символы # белые
114
ЗАПИСЬ ТЕКСТА В МНОГОУГОЛЬНИК

1450
1460
1470
1480
1490
1500
1510
1520
1530
1540
1550
1560
1570
1580
1590
1600
1610
1620
1630
1640
1650
1660
1670
1680
1690
1700
1710
1720
1730
1740
1750
1760
1770
1780
1790
GOTO 1430
! Конец IF
Mf=I-l ! Последний символ слова
Nbcar = I-Md ! Число символов слова
Длина_слова=МЬсаг*Ширина
1
!
Nbai=0 .
! Создать списки Ei, Inter
J=Tliste(Yp)
IF J=0 THEN 1610
Nbai=Nbai+l
Ei(Nbai)=J
Inter(Nbai)=Axd(J)
J=Liste(J)
GOTO 1550
Конец IF
Пока (строка записи не последняя)
и (не Конецтекста)
ВЫПОЛНЯТЬ
IF (Yb<Ymin) OR (Конец_текста=1) THEN 3470
Обрабатывать текущую строку записи
Создание текущего списка
интервалов: ВЕРШИНА
! Пропуск ребер, заканчивающихся в
интервале ] Yp, Ys[
Ki=l
IF Ki>Nbai THEN 1860
K-Ei(Ki)
IF Ayf(k)<Ys THEN 1830
J=Ki +1
IF J>Nbai THEN 1800
Ei(J-l)=Ei(J)
Inter(J-l)=Inter(J)
J=J+1
GOTO 1750
115

1800
1810
1820
1830
1840
1850
1860
1870
1880
1890
1900
1910
1920
1930
1940
1950
I960
1970
1980
1990
2000
2010
2020
2030
2040
2050
2060
2070
2080
2090
2100
2110
2120
2130
2140
2150
2160
! Конец IF
Nbai=Nbai-l
Ki=Ki-l
! Конец IF
Ki =Ki +1
GOTO 1710
Конец IF
Вычисление точек пересечения с Ys
FOR K=l TO Nbai
I nter( K) =1 nter( К) +Сдвиг*0ху( Ei (К))
NEXT К
Добавить ребра, которые начинаются,
но не заканчиваются в ]Yp,Ys]
FOR Y=Yp-l TO Ys STEP -1
J=Tlist(Y)
IF J=0 THEN 2060
IF Ayf(J)>Ys THEN 2030
Nbai=Nbai+l
Ei(Nbai)=J
Dx=Axd( J)
Dy=Y-Ys
Inter(Nbai)=Dx+Dy*Dxy( J)
! Конец IF
J=Liste(J)
GOTO I960
! Конец IF
! NEXT Y
! Упорядочить список точек
пересечения
CALL Сортировка (INTER(*), Ei(*), Nbai)
! Создание последовательности
интервалов записи
FOR 1=1 ТО Nbai
Интервал(I)=1nter(I)
NEXT I
116

2170
2180
2190
2200
2210
2220
2230
2240
2250
2260
2270
2280
2290
2300
2310
2320
2330
2340
2350
2360
2370
2380
2390
2400
2410
2420
2430
2440
2450
2460
2470
2480
2490
2500
2510
2520
Nbint=Nbai
Вычисление последовательности
интервалов записи
ДЛЯ каждой строки развертки
]Ys,Yb] ВЫПОЛНЯТЬ
FOR Y=Ys-l TO Yb STEP -1
! Пропустить ребра, заканчивающиеся
на строке Y
Ki=l
IF Ki>Nbai THEN 2400
K=Ei(Ki)
IF Ayf(K)oY THEN 2370
J=Ki +1
IF J>Nbai THEN 2340
Ei(J-l)=Ei(J)
Inter(J-l)=Inter(J)
J=J+1
GOTO 2290
! Конец IF
Nbai-Nbai-1
Ki =Ki -1
! Конец IF
Ki =Ki +1
GOTO 2250
Конец IF
Вычисление точек пересечения
FOR K=l TO Nbai
I nter( K) =1 nter( K) +Dxy( Ei (K))
NEXT К
Добавить ребра, начинающиеся на
строке Y
J=Tliste(Y)
IF J=0 THEN 2250
Nbai =Nbai +1
Ei(Nbai)=J
Inter(Nbai)=Axd(J)
117

2850
2860
2870
118
2530 J=Liste( J)
2540 GOTO 2490
2550 ! Конец IF
2560 !
2570 ! Упорядочение точек пересечения
2580 CALL CopTnpoBKa(Inter(*),Ei(*),Nbai)
2590 !
2600 ! Пересечение интервала (*) И
Inter(*)
2610 CALL Interlistes (Интервал(*),
Nbint,Inter(*),Nbai)
2620 !
2630 NEXT Y
2640
2650
2660
2670 ! Запись текста в последовательность,
заданную переменной
Интервал (*)
2680 IF Nbint=0 THEN 3370
2690 ! Последовательность не пустая
2700 ! Первый интервал записи
2710 К1=1
2720 К2=2
2730 Х1=Интервал(К1)
2740 Х2=Интервал(К2)
2750 Длина = INT(X2-X1+. 5)
2760 ! Начальная точка первого слова
2770 Xpo=INT(Xl+.5)+3
2780 IF Md=Td THEN 2810
2790 Xpo=Xpo-Ширина
2800 Длина=Длина+Ширина
2810 ! Конец IF
2820 Ypo=Yb+INT(Высота/4) ! Низ записи
2840 ! ПОВТОРЯТЬ
Обрабатывать Интервал
Пока (не конецтекста) И
(Длина >Длина_слова) выполнять

2880 IF (Конец_текста=1) OR
(Длина <Длина_слова) THEN 3180
2890 ! Записать слово
2900 PEN l
2910 CSIZE Высота/4.54, Ширина/Высота
! высота задана в единицах GDU
2920 MOVE Xpo,Ypo ! начальная точка
слова
2930
2940
2950
2960
2970
2980
2990
3000
ЗОЮ
3020
3030
3040
3050
3060
3070
3080
3090
3100
3110
3120
3130
3140
3150
3160
3170
3180
3190
LABEL TeKCT$[Md,Mf]
! Новая начальная точка слова
Хро=Хро+Длина_слова
! Новая длина интервала
Длина=Длина-Длина слова
1
! Получить следующее слово
IF MfoTf THEN 3030
Конец текста=1
GOTO 3160
Md=Mf+l
I=Md
IF (I>Tf) OR (Текст$[1,1]<>" ")
THEN 3080
1=1+1 ! пропустить белые
участки
GOTO 3050
! Конец IF
IF (I>Tf) OR
(Текст$[1,1]=" ") THEN 3120
1=1+1 ! пропустить
символы # белых участков
GOTO 3090
! Конец IF
Mf=I-l
Nbcar=I-Md
Длина слова=МЬсаг*Ширина
! Конец IF
GOTO 2780
! Конец IF
!
119

3200
3210
3220
3230
3240
3250
3260
3270
3280
3290
3300
3310
3320
3330
3340
3350
3360
3370
3380
3390
3400
3410
3420
3430
3440
3450
3460
3470
3480
3490
3500
3540
3550
3560
IF Конец_текста=1 THEN 3330
! Следующий интервал
К1-К1+2
IF Kl>Nbint THEN 3310
K2-K2+2
XI»Интервал(Kl)
Х2=Интервал(К2)
Длина=1NT(Х2-XI+. 5)+Ширина-3
! начальная точка
Xpo=INT(Xl+. 5)-Ширина+3
IF MdoTd THEN 3330
Длина=Длина-Ширина
Хро=Хро+Ширина
! Конец IF
! Конец IF
IF (Конец_текста<>1) AND (KKNbint)
THEN 2840
! ДО (Конецтекста) ИЛИ (Интервал
последний)
! Конец IF
! Следующая строка записи
Yp=Yb
Ys=Yp-Сдвиг
Yb=Ys-Высота
!
i
GOTO 6040
i
! Конец IF
i
SUBEND
I
SUB Interjistes (REAL
Интервале),INTEGER Nbint,REAL
Inter(*), INTEGER Nbai)
i
i ПЕРЕСЕЧЕНИЕ ИНТЕРВАЛОВ, ЗАДАННЫХ В
КАЖДОМ ИЗ ДВУХ СПИСКОВ
120

3570 ! ЭЛЕМЕНТАМИ 2*2, УПОРЯДОЧЕННЫМИ В
ПОРЯДКЕ ВОЗРАСТАНИЯ.
3580 ! РЕЗУЛЬТАТ СОДЕРЖИТСЯ В МАССИВЕ
Интервал(*)
3590 !
3600 OPTION BASE l
3610 INTEGER Intl,Int2,I,J,L(20),N
3620 REAL Liste(20)
3630 !
3640 ! Взаимная классификация: Интервал[*] и
Inter[*]. Результат
3650 ! в Li ste[*] и в L[*], в которых
содержатся значения и номера
3660 ! соответствующего списка
3670 CALL Fusion(MHTepBaA(*),Nbint, Inter(*),
Nbai,Liste(*),L(*),N)
3680 !
3690 ! Выделить точки пересечения
(L1ste(*),L(*))
3700 !
3710 Intl=-1 ! ложно
3720 Int2=-1 ! ложно
3730 1=0
3740 J=0
3750 ! ПОКА I<N ВЫПОЛНЯТЬ
3760 IF I>N THEN 4030
3770 !
3780 ! ПОКА (HE(Intl) ИЛИ HE(Int2)) И
KN ВЫПОЛНЯТЬ
3790 IF (I>N) OR (Intl=l) AND (Int2=l)
THEN 3870
3800 1=1+1
3810 IF L(I)=2 THEN 3840
3820 Intl=-Intl
3830 GOTO 3850
3840 Int2=-Int2
3850 ! Конец IF
3860 GOTO 3780
3870 ! Конец IF
3880 !
121

3890
3900
3910
3920
3930
3940
3950
3960
3970
3980
3990
4000
4010
4020
4030
4040
4050
4060
4110
4130
4150
4160
4170
4180
4190
4200
4210
4220
4230
4240
4250
4260
4270
4280
4290
4300
4310
IF (Intl=-1) OR (Int2=-1) THEN 4000
J=J+1
Интервал (J)=Liste(I)
1=1+1
IF L(I)=2 THEN 3960
Intl=-Intl
GOTO 3970
Int2=-Int2
! Конец IF
J=J+1
Интервал (J)=Liste(I)
! Конец IF
GOTO 3750
!
! Конец IF
Nbint=J
j
SUBEND ! Inter listes
SUB Fusion (REAL LI (*), INTEGER
N1,REAL L2(*), INTEGER N2, REAL
L3(*), INTEGER L(*),N)
! Взаимная классификация списков
LI и L2: результат в L3 и L
N=0
1=1
J=l
! ПОКА I<N1 И J<N2 ВЫПОЛНЯТЬ
IF (I>N1) OR (J>N2) THEN 4310
N=N+1
IF L1(I)>L2(J) THEN 4260
L3(N)=L1(I)
L(N)=1
1=1+1
GOTO 4290
L3(N)=L2(J)
L(N)=2
J=J+1
! Конец IF
GOTO 4180
! Конец IF
122

4330 IF I>N1 THEN 4390
4340 N=N+1
4350 L3(N)=L1(I)
4360 L(N)=1
4370 1=1+1
4380 GOTO 4330
4390 ! Конец IF
4410 IF J>N2 THEN 4470
4420 N=N+1
4430 L3(N)=L2(J)
4440 L(N)=2
4450 J=J+1
4460 GOTO 4410
4470 ! Конец IF
4480 !
4490 SUBEND ! Fusion
4500 SUB Сортировка (REAL
Ta(*), INTEGER Tb(*),N)
4510 ! Сортировка в порядке
возрастания N значений в
таблицах Та(*) и ТЬ(*)
4520
4540
4550
4560
4580
4590
4600
4610
4620
4630
4640
4650
4660
4670
4680
4690
4700
4710
4720
! Та(*) основная
OPTION BASE l
REAL Tai, Taj
INTEGER B, Inv,I,J,Nl,N2
N1=N
! Повторять
N2=N1-1
lnv=0
1=1
IF J>N2 THEN 4780
J=I+1
Tai=Ta(I)
Taj>Ta(J)
IF Taj>Tai THEN 4750
Inv=l
Ta(I)=Taj
Ta(J)=Tai
B=Tb(I)
Tb(I)=Tb(J)
123

4730 Tb(J)=B
4740 N1=1
4750 ! Конец IF
4760 1=1+1
4770 GOTO 4630
4780 ! Конец IF
4790 IF Inv=l THEN 4590
4800 ! ДО lnv=0
4820 SUBEND ! Сортировка
3.3.4. ЗАКЛЮЧЕНИЕ
Мы показали два общих подхода, использованных для запол-
нения многоугольных областей. Первый основывается на
кодировании контура в матрице точек. Второй использует струк-
турированное представление контура для заполнения путем сле-
жения за контуром.
Алгоритмы заполнения кодированием контура имеют следу-
ющие недостатки:
необходима дополнительная память изображения;
исследования проводятся в границах описывающего прямо-
угольника, превосходящего рассматриваемую область (требуются
дополнительные вычисления);
невозможно одновременное генерирование множества наклады-
вающихся друг на друга областей.
Напротив, алгоритм слежения за контуром обладает следу-
ющими достоинствами:
малый объем дополнительной памяти (пропорционально числу
ребер);
работа проходит только внутри границ области, метод обобща-
ется на случай одновременного заполнения множества областей
независимо от того, накладываются ли они друг на друга;
может быть применен к процедуре заштриховывания областей,
что будет показано в разд. 3.5.
3.4. РАЗБИЕНИЕ МНОГОУГОЛЬНИКОВ НА ПРОСТЫЕ
ЭЛЕМЕНТЫ
3.4.1. ВВЕДЕНИЕ
Существует принципиально иной способ заполнения много-
угольников, заключающийся в разбиении фигуры со сложным кон-
туром на совокупность простых фигур (трапеции, треугольники) и
в применении к каждой из таких элементарных фигур чрезвычай-
но простых алгоритмов заполнения (рис. 3.23).
124

Рис. 3.23. Смежные области фигуры с многоугольным контуром
Различия в предлагаемых методах состоят главным образом в
способе заполнения элементарных областей (слежение за конту-
ром, сортировка ребер в зависимости от их ординат, см.,
например, [9, 29]) ив возможном уменьшении числа областей.
Мы показали, что после разделения произвольного много-
угольника на совокупность треугольников, сложность алгоритмов
заполнения областей, примененных к этой совокупности, в
большинстве случаев (выпуклость, nbame2 и др.) эквивалентна
или больше сложности тех же самых алгоритмов, примененных к
исходному многоугольнику (см. [16]). В некоторых особых случаях,
когда перечисленные условия не выполняются, поскольку слож-
ность разбиения многоугольника соответствует сложности ме-
тодики заполнения, разбиение многоугольника на элементарные
фигуры не уменьшает первоначальной сложности алгоритма запол-
нения. Другой недостаток метода разбиения заключается в отступ-
лении от построчного кодирования исходной области. Сохранение
же такого кодирования, строка за строкой, было бы полезным для
передачи изображения по телевидению.
Метод разбиения обладает преимуществами только в тех слу-
чаях, когда алгоритмы заполнения трапеций или треугольников
реализуются либо микропрограммными средствами, либо на жест-
кой логике (см. [22, 25]). Можно предусмотреть также парал-
лельное заполнение элементарных областей по мере их появления
(параллелизм типа поточной обработки).
Поскольку никакой из известных алгоритмов разделения не
пригоден для фигур многоугольными контурами, имеющими пере-
секающиеся ребра, приведем далее одну идею алгоритма, основан-
ного на понятии прослеживания контура.
3.4.2. НОВЫЙ АЛГОРИТМ РАЗБИЕНИЯ
Пусть область образована множеством произвольных много-
угольных контуров, ребра которых могут пересекаться
Идея нашего алоритма базируется на идее Бентли и Оттмана,
согласно которой исследуются все взаимные пересечения в ансам-
бле отрезков. В нашем случае отрезками являются ребра контуров.
125

3.4.2.1. МЕТОД БЕНТЛИ И ОТТМАНА
Метод Бентли и Оттмана [4 ] восходит к методу Шамоса —
Хойя [39], в котором исследуются все пересечения в наборе из
N отрезков.
Алгоритм состоит из двух частей.
Часть 1 — сортировка (перебор) 2N абсцисс в порядке их
возрастания. Эта последовательность будет содержаться в структу-
ре Q.
Часть 2 — исследование полученной последовательности
Q начиная с наименьшей абсциссы. Она хранится в промежуточ-
ной структуре R, размер которой уменьшен здесь до одного эле-
мента (это, очевидно, начальная абсцисса отрезка S). Затем пере-
ходим к следующей абсциссе в последовательности Q (рис. 3.24).
О А
А А
В С
В
А А
С В
В С
D D
А
В
D
А
D
В
D D А
А А В
В В Е
Е
В
А
Е
В
Е
Е О
Рис. 3.24. Пример обработки по Бентли и Оттману
•ЕСЛИ абсцисса есть НАЧАЛО (пусть, например, хО), то
вычисляют ординаты точек пересечения прямой х=хО с отрез-
ками, которые ей встречаются при движении по вертикали. Соот-
ветствующий отрезок включают в структуру R (в том же порядке
по вертикали). Если пересечение происходит выше и ниже в
массиве R, то Q включают в первую (-ые) абсциссу (-ы) точки
(точек) пересечения.
•Если абсцисса есть КОНЕЦ, то если отрезки выше и ниже
этого отрезка в R пересекаются, вставляют абсциссу точки пере-
сечения в последовательности Q, а отрезок удаляют из R.
•ЕСЛИ абсцисса есть ПЕРЕСЕЧЕНИЕ, то следует изменить
положения рассматриваемых отрезков и удостовериться, пересека-
126

ются ли в структуре R примыкающие после этого изменения
отрезки. Абсциссы точек пересечения заносятся в Q.
•Если массив Q пуст, ш конец;
В том, что касается нас, мы рассуждаем в последовательности
убывания ординат. Но следует иметь в виду, что в алгоритме
Бентли и Оттмана возникают трудности в двух случаях:
при наличии горизонтальных отрезков; в нашем случае эта
трудность отсутствует, поскольку мы их подавляем;
при общем пересечении более двух отрезков.
3.4.2.2. ИСПОЛЬЗОВАНИЕ АЛГОРИТМА БЕНТЛИ И ОТТМАНА
Определение элементарных областей начинается с сортировки
в порядке уменьшения координаты Y концов ребер, положение ко-
торых отлично от горизонтального. Структура R упорядочивает
ребра по горизонтали, что позволяет отличать правые края от ле-
вых. В этой структуре существует 3 типа точек:
1) начала ребер;
2) концы ребер;
3) точки пересечения.
В алгоритм Бентли и Оттмана следует внести такие изменения:
в процессе обхода структуры Q перегруппировались точки,
принадлежащие одной и той же горизонтальной линии (т. е. име-
ющие одинаковые ординаты). В результате для каждой горизон-
тальной линии, где происходят изменения (одно или несколько),
будет получен упорядоченный список ребер в порядке умень-
шения абсцисс точек пересечения (структура R);
разбиение на трапеции и треугольники выполнять между дву-
мя горизонтальными линиями исходя из структуры R текущей
строки и ординаты следующей строки.
Алгоритм в общем виде можно представить следующим обра-
зом:
Разбиение
Начало
1. Перебор 2N ординат концов
негоризонтальных ребер в
убывающей последовательности
(структура Q);
2. Повторять
получить первую горизонтальную
линию (структура R);
• Пока R не пусто выполнять
Начало
получить ординату следующей строки;
разбить на простые элементы;
127

получить следующую горизонтальную
строку (структура R);
конец
до опустошения Q
конец
Рассмотрим более подробно каждый блок.
•Получение горизонтальной линии.
Для всех точек структуры Q с одинаковыми ординатами выполнять
Шыада
обрабатывать точку, как во второй части
алгоритма Бентли и Оттмана
Конец
(по окончании получаем структуру Ю.
•Разбиение на простые элементы.
Вычисляются абсциссы точек пересечения ребер, принадлежащих
структуре R, со следующей горизонтальной линией. При этом
получается множество левых и правых краев, расположенных
вдоль горизонтали.
Текущая строка
Следующая строка,
•Разбиение на трапеции. Из структуры R
выделяются пары ребер, концы которых соответствуют точкам
пересечения с текущей и следующей линиями.
•Разбиение на треугольники. Выполняется
то же, что в предыдущем пункте, а затем для каждой пары, если
нет общих точек на концах, трапеция разделяется на два тре-
угольника:
Но для действия алгоритма требуется точное определение
понятия пересечения двух ребер. Два ребра пересекаются в точке
I, если они не коллинеарны и если у них нет ни одного общего
конца:
128

Пересечение • точке I
Нет пересечения
Два общих Один общий Коллинеарность
конце конец
С другой стороны, в структуре R ребра, имеющие одну и ту же
точку пересечения с текущей горизонтальной линией, будут упо-
рядочены по степени возрастания их наклона (отрезки
ориентированы вниз).
Пример разбиения произвольной многоугольной области:
АВ
AGFB
AGHC
АС
ЕС
СЕ
CD
О
Теоретическая сложность. Метод харак-
теризуется сложностью 0(NLogN + kLogN), включая перебор для
упорядочения 2N, где К — общее число пересечений. Что же ка-
сается обращения к функции "пересечение двух отрезков пря-
мых", то его сложность составляет 0(N+k).
3.4.3. ЗАКЛЮЧЕНИЕ
В заключение можно отметить следующее. По сравнению с су-
ществующими алгоритмами этот метод позволяет разделять на
простые элементы произвольные многоугольники с учетом пересе-
чения ребер, внутренних замкнутых включений и примыкающих
X
л V /
5 - Ж. Эгрон
129

(смежных) контуров. Если же пересекающиеся ребра отсутствуют,
то можно упростить высчисления (нет необходимости вычислять
точки пересечения отрезков прямых).
Эффективность метода заполнения площадей путем их
разбиения по сравнению с прямыми методами априори вовсе не
очевидна.
3.5. ШТРИХОВАНИЕ МНОГОУГОЛЬНЫХ ОБЛАСТЕЙ
3.5.1. ВЕРТИКАЛЬНАЯ И ГОРИЗОНТАЛЬНАЯ ШТРИХОВКИ
Задача горизонтальной штриховки решается точно так же, как
задача заполнения методом прослеживания контура.
Взаимосвязь, существующую между двумя последовательными
линиями штриховки, можно выразить следующим соотношением:
если Ei — множество ребер, пересекающих строку i, то Еи-i «Ei +
{ребра, начинающиеся в полосе ]строка i, строка i+1 ] — ребра,
заканчивающиеся в полосе ] строка i, строка 1+1]}.
С другой стороны, вертикальная штриховка полностью
идентична горизонтальной штриховке, если только поменять
ролями абсциссы и ординаты.
Пример штриховки (уровни серого получены с помощью мно-
гоэлементной апертуры размером 3*3):
3.5.2. НАКЛОННАЯ ШТРИХОВКА ОБЛАСТИ С МНОГОУГОЛЬНЫМ
КОНТУРОМ
3.5.2.1. ВВЕДЕНИЕ
Поскольку мы уже умеем выполнять горизонтальную штрихов-
ку, естественно предположить, что наклонную штриховку можно
было бы осуществить следующим образом: повернуть контур на
угол - а (где а — желаемый угол наклона линий штриховки),
а затем для каждого вычисленного горизонтального отрезка
привести обратный поворот на угол а (рис. 3.25).
130

Рис. 3.25. Поворот контура:
а - угол наклона линий штриховки
Этот метод, предложенный в работе [9], кажется простым по
своей логике, однако представляется неоптимальным, из-за необ-
ходимости последовательно выполнять два поворота. Наша идея
состоит в том, чтобы, сохраняя общую схему алгоритма горизон-
тальной штриховки, избавиться от последовательных поворотов.
352.2. НАКЛОННАЯ ШТРИХОВКА МЕТОДОМ ПРОСЛЕЖИВАНИЯ КОНТУРА
Идея метода. Задача, которую предстоит решить, заключается
в нахождении всех ребер контура, пересекающих каждую линию
штриховки.
Пусть i- номер текущей линии штриховки, (i-1) — номер
предыдущей линии. Пусть также Ем — множество ребер, пересе-
кающих линию (i-1). Тогда имеем Ei—Ei-i {ребра, начинающиеся
в полосе ]линия i-1, линия i]} — {ребра, заканчивающиеся в
полосе ]линия i-1, линия i]}.
Ребро начинается ( или заканчивается) в полосе ]линия i-1,
линия i] (рис. 3.26), если его начало (или конец) принадлежит
этой плоскости (общий признак принадлежности точки плоскости).
Пусть а — наклон линий штриховки. Каждая линия штриховки
описывается уравнением y»ax+yi, где yi — константа. Если
^ Линия i-1
^L —-^*** . ^ пи*** ^—» Линия i
Рис. 3.26. Определение полосы ]линия 1-1, линия i]
131

(xl,yl) — координаты точки Р, то прямая с наклоном а, прохо-
дящая через эту точку, определяется уравнением у - ах+ур,
или ур - yi - axi (рис. 3.27). Следовательно, точка Р принад-
лежит полосе ] линия i-1, линия i], если yi-i > ур > yi .
у = ад ♦ ув
У * " ♦ У{
Рис. 3.27. Определение линии штриховки
и относительного положения точки
Алгоритм. Пусть многоугольный контур задан упорядоченным
списком S его п вершин, а наклон линий штриховки равен а.
Каждая точка s G S характеризуется значением ys, задаваемым
уравнением ys - у' - ах' , где (х' ,у') — координаты точки s.
Составим новый список вершиЦ контура, упорядочив их по ме-
ре уменьшения соответствующих вершин ys . Тогда получим пос-
ледовательность (sj ,ysj)j-i...n, где ysj-i > ysj (рис. 3.28).
Каждое ребро, заданное своими крайними точками: Sd (начало)
и Sf (конец), ориентировано таким образом, что ysd>ysf
(рис. 3.29).
Рис. 3.28. Образование упорядоченного списка вершин (последовательность
(sj, ysj), J-1.2 7)
132

*'l
->
У**|. У»*2
Рис. 3.29. Ориентация ребер
В алгоритме заполнения по методу прослеживания контура
ыполняется перемещение вдоль контура в вертикальном направ-
ении. Здесь же движение происходит по контуру в направлении,
ерпендикулярном к линиям штриховки. Расчет точек пересечения
читывает взаимосвязь, существующую между двумя последова-
ельными линиями штриховки. Это достигается тем, что для каж-
ого ребра вычисляются приращения по X и по Y на интервале
[ежду двумя линиями. Первая точка пересечения получается при
ычислении точки пересечения двух прямых: линии штриховки и
рямой - носителя ребра.
Реализация. Будем использовать следующие структуры данных.
•Список вершин, определяемый через:
s(*) — таблицу номеров вершин,
х(*),у(*) — координаты вершин контура,
ys(*) — точки пересечения прямых, проходящих через
вершины с осью Оу (прямые, параллель-
ные линиям штриховки).
•Список ориентированных ребер:
sd(*) — начальная вершина (заданная номером
вершины);
sf(*) — конечная вершина;
а(*) — приращение по х;
Ь(*) — приращение по у;
dax(*) — приращение по х между линиями штриховки;
day(*) — приращение по у между линиями штриховки.
•Список ребер, начинающихся на каждой линии штриховки и
роходящих через вершины (в порядке уменьшения ys):
133

s
LISTE
-*-k1
Ic2
m | |
• I I
• II
• I I
• I
• I
• I
•SW — точка S(i) в списке ребер kl, k2, ..., kp, начинающихся
в вершине i(i-l,2,...,nbsom размещены в соответствии с умень-
шением у si).
•Список ребер, пересекающих линию штриховки i:
Ei(*) — список ребер;
inter(x), inter(y) — координаты точек пересечения каждого ребра
с линией i.
Как и в алгоритме заполнения, контур области образован мно-
жеством многоугольников. Мы располагаем также СДВИГОМ меж-
ду двумя соседними линиями штриховки и их НАКЛОНОМ.
В общем виде алгоритм можно записать так:
НАКЛОННАЯ ШТРИХОВКА (N,T(*))
Начало
Предварительная обработка;
штрихование;
Конец;
Предварительная обработка;
Начало
Список ориентированных ребер;
упорядочить (s,ys);
перенумеровать вершины, образующие ребра;
создание списка ребер (S, LISTE)
Конец предварительной обработки;
134

Штрихование
Начало
создать список Ei, Inter;
получить первую линию штриховки;
{собственно штрихование}
Оока. линия штриховки не последняя выполнять
Начало .
вычисление пересечений ребер, имеющихся в
Ei;
добавить ребра, начинающиеся в полосе
]линия i-1 линия i ];
удалить ребра, заканчивающиеся в полосе
] линия i-1, линия i];
сортировать (Ei, Inter);
провести линии штриховки;
получить следующую линию штриховки;
шш
Конец штриховки
Модули программы предварительной обработки
в развернутом виде:
Список ориентированных ребер
Начало
{сдвиг по вертикали между линиями,
штриховки
Ecart; наклон линий штриховки Pente}
Dy := Ecart*SQRT (1+Pente2 );
{инициализация}
Nbs :=1; {число вершин}
Nba : =0; {число ребер}
i :=1; {текущий индекс Т(*)}
Пока i<N выполнять
Начало
Nbso := Nbs; {первая вершина
многоугольника}
135

io := 1;
Xd := T(i); Yd := T(i+1);
i := i+2; Xo := T(i);
x(Nbs) := Xd; y(Nbs) := Yd;
Ysd := Yd-Pente*Xd; Nsd := Nbs;
s(Nbs) := Nbs; Ys(Nbs) := Ysd;
Nbs := Nbs+1;
Fin : = ложно;
Повторять
если Xo*NIL ™ Xf: =Xo, Yf:=T(i+l);
x(Nbs):= Xf; y(Nbs) := Yf;
Ysf := Yf-Pente*Xf; Nsf := Nbs;
s(Nbs):=Nbs; Ys(Nbs): =Ysf;
Nbs := Nbs+1;
иначе Xf: =T(i o); Yf: =T(i o+l); i: =i +1;
Ysf:=Ys(Nbso), Nsf: =Nbso;
Fin:= истинно (последнее ребро
многоугольника}
{обрабатывать ребро ((Xd,Yd), (Xf, Yf))}
Если Ysd>Ysf
y_p_ Nba:=Nba+l;
sd(Nba):=Nsd, sf(Nba): =Nsf;
Ax:=Xf-Xd; Ay.=Yf-Yd;
a(Nba):=Ax; b(Nba):=Ay,
dax(Nba): =(Dy*Ax)/(Ay+Pente*Ax);
day( Nba): =Pente*dax( Nba) - Dy,
иначе если Ysd<Ysf
то Nba:=Nba+l;
sd(Nba):=Nsf; sf(Nba): =Nsd;
Ax:=Xd-Xf; Ay:=Yd-Yf;
a(Nba):=Ax; b(Nba):=Ay;
dax(Nba): =( Dy*Ax)/(Ay+Pente*Ax);
day( Nba): =Pente*dax( Nba) -Dy,
конец если
конец если
(следующее ребро}
если не (Fin) то. Xd:=Xf; Yd: =Yf;
Ysd: =Ysf; Nsd: =Nsf;
I: =1+2; Xo:= T(i);
136

Д2_ Fin
Конец пока
Nbsom: = Nbs-1;
Конец
упорядочить (s,ys);
Начало
сортировать (ys( *), s( *), х( *), у( *), nbsom) в
порядке убывания ys;
Конец
Перенумерация вершин, составляющих ребра;
Начало
Для i:=l до nbsom выполнять
начало
si(s(i)):=i;
конец
Для к: =1 до nba выполнять
Начало
sd(k):=si(sd(k));
sf(k):-si(sf(k));
конец
Конец перенумерации
Создание списка ребер S, LISTE
Начало
i:=0 (индекс s(*)}; j: =0 (индекс списка (*)}
к:=0 (индекс ребер}
s(*):=0; 1i ste(*): =0;(инициализация таблиц
нулевыми значениями}
Аля к: =1 до_ nba выполнять
i:=sd(k);
если s(i)=0
то_ s(i):=k;
иначе j:=s(i);
пока liste(j)* 0 выполнять
137

Начало
j:=liste(j);
liste( j): =k;
конец если
конец для
Конец
Рассмотрим более подробно модули ШТРИХОВАНИЯ
Создание списка Ei,Inter;
Начало
nbai:=0 (число ребер на строке i}
ns:=1 (номер вершины}
ypred: =ys(ns)
пока ypred = ys(ns) выполнять
Начало
j:=s(ns);
Пока j* 0 выполнять
nbai: =nbai+l;
Ei(nbai): =k;
(i nter- x( nbai), i nter- y( nbai)): =( x( ns), y( ns));
j:=liste(j);
конец пока
ns:=ns+l; (следующая вершина}
конец
Конец
Получение первой линии штриховки
Начало
у_текущее: =ypred-dy (строка i}
уконечное: =ys( nbsom)
Конец
Собственно штрихование:
Линяя штриховки не последняя,
если значение у текущее > у конечного.
138

Вычисление точек пересечения ребер, имеющихся
в Ei:
Начало
Аля к: =1 до nbai выполнять
Начало
i nter_x( к): =i nter_x( к) +dax( Ei (к));
i nter_y( к): =i nter_y( k) +day( Ei (k));
конец
Конец
Добавление ребер, начинающихся в полосе
1 строка i-1, строка il
Начало
Пока (ns<nbsom и_ ys(ns) > у текущее) выполнять
Начало
j=s(ns);
Пока j=0 выполнять
nbai: =nbai+l;
Ei(nbai): =k;
I nter_x( nbai): =( a( k) *y( ns) +b( k) *x( ns) -
- a( k) * утекущее) /(b( k) - pente*a( k));
I nter_y( nbai): =pente*i nter_x( nbai) +у_текущее;
j:= liste(j);
конец пока
ns:=ns+l;
конец
Конец
Отбрасывание ребер, заканчивающихся в полосе
Чстрока i-1, строка il
Начало
Для i:=l д<э nbai выполнять
Начало
к:-Е1(1);
если ys( sf(к)) < у_текущего
то. {удаление Ei(i)}
если i * nbai
то.
k:=i+l;
139

Ma j=k до. nbai выполнять
Начало
E1(j-1):-E1(j);
Inter( j-l):=inter( j);
конем
ШШ ЕСЛИ.
nbai: = nbai-1;
i:=i-l
конец если
шшц.
Конец
Сортировка (Ei, inter);
Цацадо.
сортировать (Ei, interx, intery)
interx основное (в порядке возрастания)
Конец сортировки:
Выполнение штриховки:
Начало
kl:-l;
k2: =2;
Пока k2< nbai выполнять
Начало
отобразить отрезок ((interx(kl), inter_y(kl));
((i nter_x(k2), i nter_y( k2));
kl:=kl+2; k2: =k2+2;
Конец выполнения штриховки
Получение следующей линии штриховки
Начало
y_pred: =у_текущее; {строка i-1)
утекущее :=y_pred-dy, {строка i)
Конец;
140

Примеры наклонной штриховки:
Из рисунка видно, что в процессе отображения линий
штриховки переход из пространства пользователя (вещественные
числа) в пространство экрана (целые числа) вызывает ошибки в
расстоянии между линиями штриховки (Г) (ошибки составляют от
-1 до +1 экранного пиксела).
Эта проблема не позволяет выполнять наклонное штрихование
достаточно точно, поскольку, как это видно из нижеприведенного
рисунка, не все точки области будут отображены.
Здесь отчетливо видны
ошибки в расстояниях
между линиями
штриховки
3523. ЗАКЛЮЧЕНИЕ
Оценка нашего алгоритма наклонного штрихования без поворо-
та позволяет сделать следующие выводы:
принципиальный недостаток метода состоит в необходимости
сортировки вершин, сложность которой составляет величину
0(nbsom.Log nbsom);
недостаток алгоритма наклонного штрихования с поворотом
заключается в необходимости дополнительных расчетов, вызван-
ных последовательными поворотами вначале для вершин контура,
а затем для концевых точек отрезков линий штриховки.
Задача состоит в том, чтобы понять, исходя из какого критерия
следует выбрать первое или второе решение как наиболее выгод-
ное. Нам представляется, что наш метод наклонного штрихования,
основанный на прослеживании контуров, обладает преимущест-
вами настолько, насколько число линий штриховки превосходит
число ребер (если nblh>2.nbam.nba, ще nbam — среднее число
ребер, пересекающих линию штриховки, но это неравенство тре-
буется проверить на практике).
141

3.6. ВЫВОДЫ
В общем случае характеристики и ресурсы, требующиеся для
алгоритмов заполнения или штриховки, зависят от сложности кон-
тура. Но первоначальный критерий пригодности связан с их адап-
тацией к синтезу изображений в рамках конкретного приложения,
где следует учитывать:
интенсивность яркости (переменная или постоянная),
характер областей: многоугольные или нет,
интерактивность,
имеющуюся в распоряжении память.
Для каждого класса алгоритмов заполнения можно сделать
основные замечания.
•Алгоритмы окрашивания прежде всего могут быть использова-
ны в интерактивном режиме (определение внутренней точки, связ-
ность области).
•Метод заполнения путем кодирования контура требует
значительных затрат времени и памяти дополнительного изобра-
жения и мало пригоден для обработки совокупности взаимно пере-
секающихся областей. Однако его обобщение на некоторые конту-
ры достаточно просто.
•Среди этих различных классов алгоритмов выделяется один
общий метод: прослеживание контура. Действительно, если
исходить из структурированного представления контура, то он поз-
воляет не только реализовывать заполнение области или совокуп-
ности либо многоугольных, либо более сложной формы областей,
но также легко приспосабливается к штрихованию, разделению
многоугольников на простые элементы, а кроме того, допускает
распараллеливание (см. [5]).
В следующей главе будет показано, что принципы прос-
леживания контуров обобщаются на некоторые задачи разрезания
геометрических объектов.
ГЛАВА 4
АЛГОРИТМЫ РАЗРЕЗАНИЯ И ОБРАБОТКИ
ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
4.1. ВВЕДЕНИЕ
Нередко возникают ситуации, когда во время создания рисун-
ков или изображений необходимо отобразить на экране только
часть некоторой сцены. Поскольку обычно имеют дело с плоским
изображением, то классическая задача состоит в использовании
142

Окно
Рис. 4.1. Разрезание сцены окном
окна, т.е. прямоугольника со сторонами, параллельными координа-
тным осям (рис. 4.1).
Однако может оказаться так, что необходимо производить до-
статочно много вычислений в тех случаях, когда исчезает та про-
стота, которая обеспечивалась параллельностью сторон прямоу-
гольника осям координат. Задача состоит тогда в разрезании
окном, имеющим произвольную форму, не обязательно выпуклым
многоугольником, с произвольным числом сторон.
В более общем случае можно сформулировать задачу так:
сравнить два произвольных многоугольника и определить все их
части, являющиеся общими для обеих фигур как результат их
взаимного пересечения (разрезание одним прямоугольником дру-
гого). В частности, это разрезание используется в алгоритме уда-
ления невидимых линий в трехмерных сценах Атертона и Уэйлера
[3], где исходя из множества плоских многоугольников, образу-
ющих объект, требуется получить упорядоченную последователь-
ность множества плоских граней. Такое разрезание может также
оказаться полезным в процессе преобразования изображений.
Таким образом, в зависимости от типа сцены, с которой имеем
дело (рисунок или изображение), и в соответствии с результатом,
который хотелось бы получить (структуры данных, отображение
на экране), задача разрезания может трактоваться по-разному. В
следующем разделе будут классифицированы задачи разрезания и
выделены основные геометрические задачи, характерные для каж-
дой из них.
Для множества задач, излагаемых далее, характерно широкое
разнообразие методов их решения, изложенных в литературе.
Основываясь на материале предыдущих глав, покажем некий
универсальный подход, в котором нами использован принцип ме-
тода прослеживания контура для решения задачи разрезания.
143

4.2. КЛАССИФИКАЦИЯ ЗАДАЧ РАЗРЕЗАНИЯ
Данная классификация выполнена на примере многоугольных
контуров, но она легко обобщается на контуры произвольной фор-
мы.
4.2.1. РАЗРЕЗАНИЕ МНОГОУГОЛЬНИКА ОКНОМ
Задача состоит в вычислении части многоугольника, видимой в
многоугольном окне. Можно предложить две гипотезы
а. Если выполняется простой векторный рисунок без учета
понятия контура, то элементарная задача заключается в разре-
зании отрезка прямой многоугольником.
Видимые
отрезки
Окно
Разрезаемый
многоугольник
Тогда отображаются только части сторон многоугольника, видимые
в окне.
б. Если желательно сохранить понятие контура, например
понятие плоской грани для векторного рисунка или понятие
области для синтеза изображений, то задача состоит в вычислении
результирующего многоугольника, расположенного внутри окна,
как результат разрезания окном исходного многоугольника.
Результирующий
многоугольник
Окно
Исходный
многоугольник
Здесь вычисляется множество контуров (внутренних и внешних),
составляющих результирующий многоугольник после разрезания.
144

4.2.2. РАЗРЕЗАНИЕ
ОКНОМ
ПРОИЗВОЛЬНОЙ ОБЛАСТИ МНОГОУГОЛЬНЫМ
Здесь рассматривается отображение видимой части области
(заштрихованной или заполненной) в многоугольном окне.
Можно предложить два пути решения.
а. Определить полученный многоугольник как результат разре-
зания окном исходного многоугольника (как в п.4.2.16). Затем
заштриховать или заполнить этот многоугольник (т.е. вернуться к
уже известной элементарной задаче заполнения или штрихования
площадей).
Штрижоаание
млн заполнение
результирующего
многоугольника
Результирующий
многоугольник
б. Для штрихования заштриховывают весь первоначальный
многоугольник, а отображают только видимые части линий
штриховки.
Окно
Отображаемые
линии шгрихояки
Нсотображасмыс
линии штриховки
Элементарная задача заключается в разрезании отрезка прямой
(линии штриховки) многоугольником.
Для окончательного решения заполняют весь исходный много-
угольник, а отображают только точки, расположенные внутри
окна.
Окно
Множество
видимых точек
Множество
иеотобрежаем ыя
точек (вне окна)
145

Основная задача заключается здесь в выяснении того, лежит ли
точка внутри или вне контура (путем сравнения с точками кон-
тура) .
Если в случае штрихования (а, возможно, и заполнения) необ-
ходимо отобразить видимые части контура, то возвращаемся к уже
рассмотренной задаче (п. 4.2.1а).
Для первого варианта решения время вычисления и отобра-
жения пропорционально сложности исходного изображения и не
зависит от сложности видимого изображения. Однако поскольку
время вычисления заполнения или штрихования во втором методе
б) пропорционально сложности видимого изображения, его надо
прибавить к времени вычисления разрезания, пропорционального
сложности контура. Проблема состоит в том, чтобы определить,
какое из двух решений предпочтительно в том или ином случае.
При методе б) мы предлагаем отображать видимую часть области,
выполняя заполнение или штрихование во всей первоначальной
области, но применять его только к подмножеству множества то-
чек или линий штриховки, видимых в окне. При этом принадлеж-
ность точки или отрезка к окну может быть установлена
различными методами:
либо с помощью алгоритма сравнения контурных точек или
разрезания отрезка многоугольником,
либо заполнением или штрихованием окна и области одновре-
менно, но с учетом отображения только точек или части линий
штриховки, принадлежащих внутренней части контура и внутрен-
ней части окна.
4.2.3. РАЗРЕЗАНИЕ МНОГОУГОЛЬНИКА ДРУГИМ МНОГОУГОЛЬНИКОМ
Задача здесь состоит в нахождении всех многоугольников,
образующихся в результате взаимного пересечения двух
произвольных многоугольников.
Если последовательность Р разрезает массив Q, то образуются
области Р П Q, Ql, Q2, Q3. Если контур Q разрезает Р, то обра-
146

зуются области Р П Q, Р1,Р2,РЗ,Р4,Р5. Можно получить также
Р П Q,P1,P2,P3,P4,P5 и Q1,Q2,Q3.
4.2.4. РАЗРЕЗАНИЕ ОДНОЙ ОБЛАСТИ ДРУГОЙ ОБЛАСТЬЮ
Для создания двумерного изображения мы пользуемся множе-
ством областей, которые могут накладываться друг на друга или
комбинироваться в соответствии с некоторым набором правил.
Так, в случае наложения областей следует разрезать одну из них
с помощью другой в соответствии с рассчитываемым результатом:
Q перед Р или Р перед Q
Можно наметить два пути решения.
А. Разрезание одного из контуров другим контуром области, ко-
торая находится впереди, при сохранении внешних
результирующих многоугольников этой последней. Такой путь
решения был описан в [3].
Если Q находится перед Р, то получим Р1,Р2,РЗ,Р4,Р5.
Если Р находится перед Q, то получим Q1,Q2,Q3.
Затем отображаем внешние области, определенные таким
образом, и область, находящуюся впереди, со свойственным ей
цветом. В случае неоднозначном, таком, например, как показан
на представленном рисунке, следует вычислить результат разре-
зания двух областей между собой.
Неоднозначность
147

На примере фигуры, показанной в п. 4.2.3, необходимо опре-
делить результат Р П Q, P1,P2,P3,P4,P5,Q1,Q2,Q3, где Р П Q бу-
дет иметь цвет Р, если Р находится перед Q, или, наоборот, цвет
Q, если Q ближе, чем Р, где Р1,Р2,РЗ,Р4,Р5 будут цвета Р, а
Q1,Q2 и Q3 — цвета Q. Затем, исходя из этого нового множества
областей, можно будет реализовать разрезание таким же образом
с другими областями сцены, находящимися в "конфликте". Обра-
ботка, выполненная однократно над всей представленной сценой,
отобразит этот новый набор областей.
Б. Разрезание областей, основанное на исследовании не их кон-
туров, а самих областей. Здесь вновь сталкиваемся с задачей
обработки множества областей (см. [12]). Перед началом расчетов,
связанных с разрезанием, следует попытаться определить взаимное
расположение контуров: не разъединены ли они, не входит ли
один из них в другой и пересекаются ли они (то же самое
относится и к областям).
4.2.5. ЗАКЛЮЧЕНИЕ
При классификации мы выделили четыре больших класса за-
дач разрезания:
1) многоугольника окном;
2) произвольной области окном;
3) одного многоугольника другим многоугольником;
4) одной произвольной области другой областью.
Но в каждом из этих классов целесообразно определить част-
ные упрощенные случаи, которые позволяют учитывать их особен-
ности и упрощать вычисления. К таким упрощенным можно
отнести случаи, когда окна, многоугольники или области являются
прямоугольниками со сторонами, параллельными координатным
осям, или выпуклыми фигурами.
С другой стороны, мы имели в виду использование трех эле-
ментарных задач:
1) сравнение точки и контура;
2) разрезание контуром отрезка прямой;
3) пересечение двух отрезков прямых.
В табл.3 приведены все варианты геометрических отношений
между объектами и перечислены задачи, возникающие при их
взаимодействии. Практически каждый алгоритм разрезания распа-
дается на несколько элементарных операций. Так, например, ал-
горитм Шамоса пересечения двух выпуклых контуров основан на
сравнении точки и контура, сравнении точки и прямой (или ее
отрезка) и вычислении точки пересечения двух прямолинейных
отрезков.
148

Таблица 3. Геометрическая обработка и элементарная задача разрезания
Точка
Отрезок
Прямая
Контур
Область
Точка
Совпадают
ли две
точки?
Отрезок
Положение
точки
относи-
тельно
отрезка
Пересе-
чение двух
отрезков
Прямая
Положение
точки
относитель-
но прямой
Пересе-
чение пря-
мой и
отрезка
прямой
Пересе-
чение двух
прямых
Контур
Положение
точки
относитель-
но контура
Пересе-
чение
отрезка
прямой с
контуром
Пересе-
чение пря-
мой с кон-
туром
Пересе-
чение двух
контуров
Область
Положение
точки
относитель-
но области
Пересе-
чение
области
отрезком
прямой
Разрезание
области
прямой
линией
Разрезание
области
контуром
Пересе-
чение двух
областей
4.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ
И МНОГОУГОЛЬНОГО КОНТУРА
4.3.1. ВВЕДЕНИЕ
Задача состоит в том, чтобы определить, где находится точка
относительно многоугольного контура: внутри него или снаружи.
Сопоставление точки и контура — операция, которая встречается
достаточно часто, в частности при интерактивной идентификации
контура или области, при разрезании одного контура другим, а
также в некоторых алгоритмах удаления невидимых линий.
Рассмотрим различные алгоритмы решения этой задачи, отде-
ляя те, которые применимы только к выпуклым контурам, от тех,
с помощью которых можно обрабатывать контуры произвольной
формы, определяемые лишь упорядоченной последовательностью
составляющих их вершин Si, где i=l,2, ...,nbsom (табл.4).
149

2
8
x
i
с
X
О
<
о
н
s
X
з
3
Й
о
3
я*
X
S
X
о
3
S
150
Примечание
Элементарные
вычисления
Теоретическая слож-
ность
Частные случаи
Тип контура
Название метода
Если точка
внешняя, то
осуществляет-
ся сравнение с
ребрами (не
обязательно
полное)
Уравнение прямой
Выпуклый
Ле Туана
Метод удобен,
если контур
используется
несколько раз
Тригонометрическая
функция (арктангенс)
0(п) при предвари-
тельной обработке
0(1од п) при обра-
ботке (дихотомичес-
кое разделение)
Выпуклый
ориентированный
Шамоса
Точка пересечения
отрезков
1/2 прямой
проходит через
одну или несколько
вершин
Произвольный
Вычисление
пересечений
Для выпуклого
случая метод
исчерпыва-
ющий
Тригонометрическая
функция (арктангенс)
1?
Никаких дополни-
тельных сведений,
если точка нахо-
дится на контуре
Произвольный
Допустимые
углы
Тоже
Код
Вершина принадле-
жит области, окру-
жающей точку р
Произвольный
Кодирование
Точки пересечения
Произвольный
Прослеживание
контуров

4.3.2. СРАВНЕНИЕ "ТОЧКА—КОНТУР" (ВЫПУКЛЫЙ МНОГОУГОЛЬНИК)
432.1. ВВЕДЕНИЕ
Существуют два метода, пригодные для обработки только вы-
пуклых контуров: Ле Туана и Шамоса.
Сложность первого составляет величину O(Nbsom). Напротив,
если в алгоритме Шамоса выполняется предварительная обработ-
ка выпуклого контура со сложностью O(Nbsom), то сложность со-
поставления точки с выпуклым контуром составляет О (Log
Nbsom).
43.2.2. МЕТОД ШАМОСА [37]
Принцип. Разделим плоский выпуклый многоугольник на N
треугольных секторов, вершины которых сходятся в точке С, на-
ходящейся внутри многоугольника. Точку С можно рассматривать
в этом случае как начало полярной системы координат.
ys2
$3^>/о2\-^чч^ Ось отсчета
Пусть р — точка, положение которой относительно контура
требуется определить.
Процесс вычислений состоит в том, чтобы вначале найти угол
этой точки в полярной системе координат (csi,cp), затем дихо-
томическим делением найти сектор, которому принадлежит на-
правление на точку, а после этого определить, по какую сторону
от грани, определяющей данный сектор, находится точка р.
Алгоритм. Пусть хс,ус — координаты точки С, находящейся
внутри контура, a Tangledrnbsom) — массив полярных углов,
упорядоченный в порядке их возрастания. Тогда получаем следу-
ющий алгоритм: )
Сопоставление ТОЧКА — ВЫПУКЛЫЙ КОНТУР
Начало {метод Шамоса}
граница:=ложно
vxl: =xc-x(l);
vyl:*yc-y(l);
vx2: =хс-хр;
vy2:=yc-yp;
151

угол: =arctg( vxl *vy2- vyl *vx2, vxl *vx2+vyl *vy2);
Дополнительное разделение
(угол, Тугол, nbsom, индекс)
(точка находится внутри сектора,
ограниченного
((хс, ус,) (х( индекс), у( индекс))), ((хс, ус),
(их( индекс+1), у( индекс+1)))}
а: =х( индекс+1) - х( индекс);
Ь: =у( индекс+1) - у( индекс);
с: =а. у( индекс) +Ь. х( индекс);
prod: =( а. ур+Ь. хр- с) (а. ус+b. хс- с);
если Prod<0
то если Prod=0
то если (х( индекс) - хр) (х( индекс+1) - хр)
+(у( индекс) - ур) (у( индекс+1) - ур) <0
тр_ граница: =истинно;
иначе вне:^истинно;
конец если;
иначе вне:=истинно:
кднеи если
™ вне: =ложно;
коней если
Конец
Несколько замечаний. Главным недостатком
этого метода является необходимость использования обратных
тригонометрических функций, вычисление которых требует
больших временных затрат. И наоборот, если уже известны поляр-
ные углы для большого числа точек, положение которых
относительно выпуклого контура требуется определить, то слож-
ность вычислений будет О (Log Nbsom).
4.3.3. ПОЛОЖЕНИЕ ТОЧКИ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО
КОНТУРА
433.1. ВВЕДЕНИЕ
Существуют несколько методов определения положения точки
относительно произвольного контура:
152

подсчет числа пересечений,
нахождение вмещающего угла,
кодирование.
При реализации этих алгоритмов возникают трудности в
отдельных частных случаях (см.табл.4). Чтобы обойти эти труд-
ности, предлагается алгоритм, основанный на "прослеживании
контуров".
433.2. МЕТОД ПРОСЛЕЖИВАНИЯ КОНТУРОВ
Принцип. На основе метода заполнения области путем "про-
слеживания контура" определяют четность для точки Р (рис. 4.2).
--• Рз£ области
PlG контуру
Ребро, ориентированное вниз
Рис. 4.2. Сравнение "точка — контур** методом прослеживания контуров
Для реализации предлагаемого способа подсчитывают число
пересечений горизонтальным лучом, расположенным слева от рас-
сматриваемой точки, с множеством ребер контура без учета
горизонтальных ребер и тех ребер, которые заканчиваются на пря-
мой.
Алгоритм
Сопоставление ТОЧКА - НЕВЫПУКЛЫЙ КОНТУР
Начало (метод прослеживания контура}
(исследуемая точка (хр, ур), пЬа=число ребер,
ребро контура задано начальной (xdeb, ydeb)
и конечной (xfin, yfin) точками}
внутри: =ложно: контур: =Л0ЖН0;
xdeb: =х(первая вершина); ydeb: =(первая
вершина);
xfin: =х(следующая вершина);
153

yfin: =y(следующая вершина)
Пока (ребро не последнее и. не контур)
выполнять
Начало
если ydeb=yfin (устранение
горизонтальных ребер)
то если ydeb>yfin (ребра
направлены вниз)
иначе если yfi n<yp
Lfl Ё£ДЦ ydeb >yp
LQ если yfi n >ур или
xdeb <xp
тл х BHyTp:=(ydeb-y)*
((xfi n- xdeb) /(ydeb- yfi n))
если х внутр <xp
lfl. если x внутр: =хр
lfl. контур: =
истинно
иначе внутр
:= 1 не внутр;
ШШИ если
шшц если.
Ш1£ц если
шши если
ИЫаЫ£ если yfin=yp lfl если xfin=xp
lfl. контур=И£1щнл конец если
ILQHfili если
иначе (ifl. противоположный край)
иначе если (ydeb=yp и. xdeb<xp<xfin)
lfl. контур :=истинно конец если
Ш1£Ц если
xdeb: =xf i n; ydeb: =xf i n;
xfi n: =x( следующая вершина);
xfi n: =y( следующая вершина);
154

Несколько замечаний. Достоинства метода
"прослеживания контуров" многочисленны:
особые частные случаи обрабатываются достаточно легко;
многоугольник может иметь произвольную форму; в частности,
его стороны могут пересекаться, его контур может состоять из не-
скольких фигур — внутренних и внешних;
метод легко сочетается с контролем четности; если обнаружены
два пересечения, то ясно, что точка расположена снаружи мно-
гоугольника.
Теоретическая сложность составляет величину O(nbsom).
4.3.4. ЗАКЛЮЧЕНИЕ
Если контур выпуклый, то алгоритм Шамоса обладает преиму-
ществами в случаях, когда контур используется несколько раз и
число ребер достаточно велико. Для контуров произвольной формы
(невыпуклых) из четырех методов обработки наиболее пред-
почтительным представляется метод "прослеживания контуров*9:
особые частные случаи легко преодолеваются с помощью до-
полнительных вычислений;
контуры могут содержать внутренние замкнутые области
("отверстия"), внешние грани могут пересекаться или быть разом-
кнутыми (все эти случаи представляют большие трудности для
других методов);
оценка различных алгоритмов показала, что данный метод
обладает преимуществами вследствие простоты вычислений
(см. [19]);
возможна проверка на четность.
4.4. РАЗРЕЗАНИЕ ОТРЕЗКА ПРЯМОЙ МНОГОУГОЛЬНЫМ
КОНТУРОМ
4.4.1. ВВЕДЕНИЕ
Разрезание отрезка прямой контуром используется в основном
в процессе создания векторных рисунков. В большинстве случаев
этим приемом определяют ту часть сцены, которая видна в окне.
Поскольку сцена образована множеством отрезков прямых, то
используемый алгоритм характеризуется только типом окна. Для
этого необходимо знать форму окна: в виде прямоугольника
(параллельны ли его стороны осям координат) или многоугольника
(выпуклого или произвольного).
155

В следующих подразделах будут рассмотрены алгоритмы разре-
зания применительно ко доем трем перечисленным типам окон. В
табл.5 приведена сводка характеристик различных методов.
Таблица 5. Разрезание отрезков прямой многоугольным окном
1 Название
1 метода
1 Сазерленда
1 (дихо-
1 томический
1 вариант)
1 Сазерленда
1 — Коэна
1 Павлидиса
1 Прос-
1 леживание
1 контура
Окно
Прямоу-
гольное
Прямоу-
гольное и
выпуклое
Прямоу-
гольное и
выпуклое
Произволь-
ной формы
Элементарные операции
Сравнение поло-
жения точки и кон-
тура (с
кодированием)
Вычисление се-
редины отрезка
Кодирование точки
относительно контура
Вычисление точки
пересечения отрез-
ков прямых
Сравнение точка-
отрезок (однородные
координаты)
Вычисление точки
пересечения отрез-
ков прямых
Сравнение поло-
жения точки по
отношению к прямой
Пересечение прямой
с отрезком другой
прямой
Сложность
О (Log2
(размер
отрезка))
0(2п),
где п —
число
ребер
контура
О(п)
О(п)
Примечания
Удобен для
реализации на жес-
ткой логике
Возможно распарал-
леливание
Обобщение на вы-
пуклый контур за-
труднено
Обобщение на вы-
пуклый контур за-
труднено (особые
случаи)
Сравнение с реб-
рами не обязатель-
но исчерпывающее
и произвольная
ориентация конту-
ра в случае выпук-
лости
Обобщение на не-
выпуклые контуры
очень затруднено и
дорогостоящее (осо-
бые случаи) 1
Сравнение в невы- 1
пуклом случае не
обязательно исчер- 1
пывающее 1
Очень простая 1
обработка особых 1
случаев 1
Контур невыпук- 1
лый и произволь- 1
ный: разомкнутые 1
линии, внутренние 1
области (отверстия), 1
пересекающиеся 1
ребра 1
156

4.4.2. РАЗРЕЗАНИЕ ПРЯМОУГОЛЬНЫМ ОКНОМ
44.2.1. ВВЕДЕНИЕ
Задача разрезания сцены прямоугольным окном встречается
наиболее часто:
в процессе создания рисунков или изображений;
при вырезании части сцены с помощью эффекта "вариообъ-
ектива";
в алгоритмах удаления невидимых линий при визуализации
трехмерных сцен (в частности, по методу Варнока).
•Обычный тривиальный метод состоит в том, чтобы постоянно
проверять, является ли вычисленная точка видимой или
невидимой. Этот метод, известный под названием fenetrage par
effacement, обладает заметным недостатком: он требует времени на
обработку, пропорционального сложности исходного, а не только
видимого изображения.
•Для разрезания прямолинейного отрезка прямоугольным
окном реализация на жесткой логике алгоритма Сазерленда
(дихотомический вариант) представляется наиболее удачной. Что
же касается программного обеспечения, то при достаточно боль-
шом числе горизонтальных или вертикальных отрезков метод
Павлидиса предпочтительнее метода Сазерленда—Коэна.
В следующих подразделах будет показано, что методы Сазер-
ленда и Павлидиса могут быть обобщены на случай выпуклого
окна.
АА22. АЛГОРИТМ САЗЕРЛЕНДА-СПРУЛЛА
Метод, впервые предложенный Сазерлендом и Спруллом [43],
состоит в точном вычислении видимых частей изображения,
причем список отображения содержит только их относительные
порядки. Операция разрезания применяется к отрезкам прямой, но
может быть обобщена на графические символы.
Принцип действия алгоритма заключается в следующем. Каж-
дую сторону окна продолжают в обоих направлениях так, чтобы
в пространстве пользователя образовались девять разграниченных
областей. Каждой области присваивается четырехразрядный
двоичный код. Внутренняя часть непосредственно окна кодируется
значением 0000:
(D Ю
1001
0001
0101
1000
0000
0100
1010
0010
0110
I (4)
О)
«
0) I
157

Каждой из четырех прямых присваивается один разряд. Его
значение равно 0 для всех точек, расположенных в полуплоскости,
в которой находится внутренняя часть исходного прямоугольного
окна, и 1 для точек другой полуплоскости. Алгоритм разрезания
состоит в нахождении части прямой, которая видна в окне. Для
этого начинают с определения местоположения концов прямой
относительно полученных девяти областей и присваивания каждо-
му концу кода соответствующей области.
1001
1000
1010
Рис. 4.3. Алгоритм разрезания
Из рис. 4.3. видно, что существуют три варианта расположения
отрезков прямых относительно окна:
оба конца расположены вне окна (отрезки AB,CD,EF);
оба конца расположены внутри окна и имеют поэтому код 0000
(отрезок IJ);
только один конец расположен внутри окна и имеет код 0000
(отрезок GH).
Принцип удаления невидимых частей линий очень прост:
выполняют операцию конъюнкции над кодами, присвоенными
концам отрезка;
если результат конъюнкции не нулевой, то весь отрезок на-
ходится вне окна и поэтому не виден;
если результат равен нулю, то отрезок делят на две части и к
каждой из них применяют указанную процедуру до тех пор, пока
не будут удалены его невидимые части и останется только та его
часть, оба конца которой имеют код 0000.
В этом алгоритме используются три элементарные функции:
определения кода точки;
конъюнкции двух кодов;
вычисления координат середины отрезка.
158

Последняя из операций выполняется весьма просто для отрезка,
концы которого заданы точками с координатами соответственно
xl yl и х2, у2. Точка, находящаяся в середине отрезка, имеет
координаты (x2+xl)/2, (y2+yl)/2. Если координаты концов —
целые числа, то определение средней точки сводится к двум сло-
жениям и двум сдвигам кодов вправо на один разряд.
Если алгоритм используется для обработки фигур в простран-
стве экрана, где координаты точек представляются целыми
числами, то при максимально возможной длине отрезка, равной
2 , понадобится не более к операций определения положения
отрезка относительно контура.
Временные затраты для алгоритма находятся в логарифмичес-
кой зависимости от длины отрезка.
4.423. АЛГОРИТМ ПАВЛИДИСА [33]
Павлидис также разбивает плоскость на 9 областей (рис. 4.4).
1
4
7
2
8 ,
3
6
9
Рис. 4.4. Разрезание прямоугольным окном
Он выделяет в первую очередь особые случаи расположения отрез-
ков: слева, справа, сверху и снизу от окна, а также отрезки
вертикальные и горизонтальные. В общем случае, после того как
вычислены знаки четырех углов окна относительно прямой, в ко-
торой содержится рассматриваемый отрезок, сравнением знаков уг-
лов проверяется, лежат ли взятые попарно смежные угловые точки
окна по одну или по разные стороны этой прямой. Если да (т.е.
знаки противоположные), то отрезок может разрезать одну сторо-
ну окна, соединяющую вершины двух углов.
Приводимый ниже алгоритм Павлидиса реализует разрезание
отрезка прямой, заданного своими концами (xl, yl) и (х2, у2),
прямоугольным окном с абсциссами xmin, xmax и ординатами
ymin, ymax.
РАЗРЕЗАНИЕ - ВАРИАНТ 1 (xmi n, xmax, ymi n, ymax: целые)
{разрезание прямолинейного отрезка
прямоугольным окном: алгоритм Павлидиса}
Начало
159

1- если (xl<xmin и_ x2<xmin) и/ui
(xl>xmax и^ x2>xmax)
или (yl<ymin и_ y2<ymin) или_
(yl>ymax ц y2>ymax)
то конец разрезания. Конец если
2- если (yl>y2) тр_ (переменная концов}
x:=xl, xl:=x2, х2: =х;
y=yl, yl:=y2, у2: =у,
3- если yl=y2
то если xl>x2 то^ перемена концов
конец если
если xl<xmin" то xl:=xmin
конец если
если х2>хтах то х2: =хтах
конец если
отобразить отрезок (xl, yl, х2,у2);
конец разрезания,
конец если
4- если xl=x2
то если yl<ymin, то yl:=ymin
конец если
если у2>утах, то у2: =утах
конец если
отобразить отрезок (xl, yl, х2, у2);
конец разрезания
конец если
5- dy: =yl - у2; dx: =xl - х2; dxy: =xl. у2- у2. х2;
qx: =xmi n. dy, qX: =xmax. dy,
qy =mi n, dx; qY: =ymax. dx;
ul: =qx- qy+dxy, u2: =qx- qY+dxy,
u3: =qX- qY+dxy, u4: =qX- qy+dxy
6- j: =0
7- если ul.u2<0
то (ul и u2 имеют разные знаки}
j:=j+l;
если xl <xmi n
то yl: =( xmi n. dy+dxy) /dx; xl: =xmi n;

учесть dx, dy, dxy,
если x2<xmin
Ш. y2: =( xmi n. dy+dxy) /dx; x2: =xmi n;
учесть dx, dy, dxy,
конец если
конец если
8- если u2. u3<0
10. (u2 и u3 имеют разные знаки}
j:=j+l;
если. y2>ymax
LQ. х2: =( утах. dx- dxy) /dy, y2: =ymax;
учесть dx, dy, dxy,
конец если
конец если
9- если. иЗ. и4<0
IA. {иЗ и и4 имеют разные знаки}
если xl>xmax
то. yl: =( xmax. dy+dxy) /dx; xl: =xmax;
учесть dx, dy, dxy,
конец если
если x2>xmax
то» у2: =( xmax. dy+dxy) /dx; x2: =xmax;
учесть dx, dy, dxy,
конец если
конец если
10- если u4. ul<0
то. (u4 и ul имеют разные знаки}
j:=j+l;
если yl <ymi n
то. xl:=(ymin, dx-dxy)/dy, yl:=ymin;
учесть dx, dy, dxy,
конец если
конец если
11- если j>0 то_ отобразить отрезок
(xl,yl,x2,y2)
конец если
Конец разрезания 1
161
6 - Ж. Эгрон

4.4.3. РАЗРЕЗАНИЕ ВЫПУКЛЫМ КОНТУРОМ
443.1. ВВЕДЕНИЕ
Метод Сазерленда может быть обобщен на выпуклые контуры
(см. [8 ]), но во многих особых случаях его использование сущест-
венно затруднено (отрезки, коллинеарные краям окна, и др.).
Ниже приводится алгоритм Павлидиса, в котором эти трудности
легко преодолеваются.
4.43.2. АЛГОРИТМ ПАВЛИДИСА [33]
Павлидис использует в своем алоритме представление точки Р
однородными координатами:
Р -
Чтобы изложить алгоритм Павлидиса согласованно с другими
алгоритмами, представленными здесь, примем w^l, a x и у — аб-
солютные координаты точки Р на плоскости хоу.
Постановка задачи. Пусть Si, S2, ..., Sn — вершины вы-
пуклого многоугольника, а отрезок прямой задан своими концами
Р1 и Р2. Задача состоит в определении, части отрезка, находящей-
ся внутри многоугольника.
Общая идея. Пусть (щ ,у[) — координаты вершины sj, a
(xj ,yj) — координаты точки Pj(j=l,2).
Определим п значений величин S\ следующим образом:
Si = det(Si ,pl,p2)=
- Xi (yl-y2)+Yi(x2-xl)+(xl.y2-yl.x2), (4.1)
i=l,2,...,n.
На основе этих вычислений выделим следующие случаи:
1. Значения S\ отличны от нуля и имеют один и тот же знак:
многоугольник расположен по одну сторону отрезка и последний
находится вне многоугольника.
2. Одно из значений Si равно нулю, а остальные имеют одина-
ковые знаки: прямая проходит через одну из вершин, но остается
вне многоугольника.
3. Два значения равны нулю, а остальные имеют одинаковые
знаки: прямая проходит через одну из сторон выпуклого много-
угольника, не пересекая его других сторон (выпуклость).
4. Одно или два значения равны нулю, а остальные имеют раз-
ные знаки: прямая пересекает многоугольник, переходя через одну
или две его вершины.
5. Ни одно из значений Si не равно нулю, но все значения име-
ют разные знаки: здесь при обходе периметра многоугольника име-
ем двукратное изменение знака (как в случае 4).
162

Через Sj, Sj+i и s^, s^+i обозначим пары вершин, в которых
происходит изменение знака,, а через L1 и L2 — соответственно
определяющие их отрезки (для одной из вершин одной из пар
возможно равенство S| * 0, как в случае 4).
Теперь, зная, какие две стороны многоугольника пересекаются
прямой, включающей в себя отрезок (pl,p2), необходимо опре-
делить положение точек pi и р2 по отношению к двум отрезкам
L1 и L2, проанализировав знаки четырех величин:
ul - det(pl,sj ,Sj+i)e
- xl (Yj -Yj+1)+yl(XJ+1 -Xp+CXjY^! -YjXj+i)
(положение точки pi относительно отрезка LI);
u2 « det(p2, sj, Sj+i)«
- x2 (Yj -Y^+yiCXjH -Xj)+(XjYj+1 -YjX^)
(положение точки р2 относительно отрезка LI);
u3 « det(pl,Sk, Sk+i)»
- xl (Yk -Yk+1)+yl(Xk+1-Xk)+(XkYk+1-YkXk+1)
(положение точки pi относительно отрезка L2);
u4 - det(p2,sk, Sk+i)"
- x2 (Yk -Yk+1)+y2(Xk+1 -Xk)+(XkYk+1 -YkXk+1)
(положение точки р2 относительно отрезка L2).
При обходе контура в направлении по часовой стрелке, знак U
будет отрицательным, когда точка будет находиться внутри мно-
гоугольника. Выражение (4.2) будет равно нулю, если точка
принадлежит контуру.
Пусть L — отрезок, концы которого заданы точками pl,p2, a
ql,q2 — концы отображаемого отрезка, полученного в результа-
те разрезания многоугольником отрезка L. Согласно приведенному
ниже алгоритму вычисляются точки ql и q2 с учетом различных
вариантов расположения концов pi и р2 отрезка L
Алгоритм. Будем использовать следующие структуры данных:
•Одномерные массивы XO...N) и YG...N), содержащие ко-
ординаты N вершин многоугольника.
•Координаты xl,yl и х2,у2 — точек pi и р2 соответственно.
•Двумерные массивы В(0...2,0...2) и С(0...2,0...2), содержащие
соответственно первые и вторые координаты пар вершин (Sj, Sj+i)
и (sk, sk+i).
•Массив v(0...4), содержащий знаки величин uj, i-1, ...,4,
представляющих знаки концов отрезка относительно двух сторон
многоугольника, разрезанных прямой, на которой расположен
отрезок. Здесь (qn)n*l,2 — координаты отображаемого отрезка.
РАЗРЕЗАНИЕ - ВАРИАНТ 2
(разрезание отрезка прямой L выпуклым
многоугольником: алгоритм Павлидиса}
(4.2а)
(4.26)
(4.2в)
(4.2г)

Начало
(обход контура и подсчет ребер, разрезаемых
прямой линией}
X(n+1):-X(l); Y(n+1):-Y(l);
dx:=x2-xl; dy:=yl-y2; dxy: =xl. y2-yl. x2;
S: =X( i). dy+Y( i). dx+dxy, (уравнение (1)}
u: =signe(S);
k:=0; {число разрезаемых ребер}
1:-2;
Пока (i>n+l u_ k*2) выполнять
Начало
Si: =X( i). dy+Y( i). dx+dxy,
v: =signe(Si);
если u*v и, u*0
т£ {изменение знака}
k:=k+l;
B(k,l):=X(i-l); B(k,2):=Y(i-l);
C(k,l):-X(i); C(k,2): =Y(i);
иначе если (u=0 и_ v=0 )
то конец разрезания 2
конец если
u: =v;
конец
{вычисление и отображение видимой части
отрезка прямой L}
если к=2
10 ul:=det(pl,B(l,*),C(l,*));
{уравнения 2}
u2:=det(p2,B(l,*),C(l,*));
u3:=det(pl,B(2,*),C(2,*));
u4:=det(p2,B(2,*),C(2,*));
vl: =si gne(Ul); v2: =signe(U2);
v3: =signe(U3); v4: =signe(U4);
если (v(l)=v(3) и v(l)*v(2)
и v(l)*v(3))
IQ_ конец разрезания 2
иначе Для m: =1 ДО. 2
выполнять
164

Начало
если v(m) *v(m+2)
Т£ если v(m)<0
то.
qnr =пересечение( L, L2);
иначе
qm: =пересечение( L, L1);
конец если
иначе
qirc =pm;
конец если
конец
конец если
иначе конец разрезания 2;
конец если
отобразить отрезок (ql,q2);
Конец разрезания 2
Обработка особых случаев. Рассмотрим такие положения, когда
прямая, на которой лежит отрезок, проходит через одну из вершин
многоугольника или один из концов отрезка принадлежит сто-
роне многоугольника.
•Обход контура: особенность имеет место, если есть
такое значение i, при котором знак (Si) равен нулю. В случае,
когда две соседние вершины имеют знак нуль (u-v-O), отрезок L
является невидимым. В противном случае, если одна вершина Si
имеет знак нуль, учитываем только сторону (si-i, Si), т.е. тогда
знак (Si-О^знак (Si) и знак (Si-i)*0.
•Вычисление видимой части отрез-
ка L: есть одна особенность, если одно из двух значений Ui рав-
няется нулю.
Если нулю равны два значения Ui, то qi -pi и q2 -р2 , пос-
кольку pi и р2 принадлежат контуру многоугольника, a L принад-
лежит этому многоугольнику (выпуклость). Если нулю равняется
одно из значений Ui, то только один из концов (р) отрезка L
принадлежит контуру. В этом случае, если знак другого конца (р)
по отношению к стороне Lp, которой принадлежит конец р,
положителен, он невидим. В противном случае, если этот знак
отрицателен, то qi-p, a q2-p\ если знак р относительно Lp'
отрицателен; в противном случае q2" Lp' П L (рис. 4.5).
Несколько замечаний. В процессе отыскания
ребер, пересекающих прямую, обход вершин контура не обяза-
165

p'
(->
V*
+ (")*<' ^V ^^*^*^ Рис. 4.5. Особый случай, когда один из
D ^- —^**^ концов принадлежит контуру:
в скобках — знак точки р' относительно Lp', вне
-г скобок — знак точки р относительно Lp
тельно должен быть исчерпывающим (когда имеется пересечение),
и трудности, возникающие в особых случаях, легко преодолевают-
ся. Однако следует обходить контур в направлении по часовой
стрелке (априорная ориентация).
4.4.4. РАЗРЕЗАНИЕ ПРОИЗВОЛЬНЫМ КОНТУРОМ
44,4.1. ВВЕДЕНИЕ
Алгоритм Сазерленда нельзя обобщить на контуры произволь-
ной формы, поскольку невыпуклый контур может пересекать
прямую линию более двух раз. На случай невыпуклых контуров
нами обобщен алгоритм Павлидиса [17]. Обобщение оказалось
возможным, но сложным. Было показано, что обработка особых
случаев достаточно затруднительна и требует повышенных за-
трат, поскольку для ребра (Si,S|+i), если знак одной из вершин есть
нуль (т.е. либо Si-O, либо Si-цЧ)), необходимо учесть две предше-
ствующие вершины, Si-2 и Si_i или одну предыдущую Si_i и две
следующих, Si+2 и si+з , или только одну следующую вершину Si+2.
Чтобы обойти эту трудность, мы использовали идею нашего ал-
горитма наклонного штрихования без поворота в сочетании с ме-
тодом прослеживания контура.
4ЛА2. АЛГОРИТМ ПРОСЛЕЖИВАНИЯ КОНТУРА
Итак, задача состоит в том, чтобы вычислить результат пере-
сечения отрезка прямой невыпуклым контуром (рис. 4.6).
Отрезок прямом
Видимые части
Рис. 4.6. Разрезание отрезка прямой невыпуклым окном
166

Принцип. Рассмотрим уравнение прямой, проходящей через за-
данный отрезок. Пусть а и b — приращения в направлении х и у
соответственно. Для определенности примем, что | а | £ | b |. В
противном случае все рассуждения остаются справедливыми при
замене х на у и наоборот.
Пусть у- (Ь/а)х + уО — уравнение прямой, включающей в себя
отрезок с началом в точке (xd,yd) и концом в точке (xf,yf), где
величина уО определяется выражением уО - yd(b/a)xd. Любая
вершина s\ с координатами (xi,yi) характеризуется величиной
ysi«yi-(b/a)xi. Каждое ребро многоугольника считаем
ориентированным таким образом, что ysi^ysH-i (рис. 4.7).
у = (а/Ь)х ♦ уО
Отрезок прямом
Рис. 4.7. Моделирование многоугольника и отрезка прямой
Чтобы определить точки пересечения отрезка с много-
угольником, выполним следующие операции:
вычислим все точки пересечения многоугольника с прямой и
упорядочим полученный массив точек в порядке возрастания
абсцисс. В результате образуется список частичных отрезков,
ограниченных парами точек, причем каждые две части отрезка,
будучи несмежными между собой, соединятся другим частичным
отрезком, расположенным справа от одного и слева от другого
(рис. 4.8а);
вычислим множество частичных отрезков, принадлежащих дан-
ному и расположенных внутри многоугольника, определив пересе-
чения с множеством отрезков, упорядоченных и ранее определен-
ных (рис. 4.86).
Первая фаза описываемого процесса выполняется согласно сле-
дующему алгоритму:
167

Av а. Результат
Рис. 4.8. Пересечение отрезка с многоугольником:
а - упорядоченное множество отрезков; б - пересечение разрезаемого отрезка с упорядоченным
множеством отрезков
Упорядоченный список пересечений
Начало
список LINTER пуст;
Для каждого ребра (s\ , si+i ) выполнять
Начало
если ys ,>ys 1+1
то если (ysi>yo и ysi+i<yo)
то. {ребро пересекает прямую (не
учитываются ребра,
заканчивающиеся на прямой)}
xi nter: =( ys i- yO) • (x i+i- x i) /
(yi+i-yi)-(b/a)(xi+i-Xi));
yi ner: =( b/a). xi nter+yO;
Добавить точку пересечения
(xinter, yinter) к LINTER,
соблюдая порядок возрастания
ребер.
конец если
иначе если ysi<ysi+i то. (то же, но
с переменой s\ и Si+i);
иначе (ребро принадлежит
несущей прямой}
конец
Конец;
Пересечение отрезка (xd,yd), (xf,yf), где xd<xf, с упорядочен-
ным списком отрезков, определенных списком пересечений, вы-
полняется согласно следующему алгоритму:
168

Пересечение отрезка и списка отрезков
Начало
если LINTER^nycTO
то_
внутренний: «ложно;
получить точку первого пересечения
(xint, yint);
есть пересечение: -истинно;
Пока (есть пересечение и xintxxd),
выполнять
начало
внутренний: - ] внутренний;
следующее пересечение;
учесть пересечение;
конец
если есть пересечение
то. хс: «xd;
ус: -yd;
пока (есть пересечение и
х1nt<xf) выполнять
начало
xs:»xint; ys:=yint;
если (внутренний и. xc*xs)
то_ выделить отрезок (хс,ус),
внутренний: - ] внутренний;
хс: »xs; ус: »ys;
следующее пересечение;
учесть пересечение;
конец если
если есть пересечение
то если (внутренний и xc*xf)
Т£ выделить
отрезок ((xc,yc),(xf,yf))
конец если
конец если
конец если
конец если
Конец
7-Ж.Эгрон
169

Если отрезок полностью или частично совпадает с ребрами кон-
тура, то его части, попадающие внутрь контура, определяются на
основе анализа разностей соответствующих длин отрезков и ребер
контура.
В частном случае, когда отрезок занимает вертикальное поло-
жение, следует поменять местами роль абсцисс и ординат.
Изложенный метод обладает следующими достоинствами:
при выпуклом многоугольнике нет необходимости в исчерпыва-
ющем переборе всех ребер контура;
очень простая обработка особых частных случаев, заключающа-
яся в устранении вычислений точек пересечения несущей прямой
с ребрами многоугольника, параллельными ей или заканчива-
ющимися на ней.
форма контура может быть любой: разомкнутой, с пересека-
ющимися ребрами; внутри фигуры, ограниченной контуром, могут
быть отверстия (другие замкнутые контуры).
4.4.5. ЗАКЛЮЧЕНИЕ
В этом разделе мы рассматривали разрезание отрезка прямой
окнами трех типов: прямоугольным, выпуклыми и невыпуклыми
(см. сводную табл.5). В частном случае, когда окно имеет форму
прямоугольника, метод Сазерленда (дихотомический вариант)
наилучшим образом приспособлен для реализации на жесткой
логике. В ином случае аппаратная реализация на прог-
раммируемом устройстве лучше согласуется с алгоритмом
Павлидиса, причем степень преимущества определяется харак-
теристиками сцены (содержанием в ней вертикальных и горизон-
тальных линий).
С другой стороны, мы выделили два метода сравнения точки
и отрезка прямой:
первый основан на решении уравнения прямой, проходящей че-
рез отрезок и точку;
во втором используются однородные координаты точки.
Во втором методе неявно устраняется необходимость деления на
нуль в частных случаях, когда прямая занимает горизонтальное
или вертикальное положение. Первый метод требует специальных
мер для предотвращения такого деления в частных случаях.
4.5. РАЗРЕЗАНИЕ МНОГОУГОЛЬНИКА МНОГОУГОЛЬНЫМ
ОКНОМ
4.5.1. ВВЕДЕНИЕ
Задача ставится следующим образом: найти результат пересе-
чения одного многоугольника другим (окно также имеет форму
многоугольника). В результате образуется многоугольный кон-
тур, видимый внутри окна (рис.4.9).
170

Р*эр«м«мый ^^^^ ^^^ЛАмвгоугольмо* окмо
многоугольник **^^^^ ^**^>^^^ ^ЧччЖ^
Р«эультируимци£ ^^ j^ I
многоугольник Л|''Д
Рис. 4.9. Разрезание многоугольника многоугольным окном
Одним из первых алгоритмов разрезания многоугольника, поз-
воляющим получать контур, был алгоритм разрезания много-
угольника прямой, предложенный Сазерлендом и Ходжменом [42 ].
Позднее Шамос [75 ] разработал алгоритм пересечения двух вы-
пуклых многоугольников, основанный на разбиении плоскости на
треугольные секторы. Для решения этой задачи О Турке [30]
предложил новый метод, согласно которому точки пересечения
двух многоугольников находились в процессе постепенного поша-
гового обхода одного из них. Затраты на оба метода линейно
зависят (прямо пропорциональны) от числа ребер обоих контуров,
в то время как тривиальное решение, состоящее в сравнении все-
возможных пар ребер, требует затрат, пропорциональных произве-
дению числа ребер каждого контура.
4.5.2. АЛГОРИТМ САЗЕРЛЕНДА И ХОДЖМЕНА
4.5.2.1. РАЗРЕЗАНИЕ МНОГОУГОЛЬНИКА ПРЯМОЙ
Требуется определить, какая часть произвольного много-
угольника находится в определенной полуплоскости, заданной не-
которой прямой. Задача состоит в том, чтобы для многоугольника,
описанного последовательностью вершин si,S2,...,Sp , найти новую
последовательность (в частном случае она может оказаться пус-
той) si,S2,...,Sq вершин, расположенных в рассматриваемой полуп-
лоскости. Для этого воспользуемся алгоритмом Сазерленда и Ход-
жмена, состоящим в обходе многоугольника, ребро за ребром, и
исследовании положения конечной точки каждого ребра
относительно разрезаемой прямой.
Алгоритм обработки многоугольника можно записать в следую-
щем виде:
РАЗРЕЗАНИЕ МНОГОУГОЛЬНИКА ;
Начало (разрезание многоугольника прямой линией;
функции PREMIER S0MMET (ПЕРВАЯ ВЕРШИНА) и
SOMMET SUIVANT (СЛЕДУЮЩАЯ ВЕРШИНА)
позволяют обойти последовательность ребер
7*
171

многоугольника; эта последовательность
оканчивается значением 0}
целочисленная переменная Р;
логическая переменная PREMIER;
вещественные ХР, YP, XS, YS, XJ, YJ, XI, YI;
Р: -PREMIER SOMMET; PREMIER: -истинно;
QQUL Р*0 ВЫПОЛНЯТЬ
иаыада
ХР: -Х(Р); YP:»Y(Р); (координаты вершины)
ЕСЛИ. PREMIER
то начало
PREMIER: «ложно
XJ:=XP; YJ: -YP; {сохранение первой
вершины}
конец
иначе если РЕБРО РАЗРЕЗАЕТСЯ {проверка
по отношению к прямой}
то начало
ВЫЧИСЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ (XI,YI);
ВЫХОД (Х1Д1);
конец
XS:-XP; YS: -YP; {последний конец
становится исходным}
если S вершина ВИДИМА
то ВЫХОД (XS, YS);
SOMMET SUIVANT
конец
(обработка замыкающего ребра)
если SJ РАЗРЕЗАЕТСЯ
то начало
ВЫЧИСЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ (XI,YI);
ВЫХОД (XI,YI);
конец
конец РАЗРЕЗАНИЯ МНОГОУГОЛЬНИКА;
Пересечение многоугольника прямой нельзя рассматривать как
простое расширение понятия пересечения двух прямолинейных
отрезков.
Необходимо решать два типа задач.
•Особое внимание следует уделить невыпуклым много-
угольникам, при пересечении которых могут появляться вырож-
денные многоугольники такого вида:
172

Однако нам хотелось бы получить два многоугольника, опреде-
ляемых вершинами (Si,i2,ii) и (82,14913)*
•Могут встретиться также особые случаи:
вершина принадлежит прямой;
случай коллинеарности (ребро принадлежит прямой — две со-
седние вершины лежат на этой прямой).
Особые случаи требуют особой обработки. В частности, задача
может быть решена более детальным рассмотрением понятия пере-
сечения прямолинейного отрезка (ребра) с прямой. Пусть Р — рас-
сматриваемая полуплоскость, a D — прямая. Имеются две
вершины: S| и S|+i . Можно утверждать, что ребро (si,Si+i) пере-
секает прямую, если удовлетворяется одно из перечисленных ус-
ловий:
S\ и Si+i расположены по разные стороны прямой D, причем s4
и Si+igD;
S| G Р и sh-i £ D, т.е. ребро пересекает прямую в точке Sj+i ;
^ Е D и st+i € Р, Si-i £ Р, т.е. ребро пересекает прямую в
точке si.
4S22. ОБОБЩЕНИЕ НА СЛУЧАЙ РАЗРЕЗАНИЯ МНОГОУГОЛЬНИКА ОКНОМ
Алгоритм Сазерленда и Ходжмена можно использовать для раз-
резания выпуклым окном произвольного многоугольника. На пер-
вом шаге разрезаем многоугольник прямой, проходящей через пер-
вое ребро окна, сохраняя при этом результирующий список
вершин, находящихся в полуплоскости окна. Затем, исходя из
одного результирующего многоугольника (или нескольких), таким
же образом разрезаем прямую, проходящую через второе ребро
окна, и т.д. до последнего ребра окна. В случае невыпуклого мно-
гоугольника требуется принимать особые непростые меры для пре-
дотвращения появления невырожденных многоугольников.
Кроме того, сложность такого обобщения составляет величину
0(m*n), где m , n - число вершин в каждом из пересекающихся
многоугольников. В следующем подразделе будут рассмотрены два
алгоритма разрезания выпуклых многоугольников (Шамоса и
О'Рурке), сложность которых составляет 0(m+n).
4.5.3. ПЕРЕСЕЧЕНИЕ ДВУХ ВЫПУКЛЫХ МНОГОУГОЛЬНИКОВ
Рассмотрим два многоугольника, Р и Q, содержащие пит
граней соответственно. Задача состоит в определении списка
173

вершин многоугольника, образующегося в результате пересечения
двух исходных многоугольников, Р П Q,
4.53.1. МЕТОД ШАМОСА
Пусть имеются два контура, ориентированные в произвольном
направлении.
•Принцип. Многоугольник Q разрезают на ш треугольных сек-
торов начиная с точки q, находящейся внутри контура (см. метод
Шамоса для сопоставления точки и выпуклого контура):
Начало спсчета
секторов
(Сложность такого разделения составляет О(ш).
Возможны два случая: точка q может оказаться либо внутри,
либо вне многоугольника Р.
Точка q находится внутри Р
1. Исследуем, к какому сектору принадлежит каждая вершина
контура Р.
Поскольку оба контура ориентированы и каждый контур проходит
через каждый сектор только по одному разу, то это исследование
требует затрат 0(n+m).
2. Обходя контур многоугольника Р, рассматриваем каждое его
ребро (рьРн-ih Возможны различные варианты расположения
ребер:
а) оба конца ребра (Pbft+i) принадлежат одному и тому же сек-
тору:
174

если оба расположены внутри или снаружи контура Q, то пере-
сечения нет:
если расположены по разные стороны контура, то есть пересе-
чение с ребром соответствующего сектора:
б) два конца ребра принадлежат двум различным секторам:
если оба находятся внутри многоугольника Q, то пересечения
нет (свойство выпуклости):
если расположены по разные стороны контура, то пересечение
есть:
175

если расположены снаружи контура, то или пересечения нет:
Pi
или есть два пересечения:
$■$
или бесконечное множество пересечений (коллинеарность):
&
3. Если искомый многоугольник, являющийся результатом
пересечения, существует, то он получается путем попеременного
обхода контуров Р и Q. Изменение происходит при переходе к
точке пересечения.
•Точка q находится вне контура Р
В точке q контур Р стягивается углом а. Разделим контур на
две подпоследовательности ребер, которые будут порознь обрабо-
таны методом, описываемым ниже. Приведем пример:
176

Подпоследовательности обозначены штриховой (—) и сплош-
ной ( ) линиями.
Алгоритм. Пусть многоугольники Р и Q ориентированы в на-
правлении, определяемом упорядоченными списками вершин
(sPi)hi,2, п и (sqj)j-it2, m соответственно.
В общей форме алгоритм Шамоса можно представить следу-
ющим образом:
Алгоритм Шамоса
Начало (пересечение двух выпуклых
многоугольников Р и Q}
Вычислить точку q внутри многоугольника Q ;
Разбить Q на ш направленных векторов;
Если q находится внутри Р
то. обработка 1;
иначе вычислить две подпоследовательности
вершин многоугольника Р;
для каждой подпоследовательности
выполнять обработку 1;
конец если
Обработка Р П Q * пусто;
Конец
А. Методом вмещающего угла определим, находится ли точка
q внутри многоугольника Р. Для этого выполним простые
вычисления:
177

n
если 2 угол (q spi,q spi+i)a 2 л,
i=i
то q e P,
иначе q £ P {сумма углов равна нулю}.
Для реализации этого алгоритма вначале находим углы (q sqi,
q spi), служащие, кроме того, для определения секторов, которым
принадлежат вершины (spi)j-i,2 п контура Р (здесь (q sqi)—
опорная ось системы полярных координат), а затем на основе этих
углов находим углы (q spi,q spn-i)-
Если точка q не принадлежит контуру Р, то необходимо вы-
делить две подпоследовательности вершин. Первая или последняя
вершина этих подпоследовательностей соответствует тем точкам,
в которых углы (q spi, q spt+i) заменяют знак:
Б.Процедура обработки 1 позволяет для каждой подпоследова-
тельности вершин контура Р вычислять вершины, принадлежащие
общей области РП Q. Отдельной обработки требуют некоторые
особые случаи:
вершины, общие для обоих контуров,
вершина одного контура принадлежит ребру второго контура,
ребра обоих контуров коллинеарны.
Все эти особые случаи пересечения будем рассматривать
отдельно, в зависимости от того, остается ли снаружи или внутри
текущая точка, перемещается ли она изнутри наружу или сна-
ружи проходит внутрь контура. Задача состоит в том, чтобы опре-
делить, в какой точке происходит пересечение (одно или несколь-
ко) ребра контура Р с контуром Q.
В. Определим пересечения.
Пусть (spi ,spi+i) — ребро многоугольника Р. Для каждого его
конца обозначим:
sectl и sect2 — связанные с ними секторы многоугольника Q;
178

intl и int2 — логические переменные, означающие, принадле-
жат ли концы к внутренней области фигуры Q;
contour 1 и contour 2 — логические переменные, уточняющие,
принадлежат ли концы контуру многоугольника Q.
В дальнейшем необходимо различать, принадлежат ли кЬнцы
ребра фигуры Р одному и тому же сектору или двум разным сек-
торам фигуры Q.
1. Концы ребра принадлежат одному сектору
Общий случай (He(contour 1) и не (contour 2)). Здесь
возможны четыре варианта:
•intl и int2 — (рис.4.10а);
•не (intl) и не (int2) — (рис.4.106)
-•intl и не (int2) — (рис.4.10в)
•не (intl) и (int2) — (рис.4 Л Or).
Значение Sectpred соответствует последнему сектору, в котором
находилась точка на выходе из области Q.
(intl, inty)
Рис. 4.10. Отрезки ребра многоугольника Р принадлежат
одному сектору многоугольника Q:
а - ребро находится внутри области Q: spi+i<= Р П Q; б - ребро находится вне
области О; в - выход из области Q: символом • обозначена точка пересечения
е Р П Q; г - вход в область Q: spi+i е Р П Q; точка пересечения 6 Р П Q
Частный случай (имеются два контура 1 и 2).
Здесь также возможны четыре варианта :
•intl и contour 2 — (рис.4.11а);
•contour 1 и int2 — (рис.4.116);
•(не (intl) и (contour 2) или (contour 1 и не (int2))—
(рис.4.11в);
•contour 1 и contour 2 — (рис.4.Иг).
179

«Put
ГЫ1
L^y contour 2
llntl _
llnt2
contour 2 n contour 1
ч^ ч
•—•"Uii
•Я^П 4 I
Рис. 4.11. Частный случай — концы ребра многоугольника Р принадлежат
одному сектору многоугольника Q:
а — выход из многоугольника Q: spi+i € Р П Q; б — вход в многоугольник Q:
spi+i Е Р П Q; в — предполагается, что ребро находится вне многоугольника Q
(нет пересечения); г — коллинеарность; предполагается, что ребро находится
вне многоугольника Q (нет пересечения)
2. Концы ребра принадлежат двум разным секторам
Общий случай (не (contour 1) и не (contour 2)).
Здесь возможны следующие варианты:
•intl и int2 — пересечения нет, так как Q — выпуклый мно-
гоугольник, spi+i Е Р П Q;
•если есть хотя бы одно пересечение, то возможны три варианта:
intl и не (int2) (рис.4.12а);
не (intl) и int2 (рис.4.126);
не (intl) и не (int2) (рис.4.12в-г).
Вершины многоугольника Q принадлежат одновременно и мно-
гоугольнику Р (Р П Q), т.к. они расположены внутри Р и между
двумя последовательными, точками пересечения при входе в Q или
при выходе из негб.
Частный случай (contour 1 и contour 2). Здесь
можно рассмотреть следующие случаи:
•intl и contour 2 (рис.4.13а);
•contour 1 и int2 (рис.4.136);
•одна точка пересечения и
— не (intl) и contour 2 (рис.4.13в)
180

«Put
Uit2
b*l
-]lni2
.пересечение • sqj с ребром (sqt ,sq2 ),
• К|Э с ребром (sq3 ,944 );
.коллинеарность с ребром (sq^sqj).
Рис. 4.12. Концы ребра многоугольников Р не принадлежат одному сектору:
а — выход из многоугольника Q (1 — одно пересечение (G Р П Q); 2 - два
одинаковых пересечения; проход через вершину многоугольника Q (€ Р П Q);
б — вход в многоугольник Q (1 — одно пересечение (€ Р П Q); 2 — два
одинаковых пересечения; проход через вершину многоугольника Q (е Р П Q);
в — концы находятся вне многоугольника Q (проход через) вершину много-
угольника Q (нет пересечений); г — концы находятся вне многоугольника Q
(первое пересечение) — вход в Q, второе пересечение — выход из Q (обе точки
пересечения е Р П Q); д — коллинеарность (предполагается, что Р находится
вне Q (нет пересечения))
ИЛИ
— contour 1 и не(Ы2) (рис.4ЛЗг);
•нет точки пересечения н
— (He(intl) и contour 2) или (contour 1 и He(int2)) (рис.4.13д)
или
— contour 1 и contour 2 (рис.4.13е).
181

*р**|
• Q
•Pui
Рис. 4.13. Частный случай (концы ребра многоугольника Р не принадлежат
одному и тому же сектору):
а — выход из Q (spi+i 6 Р П Q; б - вход в Q (spi Е Р П Q); в — одно пере-
сечение: вход в точку пересечения (€ Р П Q), выход из точки пересечения
spi+i: spi+i Е Р П Q; г — одно пересечение: вход в spi : spi Е Р П Q, выход
из точки пересечения (Е Р П Q); д — предполагается, что ребро находится вне
Q (нет пересечения); е — вход в spi , выход из spi+i: spi и spi+i Е Р П Q
Такое определение пересечения ребра многоугольника Р с кон-
туром многоугольника Q позволяет получать Р П Q при однократ-
ном обходе только ребер Р. Вершины многоугольника Q, принад-
лежащие одновременно Р и Q (Р П Q), расположены между
такими двумя соседними точками пересечения, в первой из кото-
рых в процессе обхода контура Р осуществляется выход из мно-
гоугольника Q, а во второй — вход в него.
182

Вход» Г* \ Выход из
многоугольник Q / j я _д_ \ многоугольника Q
ЕРПО
Для вычисления точки пересечения двух ребер многоугольников
Р и Q будем использовать алгоритм пересечения отрезков прямых
(параметрический метод, описанный в п. 4.5.3.3).
1. Если в конце обработки оказывается, что Р П Q пустое мно-
жество, то это означает одно из двух: либо Р и Q не соприкаса-
ются (разобщены), либо Q С Р. Эта альтернатива разрешается
простым исследованием следующего вида:
если q<P
IP. (Q С Р)
Р П Q:=Q;
иначе (Р и Q разъединены}
Р П Q: =пусто;
конец если
Заключение. Главное достоинство метода Шамоса состоит в
том, что его сложность составляет 0(п+т),т.е. линейно зависит от
числа ребер в контурах. Кроме того, нами было отмечено, что
"вклад" числа вершин п многоугольника Р приблизительно в
четыре раза значительнее, чем вклад числа m вершин много-
угольника Q. На практике, если m > 4п, то Р будет разрезающим
многоугольником, a Q — разрезаемым. В противном случае раз-
резаемым будет многоугольник Р.
Недостаток заключается в необходимости использования обрат-
ной тригонометрической функции (арктангенс).
4532. МЕТОД О'РУРКЕ И ДР.
Алгоритм О'Рурке и др. принципиально отличен от алгоритма
Шамоса.
Принцип. В дальнейшем будем пользоваться следующими обоз-
начениями :
р и q — вершины многоугольников Р и Q соответственно;
если р — текущая вершина, то р_ — предыдущая вершина,
а р+ — следующая;
р — прямолинейный отрезок (р_,р);
183

—hp (р)-{х:рл(х—p—)>0} — полуплоскость, в которой на-
ходится многоугольник Р, определяемая с помощью прямой, про-
ходящей через р (где символ Л означает векторное произведение).
Предикативный указатель (p,q) определим следующим обра-
зом:
указатель (p,q) - истинно, если р Е hp(q) д q Л р<0
или
р £ hp(q) д q Л р^О.
Иначе говоря, указатель (p,q) получает значение истин-
н о , если вектор р направлен к точке на прямой, проходящей
через q.
Начиная с одного из произвольно выбранных отрезков р или
q, продвигаемся вдоль одного или другого контура, от одной
"точки" к другой. Правила передвижения сведены в табл. 6.
На каждом шаге ребра q и р сравниваются на наличие пересе-
чения и получаются вершины многоугольника Р П Q. Таким
образом находятся все точки пересечения (даже дважды при обхо-
де обоих контуров). Затраты на выполнение алгоритма составляют
0(n+m).
Алгоритм. Принцип действия алгоритма заключается в повто-
ряющемся использовании описанных правил обхода, позволяющих
на каждом шаге переходить от текущего ребра к ребру, принад-
лежащему одному . или второму контуру.
Кроме того, на каждом шаге выполняется проверка на пересе-
чение и образуется соответствующая вершина. Когда петля обхода
закончена, оказываются вычисленными все вершины много-
угольника Р П Q, за исключением того случая, когда Р П Q -0.
Таблица 6. Прагала обхода хоитуров
1 Указатель (p,q)
] Указатель
l<P.q>
Упэлгль (p,q)
Продвигаться, начиная с внеш-
него ребра
Следующая вершина р
1Упзетель (pfl) I
Следующая вершина q 1
Продвигаться, начиная с|
внешнего ребра
Алгоритм в общем виде можно представить следующей записью
(без учета частных случаев):
Алгоритм (У Рурке
Начало (пересечение двух выпуклых
многоугольников Р и Q)
список вершин Р П Q »0;
взять произвольные р и q;
184

повторять
если р и q пересекаются
т£ {обработка пересечения}
езди, пересечение = первое
пересечение
Ifl коней повторения:
иначе PflQ =( P HQ) U точка
пересечения
если pGhp(q)
ю_ внутренняя :="Р";
пиане, внутренняя: ="Q";
коней если
кшец если.
клыеи если
клнец если
{р или q следующая}
если, q лр >о
ю если. pGhp(q) ш q следующая иыаые.
р следующая конец если
иначе {q Л р<0}
если. qGhp(p) ю_ р следующая иначе q
следующая коней если
до. цикл выполняется более 2(пн-п) раз
{если PDQ=0 или если P2Q или PCQ}
выбрать произвольные р и q
если. pGQ ifi. PDQ:=P иначе если qGP
т_о_ pnQ:=Q иначе PnQ=o конец если
конец еСЛИ.
конец
р следующая
начало
если внутренняя
р:=р+;
конец.
q следующая
напало.
если, внутренняя ="Q" ю_ PnQ:=(PnQ)
q конец если
185
="Р" LQ. P HQ: =( Р HQ)
р конец если
8 • Ж. Эгрон

q:=q+;
конец
Особые случаи. Рассмотрим три вида особых случаев пересе-
чения:
а) одна вершина многоугольника Р принадлежит ребру контура
Q:
б) контуры Р и Q имеют две общие вершины:
-•Р
в) ребро контура Р коллинеарно ребру контура Q.
VA
Эти трудности преодолеваются с помощью нашего определения
пересечения, которое следует ниже.
Пересечение р и q. Пусть p^Cspi, spi+i), q-(sqj,
scy+i).
Будем ли мы учитывать это пересечение, если р П q=spi, или
spi+i , или sqi, или sqi+i?
Если да, то получим две одинаковые точки пересечения (см.
случай а) или четыре одинаковые точки пересечения (см. случай
б). Для получения единственной точки пересечения в этом част-
ном случае будем считать что пересечение есть, лишь если pflq
равно spi+i или sqj+i.
186

Если р и q коллинеарны, то pflq -О (случай в).
Заключение. Затраты на алгоритм О'Рурке и др.
пропорциональны (n+m) — числу пересечений и числу вершин
PDQ. Число шагов итерации является случайным, так как оно
зависит от произвольного выбора двух первоначальных ребер. В
особых случаях, коща Р С Q, Q С Р или Р и Q разобщены, число
шагов при вычислении точек пересечения прямолинейных отрез-
ков максимально (т.е. равно 2(m+n)).
4533. ПЕРЕСЕЧЕНИЕ ДВУХ ПРЯМОЛИНЕЙНЫХ ОТРЕЗКОВ
Для вышеописанных алгоритмов общей элементарной гео-
метрической операцией является вычисление точки пересечения
двух отрезков прямых. Описать конфигурацию двух прямолиней-
ных отрезков можно различными методами:
аналитическим,
векторным,
минимаксным,
параметрическим.
Наше особое внимание привлекает параметрический метод. В
работе [2] было показано, что он обладает заметными до-
стоинствами, позволяя определять, пересекаются ли два отрезка,
и выявлять особые случаи (коллинеарность, параллельность). С
другой стороны, если отрезки пересекаются, то точка их пересе-
чения вычисляется непосредственно.
Параметрический метод
Принцип. Пусть даны два прямолинейных отрезка, АВ и CD.
Прямые (АВ) и (CD) у содержащие эти отрезки, определяются
параметрическими уравнениями:
для прямой (АВ):
Х-ХА + (ХВ-ХА) tb Y-YA + (YB-YA) ti;
для прямой (CD):
Х-ХС + (XD-XC) t2, Y-YC + (YD-YC) t2.
Значение параметра определяет положение текущей точки с ко-
ординатами (X,Y) на прямой:
187
8*

Если прямые пересекаются, то точка пересечения находится
путем решения системы уравнений.
Х- ХА + (XB-XA)ti - ХС + (XD-XCH2 ,
Y- YA + (YB-YA)ti - YC + (YD-YC)t2,
в результате чего имеем
(ХС-ХА) (YC-YD)-(XC-XD) (YC-YA)
ti : ,
(ХВ-ХА) (YC-YD)-(XC-XD) (YB-YA)
(ХВ-ХА) (YC-YA)-(ХС-ХА) (YB-YA)
(ХВ-ХА) (YC-YD)-(XC-XD) (YB-YA)
Значения параметров ti и t2 содержат всю информацию об
относительном положении отрезков прямых АВ и CD.
Алгоритм. В приведенном ниже алгоритме учитываются все
возможные случаи, которые могут встретиться (в предположении,
что ни один из отрезков не вырожден, т.е. не обращается в точку):
ПЕРЕСЕЧЕНИЕ двух отрезков АВ и CD
Начало (параметрический метод}
ХВА:-ХВ-ХА;
YBA:=YB-YA;
XCD:=XC-XD;
YCD:=YC-YD;
D:=XBA.YCD-XCD.YBA;
Если D=0
тр_ отрезки параллельны или коллинеарны
(несущие прямые совпадают);
иначе ХСА: =ХС- ХА;
YCA.--YC-YA;
Т1: =( ХСА. YCD- XCD. YCA) /D;
T2:=(XBA.YCA-YBA.XCA)/D;
если (Т1<0 или Т1>1) или (Т2<0 или Т2>1)
тр_ нет пересечения;
иначе (пересечение в точке (X, Y)}
Х:=ХА+Т1.ХВА;
Y:=YA+T1.YBA;

(особые случаи}
если Т1=0 то_ пересечение в точке А;
если Т1=1 Т£ В
если Т2=0 тр_ С;
если Т2=1 тр_ D;
конец если
конец если
Конец
А53А. ЗАКЛЮЧЕНИЕ
Алгоритм О'Рурке реализуется значительно проще, чем ал-
горитм Шамоса, и для него требуется минимальный объем данных:
список вершин обоих многоугольников и точек их пересечения.
Кроме того, в методе О'Рурке нет необходимости использовать
тригонометрические функции. Однако в методе Шамоса количест-
во вычислительных операций для определения пересечений всегда
будет меньше (или равно) числа операций, свойственных методу
О'Рурке.
4.5.4. ПЕРЕСЕЧЕНИЕ ДВУХ НЕВЫПУКЛЫХ МНОГОУГОЛЬНИКОВ
В отличие от случая выпуклых многоугольников, вычислитель-
ные затраты для которого пропорциональны сумме числа ребер
обеих фигур, вариант невыпуклых многоугольников требует за-
трат, пропорциональных произведению числа ребер одного и дру-
гого контуров. Такие затраты можно считать оптимальными, так
как число точек пересечения в этом случае может быть равно
произведению числа ребер.
4.54.1. ЧАСТНЫЙ ПОДХОД
Одна из возможностей ускорить поиск точек пересечения
состоит в разбиении многоугольников на более простые фигуры.
Пусть R1 и R2 — прямоугольники, описывающие каждый свой
вписанный в него многоугольник: Р1 и Р2 соответственно; если R1
и R2 разобщены, то Р1 и Р2 также разобщены. Если один из пря-
моугольников входит в другой, например R2 С R1, то можно рас-
смотреть вначале пересечение R2 с Р1, а затем пересечение полу-
ченной фигуры (R2 П Р1) с Р2. Если R1 П R2 не пусто, то
можно рассмотреть пересечения каждого многоугольника Р1 и Р2
с R12-R1 П R2. Это дает два новых многоугольника, к которым
рекурсивно применим тот же прием, который был использован для
Р1 и Р2 (рис.4.14).
189

R2CR1
R1
R1
(О
(2)
У
и
L
\
Ь
1
vj
/1
R12 = R1HR2
Р1П R12 = Р*1
P2HR12 = Р'2
R2CR 1
Р'1 fjR'2 = R"1
R"in Р'2
I
sTpi
^
VI
R2
<\
Л
(2)
Рис. 4.14. Процесс нахождения точек пересечения двух невыпуклых
многоугольников методом последовательного разбиения фигур
Однако уменьшение затрат может быть достигнуто только в том
случае, когда на каждом шаге разделения одного или двух много-
угольников будет удалено максимально возможное число ребер.
При этом предполагается, что число ребер достаточно велико
(»4). Такой подход не решает задачи отыскания точек пересе-
чения невыпуклых многоугольников, поскольку на каждом после-
довательном шаге разбиения получающиеся фигуры не обязатель-
но оказываются выпуклыми. С учетом сказанного следует
уточнить, какой алгоритм разбиения можно было бы использовать
для различных операций пересечения.
Для пересечения прямоугольника с выпуклым или невыпуклым
многоугольником можно применить обобщение алгоритма Сазер-
ленда и Ходжмена (см. п. 4.5.2), который реализует здесь разре-
зание многоугольника прямоугольным окном.
При пересечении двух результирующих многоугольников мож-
но выделить три случая:
а) оба многоугольника выпуклые — применяются алгоритмы
Шамоса либо О'Рурке;
б) один из двух многоугольников выпуклый — пригодно обоб-
щение метода Сазерленда и Ходжмена;
190

в) оба многоугольника невыпуклые — требуется общий метод,
типа метода Атертона и Уэйлера.
Прежде чем приниматься за детальное изучение общего метода
получения точек пересечения произвольных многоугольников, сле-
дует научиться определять, является ли многоугольник выпук-
лым или нет. Для этого предполагается следующее решение.
Пусть многоугольник Р задан упорядоченной последовательно-
стью N вершин (s^, где i-l,2,...,N. Произвольно выбрав направ-
ление их обхода, можно определить, по какую сторону (справа или
слева) от предшествующего ей ребра (S| 2 * si—1) расположена
каждая вершина S;:
*i-2 «и
У • **^
S К2 к\ ^щ
**•
Точка f4 расположена Точка S; расположена
слеаа от ребра (Si.2,sM) спрааа о? ребра (*i.2'si-l)
Полуплоскость, которой принадлежит вершина Sj, определяется
по знаку уравнения прямой, проходящей через ребро (Sj__2> Si 1),
в точке S|, или по знаку определителя det(Sj, sj_2, Si 1) квадрат-
ной матрицы размером 3x3, образованной однородными координа-
тами точек Si, Si 2» si—1 (см- алгоритм Павлидиса, п.4.4.3.2).
Зная, что у выпуклого многоугольника все вершины располо-
жены по одну сторону от предшествующего ребра, легко опре-
делить, является ли контур невыпуклым, если при последователь-
ном обходе его вершин обнаруживается, что расположение не
всегда одностороннее (т.е. изменяется знак, как на рис.4.15).
Рис. 4.15. Исследование выпуклости многоугольника:
а — выпуклый многоугольник; б — вогнутый многоугольник
Алгоритм такого исследования можно записать в следующем
виде:
191.

Проверка выпуклости многоугольника
(многоугольник задан своими вершинами
(si)1-l,2,...,n)
начало
выпуклость: =истинно;
асди. п>3
Ifl. {фигура не треугольная}
вычисление знака первой вершины si;
1:-1;
Повторять
i: =i +1; {следующая вершина}
определение знака вершины si;
если, знак (Si)**3Haic (si)
Lql (изменение знака}
выпуклость: =дожнщ_
конец если
да (J выпуклость иди. i=n)
конец если
конец
А5А2. АЛГОРИТМ АТЕРТОНА - УЭЙЛЕРА
Этот алгоритм обладает существенным достоинством: структура
данных на его выходе сохраняется такой же, какой она была на
входе. Иными словами, многоугольный контур или ориентирован-
ная грань могут в дальнейшем легко быть использованы,
например, в алгоритмах заполнения или штрихования благодаря
тому, что в процессе выполнения алгоритма удаления невидимых
линий остается неизменным понятие грани. Обрабатываемые мно-
гоугольники могут иметь произвольную форму: могут быть выпук-
лыми, невыпуклыми, могут содержать внутренние отверстия
(другие контуры). Однако действие этого алгоритма достаточно
сложное и требует больших затрат. Отличие его от таких ал-
горитмов разрезания выпуклых многоугольников, как алгоритмы
Шамоса и ОТурке, весьма велики.
Этот сложный алгоритм лежит в основе метода визуализации
реалистичных трехмерных сцен, разработанного Атертоном и
Уэйлером [3,44 ]. Здесь его рассматривать не будем, так как он не
может быть отнесен к числу элементарных базовых алгоритмов,
которым посвящена данная книга.
4.5.5. ЗАКЛЮЧЕНИЕ
Рассмотренные в этом разделе методы определения пересечений
двух многоугольников, представленные здесь как методы разре-
зания одного многоугольника многоугольным окном, позволяют
выделять два класса алгоритмов, принципиально различающихся
своей сложностью и быстродействием (табл.7).
192

I
ж
3
s
е
I
х
z
I
I
a-
x
5
Примечания
Сложность
Элементарные операции
Многоугольник,
окно
Название мето-
да
В некоторых случаях получение
вырожденных многоугольников
0(m*n), где п —
число ребер много-
угольника,
m — число сторон
окна
Пересечение прямолинейного
отрезка с прямой
Разрезание прямоугольника
прямой
Сравнение точка — прямая
Невыпуклый,
выпуклый
Сазерленда—
Ходжмена
Ориентированные контуры
При п ^4 перемена ролей много-
угольника и окна для умень-
шения вычислительных затрат
Тригонометрическая
функция (арктангенс)
0(т+п)
Сравнение точка—контур
Вычисление угла
(тригонометрическая
функция — арктангенс)
Пересечение двух отрезков
прямых
Вычисление внутренней точки
выпуклого контура
Выпуклый,
выпуклый
Шамоса
Число шагов и сравнений пар
отрезков прямых зависит от
первоначально выбранных
ребер для обхода обоих конту-
ров
+
Е
Сравнение точки и прямой
Пересечение двух
прямолинейных отрезков
Выпуклый,
выпуклый
О'Рурке
и др.
Ориентированные невыпуклые
многоугольники с отверстиями
Сложность обработки в отдель-
Форматы на входе и выходе
идентичны внешним и внут-
ренним многоугольникам
с 1
1
Пересечение отрезков прямых
Невыпуклый,
невыпуклый
Атертона—
Уэйлера
193

1. Алгоритмы, выполняющие пересечение двух выпуклых много-
угольников (Шамоса, О'Рурке), сложность которых составляет
0(m+n), ще шип — соответственно числа сторон каждого контура.
2. Алгоритмы, реализующие пересечение двух невыпуклых мно-
гоугольников (Сазерленда — Ходжмена, Атертона — Уэйлера),
сложность которых составляет 0(m*n).
Для правильного выбора того или иного алгоритма при решении
конкретной задачи следует обратить внимание на такие обстоя-
тельства:
выпуклость или невыпуклость контуров;
наличие или отсутствие необходимости сохранения исходной
структуры данных после разрезания, т.е. должен ли быть контур
(или грань) ориентированным или нет.
Например, в алгоритме Атертона — Уэйлера устранения
невидимых линий в трехмерной сцене обязательным является
использование общего метода разрезания двух невыпуклых много-
угольников, поскольку вся логика алгоритма основана именно на
этом. Однако в некоторых простых случаях, как, например, при
заполнении фигуры или штриховании части многоугольника,
видимой в окне, можно избежать общего метода разрезания, как
будет показано далее.
4.6. РАЗРЕЗАНИЕ ОБЛАСТИ МНОГОУГОЛЬНЫМ ОКНОМ
4.6.1. ВВЕДЕНИЕ
В этом разделе будем рассматривать задачу отображения в мно-
гоугольном окне видимой части области, которая либо заполнена
(окрашена), либо заштрихована. Можно наметить два пути
решения такой задачи:
1. Разрезание контура области, а затем заполнение или
штрихование результирующего многоугольника (явное разрезание
области).
2. Заполнение или штрихование всей области, а отображение
только видимых точек или линий штриховки (неявное разрезание
области).
4.6.2. ЯВНОЕ РАЗРЕЗАНИЕ
На первом шаге многоугольный контур можно разрезать с
помощью одного из алгоритмов разрезания, изложенных в преды-
дущих разделах. Затем на втором шаге, когда контур внутри окна
уже получен, можно применить к нему алгоритм заполнения или
штрихования области. Затраты на реализацию метода явного раз-
резания области равны сумме затрат на разрезание окном и на
заполнение области в полученном контуре.
4.6.3. НЕЯВНОЕ РАЗРЕЗАНИЕ
Здесь могут быть использованы два метода.
1. Первый состоит в заполнении или штриховании исходной
области, а затем в определении для каждой точки или линии
194

штриховки ее принадлежности к внутренней части окна с
помощью алгоритма сравнения точка — контур или алгоритма
разрезания отрезка многоугольником.
2. Второй заключается в одновременном заполнении или
штриховании области и окна, а отображении только тех точек или
линий штриховки, которые расположены внутри обоих контуров.
Если окно имеет форму прямоугольника, то для заполнения и
штриховки, вертикальной или горизонтальной, оба метода рав-
нопригодны. В противном случае использование второго метода
имеет тем больше преимуществ при заполнении (соответственно
при штриховании), чем больше площадь обрабатываемой поверх-
ности или число линий развертки (соответственно чем больше
линий штриховки).
Недостатком такого метода неявного разрезания являются бес-
полезные затраты времени на обработку невидимой в окне части
области, естественно возрастающие с ростом размеров этой части.
4.6.4. ЗАКЛЮЧЕНИЕ
Когда и область, и окно представлены выпуклыми много-
угольниками, преимущества на стороне явного метода. Однако в
случае невыпуклых контуров предпочтительным становится неяв-
ный метод, поскольку сложность алгоритма разрезания контуров
составляет величину 0(n*m).
Можно сделать два замечания.
•Е9ЛИ одним окном обрабатываются несколько областей, то вре-
менные затраты при неявном методе можно значительно
уменьшить, заполняя или заштриховывая окно только один раз. В
данном случае возрастает лишь требуемый объем памяти.
•При явном методе очень важно сохранить результирующий
многоугольник в тех Случаях, когда необходимо изменить цвет или
характер штриховки видимой в окне части области. Далее будет
показано, как контуры, получаемые в результате разрезания,
можно выделить и заполнить непосредственно в процессе неявного
заполнения части области, видимой в окне.
4.7. РАЗРЕЗАНИЕ ОДНОЙ ОБЛАСТИ ДРУГОЙ ОБЛАСТЬЮ
4.7.1. ВВЕДЕНИЕ
В отличие от операции разрезания области окном определим
операцию разрезания области Р областью Q более широко: резуль-
татом ее будут не только пересечение областей (Р П Q), но и их
объединение (Р U Q) и разности (Р—Q) и (Q—Р) (рис.4.16). Если
Р и Q — выпуклые фигуры, то для получения явным методом их
пересечения и объединения можно использовать только алгоритм
О'Рурке. С другой стороны, алгоритмы Сазерленда—Ходжмена
или Атертона—Уэйлера позволяет найти все результирующие мно-
гоугольники (внутренние и внешние) при взаимном разрезании
195

Рис. 4.16. Результаты операции разрезания двух областей
невыпуклых областей. Однако оба эти метода не относятся к типу
тех, которые встречались в случае выпуклых фигур, и их слож-
ность составляет 0(m*n).
Далее будет описан метод выполнения операций объединения,
пересечения и вычитания двух многоугольников (Р и Q) на осноЬе
тех же самых операций, выполняемых над двумя областями, т.е.
на основе неявного разрезания двух областей.
Можно предложить два варианта решения: область либо опре-
деляем множеством составляющих ее точек (в этом случае имеем
дело с матрицами точек), либо рассматриваем как множество
горизонтальных отрезков или интервалов, представляющих собой
части линий строчной развертки, находящихся внутри области (в
этом случае имеем дело со структурой ребер и интервалов).
4.7.2. ОБЛАСТЬ ЗАДАНА МНОЖЕСТВОМ ТОЧЕК
Пусть даны две области А и В. После того как области А и В
заполнены, а множества составляющих их точек занесены в
память соответствующих изображений (матрицы точек), можно
легко выделить желаемые подмножества и, если необходимо, за-
помнить их.
Элементарные операции очень просты и ограничены: для каж-
дой точки выполняются не более двух испытаний и два обра-
щения к таблице. Но зато приходится иметь очень большой объем
памяти и требуется просмотр всей матрицы изображения.
Можно предложить некоторое промежуточное решение, в кото-
ром используется только одна память точек. Она позволяет
записывать в нее для каждой области множество составляющих ее
точек, затем извлекать из нее список интервалов точек, строка за
строкой (кодирование областей, рис.4.17).
196

x1
д8
"Ш
Рис. 4.17. Создание списка интервалов точек:
а — заполнение точка за точкой; б — выделение интервалов строка за строкой;
в — список интервалов точек
Операции обработки обеих областей выполняются сравнением
двух списков интервалов последовательно строка за строкой. Лю-
бое желательное подмножество будет также определяться списком
интервалов. Для объединения областей вычисляется объединение
интервалов на каждой строке, для пересечения областей-пересе-
чение интервалов, для разности областей — разность интервалов.
Если выполняемые операции сложнее, чем операции, выполняе-
мых над матрицами точек, то выигрыш в объеме полезной памяти
получается заметным.
Рассмотрим более подробно различные алгоритмы объединения,
пересечения и разности двух списков интервалов точек, обозначен-
ных соответственно LISTE1 и LISTE2. Результатом выполнения
операции будет новый список интервалов точек LISTE3.
Объединение. LISTE3- LISTE U LISTE2.
На первом шаге создаем объединение двух упорядоченных
списков LISTE1 и LISTE2. В новом списке каждый элемент поме-
чен именем соответствующего первоначального списка. Зная, что
точка принадлежит объединению двух областей, если она принад-
лежит хотя бы одной из этих областей, можно выделить соответ-
ствующий список интервалов.
Пусть А и В — области, соответствующие спискам LISTE1 и
LISTE2, a int_A и int_B — логические переменные, означающие,
ведется ли расследование внутри областей А и В. Получаем сле-
дующий алгоритм.
Объединение (даны LISTE1, LI STE2; результат LISTE3)
Начало
Соединение (LISTE1, LISTE2; результат LISTE4)
{выделить объединение из LISTE4}
i nt_A: =ложно;
i nt_B: =ложно;
создать LISTE3;
ILYAELEMENT:=hcthhho; {LISTE4 не пусто}
i I»I»i i i i
I»11.1111
•i i 1»| i i |«
• 1 | 1*1 | ;• |.
»|>| | | [ | I".
I 1*1I I 1 I*
yi
IT
IT
Z
x3
x2
x1
xl
xl
x4 1
x4
x4
x4
x'8
x8 1
[IT
1 x7
~x8~]
x8
197

Пока ILYAELEMENT выполнять
начало
получить элемент LISTE4;
если текущее (LISTE4JGA
тр_ int_A := "| i nt_A;
иначе int_B:= ]int_B;
конец если
записать текущее (LISTE4) в LISTE3;
Пока (int_A) или_ int_B) выполнять
начало
получить элемент LISTE4;
если текущее (LISTE4JEA
то int_A:= ]int_A;
иначе i nt_B: = ~|int_B;
конец если
конец
записать текущее (LISTE4) в LISTE3;
учесть ILYAELEMENT;
конец
конец Объединения
Пересечение.1 USTE3-USTE1 П USTE2.
Признак принадлежности:
р е А п В, если р е А и р е В.
Используя те же обозначения, получаем следующий алгоритм:
Пересечение (даны LISTE1,.LISTE2; результат LISTE3)
Начало
Соединение (даны LISTE1,LISTE2; результат LISTE4);
{выделение пересечений из LISTE4)
i nt_A: =ложно;
i nt_B: =ложно;
создать LISTE3;
ILYAELEMENT: ^истинно; (LISTE4 не пусто}
Пока ILYAELEMENT выполнять
начало
Пример действия этого алгоритма можно увидеть в программе ТЕКСТ —
МНОГОУГОЛЬНИК (запись текста в произвольный многоугольник) в п.3.3.3.5.
198

Пока (~|int_A или_ ~]int_B) и_
ILYAELEMENT выполнять
Начало
получить элемент LISTE4;
учесть int_A и int_B;
учесть ILYAELEMENT;
конец
если (int_A и intJJ)
тр_ записать текущее (LISTE4) в LISTE3;
получить элемент LISTE4;
учесть int_A и int_B;
(имеем l(int_A и. int_B)}
записать текущее значение LISTE4 в
LISTE3;
конец если
учесть ILYAELEMENT;
конец
Конец Пересечения
Учет int_A и int_B
начало
если текущее (LISTE4JEA;
то i ntA: = | i nt_A;
иначе int_B: =~|int_B;
конец если
конец
Разности
1) LISTE3-LISTE1-LISTE2 (т.е. А-В).
Признак принадлежности: р Е А-В, если р G А и р £ В.
Получаем следующий алгоритм:
Разность А и В (даны LISTE1,LISTE2;
результат LISTE3)
Начало
Соединение (данные LISTE1, LISTE2; результат
.LISTE4);
{выделение А-В из LISTE4}
int_A: =ложно;
i nt_B: =ложно;
создать LISTE3;
ILYAELEMENT: -истинно; (LISTE4 не пусто}
199

Пока ILYAELEMENT выполнять
начало
Пока ("|int_A или int_B) и ILYAELEMENT
выполнять
начало
получить элемент LISTE4;
учесть int_A и int_B;
учесть ILYAELEMENT;
конец
если (int_A и "]int_B)
™ записать текущее (LISTE4) в LISTE3;
получить элемент LISTE4;
учесть int_A и int_B;
{имеем ] (int_A и ] int_B)}
записать текущее (LISTE4) в LISTE3;
конец если
учесть ILYAELEMENT
конец
конец Разность А-В
2) USTE3-USTE2-LISTE1 (т.е.В-А).
Признак принадлежности: р G В-А, если р 6 В и р ^ А,
Алгоритм "РАЗНОСТЬ В-А" полностью идентичен алгоритму
"РАЗНОСТЬ А-В", если в последнем выполнить две замены: ус-
ловие (] int_A шш ] int_B) на условие (int_A или "| int_B), a
условие (int_A и int_B) на условие ("| int_A a int_B).
4.7.3. ОБЛАСТЬ ЗАДАНА МНОЖЕСТВОМ ИНТЕРВАЛОВ
4.73.1. ВВЕДЕНИЕ
Вместо того, чтобы создавать список интервалов, переходя
путем заполнения точка за точкой от области к матрице точек,
можно непосредственно получать ее с помощью алгоритма прос-
леживания контура (см. п.3.3.3.2.). Различные виды обработки,
выполняемые над областями, идентичны тем, которые были описа-
ны ранее. Каждая новая область, получающаяся в результате
объединения, пересечения или вычитания двух исходных, харак-
теризуется списком составляющих ее интервалов, сорока за стро-
кой. На базе такой структуры данных операции типа заполнения
области или сдвига являются тривиальными. Однако гео-
метрические преобразования, такие, как повороты, изменение мас-
штаба, требуют описания контура области в виде списка ребер. С
другой стороны, такое описание позволит экономить объем
памяти.
200

Далее описывается алгоритм, позволяющий неявным образом
(см. п. 4.7,3.2) выполнять различные теоретико-множественные
операции над двумя многоугольными областями вычислением для
каждого получаемого подмножества соответствующего списка
ребер. Кроме того, этот алгоритм одновременно позволяет осуще-
ствлять заполнение или горизонтальную штриховку желаемого
подмножества.
4.73.2. АЛГОРИТМ РАЗРЕЗАНИЯ ДВУХ ОБЛАСТЕЙ
Пусть А и В — две многоугольные области, заданные в системе
координат экрана упорядоченными списками вершин своих конту-
ров.
Постановка задачи. Получить списки ребер, образующих кон-
туры многоугольных областей А П В, A U В, А—В и В—А.
Общий принцип. Используя метод прослеживания контура, же-
лательно вычислить ребра q, порожденные областями А и В, путем
присваивания их соответствующим подмножествам в результате
неявного разрезания А и В (рис.4.18).
d
• « А
qa A U В и А - В
qb A U В и В - А
Рис. 4.18. Неявное разрезание путем прослеживания контура»
Алгоритм. Как и для случая одновременного заполнения мно-
жества многоугольных областей, путем построчного прохода строка
за строкой образуем упорядоченный список ребер областей А и В,
пересекающих текущую строку. Вычисление ребра q, порожденно-
го областями А и В, реализуется следующим образом:
обнаружение ребра q, когда оно изменяет контекст между двумя
последовательными строками развертки. Это происходит, либо ког-
да два ребра пересекаются, либо когда ребра начинаются или за-
канчиваются. Для этого следует запомнить координаты последнего
изменения контекста ребра его контекста на предыдущей строке,
чтобы узнать, находится ли оно внутри или снаружи второго мно-
гоугольника;
201

Таблица 8
Многоугольник
Контекст
Точное
определение
1 q G Д (или р):
1 q E А (или В):
q e A
q С В
q E А П В
и
В — А
q t В
q £ A U В
и
А — В
q G В J
q С А
q G А П В
и
А — В
q <£ A
q G A U В
и
В — А
q принадлежит контуру А (или В);
q принадлежит внутренней части области А (или В),
т.е. области за вычетом контура (А — контур (А)),
или (В — контур (В)) соответственно
присваивание ребра q соответствующему подмножеству согласно
его контексту (табл.8).
В особых случаях, когда два ребра двух контуров совпадают
(т.е. имеют те же точки пересечения со строками развертки и тот
же наклон к ним, рис.4.19), присваивание ребра происходит в со-
ответствии с его контекстом по отношению к обоим много-
угольникам, А и В (табл.9).
qGAOB. А - В, В - Л
qEAOB. AUB
Рис. 4.19. Особый случай (q G А и q £ В)
Заключение. Этот метод обладает следующими достоинствами:
•Разрезание и заполнение одного или нескольких желательных
подмножеств может осуществляться одновременно: заполняются
области А П В, A U В, А — ВиВ — А, тем самым реализуются
операции пересечения, объединения и разностей списков горизон-
тальных внутренних интервалов областей А и В на каждой
строке развертки. Этот результат важен для обработки изобра-
жений.
•Структуры данных, получаемых в результате этой операции,
совместимы с дальнейшими обработками, выполняемыми на базе
202

метода прослеживания контуров (заполнение, горизонтальная
штриховка, сравнение точки с произвольным контуром), поскольку
они представляют собой множества ребер, составленных из отрез-
ков прямых и кривых линий.
Однако имеются и недостатки:
•Для выполнения таких операций, которые в дальнейшем будут
производиться над полученными подмножествами, как вертикаль-
ная или наклонная штриховка, повороты или для создания
штриховых рисунков, требуется сохранять в памяти информацию
о горизонтальных ребрах.
•Пересечение двух ребер редко происходит непосредственно на
строке развертки, а чаще между соседними строками.
Текущая строка
Следующая строка'
Пересечение
Используемая аппроксимация приводит к ошибке, значение ко-
торой зависит от наклона рассматриваемых ребер.
Таблица 9
Контекст
Много-
угольник
Опреде-
ление
q—правы
и левый
q G А
qGAHB*
и
А — В
* Вырожденные случаи (
й край А
край В
q G В
qGADB*
и
В — А
не относить с
q—левы
и правы]
q G А
qGAHB*
и
В — А
1 к АПВ).
\ край А
ft край В
q Е В
qGAHB*
и
А — В
q—правый край
А и В или
q—левый край А и В
q G А 1 q G В
qGADB qGAHB
A U В | A U В |
4.8. ОБОБЩЕНИЕ НА ОБЛАСТИ ПРОИЗВОЛЬНОЙ ФОРМЫ
Будем полагать, что контур области составлен из отрезков пря-
мых и дуг окружностей.
4.8.1. СРАВНЕНИЕ "ТОЧКА — НЕМНОГОУГОЛЬНЫЙ КОНТУР*
Задача состоит в том, чтобы определить, принадлежит ли точка
к внутренней части области, заданной контуром, не являющимся
ни многоугольником, ни выпуклой фигурой. Из всех алгоритмов
сравнения точки и многоугольного контура можно обобщить толь-
ко метод прослеживания контура. Его принцип основан на конт-
роле четности для рассматриваемой точки и на тех же рассуж-
дениях, которые использовались при заполнении областей
203

произвольной формы методом прослеживания контура
(см.п.3.3.3.2).
Основная задача, которую необходимо решить, состоит в
вычислении пересечения горизонтального луча, расположенного
слева от точки, с примитивом контура: если примитивом является
отрезок прямой, то действуем согласно алгоритму, изложенному в
п.4.3.3.2. Если же примитивом является дуга окружности и точка
не расположена над (или под) полной окружностью, то разделяем
ее с помощью квадранта (см.п.3.3.3.4) на множество прямолиней-
ных и криволинейных участков, а затем для каждого полученного
отрезка дуги окружности выполняем перечисленные ниже опе-
рации.
Точка пересечения отрезка дуги окружности с лучом
вычисляется следующим образом. Пусть (Xd,Yd), (Xf,Yf) — ко-
ординаты точек, расположенных соответственно в начале и в кон-
це отрезка дуги, a D — направление вращения (D:-l, если на-
правление против часовой стрелки, в противном случае D:-0).
Пусть также R — длина радиуса, a (Xc,Yc) — координаты центра
окружности. Координаты текущей точки (Xp,Yp). Тогда имеем
следующий алгоритм:
Если Yp>Yd или Yp<Yf или Xp<mi n( Xd, Xf)
то. нет пересечения ;
иначе пересечение с горизонталью Y=Yp в
точке с абсциссой Xi;
Xi:=Xc+(R2-(Yp-Yc)2)1/2 если D=0;
Xi:=Xc-(R2-(Yp-Yc)2)1/2 если. D-l;
если Xp=Xi тр_ точка принадлежит контуру,
если Xp<Xi T£ нет пересечения с лучом;
Сложность этого алгоритма пропорциональна числу
примитивов. Однако его можно несколько упростить за счет учета
выпуклости, если точка расположена вне контура: вычисления сле-
дует прекратить, если найдены две точки пересечения.
4.8.2. РАЗРЕЗАНИЕ ОТРЕЗКА НЕМНОГОУГОЛЬНЫМ КОНТУРОМ
Задача состоит в определении части прямолинейного отрезка,
находящейся внутри контура, не имеющего форму много-
угольника. Предлагается обобщить метод прослеживания конту-
ра, использованный для разрезания Осм. п.4.4.4. (2)) отрезка мно-
гоугольным контуром.
Основная задача, которую необходимо решить, состоит в на-
хождении точки пересечения с примитивом несущей прямой, ко-
торой принадлежит отрезок. Если примитивом является пря-
204

молинеиныи отрезок, то выполняются те же операции, что в
п.4.4.4.2. Если же примитивом является дуга окружности, то мож-
но действовать следующим образом.
Пусть у-тх+р — уравнение несущей прямой;
R — радиус, а С - (Xc,Yc) — центр окружности;
Ed - (Xd,Yd) и Ef - (Xf,Yf) — начальная и конечная точки;
D — направление обхода окружности.
Тогда точки пересечения несущей прямой с окружностью име-
ют следующие координаты:
X - Хс + "Pm±^ , Y « тХ + р,
1 +mz
где Л - p2m2-(l+m2)(p2-R2).
Могут встретиться следующие три случая:
I. Д<0 — прямая не пересекает окружности, т.е. точек пересе-
чения нет.
П. Д>0 — прямая пересекает окружность в двух различных
точках (Ik »(xk, yk)), к-1,2.
Тоща Ik G arc (Ed,Ef), если выполняется неравенство (EdCIk)<
<(EdCEf), где ориентация углов соответствует направлению D
обхода дуги окружности.
Если одна или две точки пересечения принадлежат дуге окруж-
ности, то возможны два варианта:
1) точка (или точки) пересечения отлична от точек на концах
дуги; несущая прямая пересекает дугу окружности в этой точке
(точках);
2) одна или две точки пересечения совпадают с концами дуги;
как и для отрезков прямой, концевая точка, в которой "подзвено"
заканчивается, не следует учитывать.
В точке Ed нет пересечения в точке Ed есть пересечение
(знаком -f- обозначена ( знаком * обозначена точка
точка гибели) рождения)
Здесь представляются два случая:
А. Прямая проходит только через один из концов дуги, а имен-
но через Ei.
205

Пусть Ei-(xi,yi) — один, а Ег-(х2,у2) — второй конец дуги;
D' — направление обхода дуги (Ei,E2).
Прямая проходит только через точку Ei дуги:
•yi^mxi<y2-mx2: нет пересечения в точке Ei (точка гибели);
•yi-mxi>y2-mx2: есть пересечение в точке Ei (точка рож-
дения).
Прямая проходит через точку I(xi, yi) и точку Ei дуги,
ще Ei-Ed :
•xi>xi: D'4), пересечение в точке Ei (точка рождения),
D'-l, нет пересечения в точке Ei;
D=l
Несущая прямая
•xi<xi: D'-l, пересечение в точке Ei (точка рождения);
D'4), нет пересечения в точке Еь
Ситуация противоположна при Ei -Ef .
Б. Прямая проходит через два конца, Ei и Ег, a Ei -Ed (ситу-
ация противоположна при Ei -Ef):
•xi<x2 : D'-O, нет пересечения в точках Ei и Ег (точки
гибели);
D'-l, пересечение в точках Е1 и Е2 (точки рождения);
D »0
•xi>x2 : D'4), пересечение в точках Ei и Ег (точки рож-
дения);
D'-l, нет пересечения в точках Ei и Ег (точки
гибели);
206

D = 1
J 2i! L_*
*2 *i X
III. A - 0 — прямая касается окружности в точке Т. Здесь
возможны два случая:
1) точка Т отлична от точек на концах дуги:
пересечения нет.
2) точка Т совпадает с одним из концов дуги:
если этот конец находится в точке Ei «(xi, yj), а второй в точ-
ке Е2~(х2, У2>, то:
•yi-mxi <у2-тх2: нет пересечения в точке Т (точка гибели),
•yi-mxi > у2~тхг: есть пересечение в точке Т (точка рож-
дения).
Совокупность точек пересечения на несущей прямой выделяет
на ней отрезки как внутренние по отношению к области, так и
примыкающие к ней. видимая часть разрезаемого отрезка будет
вычислена путем расчета точек пересечения их с множеством
внутренних отрезков немногоугольного контура (п.4.4.4.2).
Если отрезок прямой занимает вертикальное положение, то
роли координат X и Y меняются местами.
Сложность этого алгоритма пропорциональна числу
примитивов. Ее можно несколько уменьшить, если остановить
сравнение несущей прямой с примитивами контура, как только
найдены две точки пересечения.
Недостатком метода является необходимость использования
обратной тригонометрической функции (арктангенса) для
вычисления углов.
4.8.3. РАЗРЕЗАНИЕ ДУГИ ОКРУЖНОСТИ НЕМНОГОУГОЛЬНЫМ
КОНТУРОМ
Задача состоит в определении видимой части дуги окружности,
расположенной внутри немногоугольного контура. Алгоритм,
подобно тому, как это было в предыдущем случае, разделяется
на две части.
1. Вычисление точек пересечения контура с окружностью, со-
держащей рассматриваемую дугу ("несущей окружностью").
2. Выделение видимых частей.
4А3.1. ВЫЧИСЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ
Пересечение окружности с отрезком прямой. Вычисляются
точки пересечения несущей прямой с окружностью. Затем, если
есть две различные точки пересечения, то восстанавливаются
207

точки пересечения, принадлежащие отрезку прямой. Чтобы, как и
в случае разрезания отрезка прямой, избежать особых случаев
(окружность проходит через конец отрезка), отрезок ориентируют
по направлению вниз и не учитывают точек пересечения, совпа-
дающих с концами отрезка:
Нот пересечения
Пересечение окружности с дугой окружности. Вычисляются
точки пересечения двух окружностей. Затем, если есть две
различных точки пересечения, устанавливают точки пересечения,
принадлежащие дуге окружности (см.п.4.8.2).
Если одна из установленных точек совпадает с одним из концов
дуги окружности, то, как и в предыдущем случае, проверяют,
является ли она точкой рождения (тоща ее учитывают) или точ-
кой гибели (тоща ее отбрасывают).
Точка I несущей окружности принадлежит дуге (Ei,E2), если
угол в - (Z. EiCI) меньше или равен углу e2-(Z. E1CE2), ще
С — центр окружности.
D=1
D=i,ece2
1€ Дуге окружности
О = 0
d , о, е>е2
|£ ДУГ* окружности.
АА32. ВЫДЕЛЕНИЕ ВИДИМЫХ ЧАСТЕЙ
Пусть (1у) множество точек пересечения (k^l,2,...,N).
Упорядочим это множество в направлении увеличения углов
(Z. EiCIk), k-l,2,...,N, учитывая направление дуги Ei, Е2). Рас-
208

смотрим, находится ли точка Ei внутри или вне контура
(см.п.4.8.1.1).
Зная, находится ли точка Ei внутри или вне контура, приме-
няем контроль четности к упорядоченному списку пересечений,
принадлежащих дуге (Ei, E2), (т.е. проверяем выполнение условия
(Z.~EiCIfc)(Z. E1CE2). Каждый раз, встречая точку, мы входим в
область или выходим из нее (рис.4.20).
0 в
а б
Рис. 4.20, Пример выделения видимых частей (D-1):
а — Ei € области; б — Ei £ области
Недостатком этого алгоритма является необходимость использо-
вания обратной тригонометрической функции (арктангенса) для
вычисления углов.
4.8.4. ЗАКЛЮЧЕНИЕ
Отметим еще раз, что использование идеи прослеживания кон-
тура позволяет легко преодолевать особые случаи, встречающиеся
при обобщении на немногоугольные контуры трех элементарных
задач (сравнение точка — контур, разрезание отрезка и дуги
окружности контуром). Попутно заметим, что контуры могут быть
как выпуклыми, так и невыпуклыми.
4.9. ЗАКЛЮЧЕНИЕ
По поводу элементарных алгоритмов разрезания можно сделать
несколько замечаний.
•Отметим, что вычислительные затраты на реализацию ал-
горитма существенно зависят от вида обрабатываемых фигур: пря-
моугольная ли у них форма (в том числе параллельны ли осям
стороны прямоугольников), выпуклые ли они или невыпуклые.
Для каждого конкретного случая применения следует подбирать
адекватный алгоритм в зависимости от характеристик сцены и ее
преобразований.
•Заметим также, что хорошее действие алгоритмов, в частности
обработки особых случаев, характерных для каждой задачи, осно-
209

вывается (большую часть времени) на строгом анализе пересе-
чения двух отрезков прямых, которое меняется от одного приме-
нения к другому.
•Поскольку мы все время разграничиваем области в отличие от
векторных рисунков, можно наметить два различных подхода.
Неявное разрезание. Здесь рассматриваются участки поверх-
ности, ограниченные контуром области. Тогда области, получа-
ющиеся в результате разрезания, характеризуются множеством то-
чек (поверхностью), а не своим контуром.
Явное разрезание. Здесь обрабатывается контур области как
векторный рисунок. Образующиеся области описываются своими
контурами.
•Общий метод анализа характеризуется одним приемом — ме-
тодом прослеживания контура. Действительно, он позволяет
обрабатывать контуры независимо от того, выпуклые они или име-
ют произвольную форму, легко преодолевать любые особые слу-
чаи. Кроме того, поскольку анализ контуров, выполняемый этим
методом для разрезания, заполнения или штрихования, во всех
случаях идентичен, можно часть этих операций обработки выпол-
нять одновременно, создавая на выходе такие же структуры дан-
ных, которые используются на входе. При этом экономится тре-
буемый объем памяти и повышается быстродействие.
•Метод прослеживания контуров позволяет достаточно просто
решать некоторые элементарные задачи и в случаях немногоуголь-
ных контуров (сравнение точка — контур, разрезание отрезка и
дуги окружности). Было бы интересно исследовать и другие опе-
рации, например пересечение двух выпуклых немногоугольных
контуров.
СПИСОК РАБОТ, ПЕРЕВЕДЕННЫХ НА РУССКИЙ ЯЗЫК
10. Куэнью Ф., Гедж Р. Машинные методы генерации цветных плоских изображений
на растрах телевизионного типа ТИИЭР.—1980.—Т.68, N7.—С.177—191.
13. Фоли Дж., вэн Дэм А. Основы интерактивной машинной графики: В 2-х кн.
Пер. с англ.—М.: Мир, 1985.
25. Мартинес Ф. Синтез изображений: Пер. с франц.—М.: Радио и связь, 1990.
(Внимание! на самом деле Эгрон ссылается на диссертацию Мартинеса, но,
мне кажется, имеет смысл дать ссылку на этот перевод, тем более что
Мартинес пишет в своей книге, что в ее основе лежит его диссертация.)
28. Ньюмен У., Спрулл Р. Основы интерактивной машинной графики: Пер. с
англ.—М.: Мир, 1976.
33. Павлидис Т. Алгоритмы машинной графики и обработки изображений: Пер. с
англ.—М.: Радио и связь, 1986.

СПИСОК ЛИТЕРАТУРЫ
| В. ACKLAND, N. WESTE
The edge-flag algorithm. A fill method for raster scan displays. IEEE
Trans. Сотр., Vol. C-30, n° 1, January 1981.
2. F. ALLIAUME
Algorithmes pour identifier lee configurations glometriques de 2 seg-
ments de droite.
Rapport de recherche, Universite de Nantes, Mai 1981.
3 P. ATHERTON et K. WEILER
Hidden surface removal using polygon area sorting. Computer graphics,
vol. 11(2) : 214, Summer 1977.
4. J.L. BENTLEY, S. OTTMAN
Algorithms for reporting and counting geometric intersections. IEEE
Trans. Comp, Vol. C-28, n°9, September 1979.
5. \. BLOCH
Generation de taches bicolores - application aux caracteres d'imprime-
rie - problernes de nature ordinale.
These Docteur-Ingenieur, St-Etienne, Juillet 1981.
6. J.E. BRESENHAM
Algorithm for computer control of a digital plotter
IBM System Journal, Vol. 4, n#1 pp. 25-30, 1965.
7. J.E. BRESENHAM
A linear algorithm for incremental digital display of circular arcs
CGIP, Vol. 20, n°2, Fevrier 1977.
M. LUCAS et al.
La realisation dee logiciels graphiques interactife
Ecole d*Et4 du Breau-sans-nappe - Juillet 1979.
Ed. Eyrolles 1981.
9. K.E. BRASSEL, R. FEGEAS
An algorithm for shading of regions on vector display devices.
Computer Graphics, Vol. 13, ne3, pp. 126-133, 1979.
10. P. COUEIGNOUX, R. GUEDJ
Computer generation of colored planar patterns on TV-like rasters.
Proceedings of the IEEE, Vol. 68, n*7, July 1980.
U P. COUEIGNOUX
Character generation by computer
CGIP. 16, pp. 240-269. 1981.
12. E.A. EDMONDS, A. SEHAPFO, S.A.R. SCRIVENER
Image handling in-two-dimensional design
IEEE Computer Graphics and Applications, Vol.2, n*5, Juillet 1982.
13 J.D. FOLEY et A. VAN DAM
Fundamentals of Interactive Computer Graphics
Addison-Wetley Systems Programming Series, 1982.
14. N.R. FRANKLIN
Evaluation of algorithms to display vector plots on raster devices
CGIP, Vol. 11, pp. 377-397, 1979.
15 G. HEGRON
Algorithmes elementaires pour la production d'images par ordinateur.
Etude bibliographique.
Conv. P et T n*82 35068, RR IMI-info-3, Universite de Nantes, Juin 1982.
16. G. HEGRON
Techniques de remplissage de taches sur une surface a pointillage.
Conv. P et T n*82 35068, RR IMI-info-4, Universite de Nantes, Septem-
bre 1982.
17 G. HEGRON
Algorithmes elementaires de decoupage et traitements de nature geome-
trique pour la production d'images par ordinateur.
211

Conv. P et T n*82 35068, RR IMI-info-7, Universite de Nantes, Janvier
1983.
jg G. HEGRON
La technique du euivi de contour en synthese d'images et see applica-
tions.
PI IRISA n* 209, Universite de Rennes, Octobre 1983. *
19. G. HEGRON
Etude comparative d*algorithmes elementaires pour la eyntheae d*image
par ordinateur.
These de Зёте cycle. Universite de Rennes, Septembre 1983.
20. J-F. JARVIS, C.N. JUDICE, W.H. NINKE
A survey of techniques for the display of continuous tone pictures on
bilevel displays.
CGIP, vol.5, pp. 13-40, 1976.
21. H. LIEBERMAN
How to color in a coloring book
Сотр. graphics. Vol. 12, August 1978.
22. V.D. LITTLE, R. HEUFT
An area shading display system
IEEE Trans. Сотр., Vol. C-28, n*7, Juillet 1979.
23# M. LUCAS
Contribution a 1'etude dee techniques de communications graphiques
avec un ordinateur. Elements de base de logiciels graphiques interac-
tifs.
These d'Etat. IMAG Grenoble, Decembre 1977.
24. P.С MAXWELL, P.W. BAKER
The generation of polygenes representing circles, ellipses and hyper-
boles.
CGIP, Vol. 10, pp. 84-93, 1979.
F. MARTINEZ
Vers une approche aystematique de la synthese d*images.
Aspect logiciel et materiel. These d'Etat, INPG, Grenoble, Novembre
1982.
26 M. MERIAUX
Etude et realisation d'un terminal graphique couleur tridimensional
fonctionnant par taches.
These de Docteur-Ingenieur, Universite de Lille, Janvier 1979.
27. P. MORVAN, M. LUCAS
Images et ordinateur - Introduction a 1'infographie interactive
Ed. Larousee, Serie informatique, Paris, Septembre 1976.
28. W. NEWMAN, R.F. SPROULL
Principles of interactive computer graphics
He. Graw-Hill, New-York, First Edition 1973.
29. W. NEWMAN, R.F. SPROULL
Principles of interactive computer graphics
Mc. Graw-Hill. New-York, Second Edition 1979.
3Q J. O'ROURKE, C.B. CHIEN, T. OLSON et D. NADDOR
A new algorithm for intersection convex polygons.
CGIP, vol.19, n*4, pp. 384-391. AoQt 1982.
31. T. PAVLIDIS
Filling algorithms for raster graphics
CGIP. Vol.10, pp. 126-141, June 1979.
32. T. PAVLIDIS
Contour Filling in raster graphics
Сотр. graphics. Vol. 15. n*3, August 1981.
33. T. PAVLIDIS
Algorithms for graphics and Image Processing
Ed. Springer-Verlay, Bell Laboratories, 1982.
212

34. D.F. ROGERS, J.A. ADAMS
Mathematical element* for computer graphics
Mc Grav-Hill book company. New-York, 1976.
35. M.A. ROY
Etude comparative d'algorithmea pour 1'amelioration de detain* au trait
tur une surface point par point
IRISA Rennes, PI n*189, Universite de Nantea, RR IMI-Info 10, Janvier
1983.
36. E. SECHER
Conception et realisation d'un logiciel de aaiaie at restitution de
cartes elementaires.
IRISA Rennes, PI n*188, Universite de Nantes, RR IMI-Info 9, Janvier
1983.
37. M. SHAMOS
Geometric complexity
Proceeding of the 7th ACM symposium on the theory of Computing, May
1985.
38. H. SHANI
Filling regions in binary raster images : a graph-theorie approach
Сотр. graphics, Vol. 14, n*3, pp. 321-327, July 1980.
39. M. SHAMOS, S. HOEY
Geometric intersection problems
17th FOCS Conference, 1976.
40. С SICO
Generation de taches bicolores - Applications aux caracteres d'impri-
merie - Problem* de nature geometrique.
These de Docteur-Inglnieur, Saint-Etienne, Mars 1982.
41. A.R. SMITH
Tint fill
Proc. SIGGRAPH-ACM. pp. 276-283, August 1979.
42. I.E. SUTHERLAND, G.W. HODGMAN
Reentrant polygon clipping
CACM. Vol. 17. n*1. Janvier 1974.
43. I.E. SUTHERLAND, R.F. SPROULL
A clipping divider
FICC 1968. Thompson books. Washington, D.C., p.765.
44 K. UEILER
Polygon comparison using a graphs representation
Сотр. graphics SIGGRAPH-ACM, Vol. 14, n°3, Juillet 1980.
Примечание t CGIP • Computer Graphics and Image Processing.

ОГЛАВЛЕНИЕ
Предисловие 5
Введение 7
Глава 1 . Общее представление о базовых алгоритмах синтеза
изображений 9
1.1. Алгоритмы и элементарная обработка 9
1.2. Информационное содержание изображения 10
1.3. Кодирование изображения 11
1.4. Виды обработки при синтезе изображений 14
Глава 2 . Генерирование кривых на дискретной поверхности 16
2.1. Введение 16
2.2. Общая классификация 17
2.2.1. Численные методы 17
2.2.2. Инкрементные методы 17
2.2.3. Выводы 18
2.3. Инкрементные методы 18
2.3.1. Введение 18
2.3.2. Общие инкрементные методы 19
2.3.2.1. Общие положения 19
2.3.2.2. Метод Жордана и др 20
2.3.2.3. Выводы 23
2.3.3. Специальные инкрементные методы 23
2.3.3.1. Общие положения 23
2.3.3.2. Обобщение принципа Брезенхема 24
2.3.3.3. Выводы 25
2.4. Генерирование отрезков прямой 25
2.4.1. Алгоритм Люка 26
2.4.2. Алгоритм Брезенхема 27
2.4.3. Генерирование семейства отрезков прямых 28
2.4.3.1. Сжатие 28
2.4.3.2. Повторение 28
2.5. Генерирование окружностей 30
2.5.1. Алгоритм Брезенхема 30
2.5.2. Генерирование дуг окружности 31
2.5.2.1. Постановка задачи .31
2.5.2.2. Алгоритм Брезенхема 32
2.6. Генерирование эллипсов 36
2.6.1. Простой эллипс (алгоритм Руа) 36
2.6.2. Произвольный эллипс (алгоритм Руа) 38
2.7. Генерирование парабол 42
2.7.1. Дуга простой параболы (алгоритм Руа) 42
2.7.2. Дуга произвольной параболы . . 45
2.8. Генерирование гипербол 45
2.8.1. Обобщение метода Брезенхема на случай "простых" гипербол .45
2.8.2. Гипербола, повернутая относительно координатных осей . . .52
2.9. Улучшение качества векторных рисунков 54
2.9.1. Введение 54
2.9.2. Метод Брезенхема 55
2.9.2.1. Принцип действия 55
2.9.2.2. Улучшение изображений отрезков прямых 56
2.9.3. Улучшение изображений кривых второго порядка 58
2.9.3.1. Метод Руа 58
2.9.3.2. Улучшение изображений эллипсов 58
214

2.9.3.3. Улучшение изображений дуг параболы 66
2.9.4. Моделирование уровней яркости 67
2.9.4.1. Введение 69
2.9.4.2. Использование предопределенных ячеек 69
2.10. Заключение 74
Глава 3. Заполнение областей 74
3.1. Введение 74
3.2. Окрашивание 75
3.2.1. Основной принцип 75
3.2.2. Алгоритм Смита 78
3.2.3. Алгоритм Павлидиса 81
3.2.3.1. Принцип 81
3.2.3.2. Действие алгоритма 82
3.2.4. Заключение 86
3.3. Заполнение областей 87
3.3.1. Введение 87
3.3.2. Построчная развертка 88
3.3.2.1. Введение 88
3.3.2.2. Заполнение многоугольников 88
3.3.2.3. Заполнение областей произвольной формы 93
3.3.2.4. Заключение 95
3.3.3. Прослеживание контура 95
3.3.3.1. Принцип действия 95
3.3.3.2. Заполнение многоугольников 96
3.3.3.3. Заполнение множества многоугольников 104
3.3.3.4. Заполнение областей произвольной формы 105
3.3.3.5. Приложение: включение текста в произвольный
многоугольник , 107
3.3.4. Заключение 124
3.4. Разбиение многоугольников на простые элементы 124
3.4.1. Введение 124
3.4.2. Новый алгоритм разбиения 125
3.4.2.1. Метод Бентли и Оттмана 126
3.4.2.2. Использование алгоритма Бентли и Оттмана 127
3.4.3. Заключение 129
3.5. Штрихование многоугольных областей 130
3.5.1. Вертикальная и горизонтальная штриховки 130
3.5.2. Наклонная штриховка области с многоугольным
контуром 130
3.5.2.1. Введение 130
3.5.2.2. Наклонная штриховка методом прослеживания
контура 131
3.5.2.3. Заключение 141
3.6. Выводы 142
Глава 4. Алгоритмы разрезания и обработки геометрических объектов . . 142
4.1. Введение 142
4.2. Классификация задач разрезания 144
4.2.1. Разрезание многоугольника окном 144
4.2.2. Разрезание произвольной области многоугольным
окном. 145
4.2.3. Разрезание многоугольника другим многоугольником 146
4.2.4. Разрезание одной области другой областью 147
4.2.5. Заключение 148
4.3. Взаимное расположение точки и многоугольного контура 149
4.3.1. Введение 149
215

4.3.2. Сравнение "точка — контур" (выпуклый
многоугольник) 151
4.3.2.1. Введение 151
4.3.2.2. Метод Шамоса 151
4.3.3. Положение точки относительно произвольного контура . . .152
4.3.3.1. Введение .152
4.3.3.2. Метод прослеживания контуров 153
4.3.4. Заключение 155
4.4. Разрезание отрезка прямой многоугольным контуром 155
4.4.1. Введение 155
4.4.2. Разрезание прямоугольным окном 157
4.4.2.1. Введение 157
4.4.2.2. Алгоритм Сазерленда — Спрулла 157
4.4.2.3. Алгоритм Павлидиса 159
4.4.3. Разрезание выпуклым контуром 162
4.4.3.1. Введение 162
4.4.3.2. Алгоритм Павлидиса 162
4.4.4. Разрезание произвольным контуром 166
4.4.4.1. Введение 166
4.4.4.2. Алгоритм прослеживания контура 166
4.4.5. Заключение 170
4.5. Разрезание многоугольника многоугольным окном 170
4.5.1. Введение 170
4.5.2. Алгоритм Сазерленда и Ходжмена 171
4.5.2.1. Разрезание многоугольника прямой 171
4.5.2.2. Обобщение на случай разрезания
многоугольника окном 173
4.5.3. Пересечение двух выпуклых многоугольников 173
4.5.3.1. Метод Шамоса 174
4.5.3.2. Метод О'Рурке и др 183
4.5.3.3. Пересечение двух прямолинейных отрезков 187
4.5.3.4. Заключение 189
4.5.4. Пересечение двух невыпуклых многоугольников 189
4.5.4.1. Частный подход 189
4.5.4.2. Алгоритм Атертона — Уэйлера 192
4.5.5. Заключение 192
4.6. Разрезание области многоугольным окном 194
4.6.1. Введение 194
4.6.2. Явное разрезание 194
4.6.3. Неявное разрезание 194
4.6.4. Заключение 195
4.7. Разрезание одной области другой областью 195
4.7.1. Введение 195
4.7.2. Область задана множеством точек - 196
4.7.3. Область задана множеством интервалов 200
4.7.3.1. Введение 200
4.7.3.2. Алгоритм разрезания двух областей 201
4.8. Обобщение на области произвольной формы 203
4.8.1. Сравнение "точка — произвольный контур" 203
4.8.2. Разрезание отрезка немногоугольным контуром 204
4.8.3. Разрезание дуги окружности немногоугольным контуром . . . 207
4.8.3.1. Вычисление точек пересечения 207
4.8.3.2. Выделение видимых частей 208
4.8.4. Заключение 209
4.9. Заключение 209
Список литературы 210
Список работ, переведенных на русский язык 211
216