Текст
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО
СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ СССР
НАУЧНО-МЕТОДИЧЕСКИЙ КАБИНЕТ
ПО ЗАОЧНОМУ И ВЕЧЕРНЕМУ ОБУЧЕНИЮ
МОСКОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
имени М. В. ЛОМОНОСОВА
Е. Н. БЕРЕЗКИН
РЕШЕНИЕ ЗАДАЧ
ПО
ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Часть первая
Учебно-методическое пособие
для студентов-заочников
механико-математических факультетов
государственных университетов
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
1973
ВВЕДЕНИЕ
Настоящее пособие написано в соответствии с программой
курса теоретической механики, действующей в МГУ. Предла-
Предлагаемые в нем задачи иллюстрируют основные методы теоре-
теоретической механики и приложение этих методов к решению
конкретных задач. Последнее является особенно важным при
изучении курса."
Решение задач по теоретической механике 'представляет
серьезные затруднения для учащихся, и научиться их решать
самостоятельно весьма трудно. Кроме того, при самостоятель-
самостоятельном решеи-ии задач нет никакой уверенности в том, что из-
избранный путь решения действительно правильный. При ре-
решении задач в аудитории 'преподаватель контролирует реше-
решения и, направляя самостоятельную работу студентов, обра-
обращает их внимание на особенности изучаемых методов. Та-
Такого контроля и '.помощи лишены все те, кто изучает предмет
самостоятельно. Для них п .первую очередь и будет предназ-
предназначаться это пособие, которое в какой-то мере сможет заме-
заменить преподавателя.
В 'пособии помещены общие указания по решению задач,
даются некоторые рекомендации, приводится разбор наибо-
наиболее общих задач и методов их решения; каждый раздел за-
заканчивается задачами для самостоятельных упражнений.
Прежде чем приступать к решению задач, необходимо
изучить соответствующие разделы теоретического курса и в
дальнейшем стараться следовать изученным методам. Только
при выполнении этих условий 'пособие действительно окажет-
окажется полезным и задачи будут помотать усвоению теоретиче-
теоретических методов. Для закрепления материала необходимо решить
предлагаемые в каждом разделе задачи, краткие указания и
ответы к которым даны в конце пособия. При решении задач
необходимо стремиться к тому, чтобы решения иллюстриро-
иллюстрировали теоретические методы курса, и помнить, что основная
цель заключается в том, чтобы усвоить эти 'методы, а не в
том, чтобы решить как можно больше задач. Задачи, подо-
бранные в пособии, должны соответствовать этой цели, но на-
научиться решать их можно только не заглядывая Постоянно в
решения, приведенные в конце брошюры.
В пособии рассмотрены общие методы решения задач по
кинематике, аналитической статике, динамике точки и систе-
системы. Задачи на применение теории векторов и геометрической
статики не рассматриваются.
Настоящий выпуск пособия является первой частью, изда-
издаваемой Научно-методическим кабинетом по заочному и ве-
вечернему обучению МГУ имени М. В. Ломоносова, и включает
в себя указания к решению задач только по одному из раз-
разделов курса теоретической механики — кинематике. Части
вторая и третья пособия будут издаваться кабинетом в даль-
дальнейшем отдельными выпусками.
КИНЕМАТИКА
Основной задачей теоретической механики является опи-
описание движений механических систем, происходящих под
действием заданных сил. Такое описание может быть пол-
полностью дано только в динамике системы материальных то-
точек. Все остальные разделы теоретической механики либо
решают частные задачи, либо являются подготовкой к реше-
решению основной задачи. Последнее больше всего относится к
кинематике. Хотя в кинематике имеются свои самостоятель-
самостоятельные интересные задачи, все же основная ее цель — подготов-
подготовка материала для решения задач динамики. В кинематике
изучаются движения системы материальных точек без учета
причин, вызывающих эти движения. Все такие движения под-
подчиняются определенным правилам и законам; их можно сис-
систематизировать в следующем порядке:
1. Скорость и ускорение материальной точки в простейших
движениях.
2. Сложное движение материальной точки. Теорема о
сложении скоростей для одной 'материальной точки.
3. Теорема Эйлера о распределении скоростей в твердом
теле.
4. Теорема Кориолиса об ускорении материальной точки
в сложном движении.
5. Распределение ускорений в твердом теле.
Первый из перечисленных разделов изучает элементарные
свойства движения материальной точки, зависимость между
координатами материальной точки, возможные скорости и
ускорения материальной точки в простейших движениях. Осо-
Особое внимание следует обратить на определение проекций ус-
ускорения материальной точки на различные системы осей и
главное — на естественные оси координат.
Второй раздел изучает сложное движение материальной
точки в рассматриваемый момент времени (мгновенное сос-
состояние движения 'материальной точки). Наиболее важным яв-
ляется вопрос об определении переносной и относительной
скоростей материальной точки и о выборе подвижной систе-
системы отсчета. Теорема о сложении скоростей является одной из
важнейших теорем кинематики. Она служит основой и при
изучении распределения скоростей в твердом теле.
Теорема Эйлера о распределении скоростей в твердом те-
теле может быть .представлена формулой
-ОМ].
Наиболее существенными здесь являются представления о
сложном движении твердого тела в рассматриваемый момент
времени и о мгновенных состояниях движения твердого тела
(рассматривается лишь состояние скоростей точек твердого
тела в данный момент времени). Как частные случаи рас-
рассматриваются шюскопараллелыюе движение твердого тела и
случай движения твердого тела с одной неподвижной точкой.
Теорема Кориолиса об ускорении материальной точки в
сложном движении и формула Ривальса о распределении ус-
ускорений в твердом теле дают представление об ускорениях
точек в сложном движении. Теорема Кориолиса определяет
переход от одной системы координат к другой при нахожде-
нахождении ускорения материальной точки (системы движутся отно-
относительно друг друга). Наиболее важным является вопрос об
определении 'переносного ускорения материальной точки при
выборе различных систем отсчета. Переносное движение не
зависит от характера относительного движения материальной
точки.
Формула Ривальса раскрывает характер теоремы Корио-
Кориолиса^ давая полное представление об определении ускорения
точки подвижной системы отсчета.
В дальнейшем при решении задач будем придерживаться
представленной здесь последовательности изложения, демон-
демонстрируя на простых примерах все преимущества того или
иного метода.
Скорость и ускорение материальной точки
в простейших движениях
Первыми понятиями, связанными с представлениями о
движении материальной точки, с которыми мы встречаемся
в кинематике, являются понятия скорости и ускорения мате-
материальной точки в пространстве и характер изменения ее па-
параметров. В ряде случаев 'параметры, определяющие положе-
положение материальной точки, находятся в некоторой сложной за-
зависимости, которую необходимо раскрыть для полного опре-
определения движения материальной точки.
Рассмотрим несколько задач па раскрытие таких зависи-
зависимостей, которые могут быть представлены в виде тождест-
венных соотношений между параметрами, определяющими
положения различных материальных точек.
Пример 1. Нить ЛМС закреплена одним концом в непо-
неподвижной точке Л и продета через кольцо М, скользящее с по-
постоянной скоростью v0 no неподвижному стержню ЛВ. Другой
конец нити привязан к ползуну С, скользящему по вертикаль-
вертикальному стержню DE (рис. 1). Длина нити равна I, расстояние
AE = h. ABJ_DE. Определить скорость ползуна С в зависимо-
зависимости от расстояния АМ = х.
Рис. 1
Решение. Определим положение точки М координатой ху
определяющей расстояние точки М от точки Л, а положение
точки С — координатой у, определяющей ее расстояние от
точки D. Так как скорость точки М задана, то производная
dx г, п
=v0. Для определения скорости точки С нужно сначала
dt
установить тождественную зависимость координат х и у. Эта
зависимость сразу следует из свойств АМСЕ. Обозначим че-
через а длину стержня DE. Тогда
(h—xJ+ (а—Ур= A-хJ.
Это соотношение остается справедливым в любой момент вре-
времени и мож'ет рассматриваться как тождество по времени.
Дифференцируя это тождество1, получим
/# ч dx . ч dy /, v dx
— lh — x) (а — у) ~ = — (/ — х) — ,
V fdtKUfdt V ' dt
откуда сразу следует
dy_
dt
I — h dx
а — у dt
Здесь l>h, a>y. Исключая у и имея в виду, что
dx
dt
получим
dt
Vq.
Таким же способом решается и другая задача.
Пример 2. Ползун А приводится в движение вдоль
стержня KB при помощи нити, продетой через неподвижное
кольцо С и наматывающейся на колесо, вращающееся с по-
постоянной угловой скоростью со (рис.-2). Определить скорость
v ползуна А как функцию расстояния АВ = х, если ВС—а,
а радиус колеса равен R.
Л М
В
К
Рис. 2 Рис. 3
Решение. Скорость ползуна, совершающего прямолиней-
dx
ное движение, определяется как v =
dt
. Но изменение ве-
величины х зависит от того, как наматывается нить. Легко
устанавливается зависимость
a;2=s2—a\ A)
где s — длина отрезка нити С А. Этот отрезок уменьшается
со скоростью
ds n
dt
Дифференцируя соотношение A), получим
dx ds
dt dt
откуда
_ ds __ х dx
dt s dt
x
/a2 + x2
. В некоторых случаях указанные здесь тождественные со-
соотношения обнаружить не так просто. Рассмотрим следую-
следующий пример.
8
Пример 3. Ползун В приводится в движение посредст-
посредством нити, наматывающейся на шкив радиуса R. Определить
скорость ползуна в зависимости о г расстояния ОВ = х, если
угловая скорость шкива равна о;> (рис. 3).
Решение. В рассматриваемом случае легко устанавливает-
устанавливается простая зависимость
где х — расстояние ползуна от центра шкива; s — длина от-
отрезка нити MB {M — точка касания нити со шкивом). Это
соотношение выполняется в любой момент движения и его,
конечно, можно 'продифференцировать по времени:
dx ds
V - С -
Л —* О •
dt dt
и ds
Но здесь скорость изменения величины s, то есть — , оста-
dt
ется неопределенной, и мы не получаем решения задачи. При-
Приходится искать другую величину, изменение которой извест-
известно, и другую зависимость, связывающую эти величины. Если
в качестве такой величины принять длину участка нити АВ,
которую обозначим через /, то
или
Это соотношение остается справедливым во все время дви
жения, а потому, дифференцируя его, будем иметь
dx
dl •* dt
dt Vxz — R* dt
n
Здесь sin ro= —, а потому
x
dcp R dx
cos © — = ,
dt x2 dt
откуда
<&p _ R , dx
dt xVx* — R2 dt
9
и после подстановки получим
dl __ 1
dt ~~ /x2- R2
( R2\dx
V x J dt
x J dt
x
—Я2 dx
dt
Скорость изменения величины / теперь уже является извест-
известной величиной
dl
R
и мы легко получаем, что
dx
Vx'1 — Я2 "
Задачи для самостоятельных упражнений
1. По земле бежит человек и тащит за собой тележку, на-
находящуюся на возвышенном горизонтальном помосте (рис. 4).
Определить скорость v тележки и ее ускорение /, если извест-
известно, что скорость человека постоянна и равна и, а разность
высот конца веревки, за -который держится человек, и тележ-
Рис. 5
ки равна а.
2. Стержень ОЛ длины 2R вращается с постоянной угло-
угловой скоростью со вокруг своего неподвижного конца О. Ко-
Конец А стержня шарнир но закреплен на окружности диска
радиуса R, который свободно скользит между двумя парал-
параллельными направляющими ОВ и DE. Определить скорость
центра диска С в зависимости от величины угла ф (рис. 5).
3. Точки А и В соединены стержнем. Точка А движется
по окружности с центром на оси Oz в плоскости, параллель-
параллельной плоскости хОу. Точка В может скользить по прямой Суи
параллельной оси Оу. Определить скорость точки В в зависи-
зависимости от угла ф, если известны следующие данные: OOx=h,
ОС=а, OlA = RJ AB — l и vA—скорость точки А (рис. 6).
10
Рис. 6
Рис. 7
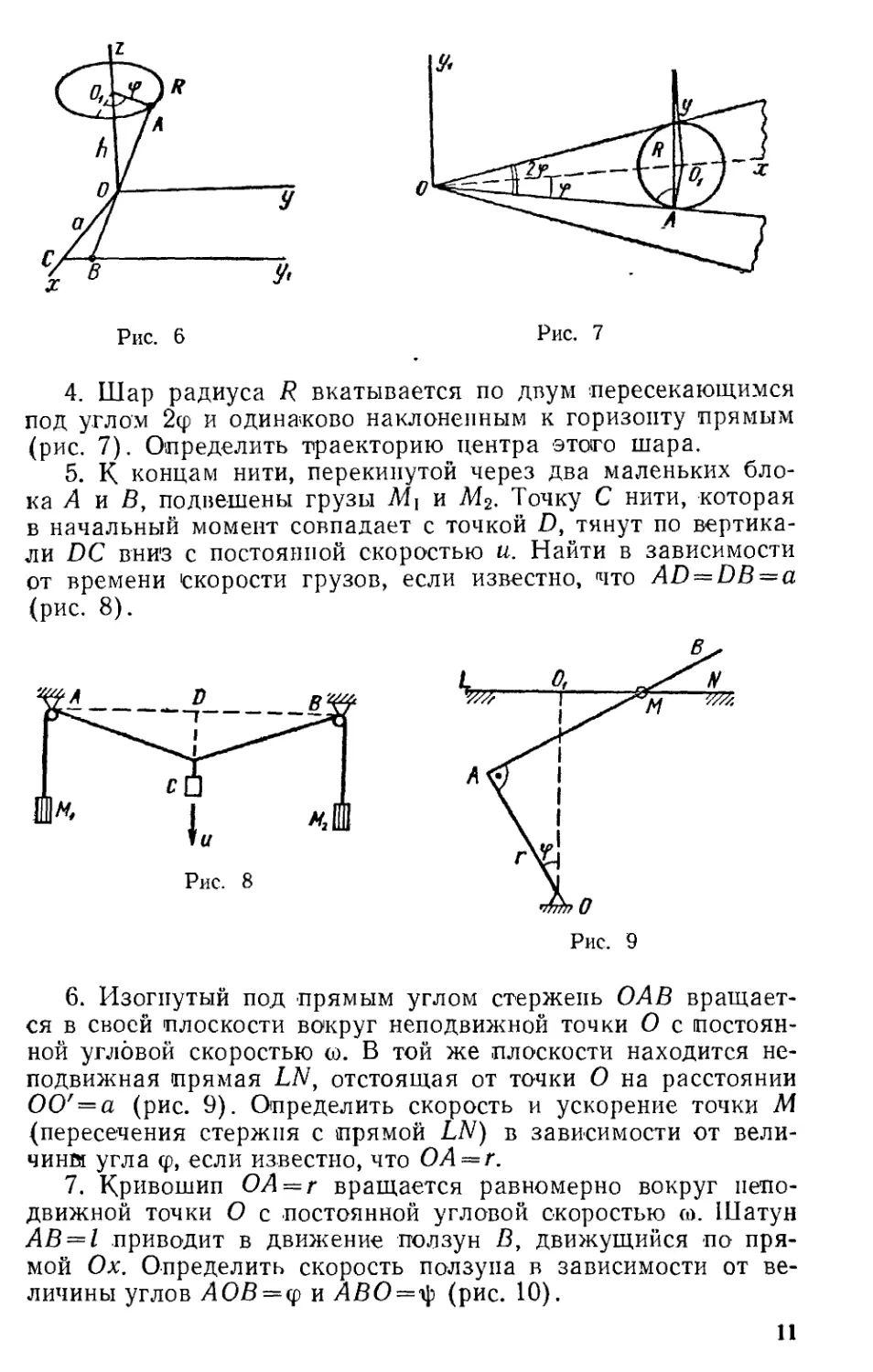
4. Шар радиуса R вкатывается по двум .пересекающимся
под углом 2ф и одинаково наклоненным к горизонту прямым
(рис. 7). Определить траекторию центра этого шара.
5. К концам нити, перекинутой через два маленьких бло-
блока Л и В, подвешены грузы М, и М2. Точку С нити, которая
в начальный момент совпадает с точкой D, тянут по вертика-
вертикали DC вниз с постоянной скоростью и. Найти в зависимости
от времени скорости грузов, если известно, что AD=DB=a
(рис. 8).
Рис. 8
6. Изогнутый под прямым углом стержень ОАВ вращает-
вращается в своей плоскости вокруг неподвижной точки О с постоян-
постоянной угловой скоростью со. В той же плоскости находится не-
неподвижная прямая LNy отстоящая от точки О на расстоянии
ООГ=а (рис. 9). Определить скорость и ускорение точки М
(пересечения стержня с прямой LN) в зависимости от вели-
чинм угла ф, если известно, что ОА = г.
7. Кривошип ОА = г вращается равномерно вокруг непо-
неподвижной точки О с постоянной угловой скоростью со. Шатун
АВ = 1 приводит в движение ползун В, движущийся по пря-
прямой Ох. Определить скорость ползуна в зависимости от ве-
величины углов АОВ = (р и ABO=ty (рис. 10).
11
Рис. 10
У////////У///7///////////////У/Л
Рис. 11
8. Прямой стержень, конец А которого скользит тю непо-
неподвижной прямой Ох с постоянной скоростью v0, проходит че-
через муфту, вращающуюся на шарнире вокруг .неподвижной
точки В. Определить траекторию, скорость и ускорение
(в функции угла ф) точки М стержня, если ЛМ=ОВ=а
(рис. 11).
9. Кривошип ОА, вращаясь с постоянной угловой ско-
скоростью со вокруг неподвижной точки О, приводит в движение
■ползун В при помощи шатуна АВ. Кривошип с шатуном со-
соединен шарниром в точке А. Определить траекторию, ско-
скорость и ускорение точки С шатуна, если ОА — АВ = 1 и АС=а
(рис. 10).
10. Точка движется по коническому сечению у2—2тх—
—пд:2 = 0 с постоянной по величине скоростью Vq. Определить
проекции скорости этой точки на оси координат.
Применение подвижных осей (полярная система коорди-
координат, естественные оси и т. д.) дает возможность глубже по-
понять некоторые свойства движения. Вместе с тем при этом
возникают и некоторые новые затруднения, которые не встре-
встречались при изучении движения в прямоугольных декартовых
осях При анализе таких движений 'применяются как геомет-
геометрические, так и аналитические методы исследования.
Пример 4. Точка описывает плоскую кривую так, что
проекция ее скорости на ось х сохраняет все время постоян-
постоянную величину с. Зная радиус кривизны траектории и скорость
точки в каждый момент времени, определить величину и на-
направление ускорения этой точки.
Решение. Согласно условию задачи, ускорение может быть
направлено только по оси Оу (рис. 12). Вектор ускорения
имеет две проекции на естественные оси, одна из которых
V*
равна —
Р
dv „
а вторая —. Проекция вектора скорости на ось
Ох равна С. Из подобия треугольников имеем
12
v-
Рис. 12
С _ V2
V р/ '
где / — ускорение точки. Отсюда получим
/ = .
ср
Аналитическое решение этой же задачи можно получить
из определения радиуса кривизны траектории
_ у*
х'у'
Х"У"
Подставляя сюда значения х', уг, ..., будем иметь
откуда непосредственно следует ответ задачи.
Пример 5. Точка описывает плоскую траекторию. Зная
радиус кривизны этой траектории и скорость изменения угла,
образуемого вектором скорости с некоторой неподвижной пря-
прямой, определить скорость точки.
Решение. Аналитическое решение задачи следует непо-
непосредственно из определения радиуса кривизны траектории
ds
р= — . Получаем
d
ds dw
— =р—!-.
dt dt
Все рассуждения и формулы становятся более сложными
при рассмотрении пространственных задач.
Пример 6. Определить тангенциальную и нормальную
составляющие ускорения материальной точки, движение кото-
которой задано уравнениями
13
'Решение. По* определению имеем
v = /*'2 + у'2 + г'2 - /[// @12 + [Л/ (О]2 + [N (Of.
откуда касательная составляющая ускорения находится про-
простым дифференцированием
• dv x'x" + y'y"-\-z'2!'
h~ di~ / x11 + yfa + z"
Величина полного ускорения точки может быть опреде-
определена из условия
Нормальную составляющую ускорения получим, восполь-
воспользовавшись формулой
(х'у" — у'х"J + {у'г" — z'y"f + {z'x" — x'z"
~ х'2 + У'2 + г'2
В случае плоского движения г'=;г"==0. Тогда
/п2 =
х'х" +у'у"
у ^
Пример 7. Точка движется по винтовой линии с постоян-
постоянной по величине скоростью v0. Определить величину и на-
направление ускорения и радиус кривизны траектории точки.
Решение. Параметрические уравнения винтовой линии име-
имеют вид:
где ф — неизвестная функция времени, г и а — постоянные.
Дифференцируя эти выражения, получим
лг' = —rq/sin(p, у' = rq/ соБф, zr = a 3
откуда
02= (r2 + a2)q>'2 = v02=const
и
= const.
Проекции ускорения получают вид:
х" = — /-ф^соэф, у" = — гф'251пф, г" — 0.
14
Из последних формул видно, что вектор ускорения распо-
расположен в плоскости, ортогональной к оси винта, а величина
ускорения равна
"■
j =Vx
Так как скорость v = const, то касательная составляющая
ускорения обращается в нуль, то есть
/,=0
и, следовательно,
р
Подставляя значение / в эту формулу, будем иметь
ra-fa2 р
откуда
р =
В этом случае вектор главной нормали к траектории точки
направлен к оси винта, но радиус кривизны траектории ока-
оказывается больше радиуса винта. Полное ускорение тоже
оказывается направленным по главной нормали. Такое рас-
расположение вектора ускорения обусловлено равномерностью
движения точки по винтовой линии. Если же движение не-
неравномерное, то появится еще и касательная составляющая
ускорения.
При применении полярной системы координат необходимо
помнить, что оси этой системы не являются неподвижными.
Они вращаются. Это обстоятельство вносит ряд особенностей
при вычислениях. Гак, если производная представляет
dt
собой проекцию скорости точки на радиус-вектор (радиаль-
(радиальная составляющая скорости), то уже (проекция ускорения
на радиус-вектор не будет равна второй шроизводной от г,
то есть
Рассмотрим некоторые примеры.
15
Пример 8. Точка описывает плоскую кривую. Радиаль-
Радиальная составляющая скорости точки положительна и постоян-
постоянна по величине, а радиальная составляющая ускорения отри-
отрицательна и обратно пропорциональна кубу расстояния от не-
некоторого полюса. Определить траекторию и секторную ско-
скорость точки.
Решение. Аналитическое решение этой задачи следует не-
непосредственно из определения радиальной и трансверсальной
составляющих ускорения материальной точки. Имеем
' "^
откуда
/
=—, г=с.
Разделив второе из последних уравнений на первое, будем
иметь
dr_ _сг*_
dq> a
Отсюда получаем конечное уравнение траектории
1 с ,
г а
где
_ l c
Ci ф0.
r0 a
Окончательно можно записать:
аг0
a —
Из формулы
Г3
непосредственно получаем
Ф'74 = а?,
так что секторная скорость точки будет равна
1 2dw a ,
— г*— =—= const.
2 dt 2
16
Из-за того, что оси полярной системы координат являют-
являются подвижными, создаются искусственные трудности и при
исследовании движения материальной точки, отнесенной к
полярным осям. Рассмотрим пример.
Пример 9. Пользуясь формулами для ускорения точки
в полярной системе координат, доказать, что если ускорение
точки равно нулю, точка будет совершать равномерное и
прямолинейное движение.
Решение. Очевидное решение задачи совсем непросто по-
получить, пользуясь только иоляргтой системой отсчета. В самом
деле, в этом случае будем иметь
dt
Отсюда следует, что
г2ц>' — а=const,
то есть
а
Далее,
Ф г2
г" = ф"г =
а2
или
, dr' Ф
dr rs *
интегрируя это уравнение, получим
/Л ХЛ/ -А ..А
Подставляя полученное значение в выражение скорости в по-
полярной системе координат, будем иметь
" -|- /V ^
+ ^+
= г" -|- /V ^-~ + ^+~ = ^ = const,
2
г
что говорит о движении точки с постоянной по величине ско-
скоростью.
С другой стороны, имеем
а
\7
откуда, интегрируя, получим
а
cos (ф -|- с)
Последнее уравнение является уравнением прямой линии в
полярной системе координат, чем и доказывается утвержде-
утверждение.
В качестве упражнений на применение полярной системы
координат и естественных осей предлагается решить следую-
следующие задачи.
Задачи для самостоятельных упражнений
11. Точка описывает плоскую траекторию с «постоянной по
величине скоростью v0. Продолжение вектора ее ускорения
все вр-емя проходит через заданную неподвижную точку О.
Начальное расстояние движущейся точки от точки О равно а.
Определить траекторию.
12. Точка движется по эллипсу
il i £1
а*
причем радиус-вектор точки, проведенный из центра эллипса,
вращается по закону ер=<рG). Определить скорость точки.
13. Зная, что в плоском движении точки 'модуль ее скоро-
скорости есть величина постоянная, равная с, а угловая скорость
вращения радиуса-вектора тоже постоянна и равна со, найти
уравнения движения и траекторию точки, если известно, что
при ф=0 имеем г = 0.
14. Материальная точка движется по эллипсу
г =
1 — e cos ф
так, что ее секторная скорость относительно фокуса эллипса
остается постоянной величиной, равной . Построить го-
годограф скорости этой точки.
15. Точка движется по поверхности прямого эллиптиче-
эллиптического цилиндра по винтовой линии, наклоненной под углом а
к образующей цилиндра. Секторная скорость проекции этой
точки на плоскость, перпендикулярную к образующей ци-
цилиндра, постоянна и равна с. Определить скорость точки.
16. Точка описывает плоскую траекторию. Известно, что
секторная скорость этой точки пропорциональна модулю ее
радиуса-вектора, а радиальная скорость постоянна, то есть
18
, b>0)
и ф=0 и r=r0 при t=0. Найти траекторию точки и уравне-
уравнения движения.
17. Точка М описывает плоскую кривую. Линия ускорения
точки в пересечении с кругом кривизны образует хорду
МЛ = 1. Выразить величину ускорения через величину скоро-
скорости и длину этой хорды.
1.8. Точка описывает окружность радиуса R с начальной
скоростью v0. Ускорение точки образует с направлением ее
скорости ^постоянный угол а. Определить величину скорости
точки как функцию времени.
19. Мост имеет форму параболы у = —0,005а:2, причем х
и у выражены в метрах. Паровоз движется ло мосту с по-
постоянной по величине скоростью, равной 72 км/час. Опреде-
Определить величину ускорения паровоза, когда он находится в зер-
шине 'параболы.
20. При 'плоском движении .материальной точки угол а
между направлениями се скорости и ускорения остается все
время 'постоянным. Показать, что в этом случае величина
скорости точки может быть представлена в виде
где ф — угол, образуемый направлением скорости и направ-
направлением некоторой неподвижной прямой, расположенной в
плоскости движения; фо и v0— соответственно начальные зна-
значения угла и скорости; c = ctga.
21. Точка описывает плоскую кривую, причем 'прямая, по
которой направлено ее ускорение /, все время проходит через
неподвижную точку О. Показать, что в этом случае
dv
dr
где v — величина скорости точки, г — модуль се радиуса-
вектора относительно точки О. Знак « + » берется в том слу-
случае, когда ускорение направлено от точки О.
22. Найти в молярных координатах (г, ф) уравнение кри-
кривой (линии погони), которую опишет корабль, сохраняющий
постоянный угол пеленга а па неподвижную точку (угол меж-
между направлением скорости и направлением на точку), если
известен угол а и г(ц> = 0) =го. Корабль принять за матери-
материальную точку, движущуюся по плоскости, а за полюс взять
произвольную точку этой плоскости. Исследовать частные
случаи: а=0, а= — и а=я.
23. Точка описывает циклоиду с постоянной по величине
19
скоростью v0. Показать, что проекция этой точки на ось Оу
движется с постоянным ускорением. Уравнение циклоиды
имеет вид
x = R(q—sincp), y = R(l—coscp).
Обратная задача. Найти кривую, если известно, что
проекция движущейся по ней с постоянной по величине ско-
скоростью v точки на некоторую пересекающую ее и лежащую
в ее плоскости прямую имеет постоянное ускорение а.
Сложное движение материальной точки.
Теорема о сложении скоростей
Теорема о сложении скоростей является одной из основ-
основных теорем кинематики. Она утверждает, что абсолютная
скорость материальной точки, участвующей в сложном дви-
движении, в каждый момент времени равна геометрической сум-
сумме ее переносной и относительной скоростей. Математически
эта теорема может быть представлена формулой
где переносной скоростью ve называется скорость той точки
подвижной системы координат, с которой в данный момент
совпадает движущаяся материальная точка. Таким образом,
переносная скорость зависит не от характера относительного
движения материальной точки, а лишь от движения подвиж-
подвижной системы отсчета и от положения материальной точки в
данный 'момент времени. Относительной скоростью vr мате-
материальной точки называется ее скорость в движении относи-
относительно подвижной системы координат. В общем случае по-
подвижная система координат совершает некоторое сложное
движение, а скорости различных точек этой подвижной систе-
системы будут различными и по величине, и по направлению. Это
обстоятельство необходимо иметь в виду при .определении стс-
репоеной скорости. Наибольшие затруднения при решении за-
задач этого раздела, 'по-видимому, заключаются в выборе по-
подвижной системы отсчета.
В ряде случаев сложное движение материальной точки
определяется одновременно относительно двух подвижных
систем отсчета. При этом полное решение задачи может быть
найдено только при учете движения обеих подвижных систем
отсчета. Рассмотрим несколько примеров, 'поясняющих это
утверждение.
Пример 10. Плоская материальная кривая, уравнение
которой, отнесенное к подвижной системе отсчета, имеет вид
y=f(x), движется в своей плоскости поступательно справа
налево с постоянной скоростью v0. Палочка ОЛ, длина кото-
20
рой равна I, шарнирно закреплена одним концом в непо-
неподвижной точке О и опирается на эту кривую другим (свобод-
(свободным) концом. Определить угловую скорость со палочки в за-
зависимости от положения системы (рис. 13).
c>
О,
Рис. 13
X
Рис. 14
Решение. Абсолютной траекторией точки А является ок-
окружность с центром в точке О. Вектор абсолютной скорости
точки А направлен по касательной в этой окружности. Из-
Известно только направление этой скорости, по не величина.
Свяжем подвижную систему отсчета с движущейся кривой.
Тогда переносное движение будет поступательным, а перенос-
переносная скорость — скоростью v0. Относительное движение точ-
точки А происходит по кривой y=f(x), а потому и относитель-
относительная скорость vr направлена по касательной к этой кривой.
Из ААВС имеем
эшф sin(90°+a —
откуда получаем
Здесь
cos (а — ф) cosoc + sina • igф
а потому
У
I f
ay
dx
dy
dx
rill
Условие постоянства скорости со получает вид
21
dy
откуда
i>oarc sin-^-
>o
co
0
/2 - уг =
C.
Если же при х=0 имеем y = 0, то С=соо/.
Пример 11. Палочка О А длины а вращается в плоско-
плоскости чертежа вокруг неподвижной точки О с постоянной угло-
угловой скоростью а>, = const (рис. И). Вокруг подвижного конца
А этой палочки в той же плоскости вращается другая палоч-
палочка АВ длины Ь так, что угол <р, заключенный между палоч-
палочками, изменяется по закону
^-co2>0,
at
где @2 постоянна по величине. Определить абсолютную ско-
скорость точки В, применяя теорему о сложении скоростей.
Решение. Построение решения зависит от выбора подвиж-
подвижной системы отсчета. Выберем сначала подвижную систему
отсчета так, чтобы ее начало координат con-падало с точкой А.
Ось Ах направим по палочке ОА, а ось Ау — ортогонально
к ней в плоскости чертежа. Тогда переносная скорость точки
будет равна со^-ОВ (рис. 15) и направлена ортогонально
'///////////////////////////////////////Л
Рис. 15
Рис. 16
к 05 Относительное положение палочки АВ определяется
углом Ф, а относительная скорость палочки равна со2-0. из
ABDC имеем
(с2
r cos у
— 2ab cos ф) +
— a cos ф)
22
■Совсем по-другому строится решение в том случае, когда
за подвижную систему выбирается система осей с началом
в точке А, но движущаяся поступательно. Тогда переносная
скорость равна vei = ы\а, а направлена ортогонально к стерж-
стержню ОЛ. Положение стержня АВ относительно подвижных
осей определяется теперь углом а+ф, который изменяется со
скоростью ом+ 002. Благодаря этому величина вектора относи-
относительной скорости равна (рис. 14)
tfr = -(@l +@2N.
Из ABD^i будем иметь
v2 = v* + ve* — 2vjVe cos ф = {щ + w2J b% +
+ со^а2 — 2 (©! + ©a) " ^i0^ cos ф = со2262 4
4- ft»!2 (а2 4- Ь2 — 2аЬ cos ф) + 2со1со26 (Ь — а cos ф).
Пример 12. Лодку М, уносимую течением реки, подтя-
подтягивают веревкой к точке А берега. Найти траекторию лодки,
принимая последнюю за точку и считая, что скорость сх те-
течения реки постоянна по всей ее ширине, скорость наматыва-
наматывания веревки постоянна по величине и равна с2 и скорость
лодки относительно реки все время направлена вдоль ве-
веревки (рис. 16).
Решение. Выберем сначала за подвижную систему коорди-
координат систему О^ХхУх, движущуюся поступательно вместе с ре-
рекой. В этой системе переносная скорость лодки vei известна
по величине и направлению. Она равна скорости течения ре-
реки С\, то есть
Относительная скорость лодки натравлена вдоль веревки,-
но не известна по величине. Исходя из этих данных, мы .мо-
.можем только сделать заключение о том, что конец вектора аб-
абсолютной скорости лежит на прямой Ai, параллельной ве-
веревке, но остается неизвестным точное значение абсолютной
скорости.
Выберем теперь другую систему подвижных координат
гУг, ось Ахч которой, про ходит все время через лодку.
В этой системе координат относительное движение лодки пол-
полностью .известно. Лодка все время находится на прямой Ах2,
а ее относительная скорость равна скорости сокращения рас-
расстояния AM, то есть скорости наматывания веревки с2. В пе-
переносном движении точка М теперь описывает окружность
с центром в точке А. Переносная скорость лодки направлена
по касательной к этой окружности, то есть ортогонально к
оси Ах2, но не известна по величине. Из теоремы о сложении
скоростей получаем, что конец вектора абсолютной скорости
должен лежать на прямой А2. Мы получили два заключения
23
о решении одной и той же задачи. Конец вектора абсолютной
скорости лежит на прямой Ai и на прямой Дг одновременно.
Эти прямые пересекаются только в одной точке N, которая и
определяет положение конца вектора абсолютной скорости.
Нетрудно теперь видеть, что в системе Ох\У\ относительная
скорость лодки
а в системе Ах2у2 переносная скорость
Для определения траектории лодки запишем проекции аб-
абсолютной скорости лодки на оси Ах2 и At/2, являющиеся по-
полярными осями:
dr
dt
Исключая время,
или
Отсюда имеем
получаем
dr
rdq>
dr _
г
г
Si
С:
Йф
~dt~~~~
С^Шф
1 Йф
или
а это и есть конечное уравнение траектории, где С — произ-
произвольная постоянная, значение которой определяется началь-
начальными условиями
Пример 13. Рассмотренный выше метод построения аб-
абсолютной скорости может быть применен для определения
направления касательных к кривым, если иметь в виду, что
вектор абсолютной скорости всегда направлен по касатель-
24
ной к траектории точки. Для определения направления абсо-
абсолютной скорости движения материальной точки представля-
представляют как сумму двух более простых движений, направление ко-
которых известно. Пусть, например, требуется построить каса-
касательную к эллипсу.
Решение. Эллипс 'представляет собой геометрическое место
точек, сумма расстояний которых до двух заданных центров
(фокусов) является величиной постоянной:
rl + r2=2af (a)
где а—большая полуось эллипса. Выберем сначала подвиж-
подвижную систему осей F\Xxyx с началом в фокусе Fu направив ось
F\Xi в сторону движущейся по эллипсу точки М (рис. 17).
Тогда относительная скорость
точки М равна скорости изме-
нения расстояния от точки М
до фокуса, то есть
drx
dt
Рис. 17
Выберем теперь подвижную систему координат F2x2y2 с
началом в фокусе F2, направив ось F2x2 в сторону движущей-
движущейся точки М. В новой системе координат относительная ско-
скорость точки М направлена вдоль оси F2x2t а ее величина рав-
равна скорости изменения расстояния от точки М до фокуса F2,
то есть
Из уравнения (а) имеем
dt ' dt
откуда
Обе подвижные системы .имеют возможность только вра-
вращаться вокруг соответствующих фокусов. Благодаря этому и
соответствующие переносные скорости направлены перпенди-
перпендикулярно к осям Fi^i и F2x2. На основании теоремы о сложе-
сложении скоростей находим, что конец вектора абсолютной ско-
скорости лежит на пересечении перпендикуляров к 'прямым F\XX
и F2x2, проведенным через концы соответствующих векторов
относительной скорости.
25
Задачи .для самостоятельных упражнений
Все приводимые ниже задачи предлагается решить с по-
помощью теоремы сложения скоростей.
24. Ползун А движется по горизонтальному рельсу с по-
постоянной скоростью v. Стержень ОВ длины / вращается с по-
постоянной угловой скоростью со вокруг оси О, связанной с пол-
ползуном и перпендикулярной к плоскости чертежа. Определить
абсолютную скорость точки В стержня (рис. 18).'
Рис. 18
Рис. 19
25. Прямая АВ совершает мгновенно-поступательное дви-
движение со скоростью vu направленной перпендикулярно к АВ.
Прямая CD совершает мгновеиио-тюстуиательное движение
в той же плоскости со скоростью V2, направленной перпенди-
перпендикулярно к CD (как показано на рис. 19). Определить вели-
величину и направления скорости колечка М, надетого одновре-
одновременно на обе прямые, если угол между прямыми равен а.
26. Кривошип ОА качающего механизма вращается с уг-
угловой -.скоростью Q. На конце кривошипа находится ползун,
который скользит по стержню, закрепленному своим концом
в неподвижной точке С. Определить угловую скорость вра-
вращения стержня в тот момент, когда угол ф, образуемый кри-
кривошипом и прямой, .соединяющей точки С и О, равен 30°.
Длина кривошипа равна г, расстояние между неподвижны-
неподвижными точками Си О равно а (рис. 20).
Рис. 20.
Рис. 21
27. Две точки движутся равномерно с противоположно
направленными скоростями v>\ и v2 соответственно по парал-
параллельным прямым I и II, г третья точка движется равномерно
26
по параллельной им прямой /// со скоростью v3. Расстояния
между соответствующими прямыми равны т и п. Определить
величину скорости и3, если известно, что во всякий момент
времени все три точки лежат на одной прямой (рис. 21).
28. Стержень ОА, который может свободно вращаться
около неподвижной оси О, расположенной па полу, опирается
на стол, имеющий высоту к и движущийся поступательно со
скоростью v. Определить абсолютную скорость точки £ стерж-
стержня, находящейся в соприкосновении с углом стола, в тот мо-
момент, когда расстояние края стола от точки О равно s
(рис. 22).
'////////////////////////////////////*
1777777777777777777777777/
Рис. 22
Рис. 23
29. Колеса А и В вагона, движущегося со скоростью v по
прямолинейному рельсу, катятся без скольжения. Радиусы
колес равны г, а расстояние между осями равно d. Опреде-
Определить скорость точки М\ колеса А относительно системы коор-
координат хВу, неизменно связанной с колесом В (рис .23).
30. Колеса А и В пагона, движущиеся со скоростью v no
прямолинейному рельсу, катятся без скольжения. Радиусы
колес равны г, а расстояние между осями равно d. Опреде-
Определить скорость точки М2 колеса А относительно системы коор-
координат, неизменно связанной с колесом В (рис. 23).
31. Колеса А и В вагона, движущиеся со скоростью v по
прямолинейному рельсу, катятся без скольжения. Радиусы
колес равны /', а расстояние между осями ранно d. Опреде-
Определить скорость центра колеса А относительно системы коорди-
координат, неизменно связанной с колесом В (рис. 23).
32. Прямая ОА, совпадающая в начальный момент с осью
Оу, вращается равномерно с угловой скоростью ш вокруг на-
начала координат. Одновременно с прямой начинает двигаться
точка М, выходя из начального положения М0(х0, у0) и со-
сохраняя во все время движения скорость vQ, постоянную по
модулю и направленную перпендикулярно к ОА. Определить
относительное движение точки М по отношению к прямой ОА
(рис. 24).
33. Изогнутый под прямым углом стержень ОАВ вра-
вращается в своей плоскости вокруг неподвижной точки О с по-
постоянной угловой скоростью (о. В той же плоскости находится
27
неподвижный стержень LN, отстоящий от точки О на рас-
расстоянии ОО' = а. Определить, применяя теорему о сложении
скоростей, абсолютную и относительную скорости кольца, на-
надетого одновременно на стержни АВ и LN (рис. 9).
Рис 24
Рис. 25
34. Стержень ОЛ вращается вокруг неподвижной точки О
со скоростью со. В точке Л с ним соединен шарнирно стер-
стержень АВ, на конце которого закреплен ползун В, скользящий
по прямой ОС. Определить скорость ползуна В, пользуясь
теоремой о сложении скоростей (р,ис. 25).
35. Шарнирный параллелограмм ОАхА2Ох имеет две непо-
неподвижных точки: О и О\. Сторона OAV вращается с постоян-
постоянной угловой скоростью со вокруг неподвижной точки О в плос-
плоскости чертежа. По стороне А\А2 с постоянной скоростью v
движется точка М. Определить величину и направление абсо-
абсолютной скорости точки М в тот момент, когда ZOiOAl = a,
считая, что OAl = a, АХА2=Ь (рис. 26).
Рис. 26
Рис. 27
36. Две палочки AD и BE вращаются в одной плоскости
со скоростями coi и оJ вокруг точек А и В соответственно.
Расстояние между точками А и В равно а. Определить ско-
скорость точки С пересечения палочек в тот момент, когда
ZABE=90°, a /.DAB = 30° (рис. 27).
37. Палочка АВ вращается в плоскости чертежа вокруг
НеПОДВИЖНОЙ ТОЧКИ А С ПОСТОЯННОЙ УГЛОВОЙ СКОрОСТЫО 0I.
В той же плоскости вторая палочка CD вращается с постоян-
постоянной угловой скоростью 0J вокруг точки С, движущейся в
свою очередь с постоянной скоростью v0 вдоль неподвижной
28
направляющей ЛЕ. Определить абсолютную скорость коль-
кольца М, надетого одновременно на палочки АВ и CD, в тот мо-
момент, когда АС=х, ZBAC=a, a ZACD=90° (рис. 28).
В
Рис. 28
Рис. 29
38. Шар радиуса 2а равномерно вращается вокруг непо-
неподвижного вертикального диаметра с постоянной угловой ско-
скоростью со. В то же время по вертикали, отстоящей на расстоя-
расстоянии а от неподвижного диаметра, движется точка М, уравне-
уравнение движения которой имеет вид z=a cos fit, где z — расстоя-
расстояние точки от экваториальной плоско'сти шара, а & = 2со. Ка-
Какой формы следует сделать канал внутри шара, чтоба оба
движения совершались не мешая друг другу?
39. Прямая FM вращается с постоянной угловой скоро-
скоростью со в плоскости данного эллипса вокруг его фокуса F.
Определить скорость точки М пересечения этой прямой с эл-
эллипсом.
40. Лодку М, уносимую течением реки, гребец все время
направляет в точку А берега, сообщая ей постоянную отно-
относительную скорость с2. Найт.и траекторию лодки, принимая
последнюю за точку и считая, что скорость с^ течения реки
постоянна по всей ее ширине. Исследовать случай С\ = с2.
41. Точка М движется по поверхности шара с постоянной
по величине скоростью v, направление которой образует с
проходящим через точку меридианом постоянный угол а.
Определить траекторию точки (рис. 29).
42. Пользуясь теоремой о сложении скоростей, доказать
следующий способ построения касательной к архимедовой
спирали r=at, q> = bt. Соединив движущуюся точку М с по-
полюсом О, восстановим из полюса О перпендикуляр к ОМ и
на этом перпендикуляре отложим в сторону вращения радиу-
радиуса-вектора отрезок ОА, равный —. Прямая, проведенная че-
Ъ
рез М перпендикулярно к МЛ, и будет касательной 'к спира-
спирали в точке М.
43. Методом Роберваля построить касательную к лемнис-
лемнискате (ati = const).
29
44. Методом Роберваля построить касательную к гипер-
гиперболе.
45. Методом Роберваля построить касательную к пара-
параболе и показать, что касательная образует с фокальным ра-
радиусом-вектором и диаметром 'параболы равные углы.
46. Шарнирный параллелограмм О ABC имеет неподвиж-
неподвижную точку О. Стержень ОЛ длины b вращается r плоскости
чертежа с постоянной угловой скоростью со2, а стержень ОС
длины а вращается с постоянной угловой скоростью щ (как
показано на рис. 30). По стержню ЛВ движется с постоянной
х м у* относительной скоростью v точ-
• *в ка М. Определить величину и на-
направление абсолютной скорости
точки М в зависимости от угла а
и расстояния AM = х.
ш,
а
Рис. 30
Кинематика твердого тела.
Распределение скоростей в твердом теле
Мгновенное состояние движения твердого тела опреде-
определяется распределением скоростей точек твердого тела в дан-
данный момент времени. Из теоремы Эйлера известно, что в об-
общем случае мгновенное движение твердого тела всегда мож-
можно представить как сложное, состоящее .из двух простейших
движений: мгновенно-поступательного и мгновенно-враща-
телыюго. Скорости точек твердого тела в общем случае опре-
определяются по формуле
где v0 — скорость мгновенно-поступательного движения; со —
мгновенная угловая скорость вращения твердого тела.
В случае плоскопараллелыюго движения твердого тела
картина распределения скоростей значительно упрощается.
В этом случае мгновенное движение твердого тела сводится
либо к одному мгновенно-поступательному, либо к одному
мгновено-вращательному движению. Изучение движения
сводится к рассмотрению движения плоской фигуры в своей
плоскости, а непрерывное движение может быть представле-
представлено как качение без скольжения подвижной центроиды по не-
неподвижной. Такое 'представление движения в ряде случаев
оказывается весьма удобным, а потому важно научиться оп-
определять положения мгновенного центра вращения и центрои-
центроиды. Мгновенный центр вращения определяется как точка
твердого тела, скорость которой равна пулю в рассматривае-
рассматриваемый момент времени.
30
Рассмотрим некоторые примеры.
Пример 14. Определить положения мгновенного центра
вращения и центроиды звена DC шарнирного антипараллело-
антипараллелограмма АСОВ, большое звено которого АВ остается непо-
неподвижным во все время движения, если известно, что АВ —
= CD=2C>AC=BD = 2a.
Решение. Точка С звена CD может двигаться только по
окружности с центром в точке А. Поэтому скорость точки С
всегда направлена перпендикулярно к АС, а мгновенный
центр вращения расположен на продолжении прямой АС
(рис. 31). Проводя аналогичные рассуждения, получим, что
А.
иеподо
центр
Рис. 31
Рис. 32
мгновенный центр вращения находится на продолжении пря-
прямой DB. Обе упомянутые прямые пересекаются в некоторой
точке S, которая и будет мгновенным центром вращения
стержня DC. Из равенства AACD и AABD непосредственно
следует равенство:
AABC=ADCSf
откуда получаем
AS—£S=2a=const,
и, следовательно, геометрическим местом точек 5 будет ги-
гипербола, фокусы которой находятся в точках А и В. Эта кри-
кривая 'будет представлять собой неподвижную центроиду.
Аналогично имеем
то есть геометрическим местом мгновенных центров по отно-
отношению к стержню CD 'будет гипербола с фокусами в точках
С и D. Непрерывное движение стержня CD можно теперь
31
представить как качение без скольжения гиперболы, связан-
связанной со стержнем CD, по неподвижной гиперболе.
Пример 15. Жесткий угол ЛО£ = ф (рис. 32) движется
в своей плоскости так, что сторона ОЛ все время проходит
через неподвижную точку М, а сторона ОБ — через непо-
неподвижную точку N. Найти центроиды этого движения.
Решение. Свяжем подвижную систему отсчета с углом АО В
и рассмотрим движение точки N. Абсолютная скорость этой
точки равна нулю. В то же время точка N все время остает-
остается на прямой ОБ и, следовательно, ее относительная ско-
скорость будет направлена вдоль прямой ОБ. Но по теореме о
сложении скоростей
и так как vn = 0, то
то есть переносная скорость направлена тоже вдоль пря-
прямой ОВ. Но переносной скоростью является скорость точки
подвижной системы отсчета, которая связана жестко с дви-
движущимся углом. Отсюда следует, что скорость точки N пря-
прямой ОВ направлена вдоль прямой ОВ. Пр,и -помощи анало-
аналогичных рассуждений приходим к заключению, что скорость
точки М прямой ОА направлена вдоль этой прямой. Зная на-
направления скоростей двух точек движущегося угла АОВ, за-
заключаем, что мгновенный центр вращения угла АОВ нахо-
находится на пересечении перпендикуляров к ОА и ОВ, восста-
восстановленных соответственно в точках М и N.
Обозначим через 5 мгновенный центр вращения угла
АОВ. Из построения нетрудно видеть, что точки М, 5, N, О
находятся на одной и той же окружности, диаметр которой
равен расстоянию 05, а центр О] делит пополам расстояние
50. Очевидно, что ZM0N=2q>, a AMO^N — равнобедренный
Отсюда следует, что точка О] является неподвижной во все
время движения, а неподвижной цептроидой будет окруж-
окружность радиуса 0\M = 0\N=r с центром в точке 0^ Подвиж-
Подвижной центроидой будет окружность радиуса 2г с центром в
точке О.
Пример 16. Прямолинейный стержень АВ скользит
своими концами по двум взаимно перпендикулярным направ-
направляющим Ох и Оу, вращающимся вокруг точки О с постоян-
постоянной угловой скоростью со. Угол наклона стержня АВ к оси Ох
изменяется по закону
Ф = Фо±со£.
Определить абсолютную траекторию произвольной точки М
стержня.
Решение. Предположим, что угол ф изменяется по закону
Ф=Фо+«£, и пусть стержень .имеет длину /. Стержень в этом
32
Рис. 33
случае участвует в двух движениях: вместе с подвижной сис-
системой (направляющими) он вращается с угловой скоростью о>
против часовой стрелки и относительно подвижной системы
отсчета вращается с такой же угловой скоростью со тто часо-
часовой стрелке. Мгновенный центр вращения в подвижной систе-
системе находится в точке S, расположенной, на пересечении пер-
перпендикуляров к осям Ох и Оу, восстановленных из концов
стержня АВ (рис. 33). Результирующее движение в этом слу-
случае представляется парой вращений, эк-
эквивалентной мгновенно-поступательному
движению твердого тела, скорость кото-
которого равна моменту пары со/. Скорость
центра стержня по все время движения
остается постоянной по величине и на-
направлена ортогонально к прямой 05,
а следовательно, центр стержня движет-
движется по окружности с постоянной скоростью.
Чтобы определить траекторию точки М,
воспользуемся тем обстоятельством, что
стержень совершает поступательное дви-
движение. Построим на прямых ООХ и 0\М
параллелограмм. Сторона 020 этого па-
параллелограмма остается неподвижной во все время движе-
движения, а точка М будет двигаться по окружности с центром, в
точке 02.
Рассмотрим второй случай, когда
ф=Фо—со/.
Угол ф убывает, и стержень совершает два происходящие
против часовой стрелки вращения. Результирующее движение
является мгновенным вращением с мгновенной угловой ско-
скоростью 2(о, причем лип.ия действия вектора мгновенной угло-
угловой скорости 'проходит через центр стержня Оь Поэтому ско-
скорость точки О\ будет 'постоянно оставаться равной нулю, а
все остальные точки стержня будут описывать концентриче-
концентрические ОКруЖНОСТИ ВОКруГ ТОЧКИ С>2.
Задачи для самостоятельных упражнений
47. Палочка ОЛ вращается в плоскости чертежа вокруг
точки О с постоянной угловой скоростью СО] = const. Вокруг
точки А этой палочки вращается в той же плоскости другая
палочка АВ, причем угол ф между палочками изменяется по
закону
dt
2 Заказ 219
33
где £02 = const (см. рис. 14). Определить абсолютную скорость
и абсолютное ускорение точки В палочки АВ, считая, что
ОЛ Л Ь
48. Палочка ЛВ движется в плоскости чертежа так, что ее
нижний конец А все время скользит по оси Ох, а сама она все
время проходит через неподвижную точку М@, К). Найти
полодии движения и мгновенную угловую скорость вращения
палочки, если скорость ее конца А равна vo = const (рис. 34).
S//////////////////A
Рис. 34
Рис. 35
49. Палочка АВ движется в плоскости хОу так, что ее
нижний конец А скользит но оси Ох, а сама она касается
окружности радиуса г с центром в точке О. Найти скорость
изменения Z.OAB, а также полодии палочки и ее мгновен-
мгновенную угловую скорость, если скорость конца А палочки равна
v (рис. 35).
50. Шарнирный плоский механизм состоит из четырех
стержней AD = BC = 2a и AB = CD = 2c<c2a, связанных шар-
нирно в точках А, В, С, D так, что сторона АВ остается все
время неподвижной. Найти зависимость между угловыми
скоростями со] и со2 звеньев AD ,и ВС соответственно (рис. 36).
О
Рис. 36
Рис 37
51. В шарнирном параллелограмме О ABC точка О остает-
остается все время неподвижной. Звенья ОА и ОС вращаются в
34
плоскости чертежа в 'противоположные стороны соответст-
соответственно с угловыми скоростями о>2 и (Оь Определить абсолют-
абсолютную угловую скорость вращения стержня АВ, его подвижную
и неподвижную центроиды, а также абсолютную скорость
точки В стержня АВ (см. рис. 30). —
52. Прямой /.ABC перемещается в плоскости таким об-
образом, что его точка А скользит по оси Ох, а сторона ВС все
время проходит через неподвижную точку D на оси у. Найти
уравнения неподвижной и «подвижной центроид, если извест-
известно, что AB = OD = a (рис. 37).
53. Парабола, уравнение которорй у\2~2рхи катится без
скольжения по неподвижной прямой. Определить траекторию
фокуса параболы.
54. Палочка О А длины а вращается в плоскости чертежа
вокруг своей неподвижной точки О с постоянной угловой ско-
скоростью соь Вокруг точки А этой палочки в той же плоскости
вращается другая палочка АВ длины Ь, причем угол ф меж-
ду палочками изменяется по закону
dt
=СО2>О, где оJ =
= const. Найти мгновенный центр вращения палочки АВ и
определить скорость движения точки В этой палочки.
55. На общей оси вращения свободно насажены колесо /
и водило //. На конце водила свободно насажено колесо ///,
которое находится в зацеплении с неподвижным колесом IV.
Зная радиусы колес, найти отношение угловых скоростей ко-
колеса / и водила, скорость которого равна соо (рис. 38).
Рис. 38 Рис. 39
56. Найти .относительную и абсолютную угловые скорости
зубчатого колеса // радиуса г2, катящегося без скольжения
по неподвижному зубчатому колесу / радиуса гх и приводя-
приводящегося в движение кривошипом ОА, вращающимся вокруг
оси неподвижного колеса О с угловой скоростью соо. Движе-
Движение кривошипа ОА принять за переносное. Определить уско-
ускорение точки В (р.ис 39).
2*
35
57. Известно, что Лупа, делая полный оборот вокруг
Земли, поворачивается за это время вокруг своей оси один
раз. Принимая орбиту Луны за окружность и допуская, что
ее ось вращения перпендикулярна к плоскости ор'биты, опре-
определить мгновенную ось вращения Луны и ее мгновенную уг-
угловую скорость вращения (принять радиус Земли за R, рас-
расстояние от центра Земли до центра Луны за /).
58. В центре О неподвижной окружности радиуса R
имеется ось, вокруг которой вращается стержень ОМ дли-
длины р. На конце этого стержня свободно насажено колесо ра-
радиуса r = R—р, лежащее в плоскости окружности и касаю-
касающееся ее внутренней стороны. Определить геометрически точ-
точку на окружности малого колеса, линия действия скорости
которой проходит через точку А, являющуюся концом диа-
диаметра, перпендикулярного к ОМ. Определить аналитически
скорость этой точки (рис. 40).
59. Колесо / неподвижно. На его оси свободно насажено
водило ОА, которое вращается вокруг точки О с угловой ско-
скоростью п. На водиле насажены колеса //, /// и IV, находя-
находящиеся в зацеплении между собой и с колесом /. Найти угло-
угловую 'Скорость оLг колеса IV относительно водила, а также его
абсолютную угловую скорость ю4 (рис. 41).
Рис. 40
Рис. 41
60. Две параллельные рейки движутся в одну сторону с
постоянными по величине скоростями vx и v2. Между рейка-
рейками зажат диск радиуса а, катящийся по рейкам без сколь-
скольжения. Найти угловую скорость диска и скорость его центра
(рис. 42).
61. Кривошип О А вращается вокруг точки О с постоянной
угловой скоростью о). При помощи шатуна ЛВ он приводит
в движение ползун В. Показать, что скорость ползуна равна
(o-OD, где D — точка пересечения АВ с перпендикуляром,
восстановленным в точке О к 'Прямой ОВ (рис. 43).
36
62. Равнобокий клин с заданными углами а помещен меж-
между двумя брусками А и В, которые движутся .поступательно
и прямолинейно по горизонтальной плоскости навстречу друг
другу с заданными скоростями о, и v2. Определить скорость
поступательного движения клина (рис. 44).
Рис. 42
Рис. 43
V/77/77/
I
Л/
Рис. 44
Рис. 45
Рис. 46
63. Две рейки движутся параллельно друг другу с посто-
постоянными скоростями Vi и и2 в противоположные стороны.
Между рейками зажат диск радиуса а, который вследствие
движения реек и трения катится по ним без скольжения. Най-
Найти уравнения центроид и определить скорость v0 центра О
диска и его угловую скорость ы (см. рис. 42).
64. Кривошип OA=U вращается вокруг неподвижной
оси О с постоянной угловой скоростью (оо. Он приводит в дви-
движение зубчатое колесо радиуса г2, которое катится без сколь-
скольжения по неподвижному колесу радиуса гх и приводит в дви-
движение связанный с ним стержень ВС = h. Определить угло-
37
вую скорость вращения стержня и скорости точек В и С в тот
момент, когда радиус АВ перпендикулярен к кривошипу ОА
(рис. 45).
65. Шестеренка //, шарнирно закрепленная на конце
стержня ОВ, катится без скольжения по внутренней поверх-
поверхности шестеренки /, которая может свободно вращаться во-
вокруг неподвижной оси О (рис. 46). С шестеренкой // жестко
связан стержень В А, шарнирно соединенный со стержнем АОи
конец О\ которого неподвижен. Стержень ОВ вращается во-
вокруг своей неподвижной точки с постоянной угловой ско-
скоростью coo. Определить угло-вую скорость со шестеренки / и
стержня О\А, принимая во внимание обозначения, указанные
на чертеже, и считая, что ZOBA = 90°, ZBAO{=45°.
66. Плоский механизм состоит из трех шарнирно соеди-
соединенных стержней ОХА, АВ, ВО, концы О и О\ которых оста-
остаются неподвижными. Шестеренка / свободно' вращается во-
вокруг неподвижной точки О и находится в зацеплении с дру-
другой такой же шестеренкой //, жестко связанной со стерж-
стержнем АВ и способной вращаться свободно вокруг шарнира В.
Стержню OiA сообщена постоянная угловая скорость соо.
Определить угловые скорости стержня ОВ и шестеренки / в
тот момент, когда а = 60°, р=90°, rl = r2=l, 0{A = l (рис. 47).
Рис. 47
Рис. 48
Рис. 49
67. Обруч радиуса г катится 'без скольжения по неподвиж-
неподвижному цилиндру радиуса R с постоянной угловой скоростью
ооо. По обручу движется точка М с постоянной относительной
скоростью vq. Определить абсолютную скорость точки М в тот
момент, когда она находится в положении, указанном на чер-
чертеже (рис. 48). Положение центра обруча определяется уг-
углом ф.
38
68. На чертеже (рис. 49) представлена схема механизма
с качающимся цилиндром, который может вращаться вокруг
неподвижной точки С. Определить угловую скорость Q ци-
цилиндра в зависимости от угловой скорости со кривошипа АВ
и угла поворота его ф, зная, что АВ = а и ВС~Ь.
Рис. 50
Рис 51
69. Два стержня АС и ВС соединены между собой шар-
нирио в точке С, а также шарнирно соединены с двумя пол-
ползунами А и В, движущимися прямолинейно со скоростями v
и V\ соответственно по прямолинейному рельсу (как показа-
показано на рис. 50). Определить скорость точки С в тот момент,
когда стержни образуют соответственно углы аире рельсом.
70. Диск катится без скольжения по неподвижной прямой
так, что его центр движется с постоянной по величине и по
направлению скоростью v0. К точке В окружности диска шар-
шарнирно прикреплен стержень АВ, свободный конец которого А
скользит по той же неподвижной прямой. Определить ско-
скорость свободного конца А стержня в зависимости от угла ср
поворота диска. Длина стержня равна /, радиус диска ра-
равен г (рис. 51).
71. К концу А стержня О А длины /, вращающегося около
неподвижной точки О с постоянной угловой скоростью со,
прикреплен стержень АВ, длина которого равна /. Конец В
этого стержня шарнирно прикреплен к 'ползуну, движущемуся
по неподвижной прямой А0С, отстоящей от точки О на рас-
расстоянии ОА0=1. Определить скорость ползуна в зависимости
от его положения, определяемого углами ф и -ф (рис. 52).
A V/////77//////y//77//77S/y/////////?T77}Y///
6
Рис. 52
39
Определить величину мгновенной угловой скорости вращения
стержня ЛВ и найти его мгновенный центр вращения.
72. Стержни ЛВ и ВС вращаются равномерно с угловыми
скоростями м и —аз вокруг неподвижного шарнира В. Стер-
Стержень DE длины а соединяет ползуны, движущиеся по ЛВ и
ВС так, что ADBE все время остается равнобедренным. Оп-
Определить скорость v поступательного движения стержня DE
и относительные скорости и скольжения ползунов по соот-
соответствующим стержням ЛВ и ВС в тот момент, когда
ZЛ£C=60o (рис.53).
73. Шарнирный антипараллелограмм ABCD состоит из че-
четырех стержней: ЛВ, ВС, CD и ЛИ. При этом AB = DC=2a,
AD = BC=2b. Стержень AD все время остается неподвижным,
0
П_
Рис. 55
а стержень ЛВ вращается вокруг точки Л с постоянной угло-
угловой скоростью соо- Определить скорость точки С стержня DC
в тот момент, когда Z/1DC=9O° (см. рис. 75).
74. Плоский механизм состоит из двух шарнирно соеди-
соединенных стержней ОЛ = г и ЛВ = 1 и ползуна В. Стержень О А
вращается вокруг неподвижной точки О с постоянной угло-
угловой скоростью щ. Ползун вынужден скользить по неподвиж-
неподвижной прямой CD, не проходящей через неподвижную точку О.
Определить скорость v движения ползуна В в тех положе-
положениях, где стержень ОЛ оказывается параллельным или пер-
перпендикулярным к прямой CD (рис. 54).
В общем случае мгновенное движение твердого тела мо-
может быть задано как сложное движение, состоящее из не-
нескольких мгновенно-поступательных и мгновенно-нращатель-
ных движений. Такое общее движение всегда можно свести
к более простому мгновенному движению — мгновенно-вин-
тоному движению твердого телТГГ При этом задача сводится
к приведению системы скользящих векторов, каковыми яв-
являются вектора мгновенной угловой скорости вращения твер-
твердого тела, к простейшему виду.
Рассмотрим пример, поясняющий сказанное.
Пример 17. Твердое тело совершает сложное движе-
движение, которое сводится к трем мгновенным вращениям вокруг
40
трех осей, расположенных по двум сторонам и одной диа-
диагонали квадрата (как указано на рис. 55), причем угловые
скорости соответственно пропорциональны длинам сторон и
диагонали квадрата. Привести эту систему мгновенных вра-
вращений к одному мгновенному вращению и найти результирую-
результирующую угловую скорость вращения.
Решение. Рассматриваемая задача сводится к приведению
системы, состоящей из трех скользящих векторов, располо-
расположенных в одной плоскости, к простейшему виду. Величина и
направление вектора определяются по правилу сложения схо-
сходящихся скользящих векторов. Таким образом, величина ре-
результирующего вектора оказывается пропорциональной отрез-
отрезку СЛ, а его линия действия параллельна отрезку СА. Для
полного определения линии действия остается указать точку,
через которую она проходит. Заметим, что два вектора (oi и
саз эквивалентны одному вектору оо = ссц + соз, линия действия
которого параллельна линиям действия векторов coi и соз и
делит пополам диагональ ВО. Отсюда следует, что вектор оJ
и вектор (о проходят через одну точку — середину диагонали
ВО, а следовательно, и результирующий вектор проходит че-
через эту же точку.
Задачи для самостоятельных упражнений
75. Куб, ребро которого равно а, совершает два одновре-
одновременных вращения € равными по величине угловыми скоростя-
скоростями (Oi и €02 вокруг двух своих непараллельных и непересека-
непересекающихся ребер AD и ОС (как указано на рис. 56). Привести
это движение к одному мгновенно-винтовому движению.
76. Дан куб ABDCFGHE с ребром, равным ам. Скорость
Vi точки А этого куба равна _а м/сек и направлена по AG\ ско-
скорость V2 точки В равна avr2 м/сек и направлена по стороне
BE; скорость же v3 точки С равна aV2 м/сек и направлена па-
параллельно стороне DF. Определить положение мгновенной вин-
винтовой оси, скорость скольжения ндоль мгновенной винтовой
оси и мгновенную угловую скорость куба (рис. 57).
Рис. 56
Рис 57
77. В винте (со, v), где v—поступательная скорость и со—
угловая скорость вращения твердого тела, найти геометриче-
геометрическое место точек, скорости которых равны vV2.
78. Твердое тело А вращается с постоянной угловой ско-
скоростью Q вокруг оси, совпадающей с одним из ребер куба,
величина которого равна а. Твердое тело В совершает мгно-
Рис. 58
Рис. 59
венно-виштовое движение (со, v), ось которого (как показано
на рис. 58) совпадает с другим ребром того же куба. Найти
движение тела В относительно тела А.
В тех случаях, когда у твердого тела закреплена только
одна точка, мгновенное движение тела сводится к одному
результирующему мгновенному вращению. При этом мгно-
мгновенная ось вращения проходит через неподвижную точку.
При определении положения мгновенной оси вращения сле-
следует помнить, что "скорости точек тела, расположенных на
мгновенной оси вращения, равны нулю.
Рассмотрим следующий пример.
Пример 18. По неподвижному круговому конусу с уг-
углом при вершине, равным 2а, катится без скольжения другой
круговой конус с углом при вершине, равным 2f>, так, что ось
симметрии последнего вращается вокруг оси симметрии не-
подвижного конуса с постоянной угловой скоростью со»!. Опре-
Определить абсолютную угловую скорость вращения подвижного
конуса и найти аксоиды.
Решение, Подвижный конус катится по неподвижному без
проскальзывания так, что точки подвижного конуса, распо-
расположенные па общей образующей, имеют нулевые скорости.
Поэтому мгновенная ось вращения совпадает с общей обра-
образующей обоих конусов. Во время движения мгновенная ось
вращения перемещается как по поверхности неподвижного,
так и по поверхности подвижного конуса. Поэтому аксоидами
будут являться эти же самые поверхности конусов. Движение
42
подвижного конуса теперь можно" представить как сложное,
состоящее из вращения подвижной системы вокруг оси сим-
симметрии неподвижного конуса с переносной угловой скоростью
<oe=coi (рис. 59) и относительного вращения подвижного ко-
конуса вокруг своей оси симметрии в подвижной системе ко-
координат. Зная направления абсолютной и относительной уг-
угловых скоростей подвижного конуса, а также величину и
направление переносной угловой скорости, легко определить
величину и направление абсолютной угловой скорости вра-
вращения конуса. Из треугольника скоростей будем иметь
откуда
_ sin (a -f p)
sinp
Пример 19. Горизонтальные колеса I и II дифференци-
дифференциального механизма вращаются вокруг одной и той же вер-
вертикальной оси Л В соответственно со скоростями o>i и Тог. Оп-
Определить мгновенную угловую скорость вращения планетного
колеса III, ось которого может свободно вращаться вокруг
осиЛВ (рис. 60).
Решение. Абсолютное мгновенное движение колеса ///
можно представить как результат сложения переносного дви-
движения (вместе с колесом /) и отно-
относительного движения колеса /// по
отношению к колесу /. В таком слу-
случае переносная уголовая скорость
колеса /// равна со,. Перенесем на-
начало вектора coi в неподвижную точ-
точку и рассмотрим относительное дви-
движение колеса ///. В этом относитель-
относительном движении мгновенная ось вра-
вращения Ai колеса /// проходит через
точку соприкосновения колеса /// с
колесом / и через точку О пересече-
пересечения осей колес /// и /. Поэтому ко-
конец вектора абсолютной угловой ско-
скорости расположен на прямой бь
проходящей через конец вектора coi
и параллельной прямой Д1р Пред-
Представляя теперь мгновенное движение колеса /// как ре-
результат сложения переносного движения (вместе с колесом
II) и относительного движения колеса /// по отношению к
колесу П, аналогичными рассуждениями получим, что конец
43
Рис. 60
вектора абсолютной угловой скорости колеса /// лежит на
прямой 6г, параллельной прямой Лг, проходящей через ко-
конец вектора шг. Величина вектора абсолютной угловой скоро-
скорости колеса /// определится из простого геометрического по-
построения и тогда
= @2
где JR и г — соответственно радиусы колес / и ///.
Задачи для самостоятельных упражнений
79. Круглый конус подвешен вершиной к неподвижной
точке О и вращается вокруг своей геометрической оси О| с
постоянной угловой скоростью (Oi и, кроме того, качается, по-
подобно маятнику, вокруг горизонтальной оси Оу, перпендику-
перпендикулярной к ОЪ, (рис. 61). В какой момент, то есть ори каком
значении угловой скорости ш2 качания маятника, мгновен-
мгновенная ось вращения будет лежать на поверхности конуса, если
его высота равна h, а радиус его основания равен R?
о
Рис. 61
Рис. 62
80. Тело вращается вокруг оси, проходящей через начало
координат. Скорость точки М(\, 0, 1) тела vx = A м/сек
и образует с осью абсцисс угол а = 45°. Скорость точки М2
C, 4, 0) тела образует с осью абсцисс угол сс2, причем
cosa2=—0,8. Найти уравнение_ мгновенной оси вращения,
мгновенную угловую скорость оз и скороть и2 точки М2 тела.
81. Диск радиуса R, плоскость которого образует угол а
с вертикалью, катится без скольжения по горизонтальной
плоскости, описывая на ней окружность, 'причем ось диска
все время шроходит через центр О этой окружности. Найти
аксоиды и абсолютную угловую скорость го диска, а также
угловую скорость G)r диска вокруг его оси, линейную ско-
44
рость v его высшей точки М, если центр диска описывает
полную окружность с-постоянной скоростью v0.
82. Круглая 'пластинка ЛВ вращается вокруг оси1 ОС, про-
проходящей через ее центр D, с 'Постоянной углопой скоростью
<оь а сама ось ОС вращается в том же направлении вокруг
вертикальной оси ОЕ с постоянной угловой скоростью сог.
Угол между осями равен а, диаметр пластинки рачзен 2d, a
расстояние OD = a. Определить скорость v самой нижней точ-
точки В пластинки (рис. 62).
Теорема Кориолиса об ускорении материальной точки
в сложном движении. Распределение ускорений в твердом теле
Зависимость между ускорениями материальной точки,
определяемыми в подвижной и неподвижной системах отсче-
отсчета, определяется теоремой Кориолиса. По этой теореме аб-
абсолютное ускорение материальной точки равно геометриче-
геометрической сумме ускорений: переносного, относительного и доба-
добавочного (кориолисова ускорения), то есть
Под переносным ускорением /« 'понимают ускорение той
точки подвижной системы отсчета, с которой в данный мо-
момент совпадает изучаемая материальная точка. Относитель-
Относительным ускорением /г называют ускорение, материальной точки
в ее движении 'относительно подвижной системы отсчета. До-
Добавочным ускорением /' называют ускорение, равное удвоен-
удвоенному векторному произведению мгновенной угловой скорости
вращения подвижной системы отсчета на относительную ско-
скорость материальной точки, то есть
Наибольшие затруднения возникают при определении пе-
переносного и добавочного ускорений. Определение переносного
ускорения связано с представлением о движении твердого те-
тела, так как всякую точку подвижной системы отсчета всегда
можно рассматривать как точку некоторого твердого тела,
жестко связанного с этой подвижной системой отсчета. Ус-
Ускорения же точек твердого тела определяются по формуле
Ривальса, на основании которой ускорение произвольной
точки твердого тела равно геометрической сумме ускорения
некоторого 'полюса, еа который может быть принята любая
точка твердого тела, вращательного и осестремительного ус-
ускорений, то есть
• • i * * •
/ /о 1 1др ~Т~ /ос*
45
Обычно в качестве полюса выбирается та точка твердого
тела, ускорение которой может быть определено без излиш-
излишних затруднений. Вращательное ускорение определяется по
формуле
где е — вектор углового ускорения твердого тела, то есть
е =
dt
Производная здесь берется_тю отношению к неподвижной си-
системе отсчета, а вектор ОМ определяет положение точки М
относительно подвижной системы координат, движущейся
поступательно вместе с полюсом. Осестремителыгое ускоре-
ускорение можно определить по формуле
/ос=ю •
~ОМ • со2,
где со — абсолютная угловая скорость вращения твердого те-
тела в рассматриваемый момент времени. Пользуясь тем, что
со — скользящий вектор, можно показать, что вектор /ос на-
направлен к линии действия вектора со, ортогонален к ней, а
его величина пропорциональна расстоянию точки М от линии
действия вектора со.
Пример 20. Пользуясь теоремой Кориолиса, определим
ускорение материальной точки в полярной системе коорди-
координат. Воспользуемся следующей схемой. Пусть движение мате-
материальной точки М по палочке О А происходит то произвольному
закону s — s(t) (рис. 63). Будем предполагать,что палочка вра-
Рис. 63
Рис. 64
46
щается в своей плоскости вокруг неподвижного конца О, при-
причем угол ф, который она образует с некоторой неподвижной
прямой этой плоскости, изменяется по произвольному зако-
закону Ф = фСО-
Для определения ускорения материальной точки восполь-
воспользуемся теоремой Кориолиса. Здесь в переносном движении
материальная точка М движется по окружности радиуса s
с центром в точке О. Определяя переносное ускорение, мы
обязаны положить s — const. Тогда получим две составляю-
составляющих переносного ускорения:
Относительное движение материальная точка совершает по
прямой О А. Следовательно, относительное ускорение будет
направлено вдоль палочки, а его величина рапиа
Добавочное ускорение получим из формулы
/' - 2 [© • v~[;
оно будет направлено ортогонально к палочке в сторону вра-
вращения, а по величине равно
Проектируя вектор ускорения на направление палочки и
на ортогональное к ней направление (см. рисунок), получим
так называемые радиальную и трансверсальную составляю-
составляющие ускорения:
jr=s" — ц>'\ /ф-= <p"s + 2<p's\
Пример 21. Палочка ЛВ длины а скользит своими кон-
концами А и В по неподвижным вертикальной и горизонтальной
прямым так, что ее конец А движется с постоянной скоростью
и (рис. 64). По палочке движется материальная точка М с
постоянной относительной скоростью vq. Определить абсолют-
абсолютное ускорение материальной точки М, принимая в качестве
параметра, определяющего положение палочки, угол ф, кото-
который она образует с вертикалью.
Решение. Для определения ускорения материальной точ-
точки воспользуемся теоремой Кориолиса. За относительное дви-
движение примем движение материальной точки М по палочке.
Переносное ускорение этой точки можно определить, пользу-
пользуясь теоремой Ривальса. Примем в качестве полюса точку А.
Тогда ускорение полюса /о = 0, а ускорение точки М палочки
47
будет зависеть лишь от вращения палочки вокруг точки А':
Заметим, что вертикальная .координата у точки А равна:
у = а cos ср.
Дифференцируем это выражение и получаем
у' =—аср 81Пф.
С другой стороны, у'=—и, откуда
и
Ф = : •
asincp
Дифференцируя последнее выражение еще раз, получим
у" — — acp'2 cos ср — аср" sin ср.
Но так как у"=0, то
,, ,
Ф — —ср
cosop a2coscp
^ — -
sincp
Определим теперь вращательное /(?1 и осестремительное
jex ускорения точки М палочки:
,, «2scoscp
- ср' s - -
Материальная точка совершает прямолинейное относи-
относительное движение с постоянной по величине относительной
скоростью v0. Поэтому относительное ускорение материаль-
материальной точки равно пулю. Остается 'подсчитать добавочное ус-
ускорение \'. Оно будет направлено ортогонально к палочке,
в сторону возрастания угла ср, а по величине равно
asincp
Величину и направление полного ускорения материальной
точки можно теперь определить, рассматривая геометриче-
геометрическую сумму составляющих ускорения материальной точки.
В результате, как нетрудно видеть, 'будем иметь
I
48
. _ / / 2uv0 us cos <р \2 w4s2
У \ asinq> а251п3ф / a^sin^cp
Следует отметить, что удачный выбор подвижной системы
отсчета в ряде случаев является залогом успеха в решении
задачи. Рассмотрим следующий пример.
Пример 22. Окружность радиуса а (рис. 65) вращается
в своей плоскости вокруг своей неподвижной точки О с по-
постоянной угловой скоростью coi против часовой стрелки. Стер-
Стержень О А вращается в той же плоско-
плоскости вокруг точки О с постоянной угло-
угловой скоростью со2 по часовой стрелке.
На стержень и на окружность надето
колечко М. Определить скорость и ус-
ускорение колечка в зависимости от ве-
величины угла ф, который образует ра-
радиус окружности со стержнем.
Решение. Определим сначала ско-
скорости. В качестве подвижной системы
координат выберем систему осей, неиз-
неизменно связанную со стержнем. Тогда
для переносной скорости получим еле-
дующее значение:
04$
= co2s = 2to2a cosq).
Рис. 65
Вектор относительной скорости точки vTi в этой системе
направлен вдоль стержня, а потому и конец вектора абсо-
абсолютной скорости точки М лежит на прямой Лг, параллель-
параллельной стержню и проходящей через конец вектора, переносной
скорости vCt.
Выберем теперь в качестве подвижной системы коорди-
координат систему осей, неизменно связанную с окружностью. То-
Тогда переносная скорость v6l по величине будет равна
Вектор относительной скорости будет направлен по касатель-
касательной к окружности и, следовательно, конец вектора абсолют-
абсолютной скорости точки М лежит на прямой Ль параллельной
касательной к окружности и проходящей через конец вектора
v6i. Нетрудно видеть, что прямые Ai и Л 2 пересекаются в
точке S, а потому конец вектора абсолютной скорости точки
М будет находиться в той же точке 5. Теперь нетрудно опре-
определить и величину скорости точки М (см. рис. 65) :
Vrt = (ав1 + ve*) tg <р = (e>i + соа) 2a sin <p;
Vri =
V
cos<p
e* =
со2) 2а = const;
va = 2а
~\- 2со2) sin2 ф.
31/4 Заказ 219
49
■Перейдем к олределению ускорений. В системе осей, неиз-
неизменно связанной с окружностью, материальная точка дви-
движется по окружности с постоянной по величине скоростью
Vrlt а потому и относительное ускорение точки в этой системе
отсчета по величине равно
о»
и направлено к центру окружности. Переносное ускорение
точки в этой системе координат равно
/<?»=<°2i S=o212a cos ф
и направлено к точке О. Добавочное ускорение по величине
равно
/1'=2о1 (с^ + Юа) 2а
и направлено от центра окружности. Проектируя эти состав-
составляющие ускорения на оси х и у, получим:
2)a sin<p,
jy= — [d)i2 + 20D2@Di + @2)]2a СОЭф.
Если в качестве подвижной системы координат выбрать
систему осей, связанную со стержнем, то, как нетрудно ви-
видеть, будем иметь:
\ег = oJ2s = со22 2а cos ф,
/' = 2<а2(со 1 + согJa sin <p.
А так как относительное движение в этой системе осей яв-
является прямолинейным движением, то для относительного
ускорения получим следующее выражение:
dvr. . . . - efo
lr = —77- = (% + ">2Ja— СОБф =
dt dt
— — (^i + ^гJ 2a cos ф.
Для проекций ускорения на оси х, у получим те же зна-
значения:
/x2(i 2) sin
jy = [2 + ( +
Формулы Ривальса для определения ускорений точек
твердого тела значительно упрощаются при рассмотрении
плоского движения твердого тела. В плоском движении век-
вектор мгновенной угловой скорости вращения твердого тела
50
может изменяться только по величине и не меняется по на-
направлению. Л это значит, что вектор углового ускорения е
и вектор мгновенной угловой скорости w становятся коллине-
аркыми векторами. Благодаря этому формулы принимают
особенно наглядный вид. Формулы значительно упрощаются,
если за полюс выбрать ту точку твердого тела, которая в
данный момент совпадает с положением мгновенного центра
вращения твердого тела. Тогда будем иметь
где ус— ускорение точки твердого тела, совпадающей в дан-
данный момент с мгновенным центром вращения, прршем
Ус= -Гсо •«].
где w — мгновенная угловая скорость вращения твердого те-
тела, и — скорость движения мгновенного центра вращения.
ут и уп— соответственно касательная и нормальная состав-
составляющие ускорения точки М тела при вращении последнего
вокруг мгновенного центра вращения. Таким образом, если
через СМ обозначить расстояние от мгновенного центра
вращения до точки Mt ускорение которой определяется, то:
уп = о2 • СМ, ух = е . СМ.
Пример- 23. Палочка АВ скользит своим концом Л по
окружности радиуса г и проходит через точку С этой окруж-
окружности. Определить ускоре-
ускорение точки В палочки, рас-
расположенной на расстоя-
расстоянии I от конца А, если точ-
точка А движется с постоян-
постоянной по величине скоро-
скоростью Uo (рис. 66).
Решение. Решим эту
задачу при помощи фор-
формул Ривальса, выбирая в
качестве полюса точку
твердого тела, совпа- Рис. 66
дающую в данный момент с мгновенным центром вращения.
Нетрудно видеть, что мгновенный центр вращения палочки
находится на пересечении диаметра окружности, проходящего"
через точку Л, и перпендикуляра к палочке, восстановленного
в точке С. Расстояние от точки А до мгновенного центра вра-
вращения равно диаметру окружности и остается постоянным
во все время движения. Благодаря этому мгновенная угло-
31/а Заказ 219 51
вая скорость вращения палочки остается постоянной во все
время движения и по величине, равна
Угловое ускорение палочки е равно нулю во все время дви-
движения. Нетрудно определить ускорение точки тела ('палоч-
('палочки), совпадающей с положением мгновенного центра враще-
вращения. По величине оно равно
Ус =
2r
и направлено к центру окружности. Нормальное ускорение уп
точки В равно
где SB=^12±-Ar2 — 4rl cos <p. Касательное ускорение равно
нулю, так как равно нулю угловое ускорение е.
Рассмотрим проекции ускорения на направление палочки
и на ортогональное к ней направление:
/ — 2r cos ф V(? V(?l
i — v,, — — cos ф — _L ,
' SB r 4r2
з + Y — = -^-sin ф.
SB r
Пример 2 4. Окружность радиуса г катится без сколь-
скольжения по неподвижной окружности радиуса R так, что ско-
скорость ее центра остается постоянной по величине и равна vQ
во все время движения. Определить ускорение точки S окруж-
окружности, совпадающей в данный момент с положением мгновен-
мгновенного центра вращения, и ускорение точки А, расположенной
на противоположном конце диаметра, проходящего через
точку S.
Решение. Так как мгновенный центр вращения находится
в точке 5, то мгновенная угловая скорость со будет по вели-
величине равна
со =
С другой стороны, точка 5 все время находится на прямой,
соединяющей центры окружностей. Поэтому скорость и дви-
52
жсния мгновенного центра вращения определяется из усло-
условия
v0 и
R + r R '
то есть
«,=3*-..
R + r
Тогда ускорение точки 5 твердого тела имеет вид
v, — сом — — ■
г (R + r)
и направлено к центру движущейся окружности^
Нетрудно видеть, что угловое ускорение е будет равно
нулю во все время движения, так как вектор мгновенной уг-
угловой скорости вращения остается во все время движения
постоянным и по величине, и по направлению. Поэтому будет
равна нулю и составляющая у-.. Для уп получим следующее
значение:
уп =
Ускорение точки Л определится из равенства
1А е V" .r(R+r) r
и будет направлено к центру подвижной окружности.
Затруднения, возникающие при определении ускорения
точки твердого тела в плоскопараллельном движении, и свя-
связанные с определением величины вектора е, иногда могут
быть устранены при рассмотрении проекций ускорения точки
на различные оси координат. Рассмотрим следующую задачу.
Пример 25. Полый цилиндр радиуса 2г вращается во-
вокруг своей неподвижной оси симметрии с постоянной угловой
скоростью со. По внутренней поверхности этого цилиндра ка-
катится без скольо/сения другой цилиндр радиуса г с'постоянной
относительной угловой скоростью ьц (как показано на
рис. 67). Определить ускорение точки С малого цилиндра,
совпадающей в рассматриваемый момент времени с осью
большого.
53
Решение. Выберем за полюс точку Оь Скорость точки Ot
может быть получена как скорость точки в сложном движе-
движении, где переносная скорость равна
03 • /*, а относительная скорость равна
03i ' г. Тогда абсолютная скорость точ-
точки О{ будет по величине равна
vOl --= (ой + щ) г
и направлена в сторону вращения по-
полого цилиндра. Точка О{ движется по
окружности радиуса г с постоянной по
Рис. 67
величине скоростью vOt
этому ускорение полюса
равно
Благодаря
по величине
Г
т
и направлено к точке О. Для определенности положим co>o)i.
Тогда абсолютная угловая 'скорость малого колеса будет
равна
и направлена против часовой стрелки. По величине Q ос-
остается постоянной во все время движения. Поэтому угловое
ускорение будет равно нулю. Ускорение точки С колеса скла-
складывается из ускорения точки О{ и из нормального ускорения
/n=(coi —соJг.
Проектируя на направление ОО\, получим
/= (о)]—(х)JГ—(co + ft)iJr=
откуда видно, что ускорение направлено от точки О{.
При решении 'пространственных задач необходимо пом-
помнить, что вектора со и е вообще не совпадают по направле-
направлению. Это обстоятельство создает некоторые осложнения при
решении задач. Рассмотрим следующие задачи.
Пример 2 6. Прямой круговой конус II с углом при вер-
вершине 2{3 катится без скольжения по внешней стороне непод-
неподвижного конуса I с углом при вершине 2а. При этом ось сим-
симметрии подвижного конуса вращается вокруг оси симметрии
неподвижного конуса с постоянной скоростью угловой wo-
54
Определить абсолютное ускорение самой верхней точки М
основания подвижного конуса.
Решение. Воспользуемся теоремой Ривальса и выберем
за полюс вершину подвижного конуса, остающуюся непод-
неподвижной во все время движения. Будем иметь
/о=О.
Остается определить осестремительное /ос и вращательное
\ер ускорения. Для- определения этих составляющих' найдем
сначала величину и направление вектора мгновенной угловой
скорости со вращения твердого тела. Из геометрических по-
построений
sin (а + Р)
СО = С00 ; .
Угловое ускорение е определяется как производная по
времени от вектора мгновенной угловой скорости со. Нетруд-
Нетрудно видеть, что конец вектора мгновенной угловой скорости
со будет описывать окружность вокруг вертикальной оси
неподвижного конуса со скоростью
[соош].
Это и есть скорость конца вектора со, то есть угловое ускоре-
ускорение е. Таким образом, величина вектора углового ускорения
гг sin (a + p) sin a
6 —■ СОп
:•
sinp
Величина вращательного ускорения точки М имеет вид
„ sin (а + 3) sin a
— wor : : -
где г — радиус основания конуса.
Нетрудно видеть, что расстояние от точки М до мгновен-
мгновенной оси вращения равно
h=2r cos p,
поэтому для величины осестремительного ускорения получим
значение
55
Рис. 68
Пример 2 7. Диск радиуса г катается без скольжения
по плоскости, описывая окружность радиуса R с постоянной
по величине угловой скоростью
o)i и сохраняя свою плоскость
вертикальной. Найти осестреми-
тельное ускорение /ос и враща-
вращательное ускорение j ep точки М,
положение которой на ободе дис-
диска определяется углом <р (как по-
показано на рис. 68).
Решение. Рассматриваемый
диск представляет собой твердое
тело с одной неподвижной точкой,
так как точка О, связанная с телом, остается неподвижной во
все время движения.
Решение задачи можно -представить в проекциях на под-
подвижные оси координат Oxyz. Линия действия вектора мгно-
мгновенной угловой скорости со будет все время проходить через
две неподвижные точки О и Л, а потому проекции вектора
со на выбранные оси координат получат вид
со @, (пу, (ог),
где od2 = coi no условиям задачи. Координаты точки А имеют
вид (О, R, —г). Определяя теперь скорость точки Л, получим
еще одно условие
откуда найдем
R ,
Ш — — o)j — Const.
г
ч
Вектор о остается 'Постоянным по величине во все время дви-
движения. Но конец вектора о) описывает окружность с угловой
скоростью o)i, благодаря чему величина вектора е будет
равна
coco ^«о»^-
г
Проекции же вектора е на оси координат получат вид
<— , 0, 0.
г
56
Для- определения ускорения точки М воспользуемся те-
теперь формулой Ривальса:
] = [(о (© .~бМ)\ -f \в • Щ =
= © fсо . ОМ] — ОМ • ш2 + [s - ОУИ].
Здесь вектор ОМ имеет проекции
г sin ф, 0, —г cos cp,
поэтому
(ш • ОМ) --= —
Для проекций ускорения на оси координат получаем следую-
следующие значения:
\х = — гшг2 ( f- I j sin ф -= — ог2 sin q-,
R R
j = cot — r(ot cos ф -f- coj2 — r cos ф == 2o>i R coi- q,
r r
D2 ч D2
/г = — CDiV COS ф + т^Г ( \- 1 ) COS ф = COi2 CCS (f,
v/-2 / /•
поэтому для полного значения ускорения точки М будем
иметь
/г>4 I
fLjLJ
Задачи для самостоятельных упражнений
83. Равнобедренный прямоугольный треугольник ОАВ
вращается с постоянной угловой скоростью м в своей плоско-
плоскости вокруг неподвижной вершины О, а некоторая материаль-
материальная точка М движется с постоянной отно-
относительной скоростью vo вдоль стороны
А В. Найти абсолютные скорость и уско-
рение материальной точки в тот момент, * м
когда она находится п положении Л, счи-
считая, что А В = а (рис. 69).
84. По хорде диска, равномерно вра-
В
щающегося вокруг неподвижной оси, про-
проходящей через его центр и перпендику- ис"
ляриой к его плоскости, движется с постоянной относитель-
относительной скоростью и точка М, выходя из середины хорды. Найти
абсолютные скорость и ускорение материальной точки М в
57
зависимости от ее положения на хорде. Угловая скорость
вращения диска равна оз, расстояние хорды от центра диска
равно а, а расстояние материальной точки от середины хорды
равно х.
85. Прямая вращается в неподвижной плоскости вокруг
своего неподвижного конца О с постоянной угловой ско-
скоростью (о. В тот момент, когда прямая находится в положе-
положении Ох, из точки О вдоль прямой начинает двигаться некото-
некоторая материальная частица М. Подобрать такой закон дви-
движения материальной частицы вдоль прямой, чтобы она име-
имела постоянную по величине абсолютную скорость v. Найти
траекторию и ускорение материальной точки.
86. На неподвижной проволочной окружности радиуса г
надето колечко М, через которое проходит стержень О А, рав-
равномерно вращающийся вокруг неподвижной точки О, распо-
расположенной на той же окружности. Угловая скорость вращения
стержня такова, что он 'поворачивается на прямой угол за
5 секунд. Определить скорость и ускорение колечка в зави-
зависимости от его положения.
87. Зубчатое колесо радиуса R зажато между двумя па-
параллельными рейками, скользящими в одну сторону соответ-
соответственно с ускорениями }\ и /г. Найти ускорение /о центра
колеса О и угловое ускорение колеса е.
88. Диск радиуса R вращается с 'постоянной угловой ско-
скоростью т вокруг оси, проходящей через его центр и перпен-
перпендикулярной к плоскости диска. По диаметру диска, выходя
из его центра, движется материальная точка М по закону
s = R simat. Найти абсолютные траекторию, скорость и уско-
ускорение материальной точки.
89. Полое кольцо ради>са г жестко соединено с валом О
так, что плоскость оси кольца перпендикулярна оси вала О.
Кольцо заполнено жидкостью, движущейся в нем в направле-
направлении стрелки, как показано на рис. 70, с .постоянной относи-
Рис. 71
58
телыюй скоростью и. Определить абсолютные скорость и ус-
ускорение частицы жидкости в положениях /, 2, 3, 4, если вал
вращается вокруг своей оси с постоянной угловой скоростью
со, а расстояние между центрами вала и кольца равно а.
90. Полое кольцо радиуса г жестко соединено с валом АВ
так, что ось вала расположена в плоскости оси кольца. Коль-
Кольцо заполнено жидкостью, движущейся в нем с постоянной
относительной скоростью и. Вал вращается по часовой стрел-
стрелке, если смотреть вдоль оси от А к В , (как -показано па
рис. 71). Угловая скорость вращения вала постоянна по ве-
величине и равна «о- Определить величины абсолютных ускоре-
ускорений частиц жидкости, расположенных в точках 1, 2, 3, 4.
91. Окружность с центром в точке О радиуса а 'Вращается
в своей плоскости вокруг неподвижной точки С окружности
с постоянной угловой скоростью ы против часовой стрелки.
Точка М движется по этой окружности по часовой стрелке
с угловой скоростью 2со. В начальный момент точки М, О и С
лежат на одной прямой. Определить абсолютную траекторию
точки М, ее скорость и ускорение в зависимости от положе-
положения.
92. Кривошип ОА длины г вращается с постоянной угло-
угловой скоростью соо и приводит в движение шатун АВ длины /.
Ползун В движется по вертикали. Определить угловую ско-
скорость и угловое ускорение шатуна, а также ускорение ползу-
ползуна В в тот момент, когда кривошип и шатун взаимно перпен-
перпендикулярны и образуют с горизонталью углы а=45° и {3 = 45°
(рис. 72).
г*
SI
2а
Рис. 72
Рис. 73
93. Топкий стержень ОА, способный свободно вращаться
около неподвижной точки О, опирается па ползун В, высота
которого равна h, движущийся поступательно с постоянной
скоростью v. Определить скорость и ускорение точки Е стер-
стержня, которая в рассматриваемый момент касается ползуна,
в зависимости от угла <р наклона стержня (см. рис. 22).
94. Плоскость Оху вращается вокруг начала координат с
переменной угловой скоростью ©@ Движение точки в этой
59
плоскости задано уравнениями *=/i@» #=f2@- Найти про-
проекции абсолютного ускорения точки на подвижные оси х и у.
95. Стержень АВ длины 2а 'вращается по часовой стрелке
в 'плоскости чертежа вокруг неподвижного конца А с посто-
постоянной угловой скоростью Q. На конце стержня свободно на-
насажено колесо радиуса а, вращающееся в той же плоскости,
но в противоположную сторону, с постоянной относительной
скоростью (о относительно 'стержня. Определить абсолютное
ускорение частицы М, которая движется по ободу колеса по
часовой стрелке с постоянной относительной скоростью v в
тот момент, когда частица М находится над стержнем
(рис. 73).
96. Колесо радиуса R зажато между двумя параллельны-
параллельными рейками, скользящими в разные стороны 'поступательно
соответственно с ускорениями ]\ и /2 и со скоростями vx и v2
в данный момент 'времени. Найти ускорение центра колеса
и угловое ускорение колеса е.
97. Палочка О А вращается в плоскости вокруг точки О
с постоянной угловой скоростью оI. Вокруг точки А
этой палочки вращается в той же 'плоскости другая палочка
ABt причем угол ф между палочками изменяется по закону
dt
где «2=const. Применяя теорему Кориолиса, определить аб-
абсолютное ускорение точки В второй палочки, считая, что
АО = а, АВ = Ь.
98. Квадрат ABCD со стороной а совершает движение в
своей плоскости. В рассматриваемый момент времени уско-
ускорения его вершин А и В соответственно равны \а и /л и на-
направлены, как показано на чертеже (рис. 74). Найти мгновен-
мгновенную угловую скорость вращения квадрата, и его угловое ус-
ускорение е. Определить ускорение точки С квадрата. *
60
ад,
Рис. 74
'//7//У////////7/////////'
Рис. 75
99. Шарнирный антипараллелограмм ABCD состоит из
двух кривошипов ЛВ и CD одинаковой длины 2а и шарнирно
соединенного с ними стержня ВС длины 2Ь. Расстояние меж-
между неподвижными точками А и D равно 2b. Кривошип АВ
D
Рис. 76
Рис. 77
вращается с постоянной угловой скоростью юо в плоскости
чертежа. Определить угловую скорость вращения и угловое
ускорение стержня в тот момент, когда Z.ADC—90° (рис. 75).
100. Квадрат ABCD со стороной а совершает движение
в своей плоскости. Найти положение мгновенного центра ус-
ускорений квадрата и ускорения его вершин С и D, если из-
известно, что в данный момент ускорения двух его вершин Л
и В по величине равны а, а направления этих ускорений сов-
совпадают с соответствующими сторонами квадрата, как указано
на чертеже (рис. 76).
101. Кривошип АО радиуса R вращается вокруг непод-
неподвижной точки О в плоскости чертежа с постоянной угловой
скоростью ojo, направленной по часовой стрелке, как указано
на чертеже (рис. 77). Вокруг точки А кривошипа вращается
с постоянной абсолютной угловой скоростью (Оь направлен-
направленной против часовой стрелки, круглый диск радиуса г. Опреде-
Определить абсолютные скорости и ускорения точек 1, 2, 3, 4 диска
и его мгновенные центры скоростей и ускорений.
102. Определить скорость и ускорение точки В четырех-
звенпого механизма, показанного на чертеже, в тот момент,
когда звено ОА горизонтально, а звено ВОХ направлено под
углом в 30° к горизонтальной линии. Кривошип О А длиной г
вращается против часовой стрелки с постоянной угловой ско-
скоростью ©о; ЛВ = 1, BOi = R. Прямая OALOB (рис. 78).
103. В эпициклической передаче ведущая шестерня радиу-
радиуса R вращается в данный момент против часовой стрелки с
угловой скоростью о)о и с угловым ускорением ео. Кривошип
длины 3R вращается вокруг оси шестерни по часовой стрелке
с такими же по величине угловой скоростью и угловым уско-
ускорением. Найти скорость и ускорение точки М ведомой ше-
шестерни радиуса R, лежащей на конце диаметра, перпендику-
перпендикулярного в данный момент времени кривошипу (рис. 79).
4 Заказ 219
61
104 Найти ускорение середины стержня АВ, если извест-
известны величины ускорений его концов }А и /в и углы, ооразо-
ваиные направлениями ускорений этих концов с прямой АВ.
а=10°, C=70° (рис.80).
Рис. 79
Рис. 80
Шестеренка радиуса R катится без скольжения по
„.еподаж^оГГстеУпке того же радиуса. Она приводится в
движение кривошипом ОС, который вращается вокруг непод-
неподвижной оси являющейся осью неподвижной шестеренки, с
угГовьш ускорением е. В рассматриваемый момент времени
=Е= лзьягдаг=лляв
ssxT=r.;.s=r
та 'времени известно, что_ускоре.ше точки А равно »а, а ус-
а Л Система состоит из трех зубчатых колес /, // и III,
rs=s?ssbXss^K
„
ненных между собой стержней ОА, АВ и
.62
скорость и ускорение точки В механизма в тот момент, когда
стержни ОА и ОХВ вертикальны. Стержень ОЛ вращается
с угловым ускорением е0 и имеет в данный момент угловую
скорость ю0; ОА = г, О,В = Я, AB = l, ZAOB=^90°. Кроме того,
определить угловую скорость вращения стержня АВ в рас-
рассматриваемом положении и положение мгновенного центра
ускорений стержня ЛВ (рис.82).
Рис. 81
Рис. 82
109. Волчок А вращается относительно оси ОВ с посто-
постоянной угловой скоростью о)ь Ось ОВ описывает равномерно
конус с постоянной по величине угловой скоростью соо.
ZBOS = a = const. Найти угловую скорость и угловое уско-
ускорение волчка (рис. 83).
НО. Конус // с углом при вершине «2=45° катится без
скольжения по внутренней стороне неподвижного конуса /
с углом при вершине cci = 90°. Высота подвижного конуса
OOx=ht а его центр основания описывает окружность с по-
постоянной по величине угловой скоростью ооо- Определить пе-
переносную, относительную и абсолютную угловые скорости
конуса //, а также его абсолютное угловое ускорение е.
111. Круглый диск вращается вокруг горизонтальной оси
CD с постоянной по величине угловой скоростью щ. Ось CD
вращается вокруг вертикальной оси А В, проходящей через
.центр диска О с постоянной по величине угловой скоростью
сог. Вычислить величину и направление мгновенной угловой
скорости со и мгновенного углового ускорения е диска.
112. Диск радиуса R вращается с постоянной по вели-
величине угловой скоростью сог вокруг горизонтальной оси ОхО2г
которая в свою очередь вращается с постоянной по величине
угловой скоростью (де вокруг вертикальной оси. Найти ско-
скорости и ускорения точек А и В, расположенных на концах
вертикального диаметра диска (рис. 84).
4* . 63
113. Конус, вершина О которого неподвижна, катится без
скольжения по плоскости так, что его центр основания дви-
движется с 'постоянной по величине скоростью ^о- Определить
абсолютную угловую скорость, угловое ускорение конуса, а
также скорости и ускорения точек Л и В диаметра основания
ЛВ конуса, если высота конуса равна /г, а угол при вершине
Z ВОЛ =90°.
114. Круглый конус с высотой h и углом при вершине 2а
катается без скольжения по плоскости так, что его ось сим-
симметрии вращается вокруг оси Oz с постоянной по величине
угловой скоростью col. Определить вращательное j ер и осе-
стремительное /ос ускорение точки М основания конуса.
115. Квадратная рама вращается вокруг оси ЛВ с посто-
постоянной по величине угловой скоростью оо. Вокруг оси ВС,
совпадающей с диагональю рамы, вращается диск с постоян-
Рис. 85
Рис. 86
ной относительной угловой скоростью соь Определить абсо-
абсолютные угловые скорость и ускорение диска, а также ускоре-
ускорение точки К диска (рис. 85).
■ 116. Тело вращается одновременно вокруг трех параллель-
параллельных осей в одну и ту же сторону с одинаковыми по величине
угловыми скоростями о. Определить положение мгновенной
оси вращения и угловую скорость результирующего движе-
движения.
117. Диск радиуса R, вращаясь вокруг неподвижной точ-
точки О (рис. 86), обкатывает без скольжения неподвижный
конус с углом при вершине 2<х=60°. Определить абсолютные
угловые скорость и ускорение диска, если ускорение нижней
точки Л обода диска в каждый момент времени постоянно
по величине и равно а.
ОТВЕТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЗАДАЧАМ
1. Задача решается тем же способом, что и пример 1. То-
Тождественное соотношение имеет вид
где х — длина веревки от человека до помоста. Дифференци-
Дифференцируя это выражение, получаем искомую скорость
dx sv
2
dt Va*+ s
Чтобы получить ускорение, следует продифференцировать
выражение для скорости. Будем иметь
] —X —
V (G2
2. Легко устанавливается тождественное соотношение
2R sin q>=R — R cos -ф,
для горизонтальной координаты центра диска получаем
Дифференцированием и исключением г|) отсюда имеем
dx _ „ Г . , A — 2 sin ф) cos ф
у = — = 2R(a sin ф + х чу т
Г .
— sin ф
3. Дифференцируя зависимость
(а — Я cos фJ+ (г/ — R sin фJ+Д2=/2,
получаем выражение для скорости
dw Г (а~/?со5фM1Пф 1
vB = -2- = cos ф _х т/ 1 t/л.
Л L 2//2-А2--(а —^собфJ]
65
4. Координаты х и у центра шара связаны условием
откуда
*2 , У2
■ ф
что является уравнением эллипса.
иН
о. и, = и» = —
6. Искомая скорость.
dx
v — — ,
di
где координаты к и ф связаны соотношением
СО8ф
отсюда дифференцированием найдем
X =— 2-<р
БтфСОБф
или после исключения х
, а — г cos ф ,
х — — Ф .
12
Дифференцируя это соотношение вторично, найдем уско-
ускорение
2
7.
СОБф
8. Здесь х—a ctg <р — a cos ф, у = a sin <p.
Исключая ф, найдем уравнение траектории
л: =
66
Дифференцируя по времени х и у, найдем
v2 = t'02(l — 2sin3(p -f- sin4 ф).
Дифференцируя по времени х' и у\ получим
а I
+ sin4 ф — 4 sin2 ф cos2 Ф + 4 cos4 q>].
9.
v = о )/(/ + яJ sin2 Ф + (/ — яJ cos2 ф,
/ = со2 /(/ + aJ cos2 ф + (/ — aJ sin2"^".
10. Дифференцируя уравнение конического сечения, полу-
получим
, т + пх ,
У = х\
У
кроме того, х' -\-у' =v%, откуда
после чего найдем
»
11. Окружность с центром п точке О.
12.
v=
13. Из определения скорости имеем
откуда получим
dr
Интегрируя это выражение, будем иметь
с
Г = 51"п(ф-|-С1).
О)
6Z
Если потребовать, чтобы при ф = 0 имело бы место условие
г=0, то получим
с .
г = — sin ф,
CD
что является уравнением окружности.
14. Будем иметь
р cos ф . р sin ф
zу Г51Пф=
, у 5ф
1—есоэф 1—
Дифференцируя по времени и исключая ф, получим
2
с2
что представляет собой уравнение окружности в переменных
х? и у'.
15.
2с
V =
h cos a
где h — длина перпендикуляра, опущенного из центра пер-
перпендикулярного сечения цилиндра на касательную к этому
сечению, проведенную через проекцию движущейся точки.
16. Здесь
Ф = — , г' =Ь,
г
откуда имеем
d<f a
ь
— ф
Интегрируя это соотношение, получим r = roe a . Уравнения
движения имеют вид
q>=-^-ln(— t+l).
b \r0 i
17. Из геометрического определения ускорения в проек-
проекциях на естественные оси будем иметь
68
18. Из определения проекций ускорения на оси естествен-
естественного трехгранника получаем
v
Rtga-tv0
19.
j=4мIсек2, p=0,01 м.
20. Следует воспользоваться выражениями для составляю-
составляющих ускорения по осям естественного трехгранника. Легко
получить дифференциальное уравнение, интегрируя которое
найдем
у = уое(Ф-Фс) ctgcs#
21. Решение непосредственно следует из рассмотрения со-
соотношений между проекциями ускорения на оси естественно-
естественного трехгранника.
22. Рассматривая составляющие скорости точки в^лоляр-
ной системе координат и исключая время, получим диффе-
дифференциальное уравнение траектории, интегрируя которое, най-
найдем конечное уравнение траектории
В частных случаях: при а=0 имеем прямую, при а =
л
= -J- — окружность, при а=я— прямую.
23. Непосредственные вычисления дают для проекций ус-
ускорения на ось Оу значение
h
Обратная задача. Если принять данную прямую за
ось Ох, а точку пересечения с кривой — за начало координат,
то найдем, что искомая кривая является циклоидой
У = ^ V 2ах (у2 — 2ах) + — arc cos
arc cos
24.
VB = /
25. (см. рис. 87)
Vv^ + у22 — 2,vtv2 cos a
и =
sis a
69
26.
со =
Qrir —a cos
— 2ar cos cp
27. Выберем систему подвижных осей, движущихся посту-
поступательно вместе с точкой А. Тогда относительные скорости
точек В и С будут находиться в соотношении
Рис. 87
Ver m +
vBr
Далее из условия vB = v1 + vBf. получаем vBf =v2 — t»lf от-
откуда
- — m + n .- —
H( )
Для модуля 'скорости отсюда получаем значение
70
—
28. 0=
29. vr -■
30. vr =
31. vr
г
32. vQ = — cor/ + — . юл; + ~ = О,
x = A cos со/ 4- В sin ш?, у = Б cos со/ — Л sin со/ -
со
33. (см. рис. 88)
= —— , ve — cos,
sin (a 4- ф) sin ф
sin (а 4-ф) , / . ч AM
ua = cos —_.. Y/ . 8Ш(а + ф) =-— ,
5 О
AM a — г cos ф со (а cos ср — г)
va = i* —- - со —— ^ , vr = -A
34. ue = 2— г й2 + б2 — 2аЬ cos ф .
a cos ф — b
35. Если систему осей жестко связать со стержнем Л^Дг,
то подвижная система координат будет двигаться поступа-
поступательно, а переносная скорость будет равна скорости точки Л.
Тогда получим
vM = yrv2 4- co2a2 —
36. (см. рис. 89)
v =—i-i- 4-co2s2tga =
cos a cos^a
vx = dJsi =co2atga,
у = V «i2 4- 2co1aJ sin2 a 4- co22 sin2 a A 4- cos2 a)
cos2 a
При a=30° имеем
37. и = y^cOiV 4- [(<% 4- w2) л; 4- v0 cos a]2 tg2 a.
cos a
38. л; = a cos — , у — asm , z = a sin
n. n n
39. o= —/ rBa — r).
71
40. В полярных координатах
г = г0
, ф Ф я,
где Го есть значение г при <р = <
41. ф = —tga
Рис. 89
Рис. 90
если при ф=0 #=0, то
43. Воспользоваться свойствами лемнискаты rrj = const.
46. (см. рис. 90)'.
Подвижную систему осей выбираем жестко связанной со
стержнем АВ. Тогда переносная скорость
и будем иметь
vex = — (аф sin a, Vg = <аф cos a — щху
после чего находим
g
cos a —
a
47. у =
to2J 62 —
oJ) a6 cos ф,
(o2L
to2J ab cos ф .
72
48. Мгновенный центр вращения палочки лежит на пере-
пересечении перпендикуляра к оси Ох, восстановленного от точ-
точки Л, и перпендикуляра к палочке, восстановленного из точ-
точки М. Из геометрических построений нетрудно получить урав-
уравнение неподвижной центроиды
и уравнение подвижной центроиды
Для мгновенной угловой скорости вращения палочки по-
получим выражение
_ Vq_ = voh
у К2 + х2'
49. Уравнение неподвижной центроиды
Х2 — Г2Х2=Г2\J
Связав подвижную систему координат с палочкой и вы-
выбрав ее начало в нижнем конце палочки, уравнение подвиж-
подвижной центроиды получим в виде
мгновенная угловая скорость выразится как
v vr
G) = =
/х2-
50. Нетрудно видеть, что @i= — @2; vc и vD — скоро-
скороде
сти точек С и D стержня, мгновенный центр вращения кото-
которого находится в точке Р пересечения стержней AD и СВ.
Поэтому будем иметь
vc PC '
Если положение системы определить углами а и р, то
можно показать, что
PD _ sin a
PC stop '
Отсюда найдем
sin a
(Dt = Crt.,.
ip
73
51 Стержень АВ остается все время параллельным
стержню ОС, а потому их абсолютные угловые скорости рав-
равны по величине и совпадают по направлению. Следовательно,
=coi. Мгновенный центр вращения стержня Л В находит-
находится на продолжении стержня ОА на расстоянии х= — b от
точки В. Центроиды: подвижная — окружность радиуса х =
= —- о с центром в точке Л; неподвижная — окружность,
центр которой расположен в точке О, а радиус
52. Мгновенный центр вращения находится на пересече-
пересечении перпендикуляров к оси Ох (в точке Л) и к оси Вс, (в точ-
точке D). Из прямоугольных треугольников имеем
Кроме того, из 'Подобия треугольников имеем £ = *, откуда
сразу находим уравнения центроид:
а), х2-\-а2=2ау.
53. Решение. Обозначим через а угол, который ось пара-
параболы образует с неподвижной осью Ох. Пусть в точке А (х0, 0)
находится мгновенный центр вращения параболы. Выберем
за подвижную систему осей систему координат x\O\yh жестко
связанную € параболой так, чтобы уравнение параболы в
этой системе приняло вид
Тогда уравнение касателыюй к параболе будет
(//1 — Ую) =0,
где Хю, ую — координаты точки касания, Х\, у\ — текущие
координаты касательной. Отсюда при //i = 0 получаем коор-
координаты точки С, связанные уравнением
—р(хх—
или
Из уравнения следует, что xi = —xl0, то есть точка В пересе-
пересечения оси i)\ с осью х делит пополам отрезок СА равнобед-
равнобедренного треугольника CFA. Значит, FB — координата у фо-
74
куса параболы. Если теперь v — скорость фокуса парабо-
параболы, то как нетрудно видеть,
а потому
dx
Но из AO^FB имеем
— о2
Р
Исключая из этих уравнении а, получаем
dy _ /4j/2 - р2
dx ~ p
Интегрируя это уравнение, находим
2 U
Если же положить, что при х=0 #=*—, то получим С=0.
54. Палочка ЛВ участвует в двух мгновенных вращениях.
Результирующая угловая скорость
Мгновенный центр вращения 5 лежит на отрезке О А на рас-
расстоянии
х = -
от точки О и на расстоянии
fi>l + fi>a
от точки Л. Центроидами являются окружности с центрами
в точках О я Л. Скорость точки В определяется из условия
х)В = [со • SB\,
откуда имеем
Г 2а2
/ \2 i " — ^ i COSQ? .
V&\ ~\~ *^2/ ®1 Т" ^2
75
00. СИ! = @0
56. Абсолютная угловая скорость
Г1
относительная угловая скорость
О) 2
О)
ускорение / = $г\гч ~\~ ^гг + г\ )•
57. Луна не вращается относительно 'системы осей, вра-
вращающейся вместе с Луной относительно Земли, а)о=юе.
Мгновенная ось вращения Луны проходит через центр Земли.
58. Искомая точка 5 лежит на пересечении продолжения
отрезка ON с окружностью малот колеса.
59. Абсолютная угловая скорость
относительная угловая скорость
60. Положим (для определенности), что V\>v2. Тогда
мгновенный центр вращения колеса будет находиться на пе-
пересечении продолжения диаметра, проходящего' через точки
касания с прямой, которая проходит через концы векторов
V\ и Vi. Мгновенная угловая скорость
CD =
vi —
2a
скорость центра диска
и = —±_j—
61. Мгновенный центр вращения шатуна АВ находится на
пересечении продолжения отрезка АО с перпендикуляром к
76
прямой ОВ, восстановленным в точке В. Отсюда непосредст-
непосредственно следует
OD
= tt -SB ^а> SB == со . OD.
SB
2 cos2 a
63 Метод решения тот же, что и для задачи 60. Мгновен-
Мгновенная угловая скорость
О) =
2а
Неподвижной центроидой является прямая, параллельная
рейкам, проходящая на расстоянии 2а ~ от точки Л. По-
движной центроидой является окружность радиуса
а
с центром в центре диска. Скорость центра диска равна
64. Мгновенный центр вращения стержня ВС находится в
точке S, расположенной на пересечении продолжения хор-
хорды DB с перпендикуляром к прямой ОС, проведенным через
точку С. Мгновенная угловая скорость
BS У /22 - г22
скорость точки В
скорость точки С
65. Угловая скорость стержня О\А
77
угловая скорость шестеренки /
66. Мгновенная угловая скорость вращения стержня ОВ
Уз .
угловая скорость вращения шестеренки /
вI = ^ B/3-1).
67. v =
68. Мгновенный центр вращения цилиндра находится на
пересечении продолжения радиуса АВ с перпендикуляром к
АС, восстановленным в точке С. Мгновенная угловая ско-
скорость цилиндра
— a)
ф _J_ ^2 _ 2^r^ Cos ф
69. При помощи теоремы о сложении скоростей получим
vc= ! X
sin (a + Р)
X У и2 sin2 (а-Ьр)+(о—УхJ cos2 р—2о (о—и,) sin а cos [3 sin (а
70. Мгновенный центр вращения стержня АВ находится
в точке 5 пересечения продолжения хорды ВС с перпенди-
перпендикуляром к прямой АС, восстановленным в точке А. Если че-
через Q обозначить угловую скорость вращения стержня АВУ
то будем иметь
С другой стороны,
откуда получим
__ _£о. §*
А г SB
78
о0 ВС • SA
n ВС • SA
Отношение определяется из геометрических гшстрое-
SB
ний, откуда имеем
vA =
rsintp
I/
71.
2 — 4r2 sin4 -|-
cos (ф -f- я|;)
2
= 1
(О
' COSlJ)
Угловая скорость вращения стержня АВ
Q = со ,
COSlJ)
где со — угловая скорость вращения стержня О А.
72. v = 2соа, и = соа т^З.
73. % =
74. Скорость движения ползуна В в горизонтальном по-
положении
h
в вертикальном положении vB = vA = o
75. Результирующее движение — мгновенно-винтовое. Ось
винта делит пополам сторону ОА и сторону FG куба. Вели-
Величина мгновенной угловой скорости вращения куба равна
Q= со V2\ скорость поступательного движения у _= ^^
где ш — величина и,-.
76. Воспользуемся формулой Эйлера
Vt =О0+ [О) -Л,-],
где о0 — скорость некоторой точки тела, принимаемой за по-
полюс, со — вектор мгновенной угловой скорости вращения те-
тела. Примем за полюс точку А. Оси к, у, z направим по реб-
ребрам куба. Проекции вектора со на эти оси обозначим через
сох, coy, (oz. Тогда,- определяя по формуле Эйлера проекции
скорости точки Б, получим:
= — 1, сож=0.
79
Далее, определяя таким же путем проекции 'скорости
точки С, получим tDj, = O. Отсюда следует, что линия действия
вектора со совпадает с направлением скорости точки А и,
следовательно, винтовая ось проходит через точку А. Мгно-
Мгновенное движение твердого тела представляется теперь век-
вектором скорости поступательного движения vx и вектором
мгновенной угловой скорости со, величина которого р_авна 1,
а направление противоположно направлению вектора V\.
77. Поверхность кругового цилиндра, ось которого являет-
v
ся осью винта, а радиус г= — .
со
78. Движение тела В относительно тела А является мгно-
мгновенно-винтовым. Ось винта пересекает ось у в точке
vQ -f- <°2я
Q2 + со2
Результирующая угловая скорость вращения со имеет проек-
проекции
(со, О, Q).
Скорость поступательного движения имеет проекции
О)
V-
со2
— Qa
+ Q2
79.
)•
со2
0,
—
R
h
со
V-
0J-
-Qa
f Q2
80. Мгновенная ось вращения проходит через 'неподвиж-
'неподвижную точку, являющуюся началом координат. Обозначим че-
через сох, coy, coz проекции вектора мгновенной угловой скорости
вращения. Тогда
3/2" oV7r 3/2
со^ = 2 У 2, со2= —у- .
Скорость точки Мг тела равна v2= 15 м/сек.
81. Пусть А является точкой касания диска и плоскости.
Линия действия вектора абсолютной угловой скорости вра-
вращения совпадает с прямой ОА. Величина и направление век-
вектора абсолютной угловой скорости о) определяется из тре-
треугольника скоростей:
со = соо ctg a,
80
где
v0 sin a
G>0 =
R cos2 a
так что
ft) =
ft cos a
Относительная угловая скорость
ft)
Г П 9
R cos*5 a
Неподвижным аксоидом является плоскость, по которой ка-
катится диск, а подвижным аксоидом — конус с углом при вер-
вершине 2а, ось которого 'совпадает с осью симметрии диска.
Скорость верхней точки равна v=2v0.
82. Пластинка участвует в сложном движении, состоящем
из двух мгновенных вращений с угловыми скоростями coi и
0J. Применяя теорему о сложении скоростей, получим:
переносная скорость точки В
vb = щ (й sin a -\- d cos а);
С
относительная скорость точки В
абсолютная скорость точки В
^а = оJ(# sina
83.
/2=
84. Абсолютная скорость
va = Vu2 + to2 (л;2 + a2) -f 2шш.
Составляющие ускорения
jr =, о, je = (о2 Ух2 + a2, \r = 2ш
81
Абсолютное ускорение точки
1а = со V со2*2 + со2я2 4- 4«2 -f- 4сош .
Q
85. х = — sin cof,
со
где с— произвольная постоянная. Уравнение траектории в по-
полярных координатах
с ,
г — — sin ф.
со
Составляющие ускорения:
/r=ccosin со^ — направлено к центру,
y соt.
л
86. со = — , ve = 2я sin ф, v — 2я = const;
dv _ . о2 2я2
— = 0, / = — = — .
rff p 5
87. Центр колеса движется прямолинейно. Его ускорение
может быть направлено только вдоль оси £, параллельной
рейкам. Для определения е имеем равенства:
• ■
h = к + 2в#, в =
Тогда
• i •
/1 +/2
/о = к + е# =
88. Траектория точки r^JRsincp; скорость точки v = (aR =
= const. Ускорение /r = cousin o)^ направлено к центру. Пере-
Переносное ускорение
je=(O2R Sin idt,
добавочное ускорение
82
абсолютное ускорение
= const.
Таким образом, точка движется с постоянными по величине
скоростью и абсолютным ускорением /. Это ускорение ортого-
ортогонально к вектору скорости точки. Радиус кривизны траекто-
R
рии точки р=— .
и2
89 Во всех точках относительное ускорение /г=—. До-
г
бавочное ускорение /' = 2(ои направлено к центру окружности.
В точке 1 имеем:
) / +
Абсолютное ускорение направлено к центру окружности.
В точках 2 и 4 переносное ускорение
je = <£>г/ а2 + г2 ,
абсолютное ускорение
В точке 3 имеем:
, / = — + 2со« + со2(а +
г
абсолютное ускорение направлено к центру окружности.
90. Относительное ускорение направлено к центру окруж-
ности и одинаково по величине во всех точках /,-=—. До-
г
бавочное ускорение в точках 2 и 4 по величине равно
// = 2cdoW и направлено ортогонально к плоскости кольца.
В точках 1 и 3 добавочное ускорение равно нулю. Перенос-
Переносное ускорение всюду направлено к оси АВ. В точках 2 и 4
оно равно ю02а, в точке 1 равно соо2(а—О-В точке 3 too2(a + r).
Поэтому будем иметь:
/i=- о>о (а — г),
г
h = h =
/з = h «о2 (а + г).
г
83
91. Рассматривая произвольное положение точки М и обо-
обозначая через г расстояние точки М от центра С, а-через ф —
угол между диаметром СО и прямой СМ, будем иметь
проекция скорости точки на направление радиуса-вектора
точки будет vr=—2coasin<p, а проекция скорости точки
на трансверсалыюе направление равна нулю.
Для ускорений получим следующие значения:
Отсюда следует, что вектор ускорения будет иметь только
радиальную составляющую, равную по величине
/=2co2acos<p.
Трансверсальная составляющая ускорения точки равна нулю.
Таким образом, направление радиуса-вектора точки остается
неизменным в пространстве, то есть точка будет совершать
прямолинейное движение независимо от ее 'положения на
окружности в начальный момент времени
= со —' = /
dt ' dt
92. Воспользовавшись формулой Ривальса, будем иметь
1а = «Д, he = ®аЛ Up =е/. «> - % —
г sin a
I stop
Из условия, что 'проекция ускорения точки В на горизонталь
равна нулю, имеем
9 9 r% sin2 а о , , о л
<D02г cos а — ш02 cos р — е/ sin p = О,
/ sin2 р
откуда находим
ftHV (/ cos a sin2 p — г sin2 a cos ft)
_
/sin
Для ускорения ползуна получим значение
о г2 sin2 a
/2 sinp
-— (/ cos а sin3 p — г sin2 а cos p) cos р.
s"
84
93. За подвижную систему координат выберем систему,
жестко связанную со стержнем ОЛ. Рассмотрим сложное
движение воображаемой точки контакта Е..Тогда искомая
скорость будет представлена как переносная скорость точки Е,
то есть ye=ysiri(p, и будет направлена в сторону уменьшения
угла ф.
Искомое ускорение будет представлять собой переносное
ускорение воображаемой точки. Одна из составляющих \еп
этого ускорения направлена к оси вращения и равна по ве-
величине
hn^— sta3<p.
Вторая составляющая \.Сх направлена ортогонально к стерж-
стержню в ту же сторону, что и скорость, а по величине равна ко-
риолисову ускорению воображаемой точки
}ех = 2 — sin2 ф cos ср.
Полное ускорение точки Е равно
V2 ,
/ = — У г — ЗбШ2ф 8Ш2ф.
h
94.
/х=— со2*—еу—2(о у' + к",
jy = —co2i/ + ex + 2со я-' + у"
95. Искомое ускорение
у = (со2 — 2о)9 — Q2)a-\-~+ 2(Q — a>)v.
а
96. /0= kk A±A
2 2R
97. Принимая точку Л за полюс, будем иметь:
ja = COi2a, /П=(ш1 + (О2JЬ, /г =0.
Полное ускорение точки
j = У <«!'а2 -|- {щ -\- со2L Ь1 — 2COJ2 (tDi -\- со2J ab cos <p .
85
Для ускорения точки С получи-м значение
99. Угловая скорость
2а2
о
У = G)
угловое ускорение
(а2—б2J
100. co = l, e = l. Мгновенный центр ускорений находится
на середине диагонали BD.
101. 01 =
102. v =
l/3(/2 — r2) — r]
103. v = R«>QVW, J = R]/ 10(s03 + G>04)-^ 12e0tD02 .
104. / = i- /м2 + /в2 — 2/и/в cos (P — a) = 5/3 см/сек2.
105. /л = 2co2/?, /л = 2R V 9oL + 4e2 .
Обозначив через М мгновенный центр скоростей, а через К —
мгновенный центр ускорений, будем иметь
мк = r °^L _^, tg лм/с -- —— .
К2 44 2со2
106. Предположим, что и^>а;в. Тогда мгновенный центр
вращения фигуры будет находиться на продолжении ЛВ на
расстоянии
л> —
wA —
86
Мгновенная угловая скорюсть вращения равна нулю, а уг-
угловое ускорение
WA — WB
з =
/
1лт о lii ^2 \
1C8. Стержень А В совершает мгновенно-поступательное
движение со скоростью 'поступательного движения vA = (o0f.
Нормальное ускорение точки В равно \Вп =u)o2r2/R.
С другой стороны, так как точка В является точкой стержня
ЛВ, проекцию ускорения точки В на нормаль определим из
равенства
Тогда
• • ■ ■
У ^п. • ft • ftPfi'
откуда будем иметь
—5— = o)oV + e Y /2 — г2 .
R
Отсюда получаем величину углового ускорения стержня
GHV(r-tf)
Полное ускорение точки В получит вид
109. Q = Y oi»!2 -j- to22 -f 210^2 cos a, e = @JCD2 sin a.
ПО. Переносная угловая скорость сое=соо- Относительная
угловая скорость вращения конуса вокруг своей оси симмет-
симметрии равна
sin 135°
юг = ©о
sin 22,5°
Вектор абсолютной угловой скорости вращения конуса на-
направлен по общей образующей, а по величине равен со0=соо.
Вектор углового ускорения е направлен ортогонально к плос-
87
кости, образованной осями конусов. По величине угловое ус-
ускорение равно
= ©о8 -2- •
1 1. О) — 0I +(rt2 , 6=COiCO2.
112. Нетрудно видеть, что и0 = ^л=сог^. Кроме того, угло-
угловое ускорение е=согсог?, а угловая скорость Qt^co^ + co,.2. От-
Отсюда получаем
\ос = ^2Р =
Полное же ускорение будет равно \а = ]в — R®r у 4®1 +
113. Абсолютная угловая скорость
переносная угловая скорость
v* /2Г
угловое ускорение
... . \(a^h . о „cos2 a
sin а sin а
115. Q = -/с»!2 -f co22 -f 2со1ю2 sin 45°, 8 = «о^а sin 45°.
116. Мгновенная угловая скорость вращения по величине
равна Зсо. Линия действия вектора мгновенной угловой ско-
скорости проходит через центр тяжести треугольника ABC, где
А, В и С — точки пересечения данных осей с перпендикуляр-
перпендикулярной к ним плоскостью.
117. Линия действия вектора мгновенной угловой скорости
вращения диска совпадает с образующей, касающейся диска.
Ускорение точки А диска равно /=е/?=const, что может быть
только в том случае, когда абсолютная угловая скорость яв-
является постоянной по величине. Нетрудно установить, что
тогда величина абсолютной угловой скорости вращения диска
равна
Rtg30° '
а угловое ускорение диска по величине равно
СОДЕРЖАНИЕ
Стр.
Введение . « . 3
Кинематика 5
Скорость и ускорение материальной точки в простейших дви-
движениях 6
Сложное движение материальной точки. Теорема о сложении
скоростей 20
Кинематика твердого тела. Распределение скоростей в твердом
теле 30
Теорема Кориолиса об ускорении материальной точки в слож-
сложном движении. Распределение ускорений в твердом теле . . 45
Ответы и методические указания к задачам 65
Евгений Николаевич Березкин
Решение задач по теоретической механике
(часть первая)
Редактор Н. В. Сысоева
Технический редактор Е. Д. Захарова
Корректор Н. Б. Казакова
Заказная
Сдано в набор 27/IV 1972 г.
Подписано к печати 29/1 1973 г.
Л-58035 Формат 60X90/16
Бумага тип. № 3
Физ. печ. л. 5,75 Уч.-изд. л. 4,88
Уч. изд. л. 4,88
Заказ 219 Тираж 4500 экз.
Цена 14 кои.
Издательство
Московского университета,
Москва, К-9, ул. Герцена, д. 5/7.
Типография Изд-ва МГУ,
Москва, Ленинские горы