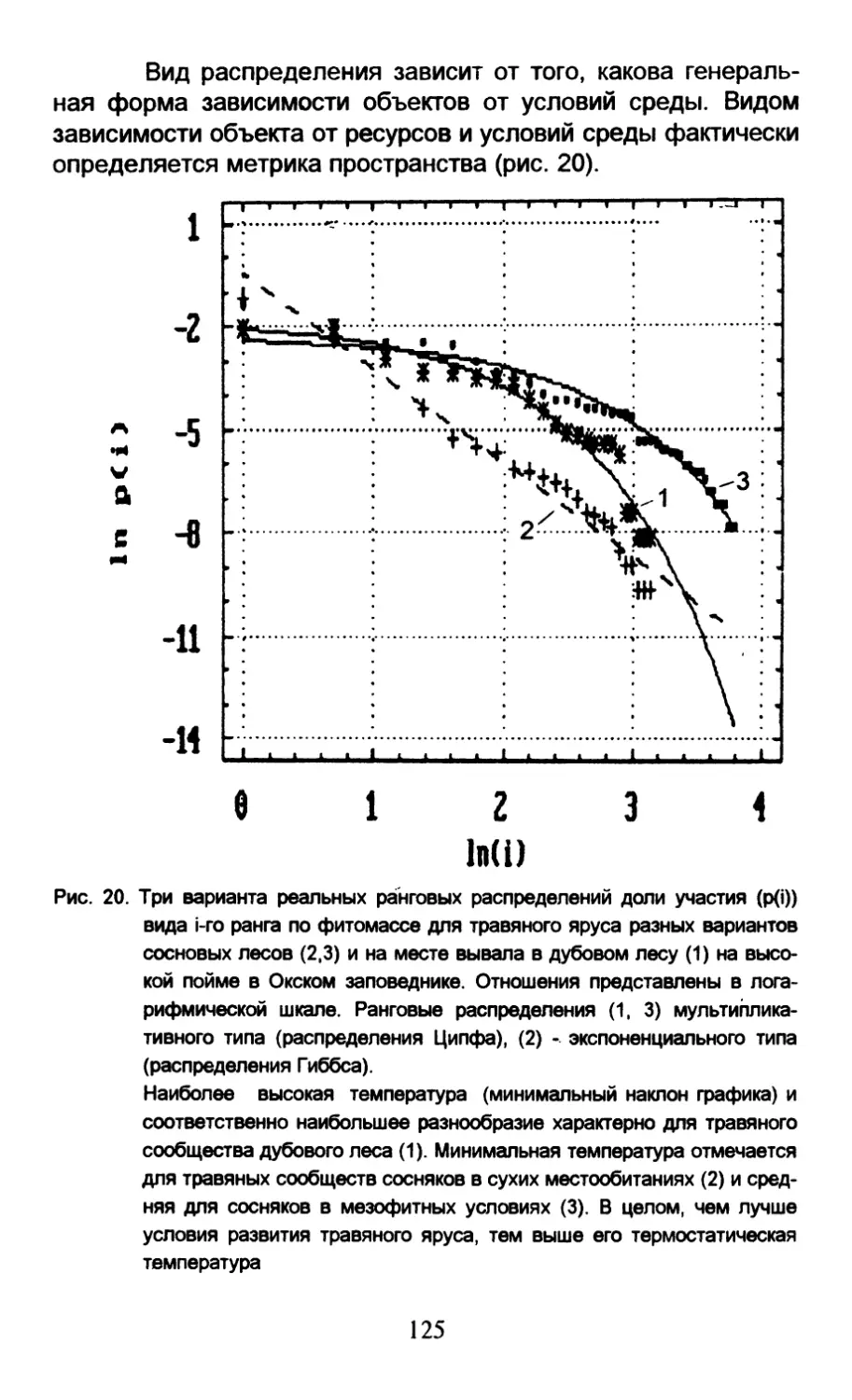
Автор: Пузаченко Ю.Г.
Теги: общая экология биоценология гидробиология биогеография географические науки экология
ISBN: 5-211-03277-2
Год: 1996
Текст
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М. В.Ломоносова
Географический факультет
Ю.Г.Пузаченко
ОСНОВЫ ОБЩЕЙ ЭКОЛОГИИ
Издательство Московского университета
1996
6БК26.8
П88
УДК 574(07)
Рецензенты д-р геогр наук К Н Дьяконов,
д-р биол нау^ А В Захаров
Печатается по постановлению
Редакционно-издательского совета
Московского университета
Пузаченко Ю Г
П88 Основы общей экологии Учеб пособие М • Изд-
во Моск. ун-та, 1996 134 с: ил.
ISBN 5-211-03277-2
Дано краткое изложение основных положений
теории популяций и сообществ, с учетом новейших
разработок в этой области. Рассматриваемые
законы применимы практически ко всем организмам,
включая важнейшие аспекты экологии человека и его
хозяйственной деятельности
Пособие ориентировано на студентов и
аспирантов географических факультетов
077 (02) - 96 - заказное ББК 26.8
ISBN 5-211-03277-2 © Московский государственный
университет, 1996
ВВЕДЕНИЕ
В последние 20 лет слово экология приобрело
исключительную популярность и всеобъемлющезначение. Чем
только ни занимаются экологи, какие только реалии природной
и общественной жизни они ни пытаются изучать и объяснять.
Люди, называющие себя экологами, занимаются
исследованием жизни микроорганизмов и млекопитающих, изучением
преобразования вещества и энергии, воздействием различных
форм деятельности человека на окружающую среду и,
наоборот, воздействием окружающей среды на человека. Но так
было далеко не всегда. Совсем недавно, в 60-ые годы слово
экология было известие только узкому кругу ученых, в
основном биологам. Экология была чисто биологической наукой, без
каких-либо особых претензий на всеобщность. Рассмотрев
историю науки, попытаемся понять, как произошло столь
резкое изменение. Сейчас же примем как факт огромный объем
современной экологии.
Но если научная дисциплина охватывает
исключительно разные предметы и явления реальности, то должно
быть что-то общее, что делает ее единой, должны
существовать какие-то общие законы или отношения, справедливые и
для "червей", и для "людей". Из этого, конечно, не следует,
что "законы червей" исчерпывают все "законы людей", и
наоборот. Но общее, что позволяет и к тем и к другим подходить
с экологических позиций, должно существовать.
Это общее, не зависящее от конкретного объекта
исследования, и является предметом общей экологии. Все
множество общих законов можно подразделить на отдельные
законы, описывающие относительно простые, элементарные
отношения, но вместе с тем при определенных условиях
приемлемые для самых различных предметов и явлений.
Каждый такой закон, взятый в отдельности, описывает
лишь небольшую часть реальности, но их осмысленное
объединение, осуществляемое по определенным правилам,
позволяет понять ход сложных процессов. Тот, кто владеет
этими основными конструктивными элементами экологического
3
знания, легче ориентируется в реальности, более адекватно
реагирует на процессы, протекающие в окружающем мире.
Но ни в коем случае не следует думать, что здание
экологии полностью построено и известны все элементарные
конструкции, необходимые для его строительства. Здесь мы в
самом начале пути, на котором человечество ждут серьезные
открытия.
Курс в целом изложен по схеме движения от частного к
общему. В первую очередь рассматриваются базовые законы
динамики популяций как частей интегрирующих их
экологических систем более высокого ранга. Затем рассматривается,
каким образом из популяций могут быть образованы
сообщества. Далее через отношения сообществ с окружающей
средой вводятся представления об экосистеме, биогеоценозе
и геосистеме. Затем рассматриваются пути их интеграции в
природно-территориальные комплексы и, в конечном итоге, в
биосферу.
Каждый уровень экологической организации обладает
свойствами, которые невоспроизводимы из интегрируемых им
частей, принадлежащих более низкому уровню. Эти свойства,
являются результатом их взаимодействий и рассматриваются
особо для каждого уровня. В заключение кратко излагаются
основные прикладные аспекты экологии, такие как
нормирование, прогноз, планирование ландшафта и т.п.
В первой части настоящего издания изложение
предмета заканчивается темой сообществ.
I. ПУТИ СТАНОВЛЕНИЯ ЭКОЛОГИИ
Большинство названий естественных и формальных
наук родилось в глубокой древности, и авторы этих названий
не известны.
Экология же имеет точную формальную дату своего
рождения и известна фамилия ее юридического отца. Им был
последователь Ч.Дарвина Э.Геккель, в 1886 г. определивший
экологию как общую науку об отношениях организмов с
окружающей средой. Это наиболее общее определение
справедливо и по сей день.
Вполне понятно, что факт рождения науки не означает,
что до этого никто не занимался ее предметом, "отношениями
организмов и среды". Тема эта столь очевидна, что она
постоянно была в поле зрения биологов, и без своего названия
наука как система знаний фактически существовала всегда.
Охотник, скотовод, землепашец далекой древности могли
достигать успеха, если имели необходимые знания об отношениях
используемых ими животных и растений с окружающей
средой. Но это были чисто эмпирические знания, которые смогли
оформиться в науку только после того, как было достигнуто
понимание всеобщности и значимости этих отношений, когда
за весьма хорошей согласованностью формы жизни и условий
жизни стали видеть не столько разум всевышнего, сколько
естественный процесс саморазвития.
Этот скачок мысль человека сделала лишь в XIX в.,
когда Ч.Дарвин в "теории происхождения видов путем
естественного отбора" обобщил многовековой опыт человечества.
В основе теории естественного отбора лежат именно
отношения организма с окружающей средой и именно эта теория
послужила одной из важнейших составных частей современной
экологии.
Однако Ч.Дарвин связывал естественный отбор с
жесткой, внутривидовой конкуренцией, которую прямо выво-
5
дил из закона Мальтуса о размножении живых организмов в
геометрической прогрессии. Этот чисто математический закон
по форме и по уровню абстракции был весьма важной
составной частью логики естественного отбора. Из теории
естественного отбора и первой математической формализации
сформировалась важная ветвь экологии, прослеживаемая до
настоящего времени.
Вторая важнейшая ветвь была порождена жесткими
требованиями практики сельского хозяйства. В конце XVIИ в.
Луавазье, Сенебье и др. установили факт разложения
углекислоты воздуха растением и показали, что это есть процесс
питания и отложения углерода в растении. Однако только
через 50 лет это открытие стало общеизвестным и повлияло на
практику сельского хозяйства. Развитие химии создало
предпосылки для того, чтобы в середине XVIII в. (1840 г.) К.Либих,
основоположник органической химии, открыл факт питания
растений элементарными химическими соединениями. До него
полагали, что растения питаются гумусом, на что, прямо
указывала положительная связь биологической продуктивности с
количеством органических удобрений и запасами гумуса в
почве. Кроме того, К.Либих сформулировал абстрактный закон
фактор-минимума: продукция растения определяется тем
элементом минерального питания, который находится в
минимуме. Ясно, что по сути это закон об отношении организма с
окружающей средой и потому его с полным основанием можно
назвать экологическим.
Примерно в то же время Буссенго документально
доказал факт увеличения продуктивности сельскохозяйственных
культур, если в севооборотах участвуют клевер и бобовые
растения. К.Либих считал, что севообороты увеличивают
продуктивность только за счет того, что разные виды растений
используют разные элементы, но в конечном итоге внесение
минеральных соединений в почву, и в том числе азотных,
совершенно необходимо. И лишь в 1885 г., только после того,
как Пастером были заложены основы учения о бактериях,
была открыта и доказана микробиологическая основа фиксации
азота клубеньковыми бактериями (Гельригль).
Это, с одной стороны, позволило объяснить важность
севооборотов с участием бобовых растений и клевера, а с
другой - осветить самое узкое место в представлении о круго-
6
вороте азота - доказать факт биологической фиксации его из
воздуха.
Вместе с тем важно отметить, что из этого этапа
развития науки вытекали и другие важные экологические
следствия: целесообразность взаимозамещений разных видов
растений во времени, эффекты, которые могут порождать
симбиотические отношения.
Наконец, в конце прошлого века К.А.Тимирязев (1875)
открыл факт фотосинтеза, показав извлечение углекислого
газа из воздуха и синтез на этой основе энергетически емких
соединений (Сахаров), с использованием солнечной энергии
при участии хлорофилла. Таким образом, в общих чертах к
концу века были заложены представления о преобразовании
энергии и круговороте химических соединений.
Обобщая достижения физики, химии, математики,
биологии в начале текущего столетия, В.И.Вернадский
сформулировал конструктивное представление о биосфере. В
конце пособия более подробно рассмотрим эти базовые
обобщающие представления, здесь же отметим, что им было
введено представление о жизни как о самостоятельной
планетарной силе.
Математической основой взглядов В.И.Вернадского
была термодинамика и представления о равновесиях,
сформулированные Гиббсом.
В целом же к концу прошлого - началу текущего
столетия было сформулировано общее здание экологии: отношения
организмов с окружающей средой через приспособление к
этим условиям на фоне внутривидовой и межвидовой
конкуренции; отношения организмов с окружающей средой через
вещественные обмены на базе преобразования солнечной
энергии растениями; общие математические представления о
саморазвитии популяций и базовые законы термодинамики как
основы представлений о равновесиях и сохранениях материи
в различных типах преобразований.
В то время все эти области научного знания прямо не
связывались с экологией. Знаний об отношениях еще было
недостаточно для того, чтобы дать необходимые основания
для формирования единой научной концепции.
Вторая половина XIX в. и первая половина XX в.
ознаменовались широкой экономической экспансией западной
7
цивилизации и высокими темпами экстенсификации
хозяйственной деятельности. Наука естественно обеспечивала сбор
необходимых знаний о состоянии ресурсов конкретных
территорий. Освоение лесов требовало развития методов
инвентаризации их состояния. Развитие сельского хозяйства -
инвентаризации свойств почв. Потребовались сведения о
вредителях сельского хозяйства, о процессах саморазвития лесов и
вообще растительных сообществ. Наконец, контакт
европейцев с новыми территориями поставил новые сложные медико-
биологические задачи, и в том числе изучение возбудителей
болезней, естественным образом циркулирующих в природе.
Все это вместе взятое определило повышенный интерес к
развитию знаний о пространственной организации природных
процессов, об их естественной динамике. Требования
практики создали материальную базу для развития географии и
экологии, между которыми на первых этапах не существовало
принципиальных различий. Постепенно возникла некоторая
дифференциация. Географические науки в большей степени
занимались проблемами типологии, картографирования,
изучением пространственной структуры. Экологи же в рамках
биологии большее внимание уделяли изучению связей между
элементами и частями природных систем, построением
моделей их динамики. Между этими крайними позициями возникла
вся гамма переходов, так что многие научные направления и
их отдельные аспекты в равной степени являлись и
географическими, и экологическими. В целом географическому типу
мышления в большей степени была присуща концепция
ведущей роли в размещении организмов, их типических
сочетаний, продуктов их жизнедеятельности, почв, внешних
факторов: климата, рельефа, литологии, а экологическому типу -
представления о ведущей роли в формировании
наблюдаемого разнообразия саморазвития жизни, на основе
взаимодействия различных видов растений и животных и их
сообществ с косными компонентами природы как в масштабах
геологического, так и исторического времени.
Взаимонеприятие этих двух позиций часто приводило к
глубокому научному и чисто эмоциональному противостоянию,
отголоски которого звучат зачастую и сегодня.
В результате этого этапа человечество получило:
8
- достаточно ясные представления о структуре
растительного и почвенного покровов суши планеты,
представленные в системах классификаций и на картах различных
масштабов;
- совокупность важнейших абстрактных, системных по
своей сути понятий, отображающих различные формы
отношений организмов с окружающей средой, таких, как биоценоз,
фитоценоз, Оиотоп, местообитание, экосистема, биогеоценоз
консорция, синузия и т.п.;
- спекулятивные представления о динамике, в первую
очередь растительности и ее территориальных единиц в
различных масштабах времени;
- обшие представления о связи структуры и
хозяйственно важных характеристик растительности, животного
населения почв с внешними факторами среды;
- развитую систему методов полевых исследований
В географии этот период ознаменовался развитием
концепций системной интеграции неживых и живых
компонентов природы в территориальные комплексы, или ландшафты
Важнейшим феноменологическим открытием географии
можно считать становление представлений о пространственной
иерархической организации территории, выраженной в
размерном соподчинении территориальных единиц.
В конечном итоге к 40»50-м годам столетия был собран
и обобщен огромный фактический материал и тем самым
обеспечена технология экстенсивного ведения хозяйства,
опирающаяся в первую очередь на знание состояния ресурсов
конкретных территорий и возможностей их использования. Из
этих же знаний вытекали и простейшие правила ограничения в
использовании соблюдение которых снижало риск
необратимой деградации земель и ресурсов
В тени господствующего направления созревали
концепции и подходы будущего. Так, в начале века начался
первый этап массового проникновения конструктивных идей
математики в экологию. В 20-х годах i оку иг о столетия трудами
В Вольтера бычи заложены основы современного здании
математической экологии, и многие полученные им результаты
стали каноническими. Практические задлч-л жеперименталь-
иых исследове ий и в том числе r польском хозяйстве спо
го^г.гвовали появлению первых ра'.рабоюг лримечеч и,« тео-
рии вероятностей и развитию статистики как науки о принятии
решений в условиях неопределенности.
Небезынтересно отметить, что в 30-х годах Костицы-
ным была разработана математическая теория глобальных
колебаний климата, строящаяся на анализе взаимодействий
суши, океана, ледниковых покровов и атмосферы. Однако в то
время она была понята и по сути дела переоткрыта уже в
60-е годы.
В первой половине текущего столетия, несмотря на
полученные фундаментальные результаты, математическое
направление не получило широкого развития. Экологи и
географы, занимающиеся решением задач инвентаризации,
накоплением фактического материала о разнообразии
изучаемых ими явлений, за редким исключением не
воспринимали математической абстракции, сводящей множество
свойств и отношений к элементарным и наиболее
существенным. Они пытались обобщить и упорядочить множество
наблюдаемых явлений и отношений через классификации,
стремясь во всех случаях добиться естественности. Под
естественностью обычно подразумевалось, что классификация
упорядочивает объекты не только по их сходству друг с
другом, но и по их генетической близости и взаимосвязи.
Предполагалось, что достижение естественности классификации
позволит описать правила взаимопреобразований изучаемых
явлений во времени и пространстве.
Послевоенные 50-60-е гг. знаменовались
становлением интереса к изучению не только структуры, но и
функционирования совокупностей организмов. В практику экологов
начали все шире приникать учеты фито- и зоомассы,
биологической продуктивности, использования солнечной энергии,
круговорота химических элементов.
Мотивацией для этих работ была естественная
необходимость интенсификации хозяйственной деятельности, в
первую очередь в сфере использования биологической
продукции и управления этими процессами.
В среде экологов господствовал наивный физикализм,
постулатом которого было представление о том, что энергия
является универсальной единицей измерения всех
отношений, своеобразной валютой экологических систем.
Соответственно допускалось, что знание правил циркуляции этой ва-
10
люты позволит с необходимой полнотой описать, по крайней
мере, важнейшие аспекты функционирования природных
систем.
Эти идеи и связанные с ними работы по исследованию
биологической продуктивности и круговорота биогенных
элементов синхронно распространялись во всем мировом
сообществе и в 60-х годах вылились в реализацию международной
биологической программы (МБП).
История реализации этой первой мировой
экологической программы заслуживает специального изучения. Ее
роль в становлении экологии и ее успех были огромны, а
практические результаты впечатляющи. Достаточно сказать, что во
всем мире множество ученых, лаборантов и студентов по
примерно сходной программе кропотливо собирали сведения
по реальной биомассе растений и животных, по ежегодному
приросту этой массы определяли ее калорийность,
содержание химических элементов в различных частях растений, в
животных и почве.
Вполне понятно, что вся эта работа могла быть
организована только на основе предшествующих результатов
инвентаризационного этапа. Знание пространственной структуры
природных образований, разнообразия и размещения
типичных комбинаций растений и почв позволяли достаточно
эффективно и независимо друг от друга спланировать
конкретные исследования, связать результаты с типологическими
единицами растительности и ландшафтов, интерполировать
данные, полученные в точке, на достаточно большие
территории.
В наиболее типичных природных ландшафтах
возникли и первые научно-исследовательские стационары, в задачу
которых входило изучение реальной динамики продуктивности
и круговорота биогенных элементов.
В конечном итоге в результате этих исследований
мировым сообществом были получены первые реальные
сведения о запасах и продукци и биологического вещества на
планете.
Обширные фактические материалы требовали
развития методов их обобщения, что естественным образом
привело к становлению союза экологов и математиков. К тому же
появление вычислительных машин создавало условия для
11
численного решения сложных задач с многими переменными.
Это определило развитие имитационного моделирования,
создание первых моделей процессов трансформации
солнечной энергии в растительном покрове, биологической
продуктивности, круговорота биогенных элементов а в конечном
итоге, привело к первым построениям и гпобапьных моделей.
Необходимость исследовать сложные многофакторные
отношения стимулировала и бурное развитие статистических
методов анализа.
В этот период исследования пространственной
структуры компонентов природы имели несколько подчиненное
значение, однако и они испытывали на себе конструктивные
идеи международной биологической программы и развитие
общенаучных идей. Особую идеологическую ропь в го время
ифала кибернетика, в рамках которой сложные для
восприятия натуралистом математические абстракции сближались с
реальностью. Именно кибернетика привнес/а в экологию
представление о фундаментальной роли в функционировании
разнообразия и структуры как основы устойчивости и гомео-
г.таза сложных природных систем Идеи кибернетики
стимулировали становление количественных исследований структуры
природных систем в их взаимосвязи с функциональными
характеристиками. В этот период получила теоретическую
основу концепция экологической ниши как многомерной области,
занимаемой видом или популяцией и определяющей его
функционирование. На смен> представлениям о жесткой
взаимосвязи совместно обитающих видов пришли идеи об их
существенной независимости друг от друга и автономности,
хотя первые факты в качестве ъазы этих идей были получены
еще в 30-е годы.
Однако функциональное направление экологии не
смогло сколь-либо существенно ассимилироваться со
структурным, и методологические основы согласованного
исследования структуры и функций остаются сложной проблемой и по
настоящее время.
Так или иначе к началу 70-х годов экология
располагала огромным фактическим материалом, опытом его сбора,
достаточно развитой теорией, многие из аспектов которой
имели конструктивное математическое представление.
Наконец она обладала первыми навыками моделирования слож-
Р
ных природных систем и процессов и располагала первыми
версиями глобальных моделей.
В ходе изучения круговорота биогенных элементов
было естественно изучать химический состав атмосферного
воздуха, твердых и жидких осадков. Эти. в то время
эпизодические исследования показали, что окружающая среда
претерпевает существенные изменения. Расчеты выбросов
двуокиси углерода и других продуктов хозяйственной
деятельности свидетельствовали об исключительных масштабах
антропогенного пресса. Возникла идея возможности
возникновения планетарного парникового эффекта и антропогенного
потепления климата, способного резко изменить условия жизни
многих стран и народов Впервые были получены прямые
данные, свидетельствующие о влиянии на наследственность
животных широко применяемых инсектицидов и в частности
ДДТ.
Эти и другие идеи и факты впервые в истории
человечества в полном объеме поставили вопрос о необходимости
сохранения окружающей среды как усповии выживания самого
человечества.
В 1972 г. в Стокгольме собрался I Международный
конгресс по окружающей среде Только на этом конгрессе
впервые понятия "экология" и "экопо!" получили современную
расширенную трактовку, и именно этот конгресс является
вехой, от которой можно вести прямой отсчет становления со
временной экологии.
Экология естественным образом включила в себя
человека со всеми его отношениями с окружающей средой и за
короткое время преобразовалась из науки с конкретной
предметной областью в очень общее и неопределенное научное
направление, скорее в очен» неясную форму мышления, чем
в науку как систему знании
Актуальность проблем привлекла под флаг экологии
новых людей не знавших ее истории научной базы
достижений. Они творили экологию в рамках и в меру своих знаний и
понимания, привнося идеи и результаты других областей
науки и техники. Экология превратилась в своеобразное
смешение "языков и народов", и самое удивительное то. что они
стали развиваться, не очень ущемляя и притесняя друг друга.
Лишь к концу 80-х годов очень постепенно начали
намечаться самые общие контуры новой экологии, но процесс ее
становления находится в самом начале.
Можно полагать, что возникновение новой экологии,
интегрирующей в себе достижения длительного периода
изучения отношений между организмами и окружающей средой,
опирающейся на идеи биологии, географии, химии, физики,
математики, современные технические средства
исследований, есть естественный процесс интеграции научного знания,
необходимого для интенсификации хозяйственной
деятельности человека, обеспечения его выживания в изменяющихся
условиях окружающего его мира. Информационная и
вещественно-энергетическая соизмеримость мощности
человеческой активности с естественными природными процессами -
естественный стимул интеграции знания как средства
уменьшения неопределенности в отношениях человека с
окружающим его миром.
Только будущее покажет, справимся ли мы с этой
сложной задачей интегрального отображения себя и
окружающего нас мира.
В заключение приведем в обобщенной и безусловно
упрощенной форме перечень и содержание основных этапов
становления экологии (табл. 1).
Таблица 1
Этапы становления экологии
Время
1
Вторая
половина
18 в.
Содержание
2
Накопление фактов в области биологии, геологии,
опыта в сельскохозяйственной деятельности и
селекции.
Установлен закон сохранения вещества
(Лавуазье).
Установлен процесс разложения углекислоты
воздуха растениями и показано, что это процесс
их питания.
Мальтус сформулировал закон размножения ор-
| ганизмов в математической формулировке.
U
Продолжение табл.1
1
Первая
половина
19 в.
Вторая
половина
19 в.
Первая
половина
20 в.
2
Первые представления о формировании
биологического разнообразия путем естественного
саморазвития и естественного отбора. Создана теория
происхождения видов путем естественного
отбора (Дарвин).
Доказано, что растения в качестве питания
используют минеральные соединения.
Сформулирован закон фактора-минимума (Либих).
Понята природа влияния севооборотов на урожай
(Буссенго).
Созданы основы теории вероятностей (Курно).
Накопление фактов о связях организмов со
средой. Сформированы представления о высотной
поясности и зональности (Гумбольдт, Докучаев).
Доказана фиксация клубеньковыми бактериями
азота из воздуха (Гельригель).
Раскрыты базовые механизмы фотосинтеза
(Тимирязев).
Доказательства роли микроорганизмов в
разложении мертвого органического вещества.
Разработана общая теория термодинамики
(Гиббс), выведено базовое уравнение
логистического роста численности популяции.
Обобщение эмпирических и теоретических
результатов 19 в. в представления о живом
веществе как независимой термодинамической
переменной и формулировка концепции
планетарных сфер (и в первую очередь биосферы) как
областей равновесия независимых
термодинамических переменных (Вернадский).
Накопление сведений о пространственной
структуре сообществ растений и животных, сведений о
связях видов с средой и формулировка базовых
понятий экологии.
Разработка математической теории экологии и
теории статистического анализа данных.
15
Окончание табл. 1
1
Вторая
половина
20 в.
Текущее
время
2
Количественное изучение биологической
продуктивности и круговорота вещества в природе,
теплобалансовых отношений. Международная
биологическая программа (МБП).
Широкое использование в исследованиях
методов моделирования. Развитие математической
теории популяций, сообществ и экосистем.
Обобщение эмпирических данных о связях видов
и их сообществ со средой.
Международная конференция по охране
окружающей среды в Стокгольме (1972 г.) - начало
расширенного понимания экологии. Широкое
развитие прикладной экологии и моделирования
глобальных процессов.
Постепенное расширение теоретического и
методологического базиса науки с учетом
представлений о неравновесных, нестационарных процессах.
Развитие моделирования сложных процессов.
Соединение эксперимента и наблюдений в
природе с моделированием.
Контрольные вопросы:
Опишите содержательные стороны основных этапов
!'<'!ЗВИТИЯ ЭКОЛОГИИ.
Как связываются друг с другом различные составные
¦ ;СТИ ЭКОЛОГИИ'?
Что общего в отношениях человека и какого-либо,
избранною Вами вида растений и животных с окружающей
средой'' Ь чем Вы усматриваете разницу?
II. ОСНОВЫ ТЕОРИИ ПОПУЛЯЦИИ
Популяцией называется совокупность особей одного
вида, способная на основе размножения поддерживать
достаточно длительное существование преемственных поколений.
Элементами этой системы являются особи. При простейшей
трактовке особи рассматриваются как неизменные и не
трансформируемые в процессе преобразований.
Следовательно, допускается, что особи, принадлежащие к одному
поколению или образующие популяцию в данный момент
времени, как и особи, принадлежащие к разным поколениям
или образующие популяцию в разные моменты времени, при-
небрежимо отличаются друг от друга. Натуралист-эколог,
прочитав это положение, сразу же заявит, что это допущение ни в
какой мере не отражает реальности, а потому все, что может
быть получено на его основе, не имеет смысла. Следует
признать, что он будет прав в первой части своего высказывания,
но не прав во второй.
Безусловно, что особи, образующие популяцию,
отличаются друг от друга по множеству свойств: они могут быть
самцами и самками, иметь разный возраст, различные
поведенческие реакции, различные размеры и т.п. В конце концов
точно так же, как нет двух абсолютно схожих людей, так и нет
двух абсолютно схожих особей любой популяции,
принадлежащей любому виду. Сколь бы детально ни учитывалось это
разнообразие, всегда можно найти то, что не учтено.
Естественно начать исследовать систему, определив
ее, в первую очередь, через наиболее общие свойства,
безусловно присущие любым ее реальным объектам, конечно, если
при таком рассмотрении выявятся следствия, которые
позволяют объяснить и предсказать существенные стороны
поведения реального объекта. Так как рассматриваются очень
общие свойства, безусловно принадлежащие всем реальным
объектам рассматриваемого типа, то соответственно можно
утверждать, что полученные следствия, по крайней мере на
качественном уровне, истинны для всех них. Далее, в элемен-
17
тарную модель отношений, полученную на основе до предела
упрощенного-определения, можно вводить все новые и новые
отношения, подразделять элементы на группы подобных и т.д.
С одной стороны, это будет приводить к приближению модели
к реальности, но, с другой - придавать ей все более частный
характер.
В первом, наиболее простом определении популяции
единственным отношением, ставящим в соответствие
элементы в один момент времени элементам в следующий
временной момент, является размножение.
Подразумевается, что популяция существует на
некоторой территории или в акватории. Подразумевается, что она
характеризуется числом элементов, или численностью
которая может изменяться во времени.
Конечно, чтобы шел процесс размножения,
необходимо, чтобы, популяция имела возможность потреблять из
окружающей среды вещество и энергию. В действительности
количество вещества и энергии, поступающих в популяцию, не
остается неизменным, однако в простейшем варианте
допускается, что флюктуации их поступления в популяцию во
времени и пространстве пренебрежимо малы.
На это упрощение необходимо обратить особое
внимание. Совершенно очевидно, что в природе популяция,
находящаяся в таких отношениях с ресурсами, - явление
совершенно исключительное. Ресурсы испытывают колебания во
времени и пространстве как в результате жизнедеятельности
самой популяции, так и по не зависящим от нее причинам.
Сколь же содержательны выводы, которые можно получить
при таком упрощении? В их содержательности можно
убедиться на очень простом примере: рост индивидуального
организма или онтогенез осуществляется на основе потребления
вещества и энергии, и если поступление обеспечивает
необходимый минимум, достаточный для поддержания жизни, то
рост будет идти по своим собственным законам,
определяемым строением самого организма. Внешние факторы вообще,
и поступление ресурсов в частности, могут замедлить рост,
модифицировать формы преобразований, но не могут
произвольно изменить само направление процесса. Процесс будет
реализован в области траекторий, допускаемых строением
организма.
18
Это фундаментальное свойстве организма и
образуемых им систем определяется тем, что жизнь добивается
устойчивости существования в условиях термодинамического
неравновесия, создавая собственное термодинамическое
поле, обеспечивающее относительную автономность
биологических систем от условий среды. Это положение отмечалось
В.И.Вернадским, и именно оно было заложено им в концепцию
биосферы.
Однако сразу же отметим, что автономность
биологических систем по отношению к внешним переменным не
является абсолютной и разные биологические системы и даже
разные виды имеют разное множество допустимых траекторий
саморазвития. В рамках этих допустимых траекторий
изменения внешних условий могут существенно влиять на ход
саморазвития.
На данном этапе рассматриваются автохтонные
законы развития в их чистом виде.
Пусть В - рождаемость, количество детей, которое
может воспроизвести,один родитель за единицу времени, D -
смертность за то же время. Численность популяции
обозначим N. Скорость роста численности популяции при принятых
условиях - соответственно
dN/dt = (В - D)N ,
где dN - приращение численности за интервал времени - dt. В
рассматриваемом варианте (В - D) константа, которую можно
назвать моментальной скоростью роста численности, или
коэффициентом размножения г.
Эта простая модель есть не что иное, как закон
экспоненциального роста численности популяции в
неограничивающей среде (закон Мальтуса).
Он истинен для любой популяции, так как всегда
обязательно присутствуют рождаемость и смертность. Но сам
экспоненциальный рост наблюдался в природе при вселении
видов на новую обширную территорию с соответствующими
ресурсами, которые до каких-то пределов не накладывают на
19
рост численности никаких ограничений. По этой схеме
размножались кролики после их вселения в Австралию. Сходно
росла численность ондатры в Евразии при ее акклиматизации
из Северной Америки.
В соответствии с этим законом.численность в момент
времени t
N(t) = N0(exp(rt)) %
где N0 - численность родителей в начальный момент времени.
На рис.1 приведены траектории роста численности для
разных г.
Н -HoEXP(rt)
Рис. 1 Экспоненциальная зависимость N, где N - численность
популяции (в общем случае количество любого вещества), от г
(коэффициента размножения или в общем случае
моментальная скорость увеличения количества вещества) и
времени t No - начальное количество родителей в популяции, а
в общем случае начальное количество любого вещества.
Эта функция фиксирует одно простое отношение между
двумя частями популяции как системы: между родителями и
потомками. Обратим внимание, что весьма длительное
время численность популяции мало отличается от начальной, а
затем стремительно, неограниченно растет
20
Введем в определение популяции дополнительные
отношения: конкуренцию особей друг с другом. Механизмы
конкуренции могут быть различными, но, в конечном итоге,
особи одной популяции могут в некоторой степени мешать
друг другу использовать ресурсы и пространство. Естественно
полагать, что чем больше особей, тем больше взаимопомех.
Такие отношения можно назвать самоингибированием.
Соответственно можно записать:
dN/dt = rN-bNa,
где b можно назвать коэффициентом самоингибирования, а - в
данной модели можно рассматривать как показатель
размерности пространства. Если проблемы конкуренции решаются на
плоскости, то естественно положить а=2, в объеме а=1.33. В
принципе а может принимать любое значение. Изменение
размерности не приводит к качественным изменениям
следствий.
В этой модели скорость роста численности и
соответственно сама численность имеют предел. Положив скорость
роста, равную нулю, получаем при а=2, предельную
численность lim N = r/b.
Как это получается?
Если система равновесна, то производная по любой
переменной, в данном случае dN/dt, должна быть равной 0.
Соответственно:
ГЫ - Ь№ = 0 И Nmax = Г/Ь.
Обозначим r/b = К - предельно возможная численность
популяции с соответствующими значениями констант. Иногда
этот показатель определяют как емкость среды.
Ускорение изменения численности изменяется в
положительной и отрицательной областях. Точка перегиба графика
численности как функции времени
N(o) exp(rt)
N(t) = , где
K + (N(o)(exprt-1))
N = r/2b в два раза меньше К.
Это выражение описывает логистический закон роста
численности.
Время, необходимое для перехода популяции на
уровень численности К/2:
21
T = 0,5r.ln((K-No)/No) ,
называют собственным временем популяции.
Очевидно, что скорость роста численности и
максимально возможные ее значения определяются
соотношениями коэффициентов размножения и самоингибирования, или
конкуренции (рис. 2.).
H4floCEXPrt)/(r*(r/J{)Ho(?XPrt-l))
* 5
" t Ю *> 25
Рис. 2. Логистическая зависимость N, где N - численность популяции
(в общем случае, количество любого вещества) от г
(коэффициент размножения или моментальная скорость
увеличения количества вещества), К (емкость среды или b = К/г -
коэффициента самоингибирований) и времени t. No - то же,
что и на рис. 1. Эта функция фиксирует два отношения между
родителями и потомками: прямое воспроизводство,
определяемое rN, и подавление воспроизводства, определяемое
bN2, записываемые в уравнении скорости роста численности
(dN/dt = rN - bN22). Обратим внимание на то, что dN/dt есть
чистая продукция, К - предельная, равновесная численность
популяции, определяемая влиянием взрослых особей на
воспроизводство в конкретных условиях среды. При фик- сиро-
ванной емкости среды время необходимое для перехода в
область равновесия зависит от скорости размножения.
Процесс, определяемый этими отношениями, справедлив
для всех систем с самоингибированием
22
Чем больше коэффициент размножения (больше
плодовитость и меньше смертность), тем соответственно быстрее
растет численность, а предел ее тем выше, чем более
терпимо особи в популяции относятся друг к другу.
С повышением масштабов конкуренции при
фиксированном коэффициенте размножения численность растет
медленнее, а максимальная численность ниже. Если емкость
среды одинакова, то виды с большим значением г, будут
достигать плато быстрее, чем с малым.
Обширный эмпирический материал показал, что в
природе встречаются виды как с медленным, так и быстрым
ростом численности, способные устойчиво существовать только
при весьма высокой или, напротив, при весьма низкой
численности.
Виды, имеющие нормально низкую численность,
обычно имеют низкий коэффициент размножения в первую
очередь за счет снижения нормы плодовитости и, в меньшей
степени, за счет уменьшения смертности. В то же время эти
виды обычно характеризуются весьма жесткой конкуренцией
за территорию и, снижая тем самым потери, очень экономно
используют ресурсы. Напротив, виды с высоким
коэффициентом размножения обычно слабо конкурируют друг с другом.
Они обычно имеют очень высокую потенциальную
плодовитость и весьма высокую смертность, что приводит к
неэкономному использованию ресурсов.
Представительность этих двух типов динамики роста
численности в природе позволила говорить о существовании,
по крайней мере, двух крайних стратегий жизни. Первую
бережливую стратегию определили как К-стратегию, вторую
назвали г-стратегией.
Две крайние формы устойчивого существования
популяций позволяют высказать предположения, в каких условиях
какая стратегия выгодна.
Так, если условия среды сильно изменяются и
соответственно меняется емкость, то явные преимущества
получают виды r-стратеги, которые способны за короткое время
поднять свою численность до очень высоких значений.
Соответственно эти виды способны быстро использовать
открывшиеся новые возможности.
23
Напротив, К-стратегия, при которой популяция
медленно изменяет свою численность и никогда не достигает
больших значений, не может обеспечить быстрой реакции на
изменение внешних условий среды и, очевидно, проигрывает
в эффективности использования сильно флуктуирующих
ресурсов среды.
Обратная ситуация складывается в относительно
стабильных условиях. Здесь высокая плодовитость приводит
только к расточительности, а виды К-стратеги, постепенно
уравновесившись с средой, экономно и эффективно
используют ее ресурсы.
Существование двух крайних стратегий в реакции на
внешние условия - явление очень общее, характерное и для
поведения. Холерические натуры (г-стратеги) быстро
реагируют на быстрые и высокочастотные изменения, сангвинические
(К-стратеги) их могут вообще не замечать, но зато надежно
реагируют на длительно действующие тенденции, которые
холерики вообще не ощущают.
С этими двумя крайними стратегиями связаны многие
важные свойства видов, в том числе имеющие и
хозяйственное значение (табл. 2.). Реальное существование двух крайних
стратегии позволяет предположить существование и
соответствующих факторов их естественного отбора.
Конечно, из сказанного не следует, что две крайние
стратегии объясняют все характерные свойства популяций и
что между ними существует непреодолимая пропасть.
Безусловно, между г и К существует широкая гамма переходов,
существуют виды, которые по одним свойствам ведут себя как
К-стратеги, по другим - как r-стратеги. Но в рамках общей
экологии представления о двух крайних формах
адаптивного поведения, возникающего на основе количественных
различий в двух формах отношений, в первом приближении
можно считать достаточным.
Предположим, что будет введено какое-либо третье
отношение, а не только размножение и самоингибирование,
влияющее на скорость роста численности. Очевидно, можно
будет рассуждать еще об одной стратегии и ее комбинации с
первыми двумя.
24
Но когда мы имеем дело со слишком большим
разнообразием типов стратегий, они просто теряют свое
познавательное значение.
Вновь усложним определение популяции и представим
ее состоящей из двух частей - взрослых и молодых особей.
Скорость увеличения численности молодых особей
будет функцией от числа особей, вступивших в размножение и
отрицательного совместного воздействия численности
взрослых особей и молодых. Скорость роста численности взрослых
особей будет функцией числа молодых, доживших до времени
вступления в размножение, и отрицательного, ингибирующего
совместного воздействия взрослых и молодых.
Модель подразумевает, что подавление приращения
численности взрослых и молодых особей осуществляется
существенно различным образом. Обычно молодые особи
испытывают существенно больший пресс, чем взрослые.
Как только популяция представляется таким образом,
то ее обязательным свойством становится возникновение
циклов с частотой, пропорциональной г0,5, где г - коэффициент
размножения, рассчитываемый относительно скорости
увеличения численности особей, еще не вступивших в
размножение.
Следовательно, чем больше коэффициент
размножения, тем за единицу времени в популяции произойдет больше
циклических колебаний численности (больше частота
колебаний).
Колебания численности популяций во времени - четко
установленный эмпирический факт. При этом разнообразие
форм колебаний очень велико. Иногда они носят весьма
строгий циклический характер и происходят с периодами в 2 - 11
лет. Причем, для млекопитающих установлено, что у мелких
животных чаще наблюдаются меньшие по продолжительности
периоды изменения численности, а у крупных - большие. Для
насекомых также обычны колебания численности, но они
часто носят исключительно нерегулярный характер, и
максимумы численности в тысячи раз больше минимумов.
Масштабы различий и характер динамики таковы, что стало
общепринятым говорить о вспышках численности. Многие вредители
сельского и лесного хозяйства ведут себя именно таким
образом. Природа динамики численности всегда была в центре
25
Таблица 2
Основные экологические характеристики видов с г и К -
стратегиями
Характеристика
1
Скорость индивидуального
роста особи
Продолжительность жизни
Половозрелость
Плодовитость
Детская смертность
Семейные отношения
Уход за потомством
у животных
Запас питательных веществ в
плодах у растений
Способность к расселению
Конкуренция за территорию
Конкуренция за пищевые
ресурсы
Тенденция к образованию
клонов, стад,колоний
Зависимость от абиотических
факторов
Зависимость от биотических
факторов
Выраженность ведущего
внешнего фактора
Продуктивность популяций
Непродуктивные потери на
поддержание численности
популяции
Средние запасы биомассы
Стратегии
г
2
большая
малая
ранняя
большая
большая
чаще
полигамия
отсутствует
или
ограниченный
ограниченный
значительные
малая
большая
высокая
высокая
низкая
большая
высокая
высокие
высокие
К
3
малая
большая
поздняя
малая
малая
чаще
моногамия
значительный
значительный
ограниченные
большая
малая
низкая
низкая
высокая
малая
низкая
низкие
низкие
26
Продолжение табл. 2
1
Дисперсии продукции и
численности во времени и
пространстве
Стадии сукцессии сообществ
Филоценогенетический
возраст сообществ
Предпочитаемая
изменчивость среды во времени и
пространстве
2
высокая
ранний
молодой
высокая
3
низкая
поздний
зрелый
низкая
экологических дискуссий. Часть исследователей связывали
периодические колебания численности с воздействием
внешних, факторов, в том числе и с периодичностью активности
Солнца. Другие усматривали в динамике действие
автохтонных, собственных механизмов популяции.
Правота последних теоретически доказывается как
только популяция представляется как система, состоящая из
двух взаимодействующих частей. Взаимодействие
осуществляется таким образом, что одна часть - вся
совокупность особей (N) отрицательно воздействует на скорость
прироста численности (г), но скорость роста положительно влияет
на общую численность:
N > - г
+ < __ 1
Таким образом возникает простой колебательный
контур, собственная частота колебания которого прямо зависит от
скорости размножения и величины запаздывания реакции
одной переменной на изменение другой в контуре обратной
связи.
Логично предположить, что воздействия одной части
популяции на другую не происходят мгновенно. Прирост
взрослых особей в момент времени t определяется тем,
сколько взрослых и молодых особей было в момент времени
t - Т, когда первые размножались и создавали новое
поколение, формирующее часть популяций, входящих в когорту
взрослых к моменту t, вторые вместе с первыми определяли
возможности их выживания.
27
Таким образом, естественно рассмотреть влияние
запаздывания Т, равного среднему времени вступления
особей в период размножения (среднее время перехода особей в
группу взрослых от момента их рождения).
Следовательно, можно записать:
dN(t)/dt = (r-bN(t-T))N(t) ,
где N(t) - численность в момент времени t = 1, 2, 3, 4 ,
N(t - Т) - численность в момент времени, имевшая место по
отношению к t, T - единиц времени назад.
Таким образом, величина самоингибирования
популяции во времени не остается постоянной.
Формальный анализ такой популяции с самоингибиро-
ванием и запаздыванием выявляет возможность нескольких
типов динамики численности, которые определяются
величиной гТ.
Если гТ < 1/е, то есть очень мала задержка, то вполне
понятно, что поведение системы мало отличается от такого
для системы без запаздывания, хотя могут возникать
колебания численности, но их период не превосходит длительности
двух поколений. Если систему вывести из состояния
равновесия, то она, совершив несколько затухающих по амплитуде
колебаний, вновь вернется в состояние равновесия (рис. 3.)
При 1/e<rT<Pi/2 о популяции всегда существуют
колебания численности, но при отсутствии внешних воздействий
они затухают.
При Pi/2<rT<Pi в популяции всегда существуют
незатухающие автоколебания с периодом, в среднем близким к 4Т, с
амплитудой, существенно зависящей от величины гТ (табл.3.).
При rt > Pi в популяции не существует устойчивого
равновесия, и она случайным образом колеблется в некоторой
допустимой области значений численности. Внешне такая
картина напоминает чисто случайные флуктуации.
Реальные ситуации, наблюдаемые в природе, по-*
видимому, более всего соответствуют третьему и четвертому
случаям.
Так, для животных с временем полового созревания в
1 год (Т=1, г > 1.57) типичны периодические колебания с
периодом 4 года, для животных (Т=2, г>1) - 8-10 лет и т.д.
Четвертый тип, по-видимому, весьма типичен для
насекомых с очень высоким коэффициентом размножения.
28
266
г=2.9 ,Т=1
г=2.5 Л«1
86
N66
20
6
г
? \ •
f : \
Е* : V >/Л""'Ч\.
Г; V J?' ^-~*
Е.:...,Ss^rrr^T I.
=6
.5,
Г
=3
: J
: j
: g
: j
6
10
20
Tin
30
40
50
Рис. З. Некоторые варианты динамики численности, порождаемые
моделью с запаздыванием реакции на самоингибирование.
Популяция представляется как система, состоящая из двух
частей: вся популяция и рожающие самки с молодняком.
При малом коэффициенте размножения г колебания в
популяции быстро уменьшаются, при среднем коэффициенте
размножения в популяции существуют автоциклические
колебания, а при высоком апериодические. При непрерывном
изменении коэффициента размножения популяция
скачкообразно переходит из одного режима динамики в другой
Первый и второй варианты характерны для организмов с
очень малым влиянием самоингибирования, например, для
тех, у которых самцы в большей своей части гибнут после
окончания периода размножения. Очень малая величина
запаздывания, по-видимому, свойственна и стадным животным,
что позволяет им поддерживать стабильность часто в весьма
нестабильных условиях среды.
У многих видов животных поколения популяций не
перекрываются, то есть родители погибают, произведя на свет
своих потомков. Это особенно характерно для большинства
насекомых, для некоторых видов рыб (например,
представителей лососевых).
29
Таблица 3
Характеристики циклов при различных rt,
(по Роберту Мею)
rt
1.57 или меньше
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
1
2.56
5.76
11.6
22.2
42.3
84.1
178
408
1040
Продолжительность
периода, лет
-
4.03
4.09
4.18
4.29
4.40
4.54
4.71
4.90
5.11
2.5 2930 5.36
В таких популяциях, как и в рассмотренном выше
случае, также действует самоингибирование, и оно, действуя на
стадии зачатия и откладки яиц, определяет в первую очередь
рождение молоди.
Модели таких популяций широко исследовались и
привели к результатам, демонстрируемых на графике (см.
рис.1). Здесь так же, как и в случае с популяцией с
перекрывающимися поколениями, в зависимости от величины
коэффициента размножения возникают разные типы динамики,
которые хорошо воспроизводят реальные ситуации.
Эти модели имеют широкое практическое применение
для прогноза и управления состоянием популяций и дают
часто очень хорошее согласие с реальностью.
Там, где уровень использования биологических
ресурсов достаточно высок и хозяйство ориентировано на
получение максимально высокой и устойчивой продукции, модели
конфетных популяций, учитывающих их реальную структуру,
особенности взаимодействия их частей, имеют очень широкое
30
применение. Такое грамотное использование позволяет в
полной мере использовать биологический ресурс при
минимальных затратах на поддержание требуемого уровня
численности и его самовоспроизводство.
Но естественно поставить вопрос, почему можно,
например, отстреливать некоторое число диких животных или,
вылавливая некоторое количество рыбы, сохраняя при этом
устойчивость популяции во времени на высоком уровне
численности, получать продукцию, не вкладывая в ее
воспроизводство практически никаких средств.
Прежде всего, обратим внимание на тот факт, что
любая популяция сама снижает скорость роста собственной
численности при ее увеличении. Она как бы сама себя поедает.
Это снижение происходит и за счет увеличения смертности и
за счет того, что многие самки при высокой численности
перестают производить потомство, а самцы не участвуют в
размножении. У растений при высокой численности резко
увеличивается смертность и замедляется индивидуальный рост,
снижается плодовитость. Естественные механизмы регуляции
численности с этих позиций весьма несовершенны и каждый
вид в конечном итоге ориентирован на создание заведомо
избыточной продукции. У К-стратегов этот избыток меньше, у
r-стратегов много больше, но у всех он всегда существует.
Если бы потенциальные возможности размножения точно
были рассчитаны на то, чтобы компенсировать естественную
смертность от элементарного физического старения, то
соответствующая популяция была бы обречена на гибель. Она не
могла бы противостоять данными ей средствами временным
ухудшениям среды, не могла бы расселяться на новые
территории, не могла бы реагировать на улучшение условий среды.
Это был бы случай предельного выражения К-стратеги^,
ведущей к неизбежному вымиранию.
Устойчиво существующие популяции всегда способны
произвести несколько большую продукцию, чем они
производят, если не осуществлять их эксплуатацию.
Сбалансированная с этими возможностями эксплуатация не только не вредит,
но, напротив, может повышать жизнестойкость популяции.
Осуществляя сбалансированную эксплуатацию, пользователь
фактически выбирает то, что и так бы погибло, и снижает тем
31
самым коэффициент самоингибирования, уменьшая
амплитуду автоколебательного процесса.
В равновесном случае мы можем изымать из
популяции долю р, равную
р = (ехрг- 1)/(ехрг).
Вместе с тем существует и некоторая величина
критической численности, при которой велик риск гибели популяции
от очень небольших внешних возмущений. Существуют
различные модели, по которым можно приблизительно оценить
критическую численность.
Большой эмпирический опыт изучения животных и
растений, на основе которого возникли представления о норме
численности, позволил выработать и чисто эмпирические
критерии. Если популяция по численности находится в состоянии,
близком к критическому, то для ее сохранения необходима
охрана. Суть охраны сводится к максимальной стабилизации
условий среды, позволяющей снизить риск даже небольших
случайных негативных воздействий, способных вытолкнуть
популяцию за границу устойчивости. Это, в первую очередь,
требует прекращения эксплуатации популяции и сохранения
ее местообитаний в максимально естественном виде. Если
этих действий недостаточно, то или осуществляют подкормку,
или расселение, а в крайних случаях прибегают к
искусственным методам воспроизводства потомства.
Охрана редких видов и популяций - важная составная
часть отношения человека с окружающей средой. Чем
эффективней он способен обеспечивать эксплуатацию и охрану
биологических ресурсов, тем соответственно выше его
собственная устойчивость.
Рассмотренные элементы теории динамики популяций
выявляют весьма общие отношения. В конечном итоге,
реальные проблемы изучения популяций являются лишь толчком
для понимания очень широкого класса систем, в которых
можно ввести отношения типа размножение и ингибирование.
Конечно, размножение можно понимать очень широко.
Например, можно смело говорить о том, что знания размножаются и
вообще информация в обществе склонна к саморазмножению.
Если какой-либо продукт хозяйственной деятельности
пользуется спросом, то он тоже начинает размножаться. Точно так
же самоингибирование как отношение обладает очень боль-
32
шой общностью и проще всего это демонстрирует избыток
товара, который автоматически снижает его производство.
Запаздывание также совершенно естественное и типичное
отношение в любой, даже не очень сложной системе.
Полученные на примере популяций результаты на
качественном уровне способны объяснить очень широкий
класс явлений, и с этих позиций их с полным основанием
можно отнести к законам с высоким уровнем общности.
Наиболее общим и важным выводом является утверждение, что в
любой популяции существуют предпосылки для
периодического или апериодического изменения численности при
неизменных условиях среды.
Контрольные вопросы:
Исследуйте зависимости численности от параметров
популяции в логистической модели?
Приведите примеры видов растений и животных с г и
К-стратегиями и определите по каким характеристикам вы
устанавливаете эти отношения?
Опишите какой-либо реальный процесс или в природе,
или в обществе, в котором текущее состояние
воспроизводства определялось бы текущим состоянием всей системы?
Где можно получить в единицу времени от
экологически сходных видов более высокий биологический урожай в
тропических или умеренных широтах и почему?
III. БАЗОВЫЕ АЛЛОМЕТРИЧЕСКИЕ ЗАВИСИМОСТИ
ПАРАМЕТРОВ ПОПУЛЯЦИЙ ОТ РАЗМЕРОВ
ОСОБЕЙ
Эмпирический факт широкого распространения в
природе аллометрических отношений типа
у = а-хь или logy = loga + blogx
был установлен очень давно. Было установлено, что
интенсивность метаболизма у животных есть функция веса
Pmet = = 800W071,
ГДе Prnet "
интенсивность метаболизма, особи; W - функция
веса, кдж/сут.
33
Одно из объяснений этой зависимости сводится к
аналогии в соотношении поверхности и объема шара:
производство энергии идет в объеме, а ее рассеивание через
поверхность.
Сразу же следует отметить, что эта зависимость не
является абсолютной, а носит статистический характер,
отражая тем самым то, что можно назвать общей нормой
отношения. Реальные данные по отдельно взятым особям одного или
разных видов в той или иной степени лежат сверху или снизу
от линии графика этой функции, отражая тем самым
индивидуальные или видоспецифичные особенности метаболизма.
Конкретные измерения заполняют некоторую область, причем
результаты измерения соотношения, почти точно
соответствующие линии графика, более часты, а значительно
отклоняющиеся более редки. Все множество достаточно вероятных
отклонений может быть определено как область генерального
равновесия или как допустимая область отношений. Можно
говорить в этом случае и об области глобальной устойчивости
отношения.
В соответствии с этим метаболизм всей популяции
будет
Pmet = = 800-N-W°71 075,
где Pmet - интенсивность метаболизма популяции.
Если предположить, что все виды, устойчиво
существующие на планете, энергетически примерно одинаково
эффективны, или допустить несколько менее жесткое условие,
что они должны быть примерно одинаково эффективны хотя
бы на какой-либо территории, то, используя параметр
плотности популяции D (число особей на единицу площади),
можно записать
D = const w071 °75
Заменяя для условий равновесия D на емкость среды
на единицу площади Km = r/b, получаем
r = b.constW*71 °75.
Соответственно численность и плотность популяции, а
также коэффициент размножения в среднем должны быть
функцией размера особи.
При этом чем больше вес, тем меньше численность и
коэффициент размножения.
34
Рассмотрим, насколько это справедливо для второго
случая. Из многих прямых определений следует, что в
среднем
г(эксп) = 1.51ЛЛ/'026,
здесь и далее вес в кг.
Что существенно выше оценки, полученной для
равновесной популяции. Такое различие можно объяснить тем, что
экспериментально определенный коэффициент размножения
(г (эксп)) обычно соответствует условиям не равновесия, а
напротив, быстрого роста численности и, соответственно,
близок к своему максимальному значению (г (эксп) = г (max)) и в
его оценке неявно присутствует вклад самоингибирования (Ь).
Отсюда можно приблизительно оценить теоретическую
зависимость самоингибирования от веса особей:
если положить г = r(max), то
b . const W*075 = const (W026) = = const (W°5) .
Таким образом, с увеличением веса особей
коэффициент размножения снижается примерно обратно
пропорционально корню четвертой степени, а самоингибирование
увеличивается пропорционально квадратному корню от веса особи.
Соответственно, чем больше размеры особей, тем
больше затраты на самоингибирование, и организмы более
крупных размеров по условию более склонны к реализации
К-стратегии.
В табя. 4 приведены эмпирические оценки
соотношения веса и плотности популяций для различных жизненных
форм млекопитающих и различных географических условий.
Приведенным эмпирическим значениям параметров
рассматриваемого отношения, конечно, не следует придавать
смысла истинности. С накоплением данных они постоянно
уточняются. Вместе с тем общие закономерности очевидны.
1. Разные трофические группы имеют различные
константы, а соответственно и разные коэффициенты
размножения г: у травоядных они максимальны, у хищников
минимальны.
2. Мелкие животные при прочих равных условиях могут
достигать существенно большей численности и соответствен-
35
Таблица 4
Соотношение плотности популяций и веса для
млекопитающих*
Трофическая группа
Травоядные
Семеноядные
Хищные
Растительноядные:
с весом < 1кг
без учета размерной
группы
Хищные
с весом < 1 кг
Всеядные
с весом < 1кг
Растительноядные:
мелкие
крупные
все
Хищные:
мелкие
крупные
Все млекопитающие
Зональная при-
уроченность
Максимальная
емкость среды
(Максимально
возможная
плотность)
Бореальные
леса
Тропики
Бореальные
леса и
тропики
а
2700
1100
16
470
213
13
36
22
2.5
13
10
0.6
98
41
Ь
Ш
0.5
1
0.66
0.61
0.94
0.66
0.49
0.3
0.6
0.87
0.47
0.77
0.86
* D = aW, где D - плотность особей на км2; W - вес особи, в
кг; а - плотность для вида с весом особей в 1 кг, b - константа. *
но имеют непропорционально больший коэффициент
размножения, чем крупные.
3. В тропической зоне во всех случаях средние
численности ниже, чем в бореальных лесах, и соответственно
36
ниже коэффициенты размножения (относительно большая
роль К-стратегии).
4. Между численностью травоядных животных и
хищников отношения в тропиках существенно уже (2-4), чем в бо-
реальной зоне (30).
Так как с величиной коэффициента размножения
прямо связана динамика численности, легко сделать вывод об
особенностях организации и продуцировании систем в
тропиках и бореальной зоне. Хотя в качестве примера
рассматриваются только млекопитающие, но аналогичные соотношения
справедливы и для других организмов.
Таким образом, можно вывести общее правило: при
прочих равных условиях чем меньше размеры организмов,
тем выше его средняя и максимальная численность, более
выражены автоколебания и больше их амплитуда.
Аллометрические отношения связывают в среднем и
продолжительность жизни с размерами особей.
Так, в среднем продолжительность жизни
Tmax = 12W°1S.
Соответственно средний возраст полового созревания
T = (1,5...2)W°15.
С размерами у млекопитающих связана также и
площадь индивидуального участка (А).
А (травоядные) = 0.023W102;
А (всеядные) = 0,339W°92;
А (хищные) = 13,2W136.
Всюду вес в кг, линейные размеры в км, площадь
в км2.
Если принять, что популяцию образуют особи, для
которых существует вероятность встречи в течение всего по-
пуляционного цикла собственной динамики, приблизительно
равной 4Т, то можно оценить примерно и площадь,
необходимую для устойчивого существования популяции:
АР (травоядные) = Р».28000\ЛГ5;
АР (хищные) = Pi 130000W0 ь.
Обратим внимание на следующее общее
соотношение: чем больше период собственных колебаний популяции,
тем при прочих равных условиях она занимает большую
территорию.
37
Следовательно, опираясь на общность аллометриче-
ских зависимостей непосредственно, по крайней мере, на
качественном уровне, получаем связь характерного времени
популяции (4Т) и характерного для нее пространства (АР).
Можно утверждать, что эта связь обладает высокой
общностью и истинна для всех форм жизни.
Конечно, в каждом частном случае существуют
несколько отличающиеся константы. Так, для r-стратегов
константа а всегда больше, чем для К-стратегов, для организмов,
использующих низкокалорийную, но массовую продукцию,
константа а и соответственно г выше; чем для организмов,
использующих высококалорийные корма и т.д.
Сходные соотношения имеются и у растений, но
разнообразие отношений здесь выше, чем у животных, а
выполнить прямые измерения констант труднее, что и определяет
отсутствие достаточных объемов эмпирических данных.
Аллометрические соотношения прямо подсказывают
ответ на вопрос: почему организмы одной функциональной
группы (растения, животные травоядные, семеноядные и т.п.)
имеют самые разные размеры? Сопоставляя особенности их
динамики и отношений к территории, можно сделать вывод, в
каких условиях могут выигрывать мелкие, а в каких крупные
организмы, в чем их преимущества и недостатки друг перед
другом.
Таким образом, вес особей является важным
собственным параметром популяции, определяющим важнейшие
особенности ее автохтонного поведения.
Однако этого параметра все-таки недостаточно для
представления о возможной численности, коэффициенте
размножения, продолжительности жизни, площади
индивидуальных участков и площади необходимой для популяции.
В первую очередь, необходимо отметить, что
стандартизованный основной обмен (коэффициент а в уравнении
у=аось) весьма существенно различается в разных группах
животных.
Здесь установлена важная эмпирическая зависимость,
связывающая стандартный основной обмен с эволюционной
прогрессивностью соответствующей формы. Показано, что
чем более прогрессивна форма, тем больше ее стандартный
обмен. То есть при прочих равных условиях энергетические
38
затраты на единицу веса древних форм существенно ниже,
чем у эволюционно более молодых и прогрессивных. Так,
например, стандартный обмен у птиц почти в 100 раз выше, чем
у насекомых, у насекомоядных млекопитающих, которые
возникли в конце палеогена, стандартный основной обмен в
четыре раза выше, чем у сумчатых, известных с начала мела.
Таким образом, в процессе эволюции возникают
формы, которые при одних и тех же размерах нуждаются для
поддержания своей жизни в большем количестве энергии и
соответственно большем количестве пищи. Соответственно, при
прочих равных условиях коэффициент размножения их будет
снижаться и расти коэффициент самоингибирования. Более
прогрессивные формы должны иметь и большие
индивидуальные участки. Казалось бы, что снижение энергетической
эффективности у прогрессивных форм должно было бы
снижать устойчивость. Однако это не так. Устойчивость их
повышается за счет усложнения строения организма,
возникновения сложных форм поведения и социальной организации.
Снижение чисто энергетической эффективности может
рассматриваться как плата за сложность.
В соответствие с этим собственные свойства
популяции, определяющие особенности ее саморазвития, зависят не
только от размеров, но и от сложности морфофизиологи-
ческой, биохимической и социально-поведенческой
организации, в процессе эволюции повышающих независимость
возникающих жизненных форм от условий среды. Это разнообразие
организаций и связанных с ними потенциальных возможностей
определяет, в конечном итоге, специфические возможности
каждого вида организмов и неизбежность качественного, или с
количественной точки зрения, приблизительного характера
общих законов. Здесь общие законы определяют, по сути
дела, лишь пределы физически возможного.
Закон увеличения стандартного основного обмена в
ходе прогрессивной эволюции справедлив для всех
самоорганизующихся, неравновесных систем. Так, самым
энергетически эффективным в истории человечества было
собирательство и охота. Пахота земли примитивной сохой с
энергетической точки зрения менее эффективна, чем собирательство,
а современная технология сельского хозяйства с тракторами,
комбайнами, химическими удобрениями в сравнении с прими-
39
тивным сельским хозяйством наших предков вообще
энергетически безумно расточительна. На этом примере
сравнительно легко увидеть, что в процессе эволюции дают
растущие затраты энергии на поддержание хозяйственной
деятельности и почему такой энергетически расточительный прогресс
необходим для выживания. Общие выводы, следующие из
такого рода анализа, можно смело распространять и на
эволюцию всего живого вещества.
Контрольные задания:
Постройте графики зависимостей, приведенных в этой
главе в логарифмической и натуральной шкале.
Исследуйте зависимость периода и амплитуды
колебаний численности в зависимости от веса для плотностноза-
висимой модели динамики численности.
Определите, где, при прочих равных условиях,
предпочтительны виды с крупными размерами особей?
Остров имеет ограниченную площадь, что снижает
численность популяции. Оцените, какого размера особи
предпочтительнее на острове? Если г зависит от индивидуальных
размеров особей, и некоторый вид заселил остров и устойчиво
на нем существует, то будут ли изменяться индивидуальные
размеры и в какую сторону?
Для ответов на вопросы используйте результаты всех
рассмотренных разделов.
Для каких реальных систем в природе, обществе и
хозяйстве можно ожидать справедливость основных алломет-
рических зависимостей? Попытайтесь найти этим
соотношениям качественные, содержательные объяснения.
IV. ЗАВИСИМОСТЬ СВОЙСТВ И СОСТОЯНИЯ ПОПУЛЯЦИИ
ОТ ОКРУЖАЮЩЕЙ СРЕДЫ
Организмы и образуемые ими популяции находятся в
сложных и противоречивых отношениях с окружающей средой.
Рассматривая их, необходимо сразу же обратить внимание на
тот факт, что отношения популяций к среде не сводимы к
отношениям организмов как индивидуумов. Дело не только в
40
том, что разные индивидуумы несколько по-разному реагируют
на одни и те же воздействия. У организованной совокупности
организмов, какой является популяция, есть собственные
параметры, такие например, как коэффициент размножения или
коэффициент самоингибирования, которые зависят не только
от реакции конкретных особей на окружающую среду, но и от
взаимодействий особей друг с другом. В результате таких
внутрипопуляционных взаимодействий, которые могут быть
разными в сходных внешних условиях, может меняться и
реакция на них.
Само по себе понятие среда очень общее. Под средой
можно понимать все то, что прямо или косвенно
воспринимается или может восприниматься некоторым субъектом, все то,
на что он прямо и косвенно влияет или может влиять.
Соответственно, в ходе саморазвития субъекта его
среда может претерпевать существенные изменения. Так,
среда, с которой субъект осуществляет взаимодействия в
данный момент времени, может быть названа реальной, а та,
с которой он может взаимодействовать в принципе,
потенциальной средой. Потенциальная среда совершенно не
обязательно переходит в реальную. Кроме того, граница
потенциальной среды в принципе не определима, и в ходе эволюции
субъект может начать взаимодействовать с такими сторонами
среды, которые на основе его прошлого поведения и строения
были совершенно не предсказуемы.
Следовательно, среду надо понимать как весьма
динамичное явление само по себе, во многом определяемое
свойствами субъекта. Вместе с тем на относительно
небольшом интервале времени для упрощения анализа среду
приходится воспринимать как независимую от субъекта.
Каждый организм воспринимает среду через свои
органы. С помощью этих органов он извлекает из среды
энергию, необходимые элементы минерального питания,
информацию.
С помощью органов с разными функциональным
назначением организм воспринимает среду дифференцированно.
Это значит, что организм с большей или меньшей точностью
идентифицирует конкретный источник воздействия и выделяет
его из всей ощущаемой им среды. Существует широкий спектр
свойств среды, которые организм не способен выделить и
41
идентифицировать, хотя они и оказывают на него
существенное воздействие. Например, человек не может почувствовать
радиоактивное излучение, магнитные и электрические
колебания, ультра- и инфразвук, как, например, он чувствует уровень
тепла, различает цвета, вкус пищи и многое другое.
Идентифицировать источник воздействия для
повышения живучести очень важно. Зная источник, обычно можно
принять своевременные действия, направленные на то, чтобы
снизить его негативное влияние и, наоборот, увеличить
позитивное.
Можно с полным основанием полагать, что величина
воспринимаемого и идентифицируемого разнообразия
воздействий среды растет по мере продвижения организма по
эволюционной лестнице.
Чем большее разнообразие воздействий может
идентифицировать организм, тем более сложно его строение
(структура).
Живое от неживого, в первую очередь, отличается
способностью к идентификации, по крайней мере, некоторых
воздействий и их источников. Человек - единственное живое
существо, которое смогло использовать для этого не только
собственные органы, но и специально сконструированные
устройства.
Очень грубо можно выделить следующие формы
воздействия среды: ресурсы, условия, пространство и время.
Под ресурсами можно понимать все то, что находится
с организмом в вещественно-энергетических отношениях. Для
растений это энергия света и элементы минерального
питания, для животных - это, в первую очередь, пища,
включающая в себя и вещество, и накопленную в нем энергию.
Высшие животные с высоким уровнем интеллектуальной
деятельности в качестве ресурса могут использовать и некоторые
материалы, из которых они, например, строят гнезда. Для
человека понятие ресурса включает всю сферу вещественно-
энергетических отношений: пищу, источники энергии и
материалы для строительства инженерно-технических сооружений,
приборов, приспособлений и т.п.
Под условиями среды удобно понимать все
идентифицируемые или не идентифицируемые воздействия, которые
повышают или понижают эффективность использования ре-
42
сурсов. Например, при низких температурах снижается
эффективность использования энергии вещества.
К условиям могут быть отнесены температура среды и
содержание в ней влаги, атмосферное давление, широкий
спектр излучений, структура почвы, структура местности,
флуктуации этих свойств во времени и пространстве и т.п.
Условия в экологии по своему действию в какой-то степени
аналогичны катализаторам в химии: они сами не вступают в
реакции, но изменяют скорость и направленность их течения и
уровни равновесия.
Следует отметить, что деление на ресурсы и условия
не абсолютно. Так, влага, потребляемая растениями,
участвует в биохимических реакциях и с этих позиций может
рассматриваться как ресурс, но та же влага, выступающая через
испарение как регулятор температуры поверхности листа, может
рассматриваться в качестве условия, определяющего
интенсивность фотосинтеза.
Время и пространство проявляют себя совершенно по-
особому.
С одной стороны, время и пространство выступают в
качестве той общей основы, которая позволяет субъекту
идентифицировать свое отношение к другим субъектам и условиям
среды. Человек изобрел свою систему измерения времени и
пространства, взяв в качестве эталона максимально
регулярные окружающие его явления: смену дня и ночи, сезонов года,
положения солнца и звезд и т.п. Однако у народов,
развивавшихся в разных географических условиях, изначально
было несколько различное восприятие времени.
А следовательно, совершенно не обязательно, чтобы
другие организмы пользовались точно теми же часами и
календарем, что и человек. Другое дело, что смена дня и ночи и
сезонов года синхронизирует многие ритмы различных
организмов, но не обязательно всех.
Существует совершенно иная форма времени,
определяемая самим организмом и их совокупностями. Это время
связывается с их внутренним циклом. Организмы однотипной
организации проходят от рождения до смерти один и тот же
цикл, который можно принять за единицу времени. То же
справедливо для всех других образуемых ими систем. Тогда,
если смотреть на мир с позиции этого собственного времени,
43
то для разных типов организмов он окажется существенно
разным. Организмы, которые в некоторой абсолютной системе
времени живут мало (короткоживущие), при сходных формах
организации будут воспринимать мир существенно более
дифференцированно, чем их долгоживущие аналоги. Такое
более дифференцированное, более детальное восприятие
мира совершенно необходимо для полного использования
ими ресурсов и условий. Так, мелкие организмы в силу
большего относительного обмена должны относительно своего
веса и больше есть, а это требует более тонкой
дифференциации кормовых объектов, их расположения в пространстве,
их свойств и т.п.
Быстрое созревание потомков требует очень тонкой
чувствительности к изменению их поведения, влекущего за
собой и изменения действий родителей.
В отличие от абсолютного эту вторую форму времени
можно определить как биологическую. Можно сказать, что все
организмы в среднем живут одно и то же биологическое
время. То же справедливо для видов и популяций.
Если обозначить абсолютное время через t, а единицу
биологического времени Т представить в единицах
абсолютного времени (например, оба параметра в минутах), то
длительность D будет
D = М.
Таким образом, Т является как бы мерой интенсивности
жизни. Физически эта мера может представлять длительность
единичного колебания.
Длительность определяет путь, пройденный в шкале
собственного времени.
Биологическое время есть результат
функционирования самого организма или, в общем случае, биологической
системы. Длительность в общем случае не зависит от
биологического времени и связывается с тем разнообразием
событий или объемом вещества, которое должно преобразовать
система за всю свою жизнь или за некоторую единицу
измерения, общую для него и биологического времени, например, за
единицу абсолютного времени.
Система может в общем случае независимо изменять
и биологическое время и длительность. Рассмотрим, как это
может происходить.
44
Для измерения собственного биологического времени
нужно выбрать и соответствующие единицы измерения. В
качестве такой единицы можно выбрать одно колебание и
биологическое время измерять частотой колебаний на
единицу абсолютного времени.
Такой естественной единицей измерения для
позвоночных может быть, например, частота колебаний сердца.
В соответствии с аллометрическими зависимостями
частота колебаний сердца у млекопитающих зависит от веса-
как
f = 241*W-025, у птиц как fc= 115,8-W"0'22.
Следовательно, мелкие животные имеют большее
биологическое время, чем крупные, а млекопитающие -
меньшее, чем птицы. Течение собственного времени у
млекопитающих более чем в два раза быстрее, чем у птиц.
Если принять, что собственная биологическая
длительность у всех одинакова, то крупные животные в
абсолютном времени будут жить дольше, чем мелкие, а птицы будут
примерно в два раза дольше, чем млекопитающие того же
веса.
Организмы научились изменять свое биологическое
время в зависимости от конкретных условий. Например, у
представителей мелких мышевидных грызунов особи,
родившиеся осенью и не размножающиеся зимой, живут 8-10
месяцев, а их сородичи, родившиеся в мае-июне и приступившие к
размножению в том же году, живут не более 3-4 месяцев. Но и
в том, и другом случае длительность их жизни была
одинаковой, но различны биологические времена.
Так, при прочих равных условиях зимоспящие
животные, способные уменьшать частоту сердцебиения, по
сравнению с незимоспящими в абсолютном времени живут заметно
дольше. Длительность же их существования в обоих случаях
одинакова.
Точно так же можно ввести единицу длительности
процесса имея в виду, что она обратно пропорциональна его
скорости.
Так, для организма естественная длительность обрат-
на пропорциональна интенсивности метаболизма, т.е.
количества энергии, выделяемой в абсолютную единицу времени.
45
Тогда
D = 1/(aWb).
Соответственно при фиксированном абсолютном
времени можно, изменяя значение констант а и Ь, менять
длительность. В табл. 5 представлены аллометрические
зависимости метаболизма покоя для рептилий, млекопитающих и
птиц, которые можно рассматривать как единицы измерения
длительности.
Таблица 5
Аллометрические зависимости метаболизма покоя
Ящерицы
0,86W082
Млекопитающие
3,35W°'b
Птицы
неворобьиные
3.31W0"'*3
воробьиные
4,98WU"4
Отсюда следует, что рептилии при том же весе в
абсолютном времени должны жить дольше, чем представители
других групп, что по-видимому, справедливо. Исходя из
собственных единиц длительности, млекопитающие и птицы
(неворобьиные) должны жить примерно одно время, но у них
существенно различалось биологическое время в полном
соответствии с этим птицы живут существенно дольше
млекопитающих.
Итак, замедляя обмен и уменьшая биологическое
время, удлиняем жизнь в абсолютном времени, и наоборот.
Манипуляции длительностью и временем дают
возможность организму и биологическим системам
приспосабливаться к широкому диапазону изменений внешних условий. Как
физически реализуются эти действия пока не ясно, но
сложность феномена времени и возможности управлять его
течением становятся все более очевидными.
Наконец, для реализации любого процесса при
неизменном биологическом времени нужно иметь необходимый
интервал абсолютного, внешнего по отношению к системе
времени. Здесь внешнее время становится уже фактором
реализации процесса, своеобразным условием среды. В
частом случае его может "не хватать", или его может быть
больше чем достаточно.
46
Не менее интересны и свойства пространства.
Прежде всего необходимо обратить внимание на тот
факт, что привычное нам Эвклидово пространство не
является чем-то абсолютным и всеобщим. Это модель пространства,
созданная человеком для решения чисто практических задач
разделения земельных участков и строительства. В
последующем оказалось, что эта модель достаточно хорошо
описывает многие относительно простые физические явления, но
и только.
Свойства пространства определяются метрикой и
размерностью. Мы научились хорошо осознавать себя в
трехмерном пространстве с Эвклидовой метрикой. Вместе с тем, в
ощущениях человека метрика заведомо не-Эвклидова. Для
того, чтобы в этом убедиться достаточно поставить в
соответствие словам "близко" и "далеко", которыми человек всегда
оценивал расстояния, крайние границы этих оценок в метрике
Эвклида (обычные километры), вполне понятно, с учетом
средств передвижения. Тогда для среднего пешехода близко
будет не более 4-5 км, а далеко не менее 16-20. Чем дальше
расстояние, тем менее точно метрическая система
переводится в понятийную.
В общем можно сказать, что человек первично в своих
ощущениях воспринимает пространство в гиперболической
метрике, искривляющей мир относительно линейной
Эвклидовой. Но гиперболическая метрика вполне реальна и ею
пользуется большинство живых организмов, а о геометрии Эвклида
они не имеют никакого представления. Вполне возможно, что
разные биологические системы воспринимают мир в разных
метриках. В этой области наши знания пока крайне
ограничены и не систематизированы. Точно так же можно полагать, что
они могут изменять метрику и соответственно существовать в
разных пространствах.
Физическое пространство, которое дано нам в прямых
ощущениях, трехмерно. Однако размерность реального
пространства может быть и существенно большей. Более того,
для разных природных систем оно может быть различным. В
общем, чем сложней устроена система, тем при прочих
равных условиях больше размерность пространства, то есть
нужно большее число независимых координат для отображения
отношений между переменными. Размерность пространства
47
может быть целочисленной и нецелочисленной. В последнем
случае она называется фракталом. Если размерность
нецелочисленная, то динамика системы имеет сложный характер и
для нее характерны скачкообразные преобразования.
Как в случае со временем, для реализации любого
процесса требуется некоторая дистанция R в пространстве,
точно так же можно рассматривать некоторое абсолютное
пространство с фиксированной метрикой 1 и биологическое
пространство L
R = 1/L.
Здесь в пространстве возникают точно те же
отношения, что и во времени, создающие огромные возможности для
приспособления.
Можно лишь добавить, что возможностей манипуляции
с пространством больше, чем с временем.
Следует отметить, что проблема времени и
пространства в экологии только-только начинает осознаваться в
научном мире, и в этой области есть богатые возможности для
развития теории и ее приложений.
При всем качественном различии ресурсов, условий,
пространства и времени, их воздействие на процессы (смену
состояний), для самых разных объектов и на различных
уровнях организации в целом, с достаточной точностью
описывается общими законами.
В биологии широко известен психофизический закон
ощущения Вебера-Фехнера, который записывается как
Y = Ыод (Р/Ро),
где Y- величина ощущения, Р - интенсивность внешнего
воздействия, Р0 - интенсивность, начиная от которой реализуется
ощущение, b - константа, характеризующая чувствительность
объекта к логарифму воздействия.
Легко увидеть, что это практически аллометрическое
отношение, рассмотренное ранее, в котором Р эквивалентно
весу, a eY - численному значению соответствующей функции.
На основе этой общей зависимости легко построить балльную
(квазиметрическую) оценку ощущения любого воздействия.
Например, для восприятия расстояния примем, что
Ртах для пешехода на один день пути составляет 75 км.
Ро = 1км. Тогда оценка ощущения расстояния по
пятибалльной шкале будет:
48
очень далеко - 5, далеко - 4, средне - 3, близко - 2,
очень близко -1. Тогда получаем:
6 = Ыод 75.
Определив константу Ь, получаем следующую шкалу,
соотносящую линейную модель пространства с
логарифмической (табл.6). Приемлемость таких оценок вполне очевидна.
Таблица 6
Формально построенная шкала восприятия расстояния
при W= 1,38
Восприятие
Очень близко
Близко
Средне
Далеко
Очень далеко
Балл
1
2
3
4
5
Реальная дистанция, км |
меньше 4
4- 9
9-18
18-36
дальше 36
Отсюда, в частности, следует, что человек во всех
своих качественных оценках свойств внешней среды
действует как измерительная система. Более того, получаемые
измерения при некоторых дополнительных оговариваемых
условиях вполне сопоставимы друг с другом.
Но сразу же следует отметить, что восприятие
пространства зависит от длительности. Соответственно, для
пешеходов разной тренированности, велосипедиста,
автомобилиста восприятие расстояния в пространстве различно. Так,
чем больше затраты энергии в единицу времени, тем меньшая
по абсолютной величине дистанция воспринимается как
достижимая. Меньшему же собственному времени соответствует
и меньшая достижимая дистанция.
В целом же этот принцип восприятия окружающего
мира широко использовался и используется в научных и
прикладных исследованиях. Специалисты таким образом
измеряют цвет, влажность почв, крутизну склонов, обилие видов
растений и многое другое. И все эти измерения при
дополнительных условиях имеют вполне достаточные основания. По
тому же закону воспринимают окружающий мир и любые
другие биологические системы на любом уровне их организации.
(Отметим весьма характерные соотношения: холерические
49
натуры с большим биологическим временем обычно
завышают оценки явлений относительно реальных значений,
сангвинические натуры - наоборот.)
Общетеоретическим основанием этого
феноменологического закона может быть количественная теория
информации, разработанная К.Шенноном. Им при некоторых
достаточно простых аксиомах выведен общий закон скорости передачи
информации С по каналу связи произвольной природы
(рис. 4):
С = w log (1 + P/N),
где w - полоса частот, в которой принимается сигнал, Р -
мощность или интенсивность сигнала, N - мощность шума (помех).
Очевидно, при P»N теоретический закон для канала связи
полностью идентичен феноменологическому закону Вебера.
Мощность сигнала адекватна интенсивности воздействия,
шум - порогу.
В теории передачи информации предполагается, что во
времени или пространстве реализуется некоторый процесс с
мощностью Р (или с амплитудой Р), на который наложен
случайный процесс с мощностью N. Приемник (биологический
объект) воспринимает этот процесс в полосе частот w.
Соответственно предполагается, что сигнал воздействия во
времени или пространстве реализуется на различных частотах, как,
например, осуществляется передача в радиосвязи.
Здесь может быть принята для всех случаев полная
ассоциация с таким типом передачи. Например, влажность
почвы, воздействуя на растения, варьирует во времени, и эти
вариации могут иметь одновременно и суточный, и
недельный, и сезонный, и многолетний режимы. Поступление пищи,
каким бы способом оно ни реализовалось, также происходит в
некотором спектре частот.
С других позиций, полосу частот можно ассоциировать
с оценкой разнообразия воспринимаемых сигналов, например,
различных видов пищи. В этом случае говорят о длине
алфавита, в котором в качестве букв выступают разные виды пищи.
Такая трактовка также не противоречит теории информации.
Шум в общем случае зависит от полосы частот. Можно
записать
N = w*N0,
50
С = и lag (1+P/uNo)
66
10
20 46
Р w ВО т
Рис.4. Закон изменения скорости передачи информации (С) от
мощности сигнала (?) и полосы частот канала связи (со).
Информация в данном случае измеряется по натуральному
основанию логарифма (nit). Количество символов,
воспроизводимых в канале связи, - ехрс. С ростом мощности сигнала и
полосы частот увеличивается нелинейно, так что при
фиксированной частоте приращение скорости передачи
информации при большой мощности сигнала практически не
наблюдается. То же имеет место и по отношению к изменению
частоты. Соответственно, при фиксированной мощности
сигнала существует оптимальное отношение C/w, а
количество информации, которое может быть передано на единицу
полосы частот имеет предел равный 1,443*(P/No). Из этого
ограничения, в частности вытекает неэффективность
системы с очень большой полосой частот
где N0 - шум на единицу полосы частот. На рис. 4 показаны
изменения С как функции от Р и w. Тогда закон скорости
передачи информации получает богатую биологическую трактовку:
1. Чем больше мощность сигнала, тем больше
информации получает система.
51
2. Чем больше полоса частот, тем, с одной стороны,
больше шум, но и больше общая пропускная способность.
Однако соотношение таково, что существует предел полосы
частот, после которого при фиксированном значении Р
приращения информации практически не будет.
3. Следовательно, если поставить в соответствие
полосе частот понятие степени специализации биологической
системы по отношению к воздействию, то получаем, что, чем
более деспециализирована система, тем больше она
допускает ошибок при преобразовании сигнала, но имеет при прочих
равных условиях большую скорость получения информации.
Если ошибки имеют какое-либо значение для жизни
системы и влияют на ее устойчивость, то биологическая
система как самоорганизующаяся должна стремиться к
специализации. Однако, если мощность сигнала мала, то при
увеличении специализации система будет получать слишком малое
количество информации (вещества, энергии), которое может
быть недостаточно для ее существования. Соответственно,
она должна искать некоторый оптимум между мощностью
сигнала и специализацией. Следовательно, можно допустить, что
сама w есть функция от мощности сигнала, например,
w = а - blog P,
где а - максимально возможная полоса частот.
Имея ввиду, что соотношения имеют смысл при P»N,
получаем, скорость пропускной способности системы с
адаптацией к мощности сигнала:
С = (а - Ыод Р)-1од Р - (а - Ыод Р)-1од (а - b log P).
Соответственно, получаем уравнение, близкое по
форме к параболе, из которого следует, что для любой
биологической системы существует некоторая оптимальная
мощность сигнала (Р), а при уменьшении и увеличении его
мощности пропускная способность снижается (рис. 5).
Полученная зависимость достаточно точно описывает
известные феноменологические отношения. Практически не
существует ни одного фактора, при больших значениях
которого не снижалось бы значение функции (соответствующего
процесса).
Различные части зависимости в экологии получили
свои наименования: область существования функции
называется областью толерантности, область, где изменение
52
C=(a-blnP)Wl*P/(a-blnP))
Рис. 5. Скорость передачи информации у системы адаптирующейся
к мощности сигнала. С увеличением мощности сигнала
полоса частот уменьшается на величину пропорциональную
логарифму его мощности (InP). В такой системе скорость
передачи информации имеет единственный максимум и при
фиксированном значении константы а этот максимум мало
зависит от изменения параметра Ь, но достигается при
различных значениях мощности сигнала. Соответственно у
каждой системы имеется свой оптимум по отношению к
мощности сигнала
функции при изменении фактора очень мало, - областью
оптимума, область, где функция очень чувствительна к
изменению значения фактора dY/dP»1, - областью границы.
В теории связи пропускная способность начинается
только с нуля. Однако для биологических систем может
существовать такое Ст1п, по достижению которого система вообще
не может функционировать и фактически не реагирует на
сигнал. Заметим, что отрицательное значение скорости передачи
информации не имеет смысла.
53
Например, для двухфакторной связи в упрощенной
форме будем иметь:
С = w(1) log P(1) + w(2) log P(2) - d(log P(1) + log P(2)),
где d - ширина пересечения полос частот.
Для трех сигналов - из суммарной пропускной
способности вычитаются 3 суммы по 2 и 1 сумма по 3 и т.д.
Легко увидеть, что увеличение числа одновременно
действующих факторов, каждый из которых сам по себе может
иметь позитивное значение, в реальной системе быстро
обращает пропускную способность в нуль. Отсюда следует
важный общий вывод: число факторов, одновременно
действующее на любой природный объект, по условию всегда
ограниченно. Выход из этого ограничения природа находит через
образование иерархических систем, разделяя прием
различных сигналов во времени, или на основе специализации
сенсорных систем по частоте, о чем будет сказано ниже.
Если рассматривать действующие факторы как
независимые, то соответственно в потенциированной форме
Y = [а(1)(Х(1) - X(1)mjn)b(1)]. [а(2)(Х(2) - X(2)mjn)]b(2).
Теперь обратим внимание на следующий факт: не
существует какого-либо внешнего фактора любой природы,
который не оказывал бы на любое произвольное
биологическое явление одновременно положительного и отрицательного
воздействия.
Например, увеличение концентрации С02 в
атмосфере, с одной стороны, повышает интенсивность фотосинтеза, а
с другой - ингибирует процессы окисления (дыхания). В
конечном итоге, продукция есть баланс между восстановительными
и окислительными реакциями, которые в сложном процессе
фотосинтеза сменяют друг друга. Точно так же избыток
времени (пространства), как и его недостаток снижают
эффективность реализации любого процесса.
Такое соотношение получается в связи с тем, что
практически любой фактор действует на объект по схеме
двухканальной компенсации: по одному каналу он действует
со знаком плюс, по другому - со знаком минус.
Результирующая действия обоих каналов имеет мультипликативную форму
(рис. 7):
Y = a(y(1)-Y(2)K,
где Y(1) - первый канал, Y(2) - второй канал;
56
\b(1).
Y(1) = (X(1)-Xmin)u
Y(2) = (Xmax-X(1))b(2);
K, (L) - чувствительность Y к переменной X1 (X2) в целом.
Y=(((X1 -X1 min)a) ((X1 max-X1 )b)K)
(((X2-X1 min)c) ((X2max-X2)d)L)
161
8
6
4
2
•[
¦T » 1 »
i i i'j i
Mill»
1
1 "¦"' "• ' ¦
¦I1 III1
1..;...
* > 111
> 11
i > г
¦ 11 i
11 il
8 18
• is xwx=ie
• X2 c=d=0
e z
i 6
XI
e le
Типичная параболическая форма зависимости произвольно
избранной экологической переменной от любого возможного
фактора (левый рисунок). Интервал Xmm...Xmax - область
определения. Не существует экологических или
биологических переменных определенных на всем интервале
значений любого физического фактора. Экологический оптимум
функции Y достигается в точке Х1 с dY/dX = 0, границы
области оптимума определяются точками, в которых
происходит смена знака второй производной. Области слева и
справа от границ области оптимума можно определить как в
целом граничные. Они характеризуются наибольшей
чувствительностью функции к изменению значений фактора.
Экологические отношения всегда сильно нелинейны. При
принятых условиях в данном случае функция Y зависит только от
внешней переменной Х1 и не зависит от Х2.
В правой части рисунка изображен тот же график, но в изо
линиях, соединяющих одинаковые значения функции
57
На рис. 8 показаны виды функций при различных
значениях коэффициентов. Очевидно, рассматриваемая модель
мало чем отличается от модели канала связи с
изменяющейся полосой частот, рассмотренной выше. В обоих случаях
рассматривается по сути двухканальная система, но при
несколько различающихся исходных допущениях.
Соответственно, если рассматривается зависимость какой-либо
функции объекта от условий среды, то по каждому фактору слева и
справа ее значения ограничены областью значений факторов,
в которых функция не реализуема, а общий вид зависимости
имеет параболическую форму.
Типичная зависимость функции от двух факторов
представлена на рис. 8. Исследуем ее экологический смысл.
В первую очередь, обратим внимание на то, что
чувствительность функции Y по отношению к обеим переменным
минимальная в области их одновременного оптимального
значения для Y.
Максимум чувствительности по одной из переменных
существует (например, Х(1)) в той области, в которой эта
переменная определяет минимальное значение функции, а
вторая, напротив, максимальное. Там, где обе функции находятся
в области минимума, производная по отношению к каждой из
них невелика.
Максимум чувствительности по отношению к Х1
достигается в условиях оптимума процесса по отношению к Х2 и
наоборот. Фактически это соотношение описывает принцип
фактор-минимума К.Либиха.
Эти соотношения позволяют, например, объяснить,
почему в области распространения любого вида существуют
условия, в которых его состояние очень слабо контролируется
внешними переменными, а также и условия, в которых
внешние переменные имеют ведущее значение. При этом в разных
частях области распространения текущее состояние будет
определяться флуктуацией различных внешних переменных.
Рассмотренные общие отношения справедливы для
описания изменения значений любых функций от любых
внешних факторов (свойств среды), изменяющихся в
пространстве или во времени
Пример 1. Продуктивность древостоев
определяется температурным режимом и содержанием влаги в поч-
58
V6 в »
a=b=cA4=8.5
О 8 19
a=b=c=d=tf5, X=L=4
4 6
XI
Рис. 8. Типичные двухфакторные формы зависимостей экологи
ческой переменной от двух факторов. Используется та же
алгебраическая форма функции, что и на рис. 7, но с
равными значениями констант для Х1 и Х2 при K=L=1 на
правом графике и при K=L=4 - на левом. Эффект, получаемый
во втором случае, можно определить как синэргетический
Он существует только, если функция зависит от двух и
более факторов. В результате его действия область оптимума
заметно сужается, а у границы существования
чувствительность функции к изменению внешних факторов резко
уменьшается
ве. В переувлажненных условиях, осушая почву, можно
добиться более высокой продукции, но не везде. Этот эффект
наиболее значителен в южной тайге при относительно богатых
почвах. В северной тайге, где температурный режим
неблагоприятен, а также на очень бедных почвах эффект от осушения
очень невелик или вообще отсутствует.
59
Пример 2. Северная граница леса в условиях
морского и океанического климата в первую очередь
определяется избыточным увлажнением, почему леса и проходят на
север по дренируемым долинам рек. В континентальных
регионах и на дренируемых поверхностях, где переувлажнение
незначительно, граница леса определяется уже термическим
режимом.
Сложный механизм влияния факторов приводит часто
к тому, что они воздействуют на процесс не только поодиноч-
ке: но и взаимодействуя друг с другом.
Так, например, на продуктивность растений влияют не
только в чистом виде температура и увлажнение почв, но и как
самостоятельный фактор соотношение между ними. На
практике это соотношение отображается каким-либо
гидротермическим коэффициентом.
На рис. 9 показаны различные варианты зависимости
функции от двух аргументов, где, кроме прямого влияния двух
факторов, действует с разным весом и их отношение друг к
другу. Такие соотношения определяют зависимость
биологической продуктивности, интенсивности минерализации
мертвого органического вещества, средние численности различных
видов растений и животных от ресурсов, условий среды,
пространства и времени.
В экологии зависимости исследуемой функции объекта
от внешних переменных получают на основе наблюдений в
природе или в результате специально поставленных
экспериментов. Большие возможности открывают исследования
зависимости избранных характеристик изучаемого объекта и
условий среды при наблюдении за их совместном изменении в
пространстве. Такой прием широко используется в эколого-
географических исследованиях.
Контрольные задания:
1. Исследуйте соответствие собственных ощущений
закону Вебера. Попытайтесь построить зависимость,
отражающую восприятие вашего ощущения, например, к
температуре воды.
2. Попытайтесь объяснить:
Почему на новом месте первые дни кажутся очень
длинными, а примерно через неделю пребывания время
начинает "течь" значительно быстрее?
60
{ a=b-0,25 c=d=0,75
Y=( ) (X1X2)q
it i mum
e=0.75 b=9.5 c-0.25 d=e.lZ5
Рис. 9. Типичные формы двухфакторных зависимостей:
Справа: чувствительность функции к Х1 в целом ниже, чем к
Х2, в соответствие с чем область оптимума по отношению к
первому фактору относительно шире, чем ко второму, а
область границ, соответственно, уже.
В центре: чувствительность функции к Х2 в целом ниже, чем
к Х1, но параметры а и b при XI, с и b при Х2, попарно
неравны, в соответствие с чем область оптимума
асимметрична относительно области определения
Слева: изменен вид функции (см. рис 7-8), к которой
дополняется неаддитивная компонента X1*X2q, отображающая
влияние на функцию соотношения или взаимодействия
факторов. В результате элептическая форма области оптимума
принимает более сложную форму, разворачивая свою
главную ось под некоторым утом к координатам и смещая
область оптимума относительно центра области определения
функции
Почему, когда Вы первый раз идете по дороге, она
кажется длиннее, чем при прохождении ее второй, третий раз?
Почему, если Вы несете груз, дорога кажется длиннее?
3. Приведите примеры, когда один и тот же фактор
одновременно "плохо" и " хорошо" влияет на состояние
объекта (функции) (в качестве объекта анализа используйте себя,
растения, наблюдаемых Вами животных)?
4. Включите одновременно телевизор и
радиоприемник и попытайтесь в равной степени воспринимать информа-
61
цию от этих двух источников; исследуйте и опишите
возникающие при этом проблемы.
5. Перечислите ресурсы и условия, влияющие на Вас
(на Ваши отдельные функции и общее состояние), на
избранные Вами виды растений или животных (отдельные
функции), попытайтесь дифференцировать их по
чувствительности к этим внешним факторам.
V. ПРЕДСТАВЛЕНИЯ О СООБЩЕСТВЕ
Каждый организм, каждая популяция находится не
только под воздействием внешних факторов, но и под
воздействием других организмов как родственных, так и
принадлежащих к другим видам. Простейшие взаимодействия между
организмами отражены, в частности, в рассмотренной выше
плотностно-зависимой модели популяции. Однако, конечно,
отношения между организмами в рамках одной популяции
существенно разнообразней. В целом, исследования внутри-
популяционных отношений являются предметом социологии и
этологии, и в данном руководстве они не рассматриваются.
Предметом настоящего раздела являются отношения
между популяциями, принадлежащими к различным видаУ/i,
приводящие к образованию сообществ. Вместе с тем
рассмотренные ниже принципы легко трансформируемы и на по-
пуляционный уровень.
Сообществом назовем совокупность популяций,
способных достаточно длительное время сосуществовать на
определенной территории.
Единство пространства и времени определяет
неизбежность каких-либо отношений между популяциями. Чисто
логически при самом простейшем рассмотрении эти
отношения можно свести к следующим трем типам:
1. Популяция вида (далее кратко "вид") А не влияет на
вид В - знак отношений 0.
2. Вид А подавляет вид В - знак отношений минус
(отрицательная связь).
62
3. Вид А способствует (поддерживает) существование
вида В - знак отношений плюс (положительная связь).
Если рассматривать только парные отношения двух
видов, то соответственно возможно 23=8 типов, для трех
видов 33=27 типов и т.д. Кроме того, положительные и
отрицательные отношения могут быть как обязательными, то есть
без них популяция не существует, так и не обязательными.
Ограничимся, в первую очередь, рассмотрением парных
отношений Для многих из них в экологии существуют
устоявшиеся термины (табл. 7).
Таблица 7
Типовые отношения между видами в сообществе,
по Ю.Одуму (1975), с дополнениями
N
1
2
3
Виды
1
+
2
-
+
Тип
взаимодействия
Хищничество
Паразитизм
Антагонизм
Конкуренция
Соперничество
Не строгое
соперничество
Характер взаимодействия
Особи вида 1 (2) поедают
особи вида 2(1)
Особи вида 1(2) подавляют,
но обычно не приводят к
моментальной и прямой
гибели особей вида 2(1)
Прямое подавление
(вытеснение видами друг друга)
Взаимовытеснения в
результате тождественного
использования одних и тех
же ресурсов или условий
среды
То же, но при неполном
сходстве потребностей
То же, но при сходстве
потребностей лишь при
некоторых дополнительных
условиях
63
Продолжение табл.7
N
4
5
6
7
Виды
+
+
0
+
0
0
0
Тип
взаимодействия
Симбиоз
(мутализм)
Содружество
Коалиция
Аменсализм
Коменсализм
Нейтрализм
Характер взаимодействия
Виды могут существовать
только совместно
Виды только при
совместном существовании
достигают наилучшего
состояния
Каждый из видов
эффективно функционирует и без
другого, но совместно они
более эффективно
противостоят по отношению к
другим видам или давлению
неблагоприятных условий
среды
Вид 1(2) подавляет вид 2(1),
но при 0 - вид 2(1) никак не
влияет на вид 1(2)
Вид 1(2) помогает виду 2(1),
но при 0 + вид 2(1) никак не
влияет на вид 1(2)
Виды никак не влияют друг
на друга
Описание такого рода отношений в общем случае яв-*
ляется предметом теории конфликтов, и любознательный
читатель может обратиться к изучению ее интересных
результатов. Здесь же эти отношения будут рассматриваться с более
традиционных позиций.
V.1. Хищничество и паразитизм
Один вид использует другой в качестве корма
(трофические отношения).
Конечно, реально в природе любой хищник использует
в качестве корма (жертвы) различные виды, которые сами
между собой могут находиться в любых отношениях.
Паразиты же часто могут быть и видоспецифичны, то есть связаны с
одним хозяином.
64
Для простоты будем полагать отношения только
парными. Это, конечно, очень сильное упрощение, но оно
позволяет исследовать важные фундаментальные закономерности.
Такое парное упрощенное представление называется
моделью "хищник-жертва".
Естественно полагать, что чем больше жертв, тем
лучше жить хищнику, и интенсивность его размножения
увеличивается. Увеличение численности хищника естественно
приводит к уменьшению численности жертвы, что, в свою
очередь, приводит к снижению численности хищника и т.д.
Фактически получаются отношения, напоминающие маятник: то
относительно увеличивается численность хищника, то жертвы.
Пусть численность жертвы х и скорость изменения
численности
dx/dt = гх,
где г - коэффициент размножения. Если жертв нет, то
численность хищника у будет уменьшаться со скоростью
dy/dt = -ay,
где а - коэффициент смертности. Смертность жертвы логично
положить пропорциональной произведению численностей
жертвы и хищника - Ьху. Произведение отображает
возможность встреч хищников и жертв в пространстве, а
коэффициент b как бы риск смертельного исхода от этих встреч для
жертв. Рождаемость хищника также пропорциональна
произведению кху. Тогда получаем следующую систему
дифференциальных уравнений:
dx/dt = гх - Ьху,
dy/dt = кху - ay.
Решение этой системы уравнений дает типичный
осциллятор с периодом собственных колебаний
Т = 2Pi/(ra)05.
При этом колебания хищника и жертвы сдвинуты по
фазе на Pi/2.
На рис. 10 приведен фазовый портрет процесса.
Численность хищника и жертвы циклически изменяется, так что
максимуму численности жертвы соответствует средняя
численность хищника, и наоборот. Траектория, по которой
происходят изменения численностей, зависят от начальных
условий: х(0) = к/а и у(0) = r/b.
65
6 Г
а = 1.3, с = 8.5
N1
6
Рис. 10. Фазовый портрет динамики численностей "жертвы - N1" и
"хищника - N2". N1, N2 - численности хищника и жертвы в
относительных единицах измерения. Точки на графике,
соединенные линиями, определяют состояние системы в
фиксированный момент времени. Стрелка указывает на
направление изменения состояния. Константы а - коэффициент
размножения жертвы, с - коэффициент самоингибирования
хищника. Диаметры эллипса траектории зависят от
начальных условий. Как видно из рисунка, максимуму численности
жертвы (N1) соответствует средняя численность хищника
(N2) и наоборот
Таким образом, получаем, что отношения типа хищник-
жертва в общем случае приводят к автоколебательному
процессу.
Если жертв несколько и параметры их популяций не
совпадают, то колебания могут быть слабо выраженными или
затухающими. Однако в силу обычной специализации хищника
66
по отношению к жертве они все-таки чаще всего будут иметь
место.
Мы помним, что для любой популяции присущи
автоциклические колебания. Период этих колебаний зависит от
коэффициента размножения. Наложение собственных попу-
ляционных колебаний и колебаний в результате
взаимодействия популяций может существенно усложнить реальную
динамику. В данном случае зафиксируем саму практическую
неизбежность автоколебательного процесса. В этой области
накоплены обширные фактические данные. Вместе с тем одни
исследователи склоняются к тому, что колебания вызываются
действием периодически изменяющихся внешних условий
(например, изменением солнечной активности), другие
говорят, что для объяснения колебаний вполне достаточно
представлений об автоколебательном процессе. Последнее время
растет понимание того, что динамика изменения состояния
реальных систем чаще всего является результатом
взаимодействия обоих типов колебаний. Как это может происходить,
мы рассмотрим ниже.
V.2. Симбиоз, содружество, коалиция
Эти отношения связываются с положительным
влиянием двух видов друг на друга. Не строя никаких моделей,
легко увидеть, что если бы не было никаких внешних и
внутренних ограничений, то такая связь приводила бы к
бесконечному росту численности обеих видов.
Так как это невозможно, то рост численности будет
ограничиваться собственными свойствами
взаимодействующих популяций или ограниченностью внешних ресурсов, что
по конечному результату одно и то же. Однако численность
каждого вида при положительном взаимодействии в пределе
может быть выше, чем в том случае, если бы такого
взаимодействия не было.
Но могут быть и другие отношения. Допустим, что
собственный период колебаний у двух взаимодействующих видов
достаточно близок. Тогда может возникать эффект резонанса:
при росте численности каждый вид усиливает рост другого, но
67
также усиливает и падение численности. Соответственно
амплитуда колебания неизбежно растет, и в какой-то момент
времени падение численности может приблизиться к
критической отметке, что приведет к гибели системы.
Совершенно иное дело будет в том случае, когда две
положительно связанные популяции по-разному реагируют на
изменение внешних условий. Тогда, в кризисной для первого
вида ситуации второй будет находиться в хороших условиях и
поможет первому, и наоборот. Здесь получаем, что каждый
вид относительно своего партнера компенсирует
неблагоприятные условия среды, и оба вида поддерживают совместное
выживание.
Примерно по этой схеме взаимодействуют водоросль
и гриб, образующие лишайник, представляющие классический
пример симбиоза. Надо отметить, что такой тип отношений в
сообществах сравнительно редок, но типичен для
социального поведения популяций.
В сообществах чаще наблюдается то, что можно
определить как коалицию, или содружество, кЪгда разные
виды помогают друг другу лишь в относительно критических
условиях или в определенные моменты времени. Причем
чаще такие отношения наблюдаются у животных и сравнительно
редко у растений. Так, например, в период гнездования
некоторые виды птиц образуют смешанные колонии с единой
системой предупреждения об опасности. Зимой многие птицы
образуют многовидовые стаи, в которых объединение, хотя и
не очень строгое, способствует лучшему поиску наиболее
кормных мест.
V.3. Антагонизм, конкуренция, соперничество
Пусть два вида используют один и тот же ресурс и
отличаются только потенциальной скоростью роста
численности г и чувствительностью b к прямому отрицательному
воздействию одного вида на другой. Этот случай можно
определить как полный антагонизм. Такая система может быть
представлена следующими уравнениями:
dN1/dt = r1N1-a1N1*N2
dN2/dt = r2N2-a2N1*N2,
68
где N1 (N2) - численность популяции первого (второго) вида, г1
(г2) - соответственно коэффициенты размножения, а1 (а2) -
коэффициенты конкурентного давления.
В условиях равновесия, то есть когда dN1/dt = 0 и
dN2/dt = 0,
N2 = r1/a1 и N1=r2/a2
M-a1N2=r2-a2N2 .
Это уравнение определяет координаты линии
отображающей область равновесия. При этом стоит лишь немного
реальным значениям численности отклониться от
равновесного состояния, как вид с лучшим соотношением коэффициентов
роста численности (г) и смертности (а) будет вытеснять
другой.
В модели популяции предполагается, что рост
численности лимитируется самоингибированием. В этом варианте
dN1/dt = r1N1 [(K1 - N1 - a1N2)/K1],
dN2/dt = r2N2 [(K2 - N2 - a2N1)/K2],
где K1 (К2) - предельно возможная численность вида 1 (2), а1
(а2) - коэффициент конкурентного подавления 1 (2) вида 1 (2).
Здесь возможны следующие 4 соотношения:
К2>К1/а1
К2<К1/а1
(К1/а1=К2/а2)
К1>К2/а2 - вид 1
может сдерживать вид 2
Каждый вид
случайным образом может
подавить противника
Первый вид всегда
побеждает второй
К1<К2/а2 - вид 1 не
может сдерживать вид 2
Второй вид всегда
побеждает первый
Ни один вид не может
победить другой
Устойчивое
сосуществование
Устойчивое сосуществование двух видов, почти
наверное, не реально. Оно требует фактически, чтобы виды были
абсолютно тождественными, и в то же время любая малая
флуктуация видовых параметров выводит систему из
равновесия. Но существование двух абсолютно тождественных
видов просто невозможно. Отсюда следует, что при антагонизме
сильный вид почти обязательно вытеснит более слабый.
69
Рассмотренная модель воспроизводит предельно
упрощенную ситуацию. Более реалистично полагать, что два
вида конкурируют не за все ресурсы или условия среды, а за
их некоторую часть. Такое допущение заставляет
предполагать наличие некоторых разноименных ресурсов (например,
разных видов кормов, разных элементов минерального
питания) или некоторого градиента среды (например, градиента
увлажнения).
Обратим внимание на то, что при исследовании
отношений типа хищник-жертва и содружества не было
необходимости в особом рассмотрении внешних ресурсов и условий
среды. Просто допускался постоянный или флуктуирующий
подвод энергии и вещества ко всем элементам системы.
При исследовании конкуренции неизбежно приходится
переходить к дифференцированному представлению условий
и ресурсов. Это требует особого рассмотрения факторов
среды и их совокупности. В соответствии с этим в экологии
возникло особое понятие экологическая ниша. Слово "ниша"
само по себе подразумевает наличие некоторого пространства,
поделенного на какие-то части (отдельные объемы), которые
по положению в пространстве факторов отличаются друг от
друга. В одной из трактовок понятия экологической ниши
подразумевается, что каждый вид занимает в соответствии с
своей специализацией свою нишу.
Поэтому часто говорят, что экологическая ниша есть
профессия вида. В рамках понятия теории информации
экологическая ниша может трактоваться как полоса частот, в
пределах которой вид воспринимает окружающую среду или
какой-либо фактор, в интервале частот от fi до f2, или как
алфавит, в котором каждая буква может трактоваться как вид
ресурса, а длина алфавита соответствует числу одновременно
воспринимаемых ресурсов.
По своему прямому смыслу ниша понимается как
замкнутая, со всех сторон ограниченная часть некоторого
объема. В случае же конкуренции многие потребности двух видов
в общем похожи, и соответственно ниши перекрываются.
Правильнее было бы говорить не о нишах, а о перекрывающихся
или не перекрывающихся экологических областях некоторого
пространства ресурсов. Однако в мировой литературе в силу
традиций обычно применяется слово "ниша".
70
Так как факторов, воздействующих на виды, много,
можно говорить о том, что они образуют многомерное
пространство. Если факторы не зависят друг от друга, например,
при любом значении температур существует любое
количество осадков, то они образуют ортогональную систему
координат, по отношению к которой рассматривается положение
каждого вида.
Множественность факторов подразумевает
многомерность пространства, где каждый фактор выступает как одна из
его координат.
Из рассмотренной выше общей модели зависимости
экологических функций от условий среды следует и одно из
возможных формальных представлений экологической ниши:
п
N = const П ((Xi - X(i)min)b(i1))*(X(i)max - X(i))b(j2)),
i=1
где N - численность (в других вариантах биомасса) вида;
Xi - i-вый фактор; П - символ, указывающий на то, что
численность есть результат умножения значений всех факторов друг
на друга.
Следует отметить, что существуют и другие модели
представления экологических ниш. Какая модель лучше
отражает реальность - предмет будущих исследований, однако
качественно выводы при применении различных моделей
существенно не изменяются.
На рис. 11 показан простой однофакторный случай
возможного размещения видов по градиенту среды.
Формально из рассмотренной выше модели следует,
что сосуществование конкурентов устойчиво, когда а1*а2<1, то
есть в ситуации, когда межвидовая конкуренция слабее само-
ингибирования.
Можно полагать, что численность уменьшается
пропорционально пересечению экологических ниш. Если принять
весь объем ниши за единицу, то очевидно, что пересечение
каждой ниши относительно любой другой будет всегда
меньше 1. Соответственно меньше единицы будет и перекрытие
пересечений. Отсюда следует, что если существует
небольшое различие в положении ниш в пространстве ресурсов и
условий среды, то, хотя виды и будут взаимно подавлять друг
друга, но все-таки их устойчивое сосуществование возможно.
71
Этот результат носит сугубо теоретический характер, но, как
будет показано ниже, он весьма реалистичен.
Рис. 11. Простая модель размещения двух видов, зависящих от одного и того
же фактора Х1, по его градиенту. Область определения каждого вида
на 50% перекрывается областью определения другого. В области
пересечения виды несколько подавляют друг друга. Совместное
сосуществование возможно, так как у каждого из видов существует
собственная область определения
Следует отметить, что исследования условий
взаимосуществования потенциально конкурирующих видов на
хорошей количественной основе по сути дела только начинаются.
Они связаны с большими методологическими трудностями,
затруднены сложностью корректного измерения пересечений
ниш и пока дают весьма разнообразные результаты. Вместе с
тем теоретический вывод о совместном устойчивом, хотя и
угнетенном существовании конкурирующих видов даже при
очень высоком, но не абсолютном подобии их в отношении к
условиям и ресурсам среды в целом получает широкое
подтверждение.
Таким образом, при конкуренции виды в одинаковой
или разной степени угнетают друг друга, но все-таки способны
к взаимососуществованию. Возможность взаимососущество-
72
вания формально связывается с тем, что у каждого вида
существует своя, может быть, и не самая лучшая область
существования, в которой он находится вне давления со стороны
своего потенциального конкурента.
V.4. Независимость двух совместно существующих видов
Представим абсолютно однородную среду, во всех
точках которой имеются и те же в равном количестве ресурсы
и условия. Каким образом в таких условиях могут
существовать абсолютно не взаимодействующие, независимые виды?
Пусть каждый вид потребляет какие-то ресурсы. Для
полной независимости необходимо и достаточно, чтобы один
вид потреблял какой-либо ресурс Х1, но не использовал
ресурс Х2, в то время как второй вид, наоборот, использовал бы
только ресурс Х2.
Тогда можно записать, что
N1 = М1 log Х1 + М2 log Х2, М1>0, М2=0,
N2 = Ь21 log Х1 + Ь22 log Х2, Ь21-0, Ь22>0.
При таких соотношениях коэффициентов следует, что
виды фактически существуют в разных пространствах, хотя и
заселяют одну территорию. Они просто не знают друг о друге.
В реальной природе, как увидим дальше, такие ситуации
весьма обычны.
Для существенной независимости могут быть и менее
строгие условия: достаточно, чтобы М1>М2, Ь21<Ь22; иначе
говоря, для независимости достаточно, чтобы у каждого вида
был бы свой видоспецифичный ведущий фактор. Виды,
подчиняющиеся таким отношениям, могут сколь угодно длительно
совместно сосуществовать на однородной территории без
конкуренции и взаимодействия.
Например, бобовые растения слабо связаны с
концентрацией почвенного азота, но более зависят от запасов
влаги в почве, а злаки, напротив, требовательны к
концентрации азота, но менее чувствительны к запасам влаги. Именно
поэтому сочетание бобовых и злаков - типичная кормовая
смесь, дающая заметно большую продукцию, чем отдельно
высаженный какой-либо вид злаков или бобовых.
73
Таким образом, для независимости видов достаточно,
чтобы к одним и тем же факторам имели существенно разную
чувствительность (коэффициенты b(i, j) - чувствительность
i-oro вида к j-овому фактору). Конкурировать они будут только
в том случае, если оба вида имеют общие ведущие факторы.
Возможность независимого сосуществования
представляется в однородных условиях только в том случае, если
виды проявляют разные потребности к разным видам
ресурсов, а сами ресурсы независимы. То есть изменение,
например, запасов влаги, не влияет на изменение запасов (или
возможность усвоения), например, азота, и наоборот.
Чем более зависимы ресурсы, тем меньше
независимость соответствующих видов и больше риск конкуренции.
Но даже при зависимости ресурсов существует
возможность совместного сосуществования двух видов в
однородной среде. Для этого достаточно, чтобы у каждого вида
была большая скорость потребления специфичного для него
ресурса и/или большая эффективность его использования.
Того же типа отношения могут складываться и в
результате разных отношений к пространству. Так, например,
ползающие виды растений сравнительно мало зависят от
своего положения относительно начальной точки роста по
горизонтальной координате, но не могут распределять свои
листья по вертикали; напротив, вертикально растущие
растения могут более свободно располагать свои листья по
вертикали и очень ограниченно изменять их положение в
горизонтальной плоскости. Соответственно ползающие и вертикально
растущие растения фактически осваивают различные
пространства и потому практически независимы при совместном
произрастании. На рис. 12 показано положение ниш двух
независимых видов.
V.5. Аменсализм и коменсализм
Эти отношения не требуют особых пояснений: здесь
один вид выступает в качестве фактора по отношению к
другому.
Так, например, деревья в лесу затеняют травы, и их
продукция соответственно зависит от плотности лесного поло-
74
га, но сами взрослые деревья от трав не зависят. Может быть
наоборот: деревья, снижая испарение с поверхности почвы,
способствуют развитию влаголюбивых мхов, хотя сами от них
не зависят. Другой пример: ствол дерева есть субстрат для
растений эпифитов, но само дерево, способствуя их
распространению, от них не зависит.
Х1 ° 10 0 2 4 6 8 18
XI
Рис. 12. Схема размещения в двухмерном пространстве, обеспечивающая
независимость двух видов. Первый вид зависит только от фактора Х1,
второй - только от Х2, в результате при любой фиксированной
численность первого вида, второй вид как отсутствует, так и существует
при любой численности, и наоборот.
Справа представлена схема в трехмерном пространстве, слева - в
двухмерном пространстве с отображением уровней численности
изолиниями
Наиболее типичны примеры таких отношений для
животных и растений. Так, семена многих растений переносятся
животными, и они положительно влияют на их
распространение, в то же время сами животные никак не зависят от этих
растений.
Если же животные, например, питаются семенами и
при этом часть их разносят в пространстве и теряют,
способствуя их распространению, то коменсализм фактически
переходит в коалицию.
75
Контрольные вопросы:
Приведите примеры различных типов отношений.
К какому типу отношений можно причислить семейные
отношения в паре "муж-жена", "родители-дети"? Как и почему
эти отношения могут изменяться в зависимости от внешних
условий и во времени?
Попытайтесь выделить пары или группы растений
совместимых в саду.
Опишите модель Вашего поведения, которая снижала
бы Вашу зависимость от членов сообщества, к которому Вы
принадлежите.
VI. ДИНАМИКА ПОПУЛЯЦИЙ
С ПОЗИЦИИ ТЕОРИИ КОЛЕБАНИЙ
VI.1. Свободные колебания
Рассматривая теоретические аспекты
функционирования популяций, мы обратили внимание на возможность
возникновения в них собственных колебаний. В основе этих
колебаний лежат фактически отношения между частями по схеме
"хищник - жертва" или "численность родителей - рождаемость
детей".
Можно утверждать, что схема отношений между
частями "положительная - отрицательная обратная связь"
определяет взаиморегулирование состояния частей, поддерживая
их значения в некоторой области фазового пространства, но, с
другой стороны, эти же отношения провоцируют
автоколебания.
Эти отношения настолько общи, что их удобно
рассматривать с общих позиций теории колебаний. Такой подход
позволяет объяснить многие важные экологические
феномены.
Если к системе осуществляется некоторый постоянный
подвод силы, то при рассмотренной выше структуре связей ее
малые свободные колебания можно описать уравнением
Y = A sin (wt + d),
76
где Аг-.амплитуда, w - частота, t - время, d - начальная фаза.
Колебания хорошо описываются простыми моделями, если
они малы. В линейных колебаниях частота не зависит от
количества энергии, подводимой к системе, и масштаба начальных
отклонений.
В нелинейных колебаниях картина, естественно, более
сложная. Конечно, в природе в подавляющем большинстве
случаев наблюдаются нелинейные колебания, но многие
очень общие отношения на качественном уровне хорошо
объясняются с позиции более простой и интуитивно понятной
линейной теории.
Частота линейных колебаний есть
w = (с/т)0'5,
где с - параметр, связанный с отношением скорости
изменения потенциальной энергии и скорости, которую можно
ассоциировать, например, со скоростью свободного падения g в
модели колебания маятника, в целом с отображает уровень
потенциальной энергии в системе; m - момент инерции
системы, в частном случае - масса.
Период колебания системы
Т = 2Pi(m/c)°5.
Чем больше момент инерции, тем больше период колебаний.
В моделях автоколебаний популяций период
колебаний был примерно равен Т = 4Тср. Выразим период
собственных колебаний через коэффициент прироста численности г. В
соответствии с аллометрическими зависимостями:
г = 1,5-W0,26 (здесь и далее масса в кг);
Тср = [1,5...2] W0'15.
Представим в логарифмической форме Тср
lnTcp=ln2 + 0,15lnW.
Выразим в логарифмической форме массу через
коэффициент скорости прироста численности
lnW = (ln 1,51 -lnr)/0,26.
Сделаем подстановку и преобразования
In ТСр = In 1,5 + 0,58 In 1,51 - 0,58 In r = In 1,9 - 0,58 In г.
Получим
Tcp=1,9/r0'58;
Т =7,6/r0;>8 = 2,41Pi/r058.
77
Таким образом, момент инерции популяции есть
приблизительно 1/г и соответственно чем больше размеры
особей и размеры популяций, тем больше период собственных
колебаний.
В модели хищник-жертва период колебаний системы
Т = 2PJ(ra)°5.
Соответственно момент инерции m = 1/ra.
Связь момента инерции с размерами
взаимодействующих особей и их популяций остается фактически той же
самой/что и для каждой отдельно взятой популяции, но
период колебания всей системы зависит от того, какие размеры
имеют особи популяций хищника и жертвы.
Любые колебания происходят в определенной среде.
Среда оказывает сопротивление. Соответственно любое
воздействие одних частей системы на другие после начального
возмущения, давшего толчок колебаниям, ослабевает. Если к
системе постоянно подводится некоторое количество энергии,
то через сопротивление, и в том числе через трение, часть ее
рассеивается, а период и амплитуда колебаний
устанавливаются на уровне, определяемом балансом между приходом
энергии и расходом ее на трение.
Влияние трения отображается специальным
коэффициентом n = u/2m, где и - константа, характеризующая
величину сопротивления. Колебания системы характеризуются
соотношением п и собственной частоты колебания w.
Возможны следующие случаи:
1. Малое сопротивление n<w.
Частота колебаний системы с сопротивлением
w" = (w2 - п2)0,5,
Y =Ae"ntsin (w"t + d).
Колебания постепенно затухают.
На рис. 13 приведена траектория колебаний и
соответствующий фазовый портрет.
2. Большое сопротивление n>m.
w" = (п2 - w2)0 5.
При большом сопротивлении после возмущения
система стремится к точке равновесия без колебаний, но в
зависимости от соотношений констант собственных колебаний,
трения и начальных условий величины возмущения и ускоре-
78
ния, движение к равновесию может иметь
характер (см. рис. 13 б,в).
различный
л
3
» г
1
е
.>...|....>...<....
lnmili.nnl.nHI
Чц;*"'.
¦ т'|Ь'щи11
1
0.8
„•.6
0.4
0.Z
0
ti>k
гН,,.,|
liaiiifciiulnuu'ln»!.! fci.nl 1
Tine
а.
2.3
„1.3
1>,г
и.?
-1.7
9 2 4 6 8 1G
Y
0 9.29.43.69.8 1
Y
Рис. 13. Варианты свободных колебаний в системах с трением. На левом
рисунке изображена траектория и фазовый портрет свободных
колебаний в системе с малым трением (фазовый портрет отображает
динамику в координатах значений функции и ее скорости). В центре и
справа траектории свободных колебаний с большим трением при
различных соотношениях параметров. На центральном рисунке
отображено поведение системы с большим сопротивлением, которая после
возмущения продолжает отклоняться от области равновесия и лишь,
достигнув некоторого предела, начинает асимптотически
приближаться к области равновесия. На рисунке справа соотношение параметров
таково, что система после возмущения без колебаний движется к
области равновесия
VI.2. Представления о формировании волн
в пространстве
Представим, что в однородной среде существует
много связанных друг с другом популяций. При увеличении
численности в одной из популяций возникает давление на сосед-
79
нюю. Действующее возмущение может приводить к снижению
ее численности и т.д. Соответственно колебание, возникшее в
одном месте, будет распространяться по всей системе.
Длина волны I. соизмерима с линейными размерами
популяции, которые в свою очередь определяются размерами
особи. Волновое число есть z = 2Pi/l. В зависимости от
собственных параметров системы ход волны и ее амплитуда
будут различными, но в пределе частоту колебаний в такой
цепочке можно считать близкой к w" = w-z.
Следовательно, чем больше линейные размеры
популяций, образующих систему, тем меньше частота колебания
всей системы и соответственно больше период (длина волны).
Таким образом, в системе популяций как бы возникает
общая волна, объединяющая частные популяции в единую
систему или популяцию более высокого уровня. В среде с
сопротивлением эта волна будет в той или иной степени
затухать, но возмущение, возникшее в какой-то индивидуальной
популяции, будет распространяться на достаточно обширных
территориях.
Для нас здесь особенно важно то, что колебания,
возникающие в одной части пространства на поверхности земли
во времени, распространяются с определенными длиной
волны и периодом, образуя тем самым пространственные
структуры. Этот эффект каждый может прямо наблюдать в
распространении волн на водяной поверхности. Полная аналогия
этому существует и в отношении любых экологических
объектов. В зависимости от физических свойств объектов скорость
движения волн и другие их параметры могут весьма
существенно отличаться, но суть дела от этого не меняется. В
результате возмущения в пространстве неизбежно возникает
иерархия волн: волны малой длины вложены в большие
волны второго порядка, волны второго порядка в более крупные
и т.д.
Эффект такого рода в популяциях давно обращал на
себя внимание исследователей. Его называли иногда
"волнами жизни". Так, при анализе заготовок шкурок
промысловых видов животных часто обнаруживалось асинхронное
изменение числа заготовленных шкур в разных, в том числе и
соседних, территориях. Во времени максимумы сменяли
средние величины заготовок, средние - минимумы и т.д. Чаще все-
80
го экологи были склонны объяснять эти колебания различием
в изменениях условий среды и, в первую очередь,
варьированием погоды. Однако хотя погодные изменения в
пространстве происходят также асинхронно, но регионы с
асинхронными колебаниями погоды в многолетних циклах имеют
значительно большие линейные размеры, чем те, которые
можно наблюдать при рассмотрении колебаний популяций.
Но здесь же следует отметить, что этот аспект
динамики экологических систем остается слабо изученным и
обычно очень трудно осознаваем практиками и учеными.
VI.3. Вынужденные линейные колебания
В любой системе, состоящей из частей, существуют
все условия для возникновения собственных колебаний с
параметрами, определяемыми строением самой системы. Эти
собственные колебания отражают ее автохтонное поведение.
Но, с другой стороны, внешние условия и ресурсы,
действующие на любую систему, есть проявление функционирования
каких-то других систем, которые также имеют собственные
колебания. В результате мы получаем, что окружающий нас
мир, в который поступает энергия Солнца и космическое
излучение, на который влияют гравитационные планетарные силы,
постоянно осциллирует во времени и пространстве.
По отношению к любой системе внешние условия и
воздействия, изменяющиеся во времени, способны вызвать ее
вынужденные колебания.
Будем считать для простоты, что возмущение
действует на систему по гармоническому закону
Q = Н sin pt,
где Н - максимальное значение или амплитуда возмущающей
силы, р - частота ее колебаний. Амплитуда колебания
системы пропорциональна h = H/m; чем больше момент инерции
или масса системы, тем труднее ее "раскачать".
Колебания системы под воздействием гармонической
вынуждающей силы описываются довольно громоздким
выражением, так что вытекающие из него следствия рассмотрим
на качественном уровне.
81
В первую очередь следует отметить, что система,
находящаяся под воздействием внешних гармонических
изменяющихся сил, испытывает сложные колебания, состоящие из
трех колебательных процессов: свободные (собственные),
сопровождающие свободные и вынужденные колебания.
Вынужденные колебания всегда происходят с частотой
вынуждающей силы и в отличие от свободных не зависят от
начальных условий, то есть от величины возмущающего
отклонения начального ускорения.
Если частота собственных колебаний w больше
частоты вынужденных колебаний р (w>p). то колебания внешней
силы и вызванные ею колебания будут находиться в одной
фазе, то есть изменение состояния системы будет
отслеживать изменения состояния среды, а собственные колебания
будут давать короткопериодную составляющую на фоне более
длиннопериодных (вынужденных) колебаний.
Если же w<p, то возмущающая сила и вызванные ею
колебания находятся в противоположных фазах, то есть когда
внешняя сила достигает максимума, система находится в
минимуме.
Если w = р, то внешняя сила раскачивает систему и
возникает эффект резонанса. Амплитуда колебаний
стремительно растет, так что система может потерять устойчивость.
В системе с сопротивлением вне зоны резонанса
амплитуда собственных и сопровождающих колебаний
постепенно уменьшается, так что, в конечном итоге, колебания
системы выглядят как чисто вынужденные. На рис. 14 показаны
вынужденные колебания без сопротивления, а на рис. 15 при
сопротивлении и их составные части: собственно свободные и
собственно вынужденные колебания. Соотношения частот в
колебании без сопротивления взяты равные двум (р = 2w), и
хотя система устойчива, но все-таки наблюдается
неаддитивный эффект, заметно увеличивающий амплитуду общего
колебания по сравнению с суммой амплитуд свободной и
вынужденной составляющих.
В установившемся режиме вынужденные колебания
описываются уравнением
h
у sjn ф* _ ф
((w2-pT + (4n'!V)05
Амплитуда вынужденных колебаний:
h
А =
((w2 - р2)2 + (4п2р)2)05
Отсюда следует, что в целом амплитуда тем больше,
чем ближе собственные и вынуждающие частоты и
соответственно ближе моменты инерции двух систем.
iee гее зев 4ве see
о lee zee зее 400 568
266^306
Рис. 14. Динамика системы как результат вынуждающих и собственных
колебаний в системе без трения. Частоты вынуждающих и собственных
колебаний различаются в два раза. Результирующие колебания
(нижний рисунок) не являются прямой суммой двух составляющих: их
амплитуда больше прямой суммы амплитуды составляющих, а
максимумы и минимумы не совпадают с ними.
Вместе с тем в результирующем колебании очевиден вклад состав
ляющих процессов.
83
108 ZOO 300 400
500
5.8 г?
200 11и(. ЗвО
Рис. 15. Динамика системы как результат вынуждающих и собственных
колебаний для системы с трением. После включения периодической
внешней силы (верхний рисунок) в равновесной системе возникают
затухающие собственные колебания, вклад которых в общий процесс
замечен лишь на коротком временном интервале, после чего
колебания системы полностью соответствует периодическому изменению
вынуждающей силы.
Максимум колебаний достигается не при равенстве
частот, а при условии р2 = w2 - 2n2, то есть при p<w. Так как
n = u/2m, то, чем меньше момент инерции (масса), тем при
меньшей частоте внешней силы достигается наибольшая
амплитуда.
Максимум вынужденных колебаний относительно
максимума действующей гармонически изменяющейся внешней
силы наступает с фазовым сдвигом tg d = 2np/(w2 - р2). При
этом максимальный сдвиг на четверть периода (Pi/2)
существует при w = р.
84
Рассмотренные соотношения показывают, что при
линейных колебаниях система увеличивает свою амплитуду и
приходит в состояние, близкое к резонансу, при близости
частот собственных и вынужденных колебаний. Увеличение
амплитуды колебания ведет к потере устойчивости. В конечном
итоге во всех инженерных конструкциях затрачиваются
большие усилия для того, чтобы исключить возникновение
разрушительного действия резонанса. Нет никаких сомнений в том,
что и природные системы должны также избегать этого
состояния. Другими словами, если природная система имеет
собственную частоту колебания, близкую к резонансной, то
какое бы ни было её внутреннее сопротивление, сколь бы ни
была велика ее масса, в конечном итоге, она может потерять
свою устойчивость и разрушиться.
Из теории колебаний следует, что если частоты
(периоды) собственных и вынужденных колебаний
различаются менее чем в два-три раза, то система переходит в область
относительно неустойчивого состояния. С уменьшением этого
соотношения система очень быстро теряет устойчивость и
разрушается.
Это исключительно важное следствие теории
колебаний, объясняющее многие наблюдаемые соотношения в
экологических системах.
Например, имеются два вида животных и растений,
которые используют абсолютно одинаковые ресурсы и
абсолютно одинаково реагируют на условия среды. Как было
показано выше, такие соотношения крайне неустойчивы, и один
вид случайным образом скорее всего вытеснит другой.
Теперь допустим, что особи этих видов по своим
линейным размерам более чем в 2 раза будут отличаться друг
от друга и соответственно иметь более чем в 2 раза
отличающиеся периоды колебаний. Через потребление ресурсов
они будут оказывать влияние друг на друга. Однако в
установившемся режиме колебания их численности будут
совершенно независимы. За время, в течение которого "крупный вид"
сделает полное колебание, "мелкий вид" успеет сделать
более двух.
Таким образом, два вида дифференцируются не по
ресурсам, а по отношению к времени, и на этой основе
успешно сосуществуют на одной территории. При этом популяция
85
вида с более крупными особями будет занимать существенно
большую площадь, чем популяция вида с особями меньших
размеров.
Правда, следует отметить, что при более сложных
отношениях, охватываемых нелинейной теорией колебаний,
резонанс возникает при отношениях частот собственных и
вынужденных колебаний, кратных 2 (2, 4. 8 и т.д.). Из этого
следует, что для устойчивого равновесного сосуществования
собственные частоты должны различаться, скорее всего, в 3,
5-7. 15 и т д. раз.
Для нас в первую очередь важно, что собственная
частота колебаний является важной координатой
экологического пространства, создающей большие возможности для
совместного сосуществования видов, сходных по своим
требованиям к ресурсам и условиям среды.
Легко предположить существование видов, которые в
достаточно широком диапазоне могут изменять собственную
частоту колебаний.
В простейшем случае это неизбежно происходит в
результате изменения индивидуальных размеров в процессе
роста. Поколение молодых деревьев в силу меньших
размеров заведомо имеет и меньшую собственную частоту
колебаний, чем поколения крупных деревьев. Многие виды растений
в зависимости от условий среды существенно изменяют
скорость роста и соответственно собственную частоту.
Многие виды по-разному во времени реализуют свои
функции. Так, некоторые растения цветут в строго
определенный период времени, другие тогда, когда благоприятствуют
внешние условия. Точно так же существуют жесткие и
скользящие режимы размножения у животных.
Следовательно, высокая специализация по
собственной частоте колебаний и деспециализированный режим, при
котором функционирование возможно в широком диапазоне
частот собственных колебаний так же, как и по всем другим
факторам, создает хорошие условия для обеспечения
нейтрализма в парных и многовидовых отношениях.
Разное отношение видов ко времени резко расширяет
возможности независимого, бесконфликтного их
существования.
S6
Следствием теории линейных колебаний является и
то, что как антагонизм и конкуренция, так и симбиоз и
содружество реализуемы лишь в том случае, если собственные
частоты систем близки. Неслучайны отношения типа хищник-
жертва, обеспечивающие равновесные циклические
колебания, возможны также при соизмеримости собственных частот
или при различии их (нелинейные отношения) в кратное число
раз. Если жертва намного меньше хищника, то динамика ее
численности почти без сдвига будет следовать за изменением
численности первого, но с очень малой амплитудой (если нет,
конечно, других внешних сил и возмущений), а хищник от нее
вообще не будет зависеть. То есть отношения переходят в
область аменсализма, и хищник становится просто
независимой внешней силой. Обратные соотношения приводят к
паразитизму ('маленький хищник" - "большая жертва').
Представления, почерпнутые из теории колебаний,
объясняют механизмы динамики системы, постоянно
получающей вещество и энергию извне, под действием внешних
по отношению к ней периодически изменяющихся по своей
величине сил. Строение системы определяет ее собственную
частоту колебания и реакцию на воздействие внешней силы.
Если скорость изменения внешней силы по отношению к
моменту инерции системы и ее собственной частоте колебания
очень мала, то система изменяет свое состояние вслед за
изменением состояния внешней силы. При этом случайные
флюктуации внешней силы могут стимулировать появление
колебаний системы на ее собственной частоте.
Любому колебанию системы во времени соответствует
пространственная структура (волна) с соответствующими ли?
нейными размерами, и соотношение между ними
определяется параметрами конкретной системы.
VII. ОБЩИЕ ПРИНЦИПЫ ОРГАНИЗАЦИИ СООБЩЕСТВА
VII.1. Основные положения
Элементами сообщества по определению являются
популяции отдельных видов Каждая популяция входит в
отношения с другими со своими собственными параметрами:
плодовитостью, способностью распространения зачатков
жизни (семян, потомков) в пространстве, продолжительностью
жизни, отношением между возрастными и половыми группами,
отношением ко времени и пространству, со специфичным
отношением этих параметров, численности и продуктивности к
ресурсам и условиям Среды, и в том числе к другим
популяциям.
Такое множество отношений заставляет вносить
некоторые упрощения и рассматривать более частные
идеализированные модели сообществ.
Удобно различать вертикальные и горизонтальные
сообщества. Вертикальные сообщества рассматривают как
совокупность видовых популяций, объединенных цепочкой
трофических (пищевых) отношений.
Первым звеном такой цепочки являются автотрофные
организмы (продуценты). Это растения - организмы,
способные синтезировать органическое вещество из
неорганического, извлекая энергию из солнечной радиации.
Второе звено образуют растительноядные животные -
гетеротрофы (плотоядные) 1-го порядка. Внутри этого звена
можно выделить две принципиально различные группы -
животные, использующие живые части растений, и организмы,
использующие отмершие части растений - деструкторы.
Деструкторы в основном обитают в почве.
Гетеротрофы 1-го порядка являются источниками
пищи (вещества и энергии) для гетеротрофов 2-го порядка -
хищников. Гетеротрофы 2-го порядка, в свою очередь, могут
быть источником пищи для гетеротрофов 3-го порядка. Это
чаще всего хищники и паразиты. Некоторые хищники 3-го
порядка могут использоваться специфическими паразитами,
которых формально можно отнести к гетеротрофам 4-го
порядка.
Такое вертикальное представление сообщества,
конечно, очень большое упрощение.
Питание различными частями растений: листьями
(фотосинтезирующие части), древесиной и стеблями, корой,
корнями, генеративными органами (цветами и плодами) -
создает принципиально различные условия для жизни
гетеротрофов 1-го порядка. Разнообразие органов растений опреде-
88
ляет и разнообразие форм жизни, строения органов
пищеварения, ферментативных структур и т.п.
Многие растительноядные организмы способны
использовать в пищу различные органы, другие узко
специализированы. Хищники 1-го порядка очень часто имеют
смешанное питание. Так, например, многие семеноядные птицы
выкармливают птенцов насекомыми, в то время как взрослые
птицы питаются семенами. Многие хищные млекопитающие
не могут существовать без растительных кормов, другие,
сохраняя морфологические признаки хищника, в основном
используют растительные корма (например, многие виды
медведей).
Исключительно богат мир паразитов, которые могут
относиться и к растительноядным, и гетеротрофам 2-го и
3-4-го порядков.
Очень сложна схема преобразования отмершей
органической массы в минеральные соединения. За последний
этап разрушения ответственны бактерии и грибы. Но они
выполняют свои функции более эффективно, если растительные
остатки предварительно разрушены растительноядными
беспозвоночными, которые извлекают из растения наиболее
доступные и питательные органические соединения.
Растительноядные почвенные беспозвоночные и микроорганизмы, в
свою очередь, являются основой для специфических
хищников и паразитов.
Таким образом, говорить о цепи питания можно лишь
весьма условно, имея в виду как бы генеральное направление
потока вещества и энергии: потока энергии Солнца через
растения к гетеротрофам 1-го и более высоких порядков и
вещества из атмосферы и почвы через растения и гетеротро-
фов в атмосферу и почву.
Под горизонтальными сообществами
подразумеваются совокупности длительно сосуществующих популяций со
сходными функционально-трофическими отношениями,
потенциальными конкурентами за пищу.
Наиболее естественно такие сообщества выделяются
для растений - их обычно называют фитоценозами. Но вполне
оправдано выделение и сообществ, например,
растительноядных насекомых (энтомоценоз), млекопитающих, почвенных
микроорганизмов (микробоценоз), почвенных беспозвоночных
89
(педоценоз). В таком выделении много условностей. Так,
например, лесной фитоценоз подразделяется на естественные
составляющие - ярусы, образованные различными видами, но
деревья и кустарники на начальных стадиях развития
находятся в среде травяного яруса.
Обобщенное рассмотрение вертикальных и
горизонтальных сообществ совершенно естественно. За этим
объединением закреплено понятие биоценоза - длительно
сосуществующей на определенном пространстве совокупности
видов, находящихся друг с другом в самых различных
экологических отношениях.
Таким образом, выделение различных типов
сообществ направлено на то, чтобы вычленить из всего
разнообразия отношений те из них, которые в конкретном случае
рассматриваются в качестве предмета исследований.
Выделение горизонтальных и вертикальных сообществ
оправдано хотя бы потому, что первое выделяется по
обобщенной координате конкуренция, а второе - по координате
трофика. Эти координаты заведомо независимы друг от друга
(ортогональны), что позволяет отдельно рассматривать
вертикальное сообщество, приняв конкуренцию на всех
трофических уровнях как константу, так и горизонтальное, приняв в
качестве константы - трофику. И то и другое - идеализация
реальности, необходимая для ее лучшего понимания и
изучения.
VII.2. Горизонтальное сообщество
Для понимания того, как организуются горизонтальные
сообщества, необходимо распространить рассмотренные
выше парные отношения на несколько видов. При этом будем
иметь два идеализированных варианта:
1) пространство, однородное во времени, по ресурсам
и условиям;
2) пространство (время), с градиентами изменения
ресурсов и условий.
Второй случай более сложный и поглощает первый.
Рассмотрим первый и наиболее простой случай.
Будем считать, что существует n-видов ресурсов (для растений
это могут быть различные соединения биогенных элементов -
90
азота, фосфора, калия, кальция и т.п., для животных -
различные виды растений, используемых в пищу и т.п.). Допускается,
что ресурсы поступают в систему с постоянной скоростью и
однородны в пространстве.
Условия среды: температура, влажность и т.п. по
определению остаются неизменными и соответственно не
влияют на отношения видов.
Каждый вид может использовать и использует самые
разнообразные ресурсы, но с различными скоростями
потребления. Чем выше скорость потребления, тем, очевидно, более
предпочтителен ресурс, тем соответственно больше
чувствительность вида к данному ресурсу. Будем для простоты
считать, что все ресурсы обладают одинаковой эффективностью,
так что единица потребления любого ресурса обеспечивает
одинаковый эффект роста или развития использующего его
организма. В принципе, конечно, можно учитывать и
различную эффективность ресурсов, но это не изменит существа
дела.
Состояние любого вида будет описываться уравнением:
Y(i) = a(i,1)X(1) + a(i,2)X(2) + ... + a(i,n)X(n),
где Y(i) - показатель состояния популяции i-ro вида
(численность, биомасса, продуктивность и т.п.), Х( j ) -
концентрация j-pecypca в среде, a(i,j) - скорость потребления j-
ресурса i-видом (элемент вектора приспособленности вида).
Так как концентрация ресурсов не изменяется во вре-
менидо имеется в виду, что они с необходимой скоростью
поступают извне.
Тогда сообщество из m видов будет описываться
матрицей коэффициентов чувствительности А
I з(1,1) а(1,2) а(1,п)|
А= |а(2,1) а(2,2) a(2,n) |
|: I
| a(m,1)a(m,2) a(m,n)|.
Эта матрица содержит информацию о трофическом
различии видов и о степени перекрывания их пищевых ниш.
Формальный анализ ее позволяет выявить условия
устойчивого сосуществования видов:
1) необходимое условие, чтобы каждый вид имел свой
предпочтительный ресурс;
91
2) необходимое и достаточное условие, чтобы
максимальные и минимальные элементы столбцов матрицы
приспособленности лежали в различных строках, а все другие
(п - 2) элемента каждого столбца монотонно не возрастали бы
или не убывали.
В такой системе число устойчиво сосуществующих
потенциально конкурирующих видов не может превышать
числа ресурсов.
Чтобы почувствовать суть этих отношений, достаточно
представить некоторый коллектив лиц и набор продуктов их
питания. Будем считать, что нет никаких других механизмов
организации этого сообщества, кроме различий в
предпочтении продуктов. Для образности в первом варианте допустим,
что различий в предпочтении не существует. Тогда можно
полагать, что все лица одновременно набросятся на один
наиболее предпочтительный продукт, и возникнет жесткая
конкуренция. Противоположная ситуация возникнет, когда
предпочтения у индивидуумов полностью различны. В этом
случае каждый из них будет использовать свой продукт, и
конкуренция не возникнет. Более реалистичный характер имеет
промежуточная ситуация, предсказываемая моделью, когда
каждый индивидуум может использовать любой продукт, но
один из продуктов является только для него наиболее
предпочтителен. В таком варианте случайное использование
каким-либо индивидуумом "чужого" продукта позволяет
достаточно легко ущемленному индивидууму найти несколько
худший, но вполне приемлемый для него другой продукт.
Основным следствием этой модели является
утверждение, что число взаимонезависимых видов в сообществе не
может превышать числа ресурсов.
В рассмотренном варианте численности популяции
видов лимитировались только ресурсами. Однако реально
популяции обладают свойством самоингибирования. В этом
случае число видов может быть больше числа ресурсов, так
как каждый вид их не доиспользует, оставляя свободные
запасы. Конечно, число видов в этом случае будет определяться
и количеством каждого ресурса Х( j).
Виды могут выделять метаболиты, которые подавляют
или. напротив, стимулируют другие виды. Число совместно
сосуществующих видов будет в этом случае определяться
92
конкретными значениями соответствующих констант, но в
целом при положительном взаимодействии число видов может
быть больше, чем без таковых.
Таким образом, основой сосуществования видов в
однородном пространстве при n-ресурсах являются видоспе-
цифичные предпочтения. Это - достаточно типичная схема.
Так, мы различаем растения светолюбивые, обладающие
высокой эффективностью использования света, и напротив,
теневыносливые, медленно увеличивающие скорость
фотосинтеза при увеличении освещенности; чувствительные и
малочувствительные к содержанию влаги; чувствительные к
изменению концентрации элементов минерального питания и
малочувствительные к ним и т.д. При прочих равных условиях
светолюбивый и теневыносливый виды легко сосуществуют.
Можно утверждать, что в достаточно обеспеченной
светом, влагой и минеральным питанием среде в одной
"точке" устойчиво может сосуществовать не менее 3 видов
растений; один более эффективно использует свет, второй -
влагу, а третий - элементы минерального питания. На этом
принципе, в частности, создаются устойчивые травосмеси.
При этом имеется в виду, что растения занимают один
вертикальный ярус.
Теперь допустим, что рассматриваемое нами
физическое пространство неоднородно как по распределению
ресурсов, так и по условиям среды. Это значит, что в различных
точках земной поверхности концентрации и соотношения
ресурсов и состояния условий среды различаются на величины,
соизмеримые с чувствительностью к их изменениям хотя бы
части видов, потенциально способных заселить эту
территорию.
Изменение условий и ресурсов в пространстве может
иметь характер тренда, или градиента (например, изменение
влажности почвы при движении по склону, изменение
гидротермического режима при движении от экватора к полюсу),
может иметь регулярный (например, при переходе из одной
долины реки в другую) и, наконец, случайный характер.
Разные ресурсы и свойства могут изменяться как
взаимосвязанно, так и независимо. Например, в горах приход
солнечной радиации на склоны никак не связан с приходом
атмосферных осадков.
93
Следует отметить, что ресурсы и условия среды могут
изменяться во времени: приход радиации, температура и
влажность воздуха имеют четко выраженный суточный ход. Те
же показатели изменяются в течение сезона года в результате
смены воздушных масс различного генезиса и т.д. При этом
изменения ресурсов и условий среды в пространстве и
времени заведомо существенно независимы.
Итак, рассмотрим, как будут размещаться виды по
некоторому условному градиенту среды в физическом
пространстве.
Как было показано выше, по отношению к любому
фактору у любого вида существует область оптимальных его
значений, а слева и справа от нее - области высокой
чувствительности. Наконец, после некоторых пороговых значений
фактора вид вообще не может существовать. Очевидно, что в
области оптимума чувствительность вида к данному фактору
близка к нулю.
Из анализа парных отношений следует, что два вида с
различными областями оптимума конкурируют друг с другом в
той степени, в какой пересекаются их ниши по градиенту. При
этом в каждой точке по градиенту в соответствии с
рассмотренным выше случаем может существовать, по крайней мере,
один вид с высокой чувствительностью, а один с низкой.
Таким образом, получаем схему размещения по
градиенту с последовательным замещением видов, как это
показано на рис. 16.
Следует отметить, что размеры области оптимума у
разных видов по отношению к одному и тому же фактору могут
быть существенно различны. Некоторые виды могут иметь
очень широкую область оптимума и при этом в целом могут
быть мало чувствительны к какому-либо фактору, другие -
наоборот. В этом случае более чувствительный вид в области
оптимума вытесняет нечувствительный. Например, сосна
обыкновенная очень мало чувствительна к запасам в почве
влаги и элементов минерального питания. Другие виды
деревьев, например ель, требуют устойчивого достаточного
увлажнения и не очень бедных почв. Если посадить сосну
искусственно, например, на вырубке, то она в большинстве
случаев будет успешно расти на любых почвах. Но в
естественных условиях сосна занимает крайне противоположные усло-
94
вия, неблагоприятные для других видов: на сухих песчаных
почвах и верховых болотах. В переходных ситуациях другие
вида деревьев, и в первую очередь ель, препятствуют росту
сосны. Могут складываться и такие соотношения, что вид с
более высокой общей чувствительностью не полностью
вытесняется более специализированным и сохраняется на всем
градиенте, хотя и с небольшим обилием.
10 h
О Ь
20 60
40 Л , 80
Grad. X
100
120
Рис. 16. Распределение пяти гипотетических видов по градиенту среды. У всех
видов отличаются области оптимума и чувствительности к градиенту
Модель такого рода сообществ показывает, что
максимально возможное пересечение может быть оценено как
1/(2cos(Pi(n +1))) и при достаточно больших п допускает
50%-го пересечения ниш, а при малом числе видов
допустимое пересечение заметно больше (при п=3 допустимое
пересечение ниш составляет около 70%).
На рис. 17 показана реальная смена видов деревьев
по градиенту уровня грунтовых вод.
Теперь допустим, что два или большее число
факторов в пространстве независимы или почти независимы друг от
95
160
120
80
40
0
tula
Ёгаий
: Alnus; L *icea
i » i i i i i » i i i i i i
-L-L.
I I I I I I
100 309 500
0 206 400 600
UGU
Рис 17. Реальное размещение видов древесного яруса по градиенту уровня
грунтовых вод (UGW) в дюнном древнеаллювиальном ландшафте в
бассейне р.Пра (Окский заповедник). Показатель обилия - сумма
площадей сечения стволов на гектар. Сосна (Pinus) имеет самую
широкую нишу по отношению к UGW (соответственно минимальную
чувствительность) с оптимумом при UGW около 400 см. Ниша березы
(Betula) несколько уже с оптимумом при UGW меньше 299 см.
Наиболее узкая ниша у серой ольхи (Alnus) с оптимумом при UGW меньше
20 см. Оптимум дуба (Qercus) лежит в интервале 60-220 см UGW. Ель
(Picea) и осина (Populus) встречаются как примесь при сходном
диапазоне уровня грунтовых вод. Пилообразный характер распределения
видов по градиенту UGW определяется влиянием микрорельефа,
перераспределяющего влагу, изменением трофности почв, условиям
дренажа при сходном уровне грунтовых вод, различной временной
стадией развития сообществ в разных точках пространства
друга, например, в пространстве могут существовать условия
с различной влажностью почв и различными запасами
минерального питания или склоны с различным приходом
солнечной радиации (северные - южные) и разными запасами влаги
96
(нижние части - верхние части склонов), то соответственно
реально виды размещаются, по крайней мере, в пространстве
трех относительно независимых градиентов. Соответственно
по каждому градиенту на некотором интервале могут
сосуществовать два взаимодополняющих и конкурирующих вида,
слабо зависящие от двух других градиентов.
Если рассмотреть проекцию такого пространства на
каждый градиент, то окажется, что четыре, но разных вида,
будут представлены практически по всему градиенту, а два -
взаимозамещать друг друга. На рис. 18 изображена
упрощенная схема размещения четырех видов в двухмерном
пространстве градиентов изменения условий среды.
Матрица коэффициентов чувствительности и знаков
связи, соответствующая этой схеме:
А
В
С
D
Вид А заменяет по градиенту Х2 вид В, и оба не
зависят от С и D, виды С и D заменяют друг друга по градиенту Х1.
Х1
0
0
-1
+1
Х2
+1
-1
0
0.
Ниша
вида С
Ниша
вида D
Х1
Ниша вида А
Ниша вида В
Х2
Рис. 18. Обобщенная схема размещения четырех видов в двухмерном
пространстве: вид А с координатами +Х1, ОХ2; вид В с координатами -Х1,
0X2; вид С с координатами 0X1, -Х2: вид D с координатами 0X1, +Х2
<Г
Таким образом, в каждой точке пространства
существуют три вида.
Объединяя две модели, получаем, что в каждой точке
пространства могут сосуществовать несколько видов за счет
разных скоростей потребления, несколько видов за счет
разных чувсгвительностей к градиентам среды.
Так как условия и ресурсы изменяются во времени, то
эти временные градиенты создают дополнительные условия
для сосуществования видов Так, разное время распускания
листьев весной и разное время начала вегетации создают
дополнительные условия для сосуществования видов.
Например, в лесах и степях широко представлены виды-эфемеры,
вегетирующие и цветущие в начале лета, когда они не
затеняются. В остальное время года они или слабо фотосинтези-
руют под тенью позднее распускающихся растений, или их
надземные части полностью отмирают.
Виды со сходными экологическими параметрами
обычно не могут существовать совместно, а с
различающимися экологическими параметрами на основе
отношений мутализма, содружества и коалиции в той или иной
степени могут тяготеть друг к другу. В результате мы наблюдаем в
пространстве и во времени относительно резкие смены типов
сообществ, каждый из которых объединяет в себя группу
видов, тяготеющих друг к другу В то же время другие виды,
независимые от них и друг друга, могут встречаться в
пространстве и времени в самых разных сочетаниях. В игоге,
опираясь на первые виды, в пространстве и во времени можно
выделить относительно дискретные сообщества, а при учете
участия вторых - те же сообщества представляются как
постепенно, без явных границ, переходящие друг в друга. При всех
условиях в одном однородном местообитании обычно все-таки
господствуют по обилию 2-3. а иногда 1 вид, в то время как
другие виды имеют подчиненное значение. Это определяется
и различиями в концентрации ресурсов, и их разной
специализацией, и, соответственно относительной эффективностью.
Наиболее жесткие схраничения на формирование
сообществ существуют у растений В конечном итоге, все
растения нуждаются в свете, влаге, в определенном наборе
элементов минерального питания Они имеют разные скорости
роста и потребления ресурсов, на возможности сосуществова-
чк
ния определяемые этими различиями довольно ограничены.
Поэтому одним из важнейших факторов их дифференциации и
сосуществования является отношение к времени,
пространству и условиям среды.
Как следует из теории колебаний, период собственных
колебаний прямо связан с моментом инерции. В наиболее
общем случае момент инерции связан с массой и
соответственно линейными размерами объекта, в нашем случае -
популяции. Период собственных колебаний популяции с
зависимостью коэффициента размножения от численности прямо
связан с продолжительностью жизни особей.
В соответствии с теорией колебаний части системы,
периоды колебаний которых различаются более чем в 2-3
раза и соответственно примерно в тех же масштабах
различаются их продолжительность жизни и линейные размеры, в
равновесном режиме практически не взаимодействуют.
Следовательно, для совместного существования необходимо и
достаточно, чтобы особи видов имели бы существенно
различные линейные размеры.
Отсюда следует, что - в растительных сообществах
должны существовать формы растений, образующие
вертикальные ярусы, с различием по высоте примерно в 3 раза.
Можно полагать, что имеет место и соответствующее
распределение корневых систем. Виды с наибольшими размерами
должны иметь и пространственно ограниченные, совместно
обитающие группы особей с линейными размерами,
пропорционально меньшими, чем у более крупных видов
На схеме (рис. 19) показано, что такая структура
действительно реализуется. Конечно, в каждом локальном месте
совершенно не обязательно выражены Е*се 5 ярусов Полная
ярусная структура реализуется на существенно большей
территории, но наличие и различная степень развития
представителей нескольких ярусов в одном месте - явление совершенно
обычное.
При этом относительно медленно изменяющаяся
структура древесного яруса создает равновесные условия для
кустарникового, изменения кустарникового яруса совместно с
изменением древесного - равновесные условия дпя крупных
трав и т.д. В результате, в пределах одного сообщества
деревьев существует вложенная мозаика сообществ кустарников и
w
сложная мозаика различных комбинаций видов трав и/или
мхов. Такие комбинации называют иногда
микроассоциациями, или синузиями.
Высота,
(глубина
81,0. к
27.0 *
0)
9.0 Ct
3,0
0,90
0.30 5
CD
0.09 о-
<0,03
0,005
0,015
0,045
0,13
0.40
1.20
3,60
10.0
) Ярус
крупные
средние
мелкие
Кустарники
очень
высокие
высокие
средние
мелкие
т
а
о
"" btL
\ t=400
t=200
t=100
t=48
t=24
t=12
t=6
t=2
"o/io"
0,30
Средняя продолжительность
собственное время, лет
0,9
2,70
Лиь
8,00
ейные
24,0
разме
72,0
жизни
эры, м
220,0
Рис. 19 Схема формирования ярусной структуры
Как показано выше, различные отношения к
пространству (виды с компактным вертикальным или диффузным
распределением листовой массы; виды, со строго
локализованным горизонтальным ее положением или с диффузным;
лианоподобные и ползучие виды) создают дополнительные
возможности к устойчивому сосуществованию большого числа
100
видов. В сообществах с очень большим числом видов ярусы
часто слабо выражены, и вертикальное распределение
листовой массы имеет один максимум на определенной высоте.
Однако, а при всех условиях существуют виды с разными
линейными размерами, как бы индуцирующие наличие разных
ярусов. Из рассмотренных выше отношений ясно, что физи-
номически ярусы должны быть более выражены там, где
ресурсы относительно ограничены.
Итак, возможности совместного устойчивого
равновесного сосуществования видов даже для растений очень велики,
что, в частности, и приводит к формированию значительного
видового богатства каждого реального сообщества. Образно
можно сказать, что разные виды стремятся заполнить всеми
способами все пустоты в гипотетическом многомерном
пространстве, образуемом ресурсами, условиями среды,
физическим трехмерным пространством и временем.
Вполне понятно, что еще больше возможностей для
совместного существования у популяций растительноядных
организмов. Разнообразие растений и их сочетаний в
пространстве и времени существенно увеличивает область
возможностей и, следовательно, потенциальное число
растительноядных видов в сообществе. Но особенно существенно
увеличивает разнообразие видов животных их,
обеспечиваемая подвижностью, относительно малая зависимость от
физического пространства.
Виды, имеющие сходные отношения к ресурсам и/или
условиям среды, часто объединяют в различные жизненные
формы, однако, подобие видов, относимых к одной жизненной
форме, условно.
При всех различиях между животными и растениями
принципы организации горизонтальных сообществ у животных
те же, что и у растений: основой сосуществования являются
различия по чувствительности к ресурсам и условиям среды,
различая областей оптимума по градиентам факторов,
различия пространственно-временных отношений. Можно
сформулировать следующее правило: если два вида имеют сходные
оптимумы по градиенту фактора, то чувствительность в их
отношении к этому фактору различна и, наоборот, при сходной
высокой чувствительности к одному фактору области
оптимума существенно разные.
101
Контрольные вопросы:
Назовите основные факторы, определяющие
возможность сосуществования видов в сообществе.
Проведите самостоятельные наблюдения по
следующей схеме:
1. В лесу, на поляне заложите 10 квадратных
площадок со стороной 50 см; подсчитайте на каждой площадке
число видов травяных растений (не обязательно определяя их
научное название, но по собственной схеме описав форму и
характер листьев, стеблей, корней); определите среднее
число видов на площадку; попытайтесь объяснить, почему, по
Вашему мнению, могут существовать совместно, по крайней
мере, некоторые виды.
2. Отберите из достаточно большого цветочного
горшка или из любой почвы наперстком поверхностные пробы
почв; в полулитровую емкость, наполненную водой, бросьте
по образцу и тщательно разболтайте; дайте воде отстояться и
тщательно под десятикратной лупой рассмотрите
поверхность. Вы обнаружите мелких животных, ногохвосток и
панцирных клещей. Подсчитайте число различающихся форм в
каждой пробе, опишите их, имея в виду размеры,
пигментацию, возможности их передвижения и попробуйте построить
гипотезы, объясняющие причины их совместного
существования
3 Выберите аналогичную схему наблюдения по
Вашему усмотрению.
Во всех случаях тщательно опишите свои наблюдения
и проиллюстрируйте их таблицами и графиками.
VII.3. Вертикальные сообщества
При трансформации энергии и вещества по цепи
питания происходит постепенное рассеивание вещества и энергии.
Если предполагать, что существует некоторое минимальное
количеств j вещества и энергии, необходимое для
поддержания устойчивого существования любой популяции, то звеньев
в этой цепи не может быть очень много
При ятом наибольшая масса будет естественно
сосредоточена в автотрофных организмах, меньшая - в гетеротро-
1П2
фах 1-го порядка, еще меньшая в хищниках 1-го порядка и т.д.
Такое соотношение масс часто называют пирамидой чисел.
Практика показывает, что больше 5 звеньев в цепи
питания не наблюдается.
Обозначим коэффициент, отражающий долю
вещества и энергии, поступивших к i-уровню и израсходованных на
восстановление биомассы - k(i), долю отмершего вещества •
m(i), долю вещества, потребленного из i уровня i + 1 уровнем
трофической цепи, - a(i). Все эти коэффициенты меньше
единицы. Коэффициент k(i) есть фактически коэффициент
полезного действия трофического уровня и пропорционален
коэффициенту размножения в модели хищник - жертва.
Моделирование такого рода цепей питания дает
соответствующие интуиции наглядные оценки зависимости числа
звеньев от параметров системы и прихода энергии.
Если q - длина цепи питания, a Q - поступление
вещества или энергии, то
m2/akq<Q<m2/ak(q*1)
при условии, что для всех звеньев цепи коэффициенты k(i)
примерно одинаковы.
Тогда 2ln m - q In ak < In Q < 2ln m - q In ak - In ak,
q = (In Q - 2ln m)/ln ak.
Соответственно получаем, что длина цепи тем больше, чем.
1) больше приход вещества и энергии (Q);
2) меньше доля отмирающей массы (т);
3) больше КПД каждого звена (к<1);
4) больше доля вещества, переходящая на
вышележащий уровень (а<1).
Так как в среднем КПД сопоставим с коэффициентом
размножения, а последний зависит от размеров организмов,
то, соответственно, если в сообществе в основном мелкие
организмы, то длина цепи при том же уровне прихода энергии
будет больше.
Из зависимости длины цепи питания от прихода
ресурсов следует, что чем меньше их приход, тем меньше длина
цепи и, следовательно, в макрогеографическом плане в
высоких широтах длина цепи должна быть короче, чем в низких.
Если же длины цепей одинаковы, то, следовательно, в
высоких широтах должны быть или больше КПД, или меньше ПОТе-
103
ри отмершего вещества, или больше доля поступления
вещества от нижнего звена к верхнему.
Так как зависимости функционирования от количества
ресурса имеют вид показательной функции у = ахь, где Ь<1, то
соответственно при малых ресурсах (х) - dy/dx КПД заведомо
выше, чем при больших. Следовательно, длины трофических
цепей питания в разных географических условиях могут
различаться незначительно, что в действительности и имеет
место.
Особый интерес имеет соотношение биомасс в
пирамиде чисел. Эмпирически было получено, что в бореальных
лесах, и особенно в степях, соотношение годовой продукции
растительности и продукции фитофагов меньше, чем в
тропических лесах. В последних все виды имеют меньшую
численность и меньший коэффициент размножения, чем в
бореальных лесах и степях.
Следовательно, в южных широтах ребра пирамиды
чисел более пологие, а в северных - более крутые.
Из моделей трофической цепи следует, что масса i-ro
трофического уровня пропорциональна к' (для всех уровней к -
примерно одинаково). Таким образом, чем больше КПД, тем
"круче" склон пирамиды. Так как с увеличением ресурсообес-
печенности КПД снижается, то в лучших условиях пирамида
чисел, как это имеет место в действительности, в среднем
будет иметь более пологие склоны.
Примерные соотношения в пирамиде чисел между
травоядными и хищниками можно получить на основе
эмпирических соотношений между биомассами жертвы и хищника по
аллометрическим зависимостям. В целом, полученные
соотношения объясняют, почему численности травоядных и
хищников в бореальной зоне выше, чем в тропиках, а в
полупустынях и даже пустынях численность фитофагов может быть
очень высокой при заведомо небольшой продукции
растительности. Однако следует иметь в виду, что видовое
богатство в тропических лесах существенно выше, чем в
бореальных.
Отметим, что передачу вещества по цепочке можно
рассматривать как аналог производственного цикла. Отсюда
следует, что умеренное ограничение в исходных ресурсах
неизбежно ведет к увеличению коэффициента полезного дей-
104
ствия каждого звена и всей системы. Система, адаптируясь к
этим условиям, будет стремиться уменьшать потери m и
увеличивать долю, передаваемую в верхнее звено.
Контрольные вопросы:
Какими факторами определяется длина цепи?
Как соотносятся массы звеньев в зависимости от
количества исходных ресурсов и масштабов их варьирования во
времени?
VIII. ОБОБЩЕННОЕ ПРЕДСТАВЛЕНИЕ О СООБЩЕСТВЕ И
ЕГО ДИНАМИКЕ
Таким образом, сообщество организуется как
объединение горизонтальных и вертикальных связей. Поскольку
каждый вид в сообществе стремится выжить и это стремление
является совершенно естественной общесистемной целью, то
каждый вид изменяет свое состояние в рамках, допускаемых
морфологической и физиологической организацией его особей
и поведенческими отношениями между ними, вымирает или
попадает в область устойчивого равновесия. Последнее
становится достижимым, если каждый вид, занимая свою
экологическую нишу, на основе преимущественного использования
видоспецифичного фактора становится практически
независимым от всех других. В такой системе общая биомасса, или
продуктивность сообщества, не будет зависеть от межвидовых
взаимодействий. Системы такого типа называются
консервативными.
Ранее были показаны широкие возможности
достижения независимости между видами за счет разной
чувствительности к разным факторам и различий областей их оптимумов,
за счет различий в пространственно-временных отношениях и
т.п. Исследование реальных сложившихся сообществ
растений и животных показывает, что они очень часто
демонстрируют существенную пространственную независимость в
размещении особей, принадлежащих разным видам. В таком
сообществе флюктуации общей биомассы определяются
собственными колебаниями численности и биомассы каждого
вида или подсистем видов, связанных достаточно хорошо
105
выраженными трофическими отношениями. Однако такое
состояние, при котором все виды независимы друг от друга,
правильнее рассматривать, скорее, как предельное.
В каждом горизонтальном сообществе по каждому
градиенту среды и ресурсов обычно неизбежно возникают
конкурентные отношения, определяемые пересечением
видовых ниш. В этих областях каждый вид испытывает некоторое
давление со стороны соседа, что приводит к потере их
совместной продукции. Такое взаимодействие можно
определить как внутреннее трение.
Сообщества с внутренним трением расходуют часть
вещества и энергии на свои взаимодействия, что и приводит к
общей потери продукции. Величина трения и, соответственно,
потери продукции определяются степенью пересечения ниш и
параметрами видов, но в целом они пропорциональны сумме
квадратов их биомасс. Такие системы с трением называются
диссипативными. Так же как и в консервативной системе, в
диссипативной возможны малые флюктуации, но внутреннее
трение снижает амплитуду и в частном случае может погашать
и сами флюктуации.
В процессе развития особи каждого вида несколько
изменяют свои свойства. Так, например, у древесных видов
каждую возрастную группу можно рассматривать как особую
часть системы с существенными различными межвидовыми
отношениями. Молодые деревья под пологом леса вступают
во взаимодействия с растениями травяного яруса, те, кто
выжил на этой стадии, начинают взаимодействовать с
кустарниковым ярусом и т.д. Хотя в целом на достаточно большом
пространственно-временном интервале популяции видов
деревьев и видов трав, в силу их резко различающихся периодов
собственных колебаний, независимы, в локальные моменты
времени и на локальном пространстве они могут вступать в
жесткие конкурентные отношения.
Точно такие же проблемы могут возникать и у других
видов. Так, семена растений поступают во времени под полог
леса порциями. Они довольно долгое время могут быть в
пассивном состоянии или находиться в стадии проростков в
травяном или кустарниковом ярусе. При густом травяном или
кустарниковом ярусе они могут погибнуть. Но если они
проросли и закрепились, то у большинства видов такие особи
106
долгое время могут находиться в угнетенном состоянии
(иногда десятки лет).
Густой травяной или кустарниковый ярус в лесу может
быть только на относительно открытых участках (в окнах
древесного полога). Такие окна образуются в результате
выпадения старых деревьев. Как будут развиваться события в таком
вновь образовавшемся окне в существенной степени зависит
от начальных условий. Если по каким-либо причинам в почве
было мало семян деревьев, а тень была столь густая, что
практически не было жизнестойких проростков, то
образовавшееся окно может быть заселено активно
расселяющимися травами или кустарниками, которые здесь надолго
исключат или ослабят развитие деревьев. В другой ситуации
подрост деревьев может быстро ускорить рост и войти в
древесный полог.
Естественно предположить, что древесный полог
образован видами с несколько различающейся
теневыносливостью. Тогда в окно, в первую очередь, устремятся более
быстро растущие виды и лишь под их пологом будут медленно
расти виды теневыносливые, которые войдут в него после
гибели более светолюбивых или под пологом светолюбивых
видов образуют второй древесный ярус.
Таким образом, на каждом небольшом участке леса,
по площади соизмеримом с линейным размером крупных
взрослых деревьев (обычно 100-400 м2), возникают
собственные колебания структуры и, естественно, биомассы и
продуктивности растительности. Такие пятна мозаики
растительности принято называть парцеллами, или гепами (gaps).
Амплитуда, частота и характер возникающих здесь
колебаний существенно зависят от начальных условий. Такого
типа колебания называются нелинейными. Они имеют
существенно более сложный характер, чем рассмотренные выше
линейные. Нелинейные колебания возникают и тогда, когда
система описывается дифференциальными уравнениями, в
которых параметры не являются константами, а явно или
неявно зависят от времени. Одной из важнейших черт такого
нелинейного колебательного процесса является то, что в
одних и тех же условиях могут существовать несколько областей
равновесия с разным сочетанием видов, с разной биомассой и
продукцией. Переход из одного равновесного состояния в дру-
107
roe з таких системах может осуществляться за очень короткое
время - скачком. В течение этого скачка система испытывает
неравновесные, нестационарные преобразования, и в какую
область равновесия она перейдет, заведомо не известно.
В результате этого процесса любое сложившееся
сообщество имеет сложную пространственную мозаику
относительно дискретных во времени и пространстве, отличающихся
друг от друга по составу пятен растительности. Причем
предсказать будущее состояние каждого пятна на достаточно
больших интервалах времени практически невозможно.
Рассмотренную пространственную структуру
сообщества, определяемую неравновесными локальными
преобразованиями, очень легко наблюдать практически в любом
лесном и луговом сообществе. Можно полагать, что она
свойственна и сообществу животных, но в силу их подвижности эта
мозаика неизбежно более размыта, а у животных скрытного
образа жизни трудно наблюдаема.
На большом интервале времени, соизмеримом с
собственным временем наиболее долго живущих видов, обычно
образующих верхний ярус, сообщество реализуется на
существенно большей площади, в сотни раз превышающей
размеры каждого пятна внутренней мозаики. Типы пятен,
отвечающие условиям локального равновесия или быстрого
неравновесного перехода, сменяют друг друга в пространстве и
во времени, так что в целом сообщество выглядит
неизменным и равновесным. Является ли оно равновесным, можно
установить, исследуя возрастную и размерную структуру
популяций каждого вида, анализируя матрицы их совместной
встречаемости, отражающие взаимоположение видовых ниш в
экологическом пространстве и степень их перекрывания.
Такие, по крайней мере, внешне равновесные сообщества
принято называть климаксными.
Теоретически любое сообщество в постоянных
условиях среды стремится к такому климаксному равновесному
состоянию, при котором оно в целом испытывает лишь малые
собственные флюктуации. Период собственных флюктуации
определяется собственным периодом колебаний видов,
образующих различные пространственно-временные структурные
части сообщества (например, ярусы). Так, для древесного
яруса лесного сообщества период собственных колебаний
108
составляет от 200 до 400 и более лет. За это время могут
циклически изменяться соотношения видов, биомасса и
продукция. В луговых сообществах период собственных колебаний
может составлять около 10-20 лет. Так как в равновесном
сообществе многие виды существенно независимы друг от
друга, то каждый из них может флюктуировать с собственной
частотой колебания.
Как теория так и практика показывают, что внедрение
новых видов в равновесное сообщество - задача весьма и
весьма трудная. Это совершенно не значит, что для вида-
вселенца в принципе нет места в сообществе. Как было
показано, каждый вид может существовать в весьма широком
диапазоне условий, определяемых его физиологическими,
морфологическими и поведенческими свойствами. Наиболее
эффективен и устойчив он в области своего экологического
оптимума, но вполне успешно может функционировать и вне ее.
Если популяция вида заселила некоторую, может быть, и не
самую лучшую для нее область экологического пространства,
то в равновесной ситуации она располагает достаточным
числом особей, способных создать необходимый
репродукционный потенциал. Любой вселяющийся новый вид проникает на
новую территорию обычно небольшим числом особей. Если
даже на этой новой территории его параметры потенциально
обеспечивают более высокую конкурентоспособность, чем у
экологически сходного вида, его популяция слишком мала и
подвержена многим случайностям. Из формальной теории
следует, что более приспособленный вид вытеснит менее
приспособленный, но очень малая начальная численность
вселенца приводит к тому, что для вселения и обеспечения
устойчивого состояния требуется очень большое время, а
неизбежные малые флюктуации делают проблему вселения
часто неразрешимой. В результате сложившиеся сообщества
весьма устойчивы к вселенцам, и для успеха последних нужны
весьма веские преимущества перед аборигенами.
Вполне понятно, что внешние условия существования
сообществ также испытывают периодические и
апериодические флюктуации. Наиболее существенными и изученными
являются колебания климата, хотя определенное значение
могут иметь и тектонические процессы.
109
В данном разделе природа колебаний климата не
рассматривается, однако обратим внимание на тот факт, что эти
колебания могут быть собственными и определяться
взаимодействием таких частей с заведомо разными моментами
инерции, как суша, океан, ледники, атмосфера. Сложная
конфигурация суши и океана при неоднородности строения их
отдельных частей может приводить к существованию
нескольких наложенных друг на друга периодов разной длительности.
К тому же механизмы изменения температурного режима и
атмосферных осадков существенно различны, и эти две
переменные также взаимодействуют нелинейно как части целого. В
результате даже без допущения изменения действия внешних
сил, например, цикличности процессов на Солнце, существуют
все необходимые предпосылки для сложного автоколебания
глобального климата.
Колебания таких сложных нелинейных систем могут
носить весьма хаотичный характер, существенно различный
на разных территориях. Действительно, анализ столетних
рядов наблюдений выявляет некоторую периодичность далеко
не во всех регионах, а в разных регионах периодические
колебания часто относительно друг друга сдвинуты по фазе.
Можно признать существование более или менее
выраженных 2-4-летних, 9-11-летних, 27-летних, 40-45-летних
циклов изменения климата. На основе исторических и
летописных данных предполагается 100-летний, 400-500-летний и
более длительные циклы.
В целом циклические колебания более выражены в
умеренных широтах, чем в тропических, но и там, как
показывают палеоматериалы за последние 10 тыс. лет, имелись
заметные изменения климата.
В общем, флюктуации климата в каждой точке
поверхности Земли изменяют в той или иной степени условия жизни
для всех существующих видов. Если изменения климата
лежат в пределах экологического оптимума вида, то он,
соответственно, их просто не замечает, и объем его ниши не
меняется. Для других видов может происходить увеличение или
•уменьшение объема экологической ниши. Соответственно,
виды, конкурируя по климатическому градиенту, могут во
времени сменять друг друга. Так как заменяющие друг друга по
градиенту виды имеют примерно равные начальные условия,
ПО
скорость их взаимозамены в сообществах будет соизмерима
только со скоростями их расселения, а скорость
преобразования сообщества - с собственным временем их колебания.
Колебания сообщества будут равновесными, если
период возбуждающей силы (климата) будет не менее чем в 2
раза больше собственного периода колебаний. При этих
условиях сообщество или его части медленно и постепенно
перестроятся. Так, например, для равновесного преобразования
лесного сообщества необходимо, чтобы период колебаний
климата был больше 1000 лет. Для равновесного
преобразования травяного яруса требуется период колебаний порядка
25 - 50 лет и т.д. Если период колебаний климата близок
периоду собственных колебаний сообщества или его отдельной
части, то возникают условия для резонанса. Резонанс может
приводить к резкой перестройке сообществ, а может быть и
погашен за счет его внутреннего трения. Здесь все зависит от
соотношения амплитуды возбуждающей силы и параметров
самого сообщества или его частей. Так или иначе
преобразования сообществ по резонансному, неравновесному типу
более чем типичны. Наиболее ярким примером является смена
сообществ в результате пожаров.
Каждое климаксное сообщество состоит из мозаики
участков с разновозрастным лесом. Опадающие листья, хвоя,
сучья создают подстилку, которая разрушается почвенной
микрофлорой и беспозвоночными животными. Масса
подстилки, накапливающаяся в каждом отдельном случае, зависит от
массы и продуктивности растительности и скорости ее
разложения. Последняя зависит от состава подстилки и локальных
микроклиматических условий.
Так, по мере роста древесных растений приход опада
(скорость поступления) постоянно увеличивается, а в билу
естественной задержки скорость разложения увеличивается
существенно медленнее. В результате подстилка
накапливается. По мере старения деревьев приход опада
уменьшается, а скорость разложения остается постоянной и запасы
подстилки стабилизируются или даже несколько снижаются. Но
так или иначе в определенном возрасте запас подстилки
оказывается очень большим. Причем в климаксном лесу всегда
найдется участок с большой массой опада.
111
Мертвое органическое вещество неустойчиво и
окисляется. Окисление идет с выделением тепла и,
соответственно, мертвое органическое вещество предрасположено к
самовозгоранию. Если подстилка влажная, то тепло идет на
испарение. Если подстилка достаточно сухая, а температура
воздуха высокая и воздух сухой, то она может самовозгореться.
Самовозгорание возможно в ограниченных условиях, когда
температура воздуха приближается к 30°С, а его
относительная влажность - к 30%. Такие ситуации наблюдаются в
условиях засух. Так как при засухе и живые растения существенно
обезвожены, то очень велик риск возникновения мощного
лесного пожара в результате самовозгорания. Все это наиболее
вероятно в относительно старом, хвойном лесу, так как опад
пород и в благоприятных условиях медленно минерализуем.
С формальных позиций это значит, что органическая
масса потеряла устойчивость и катастрофически разрушается.
Распространится самовозгорание на большую площадь кли-
максного сообщества или самолокализуется, охватит только
подстилку (низовой пожар) или перейдет на древесный ярус,
зависит от очень многих условий, но при определенном
стечении обстоятельств риск разрушительного пожара существует.
В результате сообщество естественным образом может быть
уничтожено на обширной площади. Таким образом, пожар
можно рассматривать как результат резонанса собственных
периодических изменений состояния сообщества и колебаний
климата. Пожар, конечно, катастрофа для конкретного
сообщества, но это настолько типичная катастрофа, что многие
виды растений прямо приспособлены к пожарам, и если бы их
не было, многие из них исчезли бы как виды.
Выделяется большая группа пирогенных видов,
которые наилучшим образом распространяются именно на месте
пожаров. Так, огромные площади лиственничной тайги
Восточной Сибири без периодических пожаров выродились бы в
своеобразную лесотундру.
К резонансным эффектам склонны многие виды
насекомых с очень большим коэффициентом размножения. Для
многих из них в норме численность невелика, так как
ограничена емкость среды. Ограниченная емкость среды
определяется тем. что успех их размножения во многом
определяется состоянием их корма - растений. В том случае, когда расте-
112
ния (например, деревья) ослаблены (в результате действия
засухи или загрязнения воздуха в сочетании с "преклонным"
возрастом), емкость среды резко увеличивается, и насекомые
дают вспышку численности, полностью уничтожая или
существенно угнетая своих прокормителей. Такие вспышки дают
многие виды чешуекрылых, жесткокрылых, а в степях -
прямокрылых. Этот эффект часто полностью сопоставим с
действием пожара. Такой процесс можно определить как
экологический резонанс. Резонансная динамика в целом весьма типична
и приводит к тому, что и без вмешательства человека
обширные территории периодически освобождаются от климаксной
растительности. Так как колебания климата на разных
территориях не полностью синхронны, и далеко не всякое
сообщество может быть уничтожено в данный конкретный момент
пожаром, то одновременно пожарами на обширных
территориях уничтожалось, по-видимому, не более 5-10%
растительного покрова.
В целом, пожары и/или вспышки фитофагов на каждой
территории, по-видимому, реализовались один раз в 200-500
лет и лишь в некоторых случаях чаще. Практически это было
типично для всей евразийской тайги и бореальной зоны
Северной Америки. Столь же нормальны пожары и в
африканской саванне.
Конечно, существуют условия, где пожары или
массовые размножения насекомых не типичны, но их обычно
заменяют или эпифитотии (массовые вспышки грибковых
заболеваний) в сочетании с действием ураганов или ветровалов.
Можно сказать, что для всей умеренной зоны Северного
полушария резонансные преобразования сообществ более
типичны, чем равновесные. То же, по-видимому, справедливо и
для сезонно-влажного климата тропических широт и, может
быть, резонансные преобразования сообществ не типичны
только для сообществ дождевых тропических лесов.
Пожары слабо прожигают почву, в результате чего
семена растений и многие почвенные беспозвоночные
существенно не страдают. В результате пожара или выедания
зеленой массы в почву поступает огромная масса удобрений, и
экологические условия становятся благоприятны, в первую
очередь, для светолюбивых видов с высокими требованиями к
минеральному питанию. Именно они первые и начинают ис-
113
попьзовать новые ресурсы и условия Часть этих видов в
семенах фактически находилась в исходном сообществе, часть,
обычно расселяемых ветром или животными, в большом ко-
пичестве попадает на освободившиеся территории.
Обычно на первой стадии выигрывают травяные
растения, но среди них могут выжить отдельные особи
светолюбивых деревьев и кустарников Комплекс пионерных видов
весьма обширен, и его видовое богатство, особенно богатство
травяных и кустарниковых растений, очень велико.
Конкретный видовой набор в каждом конкретном случае определяется
и характером нарушения поверхности и механическим
составом почвы, ее влажностью и микроклиматом, текущими
погодными условиями.
Каждая популяция имеет свой естественный цикл.
Будучи практически одновозрастной. она почти одновременно
стареет, резко снижает свою продуктивность и
конкурентоспособность и пропускает в сообщество популяции видов с более
длинным периодом развития, которые существовали в
угнетенном состоянии Так, пионерные травяные виды сменяются
кустарниковыми, кустарниковые -fc пионерными древесными,
пионеоные древесные - теневыносливыми и т.д. В результате
сообщество развивается в направлении создания климаксной
структуры.
Первая травяная стадия обычно не превышает 5-10
лет, вторая - 10-20, третья - 80-100 и стадия перехода к
климаксу 300-400 лет.
Число стадий, перечень сменяющих друг друга
растений зависит от исходного видового богатства и разнообразия
условий среды. В целом создается впечатление, что
восстановление сообществ после экологических резонансов идет по
достаточно устойчивой схеме и потому прогнозируемо. В
какой-то степени это действительно так, поскольку катастрофа
для отдельных сообществ не является катастрофой для их
обширных территориальных объединений. Как
катастрофические, неравновесные преобразования на уровне парцелл
внутри сообщества не нарушают его общего равновесного
состояния так и разрушения на больших площадях не
нарушают регионального равновесиях Но и на этом более
обширном пространственном уровне многие преобразования не
предсказуемы и существенно зависят от начальных условий.
114
Здесь на обширных территориях могут возникать устойчивые
комбинации видов, которых ранее не было, хотя условия и
возвращаются к исходным. В сходных условиях могут
возникать качественно различные, но равновесные и устойчивые
сообщества.
Рассмотренные выше преобразования растительности
принято называть сукцессиями. В соответствии с
определяющим их фактором они могут быть пирогенные, зоогенные. кли-
матогенные и т п. В общем случае сукцессии сообществ есть
продукт экологического резонанса, в частном случае - прямого
разрушения (лавины, сели и т.п.). В природе одновременно
действуют и равновесные, и неравновесные, вынужденные
преобразования сообществ, однако роль последних, по-
видимому, все-таки более значительна. При этом
неравновесность преобразовании относительна: неравновесные
преобразования в микромасштабе есть необходимое условие
равновесия в мезомасштабе и т.д.
Контрольные вопросы:
Опишите суть автохтонной (внутренние факторы,
собственные колебания) динамики сообществ.
Опишите механизмы алло/тонной (внешние факторы,
вынуждающие силы) динамики.
Рассмотрите эффекты взаимодействия автохтонных и
аллохтонных процессов и порождаемые ими эффекты.
IX. ПРЕДСТАВЛЕНИЕ О БИОЛОГИЧЕСКОМ
РАЗНООБРАЗИИ
Разнообразие вообще, и биологическое разнообразие
в частности, - понятие с большой семантической нагрузкой В
его основе лежит отображение феномена существования
множества объектов которые по форме, функции или другим
свойствам можно рассматривать как практически не
различимые друг от друга.
Такая совокупность объектов заменяется общим для
них всех образом. При этом объекты, принадлежащие к
разным образам, хорошо отличимы друг от друга Если говорить о
числе таких образов, то естественно применять термин мн*
115
гообразие. Если к тому же оценивать масштабы различия
образов, то соответственно правильнее говорить о
разнообразии.
Само понятие образ прямо связано с умением людей
классифицировать объекты внешнего мира. Сама же
возможность таких классификаций и их огромное значение для
упорядочения объектов и событий внешнего мира позволяют
полагать, что в природе реально существуют относительно
однородные множества объектов, хорошо отличимые от других,
по крайней мере, по некоторым признакам.
Факт существования объектов, отображаемых через не
пересекающиеся друг с другом образы, говорит о
дискретности природы. Если рассматривать природу в динамике, то
это значит, что в фазовом пространстве, образованном
всеобщими, мировыми, переменными, в процессе эволюции
могут формироваться различные, изолированные друг от друга
области равновесного, или устойчивого, состояния живого
вещества с различными структурой и организацией.
Человек в своей практической жизнедеятельности
строит свои отношения с внешним миром, определяя
принадлежность его проявления к тем или иным фиксированным
образам, с учетом их свойств и полезностей. При этом в
зависимости от целей и существующего знания одни и те же
природные объекты, используя различные признаки, можно
классифицировать самым различным способом. С другой стороны,
любые объекты, относимые к одному образу при любом
способе его выделения, в конечном итоге, все-таки отличаются
друг от друга. Но эти отличия таковы, что при принятых
условиях наблюдения или измерения выделение дискретных
образов невозможно. В этом случае изменения свойств признаков
на множестве объектов трактуются как непрерывные.
Амплитуда этих изменений может быть различна; чем больше, тем
соответственно больше и изменчивость.
Понятие изменчивость близко к понятию
разнообразие, но применимо в большей степени к свойствам или
явлениям, имеющим непрерывную природу.
Существуют, и весьма часто, ситуации» когда образы
не замкнуты относительно друг друга и частично
пересекаются, иначе говоря, размыты. В этом случае в равной степени
могут рассматриваться и разнообразие, и изменчивость. Меж-
116
ду разнообразием и изменчивостью нет абсолютной границы.
Ч.Дарвин в основе видообразования усматривал изменчивость
как непрерывное преобразование формы и функций во
времени. С позиции современной неравновесной термостатики,
теорий бифуркаций и катастроф формообразование может
происходить и скачкообразно, то есть дискретно во времени и
пространстве.
Понятие разнообразие отражает фундаментальные
свойства мироздания. В качестве формальной его основы
можно рассматривать теоретико-множественную топологию,
обобщающую отображение в мышлении человека этого
свойства окружающего нас мира.
Если в предыдущих разделах система представлялась
в основном через соотношение частей, параметры которых в
процессе преобразований обычно оставались неизменными
или изменялись по какому-либо принятому закону, то, говоря о
разнообразии, сразу же имеем в виду, что система состоит из
множества элементов, свойства которых в процессе
преобразований остаются неизменными. Следовательно, здесь речь
идет о статистическом ансамбле элементов, и
подразумевается, что число этих элементов исчисляется десятками тысяч. В
частном случае элементами являются особи, конкретные
организмы, которых мы на основе общности измеряемых свойств
относим к одному классу или на основе различий - к разным.
Формальные представления заставляют считать, что
наше текущее восприятие разнообразия никогда не может
отображать реального разнообразия окружающего мира.
Более того, в процессе эволюции человеческого общества
воспринимаемое и осмысливаемое им разнообразие постоянно
увеличивается. Соответственно наше восприятие
разнообразия всегда условно. И эта условность определяется нашими
знаниями, средствами наблюдения и их целями.
Итак биоразнообразие есть множество различающихся
образов живого вещества реального мира при принятых
условиях наблюдения.
Наиболее общепринятое понимание экологического
разнообразия (ecological diversity) связывается с двумя
компонентами: видовое богатство, или разнообразие (variety) как
число объектов разного сорта на единицу пространства или к
общему объему выборки, и как относительное обилие индиви-
117
дуумов каждого сорта (Odum ЕР 1989). По наиболее
общепринятой точке зрения биологическое разнообразие может
рассматриваться как " терминологический зонтик для
обозначения разнообразия природы, включающего в себя все виды
животных, растений и микроорганизмов, экосистем и
протекающих в них экологических процессов. При этом можно
выделить три различных уровня: генетическое разнообразие,
видовое разнообразие и разнообразие экосистем.
Генетическое разнообразие есть сумма генетической информации,
содержащейся в генах всех особей растений, животных и
микроорганизмов, обитающих на земле. Видовое разнообразие
обозначает количество (variety) видов, живущих на земле... . К
разнообразию экосистем относится количество разных (variety)
местообитаний, биотических сообществ и экологических
процессов...''
В зависимости от условий биоразнообразие
рассматривается на множестве морфологических свойств (виды, роды
и т.п. систематические категории), функциональных свойств
(жизненные формы), генетических свойств, биохимических
свойств, на уровне объединения различных форм в
пространстве и во времени (сообщества) и т.п. Во всех случаях
рассматривается или подразумевается число образов,
различая (дистанции) между ними и их представительность в
системе.
Когда идет речь о биологических системах возникают
вполне законные вопросы: Зачем природе столько разных
видов? Почему не могла возникнуть некоторая универсальная
биологическая система? Ответы на них в какой-то мере дает
теория информации.
Выше было показано, что специализация уменьшает
ошибки в канале связи и. следовательно, повышает
надежность работы системы что ни одна система не может
одновременно перерабатывать разнокачественную информацию,
поступающую из независимых источников Все это требует и
приводит к возникновению разнокачественных элементов,
различающихся по своим функциональным возможностям. С
другой стороны, с позиции теории информации можно
показать, что такие специализированные системы должны быть
дискретны
ИХ
Сущностью функционирования биологических систем,
на каком бы уровне их ни рассматривали, является
самовоспроизводство на основе преобразования вещества, энергии и
информации. В общем случае понятие "информация" может
включать в себя вещество и энергию.
Для того чтобы обеспечить свое выживание, система
должна определенным образом и с определенной скоростью
осуществлять преобразование информации. Преобразование
осуществляется по некоторым правилам. Каждое
элементарное правило можно определить как алгоритмическую
операцию. Число алгоритмических операций в секунду, которые
реализует система, можно определить как
производительность. Кроме того, система должна уметь запоминать и
количество единиц информации, запоминаемых в секунду, есть
скорость запоминания. Наконец, система с некоторой
скоростью должна передавать информацию.
Допустим, что наша система состоит из абсолютно
одинаковых элементов. При увеличении числа элементов N
растет общее время прохождения информации через систему.
Но время передачи информации t через всю систему должно
быть много меньше длительности одной алгоритмической
операции Т. В противном случае, неизбежно возникает
путаница в вычислениях, и появляются, и накапливаются ошибки и
искажения.
Отсюда следует, что число эффективно работающих
элементов в такой многосвязанной системе должно
удовлетворять требованию T»t.
Если считать, что в популяции длительность одной
алгоритмической операции составляет год, то время передачи
какого-либо сигнала, например, изъятия некоторого числа
особей из популяции, должно быть на порядки меньше. Здесь
в качестве аналогии удобно представить деревню с ее
примитивной системой передачи информации и всегда
ограниченными размерами. Современные большие города могут
существовать только на основе высоких скоростей передачи
информации, но их размеры естественно ограничены. При
превышении этих размеров город начинает испытывать
серьезные трудности, и в нем возникают внутренние относительно
автономные структуры или развиваются соответствующим
образом средства коммуникации.
119
Можно представлять информационную систему как
простой ретранслятор, где каждый элемент потенциально
связан с любым другим. Если система имеет форму шара, то
ее приемлемый радиус оценивается
R- = rN3/(bv2),
где г - константа, зависящая от физических и функциональных
свойств элементов; v - объем системы; b - константа,
изменяющаяся в диапазоне 0,5-2.
Если реальное R»R», то наступает информационный
коллапс, система поглощает информацию, но не выдает ее.
Обычно при R>R* она делится на 2 подсистемы. Наглядным
примером такой ситуации является снежный ком,
скатываемый из липкого снега. Достигнув определенных размеров,
зависящих от липкости снега (различные значения г), он обычно
распадается на два.
Таким образом, любая система, передающая или
преобразующая информацию, имеет конечные оптимальные
линейные размеры и неизбежно дискретна.
Это в равной степени справедливо и для
молекулярного, и для клеточного, и для тканевого уровней, для органов,
организмов, объединений организмов в клоны, семьи, стаи,
популяции, сообщества. На разных уровнях организации
системы образуются по принципу переработки информации или
по принципу ретранслятора. В первом случае дискретность
имеет более строгий характер, во втором - существует
намного более широкий диапазон допустимых размеров, но во всех
случаях ограничения существуют.
Конечно, если в сообществе популяции полностью не
зависимы, между ними нет обмена информацией, то
ограничения на размер сообществ отсутствуют. В этом случае будет
иметь место непрерывная смена видов. Но такое соотношение
никогда полностью не может быть реализовано, и
соответственно ограничения размеров сообществ по каким-либо
характеристикам неизбежны.
Точно так же дискретны и виды как системы
популяций, находящихся в условиях генетического обмена. При этом
размер ареала вида будет во многом определяться при
прочих равных условиях подвижностью особей, а в очень
большом ареале неизбежно будут возникать генетически
различные структуры.
120
Итак, разные образы, объединяющие сходные и
генетически близкие элементы, возникают как следствие
неизбежной и необходимой для обеспечения выживания
специализации, а число элементов, принадлежащих к ним, ограничено
возможной интенсивностью преобразования информации
между элементами и интенсивностью взаимодействия с
окружающей средой.
Из сказанного следует, что биологическое
разнообразие - весьма абстрактное понятие, отображающее
фундаментальное свойство организации макромира живого вещества.
Являясь продуктом его развития, оно не может не влиять на
такие свойства, как устойчивость живого вещества и его
функционирование.
С прагматических позиций биологическое
разнообразие можно рассматривать как характеристику качества живого
вещества как ресурса. Действительно, с одной стороны, чем
больше биологическое разнообразие в пределах какой-либо
территории, тем больше вероятность обнаружить объекты с
особо ценными свойствами, обладающие большой
потенциальной полезностью для человека. С другой стороны, чем
больше разнообразие, тем при прочих равных условиях
требуется более сложная, "разнообразная" стратегия
использования живого вещества в целом.
Имея в виду, что полезность для человека разных
видов растений и животных далеко не открыта, естественно
стоит задача и сохранения биологического разнообразия как
ресурса.
В качестве примера прагматического значения
биологического разнообразия можно привести исследования
Н.И.Вавилова.
Н.И,Вавилов в 20-е годы текущего столетия поставил
гигантскую задачу создания коллекции семян культурных
растений и их прародителей всего земного шара, как
необходимой основы для селекционной работы и выведения новых
высокоценных сортов.
Вполне понятно, что решить эту задачу, объездив весь
мир, организуя случайный поиск, было невозможно.
Исходя из эмпирического опыта и умозаключений,
Н.И.Вавилов принял, что разнообразие может порождаться
только разнообразием. Следовательно, центры культурных
Ш
растений и их предков нужно искать в горных районах, но не
во всех, а расположенных в условиях границ климатических
зон и областей. Ну и, конечно, предпочтительно там, где
известны центры древних земледельческих цивилизаций.
Выделив на карте районы, отвечающие этим требованиям, он
определил центры гипотетического биологического
разнообразия культурных растений, которых оказалось совсем немного
(около 10). Туда он ездил сам и направлял небольшие
экспедиции. Всего за пятнадцать лет им была собрана коллекция
культурных растений, объем и качество которой блестяще
подтвердили его гипотезу.
Изучение и оценка роли биологического разнообразия
в функционировании экологических систем, использования и
охраны биоразнообразия как ресурса требуют разработки
методов его измерения. Любое измерение явно или не явно
опирается на некоторые модельные представления объекта,
объясняющие логические основы введения меры. В случае с
измерением разнообразия необходимо иметь в виду, что мы
имеем дело с очень большим ансамблем элементов N
(например, особей), каждый из которых может принадлежать к
одному из классов i. Каждому классу можно присвоить номера
1,2,3,..Д...к. При этом подразумевается, что количество
классов к - конечно.
Наши элементы, вступая друг с другом в различные
взаимодействия, могут образовывать группы с различным
числом, сочетанием и последовательностью. Какие именно
труппы реализуются в природе, нам неизвестно, и поэтому
остается допустить реализуемость любых.
Тогда в пределах одного класса i с числом элементов
n(i) может быть реализовано n(i)! перестановок, а общее
множество перестановок: к
I = n(1)!n(2)!n(3)k. .n(i)!..n(k)! = П n(i)!
i=1
Очевидно, это очень большое число, экспоненциально
растущее от числа классов. Поэтому целесообразно привести
его к линейному виду операцией логарифмирования. Тогда
log I = N(-H + log-N),
^ k
U = -SUM p(i) log p(i), p(i) = n(i)/N,
где p(i) - доля участия элементов класса i в системе, Н -
энтропия.
На практике мы обычно не можем пересчитать все
множество элементов N и используем для оценки некоторую
достаточно большую выборку.
Следовательно, чтобы сравнивать измерения для
различных систем, желательно взять меру, не зависящую от
объема выборки. Такой мерой, очевидно, является Н.
В теории информации Н называют
неопределенностью, так как она характеризует насколько неопределенно
наше априорное суждение об отнесении любого произвольно
взятого элемента к конкретному классу; в термодинамике та
же мера называется энтропией, и она характеризует
внутреннюю неупорядоченность системы или неупорядоченность
внутренних превращений А. По сути дела, эти понятия
подобны. Таким образом, неопределенность может
рассматриваться как мера разнообразия, отражающая число различаемых
классов и распределение по ним элементов.
Если вероятности принадлежности элементов всем
классам равны, то
Hmax = log к.
При фиксированном числе классов Нтах -
максимальное разнообразие.
Если принять Нтах в качестве нормы, то получаем еще
одну меру (выравненности распределения элементов по
классам).
Е = Н/Нщах-
Эта мера позволяет сравнивать разнообразие систем с
разным числом выделяемых классов. Это очень важно, так как
часто классы выделяются весьма условно (например, классы
сообществ).
С другой стороны, эта мера показывает, насколько
выравнено распределение: при Е=1 распределение
максимально выравнено. Если мы предполагаем, что
функционирование системы как-то зависит от ее структуры, то такая оценка
весьма полезна.
J(i) = -log p(i),
еще одна мера, которую называют мерой неожиданности
события, или его информативностью. Неожиданность тем боль-
I23
ше, чем реже наблюдаются элементы, принадлежащие классу
j, что соответствует интуитивному восприятию смысла этого
слова. Предлагаем читателю самому обсудить вопрос: почему
редкие события более информативны.
Суммарная средняя информативность может быть
определена как
J = - (1/k)SUM log p(i).
Эта мера по смыслу близка к выравненности, но более
чувствительна к числу редких классов.
Таким образом, различные аспекты разнообразия
отображаются различными мерами.
Если допустить, что статистический ансамбль
элементов равновесен, то после соответствующих преобразований
энтропии можно получить теоретическое распределение
элементов по классам. При этом первым будет считаться класс,
имеющий наибольшее число элементов, вторым - класс,
имеющий меньшее число, и, вообще:
p(1)>p(2)>p(3)>...p(i)>p(i+1)>p(k).
Такие распределения принято называть ранговыми
(табл. 8).
Таблица 8
Примеры ранговых распределений
Метрика (dr)
(SUM|x(i)-y(i)|2)1/2
[SUM|lnx(i)-lny(i))2]1/2
[SUM|lnx(i+d)-lny(i+d))2]1/2
[SUM|lnlnx(i)-lnlny(i))2]1/2
Вид p(i)
с (exp(-bi))
cib
с (i+d)b
cA(iA-b)
Название
Гиббса
Ципфа
Ципфа-
Мандельброта
Мак-Артура
Можно утверждать, что системы самой разнообразной
природы - от электронов до лингвистических текстов, если они
рассматриваются как ансамбли элементов, принадлежащих к
различным классам, - описываются такими распределениями.
Ранговым распределениям подчиняется распределение видов
организмов по родам, родов по отрядам; распределение
видов по доли участия в сообществе, распределение сообществ
по типам и т.д.
124
Вид распределения зависит от того, какова
генеральная форма зависимости объектов от условий среды. Видом
зависимости объекта от ресурсов и условий среды фактически
определяется метрика пространства (рис. 20).
1 h
V
-2
а
с -8
-11
-И г
1 1 1 1 1 1 1 1 1 1 1 1 1 * 1 f 1 I 1 1 --I » 1
: :2^ %V Vi.
' * * * i ' ' l * ' * t * ' • * ' * ¦ * ' ' '
2
In(i)
Рис. 20. Три варианта реальных ранговых распределений доли участия (p(i))
вида i-ro ранга по фитомассе для травяного яруса разных вариантов
сосновых лесов (2,3) и на месте вывала в дубовом лесу (1) на
высокой пойме в Окском заповеднике. Отношения представлены в
логарифмической шкале. Ранговые распределения (1, 3)
мультипликативного типа (распределения Ципфа), (2) - экспоненциального типа
(распределения Гиббса).
Наиболее высокая температура (минимальный наклон графика) и
соответственно наибольшее разнообразие характерно для травяного
сообщества дубового леса (1). Минимальная температура отмечается
для травяных сообществ сосняков в сухих местообитаниях (2) и
средняя для сосняков в мезофитных условиях (3). В целом, чем лучше
условия развития травяного яруса, тем выше его термостатическая
температура
125
Параметр Ь в термостатике называется темперой, а
1/Ь - есть температура. На рис. 19 приведены реальные
ранговые распределения для травяных сообществ.
Чем "положе" ранговое распределение видов в
сообществе, тем выше его "температура".
При фиксированном объеме выборки N легко
определить, сколько различимых классов элементов можно
наблюдать в сообществе. Обратим внимание на то, что p(i) = n(i)/N.
В пределе в равновесном сообществе должен
существовать класс самого меньшего ранга к, состоящий всего из
одного элемента и соответствующий рангу к.
Тогда для первого типа рангового распределения
получаем:
1 = N-c(exp(-bk));
k>g1=log(N.c)-bk;
к = 1/Ыод (N-c).
Допустим, что исследование сообществ
осуществляются путем подсчета видов на пробных площадках
фиксированной площади, и нас интересует, как изменяется
число видов в связи с увеличением площади опробования.
Так как на каждой площадке в среднем имеется m особей
различных видов, а обследована L площадок с площадью s, то
общая обследованная площадь есть
А = Ls, N = A*m.
Следовательно, зависимость числа видов от площади
будет
k = 1/b «log A) + log (m-c)) = d + 1/b (log A).
При втором типе рангового распределения:
k = d-A1/b.
Прежде чем эти зависимости были выведены
теоретически и прежде чем стала понятна их природа, они были
получены в рамках изучения зависимости числа от площади в
островной биогеографии и при изучении выявления как функции
числа проб.
Показатель 1/Ь, обычно обозначаемый как z, есть
прямой аналог температуры и он же может рассматриваться как
важный показатель разнообразия при фиксированном числе
видов на единицу площади. Сравнивая z различных
соседствующих сообществ, можно определить примерные
интенсивности обменов между ними.
126
На рис. 21 приведена типичная зависимость числа
видов от площади.
Nsp = 6,35 Area
0,38
21 F
18
15
ft
ё
12
9
6 h
1 1 » 1 1 1 I 1 1 1
1 1 1 1 . 1
L
I .
h '
1 У
rvr
/ :
/
. #• • .-:
1 i i i 1 i ¦ i 1 » » i 1 1
А У
•»*
Л^Щ
>**r !
• i H
: : \
\ 1 \
iii i i i i i i i i i i ¦ и i i i 11 i i i 1
0
8 12 16
NPIot {0,25 m2)
ze
Рис. 21. Типичная зависимость числа видов от площади опробования для
травяного сообщества сосновых лесов. Дополнительные линии сверху и
снизу от центральной линии графика - доверительные интервалы,
определяющие область допустимых случайных отклонений
наблюдаемых данных от расчетных. Число 6,35 - среднее число видов на
четверть квадратного метра
Зависимости числа видов от площади широко
используются при первых оценках целесообразности организации
охраняемых территорий, для чего стремятся выбрать объекты
с большим значением г. В этом случае на малых территориях
удается сохранить большое число видов, которые
потенциально способны расселяться на сопредельные территории.
Все рассмотренные выше соотношения справедливы
для равновесных или стационарных условий.
127
Если система нестационарна, то реальные ранговые
распределения отличаются от теоретических. Мерой этого
отличия принимается энтропия Кульбака - мера
неупорядоченности реальной неравновесной системы с ранговым
распределением p(i), относительно равновесного (стационарного)
Р(«)ст
Hk = SUM p(i) log [p(i)CT/p(i)].
Свойства энтропии Кульбака:
1.) Hk>0 - всегда больше или равно 0;
2.) dHk/dt<0 - скорость приближения к равновесию
стремиться к нулю.
Время, необходимое для перехода системы в
стационарное состояние, пропорционально ехр(Нк). Очевидно, чем
ближе система к точке равновесия, тем медленнее ее
изменения, а при больших Hk можно ожидать очень быстрые
преобразования.
С другой стороны, для поддержания системы в
нестационарном состоянии требуется постоянный подвод к ней
извне энергии, вещества, информации - в количествах,
пропорциональных энтропии Кульбака.
Рассмотренная модель оказывается весьма полезной
при количественных исследованиях структуры реальных
экологических систем и позволяет распространить на
биологические системы многие важные результаты, полученные в
теории неравновесной термодинамики. Хотя экологи имеют
достаточный опыт измерения разнообразия и построения
ранговых распределений, однако только в самое последнее время
осуществляются попытки содержательной, теоретически
осмысленной трактовки результатов.
Теория, в частности, подсказывает, как разнообразие
может влиять на способность экологических систем
производить работу, например, создавать биологическую продукцию?
Как в среднем разнообразие должно изменяться во времени?
Каковы будут направления миграций видов между соседними
сообществами? Почему мы стремимся сохранять редкие виды
и, вообще, почему столь обычен интерес к редким событиям
или, как говорят журналисты, к "жареным (горячим) фактам"?
Попробуйте ответить на эти вопросы, опираясь на основные
положения общей экологии, и проиллюстрировать их
примерами.
I
ЗАКЛЮЧЕНИЕ
Популяция любого вида имеет собственную частоту
колебаний, определяемую принадлежностью его к
функционально-трофической группе, эволюционным возрастом,
размерами особей. Параметры популяций зависят от условий и
ресурсов среды, пространства и времени. Совокупность
популяций разных видов, заселяющих единую территорию,
образует сообщество. В рамках сообщества наиболее тесные
взаимодействия возникают между популяциями с близкими
частотами собственных колебаний. Между функционально
сходными видами возникает конкуренция, исходом которой
является или независимость, или взаимодополняемость видов
по градиентам среды во времени и пространстве.
Независимость обеспечивается, в первую очередь, за счет различной
чувствительности разных видов к одноименным ресурсам и
условиям среды, минимизация конкуренции - за счет
взаимодополнения видов по градиентам среды. В частном случае
противоречия разрешаются путем образования межвидовых
коалиций. Существенные различия видов по отношению ко
времени и пространству приводят к формированию
относительно независимых подсистем сообщества. Популяции,
принадлежащие различным подсистемам, могут вступать в
жесткие взаимодействия в локальные моменты времени в ходе
развития всего сообщества. Большую же часть времени и, в
целом, в пространстве они относительно независимы друг от
друга.
Виды, находящиеся в отношениях типа "хищник -
жертва", образуют цепи питания, по которым осуществляется
трансформация вещества и энергии. Эти потоки определяют,
в конечном итоге, круговорот вещества, обеспечивающий
стабильность всего сообщества во времени. Этот аспект в полной
мере будет рассмотрен на экосистемном уровне.
Динамика каждой популяции определяется
собственной частотой колебаний и воздействиями периодически и
апериодически флуктуирующих ресурсов и условий среды. Меж-
популяционные взаимодействия определяют частоты
собственных колебаний частей сообществ и сообщества в целом.
Таким образом, динамика сообщества определяется его
собственными параметрами и действием внешних сил. Периоди-
\2Ч
чески изменяющиеся внешние условия при близости периодов
их изменения к собственным периодам колебания сообществ
могут приводить и приводят к резонансным, по своей природе
неравновесным, нестационарным преобразованиям,
полностью или частично разрушающим сообщество. Ход процесса
восстановления разрушенных сообществ в существенной
степени зависит от начальных условий: то есть от конкретных
условий среды, запаса семян, окружения. Относительно
ограниченный исходный набор видов в региональном окружении
сообщества приводит к ограничению возможных траекторий
его саморазвития, что, однако, не исключает и значительной
многовариантности.
В целом, совокупность видов региона стремится
разместиться по отношению к ресурсам, условиям среды, друг к
другу во времени и пространстве таким образом, чтобы
максимально использовать все имеющиеся ресурсы и условия.
Такое взаиморазмещение в каждом частном случае и в целом
является результатом межвидовых взаимодействий видовых
популяций во времени и пространстве, возможности которых в
заданных условиях определяются их собственными
параметрами.
Дальнейшее усложнение экологических конструкций
связывается с рассмотрением системы отношений популяций
и сообществ с системой абиотических факторов в различных
пространственно-временных масштабах, определяемых
параметрами видов, образуемых ими сообществ и изменением
этих параметров в ходе саморазвития.
ЛИТЕРАТУРА
Основная
1. Бигон М., Харпер Дж., Таунсенд К.
Экология. М.: Мир, 1989. Т.1. 667 с; Т.2, 472 с.
2. О д у м Ю. Основы экологии. М.: Мир, 1975. 740 с.
3. О д у м Ю. Экология. М.: Мир, 1986. Т.1, 328 с; Т.2,
375 с.
4. П и а н к а Э. Эволюционная экология. М.: Мир,
1981.396 с.
5. Рифлекс Р. Основы общей экологии. М.:
Мир, 1979. 423 с.
6. Чернова Н.М., Б ы л о в а А.М. Экология. М.:
Просвещение, 1988, 269 с.
Рекомендуемая
А б р о с о в Н.С., Боголюбов А.Г. Экологические
и генетические закономерности сосуществования и
коэволюция видов. М.: Наука, 1988. 297 с.
А б р о с о в Н.С., Ковров Б.Г., Черепанов О.А.
Экологические механизмы сосуществования и видовой
регуляции. М.: Наука, 1982. 298 с.
Вольтера В. В. Математическая теория борьбы за
существование. М.: Наука, 1976. 285 с.
Д ю в е н ь о П., Т а н г М. Биосфера и место в ней
человека. М.: Прогресс, 1968. 251 с.
Жизнеспособность популяций /Под ред. М.Сулея, М.:
Мир, 1989. 222 с.
3 о т и н А.И., Владимирова ИГ.,
Кирпичников А.А. Энергетический метаболизм и направление
эволюционного прогресса в классе млекопитающих // Журнал общей
биологии, 1990. Т.51, № 6. 760-768 с.
Коли Г. Анализ популяции позвоночных М.: Мир,
1979. 361 с.
Свирежев ЮМ. Нелинейные волны, диссипа-
тивные структуры и катастрофы в экологии М Наука 1987.
366 с.
13 I
Свирежев Ю.М., Логофет Д.О. Устойчивость
биологических сообществ. М.: Наука, 1978 352 с.
У а т т К. Экология и управление природными
ресурсами. М.: Мир, 1971. 463 с.
Федоров В.Д., Г и л ь м а н о в Т.Г. Экология. М.:
Изд-во Моск.ун-та, 1980. 458 с.
Шмидт-Ниельсен К. Размеры животных:
почему они так важны? М.: Мир, 1987. 258 с.
О d u m E.P. Ecology and our endangered life-support
systems Sinauer Associates, Inc. Publishers. Sunderland.
Massachusetts, 1989. P. 1-283.
McNeely J.A., Miller K.R., R e i d W.V., M i t -
t e r m e i e r R.A., Werner T.B. Conserving the world's
biological diversity / IUCN. WRI. CI. WWF-US. The World Bank.
Gland. Switzerland. Washington DC. 1990. P. 1-191.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
I. ПУТИ СТАНОВЛЕНИЯ ЭКОЛОГИИ 5
II. ОСНОВЫ ТЕОРИИ ПОПУЛЯЦИИ 17
III. БАЗОВЫЕ АЛЛОМЕТРИЧЕСКИЕ ЗАВИСИМОСТИ
ПАРАМЕТРОВ ПОПУЛЯЦИЙ ОТ РАЗМЕРОВ
ОСОБЕЙ 33
IV. ЗАВИСИМОСТЬ СВОЙСТВ И СОСТОЯНИЯ
ПОПУЛЯЦИИ ОТ ОКРУЖАЮЩЕЙ СРЕДЫ 40
V. ПРЕДСТАВЛЕНИЯ О СООБЩЕСТВЕ 62
V.1. Хищничество и паразитизм 64
V.2. Симбиоз, содружество, коалиция 67
V.3. Антагонизм, конкуренция, соперничество 68
V.4. Независимость двух совместно существующих
видов 73
V.5. Аменсализм и коменсализм 74
VI. ДИНАМИКА ПОПУЛЯЦИЙ С ПОЗИЦИИ ТЕОРИИ
КОЛЕБАНИЙ 76
VI.1. Свободные колебания 76
VI.2. Представления о формировании волн в
пространстве 79
VI.3. Вынужденные линейные колебания 81
VII. ОБЩИЕ ПРИНЦИПЫ ОРГАНИЗАЦИИ
СООБЩЕСТВА 87
VII.1. Основные положения 87
VII.2. Горизонтальное сообщество 90
VII.3. Вертикальные сообщества 102
VIII. ОБОБЩЕННОЕ ПРЕДСТАВЛЕНИЕ О
СООБЩЕСТВЕ И ЕГО ДИНАМИКЕ 105
IX ПРЕДСТАВЛЕНИЕ О БИОЛОГИЧЕСКОМ
РАЗНООБРАЗИИ 115
ЗАКЛЮЧЕНИЕ 129
ЛИТЕРАТУРА 137
Ш
УЧЕБНОЕ ИЗДАНИЕ
Пуэаченко
Юрий Георгиевич
ОСНОВЫ ОБЩЕЙ ЭКОЛОГИИ
Редактор Л.С.Горюнова
Н/К
ЛР№ 040414 от 27.03.92.
Подписано в печать 30.09.96.
Формат 60x90/16. Бумага офсетная. Офсетная печать.
Уч.-изд.л.7,16 Усл.печ.л. 8,5 Тираж 300 экз. Заказ 546.
'Заказное.
Ордена Знак почета' Издательство Московского университета.
103009, Москва, ул. Б. Никитская, 5/7.
Отпечатано в ЛИК МГУ.
119899, Москва, Воробьевы горы. МГУ им. Ломоносова,
географический факультет.