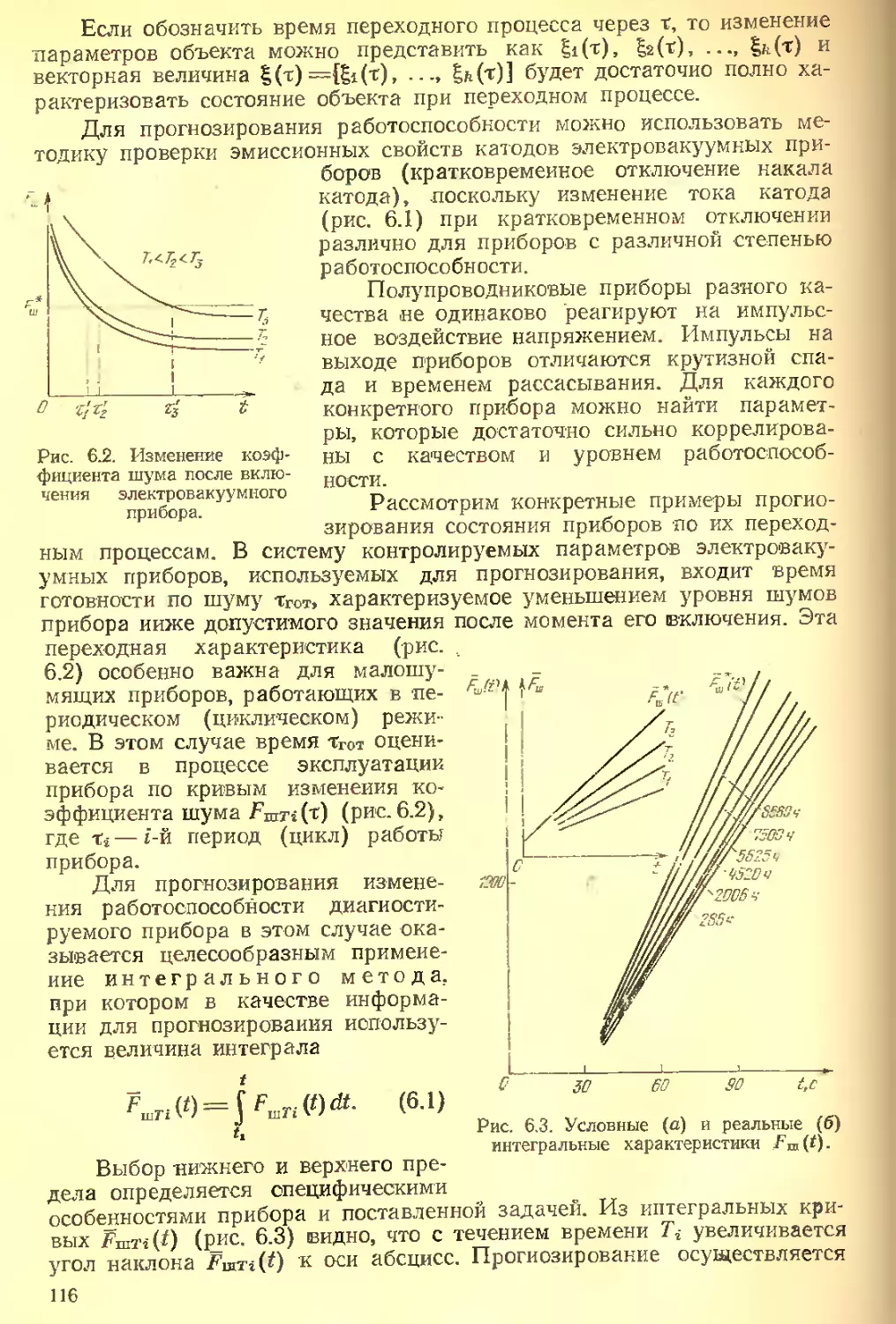
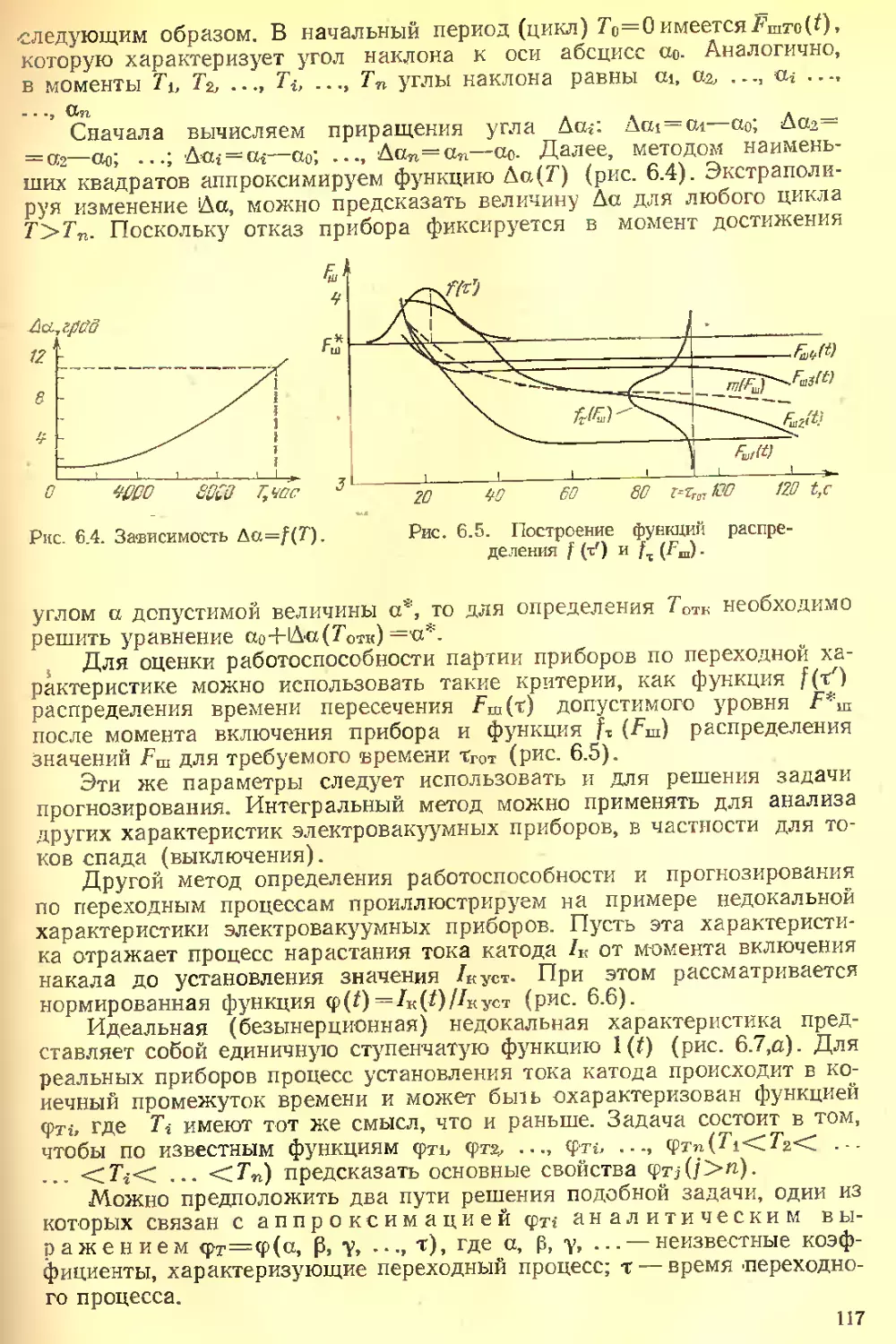
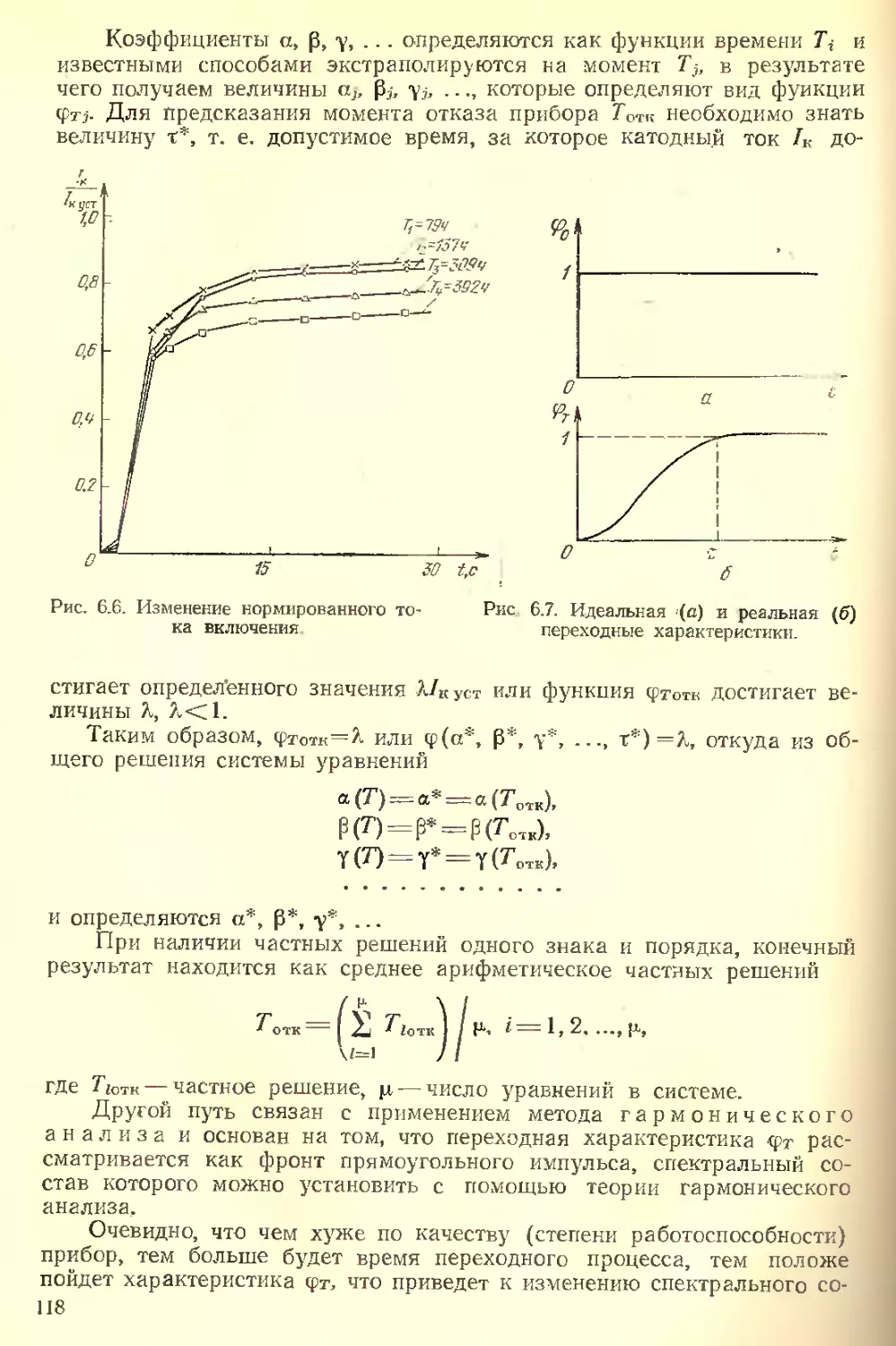
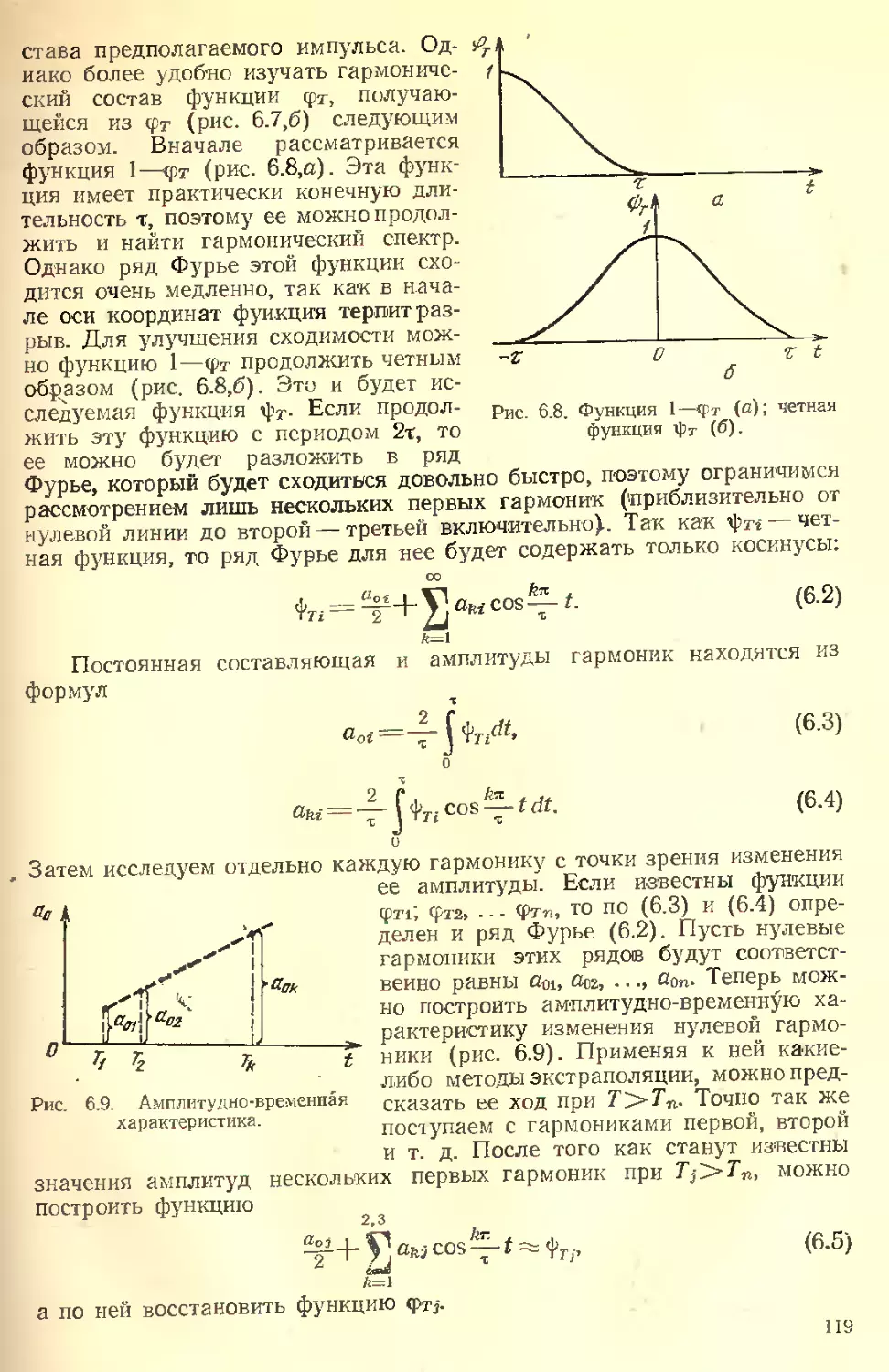
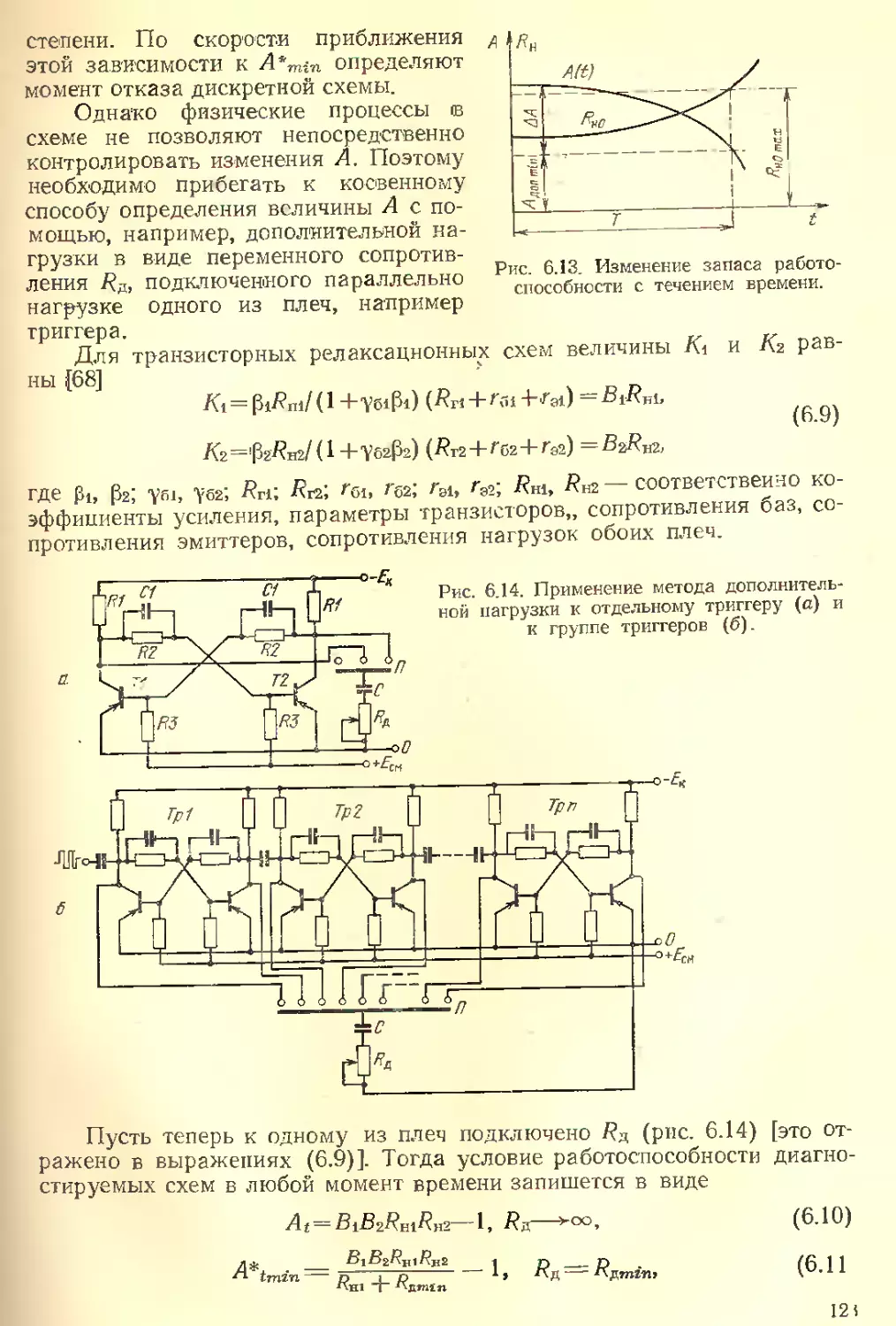
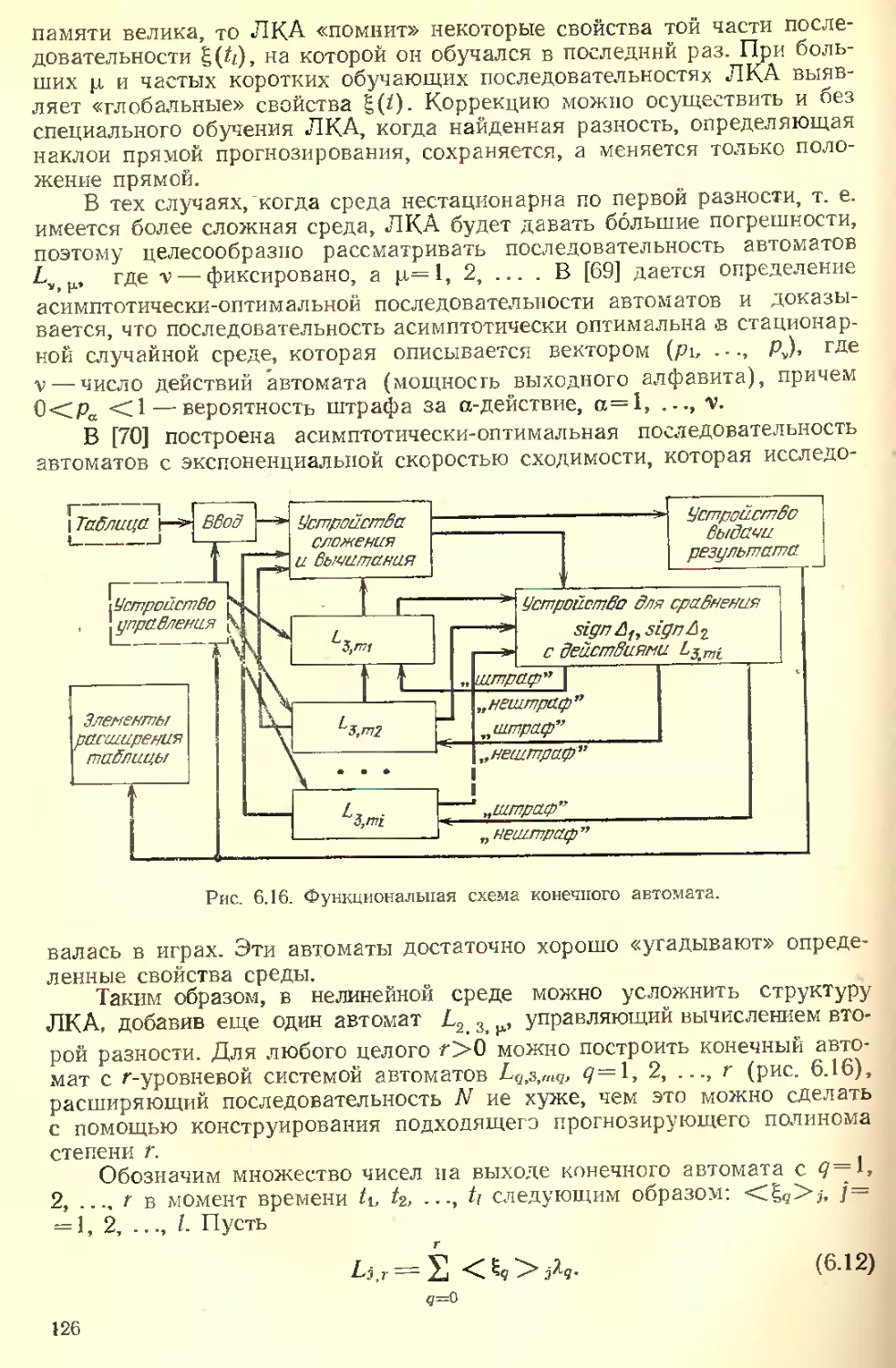
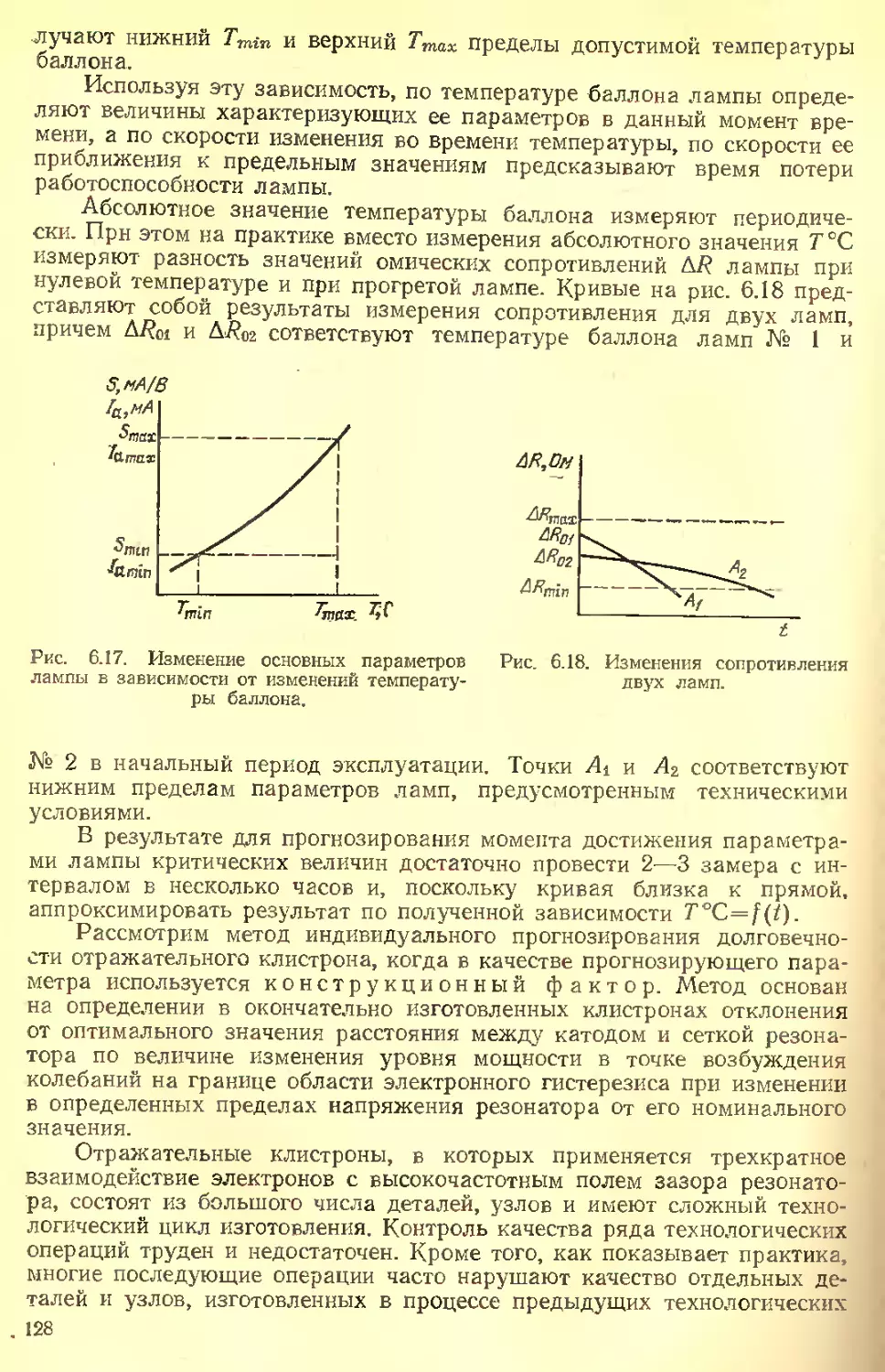
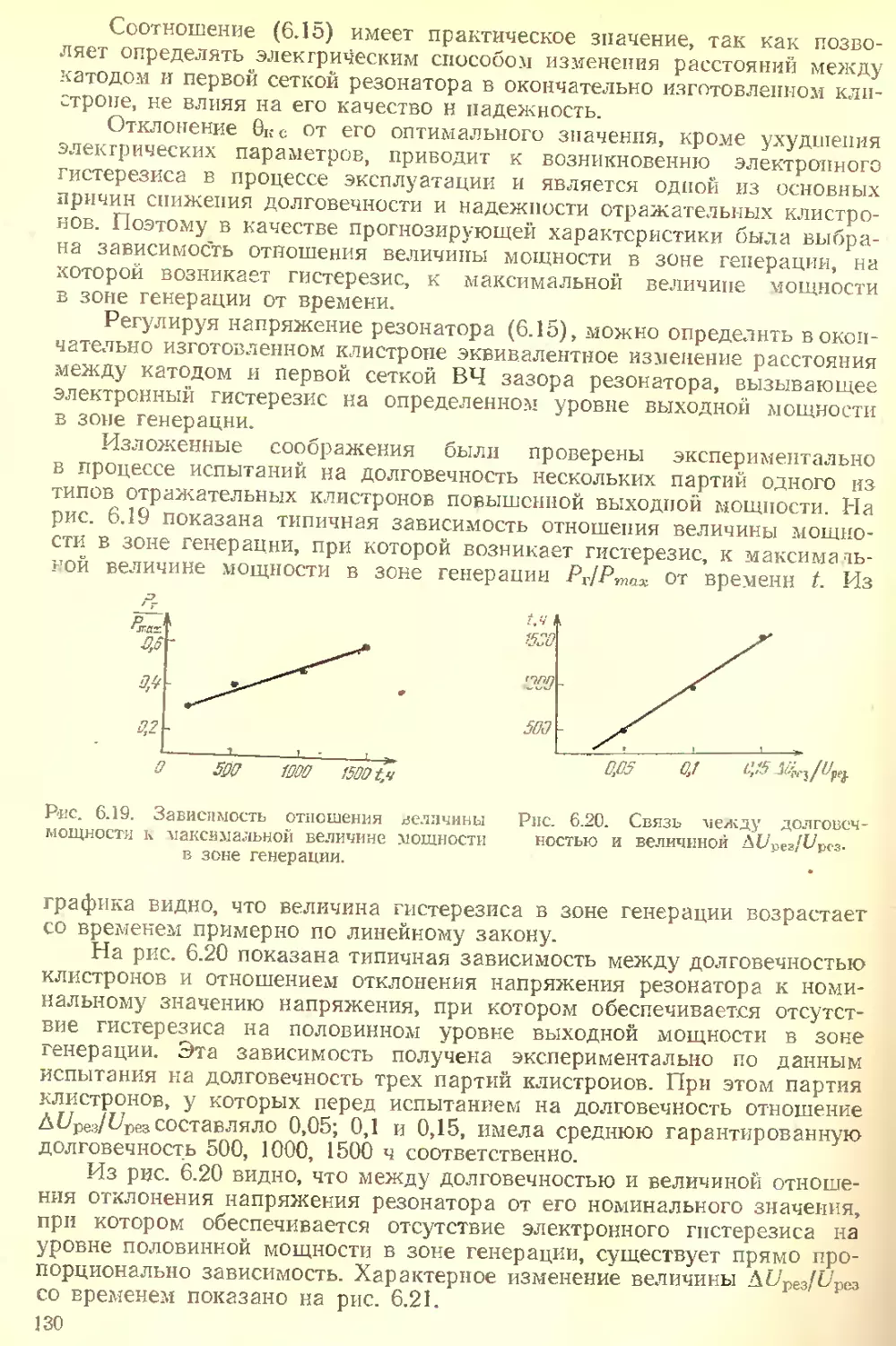
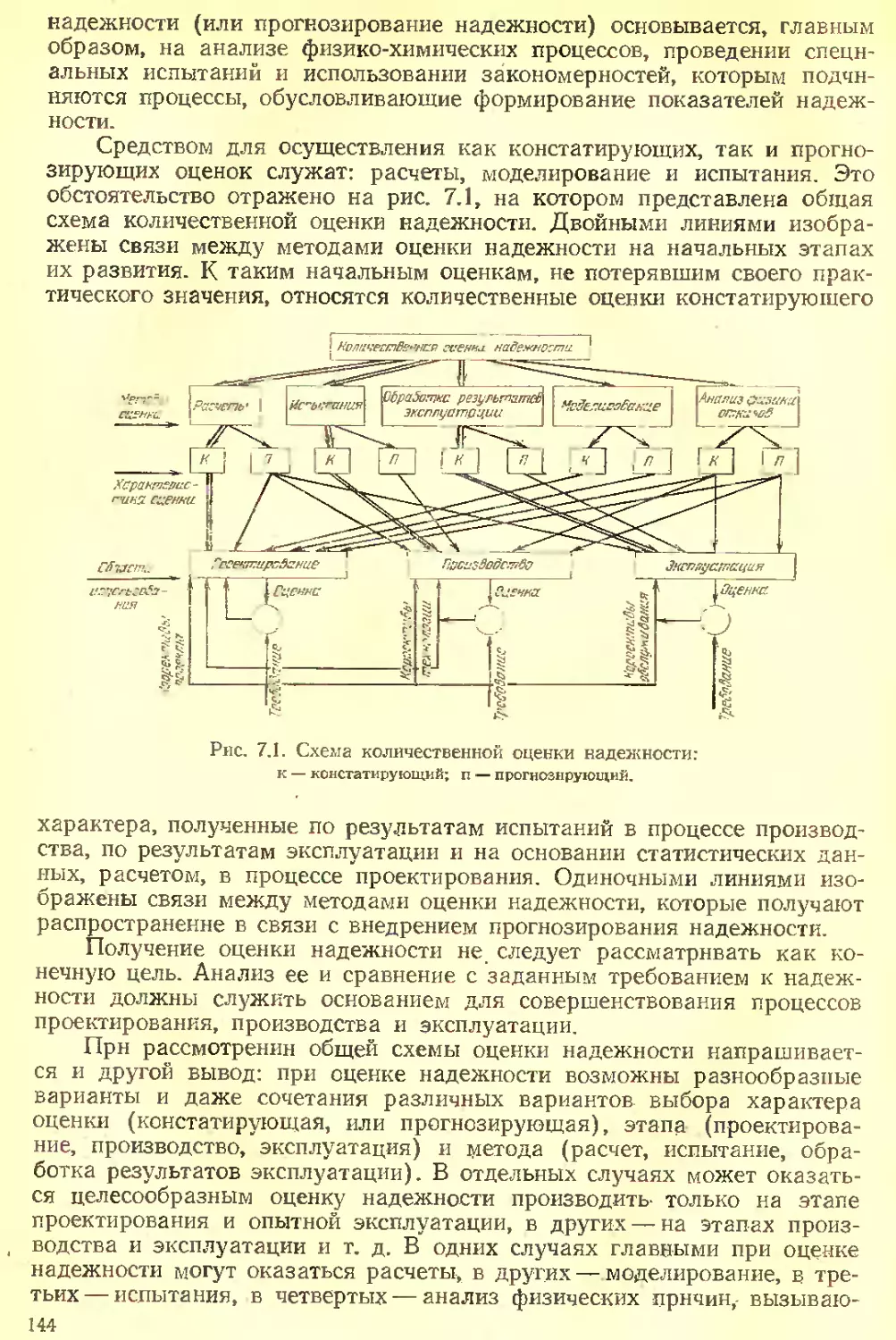
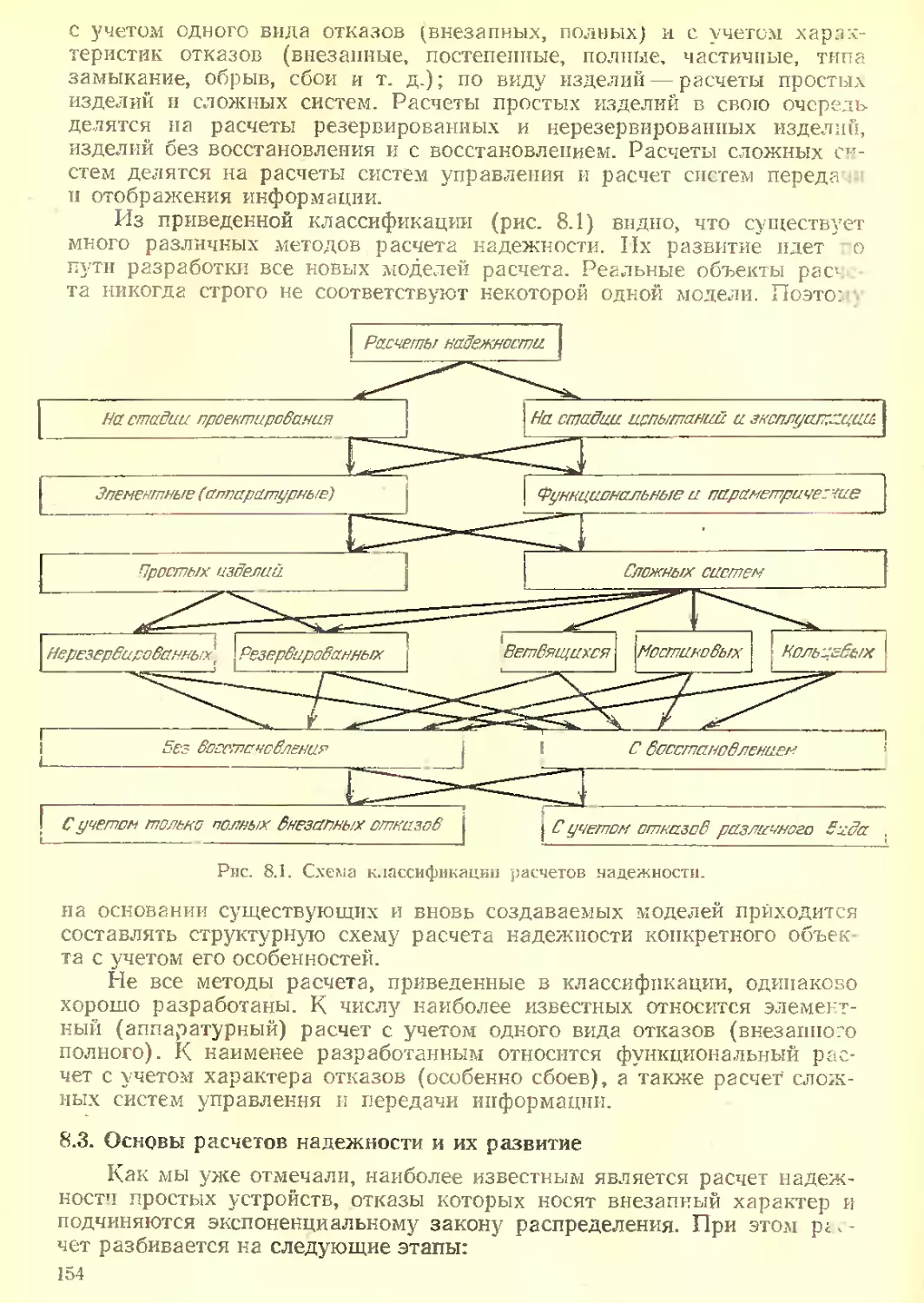
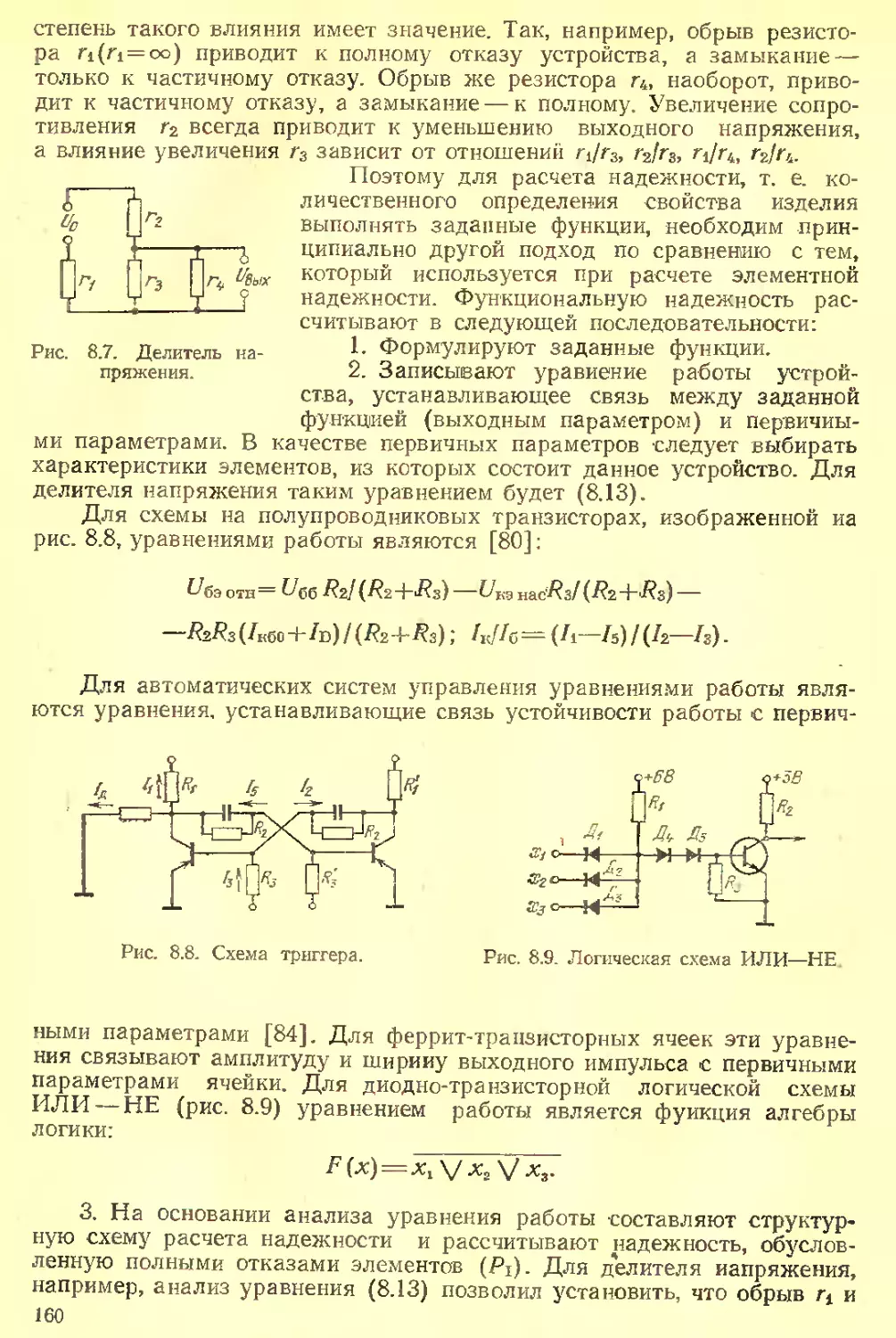
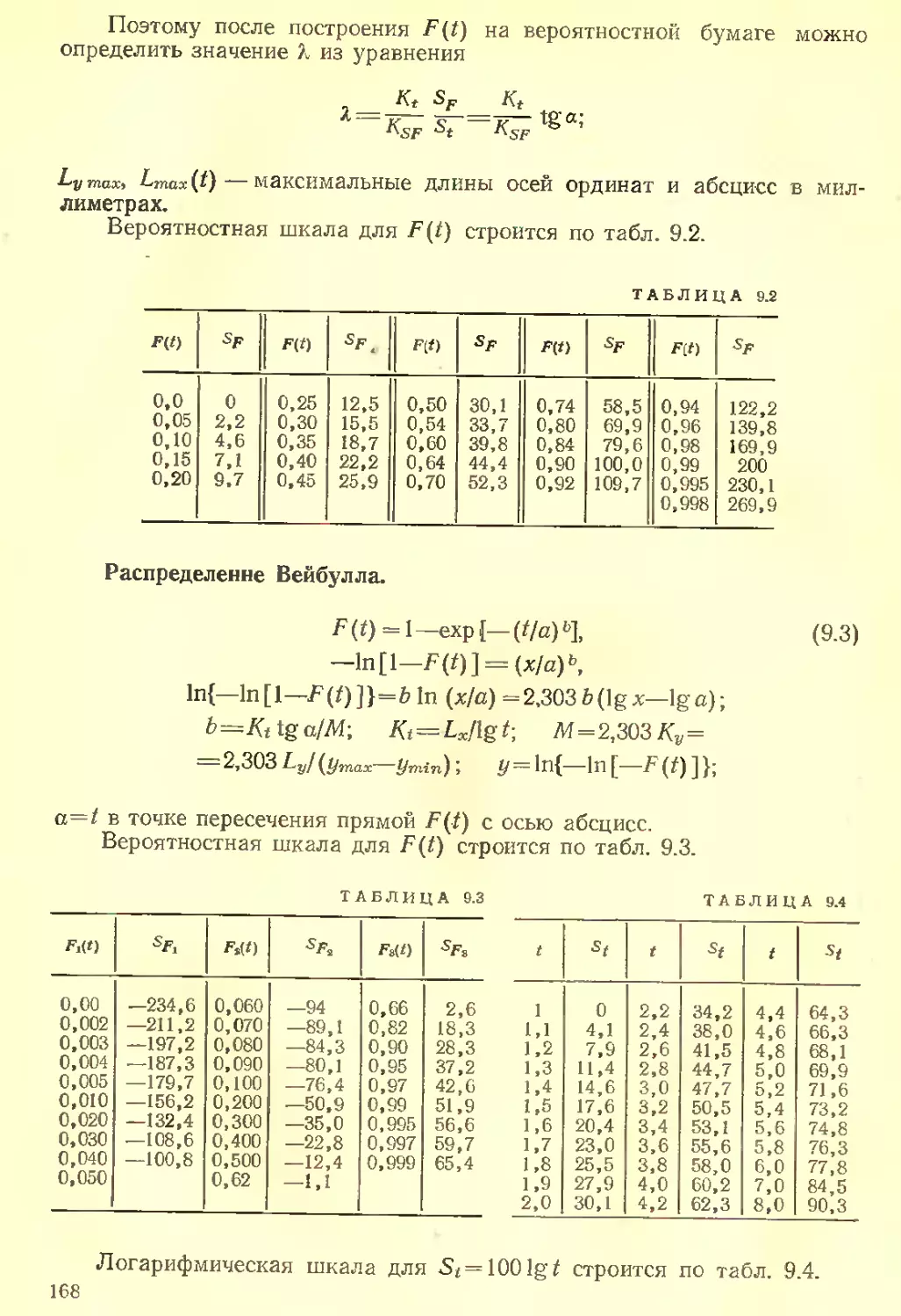
Текст
ПРОГНОЗИРОВАНИЕ
ТЕХНИЧЕСКОГО
СОСТОЯНИЯ
И НАДЕЖНОСТИ
РАДИОЭЛЕКТРОННОЙ
АППАРАТУРЫ
Д. В. Гаскаров
Т. А. Голинкевич
А.В. Мозгалевский
ПРОГНОЗИРОВАНИЕ
ТЕХНИЧЕСКОГО
СОСТОЯНИЯ
И НАДЕЖНОСТИ
РАДИОЭЛЕКТРОННОЙ
АППАРАТУРЫ
Под редакцией доктора технических наук,
профессора Т. А, Голинкевича
МОСКВА «СОВЕТСКОЕ РАДИО» 1974
6.Ф
Г 22
УДК 621.3.019
Гаскаров Д. В., Голинкевич Т. А., Мозгалевский А. В. Прогнозирование технического состоя-
ния и надежности радиоэлектронной аппаратуры. Под ред. Т. А. Голинкевича М„ «Сов, радио»,
1974, 224 с.
Излагаются общие основы прогнозирования, используемый математи-
ческий аппарат, наиболее распространенные методы прогнозирования и
примеры их применения при анализе радиоэлектронной аппаратуры. Рас-
смотрены вопросы обработки информации, методы аналитического прогно-
зирования многомерных процессов, вероятностное прогнозирование и про-
гнозирование на основе распознавания образов, Большое внимание уде-
ляется вопросам анализа надежности радиоэлектронной аппаратуры и
автоматизации процесса прогнозирования,
Книга рассчитана на широкий круг специалистов, работающих в обла-
сти проектирования и испытаний радиоэлектронной аппаратуры, и может
быть полезна специалистам других областей техники.
Рис. 108, табл. 21, библ, 101 назв.
Редакция радиотехнической литературы
30405-085
046 (01)-74 3>74
© Издательство «Советское радио», 1974 г.
Предисловие
Вопросы прогнозирования технического состояния изделий привле-
кают все большее внимание специалистов различных отраслей техники
2 в нашей стране и за рубежом. Это вызвано тем, что в связи с возра-
стающей ролью автоматических и автоматизированных систем возрас-
тает значение предвидения их состояния. Без предвидения нельзя
управлять состоянием системы, нельзя своевременно предупреждать
аварийные ситуации.
Теория прогнозирования технического состояния радиоэлектронной
аппаратуры находится в состоянии становления и развития. Многое
в ней еще не определилось и не сформировалось. Она располагается
=а стыке ряда научных дисциплин и теорий, таких, как теория надеж-
ности, техническая диагностика, основы технических измерений и дру-
гях
Прогнозирование технического состояния непосредственно примы-
кает к теории надежности, так как главная цель его заключается в свое-
временном обнаружении неблагоприятного состояния системы (изделия)
з разработке рекомендаций, которые, в конечном счете, направлены на
повышение его надежности и эффективности. Вот почему в данной кни-
ге объединены в одно целое вопросы прогнозирования технического
состояния аппаратуры и прогнозирования ее надежности. Есть все осно-
вания предполагать, что в дальнейшем развитии теории надежности
вопросы прогнозирования должны занять одно из главных мест.
Использование теории и методов прогнозирования для анализа
надежности изделий создает возможность существенно повысить эффек-
тивность оценки надежности их на различных этапах разработки, из-
готовления и эксплуатации (сокращение объема и времени испытаний,
повышение достоверности расчетов). К сожалению, применение методов
прогнозирования не получило еще достаточно широкого распростране-
ния в инженерной практике. Изданием данной книги делается попытка
содействовать этому распространению.
Естественно, что книга не может претендовать на рассмотрение
всех вопросов прогнозирования и па исчерпывающее изложение даже
отдельных из них. Целью ее является ознакомить широкий круг специа-
листов с основными положениями теории прогнозирования, показать
связь ее с другими родственными научными дисциплинами, привлечь
внимание к проблеме прогнозирования как к одному из главных разде-
лов современной теории надежности и сформулировать рекомендации,
которые могут быть полезными в инженерной практике.
Книга состоит из четырех частей. В первой части излагаются общие
вопросы и основы прогнозирования. Во второй части представлен аппа-
рат прогнозирования: расчетно-аналитического, вероятностного, осно-
3
ванного на теории распознавания образов, а также на теории случай-
ных процессов. В третьей части рассматриваются вопросы прогнозиро-
вания надежности на основе р .счетов, испытаний и моделирования.
В четвертой части излагаются вопросы автоматизации и устройства
аппаратуры для прогнозирования.
Гл. 1 написана совместно Т. А. Голинкевичем, А. В. Мозгалевским
и Д. В. Гаскаровым. Гл. 2, 3, 5 и 6 (кроме § 6.5), § 10.2—10.5 и § 11.2—
11.5 написаны Д. В. Гаскаровым, гл. 7—9 (кроме § 9.8) —Т, А. Голин-
кевичем, § 10.1 и 11.1—А. В. Мозгалевским. Гл. 4 написана совместно
А. В. Мозгалевским и Д. В. Гаскаровым, § 6.5 —Л. А. Крючковой,
§ 9.8 —В. А. Гаврилиной, § 11.6 —Е. Ф. Генераловым.
Авторы выражают глубокую признательность за ценные замечания
рецензентам книги: д-ру техн, наук Г. В. Дружинину и канд. техн, наук
А. С. Груничеву.
Книга, по-видимому, не лишена недостатков. Критические замеча-
ния читателей будут восприняты авторами с благодарностью. Их сле-
дует присылать по адресу: Москва, Главпочтамт, а/я 693, издательство
«Советское радио».
Часть I
ОБЩИЕ ВОПРОСЫ ПРОГНОЗИРОВАНИЯ
ГЛАВА 1. ОБЩИЕ ВОПРОСЫ И ОПРЕДЕЛЕНИЯ
1.1. Предварительные соображения
В процессе создания изделия, его производства и настройки, а так-
же подготовки к эксплуатации и самой эксплуатации очень важно уметь
определять его техническое состояние, т. е. знать, какими характеристи-
ками обладает изделие в данный момент времени. Эта задача решается
средствами обычного технического контроля, позволяющего получать
данные об измеряемых технических параметрах в момент нх измерения.
С появлением технических систем, выполняющих ответственные
функции, возрастает роль предвидения технического состояния в некото-
рый будущий отрезок времени, с тем чтобы можно было своевременно
принять меры по предотвращению отказов. В процессе развития тех-
ники возникла задача управления техническим состоянием больших си-
стем путем своевременного переключения на резерв, своевременного
перехода на новые рабочие режимы и т. п. Но управлять без прогнози-
рования ожидаемого состояния нельзя. Таким образом, новые этапы
развития техники вызвали к жизни новую техническую проблему —
проблему прогнозирования технического состояния..В качестве примеров
можно указать транспортные системы, системы управления производст-
венно-технологическими процессами и многие другие. Для таких изде-
лий важно установить не только то, что они исправны в данный мо-
мент времени (в период контроля), но и то, что они будут продолжать
оставаться исправными на протяжении некоторого будущего интервала
времени.
В дальнейшем оказалось, что прогнозирование технического состоя-
ния важно не только для периода эксплуатации, но и для периода про-
ектирования изделий и для процесса производства. При проектировании
следует высказать обоснованное предположение о технических харак-
теристиках, которыми будет обладать будущее проектируемое изделие.
В процессе производства по результатам испытаний ограниченного объ-
ема (малых выборок, небольших продолжительностях и т. д.) делается
предположение о технических характеристиках и работоспособности
больших партий на больших временных интервалах. По результатам
ускоренных испытаний делается прогноз о предполагаемом состоянии
"зделнй в нормальных условиях. Словом, и в процессе производства
н.-еет место прогнозирование технического состояния изделий.
Прогнозировать событие — значит предвидеть, предсказать будущее
событие на основании изучения таких факторов, от которых оно зави-
сит или которые ему сопутствуют. Научное прогнозирование основыва-
ется на изучении объективных закономерностей, которым подчиняются
интересующие нас процессы и события. При этом используются две
группы закономерностей:
— закономерности случайных событий или вероятностные (стоха-
-тические);
5
— закономерности детерминированные.
При прогнозировании события можно выделить два характерных
подхода к решению поставленной задачи:
— прогнозирование будущего состояния данного события на осно-
вании изучения закономерности изменения данного события;
— прогнозирование будущего состояния данного события на осно-
вании изучения другого события (или группы других событий), связан-
ного с данным.
Все сказанное о прогнозировании в общем плане имеет непосред-
ственное отношение к прогнозированию технического состояния и на-
дежности изделий. Техническое состояние изделия определяется значе-
нием технических параметров, от которых зависит его работоспособ-
ность: коэффициентов усиления, выходного напряжения, входного со-
противления, чувствительности, мощности, производительности, точно-
сти и т. д. Изменение этих параметров обычно вызывается многими
причинами, поэтому исключается возможность установить однозначную
связь между изменением параметра и причинами, вызывающими такое
изменение.
Прогнозирование надежности, основанное на наблюдении прямых
или косвенных прогнозирующих параметров, позволяет исследовать на-
дежность конкретных изделий в процессе их работы. Это обстоятельст-
во приобретает особую важность для-изделий, которые изготавливаются
в небольшом числе экземпляров и выполняют ответственные функции.
Для них может оказаться совершенно недопустимой ориентация на
оценку надежности по числу зафиксированных отказов, так как глав-
ным требованием может быть предупреждение отказов.
Прогнозирование технического состояния и надежности можно
осуществлять на различных стадиях создания и использования изделий:
на стадии проектирования, производства и эксплуатации. На этих ста-
диях математические основы прогнозирования сохраняются общими,
однако конкретные методики и алгоритмы различны. На стадии про-
ектирования изделий исходными данными являются предполагаемые
характеристики проектируемого изделия, рабочие режимы и предпола-
гаемые условия работы. Целевая направленность прогнозирования на
этом этапе — создание конструкции, которая наилучшим образом удов-
летворяет предполагаемым условиям работы. На стадии эксплуатации
изделий исходными данными являются предполагаемые закономерности
изменения технических параметров реального изделия. Целью прогно-
зирования технического состояния при эксплуатации является своевре-
менное предупреждение отказов и применение таких рабочих условий
и обслуживания изделий, которые наилучшим образом отвечают зада-
че обеспечения заданной надежности и эффективности.
1.2. Основные направления прогнозирования
На принцип прогнозирования влияют различные факторы, но основ-
ные из них — совокупность имеющихся параметров, целевая направ-
ленность поставленной задачи и рабочий алгоритм.
Совокупность прогнозируемых параметров £2, .. In, определяю-
щих состояние аппаратуры, можно представить различным образом:
значениями параметров в моменты времени /, распределениями пара-
метров, комплексными показателями и т. д.
е
Процесс прогнозирования преследует различные цели. Он позволяет
определить: 1) протекание процесса на протяжении будущего отрезка
времени в конкретной размерности; 2) ожидаемую вероятность того,
что исследуемый процесс не выйдет за установленные допусковые гра-
ницы; 3) к какому классу по долговечности следует отнести исследуе-
мый процесс. В зависимости от прогнозируемых параметров и целевой
направленности прогнозирования выбираются имеющиеся методы и ма-
тематический аппарат.
Сформулируем задачу прогнозирования, подходя к этому с позиции
первого направления. Пусть контролируемый процесс, характеризую-
щий состояние, можно представить в виде многомерной функции Q(gi,
-а, .., |й), которая наблюдается в период времени от 0 до tn, вследст-
вие чего известны значения этой функции Q(/o), Q(M, ..., Q(M соот-
ветственно в моменты времени to, Ц, .... Необходимо определить
значения этой функции Q(/n+i), Q(6h-2).СШп+m) в моменты време-
ни tn+2i . , tn+m^T‘2.
Подобную задачу можно решить как в явном виде, определяя непо-
средственно Q(£, /), так и косвенным путем, находя сначала каждый
параметр а затем уже Q(|, t). Подобная постановка задачи спра-
ведлива в предположении, что значения Q(|, to), Qfs, tn) предопре-
деляют величины Q(g, tn+i, ..., Q(|, /n+m); иными словами, что процесс
^информативен» во времени. Возможность подобного допущения зави-
сит от степени изученности прогнозируемого процесса, т. е. объема дан-
ных о процессе, полученных в период времени Ti от 0 до tn. Идеальным
случаем при этом является получение аналитического выражения для
функции состояния Q('g, t). Задачу прогнозирования в подобной поста-
новке можно решить различными методами, отличающимися применяе-
мым математическим аппаратом и называемыми методами аналити-
ческого прогнозирования.
Второе направление прогнозирования связано с определением ве-
роятности невыхода процесса за установленные ограничения. Эту зада-
-• можно сформулировать следующим образом: пусть известны значе-
ния параметров (5—1, 2, ..., k), полученные в моменты времени
ц’=0, 1, 2, ..., п), и в каждый момент ti функция состояния Q(£, ti)
годностью характеризуется функцией распределения F<(Q). Необходимо
гj известным значениям Q(£s, ti), Л(О), ... tn] вычислить
? n+J (е)=Р{1<Ж W-QHa)l<E},
где e=Q*(|s)- Qii(Bs), Qn(b) — номинальное (оптимальное), a Q*(|s) —
допустимое значение функции Q(g, t) в области tn+t ... tn+m для зна-
чений tn+3 (/=1, 2, ..., т). Методы, основанные на таком решении
задачи прогнозирования, назовем методами вероятностного п р о-
гпозирования.
Третье направление прогнозирования предусматривает отнесение
“озтролируемой (диагностируемой) аппаратуры к одному из временных
классов. Задача прогнозирования формулируется следующим образом:
пусть в момент времени t0 или в ограниченный начальный период вре-
мени получены значения параметров диагностируемой аппаратуры £i,
..., Ik, характеризующих функцию состояния Q(s). Необходимо по
совокупности параметров координат многомерной функции Q(|) при-
нять решение о принадлежности аппаратуры к тому или другому клас-
с} где могут быть параметрическими, временными и другими.
7
Множество и размер классов определяются специфическими технически-
ми особенностями прогнозируемой аппаратуры. Методы, основанные на
отнесении исследуемых объектов к одному из классов, будем называть
методами статистической классификации. В них использу-
ется аппарат теории распознавания образов.
В рамках указанных направлений существуют разновидности основ-
ных постановок задачи прогнозирования, которые получили название
способов прогнозирования. При этом наиболее часто используется пер-
вая группа способов, т. е. решается прямая (прямое прогнозирование)
или обратная (обратное прогнозирование) задача.
Прямое прогнозирование. В этом случае при аналитическом про-
гнозировании, предполагая наличие связей между характеристиками
процесса Q('gi, |2, ..U ^); *=0, 1, ..п и Q(gi, Ь, ..., Ь, 4+j);
tn+^T2-, /=!, 2, .m, причем Л IJ Т2, и получая из эксперимента или
расчетным путем значение Q(|s, ^), находят аналитическое выражение
зависимости
W=<p[Q& ML (1-1)
которое позволяет определить значение процесса для любого момента
времени tn+^T2\ /==1, 2....т.
Прн вероятностном решении задачи прямое прогнозирование преду-
сматривает получение зависимости, аналогичной (1.1):
[hi (У, hi(U... hiМ = [fu(Q)J, (1.2)
где — прогнозируемая вероятность; fц(Q), fti(?) — плотности
распределения вероятностей значений процесса Q н его координат
<Pi, — соответствующие функциональные зависимости, выражающие
характер связей.
Статистическая классификация позволяет также осуществить пря-
мую постановку задачи. При этом классы формируются как категории
не временное, а параметрические. Следовательно, для прямого прогно-
зирования в этом случае необходимо временное классы ... Л;
/?2т=7’1 ... Т2; ... трансформировать в параметрические
$1{:==(5ш ^12, , 5ife); ^2£=г(^21, 522, ... , ?2я),
где формируются на определенный дискретный момент времени,
обусловленный постановкой задачи.
Таким образом, сущность прямого прогнозирования заключается
в получении аналитических зависимостей вида (1.1) и (1.2) и вычисле-
нии характеристики процесса Q(g, t) или вероятности Р<М в области
'Л, или принятии решения об отнесении Q(g, t) к какому-либо парамет-
рическому классу соответствующему определенному tn+j-
Обратное прогнозирование. Идея обратной задачи заключается
в определении времени (долговечности нлн времени «жизни»
изделия), когда характеристика процесса Q(g, t) или вероятности P(Q)
достигают предельных значений, задаваемых наложенными ограниче-
ниями.
При аналитическом обратном прогнозировании в выражение (1.1)
вводится предельное значение Q*(|) и полученное уравнение решается
относительно tn+j='t*> т. е. находится в явном виде. Таким образом,
8
величину £*, как результат вероятностного обратного прогнозирования,
можно найти из следующего выражения:
P{|Qfe, ^)-Qh(|5)I<E}=P*(Q), (1.3)
где P*(Q)—допустимая вероятность нахождения функции Q в задан-
ной области.
При статистической классификации процессов и образовании времен-
ных классов /?х= 7'х_1... 7\(2= 1, 2,...) возникает задача, относящаяся
также к категории задач обратного прогнозирования, которые могут
быть решены методами теории распознавания образов. Примерами,
которые иллюстрируют необходимость решения обратных задач, может
служить определение долговечности, сроков профилактических работ,
сроков выполнения контроля и т. п.
Другая группа способов классифицируется по направлению аргу-
мента при осуществлении прогнозирования. Она объединяет три спосо-
ба, которые получили название прогнозирования вперед, в настоящем
и назад (генетическое).
Прогнозирование вперед. В подавляющем большинстве практиче-
ских случаев прогнозирование связано с определением состояния в по-
следующие значения аргумента в области будущих моментов времени,
т. е. на основе предыстории определяется предстоящая ситуация. В этом
случае для временного аргумента Q(i|, ti) и Q(g, tn+j) должно соблю-
даться условие: ... <jtn+m, т. е. аргумент всегда возрастает.
Такое прогнозирование можно определить как перспективное.
Прогнозирование в настоящем. Этот способ соответствует задаче
прогнозирования по множеству, сформулировать которую можно сле-
дующим образом. Пусть в результате контроля получена ограниченная
информация (выборка) {|}г о состоянии диагностируемого множества
(генеральной совокупности) {£}ь. Необходимо, зная состояние или свой-
ства (уровень качества, степень работоспособности и т. д.) {g}z, оценить
состояние всего множества {£}ь. В данном случае необходимо осущест-
вить экстраполяцию (распространение) свойств выборки на свойства
генеральной совокупности.
Прогнозирование назад. В некоторых случаях требуется оценить
процесс в прошлом по информации, полученной в определенный интер-
вал времени. Такие задачи возникают тогда, когда по техническим или
другим причинам нельзя определить величину Q(|, 0), а знание ее не-
обходимо. Отличие в решении подобных задач заключается в том, что
необходимо переставить местами области [0 ... tn} и [/«+1 ... tn+m\,
при этом значения аргумента не возрастают, а убывают. Подобная по-
становка задачи имеет много сходства с генезисом н поэтому удобно
назвать решение такого варианта задачи генетическим прогнозирова-
нием.
Принципиально важными для практики являются способы индиви-
дуального и группового прогнозирования.
Индивидуальное прогнозирование. Особенность решения подобной
задачи наиболее удобно объяснить на примере прогнозирования изме-
нения состояния технических изделий. В этом случае для получения
прогноза экспериментально исследуется функция состояния Q(g, t) ин-
дивидуального образца технического изделия в области Т{ и осуществ-
ляется оценка поведения этой функции в области Уз, причем, как и
раньше, Ti IJ Т2.
9
Групповое прогнозирование. При этом рассматривается целая груп-
па однородных процессов (например, изменение состояния целой группы
технических изделий), получаются и анализируются их статистические
характеристики (средние значения, элементы ковариационных матриц),
полученные в области Л.
Можно отметить еще один из подходов к решению задачи прогно-
зирования, который целиком основан на использовании определенных
эмпирических соотношений, полученных в результате изучения характе-
ра протекания некоторых физических процессов. Изменение во времени
физических процессов, происходящих в некоторых технических изде-
лиях, приводит к изменению отдельных физических величии или при-
знаков, которые могут наблюдаться визуально или вычисляться с по-
мощью простейших эмпирических соотношений. При достижении опре-
деленных значений этих величин принимается решение о качестве и на-
дежности изделия. К такому подходу относится, например, прогнозиро-
вание наступления отказов радиоэлектронной аппаратуры, основанное
на дифференцированном контроле тепловых режимов отдельных элемен-
тов аппаратуры по изменению цвета нанесенных на их поверхность
термоиндикаторных красок.
При всем принципиальном отличии указанных направлений их объ-
единяет единая цель: определение характера протекания процесса в бу-
дущем. Множество методов решения задачи прогнозирования имеет одну
общую идею: обнаружение экстраполяционных связей, существующих
между прошлым и будущим, между информацией о процессе в контро-
лируемый период времени и характером протекания процесса в после-
дующем. Очевидно, что характер экстраполяционных связей будет опре-
делять аппарат решения задачи прогнозирования, а от того, насколько
точно описаны рассматриваемые связи, будет зависеть точность прогно-
зирования. Поскольку эти связи могут быть детерминированными, ква-
зидетерминироваииыми, вероятностно-детерминированными и т. п., то
часто задачи более эффективно решаются при комбинировании методов
и математического аппарата различных направлений прогнозирования.
Так, достаточно перспективным является совместное использование ста-
тистической классификации и аналитического прогнозирования. Стати-
стическую классификацию можно рассматривать как «грубое» прогно-
зирование, определяющее временной класс обычно величиной в несколь-
ко тысяч часов, к которому относится диагностируемое изделие, а ана-
литическое прогнозирование указывает конкретную величину, например,
функцию состояния внутри соответствующего класса, т. е. уточняет ре-
зультат предварительного прогноза.
Успешность решения задачи прогнозирования зависит от ряда усло-
вий: объема и качества информации о прогнозируемом процессе; пра-
вильности формулировки задачи прогнозирования и обоснованности вы-
бора метода ее решения; наличия вычислительных средств и вычисли-
тельного аппарата для решения задачи в соответствии с выбранным
методом. Отсутствие любого из этих условий может сделать невозмож-
ным прогнозирование, Важнейшим из них является формулировка зада-
чи, так как она определяет требования к объему и качеству информа-
ции, математический аппарат и точность прогноза. Объем и качество
информации, естественно, обусловливают успех прогнозирования. Ин-
формация о прогнозируемом объекте (процессе) получается из резуль-
татов контроля. Контроль может быть непрерывным, периодическим и
однократным. Наибольшую информацию сообщает непрерывный кон-
10
троль, однако он требует специальной аппаратуры, встроенной
в объект.
Чаще всего применяется периодический (дискретный) контроль.
В этом случае информация поступает в моменты времени fo, Л, h, .tn
и весь объем ее при индивидуальном прогнозировании можно предста-
вить в виде двухмерной матрицы:
5s
^0 ?2 . . . it . . .
11 В10 111 112 » • • hi • « « 11 n
hl G22 • • » hi &2Л (1.4)
• • . - - « .
h с* &S0 1st 6s2 • ♦ • 1st . . Isn
h Sfco hl Ih2 hi . . . h«
Размер матрицы определяется условиями измерения и особенностя-
ми исследуемого объекта. Предельными случаями могут быть следую-
щие: s=k, i—О (количество объектов измерения равно k, а возможное
время измерения равно fo); s=l, i—n (количество объектов измерения
равно 1, а возможные времена измерений равны /0 • М- Требования
к точности прогнозирования и его достоверности определяют требова-
ния к размеру матрицы.
Качество информации играет не меньшую роль, чем ее количество.
Если каждый элемент матрицы будет получен с большой погрешностью,
то даже при большом объеме информации точность прогнозирования
может быть невысокой либо для обработки информации потребуются
специальные приемы фильтрации ошибок измерения и их сглаживания.
Современные методы прогнозирования основаны на использовании
большого числа различных математических теорий. К их числу отно-
сятся функциональный анализ, теория рядов, теория экстраполяции и ин-
терполяции, теория вероятностей и математическая статистика, теория
случайных функций и случайных процессов, корреляционный анализ и.
спектральный анализ, теория распознавания образов.
1.3. Показатели качества прогнозирования
Чтобы обосновать выбор того или другого метода прогнозирования,
необходимо иметь возможность количественно оценить его качество.
Каждый метод прогнозирования желательно сопровождать своим вполне
определенным значением показателя качества, изменяющимся в зави-
симости от формулировки задач и условий ее решения. Но это чрезвы-
чайно трудно. В каждом конкретном случае прогнозирования возможны
различные методы и каждый из них характеризуется не одним показа-
телем качества, а набором показателей, изменяющихся при изменении
формулировки задачи и условий ее решения. К числу наиболее важных
показателей качества прогнозирования относятся:
1. Точность прогнозирования Лт, которая характеризуется степенью
соответствия величины, полученной в результате прогноза, и величины
действительной. Она измеряется величиной ошибки Лер, равной разно-
сти между величиной tpnp, полученной в результате прогноза, и действи-
тельной, истинной величиной ф0:Дср=српр—ф0.
Если осуществляется вероятностное прогнозирование, ошибка Д<р
носит случайный характер и представляется двумя показателями: сред-
ним значением и дисперсией /)Д(р. В инженерной практике часто
бывает удобно оценивать точность прогнозирования возможным интер-
валом значений прогнозируемой величины (точность оценки) и вероят-
ностью того, что именно в этот интервал попадет истинное значение про-
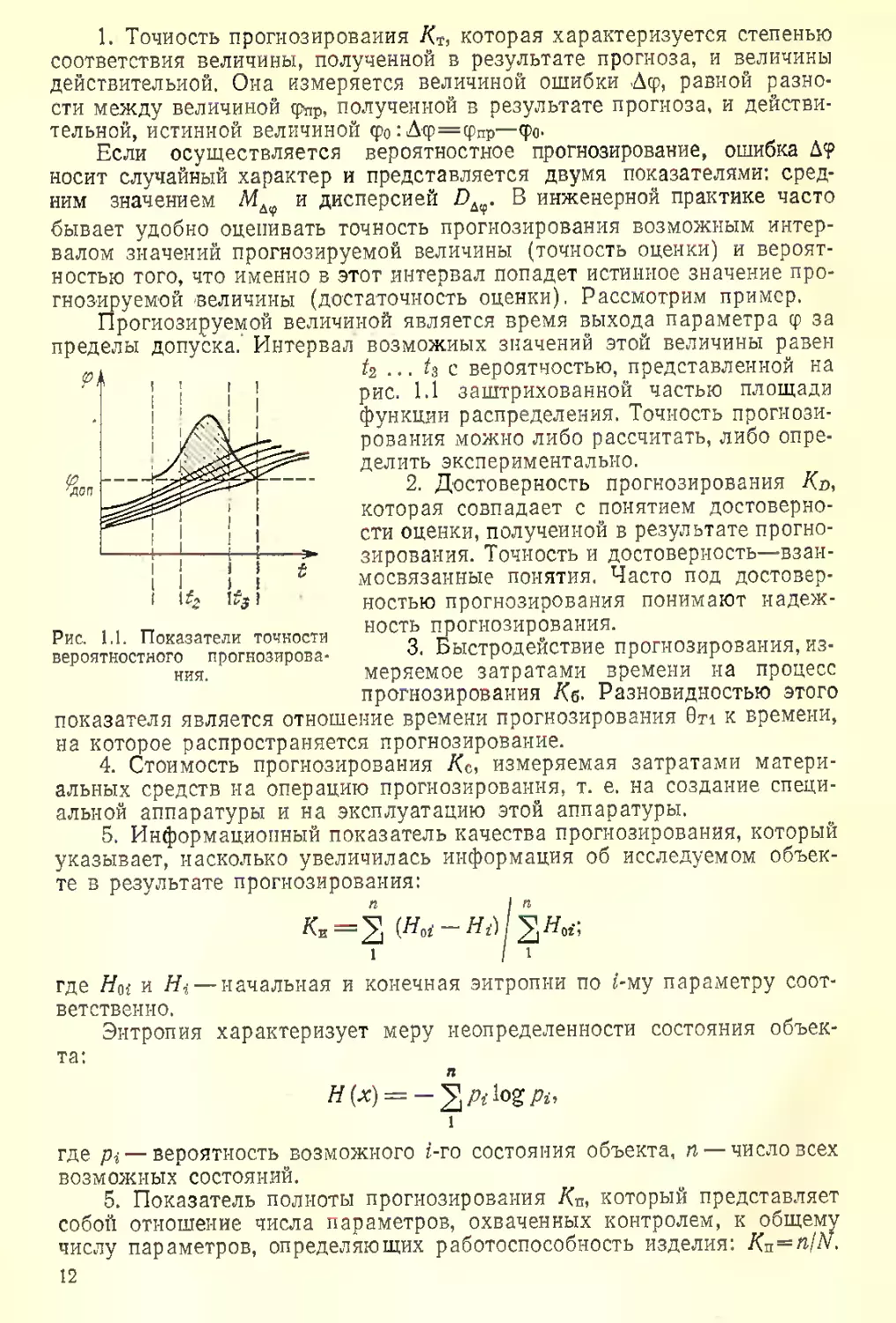
гнозируемой величины (достаточность оценки). Рассмотрим пример.
ой величиной является время выхода параметра ср за
Интервал возможных значений этой величины равен
Прогнозируем
пределы допуска.'
Рис. 1.1. Показатели точности
вероятностного прогнозирова-
ния.
t2 ... /3 с вероятностью, представленной на
рис. 1.1 заштрихованной частью площади
функции распределения. Точность прогнози-
рования можно либо рассчитать, либо опре-
делить экспериментально.
2. Достоверность прогнозирования Кл,
которая совпадает с понятием достоверно-
сти оценки, полученной в результате прогно-
зирования. Точность и достоверность—взаи-
мосвязанные понятия. Часто под достовер-
ностью прогнозирования понимают надеж-
ность прогнозирования.
3. Быстродействие прогнозирования, из-
меряемое затратами времени на процесс
прогнозирования Лб. Разновидностью этого
показателя является отношение времени прогнозирования 0п к времени,
на которое распространяется прогнозирование.
4. Стоимость прогнозирования Не, измеряемая затратами матери-
альных средств на операцию прогнозирования, т. е. на создание специ-
альной аппаратуры и на эксплуатацию этой аппаратуры.
5. Информационный показатель качества прогнозирования, который
указывает, насколько увеличилась информация об исследуемом объек-
те в результате прогнозирования:
п I п
Ки=2 (Hoi-Hi)
1 / 1
где Нщ и Hi — начальная и конечная энтропии по г-му параметру соот-
ветственно.
Энтропия характеризует меру неопределенности состояния объек-
та:
п
1
где pi — вероятность возможного г-го состояния объекта, п — число всех
возможных состояний.
5. Показатель полноты прогнозирования Кп, который представляет
собой отношение числа параметров, охваченных контролем, к общему
числу параметров, определяющих работоспособность изделия: /G = n//v.
12
6. Показатель эффективности прогнозирования который пока-
зывает, насколько улучшились эксплуатационные характеристики ис-
следуемого изделия в результате прогноза, и является обобщенным по-
казателем качества прогноза. Смысл показателя /G будет различным
для различных объектов. В случае, когда целью прогнозирования явля-
ется повышение надежности объекта, показателем эффективности будет
абсолютное, либо относительное изменение показателя надежности
в результате прогноза. В частном случае это может быть относительное
изменение коэффициента готовности изделия Кэ= (Кгг—Ян)/Ян,
Время восстановления т существенно сокращается при проведении
прогнозирования и поэтому Кт2 может становиться близким к единице,
а относительный показатель эффективности будет тем больше, чем мень-
ше начальное значение коэффициента готовности /<ri.
ГЛАВА 2. ИНФОРМАТИВНЫЕ АСПЕКТЫ ПРОГНОЗИРОВАНИЯ
2.1. Представление и первичная обработка информации
сложную функцию, включаю-
X
Рис. 2.1. Схематическое изображе-
ние влияния воздействующих фак-
торов на состояние диагностируе-
мого объекта.
Во время работы технические изделия испытывают воздействия мно-
жества внешних и внутренних факторов. В этом случае изменения па-
раметра представляют собой структурно <
щую ряд составляющих.
Пусть диагностируемый объект
(рис. 2.1) представляет собой систему
с п+яг входами и &+1 выходом. Одна
часть входов характеризуется п-мериым
вектором X=(xi, Хг, ..., хп), в какой-то
степени управляема и описывает ту
часть воздействующих факторов, которая
вызывает необратимые изменения в объ-
екте, обусловленные процессами физико-
химических превращений, старения и из-
носа. Назовем этот вектор необратимым
изменением.
Другая часть входов характеризуется
т-мерным вектором Y=(yi, у2, ут),
компоненты которого не управляемы и
ие могут быть определены прямыми из-
мерениями. Вектор ¥ характеризует влия-
ние тех факторов (внешних и внутренних),
ного в изменения параметров объекта и отражают обратимые изменения
(«помехи»), происходящие в объекте. Помеха характеризуется соответ-
ствующей стационарной плотностью распределения /(Y) и определен-
ными корреляционными свойствами [7].
Информация Q' на выходе системы характеризует ее состояние,
причем значение Q' возможно и не известно, но вполне определенным
образом зависит от состояния всех входов, т. е. Q'=q/(X, Y), где ф —
некоторая скалярная функция двух векторных аргументов. Эта функция
определяет показатель качества объекта и его работоспособность и
13
которые вносят много случаи-
в дальнейшем будет именоваться функцией состояния. Кроме того, объ-
ект имеет k выходов £'i, g'2, .£% характеристики которых зависят от
X и Y.
Величины Q' и |'г, s=l, 2, .... k подвергаются измерительным опе-
рациям. При этом на них воздействует вектор Z=(zi, z$, ..Zi), кото-
рый вносит в изменения параметров погрешности измерительных цепей
и операторов.
Таким образом, качество информации, непосредственно используе-
мой для построения алгоритма прогнозирования, зависит от трех аргу-
ментов:
W(X, Y, Z). (2.1)
Значения должны находиться в определенных пределах:
|S(X, Y, Z)«%, 5 = 1, 2, ..., k, (2.2)
где — допустимый предел изменения для s-ro параметра. Неравен-
ства (2.2) выделяют в пространстве, характеризующем работоспособ-
ность объекта, область 6, где может изменяться вектор
l=(U ь, .... Ы. (£3)
Изменение § внутри области G непосредственно зависит от харак-
тера изменений X, Y и Z, и величина % будет характеризовать опреде-
ленную степень работоспособности технического изделия. Однако вид
зависимостей (2.1) довольно часто неизвестен, что существенно влияет
на результат прогнозирования.
Если рассматривать функцию (2.1) отдельно по каждому аргумен-
ту, то зависимость
1=Фх(Х) (2.4)
будет характеризовать необратимые изменения, происходящие в изде-
лии, и закономерность изменения работоспособности контролируемого
изделия. Зависимость (2.4) намного облегчает решение задачи прогно-
зирования. Влияние остальных векторов аналогично рассмотренному,
что позволяет рассматривать функцию
Z). (2.5)
Чем сильнее влияние векторов Y и Z, тем больше случайного в изме-
нении I и тем труднее обнаружить характер изменения состояния из-
делия. Если преобладает влияние вектора X, то можно осуществлять
прогнозирование с большой точностью. Таким образом, задача пред-
варительной обработки заключается в сведении к минимуму влияния
составляющих Y, Z и формированию зависимости (2.4), определяющей
эволюцию изменения состояния изделия. Для этого можно использовать
различные математические операторы обработки, с помощью которых
можно добиться приближения <р(Х, Y, Z) к желательному пределу
<Р«(Х).
Известные операторы сглаживания случайных процессов позволя-
ют во многих случаях достичь поставленной цели на предварительном
э'1апе обработки. Среди таких операторов можно выделить [8] опера-
торы математического ожидания, текущего среднего, экспоненциально-
го сглаживания, Бернштейна и интегральные. Их исследование сводит-
ся к анализу эффективности их сглаживающих свойств и определению
оптимальных параметров сглаживания, что позволяет в каждом кон-
кретном случае выбрать оптимальный оператор.
14
Оператор математического ожидания. Под математическим ожида-
нием функции состояния подразумевают величину
Qcp(£) = M[Q(l)] = М [?(Х, Y, Z)] =
у, zj==G
= f J ?(Х, Y, Z)/>(¥)/> (Z)dYdZ, (2.6)
//SG ZSG
где G — область допустимого влияния ¥ и Z на Q(£); р(¥), p(Z) —ве-
роятности появления соответствующих величин ¥ и Z.
Если составляющие помехи ¥ и Z аддитивно накладываются на
функцию состояния
Q(l)=<p(X, Y, Z)=^(X)+Y+Z (2.7)
и являются реализациями случайного процесса с математическими ожи-
даниями I и q, то среднее значение функции состояния равно Оср(1) =
=М [(рДХ)]+/+^
Если помеха имеет нулевое математическое ожидание, то (2.7)
примет вид
Qep(g)=M[4)x(X)]> (2.8)
в котором отсутствует влияние составляющих помехи.
Оператор текущего среднего. Сущность оператора заключается
в воздействии на аддитивную сумму (2.7), рассматриваемую как функ-
цию времени, оператором вида S, т. е.
t+Tl2
S{Q(SW1}=4- J QU('t)ld't=4- J fx[x(t))^+
/—7/2 /—7/2
/+7/2
+4- C [¥(•=)+ z (t)J dt, (2.9)
/—7/2
где T — интервал обработки (сглаживания), tfT.
Интервал обработки выбирается из соображений наилучшего по-
давления составляющих помехи Y(t) и Z(t). Он может быть равным
период корреляции 7’=тк, или удвоенному периоду корреляции Т—
=2тк. Величину Т иногда удобно оценивать исходя из характера изме-
нения необратимой составляющей X(t), которая определяет закономер-
ность изменения функции состояния, однако тоже содержит колебатель-
ную составляющую. Поэтому при определении Х(1) появляются дина-
мические (систематические) ошибки, которые называются ошибками
смещения:
t+T/2
Scm=X(/)-_L J (2.10)
По величине максимально допустимой ошибки smax определяют ин-
тервал обработки Т. Выражения для некоторых е приведены в табл. 2.1
[9]. Иногда случайную функцию можно представить совокупностью
приведенных в таблице неслучайных функций.
Кроме того, оптимальный интервал обработки можно выбирать про-
порциональным отношению дисперсии контролируемого процесса к квад-
15
ТАБЛИЦА 2.1
ек<
/ + 772
1 Г
®СМ ~ X [t) ~ ’J' 1 X
4—772
sin рТ/2 1
- рТ/Г- J
р Уб |е«ак I
~ Иб |emax I e at
при a>0;
2 ,r________
a Tv I Smax I
при a < 0.
tgy*
, . l 1 Ч-tg у* Ч- tg-rr/S
t£ Y* 4у7 ln 1 — tg yf • tg у 7/2
2 ,r___________
Y * [emase 1
рату скорости (производной) изменения процесса за период Г:
Тт = DJO/I7? )=h(O/Vt (Г)]8.
Эффективность обработки Эо непосредственно влияет на качество
прогнозирования и будет тем выше, чем больше подавлены составляю-
щие помехи. Количественно эффективность обработки оценивается как
отношение
D{SH(f)j}/£>{.S[y(O+Z(O]}
DH(0J/D[y(0 +Z(01
(2.11)
где D — дисперсия соответствующих составляющих, S— оператор теку-
щего среднего, в общем случае оператор обработки.
Числитель и знаменатель этого выражения представляют собой
отношение дисперсий закономерности изменения контролируемого про-
цесса (X) и его случайных составляющих (Y+Z). Величина Эо пока-
зывает, во сколько раз это отношение увеличилось в результате обра-
ботки оператором.
Оператор экспоненциального сглаживания. Его можно представить
в интегральной форме
/ t—ъ
£[И01 = -Г (2.12)
о
и в матричной
п
1 /М_____I
77" (“77 j (2.13)
4=0
где Т, N — соответствующие параметры сглаживания, Е]»=
Кроме того, его можно определить с помощью выражения
со
(l-a)’Vi,
i=o
где >a=l/7V.
Для сглаживания случайных последовательностей используется
простой алгоритм, основанный на рекуррентном соотношении
Е [В]п=<х£тг+ (1—a)£ [£]n-i, (2.14)
причем £ [£]о=0, Е [£]1=а|1.
Особенностью применения операторов обработки и сглаживания
является необходимость в получении достаточного количества инфор-
мации, что не всегда удается
осуществить на практике.
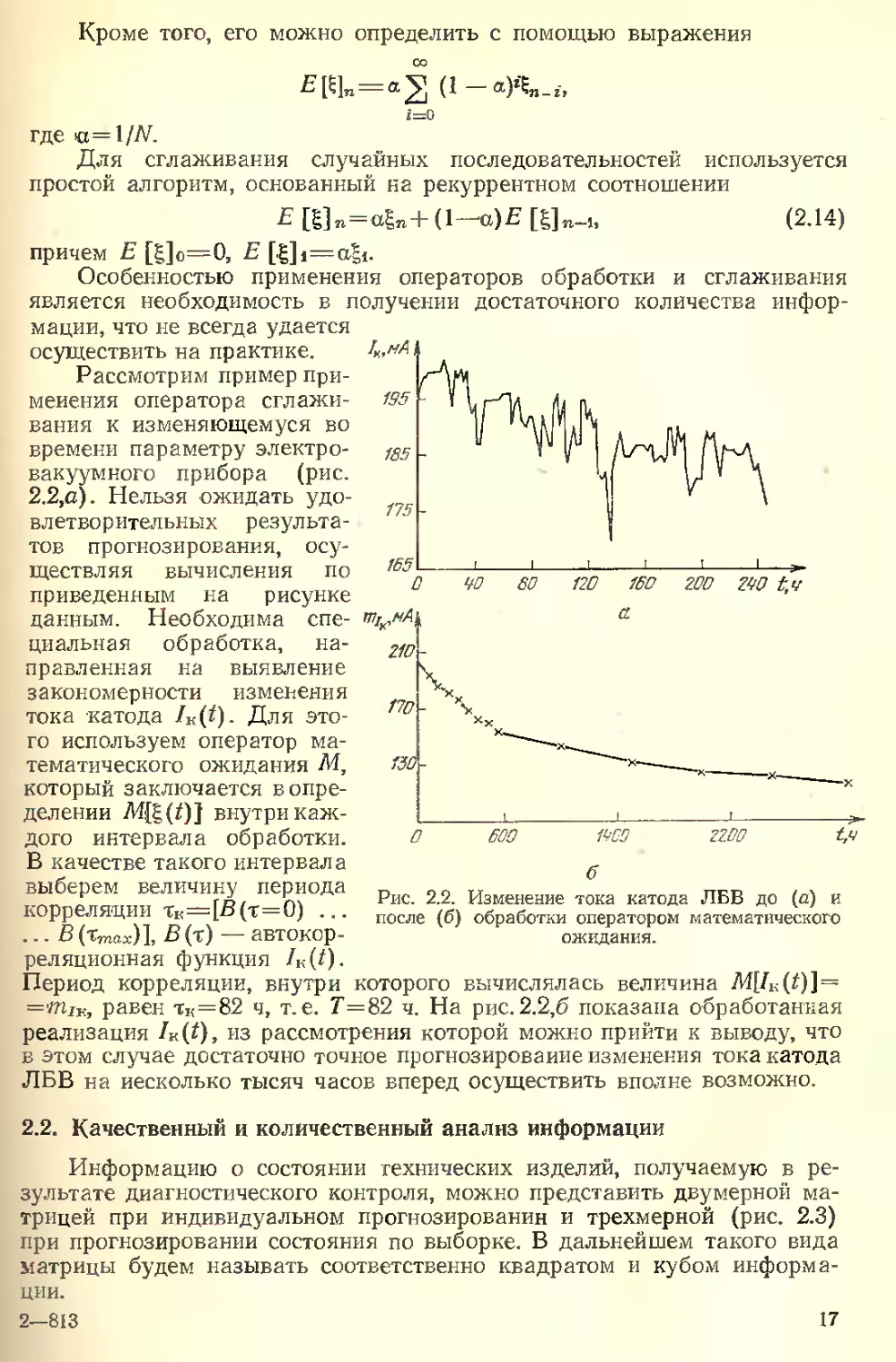
Рассмотрим пример при-
менения оператора сглажи-
вания к изменяющемуся во
времени параметру электро-
вакуумного прибора (рис.
2.2,а). Нельзя ожидать удо-
влетворительных результа-
тов прогнозирования, осу-
ществляя вычисления по
приведенным на рисунке
данным. Необходима спе-
циальная обработка, на-
правленная на выявление
закономерности изменения
тока катода /к(0- Для это-
го используем оператор ма-
тематического ожидания М,
который заключается в опре-
делении внутри каж-
дого интервала обработки.
В качестве такого интервала
выберем величину периода
корреляции тк=[£(?=0) ...
...В (Tmax)], В (т) — автокор-
реляционная функция /к(0-
Период корреляции, внутри которого вычислялась величина M(ZK(Z)]=
=mJK, равен тк=82 ч, т.е. Г=82 ч. На рис. 2.2,6 показана обработанная
реализация ZK(0, из рассмотрения которой можно прийти к выводу, что
в этом случае достаточно точное прогнозирование изменения тока катода
ЛЕВ на несколько тысяч часов вперед осуществить вполне возможно.
б
Рис. 2.2. Изменение тока катода ЛЕВ до (д) и
после (б) обработки оператором математического
ожидания.
2.2. Качественный и количественный анализ информации
Информацию о состоянии технических изделий, получаемую в ре-
зультате диагностического контроля, можно представить двумерной ма-
трицей при индивидуальном прогнозировании и трехмерной (рис. 2.3)
при прогнозировании состояния по выборке. В дальнейшем такого вида
матрицы будем называть соответственно квадратом и кубом информа-
ции.
2—813 17
Методы анализа текущей и априорной информации, представленной
матрицами, принципиально ничем не отличаются, если имеются доста-
точно большие число N изделий в выборке при групповом прогнозиро-
вании и число k параметров изделия при индивидуальном прогнози-
ровании. Обычно априорное па значительно больше текущего пт, т. е.
Рис. 2.3. Трехмерная матрица (куб) инфор-
мации.
П&^>Пч (П — ЧИСЛО ИЗВестНЫХ ТО-
чек контролируемого параметра).
Это объясняется тем, что в апри-
орные данные входят результаты
продолжительных испытаний, не
ограниченных во времени. В этом
случае (N— велико) используют-
ся классические методы обра-
ботки. Однако довольно часто при
выполнении текущего контроля
«величины k и N невелики (^20),
поэтому методы анализа и обра-
ботки будут принципиально от-
личаться от методов анализа и
обработки большого объема ин-
формации (классических мето-
дов).
При качественном ана-
лизе в первую очередь следует
составить соответствующие квадраты и кубы информации по априорным
и текущим данным по осям k и N (рис. 2.3), -взяв за основу какой-либо
критерий в зависимости от постановки задачи (например, по степени
выраженности тенденции изменения контролируемых параметров, по
степени близости совокупности k параметров изделий друг к другу
в контролируемой выборке объемом N). Далее необходимо сравнить
текущие данные с априорными, что позволяет определить близость вновь
полученной информации к прежней.
После качественного анализа принимается решение о соответствую-
щей количественной обработке. Следует особо отметить, что качествен-
ному анализу подвергается как первичная (необработанная) информа-
ция, так и вторичная (обработанная).
Количественный анализ осуществляется по всем осям квад-
рата и куба информации п, k и N. В результате обработки по времен-
ной осп п выявляется тенденция изменения каждого компонента Д Для
определения закономерности изменения используются рассмотрен-
ные ранее операторы обработки. При этом изменения £s(/) могут коли-
чественно характеризоваться коэффициентами старения, производными
различного порядка, конечными разностями и т. д.
При обработке по оси выборки N вычисляются вероятностно-стати-
стические характеристики и функции распределения параметров Допи-
сывающие состояние изделий всей выборки. В идеальном случае одно-
именные параметры различных изделий из выборки Д, 1—1, 2, ..., N
должны быть равны и их распределение должно представлять б-функ-
цию. Однако из-за множества факторов, влияющих на реальный произ-
водственный процесс, и из-за накладываемой помехи величины Д будут
иметь некоторый разброс. При этом функция распределения и статисти-
ческие характеристики достаточно полно характеризуют уровень техно-
логии и качество выборки.
18
Можно выделить две группы статистических характеристик [10].
Первая из них, к которой относятся: математическое ожидание или
среднее арифметическое, среднее геометрическое, среднее гармоническое,
мода, медиана — описывает центр распределения. Другая группа пока-
зателей: дисперсия (среднее квадратичное отклонение), среднее абсо-
лютных отклонений, коэффициент вариации, размах, коэффициент асим-
метрии или «скошенности», коэффициент эксцесса или «крутости»,
характеризует рассеяние. Каждая отдельно взятая характеристика описы-
вает одну из специфических сторон распределения по оси N (распреде-
ление выборки по каждому параметру ^5).
Обработка по оси параметров -А позволяет получить статистические
данные, характеризующие качество одного образца технического из-
делия и поэтому представляет особый интерес. Однако следует иметь
в виду, что параметры gs взятого в отдельности образца изделия могут
иметь различную размерность и тогда их нельзя рассматривать как
однородную совокупность случайных величин. Это препятствие можно
устранить с помощью одинаково обработанных безразмерных относи-
тельных величин При этом можно анализировать {£s} вероятностно-
статистическими методами.
Как уже говорилось, количественный
анализ априорной информации должен
предшествовать анализу текущей инфор-
мации, а его результаты следует сопоста-
вить с результатами обработки текущих
данных. Рассмотрим в качестве примера
один из возможных методов сравнения
результатов. Априорный куб информации
(рис. 2.3) приведем к квадрату инфор-
мации усреднением параметров £is по I
в каждой строке оси 7V:
Л'
~ N lui* s — 1, 2, ... k;
l=i
i= 0,1.....n.
Таким образом, получим квадрат
математических ожиданий:
AJ1ojVZ11A'Z12 —
••• -Мщ ... ЛГгп,
... -&fsn, (2.15)
AffcoAffc] Л1^2 Afjt,-
который представляет собой как бы эта-
лонную матрицу, характеризующую на
определенный период времени степень
изменения состояния технических изде-
лий. Матрицы текущей и эталонной
информации вида (2)15) сравниваются
поэлементно -путем нахождения алгеб-
раической разности между этими эле-
ментами {gsi—их отношения ^,dMs{
или относительного изменения (£si—
—Msi)/Mso. Обозначая результаты тако-
го сравнения через Avil составим новую
матрицу:
^10^11^12 ••• Ац ... А1п,
AzoAsjA22 ••• Azi... А^п,
AsoAglAS2 . .
Al0-AklAi2
Asi... Asti, (2.16)
• Am
которая показывает, насколько отличает-
ся текущая информация о состоянии тех-
нического изделия от аналогичной
информации, полученной ранее. По ма-
трице (2J16) можно судить, как сильно
будут отличаться результаты прогнози-
рования, осуществляемого по текущим
данным, от результатов, полученных по
априорным данным.
Составление по априорным данным
только одной эталонной матрицы вида
:(2.15) для определенного вида изделий
не всегда эффективно, так как характер
изменения состояния даже однотипных
изделий может сильно различаться и,
естественно, строки в (2.15) могут также
существенно различаться. Поэтому в ря-
де практических случаев необходимо со-
ставлять несколько эталонных матриц,
в которые закладывается информация
об изменении параметров технических
изделий, объединенных в классы с при-
близительно одинаковым характером из-
менения состояния с течением времени.
П-ри этом матрицы (2.16) позволяют
определить, к какому «классу ближе
диагностируемое изделие.
При i=0, s=fe, информация за-
дается в виде матрицы (квадрата), ко-
торая представляет нулевое временное
сечение в кубе информации (рис. 2.3).
В данном случае количественный анализ
заканчивается построением ковариацион-
ной матрицы и сравнением ее с анало-
19
• • АЛп,
•гичной априорной:
Сцб 12 . .С18.
6'216'22 • • 62s • • Cih
1С] = CSACsi. Ces. б'вЬ > (2.17)
бмбьа - •• б'лз . •• См
где Сц—коэффициенты ковариации
между i-м и j-м параметром, i, j=
= 1, 2,..., k.
Ковариационные матрицы также мо-
гут быть эталонными и найденная бли-
зость текущих ковариационных матриц
к соответствующим априорным эталон-
ным будет облегчать решение задачи
прогнозирования.
Результаты качественного и количественного анализа априорной
информации можно распространить на текущую только в том случае,
если оба вида информации однородны, т. е. изделия, по которым по-
лучена априорная и текущая информация, взяты из одной генеральной
совокупности. Проверка однородности партий представляет собой про-
верку гипотезы о том, что различные партии (выборки) извлечены из
одной и той же генеральной совокупности. Проверяемую гипотезу обыч-
но называют нулевой. Таким образом, проверка однородности сводится
к определению расхождения характеристик -v партий (выборок). При
этом в качестве нулевой гипотезы Но выдвигается предположение о со-
впадении законов распределения v выборок: Л.(£) =F2(£) = ...
... =FS(|)= ... =F.(«).
Рассмотрим частный случай провер-
ки однородности результатов испытаний
с помощью непараметрического критерия
[11, 12]. Критерий пригоден при любом
количестве выборок, не обязательно рав-
ных -по объему, и чувствителен к раз-
личию законов распределения. Им мож-
но пользоваться в том случае, если вы-
борки независимы друг от друга, а так-
же если независимы и наблюдения вну-
три каждой выборки.
Представляем результаты контроля
в виде v последовательных рядов и на-
блюдений, соответствующих данным по
надежности v изделий или v периодам
времени. При этом каждый законченный
эксперимент состоит из п, ..., rj, ...
..., rv, ... единичных наблюдений. Об-
щее число наблюдений
V
S rs = tn.
7=1
Результаты каждого ряда наблюде-
ний разобьем по значениям наблюдаемой
случайной величины на I разрядов и за-
пишем в виде табл. 22. При этом число
результатов наблюдений j-го ряда, по-
павших в i-й разряд, будем рассматри-
вать как случайную величину и обозна-
чать ее через тц.
При таком представлении гипотеза
о том, что v выборок извлечены из одной
и той же совокупности (гипотеза одно-
родности), сводится к гипотезе о том,
что существует I вероятностей pi, ..., pi,
20
Номер
разряда
т а;б Л И Ц А 2.2
Номер ряда
Сумма
таких, что
I
miv
где pi — вероятность принадлежности
отдельного результата i-му разряду во
всех v выборках.
Для проверки этой гипотезы опреде-
лим функцию результатов наблюдений:
{m.i}
Pii™
•где pij=piWj, р1=тфп—оценка веро-
ятности попадания в t-й разряд, и?г-=
=Г}(т — оценка вероятности попадания
в /-й ряд.
тц
mii
тг
т
Если проверяемая гипотеза -верна,
то предельное распределение величины
%2 имеет •(«—*>(v—1) степеней свободы.
Для обеспечения близости распределения
величины у2 'К предельному табл. 2.2
следует составлять с таким расчетом,
чтобы piitn^W.
Пусть —1)) есть (qX
Х100)%-ная точка х2 распределения
с (I—4) (v—1) степенями свободы. Тогда,
если гипотеза верна, то
^{х2>4«'-|>(>-1))} = ?-
Критическая область с уровнем зна-
чимости q определяется неравенством
Х2>^((^ — О (v—О). В противном
случае считается, что гипотеза об одно-
родности не .противоречит опытным дан-
ным. Значения для точек х2’Распределе-
ния -могут быть взяты из {20].
2.3. Обработка ограниченной по объему информации
Обработка первичной информации, представляемой в виде квадра-
тов и кубов, как было показано в § 2.2, не вызывает принципиальных
затруднений при больших k и N. При ограниченном объеме информа-
ции (при на определенной стадии требуется принципиально
иной подход.
В работе [13] предложен новый метод обработки малых выборок,
названный методом прямоугольных вкладов. Его идея заключается
в том, чтобы использовать некоторую дополнительную информацию
о неизвестном истинном распределений
и при построении эмпирической функции
распределения учесть флуктуационный
характер случайных величии д. Иначе
говоря, случайная величина не возво-
дится в некий абсолют, ей не приписы-
вается бесконечная плотность распреде-
ления, а считается, что д/ не единствен-
ное возможное, но наиболее вероятное, и
по соседству с в определенном интер-
вале плотность вероятности отлична от
нуля. Поэтому около %; строится не ё-
функция, а некоторая непрерывная функ-
ция (рь названная «функцией вклада».
В качестве был взят наиболее простой
для расчетов а графического построения
вклад в виде прямоугольника с основани-
ем d и точкой в центре (рис. 2.4,а).
В качестве функции вклада не обяза-
тельно использовать прямоугольник, тем
рая зафиксирована при конкретном изме-
более, что при применении прямоугольно-
го вклада ие выделяется точка кото-
рении величины д. Действительно, нет не-
Рис. 2.4. Функции прямоугольно-
го (а) и и треугольного (б) вклада.
обходи мости приписывать точке &
абсолютное значение, но считать в этой точке плотность вклада макси-
мальной. по сравнению с другими в интервале d вполне целесообразно.
Этому будет больше отвечать функция вклада в виде элементарного
распределения Симпсона (треугольника). Распределение Симпсона сим-
метрично, а элементарное распределение берется шириной d и высотой
h (рис. 2.4,6).
Сформулируем априорные предположения относительно истинной
плотности распределения f(E) случайной величины £, справедливые для
21
многих практических случаев. Пусть функция удовлетворяет следующим
условиям:
a) при f(£)=0 при £<а и £>&, где а и Ь-—ко-
нечные числа, ограничивающие интервал возможных значений
б) f(£) —непрерывная функция внутри (а, Ь);
в) /(£)—имеет одну основную моду и частоты спадают к грани-
цам о, Ь.
Пусть Z=0, т. е. нет ни одного значения Казалось бы, не имеет
смысла спрашивать, какова плотность распределения величины Одна-
ко, учитывая предварительные условия, можно записать плотность рас-
пределения в виде, не противоречащем имеющейся информации о
О
— 0,5 (Зе — &)]/(« — 6)2
[0,5(ЗЬ —
0
При
при а
при
при
где с—(Ь+а)/2.
Удобно назвать базовым или априорным вкладом (рис. 2.5,а).
Рис 25 Нормированная функция распределенья при треугольной функции вклада при
(с) и Л=5 (б).
При поступлении информации о & строится функция вклада cpi(^) —
треугольник с центром в точке £i над базовым вкладом. Плотность рас-
пределения fi(l) =&(£) +<pi(£).
При наличии N значений параметра g плотность распределения
определяется как
N
Ц® = )«(?) +2^). (2-18)
1=1
Необходимо отметить, что вклады не перекрываются, а надстраи-
ваются друг над другом.
Нормирование распределения (2.18) или построение многоуголь-
ника вероятностей, соответствующего (2.18), осуществляется следую-
щим образом. Диапазон [я, 6] разбивается на ряд интервалов (5... 10)
и подсчитываются площади Si, попавшие в каждый интервал. Отноше-
ния Si/S, где S— общая площадь, определяют вероятности попадания
в £-й интервал.
22
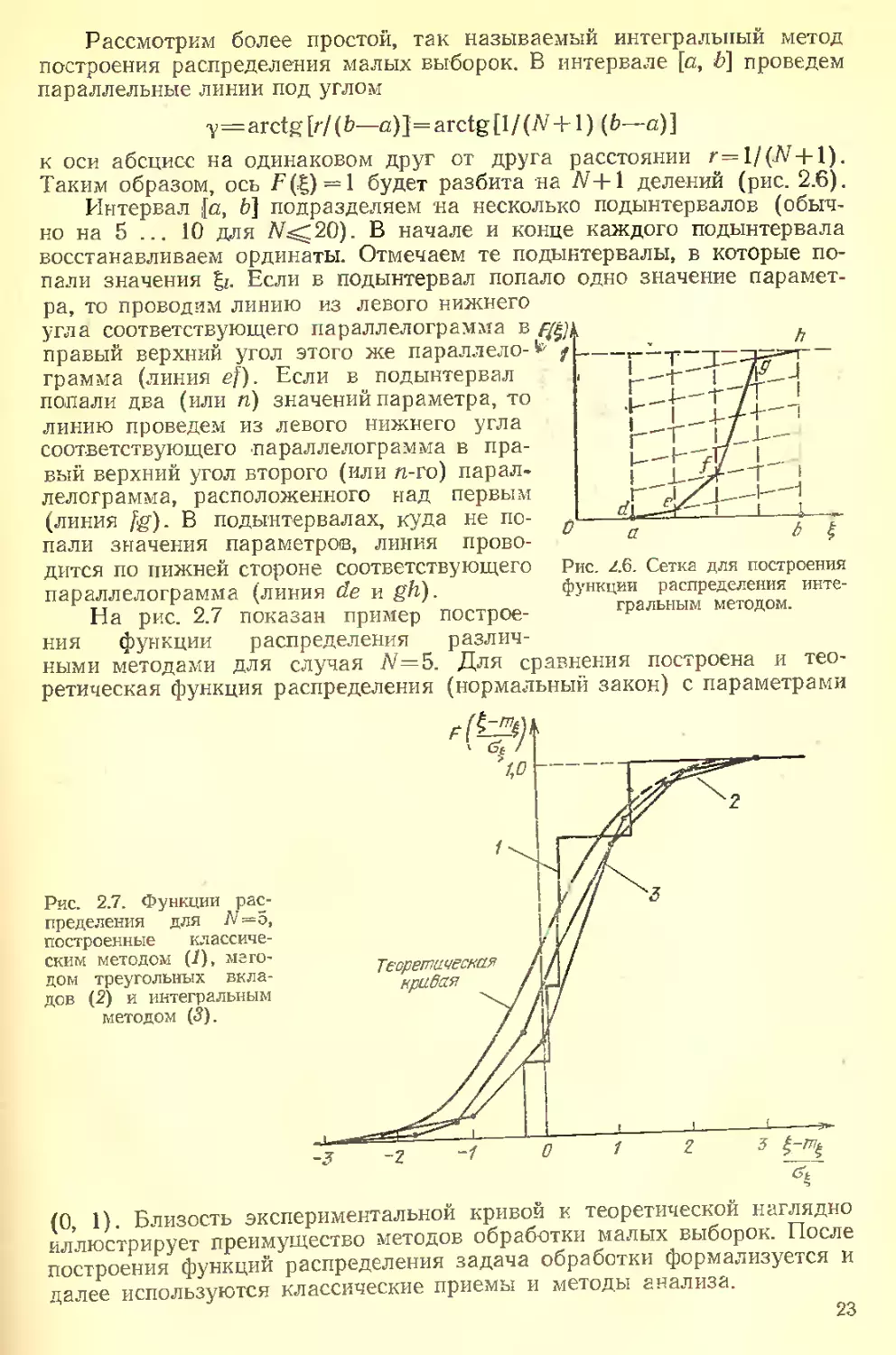
Рассмотрим более простой, так называемый интегральный метод
построения распределения малых выборок. В интервале [а, &] проведем
параллельные линии под углом
Рис. 2.6. Сетка для построения
функции распределения инте-
гральным методом.
<Y=arctg[г/(b—a)] —arctg[I/(N+1) (b—a)]
к оси абсцисс на одинаковом друг от друга расстоянии г = I/(.N +1).
Таким образом, ось F(£) = 1 будет разбита на JV+1 делений (рис. 2.6).
Интервал [а, Ь] подразделяем на несколько подынтервалов (обыч-
но на 5 ... 10 для Л'^20). В начале и конце каждого подынтервала
восстанавливаем ординаты. Отмечаем те подынтервалы, в которые по-
пали значения Если в подынтервал попало одно значение парамет-
ра, то проводим линию из левого нижнего
утла соответствующего параллелограмма в f/gn
правый верхний угол этого же параллело-^ f
грамма (линия ef). Если в подынтервал
попали два (или п) значений параметра, то
линию проведем из левого нижнего угла
соответствующего параллелограмма в пра-
вый верхний угол второго (или n-го) парал-
лелограмма, расположенного над первым
подынтервалах, куда не по-
пали значения параметров, линия прово-
дится по пижней стороне соответствующего
параллелограмма (линия de и gh).
На рис. 2.7 показан пример построе-
ния функции распределения различ-
ными методами для случая N=5. Для сравнения построена и тео-
ретическая функция распределения (нормальный закон) с параметрами
(линия fg). В
Рис. 2.7. Функции рас-
пределения для N=5,
построенные классиче-
ским методом (/), мето-
дом треугольных вкла-
дов (2) и интегральным
методом (5).
(0, 1). Близость экспериментальной кривой к теоретической наглядно
иллюстрирует преимущество методов обработки малых выборок. После
построения функций распределения задача обработки формализуется и
далее используются классические приемы и методы анализа.
23
2.4. Выбор прогнозирующих параметров
Выбор прогнозирующих параметров технических изделий в настоя-
щее время представляется весьма трудной задачей. В каждом конкрет-
ном случае приходится решать задачу их выбора своим оригинальным
путем, особенно если задачи прогнозирования решаются различными
методами. Однако можно сформулировать некоторые рекомендации
(методы) по выбору прогнозирующих параметров применительно к раз-
личным техническим изделиям.
Метод выбора, учитывающий производные параметров. Пусть из-
менение состояния изделия описывается вектором !(/) = [£i(0,
..., МО], гДе 'МО —координаты вектора, характеризующие состояния
отдельных узлов, q={, 2, ..., г. Требуется, оценив величины ^q(t) и
B'g(O, £%(0, определить, какими из координат (мало изменяющимися
во времени) можно пренебречь по сравнению с остальными.
Введем норму q-ro параметра — координаты
где hq = d^q/dtt tg = d£g!dt...
Обозначим р(/) =max||£e(2)H, i^zq^r, и зададим б(/)<1. Коор-
динаты, для которых И1е(/) И/р(£) <6(0, заменим нулями. В этом случае
1 (0 = (0» Ь(0, • •& (О ], причем
Для всех q, для которых ||gQ(Z)||/р(/)>б(/),
^s(t)= 0 для всех s, для которых |Ц£(0 Н/р(О <6(0, (2.19)
s=l, 2, ..., А.
В частном случае, если £,(/) обладает свойством «монотонности»
координат, т. е. если Illell>ll£s|| для всех q>kt то вектор |(/) можно*
заменить на вектор 1(0 = [Ы0, Ь('0, 0, ..., 0] = [МО, • ЫОЬ
где для Л-го параметра впервые выполняется неравенство (2.19), при-
чем Если координаты |(0 не обладают свойством монотонности,
то их можно упорядочить по величине отношения (2.19).
Этот метод целесообразно использовать при аналитическом прогно-
зировании в случае, если учитываются производные прогнозирующих,
параметров.
Информационный подход к выбору параметров. Контроль с инфор-
мационной точки зрения позволяет снять неопределенность состояния
объекта, которая количественно характеризуется энтропией этого со-
стояния. Пусть координаты 1? (s~l, 2, ..., k) вектора состояния |—
независимые величины. Тогда, используя известное свойство, заключаю-
щееся в том, что энтропия совокупности независимых величин равна
сумме энтропии этих величин, можно записать
k
НЪ=%Н.®, (2.20)
1
где Ну.—энтропия состояния диагностируемого изделия, Hs(t,) —
безусловная энтропия s-ro параметра. Количество информации /е(1с, 2),.
24
которую несет параметр, о состоянии изделия, можно оценить выраже-
нием [14]
Л&, 2) = /7£~//£(Z/y,
где ЯД2/д£)—условная энтропия состояния изделия после контроля
параметра
Выбор параметров следует начинать с параметра |8, несущего ма-
ксимальное количество информации Энтропию по s-му параметру
в (2.20) можно вычислить с помощью следующего выражения [15]:
со
я, (6) = - J f (У log2 f (У <Й2, (2.21)
—со
где f(gs) — функция плотности распределения по s-му параметру. По-
скольку f(£) практически всегда определяется как многоугольник веро-
ятностей, то выражение (2.21) можно представить в виде
= Рг^&Рг, (2.22)
i=l
где рг — вероятность попадания параметра £s в г-й интервал диапазона
его изменения.
Параметры можно выбирать и по критерию минимума величины
Я(£). Если распределение f(is) подчинено нормальному закону, что на
практике встречается часто, то энтропия отдельного параметра соглас-
но (2.21) равна
1 г Г ( ?2 \1 / Е2 \
= ~ J [ехр 2D^J ( ~ 1о^£ “ 2D 1о&2 е)
где D^s — дисперсия распределения параметра £s.
Осуществляя преобразования, ^получаем
//.Л) = log2 j/Wy.
Таким образом, упорядочение параметров по степени информатив-
ности можно осуществлять по величине дисперсии распределения пара-
метра. Это можно объяснить иначе: чем меньше дисперсия параметра,
тем плотнее распределение и тем больше вероятность того, что изделия
принадлежат к одному классу, который характеризуется определенной
степенью работоспособности или сроком службы. И наоборот, чем боль-
ше тем менее однородной является партия изделий. Этот метод
можно рекомендовать при вероятностном прогнозировании, когда вы-
числяются и анализируются величины дисперсий компонентов прогно-
зируемого процесса.
Прогнозирующие параметры некоторых технических изделий. В ряде
практических случаев при диагностике изделий оказывается выгодным
отвлечься от их функционального назначения, так как основные пара-
метры функционирования часто оказываются нечувствительными к из-
менениям состояния изделия. Например, выходные параметры системы,
которые характеризуют влияние нескольких подсистем и большого чис-
ла разных узлов, очевидно, не могут быть чувствительны к малым из-
менениям, происходящим в каждом из них.
25
Рассмотрим конкретные примеры ча-
сто .встречающихся параметров, чувстви-
тельных к изменению состояния и, сле-
довательно, к работоспособности техни-
ческих изделий
1. Температура поверхностей узлов
аппаратуры зависит от мощности рас-
сеяния. Измерение сопротивления обмо-
ток трансформатора позволяет судить
о температуре обмоток и часто обеспе-
чивает достаточно точную индикацию
локальной окружающей температуры.
2. Ток холостого хода трансформа-
тора очень чувствителен к отклонениям
от нормального рабочего режима транс-
форматора и к нагрузкам выходных це-
пей. Дополнительная проверка трансфор-
матора в рабочем состоянии дает ценные
данные, но они часто имеют не столь
большое значение.
3. Такие параметры, как отношение
прямого и обратного сопротивлений дио-
дов, ток базы транзисторов, ток сетки
вакуумных ламп или сопротивление
утечки конденсаторов весьма чувстви-
тельны к некоторым часто встречающим-
ся дефектам, предшествующим отказам
элементов на их ранних стадиях.
4. Многие измерения в системах
управления с незамкнутым контуром ре-
гулирования, например контроль покас-
кадного усиления, указывают на прибли-
жающееся повреждение.
5. Измерения коэффициента стоячей
волны с выходного конца волноводной
линии, ведущей к нагрузке, могут ука-
зать на возникновение ряда типовых
неисправностей.
Для различных изделий можно со-
ставить перечни параметров, измеряемых
как в статическом, так и в динамиче-
ском режиме работы. Такими параметра-
ми в динамическом режиме, например
у -электровакуумных приборов, могут
быть: ток включения, ток спада, время
установления шума после включения,
вакуум-фактор и другие; у транзисторов:
длительность спада, время рассасывания,
шумы на различных частотах и другие.
Кроме того, иногда для прогнозирования
следует выбирать интегральные параме-
тры, -например площадь под кривой тока
спада, интеграл по кривой шума в опре-
деленном диапазоне частот и т. д. Таким
образом, можно прийти к выводу, что
выбор прогнозирующих параметров явля-
ется достаточно сложной задачей и тре-
бует от проектировщика инженерией
интуиции, изобретательности и глубоких
знаний контролируемого изделия.
2.5. Выбор прогнозирующих параметров методами
статистической классификации
В различных задачах число начальных, первичных параметров (из-
мерений) может колебаться от нескольких единиц и десятков до сотен
и тысяч. Обычно число параметров-признаков стремятся свести к мини-
муму как с точки зрения простоты распознающей системы, так и с точ-
ки зрения сокращения затрат на выполнение измерений электрических
параметров, подчас весьма трудоемких, требующих специально разра-
ботанной аппаратуры.
Метод весовых коэффициентов. При оценке работоспособности
диагностируемой системы не все параметры имеют одинаковую значи-
мость, т. е. каждый параметр в большей или меньшей степени содер-
жит в себе информацию о состоянии системы. Всю совокупность пара-
метров можно упорядочить таким образом, что на первых местах ряда
будут находиться наиболее «полезные» параметры и с ростом поряд-
кового номера члена ряда их информативность будет убывать.
Для оценки значимости каждого конкретного параметра можно
ввести некоторое множество чисел, каждое из которых будет характе-
ризовать «полезность» отдельного параметра. Такие числа называются
«весами», потому что они описывают как бы веса параметров в общей
оценку работоспособности. Эти числа образуют поле действительных
положительных чисел, и параметру, имеющему наибольшую значимость,
должен быть приписан наибольший вес. Допустим, имеется множество
N объектов. И пусть для простоты пояснения это множество состоит
только из двух классов объектов, характеризующихся, например, тем,
что объекты, относящиеся к этим классам, имеют различный срок служ-
бы Л и Т2, причем Ti=^T2.
26
Каждый объект множества N описывается одним и тем же набором
k параметров: gi, 52, ..., ел, значения которых в совокупности и опре-
деляют принадлежность объекта к своему классу. Если пространство
параметров рассматривать как линейное метрическое, то набор пара-
метров порождает две суммы, характеризующие близость объектов
к классу TVi и N&:
k _ k
=S as ^»s ~ =S ^ss ~
8=1 5=1
где £is и £2s— средние значения s-го параметра, определенные по сово-
купности приборов 1-го и 2-го классов соответственно; as — весовой ко-
эффициент s-ro пара1метра.
Задача сводится к нахождению такой совокупности весовых коэф-
фициентов, которая позволила бы уменьшить расстояние между объек-
тами внутри одного класса и увеличить расстояние между объектами
различных классов. Тогда принадлежность Z-го объекта к одному из
классов можно оценить с помощью разности y=Si—s2, причем
если S1C6, s2>0; если SiX), s2<6, где 6—некоторый порог,
относительно которого оценивается принадлежность объекта В; к соот-
ветствующему классу. Величина этого порога зависит от степени пере-
крытия классов, т. е. от множества G={yi} объектов yi<^Ni(~} N2, обра-
зующих пересечение классов. Таким образом, необходимо найти сово-
купность весовых коэффициентов, входящих в соотношение y=Si—s2,
таких, чтобы максимально уменьшить пересечение классов.
Пусть множество G есть множество объектов yi, принадлежащих
пересечению классов и Каждый элемент множества можио ха-
рактеризовать суммой
k
= 2 Es2as-
s=l
Средняя величина таких сумм для объектов равна
где Ej — среднее значение s-ro параметра по всем объектам множест-
ва G.
Для того чтобы можно было максимально точно разделить объек-
ты множества G, принадлежащие различным классам, необходимо
в пространстве параметров найти направление максимальной дисперсии
объектов. Очевидно, что в этом направлении должен быть расположен
вектор, компонентами которого являются весовые коэффициенты щ.
Тогда эти весовые коэффициенты будут порождать такие значения si,
что множество G будет представлено в виде двух групп, за исключе-
нием объектов, для которых si имеет значение, близкое или равное 6.
Составим выражение вида
т _ Ik
4 = S(st-Sr
1=1 / 8=1
27
Числитель этого выражения будет тем больше, чем меньше сумма
k
2 при этом будет иметь место наилучшее разделение объектов.
5=1
Выражение для у можно записать в матричной форме: у=
=а-A-a'/ia-Б-а', где -а — вектор строки, а' — вектор столбца, Б — еди-
ничная матрица, а А—матрица, пропорциональная выборочной кова-
риационной матрице, элементами которой являются числа
т
as3 2 -- Е») - Es)-
1=1
Поскольку матрица А задана в области вещественных чисел и явля-
ется симметричной, то все ее собственные значения являются действи-
тельными числами. Дифференцируя выражение для у по каждому as,
получаем систему уравнений:
|уБ—А|а'=0.
Для ненулевых as система уравнений разрешима только в том слу-
чае, если ее определитель |уБ—А|=0. Если раскрыть это выражение,
то получим характеристический многочлен матрицы А, корни которого
образуют спектр матрицы yi> Уъ ♦ > Уь- Среди всех собственных чисел
матрицы имеется максимальное ys; собственный вектор, соответствую-
щий этому числу, является тем вектором, компоненты которого образу-
ют искомый набор весовых коэффициентов.
Собственный вектор будем искать методом итераций. Так как А —
действительная симметричная матрица порядка ky то собственные зна-
чения этой матрицы есть действительные числа, а собственные векторы
си, 02, ..cik образуют ортогональный базис. Тогда любой произвольный
^-мерный вектор f можно единственным образом разложить в этом
базисе: £10*1 + 020*2+ ... + ЩгА, где — собственные векторы ма-
трицы А.
Умножая f на Ат, получаем km-f=tziyrnai+ ... Если у4 является
наибольшим собственным числом матрицы А, а т достаточно велик, то
членами, не содержащими yi, можно пренебречь. Тогда среди слагае-
мых, обозначенных многоточием, содержатся лишь члены, имеющие со-
множителями Ут2, Щу(тп-1)2, - . Утз И Т. Д. В ЭТОМ Случае Am'flymi —
=010*1+ ..., где невыписанные члены содержат yWYmi ... и т. д.
Так как IyJXyJ, |>{уД, то при т — сю
lim (Ат-//уда1)=о1а1.
т-кю
Обозначая Z-й компонент вектора Am-f в произвольном фиксиро-
ванном базисе через Vmi, а l-й компонент вектора а в этом же базисе
через .щ и определяя пределы
lim =6^011; lim ^^=0^,
т->со Нт —1)1 т->сх> Ymi
можно записать
lim 'угЧ~=Т1-
rn-»co * vm-1)1
Таким образом, числа Vmi, Vms, ..., Vmk при больших т пропор-
циональны числам ai, а2, а вектор приблизительно пропор-
28
ционален собственному вектору, соответствующему собственному чис-
лу yi.
Таким образом, метод нахождения необходимого набора весовых
коэффициентов состоит в следующем. Берем произвольный вектор f и
составляем последовательность AJ; A2f; Asf; ..A„J; ... Начиная с не-
которого т строка Awf приблизительно пропорциональна строке A^-if.
Коэффициент пропорциональности есть собственное число yi, а сам
вектор A^jf — собственный вектор, компоненты которого и есть искомый
набор весовых коэффициентов.
Располагая коэффициенты в порядке убывания |>]ш|>
упорядочиваем выбранную систему параметров по значимости.
Эмпирический метод. Для получения «наилучшего» (по какому-то
определенному критерию) набора признаков можно рекомендовать сле-
дующее правило [11, 18]. Из всех признаков выбирается один (или не-
сколько), наиболее информативный («ценный»); далее, к первому при-
знаку добавляется такой признак из г—1 оставшихся, чтобы информа-
тивность пары признаков для прогнозирования была наибольшей; затем
к полученной паре признаков добавляется наилучшим образом новый
признак и так далее. Процесс заканчивается тогда, когда информатив-
ность некоторой совокупности признаков незначительно превосходит
информативность совокупности, полученной на предыдущем шаге, или
когда достигнут требуемый уровень информативности (или требуемый
уровень точности распознавания).
Процесс отбора признаков можно вести и в обратном порядке: сна-
чала выбирается наиболее «информативное» подмножество (г—1) при-
знаков при исходной совокупности г признаков, затем из этого подмно-
жества отбирается наиболее «информативное» подмножество (г—2)
признаков из всех возможных подмножеств и так далее.
В [18] для упрощения правила отбора признаков рекомендуется
использовать такие свойства признаков, как статистическая независи-
мость. При этом различают случаи, когда признаки статистически не-
зависимы при объединении классов и когда признаки независимы вну-
три каждого класса.
В случае статистической независимости «объединенных» признаков
(при объединении классов) рекомендуется в качестве критерия для от-
бора признаков использовать информационную меру Шеннона. Тогда
процедура отбора сводится к упорядочению признаков по убыванию
количества обеспечиваемой ими информации при прогнозировании (или,
что то же самое, возрастанию неопределенности решения — энтропии).
Критерий знаков. Пусть прогнозироваине предусматривает разде-
ление изделий на два класса RlT и 7?2т, при этом параметры {£}, описы-
вающие состояния изделий, принадлежащих к R\T, обозначим £ц, £.12, ...
..., £ts, ..., &г, а принадлежащих к Егт — <21, %zz, . -ias, - •Ьг. Если
функции распределения и Е2(^₽) s-ro параметра равны Л(£к) =
= E2(|S), то, очевидно, параметр gs не несет никакой информации о при-
надлежности объекта к классам и R^t- В противном случае £s обла-
дает определенной информацией при условии, что различие между Ej (|s)
и E2(£s) не является случайным (например, из-за ограниченности объе-
ма выборок). Таким образом, задачу выбора информативных парамет-
ров можно свести к проверке тождества распределений
Л(|)=Е2(Ю- (2.23)
29
Если эта проверка позволит выбрать такие £, для которых тожде-
ство (2.23) не выполняется, то наиболее информативным может счи-
таться тот параметр, у которого разность между распределениями раз-
ных классов максимальна. Гипотезу (2.23) для случая, когда вид рас-
пределения неизвестен, можно проверить с помощью критерия знаков,
который основан на оценке вероятности появления знаков ( + ) и (—)
В ряду [1—9]:
Ей—E-2i; £12—£22; ..£ъ-—£гг- (2.24)
Пусть гипотеза /70 утверждает, что все '£i и £2 имеют одинаковые
функции распределения и наблюдаемое различие между ними чисто
случайное. Тогда вероятности появления в ряд}' (£1—£2) положительных
и отрицательных чисел равны Р(£ы—£ге>0) =P(£is—£2s<0). Случай
£is-—s2s=0 можно исключить из рассмотрения.
Аналитический метод определения допустимого отклонения числа
знаков ( + ) или (—) от г/2 при заданном уровне значимости р доста-
точно сложен. Поэтому целесообразно пользоваться простым графиче-
ским решением задачи выбора параметров, построенным по соответст-
вующим зависимостям в [20] для р=0,1. Последовательность исполь-
зования графической зависимости следующая:
а) по данным контроля строится' ряд (2.24) и находится значение
6 = т—rj2, где т— количество преобладающих знаков в ряде (2.24);
б) полученное значение 6 сравнивается с граничным значением бгр,
определенным при р=0,1 [20]. Это соответствует тому, что допустимые
величины отклонений в (2.24), при которых вероятность отвергнуть
правильную гипотезу Но, не превышают р. Параметр следует считать
информативным, если -б>6гр, и не несущим информации, если б<бгр.
При 6~6гр сделать достоверный вывод трудно, и этот случай следует
проверить с помощью других методов.
Часть II
АППАРАТ ПРОГНОЗИРОВАНИЯ
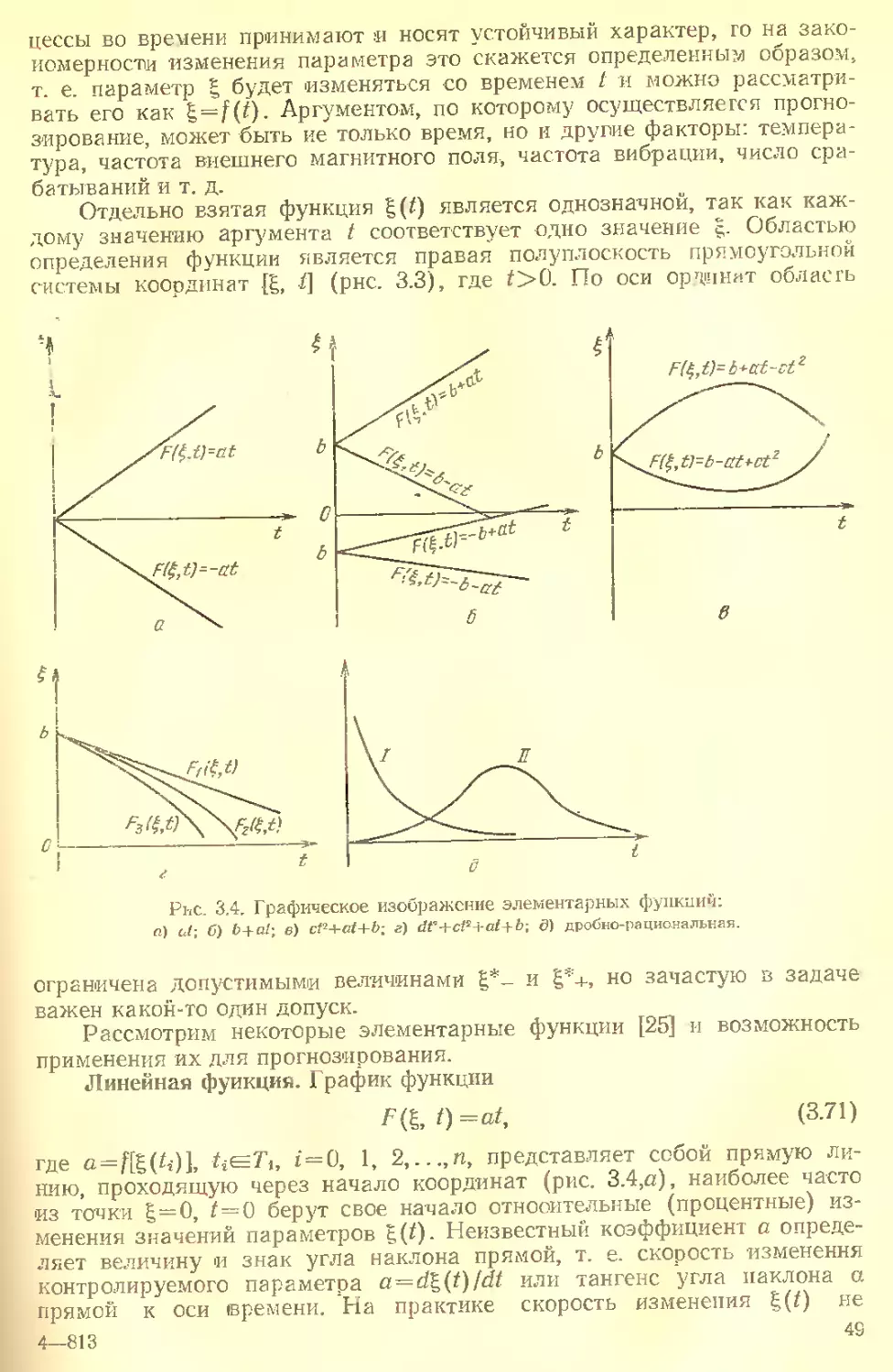
ГЛАВА 3. ОСНОВЫ АНАЛИТИЧЕСКОГО ПРОГНОЗИРОВАНИЯ
3.1. Методы аналитического прогнозирования
многомерных процессов
Изменение состояния подавляющего большинства технических си-
стем можно рассматривать как процесс, характеризуемый изменениями
некоторого множества параметров. В связи с этим изменение степени
работоспособности целесообразно определять совокупностью такого чис-
ла параметров, контроль которых позволяет достаточно полно пред-
ставить процесс изменения состояния диагностируемой системы. Тогда
состояние системы удобно характеризовать вектором в ^-мерном про-
странстве, где координатами пространства служат k параметров систе-
мы s=l, 2, k.
Положение вектора состояния в пространстве при этом будет опре-
делять некоторую степень работоспособности системы. В период экс-
плуатации степень работоспособности систем изменяется, вследствие
чего точка (конец вектора |) в пространстве состояний перемещается и
ее местонахождение определяется значениями k параметров. При
диагностике и прогнозировании целесообразно выделить области, соот-
ветствующие определенным степеням работоспособности, и определить
границу допустимого уровня работоспособности.
Таким образом, возникает задача, заключающаяся в предваритель-
ном периодическом контроле параметров &(/)> являющихся функция-
ми времени, определении в моменты контроля функции состоя-
ния Q[|(/)] =Q[£i(0, •••> £ь(0] и расчете значений функции Q(g)
состояния в области значений времени Т^>Т^
При этом чем дальше будет расположен вектор состояния от гипер-
поверхности допустимых значений степени работоспособности Q(^),
тем выше степень работоспособности диагностируемой системы. Чем
меньше разность ||—1*[, тем ниже уровень работоспособности. Степень
работоспособности системы тем ниже, чем больше вектор скорости
определенный в момент контроля, и чем ближе направление к пер-
пендикуляру к гиперповерхности
Использование методов аналитического прогнозирования предпола-
гает в определенной мере регулярность изменения компонентов процес-
са во времени. При этом под алгоритмом прогнозирования регулярных
процессов подразумевается такая система вычислительных операций,
которая строго предопределяется сложившейся ситуацией.
Иначе говоря, в одинаковых ситуациях используется один и тот
же алгоритм в противоположность алгоритмам прогнозирования слу-
чайных процессов, которые допускают неодинаковую систему вычисли-
тельных операций в идентичных ситуациях (задачах) .
Весьма перспективным методом прогнозирования регулярных про-
цессов является градиентный метод. В этом случае экстраполи-
руется функция работоспособности Q[£(/)] в градиентном направлении,
31
т. е. в направлении вектора градиента функции работоспособности. Как
известно, вектор градиента определяет направление наибольшего изме-
нения функции. Поэтому в данном случае этот метод является опти-
мальным в том смысле, что он оценивает работоспособность системы
в направлении наибольшего изменения функции работоспособности, т. е.
в направлении более быстрого достижения допустимых значений, или
в «опасном» направлении. Градиентное прогнозирование разделяется
на два этапа. На первом этапе определяют составляющие градиента,
т. е. частные производные функции работоспособности, по координа-
там— параметрам dQ/d£s (s=l, 2, ..., k). На втором этапе осуществ-
ляют прогнозирование в градиентном направлении, т. е. находят
Q [I (W ] = Q [I (М ] + уп+1 vq [| (М ], (3.1)
где Q[|(0функция состояния (работоспособности) в существующие
моменты времени; уп+4>0 — параметр, характеризующий длину шага
прогнозирования; V-Q^(Zn)] — вектор градиента функции состояния,
в общем случае равный
vQ(s)—[ >••••> ]• {^)
Имея в виду, что
vQ(D=li.+f +••• + < (3.3)
где <2=^111+^24- ... ii, 12, .... К —единичные орты, получим
аналогично (3.1)
^(in+.)=E,W + Wgg, s=l. 2,..., k. (3.4)
В тех случаях, когда функция состояния неизвестна, система уравне-
ний (3.4) позволяет найти ее. Пусть уп-н=^п-ь1—in—^n+i. Тогда, заме-
няя [£s(^n+i)—€s(^n)^Mn+i на d^ddt, получаем
d&fdt=dQ/dU (3.5)
Следовательно, зависимость (3.2) с учетом (3.5) можно заменить на
VQR(OJ=[$, >]. (3.6)
что существенно облегчает практическое решение задачи прогнозиро-
вания.
Заменяя d^dt простейшей функцией времени <ре(£), получаем
<Ps(0 = dQldls, s = 1,2.Ли d^ddt=<ps(t), (3.7)
откуда
Е,= С¥,(О<й=Ф.(Э- (3-8.'
О
Обращая уравнение (3.8) f=©(£s), можно получить
(0 =ф4© (£0 ]=Р (Ы. 1 (3.9
Таким образом, из (3.7) и (3.9) имеем
p(y=dQ/& s=l, 2,.., k. (3.10
32
। . - в (3.10) не входят другие координаты, кроме то частную
Ьиводную можно заменить на обыкновенную:
pfe)=d<M, s=l, 2....Л (3.11)
Г. 1я (3.11), получаем
+ (3.12)
В выражении (3.12) постоянная интегрирования С зависит от всех
z ^роме cs. На основе (3.12) имеем
<Э(е„ 5,,..., M = S <3-13>
5=1 '
Неопределенные интегралы в (3.13) можно брать с любой констан-
“ и, так как VQ от этого не изменится. Подставляя выражение (3.13)
• (3.1), можно осуществлять прогнозирование. В тех случаях, когда
z нкция работоспособности известна, решение поставленной задачи
ощается. В выражении (3.4) можно выбрать yn+i более сложным
азом, например: Yn+i=(/«+i—tn)q(tn) —&tn+lq(tn). Тогда вместо
(3 5) получим
1 —^dQ /о 1д\
<7(0 Л4'
Далее структуру ищут аналогично рассмотренному случаю.
Необходимо отметить, что величина параметра у может опреде-
,• дься двояким образом. Если y—const, то модуль шага прогнозиро-
:_ния для градиентного метода оказывается пропорциональным модулю
адиента:
(tn+1) - (Q = I (n+1) I = Yn+11 VQ (M I, (3-15)
т e. не является величиной постоянной. Если же в (3.15) выбрать
1 4=fc| ?<Ж(М)Г‘, то модуль шага прогнозирования оказывается
71 эстоянным для любой ситуации.
Выбор того или иного значения параметра у зависит от априорных
лэелставлен'ий о форме гиперповерхности (в том числе допустимой), со-
ответствующей равным уровням функции работоспособности Q(|).
В тех случаях, когда поверхность Q(£)—const имеет ярко выражен-
ие экстремумы, для повышения точности прогнозирования целесооб-
р: 1но ввести в (3.1) вместо y.„+i матрицу [21]
Г[п+1]=ЬЛ«+1)Н, s, /=1, 2,...,Л. (3.16)
7' ла (3.1) примет более общий вид:
Q[V4+i)] = ® (М1-Г[«+ l]VQ[g(/n)J. (3.17)
В этом случае величины шагов по различным координатам—пара-
* етрам различны и могут быть взаимозависимыми. В общем случае
П/z + l] может зависеть от значений векторов |(£n-i), К^г-2),...
Градиентный метод, вообще говоря, является линейным и эффек-
~ 1зно применяется в тех случаях, когда функция работоспособности си-
семы изменяется по линейному или близкому к линейному закону.
Анализ изменений функций работоспособности реальных систем по-
казал, что в большинстве случаев Q(£) изменяется не быстрее, чем ги-
813 33
перповерхность второго порядка. Поэтому для прогнозирования в этих
случаях целесообразно использовать операторный метод. Мате-
матическое выражение, используемое для прогнозирования оператор-
ным методом, включает в себя вторые частные производные функции
р а ботоспособн ости:
Q Н («»+.)] =Q [ (I (MJ - т„+. VQ i- (4)J - <+1 AQ [i (<„)], (3.18)
где в общем случае
AQ(|)=/^ (3.19)
— оператор Лапласа, учитывающий нелинейность второго порядка кон-
тролируемого процесса.
Для вычислений применимо и упрощенное выражение
QlSlU.)]=<3(1(4.)] - AQ(S(4)]. (3.20)
Если известна функция ('()], то вычисление AQ{|(/)] не вызы-
вает принципиальных трудностей. Когда же функция работоспособно-
сти выбирается произвольно, то для определения оператора Лапласа
следует выполнить некоторые преобразования. Поскольку (3.5) спра-
ведливо и для операторного метода, продифференцируем его:
___ 19 h
dt* ” ag dt' s~~
(3-21)
Первую и вторую производные от £s по t в (3.21) вычисляем сле-
дующим образом. Вместо dfcddt строим функцию
5s Ci+1) Is Ci) _v (+ \ -^
—дГ— de
а вместо d%/dts
rs Ct + l) rs Ci) _ // \_
_msта
Таким образом, получаем уравнение вида (3.21) для приращений
вторых порядков. Аппроксимируем rs(ti) и элементарными не-
прерывными функциями rs(t) и В результате
(0 := ле2 (^
(3.22)
и для всех s
n k
4=1 4=1 S
(3.23)
Уравнения (3.23) решаем численными методами и находим значе-
ния Ф(5). Однако с помощью (3.23) трудно вычислить Q(£s), так как
в это соотношение входит величина I в явном виде. Этой трудности
можно избежать, применив преобразования, аналогичные (3.7)... (3.13).
Действительно, поскольку (() —d£,sldt* то
t
^=\rs(t)dt^£(t)- (3.24)
о
34
- з (3.24) можно явно выразить ty т. е. получить зависимость t—
1 ' ): тогда
г. (О =Gfc>(b)]=ps(^) (3.25)
Ws (i) — /72sfО) (Ь) ] — '^>s ('Gs) • ( 3.26 )
С учетом (3.25) и (3.26) перепишем (3.23) следующим образом:
k k
Уя5(У = У]^-р6(у. (3.27)
ь +1 -S’—1
Решая это уравнение численными методами, находим Q(£i, £2,...
с ) для всех t^Ti. Описанный метод обладает достоинствами гра-
чтного метода и позволяет учитывать квадратичный характер из-
делия координат функции состояния |s.
Рассмотрим еще один метод, также учитывающий производные
пщин работоспособности первого и второго порядка и получивший
лзание метода суммирования производных. Применение
предусматривает, что функция Q(|i, £2 ••-,£&) известна, а частные
эизводные в выражении для прогнозирования представлены в виде
г мы.
Задача заключается в том, чтобы по известной Q(|) в области
осуществить прогнозирование значений Q(£) на интервале
’ -1 - •. ^п+т] и оценить погрешность прогнозирования. Рассмотрим ли-
Квое выражение, использующее производные первого порядка:
k
Q [«. (U А -, (Uj)] = Q в (М.....(«] + V -Ц- ДЕ» (3.28)
«=1
гд A^s — приращение по s-й координате.
Пусть существуют k функций (gi, ..., £ft)» • - Ы) таких,
(бь где D — гиперпараллелепипед, ^(MsCSs^^Gn+m),
5=1,2,...,Л,
|Q^(^-, 5=1, 2,..., k. (3.29)
Тогда погрешность <5(|i,...,ЕЭТ) прогнозирования, осуществляемого
4 > формуле (3.28), удовлетворяет неравенству
k
18(?,...ад |<2 % [S. (ад,..., е*(ад] дад (з.зо>
8=1
Доказательство. Считая A£s (s = l, 2,...,k) достаточно малыми,
•чедполагая, что существуют все частные производные, и пренебрегая
[иенами, содержащими произведения A£sA|z (s=/=Z), как величинами
рого порядка малости, получим
1Q^(Z),..., MU1I =
k k
У а?ге,(ад.... . WI у ft [6, (ад,..., (ад] &s.
s=l s=l
Прогнозирование осуществляем следующим образом: выбирая А£3
д я каждого s достаточно малым, по формуле (3.28) определяем зиа-
35
чения QU'1 (С), -.£'й(Z„)], где (tn) (tn) + Лщ (O, s=1, 2,. k
Затем с помощью (3.28) находим
k
; <П -»^(Ш
<%* (tn)
Погрешность вновь оцениваем по формуле (3.30), для чего заменяем.
ts(in) в первой части (3.30) на %'s (tn), а затем действуем, как и в пре-
дыдущем случае. На каждом шаге прогнозирования до момента tn+m
погрешность оцениваем с помощью (3.30).
Выражение для прогнозирования, содержащее производные второ-
го порядка, имеет вид
k
q(б„..., ад=qща„),..., ?„(/„я+2 q-(s[6,(tn),(«„)] де8 +
s— 1
k
+ 2 в (3-31>
Р. Г=1
Пусть существуют /г2 функций ^„(^,..., ^),..., qnn$i, , М» таких
что (£„ ..., и
Ъ), s, 1=1, 2,..., k. (3.32)
Тогда погрешность 6(£i,...»|й) прогнозирования, вычисленная по
формуле (3.31), удовлетворяет неравенству
|8(5„.... М|< 3 ЬОде.дЕ,.
5.
Доказательство. Считая Xt,s достаточно малым, предполагая, что су-
ществуют все частные производные, и пренебрегая членами, содержа-
щими произведения A£SA^/A;g?l, получаем
k
Q[e,(M.... MQi+2
S = ]
< S < S IQ"EsyI^A : S feAMS;-
s, /=1 s, l—l *. ’ =1
Прогнозирование по формуле (3.31) можно осуществить на т
шагов, как и по формуле (3.28). Существенный эффект может дать ком-
бинация выражений (3.1) и (3.18), (3.28) и (3.31). Если обозначить
линейные выражения через Qv (/), а нелинейные — через <2Д (£), то
(3-33)
где Лд — соответствующие коэффициенты (матрицы коэффициентов)
адаптации, определяемые в период обучения (в области TJ модели
(3.33) и уточняемые в момент очередного контроля.
Решение задачи прогнозирования значительно облегчается, если
изменение функции работоспособности в области удается описать
36
с приемлемой точностью сравнительно простыми математическими мо-
Z ями.
Линейная модель является наиболее простой. Она характери-
зуется линейной зависимостью Q от координат параметров ts, s=l,
-
Q„ ft,.... м= <2п + 2 °» &|Z’ «*М» (3-34)
5=1
или в векторном виде
QT2 [I (0]=Qn + {u (0 -1 (Ml VQ [§ (4-)]},
"де фигурными скобками обозначено скалярное произведение, а вектор
~ клиента функции! работоспособности предполагается постоянным в об-
J4cni прогнозирования.
Линейная модель распространяется, в основном, на достаточно мо-
нотонные и «гладкие» функции работоспособности, в других случаях
1 fee целесообразно применять только при прогнозировании на один-два
триода контроля системы.
Центральная модель удобна для применения в районе до-
пустимых границ функции работоспособности:
(3.35)
где f — заданная монотонно уменьшающаяся функция от расстояния до
Баннцы допусков £*=£*1, £*2,..1*и:
В простейшем случае, когда /(г) =г, получаем
0(1) ==<2*+М£-Г|,
(3.36)
' 0*=!0(|*)—допустимое значение функции работоспособности, /г —
1ЭСТОЯННЫЙ коэффициент, ||—£*|— модуль соответствующего вектора.
Центральная модель хорошо согласуется с линейной при больших
расстояниях до допустимых значений параметров.
Эллиптическую модель функции работоспособности можно исполь-
зс *ать в области допустимых значений:
Г k
1/2
Q&, е2,..., M=Q* + 2 а^-^У (3.37)
-i
гл. us>0 пропорциональны составляющим градиента функции работо-
Г особности. При ^—О2=...=ак модель вырождается в центральную
(3.36). Размерность модели k совпадает с числом переменных, для кото-
рых dQfd^s по модулю существенно больше, чем для других. В данном
iae эти параметры соответствуют большим значениям as.
Рассмотренные модели обладают ограниченной неопределенностью,
вторую, однако, можно один раз преодолеть и использовать модели
.-е на весь период прогнозирования. При случайных помехах, накла-
37
дывающихся на функцию работоспособности, начальная неопределен-
ность возрастает и затрудняет определение модели прогнозирования.
Если в реальных объектах изменение состояния описывается непря-
молинейными градиентными линиями, то для прогнозирования можно
использовать модель, в которой учитывается случайный, стохастический
характер градиентных линий. Такие мотели называются стохастиче-
скими.
Рассмотренные принципы можно использовать для прогнозирова-
ния изменения работоспособности широкого класса многопараметриче-
ских приборов и систем. При этом эффективность методов значительно
возрастает с применением ЭЦВМ
3.2. Метод обобщенного параметра
Идея метода обобщенного параметра при прогнозировании заклю-
чается в том, что процесс, характеризуемый многими компонентами,
описывается одномерной функцией, численные значения которой зави-
сят от контролируемых компонентов процесса. Такая функция рассмат-
ривается как обобщенный параметр процесса. При этом может ока-
заться, что обобщенный параметр не имеет конкретного физического
смысла, а является математическим выражением, построенным искусст-
венно из контролируемых компонентов прогнозируемого процесса.
Примером такого рода процессов может служить процесс измене-
ния состояния ряда электронных н электротехнических приборов и
устройств, характеризующий степень их работоспособности. При обоб-
щении параметров, характеризующих степень работоспособности при-
боров, приходится решать следующие задачи:
— определение относительных значений первичных параметров, т. е.
параметров узлов,
— оценка значимости первичного параметра для оценки состояния
прибора,
— построение математического выражения для обобщенного пара-
метра.
Определение относительных значений первичных параметров не-
обходимо в связи с тем, что состояние объекта может характеризовать-
ся параметрами, имеющими различную размерность. Поэтому все кон-
тролируемые первичные параметры следует привести к единой системе
исчисления, в которой они могут быть сравнимыми. Такой системой яв-
ляется система безразмерного (нормированного) относительного исчис-
ления.
Реально для каждого параметра gs, s=l, 2, ...,k можно выделить
допустимое значение при достижении которого объект теряет ра-
ботоспособность, и оптимальное с точки зрения надежности значение
ssout (зачастую оно равно номинальному значению £SH). Пусть в про-
цессе эксплуатации объекта соблюдается условие Если
достаточно ввести вместо £S(Z) новый параметр т]8Ц)>т]%
и тогда для будет соблюдаться требуемое условие.
Запишем безразмерный (нормированный) параметр в виде
С(0=& (О - ?J/(U - 5*s), (3.38)
где причем при М0 = ^опт ^=1, а при £fi = 0.
38
Таким образом, с помощью выражения (3.38) нормируется параметр
(f), а безразмерная нормированная величина С (t) изменяется с течением
времени от 1 до 0. Отсюда по величине ts(t) можно судить о степени
работоспособности объекта по данному параметру. Теоретически может
«Г*'"
быть < 0, но это означает, что на практике объект неработоспособен.
Можно указать различные нормирующие выражения, которые ока-
зываются удобными при решении частных задач, например:
€ (0 = (0/^0 или (t) =
€ (0 = € (0 =
Z (t) = & (0 - а = 1, 2,., /г,
(3.39)
(3.40)
где ^s(f), Etc, КТу> — соответственно текущее, нулевое, мак-
снмум-максиморум, заданное по ТУ значения и математическое ожида-
ние 5-го параметра.
Использование нормирующих выражений позволяет получить сово-
купность безразмерных величин, которые характеризуют состояние объ-
екта. Однако количественно одинаковое изменение этих величин не яв-
ляется равнозначным по степени влияния на изменение работоспособ-
ности объекта, поэтому необходимо дифференцировать первичные пара-
метры. Этот процесс осуществляется с помощью весовых коэффициен-
тов, величины которых характеризуют важность соответствующих па-
раметров для физической сущности задачи. Пусть в таком случае пара-
метрам объекта соответствуют весовые коэффициенты v4,
V2,..., Vfe, удовлетворяющие тем или иным заданным критериям, причем
0<v8<l.
Степень работоспособности объекта по множеству контролируемых
параметров можно оценить с помощью обобщающего выражения [22]
k f k,
<2.(0 = 2 *Х(01 /3 vs>
S=1 / S=1
(3-41)
где — обобщенный параметр объекта. »
Выражение (3.41) представляет собой линейное среднее, которое
обладает следующим свойством (будем считать его необходимым для
любого обобщенного критерия):
k
S vs= i-
£—1
QJ0
(0=1
Из определения обобщенного параметра следует, что чем больше
величины ts(f) и vs, тем больше вклад s-ro слагаемого (параметра)
в Qv(t), что соответствует и физическому смыслу. Однако весовые
коэффициенты vs могут выбираться не только из рассмотрения физиче-
ской значимости 5-го параметра, но и с учетом флюктуаций в функциях
£(0 и QjG).
39
Обобщенный параметр можно определить помощью выражения
вида
k
я %
f 11 I/v 1 S=1
[U£)] J (3.42)
которое представляет собой нелинейное среднее. Здесь также Qv(0=l
при всех (0=1- Кроме того, чем больше (t) и vs, тем больший
вклад вносит слагаемое [М01 8 в величину Qt(t).
Заслуживает внимания и другой вариант нелинейного среднего:
Qs(0 = Sv.[S(i)]1','/2 Ч, (3.43)
.4=1 / * = 1
где при ^(t)= 1, s — I, 2,..., k Q v(t)= 1.
Чем больше £S(Z) и %, гем больший вклад вносит слагаемое
ХЧ 1 у У
vs[^(01 8 в обобщенный параметр Qv(0-
Для определения обобщенного параметра можно использовать вы-
ражение для параметрического среднего:
f ’ <3,44)
4 =1 j
rie подбирается так, чтобы критерий (3.44) давал лучшее при-
ближение к результатам, полученным экспериментальным путем. Коли-
чественно р определяется на стадии обучения математических моделей
прогнозирования.
При рассмотрении выра/кений для'обобщенных параметров считалось,
что 1 (/) не меняет знака, т. е. всегда % (t) > £%,. Если же необходимо
учитывать знак, то нужно каждое слагаемое в выражениях (3.41)...
... (3.44), стоящее под знаком суммы, дополнительно умножить на член
вида sign[gs(0 —g%]_ В этом случае выражение (3.41) можно пере-
писать:
k / k
Qv (о=j (of8 sign (о—^*6] / 2 vb.
S=I / S=1
В тех случаях, когда в изменениях £ч(0 много случайного н по-
грешности измерений велики, в обобщенные параметры целесообразно
вводить интегральные значения безразмерных параметров £s(0:
Л ^4 + 1^
QJ0 = S vs f (3.45)
К
где (ti... ti+i) —интервал обработки или контроля. В зависимости от
изменений &(t) значения интегралов вида (3.45) также будут меняться,
однако более плавно и монотонно.
40
Применение выражения вида
k ft+i
QL(O=-Svfi J [X(OJ lpdtf
.^1 t.
г
(3.46)
где p целое положительное число, для построения обобщенного пара-
метра еще больше уменьшает влияние флюктуации первичных пара-
метров.
Применимо на практике и следующее выражение:
А *г + 1
<2._(П = Улв f —'----------Л, (3.47)
J ё» (О + ?.
где ps>0.
Можно, например, использовать оба выражения, (3.45) и (3.47),
сразу. Так, в тех ’Случаях, когда часть параметров g; возрастает,
а часть £м-1,...,£ь— убывает, следует пользоваться выражением
‘ 0 + 1 А
Qr(0=y *. j is(t)dt+ J; ve
6=1 t s~l+\
0+1
f dt
7 £ (0 + .<
Если обобщенный параметр брать в виде произведения первичных
параметров
С-.(О=(п^(ЧнГ • (3.48)
S=1 J
то выход любого параметра за допустимые пределы, т. е. ?(0=О, при
водит к равенству Qr(^)=0. Это несомненное достоинство выражения
(3 48) .
Обобщенные выражения позволяют определить запас работоспособ-
ности многопараметрического объекта и проследить характер измене-
ния работоспособности во времени. Матрица информации (1.4) после
нормировки и обобщения перепишется в виде
Q. (Q, Q. (К),Qx (ti),..., Q, (tn). (3.49)
Таким образом, задачу прогнозирования изменения работоспособ-
ности многопараметрического объекта, как уже говорилось, можно
свести к прогнозированию одномерной временной функции вица (3.49).
Пример. Испытания генераторной
усилительной лампы (типа ГУ) в тече-
ние 250 ч, у которой контролировались
6 -параметров, дали результаты, приве-
~чнныс в табл. ЗЯ. После нормирования
значений параметров с помощью выра-
жения (3.38) табл. 3.1 принимает иной
вид (табл. 3.2).
Обобщенный параметр вычисляем
с помощью выражения (3.41), где весо-
вые коэффициенты определялись из со-
ображений значимости контролируемых
параметров для прогнозирования долго-
вечности лампы. При этом они удовле-
6
творяти условию У, 'Ц 1 и бытиопре-
с=1
делены гак:
Vi(Jn) =0,05; V2((7^0 =0,20; Тз(5)=0,25;
V4 (/.то) =0,15; V5 (Д,3) =0/1; т?е(Р)=0,25.
В результате обобщенный пара-
метр принимает следующие значения
(табл. 3.3). Для прогнозирования вос-
пользуемся полиномом Ньютона первой
41
ТАБЛИЦА 3.1
t, Ч /_ „«„=9,5 А, н ном . ' /* =10,5 А н CQ S «а e|i И tw tu* 1 1 сс 2“и о 2 со и S §и и* со со < U ю §« Д о о «С» —мА, “3io мА 83 m g е т § ° 11 й* о. О.
0 10 126 5,4 2 76 814
120 10 131 5,4 4 88 874
250 10 136 5,2 5 84 870
ТАБЛИЦА 3.3
t, ч 0 120 250
Q. 0,689 0,671 0,579
ТАБЛИЦА 3.2
t, ч К S Zg3 "р
0 0,5 0,7 0,6 1,о 0,85 0,656
120 0,5 0,45 0,6 0,846 0,55 0,897
250 0,5 0,2 0,466 0,769 0,65 0,88
степени: F{m) =£(/») +A£n-im, где т —
чисто шагов прогнозирования (контро-
ля). Д^п-i = *(tn) = — 0,092,
g(fn) =0,579
Поскольку неизвестным в полиноме
является т, то воспользуемся способом
обратного прогнозирования, помня, что
Q®, (0 = 0 и F (m*) = Q% (/).
Отсюда прогнозирующее уравнение пе-
репишется как 0=0,579—0,092m*. В ре-
зультате т* =0,579/0,092—0,3. Таким об-
разом, отказ по результатам прогноза
наступит через 6,3 шага прогнозирова-
ния, т. е. через /=тД/=6,3-|125=788 ч.
На практике же лампа отказала через
820 ч. Такая точность вполне удовлетво-
ряет с точки зрения технических прило-
жений методов прогнозирования.
3.3. Прогнозирование одномерных временных рядов
На практике прогнозируемые процессы можно представить в виде
временного ряда чисел, определяющих их характер. При этом резуль-
тат прогнозирования получаем в виде одного числа. Иногда и прогнози-
рование многомерного процесса можно свести к этому случаю, если рас-
сматривать характер изменения его компонентов в отдельности.
Кроме того, существует достаточно много задач, когда требуется
осуществить прогнозирование отдельных временных функций (парамет-
ров). В этом случае постановка задачи принципиально ничем не отли-
чается от ранее сформулированной, только речь будет идти об одном
временном ряде. При индивидуальном прогнозировании следует анали-
зировать отдельные строки информационной матрицы или пересчиты-
вать ее во временной ряд (3.49). При групповом прогнозе исследуют
строки матрицы математических ожиданий (2.15). Например, в резуль-
тате контроля выбранного параметра объекта получен ряд значений
g(/o), соответствующих моментам времени /о,
tlf..., U,взятым через постоянный интервал Ы в известный пери-
од эксплуатации 7\ (рис. 3.1). Требуется на основе известных значений
о £(^)> ii^T± вычислить значения параметра g(£n+i), ...» £(£«+•?), ...
...,^(/n+m) в будущие моменты времени tn+^T^ /=1, 2,..., т, где Тг —
предстоящий период эксплуатации объекта.
При такой постановке задачи основным является построение та-
кого аналитического выражения W(/), которое давало бы минимальную
ошибку прогноза. Каким -бы, однако, ни было полученное выражение,
в области Ti необходимо соблюсти условия
[Г (0 - £ (01,=#4 - о, I = О, 1, 2,..., п, (3.50)
•42
Выполнение условия (3.50) позволяет с помощью прогнозирующего
выражения учесть тенденцию изменения £(/) в интервале Об-
ласть времени 7\, где известно изменение £(/), вообще говоря, исполь-
зуется для обучения математической модели прогнозирования, т. е. для
количественного определения неизвестных коэффициентов модели, ко-
торые оптимальны для решения именно отдельной рассматриваемой за-
дачи. При этом следует отметить, что насколько точно будут найдены
неизвестные коэффициенты, настолько точен будет и результат прогно-
зирования.
Условие (3.50) не является столь строгим и практически всегда вы-
полнимо, если пользоваться методами теории интерполяции. Более
сложным для выполнения является другое условие, накладываемое на
Рис. 3.1. Область известных
и прогнозируемых значений
контролируемого парамет-
ра g(0-
прогнозирующую модель в области значений аргументов 7’2=^+i...
• - -
/ = 1, 2,.. ,,m, (3.51)
где — заданная (допустимая) ошибка прогнозирования на /-м шаге.
Соблюдение требования (3.51) с минимальными приводит к наиболее
эффективным выражениям для прогнозирования.
Для конкретных задач необходимо вводить дополнительные усло-
вия, которые определяются различными физическими условиями и по-
зволяют провести более точные вычисления. Можно ввести разнообраз-
ные ограничения, использующие, например, уменьшение со временем
запаса работоспособности технических объектов, которое количественно
выражается изменением значений параметров.
Таким образом, можно сформулировать одно из ограничений, кото-
рое применимо ко многим задачам: величина £(/) должна с течением
времени убывать (возрастать). Тогда из-за d£jd.t<X) прогнозирующее
выражение в области Т2 должно удовлетворять условию
dW nl
dt
(3.52)
Для того чтобы коэффициенты модели W(t) учитывали условие
(3.52), они должны удовлетворять системе неравенств
Г'ап+1)<0,
(3.53)
W"(«n+ra)<0,
43.
в pt ;ультате решения которой совместно с системой (3.51) методами
линейного программирования можно вычислить коэффициенты прогно-
зирующего выражения.
Часто вводят ограничение другого типа: значения параметра g(/n+3)
не- должны превышать какой-то величины с,. Тогда вместо системы
(3.53) получим W(tn+j) <Cj, / = 1,2,..., т.
Дополнительные условия позволяют расширить возможности мето-
дов прогнозирования, разнообразить их, а также повысить точность про-
гнозирования при ограниченном числе данных.
Выбор и построение аналитического выражения для прогнозирова-
ния является одним из основных вопросов, который принципиальным
образом влияет на конечный результат. При этом к прогнозирующему
выражению предъявляются следующие два требования: оно должно
быть только индивидуально детерминированным и содержать элемент
адаптации, используемый в процессе решения задачи.
Здюь говори гс-с о простоте ычислений, точности <и др., эти усло-
вия очевидны и остаются всегда при решении подобных вопросов. Пер-
вое требование имеет в виду возможность учета прогнозирующей фор
мулой индивидуальных особенностей каждой отдельной задачи, при-
спосабл1иваемости к новой задаче, выражающееся в способе вычисления
неизвестных коэффициентов, отбрасывании ненужных членов и т. д.
Второе требование подразумевает необходимость введения в оконча-
те ьный вп ; и. шв кого выражения членов (коэффициентов) адап-
тации, которые бы вычислялись <и корректировались в процессе решения
3* W’l.
В качестве подобных выражений, используемых для прогнозирова-
ния величины контролируемых параметров, можно использовать раз-
личные полиномиальные и степенные многочлены, аппроксимирующие
выражения, элементарные временные функции и т. п. Однако брать
в качестве искомого выражение качой-то отдельный многочлен или по-
лином определенной степени нецелесообразно, так как при этом значи-
тельно сужаются его прогнозирующие возможности. Нужно получить
формулу такой структуры, которая содержала бы полиномы различных
степеней и различные адаптационные коэффициенты, повышающие точ-
ность прогнозирования.
Рассмотрим в качестве прогнозирующего аналитического выраже-
ния IF(tf) многочлен следующего вида [23]:
IF (О — 2 1 (3.54)
/=1
где t) представляют собой базовые выражения, составляющие ос-
нову прогнозирующей формулы; Ai—степенные адаптационные коэф-
фициенты, 1= 1, 2,..., р — степень базовых выражений.
В пользу использования зависимостей вида (3.54) в качестве про-
тезирующих выражений можно привести следующие доводы. Старение
а износ объекта, если отсутствуют конструктивные и технологические
просчеты в его исполнении, происходят в определенной степени посте-
пенно. Монотонность в большинстве случаев заложена в явной или
скрытой форме в этих постепенных изменениях работоспособности объ-
екта. Иногда характер этих изменений трудно определить, но его выяв-
лению часто помогают различные способы обработки первичной инфор-
мации.
44
Если в контролируемом процессе наблюдается в определенной сте-
пени монотонность и постепенность и налицо инерционность изменения
во времени, то количественное выражение изменения процесса—изме-
нения параметра £(/) —можно разложить в ряд с помощью полиномов
различных степеней. Такое разложение, например с помощью выраже-
ния (3.54), весьма удобно и имеет определенные преимущества. Оно
аналогично спектральному ана-
лизу (разложению) колебатель-
ных функций. Иначе говоря, мо-
нотонные и инерционные функ-
ции можно представить в виде
суммы полиномов различных сте-
пеней от J до ц, вклад которых
в изменениях функции различен и
характеризуется зависимостью
A=f(l), 1=1, 2, ..., ц. Адаптации
онные коэффициенты показывают
«полиномиальный спектр» функ-
ции g(Z).
Состав полиномиального
Рис. 3.2. Временное подобласти вычисления
слагаемых a tpp и корректировочных коэф-
фициентов у и
спектра позволяет ограничиться
соответствующими базовыми вы-
ражениями Fitt» /), что сказывается на простоте и быстроте решения за-
дачи прогнозирования. Кроме того, использование выражений вида
(3.54) дает следующее преимущество. Базовые выражения при распро-
странении их на область времени 7?. перекрывают значительные зоны
возможных значений параметров. Коэффициенты Ai, вычисляемые на
основе последних данных о £(£), сужают эти зоны и с каждым после-
дующим контролем параметра корректируются и повышают точность
прогнозирования.
Величины степенных адаптационных коэффициентов целесообразно
ограничить следующим образом:
или
2 А=1
Г—1
R
ПА^1-
(3.55)
(3.56)
Условие (3.56) является более жестким и поэтому лучше использо-
вать именно его. Базовые выражения в (3.54) различных степеней мож-
но выбирать однотипными, что упрощает вычисления, и различными,
что увеличивает возможности прогнозирующего выражения. При этом
корректировку и адаптацию осуществляют внутри базовых выражений.
Наиболее общее выражение, которое можно использовать в качестве
базового, представим следующим образом:
F 0, 0 = ад0 К) + (0 + - - + (0, (3.57)
где ap = f [Ц4)1 — неизвестные коэффициенты, р=0, 1,..., ц; ti& i
? (0 — временные функции простейшего вида. При % (0 = 1, ?i(0 = ^p
45
(?2(t) = t2p, , ?j*(0=выражение (3.57) примет вид
p-
F(l, t)=^ apt*\ (3.58>
p—п
где p может быть любым положительным числом, целым или дроб-
ным.
Если необходимо ослабить или усилить влияние некоторых сла-
гаемых, то в (3.58) вводятся дополнительные коэффициенты у, которые
называют первичными адаптационными:
н
о=2 ypvf* <2 3’59)
Р=о
где то=1.
В этом случае общее прогнозирующее выражение (3.54) можно
переписать:
^(0=3 А2 feaptfp. (3.60)
Z=I р-0
Рассмотрим последовательность вычисления составляющих элемен-
тов многочлена №(2), т- в. базовых выражений F(£, t) и адаптацион-
ных коэффициентов А.
Поскольку значения £ (/) известны только в области Ти то F (£, t), у,
и А можно определить только для этой области, причем коэффициенты
ур вычисляются только после определения неизвестных ар и р в базовом
выражении (3.58), а коэффициенты At вычисляются после того, как най-
дены ур и составлено выражение (3.59). Такая последовательность дик-
тует распределение известной информации о £(/) в области 7\. Посколь-
ку ур вычисляются по известным слагаемым выражения F(^, f), a At—
по известным F(g, t) и у, то базовые выражения н адаптационные ко-
эффициенты нельзя найти по одним и тем же значениям £(/). Необхо-
димо область обучения 7\ разбить на три подобласти (рнс. 3.2).
В некоторых случаях величины ур и Ai можно находить по априорным
данным или получать при решении идентичных задач. Иногда для упро-
щения решения задачи можно опускать коэффициенты у . В подобла-
сти Гц=[/0 ... ir] методами, встречающимися в теории интерполяции,
теории аппроксимации и др., вычисляются неизвестные коэффициенты
базовых выражений Е(£, /), а «именно <2р <и р без первичных адаптаци-
онных коэффициентов у . Далее в Е(£, /) (3.58) подставляют значения
аргументов нз подобласти Т21=$г-и. - Дп], т. е. осуществляется экстра-
поляция на известную подобласть Т21. При этом будут существовать от-
клонения di расчетных величин от экспериментальных:
apep~Z(ti) = dit i = h. (3.61)
р=0
Решая систему уравнений
2 Гр«р^-Ц.)=0. 1=г + 1.... h (3.62)
р—о
относительно у добиваются равенства di нулю.
46
В подобласти 7si=«£fi+i.. .tn определяются коэффициенты Alr 1=1,
2,..., jx. В данном случае осуществляется экстраполяция базовыми вы-
ражениями (3.59) на подобласть 731. По полученным результатам (ре-
зультатам экзамена) решается система уравнений:
E(ifc+1)=2 тЛС,-
7=1 р=о
?(«ft+2)=2 а 2 yp<v£2,
7=1 р=о
р. I
4U=3A3V₽e. (3-63)
1=1 р=о
где неизвестными являются только степенные адаптационные коэффици-
енты At.
Таким образом, с помощью ур осуществляется корректировка вы-
числений внутри базового выражения, а с помощью Ai — базовых выра-
жений в рамках общего прогнозирующего выражения TF(Z). В тех слу-
чаях, когда Тр и At слишком малы, соответствующе мп слагаемыми и
полиномами в выражениях (3.59) и (3.60) можно пренебречь. Так, на-
пример, при изменениях £(£), весьма близких к линейным, в (3.59) прн
р=1 останется только двучлен, а в (3.60)—полином первой степени,
причем получим y'i = 1 и А{= 1.
При прогнозировании в области Т2 удобно представлять W(t) функ-
цией от числа шагов прогнозирования т. Учитывая, что m=(t—tn)/&t,
где Л1/ — интервал контроля, и принимая Д/=1, т. е. равным относитель-
ной единице времени, выражение (3.54) можно переписать:
Г(т>=2 AFZ(^, m). (3.64)
i=i
В качестве базовых можно использовать следующие выражения:
1) преобразованную интерполяционную формулу Лагранжа [24]
ГД1-, m)=Z.^(/<,) + Z.ul4O4--.. + ^«f) + - + ^(y. (3.64)
где
7=Н I t'—V-
m) = Ц (m-H) ГР~/) (3-65)
7=0 I 7=0
&V-—i I
— коэффициенты Лагранжа; m — число шагов прогнозирования; i, j—
индексы интервалов времени в Ли Т^\
2) вторую интерполяционную формулу Ньютона, которая после
преобразования имеет вид
Fh(e, m) = ^(fn)4- + Д%-Л.4- ..., (3.66)
где
А=р.
= f (т)=~т П(т— 14-Л)
(3.67)
— коэффициенты Ньютона;
47
3) полиномиальное выражение вида
|Л р,
m) =S
Z=0 i=-0
(3.68)
где git=f(p, t) — постоянные коэффициенты;
4) преобразованный ряд Тейлора
т)^^(/п) + ^(Гп)61 + Г(^)6г + -. ЖЯ, (З-69)
где Vх(tn) — Р--я производная в точке О,
6,. (т)—(3.70)
— коэффициенты Тейлора.
Численные значения указанных коэффициентов (3.65), (3.67),
(3.70), а также gu в (3.68) в функции от числа шагов прогнозирования
и степеней базовых выражений приведены в [23].
Кроме того, в качестве базовых выражений можно использовать
ортогональные полиномы Чебышева; многочлены вида (3.57), где неиз-
вестные коэффициенты ар вычисляются методом наименьших квадра-
тов; различные эмпирические выражения, учитывающие наиболее пол-
но индивидуальную специфику поставленной задачи; разнообразные
элементарные математические функции и множество других выражений,
используемых в численном анализе и других областях математики. Не-
обходимо заметить, что эффект от использования прогнозирующих вы-
ражений вида (3.60) во многом зависит от физических процессов, про-
текающих в техническом объекте.
3.4. Применение элементарных функций для прогнозирования
изменения параметров объектов
Элементарные математические функции с успехом применяются при
решении многих практических задач. Анализ кривых изменения пара-
метров отдельных элементов, приборов и узлов систем говорит о воз-
можности их аппроксимации сравнительно простыми выражениями. Это
Рис. 3.3. Область определения
исследуемой функции £(/).
объясняется тем, что при изменениях па-
раметров этих элементов преобладает не-
обратимая составляющая, которая в ос-
новном и определяет закономерность из-
менения параметра и носит характер,
близкий к детерминированному, почти
детерминированному, квазндетерминиро-
ваниому.
Каждый параметр технического обь-
екта является количественным выраже-
нием тех физических процессов, которые
протекают в нем. Однако для большин-
ства элементов и приборов функциональ-
ную .зависимость параметра от указан-
ных процессов практически невозможно
определить в связи со сложностью и ма-
лоизучеппостью их. Если же про-
48
цессы во времени принимают я носят устойчивый характер, го на зако-
номерности изменения параметра это скажется определенным образом,
т. е. параметр £ будет изменяться со временем / и можно рассматри-
вать его как Аргументом, по которому осуществляется прогно-
зирование, может быть ие только время, но и другие факторы: темпера-
тура, частота внешнего магнитного поля, частота вибрации, число сра-
батываний и т. д.
Отдельно взятая функция £(Q является однозначной, так как каж-
дому значению аргумента t соответствует одно значение Областью
определения функции является правая полуплоскость прямоугольной
системы координат [£, i] (рнс. 3.3), где £>0. По оси ординат область
Рис. 3.4. Графическое изображение элементарных функции:
о) at; б) b-t-at; в) cf2+at+b; г) dr+ct^+at+b; а) дробно-рациональная.
ограничена допустимыми величинами g*_ и но зачастую в задаче
важен какой-то один допуск.
Рассмотрим некоторые элементарные функции [25] и возможность
применения их для прогнозирования.
Линейная функция. График функции
a a,
(3.71)
где a=f[£(ML i—0, 1, 2,. ..,п, представляет собой прямую ли-
нию, проходящую через начало координат (рис. 3.4,а), наиболее часто
из точки £ —О, /=0 берут свое начало относительные (процентные) из-
менения значений параметров &(/). Неизвестный коэффициент а опреде-
ляет величину и знак угла наклона прямой, т. е. скорость изменения
контролируемого параметра a=d^(t)(dt или тангенс угла наклона а
прямой к оси «времени. На практике скорость изменения не
4—813 49
является постоянной, поэтому точность прогноза зависит от того, на-
сколько вычисленная а близка к реальной.
Более общее выражение линейной функции (рис. 3.4,6) имеет вит
f(|, t)=b+at, (3.72)
где 6=f[£(4)] характеризует начальное значение параметра ^(t), 6^0.
Учитывая псе сказанное относительно коэффициента а в (3.71), от-
метим, что величины а и b в общем случае являются случайными ве-
личинами. При пери одическом контроле они уточняются на каждом
шаге.
При прогнозировании а и b можно вычислить по двум последним
значениям параметра B('/n-i) н £(А) и тогда F(g, т) =£(tn) ±A>«_i?n,
где A^K-i=i(^n)——первая конечная разность.
При прогнозировании на несколько шагов вперед, тем более на
один интервал контроля, линейная функция (3.72) является весьма
эффективной, так как часто технические параметры на отдельных
участках достаточно хорошо аппроксимируются прямыми.
Квадратичная функция. В общем случае она имеет вид
F(lt t)=ct4-at+b, (3.73)
где с=Л1(/г)]¥=О, i=0, 1, 2,
Из (3.73) можно получить частные выражения при следующих усло-
виях: а#=0, 6 = 0: ц=0, 6^=0, а=0, 6=0.
Коэффициент с идентичен ускорению процесса, иными словами,
его второй производной. Величина с может быть как положительной,
так и отрицательной, что соответствует увеличению или уменьшению
скорости старения и износа. Если коэффициенты с и а очного знака,
функция (3.73) не имеет экстремума; он появляется прн разнополяр-
ных с и а. Анализируя коэффициенты с (вторую производную), можно
сделать вывод о выпуклости или вогнутости кривой £(/). Применение
выражения (3.73) особенно целесообразно тогда, когда в изменениях
£(•/) наблюдается определенная нелинейность, и с течением времени
параметр изменяется по параболическому закону (рнс. 3.4,в).
Кубическая функция. Для аппроксимации кривых изменения g(Z)
функция
Г(£, 0=^3+^+а/+6, (3.74)
где i = 0, 1, 2,..., и, используется значительно реже.
Однако с ее помощью можно определить величину, важную для про-
гнозирования. Выражение (3.74) указывает на практическую границу
закономерности изменения %(1). Анализ экспериментальных данных по-
казывает, что для огромного большинства технических изделий уравне-
ние (3.74) представляет собой своего рода гарантированную границу
изменения работоспособности технических объектов.
Дробно-рациональная функция. В общем виде функция
t) =
ai* + «р,—1 1 + + ad + ао
Vlt1 + + •• + М + ро
(3.75)
мало пригодна для прогнозирования, но получаемые из нее простыми
преобразованиями элементарные выражения также можно использовать.
50
Обратно пропорциональная зависимость F(£, t) =«o/0^+Po) гра-
фически -представляет собой гиперболу, которая нередко встречается на
практике (рис. 3.4,д).
Аналогичный характер изменения -имеет и дробно-линейная функ-
ция F(g, 0 = (а^+'ао)/(!М+!М-
У некоторых объектов кривые изменения параметров g(£) имеют
точку перегиба, т. е. вторая призводная %'(t) меняет знак. Такие функ-
ции трудно аппроксимировать и экстраполировать, поэтому в общем
наборе элементарных функций желательно иметь такую, которая по-
зволяет моделировать изменение параметра. Подобную зависимость
имеет график простейшей Дроби F(g, t) = (ai£+feo)/(P2F4-[3iZ + Po). Во
всех приведенных дробных выражениях коэффициенты а и (3 являются
функциями S(F),
Показательная функция. Весьма распространенной на практике
является зависимость (рис. 3.5)
F(g,
(3.76)
где a, b, c=/Is(/i)] — неизвестные коэффициенты, а>0. Если вместо а
в (3.76) ввести экспоненту, то получим экспоненциальную функцию
F(£, 1)=Ь&\ (3.77)
где знаки коэффициентов b <и с
Ш-
определяются характером изменения-
Рис. 3.5. Графическое изображение по-
казательной функции.
Рис. 3.6- Примерный график функции
Ffc, 0 = 2»^ .
Пример. Пусть для нахождения не-
известных коэффициентов b <и с исполь-
зуются два значения контролируемого
параметра £(/и-1) и £(Гп):
F (L
F(|, =
Решая эту систему, -получаем про-
гнозирующее выражение:
_, г ж— ) I V
т)—§(/„_)) £(£те) I
(рис. 3.6), то для экстраполяции можно-
использовать функцию
(3-78)
(»)
где -число слагаемых в ’(3.78) опреде-
ляется эмпирически.
Пример выбора прогнозирующей
функции. В табл. 3.4 приведены отно-
сительные значения тока спада катода,
усредненные по целой партии маломощ-
ных клистронов.
ТАБЛИЦА 3.4
где Lt = tn —
Когда у -контролируемой функции
встречается экстремум — максимум
t, ч 200 600 юоо 1400 1800
23.7 52 59.2 73 83.2
51
4*
II родолэкение табл. 3.4
t, Ч 2220 2690 З'ЮО 340И 380')
А/ // к' и 83,9 84.2 85,2 89 93,7
5(М
U>x(0 ‘
юо (А/ /)0
(Л/ /)о
Требовалось ...шти функцию, кото-
рая наилучшим образом описывала бы
эти изменения <л, следовательно, могла
•быть использована для осуществления
прогнозирования. Исследовались четыре
ида функции: а) полиномиальная F(Z)
—аь+а^+а2&:, б) логарифмическая
f2(/)_log a(l+6Z); чз) натуральный ло-
ирифм Fs(t) = 1п(| +bt); г) показатель-
ная )-/1(Z)=,l—д) .показательно-сте-
пенная /-.(/)
Для упрощения вычислений прово-
дились преобразования:
t - 200
100 ’
(ДЛ/)о '
23,7;
.Методом наименьших квадратов
определялись известные коэффициенты
в полиномиальной функции и функции
ншурального логарифма: F} (т) -—0,185
+ 1,745т+0,2975-t2, Fs(t) =ln(l +6,443t).
Меч-од ом средних вычислялись ко-
эффициенты в остальных формулах:
- I,f55 lg (115,22т),
(т) = 1 - е
F^) I- е-о^.бЗ
В табл. 3.5 приведены значения сум-
мы квадратов отклонений между истин-
ными величинами тока катода (табл. 3.4)
и полученными с помощью аппроксими-
рующих функций.
Таким образом, функция F(t) =
=•1— ехр[—0,972t*j-G5] наилучшим образом
описывает процесс изменения Ы/1 кли-
строна и се применение более эффектив-
но при прогнозировании долговечности
клистро1 1 по рассматриваемому пара-
метру.
т 1Б л и ц А
0
Вид функции й'.0+<71‘+^2'Г2 1п(1+(гс) loga(l+frc) 1- е~ят 1 -ехр[-
10 1 0,4649 0,4558 0,2262 0,4604 0,180?
3.5. Обратное прогнозирование и вопрос точности
Обратное прогнозирование удобно тем, что результатом вычисле-
ний является не величина контролируемого компонента в будущие мо-
менты времени (прямое прогнозирование), а момент времени выхода
процесса за допустимые границы.
Применение обратного прогнозирования существенно расширяет
круг практических задач, которые могут быть решены. С другой сто-
роны, для решения этих задач пригодны методы прямого прогнозиро-
вания после некоторого преобразования. При этом принципиальным от-
личием являемся только то, что при прямом прогнозировании задаются
моменты времени в будущем и необходимо вычислить величины компо-
нентов (параметров) в эти моменты, а при обратном задается величина
компонента (параметра) в будущем (допустимая граница) и необхо-
димо вычислить момент времени, когда процесс достигает такого уров-
ня, что компонент выйцет за допустимые пределы. Перепишем урав-
нение (3.1) в упрощенном виде:
Qn+j=-<2n+Yn+3-VQr), /=1, 2,..., т, (3.79)
52
i значения функции работоспособности в будущие моменты эксплуа-
гак 11 являются функцией всех слагаемых в правой части:
Q»u-i—f[Qn, VQW, (3.80)
Поскольку при обратном прогнозировании необходимо определять
момент достижения функцией допустимой границы Q*, т. е. когда
Qnq = Q*. то (3.79) можно переписать:
О* = д,,.+Гя^л, (3.81)
где неизвестной величиной является Tw — время жизни илн долговеч-
ность объекта Гж=/Д/. Отсюда
^=(Q*-Q«)/VQn (3.82)
и зависимость, аналогичная (3.80), может быть записана как
F«=<p[Qn, VQn, Q*], (3.83)
т. е. две величины меняются местами.
В одномерном варианте при использовании выражения (3.60) пра-
вая часть его приравнивается величине £*:
е* =2 a 2 wr- <3 84)
1-1 р=0
где у — первичные адаптационные коэффициенты.
Таким образом, получили одно уравнение с одним неизвестным, ре-
шая которое можем найти Тж. При линейном прогнозе, когда g=l, А =
= 1 (уо=1), получим
Гж=1«* a«)Z(Y,а,)]'"’•
При большем числе слагае>мых в (3.84) при р=1 решается квадра-
тическое, кубическое и т. д. уравнения. Вычисления в определенной сте-
пени усложняются, но алгоритм решения получаемых уравнений обыч-
но разрабатывается заранее, что облегчает прогнозирование [23].
Точность прогнозирования — весьма сложный вопрос, поскольку аб-
солютно точный прогноз невозможно получить, а насколько прогнозиру-
емая величина близка к истинной, можно оценить только ориентиро-
вочно. Причина этого — множество факторов, которые могут влиять на
процесс, в результате чего при изменениях параметров случайная со-
ставляющая играет более или менее заметную роль. Поэтому для
уменьшения погрешности необходимо тщательно подготавливать и осу-
ществлять прогнозирование. В самом общем случае величина ошибки
зависит от трех основных причин: 1) от степени изученности исследуе-
мого процесса; 2) от количества и качества имеющейся информации
(априорной и текущей) о контролируемом процессе; 3) от выбранного
метода прогнозирования.
При решении каждой конкретной задачи будет, естественно, свой
путь определения ошибок, однако можно отметить общие моменты.
Оценку ошибок прогнозирования е можно произвести как эмпирически-
ми, так и аналитическими способами. Эмпирический путь определения
е можно осуществить двумя методами. Метод определения ошибок по
априорной информаций связан с набором статистических данных ре-
53
зультатов лабораторных испытаний н эксплуатации. Метод определе-
ния е по текущей информации предусматривает вычисления ошибки
предыдущего прогноза на каждом шаге контроля и экстраполирования
полученного ряда ошибок на будущее.
Ошибки прогнозирования изменения -состояния технических объек-
тов по априорной информации можно оценить при выполнении трех
условий:
а) необходимо иметь информацию об изменении функции работоспо-
собности во времени для большого количества интересующих нас тех-
нических изделий;
б) указанные изделия должны пронтн длительные эксплуатацион-
ные или полевые (лабораторные) испытания для определения их фак-
тической долговечности;
в) необходимо произвести прогнозирование хода кривых изменения
параметров, полученных в зада ной области 7\ до выхода параметра за
допустимый предел.
Таким образом, при прогнозировании хода известных кривых пара-
метров в заданной области на /=1, 2,..., m шагов вперед и
сравнении истинного £и(ФнД и прогнозируемого ьп(Ф-н) получим отно-
сительные значения ошибок 8j:
100 од, 2,..., m, (3.85)
£н
где £н—номинальное или начальное значение исследуемого параметра
£(£). Исследование множества кривых идентичных параметров позво-
ляет получить наиболее устойчивые (усредненные) значения ошибок на
каждый интервал времени прогнозирования, т. е. получить статистиче-
ские значения ошибок. Важность получения подобной информации для
повышения точности прогнозирования подчеркивалась еще Н. Вннером
[26].
При отсутствии данных об ошибках на каждом шаге прогнозиро-
вания их можно определить по текущей информации" следующим обра-
зом. Известная область Ti разбивается на ряд подобластей (больше 3),
где в первых трех определяются компоненты прогнозирующего выра-
жения П7(/), а в последующих, например в четвертой подобласти, по
результатам прогнозирования находят ряд ошибок s(tn),
который можно экстраполировать дальше до момента tm. Это становит-
ся возможным благодаря перенесению начала прогнозирования внутрь
области Ti, в частности в начало четвертой подобласти.
Для определения ошибок аналитическим путем можно дать только
общую идею, поскольку для каждого конкретного метода будут свои
ошибки. Этот путь позволяет получить как бы ошибку метода прогно-
зирования, которая зависит и от качества информации. Идея заключа-
ется в том, что ряд значений параметров £(й)), £(/i),..., £(/эт), получен-
ных в результате контроля, предполагают по тем или иным причинам
не равными истинным и этот ряд представляется как
со+Д^о, £1+|Д£1,..., gn+A£n, (3.86)
где Д£< — например, погрешности контроля.
В результате коэффициенты прогнозирующего выражения будут вы-
числены с погрешностью ар + Д«р, Тр + Дур, А-фДА, отсюда результат
прогнозирования £(^i+j) также будет получен с ошибкой Д£п+д которая
54
зависит от качества ряда (3.86) и выбранного метода прогнозирования.
Очевидно, погрешности в (3.68) будут влиять и на время прн обратном
прогнозировании.
Определим точность вычислений на примере метода обобщенного
параметра при наличии погрешностей в исходной информации. Пусть
значения контролируемых параметров £s(0> $=Е 2,..., \k поступают
с некоторой дисперсией ^(/)±q]os, где щ— среднее квадратическое от-
клонение s-ro параметра т]^3 и может быть целым и дробным. Тогда
относительное значение параметров (3.38) будет получено также с по-
грешностью
с {/ч k (0-Ге +
-- t fc* t ____ t* -- fc _____t* *
r--- r _ bSOUT Ъ $ ЬСОПТ Ъ s
(3.87)
Если t)os<C (Ьопт—£%), то вторым членом можно пренебречь и диспер-
сия параметра не будет влиять на точность прогноза. Если ^os сравни-
ма со знаменателем, то будем иметь
где СоЮ, ^(^ — соответственно первое и второе слагаемые в (3.87).
Обобщенный параметр (3.41) примет вид
k k k
2 v. fi.« ю ±f„ (о)’* 2 2 ’•ft. <оГ‘
<?s (0=—-------1-------------------------------------=
2 2>. 2-.
8=1 8=1 8=1
=Qso(0±Q£o(0- (3.88)
Здесь сделано допущение о малости величин <jso {f), (/), a (t) — со-
ставляющая обобщенного параметра, 1 появляющаяся при наличии дис-
персии у контролируемых параметров.
Время жизни или долговечности при линейном прогнозе определя-
ется с помощью выражения, подобного (3.82):
Д.< ЧСД - Q,O/[Qe0(U - Qs (*«->/]• (3.89)
Подставив в (3.89) выражение (3.88) получим
у, [@£0 On) ± @£а On)]
ж = [Qvo On) ± Qse On)] - [Qso 0»-0 ± Q^On-ж) 1 =
Q*l! ^£0 On) + ^£а On) ,Q qp.
— IQio On) -0«-ж)1 ± [QEc On) - On-01' 1 J
Допустим, что РУо(Д) == Qvc(^-i), тогда вторым слагаемым в знаме-
нателе (3.90) можно пренебречь и выражение можно переписать:
т№=т^т>гл> (3.91)
где Т^.а определяет достоверность метода ппогнозировання н равно
'Щ(t)i[Q№ (Z„) - <?Е0 (1п_ ,)]•
55
Если указанное допущение ввести нельзя, то следует осуществить
более сложные преобразования, после которых также можно опреде-
лить величину 7^. Иногда целесообразно таким образом строить
прогнозирующие выражения, чтобы уменьшились значения '\£п.(и
ГЛАВА 4. ВЕРОЯТНОСТНОЕ ПРОГНОЗИРОВАНИЕ
4.1. Вероятностное прогнозирование многомерных процессов
Необходимость вероятностного прогнозирования многомерных про-
цессов определяется сильным влиянием внешних и внутренних факто-
ров, имеющих случайный характер. Такая ситуация складывается, на-
пример, при эксплуатации электронных систем в условиях воздействия
переменной температуры, влажности и т. п. В этом случае преоблада-
ние случайной составляющей при изменениях £S(Z) приводит к большим
случайным изменениям функции работоспособности Q(|).
Метод статистического градиента. Закономерность движения
Q(£) к допустимым границам Q*(£) можно оценить статистически,
В момент tn из k координат вектора Q(|) выбираются случайным об-
разом группы по I и определяются соответствующие приращения коор-
динат yii,..., yi/, где i.s— единичные случайные векторы, y—tn—tn~i-
Приращение функции работоспособности вычисляется из
+yis] ®(U-i)].
После этого для момента tn можно составить векторную сумму [7]:
i
= 2 'М,
S-1
(4.1)
которая для линейного пространства при I—>оо представляет собой
градиент функции работоспособности:
lira dir Rz — dir V Q,
l-ьоо
где dir R = R/|R| —направление вектора R.
С другой стороны, среднее значение R по всем возможным резуль-
татам Контроля групп из I координат также совпадает с направлением
градиента;
M(dir/?z) = dirVQ.
Таким образом, найденное направление вектора R при конечном I
является статистической оценкой градиентного направления, которое и
нужно выбирать при прогнозировании. Поэтому направление прогнози-
рования на каждом шаге следует выбирать в соответствии с оценкой
A«;=yR/|R|. ^Ри I—k и неслучайных векторах i рассмотренный метод
вырождается в метод градиента, который является частным случаем
метода статистического градиента.
Запишем формулу (4.1) в виде рекуррентного соотношения:
Rn+i—г Rn + i AQn-f-i,
(4.2)
оЬ
где 0<r^l—параметр, учитывающий предысторию. В линейном про-
странстве AQn+i = dcosq>n+i, где <pn+t — угол между вектором случайно-
го niara in+i и направлением градиента функции работоспособности, 6 =
=y|vq|.
Существенной особенностью метода статистического градиента
является возможность принять решение о направлении прогнозирова-
ния при любом /</г, в то время как метод градиента требует проверки
всех направлений, т. е. контроля всех k параметров.
Метод, использующий байесов критерий. При этом методе рассмат-
ривается плотность распределения f(VQ). В общем случае для нор-
мально распределенной помехи выражение (3.1) примет вид
Qn-p — Qn “h Tn-м | eXP 2a2 Q* VQ") (4-3)
где VQ°— наиболее вероятное значение градиента функции состояния,
о2 — дисперсия градиента функции состояния. Для определения наибо-
лее вероятного направления градиента в этом случае необходимо
строить распределение приращений Л| по каждой координате вектора
функции состояний. Для этого необходимо изменения сд отобразить
в безразмерном пространстве [0,1], где At^>0. Тогда для каждого мо-
мента I получим условную плотность jP{VQ/A£) распределения значе-
ния градиента функции состояния при фиксированном A'g.
В соответствии с формулой Байеса получаем выражение для апо-
стериорного распределения градиента вектора функции состояния после
п шагов контроля:
Р (ДЕ/V Q)=Р (М)П Pi (V W (ДЕ) П Pi (V Q/ДЕ), (4.4)
1=1 1=1
где r(Ag)—априорное распределение приращений координат функции
состояния. Изменение функции состояния вдоль градиентного направ-
ления оценивается с помощью формулы
AQn+j=T„+j |\Q/-(WVC)<WVQ). (4.5)
n
Тогда прогнозирование значений функции состояния можно осуще-
ствлять с помощью выражения
Qn-м — Qn + A Qn + j.
(4.6)
При достижении функцией работоспособности допустимого уровня
Q* считается, что объект не удовлетворяет заданным требованиям, т. е.
потерял работоспособность. Отсюда количество временных интервалов,
через которое наступит потеря работоспособности, равно
/1
(4.7)
о
Метод гипотез и фильтрации. Наличие помех увеличивает дисперсию
функции работоспособности и уменьшает точность прогноза, поэтому
оказывается необходимым вводить дополнительные условия.
Введем, например, гипотезу, что функция работоспособности со вре-
менем только уменьшается н затем отфильтруем все результаты конт-
57
роля и прогнозирования, которые не удовлетворяют принятой гипотезе
Пусть это положение соответствует тому, чго приращения функции ра-
ботоспособности отрицательны, т. е. Д<2<0; тогда будем отбрасывать
все случаи, когда AQ>0, и считать Qn+t = Qn- Помеха е накладывается
на Q(b- В этом случае Q'(£) =!Q (£) +е- Это может привести к ошибочно-
му выводу о знаке приращения AQ. Если же signAQ = sign (Дф + е), тс
в этом случае можно принять полученное приращение, причем AQ сле-
дует оценивать с помощью (4.5). Кроме того, в качестве дополнитель-
ного условия фильтрации можно ввести условие, которое учитывает
приращение A'QA(|), превышающее некоторый порог б>0:
— YlssignAQ' при j AQ' | >6, AQ’ <0,
0 при [ AQ' | 6.
Метод покоординатного самообучения. Важным элементом, повышаю-
щим точность вычислений, является введение самообучения в процесс
прогнозирования. В этом случае необходимо запоминать предыдущие
удачные направления прогноза и с определенной вероятностью изме-
нять эти направления на новом шаге контроля. Самообучение при ве-
роятностном прогнозировании проявляется в адаптации вероятностных
характеристик объекта, в результате чего отдается преимущество опре-
деленным направлениям.
В процессе пакрпления текущей информации постепенно оптими-
зируется оценка направления наибольшего изменения работоспособно-
сти объекта, которое и выбирается за направление прогнозирования.
По мере возрастания информации дисперсия этих оценок должна умень-
шаться. Таким образом, процесс обучения должен стремиться «задетер-
минировать» прогнозирование в выбранном направлении. С другой сто-
роны, алгоритм обучения должен иметь возможность «переучитывать-
ся», если ситуация изменилась или обучение было неточно.
При самообучении методом исключения из числа возможных на-
правлений прогнозирования исключаются те направления, которые
уменьшают вероятность точного прогноза, что увеличивает точность
окончательного результата.
Рассмотрим один из методов прогнозирования, использующий са-
мообучение. Пусть вероятность выбора направления прогнозирования
вдоль s-н координаты является определенной функцией некоторого па-
раметра wns, который назовем параметром памяти или просто «па-
мятью» по s-й координате на /г-м шаге контроля: Pns=p(<i>ns)-
Функция р(<о) может иметь различный вид, но она всегда должна
быть монотонной и неубывающей. Например [7]:
а) экспоненциальная зависимость
/?(<») =
0,5ес<и
I—0,5ег:о
при <о’=С 0,
при со^>0;
б) линейная зависимость
I 0
р (со) — j 0,5 (1 — со)
1
при W < — 1,
при — 1 1>
при 1 < со;
в) гауссова зависимость
р((о) =0,5[1—Ф(©)];
58
г) ступенчатая зависимость
Р(®) =
О
0,5
1
ПОИ — I,
при — К со < 1,
при <0 • 1.
Алгоритм обучения в этом случае реализуется путем соответствую-
щего изменения параметра памяти, например при помощи следующей
рекуррентной зависимости:
(0(n+i)s=(0nS—^sign (Ai|nsAQn), (4.9)
где 6 — «шаг по памяти» — величина, определяющая скорость обучения;
Asns=|n« •!(«—AQn=Qn(|) —Q»—1(^)-
Чем больше б, тем быстрее обучается алгоритм прогнозирования.
При 6=0 обучение отсутствует. Смысл выражения (4.9) заключается
в следующем. Если произведенный шаг контроля или прогнозирования
привел к увеличению функции работоспособности, т. е. был сделан
в неблагоприятном направлении, то вероятность выбора этого направ-
ления при последующем шаге уменьшается. И наоборот, в случае умень-
шения функции работоспособности вероятность выбора этого направле-
ния увеличивается. Таким образом, описываемый алгоритм обучения
работает в двух режимах: режиме поощрения (при XQ<0) и режиме
наказания (при AQ>0).
Необходимость обучения по определенной координате ^(t) зависит
прежде всего от полученного результата AQ и степени участия |s(/)
в указанном результате. Поэтому часто оказывается более целесооб-
разным применять дифференцированный алгоритм обучения, который
можно представить в виде
(0(n+i)s=(07is (4.10)
Дифференцированный алгоритм уже реагирует как на результат
шага прогнозирования, так и на степень участия параметра ^(0 в этом
результате. Выражение (4.10) устанавливает связь между новым н ста-
рым направлением. При малых 6 эта связь большая, а при больших —
малая.
Дифференцированная оценка делает этот алгоритм весьма чувст-
вительным к определению наилучшего направления прогнозирования.
При этом выбор производится не среди всех возможных, а лишь среди
ограниченного числа направлений.
Построение Л-мерного вектора памяти <в= (он, 02, устанав-
ливает определенную зону — конус, в котором необходимо искать наи-
лучшее направление. При этом искомое направление определяется за-
данным многомерным распределением Р(|8/о), которое должно обла-
дать свойством: скорректированное направление математического ожи-
дания |s, s = I, ..., k по всем возможным реализациям должно совпа-
дать с направлением вектора со.
Подобный алгоритм прогнозирования обладает определенной плав-
ностью и инерционностью, так как направление прогнозирования в ря-
де практических случаев не может значительно измениться за один
шаг.
Б9
4.2. Прогнозирование изменений одномерных функций
распределения
Влияние помехи и преобладание случайной составляющей при изме-
нениях £(£) приводит к необходимости анализа не отдельных величин
Ь(^) (по своему поведению случайных), а их совокупности. При груп-
повом прогнозировании совокупность рассматривается как совокупность
составляющих, расположенных по оси N куба информации (рис. 2.3),
а при индивидуальном прогнозировании — по столбцу. Хотя форма
представления информации в обоих случаях различна, вероятностно-
статистическая обработка и построение функций распределений ука-
занных совокупностей идентичны.
Поскольку методы анализа совокупности случайных величин под-
робно изложены в -работах по теории вероятности и математической ста-
тистике, рассмотрим лишь некоторые моменты обработки множеств
{ъ/}> ^=1» /V и {gsJ, s = l,..., k, характерных для процесса прогнози-
рования изменения состояния технических систем.
Групповое прогнозирование. Пусть требуется обработать совокуп-
ность значений параметров gi, принадлежащих N однотипным
изделиям контролируемой группы (партии). Смысл обработки заклю-
чается в том, чтобы оцепить, как распределены значения 5/, около ка-
кой величины они сосредоточены, насколько велика разбросанность и
т. д., т. е. в конечном счете оценить уровень производства изделий, сте-
пень работоспособности и качество. В количественном отношении эта
оценка заключается в определении местонахождения {сф в интервале,
ограниченном величинами [£*-----£*+] при двухстороннем ограничении
или [£п...£*] при одностороннем ограничении, установленными раз-
личными техническими требованиями. Очевидно, чем дальше от £*,
тем больше запас работоспособности н выше качество изделия, и наобо-
рот.
В большинстве случаев вероятностно-статистическая обработка за-
канчивается вычислением статистических характеристик и построением
функций распределения. Функция распределения Г(£) является наибо-
лее полной характеристикой -случайных величин, так как связывает слу-
чайную величину с вероятностью се появления. Поэтому, зная функцию
распределения, можно определить вероятность потери работоспособно-
сти изделием для каждого момента времени.
60
На первом этапе обработки весь диапазон значений параметров
в который входит и поле допуска, разбивается на я интервалов [$v0...
Подсчитывается количество значе-
ний, попавших в каждый интервал, и составляется статистический ряд
ГС
А, /г2,..., «я, где п. е - ^1, - , пк<Е R(V <г_0 ... BVJ, J nv =N, а затем
41 = 1
статистический ряд вероятностей p,==nJN, p*=nJN,...,p7=riJN, где д -
частота или вероятность попадания значений параметра в v-й интервал.
Графическое представление о статистическом ряде дает гистрограмма
(рис. 4.1), которая является аналогом статистической дифференциаль-
ной функции распределения или плотности распределения £v(g). Далее
строится статистическая интегральная функция распределения
удовлетворяющая следующим соотношениям:
(«.») = 0
Лу (^vi) = А»
^(W = A +А» (411>
v-1
Целесообразность использования функции распределения объясня-
ется тем, что значение 1%7('S*) задает вероятность потери работоспособ-
ности:
(4.12)
Плотность распределения Д<(1) в этом случае показывает, как
размещено множество fe} в поле допуска и насколько оно рассеяно.
Таким образом, после обработки при групповом прогнозировании
куб информации заменяется квадратом информации вида
fivfe), Ь(?м).....MU). МЫ), 2. ...,Л (4.13)
или
Av(U), Av(^si), ..., Avfc), Лу(Ы), s=I, 2, k. (4.14)
Если в результате обработки вычислялись статистические характе-
ристики (математическое ожидание дисперсия DN и другие), то
матрица дополнится и примет вид
Руо Руу Pis Аг' Pvn-i
Рго Ры Аг ••• Аг' ••• Ап,
.................................................... (4.16)
Au Psi Рб2 — Psi Psni
Ao Ai Аг —Аг —An,
61
где psi—вероятность потери работоспособности группой N объектов
по каждому параметру s в г-й момент времени в области
Отметим, что обработка первичной информации при вероятностном
прогнозировании считается выполненной при условии построения матри-
цы информации вида (4.15) — (4.16).
Индивидуальное прогнозирование. В этом случае полученная теку-
щая информация представляется только квадратом и задача обработки
заключается в приведении матрицы (1.4) к виду (4.13) — (4.16). Если
это удается, то в дальнейшем можно будет пользоваться методами
группового прогнозирования.
Для получения .вероятностно-статистических характеристик <в каж-
дом временном сечении ti в (1.4) необходимо, чтобы информация по
столбцам могла быть статистически обработана. Для этого все элемен-
ты столбца должны иметь одну размерность (или быть безразмерны-
ми). Получить относительные (безразмерные) величины gs можно с по-
мощью нормирующих выражений (3.38)—(3.40). В этом случае (1.4)
может быть представлено так:
^io £и ••• £1/ •••
£21 ^2?1»
.................................... (4.17)
£^0 £si £s2*••• £sn>
£fto £fei ••• £az ••• £j<n-
Относительные значения параметров в каждом столбце можно рас-
сматривать как совокупность случайных величин, характеризующих ра-
ботоспособность и качество индивидуальных изделий. Дальнейшую об-
работку можно формализовать и строить функцию распределения из-
вестным методом. Тогда аналогично (4.14)—(4.16) получим одномер-
ные временные ряды для многомерного индивидуального объекта:
А(Х). А(Х),-4ИМ,-. Mt),
•или
-ИЛИ
(Х)> Аг (X), -, (X),... • A (U
А(Х)> А А(Х),-.Af£n),
(4.18)
где fk (X). Рк (X) — индивидуальные плотность и функция распределения,
—вероятность потери работоспособности в i-й момент времени.
Следует отметить, что название для (4.18) «индивидуальная функ-
ция распределения» справедливо, когда £s, s=l, 2,..., k между собой
некоррелированы. В тех случаях, когда между- параметрами существу-
ет зависимость, А(£Т корректнее назвать «индивидуальной функцией
состояния».
Если имеется небольшое количество (малые партии) изделий, то
можно увеличить информацию, построив обобщенные функции распре-
деления для всего массива информации [/гХА^] в i-м временном сече-
62
нии. Необходимо только весь массив [ЛхЛ7] представить в виде отно-
сительных величин, как это делалось для случая индивидуальной функ-
ции распределения. Однако по сравнению с (4.13) — (4.16) в данном
случае информации получается больше в k раз, а по сравнению
с (4.18) — в N раз. После обработки случайных величин получаем ря-
ды обобщенных функций распределения и обобщенные вероятности по-
тери работоспособности:
fkN (^о)> f kN (М> ’ f kN
^kN ^kN X -" » ?kN (^л)>
(4-19)
В заключение сформулируем общую для всех рассмотренных слу-
чаев задачу, которую можно решить с помощью прогнозирования в од-
номерном варианте. Пусть известные значения параметра объекта
в области 7]
UM, им, и^п), Ко..Un].
Необходимо вычислить вероятность потери объектом работоспособно-
сти:
(4.20)
или вероятность нахождения работоспособности в допустимых преде-
лах 1—7(£*) =P{U/n+j)>U} в моменты tn+j^T2, j=l. 2, ..., т, где 72—
область времени в период будущей эксплуатации.
Методы прогнозирования известных функций распределения параме-
тров. Здесь речь .идет о функциях распределения параметров £(0) в f-м
временном сечении и о прогнозировании их изменений, в результате
чего вычисляется искомая вероятность в области 72.
Поскольку в большинстве случаев распределение параметров во
временных сечениях 0 подчинено нормальному закону, то наибольший
интерес представляет метод прогнозирования нормальной функции рас-
пределения. Нормальная функция распределения
]
f г (£) {Л2я сц(^)
exp
— (О))2
(О)
(4-21)
достаточно полно описывается математическим ожиданием m^(t) и сред-
ним квадратическим отклонением с (/), которые вследствие 5 = f (/)
являются также функциями времени, что приводит к временной зависи-
мости и функции распределения.
Статистические характеристики количественно описывают наиболее
устойчивые стороны распределения, например, — центр распределе-
ния. а — меру рассеяния. С течением времени устойчивые стороны
распределения меняются мало и при их изменениях случайная состав-
ляющая параметров %(t) играет незначительную роль. Отсюда появляется
возможность аппроксимации, а затем прогнозирования изменения я^(?)
и at(Z) с помощью аналитических прогнозирующих выражений (3.58) или
(3.60).
63
Таким об р а зол!, плотность распре целен и я для моментов времени
можно предсказать с помощью выражения
—L---------
j At 2 Yp«paw₽^
l~i р=о
I
ехр {
2 Лг S ^рарт^РРт
2=1 р—о_ _
и
рра
р"рс^
(4.22)
)
где a ni Pm = f [m. (ti}}, CL^, p°=f ]з^ (4)] обозначают соответствующие
зависимости, позволяющие вычислить и az(t„}, m — количество
шагов прогнозирования. Тогда вероятность потери работоспособности
(4.20) в области Т2 вычисляется с помощью
F (Е*) = Р {Е (tm) < Г} = ( Лп (В) =
е* - sа2W1"”)lsA‘SW””’
Z=1 р=О /1/1 P=0
(4.23)
где величина Fo может быть табулирована как это сделано в [27].
При обратном прогнозировании, когда вычисляется время «жизни»
7Ж, необходимо задавать допустимое значение вероятности Р\ потери
работоспособности. Величина Tw находится в результате решения урав-
нения
P^FJZ*), (4.24)
где Z*— допустимое значение величины в скобках в (4.23).
Решим уравнение (4.24), когда в качестве прогнозирующего выра-
жения используется линейный двучлен вида a0+ai/p при условии yi — Е
Строго говоря, в этом случае вместо (4.24) решается уравнение вида
(f—Тш):
Z* = [$* - + атТ^]/(аа, + с,/'),
где р принято равным для обоих двучленов, Z* соответствует Р*^ и бе-
рется из таблиц [27]. После некоторых преобразований получаем
= {[Г - (a„m + Z»aJ]/(aim + Z*a,o)},/?. (4.25)
Неизвестные коэффициенты в (4.25) находятся ранее рассмотренными
способами.
Значительно реже на практике встречаются случаи, когда распреде-
ление параметра %(t) объектов во временных сечениях подчинено закону
Всйбулла:
Р {5 > **} - 1 ~ F (Е*) — ехр [— (Е* 'а)3], (4.26)
где а, ₽=fl&(ML причем ₽ задает остроту и асимметрию распределе-
ния, а а — масштаб кривой распределения по осп абсцисс. Если аир
являются функциями времени, то используя прогнозирующие выраже-
ния U7(/) (3.60), можно вычислять вероятность сохранения работоспо-
собности объектом в последующий период эксплуатации с помощью вы-
ражения
Pt(i„+j)=exP[-(r/»a (<»+i’ ], (4.27)
54
где неизвестные коэффициенты прогнозирующих выражений определя-
ются на основе информации о а(^) и Р(^). Величину Тщ в этом случае
можно получить из решения уравнения
In [- In Р* J = (Tffi) [In e* - In uza(Тж)].
Существует другой путь решения задачи, который базируется на
предварительно табулированных [27] зависимостях Р(£/а) и Р(р).
В этом случае для допустимой вероятности сохранения работоспособно-
сти можно найти значения и 0* и решать уравнения
FS(7’H1)=(3* и Г.(Тж)=Г/а* выбирая min(7>га, Т^.
При этом прогнозируются функции распределения каждого из k
контролируемых параметров и для определения долговечности берутся
$=1, 2, ..., k. Следует заметить, что методы прогнозирова-
ния обобщенной и индивидуальной функции распределения имеют суще-
ственное преимущество, которое заключается в устранении многознач-
ности при вычислении 7».
Доверительные интервалы, определяющие точность решения задачи,
моя-но оценить при прогнозировании и ~>(0, в результате чего
получаем среднее значение Тжср и меру расстояния аГк.
Для оценки погрешностей прогнозирова-
ния при использовании рассмотренных мето-
дов можно рекомендовать следующий способ.
Пусть в сечениях 4-1 и tn имеются значения
контролируемого параметра £(£), распределе-
ния которого, возникающие за счет влияния
случайной составляющей, подчинены нормаль-
ному закону (рис. 4.2). При измерении может
быть зарегистрировано одно из значений
и g(/n), лежащих в пределах 6^ рас-
пределений в tn__i и tn- Полученное значение
£(£<), вообще говоря, не будет равно истинно-
му. Можно выделить зоны, определяющие
величину ошибки прогноза (рис. 4.3). Если
в качестве прогнозирующего выражения ис-
пользуем линейную зависимость, то границы
зон могут быть определены следующим об-
Рис. 4.2. Изменение ма-
тематического ожида-
ния (——) и дисперсии
партии (-------) полупро-
водниковых приборов.
разом.
1. Если в результате измерений получено, что fc(fn-i) = ^(£n-i) и
Е (/n) = (tn), то считаем, что случайная составляющая ие повлияла на
результат контроля, ошибкой, появляющейся за счет случайных измене-
ний можно практически пренебречь и вычисленное значение рав-
но Гж0-
2. Если £04-0 = ^ (^n-i) 4- и 5(^)—— Зз£, то получаем
максимальную отрицательную погрешность (—етж), причем долговеч-
ность равна Тж—етж.
3. Если £(£„_,) — — Зз£ и l(tn) = (tn) Зз£> то получаем
максимальную положительную погрешность (-]- еГж), причем'долговечность
равна Лк + еТж-
5—813
65
Зона [Уж-4*’].. • IT»- охватывает весь диапазон возможных
максимальных ошибок. Этот диапазон можно подразделить на ряд
интервалов и оценить вероятность появления ошибки той или иной ве-
личины. Так, например, вероятность появления ошибки Равна
0,9-10~5.
4. Если и t(tn) = тД/?1) — 2х; £(^_,) =
= /nJ^_i)±=ot и ^(tn)=mk(tn)~a то ошибки прогноза соответственно
равны 0=4»’) и <^4». )
Вероятности появления подобных ошибок соответственно равны
0,00208 и 0,1, т. е. ошибка е>е^ фактически исключается, a
сравнительно редка.
4.3. Методы упрощенного вероятностного прогнозирования
Для ориентировочного, предварительного или оперативного про-
гноза могут быть полезными методы упрощенного вероятностного прог-
нозирования. Эти методы можно выделить в отдельную группу и опреде-
лить их как методы прогнозирования искомой вероятности при неизвест-
ных функциях распределения.
Неравенство Чебышева. При неизвестном законе распределения
t,(t) для прогнозирования можно пользоваться вероятностными нера-
венствами. Наиболее распространенным из них является неравенство
Чебышева [28]:
Р (] е — т J s) < DJe2, (4.28)
где Р — вероятность потери работоспособности, в — величина поля
допуска, (gn—£*).
Однако неравенство Чебышева дает только верхнюю границу вероят-
ности потери работоспособности. Выше этой границы вероятность по-
тери работоспособности не примет значений ни при каком законе рас-
пределения.
Применение неравенства Чебышева позволяет быстро выполнить
ориентировочный этап прогнозирования. Но здесь следует отметить осо-
бенности изменения со временем выражения (4.28). Если выбрать вели-
чину в постоянной относительно начального значения параметров систе-
мы, а дисперсию О, вычислять с помощью выражения
i=l
где рг — вероятность, соответствующая г-му значению параметра ^(0
в распределении, то результаты расчетов будут неточными. Это объяс-
няется тем, что вероятность потери работоспособности вычисляется
с помощью неравенства Чебышева без учета изменения со временем
математического ожидания, а учитывается только изменение дисперсии.
Допустим, что распределение параметров диагностируемой системы
подчинено нормальному закону с изменяющимися во времени парамет-
рами т£(0 и o£(f). Тогда для использования неравенства Чебышева
необходимо, чтобы характеристики распределения параметров имели
вид
т'^ = т0 — const, =
(4.29)
66
Таким образом, вместо реального распределения (4.21) с характе-
ристиками и вводим некоторое „фиктивное" распределение с па-
раметрами т'^ и Вследствие сделанного допущения о том, изо
первичное распределение является нормальным (рис. 4.4), искомую
вероятность определяем через функцию Лапласа. Чтобы стало возмож-
ным практически использовать «фиктивное» распределение, необходимо
связать его с реально существующим. Для этого при выборе характе-
ристик фиктивного распределения вполне естественно потребовать, что-
бы вероятность того, что определенная по фиктивному распреде-
Рис. 4.4. Фиктивное и реальное распределение параметров во временных сечениях
лению, была равна вероятности отказа, вычисленной по реальному рас-
пределению для того же значения g*, т. е.
г
Й! ех₽
—ОО
2о?
J 1
(g — -1
2с|
dt
67
или
1 С Л Г (I— 1 Г
----77=- 1 ехр ——огаТТч шё= ——— I ехр
f(O/27v J 2f2 (О J ¥г(0^2л J 1
—со —со
(В—у.Ю)-
2?! (о
отсюда
- /га0)//2 f (/)] = Ф [(ё* - % (t))//2 <?= (О]-
(4.30)
Очевидно, что значения функций Лапласа (4.30) равны тогда, когда
равны их аргументы, т. е. (£*—tn0)/f{t)= (£*—<pi(/))/(p2(0; следова-
тельно,
f (О =’(^“^)<Р2(О/И*-Ф1(О] (4.31)
и для моментов времени t=ti
f(h} = (g*—яМ<рг(^)/[£*—<₽1(н)].
(4.32)
Выражение (4.32) определяет связь между параметрами фиктивно-
го и реального распределения в нм времени сечення. Заменяя значения
функции через характеристики распределений, (4.31) можно переписать;
(0 = ($* — т0) (0z[5* — (f)]. Заменив = (ё* — (01, полу
чим
После преобразований неравенство Чебышева примет вид
(4-33)
Если учесть, -что нередко |*—m0=s, то неравенство (4.33) можно
переписать:
^(0^k(W-^(0)F, (4.34)
где — математическое ожидание и среднее квадратическое
отклонение реального распределения соответственно. Таким образом,
формула (4.34) представляет собой неравенство Чебышева для случая,
когда и а являются функциями времени.
В наиболее общем виде неравенство Чебышева можно сформулиро-
вать следующим образом.
Если имеется нестационарная случайная функция ё(/) с математи-
ческим ожиданием (t) и дисперсией (/) — (Q, то, как бы ни умень-
шалось положительное число £(/) = ё*— /№,(/), вероятность того, что
значения функции ё(0 отклоняются от своего математического ожидания
не меньше, чем на £(/), ограничена сверху величиной D,_ (t) [ Е& (/),
С учетом определения неравенство (4.34) перепишется:
Pj-S^W
Очевидно, устаиавлйвая тенденцию изменений а£(0 и E^(t) и экстра-
полируя их, можно оценить вероятность потери работоспособности систе-
мой в период эксплуатации. Для экстраполяции можно использовать
математические модели аналитического прогнозирования (3.58), (3.60).
В результате подстановки формул экстраполяции неравенство Чебышева
68
непосредственно для прогнозирования примет вид
(4.35)
где Fa, Fe — базовые выражения прогнозирующих формул для ^(f) и
EJJ) соответственно; т — число шагов прогнозирования.
Если задано допустимое значение вероятности потери работоспо-
собности Р*, то можно определить критический момент при котором
P(t) достигает Р*. Решение уравнения
wE(T^p'’2=\vQ(T.M\
(4.36)
где WE(t) и Wa(t) — экстраполирующие выражения для E^(f) и ^(t) соот-
ветственно, позволяет рассчитать величину
В качестве примера, часто встречающегося на практике, можно рас-
смотреть случай, когда WE(l) и (/) представляют собой линейные
двучлены. При этом
[«0£ + а1£Тж] Р1/2 =аРо + «ь/ж, (4-37)
Где = f (//)], t/ [Zj ... О)а, C!jo ^n],
£=1,2,...,-, [Л ...и — область диагностики, область известных зна-
чений E£(f) и
Выражение (4.37) можно преобразовать к виду
Тж =-- (О„Е₽,/2 - СВ),'(С1<, - а1ЕР'12). (4.38)
Естественно, для более сложных моделей экстраполирования это выра-
жение становится более громоздким.
Подводя итоги изложенного, можно рекомендовать следующую
последовательность прогнозирования этим методом:
1. Определить в результате контроля значения интересующих нас
параметров |(/) в области [Л... /п]-
2. Вычислить статистические характеристики для отдельных мо-
ментов h или отдельных временных интервалов. В частности, такими
характеристиками могут быть математическое ожидание ^(^) и сред-
нее квадратическое отклонение у (tz).
3. Основываясь на результатах эксперимента и опыта, выбрать
наиболее эффективную 'математическую модель прогнозирования I^(Z).
4. В соответствии с техническими условиями установить значение
допустимой вероятности Р*о потери работоспособности или допустимой
вероятности Р*н надежного функционирования.
5. В зависимости от того, что требуется прогнозировать — Ро(/п-н)
и P.t(tn+j) или Т)К, выбрать соответствующие выражения функций рас-
пределения или вероятностных неравенств.
6. Подставить математические модели прогнозирования в соответст-
вующие вероятностные выражения и произвести расчеты для необходи-
мого числа временных -интервалов.
Неоавенство Кемп-Мейдель. Можно улучшись результаты прогнози-
рования с помощью неравенства Чебышева, если будут справедливы
следующие положения:
69
1) распределение может иметь одну ил-и несколько *мод — макси-
мумов плотности вероятностей;
2) единственная или 'максимальная мода приближенно равна ма-
тематическому ожиданию;
3) частоты распределения спадают непрерывно (хотя, возможно, не
одинаково) по обеим сторонам от моды.
Соблюдение этих условий позволяет применить неравенство Кэмп-
Мсйдель, утверждающее, что для любого распределения, удовлетворяю-
щего упомянутым требованиям, часть, большая чем (1—4/9г), должна
лежать внутри границ т^~
Неравенство Кэмп-Мейдель записывается в виде
Д (0 С [2а6 (0/3 (5* - тЕ (О)]8 (4.39)
и дает более точное значение вероятности потери работоспособности.
ТАБЛИЦА 4.1
Граница Неравен- ство Чебышева Неравен- ство К.ЗМН- Мейдель Нормаль- ное распреде- ление
+2о 0,250 0,111 0,00455
-р-2,5а 0,160 0,071 0,0124
-{-За 0,111 0,049 0,0027
+3,5а 0,082 0,036 0,00005
±4а 0,063 0,028 0,00006
В табл. 4.1 для сравнения при-
ведены значения вероятностей поте-
ри работоспособности, определяемые
с помощью неравенства Чебышева,
Кэмп-Мейдель и для случая нор-
мального распределения. При этом
для расчетов при прогнозировании
используются выражения, аналогич-
ные (4.35).
Неравенство Колмогорова. Это
неравенство является наиболее
общим из вероятностных неравенств,
учитывает максимальные измене-
ния всех параметров £»(=/), s=l, 2, ...,& и позволяет вычислить общую
вероятность потери работоспособности
Pl шах
(4.40)
S & — mis)
1
где е — запас работоспособности по всем параметрам.
Нетрудно заметить, что из (4.40) при определенных условиях можно
получить неравенство Чебышева. Осуществляя аналогичные преобразо-
вания, из (4.40) можно получить прогнозирующее выражение, по форме
аналогичное (4.35).
Пример. Количественное изменение
математического ожидания «и средне-
квадратического отклонения относитель-
ной магнитной проницаемости магнито-
мягких ферритов марки 2000 НМ1
за 1000 ч испытаний приведено в
табл. 4.2.
ТАБЛИЦА 4.2
Статистические параметры, %
t, ч 250 500 750 1000
М^др/р1 3 23 4.31 —3,63j 4.35 —4.17 4,61 —4,03 4,7
Необходимо определить вероятность
выхода за допуск (Ap,*/ji='15%) пара-
метров (используемых ферритов. По-
скольку распределение во временных се-
чениях не подчинялось явно какому-ли-
бо закону, то искомая вероятность вы-
числялась с помощью неравенства Чебы-
шева (4.34), где параметры .неравенства
прогнозировались на необходимое время
вперед.
В качестве прогнозирующего выра-
жения для экстраполяции как
так и о(0 возьмем функцию вида
F(t)=axcl, где a, (Api/p.]; q<l; т=
=//1000.
Для вычисления неизвестных коэф-
фициентов приведенное выражение ло-
70
гарифмируется: Inf (/) =lna+Q In т. За-
меняя логарифмы, получаем линейный
двучлен <р(/) “Ко+^б, неизвестные коэф-
фициенты которого для обоих случаев
определялись методом наименьших квад-
ратов. В результате
/ ы(т) = — 4,12тМ«;
fa(/)= — 4,57-тЛ213.
Искомую вероятность для будущих
моментов времени вычисляем с помощью
преобразованного неравенства Чебы-
шева:
Г — 4,53-т°.213 :-2
Р (0^1 __ (Др./р-)* + 4,12--t°.s« j '
Для т—2 (/=2000 ч) Рп (0 <0,365, а
истинная вероятность Диет (0 <0,35.
К распределениям Лр/р в рассмат-
риваемых временных сечениях с опреде-
ленными допущениями применимы усло-
вия неравенства Кемп-Мейдель, что по-
зволяет воспользоваться формулой
(4 39) и уточнить значения найденных
(вероятностей, которые, как известно, яв-
ляются граничными значениями. При
этом прогнозируемая вероятность
Г 2Г„(г = 2) у
<0,157,
а Лгст(0 <0,151.
Метод оперативного вычисления вероятности. При анализе измене-
ний функции распределения считается, что критический момент насту-
пает тогда, когда уровень распределения 3^ достигает допустимого
значения £*. Известно, что 'вероятность нахождения значений пара-
метра в области 3^] при нормальном законе распределения
равна 0,9972. Отсюда, прогнозируя момент достижения величиной 3^
границы е* для -нормального распределения, можно решить задачу
прогнозирования.
Если выбрать величину запасов работоспособности большей Зег, то
расчеты при прогнозировании можно значительно сократить, вводя
вместо нормального закон равномерного распределения [63].
Пусть значение среднего квадратического отклонения остается
постоянным = const, а изменяется только myt). Равномерное распре-
деление, для которого f(B) = /z, можно выбрать из условия
₽ 6
(^) ^=| А^ = А(сс — р),
а а
где а~ (£o4-!Ag)/go, 3= (§o'-Ag)/co — нормированные верхний и нижний
допустимые пределы; £о — начальное значение (рис. 4.5).
Нормирование производится для удобства анализа отклонений, ко-
торые отсчитывают от единицы. Нетрудно видеть, что 1/(сх—р) =
= £о/2А£, где £0| или ja—£о|-
Для равномерного распределения сг постоянна и определяется с по-
мощью уравнения
с/,
в котором предполагается, что ar = У1/3 (Д£/Ео) = 0,578 (M/Q.
Соответствующая площадь, ограниченная кривой нормального рас-
пределения, равна 2<p(Z) или 0,578. Таким образом, в этом распределе-
нии зона в одну <у соответствует 58% благоприятных событий в отличие
от 68% при нормальном распределении.
71
Ряс. 4.5. Аппроксимация нормального рас-
пределения прямоугольным
Для экстраполяции статисти-
ческих характеристик можно ис-
пользовать математические моде-
ли аналитического прогнозирова-
ния. Так, при изменении rn^(t)
по закону, близкому к экспонен-
циальному, значения для мо-
ментов времени в будущем моле-
но определить из выражения
5(«п+Л = е»е-0'Ь.
где а, b характеризуют времен-
ной характер экспоненты и опре-
деляются методом наименьших
квадратов.
Запас работоспособности исчерпывается в момент, когда £=$*, где
=£р e~at — Д£ или
(4.41)
Отсюда критическое значение времени, когда система теряет рабо-
тоспособность, равно
Для всех t>T№ вероятность надежного функционирования опреде-
ляется как
м>&*! Н-
Таким образом, вероятность того, что система будет работоспособна
после Т-,к, равна
Р„ = h (е-°'Ь+Д5Д,
Подставляя сюда значение h, после преобразований получаем
Рв = 0,5 4-(^0/2Д^) (е -a(b - ^). (4.42)
4.4. Прогнозирование многоэкстремальных параметров
При решении ряда технических задач часто требуется предсказать
форму временного рада. При этом исследование временных рядов осно-
вывается на двух предположениях; а) любой ряд является отрезком
более длительного ряда; б) законы, управляющие событиями, на любом
отрезке инвариантны, так что характер изменения ряда на одном отрез-
ке времени будет похож иа характер изменения на другом. При этом
изучаемый отрезок ряда можно рассматривать как совокупность выбо-
рочных значений и оценивать значения других отрезков аналитическими
илн статистическими методами в зависимости от требований.
При постоянных и циклически изменяющихся величинах воздейст-
вий определение средних, эффективных и максимальных значений пара-
72
метров выполняется достаточно просто. С учетом принятых допущений
именно эти величины необходимы для предсказания формы ряда.
Для других форм изменений 'Можно показать, что среднее значение
не зависит от длины временного отрезка, однако неопределенность
в оценке среднего значения, безусловно, возрастает с уменьшением дли-
ны отрезка. Можно показать, что вероятная величина максимального
(минимального) значения возрастает с увеличением длины отрезка.
В общем виде это формулируется так: вероятность превышения данного
значения переменной зависит от числа наблюдений над ней [30].
Рассмотрим необходимые для понимания метода прогнозирования
элементы теории экстремальных значений. Пусть Е(£) есть вероятность
того, что некоторая случайная величина имеет значение, меньшее и
пусть f(g)=/?/(^)— плотность вероятности. Вероятность того, что п.
независимых наблюдений дадут значения, меньшие равна Е??(£). Это
есть вероятность того, что £ — наибольшее значение среди п независи-
мых наблюдений. Другими -словами, вероятность того, что данное 'наи-
большее значение будет меньше равна
Ф(|п)-=^(бп), (4.43)
а ее производная
<p(gn)=n^(U)f(B„) (4.44)
будет распределением наибольших значений п независимых наблюде-
ний.- Это уравнение лежит в основе точной теории экстремальных значе-
ний [31].
Если известно начальное распределение, то можно непосредственно
вычислить распределение крайних значений. Однако начальное распре-
деление известно не всегда, Кроме того, в любом случае оно ведет к ин-
тегральным выражениям, которые можно аппроксимировать только чис-
ленными методами, поэтому целесообразно пользоваться асимптотиче-
скими формулами теории экстремальных значений.
Пусть определенное значение распределения рп однозначно описы-
вается тем, что его вероятность равна
Е(цп) = 1—1/п. (4.45)
Иначе это можно записать так;
п[1—Р(цп)]=1. (4.46)
Произведение, стоящее в левой части, есть вероятное число значе-
ний, равных или больших ;р,эт, поэтому называют наибольшим вероят-
ным значением. Из этого уравнения видно, что значение рте возрастает
с объемом выборки п.
Кроме того, введем величину ап, определив ее следующим образом:
&П--flf (р-п) -
Дифференцируем уравнение (4.45):
dn
(4.47)
,2 ’
или используем уравнение (4.47):
d In п
(4,48)
73
Таким образом, величина является мерой 'повышения наиболь-
шего вероятного значения в зависимости от логарифма объема выборки.
Другими словами, она является мерой дисперсии распределения. Если
ап не зависит от п, то наибольшее вероятное значение будет возрастать
как логарифм объема выборки. Если ап увеличивается или уменьшает-
ся с ростом п, то наибольшее вероятное значение будет расти быстрее
или медленнее, чем логарифм объема выборки. Из уравнения
(4.48) следует, что логарифм объема выборки является мерой возра-
стания наибольшего значения. Это соотношение называется логарифми-
ческим законом роста экстремальных значений.
В зависимости от того, будет ап постоянным или будет меняться
с ростом п, возможны три различные формы распределения. Обычно
мера дисперсии ап не зависит от объема выборки, поэтому-первая форма
распределения встречается чаще.
Моду .наибольшего значения можно определить с помощью (4.44)
как решение соотношения (и—1)И»)/Е(£) =—Если £ будет
очень велико, то плотность [(£) будет очень малой, и если размах варь-
ирования не ограничен, то /'(!) будет сходиться -к нулю. Применяя пра-
вило Л опита л я, получаем f(£)/[l—
Таким образом, мода наибольшего значения сходится к наиболь-
шему вероятному значению. Применяя то же правило <к следующей про-
изводной, получаем, что ряд Тейлора для вероятностей в окрестности
сходится к следующей величине: F(^) —1—(1/п) ехр{——рл)}-
Следовательно, асимптотическая вероятность Ф (В) — lim Ф (п) соот-
п-^оа
ветствует то?лу, что % есть наибольшее среди значений, и асимптоти-
ческая функция распределения Ф(£) будут сходиться к следующим вы-
ражениям:
Ф(£) =ехр{—ехр[—Y)]}; Ф(1) —ап ехр{—?]—ехр[-—и]}, (4.49)
где ц=ап(£—Рп) представляют собой распределение наибольшего зна-
чения при большом объеме выборки [30, 31].
Известно несколько методов использования выведенных выше функ-
ций распределения. Простейшим из них с инженерной точки зрения
является построение графиков на экстремально-вероятностной бумаге.
График дает зависимость значений £ исследуемых экстремумов от нор-
мированных уклонений т], представляющих аргументы функции
ехр[—ехр(—т))]. Значения ц откладываются по горизонтали. Параллель-
но основной шкале ц дается дополнительная функциональная шкала, на
которой откладывается накопленная частота. Обычно эта шкала нерав-
номерная (логарифмическая). По вертикальной оси трафика отклады-
ваются наблюдаемые значения £ экстремумов. Совокупность точек на
графике аппроксимируется соответствующей линией, которая и позволя-
ет прогнозировать значения экстремумов.
Для прогнозирования рассмотренным методом необходимо выпол-
нить следующие операции:
1. Расположить данные наблюдений в порядке их возрастания от
наименьшего значения к наибольшему. Обозначить наименьшее значе-
ние п=1, следующее за ним п=2, и так далее для всех 7V наблюдений:
£1<£г<- - -<£л-
2. Вычислить для каждой выборки ее «накопленную частоту»
«/(7V + 1).
74
3. Вычислить моду и и стандартное отклонение этих данных
обычным способом.
4. Вычислить значения меры дисперсии ап -и р,п -по формулам
!/«« = , (4.50)
где величины сгЛ и Цп в зависимости об объема выборки п -находятся
по специальным таблицам, приведенным в [31J.
5. Нанести г] 'полученных точек на график и провести прямую, наи-
лучшим образом аппроксимирующую полученный график. Для этого
следует воспользоваться уравнениями (4.49) и (4.50). Доверительные
интервалы можно построить, как описано в (31]. Однако для большин-
ства технических задач можно пользоваться весьма простой оценкой;
искомое максимальное значение с вероятностью, приблизительно равной
0,67, должно лежать между границами, равными 0,32 и 3,13 от точки на
прямой, соответствующей объему выборки п.
Во многих случаях этапы 3 и 4 можно опустить, а прямую линию,
проходящую через отложенные точки, провести на глаз. С помощью
построенных таким образом границ можно оценить вероятность появле-
ния величин, равных или превышающих данное значение.
Характерным примером, требующим применения изложенного ме-
тода, является прогнозирование работоспособности некоторых радио-
электронных приборов, для которых из общей совокупности воздействий
можно выделить постоянное, циклически изменяющееся и нерегулярное
или мгновенное воздействия.
Соответственно изменениям нагрузочных воздействий -будут изме-
няться параметры контролируемых приборов, количественно характери-
зующих изменение их работоспособности. Иначе говоря, в этом случае
временному ряду воздействий -(нагрузок) соответствует временной ряд
изменений параметров. При этом чем больше факторов воздействует на
прибор, тем более сложный характер носят изменения параметров.
Пример. Рассмотрим возможности
предлагаемого метода на примере прог-
нозирования долговечности двух ламп
бегущей волны. На экстремально-вероят-
ностной бумаге (рис. 4.6) осуществляет-
ся экстраполяция одного параметра.
Рис. 4.6. К вопросу
определения долго-
вечности ЛБВ с по-
мощью экстремально-
вероятностной бу-
маги.
Нормированное отклонение от модь/
75
ТАБЛИЦА 4.3
Час изме- рение Ток катода. мкА Час измерения Ток катода, кмА Час измерения Ток катода. мкА
При'ор А 1 Приаор № 2 При. ор Лы 1 Прибор \ 2 Прибор № 1 Приюр A. 2
2 105 114 70 Ш 114 138 Ill ИЗ
4 106 114 72 112 113 140 110 2
6 106 115 74 112 113 142 111 112
8 106 116 76 113 ИЗ 144 Ill 112
10 106 116 78 ИЗ ИЗ 146 103 113
12 106 115 80 112 112 148 105 112
14 110 115 82 112 113 150 105 ИЗ
16 110 115 84 113 113 152 lUj 112
18 109 115 86 112 113 154 ИЛ Н2
20 ПО 115 88 112 114 156 105 112
22 109 116 90 112 ИЗ 158 103 U2
24 108 115 92 113 ИЗ 160 1C J 112
•>6 108 115 94 112 114 162 105 112
28 107 114 96 из 113 164 105 111
30 107 115 98 113 113 166 К ) 112
32 108 115 100 из 113 168 109 111
34 109 114 102 114 113 170 103 111
36 109 Г.5 104 113 112 172 103 111
38 108 114 106 114 113 174 103 111
40 109 114 108 113 113 176 103 112
12 109 115 ПО По 113 178 105 111
44 108 114 112 112 114 180 105 Ill
46 109 114 114 112 113 182 106 112
48 109 114 116 ИЗ 113 184 106 Ш
50 109 114 118 113 113 186 103 111
52 108 115 120 113 114 188 105 НО
54 109 115 122 113 113 190 105 ПО
56 109 115 124 115 ИЗ 192 104 111
58 108 115 126 ИЗ из 194 109 ПО
60 107 114 128 112 114 196 110 110
62 109 115 130 112 114 198 109 НО
64 108 115 132 112 114 200 109 по
66 108 115 134 112 114
68 108 114 136 112 114
ТАБЛИЦА 4.4
Прибор .Xs 1 Прибор л*’ 2
Час Номер Ток " Нан ояленная; Час Номер Ток Накопленная
измерения выборки катода, мкА частота измерения выборка катода, мкА частота
98 1 ИЗ 0,02 6 1 1 115 0,02
104 2 ИЗ 0,04 12 2 115 0,04
108 3 113 0,06 16 3 115 0,06
120 4 113 0,08 20 4 115 0,08
122 5 113 0,10 22 5 115 0,10
74 6 112 0,12 32 6 115 0,12
80 7 112 0,14 56 7 115 0,14
82 8 112 0,16 64 8 115 0,1
86 9 112 0,18 4 9 114 0,lQ
90 10 112 0,20 28 10 114 0,29
94 11 112 0,22 34 И 114 0.22
112 12 112 0,24 40 12 114 0,24
114 13 112 0,26 44 13 114 0,26
128 14 112 0,28 48 14 114 0,28
132 15 112 0,30 50 15 114 0,30
76
Продолжение табл. 4Л
Прибор Л 1 [ Прибор № 2
Час ( измерения | Номер выборки Ток като- j да, мкА j Накоплю пая частота Час измерения Номер выборки Ток като- да, мкА Накопленная частота
136 1 16 112 0,32 60 16 114 ! С, 32
70 17 111 0,34 68 17 114 0,34
142 18 111 0,36 130 18 114 0,36
14 19 НО 0,38 136 19 114 0,38
140 20 ПО 0,40 72 20 ИЗ 0,40
18 21 109 0,42 76 21 113 0,42
36 22 109 0,44 94 22 113 0,44
48 23 109 0,46 86 23 113 0,46
56 24 109 0,48 92 24 113 0,48
166 25 1CS 0,50 96 25 113 0,50
194 26 109 0,52 100 26 113 0,52
198 27 109 0,54 108 27 113 0,54
22 28 108 0,56 110 28 113 0,56
138 29 108 0,58 116 29 113 0,58
44 30 108 0,60 118 30 113 0,60
52 31 108 0,62 124 31 113 0,62
G4 32 108 0,64 126 32 из 0,64
68 33 108 0,66 80 33 112 0,66
28 34 107 0,68 104 34 И2 0,68
30 35 107 0,70 140 35 112 0,70
60 36 107 0,72 144 36 112 0,72
8 37 106 0,74 148 37 112 0,74
12 38 106 0,76 152 38 112 0,76
2 39 105 0,78 156 39 112 0,78
52 40 105 0,80 160 40 112 0,80
156 41 105 0,82 164 41 Ill 0,82
162 42 105 0,84 168 42 111 0,84
178 43 105 0,86 172 43 Ill 0,86
188 44 105 0,88 174 44 111 0,88
192 45 104 0,90 180 45 111 0,90
158 46 103 0,82 182 46 I 110 0,92
172 47 103 0,94 188 47 ПО 0,94
176 48 103 0,96 190 48 110 0,96
186 49 103 0,98 1 196 49 110 0,98
При наличии нескольких контролируе-
мых, -параметров строятся графики для
каждого из них, либо используется
обобщенный параметр, В качестве прог-
нозирующего параметра малошумящих
ЛБВ используется ток катода I».
В связи с тем, что потеря работо-
способности прибора может наступить
при уменьшении 1К, т. е. при
то целесообразно анализировать экстре-
мальные значения — минимумы -случай-
ной функции /к(0-
Для прогнозирования использова-
лись результаты измерения тока катода
двух ЛБВ, полученные в течение 200 ч
эксплуатации и приведенные -в табл. 4.3.
Результаты измерений IK(t) разбивались
на группы из двух измерений; из них
выбирались экстремальные (минималь-
ные) значения, которые располагались
з порядке уменьшения (табл. 4.4).
В этом случае каждой группе (выборке)
можно дать свой номер 4, 2.... п и ей
будет соответствовать своя «накоплен-
ная частота». Значения /К(О наносятся
на экстремально-вероятностную бумагу
в соответстви-и с «накопленной часто-
той». Прогнозирующая прямая прово-
дится методом наименьших квадратов.
Экстремальное значение тока катода
ZK(/), равное допустимому и соот-
ветствующее ему время «жизни» 7»
можно непосредственно определить из
трафика. Для -прибора № 1 это время
равно 600 ч, а для прибора № 2 6000 ч
(рис. 4.6). В действительности отказ
приборов из-за ухудшения коэффициен-
та шума (измерение которого не было
автоматизировано, как это было сдела-
но с /к, поэтому информации было не
достаточно дли применения этого -мето-
да) произошел через 715 ч (прибор № 1)
и через 4'130 ч (.прибор № 2), т. е.
ошибка вполне приемлема, если учесть,
77
что приборы контролировались только
200 ч в начале эксплуатации. П.ри авто-
матизации контроля коэффициента шу-
ма появилась бы возможность контро-
лировать его через каждый 2 ч эксплуа-
тации (как это было с /к) и есть все
предпосылки, что прогнозирование было
бы еще более точным. Результат прогно-
зирования можно получить <и в виде
вероятности <!?*], которая опре-
деляется по нижней горизонтальной
оси.
Одним из требований данного ме-
тода является непрерывный контроль
параметров диагностируемого изделия
или сравнительно частый дискретный,
что удается выполнить в случае авто-
матического контроля.
4.5. Прогнозирование марковских процессов
Марковский процесс характерен тем, что закон распределения па-
раметра процесса в любой будущий момент времени зависит только
от значения параметра в данный момент времени и «е зависит от того,
какие значения случайная функция имела в прошлом. Математически
основное свойство марковского процесса формулируется следующим
образом (39]. Если для любых момент о® вре.мени
... 1 (4.51)
f (W£1, - - .Лп-1) (Ufen-0, (4.52)
то процесс будет марковским.
Известно, что все законы распределения 'марковского процесса одно-
значно можно выразить через двумерные законы распределения. Это
означает, что двумерный закон распределения для любых значений вре-
мени t и т полностью определяет значения случайного процесса.
При соответствующих начальных и граничных условиях условная
плотность вероятности марковского процесса /(/, т, ц) удовлетво-
ряет уравнениям Колмогорова, которые обычно представляют в следую-
щем виде. Если f(t, т, *1) рассматривается как функция параметров
первоначального состояния t и то
^-+а(/Л)^.+4-6(<Л)^- = °. (4.53)
Если /(/, т, ц) рассматривается как функция параметров конечного
состояния т и ц, то
(г, 4) fl - 4- [6 (Ъ 4) fl = 0. (4.54)
Здесь ci(t, •£), b(t, £), а(т, ц), &(т, ц)—неслучайные функции времени,
которые определяют особенности рассматриваемого 'марковского про-
цесса.
Для процессов, удовлетворяющих указанным условиям, можно
сформулировать задачу прогнозирования, близкую к задаче прямого ве-
роятностного прогнозирования, а именно: известна случайная функция
времени f (/) и ее значение £ в момент времени t, требуется определить
вероятность того, что в некоторый будущий момент времени т функция
/(/) будет иметь значение ц, ни разу не заходя >в течение интервала
времени (t, т) за установленные пределы. Возможность и сложность
решения этой задачи определяется видом функции а и Ь.
Для получения решения дифференциальных уравнений в частных
производных, например в виде первого и второго уравнений Колмого-
рова, необходимо знать начальные и граничные условия для искомой
78
функции. При этом начальные условия должны определять зависимость
искомой функции [ от пространственной координаты (£ или т]). Примем
/, Р>0, (4.55)
f(g, £)|f=0=<p(g) (функция заданного (вида).
Граничные условия должны характеризовать значения функции f
для любого момента времени на .границе допустимой области ’изменения
пространственной координаты (£ или tj) . В нашем случае f(£, t) огра-
ничена у ^>0 и при каждом | К00* 't) = 0у t или, точнее,
lira (4.56)
£~>оо
Решение уравнения <(4.53) получено для случаев, когда можно
разделить переменные, а случайные функции времени имеют вид
Ь—Ь(%) и а=а(1). Полагая f(£, 0 = ^(Ф(ё)> 'Можно получить
^-й(5) + -^-с(5)=-Д-=Я. (4.57)
Разделим переменные? и получим Т(t) = С*. Из условия (4.56)
ограниченности функции f(^, t) у/>0 следует, что 2,^>0. Тогда <из (4.57)
Х"Ь(%) +Х'а(£)—АЛ=0. (4.58)
1-й случай: а(£)=а, b{^)=b и таковы, что корни характеристи-
ческого уравнения (4.58) вещественны и различны: ai(X), а2(Х)- Допу-
стим ai(k)<0, а а2(Х)>0. В этом случае
X (£) = С, (2) eai {Х) Ц- С2 (2) e“s (Х}
Поскольку АЛ(^)—>0 при то С2(2) = 0, так как а2>0. Поэтому
с учетом (4.56) X (£) = Сх (2) е“1
Обозначив at (2) = — р (2), получим X(Е) — Ct (2) е-₽ (>) Частное
решение в этом случае будет иметь вид
f, (?,«) = С (Я) е~и е~° а> Е= С (Х)е~(,г+ю (₽ >0, Я > 0).
Так как 2^=0 и меняется .непрерывно, то общее решение можно пред-
ствить в виде
f (6, i)=С fх (Е, t) d>.="\C (₽ (Я)) е“(J,+? w 61 d (₽ (Я)). (4.59)
о 6
Из условия (4.56) и f(E, 0|t=o=^(^) имеем
СО СО
¥ (Е) = ф (₽ (Я)) е~? w s d (р (Я)) = Г С ©е"*1 w Е ф
о О
Существование подобной связи между <р(|) и С(р) позволяет предста-
вить функцию <р(£) как преобразование по Лапласу функции С(р),
Тогда
a0+ico <r0+ioo
С© = -А- f e₽W6C(?)dE = -5F J efWE¥(E)<fi.
c0—ico —ico
79
Наконец решение (4.53) при t, будет иметь вид
со/ c0+ioo \
J egp)^0)dde-<^+₽a>u/f8(2).
О ' с0—ioo J
Из-за симметрии ft) относительно | решение в
£(—оо, Ч-оо) можно получить из (4.60) заменой | на |||.
(4.60)
пределах
Пример. Рассмотрим решение этой
задачи прогнозирования для случая,
когда марковский процесс удовлетворя-
ет первому уравнению Колмогорова
(4.53). Пусть плотность распределения
t) в начальный момент времени
(*=0):
е—
= ?(!) = *-у-* £>°-
Отсюда
НЕ. 0 = » fexpl-lb Кй+
J I Lk 2 У bt;
4W j)
где р. > 0 — произвольный параметр, у —
нормирующий множитель, выбираемый из
СО
условия | <f III d% = ~2~ •
б
Необходимо предсказать вероят-
ность сохранения работоспособности из-
делиями в будущие моменты времени.
Йз рассмотренных условий следует, что
С(0) ->.<р(|). Воспользуемся таблицей
оригиналов и изображений по Лапласу
и найдем
xW-0Kw+-WHJx
р-
х^б Уьг+ g7z—)•
V 2 г bt )
С(Р) =
/ор<|х- т
Тогда в соответствии с (4.60)
со
f (£, t) = J С (₽ (Л)) (X),
о
Если в полученном выражении обозначить
р У ~ьГ + (|—«о/2 VbT= z, то получим
известный интеграл Лапласа со следую-
щими пределами: если ₽ ~»со, то Z-»co,
если р = |}х, то Z — j* V bt + (| —
— Vbt:
со
X f e~z2dz.
ехр |j
Г(£-^)2. 1
_ 4W J у bt
е
£
Поскольку ц>0, а Р(Х)=—а, где
а — корень характеристического уравне-
ния а2£+сш—Х=0, то Л=Л(₽)=р26+₽а.
Следовательно,
f (I, 0 = V |е-|Х(₽)+?^ =
р-
и
CO
/•
Поскольку известно, что I e~zarfZ —-
и
1 (l- °=wexp L « j x
Произведем преобразование показате-
ля степени:
/ .г- %—at \2
рМ_р„; + К= -
№—а<)*
4W
wex₽
r(E-«O! j
L 4« J
80
-Днгтг-^)].
где Ф(2) —интеграл Лапласа, значение
которого для любого интересующего нас
момента времени можно взять из таб-
лицы.
Искомая вероятность определяется
как
р,&<$*) = p(i.o di
i*
и дает нам результат прогнозирования.
2-й случай: a(fe) — (cc-rd)/a, &(£) = (с£+ф)26, где а, Ь, с и d —
произвольные постоянные величины.
Допустим для упрощения выкладок, что а(£) =а% и Ь($) = Ь^г,
тогда уравнение (4.58) примет вид ЬХ'^+аХ'^—ХХ=0. Ищем решение
этого уравнения в виде L=X. Тогда
ba(a — 1) В'х~2Е3-}-аа^я“Ц — /Xх — 0 или Ьа (а — 1)-}-ш— Л—0. (4.61)
Отсюда следует A"(^) = C^rei -f-C,tT2, где а, и а2 —корни характеристи-
ческого уравнения (4.61). Допустим, что «1<0, а2>0, тогда С2—0.
Обозначим а4=—а(Х), тогда X(g) =С1$-о(>)иХ(д)—>0, £—>оо. При этих
условиях частное решение будет fу (£,t)— С (z)e~' (<) .Поскольку Л
изменяется плавно при общее решение примет вид
f (5, о = J И Л 0 dl =7с (Я) t 1Г “ ^dl.
Или если произвести интегрирование по а (Я), то
f ft, t) =Jc (a U)) е~и Га (>) d (а (Z)). (4.62)
о
Для определения постоянной воспользуемся начальным условием
f(g, /) |f==0=<p(£, 0)=ф(^). Тогда
СО
<?(?)= СС(а(Я))Га(Чй(а(Я)).
Если представить A’=e'nt, то
<f (?) ='[С(а(Я)) е~“ 1,1Е d (а(Я)) = С(1п?), (4.63)
о
где С (1п£) —преобразованная по Лапласу функция С (1п£). Таким образом,
чтобы -найти постоянную C(a(Z,)), достаточно выполнить обратное пре-
образование Лапласа в (4.63).
В общем виде получим
сто+ too а0+ IQO
C(“)=1ST J е’ w “Е С (In 5) d (In t)=Ш j e“ w'"4<e)d(ln?). (4.64)
a0—ico a0—ioo
Подставив (4.64) в (4.62), получим решение, справедливое для .всех
£>0, в следующем виде:
f ea(X>!n£^(^^(itl^),)e_Wr“iriW“))- <4-65)
О Со—гео
Для того чтобы распространить полученное решение и на случаи
д<0, достаточно заменить g иа |§|.
ь—813 81
4.6. Каноническое разложение случайных процессов
Довольно большой класс аналитических случайных процессов обра-
зуется в случае так называемого канонического представления процес-
са [29], когда функции, по которым ведется разложение процесса,
являются аналитическими и в качестве приближения процесса рассмат-
ривается конечное число членов канонического разложения. В этом слу-
чае диагностируемый процесс можно представить в виде
(4.66)
где тД£)— математическое ожидание £(/), Vv, v=l, 2,... — некоррели-
рованные случайные величины, математические ожидания которых рав-
ны нулю (случайные коэффициенты канонического разложения), £(/) —
неслучайные функции времени (координатные функции разложения).
При каноническом разложении должны быть справедливы следующие
соотношения:
= при n=/=v, D,[VJ = M[1VJ2], (4.67)
где — дисперсия случайных величин Vv.
Поскольку СД/)—элементарные функции времени, a не зависит
от t, то воздействуя оператором прогнозирования, например, W на про-
цесс £(0, описываемый уравнением (4.66), можно предсказать процесс
в моменты tn+^T2, j=l, 2,.. .,т:
Е (Ui) = V7 {Е (4)} = W {mE (/)} + 2 ЦГ К. (ti)}. (4.68)
При этом коэффициенты разложения Vv остаются неизменными, а мате-
матическое ожидание и координатные функции подвергаются преобра-
зованию оператором прогнозирования.
Таким образом, для решения задачи прогнозирования методом кано-
нического разложения необходимо определить закономерность изменения
и вид координатных функций Cv(0. Случайные величины Vv можно
определить по значениям их дисперсии Dv.
Каноническое разложение типа (4.66) позволяет осуществить прог-
нозирование только приближенно, однако для практических целей такое
представление часто оказывается достаточным.
Рассмотрим возможные пути определения Dv и СД£), Для этого пе-
рейдем от к центрированному случайному процессу:
Йо=Е (0 - "Ч (0 = S КА, <4 -69)
V
б п временных сечениях /2, ..-Лп; t^Ti (рис. 4.7).
В моменты ti разложение (4.69) должно точно представлять случай-
ный процесс Е(/). Учитывая это, можем записать п равенств [40]:
• 82
i(4)=Svxft),
У
5fc) = Sv?,(iz),
V
(4.70)
?(U = SVA(Q.
Пусть -при этом число членов канонического разложения конечно и
равно q, v=l, 2, ...,q. Рассмотрим первое из равенств (4.70). Для того
чтобы соблюдались равенства (4.70) и условие некоррелированности
Vi, Ка,..., Vq, достаточно ввести в его правую часть только одну вели-
Рис. 4.7. Центрированные значения £(£)
чину Vt, положив коэффициент равным единице: £1(Л) =£ц= 1, а все-
остальные коэффициенты — нулю: у21=^31=.. ,=£д1 = 0. Тогда первое
из равенств (4.70) примет вид £(/i) = Vi. Второе равенство (4.70) с уче-
том того, что Vt и Vz должны быть некоррелированными, можно пере-
писать так:
1(М=С121Л + К, (4.71)
где ^22=1, а £з2=£42= ... —£д2=0. Коэффициент £12 определяется из
условия некоррелированности Vi и V2.
Поступая аналогичным образом с остальными равенствами (4.70) и
полагая при любом Kv£ = l, v = t Су+1 . = Cv+2 z = £v+s, . = г- = 0,
получаем систему уравнений:
Ч4)=с.2к + ^,
к)==^.+уи2 + ^,
(4-72)
4^)-^+^ + ... + ^-,
l(tn) = + ... + Vn.
6*
83
Далее необходимо определить коэффициенты в (4.72) и дисперсии
Dif i=l, 2,..гс, чтобы Vl} Vn (q—n) были некоррелированными.
Чтобы найти коэффициент ti2, следует перемножить первое и второе
равенства (4.72) и к результату «применить операцию математического
ожидания {29, 40]:
м [*((,)? (01=[V? ] + м [У.К].
Так как
M[I/,V2]=O, M[V; ]=£>.,
4),
получим
откуда
-ia = Bt(flt Q/Д. (4.73)
Величина Di находится при определении дисперсий обеих частей
первого из равенств (4.72):
D1 Q.
Последующие коэффициенты и дисперсии находятся с помощью
аналогичных приемов. Можно выделить систему рекуррентных соотно-
Рис. 4.8. Семейство координатных функ-
ций.
Рис. 4.9. Примерные зависимости £(/).
шений, достаточную для построения всех координатных функций -и дис-
персий:
t,),
D,=Bt{t„ О-К,(О1'П„ (4.74)
0,=£t(C O-StWFA.
1=1
uo=h е(%. о
L
2
/=i
D
где tv&\.
Необходимо отметить, что функции £,v(t) можно представить б виде
(4.74) только при t lv (рис. 4.8), при Cv(/) = 0.
Рассмотрим другой вариант практического построения канониче-
ского разложения случайного процесса. Положим, что
4+i,^4+2,^---^- = 0, D1 = D2=±=... = О9—1. (4.75)
Второе условие в (4.75) введено вместо CVJ = 1, v — i. Тогда, учи-
тывая эти условия (рис. 4.9), уравнения (4.70) можно переписать сле-
дующим образом:
foWuK,
............................... (4-76)
? (tj=C1/V1 + 4-... + (Л
£ (&п) = ^inVi 4" ^тУг. 4" - + ЧтУд-
Выполнив преобразования, аналогичные приведенным выше, можно
получить .выражения для координатных функций в следующем виде:
t)/c^)=^(t)B(tlt t),
Ъ (У) = Я{ (у yi-B*(tt, t„), (4.77)
= tf — Bft,, t)B(tu t2)]/yi у
и т. д., где B(tit i] = B^(tit t)/c^(t/)(t) — нормированная корреляцион-
ная функция.
Поскольку не стационарность процесса обычно отражается на зако-
номерности изменения т. е. m£(f), то центрированный процесс НО
•с большим основанием можно полагать стационарным. Тогда справед-
лива запись
B(t, ti=t+r)=B[t— G+t)]=B(t).
Решение задачи прогнозирования существенно упрощается, если
известно изменение коэффициента корреляции Б(т), в частности, если
он имеет вид
В(т) = е^\ (4.78)
С учетом (4.78) расчетные формулы для координатных функций
значительно упростятся. Опуская промежуточные выкладки, можно
записать
^(/) = а^1(/), (4.79)
85
где ^(О = ^(Ое (рис. 4.10),
а = е
причем аг — 1.
С учетом (4.79) имеем каноническое разложение случайного про-
цесса б -фиксированные моменты (времени
I
Е (4) = (/г) + С, (ti)
V=1
(4.80)
Если случайный процесс в промежутке {70---М представлен кано-
ническим разложением, то оптимальное прогнозирование процесса за
пределами этого промежутка [i>tn, t^T2] можно осуществить, вычис-
ляя координатные функции аргумента для t^T2=tn+l - - . tm-
Рис. 4.10. Примерные зависимости £(0 для
случая, когда нормированная корреляцион-
ная функция—экспонента.
Однако если учесть, что закономерность изменения £(/) определяет
mt(Z), то дополнительно к сказанному необходимо осуществлять экстра-
поляцию m, (t), например с помощью рассмотренных ранее аналитических
прогнозирующих выражений. Тогда выражение, непосредственно исполь-
зуемое для 'Прогнозирования при каноническом разложении процесса,
примет (вид
(£, т? m) + (m) 2 (4-81)
V=1
где W($, т)—выражение, подобное (3.60); т — количество шагов
прогнозирования.
Безусловно, метод прогнозирования, основанный на каноническом
разложении диагностируемого процесса, расширяет круг решаемых прак-
тических задач. Однако в данном случае обязательно знание корреля-
ционных функций.
4.7. Эргодическое свойство случайных процессов
и прогнозирование
На практике часто возникает необходимость осуществлять прогно-
зироеание по ограниченной информации. При рассмотрении информа-
ционной трехмерной матрицы (рис. 2.3) условия ограничения информа-
ции, например, -могут быть записаны как 7V=1, s=l, i=n, что означает
86
наличие только одной реализации процесса в виде случайного измене-
ния одного параметра в интервале t0...tn=Ti.
Необходимая для прогнозирования обработка единственной реали-
зации случайной функции при этом осуществляется следующим
образом. Функция £(/) рассматривается как стационарная случайная,
что не совсем точно, поскольку процессы, характеризующие деградацию
состояния объекта во времени, вообще говоря, не являются стационар-
ными, так как их математическое ожидание изменяется с течением вре-
мени. Естественно, что изменение (/) во времени может вносить су-
щественные погрешности в расчеты, если •§(./) предположить стационар-
ной на протяжении всего времени существования функции. Однако если
рассматривать ограниченные интервалы времени, то практически можно
принять (t)= const м §(f) считать стационарной случайной функцией.
В этом случае можно воспользоваться эргодическим свойством ста-
ционарных случайных процессов, что позволяет экспериментально опре-
делить математическое ожидание, использовав вместо значений-большого
числа различных реализаций при одном и том же значении аргумента
значения одной его реализации при различных значениях аргумента.
Кроме того, поскольку вероятностные характеристики стационарных
случайных процессов не изменяются при любых сдвигах во .времени, то
можно определить функции распределения по одной реализации про-
цесса.
Поскольку для прогнозирования случайного процесса необходимо
знать изменение его математического ожидания во времени ^(/) и
вероятностные характеристики в последовательных временных сечениях,
аю, считая диагностируемый процесс почти стационарным, можно вы-
числить необходимые характеристики процесса. Математическое ожида-
ние процесса равно
^(Т^-Г-рр)*, (4.82)
О
где То — период обработки, внутри которого нестационарный случай-
ный процесс считается стационарным; 7о<сЛ, Т^Т±.
Дисперсия определяется с помощью
Д(Т0)=М [/Н.
О
То То
=И-СГве(/-Г)<!<Л'. (4.83)
О о
Следовательно, среднеквадратическую ошибку приближенного ра-
венства (4.82) можно сделать сколь угодно малой путем выбора доста-
точно большого То при условии, что квазистационарность сохраняется
и среднее значение корреляционной функции стремится к нулю при
увеличении t—t'=x. Основным условием для этого является существо-
вание такого значения то, чтобы В (т) можно было считать практически
равной нулю при |т] >то. А условие В^ (т)—>-0 при т—^оо является
достаточным условием эргодичности стационарной случайной функции
по отношению к математическому ожиданию.
87
говоря, могут
нахождения
Рис. 4.11. Функция распределения по множеству (а)
и то индивидуальной (б) реализациям.
Таким образом, поскольку квазистационарность случайного про-
цесса подразумевает его стационарность на определенных временных
отрезках или периодах, то эти периоды можно принять за периоды^ об-
работки То, внутри которых используют эргодическое свойство. Пути
различными, например од-
ним нз способов прибли-
женного определения пе-
риода обработки являет-
ся способ вычисления ав-
токорреляционной функ-
ции по единственной реа-
лизации диагностируемо-
го процесса |(/). В этом
случае То=[1 ... 0,5]X
0). При этом так
как значения реализации
процесса g(^) и
рассматриваются как не-
зависимые, предполагает-
ся, что значения g(Z) в
любых периодах обработ-
ки независимы и их мож-
но рассматривать как от-
дельные выборки из одной
генеральной совокупности
случайных величин.
Рассмотрим две плот-
ности распределения J? (?)
и (рис. 4.11), одна
из которых fi(£) построе-
на по мгновенным значе-
ниям для сечения ti
(рис. 4.11, а), а другая
?г(£)—по мгновенным
значениям единственной
она принимает в ин-
справедливо эргодическое
свойство, то рассматриваемые плотности распределения верно отража-
ют структуру случайного процесса £(t). Совокупность значений множе-
ства реализаций в сечении U эквивалентна совокупности множества
значений одной реализации на интервале То. В результате одна
реализация дает достаточно полное представление о свойствах случай-
ного процесса в целом. В частности, усредняя значения этой реализации
вдоль оси абсцисс (оси времени), получаем приближенное значение
математического ожидания процесса т^ (Т0); усредняя квадраты откло-
нений от этого среднего, получаем приближенное значение дисперсий, и
Т. д.
В ряде случаев изменения параметров технических изделий и объ-
ектов прн их подробном анализе (частом контроле) можно принять за
квазистационарные случайные функции и для решения задачи прогно-
зирования использовать свойство эргодичности.
реализации £(£) (рис. 4.11,6), которые
тервале 70. Если на указанием интервале
88
4.8. Прогнозирование с помощью уравнений регрессии
Задачу прогнозирования временных рядов можно решить с помо-
щью авторегрессионной модели. Методы теории статистической регрес-
сии позволяют предсказать одну или несколько величин у и у2,-.уд на
основе информации о параметрах объекта gi, £2,. • •» ёь Величина У мо-
жет представлять собой какой-либо обобщенный критерий состояния,
или, в частном случае, будущие значения параметра £.s (/«+;), / = 1, 2,...,
т, tn+j^T2.
Задача заключается в определении такой функции (модели):
У-ИЧВ1, Ы, (4-84)
зная которую можно с некоторой достоверностью судить об изменении
величины У в зависимости от аргументов gs, s— 1, 2,..., k. Наиболее
распространенной формой представления функции W является линей-
ное соотношение вида
y=e + ati^i-ba2^+.. (4.85)
где а$— неизвестные коэффициенты, е— некоторая случайная величи-
на.
В некоторых задачах, связанных с передачей информации по кана-
лам связи, величина У представляет сумму, зависящую от времени t,
определенной (неслучайной) функции и случайного компонента «(/),
отражающего влияние «помех» или «шума» [42]: Y=a$+alt+a2t2+ ...+
+аь/*+е(/). В других случаях W может иметь вид У=а0+«1соз(л/ +
4-р) +... +в(0- При этом в(0 предполагается нормально распреде-
ленной переменной с центром в нуле и постоянной дисперсией о2, при-
чем для любых моментов времени t2,..., tn величины е(^) предпола-
гаются независимыми.
Функция W и ее коэффициенты определяются из условия достиже-
ния экстремального значения некоторым выбранным критерием. В каче-
стве такого условия можно принять достижение минимума среднеквад-
ратической ошибки: Л4[У—IT(|)]2=min. Пусть £(§) =М(УД).
Тогда 7И[У—IF(|)]2 достигает минимума при IF(|)=£‘(|), где
£(S) —условное математическое ожидание У при данном § ([43].
По определению условного математического ожидания
М[ (У—Я) (£—№)]=М[ (£— IF) М (Y—E/1) ]=0,
так что
/И(У—1П2=2ЩУ—£+£—№)2-Л4(У—£)2+
+ М Y—E) z.
Нижн>5« граница М(У—IF)2 достигается при W—E, поэтому наи-
лучшей предсказывающей функцией, которая минимизирует среднюю
квадратическую ошибку, является Е(§). Функция Л4(У/|) называется
регрессией У на gj,.£>.. Средняя квадратическая ошибка 7И(У—Е)2
представляет собой среднее значение условной дисперсии У при данном
Кроме рассмотренного условия можно использовать условия дости-
жения максимальной корреляции W с У.
Рассмотрим один нз методов прогнозирования • чучайных процессов
с помощью авторегрессионной модели. По известному ряду g(Zi), g( ?.),
...» КМ; i==i, 2,..., n необходимо определить величину
£ (/jl-lK tn+j^Tz.
ay
Если выбрана модель линейной регрессии, то задачу решаем с по-
мощью средних значений и функций ковариации и нет необходимости
знать точное распределение значений Учитывая сказанное, уравнение
(4.85) можно переписать:
Sn-!1 — S (/п+1) = + - - - 4-£п+1, (4.86)
где & = l(ti),
Для определения неизвестных коэффициентов щ в уравнении (4.86)
применим метод наименьших квадратов. При этом величину опре-
делим с помощью линейной комбинации п функций Vi(£Zi+i), ...,
Vn(/n+i), которые принимают значения Vi(Д-и) i=0, 1, 2, ...
Эти функции являются независимыми переменными. Все данные, подле-
жащие обработке, сведены в табл. 4.5.
ТАБЛИЦА 4.5
Бремя контроля Зависимая переменная Независимые переменные
VJt) vs<f)
0 So — .—
1 Si So — — —
^71 “2 tn-2 Sn-3 Sri-4 Sn-5 — —
Sn-X tn-2 fen— 3 So —
6. tn tn - 1 tn-2 tn-3 Si So
Из всей совокупности независимых переменных, приведенных
в табл. 4.5, с помощью статистического критерия, рассматриваемого
далее, выбираются те, которыми можно ограничиться при построении
линейной модели:
S(M — СоУ1(М +щУ2(гп) + ... k<Zn.
При выборе многочлена регрессии следует исходить из объема име-
ющейся информации и результатов предварительного анализа. Если вы-
браны переменные Vi(t),..Ел(/), k<n, то коэффициенты а0...... ah-i
находятся из условия
2 (4) - (t^- (U) - ... -~ак_У^ № =
i =n—ft+1
— 2 1И/г) — Ь — a£(ti — 2) — ... — ak_£(ti — £)]2 = mm.
Это условие минимизирует сумму квадратов отклонений от получен-
ных в результате выполнения эксперимента данных. Чтобы распростра-
нить полученную зависимость на область аналогичных задач, достаточ-
но выполнить следующие условия: 1) ряд £(/)—е(/)=аОд(/—1) +
—2)+ ... ограничивается конечным числом членов; 2) е(£)—не-
зависимые случайные величины.
Первое условие практически всегда соблюдается. Для проверки вы-
полнения второго условия необходимо вычислить корреляционную функ-
90
дию по значениям £(^)> Z=E 2, .... п, —Ве (и), где т='(/г+т)—ti. Если
/?Дт), т=1, 2, ... принимает значения, близкие к нулю, то можно счи-
тать величины e(t) и в(/+т) некоррелированными. Для их независимо-
сти достаточно, чтобы они были нормально распределены.
Для определения величины k ® {46] предложен критерий, удобный
тем, что в нем используются непосредственно вычисляемые, а не оцени-
ваемые величины. Чтобы оценить степень приближения в результате
аппроксимации экспериментальных данных рядом (4.86) порядка 'k, не-
обходимо определить отклонения, которые возникают при повышении
порядка авторегрессии. Для этого нужно строить модели порядка q, где
k<.q<.nl^ п — число экспериментальных значений, и определить суммы
квадратов отклонений тех значений, для которых величину мож-
но вычислять с помощью рядов порядка k, так и с помощью рядов по-
рядка q.
Пусть 21 — сумма квадратов £(0 для ряда порядка k, а 2а — для
ряда порядка q. В этом случае величина — (п—q) In (2й/21) имеет рас-
пределение х2 с q—k степенями свободы [46]. Задавшись определенным
уровнем значимости принятия решения, можно проверить гипотезу
о том, что диагностируемый процесс действительно представляет собой
авторегрессию заданного порядка.
Если считать, что определена оптимальная величина k и е распреде-
лены нормально с математическим ожиданием, равным нулю, и с диспер-
сией о2, то можно получить доверительные границы предсказанного
значения. Если случайная величина е имеет оценку дисперсии <у2-, где
az—2e2/(fi—k), то случайная величина <л==е/о имеет /-распределение
Стьюдента с п—k степенями свободы. Отсюда можно определить преде-
лы ta, в которых величина to находится с заданной вероятностью а.
Таким образом Р{| &/о| /а}.
В результате
Р {|*п+Э (п+э) == Л
ИЛИ
Р {^Н («4-3) (п+3} “F taj} = ОС,
gn-н, — соответственно истинное и прогнозируемое значения
параметра g на (п+/)-м шаге прогнозирования.
ГЛАВА 5. ПРОГНОЗИРОВАНИЕ НА ОСНОВЕ ТЕОРИИ СТАТИСТИЧЕСКОЙ
КЛАССИФИКАЦИИ (РАСПОЗНАВАНИЕ ОБРАЗОВ)
5.1. Формулировка задачи
Задача прогнозирования как задача статистической классификации
{47] формулируется следующим образом:
Пусть на основе априорной информации (обучающей выборки) из-
вестны плотность распределения вероятностей f(|//<\) вектора § при
условии, что он принадлежит к классу Z—1, 2..., т, и ^—априор-
ные вероятности классов.
91
Необходимо выбрать такое решающее правило б(|), представлен-
ное как распределение вероятности на пространстве возможных реше-
ний D — (d0, dlt ..dm)
6(^)={3(d0/^, 8(^/g),..., S(dm!&],
при
2 8(^/1)=! и 8(4/J)>0, у/; g,
1=0
которое минимизировало бы математическое ожидание функции потерь
(ожидаемый риск) в:
т т
6 (<7, 8) = 2 2 J 6 dl, (5.1)
г=0 Х=1|
где di — решение, соответствующее принадлежности объекта Л классу
Rt, do — решение, означающее отказ от классификации (распознавания),
o)(rft, ^}=(Оа—весовая функция (функция потерь), представляющая
потери, понесенные в результате того, что принято решение di, в то вре-
мя как истинно d^ (ф.7 > <в0> > свп, i Л 0).
Минимум ожидаемого риска 6(</, 6) достигается при решающем
правиле 6°, называемом бейесовым и определяемым
S°ШЛ) = 1 8° (d^ = 0, Ni=£l, (5.2)
если
т т
3 ъ.==3
1 Х=1 Т=1
Различные алгоритмы, используемые для прогнозирования с пози-
ции статистических решений, отличаются видом аппроксимации много-
мерной функции плотности f(|/^x). простейшем случае используется
предположение о статистической независимости признаков и многомер-
ное распределение представляется как произведение одномерных гаус-
совых распределений. В более общем случае применяют многомерную
гауссову аппроксимацию, причем может предполагаться равенство или
неравенство ковариационных матриц классов. Имеются также предло-
жения по представлению плотностей вероятности в виде разложения по
ортогональной системе функций [58].
Рассмотрим случай двух распознаваемых классов, что, вообще го-
воря, не является сильным ограничением общности, так как, применяя
метод последовательной дихотомии, можно получить большее число
классов. В случае двух классов и J?2 бейесово правило б°(ё) имеет
вид [56]
(если ’AJ,
= если ^G{g:£(^)<AJ, (5.3)
I d0, если I? е {I: Ла <£(£)< AJ,
/ = 1, 2,..., N,
где
д — f (£/&)_.—J1 (%) (5 4}
— отношение правдоподобия, fi(|), fz(|) —условные плотности распре-
деления вероятностей объектов 1-го и 2-го классов соответственно, Ai,
92
Л2 — некоторые пороги сравнения, определяемые априорными вероятно-
стями q\ и Цъ и задаваемой матрицей потерь
<о = (л^), г = 0, 1, 2; 2 = 1, 2.
При од.=<»22 = 0, со.. = 1й — с» —----------поиоги сравнения Л,,
Л2 определяются:
Л1— (<72/91) (<012—<£>о)/соо» Лг= (qz/tfi) <оо/(е>21—(,Jc). (5.5)
Очевидно, что чем больше удалены друг от друга пороги, тем мень-
ше будет ошибок при распознавании (прогнозировании).
При гауссовой аппроксимации условных плотностей вероятностей
fi(|), Ь(|) логарифм отношения правдоподобия (5.4) равен
in L (S)=In 4- (S - .«.)* Up « - М.) +
+4-(^-^)*tv'^-w+4-lnjun-’ <5-6>
где £7, — ковариационные матрицы для объектов классов 2 = 1,2;
обратные матрицы; [tAJ— определители матриц; — векторы средних
значений признаков для объектов классов 2=1,2; >{<—знак транспони-
рования.
Элементы ковариационных матриц и векторы средних значений для
каждого класса 2 (2=1,2) оцениваются из обучающей выборки (апри-
орной информации) объектов
.V)
е =_5_/3-Г'Е 8 -» » к
СУвг fa' i /Д j Or j
Л—1 \ f.
х z=i
/=1
где s, г—1, 2,..., k—число признаков, — число априорных объектов
для обучения в классе 2.
Априорные вероятности классов 91 и <7з равны
<71===: А1/ (Лй “F ЛА) > <7 == А 2/ (.Vi 4- ЛА),
если обучающая выборка сформирована случайным образом.
Следует отметить, что число объектов N. в обучающих выборках
каждого класса должно быть не меньше размерности пространства приз-
наков, т. е. Ny k. Это необходимо для того, чтобы ковариационная
матрица не оказалась особой и, следовательно, имела требующуюся
для вычисления выражения (5.6) обратную матрицу U^1 .
При использовании гауссовой аппроксимации для fx(l) решающее
правило (5.3) получается квадратичным. Когда условные распределе-
ния классов описываются законом, отличным от нормального,
использование квадратичного решающего правила может привести
к значительным ошибкам. Для получения более гибкого решения можно
93
применить эмпирические (частотные) оценки для |г(1) —многомерные
гистограммы. При этом решающее правило (разделяющая классы ги-
перповерхность) будет иметь «ступенчатый» вид.
Рассмотрим дискретное пространство признаков размерности Л с ко-
ординатными осями gi, S2, - - и числом интервалов п (градаций) по
осям Л1, зг2, -.лп соответственно. Однако из-за ограниченного объема
памяти и быстродействия электронных вычислительных машин эмпири-
ческие оценки распределений вероятностей при построении отношения
правдоподобия £(£) ~Л(1)/М1) на этапе обучения в каждой дискрет-
ной точке | могут быть вычислены лишь при весьма малом количестве
признаков и числе градаций по ним. Так, уже при &=10 и зг=8 (ш=
= Л2= =лЛ) требуется память ЭВМ порядка 7-108 ячеек.
Рассмотрим подход, реализующий метод статистических решений,
при эмпирических оценках для /х(|) [или Т(|) =/1(|)//2(^)1 при сравни-
тельно больших размерности пространства признаков ife и числе интер-
валов (градаций) по каждому признаку Статистическая оценка Л(|)
производится не для всех точек пространства £ сразу, а последователь-
но, в процессе собственного прогнозирования, и только для тех точек
(или их некоторых «окрестностей»), которые необходимы для распозна-
вания из текущей информации («экзамена»). Выражение для эмпириче-
ской (статистической) оценки отношения правдоподобия можно пред-
ставить в виде
/ __Г1 + 1 'v2 + 2 /Г У'
Л(|) ~~гг+1 ЛЙ + 2 ’
где — (п4-1)/(Мч-2), f2(t) — (Г2-М)/(УУ2-Р2 — байесовы оценки ве-
роятностей попадания объектов из 1-го или 2-го классов соответственно
в некоторую точку | (или «окрестность» ее) ; п, г2—число объектов 1-го
и 2-го классов, лопавших в точку | из априорной информации; /V4, Nz —
количество объектов 1-го и 2-го классов обучающей выборки (априор-
ной информации).
При диагностике объекта с вектором состояния & каждый раз вы-
числяется функция L(^i) с помощью (5.7) в некоторой окрестности 1? и
в соответствии с правилом (5.3) принимается решение о принадлежно-
сти к тому или иному классу.
«Окрестность» точки (например, многомерный брус) рассматри-
вается в связи с ограниченностью априорной информации. Она форми-
руется относительно точки как центра, так, чтобы в ней содержалось
некоторое число объектов из обучающей выборки (1-го и 2-го классов),
например irj=34-0,2(JVi+Ar2). Этап обучения здесь заключается в запо-
минании объектов из обучающей выборки, а вычисление £(|) произво-
дится всегда при осуществлении распознавания.
Использование метода «локальной» оценки Т(|) позволяет решать
задачи прогнозирования с числом параметров 6^50 и числом градаций
по каждому параметру л=С8 (при не слишком больших выборках изде-
лий) .
Таким образом, формально решение задачи прогнозирования с по-
мощью математического аппарата статистической классификации ие
имеет принципиальных отличий от решения других технических задач,
требующих распознавания, ио существует ряд специфических особенно-
стей, которые необходимо учитывать. При этом основными этапами ре-
шения задачи распознавания являются следующие:
94
1. Выбор модели распознавания, которая может быть детерминиро-
ванной, вероятностной и индетерминированпой и зависит от того, на-
сколько перемешаны множества {Ы, принадлежащие разным клас-
сам
2. Описание эталонов классов на основании априорной информа-
ции и обучение (самообучение) модели распознавания. Оценка инфор-
мативности (значимости для распознавания) параметров позволяет
оптимизировать описание эталонов.
3. Сопоставление текущей информации о контролируемом приборе
с априорно заданными эталонами классов
4. Принятие решения о качестве или степени работоспособности
прибора по данным контроля.
5. Оценка надежности распознавания путем экзамена выбранной
модели распознавания.
Методы распознавания образов можно классифицировать следую
щим образом:
а) детерминированные, вероятностные и мидетерминированные;
б) с обучением («обучение с учителем») и самообучением («обуче-
ние без учителя»);
в) параметрические и непараметрические;
г) нерекуррентные и рекуррентные (адаптивные);
д) линейные и нелинейные (квадратичные и др.).
5.2. Прогнозирование как распознавание образов
(одномерный случай)
В методах аналитического и вероятностного прогнозирования экс-
траполяция фукнций времени заложена в явном виде. Если же контроль
возможен только в ограниченном интервале или в отдельном временном
сечении, то в начале эксплуата-
ции отсутствуют предпосылки для
экстраполяции с помощью рас-
смотренных математических вы-
ражений. Это объясняется недо-
статочным количеством информа-
ции, которую можно получить в
начальный период эксплуатации
или испытания диагностируемых
объектов.
Рассмотренная ранее поста-
новка задачи прогнозирования с
помощью аппарата статистиче- Ркс- 0,1 • вопросу обучения акстраполя-
V . г ционпым связям,
скои классификации предполага-
ет, что k параметров £2, ..., £/it
характеризующих состояние системы, будут иметь идентичную совокуп-
ность {£,} для систем с равным или примерно равным запасом работо-
способности. Иными словами, группа приборов (систем), имеющая оди-
наковую долговечность, будет отличаться от приборов, не входящих
в эту группу, вектором или функцией состояния, которые описываются
координатами — параметрами Es, s = l, 2, k.
В подобных случаях элементы экстраполяции закладываются в ме-
тоды прогнозирования на основе статистической классификации тех
95
устойчивых связей, которые обнаруживаются между классом с соот-
ветствующим запасом работоспособности и сочетанием Процесс уста-
новлений экстраполяционных связей осуществляется на основе априор-
ной информации и называется процессом об\ чепия экстраполяционным
связям (рис. 5.1). При прогнозировании по результатам текущего кон-
троля обнаружение и распознавание экстраполяционных связей произ-
водится с помощью той или иной математической модели.
Таким образом, из общего круга решаемых при статистической
классификации вопросов необходимо выделить два основных: количест-
венная оценка обучения экстраполяционным связям и формирование
оптимальной модели распознавания.
Пусть имеется априорная выборка приборов или систем одного
типа с диагностируемыми. Состояние каждого прибора (системы) ха-
рактеризуется совокупностью k параметров, которые являются коорди-
натами вектора состояния
• • > S&- (5.8)
В процессе обучения устанавливается, какие векторы (5.8) форми-
руют класс с запасом работоспособности Ri, какие — с запасом работо-
способности R% и т. д. Иначе говоря, осуществляя вероятностную и ста-
тистическую обработку векторов ^^Rz, ... внутри каждого клас-
са, можно описать R\ Л.=1, 2, ..., m с помощью эталонного вектора
11э, ы ..., пли функции плотности распределепия Л(|), /г (£),...
В зависимости от того, как описывается класс или как того требует
постановка задачи, векторы | классифицируют либо детерминированны-
ми, либо вероятностными методами. Детерминированные методы целе-
сообразно использовать тогда, когда векторы состояний принадле-
жащие различным классам, не сильно перемешаны. В этом случае век-
тор определяемый в результате обработки текущей информации, срав-
нивается с эталонными |Хэ, Х=1, 2, ..., т, и определяется, к какому
из эталонных векторов он «ближе». Мера близости может выражаться
расстоянием между сравниваемыми векторами. При этом метрика долж-
на обладать общими для объектов класса свойствами. Затем отыски-
вается наплучшая метрика, максимальным образом сближающая
(уплотняющая) векторы одного класса.
Как уже отмечалось, задача распознавания образов имеет двойст-
венный характер: с одной стороны, необходимо построить характери-
стики (описание) класса на основе априорной информации (обучение);
с другой стороны, необходимо принять решение об отказе (объекте) из
текущей информации (распознавание — экзамен).
Существуют различные способы описания классов, однако наиболее
пригодным для практики является способ, связанный с вычислением
статистических параметров и характеризующий центр рассеивания слу-
чайных величии (значений параметров объектов из априорной инфор-
мации).
Пусть характеризует статистически центр Л-го класса по s-й
координате (параметру). Тогда соотношение между и £)s, где — $-й
параметр диагностируемого объекта, будет говорить о близости объекта
к л-му классу.
96
Перечислим некоторые меры близости, отличающиеся как видом
функции, так и способом нормирования [54]:
1. Квадрат расстояния
k
^==2
8=1
2. Скалярные произведения
k
+ ^1x2 + - • + = 2
»=1
3. Скаляриые произведения при различных способах нормирования:
k I k
<4=2«Js
8=1 I s=i
4. Корреляционный метод
5. Расстояние по Хеммингу
л-
^=2 l«.-U
8=1
Здесь везде Х=1, 2, ..., т.
Вообще, нормирование желательно осуществлять во всех случаях,
поскольку при этом становится более ясной степень близости экзаме-
нуемого объекта к тому или иному классу. Для этого вполне пригодны
выражения (3.38) — (3.40), однако они никоим образом не учитывают
значимость и вес того или иного параметра. Введение весовых коэффи-
циентов позволяет повысить точность распознавания (прогнозирования)
[57]. Таким образом, мера близости в линейном пространстве признаков
с учетом сказанного определяется следующим образом:
ft
1/2
Я = 1, 2,.... т,
(5-9)
где а5 — весовой коэффициент s-ro параметра-признака, определяемый
на стадии обучения из соображений наилучшего прогнозирования диаг-
ностируемого объекта; при этом должно соблюдаться условие
ft ft
2 as=l или П as = l-
8=1 8=1
7—813
97
Мера близости, вычисленная в нелинейном пространстве признаков,
во многих случаях дает повышенную точность прогноза:
k
<[«.)”-(кП (5.10)
S=1
где р — степень нелинейности, вычисляемая на стадии обучения модели
и предназначенная уменьшить ошибку классификации. Обычно на прак-
тике р=2,3.
После этапа обучения обычно оказывается необходимым решать
задачу построения разделяющей функции, т. е. определять уравнение
поверхности, разделяющей классы R> в пространстве образов-объек-
тов. Разделяющая функция строится на основе функций подобия (мер
близости) диагностируемого образа к априорному подмножеству
образов.
Метод зои позволяет в некоторых случаях достаточно быстро
и просто осуществлять прогнозирование. Общую схему метода можно
представить следующим образом.
Все параметры объекта разносятся по трем зонам (областям) (слу-
чай двух классов). Границами зон являются величины и кото-
рые определяются различными способами, в частности, как
и £*2s~&S—ГХЗЪъ
где — среднее квадратическое отклонение $-го параметра, а г может
быть целым и дробным, ио практически г<3. Будем считать, что объект
по параметру относится к 1-му классу, если IssCB**®, и ко 2-му, если
£s^>£*2s- При l*is<^e<|*2s решение не принимается и целесообразно
применить более точный метод. Подобный анализ необходимо осуществ-
лять по всем параметрам. Математическая основа метода может быть
представлена следующим образом.
Считаем, что мера близости (функция подобия) для s-ro параметра
дискретна и принимает три значения:
(5.11)
Общая мера близости (по
ная сумма функций подобия
k параметрам) вычисляется как лиией-
(5.12)
Принадлежность диагностируемого образа к той или иной зоне
определяется знаком меры близости (5.12): I Rrt если и
если Qx>0. Если £>г=0, то значение вектора состояния £
попадает в зону отказа от распознавания ft-мерного пространства при-
знаков. Для практических целей удобно все оси параметров разместить
в одномерной плоскости (рис. 5.2). В (5.12) можно ввести весовые коэф-
фициенты, как это сделано в (5.9), которые можио определить на стадии
обучения.
98
Метод обобщенной точки является дальнейшим разви-
тием рассмотренного метода. Его идея заключается в том, что все оси k
параметров сводятся к одной обобщенной оси Qo, на которой выделяют-
ся три зоны с границами Q*io и Q*2o. Положение обобщенной точки на
этой оси будет говорить о принадлежности объекта к тому или иному
классу или о необходимости отказаться от распознавания. Точность
распознавания, очевидно, будет во многом зависеть о г того, насколько
хорошо выбрано обобщающее выражение. Одним из основных крите-
риев при создании подобных выражений, безусловно, является как мож-
но большее удаление классов друг от друга и сжатия объектов внутри
класса. В данном случае это осуществляется следующим образом. Мно-
Рис. 5.2 Представление
параметров электронно-
лучевой трубки в одно-
мерной плоскости.
жество k параметров объекта, отнесенного к 1-му классу, разделяется
на две части, из которых одна часть параметров 1=1, 2, ..., k, боль-
ше по своим значениям, чем параметры объекта, отнесенного ко 2-му
классу 5=1, 2, ..к—k, а часть параметров меньше, т. е.
Z=l, 2, ..., k и bs<bs, 5=1, 2, ..., к—k, s=£l. Например, на рис. 5.2
в первую часть входят 1-й, 2-й, 3-й, 7-й, 8-й, 9-й, 10-й параметры, а во
вторую — все остальные. Если в обобщенном выражении учесть отноше-
ние сумм параметров, отнесенных к разным частям, то тем самым
удастся более четко разделить классы по обобщенной оси Qo. Обобщен-
ную точку можно найти с помощью выражений
ft I __
^ = 2 MS*- <5-13)
l~l I 3~1
' й 1 к____k
ч=ПчП s^1- <5-14)
г=1 / $=i
Выражение (5.14) является более эффективным с точки зрения точ-
ности распознавания. Границы классов на обобщенной оси опреде-
ляются:
k I к—к k I к—k
= S Ms ИЛИ Й»„= П / П е*16,
/=1 / s=l 1=1 I S=1
k I k—k k I к—k
= / 2 ^2S КЛИ = H / П S=^1-
Z=1J I $=] / = 1 / s=l
7»
99
Введение весовых коэффициентов для параметров повышает точ-
ность распознавания, а использование безразмерных (нормированных)
величин упрощает решение и делает его более наглядным. Следует
заметить, что использование различных мер близости довольно мало
влияет на изменение границ, разделяющих классы, однако при этом
в зависимости от количества и качества информации можно достигнуть
большей разрешающей способности экзаменуемых объектов. Совместное
использование весовых коэффициентов и обобщенных мер близости
иногда позволяет повысить процент правильных решений до 90 ... 95%,
что делает детерминированные методы в одномерном варианте прием-
лемыми для практических целей.
Пример. Рассмотрим приложение
изложенного метода к прогнозированию
долговечности мощных клистронов типа
КИУ42. В результате анализа априор-
ной информации были сформированы
три временных класса, которые описы-
вались средними арифметическими зна-
чениями параметров клистронов, входя-
щими в свой класс (табл. 5.4). Необхо-
димо было осуществить классификацию
приборов в начале их эксплуатации по
долговечности.
Анализируя изменение средних зна-
чений по классам, -можно установить, что
при применении выражения (5.14) в чис-
лителе его будут два параметра РВЫх
и 7а, которые растут с увеличением дол-
говечности, а в знаменателе остальные,
которые для старших классов уменьша-
ются. Вычисляя обобщенные точки
(5.14) для каждого класса, получим эта-
лонные значения, около которых группи-
руются классы:
Й10=0,536 • ПО-5; .Й2о=О,776 10~5;
Йзо=О,9М-10-5.
Пусть экзаменуются три прибора,
для которых вычислены следующие
обобщенные точки:
20,3-180
о---------------------- - 0 444 • 10 - 5
1x21 — 280-18-10.5-150-10 ’
Далее определяется близость вычис-
ленных обобщенных точек к эталонным.
Значение (Qi—Qw) минимально, что
говорит о близости первого прибора
к 1-му классу, на основании чего он
был отнесен к классу с долговечностью
0...3000 ч. Истинный же срок службы
прибора был равен 14’53 ч. Значение Йз
ближе к £23о, что также соответствовало
истине, у третьего прибора долговеч-
ность была равна 10614 ч. А вот для
второго прибора оказалось (й2—Н2о)>
>(.П2—Изо), хотя прибор и принадле-
жит ко 2-му классу. Ошибка объясняет-
ся тем, что долговечность прибора рав-
на 5717 ч; это, как не трудно заметить,
находится вблизи границы между клас-
сами '(6000 ч). Чтобы быть уверенными
в принятом решении, необходимо осу-
ществить классификацию каким-либо
другим методом, отличающимся от пред-
ложенного. Такой метод будет рассмот-
рен позднее.
ТАБЛИЦА 5.1
20,3-185
= 270-15-9,5-1460-7,55
= 0,876-10-®,
20,1-200
2з = 285-15-9,5-1425-7,85
= 0,889-10-®.
Параметры КИУ-12 1 класс О...ЗЭОО ч 2 класс 3000...6000 ч 3 класс 6000...оэ ч
20,200 20,200 20,282
МВт
иа, кВ 283,571 281,857 281,250
А 185,285 192,428 188,875
7Ф. А 16,500 15,000 13,625
4/н. В 10,000 9,642 9,565
Ом 1525,0 1480,6 1447,5
PEZ, кВт 9,787 8,29 7,75
При наличии помех и преобладании случайной составляющей в |
образы-объекты различных классов оказываются существенно переме-
шанными, что затрудняет распознавание. В этом случае целесообразно
применять вероятностные методы. Мерой близости при этом является
апостериорная (условная) вероятность принадлежности диагностируемо-
го объекта по s-му параметру к Х-му классу Наиболее про-
стыми способами разделения объектов на классы по известному векто-
ру состояния | являются:
100
а) по сумме вероятностей
k k k
2 P(W)>..., S -> 3 W^);
5=1 5=1 6=1
б) по произведению вероятностей
k k k
П ₽(W.).....П P^IR>)’ П
s—l 5=1 5=1
Однако способы сумм и произведений вероятностей, являясь спосо-
бами быстрой оперативной проверки гипотез о принадлежности объек-
тов, ие учитывают априорную вероятность появления каждого класса
в генеральной совокупности классов, без использования которой невоз-
можно обойтись в некоторых сложных задачах распознавания. Этого
недостатка лишена бейесова схема распознавания, в которую вводятся
весовые коэффициенты:
А / т k
p(rjd=p(^) р (W1 73 р(р>) П • <5-15)
5=1 / Х=1 5=1
где P(Ry/^) — апостериорная вероятность гипотезы о принадлежности
вектора Z-му классу; Р (Ру) — априорная вероятность принадлежности
к Х-му классу; ys — корректировочный коэффициент, определяемый на
стадии обучения.
Коэффициент ys позволяет повысить точность распознавания. Ко-
личественные значения его выбирают исходя из физической значимости
параметров или степени флюктуации и т. п.
При вероятностных способах распознавания в качестве критериев
могут служить как максимальные величины
k
12
5=1
’ k
П р&'*>)
5=1
так и заданное превышение максимальной вероятности гипотезы над
ближайшей к ней по величине вероятности, например
[^ л
где Л — порог сравнения, зависящий от требуемой точности распозна-
вания.
В [54] справедливо отмечена нецелесообразность (и ошибочность)
принципиального разграничения методов распознавания с точки зрения
их строгости и объективности. Критерием выбора метода может слу-
жить простота определения меры близости, сложности описания границ
классов и образов, разрешающая способность и т. д. При этом весьма
важным является знание индивидуальных физических особенностей рас-
познаваемых объектов, информативности выбранных признаков, количе-
ство и качество априорной и текущей информации, возможность введе-
ния адаптационных (весовых) коэффициентов и др.
101
5.3. Метод потенциальных функций
В [60] предлагается метод распознавания, в основу которого поло-
жено построение так называемых потенциальных функций. Метод бази-
руется на гипотезе о характере функций, разделяющих множества, со-
ответствующие различным образам (классам). Большим преимущест-
вом метода является то, что к нему можно свести многие известные
алгоритмы распознавания.
Пусть в пространстве признаков-параметров диагностируемому при-
бору соответствует единственная точка (конец вектора состояния 1) и
пусть задача прогнозирования решается относительно двух классов (па-
раметрических или временных) Ri и JRz- Если предположить, что jRi и
A*2 не пересекаются, то должна существовать по крайней мере одна раз-
деляющая функция. Задача состоит в том, чтобы в период обучения на
основе априорной информации построить какую-либо из разделяющих
функций. При этом распознающий алгоритм на основе анализа текущей
информации позволяет отнести объекты к одному из классов, или А'г-
Метод потенциальных функций предусматривает следующую после-
довательность действий. При появлении в процессе обучения некоторой
точки (объекта) с ней связывается функция /(('§, &), заданная на
всем пространстве признаков Й и зависящая от у как от параметра.
Такая функция называется потенциальной. Последовательности £i,
§2, ... появляющихся в процессе обучения точек соответствует последо-
вательность /((£, £i), K(g, 52), ... потенциальных функций, которая при
помощи определенных правил используется для построения функции
<p(g, £2, -••). Правила формирования функции устанавливаются та-
ким образом, чтобы по мере увеличения числа предъявляемых в процес-
се обучения точек (объектов) функция ср стремилась к разделяющей
функции.
Метод потенциальных функций предполагает существование в про-
странстве £ системы функций (р<(£), 1=1, 2. ..., позволяющих
для каждой пары разделяемых множеств- найти такое число /V, при
котором разделяющую функцию можно представить в виде
Если в пространстве £ существует полная система функций, то
(piU) можно считать элементами ее, и любая функция этой системы,
в том числе и разделяющая, может быть представлена в виде бесконеч-
СО
него ряда S
t=i
Условие (5.16) требует, чтобы разделяющие функции разлагались
в ряды с конечным числом членов. При этом в пространстве g эти функ-
ции должны быть не очень сложными («равными» или «вычурными»)
и не должны иметь большого числа экстремумов в малой области,
в близкорасположенных точках их значения должны мало отличаться
друг от друга.
Алгоритм распознавания, основанный па рассматриваемом методе,
заключается в следующем. В качестве потенциальной принимается ска-
102
л яркая функция двух векторных аргументов вида
U=2 «>(5)?г(5о), (5-17)
1=1
где <j>z(g) —линейно независимая система функций, щ — действительные
числа, отличные от нуля для всех 1=1, 2, ..N, go— точки, появляю-
щиеся в процессе обучения. Предполагается, что qpi(g) и /<(g, go) огра-
ничены при ge/?l.UJ?2-
Пусть в процессе обучения появляются точки gi, gg, ...» gz, ..каж-
дая из которых принадлежит iRi или Яг- Будем считать множество Я1
положительным, а множество -Я2— отрицательным.
При появлении первой точки g! строится потенциальная функция
ZG(g), значение которой равно потенциалу, соответствующему точке gz,
взятому со знаком множества, к которому принадлежит точка gi, т. е.
если
если
(5-18)
Далее пусть для /-го предъявления построен потенциал Я/ (g) и на сле-
дующем (/-Н)-м шаге обучения появляется точка gz+i. В результате
возможны четыре случая:
I) ^.м^Яа, /<z(g,+I)>0;
2) ьн-1^А*2, Az(g?+i) <0;
3) Kz(W<0;
4) Аг(^+,)>0.
(5.19)
В случаях 1 и 2 знак множества, которому принадлежит предъяв-
ляемая точка gz+i, и знак функции Kz(gzj-i) совпадают, т. е. алгоритм
правильно классифицирует объект gz+i («ошибки нет»). При этом при-
нимается 7</+i(g) =/<((g).
В случаях 3 и 4 существует ошибка, т. е. знак множества, которому
принадлежит gz+i, и знак функции ZG(g/+i) не совпадают. Тогда следует
исправить ошибку, т. е. для случая 3 приняты АнмШ = A'z(g) + g?+i),
а для случая 4 Xz+i(g) =-Az(g)—K(g, gz+i).
Таким образом, при предъявлении (/Т 1)-й точки делается предпо-
ложение о том, что потенциал, построенный при распознавании /-й точ-
ки, разделяет классы, т. е- функция Kz(g) и есть искомая разделяющая
функция. Такая же процедура повторяется и для (/+1)-й точки. Если
это предположение оказывается для нее справедливым, то потенциал на
этом шаге не изменяется. В противном случае потенциал меняется пу-
тем добавления к нему потенциала (/+ 1)-й точки с таким знаком, что-
бы это изменение было направлено на ликвидацию ошибки.
Построенный после Z-го шага потенциал можно записать следую-
щим образом:
лт(^)=2ка ^)-2kg, м, (5.20)
где точки gz(_) принадлежит классу Ai, подстановка их в предыдущий
потенциал приводила к ошибке, точки gQ(_) принадлежат классу Яг, их
подстановка в предшествующий потенциал приводила к ошибке.
103
В [60] предложены две конкретные реализации алгоритма метода
потенциальных функций. В первом случае разделяющая функция
<pJ+i(g) строится по следующему рекуррентному правилу:
Wi(g) =<p/(g) +az+isign[q)(^+i)—-<pf (gt+-i)]/C(g, &+i), (5-21)
где az+1 — любая последовательность положительных чисел, удовлетво-
ОО 00
ряющих условию: ряд at расходится, а ряд % сходится (напри-
i=i i=i
мер, ai=l/l).
Второй алгоритм осуществляет переход от функции <pz(g) к функ-
ции согласно формуле
%+.©=й© + [¥Й+,)-?^г+1)]4-К(Е, =.ч,), (5.22)
где g—произвольная положительная константа, удовлетворяющая усло-
вию g=0,5max f((g, go), (pz+i(£) —действительное значение разделяющей
функции.
При практическом использовании рассматриваемого метода возни-
кает задача выбора потенциальной функции. Иногда не обязатель-
но заботиться о предварительном выборе системы функций срг(^) и кон-
стант а/. Можно сразу задать потенциал /((g, go) таким, чтобы, во-пер-
вых, функция go), рассматриваемая как функция g при фиксиро-
ванных значениях go, была достаточно гладкой, а во-вторых, чтобы
функция go) принимала максимальное значение при g=go.
Кроме того, следует принимать во внимание возможность варьиро-
вать потенциальные (функции в значительных пределах, а также требо-
вать симметрии 7<(g, go) = A (go, g). Поскольку указанные требования
к потенциальным функциям имеют достаточно общий характер, то при
практическом использовании метода можно задавать /<(g, go) в форме
простых убывающих функций. Кстати, представляя точку —объект
в виде точечного заряда (источника потенциала)—в пространстве па-
раметров по аналогии с моделью электрического поля, можно потен-
циальную функцию принять за меру1 удаления прогнозируемого объекта
от всех точек класса, т. е. считать ее максимальной в точке-источнике
и убывающей по какому-то знаку по всем направлениям от нее.
Если в пространстве g ввести понятие о расстоянии £?(g, go) между
двумя точками g и go, то в качестве потенциальной функции K(-g, go)
можно выбрать достаточно простую убывающую функцию этого рас-
стояния, например,
&>) = 1Д1— ad’ (g ад] или К(|, ад =а/[1—<₽(£. go)], (5.23)
где а и г определяют скорость изменения K(g ад. Кроме того,
K(g, go) =ехр [-U.& (g, go)], (5.24)
где зачастую г=2, или K(g, go) =sin]cuZ(g, g0)/^(g, go)].
Особое внимание следует уделить выбору параметра а, имея
в виду, что чем сложнее задача (сложнее разделяющая функция),
тем быстрее должен убывать потенциал K(g, go). При практическом
использовании алгоритма параметр крутизны потенциальной функции
рекомендуется подбирать экспериментально [60].
104
Метод потенциальных функций рассматривался в предположении,
что классы не пересекаются и что всегда существует одна или несколь-
ко разделяющих их функций. Такой подход к решению задачи является
детерминистским и не -всегда применим на практике. В [60] рас-
смотрена возможность применения метода потенциальных функций
в случае, когда Ri и R2 пересекаются и ие существует разделяющих их
функций. Но при этом предполагается существование функции степени
достоверности. В этом случае мы имеем дело с вероятностной
реализацией метода потенциальных функции.
Очевидно, для каждого объекта существует вероятность принадлеж-
ности его к Ri и R2 и в процессе обучения каждый объект относится
к классам Ri или Rz в соответствии с этими вероятностями. Предполо-
жим, что в пространстве признаков £ объективно существуют функции
£(^1, I) и L(R2, £)=1—L{Ri, I)- Эти функции соответствуют вероятно-
стям того, что объект, ‘представленный точкой принадлежит к одному
из классов Ri или R2, и называются степенями достоверности. Предъяв-
ляемые для распознавания точки относятся к R\. и R% не однозначно,
а в соответствии с объективно существующими степенями достоверно-
сти. Задача состоит в том, чтобы по предъявляемым в процессе обуче-
ния точкам и по априорной информации о принадлежности этих точек
к какому-либо образу восстановить L(Ri, |) и L(A*2, £) как функции,
'Заданные на всем пространстве параметров
Для этого можно использовать рекуррентную процедуру, подобную
(5.21), при этом фг(&) дает /-е приближение для L(R\, £), где
{0, если —со < <f>i (Е) < 0,
если 0 <?/(£)< 1,
1, если 1 (£)•< ©о.
Числа щ определяются следующим образом:
[°, если titERt И или и Е/- ^R2',
к, если ti(ERi и
.-и если %i£ER2 И ti — Ri,
где sz—ЧЪ, обозначают события, относящие & (в результате
случайного акта) к классу Ri с вероятностью cpz-i(^) или к классу
R2 с вероятностью 1—9?-i(^), Yz— последовательность положительных
чисел, удовлетворяющая условиям
СО ОС
2^ = 00. .
1=1 2=1
Степени достоверности можно определять и с помощью бейесового
правила принятия решения. В [21] показано, что все алгоритмы, реали-
зующие метод потенциальных функций, являются частными случаями
общего алгоритма стохастической аппроксимации.
5.4, Дискриминантный анализ
Одним из основных результатов, получаемых в процессе обучения
при решении задачи прогнозирования методами распознавания, как
уже отмечалось,- является построение разделяющей функции (поверх-
ности), которая разграничивает выделенные классы Rr.
105
Разделяющие поверхности в любом случае при классификации объ-
ектов можно полностью определить скалярными функциями gi(|), ...,
..., g’m(l), где |=£ц — вектор состояния диагностируемого
объекта. Эти функции, названные дискриминантными [62], выби-
раются так, чтобы для всех выполнялось условие gy (|)>£г(1)
при X, г=1, т, Х=Ал
Иначе говоря, Х-я дискриминантная функция в области Ry принимает
наибольшее значение по сравнению с другими дискриминантными функ-
циями.
Если предположить, что дискриминантные функции непрерывны на
разделяющих поверхностях, то поверхность, разделяющая смежные
классы Ri и R& определяется уравнением
= (5.25)
Разделяющие поверхности в плоскости £1, g2 (рис. 5.3) являются проек-
циями на эту плоскость линий пересечения дискриминантных функций.
‘ С помощью дискриминантных функций можно получить стандарт-
ный и удобный для практического использования метол задания разде-
ляющих поверхностей. В достаточно распространенном на практике слу-
чае, когда Х=2, при осуществлении классификации необходимо опре-
делить, какое из чисел gi(|) и £г(£) больше, а это можно сделать, опре-
делив знак дискриминантной функции g(|)=gi(|)—£2(5). Если
>0, то объект принадлежит к классу Rit если g(|)<CO, то к Rz- Соотно-
шение g'(|)~0 характеризует в этом случае разделяющую поверхность.
Таким образом, при X—чп можно найти m-дискриминантные функции
gi, ..., gm, при Х = 2—ТОЛЬКО одну фуНКЦИЮ £(!).
Дискриминантные функции можно выбирать различными способа-
ми. Иногда функции точно определяются на основе полной априорной
информации об объектах, подлежащих
классификации. В других случаях можно
сделать предположения, опираясь па каче-
ственные характеристики обьектов. В каж-
дом из этих случаев, особенно во втором,
может оказаться необходимым корректиро-
вать функции для иолучения приемлемой
точности прогнозирования. Адаптация и
корректировка нужна и тогда, когда в объ-
ект вносятся конструктивные и технологи-
ческие изменения.
Как уже упоминалось, дискриминант-
ные функции определяются на стадии обу-
чения. При использовании параметриче-
ских и непараметрических методов
обучения построение дискриминантных
функций будет различным.
Параметрические методы целесообраз-
но применять в тех случаях, когда
каждый класс объектов X (Х=1, 2, ..., т)
параметров, причем значения некоторых из
Рис. 5.3.
функции
Дискриминантные
для двумерных
объектов.
априорно известно, что
характеризуется системой
них могут быть неизвестными. При этом обучающая выборка объектов
используется для определения параметров, по которым затем находятся
дискриминантные функции.
106
Пусть, например, необходимо разделить объекты на два класса Ri
и Rz, которые описываются векторами & и & с координатами (&и,
£12, - и (сз.ъ Вгь)- Дискриминантную функцию, которая раз-
деляла бы эти два класса, можно представить в виде
g (I) = (|i-g2) I+0,5 ] & 12—0,51 & Р, (5.26)
где (|1—— скалярное произведение векторов, 1£]2=1*|— квадрат
модуля вектора |.
Параметрический метод в этом случае используется для определе-
ния и Если в Ri находится Ni объектов, а в Rz—N2, то соответст-
вующие средние могут служить разумными оценками |i и Затем
оценку этих средних можно использовать для определения g(£) с по-
мощью уравнения (5.26). На этом процесс обучения заканчивается.
Когда же нельзя сделать каких-либо предположений относительно
параметров, характеризующих классы, наиболее уместным является
применение пепараметрических методов обучения. При этом на форму
дискриминантных функций накладывают ограничения. Например, пред-
полагают, что эти функции являются либо линейными, либо квадратич-
ными, либо кусочно-линейными. Эти функциональные формы содержат
неизвестные коэффициенты, подбираемые таким образом, чтобы дискри-
минантные функции осуществляли требуемое разделение на обучаемой
выборке.
При использовании линейной дискриминантной функ-
ции вида [63]
£(£) =Pi£i+'[Mh+ - +0ь|л (5.27)
необходимо в процессе обучения определить коэффициенты •£ таким об-
разом, чтобы величина g(|) могла быть использована для классифи-
кации объектов. Обозначим дискриминантные функции для обоих клас-
сов Ri и R2 как gi(l) и gz(i). Взаимное распределение величин
g(i)[A(g) Для gi(|) и fz(g) для g2(|)] позволяет сделать вывод об эф-
фективности дискриминантной функции (рис. 5.4).
Если распределения значительно перекрывают друг друга, то приме-
нение дискриминантной функции не эффективно. Ее целесообразно ис-
пользовать в случае, когда разность [gi(|)—£г(1)] велика по сравнению
с дисперсиями распределений fi(g) и fz(g). Комбинация изменений ве-
личин £(|) для обоих классов объектов определяется выражением
2
2 S tex; -ix)!> (5-28)
)=1 /=1
где gy — среднее значение распределения Z-го класса, — значения
величин g(£) внутри Z-го класса, пг—количество приборов в Я-м классе.
Наилучшее разделение получается при максимизации выражения
/2
S3 tex;-gx)s. (5.29)
Х=1 /=1
что приводит к следующим уравнениям:
“К Ч" •** Ч" fimsrm = Cdr, (5.30)
С = (Яг^1 (5.31)
107
2 «X
«и = =2 2 - V - Гв>), (5.32)
}.=! /=1
«X
(5-33)
/=1
с?р>= §р1 ^рг- (5.34)
Индексы р, q, г обозначают специфические параметры и лежат в пре-
делах от J до т. Точное значение С несущественно и на практике мож-
Рис. 5.4. Неэффективные (а) и эффективные (б) дискриминантные функции.
но считать С=1. Система (5.30) — (5.34) состоит из т независимых
уравнений и позволяет найти tn неизвестных {%
Пример. Рассмотрим -решение зада-
чи прогнозирования для кинескопов
типа 47ЛК2Б, работоспособность кото-
рых оценивалась по трем параметрам:
максимальный ток луча 1тах, яркость В
к коэффициент качества q. Необходимо
•о помощью дискриминантной функции
предсказать, -принадлежит лн прибор
к 1-му классу с [0...7\]=0...6000 ч или
яопадет в класс с Т’>6000 ч.
По результатам контроля парамет-
ров при tfo с помощью уравнений
(5.30)—(5.34) были вычислены Pi, р2,
Рз и ijслучена дискриминантная функция
£(|) —0,299/Яюх +1,83В—2,45?. (5.35)
Граничное значение g*t(B)=0,4 да-
вало точность прогноза, равную 88%,
а при g*(£) =0,430 точность равнялась
94%.
Рассмотренный метод можно успеш-
но применять для прогнозирования и
оценки работоспособности только одно-
типных приборов с 'идентичной техноло-
гией. Так, для партии кинескопов с из-
мененной технологией .прогнозирование,
осуществляемое с помощью дискрими-
нантной функция (5.35), дало точность
только 50.-60%, что подтверждает не-
обходимость корректировки функции
При сильном смешивании классов
необходим вероятностный подход к по-
строению искомых функций. В этом слу-
чае дискриминантная функция будет
зависеть от (вероятности Р(|Д) появле-
ния объекта | при условии, что он
принадлежит к классу X, и априорной
вероятности Р(Х) каждого класса.
В частности, дискриминантные функции
можно выразить в виде
= Р (ВД Р(X), Х= 1,2, ... m (5.36)
или. что то же самое,
gx(|) = lgP(£A)4-lgP(X),
Х= 1, 2,..., т, (5.37)
При т = 2
s U) — igq (g/2) +ig К — рг -
(5.38)
Определение на стадии обучения ве-
роятностей, входящих в (5.38), позволя-
ет построить вероятностную дискрими-
нантную функцию.
5.5. Распознавание траекторий изменения состояния
диагностируемого объекта
Влияние внешних и внутренних факторов приводит к тому, что
с течением времени состояние технических объектов изменяется. При
этом показатели характеристик или параметры можно рассматривать
108
как функции времени, представляющие собой траектории, описываю-
щие перемещения этих величин с течением времени. Если есть возмож-
ность заранее определить и задать эталонные траектории, то, сравни-
вая действительные траектории с эталонными, можно установить, к ка-
кому из классов относится объект по своему состоянию. Эталонные
траектории, характеризующие изменения состояния конкретных объек-
тов, можно получить в результате либо длительного наблюдения за по-
ведением подобных объектов в период эксплуатации, либо физического
или математического моделирования процессов, протекающих в объекте
с течением времени. Таким образом, определение состояния объектов
в этом случае сходно с задачей распознавания образов, определяемых
траекториями показаний или параметров.
Рассмотрим некоторые особенности решения задачи распознавания
траекторий изменения состояния (работоспособности) объекта диагно-
стики. Пусть Въ ..., Вт — множество эталонных траекторий, характери-
зующихся определенной степенью работоспособности, т. е. траектории
соответствуют определенным классам объектов, в частности, может
быть: B^Ri, ..., B^R2f Bm^Rm; —множество призна-
ков отдельной траектории в каждый момент времени; gs (т), <8=1, 2, ..
i = l, 2, ..., п—-множество значений s-ro признака траектории, где i —
выбранные моменты времени; Л(£С1(£), ..., gaft(i)), 2, .п— тра-
ектория изменения состояния объекга. Необходимо в процессе решения
задачи распознать траекторию А, т. е. отнести ее к наиболее близкой
ей эталонной траектории.
Назовем интервалом Dab между траекториями А и В положитель-
ную величину, квадрат которой определяется выражением
k
D2Ab^ [ем(1)-?ьЛ1)]! + ...4-[^(л)-^(к)Г. (5.39)
г=1
Пусть множество признаков траекторий представляет собой бинар-
ную последовательность, т. е. £s(i) равно либо 1, либо 0. Отсюда
[U (0 - «и (01 = [ °; еСЛИ !“ ® = J68 JJ’ (5.40)
I 1 у если
Таким образом, если рассматривать совокупность gs(i), s=l, ..., k,
n как [£Xпоразрядное двоичное число, то квадрат интервала
между траекториями А и В будет равен количеству поразрядных несов-
падений в двух [ЙХ поразрядных двоичных числах А (gas(l), .£as(n))
и B(gds(l), ..., &Дп)):
£>2дв=/. (5.41)
Выражение (5.39) удовлетворяет следующим топологическим усло-
виям:
Dab^Dea, Dab—Dac-ttDcb, Dab^Q, (5.42)
причем Рав=0 тогда и только тогда, когда А совпадает с В.
Каждая траектория Ву, определяемая некоторым множеством призна-
ков в пространстве признаков, будет занимать определенную область,
которую можно характеризовать величиной диаметра этого множе-
ства. Диаметром множества можно, в частности, считать наибольшее
109
расстояние между двумя его точками, т. е. величину, пропорциональную
мере множества в г'-ом временном сечении:
Dx(i) = TDm(0 (5.43)
где
k N
О = S 4-S-К(OF (5.44)
s=i r=l
— мера множества Вх в i-й момент времени, N — число траекторий,
принадлежащих
Л'
ь.-4-JX (5л5)
Г —1
— центр множества Вг по s-му параметру.
Коэффициент у зависит от закона распределения точек множества
в пространстве признаков и точности, с которой желательно определить
границу множества Ву.
Определим меру близости и центр множества через условные ве-
роятности появления множества {£,} s-ro параметра в i-м временном се-
чении, принадлежащего В^:
Р({^1Ву)=Рм.
Так как равно либо 1, либо 0, и при увеличении N, согласно закону
больших чисел, частота события стремится к ее вероятности, можно за-
писать
N
lim Л- V (i) = Р ({У,/Д). (5.46)
Л’->сю
г=1
Пользуясь выражениями (5.45) и (5.46), можно определить коор-
динаты 5=1, 2, ..., k центра области В^.
1^(i)=P({is}i/B>)- (5-47)
Произведем некоторые преобразования в выражении меры множе-
ства (5.44), которая представляет собой средний квадрат отклонения
точек множества от его центра:
k кг
1 -(/) “ 2Е,Г 0 0+01’
4=1 Г = 1
Так как gSr(t) может быть равным либо 1, либо 0, то
N N
~N~ 2 С W = АГ } ( W =
г-1 /=1
Тогда
а _ _ _ ~ -
ok(o=S imo-23,(*)+£(O1=s
4=1
но
или
k
ok«)=s M>[1
5—1
Наконец, имея в виду выражение (5.47), можем записать
и окончательно получить
ok<0=S р(Шву)ч(ШВ^
5=1
(5.48)
Формулы (5.47) и (5.48) позволяют определить центр и меру в г-м се-
чении каждой траектории
Введем критерий различимости траекторий. Это понятие весьма су-
щественно, ибо чем меньше интервал DByBl между центрами двух об-
ластей и чем больше их диаметр, тем больше эти области перекрыва-
ют друг друга и тем большее число точек можно с равным основанием
отнести как к одной области, так и к другой.
Критерий различимости двух траекторий можно выразить следую-
щим образом:
5(/)х + Д). (5.49)
В соответствии с (5.39) и (5.47)
k
&B\Bl= (О ^>ls (01
5—1
или
k
5=1
Метод распознавания траекторий изменения состояния (работоспо-
собности) технических объектов может оказаться весьма эффективным
в тех случаях, когда имеется априорная информация об эталонных тра-
екториях и по каким-либо причинам невозможно применить для решения
задачи прогнозирования аналитические и вероятностные методы и ме-
тоды статистического распознавания образов.
В заключение отметим еще один способ решения задачи прогнози-
рования с использованием так называемого метода функции отка-
зов. Суть метода заключается в следующем. Все отказы объектов упо-
рядочиваются по времени их возникновения тг: Тц т$, ..., тьч где
<т2< ... <tjv и N— количество отказов. Каждому объекту, отказав-
шему в момент т?-, очевидно, в начальный момент времени соответствует
совокупность параметров {£}i={£i, £2, --•> Ыъ т- е- Шъ Шг, - или
векторы |1, & ..., Ijv-
Применяя предположение (которое уже использовалось в методах
статистической классификации), что значение векторов состояния | со-
ответствуют определенным образом подготовленности объектов, можно
ill
говорить о зависимости вектора состояния | от времени отказа объек-
та т. В общем случае —нелинейная функция и в связи с этим
возникает задача аппроксимации ее простейшими функциями, напри-
мер, вида
k s k
?®=2 2 + 2 *&'+ v„ (5.50)
s=l r—1 S=1
где v— весовые коэффициенты, которые определяются из условия ми-
нимизации средней квадратической ошибки отклонения.
Существенным достоинством этого метода является то, что он мо-
жет быть заложен в простую опознающую систему.
5.6. Индивидуальная функция состояния
Прогиозирование изменения состояния технических систем в ряде
случаев можно осуществить, используя совокупность значений отдель-
ных параметров или показаний, характеризующих состояние системы,
с помощью так называемой индивидуальной функции состояния.
Для этого всю совокупность {Ы, s—1, 2, ..., k, параметров или показа-
телей, характеризующих состояние системы, значения которых могут
быть случайными, нормируют с помощью выражений вида
г=|^-^|/г=б5 (5.51)
или
X = IГ4— W/(^ - ^)|, (5.52)
где X—относительное значение m^t <j— соответственно математи-
ческое ожидание и среднеквадратическое отклонение величин s-ro па-
раметра или показателя, г — числовой коэффициент, который может
быть как целым, так и дробным. Обычно г^З.
В результате получается совокупность случайных чисел, которые
характеризуют конкретную систему:
.s=l,2...k. (5.53)
Если предположить, что £s независимы между собой, то эту сово-
купность можно описать функцией распределения Ф(£), которую в даль-
нейшем будем называть индивидуальной функцией состоя-
ния.
В том случае, когда X зависят друг от друга и известны коэффици-
енты корреляции, то функцию Ф(^) можио построить лишь после декор-
реляции всех [Функцию Ф(£) можно построить двумя путями. Выбор
того или иного пути определяется мощностью множества {gs}, т. е. ко-
личеством параметров или показателей, характеризующих состояние си-
стемы. Первый путь выбирается при большом k (классический метод),
а второй — при /г^2С (методы построения распределения для малых
выборок).
112
Рассмотрим особенности прогнозиро-
вания с использованием функции Ф (|).
Пусть нормирование контролируемых
параметров объекта с помощью (5.51)
или ‘(5.52) позволило получить ряд без-
размерных нормированных значений па-
раметров |s, которые могут изменяться
в пределах от 1 до со. Строя функцию
плотности распределения по k величи-
во по оси абсцисс. В этом случае сте-
пень работоспособности объекта можно
оценить с помощью следующего выра-
жения:
где т] — коэффициент специфичности--
Рис. 5.5. Идеальная (а) и реальная
(б) индивидуальные функции состояния.
нам и учитывая, что для идеального
прибора -справедливо |в=|в опт, £«=
=!] (2=0), получаем 6-функцию
(рис. 5.5,а).
Чтобы решить задачу прогнозирова-
ния изменения работоспособности объ-
екта, удобно представить б-функцию на
оси абсцисс (Is—П] в виде прямоугольни-
ка с координатами ((0, 1); (0, 1)].
Функция плотности распределения,
имеющая форму прямоугольника, 'пред-
ставляет идеальную индивидуальную
функцию состояния Ф(|) ‘(<рис. 5.5,6).
Для нее справедливы следующие на-
чальные условия (2=0):
(
]Ф(1)4=0, -со<1<0,
—00
объекта, который при отсутствии специ-
альных оговорок может быть принят
равным 1.
При (выполнении условий (5.54)
1Гс=оо, на практике же 17с<§Ссо, При
прогнозировании <в качестве исходной
информации можно использовать изме-
нения во времени 6(|, t) или ТГС(|, f).
Функция J Ф (|) может служить «образом»
объекта, который нужно отнести к тому
или иному классу. В этом случае отно-
шение правдоподобия определяется как
а®
1-41)
0=С|<1,
f Ф(1)^1=о.
1
(5.54)
где 6(|) получило -название 6-функ-
ции работоспособности.
На практике для реальных объек-
тов б-функция работоспособности отли-
чается от идеальной и практически всег-
да 6(£)<11- При этом чем выше степень
работоспособности, тем ближе 6(|)
£ единице, а Ф(|) к прямоугольному
виду, и наоборот, с ухудшением состоя-
ния Ф(|) начинает «расползаться» впра-
Сравнение полученного порога Л с
эталонным Ло позволяет принять опре-
деленное решение о принадлежности
объекта к классам 2?^, А. — 1,2, ..., т.
Кроме того, б-функцию работоспо-
собности можно рассматривать как объ-
ем, из которого «вытекает» ресурс рабо-
тоспособности, т. е. уменьшается с тече-
нием времени часть Ф(|), ограниченная
интервалом (О, 1] и характеризующая за-
пас работоспособности ТГ3(|). Величи-
на Ws(|) определяется как
^©=4
и изменяется от со до 0.
w=
1
]‘ф(1)4=1,
о
&—813
113^
1,0 1,6 2,0 2,4 2,В 3,2 (
Рис 5.6. Индивидуальные функции состояния для экзаменуемых приборов с различной
долговечностью (б) и функции состояния для трех классов приборов (с): #1=
=0 ... 3000 ч; /?2=3000 ... 6000; #в=6000 ... со.
Такая интерпретация 6-функции по-
зволяет использовать скорость уменьше-
ния запаса работоспособности
и уровень запаса V23 (%), .который для
каждого класса будет принимать опре-
деленное значение.
Если степень работоспособности
уменьшается по линейному закону» вре-
мя «жизни» объекта можно определить
из следующего выражения;
сти упомянутых приборов. Нормирова-
ние параметров осуществляется с
помощью выражения (5.52). По полу-
ченной совокупности нормированных
случайных величин строятся гистограм-
мы для всех трех классов '(рис. 5.6,а).
Эталонные пороги А вычисляются
с помощью соотношения
2
Ъ-------=д1О=Ь05:
[ф®4
2
Д2О = 2,20; Дз0 = 4,62.
Величина Ф (f) является наиболее инфор-
мативным показателем состояния и -мо-
жет быть рекомендована для прогнози-
рования изменения степени работоспо-
собности многопараметрических систем.
Пример. Пусть имеем партию мощ-
ных клистронов, из которой сформиро-
вано три временных класса (их описа-
ние дано в предыдущем примере).
Рассмотрим применение индивидуаль-
ной функции состояния Ф (£) для прогно-
зирования индивидуальной долговечно-
114
На рис. 5.6, а в качестве оси абсцисс
взята ось £ а не [£-— 1], поэтому в
интеграле берутся именно такие пределы.
Вообще говоря, предел, который разде-
ляет интегралы (в данном случае £ = 2),
следует выбирать из условия наилуч-
шей классификации. Кроме того, для
простоты в интервал гистограммы (3,0);
(3, 2) отнесены все параметры, для ко-
торых g^>3,0. Для трех экзаменуемых
•приборов методом прямоугольных вила-
дов строятся индивидуальные функции
состояния, которые приведены на
рис. 5.6,6.
С помощью вышеприведенного со-
отношения определяются пороги сравне-
ния для всех трех приборов Ai=0,-604,
Л2=2,49, Л3=5,15. Очевидна близость
Ai к J?i, Лг к /?г и Аз к /?3- На практике
это и имело место (7'il<t=203 ч, 7'Ж2=
=5817 'ч, з=6200 ч).
Возвращаясь к предыдущему приме-
ру, отметим, что 2-й прибор, один и
тот же для обоих случаев, здесь был
-верно отнесен .ко второму классу. По-
скольку функция состояния представля-
ет собой плотность распределения пара-
метров, которая является более полной
характеристикой совокупности случай-
ных величин, то данный метод является
более достоверным.
ГЛАВА 6 ПРОГНОЗИРОВАНИЕ НА ОСНОВЕ ИССЛЕДОВАНИЯ
ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССОВ
6.1. Прогнозирование по переходным процессам
Под переходным процессом будем понимать изменение одного или
совокупности параметров при переходе объекта из одного режима ра-
боты в другой или из одного устойчивого состояния в другое. Приме-
нение результатов анализа переходного процесса к решению задачи
прогнозирования обусловлено тем, что такой процесс является наиболее
информативным. Это объясняется тем, что переходный процесс пред-
ставляет собой динамический режим работы диагностируемого объекта,
в котором наиболее полно проявляется истинный уровень состояния
объекта.
При рассмотрении переходных процессов остановимся только на
трех их видах:
— реакциях (изменение параметров) объекта на ступенчатый или
импульсный входной сигнал,
— процессах, происходящих при включении объектов, когда пара-
метры от начальных значений (часто нулевых) изменяются до значе-
ний, характерных для установившегося режима,
— процессах, происходящих при выключении (частичном выключе-
нии) объектов, когда параметры от рабочего уровня изменяются до
уровней, характерных для выключения состояния.
Рис. 6.1. Изменение тока катода при кратковременном отключении накала.
Если обозначить время переходного процесса через г, то изменение
параметров объекта можно представить как 11(т), £г(г), ..., £ь(т) и
векторная величина |(т)={£г(т), ..., £ь(т)] будет достаточно полно ха-
рактеризовать состояние объекта при переходном процессе.
Для прогнозирования работоспособности можно использовать ме-
тодику проверки эмиссионных свойств катодов электровакуумных при-
боров (кратковременное отключение накала
катода), .поскольку изменение тока катода
(рис. 6.1) при кратковременном отключении
различно для приборов с различной степенью
работоспособности.
Полупроводниковые приборы разного ка-
чества не одинаково реагируют на импульс-
ное воздействие напряжением. Импульсы на
выходе приборов отличаются крутизной спа-
да и временем рассасывания. Для каждого
конкретного прибора можно найти парамет-
ры, которые достаточно сильно коррелирова-
ны с качеством и уровнем работоспособ-
ности.
Рассмотрим конкретные примеры прогно-
зирования состояния приборов по их переход-
ным процессам. В систему контролируемых параметров электроваку-
умных приборов, используемых для прогнозирования, входит время
готовности по шуму Тгот> характеризуемое уменьшением уровня шумов
прибора ниже допустимого значения после момента его включения. Эта
переходная характеристика (рис.
6.2) особенно важна для малошу-
мящих приборов, работающих в пе-
риодическом (циклическом) режи-
ме. В этом случае время тГот оцени-
вается в процессе эксплуатации
прибора по кривым изменения ко-
эффициента шума Л’штДт) (рис. 6.2),
где т$ — i-й период (цикл) работы
прибора.
Для прогнозирования измене-
ния работоспособности диагности-
руемого прибора в этом случае ока-
зывается целесообразным примене-
ние интегрального метода,
при котором в качестве информа-
ции для прогнозирования использу-
ется величина интеграла
t
(0 =(^г. (')<«• (6.1)
£
Выбор нижнего и верхнего пре-
дела определяется специфическими
особенностями прибора и поставленной задачей. Из интегральных кри-
вых ЛнтД/) (рис. 6.3) видно, что с течением времени Ti увеличивается
угол наклона Рштг(О к оси абсцисс. Прогнозирование осуществляется
Рис. 6.2. Изменение коэф-
фициента шума после вклю-
чения электровакуумного
прибора.
Рис. 6.3. Условные (а) и реальные (6)
интегральные характеристики (/).
116
следующим образом. В начальный период (цикл) Го=О имеется/што(О»
которую характеризует угол наклона к оси абсцисс «о- Аналогично,
в моменты Ti, Т% ..., Тг, ..., Тп углы наклона равны си, а^ ..., а* ....
- - (Х?г
Сначала вычисляем приращения угла Да-;: Aai=ai—а0; Ла2=
= аг—«о; ..Лаг — —сю; .Аате=ап—ао- Далее, методом наимень-
ших квадратов аппроксимируем функцию Аа(Г) (рис. 6.4). Экстраполи-
руя изменение Да, можно предсказать величину Да для любого цикла
Т>Тп. Поскольку отказ прибора фиксируется в момент достижения
Рис. 6.5. Построение функций распре-
деления f (г') и (Гш).
Рис. 6.4. Зависимость Ao.=f(T).
углом а допустимой величины а*, то для определения Го™ необходимо
решить уравнение ао+Да(Г0тИ) =а*.
Для оценки работоспособности партии приборов по переходной ха-
рактеристике можно использовать такие критерии, как функция f(t')
распределения времени пересечения ЛДт) допустимого уровня А*ш
после момента включения прибора и функция fx (Гш) распределения
значений Ги, для требуемого времени хГот (рис. 6.5).
Эти же параметры следует использовать и для решения задачи
прогнозирования. Интегральный метод можно применять для анализа
других характеристик электровакуумных приборов, в частности для то-
ков спада (выключения).
Другой метод определения работоспособности и прогнозирования
по переходным процессам проиллюстрируем на примере нелокальной
характеристики электровакуумных приборов. Пусть эта характеристи-
ка отражает процесс нарастания тока катода /к от момента включения
накала до установления значения /куст. При этом рассматривается
нормированная функция <р(/)=/к(/)//куст (рис. 6.6).
Идеальная (безынерционная) нелокальная характеристика пред-
ставляет собой единичную ступенчатую функцию !(/) (рис. 6.7,п). Для
реальных приборов процесс установления тока катода происходит в ко-
нечный промежуток времени и может бьпь охарактеризован функцией
<Рть где Ti имеют тот же смысл, что и раньше. Задача состоит в том,
чтобы по известным функциям фп, (ртг, ..., фг$, . -, (pTn(Ti<ZTz<Z
... <Ъ< ... <Тп) предсказать основные свойства фгД/>п).
Можно предположить два пути решения подобной задачи, один из
которых связан с аппроксимацией (рп аналитическим вы-
ражением фГ=ф(а, р, у, ..., т), где а, р, у, ... — неизвестные коэф-
фициенты, характеризующие переходный процесс; т — время переходно-
го процесса.
117
Коэффициенты а, 0, -у, ... определяются как функции времени 7\ и
известными способами экстраполируются на момент Tj, в результате
чего получаем величины а}, 0д yj, ..которые определяют вид функции
(pTj. Для предсказания момента отказа прибора ГОТк необходимо знать
величину т*, т. е. допустимое время, за которое катодный ток 7К до-
стигает определенного значения А/Иуст или функция фтоть достигает ве-
личины Z, Х<1.
Таким образом, фтотк=^ или ф(а*, 0*, у*, г*) =К откуда из об-
щего решения системы уравнений
а(Т)=а*=а(Тогк),
Р(7') = ₽* = ₽(ГО,В),
Y(7} = y* = y(7’o„),
и определяются а*, р*, у*, ...
При наличии частных решений одного знака и порядка, конечный
результат находится как среднее арифметическое частных решений
где Тготк — частное решение, р— число уравнений в системе.
Другой путь связан с применением метода гармонического
анализа и основан на том, что переходная характеристика фт рас-
сматривается как фронт прямоугольного импульса, спектральный со-
став которого можно установить с помощью теории гармонического
анализа.
Очевидно, что чем хуже по качеству (степени работоспособности)
прибор, тем больше будет время переходного процесса, тем положе
пойдет характеристика фт, что приведет к изменению спектрального со-
118
Рис. 6.8. Функция 1—<рт (с); четная
функция фт- (б).
става предполагаемого импульса. Од-
нако более удобно изучать гармониче-
ский состав функции фТ, получаю-
щейся из (рт (рис. 6.7,6) следующим
образом. Вначале рассматривается
функция 1—<рт (рис. 6.8,й). Эта функ-
ция имеет практически конечную дли-
тельность т, поэтому ее можно продол-
жить и найти гармонический спектр.
Однако ряд Фурье этой функции схо-
дится очень медленно, так как в нача-
ле оси координат функция терпит раз-
рыв. Для улучшения сходимости мож-
но функцию 1—<рт продолжить четным
образом (рис. 6.8,6). Это и будет ис-
следуемая функция фг- Если продол-
жить эту функцию с периодом 2т, то
ее можно будет разложить в ряд
Фурье, который будет сходиться довольно быстро, поэтому ограничимся
рассмотрением лишь нескольких первых гармоник (приблизительно от
нулевой линии до второй — третьей включительно).. Так как фтг — чет-
ная функция, то ряд Фурье для нее будет содержать только косинусы:
оо
Фп = cos Л (6-2)
Л=1
Постоянная составляющая и амплитуды гармоник находятся из
формул
о
cos ~ t di. (6.4)
и
Затем исследуем отдельно каждую гармонику с точки зрения изменения
ее амплитуды. Если известны функции
фп; (р7-2, - - - фтп, то по (6.3) и (6.4) опре-
делен и ряд Фурье (6.2). Пусть нулевые
гармоники этих рядов будут соответст-
венно равны ftoi, йог, •.Gon. Теперь мож-
но построить амплитудно-временную ха-
рактеристику изменения нулевой гармо-
ники (рис. 6.9). Применяя к ней какие-
либо методы экстраполяции, можно пред-
сказать ее ход при Т>Тп. Точно так же
поступаем с гармониками первой, второй
и т. д. После того как станут известны
значения амплитуд нескольких первых гармоник при TjZ>Tn, можно
построить функцию
(6.5)
k=l
а по ней восстановить функцию (pyj.
Рис. 6.9. Амп литу дно-временна я
характеристика.
119
Отметим, что в выражениях (6.2), (6.3), (6.4), (6.5) величина г
является постоянной и выбирается в 2—3 раза большей величины
Тцоп (Тдоп— длительность функции фтдоп).
Здесь для предсказания ГОТк нужно также знать тДоп. Тогда, опре-
делив а*; р*; у*; ... получим функцию ^tOtk=1—Фто-гк (для’^0).
С помощью (6.3) и (6.4) вычисляем а*о и сС'и- Далее из системы урав-
нений
До(Т) = СС 'о До(Тотк), йй(Т) = а ‘ £ = CLfi (Тснк) у
k
определяем 70ТК = 2 где ^отк — частное решение, k—число ис-
i=l
пользуемых гармоник, Z = 0,1, 2,..., k — номер гармоник.
В заключение следует отметить, что задача прогнозирования ре-
шается тем эффективнее, чем больше параметров исследуется в пере-
ходном режиме.
6.2. Прогнозирование изменения работоспособности
дискретных устройств
Эта задача является одной из актуальнейших и выделяется не спо-
собом прогнозирования (здесь можно применить и ранее рассмотрен-
ные методы), а трудностью выбора и контроля прогнозирующих пара-
метров.
Дискретные устройства, обычно характеризующиеся двумя устой-
чивыми или квазиустойчивыми состояниями, широко применяются
в вычислительной и радиоэлектронной аппаратуре. Однако из-за нели-
нейности их рабочей характеристики практически трудно оценить посте-
пенное изменение работоспособности схем по результатам контроля
общепринятых параметров, как это делается для аналоговых схем. Это
обстоятельство влечет за собой сложности в определении запаса рабо-
тоспособности и осуществлении прогнозирования.
Рассмотрим возможные методы прогнозирования постепенного из-
менения состояния дискретных схем. Известные различные логиче-
ские методы, использующие комбинации разнообразных тестсигналов,
позволяют решить задачу определения работоспособности только по
принципу «годен — не годен», что оказывается недостаточным для про-
гнозирования.
Опыт эксплуатации дискретных устройств показывает, что отказ су-
щественно зависит ие только от схемы устройства и надежности эле-
ментов, но и от степени удаленности параметров элементов от границ
области допустимых изменений параметров, при которых нарушается
работоспособность, т. е. от запаса работоспособности устройства. Запас
работоспособности можно оценить в результате контроля прогнозирую-
щих параметров.
Для ламповых дискретных устройств в качестве диагностического
метода иногда используется метод понижения напряжения и а-
к а л а, сущность которого заключается в выявлении ламп с понижен-
ным запасом работоспособности путем контроля параметров при пони-
жении напряжения накала. Однако применение этого метода для про-
гнозирования постепенного изменения состояния малоэффективно по
следующей причине: триггеры, наиболее часто применяемые в дискрет-
ных устройствах, работают на двойных триодах, поэтому понижение'
120
напряжения накала приводит к одновременному уменьшению анодных
токов обоих триодов лампы, что мало сказывается на работе триггера.
Работоспособность триггера (счетчика) при эксплуатации зависит от
суммарного изменения во времени параметров его элементов: ламп, по-
лупроводниковых приборов, сопротивлений плеч сеточных делителей,
питающих напряжений, в то время как понижение напряжения накала
является в основном недостатком лампы с недостаточной эмиссией. Та-
ким образом, данный метод позволяет решить задачу лишь частично.
На практике, кроме того, применяется метод изменения на-
пряжения питания. Его идея заключается в том, что если пара-
метры элементов пересчетного устройства (регистра) находятся вблизи
границ области допустимых изменений, то изменение напряжения пи-
тания в некоторых пределах может привести к отказу устройства. По
величине изменения напряжения питания, при которой произошел от-
каз, можно судить о запасе работоспособности устройств. Поэтому ве-
личину изменения питающих напряжений можно рассматривать как
прогнозирующий параметр. Данный метод, как и предыдущий, оказы-
вается эффективным только при малом запасе работоспособности дис-
кретного устройства.
Определенное преимущество перед указанными методами имеет ме-
тод дозированных помех. Изменения во времени параметров эле-
Рис. 6.11. Схема подачи дозированной по-
мехи на транзисторный триггер
ментов триггера (ламп, полупроводниковых приборов, сопротивление
плеч сеточных делителей, питающих напряжений) можно привести
к эквивалентному изменению напряжений на управляющих электродах
ламп триггера. Поэтому изменением напряжения на управляющих
электродах лампы путем подачи на одно из плеч сеточных делителей
триггера дозированной помехи определенного вида можно имитировать
комплексное изменение параметров элементов триггера (рис. 6.10, 6.11)
во времени. В данном случае дозированная помеха ип является прогно-
зирующим параметром, т. е. по ее величине можно судить о степени
работоспособности устройства.
Данный метод можно применять для прогнозирования изменения
работоспособности пересчетной декады, при этом дозированная помеха
подается одновременно на четыре триггера. Результаты эксперимента,
121
приведенные на рис. 6.12, показывают, что между величиной дозирован-
ной Помехи и вероятностью исправной работы пересеченной декады за
время Д£=100 ч существует зависимость, позволяющая оценить вероят-
ность Р сохранения работоспособности пересчетной декадой по величи-
не и дозированной помехи, при которой не нарушается работа, т. е. Р=
=<р(м). Максимальную величину дозированной помехи, при которой не
нарушается работа декады, называют общим запасом работоспособно-
сти схемы.
Однако метод дозированных помех практически неприменим для
диагностики непосредственно в период эксплуатации дискретных
устройств с большим числом триггеров (пересчетных схем). Для реше-
ния же задач технической диагностики желательно иметь такой метод,
между величиной дозиро-
ванной помехи и вероят-
ностью исправной работы.
который можно использовать, когда диагно-
стируемый объект находится в рабочем (экс-
плуатационном) режиме или режиме профи-
лактики. При минимальном влиянии на объ-
ект он должен оценивать запас работоспособ-
ности, т. е. давать исходную информацию для
осуществления прогнозирования. Таким мето-
дом является метод дополнительной
нагрузки, который требует значительно
меньшего числа выводов с объекта диагности-
ки по сравнению с методом дозированных по-
мех, более прост и способствует повышению
быстродействия.
Дискретные схемы характеризуются двумя
устойчивыми (триггерные схемы) или квази-
устойчивым (мультивибраторные схемы) состояниями. В момент пере-
хода из одного состояния в другое, т. е. в момент опрокидывания схе-
мы, когда ток протекает через оба плеча, работа подобных схем описы-
вается дифференциальным уравнением [67]
dW_____2_ 1 dU 1 1 77__п
dt2 Ъ KiK2 — 1 % Л1Ка — 1 U
(6-6)
где Ль Лг— коэффициенты передачи соответственно с 1-го плеча на 2-е
и со 2-го на 1-е, ту — постоянная времени цепи управления.
Из анализа уравнения (6.6) вытекает, что для обеспечения опро-
кидывания схемы, т. е. работоспособного состояния, необходимо выпол-
нить условие
А = К1Кг~^ 1>о. (6.7)
Зададимся минимально допустимым значением А—А^т1п, необхо-
димым для каждого срабатывания схемы. Тогда условие работоспособ-
ности (6.7) запишется в виде
Д=Л2Л1—(6.8)
Степень обеспечения условия (6,8) характеризует степень работо-
способности схемы, а величина А характеризует запас работоспособно-
сти схемы при опрокидывании. Иначе говоря, с точки зрения задачи
прогнозирования А является наиболее информативным параметром.
Зависимость параметра А от времени для большинства рассматривае-
мого типа схем, как ламповых, так и транзисторных, аналогична пока-
занной на рис. 6.13, и может быть аппроксимирована полиномом второй
122
Рис. 6.13. Изменение запаса работо-
способности с течением времени.
степени. По скорости приближения
этой зависимости к A*min определяют
момент отказа дискретной схемы.
Однако физические процессы вз
схеме не позволяют непосредственно
контролировать изменения А. Поэтому
необходимо прибегать к косвенному
способу определения величины А с по-
мощью, например, дополнительной на-
грузки в виде переменного сопротив-
ления подключенного параллельно
нагрузке одного из плеч, например
триггера.
Для транзисторных релаксационных схем величины Ki и К2 рав-
ны (68]
Л1 = Р1Дп1/(1 + Уб1р1) + 4"’Гэ1) —BiRfii,
(6.9)
Л2~!р2^н2/ (1 +Т62Р2) (А'тг + Г62 + ^92) =^2^н2,
где fa, fa; Y61, У62-, Rm; Rtf, Rni, Rl& — соответственно ко-
эффициенты усиления, параметры транзисторов,, сопротивления баз, со-
противления эмиттеров, сопротивления нагрузок обоих плеч.
Пусть теперь к одному из плеч подключено /?д (рис. 6.14) [это от-
ражено в выражениях (6.9)]. Тогда условие работоспособности диагно-
стируемых схем в любой момент времени запишется в виде
—1, Ra—(6.10)
д* . _ B1B2RihRK2 ip __р (р. 11
Л trnin — р । р 1» ^Д — 11
Ahi Т" ''zmtn
121
где Rp,min — дополнительное нагрузочное сопротивление, при котором
происходит потеря работоспособности схемы (срыв колебаний).
Вычитая (6.11) из (6.10), можно оценить запас работоспособности:
= At А ' train ~ ВiBzRvlRnzRnll (>Rh1 +Rimin') .
При старении элементов схемы величина RRmin во времени будет
увеличиваться, что приведет к снижению работоспособности ('рис. 6.13).
К моменту отказа схемы Ramin достигнет значения Ramin max- Из ска-
занного ясно, что для прогнозирования отказов дискретных схем вместо
зависимости параметра А от времени можно пользоваться зависимостью
значения Ramin от времени.
Таким образом, работоспособность схемы характеризуется разно-
стью Ramin max—Ramin. Переменное сопротивление Rr можно отградуи-
ровать в омах или непосредственно в единицах работоспособности.
В некоторых случаях удобно рассматривать коэффициент т) =
= А/A*min, характеризующий кратность запаса работоспособности.
В этом случае применение метода дополнительной нагрузки значительно
ускоряет и упрощает оценку степени (запаса) работоспособности и про-
гнозирование изменения работоспособности в будущие моменты экс-
плуатации дискретных схем, причем для этого можно ие отключать схе-
мы от всего диагностируемого объекта (радиотехнической системы или
вычислительной машины). Кроме того, подобный метод с некоторыми
модификациями применим для различного класса нелинейных устройств.
6.3. Метод конечных автоматов
Задачу прогнозирования можно решить с помошью аппарата тео-
рии конечных автоматов. Пусть £(/г), 2, • ••♦ Ч п+1, ..., !, ---
.., т — конечная последовательность чисел и известны некоторые чле-
ны этой последовательности £(/*), t'=I, 2, ..., п; Необходимо по
известным восстановить неизвестную часть последовательности
с(^), /=п+1, ..., m;
При этом следует выявить некоторые зависимости между £(/г) и,
предположив, что они справедливы для всех членов последовательно-
сти, «строить» недостающие члены. В это время могут стать известными
некоторые новые или некоторые соотношения, справедливые для
всей последовательности (сообщается дополнительная информация), что
позволяет внести коррекцию в процесс построения новых £(Л).
Таким образом, рассматривается задача о конечных расширениях
конечных числовых множеств. Множество называется конечным, если
оно задано таблицей, перечисляющей его элементы. Всякое множество
М, включающее в себя конечное множество М(Л1=>М), называется рас-
ширением N. Будем называть расширение конечным, если оно удовле-
творяет двум условиям: 1) оно есть конечное множество; 2) каждый
его элемент может быть получен из явно указанных элементов расши-
ряемого множества за конечное число шагов, однозначно определяемых
с помощью таблиц.
Таблица чисел вместе с экспериментатором или подходящим обра-
зом построенной программой для ЭЦВМ может рассматриваться как
среда, с которой взаимодействует автомат, распознающий свойства сре-
ды. Автоматы, имеющие дело с конечным множеством чисел, получили
название конечных. Конечный автомат можно научить расширять по-
следовательность £(б) (множество =ZV).
124
Учитывая физический смысл параметров, описывающих диагности-
руемый объект, можно делать определенные предположения об анали-
тической структуре функций, характеризующих изменение этих пара-
метров, и строить взятые из определенного класса функции, которые
принимают в точках ^е7,27=«4-1, т, те же (или почти те же) зна-
чения, что и соответствующие элементы таблицы чисел
Приняв гипотезу о подобном классе функций, следует построить
программму для ЭЦВМ или специализированное вычислительное устрой-
ство для нахождения конечного расширения известной последователь-
ности [69].
Автомат с линейной тактикой L представляет"; собой конечный
автомат с одним входом, одним выходом, v действиями, uv состояниями,
входным алфавитом {0, 1} (1 — «штраф», 0 — «нештраф») и выходным
„нештраф”-„о”
„штраф”
Рис. 6.15. Графы переходов автомата.
алфавитом (xi, х&, хЦ (рис. 6.15). Назовем его для краткости ЯКА
(линейный конечный автомат).
ЯКА функционирует следующим образом. Первое число из таблицы
запоминается, второе число также запоминается, причем из него вычи-
тается первое (вычисляется разность).
Затем знак разности сравнивается с выходным [сигналом автомата
£3 р- ® данном случае взят [автомат £3 выполняющий три действия:
«-(-», «О» и «—». Если знаки различны, £3 получает «штраф», если
совпадают — «нештраф». Если автомат £3 получает «нештраф», то за-
поминается вычисленная разность, если же «штраф», то сохраняется
прежняя разность.
Рассмотренная последовательность действий применяется к новым
членам таблицы (процесс обучения автомата). Затем входное устройст-
во ЯКА отключается от среды и на выходе присутствует последнее из
запоминавшихся чисел £(А). В следующем такте из £(£г) вычитается
(или прибавляется) последняя из запоминавшихся разностей. Этот про-
цесс сложения с разностью повторяется столько раз, сколько потребует-
ся (т—число шагов прогнозирования) и представляет собой не что
иное, как линейное прогнозирование. Но все дело в том, что ЯКА вы-
бирает такую первую разность, которая чаще всего встречается в из-
вестной последовательности чисел. Иначе говоря, ЯКА выбирает из
всех просмотренных разностей наиболее вероятную (полномочного
представителя), т. е. является автоматом с «осторожной» тактикой.
Если первая разность последовательности сцационарна, то ЯКА дает
хорошие результаты.
Преимущество ЯКА перед другими методами линейного прогно-
зирования заключается в том, что его поведение можно легко коррек-
тировать по мере получения дополнительной текущей информации пу-
тем перевода автомата в режим обучения свойствам вновь ставшей
известной части диагностируемой последовательности. Если глубина ц
125-
памяти велика, то ЯКА «помнит» некоторые свойства той части после-
довательности на которой он обучался в последний раз. При боль-
ших р и частых коротких обучающих последовательностях ЯКА выяв-
ляет «глобальные» свойства £(/). Коррекцию можно осуществить и без
специального обучения ЯКА, когда найденная разность, определяющая
наклон прямой прогнозирования, сохраняется, а меняется только поло-
жение прямой.
В тех случаях, когда среда нестационарна по первой разности, т. е.
имеется более сложная среда, ЯКА будет давать большие погрешности,
поэтому целесообразно рассматривать последовательность автоматов
Av>p_, где v — фиксировано, а р=1, 2, ... . В [69] дается определение
асимптотически-оптимальной последовательности автоматов и доказы-
вается, что последовательность асимптотически оптимальна .в стационар-
ной случайной среде, которая описывается вектором (рь . •., Ру), где
v — число действий автомата (мощность выходного алфавита), причем
Q<ZPa <1 — вероятность штрафа за a-действие, а=1, ..., т.
В [70] построена асимптотически-оптимальная последовательность
автоматов с экспоненциальной скоростью сходимости, которая исследо-
Рис. 6.16. Функциональная схема конечного автомата.
валась в играх. Эти автоматы достаточно хорошо «угадывают» опреде-
ленные свойства среды.
Таким образом, в нелинейной среде можно усложнить структуру
ЛКА, добавив еще один автомат L2 3> , управляющий вычислением вто-
рой разности. Для любого целого г>0 можно построить конечный авто-
мат с r-уровневой системой автоматов Lq,3,(,iq> <7=1, 2, ..., г (рис. 6.16),
расширяющий последовательность N ие хуже, чем это можно сделать
с помощью конструирования подходящего прогнозирующего полинома
степени г.
Обозначим множество чисел на выходе конечного автомата с <7 = 1,
2, .... г в момент времени tb t2, ..., ti следующим образом: j—
= 1, 2, ..., I. Пусть
O.r=S<^>A- (6-12)
<?=0
126
— линейная комбинация результатов с разными коэффициента-
ми. Здесь <£о>— выход нулевого конечного автомата, одно и ^о же
число для всех моментов времени, которое подбирается с помощью £03uf
во время обучения. Все автоматы можно обучить одновременно, а ре-
зультатом работы совокупности q автоматов KAg, q=\, 2, ..., г считать
величину L^r.
Разные автоматы из этой совокупности можно обучать в разных
частях последовательности £(/). Для получения прогнозируемых значе-
ний как результата работы совокупности всех автоматов можно вы-
числять Ljfq, причем сначала полагаем все К в (6.12) равнозначными,
а затем увеличиваем на если ^-й конечный автомат обучался и
не изменяет если он не обучался. Иначе говоря, вклад конечных
автоматов в сумму растет по мере обучения этого автомата.
В общем случае под структурой конечного автомата можно пони-
мать специализированное вычислительное устройство или программу
для ЭЦВМ.
6.4. Некоторые частные методы прогнозирования
работоспособности элементов радиоэлектронной техники
Одним из таких способов прогнозирования для различной радио-
электронной аппаратуры является метод, основанный на дифференци-
рованном контроле типовых режимов отдельных элементов аппаратуры
по изменению цвета нанесенных на поверхность этих элементов термо-
индикаторных (термочувствительных) красок {16, 72]. При
повышении температуры краска меняет свой цвет, причем критическая
температура элемента вызывает появление определенного оттенка
у краски. Таким образом, цвет краски может быть использован для
прогнозирования.
Визуальную индикацию изменения цвета термоиндикаторной крас-
ки в процессе работы контролируемых элементов можно облегчить,
если на участки поверхности элементов, соседние (смежные) с покрыты-
ми термоиндикаторной краской, нанести термостойкую краску, цвет
которой соответствует цвету термоиндикаторной- краски при температу-
ре ниже критической. Значение критической температуры термоиидика-
торной краски выбирается на линейном участке ее температурно-вре-
менной характеристики.
Указанные две краски наносят на поверхность деталей в виде пе-
ремежающихся продольных или поперечных полос либо в виде концен-
трических окружностей. Предельная погрешность фиксации температу-
ры современными отечественными термоиндикаторпыми красками при
этом равна ±5°C.
Сравнительно простой способ прогнозирования для приемно-усили-
тельных ламп может быть применен при их испытании. В этом слу-
чае измеряется температура баллона лампы и по полученной зависимо-
сти Т°C—f(t) рассчитывается ожидаемое время сохранения работоспо-
собности.
Известно, что основные параметры ламп (/а — анодный ток, S —
крутизна) имеют граничные отклонения, установленные техническими
условиями. Значение температуры баллона связано со значениями
основных параметров (рис. 6.17). Проектируя точки пересечения кривой
с верхней и нижней границами параметров лампы на ось абсцисс, по-
127
лучают нижний Ттгп и верхний Т^ах пределы допустимой температуры
баллона.
Используя эту зависимость, по температуре баллона лампы опреде-
ляют величины характеризующих ее параметров в данный момент вре-
мени, а по скорости изменения во времени температуры, по скорости ее
приближения к предельным значениям предсказывают время потери
работоспособности лампы.
Абсолютное значение температуры баллона измеряют периодиче-
ски. Прн этом на практике вместо измерения абсолютного значения Т °C
измеряют разность значений омических сопротивлений AR лампы при
нулевой температуре и при прогретой лампе. Кривые на рис. 6.18 пред-
ставляют собой результаты измерения сопротивления для двух ламп,
причем Д/?о1 и ДТ?о2 сответствуют температуре баллона ламп № 1 и
Рис. 6.17. Изменение основных параметров
лампы в зависимости от изменений температу-
ры баллона.
Рис. 6.18. Изменения сопротивления
двух ламп.
№ 2 в начальный период эксплуатации. Точки Ai и А2 соответствуют
нижним пределам параметров ламп, предусмотренным техническими
условиями.
В результате для прогнозирования момента достижения параметра-
ми лампы критических величин достаточно провести 2—3 замера с ин-
тервалом в несколько часов и, поскольку кривая близка к прямой,
аппроксимировать результат по полученной зависимости Т°C
Рассмотрим метод индивидуального прогнозирования долговечно-
сти отражательного клистрона, когда в качестве прогнозирующего пара-
метра используется конструкционный фактор. Метод основан
на определении в окончательно изготовленных клистронах отклонения
от оптимального значения расстояния между катодом и сеткой резона-
тора по величине изменения уровня мощности в точке возбуждения
колебаний на границе области электронного гистерезиса при изменении
в определенных пределах напряжения резонатора от его номинального
значения.
Отражательные клистроны, в которых применяется трехкратное
взаимодействие электронов с высокочастотным полем зазора резонато-
ра, состоят из большого числа деталей, узлов и имеют сложный техно-
логический цикл изготовления. Контроль качества ряда технологических
операций труден и недостаточен. Кроме того, как показывает практика,
многие последующие операции часто нарушают качество отдельных де-
талей и узлов, изготовленных в процессе предыдущих технологических
128
операций. Поэтому окончательно качество выполнения некоторых опе-
раций можно определить непосредственно или косвенно только лишь
в изготовленном клистроне.
Разнообразие требований, предъявляемых к отражательным кли-
стронам, а отсюда и различные их конструкции и технология изготов-
ления, сложность и трудность управления происходящими в них физико-
химическими процессами затрудняют нахождение общих методов про-
гнозирования клистронов и стимулируют разработки и внедрение ин-
дивидуальных методов прогнозирования.
Как известно, работоспособность отражательных клистронов опре-
деляется различными факторами и условиями: режимами эксплуатации,
конструктивно-технологическим оформлением, величиной и постоянством
вакуума, стабильностью геометрических размеров межэлектродных рас-
стояний в процессе эксплуатации. Поэтому для того чтобы выяснить,
насколько влияет качество, надежность и долговечность того или иного
узла или детали иа работоспособность клистрона в целом в зависимости
от критичности параметров к величине и постоянству вакуума в процес-
се эксплуатации и длительного хранения, в последнее время были пред-
ложены и опробированы некоторые методы индивидуального прогнози-
рования для вакуумных приборов,, в частности отражательных клистро-
нов. Данный метод применим при изготовлении клистронов, для кото-
рых критичным параметром является уровень мощности в точке воз-
буждения колебаний и изменение этого уровня в ходе эксплуатации
клистрона.
При разработке методов прогнозирования и выборе прогнозирую-
щих параметров или характеристик обычно исходят из принципа дей-
ствия диагностируемого прибора, его конструктивно-технологического
оформления и устойчивости того или иного параметра или характери-
стики при длительной работе в условиях воздействия различных деста-
билизирующих факторов.
В отражательном клистроне происходит трехкратное взаимодейст-
вие электронов с ВЧ полем зазора резонатора. При этом в зависимости
от интенсивности электронного потока, многократно пролетающего че-
рез ВЧ поле зазора резонатора, и фазы влета электронов в него при
третьем пролете возможно улучшение или ухудшение электрических
параметров и характеристик клистрона (по сравнению с двукратным
взаимодействием электронов): повышение или снижение выходной мощ-
ности и к. п. д., расширение или сужение диапазона электронной пере-
стройки частоты и т. д. Угол пролета электронов в пространстве катода
при третьем взаимодействии электронов с ВЧ полем зазора резонатора
на заданной длине волны X зависит от напряжения резонатора t/рез и
расстояния между катодом и центром ВЧ зазора резонатора dKC и
определяется согласно кинематической теории отражательного клистро-
на по формуле
6к с= 1,9 10Мк с/l/t/рез [см/см - В]. (6.13)
Пользуясь формулой (6.13), можно найти связь между отклонением
Ок с, изменением Г7рвз—Дt/рез и AdKC:
Отсюда при условии изменения 0Кс на одну и ту же величину
Д^к c/du с == Д t/рез/2 Uрез. (6.15)
9—813 129
Соотношение (6.15) имеет практическое значение, так как позво-
ляет определять электрическим способом изменения расстояний между
катодом и первой сеткой резонатора в окончательно изготовленном кли-
строне, не влияя на его качество н надежность.
Отклонение 6Кс от его оптимального значения, кроме ухудшения
электрических параметров, приводит к возникновению электронного
гистерезиса в процессе эксплуатации и является одной из основных
причин снижения долговечности и надежности отражательных клистро-
нов. Поэтому в качестве прогнозирующей характеристики была выбра-
на зависимость отношения величины мощности в зоне генерации, на
которой возникает гистерезис, к максимальной величине мощности
в зоне генерации от времени.
Регулируя напряжение резонатора (6.15), можно определить в окон-
чательно изготовленном клистроне эквивалентное изменение расстояния
между катодом и первой сеткой ВЧ зазора резонатора, вызывающее
электронный гистерезис на определенном уровне выходной мощности
в зоне генерации.
Изложенные соображения были проверены экспериментально
в процессе испытаний на долговечность нескольких партий одного нз
типов отражательных клистронов повышенной выходной мощности. На
рис. 6.19 показана типичная зависимость отношения величины мощно-
сти в зоне генерации, при которой возникает гистерезис, к максима ть-
ной величине мощности в зоне генерации PrjPmnx. от времени t. Из
Р-ис. 6.19. Зависимость отношения величины
мощности к максимальной величине мощности
в зоне генерации.
Рис. 6.20. Связь между долговеч-
ностью и величиной А17рег/£/Рсз.
графика видно, что величина гистерезиса в зоне генерации возрастает
со временем примерно по линейному закону.
На рис. 6.20 показана типичная зависимость между долговечностью
клистронов и отношением отклонения напряжения резонатора к номи-
нальному значению напряжения, при котором обеспечивается отсутст-
вие гистерезиса на половинном уровне выходной мощности в зоне
генерации. Эта зависимость получена экспериментально по данным
испытания на долговечность трех партий клистронов. При этом партия
клистронов, у которых перед испытанием на долговечность отношение
Дб/рез/t/рез составляло 0,05; 0,1 и 0,15, имела среднюю гарантированную
долговечность 500, 1000, 1500 ч соответственно.
Из рис. 6.20 видно, что между долговечностью и величиной отноше-
ния отклонения напряжения резонатора от его номинального значения,
при котором обеспечивается отсутствие электронного гистерезиса на
уровне половинной мощности в зоне генерации, существует прямо про-
порционально зависимость. Характерное изменение величины AU-рез/^рсз
со временем показано на рис. 6.21.
130
Рассмотренный метод прогнозирования позволил избежать возник-
новения гистерезиса на заданном уровне выходной мощности при дли-
тельной работе клистрона и, таким образом, гарантировать определен-
ные величины долговечностей без непосредственных испытаний клист-
ронов на долговечность. Достоинством этого метода является быстрота
и простота, проведение испытаний без
использования специальной аппаратуры и
установок. При испытаниях не возникает
внутренних изменений и процессов, приво-
дящих к снижению долговечности и надеж-
ности клистронов при последующей их ра-
боте в течение длительного времени.
Весьма большие возможности для ре-
шения задач прогнозирования таят в себе
шумовые характеристики различ-
ных изделий. У всех проводников электри-
чества возникают электрические шумы, по-
явление которых обусловлено флюктуация-
Рис. 6.21. Типичная зависи-
мость Аб^рез/брез.
ми электрического напряжения (тока),
причем у многих изделий уровень и спектр шумов находится в прямой
зависимости от их состояния и степени работоспособности. В этой связи
шумы могут быть исходной информацией для решения поставленных
задач. Шумы по своему виду могут быть тепловые, дробовые, избыточ-
ные. Рассмотрим их связь с состоянием различных изделий .[59, 102].
Резисторы. По величине избыточного шума можно судить о состоя-
нии структуры резисторов, о качестве их изготовления. Величина э. д. с.
шума порядка 5 мкВ/B свидетельствует о высокой степени работоспо-
собности резисторов, ухудшение состояния приводит к возрастанию
э. д. с. в десятки раз. В табл. 6.1 приводятся обобщающие эксперимен-
тальные данные для металлизированных резисторов МЛТ.
ТАБЛИЦА 6.1
Тип сопротивления Характер дефекта Уровень э.д.с. шумов, мкВ/В
А (/(=03) В (/(=1.0)
МЛТ-0,25 Продольная царапина 20 50
МЛТ-0,5 62 79
МЛТ-0,25 В пределах одного витка 50 93
МЛТ-0,5 28 91
МЛТ-0,25 В пределах двух витков 17 125
МЛТ-0,5 17 98
МЛТ-0,25 Точечное нарушение 13 50
МЛТ-0,5 58 65
Эти данные показывают, что независимо от характера дефекта
уровень э. д. с. шумов значительно выше допустимых, устанавливаемых
техническими требованиями, поскольку для группы А шумы должны
быть не более 1 мкВ/B, а для группы В — не более 5 мкВ/B. Повышен-
ный уровень шумов приводит к возрастанию интенсивности отказов, на-
пример резисторы с уровнем э. д. с. шумов менее 0.25 мкВ/B имели
9* 131
X—5-10 7 1/ч, а при уровне шумов, превышающем эту границу, X воз-
растала до 10~5 ... 10~4 1/ч.
Электровакуумные приборы. У ЭВП величина дробового шума хо-
рошо характеризует состояние катодов ламп различного качества. Из-
менение шума ЭВП при недокале показывает, что при плохо активиро-
ванном катоде лампы имеют гораздо большую величину шума, чем
при хорошо активированном (рис. 6.22).
Для оценки работоспособности ламп по шумовым характеристикам
напряжение накала целесообразно понижать до 4,5 ... 5 В. Примерным
критерием годности лампы можно считать относительное изменение
дробового шума в 1,5 ... 2 раза. Осуществление прогнозирования по
Рис. 6.22. Зависимость относительного измене-
ния напряжения шума от напряжения накала
ламп 6П15П:
1—4— новые лампы: 5—8— лампы, снятые с прогона.
Рис. 6.23. Зависимость коэффициента
шума транзисторов МП 13 от вре-
мени.
результатам контроля дробового шума рекомендуется для приемно-
усилительных ламп.
Полупроводниковые приборы. Собственные шумы в транзисторах
обычно разделяют на высокочастотные й низкочастотные. Составляю-
щие шума на частотах выше 1000 Гц, связанные с протекающими через
переходы токами дробового и теплового шумов, не содержат надежной
информации о состоянии качества транзисторов. Эти шумы изменяются
в процессе старения транзисторов и диодов незначительно, чего нельзя
сказать о низкочастотных составляющих шума, чувствительных к со-
стоянию поверхностей полупроводникового кристалла и составу запол-
няющего корпус транзистора газа.
Величина низкочастотных шумов является для полупроводниковых
приборов одним из наиболее информативных признаков диагностики.
Полученные экспериментально данные (рис. 6.23) показали, что быстрее
теряют работоспособность транзисторы с повышенным уровнем шума.
Было замечено, что у отказавших транзисторов до £Исп~108 ч наблюда-
лось изменение не только коэффициента шума, но и величины обрат-
ного тока коллектора.
Таким образом, при квалифицированном подходе к объекту диагно-
стики эмпирические методы анализа изменения состояния представляют
собой достаточно эффективное средство для решения задачи прогнози-
рования.
132
6.5. Особенности прогнозирования отказов интегральных схем
Основные отказы н причины, вызывающие их. Требования высокой
точности при изготовлении интегральных схем (ИС), а также бол.ьшое
количество технологических операций (~100) приводят к большому
проценту брака. По данным иностранной литературы, примерно 80%
схем в процессе производства отбраковывается и только 20% постав-
ляется потребителю.
Возможными причинами отказов при производстве кремниевых ин-
тегральных схем являются:
— во время механических процессов: 1) откалывание краев кри-
сталла, 2) трещины в пластине, 3) растрескивание кристаллов;
— во время присоединения контактов и монтажа: 1) разбрызги-
вание металла, 2) трещины, механические напряжения и разрывы,
3) отделение кристалла от держателя, 4) низкое качество присоедине-
ния выводов, 5) обрыв проводов, 6) слабое контактирование токопро-
водящих поверхностей, 7) коррозия;
— при герметизации: 1) низкое качество сварной герметизации и
спая со стеклом, 2) появление инородных частиц;
— при фотолитографии: 1) низкое качество очерчивания и регист-
рации маски, 2) неправильная экспозиция, 3) неправильное время
травления, 4) царапины или поры, 5) плохая промывка (остаются сле-
ды травителя);
— во время диффузии и эпитаксильного процесса: 1) дефекты
в основном кристалле (дислокации, дезориентация, дефекты упаковки
и т. п.), 2) искажение удельного сопротивления, 3) неправильная ско-
рость диффузии, 4) неправильный градиент диффузии, 5) эпитаксиаль-
ное размытие рисунка;
— при металлизации: 1) некачественное совмещение маски, 2) не-
качественный омический контакт, 3) слишком тонкий слой металла,
4) некачественная адгезия, 5) неправильное вплавление, 6) царапины
или поры, 7) разломы металлизации.
Анализ причин выхода из строя ИС при эксплуатации и испытаниях
также устанавливает преобладание отказов, обусловленных низким ка-
чеством выполнения отдельных технологических операций. Постепенные
отказы выражаются, главным образом, в увеличении токов утечки и
вызываются такими причинами, как появление каналов с инверсной
проводимостью и загрязнение поверхности полупроводникового кри-
сталла.
Отказы ИС можно условно разделить на три категории:
— связанные с явлениями в объеме кристалла,
— зависящие от состояния контактных соединений,
— обусловленные явлениями на поверхности кристаллической
структуры.
Первая категория отказов объясняется перераспределением леги-
рующих примесей в объеме кристалла и структурным несовершенством
полупроводникового материала (дислокации, трещины и т. д.).
Перераспределения легирующих примесей происходят в результате
процессов диффузии, однако влияние их не столь значительно, посколь-
ку коэффициенты диффузии легирующих примесей (бора, фосфора
и др.) в монокристалле кремния ничтожно малы при температурах ис-
пользования ИС.
133
Болес вероятны отказы, обусловленные дефектами в полупровод-
никовом материале. Дислокации и прочие дефекты структуры, трещины
и деформации, механические напряжения в кристалле кремния, разви-
ваясь в процессе эксплуатации под воздействием термических и меха-
нических нагрузок, могут существенно изменять электрические харак-
теристики схемы, приводя как к постепенным, так и к внезапным от-
казам-
В ИС используют два типа соединений: металлизированная раз-
водка между отдельными компонентами и соединения алюминиевых
контактных площадок с внешними выводами с помощью золотых про-
водников, которые привариваются к контактным площадкам на кри-
сталле кремния и траверзам выводов корпуса. Для получения метал-
лизированных дорожек используют метод напыления алюминия на по-
верхность окисла кремния с последующим вжиганием. Отказы, связан-
ные с металлизированной разводкой, обычно возникают из-за механи-
ческих повреждений ее разводки или из-за недостаточной толщины
пленки алюминия, что в процессе эксплуатации ИС может вызывать
локальные перегревы металлизированной дорожки, а это в свою оче-
редь приводит к коррозии или к расплавлению алюминия в повреж-
денных областях. Нарушение целостности электрической цели из-за об-
разования на границе раздела алюминий — кремний электроизолирую-
щей пленки также приводит к отказу ИС.
Отказы в ИС возникают в случае попадания влаги внутрь корпуса
до герметизации прибора, или из-за недостаточной герметичности кор-
пуса. Попадание влаги приводит к образованию гидрата окиси алюми-
ния. При этом нарушается целостность электрической цепи из-за высо-
кого электрического сопротивления дефектных участков металлизиро-
ванной разводки.
При соединении металлизированных площадок с внешними выво-
дами корпуса ИС используется золотая проволока, которая методом
термокомпрессионпой сварки присоединяется к соответствующим кон-
тактным площадкам. Основными причинами отказов термокомпрессион-
ных контактов являются образование интерметаллических соединений
на границе раздела золото — алюминий, отрыв алюминиевых контакт-
ных площадок от поверхности кристалла и иногда малая механическая
прочность термокомпрессионных контактов. Состав интерметаллических
соединений, приводящих к обрывам 1ермокомпрессионных золото-алю-
миниевых контактов, сложен и меняется в зависимости от условий его
образования: концентрации золота и алюминия, присутствия свободного
кремния, температуры и давления в процессе термокомпрессии, темпе-
ратуры окружающей среды, времени эксплуатации и многих других
факторов.
Образование интерметаллических соединений и изменение их со-
става в процессе эксплуатации приводит к образованию механических
напряжений на поверхности раздела золото—алюминий и ослаблению
контактного соединения. Непосредственно после сварки контактные со-
единения обладают хорошими механическими и электрическими свой-
ствами, однако в процессе последующей работы или при хранении
в условиях повышенной температуры возникают необратимые явления,
вызывающие увеличение сопротивления и обрыв термокомпрессионных
контактов.
Одной из основных причин обрыва термокомпрессионных контактов
являются механические напряжения. Они возникают на поверхности
134
раздела золото — алюминий при появлении интерметаллических соед
нений, которое связано с изменением объема и несовпадением кристал-
лических решеток вновь образованных соединений. Эти напряжения
дополняются остаточными механическими напряжениями контакта зо-
лота с алюминием, а также напряжениями, возникающими вследствие
различия термических коэффициентов расширения отдельных интерме-
таллических соединений. Все это усугубляется повышенной хрупкостью
большинства интерметаллических соединений, что приводит к отрывам
золотых проводников от алюминиевых контактных площадок. Часто об-
разование интерметаллического соединения сопровождается значитель-
ным увеличением сопротивления контакта, что приводит к его разогре-
ву и обрыву.
Образование интерметаллического соединения AIxAutfSi2 приводит
к еще одному виду отказов ИС. Обычно поверхность кристалла защи-
щена пленкой двуокиси кремния. При наличии дефектов в окисной
пленке (отверстий, проколов, недостаточной толщины слоя окисла и до.)
в области термокомпрессионного соединения может присутствовать сно
бедный кремний, который при взаимодействии с алюминием и золоюм
приводит к быстрому образованию интерметаллического соединения
типа AlxAuySi2 темно-красного или черного цвета. Электропроводность
и механическая прочность этого соединения низки, что и служит в ряде
случаев причиной обрыва термокомпрессионных контактов схем в экс-
плуатации.
После изготовления прибора окисный слой остается и защищает
р—«-переходы от воздействия окружающей среды. При эксплуатации
ИС в приповерхностной области полупроводниковой структуры накап-
ливаются заряды, вызывающие значительные изменения в состоянии
электронно-дырочных переходов и иногда обусловливающие появление
поверхностных каналов с инверсной проводимостью.
Тонкий окисный слой, приобретая заряд, изменяет состояние по-
верхности, что влияет на свойства полупроводниковых приборов, вызы-
вая нежелательные эффекты: возрастание токов утечки, отсутствие на-
сыщения вольт-амперной характеристики перехода коллектор — база,
омическое шунтирование эмиттера с коллектором; снижение и неста-
бильность величины обратного пробивного напряжения па коллекторе,
уменьшение коэффициента усиления по току, уменьшение эффективно-
сти эмиттера из-за омического шунтирования эмиттера с базой, увеличе-
ние шумов.
Экспериментально установлено, что по закону распределения пара-
метры можно разделить на две группы. Прямое падение напряжения
на переходе пПр, напряжение стабилизации и<-г, дифференциальное со-
противление диода емкость перехода С, коэффициенты усиления по
току транзисторов Вст, h^u имеют распределения, близкие к нормально-
му. Эгн параметры зависят от удельного сопротивления исходного
материала, геометрических размеров структуры и ряда факторов,
достаточно хорошо контролируемых в процессе изготовления приборов.
Вторая группа параметров, таких, как обратные токи диодов
коллекторного и эмиттерного переходов транзисторов /ко и Л,с, а также
токи 7КН и 1из трудно управляются в процессе производства. Реальная
величина обратного тока много больше расчетной. Обычно нормы ТУ
на эти величины выбираются с достаточно большим запасом, в резуль-
тате распределения таких величин близки к логарифмически нормаль-
ным и «вытянуты» в сторону больших значений.
135
Часто изменение формы распределения параметров в процессе
испытаний или отклонение начального распределения от нормального
может служить признаком происходящих в приборах явлений, вызы-
вающих отказ. На рис. 6.24 и 6.25 показаны характерные распределе-
ния параметров.
Для анализа результатов испытаний строят также корреляционные
поля. Пример такого поля показан на рис. 6.26. Координаты по гори-
Рис. 6.24. Интегральное распределение стати- Рис. 6.25 Интегральное распределе-
ческого коэффициента усиления транзисторов ние обратного тока транзистора.
П416.
зонтали равны начальному значению параметра I'KG, а по вертикали —
конечному значению /"Е0 после испытаний. При одинаковых масштабах
по обеим осям токн, соответствующие стабильным приборам, распола-
Рис. 6.26. Корреляционное по-
ле обратного тока транзистора.
гаются по прямой, проходящей под углом
45°. В данном примере имеется группа ста-
бильных приборов, у которых /ко<2 мкА,
и нестабильных, у которых /ко>2 мкА. По-
сле испытаний величина обратного тока
у них значительно возрастает.
Явления на поверхности кристаллов
с переходами. Основной причиной неста-
бильности параметров полупроводниковых
приборов, вызывающей основную часть де-
градационных отказов, является изменение
поверхности кристалла полупроводника с
переходами во время работы или хране-
ния.
Одной из основных причин, вызываю-
щих такую сильную зависимость электри-
ческих параметров полупроводниковых приборов от процессов, происхо-
дящих на поверхности, является возникновение электрических зарядов
па поверхности и в объеме, близком к поверхности. Источники возник-
новения этих зарядов могут быть самыми различными.
1. Заряд может быть образован ионами на внешней поверхности
окисной пленки. Их количество зависит от способа обработки кристал-
ла, влажности, окружающей среды. Влага сильно увеличивает подвиж-
ность ионов под действием напряжений, приложенных к электродам.
136
2. Ионы, находящиеся внутри окисной пленки, также могут обра-
зовать заряд. Так, например, положительные ионы натрия, от присут-
ствия которого очень трудно избавиться даже при тщательно контроли-
руемом технологическом процессе, при температуре 100 ... 200 °C и
наличии электрического поля перемещаются к границе кремний — оки-
сел. Величина перемещенного заряда, образованного ионами натрия
Арка за время t, определяется по следующей формуле:
ДО.,
^Na
где энергия активации Ez — 0,7 эВ. Таким образом, величина заряда
сильно зависит от температуры. Кроме натрия, внутри окисной пленки
могут перемещаться и другие ионы, например ионы золота. В отличие
от натрия его ионы создают отрицательный заряд в пленке.
3. Заряд может быть образован избыточными атомами кремния
вблизи границы с кристаллом. При этом сначала должен образоваться
свежий окисел на границе с кристаллом. Этим создается избыток атомов
кремния. Они создают положительный заряд, величина которого зави-
сит от условий и способа выращивания окисла, ориентации пластины
относительно кристаллографических осей. При нормальной температуре
заряд неподвижен, а при высокой температуре и при сильном поле за-
ряд начинает перемещаться, атомы кремния выходят нз кристалла на-
встречу SiO2 и двигаются к внешней поверхности пленки.
4. Вследствие обрыва кристаллической решетки на границе появля-
ются атомы полупроводника с нарушенными электронными связями.
Это означает, что электроны переходят в энергетические состояния вну-
три запрещенной зоны энергий для данного полупроводника. Электроны
с такой энергией не могут проникать в глубь кристалла и остаются
вблизи поверхности.
Наличие поверхностных энергетических состояний и поверхностных
зарядов приводит к образованию под поверхностью объемного заряда,
равного по величине, но противоположного по знаку, заряду на поверх-
ности. При этом толщина слоя объемного заряда сравнима с размерами
элементов перехода транзисторов и диодов (~10~4 см). Образование
заряда на поверхности приводит к изменению электропроводности по-
лупроводника.
Поверхностные энергетические состояния могут служить эффектив-
ными центрами рекомбинации, они увеличивают вероятность столкно-
вения подвижных носителей заряда и рекомбинацию носителей заряда
другого знака.
Итак, образование заряда на поверхности полупроводника приво-
дит к изменениям электропроводности и скорости поверхностной реком-
бинации, что, в свою очередь, вызывает изменение электрических пара-
метров полупроводниковых приборов: увеличение обратного тока и
уменьшение напряжения пробоя вследствие уменьшения ширины пере-
хода, вызванного увеличенной концентрацией носителей заряда вблизи
поверхности. Это явление наблюдается, когда к переходу приложено
запирающее напряжение.
В результате действия этих эффектов все характеристики планар-
ных приборов могут изменяться со временем как при хранении, так и
в процессе эксплуатации и приводить к постепенным отказам ИС.
К отказам, обусловленным неудовлетворительным состоянием по-
верхности планарной структуры, следует отнести и такой широко рас-
137
пространенный вид отказа, как короткое замыкание металлизированной
разводки на поверхности кремния через отверстие в окисной пленке.
Причинами этого являются различные дефекты окнсла (отверстия, про-
колы, царапины, трещины и др.), снижающие его диэлектрическую
прочность или обнажающие поверхность кремния. Трудность обнаруже-
ния подобных потенциально ненадежных схем объясняется тем, что
дефект проявляется чаще всего лишь в эксплуатации.
Явления, сопутствующие отказам ИС. Одним из основных внешних
проявлений изменения состояния ИС является изменение обратного
тока /к0 и нулевого тока коллектора /кзо на величину тока утечки /у.
Появление тока утечки объясняется возникновением проводимости, па-
раллельной р— «-переходу, вследствие поверхностных дефектов ИС.
Дрейф параметров ИС (0 и /ко) является следствием нарушения
теплового режима ИС и может вызывать пробой или короткое замыка-
ние. Анализ отказов и явлений, сопровождающих постепенные отказы,
показывает, что основными сопутствующими явлениями являются: из-
менение электрических параметров ИС; изменение теплового режима
ИС и изменение распределения потенциалов ИС.
При решении задачи прогнозирования отказов ИС исключительно
важное значение имеет выбор прогнозирующего параметра. От решения
этого вопроса зависит эффективность прогнозирования. Необходимо
различать прогнозирование отказов ИС при производственных испы-
таниях па за воде-изготовителе и прогнозирование отказов при эксплуа-
тации. При производственных испытаниях и контроле качества ИС на
заводах-изготовителях для прогнозирования постепенных отказов ИС
широко применяются методы неразрушающего контроля: инфракрасная
радиометрия (ИК метод); растровая электронная микроскопия, осно-
ванная на контроле распределения электрического потенциала рабо-
тающей схемы; определение герметичности корпусов; рентгенография.
Более перспективными являются первые два метода, в которых
предсказание отказов основано на сравнении теплограмм и потенцна-
лограмм с эталонными. Метод ИК радиометрии основан на зависимости
интенсивности ИК излучения от рассеиваемой элементами ИС мощ-
ности.
Плотность потока излучения серых тел Р( при е = const равн;
Р(=воГ4, где в—степень черноты тела; о~5,67-10“12 Вт/см2-(К)4 — по-
стоянная Стефана — Больцмана, Т температура тела.
Температура на поверхности ИС отражает влияние окружающей
среды и собственное тепловыделение. Измерение ИК излучения тепло-
рассеивающих элементов электронных схем позволяет судить не только
об их температуре, но и о величине электрического тока в них.
Главными преимуществами ПК метода являются универсальность;
отсутствие физического контакта, нарушающего электрическое или те-
пловое равновесие; возможность определения динамических термических
характеристик; быстрота и наглядность; возможность автоматизации
и осуществимость на любой стадии технологического процесса произ-
водства микросхемы.
Исследования тепловых карт ИС (рис. G.27) показывают, что наи-
более нагретые области находятся в р—/1-переходах, сопротивлениях,
а’ также в зоне таких дефектов, как малое поперечное сечение метал-
лизированной дорожки и др.
Прогнозирование отказов заключается в обнаружении расхождения
тепловых карт исследуемых ИС с эталонными картами для данного
138
типа схемы, при этом любое нарушение электрического режима работы
схемы легко и быстро обнаруживается по тепловой карте.
Интегральная схема (рис. 6.27) представляет собой мощный им-
пульсный усилитель с диодной логикой на входе, выполнена по пла-
нарной технологии, на монолитном кристалле кремния размером 1X
X 1X0,2 мм. По линии А А с помощью ИК микроскопа сняты яркост-
ные температуры в точках с шагом 20 мкм для невключенпой схемы
(кривая /). Для включенной схемы в режиме максимальной рассеивае-
Рис. 6.27. Топология ИС и профили тепловых карт.
мой мощности получена кривая II. Кривая III представляет собой раз-
ность яркостных температур для включенной и невключенной схем.
Для иллюстрации метода обнаружения дефектов по локальным
перегревам на рис. 6.28 представлены профили яркостных температур,
снятые вдоль шины печатной схемы при различных протекающих по
ней токах, причем сечение шины в точке А было искусственно умень-
шено на 30%. На кривой III отчетливо видно резкое увеличение ярко-
стной температуры в ючке .4 по сравнению с соседними точками при
увеличении протекающего тока.
Рассматривая кривую I, можно отметить значительный разброс из-
лучаемой способности поверхности шины в различных точках, что ха-
рактеризует качество обработки поверхности.
Анализ тепловых карт позволяет выявить образцы с плохой адге-
зией пленок с подложкой; с плохими тепловой и электрической прово-
димостью, с неравномерной плотностью тока и др., которые не могу г
быть обнаружены путем обычных электрических измерений. Ограничен-
ность этого метода заключается в том, что технологический процесс из-
готовления ИС заканчивается герметизацией корпуса, а существующие
материалы, из которых изготовлен корпус, непрозрачны для ИК спектра
частот.
139
Рис 6.28. Профиль яркостных темпе-
ратур.
Метод растровой электронной микроскопии состоит в том, что при
использовании растрового электронного микроскопа проявляется эффект
вторичного отражения электронов от поверхности исследуемой ИС, ко-
торая находится во .включенном со-
стоянии. При этом траектория рассеи-
вания вторичных электронов опреде-
ляется потенциалами различных обла-
стей исследуемой схемы. В результате
электронного сканирования формиру-
ется лотенциолограмма испытуемой
схемы.
Однако методы неразрушающего
контроля не являются универсальны-
ми для прогнозирования отказов ИС
и неприменимы для прогнозирования
отказов ИС при эксплуатации их в ап-
паратуре. Более перспективными сле-
дует считать методы, основанные на
радиотехнических измерениях, которые
дают интегральные сведения о состоя-
нии прибора.
Для прогнозирования постепенных
отказов ИС дискретного действия
можно использовать следующие ме-
тоды:
1. Метод моделирования. Он за-
ключается в замене физического маке-
тирования схем математическим. Это
важно для микроэлектроники, где фи-
зическое макетирование и дорого, и
длительно. Моделирование должно
обеспечить решение следующих задач:
определение законов функционирова-
параметров при изменении внешних воз-
ния ИС и оценка основных ее
действий на схему (входных сигналов, температуры и т. д.) и внутрен-
них (изменение номиналов под действием внешних условий и времени,
напряжения питания, помех и т. д) Однако этот метод пригоден лишь
на этапе проектирования при достаточной априорной информации.
2. Метод изменения питающих напряжений (метод граничных испы-
таний). Величину изменения питающих напряжений в данном случае
можно рассматривать как прогнозирующий параметр. Этот метод эф-
фективен-лишь для схем с низкой надежностью.
3. Метод изменения входных воздействий. Здесь прогнозирующим
параметром является коэффициент отпускания 6=мОтп/«ср, нли ширина
пути отпускания Д&отп=&ср—аотп, где мср, &отп — входные напряжения
срабатывания и отпускания.
4. Метод дозированных помех. Изменение параметров ИС можно
представить эквивалентным напряжением на входе ИС. Подавая дози-
рованную помеху определенного вида, можно имитировать комплексное
изменение параметров элементов во времени. В этом случае дозирован-
ная помеха является прогнозирующим параметром, по ее величине
можно судить о расположении параметров НС относительно допусти-
мых значений.
ио
5. Метод контроля вольт-амперной характеристики. Изменение па-
раметров вольт-амперной характеристики приборов с р — «-переходами
может служить предвестником отказа. Таким образом, вольт-амперная
характеристика также может служить прогнозирующим параметром.
Типичные изменения вольт-амперных характеристик микродиодов пред-
ставлены на рнс. 6.29. Они вызваны следующими причинами:
а) в результате загрязнения поверхности р— «-перехода образует-
ся слой объемного заряда, который обычно не сильно влияет на прямой
Рис. 6.29. Изменения вольт-амперной характеристики микродиодов в зависимости от
различных факторов.
и обратный токи. Исключение составляет случай, когда приложенное
напряжение достигает значения, при котором начинается лавинная
ионизация, что приводит к уменьшению напряжения пробоя;
б) вследствие загрязнения поверхности переходов ионами материал
может изменить свой тип проводимости. Обычно ток, возникающий
из-за инверсионных слоев, настолько мал, что не может служить причи-
ной выхода прибора из строя. Если же инверсный слой контактирует
с дефектным центром, то происходит резкое увеличение обратного
тока;
в) из-за конденсации паров на поверхности р—«-перехода и обра-
зования при этом проводящих каналов поверхность перехода приходит
в негодность. В этом случае вольтамперная характеристика пропорци-
ональна приложенному напряжению, а коэффициентом пропорциональ-
ности служит поверхностная проводимость;
г) из-за выпадения в осадок ионов или атомов металла, находя-
щихся в твердом растворе в области, близкой к р—«-переходу из-за
большого тепловыделения при протекании прямого тока, параметры
прибора ухудшаются. В литературе это явление носит название мягкого
пробоя. Такой осадок обычно образуется около дислокаций или вдоль
границ зерен. В этом случае 70бр пропорционален приложенному напря-
жению в п-й степени, где «=3 ... 7. Обнаружено, что такие нарушения
обратимы и образуемый в переходе осадок может снова перейти в твер-
дый раствор;
д) из-за увеличения сопротивления омического контакта, когда та-
кой контакт включен последовательно с переходом.
6. Метод, основанный на измерении характеристики вход — выход
интегральных схем. Дискретные элементы по характеристикам вход —
выход разбиваются на 2 группы: элементы-повторители и элементы-ин-
верторы (рис. 6.30).
Обычно различают три участка линии, показывающей связь между
входом и выходом схемы. Для первого, участка характерно
141
|Д«вых/Д«вх|<1; для второго |Д«вых/Д^ех| >1; для третьего
I Д&ВЫх/Д ^ВХI = 1 -
Устойчивой работе элемента соответствует вполне определенная
линия связи между входом и выходом. Отклонение реальной линии
вход — выход от оптимальной служит характеристикой запаса работо-
способности элемента и может быть использовано в качестве прогнози-
рующего параметра.
Рис. 6.30. Характеристики вход—выход дискретных элементов.
7. Метод, основанный на определении динамической устойчивости..
Для работы дискретных элементов необходимо, чтобы импульс вход-
ного сигнала имел продолжительность, достаточную для перехода из
нулевого состояния в единичное, а время перехода из единичного со-
стояния в нулевое должно быть меньше времени паузы Л При задан-
ных скважности, форме и амплитуде входного сигнала величины ма-
ксимальной fMaKC и минимальной /мин частот входного сигнала, при ко-
торых дискретный элемент выполняет возложенные на него функции,
являются мерой динамической работоспособности.
При последовательном соединении дискретных элементов на выходе
последнего продолжительности импульса и паузы будут равны
п п
t-гм == 2 == Лх 2
i-1 =1
мин'Смакс, ta мин4С^пп4С tn макс-
Для устойчивой работы дискретного устройства необходимо, чтобы
t-nii И tnn не выходили за допустимые пределы. Таким образом, величи-
ны Д/макс и Д/мин являются мерой запаса динамической работоспособ-
ности устройства, а их уменьшение является предвестником отказа, про-
гнозирующим параметром.
Часть 1П
ПРОГНОЗИРОВАНИЕ НАДЕЖНОСТИ
ГЛАВА 7. ИСХОДНЫЕ ПОЛОЖЕНИЯ ПО ПРОГНОЗИРОВАНИЮ
НАДЕЖНОСТИ
7.1. Общая схема оценки надежности изделий
Как н многие из технических параметров, надежность на первых
этапах использования подвергалась только качественной оценке. В тех-
нической документации можно было встретить выражения: «обеспечить
высокую надежность», «изделие обладает повышенной надежностью»
и’т. д. Для простых изделий, а также для изделий со строго определен-
ной структурой, конструкцией, используемыми материалами и применяе-
мой технологией, по-видимому, никакого другого определения и не тре-
бовалось. Но как только появились сложные технические системы, на-
дежностью которых стало возможным и необходимым управлять, сразу
же возникла задача количественной оценки надежности.
Только количественная оценка надежности позволяет обоснованно
сравнить конструктивные варианты, выбирать оптимальную технологию
и режимы использования, делать содержательными понятия «высокая
надежность» и «низкая надежность».
Изделие может обладать некоторой надежностью, т. е. оно может
обладать способностью выполнять требуемые функции в некоторых за-
данных условиях. Эту способность можно количественно оценить по ре-
зультатам эксплуатации или испытаний. В этом случае оценкою на-
дежности данного изделия может быть заключение: «изделие прорабо-
тало до отказа столько-то часов». Для группы однотипных изделий
в качестве количественных показателей надежности могут быть «вероят-
ность работоспособного состояния», «среднее время наработки до отка-
за» и т. д.
Оценки надежности, полученные по результатам испытаний и экс-
плуатации, носят, как правило, характер констатации -результатов ра-
боты изделия. В отдельных случаях они могут приобретать характер
прогнозирующих оценок, если, например, на основании результатов вы-
борочных испытаний делается прогноз о будущем состоянии партии из-
делий.
Оценка надежности становится прогнозирующей тогда, когда на
основании изучения закономерностей, которым подчиняется процесс
формирования показателей надежности, делается предположение о бу-
дущем состоянии надежности изделия, которого в данный момент мо-
жет еще и не быть (оно может существовать в проекте). Такое прогно-
зирование надежности осуществляется на этапе проектирования изде-
лий.
Таким образом, количественная оценка надежности может иметь
различную направленность, а именно: констатацию уровня надежности
и прогнозирование ее.
Констатация уровня основывается на результатах опыта (испыта-
ний, эксплуатации, статистических данных). Прогнозирующая оценка
143
надежности (или прогнозирование надежности) основывается, главным
образом, на анализе физико-химических процессов, проведении специ-
альных испытаний и использовании закономерностей, которым подчи-
няются процессы, обусловливающие формирование показателей надеж-
ности.
Средством для осуществления как констатирующих, так и прогно-
зирующих оценок служат: расчеты, моделирование и испытания. Это
обстоятельство отражено на рис. 7.1, на котором представлена общая
схема количественной оценки надежности. Двойными линиями изобра-
жены связи между методами оценки надежности на начальных этапах
их развития. К таким начальным оценкам, не потерявшим своего прак-
тического значения, относятся количественные оценки констатирующего
Рис. 7.1. Схема количественной оценки надежности:
к — констатирующий; п — прогнозирующий.
характера, полученные ло результатам испытаний в процессе производ-
ства, по результатам эксплуатации и на основании статистических дан-
ных, расчетом, в процессе проектирования. Одиночными линиями изо-
бражены связи между методами оценки надежности, которые получают
распространение в связи с внедрением прогнозирования надежности.
Получение оценки надежности не следует рассматривать как ко-
нечную цель. Анализ ее и сравнение с заданным требованием к надеж-
ности должны служить основанием для совершенствования процессов
проектирования, производства и эксплуатации.
Прн рассмотрения общей схемы оценки надежности напрашивает-
ся и другой вывод: при оценке надежности возможны разнообразные
варианты и даже сочетания различных вариантов выбора характера
оценки (констатирующая, или прогнозирующая), этапа (проектирова-
ние, производство, эксплуатация) и метода (расчет, испытание, обра-
ботка результатов эксплуатации). В отдельных случаях может оказать-
ся целесообразным оценку надежности производить- только на этапе
проектирования и опытной эксплуатации, в других — на этапах произ-
водства и эксплуатации и т. д. В одних случаях главными при оценке
надежности могут оказаться расчеты, в других — моделирование, в тре-
тьих— испытания, в четвертых — анализ физических причин,- вызываю-
144
тих отказы и т. д. Поэтому при разработке, изготовлении и эксплуа-
тации изделий необходимо планировать мероприятия по обеспечению и
оценке надежности. Такой план должен включать сочетание таких при-
емов и методов количественной оценки надежности, которые в каждом
конкретном случае приводят к достижению поставленной цели наиболее
быстро и с меньшими затратами.
7.2. О связи прогнозирования технического состояния
и прогнозирования надежности
Надежность принадлежит к числу характеристик, определяющих
техническое состояние изделия. Однако прогнозирование надежности
имеет смысл выделять отдельно. Можно указать следующие особенно-
сти определения этой технической характеристики. В отличие от всех
других характеристик надежность нельзя непосредственно измерить.
Причинами отказов могут быть не только закономерные постепенные
изменения технических параметров, но также и внезапно возникающие
повреждения. Для определения вероятности возникновения постепенных
отказов необходимы длительные наблюдения. Отказ по одному из пара-
метров либо отказ одного из элементов изделия может не приводить
к отказу изделия. Все сказанное ранее относительно прогнозирования
технического состояния имеет непосредственное отношение также и
к прогнозированию надежности, но не исчерпывает полностью эту про-
блему.
Задачей прогнозирования технического состояния является пред-
сказание количественных значений технических параметров, либо отне-
сение этих параметров к некоторому классу, а также определение веро-
ятности выхода параметров за пределы допуска, т. е. прогнозирование
отказов. Задачей прогнозирования надежности является предсказание
количественных показателей надежности изделия на основе прогнози-
рования постепенных и внезапных отказов.
В частном случае, когда работоспособность изделия определяется
одним параметром, а отказы изделия вызываются постепенным измене-
нием этого параметра, тогда прогнозирование технического состояния и
прогнозирование надежности совпадают. В общем случае, надежность
изделия зависит от большого числа разнообразных факторов и осуще-
ствляется на основе расчетов, испытаний и моделирования с учетом
всей совокупности действующих факторов.
7,3. Прогнозирование отказов и прогнозирование
количественных показателей надежности
Прогнозирование надежности аппаратуры означает предвидение по-
казателей ее надежности в будущем. Прогнозирование отказа означает
предвидение определенного отказа с указанием возможного интервала
времени и вероятности его возникновения. В результате прогнозирова-
ния надежности определяются ожидаемые значения’показателей надеж-
ности. К ним относятся следующие показатели:
— ожидаемая вероятность безотказного состояния в заданном бу-
дущем интервале времени или в пределах заданной наработки;
— ожидаемая интенсивность отказов либо параметр потока отказов
н интенсивность восстановления (для восстанавливаемых изделий).
10-813 145
Прогнозирование отказов ориентировано на изучение вполне опре-
деленных отказов п предсказание некоторых из них может быть не
связано с оценкой надежности. Так, например, может оказаться, что
отказ некоторого резервного блока не влияет на показатель надежности
аппаратуры на интервале времени А/ (она продолжает сохранять ра-
ботоспособность на этом интервале). Однако прогнозирование отказа
этого блока имеет большое значение для предупреждения накопления
отказов и своевременного профилактического ремонта для обеспечения
безотказного состояния аппаратуры на интервале времени, превышаю-
щем АЛ Таким образом, прогнозирование отказов может сопровождать-
ся прогнозированием показателей надежности.
Прогнозирование отказов требует четкого представления о природе
и характере отказов. По источникам возникновения отказы радиоэлек-
тронной аппаратуры делятся на следующие четыре группы:
— отказы аппаратурные, вызванные тем, что элементы аппаратуры
переходят в отказовое состояние (изнашиваются, ломаются, перегорают
и т. д_);
— отказы программные, вызванные несовершенством программы,
а также тем, что программы часто составляются прн условии ограниче-
ний, за пределы которых выходит фактический процесс работы машины;
• — отказы информационные, представляющие искажение информа-
ции при ее передаче и обработке;
— отказы, вызванные ошибками оператора, обслуживающего аппа-
ратуру.
При разработке программы прогнозирования отказов необходимо,
прежде всего, четко сформулировать задачу и определить, какие отказы
прогнозируются. По характеру проявления отказы могут быть внезап-
ными и постепенными.
Наиболее разработанными являются методы прогнозирования аппа-
ратурных устойчивых постепенных (параметрических) отказов, так как
существуют достаточно разработанные методы измерения параметров
аппаратуры и даже некоторые априорные закономерности их изменений.
Труднее прогнозировать сбои (самоустраняющиеся отказы) и внезап-
ные отказы. Они относятся к разряду случайных событий, поэтому
к ним нельзя применять методы, основанные на детерминированных за-
кономерностях. Для прогнозирования сбоев и внезапных отказов исполь-
зуются косвенные параметры и вероятностные закономерности. Так,
например, установлено, что сбои в работе аппаратуры на интегральных
схемах вызываются, главным образом тем, что уровень действующих
помех соизмерим с уровнем полезного сигнала. Поэтому вероятность
сбоя можно определить вероятностью превышения уровня помехи пре-
дельно-допустимого уровня. Для прогнозирования внезапных устойчи-
вых отказов можно также использовать косвенные прогнозирующие
параметры (увеличение «шума», увеличение теплового излучения
и т. и.).
Прогнозировать отказы, вызванные ошибками программы, не име-
ет смысла, как и отказы, вызванные грубыми дефектами производства.
Контроль качества программы и производственного процесса должен
быть таким, чтобы грубые дефекты выявлялись и устранялись своевре-
менно и с достаточной полнотой.
Анализ информационных отказов приобретает очень большое зна-
чение в связи с широким внедрением информ ационно-логических си-
стем. Сущность этих отказов заключается в том, что при передаче ин-
146
формации и ее обработке могут появиться искажения даже при исправ-
ной аппаратуре и нормально составленной программе. Искажения могут
возникнуть в результате неблагоприятного сочетания допусковых откло-
нений параметров, неблагоприятных рабочих режимов, под воздействи-
ем помех, при плохой различимости признаков в представлении инфор-
мации и команд н других аналогичных причин. Трудность прогнозиро-
вания информационных отказов определяется тем, что они могут
вызываться аппаратурными отказами и факторами, не зависящими от
отказов аппаратуры.
По-видимому, на данном уровне наших представлений об отказах
следует внедрять в инженерную практику прогнозирование аппаратур-
ных устойчивых отказов и принимать меры по исключению сбоев, про-
граммных отказов, отказов информационных и отказов, вызванных
ошибками оператора. При предъявлении требований к надежности
полезно оговорить требования, обусловленные отдельными вадами от-
казов. При анализе отказов по результатам эксплуатации и испытаний
совершенно необходимо распределять их по видам отказов и устанав-
ливать причину возникновения.
7.4. Типовые задачи прогнозирования надежности изделий
Методы прогнозирования надежности, ее целевая направленность,
исследуемый аппарат и исходные данные зависят от задачи прогнози-
рования. Можно указать следующие пять задач, которые возникают
в области прогнозирования надежности.
1. Прогнозирование надежности для предсказания закономерности
изменения надежности некоторого класса изделий в связи с перспекти-
вами развития техники производства и внедрения новых материалов.
Так, например, можно поставить задачу обосновать предположение
о надежности вычислительных машин будущего пятилетия в связи с на-
метившейся тенденцией внедрения новых элементов, новых материалов
и новых принципов конструирования. Такое прогнозирование необходи-
мо при планировании работ по созданию больших технических систем.
Оно основано на изучении статистических материалов, связанных с ис-
следованием перспектив развития производства, и осуществляется с по-
мощью моделирования и расчетов.
2. Определение надежности проектируемого изделия до того, как
оно будет изготовлено. Эта задача возникает на стадии проектирования
при выборе конструктивного варианта, структуры и принципиальной
схемы изделия. Сравнение вариантов сложных изделий до их изготов-
ления должно сопровождаться оценкой их возможной надежности. Та-
кая оценка для создания изделия представляет собой ни что иное, как
прогнозирование. Ойо может быть реализовано на основе расчета либо
моделирования по информации о надежности элементов, структуры
устройства и условиях работы.
3. Предсказание надежности на основе информации о возможном
изменении внешних факторов, обусловливающих надежность. Так, на-
пример, может быть поставлена задача высказать предположение о на-
дежности работы изделия при условии, что температура и влажность
окружающей среды будут изменяться в некоторых пределах, или прн
условии, что вероятность ошибок обслуживающего персонала возрастет
до некоторого уровня и т. д.
10* 147
Если в предыдущей задаче фиксированными были условия работы
и воздействующие факторы, а переменными — структура и элементы, то
здесь фиксированными становятся структура и элементы изделия, а пе-
ременными— воздействующие факторы и условия работы. При решении
этой задачи используются эксперимент, расчет и моделирование.
4. Индивидуальное прогнозирование надежности изделия на осно-
вании результатов измерения его прогнозирующих параметров. В отли-
чие от предыдущих задач в данном случае объектом исследования
является вполне определенное изделие. Предварительно выбираются
прогнозирующие параметры, т. е. такие, по изменению которых можно
сделать вывод об изменении надежности. В частном случае, при про-
гнозировании надежности такими параметрами могут быть либо основ-
ные, непосредственные, либо дополнительные косвенные. К основным
прогнозирующим параметрам относятся такие, выход которых за тех-
нический допуск рассматривается как отказ. Например, если в техниче-
ской документации записано, что выходное напряжение должно быть
в пределах ±10% от номинального, то выходное напряжение будет
прямым прогнозирующим параметром надежности. Косвенными прогно-
зирующими параметрами будем называть такие, которые не определя-
ют работоспособность изделия, но изменение которых связано с изме-
нением основных параметров, определяющих работоспособность изде-
лия. Так, например, для резисторов и полупроводниковых транзисторов
характерно заметное изменение уровня «шумов» задолго до отказа их
по основным параметрам.
После того, как прогнозирующие параметры (один или несколько)
выбраны, ведется наблюдение за их изменением и делается вывод
о предполагаемой надежности изделия для некоторого будущего интер-
вала времени.
5. Групповое прогнозирование надежности, т. е. такое прогнозиро-
вание, когда на основании изучения группы изделий либо отдельных
представителей группы высказывается предположение о надежности
группы изделий в будущем. Часто, например, из некоторой совокупно-
сти изделий выделяется одно или несколько изделий для «опытной» экс-
плуатации, которая сопровождается тщательным наблюдением за тех-
ническими параметрами. На основании изучения материалов эксплуа-
тации опытного изделия или группы изделий делается вывод о надеж-
ности совокупности изделий, из которой взяты данные изделия. По сво-
ей формулировке эта задача внешне похожа на задачу оценки изделий
на основании выборочного метода. Но это только внешнее сходство.
При выборочном методе оценки возможны несколько случаев:
I) исследуемая совокупность состоит из разных изделий (шары
черные и белые, изделия годные и негодные и т. д.). Необходимо оце-
нить долю разных изделий в совокупности по результатам подсчета их
в выборке;
2) исследуемая совокупность состоит из одинаковых изделий, но
степень «одинаковости» будет разной в зависимости от объема сово-
купности. На основании изучения выборки делается вывод о ее харак-
теристике, и она —эта характеристика выборки — распространяется на
всю совокупность. Такая задача типична для выборочной оценки на-
дежности.
Формулировка задачи 5 близка ко второму случаю. Отличие за-
ключается в том, что здесь требуется не только определить показатель
надежности некоторой совокупности изделий по показателю надежно-
148
сти выборки на некоторый фиксированный момент времени, ио и вы-
сказать также предположение о будущем состоянии надежности сово-
купности изделий на основании прогнозирующей оценки опытных из-
делий.
7.5. О прогнозировании надежности сложных систем
Терминология по вопросам надежности к данному моменту разпа
ботана применительно к таким изделиям, которые могут находиться
в двух возможных состояниях: работоспособном и отказовом. Но в ин-
женерной практике имеют место более сложные случаи. Телевизор, рас-
считанный на работу по трем программам, может отказать при работе
на одну из них, но продолжать работу по остальным двум программам.
В системе освещения часть светильников может отказать, но система
будет продолжать действовать с некоторым уменьшением освещенности
и т. д.
В практике широко распространены изделия, которые могут нахо-
диться в нескольких возможных рабочих состояниях. Для таких изде-
лий нельзя применять рекомендуемые показатели надежности, прежде
чем будет определено понятие «отказ изделия», которое должно учи-
тывать, что изделие может находиться в большом числе работоспособ-
ных состояний.
Это обстоятельство вызвало необходимость делить все изделия на
следующие две группы: с одним состоянием работоспособности и с не-
сколькими. В существующей терминологии по надежности эти понятия
все еще не установились и в различных работах называются по-разно-
му. Чаще всего изделия первой группы (с одним рабочим состоянием)
называются простыми, а изделия второй группы (с несколькими рабо-
чими состояниями) — сложными. Сложными будем называть системы,
обладающие следующими признаками:
— в состав их входят конструктивно-независимые подсистемы и
части системы, выполняющие самостоятельные функции;
— подсистемы и части системы соединены между собой разветв-
ленной передачей информации, которая позволяет осуществлять пере-
строение структуры системы;
— отказ отдельных частей системы не приводит к отказу системы,
а может вызывать снижение ее эффективности, т. е. система может
находиться в двух и более состояниях работоспособности, каждое из
которых характеризуется своей эффективностью.
Одной из основных характеристик качества сложных систем явля-
ется показатель эффективности. Под эффективностью изделий, в самом
общем виде, принято понимать степень приспособленности их для вы-
полнения поставленной эксплуатационной задачи (управление объек-
том, поражение цели, перевозка груза и т. д.).
Эффективность характеризуется показателем или набором показа-
телей, которые выбирают с учетом особенностей поставленной эксплуа-
тационной задачи. Существует много различных направлений анализа
эффективности технических изделий, в том числе анализ эффективности
экономической, технической, оперативной и др.
Так как вопросы надежности связаны, главным образом, с поня-
тием технической эффективности, поэтому в дальнейшем будем рассма-
149
тривать только этот вид. Под технической эффективностью будем по-
нимать эффективность, обусловленную техническими характеристиками
исследуемого объекта (его мощностью, надежностью, приспособленно-
стью к преодолению противодействующих факторов, способностью к пе-
рестройке структуры и т. д.).
Показателями технической эффективности могут быть вероятность
выполнения поставленной задачи; объем выполненной работы (произ-
водительность); число объектов, управляемых данной системой управ-
ления в заданный промежуток времени; время обработки и передачи
заданного объема информации и т. д.
В отличие от простых изделий надежность сложных систем долж-
на определяться на основании набора первичных показателей надеж-
ности, а именно: показателей надежности отдельных каналов передачи
информации и простых систем, входящих в состав сложной системы:
показателей надежности сложной системы в каждом из возможных ее
рабочих состояний [Р*].
Для каждого из работоспособных состояний системы следует опре-
делять частный показатель эффективности системы (£г). В качестве
обобщенного показателя надежности сложной системы может быть
использована сумма вероятностей безотказного состояния системы
в каждом из возможных работоспособных состояний.
Обобщенный показатель технической эффективности сложной систе-
мы равен — Таким образом, для сложной системы [с охран я-
i=l
ется понятие надежности системы, на базе которого формируется обя-
зательная для сложных систем оценка эффективности системы.
Понятие надежность используется для оценки технического состоя-
ния системы, понятие эффективность — для оценки результата приме-
нения системы. Эти понятия не следует ни смешивать, ни противопо-
ставлять.
Для простых изделий также возможно, а иногда необходимо при-
менять понятие эффективности, так как в ряде случаев изолированное
рассмотрение показателя надежности может привести к неправильным
заключениям. Можно, например, формально повысить надежность вы-
числительной машины, снизив ее производительность. Можно уменьшить
число параметрических отказов, расширив поле допуска, продлить срок
службы осветительного прибора, снизив интенсивность свечения, и т. д.
Но такие методы повышения надежности не улучшают качества функ-
ционирования и потому оценка полученного выигрыша в показателях
надежности должна сопровождаться оценкой проигрыша в эффективно-
сти использования изделия.
Для простых изделий это сопоставление не всегда актуально, так
как для них, как правило, устанавливается один режим использования.
Для сложных систем на первый план выступает оценка эффективности,
так как различные режимы использования являются правилом, а не
исключением.
Проблема прогнозирования надежности сложных систем значитель-
но усложняется по сравнению с прогнозированием надежности простых
изделий. Она распадается на прогнозирование ряда показателей надеж-
ности системы для каждого из возможных состояний и завершается
прогнозированием технической эффективности.
150
ГЛАВА S. ПРОГНОЗИРОВАНИЕ ПО РЕЗУЛЬТАТАМ РАСЧЕТОВ
НАДЕЖНОСТИ
S.I. Характерные особенности расчетных методов и их виды
Определение количественных показателей надежности всегда сопро-
вождается некоторыми расчетами. Они проводятся и при проектирова-
нии, и на заключительном этапе испытаний, и при анализе результатов
эксплуатации. Расчеты принято делить на две группы. К первой отно-
сятся расчеты, основанные на анализе структуры изделия и заданных
условий работы. Их принято называть расчетно-аналитическими, пли
расчетами надежности. Ко второй — расчеты, связанные с обработкой
результатов эксперимента. Они называются расчетно-эксперименталь-
ными, или обработкой опытных данных.
Характерной особенностью расчета надежности является то, что
показатели надежности объекта определяются в виде зависимостей от
первичных факторов, обусловливающих его надежность. Такие расчеты
имеют все признаки прогнозирования, так как они служат обосновани-
ем предполагаемых (прогнозируемых) показателей надежности объек-
та, который может не существовать в реальном исполнении.
Вообще говоря, признаки прогнозирования присущи всем расчетам
в разной степени. Пусть, например, при расчете определяется интенсив-
ность отказов объекта, состоящего из двух последовательно связанных
частей, интенсивности отказов которых известны. Суммирование интен-
сивностей отказов частей объекта не имеет смысла относить в разряд
прогнозирования, так как в данном случае отсутствует анализ процес-
са, в результате которого высказывается прогнозируемая оцецка.
Обычно расчеты надежности связаны с предварительным выявлени-
ем закономерностей, которым подчиняются изменения действующих
факторов, а именно: характер процесса возникновения отказов и про-
цесса восстановления работоспособности, связь между набором вход-
ных величин и действием отказов элементов объекта, предполагаемый
закон распределения входных величин, влияние используемого способа
резервирования, внешних факторов и т. д. Поэтому, как правило, рас-
четы надежности приобретают все черты, присущие исследованиям
сложных, изменяющихся во времени процессов, предсказание характе-
ристики которых называется прогнозированием. По так как исходные
данные, используемые при расчетах, могут определяться с различной
степенью прогнозирования, поэтому и расчеты надежности по степени
прогнозирования могут быть различными.
Методы расчета надежности находятся в состоянии непрерывного
развития. Первые рекомендации сводились к расчетам простых изделий
без учета постепенных отказов и влияния контроля и профилактики.
Развитие теории надежности сопровождалось большим числом работ
в области расчетов. Главное внимание на первых этапах этих работ
обращалось на разработку способов резервирования и методов расчета
надежности при различном резервировании. Это объяснялось тем, что
резервирование оказалось наиболее эффективным средством повышения
надежности при рациональном его использовании.
Для того чтобы разобраться, когда и какой эффект даст тот или
другой вид резервирования, понадобились предварительные расчеты.
J51
Так возник большой перечень работ в области расчетов резервирован-
ных изделий.
Работы в этой области далеко не закончены. Возникают все новые
и новые виды резервирования, а вслед за ними и потребность в новых
способах расчетов. Наиболее употребительные методы резервирования
можно разделить на следующие три группы:
— элементное или аппаратурное резервирование, при котором
в объекте наряду с основными элементами имеют место резервные. Спо-
собы включения их чрезвычайно разнообразны (параллельное, последо-
вательное, комбинированное, поэлементное, общее, мостиковое, по из-
бирательной схеме, постоянное, с переключающими устройствами
И т. д.);
— временное резервирование, при котором предусматривается за-
пас (резерв) времени на выполнение заданных функций. Этот резерв
времени позволяет многократно повторять рабочую операцию, обнару-
живать отказ и устранять его. Отказ в период резервного времени не
приводит к катастрофическим последствиям и его можио ие учитывать
при расчетах;
— информационное резервирование, когда при передаче и пред-
ставлении информации используются добавочные (резервные, избыточ-
ные) средства представления (дополнительные кодовые разряды, коды
с обнаружением ошибок и т. п.).
Информационная избыточность позволяет исключить искажения
в передаче информации даже при наличии отказов в аппаратуре пере-
дачи и отображения и поэтому по своему воздействию на надежность
относится к категории резервирования.
Итак, разработка и совершенствование методов расчета резервиро-
ванной аппаратуры, включая и аппаратуру с автоматическим перестрое-
нием структуры (адаптирующаяся аппаратура), явилось одним из глав-
ных направлений совершенствования расчетных методов.
Вторым направлением совершенствования расчетных методов явля-
ется разработка методов расчета, учитывающих влияние контроля и
восстановления работоспособности. Это направление работ также было
вызвано потребностью практики, так как при использовании высокона-
дежной и сложной аппаратуры было обнаружено, что для обеспечения
высокой надежности такой аппаратуры необходим контроль за ее тех-
ническим состоянием и рационально организованное обслуживание, свя-
занное с заменой деталей и узлов.
В практике использования радиоэлектронной аппаратуры возникли
разнообразные виды контроля, а именно: контроль полный и ограни-
ченный; контроль программный и аппаратурный; контроль непрерывный,
периодический и контроль в случайные интервалы времени.
Восстановление работоспособности аппаратуры также стало разно-
образным (полное и частичное, с потерей и без потери времени и т. д_).
Все это потребовало разработки новых приемов расчета надежности,
учитывающих влияние на надежность разнообразных способов контро-
ля и восстановления работоспособности.
Третьим направлением явились работы в. области расчетов надеж-
ности сложных систем. Обычные методы расчета надежности, ориенти-
рованные на простые изделия, оказались непригодными для расчета
сложных систем. Это сделало необходимым разработку специальных
методов расчета.
152
Четвертое направление объединяет работы по расчетам так назы-
ваемой функциональной и параметрической надежности. Все расчетные
методы на первых этапах развития теории надежности были основаны
на учете внезапных, полных отказов и на предположении о том, что
они подчиняются экспоненциальному закону распределения. Общепри-
нятым считалось также, что отказ устройства вызывается отказами его
составных частей, поэтому интенсивность отказов устройства определя-
ется как сумма интенсивностей отказов ее составных элементов, скор-
ректированная с учетом применяемого резервирования и восстановле-
ния. Такой подход, т. е. элементный расчет надежности, не потерял
своего значения и на современном этапе, однако он стал недостаточным.
Очень часто требуется определить не вероятность того, что откажет
элемент или группа элементов устройства, а вероятность того, что
устройством будет выполнена заданная рабочая функция. Такая задача
стала особенно актуальной с внедрением в технику логических элемен-
тов, т. е. устройств, с помощью которых решаются логические задачи.
Расчет надежности, при помощи которого решают такую задачу, полу-
чил наименование расчета функциональной надежности.
Расчетом параметрической надежности принято называть расчет,
в результате которого определяется вероятность того, что некоторый
параметр или группа параметров, определяющих работоспособность
изделия, не выйдут за пределы допуска.
Расчет параметрической надежности по существу своему является
продолжением обычных инженерных расчетов, которые проводятся
в процессе проектирования аппаратуры. При проектировании рассчи-
тываются основные параметры: напряжения в определенных точках
цепи, устойчивость, точность, коэффициенты усиления и т. д. Расчет
параметрической надежности является продолжением расчетов указан-
ных параметров и сопровождается изучением изменений параметров
с течением времени и определением вероятности выхода их за допусти-
мые пределы. Разработку инженерных методов расчета функциональ-
ной и параметрической надежности следует считать одним из актуаль-
ных направлений работ по расчетам надежности.
Уже отмечалось, что все расчеты надежности на стадии проектиро-
вания в той или другой степени носят характер прогнозирования. Сте-
пень прогнозирования расчетов тем выше, чем в большей степени учи-
тывается в них характер процессов изменения факторов, влияющих на
надежность.
Расчеты параметрической и функциональной надежности в наи-
большей степени отвечают этому требованию, поэтому они в наиболь-
шей степени соответствуют наименованию прогнозирующих расчетов.
Расчеты, в результате которых дается констатирующая оценка надеж-
ности, будем называть оценкой надежности.
8.2. Классификация методов расчетов надежности
По целевому назначению различают расчеты на стадии проектиро-
вания (прогнозирующие расчеты) и на стадии эксплуатации и испыта-
ний (главным образом — констатирующие расчеты). По принципиаль-
ным основам своим расчеты делятся на элементные (аппаратурные) н
функциональные (частым случаем которых являются расчеты парамет-
рические). По характеру учитываемых отказов различают расчеты
153
с учетом одного вида отказов (внезапных, полных) и с учетом харак-
теристик отказов (внезапные, постепенные, полные, частичные, типа
замыкание, обрыв, сбои и т. д.); по виду изделий — расчеты простых
изделий и сложных систем. Расчеты простых изделий в свою очередь
делятся на расчеты резервированных и нерезервированных изделий,
изделий без восстановления и с восстановлением. Расчеты сложных си-
стем делятся на расчеты систем управления и расчет систем переда
п отображения информации.
Из приведенной классификации (рис. 8.1) видно, что существует
много различных методов расчета надежности. Пх развитие идет -о
пути разработки все новых моделей расчета. Реальные объекты pacv-
та никогда строго не соответствуют некоторой одной модели. Поэто: •.
Расчеты надежности.
На стадии испытании и эксплуатации.
На стадии проектирования
Р Элементные (аппаратурные)
Простых изделий
| Функциональные и параметриче:чие~\^
1
Сложных систем
вольигвых I
Ветвящихся Мостиковых
Нерезервированных г резервированных
L
С восстановлением
I С учетом только полных внезапных отказов
5ез вооотсосвоения
| С учетом отказов различного вида ,
Рис. 8.1. Схема классификации расчетов надежности.
на основании существующих и вновь создаваемых моделей приходится
составлять структурную схему расчета надежности конкретного объек-
та с учетом его особенностей.
Не все методы расчета, приведенные в классификации, одинаково
хорошо разработаны. К числу наиболее известных относится элемент-
ный (аппаратурный) расчет с учетом одного вида отказов (внезапного
полного). К наименее разработанным относится функциональный рас-
чет с учетом характера отказов (особенно сбоев), а также расчет слож-
ных систехм управления и передачи информации.
8.3. Основы расчетов надежности и их развитие
Как мы уже отмечали, наиболее известным является расчет надеж-
ности простых устройств, отказы которых носят внезапный характер и
подчиняются экспоненциальному закону распределения. При этом р<, -
чет разбивается на следующие этапы:
154
— составляют структурную схему расчета надежности на оспоз:-
нии физических представлений о работе устройства. Структурная схема
расчета надежности представляет в общем случае цепь расчета после-
довательно и параллельно соединенных элементов устройства;
— записывают уравнения расчета на основании структурной схемы;
— в эти уравнения подставляют числовые значения показателей
надежности элементов;
— • решая уравнения надежности, определяют показатели надеж-
ности исследуемого устройства.
При такой методике расчета определяют следующие показатели:
Вероятность безотказного состояния простого устройства
а) для структуры с последовательным соединением элементов:
pipz Рп,
(8.1)
где pi — вероятность безотказной работы элементов, соединенных по-
следовательно в структурной схеме расчета;
б) для структуры с параллельным соединением элементов:
п с\ fC'n
П АЯА) —- (8.2)
\ / \ /
где Ед-— сумма вероятностей безотказной работы параллельно соеди-
/с2 \
Iя I
ненных элементов; Я\Нр{Рз1— сумма парных произведений вероятно-
стей безотказной работы этих же элементов (число слагаемых С2);
/с3 \
I /г I
Е ’ /i— сумма произведений вероятностей безотказной работы па-
раллельно соединенных элементов, взятых по три из общей совокупно-
сти (число слагаемых ).
Вероятность работоспособного состояния сложного устройства рав-
на сумме вероятностей его работоспособных состояний (д)
P=3₽f... (8.3)
Последующее развитие расчетных методов связано с расчетами
восстанавливаемых устройств. Возникли структурные схемы расчетов
в виде графов состояний с обозначением вероятностей возможных пере-
ходов из одного состояния в другое.
Вначале на основании анализа изделия
составляют граф (рис. 8.2) возможных со-
стояний, на котором указывают номера со-
стояний, направления (стрелки) и интен-
сивности переходов. На основании графа
состояний составляют систему дифференци-
альных уравнений, каждое из которых со-
ответствует определенному состоянию и за-
писывается по следующему правилу.
В левой части уравнения записывают
где Pk(t)—вероятность &-го со-
стояния, в правой части — столько членов,
Рте 8.2. Граф, возможных со-
стояний.
155
сколько стрелок непосредственно связано с данным Л-м состоянием.
Каждый член равен интенсивности потока событий, обозначенной на
стрелке, умноженной на вероятность того состояния, из которого исхо-
дит стрелка (знак плюс, если стрелка направлена в данное А-е состоя-
ние, н минус в противном случае).
Для состояния Xj, изображенного на рис. 8.2, уравнение состояния
имеет следующий вид:
dPt (t)/dt===faP2(t) +ЬВД - (Х12+Х1з) Pi (0. (8.4)
Решая полученную систему уравнений, определяют вероятность на-
хождения изделия в каждом из возможных состояний. Это решение су-
щественно облегчается для случая, когда имеет место установившийся
режим работы изделия, позволяющий принять Лг== const; dPildt—Q.
Тогда система дифференциальных уравнений переходит в систему алге-
браических уравнений.
Суммарная вероятность безотказной работы изделия, т. е. коэффи-
циент готовности изделия, равна сумме вероятностей работоспособных
состояний его:
k
Pz=2A‘. (8-5)
i
Среднее время до первого отказа изделия равно сумме значений
среднего времени работы в каждом из частных работоспособных со-
стояний, т. е.
k
^=2^-, («О
1
где k — множество работоспособных состояний.
Значения Л и Pi вычисляют в результате решения системы урав-
нений вида
— Рк (O) = ^(fc-I)fc^ft-1 — Тк + %(к+1)к'1 к+и
Рп(^)== ,
При определении среднего времени до отказа принимают ро(0) —1,
а рг(0)=0. При определении среднего времени, приходящегося на от-
каз, вероятность предотказового состояния принимается равной 1,
а всех остальных — равной нулю. При этом
Ti= ^pi{t)dt. (8.8)
о
В основе вывода расчетных уравнений (8.1) — (8.8) лежит учет
всех возможных состояний работоспособности. Рассмотрим, каким об-
разом получено уравнение (8.2) для трех параллельно соединенных
элементов (рис. 8.3). Существует семь возможных работоспособных со-
стояний устройства:
первое — все три элемента работоспособны (его вероятность равна
Pipzps);
второе, третье и четвертое — работоспособны любые два элемента
из трех [вероятности их равны pip2(l—рз), Р1Рз(1—рг), р2рз(1 — Pi)];
156
8.3. Структурная схема рас-
чета надежности.
пятое, шестое и седьмое — работоспособен один из трех элементов
[вероятности их равны: pt (I —р2) (1 — р3): pz(i— pi) (1— р3); — pt)X
Просуммировав вероятности всех возможных работоспособных со-
стояний, получим вероятность работоспособности устройства
Р= (Р14-Р24-Рз)~(Р1Р2+Р1Рз+Р2Рз) 4-/адр3. (8.9)
Выявление и учет всех возможных состояний исследуемого устрой-
ства становится более трудным при переходе к расчету сложных струк-
тур. Для мостиковой структуры, напри-
мер, трудно подобрать структурную схе- а.
му расчета надежности, состоящую из °
последовательных и параллельных уча-
стков цепи.
Для расчета сложных структур, а
также для расчета логических устройств
оказались удобными так называемые ло-
гико-вероятностные методы расчета, суть
которых заключается «в следующем. На Рис'
основании анализа физических особен-
ностей работы устройства составляется
логическая функция работоспособности устройства, т. е. уравнение, левая
часть которого представляет признак работоспособного состояния
устройства, а правая — условие работоспособного состояния, записан-
ное на языке алгебры логики, т. е. логическая функция работоспособ-
ности.
От логической функции переходят к уравнению работоспособности
в символах обычной алгебры на основании следующих зависимостей:
— если х4 и xz связаны логической операцией дизъюнкция, то
х, V х2=л2 — xt х2; (8.1 Оа)
— если Xi и х2 связаны логической операцией «исключающее ИЛИ»,
то
Xi ИЛИ... ИЛИ Х2=Х1+х2—2xiX£ (8.106)
— если Xi и х2 связаны логической операцией конъюнкция, то
х1Дл8=х1х2. (8.10в)
При этом следует иметь в виду, что XiXi=Xi.
Вероятность работоспособного состояния устройства определяется
путем подстановки в правые части зависимостей (8.10) вместо обозна-
чений простых событий Xi вероятностей этих событий рх^
Ипользуем, например, этот метод для вывода уравнения (8.9) в со-
ответствии с рис. 8.3. Под работоспособностью исследуемой схемы бу-
дем понимать проводимость ее от точки с к точке Ь. Если проводимости
отдельных элементов схемы обозначить Xi, xZ) xs, а вероятность этих
событий — pxt, Рх2, Рхз> то:
— логическая функция работоспособности устройства, изображен-
ного на рис. 8.3, равна
F — хг xz х5,
— уравнение работоспособности в сшмволах обычной алгебры имеет
вид
F=Xi 4- х24-х3— (Х1Х2 4- XfXs 4- х2х3) 4- Х1Х2Хз‘,
157
— вероятность работоспособного состояния схемы равна P = pxi +
4“рх24-рхЗ-(Рх\Рх2 4“ pxipx3 4“Рх2.Рхз} 4“ pxi.px"2.PxZ-
Логико-вероягностнын метод наиболее эффективен для расчета на-
дежности сложных структур, сведение которых к последовательно-па-
раллельным структурным схемам встречает затруднения.
Укажем наиболее распространенные уравнения алгебры логики, ко-
торые можно рекомендовать для расчета надежности сложных струк-
тур:
а Д (Ь V г) = (а Д b) V (« Д с),
а V Ф А с) = (а V Ь) Д (а V с),
а\/ Ь~а /\Ь,
а /\Ь = а\/b, } (8.11)
- - I
а V (a A b) = b V (6 A CL) = а\/ /?,
f (^ I г ^2 ’ • • t — ^n)-I (fl t» f •. - 1 - -
... an) \/ак1 (au az ... 0 ... atl),
где A — знак конъюнкции (логического умножения — операции И),
V — знак дизъюнкции (логического суммирования—операции ИЛИ), черта
над символом — операция отрицания события.
Пример I. Записать уравнение на-
дежности для устройства, изображенно-
го на рис. 8.4.
Рис. 8 4. К примеру расчета надежности.
Решение. 1. Логическое уравне-
ние работоспособности (прохождение
сигнала по схеме)
I — ub< V ое V de — abc -j- ае 4- de —
— (abce -j- abed -j- aedc) 4- a be de.
2. Вероятность работоспособного со-
стояния устройства за заданное 'время t
Р =‘Paptpc flpaPe + Pdpc—
’ kPaPt>PcPe + pap bPcPd +
4" PapcPdPc) + Pupt>Pcpd.Pe.
Пример 2. Записать уравнение на-
дежности для устройства, изображенно-
го на рис. 8.5.
Решение 1. Логическое уравне-
ние работоспособности
XI /\ [(*3 /\ X?) V (X j /\ Х8) j \/
V Хг /\ {(Xi Х7) (Х6 /\ XS)J.
2. Запись на языке обыкновенной
алгебры
F= (Х1ХэГ7 + Х1ХзХ8—Х1ХзХчХ$Х&) +
+ (Х2Х.-.Х7 + x2xexs—Х2Х.5 Х7Х6Х8) —
--[ (*1X3X7 + X]X5Xs—Х1ХзХ7Х5Хв) +
4- (х2х4х7 4- х2Хб*8—XoXiXvXGXe)].
3, Подстановка вместо значений со-
бытий их вероятностей
Р=Р1Рзр7 {1—Pspsl'l — Р2Рб( 1—Pi)]—
—[Р2р4 (1— P^Ps—peps) — PzpGps]} +
4- piP5ps[ 1 —Р2ре (I —pepi) —p^pepi) 4-
4-ргр4р7(!1—Peps) -YPzPePs-
Пример 3. Записать уравнение на-
дежности для мостиковой схемы, изоб-
раженной на рис. 8.6.
Решение. 1. Логическое уравне-
ние работоспособности
Г — (х3 V V х2 (х4 V *5*3) =
= XjX3 V Х 1X5X4 V *2*4 V Х2Х5Х3-
2. Запись F на языке обычной ал-
гебры
F=XtXs -г Х1Х4Х5 4- х2Х14- Х2Х3Х5—
—(Х1Х3Х4Х5 4- Xj Х3Х2Х4+Х1Х3Х2Х5 +
+ Х1Х4Х5Х2 4- Х1Х4Х5Х2Хз 4- Х2Х4Х3Х5) +
+ Xj X3XtX5X2 4- Х1ХгХ4Х5Х2 4- Х1Х3Х2Х4Х5 4-
4- Х1Х4х5х2Хз—xix2x3x4x5=
— Х1Х3 4- Х1Х4 хя 4- х2х4 4- х2х3х5—
—Х1Х3Х4Х5—X1X2XSX4—Х1Х2Х3Х5—
—Х1Х2Х4Х3—Х2Х3Х4Х5 +
4-2Х1Х^.гзх4х5.
158
3. Вероятность работоспособного со-
стояния мостиковой схемы
Р = Рх 1рх 3 + PxiPx -.Рха 4- Px2pxi +
+ px2PxzPx'j,---pxlpxzPxipxZ---
--pxipxzPxSPxi----PxiPxZpxipxS
--pxipxipxiPxa—рк->Рхп.рхъРх-% +
-I~~px^px2px3pxipx:i-
При равенстве pi=p пряуч :гм
P=2[P -г 2ps—5р4 4- 2р:'
Третий пример можно решить с по-
мощью дру;чх приемов, основанных на
применении уравнений алгебры логики.
Рас • >м v перекрестными <яя
ЗЯМЙ.
Послезнее уравнение системы (811) по-
зволяет ра^тожить уравнение алгебры
логики на две составляющие.
Логическое уравнение 'В этом приме-
пе имеет вид
f ^х,х, V Х1Х4Х5 V х2х4 V х-х3х3-
Разложим его по аргументу х3:
Р = Х3 [Xi (Х3 \/ Х.1) V Х2 (X.j. V Х2)] V
X/jXj [XjXj \/ Х2Х4] = Xg [(Хз \/ Х4) /\
/\ (Х3 \/ Xg)J -pJXg (XjXj \/ Х2Х4) =
= х5 [(х3 4-xt — х3х4) (х, 4- х2 —
— xtx2) J 4- (1 —х5) (XjXs 4- x2xt —
— XjX2x3x4) (8.1х,)
Полученный результат совладает с ре-
шением примера по первому варианту.
Можно предложить также и третий
вариант решения третьего примера. Ум-
ножив логическое уравнение на (х5Д
Х/хэ), равное единице» получим
Р = Х3 (Х3Х3 \/ Х2Х4 \/ XjXj \/ Х2Х-|) \/
V x5(xjX3 v х2х4) - *;, Г*, (х.-< V X.) V
V X» (Х3 V Х4)] V Х5 (Х,Х3 V X2Xj)
~= Х5 (Х» V Xj) (Xj \/ Х2) \/ Xg (XjX3 \/
V х2х.,) .
Это логическое уравнение совпадает с
выражением, полученным при втором
варианте решения.
Уместно заметить, что известный
способ решения, основанный на разло-
жении мостиковой схемы на две экви-
валентные схемы с последовательно-па-
раллельным соединением элементов
(рис. 8.6), приводит к расчетному урав-
нению (8.12).
Рис. S 6. Мостиковая схема.
Таким образом, уже на данном этапе развития теории надежности
имеется достаточно большое количество средств, позволяющих получить
уравнения надежности.
8.4. Прогнозирование функциональной надежности
В основе-расчета функциональной надежности лежит, анализ функ-
ций, выполняемых изделием. Пусть, например, требуется определить на-
дежность делителя напряжения, изображенного на рис. 8.7. Его функ-
циональное назначение — создавать напряжение на выходе (£7ВЫХ), рав-
ное GBbJ х—U0Г3Х4Д (Гз 4- ) (г 1 + г г) + ГзГь . Это у р а*вн ение можно также
представить в следующем виде:
^вых== ПсГз/(Г1-ЬГ2-гГз4-Г1Хз/Г4 4-Г2Гз/Х4) - (8.13)
При элементном расчете надежности не учитывают степень влия-
ния отдельных элементов на надежность устройства. На самом же деле
159
а влияние увеличения
Рис. 8.7. Делитель на-
пряжения.
степень такого влияния имеет значение. Так, например, обрыв резисто-
ра п(Г1 = оо) приводит к полному отказу устройства, а замыкание —
только к частичному отказу. Обрыв же резистора г4, наоборот, приво-
дит к частичному отказу, а замыкание — к полному. Увеличение сопро-
тивления г2 всегда приводит к уменьшению выходного напряжения,
г3 зависит от отношений ri/r3, г2Лз> п/>4,
Поэтому для расчета надежности, т. е. ко-
личественного определения свойства изделия
выполнять заданные функции, необходим прин-
ципиально другой подход по сравнению с тем,
который используется при расчете элементной
надежности. Функциональную надежность рас-
считывают в следующей последовательности:
1. Формулируют заданные функции.
2. Записывают уравнение работы устрой-
ства, устанавливающее связь между заданной
функцией (выходным параметром) и первичиы-
ачестве первичных параметров следует выбирать
характеристики элементов, из которых состоит данное устройство. Для
делителя напряжения таким уравнением будет (8.13).
Для схемы на полупроводниковых транзисторах, изображенной иа
рис. 8.8, уравнениями работы являются [80]:
ми параметрами. В
^бэ отн— ^бб -РгДРгН-Рз) —t/кэ насРз/(Р2Н_,Рз) —
—JR2R3 (Дбо+7п) / №+Рз); ЛсДб=(Л-Д) / (Д—/з) -
Для автоматических систем управления уравнениями работы явля-
ются уравнения, устанавливающие связь устойчивости работы с первич-
Рис. 8.8. Схема триггера.
Рис. 8.9. Логическая схема ИЛИ—НЕ
ными параметрами [84]. Для феррит-трапзисторных ячеек эти уравне-
ния связывают амплитуду и ширину выходного импульса с первичными
параметрами ячейки. Для диодно-транзисторной логической схемы
ИЛИ — НЕ (рис. 8.9) уравнением работы является функция алгебры
логики:
F(x)=xl \/ xs V хя.
3. На основании анализа уравнения работы составляют структур-
ную схему расчета надежности и рассчитывают надежность, обуслов-
ленную полными отказами элементов (Pi). Для делителя напряжения,
например, анализ уравнения (8.13) позволил установить, что обрыв и
160
Гц, замыкание г4 и обрыв либо замыкание г3 приводит к полному отказу
устройства.
4. Дифференцируя уравнение работы по каждому из первичных
параметров, определяют коэффициенты влияния первичных параметров
на выходной параметр. В результате получают уравнение точности
устройства:
<8л4>
i=l
Для делителя напряжения
. ди лТ1 . ди. . . ди . .ди . .ди .
Дцвых = ттт- + — Дг, 4- -г- Дг2Ч- Дг, 4- -j— Дг4.
вых ° 1 д/з 1 ’ drz 21 дг& 8 1 ст4 4
5. Решая уравнения (8.14), определяют область возможных значе-
ний выходного параметра и тем самым вероятность отсутствия выхода
его за пределы допуска. Эта вероятность принимается равной вероят-
ности Рп отсутствия отказа устройства, вызванного постепенными от-
казами элементов.
6. Полная вероятность безотказной работы устройства равна Р~
= PiPn.
Необходимость решения уравнения (8.14) может возникнуть в двух
случаях:
1. По известным допускам на первичные параметры Дхг необходи-
мо определить область возможных значений выходного параметра <р
(задача точности в момент сборки изделия). В этом случае ошибки пер-
вичных параметров следует определять из допусков на эти параметры.
2. По изменению первичных параметров в процессе эксплуатации
необходимо найти вероятность отсутствия выхода основного параметра
за пределы допуска (задача расчета надежности). В этом случае зна-
чения Д-Х{ следует определять на основании изучения изменений пер-
вичных параметров в процессе эксплуатации изделия.
Известную трудность при решении уравнения (8.14) может выз-
вать процедура дифференцирования по первичным параметрам. Для
упрощения ее можно использовать метод преобразованной электриче-
ской цепи [84].
Расчет функциональной надежности дискретных логических схем
обладает некоторыми специфическими особенностями. При определении
Pi рекомендуется [82] составлять таблицу состояний работы устройст-
ва с указанием возможных комбинаций входных сигналов.
При различных наборах входных сигналов различно влияние отка-
зов элементов схемы на ее надежность. Так, например, при подаче на
вход схемы рис. 8.9 сигналов [101] (xi=xs= 4-Зв, х2=Ов) обрыв дио-
дов Д1 и Д3 не повлияет на работоспособность схемы.
Показатель надежности схемы определяют для каждого из ее ра-
бочих состояний. Суммарная вероятность работоспособного состояния
схемы находится по уравнению полной вероятности: Pi — Pipi-\-P2Pz+
4- ... +Pnpn, где Pi — вероятность безотказного состояния при i-м на-
боре; Pi — вероятность г-го набора.
Расчет функциональной надежности сопровождается исследованием
процессов изменения первичных параметров и прогнозированием функ-
ционирования устройства. Поэтому есть все основания расчет функцио-
нальной надежности называть прогнозирующим.
11—813 161
8.5. Расчет надежности с использованием производящих
функций
Производящей функцией распределения случайной величины х,
принимающей значения 0, 1, 2..., называется следующее выражение:
(5) = p0So+piSi 4-...pnSn, (8.15)
где ро, pi,..., рп - - вероятности того, что случайная величина х прини-
п
мает значения: 0, 1, 2 ...; Pi=z «Si—параметр производящей фуик-
1
ции.
При известном распределении случайной величины х выражению
(8.15) можно придать более компактный вид. Если х имеет биноми-
нальное распределение, т. е. вероятность т событий при п опытах (ртп)
представляет собой член разложения бинома (<74р)к, тогда производя-
щая функция вероятностей числа событий т при числе опытов п (про-
сто производящая функция) принимает следующий вид:
<Pn(S) = (<7+P-S)n, (8-16)
где q=\—р.
Выражение (8.16) справедливо для случая, когда вероятность р не
меняется от опыта к опыту. В общем случае, когда р в каждом из опы-
тов разные, справедливо уравнение
?п(5)=П -FA’S).
i=l
Для распределения Пуассона
Pk=ake~a/kl (8.17)
производящая функция после подстановки в (8.15) значений Ph, где k
изменяется от 0 до п, принимает следующий вид:
фп(£) (8-18)
Для геометрического распределения — распределения числа опытов
до успешного результата, т. е. для распределения вида
Pk=pqh (8.19)
производящая функция после подстановки Ph в уравнение (8.15) при-
обретает вид
<M-S)=p/(1-<7«S). (8.20)
Производящие функции позволяют сократить вычисления в ряде
случаев расчета надежности. Пусть, например, требуется определить ве-
роятности отказов числа элементов 0, 1, 2, 3, .т. е. tfo, Qi, ?2, Уз, в схеме,
изображенной на рис. 8.3. Решение этой задачи методом перебора всех
возможных состояний достаточно громоздко. Применяя понятия произ-
водящей функции, получим
фз(5) = (p+qS)3==p3+3pzqS+3pq2S2+q3S3. (8.21)
Из уравнения (8.21) следует, что
— вероятность отсутствия отказов всех трех элементов равна р3;
— вероятность того, что откажет один элемент из трех, равна Зр2<у;
— вероятность того, что откажут два элемента из трех, равна Зрр2;
— вероятность того, что откажут все три элемента, равна «у3.
Наиболее эффективно применение про-
изводящих функций при расчете надежно-
сти сложных систем.
Введем следующие определения. Систе-
ма называется иерархичной, если она со-
стоит из нескольких уровней. Верхний уро-
вень называется нулевым рангом системы.
Каждый последующий получает соответст-
венно номера рангов: первый, второй и т. д.
На каждом ранге расположены элементы,
от которых идут разветвления к элементам
нижних рангов. Число разветвлений назы-
вается коэффициентом разветвления (а).
Если на каждом ранге имеет место один
коэффициент разветвления — система назы-
вается симметричной. Для разветвленной
схемы передачи информации, обладающей
симметричным характером (рис. 8.10), ко-
эффициентом разветвления а и вероят-
ностью Р работоспособного состояния от-
Рис. 8.10. Схема разветвленной
структуры.
дельного канала, справедливо следующее выражение для производя-
щей функции распределения числа работоспособных каналов на
и-м ранге:
<р„С$) =(РФп-1(£) 4-9?- (8.22)
Заметим, что <р0 (<S) =S.
Выражение (8.22) позволяет непосредственно из схемы рис. 8.10
при а=2 установить, что
— на первом ранге системы число работоспособных каналов рас-
пределяется по закону <pi(S) = (pS+q)z=p2Sz+2pqS+q2S°',
— на втором ранге <p2(S) — [p(pi(S) +q]z;
— на третьем ранге фз(*$) =[p<p2(S)
При использовании производящих функций полезно иметь в виду,
что среднее значение случайной величины х равно
М(х) =Жр (S) !dS, при $ = 1; (8.23)
дисперсия случайной х
ВД; <>»«>
производящая функция C(S) суммы неотрицательных целочисленных
случайных величин х и у, имеющих производящие функции Л(5) и
B(S), равна
C(S)=,1(S)B(S). (8.25)
Пример. Найти распределение числа
•и среднее число работоспособных кана-
лов на втором ранге схемы рис. 8.10 при
условии, что вероятность работоспособ-
ности канала равна 0,9.
Решение. И. Производящая функ-
ция для второго ранга равна
11*
Фе ($) ={р352+^p^-qS+pq2 + с]2 -
- 0,531 S4+0,23653+0,'185S2+
+0,0355+0,012.
Отсюда вероятность того, что все кана-
лы второго ранга системы будут ис-
пр шы, равна 0,531;
163
— вероятность исправности трех,
двух и одного каналов соответственно
равна 0,236; 0,185; 0,035; вероятность
того, что хотя бы один канал будет ис-
правен, I-—0,012=0,988, и среднее число
работоспособных каналов на втором
ранге системы М (х) =4 • 0,5314-3 - 0,236+
2.0,185+0,035=3,237.
8.6. Заключение по расчетным методам оценки
и прогнозирования надежности
Надежность любого изделия, в том числе и радиоэлектронной аппа-
ратуры, зависит от большого числа разнообразных факторов, часто свя-
занных между собой сложными зависимостями. Учесть все эти факторы
и связи при расчетах чрезвычайно трудно.
На данном этапе расчетные методы развиваются в направлении
разработки более сложных моделей и отыскания для иих расчетных
уравнений, удобных в использовании и учитывающих возможно боль-
шее число действующих факторов. В каждом случае расчета подбира-
ется наиболее подходящая модель расчета. Но никакие модели ие могут
полностью обеспечить учет всех своебразий исследуемых устройств. По-
пытки учесть возможно полнее своеобразие рассчитываемых устройств
привели к разработке ряда новых методов расчета, а именно: расчетов
параметрической надежности, расчетов функциональной надежности,
расчетов, основанных на анализе физико-химических процессов и т. д.
Некоторые из перечисленных методов находятся в начальной стадии
их разработки, другие уже применяются иа практике.
Результаты расчетов существенно зависят от того, при каких исход-
ных данных, с помощью каких методов и при каких допущениях прово-
дился расчет. Поэтому очень важно при использовании расчетных пока-
зателей надежности каждый раз указывать условия, при которых полу-
чены эти показатели, целевое назначение показателей и область их ис-
пользования. Отсутствие таких указаний часто приводит к серьезным
недоразумениям. Результаты расчета, основанного на показателях про-
изводственно-технологической надежности, иногда сравниваются с ре-
зультатами эксплуатации, в условиях которой действуют совсем другие
факторы, обусловливающие надежность. Естественно, что при таком
сравнении обнаруживаются расхождения, как бы порочащие расчетные
методы.
Главным назначением расчетов надежности следует считать:
- - сравнительный анализ различных конструктивных (схемных) ва-
риантов изделия на стадии его проектирования для обоснованного вы-
бора комплектующих элементов, общей структурной схемы, способов
резервирования, методов контроля и обслуживания,
— ориентировочная, прогнозируемая оценка надежности изделия
на этапе утверждения технического проекта для обоснования вывода
о том, что проектируемое изделие может быть изготовлено удовлетво-
ряющим требованиям по надежности;
— ориентировочная, прогнозируемая оценка надежности сложного
изделия на этапе отработки опытного образца для обоснования рас-
пределения требований к надежности частей изделия и обоснованного,
хотя и ориентировочного, определения состава и количества запасных
частей и сроков обслуживания.
164
ГЛАВА 9. ПРОГНОЗИРОВАНИЕ НАДЕЖНОСТИ В ПРОЦЕССЕ
ИСПЫТАНИИ И МОДЕЛИРОВАНИЯ
9.1. Виды испытаний на надежность
Проблема испытаний на надежность приобретает все большую ост-
роту и актуальность. Из всех существующих в данное время методы
оценки надежности, основанные на результатах 'испытаний, являются
наиболее достоверными. По существу расчеты и моделирование строят-
ся на результатах испытаний, так как исходные данные — информация
о надежности элементов изделий — берутся нз сферы испытаний и экс-
плуатации. В ряде случаев, например при анализе надежности элемен-
тов радиоэлектронной аппаратуры, практически возможным способом
оценки надежности все еще остается эксперимент, испытания либо экс-
плуатация. Это объясняется большим числом факторов, обусловливаю-
щих надежность и связанных между собой сложными зависимостями.
Методы испытаний на надежность продолжают бурно развиваться.
На первых этапах внедрения они представляли заключительный этап
сдачи изделий заказчику и предназначались для разделения изделий на
годные, удовлетворяющие требованиям к надежности, и негодные, не
удовлетворяющие этим требованиям. На последующих этапах к этим
задачам добавились новые. Потребовалось управлять процессом фор-
мирования надежности на всех этапах создания изделия. Но для этого
нужно знать состояние процесса в каждый данный момент времени и
предвидеть состояние будущее. Это сделало необходимым переход к си-
стеме разнообразных испытаний и проверок, проводимых для решения
разных задач, ио преследующих одну цель — обеспечить требуемую на-
дежность изделия. Так возникли разнообразные виды испытаний на-
дежности. Они пока еще представляют разрозненные испытания, но ста-
новится очевидной очередная проблема — наряду с дальнейшим совер-
шенствованием отдельных видов испытаний создание единой системы
связанных между собой и дополняющих друг друга испытаний и прове-
рок для каждого из конкретных типов промышленных изделий.
К основным группам испытаний на надежность следует отне-
сти [85]:
1. Испытания для определения количественных показателей надеж-
ности. Их принято называть определительными и можно проводить по
различным планам, а именно: без восстановления до отказа всех изде-
лий (план 7VB/V), без восстановления до фиксированного времени испы-
таний (план А/БТ), без восстановления до фиксированного числа отка-
зов (план NBn), с восстановлением до фиксированного времени испыта-
ний (план /VBT) и т. д. Характерной особенностью этой группы испыта-
ний является то, что они фиксируют (констатируют) показатель на-
дежности изделий, которые прошли испытания, т. е. в данном случае
производится оценка надежности, обращенная в прошлое, определяется
уровень надежности, которым обладали изделия до испытания и который
был обнаружен (зафиксирован) при испытаниях. Вместе с тем эти планы
содержат элементы прогнозирования, так как они основаны на прогно-
зируемом (предполагаемом) законе распределения времени работы до
отказа изделия. Если испытаниям подвергается выборка из партии
изделий, то оценка надежности партии изделий по результатам испы-
таний выборки приобретает характер прогнозирования надежности пар-
165
тии на основании .предположений о степени совпадения свойств изделий,
входящих в партию и в выборку.
2. Испытания, в результате которых контролируется некоторый
признак, позволяющий утверждать, что уровень надежности не ниже
заданного. Этим признаком может быть число отказов изделий в про-
цессе их испытания и характер отказов либо некоторый косвенный по-
казатель надежности (уровень «шумов», количество выделяемого тепла,
спектральный состав излучения и т. д.). Такие испытания принято назы-
вать контролирующими. Качество контролирующих испытаний опреде-
ляется оперативной характеристикой, т. е. функцией, связывающей ве-
роятность приемки изделия в качестве годного и показатель качества
исследуемого изделия (показатель надежности, процент «засоренности»
исследуемой выборки негодными изделиями и т. д.). Эта группа испыта-
ний содержит большее число признаков прогнозирования по сравнению
с первой группой. Результаты испытаний основаны на изучении таких
процессов, событий и связей между ними, которые обусловливают пред-
полагаемую надежность изделия.
9.2. О прогнозировании надежности по результатам
определительных испытаний
В результате определительных испытаний получают информацию
о времени возникновения отказов испытуемых изделий. На основании
обработки этой информации получают сведения о параметрах функции
F (t) распределения до возникновения отказов. Для того чтобы можно
было на основании опытных данных прогнозировать вероятность безот-
казной работы изделия в течение времени необходимо знать функцию
распределения F(t), так как для каждой функции распределения суще-
ствует своя зависимость между ее параметрами и вероятностью от-
каза.
Прежде чем обрабатывать опытные данные изучается модель воз-
никновения отказов и высказывается предположение о функции распре-
деления F(t). В основе таких предположений лежит следующее. Отка-
зы, возникающие по модели постепенного накопления повреждений
(износ, старение и т. п.), подчиняются нормальному закону с функцией
распределения
F(0
оо
—оо
2с*
di.
Параметрами функции распределения являются среднее время Mt
работы до отказа и среднее квадратическое отклонение времени до
отказа.
Внезапные отказы подчиняются экспоненциальному закону с функ-
цией распределения £(/)=!—ехр (—М) = 1—ехр (—t/T), где 1 —пара-
метр функции распределения.
В качестве промежуточного распределения можно использовать
распределение Вейбулла с функцией распределения F(t) =
= !•—ехр[— где а и b — ее параметры. Когда & = 1, распределе-
ние Вейбулла совпадает с экспоненциальным.
После того как произведен предварительный выбор закона распре-
деления, строится теоретическая функция распределения F(t). На осно-
вании результатов испытаний на том же графике F(t) строится опыт-
ная функция распределения 7\(/). При совпадении опытной и теорети-
166
ческой функций делается вывод о достоверности первоначального пред-
положения о функции распределения. На этом основании производится
оценка параметров распределения и прогнозирование вероятности без-
отказной работы за заданное время t.
Чтобы облегчить сравнение теоретической и опытной функций рас-
пределения, масштабы для построения графиков выбираются такими,
чтобы функция F(t) была прямой линией. Часто это обеспечивается
применением так называемой вероятностной бумаги.
Приведем без вывода формулы для обработки опытных данных
и примеры их применения.
Нормальное распределение. Величина отрезка на оси ординат, соот-
ветствующая значению F(t],
Sfklm.:=='^fFuf/(Upmax' UFmin) j
Lvf! ( Upraax—Upmin) =
где UF=(t—^cp)/o — число о, откладываемых по оси абсцисс, которым
соответствует значение F(f) .по оси ординат. При построении графика
SF берется из табл. 9.1. Для F(t)<C0,o принимается SF=—SF.
Величина £ср определяется по графику. Прямая F(t) пересекает
ось t, проведенную через F(t)— 0,5, в точке А, отстоящей на расстоянии
^сР (рис. 9.1).
Значение о определяется уравнением (jnsrlKt} etga, где Kt —
= Liftman, Lt — максимальная длина линии абсцисс.
Рис. 9.1. Графическое представление зависимостей
параметров функции распределения.
F(O SF Fit) SF F(t) SF Fit)
0,50 0 0,66 20,0 0,82 44,4 0,98 99,6
0,52 2,4 0,68 22,7 0,84 48,2 0,985 106,2
0,54 4,8 0,70 25,4 0,86 52,4 0,990 112,9
0,56 7,3 0,72 28,3 0,88 57,0 0,992 116,9
0,58 9,8 0,74 31,2 0,90 62,2 0,994 121,9
0,60 12,3 0,76 34,2 0,92 68,1 0,996 128,7
0,62 14,8 0,73 37,4 0,94 75,4 0,998 139,5
0,64 17,4 0,80 40,8 0,96 82,3 0,999 150
Экспоненциальное распределение.
F(Z)=l-e-;', (9.1)
Л=—1п[1— (9.2)
FN{t)=ib{t)fN', St—Krt\ Kt=L(t)maxft7nax\
Sf=—KsfIn [1—^(0]; Ksr—L(SF)max/—In[1—F(/)mox].
167
Поэтому после построения F(t) на вероятностной бумаге можно
определить значение 1 из уравнения
Kt SF____
Ksf KSF
tg«;
Lymaxi l^nax(t) — максимальные длины осей ординат и абсцисс в мил-
лиметрах.
Вероятностная шкала для F(t) строится по табл. 9.2.
ТАБЛИЦА 9.2
F(0 F(0 SF4 F(O SF F(O SF F(/) SF
0,0 0 0,25 12,5 0,50 30,1 0,74 58,5 0,94 122,2
0,05 2,2 0,30 15,5 0,54 33,7 0,80 69,9 0,96 139,8
0,10 4,6 0,35 18,7 0,60 39,8 0,84 79,6 0,98 169,9
0,15 7,1 0,40 22,2 0,64 44,4 0,90 100,0 0,99 200
0,20 9.7 0,45 25,9 0,70 52,3 0,92 109,7 0,995 0,998 230,1 269,9
Распределение Вейбулла.
F(t) = 1— ехр{— (//a)b]> (9.3)
—In [ 1—F (t) ] — (x/a)b,
ln{—In [ 1 —F (/) ]}=b In (x/a) = 2.303 b (1 g x—1g a);
b=Kttga/M; /(t = Lx/lgt; M=2,303Ky=
= 2,303 Lyf (ymax—Утгп) У~ 1п{—In [—F (f) ]};
а=/ в точке пересечения прямой F(t) с осью абсцисс.
Вероятностная шкала для F(t) строится по табл. 9.3.
ТАБЛИЦА 9.3
ТАБЛИЦА 9.4
SF, 5F2 W) sf8 t St t St t 5/
0,00 —234,6 0,060 —94 0,66 2,6 1 0 2,2 34,2 4,4 64,3
0,002 —211,2 0,070 —89,1 0,82 18,3 1,1 4,1 2,4 38,0 4,6 66,3
0,003 —197,2 0,080 —84,3 0,90 28,3 1,2 7,9 2,6 41,5 4,8 68,1
0,004 —187,3 0,090 —80,1 0,95 37,2 1,3 11,4 2,8 44,7 5,0 69,9
0,005 —179,7 0,100 —76,4 0,97 42,6 1,4 14,6 3,0 47,7 5,2 71,6
0,010 —156,2 0,200 —50,9 0,99 51,9 1,5 17,6 3,2 50,5 5,4 73,2
0,020 —132,4 0,300 —35,0 0,995 56,6 1,6 20,4 3,4 53,1 5,6 74,8
0,030 —108,6 0,400 —22,8 0,997 59,7 1,7 23,0 3,6 55,6 5,8 76,3
0,040 —100,8 0,500 —12,4 0,999 65,4 1,8 25,5 3,8 58,0 6,0 77,8
0,050 0,62 —1,1 1,9 27,9 4,0 60,2 7,0 84,5
2,0 30,1 4,2 62,3 8,0 90,3
Логарифмическая шкала для St = 100 lg t строится по табл. 9.4.
168
Рис. 9.2. Пример построения функции распределения.
Пример. В результате испытания
18 образцов 15 из них отказали в сле-
дующие интервалы времени:
t 0...100 100—.200 200...300 300...400
Число 5 5 3 2
отказов
По условиям .возникновения отказов
предполагается экспоненциальный закон
распределения. Требуется проверить
прогнозирование и определить прогнози-
руемое значение X, а также прогнози-
руемую вероятность появления отказов
на интервале времени, большем 400 ч.
Решение.
1. Задаемся следующими значения-
ми предельной длины осей абсцисс и
ординат: L(t)tnax—:140 мм, /*(у) тпах~~
= 100 мм, масштаб по оси ординат:
в 1 см 10 ед. SF.
2. Предельное значение вероятности
отсутствия отказа объектов испытания,
которую следует воспроизвести на оси
ординат, примем равным [1—F(/)]min =
=0,001 при предельном значении вре-
мени испытания, которое следует вос-
произвести на оси абсцисс, t-max —
= 700 ч.
3. Определяем значения Kt и Кб г'-
Kt == L (t)max/t-max 0,2 ММ/Ч,
L(Sf)
tnax
KSF^ “in [I— FtOki» =
100 и a
— In 0,001 “ 14,4'
4. Результаты расчетов внесем
в табл. 9.5 и построим график SF=f(t,
Si) (рис. 9.2).
5. Убеждаемся в подтверждении
предположения об экспоненциальном
распределении вероятностей отказов,
так как экспериментальная зависимость
SF от t хорошо интерполируется пря-
мой линией.
6. Продолжим линию на графике до
пересечения с горизонтальной .прямой,
отвечающей значению [1—F(f)]=0,001,
и заметим, что эта точк'а пересечения
соответствует /=700 ч.
7. По графику определяем:
Sfгпax/Sf т,ах = &= о0/’140=0,356j
X = fG’tg <xiKsF~V • 10~
/сp=4/X=200 я.
8. Из графика находим, что прира-
щение вероятности отказов на интерва-
лах 400...500, 500...600, 600...700 ч равно
1/18. Это соответствует предположению
о том, что в этих интервалах возникает
ТАБЛИЦА 9.5
t Опытные Прогнозируемые
100 200 300 400 *00 600 700
St=Kt* 20 40 60 80 100 120 140
5 10 13 15 16 17
N(t) 18 18 18 18 IF ~TF 0,98
13 18 _8_. 18 5 IF 3 18 2 18 1 18 0,018
—0,33 —0,81 — 1.3 —1,8 —2,2 —2,9 —
SF 4,75 11,66 18,72 25,9 31,7 41,7 54,0
169
по одному отказу, т. е. откажут все
18 объектов за 700 ч испытаний с ве-
роятностью 0,98.
При предыдущих графических по-
строениях мы пренебрегали ошибками
вычислений статистических вероятностей
Fnfi) « [1—Fw(0L На самом деле ста-
тистическая вероятность является вели-
чиной случайной, т. е. находится ® не-
которых пределах с некоторой довери-
тельной вероятностью, зависящей от
объема испытаний. Поэтому на графике
рис. 9.2 при исследованиях с учетом
доверительной вероятности должна про-
водиться «е одна, а две линии, опреде-
ляющие предел возможных значений
Sf с заданной доверительной вероятно-
стью
9.3. Ускоренные испытания — разновидность прогнозирующих
определительных испытаний
В основе ускоренных испытаний, в той или другой степени,
используется принцип прогнозирования. По характеру рабочих режимов
различают ускоренные испытания в нормальных и в форсированных ре-
жимах работы. Нормальный режим эксплуатации оговаривается в тех-
нических условиях и б инструкциях по эксплуатации изделий. В [38]
указываются, например, следующие «нормальные климатические усло-
вия»: температура 4-20° ±5 °C; относительная влажность 65±15%;
атмосферное давление 750±30 мм. рт. ст.
Испытания, проводимые в нормальных условиях, можно ускорить
следующим образом:
1. На выходной контролируемый параметр устанавливается более
«жесткий» допуск по сравнению с указанным в технических условиях.
Естественно, что время, в течение которого контролируемый параметр
может находиться в поле «жесткого» допуска, будет меньше, что позво-
ляет сократить время испытаний. Пусть, например, установлено, что
контролируемый параметр изменяется по закону
х=х0+/'(/). (9.4)
В простейшем случае уравнение (9.4) может иметь вид х=х0 +
±ПоА Тогда приращение выходного параметра (Ах) будет равно Ах=
=х—Хо=а^. Если допустимое приращение принять равным Axi, то
время испытаний данного объекта, т. е. время до появления отказа
Ап ~ Ах/Од.
При уменьшении допустимого значения Ах сокращается время
испытаний (быстрее наступает отказовое состояние).
Полученное в результате ускоренных испытаний значение 1К позво-
ляет определить время возникновения отказа при нормальном допусти-
мом значении Ах
Однако этот метод требует предварительного изучения закономер-
ности изменения контролируемого параметра, определения числовых
значений х0 и коэффициентов, входящих в уравнение (9.4), а также
постоянной проверки стабильности этой закономерности и коэффи-
циентов.
2. Испытания можно ускорить, если использовать информацию
о характере случайного процесса возникновения отказов. Задачу уско-
рения определительных испытаний в нормальном режиме можно сфор-
мулировать следующим образом. На испытании находятся п объектов.
Измерения параметров изделий производятся на интервале от 0 до А
в моменты А, А, . •tu. Требуется по результатам измерений на интер-
вале 0 ... Аь определить вероятность отказа изделий на интервале 0 ...
... А, который больше интервала измерений.
170
Из формулировки задачи очевидно, что она является задачей прог-
нозирования случайного процесса. Если о характере прогнозируемого
процесса ничего ие известно, то прежде чем осуществлять прогнозиро-
вание, необходимо изучить процесс на всем интервале времени от 0 до
С, определить функцию распределения отказов и только после этого
ускорять испытания, т. е. проводить их на сокращенном участке време-
ни 0 ... /и с последующим прогнозированием показателей надежности
для интервала 0 ... /г.
3. Испытания можно также ускорить, либо увеличивая объем испы-
туемой партии, либо снижая доверительную вероятность получаемого
результата. Последнее часто является наиболее целесообразным, гак
как снижение доверительной вероятности можно в дальнейшем компен-
сировать накоплением информации о надежности, т. е. объединением
оценок надежности, полученных на различных этапах испытаний, либо
уточнением априорной оценки по уравнению теории гипотез.
4. В ряде случаев процесс появления отказов, возникающих по схе-
ме «накопления повреждений» (износ, старение и др.), сопровождается
косвенными признаками, наблюдение за которыми позволяет прогнози-
ровать время возникновения отказов. В § 2.4 даны сведения о подобных
косвенных признаках, которые позволяют прогнозировать отказы.
В практике проведения ускоренных испытаний используются сле-
дующие косвенные признаки отказов:
— изменение «шумовых» характеристик (при испытании полупро-
водниковых приборов и пленочных резисторов);
— изменение крутизны анодной характеристики электровакуумных
приборов;
— изменение помехоустойчивости при подаче на вход прибора до-
зированной помехи (интегральные схемы);
— изменение теплового поля, создаваемого работающими объекта-
ми (печатный монтаж, резисторы, мнкромашины и др.).
Перечисленные четыре способа ускорения испытаний на надеж-
ность при проведении их в нормальных условиях не исчерпывают всех
возможных способов ускорения. Общей чертой этих способов является
использование дополнительной информации (информации о закономер-
ности изменения контролируемого параметра, о функции распределения
отказов, о связи определяющих и косвенных параметров и т. п.), а так-
же то, что для сокращения времени испытаний используются в той
или иной степени приемы прогнозирования. Указанная общая черта
сохраняется также и при проведении форсированных ускоренных испы-
таний.
Форсированными испытаниями принято называть такие, которые
проводятся в условиях форсирования процесса возникновения отказов.
Такое форсирование можно осуществить различными способами,
а именно: изменением температуры, нагрузки, рабочей частоты, повы-
шением влажности, комплексным (одновременным и последовательным)
изменением температуры н нагрузки н т. д.
Существо форсированных режимов заключается в том, что они
ускоряют процессы износа и старения, а также изменяют физико-хими-
ческие характеристики материалов так, что это изменение приводит
к повышению вероятности отказовых состояний.
Основным ускоряющим фактором, чаще всего используемым для
форсирования испытаний, является температура. Под влиянием темпе-
ратуры изменяется механическая и электрическая прочность материа-
171
лов, падает напряжение разрыва, увеличивается износ, ускоряется ста-
рение, изменяются электропроводность, диэлектрическая проницаемость
и магнитные свойства материалов *. Все это, а также сравнительная
простота аппаратуры для обеспечения тепловых воздействий, способст-
вуют широкому использованию их при форсированных испытаниях.
В основе ускоренных испытаний при форсированных режимах лежат
уравнения [90, 93]:
Рис. 9.3. График ускоренных испы-
таний.
<7о(ео4) — ср[<7* (А)], (9.5)
Wr=X*ZH, (9.6)
где <7* — вероятности отказов в нормальном и форсированном режи-
мах; во, в* — характеристики нормального и форсированного режима;
tr — время работы, гарантируемое для нормального режима; /и—время
испытаний в форсированном режиме; Хо, V — интенсивности отказов
при нормальном и форсированном режимах.
На рис. 9.3 показана возмож-
ность использования уравнения (9.5).
В результате предварительных иссле-
дований строят график функции
<7о(еоМ- Испытания в режиме е* про-
водят в течение времени /и. По резуль-
татам испытаний определяют значе-
ние q* и приравнивают его q®. Далее
по левому графику ^r=f(^o8o) находят
значение tT. Отношение tr/tn=K назы-
вается коэффициентом ускорения ис-
пытаний; К=£г#и=^*До.
Ускоренные испытания в форсиро-
ванном режиме содержат больше
испытания в нормальном режиме, так
элементов прогнозирования, чем
как в этом случае прогнозируется не только процесс изменения опре-
деляющих параметров, но и связь параметров в нормальных и форси-
рованных условиях. Поэтому ускоренные испытания в форсированных
режимах позволяют еще больше сократить время испытаний, однако
точность (достоверность) результатов их будет меньше, так как к ошиб-
кам, имеющим место при ускоренных испытаниях в нормальном режи-
ме, добавляются ошибки определения основных уравнений связи между
результатами форсированных и нормальных испытаний.
9.4. Контролирующие испытания на надежность и их
связь с прогнозированием надежности
В процессе разработки, производства и эксплуатации проводятся
разнообразные испытания для оценки и обеспечения надежности. Было
бы совершенно неразумно сводить все испытания на надежность только
к определительным, так как это привело бы к неоправданным потерям
времени и средств. Контролирующими испытаниями на надежность при-
нято называть следующие два вида испытаний:
1. Испытания и проверки, служащие средством контроля за факто-
рами, влияющими на надежность изделий. В результате таких испыта-
*> Уравнения, устанавливающие связь между изменением температуры и измене-
нием перечисленных характеристик, даны в [80].
172
ний устанавливается, например, что нагрузка на элементы изделия не
превышает допустимую или что при работе изделия не возникает резо-
нансных колебаний, помехозащищенность достаточно эффективна, каче-
ство присоединения навесных элементов не ниже требуемых норм
и т. д.
Если можно было бы контролировать все действующие на надеж-
ность факторы и не только каждый из ннх в отдельности, но н совмест-
ное влияние их, то отпала бы нужда во всех других испытаниях на на-
дежность. Однако, к сожалению, это сделать практически невозможно.
Поэтому наряду с указанным видом контролирующих испытаний необ-
ходим и другой вид испытаний.
2. Испытания, в результате которых с определенной доверительной
вероятностью устанавливается, что изделия по уровню своей надежнос-
ти относятся к определенной группе изделий или что надежность их не
ниже некоторого уровня.
В дальнейшем под контролирующими испытаниями на надежность
будем понимать именно этот вид испытаний, так как первый хотя и
имеет непосредственное отношение к контролю надежности, но сливает-
ся (совпадает) с конструкторскими и техническими проверками, выде-
ляемыми обычно в особую группу.
Контролирующие испытания в общей системе испытаний занимают
важное место. Они играют роль своеобразного фильтра на пути дви-
жения изделий от изготовителя к потребителю. Не отвечая непосредст-
венно на вопрос о том, какова надежность испытуемых изделий, они
обеспечивают выполнение условия: если надежность изделия ниже неко-
торого уровня, то оно будет забраковано с определенной вероят-
ностью.
Контролирующие испытания можно классифицировать следующим
образом. По контролируемым параметрам различают прямые и косвен-
ные испытания; по объектам контроля — индивидуальные и массовые;
по режимам работы — нормальные н форсированные. При прямых
испытаниях ведут наблюдение за основными параметрами, непосредст-
венно (прямо) определяющими работоспособность изделия (например,
значение сопротивления току для резистора). При косвенных — наблю-
дают за косвенными параметрами (например, «шумовые» токи резис-
тора). Индивидуальные испытания представляют собой испытания кон-
кретного изделия, массовые испытания — испытания некоторой массы
изделий (партий, группы, серии, выборки, генеральной совокупности).
Нормальные испытания проводят в нормальных режимах н условиях ра-
боты, форсироваздтые — в форсированных режимах.
Все виды контролирующих испытаний по существу своему являют-
ся прогнозирующими. При проведении их используют аппарат теории
прогнозирования, а именно:
— предварительно изучают закономерности отказов контролируе-
мого объекта и определяют наиболее подходящий вид функции распре-
деления отказов. Затем устанавливают такие контрольные значения па-
раметров, которые позволяют предполагать (прогнозировать), что изде-
лия, прошедшие контроль, относятся к той илн другой группе с опреде-
ленной, заранее установленной вероятностью.
Испытания по так называемому методу последовательного анализа
и испытания, основанные на числе допустимых отказов, равном нулю,
относятся к категории контролирующих. Их методика широко известна.
Заметим, что наиболее распространенным приемом, разработанным
173
в теории прогнозирования и используемым в контролирующих испыта-
ниях, является распознавание образа.
Процесс контролирующих испытаний можно представить в следую-
щем виде. Вначале создают «образ» изделия, удовлетворяющего требо-
ваниям к надежности, или несколько «образов», удовлетворяющих не-
которым уровням требований. Затем наблюдают за признаками, по ко-
торым делается заключение о принадлежности изделий к тому или дру-
гому «образу».
9.5. Прогнозирующие индивидуальные испытания
иа надежность на основе распознавания образов
Прогнозирующие испытания на надежность, основанные на теории
распознавания образов, могут быть индивидуальными и массовыми. Прн
индивидуальном испытании проверке подвергается одни объект. В ре-
зультате испытаний он относится к тому или другому классу по уров-
ню своей надежности.
При массовых испытаниях проверке подвергается некоторая масса
объектов. Однако и в этом случае используется методика индивидуаль-
ного прогнозирования. Каждый из контролируемых объектов исследует-
ся по методике индивидуального прогнозирования и в результате вся
совокупность их распределяется на классы в соответствии с их на-
дежностью.
Теоретические основы таких испытаний изложены в гл. 5.
Из множества различных методов распознавания образов в обла-
сти испытаний па надежность наибольшее применение получил метод
потенциалов, суть которого заключается в следующем. На первом этапе
исследуемые объекты в результате обычных определительных испыта-
ний разбивают на группы по показателям надежности (в простейшем
случае на две группы — удовлетворяющие требованиям к надежности
и не удовлетворяющие им).
Для каждой нз групп составляют набор значений параметров, от
которых зависит работоспособность (надежность) исследуемого объек-
та (значение тока, напряжения в отдельных точках схемы, выделяемая
мощность и т. д.). Этот набор параметров является описанием «обра-
за», определение принадлежности к которому и является конечной
целью исследования. В состав «параметров», описывающих «образ»,
могут входить и косвенные параметры (шум, тепловые излучения, ре-
зультаты проверки изделий на предыдущих этапах изготовления
и др.).
Степень близости некоторого неизвестного исследуемого объекта
к данному образу определяется так же, как определяется значение по-
тенциала в точке, удаленной на некоторое расстояние от источника
электрического заряда, т. е. потенциальной функцией распознавания.
Ей обычно придают следующий вид:
<p(/?) = l/(l+a/?fe), (9.7)
где Я — расстояние между зарядом и точкой, в которой определяется
потенциал; a, k — коэффициенты, которые подбираются при оптимиза-
ции функции распознавания на основании экспериментов. В первом
приближении для функциональных узлов «расстояние R принимается
174
равным
R=\/ W, (9*8)
’ k
где n — число контролируемых параметров; Хм, xkj— контролируемые
параметры исследуемого объекта и объекта, принадлежащего к данно-
му «образу»; [Xk — поправочный коэффициент (в первом приближении
рекомендуется принимать р=1).
На втором этапе исследования производится «обучение» — оптими-
зация распознающей функции, оценка информативности контролирую-
щих параметров и определение продолжительности испытаний при
индивидуальном прогнозировании. Для решения задач «обучения» из
состава изделий, прошедших испытания на первом этапе исследования,
методом случайного отбора формируют обучающие партии не менее
15 экземпляров изделий каждого «образа». Каждое из изделий прове-
ряют на принадлежность к своему «образу» путем использования потен-
циальной распознающей функции. При этом обнаруживается целесо-
образность внесения корректив в внд функции и значения исполь-
зуемых коэффициентов. Для удобства вычислений контролирующие па-
раметры нормируются по формуле XkE=Xkfcxk.
На третьем этапе исследований производится, собственно, индиви-
дуальное прогнозирование, так как первые два этапа по существу явля-
ются предварительными. Прогнозирующее испытание заключается
в измерении контролируемых параметров в одной или нескольких вре-
менных точках. По результатам измерений с помощью распознающей
функции определяют, к какому из «образов» относится исследуемый
объект. Для этого находят суммарные нормированные потенциалы
исследуемого изделия X и образов А, В, С} ..., М:
« т- «•
Изделие считается принадлежащим к тому образу, суммарный по-
тенциал которого и данного изделия имеет наибольшее значение. Прн
правильно выбранной распознающей функции и наличии границ между
«образами» переход от одного потенциала к другому осуществляется
скачком.
В [95] приводятся следующие данные об опыте испытаний, осно-
ванных на распознавании образов. Испытаниям подвергались клистро-
ны. Показатель надежности — срок службы. Число контролируемых
параметров — 9 (анодное напряжение, ток луча, время тренировки, глу-
бина вакуума и т. п.). Число клистронов, поставленных на предвари-
тельные испытания — 217. Объем обучающей партии—117. Количество
«образов», т. е. групп клистронов по продолжительности срока служ-
бы— 8. После предварительных испытаний и обучения каждый контро-
лируемый клистрон относился к тому или другому классу по сроку
службы с достоверностью 0,8 по результатам измерений контролируе-
мых параметров.
Прогнозирующие индивидуальные испытания на надежность имеют
ряд несомненных преимуществ по сравнению с другими методами испы-
таний. Главное преимущество их состоит в том, что они позволяют оце-
нивать надежность каждого изделия без существенных затрат времени
и без расхода рабочего ресурса. Это делает их исключительно актуаль-
175
ными для высоконадежных изделий, выпускаемых небольшим числом
экземпляров.
Для применения указанного метода необходима устойчивость тех-
нологического процесса, так как только при этом условии возможно
использование распознающей функции, полученной на этапе предвари-
тельных испытаний и обучения.
Для случая, когда невозможно провести предварительные испыта-
ния на надежность и обучение на обучаемой партии, распознающую
функцию можно получить на основании предварительных расчетов и
моделирования процессов, обусловливающих надежность исследуемого
изделия. Это может иметь место в случае изготовления уникальных
сложных изделий.
Испытания на надежность, основанные на использовании косвенно-
го параметра, можно рассматривать как частный случай распознавания
образа.
В приложении дается пример прогнозирования надежности на
основе распознавания образов.
9.6. Один нз возможных вариантов прогнозирующих
испытаний, основанных на использовании температурных влияний
В практике производства получили распространение ускоренные
испытания унифицированных функциональных узлов, построенных на
маломощных германиевых полупроводниковых приборах. Сущность этих
испытаний заключается в следующем. Предварительно исследуют опти-
мизацию аппроксимирующей функции, связывающей интенсивности от-
казов в эксплуатационном режиме и в режиме испытаний прн повы-
шенной температуре. На стадии предварительной подготовки выбирают
также значение коллекторного напряжения, с тем чтобы обеспечить
одинаковое значение выделяемой мощности на выходе прибора при раз-
личных температурах.
Испытуемые изделия разбивают на четыре группы по 20 ... 30 штук
в каждой группе. Изделия каждой группы подвергаются испытаниям
прн температурах: 85°C (1-я группа), 96°C (2-я группа), 108°C
(3-я группа) и 122°C (4-я группа).
Связь между интенсивностью отказов в эксплуатационных условиях
(при температуре и частотой отказов в условиях испытаний опреде-
ляется следующим уравнением*:
Яэ = 2 d, % N}tsw>-', (9.9)
где ла— интенсивность отказов в эксплуатационных условиях; —
коэффициент, учитывающий число отказов, получаемое в каждом из
температурных режимов; b — коэффициент, учитывающий перепад тем-
пературы при испытаниях; dj — число отказов при /-м режиме испыта-
ний; Nj — число испытуемых объектов при j-м режиме; tj—?продолжи-
тельность /-го испытания; Wo определяется решением уравнения:
TFo=H-0,1(Z-1)+0,1|G1/(|Cz| + 1G+i|) (9.10)
* Уравнение (9.9) справедливо для типичных условий производства унифициро-
ванных узлов.
176
где I — иомер последнего шага при последовательном решении урав-
нения
4 4
с = S S diNktkW"~' (?7---тг) = °’ (э- ’1 >
/=*1 /г=1
/— номер температурного режима; k — номер группы испытуемых
изделий.
Первым шагом решения уравнения (9.11) является решение прн
Wo— 1 и продолжается оно до изменения значения С с минуса на плюс.
Этому последнему шагу присваивается индекс Z+l (G+i). В данном
случае использован один ускоряющий фактор — повышенная темпе-
ратура. Одновременное нспользованне наряду с тепловым воздействием
повышенной нагрузки и других ускоряющих факторов, по-видимому^
позволило бы повысить коэффициент ускорения, однако это потребовало
бы проведения сложных предварительных исследований.
В использованной методике обработки результатов испытаний за-
ложена идея обобщения информации, полученной при различных тем-
пературных режимах, и уточнение аппроксимирующей функции каждый
раз при проведении испытаний. Это усложняет процесс проведения
испытаний и обработку полученных результатов, но повышает достовер-
ность прогнозирования.
Общее заключение по рассмотренным методам испытаний, содер-
жащим элементы прогнозирования, можно сформулировать следующим
образом.
Основная идея прогнозирования в процессе испытаний заключается
в увеличении информативности испытаний, в использовании кроме чис-
ла зафиксированных отказов, закономерностей изменения прямых и
косвенных параметров, обусловливающих возникновение отказов. Про-
гнозирование в процессе испытаний позволяет проводить испытания
малого числа объектов и даже одиночных объектов, а также сущест-
венно сократить либо число испытуемых объектов, либо время испыта-
ний в условиях массового производства.
9.7. Заключение о производственных испытаниях на надежность
Необходимость большого объема испытаний в процессе производст-
ва, в том числе испытаний иа надежность, вызвана тем, что производ-
ственно-технологические операции все еще не поддаются строгому
управлению. Физико-химические свойства материалов, качество поверх-
ностного слоя, свойства внутренних областей, точность геометрических
размеров, прочность соединений и другие характеристики, определяю-
щие надежность изделия, получаются различными при одних и тех же
условиях, предписанных технологической документацией. Поэтому необ-
ходим контроль, проверки и испытания и иа отдельных этапах произ-
водства готовых изделий.
Одной из важнейших задач совершенствования производственного
процесса является внедрение таких систем автоматизированного и авто-
матического управления технологическими процессами, которые устра-
няли бы их случайный характер. Тогда роль и значение испытаний го-
товых изделий будет снижаться. Известно, например, что внедрение
автоматизации проектирования вычислительных машин существенно
снижает объем контрольных операций. Однако на данном этапе про-
12—813 177
изводства эта задача далеко еще не решена. Производственные испы-
тания играют чрезвычайно важную роль в решении проблемы обеспече-
ния качества изделий. Одним из важнейших направлений совершенст-
вования производственных испытаний является повышение их информа-
тивности с помощью методов прогнозирования.
9.8. Решение задачи прогнозирования с помощью
математического моделирования
Математическое моделирование, или, точнее, машинный экспери-
мент, позволяет в некоторых случаях предсказать ход протекания физи-
ческих процессов и, следовательно, может использоваться как инстру-
мент прогнозирования. Рассмотрим несколько подходов к решению за-
дачи прогнозирования с помощью математического моделирования.
Если имеются математические зависимости, описывающие исследуемое
техническое устройство, то с помощью математического моделирования
можно имитировать изменения во времени параметров элементов схе-
мы и, зная кривые старения комплектующих элементов, установить сро-
ки профилактического контроля устройства, находящегося на хранении,
и выделить наиболее вероятные типичные кривые изменения параме-
тров устройства и тем самым наиболее типичные закономерности поте-
ри устройством работоспособности.
Закономерность изменений во времени параметров элементов диаг-
ностируемых объектов лежит в основе метода моделирования функций
старения. В качестве примера рассмотрим простую пассивную цепь,
описываемую уравнением
U(t) =L(t)di/dt+R(t)t-t-q/c(t), (9.12)
где U, i, q — соответственно падение напряжения, ток в цепи и заряд
конденсатора; L(t), R(t), c{t)—индуктивность, сопротивление и
емкость, рассматриваемые как функции времени.
Предполагая изменения L(Q, R(t), c(t) во времени случайными,
определим, когда из-за старения элементов цепи U(t) достигнет пре-
дельного уровня U* и перестанет удовлетворять предъявляемым требо-
ваниям
Если известна зависимость (9.12) и закономерности изменения L,
R, с во времени, а также функции распределения ft(R), ft(c)
в различных временных t сечениях, то, моделируя изменения парамет-
ров элементов, можно определить для каждого момента времени ве-
роятность Pt{lJ (t) < U*} и, в конечном счете, время достижения U(t)
уровня U. Если известны кривые L(t), R(t), c(t), то можно построить
своего рода эталонные траектории U(t) для различных значений токов
(нагрузки) и внешних воздействующих факторов (температуры и др.).
Математическое моделирование можно осуществить с помощью различ-
ных технических средств (ЭЦВМ и специальных моделирующих уста-
новок).
Метод статистического моделирования позволяет исследовать нели-
нейные схемы при произвольных распределениях параметров объекта,
а также учитывать флуктуацию параметра. Однако здесь также необ-
ходима априорная информация о процессах старения, износа и дегра-
дации элементов объекта.
178
Процесс статистического моделирования сводится к получению вы-
борок определенного объема из генеральной совокупности. На основа-
нии этих выборок определяются числовые характеристики генеральной
совокупности. Объем выборок определяет точность полученного резуль-
тата. Поскольку объем выборок, как правило, ограничен, в результате
моделирования получаются лишь оценки числовых характеристик.
Несмещенной оценкой математического ожидания является среднее
арифметическое результатов п опытов:
п
**=4£*-
4=1
Несмещенной оценкой дисперсии будет
п
Оценкой вероятности события является частота его появления в п
опытах: P*=kjn, k — количество испытаний, в течение которых про-
изошло событие.
Погрешность определения искомых числовых характеристик из-за
ограниченности объема выборок носит вероятностный характер. Нельзя
утверждать категорически, что ошибка не превысит определенной вели-
чины. Можно лишь указать границы, за пределы которых ошибка не
выйдет с заданной вероятностью.
Таким образом, оценки прогнозируемых числовых характеристик
являются случайными величинами. В общем случае закон распределе-
ния оценок зависит от распределения оцениваемой случайной величины
и от числа испытаний. При использовании метода Монте-Карло число
испытаний обычно велико, поэтому (на основании центральной предель-
ной теоремы) можно считать, что закон распределения оценок нор-
мальный.
Практически необходимо определить погрешность результата по из-
вестному числу реализаций, или наоборот, по заданной точности вы-
брать необходимое число реализаций. Решить эту задачу помогает взаи-
мосвязь количества опытов, точности и достоверности полученных
результатов. Под достоверностью понимается доверительная вероят-
ность а того, что интервал (а*—е, а*-Ье) накроет неизвестный пара-
метр а-. а~Р(а*—8<а<а* + Е), где а*— оценка а.
Доверительные интервалы для вероятности Р зависят от числа
реализаций пр:
Р = ± 2 |ЛР*(1 — Р*);/7р.
Необходимое число реализаций нР, обеспечивающее вычисление иско-
мой вероятности Р с погрешностью нс больше 8, равно пртр=
=4Р(1—Р)/е2.
Доверительные интервалы для математического ожидания:
12*
179
где Xi — значение случайной величины в х-й реализации. Необходимое
число реализаций для получения среднего с ошибкой не более е: /2рТр=
=4D3c/e2, где Dx — дисперсия случайной величины х.
Дисперсию следует вначале вычислить ориентировочно:
а затем уточнять по мере накопления данных.
Как следует из формул, для задания необходимого числа реализа-
ций, обеспечивающего вычисление искомого параметра с заданной точ-
ностью, требуется знать хотя бы ориентировочно значение определяе-
мого параметра. Это не всегда возможно. Поэтому существует другой
подход, широко применяемый на практике. Этот подход позволяет вести
текущий автоматический контроль точности решения и устанавливать
момент останова ЭВМ по достижении заданной точности.
Задается первоначальное заведомо заниженное число реализаций,
а затем после каждой последующей реализации проверяется условие
Е<Етр. При этом для оценки точности е математического ожидания
можно использовать выражение
/г/\ / >
где е — значение точности в долях от полученного результата, ^а =
= Ф''1(а) (табл. 9.6), Ф~\(а)—функция,’^обратная функции Лапласа,
т. е. такое значение аргумента, при котором функция Лапласа равна
доверительной вероятности а.
ТАБЛИЦА 9.6
а а 1 а а ta
0,80 1,282 0,85 1,439 0,91 1,694 0,96 2,053
0,81 1,310 0,86 1,475 0,92 1,750 0,97 2,169
0,82 1,340 0,87 1,513 0,93 1,810 0,98 2,325
0,83 1,371 0,88 1,554 0,94 1,880 0,99 2,576
0,84 1,404 0,89 1,597 0,95 1,960 0,9973 3,000
Для оценки относительной погрешности при вычислении вероятно-
сти используется выражение е = ^р"(1 — р*)/р*пр. Задачи статистичес-
кого моделирования можно разделить на следующие три группы по
способу повышения достоверности определения показателей прогнози-
руемого процесса.
1. Показатели, вычисляемые моделированием, можно получить
с помощью эксперимента для ограниченной области изменения входных
параметров. Тогда можно использовать эксперимент для контрольной
проверки модели в ряде выборочных точек, и в случае несовпадения ре-
зультатов модель корректируется, «настраивается».
1 80
2. Показатели можно вычислить только с помощью моделирования.
.Исходные данные (законы распределения случайных характеристик эле-
ментов системы) получены в результате экспериментов. Тогда избежать
ошибок можно только тщательной формализацией процесса, исключаю-
щей непроверенные допущения и ограничения. Все последующие огра-
ничения и допущения при доработке модели следует тщательно оцени-
вать по их влиянию на величину определяемого параметра.
3. Показатели можно вычислить только с помощью моделирова-
ния, но законы распределения исходных случайных величин получены
в результате теоретических исследований на основе априорных данных
или же частично с помощью натурного эксперимента. Здесь также
основную роль играет точность начального математического описания
системы. Но, поскольку исходные данные недостоверны, оценка допу-
щений и ограничений для этих задач является значительно более слож-
ной.
После тщательной формализации процесса составляется модели-
рующий алгоритм. Моделирующий алгоритм представляет собой систе-
му правил, определяющих последовательность действий, которые необ-
ходимо выполнить иад исходными данными, чтобы получить численное
значение величин, выбранных в качестве оцениваемых показателей.
Алгоритм можно представить различными способами: в виде логи-
ческого описания, логической схемы или описания на одном из спе-
циальных языков.
При разработке алгоритмов необходимо тщательно учитывать все
возможные ситуации, которые могут возникнуть в процессе решения,
т. е. необходимо предусмотреть все возможные состояния процесса. По-
этому даже для сравнительно простых задач строятся разветвленные
алгоритмы. Если упустить хотя бы одно из возможных состояний, то
алгоритм будет работоспособным только для частных случаев.
Метод Монте-Карло позволяет строить универсальные алгоритмы,
охватывающие большое число вариантов системы и позволяющие опре-
делять все характеристики надежности. Но для инженерной практики
это неоправдан©, так как обычно при проектировании рассматривают
ограниченное число вариантов системы и, как правило, интересуются
не всеми показателями надежности. Универсальный алгоритм составить
сложно: он получается громоздким, трудно поддается отладке и требует
больших затрат машинного времени. Поэтому удобнее иметь набор бо-
лее простых алгоритмов, каждый из которых предназначен для иссле-
дования определенного класса систем. Для составления алгоритмов
обязательно знать основные принципы работы ЭВМ и ее возможности.
В настоящее время основными способами воспроизведения на ЭВМ
процессов функционирования радиоэлектронных систем являются:
1) Д/-способ; 2) способ, основанный на формировании и анализе мо-
ментов перехода системы из состояния в состояние; 3) комбинирован-
ный способ, сочетающий два первых.
Коротко рассмотрим каждый из них.
Af-способ. Весь промежуток времени Т, в течение которого предпо-
лагается моделировать процесс функционирования, разбивается на от-
дельные моменты времени ti через интервалы At. Интервал А/ выби-
рается с учетом особенностей функционирования системы, требований
к точности результатов и времени, отводимого на решение задачи. В мо-
менты ti моделируется процесс работы системы. Все числовые значения
•параметров, характеризующих качество функционирования, фиксиру-
181
ются в памяти машины. При переходе к моменту времени = +
учитываются все изменения, происшедшие в -процессе функционирова-
ния, и вычисления повторяются. Накопление статистических данных за
и обработка их позволяют определить числовые характеристики
качества функционирования.
Этот способ, как правило, применяется в моделях идеального
функционирования, т. е. моделируется сам процесс функционирования
в предположении, что элементы системы идеально надежны. Исследо-
вание подобной модели позволяет получить выходные характеристики
системы, которые в дальнейшем используются для оценки влияния раз-
личных факторов, в том числе и ненадежности, на качество функцио-
нирования систем.
Способ формирования и анализа моментов перехода системы из
одного состояния в другое. Этот способ используется в моделях работо-
способности, предназначенных для исследования надежности радио-
электронных систем путем воспроизведения процесса отказов и восста-
новлений элементов системы. Здесь конкретный процесс функциониро-
вания косвенно учитывается на предварительном этапе до построения
модели при формулировании критерия отказа системы.
Сущность способа заключается в формировании для каждого эле-
мента системы последовательности случайных чисел времени работы —
Трг- и времени восстановления — тВг, характеризующих времена пребы-
вания элемента в исправном состоянии или неисправном. Случайные
величины и Твг формируются в соответствии с законами распреде-
ления времени безотказной работы F(t) и времени восстановления
G(l).
Далее состояния системы анализируются в точках изменения со-
стояний элементов и формируются показатели надежности в соответст-
вии с принятым критерием отказа системы. В зависимости от метода
воспроизведения с помощью ЭВМ траектории изменения состояний си-
стемы различают последовательное и параллельное решение задачи.
При последовательном решении вначале моделируются моменты только
первого изменения состояния у каждого из элементов системы. По наи-
меньшему из полученных моментов времени формируется первый пере-
ход системы в другое состояние (Si—*S2) и это состояние анализирует-
ся. Затем моделируется момент времени следующего изменения состоя-
ния для элемента, имевшего наименьший момент первого изменения и
использованного для образования S2. Новый момент записывается в па-
мять машины па место старого. Далее процесс повторяется, т. е. по
наименьшему моменту для элементов формируется переход S2—*Ss
и т. д. до тех пор, пока время очередного состояния системы Si не пре-
высит заданное время Т. После этого сформированные в процессе мо-
делирования счетчики используются для вычисления по соответствую-
щим формулам показателей надежности и результаты выдаются на
печать.
При параллельном решении необходимо для каждого элемента си-
стемы сначала определить интервалы трг, твг (г=1, 2, ...), а затем рас-
считать моменты отказов и восстановлений элементов /Отк<, которые
могут произойти при выбранных законах распределения за весь интер-
вал моделирования Т:
== === ^оТК1 ^FlJ
Дтх г — Gt -1 -F "^рО Au:== Дткг "4" •
182
Выполнив такую работу параллельно по всем элементам и за весь
период Г, можно затем расположить моменты ti изменения состояний
системы в порядке возрастания времени ее функционирования. Зная
теперь траекторию состояний системы, можно определить интересующие
нас показатели надежности.
Параллельное решение заранее предполагает независимое функцио-
нирование элементов, последовательное решение позволяет учесть и
зависимые события, кроме того, последовательное решение в большей
мере отвечает естественному процессу функционирования системы.
Комбинированный способ. Этот метод применяется в моделях реаль-
ного функционирования, представляющих собой модели совместного
воспроизведения двух процессов: процесса изменения работоспособности
элементов системы и реального процесса функционирования. Чтобы
связать эти два процесса, необходимо иметь информацию о поведении
элементов системы в различных режимах, обусловленных отказами от-
дельных элементов или изменениями условий окружающей среды.
Комбинированный способ основан на сочетании двух первых: про-
водится анализ процесса в точках изменения состояния системы и моде-
лируется процесс функционирования через небольшие интервалы време-
ни АЛ Этот подход применим к функционально-избыточным системам,
у которых можно различить несколько уровней функционирования.
В таких случаях оценка качества системы осуществляется по выходному
эффекту, т. е. определяется оперативная эффективность системы с уче-
том надежности входящих в иее элементов.
Комбинированный способ является наиболее эффективным способом
исследования на ЭВМ процессов функционирования сложных радио-
электронных систем. Но необходимо учитывать, что исследование мо-
делей реального функционирования сложно и трудоемко даже при
использовании современных ЭВМ. Поэтому при исследовании таких
моделей необходимо сочетать аналитические методы и -статистическое
моделирование.
Для воспроизведения процессов функционирования сложных систем
на ЭВМ необходимо иметь возможность получать случайные числа
с различными законами распределения.
Основой получения случайных чисел с заданным законом распре-
деления являются случайные числа с равномерным распределением на
интервале (0, 1). Программы получения случайных чисел с равномер-
ным распределением на интервале (0, 1) входят в библиотеку стандарт-
ных программ (БСП).
Подробно вывод формул, дающих преобразование равномерно рас-
пределенных случайных чисел в случайные величины с заданным зако-
ном распределения, дается в [97]. Там же рассмотрены вопросы моде-
лирования дискретных распределений. В табл. 9.7 приведены формулы
для вычисления случайных чисел xif распределенных по различным не-
прерывным законам [£$— случайное число, равномерно распределенное
в (О, I)].
Обобщенную схему алгоритма можно представить -следующим об-
разом (рис. 9.4). Блок 1 предусматривает ввод исходных данных, необ-
ходимых для моделирования. Необходимо вводить: точность моделиро-
вания [е-гр], первоначальное число реализаций [ир], длительность ин-
тервала 7, на котором моделируется поведение системы, значение £«
для заданной доверительной вероятности (см. табл. 9.5), параметры
законов распределения случайных величин, характеризующих работу
183
ТАБЛИЦА 9.7
Характер распределения и его параметры
Формула плотности распре-
деления f (х)
Формула для вычисле-
ния случайного числа
Равномерное распределение в ин-
тервале (а, Ь)
X Экспоненциальное распределение,
— интенсивность отказов
Нормальное распределение, а—мате-
матическое ожидание, с2 — дисперсия
Распределение Эрланга, k. —пара-
метры распределения
Распределение Вейбулла, к—масштаб
параметра, k — параметр, определяю-
щий асимметрию и эксцесс
%2 — распределение, п — число сте-
пеней свободы
Г 1
'у а при а^х^Ь
О при х < а, х^> b
Хе~^х , О < х < со
(х—а)»
1 2а-
•—СО <Z X <^со
X
х*-1
ркГ (k) е
OsJZX <«
a.kxh~1 е—кх*
0-сБх <со
П X
I ~2 1 2
2«/2Г (п/2) х е
a + (b~a)li
системы (времени'безотказной работы, времени восстановления и др.),
неслучайные характеристики системы (число ремонтных бригад, число
основных и резервных элементов, вероятность переключения на резерв,
Ввод исхсвкых Ратл-tx
выра^тяа исхо/Уа»* Заняь/х
Вт моделирования
А лгтштм. лойе.сирующий
исслевуепьй процесс
Блок овраболжа результатов
одной реализации
Проверка е<е,
Via
Ооеоатор одоавотки результатов
всех реализаций
Пеиать результатов, останов ЗВН
Рис 9.4. Обобщенная схема алгоритма
моделирования.
допустимое время простоя системы,
периодичность контроля, полнота
контроля и пр.) и другие исходные
данные для решения.
В блоке II реализуются случай-
ные зависимости для принятой ве-
роятностной схемы, вырабатываются
последовательности случайных чи-
сел с заданными законами распре-
деления иа основе программы полу-
чения таких чисел. Исходной ин-
формацией для этого блока явля-
ются параметры заданных законов
распределения.
Блок III представляет собой
собственно алгоритм моделирования
сложной системы, т. е. воспроизво-
дит поведение сложной системы. Для
I
I
S
I
184
построения статистической модели изучаемой сложной системы исполь-
зуется метод эквивалентных подсистем. Сущность его заключается
в следующем. На первом этапе исследуется надежность резервирован-
ных подсистем и каждая из таких подсистем заменяется эквивалент-
ным элементом с характеристиками надежности, соответствующими
замененной подсистеме.
После этого этапа мы имеем дело с системой, состоящей только из
последовательно соединенных элементов, для которой оцениваются по-
казатели надежности. Такой подход упрощает алгоритм исследования
-системы. Для исследования резервных подсистем используется один из
вышеприведенных способов моделирования.
Блок IV производит обработку результатов одной реализации по-
ведения системы. Он включает, в основном, счетчики, которые подсчи-
тывают различные величины, необходимые для получения моделируе-
мых показателей, для построения гистограмм (количество реализаций,
количество отказов системы, количество выходов параметров системы
Рис. 9.5. Обобщенный алгоритм моделирования.
за допустимые границы, количество отказавших элементов в резервных
группах, сумму отрезков времени исправной работы, сумму отрезков
времени восстановления и т. д.).
В блоке V оценивается точность полученных результатов. В зави-
симости от результата проверки дается команда иа продолжение или
прекращение испытаний.
В блоке VI обрабатываются результаты всех реализаций. Здесь,
в основном, по общеизвестным формулам рассчитывается статистическое
185
определение показателей надежности. В расчетах используются пока-
зания счетчиков из блока IV.
После расчетов производится печать результатов и останов ЭВМ
(блок VII).
Таким образом, при решении задач надежности используется мо-
дель работоспособности, реализуемая способом формирования и анали-
за моментов перехода системы из одного состояния в другое. При по-
строении такой модели для любой задачи можно выделить типовые опе-
рации, которые -выполняются всегда независимо от особенностей решае-
мой задачи. Обобщенный алгоритм с учетом этих типовых операций
представлен на рис. 9.5.
Часть TV
АВТОМАТИЗАЦИЯ ПРОГНОЗИРОВАНИЯ
ГЛАВА 10. ОСНОВЫ АВТОМАТИЗАЦИИ ПРОГНОЗИРОВАНИЯ
10.1. Причины автоматизации прогнозирования
Из всех предшествующих разделов дайной книги должно быть оче-
видно, что прогнозирование технического состояния изделий и их на-
дежности открывает новые большие возможности управления качеством
изделий. Управлять —это прежде всего уметь предвидеть. Возможность
предвидения покупается дорогой пеной. Требуется больший объем ра-
бот, обеспечивающих предвидение, а именно: необходимо собирать ин-
формацию непрерывно на некотором отрезке времени по ряду парамет-
ров, необходимо не только фиксировать отказовые состояния, но изме-
рять значения параметров, и не только основных, но и косвенных,
необходим переход от датчиков, работающих по признаку «да — нет»
к датчикам-измерителям. Информацию необходимо практически мгно-
венно обработать, с тем чтобы можно было выявить закономерности
изменения процессов без искажений, вызываемых запаздыванием ввода
входных данных.
Все эти обстоятельства делают совершенно необходимым автомати-
зацию прогнозирования. Так называемые ручные методы обработки ин-
формации и решения уравнений прогнозирования не исключаются, но
ограниченность их очевидна. Области применения ручных методов, ча-
стично автоматизированных и автоматизированных определяются слож-
ностью задач, объемом вычислений и предъявляемыми к ним требо-
ваниями.
10.2. Пути реализации прогнозирующих устройств
Автоматизация прогнозирования осуществляется с помощью специ-
альных устройств, называемых лрогнозаторами. В качестве прогнозато-
ров можно использовать универсальные цифровые машины (ЦВМ), спе-
циализированные вычислительные машины (СВМ), аналого-цифровые
машины, аналоговые вычислительные машины (АВМ) и др.
В случае, когда в системе технической диагностики (СТД) приме-
няются универсальные вычислительные машины, задача прогнозирова-
ния может решаться несколькими методами, что повышает его точность.
Кроме того, осуществляется хранение и обработка большого количества
информации, сравниваются различные варианты решения задачи, вы-
бирается наилучший из них в соответствии с определенными критерия-
ми, учитываются изменения воздействия и т. д. Однако использование
ЭЦВМ в СТД приводит к значительному увеличению стоимости, веса,
габаритов и т. п., поэтому такой путь реализации СТД и, соответствен-
но, прогиозаторов, несмотря на их информационные и логические воз-
можности, используется только в тех случаях, когда поток входной и
выходной информации, сложность вычислительных операций и требуе-
мая точность исключают возможность иной реализации структуры СТД.
187
Применение специализированных машин, решающих конкретные за-
дачи прогнозирования, представляет собой другой путь автоматизации
процесса предсказания. Обычно в зависимости от обеспечения аппара-
турой ввода и вывода, от задач, которые решает СВМ в обшей СТД, и
от способа подключения СТД к диагностируемому объекту различают
организацию системы в виде СТД информационного типа, типа совет-
чика оператора и управляющего типа.
СТД информационного типа (рис. 10.1) состоит из устройства вво-
да СВМ, схемы индикации и объекта диагностики. Все основные задачи
технической диагностики можно решить при помощи СВМ, в которых
используется одна или несколько программ прогнозирования изменения
состояния диагностируемого объекта. На схеме индикации показывает-
ся текущее и прогнозируемое состояния системы. На основании этих
данных оператор принимает решение о работоспособности системы на
период /А/, /=1, 2, ..., т с момента прогнозирования. При такой струк-
туре СТД процесс прогнозирования разбивается на следующие этапы.
Рис. 10.2. Система технической диагно-
стики, организованной по принципу со-
ветчика-оператора.
Рис. 10.1. Система технической диагно-
стики информационного типа.
1. Непрерывно или периодически контролируется значение входных
величин и проверяется их соответствие допустимым значениям.
2. Регистрируются все контролируемые параметры.
3. Производится вероятностно-статистическая обработка текущей
информации.
4. Вычисляется значение функции работоспособности согласно пред-
лагаемому алгоритму.
5. Фиксируются скоростные характеристики контролируемых пара-
метров и функции раоотоспосоон
।--- —< Бь'хзЗные 1----------—- —>
" . т । " •
•flfr I—-----Д Л' &
_______j 1— -----.— -----1
*
свм
--------т-------‘упри&лыия
f___ _____,_________. У____. ____ j
ь г/ ] IПрес5рязб-'‘”пЕяьВмjBxH u»C)Gayayiiu\
р xtfa/e |В ггнклы упраЬгчхя |
6. Осуществляется прогнози-
рование по одному или нескольким
предлагаемым алгоритмам.
7. Выводятся на индикацию
прогнозируемые и текущие значе-
ния параметров функции работоспо-
собности.
При организации СТД по
принципу
функции вычислительной машины
советчика-оператора
Рис. 10.3. Система технической диагно-
стики управляющего типа.
как прогнозатора расширяются
(рис. 10.2). В этом случае, помимо сказанного, на основании текущей и
предсказанной информации о работоспособности системы вырабатыва-
ются рекомендации относительно эксплуатационного (или производст-
венного) режима системы в настоящем и будущем, даются рекоменда-
188
ции по замене или профилактике узлов системы с наихудшей сте-
пенью работоспособности как в период контроля, так и в период
предстоящей эксплуатации. В результате роль оператора сводится
к выполнению рекомендаций («советов») прогнозатора (СВМ).
В СТД управляющего типа (рис. 10.3) осуществляется контроль
режима работы диагностируемого объекта и оптимальное управление
им. На практике часто оказывается достаточным решить задачу опре-
деления степени работоспособности и прогнозирования с помощью эле-
ментов встроенного контроля и простых классификаторов. В этом случае
вычислительные устройства могут быть как аналогового, так и дискрет-
ного типа. Они являются достаточно простыми и позволяют решить
поставленную задачу с незначительными экономическими затратами.
Обычно эти устройства реализуют простые математические выражения,
позволяющие с достаточной точностью получить результат прогнозиро-
вания информационного характера.
10.3. Устройство автоматического прогнозирования
многопараметрических объектов
Рассмотрим устройство, в основу которого положен математический
аппарат метода обобщенного параметра. В этом случае все входные
величины (контролируемые параметры) &(/), &(t), ..., h(0 нормиру-
ются с помощью, например, выражения (3.38) и получается нормиро-
ванный ряд gi(£), £з(£), ..., Степень работоспособности СТД и ее
изменение можно оценить с помощью следующего обобщенного выра-
жения:
k Ik
Q(t)==^v&(t) r£vs,
i / i
представляющего собой линейное среднее, где vs—веса контролируемых
параметров. Естественно, при прогнозировании интересует момент, когда
обобщенный параметр достигнет допустимого значения Q*r . Про-
гнозирование изменения (t) позволяет определить гнаиболее вероятное
время Тер, в течение которого контролируемая система будет сохранять
свою работоспособность. Однако какой-то из k параметров МО достиг-
нет раньше остальных допустимого значения |*s, а так как выход лю-
бого параметра за допустимые пределы ведет к отказу системы, то
прогнозируемое первое достижение допуска будет определять мини-
мальное время Т-min работоспособного состояния системы. Таким обра-
зом, целесообразно прогнозировать величины как 7Ср, так и 7?nin. Для
этого необходимо прогнозировать изменения как обобщенной . так и
отдельного параметра с максимальной скоростью изменения.
Рассмотрим работу устройства автоматического прогнозирования
(УАП) (рис. 10.4). С помощью датчиков, находящихся на диагности-
руемом объекте или подключаемых к нему, в УАП подаются значения
прогнозирующих параметров МО- В момент времени опера ор дает
команду: «Пуск», в результате чего напряжение с датчиков поступает
в каналы определения конечных разностей э=1, 2, ..., k, В канале
предварительно параметр нормируется, затем преобразуется в двоичный
код и запоминается. При большом интервале контроля УАП выключа-
ется, поэтому значение ММ необходимо запомнить в долговременном
189
ЗУ илн занести в карточку учета. Во втором случае требуется вмеша-
тельство оператора, но в то же время отпадает необходимость в ЗУ и
оператор имеет представление о величинах параметров.
В момент времени оператор опять нажимает кнопку «Пуск» и тем
самым вводит напряжение с датчиков в те же каналы, где получаются
безразмерные значения параметров £(£>)- Затем вычисляется первая ко-
нечная разность Д^5 = С(4) — МЛ), которая поступает на блоки сравне-
ния, имеющиеся в каждом канале. В блоках сравнения выделяется
Д^ш, и указывается номер канала (параметра) S, где скорость измене-
ния максимальна. В канал S тут же подается напряжение (f3) (t3 t2)
н определяется С (Л) € (4)- Это равенство справедливо с большой
точностью, так как t2— —12.
В блоке распознавания на основе Д^ тах и (t3) = (4) определяет-
ся время выхода параметра системы £s(/) за допустимые пределы. Его
основой (рис. 10.5) является диодный дешифратор, который управляет
Рис. 10.4. Функциональная схема устройства
автоматического прогнозирования.
Рис. 10.5. Блок распознавания У АП.
схемой индикации, собранной на лампах ИН1, где и фиксируется время
выхода параметра за допустимый предел.
Блок распознавания функционирует следующим образом. При по-
даче команды «Пуск» в момент /2 из устройства управления У У по
шине 1 в реверсивный счетчик PC подаются импульсы, количество ко-
торых соответствует максимально возможному Д£6. С каждого разряда
реверсивного счетчика идут шины связи 2 на блоки сравнения в каж-
дом из k каналов.
Блок сравнения выдает сигнал лишь в случае совпадения числа, за-
писанного в PC, с числом Д^, вычисленным в канале. Если после запи-
си Д£1тсх в PC и вычисления Д^ в каналах окажется, что ни одна раз-
ность не равна максимальной, то из УУ в реверсивный счетчик через
ключ К подается последовательность импульсов, которая уменьшает
число, записанное в PC (счетчик работает на вычитание). В некоторый
момент число в реверсивном счетчике, постепенно уменьшаясь, сравня-
ется с наибольшей конечной разностью в одном из каналов. В то же
время на выходе соответствующего блока сравнения появится сигнал,
190
который закроет ключ К. Таким образом, в реверсивном счетчике ока-
зывается записанным число, равное максимальной конечной разности
которая и подается иа дешифратор.
Сигнал с блока сравнения S-ro канала поступает на ключ К, кото-
рый повторно запускает устройства канала для записи максимально
изменяющегося значения параметра в регистре максимально изменяю-
щегося параметра РИП, откуда поразрядно величина параметра по-
дается на дешифратор.
Последовательность импульсов, подаваемая па дешифратор, состоит
из двух частей. Первая обусловливается величиной ДЕ«, а вторая — ве-
личиной Варьируя возможными значениями этих двух величин,
составляют таблицу значений /А/, /'=1, 2, ..., т; At— интервал кон-
троля.
Рассмотрим работу канала определения конечной разности Д^„
(рис. 10.6). На его вход поступает напряжение с датчика контролируе-
мого параметра. В нормирующем уст-
ройстве НУ в результате обработки
получаем значение безразмерного па-
раметра. В момент ti запускается пре-
образователь напряжения в код ПНК,
переключатель при этом находится
в положении П1 и на выходе ПНК по-
лучаем число импульсов, пропорцио-
нальное значению которое запи-
сывается в реверсивном счетчике ка-
нала РСК- Через интервал контроля
At в момент h, оператор переводит
командой «Пуск» переключатель в по-
.чзВания
Рис. 10.6. Функциональная схема ка-
нала определения конечной разности.
ложение П2 и запускает ПНК, который подает код числа ^(/2), выра-
ботанного нормирующим устройством, на вычитающий вход РСК-
В РСК осуществляется вычитание МС)— М^) и полученная раз-
ность Д£5 поразрядно подается на блок сравнения.
Кроме того, на блок сравнения из блока распознавания с PC пораз-
рядно подается значение Д£тйх, которое уменьшается от максимально воз-
можного до ближайшего к нему значения Д^ в каком-либо из каналов.
Рис. 10.7. Ячейка сравне- Рис. 10.8. Структурная схема Рис. 10.9. Изменение
ния. экстраполятора: функции с (Л
Д — задержка; 1. 2, 3— блок умноже-
ния; 4 — сумматор.
191
В том из каналов, где наступает указанное равенство, на все входы ло-
гической схемы И1 -с выхода блока сравнения подаются высокие потен-
циалы. На выходе схемы И1 также появится высокий потенциал, кото-
рый, поступая в блок распознавания, закрывает ключ К (рис. 10.5) и
прекращает подачу импульсов на PC, где записывается ЛЕ max-
Скачок напряжения иа выходе И1 запускает ПНК, который преоб-
разует величину = в код (рис. 10.6). Импульсы поступают
через схему И2, которая открывается также напряжением с выхода И1
в блок распознавания. Ключ К закрывается напряжением с И1 до на-
ступления момента t3.
В блоке сравнения поразрядно сравниваются два числа, при ра-
венстве которых на все входы схемы И1 поступают высокие потенциа-
лы. Ячейка сравнения в каждом разряде работает по следующей логи-
ке, которую можно реализовать с помощью схемы на рис. 10.7:
PC 0 0 11
РСК 0101
Вход И1 1 0 0 0
Выходы ячеек сравнения соединены со входами схемы И1, которая
и регистрирует момент равенства обоих кодов.
10.4. Экстраполяторы
Задачу прогнозирования можно решить с помощью автоматических
устройств, осуществляющих экстраполяцию изменения контролируемых
параметров — экстраполяторов (рис. 10.8). Они в основном применяют-
ся в тех случаях, когда производится периодический контроль пара-
метров диагностируемой системы.
Пусть необходимо предсказать величину параметра £(/) в точке
/тг-i-i по известным значениям в точках tn, tn-i, ... (рис. 10.9). Через
известные точки проводим кривую второго порядка £(£) —*W2+ai(0+
+ п0. При t—Q, —At, t получаем [98]
t(tn) = a0,
(M — а, Д/ -Ь <№,
е = — 2С1Д/ + 4aaAf,
где At — интервал контроля. Из этих уравнений находим прогнозирую-
щий многочлен в виде
Z(t) = ^(tn) + (2A/)-4^(/n_2)-4^(fn_i) +ЗНМ1 + (2AH-4X
X [£Gn-2)—^(/n-1) +£(M]^2
£Gn+i) =3^(?п-г)—3g(/n-i) +s(M-
Прогнозируемое значение параметра равно сумме предшествующих
значений, отстоящих друг от друга на интервал At и умноженных на
соответствующие коэффициенты веса.
Если необходимо экстраполировать непрерывное изменение пара-
мегра на время т, то прогнозируемое значение параметра вычисляется
в виде суммы:
= (Ю.1)
о
где —значения параметра £(/) в моменты t^Tr, a — коэффициент
веса Его значения ^(t).
192
Приведенная формула представляет собой первый член расширен-
ного оператора предсказания Колмогорова. Схема экстраполятора, реа-
лизующего форму (10.1) приведена на рис. 10.10.
Непрерывно изменяющийся параметр подается в запоминающее
устройство, где разбивается на n~T-Ji\t равноотстоящих значений. Зна-
чение параметра с каждой ячейки памяти, умноженное на свой коэф-
фициент веса а, поступает на сумматор. Так как контролируемый пара-
Рис. 10.10, Экстр а поля тор непрерывного сигнала:
Д — задержка, 1 фильтр, 2 — блок выдачи задержанных значений; 3 — сумматор.
метр на входе устройства изменяется непрерывно, на выходе сумматора
получаем его непрерывное упрежденное значение. Подобный экстрапо-
лятор может быть реализован как в аналоговом, так и в цифровом
варианте.
В преобразователе 2 дискретного экстраполятора (рис. 10.11) зна-
чения непрерывного входного сигнала преобразуются в цифровую фор-
му. С помощью сдвигающего регистра 3 и блока весовых коэффициен-
тов 4 можно в соответствии с (10.1)
последовательно перемножить дис-
кретные значения экстраполируемой
функции на коэффициенты а*. Схема
формирования адреса 5 обеспечивает
запись произведений g(^)cti в опре-
деленные ячейки запоминающего
устройства 6. Произведения £(£г)а»
затем суммируются в сумматоре 7.
Часто значения контролируемого
параметра можно получить только в
дискретные моменты времени. При
этом требуется зиатъ вероятное значе-
ние параметра не только в некоторый
будущий момент г^ + А/, но и в тече-
ние некоторого интервала времени
[£« ... 6г + А/]. Пользуясь известными
математическими приемами, можно отыскать закономерность изменения
коэффициентов веса в течение одного интервала дискретности. Схема
устройства, реализующего задачу экстраполирования © такой форме,
приведена на рис. 10.12.
13—813
Рис. 10.11. Экстраполятор дискретно-
го действия:
1 — блок умножения; 2 — преобразователь;
3 — сдвигающий регистр; 4 — блок весовых
коэффициентов; 5 — схема формирования
адреса; 6 — запоминающее устройство;
7 — сумматор
193
Дискретный сигнал подается в ячейки памяти со сдвигом после-
дующего значения параметра относительно предыдущего на величину
Дд Запомненные значения параметров в виде постоянного в интервале
Дг напряжения непрерывно подаются на масштабные потенциометры.
Сопротивление этих потенциометров меняется по закону ср(/+/Л/), где
/— целое число. Сигнал с потенциометров, умноженный на ш, посту-
пает на вход сумматора. На выходе получаем непрерывное сглаженное
значение прогнозируемого параметра. Таким образом, при непрерывной
экстраполяции по известным дискретным значениям необходимо, чтобы
Рис. 10.12. Экстраполятор для получения непрерывного упреждения сигнала по дискрет-
ным входным данным.
коэффициенты веса представляли собой некоторые функции времени
щ(/).
Рассмотрим еще одно автоматическое устройство — аналого-цифро-
вой экстраполятор отношения функций (ЭОФ), позволяющий решать
задачу прогнозирования [99]. Такие устройства необходимы для реше-
ния многих задач в области измерительной техники и техники автома-
тического управления.
Рассматриваемый аналого-цифровой ЭОФ разработан применитель-
но к решению одной из задач автоматического контроля состояния слож-
ных технических устройств — для предсказания по данным измерений
наиболее вероятных значений параметров, определяющих состояния
контролируемых элементов автоматической системы, для прогнозирова-
ния отказов по точности в процессе эксплуатации.
Определяющий параметр ОП, характеризующий состояние элемен-
та, обычно не доступен для измерения и поэтому его значение можно
найти только путем преобразования измеренной информации при помо-
щи вычислительных устройств.
В большинстве случаев в качестве ОП может служить у — отноше-
ние уровня |3 выходной величины к уровню а входной величины при
определенном установившемся режиме работы контролируемого элемен-
та. Однако измеренные в реальных условиях эксплуатации значения
выходной и входной величии представляют собой сложные функции
194
Рис. 10.13. Совмещение возмож-
ных изменений уровня входного и
выходного сигнала элемента при
наличии в нем нестационарных
задержек.
температуры окружающей среды 6 и подвержены влиянию частотных и
нелинейных искажений, а также случайных воздействий. Поэтому для
определения ОП при помощи делительного устройства необходимо преж-
де всего преобразовать данные измерений к определенному базовому
режиму, чтобы обеспечить инвариантность у в отношении температуры
•6, уровня а и частоты со входного сигнала.
Сложнее осуществить инвариантность у по отношению к случайным
воздействиям, которые могут проявляться в виде внутренних помех и
нестационарных фазовых сдвигов т3 (рис. 10.13) компенсация которых
несомненно необходима: если без компенсации т3 вычислить отношение
сигналов р и а в некоторый момент времени Zi, то получим ложную
информацию о величине ОП.
Влияние внутренних помех можно уменьшить, сглаживая данные
измерений, а влияние нестационарных задержек свести к минимуму,
определяя у как отношения смежных максимумов уровней р и а.
Для построения ЭОФ на основе ука-
занных принципов необходимо знать:’
статическую зависимость коэффициента
преобразования Кп=='р/а=/ (а) при ба-
зовых значениях частоты и температуры;
зависимость от температуры: ампли-
тудно-частотную характеристику контро-
лируемого элемента. Получение этих за-
висимостей ие представляет трудностей.
Разработанный ЭОФ состоит из бло-
ка функциональных преобразователей
БФП, аналого-цифрового блока деления
БД н органически связанного с ним бло-
ка экстраполяции БЭ.
БФП (рис. 10.14) состоит из пассив-
ного фильтра ПФ, нелинейного элемента
ПЭ, термокомпенсатора Т и устрой-
ства обнаружения максимумов УОМ.
Фильтр ПФ обеспечивает инвариантность у по отношению к изме-
нению частоты входного сигнала контролируемого элемента КЭ.
Он имеет амплитудно-частотную характеристику, подобную амплитудно-
частотной характеристике КЭ. НЭ со стабильной характеристикой мо-
делирует первоначальную статическую характеристику КЭ, в результа-
те чего отношение p/а приводится к базовому режиму. Термокомпенса-
тор Т служит для приведения величины р к базовому режиму при по-
мощи термосопротивления, встроенного в КЭ.
Устройство обнаружения максимумов УОМ фиксирует преобразо-
ванное максимальное значение входной величины maxeBXi и следующее
за ним максимальное значение выходной величины тахеВХ2 и выдает
сигнал на сравнение этих величин в БД, если максимальное значение
выходной величины не превосходит определенного уровня (что необхо-
димо для элементов с резко выраженным насыщением). Такой алгоритм
можно реализовать с помощью известных устройств для запоминания
максимума и простого дискретного автомата, одновременно используе-
мого и для управления блоками БД и БЭ. В случае экстраполяции ОП
элементов без существенной задержки УОМ может отсутствовать.
Блок деления БД осуществляет операцию деления двух аналоговых
величин с получением частного в виде временного интервала, который
аз* 195
в свою очередь можно легко преобразовать в цифровую форму. Схема
БД (рис. 10.15) состоит из интегратора, вентилей, индикатора нуля.
В качестве одного из вентильных элементов применена лампа Л1, пра-
вый диод которой отпирается триггером Т1, когда последний находится
в положении «0». При открытом вентиле сигнал maxe^i через входное
сопротивление ₽1 подается па вход интегрирующего усилителя КРУ.
Напряжение выхода 1 РУ:
t
[ max
о
где UVT — напряжение на выходе триггера Т1.
Для упрощения пробной реализации целесообразно, чтобы Z7MT=0.
Рис. 10.14. Схема экстраполятора отно-
шения функций.
Рис. 10 15. Схема блока деления.
Напряжение t7py суммируется с напряжением тахевх2 на суммиру-
ющем усилителе 2 РУ. Напряжение па его выходе:
t
Uя = k:i шах еВХ2 — J шах e^dt.
о
Когда Ц, =0, индикатор пуля ИН выдает импульс на вход триг-
гера Т1, после чего процесс интегрирования прекращается. Время инте-
грирования /и определяется из равенства
kt J max eKXldt = k3 шах еВХ2,
о
откуда
tn==ks max eBX2//?t max евхь
Из-за внутренних шумов в контролируемом элементе н случайных
ошибок, возникающих в БД, выходная величина /п, наряду с величиной
у содержит помеху б(/). Уровень помехи можно снизить при помощи
многократных измерений.
196
Отрезок времени /и можно измерить с высокой точностью и резуль-
тат измерения представить как в цифровом, так и в аналоговом виде.
В рассматриваемом случае, исходя из условий передачи результатов
вычислений в блок экстраполяции, целесообразно представить получен-
ную величину tn в. число-импульсном коде, производя отсчет путем за-
полнения счетчика СЧ импульсами со стабильной частотой следования.
Эти импульсы генерируются генератором КГИ с кварцевой стабилиза-
цией частоты.
Для управления заполнением счетчика СЧ служит вентиль В1, ко-
торый отпирается триггером Т1, если последний находится в положении
«О». Импульс на переброс триггера в положение «О» поступает от У ОМ,
а импульс на возврат триггера в положение «1» — от ИН. За время
нахождения триггера в положении «1» интегрирующий усилитель 1 РУ
и устройство УОМ должны возвратиться в исходное, т. е. нулевое со-
стояние. Для установки нулевых начальных данных па интегрирующем
усилителе 1 РУ применен импульсный трансформатор ИТ, одна обмотка
которого включена через сопротивление Ro на вход интегрирующего
усилителя 1 РУ. Если триггер Т1 находится в положении /, импульсы
от какого-либо источника через открытый вентиль В2 поступают на
входную обмотку ИТ. Возникающие во вторичной обмотке ИТ импуль-
сы имеют полярность, противоположную полярности входного сигнала
max еВх2- Поэтому при поступлении импульсов от ИТ иа вход 1 РУ его
выходное напряжение С7РУ начинает уменьшаться до нуля. Разрядная
цепь, состоящая из R3, Л1 и С1, предотвращает возможность изменения
полярности на выходе 1 РУ.
Схемы запоминания можно установить на нуль импульсом, возни-
кающим при перебросе триггера Т1 в нулевое положение.
Блок экстраполятора БЭ служит для предсказания будущего зна-
чения определяющего параметра У по совокупности измеренных значе-
ний у. Поскольку ОП является медленно изменяющейся величиной, ин-
формация о прошлых значениях у должна храниться в ЭОФ в течение
длительного времени. Это исключает применение аналоговых запоми-
нающих устройств и предопределяет различное внутреннее представле-
ние величин.
Нахождение наиболее вероятного значения величины У
в момент времени ^=^о+Д^» с точки зрения наиболее простой при-
борной реализации, целесообразно осуществлять по ранее рассмотрен-,
ному методу. Согласно этому методу искомое значение ЛДНД опреде-
ляется формулой
С10-2)
О
где у~г — измеренное значение ОП в г-й момент времени, отсчитывае-
мый от момента времени to последнего измерения; Li — весовой коэф-
фициент Сго слагаемого.
Вычисление Л1{ЕТ} по формуле (10.2) требует, чтобы измерения
производились через одинаковые промежутки времени A/=£-i—fi-j,
а упреждение производилось на время уД/ при целочисленных у.
Весовые коэффициенты Д можно ввести при помощи несложных
коммутаций в цепях БД. В самом деле, получаемое на выходе БД чис-
ло пропорционально величине у, причем коэффициент пропорциональ-
197
нести является функцией передаточных коэффициентов решающих уси-
лителей и частоты КГИ. Следовательно, с помощью переключателя,
включенного в цепь КГИ (или посредством переключения входных со-
противлений 1 РУ), можно получать значения у с различными весовы-
ми коэффициентами.
Для получения упрежденного значения У необходимо полученное -
значение у с весовыми коэффициентами, соответствующими всем точ-
кам интерполяции, перезаписать в регистр Р1 блока экстраполяции
(рис. 10.16), а затем в устройство внешней памяти УВП. После записи
информации о текущем значении ОП элемента можно приступать к вы-
бору информации о прошлых значениях ОП. Выборка заключается
в считывании с УВП тех значений y~iL^ для которых <=/, и передаче
считываемого числа на одноразрядный сумматор 2, где производится
суммирование считываемого и находящегося в регистре Р2 числа. Полу-
ченный результат направляется далее снова в Р2. После п циклов, со-
гласно выражению (10.2) в Р2 накапливается значение М{УД. Это чис-
ло можно выдать на регистрирующее устройство или подать на другое
автоматическое устройство.
После каждого цикла все ранее записанные в УВН значения ytL,
изменяют свой порядковый номер, поскольку нумерация их производит-
ся от последнего измерения. Так как для вычисления У необходимо
только п+1 значение у, после каждого цикла предсказания определен-
ная часть информации должна быть удалена с УВП.
Работой ЭОФ управляет дискретный автомат, выполняющий необ-
ходимые переключения в схеме. Конкретная схема дискретного автома-
__________________ та зависит, в основном, от вида
• С- - v । Jstf/yi—*' I-, УВП, и его синтез из стандарт-
• 1 _J L — r*f—- ных элементов не встречает за-
------------ труднений.
Рис. 10.16. Охема блока экстраполятора. Погрешность описанного ЭОФ
определяется в основном дискретно-
стью отсчета импульсов от КГИ в счетчике СЧ, случайными ошибками,
вызванными в линии связи, и, наконец, ошибками, вызванными неста-
бильностью питающих напряжений и постепенным изменением перепа-
дов напряжения триггера Т1. Так как в большинстве случаев нас инте-
ресует относительное изменение ОП элемента, большинство. методиче-
ских ошибок, возникающих при работе ЭОФ, не оказывает существен-
ного влияния на точность получаемого результата. Некоторое уменьше-
ние случайных ошибок, вызываемых дискретностью отсчета, нестабиль-
ностью напряжений и помехами в линии связи, обусловливается много-
кратным изменением величины у в каждой точке. Наибольшее влияние
на точность предсказания может оказать ошибка компенсации действия
внешних условий (температуры 6) и изменения входных воздействий
(а, со). Эта ошибка, вследствие стохастического изменения параметров
а, со и 0 также будет случайной во времени и частично сглаживается
при экстраполяции. Естественно, чем больше точек п, в которых изме-
няется параметр у, тем меньше эта ошибка. Одиако при увеличении п
понижается точность ЭОФ, так как изменение ОП для реальных эле-
ментов имеет, как правило, нестационарный характер, а описанный
метод экстраполяции основан на предположении стационарности изме-
нения у на отрезке времени от to—nAt до /о+уД?-
Решение вопроса о выборе оптимальных п и у относится к вариа-
ционным задачам и должно решаться конкретно для каждого элемента.
198
10.5. Устройство контроля с экстраполятором
производить научно-
Рис. 10.17. Схема устрой-
ства контроля с экстра-
полятором.
Очевидно, с помощью устройств контроля можно решить только
ограниченную задачу: определить состояние системы в текущий момент
времени. Возможности подобного устройства значительно возрастают,
если в него включить экстраполятор (прогнозатор), позволяющий оце-
нить работоспособность системы в будущие моменты времени эксплуа-
тации.
Рассмотрим устройство контроля с экстр о полито ром (рис. 10.17),
позволяющее определить вероятность отказа диагностируем о го изде-
лия. На основании подобной информации можно
обоснованные замены изделий и поддерживать
в процессе эксплуатации требуемый уровень ра-
ботоспособности. Такое устройство дает более
достоверные результаты контроля, поскольку
реализуемый этим устройством метод определе-
ния вероятности отказа учитывает лишь индиви-
дуальные свойства изделия, а не свойства их
статистической совокупности.
Объекты контроля 1 (число их может быть
достаточно большим) с помощью системы обе-
гающего контроля 2 соединены со входом экс-
траполятора 3 и с одним из входов блока раз-
ности 4. Второй вход блока разности через блок
задержки 5 соединен с выходом экстраполято-
ра 3. Задержка блока 5 должна быть равна пе-
риоду экстраполяции (прогнозирования). Вы-
ход блока разности через квадратор 6 соеди-
нен со входом сумматора 7 накапливающего ти-
па. Счетчик 3, предназначенный для регистра-
ции количества произведенных предсказаний,
соединен с выходом экстраполятора. Сигналы с
подаются на блок деления 9. Вывод делительного устройства 9 соеди-
нен с входом многоаргументного преобразователя 10. Другие входы
преобразователя 10 соединены с выходами блока 2 и экстраполятора 3.
Многоаргументный функциональный преобразователь 10 соединен после-
довательно с блоком печати 11 (можно использовать и другое регист-
рирующее устройство), который является оконечным блоком всего
устройства контроля. Блок печати фиксирует вероятности отказов диаг-
ностируемых изделий до следующего момента контроля. В качестве
узла экстраполяции можно использовать описанный ранее аналого-циф-
ровой экстраполятор отношения функций.
В момент контроля информация о значении параметра £(k), харак-
теризующего текущую работоспособность контролируемого изделия /,
через систему обегающего контроля 2 поступает на блок экстраполято-
ра 3, с помощью которого определяется наиболее вероятное значение
параметра S(/-h-i) в будущий момент времени £нВ(^+1). В экстрапо-
ляторе 3 для определения EHB(^+i) должно сохраняться определенное
количество ранее измеренных значений параметров £(/) (предыстория
изменения состояния изделий), что предопределяет использование в экс-
траполяторе блока магнитной памяти.
После задержки в блоке 5 предсказанная величина £Нв(^-н) срав-
нивается в блоке 4 с истинными значениями параметра £(/<+i) в
199
выхода блоков 7 и 8
момент времени. Очевидно, что такое сравнение следует производить
через период контроля, за время которого предлагаемое устройство осу-
ществило контроль всех объектов с помощью системы 2.
В блоке 4 определяется разность £нВ(^+1)—£(£*+i)> которая в узле 6
возводится в квадрат. Полученный на выходе узла 6 квадрат разности
накапливается сумматором 7. Таким образом, на вход узла 9 поступает
величина, равная
i=0
На второй вход узла 9 от счетчика 8 подается число п произведенных
для контролируемого изделия сравнений, предсказанных и измеренных
значений параметра £(•£). В делительном устройстве 9 определяется ве-
личина
п
(п-i)- 2 [е.в(^+,)-ч«!+.)Г.
£=0
характеризующая дисперсию (точность) произведенных предсказаний.
Эта величина с выхода блока 9 подается на вход многоаргументного
функционального преобразователя 10. Одновременно на блок 10 посту-
пают величины и £нв (ti+i) - Многоаргументный функциональный
преобразователь выполняет следующее преобразование:
£ (*р
J exp-{[g-U(^+I)r/2^}di
I*_________________________
t (Q
J exp-{^-U(^+i)]2/2c2}^
о
Результат преобразований, выполненных блоком 10, представляет
собой вероятность безотказной работы контролируемого изделия до мо-
мента следующего контроля. Этот результат поступает в блок печати
11, который фиксирует вероятность безотказной работы изделия до сле-
дующей проверки.
ГЛАВА II СПЕЦИАЛИЗИРОВАННЫЕ АВТОМАТИЧЕСКИЕ УСТРОЙСТВА
ДИАГНОСТИКИ И ПРОГНОЗИРОВАНИЯ
ИЛ. Устройства для оценки работоспособности
технических объектов
Для диагностики и прогнозирования изменения состояния сложных
объектов не массового производства более целесообразно использовать
специализированные автоматические устройства, которые решают огра-
ниченный круг задач. К числу таких задач относится определение сте-
пени и запаса работоспособности диагностируемого изделия и прогно-
зирование с учетом известной предыстории. Такая задача возникает
в сфере эксплуатации изделий.
200
Типовая структурная схема (рис. 11.1) такого устройства состоит
из нескольких однотипных электронных приборов. Двухступенчатый ком-
бинированный коммутатор К предназначен для подключения контроли-
руемых объектов (шаговыми селекторами, первая ступень) и выбора
отдельных параметров объекта для измерения и оценки степени рабо-
тоспособности любого электронного прибора (с помощью электромаг-
нитных реле, управляемых схемой, в которую входят двоичный трех-
разрядный счетчик и координатная сетка; вторая ступень).
Напряжение постоянного тока с выхода
коммутатора поступают в преобразователь
П, который кодирует двоичным кодом по-
ступающее (в к напряжение. Преобразова-
ние постоянного напряжения в дискретную
форму осуществляется путем сравнения
контролируемого напряжения с напряже-
нием обратной связи, вырабатываемым
цифро-аналоговым •преобразователем. Эти
операции выполняют аналого-цифровой пре-
образователь и регистр выходного кода.
Блок логической обработки БЛО опре-
деляет знак и величину отклонения действи-
Рис. 11.1. Типовая структурная
схема устройства автоматиче-
ского определения работоспо-
собности.
тельного значения контролируемого пара-
метра от эталонного и оценивает результаты контроля ib соответствии с
выбранным принципом. В соответствии с решаемыми задачами БЛО име-
ет два субблока: арифметический и классификатор. Арифметический
субблок выполняет операцию вычитания кодовых комбинаций эталон-
ного и измеренного значений контролируемого параметра, т. е. опреде-
ляет величину отклонения действительного значения контролируемого па-
раметра от эталонного, представленных в параллельном двоичном коде,
для чего в него входят (рис. 11.2): схема определения знака модуля
разности, схема определения кода модуля разности периода параметра
Рис. 11.3. Классификатор.
Рис. 11.2. Арифметический блок.
таты классифицируются по зонам; 1 -я зона соответствует отклонению, не
превышающему 5% от номинального значения; 2-я зона соответствует от-
клонению в пределах от 5 до 15% номинального значения. В соответст-
вии со своим назначением классификатор включает в себя буферные
инверторы, диодную матрицу, коммутатор и собственно классификатор
(рис. 11.3). Классификатор имеет столько каналов, сколько контроли-
201
руется параметров. Управление им осуществляется импульсами посто-
янного напряжения, в данном случае поступающими с коммутатора
параметров.
Диодная многоступенчатая дешифраторная матрица в виде избира-
тельной схемы с определенным числом входов и выходов преобразовы-
вает величину отклонения параметра от номинального значения, пред-
ставленную в двоичном коде, в десятичный код. При поступлении им-
пульса управления в дешифраторе набирается определенная кодовая
комбинация и на одном из выходов появляется импульс напряжения.
Коммутатор переключает выходы дешифратора и входы классифи-
катора, число которых одинаково. Строится коммутатор из диодных
схем совпадения с двумя входами, один из которых связывается с де-
шифратором, а на другой подаются импульсы управления.
Классификатор собирается из типовых элементов ИЛИ и обеспечи-
вает отнесение классифицируемого напряжения по величине отклонения
к одной из зон (5 или 15%). Выходы классификатора связаны с им-
пульсными инверторами, формирующими импульсы управления необ-
ходимой длительности и полярности, которые могут быть использованы
для управления индикаторными схемами.
Блок формирования эталонов ФЭ. (рис. 11.1) предназначен для
выдачи эталонных значений контролируемых напряжений, представлен-
ных в восьмиразрядном двоичном коде. ФЭ состоит из запоминающего
и логического устройств. Запоминающее устройство представляет собой
накопительный регистр, собранный на потенциальных инверторах. Логи-
ческое устройство, состоящее из типовых логических элементов, обес-
печивает фиксацию соответствующего закодированного напряжения
в регистре.
Программный блок ПБ, программоносителем в котором является
диодная матрица, управляет всеми блоками, участвующими в оценке
работоспособности. Он включает в себя схемы формирования импуль-
сов управления и опроса.
Регистр Р преобразует сигналы устройства в форму, удобную для
управления печатающим устройством ПУ, и проектируется в соответ-
ствии с условиями, налагаемыми ПУ. Преду-
сматривается в течении одного' цикла, соот-
ветствующего обработке и фиксации одного
параметра, регистрировать условный номер
объекта, знак и (величину отклонения и инфор-
мацию о допустимости или недопустимости
отклонения по величине.
Bxcdmt
инп&ьс
Рис. 11.4. Схема канала Индикатор обеспечивает последователь-
индикатора. ную визуальную индикацию знака и зоны, к
которой относится контролируемый параметр
по величине отклонений от номинального значения. Для повышения на-
дежности фиксации признаков предусматривается определенная продол-
жительность горения <сигнальных лампочек индикатора, что достигается
введением элемента памяти на выходе каждого канала индикатора. На
рис. 11.4 представлена схема одного из каналов индикатора, в котором
число таких каналов равно произведению числа параметров на число
признаков одного параметра. Операции по самоконтролю устройства
производятся в канале каждого цикла контроля параметров групп объ-
ектов. При этом эталонные значения параметров в форме напряжения
постоянного тока подаются в виде стимулирующих сигналов на вход
202
устройства и подвергаются обработке по полному алгоритму функцио-
нирования устройства контроля. Результаты регистрируются и сравни-
ваются с заданными значениями. При условии совпадения полученных
результатов с заданными устройство признается работоспособным.
Работу устройства обеспечивает автономный источник питания, вы-
рабатывающий стабилизированные напряжения постоянного тока, по-
даваемые непосредственно на отдельные его блоки.
11.2. Статистический классификатор
В настоящее время достаточно распространены автоматические
устройства, которые осуществляют допусковую оценку совокупности па-
раметров по принципу «годен — негоден». Подобная оценка не позволя-
ет определить степень работоспособности диагностируемой системы, что
является его существенным недостатком.
Рассмотрим устройство, которое позволяет автоматически оценить
по степени отклонения параметров от их номинальных значений степень
работоспособности контролируемого объекта. В таком устройстве эти
операции осуществляются автоматически и решение достигается тем, что
каждое измеренное значение параметра подается на блок, содержащий
т пороговых устройств, которые разделяют всю шкалу значений пара-
метров на ряд градаций, соответствующих той или иной степени работо-
способности. В этом блоке с помощью пороговых устройств оценивается
значение каждого параметра, т. е.
определяется номер градации. По по-
лученной совокупности ‘номеров гра-
даций измеряемых параметров на
основании заранее заложенной -в раз-
деляющем устройстве программы опре-
деляется степень работоспособности
диагностируемого объекта.
Градация значений параметров
осуществляется на основе статистиче-
ских данных, которые 'накапливаются
в период эксплуатации и соответст-
вующим образом обрабатываются. По-
добные устройства получили название
статистических классификаторов. Оп-
ределенной степени работоспособности
соответствует характерное значение
всех параметров объекта и прибор как
бы «опознает» ту или иную степень
работоспособности (класс), основные
черты которой заложены в развязы-
вающем устройстве.
Устройство (рис. 11.5) состоит
Рис 11.5. Функциональная схема ста-
тистического классификатора.
из входного нормирующего блока
ВНБ, п блоков формирования кода класса БФКК, разделяющего
устройства РУ и ряда схем индикации СИ, число которых равно числу
распознаваемых дефектов или уровней работоспособности. Число п со-
ответствует числу контролируемых параметров (признаков) прибора,
состояние которого определяется. Каждый БФКК (рис. 11.5) содержит
203
схему управления СУ, состоящую из задержанного мультивибратора
ЗМ, дифференцирующей цепочки ДЦ, ограничителя О и ключа-инвер-
тора КН, а также т каналов РЗУ, состоящих из порогового устройст-
ва ПУ, схемы совпадения И$_1, ключа Ki-i, схемы совпадения Йг_2 и
запоминающего устройства ЗУ. Число каналов РЗУ т соответствует
числу градаций (числу дискретных интервалов), на которое разбивается
весь диапазон значений измеряемого параметра.
Устройство работает следующим образом. Испытуемый прибор под-
ключается ко входному нормирующему блоку, которое поочередно из-
меряет все п различительных признаков (параметра), и преобразует их
в напряжение, меняющееся в пределах от до t/2, в том случае, когда
какой-либо признак не может быть измерен непосредственно в единицах
напряжения (например, когда в качестве различительного признака
используется длительность выходного импульса испытуемого прибора
и т. д.). Напряжение с выхода ВНБ, соответствующее значению изме-
Рис. 11.6. Принципиальная схема блока формирования кода класса.
ренного признака, поступает на вход БФКК, число которых соответст-
вует числу измеряемых параметров (признаков), т. е. равно п.
Весь диапазон выходного напряжения ВНБ, меняющийся в преде-
лах от Ui до U2 и соответствующий изменению признака от его значе-
ний до ^тах, разбивается на т градаций Уровни срабатывания
каналов РЗУ тоже разбиты на т градаций, причем сигнал на дешиф-
ратор поступает с того канала РЗУ, номер которого соответствует уров-
ню выходного напряжения ВНБ. Это осуществляется следующим обра-
204
зом (рис. 11.6). На входе каждого канала РЗУ стоят пороговые устрой-
ства— триггеры Шмитта, собранные иа транзисторах Ti-i, Ti-s, T2-i,
Т2-2, - -Tm-i, Ттп-2- Пороги срабатывания этих устройств Uci, (/С2,
. . ., Uст подбираются С ПОМОЩЬЮ сопротивлений Ri-i, R2-1, . • Rm-1-
'Если величина входного напряжения такова, что то
срабатывает /-е пороговое устройство. При этом транзистор Т<_1 запи-
рается и отрицательное напряжение, через диод Д?-_1 поступает на базу
Ti ждущего мультивибратора СУ и отпирает его. Отрицательный им-
пульс с коллектора Т2 поступает на дифференцирующую цепочку RiCi,
с выхода которой первый отрицательный всплеск через диоды Д1-2,
Д2_2, ..., Дто-2 поступает на запоминающие устройства ЗУ (на базы
Ti-5, Т2-5, •.Ъп-з триггеров с эмиттерпой связью) и приводит их в ис-
ходное состояние, т. е. состояние, при котором выходное напряжение
ЗУ равно нулю.
Положительный всплеск с выхода дифференцирующей цепи через
диод Д1 поступает па базу ключа Т3 и закрывает его. Отрицательное
напряжение с коллектора Т3 поступает на схемы совпадений И1_2,
И2-2, .- Итп-2 (рис. 11.5). Одновременно при срабатывании порогового
устройства транзистор Тг-2 отпирается и на его коллекторе устанавли-
вается напряжение близкое к нулю. Если при этом пороговое устрой-
ство /4-1-го канала не сработало, т. е. на коллекторе транзистора
T(i+i)-i напряжение близко к нулю, то на схему Иг-1 подаются два на-
пряжения, близкие к пулю, что приводит к запиранию ключа Тг-з- От-
рицательное напряжение с коллектора Тг--з поступает на схему совпа-
дения Иг-2, с выхода которой отрицательный сигнал через диод Дг-~з
поступает на базу транзистора Тг_4 ЗУ (триггера). При этом триггер
ЗУ опрокидывается так, что транзистор Тг--4 будет открыт, а триод Тг_&
будет заперт, т. е. на выход схемы с /-го капала поступает отрицатель-
ное напряжение, равное напряжению коллектора, запертого триода Tj-s.
В таком положений схема будет находиться до тех пор, пока на вход
БФКК не поступит напряжение от нового диагностируемого прибора.
Следует отметить, что при выполнении условия Uci>UBX>Uci сра-
батывает пороговое устройство /-го канала РЗУ, а также всех каналов,
номера которых меньше /. Одиако на схемы совпадений И1-1, И2-1, ...
..., поступает отрицательное напряжение с коллекторов тран-
зисторов соответственно Т2-1, T3_i, ..., T<-i, что поддерживает ключи
Ki-t, К2-1, - - на транзисторах Tt_3, Т2-3, -.Т(г-1)-з открытыми.
При этом схемы совпадений Hi_2, И2-2, - -И(г-1)-2 не срабатывают и
на запоминающие устройства 1, 2 ... (2—1)-го каналов РЗУ никакой
сигнал не поступает.
Развязывающее устройство (рис. 11.7) включает в себя диодную
матрицу, имеющую тХп входов, где и— число блоков БФКК (число
измеряемых признаков), а т — число выходов блоков БФКК (число
градаций, па которое разбивается каждый признак). Количество выхо-
дов матрицы равно количеству распознаваемых классов (дефектов) и
может меняться от 2 до 2'т+п. На каждый вход матрицы сигнал с выхо-
да блока БФКК подается через схему ИЛИ, имеющую т входов. Не-
обходимость схем ИЛИ вызвана следующим. Каждому классу по лю-
бому из измеряемых признаков может соответствовать не одно значе-
ние градации, а любая совокупность из нескольких значений градации
(в предельном случае из т градаций). В этом случае к каждому из
входов Ц диодной матрицы должно быть подключено столько выходов
блока БФКК /, сколько значений градаций по /-му признаку соответ-
205
ствует t-му классу. Таким образом, несколько выходов блока БФКК
j оказываются запараллеленными и для их развязки (для устранения
взаимного влияния друг на друга) служат схемы ИЛИ.
Описанное устройство предназначалось для оценки состояния гер-
маниевых транзисторов. В качестве измеряемых признаков были вы-
Рис. 11.7. Развязывающее устройство статистического классификатора.
браны время рассасывания тр и время спада импульса транзистора при
работе его в импульсном переключающем устройстве, причем эти пара-
метры измерялись для трех схем включения: с общим эмиттером, об-
щим коллектором и общей базой. Таким образом, число признаков,
а значит и блоков БФКК, было выбрано п=6. Число градаций каждого
признака также было выбрано т=6. Устройство позволяет выделить
6 классов степеней работоспособности транзисторов. Если в разделяю-
206
а пес устройство закладывать информацию о временных классах, то ре-
зультатом прогнозирования будет не степень работоспособности, а дол-
говечность или срок профилактических работ.
11.3. Устройства для диагностики дискретных схем
Рассмотрим работу двух устройств для определения работоспособ-
ности схем дискретного действия, которые реализуют метод дополни-
тельной нагрузки. Принцип работы одного из них иллюстрируется схе-
мой, изображенной на рис. 11.8. Коммутатор К периодически опраши-
вает диагностируемые объекты Oi, О2, ..., О,-, ..., Оп, где О — схема
дискретного действия, например триггер, мультивибратор. При этом
параллельно выходу диагностируемого объекта подключается перемен-
ная нагрузка величина которой регулируется исполнительным меха-
низмом ИМ. При срыве колебаний в контролируемом объекте, что ре-
гистрируется индикатором И, исполнительный механизм останавливает-
ся и фиксирует величину сопротивления Ramin, определяющего запас
работоспособности Величину нагрузки можно отградуировать в еди-
ницах сопротивления или непосредственно
в единицах, оценивающих степень работо-
способности.
В качестве коммутатора такого устрой-
ства (рис. 11.9) используются транзистор-
ные ключи, которые управляются триггер-
ным счетчиком ТСЪ состоящим из триггеров
Ti, Тг, -. Т« и диодной матрицы ДМц со
схемой ИЛИ. Количество разрядов счетчи-
ка ТС определяется числом транзисторных
ключей ТК-
Переменная нагрузка Ra представля-
ет собой магазин на $ сопротивлений,
которые коммутируются контактами реле _______ г
подключены к выходу диодной матрицы ДМ2, которая управляется
триггерным счетчиком ТС2, состоящим из триггеров ТТ, Т 2, ..., Т'щ-
'Число разрядов триггерного счетчика ТС2 равно числу сопротивле-
ний Rs. Сигнал с выхода диодной матрицы ДМ2 поступает на
цифровой индикатор ДЯ, фиксирующий число сработавших реле, т. е.
/величину сопротивления Кроме того, этот сигнал подается на запо-
Рис. 11.9. Функциональная схема устройства диагностики.
207
минающее устройство ЗУ или записывается на магнитной ленте (само-
писце) .
Триггерные счетчики TCi и ТС2 управляются блоком синхронизации
БС, состоящим из задающего генератора ЗГ, делителя частоты Д, линий
задержки ЛЗ и выходных эмиттер ных повторителей ЭП. Задающий
генератор вырабатывает импульсы с частотой F2, запускающие триггер-
ный. счетчик ТС2- Линия задержки задерживает импульсы с частотой
F-z на величину где tn— время переключения триодных ключей
ТК. Импульсы напряжений, поступающие с выхода делителя Д с ча-
стотой Fi, запускают триггерный счетчик TCi. Коэффициент деления
делителя частоты
Блок синхронизации Б С запускается и прерывается контактами
реле Ро, обмотка которого подключена к выходу индикатора колебаний
диагностируемого объекта, состоящего из дифференцирующей цепочки
Рис. 11.10. Функциональная схема устройства диагностики сложных объектов по ограни-
ченной информации.
ДЦ, задержанного мультивибратора ЗМ и выпрямителя В. В схеме
предусмотрен также ручной запуск и остановка работы блока синхро-
низации.
Теперь рассмотрим работу устройства (рис. 11.10), которое пред-
назначено для контроля работоспособности более сложных объектов
диагностики при ограниченной информации о его состоянии. Оно по-
зволяет восстанавливать функцию работоспособности диагностируемого
объекта методом вкладов.
Устройство состоит из одного блока формирования базового вклада
(ФБВ) и блоков формирования элементарных вкладов (БФЭВ), блока
определения средиеквадратического значения функции распределения
работоспособности, блока синхронизации устройства и элементов инди-
кации, позволяющих визуально наблюдать функцию распределения ра-
ботоспособности диагностируемого объекта и его запас работоспособ-
ности.
Случайная величина характеризующая степень работоспособно-
сти s-ro узла сложного объекта диагностики, поступает на вход s-ro
блока формирования элементарных вкладов БФЭВ, который состоит из-
нормирующего устройства НУ, сравнивающего устройства СУ, форми-
рователя импульсов вкладов ФИВ, линии задержки и выходного устрой-
ства ВУ. Нормирующее устройство преобразовывает входную случайную'
208
величину £s в постоянное напряжение lh, величина которого пропорцио-
нальна Ь- В сравнивающем устройстве постоянное напряжение ^срав-
нивается с пилообразным, вырабатываемым генератором пилы ГП, и
преобразуется во временной интервал (импульс), длительность которо-
го пропорциональна величине напряжения Us. В момент спада этого
импульса запускается ФИВ, представляющий собой задержанный муль-
тивибратор.
Импульсы вкладов, задержанные на величину /3=^п—^ив/2, где
— длительность пилообразного напряжения, в — длительность
импульса вклада, через выходное устройство поступают па сумматор.
Кроме того, на сумматор поступает импульс базового вклада, длитель-
ность которого пропорциональна величине ^тах—Ъмп- Запуск блока
формирования базового вклада ФБВ осуществляется первым импульсом
вклада, а срыв — последним, для чего на ФБВ подается напряжение со
всех сравнивающих устройств через схему ПЛИ.
С сумматора напряжение поступает на функциональный преобразо-
ватель ФП, играющий роль сглаживающего устройства, на выходе ко-
торого напряжение принимает вид функции работоспособности диагно-
стируемого объекта. Это напряжение поступает одновременно в элек-
тронно-лучевую трубку ЭЛТ для визуального наблюдения и на триггер
Шмитта ТШ, фиксирующий момент, при котором функция работоспо-
собности достигает уровня от максимального значения, т. е. уровня
соответствующего значению т±3о при нормальном законе распределе-
ния функции работоспособности. Этот уровень характеризует ми-
нимальную степень работоспособности узлов диагностируемого объекта.
Определяя разность между допустимым значением степени работо-
способности I* и минимальным ее значением £3(J, получаем запас работо-
способности объекта по критерию Зо как Д3^ = £* — £3а, который вычис-
ляется с помощью устройства, состоящего из задержанного мультиви-
братора ЗМ, генератора импульсов ГИ, триггерного счетчика ТС и фик-
сируется цифровым индикатором ЦИ.
Для нормирования величины функции работоспособности при изме-
нении числа контролируемых блоков (параметров) в схему введена
автоматическая регулировка уровня напряжения сумматора АРУ.
Управление осуществляется блоком синхронизации БС.
Рассмотренные устройства позволяют оценить степень и запас рабо-
тоспособности диагностируемого объекта, что является исходной инфор-
мацией для прогнозирования. Таким образом, подобные устройства
можно рассматривать как составные части автоматических прогиоза-
торов.
11.4. Устройство для оценки состояния объектов,
описываемых множеством параметров
В настоящее время определение состояния и характера изменения
многопараметрических объектов в большинстве случаев осуществляется
с помощью набора измерительных приборов различного назначения,
позволяющих оператору периодически контролировать множества пара-
метров объекта. Некоторые операции по определению запаса работоспо-
собности и непосредственному прогнозированию осуществляются вруч-
ную. Поэтому понятна необходимость разработки устройства, позволяю-
14—813 209
щего определить степень и запас работоспособности контролируемой
системы и осуществить прогнозирование состояния объекта (системы).
Эти задачи можно решить с помощью устройства, которое реализует
способ, заключающийся в том, что, применяя специальное нормирова-
ние, все полученные относительные величины параметров располагают
в пространстве (1 ... 0), которое разбивается на старшие (например,
1 ... 0,9) и младшие (например, 0 ... 0,1; 0,1 ... 0,2; и т. д.) разряды.
Чем выше степень работоспособности, тем больше информации (значе-
ний параметров) находится в старших разрядах и тем меньше
в младших.
Таким образом, определяя отношение количества информации, за-
ложенной в старших размерах, к количеству информации в младших
разрядах, можно оценить запас работоспособности контролируемой си-
стемы. Для систем различной долговечности результаты отношений (и
запас работоспособности) будут различными, а для систем с одинаковой
долговечностью — одинаковыми. Отсюда, сравнивая итоги отношения
количества информации с эталонными значениями, принадлежащими
определенным классам качества, осуществляем непосредственное про-
гнозирование.
Такое устройство (рис. 11.11) содержит блок нормирования, деши-
фратор, накапливающие счетчики, дискриминаторы, анализатор и схемы
индикации. Анализатор, составляющий прогнозирующую часть, пред-
ставляет собой один из вариантов статистического классификатора.
Датчики, установленные (или подключенные) в контролируемой систе-
ме, соединены со входами нормирующего устройства, выходы которого
соединены со входами 1 дешифратора 2.
Дешифратор представляет собой переключательную систему диод-
ного типа, преобразующую двоичный код в натуральный ряд чисел де-
сятичной системы счисления. Выходы дешифратора соединены с накап-
ливающими счетчиками 3, каждый из которых в конце опроса парамет-
ров содержит код — число, пропорциональное количеству информации,
находящейся во всех разрядах, например, 1 ... 0,9 (старший разряд);
0,9 ... 0,8; ...; 0,1 ... 0 (младшие разряды). При этом в старшем счетчи-
ке 4 записано число, пропорциональное числу значений .параметров, на-
ходящихся в старшем разряде, например, I ... 0,9. Чем больше это
число, тем выше степень работоспособности, тем больше ее запас.
Запас работоспособности можно определить, если вычислить, на-
сколько число, записанное в старшем разряде, больше каждого из чи-
сел, записанных в младших разрядах. Для этого старший накапливаю-
щий счетчик соединен со входом каждого цифро-аналогового дискрими-
натора 5, вторые входы которых подключены к соответствующим млад-
шим счетчикам. Цифро-аналоговым дискриминатором кодов является
устройство, имеющее на выходе напряжение постоянного тока, пропор-
циональное разности двух чисел-кодов, которые поступают на его вход.
При этом вывод кода из накапливающих счетчиков может быть как по-
следовательным, так и параллельным. При переходе изменится только
тип дискриминатора [101].
Выходы дискриминаторов соединены с соответствующими входами
анализатора 6. Анализатор содержит число входов и соответственно им
число каналов, равных числу младших счетчиков, выходы которых
соединены со своим каналом в анализаторе. Выход дискриминатора не-
посредственно соединен с пороговыми элементами канала, число кото-
рых соответствует числу линии в канале и может быть различным
210
в зависимости от требуемой точности прогнозирования. Пороговые эле-
менты представляют собой обыкновенные ключи (например, электрон-
ные), выходы которых соединены со входами несимметричных тригге-
ров. В свою очередь в линии за несимметричным триггером следует сим-
метричный триггер, играющий роль запоминающего устройства. Выход
симметричного триггера подклю-
чен как ко входу различителя,
так и ко ©ходу первого индика-
торного устройства 7 (индикатор
запаса работоспособности). Све-
товая индикация дает информа-
цию о запасе работоспособности.
В каждом канале напряже-
ние присутствует только в одной
линии. Несрабатывание симме-
тричных триггеров соседних ли-
ний обеспечивается обратными
Рис. 11.11. Устройство для оценки состоя-
ния индивидуальных объектов.
связями в линиях одного канала.
Выходы линий соединены со
входами ‘различителя, построенного в виде диодной матрицы..
К различителю также подключен блок набора классов БНК, который,
осуществляет набор классов качества (например, классов долговечнос-
ти), объединяющий системы с идентичными характеристиками качества
(например, запасом работоспособности или долговечностью). Набор
классов осуществляется на базе априорного статистического материа-
ла и основывается иа том, что у систем с приблизительно равным запа-
сом работоспособности и долговечностью будет идентичная совокуп-
ность напряжений после сравнения в дискриминаторе. Выходы
различителя соединены с блоком индикации класса 8 (индикатор клас-
са качества — результата прогнозирования).
Устройство работает следующим образом. Значения параметров,
снятые с датчиков, нормируются в нормирующем устройстве таким
образом, что все значения параметров для работоспособности системы
находятся в интервале 1 ... О, причем значения, близкие к 1 (например,
в промежутке 1 ... 0,9), формируют старший разряд, а значения, уда-
ленные от 1 (например, в промежутках 0,9 ... 0,8; 0,8 ... 0,7; ...; 0,1 ...
... 0), формируют младшие разряды. Заметим, что чем больше инфор-
мации в старшем разряде, тем выше качество системы, больше запас ее
работоспособности, больше долговечность. Нормированные значения па-
раметров поступают в двоичном коде иа входы 1 дешифратора 2.
Импульсы с выхода дешифратора подаются на соответствующие накап-
ливающие счетчики. Числа, записанные в счетчике после опроса всех
датчиков, представляют собой функцию состояния.
В рассматриваемом устройстве число, записанное в старшем счет-
чике, параллельно или последовательно в виде кода подается на первый
вход всех цифро-аналоговых дискриминаторов, а иа их вторые входы
подаются коды с соответствующих младших разрядов. Напряжение
с выхода каждого дискриминатора, пропорциональное разности кодов,
поступает в свой канал в анализаторе.
Таким образом, ко входам анализатора подводятся напряжения,
характеризующие запас работоспособности системы. Очевидно, чем
больше напряжения на выходе более младших дискриминаторов, тем
больше запас работоспособности. Для систем разного уровня работо-
14*
21k
способности (качества, долговечности) этот ряд напряжений будет раз-
личен.
Напряжение с выхода дискриминатора проходит в ту линию своего
канала, пороговый элемент которой пропускает его. Срабатывает несим-
метричный триггер этой линии, импульс которого опрокидывает симме-
тричный триггер. Напряжение на выходе каждого каиала присутствует
только в одной линии, т. е. только на выходе одного симметричного
триггера. При этом оно включает схему индикации запаса работоспо-
собности и подается на различитель. В итоге на различитель поступает
напряжение с каждого канала. Совокупность напряжений, соответст-
вующих одному из классов, включает блок индикации класса. Индика-
ция класса и есть результат прогнозирования.
11.5. Устройства для диагностики больших систем, типа
автоматизированных систем управления (АСУ)
Разработка средств контроля сложной системы типа АСУ сущест-
венно отличается от разработки средств и методов контроля отдельного
вида аппаратуры, так как система состоит из целого ряда технических
средств, объединенных в единый комплекс средств автоматизации
(КСА). Рассмотрим некоторые особенности контроля АСУ.
Современные АСУ характеризуются сложной, разветвленной иерар-
хической структурой, большим количеством, отдельных подсистем, кото-
рые часто отстоят друг от друга на большие расстояния, и для их
объединения требуются специальные каналы связи. Они работают, как
правило, в реальном или близком к реальному масштабу времени. Ре-
шение задачи создания средств контроля АСУ требует системного под-
хода. В отличие от ранее применяемых средств и методов контроля,
когда основными контролируемыми параметрами являлись различные
технические параметры аппаратуры, при контроле АСУ в качестве глав-
ных контролируемых параметров выбираются алгоритмы функциони-
рования, контролируется способность комплекса средств автоматизации
нормально функционировать в соответствии с возложенными на них
алгоритмами. С учетом этой особенности контроль АСУ принято назы-
вать функциональным контролем (ФК), а комплекс средств и меро-
приятий, обеспечивающих его проведение — системой функционального
контроля (СФК)-
Задачей СФК является не только обнаружение, но также локализа-
ция места отказа, оперативное подключение резервных комплексов
вместо отказавших и выдача требования на перераспределение задач.
Систему функционального контроля целесообразно строить как автома-
тизированную, так как она решает задачи, которые требуют участия
человека-оператора. Поэтому неотъемлемой частью технических средств
СФК является специальное рабочее место (РМ СФК), которое через
«человека-оператора» объединяет систему контроля и систему восста-
новления КСА АСУ.
Процесс разработки СФК складывается из последовательного ре-
шения следующих вопросов: исследования структурной и функциональ-
ной схемы АСУ; исследования задач и назначения отдельных элементов
КСА; определения назначения и задач СФК в составе КСА АСУ; раз-
работки принципов организации СФК; выбора варианта технической
реализации СФК, определения состава технических средств СФК, опре-
-212
деления уровня централизации и децентрализации размещения средств
контроля.
В настоящее время определились два основных подхода к вопросу
организации СФК АСУ. Первый состоит в создании специальной СФК,
повторяющей структуру и иерархию контролируемой АСУ. Второй пред-
полагает блочное построение СФК без жесткой привязки к структуре и
иерархии контролируемой АСУ. В этом случае СФК складывается из
отдельных подсистем ФК (ПФК), выполняющих независимо друг от
друга функциональный контроль КСА звеньев АСУ и специального
блока (БФК), объединяющего их в единую систему функционального
контроля АСУ.
ПФК реализуют единые принципы и методы контроля на всех
звеньях АСУ. На него возложены задачи контроля работоспособности,
поиска и локализации места отказа с заданной подробностью, управле-
ния режимами контроля и режимами работы КСА по результатам кон-
троля, прогнозирования состояния КСА, прогнозирования расхода ЗИП
и необходимого количества обслуживающего персонала на определен-
ный период эксплуатации, а также наглядное отображение состояния
и режимов работы КСА звена управления. БФК решает задачи контро-
ля состояния трактов обмена информацией между отдельными звеньями
АСУ.
Вся информация о состоянии КСА звеньев управления в этом слу-
чае сосредоточивается на одном РМ СФК, объявляемом старшим и раз-
мещаемом на одном из звеньев управления. Для этого на алгоритмы
ПФК и БФК звеньев АСУ накладываются определенные ограничения,
позволяющие направить потоки контрольной информации от ПФК
звеньев в адрес старшего РМ СФК. В зависимости от сложности КСА
звеньев управления в состав технических средств ПФК других звеньев
РМ СФК либо включаются, либо не включаются. Для АСУ с не ярко
выраженными звеньями управления, имеющими компактное террито-
риальное размещение, применяются СФК, повторяющие структуру АСУ
с единым РМ СФК.
На рис. 11.12 показана упрощенная схема организации СФК услов-
ной АСУ. Здесь звено А выделено как главное по иерархии. На его
РМ СФК сосредоточивается информация о состоянии КСА за всю АСУ.
На звеньях А, В, Г, Ду Е размещены ПФК и унифицированный блок
БФК, с помощью которого создана единая СФК АСУ.
Возможны различные варианты организации системы контроля
звеньев управления (ПФК) и СФК, повторяющих структуру контроли-
руемой АСУ, в частности на базе встроенного аппаратного контроля
с использованием кодовой избыточности; на базе контрольных контуров
с использованием информационной избыточности; комбинированный,
на базе встроенного аппаратного, контурного и визуального кон-
троля.
Для контроля работоспособности АСУ в состав каждого комплекта
аппаратуры вводятся специальные устройства аппаратного контроля.
Они же обеспечивают передачу результатов контроля на РМ СФК-
Аппаратиый контроль основывается на введении различного рода избы-
точности в кодирование рабочей информации. В настоящее время изве-
стны и применяются такие способы кодирования, как контроль по
модулю, код Хемминга, циклические коды, рекуррентные коды и т. д.
Однако использование избыточного кодирования не позволяет прове-
рить все цепи, например цепи управления, поэтому для их контроля
213
Звено А
Рис. 11.12. Схема организации СФК.
разрабатываются специальные методы аппаратного контроля, такие,
как дублирование, голосование «2 из 3» и другие.
Вариант организации СФК на базе встроенного аппаратного кон-
троля следует применять в тех случаях, когда состав технических
средств АСУ небольшой и представляется возможным выбрать единый
закон избыточного кодирования для большинства аппаратуры.
Сущность метода контуров состоит в том, что контролируемая
аппаратура включается в цепочку средств, являющихся частью общего
контура АСУ, при этом источник контрольной информации является и
ее приемником. Для такой схемы организации СФК является ха-
рактерным введение в состав информации, циркулирующей в кои-
туре АСУ, специальной контрольной информации (тестов). Кон-
троль при этом осуществляется таким образом, что позволяет судить
о работоспособности не только контролируемой аппаратуры, но и о всей
цепочке связанных с ней технических средств. Вариант организации
СФК на базе контрольных контуров подразумевает наличие специаль-
ного централизованного устройства контроля, на которое замыкаются
контрольные контуры. Это устройство располагает набором тестов, ко-
торые в соответствии с алгоритмом контроля с заданным периодом
вводятся в контрольные контуры й после их возвращения по цепи
обратной связи обрабатываются. Результатом обработки является
информация о состоянии технических средств АСУ. Эта информация
выдается на РМ СФК- В качестве централизованного устройства кон-
троля может служить ЭВМ, если она входит в состав технических
средств АСУ и имеет необходимый запас производительности.
Комбинированный вариант организации системы контроля опти-
мальным образом совмещает встроенный аппаратный контроль, контур-
214
1ый контроль и визуальный контроль. Для одной и той же аппарату-
ры, входящей в состав технических средств АСУ, можно применить
одновременно все перечисленные способы контроля. Для этого рекомен-
дуется функциональную схему аппаратуры разделять на области, кото-
рые могут частично пересекаться, но при этом не должно оставаться ни
одного элемента схемы, ие вошедшего ни в одну из областей контроля.
Прежде всего выделяют ту область, которая охватывается оперативным
контурным контролем. В нее должны войти все стыки данной аппарату-
ры с другой аппаратурой АСУ и устройства, выполняющие основные
логические функции. Далее выделяют область визуального контроля.
Визуальный контроль может быть распространен только на ту аппара-
гуру АСУ, которая по своему назначению подразумевает наличие чело-
века-оператора.
В зависимости от структуры и состава технических средств АСУ,
методов контроля, оснащенности АСУ вычислительными средствами
применяют различные типы рабочих мест РМ системы контроля. Они от-
личаются по составу и методу построения средств наглядного отобра-
жения, объему выполняемых задач и способу включения в состав функ-
циональной (структурной) схемы АСУ. Наиболее простым является
РМ СФК с представлением информации в табличном виде со съемом
информации непосредственно от встроенных устройств аппаратного кон-
троля.
Решение проблемы прогнозирования состояния объекта контроля
и выбор оптимальной стратегии эксплуатации КСА АСУ становится
важнейшей и актуальной задачей создания АСУ.
Проблема прогнозирования распадается на две составные части:
— разработку методов и средств выделения и сбора информации,
необходимой для прогнозирования;
— определение необходимых апостериорных критериев качества
функционирования объекта контроля на основе данных, полученных
СФК в результате контроля, а также алгоритмизации решения задач
прогноза с учетом технических средств СФК-
Техническая оснащенность современных СФК АСУ позволяет с до-
статочной для практики полнотой решать эти задачи
ПРИЛОЖЕНИЕ
ПРИМЕР ПРОГНОЗИРОВАНИЯ НАДЕЖНОСТИ НА ОСНОВЕ
РАСПОЗНАВАНИЯ ОБРАЗОВ
Определить, будет ли исследуемый усилитель ко времени 2=1000 ч работы у.дов-
четворять требованиям к надежности, если известно, что: 1) признаком отказа яв-
ляется снижение коэффициента усиления К до 50 и ниже; 2) в результате -постепенных
отказов К измняется монотонно; 3) в результате предварительного «обучения» полу-
чены следующие нормированные значения параметров усилителей: /, Ult Uz в момент
t—Q и значения Л через 1-000 ч работы (см. таблицу)
Параметры М усилителей
1 2 3 4 5 6 7 8 9 10
/ и* К 7,50 44,44 5,62 40 8,75 47,22 4,73 44 9,38 50,00 4,59 45 10,63 52,78 4,14 47 11,88 53,33 3,50 50 13,13 57,22 2,37 56 14,38 58,89 2,07 59 15,63 61,11 1,48 60 16,25 63,89 1,18 61 18,13 66,67 0,59 64
215
Решение.
I По уравнению (9.8), принимая g=l, определяем расстояния /?fj. Например:
/?12 = К(8?75 —7,5)2+ (47,22 —44,44)2-|- (5,62 —4.73)2 = 3,18
2. По уравнению (9.7), принимая а~3, k—4, определяем значения «потенциаль-
ной» функции (pij, приписывая знак минус всем (pij, у которых i^5, так как все уси-
лители до 5-го включительно находятся в зоне надежности. Например:
¥16 = “ 1 + 3-14,34* = — 8-10"6-
3. Измеряем нормированные параметры исследуемого усилителя. Пусть они рав-
ны: /=10,00; 64=52,78; 64=4,43.
4. По уравнениям (9.8) и (9.7) определяем /?ц,j и фи.д
5. Вычисляе*м значение суммарного потенциала исследуемого усилителя по фор-
муле:
ю
=2 = —6-10-8 —3-10-* —5.10-3 _59. ю-2— 15-IO-3 4-3-10—4 +
/=1
4-9.10-5-1-3-10-3-1- 1-10-5 _{_ 15-10-3 —60-10-2
Суммарный потенциал имеет знак минус, поэтому делаем заключение о том, что
исследуемый усилитель относится к разряду ненадежных.
•СПИСОК ЛИТЕРАТУРЫ
1. Колмогоров А. Н. Интерполирование и экстраполирование-стационарных
случайных последовательностей. — «Известия АН СССР. Сер. математиче-
ская», 4971, т. 5, № 1.
2. W i е n е г N. Extrapolation, Interpolation 'and Smoothing of Stationary Time
Series, with Engineering Applications. The Technology Press. New York, 1949.
3. 'Васильев Б. ‘В. Прогнозирование -надежности и эффективности радио-
электронных устройств. М., «Сов. радио», 1970.
, 4. Дружинин Г. В. Надежность систем автоматики. М., «Энергия», 1967.
5. Пол оз к о А. М. Основы теории надежности. -М., '«Наука», 1964.
6. Основные вопросы теории и практики надежности. М., «Сов. радио», 1971.
7. Растр 1йгин Л. А. Статистические методы поиска. М., «Наука», 1968.
8. Ромамеако А. Ф., Сергеев Г. А. Вопросы прикладного анализа слу-
чайных процессов. М., «Сов. радио», 1968.
9. Чижов А. В., Добжи некий Б. Н. О погрешностях измерения изменяю-
щейся частоты методом счета нулей. — «Радиотехника», 1964, т. 19, № <1.
10. Справочник по надежности Пер. с англ. М., «Мир», 1969.
11. Крамер Г. Математические методы статистики. Пер. -с англ. М., ИЛ,
1948.
12. Я стребенецкий М. А., Соляник Б. Л. Определение -надежности
аппаратуры -промышленной автоматики -в условиях эксплуатации. М., «Энер-
гия», 1968.
13. Ч а вч а ни д з е В. В., -Кумсишвмли В. А Об определении законов
распределения на основе малого числа наблюдений. — В кн.: Применение
вычислительной техники для автоматизации производства. М., Машгиз, '1961.
14. Спра-вочник по основам электронной техники. Под ред. Б. С. Гершунского.
Изд-во Киевского университета. 1972. Авт.: Б. С. Гершунский, А. В. Романов-
ская, И. М. Ващенко, В. <В. Власенко.
15. Пугачев В. С. Введение в теорию .вероятностей. М., «Нау-ка», 1968.
16. Kirkman К. A. Failure prediction in electronic system.—«IEEE Trans.»,
1966, AES-2, № 6.
17. Лисичкин В. А, Отраслевое -научно-техническое прогнозирование. М.»
«Экономика», 1971.
18. Б р аил о.век и й В. Л. Алгоритм распознавания объектов -со многими
параметрами .и его приложения. — «Известия АН СССР. Техническая кибер-
нетика», 1964, № 2
19. В а и дер Варден Б Л. Математическая статистика. Пер. с нем. М.,
ИЛ, 1960.
20. Большо-в Л. Н., Смирнов Н. В. Таблицы математической статистики.
М., «Наука», 1965.
21. Цыпким Я. 3., Адаптация и обучение в автоматических системах. М.,
«Наука», 1968.
22. Г а с -к а р о в Д. В. Вопросы прогнозирования изменения состояния техни-
ческих объектов. ЛДНТП, «Знание», 1968.
23 Блинов И Н., Г а с к а ров Д. В., Моз г ал е веки й А. В. Автоматиче-
ский контроль систем управления. Л., «Энергия», 1968.
21. Г а с-к а ров Д. В., М о з г а л е в ски й А. В. Некоторые технические при-
ложения метода экстраполяции при помощи полиномов. — «Радиотехника».
1967, № 2.
25. Крейн С. Г., Ушаков В. -Н. Математический анализ элементарных функ-
ций. М., «Наука», 1966.
26. Винер Н. Я- — математик. Пер. с англ. М., «Наука», 1967.
27 Шор Я. 'Б., -Кузьмин Ф. И. Таблицы для анализа и контроля надежно-
сти. М., «Сов радио», 1968.
28. Вентцел ь Е. С. Теория -вероятностей. М., «Наука», 1969.
29. Пугачев В. С. Статистические методы в технической кибернетике. М„ «Сов.
радио», 1971.
30. Хевмлеид Р. Инженерная надежность и -расчет на долговечность. Пер.
•с англ., М.—Л., «Энергия», 1966.
2J7
31. Гумбель Э. 'Статистика экстремальных значений. Пер. с англ. М., «Мир»,
1905.
32. Казаков В. А. Введение в теорию марковских процессов и «©которые
радиотехнические задачи. (М., «Сов. радио», 1973.
33. X е н н а н Э. Анализ временных рядов. Пер. с англ. М., «Наука», 1964.
34. И в а х н ен.ко А. Г., Лапа В. Г. Кибернетические предсказывающие
устройства. Киев, «Наукова думка», 1965.
35. Яглом А. М., Ятлом И. М. Вероятность и информация. >М., «Наука»»
1973.
36. Пр охор о-в Ю. В., Розанов Ю. А. Теория вероятностей. М., «Наука»»
1967.
37. Зельдович Я. Б.» Мышки с А. Д. Элементы прикладной математики.
М., «Наука», 1967.
38. Куликов В. А. Обеспечение надежности сложной радиоэлектронной аппа-
ратуры. М., «Сов. радио», 1966.
39. С вешников А. А. Прикладные методы теории случайных функций. М.»
«Паука», 1968.
40. Пугачев В. С. Теория случайных функций и ее применение к задачам
автоматического управления. М., Физматгиз, 1962.
41. Гренамдер У. Случайные процессы и статистические выводы. Пер. с англ.
М., ИЛ, 1961.
42. Смирнов Н. В., Д ун и н - Б ар к о в с к и й И. В. Курс теории вероятно-
стей и математической статистики. М., «.Наука», 1969.
43. Рао С. Р. Линейные статистические методы и их применение. Пер. -с англ
М., «Наука», 1968.
44. Левин Б. Р. Теоретические вопросы статистической радиотехники М,
«Сов. радио», 1968.
45. Гаск а ров Д. .Б, Мозга л ев с кий А. В. Проблемы прогнозирования
изменения состояния технических объектов. — «Известия ЛЭТИ», 1972,
выл. 118.
46. Бартлетт М. С. Введение в теорию случайных процессов. Пер. с англ
М„ ИЛ, 1958.
47. Вальд А. Статистические решающие функции. — В кн.: Позиционные
игры. Пер. с англ. М., ИЛ, 1967.
48. Б лек у эл Д.( Гирш их М. Д. Теория игр и статистических решений.
Пер. с англ. М., ИЛ, 1958.
49. Загоруйко Н. Г. Методы распознавания и их применение. М., «Сов.
радио», 1972.
50. Пе рв о з в а >я ски й А. А. Распознавание абстрактных образов как задача
линейного прогнозирования. — «Известия АН СССР. Техническая киберне-
тика», 1965, № 4.
51. Поспелов Д. А. Игры и автоматы. М., «Энергия», 1966.
52 Беляков-Бодин В. И. Геометрический метод распознавания образов. —
В кн.: Работа по технической кибернетике. Вып. 2. М., ВЦ АН СССР, 1968.
53. Розен блат Ф. Принципы .нейродинамики. Пер. с англ. «М., «Мир», 1965.
51. И вахненко А. Г. Самообучающиеся системы распознавания и автомати-
ческого управления. Киев, «Техника», 1969.
55. Розенфельд А Распознавание и обработка изображений. Пер. с англ.
М., «Мир», 1972.
56. А н д е р с о н Т. Введение в многомерный статистический анализ. М., Физ-
матгиз, 1963.
57. Себсстиан Г. С. Процессы принятия решений при распознавании обра-
зов. Киев, «Техника», 1965.
58. Левин И. Я. Некоторые вопросы теории опознавания образов. — «Изве-
стия АН СССР. Техническая кибернетика». 1964, № 2.
59. Б е б и а ш в и л и Ш. Л., Гаск а ров Д. В., Гугуш-вили Дж. Ф., На-
мине йшв ил и О. М. Некоторые результаты прогнозирования состояний
полупроводниковых триодов по шумовым признакам на основе статистиче-
ской теории распознавания образов. — «Сообщения АН ГрССР», 1973, т. 71,
№ 1.
60. А й з е .р .м а н М. А., Б р а вер м ан Э. М.» Розн оэ р Л. И. Метод по-
тенциальных функций в теории обучения машин. М., «Наука», 1970.
61. Гаскаров Д. Б. О (возможности многопараметрического индивидуального
npoiпозирования.— В кн.: Техническая диагностика.' Труды I Всесоюзного
совещания по технической диагностике. М., «Наука», 1972.
218
62. Нильсон Н. Обучающие машины. Пер. с англ. М., «Мир», 1967.
63. Надежность радиоэлектронных систем. Пер. с англ. М., «Сов. радио», 1968.
64 К о р я Г. Моделирование случайных процессов на аналоговых и аналого-
цифровых машинах. Пер. с англ., М., «Мир», 1968.
65. М о з г а л ев с к и й А. В., Волынский В. И., Г а ска.ров Д. В. Тех-
ническая диагностика судовой автоматики. Л., «Судостроение», 1972.
66. Сил ин В. Б., ЗаковряшЯ'Н А. И. Автоматическое прогнозирование
состояния аппаратуры управления и наблюдения. М., «Энергия», 1973.
67. Калинин В. И., Г е р ште й н Г. М. Введение в радиофизику. М., «Энер-
гия», 1957.
68. Степаненко И. П. Основы теории транзисторов и транзисторных схем.
М., «Энергия», 1965.
69. Цетлин М. Л. Поведение автоматов в случайных средах. — «УМ’Н», 1963,
т. 18, выл. 4.
70. Кри некий В. И. Асимптотически оптимальная последовательность авто-
матов с экспоненциальной скоростью сходимости.—«Биофизика», 1963,
выл. 6.
71. Кудрицкнй В. Д. Прогнозирование надежности радиоэлектронных
устройств. Киев, «Техника», 1973.
72. Ш у с т е р о ® и ч А. Н. Обнаружение неисправностей радиоэлектронного обо-
рудования. М, «Энергия», 1970.
73. М о з га л е® с к и й А. В.. Шарапов В. П. Техническая диагностика.
Л., ЛД НТ. 1968.
74. Меламедов И. М. Физическая основа надежности. М.—Л., «Энергия»,
1970.
75. Еф имев И. Е., К а л ь м а н Н. Г., Марты н ов В. И. Надежность инте-
гральных полупроводниковых схем. М., Изд-во стандартов, 1969.
76. Сандлер Дж. Техника надежности систем. Пер. с англ. А!., «Наука», 1966.
77. Гол инке вич Т. А. Оценка надежности радиоэлектронной аппаратуры. М..
«Сов. радио», 1969.
78. Неч ил о р е н к о В. И. Структурный анализ и методы построения надеж-
ных схем. М., «Сов. радио», 1968.
79. Рябинин И. А. Основы теории и расчета надежности судовых электро-
энергетических систем. Л., «Судостроение», 1971.
80. С о т с к о в Б. С. Основы теории и расчета надежности элементов -и устройств
авто.мат-ики и вычислительной техники. М., «Высшая школа», 1970.
81. Туркельтауб Р. М. Методы исследования точности и надежности схем
аппаратуры. М.—Л., «Энергия», 1966.
82. Д о м а н и ц к и й С. М. Построение надежных логических устройств. М.—Л.,
«Энергия», 1971.
83. Козлов В. А., Ушаков И. А. Краткий справочник по расчету надеж-
ности радиоэлектронной аппаратуры. М., «Сов. радио», 1966.
84. Бессонов А. А. Прогнозирование характеристик надежности автомати-
ческих систем. М., «Энергия», 1971.
85. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Математические
•методы в теории надежности. М., «Наука», 1965.
86. Ш о р Я. Б. Статистические методы анализа и контроля качества и надеж-
ности. iM., «Сов. радио», 1962.
87. О надежности сложных технических систем. М., «Сов. радио», 1966.
88. Груничев А. С., К у зя е ц о в В. А., Шипов Е. В. Испытания радио-
электронной аппаратуры на надежность. М., «Сов. радио», 1969.
89. Б а з о веки й И. Надежность. Теория и практика. Пер. с англ. М., «Мир»,
1965.
90. Цветаев К- Н. Сокращение времени испытаний на надежность при изве-
стном виде функции распределения. М., «Знание», 1969.
91. Барлоу Р., Прошан Ф. Математическая теория надежности. Пер.
с англ. М., «Сов. радио», 1969
92. Фир се нк о® Г. Ф. К планированию испытаний на надежность унифи-
цированных функциональных узлов. — В -кн.: Стандарты и качество. Изд-во
стандартов, 1967, № 3.
93. Пер роте А. И., К ар та ш о в Г Д., Цветаев К. Н. Основы ускорен-
ных испытаний радиоэлементов на надежность. М., «Сов. радио», 1968.
94. Я в рн ян А. Н. Ускоренные определительные и приемно-сдаточные испы-
тания на надежность, основанные на линейной апроксимации изменений
технических параметров М., «Знание», 1969.
219
^5. Аркадьев А. Г., Б-р а верман Э. М. Обучение машины классификации
объектов. М., «Наука», 1971.
96. Г ро дзен ски ii С. Я. Прогнозирование срока службы электровакуумных
приборов.—«Обзоры но электронной технике. Сер. Электроника СВЧ»,
-вып. № 10(297). М., ЦНИИ «Электроника», 1971.
97. Решение задач надежности и эксплуатации <на универсальных ЭЦВМ. М.,
«Сов. радио», 1967. Авт.: Б. П. Креденцер, iM. iM. Ластовченко, С. А. Сенеч-
кин, Н. А. Шшпонок.
98. Зельк ин Э. Г. Построение экстраполяторов— «Автоматика и телеме-
ханика», 1962, т. XXII, № 9.
99 Кар'нюшин Л. В., Курт-Умер ов В. О. Аналого-цифровой экстрапо-
лятор ^отношений. -- В кн.: Вычислительная техника в управлении. М., «Нау-
100 Касаткина А. С., Кузьмин И. В. Оценка эффективности автомати-
зированных систем контроля. М., «Энергия», 1967.
101. Б р уф май С. С Цифровые элементы сравнения. М., «Энергия», 1967.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомат линейный конечный 125
Алгоритм моделирующий 181
— ’— обобщенный 185
— 'обучения 59
Анализ гармонический 118
Блок распознавания 190
— сравнения 190
Вектор состояния 31
Выражения математические базовые 47
Граф возможных состояний Г55
Группы статистических характеристик
Дешифратор 210
Диаметр множества 109
Дискриминатор 210
Достоверность прогнозирования 12
Замыкание короткое 138
Изменение необратимое 13
Интервал доверительный 179
Испытания контролирующие 1'66, 172
--- на основе распознавания образов
174
— определительные 165
— ускоренные 170
— форсированные 171
Карта тепловая 139
Качество информации 14
Квадрат информации 17
Классификатор статистический 203
Классификация статистическая 8
Контроль функциональный 212
— аппаратный 213, 214
---встроенный 214
Контура контрольные 215
Коэффициенты весовые 97
— разветвления 163
— первичные адаптационные 46
Краска термоиндикаторная 127
Критерий -минимума энтропии 25
— знаков 29
Куб информации 17
220
Матрица двумерная 17
— ковариационная 20
— трехмерная 17
— эталонная 191
Метод весовых коэффициентов 26
— гипотез и фильтраций 57
— градиентный 31
— дозированных помех 121, 140
— дополнительной нагрузки 122
— зон 98
—• измерения напряжений питания 121,
140
— инфракрасной радиометрии 138
— итераций 28
— конечных автоматов 124
— логический 120
— обобщенного параметра 38
— обобщенной точки 99
— операторный 34
— понижения напряжения накала 120
— потенциальных функций 102
— прямоугольных вкладов 2'1
— растровой электронной микроскопии
140
— эмпирический 29
Моделирование математическое 178
— статистическое '179
Модель линейная 37
— центральная 37
— стохастическая 38
Надежность 143
Неравенство Кемп — /Мендель 69
— Чебышева 66
Оператор математического ожидания 15
— сглаживания 14
--- экспоненциального 16
— текущего среднего 15
Отказы аппаратурные 146
— внезапные 146, 166
— информационные 146
— постепенные 146, 166
— программные 146
Отношение правдоподобия 92
Оценка надежности 143
Параметры интегральные 26
— информативные 30
— прогнозирующие 25
— технические 5
Планы испытаний 165
Плотность потока излучения 138
Показатель качества прогнозирования
11
—- полноты прогнозирования 12
— надежности 143
— технической эффективности 151
— эффективности прогнозирования 13
Последовательность расчета надежно-
сти 155, 157, 160
Поля корреляционные 136
Правило Бейеса 92
Причины отказов ИС 133
Производящая функция 162
Прогнозаторы 187
Процесс марковский 78
Прогнозирование аналитическое 7, 31
— вероятностное 7, 56, 66
— в настоящем 9
— вперед 9
— индивидуальное 9, 62
— .марковских процессов 78
— надежности 148
— назад 9
— научное 5
— обратное 8, 52
— прямое 8
— событий 5
Расчет надежности 151
---параметрический 153
--- функциональный 153
---элементный 153
Распределение Вейбулла 168
— нормальное 167
— Симпсона 21
— экспоненциальное 167
Разложение случайных процессов
82
Свойство случайных процессов эргоди-
ческое 86
Система иерархическая 163
— простая 149
— сложная 149
— технической диагностики 187, 188
— функционального контроля 212
Стадии создания изделий 6
Стоимость прогнозирования 12
Схема алгоритма моделирования 183, 184
- — «накопления повреждений» 171
— оценки надежности 144
— расчет надежности структурная 155
Точность прогнозирования 12
Траектория изменения состояния объек-
та 108
Условия климатические нормальные 170
Устройство автоматического прогнозиро-
вания 189
— контроля 199
— для оценки работоспособности 200
------- состояния объектов 209
О-к юры. влияющие на прогнозирова-
ние 6
Функция дискриминантная неэффектив-
ная 108
---эффективная 108
Функция дробно-рациональная 50
— квадратичная 50
— кубическая 50
— подобия 98
— показательная 51
— прогнозирующая 51
Характеристики шумовые 131
Цели прогнозирования 7
Экстраполятор 192
— • аналоге цифровой 194
— дискретного действия 193
— непрерывного сигнала 193
Энтропия 12, 24
Этапы прогнозирования 188
— решения задачи распознавания 94
Эффективность '149
— техническая 149
Оглавление
Предисловие 3
ЧАСТЬ I
ОБЩИЕ ВОПРОСЫ
ПРОГНОЗИРОВАНИЯ
Глава 1. Общие вопросы и опре-
деления ................... . 5
1.1. Предварительные сообра-
жения ......................... 5
1.2. Основные направления про-
гнозирования ................... 6
1.3. Показатели качества про-
гнозирования....................11
Глава 2 Информативные аспекты
прогнозирования . . » , 13
2.1. Представление и первичная
обработка информации . . 13
2.2. Качественный и количест-
венный анализ информации. . 17
2.3. Обработка ограниченной по
объему информации ... 21
2.4. Выбор прогнозирующих па-
раметров .......................24
2.5. Выбор прогнозирующих па-
раметров методами статистиче-
ской классификации ... 26
ЧАСТЬ II
АППАРАТ ПРОГНОЗИРОВАНИЯ
Глава 3. Основы аналитического
прогнозирования .... 31
3.1. Методы аналитического про-
гнозирования многомерных про-
цессов ........................31
3.2. Метод обобщенного пара-
метра .........................38
3.3. Прогнозирование одномер-
ных .временных .рядов ... 42
3.4. Применение элементарных
функций для прогнозирования
изменения параметров объектов 48
3.5. Обратное прогнозирование
и вопрос точности ... 52
Глава 4. Вероятностное прогно-
зирование ... 56
4.1. Вероятностное прогнозиро-
вание многомерных процессов 56
4.2. Прогнозирование изменений
одномерных функций распреде-
ления .........................60
4.3. Методы упрощенного веро-
ятностного прогнозирования . 66
222
4.4. Прогнозирование многоэкс-
тремальных параметров . . 72
4.5. Прогнозирование марков-
ских процессов .... 78
4.6. Кононическое разложение
случайных процессов ... 82
4 7. Эргодическое свойство слу-
чайных процессов и прогнози-
рование .......................86
4.8. Прогнозирование с помо-
щью уравнений регрессии . 89
Глава 5. Прогнозирование на ос-
нове теории статистической клас-
сификации (распознавание об-
разов) . . .91
5.1. Формулировка задачи . 91
5.2. Прогнозирование как рас-
познавание образов (одномер-
ный случай)....................95
5.3. Метод потенциальных функ-
ций ........................102
5.4. Дискриминантный анализ 105
5.5. Распознавание траекторий
изменения состояния диагности-
руемого объекта . . . . 108
5.6. Индивидуальная функция
состояния.....................112
Глава 6. Прогнозирование на ос-
нове исследования физико-хи-
мических процессов . . . 115
6.1. Прогнозирование по пере-
ходным процессам . , . . 115
6.2. Прогнозирование изменения
работоспособности дискретных
устройств.....................120
6.3. Метод конечных автоматов 124
6.4. Некоторые частные методы
прогнозирования работоспособ-
ности элементов радиоэлектрон-
ной техники...................127
6.5. Особенности прогнозирова-
ния отказов интегральных схем 133
ЧАСТЬ III
ПРОГНОЗИРОВАНИЕ НАДЕЖНОСТИ
Глава 7. Исходные положения по
прогнозированию надежности . 143
7.1. Общая схема оценки на-
дежности изделий . . . . 143
7.2. О связи прогнозирования
технического состояния и про-
гнозирования надежности . . 145
7.3. Прогнозирование отказов и
прогнозирование количественных
показателей надежности . . 145
7.4. Типовые задачи прогнози-
рования надежности изделий . 147
7.5. О прогнозировании надеж-
ности сложных систем 149
Глава 8. Прогнозирование по ре-
зультатам расчетов надежности 151
8.1. Характерные особенности
«расчетных методов и их виды 151
8.2. Классификация методов рас-
четов надежности . . . . 153
8.3. Основы расчетов надежно-
сти и их развитие . . . 154
8.4. Прогнозирование функци-
ональной надежности . . . 159
8.5. Расчет надежности с ис-
лользованием производящих
функций . . . ... 162
8.6. Заключение по расчетным
методам оценки и прогнозиро-
вания надежности . . . 164
Глава 9. Прогнозирование надеж-
ности в процессе испытаний и
моделирования . . . 165
9.1. Виды испытаний на надеж-
ность ........................165
9.2. О прогнозировании надеж-
ности по результатам опреде-
лительных испытаний . . . 166
9.3. Ускоренные испытания —
разновидность прогнозирующих
определительных испытаний . 170
9.4. Контролирующие испытания
на надежность и их связь с про-
гнозированием надежности . 172
9.5. Прогнозирующие индивиду-
альные испытания на надеж-
ность на основе распознавания
образов.......................174
9.6. Один из возможных вари-
антов протезирующих испыта-
ний, основанных на использова-
нии температурных влияний 176
9.7. Заключение о производст-
венных испытаниях на надеж-
ность ........................177
9.8. Решение задачи прогнози-
рования с помощью математи-
ческого моделирования . . 178-
ЧАСТЬ IV
АВТОМАТИЗАЦИЯ
ПРОГНОЗИРОВАНИЯ
Глава 10. Основы автоматизации
прогнозирования .... 187
10.1. Причины автоматизации
прогнозирования . ... 187
10.2. Пути реализации прогно-
зирующих устройств . . . 187
10.3. Устройство автоматическо-
го прогнозирования многопара-
метрических объектов . . 189
10.4. Экстраполяторы . - - 192
10.5. Устройство контроля с эк-
стр ап олятором ..............199
Глава 11. Специализированные
автоматические устройства ди-
агностики и прогнозирования 200
1'1.1. Устройства для оценки
работоспособности технических
объектов.......................200
11.2. Статистический классифи-
катор .........................203
11.3. Устройства для диагности-
ки дискретных схем . . . 207
11.4. Устройства для оценки
состояния объектов, описыва-
емых множеством параметров 209
11.5. Устройства для диагности-
ки больших систем, типа авто-
матизированных систем управ-
ления (АСУ).................212
Приложение................. 215
Список литературы . . . 217
Предметный указатель . . . 220
Гаскаров Д. В. и др.
22 Прогнозирование технического состояния и на-
дежности радиоэлектронной аппаратуры. М., «Сов.
радио», 1974.
224 с. с ил.
Перед загл. авт.: Д. В. Гаскаров, Т. А Голннкевич,
А. В. Мозгалевский.
Излагаются общие основы прогнозирования, используемый мате-
матический аппарат, наиболее распространенные методы прогнозиро-
вания и примеры их применения при анализе радиоэлектронной аппа-
ратуры. Рассмотрены вопросы обработки информации, методы анали-
тического прогнозирования многомерных процессов, вероятностное
протезирование и прогнозирование на основе распознавания образов.
Большое внимание уделяется вопросам анализа надежности радио-
электронной аппаратуры и автоматизации процесса прогнозирования.
Книга рассчитана на широкий круг специалистов, работающих
в области проектирования и испытаний радиоэлектронной аппаратуры
и может быть полезна специалистам других областей техники.
30405-085
046(01)-74 Зо*74
6.Ф