Автор: Калашников С.Г.
Теги: электричество магнетизм электромагнетизм физика
ISBN: 5-9221-0312-1
Год: 2003
Текст
С.Г. КАЛАШНИКОВ
ЭЛЕКТРИЧЕСТВО
ИЗДАНИЕ ШЕСТОЕ, СТЕРЕОТИПНОЕ
Допущено Министерством образования
Российской Федерации
в качестве учебного пособия
для студентов физических специальностей
высших учебных заведений
МОСКВА
ФИЗМАТЛИТ
2003
УДК 537
ББК 22.33
К17
Калашников С. Г. Электричество: Учебн. пособие. — 6-е изд.,
стереот. — М.: ФИЗМАТЛИТ, 2003. - 624 с. — ISBN 5-9221-0312-1.
Книга написана на основе курса лекций, читанных автором в течение
многих лет на физическом факультете Московского государственного уни-
университета. В результате обобщения опытных фактов формулируются в сжа-
сжатой, но ясной форме основные законы электродинамики и выясняется их
физический смысл. Изложение построено на основе СИ.
5-е изд. — 1985 г.
Для студентов физических и физико-математических факультетов уни-
университетов, физико-технических и инженерно-физических институтов, а так-
также для всех вузов, где физика является основной дисциплиной; книга может
быть также полезна для преподавателей физики в высшей школе.
Табл. 20. Ил. 448.
Учебное издание
КАЛАШНИКОВ Сергей Григорьевич
ЭЛЕКТРИЧЕСТВО
Редактор Д-А. Миртова
Оригинал-макет: О. Б. Широкова
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 03.12.02. Формат 60x90/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 39. Уч.-изд. л. 38,13.
Тираж 3000 экз. Заказ Л» 4fc7.
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ФГУП «Московская
типография № в» Министерства РФ по делам печати,
телерадиовещания и средств массовых коммуникаций.
115088 Москва, Ж-88, Южнопортовая ул., 24
ISBN 5-9221-0312-1
9»78 922И1 03121
ISBN 5-9221-0312-1
© ФИЗМАТЛИТ, 1985, 2003
ОГЛАВЛЕНИЕ
От редакции
Из предисловия к первому изданию
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Глава I. Электрические заряды 11
§ 1. Введение A1). § 2. Закон взаимодействия электрических за-
зарядов A2). § 3. Абсолютная электростатическая система единиц
A5). § 4. Международная система единиц (СИ) A6). § 5. Гальва-
Гальванические элементы A8). § 6. Электризация как разделение зарядов
A9). § 7. Электроны A9).
Глава II. Электрическое поле 21
§ 8. Понятие об электрическом поле B1). § 9. Напряженность
электрического поля B2). § 10. Сложение электрических полей
B4). § 11. Объемная и поверхностная плотности заряда B4).
§ 12. Линии напряженности электрического поля B5). § 13. Тео-
Теорема Остроградского-Гаусса B9). § 14. Уравнение Пуассона C6).
§ 15. Диполь в электрическом поле C8).
Глава III. Разность потенциалов 40
§ 16. Работа в электростатическом поле D0). § 17. Разность по-
потенциалов D1). § 18. Условия равновесия зарядов в проводниках
D4). § 19. Разность потенциалов и напряженность поля D4). § 20.
Эквипотенциальные поверхности D6). § 21. Измерение напряже-
напряжения между проводниками D7). § 22. Нормальные элементы D9).
§ 23. Электрический зонд E0). § 24. Потенциал в простейших элек-
электрических полях E1). § 25. Вычисление потенциала в поле задан-
заданных зарядов E3). § 26. Общая задача электростатики E5). § 27.
Проводники в электрическом поле E7). § 28. Точная проверка за-
закона Кулона E8). § 29. Острия F0). § 30. Электростатический ге-
генератор F1).
Глава IV. Энергия электрического поля 63
§ 31. Электрическая емкость F3). § 32. Емкость простых конденса-
конденсаторов F4). § 33. Метод зеркальных изображений F8). § 34. Энергия
заряженного конденсатора F9). § 35. Соединение конденсаторов
ОГЛАВЛЕНИЕ
G0). § 36. Сложные конденсаторы G2). § 37. Энергия электричес-
электрического ноля G4).
Глава V. Диэлектрики 77
§ 38. Поляризация диэлектриков G7). § 39. Поляризованность (80).
§ 40. Напряженность электрического поля внутри диэлектрика
(83). § 41. Электрическое смещение в диэлектрике (85). § 42. Изо-
Изотропные и анизотропные диэлектрики (88). § 43. Преломление ли-
линий смещения и напряженности поля (89). § 44. Законы электри-
электрического поля в диэлектриках (90). § 45. Механические силы при на-
наличии диэлектриков (93). § 46. Электронная теория поляризации
диэлектриков (94). § 47. Диэлектрическая проницаемость неполяр-
неполярных диэлектриков (96). § 48. Диэлектрическая проницаемость по-
полярных диэлектриков (98). § 49. Определение дипольных моментов
молекул (99). § 50. Сегнетоэлектрики A01). § 51. Пьезоэлектриче-
Пьезоэлектрический эффект A04). § 52. Обратный пьезоэлектрический эффект
(ПО).
Глава VI. Постоянный электрический ток 115
§ 53. Характеристики электрического тока A15). § 54. Уравнение
непрерывности A17). § 55. Действия электрического тока A18).
§ 56. Баллистический гальванометр A21). § 57. Закон Ома A23).
§ 58. Измерение сопротивлений A24). § 59. Сопротивление прово-
проволок A26). § 60. Зависимость сопротивления от температуры A27).
§ 61. Закон Ома в дифференциальной форме A28). § 62. Элек-
Электролитическая ванна A32). § 63- Заземление в линиях связи A33).
Глава VII. Электродвижущая сила 136
§ 64. Источники тока A36). § 65. Работа и мощность постоянного
тока. Закон Джоуля-Ленца A36). § 66. Энергия, освобождаемая в
гальваническом элементе A38). § 67. Электродвижущая сила галь-
гальванического элемента A38). § 68. Напряжение на зажимах источ-
источника тока A41). § 69. Электродвижущая сила и работа источника
тока A43). § 70. Разветвленные цепи. Правила Кирхгофа A46).
§ 71. Мощность во внешней цепи и коэффициент полезного дей-
действия источника тока A52). § 72. Закон сохранения энергии для
электрического поля A54). § 73. Квазистационарные токи A57).
§ 74. Конденсатор в цепи с сопротивлением A59).
МАГНИТНОЕ ПОЛЕ
Глава VIII. Магнитное поле токов в вакууме 162
§ 75. Магнитное взаимодействие токов A62). § 76. Магнитная ин-
индукция A64). § 77. Абсолютная электромагнитная система еди-
единиц A68). § 78. Магнитная постоянная A70). § 79. Напряженность
магнитного поля A71). § 80. Линии индукции магнитного поля
A73). § 81. Вихревой характер магнитного поля A74). § 82. Маг-
Магнитный момент тока A79). § 83. Два параллельных проводника с
ОГЛАВЛЕНИЕ
током A81). § 84. Механическая работа в магнитном поле. Маг-
Магнитный поток A82). § 85. Контур с током в магнитном поле A85).
§ 86. Магнитное поле движущегося заряда A88). § 87. Опыты Ро-
уланда и Эйхенвальда A89). § 88. Сила Лоренца A91).
Глава IX. Электромагнитная индукция 192
§ 89. Электромагнитная индукция A92). § 90. Закон Ленца A94).
§ 91. Основной закон электромагнитной индукции A95). § 92. Из-
Измерение магнитного напряжения B00). § 93. Самоиндукция B01).
§ 94. Магнитная проницаемость вещества B05). § 95. Исчезновение
и установление тока B06).
Глава X. Энергия магнитного поля 208
§ 96. Собственная энергия тока B08). § 97. Энергия магнитного
поля B10). § 98. Взаимная индукция B12). § 99. Взаимная энергия
двух токов B14). § 100. Закон сохранения энергии при наличии
магнитного поля B15). § 101. Механичес кие силы в магнитном поле
B18). § 102. Давления и напряжения Фарадея-Максвелла B21).
Глава XI. Магнетики 222
§ 103. Намагничивание сред B22). § 104. Напряженность магнит-
магнитного поля внутри магнетика B24). § 105. Магнитная индукция в
магнетике B25). § 106. Законы магнитного поля в магнетиках B27).
§ 107. Влияние формы тела на намагничивание B30). § 108. Пре-
Преломление линий индукции магнитного поля B32). § 109. Маг-
Магнитные свойства веществ. Диамагнетизм и парамагнетизм B36).
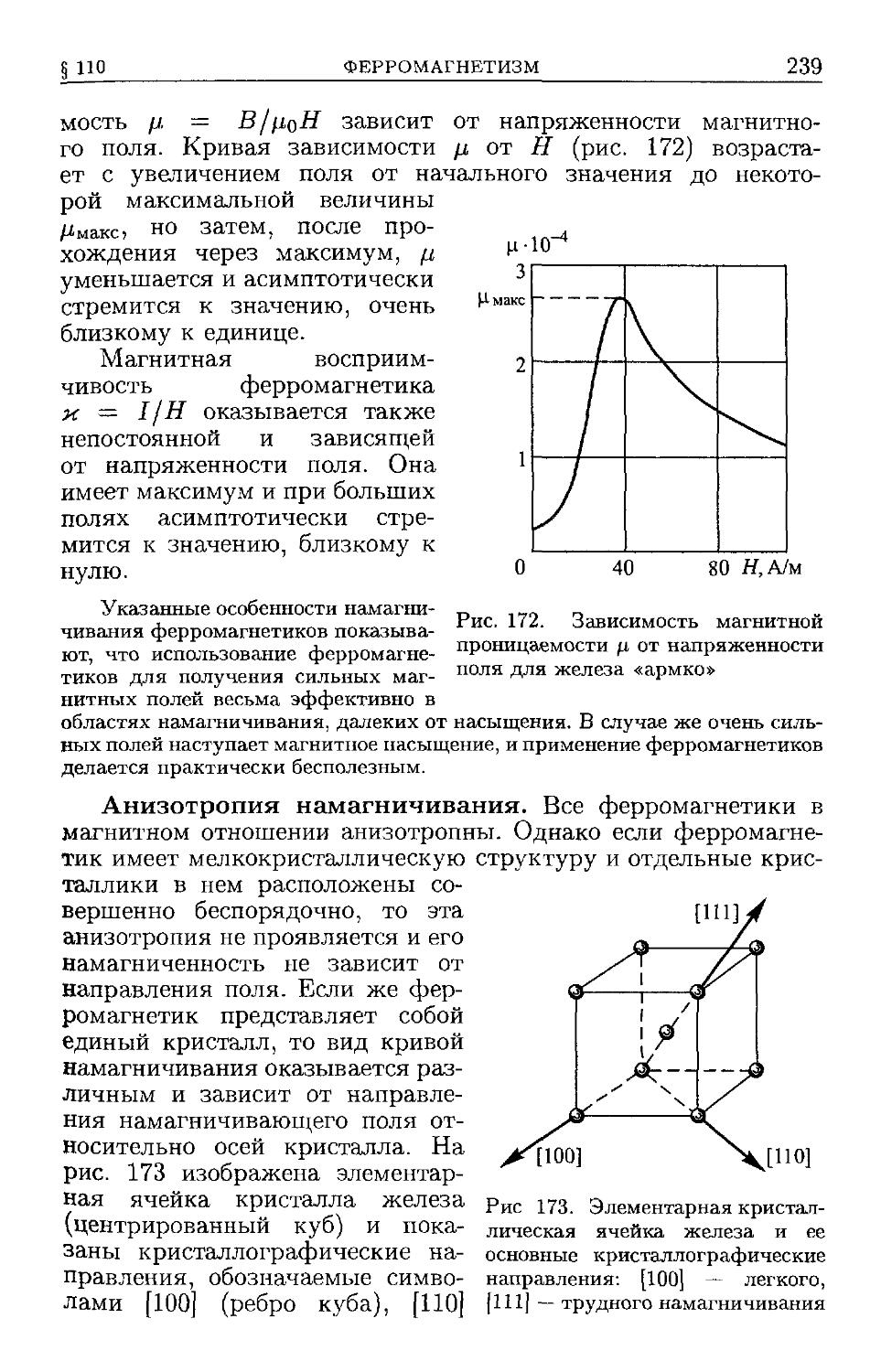
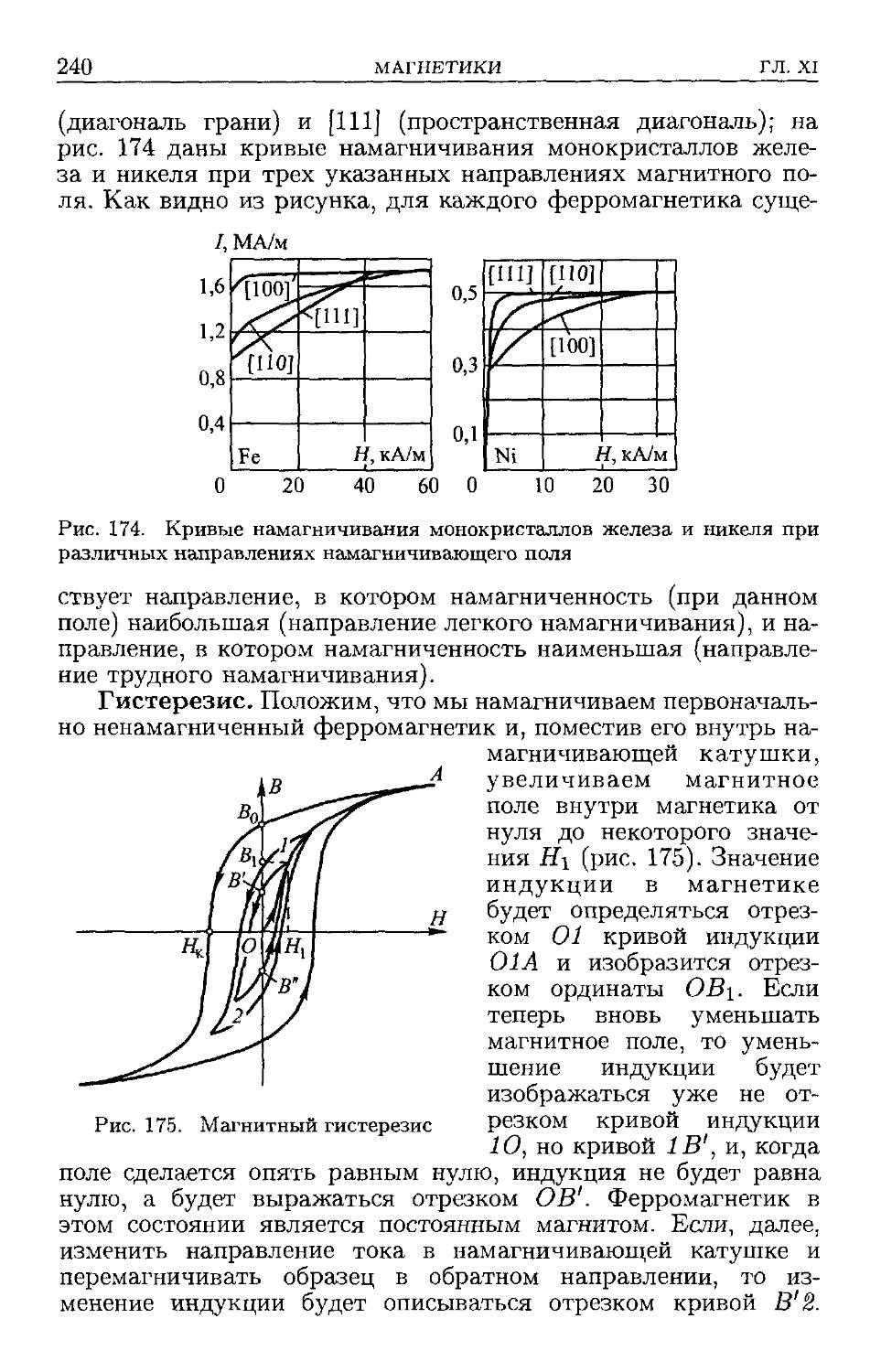
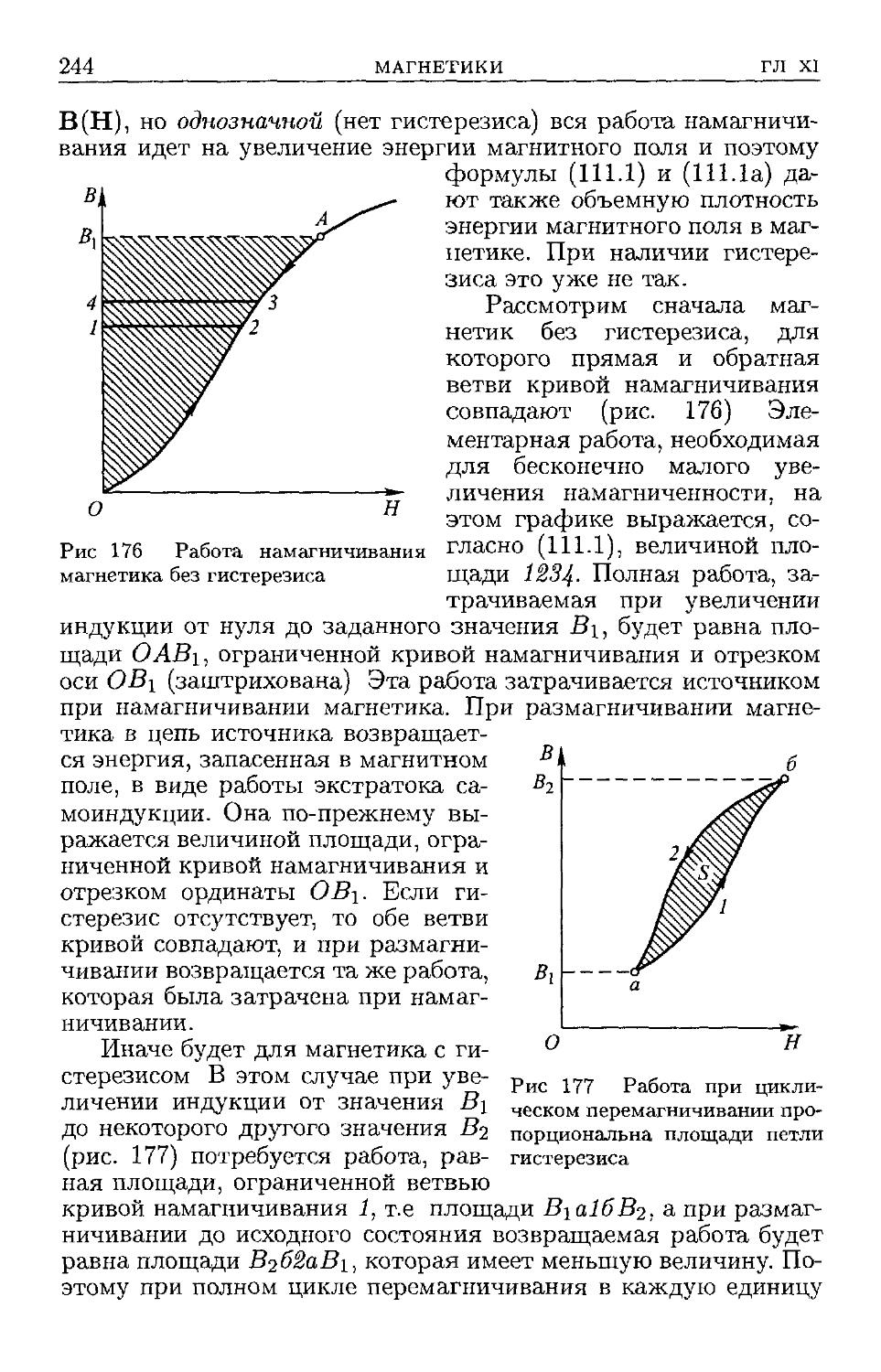
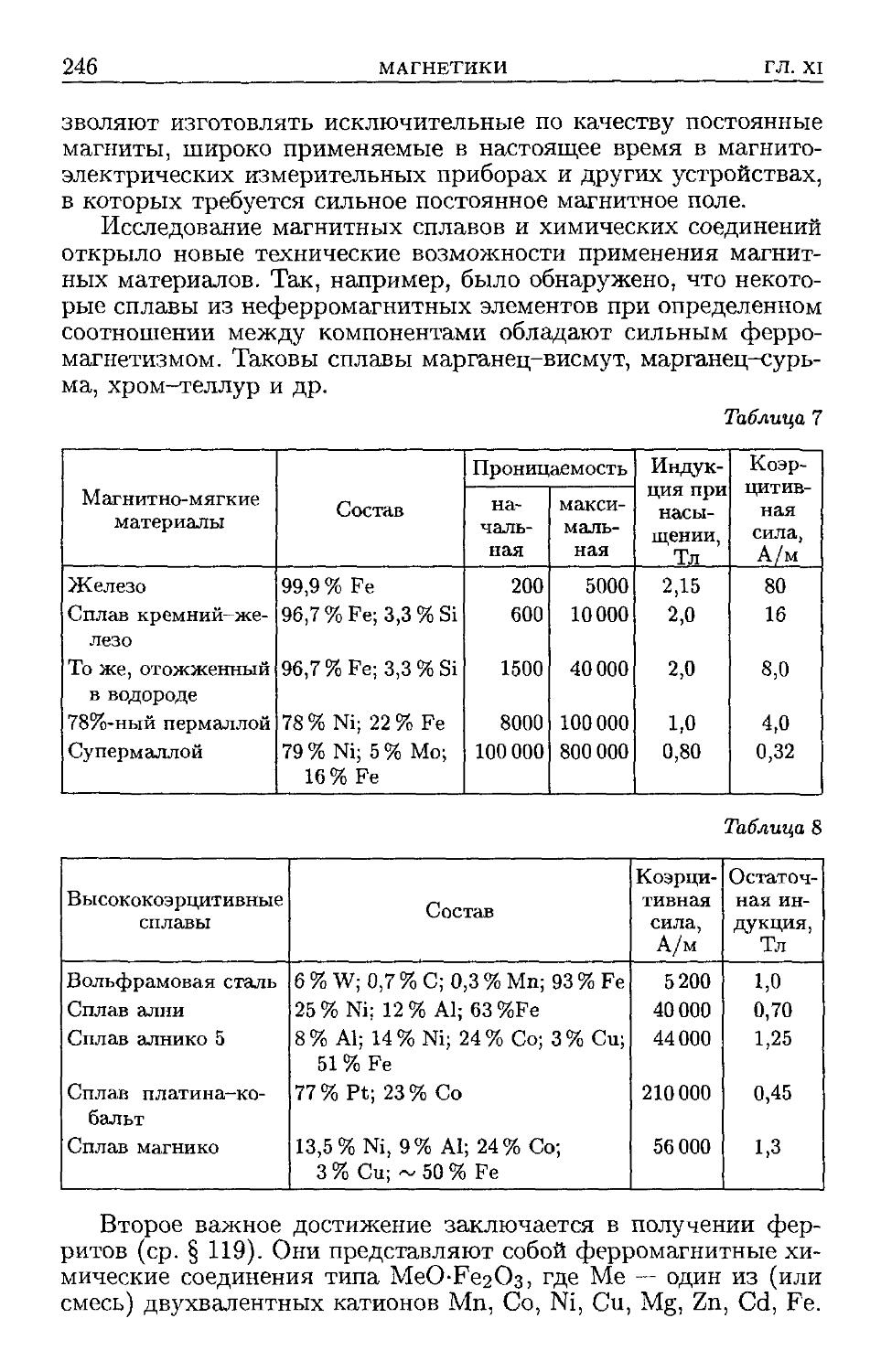
§ ПО. Ферромагнетизм B38). § 111. Работа при намагничивании
B42). § 112. Магнитные материалы. Ферриты B45). § 113. Магнит-
Магнитные заряды. Формальная теория магнетизма B47). § 114. Влияние
среды на магнитное взаимодействие B53). § 115. Природа моле-
молекулярных токов B55). § 116. Магнитомеханическое и механомаг-
нитнос явления B57). § 117. Магнитный и механический моменты
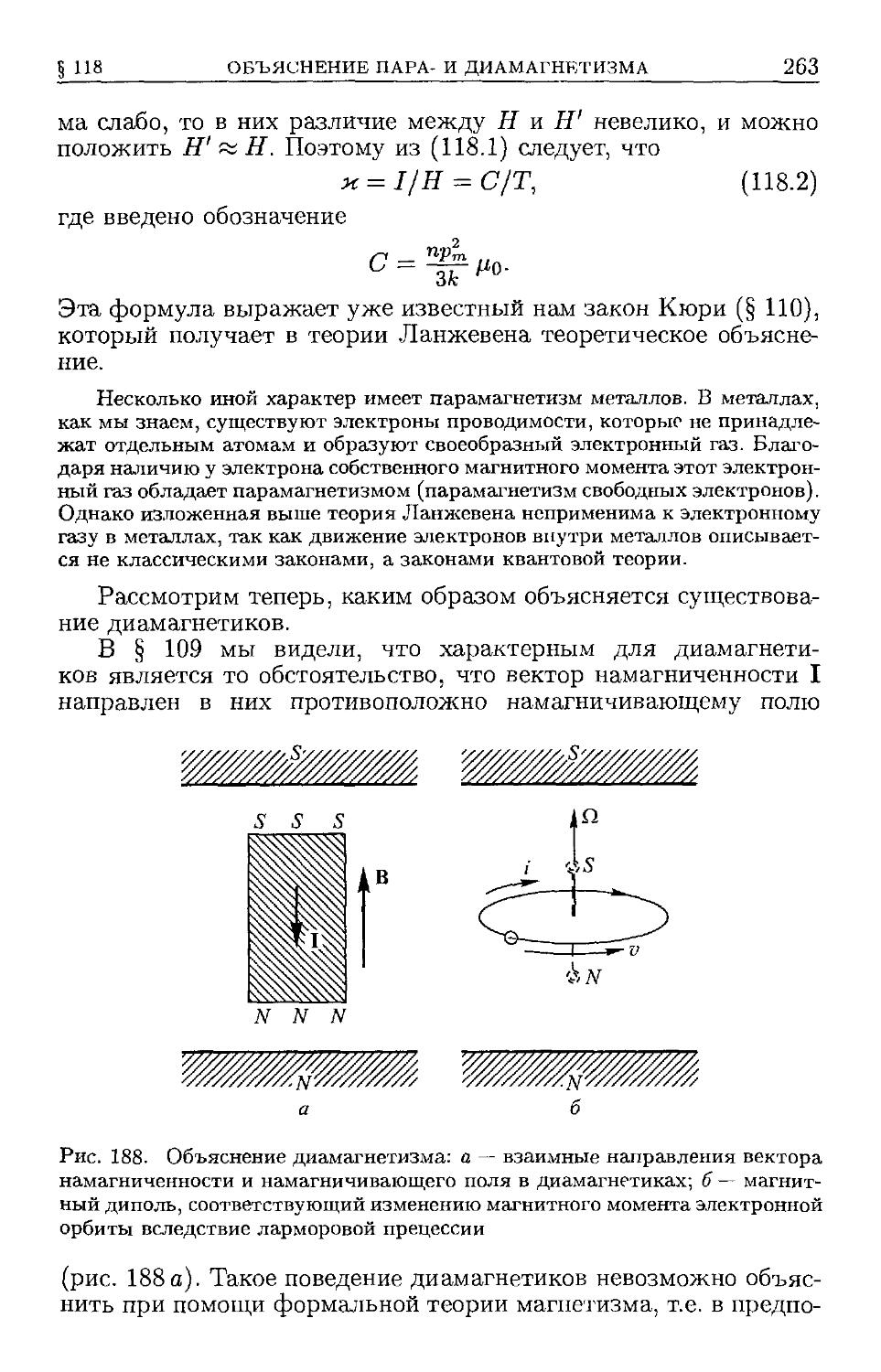
электрона B59). § 118. Объяснение пара- и диамагнетизма B61).
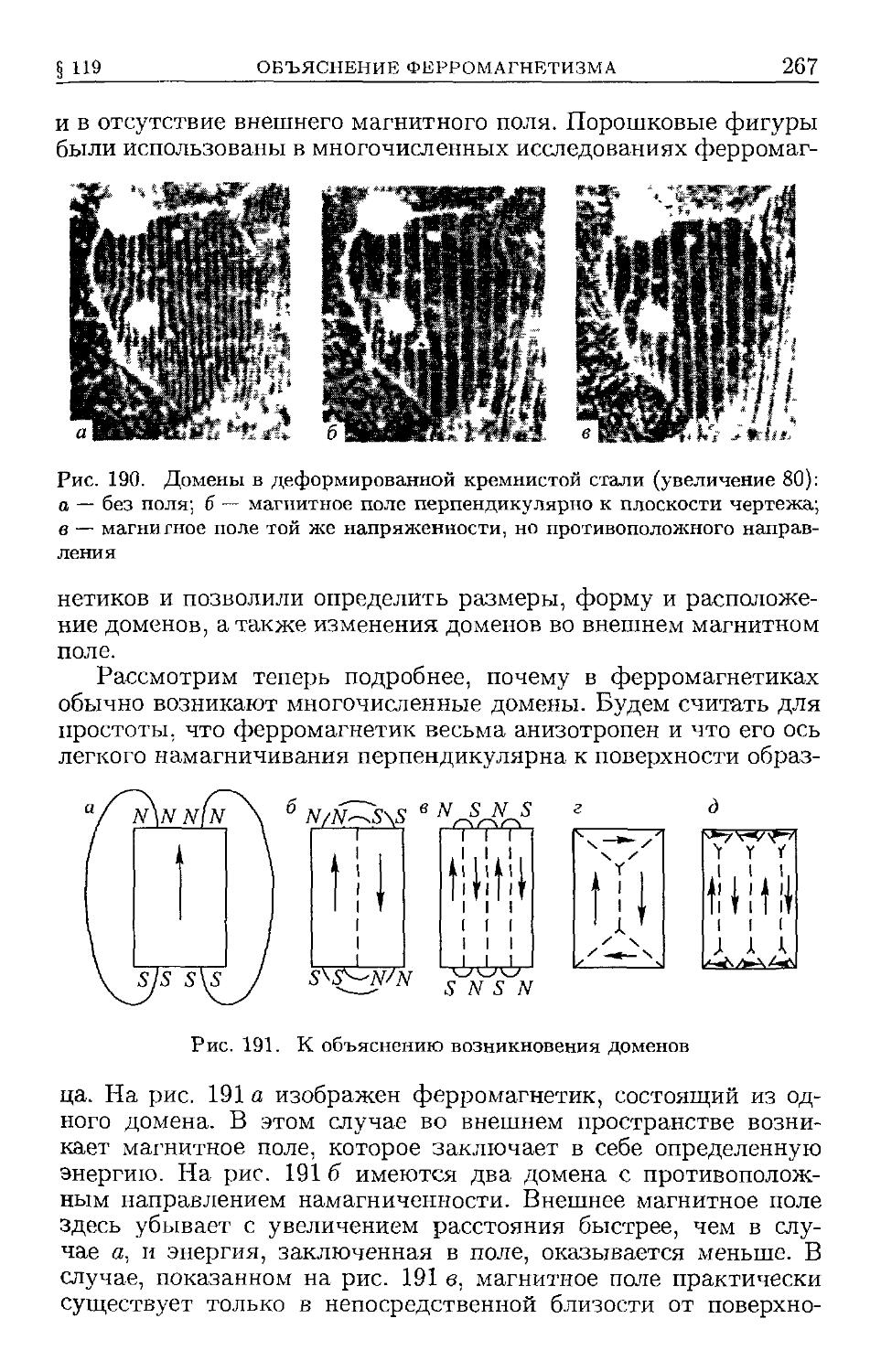
§ 119. Объяснение ферромагнетизма B65).
Глава XII. Техническое использование магнитного потока.
Генераторы и двигатели 271
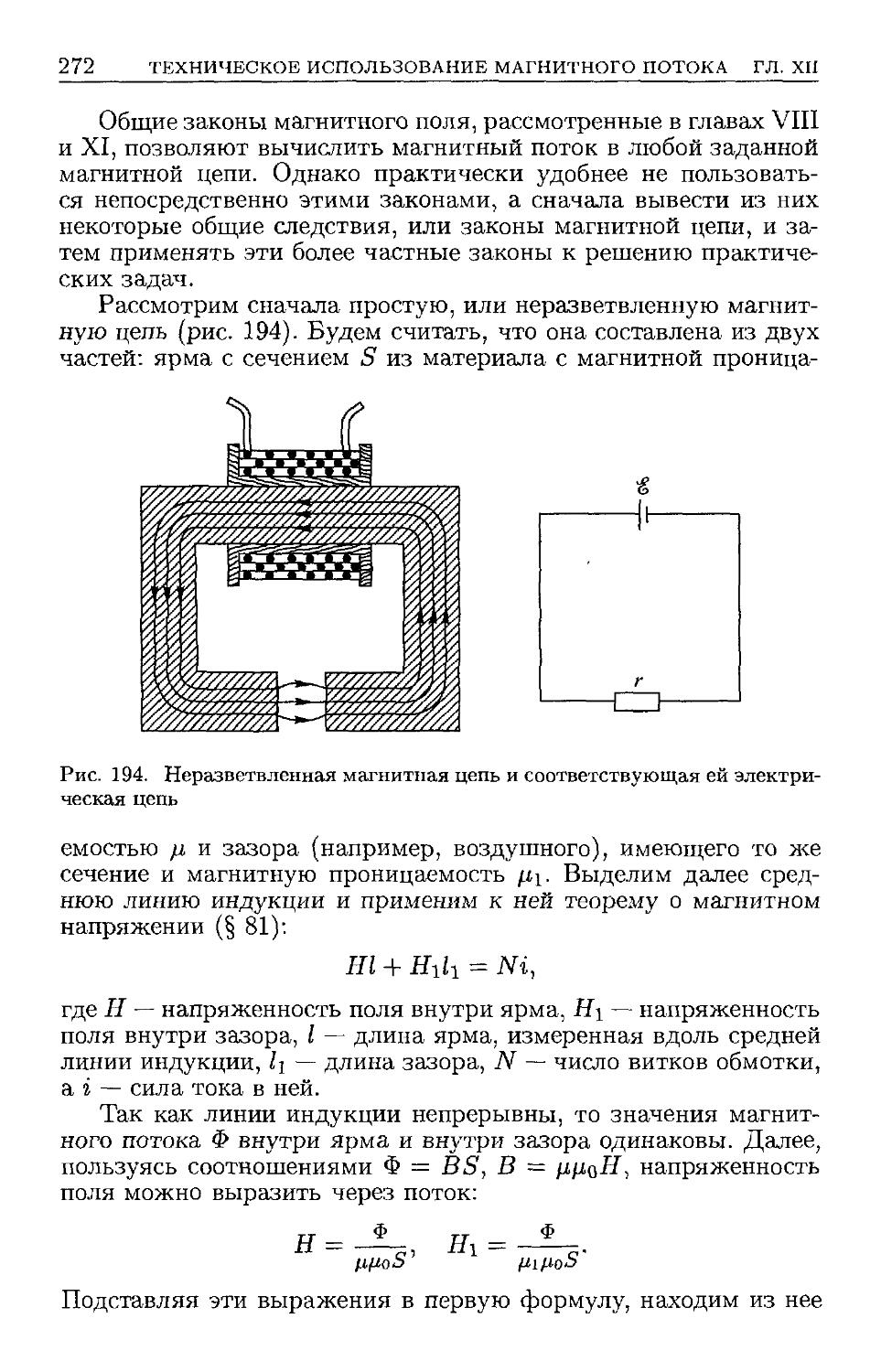
§ 120. Магнитные цепи B71). § 121. Электромагниты B74).
§ 122. Разветвление магнитного потока B76). § 123. Генераторы
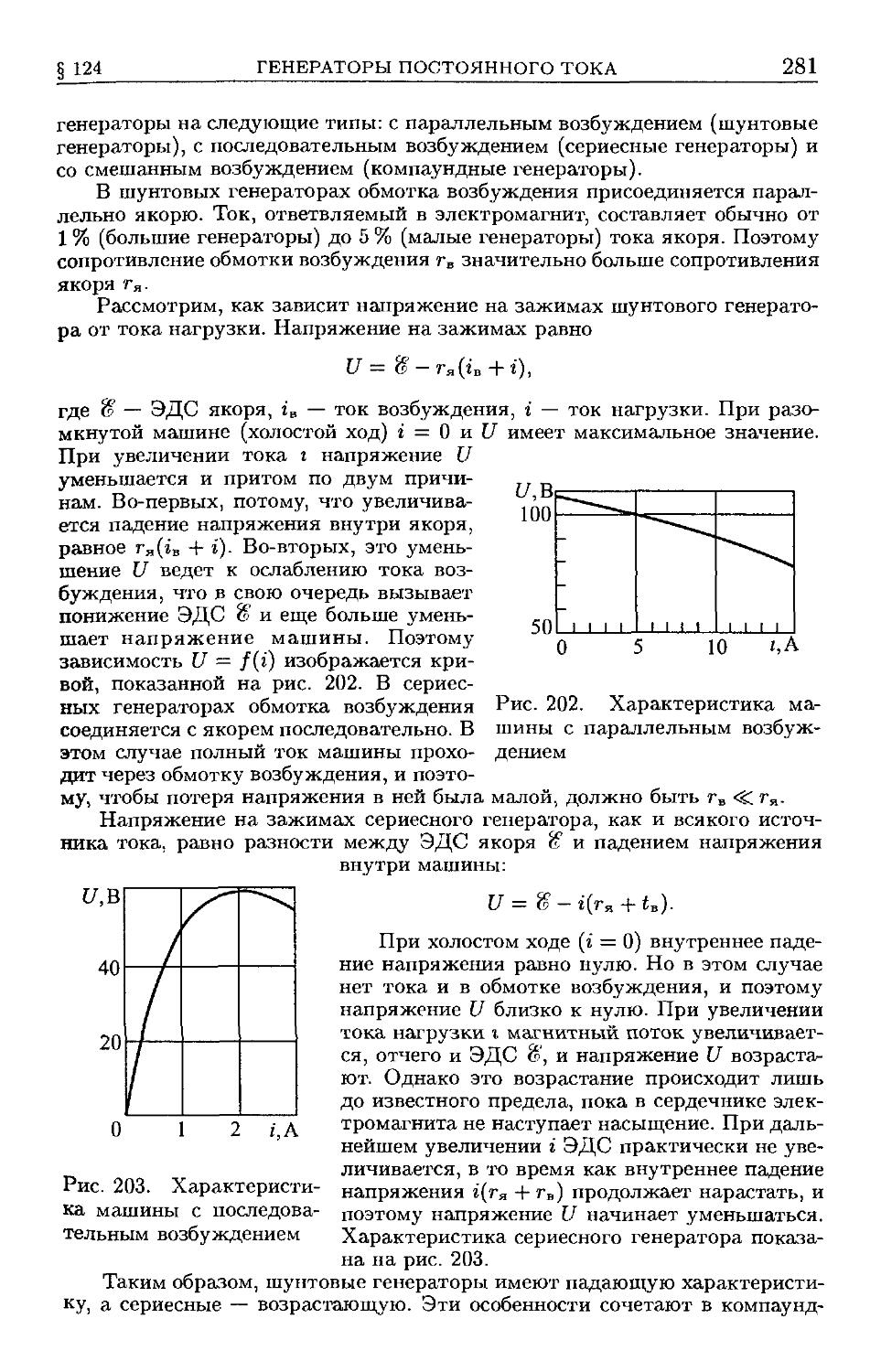
переменного тока B78). § 124. Генераторы постоянного тока B80).
§ 125. Электродвигатель постоянного тока B82). § 126. Синхронные
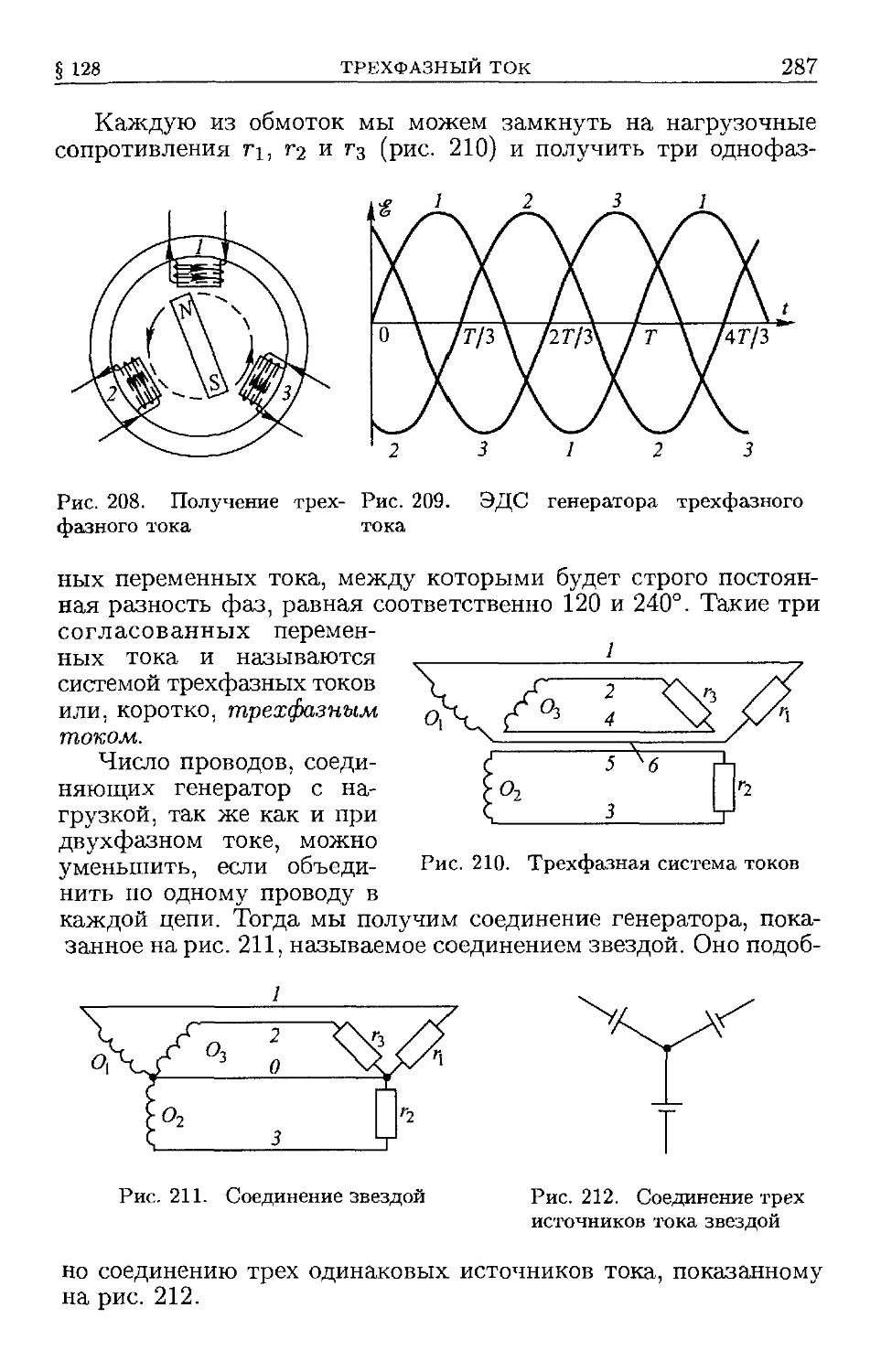
двигатели B83). § 127. Двухфазный ток B84). § 128. Трехфазный
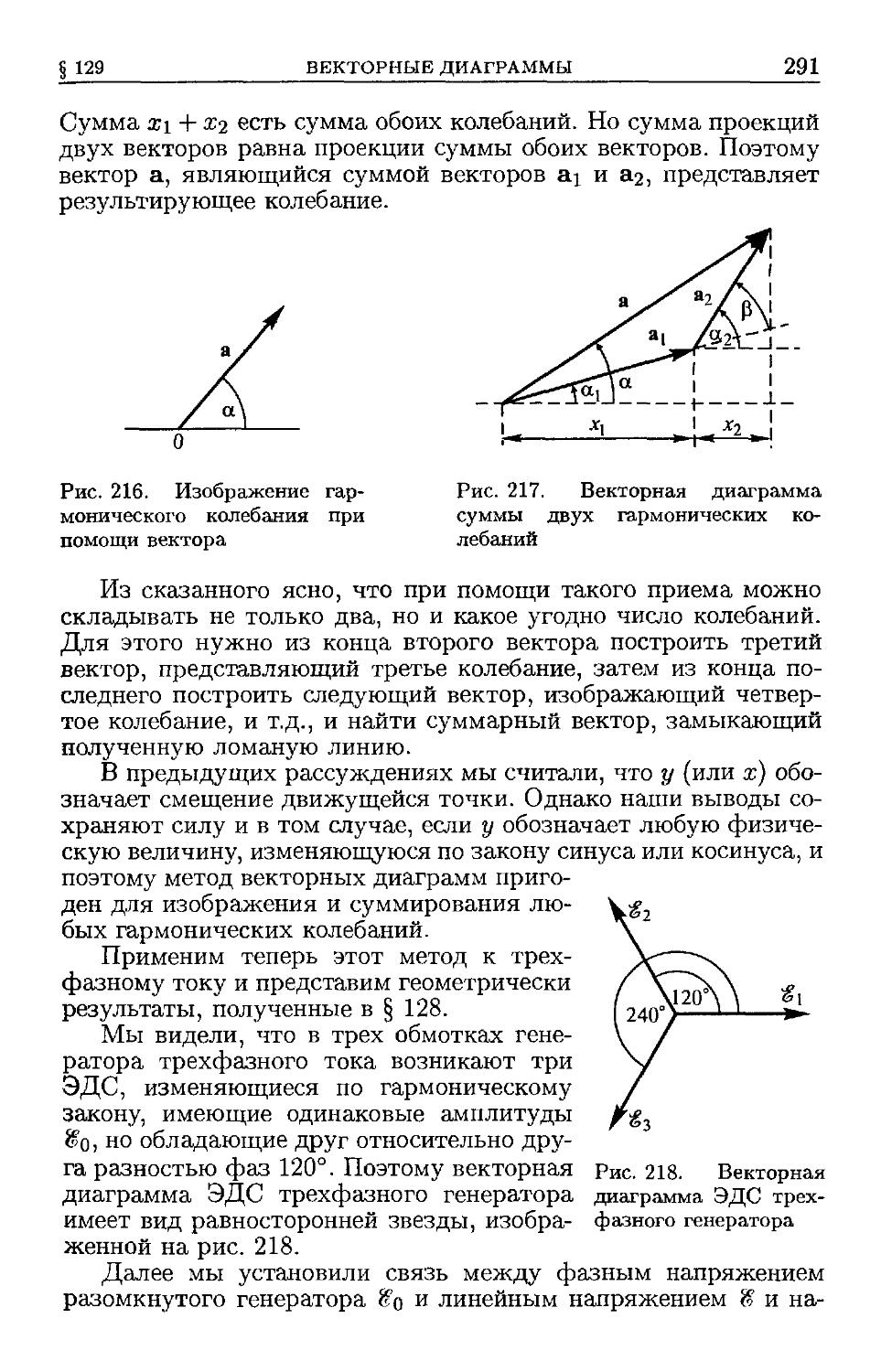
ток B86). § 129. Векторные диаграммы B90). § 130. Вращающееся
магнитное поле B93).
Глава XIII. Взаимные превращения электрических и маг-
магнитных полей. Теория Максвелла 296
§ 131. Вихревое электрическое ноле B97). § 132. Вихревые токи
B99). § 133. Трансформатор C01). § 134. Вытеснение переменного
ОГЛАВЛЕНИЕ
тока (скин-эффект) C04). § 135. Индукционный ускоритель C06).
§ 136. Ток смещения C08). § 137. Уравнения Максвелла C11).
§ 138. Уравнения Максвелла в дифференциальной форме C13).
§ 139. Значение теории Максвелла C16). § 140. Электромагнит-
Электромагнитное ноле в движущихся толах C17). § 141. Для электромагнитных
явлений важно относительное движение C20). § 142. Электромаг-
Электромагнитная индукция в движущихся проводниках C23). § ]43. Преоб-
Преобразование Лоренца C25).
ЭЛЕКТРОННЫЕ И ИОННЫЕ ЯВЛЕНИЯ
Глава XIV. Природа электрического тока в металлах и по-
полупроводниках 329
§ 144. Измерение заряда электрона C29). § 145. Природа носите-
носителей заряда в металлах C32). § 146. Причина электрического со-
сопротивления C34). § 147. Классическая электронная теория ме-
металлов C36). § 148. Сверхпроводимость C40). § 149. Пределы
применимости классической электронной теории металлов C44).
§ 150. Концентрация и подвижность электронов в металлах C46).
§ 151. Полупроводники и диэлектрики C48). § 152. Собственная
проводимость полупроводников C50). § 153. Примесная проводи-
проводимость полупроводников C52). § 154. Понятие об энергетических
зонах C54). § 155. Распределение импульса и энергии у электро-
электронов C59).
Глава XV. Электрические токи в вакууме 363
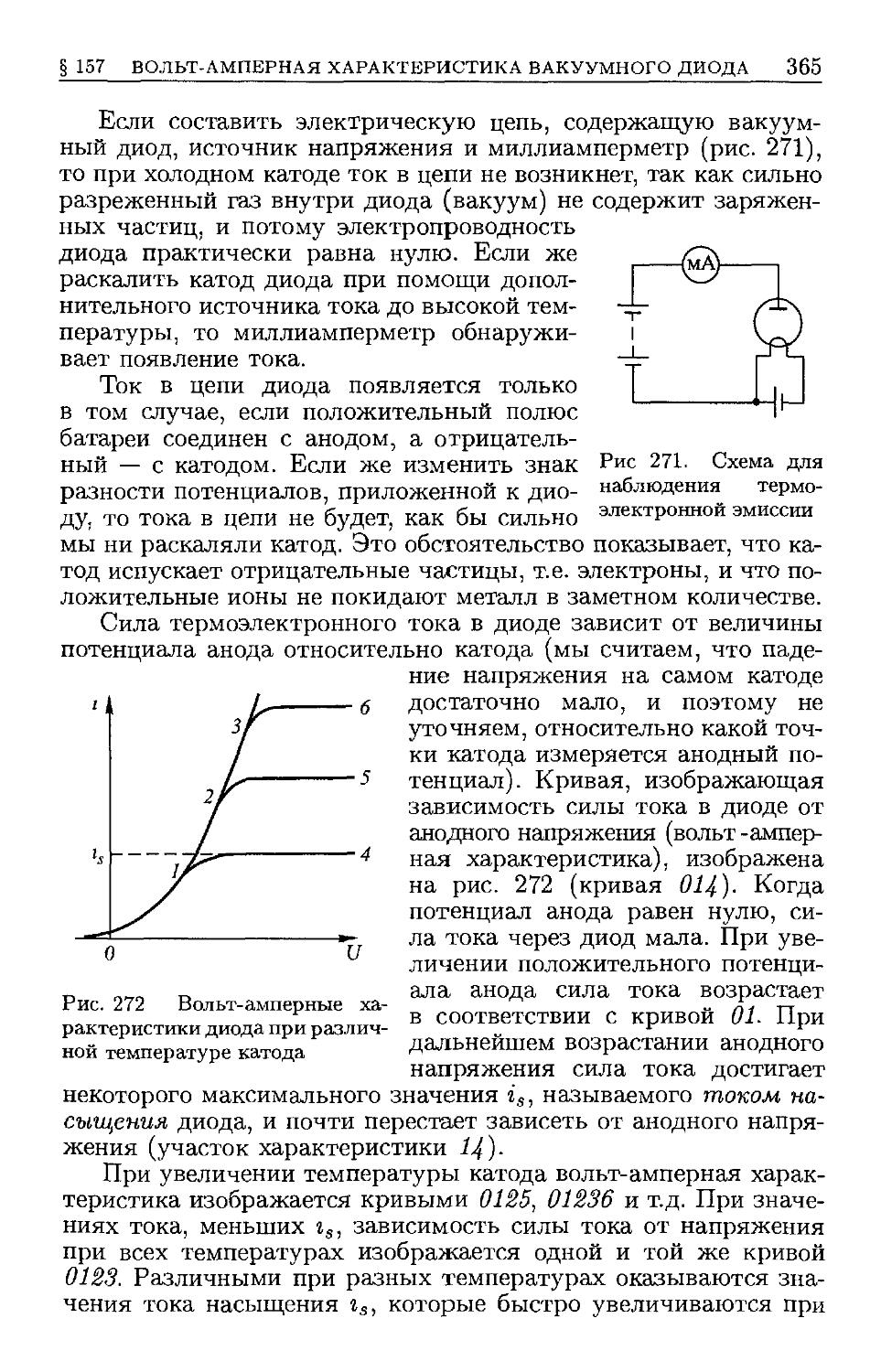
§ 156. Электронная эмиссия C63). § 157. Вольт-амперная харак-
характеристика вакуумного диода C64). § 158. Зависимость тока насы-
насыщения от температуры C67). § 159. Электронная лампа как вы-
выпрямитель C69). § 160. Трехэлектродная электронная лампа (три-
(триод) C70). § 161. Усиление электрических сигналов C74). § 162.
Электрические флуктуации C77). § 163. Вторичная электронная
эмиссия C79). § 164. Многосеточные лампы C81). § 165. Автоэлек-
Автоэлектронная эмиссия C82).
Глава XVI. Разряды в газах 383
§ 166. Ионизация газов C83). § 167. Ионизация электронными уда-
ударами C85). § 168. Движение ионов в газах C86). § 169. Несамо-
Несамостоятельные и самостоятельные разряды C88). § 170. Возникно-
Возникновение самостоятельных разрядов C90). § 171. Тлеющий разряд
C94). § 172. Коронный разряд C97). § 173. Искровой разряд D00).
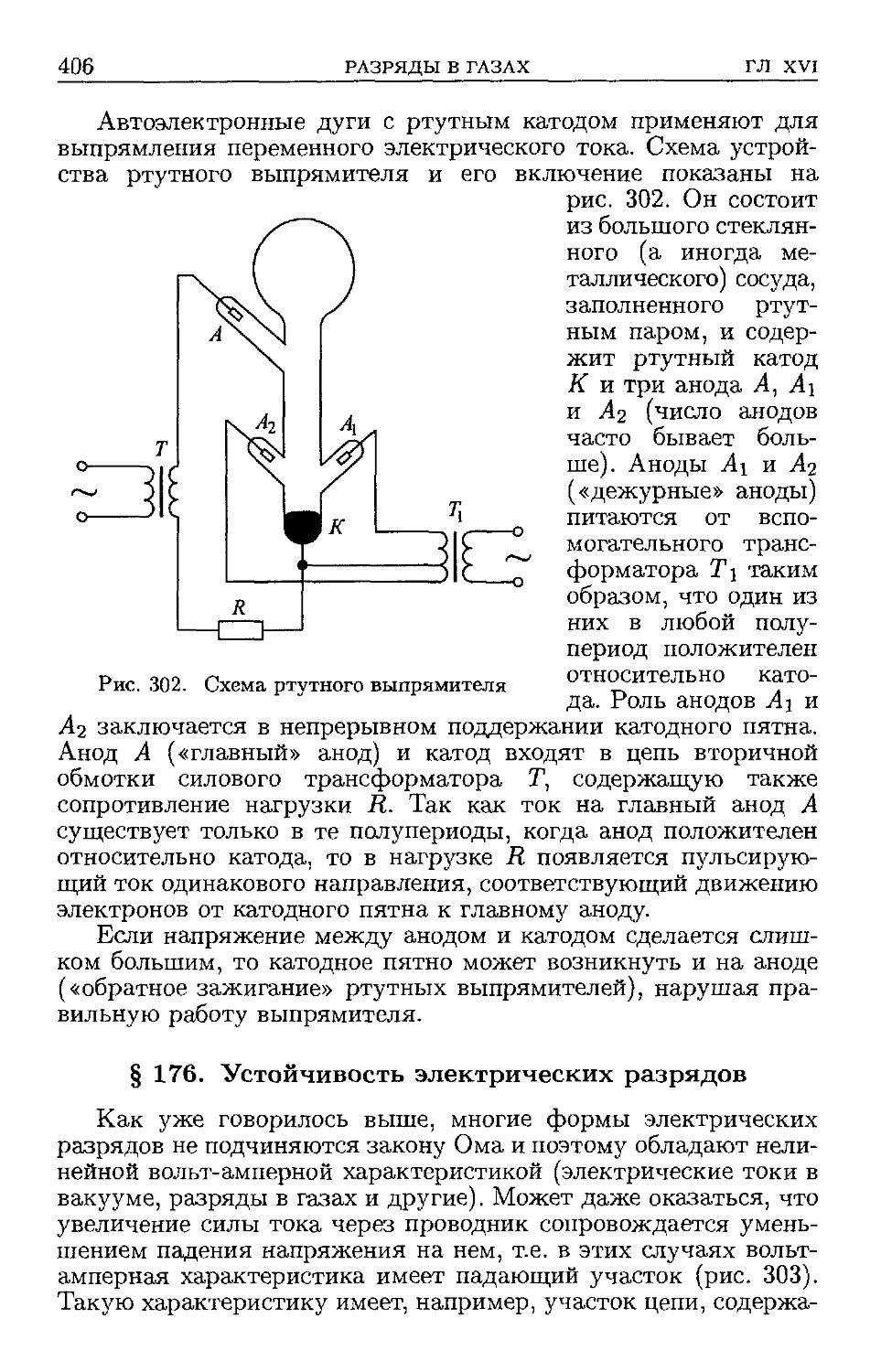
§ 174. Молния D02). § 175. Дуговой разряд D03). § 176. Устойчи-
Устойчивость электрических разрядов D06). § 177. Плазма D10).
Глава XVII. Движение заряженных частиц в электрических
и магнитных полях 412
§ 178. Движение заряженных частиц в однородном электрическом
поле D12). § 179. Движение заряженных частиц в однородном
ОГЛАВЛЕНИЕ
магнитном поле D13). § 280. Циклотрон D16). § 181. Определе-
Определение удельного заряда электронов методом магнитной фокусиров-
фокусировки D18). § 182. Магнегрон D19). § 183. Определение удельного
заряда /3-частиц D22). § 184. Результаты измерений удельного за-
заряда электрона D24). § 185. Циклотронный (диамагнитный) резо-
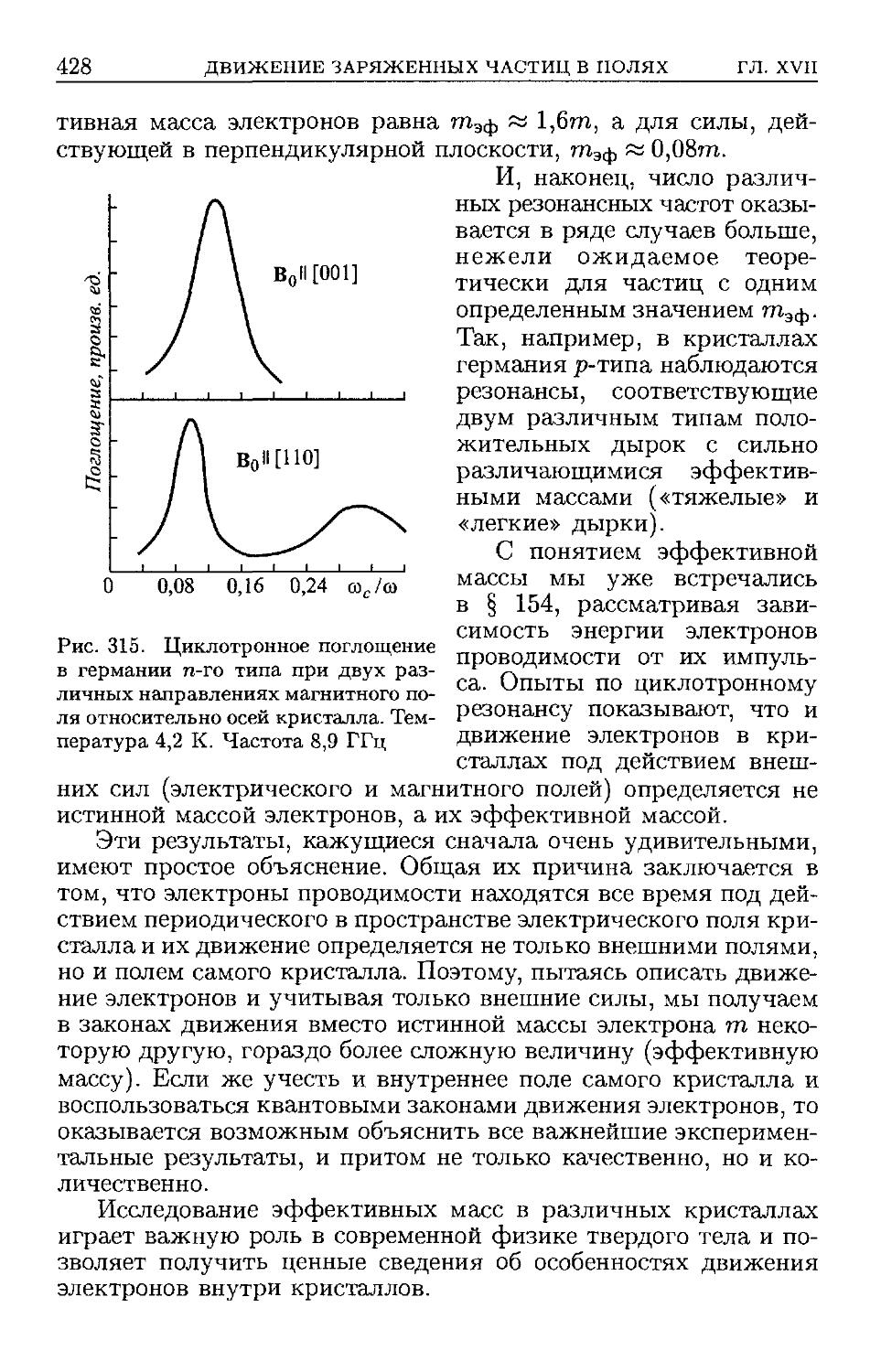
резонанс D25). § 186. Эффективная масса D27). § 187. Отражение и
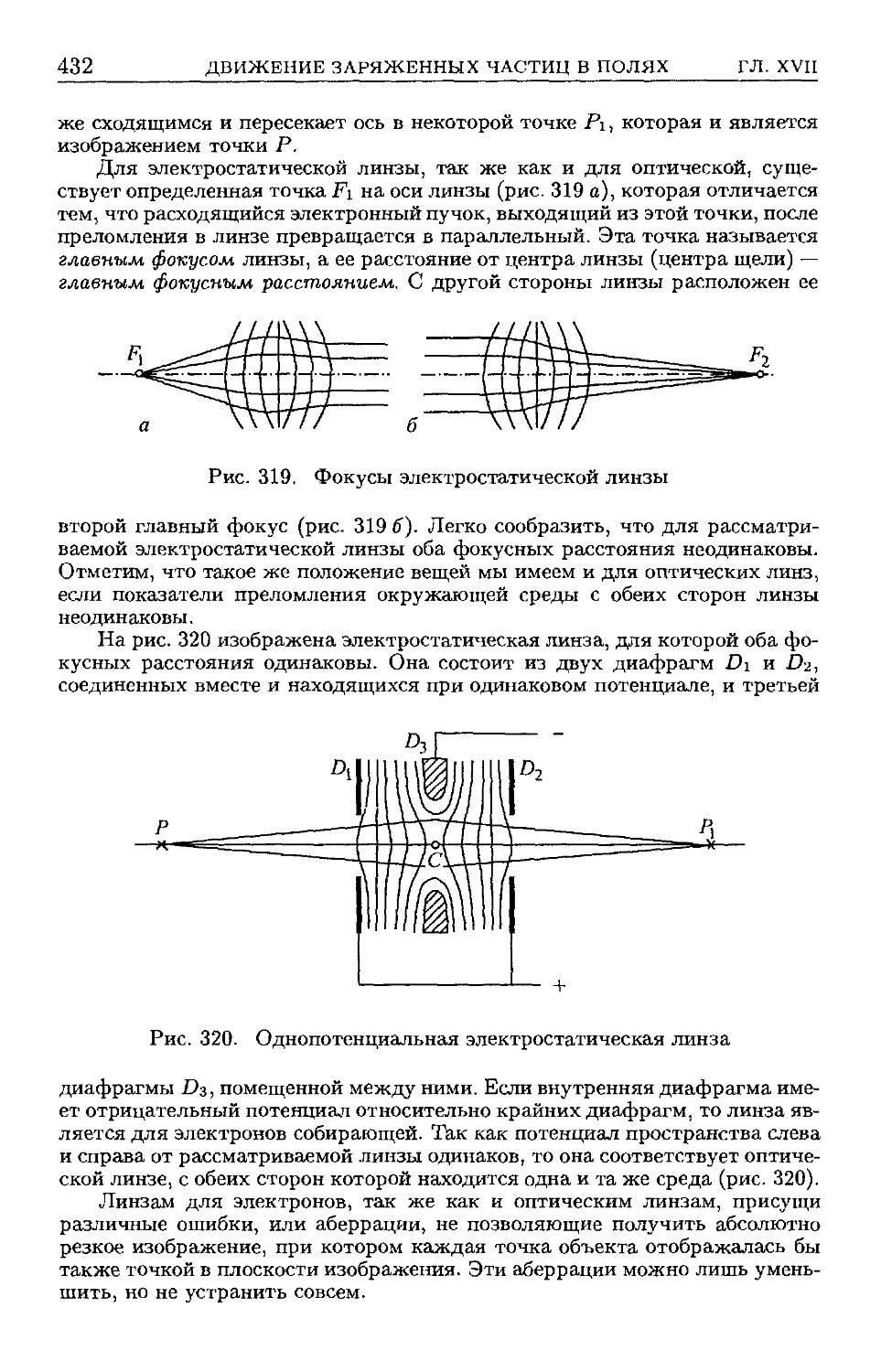
преломление электронных пучков. Электронная и ионная оптика
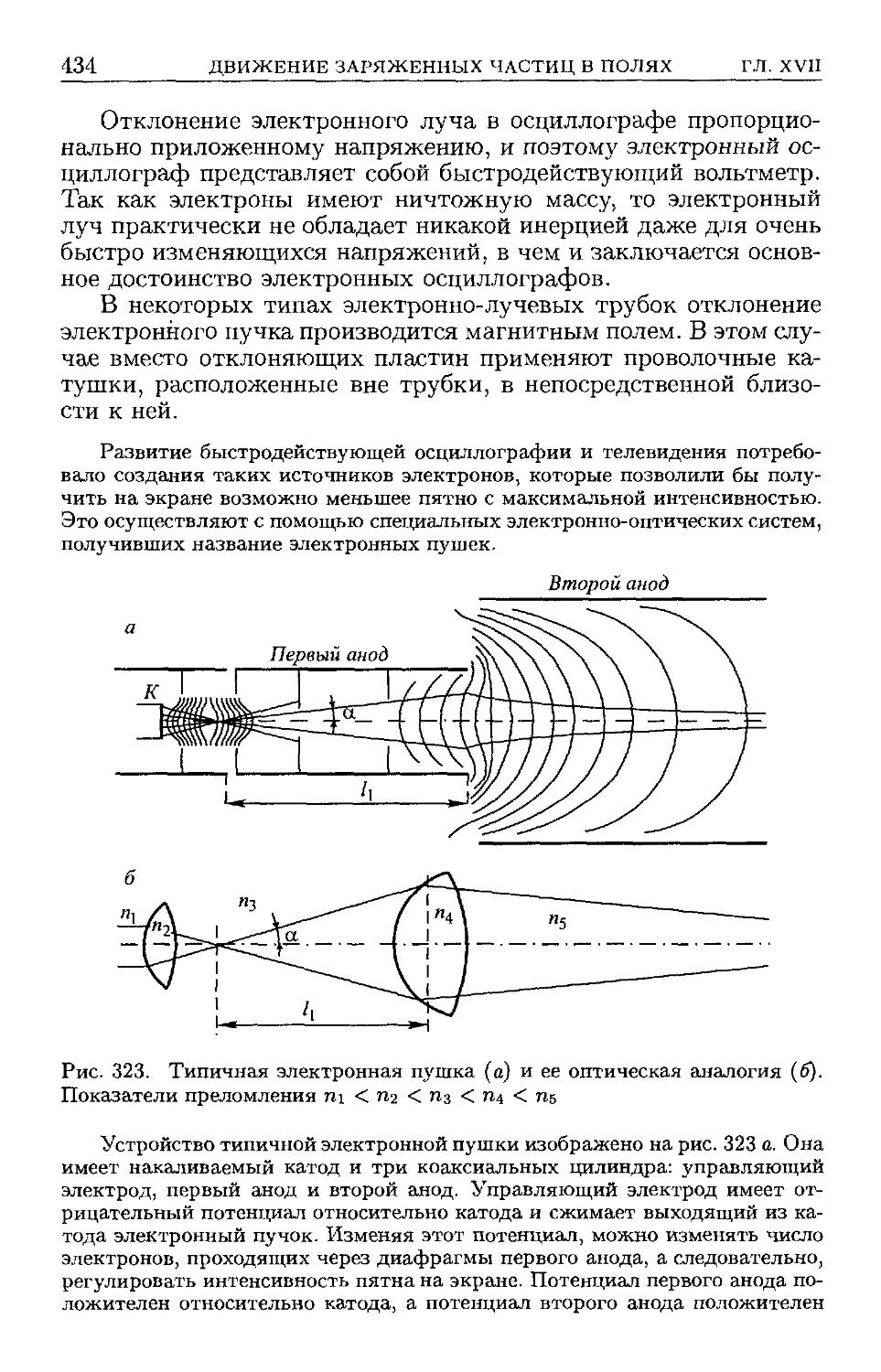
D29). § 188. Электронный осциллограф D33).
Глава XVIII. Электрический ток в электролитах 435
§ 189. Законы электролиза Фарадея D35). § 190. Электролитиче-
Электролитическая диссоциация D38). § 191. Движение ионов в электролитах
D41). § 192. Проводимость электролитов D43). § 193. Числа пере-
переноса. Подвижности ионов в электролитах D44). § 194. Электрод-
Электродные потенциалы D47). § 195. Химические источники тока D51).
§ 196. Напряжение разложения электролита D55). § 197. Аккуму-
Аккумуляторы D57).
Глава XIX. Электрические явления в контактах 459
§ 198. Контактная разность потенциалов D59). § 199. Термо-
Термоэлектричество D63). § 200. Эффект Пельтье D67). § 201. Эф-
Эффект Томсона D70). § 202. Применения термоэлектричества D72).
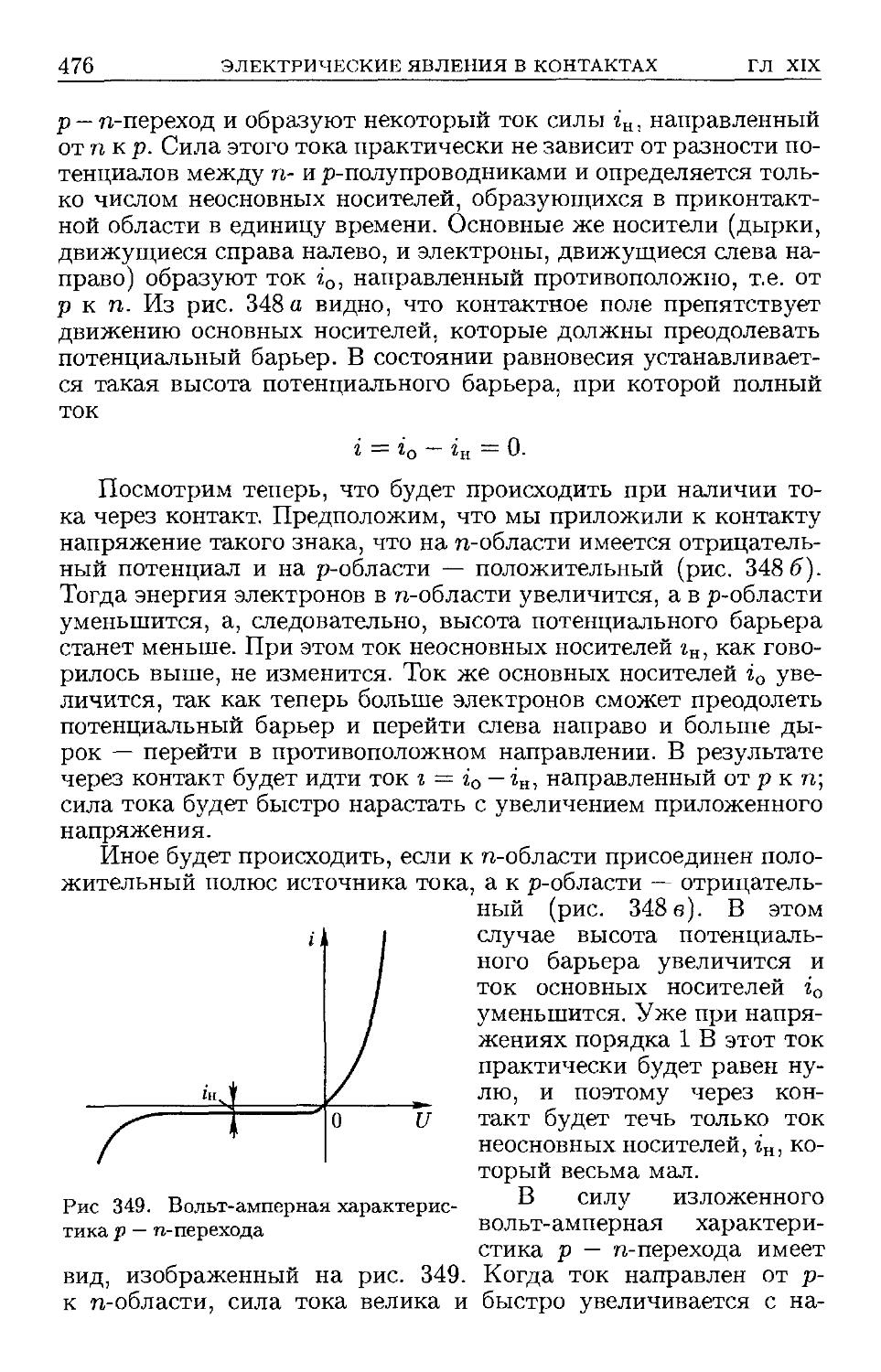
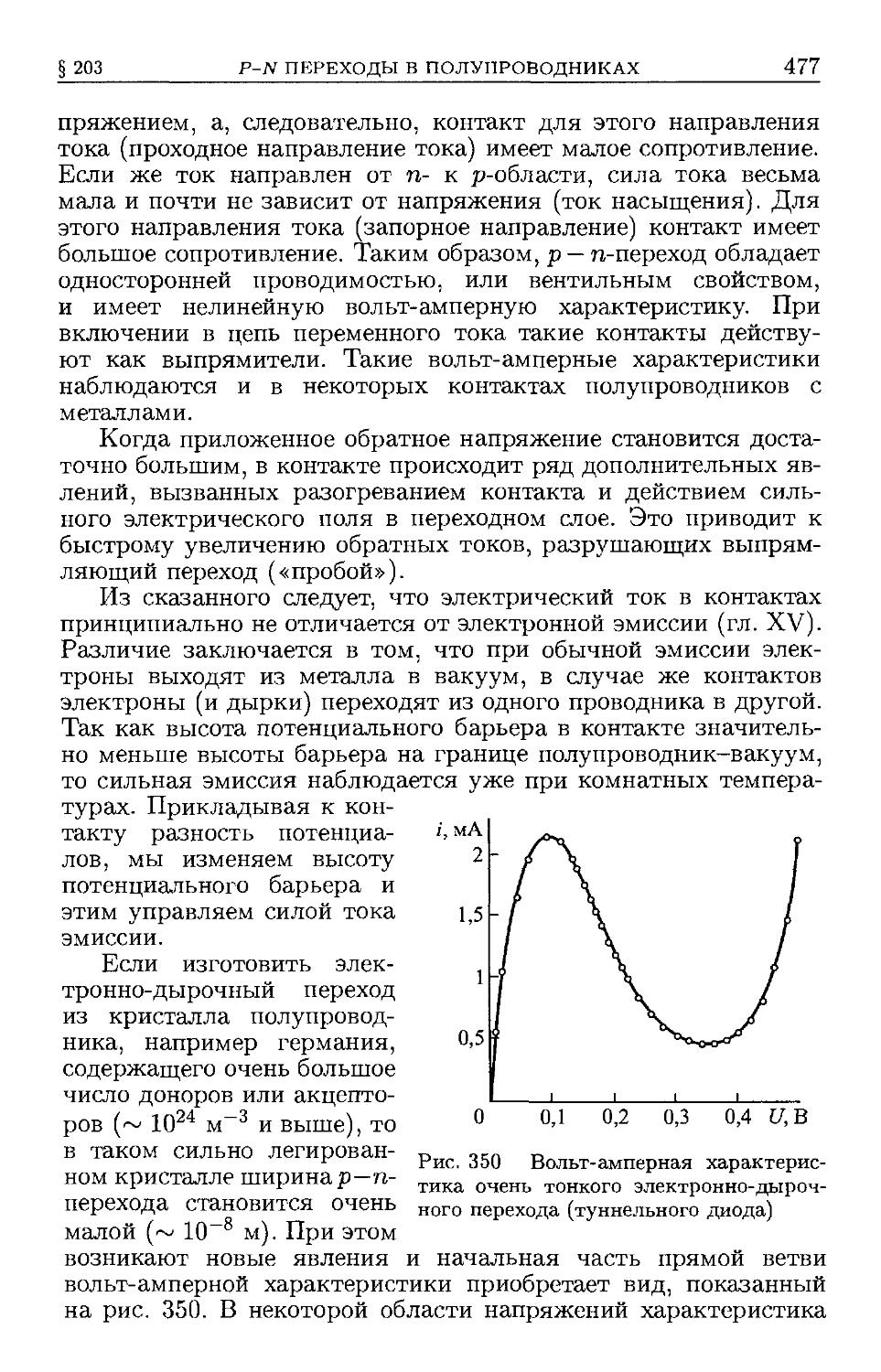
§ 203. Электронно-дырочные переходы в полупроводниках D73).
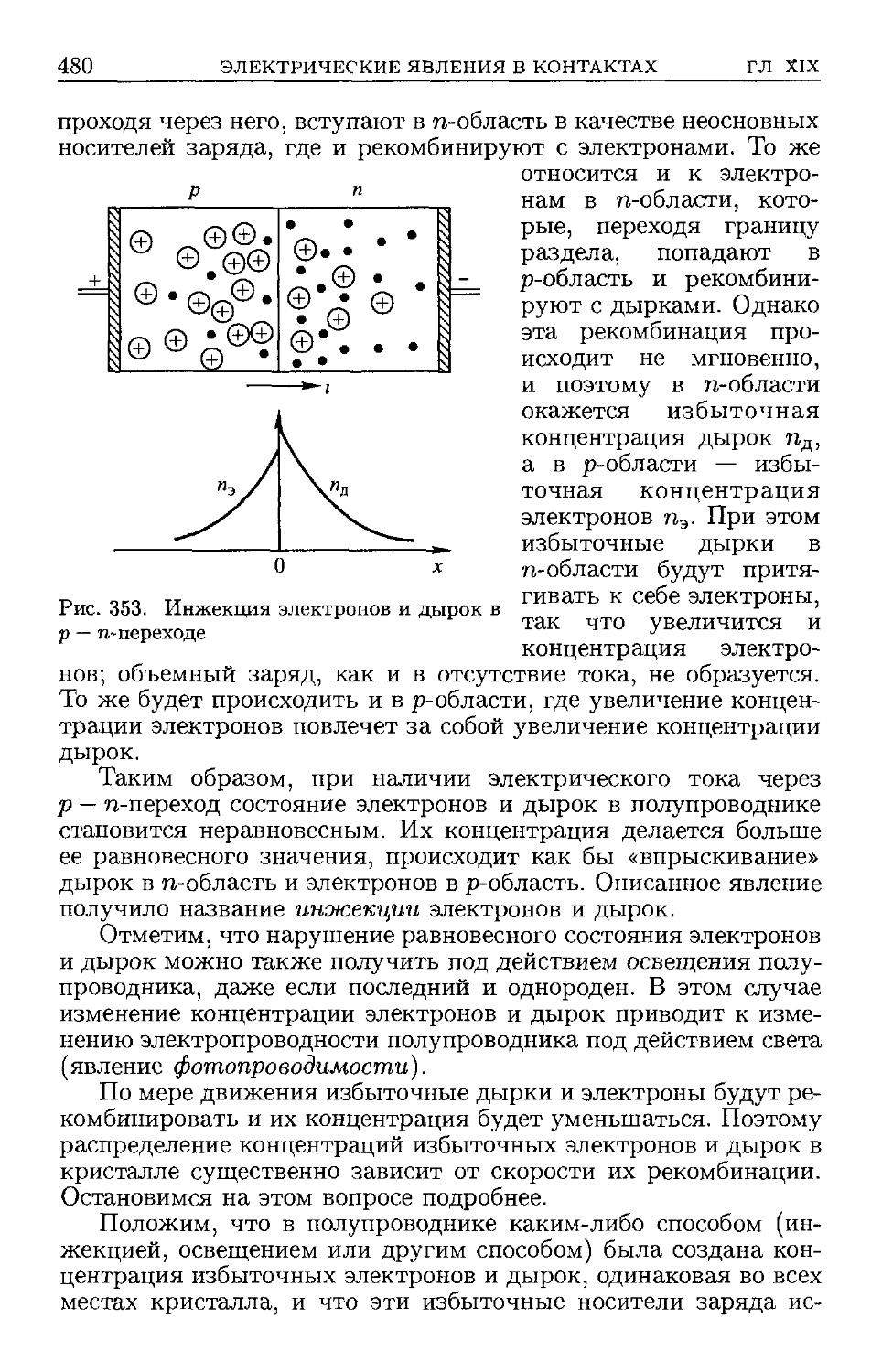
§ 204. Полупроводниковые диоды D78). § 205. Неравновесные элек-
электроны и дырки с полупроводниках D79). § 206. Полупроводнико-
Полупроводниковые усилители D82).
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
Глава XX. Собственные электрические колебания 485
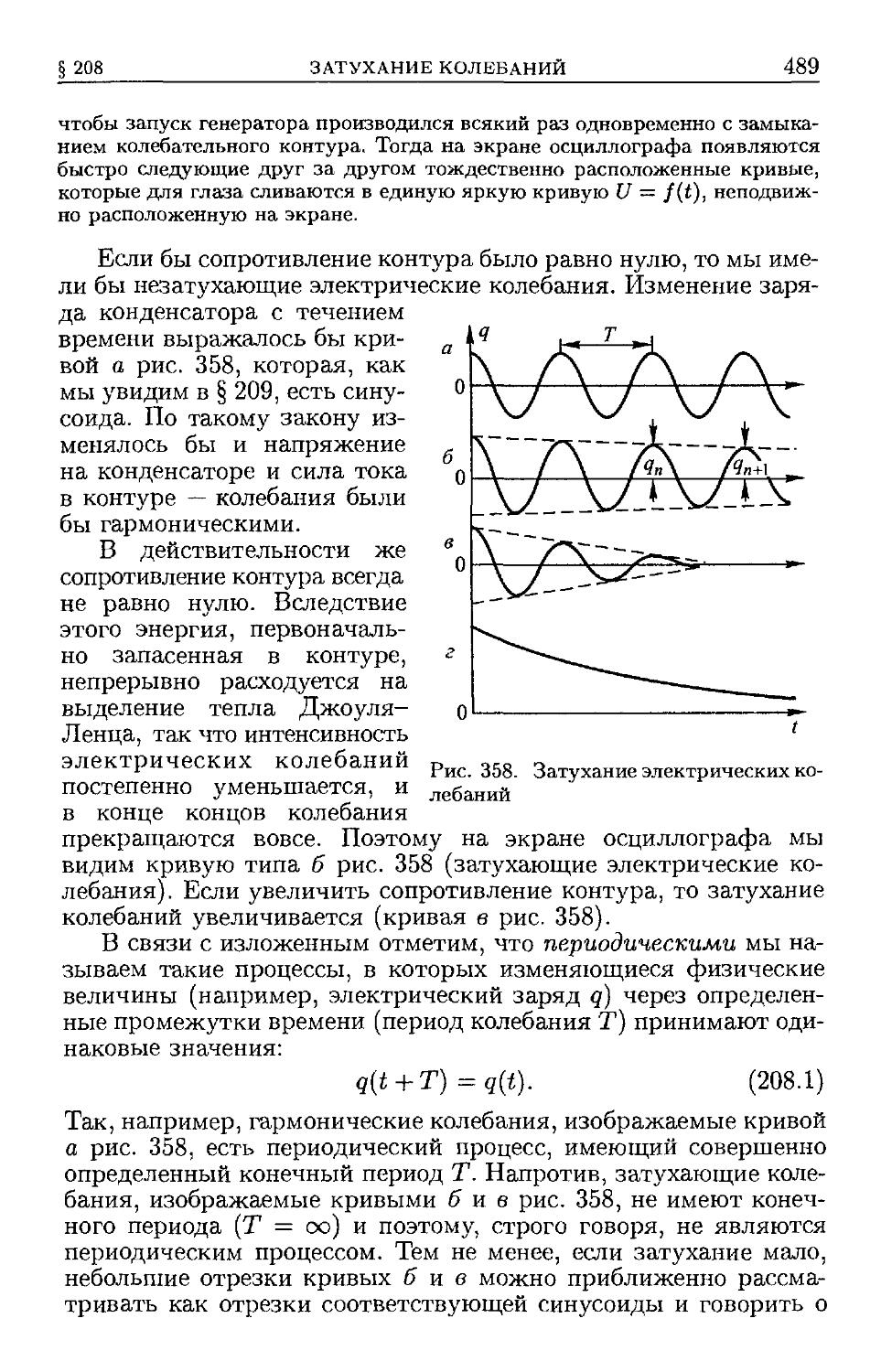
§ 207. Собственные электрические колебания D85). § 208. Затуха-
Затухание колебаний D88). § 209. Уравнение собственных электрических
колебаний. Колебания в отсутствие затухания D90). § 210. Коле-
Колебания при наличии затухания D93). § 211. Поддержание колеба-
колебаний. Искровой контур D96). § 212. Автоколебательные системы
D97). § 213. Использование отрицательных сопротивлений D98).
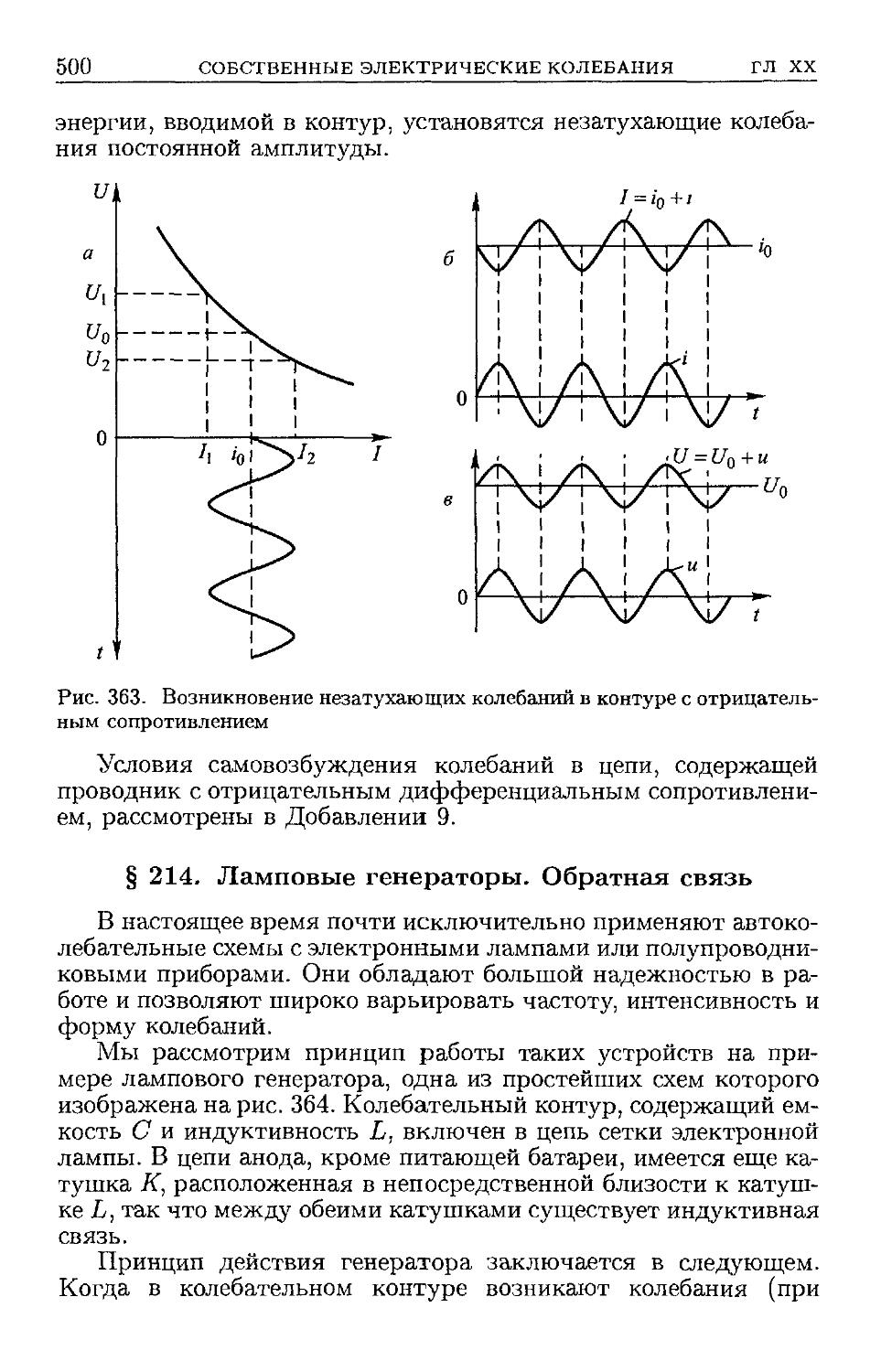
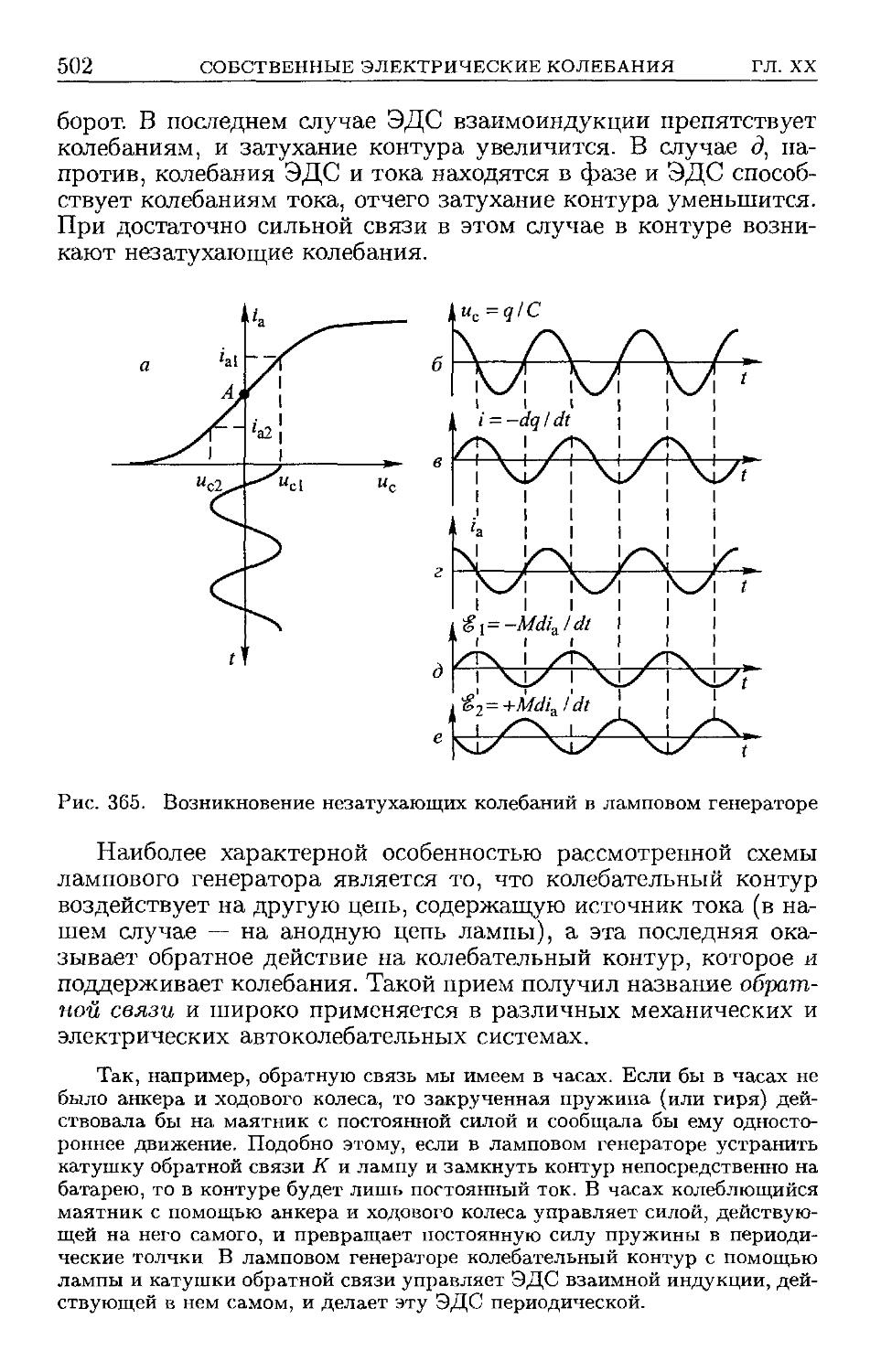
§ 214. Ламповые генераторы. Обратная связь E00). § 215. Условие
самовозбуждения E03). § 216. Релаксационные колебания E05).
Глава XXI. Вынужденные электрические колебания. Пере-
Переменные токи 506
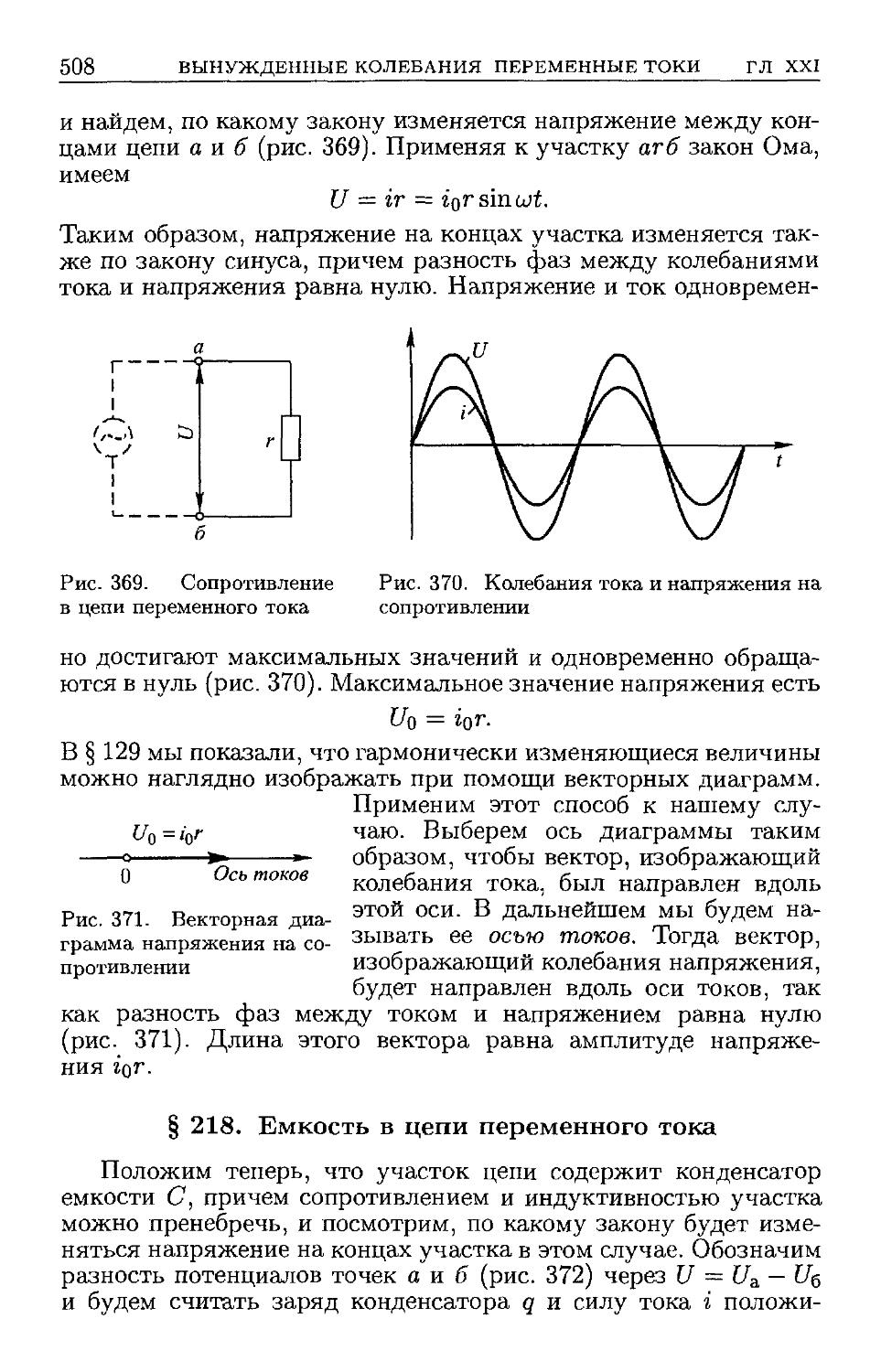
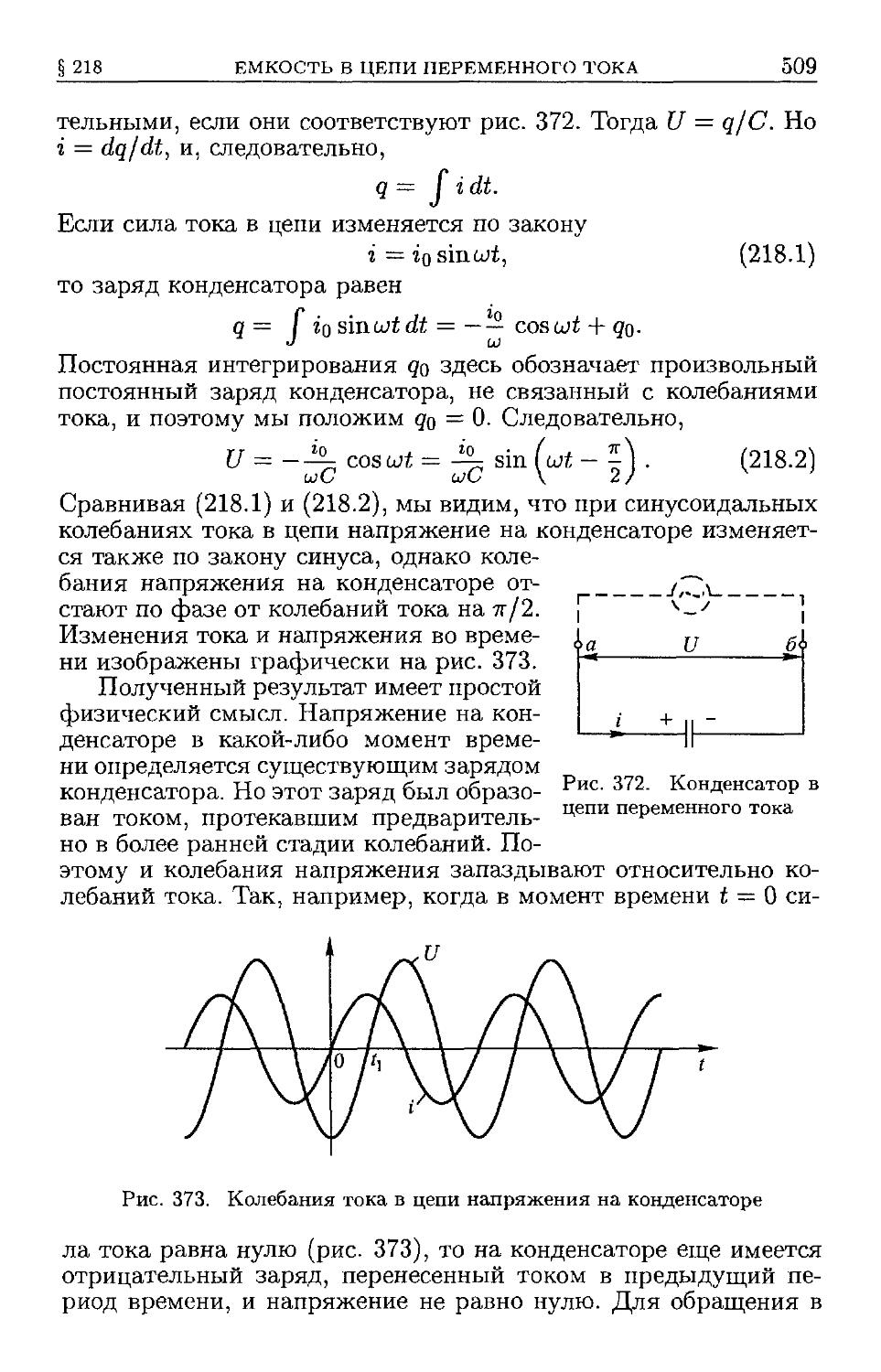
§ 217. Сопротивление в цепи переменного тока E07). § 218. Ем-
Емкость в цепи переменного тока E08). § 219. Индуктивность в цепи
переменного тока E11). § 220. Закон Ома для переменных токов
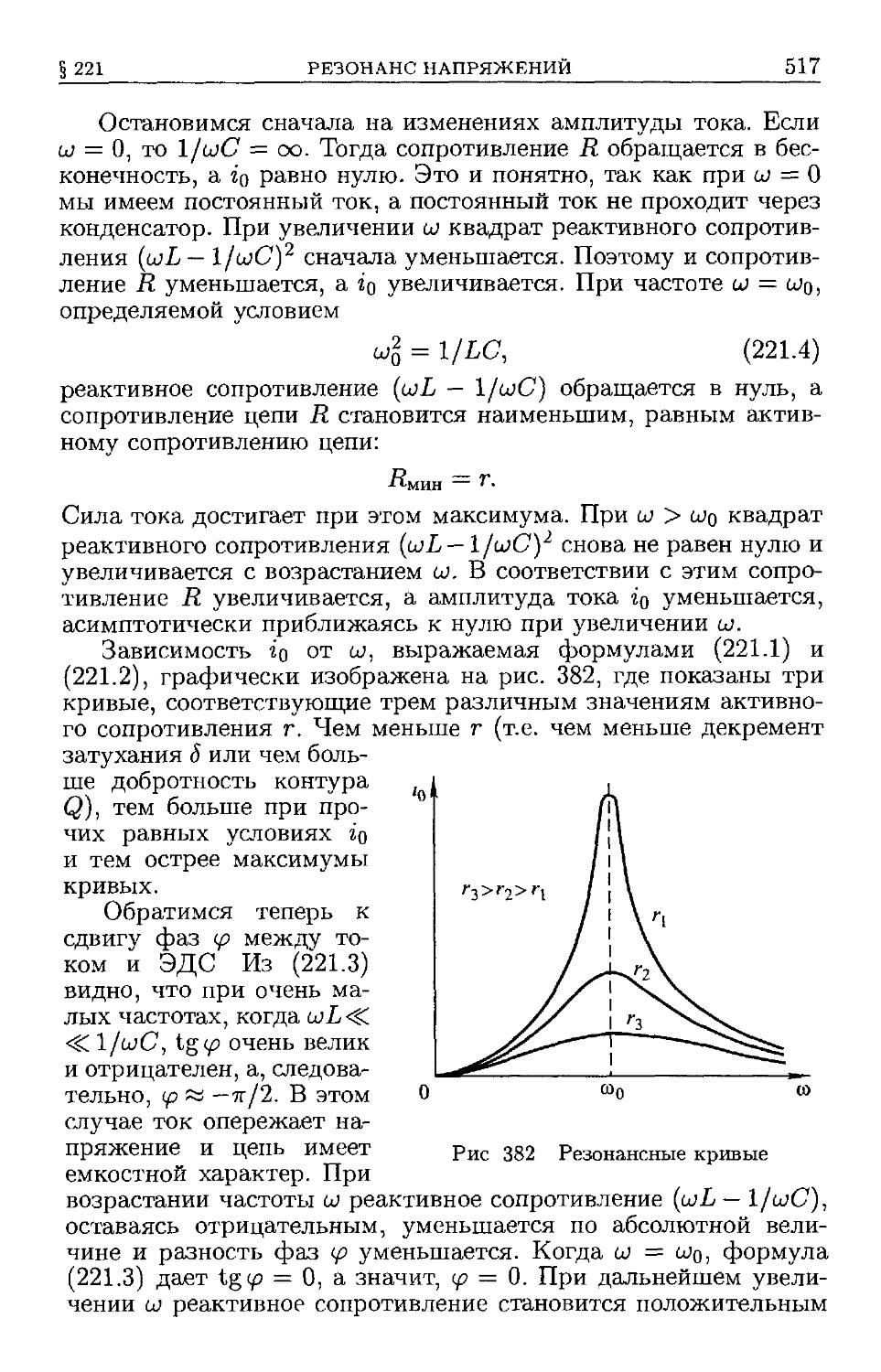
E14). § 221. Резонанс напряжений E16). § 222. Установление ко-
колебаний E20). § 223. Работа и мощность переменного тока E22).
ОГЛАВЛЕНИЕ
§ 224. Разветвление переменных токов E25). § 225. Резонанс токов
E27). § 226. Параметрический резонанс E30). § 227. Комплексные
величины E32). § 228. Комплексные сопротивления E36).
Глава XXII. Электромагнитные волны вдоль проводов . . . 541
§ 229. Распределенные системы E41). § 230- Электромагнитный
импульс вдоль проводов E42). § 231. Электромагнитные волны
E45). § 232. Стоячие электромагнитные волны E47). § 233. Соб-
Собственные колебания двухпроводной линии E51). § 234. Экспери-
Экспериментальное исследование стоячих электромагнитных волн E53).
§ 235. Открытый вибратор E55). § 236. Стоячие волны в катушках
E56).
Глава XXIII. Свободные электромагнитные волны 557
§ 237. Образование свободных электромагнитных волн E57).
§ 238. Волновое уравнение E58). § 239. Плоские электромагнит-
электромагнитные волны E60). § 240. Свойства электромагнитных волн E62).
§ 241. Экспериментальное исследование электромагнитных волн
E63). § 242, Энергия электромагнитных волн E67). § 243. Эле-
Элементарный диполь E71). § 244. Давление электромагнитных волн
E74). § 245. Импульс и масса электромагнитного поля E75).
§ 246. Электромагнитная масса движущегося заряда E79).
Глава XXIV- Применение электромагнитных волн для целей
связи 582
§ 247. Принцип радиосвязи E82). § 248. Модуляция колебаний
E83). § 249. Радиопередатчик E86). § 250. Демодуляция коле-
колебаний. Радиоприемник E88). § 251. Гетеродинный прием E91).
§ 252. Супергетеродинный приемник E91). § 253. Полусвободные
электромагнитные волны E93).
Добавления 595
1. Теория опытов Кавендиша и Максвелла (к § 28) 595
2. Ориентировка полярных молекул в электрическом поле (к § 48) . 598
3. Лилии напряженности и тока (к § 61) 599
4. Метод контурных токов (к § 70) 600
5. Максвелловское время релаксации (к § 73) 601
6. Взаимная энергия двух токов (произвольные контуры) (к § 90) . 602
7. Теорема Лармора (к § 115) 603
8. Закон Богуславского-Лэнгмюра 604
9. Устойчивость электрических разрядов (к § 176, 213) 605
10. К объяснению циклотронного резонанса (к § 185) 608
11. Электромагнитное поле диполя (к § 243) 610
12. Давление электромагнитных волн (к § 244) 612
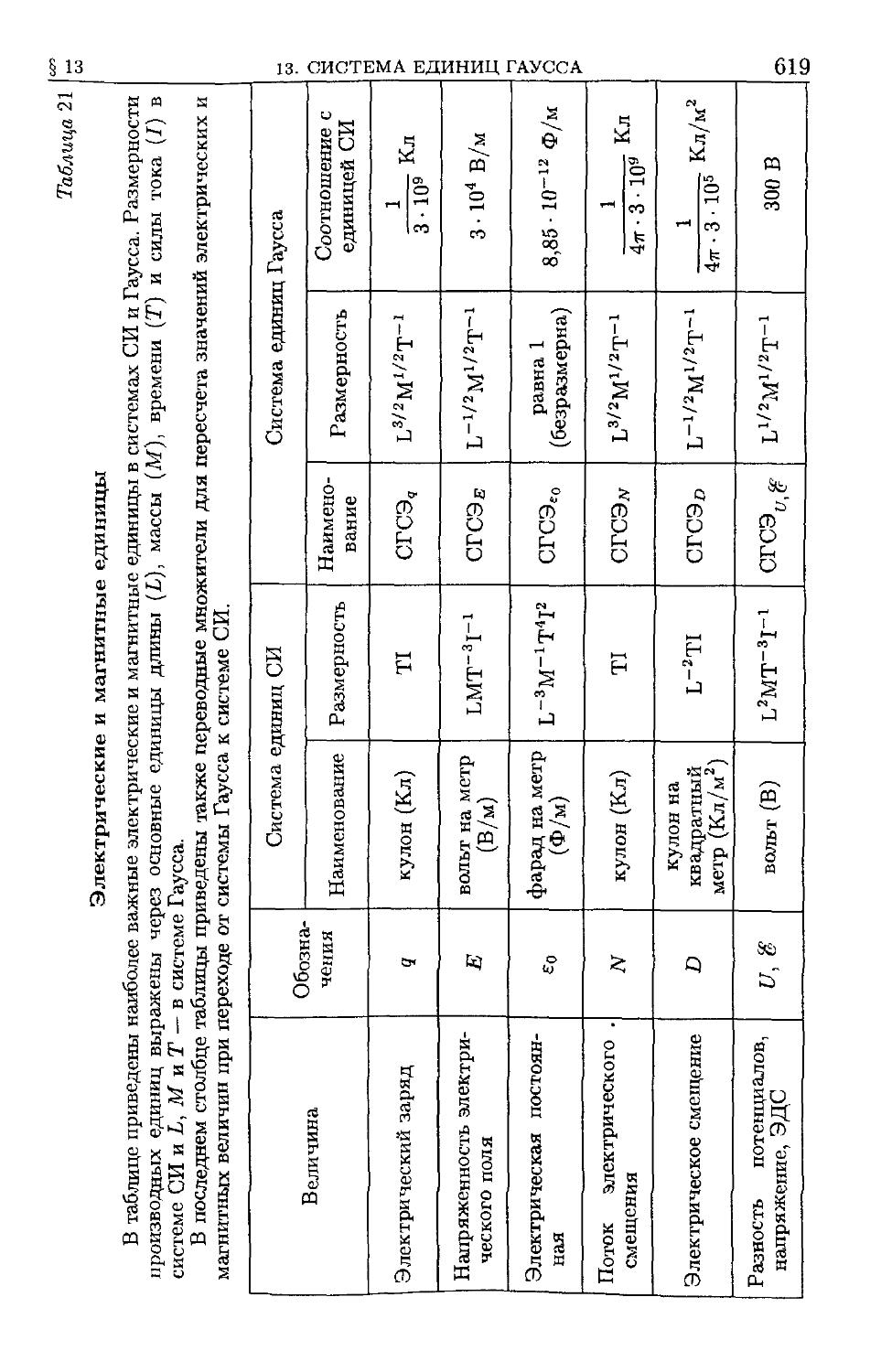
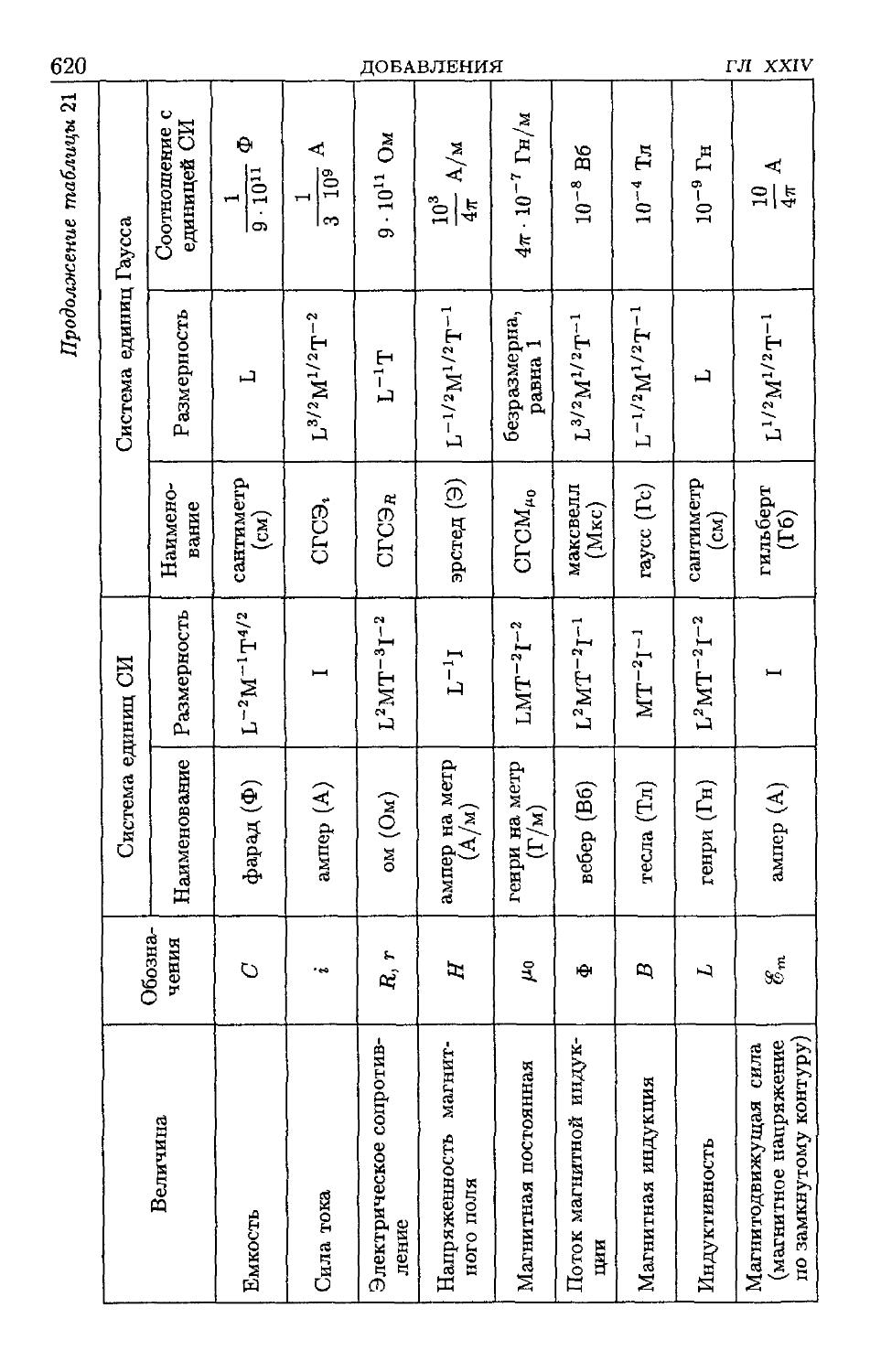
13. Система единиц Гаусса 6]4
14. Таблица электрических и магнитных единиц 619
Предметный указатель 621
ОТ РЕДАКЦИИ
Предлагаемая вниманию читателей книга профессора
С.Г. Калашникова «Электричество» написана на основе лек-
лекций, которые автор читал в течение ряда лет на физическом
факультете Московского государственного университета. Лек-
Лекции С.Г. Калашникова по курсу общей физики и созданный им
курс по физике полупроводников всегда отличались глубиной
содержания, точностью и прозрачной ясностью изложения
и неизменно современным уровнем. Эта особенность лекций
привлекала к ним не только студентов, на которых они прежде
всего были рассчитаны, но и аспирантов, преподавателей и
научных сотрудников всех рангов.
Книга впервые увидела свет в 1956 году, быстро получила
широкое признание и стала одним из основных учебных посо-
пособий для студентов физических специальностей высших учебных
заведений. При подготовке переизданий автор постоянно совер-
совершенствовал курс, дополняя его новым материалом и расширяя
содержание. За несколько дней до своей кончины, последовав-
последовавшей 23 апреля 1984 года, Сергей Григорьевич Калашников за-
завершил работу над основным текстом настоящего, пятого, из-
издания «Электричества»; не написанным осталось только преди-
предисловие.
Как и в предыдущих изданиях, автор внес в книгу некото-
некоторые улучшения и изменения, сохраняя при этом общий замысел,
структуру курса и стиль изложения. Так, расширены и перера-
переработаны § 113 (Магнитные заряды. Формальная теория магне-
магнетизма), § 117 (Магнитный и механический моменты электрона),
§ 246 (Электромагнитная масса движущегося заряда). Добав-
Добавлены важные сведения об изотропных и анизотропных диэлек-
диэлектриках (§ 42), прямом и обратном пьезоэлектрических эффектах
(§ 42, 51), энергии заряженного конденсатора (§ 34) и энергии
магнитного поля (§ 47), а также о термоэлектричестве (§ 199).
Включен вопрос об ориентировке полярных молекул в электри-
электрическом поле (Добавление 2). Кроме того, сделано значительное
число более мелких вставок и замен в других местах книги.
В процессе редактирования и окончательной подготовки ру-
рукописи к публикации проведено уточнение терминологии; обо-
обозначения единиц физических величин приведены в соответствии
с действующим ГОСТ 8.417-81 (СТ СЭВ 1052-78).
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Настоящая книга задумана как учебное пособие по разде-
разделу «Электричество» общего курса физики, который я читал в
течение ряда лет на физическом факультете Московского уни-
университета.
В основу изложения материала, за редкими исключениями,
обусловленными методическими соображениями, я стремился
положить опыт. Я старался также уделить внимание разъясне-
разъяснению принципов измерения основных электрических и магнит-
магнитных величин, которое, по возможности, следует непосредствен-
непосредственно за введением соответствующих физических понятий. Однако
описание различных опытов отнюдь не претендует на полно-
полноту и, кроме того, касается только принципов этих опытов, так
как предполагается, что читатели этой книги слушают лекци-
лекционный курс с демонстрациями и работают в учебных лаборато-
лабораториях. По этой же причине большинство рисунков выполнено в
виде умышленно простых схем, легко доступных воспроизведе-
воспроизведению студентами.
Текст книги разделен на три группы. Материал, набранный
основным шрифтом, соответствует принятой программе и, по
мнению автора, является обязательным для изучения. Факуль-
Факультативный материал дан петитом. Наконец, в добавления вынесе-
вынесены некоторые (факультативные) вопросы, которые имеют чисто
вычислительный характер.
Так как в настоящее время имеются задачники, соответству-
соответствующие университетскому курсу физики, то включение в книгу
задач и упражнений казалось мне излишним. Поэтому в кни-
книге приведены лишь сравнительно немногочисленные примеры,
иллюстрирующие применение наиболее важных законов и со-
составляющие, как правило, органическую часть текста.
Июнь 1956 С. Г. Калашников
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛАВА I
ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
§ 1. Введение
Напомним некоторые элементарные факты, касающиеся
электрических зарядов. Так как они должны быть известны чи-
читателям из курса физики средней школы, мы остановимся на
них лишь очень кратко.
Уже в глубокой древности было известно, что янтарь, по-
потертый о шерсть, приобретает способность притягивать легкие
предметы. Однако только в конце XVI века английский врач
Джильберт подробно исследовал это явление и нашел, что ана-
аналогичным свойством обладают многие другие вещества. Тела,
способные, подобно янтарю, после натирания притягивать лег-
легкие предметы, он назвал наэлектризованными (от греческого
электрон — янтарь). Теперь мы говорим, что на телах в та-
таком состоянии имеются электрические заряды, а сами эти тела
называем заряженными.
Укажем, что само трение при «электризации трением» не
играет никакой принципиальной роли. Электрические заряды
всегда возникают при тесном соприкосновении различных ве-
веществ. В случае твердых тел тесному соприкосновению препят-
препятствуют микроскопические выступы и неровности, всегда имею-
имеющиеся на поверхности. Сдавливая тела и притирая их друг к
другу, мы лучше сближаем поверхности обоих тел, которые без
притирания соприкасались бы только в немногих точках.
В некоторых телах электрические заряды могут свободно пе-
перемещаться между различными частями тела, в других же те-
телах это не имеет места. Тела первого рода называют проводни-
проводниками электричества, а тела второго рода — диэлектриками или
изоляторами. Проводниками являются все металлы в твердом
и жидком состояниях, водные растворы солей и кислот и многие
другие вещества. Примерами изоляторов могут служить янтарь,
кварц, эбонит и все газы в нормальных условиях.
Отметим, что разделение тел на проводники и диэлектрики
весьма условно. Все известные вещества в большей или мень-
12 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ГЛ. I
шей степени проводят электричество. Когда мы говорим, что
данное тело есть изолятор, то этим мы выражаем только то об-
обстоятельство, что в данных условиях опыта заряд, прошедший
через тело, мал по сравнению с другими зарядами, участвую-
участвующими в рассматриваемом явлении.
Опыт показывает, далее, что два заряженных тела могут ли-
либо отталкиваться, либо притягиваться друг к другу. Если заря-
зарядить два легких тела, подвешенных на изолирующих шелковых
нитях, прикасаясь к ним стеклянной палочкой, потертой о шелк,
то оба тела отталкиваются. То же наблюдается, если оба тела
заряжены при помощи эбонитовой палочки, потертой о мех. Но
если зарядить одно из тел от стеклянной палочки, а другое —
от эбонитовой, то оба тела притягиваются друг к другу. Это
означает, что заряды стекла и эбонита качественно различны.
Несмотря на обилие различных веществ в природе, существу-
существуют только два вида электрических зарядов: заряды, подобные
возникающим на стекле, потертом о шелк, и заряды, подобные
появляющимся на эбоните, потертом о мех. Первые из них по-
получили название положительных зарядов, а вторые — отрица-
отрицательных зарядов. Следовательно, одноименные заряды оттал-
отталкиваются, а разноименные притягиваются.
Явление электрического отталкивания используют для
устройства электроскопа, предназначенного для обнаружения
электрических зарядов. Он состоит из изолированного метал-
металлического стержня, к которому прикреплены легкие металли-
металлические или бумажные листочки. При соприкосновении с заря-
заряженным телом часть заряда тела переходит на электроскоп и
листочки под действием сил электрического отталкивания от-
отклоняются на некоторый угол.
§ 2. Закон взаимодействия электрических зарядов
Начало количественного изучения электрических явлений
относится к концу XVIII века, когда Кулон A785 г.) установил
на опыте закон взаимодействия электрических зарядов.
Для заряженных тел произвольных размеров такой закон в
общей форме дать нельзя, так как сила взаимодействия протя-
протяженных тел зависит от их формы и взаимного расположения.
Однако форма тел и их взаимная ориентировка перестают ска-
сказываться, если размеры тел весьма малы по сравнению с рас-
расстоянием между ними. Поэтому закон взаимодействия, имею-
имеющий общее значение, можно установить только для точечных
зарядов.
Так как электрические заряды всегда распределены в объ-
объеме, то никаких конечных зарядов в математической точке, ра-
разумеется, быть не может. Под точечным зарядом в физике все-
§2
ЗАКОН ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
13
гда понимают протяженное заряженное тело, размеры которого
весьма малы по сравнению с расстоянием от других зарядов.
Схема опытов Кулона изображена на рис. 1 (а — общий вид
прибора, б — его головка, в — проводник для зарядки шари-
шариков А я Б). На тонкой металлической нити Н подвешено легкое
изолирующее коромысло К, имею-
имеющее на одном из концов ша-
шарик А, а на другом — противо-
противовес П. Верхний конец нити за-
закреплен на вращающейся головке
прибора, позволяющей точно от-
отсчитывать угол закручивания ни-
нити. Внутрь прибора можно вно-
вносить второй изолированный ша-
шарик Б такого же размера, как и
шарик А. Большой стеклянный
цилиндр защищает чувствитель-
чувствительные части прибора от движения
воздуха.
Чтобы установить, как зави-
зависит сила взаимодействия от рас-
расстояния между зарядами, шари-
шарикам А и Б сообщают произволь-
произвольные заряды, касаясь их третьим
заряженным шарикбм, укреплен-
укрепленным на изолирующей ручке. Ша-
Шарики отталкиваются и устанавливаются на некотором расстоя-
расстоянии, которое измеряют, пользуясь шкалой прибора. Затем вра-
вращают головку прибора и закручивают нить подвеса, замечая
при этом расстояния, до которых сближаются шарики при раз-
различных углах закручивания нити. Как известно из механики,
при деформации кручения (в области обратимых упругих де-
деформаций) угол закручивания пропорционален моменту крутя-
крутящей силы; зная, во сколько раз мы увеличили угол закручива-
закручивания нити, мы тем самым определяем, во сколько раз увеличился
момент силы, а отсюда можно определить и силу, действующую
на шарик коромысла. В результате этих опытов Кулон заклю-
заключил, что сила взаимодействия двух точечных зарядов направле-
направлена вдоль линии, соединяющей оба заряда, и обратно пропорци-
пропорциональна квадрату расстояния между зарядами:
F-1/r2.
Сила взаимодействия между шариками зависит еще от заря-
зарядов шариков. Эту зависимость можно выяснить при помощи сле-
следующего опыта. Если коснуться на короткое время одного из ша-
шариков, А или Б, другим шариком, имеющим такие же размеры,
Рис. 1. Крутильные весы Кулона
14 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ГЛ. I
но не заряженным, то в силу тождественности обоих соприка-
соприкасающихся шариков заряд распределяется между ними поровну.
При этом оказывается, что сила взаимодействия между шарика-
шариками А и Б, на одном из которых теперь находится лишь половина
первоначального заряда, при том же расстоянии уменьшается в
два раза. Повторяя этот прием, можно уменьшить заряд шарика
в два, четыре и т.д. раз и убедиться, что сила взаимодействия
пропорциональна заряду каждого из шариков.
Более точно этот вопрос можно исследовать следующим
образом. Сообщим шарикам А и В некоторые (неизвестные)
заряды и измерим силу взаимодействия Fab между ними при
некотором определенном расстоянии. Заменим, далее, шарик Б
другим заряженным шариком В и измерим снова силу взаи-
взаимодействия Fab между А и В при том же расстоянии, что и
в первом случае. Если теперь изменить произвольным образом
заряд шарика А и опять измерить силы взаимодействия шарика
А с шариками Б и В, то опыт показывает, что отношение сил
Fab /Fab в обоих случаях одинаково, т.е. не зависит от заря-
заряда шарика А. Это значит, что указанное отношение сил зависит
только от зарядов шариков Б и В, а следовательно, можно по-
положить его равным отношению зарядов обоих шариков, т.е.
Fab /Fab =Яб/чв-
Это соотношение является определением отношения двух заря-
зарядов и указывает способ сравнения зарядов..
Полученный результат показывает, что сила взаимодействия
пропорциональна заряду одного из шариков (А). Так как оба
шарика в этих опытах равноправны, то отсюда следует, что сила
взаимодействия пропорциональна каждому из зарядов q\ и qi-
Таким образом, сила взаимодействия двух точечных зарядов
равна
F = /??. B.1)
Здесь / — коэффициент пропорциональности, зависящий от вы-
выбора единиц заряда, расстояния и силы.
Для того чтобы выразить не только модуль силы, но и ее на-
направление, закон Кулона можно представить в векторной форме:
Fi2 = /^r12, B.1а)
*i
где Fi2 — вектор силы, действующей на заряд 2 со стороны
заряда 1, а Г12 — радиус-вектор, направленный от заряда 1 к
заряду 2.
Опыты Кулона, конечно, не являются единственным дока-
доказательством справедливости закона обратных квадратов. В на-
настоящее время имеется большое количество других эксперимен-
экспериментальных данных, показывающих, что закон Кулона выполняется
§ 3 АБСОЛЮТНАЯ ЭЛЕКТРОСТАТИЧЕСКАЯ СИСТЕМА ЕДИНИЦ 15
очень точно и притом как для очень больших, так и для очень
малых расстояний. В частности, исследования атомных явле-
явлений позволяют заключить, что он справедлив, по крайней мере,
вплоть до расстояний порядка 10~15 м.
§ 3. Абсолютная электростатическая система единиц
Для определения коэффициента пропорциональности / в за-
законе Кулона мы должны остановиться на какой-либо определен-
определенной системе единиц.
Всякая система единиц состоит из некоторого числа основ-
основных единиц, выбираемых независимо друг от друга, и сово-
совокупности производных единиц. Последние образуются из основ-
основных (и других производных) единиц с помощью подходящим
образом выбранных соотношений, выражающих определенные
физические законы и связывающих между собой данную фи-
физическую величину, для которой устанавливается единица, с
другими величинами, единицы которых уже определены. Каж-
Каждое такое соотношение, используемое для установления той или
иной производной единицы, мы будем называть определяющим
соотношением для данной единицы.
В физике до настоящего времени часто употребляют абсо-
абсолютную систему единиц (механических, электрических и маг-
магнитных) СГС, построенную на трех основных единицах: длины
(сантиметр), массы (грамм) и времени (секунда). Единицей си-
силы в этой системе служит дина. Если выражать расстояние г в
сантиметрах, а силу F в динах, то в законе Кулона будет един-
единственная неопределенная единица — единица заряда. Поэтому
можно выбрать эту единицу таким образом, чтобы было / = 1,
т.е. чтобы закон Кулона приобрел наиболее простую форму. Та-
Такая единица заряда получила название абсолютной электро-
электростатической единицы заряда.
Полагая в формуле B.1) г = 1, q\ = q2 = 1, получаем F = 1.
Это значит, что абсолютная электростатическая единица за-
заряда есть такой заряд, который действует в вакууме на рав-
равный ему заряд, удаленный на расстояние 1 см, с силой 1 дин.
Если выражать заряды в абсолютных электростатических
единицах, силу — в динах, а расстояние —- в сантиметрах, то
закон Кулона B.1) принимает вид
Выбирая за основные единицы сантиметр, грамм и секунду
и пользуясь абсолютной электростатической единицей заряда,
можно определить единицы всех электрических и магнитных
величин, с которыми мы познакомимся в дальнейшем. Такая
16 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ГЛ I
система единиц называется абсолютной электростатической
системой и обозначается символом СГСЭ.
Таким образом, в системе СГСЭ единица заряда есть произ-
производная единица. Определяющим соотношением для нее служит
закон Кулона.
В дальнейшем мы будем пользоваться общепринятым спосо-
способом обозначения производных единиц. Для этого данную вели-
величину будем выражать из определяющего соотношения и в полу-
полученное выражение подставлять вместо физических величин их
единицы. Так, например, из формулы C.1) имеем
отсюда единица заряда в системе СГСЭ равна
1 СГСЭд = 1 см • дин1/2.
Такой способ обозначения производных единиц удобен пото-
потому, что он определяет их размерность, т.е. показывает, как из-
изменяется единица данной физической величины при изменении
других единиц системы. Так, например, приведенное выраже-
выражение показывает, что при увеличении единицы длины в а раз и
единицы силы в Ь раз единица заряда увеличивается в аб1/2 раз.
Производные единицы можно также выразить только через
основные единицы. Так, например, учитывая, что 1 дин есть
1 г-см-с", получаем
1 СГСЭ, = 1 см3/2 ¦ г1'2 ¦ с.
§ 4. Между народная система единиц (СИ)
Помимо системы СГСЭ, можно построить и другие абсолют-
абсолютные системы электрических и магнитных единиц. Так, напри-
например, в § 77 мы познакомимся с электромагнитной системой еди-
единиц СГСМ, которая, как и система СГСЭ, построена на трех
основных единицах: длины (сантиметр), массы (грамм) и вре-
времени (секунда), но основана не на законе электростатическо-
электростатического взаимодействия зарядов, а на законе магнитного взаимодей-
взаимодействия токов. Эта система является также абсолютной, так как в
ней все магнитные единицы определяются таким образом, что-
чтобы коэффициенты пропорциональности в законах магнетизма
обратились в единицу. Система единиц СГСЭ весьма удобна
для описания электрических явлений, а система СГСМ — для
магнитных явлений. Особенно широко в физической литерату-
литературе применяется также так называемая симметричная система
электрических и магнитных единиц (система единиц Гаусса),
представляющая собой сочетание обеих систем СГСЭ и СГСМ
(см. Добавление 13).
§ 4 МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ) 17
Однако эти абсолютные системы единиц, наряду с весьма
большими их достоинствами, обладают тем недостатком, что
единицы многих электрических и магнитных величин получа-
получаются в них неудобными для целей практики, так как оказыва-
оказываются или слишком большими, или слишком малыми. Поэтому
в настоящее время получила широкое распространение Меж-
Международная система единиц, сокращенно обозначаемая латин-
латинскими буквами SI (The system international of units) и русскими
буквами СИ (система интернациональная). При разработке этой
системы стремились к тому, чтобы единицы основных электри-
электрических и магнитных величин совпали с соответствующими прак-
практическими единицами, давно установившимися и принятыми в
электротехнике и радиотехнике 1).
Система СИ построена на основе семи основных единиц: еди-
единица длины — метр (м), единица массы — килограмм (кг), еди-
единица времени — секунда (с), единица силы тока — ампер (А),
единица термодинамической температуры — кельвин (К), еди-
единица силы света — кандела (кд) и единица количества веще-
вещества — моль (моль). Кроме семи основных, система СИ имеет
две дополнительные единицы: единицу плоского угла - радиан
(рад) и единицу телесного угла — стерадиан (ср).
Каждая из этих единиц позволяет образовать все производ-
производные единицы для величин, имеющих немеханическую природу:
ампер — единицы электрических и магнитных величин, кель-
кельвин — единицы тепловых величин, кандела — единицы свето-
световых величин, моль — единицы величин молекулярной физики и
химии.
Единица электрического заряда в системе СИ есть кулон
(Кл) — заряд, проходящий за 1 с через сечение проводника, в
котором имеется неизменяющийся ток силой 1 А, т.е.
1 Кл = 1 А • 1 с = 1 А • с.
Определение ампера основано на законе магнитного взаи-
взаимодействия токов и будет дано в § 83. Из этого определения
следует, что 1 кулон содержит 0,1с единиц заряда СГСЭ, где
с = 2,99792458 • 1010 есть скорость света в вакууме, выраженная
в см/с. В дальнейшем мы будем пользоваться округленным зна-
значением этой величины и считать, что заряд
1 Кл = 3 • 109 СГСЭ9.
1) Постановлением Государственного комитета СССР по стандартам от
19 марта 1981 г с 1 января 1982 г в Советском Союзе введен в действие
государственный стандарт ГОСТ 8 417-81 (СТ СЭВ 1052-78), согласно ко-
которому обязательному применению подлежат единицы Международной си-
системы (СИ), а также десятичные кратные и дольные от них. (Примеч. ред.)
18 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ГЛ. I
Отличие системы СИ от системы СГСЭ заключается еще и в
том, что в ней используется так называемая рационализованная
форма записи законов электричества Это изменение заключа-
заключается в следующем. Во многие формулы электричества, в осо-
особенности в те, которые часто встречаются в практике, входит
множитель 4тг. Чтобы избавиться от него в практически важ-
важных формулах, в выражение для закона Кулона с самого нача-
начала вводят множитель 1/4тг. Такой же множитель оказывается
удобным ввести и в основной закон магнитного взаимодействия
токов (ср. § 79). Поэтому закон Кулона в системе единиц СИ
записывают в виде
F =-!-*?, D.1)
где вместо коэффициента пропорциональности /, входящего в
формулу B.1), написано 1/Dтгео). Здесь е0 — некоторая посто-
постоянная, зависящая от выбора единиц. Однако, так как едини-
единица заряда уже определена, эту постоянную нельзя обратить в
единицу. Поэтому в системе СИ, в отличие от системы СГСЭ,
в законы электричества входит новая постоянная бо, имеющая
определенную размерность. Эту постоянную мы будем называть
в дальнейшем электрической постоянной.
Нетрудно найти, чему равно значение ?о в системе единиц
СИ. Положим, что два точечных заряда q\ = qi = 1 Кл, удален-
удаленных на расстояние 1 м = 102 см, взаимодействуют в вакууме.
Тогда, согласно формуле C.1), сила взаимодействия равна
С другой стороны, согласно формуле D.1), та же сила есть
F= 1 ''= 1 н
4 I2 4
Отсюда
О единице электрической постоянной ео см. § 32.
§ 5. Гальванические элементы
Электрические заряды можно получить различными спосо-
способами, с которыми мы познакомимся в дальнейшем. Сейчас же
мы упомянем о получении зарядов с помощью гальванических
элементов.
Гальваническим элементом называют два различных провод-
проводника, соединенных электропроводящим раствором (обычно вод-
ЭЛЕКТРИЗАЦИЯ КАК РАЗДЕЛЕНИЕ ЗАРЯДОВ
19
Си
ным раствором кислоты или соли). На рис. 2 показан один из
простейших элементов — элемент Вольты. Он состоит из медной
и цинковой пластин, называемых элек-
электродами элемента, погруженных в сла-
слабый водный раствор серной кислоты.
Медь заряжается положительно, а цинк —
отрицательно. Положительный электрод
часто называют анодом, а отрицатель-
отрицательный — катодом.
Устройство различных гальваниче-
гальванических элементов и процессы, в них проис-
происходящие, будут рассмотрены в ГЛ. XVIII. Рис. 2. Элемент Вольты
§ 6. Электризация как разделение зарядов
Опыт показывает, что возникновение заряда на любом теле
всегда сопровождается появлением другого заряда, равного ему
по модулю, но противоположного по знаку. Так, например, в
гальванических элементах мы имеем всегда два электрода, один
из которых заряжается положительно, а другой — отрицатель-
отрицательно. При электризации трением также всегда заряжаются оба
притираемых тела и притом равными по модулю, но противо-
противоположными по знаку зарядами.
Одновременное появление разноименных зарядов при всяком
процессе заряжения привело к заключению, что во всех телах
всегда содержатся положительные и отрицательные заряды. В
обычных условиях, однако, количество положительного заряда
в каждом объеме тела равно количеству отрицательного заря-
заряда, и поэтому тело представляется нам незаряженным. Всякий
процесс заряжения есть процесс разделения электрических за-
зарядов, при котором на одном из тел (или части тела) появляется
избыток положительного заряда, а на другом (или другой части
тела) — избыток отрицательного заряда. Общее количество по-
положительного и отрицательного зарядов, содержащихся в телах,
не изменяется, а эти заряды только перераспределяются между
телами. Поэтому алгебраическая сумма зарядов, возникающих
при любом электрическом процессе на всех телах, участвующих
в процессе, всегда равна нулю.
§ 7. Электроны
В настоящее время твердо установлено, что электрические
заряды существуют в природе в виде заряженных частиц, кото-
которые мы считаем простейшими, или элементарными. Элементар-
Элементарная отрицательно заряженная частица, с которой нам приходит-
приходится встречаться в электрических явлениях, получила название
20 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ГЛ. I
электрона. Заряд каждого из электронов равен 1,60 • 109 Кл
(§ 144). Масса электрона чрезвычайно мала и составляет все-
всего около 10~30 кг. Поэтому можно принести на тело и убрать с
него огромное число электронов без заметного изменения массы
тела.
В состав атома каждого элемента входит определенное свой-
свойственное ему число электронов. Атом в целом, однако, не заря-
заряжен, так как в нем имеется и положительный заряд, равный по
модулю сумме зарядов всех электронов атома. Положительный
заряд атома заключен в ядре атома, в котором сосредоточена
практически вся масса атома.
Если атом теряет один или несколько электронов, то он обра-
обращается в положительно заряженный атом, или положительный
ион. Если атом захватывает дополнительные электроны, образу-
образуется отрицательно заряженный атом, или отрицательный ион.
Процесс заряжения какого-либо тела представляет собой либо
перенос на это тело, либо увод с него некоторого количества
электронов или ионов.
Теория, объясняющая различные свойства вещества наличи-
наличием в нем электронов и их движением, носит название электрон-
электронной теории.
Хорошие проводники электричества — это такие тела, в ко-
которых электрические частицы могут свободно перемещаться.
Электропроводность металлов обусловлена тем, что часть элек-
электронов, содержащихся в металле, находится в подвижном со-
состоянии. Такие электроны называются свободными электронами
или электронами проводимости.
Если к изолированному незаряженному металлическому про-
проводнику приблизить заряженное тело, то на проводнике появ-
©•©•©•©•\ "/• © • © • © ©
©•©•©•©• \ /т\ /•©•©•©•©
©•©•©•©• / <& \т ©•©•©•©
©•©•©•©•У f. V© • © • © ©
Рис. 3. Схема объяснения электрической индукции в электронной теории
ляются наведенные, или индуцированные, заряды (рис. 3, где
кружки с плюсом — положительные ионы металла, темные точ-
точки — электроны проводимости). В рамках электронной теории
это объясняется тем, что приближение влияющего тела вызыва-
вызывает появление сил, действующих на электроны проводимости ме-
металла, отчего они перемещаются и перераспределяются, пока не
будет достигнуто новое положение равновесия. Если, например,
влияющее тело заряжено положительно, то электроны проводи-
проводимости будут притягиваться к нему и на ближнем к телу конце
§ 8 ПОНЯТИЕ ОБ ЭЛЕКТРИЧЕСКОМ ПОЛЕ 21
проводника появятся избыточные электроны, т.е. отрицатель-
отрицательный заряд; на удаленном конце образуется недостаток электро-
электронов, а следовательно, здесь появляется избыток положительных
ионов, т.е. возникает положительный заряд (рис. 3 6).
В дальнейшем мы рассмотрим основные опыты, доказываю-
доказывающие существование электронов, позволяющие определить их
свойства и выясняющие участие электронов в различных элек-
электрических явлениях. Однако существование электронов целесо-
целесообразно учесть уже с начала изучения электричества, так как
это сразу позволяет просто и наглядно объяснить многие элек-
электрические явления.
ГЛАВА II
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
§ 8. Понятие об электрическом поле
При исследовании взаимодействия электрических зарядов,
естественно, возникает вопрос, почему появляются силы, дей-
действующие на заряды, и как они передаются от одного заряда
к другому? Совершенно так же можно поставить и следующий
вопрос: механические силы возникают только при наличии двух
зарядов; происходят ли, однако, какие-либо изменения в окру-
окружающем пространстве при наличии только одного заряда, когда
второго нет вовсе?
В процессе развития физики существовали два противопо-
противоположных подхода к ответу на поставленные вопросы. При одном
из них предполагалось, что телам присуще свойство действовать
на другие тела на расстоянии, без участия промежуточных тел
или среды, т.е. предполагалось, что силы могут передаваться от
одного тела к другому через пустоту и притом мгновенно (тео-
(теории дальнодействия). С этой точки зрения при наличии только
одного заряда никаких изменений в окружающем пространстве
не происходит.
Согласно второму взгляду силовые взаимодействия между
разобщенными телами могут передаваться только при наличии
какой-либо среды, окружающей эти тела, последовательно от
одной части этой среды к другой, и с конечной скоростью (тео-
(теории близкодействия); даже при наличии одного-единственного
заряда в окружающем пространстве происходят определенные
изменения.
Современная физика сохраняет только идею близкодействия
и отвергает дальнодействие. Действительно, допущение возмож-
возможности передачи силовых взаимодействий, т.е. движения, через
22 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ГЛ. II
пустоту, без участия материи, равносильно допущению возмож-
возможности движения без материи, что бессодержательно.
Таким образом, для понимания происхождения и переда-
передачи сил, действующих между покоящимися зарядами, необходи-
необходимо допустить наличие между зарядами какого-то физического
агента, осуществляющего это взаимодействие. Этим агентом и
является электрическое поле. Когда в каком-либо месте появля-
появляется электрический заряд, то вокруг него возникает электриче-
электрическое поле. Основное свойство электрического поля заключается
в том, что на всякий другой заряд, помещенный в это поле, дей-
действует сила.
Рассматривая взаимодействие покоящихся зарядов, мы при-
приходим к понятию электрического поля. Подобным же образом,
рассматривая магнитное взаимодействие движущихся зарядов
(токов) или постоянных магнитов, мы придем к понятию маг-
магнитного поля. Мы увидим (гл. XIII), что электрические и маг-
магнитные поля могут превращаться друг в друга и что каждое из
них есть лишь частный случай более общего электромагнитного
поля. Далее будет показано, что электрические (и магнитные)
поля могут существовать и без зарядов (и токов), первоначаль-
первоначально их породивших (гл. XXIII), и что именно в электромагнитном
поле нужно видеть основную причину электрических и магнит-
магнитных явлений. Электромагнитное поле заключает в себе и пере-
переносит определенную энергию (§ 242), а также обладает импуль-
импульсом и массой (§ 245). Следовательно, электромагнитное поле не
есть абстрактный образ, введенный нами для описания элек-
электрических и магнитных взаимодействий, но представляет собой
объективную реальность, обладающую физическими свойства-
свойствами. Оно является определенной формой материи, которая осу-
осуществляет электрические и магнитные взаимодействия. Таким
образом, современная физика при помощи понятия поля расши-
расширяет представление о близкодействии и распространяет его на
немеханические явления.
§ 9. Напряженность электрического поля
Для количественной характеристики электрического поля
служит специальная физическая величина — напряженность
электрического поля.
Рассмотрим точечный электрический заряд q и будем вно-
вносить в электрическое поле этого заряда другой точечный проб-
пробный заряд <7ь На пробный заряд q\ будет действовать сила F,
различная в разных точках поля, которая, согласно закону Ку-
Кулона, будет пропорциональна пробному заряду q\. Поэтому от-
отношение этой силы к пробному заряду F/q\ уже не зависит от
выбора пробного заряда и характеризует электрическое поле в
|9 НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 23
той точке, где находится пробный заряд. Эта величина и полу-
получила название напряженности поля.
Если электрическое поле вызвано одним точечным зарядом
q, то напряженность поля получается непосредственно из зако-
закона Кулона путем деления обеих частей равенства на пробный
заряд. Обозначая напряженность поля через Е, имеем
()
Г2 Ч '
Напряженность поля точечного заряда убывает обратно пропор-
пропорционально квадрату расстояния от заряда.
Так как электрический заряд есть скаляр, а сила — вектор, то
напряженность поля, получаемая от деления вектора на скаляр,
есть вектор. Направление этого
вектора определяет направление
силы, действующей на положи-
положительный заряд, помещенный в рас-
рассматриваемую точку поля. Так,
например, если поле вызвано по-
положительным зарядом, то вектор
напряженности направлен вдоль Рис' 4- Направление напряжен-
радиус-вектора от заряда во внеш- ности электрического поля соз-
^ J ^ Г даваемого положительным (а) и
нее пространство (отталкивание отрицательными (^ зарядами
положительного пробного заряда);
если поле вызвано отрицательным зарядом, то вектор напря-
напряженности направлен к заряду (рис. 4).
Пользуясь законом Кулона в векторной форме, можно на-
написать выражение для напряженности электрического поля то-
точечного заряда также в векторной форме:
Е ^ (9.1а)
Г3
Здесь г — модуль расстояния от заряда до рассматриваемой точ-
точки поля, а г — радиус-вектор, направленный от заряда в данную
точку. Из сказанного следует, что если известна напряженность
поля в какой-либо точке, то тем самым определена и сила, дей-
действующая на электрический заряд, помещенный в эту точку. А
именно:
F = qB. (9.2)
Отметим в заключение, что для случая поля, вызванного то-
точечным зарядом, выбор величины пробного заряда безразличен.
В более сложных случаях, рассматриваемых ниже, может ока-
оказаться, что само его внесение вызывает перераспределение заря-
зарядов, создающих поле, и поэтому пробный заряд может вызвать
искажение поля. Чтобы это не имело места, пробный заряд дол-
должен быть достаточно малым.
24 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ГЛ. II
§ 10. Сложение электрических полей
Рассмотрим теперь электрическое поле двух точечных заря-
зарядов q\ и <72- Пусть Ei — напряженность поля в точке а, создава-
создаваемая зарядом q\ (когда заряда qi нет вовсе), а Е2 — напряжен-
напряженность поля заряда qi (когда нет заряда q\). Опыт показывает,
что напряженность Е результирующего поля (при наличии обо-
обоих зарядов) может быть найдена по правилу сложения векто-
векторов (по правилу параллелограмма)
(рис. 5). Или, иначе, напряженность
результирующего электрического по-
поля есть векторная сумма напряжен-
ностей полей, создаваемых отдельны-
отдельными зарядами.
Правило векторного сложения
~ электрических полей справедливо
Рис. 5. Сложение электриче- не только для двух, но и для какого
ских полей угодно числа зарядов. Если Еь Ег,
Ез, ... — напряженности полей,
создаваемых отдельными зарядами в какой-либо точке, то
напряженность Е результирующего поля в той же точке равна
E = Ei +E2+B3 + ...
Соотношение A0.1) выражает принцип суперпозиции (или на-
наложения) электрических полей и представляет важное свойство
электрического поля.
Отметим, что справедливость этого принципа заранее не оче-
очевидна и в его правильности нас убеждает только опыт. А именно,
вычисляя электрические поля при помощи принципа суперпози-
суперпозиции, мы всегда получаем результаты, согласующиеся с опытом.
Однако при очень малых расстояниях (~ 10~13 см) и экстре-
экстремально сильных электрических полях (ср. § 245) принцип су-
суперпозиции электрических полей, возможно, и не выполняется.
§ 11. Объемная и поверхностная плотности заряда
Пользуясь формулами (9.1а) и A0.1), можно вычислить на-
напряженность электрического поля, создаваемого любыми заря-
заряженными телами.
Если линейные размеры каждого из заряженных тел малы
по сравнению с расстояниями между этими телами и рассма-
рассматриваемой точкой поля, то каждое из тел можно рассматривать
как точечный заряд. В этом случае по формуле (9.1а) можно
вычислить напряженность поля, создаваемого каждым из заря-
§ 12 ЛИНИИ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 25
женных тел, и затем, пользуясь принципом суперпозиции полей
A0.1), найти их векторную сумму.
Если заряженное тело настолько велико, что его нельзя рас-
рассматривать как точечный заряд, то в этом случае необходимо
знать распределение зарядов внутри тела.
Выделим внутри заряженного тела малый объем Дт и обо-
обозначим через Д<7 электрический заряд, находящийся в этом
объеме. Предел отношения Aq/Ат, когда объем неограниченно
уменьшается, называют объемной плотностью заряда в данной
точке. Обозначая ее через р, имеем
lim ^-=p. A1.1)
Таким образом, объемная плотность заряда измеряется зарядом
единицы объема тела. Заряд, находящийся в элементе объема
dr, равен pdr. В общем случае неравномерно заряженного тела
р различно в разных точках. Распределение заряда в объеме
тела задано, если известно р как функция координат.
Очень часто заряды распределяются в телах только внутри
тонкого слоя, прилегающего к поверхности. В этом случае удоб-
удобно пользоваться поверхностной плотностью заряда, которая,
по определению, есть
lim #f = <т. A1.2)
Здесь Дд — заряд, находящийся на элементе поверхности Д5.
Иными словами, поверхностная плотность заряда измеряется
зарядом единицы поверхности тела. Заряд, находящийся на эле-
элементе поверхности dS, равен a dS. Для задания распределения
зарядов на поверхности тела нужно знать а как функцию коор-
координат поверхности.
Если известно распределение зарядов внутри тела, то мож-
можно вычислить и создаваемое ими электрическое поле. Для этого
заряженное тело разбивают на бесконечно малые части и, рас-
рассматривая их как точечные заряды, вычисляют напряженность
поля, создаваемую отдельными частями тела. Полное поле нахо-
находят затем суммированием полей, вызываемых отдельными ча-
частями тела; суммирование обычно сводится к интегрированию.
Следует, однако, отметить, что определение электрического
поля по заданным зарядам чаще всего производят посредством
вычисления разности потенциалов (гл. III), так как в этом случае
расчеты проще.
§ 12. Линии напряженности электрического поля
Для описания электрического поля нужно задать вектор на-
напряженности в каждой точке поля. Это можно сделать аналити-
аналитически, выражая зависимость напряженности поля от координат
26
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. II
Рис. 6. К
линии напряженности
в виде формул. Однако такую зависимость можно представить
и графически, используя линии напряженности электрического
поля.
Линиями напряженности электрического поля (или линия-
линиями вектора Е) называют линии, касательные к которым направ-
направлены так же, как и вектор напряженности Е в данной точке поля
(рис. 6). Поскольку касательная, как и
всякая прямая, определяет два взаимно
противоположных направления, то ли-
линии напряженности приписывают опре-
определенное направление, отмечая его на
чертеже стрелкой.
Чтобы при помощи линий напряжен-
определению ности изобразить не только направле-
направление, но и модуль напряженности поля,
условились на графиках поля проводить
линии напряженности с определенной густотой, а именно так,
чтобы число линий, проходящих через единицу поверхности,
перпендикулярной к ним, было равно (или пропорционально)
напряженности поля в данном месте.
Изображая линии электрического поля, мы получаем своеоб-
своеобразные графики или карты поля, которые сразу наглядно пока-
показывают, чему равна напряженность в разных частях поля и как
она изменяется в пространстве. Вследствие большой наглядно-
наглядности этот способ представления полей широко применяют в элек-
электротехнике.
Из сказанного следует, что линию напряженности можно
провести через всякую точку поля. Далее, так как в каждой
точке поля вектор напряженности имеет вполне определенное
направление, то линии напряженности нигде не пересекаются.
Линии напряженности закан-
заканчиваются (или начинаются)
на окружающих предметах,
на которых возникают ин-
индукционные заряды.
На рис. 7 в качестве при-
примера дана картина линий
напряженности точечного за-
заряда. Густота линий напря-
напряженности на каком-либо рас-
расстоянии г от заряда равна
отношению полного числа N линий напряженности, вышедших
из заряда, к поверхности сферы радиуса г, т.е. ЛГ/Dя"г2). Она
убывает обратно пропорционально квадрату расстояния от за-
заряда, т.е. так же, как и напряженность поля.
Рис. 7. Линии напряженности точеч-
точечного заряда
12
ЛИНИИ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
27
Если удается вычислить напряженность электрического по-
поля, то можно построить и чертежи линий напряженности этого
поля. Однако в случае заряженных тел сложной формы такие
вычисления могут быть
трудны. В ¦ этих случа-
случаях картину линий напря-
напряженности можно полу-
получить на опыте.
Если в электричес-
электрическом поле поместить ка-
какие-либо мелкие части-
частицы, то на них возник-
возникнут индукционные заря-
ОООг
Мелкие частицы в электрическом
Рис. 8.
ды (рис. 8 а). Такие ча- поле
стицы будут перемещаться под влиянием взаимного притяже-
притяжения разноименных зарядов и отталкивания одноименных, пока
не установятся в виде цепочки, направленной вдоль линии на-
напряженности (рис. 8 б). Этим и пользуются для эксперименталь-
экспериментального исследования электрического поля: в изучаемое поле вносят
подходящий жидкий изолятор, к которому подмешан порошок
из мелких твердых частичек; частицы порошка образуют в элек-
электрическом поле множество цепочек, простирающихся от одного
заряженного электрода до другого, и воспроизводят форму и
расположение линий напряженности.
Рис. 9. Линии напряженности электрического поля между двумя разно-
разноименно заряженными шариками
На рис. 9 показано электрическое поле между двумя одина-
одинаковыми шариками, заряженными разноименно. Изображенное
28
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. II
поле возникает в том случае, если другие окружающие тела рас-
расположены достаточно далеко, т.е. на расстояниях, значительно
больших, чем расстояние между шариками.
Рассмотрим еще электрическое поле между двумя парал-
параллельными металлическими пластинами, заряженными разно-
разноименными зарядами. Такая система называется плоским кон-
конденсатором.
Электрическое поле плоского конденсатора показано на
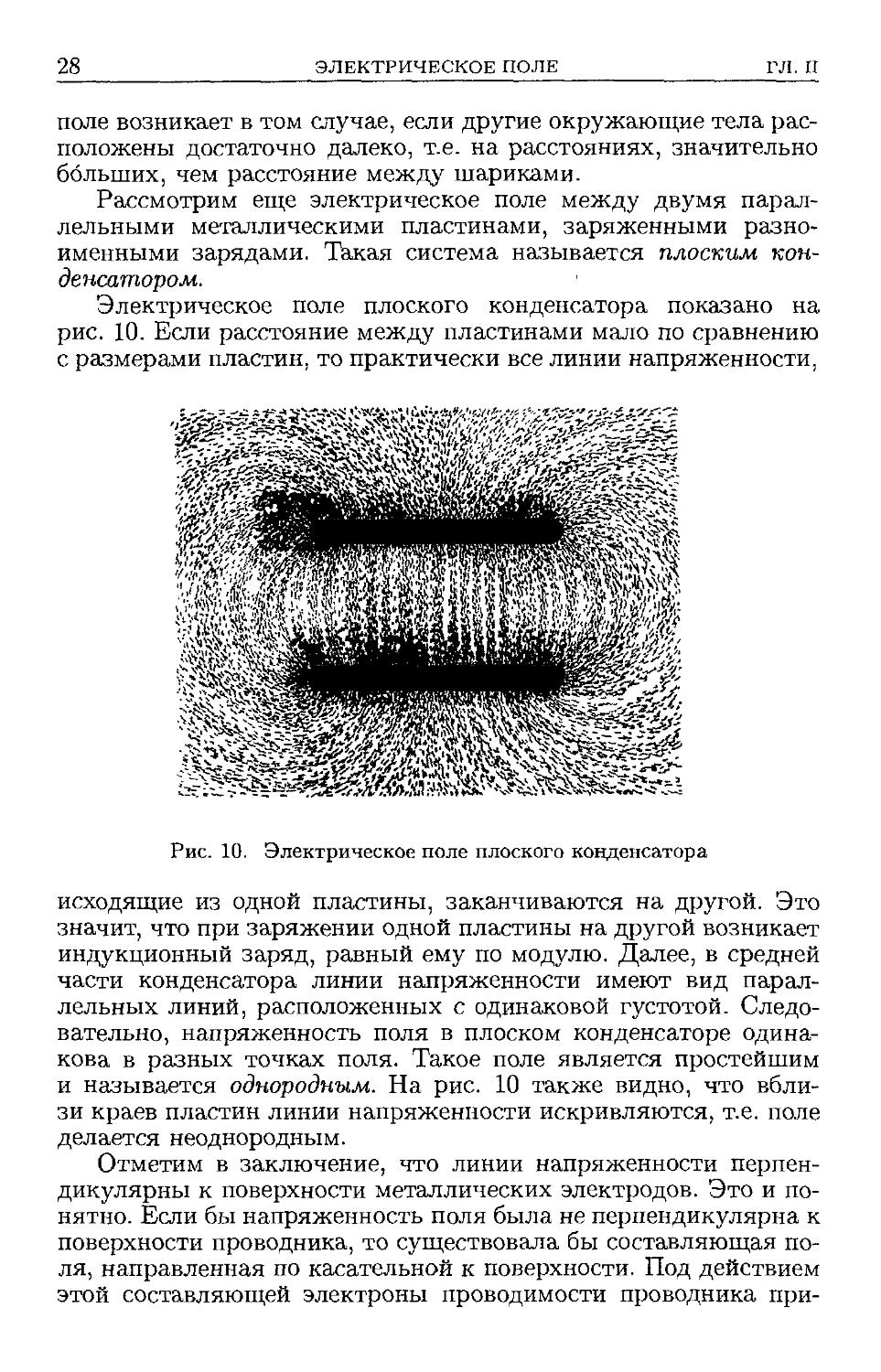
рис. 10. Если расстояние между пластинами мало по сравнению
с размерами пластин, то практически все линии напряженности,
тттшшттттжж
Рис. 10. Электрическое поле плоского конденсатора
исходящие из одной пластины, заканчиваются на другой. Это
значит, что при заряжении одной пластины на другой возникает
индукционный заряд, равный ему по модулю. Далее, в средней
части конденсатора линии напряженности имеют вид парал-
параллельных линий, расположенных с одинаковой густотой. Следо-
Следовательно, напряженность поля в плоском конденсаторе одина-
одинакова в разных точках поля. Такое поле является простейшим
и называется однородным. На рис. 10 также видно, что вбли-
вблизи краев пластин линии напряженности искривляются, т.е. поле
делается неоднородным.
Отметим в заключение, что линии напряженности перпен-
перпендикулярны к поверхности металлических электродов. Это и по-
понятно. Если бы напряженность поля была не перпендикулярна к
поверхности проводника, то существовала бы составляющая по-
поля, направленная по касательной к поверхности. Под действием
этой составляющей электроны проводимости проводника при-
§13
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
29
шли бы в движение вдоль поверхности, и мы не имели бы рав-
равновесия электрических зарядов.
§ 13. Теорема Остроградского-Гаусса
Вычисление электрического ноля во многих случаях силь-
сильно упрощается применением важной теоремы, излагаемой ниже.
Она была установлена М.В. Остроградским в виде некоторой
общей математической теоремы и Гауссом — применительно к
случаю электрического поля.
Чтобы сформулировать эту теорему, введем новое понятие
электрического смещения. Для вакуума электрическое смеще-
смещение, по определению, равно
D = е0Е. A3.1)
Обобщение этого понятия на случай произвольной среды будет
дано в § 41. Если электрическое поле создается одним точечным
зарядом, то электрическое смещение на расстоянии г от заряда
равно по модулю
D = hi> A3-2)
а направление смещения D совпадает с направлением поля Е.
Отметим, что в системе СГСЭ напряженность поля и электрическое
смещение в вакууме равны друг другу. В системе же СИ они различны.
По аналогии с линиями напряжен-
напряженности электрического поля (§ 12) для
графического изображения распреде-
распределения электрического смещения в про-
пространстве мы будем пользоваться ли-
линиями электрического смещения. На-
Направление этих линий в каждой точке
пространства совпадает с направлени-
направлением вектора электрического смещения, а
их густота равна электрическому сме-
смещению.
Введем далее понятие потока
электрического смещения. Рассмотрим
в электрическом поле плоскую по-
поверхность S и выберем определенное направление нормали п
к ней (рис. 11). Будем считать сначала, что поле однородно,
но составляет произвольный угол а с направлением нормали.
Величину
N = SD cos a = SDn A3.3)
называют потоком электрического смещения через данную по-
поверхность. Здесь через Dn обозначена проекция D на направ-
направление нормали п. Так как густота линий электрического сме-
Рис. 11. Поток электри-
электрического смещения через
данную поверхность
30
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. II
щения равна D, то можно сказать также, что поток вектора
электрического смещения через данную поверхность равен пол-
полному числу линий электрического смещения, проходящих через
эту поверхность.
Если поле неоднородно и поверхность, через которую разыс-
разыскивают поток, не является плоскостью, то эту поверхность мож-
можно разбить на бесконечно малые элементы dS и каждый элемент
считать плоским, а поле возле него — однородным. Поэтому для
любого электрического поля поток смещения через элемент по-
поверхности есть dN — Dn dS. Полный поток смещения через по-
поверхность S в любом неоднородном электрическом поле равен
N=fDn
dS.
A3.4)
Отметим, что поток смещения, определяющий число проходя-
проходящих линий смещения, есть скаляр.
Из A3.3) видно, что поток может быть как положительным,
так и отрицательным. Если направление линий смещения соста-
составляет острый угол с направлением нормали (cos a > 0), то поток
будет положительным. Если же этот угол тупой (cos a < 0), по-
поток будет отрицательным.
Рассмотрим теперь точечный положительный заряд q и вы-
вычислим поток электрического смещения через замкнутую сфе-
сферическую поверхность S (рис. 12), окружающую этот заряд и
имеющую центр в точке на-
нахождения заряда. За поло-
положительное направление нор-
нормали выберем направление
внешней нормали. В этом
случае D во всех точках сфе-
\S) ры одинаково и, кроме того,
везде cos a = 1. Поэтому
Легко видеть, что этот ре-
результат справедлив не только
для сферической поверхно-
поверхности, но и для любой замкну-
замкнутой поверхности и для любого
произвольного расположения
Рис. 12. К выводу теоремы Остро- Заряда внутри этой поверх-
градского-Гаусса НОСТИ.
Действительно, полученный результат показывает, что поток
смещения через сферическую поверхность не зависит от радиу-
радиуса сферы, он один и тот же для сферы S и любой другой кон-
§13 ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА 31
центрической с ней сферы Sy (рис. 12). Это значит, что линии
смещения в пространстве между S и Si, где не имеется заря-
зарядов, непрерывны. Линии электрического смещения начинаются
и заканчиваются только на электрических зарядах.
Но из непрерывности линий смещения следует, что полное
число линий смещения, проходящих через произвольную по-
поверхность ^2 (рис. 12), охватывающую заряд, т.е. поток смеще-
смещения N, имеет такое же значение, как и для сфер Si и S, т.е.
N = J DndS = q. A3.5)
Напротив, если замкнутая поверхность не охватывает заряда Eз
на рис. 12), то поток смещения через эту поверхность равен ну-
нулю, так как число линий смещения, входящих через поверхность,
равно числу линий, выходящих из нее.
Из A3.5) также следует, что поток через замкнутую поверх-
поверхность не зависит от расположения заряда внутри поверхности.
Это значит, что полученный результат справедлив не только для
одного заряда, но и для какого угодно числа произвольно рас-
расположенных зарядов, если только подразумевать под q алгебра-
алгебраическую сумму всех зарядов, находящихся внутри поверхности.
Формула A3.5) выражает теорему Остроградского-Гаусса:
поток электрического смещения через замкнутую поверх-
поверхность равен алгебраической сумме всех зарядов, расположен-
расположенных внутри поверхности.
Отметим, что при доказательстве этой теоремы мы исходили
из закона Кулона, и потому она есть следствие этого закона.
Если бы показатель степени у расстояния в формуле B.1) был
не 2, а каким-либо другим, то и доказанная теорема была бы
несправедливой.
Из формулы A3.5) видно, что размерность потока смещения
такая же, как и электрического заряда. Поэтому единицей по-
потока смещения, как и заряда, служит кулон. Это — поток через
замкнутую поверхность, окружающую заряд 1 Кл.
Электрическое смещение можно определить как поток сме-
смещения через единицу поверхности, нормальной к направлению
смещения, или, иначе, как плотность потока смещения. Поэто-
Поэтому единица электрического смещения есть кулон на квадратный
метр (Кл/м2).
Рассмотрим некоторые простые примеры вычисления
электрического поля с помощью теоремы Остроградского-
Гаусса.
Пример 1. Равномерно заряженная плоскость. Имеет-
Имеется безграничная плоскость, заряженная равномерно с поверх-
поверхностной плотностью заряда а. Из симметрии задачи очевидно,
что линии смещения могут быть направлены только перпен-
32
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. II
,
1
'-
n
т
n
E
-S-
-s-
E
]
Рис. 13. Электрическое поле
равномерно заряженной плос-
плоскости
дикулярно к плоскости. В этом случае в качестве замкнутой
поверхности в теореме Остроградского-Гаусса удобно выбрать
прямой цилиндр, перпендикуляр-
перпендикулярный к заряженной плоскости и огра-
ограниченный двумя плоскими основа-
основаниями перпендикулярными к лини--
ям напряженности поля и располо-
расположенными по обеим сторонам заря-
заряженной плоскости (рис. 13). Так как
образующие цилиндра параллельны
линиям смещения (cos a = 0), то
поток смещения через боковую по-
поверхность цилиндра равен нулю и
поэтому полный поток сквозь ци-
цилиндр равен сумме потоков через
его основания: N — 2DS. Пол-
Полный заряд, заключенный внутри ци-
цилиндра, равен aS. Поэтому, применяя теорему Остроградского-
Гаусса, имеем
2DS = aS,
откуда
D = а/2.
Напряженность поля равномерно заряженной плоскости в
вакууме равна
Е = а/2е0. A3.6)
Пример 2. Поверхность заряженного проводника. По-
Посмотрим теперь, чему равна напряженность поля вблизи поверх-
поверхности произвольного заряженного металлического проводника,
если заряды на нем находятся в равновесии.
При решении задачи мы учтем, что в отсутствие электри-
электрического тока линии напряженности всегда перпендикулярны
к поверхности проводника (§ 12). Да-
Далее очевидно, что в этом случае на-
напряженность поля внутри проводни-
проводника всегда равна нулю. Действительно,
если бы это было не так, то электро-
электроны проводимости металла пришли
бы в движение, т.е. в проводнике
возник бы электрический ток, что
противоречит условию.
Выделим на поверхности провод-
проводника бесконечно малый элемент по-
поверхности dS (рис. 14) и обозначим
поверхностную плотность заряда на нем через а. В качестве за-
замкнутой поверхности выберем опять прямой цилиндр с осно-
/dS
w
L
'
Рис. 14. Электрическое по-
поле у поверхности заряженного
проводника
§13
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
33
ваниями dS и бесконечно малой высотой dh. В данном случае
нужно рассматривать бесконечно малый элемент поверхности
проводника, так как в общем случае а меняется от точки к точке
поверхности. Высота цилиндра должна быть также бесконечно
малой, потому что в случае проводника произвольной формы
линии смещения будут перпендикулярными к поверхности про-
проводника только в непосредственной близости от нее. В этом слу-
случае полный поток смещения равен потоку через одно основание,
и мы имеем
DdS = adS.
Поэтому
D = a, E = а/е0. A3.7)
Таким образом, значение D у поверхности проводника рав-
равно непосредственно поверхностной плотности заряда, т.е. заря-
заряду, сместившемуся внутри проводника, в расчете на единицу
поверхности. Этим объясняется происхождение термина «элек-
«электрическое смещение». Замечательным в этом результате являет-
является то обстоятельство, что напряженность поля и электрическое
смещение вблизи рассматриваемой точки поверхности не зави-
зависят явно от формы проводника, от распределения зарядов на
нем, а также от расположения других соседних проводников.
При сравнении формул A3 6) и A3.7) возникает кажущееся противо-
противоречие: в обоих случаях мы имеем заряженные поверхности, однако напря-
напряженность поля около них отличается в два раза. На самом же деле ни-
никакого противоречия здесь нет. Формула A3.6) выражает поле, вызванное
только зарядами, располо-
расположенными на плоскости. В
случае же поверхности про-
проводника исходящие из нее
линии напряженности все-
всегда заканчиваются на дру-
других телах, на которых воз-
возникают индукционные заря-
заряды. Формула A3.7) учитыва-
учитывает действие всех фактически
существующих зарядов как
на рассматриваемой поверх-
поверхности, так и на окружающих
телах.
Сказанное можно пояс-
пояс, 2е0
Е-, = —
Рис. 15. Электрическое поле внутри плоско-
плоского конденсатора есть сумма полей, создава-
создаваемых заряженными плоскостями его обкла-
обкладок
нить на примере плоско-
плоского конденсатора (рис. 15).
При появлении на какой-
либо пластине заряда с плот-
плотностью +а на второй пла-
пластине всегда возникает заряд противоположного знака с плотностью —а.
Эти заряды под влиянием взаимного притяжения будут сосредоточены на
внутренних поверхностях пластин. Заряженная плоскость каждой пласти-
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. II
ны создает по обе стороны от себя напряженность поля, выражаемую фор-
формулой A3.6) и равную ±<т/2ео. Внутри металлических пластин и вне кон-
денгатора эти поля направлены противоположно и поэтому в сумме дают
нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и,
складываясь, дают у поверхности пластин напряженность а/еа в соответ-
соответствии с A3.7). В данном частном случае электрическое поле однородно, и
поэтому его напряженность у поверхности пластин такая же, как и в других
точках ноля. Это мы и видели на опыте, описанном в § 12.
Пример 3. Равномерно заряженный шар. Рассмотрим
электрическое поле между двумя шаровыми концентрически-
концентрическими электродами (рис. 16). Такая си-
система электродов называется шаро-
шаровым конденсатором.
Если заземлить внешний элек-
электрод и сообщить внутреннему шару
заряд +q, то на внешнем электро-
электроде возникает индуцированный за-
заряд — q. Под действием взаимного
притяжения эти заряды располо-
расположатся только на поверхности вну-
внутреннего шара и на внутренней по-
поверхности внешнего электрода.
_ Из условий симметрии задачи
Электрическое поле очевиднО) чт0 зарЯды на обоих ша-
шарах будут распределены равномер-
равномерно и что линии смещения могут быть только радиальными
прямыми. Поэтому в качестве замкнутой поверхности удобно
выбрать сферу с радиусом г, расположенную между электрода-
электродами и имеющую общий центр с обоими электродами. Тогда из
теоремы Остроградского-Гаусса следует
Рис. 16.
шарового конденсатора
N = D ¦ 4тгг2 = q,
откуда
E=~\. A3.8)
4тг?0 r2 v '
Эта формула показывает, что напряженность поля между элек-
электродами зависит от расстояния г рассматриваемой точки ноля
от центра внутреннего шара, но не зависит вовсе от размеров
внешнего электрода. Поэтому мы получим ту же напряженность
поля, если радиус внешнего электрода будет как угодно велик.
Если внешний электрод значительно больше внутреннего, то
электрическое поле вблизи внутреннего шара не зависит и от
формы внешнего электрода. Это происходит по той причине, что
при удаленном внешнем электроде изменение его формы не ока-
оказывает влияния на распределение зарядов на внутреннем шаре,
которое остается по-прежнему равномерным. Следовательно, и
§13 ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА 35
в том случае, когда роль внешнего электрода играют различ-
различные удаленные заземленные предметы, например стены, пол и
потолок комнаты, формула A3.8) будет также применима для
участков поля вблизи шара. Поэтому часто говорят просто о по-
поле заряженного шара, не указывая, что именно является вторым
электродом.
Электрическое поле шара, равномерно заряженного ио по-
поверхности, во внешнем пространстве совпадает с полем точечно-
точечного заряда, равного полному заряду шара и помещенного в центре
шара.
Если бы мы рассмотрели шар, заряженный равномерно ио
объему, то напряженность поля вне шара выражалась бы то-
тоже формулой A3.8). Напряженность же поля внутри шара в
обоих случаях различна. В случае шара, равномерно заряжен-
заряженного по поверхности, напряженность поля в любой внутренней
точке равна нулю. Если же шар заряжен равномерно по объ-
объему, то напряженность поля равна нулю только в центре шара
и с увеличением расстояния г от центра возрастает пропорцио-
пропорционально г. В справедливости этого можно убедиться также при
помощи теоремы Остроградского-Таусса.
Пример 4. Равномерно заряженный цилиндр. Вычислим
напряженность электрического поля между двумя коаксиаль-
коаксиальными металлическими цилиндрами. Такая система называется
цилиндрическим конденсатором.
Предположим, что внешний цилиндр соединен с землей, а
внутреннему цилиндру сообщен заряд +q\ на каждую единицу
длины цилиндра. Тогда на внешнем цилиндре появится заряд
—qi на единицу его длины и эти заряды будут сосредоточены
только на обращенных друг к другу поверхностях обоих ци-
цилиндров. Длину цилиндров будем
считать весьма большой по срав-
сравнению с их радиусами.
Из условий симметрии ясно,
что заряды будут распределены
равномерно по поверхности ци-
цилиндров, а линии смещения будут
радиальными прямыми, перпен-
перпендикулярными к поверхности обо- Рис 17- К вычислению поля ци-
ИХ цилиндров. В этом случае в ка- ливдрического конденсатора
честве поверхности для вычисления потока электрического сме-
смещения удобно выбрать цилиндрическую поверхность, показан-
показанную на рис. 17. Так как поток электрического смещения через
основания цилиндра равен нулю (cosа = 0), а боковая поверх-
поверхность перпендикулярна к линиям смещения (cos a = 1), то фор-
формула A3.5) дает
D-2-itrl = qil.
36
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ГЛ. П
Отсюда получаем, что напряженность ноля между электродами
в точке, отстоящей на расстоянии г от оси цилиндров, равна
? = — 21. A3.9)
Это выражение справедливо для всех участков конденсато-
конденсатора, не слишком близких к его краям. Практически его можно
применять уже на расстоянии от края порядка одного диаметра
внешнего цилиндра.
Так же как и в предыдущем примере, напряженность поля
между электродами не зависит от радиуса внешнего цилиндра.
Если размеры внешнего электрода значительно больше радиуса
внутреннего цилиндра, то напряженность поля вблизи него не
зависит и от формы внешнего электрода. Поэтому и здесь ча-
часто говорят о поле равномерно заряженного цилиндра. Напря-
Напряженность поля, выражаемую формулой A3.9), мы имеем возле
металлических проволок, удаленных от окружающих предметов
на расстояния, значительно превышающие их радиус.
§ 14. Уравнение Пуассона
Теорема Остроградского-Гаусса в форме A3.5) связывает
электрическое смещение в точках некоторой замкнутой поверх-
поверхности с зарядом, находящимся внутри объема, ограниченного
этой поверхностью, т.е. связывает величины, относящиеся к раз-
разным точкам поля. Можно, однако,
придать этой теореме такую форму,
чтобы в нее входили величины, от-
относящиеся к одной и той лее точке
поля. Для этого нужно применить
теорему к бесконечно малому объ-
объему.
Введем прямоугольную систе-
^^Х " МУ координат X, Y, Z и обо-
обозначим электрическое смещение в
Рис.18. К выводу теоремы какой-либо точке a(x,y,z) через
Остроградского-Гаусса в диф- D{DX, Dy, Dz). Рассмотрим беско-
ференциальной форме нечно малый прямоугольный парал-
параллелепипед с вершиной в точке а
и ребрами dx, dy, dz, параллельными координатным осям
(рис. 18), и вычислим поток смещения через его поверхность.
Поток через грань dydz, проходящую через а, есть
—Dx dy dz,
где знак минус означает, что внешняя нормаль к dydz и поло-
положительное направление Dx составляют угол а = тг (cos а = — 1).
Поток через параллельную ей грань, смещенную вдоль X на dx
a{x,y,z)
§ 14 УРАВНЕНИЕ ПУАССОНА 37
(она заштрихована), есть (Dx -~-dx\ dydz. Поэтому поток че-
через обе эти грани равен
(Dx + ^ dx) dydz -Dxdydz = ^dr,
где dr = dxdydz — объем параллелепипеда. Вычисляя анало-
аналогичным образом потоки через две другие пары граней и скла-
складывая их, получим полный поток через всю поверхность парал-
параллелепипеда
дх ду d
Если в рассматриваемом пространстве имеется распределен-
распределенный в объеме заряд с объемной плотностью р — p(x,y,z), то ве-
величина заряда, содержащегося в объеме параллелепипеда, равна
pdr. Приравнивая ее, согласно A3.5), значению полного потока
через поверхность параллелепипеда, мы получим
Ё°.+Ё°л+ §»-. = р. A4.1)
дх ду dz ч '
Это соотношение, выражающее теорему Остроградского-Гаусса
в дифференциальной форме, носит название уравнения Пуассо-
Пуассона.
В векторном анализе показывают, что предел отношения по-
потока какого-либо вектора А через замкнутую поверхность S к
объему т, ограниченному поверхностью S, при т —> 0 (если этот
предел существует) не зависит от формы поверхности S. Предел
этого отношения получил название дивергенции или расхожде-
расхождения вектора А и обозначается специальным символом divA.
Таким образом, по определению,
1 с
div А = lim - I An dS.
т—»0 т J
т->0
Так как поток вектора и объем суть скаляры, то и дивергенция
вектора тоже есть скаляр.
Пользуясь этим понятием, можно записать уравнение Пуас-
Пуассона в виде
div D = р.
Если составляющие электрического смещения D заданы в
какой-либо системе координат в виде функции этих координат,
то всегда можно вычислить и значение div D в каждой точке.
Так, например, мы видели выше, что если пользоваться прямо-
прямоугольными декартовыми координатами, то
^ + ^ + ^.
дх ду dz
¦±
38 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ГЛ. II
§ 15. Диполь в электрическом поле
Рассмотрим два точечных заряда +q и —q, жестко связан-
связанных между собой и смещенных на расстояние I друг от друга.
Смещение обоих зарядов будем характеризовать вектором 1, на-
направленным от отрицательного заряда к положительному. Та-
Такую пару зарядов называют электрическим диполем.
С электрическими диполями нам приходится встречаться
весьма часто. Небольшое проводящее тело в электрическом поле
можно приближенно рассматривать как диполь, так как на его
концах возникают индукционные заряды, равные по модулю и
противоположные по знаку. В гл. V мы увидим, что подобные
заряды возникают и на диэлектриках, и поэтому небольшое ди-
диэлектрическое тело в электрическом поле также можно рассма-
рассматривать как диполь. Наконец, многие молекулы построены из
положительных и отрицательных ио-
нов, центры которых смещены друг
относительно друга. Такие молеку-
лы можно считать во многих случаях
электрическими диполями.
Найдем силу, действующую на
"¦" диполь в электрическом поле, причем
D 1П г, будем считать сначала, что поле од-
РИС. 19. ДИПОЛЬ В ОДПОрОД- J" , 1П\ тт
ном поле породно (рис. 19). На концы диполя
действуют равные по модулю силы
F = qE, где Е — напряженность поля. Эти силы направлены
в противоположные стороны и образуют пару сил. Момент М
этой пары равен
М = qEl sin a,
где а — угол между вектором 1 и напряженностью поля Е.
Мы видим, что момент пары сил зависит от произведения
заряда q на длину диполя I. Это произведение называют элек-
электрическим моментом диполя. Момент диполя р есть вектор,
равный
p = ql. A5.1)
Он направлен так же, как и 1, т.е. от отрицательного заряда к
положительном}'. Единица электрического момента диполя есть
кулон-метр (Кл-м).
Пользуясь понятием электрического момента диполя, можно
написать выражение для момента пары сил, действующей на
диполь, в виде
М = рЕ sin (p,E). A5.2)
Направление момента этой пары совпадает с направлением оси
вращения диполя, т.е. перпендикулярно к р и Е.
§ 15
ДИПОЛЬ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
39
Рис. 20. Векторное произ-
произведение двух векторов
Модуль и направление момента пары М можно выразить од-
одной формулой, если воспользоваться обозначениями векторной
алгебры. Как известно, векторным про-
произведением [аЬ] двух векторов а и b на-
называют вектор, модуль которого равен
aft sin (а, Ь), т.е. равен площади парал-
параллелограмма, построенного на векторах
а и b как на сторонах. Этот вектор пер-
перпендикулярен к а и b и направлен в сто-
сторону перемещения буравчика с правой
нарезкой, вращаемого от а к b (рис. 20).
Поэтому вектор момента пары сил М,
действующей на диполь, можно выразить формулой
М = [рЕ]. A5.3)
Мы видим, что в однородном поле на диполь действует только
пара сил, которая стремится повернуть диполь таким образом,
чтобы р и Е были параллельны.
Для того чтобы повернуть диполь в электрическом поле па
некоторый угол, нужно совершить определенную работу. Так
как эта работа равна увеличению потенциальной энергии дипо-
диполя, то можно найти выражение для энергии диполя в электриче-
электрическом поле. Примем за нуль энергию диполя, перпендикулярного
к направлению поля (а = 7г/2). Тогда энергия диполя, момент
которого составляет угол а с направлением поля, равна
а
W= Г pEsinada = — pEcosa. A5.4)
тг/2
Рассмотрим теперь диполь в неоднородном поле и положим
для простоты, что момент диполя параллелен направлению по-
поля (а = 0). В этом случае си-
силы, действующие на концы ди-
диполя, уже неодинаковы, и по-
поэтому их результирующая не
равна нулю (рис. 21). На диполь
в неоднородном поле действует
сила, стремящаяся передвинуть
диполь в область поля с большей
напряженностью.
Найдем эту силу. Направим
координатную ось X вдоль мо-
момента диполя и будем считать,
что длина диполя А/ весьма мала (элементарный диполь). Си-
Сила, действующая на отрицательный конец диполя, есть — qE,
где Е — напряженность поля в точке нахождения заряда —q.
Рис- 21
поле
Диполь в неоднородном
40 РАЗНОСТЬ ПОТЕНЦИАЛОВ ГЛ. III
Сила, действующая на положительный конец диполя, равна
+q[E + (dE/dx)Al], где Al — длина диполя. Поэтому полная си-
сила F оказывается равной
^AlE)qAl^=p^. A5.5)
dx I dx dx '
В однородном поле dE/dx = 0 и результирующая сила равна
нулю.
Если диполь находится в неоднородном поле и не паралле-
параллелен полю, то на него действуют и пара сил, стремящаяся повер-
повернуть диполь параллельно полю, и сила, втягивающая диполь в
область более сильного поля.
Пусть Ех, Еу, Ez — составляющие напряженности электри-
электрического поля в прямоугольных осях координат, а рх, ру, pz —
составляющие момента диполя в тех же осях. Тогда, поступая
так же, как и выше, легко получить, что составляющая силы по
оси X равна
о п дЕх дЕх дЕх h_ ,
Составляющие силы Fy и Fz выражаются аналогичными фор-
формулами.
Этот результат можно выразить векторной формулой:
F = (pgrad)E, A5.7)
где введен дифференциальный оператор
(pgrad)= Px-^+Py^+Pz^;- A5.8)
ГЛАВА III
РАЗНОСТЬ ПОТЕНЦИАЛОВ
§ 16. Работа в электростатическом поле
Для понимания свойств электрического поля большое значе-
значение имеет понятие разности потенциалов, или электрического
напряжения. К этому понятию мы приходим, рассматривая ра-
работу сил электрического поля.
Предположим, что электрический заряд перемещается в
каком-нибудь электрическом поле из некоторой точки 1 в дру-
другую точку 2. Так как на заряд в электрическом поле действует
сила, то при таком перемещении будет произведена определен-
определенная работа, которую мы обозначим через А]2- Ясно, что если
§17
РАЗНОСТЬ ПОТЕНЦИАЛОВ
41
тот же заряд перемещается по прежнему пути в обратном на-
направлении (от точки 2 к точке i), то работа будет той же, но
изменится ее знак, т.е. А\2 = —А21.
Рассмотрим теперь электрическое поле, созданное неподвиж-
неподвижными зарядами (электростатическое поле). Легко видеть, что
в электростатическом поле работа при перемещении заряда не
зависит от формы пути, по которому движет-
движется заряд, и определяется только положением
точек 1 и 2 — начала и конца пути заряда.
Действительно, допустим, что это не так
и что работа А12 при перемещении заряда
вдоль контура L (рис. 22) не равна работе
А\2 для контура L\, причем оба они соеди-
соединяют одни и те же точки 1 и 2. Тогда, пе-
перемещая заряд по замкнутому контуру, со-
составленному из путей L и L\, мы найдем, что
электрические силы совершили работу
ЛЬ)
"г
,(?i)
которая не равна нулю. Но это противоречит Рис- 22' Работа ПРИ
общему закону сохранения энергии. Если за- пеРеме1чении заРя'
J ^ ^ да в электростати-
ряды, создающие поле, неподвижны, то при ческом поле не зави-
перемещении подвижного заряда в окружаю- сит от формы пути
щих телах не происходит никаких процессов.
После возвращения заряда в исходную точку 1 мы не имеем ни-
никаких изменений в рассматриваемой системе тел и поэтому не
можем получить ни выигрыша работы, ни ее потери. Это значит,
что наше предположение неверно и что в действительности
Таким образом, в электростатическом поле работа переме-
перемещения заряда между двумя точками не зависит от формы пути,
соединяющего эти точки. При перемещении заряда по замкну-
замкнутому контуру работа равна нулю.
§ 17. Разность потенциалов
Положим теперь, что в электростатическом поле из точки
1 в точку 2 перемещается положительный заряд +1. Согласно
§ 16 работа, совершаемая силами поля при этом перемещении,
не зависит от формы пути. Так как заряд выбран определенным
(+1), то эта работа зависит только от существующего электри-
электрического поля и поэтому может служить его характеристикой.
Она называется разностью потенциалов точек 1 и 2 в данном
электрическом поле или электрическим напряжением между
42 РАЗНОСТЬ ПОТЕНЦИАЛОВ ГЛ III
точками 1 и 2. Разность потенциалов двух точек 1 и 2 в элек-
электростатическом поле измеряется работой, совершаемой силами
поля при перемещении заряда +1 из точки 1 в точку 2.
Зная напряженность ноля в каждой точке, можно вычислить
и разность потенциалов любых двух точек. Если ds — элемент
перемещения заряда, Es — проекция век-
вектора напряженности поля на направле-
направление ds (рис. 23), то работа при перемеще-
перемещении заряда +1 на отрезок ds есть Esds.
Поэтому разность потенциалов точек 1
и 2 равна
2
Ul2=jEsds, A7.1)
1
где интегрирование производится вдоль
Рис. 23. К определению любого контура L, соединяющего рае-
разности потенциалов сматриваемые точки, в направлении от
точки 1 к точке 2.
Если в электрическом поле перемещается не единичный за-
заряд, а заряд произвольной величины q, то в каждой точке сила,
действующая на заряд, увеличится в q раз. Поэтому работа А\2,
совершаемая силами поля при перемещении заряда q из точки
1 в точку 2, равна
Ап = qUn. A7.2)
Из сказанного следует, что физический смысл имеет только
разность потенциалов, или напряжение, между двумя точками
поля, так как работа определена только тогда, когда заданы две
точки — начало и конец пути. Несмотря на это, часто говорят
просто о потенциале, или напряжении, в данной точке, но всегда
имеют в виду разность потенциалов, подразумевая, что одна из
точек выбрана заранее. Такую постоянную точку часто выби-
выбирают «в бесконечности», т.е. на достаточном удалении от всех
заряженных тел.
Мы видели, что в электростатическом поле напряжение меж-
между двумя точками не зависит от формы пути, соединяющего
эти точки. Поэтому, если заряд +1 перемещается по замкнуто-
замкнутому контуру, например, сначала из точки 1 к точке 2 по контуру
L (рис. 22), а затем от 2 к 1 вдоль L\, то работа будет равна
и12 + u2i = и12 - ии = о.
В электростатическом поле напряжение вдоль замкнутого кон-
контура всегда равно нулю.
Последнее утверждение выражает важное свойство электро-
электростатического поля. Именно по этой причине для электростати-
электростатического поля можно ввести разность потенциалов, которая одно-
§ 17 РАЗНОСТЬ ПОТЕНЦИАЛОВ 43
значно определяется действующим полем (не зависит от формы
пути) и поэтому может служить характеристикой поля.
Пользуясь формулой A7.1), можно выразить это свойство
электростатического поля в следующей форме:
sc/s = O, A7.3)
где кружок у интеграла означает, что интегрирование произво-
производится по замкнутому контуру. Криволинейный интеграл какого-
либо вектора вдоль замкнутого контура называется циркуляци-
циркуляцией вектора вдоль этого контура. Следовательно, можно также
сказать, что циркуляция напряженности электрического поля
вдоль любого контура равна нулю.
Понятие разности потенциалов широко используют по двум
основным причинам. Во-первых, описание электрического ноля
при помощи потенциала гораздо проще, чем при помощи напря-
напряженности поля. Напряженность поля есть вектор, и поэтому для
каждой точки поля нужно знать три скалярные величины —
составляющие напряженности по координатам. Потенциал же
есть скаляр и вполне определяется в каждой точке одной вели-
величиной — своим числовым значением. В § 19 мы увидим, что,
зная потенциал в каждой точке поля, можно найти и вектор
напряженности.
Во-вторых, разность потенциалов гораздо легче измерить на
опыте, чем напряженность поля. Д/гя измерения напряженности
поля нет удобных методов. Напротив, для измерения разности
потенциалов существуют многочисленные методы и разнообраз-
разнообразные приборы. Поэтому и описывать электрическое поле гораздо
удобнее при помощи потенциала.
Единица разности потенциалов (напряжения) в системе СИ
есть вольт (В). Вольтом называется потенциал в такой точке,
для перемещения в которую из бесконечности заряда, равного
1 Кл, надо свершить работу 1 Дж.
Отметим, что, пользуясь формулой A7.2), можно выражать
энергию не в механических единицах (эргах, джоулях и т.п.), а
в электрических. Для этого служит внесистемная единица энер-
энергии, называемая электронвольтом (эВ). Электронвольт -- это
энергия, которую приобретает частица с зарядом, равным заря-
заряду электрона е = 1,60 - 10~19 Кл, пробегая в вакууме разность
потенциалов 1 В, т.е.
1 эВ = 1,60 • 10~19 Дж = 1,60 ¦ 10~12 эрг.
В электронвольтах обычно выражают энергию различных эле-
элементарных частиц (электронов, протонов и др.). При этом при-
применяют также более крупные единицы энергии: 1 килоэлектрон-
килоэлектронвольт (кэВ) = 103 эВ, 1 мегаэлектронвольт (МэВ) = КN эВ и др.
44 РАЗНОСТЬ ПОТЕНЦИАЛОВ ГЛ. III
§ 18. Условия равновесия зарядов в проводниках
Если электрические заряды находятся в равновесии в каком-
либо проводнике, т.е. в этом проводнике нет электрического то-
тока, то напряженность поля Ei в любой точке внутри проводника
равна нулю. Действительно, если бы это условие не выполня-
выполнялось, то подвижные электрические частицы, имеющиеся во вся-
всяком проводнике, под действием сил поля пришли бы в движение
и равновесие было бы нарушено. Кроме того, в § 12 мы нашли,
что при равновесии зарядов вектор напряженности поля у по-
поверхности проводника перпендикулярен к поверхности. Отсюда
следует, что для перемещения заряда из любой точки проводни-
проводника в любую другую его точку не требуется никакой работы. Но
согласно A7.1) это обозначает, что разность потенциалов любой
пары точек как внутри проводника, так и на его поверхности
равна нулю. В отсутствие электрического тока все точки про-
проводника имеют одинаковый электрический потенциал.
Земля является также проводником. Хотя в земле существу-
существуют токи, но они невелики, и можно считать, что заряды земли
близки к равновесию. Поэтому для многих случаев можно при-
принять, что все точки земли имеют одинаковый потенциал. По
этой причине постоянную точку при измерении потенциала ча-
часто выбирают в земле и говорят о потенциале относительно зем-
земли.
Если соединить два проводника металлической проволокой,
то оба проводника и проволока образуют единый проводник. Ес-
Если до соединения между проводниками существовала разность
потенциалов, то равновесие зарядов будет невозможно. Напря-
Напряженность поля Е внутри проволоки не будет равна нулю, и элек-
электроны проводимости в проволоке придут в движение, т.е. в ней
возникнет электрический ток. Этот ток будет продолжаться до
тех пор, пока потенциалы обоих проводников не сделаются рав-
равными.
§ 19. Разность потенциалов и напряженность поля
Если известно распределение потенциала, т.е. его значение
в каждой точке поля, то можно найти и напряженность этого
поля в каждой точке.
Рассмотрим в однородном электрическом поле две точки 1
и 2 и предположим, что заряд +1 переходит из точки 1 в точ-
точку 2 вдоль прямолинейного отрезка As (рис. 24). Работу элек-
электрических сил АА при этом перемещении можно выразить, во-
первых, через напряженность поля:
АА = Es As,
19
РАЗНОСТЬ ПОТЕНЦИАЛОВ И НАПРЯЖЕННОСТЬ ПОЛЯ
45
где Es — проекция вектора напряженности Е на направление
As. С другой стороны, ту же работу можно выразить через раз-
разность потенциалов AC/i2 точек 1 и 2:
АА =
Рис. 24. К соотноше-
соотношению между разностью
потенциалов и напря-
напряженностью поля
Введем теперь приращение потенциала
при перемещении As, т.е. разность потен-
потенциалов AU21 точки 2 (конец пути) и точки
1 (начало пути), и обозначим его через AU.
Тогда
Д17 = Д1721 = -Д1712.
Приравнивая оба выражения для работы,
получаем для напряженности электричес-
электрического поля выражение
Es = -AU/As.
В общем случае неоднородного поля обе точки 1 и 2 нужно
выбирать достаточно близко друг от друга, строго говоря, беско-
бесконечно близко, чтобы можно было считать напряженность поля
на отрезке As постоянной. Переходя к пределу при As —> О,
получим
Es = -dUjds. A9.1)
Производная, стоящая в правой части равенства, выражает бы-
быстроту изменения потенциала в данном направлении. Мы ви-
видим, что проекция вектора напряженности на данное направле-
направление равна быстроте изменения потенциала в этом направлении
с обратным знаком.
Градиентом любой скалярной величины </э в векторном ана-
анализе называют вектор, направление которого совпадает с на-
направлением быстрейшего увеличения кр. Модуль же этого век-
вектора равен изменению <р при перемещении на единицу длины в
направлении быстрейшего изменения. Этот вектор обозначает-
обозначается символом gradt/з. Из сказанного следует, что напряженность
электрического поля равна градиенту потенциала с обратным
знаком:
E = -grad?7. A9.2)
Таким образом, зная распределение потенциала, мы всегда
можем определить и проекцию напряженности поля на любое
направление, а значит, и проекции Ех, Еу, Ez на координатные
оси.
Если поле однородно, т.е. создается плоским конденсатором,
a U — напряжение между пластинами, d — расстояние между
ними, то
Е = U Id. A9.3)
Это соотношение используют для опредапения единицы напря-
напряженности электрического поля. Единица напряженности вольт
46 РАЗНОСТЬ ПОТЕНЦИАЛОВ ГЛ. III
на метр (В/и) — это напряженность однородного электрическо-
электрического поля, создаваемая разностью потенциалов 1 В между точка-
точками, находящимися на расстоянии 1 м на линии напряженности.
Из сказанного ясно, что если между какими-нибудь провод-
проводниками есть электрическое напряжение, то между ними суще-
существует и электрическое поле. Это обстоятельство разъясняет так
называемое отведение зарядов в землю. Когда мы желаем раз-
разрядить какой-либо проводник, то соединяем его с заземленным
предметом, например, с водопроводным краном, или даже про-
просто касаемся его рукой, и говорим, что заряды с проводника
«ушли через наше тело в землю».
Более точно это явление заключается в следующем. Все элек-
электрические действия обусловлены электрическим полем. Поэто-
Поэтому мы наблюдаем их только тогда, когда имеется напряжение
между рассматриваемым телом и окружающими предметами.
При соединении тела с землей исчезает напряжение между этим
телом и окружающими заземленными предметами, а значит, и
электрическое поле, и все электрические действия прекращают-
прекращаются. Само соединение с землей не играет принципиальной роли.
Мы наблюдали бы то же самое, если бы вместо заземленных
предметов, например стен комнаты, имели замкнутый провод-
проводник, изолированный от земли.
§ 20. Эквипотенциальные поверхности
Объединяя в электрическом поле точки, обладающие одина-
одинаковым потенциалом, мы получаем некоторые поверхности, на-
называемые поверхностями равного потенциала или эквипотен-
эквипотенциальными поверхностями. Пользуясь эквипотенциальными
поверхностями, можно изображать электрические поля графи-
графически, подобно тому как мы это делали с помощью линий на-
напряженности. Пересекаясь с плоскостью чертежа, эквипотенци-
эквипотенциальные поверхности дают эквипотенциальные линии (рис. 25).
Прочерчивая эквипотенциальные линии, соответствующие раз-
различным значениям потенциала, мы получаем сразу наглядное
представление о том, как изменяется потенциал в данном поле.
Так как все точки эквипотенциальной поверхности находят-
находятся при одинаковом потенциале, то перемещение заряда вдоль
нее не требует работы. Это значит, что сила, действующая на
заряд, все время перпендикулярна к перемещению. Отсюда мы
заключаем, что линии напряженности всегда перпендикулярны
к эквипотенциальным поверхностям.
Если прочерчивать эквипотенциальные линии так, чтобы они
соответствовали одинаковым приращениям потенциала, напри-
например 1, 2, 3 и т.д. вольт, то быстрота изменения потенциала в
направлении линий напряженности будет обратно пронорцио-
§21
ИЗМЕРЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ПРОВОДНИКАМИ
47
нальна расстоянию между соседними эквипотенциальными ли-
линиями. Это значит, что густота эквипотенциальных линий про-
Рис. 25. Эквипотенциальные линии (сплошные) и линии напряженности
(штриховые) поля двух одноименно заряженных металлических шаров
порциональна напряженности поля: там, где больше напряжен-
напряженность поля, там и эквипотенциальные линии располагаются
теснее друг к другу.
Мы видим, что, зная эквипотенциальные поверхности,
можно всегда построить линии напряженности данного поля и
наоборот. Поэтому любое электрическое поле можно графиче-
графически изобразить при помощи эквипотенциальных поверхностей
так же хорошо, как и при помощи линий напряженности.
В § 18 мы видели, что если заряды находятся в равновесии,
то все точки проводника имеют одинаковый потенциал. Это зна-
значит, что в отсутствие тока поверхность проводника есть одна из
эквипотенциальных поверхностей.
§ 21. Измерение напряжения между проводниками
Электрическое напряжение можно просто измерить на опы-
опыте. Для этого служат приборы, называемые электромет,рами
или электростатическими вольтметрами.
На рис. 26 изображен один из простейших электромет-
электрометров. Штриховыми линиями изображены сечения эквипотенци-
эквипотенциальных поверхностей плоскостью чертежа, сплошными линия-
линиями — линии напряженности электрического поля. Электрометр
содержит легкую алюминиевую стрелку а, укрепленную на ме-
металлическом стержне б. Стрелка может поворачиваться вокруг
горизонтальной оси. Стержень со стрелкой заключены внутри
металлического корпуса в и хорошо изолированы от него при
помощи пробки г из непроводящего материала (янтарь, кварц,
48
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ. III
эбонит и т.п.). Прибор имеет шкалу, позволяющую отсчитывать
угол отклонения стрелки.
Рассмотрим сначала, как измеряют напряжение между дву-
двумя проводниками. Для этого соединяют корпус электрометра с
одним из проводников, а его стер-
стержень — с другим. Бели нужно из-
измерить напряжение между заря-
заряженным проводником и землей, то
корпус электрометра соединяют с
землей, а стержень присоединяют
с помощью металлической прово-
проволоки к заряженному проводнику
(рис. 27).
Легко видеть, что отклонение
стрелки электрометра будет зави-
зависеть от напряжения, существую-
существующего между стрелкой и корпусом.
Действительно, на стрелку дей-
действуют силы, поворачивающие ее,
потому, что внутри электромет-
электрометра возникает электрическое поле.
Так как электрометр имеет корпус
неизменной формы, то это поле бу-
будет зависеть только от напряжения,
приложенного к электрометру.
Создавая каждый раз одно и то же напряжение между стрел-
стрелкой и корпусом, мы будем получать одну и ту же напряжен-
напряженность поля у поверхности стрелки,
а значит, будут одинаковы и силы,
действующие на стрелку, и ее от-
отклонение. А это и означает, что
электрометр измеряет напряжение.
Такой прибор можно проградуи-
ровать, т.е. определить, каким
напряжениям соответствуют раз-
различные углы отклонения стрелки.
Таким образом, электрометр
всегда измеряет напряжение, су-
существующее между его стрелкой и
корпусом. Поэтому в опыте, изо-
изображенном на рис. 27, можно бы-
было бы изолировать корпус и соеди-
соединить его с исследуемым телом, а стержень соединить с землей,
и при этом показания электрометра не изменились бы.
Пользуясь электрометром, легко убедиться, что поверхность
проводника всегда является эквипотенциальной поверхностью.
Рис. 26.
кой
Электрометр со стрел-
Рис. 27. Измерение напряже-
напряжения между заряженным провод-
проводником и землей
22
НОРМАЛЬНЫЕ ЭЛЕМЕНТЫ
49
Если в опыте, изображенном на рис. 27, соединять электрометр
с различными точками проводника, то, как бы сложна ни была
форма проводника, отклонение стрелки электрометра не изме-
изменяется.
Описанный электрометр удобен для измерения высоких на-
напряжений (тысячи и десятки тысяч вольт). Для измерения ма-
малых напряжений применяют электрометры других типов.
§ 22. Нормальные элементы
Для того чтобы с помощью электрометров измерять напря-
напряжение, их необходимо проградуировать. Для градуировки элек-
электрометров в настоящее время часто пользуются нормальными
элементами, которые представляют собой гальванические эле-
элементы, составленные из таких веществ, которые обеспечивают
весьма большое постоянство напряжения между электродами.
Это напряжение было тщательно измерено и теперь хорошо из-
известно, поэтому нормальные элементы являются удобными эта-
эталонами напряжений, которые легко воспроизвести в любой ла-
лаборатории. Нормальные элементы играют в электрической из-
измерительной технике ту же роль, что и эталоны длины (метра)
и массы (килограмма) при измерении механических величин.
Большое распространение получил кадмиевый нормальный
элемент. Его напряжение при 20 °С равно 1,0186 В.
При комнатных температурах напряжение этого элемента
почти не зависит от температуры: при повышении температу-
температуры на 1 °С оно уменьшается менее чем на 0,0001 В.
Устройство кадмиевого нормального элемента показано на рис. 28. Он
состоит из двух соединяющихся стеклянных пробирок, в дно которых впая-
впаяны платиновые проволоки. На дне одной из пробирок находится небольшое
количество ртути, а поверх наложена паста из смеси сернокислой ртути
и сернокислого кадмия. На
дне другой пробирки имеет-
имеется амальгама кадмия. Про-
Пробирки заполнены насыщен-
насыщенным раствором сернокисло-
сернокислого кадмия. В этом элементе
положительным электродом
(анодом) служит ртуть, а
отрицательным (катодом) —
амальгама кадмия.
От такого элемента мож-
можно брать только очень сла-
слабые токи, не превышающие
нескольких микроампер, так
как только при этом условии его напряжение можно считать неизменяю-
неизменяющимся. Однако этого вполне достаточно для проведения измерений.
Для получения более высоких напряжений нормальные эле-
элементы можно соединять между собой последовательно в бата-
Раствор
CdSCV
CdSO
HgCd
Парафин
CdSO4, HgSO4
Hg
Рис. 28. Кадмиевый нормальный элемент
50
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ III
реи так, чтобы положительный полюс каждого предыдущего
элемента был соединен с отрицательным полюсом последующе-
последующего. При п элементах, соединенных последовательно, напряжение
между крайними электродами батареи будет в п раз больше, чем
у одного элемента.
Отметим, однако, что на практике соединение нормальных
элементов применяют редко. При использовании компенсацион-
компенсационных схем измерения напряжений (§ 70) оказывается возможным
измерить напряжение какого-нибудь источника, применяя всего
один нормальный элемент, даже если измеряемое напряжение
намного больше или намного меньше, чем у нормального эле-
элемента.
§ 23. Электрический зонд
Посмотрим теперь, как можно измерить потенциал внутри
диэлектрика.
Пусть требуется измерить потенциал в какой-либо точке в
воздухе относительно земли. Если мы поместим в эту точку
металлический шарик, то на шарике возникнут индукционные
заряды. Эти заряды вызовут дополнительное поле, и поэтому
результирующее поле изменится. Электрическое поле будет ис-
искажено внесением шарика.
Если, однако, шарик мал, то и разноименные индукционные
заряды будут расположены близко друг к другу, и искажение,
вносимое ими, будет проявляться только в непосредственной
близости от шарика (рис. 29 а). Поэтому шарик практически
Рис. 29. Маленький металлический шарик слабо искажает поле (а), но при
соединении шарика с электрометром искажение поля увеличивается (б):
сплошные линии — линии напряженности, штриховые — эквипотенциаль-
эквипотенциальные линии
примет потенциал, который существовал в данной точке до вне-
внесения шарика.
§24 ПОТЕНЦИАЛ В ПРОСТЕЙШИХ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ 51
Однако мы получим совсем иную картину, если, желая из-
измерить этот потенциал, соединим шарик проволокой с электро-
электрометром (рис. 29 6). В этом случае на шарике будут находиться
индукционные заряды только одного знака, а заряды противопо-
противоположного знака будут внутри электрометра. Поэтому возникнет
сильное искажение первоначального поля и его эквипотенциаль-
эквипотенциальные поверхности и линии напряженности существенно изменят-
изменятся. Электрометр и в этом случае, как и всегда, покажет потен-
потенциал стрелки относительно корпуса, равный потенциалу шарика
относительно земли. Однако этот потенциал будет совсем дру-
другим, нежели тот, который существовал до внесения шарика.
Из сказанного ясно, что мы получим правильное значение по-
потенциала, если уберем индукционные заряды, искажающие по-
поле. Это можно сделать, если вблизи шарика создать в воздухе
небольшое количество ионов. Тогда ионы, противоположные по
знаку заряду шарика, будут переходить на шарик до тех пор, по-
пока индукционный заряд не исчезнет вовсе. Это обстоятельство
используют на практике для устройства электрического зонда.
Электрический зонд представляет собой небольшой метал-
металлический электрод, вокруг которого создается ионизация газа.
Бе можно осуществить, помещая зонд в небольшое пламя горя-
горящего светильного газа (пламенный зонд). Для этого можно так-
также использовать металлическую проволоку, накаливаемую то-
током (зонд с накаленной нитью), или применить любой другой
прием ионизации газа. Зонд соединяют металлической проволо-
проволокой с электрометром, корпус которого заземлен. Тогда показа-
показание электрометра даст потенциал относительно земли той точки
поля, где находится зонд.
§ 24. Потенциал в простейших электрических полях
Вычислим потенциал в электрическом поле, создаваемом од-
одним точечным зарядом q. Рассмотрим в этом поле некоторую
точку, удаленную на расстояние г от заряда, и найдем потенци-
потенциал в этой точке относительно бесконечности. Так как разность
потенциалов не зависит от формы пути, то мы предположим,
что заряд +1 перемещается из точки г в бесконечность вдоль
радиуса, т.е. вдоль линии напряженности электрического поля.
Тогда
U= Г Edr = -2— Г'^ = _1_?. B4.1)
г г
Потенциал убывает обратно пропорционально первой степени
расстояния от заряда.
Поступая подобным образом, можно вычислить распределе-
распределение потенциалов и в других полях, если известна напряженность
52
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ. Ш
поля в каждой точке. Рассмотрим некоторые практически важ-
важные примеры.
Пример 1. Шаровой конденсатор. Имеются два электро-
электрода в виде концентрических сфер с радиусами а (внутренняя) и
Ь (внешняя). Напряженность поля Е между такими электрода-
электродами выражается формулой A3.8) и изменяется в пространстве
так же, как и в случае точечного заряда. Следовательно, раз-
разность потенциалов между внутренней сферой и какой-либо точ-
точкой внутри конденсатора, удаленной на расстояние г от центра
конденсатора, равна
В этой формуле можно выразить заряд q через разность потен-
потенциалов Щ между электродами:
9
B4.2)
откуда окончательно получаем
Таким образом, измеряя Щ между электродами, по формуле
B4.2) можно вычислить потенциал в любой точке поля.
Пример 2. Плоский конденсатор.
Вычислим разность потенциалов между
положительно заряженной пластиной и
произвольной точкой, удаленной на рас-
расстояние х от нее. Напряженность поля в
плоском конденсаторе выражается фор-
формулой A3.7). Поэтому
U
X X
= Г Edx= — Г
J eo J
= -х.
So
B4.3)
Рис. 30. Эквипотенци-
Эквипотенциальные линии и линии
напряженности поля
плоского конденсатора
Полная разность потенциалов С/о между
электродами равна
B4.3а)
где d — расстояние
Поэтому также
между пластинами.
.
В плоском конденсаторе потенциал изменяется
по линейному закону.
B4.36)
с расстоянием
§ 25 ВЫЧИСЛЕНИЕ ПОТЕНЦИАЛА В ПОЛЕ ЗАДАННЫХ ЗАРЯДОВ 53
В этих расчетах мы не учитывали искажение электрическо-
электрического поля вблизи краев пластин. Поэтому полученные формулы
применимы только для средней части конденсатора. Электри-
Электрическое поле плоского конденсатора конечных размеров показано
на рис. 30.
Пример 3. Цилиндрический конденсатор. Рассмотрим еще
распределение потенциала между коаксиальными цилиндрами.
Напряженность этого поля выражается формулой A3.9). Поэто-
Поэтому разность потенциалов между внутренним цилиндром и про-
произвольной точкой между электродами равна
2я-?о J г 2п?о а'
а
Здесь г — расстояние от рассматриваемой точки до оси цилин-
цилиндров, а — радиус внутреннего цилиндра, q\ — заряд внутреннего
цилиндра на единицу его длины. Полная разность потенциалов
Щ между цилиндрами равна
U°= btolna>
где Ь — радиус внешнего цилиндра. Отсюда
U ~ °
Потенциал в цилиндрическом конденсаторе изменяется по лога-
логарифмическому закону.
§ 25. Вычисление потенциала в поле заданных зарядов
В примерах предыдущего параграфа мы вычисляли потен-
потенциал по напряженности поля, которая была известна заранее.
Однако часто напряженность поля бывает неизвестна и именно
ее и требуется вычислить. В этих случаях находят сначала по-
потенциал, что оказывается гораздо проще, а затем вычисляют и
напряженность поля по формуле A9.1).
При вычислении потенциала следует различать два случая:
а) задано распределение зарядов, вызывающих поле, и б) зада-
заданы потенциалы заряженных тел, создающих поле. Рассмотрим
сначала первый случай.
Если поле создается одним-единственным точечным заря-
зарядом, то потенциал этого поля выражается формулой B4.1).
Если имеется несколько точечных зарядов, то, согласно
принципу наложения электрических полей (§ 10), результирую-
результирующее поле равно сумме полей, создаваемых отдельными заряда-
зарядами. Поэтому и потенциал этого поля равен сумме потенциалов,
54
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ. III
вызываемых отдельными зарядами, т.е.
1
B5.1)
Здесь U — потенциал результирующего поля в рассматриваемой
точке относительно бесконечности, гг — расстояние этой точки
до г-го заряда, а суммирование производится по всем точечным
зарядам.
Подобным образом можно рассчитать потенциал поля и про-
протяженных заряженных тел. В этом случае нужно сначала найти
потенциал, создаваемый отдельным бесконечно малым элемен-
элементом объема тела dr, который можно рассматривать как точеч-
точечный заряд. Этот потенциал есть
47Г60 Г
где р —- объемная плотность заряда, а г — расстояние от рас-
рассматриваемой точки поля до dr. Полное значение потенциала
равно
1 Г pdr
U =
47ГЕО
B5.2)
где интегрирование распространяется на весь объем г заряжен-
заряженного тела.
Если заряды расположены только на поверхности тела, то
1 Г crdS
U =
47Г?о
B5.3)
Здесь а — поверхностная плотность заряда, dS — элемент
поверхности тела, г — расстояние рассматриваемой точки поля
до dS, а интегрирование распро-
распространяется по всей заряженной по-
поверхности S.
Электрическое поле дипо-
диполя. Применим результаты преды-
предыдущего параграфа к вычислению
электрического поля, создаваемого
диполем (рис. 31). Согласно B5.1)
потенциал в некоторой точке поля
а есть
U =
_ Я.
47ГЕ-0 V Г2
_ q ri - r-j
Г1Г2
Будем теперь считать, что длина
Рис. 31 К вычислению элек- диполя I весьма мала по сравнению
трического поля диполя с расстояниями г\ и ri до точки а
§ 26 ОБЩАЯ ЗАДАЧА ЭЛЕКТРОСТАТИКИ 55
(элементарный диполь). В этом случае можно положить
Г\ — Г2 = I COS а, Г\Г2 = Г2
и выражение для потенциала принимает вид
и= 1 pcosa }
Здесь р есть модуль момента диполя, а а — угол между на-
направлением момента диполя р и направлением радиус-вектора
г, проведенного из диполя в рассматриваемую точку поля.
Зная U в зависимости от координат, мы можем вычислить
напряженность поля Е по формуле A9.1), дифференцируя вы-
выражение для U по координатам. Будем пользоваться полярными
координатами г и а с началом в точке нахождения диполя и на-
направим полярную ось в направлении момента диполя р. Тогда
составляющая напряженности в направлении радиуса г есть
Ег=Ы = jcosa ( 5)
Составляющая, перпендикулярная к г:
7-, dU p sin a
Полная напряженность поля в точке а(г,а) будет
os2a + l. B5.7)
Вектор напряженности образует с
направлением г угол /3:
tg/3 = Ea/Er = {1 /2) tg a. B5.8)
Эти формулы вполне определяют
напряженность поля по модулю и
ПО направлению В каждой его точке. Рис. 32. Линии напряженно-
На рис. 32 изображены линии поля сти элементарного диполя
диполя.
§ 26. Общая задача электростатики
Наиболее часто встречаются такие случаи, когда распреде-
распределение зарядов неизвестно, но заданы потенциалы проводников.
Такие задачи могут быть сформулированы следующим общим
образом: имеется система проводников А, Б, В и т.д. заданной
формы и заданного взаимного расположения и известны потен-
потенциалы всех проводников Ua, Ub и т.д. (например, относительно
56 РАЗНОСТЬ ПОТЕНЦИАЛОВ ГЛ. III
бесконечности или относительно одного из проводников); требу-
требуется определить значение потенциала в любой точке поля между
проводниками.
Математически эта задача сводится к следующей. Состав-
Составляющие напряженности поля Е по координатам можно выра-
выразить, согласно A9.1), через потенциал:
тр __dU „ _ _dU „ _ dU
Подставляя эти выражения в уравнение Пуассона A4.1), мы по-
получим общее уравнение, которому удовлетворяет потенциал, в
виде
?
Если между проводниками нет зарядов, то во всех точках
р = 0, и уравнение B6.1) переходит в более простое:
d?V_ ,д^Ц_ ,dHJ_ __ n (Of. „v
ax2 ay2 az2 v '
называемое уравнением Лапласа. Поэтому вычисление потен-
потенциала в общем случае сводится к нахождению такой функции
координат U(x,y,z), которая во всем пространстве между
проводниками удовлетворяет дифференциальному уравнению
B6.2), а на самих проводниках принимает заданные постоян-
постоянные значения Ua, Ub и т.д. Можно показать, что решение такой
задачи однозначно.
Легко убедиться, что найденные нами в § 24, 25 выражения для потен-
потенциала в простейших полях удовлетворяют уравнению B6.2) и граничным
условиям.
Действительно, для однородного поля плоского конденсатора потенци-
потенциал выражается формулой B4.3). Потенциал зависит лишь от одной коор-
координаты х, и поэтому в уравнении Лапласа B6.2) имеется всего один член.
Вычисляя производные от потенциала по координатам, имеем
a dU _ a d2U
U — х, — , „ — U.
?о ах ?о ах*
Потенциал, кроме того, удовлетворяет граничным условиям, так как оста-
остается постоянным во всех точках одной обкладки (х = 0) и другой обкладки
(х = d).
Для радиального поля шарового конденсатора мы нашли формулу
B4.2), где г = у/х2 +у2 + z2. Дифференцируя выражение для потенциа-
потенциала по координатам, получаем
г2 — Чт2
со^ —.
дх дх \ rj r2 r' дх2
И аналогично
d2U ej г2 - Зу2 д2Ц с2 г2 - Зг2
ду2 °° г5 ' дг2 г5
§ 27 ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ 57
Поэтому
&V_ д^и_ d2U gj Зг2 - 3(х2 + у2 + z2) _ Q
дх2 ду2 dz2 r5
Потенциал, выражаемый формулой B4.2), удовлетворяет и граничным
условиям, так как постоянен во всех точках каждой обкладки (при г = а и
г = Ь).
Подобным же образом можно проверить, что формула B4.4), найденная
для потенциала в поле цилиндрического конденсатора, также удовлетворя-
удовлетворяет и уравнению B6.2), и граничным условиям.
Решение уравнения B6.2), вообще говоря, сложно и составля-
составляет содержание специального раздела математической физики —
теории потенциала.
Если форма электродов настолько сложна, что распределе-
распределение потенциала трудно вычислить, то его всегда можно опре-
определить экспериментально. Для этого может служить электри-
электрический зонд (§ 23). Еще удобнее применение электролитической
ванны, описанной в § 62.
§ 27. Проводники в электрическом поле
Рассмотрим теперь, каким образом распределяются электри-
электрические заряды внутри проводников в отсутствие электрического
тока.
В § 18 мы видели, что для равновесия зарядов необходимо,
чтобы напряженность поля Е{ в любой точке внутри провод-
проводника была равна нулю. Но тогда из уравнения Пуассона A4.1)
следует, что объемная плотность заряда pi внутри проводника
также равна нулю. В отсутствие электрического тока заряды
распределяются только на поверхности проводника.
Если мы представим себе, что из сплошного проводника уда-
удалена внутренняя часть, то получится полый замкнутый провод-
проводник. Так как внутренняя часть не имела зарядов, то ее удаление
не изменит ни распределение поля, ни распределение зарядов
внутри оставшейся части проводника. Поэтому равновесное рас-
распределение зарядов в полом проводнике будет таким же, как и в
сплошном проводнике, т.е. заряды будут только на внешней по-
поверхности. Напряженность же поля будет равна нулю в любой
точке внутри стенок и в любой точке внутри полости.
Заряды в состоянии равновесия распределяются на поверх-
поверхности проводника всегда, независимо от того, каким образом они
возникли. Если замкнутый полый металлический проводник на-
находится во внешнем электрическом поле (рис. 33 а), то на нем
появятся индукционные заряды. Эти заряды будут также сосре-
сосредоточены только на внешней поверхности, а электрическое поле
и в толще металла, и внутри полости будет равно нулю. Поэтому
58
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ Ш
полый металлический проводник экранирует электрическое по-
поле всех внешних зарядов. Этим широко пользуются на практи-
практике для устройства электростатической защиты. Для того чтобы
оградить чувствительные электрические приборы от возмуща-
возмущающего действия внешних электрических полей, их заключают в
замкнутые металлические ящики, которые соединяют с землей.
Отметим, что замкнутый полый проводник экранирует толь-
только поле внешних зарядов. Если электрические заряды находят-
находятся внутри полости, индукци-
индукционные заряды возникнут не
только на внешней поверхности
проводника, но и на внутрен-
внутренней (рис. 33 5). Распределение
этих индуцированных зарядов
будет таким, чтобы полное по-
поле, равное сумме полей, созда-
создаваемых зарядом внутри полости
и индукционными зарядами, в
любой точке в толще металла
было равно нулю (условие рав-
равновесия) . Однако внутри полос-
полости поле не будет равно нулю,
и здесь будут проходить линии
Рис. 33. Заряд вне (а) и внутри (б)
металлической полости
напряженности, соединяющие
заряд, заключенный в полости,
с индукционными зарядами на
внутренней поверхности. Индукционные же заряды на внешней
поверхности вызовут поле во внешнем пространстве, и поэтому
замкнутая проводящая полость не экранирует поле электриче-
электрических зарядов, помещенных внутри нее.
В связи с изложенным выше находится важный практиче-
практический прием передачи заряда от одного проводника к другому.
Пусть, например, требуется передать заряд с металлического
проводника на электрометр. Чтобы осуществить эту переда-
передачу полностью, электрометр соединяют с полым проводником,
приближающимся по форме к замкнутой полости, например с
металлическим цилиндром («фарадеев цилиндр»), и вносят за-
заряженный проводник внутрь этой полости. Тогда проводник
разряжается полностью и его заряд целиком переходит на элек-
электрометр.
§ 28. Точная проверка закона Кулона
В предыдущем параграфе, объясняя, почему заряды рас-
распределяются только на поверхности проводника, мы основыва-
основывались на теореме Остроградского-Таусса. Но эта теорема есть
§ 28
ТОЧНАЯ ПРОВЕРКА ЗАКОНА КУЛОНА
59
следствие закона Кулона, и поэтому найденные нами особен-
особенности распределения зарядов являются также следствием этого
закона.
И наоборот: можно показать, что если бы сила взаимодей-
взаимодействия точечных зарядов выражалась законом
то при любом S, отличном от нуля, теорема Остроградского-
Гаусса не имела бы места и заряды распределялись бы не только
на поверхности, но и в объеме проводника (см. Добавление 1).
Поэтому, исследуя на опыте, действительно ли в объеме про-
проводника нет зарядов, можно проверить справедливость закона
Кулона и притом гораздо более точно, нежели в опытах с кру-
крутильными весами.
Такие опыты произвел впервые Кавендиш, который за
несколько лет до Кулона установил, что сила взаимодействия
зарядов обратно пропорциональна квадрату расстояния. В этих
опытах металлический шар 1 (рис. 34) был укреплен на изоли-
изолирующей подставке 2. Две металлические полусферы 3, изоли-
изолированные от земли, были укреплены на подвижных подставках
(на рисунке не изображены) и могли быть
соединены в одну сферу, охватывающую
шар 1. В одной из полусфер имелось малое
отверстие, в которое можно было вставлять
короткий металлический проводник 4, под-
подвешенный на изолирующей нити 5, и соеди-
соединять шар и сферу, не разряжая прибора.
Сам опыт заключался в следующем. По-
Полусферы 3 складывали вместе, соединяли
их проводником 4 с шаром 1 и заряжали.
О заряде сферы судили по показаниям элек-
электрометра. Затем проводник 4 с помощью
нити 5 удаляли, обе полусферы раздвигали
и разряжали, соединяя их с землей. После вендиша
этого электрометр присоединяли к шару 1
и проверяли, имеется ли на нем какой-либо заряд. Опыт всегда
показывал, что на шаре нет никаких следов заряда.
Вследствие большого принципиального значения вопроса о
законе силового взаимодействия зарядов подобные опыты бы-
были повторены позднее Максвеллом в улучшенной форме. Исхо-
Исходя из чувствительности своих опытов, Максвелл рассчитал, что
отклонение S от величины 2 в показателе закона Кулона если
и существует, то не превышает 1/21600. В настоящее время за-
закон Кулона для макроскопических расстояний проверен гораздо
точнее.
Рис. 34. Опыт Ка-
60
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ. III
§ 29. Острия
При исследовании распределения зарядов на проводнике
сложной формы (рис. 35 а) оказывается, что поверхностная
плотность заряда различна в разных точках поверхности: она
близка к нулю внутри углубления (точка 1), принимает наиболь-
наибольшее значение на заострении (точка 2) и имеет промежуточную
величину в точках боковой поверхности C).
Но напряженность поля Е, согласно A3.7), пропорциональна
поверхностной плотности заряда о. Поэтому и напряженность
поля у поверхности проводника сложной формы также весьма
неодинакова. Она особенно велика возле участков с малым ра-
радиусом кривизны, т.е. у заострений.
Это приводит к своеобразному явлению «стекания» зарядов
с металлических острий. Если соединить изолированное метал-
металлическое острие с источником высокого напряжения, то находя-
находящиеся поблизости изолированные проводники заряжаются. По-
Помещая недалеко от острия электрометр, соединенный с метал-
металлической пластиной, можно видеть, что пластина заряжается до
значительного напряжения и притом зарядом того же знака, что
и на острие. Если, наоборот, предварительно зарядить пластину
с электрометром, а острие присоединить к земле, то при подне-
поднесении острия к пластине последняя разряжается: индукционные
заряды стекают с острия и нейтрализуют заряд пластины.
Причина этого явления заключается в большой напряжен-
напряженности поля возле острия. Когда эта напряженность становится
достаточно большой, в окружающем воздухе начинается иони-
ионизация (подробнее см. § 166) и появляются положительные и от-
отрицательные ионы (рис. 35 5). Ионы с тем же знаком заряда,
Рис. 35. Напряженность электрического поля и поверхностная плотность
у заострения проводника (а); причина стекания зарядов (б)
что и у острия, движутся от острия; ионы с противоположным
знаком заряда движутся к острию и уменьшают его заряд.
Ионы, движущиеся от острия, увлекают в своем движении и
нейтральные молекулы, отчего возникает направленное течение
§ 30
ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР
61
воздуха от острия, или электрический ветер. Его можно обнару-
обнаружить, поднося к острию зажженную свечу: пламя свечи сильно
отклоняется от острия и может быть погашено струей электри-
электрического ветра.
Рассмотренное свойство заостренных проводников использу-
используют на практике для съема зарядов в различных устройствах.
Для предотвращения стекания зарядов у всех приборов и
машин, работающих под высоким электрическим напряжением,
металлические части делают хорошо закругленными, а концы
металлических стержней снабжают гладкими шариками; нали-
наличие заострений вызвало бы стекание зарядов и нарушение изо-
изоляции.
§ 30. Электростатический генератор
То обстоятельство, что заряды всегда распределяются толь-
только на внешней поверхности проводника, используют для устрой-
устройства электростатических генераторов, предназначенных для по-
получения весьма высоких напряжений. Принцип их действия
разъясняется опытом, изображенным на рис. 36. Соединим изо-
изолированный проводник а с источником напряжения В (удобно
воспользоваться заря-
заряженным конденсатором
или техническим выпря-
выпрямителем на 2-3 тысячи
вольт) и расположим
поблизости полый изоли-
изолированный проводник б,
соединенный с электро-
электрометром. Соединим на
момент проводники а и б
металлическим стерж-
стержнем (на изолирующей
ручке). Проводник б за-
зарядится до напряжения ~ ~
проводника а, которое и „ „,, „
_ Рис. 36. Принцип действия электростати-
определим по показаниям ческого генератора
электрометра. Возьмем
теперь металлический шар е, укрепленный на изолирующей
ручке, коснемся им проводника а, а затем внутренней поверх-
поверхности проводника б. Заряд шара в перейдет полностью на
проводник б, отчего напряжение на б увеличится. Повторяя
этот процесс многократно, мы сможем сделать напряжение
на проводнике б намного бблыпим, чем на проводнике а; в
принципе можно увеличивать его неограниченно.
62
РАЗНОСТЬ ПОТЕНЦИАЛОВ
ГЛ IV
При помощи описанного процесса мы переносим положительные заря-
заряды от тела с более низким потенциалом к телу с более высоким потенци-
потенциалом. На первый взгляд это может показаться удивительным, так как при
соединении двух проводников положительные заряды всегда перемещают-
перемещаются от более высокого потенциала к более низкому. На самом же деле здесь
никакого противоречия нет, так как при перемещении шара в от а к б мы
преодолеваем силу отталкивания и совершаем механическую работу. Поэто-
Поэтому, перемещая в по направлению к б, мы увеличиваем потенциал шара в.
Когда в окажется внутри полости б, его потенциал сравняется с потенциа-
потенциалом б. Таким образом, ценой совершения механической работы мы можем,
располагая источником небольшого напряжения, зарядить какой-либо про-
проводник до напряжения более высокого.
Это и осуществляется в электростатическом генераторе. Он
состоит из большого полого проводника 1 (рис. 37), обычно ша-
шарообразной формы, укрепленного на изолирующей колонне 2.
Внутри колонны проходит бесконечная лента 3 из прорезинен-
прорезиненной ткани, движущаяся на двух шкивах 4 и играющая роль ша-
шара в на рис. 36. Лента заряжается при
помощи системы острий 5, соединенных
с одним из полюсов источника напря-
напряжения, второй полюс которого заземлен.
Против острий, с обратной стороны лен-
ленты, помещают заземленную пластину 6,
которая увеличивает заряды, стекающие
с острия 5 на ленту. Проходя мимо си-
системы острий 7, соединенных с шаром 1,
резиновая лента отдает им принесенные
заряды, которые полностью переходят
на внешнюю поверхность шара незави-
независимо от того, какое напряжение имеется
между шаром и землей.
Максимальное напряжение, которое
практически можно получить на шаре,
определяется утечками зарядов с шара
(главным образом вследствие ионизации
лектростати- ВОЗдуха). Напряжение шара перестает
повышаться, когда заряд, приносимый
лентой в единицу времени (ток ленты), делается равным заряду,
теряемому вследствие утечки (току утечки). Поэтому на прак-
практике стремятся по возможности увеличить ток ленты.
Электростатические генераторы применяют в настоящее время
для ускорения заряженных частиц (электронов и ионов). С их по-
помощью удается получить напряжения до 3-5 миллионов вольт.
Высота таких генераторов достигает 10-15 м, а диаметр шара -
нескольких метров. Электростатические генераторы иногда
помещают в камеры со сжатым газом, так как ионизация газа
при повышении давления наступает при больших напряжениях.
Рис. 37.
ческий генератор
§31 ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ 63
ГЛАВА IV
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
§ 31. Электрическая емкость
Рассмотрим два проводника, между которыми существует
электрическое напряжение, и предположим, что все линии сме-
смещения, исходящие из одного проводника, заканчиваются на дру-
другом. Такую пару проводников мы будем называть простым кон-
конденсатором или просто конденсатором.
Простым конденсатором является шаровой конденсатор, со-
состоящий из двух проводников в виде концентрических сфер
(§ 24), так как линии смещения, исходящие из внутренней сфе-
сферы, обязательно все заканчиваются на внешней сфере. Две
параллельные проводящие пластины (плоский конденсатор)
можно считать также простым конденсатором, если расстояние
между пластинами мало по сравнению с их размерами. Простым
конденсатором является и цилиндрический конденсатор (§ 24),
если длина цилиндров велика по сравнению с зазором между ни-
ними. Оба проводника, образующие конденсатор, называются его
обкладками.
Так как линии смещения начинаются и заканчиваются на
электрических зарядах, то отсюда следует, что заряды, нахо-
находящиеся на обкладках простого конденсатора, всегда равны по
модулю и противоположны по знаку.
Напряженность поля в любой точке между обкладками кон-
конденсатора всегда пропорциональна заряду обкладок. Поэтому,
согласно A7.1), и напряжение U между обкладками всегда про-
пропорционально заряду обкладок q:
q=CU. C1.1)
Коэффициент С в этой формуле называют электрической ем-
емкостью конденсатора или просто его емкостью.
Из C1.1) следует, что q = С при [7 = 1. Это значит, что
емкость конденсатора измеряется зарядом, находящимся на
каждой из обкладок, если напряжение между обкладками равно
единице.
Единицей емкости служит фарад (Ф) — емкость такого уеди-
уединенного проводника, потенциал которого повышается на 1 В при
сообщении ему заряда 1 Кл:
1 Ф = 1 Кл/1 В = 1 Кл/В.
На практике применяют также более мелкие единицы емкости:
1 микрофарад (мкФ) = 10~6 Ф и 1 пикофарад (пФ) — 10~12 Ф.
64
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
ГЛ. IV
Емкость конденсатора зависит от его размеров, формы и от
свойств среды, находящейся между его обкладками.
Пусть Со — емкость любого конденсатора, когда его об-
обкладки находятся в вакууме. Практически мы получим ту же
емкость, если между обкладками будет атмосферный воздух.
Пусть далее С — емкость того же конденсатора, если все про-
пространство между его обкладками заполнено каким-либо другим
однородным диэлектриком. Отношение
С/Со = е C1.2)
называют относительной диэлектрической проницаемостью
или просто диэлектрической проницаемостью диэлектрика. Ди-
Диэлектрическая проницаемость е есть величина, характеризую-
характеризующая электрические свойства вещества и зависящая от рода ве-
вещества и от его состояния (температуры, давления и т.д.).
Отметим, что величина, определяемая формулой C1.2), есть
отношение абсолютной диэлектрической проницаемости данно-
данного вещества (eqe) и вакуума {eq). Как видно из C1.2), эта вели-
величина безразмерна. Значение абсолютной диэлектрической про-
проницаемости eqe зависит от того, какую размерность и какое зна-
значение приписать eq. В абсолютной электростатической системе
единиц полагают е$ — \ к считают величиной безразмерной.
Поэтому C1.2) определяет одновременно и абсолютную диэлек-
диэлектрическую проницаемость в системе единиц СГСЭ.
В системе единиц СИ ео есть величина размерная и не равная
единице (§4). Поэтому абсолютная диэлектрическая проницае-
проницаемость вещества в системе единиц СИ есть eqe.
В качестве примера приводим в табл. 1 диэлектрические про-
проницаемости е некоторых веществ:
Таблица 1
Вещество
Вакуум
Воздух *)
Эбонит
е
1
1,000594
2,7-2,9
*) При 0 °С и 760 мм
**) В зависимости от
Вещество
Стекло
Спирт этиловый
Вода
рт. ст.
сорта.
е
5-10 *¦)
27
81
§ 32. Емкость простых конденсаторов
Емкость конденсаторов простой формы можно вычислить.
Для этого предполагают, что на каждой из обкладок находит-
находится некоторый заряд q, и вычисляют потенциал в электрическом
§ 32 ЕМКОСТЬ ПРОСТЫХ КОНДЕНСАТОРОВ 65
поле рассматриваемого конденсатора U(x:y, z). Если удается ре-
решить эту задачу, то отсюда получается и значение напряжения
между обкладками конденсатора U. После этого емкость можно
найти по формуле C1.1).
Рассмотрим некоторые примеры.
Пример 1. Плоский конденсатор. Будем считать, что
зазор между пластинами мал по сравнению с их размерами, так
что краевыми эффектами можно пренебречь. Распределение по-
потенциала в поле плоского конденсатора нами уже вычислено в
§ 24. Если на единице поверхности обкладок имеется заряд а и
диэлектриком является вакуум, то полное напряжение между
обкладками равно
U = ad/sQ,
где d — расстояние между пластинами. Если площадь каждой
пластины равна S, то полный заряд пластины есть q = aS. По-
Поэтому
C = q/U = ?0S/d. C2.1)
Если диэлектриком является не вакуум, а вещество с диэлек-
диэлектрической проницаемостью е, заполняющее все пространство,
где имеется электрическое поле (пространство между обкладка-
обкладками), то емкость будет в е раз больше:
С = ee0S/d. C2.1а)
При уменьшении расстояния d между обкладками емкость уве-
увеличивается.
Пример 2. Шаровой конденсатор. Если на обкладках кон-
конденсатора имеется заряд q, то напряжение между обкладками в
вакууме (§ 24)
A 1 \
а Ь) '
где а и Ь — радиусы внутренней и внешней обкладок. Поэтому
емкость в вакууме
С- q -
Если внешний радиус Ь гораздо больше внутреннего а, то фор-
формула упрощается:
С = 4тге0а. C2.3)
Этот результат справедлив и в том случае, если внешняя об-
обкладка имеет не сферическую форму, а какую угодно, при усло-
условии, что ее размеры намного больше радиуса внутренней сфе-
сферы. В таком смысле часто говорят о емкости уединенного шара,
хотя это выражение всегда обозначает емкость конденсатора,
у которого роль внешней обкладки играют удаленные предме-
предметы, находящиеся при одинаковом потенциале (стены комнаты и
т.п.).
66 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ГЛ IV
Если, наоборот, зазор между обкладками Ь — а = d весьма
мал по сравнению со средним радиусом сфер г, то C2.2) можно
представить в виде
ob , г2 S
^??
где S = 4тгг2 есть площадь поверхности обкладок. Мы видим,
что при малом зазоре выражения для емкости сферического и
плоского конденсаторов совпадают.
Пример 3. Цилиндрический конденсатор. Пусть конден-
конденсатор состоит из двух коаксиальных цилиндров с радиусами а
(внутренний) и Ь (внешний). Длину цилиндров будем считать
весьма большой по сравнению с зазором между ними. Напряже-
Напряжение между обкладками (§ 24)
2тг?0 а
где q\ — заряд на единицу длины цилиндров. Поэтому емкость
цилиндрического конденсатора в вакууме на каждую единицу
длины равна
с' - % = im- <32-4>
Эта формула выражает, в частности, емкость кабеля, который
состоит из металлического провода, окруженного слоем изолято-
изолятора и металлической броней; выражение C2.4) следует умножить
еще на диэлектрическую проницаемость е вещества изолятора.
Если расстояние между цилиндрами Ъ — а = d мало по срав-
сравнению с их радиусами, то C2.4) упрощается. В этом случае
In (b/a) можно разложить в ряд и ограничиться только членом
первого порядка:
In (Ь/а) =ln(l + d/a)»d/o.
Поэтому
где через S обозначена площадь поверхности обкладок на еди-
единицу длины конденсатора: S = 2тга. И в этом случае емкость
выражается той же формулой, что и для плоского конденсато-
конденсатора.
Отметим, что этот результат имеет общий характер и спра-
справедлив для конденсаторов с обкладками любой формы, если
только зазор между обкладками мал по сравнению с радиусом
кривизны обкладок. Он является следствием того, что любое
неоднородное поле на малых расстояниях можно рассматривать
как однородное.
§ 32 ЕМКОСТЬ ПРОСТЫХ КОНДЕНСАТОРОВ 67
Пример 4. Двухпроводная линия. Рассмотрим теперь
два параллельных цилиндрических провода с радиусами а и
расстоянием между осями d (рис. 38). Будем считать, что все
остальные тела, включая и землю, на-
находятся на расстояниях, больших по
сравнению с d, и поэтому будем рассма-
рассматривать оба провода как простой конден-
конденсатор.
Если расстояние d сравнимо с а, то
заряды будут распределены по поверх- r**-1* d I
ности проволок неравномерно, и вычис- <~т т^
ление электрического поля будет слож- Рис 3§ Электрическое
ным. Поэтому мы предположим, что поле двухпроводной ли.
а ^>а. В этом случае оба цилиндра заря- нии
жены равномерно, и напряженность по-
поля, создаваемую ими, можно найти по формуле A3.9). Так как
напряжение в электростатическом поле не зависит от формы пу-
пути, то для его вычисления мы выберем простейший путь в виде
прямой линии, соединяющей оси проводов и перпендикулярной
к их поверхности. Напряженность поля Е в какой-либо точке х
на этой линии (рис. 38) равна
27Г?о X 2iT?0 d — X '
где q\ — заряд на единицу длины проволок. Поэтому напряже-
напряжение U между проводами
d — a d — a d — а
Edx = / 1 j — = —— In ~— In -
27Г?о J х 2гг?о J a — х тгео а 7Г?о с
а а а
Емкость двухпроводной линии на каждую единицу длины
U In [d/a) ' '
Единица электрической постоянной ео- Понятие элек-
электрической емкости используют в системе единиц СИ для опре-
определения единицы электрической постоянной Eq. Пользуясь, на-
например, формулой C2.1), имеем
е0 = Cd/S.
Подставляя сюда вместо С, d и S их единицы, находим единицу
электрической постоянной:
1 ?о = 1 Ф • 1 м/1 м2 = 1 Ф/м;
она получила название фарад на метр (Ф/м).
68
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
ГЛ. IV
§ 33. Метод зеркальных изображений
При расчете электрического поля и вычислении емкости
бывает полезен вспомогательный прием, называемый методом
зеркальных изображений зарядов. Этот метод основан на сле-
следующем очевидном положении: если в электрическом поле заме-
заменить какую-либо эквипотенциальную поверхность проводником
той же формы и создать на нем
потенциал, равный потенциалу рас-
рассматриваемой эквипотенциальной по-
поверхности, то электрическое поле не
изменится.
Применим это положение к элек-
электрическому полю двух точечных заря-
зарядов +q и —q, расположенных на рас-
расстоянии 2/г друг от друга (рис. 39).
Рассматриваемое поле можно разде-
разделить плоскостью А А на две равные ча-
части. Эта плоскость будет везде перпен-
Рис. 39. Электрическое по- дикулярна к линиям напряженности
ле между точечным заря- П0ЛЯ; а следовательно, будет эквипо-
дом^и проводящей плоско- тенциальной поверхностью. Поэтому
если в АА находится неограниченная
проводящая плоскость, то поле между этой плоскостью и заря-
зарядом +q не изменится и будет совпадать с полем двух точечных
зарядов +q и —q. Это позволяет просто учесть действие инду-
индуцированных зарядов на проводящей плоскости.
Заряд — q расположен за плоскостью на том же расстоянии h,
что и заряд +q над плоскостью, и поэтому является его зеркаль-
зеркальным изображением в проводящей плоскости. Поэтому найден-
найденный результат можно сформулировать так: электрическое поле
между точечным зарядом и бесконечной проводящей плоско-
плоскостью совпадает с полем, создаваемым рассматриваемым заря-
зарядом и его зеркальным изображением в проводящей плоскости.
Или, иначе: действие проводящей плоскости с ее индуцирован-
индуцированными зарядами можно заменить действием точечного заряда,
являющегося зеркальным изображением данного заряда в про-
проводящей плоскости.
Применим рассмотренный метод к вычислению емкости ци-
цилиндрического провода с радиусом а, подвешенного на высоте
h над землей. Такой случай мы имеем в воздушной телеграф-
телеграфной линии. Линии напряженности этого поля (в плоскости, пер-
перпендикулярной к проводу) будут изображаться так же, как на
рис. 39. Поле в пространстве между проводом и землей будет
совпадать с полем провода и его зеркального изображения, и
поэтому задача сводится к случаю двух параллельных прово-
§34
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
69
дов. Однако напряжение между поверхностью земли и прово-
проводом при том же заряде провода будет равно только половине
напряжения между двумя проводами, а, значит, емкость будет
в два раза больше. Умножая на 2 соотношение C2.5) и полагая
в нем d = 2/i, найдем выражение для емкости единицы длины
провода над землей в виде
к
1
Б
т
% 34. Энергия заряженного конденсатора
Если обкладки заряженного конденсатора замкнуть метал-
металлическим проводником, то в нем возникнет электрический ток, а
конденсатор разрядится. Электрический ток разряда конденса-
конденсатора выделяет в проводнике определенное количество теплоты,
а это значит, что заряженный конденсатор обладает энергией.
Так, если в схеме рис. 40 перевести переключатель К в по-
положение 1, то конденсатор С окажется соединенным с батареей
элементов Б и зарядится до напряже-
напряжения батареи. При перебрасывании пе-
переключателя в положение 2 конденса-
конденсатор разряжается через электрическую
лампочку, которая дает вспышку.
Вычислим энергию заряженного
конденсатора. Для этого представим
себе, что конденсатор заряжается, и
обозначим через и мгновенное значе-
значение напряжения между его обклад-
обкладками. Процесс зарядки будем счи-
считать бесконечно медленным (квазиста-
(квазистатическим), полагая, что напряжение батареи и равное ему на-
напряжение между обкладками бесконечно медленно увеличива-
увеличиваются. В этом случае потенциал каждой из обкладок в любой
момент времени будет иметь везде одно и то же значение. Если
заряд обкладок увеличивается на малую величину dq, то совер-
совершаемая при этом внешняя работа 6А (в данном случае батареи),
согласно § 17, равна
6А — и dq.
Выражая в этой формуле заряд обкладок q через напряжение
по формуле C1.1), получим
6A = Cudu.
Если емкость не зависит от напряжения (электрического поля),
то работа 5А идет на увеличение энергии конденсатора dW. Ин-
Рис. 40. При разрядке кон-
конденсатора через электриче-
электрическую лампу его энергия пре-
превращается в тепло
70 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ГЛ IV
тегрируя выражение для 5А между значениями напряжения 0
(начало зарядки) и U (конец зарядки), получаем
и
A = W = C fudu = lcU2. C4.1)
0
Зависимость энергии конденсатора от емкости и напряжения
можно также показать в описанном выше опыте (рис. 40). Если
увеличить напряжение батареи (увеличивая, например, число
последовательно соединенных элементов), то лампочка вспыхи-
вспыхивает гораздо ярче. Если, оставляя батарею неизменной, изме-
изменять емкость конденсатора, то с увеличением емкости накал
лампочки увеличивается.
Пользуясь соотношением C1.1), можно представить выраже-
выражение для энергии заряженного конденсатора также в любом из
следующих видов:
Благодаря способности запасать в себе энергию конденсато-
конденсаторы играют большую роль в электро- и радиотехнике.
§ 35. Соединение конденсаторов
Если напряжение на конденсаторе сделать слишком боль-
большим, то конденсатор «пробивается», те. между его обкладка-
обкладками возникает искра (внутри диэлектрика или по его поверхно-
поверхности) и конденсатор портится вследствие нарушения изоляции.
Поэтому каждый конденсатор характеризуется не только своей
емкостью, но еще и максимальным рабочим напряжением.
Для того чтобы, располагая определенными конденсаторами,
осуществить желаемую емкость при нужном рабочем напряже-
напряжении, конденсаторы соединяют в батареи.
ННН
Рис 41 Соединения конденсаторов
На рис. 41 а показано параллельное соединение конденсато-
конденсаторов. В этом случае общим для всех конденсаторов является на-
напряжение U, и мы имеем
qi=CiU, q2
§ 35 СОЕДИНЕНИЕ КОНДЕНСАТОРОВ 71
Суммарный заряд, находящийся на батарее, равен
и поэтому емкость батареи
Емкость батареи конденсаторов, соединенных параллельно,
равна сумме емкостей отдельных конденсаторов. Так как в этом
случае напряжение на каждом конденсаторе равно напряжению
на батарее, то и допустимое рабочее напряжение батареи будет
таким же, как и у одного конденсатора
На рис. 41 б изображено последовательное соединение кон-
конденсаторов. В этом случе одинаков для всех конденсаторов за-
заряд q, равный полному заряду батареи, и мы можем написать
Ui = q/C\, U2 = q/C2.
Напряжение же батареи будет равно сумме напряжений на от-
отдельных конденсаторах, т.е.
Поэтому для емкости С всей батареи, находим
- C5-2)
При последовательном соединении конденсаторов суммиру-
суммируются обратные значения емкостей В этом случае напряжение
на каждом конденсаторе будет меньше напряжения на батарее,
и поэтому допустимое рабочее напряжение будет больше, чем у
одного конденсатора.
На рис. 41 в показано смешанное соединение конденсаторов.
Емкость такой батареи легко определить, пользуясь формулами
C5.1) и C5.2), что предоставляем сделать самим читателям.
Используя на практике соединение конденсаторов, следует всегда иметь
в виду, что диэлектрик любого конденсатора не является идеальным изо-
изолятором и, хотя бы очень слабо, проводит электричество Поэтому всякий
С2 Сх С2 С,
шг гчхг дихт
Рис 42 Эквивалентные схемы конденсаторов с утечками
реальный конденсатор имеет некоторую утечку зарядов и может быть изо-
изображен эквивалентной схемой (рис 42 а) в виде идеального конденсатора
72
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
ГЛ IV
С (без утечки) и параллельно присоединенного большого сопротивления г.
В случае параллельного соединения конденсаторов утечки не играют осо-
особой роли и напряжение на каждом конденсаторе будет равно по-прежнему
полному напряжению батареи. Не то, однако, будет при последовательном
соединении. Если конденсатор Сг (рис. 42 б) без утечки соединен последова-
последовательно с конденсатором С\, обладающим утечкой п, то с течением времени
конденсатор С\ будет разряжаться, и в конце концов на конденсаторе Сг
окажется полное напряжение батареи. В реальном случае обоих конденса-
конденсаторов с утечками (рис. 42 е) установившиеся напряжения будут зависеть не
от емкостей, а от утечек. На конденсаторе с меньшей утечкой будет большее
напряжение, и он может быть пробит. Поэтому последовательное соедине-
соединение конденсаторов не применяют при работе с постоянными напряжениями,
а используют его в цепях переменного тока.
§ 36. Сложные конденсаторы
До сих пор мы рассматривали лишь простые конденсаторы,
в которых все линии смещения, исходящие из одной обкладки,
заканчивались на другой обклад-
обкладке. Однако могут быть и более
сложные случаи, когда линии
смещения распределяются меж-
между несколькими проводниками
(рис. 43). Такую систему про-
проводников мы будем называть
сложным конденсатором.
В этом случае заряд какого-
либо из тел будет зависеть от
потенциалов всех проводников,
участвующих в образовании
Поле сложного конден- электрического поля. Этот заряд
можно найти следующим образом.
Рассмотрим проводник 1 (рис. 43)
и выделим на нем часть поверхности аб, которая соединяется
линиями смещения только с проводником 2. Заряд такого
участка равен qae — C^Uiz, где С^ — емкость участка аб
относительно тела 2, a TJ\i — напряжение между телами 1
и 2. Аналогично для другого участка поверхности бе имеем:
Чбв — Сбви\з и т.д. Поэтому полный заряд тела 1 будет равен
Рис. 43.
сатора
= Ca6Ul2
CeoUU-
C6.1)
Здесь через Un обозначено напряжение между проводником 1 и
тем телом, на котором заканчиваются линии смещения, идущие
с участка ва.
Вместо напряжений или разностей потенциалов между каж-
каждой парой проводников U12, C/13, ... мы можем ввести в C6.1)
потенциалы Ui, С/2, ¦ •• каждого из проводников (например, от-
§36
СЛОЖНЫЕ КОНДЕНСАТОРЫ
73
носительно бесконечности):
= Ui- U2,
Подставляя эти выражения в C6.1), получим для заряда q\
опять линейную функцию потенциалов всех проводников в виде
Cl2U2
C6.2)
И аналогично для зарядов других проводников имеем
C6.2а)
где i — номер проводника. Коэффициенты Сц- в этих формулах
имеют простой физический смысл. Из C6.2) видно, что Сц рав-
равно заряду проводника 1, когда его потенциал равен единице, а
потенциалы всех других проводников равны нулю; коэффици-
коэффициент Суг равен заряду на теле 1, когда потенциал тела 2 равен
единице, а потенциалы всех остальных тел (включая и тело 1)
равны нулю, и т.д. С^ зависят от формы и размеров рассма-
рассматриваемых проводников, от их взаимного расположения и от
свойств окружающей среды.
Систему уравнений C6.2а) можно разрешить относительно потенциа-
потенциалов Uk и выразить, наоборот, все потенциалы через полные заряды про-
проводников. Потенциалы проводников будут также линейными функциями
зарядов, и мы можем написать:
Uk — / PikQi- C6.3)
о
+
+
++
+
+
+
+
V
^ -
E
+
i
-
=
Можно показать, что коэффи-
коэффициенты С,к и р,к удовлетворяют
условиям симметрии
Cik = Скг, Ргк = Pki,
на чем, однако, мы не останавли-
останавливаемся.
Мы видим, что в ел у-
чае сложного конденсатора
Заряд любого из проводни- Рис. 44. Пример сложного конденса-
ков определяется потенциа- тора
лами всех проводников. По-
Поясним это на простом примере. Рассмотрим цилиндрический
конденсатор вблизи поверхности земли (заземленных предме-
предметов) (рис. 44). Мы имеем здесь три проводника: внешнюю об-
обкладку, внутреннюю обкладку и землю, и в правой части фор-
формулы C6.1) будут два члена. Обозначим через С емкость обеих
74 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ГЛ IV
обкладок, а через с — емкость внешней обкладки относитель-
относительно земли (емкостью стержня относительно земли пренебрегаем).
Если соединить внешнюю обкладку с землей, то U\3 = 0. Поэто-
Поэтому при заряжении конденсатора до напряжения U он накопит
заряд
gi = CU.
Если же соединить с землей внутреннюю обкладку, то Ui$ не
равно нулю и равно напряжению на конденсаторе U. Поэтому
при том же напряжении заряд конденсатора будет больше, чем
в первом случае, а именно
д2 = CU + cU.
§ 37. Энергия электрического поля
Мы видели, что заряженный конденсатор обладает опреде-
определенной энергией. Поэтому можно поставить вопрос о том, где
именно сосредоточена, локализована эта энергия. Можно, на-
например, предполагать, что энергия сосредоточена на обклад-
обкладках конденсатора, т.е. на электрических зарядах. Однако мож-
можно также допустить, что энергия конденсатора сосредоточена в
его электрическом поле, т.е. в пространстве между обкладками.
Только опыт, очевидно, может дать решение этого вопроса.
Пока мы рассматриваем постоянные электрические поля, та-
такой опыт невозможен, так как в этом случае мы всегда имеем
заряды, окруженные электрическим полем, и, наоборот, — элек-
электрические поля совместно с электрическими зарядами. Одна-
Однако интересующие нас опытные данные можно получить, рас-
рассматривая поля, переменные во времени. Ниже мы увидим
(гл. XXIII), что существуют электромагнитные волны, предста-
представляющие собой электрические и магнитные поля, изменяющиеся
во времени и распространяющиеся с определенной скоростью в
пространстве. Электрические поля в электромагнитных волнах
можно получить без электрических зарядов, первоначально по-
породивших эти поля (так же как и магнитные поля — без элек-
электрических токов, их поддерживающих). Опыт показывает, что
электромагнитные волны заключают в себе и переносят энер-
энергию, и эту энергию мы с успехом используем в радиотехнике
для целей связи и в других технических устройствах. Факт су-
существования электромагнитных волн позволяет ответить на по-
поставленный выше вопрос и заключить, что энергия сосредото-
сосредоточена в электрическом поле.
Учитывая этот результат, мы можем преобразовать выраже-
выражение C4.1) для энергии конденсатора таким образом, чтобы в
него входила характеристика поля — его напряженность.
§ 37 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 75
Рассмотрим сначала однородное поле и применим C4.1) к
плоскому конденсатору. Мы получим
Но U/d (ср. § 19) есть напряженность поля Е, a Sd — объем,
занимаемый полем. Мы видим, что энергия однородного поля
пропорциональна объему, занимаемому полем. Поэтому целесо-
целесообразно говорить об энергии каждой единицы объема, или об
объемной плотности энергии электрического поля. Она равна
u = \eeQE2. C7.1)
При получении формул C4.1) и C7.1) мы предполагали, что
емкость конденсатора, а значит, и диэлектрическая проницае-
проницаемость постоянны. При этом мы считали, что вся внешняя работа
(источника тока) превращается в энергию электрического поля.
Это совершенно точно для вакуума, и поэтому формула C7.1)
при е = 1 выражает объемную плотность энергии электрическо-
электрического поля в вакууме. В диэлектриках, вообще говоря, это не так.
При создании электрического поля диэлектрики могут нагре-
нагреваться. Их объем и плотность в электрическом поле, даже при
неизменной температуре, могут изменяться (вследствие явления
электрострикции § 45). Диэлектрическая же проницаемость за-
зависит от температуры и плотности вещества и не остается по-
постоянной. Кроме того, внешняя работа источника тока может
не целиком переходить в энергию поля. Поэтому в общем слу-
случае формула C7.1) не точна.
В дальнейшем мы будем считать, что объем г среды и ее
плотность остаются постоянными (не изменяются в электриче-
электрическом поле или поддерживаются неизменными).
Формула C4.1) выражает точно внешнюю работу (источни-
(источника тока) Л, если температуру диэлектрика, а следовательно и е,
поддерживать постоянной. Эта работа расходуется на увеличе-
увеличение энергии поля W и на выделение тепла Q, которое нужно от-
отводить от диэлектрика (или подводить к нему, тогда оно войдет
со знаком минус) для поддержания неизменной температуры:
А = W + Q. C7.2)
Но из термодинамики известно, что работа внешних сил, со-
совершаемая над системой при квазистатическом изотермическом
процессе, равна приращению функции состояния системы, на-
называемой свободной энергией. Поэтому формула C7.1) выража-
выражает не внутреннюю энергию электрического поля в диэлектри-
диэлектрике, а слагаемое в свободной энергии диэлектрика, зависящее от
электрического поля, являющееся мерой внешней работы при
изотермическом изменении электрического поля.
76 ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ГЛ. IV
Если диэлектрическую проницаемость при постоянном объ-
объеме т можно считать не зависящей от температуры: (ds/дТ) =
— О, то е = const при Q = 0, и формула C7.1) опять дает объ-
объемную плотность энергии электрического поля. В этом случае
электрические части свободной энергии и внутренней энергии
диэлектрика совпадают друг с другом.
В дальнейшем мы будем предполагать, что тепло Q в фор-
формуле C7.2) мало по сравнению с энергией поля W и, если не
оговорено обратное, будем считать внешнюю работу при созда-
создании электрического поля в диэлектрике равной энергии этого
поля.
При выводе формулы C7.1) было сделано также предполо-
предположение, что электрическое смещение D = eeqE> есть линейная
функция напряженности поля Е (е = const). Между тем для
некоторых веществ зависимость D от Е, даже при постоянной
температуре, оказывается более сложной. Нетрудно обобщить
полученные результаты на случай нелинейной зависимости D
от Е. Для этого учтем, что поверхностная плотность заряда а
на проводниках (обкладках) равна нормальной составляющей
вектора электрической индукции Dn (§ 13, пример 2; см. также
§ 41). Поэтому, рассуждая, как и выше (§ 34) в случае однородно-
однородного электрического поля, мы получим для приращения внешней
работы при зарядке конденсатора
6 А = udq = uSdDn.
Здесь и = Ed, a Sd = т есть объем поля. Следовательно,
5 А - Ed • SdDn = т(Е <Ш).
Полная работа при создании электрического поля в диэлектрике
равна
A = rf(EdD). C7.3)
Смещение D зависит не только от электрического поля Е,
но еще и от температуры тела и его плотности. Поэтому функ-
функция D(E), а значит, и работа А зависят от условий создания
электрического поля и различны для теплоизолированного тела,
поддерживаемого при постоянной температуре, и т.д. В случае
изотермического процесса формула C7.3) дает общее выраже-
выражение для приращения свободной энергии тела в электрическом
поле.
Если выделяющимся теплом (и внешней работой при изме-
изменении объема тела) можно пренебречь по сравнению с энергией
поля, то вся внешняя работа А превращается в энергию поля.
Из формулы C7.3) следует, что в этом случае объемная плот-
плотность энергии электрического поля равна
и= J(EcflD). C7.4)
§ 38
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
77
При исчезновении электрического поля (разряде конденса-
конденсатора) эта энергия выделяется во внешней цепи. Для линейной
связи D = ееоЕ (формула C7.4) переходит в формулу C7.1)).
Если электрическое поле неоднородно, то его можно разбить
на элементарные объемы dr и считать, что в пределах бесконеч-
бесконечно малого объема это поле однородно. Полная энергия электри-
электрического поля равна
W = fudr, C7.5)
т
где и выражается формулой C7.4), а интегрирование произво-
производится по всему объему т электрического поля.
Отметим в заключение, что при наличии диэлектрического
гистерезиса (сегнетоэлектрики, см. § 50) внешняя работа при со-
создании электрического поля по-прежнему определяется форму-
формулой C7.3). Однако в этом случае внешняя работа уже не равна
приращению энергии поля, так как ее заметная часть превра-
превращается в тепло (ср. § 111). Поэтому и формула C7.4) уже не
выражает объемную плотность энергии поля.
ГЛАВА V
ДИЭЛЕКТРИКИ
§ 38. Поляризация диэлектриков
При внесении в электрическое поле каких-либо диэлектриков
электрическое поле изменяется. В настоящей главе мы рассмо-
рассмотрим, как оно изменяется в присут- _-,
сугвии диэлектриков и в чем заключа- [+• ±';± '1yt\
ются причины его изменения.
Для выяснения этого вопроса обра-
обратимся к опытам. Зарядим электрометр
и отметим его показание. Приблизим к
электрометру какое-либо незаряженное
диэлектрическое тело, например тол-
толстую стеклянную пластину (рис. 45).
Мы увидим, что показания электромет-
электрометра уменьшаются, когда пластина на-
находится вблизи электрометра, и вновь Рис- 45-
восстанавливаются при удалении пла-
пластины.
Если бы вместо диэлектрика мы
приближали к электрометру проводник, то мы наблюдали бы
подобное же явление. Но мы знаем, что на проводнике возника-
При поднесении
незаряженного диэлектри-
диэлектрика показания электрометра
уменьшаются
78
ДИЭЛЕКТРИКИ
ГЛ V
ют индукционные заряды, которые и изменяют электрическое
поле Отсюда можно заключить, что на диэлектрике в электри-
электрическом поле также возникают заряды, на ближайшей к телу ча-
части диэлектрика появляются заряды, разноименные с зарядом
влияющего тела, а на удаленной ча-
части диэлектрика — одноименные за-
заряды (рис 45)
Появление зарядов на диэлектри-
диэлектриках ведет к возникновению сил,
действующих на диэлектрики, даже
если они первоначально были неза-
незаряженными Подвесим на тонкой ни-
нити стеклянную или парафиновую па-
палочку (рис 46) и приблизим к ней
Рис 46 Диэлектрическая па- заряженный шар Палочка начнет
лочка в электрическом поле поворачиваться и установится сво-
поворачивается и устанавли- ^ J „
вается вдоль линий напряжен- еи осью ВДОЛЬ линии напряженно-
ности поля сти п°ля, т е таким образом, что ее
ось окажется направленной к центру
шара Это свидетельствует опять о том, что на ближайшей к ша-
шару части палочки появляются заряды, разноименные с зарядом
шара, а на удаленной части — одноименные
Подобные силы можно наблюдать и в таком опыте Укрепим
неподвижно две изолированные металлические пластины плос-
плоского конденсатора Подвесим на одном
конце коромысла весов стеклянную
пластину, поместив ее между обклад-
обкладками конденсатора без соприкоснове-
соприкосновения с ними так, чтобы она заполняла
только часть пространства конденса-
конденсатора, и уравновесим весы Создадим
теперь между обкладками конденса-
конденсатора электрическое поле, соединив их
с источником напряжения в несколь-
несколько тысяч вольт Мы увидим, что стек-
стеклянная пластина начнет втягиваться в
электрическое поле, и равновесие весов
нарушится Причину появления сил,
действующих на стеклянную пласти-
пластину, разъясняет рис 47 На стеклянной
пластине в электрическом поле появ-
появляются заряды В области неоднород-
неоднородного поля (вблизи краев обкладок) на-
напряженность поля конденсатора Е имеет составляющую Ej,
параллельную обкладкам а и б, и поэтому на стеклянную плас-
пластину действуют силы F, втягивающие ее внутрь конденсатора
Рис 47 Пластина диэлек-
диэлектрика втягивается в элек-
электрическое поле
§38
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
79
Рассмотрим в заключение еще один поучительный опыт Соединим по-
последовательно плоский конденсатор, источник напряжения Б и чувстви-
чувствительный гальванометр (рис 48) Если изо-
изоляция конденсатора достаточно хороша, то
гальванометр не покажет никакого тоха Бы-
Быстро вдвинем теперь в конденсатор стеклян-
стеклянную пластину Мы заметим, что при вдвигании
диэлектрика гальванометр показывает кратко-
кратковременный ток, который исчезает, как только
пластина перестает перемещаться При выдви-
выдвигании пластины в цепи появляется ток обрат-
обратного направления
Возникновение тока в этом опыте опять
свидетельствует о появлении зарядов на диэлек-
диэлектрике Эти заряды частично компенсируют
действие зарядов на обкладках Чтобы напря-
напряжение между обкладками осталось неизмен-
неизменным (конденсатор подключен к источнику),
на пластины должны перейти с источника
дополнительные заряды, равные зарядам на
диэлектрике, и поэтому в цепи возникает ток
При выдвигании диэлектрика эти дополни-
дополнительные заряды уходят снова в источник и
в цепи появляется ток обратного направления
Рис 48 При вдвигании
диэлектрической пласти-
пластины в конденсатор в цепи
возникает электрический
ток
Приведенные опыты показывают, что на первоначально неза-
незаряженных диэлектриках в электрическом поле возникают элек-
электрические заряды На диэлектрике появляются электрические
полюсы, отчего и самое явление получило название поляризации
диэлектриков Заряды, возникающие на диэлектриках в электри-
электрическом поле, мы будем называть поляризационными зарядами
Явление поляризации диэлектриков имеет сходство с индук-
индукцией в проводниках Однако между обоими явлениями имеется и
важное различие Разъединяя в электрическом поле проводник
на части, можно отделить друг от друга индукционные заряды,
и поэтому после исчезновения поля разъединенные части про-
проводника остаются заряженными Разъединяя же в электриче-
электрическом поле диэлектрики, мы найдем, что после устранения поля
каждая часть диэлектрика остается по-прежнему незаряженной
Отделить друг от друга поляризационные заряды невозможно
Это различие объясняется тем, что в металлах отрицатель-
отрицательный заряд существует в подвижном состоянии в виде электронов
проводимости, которые могут перемещаться на значительные
расстояния Поэтому индукционные заряды в металлах можно
отделить друг от друга В диэлектриках же заряды обоих зна-
знаков связаны друг с другом и могут только смещаться на малые
расстояния в пределах одной молекулы
Неполяризованный диэлектрик (в отсутствие электрического
поля) можно схематически изобразить в виде собрания молекул,
80
ДИЭЛЕКТРИКИ
ГЛ V
в каждой из которых равные положительные и отрицательные
заряды распределены равномерно по всему объему молекулы
(рис. 49 а). При поляризации диэлектрика заряды в каждой мо-
ооооо
ооооо
ооооо
о
э
э
о
о
о
о
о
о
о
э
о
8fiS$$S888&5&§&b
6/ ',
Рис. 49. Модель непсшяризованного (а) и поляризованного (б) диэлектрика
лекуле смещаются в противоположные стороны, и на одном кон-
конце молекулы появляется положительный заряд, а на другом —
отрицательный (рис. 49 <з). При этом каждая молекула превра-
превращается в электрический диполь.
Смещение зарядов внутри молекул будет проявляться как
возникновение некоторых зарядов на диэлектрике. Действи-
Действительно, неполяризованный диэлек-
диэлектрик можно представить как два
тождественных объема, совпада-
совпадающих друг с другом, каждый из
которых равномерно заполнен по-
положительным или отрицательным
зарядом (рис. 50 а). Поляризацию
диэлектрика можно рассматривать
как смещение этих объемов на ма-
малое расстояние в противоположные
Рис 50 Поляризация диэлек- стороны (рис. 50 6). При этом вну-
трика как смещение зарядов: ТРИ Диэлектрика по-прежнему коли-
а - неполяризованный, б - по- чество положительного заряда будет
ляризованный диэлектрик равно количеству отрицательного,
но на одном из концов диэлектрика
возникнет тонкий слой с некомпенсированным положительным
зарядом, а на другом появится некомпенсированный отрица-
отрицательный заряд, т.е. возникнут поляризационные заряды.
§ 39. Поляризованность 1)
При поляризации диэлектрика каждая его молекула превра-
превращается в электрический диполь и, следовательно, приобретает
определенный электрический момент (§ 15), равный
х) Прежнее наименование этой физической величины — вектор поляри-
поляризации {Примеч. ред.)
§ 39 ПОЛЯРИЗОВАННОСТЬ 81
При этом, как и прежде, вектор смещения 1 считается направ-
направленным от отрицательного заряда к положительному.
Для количественной характеристики поляризации диэлек-
диэлектрика служит специальная физическая величина, называемая
поляризованностъю. Поляризованностью диэлектрика называ-
называют электрический момент единицы объема диэлектрика. Он
равен векторной сумме электрических моментов всех молекул,
заключенных в единице объема:
Р = -Х)Р»- C9Д)
Если диэлектрик однороден и смещение зарядов 1 одинаково
во всех точках, то и вектор Р будет одинаков по всему диэлек-
диэлектрику. Такую поляризацию называют однородной.
Зная поляризованность Р,
можно определить поляризаци-
поляризационные заряды, и наоборот. Будем
считать поляризацию однородной
и рассмотрим в электрическом
поле кусок диэлектрика в виде на- (-• *-\ Р„
клонной призмы с основанием S и
ребром L, параллельным вектору Рис 51 К определению поля-
Р (рис. 51). На одном из оснований ризованности Р
призмы появятся отрицательные
поляризационные заряды с поверхностной плотностью —а', а на
другом — положительные заряды с плотностью +<т', и призма
приобретет электрический момент
р = a'SL.
Если а — угол между направлением нормали к основанию приз-
призмы и вектором Р, то объем призмы т равен
т = SL cos a,
и поэтому
а'т
COS Q '
Но, с другой стороны, эту же величину можно выразить через
электрический момент единицы объема:
р = Рт.
Сравнивая оба последних равенства, мы находим соотношение
c/ = Pcosa = Pn. C9.2)
В этой формуле Рп обозначает проекцию вектора Р на направ-
направление внешней нормали к рассматриваемой поверхности. Для
правой грани призмы на рис. 51 угол а острый (cos a > 0) и а'
положительно. Для левой грани угол а тупой (cos a < 0) и а'
отрицательно.
82
ДИЭЛЕКТРИКИ
ГЛ V
Полученный результат показывает, что поверхностная плот-
плотность поляризационных зарядов равна нормальной составляю-
составляющей поляризованности в данной точке поверхности. Он также
означает, что электрический заряд, прошедший через единицу
поверхности, перпендикулярной к направлению смещения заря-
зарядов, равен модулю поляризованности.
Если вектор Р различен в разных точках (неоднородная по-
поляризация), то в диэлектрике могут возникнуть еще объемные
заряды.
Объемные поляризационные заряды можно найти следующим образом.
Рассмотрим внутри поляризованного диэлектрика бесконечно малый па-
параллелепипед с ребрами dx, dy и dz, параллельными прямоугольным осям
координат X,Y и Z Пусть, далее, поляризо-
ванность имеет в точке (x,y,z), где находит-
находится одна из вершин параллелепипеда, состав-
составляющие по осям Рх, Ру, Pz (рис 52). Тогда,
согласно C9 2), положительный заряд, выхо-
выходящий из параллелепипеда через заштрихо-
заштрихованную грань, равен
dydz.
Положительный заряд, входящий в паралле-
Рис 52 К определению лепипед через другую параллельную грань,
объемных поляризационных есть
зарядов Pxdydz
Поэтому приращение положительного заряда равно
где dr — dx dy dz — объем параллелепипеда Рассматривая подобным обра-
образом две другие пары граней, перпендикулярные к осям Y и Z, мы найдем,
что полный положительный заряд, вошедший внутрь параллелепипеда при
поляризации, дается выражением
(эрх дру дРЛ
\ ах ду dz )
С другой стороны, тот же заряд равен р dr, где р — объемная плотность
искомых поляризационных зарядов Поэтому
-Р =
дРх
дх ду
дРг
dz
C9.3)
Если поляризация однородна, то Р = const и C9 3) дает р = 0. Заме-
Заметим, что в некоторых случаях и при неоднородной поляризации выражение
C9.3) также может обращаться в нуль (ср. § 44)
§40 НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ 83
§ 40. Напряженность электрического поля внутри
диэлектрика
В гл. II мы определили напряженность электрического поля в
вакууме как силу, действующую на единичный положительный
пробный заряд. При переходе к диэлектрикам это определение
требует дополнительного уточнения.
Представим себе, что размеры пробного заряда малы по
сравнению с расстояниями между молекулами диэлектрика. То-
Тогда мы найдем, что электрическое поле внутри диэлектрика
весьма различно в разных точках и достигает особенно больших
значений вблизи заряженных концов молекул — диполей. Эти
изменения поля происходят лишь в микроскопических масшта-
масштабах и недоступны непосредственному наблюдению. Определен-
Определенное подобным образом поле носит название микроскопического
поля (Ем).
Однако во всех реальных опытах мы имеем дело с телами
(или частями этих тел), размеры которых велики по сравне-
сравнению с межатомными расстояниями. В таких случаях нас инте-
интересует усредненное по объему значение микроскопического поля
Ем, т.е. макроскопическое поле. Это среднее значение напря-
напряженности электрического поля и называют напряженностью
электрического поля внутри диэлектрика. Таким образом, по
определению
! fMdr. D0.1)
Отметим, что объем т в этой формуле должен быть велик
микроскопически, те в нем должно содержаться большое число
молекул. Однако он должен быть достаточно мал макроскопи-
макроскопически, т.е на протяжении его размеров макроскопическое значе-
значение поля должно оставаться практически неизменным. Подоб-
йые малые объемы, удовлетворяющие обоим этим требованиям,
называются физически бесконечно малыми (в отличие от мате-
математически бесконечно малых).
Совершенно аналогично потенциалом внутри диэлектрика
называют макроскопический потенциал, т.е. среднее его значе-
значение по некоторому физически малому объему. Макроскопиче-
Макроскопические значения поля Е и потенциала U связаны теми же соотно-
соотношениями, что и в вакууме. В случае плоского конденсатора мы
имеем
Е = U/a, D0.2)
где U — разность потенциалов между обкладками, а — расстоя-
расстояние между ними.
Рассмотрим плоский конденсатор (однородное поле), цели-
целиком заполненный однородным диэлектриком. Напряженность
84
ДИЭЛЕКТРИКИ
ГЛ. V
поля Е внутри диэлектрика есть сумма двух полей: поля
созданного зарядами на металлических обкладках, и поля Е',
вызванного поляризованным диэлектриком (рис. 53). Поле Eq
равно ст/ео, гДе <? — поверхностная
" Ёо ~^ - плотность заряда на металлических
с обкладках. Действие же поляри-
поляризованного диэлектрика можно вы-
выразить через поляризационные за-
заряды (§ 39), возникающие на его
поверхности. Поэтому Е' = —cf'/cq,
где а' — поверхностная плотность
поляризационных зарядов. Следо-
Следовательно,
Е = (а- а')/е0.
Напряженность поля
диэлектрика совпадает с
Е-
Рис. 53. Напряженность элек-
электрического поля Е внутри ди-
диэлектрика есть разность меж-
между полем Ео зарядов обкладок
и полем Е' поляризационных
зарядов
внутри
напря-
напряженностью поля в вакууме, когда
поверхностная плотность заряда
на обкладках конденсатора равна
(ст — а'). Эту разность между зарядом обкладок и поляризаци-
поляризационным зарядом часто называют свободным зарядом.
В связи со сказанным выше необходимо особо отметить, что
сила, действующая на макроскопическое тело с зарядом q, по-
погруженное в диэлектрик, в общем случае уже не равна qE, как
это имело место в вакууме.
Действительно, рассмотрим сначала твердый диэлектрик.
Чтобы внести в него заряженное тело, мы должны сделать в
нем полость. Но на ее поверхности будут возникать поляриза-
поляризационные заряды, и поэтому сила, действующая на тело, будет
зависеть от формы полости.
В случае жидких и газообразных диэлектриков это также
справедливо, так как при внесении заряженного тела мы вы-
вытесняем телом часть среды и создаем в нем тоже «полость»,
совпадающую по форме с заряженным телом. Однако в случае
жидкостей и газов на тело будет действовать еще дополнитель-
дополнительная механическая сила, вызванная деформацией диэлектрика в
электрическом поле (электрострикция, см. § 45).
Тем не менее напряженность поля внутри диэлектрика мож-
можно определить и с помощью силы, действующей на пробный за-
заряд. Для этого представим себе узкую длинную щель, прорезан-
прорезанную внутри диэлектрика параллельно направлению смещения
зарядов (рис. 54), и будем считать, что пробный заряд не каса-
касается стенок полости. Поляризационные заряды будут возникать
только на торцах полости, и если ее диаметр мал по сравне-
сравнению с длиной, то и поле, создаваемое этими зарядами, будет
§41
ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ В ДИЭЛЕКТРИКЕ
85
+c
Рис. 54. К определению на-
напряженности электрическо-
электрического поля внутри диэлектрика
пренебрежимо мало. Поэтому внутри полости будет напряжен-
напряженность поля, создаваемая только свободными зарядами (а — а') у
внешней поверхности диэлектрика, а
это, как мы видели, и есть напряжен-
напряженность поля внутри диэлектрика. На-
Напряженность поля внутри диэлектри-
диэлектрика равна напряженности поля внутри
узкой полости, вырезанной в диэлек-
диэлектрике параллельно направлению сме-
смещения зарядов. Она равна силе, дей-
действующей на заряд +1 внутри этой
полости.
Для практического определения
напряженности поля внутри диэлек-
диэлектрика достаточно измерить напряже-
напряжение между обкладками конденсатора.
Тогда для плоского конденсатора напряженность поля можно
найти по формуле D0.2), а для конденсаторов другой формы —
по соответствующим формулам, полученным нами ранее для ва-
вакуума.
§ 41. Электрическое смещение в диэлектрике
Рассмотрим теперь границу двух однородных и однородно
поляризованных диэлектриков 1 и 2 (рис. 55). В каждом из
диэлектриков вблизи поверхности раздела появятся поляриза-
поляризационные заряды с плотностями а[ и а2, которые будут иметь
противоположные знаки. Грани-
Граница раздела окажется заряженной
с поверхностной плотностью за-
¦ ' ряда а1 — о2, отчего появится до-
, полнительное электрическое поле
'' (а[ — а'2)/2е$) перпендикулярное
к границе раздела и направ-
направленное в каждом из диэлектри-
диэлектриков в противоположные стороны
Рис. 55. Поляризационные заря- (рис. 55).
ды на границе двух диэлектриков иоозначим напряженность
и создаваемое ими электрическое полного поля в каждом из ди-
диполе электриков через Ei и ~Е2 и
разложим каждое из этих полей
на две составляющие: касательную к границе раздела (Ец и
Et2) и нормальную к границе (Еп\ и Еп2). Нормаль будем
считать направленной от диэлектрика 1 к диэлектрику 2. Так
как электрическое поле зарядов поверхности раздела перпен-
перпендикулярно к этой поверхности, то касательные составляющие
86 ДИЭЛЕКТРИКИ ГЛ V
поля не изменятся и их значение в обоих диэлектриках будет
одинаково:
Еп = Et2. D1.1)
Напротив, нормальные составляющие поля будут различны; их
разность равна
ЕП2 - ЕпХ = {а[ - а'2)/е0 = {Рщ - Рп2)/ео,
где Рп\ и РП2 — нормальные составляющие поляризованности в
каждом из диэлектриков. Но, согласно § 13, нормальная состав-
составляющая напряженности поля есть поток линий напряженности
через единицу поверхности. Поэтому число линий напряженно-
напряженности, проходящих через единицу поверхности раздела, в диэлек-
диэлектриках 1 и 2 не равно друг другу, а значит часть линий преры-
прерывается на границе раздела
Если на поверхности раздела кроме поляризационных заря-
зарядов имеется заряд с поверхностной плотностью а, то вместо пре-
предыдущего соотношения имеем
ЕП2 - Еп1 = {Рп1 - Рп2)/е0 + ст/е0.
В § 13 мы ввели электрическое смещение в вакууме ?оЕ.
Обобщим теперь это понятие на случай произвольного диэлек-
диэлектрика и определим электрическое смещение в диэлектрике как
D=?0E + P. D1.2)
Тогда из сказанного выше следует, что
Аг2 - Ai = сг-
В случае заряженной поверхности раздела нормальная состав-
составляющая электрического смещения испытывает скачок, равный а.
Если вместо диэлектрика 1 имеется металл, то
Dnl = 0 и Dn = a, D1.3)
где индекс 2 у Dn опущен. Нормальная составляющая электри-
электрического смещения в диэлектрике у поверхности металла в отсут-
отсутствие тока равна поверхностной плотности заряда металла. Этот
результат мы уже получили в § 13 для поверхности металла в
вакууме.
Для незаряженных диэлектриков (о = 0) нормальные к гра-
границе раздела составляющие электрического смещения непре-
непрерывны:
Аи = Dn2. D1.4)
Так как Dn\ равно числу линий смещения, пересекающих
единицу поверхности раздела в диэлектрике 1, a Dn2 — числу
линий смещения для той же площадки в диэлектрике 2, то из
D1.4) следует, что линии электрического смещения не преры-
прерываются на границе раздела диэлектриков. Поэтому для описа-
описания электрического поля в неоднородных диэлектриках гораз-
гораздо удобнее пользоваться электрическим смещением D вместо
§41
ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ В ДИЭЛЕКТРИКЕ
87
напряженности поля Е, и в этом заключается основной смысл
введения электрического смещения.
Легко показать, что линии электрического смещения остаются непре-
непрерывными и при неоднородной поляризации, когда в диэлектрике возникают
объемные поляризационные заряды Действительно, согласно C9 3), объем-
объемная плотность зарядов в диэлектрике равна
, (дРХ ЭРу
р - - \~дх~ + ~ду~
Поэтому по теореме Остроградского-Таусса
дР
?о
(дЕх дЕу дЕЛ _ (дР^
\ дх + ду + dz ) - \ дх
или
А)+ ?
эр
{e0Ez+Pz) = i
Но полученный результат показывает, что поток вектора D = еоЕ + Р че-
через замкнутую поверхность равен нулю, а это значит, что линии смещения
нигде не возникают и не обрываются внутри диэлектрика
Рассмотрим опять плоский конденсатор, заполненный одно-
однородным диэлектриком (рис 53) Тогда, согласно § 40, напряжен-
напряженность поля внутри диэлектрика равна
Следовательно,
D = е0Е + Р = ?0Е0, D1.5)
т.е. в случае однородного диэлектрика электрическое смещение
внутри диэлектрика совпадает с электрическим смещением в ва-
вакууме, создаваемым одними зарядами
обкладок конденсатора. Если q — заряд
обкладок конденсатора, S — площадь
каждой обкладки, то
D = а = q/S. D1.6)
Из этой формулы вытекает практи-
практический способ измерения D. Чтобы из-
измерить электрическое смещение внутри
диэлектрика, достаточно измерить за-
заряд на обкладках, ограничивающих ди-
диэлектрик.
Определение электрического смеще-
смещения можно представить и в другой фор-
форме. Рассмотрим в однородном диэлек-
диэлектрике узкую длинную щель, вырезанную перпендикулярно к на-
направлению смещения зарядов (рис. 56). Тогда, согласно формуле
D1.4), электрическое смещение внутри щели будет такое же, как
и внутри диэлектрика. Поэтому электрическое смещение вну-
внутри диэлектрика равно электрическому смещению внутри узкой
Рис 56 К определению
электрического смещения
внутри диэлектрика
ДИЭЛЕКТРИКИ ГЛ. V
длинной полости, вырезанной в диэлектрике перпендикулярно
к направлению смещения зарядов. Сила, действующая на заряд
+1 в этой полости, равна D/
§ 42. Изотропные и анизотропные диэлектрики
Если измерять электрическое смещение в стеклянных пла-
пластинках, вырезанных различным образом из массивного куска,
то при одинаковом значении поля Е электрическое смещение во
всех пластинках оказывается одинаковым. Согласно D1.2) это
значит, что и поляризованность Р одна и та же во всех пластин-
пластинках, а следовательно, поляризация не зависит от направления
поля. Такие диэлектрики называются изотропными. В изотроп-
изотропных диэлектриках смещение зарядов происходит в направлении
электрического поля, и поэтому векторы Е и Р параллельны.
Для многих кристаллов это, однако, не имеет места. Если
исследовать электрическое смещение в пластинках, вырезанных
различным образом из таких кристаллов, то D при одном и том
же поле Е будет различно. Это показывает, что диэлектрические
свойства зависят от направления поля относительно осей кри-
кристалла. Подобные диэлектрики называются анизотропными. В
анизотропных диэлектриках направления Е и Р, вообще говоря,
не совпадают, и поэтому направления Е и D также различны.
Опыт показывает, что в широком интервале изменения
электрического поля поляризованность можно считать пропор-
пропорциональной напряженности поля Е в данной точке. Поэтому для
изотропного диэлектрика можно написать
P = Q?oE, D2.1)
где а — скалярная величина, получившая название диэлектри-
диэлектрической восприимчивости данного вещества. В эту формулу мы
вводим ?о, чтобы а было безразмерным.
Подставляя D2.1) в D1.2), получаем
D = ееоЕ, D2.2)
где через е обозначено:
? = 1 + а. D2.3)
Легко видеть, что определяемая таким образом величина е
есть диэлектрическая проницаемость вещества (относительная),
которую мы уже ввели в § 31, рассматривая зависимость емко-
емкости конденсатора от свойств диэлектрика. Действительно, поло-
положим для определенности, что при заполнении конденсатора ди-
диэлектриком конденсатор остается присоединенным к источнику
напряжения. Это значит, что напряжение между обкладками, а
следовательно, и напряженность поля в конденсаторе не изменя-
изменяются. Тогда из формулы D2.2) следует, что электрическое сме-
§ 43 ПРЕЛОМЛЕНИЕ ЛИНИЙ СМЕЩЕНИЯ И НАПРЯЖЕННОСТИ ПОЛЯ 89
щение внутри конденсатора увеличивается в е раз. Но, согласно
формуле D1.6), это значит, что во столько же раз увеличится и
заряд обкладок, а следовательно, и емкость конденсатора
В анизотропных средах (кристаллах) линейная зависимость D от Е
имеет вид
Dv = SyxSoEx + EyyEo-Ej, 4- EyZEQEz, D2.4)
Dz = EzxEqEx + EzyEoEy + SzzEoEz,
или, в сокращенной записи,
Ог-'^ЕгкЕйЕк, i,k = x,y,z. D2.5)
к
Девять величин ?гк образуют компоненты тензора диэлектрической прони-
проницаемости 2-го ранга. Этот тензор симметричен: etk = ?ь, а поэтому имеется
только шесть независимых компонент.
Из математики известно, что для всякого симметричного тензора
2-го ранга можно выбрать такие оси координат (главные оси тензора), что-
чтобы недиагональные компоненты со смешанными индексами обратились в
нуль. В этом случае остаются только три независимых значения тензора:
?xx=?i, e»»=?2, ?zz=E3, называемые главными диэлектрическими проница-
емостями кристалла. Если ?\ = ег = ?з, то направления D и Е совпадают
и кристалл ведет себя как изотропная среда.
В очень сильных электрических полях соотношения D2.4) нарушаются
и связи между Р и Е и соответственно D и Е становятся нелинейными.
Такие поля существуют в излучении так называемых оптических кванто-
квантовых генераторов, или лазеров. Нелинейная зависимость D от Е существенна
для явлений нелинейной оптики. Линейная зависимость D от Е нарушается
также в сравнительно слабых электрических полях в веществах с большой
поляризуемостью, например в сегнетоэлектриках (§ 50).
§ 43. Преломление линий смещения и напряженности
поля
Соотношения D1.1) и D1.4) выполняются всегда на границе
раздела двух сред и представляют собой граничные условия для
электрического поля. Из них сле-
следует, что направления линий сме- Dn
щения и напряженности поля изме-
изменяются при переходе через границу
раздела.
Пусть Dnx и Оц — составляю-
составляющие электрического смещения Di
по нормали к поверхности раздела и !
вдоль нее в диэлектрике 1 (рис. 57),
а Dn2 и Dt2 — составляющие смеще-
смещения D2 в диэлектрике 2. Обозначим рис. 57. Преломление линий
через Q2 угол между вектором D2 в смещения на границе двух ди-
Диэлектрике 2 и нормалью к грани- электриков
90 ДИЭЛЕКТРИКИ ГЛ V
це раздела, а через а.\ — соответствующий угол для вектора Di
в диэлектрике 1. Из рис 57 видно, что
tg «1 = Da /Dni, tg q2 = Dt2 /Dn2
Ho Dn\ — Dn2, и поэтому
tga2/tgai = Dt2jDn.
Далее, из D2.2) и граничного условия D1.1) имеем
Dt2 = e2e0Et2, Dn = eie0Etl, Etx = Et2.
Отсюда получаем окончательно
tgQ2/tgQl =tijt\. D3.1)
Эта формула выражает закон преломления линий смещения
Она показывает, что, входя в диэлектрик с большей диэлектри-
диэлектрической проницаемостью е, линии смещения удаляются от нор-
нормали
Закон преломления линий напряженности поля в изотроп-
изотропных диэлектриках, очевидно, такой же, как и закон преломления
линий смещения, поскольку в
каждом из диэлектриков на-
направления D и Е совпадают.
Однако картины линий
смещения и линий напря-
напряженности будут все же раз-
различны. Различие заключает-
заключается в том, что линии смещения
непрерывны, в то время как
часть линий напряженности
Рис 58 Линии смещения (а) и линии прерывается на границе раз-
напряженности (б) в пластине диэлек- дела (§ 41) На рис 58 по-
тРика казаны в качестве примера
линии смещения и линии напряженности в диэлектрической
пластинке
При этом предполагается, что длина и ширина пластинки
очень велики, так что искажения поля, вносимые краями пла-
пластинки, не сказываются в рассматриваемой части пластинки В
соответствии с D2 2) густота линий напряженности внутри пла-
пластинки меньше, чем вне пластинки Отметим еще, что линии
смещения внутри пластинки вследствие преломления сгущают-
сгущаются, что указывает на увеличение смещения D в пластинке
§ 44. Законы электрического поля в диэлектриках
Основным законом в электростатике является закон Кулона
Поэтому прежде всего рассмотрим, как изменится этот закон
Пусть в однородном изотропном диэлектрике с диэлектриче-
диэлектрической проницаемостью е находится точечный заряд +q, который
§44
ЗАКОНЫ ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКАХ
91
мы будем представлять себе в виде равномерно заряженного ша-
шара (рис 59) Вычислим напряженность поля на расстоянии г от
центра шара На границе диэлектрика, прилегающей к шару, по-
появится отрицательный поляризационный заряд с поверхностной
плотностью —а', которая, согласно
сказанному в § 42, равна
о' — аеоЕ(а) = (е - 1)еоЕ(а).
Здесь Е(а) — напряженность поля в
диэлектрике на расстоянии а от цен-
центра шара, а — радиус шара. Поэтому
полный поляризационный заряд ра-
равен v-~———*- '
q1 = 4тга2сг' = 4тга2?0(? - 1)Е(а). Рис 59 К определению на-
Из симметрии задачи ясно, что ли- пряженности поля точечного
нии напряженности могут быть толь- заРяДа в диэлектрике
ко радиальными прямыми, густота которых обратно пропорцио-
пропорциональна квадрату расстояния от заряда, а значит,
Е{а)/Е(г) = г2/а2.
Поэтому
д' = 4тгг2?о(? - 1)Е(г)
Напряженность поля в точке г равна напряженности поля,
создаваемого свободным зарядом (q — q') в вакууме Следова-
Следовательно,
тп/ \ 1 Q - </ 1
^ ( ч-ч
J~Jy' ' 4тгео г2 4тг?о
Выражая отсюда Е(г), находим
Е(г) =
i - (е - 1)Е(г).
_q_ =ЁШ D41)
4тгео? г2 ? v '
где через Ео(г) обозначена напряженность поля, создаваемая
точечным зарядом в вакууме
Полученная формула выражает закон Кулона для диэлек-
диэлектриков. Она показывает, что напряженность поля точечного за-
заряда в однородном диэлектрике уменьшается в е раз по срав-
сравнению с его значением в вакууме Мы видим, что физическая
причина этого заключается в появлении поляризационных за-
зарядов в диэлектрике, уменьшающих электрическое поле.
Однако если бы мы, желая получить силу взаимодействия
двух точечных зарядов, разделили выражение B 1) на ?, то мы
получили бы в общем случае неверный результат, так как сила
может зависеть от формы полости, где находится пробный заряд
(ср. § 40)
92
ДИЭЛЕКТРИКИ
ГЛ V
При выводе формулы D4 1) мы считали, что объемных поляризаци-
поляризационных зарядов нет Легко убедиться, что в случае радиального поля это
действительно так Мы имеем
Р =
D
Так как линии смещения непрерывны всегда, то в силу сферической сим-
симметрии задачи
D(r) = D(a)a2/r2, D = D(a)a2r/r3
Поэтому, вычисляя по формуле C9 3) объемную плотность поляризацион-
поляризационных зарядов р , имеем
дРх ?-1 2 д х е-1 2г3-Ъгх2
=D(a)a = D(a)a g ,
дх
ду
dpz
dz
Р ~
?
?
е-1
В
дРх
дх
^">" дх
\а)а
Г)(п\2Г
'J{a)a
дРу
ду
гз
г6
т
дРг
dz
В
1
= 0
Из D4.1) следует, что потенциал (относительно бесконечно-
бесконечности), создаваемый точечным зарядом в диэлектрике, есть
D4.2)
Обратимся теперь к теореме Остроградского-Гаусса (§ 13).
Из формул D2 2) и D4.1) следует, что электрическое смещение,
создаваемое точечным зарядом в диэлектри-
диэлектрике, есть
D = д/Dтгг2).
Оно такое же, как и в отсутствие ди-
диэлектрика в вакууме. Поэтому теорема
Остроградского-Гаусса для диэлектриков
имеет тот же вид A3.5), что и для вакуу-
вакуума, где q обозначает фактические заряды
тел без учета поляризационных зарядов
диэлектрика.
Отсюда, в частности, следует, что при за-
Конденса- полнении любого конденсатора (отключенно-
(отключенного от источника) однородным диэлектриком
электрическое смещение D не меняется. На-
Напряженность же поля Е = D/eo? в любой
точке поля уменьшится в е раз. Однако нужно иметь в виду, что
поле уменьшается в е раз только в том случае, когда диэлектрик
заполняет все пространство конденсатора. Если это условие не
выполнено, то напряженность поля может быть как меньше, так
Рис 60
тор с неоднородным
диэлектриком
J» 45
МЕХАНИЧЕСКИЕ СИЛЫ ПРИ НАЛИЧИИ ДИЭЛЕКТРИКОВ
93
и больше его значения в вакууме Eq. Так, например, в случае,
изображенном на рис 60, напряженность поля в точке б меньше
fio, но в точках а и в — больше Eq
§ 45. Механические силы при наличии диэлектриков
Опыты, описанные в § 38, показывают, что на диэлектрики в
электрическом поле действуют механические силы Они возни-
возникают и в том случае, если диэлектрик в целом не заряжен.
Объяснение происхождения этих сил мы уже дали выше.
Они возникают потому, что на диэлектриках в электрическом
поле появляются поляризационные заряды (как поверхностные,
так и объемные), и поэтому на каждый элемент поверхности и
объема диэлектрика действует определенная сила.
Если тело находится не в вакууме, а в какой-либо другой
среде, то поляризация будет происходить и в окружающей сре-
среде, и поэтому силы, действующие на тело, будут зависеть как
от поляризационных зарядов тела, так и от поляризационных
зарядов окружающей среды.
Хорошей иллюстрацией сказанному служит опыт, изобра-
изображенный на рис 61. Подвесим на нити парафиновый шарик а
и поместим его вблизи изолированно-
изолированного металлического шарика б Когда
оба шарика находятся в воздухе, то
при заряжении металлического шари-
шарика парафиновый шарик притягивается
к нему. Если же погрузить оба шарика
в ацетон, у которого диэлектрическая
проницаемость больше, чем у парафи-
парафина, то парафиновый шарик отталкива-
отталкивается от металлического шарика
Объяснение этого опыта заключа-
заключается в следующем. На поверхности ша- Рис 61 Парафиновый ша-
шарика появляются поляризационные за-
заряды с некоторой поверхностной плот-
плотностью а[, а на границе среды, при-
прилегающей к шарику, — поляризацион-
поляризационные заряды противоположного знака с
другой плотностью ст2, поэтому сила, действующая на поверх-
поверхность шарика, зависит от результирующего заряда а[ — <т'2 Если
диэлектрическая проницаемость среды ?2 < ?i, то ст2 < ®'\- Если
?2 > ?i, то <72 > <7], результирующий заряд изменяет знак, и
поэтому сила притяжения переходит в силу отталкивания.
Сила, действующая на тело в диэлектрике, зависит, однако,
не только от свободных зарядов, находящихся на теле. Вслед-
рик а притягивается к за-
заряженному металлическому
шарику б в воздухе, но от-
отталкивается от него в аце-
ацетоне
94 ДИЭЛЕКТРИКИ ГЛ V
ствие поляризации на каждый элемент объема диэлектрика дей-
действуют силы, и поэтому диэлектрики в электрическом поле де-
деформируются. Это явление носит название электрострикции.
Вследствие электрострикции внутри диэлектрика возникают ме-
механические силы. Поэтому непосредственное вычисление полной
механической силы, действующей на какое-либо тело в диэлек-
диэлектрике, как правило, сложно. Однако во многих случаях механи-
механические силы можно просто вычислить без детального разбора их
происхождения, с помощью закона сохранения энергии. К этому
вопросу мы вернемся в § 72.
§ 46. Электронная теория поляризации диэлектриков
Мы уже говорили, что причина поляризации диэлектриков
заключается в том, что атомы и молекулы всех тел содержат
элементарные заряженные частицы. В электрическом поле про-
происходит смещение этих частиц, и поэтому возникает электриче-
электрический момент. Однако в различных диэлектриках эти смещения
имеют разный характер.
Молекулы многих веществ построены из незаряженных ато-
атомов. Примером может служить молекула водорода (рис. 62 а).
Подобные молекулы названы неполяр-
неполярными. Молекулы многих других ве-
веществ, напротив, содержат атомы в заря-
заряженном состоянии, т.е. ионы (полярные
молекулы). Полярной является молеку-
молекула воды, которая содержит отрицатель-
отрицательный ион кислорода и два положитель-
положительных иона водорода (рис. 62 6).
Неполярную молекулу в отсутствие
электрического поля в грубом (но доста-
достаточном для наших целей) приближении
можно представить в виде двух рав-
Рис. 62. Грубые модели н°мерно заряженных сфер, центры ко-
неполярной молекулы во- ТОРЫХ совпадают. Так как поле равно-
дорода (а) и полярной мо- мерно заряженной сферы во внешнем
лекулы воды {б) пространстве равно полю точечного за-
заряда той же величины, помещенного в
центре сферы, то очевидно, что электрический момент такой
молекулы равен нулю. В электрическом поле оба заряда смеща-
смещаются в противоположные стороны, и поэтому молекула будет
вызывать электрическое поле, совпадающее (вне молекулы) с
полем диполя, у которого каждый из точечных зарядов равен
заряду соответствующей сферы, а расстояние между зарядами
равно смещению центров сфер (рис. 63).
§46
ЭЛЕКТРОННАЯ ТЕОРИЯ ПОЛЯРИЗАЦИИ ДИЭЛЕКТРИКОВ
95
Смещение зарядов в молекуле при не очень сильных полях
можно положить пропорциональным напряженности электри-
электрического поля. Поэтому дипольный мо-
момент молекулы р можно считать пропор-
пропорциональным напряженности поля:
р = /0?ОЕ', D6.1)
где Е' — напряженность поля, действую-
действующего на молекулу. Это поле отличается
от среднего поля Е внутри диэлектрика
(подробнее см. § 47), поэтому мы и ввели
для него специальное обозначение. Ко-
Коэффициент пропорциональности /?, на- Рис- 63. Схема электрон-
зываемый поляризуемостью молекулы, ной поляризации
зависит от строения молекулы. Описанный тип поляризации на-
называют электронной поляризацией смещения.
Рассмотрим теперь диэлектрик с полярными молекулами. В
этом случае каждая молекула имеет определенный дипольный
момент ро уже в отсутствие поля. Однако, вследствие теплового
движения, в отсутствие поля молекулы расположены совершен-
совершенно хаотично (рис. 64 а), и поэтому векторная сумма всех момен-
моментов диполей в среднем близка к нулю. При наложении внешнего
электрического поля на каждый диполь действуют силы, стре-
стремящиеся ориентировать его параллельно электрическому полю.
Поэтому возникает частичное упо-
упорядочение в расположении диполей
(рис. 64 6), тем большее, чем сильнее
внешнее поле и чем ниже температу-
температура. В этом случае сумма всех диполь-
ных моментов молекулы уже не равна
нулю, и диэлектрик приобретает элек-
электрический момент. Такой тип поляри-
поляризации называют ориентационной или
диполъной поляризацией.
В твердых диэлектриках мы нахо-
находим еще один тип смещения зарядов,
приводящий к поляризации. Кристал-
Кристаллические решетки многих веществ по-
построены из положительных и отрица-
отрицательных ионов. Примером может слу-
служить кристалл хлористого цезия. Элементарная ячейка его ре-
решетки представляет собой центрированный куб (рис. 65), в
вершинах которого находятся положительные ионы Cs+, а в
центре — отрицательные ионы С1~. Рассматривая все ионы Cs+
и все ионы С1~ порознь, мы находим, что они образуют две про-
простые кубические решетки, сдвинутые по отношению друг к дру-
Рис. 64. Схема дипольной
поляризации
96
ДИЭЛЕКТРИКИ
ГЛ. V
гу в направлении диагонали куба на расстояние половины диа-
диагонали.
В электрическом поле на каждую из простых решеток дей-
действуют различные по модулю и направлению силы и решет-
решетки смещаются по отношению друг к
другу. Вследствие этого в некоторых
кристаллах может возникнуть элек-
электрический момент. Этот тип поляри-
поляризации называют поляризацией ион-
ионного смещения или просто ионной
поляризацией.
Рассмотренные типы поляриза-
поляризации могут сочетаться друг с другом.
Так, например, в полярных жидких и
газообразных диэлектриках молеку-
молекулы могут не только ориентироваться
под действием поля, но и деформиро-
деформироваться, и поэтому в них может проис-
происходить одновременно электронная и
дипольная поляризации.
Рис. 65. Элементарная ячей-
ячейка кристалла хлористого це-
цезия CsCl
§ 47. Диэлектрическая проницаемость неполярных
диэлектриков
Исходя из представлений, изложенных в предыдущем па-
параграфе, можно вычислить диэлектрическую проницаемость и
связать ее с атомарными постоянными диэлектрика. Рассмо-
Рассмотрим сначала неполярные диэлектрики.
Пусть диэлектрик находится в электрическом поле, и будем
считать сначала, что поле Е', действующее на молекулу, сов-
совпадает со средним полем Е внутри диэлектрика. Тогда каждая
молекула диэлектрика имеет дипольный момент р, выражаемый
формулой D6.1), где Е' = Е. Если п — число молекул в единице
объема диэлектрика, то электрический момент единицы объема
(поляризованность) равен
Р = п/ЗеоЕ,
а для смещения D, согласно D1.2), имеем
D = ?0Е + Р = ?0ЕA + пр).
Так как, с другой стороны, D = ??оЕ, то отсюда
е=1 + п/3. D7.1)
Полученное соотношение связывает диэлектрическую проница-
проницаемость ? с концентрацией п молекул внутри диэлектрика и по-
поляризуемостью молекул /3.
§ 47 ПРОНИЦАЕМОСТЬ НЕПОЛЯРНЫХ ДИЭЛЕКТРИКОВ 97
Формула D7.1) весьма приближенна. При выводе ее мы счи-
считали, что электрическое поле Е\ вызывающее смещение заря-
зарядов в молекуле, равно среднему электрическому полю Е. Это,
однако, неверно. При вычислении поляризации молекулы нас
интересует не среднее поле, а поле в точке, где находится дан-
данная молекула. Среднее поле Е учитывает действие всех зарядов,
т.е. зарядов на обкладках конденсатора и зарядов всех молекул,
включая и рассматриваем)'Ю. Поле же Е' выражает действие
всех зарядов при исключении рассматриваемой молекулы. Хотя
заряды одной молекулы и малы по сравнению с зарядами мно-
множества других молекул диэлектрика, но эти заряды находятся
в непосредственной близости от рассматриваемой точки и по-
поэтому их исключение приводит к поправке конечной величины.
Различие полей Е и Е' не существенно только в газах, для ко-
которых е близко к единице.
Чтобы получить выражение для диэлектрической проница-
проницаемости плотных диэлектриков, нужно определить напряжен-
напряженность поля Е', действующего на молекулу (внутреннее поле).
Это является, вообще говоря, сложной задачей, так как внутрен-
внутреннее поле существенно зависит от структуры диэлектрика.
Внутреннее поле можно просто вычислить только для кри-
кристаллов с кубической решеткой. Для них
Е' = Е + Р/3?0, D7.2)
где Р — поляризованность кристалла. Эту формулу можно при-
приближенно применять и к неполярным жидкостям и газам, в ко-
которых расположение молекул хаотично.
Пользуясь формулой D7.2), можно вычислить электронную
поляризованность плотных диэлектриков. Электрический мо-
момент единицы объема в этом случае будет равен
р = пр = прео{Е + Р/Зе0).
Поэтому для смещения D получаем
D = е0Е + Р =
= е0Е + п/3 \eqE + i (D - e0E)j = e0E + 1 nj3(D + 2e0E).
Так как D = ssqE, to отсюда следует
(
5 + 2 3 [i'-6)
(формула Клаузиуса-Моссотти).
Соотношение D7.3) показывает, что для неполярных диэлек-
диэлектриков величина (е — 1)/(е + 2) прямо пропорциональна концен-
концентрации молекул, а следовательно, плотности данного диэлектри-
диэлектрика. Этот результат хорошо оправдывается на опыте, например
для газов в широком интервале изменения давлений. Кроме то-
того, из D7.3) видно, что при неизменной концентрации молекул
98 ДИЭЛЕКТРИКИ ГЛ V
(плотности) диэлектрическая проницаемость не зависит от тем-
температуры, так как поляризуемость молекул /3 зависит лишь от
их строения, но не от температуры. Этот результат также хо-
хорошо подтверждается на опыте, который показывает, что при
нагревании или охлаждении неполярных диэлектриков при по-
постоянном объеме их диэлектрическая проницаемость не изменя-
изменяется.
Формулу D7.3) часто пишут в несколько ином виде. Концен-
Концентрацию молекул п можно выразить через молярную массу ве-
вещества [I, его плотность d и постоянную Авогадро iV, а именно
п — Nd/fi. Подставляя это в D7.3), имеем
? = ТГ21 = const
Величину, стоящую в левой части, называют молярной поляри-
зованностъю данного вещества. Она зависит только от поля-
поляризуемости молекул j3, т.е. от рода вещества, но не зависит от
температуры и давления, и, следовательно, остается постоянной
для данного вещества при изменении его состояния. Измеряя на
опыте е при данном d, можно определить молярную поляризо-
ванность и по формуле D7.3а) найти поляризуемость молекул.
§ 48. Диэлектрическая проницаемость полярных
диэлектриков
Рассмотрим теперь, от чего зависит диэлектрическая прони-
проницаемость газообразных полярных диэлектриков и как именно.
Сначала будем считать, что молекулы недеформируемы, т.е. не
будем учитывать электронную поляризацию.
Электрический момент единицы объема такого диэлектрика
есть
где рЕг — проекция электрического момента какой-либо г-й моле-
молекулы на направление внешнего поля, а т — объем диэлектрика.
Но, по определению среднего значения,
г
где п — число молекул в единице объема, а Ре — среднее зна-
значение проекции дипольного момента молекул на направление
поля. Поэтому вычисление поляризованности сводится к опре-
определению Ре-
Расчет, согласно законам статистической физики, дает (см.
Добавление 2)
ё
§ 49 ОПРЕДЕЛЕНИЕ ДИПОЛЬНЫХ МОМЕНТОВ МОЛЕКУЛ 99
Здесь ро — постоянный дипольный момент одной молекулы, к =
= 1,38 • 10~23 Дж/К — постоянная Больцмана, Т — термодина-
термодинамическая температура диэлектрика, Е' — напряженность поля,
действующего на диполь. При выводе D8.1) предположено, что
поле Б' не очень велико и вызывает только слабую упорядочен-
упорядоченность в расположении диполей.
Отметим, что результат, выраженный формулой D8.1), каче-
качественно понятен и без расчетов: чем больше поле Е', тем сильнее
ориентация диполей, тем больше будет и проекция дипольного
момента на направление поля; напротив, чем выше температу-
температура, тем сильнее дезориентирующее влияние теплового движе-
движения, тем меньше и проекция дипольного момента. Сравнивая
D8.1) с D6.1), мы видим, что при дипольной поляризации вели-
величина рп/ЗеокТ играет ту же роль, что и поляризуемость моле-
молекулы р в неполярных диэлектриках. Подставляя эту величину
в D7.3), получим
(е - 1I {е + 2) = р20п/(9еокТ). D8.2)
Диэлектрическая проницаемость полярных диэлектриков зави-
зависит от температуры и уменьшается при нагревании.
Отметим еще раз, что последняя формула, так же как и
формула D7.3), справедлива лишь тогда, когда внутреннее поле
можно представить в виде D7.2). В жидкостях с полярными мо-
молекулами, в отличие от неполярных жидкостей, формула D7.2)
для внутреннего поля, по-видимому, оправдывается плохо.
Положение упрощается для газообразных диэлектриков.
Вследствие слабой их поляризуемости в них можно считать вну-
внутреннее поле Е' равным среднему полю Е. Это значит, что в
левой части формулы D8.2) нужно положить е + 2 « 3.
Если в газообразном диэлектрике молекулы обладают в от-
отсутствие поля постоянным дипольным моментом и, кроме того,
могут деформироваться в электрическом поле, то диэлектриче-
диэлектрическая проницаемость газа равна
? = 1 + n[/3 + p§/Ce0fcT)]. D8.3)
Здесь второе слагаемое описывает электронную поляризацию
смещения, а третье — дипольную (ориентационную) поляриза-
поляризацию.
§ 49. Определение дипольных моментов молекул
Рассмотренная выше теория поляризации диэлектриков,
принадлежащая в основном Дебаю и Ланжевену, приводит к
зависимости диэлектрической проницаемости от температуры,
показанной на рис. 66. По оси ординат отложено значение мо-
молярной поляризованности, а по оси абсцисс — величина, обрат-
100
ДИЭЛЕКТРИКИ
ГЛ V
ная термодинамической температуре. Для чисто неполярных
диэлектриков (ро = 0) молярная поляризованность не зависит от
температуры и изображается прямой 1, параллельной оси 1/Т.
Для чисто полярных диэлектриков
/ = 0) эта зависимость, согласно
48.2), выражается прямой 2, прохо-
проходящей через начало координат. Если
молекулы имеют и постоянный диполь-
ный момент ро, и заметно деформиру-
деформируются (/3^0), то наблюдаются оба типа
поляризации и рассматриваемая зави-
зависимость изображается прямой 3, полу-
получаемой сложением прямых 1 и 2.
Исследуя на опыте температурную
зависимость диэлектрической прони-
проницаемости е, можно определить, какой
тип поляризации имеет место в данном
диэлектрике, и выделить электронную поляризацию смещения
и ориентационную (дипольную) поляризацию. А отсюда можно
найти по формулам D7.3) и D8.2) поляризуемость молекулы ft
или соответственно ее дипольный момент щ. Значения диполь-
ных моментов молекул, полученные таким образом для некото-
некоторых веществ, приведены в табл. 2.
Таблица 2
Рис. 66. Теоретическая за-
зависимость молярной поля-
ризованности от темпера-
температуры
Вещество
Водород, азот, кислород
Четыреххлористый углерод
Хлористый водород
Бромистый »
Окись углерода
Этиловый эфир
Вода
Химическая
формула
H2,N2,O2
СС14
НС1
НВг
СО
(CaHsbO
Н2О
Дипольный момент
ро, 1(Г30 Клм
0
0
3,4
2,6
0,40
3,8
6,2
Зная дипольный момент, можно оценить размеры молекул.
Простейший случай представляет молекула из двух ионов, для
которой ро — Ф {я — заряд ионов, I — расстояние между их
центрами). Так, например, для молекулы НС1 q равно заряду
электрона е = 1,60 • 10~19 Кл, так как известно, что водород
содержит всего один электрон. Поэтому для расстояния между
центрами ионов мы находим I = C,4 • 10~30) : A,60 ¦ 10~19) ~
рз 2 • 101 м = 0,2 ¦ 10~8 см, что по порядку величины хорошо
совпадает с размером молекул, определяемым из данных химии
и молекулярной физики.
§50
СЕГНЕТОЭЛЕКТРИКИ
101
Рис. 67. Кристалл сегне-
товой соли
§ 50. Сегнетоэлектрики
Некоторые химические соединения в твердом состоянии име-
имеют весьма необычные и интересные диэлектрические свойства.
Первоначально эти свойства были обнаружены в кристаллах
сегнетовой соли, и поэтому все подобные диэлектрики получили
название сегнетоэлектриков. Деталь-
Детальное исследование диэлектрических
свойств сегнетовой соли было впер-
впервые произведено в 1930-1934 гг. И.В.
Курчатовым и П.П. Кобеко, которы-
которыми были установлены все основные
свойства сегнетоэлектриков.
Сегнетова соль представляет собой
двойную натрий-калиевую соль винной
кислоты NaKGjKUOe • 4НгО. Ее кри-
кристаллы принадлежат к ромбической си-
системе и обычно имеют вид, показанный
на рис. 67, где а, Ь, с — кристаллографи-
кристаллографические оси. Кристаллы сегнетовой соли
обнаруживают резкую анизотропию свойств. Сегнетоэлектриче-
ские свойства, описываемые ниже, наблюдаются, если электри-
электрическое поле конденсатора направлено вдоль кристаллографиче-
кристаллографической оси а (рис. 67).
Первая особенность сегнетовой соли заключается в том, что
в некотором температурном интервале ее диэлектрическая про-
проницаемость весьма велика и достигает огромного значения: око-
около 10 000.
Второе важное свойство сегнетовой соли обнаруживается
при исследовании зависимости электрического смещения от на-
напряженности поля. Смещение оказывается не пропорциональ-
пропорциональным полю, а значит, диэлектрическая
проницаемость зависит от напряжен-
напряженности поля. Эта зависимость для раз-
разных сегнетоэлектриков различна.
Третья особенность состоит в
том, что значение электрического
смещения в сегнетовой соли опре-
определяется не только значением на-
напряженности поля, но зависит еще
от предшествовавших состояний по-
поляризации. Это явление называется
диэлектрическим гистерезисом (ср.
§ 110). Зависимость смещения D от
А
Рис. 68. Диэлектрический
гистерезис в сегнетоэлектри-
ках
напряженности поля Е имеет вид, изображенный на рис. 68.
При первоначальном увеличении поля нарастание смещения
102 ДИЭЛЕКТРИКИ ГЛ V
описывается ветвью кривой J, которая не линейна. Если затем
уменьшать электрическое поле (напряжение на конденсаторе),
то уменьшение смещения будет происходить в соответствии с
ветвью 2. Когда поле становится равным нулю, смещение не
равно нулю и изображается отрезком D\. Это показывает, что
в сегнетовой соли имеется остаточная поляризация и сегнето-
ва соль остается поляризованной даже в отсутствие внешнего
электрического поля. Чтобы уничтожить остаточную поляриза-
поляризацию, нужно создать электрическое поле Е\ обратного направле-
направления. При дальнейшем циклическом изменении электрического
поля изменение смещения описывается изображенной петлеоб-
петлеобразной кривой — петлей гистерезиса.
Эти свойства присущи не только сегнетовой соли, но и всем
сегнетоэлектрикам.
Сегнетоэлектрические свойства сильно зависят от темпера-
температуры. При температурах, превышающих определенное значе-
значение Tki различное для разных веществ, сегнетоэлектрические
свойства исчезают и сегнетоэлектрик превращается в обычный
диэлектрик. Эта температура называется температурой Кюри
или точкой Кюри в честь Кюри, который впервые обнаружил
существование подобной критической температуры при иссле-
исследовании магнитных свойств железа и сходных с ним веществ
(ферромагнетиков). В некоторых случаях, как, например, для
сегнетовой соли, существуют две температуры Кюри (+24 °С и
—18 °С) и сегнетоэлектрические свойства наблюдаются только
при температурах, лежащих между обеими точками. Наличие
одной или нескольких точек Кюри является четвертым харак-
характерным свойством всех сегнетоэлектриков.
Помимо сегнетовой соли сегнетоэлектрическими свойствами
обладают и другие соединения, например КН2РО4 (фосфат ка-
калия) и KH2AsO4- Практически важным сегнетоэлектриком яв-
является титанат бария ВаТЮз- Его точка Кюри лежит около
120 °С, а диэлектрическая проницаемость достигает в макси-
максимуме 6000-7000.
Сегнетоэлектрики имеют важные практические применения
Приготовляя сложные диэлектрики на основе сегнетоэлектри-
сегнетоэлектриков и добавляя к ним различные примеси, можно получить кон-
конденсаторы большой емкости при малых размерах и придать им
высокие качества
Причиной сегнетоэлектрических свойств является самопро-
самопроизвольная поляризация сегнетоэлектриков, возникающая в них
под действием особенно сильного взаимодействия между части-
частицами. Под влиянием этого взаимодействия сегнетоэлектрик под-
подразделяется на отдельные области — области самопроизвольной
(спонтанной) поляризации, или диэлектрические домены, в ко-
§50
СЕГНЕТОЭЛЕКТРИКИ
103
торых возникает большой электрический момент даже в отсут-
отсутствие внешнего электрического поля
Спонтанная поляризация в обычных условиях, однако, не
проявляется. Если указанные области малы, то поляризован-
ность направлена в
разных областях раз-
различно и результирую-
результирующее значение электри-
электрического момента всего
сегнетоэлектрика близ-
близко к нулю (рис 69 а).
Такое расположение
соответствует мини-
минимуму энергии, так как
в противном случае
вокруг гегнетоэлектри-
ка возникло бы элек-
Е
Рис. 69. Области самопроизвольной поляри-
поляризации в сегнетоэлектриках и направление век-
вектора поляризованное™ в них (схематически)
а) сегнетоэлекгрик в целом неполяризован,
б) сегнеюэлектрик поляризован
трическое поле, кото-
которое содержало бы в
себе дополнительную
энергию. Если области
спонтанной поляризации велики или если даже весь кристалл
представляет собой одну такую область, то поляризация обыч-
обычно все же не проявляется, так как на поверхности кристалла
возникают поверхностные заряды (вследствие осаждения ионов
из воздуха или за счет электропроводности кристалла), ком-
компенсирующие поляризационные заряды кристалла Поэтому в
обоих случаях могут наблюдаться только изменения электри-
электрического момента сегнетоэлектрика, возникающие по каким-либо
причинам.
Во внешнем электрическом поле происходит изменение на-
направления поляризованности в отдельных областях Это измене-
изменение таково, что векторы поляризованности приближаются к по-
положению, параллельному направлению поля, и тем ближе, чем
сильнее поле (рис. 69 6). Кроме того, границы между отдель-
отдельными областями могут смещаться таким образом, чтобы объем
энергетически более выгодных областей увеличивался за счет
объема энергетически менее выгодных. Поэтому электрический
момент всего сегнетоэлектрика изменяется и это изменение вос-
воспринимается как его поляризация
Наличие областей спонтанной поляризации является наибо-
наиболее общим и точным признаком сегнетоэлектриков
Кристаллы, в которых возникает спонтанная поляризация без внешнего
Электрического поля, образуют более широкую группу, нежели сегнетоэлек-
трики Они получили название пир о электриков Помимо упомянутой выше
причины, спонтанная поляризация может возникнуть вследствие особенно-
104 ДИЭЛЕКТРИКИ ГЛ V
стей структуры кристалла. Так, расположение положительных и отрица-
отрицательных ионов в элементарной ячейке кристалла может быть таким, что их
электрический дипольный момент не равен нулю. Тогда и кристалл в це-
целом приобретает электрический момент, т.е. оказывается поляризованным.
Поляризованность при этом направлена вдоль некоторой, характерной для
данного кристалла, оси. Для возникновения спонтанной поляризации та-
такого рода необходимо, чтобы у кристалла было выделенное направление и
притом единственное. Поэтому спонтанная поляризация имеет место только
у кристаллов определенных кристаллографических классов. В отличие от
сегнетоэлектриков, рассматриваемая спонтанная поляризация практически
не изменяется внешним электрическим полем.
Вследствие компенсации поляризационных зарядов из-за проводимо-
проводимости кристалла, а также в результате оседания ионов из воздуха, постоян-
постоянная спонтанная поляризация не наблюдается Однако она проявляется при
нагревании кристалла Вследствие теплового расширения изменяется рас-
расположение ионов в элементарной ячейке, а следовательно, изменяются ее
дипольный момент и поляризованность кристалла Это изменение и прояв-
проявляется как возникновение поляризационных зарядов на гранях кристалла.
Электризация при нагревании кристаллов получила название пироэлектри-
пироэлектрического эффекта. Отсюда произошло и название веществ, в которых на-
наблюдается это явление Классическим примером пироэлектрика являются
кристаллы турмалина.
Из 32 кристаллографических классов симметрии только 10 являются
пироэлектрическими.
Таким образом, сегнетоэлектрики представляют собой частный случай
пироэлектриков, в которых спонтанную поляризацию можно обратимо из-
изменять электрическим полем. По аналогии со свойствами ферромагнитных
материалов (§ 112) сегнетозлектрики можно назвать «мягкими» пироэлек-
триками. По этой же аналогии их часто называют ферроэлектриками.
§ 51. Пьезоэлектрический эффект
До сих пор мы рассматривали поляризацию диэлектриков,
вызванную внешним электрическим полем. В некоторых кри-
кристаллах поляризация может возникнуть и без внешнего поля,
если кристалл подвергается механическим деформациям. Это
явление, открытое в 1880 г. Пьером и Жаком Кюри, получи-
получило название пьезоэлектрического эффекта.
Чтобы обнаружить пьезоэлектрические заряды, на грани
кристаллической пластинки накладывают металлические об-
обкладки. При разомкнутых обкладках между ними при дефор-
деформации появляется разность потенциалов. При замкнутых об-
обкладках на них образуются индуцированные заряды, равные по
модулю поляризационным зарядам, но противоположные им по
знаку, и в цепи, соединяющей обкладки, в процессе деформации
возникает ток.
Рассмотрим основные особенности пьезоэлектрического эф-
эффекта на примере кварца. Кристаллы кварца ЭЮг существуют в
различных кристаллографических модификациях. Интересую-
§51
ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
105
щие нас кристаллы (а-кварц) принадлежат к так называемой
тригональной кристаллографической системе и обычно имеют
форму, показанную на рис. 70. Они
напоминают шестигранную призму,
ограниченную двумя пирамидами,
однако имеют еще ряд дополни-
дополнительных граней. Такие кристаллы
характеризуются четырьмя кристал-
кристаллическими осями, определяющими
важные направления внутри кри-
кристалла. Одна из этих осей — Z соеди-
соединяет вершины пирамид. Три другие
Х\, Х2, Х$ перпендикулярны к оси
Z и соединяют противолежащие реб-
ребра шестигранной призмы. Направле-
Направление, определяемое осью Z, пьезоэлек-
пьезоэлектрически неактивно: при сжатии или
растяжении по этому направлению
никакой поляризации не происходит.
Напротив, при сжатии или растяже-
Рис. 70. Кристалл кварца
нии в любом направлении, перпендикулярном к оси Z, возни-
возникает электрическая поляризация. Ось Z называется оптичес-
оптической осью кристалла, а оси Х\, Х^1
Хз — электрическими или пьезо-
пьезоэлектрическими осями.
Рассмотрим пластинку кварца,
вырезанную перпендикулярно к од-
одной из пьезоэлектрических осей X.
Ось, перпендикулярную к Z и X,
обозначим через Y (рис. 71). То-
Тогда оказывается, что при растяже-
растяжении пластинки вдоль оси X на пер-
перпендикулярных к ней гранях А В CD
и EFGH появляются разноименные
Рис 71. Кварцевая пластин- поляризационные заряды. Такой пье-
ка, вырезанная перпендику- зоэлектрический эффект называется
лярно к пьезоэлектрической продольныж Если изменить знак де-
деформации, т.е. перейти от растяже-
растяжения к сжатию, то и знаки поляризационных зарядов изменятся
на обратные.
Возникновение поляризационных зарядов определенных знаков при
данном типе деформации (растяжение или соответственно сжатие) показы-
показывает, что концы осей X неравноправны, и осям X можно приписать опреде-
определенные направления (что отмечено на рис 70 стрелками) Это значит, что
при данной деформации знак заряда зависит от того, направлена ли ось X
по внешней нормали к грани или по внутренней. Такие оси с неравноправ-
106
ДИЭЛЕКТРИКИ
ГЛ V
ными концами получили название полярных осей. В отличие от полярных
осей Xi, Х-г, Хз, концы оси Z совершенно равноправны и она является
неполярной осью.
Неравноправность концов полярной оси проявляется, конечно, не толь-
только в пьезоэлектрическом эффекте, но и в других явлениях. Так, например,
скорость химического травления граней, расположенных у разных концов
полярной оси, оказывается различной и получающиеся при этом фигуры
травления отличаются друг от друга.
Наряду с продольным пьезоэлектрическим эффектом суще-
существует также поперечный пьезоэлектрический эффект. Он за-
заключается в том, что при сжатии или растяжении вдоль оси Y
возникает поляризация вдоль оси X и на тех же гранях ABCD
и EFGH появляются поляризационные заряды. При этом ока-
оказывается, что знаки зарядов на каждой грани при сжатии вдоль
Y (в поперечном эффекте) такие же, как при растяжении вдоль
X (в продольном эффекте).
Пьезоэлектрический эффект объясняется следующим обра-
образом. В § 46 мы уже говорили, что в ионных кристаллах вслед-
вследствие несовпадения центров положительных и отрицательных
ионов имеется электрический момент и в отсутствие внешнего
электрического поля. Однако эта поляризация обычно не прояв-
проявляется, так как она компенсируется зарядами на поверхности.
При деформации кристалла положительные и отрицательные
ионы решетки смещаются друг относительно друга, и поэтому,
вообще говоря, изменяется электрический момент кристалла.
Это изменение электрического момента и проявляется в пьезо-
пьезоэлектрическом эффекте.
Рис. 72. К объяснению пьезоэлектрического эффекта
Рисунок 72 качественно поясняет возникновение пьезоэлек-
пьезоэлектрического эффекта в кварце. Здесь схематически показаны
проекции положительных ионов Si (заштрихованные кружки) и
отрицательных ионов О (светлые кружки) в плоскости, перпен-
перпендикулярной к оптической оси Z. Этот рисунок не соответствует
§ 51 ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ 107
фактической конфигурации ионов в элементарной ячейке квар-
кварца, в которой ионы не лежат в одной плоскости, а их число боль-
больше показанного. Он, однако, правильно передает симметрию
взаимного расположения ионов, что уже достаточно для каче-
качественного объяснения. Рисунок 72 а соответствует недеформи-
рованному кристаллу. На грани Л, перпендикулярной к оси Х\,
имеются выступающие положительные заряды, а на параллель-
параллельной ей грани В — выступающие отрицательные заряды. При
сжатии вдоль оси Х\ (рис. 72 б) элементарная ячейка деформи-
деформируется. При этом положительный ион 1 и отрицательный ион
2 «вдавливаются» внутрь ячейки, отчего выступающие заряды
(положительный на плоскости А и отрицательный на плоскости
В) уменьшаются, что эквивалентно появлению отрицательного
заряда на плоскости А и положительного заряда на плоскости В.
При растяжении вдоль оси Х\ имеет место обратное (рис. 72 е):
ионы J и 2 «выталкиваются» из ячейки. Поэтому на грани А
возникает дополнительный положительный заряд, а на грани
В — отрицательный заряд.
Анализ симметрии в теории твердого тела в согласии с опы-
опытом показывает, что пьезоэлектрический эффект может суще-
существовать только в таких кристаллах, в которых элементарная
ячейка не имеет центра симметрии. Так, например, элементар-
элементарная ячейка кристаллов CsCl (рис. 65) имеет центр симметрии
и эти кристаллы не обнаруживают пьезоэлектрических свойств.
Расположение же ионов в ячейке кварца таково, что в нем центр
симметрии отсутствует, и поэтому в нем возможен пьезоэлектри-
пьезоэлектрический эффект.
Из 32 кристаллографических классов симметрии 21 класс не имеет цен-
центра симметрии, однако один из них пьезоэлектрически неактивен и пьезо-
электриками являются кристаллы 20 классов.
Отметим, что для существования пироэлектрических свойств (§ 50) то-
тоже необходимо отсутствие центра симметрии, но одного этого условия еще
недостаточно. Поэтому пироэлектричество, как уже отмечалось, наблюда-
наблюдается только у 10 кристаллографических классов, которые относятся к чис-
числу 20 пьезоэлектрических. Следовательно, все пироэлектрики (включая и
сегнетоэлектрики) являются и пьезоэлектриками, но не каждый пьезоэлек-
трик обладает пироэлектрическими свойствами.
Поляризованность Р в широком интервале изменения пропорциональна
механическим деформациям. Так, при растяжении вдоль оси X в продоль-
продольном эффекте
где d — толщина пластинки, a Ad — ее изменение при деформации. При
растяжении вдоль оси У при поперечном эффекте
где I — длина пластинки (см. рис 71) Величина /3 называется пьезоэлек-
108 ДИЭЛЕКТРИКИ ГЛ V
трическим коэффициентом. Знак /? может быть как положительным, так
и отрицательным. Так как относительная деформация безразмерна, то ве-
величина /3 измеряется в тех же единицах, что и Р, т.е. кулон на квадрат-
квадратный метр (Кл/м2). Поверхностная плотность пьезоэлектрических зарядов
на гранях, перпендикулярных к оси X, равна <г' — Рх-
Пьезоэлектрический эффект возникает не только при деформации од-
одностороннего растяжения, но и при деформации сдвига. В общем случае де-
деформация характеризуется симметричным тензором деформации 2-го ран-
ранга. Если смещения точки среды с координатами х, у, z вдоль координатных
осей X,Y и Z есть и, и и го, то компоненты тензора деформации, по опре-
определению, равны
du dv dw 1 (dw dv\
UXx ~ C > ^УУ == "o~> Uzz ~ ~7i } Wyz = UZy = ~ I -7т + 77— I ,
ox ay oz 2 \dy ozj
1 (ди dw\ 1 (dv du
Компоненты с одинаковыми индексами дают линейные растяжения вдоль
координатных осей, а компоненты со смешанными индексами описывают
деформации сдвига. В общем случае каждая составляющая поляризован-
ности Рх, Ру и Рг есть линейная функция всех компонент тензора дефор-
деформации.
В кристаллофизике вместо тензорных соотношений часто употребля-
употребляют более простую, так называемую матричную форму записи. Для этого
вводят сокращенные обозначения:
tin = mi, Uyy = иг, uzz = из,
2uzy — 2uyz = Ui, 2uzx = 2uxz = U5, 2uxy = 2uyx = tie-
Тогда общее выражение для поляризованности принимает вид
Рх = fillUl + /?12 + /?13 + /9l4«M + /?I5U5 + /?16И6,
Ру = #21 + /?22 + /З23М3 + /З24И4 + /?25 + /326"e, E1-1)
Рг = folUl + /З32М2
Таким образом, в общем случае пьезоэлектрический эффект описыва-
описывается матрицей из 18 пьезоэлектрических коэффициентов /?п, ..., /Зге- Одна-
Однако все эти коэффициенты отличны от нуля только для кристаллов наиме-
наименее симметричной триклинной системы. С повышением степени симметрии
кристалла увеличивается число коэффициентов, обращающихся в нуль, а
отличные от нуля коэффициенты оказываются связанными друг с другом.
Поэтому число независимых пьезоэлектрических коэффициентов уменьша-
уменьшается и тем сильнее, чем выше симметрия кристалла.
Так, например, для кварца
/3i2 = -/9u, 025 = -Ры, /326 = -/?ii, E1.2)
а остальные коэффициенты равны нулю. Таким образом, остается лишь
пять коэффициентов, из которых независимы только два. За них принима-
принимают ^и и /?i4 При выборе координатных осей так, как показано на рис 70,
эти коэффициенты равны
?и = +5,2 • 104 СГСЭ = +0,18 Кл/м2,
/Зн = +1,2 104 СГСЭ = +0,040 Кл/м2.
§ 51 ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ 109
Следовательно, пьезоэлектрический эффект в кварце описывается уравне-
уравнениями
Рх — /3llUl - /3uU2 + /3uli4,
Ру = -Рииъ- gillie, E1.3)
Pz=0.
Вследствие возникновения поляризации при деформации изменяется и
электрическое смещение D внутри кристалла. В этом случае в общем опре-
определении смещения D1.2) под Р нужно понимать сумму Ре + Р«, где Ре
обусловлено электрическим полем, аР, — деформацией:
D = e0E + PB + P«. E1.4)
Здесь поляризованность Ри в общем случае определяется соотношениями
E1.1). Если поляризованность в электрическом поле Ре не зависит от на-
направления Е, то можно ввести скалярную диэлектрическую проницаемость
е (§ 42) и написать еоЕ + Ре = ееоЕ. Тогда
D = ??OE + PU. E1.5)
Оценим теперь порядок величины пьезоэлектрического эффекта на
примере кварца. Для этого рассмотрим пластинку, вырезанную перпенди-
перпендикулярно к электрической оси X (си. рис. 71), и положим, что она подвер-
подвергается одностороннему растяжению вдоль этой оси.
Пусть растягивающее напряжение равно si = 105 Па. Возникающая
деформация равна и\ = si/C, где С — модуль упругости (модуль Юн-
Юнга), зависящий от направления растяжения и от того, закреплены боковые
грани пластинки или свободны (зависит от граничных условий при дефор-
деформации). Будем считать боковые грани пластинки свободными. Тогда при
растяжении вдоль оси X для кварца С = 7,8 • Ю10 Па. Тогда деформация
равна
Ad si Ю5 , , 1П-в
U 13 10
Возникающая вследствие этой деформации поляризованность, согласно
первому из уравнений E1.3), равна
Рх\ = ?п«1 = 0,23 ¦ 10~6 Кл/м2.
Найдем теперь напряженность электрического поля, вызываемого этой
поляризацией. Ее можно определить из выражения для электрического сме-
смещения. У кварца е слабо зависит от направления и можно воспользоваться
формулой E1.5).
Так как объемная плотность заряда р внутри пластинки равна нулю,
то, согласно уравнению Пуассона A4.1), divD = 0, а следовательно, D =
= const Это значит, что возникновение в каком-либо сечении пластинки
X = const поляризации Р„ будет сопровождаться появлением в том же
сечении электрического поля Е противоположного направления и такой ве-
величины, чтобы изменения обоих членов в правой части формулы E1 5)
компенсировали друг друга. Поэтому найденная выше поляризованность
¦Pxi = j3nui вызовет электрическое поле
Bxi = -^ui. E1.6)
??0
Подставляя сюда для кварца е = 4,5 и используя приведенные выше значе-
значения /?ц и «1, находим \Е\ = 5900 В/м = 59 В/см. При толщине пластинки,
скажем, d = 0,5 см напряжение между обкладками будет U = Ed и 30 В.
110
ДИЭЛЕКТРИКИ
ГЛ V
IF,
Как уже говорилось, пьезоэлектрические свойства наблюдаются, кро-
кроме кварца, у большого числа других кристаллов. Гораздо сильнее, чем у
кварца, они выражены у сегнетовой соли. Сильными пьезоэлектриками яв-
являются кристаллы соединений элементов П-й и VI-й групп периодической
системы (CdS, CdSe, ZnO), а также многих других химических соедине-
соединений. Применяя вместо кварца более сильные пьезоэлектрики и используя
должным образом выбранные типы деформаций, можно получать пьезо-
пьезоэлектрические напряжения, измеряемые многими тысячами вольт.
§ 52. Обратный пьезоэлектрический эффект
Наряду с пьезоэлектрическим эффектом существует и обрат-
обратное ему явление: в пьезоэлектрических кристаллах возникнове-
возникновение поляризации сопровождается механическими деформация-
деформациями. Поэтому, если на металлические
обкладки, укрепленные на кристалле,
подать электрическое напряжение, то
кристалл под действием поля поляризу-
поляризуется и деформируется.
Легко видеть, что необходимость су-
существования обратного пьезоэффекта
следует из закона сохранения энергии
и факта существования прямого эф-
эффекта. Рассмотрим пьезоэлектрическую
пластинку (рис. 73) и предположим, что
мы сжимаем ее внешними силами F. Ес-
Если бы пьезоэффекта не было, то работа
внешних сил равнялась бы потенциаль-
потенциальной энергии упруго деформированной
пластинки. При наличии пьезоэффекта на пластинке появляют-
появляются заряды и возникает электрическое поле, которое заключает
в себе дополнительную энергию. По закону сохранения энергии
отсюда следует, что при сжатии пьезоэлектрической пластинки
совершается большая работа, а значит, в ней возникают допол-
дополнительные силы Fi, противодействующие сжатию. Это и есть
силы обратного пьезоэффекта.
Из приведенных рассуждений вытекает связь между знака-
знаками обоих эффектов. Если в обоих случаях знаки зарядов на
гранях одинаковы, то знаки деформаций различны. Если при
сжатии пластинки на гранях появляются заряды, указанные на
рис. 73, то при создании такой же поляризации внешним полем
пластинка будет растягиваться.
Обратный пьезоэлектрический эффект имеет внешнее сход-
сходство с электрострикцией (§ 45). Однако оба эти явления раз-
различны. Пьезоэффект линейно зависит от электрического поля
и при изменении направления последнего на противоположное
Рис. 73. Связь прямого и
обратного пьезоэлектри-
пьезоэлектрических эффектов
§52 ОБРАТНЫЙ ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ 111
изменяет знак. Электрострикция же пропорциональна и элек-
электрическому полю и поляризации, производимой этим же полем,
т.е. пропорциональна квадрату напряженности электрического
поля и поэтому не зависит от направления поля. Пьезоэффект
наблюдается только в кристаллах, и притом только некоторых
кристаллографических классов, не обладающих центром сим-
симметрии. Электрострикция же имеет место во всех диэлектри-
диэлектриках — твердых, жидких и газообразных.
Будем характеризовать обратный пьезоэлектрический эффект механи-
механическими напряжениями, соответствующими возникающим деформациям.
Как известно из механики, упругие напряжения в твердом теле описывают-
описываются симметричным тензором 2-го ранга, имеющим шесть независимых ком-
компонент:
Sxx, Syy, Szz, &yz — Szy, Szx — Sxzi Sxy — Syx.
Каждая из этих компонент выражает некоторую силу, действующую на
единичную площадку внутри твердого тела. Первый индекс указывает на-
направление внешней нормали к площадке, а второй дает координатную ось,
вдоль которой рассматривается составляющая силы, действующей на пло-
площадку. Как и в случае упругих деформаций (§ 51), в кристаллофизике обыч-
обычно используют упрощенную запись, обозначая:
Sxx = S\, Syy = «2, Szz = S3,
Szy — Syz ~~ S4, Szx "-" Sxz *— 55, Sxy = Syx — S(j.
Во избежание недоразумений в дальнейшем, необходимо условиться о знаке
напряжений. Мы будем понимать под st внутренние напряжения в кристал-
кристалле. Сжимающие напряжения будем считать положительными, а растя-
растягивающие — отрицательными.
Опыт показывает, что в широком интервале изменения напряжений,
компоненты тензора напряжений линейно зависят от составляющих напря-
напряженности электрического поля Ех, Еу и Ez. Поэтому общие уравнения,
описывающие линейный обратный пьезоэлектрический эффект, можно за-
записать в виде
— «2 = y
s3=j3i3Ex + pKEy+fr3Ez,
—Si = j3nEx + &i\Ey + PzaEz,
-s5 =
где восемнадцать величин /Зп, ..., /Зге есть те же самые пьезоэлектрические
Коэффициенты, которые входят в уравнения E1.1) для прямого пьезоэлек-
пьезоэлектрического эффекта.
Как уже говорилось в § 51, часть пьезоэлектрических коэффициентов
может быть равна нулю, и их число тем больше, чем выше симметрия кри-
кристалла. Возвращаясь опять к а-кварцу, мы находим в нем только пять от-
отличных от нуля коэффициентов, между которыми имеются соотношения
E1.2). Поэтому уравнения, описывающие обратный пьезоэффект в кварце,
112 ДИЭЛЕКТРИКИ ГЛ. V
имеют вид
si = -рпЕх, s2 = +рцЕх, Si = О,
S4 = -puEx, s5 = +j3i4Ey, s6 — +fiuEy.
Уравнения E2.1) и E2.2) выражают упругие напряжения, вызываемые
электрическим полем. Помимо них, в кристалле могут быть еще и напря-
напряжения, не связанные с электрическим полем, а обусловленные упругими де-
деформациями кристалла. Полная величина упругих напряжений есть сумма
обоих этих напряжений.
В формулах E1.1) и E2.1) мы выбирали в качестве независимых пере-
переменных деформации и, и напряженность электрического поля Е и считали
поляризованность Р и упругие напряжения Sk их функциями. Это, конечно,
не обязательно, мы могли бы считать независимыми переменными другую
пару величин, одна из которых — механическая, а другая — электрическая.
Тогда мы получили бы тоже два линейных соотношения между Uj, sj, E и
Р, но с другими пьезоэлектрическими коэффициентами. В зависимости от
типа рассматриваемых задач удобны различные формы записи основных
пьезоэлектрических соотношений.
Оценим теперь порядок величины обратного пьезоэффекта, опять на
примере кварца. Положим, что пластинка толщины d = 0,5 см выреза-
вырезана перпендикулярно к электрической оси X и что к обкладкам пластинки
приложено напряжение U = 103 В, вызывающее электрическое поле напря-
напряженности Е = Ех — 2 • 105 В/м. Пусть это поле Е > 0, т.е. направлено
вдоль электрической оси X. Тогда, учитывая значение /?п (§ 51), из пер-
первого уравнения E2.2), находим, что, например, сила в направлении оси X
на единицу площади равна s\ = —0,18 • 2 • 105 = —0,36 • 105 Па. Знак ми-
минус обозначает, что механическое напряжение s\ соответствует растяжению
пластинки вдоль оси X.
Нетрудно видеть, что это соответствует соотношению между знаками
прямого и обратного эффектов, о котором говорилось выше. Действитель-
Действительно, из формулы E1.6) видно, что в прямом пьезоэлектрическом эффекте
для создания электрического поля Ех\, направленного вдоль оси X, необ-
необходимо ui < 0, т.е. сжатие, пластинки. В обратном же эффекте, как мы
видели, при том же самом направлении электрического поля пластинка бу-
будет растягиваться. Это растяжение можно найти по формуле и\ = Ad/d —
— si/C, где С = 7,8 ¦ 1010 Па есть модуль Юнга для данного направления
деформации. Это дает и\ = 0,46 • 10~6.
Уравнения пьезоэлектрического эффекта в некоторых специальных
случаях можно представить в простой скалярной форме. А именно, во мно-
многих кристаллах можно выбрать такое направление (обычно оно совпадает
с одной из осей симметрии высокого порядка), чтобы при простой дефор-
деформации, скажем одностороннем растяжении и вдоль этой оси, возникающие
поляризованность Ри и электрическое поле Е были тоже параллельны (или
антипараллельны) этой оси. В этом случае Ри = ри и пьезоэлектрический
эффект характеризуется только одним коэффициентом /5. Если при этом
Ре и Е тоже коллинеарны, то для электрического смещения вместо фор-
формулы E1.5) получаем скалярное соотношение
D = ее0Е + ри, E2.3)
где е — диэлектрическая проницаемость при постоянной деформации и.
§52 ОБРАТНЫЙ ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ 113
Аналогично, для единственной составляющей механического напряже-
напряжения имеем
а = Си - J3E. E2.4)
Здесь, как и раньше, s считается положительным, если оно соответствует
сжатию, С — модуль Юнга для данной деформации, взятый при постоян-
постоянном поле. Формулы E2.3) и E2.4) широко используются при исследовании
распространения упругих волн в пьезоэлектрических кристаллах.
Пьезоэлектрический эффект проявляется и в упругих свойствах кри-
кристаллов. Поясним это с помощью простых соотношений E2.3) и E2.4).
Для этого рассмотрим пластинку, вырезанную перпендикулярно к соответ-
соответствующему направлению, и представим, что она испытывает растяжение
и вдоль этого направления. Так как объемных зарядов в кристалле нет,
то электрическое смещение при деформации остается постоянным. Поэто-
Поэтому, рассуждая так же, как и при получении формулы E1.6), мы найдем
из формулы E2.3), что при деформации и возникает электрическое поле с
напряженностью
Е=--$-и. E2.5)
Подставляя это выражение в формулу E2.4), находим для механиче-
механического напряжения в пластинке
^\( ^Л E2.6)
Напряжение, как и в отсутствие пьезоэлектрического эффекта, пропорци-
пропорционально деформации. Однако упругие свойства пластинки теперь характе-
характеризуются эффективным модулем упругости
С = С
который больше С. Увеличение упругой жесткости вызвано появлением до-
добавочного напряжения при обратном пьезоэффекте, препятствующего де-
деформации. Влияние пьезоэлектрических свойств кристалла на его механи-
механические свойства характеризуется величиной
? E2.8)
Квадратный корень из этой величины (К) называется константой элек-
электромеханической связи. Пользуясь приведенными выше значениями е, С
и /3, находим, что для кварца К2 к 0,01. Для всех других известных пье-
пьезоэлектрических кристаллов К2 оказывается также малым по сравнению с
единицей и не превышает 0,1.
Пьезоэлектрический эффект (прямой и обратный) широко
применяется для устройства различных электромеханических
преобразователей. Для этого иногда используют составные пье-
зоэлементы, предназначенные для осуществления деформаций
разного типа.
На рис. 74 показан двойной пьезоэлемент (составленный из
двух пластинок), работающий на сжатие. Пластинки вырезаны
из кристалла таким образом, что они одновременно либо сжи-
сжимаются, либо растягиваются. Если, наоборот, сжимать или рас-
растягивать такой пьезоэлемент внешними силами, то между его
114
ДИЭЛЕКТРИКИ
ГЛ VI
обкладками появляется напряжение. Соединение пластинок в
этом пьезоэлементе соответствует параллельному соединению
конденсаторов.
|E
Рис 74. Двойной пьезоэлемент,
работающий на сжатие
Рис. 75 Двойной пьезоэлемент,
работающий на изгиб
На рис. 75 показан двойной пьезоэлемент, работающий на
изгиб. При появлении напряжения на обкладках одна из пла-
пластинок сжимается в поперечном направлении и удлиняется в
продольном, а другая — растягивается и укорачивается, отче-
отчего и возникает деформация изгиба. Если изгибать такой пье-
пьезоэлемент внешними силами, то между его обкладками возни-
возникает электрическое напряжение. Соединение пластинок в этом
случае соответствует последовательному соединению конденса-
конденсаторов. Очевидно, что такой пьезоэлемент не отвечает на сжатия
и растяжения: в этом случае в каждой из пластинок возника-
возникает электрическое поле, но поля направлены противоположно, и
поэтому напряжение между обкладками равно нулю.
Электромеханические преобразователи находят многочис-
многочисленные применения в разнообразной электроакустической и
измерительной аппаратуре. Укажем на пьезоэлектрические
микрофон и телефон, пьезоэлектрический адаптер (в электриче-
электрических проигрывателях патефонных пластинок), манометры, из-
измерители вибраций и др. Особенно важные применения имеют
пьезоэлектрические колебания кварца. Если поместить квар-
кварцевую пластинку между пластинами конденсатора и создать
между пластинами переменное напряжение, то при частоте
электрических колебаний, совпадающей с одной из собственных
механических частот пластинки, наступает механический резо-
резонанс и в пластинке возникают очень сильные механические ко-
колебания. Такая кварцевая пластинка является мощным изл}'-
чателем волн сверхзвуковой частоты (кварцевые излучатели),
используемых в технике, биологии и медицине, а также в мно-
многочисленных физических и физико-химических исследованиях.
Пьезоэлектрические колебания применяются также для стаби-
стабилизации частоты генераторов электрических колебаний в радио-
радиотехнике и в других технических устройствах
§53 ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ТОКА 115
ГЛАВА VI
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
§ 53. Характеристики электрического тока
Всякое движение электрических зарядов мы называем элек-
электрическим током.
В металлах могут свободно перемещаться только электроны.
Поэтому электрический ток в металлах есть движение электро-
электронов проводимости. В гл. XVIII мы увидим, что в проводящих
растворах нет свободных электронов, а подвижными заряжен-
заряженными частицами являются ионы. В газах могут существовать в
подвижном состоянии и ионы, и электроны (гл. XVI).
Направлением тока условились считать направление движе-
движения положительных частиц. Поэтому направление тока в метал-
металлах противоположно направлению движения электронов.
Линии, вдоль которых движутся заряженные частицы, на-
названы линиями тока. За направление линий тока принимают
направление движения положительных зарядов. Прочерчивая
линии тока, мы получаем сразу нагляд-
наглядное представление о движении электро-
электронов и ионов, образующем ток.
Если внутри проводника с током
мысленно выделить трубку, у которой
боковая поверхность состоит из линий
тока, то заряженные частицы при дви-
жении не будут пересекать боковую по- Рис 76 т бка тока
верхность трубки и не будут ни выхо-
выходить из трубки наружу, ни входить извне в трубку. Такая трубка
называется трубкой тока (рис. 76). Поверхность металлической
проволоки, находящейся в изоляторе, есть одна из трубок тока.
Для количественной характеристики электрического тока
служат две основные величины: плотность тока и сила тока.
Плотность тока равна заряду, про-
проходящему в единицу времени через
1 \///Ш единицу поверхности, перпендикуляр-
) Я ной к линиям тока.
Выделим внутри проводника пло-
площадку с S = 1, расположенную пер-
Рис. 77 К определению пендикулярно к линиям тока, а зна-
Илотности тока ЧИТ! и перпендикулярно к направле-
направлению скорости v заряженных частиц
(рис. 77). Построим на этой площадке прямоугольный парал-
параллелепипед с длиной, равной скорости движения частиц v. Тогда
Число частиц, которые пройдут через рассматриваемую площад-
116 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК ГЛ VI
ку в единицу времени, будет равно числу частиц, заключенных
внутри параллелепипеда. Если п есть концентрация заряжен-
заряженных частиц, то число частиц внутри параллелепипеда равно nv,
а заряд, переносимый ими, есть nev, где е — заряд одной части-
частицы (например, электрона). Поэтому плотность тока j равна
j = nev. E3.1)
Так как п и е суть скалярные величины, а скорость — вектор, то
можно ввести вектор плотности тока j, определяемый следую-
следующим образом:
j = nev. E3.1a)
Так как скорость v характеризует движение заряженных частиц
в данной точке, то и вектор плотности тока j определяет элек-
электрический ток в данной точке проводника.
Если выделить внутри проводника бесконечно малую пло-
площадку dS, перпендикулярную к вектору плотности тока j, то
заряд, проходящий через нее за время dt, равен
dq — j dS dt.
Бели площадка dS не перпендикулярна к j, то в этом выражении
вместо j нужно взять составляющую плотности тока jn, перпен-
перпендикулярную к dS.
Сила тока i в каком-либо проводнике равна заряду, проходя-
проходящему в единицу времени через полное сечение проводника. Если
dq — заряд, прошедший через сечение проводника за время dt,
то
i = dq/dt. E3.2)
Так как заряд dq и время dt суть скаляры, то и сила тока есть
скалярная величина.
Зная вектор плотности тока j в каждой точке проводника,
можно выразить через него и силу тока. Из сказанного выше
следует, что
i= fjndS, E3.3)
5
где интегрирование производится по всей поверхности S любого
сечения проводника (рис. 76).
Единицей силы тока служит ампер (А). Эта единица явля-
является одной из основных единиц системы СИ и определяется в
§ 83. При токе в 1 А через полное сечение проводника протека-
протекает заряд 1 Кл за время 1 с. На практике употребляют и более
мелкие единицы: 1 миллиампер (мА) = 10~3 А и 1 микроампер
(мкА) = 10~6 А.
Единица плотности тока есть ампер на квадратный метр
(А/и2).
§54 УРАВНЕНИЕ НЕПРЕРЫВНОСТИ 117
Если плотность тока и сила тока не меняются во времени,
то мы говорим, что в проводнике имеется постоянный, или ста-
стационарный, ток. Для постоянного тока сила тока одинакова во
всех сечениях проводника. Действительно, если бы сила тока
для двух каких-либо сечений S и S\ (рис. 76) была различна,
то заряд, заключенный между этими сечениями, изменялся бы
во времени, так как заряд, входящий через Si, был бы не равен
заряду, выходящему через S. Но тогда изменялось бы и элек-
электрическое поле внутри проводника и ток не мог бы оставаться
постоянным.
§ 54. Уравнение непрерывности
Рассмотрим внутри проводника с током какую-либо замкну-
замкнутую поверхность S и будем понимать под jn проекцию вектора
плотности тока j на внешнюю нормаль к элементу поверхности
dS. Тогда из определения плотности тока следует, что положи-
положительный заряд, уходящий в единицу времени через всю поверх-
поверхность S наружу, есть
§ Зп dS,
где интегрирование проводится по всей замкнутой поверхности.
Вместе с тем, согласно одному из основных законов электриче-
электричества, электрические заряды сохраняются: они только перерас-
перераспределяются между телами (или различными частями тела), но
долная сумма возникающих положительных и отрицательных
зарядов равна нулю (ср. § 6). Поэтому если dq/dt есть измене-
изменение за единицу времени положительного заряда, заключенного
внутри замкнутой поверхности S, то
JndS. E4.1)
s
5то соотношение называется уравнением непрерывности.
Поступая так же, как при преобразовании уравнения Пуас-
Сона (§ 14), мы можем записать уравнение E4.1) в дифферен-
дифференциальной форме, связывающей токи и заряды в одной и той же
Точке среды. Для этого рассмотрим опять бесконечно малый
Йараллелепипед с ребрами, параллельными координатным осям
X, Y и Z (см. рис. 18), и воспользуемся соотношением E1.1).
Тогда, рассуждая как и в § 14, мы найдем, что правая часть
формулы E4.1) равна
х ду oz )
Где dr = dx dy dz — объем параллелепипеда. С другой стороны,
118
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ VI
если р есть объемная плотность заряда, то q = р йт и мы полу-
получаем уравнение непрерывности в дифференциальной форме:
_др _ djx
~dt ~ Ih
ду
E4.2)
Отметим, что мы употребляем здесь символы частных произ-
производных, поскольку р и j могут зависеть как от координат, так и
от времени.
Пользуясь понятием дивергенции вектора (ср. § 14), уравне-
уравнение E4.2) можно записать в более компактной форме:
— ~- = divj. E4.3)
Если токи постоянны, то все электрические величины не за-
зависят от времени и в уравнении непрерывности нужно положить
dpjdt равным нулю. Тогда получается, что поток вектора j че-
через любую замкнутую поверхность равен нулю, а, значит, для
постоянных токов линии тока непрерывны.
§ 55. Действия электрического тока
Движение электронов и ионов непосредственно невидимо.
Однако это движение вызывает различные сопутствующие ему
явления, по которым мы и судим о наличии тока и его величине.
Магнитное действие тока. Еще в 1820 г. копенгагенский
профессор физики Эрстед открыл, что проводник с током вызы-
вызывает появление сил, действующих на магнитную стрелку. Если
расположить прямую металлическую
»-, N проволоку в направлении магнитно-
~ " го меридиана (в направлении север —
юг) и поместить под ней магнитную
стрелку (рис. 78), то при соединении
концов проволоки с электродами
гальванического элемента магнитная
стрелка отклоняется. Направление
отклонения стрелки можно найти
при помощи следующего правила: ес-
Рис. 78. Магнитное действие ли положить ладонь правой руки на
провода с током провод сверху и направить средние
пальцы в направлении тока, то ото-
отогнутый большой палец укажет направление отклонения север-
северного конца стрелки. Помещая магнитную стрелку над проводом,
мы найдем, что отклонение стрелки изменилось на обратное.
Если заменить металлическую проволоку стеклянной труб-
трубкой, наполненной каким-либо проводящим раствором, например
раствором серной кислоты в воде, и присоединить проводящий
столб раствора при помощи металлических проводников, опу-
§55 ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 119
щенных в него, к полюсам батареи, то магнитная стрелка также
отклоняется. Отклонение стрелки наблюдается и в том случае,
если вместо проволоки использовать газоразрядную трубку (на-
(например, неоновую рекламную трубку), питаемую постоянным
током. Магнитное действие наблюдается во всех случаях неза-
независимо от природы проводника и является самым общим при-
признаком тока.
Магнитное действие тока используют для измерения силы
тока с помощью магнитоэлектрических приборов. Они содержат
легкую рамку с проволокой, укрепленную на упругой пружине
и помещенную между полюсами магнита. В § 85 мы увидим,
что в этом случае на рамку с током действует момент силы М,
пропорциональной силе тока:
М = аг. E5.1)
Коэффициент пропорциональности а зависит от устройства
прибора (от числа витков проволоки, силы магнита и т.п.). По-
Поэтому по отклонению рамки можно судить о силе тока. Прибо-
Приборы, показания которых зависят от силы то-
тока, получили общее название гальваномет- ~^Гфг-Уголь.
ров.
Химическое действие тока. Электри-
Электрический ток может выделять в некоторых ЧЧ-CuSO
проводниках их составные химические ча- *^"—
сти.
Химическое действие тока можно наблю-
наблюдать в простых опытах. Опустим в водный
раствор медного купороса CuSO4 две уголь- Рис 79- Разложение
ные пластины (рис. 79) и соединим их с по- током медного купо-
люсами батареи гальванических элементов. роса
Через несколько минут вынем пластины из раствора. Мы обна-
обнаружим, что на пластине, соединенной с отрицательным полю-
полюсом батареи, выделился блестящий слой меди, хорошо заметный
На черном фоне угля. На второй пластине, соединенной с поло-
положительным полюсом батареи, выделяется остаток SO4- Однако,
Соприкасаясь с водой, он вступает во вторичную реакцию, не
Связанную с наличием тока, по суммарной формуле
2SO4 + 2Н2О = 2H2SO4 + О2;
в растворе появляется серная кислота и на пластине выделяется
газообразный кислород.
В качестве второго примера рассмотрим разложение током
водного раствора бромистого калия КВг. В этом случае у поло-
положительной пластины выделяется Вг, который хорошо заметен
вследствие своей бурой окраски. У отрицательной пластины по-
120 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК ГЛ VI
является К, который вступает во вторичную реакцию с водой
2К + 2Н2О = 2КОН + Н2,
так что у отрицательной пластины выделяется вместо калия во-
водород.
Явление выделения током химических составных частей про-
проводника получило название электролиза (от греческого л и о —
разлагаю). Электролиз имеет место не во всех проводниках
Проводники, в которых не наблюдается химическое действие
тока, называются проводниками 1-го рода К их числу принадле-
принадлежат все металлы, уголь и многие химические соединения. Про-
Проводники, в которых происходит электролиз, называются провод-
проводниками 2-го рода или электролитами. Электролитами являются
многие водные растворы кислот и солей и некоторые химические
соединения как в жидком, так и в твердом состояниях.
Явление электролиза обычно осложняется вторичными реак-
реакциями, примеры которых были рассмотрены выше. Вторичные
реакции не связаны с наличием тока и не имеют прямого от-
отношения к электролизу. Если, однако, отделить первичное дей-
действие тока от вторичных реакций, то можно обнаружить простое
правило на отрицательном полюсе (катоде) всегда выделяются
металлы и водород, а на положительном полюсе (аноде) — оста-
остаток химического соединения При этом составные части элек-
электролита выделяются только на электродах
Масса любого вещества, отложившегося на электроде, всегда
пропорциональна полному заряду, прошедшему через электро-
электролит.
Однако масса вещества, выделяемая единицей заряда, раз-
различна для разных веществ Так, например, при прохождении
1 Кл через водный раствор какой-либо серебряной соли на ка-
катоде выделяется 1,1180 мг металлического серебра, а при про-
прохождении 1 Кл через раствор медной соли выделяется 0,3294 мг
металлической меди (подробнее см. § 189)
Явление электролиза используют в кулонометрах, представ-
представляющих собой электролитические ванны, включаемые последо-
последовательно в цепь тока. Одним из точных приборов является се-
серебряный кулонометр, который имеет серебряные электроды и
содержит в качестве электролита водный раствор азотнокислого
серебра AgNO3
Кулонометры непосредственно измеряют заряд, прошедший
через цепь Если т — масса выделенного Ag в миллиграммах, а
t — время пропускания тока в секундах, то сила тока в амперах
равна
г = l,1180m/i.
Тепловое действие тока. Электрический ток вызывает на-
нагревание проводников Если пропускать ток через металличе-
§ 56 БАЛЛИСТИЧЕСКИЙ ГАЛЬВАНОМЕТР 121
ский проводник, то при достаточной силе тока его можно на-
нагреть до желаемой температуры, довести до плавления и испа-
испарить. На тепловом действии тока основано устройство тепло-
тепловых гальванометров. Они содержат металлический проводник
из неокисляемого упругого материала, через который пропуска-
пропускают измеряемый ток О силе тока судят по удлинению проводни-
проводника вследствие его нагревания током.
Магнитоэлектрические и тепловые гальванометры не явля-
являются абсолютными приборами и требуют градуировки.
§ 56. Баллистический гальванометр
При помощи гальванометров можно измерить не только силу
тока, но и заряд, находящийся на каком-либо конденсаторе.
Рассмотрим магнитоэлектрический гальванометр и будем
считать, что трение при движении рамки настолько мало, что им
можно пренебречь. Рамка является механической колебательной
системой, Она имеет определенный момент инерции I и на нее
действует сила упругости подвеса Момент сил упругости подве-
подвеса Мп можно считать пропорциональным углу поворота рамки:
Мп = -fa,
где / зависит от устройства подвеса или спиральных пружин.
Поэтому, будучи выведена из положения равновесия, рамка со-
совершает механические крутильные колебания с периодом
Т = 2тгл//77-
Положим теперь, что мы замкнули на гальванометр какой-
нибудь заряженный конденсатор. Конденсатор начнет разря-
разряжаться и в гальванометре возникнет кратковременный ток
(импульс тока). Будем считать, что время импульса т мало по
сравнению с периодом колебаний рамки: т <С Т (баллистический
режим). Тогда за все время импульса рамка не успеет заметно
сместиться и все явление будет подобно явлению удара в меха-
механике.
За время т на рамку подействует импульс момента силы,
равный, согласно E5.1),
Г М dt = a I idt = aq,
где q — полный заряд, прошедший через гальванометр. Поэтому
рамка приобретает момент импульса
/а>о = aq
(а>о — угловая скорость рамки) и кинетическую энергию
WK = Iu>l/2.
122
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ. VI
После окончания импульса тока рамка начнет поворачивать-
поворачиваться и ее кинетическая энергия будет превращаться в потенциаль-
потенциальную энергию закрученного подвеса:
Wn = fa2/2.
Поэтому, если ат есть максимальный отброс, то
/с&/2 = 1шЦ2.
Из этих уравнений находим
=
Ч =
= Ьа
т,
E6.1)
где b — постоянная для данного прибора, называемая балли-
баллистической постоянной. Мы видим, что, измеряя первый макси-
максимальный отброс гальванометра, можно определить полный за-
заряд, прошедший через гальванометр.
Баллистический метод измерения заряда весьма удобен и
широко применяется на практике. Употребляемые для таких
измерений гальванометры называют баллистическими гальва-
гальванометрами. В отличие от обычных гальванометров, в которых
затухание колебаний рамки долж-
должно быть значительным (чтобы вре-
время установления рамки было малым),
в баллистических гальванометрах за-
затухание делают возможно меньшим.
Т Кроме того, для лучшего выполнения
¦ ' условия баллистического режима уве-
_ личивают момент инерции рамки, что
Рис. 80. Принципиальная обеспечивает большой период ее соб-
схема для определения ственных колебаний AО„2о с)
Г
баллистической постоянной
и для сравнения емкостей
В предыдущих рассуждениях мы
не учитывали затухания колебаний
рамки вследствие трения. При учете трения теория получается
более сложной. Однако это не имеет особого значения, так как
обычно баллистическую постоянную Ь определяют не расчетом,
а на опыте, т.е. градуируют гальванометр на заряды. Употребля-
Употребляемая для этого принципиальная схема показана на рис. 80. Здесь
С — конденсатор известной емкости, а Б — батарея с известным
напряжением U. В этом случае известен и заряд конденсатора
q = CU, и поэтому, наблюдая отброс гальванометра ат, можно
по формуле E6.1) найти Ъ.
Если в схему рис. 80 один раз включить конденсатор с емко-
емкостью С\, а другой раз — с емкостью С2, то отношение отбросов
гальванометра в обоих случаях будет равно отношению емко-
емкостей:
= Сх/С2.
§57
ЗАКОН ОМА
123
Рис. 81. Падение напряжения
вдоль проводника с током
Поэтому баллистический гальванометр позволяет просто срав-
сравнивать емкости, причем напряжение батареи знать не нужно.
§ 57. Закон Ома
Если в проводнике имеется ток, то потенциал в различных
его точках уже не одинаков. Присоединив корпус электрометра
к одному из концов а прово-
проволоки аб с током, а стрелку —
к какой-либо другой точке Ъ
(рис. 81), мы обнаружим, что
между этими точками имеется
напряжение, которое тем боль-
больше, чем ближе точка Ъ ко вто-
второму концу проволоки. При на-
наличии тока существует падение
напряжения вдоль проводника.
Падение напряжения, со-
согласно § 19, означает, что су-
существует составляющая напря-
напряженности поля Et, направленная вдоль проводника (рис. 82).
Это значит, что напряженность поля у поверхности проводни-
проводника с током, а следовательно, и линии на-
напряженности уже не перпендикулярны к по-
поверхности проводника. Они наклонены в на-
направлении тока на некоторый угол а, при-
причем tga = En/Et.
Мы видим, что для поддержания посто-
постоянного тока, т.е. движения электронов с по-
постоянной скоростью, необходимо непрерыв-
непрерывное действие силы (равной eEt, где е — за-
заряд электрона). А это значит, что электро-
электроны в проводниках движутся с трением, или, иначе говоря, что
проводники обладают электрическим сопротивлением.
Если состояние проводника остается неизменным (не меняет-
меняется его температура и т.д.), то для каждого проводника существу-
существует однозначная зависимость между напряжением U, приложен-
приложенным к концам проводника, и силой тока г в нем: г = f(U). Она
называется вольт-амперной характеристикой данного провод-
проводника.
Для многих проводников, в особенности для металлов, эта
зависимость особенно проста — сила тока пропорциональна при-
приложенному напряжению, т.е.
t = A.U. E7.1)
Этот закон носит название закона Ома.
Рис. 82. Электриче-
Электрическое поле проводника
с током
124 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК ГЛ VI
Коэффициент пропорциональности Л называется электри-
электрической проводимостью, а величина, обратная проводимости, —
электрическим сопротивлением. Если обозначить сопротивле-
сопротивление проводника через R, то
Л = 1/R. E7.2)
Электрическая проводимость и сопротивление зависят от ро-
рода вещества проводника, от его геометрических размеров и фор-
формы, а также от состояния проводника
Единицей сопротивления служит ом (Ом) сопротивление та-
такого проводника, в котором при напряжении между его концами
1 В течет постоянный ток силой 1 А:
1 Ом = 1 В/1 А = 1 В/А.
Для измерения больших сопротивлений употребляют более
крупные единицы: 1 килоом (кОм)= 103 Ом и 1 мегаом (МОм) =
= 106 Ом. Единицей электрической
проводимости является сименс (См).
По определению 1 См = 1 Ом".
На использовании закона Ома
основано измерение напряжений
при помощи вольтметра. Вольтметр
Рис 83 Вольтметр представляет собой гальванометр,
последовательно с которым со-
соединено большое сопротивление (рис. 83). При подключении
вольтметра к каким-либо точкам а и б участка цепи в вольтметр
ответвляется часть тока; сила ответвленного тока г по закону
Ома пропорциональна напряжению U между этими точками:
i = U/г.
Поэтому, зная чувствительность вольтметра по току и его сопро-
сопротивление г, можно определить и напряжение U. Это напряжение
наносят непосредственно на шкалу прибора.
Чтобы подключение вольтметра существенно не изменяло
силу тока и распределения напряжения в цепи, ток в вольтмет-
вольтметре должен быть мал по сравнению с током в цепи, а для этого
сопротивление вольтметра г должно быть велико по сравнению
с сопротивлением R участка цепи аб.
§ 58. Измерение сопротивлений
Сопротивление какого-либо проводника можно измерить
наиболее просто при помощи амперметра и вольтметра. Если г —
сила тока в амперах, показываемая амперметром, at/ — напря-
напряжение в вольтах на концах проводника, измеряемое вольтмет-
вольтметром, то сопротивление проводника в омах равно R = U/г. При
§58
ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ
125
этом предполагается, что ток, ответвляющийся в вольтметр, мал
по сравнению с током в проводнике. Если током вольтметра пре-
пренебречь нельзя, то в написанной формуле под г нужно понимать
ток в проводнике, равный г = г а — ty, где г а — показания ам-
амперметра, и iy — ток вольтметра. Последний можно найти по
закону Ома, зная сопротивление вольт-
вольтметра. Ток вольтметра можно также
определить, зная чувствительность вольт-
вольтметра по току, т.е. ток, соответствующий
отклонению вольтметра на одно деление.
Точность этого метода определяется
точностью амперметра и вольтметра и
обычно бывает не очень велика (~ 1%).
Поэтому для точного измерения сопро-
сопротивлений употребляют метод сравнения
сопротивлений, не требующий измерения
тока и напряжения. Это осуществляют
в схеме моста, изображенной на рис. 84. Рис g4
Здесь ri, Г2, гз и Г4 — четыре сопротивле-
сопротивления, одно из которых неизвестно. Сопро-
Схема
сопротивлений
моста
тивления плеч моста изменяют и подбирают их таким образом,
чтобы ток гальванометра был равен нулю. В этом случае
гг/г2 = гз/г4. E8.1)
Поэтому, зная сопротивление трех плеч моста, можно опреде-
определить и неизвестное четвертое сопротивление.
Условие E8.1) можно получить следующим образом. Пусть
п, *2, h и «4 — силы токов в плечах моста г\, Е
ток гальванометра равен нулю, то в точках в
и г
у
и г±. Если
не имеется
разветвления токов, и поэтому г\ = 12, «з = «4- Напряжения
между концами плеч моста:
Uae = i\r\, Ue6 = «2^2 = ii?,
= 23Г4.
В отсутствие тока в гальванометре напряжение между точ-
точками виг равно нулю. Это дает
= иаг = г3гз,
Деля почленно оба равенства, получим соотношение E8.1). В
него входят сопротивления плеч моста, включающие в себя и
сопротивления соединительных проводов. Поэтому измеряемое
сопротивление и сопротивления остальных плеч моста должны
быть велики по сравнению с сопротивлением соединительных
проводов.
126
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ VI
§ 59. Сопротивление проволок
В § 57 мы говорили, что сопротивление проводников зависит
от их формы и размеров. Эта зависимость особенно проста, если
проводники имеют форму цилиндров постоянного поперечного
сечения (проволоки). Тогда
R = pl/S, E9.1)
где / — длина проводника, a S — его поперечное сечение. Коэф-
Коэффициент пропорциональности р зависит от рода вещества и его
состояния и называется удельным электрическим сопротивле-
сопротивлением данного вещества. Величина, обратная удельному сопро-
сопротивлению, Л = 1/р, получила название удельной электрической
проводимости вещества.
Единица удельного сопротивления есть ом-метр (Ом-м) Ес-
Если в E9.1) положить / = 1, S = 1, то R = р. Следовательно,
удельное сопротивление вещества есть сопротивление куба с ре-
ребром 1 м из данного вещества, выраженное в омах, при токе, па-
параллельном одному из ребер куба. В табл. 3 приведены удельные
сопротивления некоторых веществ при комнатной температуре.
Таблица 3
Вещество
Серебро
Медь тянутая
Платина
Константин (сплав
60 % Си, 40 % №)
Нихром F7,5% N),
15%Сг, 16% Fe,
1,5 % Мп)
Графит
Удельное
сопротивление р,
Ом м
A,66-1,63)-КГ8
1,78 1СГ8
11,0 10~8
49,0 1(Г8
110 10"8
~3 1(Г6
Вещество
10 %-ный водный
раствор NaCl
Химически чис-
чистая вода
Стекло натровое
Фарфор
Янтарь, плав-
плавленый кварц
Удельное со-
сопротивление
р, Ом м
0,0825
~106
~109
~1013
> 1018
Простой зависимостью E9.1) пользуются на практике для
изготовления различных сопротивлений из проволок. Если со-
сопротивления нужно изменять во вре-
время опыта, то употребляют реостаты со
скользящим контактом Они состоят из
однослойной обмотки голой проволоки
из сплава с высоким удельным сопротив-
сопротивлением (нихром, никелин), намотанной
на жаростойкий изолирующий цилиндр
(фарфор, стеатит), и скользящего кон-
Рис 85 Делитель на- такта В цепь тока включают один конец
пряжения обмотки и скользящий контакт
Г
I
I
U
§ 60 ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ 127
На рис 85 показана схема делителя напряжения. Если Щ
есть напряжение между концами реостата а и б, то напряжение
U между точками виг (разомкнутыми) равно
U = U0n/r,
где г — полное сопротивление реостата, а г\ — сопротивление
его части между зажимом б и скользящим контактом.
§ 60. Зависимость сопротивления от температуры
Удельное сопротивление зависит не только от рода вещества,
но и от его состояния, в частности от температуры. Зависимость
удельного сопротивления от температуры можно охарактеризо-
охарактеризовать температурным коэффициентом сопротивления данного
вещества:
Он дает относительное приращение сопротивления при увели-
увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного
вещества различен при разных температурах, т.е. удельное со-
сопротивление изменяется с температурой не по линейному зако-
закону, а зависит от нее более сложным образом. Однако для многих
проводников, к которым относятся все металлы, изменение а с
температурой не очень велико. Если интервал изменения темпе-
температуры достаточно мал, то приближенно можно считать а по-
постоянным, равным среднему его значению внутри рассматрива-
рассматриваемой области температур. Так, например, если ро есть удельное
сопротивление при 0 °С, а р — его значение при t °С, то можно
положить
p = P0(l + at). F0.2)
Температурный коэффициент сопротивления может быть
как положительным, так и отрицательным. У всех металлов со-
сопротивление увеличивается с увеличением температуры, а сле-
следовательно, для металлов а > 0 Для многих других проводни-
проводников 1-го рода наблюдается обратное и, по крайней мере в некото-
некотором температурном интервале, их сопротивление уменьшается с
увеличением температуры. Наконец, у всех электролитов (про-
(проводники 2-го рода), в отличие от металлов, сопротивление при
нагревании всегда уменьшается, и для них также а < 0.
В табл. 4 приведены средние значения температурного ко-
коэффициента сопротивления для некоторых веществ. Для всех
чистых металлов температурный коэффициент сопротивления
близок к 1/273 = 0,00367, т.е. к температурному коэффициен-
коэффициенту расширения газов. Следует также отметить, что некоторые
сплавы имеют весьма малое а, примером чего может служить
128
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ. VI
константан. Поэтому проволоки из таких сплавов применяют
для изготовления точных образцов (эталонов) сопротивлений.
Таблица 4
Вещество
Серебро
Медь
Платина
Константан
10 %-ный водный
раствор NaCl
Графит
Стекло
Температура, °С
0-100
18
0-100
18
18
18
100
*) В зависимости от образца.
Температурный коэффициент
сопротивления а, К
40 • Ю-4
43 -10~4
38 • Ю-4
(от-0,4 до+0,1)-КГ4 *)
-0,021
-5-10-"
от -0,1 до -0,2
Зависимость сопротивления металлов от температуры ис-
используют в различных измерительных и автоматических
устройствах. Наиболее важным из них является термометр со-
сопротивления. Он представляет собой сопротивление из плати-
платиновой проволоки, которое включают в схему моста в качестве
одного из плеч. Сопротивление платины весьма постоянно во
времени и хорошо изучено в широком интервале температур.
Поэтому, измеряя сопротивление платиновой проволоки, можно
очень точно измерить и температуру. Термометры сопротивле-
сопротивления обладают тем важным достоинством, что могут служить
как при очень низких, так и при высоких температурах, при
которых применение обычных жидкостных термометров невоз-
невозможно.
При очень низких температурах в некоторых веществах воз-
возникает удивительное состояние сверхпроводимости, в котором
электрическое сопротивление исчезает вовсе. Однако этот во-
вопрос будет рассмотрен позднее (§ 148).
§ 61. Закон Ома в дифференциальной форме
Закон Ома E7.1) и формула E9.1) позволяют найти силу
тока в проволоках и вообще в тех случаях, когда трубки тока
являются цилиндрами постоянного сечения. Однако часто при-
приходится вычислять силу тока в проводящих средах, в которых
трубки тока не имеют цилиндрической формы. Примерами мо-
могут служить сферический и цилиндрический конденсаторы, в
которых пространство между обкладками заполнено проводя-
проводящей средой. В этом случае формула E9.1) уже неприменима,
так как расстояние / различно для разных точек поверхности
§ 61
ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
129
обкладок, а площадь S у каждой обкладки имеет разную вели-
величину.
Однако закон Ома можно представить в другой форме, кото-
которая пригодна и для решения задач о токах в проводящих средах.
Рассмотрим в однородной и изо-
изотропной проводящей среде небольшой
отрезок трубки тока длины Д/ (рис. 86)
и два близких эквипотенциальных ее
сечения 1 и 2. Обозначим их потенциа-
потенциалы через C/i и С/г, а среднюю площадь
сечений — через AS. Применяя к это-
этому отрезку закон Ома E7.1) и формулу
E9.1), получим
=jAS=
Рис. 86. К закону Ома в
дифференциальной форме
или, сокращая на AS и вводя удельную электрическую прово-
проводимость среды А = 1/р, получим
- _ х U\ - U? _ \U2-Ux _ ХД?/
;~л~дг л~дг л^Г
Чтобы последняя формула была совершенно точна, нужно пе-
перейти к пределу при А1 —> О, так как только в этом случае рас-
рассматриваемый отрезок трубки можно считать цилиндрическим
и применять к нему формулу E9.1). Но
где Е — напряженность электрического поля внутри провод-
проводника. Учитывая далее, что j и Е суть векторы, и что внутри
изотропных сред они направлены одинаково, находим
j = ЛЕ. F1.1)
Это соотношение носит название дифференциальной формы за-
закона Ома. В отличие от E7.1) (интегральной формы закона
Ома), оно содержит величины, характеризующие электрическое
состояние среды в одной и той же точке.
В анизотропных средах, каковыми, например, являются мно-
многие кристаллы, направления j и Е, вообще говоря, уже не сов-
совпадают. В этом случае вместо формулы F1.1) получается более
сложное соотношение.
В анизотропных средах в широкой области электрических попей ли-
линейная связь между j и Е сохраняется. Поэтому дифференциальный закон
Ома в общем виде выражается формулой
где индексы i и к пробегают значения х, у, z. Девять величин А,* суть ком-
компоненты тензора удельной электрической проводимости. Этот тензор 2-го
130 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК Г Л VI
ранга симметричен. Ал = А*,, и поэтому независимыми являются только
шесть компонент Так же как и в случае тензора диэлектрической проница-
проницаемости (§ 42), при выборе осей координат, совпадающих с главными осями
тензора, отличны от нуля только три диагональных компоненты: \хх — Ai,
\уУ = \2 и \zz = A3, которые называются главными значениями удельной
электрической проводимости.
Поле Е, входящее в F1.1), есть поле внутри проводящей сре-
среды при наличии тока. Можно, однако, показать, что если про-
проводящая среда однородна, то во всех практически интересных
случаях это поле совпадает с электростатическим полем Ест, т.е.
с полем, которое существовало бы между данными электрода-
электродами, если бы между ними было то же напряжение, что и при
наличии тока, а вместо проводящей среды был бы вакуум. От-
Отсюда следует, что в однородном проводнике линии напряжен-
напряженности электростатического поля совпадают с линиями тока (см.
Добавление 3).
Для вычисления силы тока в проводящих средах поступают
следующим образом. Сначала находят по заданному напряже-
напряжению между электродами напряженность поля внутри проводя-
проводящей среды, т.е. решают задачу электростатики, и потом, поль-
пользуясь формулой F1.1), определяют плотность тока j в каждой
точке среды. Затем мысленно выделяют какую-либо замкнутую
поверхность S, целиком окружающую один из электродов, и на-
находят силу тока г, согласно E3.3), как поток вектора j через
эту поверхность. Разумеется, замкнутую поверхность S следу-
следует выбирать, сообразуясь с условиями симметрии задачи, чтобы
вычисления были простыми.
Пример 1. Сферический конденсатор с утечкой. Пусть
имеется сферический конденсатор, у которого пространство
между обкладками заполнено веществом с удельной электри-
электрической проводимостью Л. Потенциал U его электрического поля
нами уже вычислен, он выражается формулой B4.2). Отсюда
находим напряженность поля:
F = -QL = и° 1
dr 1/а - l/b г2 "
Поэтому, согласно F1 1), плотность тока на расстоянии г от цен-
центра равна
3 = Uo TJa^TTb И'
В данном случае удобно выбрать в качестве поверхности S в
E3.3) сферу некоторого радиуса г, проходящую между обклад-
обкладками. Тогда jn = j и, кроме того, j постоянно во всех точках
сферы. Поэтому
•о тт А 1 . 2 4тгА тт
1/а — 1/6 г2 1/а — 1/Ь
§ 61 ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ 131
Сила тока через конденсатор, в соответствии с E7.1), пропор-
пропорциональна напряжению Uq между обкладками. Проводимость
конденсатора Л оказывается равной
4тгЛ
С/о l/a-1/Ь'
По этим формулам можно вычислить ток утечки г и сопротив-
сопротивление утечки R = 1/Л сферического конденсатора.
Пример 2. Цилиндрический конденсатор с утечкой. В
этом случае напряженность поля находим из формулы B4.4):
Е = -— = Uo 1
dr In (b/a) r'
Плотность тока j равна
Так как нас не интересует направление тока, а лишь его зна-
значение, мы опустим в дальнейшем знак минус. В качестве зам-
замкнутой поверхности целесообразно выбрать цилиндр радиуса г,
проходящий между обкладками. В этом случае опять jn = j и
постоянно на поверхности цилиндра. Поэтому сила тока на еди-
единицу длины конденсатора получается равной
I • п тт ^ 1 л 2тгЛ тт
т = 3s — Uo . ,, , ч - • 2тгг = -¦-, С/о.
I In (b/a) r In (b/a)
И в данном случае, как и во всех подобных задачах, сила то-
тока пропорциональна напряжению между обкладками. Проводи-
Проводимость конденсатора длины / есть
а 27гЛ /
Этими формулами пользуются для вычисления тока и сопро-
сопротивления утечки кабеля.
Сравнивая полученные выражения для проводимости Л сфе-
сферического и цилиндрического конденсаторов с выражениями
для емкости С (§ 32), мы видим, что отношение этих величин
равно
С/Л = еое/Х. F1.2)
Оно одинаково для обоих типов конденсаторов и зависит
только от свойств среды между электродами. Этот результат
справедлив и в общем случае проводников произвольной фор-
формы, как угодно расположенных относительно друг друга.
Для правильности полученного результата необходимо, что-
чтобы удельная электрическая проводимость среды была значи-
значительно меньше удельной электрической проводимости провод-
проводников.
132
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ VI
Формула F1.2) оказывается во многих случаях полезной.
Так, если нужно определить емкость какой-либо пары проводни-
проводников, то вместо непосредственного измерения их емкости (что при
малой ее величине не очень просто) можно поместить проводни-
проводники в среду с известной величиной А и измерить электрическую
проводимость, после чего найти их емкость по формуле F1.2).
И обратно, полученное соотношение позволяет свести измерение
электрической проводимости к измерению емкости.
§ 62. Электролитическая ванна
В § 61 мы говорили, что в однородной среде линии напряжен-
напряженности электростатического поля совпадают с линиями тока. На
этом основан ценный практический метод экспериментального
исследования электрических полей.
Если имеется какое-либо двумерное электрическое поле и же-
желают определить на опыте его эквипотенциальные поверхности,
то изготовляют металлические модели электродов, создающих
поле, и помещают их в слабо проводящую сред}'. Модели могут
и не совпадать по своим размерам с оригиналом, но должны
быть им подобны и подобным образом расположены. На элек-
электроды подают напряжения, пропорциональные напряжениям на
действительных электродах. Тогда распределение потенциала
между моделями электродов будет подобно распределению по-
потенциала между действительными электродами. Для измерения
потенциала в различных точках среды в них помещают неболь-
небольшой проводник — зонд, например в виде короткого металличе-
металлического штифта. В качестве проводящей среды часто употребляют
какой-либо электролит, налитый
в достаточно большую ванну, от-
отчего указанный метод получил
название метода электролитиче-
электролитической ванны.
На рис. 87 показана схема од-
одной из простейших электролити-
электролитических ванн. В деревянный ящик,
наполненный влажным песком,
погружены исследуемые электро-
Рис 87. Простая электролитиче- ды а и б Размеры ящика должны
екая ванна в несколько рэз превышать рас-
расстояние между электродами. На электроды подают напряжение
от батареи и делителя напряжения. В песок погружают два зон-
зонда 1 и 2, присоединенных к зажимам вольтметра. Для определе-
определения эквипотенциальной линии один из зондов оставляют непо-
неподвижным, а другой помещают в разные точки и находят такие,
для которых отклонение вольтметра равно нулю. Таким обра-
§ 63 ЗАЗЕМЛЕНИЕ В ЛИНИЯХ СВЯЗИ 133
зом определяют одну из эквипотенциальных линий. Затем пер-
первый зонд помещают в другую точку, с другим значением потен-
потенциала, и при помощи второго зонда находят точки, лежащие на
другой эквипотенциальной линии, и т.д. Поступая подобным об-
образом, можно определить форму и расположение эквипотенци-
эквипотенциальных линий электрического поля данных электродов. Вместо
вольтметра удобнее применять нулевой гальванометр, в котором
нулевое деление расположено в центре шкалы.
Отметим, что в § 61, говоря о совпадении поля в проводящей среде
с электростатическим полем, мы предполагали, что проводящая среда од-
однородна В электролитической же ванне мы имеем неоднородную среду,
состоящую из электролита и воздуха, имеющую границу раздела между
ними. Однако это не изменяет результата. Действительно, в случае цилин-
цилиндрических электродов с параллельными осями (двумерное поле) все линии
тока лежат в плоскостях, перпендикулярных к электродам. Но поверхность
электролита есть одна из таких плоскостей Это значит, что линии тока и
напряженности не пересекают эту поверхность, а, значит, ее наличие и не
искажает распределения этих линий
Электролитическая ванна имеет большие преимущества пе-
перед электрическим зондом (§ 23). То обстоятельство, что вну-
внутри электролита текут токи, делает возможным употребление
токопотребляющих вольтметров и гальванометров, которые го-
гораздо удобнее и надежнее электрометров. Кроме того, распреде-
распределение токов и напряжений в ванне нечувствительно к посторон-
посторонним электростатическим влияниям. Поэтому электролитическая
ванна обеспечивает наиболее простой и удобный метод исследо-
исследования электрических полей и широко применяется на практике.
Если нужно произвести точные измерения, то ванна, изображенная на
рис. 87, малопригодна. Один из ее недостатков заключается в том, что при
постоянном токе происходит электролиз и на электродах выделяются со-
составные части электролита (электроды поляризуются, см. § 195). В резуль-
результате напряжение между электродами в течение опыта несколько изменяется
и измерения становятся неточными Чтобы избавиться от этого неудобства,
применяют переменный ток. К электролитической ванне часто присоединя-
присоединяют еще пантограф, состоящий из системы рычагов, на одном конце которой
находится зонд, а на другом — пишущее приспособление, отмечающее на
листе бумаги положение зонда.
§ 63. Заземление в линиях связи
Результаты § 61 позволяют понять действие заземления в
линиях связи. Схема заземления изображена на рис. 88. При
сооружении телеграфных и телефонных линий прокладывают
всего один провод (Л). С этим проводом соединяют лишь один
полюс источника тока Б отправительной станции, а второй его
полюс присоединяют к металлическому листу 3, который зака-
закапывают в землю. Аппарат приемной станции (показанный на
134
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
ГЛ VI
рис. 88 в виде гальванометра) присоединяют к линии и к друго-
другому такому же листу. Роль второго провода, замыкающего цепь,
играет земля. Существенным
является то обстоятельство,
что сопротивление заземления
практически не зависит от
расстояния между станциями.
Сопротивление заземления
получается сравнительно ма-
малым (в хороших заземлениях—
десятки омов и омы), хотя
среда между его электродами
Рис 88 Заземление в линиях связи плохо проводит электричество
(сухие почвы, граниты и т.п.)
Чтобы понять свойства заземления, рассмотрим электроды
простой формы в виде двух одинаковых шаров радиуса а и бу-
будем предполагать, что они погружены в безграничную однород-
однородную среду с удельной электрической проводимостью А (рис. 89).
Среду между шарами мы можем
разбить на трубки тока и рассма-
рассматривать их как параллельно соеди-
соединенные проводники (одна из тру-
трубок тока на рис. 89 заштрихована).
Увеличивая расстояние между ша-
шарами, мы будем удлинять каждую
трубку тока, отчего ее сопротивле-
сопротивление будет увеличиваться. Однако
при этом линии тока в среде бу-
будут все больше и больше удаляться
от обоих шаров (в предельном слу-
случае бесконечно большого расстоя-
расстояния между шарами линии тока направлены вдоль радиусов ша-
шаров и уходят в бесконечность). Поэтому и сечения трубок тока,
на которые мы разбили среду, будут увеличиваться, что приве-
приведет к уменьшению сопротивления каждой трубки. Физическая
причина независимости сопротивления от расстояния и заклю-
заключается в том, что увеличение сечения как раз компенсирует уве-
увеличение длины.
Вычислим сопротивление между шарами, пользуясь мето-
методом, изложенным в § 61. Окружим один из шаров замкнутой
поверхностью S, вплотную прилегающей к поверхности шара, и
вычислим силу тока через нее. Будем считать, что расстояние
между шарами г>а. В этом случае можно пренебречь индук-
индукционным влиянием шаров друг на друга и считать, что заряды
распределяются на шарах равномерно. Если заряды на шарах
равны +д и —</, то их потенциалы (относительно бесконечности)
Рис. 89 К объяснению
ствия заземления
дей-
§ 63 ЗАЗЕМЛЕНИЕ В ЛИНИЯХ СВЯЗИ 135
выражаются соотношениями
°° 4тг??о а' 4тг??о a'
Разность потенциалов, или напряжение между шарами, есть
а
Поэтому напряженность поля у поверхности каждого шара, вы-
выраженная через напряжение, равна
Е= 1 * = и.
4тг??о а2 2а'
Отсюда находим силу тока через поверхность шара:
i= JjdS = \fEdS = \^- 4тга2 = 2жа\и.
s s
Следовательно, сопротивление R среды между шарами равно
г 2тгаЛ
Мы видим, что сопротивление вовсе не зависит от расстояния
между электродами и определяется только радиусами шаров и
удельной электрической проводимостью среды.
Полученный результат легко продемонстрировать на опыте.
Для этого опустим в какой-либо электролит, налитый в боль-
большую ванну, два малых металлических шарика и включим их в
цепь тока, содержащую батарею и амперметр. Чтобы с электро-
электролитом соприкасалась только поверхность шариков, подводящие
провода нужно изолировать стеклянными трубками. Отметим
показания амперметра и будем изменять расстояние между ша-
шариками. Мы увидим, что пока расстояние между ними превы-
превышает несколько радиусов, показания амперметра практически
не зависят от расстояния между шариками, а значит, и сопро-
сопротивление остается постоянным. И только при сближении шари-
шариков на расстояние порядка их радиуса амперметр показывает
увеличение тока.
Обращаясь вновь к рис. 89, мы видим, что густота линий
напряженности велика только в непосредственной близости к
шарам. Это значит, что напряженность поля значительна толь-
только вблизи шаров и, следовательно, основная часть напряжения
приходится на участки среды, непосредственно прилегающие к
электродам. Поэтому и сопротивление заземления практически
зависит только от удельной электрической проводимости этих
участков. Чтобы уменьшить сопротивление заземления, элек-
электроды закапывают на глубине подпочвенных вод, где прово-
проводимость велика вследствие растворения солей, содержащихся в
земле.
136 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
ГЛАВА VII
ЭЛЕКТРОДВИЖУЩАЯ СИЛА
§ 64. Источники тока
Легко видеть, что нельзя получить в проводнике постоян-
постоянный ток, если для создания напряжения на концах проводни-
проводника пользоваться заряженными конденсаторами. Действительно,
наличие тока будет всегда сопровождаться переходом зарядов с
одной обкладки на другую и притом в таком направлении, что
заряды обкладок будут уменьшаться. В результате будет непре-
непрерывно уменьшаться напряжение между обкладками и, согласно
закону Ома (§ 57), сила тока в проводнике будет падать. Это об-
обстоятельство является общим для любого электростатического
поля: такое поле всегда перемещает заряды так, чтобы разности
потенциалов уменьшались.
Для получения постоянного тока на заряды в электрической
цепи должны действовать какие-либо силы, отличные от сил
электростатического поля. Такие силы получили общее назва-
название сторонних сил. Всякое устройство, в котором возникают
сторонние силы, мы называем источником тока. Источниками
тока являются, например, гальванические элементы.
Если воспользоваться гидростатической аналогией, то силы
электростатического поля можно уподобить силе тяжести, стре-
стремящейся выравнять уровни жидкости в сообщающихся сосудах;
источник же тока можно сравнить с насосом, работающим про-
против силы тяжести и восстанавливающим разность уровней в со-
сосудах, несмотря на наличие тока жидкости.
Ближайшей нашей задачей будет установление количествен-
количественных характеристик источников тока и выяснение связи между
ними и силой тока в цепи. Мы будем считать, что источник то-
тока есть гальванический элемент, а затем обобщим полученные
результаты на случай любого источника. При разборе этих во-
вопросов мы будем исходить из первого начала термодинамики
(общего закона сохранения энергии) и рассмотрим, какие пре-
превращения энергии происходят в замкнутой цепи тока.
§ 65. Работа и мощность постоянного тока.
Закон Джоуля-Ленца
Электрический ток совершает в любом участке цепи опре-
определенную работу. Пусть имеется произвольный участок цепи
(рис. 90), между концами которого существует напряжение U.
По определению электрического напряжения (§ 17) работа, со-
совершаемая при перемещении единицы заряда между точками а
§ 65 РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА 137
и б, равна U. Если сила тока в участке цепи равна г, то за время
t пройдет заряд it, и поэтому работа электрического тока в этом
участке будет
А = Uit. F5.1)
Это выражение справедливо для постоянного тока в любом слу-
случае, для какого угодно участка цепи, который может содержать
проводники 1-го и 2-го рода, электромоторы и т.д. Мощность
тока, т.е. работа в единицу времени, равна
Р = A/t = Ui. F5.2)
Формулу F5.2) используют в системе СИ для определения
единицы напряжения. Единица напряжения вольт (В) есть
1 В = 1 Вт/1 А = 1 Вт/А.
Вольт — электрическое напряжение, вызывающее в электриче-
электрической цепи постоянный ток силой 1 А при мощности 1 Вт.
Будем теперь считать, что участок цепи представляет собой
неподвижный проводник 1-го рода. Тогда вся работа тока пре-
превращается в тепло, которое выделяется в проводнике. Если про-
проводник однороден и подчиняется закону
Ома (сюда относятся все металлы и элек- ^ и ж |
тролиты), то U = гг, где г — сопротивле- I 1
ние проводника. В таком случае А—Н> ——/ °Ц—-А
А = ri2t. F5.3)
Рис. 90. К вычисле-
Этот закон был впервые установлен на нию работы электри-
опыте Э-Х. Ленцем и, независимо от него, ческого тока
Джоулем.
Отметим, что нагревание проводников током находит много-
многочисленные технические применения. Наиболее важное из них —
осветительные лампы накаливания.
Современные лампы накаливания являются результатом настойчивых
и длительных работ ряда ученых. Большое значение в развитии ламп на-
накаливания имели работы А.Н. Лодыгина, который уже в 1873 г. публично
демонстрировал в Петербурге различные типы своих ламп. Первые лам-
лампы Лодыгина имели форму стеклянного шара, в котором на двух медных
стержнях был укреплен стерженек специального угля. В поисках способов
увеличения срока службы ламп им совместно с сотрудниками была введена
откачка ламп и найдены более долговечные тела накала в виде различных
обугливаемых органических волокон. В 1890 г. Лодыгин ввел лампы накали-
накаливания с металлической нитью из тугоплавких металлов: вольфрама, молиб-
молибдена и др. Работы Эдисона, поставленные в очень широком промышленном
масштабе, привели к внедрению ламп накаливания в практику. В после-
последующее время были сделаны только два существенных усовершенствова-
усовершенствования: тело накала стали изготовлять в виде тонкой спирали, что уменьшило
теплоотдачу, и баллоны ламп начали наполнять инертным газом, чтобы
иметь возможность повысить температуру нити накала без заметного ее
распыления (Лэнгмюр).
138 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
§ 66. Энергия, освобождаемая в гальваническом
элементе
Когда какой-либо гальванический элемент создает в цепи
ток, то внутри элемента происходят химические реакции. В
большинстве элементов основная реакция состоит в соединении
цинкового электрода, являющегося катодом элемента, с электро-
электролитом, и поэтому во время работы элемента расходуется метал-
металлический цинк, а в растворе появляются новые вещества — про-
продукты реакций. В простейшем элементе Вольты (см. рис. 2) эта
реакция такова:
Zn + H2SO4 = ZnSO4 4- Н2-
Но опыт показывает, что при всякой химической реакции ли-
либо поглощается, либо выделяется определенное количество энер-
энергии. В дальнейшем мы будем предполагать, что химическая ре-
реакция происходит при постоянном внешнем давлении. При этом
выделяется количество теплоты Qx, равное
Qx=pm, F6.1)
где т — масса прореагировавшего вещества. Величина р опре-
определяет тепловой эффект химической реакции и указывает, ка-
какое количество теплоты выделяется при вступлении в данную
реакцию единицы массы рассматриваемого вещества. Если ре-
реакция идет с выделением тепла, то р положительно, если с по-
поглощением тепла, — отрицательно. Так, например, в указанной
реакции образования сернокислого цинка при взаимодействии
1 г цинка с серной кислотой выделяется 6900 Дж, и поэтому
тепловой эффект данной реакции, рассчитанный по цинку, есть
р = 6,9 • 106 Дж/кг.
Энергия химических реакций и есть та энергия, которая
освобождается в гальванических элементах. Ее мерой является
тепловой эффект реакции.
§ 67. Электродвижущая сила гальванического
элемента
Рассмотрим теперь какой-либо гальванический элемент, зам-
замкнутый на проводник с сопротивлением R (рис. 91). Будем счи-
считать, что в отсутствие тока в элементе не происходит никаких
химических реакций. Это имеет место не для всех комбинаций
металлов с электролитами. Так, например, в элементе Вольты
цинк растворяется в серной кислоте и при разомкнутой цепи, хо-
хотя и в меньшей степени. Если же цинк покрыть слоем амальгамы
цинка путем обработки его ртутью и в качестве электролита вы-
выбрать раствор хлористого цинка ZnC^ или хлористого аммония
NH4CI, то цинк в отсутствие тока растворяется очень медленно,
§ 67 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА 139
Рис. 91. Электрическая
цепь с гальваническим
элементом
и наше предположение будет ближе к действительности. При
наличии тока масса электрода, перешедшая в электролит, равна
т = Kq,
где К — электрохимический эквивалент металла электрода (ср.
§ 189), ад — полный заряд, прошедший через элемент. Поэто-
Поэтому для энергии, освобождаемой в химиче-
химических реакциях у обоих электродов, имеем
Qx = (piKi + P2K2)q.
При замкнутом элементе в цепи бу-
будет совершаться еще работа тока, кото-
которая будет превращаться в тепло Джоуля-
Ленца. При этом мы должны учесть, что
электрические заряды нигде не накап-
накапливаются в цепи, а, значит, ток суще-
существует не только во внешней цепи, но и
внутри элемента. Гальванический элемент
представляет для тока определенное со-
сопротивление, называемое внутренним со-
сопротивлением, которое складывается из
сопротивлений электролита и электродов. Далее, будем считать,
что элемент поддерживается при постоянной температуре и что
мы отбираем от него только очень слабый ток (строго говоря —
бесконечно слабый). В этом случае внутри элемента не будут
возникать ни заметные разности концентраций в электролите,
Ни заметные разности температур, и состояние элемента в лю-
любой момент времени будет лишь бесконечно мало отличаться
от состояния равновесия в отсутствие тока. Такой режим рабо-
работы элемента часто называют квазистатическим. Однако если
температура элемента поддерживается постоянной, то при на-
наличии тока элемент будет передавать окружающей среде (или,
наоборот, заимствовать от нее) некоторое количество теплоты
Qt-i необходимое для поддержания постоянства температуры.
Применим теперь к рассматриваемой замкнутой цепи пер-
первое начало термодинамики (общий закон сохранения энергии).
Тогда
<3х = А + QT, F7.1)
Где А — работа тока. Разумеется, все входящие сюда величины
Должны быть выражены в одинаковых (тепловых или механи-
механических) единицах.
Рассуждая совсем точно, мы должны были бы еще учесть, что в кон-
контактах двух различных проводников в присутствии тока выделяется или
Поглощается (в зависимости от направления тока) дополнительное коли-
количество теплоты. Однако это так называемое тепло Пельтье (§ 200) обычно
мало по сравнению с теплом химических реакций и теплом Джоуля-Ленца,
и поэтому им можно пренебречь
140 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
Мы видим, что даже в квазистатическом режиме в работу
тока превращается не вся энергия химических реакций, а лишь
разность
А = Qx - QT.
Если бы мы отбирали от элемента ток конечной силы, то вну-
внутри элемента происходили бы еще дополнительные процессы,
обусловленные появлением разностей концентраций и темпера-
температур, и полезная работа тока была бы еще меньше. Величина А
для квазистатического процесса называется максимальной ра-
работой химической реакции. Максимальная работа при данной
температуре представляет собой определенную долю энергии Qx
и, подобно Qx, пропорциональна заряду, прошедшему по цепи.
Поэтому можно положить
А = Щ,
где & — максимальная работа данной химической реакции (или
реакций), рассчитанная на единицу заряда. Она получила на-
название электродвижущей силы гальванического элемента.
Приравнивая А полной работе тока (во внешней цепи и вну-
внутри источника), имеем
Щ = Ri2t + ri2t,
где г — внутреннее сопротивление элемента. Деля обе части ра-
равенства на заряд q = it, находим
Полученный закон F7.2) называется законом Ома для замкну-
замкнутой цепи. Сумму (R+r) внешнего и внутреннего сопротивлений
называют полным сопротивлением цепи. Формула F7.2) пока-
показывает, что для всякого гальванического элемента можно ввести
характерную для него величину — электродвижущую силу — та-
таким образом, что частное от деления ее на полное сопротивление
цепи будет равно силе тока в цепи.
Из F7.2) видно, что размерность % совпадает с размерностью
напряжения, и поэтому ЭДС выражают в тех же единицах, что
и напряжение.
Максимальная работа А, так же как и энергия химических
реакций <5Х, при известном прошедшем заряде зависит только от
природы электродов и электролита. Поэтому и ЭДС гальваниче-
гальванического элемента зависит только от рода веществ, входящих в его
состав, и не зависит от размеров элемента. Напротив, внутрен-
внутреннее сопротивление элемента, как и всякого проводника, зависит
от его размеров и формы.
Выше мы определили ЭДС гальванического элемента через максималь-
максимальную работу химической реакции. Однако ЭДС можно выразить и непо-
непосредственно через тепловой эффект химической реакции. В термодинамике
§ 68 НАПРЯЖЕНИЕ НА ЗАЖИМАХ ИСТОЧНИКА ТОКА 141
показывается, что работа А, совершаемая в любом изотермическом квази-
квазистатическом процессе, связана с количеством теплоты Qp, отбираемым от
источника тепла, соотношением
где индекс р указывает, что соответствующие величины измерены при по-
постоянном внешнем давлении (формула Гиббса-Гельмгольца). Подставляя
Сюда вместо Qp выражение Qx, приведенное в тексте, и А = 8'д, получаем
' p
где первое слагаемое в правой части есть тепловой эффект химических ре-
реакций в элементе, рассчитанный на единицу прошедшего заряда. Это соот-
соотношение было получено Гельмгольцем и является основным в теории галь-
гальванических элементов.
Мы получили закон Ома F7.2), рассматривая источник то-
тока в виде гальванических элементов. Однако этот закон имеет
общее значение. Всякий источник тока можно охарактеризовать
его электродвижущей силой таким образом, что будет справед-
справедлив закон Ома F7.2). Так как ЭДС любого источника легко из-
измерить на опыте (§ 68), то формула F7.2) имеет большое значе-
значение и позволяет вычислить силу тока в любой цепи.
Отметим, что закон F7.2) был впервые установлен Омом на опыте со-
совсем другим путем. Ом экспериментировал не с гальваническими элемента-
элементами, а с термоэлементами, и при теоретическом объяснении закона исходил
из аналогии между электрическим током и течением жидкости и тепла.
§ 68. Напряжение на зажимах источника тока
Пусть имеется цепь, содержащая источник тока, переменное
внешнее сопротивление R и амперметр А (рис. 92), и положим,
что мы измеряем напряжение на за-
зажимах источника с помощью вольт- г
метра V. Сопротивление вольтметра
выберем достаточно большим, чтобы ]>•
подключение вольтметра не изменя-
изменяло напряжение между точками 1 я 2. /
Мы найдем, что напряжение, показы-
показываемое вольтметром, зависит от си-
силы тока в цепи. Оно наибольшее при
разомкнутой цепи (г = 0) и стремит- Рис- 92- Измерение напря-
ся к нулю при уменьшении до нуля жения на зажимах работаю-
_ ^ J ту f щего источника
внешнего сопротивления К (включая
и сопротивление амперметра). Напряжение на зажимах рабо-
работающего источника есть величина переменная, зависящая от на-
нагрузки источника.
-g r
1| •—
142
ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ГЛ VII
Объяснение этого мы находим в законе Ома. Напряжение,
показываемое вольтметром, есть напряжение между точками 2
и 1. Применяя к внешней цепи 2R1 (не содержащей ЭДС) закон
Ома E7.1), имеем
U2i = Ri.
Но сила тока в цепи выражается законом Ома F7.2), и поэтому
Мы видим, что напряжение на зажимах меньше ЭДС на вели-
величину ri, которая есть падение напряжения внутри самого источ-
источника.
Полученная формула показывает, что чем больше внешнее
сопротивление Я по сравнению с внутренним сопротивлением г,
тем меньше падение напряжения внутри источника и тем ближе
напряжение на зажимах к ЭДС. Если R^>r (цепь разомкнута),
то U = Ш: электродвижущая сила равна напряжению на зажи-
зажимах разомкнутого источника. Это позволяет весьма просто опре-
определить ЭДС любого источника и лежит в основе всех методов
измерения ЭДС.
Чтобы пояснить смысл формулы F8.1), рассмотрим распре-
распределение потенциала в цепи гальванического элемента. При разо-
разомкнутой цепи (нет тока) потенциал внутри металлических элек-
электродов, проводов и в толще электролита (где нет сторонних сил)
постоянен (рис. 93 а). В тонких же пограничных слоях между
+
a
и
1
I
i
т
\
«2,
X
б
и
¦
ri--4
;
/
п
X
Рис 93. Распределение потенциала в цепи разомкнутого (а) и замкнутого
(б) гальванического элемента
электродами и электролитом существуют сторонние силы, вы-
вызывающие быстрое изменение (скачки) потенциала Ь\ и #2- Сум-
§ 69 ЭЛЕКТРОДВИЖУЩАЯ СИЛА И РАБОТА ИСТОЧНИКА ТОКА 143
ма этих скачков равна напряжению между электродами и пред-
представляет собой полную ЭДС элемента. При замыкании точек
а и б цепи получается распределение потенциала, показанное
на рис. 93 б. Из рисунка видно, что в этом случае напряжение
между точками 2 и 1 (между электродами) уже не равно сумме
$1 + ^2 > а уменьшается на величину падения напряжения внутри
элемента гг.
Обратим еще внимание на то, что заряды в замкнутой цепи
движутся кругообразно: во внешней части цепи положительные
заряды перемещаются от положительного электрода к отрица-
отрицательному, а внутри источника — от отрицательного электрода
к положительному. Это и понятно. Из рис. 93 б видно, что в
толще электролита это соответствует движению от более высо-
высокого потенциала к более низкому, т.е. так же, как и во внешней
цепи. В пограничных же слоях, где имеются скачки потенциа-
потенциала, положительные заряды движутся в направлении увеличения
потенциала, что осуществляется с помощью сторонних сил.
Если внешнее сопротивление R намного меньше г, то из
F8.1) следует, что U < %. Если R -? 0, то и U -? 0. Случай
R <С т называют коротким замыканием источника. При этом
сила тока, согласно F7.2), делается максимальной:
We = 8/г F8-2)
(ток короткого замыкания).
Мы видим, что качество источника определяется не только
его ЭДС, но и внутренним сопротивлением.
Формула F8.1) связывает напряжение на участке цепи с си-
силой тока в нем и поэтому может быть названа законом Ома для
участка с ЭДС (ряс. 94). В дальнейшем
мы будем писать ее в виде ,• €, г
Uvt = ri-«. F8.3) 1О~* 'I °2
Здесь г — полное сопротивление участ- Рис. 94. Участок цепи с
ка (сопротивление источника и про- ЭДС
водников). При пользовании формулой
F8.3) необходимо соблюдать следующее правило знаков: ток
считается положительным, если он направлен от точки 1 к точке
8, ЭДС считается положительной, если, перемещаясь от точки
1 к точке 2, мы проходим источник от отрицательного полюса
к положительному.
§ 69. Электродвижущая сила и работа источника тока
Понятие электродвижущей силы, введенное выше на приме-
примере гальванических элементов, можно обобщить так, чтобы оно
охватывало любые источники тока. Рассмотрим произвольный
144 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ УП
источник тока, который посылает ток во внешнюю цепь, состоя-
состоящую из неподвижных проводников 1-го рода. Напишем выраже-
выражение для силы тока в цепи в прежнем виде
g
1 R + r
(закон Ома для замкнутой цепи) и выясним, какой физический
смысл имеет & в общем случае. Умножим обе части этого ра-
равенства на it = q, где t — время протекания тока, a q — полный
заряд, прошедший по цепи. Тогда
i2Rt + i2rt = Ы = Щ.
Но слева стоит полная работа, совершенная током во всей цепи,
т.е. работа источника. Обозначая ее через Л, получаем
А=Ш = Щ. F9.1)
Следовательно, работа любого источника тока выражается про-
произведением его ЭДС на полный заряд, прошедший по цепи.
Полагая в F9 1) q — +1, мы получим & = А. Это позволя-
позволяет дать определение ЭДС через работу: электродвижущая сила,
действующая в какой-либо цепи, измеряется работой, соверша-
совершаемой при перемещении заряда +1 по этой цепи.
В § 64 мы говорили, что во всяком источнике тока на заря-
заряды обязательно действуют какие-либо силы (сторонние силы),
отличные от сил электростатического поля. Работа, которая со-
совершается в цепи с ЭДС, и есть работа сторонних сил, и поэтому
ЭДС можно выразить через эти силы
= +1 Введем новую величину, которую назовем
напряженностью поля сторонних сил.
Мы определим ее как силу, действующую
на заряд +1, которая обусловлена любы-
любыми причинами, кроме электростатическо-
электростатического поля. Тогда полная сила, действующая
на заряд +1, будет суммой
Е + Е*,
где Е — напряженность электростатиче-
Рис ^' К опРеДеле- ского поля, а Е* — напряженность поля
нию ЭДС сторонних сил.
Рассмотрим теперь замкнутую цепь I (рис. 95) с ЭДС и пред-
предположим, что заряд +1 обходит эту цепь. Тогда совершаемая
работа есть
§
dl,
где индекс / обозначает проекцию соответствующей величины
на направление перемещения dl, а интегрирование производится
§ 69 ЭЛЕКТРОДВИЖУЩАЯ СИЛА И РАБОТА ИСТОЧНИКА ТОКА 145
по всей замкнутой цепи I. Но, согласно § 17, напряжение вдоль
замкнутого контура в электростатическом поле равно нулю, т.е.
idl = 0.
Поэтому
Ш= § Efdl. F9.2)
Если Е* отлично от нуля только в части цепи, например на от-
отрезке 1\ (рис. 95), то для всех других участков подынтегральное
выражение в F9.2) будет равно нулю, и поэтому интегрирование
можно производить только по участку цепи /i.
Формула F9.2) дает самое общее определение ЭДС и пригод-
пригодна для любых случаев. Если известно, какие именно силы вы-
вызывают движение зарядов в данном источнике, то всегда можно
найти напряженность поля сторонних сил Е* и по F9.2) вычис-
вычислить полную ЭДС источника Измерить же ЭДС в любом случае
можно по напряжению разомкнутого источника.
Физическая природа электродвижущих сил в разных источ-
источниках весьма различна. Так, например, в гальванических эле-
элементах — это силы молекулярного взаимодействия (§ 195), в тер-
термоэлектрических явлениях — силы давления электронного газа
(§ 199), в электромагнитной индукции — силы электрического
поля (однако не электростатического, а
вихревого; см. § 131). Ниже будут рас-
рассмотрены подробнее причины возникно-
возникновения этих сил и будет показано, как
в отдельных случаях можно вычислить
ЭДС
Сейчас мы ограничимся лишь одним особен-
особенно простым примером Пусть имеется металли-
металлический диск радиуса а (рис 96), вращающийся с
угловой скоростью ш Диск включен в электри-
электрическую цепь при помощи скользящих контак- п „_ _
т-* "не У6. Ниимеи вычис-
тов, касающихся оси диска и его окру ясности В " „~F
этом случае на каждый электрон металла дей- "=""¦» ^-v-w
ствует центробежная сила, которая и является сторонней силой Поэтому
в диске появляется ЭДС и между осью диска и его наружным краем воз-
возникает напряжение Вычислим эту ЭДС. Центробежная сила равна
F = тгш2,
где г — расстояние от оси диска, am — масса электрона Эта сила действует
на эаряд электрона е, и поэтому
» _ F _ тгш2
е е
Возникающая ЭДС равна
О 2 О 9 9
с? (• * tnuj n тпш а
' ~ j r - е J r r - 2е
146 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ. VII
Полагая о = 0,1 м, ш = 103 рад/с, т - 9 • 1СГ31 кг и е = 1,6 • 1СГ19 Кл,
находим ЭДС:
2-1,6-10-"
§ 70. Разветвленные цепи. Правила Кирхгофа
До сих пор мы имели дело с простыми электрическими це-
цепями, представляющими собой один замкнутый контур. Рассмо-
Рассмотрим теперь более сложный случай разветвленной цепи, пример
которой изображен на рис. 97. Здесь имеются точки разветвле-
разветвления А, В, С, D, F, где сходятся три и более проводов. Между
точками разветвления находятся участки цепи 1,2,..., 7, кото-
которые имеют определенные сопротивления г\, г%, .. -, r-j и могут
содержать источники с ЭДС Ш\,
82, -.-, Щ- Изображенный контур
может в свою очередь входить в
состав более сложной цепи. Сопро-
Сопротивления участков и действующих
в них ЭДС будем считать заданны-
заданными. Задача заключается в вычис-
вычислении силы тока во всех участках
цепи.
Рассмотрим какую-либо точку
разветвления, например точку F. В
D n-7 d этой точке сходятся три участка E,
гис. 97 Разветвленная цепь i /у\ ¦
4 и 7), в которых имеются токи ?з>
«4 и «7- Припишем этим токам определенные знаки: будем счи-
считать их положительными, если они направлены к точке развет-
разветвления («з), и отрицательными, если они направлены от нее (г4
и ii). Выбор знаков токов произволен, и мы могли бы считать,
наоборот, токи, притекающие к узлу, отрицательными, а токи,
уходящие от узла, — положительными.
Алгебраическая сумма токов «з ~ Н — *7 есть заряд, прихо-
приходящий к точке F за единицу времени. Если в данной цепи токи
постоянны, то эта сумма токов должна равняться нулю, так как
в противном случае потенциал рассматриваемой точки изменял-
изменялся бы со временем, а значит, изменялись бы и токи в цепи. Это
справедливо по отношению ко всякой точке разветвления, и по-
поэтому для любой точки разветвления
5> = °- G0-1)
Эта формула выражает первое правило Кирхгофа: алгебраиче-
алгебраическая сумма сил токов в участках цепи, сходящихся в любой точке
разветвления, равна нулю.
§ 70 РАЗВЕТВЛЕННЫЕ ЦЕПИ ПРАВИЛА КИРХГОФА 147
Выделим теперь в разветвленной цепи какой-либо замкну-
замкнутый контур, например контур ABCFA (рис. 97). К отдельным
его участкам можно применить закон Ома для участка цепи
F8.3). Тогда для разности потенциалов точек А я В имеем
Аналогично для других участков:
Uв — Uc =
UC-UF = i3r3 - g'3,
Up — UA = ЧГА — <$4-
Складывая почленно эти равенства, мы найдем, что сумма ле-
левых частей равна нулю, откуда
Подобное соотношение мы получим для любого замкнутого кон-
контура, и поэтому
Х> Х>п- G0.2)
Написанное соотношение выражает второе правило Кирхгофа.
Каждое из произведений ir определяет разность потенциалов,
которая существовала бы между концами соответствующего
участка, если бы ЭДС в нем была равна нулю, т.е. это произ-
произведение есть падение напряжения, вызываемое током. Поэтому
второе правило Кирхгофа можно выразить следующим образом:
для любого замкнутого контура сумма всех падений напряже-
напряжения равна сумме всех электродвижущихся сил в этом контуре.
Правила Кирхгофа не выражают новых свойств электричес-
электрического поля. Выше мы видели, что первое правило обозначает не
что иное, как условие стационарности токов. Второе правило
вытекает из того, что электрическое напряжение по замкнуто-
замкнутому контуру равно нулю, а значит, это правило есть следствие
основного свойства электростатического поля, согласно которо-
которому работа при движении заряда по замкнутому контуру равна
нулю (§ 17).
Однако оба правила Кирхгофа весьма полезны при решении
задач на разветвленные цепи. Применяя эти правила к точкам
разветвления и к различным замкнутым контурам, входящим в
состав сложной цепи, мы получаем уравнения для определения
всех неизвестных токов. Можно показать, что получаемое при
этом число независимых уравнений всегда равно числу неизвест-
неизвестных токов, и поэтому оба правила Кирхгофа дают общий метод
решения задач на разветвленные цепи.
При составлении уравнений с помощью правил Кирхгофа
G0.1) и G0.2) следует тщательно соблюдать правило знаков,
приведенное в § 68. Так, например, в цепи рис. 97 ЭДС в участ-
148 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ. VII
ке 1 следует брать со знаком плюс, а ЭДС в участке 6 — со
знаком минус.
В связи с этим правилом знаков может возникнуть кажуще-
кажущееся затруднение при составлении уравнений. Ведь направления
отдельных токов заранее неизвестны и должны быть найдены из
решения задачи, тогда как само составление уравнений требует
знания этих направлений. Однако на самом деле этой трудно-
трудности не существует. При составлении уравнений можно с самого
начала произвольно выбрать для каждого участка некоторые
направления токов и считать их положительными. Иными сло-
словами, можно сначала произвольно предположить, что токи в
участках текут в определенных направлениях, и в соответствии
с этим применить правило знаков для ЭДС. Действительное на-
направление токов определится решением задачи: если какой-либо
ток окажется положительным, то, значит, его направление сов-
совпадает с предположенным; если он окажется отрицательным,
то, значит, в действительности он направлен противоположно
принятому положительному направлению.
Отметим в заключение, что метод Кирхгофа приводит к
необходимости решать систему алгебраических уравнений пер-
первого порядка. Для сложных цепей это тре-
требует вычисления детерминантов высокого
порядка, что весьма кропотливо. Поэто-
Поэтому были предложены различные вспомо-
вспомогательные приемы, позволяющие умень-
уменьшить число уравнений системы. Один из
них рассмотрен в Добавлении 4.
Пример 1. Параллельное соединение со-
Рис. 98. Параллельное противлении. Шунт. Пусть в цепь источника с
соединение сопротивле- ЭДС % и внутренним сопротивлением г включе-
включений ньг два сопротивления п и гг, соединенные свои-
своими концами в точках разветвления аи б (рис. 98).
Вычислим силу тока в цепи. Выберем положительные направления токов
так, как показано на рисунке. Тогда первое правило Кирхгофа для точки а
дает
i — i\ — гг = 0.
Применяя второе правило Кирхгофа к контурам аг^бгх и аг\бШа и обходя
их по часовой стрелке, имеем
—r\i\ + гггг = 0, ri + nil = Щ.
Мы получили три уравнения для определения трех неизвестных токов,
и легко убедиться, что больше независимых уравнений нет.
Исключим из первых двух уравнений ток ti. Это дает соотношение
i2/i = п/(п +г2).
Исключая из тех же уравнений ток г'г, найдем аналогично
ii/i = г2/(г1 +г2).
§ 70
РАЗВЕТВЛЕННЫЕ ЦЕПИ. ПРАВИЛА КИРХГОФА
149
Поэтому
Отношение сил токов в двух проводниках, соединенных параллельно,
обратно пропорционально отношению их сопротивлений.
Подставляя выражение для i\ в третье уравнение системы, находим
i[r + Г1Г2/(г1 + г2)] = 8".
Сравнивая полученное выражение с законом Ома F7.2), мы видим, что оба
параллельно соединенных проводника имеют сопротивление
R = пгг/(г1 +г2).
Полученный результат можно записать в более удобном виде
1/Я=1/п + 1/г2.
Если бы мы рассмотрели не два проводника, а какое угодно их количе-
количество, то результат был бы аналогичен:
R
G0.3)
г а
Участок цепи, составленный из параллельно соединенных проводников,
имеет проводимость, равную сумме проводимостей отдельных проводни-
проводников.
Параллельное соединение сопротивлений /~Г\
используют при устройстве шунта в измери-
измерительных приборах. Пусть требуется измерить
силу тока в какой-либо цепи при помощи ам- i_
перметра, который рассчитан на меньшую
силу тока. В этом случае параллельно ампер-
амперметру включают сопротивление г (рис. 99), гис. 99. Шунт
называемое шунтом. Тогда, согласно полученным выше результатам, сила
тока в цепи г связана с током амперметра гл соотношением
г
-CD-
#!,/-, ?[,/-(
R
-сэ-
Рис. 100. Батарея из п
последовательно соеди-
ненных источников тока,
питающих нагрузку R
Сравнивая эту формулу с
ствует как один источник
ление г имеют значения
где га — сопротивление амперметра. Так, на-
например, если при помощи амперметра, рассчи-
рассчитанного на токи до 10 А, нужно измерять токи
силой до 100 А, то должно быть (г + га)/г = 10,
откуда г = г а/9.
Пример 2. Соединение источников то-
тока. Пусть п одинаковых источников соединены
последовательно и замкнуты на внешнюю цепь
(рис. 100). Обозначим ЭДС каждого источника
а,
через ©1, его внутреннее сопротивление через
а сопротивление внешней цепи - через Я.
Тогда Qe п л0 к гофа
г(пп + Щ = пШ\.
законом Ома F7.2), мы видим, что батарея дей-
дейтока, у которого ЭДС "& и внутреннее сопротив-
сопротив$' = nisi, г — nri.
150
ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ГЛ. VII
При последовательном соединении п одинаковых источников тока ЭДС
батареи и ее внутреннее сопротивление в п раз больше, чем у одного
источника.
Рассмотрим теперь параллельное соединение, показанное на рис. 101.
В этом случае все положительные полосы отдельных источников и все
отрицательные полосы соединяются между собой и образуют два по-
полюса а и. б батареи. Выберем положительные направления токов, как
показано на рис. 101, и применим к изображенной цепи оба правила
Кирхгофа. Первое правило для точки а дает
г =ii +«г + ... +гт.
Применяя второе правило к отдельным про-
простым контурам цепи, получаем
= W\ - %i - 0,
i2 - пг3 = 0,
im-i — r\im = 0,
Рис. 101. Батарея из т Из этих уравнений (кроме последнего) находим
^ = j2 = j3 = . i ^
последнее уравнение дает
параллельно соединен-
ных источников тока,
питающих нагрузку R
im _
Отсюда видно, что такая батарея действует как один источник, для кото-
которого
% = isi, г = гх/т.
При параллельном соединении т одинаковых источников тока ЭДС бата-
батареи равна ЭДС одного источника, а внутреннее сопротивление батареи в т
раз меньше, чем у одного источника.
На рис. 102 показано смешанное со-
соединение источников. Такая батарея со-
состоит из т параллельно соединенных
звеньев, в каждом из которых имеется
п последовательно соединенных источни-
источников. Легко сообразить, что ЭДС и вну-
внутреннее сопротивление этой батареи име-
имеют значения iS = n<S\, r = пп/т.
Пользуясь соединением источников в
батареи, можно изменять ЭДС и вну-
внутреннее сопротивление в широких преде-
пределах и осуществлять такие их значения,
которые необходимы для питания данной
внешней цепи.
Пример 3. Компенсационный метод измерения ЭДС.
Рассмотрим важный метод измерения ЭДС при помощи компен-
Рис. 102. Смешанное соедине-
соединение источников тока в батарею
§70
РАЗВЕТВЛЕННЫЕ ЦЕПИ ПРАВИЛА КИРХГОФА
151
сации. Схема этого метода показана на рис. 103. Два источника
с ЭДС $ и is/ включены навстречу друг другу. Сопротивления
П и Г2 — переменные, причем
все время выполняется условие
т\ + Г2 = R = const.
Если можно ограничиться
не очень высокой точностью
(~1%), то осуществляют оба
сопротивления г\ и Г2 в виде
однородной проволоки, натяги-
натягиваемой между точками а и б, a
точка в определяется скользя-
скользящим контактом. В точных из-
измерениях сопротивления Г\ И Г2 Рис. 103. Принципиальная схема
представляют собой магазины потенциометра
сопротивлений.
Выберем положительные направления токов, как показано
на рисунке, и применим к рассматриваемой схеме правила Кирх-
Кирхгофа. Первое правило для точек а и в дает
ti — i — »' = 0.
Второе правило для контуров а'ёбва и а&'ва приводит к урав-
уравнениям
ir + i{R — n)
Эти уравнения вполне определяют все неизвестные токи. Од-
Однако мы ограничимся частным случаем и предположим, что со-
сопротивления п и Г2 подобраны таким образом, что ток в цепи
гальванометра i' = 0. В этом случае написанные уравнения дают
Н = г, i(R + r) = %, in = %'.
Из двух последних уравнений находим
Предположим теперь, что вместо источника с ЭДС ?' мы
включили в схему другой источник с ЭДС if" и изменением пе-
переменных сопротивлений вновь добились компенсации. Пусть
Для этого вместо сопротивления т\ потребовалось ввести сопро-
сопротивление г". Тогда
щ" =
R + r
Деля почленно оба последних равенства друг на друга, находим
152 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
Это равенство и лежит в основе сравнения ЭДС при помощи
метода компенсации.
Отметим, что отношение сравниваемых ЭДС не зависит во-
вовсе от внутренних сопротивлений источников и от других сопро-
сопротивлений схемы и определяется только сопротивлениями участ-
участка цепи, к которому подключаются сравниваемые источники. Не
требуется знать и ЭДС вспомогательного источника 8", которая
только должна быть достаточно постоянна во время измерения
и должна быть больше обеих сравниваемых ЭДС ft' и Ш . Для
измерения ЭДС этим методом в качестве одного из сравнива-
сравниваемых источников выбирают нормальный элемент (§ 22), ЭДС
которого известна очень точно.
Для практического измерения ЭДС компенсационным мето-
методом служат потенциометры, устроенные в принципе по схеме
рис. 103. Переменные сопротивления г\ и Г2 выполняются в них
обычно в виде точных магазинов сопротивления с кнопочны-
кнопочными контактами и спаренными рукоятками и увеличение одного
из сопротивлений автоматически сопровождается соответствую-
соответствующим уменьшением другого.
§ 71. Мощность во внешней цепи и коэффициент
полезного действия источника тока
Рассмотрим теперь практически важный вопрос об использовании энер-
энергии источника тока.
Пусть какой-либо источник с ЭДС iS и внутренним сопротивлением г
замкнут на внешнюю цепь с сопротивлением R. Во внешней цепи будет
выделяться мощность Ра, равная
Ра = Ui = Ri2 ~ I ~
Предположим теперь, что мы желаем получить во внешней цепи макси-
максимальную мощность (Ра)макс, возможную при данном источнике, и для это-
этого меняем внешнее сопротивление R. Значение R = Rm, соответствующее
максимальной мощности, мы получим, дифференцируя выражение Ра по
R и приравнивая первую производную нулю Это дает
dR ~С> (r
откуда, учитывая, что г и R всегда положительны, получаем
Rm =Г.
Мощность, выделяемая во внешней цепи, достигает наибольшего значения,
если сопротивление внешней цепи равно внутреннему сопротивлению ис-
источника. При этом ток в цепи равен <s/2r, те. половине тока короткого
замыкания, а наибольшее возможное значение мощности есть
(Ра )макс = 82/4г.
§71
МОЩНОСТЬ ВО ВНЕШНЕЙ ЦЕПИ И КПД ИСТОЧНИКА ТОКА
153
Однако при практическом использовании источников тока важна не
только мощность, но и их коэффициент полезного действия (КПД). Когда
источник работает на внешнюю цепь, то ток протекает также и внутри ис-
источника, и поэтому некоторая мощность тратится бесполезно на выделение
тепла внутри источника. Эта мощность имеет значение
Р, = П\
тогда как полная мощность источника
р = т2 + н
Поэтому КПД источника равен
г, = Ра/Р =
Так как всегда [/ ^ ё, то и т; ^ 1.
Рассмотрим подробнее, как зависят Ра и 7/ от силы тока г, отбираемой от
источника. Полезную мощность Ра можно представить в следующем виде:
= т.
Мощность во внешней цепи Ра меняется с изменением г по параболическому
закону; Ра обращается в нуль, если
i(e-ri) =0.
Это дает два значения тока: i\ = 0 и г'г = <s/r. Первое решение соответству-
соответствует разомкнутой цепи (Д> г), а второе — короткому замыканию (R <С г).
Зависимость КПД от силы тока выражается следующей формулой:
т, = Ра/Р = (Ш - ri2)/&i = 1 - п/Ш.
КПД достигает наибольшего значения i/=1b случае разомкнутой цепи и
затем уменьшается по линейному закону, обращаясь в нуль при коротком
замыкании
Зависимость Р, Р, и ij от силы тока i изображена графически на
рис. 104. Мы видим, что условия получения наибольшей полезной мощности
Ра и наибольшего КПД т] несовмести-
несовместимы. Когда Ра достигает наибольше-
наибольшего значения, сила тока равна <§/2г
и КПД 7/ = 1/2, или 50%. Когда
же КПД т] близок к единице, полез-
полезная мощность Ра мала по сравнению
С МакСИМаЛЬНОЙ МОЩНОСТЬЮ (Ра)макс,
которую мог бы развить данный ис-
источник.
В силовых электрических уста-
установках важнейшим требованием яв-
является получение высокого КПД. А
для этого должно быть
п
п
Рис. 104. Зависимость мощности
источника Р, мощности во внешней
цепи Ра и КПД источника т/ от силы
тока
g (R + r)i R + r '
т.е. внутреннее сопротивление г ис-
источника должно быть мало по срав-
сравнению с сопротивлением R нагрузки (сети). При этом мощность Р,, выде-
выделяемая внутри источника, мала по сравнению с полезной мощностью Ра в
нагрузке.
154 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
В случае короткого замыкания, как мы видели выше, Рй = 0 и вся
мощность выделяется внутри источника, что может привести к перегре-
перегреву внутренних частей источника и выходу его из строя По этой причине
короткие замыкания мощных источников (генераторы постоянного тока,
аккумуляторные батареи) недопустимы.
§ 72. Закон сохранения энергии для электрического
поля
Закон сохранения энергии есть общий закон природы, и по-
поэтому он применим и к электрическим явлениям. При разборе
превращений энергии в электрическом поле удобно различать
два случая: 1) заряды проводников не изменяются (т.е. провод-
проводники изолированы) и 2) потенциалы проводников не изменяют-
изменяются (проводники присоединены к источникам тока). Рассмотрим
сначала второй случай.
Положим, что мы имеем систему тел (проводников и диэлек-
диэлектриков) и даем возможность этим телам совершить бесконечно
малые и бесконечно медленные (квазистатические) возможные
перемещения. Температуру тел будем поддерживать постоян-
постоянной, для чего потребуется отводить тепло от тел, если оно выде-
выделяется, или сообщать его телам, когда оно поглощается. Диэлек-
Диэлектрики будем считать изотропными и слабо сжимаемыми и со-
соответственно плотность их постоянной. При этих условиях доля
внутренней энергии тел, не связанная с электрическим полем, не
будет изменяться. Кроме того, диэлектрическая проницаемость
диэлектриков (которая зависит от плотности и температуры)
тоже будет оставаться постоянной. Посмотрим, какие превра-
превращения энергии будут происходить в рассматриваемой системе.
На всякое тело, находящееся в электрическом поле, действу-
действуют силы. Эти силы называют иногда пондеромоторными сила-
силами поля, т.е. действующими на тела, в отличие от электродвижу-
электродвижущих сил неэлектростатического происхождения, действующих
на заряды внутри тел. При бесконечно малом перемещении тел
пондеромоторные силы поля произведут бесконечно малую ра-
работу, которую мы обозначим через 5А.
Далее, в § 37 мы видели, что электрическое поле заключа-
заключает в себе определенную энергию. Если тела перемещаются, то
электрическое поле между ними изменяется, а следовательно, и
его энергия также изменяется. Обозначим увеличение энергии
поля при бесконечно малом перемещении тел через dW.
При перемещении проводников изменяется их взаимная ем-
емкость, и поэтому, чтобы их потенциалы оставались постоянны-
постоянными, к проводникам нужно либо подводить, либо убирать с них
некоторые заряды. Тогда каждый из источников тока совершит
работу 8 dq = tfidt, где 9 - ЭДС источника, г — сила тока в
§ 72 ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 155
нем, a dt — время перемещения. При этом в рассматриваемой
системе тел появятся электрические токи и в каждой ее части
будет выделяться соответствующее тепло Джоуля-Ленца ri dt.
Вследствие закона сохранения энергии работа всех источников
тока должна быть равна механической работе сил электричес-
электрического поля + увеличение энергии электрического поля + тепло
Джоуля-Ленца:
]Г Ш dt = 5 А + dW + ]Г ri2 dt. G2.1)
Если все проводники и диэлектрики неподвижны, то 5А =
= dW = 0и вся работа источников тока превращается в тепло.
Рассмотрим теперь другой случай, когда не изменяются за-
заряды проводников. Здесь источники тока не входят в рассматри-
рассматриваемую систему, и поэтому левая часть в формуле G2.1) равна
нулю. Кроме того, тепло Джоуля-Ленца (которое может воз-
возникать в результате перераспределения зарядов в телах при их
перемещении) обычно пренебрежимо мало по сравнению с дру-
другими слагаемыми. Тогда закон сохранения энергии дает
SA + dW = 0. G2.2)
В этом случае механическая работа сил электрического поля
равна уменьшению энергии электрического поля.
Пользуясь законом сохранения энергии, во многих случаях
можно вычислить механические силы в электрическом поле го-
гораздо проще, чем непосредственно рассматривая действие поля
на отдельные части тел. Для этого поступают следующим об-
образом. Если нужно найти силу F, действующую на какое-либо
тело в поле, то предполагают, что это тело совершает какое-
либо малое возможное перемещение dr. Тогда работа неизвест-
неизвестной силы будет Frfr = Frdr. Потом вычисляют все остальные
изменения энергии, вызванные этим перемещением, и затем из
закона сохранения энергии G2.1) или G2.2) находят проекцию
неизвестной силы Fr на направление dr. Выбирая рассматрива-
рассматриваемые перемещения параллельными координатным осям, можно
найти составляющие силы по этим осям, а значит, определить
неизвестную силу по модулю и направлению.
Пример 1. Вычислим силу притяжения F между пластинами плос-
плоского конденсатора, находящегося в однородном и изотропном диэлектрике
с диэлектрической проницаемостью е. Диэлектрик будем представлять се-
себе в виде жидкости, которая при перемещении пластин может входить в
конденсатор или выходить из него Пластины отключены от источника.
Из соображений симметрии ясно, что в данном случае сила может быть
только перпендикулярна к поверхности пластин, и поэтому возможное пе-
перемещение следует выбирать по нормали к пластинам.
Если расстояние между пластинами уменьшается на dx, то механиче-
механическая работа равна
6A = Fdx
156
ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ГЛ VII
Изменение энергии поля
dW = -{ееоЕ2 /2M dx
и уравнение G2.2) дает
F = (??0E2/2)S.
Таким образом, сила, действующая на единицу поверхности пластины (ме-
(механическое напряжение), равна
/ = F/S = ??ОЕ2/2, G2.3)
т.е. объемной плотности энергии электрического поля.
Если бы между пластинами был вакуум (е = 1), то сила была бы равна
Fo = {e0E2/2)/S.
При заполнении конденсатора, отключенного от источника, диэлектриком
напряженность поля внутри диэлектрика уменьшается в е раз, а, следова-
следовательно, сила притяжения изменяется в еA/еJ = 1/е раз, т.е. становится в
? раз меньше.
Отметим, что полученный результат на первый взгляд кажется непо-
непонятным. Действительно, ведь заряды обкладок находятся вне диэлектрика,
где напряженность поля такая же, как и в вакууме, и поэтому неясно, поче-
почему же сила взаимодействия уменьшается в е раз. Объяснение заключается
в том, что в случае жидких и газообразных диэлектриков появляются еще
силы электрострикции (§ 45), которые расталкивают пластины конденса-
конденсатора. Результирующая сила равна разности между силой электростатиче-
электростатического притяжения между пластинами (которая не изменяется при введении
диэлектрика) и силой электрострикции. Закон
сохранения энергии автоматически учитыва-
учитывает все силы, действующие в системе, и пока-
показывает, что эта результирующая сила умень-
уменьшается в е раз. Если бы между диэлектриком
и пластинами конденсатора был хотя, бы
очень тонкий зазор, то силы электрострикции
не передавались бы пластинам и сила взаи-
взаимодействия между ними не менялась бы при
введении диэлектрика.
Пример 2. Рассмотрим плоский кон-
конденсатор, частично погруженный в жидкий
диэлектрик (рис. 105). При заряжении пла-
пластин на жидкость в области неоднородного
поля действуют силы (§ 38) и жидкость втя-
втягивается в конденсатор. Вычислим силу /,
с которой электрическое поле действует на
каждую единицу горизонтальной поверхности
жидкости. При расчете будем считать, что пластины присоединены к источ-
источнику напряжения, а, следовательно, напряжение U и напряженность поля
Е = U/d между пластинами постоянны.
Если высота жидкости h увеличится на dh, то работа искомой силы
равна
dA = Sf dh,
где 5 — горизонтальное сечение конденсатора. Изменение энергии электри-
электрического поля равно
dW = (??0Е2/2 - ?OE2/2)Sdh.
Рис. 105. Втягивание жид-
жидкого диэлектрика в элек-
электрическое поле
§ 73 КВАЗИСТАЦИОНАРНЫЕ ТОКИ 157
На пластины перейдет дополнительный заряд dq = {ее0Е — EoE)adh (a —
ширина пластин), и работа источника тока будет
&dq = Udq = U{ee0E - Е0Е)а dh = {ee0E2 - e0E2)Sdh.
Мы предположили, что сопротивление проводов весьма мало, и в соответ-
соответствии с этим считали Ш = U. Подставляя эти выражения в уравнение G2.1),
находим
/ = ее0Е2/2 - ?0Е2/2. G2.4)
Механическое напряжение / равно разности объемных плотностей энергии
электрического поля с обеих сторон границы раздела (ср. § 101).
Отметим, что полученный результат, разумеется, не зависит от сопро-
сопротивления проводов. Если бы мы положили это сопротивление не малым, то,
объединяя в G2.1) два члена: ffAdt и ri2 dt, мы нашли бы, что
Ш dt = ri2 dt = ($- ri)i dt = Ui dt,
т.е. то же, что и раньше.
§ 73. Квазистационарные токи
До сих пор мы рассматривали только постоянные токи. Од-
Однако полученные законы во многих случаях можно применять и
к изменяющимся токам, если только изменение силы тока про-
происходит не слишком быстро.
Действительно, представим себе, что в некотором контуре с
постоянным током электродвижущие силы изменились на ма-
малую величину. Сила тока в контуре начнет изменяться, но через
некоторое время достигнет нового установившегося значения.
Изменяя ЭДС небольшими ступенями, мы создадим в конту-
контуре ступенчато изменяющийся ток, к отдельным установившимся
Значениям которого будут применимы все законы постоянного
тока.
Представим себе теперь, что мы увеличиваем число ступеней
тока, уменьшая одновременно величину каждой ступени. Тогда
в пределе мы получим непрерывно изменяющийся ток. Если из-
изменения тока настолько медленны, что за время установления
Электрического равновесия в цепи относительные изменения то-
токов и ЭДС малы, то мгновенные значения токов и ЭДС будут
подчиняться всем законам постоянных токов, как и при ступен-
ступенчатом изменении тока. Такие токи называют медленно меняю-
меняющимися или квазистационарными.
Отметим, что скорость установления электрического равно-
равновесия весьма велика, и поэтому под понятие квазистационарных
Токов подпадают в обычном смысле весьма быстрые процессы.
Все технические переменные токи являются квазистационарны-
квазистационарными. Даже очень быстрые электрические колебания, употребляе-
употребляемые в радиотехнике, с частотами порядка миллиона колебаний
В секунду, очень часто можно еще рассматривать как квазиста-
Ционарные.
158 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ VII
Из сказанного следует, что задачи на квазистационарные
электрические процессы можно решать при помощи законов по-
постоянных токов, если применять эти законы к мгновенным зна-
значениям электрических величин Однако при этом вместо алге-
алгебраических соотношений мы приходим к дифференциальным
уравнениям, интегрирование которых и дает зависимость иско-
искомых величин от времени
Чтобы неустановившийся электрический процесс был квазистационар-
квазистационарным, необходимо выполнение двух условий Первое из них относится к про-
процессам внутри проводника А именно, можно показать (см Добавление 5),
что если внутри проводящей среды возник избыточный объемный заряд с
плотностью р, то этот заряд под действием вызванного им самим электро-
электростатического поля будет уменьшаться с течением времени по закону
р = ро ехр (-t/тм) G3 1)
Здесь ро — объемная плотность заряда в момент времени t — О, а
тм = еое/Х, G3 2)
где е — диэлектрическая проницаемость среды, А — ее удельная элек-
электрическая проводимость Время тм называется временем диэлектрической
релаксации или временем релаксации Максвелла Оно равно времени, в те-
течение которого объемный заряд уменьшается в е = 2,71 раза Время ре-
релаксации Максвелла, следовательно, определяет порядок времени, в тече-
течение которого восстанавливается стационарность электрических процессов
Чтобы токи можно было считать квазистационарными, характерное вре-
время рассматриваемого неустановившегося процесса Г должно удовлетворять
условию
тм < Т G3 3)
Если токи изменяются со временем периодически (электрические коле-
колебания), то под Г следует понимать период колебаний и сформулированное
условие примет вид
LJTM "С 1,
где ш = 27г/Т — круговая частота колебаний
Однако при рассмотрении электрических контуров (цепей) следует на-
наложить еще одно условие на размеры контура Дело в том, что при любом
изменении электрического состояния в какой-либо части контура электри-
электрическое возмущение распространяется вдоль контура с конечной скоростью,
равной (гл XXII)
Здесь с ~ 3 108 м/с — скорость света в вакууме, а е и ц — диэлектри-
диэлектрическая и магнитная проницаемости среды, окружающей проводники Если
/ — длина контура, то время прохождения возмущения вдоль контура равно
r = l/v = (l/c)y/Ejl G3 4)
Поэтому второе условие квазистационарности токов есть
г < Т G3 5)
Для периодически изменяющихся токов оно имеет вид
изт < 1 G3 5а)
§74
КОНДЕНСАТОР В ЦЕПИ С СОПРОТИВЛЕНИЕМ
159
При выполнении этого условия мгновенные значения всех электрических
величин в каждой части контура будут такими же, как и в случае постоян-
постоянного тока В частности, для простого неразветвленного контура мгновенная
сила тока в любом сечении проводника одинакова
Значение тм изменяется в широчайших пределах В плохо проводящих
веществах (диэлектриках) оно может измеряться многими минутами В ме-
металлах вследствие их большой электропроводности тм равно по порядку
величины 10 ~17 с
В зависимости от свойств проводников одно из условий квазистацио-
квазистационарности G3 3) и G3 5) обычно гораздо сильнее другого, и поэтому лишь
одно из них является определяющим
§ 74. Конденсатор в цепи с сопротивлением
В качестве примера квазистационарных токов рассмотрим
процессы зарядки и разрядки конденсатора. Пусть конденсатор
с емкостью С включен в схему рис. 106 Тогда, ставя переклю-
переключатель в положение 1, мы будем заряжать конденсатор от ис-
источника тока, а перебрасывая переключатель в положение 2, —
разряжать конденсатор
Рассмотрим сначала процесс зарядки конденсатора Обозна-
Обозначим через Ш ЭДС источника, через г — сопротивление цепи
(включая и внутреннее сопротивление
источника) и выберем положительное
направление тока, как показано на ри-
рисунке Применяя к контуру &гС& вто-
второе правило Кирхгофа, получим
п + U = Щ
I
г
1——1
1 1
/¦
1
1
1
+ 1
1
- -*i
-
С
здесь г — мгновенное значение силы то-
тока, U — мгновенное значение напряже-
напряжения на конденсаторе Но
U = q/C, г = dq/dt,
где q — заряд конденсатора. Из напи- рИс 106 Заряжение и
санных трех равенств мы можем исклю- разряжение конденсатора
чить две из трех переменных величин q,
г и U и получить уравнение для какой-либо одной из них Ис-
Исключая q и г, находим
dt
гС гС
Мы получили для определения U дифференциальное уравнение
первого порядка с постоянными коэффициентами
Введем новую переменную u = U — Ш. Тогда
du
160 ЭЛЕКТРОДВИЖУЩАЯ СИЛА ГЛ. VII
В этом уравнении переменные разделяются, и в результате ин-
интегрирования находим
Постоянная интегрирования А зависит от начального усло-
условия. Положим, что мы начинаем отсчет времени с момента за-
замыкания переключателя. Тогда начальное условие имеет вид
t = 0: G = 0, и = -Ш.
Это дает
А = -$.
Возвращаясь к прежней переменной U, находим окончательно
для напряжения на конденсаторе выражение
G4.1)
При t = 0 это выражение дает U = 0 в соответствии с началь-
начальным условием задачи. С увеличением времени t напряжение U
непрерывно увеличивается и асимптотически приближается к
ЭДС источника.
Зависимость зарядного тока от времени имеет вид
. -С/Ч-8" » ( t
Сила тока имеет наибольшее значение в начальный момент вре-
времени и асимптотически стремится к нулю в процессе зарядки.
В случае разрядки конденсатора исходные уравнения будут
ri = U, U = q/C, i = -dq/dt.
В отличие от предыдущего, в выражение для тока г входит знак
минус, так как выбранное нами положительное направление то-
тока соответствует уменьшению заряда конденсатора. Исключая
из написанных равенств q и г, получим
dt + rC U'
откуда
(
Если начало отсчета времени совпадает с началом процесса раз-
разрядки, то начальное условие будет
t = 0: U = П.
В этом случае постоянная интегрирования равна В = Ш, и
зависимость напряжения конденсатора от времени имеет вид
G4.2)
§ 74 КОНДЕНСАТОР В ЦЕПИ С СОПРОТИВЛЕНИЕМ 161
Полученные результаты показывают, что процессы заряже-
заряжения и разряжения (установление электрического равновесия)
происходят не мгновенно, а с конечной быстротой. Для рас-
рассмотренного контура, содержащего сопротивление и емкость,
быстрота установления зависит от произведения
Т - гС, G4.3)
которое имеет размерность времени и называется постоянной
времени данного контура. Постоянная времени показывает, че-
через какое время после выключения ЭДС напряжение (а значит,
и напряженность поля внутри конденсатора) уменьшается в е =
= 2,71 раза. Если г и С выражать в единицах системы СИ (в
омах и фарадах), то Т будет выражено в секундах. Мы полу-
получим Т в секундах и в том случае, если будем выражать г и С в
единицах системы СГС, так как в обеих этих системах единицей
времени служит секунда.
При решении задачи мы сразу предположили, что процессы являют-
являются квазистационарными. Правильность этого можно выяснить a posteriori,
проверяя, удовлетворяет ли полученное решение условиям квазистационар-
квазистационарности G3.3) и G3.5). Характерным временем рассматриваемых процессов
является постоянная времени Т = гС.
Так, например, если емкость конденсатора С = 1 мкФ, а сопротивление
контура г = 1 Ом, то Т = 10~6 ¦ 1 = 10~6 с. Таким образом, условие G3.3)
выполняется с большим запасом, так как гм внутри металлов на много
порядков меньше Т (ср. § 73). Если, далее, длина контура / = 1 м, то время
распространения возмущения т = l/v и 10~8 с. Поэтому и условие G3.5)
тоже выполняется и, следовательно, наше решение правильно. Однако при
уменьшении Сиг условие G3.5) может оказаться нарушенным. В этом
случае мы должны уже рассматривать процессы совсем иначе, а именно,
как распространение электромагнитных волн вдоль контура (см. гл. XXII).
МАГНИТНОЕ ПОЛЕ
ГЛАВА VIII
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
§ 75. Магнитное взаимодействие токов
Мы уже говорили, что электрические токи действуют на маг-
ниаы и, обратно, магниты действуют на электрические токи
(§ 55). Подобным образом взаимодействуют и два проводника
с током.
Взаимодействие токов было открыто практически одновре-
одновременно с действием тока на магнитные стрелки в 1820 г. и подроб-
подробно изучено Ампером, который исследовал поведение подвижных
проволочных контуров различной формы, укрепленных в специ-
специальных приспособлениях (станки Ампера)
Рис 107 Станок Ампера с прямоугольной рамкой Взаимодействие двух
прямых токов
На рис. 107 изображен станок Ампера с прямоугольным кон-
контуром. Он содержит прямоугольную проволочную рамку, укреп-
укрепленную на двух вертикальных остриях, опирающихся о днища
двух чашек с ртутью. Вследствие ничтожного трения в игольча-
игольчатых подшипниках рамка может свободно поворачиваться вокруг
§75
МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ТОКОВ
163
вертикальной оси, оставаясь все время включенной в цепь тока
при помощи ртутных контактов
Если приблизить к подвижной рамке другую (неподвижную)
рамку с током, то можно наблюдать взаимодействие токов. При
достаточном сближении одного из ребер подвижной рамки с
каким-либо из ребер неподвижной рамки можно считать, что
практически взаимодействуют только сближенные ребра, и та-
таким образом исследовать взаимодействие двух прямолинейных
токов. При этом легко обнаружить, что токи, направленные
одинаково (параллельные), притягиваются друг к другу, а то-
токи, направленные противоположно (антипараллельные), оттал-
отталкиваются друг от друга.
Пользуясь таким станком, можно исследовать взаимодей-
взаимодействие тока и магнита и двух токов между собой Если подне-
поднести к одному из вертикальных ребер подвижной рамки с током
прямой магнит, то рамка поворачивает-
поворачивается. При замене северного полюса магни-
магнита на южный направление силы изменя-
изменяется и рамка начинает поворачиваться
в обратную сторону Направление силы
изменяется и в том случае, если изме-
изменить направление тока в рамке.
На рис. 108 показан станок Ампера
с прямой длинной катушкой (соленоид).
Если подносить к концам такого солено-
соленоида прямой магнит, то обнаруживается,
что один из концов соленоида отталки-
отталкивается oi северного полюса магнита, но
притягивается к южному полюсу, в то
время как для второго конца соленоида Рис 108 Прибор Ампе-
наблюдается обратное. Этот опыт пока- p&j B котором рамка заме-
зывает, что соленоид с током ведет себя Нена соленоидом
как прямой магнит. Тот конец соленоида,
который обтекается током против часовой стрелки (если смо-
смотреть в торец катушки), соответствует северному полюсу маг-
магнита (указывающему на север), а конец, обтекаемый током по
часовой стрелке, соответствует южному полюсу магнита Если
убрать магнит, то соленоид с током устанавливается так же, как
магнитная стрелка компаса, в направлении магнитного мериди-
меридиана Земли
Заменяя в предыдущем опыте магнит другим (неподвиж-
(неподвижным) соленоидом, можно исследовать взаимодействие двух со-
соленоидов. При этом вновь легко убедиться, что каждый из со-
соленоидов по своим действиям подобен прямому магниту.
Описанные опыты и им подобные показывают, что взаимо-
взаимодействие контуров с током подобно действию токов на магниты,
164 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ VIII
а также действию магнитов на токи. Поэтому рассмотренное
взаимодействие проводников с током получило название маг-
магнитного взаимодействия.
Магнитное взаимодействие проводников отлично от электри-
электрического взаимодействия, рассмотренного в гл. I. Электрическое
взаимодействие возникает при наличии зарядов на проводниках
и зависит от этих зарядов; магнитное же взаимодействие не за-
зависит от зарядов проводников, возникает только при наличии
токов в проводниках и зависит от этих токов. Если заряжен-
заряженное тело находится внутри замкнутой металлической оболочки,
то действие на него других зарядов, находящихся вне оболоч-
оболочки, не наблюдается. Если же заэкранировать проводящей обо-
оболочкой один из контуров с током, то магнитное взаимодействие
сохраняется. При истолковании магнитного взаимодействия то-
токов мы встречаемся с теми же вопросами, что и при объяснении
электрического взаимодействия зарядов. И здесь можно спро-
спросить, почему возникают силы, действующие на контур с током
в присутствии другого контура, и как эти силы передаются от
одного проводника к другому? Происходят ли какие-либо из-
изменения в пространстве возле провода с током, когда другого
провода нет и магнитное взаимодействие не проявляется?
По тем же причинам, которые изложены в § 8, современная
физика отвергает возможность дальнодействия в магнитных яв-
явлениях, так же как и в электрических. Причину возникновения
сил магнитного взаимодействия мы видим в появлении вокруг
проводников с током магнитного поля. Мы увидим далее, что
магнитное поле является носителем ряда физических свойств.
Основное свойство магнитного поля заключается в том, что на
проводники с током, находящиеся в нем, действуют силы.
Магнитное поле возникает вокруг провода с током всегда,
даже в отсутствие других проводников, когда магнитное вза-
взаимодействие не наблюдается. И в этом случае в окружающем
проводник пространстве происходят определенные физические
изменения. Основная задача исследования магнитных явлений
заключается в изучении свойств магнитного поля и законов, ко-
которым оно подчиняется.
Мы начнем изучение магнитных явлений с исследования вза-
взаимодействия между токами. Сначала мы рассмотрим это взаи-
взаимодействие в вакууме, а затем учтем влияние среды на магнит-
магнитные явления.
§ 76. Магнитная индукция
В опытах Ампера было прежде всего установлено, что сила
взаимодействия двух проводников пропорциональна силе тока
в каждом из них. Далее опыты показали, что если провод с то-
§76
МАГНИТНАЯ ИНДУКЦИЯ
165
б Ж
2
4%5
Рис 109 Изогнутые про-
проводники (а, б) не произво-
производят магнитного действия
ком изогнуть, как показано на рис. 109 а, то он не производит
магнитного действия. И, обратно, такой проводник не испыты-
испытывает действия силы со стороны других проводников. Магнитное
действие не наблюдается и в том слу-
случае, если одну часть провода (и притом
произвольным образом) обвить вокруг
другой (рис. 109 6).
Из этих результатов вытекает за-
заключение, что какие-либо элементы
проводника dli, dl? и dlz совместно
(рис. 110) производят такое же магнит-
магнитное действие, как один элемент dl, за-
замыкающий эти отрезки. В частности,
действие изогнутых отрезков 12 и 23
проводника на рис. 109 б оказывается
таким, как если бы вместо них был
прямолинейный отрезок, соединяющий
точки 1 и 3, действие 34 и ^5 равно действию 35 и т.д., поэто-
поэтому действие всего этого проводника такое же, как и проводника
на рис. 109 а, т.е. равно нулю. Из сказанного следует, что маг-
магнитное действие бесконечно малого отрезка
du провода зависит от произведения i dl, где i —
сила тока, a dl — вектор, имеющий длину от-
отрезка dl и направленный вдоль тока. Это про-
произведение называют элементом тока.
Сила взаимодействия контуров конечных
размеров складывается из взаимодействия
отдельных элементов тока. Она зависит от
размеров контуров, их формы и взаимного
расположения, и поэтому сформулировать об-
общий закон взаимодействия контуров с током
нельзя. Однако такой закон можно дать для
элементов тока. Понятие элемента тока в законах магнитного
взаимодействия играет ту же роль, что и понятие точечного за-
заряда в законах электрического взаимодействия.
Результаты опытов Ампера и последующих многочисленных
исследований можно сформулировать следующим образом. Спо-
Способность магнитного поля вызывать появление механической си-
силы, действующей на какой-либо элемент тока, можно количест-
количественно описать, задавая в каждой точке поля некоторый вектор В.
При этом сила, действующая на элемент тока г dl, равна
dF = i[dlB]. G6.1)
Величина В называется магнитной индукцией и является
основной характеристикой магнитного поля. Соотношение же
G6.1) есть определение магнитной индукции.
Рис. 110 К поня-
понятию элемента тока
166
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ VIII
G6.1а)
векторного произведения
Полную силу, действующую на проводник конечных разме-
размеров, можно найти, суммируя силы на отдельных его элементах.
Если имеется прямолинейный отрезок провода и магнитная ин-
индукция во всех его точках постоянна, то из формулы G6.1) по-
получаем
F = г[1В].
В соответствии с определением
двух векторов (§ 15) эта сила равна
F = *?Bsin(l,B). G6.16)
Направление силы перпендикулярно к 1 и В и подчиняется пра-
правилу правого буравчика: при движении рукоятки буравчика от
вектора 1 к вектору В поступательное дви-
движение буравчика происходит в направле-
направлении силы F. Взаимное расположение век-
векторов 1, В и F показано на рис. 111.
Посмотрим теперь, как можно найти
магнитнз'ю индукцию, входящую в форму-
формулу G6.1). Опыт показывает, что для маг-
магнитного поля, так же как и для электри-
электрического, в широкой области изменения
магнитной индукции справедлив принцип
наложения, или суперпозиции: если имеет-
имеется несколько контуров с током, каждый из
которых создает магнитные индукции Bi, B2 и т.д., то магнит-
магнитная индукция результирующего поля равна векторной сумме ин-
индукций отдельных контуров:
В = Bi + В2 -+- .
Отсюда можно заключить, что принцип суперпозиции справед-
справедлив и для элементов тока.
Поэтому магнитную индукцию, создаваемую каким-либо
контуром с током, можно найти, суммируя магнитные индук-
индукции от отдельных элементов тока, на которые можно разбить
данный контур. Чему же равна индукция, создаваемая элемен-
элементом тока?
Опыт дает, что правильные значения сил магнитного взаимо-
взаимодействия мы получим в том случае, если примем, что индукция
магнитного поля элемента тока равна
dB = K—sT- I76-2)
Рис Ш
магнитного
ток
Действие
поля на
Здесь г — радиус-вектор, проведенный из элемента тока в рас-
рассматриваемую точку, а К — коэффициент пропорциональности,
зависящий от выбора единиц.
§76
МАГНИТНАЯ ИНДУКЦИЯ
167
Из G6.2) следует, что магнитная индукция в точке, удален-
удаленной на расстояние г от элемента тока, равна
dB = к1-^^-, G6.2а)
где i9 — угол между d\ и г (рис. 112). Направление dB перпенди-
перпендикулярно к d\ и г, т.е. перпендикулярно к плоскости, в которой
они лежат. Это направление подчиняется правилу правого бу-
буравчика; направление магнитной индукции совпадает с направ-
направлением движения конца
рукоятки буравчика с пра-
правой нарезкой, движущегося
поступательно в направле-
направлении тока. Так, например,
если ток течет вертикально
сверху вниз (рис. 112), то
правый буравчик нужно
вращать по часовой стрелке
(глядя сверху); поэтому
магнитная индукция в
точке а будет направлена
от чертежа к читателю, в
точке б она направлена
противоположно, от чита-
читателя за чертеж. Формула
G6.2) носит название зако-
закона Био-Савара-Лапласа.
Формулы G6.1) и G6.2)
совместно вполне опреде-
определяют закон взаимодействия
двух элементов тока.
Рассмотрим в качестве примера два параллельных элемента
тока i\ d\\ и 12 db, показанные на рис. 113. Так как sin (dl\, Г12) =
= 1, то формула G6.2а)
дает, что индукция, со-
создаваемая элементом то-
тока iidli, равна dB\ =
= Ki\ dlijr\2. Она пер-
перпендикулярна плоскости
_, 11О _ чертежа и направлена от
Рис. ИЗ Два параллельных элемента тока Ч1?атедя за чертеж. То-
гда по формуле G6.16) получаем, что сила, действующая на эле-
элемент тока %i dl.2, равна
dF = К j ? G6.3)
так как sin(cfl2,B) = 1. Она направлена вдоль линии, соединя-
Рис 112
аа тока
Магнитная индукция элемен-
i\(u\
168 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ VIII
ющей оба элемента тока, от элемента тока 2 к элементу тока 1.
Сила, действующая на второй элемент тока i\ d\\, имеет такую
же величину, но направлена противоположно.
Отметим, что закон взаимодействия токов, выражаемый формулами
G6.1) и G6.2), на первый взгляд не удовлетворяет третьему закону Нью-
Ньютона, Так, например, для двух элементов тока 1 и 2, изображенных на
рис. 114, индукция, создаваемая током 1 в точке 2, равна нулю, так как
sin(cWi,ri2) = 0. Поэтому и dF\2 — 0.
(Индукция же, создаваемая током 2 в
2 точке 1, отлична от нуля и направле-
1на перпендикулярно току 1, а следо-
_ „ вательно, cfi<2i не равна нулю. Такой
clY dt\2-u результат получился потому, что на
опыте можно исследовать только вза-
взаимодействие замкнутых контуров ко-
Рис. 114. Два взаимно перпенди- нечной величины. Поэтому из опыта
кулярных элемента тока можно вывести закон взаимодействия
элементов тока только с точностью до
некоторого слагаемого, обращающегося в нуль при суммировании по зам-
замкнутому контуру. Такое слагаемое опущено в G6.2), что и является при-
причиной кажущегося нарушения третьего закона Ньютона. Однако это сла-
слагаемое не играет никакой роли, так как, применяя формулы G6.1) и G6.2)
к замкнутым контурам, мы всегда получаем результаты, согласующихся с
третьим законом Ньютона.
§ 77. Абсолютная электромагнитная система единиц
В выражение G6.2) для магнитной индукции входит коэф-
коэффициент пропорциональности Л", зависящий от выбора единиц.
Поэтому для вычисления сил магнитного взаимодействия мы
должны остановиться на какой-либо определенной системе еди-
единиц и определить, какое значение имеет К в выбранной системе.
Если пользоваться абсолютной системой единиц СГС, по-
построенной на трех основных механических единицах, то длины
dl-y, dl2, т\2 нужно измерять в сантиметрах, а силу — в динах.
Единица силы тока при этом будет производной, и поэтому ее
можно выбрать такой, чтобы коэффициент пропорционально-
пропорциональности К обратился в единицу. Такая единица силы тока получила
название абсолютной электромагнитной единицы силы тока
(СГСМ{).
Выражая из формулы G6.3) силу тока и заменяя (в соответ-
соответствии с правилом образования производных единиц) в получен-
полученном выражении физические величины их единицами, находим
1 СГСМ; = 1 дин1/2.
Эта единица отличается от единицы силы тока в системе
СГСЭ. Учитывая выражение единицы заряда в системе СГСЭ
§ 77 АБСОЛЮТНАЯ ЭЛЕКТРОМАГНИТНАЯ СИСТЕМА ЕДИНИЦ 169
(§ 3), имеем
1 СГСЭ; = 1 дин1/2 . см/с.
Если г'э — сила некоторого тока, измеренная в системе СГСЭ,
а гы — сила того же тока в системе СГСМ, то можно написать
*м = -гэ, G7.1)
где с — некоторая размерная постоянная, называемая электро-
электродинамической постоянной. Ее размерность совпадает с размер-
размерностью скорости.
Значение постоянной с можно определить только из опытов.
Такие опыты были произведены А.Г. Столетовым, Вебером и
другими исследователями. Тщательно изготовленный конденса-
конденсатор, емкость которого была точно определена, заряжался много
раз в секунду и разряжался через цепь, содержащую гальвано-
гальванометр. Напряжение, до которого заряжался конденсатор, измеря-
измерялось электростатическими методами, откуда можно было опре-
определить заряд конденсатора и силу тока в электростатических
единицах. Измеряя тот же ток гальванометром, основанным на
магнитном действии тока, можно было найти его значение в маг-
магнитных единицах и отсюда определить с. Эти опыты привели к
заключению, что электродинамическая постоянная равна скоро-
скорости распространения света в вакууме 3 • 1010 см/с.
Такое совпадение не случайно. Еще во второй половине
XIX в. Максвелл развил электромагнитную теорию света, со-
согласно которой свет есть электромагнитные волны, и теорети-
теоретически показал, что в вакууме скорость света, как и скорость
распространения любых электромагнитных волн, должна быть
равна электродинамической постоянной.
Исходя из закона магнитного взаимодействия токов, можно
построить новую систему электрических единиц — абсолютную
электромагнитную систему. В этой системе все механические
единицы остаются такими же, как в системе СГСЭ (сантиметр,
грамм, секунда), но в основу определения электрических и маг-
магнитных единиц кладется не электростатическая единица заряда
(как в системе СГСЭ), а электромагнитная единица силы тока.
Нетрудно найти соотношение между основными электрическими вели-
величинами в обеих системах.
Заряд есть произведение силы тока на время: q = it. Поэтому соотно-
соотношение зарядов в обеих системах такое же, как и токов. Если дм — заряд,
измеренный в системе СГСМ, а дэ — тот же заряд, измеренный в системе
СГСЭ, то
1
дм = -дэ.
Если заряд какого-либо тела равен 1 СГСМ,, а заряд другого тела есть
1 СГСЭЧ, то, сравнивая оба заряда, мы найдем, что заряд у первого тела в
3 • 1010 раз больше, чем у второго тела.
170 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ VIII
Произведение силы тока на напряжение есть мощность: Ш = Р, ко-
которая измеряется в одних и тех же единицах в обеих системах (в эрг/с).
Поэтому
и, следовательно,
г'м
Напряжение, равное единице в системе СГСМ, в 3 • 1010 раз меньше, чем
напряжение, равное единице в системе СГСЭ
Поступая подобным образом, можно выразить все электрические вели-
величины в системе СГСМ.
Однако в физической литературе системы СГСЭ и СГСМ
обычно не применяют, а широко используют так называемую аб-
абсолютную симметричную систему электрических и магнитных
единиц, или, иначе, систему единиц Гаусса. Она построена на
трех основных единицах: сантиметре, грамме и секунде, но пред-
представляет собой сочетание обеих систем СГСЭ и СГСМ. Система
единиц Гаусса рассмотрена в Добавлении 13.
§ 78. Магнитная постоянная
В Международной системе СИ единица силы тока являет-
является одной из основных единиц, а следовательно, уже установ-
установлена. Поэтому коэффициент пропорциональности в ней нельзя
сделать безразмерным. Далее выражение для магнитной индук-
индукции записывают в рационализованной форме, т.е. добавляют в
знаменателе множитель An, чтобы этот множитель не входил
впоследствии в другие, часто встречающиеся формулы. Поэто-
Поэтому магнитная индукция, создаваемая элементом тока, в системе
единиц СИ, выражается формулой
dB G81)
4тг г2
Здесь /uq — новая размерная постоянная, которая называется
магнитной постоянной.
Если в формуле G8.1) все величины измерять в единицах
системы СИ, т.е. длину — в метрах, силу тока — в амперах,
механическую силу — в ньютонах, то
Это значение /j.q непосредственно следует из определения ампе-
ампера, которое будет дано в § 83. Сама же единица для измерения цо
в системе СИ получила название генри на метр (Гн/м). Смысл
этого наименования будет разъяснен в § 94.
Вычисляя магнитную индукцию по формуле G8.1), мы по-
получим ее выраженной в системе СИ; в этой системе единица
§ 79 НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ 171
магнитной индукции называется тесла (Тл). В однородном маг-
магнитном поле с индукцией 1 Тл на 1 м длины перпендикулярного
к вектору В прямого проводника, по которому течет ток 1 А,
действует сила 1 Н:
1 Н = 1 А • 1 м • 1 Тл,
отсюда
1 Тл = 1 Н/A А • 1 м) = 1 Н/(А • м).
§ 79. Напряженность магнитного поля
Для описания магнитного поля наряду с магнитной индук-
индукцией широко используют еще другую физическую величину —
напряженность магнитного поля. Если В — магнитная индукция
в какой-либо точке поля в вакууме, то напряженностью магнит-
магнитного поля в той же точке поля называется
Н = B/V G9.1)
Так как Цо есть скаляр, то Н, как и В, есть вектор.
В абсолютной системе единиц СГСМ цо — безразмерная ве-
величина, равная единице. Поэтому Н и В в вакууме в этой си-
системе совпадают друг с другом.
В системе единиц СИ В и Н даже в вакууме имеют различ-
различную размерность и отличаются друг от друга. Из формул G8.1)
и G9.1) следует, что напряженность магнитного поля, создавае-
создаваемого элементом тока г ей есть
G9 2)
или в векторной форме
dH = -?-&]. G9.2а)
Пока мы рассматриваем магнитные поля в вакууме, нам до-
достаточно знать лишь один из векторов В или Н, безразлично
какой, так как, зная В, можно по формуле G9.1) найти Н, и
обратно. Однако внутри намагничивающихся сред это уже не
так (гл. XI).
Найдем напряженность магнитного поля в вакууме для неко-
некоторых простых контуров с током.
Пример 1. Магнитное поле в центре кругового провод-
проводника (рис. 115). В этом случае все элементы проводника пер-
перпендикулярны к радиус-вектору и sin?? = 1. Расстояние всех
элементов провода до центра круга одинаково и равно радиусу
круга R. Поэтому G9.2) дает
172
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ VIII
Все элементы тока создают магнитное поле одинакового направ-
направления, перпендикулярное к плоскости витка, и поэтому полная
напряженность поля в центре кругового витка
равна
тт __
Jdl =
= ъ- G9-3)
Рис. 115.
ное поле в центре
кругового тока
4тгД2 J 4тгЯ2
Направление магнитного поля находим по
правилу правого буравчика, который нужно
расположить параллельно касательной к кругу
Магнит- (в направлении тока). Если ток обтекает виток
против часовой стрелки, то правило правого
dl
буравчика дает, что магнитное поле направ-
направлено от витка к наблюдателю (рис. 115).
Пример 2. Магнитное поле прямого тока. Найдем на-
напряженность поля, создаваемого прямым проводом в точке а
(рис. 116), удаленной на расстояние R от оси провода. Длину
провода будем считать весьма
большой по сравнению ей. Ив
этом случае направление магнит-
магнитного поля всех элементов прово-
провода одинаково (перпендикулярно к
плоскости чертежа, рис. 116), и
поэтому можно складывать мо-
модули напряженностей. Напряжен-
Напряженность поля какого-либо элемента
проводника dl выражается фор-
формулой G9.2). Из рис. 116 видно,
что
cMsini? d/cosa ds ,
da
Рис. 116. К вычислению магнит-
магнитного поля прямого тока
Г =
R
cos a
Подставляя эти выражения в G9.2), мы находим, что напряжен-
напряженность, создаваемая одним элементом провода, равна
, о- 1 г dl sin ¦д
an — - —
4тг г2
cos a da.
г* 4тгД
Поэтому для полной напряженности поля получаем
+7Г/2
if* 1
Н = —- / cos ada = .
-тг/2
Это поле направлено перпендикулярно к плоскости, содержащей
провод и отрезок R. Если в формулах G9.3) и G9.4) выражать
силу тока в амперах, а длину — в метрах, то напряженность
G9.4)
§80
ЛИНИИ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ
173
магнитного поля будет выражена в единицах системы СИ. Эта
единица называется ампер на метр (А/м).
§ 80. Линии индукции магнитного поля
Магнитные поля, так же как и электрические, можно изобра-
изображать графически при помощи линий индукции. Линиями ин-
индукции (или линиями вектора В) называют линии, касательные
к которым направлены так же, как и вектор В в данной точке
поля.
Очевидно, что через каждую точку магнитного поля мож-
можно провести линию индукции. Так как индукция поля в любой
точке имеет определенное направление, то и направление ли-
линии индукции в каждой точке данного поля может быть толь-
только единственным, а значит, линии магнитного поля, так же как
и электрического, нигде не пересекаются. Подобно линиям на-
напряженности электрического поля, линии индукции магнитного
поля прочерчивают с такой густотой, чтобы число линий, пере-
пересекающих единицу поверхно-
поверхности, перпендикулярной к ним,
было равно (или пропорцио-
пропорционально) индукции магнитного
поля в данном месте. Поэтому,
изображая линии индукции,
можно наглядно представить,
как меняется в пространстве
индукция, а следовательно, и
напряженность магнитного по-
поля по модулю и направлению.
Рассмотрим линии индук-
индукции поля прямого тока. В § 79
мы видели, что напряженность
Н (а следовательно, и В) всегда
перпендикулярна к плоскости,
содержащей проводник и рас-
рассматриваемую точку поля. По-
Поэтому линии индукции в данном случае суть концентрические
окружности, центр которых расположен на оси тока (рис. 117).
Представление о виде линий индукции можно получить на
опыте. Для этого пользуются тем обстоятельством, что подвиж-
подвижная магнитная стрелка всегда устанавливается своей осью в на-
направлении линий магнитного поля, т.е. линий индукции.
Еще удобнее пользоваться железными опилками. Крупинки
железа в магнитном поле намагничиваются и становятся подоб-
подобными магнитным стрелкам. При практическом осуществлении
этих опытов исследуемый провод с током пропускают сквозь
Рис. 117. Линии индукции магнит-
магнитного поля прямого тока
174
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ. VIII
горизонтальную стеклянную пластину (или листок картона),
на которую насыпают небольшое количество железных опилок.
При легком встряхивании пластинки (постукивании) частицы
опилок образуют цепочки, форма которых близко соответству-
соответствует линиям исследуемого магнитного поля
Рис. 118. Линии индукции магнитных полей кругового тока (а) и соленои-
соленоида (б)
На рис. 118 приведены полученные таким способом картины
линий индукции магнитного поля кругового тока и поля соле-
соленоида.
Из рисунка видно, что в средней части соленоида линии ин-
индукции суть прямые параллельные линии. Это показывает, что
здесь индукция одинакова во всех точках, т.е. что в средней
части соленоида поле однородно. У концов соленоида линии ис-
искривляются и расходятся, а значит, поле становится неоднород-
неоднородным.
§ 81. Вихревой характер магнитного поля
На рис. 118 видно, что линии индукции магнитного поля
непрерывны: они не имеют ни начала, ни конца. Это имеет место
для любого магнитного поля, вызванного какими угодно кон-
контурами с током. Векторные поля, обладающие непрерывными
линиями, получили название вихревых полей. Мы видим, что
магнитное поле есть вихревое поле. В этом заключается суще-
существенное отличие магнитного поля от электростатического.
В электростатическом поле линии напряженности всегда
разомкнуты: они начинаются и заканчиваются на электриче-
электрических зарядах. Линии же индукции магнитного поля не имеют
ни начала, ни конца. Это соответствует тому, что в природе нет
магнитных зарядов.
§ 81
ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ
175
Движение электрических зарядов есть электрический ток.
Так как магнитных зарядов нет, то магнитного тока не суще-
существует.
В § 17 мы ввели понятие электрического напряжения вдоль
заданного контура. В электростатическом поле напряжение не
зависит от формы контура и для замкнутого контура всегда
равно нулю. Это позволило ввести разность потенциалов двух
точек поля, зависящую только от положения этих точек.
Аналогично этому мы введем понятие магнитного напряже-
напряжения вдоль контура L:
= f
Hs ds,
ds
где ds — элемент длины контура L, a Hs — проекция напряжен-
напряженности магнитного поля на направление ds. Однако, в отличие от
электрического напряжения в поле неподвижных зарядов, маг-
магнитное напряжение зависит от формы контура L и не опреде-
определяется только положением точек начала и конца этого контура.
Поэтому однозначной раз-
разности потенциалов в маг-
магнитном поле не существует.
Магнитное напряжение по
замкнутому контуру, вооб-
вообще говоря, не равно нулю.
Рассмотрим, от чего за-
зависит магнитное напряже-
напряжение. Наиболее просто это
можно сделать на примере
поля, создаваемого прямым
длинным проводом. Пред-
Предположим сначала, что кон-
контур есть часть окружно-
окружности между точками 1 и 2
(рис. 119), совпадающая с одной из линий индукции. В этом слу-
случае во всех точках контура (окружности) напряженность поля
одинакова. Далее, так как контур совпадает с линией индукции,
то во всех точках Hs = Н — -—, и поэтому
Рис. 119. К вычислению магнитного на-
напряжения
где s — длина дуги окружности между точками 1 и 2. Но s/r
есть угол ip, составленный радиус-векторами, проведенными в
точки начала (./) и конца B) контура Поэтому
Uu = f Hsds =
(81.1)
176
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ VIII
Рассмотрим теперь произвольный контур L (рис. 119), одна-
однако лежащий в плоскости, перпендикулярной к току. Магнитное
напряжение вдоль элемента <is этого контура есть
= Hsds = Н cos ads = ~^— cos a ds,
2irr
где а
угол между Н и ds. Но
ds cos a
= dip,
ds2
и поэтому, суммируя магнитное напряжение по всему контуру,
мы получим опять формулу (81.1).
Если контур L не лежит в плоскости, перпендикулярной к
току, то любой элемент этого контура ds можно разложить на
составляющую ds\, перпендикулярную к току, и составляющую
ds2, параллельную к току (рис. 120). Так как составляющая ds2
перпендикулярна к Н, то для нее Нs = 0 и dUu — 0- Это зна-
значит, что магнитное напряжение вдоль ds такое же, как вдоль
cfei- Отсюда следует, что магнитное напряжение вдоль произ-
произвольного контура такое же, как
и для проекции этого контура
на плоскость, перпендикулярную к
току.
Рассмотрим теперь магнитное
напряжение вдоль замкнутого кон-
контура, охватывающего провод с то-
током (рис. 121а), или циркуляцию
напряженности магнитного поля
(ср. § 17) В этом случае ip = 2ж,
и поэтому
Isds = i. (81.2)
Рис 120. Магнитное напряже- Для формулы (81.2) также
ние вдоль отрезка ds равно маг- справедливо правило правого бу-
нитному напряжению вдоль dsi равчика: положительное направле-
направление обхода контура совпадает с на-
направлением вращения правого буравчика, который движется
поступательно в направлении тока. Так, например, на рис. 121
ток предполагается текущим от читателя за чертеж, и поэтому
контур нужно обходить по часовой стрелке.
Если замкнутый контур не охватывает провод с током
(рис. 1216), то при обходе такого контура, например, начиная
от точки 1 по часовой стрелке, радиус-вектор будет занимать
последовательно положения ri, гг, гз и угол ср будет увеличи-
увеличиваться. Если продолжать обход, начиная с точки 2, то после-
последовательные положения радиус-вектора будут гз, г±, г§ и т.д. и
угол tp будет уменьшаться; когда мы вернемся в точку 1, угол
§81
ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ
177
(р = 0. Поэтому магнитное напряжение для любого замкнутого
контура, не охватывающего ток, равно нулю.
В том случае, когда замкнутый контур охватывает ток не
один, а п раз (рис. 121 б, п — 2), магнитное напряжение будет в
п раз больше.
Рис. 121. Контуры, охватывающие (аи в) ш не охватывающие (б) ток
Формула (81.2) выражает важнейшее свойство магнитного
поля. Можно показать, что она справедлива не только для по-
поля прямого провода, но и для любого постоянного во времени
магнитного поля, вызванного каким угодно распределением то-
токов. Таким образом, магнитное напряжение вдоль замкнутого
контура равно полной силе тока, протекающего сквозь поверх-
поверхность, ограниченную рассматриваемым контуром.
Из формулы (81.2) видно, что магнитное напряжение изме-
измеряется в тех же единицах, что и сила тока, т.е. в амперах.
Рассмотренная теорема позволяет
во многих случаях просто вычислить
напряженность магнитного поля. Обра-
Обратимся к некоторым важным примерам.
Пример 1. Тороидальная катуш-
катушка. Вычислим напряженность поля вну-
внутри замкнутой тороидальной катушки
(рис. 122). Из соображений симметрии
ясно, что напряженность Н одинако-
одинакова во всех точках окружности, центр
которой совпадает с центром тороида.
Поэтому магнитное напряжение вдоль
этой окружности равно Н ¦ 2жг.
Рассматриваемая окружность охва-
охватывает токи всех витков катушки. Если
полное число витков катушки есть N, а
сила тока в ней равна г, то наша окружность охватывает ток си-
силы Ni. Поэтому по теореме о магнитном напряжении мы имеем
Н ¦ 2irr = Ni, откуда
H = N^. (81.3)
Рис 122.
катушка
Тороидальная
178 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ VIII
Следует иметь в виду, что поле внутри тороида не вполне
однородно. Напряженность наибольшая у внутренней сторо-
стороны катушки [Н\ = N | и наименьшая у внешней стороны
2 = N——). Относительная разность обоих полей равна
27ГГ2 /
(Я1-Я2)/Я1 = (г2-п)/г2.
Пример 2. Соленоид. Будем теперь неограниченно уве-
увеличивать радиус тороида г. Тогда отношение {г2 — гг)/гг будет
стремиться к нулю и поле сделается однородным. Любой отрезок
тороида перейдет при этом в прямую катушку или соленоид. На-
Напряженность поля внутри соленоида можно найти из формулы
N
(81.3). Замечая, что -— = п, где п — число витков на единицу
длины катушки, находим
Н = т. (81.4)
Мы видим, что напряженность магнитного поля в достаточно
длинном соленоиде равна произведению силы тока и числа вит-
витков на единицу длины катушки. Это произведение называют
числом ампер-витков на метр.
Соленоиды широко используют в технических устройствах и
в лабораторной практике, так как с их помощью можно просто
создать однородное магнитное поле и притом известной напря-
напряженности.
Пример 3. Прямой длинный провод. Рассмотрим еще
вычисление магнитного поля длинного прямого провода в точ-
точке, лежащей вне провода на расстоянии R от его оси. В этом
случае в качестве контура для вычисления магнитного напря-
напряжения удобно выбрать окружность радиуса R, перпендикуляр-
перпендикулярную к току и имеющую центр на оси тока. Теорема о магнитном
напряжении дает
2ttRH = г,
откуда
Я = —^— (вне провода). (81.5)
Этот результат мы получили уже в § 79. Мы видим, что рас-
расчет при помощи магнитного напряжения гораздо проще, неже-
нежели непосредственное суммирование полей отдельных элементов
тока.
Вычислим теперь напряженность поля в какой-либо точке
внутри провода, отстоящей на расстоянии г от оси провода. Зам-
Замкнутый контур выберем опять в виде окружности, проходящей
через эту точку с центром на оси провода (на рис. 123 а указана
§82
МАГНИТНЫЙ МОМЕНТ ТОКА
179
штриховой линией). Тогда но теореме о магнитном напряжении
имеем
2-кгН - жг2],
где j — плотность тока (постоянная во всех точках проводника)
Отсюда получается
(внутри провода). Здесь
г — полная сила тока через
все сечение провода, а —
радиус провода.
Таким образом, напря-
напряженность поля внутри про-
провода увеличивается с рас-
расстоянием от оси по линей-
линейному закону, а во внешнем
пространстве уменьшается
по гиперболическому зако-
закону. Эта зависимость изо-
изображена графически на
рис. 123 6.
Рис. 123 Магнитное поле прямого про-
провода с током
§ 82- Магнитный момент тока
Во многих случаях нам приходится иметь дело с замкнутыми
токами, размеры которых весьма малы по сравнению с расстоя-
расстоянием от них до точки наблюдения Такие токи мы будем назы-
называть элементарными. Пример подобных токов мы имеем во всех
атомах, так как в них имеются движущиеся электроны, обра-
обращающиеся по замкну-
замкнутым орбитам (гл. XI).
Эти токи вследствие
малости атомов мож-
можно рассматривать по-
почти во всех задачах
как элементарные.
Посмотрим, от че-
чего зависит магнитное
поле, создаваемое эле-
элементарным током. По-
Положим, что мы имеем
круговой ток силы г
с радиусом R. Вычис-
Матнитное поле кругового витка с
Рис 124
ТОКОМ
лим магнитное поле в некоторой точке А, находящейся на оси
тока на расстоянии г от его центра (рис. 124). В этом случае все
180 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ. VIII
элементы тока перпендикулярны к радиус-векторам р и поэтому
в формуле G9.2) sini9 = 1. Далее, из рис. 124 видно, что магнит-
магнитные поля dHi и dH-2, создаваемые какой-либо парой элементов
тока 1 и 2, расположенных на одном диаметре, складываясь,
дают поле dH, направленное вдоль оси тока. Поэтому и полное
поле всего кругового тока направлено по его оси.
Составляющая поля по оси тока, создаваемого одним элемен-
элементом тока, есть
J_ г off sin ^ _ J_ idlR
4тг р2 4-jt р3
Суммируя это выражение по всем элементам тока, получаем
где S = 7ГЙ2 — площадь, обтекаемая током.
Бели ток является элементарным, т.е. если р~Э> R, то с точно-
точностью до малых второго порядка в полученной формуле можно
положить р ~ г. Окончательный результат удобно представить
в виде
Если бы мы имели элементарный электрический диполь, на-
направленный вдоль оси тока (он изображен на рис. 124 штриховой
линией), то создаваемое им электрическое поле было бы направ-
направлено так же, как и магнитное поле в рассматриваемом примере,
т.е. тоже по оси тока. Электрическое смещение D = EqE, соглас-
согласно B5.5) (где нужно положить cos a = 1), было бы равно
D = ?
где р — электрический момент диполя. Формула (82.2) имеет
тот же вид, что и (82.1). Однако роль электрического момента р
диполя играет произведение iS; оно получило название магнит-
магнитного момента тока. Единицей магнитного момента в системе
СИ является ампер-квадратный метр (А-м2).
Электрический момент диполя есть вектор
(§ 15). Аналогично магнитный момент тока
есть также вектор. За его направление прини-
w мают направление нормали к плоскости вит-
* ка (рис. 125). Если п есть единичный вектор
вдоль нормали, то магнитный момент тока рт
равен
рт = iSn. (82.3)
„¦ " Выше мы ограничились частным случаем
ныи момент тока L CJ
кругового тока и считали, что точка наблюде-
наблюдения лежит на оси тока. Однако понятие магнитного момента
тока имеет общее значение. Легко показать, что напряженность
§ 83
ДВА ПАРАЛЛЕЛЬНЫХ ПРОВОДНИКА С ТОКОМ
181
магнитного поля элементарного тока любой формы и в произ-
произвольной точке наблюдения можно найти по формулам B5.5)
и B5.6), если выразить из них ?qEt и ?оД» и затем заменить
электрический момент диполя р на магнитный момент тока рт,
определяемый формулой (82.3). Мы видим, что магнитное дей-
действие элементарного замкнутого тока определяется его магнит-
магнитным моментом.
§ 83. Два параллельных проводника с током
Зная магнитное поле, создаваемое каким либо проводником
с током, можно вычислить и силу, действующую на другой про-
проводник с током в этом поле.
Рассмотрим в качестве примера два бесконечно длинных па-
параллельных проводника 1 и 2 с током (рис. 126) и вычислим
силу, действующую на отрезок длины / проводника 2 со стороны
проводника 1. Напряженность маг-
нигного поля, создаваемого провод-
проводником 1 в месте нахождения провод-
проводника 2, выражается формулой G9.4),
а следовательно, магнитная индук- /""' i
ция равна 'ч
2-nR
Индукция перпендикулярна к
проводнику 2, а следовательно,
sin(l,B) = 1. Поэтому G6.16) дает
(83.1)
Рис. 126. Взаимодействие
Если бы мы вычислили индукцию двух параллельных провод-
02, создаваемую током й, а затем на- ников с током
шли силу, действующую на провод-
проводник 1, то получили бы ту же формулу (83.1). Это и понятно,
так как при магнитном взаимодействии выполняется закон ра-
равенства действия и противодействия.
Применяя правило правого буравчика к рис. 126, легко ви-
видеть, что если направления токов в обоих проводниках одинако-
одинаковы, то возникающие силы стремятся уменьшить расстояние R
между проводниками; если же токи направлены противополож-
противоположно, то эти силы стремятся увеличить расстояние R: параллель-
параллельные токи притягиваются, антипараллельные — отталкиваются.
Определение ампера. В § 4 мы уже говорили, что четвер-
четвертая основная единица системы СИ — ампер — определяется че-
через магнитное взаимодействие токов. Для этого как раз исполь-
используют закон взаимодействия двух параллельных токов (83.1).
182 МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ ГЛ VIII
Ампер — сила неизменяющегося тока, который, проходя по двум
параллельным прямолинейным проводникам бесконечной дли-
длины и ничтожно малой площади кругового поперечного сечения,
расположенным в вакууме на расстоянии 1 м один от другого,
вызвал бы на каждом участке проводника длины 1 м силу вза-
взаимодействия, равную 2•10~7 Н.
Отсюда непосредственно получается значение цо, уже при-
приведенное нами в § 78. Действительно, из формулы (83.1) и опре-
определения ампера следует, что
2 - 1СГ7 = Ь1 1
откуда
цо = 47г ¦ 10~7 СИМ0.
Найдем еще соотношение между ампером, с одной стороны, и единица-
единицами силы тока в системах СГСМ и СГСЭ, с другой. В нерационализованной
системе СГСМ /хо = 1- Кроме того, мы во все формулы должны ввести еще
множитель 47г. Поэтому в системе СГСМ вместо формулы (83.1) имеем
„ 2гщ*2М , ,„„ „ч
F = —— I, (83.2)
где силы тока измеряются в единицах СГСМ, длины — в сантиметрах, а
сила — в динах.
Если силы обоих токов равны 1А, a, R = I (I = 1 м), то сила будет
2 ¦ 10~7 Н = 2 ¦ 10~2 дин, и мы имеем
2-10 =2iiMi2M-
Отсюда видно, что »ш = »2М = 0,1. Это значит, что сила тока, которая в
системе СИ равна 1 А, в системе СГСМ равна 0,1 СГСМг.
Так как, с другой стороны, сила тока, равная 1 СГСМг, в системе СГСЭ
равна 3 ¦ 10io СГСЭ,, то 1 А соответствует 3 • 109 СГСЭг.
§ 84. Механическая работа в магнитном поле.
Магнитный поток
Так как на провод с током в магнитном поле действуют си-
силы, то при движении провода совершается определенная работа.
Найдем эту работу.
Предположим, что прямой проводник длины /, входящий в
цепь тока, перемещается поступательно параллельно самому се-
себе на отрезок dx и переходит из положения 1 в положение 2
(рис. 127). Направление магнитной индукции В будем считать
перпендикулярным к I и к dx. На проводник действует сила
и поэтому механическая работа 6А выразится формулой
6А = ИВ dx = iB dS,
§84
МЕХАНИЧЕСКАЯ РАБОТА В МАГНИТНОМ ПОЛЕ
183
где dS = Idx — площадь, описанная проводником с.током при
движении (на рис. 127 заштрихована).
Если индукция В направлена иначе, то ее всегда можно раз-
разложить на составляющую В„, перпендикулярную к dS, и со-
составляющую В{, параллельную dS. Так как сила F всегда пер-
перпендикулярна к В (§ 76), то составляющая В< вызовет силу,
перпендикулярную к dx, и работа этой силы будет равна нулю.
Поэтому
SA = iBndS. (84.1)
Рассмотрим теперь вращательное движение проводника.
Пусть элемент проводника dl, входящий в цепь тока, повора-
поворачивается в магнитном поле на угол da (рис 128). При движении
он описывает площадь dS = Idadl, где / — расстояние элемента
Ш
I •
Рис. 127. К вычислению механи-
механической работы при поступательном
движении проводника
4
О
Рис. 128. К вычислению меха-
механической работы при вращатель-
вращательном движении проводника
от оси вращения О- Сила, действующая на элемент dl в направ-
направлении его перемещения, есть idlBn, где Вп — составляющая
напряженности, перпендикулярная к dS. Поэтому совершаемая
работа равна
6 A = idl Bnl da = iBn dS
и выражается той же формулой (84.1), что и при поступатель-
поступательном движении.
Но любое движение проводника можно свести к поступатель-
поступательному и вращательному движениям. Это значит, что формула
(84.1) определяет механическую работу для произвольного пе-
перемещения проводника.
Полученный результат можно представить в более удобном
виде, если ввести понятие магнитного потока.
Рассмотрим сначала плоскую площадку S (рис. 129), нахо-
находящуюся в однородном магнитном поле с индукцией В. Маг-
Магнитным потоком или потоком вектора магнитной индукции
184
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ VIII
сквозь площадку S называют величину
Ф = BScos a = BnS. (84.2)
Здесь а — угол между направлением нормали п к площадке и
направлением индукции В, и Вп — проекция вектора В на нор-
нормаль п. Так как Вп — скаляр, то и магнитный поток есть ска-
скалярная величина. Магнитный поток BnS равен полному числу
линий магнитной индукции, проходящих через данную поверх-
поверхность.
Магнитный поток характеризуется не только своей величи-
величиной, но и знаком, который зависит от того, какой знак имеет
cos а. Этот знак зависит от выбора положительного направ-
направления нормали п. Во всех электромагнитных явлениях всегда
приходится рассматривать магнитный поток в связи с током,
обтекающим контур,
ограничивающий рассма-
рассматриваемую поверхность.
Поэтому положительное
направление нормали
естественно связать с на-
направлением этого тока.
Мы будем везде считать,
что положительное на-
Рис 129
тока
К определению магнитного по-
правление нормали к пло-
площадке совпадает с на-
направлением перемещения
буравчика с правой нарезкой, вращаемого в направлении тока
(ср. рис. 129) Отсюда, в частности, следует, что магнигный по-
поток, создаваемый каким-либо проволочным контуром с током,
сквозь поверхность, ограниченную им самим, всегда положите-
положителен.
Если магнитное поле неоднородно, а рассматриваемая по-
поверхность не плоская, то ее можно разбить на бесконечно малые
элементы dS. Каждый элемент поверхности можно рассматри-
рассматривать как плоскую площадку, а любое поле на протяжении этого
элемента — как однородное. Поэтому магнитный поток через
элемент поверхности есть
d<$> = Вп dS,
а полный магнитный поток через всю поверхность
Ф = f Bn dS.
(84.3)
Если в (84.2) и (84.3) выражать В в Тл, a S — в м2, то маг-
магнитный поток окажется также выраженным в единицах системы
СИ веберах (Вб) (§91)
§85
КОНТУР С ТОКОМ В МАГНИТДОМ ПОЛЕ
185
Пользуясь понятием магнитного потока, мы можем предста-
представить (84.1) в следующем виде:
5 А = i е*Ф. (84.4)
Здесь 5А — работа, совершаемая силами поля, а ёФ — увеличе-
увеличение магнитного потока сквозь поверхность, ограниченную кон-
контуром с током
Если проводник совершает конечное перемещение, то
А = г(Ф2-Ф,), (84.5)
где $2 ~ магнитный поток сквозь контур в конце перемещения,
а Ф\ — поток сквозь контур в начале перемещения; при этом мы
считаем, что сила тока в контуре при его перемещении поддер-
поддерживается постоянной.
Выражая в этой формуле магнитный поток в веберах, а силу
тока — в амперах, мы получим работу в джоулях.
§ 85. Контур с током в магнитном поле
Найдем теперь механические силы, действующие на замкну-
замкнутый контур с током в магнитном поле. Положим сначала, что
контур имеет форму прямоугольной рамки (рис 130) и магнит-
магнитное поле однородно Согласно формуле G6.1а) силы, действую-
действующие на ребра а, перпендикулярны к ним и к магнитной индук-
индукции В и поэтому стремятся только растянуть (или сжать) виток.
Силы же F, действующие на ребра Ь, стремятся повернуть виток
м
Рис. 130 Прямоугольная рамка с током в магнитном поле' а — вид сбоку,
б — вид сверху
так, чтобы его плоскость стала перпендикулярна к В. Следова-
Следовательно, на виток действует пара сил с некоторым моментом М.
186
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ VIII
Это справедливо, очевидно, не только для прямоугольной рам-
рамки, но и для контура произвольной формы.
Момент пары сил М (и притом для плоского контура про-
произвольной формы) можно непосредственно найти из формулы
(84.4). Для этого представим себе, что мы даем возможность
контуру повернуться под действием сил поля на бесконечно ма-
малый угол da. Силу тока в контуре i будем считать неизменяю-
неизменяющейся, и следовательно, магнитный момент контура рт = iS —
постоянным. Тогда механическая работа сил поля будет равна
5А = М da. Вместе с тем магнитный поток, пронизывающий
контур, есть Ф = SB cos а, а его изменение при уменьшении
угла а на da равно о!Ф = SB sin a da. Поэтому из формулы (84.4)
имеем
М da = iSB sin a da,
откуда
М = ртВ sin a. (85.1)
Полученные результаты можно выразить векторной форму-
формулой, дающей и модуль, и направление момента пары сил:
М = [РтВ]. (85.2)
Эта формула аналогична выражению A5.3) для момента па-
пары сил, действующих на электрический диполь в электрическом
поле.
Рассмотрим теперь малый виток с током в неоднородном
магнитном поле (рис. 131) и будем считать сначала, что линии
индукции симметричны относительно нормали к плоскости вит-
витка. Силы g!F, действующие на от-
отдельные участки витка, будут по-
прежнему перпендикулярны к току
и к магнитному полю. Однако те-
теперь, так как линии индукции уже
не параллельны, эти силы будут со-
составлять некоторый угол с плоско-
плоскостью витка. Составляющие этих сил
dJ?t, параллельные витку, создадут
усилия, растягивающие или сжима-
сжимающие виток. Составляющие же dFn.
перпендикулярные к плоскости вит-
витка, складываясь, дадут некоторую
силу F, стремящуюся перемещать
виток в магнитном поле.
Применяя правило правого бу-
буравчика, легко видеть, что если мо-
момент тока рт параллелен магнитной индукции (как изображено
на рисунке), то виток будет втягиваться в область более сильно-
сильного поля. Если же вектор рт антипараллелен индукции, то виток
Рис 131 Виток с током в
неоднородном поле
§ 85 КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ 187
будет выталкиваться и перемещаться в область более слабого
поля.
Найдем эту силу, пользуясь тем же приемом, что и выше.
Положим, что виток смещается в направлении рт на малый
отрезок dx. Тогда механическая работа 5А = F dx. Изменение
магнитного потока есть dФ = S(dBn/dx) dx, где Вп — состав-
составляющая В, нормальная к плоскости витка. Поэтому формула
(84.4) принимает вид
^dx,
ах
а следовательно,
F = pJ-^. (85.3)
Сила, действующая на малый виток с током в магнитном по-
поле, пропорциональна быстроте изменения магнитной индукции
в рассматриваемом направлении.
Рассуждая указанным образом, легко найти и общее выра-
выражение для силы при произвольной ориентации малого конту-
контура с током относительно магнитной индукции. Если ртх. Рту
и Pmz — составляющие магнитного момента контура с током в
Прямоугольных осях координат, а Вх, Ву и Bz — составляющие
магнитной индукции, то сила в направлении оси X выражается
формулой, подобной A5.6):
дВ* л п дВ* л -п дВ* /-«г; л\
+P+Pz-Q^- (85.4)
Для составляющих силы Fy и Fz справедливы аналогичные фор-
формулы. Эти результаты можно записать в виде векторной фор-
формулы
F = (pmgrad)B, (85.4а)
где введен дифференциальный оператор (ср. § 15)
(pmgrad) =pmx— +Pmy-^+Pmz-Q-z-
В общем случае неоднородного поля, не перпендикулярного
К плоскости витка, будут действовать и пара сил, стремящихся
Довернуть виток, и сила, вызывающая поступательное переме-
перемещение.
Силу, действующую на контур конечных размеров с током,
можно найти, разбивая площадь S, ограниченную этим конту-
контуром, на элементы dS, обтекаемые током той же силы г и в том
же направлении, что и в ограничивающем контуре. Полная сила
есть сумма сил, действующих на отдельные элементы с магнит-
магнитными моментами idS.
188
MAI НИТНОЕ ПОЛБ ТОКОВ В ВАКУУМЕ
ГЛ VIII
§ 86. Магнитное поле движущегося заряда
Мы видели выше, что каждый проводник с током создает в
окружающем пространстве магнитное поле. Но электрический
ток в любом проводнике есть движение заряженных частиц:
в металлах — это движение электронов, в электролитах — ио-
ионов, в газовом разряде — и ионов, и электронов. Отсюда можно
заключить, что всякий движущийся заряд создает вокруг себя
магнитное поле. Найдем напряженность этого поля.
Рассмотрим малый отрезок провода длиной I с током г. Со-
Согласно G9.2) этот отрезок создает в некоторой точке, удаленной
на расстояние г, напряженность поля
1_ г! sun?
4^ г2
Но силу тока можно выразить через плотность тока j и сечение
провода S (г = jS), а плотность тока — через концентрацию
заряженных частиц п и их скорость v (j = nqv, где q — заряд
частицы). Это дает
И = jSl = nqvSl = Nqv,
где N — полное число частиц в отрезке провода Поэтому на-
напряженность поля можно
представить в виде
1 Nqv sin •&
4^ г5 '
Отсюда следует, что на-
напряженность поля, вызы-
вызываемого одной заряженной
частицей, имеет значение
1 qv sin ¦д
47Г Г2
н =
Магнитное поле движущегося
(86.1)
Направление этого по-
поля перпендикулярно к ско-
скорости v частиц и к радиус-
вектору г, проведенному
из заряда в рассматривае-
рассматриваеРис 132
заряда
мую точку, и подчиняется, как и прежде, правилу правого бу-
буравчика (рис. 132).
Пользуясь обозначениями векторной алгебры, можно выра-
выразить модуль и направление поля движущегося заряда одной
формулой:
Н = -1 Щ. (86.2)
47Г Гл
Эта формула выражает напряженность поля положительного
заряда, движущегося со скоростью v. Если движется отрица-
отрицательный заряд, то в формуле нужно заменить q на —q.
§87
ОПЫТЫ РОУЛАНДА И ЭЙХЕНВАЛЬДА
189
Сравнивая (86 2) с G9.2а), мы видим, что движущийся заряд
по своим магнитным действиям эквивалентен элементу тока
г\ = qv. (86.3)
Формулы (86.1) и (86.2) мы получили из результатов § 79,
которые в свою очередь были установлены в опытах с непо-
неподвижными (относительно наблюдателя) проволочными конту-
контурами. Поэтому и скорость v, входящая в эти формулы, есть от-
относительная скорость, те. скорость относительно наблюдателя
и тех приборов, которые измеряют магнитное поле (ср. § 141).
§ 87. Опыты Роуланда и Эйхенвальда
Результаты, полученные в § 86, должны быть справедливы
не только для движущихся электронов или ионов, но и для лю-
любого заряженного тела Если заряженное тело неподвижно от-
относительно наблюдателя, то для него существует только элек-
электрическое поле. Если же заряженное те-
тело движется относительно наблюдателя,
то для него, помимо электрического поля,
существует еще и магнитное поле. Эти вы-
выводы были качественно проверены на опы-
опыте Роуландом и тщательно изучены А.А
Эйхенвальдом в 1901 г
Схема одного из опытов Эйхенвальда
показана на рис. 133. Два параллельных
металлических диска D\ и D2 могли вра-
вращаться вокруг осей О и О\. Вблизи дисков
была подвешена на тонкой нити неболь-
небольшая магнитная стрелка, ось которой па-
параллельна плоскости дисков. Для наблю-
наблюдения за поворотом стрелки к ней было
прикреплено небольшое зеркальце 3.
Стрелка помещалась внутрь проводящего
кожуха, предохранявшего ее от действия
Электрического поля и от токов воздуха
при вращении дисков Оба диска заряжа-
заряжались разноименно и приводились в быстрое вращение. При этом
вращался либо один из дисков, либо оба диска вместе, как в оди-
одинаковом направлении, так и в противоположном. Опыты пока-
показали, что при вращении дисков магнитная стрелка отклоняется,
Что указывает на появление магнитного поля.
Для количественной проверки формулы (86.3) диски оста-
останавливали, по ним пропускали ток от постороннего источника и
определяли силу тока, вызывающую то же отклонение стрелки,
что и при вращении дисков. Опыты показали, что эта сила тока
соответствует формуле (86 3)
Рис. 133
вальда
Опыт Эйхен-
190
МАГНИТНОЕ ПОЛЕ ТОКОВ В ВАКУУМЕ
ГЛ. VIH
Расчет особенно прост, если диск изготовлен из изолирующего материа-
материала и имеет металлическую обкладку в виде кольца с разрезом (рис. 134).
Малый отрезок I такого кольца имеет поверхность
al (а — ширина кольца), а заряд на нем есть ala
(а — поверхностная плотность заряда). Если v —
линейная скорость движения кольца, то, соглас-
согласно (86.3), рассматриваемый отрезок эквивалентен
элементу тока:
И = alav,
откуда
г = auv.
Если средний радиус кольца есть г, а диск дела-
делает в секунду п оборотов, то и = 2тггп. Учитывая
еще, что 2тгго = S есть полная поверхность кольца,
имеем
i = аа ¦ 2тггп = qn,
где q — полный заряд кольца.
Рассмотрим численный пример. Пусть площадь кольца S = 100 см2 =
3~2 м2, а расстояние между дисками d = 1 см = 10~2 м. Тогда емкость
Рис. 134 К
Эйхенвальда
опытам
дисков
10"
ИГ9 Ф.
" d 4тг • 9 • 109 Ю-2 " Збтг
Если напряжение между дисками U = 104
—— 1U 11) — ——
56тг Збтг
При частоте вращения п = 100 об/с сила тока бу-
будет
= CU =
В, то
Кл
1
Збтг
= —- Ю-5 • 10я а 0,9
10~5 А.
I
д
- +¦
Присоединяя концы 1 и 2 кольца (рис. 134) к ис-
источнику тока и создавая в кольце ток такой силы,
мы получим то же отклонение стрелки, что и при
вращающемся диске.
Приведенный пример показывает, что сила то-
тока получается очень малой, и поэтому возникаю-
возникающие в подобных опытах поля очень слабы. Обычно
они в десятки тысяч раз меньше магнитного поля
Земли, что делает опыты очень трудными.
Если между дисками D\ и D^ поме-
поместить диэлектрик А с диэлектрической
/ ioc\ щимся диэлектриком
проницаемостью е (рис. loo), то заряд на
металлических дисках увеличится в е раз и будет eq. Поэто-
Поэтому при вращающихся металлических дисках и неподвижном ди-
диэлектрике магнитное поле увеличится тоже в е раз.
На поверхности диэлектрика возникают поляризационные
заряды, которые на каждой поверхности диска А равны (е — l)q.
Если оставить диски D\ и Di неподвижными, но вращать ди-
диэлектрик А, то также возникает магнитное поле. Это поле будет,
Рис. 135.
хенвальда
Опыт Эй-
с движу-
§ 88 СИЛА ЛОРЕНЦА 191
однако, намного меньше, чем при вращении дисков D\ или D2,
так как на диэлектрике А возникают заряды двух знаков и его
действие соответствует двум круговым близким токам, направ-
направленным противоположно.
Если, наконец, вращать весь конденсатор с диэлектриком как
целое, то на каждом металлическом диске будет движущийся
заряд eq, а на прилегающей к нему поверхности диэлектрика —
заряд противоположного знака — (е — \)q. Поэтому магнитное
действие будет пропорционально eq — (е — l)q = q, т.е. будет
таким же, как и в отсутствие диэлектрика.
Все эти случаи были проверены на опыте Эйхенвальдом. Эти
опыты, следовательно, показали, что любые движущиеся заря-
заряды, независимо от их природы, в том числе и поляризационные
заряды, вызывают магнитное поле.
§ 88. Сила Лоренца
Вернемся теперь к действию магнитного поля на ток. Так
как всякий ток есть движение заряженных частиц (электронов
или ионов), то отсюда следует, что на дви-
движущийся заряд в магнитном поле дей-
действует сила.
Нетрудно определить эту силу. На
проводник длины I с током г в магнитном
поле действует сила
tZSsin(l,B), • •
где В — магнитная индукция. С другой
стороны,
Ц = JSfnv Рис. 136. Направление
силы, действующей на
где N — полное число движущихся заря- движущийся заряд в
женных частиц внутри проводника. Учи- магнитном поле. Поле
Тывая, что направление 1 совпадает с направлено к читателю
направлением скорости v движения поло-
положительных частиц (с направлением тока), мы можем выраже-
выражение для силы представить в виде
NqvB sin {v,В).
Сила, действующая на проводник, пропорциональна полному
Числу движущихся частиц, а значит, сила, действующая на одну
Частицу, равна
F = qvB sin (v, В).
Направление этой силы перпендикулярно к направлению скоро-
скорости v и магнитной индукции В и подчиняется правилу правого
буравчика (рис. 136).
192
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ГЛ. IX
Полученный результат можно выразить в виде векторной
формулы
F = g[vB]. (88.1)
Если имеется еще электрическое поле, то полная сила равна
F = qE + q[vB]. (88.2)
Выражение (88.2) было впервые получено из опыта Г. Ло-
Лоренцем, и поэтому силу, действующую на движущийся заряд,
называют силой Лоренца.
Формулу (88.2), так же как и результаты § 86, мы получи-
получили, анализируя опытные данные о взаимодействии неподвиж-
неподвижных контуров с током. Поэтому скорость, входящая в (88.2),
есть скорость относительно магнитного поля (ср. § 143).
Сила Лоренца проявляется при движении электронов и ио-
ионов в магнитных полях. Эти явления будут рассмотрены в
гл. XVII.
ГЛАВА IX
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
§ 89. Электромагнитная индукция
В предыдущей главе мы видели, что электрические токи соз-
создают вокруг себя магнитное поле. Существует и обратное явле-
явление: магнитное поле вызы-
вызывает появление электриче-
электрических токов. Это явление
было открыто М. Фараде-
ем в 1831 г. и получило на-
название электромагнитной
индукции.
Рассмотрим некоторые
опыты, иллюстрирующие
электромагнитную индук-
индукцию. Для этого восполь-
воспользуемся двумя проволоч-
проволочными катушками 1 и 2
(рис. 137), одну из кото-
Рис. 137. При движении катушки 1 в рых (_f) можно надевать
магнитном поле катушки 2 в цепи катуш- на другую B) Соединим
ки 1 появляется ток катушку 1 с гальваномет-
ром, а катушку 2 с источником тока. Если катушка 1 неподвиж-
неподвижна относительно катушки 2 (т.е. относительно магнитного поля),
то в цепи 1 не будет тока, как бы сильно ни было магнитное поле
§ 89
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
193
катушки 2. Начнем теперь перемещать катушку 1. Мы увидим,
что гальванометр покажет появление тока. Этот ток существует
только при движении катушки, и он тем сильнее, чем быстрее
движется катушка. Ток в цепи катушки 1 возникает и при сбли-
сближении катушек, и при удалении их, однако токи в обоих случаях
имеют противоположные направления.
Если оставить катушку 1 неподвижной, а двигать катушку с
током 2, то гальванометр также показывает ток при движении
катушки.
Мы могли бы оставить обе катушки 1 и 2 неподвижными,
но изменять силу тока в катушке 2 при помощи реостата. Тог-
Тогда при всяком изменении силы тока (т.е. магнитного поля) в
цепи катушки 1 возникал бы ток. Направление тока в катушке
1 при усилении магнит-
магнитного поля противополож-
противоположно направлению тока при
ослаблении поля; ток в ка-
катушке 1 не возникает, ес-
если магнитное поле остает-
остается постоянным.
Эти опыты показыва-
показывают, что причиной появ-
появления индукционного тока
является изменение маг-
магнитного поля. Каким обра-
образом создается это измене-
изменение, безразлично. В опыте,
изображенном на рис. 138,
обе катушки 1 и 2 непо-
неподвижны, но в катушку 2
мы вдвигаем или выдвига-
выдвигаем из нее железный сердеч-
сердечник С. При вдвигании сер-
сердечника он намагничивается, и магнитное поле усиливается; при
выдвигании сердечника поле уменьшается. Ток в цепи катушки
1 течет только при движении сердечника.
Изменяющееся магнитное поле мы можем создать и движе-
движением постоянного магнита. Если вовсе удалить катушку с током
2 и вдвигать (или выдвигать) в катушку 1 постоянный магнит,
то гальванометр также показывает ток. Этот ток возникает и в
том случае, если движется катушка, а магнит находится в покое.
Наблюдая направления тока при сближении магнита и катуш-
катушки и при удалении, можно убедиться, что они противоположны,
так же как и в предыдущих опытах.
Результаты своих многочисленных опытов Фарадей выразил
в следующей наглядной форме. Будем изображать магнитное
Рис. 138. При движении железного сер-
сердечника С магнитное поле катушки 2 из-
изменяется и в цепи катушки 1 появляется
ток
194
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ГЛ IX
Рис 139 Замкнутый проводник и линии маг-
магнитной индукции «сцеплены» между собой
поле при помощи линий магнитной индукции. Тогда магнитная
индукция будет характеризоваться густотой линий индукции.
Представим себе теперь, что замкнутый проводник движется
в магнитном поле и переходит в область более сильного поля.
Тогда число линий индукции, охватываемых проводником, уве-
увеличится. Напротив, при движении проводника в область более
слабого поля число линий индукции, охватываемых проводни-
проводником, уменьшится. Но магнитное поле есть поле вихревое (§ 81),
и его линии индук-
индукции не имеют кон-
концов. Вследствие этого
линии индукции по-
поля сцеплены с прово-
проволочным контуром на-
наподобие звеньев цепи
(рис. 139). Поэтому
всякое изменение чис-
числа линий индукции,
охватываемых конту-
контуром, может произой-
произойти только в результате
пересечения ими про-
проволочного контура. Точно так же, если проводник находится в
покое, но изменяется магнитная индукция, то при усилении по-
поля густота линий индукции будет увеличиваться и они будут
стягиваться друг к другу, а при ослаблении поля — расходиться
друг от друга И в этом случае произойдет пересечение неко-
некоторого числа линий индукции проводником. Поэтому Фарадей
заключил, что индукционный ток возникает в проводнике в том
случае, если проводник или какая-либо его часть пересекает ли-
линии магнитной индукции.
Открытие электромагнитной индукции имело огромное на-
научное и техническое значение Это явление показало, что мож-
можно не только получить магнитное поле при помощи токов, но и,
обратно, получить электрические токи при помощи магнитно-
магнитного поля. Этим была установлена окончательно взаимная связь
между электрическими и магнитными явлениями.
§ 90. Закон Ленца
Э.Х. Ленц установил важный закон, позволяющий опреде-
определить направление индукционного тока. Он сформулировал най-
найденный им закон следующим образом: «Если металлический
проводник передвигается вблизи гальванического тока или вбли-
вблизи магнита, то в нем возбуждается гальванический ток такого
направления, которое вызвало бы движение покоящегося прово-
§91 ОСНОВНОЙ ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 195
да в направлении, прямо противоположном направлению дви-
движения, навязанного здесь проводу извне, в предположении, что
находящийся в покое провод может двигаться только в направ-
направлении этого последнего движения или в прямо противополож-
противоположном».
В более сжатой форме закон Ленца можно выразить так:
индукционный ток во всех случаях направлен таким образом,
что его действие противоположно действию причины, вызвав-
вызвавшей этот ток.
Закон Ленца применим и к случаям, когда проводники непо-
неподвижны, а изменяется магнитное поле (сила тока). В таком слу-
случае индукционные токи всегда вызывают поле, которое стремит-
стремится противодействовать изменениям внешнего поля, вызвавшим
эти токи. Так, например, если в опыте (см. рис. 137) катушки
неподвижны, то при включении тока в катушку 2 (его нара-
нарастании) направление тока в катушке 1 будет противоположно
(индукционный ток стремится ослабить нарастающее поле ка-
катушки 2), а при выключении тока (его убывании) ток в катуш-
катушке 1 будет направлен так же, как и в катушке 2 (стремится
поддержать ослабевающее магнитное поле).
Закон Ленца вытекает из закона сохранения энергии Дей-
Действительно, индукционные токи, как и всякие электрические то-
токи, производят определенную работу Но это значит, что при
движении замкнутого проводника в магнитном поле должна
быть произведена дополнительная работа внешних сил. Эта ра-
работа возникает потому, что индукционные токи, взаимодействуя
с магнитным полем, вызывают силы, направленные противопо-
противоположно движению, т.е. препятствующие движению.
§ 91. Основной закон электромагнитной индукции
В результате многочисленных опытов Фарадей установил
основной количественный закон электромагнитной индукции.
Однако мы рассмотрим сначала другую формулировку этого
закона, данную впоследствии Максвеллом.
Возникновение индукционного тока показывает, что при
электромагнитной индукции в проводнике появляется опреде-
определенная электродвижущая сила. В § 89 мы видели, что индукци-
индукционный ток, а следовательно, и ЭДС индукции появляются толь-
только в том случае, если проводник пересекает линии магнитной
индукции, т.е. если полное число линий индукции, проходящих
через площадь, ограниченную проволочным контуром, изменя-
изменяется. Но полное число линий магнитной индукции, проходящих
через какую-либо поверхность, есть магнитный поток через эту
поверхность. Отсюда можно заключить, что причина появле-
появления ЭДС электромагнитной индукции есть изменение магнитно-
196 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ГЛ IX
го потока. Анализируя результаты опытов Фарадея, Максвелл
установил, что во всех случаях ЭДС электромагнитной индук-
индукции пропорциональна быстроте изменения магнитного потока
через площадь, ограниченную контуром, т.е.
где / — множитель пропорциональности, зависящий только от
выбора единиц.
В системе единиц СИ ЭДС измеряют в вольтах, а время —
в секундах. Закон же электромагнитной индукции используют
для определения единицы магнитного потока — вебера, с кото-
которой мы уже встречались в § 84. А именно, ее выбирают таким
образом, чтобы множитель / обратился в единицу.
Остановимся теперь на знаке ЭДС электромагнитной индук-
индукции. В § 84 мы приписали магнитному потоку определенный
знак, который зависит от выбора положительной нормали к
плоскости контура. Это направление нормали мы связали при
помощи правила правого буравчика с положительным направ-
направлением тока в контуре. Поэтому, выбирая (произвольно) опре-
определенное положительное направление нормали, мы определяем
как знак потока, так и положительное направление тока и ЭДС
в контуре. Пользуясь этим, можно выразить ЭДС индукции и
по модулю, и по знаку следующей формулой:
которая и представляет собой основной закон электромагнитной
индукции в форме, данной Максвеллом.
Знак минус в этой формуле соответствует закону Ленца.
Поясним это на конкретном примере. Пусть положительное на-
направление нормали совпадает с направлением магнитной индук-
индукции (см. рис. 139). Тогда поток сквозь контур будет положитель-
положительным. Положительное направление тока определяется выбором
направления нормали и на рис. 139 показано штриховой лини-
линией. Если теперь магнитное поле увеличивается, т.е. d&/dt > О,
то, согласно (91.1), Ш < О, а следовательно, и г < 0. Это значит,
что направление индукционного тока противоположно выбран-
выбранному нами положительному направлению.
Формула (91.1) выражает закон электромагнитной индукции
в общей форме. Она применима как к неподвижным контурам,
так и к движущимся проводникам в магнитном поле. Входящая
в нее производная от магнитного потока по времени в общем слу-
случае состоит из двух частей, одна из которых обусловлена изме-
изменением магнитной индукции во времени, а другая — движением
контура относительно магнитного поля (или его деформацией).
Рассмотрим некоторые примеры применения этого закона.
§ 91 ОСНОВНОЙ ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 197
Пример 1. Прямолинейный проводник длины / движет-
движется параллельно самому себе в магнитном поле (рис. 140). Этот
проводник может входить в состав за-
замкнутой цепи, остальные части которой
неподвижны. Найдем ЭДС, возникаю-
возникающую в проводнике.
Если мгновенное значение скорости
проводника есть v, то за малое время
dt он опишет площадь dS = Ivdt и за
это время пересечет все линии магнит-
магнитной индукции, проходящие через dS.
Поэтому изменение магнитного потока рис 140 Движение про-
через контур, в состав которого входит водника в магнитном поле
движущийся проводник, будет о!Ф =
= Bnlvdt. Здесь Вп — составляющая магнитной индукции, пер-
перпендикулярная к dS. Подставляя это в формулу (91.1), получаем
эдс
8 = BJv. (91.2)
Направление индукционного тока и знак ЭДС определяют-
определяются законом Ленца: ток направлен так, что механическая сила,
действующая на движущийся проводник, противоположна ско-
скорости (тормозит движение).
Рассмотрим численный пример. Вертикальный проводник (автомобиль-
(автомобильная антенна) длины 1 = 2м движется с востока на запад в магнитном поле
Земли со скоростью v = 60 км/ч = A03/60) м/с. Вычислим напряжение
между концами проводника.
Так как проводник разомкнут, то тока в нем не будет и напряжение
на концах будет равно ЭДС индукции. Учитывая, что горизонтальная со-
составляющая магнитной индукции поля Земли (т.е. составляющая, перпен-
перпендикулярная к направлению движения) для средних широт равна около
0,2 - 10~4 Тл, по формуле (91.2), находим U = Bnlv = 0,2 10~4 ¦ 2 103/60 =
= B/3) 10~3 Вй1мВ
Магнитное поле Земли направлено с юга на север. Поэтому мы находим,
что ЭДС направлена сверху вниз. Это значит, что нижний конец провода
будет иметь более высокий потенциал (зарядится положительно), а верх-
верхний — более низкий (зарядится отрицательно).
Пример 2. В магнитном поле находится замкнутый про-
проволочный контур, пронизываемый потоком магнитной индук-
индукции Ф. Положим, что этот поток уменьшается до нуля, и вычис-
вычислим полный заряд, прошедший по цепи.
Мгновенное значение ЭДС в процессе исчезновения магнит-
магнитного потока выражается формулой (91.1). Следовательно, со-
согласно закону Ома, мгновенное значение силы тока есть
_ _1 d$
1 ~ г dt>
198 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ГЛ IX
где г — полное сопротивление цепи. Прошедший заряд равен
о
q= f tdt = -- [ йФ= -. (91.3)
ф
Полученное соотношение выражает закон электромагнитной ин-
индукции в форме, найденной Фарадеем, который из своих опы-
опытов заключил, что заряд, прошедший по цепи, пропорционален
полному числу линий магнитной индукции, пересеченных про-
проводником, и обратно пропорционален сопротивлению цепи.
Отметим, что входящий в выражение для i магнитный по-
поток есть сумма потоков, создаваемых внешними источниками и
током (в самом рассматриваемом контуре), возникающим в про-
процессе исчезновения магнитного поля. Однако после интегриро-
интегрирования остаются только значения магнитного потока в начале и
конце процесса, когда ток в рассматриваемом контуре равен ну-
нулю. Поэтому магнитный поток, создаваемый самим контуром,
выпадает из окончательного результата и Ф в формуле (91.3)
обозначает магнитный поток, создаваемый только внешними ис-
источниками.
На соотношении (91.3) основано определение единицы маг-
магнитного потока в системе СИ: вебер — магнитный поток, при
убывании которого до нуля в сцепленном с ним контуре сопро-
сопротивлением 1 Ом проходит количество электричества 1 Кл.
Отсюда также следует определение еди-
единицы СИ для магнитной индукции: те-
тесла — магнитная индукция, при которой
магнитный поток сквозь поперечное сече-
сечение площадью 1 м2 равен 1 Вб.
Формула (91.3) лежит в основе про-
простого и удобного способа измерения маг-
магнитной индукции. Для этого служит
флюксметр. Он состоит из небольшой
плоской проволочной катушки, соединен-
Рис. 141 Принцип ной с баллистическим гальванометром
флюксметра (рис. 141). Чтобы в случае неоднородного
поля по возможности приблизиться к зна-
значению индукции в определенной точке поля, размеры катушки
делают малыми (диаметр около 1 см).
При измерениях катушку флюксметра ориентируют перпен-
перпендикулярно к направлению магнитной индукции. Тогда магнит-
магнитный поток через катушку равен Ф = BSn, где S — площадь
катушки, an — число витков проволоки. Затем магнитный по-
поток через катушку быстро уменьшают до нуля. Это можно осу-
осуществить, быстро выдергивая катушку из области магнитного
поля или выключая токи, создающие магнитное поле, или, на-
§91
ОСНОВНОЙ ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
199
При этом по цепи пройдет
конец, поворачивая катушку на 90°
заряд
q = — = — В = аВ.
г г
Поэтому, измеряя заряд q баллистическим гальванометром и
зная постоянную прибора а, можно определить магнитную ин-
индукцию В. Значение постоянной а
обычно не вычисляют, а определя-
определяют опытным путем при помощи по-
полей с известной индукцией (длин-
(длинные соленоиды).
Пример 3. Замкнутый виток про-
проволоки движется поступательно в одно-
однородном магнитном поле (рис. 142)
В этом случае магнитный поток
сквозь площадь витка остается при дви-
движении постоянным и, согласно (91 1),
ЭДС индукции W = 0. Поэтому и тока в
витке не будет В рассматриваемом при-
примере линии магнитной индукции пересе-
пересекают отдельные части витка и в них име-
имеются ЭДС Однако полная ЭДС контура,
равная сумме ЭДС, возникающих в отдельных его частях, оказывается рав-
равной нулю
Чтобы в замкнутом жестком контуре, движущемся в однородном поле,
возникла ЭДС, контур должен поворачиваться (рис. 143)
Рис 142 Движение витка в
магнитном поле без изменения
магнитного потока
Рис. 143 Вращение витка в маг-
магнитном поле
Рис 144 Вращение диска в маг-
магнитном поле
Пример 4 Рассмотрим металлический диск, вращающийся в маг-
магнитном поле. Диск может быть включен в цепь при помощи скользящих
контактов, касающихся его оси О и точки окружности А (рис 144) Маг-
Магнитное поле перпендикулярно к плоскости диска Найдем ЭДС индукции,
возникающую при вращении диска
В этом примере движущимся проводником, входящим в состав цепи,
является радиальная часть диска, замыкающая точки О и А Так как ЭДС
индукции не зависит от вещества проводника и его сечения, то она такая же,
200
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ГЛ IX
как и в примере 1, и равна числу линий магнитной индукции, пересекаемых
радиусом диска ОА в 1 с.
§ 92- Измерение магнитного напряжения
Пользуясь электромагнитной индукцией, можно просто из-
измерить и магнитное напряжение, введенное нами в § 81.
Рассмотрим длинную катушку в магнитном поле (рис. 145 а).
Ее можно представить как совокупность замкнутых витков и
прямолинейных отрезков, со-
соединяющих витки (рис. 145 б).
Если магнитное поле быстро
уменьшается до нуля, то по
цепи катушки протечет неко-
некоторый заряд, обусловленный
кратковременным импульсом
напряжения в круговых витках
и в прямолинейных отрезках.
Действие прямолинейных от-
отрезков можно исключить, если
сделать катушку двухслойной
(рис. 145 в), так как в этом
случае прямолинейные отрез-
Рис 145. Схема пояса Роговского ки внутренней и наружной
обмоток вызывают противо-
противоположные токи во внешней цепи, и поэтому остается только
действие витков катушки.
Вычислим заряд, протекающий в цепи за время исчезновения
поля. Если п — число витков катушки на единице длины (в обоих
слоях), то на элементе длины ds катушки будет nds витков,
которые, согласно сказанному в § 91, дадут заряд
dq^ —Bsds = uu—Hsds.
Т V
Здесь Bs и Hs — проекции магнитной индукции и соответствен-
соответственно напряженности магнитного поля на направление ds, до ~
магнитная постоянная, а остальные обозначения имеют прежние
значения Поэтому полный заряд, прошедший по цепи, будет
= Ho^y f
(92.1)
Здесь интегрирование производится по контуру /, совпадающе-
совпадающему с осью катушки. Заряд оказывается пропорциональным маг-
магнитному напряжению Um, и поэтому, изгибая катушку долж-
должным образом, можно измерить магнитное напряжение но любо-
любому контуру.
93
САМОИНДУКЦИЯ
201
Для подобных измерений служит пояс Роговского, представ-
представляющий собой узкую двухслойную катушку, намотанную на
гибкий ремень (рис. 146). Кон-
Концы обмотки, сходящиеся в се-
середине внешнего слоя, при-
присоединяют к баллистическому
гальванометру.
Пользуясь поясом Ро-
Роговского, можно проверить
основную теорему о магнит-
магнитном напряжении, установлен-
установленную в § 81. Если изогнуть пояс
Роговского таким образом,
чтобы образовался замкнутый
контур, охватывающий ток
(рис 146), и затем выключить
ток, создающий магнитное по-
поле, то отброс баллистического
гальванометра укажет маг-
магнитное напряжение по зам-
замкнутому контуру При этом
легко убедиться, что отброс
гальванометра не изменяется
при любом изгибании пояса
Роговского, пока образованный им контур охватывает ток один
раз. Если замкнутый контур охватывает ток два раза, то и
отброс гальванометра возрастает вдвое. Если пояс образует
замкнутый контур, не охватывающий ток, то гальванометр не
дает никакого отброса.
Пользуясь поясом Роговского, можно измерить магнитное
напряжение по любому контуру, замкнутому или разомкнуто-
разомкнутому, и в любом магнитном поле, независимо от того, создано ли
это поле контурами с током или магнитами.
§ 93. Самоиндукция
Явление электромагнитной индукции наблюдается во всех
случаях, когда изменяется магнитный поток, пронизывающий
контур. В частности, этот поток может создаваться током, те-
текущим в самом рассматриваемом контуре. Поэтому при вся-
всяком изменении силы тока в каком-либо контуре в нем возникает
ЭДС индукции, которая вызывает дополнительный ток в конту-
контуре. Это явление называется самоиндукцией, а дополнительные
токи, вызываемые ЭДС самоиндукции, — экстратоками само-
самоиндукции.
Рис 146 Изменение магнитного на-
напряжения в поле прямого тока Пояс
Роговского охватывает ток один раз
202 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ГЛ IX
На рис. 147 дана схема опыта для наблюдения экстратоков.
Катушка L, имеющая несколько тысяч витков проволоки, вклю-
включена в цепь, содержащую батарею В, реостат г и ключ К. Па-
Параллельно катушке присоединен грубый гальванометр. При за-
замкнутом ключе ток батареи разветвляется: его часть г проходит
через катушку, а часть г'х — через гальванометр. Если разом-
разомкнуть ключ, то магнитный поток в катушке будет исчезать и в
ней возникнет экстраток самоиндукции / (экстраток размыка-
размыкания). В соответствии с законом Ленца он будет препятствовать
убыванию магнитного потока, т.е. будет
направлен в катушке так же, как и убыва-
убывающий ток. Этот экстраток проходит цели-
целиком через гальванометр, где его направ-
направление противоположно первоначальному
току г\. Поэтому гальванометр дает от-
отброс в обратную сторону.
При замыкании ключа (установлении
Б К тока) в катушке также возникает экстра-
——(| 1| -> ток (экстраток замыкания). Его направ-
направление в катушке противоположно нара-
стающему току батареи. Однако в случае
Рис. 147. Наблюдение замыкания экстраток делится между ба-
экстпатока самоиндук- г ¦*
и^ ^ тареей и гальванометром и, кроме того,
его направление в гальванометре — такое
же, как и нарастающего тока батареи i\. Поэтому экстраток за-
замыкания заметен гораздо хуже.
Если поместить в катушку железный сердечник, то экстра-
экстратоки значительно увеличиваются. В этом случае гальванометр
можно заменить небольшой лампой накаливания. При размыка-
размыкании ключа лампа дает яркую вспышку.
Рассмотрим, от чего зависит ЭДС самоиндукции. Магнитная
индукция (плотность магнитного потока) в любой точке поля
пропорциональна силе тока г в катушке. Поэтому и магнитный
поток Ф, пронизывающий катушку, пропорционален току:
Ф = Li. (93.1)
Коэффициент пропорциональности L называется индуктивно-
индуктивностью контура. Если г', — 1, то Ф = L, т.е. индуктивность конту-
контура равна магнитному потоку через этот контур при силе тока в
контуре, равной единице.
Единицей индуктивности в системе СИ служит генри (Гн).
Это индуктивность такого контура, в котором при силе тока 1 А
возникает магнитный поток 1 Вб:
1 Гн = 1 Вб/1 А = 1 Вб/А.
Применяя к явлению самоиндукции основной закон электро-
электромагнитной индукции (§ 91), мы получаем для ЭДС самоиндук-
§ 93 САМОИНДУКЦИЯ 203
ции выражение
% = -L^. (93.2)
ЭДС самоиндукции пропорциональна производной тока по вре-
времени, т.е. быстроте изменения тока.
Индуктивность какого-либо контура зависит от его формы и
размеров, а также от свойств окружающей среды.
При получении формулы (93.2) мы считали, что L постоян-
постоянно. Это справедливо, если контур жесткий и находится в ва-
вакууме или в среде, магнитные свойства которой не зависят от
магнитного поля. Однако в железе и некоторых других веще-
веществах (ферромагнетиках, см. § 110) последнее не имеет места, и
поэтому индуктивность контура, содержащего такие вещества,
зависит от силы тока (магнитного поля) и при меняющемся то-
токе изменяется со временем. В этом случае ЭДС самоиндукции
равна
Будем считать сначала, что контур находится в вакууме или,
что практически то же, в атмосферном воздухе. Чтобы вычис-
вычислить индуктивность контура, нужно найти сначала магнитный
поток Ф через этот контур, создаваемый током некоторой силы г.
После этого индуктивность можно найти по формуле (93.1). Рас-
Рассмотрим некоторые примеры.
Пример 1. Индуктивность соленоида. Длину солено-
соленоида будем считать большой по сравнению с его диаметром, и
поэтому будем пренебрегать искажением поля вблизи концов со-
соленоида. При этом предположении напряженность поля во всех
точках внутри соленоида можно считать одинаковой и, согласно
§ 81, имеющей величину
Я = га = Ni/l.
Здесь п — число витков на единицу длины, N — полное чис-
число витков, а / — длина соленоида. Если S — площадь сечения
соленоида, то магнитный поток через один виток равен
а полный поток через все N витков
, N2S ¦
Ф = М0— г.
Поэтому индуктивность длинного соленоида в воздухе равна
L = fM0^. (93.3)
Эта формула определяет и индуктивность замкнутой торои-
тороидальной катушки.
204
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ГЛ IX
Если длина соленоида невелика по сравнению с его диамет-
диаметром, то формула (93.3) становится неточной. В этом случае вво-
вводят поправочный множитель, значение которого можно найти в
справочниках по радиотехнике.
Пример 2 Индуктивность двухпроводной линии Пусть имеются
два длинных параллельных провода, входящих в цепь тока (рис. 148). Ра-
Радиус каждого из проводов равен а, а расстояние между их осями равно d.
Вычислим магнитный поток через площадь, ограниченную осями проводов,
для отрезка линии длины I Рассмотрим сначала магнитное поле одного ле-
левого провода. В области 0 < х < а (внутри провода) напряженность поля
%х
равна (§ 81) -—j, и поэтому поток через часть рассматриваемой площади,
лежащей внутри провода, есть
иО л7 / X ах — - Л.
2naz •> 4ж
Напряженность поля в области х > а, согласно § 81, равна -—, что дает
27ПЕ
для потока через остальную часть площади
d
г1 f dx il , d
2ir J х 2тг а
Так как токи в обоих проводах направлены противоположно, то направ-
направления полей, создаваемых обоими проводами между их осями, одинаковы
(см рис 148) Поэтому полный
-'""" поток Ф, создаваемый обоими
проводами, будет в два раза
больше потока от одного прово-
провода
X
тг \2 а
Отсюда получаем формулу для
индуктивности двухпроводной
линии
(93 4)
п ._ т. Если длина линии I выра-
Рис 148. К вычислению индуктивности жена в т0 ин т^в.
двухпроводной линии ность L будет выражена в ген.
ри Обычно радиус проводов а
очень мал по сравнению с расстоянием d между ними, и поэтому дробью
1/2 в скобках можно пренебречь по сравнению с In (d/a).
Единица магнитной постоянной /^о* Понятие индуктив-
индуктивности используют в системе единиц СИ для обозначения еди-
единицы магнитной постоянной /j.q. Так, например, если восполь-
воспользоваться для индуктивности соленоида соотношением (93.3),
§94 МАГНИТНАЯ ПРОНИЦАЕМОСТЬ ВЕЩЕСТВА 205
выразить из него ^о и затем заменить все другие величины их
единицами, то получим единицу магнитной постоянной ^о в си-
системе СИ в виде
1^0 = 1 Гн • 1 м/1 м2 = 1 Гн/м.
Как уже говорилось раньше, она получила название генри на
метр.
§ 94. Магнитная проницаемость вещества
Опыт показывает, что индуктивность всякого контура зави-
зависит еще от свойств среды, в которой он находится. В этом можно
убедиться при помощи опыта, описанного в § 93 (см. рис. 147).
Если вдвинуть в катушку L железный сердечник, то при всех про-
прочих одинаковых условиях сила экстратоков возрастает во много
раз, а значит, сильно увеличивается и индуктивность катушки.
Будем считать, что окружающая среда однородна и заполня-
заполняет все пространство, где имеется магнитное поле. Для замкнутой
тороидальной катушки это практически значит, что среда нахо-
находится везде внутри катушки, так как поле вне тороида весьма
мало (поле одного замкнутого витка). Это справедливо и для
длинного соленоида.
Пусть Lo есть индуктивность некоторого контура в вакууме,
a L — индуктивность того же контура в однородном веществе,
заполняющем все магнитное поле. Отношение
L/Lo = \х (94.1)
называют относительной магнитной проницаемостью или
просто магнитной проницаемостью вещества. Магнитная про-
проницаемость есть величина, характеризующая магнитные свой-
свойства вещества, она зависит от рода вещества и его состояния
(например, от температуры).
Мы ввели магнитную проницаемость ц аналогично диэлек-
диэлектрической проницаемости е (§ 31). И в этом случае величина
ц, определяемая формулой (94.1), есть отношение абсолютных
магнитных проницаемостей рассматриваемого вещества (/i^o) и
вакуума (^о) Очевидно, что р, как и е, есть безразмерная вели-
величина Абсолютная же магнитная проницаемость вещества /j,/j,q
имеет ту же размерность, что и ^о-
Тот факт, что среда влияет на индуктивность контура, по-
показывает, что с изменением среды меняется и магнитный поток,
пронизывающий контур, а следовательно, и индукция в каждой
точке поля. В среде с магнитной проницаемостью ц при том же
токе в контуре индукция в ц раз больше, нежели в вакууме:
В = jt/ioH. (94.2)
Физические причины этого будут рассмотрены в гл. XI
206 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ГЛ. IX
Из формулы (94.2) следует, что единица абсолютной маг-
магнитной проницаемости 1 Гн/м есть магнитная проницаемость
среды, в которой при напряженности магнитного поля 1 А/м
создается магнитная индукция 1 Тл.
§ 95. Исчезновение и установление тока
Экстратоки самоиндукции в соответствии с законом Лен-
Ленца всегда препятствуют изменениям тока, их вызвавшим. При
включении в цепь источника тока экстра-
экстратоки направлены противоположно току,
создаваемому источником. При выключе-
выключении источника тока экстратоки имеют то
же направление, что и ослабевающий ток
источника. Поэтому индуктивность цепи
проявляется в замедлении процессов ис-
исчезновения и установления тока. Рассмо-
Рассмотрим это явление подробнее.
Пусть имеется цепь, содержащая ис-
Рис. 149. Цепь с индук- Т0Чник тока с ЭДС Ш, сопротивление г и
тивностью, сопротивле- ИНДуктивность L (рис. 149). При разом-
нием и источником тока KHyTQM кдюче R в цепи будет деиствовать
ЭДС источника и в ней установится ток силы г'о = ЗГ/г. Если за-
замкнуть ключ К, то источник тока будет выключен из цепи и ток
начнет исчезать.
Будем считать ток квазистационарным и найдем закон исчез-
исчезновения тока. Обозначим через г мгновенную силу тока в момент
времени t и применим к контуру LKrL второе правило Кирхго-
Кирхгофа (§ 70). Учитывая, что в цепи действует ЭДС самоиндукции
—Ldi/dt, имеем
г di
гг = —L—.
dt
В этом уравнении переменные разделяются:
?¦=-?*¦
и поэтому интегрированием находим
i = Cexp(-j-tj .
Постоянная интегрирования С может быть определена из на-
начального условия. Положим, что источник был выключен в мо-
момент времени t — 0. Тогда начальное условие есть t = 0, ъ — го>
откуда С = г'о- Поэтому закон убывания тока принимает вид
« = ioexp(-i/T), (95.1)
где
Т = L/r. (95.2)
§ 95 ИСЧЕЗНОВЕНИЕ И УСТАНОВЛЕНИЕ ТОКА 207
Величина Г имеет размерность времени и называется посто-
постоянной времени цепи с индуктивностью и сопротивлением. Из
(95.1) видно, что Г есть время, в течение которого сила тока
уменьшается в е — 2,71 раза. Чем больше индуктивность и мень-
меньше сопротивление, тем медленнее происходит исчезновение тока.
Отметим, что, согласно (95.1), сила тока асимптотически
стремится к нулю, так что полное исчезновение тока (г = 0)
наступает только через время t = oo. Однако практически ис-
исчезновение тока обозначает, что его сила сделалась достаточно
малой. А такое почти установившееся состояние достигается в
конечное время, однако тем большее, чем больше постоянная
времени Т.
Рассмотрим численный пример. Пусть L = 1 Гн, а г = 100 Ом. Тогда
Г = 0,01 с и через это время ток уменьшится в е = 2,71 раза. Ток умень-
уменьшится до 0,001 первоначальной величины через время t, которое можно
определить из (95.1):
lnlOOO = t/0,01,
откуда t = 0,069 с.
Если в цепи, изображенной на рис. 149, ключ К сначала был
замкнут и затем внезапно разомкнут, то в цепи начнется процесс
установления тока. В этом случае в цепи будут действовать ЭДС
источника & и ЭДС самоиндукции —Ldi/dt, и второе правило
Кирхгофа дает
ri = %- Ldi/dt.
Здесь г — полное сопротивление цепи, в которое в данном случае
должно быть включено и внутреннее сопротивление источника.
Введя новую переменную
и = ri - g,
преобразуем это уравнение к тому же виду, что и выше:
du/u = -dt/T,
где через Т обозначена постоянная времени, выражаемая фор-
формулой (95.2). Поэтому
u = Cexp(-t/T).
Если начало отсчета времени совпадает с моментом включения
источника, то начальное условие имеет вид
Это дает С = — &, и мы имеем
и = гг - Ш = -? exp (-t/T).
Выражая отсюда силу тока г, находим окончательно
г = (g/r)[l - exp {-t/T)]. (95.3)
208
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
ГЛ. X
Сила тока возрастает от начального значения i = 0 и
асимптотически стремится к установившемуся значению if/г.
Быстрота установления тока определяется той же постоянной
времени Г, что и исчезновение тока.
Влияние индуктивности можно продемонстрировать на опы-
опыте, схема которого показана на рис. 150. Здесь имеются две па-
параллельно соединенные ветви, одна из которых содержит боль-
большую индуктивность L в несколько десятков генри (вторичная
обмотка высоковольтного трансформатора), а другая — сопро-
сопротивление г, равное сопротивлению катушки L. Л\ и Лч ~ одина-
одинаковые лампы накаливания, играющие роль демонстрационных
амперметров; П — переключатель, позволяю-
позволяющий изменять направление тока; В — бата-
батарея. При замыкании цепи на батарею лампа
Лг накаливается быстро, практически мгно-
мгновенно. Лампа же Л\ накаливается с заметным
запозданием (порядка 1 с) и ее свечение уси-
усиливается постепенно.
При быстрых непрерывных переключени-
переключениях батареи лампа Л\ вообще не успевает на-
накалиться за время между переключениями и
остается темной. Этот опыт разъясняет при-
причину так называемого «кажущегося сопротив-
сопротивления» индуктивности в цепи переменного то-
тока, которое мы рассмотрим подробнее в § 219.
Для многих целей, например при измере-
измерениях на переменном токе, желательно иметь
катушки сопротивлений, индуктивность кото-
установле- рЫХ по возможности мала. Для устройства
таких безындукционных катушек проволоку
сгибают посредине и получившуюся двойную проволоку исполь-
используют для обмотки. Такие бифилярные (двунитные) катушки
можно рассматривать как состоящие из двух катушек, токи в
которых направлены противоположно. Магнитное поле таких
катушек почти равно нулю, и поэтому их индуктивность ни-
ничтожно мала.
Рис. 150. Демон-
Демонстрация влияния
индуктивности на
время
ния
ГЛАВА X
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
§ 96. Собственная энергия тока
Для увеличения тока в электрической цепи необходима неко-
некоторая работа. Эту работу производит источник тока, включен-
§ 96 СОБСТВЕННАЯ ЭНЕРГИЯ ТОКА 209
ный в цепь. Напротив, при всяком уменьшении тока в цепи
освобождается некоторая энергия и источник тока совершает
меньшую работу, нежели при постоянном токе. Рассмотрим этот
вопрос подробнее.
Вернемся к цепи, изображенной на рис. 149, содержащей ин-
индуктивность L и имеющей полное сопротивление г, и предпо-
предположим сначала, что в ней имеется установившийся постоянный
ток. Сила этого тока определяется ЭДС источника тока Ш и со-
сопротивлением цепи: i = 8/г. За время dt в цепи будет выделено
тепло Джоуля-Ленца ri2 dt. Так как ri — ?, то
ri2 dt — Ш dt.
Но правая часть этого равенства выражает работу источника
тока за то же время dt. Мы видим, что работа источника в точ-
точности равна теплу Джоуля-Ленца, а, значит, для поддержания
постоянного магнитного поля не требуется никакой работы.
Представим себе теперь, что ток в цепи увеличивается с бы-
быстротой di/dt. В этом случае в цепи появится еще ЭДС самоин-
самоиндукции iFc, которая вызовет экстраток
г г dt
Он направлен против тока г, и поэтому полная сила тока в цепи
будет г — Si.
В дальнейшем мы будем считать, что процесс увеличения
тока происходит весьма медленно (Si<^i), и при расчетах будем
удерживать только члены первого порядка малости.
В рассматриваемом процессе за время dt выделится тепло
Джоуля-Ленца г(г — SiJ dt. Оно меньше по сравнению со слу-
случаем постоянного тока на величину
ri2 dt - r(i - SiJ dt = 2ri Si dt = 2Li ^ dt = 2Li di.
Здесь di — увеличение тока в цепи за время dt.
За то же время источник тока совершит работу <?(г — Si) dt и
поэтому произойдет «разгрузка» батареи на величину работы:
Ш dt - %{i - Si) dt=c6 8idt = Li di.
Следовательно, в случае нарастающего тока работа источни-
источника тока больше количества выделившегося тепла. Избыток ра-
работы источника
dW = Li di
и есть та работа, которая необходима для увеличения силы тока
в цепи от значения г до г + di. Полная работа, необходимая для
210 ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ГЛ X
установления тока г, равна
г
W = L fidi = Li2/2. (96.1)
о
При выключении источника тока работа W выделяется в це-
цепи; ее совершают экстратоки размыкания. Поэтому выражение
(96.1) дает энергию, запасаемую контуром с током. Она полу-
получила название собственной энергии тока. Именно эта энергия
и проявлялась в опыте (рис. 147) в виде отброса стрелки галь-
гальванометра и вспышки лампы от экстратоков размыкания.
Полезно сопоставить выражения для собственной энергии
контура с током и энергии заряженного конденсатора, равной
(§34)
д2/2С.
Энергия конденсатора пропорциональна квадрату заряда, энер-
энергия же тока пропорциональна квадрату силы тока, т.е. зависит
от скорости движения зарядов.
В механике мы встречались с двумя видами энергии: потен-
потенциальной и кинетической. Потенциальная энергия сжатой пру-
пружины равна
кх2/2,
где х — смещение конца пружины, а к — ее жесткость, а кине-
кинетическая энергия движущегося тела есть
mv2/2,
где т — масса тела, a v — его скорость. Развивая аналогию меж-
между электрическими и механическими явлениями, мы видим, что
энергия конденсатора соответствует потенциальной энергии в
механике, а собственная энергия тока — кинетической энергии.
При этом величина 1/С, обратная емкости, аналогична жестко-
жесткости пружины, а индуктивность L — массе тела.
§ 97. Энергия магнитного поля
Всякий электрический ток всегда окружен магнитным по-
полем. Поэтому можно спросить, где именно сосредоточена, лока-
локализована, собственная энергия тока: внутри проводов, где дви-
движутся электрические заряды, или в магнитном поле, т.е. в среде,
окружающей токи?
Ответ на вопрос может быть дан только опытом. Однако по-
пока мы имеем дело с постоянными токами, такие опыты невоз-
невозможны, так как в этом случае токи всегда окружены магнит-
магнитным полем и, наоборот, магнитное поле всегда сопровождается
токами, его поддерживающими, что относится и к постоянным
магнитам, которые также содержат замкнутые молекулярные
токи (гл. XI).
§ 97 ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ 211
Ответ на поставленный вопрос можно получить, иссле-
исследуя переменные магнитные поля или электромагнитные волны
(гл. XXIII). В электромагнитных волнах мы имеем магнитные
поля, изменяющиеся в пространстве и времени и способные су-
существовать без токов, их поддерживающих. Так как электро-
электромагнитные волны заключают в себе и переносят определенную
энергию, то отсюда мы делаем вывод, что энергия сосредоточе-
сосредоточена в магнитном поле.
Найдем энергию, заключающуюся в единице объема магнит-
магнитного поля. Рассмотрим замкнутую тороидальную катушку. Ее
индуктивность (§ 93, 94) есть
L = fifi0N2S/l,
где [л — магнитная проницаемость среды, а ^о ~ магнитная по-
постоянная. Подставляя это выражение в (96.1), имеем
т„ 1 N2S .2
Но Ni/l = Н есть напряженность поля внутри катушки (§ 81).
Поэтому
W = woH2t/2,
где т = SI — объем катушки. Мы видим, что энергия одно-
однородного магнитного поля пропорциональна объему г, занятому
полем. Поэтому энергия единицы объема поля, или объемная
плотность энергии магнитного поля, равна
w = /i/iO#2/2- (97.1)
Если магнитное поле неоднородно, то его можно разбить на бес-
бесконечно малые элементы объема dr, в каждом из которых поле
можно считать однородным. Энергия, заключенная в элемен-
элементе объема, есть wdr. Полная энергия любого магнитного поля
равна
W = fwdr, (97.2)
т
где интегрирование распространяется на весь объем т, занятый
магнитным полем.
При выводе формул (96.1), а следовательно, и (97.1) мы счи-
считали, что индуктивность контура, а значит, и магнитная про-
проницаемость среды остаются постоянными. Мы считали также,
что вся работа источника тока превращается в энергию маг-
магнитного поля. Это точно выполняется только для вакуума, так
что формула (97.1) при ц = 1 выражает объемную плотность
энергии магнитного поля в вакууме. Если же контуры с током
находятся в какой-либо среде, то приходится учитывать допол-
дополнительные обстоятельства, аналогичные указанным в § 37 для
электрического поля, а именно, при намагничивании среды она
212 ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ГЛ X
может нагреваться. Ее объем и плотность, даже при неизмен-
неизменной температуре, в магнитном поле могут изменяться (явление
магнитострикции). Поэтому магнитная проницаемость, зави-
зависящая от температуры и плотности среды, не остается постоян-
постоянной при намагничивании. Помимо этого, работа источника тока
может и не превращаться целиком в энергию магнитного поля.
По этим причинам в общем случае формула (97.1) не выражает
точно работу при намагничивании и не дает объемную плот-
плотность энергии магнитного поля в среде.
В дальнейшем мы будем считать, что влияние изменения
объема среды пренебрежимо мало (или что объем поддержи-
поддерживается постоянным).
Однако формула (97.1) дает внешнюю работу А при намаг-
намагничивании, если температуру среды поддерживать постоянной.
Как и в случае электрического поля, эта работа идет на уве-
увеличение энергии магнитного поля й^ина выделение тепла Q,
отводимого от тела (или сообщаемого ему) для поддержания
постоянной температуры. В § 37 мы уже говорили, что работа
внешних сил (в данном случае источника тока), совершаемая
над телом при квазистатическом изотермическом процессе, рав-
равна приращению свободной энергии тела Следовательно, форму-
формула (97.1) выражает не внутреннюю энергию магнитного поля, а
ту часть свободной энергии намагниченной среды, которая за-
зависит от магнитного поля.
Если тепло Q мало по сравнению с энергией поля W, то внеш-
внешняя работа при создании магнитного поля равна энергии этого
поля. Это мы и будем предполагать в дальнейшем, если не ска-
сказано обратное.
Предположение о постоянстве /л обозначает также, что маг-
магнитная индукция В = /i^oH есть линейная функция магнитного
поля Н. Такая зависимость точно справедлива для вакуума (/л =
= 1). Ее можно также применять с хорошей точностью для мно-
многих веществ (парамагнетиков и диамагнетиков, § 109). Однако
в ферромагнетиках (§ 110) зависимость В от Н сильно нели-
нелинейна даже при неизменной температуре, и поэтому формула
(97.1) к ним неприменима. Более общее выражение для энергии
магнитного поля, справедливое при нелинейной, но однозначной
зависимости В от Н (отсутствие магнитного гистерезиса), будет
дано в § 111.
§ 98. Взаимная индукция
Рассмотрим теперь два контура с током, например два кру-
круговых витка 1 и 2 (рис. 151). Часть линий индукции поля, созда-
создаваемого контуром 1, будет проходить через контур 2, т.е. будет
сцеплена с этим контуром. И, обратно, определенное число ли-
§ 98 ВЗАИМНАЯ ИНДУКЦИЯ 213
ний индукции, создаваемых контуром 2, будет сцеплено с конту-
контуром 1. В этом случае мы говорим, что между обоими контурами
существует магнитная связь.
Индукция поля контура 1 пропорциональна силе тока г-^ в
этом контуре. Поэтому магнитный поток Ф12 через контур 2,
создаваемый контуром 1, также
пропорционален току iy.
Ф12 = Ln.ii. (98.1)
Коэффициент Li2 называется
взаимной индуктивностью кон-
контуров 1 и 2. Она, очевидно,
равна магнитному потоку через
контур 2, создаваемому конту- „
ром 1 при силе тока в нем, рав- Рис 15L м<™ная связь двух
* „ ^ контуров
нои единице.
Из сравнения (98.1) с (93.1) видно, что размерность L\2 та же,
что и размерность индуктивности, и поэтому взаимная индук-
индуктивность измеряется в тех же единицах, что и индуктивность.
Совершенно так же, если в контуре 2 имеется ток некоторой
силы i2, то он создает магнитный поток Ф21 через контур 1,
причем
Ф21 = L2ii2- (98.1а)
Здесь Li\ есть взаимная индуктивность контуров 2 и 1.
Можно показать (§ 99), что для любых двух контуров вза-
взаимные индуктивности всегда равны:
Lu = L21. (98.2)
Наличие магнитной связи между контурами проявляется в
том, что при всяком изменении силы тока в одном из контуров в
другом контуре появляется ЭДС индукции. Согласно основному
закону электромагнитной индукции (§91) имеем
82 = = -?,12 —, <*! = -_ =-L12_, (98.3)
где (?2 — ЭДС индукции, возникающая в контуре 2, а Ъ.\ — ЭДС
индукции в контуре 1.
Взаимная индуктивность зависит от формы и размеров кон-
контуров и от их взаимного расположения. Она зависит также от
свойств окружающей среды.
Рассмотрим простой пример вычисления взаимной индук-
индуктивности. Пусть имеются две тороидальные однослойные катуш-
катушки 1 и 2, вплотную прилегающие друг к другу (рис. 152). В этом
случае все линии индукции, создаваемые одной катушкой, про-
проходят и через вторую катушку. Напряженность магнитного поля
катушки 1 равна (§81)
Их =
214
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
ГЛ X
Это поле создает магнитный поток сквозь один виток катушки 2-,
равный /j,qHiS = jUoiViiiSy/, где S — площадь сечения катушек.
Полный поток сквозь все
N2 витков катушки 2 есть
Ч,
откуда для взаимной ин-
индуктивности получается
выражение
Рис.152. Две обмотки с магнитной связью
тт
Н-2 =
21 =
(98.4)
Если вычислить маг-
магнитный поток, создавае-
создаваемый катушкой 2 сквозь
катушку 1, то получится
г2.
Отсюда мы находим для взаимной индуктивности L2i преж-
прежнее выражение (98.4) в соответствии с формулой (98.2).
В том случае, когда внутри катушек имеется сердечник из
вещества с магнитной проницаемостью ^, магнитный поток уве-
увеличивается в [1 раз и коэффициент взаимной индукции будет в
/i раз больше.
§ 99. Взаимная энергия двух токов
Вычислим энергию магнитного поля, созданного двумя кон-
контурами с током. Рассмотрим самый простой случай двух торо-
тороидальных катушек (см. рис. 152), находящихся в вакууме, в ко-
которых магнитное поле однородно. Напряженность суммарного
поля внутри катушек
Н = Н1±Н2 = №х ± N2i2)/l;
выбор знака + или — зависит от того, одинаковы или противопо-
противоположны направления токов в обеих катушках. В единице объема
этого поля заключена энергия (§ 97) цоН2/2, а полная энергия,
находящаяся во всем объеме поля г = SI, равна
W -
Воспользовавшись выражениями для индуктивностей L\ и L2
обеих катушек (§ 93) и их взаимной индуктивности L\2 (§ 98),
полученный результат можно представить в виде
W =
(99.1)
§ 1QQ СОХРАНЕНИЕ ЭНЕРГИИ В МАГНИТНОМ ПОЛЕ 215
Первый член этой формулы дает собственную энергию тока кон-
контура 1 (§ 96), а второе слагаемое выражает собственную энергию
тока контура 2. Формула показывает, что энергия двух токов в
контурах, обладающих магнитной связью, отличается от суммы
собственных энергий токов на величину
Wn = ±?12*1*2- (99.2)
Она получила название взаимной энергии двух токов.
Из сказанного видно, что причина возникновения взаимной
энергии токов заключается в том, что в поле нескольких конту-
контуров с током складываются напряженности поля (принцип нало-
наложения или суперпозиции полей, см. § 76), в то время как энергия
магнитного поля пропорциональна квадрату напряженности, а
квадрат суммы не равен сумме квадратов.
Представим себе, что мы сначала создаем ток %\ в контуре 1,
а ток в контуре 2 %2 = 0. Для этого потребуется работа L\i\/2.
Создавая затем ток в контуре 2, мы совершим работу, согласно
(99.1) равную I^i!/^ ±?i2M2- Если бы мы сначала создали ток
12 (а ток ix был бы равен нулю), то для этого была бы необ-
необходима работа Lii\l2. Но тогда последующее создание тока i\
потребовало бы работы Liif/2 ± Lyiii^i- Мы видим, что работа
образования тока в контуре в присутствии другого контура с
током не равна работе образования того же тока в уединенном
контуре; она отличается на величину взаимной энергии обоих
токов Wyi-
Мы получили формулы (99.1) и (99.2), рассматривая част-
частный случай тороидальных катушек. Легко убедиться, однако,
что этот результат справедлив для контуров произвольной фор-
формы, находящихся в любой среде (см. Добавление 6).
§ 100. Закон сохранения энергии
при наличии магнитного поля
Магнитные явления, как и любые другие процессы в приро-
природе, подчиняются закону сохранения энергии. Рассмотрим этот
вопрос на примере двух контуров.
Пусть имеются два произвольных контура с токами ii,i2, ис-
источниками тока с ЭДС l?i, <?2 и полными сопротивлениями г\ и
т%. Контуры могут быть как неподвижными, так и движущими-
движущимися, а токи в них могут изменяться. В каждом из контуров, во-
первых, производят определенную работу источники тока. Их
работа за бесконечно малое время dt равна
$liidt + %2i2 dt.
Если источниками тока являются гальванические элементы, то
эта работа совершается за счет химических реакций в элементах.
216 ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ГЛ. X
Далее, в контурах выделяется тепло Джоуля-Ленца:
\ dt + rw\ dt.
На каждый контур действуют силы магнитного взаимодей-
взаимодействия. Поэтому при перемещении контуров (или при их де-
деформации) будет совершена определенная механическая работа.
Обозначим ее через 5А.
Наконец, при движении контуров или при изменении силы
токов в них будет изменяться магнитное поле, а следовательно,
будет изменяться и его энергия. Согласно § 99 изменение энер-
энергии магнитного поля равно
dW = d{Lii\j2 + LihJI ± Li2«i«2)-
Мы будем считать, что емкость контуров весьма мала, и поэто-
поэтому энергию электрического поля учитывать не будем. Согласно
закону сохранения энергии имеем
работа источников тока =
= тепло Джоуля-Ленца 4- механическая работа+
+ увеличение энергии магнитного поля.
Или, иначе:
?iii dt + %ih dt = (nij dt + r2i\ dt) + SA + dW. A00.1)
Если контуров не два, а больше, то закон сохранения энергии имеет вид
Y^^ Y^2 + SA + dY^J2Lkliki'f2- A00.1a)
В этой формуле последний член выражает изменение энергии магнитно-
магнитного поля, Lkk обозначает коэффициент самоиндукции k-ro контура, a Lki —
коэффициент взаимной индукции контуров к и I. При к = I соответствую-
соответствующий член суммы дает собственную энергию к-го контура ifcfci|/2, а при
к ф I каждая пара членов суммы Lkiikii/2 + Likiiik/2 = Lkiikii представля-
представляет взаимную энергию к-го и 1-го контуров.
Поясним сказанное на примерах.
Пример 1. Один контур с постоянным током. Так как в данном
случае магнитное поле постоянно, то изменение энергии поля равно нулю.
Если контур не деформируется, то и механическая работа 5А = 0. Поэтому
A00.1) дает
Ш dt = ri2 dt.
В этом случае работа источника тока целиком превращается в тепло
(рис. 153 а)
Пример 2. Один контур, в котором устанавливается ток. За-
Зависимость силы тока от времени в процессе его установления выражается,
согласно § 95, формулой
• = .-„ [l-exp (-?
100
СОХРАНЕНИЕ ЭНЕРГИИ В МАГНИТНОМ ПОЛЕ
217
Работа источника тока за время dt равна ffidt. По сравнению со случаем
установившегося тока она уменьшается на величину
— Widt = $i0 exp
(--() dt.
ния ток
I exp f — yt) dt = Lig.
0
выделенного тепла ест
со со
/ (rig - ri2) dt = ril f [2exp (-It) - exp ( - \ t)J dt=\ Li*.
Поэтому в течение всего процесса установления тока произойдет «разгруз-
«разгрузка» батареи, равная
сю
Уменьшение количества выделенного тепла есть
со со
0 0
Поэтому получается «экономия» энергии
3 Т .2 т .2 _ 1 т .2
— Ы§ — Ыо — — 1Л0.
Но это выражение как раз равно энергии возникающего магнитного поля
(собственной энергии тока, § 96). Мы видим, что в данном процессе энер-
энергия магнитного поля возни-
возникает за счет экономии рабо-
работы, затрачиваемой на тепло
Джоуля-Ленца (рис. 153 5).
Пример 3. Два конту-
контура с токами медленно сбли-
сближаются. При неподвижных
контурах
Работа
источника
Работа
источника
Тепло
где Ш\ и $2 — ЭДС источни-
источников тока, a ri и гг — сопро-
сопротивления контуров.
При движении контуров
магнитный поток, пронизы-
вающии контуры, изменяет-
ся, отчего появляется допол-
б Энергия поля
рис 153 превращения энергии в контуре
постоянньм тОКОМ (о) и устанОвлении
ся, отчего появляется допол- ,g. у ' v J
нительная ЭДС индукции, и ^ '
токи в контурах меняются. Сила тока в контуре 1 при движении будет
1\+дц,
- —
П at
где Фх — магнитный поток сквозь контур 1, создаваемый контуром 2.
В дальнейшем мы будем считать, что контуры сближаются весьма мед-
медленно, так что Si <K г, и будем удерживать только малые первого порядка.
Уменьшение работы источника за время dt вследствие движения равно
<?i»i dt — <?i(ii +&i\)dt = — $i 8ii dt = —riii <Hi dt = ii
Уменьшение тепла Джоуля-Ленца есть
218
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
ГЛ X
Поэтому выигрыш энергии в контуре 1 равен 2г\ d<?i — i\ d§\ = %\d&\.
Аналогично, выигрыш энергии в контуре 2 есть t2 BФг- Поэтому экономия
энергии на тепле Джоуля-Ленца в обоих контурах равна
Но, согласно § 98, Ф1 = Li2(i2 + Si2), Фг = ?12A1+ <5ii), где La — коэффици-
коэффициент взаимной индуктивности обоих контуров. Поэтому, удерживая только
малые первого порядка, имеем
612)
12
i\ d$\ + 42 d$2 ~ 2llJ2 dh\2-
Механическая работа при сближении контуров, согласно § 84, равна
5А — (ii + Sit) d$i = (г'2 + S12) d$2 ~ u»2 dLi2
Наконец, изменение энергии поля есть
dW=
Jt
где токи за время dt нужно считать постоянными Если контуры не дефор-
деформируются, то dLi/dt = dL2/dt = 0, и
~-
dL
l2.
Работа
источника
Работа
источника
Тепло
Тепло
Энергия поля
Механическая
работа
Рис. 154. Превращения энергии в двух медленно сближающихся контурах
с током
В рассматриваемом случае половина энергии, сэкономленной па умень-
уменьшении тепла, переходит в энергию магнитного поля, а вторая ее половина
расходуется на механическую работу (рис. 154).
§ 101. Механические силы в магнитном поле
Мы знаем, что на всякий проводник с током в магнитном по-
поле действуют силы. Эти пондеромоторные (т.е. действующие на
§ 101 МЕХАНИЧЕСКИЕ СИЛЫ В МАГНИТНОМ ПОЛБ 219
тела) силы магнитного поля во многих случаях можно просто
вычислить при помощи закона сохранения энергии. Для этого
нужно представить себе, что рассматриваемый проводник со-
совершает бесконечно малое возможное перемещение и, вычислив
происходящие при этом превращения энергии, найти из уравне-
уравнения энергии A00.1) работу 5А пондеромоторных сил. Зная же
работу и перемещение, можно определить и эти силы.
Вычислим работу пондеромоторных сил, совершаемую при
деформации какого-либо контура с током. Рассмотрим уединен-
уединенный контур, содержащий источник тока с ЭДС 8 и обладающий
индуктивностью L и сопротивлением г. Сила установившегося
тока в контуре равна i — Ш/r. Представим себе далее, что этот
контур очень медленно произвольным образом деформируется,
так что изменяется его индуктивность L. В процессе деформа-
деформации ток в контуре изменяется на величину
где Ф — магнитный поток, пронизывающий контур. Поэтому
уменьшение работы источника тока за время dt будет
%idt- %(i + 8i)dt = -%Sidt = id$.
Уменьшение тепла Джоуля-Ленца есть
п2 dt - r{i + SiJ dt = -2ri Si dt = 2i d$.
Таким образом, за время dt получается выигрыш энергии гс?Ф,
а в течение всего процесса деформации
где AL — изменение индуктивности контура вследствие дефор-
деформации. Увеличение энергии магнитного поля есть
L2i2/2 - L^2/2 = г2Д?/2.
Поэтому из закона сохранения энергии следует, что искомая ме-
механическая работа равна
ДА = i25L - i2AL/2 = i2AL/2.
Полученное выражение при i = const можно записать и так:
АА = А(Ы2/2)г = const, A01.1)
т.е. механическая работа равна изменению энергии магнитного
поля при неизменной силе тока в контуре.
Применим теперь найденный результат A01.1) к случаю со-
соленоида. Вследствие взаимного притяжения его витков возника-
возникают силы Fi, стягивающие соленоид (рис. 155). Чтобы удержать
соленоид в неизменном состоянии, к его концам нужно прило-
приложить внешние силы — F[. Точно так же, вследствие действия
220
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
ГЛ X
магнитного поля соленоида на каждый виток, появляются ра-
радиальные силы Fr, стремящиеся разорвать соленоид (рис. 155).
Найдем эти силы, пользуясь формулой A01.1).
Индуктивность соленоида выражается формулой (§ 93)
L = noN2S/l.
Поэтому при бесконечно малом укорочении соленоида на dl ра-
работа пондеромоторных сил, согласно A01.1), выразится соотно-
соотношением
С другой стороны,
6 А = Ft dl.
Приравнивая оба выра-
выражения для работы, на-
находим
Полученное выра-
выражение можно предста-
Рис. 155 Силы, действующие на соленоид с вить в более удобНом
током виде. Вычислим силу
/г, действующую на единицу поверхности торца соленоида
(сжимающее напряжение), и введем напряженность магнитного
поля в соленоиде Н = Ni/l. Тогда
fi = Fi/S = МЯ2/2. A01.2)
Сжимающее напряжение равно объемной плотности энергии
магнитного поля соленоида.
Посмотрим теперь, чему равны растягивающие поперечные
силы. При бесконечно малом увеличении радиуса г соленоида на
dr пондеромоторные силы, согласно A01.1), совершают работу
6А = \ i2 dL = l- г2 d
i2 dr.
2 V I
Но ту же работу можно выразить и иначе:
6A-fr- 2vrr/ dr,
где fr — радиальная сила, рассчитанная на единицу боковой
поверхности (радиальное напряжение). Отсюда получаем
Вводя в это выражение напряженность магнитного поля Н вну-
внутри соленоида, находим окончательно
'2. A01.3)
§102
ДАВЛЕНИЯ И НАТЯЖЕНИЯ ФАРАДЕЯ-МАКСВЕЛЛА
221
Радиальное напряжение, так же как и сжимающее, равно объ-
объемной плотности энергии магнитного поля.
Если бы соленоид находился в среде с магнитной проницае-
проницаемостью /i, то и напряжения были бы в /i раз больше.
Рассмотрим численный пример. П Л. Капица, пропуская через соленоид
кратковременные токи короткого замыкания от специального генератора,
получал магнитные поля с напряженностью до 3 • 107 А/м. При этом меха-
механические напряжения в катушках достигали огромных значений.
/, = /г = I 4тг ¦ 1(Г7C • 107J ~ 109 Н/м2
Чтобы катушки выдерживали эти напряжения, они должны были иметь
специальную механическую конструкцию.
§ 102. Давления и натяжения Фарадея—Максвелла
Результаты, найденные в предыдущем параграфе, допускают
весьма наглядное истолкование. Механические напряжения fi
и /г, действующие на соленоид, оказываются такими, как если
бы линии индукции были
подобны растянутым
упругим нитям, которые
стремятся сократиться
и развивают продольное
натяжение /х/хо#2/2 на
единицу поверхности и,
кроме того, расталкива-
расталкивают друг друга, создавая
боковое давление, также
равное объемной плотно-
плотности энергии /i/io-?f2/2.
Оказывается, что это
справедливо не только
для соленоида, но и для
всех других случаев пон-
деромоторных сил в маг-
магнитном поле.
Аналогично положе-
положение вещей и в электри-
электрическом поле. Электри-
Электрические пондеромоторные
силы имеют такую же
величину, как если бы
Линии напряженности Рис.156. Сила, действующая на ток в маг-
Имели продольные на- нитном поле, как резулыат давлений и на-
натяжения и боковые тяжений линий индукции
222 МАГНЕТИКИ ГЛ XI
давления, каждое из которых равно объемной плотности
энергии поля ее$Е2/2 (ср. § 72, примеры 1 и 2).
Представление о натяжении и боковом давлении электриче-
электрических и магнитных линий было введено Фарадеем и Максвеллом.
Хотя в действительности никаких физических линий и не суще-
существует (линии напряженности и индукции есть геометрический
образ, введенный нами для графического изображения полей),
тем не менее представления Фарадея и Максвелла в ряде слу-
случаев весьма полезны, так как позволяют просто определить ха-
характер механических сил в электромагнитном поле.
Рассмотрим в качестве примера прямой ток в однородном
магнитном поле (рис. 156). Линии индукции поля В до внесе-
внесения тока имеют вид параллельных прямых линий, направлен-
направленных справа налево. Линии же тока представляют собой концен-
концентрические окружности. Складываясь, оба поля дают картину
линий, изображенную на рисунке, откуда сразу можно заклю-
заключить, что на провод действует сила, перпендикулярная к прово-
проводу и к первоначальному магнитному полю.
ГЛАВА XI
МАГНЕТИКИ
§ 103. Намагничивание сред
До сих пор мы рассматривали магнитное поле в вакууме. Ес-
Если проводники с током находятся не в вакууме, а в другой среде,
то магнитное поле изменяется. Это показывает, что различные
вещества в магнитном поле намагничиваются, т.е. сами стано-
становятся источниками магнитного поля. Результирующее магнит-
магнитное поле в среде является суммой полей, создаваемых проводни-
проводниками с током и намагниченной средой, и поэтому не равно полю
в вакууме. Вещества, способные намагничиваться, называются
магнетиками.
Причина намагничивания заключается в том, что во всех
веществах существуют мельчайшие электрические токи, замы-
замыкающиеся в пределах каждого атома (молекулярные токи). В
дальнейшем мы рассмотрим опыты, доказывающие существо-
существование молекулярных токов внутри магнетиков и позволяющие
определить природу этих токов (§ 115, 116). Однако существо-
существование молекулярных токов мы учтем с самого начала.
Если магнетик не намагничен, то он не создает магнитного
поля. Это значит, что молекулярные токи расположены в нем
беспорядочно, так что суммарное их действие равно нулю. При
намагничивании магнетика расположение молекулярных токов
о
о
"о
о
о
о
о
о
о
о
о
о
о
о,
о
о
§ 103 НАМАГНИЧИВАНИЕ СРЕД 223
становится частично или полностью упорядоченным. Поэтому
намагниченный магнетик можно представить как систему мель-
мельчайших ориентированных токов
(рис. 157).
В § 82 и 85 мы видели, что
все магнитные действия замкну-
замкнутых токов определяются их маг-
магнитным моментом:
pm = iSn,
где i — сила тока, S — площадь,
обтекаемая током, п — единичный
вектор нормали к плоскости витка
с током. Каждый молекулярный
ток в магнетике обладает опреде-
определенным магнитным моментом, а
значит, и магнетик в целом при Рис. 157 Модель молекулярных
намагничивании приобретает маг- токов в однородно намагничен-
нитный момент, равный вектор- ном магнетике и соответствую-
ной сумме моментов всех молеку- Щ™ им поверхностный ток
лярных токов. Поэтому магнитное состояние вещества можно
вполне охарактеризовать, задавая магнитный момент каждой
единицы его объема. Эта величина получила название намагни-
намагниченности.
Обозначая вектор намагниченности через I, мы имеем, сле-
следовательно, по определению
1 = ?Ртв/т, A03.1)
где г — физически малый объем (§ 40), а суммирование распро-
распространяется на все молекулярные токи в объеме т.
Вектор намагниченности является основной величиной, ха-
характеризующей магнитное состояние вещества. Зная его в каж-
каждой точке какого-либо тела, можно определить и магнитное по-
поле, создаваемое рассматриваемым намагниченным телом.
Задача сильно упрощается, если вектор намагниченности
одинаков во всех точках магнетика (однородное намагничива-
намагничивание). В этом случае при сложении молекулярных токов их при-
прилегающие отрезки, имеющие противоположные направления то-
токов, взаимно компенсируются и остаются только отрезки токов,
примыкающие к поверхности магнетика. Поэтому действие всех
Молекулярных токов будет такое же, как действие некоторо-
некоторого поверхностного тока, обтекающего намагниченный магнетик
(рис. 157). В этом смысле можно сказать, что при вдвигании в
соленоид железного сердечника на поверхности сердечника как
бы появляются дополнительные невидимые ампер-витки, кото-
которые добавляются к ампер-виткам намагничивающей катушки
(рис. 158).
224 МАГНЕТИКИ ГЛ XI
Величина указанного поверхностного тока определяется
значением намагниченности /. Рассмотрим в однородном маг-
магнитном поле (длинный соленоид) достаточно длинный цилин-
цилиндрический стержень (рис. 158) и обозначим через j\ линейную
плотность поверхностного тока,
т.е. силу тока на единицу длины
стержня. Тогда полная сила по-
поверхностного тока стержня есть
jil, где I — длина стержня. Если
5 — площадь сечения стержня, то
его магнитный момент равен
Рис. 158 Поверхностные токи в
намагниченном цилиндре (г — объем стержня). С другой
стороны, по определению намагни-
намагниченности /, этот же момент равен 1т. Приравнивая оба выра-
выражения, находим
1 = 31. (Ю3.2)
При однородном намагничивании намагниченность / равна
линейной плотности поверхностного тока магнетика.
Единица намагниченности есть ампер на метр (А/м). Это та-
такая намагниченность, при которой вещество объемом 1 м3 имеет
магнитный момент 1А-м2.
§ 104. Напряженность магнитного поля внутри
магнетика
При изучении поляризации диэлектриков мы определили
напряженность электрического поля внутри диэлектрика как
среднюю напряженность микроскопического поля в объеме ди-
диэлектрика. Мы видели также, что эта величина совпадает с на-
напряженностью поля внутри узкой щели, прорезанной в диэлек-
диэлектрике параллельно направлению поляризованности (§ 40).
В начале изучения магнетизма предполагали, что процесс
намагничивания вещества совершенно подобен поляризации ди-
диэлектриков, и объясняли его существованием внутри веществ
мельчайших элементарных магнитов (магнитных диполей). По-
Поэтому и напряженность магнитного поля внутри магнетика
определяли так же, как и напряженность электрического по-
поля внутри диэлектрика, т.е. как напряженность поля в узкой
щели, прорезанной в магнетике параллельно направлению на-
намагниченности.
Впоследствии, однако, выяснилось, что магнитных зарядов
в природе не существует и что намагничивание тел обусловле-
обусловлено существованием в них молекулярных токов. Но магнитное
§ 105 МАГНИТНАЯ ИНДУКЦИЯ В МАГНЕТИКЕ 225
поле токов есть поле вихревое, в то время как электрическое
поле зарядов — безвихревое. Оба эти поля обладают различ-
различными свойствами, и поэтому физический смысл напряженности
электрического поля в диэлектриках и магнитного поля в маг-
магнетиках оказался различным.
Выясним, какой физический смысл имеет определенная вы-
выше напряженность поля внутри магнетика. Будем считать, что
магнетик заполняет все пространство, где имеется магнитное
поле. В случае тороидальной катушки это значит, что магнетик
имеет вид замкнутого тороидального сердечника. Если намаг-
намагничивающей катушкой служит прямой соленоид, то мы будем
считать, что магнетик имеет фор-
форму очень длинного цилиндра, дей-
действием концов которого можно пре-
пренебречь. ) L..L...1
Напряженность поля внутри ще- \ Ч f ;
ли, параллельной направлению на- и~
магниченности (рис. 159), склады-
вается из трех частей: поля Но, соз- Рис 159 к определению на_
даваемого витками намагничиваю- пряженности магнитного поля
щей катушки, поля Hi токов на внутри магнетика. Схематиче-
внешней поверхности магнетика и ски изображен один из молеку-
поля Нг токов на внутренней по- лярных токов
верхности полости. Так как линей-
линейная плотность поверхностных токов дается выражением A03.2),
то напряженность поля Hi можно найти по формуле (81.4),
положив в ней га = j\ = /. Это дает: Hi = I. Токи же на
внутренней поверхности имеют противоположное направление
(рис. 159), и поэтому создаваемое ими поле есть Н2 = —I. Пол-
Полная напряженность поля в щели
Н = Но+ 1-1 = Но. A04.1)
Мы видим, что напряженность магнитного поля внутри без-
безграничного магнетика равна напряженности магнитного поля
намагничивающей катушки.
Из сказанного вытекает и метод измерения напряженности
поля внутри магнетика. Для этого можно измерить (например,
при помощи флюксметра, § 91) поле в указанной выше щели или,
что гораздо проще, удалить магнетик из катушки и измерить
напряженность поля, создаваемого катушкой без магнетика.
§ 105. Магнитная индукция в магнетике
Рассмотрим теперь магнетик, в котором прорезана уз-
узкая щель, перпендикулярная к направлению намагниченности
(рис. 160). Магнитную индукцию внутри такой щели называ-
226 МАГНЕТИКИ ГЛ XI
ют магнитной индукцией внутри магнетика. Таким образом, мы
определяем магнитную индукцию аналогично электрическому
смещению (§ 41). Однако по причинам, указанным в § 104, физи-
физический смысл магнитной индукции оказывается совсем другим.
Обозначим через Вм среднее по объему от полного микроско-
микроскопического значения магнитной индукции в магнетике (ср. § 40),
т.е. индукции (в вакууме) в любой заданной точке внутри маг-
магнетика, созданной как намагничивающей обмоткой, так и всеми
молекулярными тока-
токами. Тогда магнитная
индукция равна
В = Вм - В',
где через В'обозначена
магнитная индукция,
/ *~ создаваемая удален-
„ , .„ т. ной частью магнетика,
Рис 160. К определению магнитной индукции заполнявшей ранее по-
внутри магнетика ,-т ^
л ость. Положим, что
полость имеет форму круговой щели (результат расчета не зави-
зависит от формы полости). Тогда удаленная часть магнетика будет
иметь вид диска (рис. 160). Если намагниченность магнетика
есть /, то сила тока, обтекающего диск, равна а/, где а — тол-
толщина диска (§ 103). Поэтому, согласно формуле G9.3),
где г — радиус диска (полости). Отсюда видно, что если а/г —*• 0
(что требуется по условию), то В' —» 0, и поэтому
В = ВМ. A05.1)
Таким образом, по определению, магнитная индукция в маг-
магнетике равна среднему по объему от микроскопического значе-
значения магнитной индукции внутри магнетика.
Выражение A05.1) для магнитной индукции можно предста-
представить и иначе. Среднее значение магнитной индукции Вм скла-
складывается из индукции /ioH, создаваемой намагничивающей ка-
катушкой (где Н — поле, создаваемое катушкой, совпадающее с
полем внутри магнетика), и индукции, создаваемой поверхност-
поверхностными токами магнетика. Но, согласно сказанному в § 104, напря-
напряженность поля поверхностных токов равна I, а, следовательно,
создаваемая ими индукция есть /jqI. Поэтому полная магнитная
индукция в магнетике равна
B = /i0H + /i0I. A05.2)
Эта формула дает другое определение магнитной индукции в
магнетике и выражает магнитную индукцию через напряжен-
§ 106 ЗАКОНЫ МАГНИТНОГО ПОЛЯ В МАГНЕТИКАХ 227
ность магнитного поля внутри магнетика и его намагничен-
намагниченность. Она аналогична формуле D1.2), определяющей электри-
электрическое смещение.
Направления напряженности поля Н и намагниченности I
могут не совпадать друг с другом. Это наблюдается для ряда
магнитных кристаллов. В таких кристаллах намагниченность
зависит еще от направления поля относительно осей кристал-
кристалла. Подобные вещества называют анизотропными магнетиками.
Для них направления индукции В и напряженности Н, вообще
говоря, различны.
Напротив, для многих веществ направления Н и I всегда
совпадают. Намагниченность таких веществ не зависит от на-
направления намагничивающего поля, и поэтому они получили
название изотропных магнетиков. В них направления В и Н
также одинаковы.
В изотропных магнетиках связь между индукцией и напря-
напряженностью поля значительно упрощается. В этом случае можно
положить, что
I = хН, A05.3)
где л — скалярная величина, зависящая от рода магнетика и
его состояния (температуры и т.д.); она называется магнитной
восприимчивостью данного вещества и аналогична диэлектри-
диэлектрической восприимчивости диэлектриков (§ 42). Однако, в отличие
от формулы D2.1), в формуле A05.3) мы не пишем /io, чтобы к
(как и диэлектрическая восприимчивость а) была безразмерной
величиной. Подставляя A05.3) в A05.2), находим
В = A*/i0H, A05.4)
где /j, — магнитная проницаемость вещества (§ 94), выражаемая
соотношением
ц = \+х. A05.5)
Магнитная проницаемость вещества /х показывает, во сколь-
сколько раз магнитная индукция, т.е. средняя плотность магнитно-
магнитного потока в магнетике, больше плотности магнитного потока,
создаваемого одной намагничивающей катушкой. Поэтому при
заполнении пространства магнетиком увеличивается в рь раз и
полный магнитный поток, пронизывающий контур с током, а
следовательно, определение магнитной проницаемости, выражае-
выражаемое формулой A05.5), и определение, данное в § 94, совпадают.
§ 106. Законы магнитного поля в магнетиках
При изучении электрического поля нам оказалось необходи-
необходимых ввести две основные величины — напряженность электри-
электрического поля Е и электрическое смещение D. Аналогично этому
для описания магнитного поля тоже необходимы две основные
228 МАГНЕТИКИ ГЛ. XI
величины — напряженность магнитного поля Н и магнитная
индукция В. Поэтому для лучшего уяснения смысла напряжен-
напряженности Н и индукции В магнитного поля в магнетиках полез-
полезно их сопоставить с аналогичными величинами напряженности
электрического поля Е и электрического смещения D в диэлек-
диэлектриках.
Мы видели (§ 40), что напряженность электрического поля Е
внутри диэлектрика есть среднее по объему от полной, фактиче-
фактически существующей напряженности Ем, созданной как зарядами
обкладок конденсатора, так и молекулами-диполями диэлектри-
диэлектрика. При этом силы, действующие на заряды, определяются имен-
именно напряженностью поля Е (а не электрическим смещением D).
Аналогичное положение мы имеем для магнитной индукции; В в
магнетиках есть среднее по объему от полной плотности магнит-
магнитного потока Вм, созданного как намагничивающими катушками,
так и молекулярными токами самого магнетика (§ 105). Далее
мы видели (§ 76), что сила, действующая на токи в магнитном
поле, пропорциональна как раз индукции В (а не напряжен-
напряженности поля Н). Поэтому магнитная индукция В в магнетиках
соответствует напряженности электрического поля Е в диэлек-
диэлектриках.
С другой стороны, электрическое смещение D совпадает
с электрическим смещением в вакууме, создаваемым одними
зарядами обкладок конденсатора (без учета поляризационных
зарядов диэлектрика). Аналогично этому напряженность маг-
магнитного поля в магнетике представляет магнитное поле одних
намагничивающих катушек (без учета молекулярных токов маг-
магнетика). Следовательно, напряженность магнитного поля Н в
магнетиках соответствует электрическому смещению D в ди-
диэлектриках. Поэтому было бы правильнее назвать магнитную
индукцию напряженностью магнитного поля, а напряженность
магнитного поля — индукцией; однако это не сделано до настоя-
настоящего времени в силу исторических традиций.
Выяснив физический смысл индукции В и напряженности
поля Н, мы можем легко понять, каким образом изменяются
законы магнитного поля при переходе от вакуума к магнетикам.
Так как напряженность Н выражает напряженность магнит-
магнитного поля только намагничивающих катушек, то очевидно, что
эта напряженность будет одна и та же в вакууме и в любом
магнетике. Поэтому все формулы, выражающие напряженность
магнитного поля токов, не изменяются. В частности, выражение
для напряженности поля, создаваемого элементом тока (§ 79),
будет иметь такой же вид, как и для вакуума, а именно
<ш = -!- г.Ц11. (Ю6.1)
47Г Г3 '
Это поле не зависит от магнитной проницаемости среды.
§ 106 ЗАКОНЫ МАГНИТНОГО ПОЛЯ В МАГНЕТИКАХ 229
По той же причине не изменится и теорема о магнитном на-
напряжении (§ 81):
<fHsds = i, A06.2)
где в левой части по-прежнему Hs обозначает напряженность
магнитного поля в магнетике, а г — алгебраическую сумму токов
в проводниках (без учета молекулярных токов магнетика).
Напротив, механические действия магнитного поля на элек-
электрические токи при переходе от вакуума к магнетику изменяют-
изменяются. Эти действия определяются суммарной плотностью магнит-
магнитного потока (намагничивающих катушек и молекулярных токов),
т.е. индукцией В в магнетике. При заполнении пространства
магнетиком с относительной магнитной проницаемостью веще-
вещества /i (и неизменном токе в намагничивающих катушках) маг-
магнитная индукция становится равной /i/^oH, т.е. увеличивается в
/i раз и во столько же раз возрастают механические силы. По-
Поэтому, например, сила, действующая на провод с током в маг-
магнитном поле (ср. формулу G6.1а)), внутри магнетика равна
F = *[1В] = i/i/iO[lH]. A06.3)
Вернемся, наконец, к явлению электромагнитной индукции. В
§ 91 мы видели, что ЭДС индукции зависит от быстроты измене-
изменения магнитного потока, пронизывающего рассматриваемый кон-
контур. Это справедливо и для магнетиков. Однако в данном случае
суммарный магнитный поток складывается из потока, создавае-
создаваемого намагничивающими катушками, и потока, обусловленного
молекулярными токами, и поэтому в основном законе электро-
электромагнитной индукции (91.1) под Ф следует понимать поток век-
вектора магнитной индукции В = /i/ioH внутри магнетика. При
заполнении пространства магнетиком с магнитной проницаемо-
проницаемостью /х поток, а следовательно, и ЭДС индукции увеличиваются
в /i раз.
В § 81 мы видели, что линии магнитного поля токов непре-
непрерывны. Это значит, что и линии магнитной индукции /хоН в ва-
вакууме тоже непрерывны. С другой стороны, в § 105 мы говорили,
что магнитная индукция внутри магнетика есть суммарная маг-
магнитная индукция в вакууме, созданная намагничивающими ка-
катушками и элементарными токами магнетика. Отсюда следует,
что и линии магнитной индукции внутри магнетика также везде
непрерывны. Это значит, что для любой замкнутой поверхности
число входящих через нее линий индукции равно числу выходя-
выходящих, т.е. полный поток магнитной индукции через замкнутую
поверхность всегда равен нулю:
fBndS = 0. A06.4)
Эта формула выражает теорему Остроградского-Гаусса для
магнитного поля.
230 МАГНЕТИКИ ГЛ XI
§ 107. Влияние формы тела на намагничивание
До сих пор мы рассматривали неограниченные магнетики
или, точнее, тела такой формы, при которой линии намагничи-
намагничивающего поля не пересекали поверхность тела (тороидальный
замкнутый сердечник, неограниченно длинный прямой цилиндр
внутри соленоида). Мы видели, что в этом случае напряжен-
напряженность поля внутри магнетика
Т1Й^ЕетЛь, н = но, где Но - напряжен-
{ JJ ЩЩЩЩшй I 5 НОСТЬ ПОЛЯ намагничивающей
катушки.
Рассмотрим теперь огра-
ограниченный магнетик, например
Рис 161 Ограниченный магнетик имеющий форму короткого ци-
в магнитном поле линдра 1 (рис. 161). В нем от-
отсутствуют боковые части 2 и 3,
которые содержали молекулярные токи и участвовали в образо-
образовании магнитного потока. Поэтому плотность магнитного пото-
потока, т.е. магнитная индукция В, в ограниченном магнетике будет
меньше, а следовательно, и напряженность поля Н = B/fifio
также будет меньше Hq на некоторую величину На:
Н = Н0-На. A07.1)
Поле На называют размагничивающим полем. Так как дей-
действие частей 2 и 3 магнетика пропорционально намагниченно-
намагниченности данного вещества /, то можно положить
#о = /3/, A07.2)
где /3 — безразмерный множитель, зависящий от формы и раз-
размеров тела; он получил название размагничивающего фактора.
Выражая размагничивающее поле формулой A07.2), мы
предполагаем намагниченность / постоянной во всех точках те-
тела Расчет показывает, что это точно выполняется только для
эллипсоида. Указанное предположение справедливо и для шара
(частный случай эллипсоида), а также для бесконечно тонких
стержня и диска, которые можно рассматривать как предель-
предельные случаи эллипсоида. Для тел иной формы формула A07.2)
справедлива только приближенно и под I нужно понимать неко-
некоторое среднее значение намагниченности.
Из сказанного ясно, что в действительности никакого «раз-
«размагничивающего» поля не существует Этим термином мы вы-
выражаем только то, что магнитное поле внутри какого-либо тела
зависит от формы тела и что оно меньше, чем внутри замкну-
замкнутого тороида.
Рассмотрим теперь значения размагничивающего фактора
для тел простейшей формы. Для замкнутого тороида Й = Hq,
§ 107 ВЛИЯНИЕ ФОРМЫ ТЕЛА НА НАМАГНИЧИВАНИЕ 231
Н<=> = 0, и поэтому /3 = 0. Для очень длинного стержня, для
которого отношение длины к диаметру весьма велико, размаг-
размагничивающий фактор /3 очень мал и практически его можно счи-
считать также равным нулю.
Вычислим размагничивающий фактор для тонкого диска,
перпендикулярного к направлению намагничивающего поля. В
§ 105 мы видели, что элементарные токи в диске, складываясь,
дают поверхностный круговой ток силой al (a — толщина дис-
диска), который создает в центре диска поле
Я' = al/2r
(г — радиус диска). Поэтому индукция внутри диска равна
В = ^
Для бесконечно тонкого диска а/г —> 0, и поэтому
В = fj,oHo, Я = B/fifio = Но/р.
Подставляя этот результат в A07.1), имеем
#о = Но - Я = Я (/х - 1) = хЯ,
так как /i = 1 + к Но, согласно A05.3), I = кН. Поэтому
а следовательно,
/3 = 1 (бесконечно гонкий диск).
Можно также легко показать, что для магнетика шарообраз-
шарообразной формы
/3 = 1/3 (шар).
Полученные результаты разъясняют влияние формы тела
на намагничивание. Намагничивание вещества какого-либо те-
тела тем больше, чем больше напряженность ноля Я внутри тела.
Помещая тела из одинакового вещества, но различной формы,
в одно и то же внешнее поле, мы будем иметь различную напря-
напряженность поля внутри тел, и поэтому тела разной формы будут
намагничиваться по-разному. Сильнее намагнитится то тело, у
которого размагничивающий фактор /3 меньше.
На рис. 162 изображен наглядный опыт, подтверждающий
сказанное. Расположим у нижнего конца вертикальной прово-
проволочной катушки А пучок железных проволок, стянутых вместе
в виде стержня, и подберем в катушке такую силу тока, чтобы
она была лишь немного меньше той, которая необходима для
втягивания стержня внутрь катушки. Вынем теперь пучок про-
проволок, удалим проволочные петли, стягивающие проволоки вме-
вместе, и поместим опять наши проволоки на прежнее место. Мы
232
МАГНЕТИКИ
ГЛ XI
увидим, что при той же силе тока проволоки сильно втягивают-
втягиваются внутрь катушки.Это происходит потому, что во втором слу-
случае каждая из проволок намагничивается раздельно, а так как
размагничивающий фактор для тонкой проволоки меньше, чем
для толстого стержня, то и намагничивание во втором случае
оказывается больше.
Сказанное выше применимо и к постоянным магнитам. Они
представляют собой магнетики, в которых молекулярные токи
находятся в ориентированном состоянии в отсутствие внешнего
поля. Замыкая концы магнита железной пластиной, мы умень-
уменьшаем размагничивающий фактор, отчего и напряженность по-
поля, и магнитная индукция внутри магнита увеличиваются.
Рис 162. Железные проволоки порознь намагничиваются сильнее, чем
толстый стержень, составленный из этих проволок
Чтобы при случайных внешних воздействиях (механиче-
(механические сотрясения, внешние размагничивающие поля) намагни-
намагниченность постоянных магнитов не уменьшалась, нужно, чтобы
напряженность поля внутри магнита была возможно большей.
Поэтому при хранении постоянных магнитов их концы (полюсы)
всегда замыкают железными пластинами («якорями»).
§ 108. Преломление линий индукции магнитного поля
На границе раздела двух различных сред с разными значе-
значениями магнитной проницаемости линии магнитной индукции,
подобно линиям электрического смещения (§ 43), изменяют на-
направление, т.е преломляются.
Для того чтобы выяснить, как преломляются линии индук-
индукции, рассмотрим прямоугольный параллелепипед, одно из осно-
108
ПРЕЛОМЛЕНИЕ ЛИНИЙ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ
233
ваний которого лежит в среде 1 с магнитной проницаемостью
Мь а ДРУгое ~~ в среде 2, магнитная проницаемость которой fi2
(рис. 163), и вычислим поток
магнитной индукции сквозь его
поверхность. Если S есть пло-
площадь основания, а Вп2 — нор-
нормальная составляющая индук-
индукции в среде 2, то поток сквозь
верхнюю грань параллелепипе-
да есть Bn2S. Аналогично по-
ток сквозь нижнюю грань ра- Рис ш к выводу граничных
вен BnlS. Высоту параллелепи- условий для магнитНого поля
педа будем считать бесконечно
малой, и поэтому поток через его боковую поверхность учи-
учитывать не будем. Согласно A06.4) поток магнитной индукции
сквозь замкнутую поверхность всегда равен нулю:
Bn2S — BnlS = 0,
или
Вщ = Вп2. A08.1)
Нормальная составляющая магнитной индукции непрерывна.
В противоположность этому, нормальные составляющие на-
напряженности магнитного поля в обеих средах будут различны.
Так как Bni = /ii/io#ni и Вп2 =
, т0
Hni/Hn2 =
Рассмотрим теперь прямоуголь-
прямоугольный контур с бесконечно малой высо-
высотой h (рис. 164), одно ребро которого
длиной I лежит в среде 1, а другое —
„ ,„, т, в среде 2, применим к нему теорему
Рис. 164 К выводу гранич- магнитном напряжении (§ 81). Маг-
кых условий для магнитно- ^ vc '
™ ттг,\тО нитное напряжение вдоль рассматри-
1О ПОЛЯ -. yy 7 ТТ
ваемого контура равно irli2 — Шц, где
Нц и Ht2 — касательные к поверхности раздела составляющие
напряженности магнитного поля в обеих средах. Если h —> 0, то
и площадь, ограниченная контуром, стремится к нулю, а значит,
стремится к нулю и сила тока, проходящего через эту площадь.
Поэтому
1На - Ша = 0,
откуда
На = Щ2. A08.2)
При переходе через границу раздела двух сред касательные
составляющие напряженности магнитного поля не изме-
изменяются.
234
МАГНЕТИКИ
ГЛ XI
Напротив, касательные составляющие индукции испытыва-
испытывают скачок, причем
Соотношения A08.1) и A08.2) выполняются во всех случаях
и выражают граничные условия для магнитного поля. Они со-
совершенно аналогичны граничным условиям для электрического
поля (§ 41).
Из этих формул вытекает закон преломления линий индук-
индукции:
tgai/tga2 = /xi//x2, A08.3)
где а\ — угол между линиями индукции в среде 1 и нормалью
к поверхности раздела, а «2 — соответствующий угол в среде 2.
Так как в изотропных магнетиках направления индукции и
напряженности поля совпадают, то A08.3) выражает также и
закон преломления линий напряженности поля.
Из A08.3) следует, что линии индукции, вступая в среду с
большей магнитной проницаемостью, удаляются от нормали, а
следовательно, сгущаются.
Вычисление хода линий индукции довольно сложно даже для
тел простой формы, и поэтому мы ограничимся только каче-
качественным разбором. Рассмотрим, например, кусок магнетика в
виде прямоугольного бруска в магнитном поле, которое до внесе-
внесения магнетика было однородным (рис. 165). Магнитную прони-
проницаемость магнетика будем считать большей, чем у окружающей
среды. Рассматриваемый брусок в магнитном поле намагнитит-
© ©
_©_
© 0
© ©_
© © ^^
Рис. 165 Сгущение линий индукции внутри магнетика
ся и станет сам источником магнитного поля, линии индукции
которого показаны штриховыми линиями. Это поле будет скла-
складываться в каждой точке с первоначальным однородным по-
полем по правилу параллелограмма, отчего возникнет результи-
§ 108 ПРЕЛОМЛЕНИЕ ЛИНИЙ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ
235
рующее поле, изображенное утолщенными линиями индукции.
Из рис. 165 видно, что линии индукции стягиваются к бруску,
испытывают на его поверхности преломление и располагаются
внутри бруска гораздо гуще.
На рис. 166 показаны линии индукции в теле шаровой фор-
формы, помещенном в первоначально однородное магнитное поле.
В этом случае оказывается, что линии индукции внутри ша-
Рис. 166. Магнитная проницаемость вещества шара больше (о) и меньше
(б), чем у окружающей среды
ра представляют собой параллельные прямые линии, а следо-
следовательно, и значение индукции во всех точках шара одинаково.
При этом будут постоянны и напряженность поля Н, и намаг-
намагниченность I, т.е. шар будет намагничен однородно.
Если в однородное магнитное поле поместить полое тело,
например цилиндр, из вещества с магнитной проницаемостью,
большей чем у окружающей среды,
то линии индукции будут сгущаться
в теле цилиндра (рис. 167). В поло-
полости же цилиндра густота линий индук-
индукции уменьшится, а следовательно, и
магнитное поле внутри цилиндра бу-
будет ослаблено (внутри воздушной по-
полости магнитного поля практически
нет). Этим обстоятельством пользуют-
пользуются для устройства магнитной защиты.
Чтобы предохранить чувствительные
измерительные приборы от действия
внешних магнитных полей, их заклю- Рис. 167. Линии магнитной
чают в замкнутые оболочки из веще- индукции внутри железно-
ства с большой магнитной проницае- го цилиндра, помещенного
мостью (железо). Однако, в отличие в первоначально однородное
от электростатической защиты (§ 27), магнитное поле
таким приемом можно только осла-
ослабить внешнее поле (в сотни и тысячи раз), но нельзя исключить
его вовсе, так как в природе существуют проводники электри-
электричества, но нет проводников магнетизма.
236 МАГНЕТИКИ ГЛ XI
Из сказанного ясно, что если конфигурация первоначального
поля и форма тела таковы, что линии индукции не пересекают
поверхность тела, то не будет и преломления линий индукции
и магнитное поле вне тела не будет изменяться при внесении
тела. Так, например, если на прямой длинный провод с током
надеть длинную железную трубу, коаксиально с проводом, то
линии индукции, имеющие в этом случае вид концентрических
окружностей, не будут пересекать ни внутреннюю, ни внешнюю
поверхности трубы, и магнитное поле во всем пространстве, кро-
кроме толщи самой трубы, будет таким же, как и до надевания тру-
трубы. В самом же теле трубы магнитная индукция увеличится в
/i раз.
§ 109. Магнитные свойства веществ. Диамагнетизм и
парамагнетизм
Магнитные свойства различных веществ гораздо разнообраз-
разнообразнее, нежели электрические свойства. В то время как диэлектри-
диэлектрическая проницаемость е у всех веществ всегда больше едини-
единицы, магнитная проницаемость /i может быть как больше, так
и меньше единицы. Вещества, для которых /i < 1, называются
диамагнитными или диамагнетиками, а вещества с /i > 1 — па-
парамагнитными или парамагнетиками. Так как магнитная вос-
восприимчивость >с — /i — 1, то для парамагнетиков х положитель-
положительна, а для диамагнетиков — отрицательна.
Намагниченность вещества I (магнитный момент единицы
объема), как мы видели в § 105, связана с напряженностью маг-
магнитного поля соотношением I = хН. Отрицательное значение
ус в диамагнетаках обозначает, что в этих веществах намагни-
намагниченность направлена противоположно намагничивающему по-
полю. Объяснение такого, неожиданного на первый взгляд, харак-
характера намагничивания будет рассмотрено ниже.
Наличие диа- и парамагнитных веществ качественно легко
обнаружить, наблюдая поведение вещества в сильном магнит-
магнитном поле. Атмосферный воздух является парамагнетиком, его
магнитная восприимчивость ус при 760 мм рт. ст. и комнатной
температуре равна 0,38 ¦ 10~6. Поэтому все парамагнетики, у
которых ус > 0,38 • 10~6, ведут себя подобно диэлектрикам с ди-
диэлектрической проницаемостью ?\ бблыпей, чем e<i окружающей
среды, т.е. втягиваются в область сильного поля. Напротив, на
диамагнетики действуют силы того же знака, что и на диэлек-
диэлектрики с ei < ?2, и они выталкиваются из магнитного поля.
Примером парамагнетика может служить хлористое железо.
Стеклянная ампула с водным раствором этой соли, подвешенная
на тонкой нити в магнитном поле, втягивается полем и устанав-
устанавливается параллельно направлению поля (рис. 168).
109
ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
237
Примером диамагнетика является висмут. Висмутовая па-
палочка выталкивается из магнитного поля и устанавливается пер-
перпендикулярно к направлению поля (рис. 169).
Рис. 168. Ампула с парамагнит-
парамагнитным раствором хлористого железа
в магнитном поле
Рис. 169. Диамагнитная палочка
висмута в магнитном поле
Если тело находится в среде, которая сама способна намаг-
намагничиваться, то силы, действующие на него, зависят не только
от намагничивания тела, но и от намагничивания окружающей
среды. В частности, парамагнетик, помещенный в парамагнит-
парамагнитную же среду с большим х, ведет себя как диамагнетик.
Так, например, если ампулу с парамагнитным раствором
хлористого железа погрузить в кювету с более крепким раство-
раствором той же соли, то ампула будет выталкиваться из магнитного
поля.
В табл. 5 приведены значения магнитной восприимчивости
для некоторых веществ. Данные для газов относятся к давлению
760 мм рт. ст. и комнатной температуре. Как видно из таблицы,
значения я весьма малы, и поэтому магнитная проницаемость
/i = 1 + х близка к единице: все диа- и парамагнетики суть
вещества, намагничивающиеся весьма слабо.
Отметим, что для данного вещества х приблизительно про-
пропорциональна плотности вещества. Поэтому в различных табли-
таблицах часто приводят удельную магнитную восприимчивость xi =
= x/d, где d — плотность вещества. В отличие от х, которая
есть величина безразмерная, щ имеет размерность, обратную
размерности плотности.
Таблица 5
Вещество
Азот
Углекислота
Вода
Серебро
Висмут
яг- 106
-0,0062
-5,3
-9,0
-26
-170
Тип
магнетика
Диамагне-
Диамагнетик
Вещество
Кислород
Алюминий
Платина
Хлористое же-
железо (FeCl3)
яг-106
1,8
21
300
2500
Тип
магнетика
Парамагне-
Парамагнетик
»
238
МАГНЕТИКИ
ГЛ XI
§ 110. Ферромагнетизм
Наряду с диа- и парамагнетиками имеются вещества, спо-
способные намагничиваться весьма сильно. Они получили назва-
название ферромагнетиков. Магнитная проницаемость большинства
ферромагнетиков при обычных температурах измеряется мно-
многими сотнями и тысячами единиц, а у некоторых специально
приготовленных и обработанных ферромагнетиков она достига-
достигает миллиона.
Ферромагнетики, помимо способности сильно намагничи-
намагничиваться, обладают рядом свойств, существенно отличающих их
от диа- и парамагнетиков.
Кривая намагничивания. Характерной особенностью
ферромагнетиков является сложная нелинейная зависимость
между индукцией В
и напряженностью по-
поля Н. Эта зависи-
зависимость была установ-
установлена в классических
работах А.Г. Столе-
Столетова на примере мяг-
мягкого (отожженного)
железа. Зависимость
индукции В от напря-
напряженности магнитного
поля Н в ферро-
ферромагнетиках имеет
Рис. 170. Зависимость магнитной индукции от вид показанный на
напряженности магнитного поля- 1 — электро- рис 170 Индукция
литическое железо, 2 - малоуглеродистое же- сначала быстро увели-
лезо, 3 - литая сталь, 4 ~ чугун чивается, но по мере
намагничивания магнетика ее нарастание замедляется.
По значениям индукции В и поля Н можно определить на-
намагниченность магнетика I = B/fiQ—H (магнитный момент еди-
единицы объема). Характер зависимости
I от Н для ферромагнетиков изо-
изображен на рис. 171. Намагниченность
/, подобно индукции, сначала быстро
возрастает, но затем наступает маг-
магнитное насыщение, при котором на-
намагниченность достигает некоторого
максимального значения Is и практи-
практически перестает зависеть от напряжен-
напряженности поля.
Рис. 171. Кривая намагни- Вследствие нелинейной зависимо-
чивания ферромагнетиков Сти В от Н магнитная проницае-
If
——
-
^—¦
заян
ии
,
-
8 10 12 Я, кА/м
§ I10
ФЕРРОМАГНЕТИЗМ
239
ц-10
3
мость fj, = в I [ion зависит от напряженности магнитно-
магнитного поля. Кривая зависимости /i от Н (рис. 172) возраста-
возрастает с увеличением поля от начального значения до некото-
некоторой максимальной величины
Ммакс, но затем, после про-
прохождения через максимум, ц
уменьшается и асимптотически
стремится к значению, очень
близкому к единице.
Магнитная восприим-
восприимчивость ферромагнетика
ус = I/H оказывается также
непостоянной и зависящей
от напряженности поля. Она
имеет максимум и при больших
полях асимптотически стре-
стремится к значению, близкому к
нулю.
/
J
\
ч
о
40
80 Я,А/м
Рис. 172. Зависимость магнитной
проницаемости р, от напряженности
поля для железа «армко»
[1П],
Указанные особенности намагни-
намагничивания ферромагнетиков показыва-
показывают, что использование ферромагне-
ферромагнетиков для получения сильных маг-
магнитных полей весьма эффективно в
областях намагничивания, далеких от насыщения. В случае же очень силь-
сильных полей наступает магнитное насыщение, и применение ферромагнетиков
делается практически бесполезным.
Анизотропия намагничивания. Все ферромагнетики в
магнитном отношении анизотропны. Однако если ферромагне-
ферромагнетик имеет мелкокристаллическую структуру и отдельные крис-
кристаллики в нем расположены со-
совершенно беспорядочно, то эта
анизотропия не проявляется и его
намагниченность не зависит от
Направления поля. Если же фер-
ферромагнетик представляет собой
единый кристалл, то вид кривой
намагничивания оказывается раз-
различным и зависит от направле-
направления намагничивающего поля от-
относительно осей кристалла. На
рис. 173 изображена элементар-
элементарная ячейка кристалла железа
(центрированный куб) и пока-
показаны кристаллографические на-
направления, обозначаемые симво-
символами [100] (ребро куба), [110]
[ПО]
Рис 173. Элементарная кристал-
кристаллическая ячейка железа и ее
основные кристаллографические
направления: [100] — легкого,
[111] — трудного намагничивания
240
МАГНЕТИКИ
ГЛ. XI
(диагональ грани) и [111] (пространственная диагональ); на
рис. 174 даны кривые намагничивания монокристаллов желе-
железа и никеля при трех указанных направлениях магнитного по-
поля. Как видно из рисунка, для каждого ферромагнетика суще-
/,МА/м
1,6
1,2
п о
0,4
'[iooj;
'[ПО]
Fe
^^
[41]
Я,кА/м
0
20
0,5
0,3
0,1
40 60 0
[ill]
Y
Ni
?110]
К-
[ЮО]
Я,кА/м
10 20 30
Рис. 174. Кривые намагничивания монокристаллов железа и никеля при
различных направлениях намагничивающего поля
ствует направление, в котором намагниченность (при данном
поле) наибольшая (направление легкого намагничивания), и на-
направление, в котором намагниченность наименьшая (направле-
(направление трудного намагничивания).
Гистерезис. Положим, что мы намагничиваем первоначаль-
первоначально ненамагниченный ферромагнетик и, поместив его внутрь на-
намагничивающей катушки,
А увеличиваем магнитное
поле внутри магнетика от
нуля до некоторого значе-
значения Hi (рис. 175). Значение
индукции в магнетике
будет определяться отрез-
отрезком 01 кривой индукции
01А и изобразится отрез-
отрезком ординаты ОВ\. Если
теперь вновь уменьшать
магнитное поле, то умень-
уменьшение индукции будет
изображаться уже не от-
Рис. 175. Магнитный гистерезис резком кривой индукции
10, но кривой 1В', и, когда
поле сделается опять равным нулю, индукция не будет равна
нулю, а будет выражаться отрезком ОВ'. Ферромагнетик в
этом состоянии является постоянным магнитом. Если, далее,
изменить направление тока в намагничивающей катушке и
перемагничивать образец в обратном направлении, то из-
изменение индукции будет описываться отрезком кривой В'2.
§ НО ФЕРРОМАГНЕТИЗМ 241
При последующем изменении поля в обратном направлении
индукция будет изменяться в соответствии с кривой 2 В" 1. При
циклическом перемагничивании ферромагнетика изменение
индукции в нем будет изображаться петлеобразной замкнутой
кривой 1В'2В.
Мы видим, что значение индукции в ферромагнетике опреде-
определяется не только существующим магнитным полем, но еще зави-
зависит от предыдущих состояний намагничивания, причем проис-
происходит своеобразное отставание изменения индукции от изменений
напряженности поля. Это явление получило название магнитно-
магнитного гистерезиса, а указанная выше петлеобразная кривая зависи-
зависимости В от Н при циклическом перемагничивании называется
петлей гистерезиса. Магнитный гистерезис подобен диэлектри-
диэлектрическому гистерезису в сегнетоэлектриках (§ 50).
Из кривых рис. 175 видно, что при устранении намагничиваю-
намагничивающего поля ферромагнетик сохраняет остаточную намагничен-
намагниченность, причем внутри магнетика существует некоторая остаточ-
остаточная индукция. При увеличении амплитуды намагничивающего
поля она стремится к предельному значению Bq (рис. 175).
Чтобы уничтожить эту остаточную намагниченность внутри
ферромагнетика, необходимо создать определенное поле, на-
направленное против первоначального намагничивающего поля,
изображаемое отрезком ОНК. Это поле называют задерживаю-
задерживающей или коэрцитивной силой ферромагнетика.
В связи со сказанным выше находится практический прием, употреб-
употребляемый для размагничивания ферромагнетиков. Для этого ферромагнетик
помещают внутрь катушки, питаемой переменным током, и силу тока посте-
постепенно уменьшают до нуля. При этом ферромагнетик подвергается много-
многократным циклическим перемагничиваниям, соответствующим различным
петлям гистерезиса, которые, постепенно уменьшаясь, стягиваются к точке
О (рис. 175), где намагниченность равна нулю.
Гистерезис зависит в сильнейшей степени от состава фер-
ферромагнетика и от его обработки. Для чистого мягкого железа,
т.е. отожженного и затем медленно охлажденного, гистерезис
выражен весьма слабо и петля гистерезиса очень узка. Но у за-
закаленной стали гистерезис значителен.
Температура Кюри. Способность пара- и ферромагнети-
ферромагнетиков намагничиваться различна при разных температурах, т.е.
их магнитная восприимчивость зависит от температуры. Она
уменьшается с увеличением температуры. Напротив, магнитная
восприимчивость диамагнетиков практически не зависит от тем-
температуры.
Для многих парамагнитных веществ изменение я с темпера-
температурой подчиняется закону, установленному Кюри:
х = С/Т, A10.1)
242
МАГНЕТИКИ
ГЛ XI
где Т — термодинамическая температура, а С — постоянная Кю-
Кюри, зависящая от рода вещества. Магнитная восприимчивость
таких веществ монотонно изменяется с изменением температу-
температуры. Подобные вещества называются нормальными парамагне-
парамагнетиками.
Зависимость магнитной восприимчивости от температуры
для ферромагнетиков имеет более сложный характер. При по-
повышении температуры способность ферромагнетиков намагни-
намагничиваться уменьшается. При этом падают значения их магнитной
восприимчивости и проницаемости при любом значении магнит-
магнитного поля, ослабляется гистерезис и уменьшается намагничен-
намагниченность насыщения Is. При некоторой температуре Тк, называе-
называемой температурой Кюри, ферромагнитные свойства исчезают
вовсе.
Температура Кюри различна для разных ферромагнетиков;
ее значения для некоторых веществ приведены в табл. 6.
Таблица 6
Вещество
Кобальт
Железо
78 %-ный пермаллой
(сплав 22 % Fe, 78 % Ni)
ТК,°С
1150
770
550
Вещество
Никель
30 %-ный пермаллой
Гадолиний
Гк,°С
360
70
17
При температурах более высоких, нежели температура Кю-
Кюри, ферромагнетик превращается в парамагнетик. Зависимость
магнитной восприимчивости л от температуры для таких пара-
парамагнетиков подчиняется закону Кюри-Вейсса:
*=Г^г- (И0.2)
1 1к
Здесь С — постоянная, зависящая от рода вещества.
§ 111. Работа при намагничивании
При намагничивании любого магнетика совершается опреде-
определенная работа. Вычислим эту работу, пользуясь законом сохра-
сохранения энергии (§ 100),
Пусть магнетик имеет форму замкнутого тора и намагничи-
намагничивается равномерно расположенной на нем обмоткой, сила тока
в обмотке г, ЭДС батареи Ш, полное сопротивление цепи г. Если
сила тока постоянна, то будет постоянным и магнитное поле и
его энергия не будет изменяться. В этом случае работа источ-
источника тока превращается целиком в тепло Джоуля-Ленца, и мы
имеем
§ 111 РАБОТА ПРИ НАМАГНИЧИВАНИИ 243
Допустим теперь, что сила тока в обмотке очень медленно
увеличивается. Тогда при том же значении сопротивления г си-
сила тока будет меньше на малую величину Si, так как вследствие
электромагнитной индукции в цепи будет еще экстраток самоин-
самоиндукции, направленный противоположно току i. При этом за вре-
время dt увеличится и магнитное поле, на что затрачивается неко-
некоторая работа 6А. Согласно закону сохранения энергии должно
быть
&(г - Si) dt = r{i - SiJ dt + 6A.
Работа источника уменьшилась на величину if Sidt = ri Si dt,
а уменьшение количества теплоты равно ri dt — r(i — Si) dt ~
« 2ri Si dt. Разность этих работ ri Si dt равна работе намагничи-
намагничивания, и поэтому
SA = ri Si dt.
Но, согласно основному закону электромагнитной индукции,
ЭДС индукции в обмотке равна —S(dB/dt)N, где В — индук-
индукция в магнетике, 5 — его сечение (равное площади витка), N —
полное число витков обмотки. Отсюда получается
а следовательно,
= SNidB.
SA ri^
г dt
Умножая и деля правую часть этого равенства на длину магне-
магнетика (тороида) I и замечая, что Ni/l — Н есть напряженность
поля внутри магнетика, находим
SA = HdBnr = (Htffi)r,
где т = SI — объем магнетика. Мы отметили индексом п у В то
обстоятельство, что в закон индукции в действительности вхо-
входит составляющая магнитной индукции, нормальная к плоско-
плоскости витков, т.е. проекция магнитной индукции на направление
магнитного поля. Работа dw, необходимая для увеличения ин-
индукции на dB в единице объема магнетика, равна
dw = {UdB). AH-1)
Так как работа намагничивания зависит лишь от процессов
внутри магнетика, то выражение A11.1) будет справедливым,
очевидно, для магнетика любой формы.
Полная работа намагничивания (на единицу объема) есть
w= f (HdB). A11.1a)
Полученное общее выражение справедливо при любой зави-
зависимости В от Н. В случае линейной связи В = /u/uoH эта фор-
формула переходит в формулу (97.1). При нелинейной зависимости
244
МАГНЕТИКИ
ГЛ XI
В
В(Н), но однозначной (нет гистерезиса) вся работа намагничи-
намагничивания идет на увеличение энергии магнитного поля и поэтому
формулы A11.1) и A11.1а) да-
дают также объемную плотность
энергии магнитного поля в маг-
магнетике. При наличии гистере-
гистерезиса это уже не так.
Рассмотрим сначала маг-
магнетик без гистерезиса, для
которого прямая и обратная
ветви кривой намагничивания
совпадают (рис. 176) Эле-
Элементарная работа, необходимая
для бесконечно малого уве-
увеличения намагниченности, на
этом графике выражается, со-
Рис 176 Работа намагничивания гласно A11.1), величиной пло-
магнетика без гистерезиса щади 1234- Полная работа, за-
затрачиваемая при увеличении
индукции от нуля до заданного значения В\, будет равна пло-
площади ОАВ\, ограниченной кривой намагничивания и отрезком
оси ОВ\ (заштрихована) Эта работа затрачивается источником
при намагничивании магнетика. При размагничивании магне-
магнетика в цепь источника возвращает-
возвращается энергия, запасенная в магнитном
поле, в виде работы экстратока са-
самоиндукции. Она по-прежнему вы-
выражается величиной площади, огра-
ограниченной кривой намагничивания и
отрезком ординаты ОВ\. Если ги-
гистерезис отсутствует, то обе ветви
кривой совпадают, и при размагни-
размагничивании возвращается та же работа,
которая была затрачена при намаг-
намагничивании.
Иначе будет для магнетика с ги-
стерезисом В этом случае при уве- Рис т Работа .
личении индукции от значения Вг ческом перемагничивании пРо-
до некоторого другого значения В2 порциональна площади петли
(рис. 177) потребуется работа, рав- гистерезиса
ная площади, ограниченной ветвью
кривой намагничивания 1, т.е площади В\а1бВ2, а при размаг-
размагничивании до исходного состояния возвращаемая работа будет
равна площади В2б2аВх, которая имеет меньшую величину. По-
Поэтому при полном цикле перемагничивания в каждую единицу
В
В2
В,
1
О
н
§ 112 МАГНИТНЫЕ МАТЕРИАЛЫ ФЕРРИТЫ 245
объема магнетика вводится энергия
w = S, A11.2)
где S — площадь петли гистерезиса Эта энергия расходуется на
совершение работы против коэрцитивных сил в магнетике и в
конечном счете превращается в тепло. Поэтому ферромагнетики
при циклическом перемагничивании нагреваются, и тем больше,
чем сильнее выражен гистерезис.
Тепло гистерезиса всегда учитывают при расчете различ-
различных электрических устройств переменного тока, содержащих
ферромагнетики, подвергающиеся периодическому перемагни-
чиванию. Таковы, например, железные сердечники трансфор-
трансформаторов (§ 133) и вращающиеся железные якори генераторов
постоянного тока. Наличие гистерезиса в них приводит к беспо-
бесполезной затрате части энергии на тепло гистерезиса и снижает
коэффициент полезного действия установок. Поэтому для по-
подобных устройств применяют специальные сорта мягкого желе-
железа (трансформаторное железо), в которых гистерезис выражен
слабо.
§ 112. Магнитные материалы. Ферриты
В современной электротехнике ферромагнетики играют вы-
выдающуюся роль. Используя ферромагнетики, мы заставляем
элементарные токи принимать участие в образовании магнитно-
магнитного поля и, можно сказать, «бесплатно» увеличиваем магнитное
поле в тысячи раз по сравнению с полем одних намагничиваю-
намагничивающих катушек.
В зависимости от назначения ферромагнетиков к ним предъ-
предъявляют различные требования. Так, например, для их при-
применения в трансформаторах важнейшими требованиями явля-
являются высокая магнитная проницаемость и слабый гистерезис
(«магнитно-мягкие» материалы). Для изготовления же посто-
постоянных магнитов наиболее важны остаточное намагничивание и
большая коэрцитивная сила.
В качестве ферромагнитных материалов в настоящее время
широко применяют железо и его сплавы с другими элемента-
элементами. Подбирая состав сплавов и варьируя их обработку, оказы-
оказывается возможным получить различные ферромагнитные мате-
материалы, отличающиеся чрезвычайным разнообразием магнитных
свойств. В таблицах 7 и 8 приведены магнитные характеристики
некоторых веществ, применяемых в современной технике
Приведенные данные показывают, что в изготовлении маг-
магнитных материалов достигнуты выдающиеся успехи. Некоторые
сплавы (алнико, магнико) отличаются весьма высокими значе-
значениями коэрцитивной силы и остаточной индукции и поэтому по-
246
МАГНЕТИКИ
ГЛ. XI
зволяют изготовлять исключительные по качеству постоянные
магниты, широко применяемые в настоящее время в магнито-
магнитоэлектрических измерительных приборах и других устройствах,
в которых требуется сильное постоянное магнитное поле.
Исследование магнитных сплавов и химических соединений
открыло новые технические возможности применения магнит-
магнитных материалов. Так, например, было обнаружено, что некото-
некоторые сплавы из неферромагнитных элементов при определенном
соотношении между компонентами обладают сильным ферро-
ферромагнетизмом. Таковы сплавы марганец-висмут, марганец-сурь-
марганец-сурьма, хром-теллур и др.
Таблица 7
Магнитно-мягкие
материалы
Железо
Сплав кремний-же-
кремний-железо
То же, отожженный
в водороде
78%-ный пермаллой
Супермаллой
Состав
99,9 % Fe
96,7 % Fe; 3,3 % Si
96,7 %Fe; 3,3% Si
78 % Ni; 22 % Fe
79 % Ni; 5 % Mo;
16% Fe
Проницаемость
на-
чаль-
чальная
200
600
1500
8000
100 000
макси-
маль-
мальная
5000
10000
40000
100000
800 000
Индук-
Индукция при
насы-
насыщении,
Тл
2,15
2,0
2,0
1,0
0,80
Коэр-
Т ТТЛ" Т* ТТТС
1-Ц-11 Ий-
ная
сила,
А/м
80
16
8,0
4,0
0,32
Таблица 8
Высококоэрцитивные
сплавы
Вольфрамовая сталь
Сплав алии
Сплав алнико 5
Сплав платина-ко-
платина-кобальт
Сплав магнико
Состав
6 % W; 0,7 % С; 0,3 % Мп; 93 % Fe
25% Ni; 12% Al;63%Fe
8% Al; 14% Ni; 24% Co; 3% Cu;
51 % Fe
77% Pt; 23% Co
13,5% Ni, 9% Al; 24% Co;
3 % Cu; ~ 50 % Fe
Коэрци-
Коэрцитивная
сила,
А/м
5200
40000
44000
210000
56 000
Остаточ-
Остаточная ин-
индукция,
Тл
1,0
0,70
1,25
0,45
1,3
Второе важное достижение заключается в получении фер-
ферритов (ср. § 119). Они представляют собой ферромагнитные хи-
химические соединения типа МеО-РегОз, где Me — один из (или
смесь) двухвалентных катионов Mn, Co, Ni, Cu, Mg, Zn, Cd, Fe.
§113 МАГНИТНЫЕ ЗАРЯДЫ ФОРМАЛЬНАЯ 1ЕОРИЯ МАГНЕТИЗМА 247
В отличие от железа и других ферромагнитных металлов фер-
ферриты являются магнитными полупроводниками (§ 151) и имеют
большое удельное электрическое сопротивление порядка 102 —
—106 Ом-см. Этим и обусловлено большое техническое значение
ферритов. Ферромагнитные металлы нельзя использовать в ра-
радиотехнике высоких частот вследствие их большой электропро-
электропроводности и возникающих отсюда больших потерь на вихревые
токи (см. § 132). Ферриты же лишены указанного недостатка и
позволяют по-новому решать ряд задач радиотехники.
§ 113. Магнитные заряды.
Формальная теория магнетизма
На ранней стадии исследований магнетизма предполагали,
что причины магнитного взаимодействия токов между собой и
причины взаимодействия магнитов различны. Взаимодействие
магнитов объясняли существованием в них магнитных зарядов
и считали, что в природе существуют два вида «магнитных заря-
зарядов», причем одноименные магнитные заряды отталкиваются, а
разноименные притягиваются. Заряды, сосредоточенные в том
конце магнитной стрелки, которая указывает на север, назвали
северными, находящиеся на другом конце магнитной стрелки —
южными.
Однако сразу же после открытия магнитного взаимодей-
взаимодействия токов Ампер высказал предположение, что причина вза-
взаимодействия магнитов — та же, что и причина взаимодей-
взаимодействия проводников с током, и что внутри магнитов имеются
мельчайшие замкнутые электрические токи (молекулярные то-
токи Ампера). Дальнейшие исследования магнетизма подтвердили
правильность гипотезы Ампера и показали, что в природе нет
«магнитных зарядов». В соответствии с этим мы и начали изу-
изучение магнитных явлений с исследования магнитного поля то-
токов. Теория магнетизма, основанная на представлениях о маг-
магнитных зарядах и использующая чисто внешнее, формальное
сходство взаимодействия магнитов с взаимодействием вообра-
воображаемых магнитных зарядов, может быть названа формальной
теорией магнетизма.
Пользуясь приемом, описанным в § 80, легко получить карти-
картины линий поля, создаваемого постоянными магнитами. Пример
такой картины приведен на рис. 178. Подобные опыты показы-
показывают, что линии поля входят и выходят из магнитов преимуще-
преимущественно вблизи их концов. Это обстоятельство привело к пред-
представлению о существовании в магнитах двух полюсов, северного
и южного, вокруг которых распределяются магнитные заряды.
Чем больше отношение длины магнита к его диаметру, тем
в меньшей части магнита сосредоточены его магнитные заряды.
248
МАГНЕТИКИ
ГЛ XI
Поэтому для очень длинных и тонких магнитов можно прибли-
приближенно говорить о точечных «магнитных зарядах», расположен-
расположенных на концах магнита.
Взаимодействие полюсов длинных и тонких магнитов было
исследовано на опыте Кулоном, который пришел к заключению,
что магнитные заряды взаимодействуют по тому же закону, что
Рис 178 Линии поля прямого магнита
и электрические заряды: сила взаимодействия двух точечных
«магнитных зарядов» направлена вдоль линии, соединяющей
заряды, и обратно пропорциональна квадрату расстояния меж-
между зарядами.
= /—5-г. A13.1)
Здесь mi и тп2 — величины обоих «магнитных зарядов» или ко-
количества магнетизма, а / — коэффициент пропорциональности.
Напряженность магнитного поля Н определяется, аналогич-
аналогично напряженности электрического поля в электростатике, соот-
соотношением
F = тН, A13.2)
где F — сила, действующая на «магнитный заряд» m
Так как нельзя отделить друг от друга магнитные заряды
противоположных знаков, то намагничивание вещества в фор-
формальной теории объясняют тем, что атомы и молекулы по своим
магнитным свойствам подобны элементарным магнитным дипо-
диполям, т.е. двум одинаковым по модулю, но разным по знаку маг-
магнитным зарядам, смещенным друг относительно друга на малый
отрезок 1 Магнитные свойства таких диполей характеризуют их
магнитным моментом р^, определяемым аналогично моменту
§113 МАГНИТНЫЕ ЗАРЯДЫ ФОРМАЛЬНАЯ ТЕОРИЯ МАГНЕТИЗМА 249
электрических диполей:
p'm = ml. A13.3)
Магнитный момент считается направленным от отрицательного
(южного) магнитного заряда к положительному (северному).
Чтобы установить связь между магнитными действиями ди-
диполей и магнитными действиями токов, можно поступать по-
разному. Выбранный ниже способ кажется нам наиболее есте-
естественным, хотя он и не является единственным.
Коэффициент пропорциональности в формуле A13 1) зави-
зависит от выбора единиц. В абсолютной системе СГС полагают / =
= 1 и таким образом определяют единицу магнитного заряда.
Единичный магнитный заряд есть такой заряд, который, будучи
точечным, действует на равный ему точечный магнитный заряд,
удаленный на расстояние единицы A см) с силой, равной еди-
единице A дин). В системе СИ / является размерной величиной,
не равной единице.
Так как единицы напряженности Н (ампер на метр) и силы
jP (ньютон) в системе СИ уже установлены, то из A13.2) полу-
получается единица количества магнетизма: ныотон-метр на ампер
(Н-м/А). Ее размерность, выраженная через основные единицы,
есть L2MT~2I~2 и совпадает с размерностью потока магнитной
индукции (ср. таблицу Приложения 2 в конце книги), измеряе-
измеряемой в веберах (Вб). Поэтому и единица количества магнетизма
в системе СИ есть вебер (Вб). Единица магнитного момента ди-
диполя есть вебер-метр (Вб-м).
Поскольку теперь единицы для всех величин в формуле
A13.1) установлены, коэффициент пропорциональности / по-
получает вполне определенное значение. Для вакуума оно равно
/ = 1/D7фо), где hq — введенная ранее магнитная постоянная.
Таким образом, закон Кулона для взаимодействия точечных
магнитных зарядов в вакууме в системе СИ имеет вид
- <ш-4>
аналогичный закону взаимодействия точечных электрических
зарядов (§ 4). Если магнитные заряды находятся не в вакууме,
а в однородной среде с магнитной проницаемостью ц, то вместо
Но в формулу войдет произведение ццо
Найдем теперь связь между магнитным моментом элемен-
элементарного тока (§ 82) pm = iSn и магнитным моментом р^ = ml
элементарного диполя, эквивалентного по магнитным действи-
действиям элементарному току.
В дальнейшем мы будем считать, что диполи и токи находят-
находятся в вакууме (или, что практически то же самое, в атмосферном
воздухе) О влиянии окружающей среды на магнитные взаимо-
взаимодействия будет кратко сказано в следующем параграфе.
250 МАГНЕТИКИ ГЛ. XI
Рассмотрим сначала механические силы в магнитном поле.
На элементарный ток действует пара сил (§ 85, формула (85.2))
М - [ртВ],
пропорциональная магнитной индукции В. В случае элементар-
элементарного магнитного диполя из формул A13.2) и A13.3) следует, что
пара сил, действующих на магнитный диполь, есть (ср. § 15)
М = [р^Н]. A13.5)
Она пропорциональна напряженности поля Н. Так как В =
= ?/оН, то сравнение обеих формул дает
Pm=W)Pm- (П3.6)
Полученное соотношение выражает условие эквивалентности
элементарных токов и элементарных магнитных диполей.
В системе СГС /ио = 1. Поэтому в вакууме магнитный момент
элементарного тока и момент эквивалентного ему магнитного
диполя равны друг другу: р^ = pm = iSn.
Такой же результат A13.6) мы получим, рассматривая силы, действую-
действующие на элементарный ток и элементарный магнитный диполь в неоднород-
неоднородном магнитном поле. Действительно, согласно § 85, на элементарный ток
действует сила
F = (pmgrad)B. (85.4а)
Для магнитного диполя мы должны опять исходить из соотношений A13.2)
и A13.3), которые аналогичны формулам (9.2) и A5.1) электростатики. По-
Поэтому, рассуждая так же, как и в § 15, мы получим формулу типа A5.6),
с тем отличием, что вместо момента электрического диполя в нее войдет
момент магнитного диполя р'го, а вместо напряженности электрического
поля — напряженность магнитного поля Н:
F = (р™ grad)H. A13.7)
Сравнивая формулы A13.7) и (85.4а), мы видим, что силы в обоих слу-
случаях будут одинаковы, если рт и р'го связаны соотношением эквивалент-
эквивалентности A13.6).
Элементарные токи и магнитные диполи, моменты которых
связаны соотношением A13.6), не только испытывают одинако-
одинаковые механические силы в магнитных полях, но и сами создают
во внешнем пространстве одинаковые магнитные поля. Покажем
это на конкретном примере. Рассмотрим элементарный контур
с током и точку, лежащую на его оси на расстоянии г от центра
контура (см. рис. 124). Напряженность магнитного поля в этой
точке направлена вдоль оси тока и равна (§ 82, формула (82.1))
Пусть теперь имеется магнитный диполь, совпадающий с эле-
элементарным током, с моментом р'т, параллельным моменту эле-
элементарного тока рт. Для вычисления создаваемой им напря-
напряженности магнитного поля мы имеем формулы A13.4), A13.2)
§ 113 МАГНИТНЫЕ ЗАРЯДЫ. ФОРМАЛЬНАЯ ТЕОРИЯ МАГНЕТИЗМА 251
и A13.3), которые аналогичны формулам электростатики D.1),
(9-2) и A5.1), лежащим в основе вычисления напряженности по-
поля электрического диполя. Поэтому мы можем сразу воспользо-
воспользоваться формулой B5.5), заменив в ней р на величину момента
магнитного диполя р'т, ео — на цо, и положив cos a = 1 (так как
мы ищем поле в точке, лежащей на оси диполя). Тогда
Это поле направлено вдоль оси диполя (На — 0), т.е. так же,
как и поле элементарного тока. Учитывая соотношение A13.6),
находим, что оба поля Н и Н' равны друг другу. Можно пока-
показать, что найденный результат справедлив не только для точек
на оси диполя (тока), но и в произвольной точке поля.
Если контур с током имеет конечные размеры, то его все-
всегда можно представить как совокупность элементарных замкну-
замкнутых токов одинакового направления, текущих на поверхности,
ограниченной контуром с током (ср. рис. 157). Так как каждый
элементарный ток эквивалентен некоторому элементарному маг-
магнитному диполю, то весь контур с током эквивалентен магнит-
магнитному листку, или магнитному двойному слою. Обе стороны та-
такого слоя имеют магнитные заряды противоположных знаков,
разведенные на малое расстояние. Если контур с током плоский
и поверхность, опирающаяся на контур, есть плоскость с пло-
площадью S, то, согласно соотношению эквивалентности A13.6),
магнитный момент магнитного листка есть
т = noiSn. A13.9)
Здесь п — единичный вектор нормали к плоскости листка, на-
направление которого связано с направлением тока в контуре пра-
правилом правого буравчика (см. рис. 125).
Если опирающаяся на контур поверхность не есть плоскость,
то под Sn нужно понимать величину
Sn= lim VA5ii/»= [vdS, A13.10)
где v — единичная нормаль к элементу поверхности dS. При
этом сама поверхность может быть произвольной, важно только,
чтобы она опиралась на данный контур с током. Магнитный
момент, отнесенный к единице поверхности магнитного листка,
называется мощностью магнитного листка. Она равна
m = цогп. A13.11)
Единица мощности m есть вебер на метр (Вб/м).
Магнитные действия трехмерных тел в формальной теории
магнетизма, по аналогии с поляризацией диэлектриков (§ 39),
252 МАГНЕТИКИ ГЛ XI
характеризуют магнитной поляризованностъю. Она равна маг-
магнитному моменту, создаваемому магнитными диполями в едини-
единице объема,
i?m = ^5>m> A13.12)
где т — рассматриваемый объем. Так как единица магнитного
момента есть Вб-м, а т — м3, то единица магнитной поляри-
зованности есть Вб/м2. Она совпадает с единицей магнитной
индукции — тесла (Тл).
Однако в действительности, как мы знаем, существуют мо-
молекулярные токи, и, исходя из этих представлений, мы уже
ввели характеристику намагничивания — вектор намагничен-
намагниченности I (§ 103), определяемый формулой A03.1). Связь между
двумя этими величинами получается непосредственно из соотно-
соотношения эквивалентности элементарных токов и диполей A13.6).
Мы имеем
В системе СГС магнитная поляризованность и намагниченность
совпадают друг с другом.
Развивая внешнюю аналогию между электрическими и маг-
магнитными диполями, можно построить полную теорию магнит-
магнитного поля покоящихся магнитных зарядов, или магнитостатику.
При этом магнитные действия контуров с постоянными тока-
токами можно описывать с помощью представлений о магнитных
диполях или соответственно магнитных листках и магнитно-по-
магнитно-поляризованных телах.
Формальной теорией магнетизма пользуются иногда и в на-
настоящее время, так как многие результаты в ней можно полу-
получить непосредственно из аналогии с электростатикой. Однако
при этом всегда нужно помнить, что на самом деле магнитные
явления обусловлены взаимодействием токов. Это, в частности,
проявляется в том, что эквивалентность между токами и маг-
магнитными диполями существует только во внешнем простран-
пространстве по отношению к контурам с током и намагниченным те-
телам и не имеет места внутри них. Так, например, рассматривая
соленоид с током и равновеликий с ним эквивалентный магнит,
мы найдем, что создаваемые ими магнитные поля во внешнем
пространстве совпадают. Внутри соленоида, вследствие непре-
непрерывности линий индукции, магнитное поле направлено от юж-
южного конца соленоида к северному. В постоянном же магните
с точки зрения формальной теории, вследствие магнитной по-
поляризации, на торцах находятся магнитные заряды. Поэтому
магнитное поле внутри магнита будет направлено от северного
конца к южному, т.е. противоположно полю в соленоиде
ВЛИЯНИЕ СРЕДЫ НА МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
253
Рис 179 Постоянный магнит есть
полости, непроницаемой для внеш-
внешней среды
§ 114. Влияние среды на магнитное взаимодействие
Взаимодействие токов и магнитов зависит от свойств окру-
окружающей среды. Это происходит потому, что окружающая сре-
среда намагничивается полем, создаваемым токами и магнитами, и
сама становится источником магнитного потока, вызывающего
дополнительные силы.
Если в безграничном магнетике имеются два контура с то-
током, то суммарная плотность магнитного потока, создаваемого
каждым из этих токов, как мы видели (§ 105), выражается ин-
индукцией В = ццоН, и поэтому
сила взаимодействия двух то-
токов пропорциональна магнит-
магнитной проницаемости fj, окружаю-
окружающей среды.
Так как всякий постоянный
магнит есть система токов (эле-
(элементарных токов), то может по-
показаться, что и силы, действую-
действующие между магнитами, также
пропорциональны р. Однако в система молекулярных токов внутри
действительности эта зависи-
зависимость сложнее, так как между
токами и магнитами существует важное различие: окружаю-
окружающая среда проникает внутрь контуров с током, но не проникает
внутрь магнитов Поэтому внесение любого магнита внутрь маг-
магнетика неизбежно нарушает сплошность магнетика и делает его
неоднородным. Магнит внутри магнетика есть полость, запол-
заполненная веществом, имеющим иную магнитную проницаемость
fj,', нежели у окружающей среды (рис. 179).
Вопрос существенно упрощается, если магниты намагниче-
намагничены до насыщения. Тогда у! ~ 1 и магнит можно представить
в виде полости, внутри которой имеется вакуум Чтобы лучше
выяснить сущность дела, мы в дальнейшем ограничимся только
этим случаем.
Рассмотрим сначала взаимодействие тока и магнита Сила,
действующая на магнит (т.е. на молекулярные токи), определя-
определяется значением магнитной индукции внутри магнита. Она скла-
складывается из индукции ?/оН, создаваемой током в вакууме, и
индукции В', вызываемой намагниченной средой. Но В' суще-
существенно зависит от формы полости Поэтому и сила, действую-
действующая на магнит, зависит от формы магнита, и никакого общего
закона влияния магнитной проницаемости среды на силу, дей-
действующую на магниты, дать нельзя.
Рассмотрим частный случай длинного магнита, расположен-
расположенного параллельно полю (рис. 180). Напряженность поля внутри
254
МАГНЕТИКИ
ГЛ. XI
магнита Щ (т.е. в щели, параллельной полю, ср. § 104) есть на-
напряженность поля внутри магнетика, которая совпадает с на-
напряженностью поля До в вакууме. Поэтому индукция внутри
магнита равна //оДои сила F взаимодействия между током и
магнитом внутри магне-
магнетика будет такая же, как
и в вакууме (Fo):
F=^F0, A14.1)
и не будет зависеть от
магнитной проницаемо-
проницаемости среды.
Согласно третьему
закону Ньютона на ток
Рис.180. Контур с током и постоянный маг- со стороны магнита дей.
нит в магнетике тр
ствует сила ~г , равная
по модулю, но противоположная по направлению. Но сила,
действующая на ток, определяется индукцией В = /i/uoH. От-
Отсюда следует, что индукция, создаваемая длинным магнитом,
не зависит от ц, а, следовательно, напряженность поля магнита
уменьшается в ц раз:
Н = Но///. A14.2)
Перейдем теперь к взаимодействию двух магнитов. Рас-
Рассмотрим два очень длинных магнита, оси которых совпадают
(рис. 181). Если бы магнита 2 не
было вовсе, то магнит 1 создавал
бы во внешнем пространстве на-
напряженность поля Н\а, выражае-
выражаемую формулой A14.2). Эта на-
напряженность поля будет и внутри
магнита 2 (ср. § 104):
Д2г = Н\а = HqJ fJt.
Рис. 181. Два постоянных магни-
Поэтому индукция внутри та внутри магнетика
магнита 2 будет hqHq/ц, т.е. в \х
раз меньше, чем в вакууме, а, следовательно, сила взаимодей-
взаимодействия полюсов длинных магнитов обратно пропорциональна
магнитной проницаемости среды:
F = FQ/(i. A14.3)
Если бы магниты имели другую форму, то и результаты по-
получились бы иные.
В случае магнитов, намагниченных не до насыщения, внутри
рассмотренных выше полостей имелось бы вещество магнита с
д'^1и силы взаимодействия зависели бы еще от д'.
§ 115 ПРИРОДА МОЛЕКУЛЯРНЫХ ТОКОВ 255
§ 115. Природа молекулярных токов
Для объяснения намагничивания вещества мы положили в
основу представление о том, что внутри атомов и молекул су-
существуют замкнутые электрические токи (молекулярные то-
токи). Рассмотрим теперь, какую физическую природу имеют эти
токи.
Мы уже говорили (§ 7), что все атомы построены из поло-
положительно заряженных ядер, в которых сосредоточена практиче-
практически вся масса атома, и некоторого количества электронов. Число
электронов в атоме таково, что полный их отрицательный заряд
равен положительному заряду ядра, так что атом в нормальном
состоянии электрически нейтрален.
Заряд ядра, а следовательно, и количество электронов в ато-
атоме тесно связаны с положением элемента в периодической си-
системе. Если Z — порядковый номер элемента, а е — заряд элек-
электрона, то заряд ядра равен Л-Ze и атом содержит Z электронов.
Так, например, атом водорода (Z = 1) имеет всего один элек-
электрон, атом Na (Z = 11) — 11 электронов, атом железа [Z = 26) —
26 электронов.
Электроны в атоме находятся в состоянии непрерывного дви-
движения. Для многих целей, в том числе и для объяснения ряда
магнитных явлений, с достаточным приближением можно счи-
считать, что электроны обращаются вокруг ядра по круговым или
эллиптическим орбитам, подобно планетам Солнечной системы
(планетарная модель атома). Каждый из атомных электронов
движется по своей собственной орбите, а разные электронные
орбиты лежат в различных плоскостях.
Такие электроны, обращающиеся по орбитам, представля-
представляют собой замкнутые электрические токи, и потому естественно
предположить, что именно они являются молекулярными то-
токами (существование которых предполагал еще Ампер), ответ-
ответственными за намагничивание вещества. В § 116 мы рассмотрим
опыты, доказывающие, что это действительно так.
Так как электронам присущ не только заряд, но еще и мас-
масса, то каждый орбитально движущийся электрон обладает не
только магнитным моментом (как и всякий замкнутый ток), но
еще и определенным механическим моментом или вращатель-
вращательным импульсом, т.е. подобен волчку.
Между магнитным моментом электрона на орбите и его мо-
моментом импульса существует простая связь. Выясним ее на при-
примере круговой орбиты (рис. 182). Если электрон совершает и
оборотов в секунду, то сила тока равна г = ей.
Орбитальный магнитный момент электрона рт есть
рт = evS,
256
МАГНЕТИКИ
ГЛ. XI
где S — площадь орбиты. Если, как показано на рис. 182, элек-
электрон обращается по часовой стрелке, то ток направлен против
часовой стрелки (заряд электрона отрицательный) и орбиталь-
орбитальный магнитный момент направлен, в соответствии с правилом
правого буравчика, перпендикулярно
к плоскости орбиты снизу вверх.
Движущийся по орбите электрон
обладает орбитальным механическим
моментом (или моментом импульса),
равным
I — тшг = 2mvS,
где ш = 2irv — угловая скорость элек-
Рис. 182. Магнитный (Рт) трона. Направление вектора 1 также
и механический A) моменты подчиняется правилу правого бурав-
буравэлектронной орбиты
чика. Из рис. 182 видно, что направ-
направления 1 и рт противоположны. Из
сказанного следует, что отношение магнитного момента орбиты
к ее механическому моменту не зависит от и и 5 и определяется
только универсальными постоянными:
Г = pm/l = ~e/2m, A15.1)
где е/т — отношение заряда электрона к его массе, равное
1,76 ¦ 1011 Кл/кг. В этой формуле знак минус выражает противо-
противоположность направлений рт и 1. Отношение
Г = рт/1 называют гиромагнитным отно-
отношением.
Формула A15.1) выведена нами для кру-
круговой орбиты. Однако легко показать, что
она справедлива и для эллиптических орбит.
Рассмотрим теперь, что произойдет, если
на электрон, вращающийся на орбите, будет
действовать внешнее магнитное поле.
На замкнутый ток в магнитном поле дей-
действует пара сил (§ 85). Так как электрон на
орбите подобен волчку, то под действием этой
пары сил он будет совершать, как и всякий
волчок, прецессионное движение, т.е. полу-
получит дополнительное равномерное вращение,
при котором вектор 1 будет описывать конус вокруг направле-
направления индукции В с некоторой угловой скоростью tl (рис. 183).
Простой расчет показывает (см. Добавление 7), что если вра-
вращающаяся частица имеет отрицательный заряд (электрон), то
вектор угловой скорости С1 направлен параллельно В, а угловая
скорость прецессии равна
П = еВ/2т. A15.2)
Рис. 183. Ларморо-
ва прецессия
§116 МАГНИТОМЕХАНИЧЕСКОЕ И МЕХАНОМАГНИТНОЕ ЯВЛЕНИЯ 257
Скорость этой прецессии не зависит от ориентировки орбиты,
т.е. от угла между векторами 1 и В.
Сформулированный нами результат составляет содержание
теоремы Лармора: действие магнитного поля на движущийся
электрон заключается в наложении на первоначальное движе-
движение равномерного вращения вокруг направления внешнего маг-
магнитного поля.
Таким образом, внешнее магнитное поле не вызывает непо-
непосредственно переориентировки электронных орбит, а вызывает
только их прецессию. Однако если имеются какие-либо при-
причины, тормозящие прецессию, например соударения с соседни-
соседними атомами, то электронная орбита будет постепенно изменять
свою ориентировку и будет стремиться в конце концов устано-
установиться таким образом, чтобы магнитный момент орбиты оказал-
оказался параллельным магнитному полю.
Атом в целом представляет собой совокупность электронов и
поэтому обладает и магнитным, и механическим моментами, ко-
которые представляют собой векторные суммы моментов отдель-
отдельных электронов атома. Во внешнем поле атомы будут сначала
прецессировать, по затем, под действием соударений, ориенти-
ориентироваться в направлении поля, отчего вещество приобретет опре-
определенный суммарный магнитный момент, т.е. намагнитится.
§ 116. Магнитомеханическое и механомагнитное
явления
Рассмотренные выше представления о том, что молекуляр-
молекулярными токами являются движущиеся электроны атома, приво-
приводят к заключению, что всякое изменение намагниченности ве-
вещества должно сопровождаться определенными механическими
явлениями. Действительно, механический момент электронной
орбиты 1 связан с ее магнитным моментом рт соотношением
A15.1). Если 1 — вектор намагниченности, а т — объем тела,
то полный магнитный момент тела есть Ir. Он равен векторной
сумме моментов всех молекулярных токов:
Согласно A15.1) этому магнитному моменту соответствует ме-
механический момент импульса L:
Если тело вначале было не намагничено, то I = 0 и суммарный
механический момент всех элементарных токов L = 0. При на-
намагничивании элементарные токи приобретают суммарный ме-
механический момент L, выражаемый формулой A16.1). Йо ориен-
258
МАГНЕТИКИ
ГЛ XI
Рис 184 Схема
опыта для наблю-
наблюдения магнитомеха-
нического явления
тирование элементарных токов происходит под действием соуда-
соударений, т.е. внутренних сил, и поэтому должен соблюдаться закон
сохранения момента импульса. Это значит, что намагничивае-
намагничиваемое тело должно приобрести момент импуль-
импульса —L, т.е. прийти во вращение вокруг оси,
параллельной вектору намагниченности I.
Возникновение вращения при намагни-
намагничивании получило название магнитомеха-
нического явления. Оно совершенно подоб-
подобно известному опыту в механике со скамьей
Жуковского, если человек, сидящий на вра-
вращающейся скамье, поворачивает раскручен-
раскрученный маховик, то скамья с экспериментатором
вследствие сохранения момента импульса си-
системы приходит во вращение.
Магнитомеханическое явление было впер-
впервые наблюдено на опыте Эйнштейном и Гаа-
Гаазом в 1915 г. В этих опытах небольшой желез-
железный цилиндрик был подвешен на тончайшей
нити и помещен внутри соленоида (рис. 184).
При намагничивании цилиндра он начинал поворачиваться,
причем направление вращения изменялось при изменении на-
направления магнитного поля. Поворот цилиндра отмечался при
помощи небольшого зеркальца, скрепленного с цилиндром.
Возникающие при этом угловые скорости весьма малы. Так,
например, для железного цилиндра диаметром несколько мил-
миллиметров в поле напряженности 10 А/м угловая скорость имеет
порядок только 10~3 рад/с. Поэтому,
чтобы усилить наблюдаемый эффект,
Эйнштейн и Гааз использовали явле-
явление механического резонанса: частоту
крутильных колебаний цилиндра делали
равной частоте переменного тока.
Наряду с магнитомеханическим яв-
явлением существует и ему обратное явле-
явление, механическое вращение тела вызы-
вызывает намагничивание этого тела.
Известно, что если вращающийся
волчок заставить участвовать в дополни-
дополнительном вращении вокруг некоторой оси
(вынужденная прецессия), то на волчок
начинает действовать пара сил, стре-
стремящаяся уменьшить угол между осью
волчка и осью вынужденной прецессии и установить волчок та-
таким образом, чтобы обе эти оси были параллельны (рис. 185).
Рис 185 Вынужденная
прецессия волчка
§ 117 МАГНИТНЫЙ И МЕХАНИЧЕСКИЙ МОМЕНТЫ ЭЛЕКТРОНА 259
Так как атомы обладают определенным моментом импульса,
то при вращении тела они, подобно волчку, будут ориентиро-
ориентироваться, а, следовательно, тело намагнитится.
Намагничивание при вращении (механемагнитное явление)
действительно наблюдается на опыте и было впервые обна-
обнаружено Барнеттом. В этих опытах небольшой железный ци-
цилиндр приводился в быстрое вращение вокруг своей оси и затем
измерялось намагничивание, вызванное вращением. За коли-
количественную меру наблюдаемого эффекта обычно принимают на-
напряженность внешнего магнитного поля Н, вызывающего то же
намагничивание, что и вращение (эквивалентное поле). Это эк-
эквивалентное поле оказывается весьма малым. Так. например,
даже при скорости вращения в 6000 об/мин оно равно приблизи-
приблизительно 10~2 А/м, т.е. примерно в тысячу раз меньше магнитного
поля Земли.
Механомагнитное явление (так же как и магнитомеханиче-
ское) доказывает, что молекулярные токи, обусловливающие на-
намагничивание, обладают механиче-
механическим моментом Далее, определяя
знак возникающего намагничивания,
можно установить и знак заряда
движущихся частиц. Так, например,
если частицы имеют отрицательный
заряд, то магнитный и механический
моменты каждого элементарного тока
направлены противоположно (§ 115),
и поэтому магнитный момент тела
и направление эквивалентного поля
будут также противоположны угловой
скорости вращения (рис. 186 а). Если
же заряд частиц положительный, то
магнитный момент тела и угловая
скорость вращения должны быть
направлены одинаково (рис. 18G6). Опыты показывают, что
возникающее намагничивание соответствует отрицательному
заряду частиц, и поэтому механомагнитное явление, так же
как и магнитомеханическое, подтверждает предположение
о том, что намагничивание тел обусловлено движущимися
электронами.
б е>0
Рис 186 Механомагнит-
Механомагнитное явление
§ 117. Магнитный и механический моменты электрона
Детальное исследование магнитомеханического и механомаг-
нитного явлений показало, однако, что вопрос о природе элемен-
элементарных токов более сложен, чем казалось вначале.
260 МАГНЕТИКИ ГЛ XI
Оба эти явления зависят от величины гиромагнитного от-
отношения Г. Поэтому по данным опыта можно определить гиро-
гиромагнитное отношение и сравнить его с теоретически ожидаемым
значением для электронной орбиты A15.1). Первые же опыты в
этом направлении показали, что экспериментальное значение Г
в ферромагнетиках не согласуется с A15.1) и оказывается при-
приблизительно в два раза бблыпим. Последующие многочисленные
определения гиромагнитного отношения подтвердили этот ре-
результат. Аномальное значение гиромагнитного отношения при-
привело к заключению, что внутри атома, помимо орбитального
движения электрона, имеется и другой тип движения, приво-
приводящий к возникновению магнитного и механического моментов.
Поэтому было сделано предположение, что самому электрону,
как таковому, присущи и магнитный, и механический моменты,
причем их отношение для электрона Ге равно
Ге = -е/т. A17.1)
Впоследствии это предположение полностью подтвердилось.
Таким образом, электрон по своим магнитным и механическим
свойствам оказывается подобным заряженному телу, вращаю-
вращающемуся вокруг своей оси. Поэтому вначале возникло представ-
представление о «вращающемся электроне», и в физической литературе
появился термин спин электрона, обозначающий собственный
механический момент количества движения электрона.
Следует, однако, отметить, что, хотя термин спин электрона
широко применяется и в настоящее время, с ним уже не связы-
связывают представление о механическом вращении электрона Раз-
Развитие современной квантовой физики атома показало, что пере-
перенесение образов макроскопической механики в область атомного
мира невозможно. В настоящее время мы рассматриваем элек-
электрон как одну из элементарных частиц, которая характеризуется
своим зарядом, массой, магнитным и механическим моментами.
Магнитный и механический моменты электрона проявляют-
проявляются не только в магнитных свойствах вещества, но и в других
многочисленных явлениях и, в частности, в особенностях опти-
оптических спектров Поэтому существование этих свойств у элек-
электрона в настоящее время установлено с большой надежностью.
Совокупность всех имеющихся опытных данных, в согласии
с выводами квантовой механики, приводит к следующим резуль-
результатам. Направление собственного механического момента элек-
электрона 1е (спина) квантуется. А именно, проекция спина на вы-
выделенное направление (например, на направление магнитного
поля) /ен может принимать только два различных значения:
Здесь h - универсальная постоянная квантовой теории — по-
§ 118 ОБЪЯСНЕНИЕ ПАРА- И ДИАМАГНЕТИЗМА 261
стоянная Планка, равная
h = 6,62 • 1(Г34 Дж • с = 6,62 • 1(Г27 эрг • с.
Поэтому квантуется и направление собственного магнитного мо-
момента электрона рше Его проекция на направление магнитного
поля рея (где индекс т для краткости мы опускаем), согласно
формулам A17.1) и A17.2), равна
РеЯ = 1енГе = ±А ±, (Ц7.3)
и может иметь тоже только два значения. Величина
»в = ~ (П7.4)
получила название магнетона Бора. Она равна
цв = 9,27 • 1(Г24 А • м2 = 9,27 • 1(Г21 СГС^В.
Таким образом, проекция собственною магнитного момента
электрона на направление магнитного поля может равняться
только одному магнетону Бора- +цв или — цв-
Понятие магнетона было введено Бором задолго до открытия спина
электронов в элементарной квантовой теории, в которой рассматривается
движение электронов в атоме по определенным круговым или эллипти-
эллиптическим орбитам вокруг положительного ядра При этом момент импуль-
импульса электрона / на орбите квантуется, т е может принимать только дис-
дискретные значения I = nh/2ir, где h постоянная Планка, а п = 1,2,3,
Наименьший возможный механический момент есть h/2n, и ему, соглас-
согласно формуле A15 1), соответствует наименьший магнитный момент орбиты
{ej2m)hj2-K — he/(inm) А это и есть магнетон Бора цв Таким образом,
магнетон Бора есть наименьшее возможное значение магнитного момента,
которое можно назвать атомом магнитною момента Квантовая механика
отказывается от представления об электронных орбитах. Однако величи-
величина магнетона Бора A17 4) в ней сохраняется как наименьшее изменение
проекции магнитного момента на направление магнитного поля
Мы видим, что магнетизм атомов обусловлен двумя причинами во-
первых, движением электронов в атоме и, во-вторых, магнетизмом самих
электронов, которые являются источниками магнитного поля независимо
от их движения внутри атома
§ 118. Объяснение пара- и диамагнетизма
Выяснив основные магнитные свойства атомов, мы можем
перейти к объяснению магнитных свойств вещества.
Парамагнитные свойства вещества объясняются наличием
у атомов определенного магнитного момента. В отсутствие
магнитного поля магнитные моменты атомов в парамагнетике
вследствие теплового движения ориентированы совершенно бес-
беспорядочно (рис. 187 а). Поэтому магнитный момент тела, рав-
равный векторной сумме моментов отдельных атомов, близок к ну-
нулю, а, следовательно, тело не намагничено
262
МАГНЕТИКИ
ГЛ. XI
a
Рис
\
\
. 187.
¦
\
/
Объ
Во внешнем магнитном поле на каждый атом действует па-
пара сил, стремящаяся установить магнитные моменты атомов па-
параллельно полю. В результате этого внутри парамагнетика воз-
возникает упорядоченное расположение атомов и намагниченность
становится не равной нулю
(рис. 187 6). При этом на-
направление намагниченности
I (от южного полюса к се-
северному) оказывается парал-
параллельным направлению ин-
индукции В, что характерно
для парамагнетиков.
Чем выше температура
парамагнетика, тем сильнее
Объяснение парамагнетизма тепловое движение атомов и,
следовательно, тем слабее их
ориентировка в данном поле, т.е. тем слабее намагничивание.
Этим объясняется уменьшение магнитной восприимчивости па-
парамагнетиков при нагревании.
Из сказанного видно, что объяснение парамагнетизма в точ-
точности совпадает с объяснением поляризации диэлектриков с
полярными молекулами (§ 48) и единственное различие заклю-
заключается лишь в том, что для диэлектрической поляризации суще-
существен электрический момент атомов, а для намагничивания --
их магнитный момент. Отметим, что исторически теория пара-
парамагнетизма была развита Ланжевеном раньше, нежели теория
диэлектриков, и лишь затем представления этой теории были
перенесены Дебаем на диэлектрики.
Остановимся подробнее на некоторых результатах теории па-
парамагнетизма. Пусть РтН есть среднее значение проекции маг-
магнитного момента атома рт на направление внешнего магнит-
магнитного поля. Тогда, рассуждая так же, как при выводе формулы
D8.1) (Добавление 2), для случая слабой ориентировки атомов
получим
Здесь Н' — напряженность поля, действующего на атом, Т —
термодинамическая температура, к — постоянная Больцмана.
Обозначим далее через п число атомов в единице объема веще-
вещества. Тогда магнитный момент единицы объема (намагничен-
(намагниченность) есть
С другой стороны, / = иН, где и — магнитная восприимчи-
восприимчивость. Так как, далее, все парамагнетики намагничиваются весь-
§
ОБЪЯСНЕНИЕ ПАРА- И ДИАМАГНЕТИЗМА
263
ма слабо, то в них различие между Л и Л' невелико, и можно
положить Н' « Н. Поэтому из A18.1) следует, что
х = 1/Н = С/Т, A18.2)
где введено обозначение
Эта формула выражает уже известный нам закон Кюри (§ ПО),
который получает в теории Ланжевена теоретическое объясне-
объяснение.
Несколько иной характер имеет парамагнетизм металлов. В металлах,
как мы знаем, существуют электроны проводимости, которые не принадле-
принадлежат отдельным атомам и образуют своеобразный электронный газ. Благо-
Благодаря наличию у электрона собственного магнитного момента этот электрон-
электронный газ обладает парамагнетизмом (парамагнетизм свободных электронов).
Однако изложенная выше теория Ланжевена неприменима к электронному
газу в металлах, так как движение электронов внутри металлов описывает-
описывается не классическими законами, а законами квантовой теории.
Рассмотрим теперь, каким образом объясняется существова-
существование диамагнетиков.
В § 109 мы видели, что характерным для диамагнети-
диамагнетиков является то обстоятельство, что вектор намагниченности I
направлен в них противоположно намагничивающему полю
S S S
N N N
Рис. 188. Объяснение диамагнетизма: а — взаимные направления вектора
намагниченности и намагничивающего поля в диамагнетиках; б — магнит-
магнитный диполь, соответствующий изменению магнитного момента электронной
орбиты вследствие ларморовой прецессии
(рис. 188 а). Такое поведение диамагнетиков невозможно объяс-
объяснить при помощи формальной теории магнетизма, т.е. в предпо-
264 МАГНЕТИКИ ГЛ XI
ложении, что внутри магнетиков существуют магнитные дипо-
диполи. Действительно, в этом случае нужно было бы допустить, что
диполи во внешнем поле устанавливаются так, что северные их
концы обращаются к северному же полюсу влияющего магнита,
а южные концы — к южному полюсу, или, иначе, что одноимен-
одноименные магнитные полюсы притягиваются, а не отталкиваются. На-
Напротив, существование диамагнетиков естественно объясняется
наличием молекулярных токов
Объяснение диамагнетизма было дано впервые также Лан-
жевеном. Основную идею его теории разъясняет рис. 188 б.
Рассмотрим какую-либо электронную орбиту внутри атома и
предположим, что в некоторый момент времени мы включили
внешнее магнитное поле. Движение электрона изменится, а
именно — возникнет ларморова прецессия; причем для случая
движения электрона (е < 0) вектор угловой скорости прецессии
ft будет направлен параллельно направлению поля В (§ 115). На
рис. 188 это соответствует дополнительному вращению электро-
электрона против стрелки часов (если смотреть сверху) Но вращение
отрицательной частицы против часовой стрелки есть ток, теку-
текущий по часовой стрелке. При этом северная сторона тока будет
расположена снизу, а южная — сверху, т.е. возникающий вслед-
вследствие прецессии дополнительный магнитный момент орбиты бу-
будет соответствовать диполю, у которого южный конец обращен
к южному полюсу магнита, а северный конец — к северному
полюсу (диамагнитный эффект). Таким образом, существова-
существование диамагнетизма вполне объясняется ларморовой прецессией.
Теория диамагнетизма Ланжевена объясняет диамагнетизм не
только качественно, но приводит и к правильному порядку ве-
величины магнитной восприимчивости.
Выше мы рассмотрели диамагнетизм, возникающий вследствие лармо-
ларморовой прецессии электронных орбит внутри атома Если вещество явля-
является металлом, то возникает еще дополнительный диамагнитный эффект,
обусловленный электронами проводимости Этот эффект был открыт те-
теоретически ЛД Ландау, который показал, что искривление путей элек-
электронов в магнитном поле, вызываемое силой Лоренца, приводит также к
появлению диамагнетизма (диамагнетизм свободных электронов) Расчеты,
однако, показывают, что этот диамагнетизм в три раза меньше парамагне-
парамагнетизма, обусловленного собственными магнитными моментами электронов
Поэтому диамагнетизм свободных электронов непосредственно на опыте не
наблюдается и электронный газ в металлах в результате одновременного
наложения обоих эффектов оказывается всегда парамагнитным
Суммируя сказанное выше, мы можем также понять, почему
одни вещества являются парамагнетиками, а другие — диамаг-
нетиками. Так как ларморову прецессию в магнитном поле ис-
испытывают все электроны любого атома, то атомы всех веществ
являются носителями диамагнитных свойств. Однако это еще
§ 119 ОБЪЯСНЕНИЕ ФЕРРОМАГНЕТИЗМА 265
не значит, что вещество будет диамагнетиком, так как атомы
имеют и постоянный суммарный магнитный момент, который
обусловливает их парамагнитные свойства. Если магнитный мо-
момент атомов велик, то парамагнитные свойства преобладают
над диамагнитными и вещество оказывается парамагнетиком.
Если магнитный момент мал, то преобладают диамагнитные
свойства и вещество является диамагнетиком. В частности, ато-
атомы всех инертных газов имеют полный магнитный момент, рав-
равный нулю. Поэтому для них имеется только один диамагнитный
эффект и все инертные газы диамагнитны.
§ 119. Объяснение ферромагнетизма
Перейдем теперь к объяснению ферромагнетизма.
Современная теория ферромагнетиков опиралась в своем
развитии на следующие основные опытные факты. Во-первых,
мы видели в § 110, что у некоторых ферромагнетиков можно
изменять намагниченность от начального нулевого значения до
огромного значения насыщения под действием ничтожного на-
намагничивающего поля. Это обстоятельство характерно для фер-
ферромагнетиков и резко отличает их от парамагнетиков. Укажем
для сравнения, что нормальная парамагнитная соль, например
FeSO4, при комнатной температуре под действием поля в 10 А/м
увеличивает свою намагниченность в сотни миллионов раз мень-
меньше, чем некоторые магнитно-мягкие ферромагнитные сплавы.
Вторая особенность касается магнитного момента атомов
ферромагнитных веществ. Прямые опыты показывают (опыты
Штерна и Герлаха), что магнитные моменты атомов ферромаг-
ферромагнитных веществ имеют тот же порядок величины, что и ато-
атомы парамагнетиков, и измеряются немногими магнетонами Бо-
Бора цв- Отсюда следует, что ферромагнетизм нельзя объяснить
при помощи теории, подобной теории парамагнетизма, и что
ферромагнитные свойства не обусловлены наличием магнитного
момента атома в целом
Третий важный опытный факт связан с величиной гиромаг-
гиромагнитного отношения Г. В ферромагнетиках Г оказывается при-
приблизительно в два раза большей, чем ожидаемое теоретически
значение для электронных орбит, и соответствует отношению
собственных магнитного и механического моментов электрона.
Это обстоятельство указывает, что намагничивание ферромаг-
ферромагнетиков обусловливается очень сильной ориентировкой соб-
собственных магнитных моментов электронов (электронных спи-
спинов), но не магнитных моментов атомов в целом.
Согласно современным представлениям, надежно обоснован-
обоснованным на опыте, сущность ферромагнетизма заключается в том,
что сильная ориентировка элементарных магнитных моментов
266
МАГНЕТИКИ
ГЛ XI
Рис. 189. Схематические изо-
изображения расположения элек-
электронных спинов при самопроиз-
самопроизвольном намагничивании (низ-
(низкая температура) (а) и направ-
направления намагниченности в от-
отдельных доменах (б)
возникает в ферромагнетиках независимо от внешнего маг-
магнитного ноля, так что ферромагнетик намагничен до насыще-
насыщения, отвечающего данной температуре, уже без всякого поля
(рис. 189 а). Наличие такого само-
произвольного, или спонтанного,
намагничивания является наибо-
наиболее характерным свойством ферро-
ферромагнетиков.
Указанные представления были
высказаны в работах Б.Л. Розин-
га еще в 1892 г. Однако они не по-
получили в то время должного раз-
развития и были выдвинуты вновь в
1907 г. Вейссом. Так как опыт по-
показывает, что ферромагнетики в
отсутствие внешнего поля могут
быть и не намагничены, то для
объяснения этого кажущегося про-
противоречия Вейсс выдвинул вторую
основную гипотезу, согласно которой ферромагнетик разбива-
разбивается на большое число малых (но макроскопических) областей,
или доменов. Каждая из этих областей при температурах ниже
температуры Кюри намагничена весьма сильно, но направления
намагничивания в отдельных доменах различны, а именно тако-
таковы, что полный магнитный момент ферромагнетика равен нулю
(рис. 189 6).
Вопрос о физической причине самопроизвольного намагни-
намагничивания был принципиально разрешен в 1928 г. Я.И. Френкелем
и затем Гейзенбергом, которые показали, что сильная ориенти-
ориентировка электронных спинов вызывается силами обменного взаи-
взаимодействия. Наличие этого нового класса сил, необъяснимого в
классической физике, было выяснено лишь с развитием кванто-
квантовой физики атома.
Существование доменов в ферромагнетиках в настоящее вре-
время доказано различными опытами. Наиболее прямой метод за-
заключается в получении так называемых порошковых фигур.
Если на хорошо отполированную поверхность ферромагнети-
ферромагнетика поместить слой жидкости, в которой взвешены мельчайшие
крупинки ферромагнитного порошка (например, РегОз), то эти
крупинки будут оседать преимущественно на те места, вблизи
которых магнитное поле неоднородно. Но как раз вблизи границ
доменов и возникают неоднородности поля, и поэтому осевший
порошок обрисует границы областей самопроизвольного намаг-
намагничивания. На рис. 190 приведены фотографии порошковых фи-
фигур, видимых в микроскоп при небольшом увеличении. Особен-
Особенно следует отметить, что домены действительно наблюдаются
§ И9
ОБЪЯСНЕНИЕ ФЕРРОМАГНЕТИЗМА
267
и в отсутствие внешнего магнитного поля. Порошковые фигуры
были использованы в многочисленных исследованиях ферромаг-
Рис. 190. Домены в деформированной кремнистой стали (увеличение 80):
а — без поля; б — магнитное поле перпендикулярно к плоскости чертежа;
в — магнитное поле той же напряженности, но противоположного направ-
направления
нетиков и позволили определить размеры, форму и расположе-
расположение доменов, а также изменения доменов во внешнем магнитном
поле.
Рассмотрим теперь подробнее, почему в ферромагнетиках
обычно возникают многочисленные домены. Будем считать для
простоты, что ферромагнетик весьма анизотропен и что его ось
легкого намагничивания перпендикулярна к поверхности образ-
7
/
[
\
N\N NIN
s/s
s\s
\
\
0 ,
)
1
V/N-
\
\
1
I
—
, в
N S N S
1 1 1
III
1 1 1
I I 1
i i i
S N S N
Y Y Г
tililil
I I I
X А к
Рис. 191. К объяснению возникновения доменов
ца. На рис. 191 а изображен ферромагнетик, состоящий из од-
одного домена. В этом случае во внешнем пространстве возни-
возникает магнитное поле, которое заключает в себе определенную
энергию. На рис. 191 б имеются два домена с противополож-
противоположным направлением намагниченности. Внешнее магнитное поле
здесь убывает с увеличением расстояния быстрее, чем в слу-
случае а, и энергия, заключенная в поле, оказывается меньше. В
случае, показанном на рис. 191 в, магнитное поле практически
существует только в непосредственной близости от поверхно-
268 МАГНЕТИКИ ГЛ XI
сти магнетика и энергия поля еще уменьшается. На рис. 191 г
изображен случай, когда во внешнем пространстве магнитного
поля вовсе нет. Здесь имеются «замыкающие» домены в форме
трехгранных призм, боковые поверхности которых везде состав-
составляют угол 45° с вектором намагниченности. Вследствие этого
магнитный поток проходит исключительно внутри ферромагне-
ферромагнетика, он замыкается граничными доменами, чем и обусловлено
их название — замыкающие домены. Состояние г энергетиче-
энергетически более выгодно, нежели предыдущие состояния, и поэтому
ферромагнетик, находящийся, например, в состоянии а, будет
стремиться перейти в состояние г. Наконец, на рис. 191 д пока-
показана целая совокупность доменов совместно с замыкающими их
доменами, у которой также нет внешнего поля. Подобная форма
доменов действительно наблюдается на опыте. Таким образом,
разбиение ферромагнетика на домены происходит потому, что
при образовании доменных структур энергия ферромагнетика
уменьшается (Л.Д. Ландау и Е.М. Лифшиц).
Выше мы рассматривали ферромагнетик в отсутствие внешнего маг-
магнитного поля и учитывали только его собственную магнитную энергию
Если бы имелись еще и другие источники энергии, например, механические
напряжения или внешнее магнитное поле, то форма доменов определялась
бы полной энергией системы Поэтому при наличии механических напря-
напряжений и внешнего поля доменная структура изменяется
При возникновении самопроизвольного намагничивания
(ориентировки электронных спинов) магнетик деформируется.
Если при температуре более высокой, чем температура Кюри,
вырезать из монокристалла ферромагнетика шар, то при охлаж-
охлаждении ниже температуры Кюри шар превратится в эллипсоид.
Форма и размеры доменов изменяются и при перемагничива-
нии. Поэтому ферромагнетик, в целом не намагниченный, при
намагничивании деформируется.
Явление деформации при намагничивании было открыто в
середине прошлого столетия Джоулем и получило название маг-
нитострикции. Возникающие при этом деформации весьма ма-
малы: относительные удлинения образца А/// в полях порядка
105 А/м обычно имеют порядок 10~5 — 10~6. Магнитострик-
цию используют, подобно обратному пьезоэлектрическому эф-
эффекту (§ 52), для устройства мощных излучателей ультразвуко-
ультразвуковых волн и для других целей.
Силы обменного взаимодействия вызывают в ферромагнети-
ферромагнетиках параллельную ориентировку электронных спинов. Однако
обменные силы зависят от структуры тела, и поэтому харак-
характер вызываемой им ориентировки спинов может быть различен.
Оказывается, что существуют вещества, в которых также воз-
возникает сильная ориентировка электронных спинов, но, в отли-
§ 119 ОБЪЯСНЕНИЕ ФЕРРОМАГНЕТИЗМА 269
чие от ферромагнетиков, электронные спины ориентированы в
них попарно антипараллельно. В простейшем случае электрон-
электронные спины образуют как бы две пространственные подрешетки,
вставленные друг в друга и на-
намагниченные в противополож-
противоположных направлениях (рис. 192).
Вещества, в которых на-
намагниченность обеих подре-
шеток одинакова по модулю,
получили название антифер-
антиферромагнетиков. Их существо-
существование было предсказано теоре-
теоретически Л.Д. Ландау в 1933 г.
Антиферромагнетиками явля-
являются некоторые соединения
марганца (MnO, MnS), хрома
(NiCr, Cr2O3), ванадия (VO2) рис 192 Характер намагничивания
И др. Подобные вещества при в антиферромагнетиках (а) и ферри-
низких температурах имеют тах (б) (схематически)
ничтожно малую магнитную
восприимчивость. При повышении температуры строгая попар-
попарная антипараллельность электронных спинов нарушается и маг-
магнитная восприимчивость увеличивается. При некоторой темпера-
температуре (антиферромагнитная температура Кюри или температура
Нееля) области самопроизвольной ориентировки электронных
спинов разрушаются и антиферромагнетик превращается в па-
парамагнетик При дальнейшем повышении температуры магнит-
магнитная восприимчивость, как у всякого парамагнетика, уменьша-
уменьшается, а следовательно, при антиферромагнитной температуре
Кюри магнитная восприимчивость имеет максимум.
Если намагниченность обеих подрешеток неодинакова по мо-
модулю, то появляется некомпенсированный антиферромагнетизм
и вещество может приобрести значительный магнитный мо-
момент. Такой характер намагничивания имеет место в ферритах
(ср. § 112).
Процессы намагничивания ферромагнетика. Одной из
основных задач теории ферромагнетизма является объясне-
объяснение технической кривой намагничивания, т.е. зависимости на-
намагниченности / от напряженности намагничивающего поля.
В результате многочисленных исследований была установлена
следующая общая картина процесса намагничивания ферромаг-
ферромагнетиков
В отсутствие внешнего поля ферромагнетик разбивается на
домены таким образом, что его результирующий магнитный мо-
момент близок к нулю Это схематически показано на рис. 193 а,
где изображены четыре домена одинакового объема, намагни-
270
МАГНЕТИКИ
ГЛ XI
/
ч
ч
/
\
ч
н
Is/2
\
ченные до насыщения и обладающие магнитным моментом Js/4,
равным четверти полного момента всего магнетика в состоянии
насыщения. При включении
внешнего поля энергии от-
отдельных доменов делают-
делаются неодинаковыми: энергия
меньше для тех доменов, в
которых вектор намагничен-
намагниченности образует с направле-
направлением поля острый угол, и
больше в том случае, если
этот угол тупой. Поэтому
возникает процесс смещения
границ доменов, при кото-
котором объем доменов с мень-
меньшей энергией возрастает, а с
большей энергией уменьша-
уменьшается (рис. 193 6). Этот про-
процесс можно рассматривать
как фазовое превращение, а
домены с различным направ-
направлением намагниченности —
как разные фазы ферромаг-
о
нетика.
В случае
очень слабых
Рис. 193 Различные типы процессов
намагничивания ферромагнетика (схе-
(схематически), а-в — смещение границ, пол ей эти смещения границ
г — намагничивание вращения, д — на- обратимы И ТОЧНО следуют
магничивание насыщения за изменением поля. Началь-
Начальная восприимчивость ферро-
ферромагнетиков и область 1 кривой намагничивания (рис. 193 е) обу-
обусловлены процессами обратимого смещения границ
При увеличении поля смещения границ доменов делают-
делаются необратимыми. При достаточной величине намагничиваю-
намагничивающего поля энергетически невыгодные домены исчезают вовсе
(рис. 193 в). Этому соответствует область 2 кривой намагничи-
намагничивания (рис. 193 е).
Если поле увеличивается еще больше, то возникает новый
тип процесса намагничивания, при котором изменяется направ-
направление магнитного момента внутри домена (намагничивание вра-
вращения, рис. 193 г; этому соответствует область 3 на рис. 193 е).
Наконец, в очень сильном поле магнитные моменты всех
доменов устанавливаются параллельно полю. В этом состоя-
состоянии ферромагнетик имеет наибольший, возможный при данной
температуре магнитный момент, т.е. намагничен до насыщения
(рис. 193 д).
§ 120 МАГНИТНЫЕ ЦЕПИ 271
Указанные процессы намагничивания (за исключением сме-
смещения границ в слабых полях) происходят с некоторой задерж-
задержкой, т.е. смещение границ и поворот вектора намагниченности
отстают от изменения поля, что приводит к появлению гистере-
гистерезиса.
Гистерезис может возникнуть и по другой причине. Мы го-
говорили выше, что при наличии поля вследствие смещения гра-
границ доменов происходит увеличение объема той магнитной фа-
фазы (тех доменов), которая обладает меньшей энергией. Однако
может оказаться, что данная фаза при данном состоянии фер-
ферромагнетика или данном направлении поля не существует, и по-
поэтому должны возникнуть и вырасти малые области этой фазы
или зародыши перемагничивапия. Такие зародыши возникают
не точно при том значении поля, при котором существова-
существование этой фазы делается энергетически выгодным, а происходит
задержка роста зародышей перемагничивания, которая также
приводит к появлению гистерезиса. Это явление подобно пере-
пересыщению пара и переохлаждению жидкости, т.е. существованию
неустойчивых фаз вследствие задержки роста зародышей устой-
устойчивой фазы. Если ферромагнетик имеет мелкокристаллическую
структуру, так что отдельные его кристаллики состоят всего из
одного домена, то возможно получение особенно большой коэр-
коэрцитивной силы.
ГЛАВА XII
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ
МАГНИТНОГО ПОТОКА.
ГЕНЕРАТОРЫ И ДВИГАТЕЛИ
§ 120. Магнитные цепи
Магнитные потоки широко используют в современной элек-
электротехнике. Действие электромагнитов, мощных генераторов
электрического тока, электродвигателей, трансформаторов и
многих измерительных приборов основано на существовании в
них магнитного потока.
Для усиления магнитного потока почти всегда применяют
ферромагнитные материалы. Изготовляя из этих материалов
тела различной формы и размеров, оказывается возможным со-
создавать магнитные потоки нужной величины и направлять их
в желаемом направлении. Совокупность тел, внутри которых
проходят замкнутые линии магнитной индукции, называют маг-
магнитной цепью.
272
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ. XII
Общие законы магнитного поля, рассмотренные в главах VIII
и XI, позволяют вычислить магнитный поток в любой заданной
магнитной цепи. Однако практически удобнее не пользовать-
пользоваться непосредственно этими законами, а сначала вывести из них
некоторые общие следствия, или законы магнитной цепи, и за-
затем применять эти более частные законы к решению практиче-
практических задач.
Рассмотрим сначала простую, или неразветвленную магнит-
магнитную цепь (рис. 194). Будем считать, что она составлена из двух
частей: ярма с сечением S из материала с магнитной проница-
Рис. 194. Неразветвленная магнитная цепь и соответствующая ей электри-
электрическая цепь
емостью р, и зазора (например, воздушного), имеющего то же
сечение и магнитную проницаемость ц\. Выделим далее сред-
среднюю линию индукции и применим к ней теорему о магнитном
напряжении (§ 81):
HI + Hili = Ni,
где Н — напряженность поля внутри ярма, Н\ — напряженность
поля внутри зазора, I — длина ярма, измеренная вдоль средней
линии индукции, 1\ — длина зазора, N — число витков обмотки,
а г — сила тока в ней.
Так как линии индукции непрерывны, то значения магнит-
магнитного потока Ф внутри ярма и внутри зазора одинаковы. Далее,
пользуясь соотношениями Ф = BS, В = /i/io-ff, напряженность
поля можно выразить через поток:
Н =
#1 =
Подставляя эти выражения в первую формулу, находим из нее
§ !20 МАГНИТНЫЕ ЦЕПИ 273
поток Ф:
ф Nl
Полученная формула подобна закону Ома для замкнутой элек-
электрической цепи, изображенной на рис. 194. При этом величина
Шт = Ni A20.1)
играет роль электродвижущей силы, и поэтому по аналогии она
получила название магнитодвижущей силы. Единица магнито-
магнитодвижущей силы в системе СИ есть ампер. Сумма
Rm = -Ц + -Ц A20.2)
входит в формулу так же, как и полное сопротивление элек-
электрической цепи в закон Ома, и поэтому ее называют полным
магнитным сопротивлением цепи. Величины
Гт = 1/woS, rmi = li/mfioS A20.3)
дают магнитные сопротивления участков цепи. Магнитное со-
сопротивление зависит от длины магнитопровода I и его сечения
S, так же как и электрическое сопротивление, но роль удель-
удельной электрической проводимости А играет магнитная проница-
проницаемость flflQ.
Пользуясь этими понятиями, мы можем представить полу-
полученные результаты следующим образом:
Ф = VmlRm- A20.4)
Иными словами, в неразветвленной магнитной цепи магнитный
поток равен частному от деления магнитодвижущей силы на
полное магнитное сопротивление.
Из формулы A20.4) видно, что магнитное сопротивление в
системе единиц СИ измеряется в амперах на вебер (А/Вб).
Сравнивая A20.2) и A20.3), мы также видим, что полное со-
сопротивление нашей цепи равно сумме сопротивлений ее частей:
Этот результат, очевидно, справедлив и в том случае, если цепь
составлена из какого угодно числа частей, если только магнит-
магнитный поток проходит целиком последовательно через эти части:
при последовательном соединении магнитопроводов их магнит-
магнитные сопротивления складываются.
На рис. 195 изображена схема опыта, показывающего влия-
влияние магнитного сопротивления. П-образный железный сердеч-
сердечник намагничивается обмоткой 1, включенной последователь-
последовательно с амперметром А и реостатом в цепь переменного тока. В
обмотке 2 наводится ЭДС индукции, и показания вольтметра
V пропорциональны магнитному потоку в сердечнике. Если,
274
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ. XII
сохраняя неизменной силу тока в обмотке 1, замкнуть сердечник
железной пластиной, то магнитное сопротивление цепи умень-
уменьшается и показание вольтметра увеличивается.
Следует отметить, что введенные термины и понятия име-
имеют лишь формальный характер. В магнитном потоке не дви-
движутся никакие частицы, и поэтому нет основания говорить ни
о «магнитодвижущей силе», ни о «магнитном сопротивлении».
Рис. 195. При замыкании железного сердечника его магнитное сопротив-
сопротивление уменьшается и магнитный поток внутри него становится больше
Как разъяснялось в гл. XI, физический смысл описанного опыта
и ему подобных заключается в том, что, вводя в магнитную цепь
намагничивающиеся тела, мы вводим в действие молекулярные
токи магнетиков, которые и создают добавочные магнитные по-
потоки. Однако указанное выше формальное описание удобно для
решения практических задач и поэтому применяется в электро-
электротехнике.
§ 121. Электромагниты
Пример неразветвленной магнитной цепи мы имеем в про-
простом электромагните (рис. 196).
Подъемная сила электромагнита (или максимальная мас-
масса, удерживаемая электромагнитом) приближенно выражается
формулой
= ~B2S.
A21.1)
§ 121
ЭЛЕКТРОМАГНИТЫ
275
Здесь В — индукция внутри сердечника, S — площадь сопри-
соприкосновения сердечника и якоря. Если в формуле A21.1) В выра-
выражено в Тл, a S — в м2, то ^о =
= 47Г • 10~7 Гн/м и сила F полу-
получится выраженной в ньютонах.
Формулу A21.1) можно получить
следующим образом. Предположим,
что между якорем и сердечником
имеется малый зазор х (рис. 196)
и якорь удаляется от сердечника на
отрезок dx. Поток через намагни-
намагничивающую обмотку изменяется при
этом на некоторую величину ЙФ и в
цепи возникает дополнительный ток
1 ЙФ
дг = —.
г dt
Здесь г обозначает полное сопротив-
сопротивление цепи, включая и сопротивле-
сопротивление источника тока. Далее, мы будем
считать, что якорь движется бесконечно медленно, так что Si есть беско-
бесконечно малая величина.
Согласно закону сохранения энергии (§ 100) при таком перемещении
изменение работы источника тока =
= изменение количества теплоты Джоуля-Ленца +
+ механическая работа + изменение энергии магнитного поля.
Изменение работы источника тока:
г dt
Рис. 196. Электромагнит
Шг + Si)dt -
Изменение количества теплоты:
r(i + SiJ dt - ri2 dt = 2ri Si dt = -2ri - — dt = -
r dt
Изменение энергии поля есть разность энергий в конце и в начале переме-
перемещения:
где dL — увеличение индуктивности электромагнита при увеличении зазора
на dx. Но Ф = Ы, и поэтому
1
dW = - idty.
Наконец, механическая работа 5А = F dx. Поэтому
—i f/Ф = —2t f/Ф 4- F dx 4- — i f/Ф или F = — г —
2 2 dx'
В этих формулах Ф есть поток, пронизывающий обмотку. Если Ф — поток
в сердечнике, а обмотка имеет N витков, то Ф = Л^Ф.
276
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ ХП
Но, согласно § 120, поток в сердечнике можно выразить следующим
образом {/л = 1, h — 2х):
Ni „ Ni
где I — длина линии индукции в сердечнике и в якоре, a S — сечение сер-
сердечника. Поэтому
Jx~~ !Ь~ A + 2цхJ '
Подставляя это выражение в формулу для подъемной силы, имеем
F=i =
2 dx ц
Знак минус показывает, что сила, действующая на якорь, стремится умень-
уменьшить зазор х. Выражение, стоящее в скобках, есть индукция В в сердечни-
сердечнике электромагнита, a 2S — площадь соприкосновения сердечника и якоря.
Обозначая эту площадь через S, получим формулу A21.1).
Формула A21.1) показывает, что подъемная сила электро-
электромагнита пропорциональна квадрату индукции. Поэтому для по-
получения большой подъемной силы нужно применять материалы
с высокой магнитной проницаемостью и обеспечить хорошее за-
замыкание сердечника и якоря.
§ 122. Разветвление магнитного потока
Наряду с простой магнитной цепью на практике приходит-
приходится встречаться с более сложными цепями, в которых происхо-
происходит разветвление магнитного потока. Пример такой магнитной
цепи показан на рис. 197. Пользуясь теоремой о магнитном на-
е д г
Рис 197. Магнитная цепь с разветвлением магнитного потока
пряжении, можно и в этом случае дать простые правила для
вычисления магнитного потока.
§ 122 РАЗВЕТВЛЕНИЕ МАГНИТНОГО ПОТОКА 277
Рассмотрим замкнутый контур абдеа (рис. 197), входящий в
состав*нашей цепи, и обозначим длину участка бд через 1\, его
сечение — через Si и напряженность поля в нем — через Hi,
а соответствующие величины для участка деаб — через I2, S2
и i?2- Так же, как и раньше, Hi и Нъ можно выразить через
потоки Ф\ и Ф2 в рассматриваемых участках:
fJ.2tJ.0S2'
где Hi и fj,2 — магнитные проницаемости материала на участках
бд и деаб. Поэтому
Но
— магнитные сопротивления участков цепи бд и деаб, а
Nlh = %m\
— магнитодвижущая сила этой цепи, и предыдущая формула
принимает простой вид
В выделенный замкнутый контур могут входить не два
участка с различными потоками, а какое угодно их число, и в
каждом из этих участков может быть своя намагничивающая
обмотка. Поэтому в общем случае
^фкгтк = ^гпк. A22.1)
Эта формула имеет тот же вид, что и второе правило Кирх-
Кирхгофа для разветвляющихся токов (§ 70), причем вместо силы
тока i входит магнитный поток Ф, а роль электрического со-
сопротивления г и ЭДС 8" играют магнитное сопротивление гт и
магнитодвижущая сила $ш.
При пользовании формулой A22.1) нужно, очевидно, учиты-
учитывать правило знаков для <?т и Ф. Магнитодвижущая сила счита-
считается положительной, если соответствующая обмотка создает по-
поток, направление которого совпадает с выбранным направлением
обхода контура. Положительное значение потока Ф означает,
что направление потока совпадает с выбранным направлением
обхода.
Рассмотрим теперь какой-либо узел разветвления магнитной
цепи (рис. 198), в котором сходятся три или более магнитопро-
вода. Так как линии индукции непрерывны, то общее число этих
линий, идущих к узлу разветвления, равно числу линий, уходя-
уходящих от узла разветвления. Или: сумма всех потоков, направлен-
278
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА Г Л XII
ных к месту разветвления, равняется сумме всех потоков, ухо-
уходящих от него. Приписывая этим потокам разные знаки, имеем
для каждого узла разветвления:
>к = 0. A22.2)
Эта формула имеет тот же вид, что и первое правило Кирхгофа
(§ 70).
Таким образом, задача вычисления потоков в любой магнит-
магнитной цепи оказывается аналогичной задаче вычисления токов в
электрической цепи, причем каждой магнитной цепи можно со-
сопоставить соответствующую ей электрическую цепь (рис. 197).
Применяя эту аналогию, можно в ряде случаев не решать за-
задачу вовсе, а воспользоваться уже известным решением электри-
электрической задачи. Так, например, мы знаем, что при параллельном
соединении проводников токи в
них обратно пропорциональны
сопротивлениям. Поэтому можно
утверждать, что и при параллель-
параллельном соединении магнитопроводов
магнитные потоки в них будут
обратно пропорциональны маг-
магнитным сопротивлениям.
При пользовании аналогией
между магнитными и электри-
электрическими цепями следует иметь
в виду, что здесь имеется и су-
существенное различие. Удельная электрическая проводимость
металлов практически не зависит от плотности тока, и поэтому
сопротивления участков электрической цепи можно считать
постоянными. Магнитная же проницаемость ц зависит от
напряженности магнитного поля, а следовательно, и магнитные
сопротивления в формуле A22.1) являются переменными
величинами, зависящими от значения потока Ф.
§ 123. Генераторы переменного тока
Наиболее важно применение магнитного потока в электри-
электрических машинах, предназначенных для превращения механиче-
механической энергии в электрическую (генераторы) или электрической
энергии в механическую (электродвигатели).
В настоящее время имеется много типов генераторов и двига-
двигателей. Их конструкция доведена до высокой степени совершен-
совершенства, что потребовало разрешения ряда важных вспомогатель-
вспомогательных технических задач. Мы, однако, не будем вовсе касаться
деталей конструкции электрических машин (это относится к
Рис 198 Разветвление магнит-
магнитного потока
§ 123 ГЕНЕРАТОРЫ ПЕРЕМЕННОГО ТОКА 279
специальному курсу электротехники) и ограничимся только
принципами их устройства.
Все современные мощные генераторы электрического тока
основаны на явлении электромагнитной индукции при движе-
движении проводников в магнитном поле. Остановимся сначала на ге-
генераторах переменного тока.
Рисунок 199 разъясняет принцип получения технического
переменного тока. Электродвижущая сила возникает вследствие
вращения проволочной обмотки. Концы обмотки подведены к
двум изолированным медным коль-
кольцам (контактные кольца), укреп-
укрепленным на оси машины, и при по-
помощи прижимных проводников из
меди или графита (щетки) могут
быть включены в замкнутую цепь
тока без нарушения вращения об-
обмотки.
Если а — угол, составленный
нормалью п к плоскости витка
и индукцией поля В, то поток
сквозь виток равен
Ф = BS COS а = Ф0 COS а, рис 199 Принцип получения
где S — площадь витка, а Фо — пеРеменног° тока
максимальное значение потока
при а = 0. При равномерном вращении витка с угловой
скоростью ш угол а = uit + ао, и поэтому ЭДС одного витка
? = -^ = <&owsin(wf+ а0) = 80sin(wf+ а0). A23.1)
(ль
Если имеется не один, a TV витков проволоки, то амплитуда
ЭДС &о будет в N раз больше. Если Фо выражено в Вб, аш-в
рад/с, то &о выражено в вольтах.
Из A23.1) видно, что для повышения ЭДС необходимо уве-
увеличивать магнитный поток Фо, а для этого сопротивление маг-
магнитной цепи машины выгодно сделать возможно меньшим. По-
Поэтому магнитную систему генераторов делают из двух железных
сердечников: наружного кольцеобразного неподвижного сердеч-
сердечника и внутреннего вращающегося цилиндрического сердечни-
сердечника, а воздушный зазор между ними доводят до минимальных
размеров. Машина имеет, как правило, две обмотки, одна из
которых размещается в пазах неподвижного сердечника (стато-
(статора) с внутренней его стороны, а другая расположена в пазах
вращающегося сердечника (ротора). Одна обмотка использует-
используется для создания магнитного потока, а другая служит рабочей
обмоткой, в которой индуцируется переменная ЭДС.
280
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ. XII
§ 124. Генераторы постоянного тока
В генераторах постоянного или прямого тока переменная
ЭДС, возникающая во вращающейся обмотке, выпрямляется
при помощи коллектора, который
представляет собой вращающийся
переключатель.
Простейший генератор прямого
тока изображен на рис. 200. Он име-
имеет обмотку из одного витка, а его
коллектор состоит из двух медных
изолированных полуцилиндров, на-
насаженных на ось машины, к которым
присоединены концы обмотки. К пла-
пластинам коллектора прижимаются две
щетки, осуществляющие включение
обмотки в цепь тока. Рисунок 201 по-
поясняет действие коллектора. Кривая
а представляет напряжение между концами обмотки, которое
изменяется в соответствии с A23.1) по закону синуса. Через
каждую половину оборота коллектор переключает (коммути-
(коммутирует) концы обмотки, и поэтому на щетках получается напря-
напряжение, изображаемое кри-
кривой б. Такой простейший
генератор, следовательно,
дает пульсирующий ток,
направление которого хотя и
остается постоянным, но сила
изменяется.
Так как коллектор враща-
ется, то и рабочую обмотку,
соединенную с ним, делают
Рис. 200. Простейший гене-
генератор прямого тока
0
Рис. 201. Действие коллектора
всегда вращающейся. Ее рас-
располагают на внутреннем же-
железном сердечнике, насаженном на ось машины. Для получения
постоянного тока без пульсаций обмотку разделяют на много
секций и применяют коллекторы из многих пластин.
Для получения магнитного потока в современных мощных генераторах
применяют исключительно электромагниты. Для питания обмотки элек-
электромагнита в некоторых специальных случаях пользуются вспомогатель-
вспомогательным источником (генератором с внешним возбуждением). Однако гораздо
чаще строят генераторы с самовозбуждением, в которых для создания тока
в электромагните (обмотке возбуждения) используют напряжение, разви-
развиваемое самим генератором.
Свойства генераторов постоянного тока существенно зависят от способа
соединения обмотки возбуждения с якорем. По этому принципу разделяют
§
ГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
281
генераторы на следующие типы: с параллельным возбуждением (шунтовые
генераторы), с последовательным возбуждением (сериесные генераторы) и
со смешанным возбуждением (компаундные генераторы).
В шунтовых генераторах обмотка возбуждения присоединяется парал-
параллельно якорю. Ток, ответвляемый в электромагнит, составляет обычно от
1 % (большие генераторы) до 5 % (малые генераторы) тока якоря. Поэтому
сопротивление обмотки возбуждения гв значительно больше сопротивления
якоря гя.
Рассмотрим, как зависит напряжение на зажимах шунтового генерато-
генератора от тока нагрузки. Напряжение на зажимах равно
U,В
100
50
1—-^_
1 1 1 1
---^
1 1 1 1
1 1 1 1
о
10
Рис. 202. Характеристика ма-
машины с параллельным возбуж-
возбуждением
где <? — ЭДС якоря, г'в — ток возбуждения, г — ток нагрузки. При разо-
разомкнутой машине (холостой ход) г = 0 и U имеет максимальное значение.
При увеличении тока г напряжение U
уменьшается и притом по двум причи-
причинам. Во-первых, потому, что увеличива-
увеличивается падение напряжения внутри якоря,
равное гя(гв + i)- Во-вторых, это умень-
уменьшение U ведет к ослаблению тока воз-
возбуждения, что в свою очередь вызывает
понижение ЭДС <S и еще больше умень-
уменьшает напряжение машины. Поэтому
зависимость U = f(i) изображается кри-
кривой, показанной на рис. 202. В сериес-
ных генераторах обмотка возбуждения
соединяется с якорем последовательно. В
этом случае полный ток машины прохо-
проходит через обмотку возбуждения, и поэто-
поэтому, чтобы потеря напряжения в ней была малой, должно быть rB <К гя.
Напряжение на зажимах сериесного генератора, как и всякого источ-
источника тока, равно разности между ЭДС якоря Ж и падением напряжения
внутри машины:
U,В
U= %-i(r* + tB).
При холостом ходе (г = 0) внутреннее паде-
падение напряжения равно нулю. Но в этом случае
нет тока и в обмотке возбуждения, и поэтому
напряжение U близко к нулю. При увеличении
тока нагрузки i магнитный поток увеличивает-
увеличивается, отчего и ЭДС 8', и напряжение U возраста-
возрастают. Однако это возрастание происходит лишь
до известного предела, пока в сердечнике элек-
электромагнита не наступает насыщение. При даль-
дальнейшем увеличении г ЭДС практически не уве-
увеличивается, в то время как внутреннее падение
напряжения г(гя +гв) продолжает нарастать, и
поэтому напряжение U начинает уменьшаться.
Характеристика сериесного генератора показа-
показана на рис. 203.
Таким образом, шунтовые генераторы имеют падающую характеристи-
характеристику, а сериесные — возрастающую. Эти особенности сочетают в компаунд-
Рис. 203. Характеристи-
Характеристика машины с последова-
последовательным возбуждением
282
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
ных генераторах, электромагниты которых имеют две обмотки одна из них
присоединяется параллельно якорю, а другая — последовательно Подбирая
должным образом обмотки, можно добиться, чтобы в известном интервале
изменения токов нагрузки напряжение оставалось приблизительно посто-
постоянным
§ 125. Электродвигатель постоянного тока
Если в машине постоянного тока, рассмотренной в предыду-
предыдущем параграфе, создать ток от внешнего источника, то ее якорь
приходит во вращение. Поэтому коллекторные машины могут
служить как генераторами,
так и двигателями, т.е. они
обратимы.
Для лучшего уяснения
превращения энергии в
генераторах и двигателях,
рассмотрим силы, действую-
действующие на якорь. На рис. 204
схематически изображена
машина постоянного тока,
Рис 204. Электродинамические силы, работающая в качестве
действующие на якорь генератора (а) и генератора (а) и в качестве
двигателя (б) постоянного тока двигателя (б). В случае
генератора направление
тока индукции в якоре определяется законом Ленца (§ 91): у
северного полюса ток направлен от чертежа к читателю, а у
южного полюса — от читателя за чертеж. На проволоки якоря
действуют электродинамические силы, которые пропорцио-
пропорциональны току якоря. Они стремятся вызвать вращение якоря по
часовой стрелке, т.е. в сторону, противоположную вращению
генератора. Для поддержания вращения якоря необходимо
действие внешних сил, равных по модулю и противоположных
по направлению, которые создаются двигателем, вращающим
генератор. Поэтому двигатель непрерывно производит меха-
механическую работу против электродинамических сил, которая
тем больше, чем сильнее ток, отбираемый от генератора, и
мы имеем, следовательно, превращение механической работы
двигателя в электрическую энергию.
При работе машины в качестве электродвигателя внешне-
внешнего двигателя нет и на обмотку якоря действуют только элек-
электродинамические силы, под действием которых якорь приходит
во вращение. В этом случае работу совершают электродинами-
электродинамические силы, и мы имеем превращение электрической энергии
источника, питающего двигатель, в механическую работу. Из
рис. 204 видно, что при одинаковом направлении вращения re-
§ 126 СИНХРОННЫЕ ДВИГАТЕЛИ 283
нератора и электродвигателя направления токов в якоре проти-
противоположны.
При вращении якоря двигателя его обмотка пересекает ли-
линии индукции магнитного поля, и поэтому в ней возникает ЭДС
индукции #\ Эта ЭДС, как разъяснялось выше, стремится соз-
создать ток, противоположный току якоря, и поэтому она получила
название протпивоэлектпродвижущей силы. Сила тока в якоре
зависит как от напряжения U на якоре, так и от противоэлек-
тродвижущей силы (закон Ома для участка цепи с ЭДС):
где гя — сопротивление якоря.
Противоэлектродвижущая сила уменьшает ток якоря. При
работе двигателя без нагрузки (холостой ход) скорость враще-
вращения якоря велика и противоэлектродвижущая сила лишь немно-
немного меньше напряжения U. Поэтому ток холостого хода мал. При
увеличении нагрузки скорость якоря уменьшается и противо-
противоэлектродвижущая сила падает. В соответствии с этим ток, по-
потребляемый двигателем, увеличивается, и тем больше, чем силь-
сильнее нагрузка.
Это обстоятельство приходится учитывать при пуске двига-
двигателя. В момент пуска якорь не вращается вовсе и противоэлек-
противоэлектродвижущая сила равна нулю. Поэтому в первые моменты по-
после пуска ток якоря может оказаться настолько большим, что
вызовет порчу обмотки и пластин коллектора. Для устранения
этого явления при пуске мощных двигателей всегда употребля-
употребляют так называемые пусковые реостаты, которые включают по-
последовательно с двигателем и выводят постепенно, по мере роста
числа оборотов двигателя.
§ 126. Синхронные двигатели
Генераторы переменного тока могут быть использованы и в
качестве электродвигателей, те. они, так же как и машины по-
постоянного тока, обладают обратимостью
Для разъяснения способа действия таких двигателей обра-
обратимся к рис. 205, на котором показана часть машины с внешни-
внешними полюсами Ее электромагниты S, N, S, ... питаются, как в
генераторе, от внешнего источника постоянного тока, например
от вспомогательного генератора, насаженного на общую ось ма-
машины, а ротор присоединяется к сети переменного тока. Пусть
один из полюсов ротора находится в положении 1 и ток в об-
обмотке ротора создает на этом полюсе южное намагничивание.
Полюс ротора будет отталкиваться от южного полюса S и при-
притягиваться к северному полюсу N, и ротор начнет поворачи-
поворачиваться по часовой стрелке Допустим теперь, что в положении
284
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
ротора 2 (рис. 205) сила тока обращается в нуль, а в более позд-
позднем положении 3 ток в обмотке ротора изменяет направление.
Тогда рассматриваемый полюс ротора в положении 3 перемаг-
перемагнитится и будет уже отталкиваться от северного полюса N и
притягиваться к южному полюсу S. Поэтому ротор будет про-
продолжать вращаться по часовой стрелке до тех пор, пока в его
обмотке существует переменный ток.
Из сказанного ясно, что вращение ротора будет происходить
только при строго определенной скорости вращения. Эта ско-
скорость должна быть такой, чтобы время, необходимое для про-
прохождения каждым полюсом ротора расстояния между двумя
соседними одноименными полюсами статора, точно равнялось
Рис 205 Принцип синхронного двигателя переменного тока
периоду переменного тока. Или, как принято говорить, ротор
должен вращаться синхронно с изменением переменного тока.
Поэтому и двигатели такого типа получили название синхрон-
синхронных двигателей.
Синхронные двигатели обладают тем неудобством, что они
не запускаются сами; для их пуска необходимо раскрутить ро-
ротор до синхронной скорости с помощью постороннего двигателя
или какого-нибудь иного приема. Точно так же, если вследствие
значительной перегрузки скорость ротора уменьшится (двига-
(двигатель выйдет из синхронизма), то двигатель остановится. Тем не
менее синхронные двигатели находят себе применение, в особен-
особенности в тех случаях, когда необходимо иметь строго постоянное
число оборотов.
Наряду с синхронными двигателями имеются и другие типы
электродвигателей переменного тока. Однако широкое внедре-
внедрение в технику двигателей переменного тока сделалось возмож-
возможным лишь после того, как М.О. Доливо-Добровольским были
разработаны так называемые системы многофазных токов, к
рассмотрению которых мы и обратимся.
§ 127. Двухфазный ток
Рассмотрим генератор (рис. 206), подобный обычному гене-
генератору переменного тока, но содержащий две независимые об-
обмотки: одну состоящую из катушек 1 и 3, и другую — из катушек
§ 127
ДВУХФАЗНЫЙ ТОК
285
2 я 4, повернутую относительно первой на угол тг/2. При враще-
вращении ротора в каждой из обмоток будет наводиться переменная
ЭДС, но максимум ЭДС Щ в обмотке 2~4 будет достигаться
позднее, чем максимум ЭДС Ш\ в обмотке 1-3, на время в чет-
четверть периода обращения ротора, и ЭДС <?2 будет обращаться
в нуль с таким же опозданием. Иными словами, между колеба-
колебаниями ЭДС в обеих обмотках будет существовать разность фаз
в 90°, или тг/2. Если обозна-
обозначить максимальное значение ЭДС
в каждой обмотке через 8о (ам-
(амплитуда ЭДС), а угловую скорость
вращения ротора — через ш, то за-
закон изменения ЭДС в обеих катуш-
катушках будет иметь вид
= &osmujt,
A27.1)
Получение двухфаз-
ного тока
Каждую из двух обмоток гене-
генератора, которые мы будем обозна- р
чать в дальнейшем через О\ и 02,
мы можем соединить с нагрузоч-
нагрузочными сопротивлениями ri и гг (рис. 207), и тогда получатся
две цепи, в каждой из которых будет переменный ток. Одна-
Однако оба эти тока будут согласованы, между ними также будет
существовать определенная разность фаз. Два таких тока на-
называются двухфазной системой токов или просто двухфазным
током.
А
>о,
О2
Рис 207. Схема двухфазной системы токов
На рис. 207 а показаны четыре провода, соединяющие гене-
генератор с нагрузкой. Однако число проводов можно уменьшить.
Так как для электрических явлений важны только разности по-
потенциалов, то один провод каждой цепи можно сделать общим,
и тогда мы получим трехпроводную цепь двухфазного тока, по-
показанную на рис. 207 б.
Напряжения между концами обмоток О\ и 02 называют фаз-
фазными напряжениями, токи в О\ и 02 — фазными токами. Эти-
Этими же названиями обозначают напряжения и токи в нагрузоч-
286 ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
ных сопротивлениях 7*i и Г2- Напряжения же между проводами
линии 1, 2 и 3 называют линейными напряжениями, а токи в
этих проводах — линейными токами. Если генератор разомкнут
(п = Г2 = оо), то фазные напряжения равны ЭДС в каждой об-
обмотке. Если принять потенциал провода 1 за нуль, то потенциал
провода 2, или линейное напряжение между проводами 1 я 2,
равен
а линейное напряжение между I а 3 равно
f/13 = g0sin(cj«-90°).
Линейное же напряжение между проводами 2 и 5 есть разность
потенциалов проводов 2 и 3:
U23 = Ч sin^t - g0 sin (ut - 90°) = 280 sin 45° cos (ut - 45°) =
= \/2 80sin(w* + 45o). A27.2)
Таким образом, в трехпроводной системе двухфазного тока мы
можем получить три обычных (однофазных) тока одинаковой
частоты ш, но с разностью фаз 90 и 45° и с двумя разными
амплитудами ЭДС, %о и $о\/2-
Подобным образом мы можем себе представить не два, а три,
четыре и вообще п переменных согласованных токов, получае-
получаемых в одном генераторе с п обмотками, обладающих определен-
определенной разностью фаз, или систему многофазных токов. Однако
широкое практическое применение получил только трехфазный
ток.
§ 128. Трехфазный ток
Схема устройства генератора трехфазного тока показана на
рис. 208. Генератор имеет три обмотки, смещенные друг отно-
относительно друга на 1/3 окружности. При вращении ротора мы
получим в каждой из обмоток, обозначаемых в дальнейшем че-
через Oi, Ог и Оз> переменные ЭДС <гь $2 и $з, между которыми
будет разность фаз 120 и 240°. Поэтому, если колебания ЭДС в
обмотке О\ выражаются формулой
&1 = %osmut,
то для ЭДС в других обмотках мы имеем
Й'з = % о sin (wt-240°).
Изменение во времени ЭДС в трех обмотках графически пред-
представлено на рис. 209.
§128
ТРЕХФАЗНЫЙ ТОК
287
Каждую из обмоток мы можем замкнуть на нагрузочные
сопротивления г\, г^ и гз (рис. 210) и получить три однофаз-
л
0
>—у
2
1
г-
у
V
X
/г/з>
\^
3
/
Y
А
г
V
л
V
л
г
^-/
2
у
/ \ *
Аг/з
Ч.
3
1
Рис. 208. Получение трех- Рис. 209. ЭДС генератора трехфазного
фазного тока тока
ных переменных тока, между которыми будет строго постоян-
постоянная разность фаз, равная соответственно 120 и 240°. Такие три
согласованных перемен-
переменных тока и называются
системой трехфазных токов
или, коротко, трехфазным
током.
Число проводов, соеди- rj
няющих генератор с на- ? О2
грузкой, так же как и при
двухфазном токе, можно
уменьшить, если объеди-
объединить по одному проводу в
каждой цепи. Тогда мы получим соединение генератора, пока-
показанное на рис. 211, называемое соединением звездой. Оно подоб-
7
Рис. 210. Трехфазная система токов
Рис.211. Соединение звездой
Рис. 212. Соединение трех
источников тока звездой
но соединению трех одинаковых, источников тока, показанному
на рис. 212.
288 ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
Предположим, что генератор разомкнут (г\ = гг = гз = сю),
и найдем связь между фазным напряжением (существующим
в каждой из обмоток О\, 02, Оз) и линейными напряжениями
(между проводами 0, 1, 2, 3). Очевидно, что линейное напря-
напряжение между проводом 0 и любым из других проводов равно
фазному напряжению и его амплитуда есть <?о- Линейное на-
напряжение между любой парой проводов 1, 2 и 3 будет другим.
Вычислим, например, напряжение между проводами 1 я 3. Оно
равно разности потенциалов между свободными концами обмо-
обмоток О\ и Ог'-
П = gosincjf-^osin(cj«-12O0) = 2?0sin60° cos (ut - 60°).
Ho sin60° = ч/3/2, cos (ujt - 60°) = sm(wt + 30°), и поэтому
g= ^ол/3 sin(wi + 30°).
Мы имеем, следовательно, линейное напряжение, изменяюще-
изменяющееся с той же частотой и, что и фазное, но с амплитудой в л/3
раз больше фазного. Таким образом, при соединении генератора
звездой мы можем получить в линии два напряжения, а именно
фазное 8 о и #о\/3-
Допустим теперь, что генератор нагружен на сопротивления,
также соединенные звездой (рис. 211), причем г\ = Г2 = гз (сим-
(симметричная нагрузка). В этом случае в каждом из проводов 1, 2
и 5 амплитуда токов го будет одинакова и токи в них будут
изменяться по закону i\ = iosincji, г'г = iosin(w? — 120°), i% =
= го sin(cjt — 240°). В проводе 0, являющемся общим, сила тока
г будет равна сумме всех линейных токов:
i = %\ + %2 + гз = г'о sincjt + г'о sin (ut — 120°) + г'о sin (cot — 240°).
Но sm(wt - 120°) + sm(ut - 240°) = 2sin(ojj: - 180°)cos60° =
= sin(aji — 180°) = — smut. Поэтому
i = i\ + %2 + г'з = 0.
Таким образом, при симметричной нагрузке сила тока в про-
проводе 0 равна нулю, отчего этот провод называют нулевым. В
случае симметричной нагрузки (или даже приблизительно сим-
симметричной) нулевой провод можно удалить вовсе и линия будет
работать исправно.
Возможно и другое соединение обмоток генератора, показан-
показанное на рис. 213 (соединение треугольником). Ему соответствует
соединение трех источников тока, изображенное на рис. 214.
На первый взгляд может показаться, что в этом случае об-
обмотки замкнуты сами на себя (накоротко). Это действительно
так и было бы, если бы мы имели три источника постоянного то-
тока. На самом же деле мы имеем переменные ЭДС, обладающие
разностью фаз, что существенно изменяет дело. Действительно,
§ 128 ТРЕХФАЗНЫЙ ТОК 289
полная ЭДС треугольника равна
Но мы уже вычислили выше эту сумму и видели, что она равна
нулю. Таким образом, полная ЭДС треугольника равна нулю, и
Рис. 213. Соединение треугольником Рис. 214. Последова-
Последовательное соединение трех
источников тока
если генератор не нагружен, то не только не получается корот-
короткого замыкания, но в его обмотках вовсе нет тока.
Из рис. 213 ясно без расчетов, что при соединении треуголь-
треугольником линейные напряжения равны фазным напряжениям; при
разомкнутом генераторе амплитуда линейных напряжений рав-
равна амплитуде ЭДС в одной обмотке $о.
Отметим в заключение, что на рисунках 211 и 213 мы пред-
предполагали, что и генератор и нагрузки соединены одинаково —
либо звездой, либо треугольником. Разумеется, можно употреб-
употреблять и комбинированные схемы, соединяя, например, генератор
звездой, а потребителей энергии — треугольником, или, наобо-
наоборот, генератор — треугольником, а потребителей — звездой.
Попутно отметим одно существенное обстоятельство Вернемся к схеме
рис. 211 и предположим, что один из проводов, например провод 1, оборвал-
оборвался или перегорел. Это приведет к выключению нагрузки г\, но не нарушит
нормальной работы нагрузок гч и гз, на которых по-прежнему будут фаз-
фазные напряжения. Не то, однако, произойдет при обрыве нулевого провода.
В этом случае каждая пара сопротивлений, например п и гг, окажется со-
соединенной последовательно и включенной под напряжение в -\/3 раз больше
фазного. Это напряжение распределится, как при всяком последовательном
соединении, неравномерно, пропорционально сопротивлениям г\ и гг. Так,
если сопротивление г\ есть одна лампочка, а сопротивление гг — девять
лампочек (соединенных параллельно), то на ветви гг окажется лишь 1/10
полного напряжения, а на ветви п — 9/10 напряжения. Если напряжение
сети (фазное) было 220 В, то на обеих ветвях окажется 220\/§ = 380 В, из
которых 380 • 1/10 = 38 В придется на лампочки ветви гг, а 380 • 9/10 =
= 342 В — на лампочку ветви п. Поэтому лампочка перегорит и ток в
обеих ветвях прервется. По этой причине на нулевой провод никогда не
ставят плавкие предохранители, чтобы случайное короткое замыкание не
привело к отключению этого провода, а защищают сеть предохранителями,
поставленными на остальные провода.
290
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ. XII
§ 129. Векторные диаграммы
Выше мы рассматривали переменные токи, которые изме-
изменяются по закону синуса или косинуса, т.е. по тому же зако-
закону, что и гармонические колебания в механике. Такие гармо-
гармонические изменяющиеся токи и напряжения нам приходилось
складывать, что мы и делали аналитически, складывая соот-
соответствующие тригонометрические
функции. Однако гармонические
колебания можно изображать гра-
графически и производить их сложе-
сложение графическим методом, кото-
который во многих случа- ях гораздо
проще, нежели метод аналитиче-
аналитический. Для этой цели служат вектор-
векторные диаграммы колебаний.
Как известно из механики, гар-
гармоническое колебание точки можно
представить как проекцию равно-
равномерно вращающегося вектора. Дей-
л oir I-. ствительно, рассмотрим произволь-
Рис. 215. Гармоническое коле- v / r»ir\
бание как проекция равномерно НУЮ ПР™УЮ Х (РИС" 215) И векТ0Р>
вращающегося вектора имеющий длину а и составляющий
с прямой X угол <?>. Предположим
далее, что этот вектор равномерно вращается против часовой
стрелки с угловой скоростью ш, так что
tp = tot -\- а,
где а — значение угла </? в момент времени t = 0. Тогда проекция
рассматриваемого вектора на ось X выразится формулой
х = о cos (ojt + а),
а проекция на перпендикулярную к ней ось Y — формулой
у = a sin (ut + а).
Поэтому при известной и постоянной частоте колебаний ш мы
вполне определим гармоническое колебание, если изобразим век-
вектор с длиной а, составляющий с выбранным направлением X
угол а (рис. 216).
Рассмотрим теперь сложение двух гармонических колебаний
одинаковой частоты. Построим вектор, изображающий первое
колебание. Его длина а\ (рис. 217) равна амплитуде колебаний, а
угол cci, составляемый с осью диаграммы, дает начальную фазу.
Из конца этого вектора построим второй вектор, изображающий
второе колебание, имеющее амплитуду ai и начальную фазу ai •
Угол /3 = ai — а.\ есть разность фаз колебаний. Проекция ху век-
вектора ai дает одно из колебаний х\ = а\ cos {not + a\), а проекция
Х2 второго вектора дает второе колебание xi = a<i cos (u:t + ai).
§129
ВЕКТОРНЫЕ ДИАГРАММЫ
291
Сумма х\ + Х2 есть сумма обоих колебаний. Но сумма проекций
двух векторов равна проекции суммы обоих векторов. Поэтому
вектор а, являющийся суммой векторов ах и аг, представляет
результирующее колебание.
О
Рис. 216. Изображение гар-
гармонического колебания при
помощи вектора
Рис. 217. Векторная диаграмма
суммы двух гармонических ко-
колебаний
Из сказанного ясно, что при помощи такого приема можно
складывать не только два, но и какое угодно число колебаний.
Для этого нужно из конца второго вектора построить третий
вектор, представляющий третье колебание, затем из конца по-
последнего построить следующий вектор, изображающий четвер-
четвертое колебание, и т.д., и найти суммарный вектор, замыкающий
полученную ломаную линию.
В предыдущих рассуждениях мы считали, что у (или х) обо-
обозначает смещение движущейся точки. Однако наши выводы со-
сохраняют силу и в том случае, если у обозначает любую физиче-
физическую величину, изменяющуюся по закону синуса или косинуса, и
поэтому метод векторных диаграмм приго-
пригоден для изображения и суммирования лю-
любых гармонических колебаний.
Применим теперь этот метод к трех-
трехфазному току и представим геометрически
результаты, полученные в § 128.
Мы видели, что в трех обмотках гене-
генератора трехфазного тока возникают три
ЭДС, изменяющиеся по гармоническому
закону, имеющие одинаковые амплитуды
$о> но обладающие друг относительно дру-
друга разностью фаз 120°. Поэтому векторная рИс. 218. Векторная
диаграмма ЭДС трехфазного генератора диаграмма ЭДС трех-
имеет вид равносторонней звезды, изобра- фазного генератора
женной на рис. 218.
Далее мы установили связь между фазным напряжением
разомкнутого генератора ?о и линейным напряжением Ш и на-
292
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
шли, что при соединении звездой Ш = Йо>/3. Поясним это соот-
соотношение при помощи векторной диаграммы (рис. 219). Линей-
Линейное напряжение ё есть разность ЭДС &i и Ш^ в двух соседних
обмотках и изображается, следовательно, суммой векторов Ш\ и
— ft2- Из рисунка видно, что Ш яв-
является основанием равнобедренно-
равнобедренного треугольника с углом при осно-
основании в 30°, а следовательно,
Ш = 2&Q cos 30° = 2?о \/3/2 =&оу/3,
что мы и получили раньше, скла-
складывая колебания аналитически.
Наконец, рассматривая четы-
рехпроводную линию трехфазного
тока, мы видели, что ток в нуле-
нулевом проводе есть сумма трех токов,
сдвинутых по фазе на 120°. При
симметричной нагрузке амплиту-
амплитуды этих токов одинаковы и вектор-
векторная диаграмма токов имеет вид равностороннего замкнутого
треугольника (рис. 220) Длина замыкающей этих трех векто-
векторов равна нулю, и поэтому результирующая сила тока в любой
момент времени также равна нулю.
Если нагрузка несимметрична, то длины векторов, изобра-
изображающих токи i\, %2 и гз> неодинаковы, и мы получим векторную
диаграмму рис. 221. В этом случае в нулевом проводе будет су-
существовать переменный ток, амплитуда и фаза которого изо-
изображаются вектором i.
Рис. 219. Векторная диаграмма
фазного и линейного напряже-
напряжений; соединение звездой
120
Рис. 220. Векторная диаграм-
диаграмма токов в нулевом проводе.
Симметричная нагрузка
Рис. 221. Векторная диаграмма то-
токов в нулевом проводе. Несимметрич-
Несимметричная нагрузка
Приведенные примеры показывают, что векторные диаграм-
диаграммы позволяют весьма наглядно изображать колебания токов и
напряжений и легко производить их суммирование. Поэтому ме-
§130
ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
293
тод векторных диаграмм получил широкое распространение в
электротехнике.
§ 130. Вращающееся магнитное поле
Представим себе вращающийся постоянный магнит. Вместе с
магнитом будет перемещаться и создаваемое им магнитное поле,
и мы получим вращающееся магнитное
поле.
Если в такое поле поместить магнит-
магнитную стрелку, то она будет стремиться
установиться вдоль линий поля и поэто-
поэтому придет во вращение в ту же сторону,
в которую вращается поле.
Подобно магнитной стрелке будет ве-
вести себя замкнутый виток проволоки.
Вследствие движения поля относительно
витка в проволоке возникнет индукцион-
индукционный ток, который будет направлен так,
как показано на рис. 222. На этот ток со
стороны магнитного поля будут действо- Рис 222- Действие вра-
вать силы, стремящиеся вращать виток
вместе с полем, и виток придет во вра-
вращение.
Таким же образом будут вести себя массивные металличе-
металлические диск или цилиндр, так как в них также будут наводиться
индукционные токи, которые
будут замыкаться в толще ме-
металла диска или цилиндра (так
называемые вихревые токи;
см. § 132), однако, так же как
и токи в проволоках, они будут
взаимодействовать с магнитным
полем. Возникающие при этом
силы, согласно закону Ленца,
будут направлены так, чтобы
уменьшить скорость вращения
диска относительно поля, отчего
диск (или цилиндр) придет во
вращение в том же направлении,
как и поле.
Вращающееся магнитное по-
поле можно получить и с помощью
переменных токов. Рассмотрим
щающегося магнитного
поля на замкнутый ви-
виток проволоки
:•:
i
i
n
У
J
/ 1 x
Рис. 223. Возникновение вращаю-
вращающегося магнитного поля двухфаз-
двухфазного тока
сначала получение вращающегося ноля при помощи двухфазно-
двухфазного тока. Пусть имеются две катушки 1 vl 2 (рис. 223), повернутые
294
ТЕХНИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ МАГНИТНОГО ПОТОКА ГЛ XII
друг относительно друга на угол 90°, питаемые двухфазным то-
током Это значит, что если ток в катушке 1 меняется по закону
i\ = «о sinuit, то ток в катушке 2 будет, ii = Zq sin {cot — 90°). Ка-
Катушка 1 создает переменное магнитное поле Нх, изменяющееся
по закону
Нх =
Катушка 2 создает магнитное поле Ну, направленное перпенди-
перпендикулярно к полю Нх и отстающее от него по фазе на 90°.
Ну = Но sin (ut - 90°) = -Но cos wt.
Напряженность результирующего поля
' = Но A30.1)
остается постоянной во времени. Направление же этого поля
изменяется Будем характеризовать это направление углом а
(рис 223), составленным вектором Н и осью Y Тогда
tg а = Нх/Ну = - tg ut, a = -иЛ. A30.2)
Мы видим, что вектор Н результирующего поля равномерно
поворачивается против часовой стрелки с угловой скоростью ш,
те. мы имеем вращающееся
магнитное поле, подобное по-
полю вращающегося постоянно-
постоянного магнита
В рассмотренном примере
мы получили поле, вращаю-
вращающееся против часовой стрел-
стрелки Легко видеть, что если бы
мы пересоединили концы од-
одной из катушек 1 или 2, то мы
изменили бы знак одного из
полей Нх или Ну и при этом
получили бы а = +u)t, те
вращение по часовой стрелке
Для получения вращаю-
вращающегося магнитного поля с
помощью трехфазного тока
нужны три катушки (или их
число, кратное трем) соответ-
соответственно трем переменным токам в системе трехфазных токов.
Катушки 1, 2 и 3 должны быть повернуты друг относительно
друга на углы 120°, как показано на рис 224. В этом случае мы
имеем три переменных магнитных поля Hi, H2 и Нз, которые
составляют друг с другом, так же как и катушки, углы в 120°
Рис 224 Возникновение вращающе-
вращающегося магнитного поля трехфазного
тока
§ 130 ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ 295
Колебания этих полей выражаются формулами
Н\ = Hos'mojt,
Н2 = #0 sin (wt - 120°), A30.3)
#з = Щ sin (wt -240°).
Нетрудно показать, что эти три поля, складываясь, дают ре-
результирующее поле, вращающееся с угловой скоростью w На-
Напряженность результирующего поля остается постоянной и рав-
равной C/2)#о
Если поменять местами концы любой пары проводов, при-
присоединенных к катушкам поля (или к зажимам генератора), то
направление вращения поля изменяется на обратное
Введем две взаимно перпендикулярные координатные оси ХиУи на-
направим ось X параллельно полю Hi Тогда составляющие полей по оси X
будут
Н\х = Н1 = Hosmut,
Н2х = Н2 cos 120° = -A/2)Я0 sin (wt - 120°),
Н3х = Н3 cos 240° = -A/2)Я0 sin (wt - 240°)
Сложим сначала два последних поля
#2* + Н3х = -(l/2)H0[sin (wt - 120°) + sin M - 240°)] =
= -A/2)Я0 2sm(wt - 180°)cos60° = (l/2)#osinwt
Поэтому полная составляющая результирующего поля по оси X равна
Нх = Я1* + Н2х + Яз* = C/2) tfo sin ut
Найдем теперь составляющую поля по оси У
Н1у = 0,
Н2у = Hi cos 30° = (\Д/2)Н0 sin (wt - 120°),
Я3„ = H3cos 150° = -(л/3/2)Я0sin (wt - 240°)
Поэтому
Ну = Я2„ + Н3у = (\/3/2)Я0 2 sin 60° cos (wt - 180°) = -C/2)Я0 cos wt
Поступая, как и раньше, находим модуль результирующего поля
Я = у/щ + Щ = C/2)ЯО,
угол q, образованный вектором Н и осью Y, определяется из соотношения
tga = Нх/Ну — — tgwt, a = -wt
Таким образом, и здесь мы получаем магнитное поле, вращающееся с угло-
угловой скоростью w
Вращающееся магнитное поле используют в асинхронных
двигателях переменного тока. В двигателях трехфазного тока
три обмотки, создающие вращающееся магнитное поле, разме-
размещены в пазах статора. Они соединяются либо по схеме треуголь-
треугольника, либо по схеме звезды и включаются в сеть трехфазного
тока
296 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
Ротор двигателя представляет собой железный сердечник, в
пазах которого помещается обмотка. В двигателях небольшой
мощности эта обмотка замыкается сама на себя накоротко. Об-
Обмотка ротора часто выполняется в виде толстых стержней, замк-
замкнутых на концах медными кольцами, так что вся обмотка имеет
вид «беличьего колеса»
Вследствие возникновения вращающегося поля в обмотке ро-
ротора возникает индукционный ток, взаимодействие которого с
магнитным полем статора приводит к силам, поворачивающим
ротор.
Сила тока ротора зависит от относительной скорости вращения поля и
ротора Эту скорость принято характеризовать коэффициентом скольже-
скольжения ротора
К = (ип - ир)/ип,
где i/ц — число оборотов поля, а, ир — число оборотов ротора в секунду
Если ротор вращается со скоростью поля (относительная скорость равна
нулю), то К — 0 Если ротор неподвижен (момент пуска), то К = 1 Чем
больше нагрузка двигателя, тем сильнее должен быть ток в роторе, тем
больше будет коэффициент скольжения и тем меньше будет число оборо-
оборотов ротора Поэтому число оборотов двигателя не остается постоянным, а
несколько изменяется с изменением нагрузки, отчего этот двигатель, в от-
отличие от синхронного двигателя, рассмотренного в § 126, получил название
асинхронного двигателя
В момент пуска К = 1 и относительная скорость вращения наиболь-
наибольшая. В это время сила тока в роторе наибольшая и в роторах мощных
двигателей, сопротивление обмотки которых ничтожно мало, может дости-
достигать опасных значений Чтобы уменьшить эту начальную силу тока, роторы
больших двигателей не делают короткозамкнутыми, а снабжают контакт-
контактными кольцами С помощью колец и щеток обмотку ротора замыкают на
пусковой реостат, который постепенно выводят по мере увеличения числа
оборотов двигателя.
Асинхронный двигатель трехфазного тока отличается боль-
большой простотой устройства. Он обладает также хорошими меха-
механическими характеристиками. Поэтому этот двигатель получил
весьма широкое распространение
ГЛАВА XIII
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЭЛЕКТРИЧЕСКИХ
И МАГНИТНЫХ ПОЛЕЙ. ТЕОРИЯ МАКСВЕЛЛА
Между электрическими и магнитными полями существует
глубокая внутренняя связь, проявляющаяся в том, что эти поля
могут превращаться друг в друга. Всякое изменение магнитно-
магнитного поля всегда сопровождается появлением электрического по-
поля и, наоборот, всякое изменение электрического поля приво-
§ 131
ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
297
дит к появлению магнитного поля. Это взаимное превращение
электрического и магнитного полей было открыто в начале вто-
второй половины прошлого века Максвеллом, который развил об-
общую теорию электромагнитного поля в покоящихся средах. Тео-
Теория Максвелла позволяет с единой точки зрения охватить всю
совокупность рассмотренных выше фактов, касающихся свойств
электрических и магнитных полей, а также новые важные яв-
явления В настоящей главе мы рассмотрим основные идеи этой
теории.
§ 131. Вихревое электрическое поле
Вернемся к явлению электромагнитной индукции и рассмо-
рассмотрим неподвижный замкнутый проводник в магнитном поле. В
гл. IX мы видели, что при всяком изменении магнитного поля
в таком проводнике возникает электродвижущая сила и вслед-
вследствие этого появляется индукционный ток.
С другой стороны, из сказанного в гл. VII мы знаем, что
электродвижущая сила в любой цепи возникает только в том
случае, если в ней на заряды действуют какие-либо сторонние
силы, т.е. силы неэлектростатического происхождения. Поэтому
возникает вопрос, какова физическая природа сторонних сил в
этом случае7
Опыт показывает, что ЭДС индукции не зависит вовсе от ро-
рода вещества проводника, который может быть как однородным,
так и неоднородным, как проводником 1-го рода, так и проводни-
проводником 2-го рода (электролит). Она не зависит также от состояния
проводника и, в частности, от
его температуры, которая мо-
может быть и одинаковой, и нео-
неодинаковой вдоль проводника.
Это показывает, что в данном
случае сторонние силы не свя-
связаны с изменением свойств про-
проводника в магнитном поле, а
обусловлены самим магнитным
полем.
Анализируя явление элек-
электромагнитной индукции, Мак-
Максвелл заключил, что причи-
причина появления ЭДС индукции
заключается в возникновении
электрического поля (рис. 225), теже напРавл|
у \r n возрастанию В
а проводники играют второсте-
второстепенную роль и являются только своего рода прибором, обна-
обнаруживающим это поле. Под действием поля электроны прово-
Рис 225 При изменении магнитно-
магнитного поля появляется вихревое элек-
электрическое поле Показанное на чер-
теже HanP*B™ Е соответствует
298
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
димости в проволоке приходят в движение и, если проволока
замкнута, в ней возникает индукционный ток.
Существенная особенность рассматриваемого явления заклю-
заключается в том, что возникающее электрическое поле не является
электростатическим. Линии напряженности электростатическо-
электростатического поля всегда разомкнуты; они начинаются и заканчиваются
на электрических зарядах, в соответствии с чем напряжение
по замкнутому контуру в электростатическом поле всегда рав-
равно нулю. По этой причине электростатическое поле не может
поддерживать замкнутое движение зарядов и, следовательно, не
может привести к возникновению электродвижущей силы. На-
Напротив, электрическое поле, возникающее при электромагнит-
электромагнитной индукции, имеет непрерывные линии напряженности, т.е.
представляет собой вихревое поле Такое поле вызывает в про-
проволоке движение электронов по замкнутым траекториям и при-
приводит к возникновению электродвижущей силы — сторонними
силами являются силы вихревого электрического поля. Элек-
Электрическое напряжение по замкнутому контуру в таком поле не
равно нулю; его значение между двумя какими-либо точками
уже не определяется только положением этих точек, как было
в случае электростатического поля, но зависит еще от формы
контура (проводника), соединяющего данные точки (ср. § 133).
Таким образом, углубленное истолкование явления электро-
электромагнитной индукции приводит к следующему выводу, выражаю-
выражающему первое основное положение тео-
теории Максвелла- всякое изменение
магнитного поля вызывает появле-
появление вихревого электрического поля.
Полученный результат можно
выразить в количественной форме
Согласно основному закону электро-
электромагнитной индукции (§91) ЭДС ин-
индукции равна быстроте изменения
формулировке магнитного потока
g = -d$/dt, A31.1)
Рис 226 К
уравнения Максвелла
где Ф — поток магнитной индукции В через площадь S, огра-
ограниченную рассматриваемым контуром I (рис. 226).
Ф = Вп dS.
s
A31.2)
С другой стороны, согласно § 69, электродвижущая сила,
действующая в каком-либо контуре I, равна
П= J Efdi,
A31.3)
jj 132 ВИХРЕВЫЕ ТОКИ 299
где Е* — напряженность поля сторонних сил. В данном случае
Е* есть напряженность вихревого электрического поля Е. По-
Поэтому, подставляя A31.3) с Е* = Е в A31.1), находим
d^ tdt. A31.4)
Это соотношение выражает количественную связь между изме-
изменяющимся магнитным полем (В) и вихревым электрическим по-
полем (Е) и является одним из основных уравнений в теории Мак-
Максвелла.
Напомним, что в формуле A31.1) мы приписываем магнит-
магнитному потоку определенный знак, зависящий от выбора поло-
положительного направления нормали п к площадке S. Это на-
направление нормали определяет и знак ЭДС, который связан с
направлением п правилом правого буравчика (§ 91). Поэтому
и в уравнении Максвелла A31.4) направление нормали п и на-
направление обхода по контуру / связаны также правилом правого
буравчика.
Поясним сказанное на примере. На рис. 226 указано выбран-
выбранное направление нормали п и соответствующее ему направле-
направление обхода контура /. Если вектор В направлен параллельно п
(или составляет с п острый угол), то поток Ф будет положите-
положителен. Если при этом магнитное поле увеличивается, то d$jdt > О
и из A31.4) следует, что §E[dl < 0. Это значит, что вихревое
i
электрическое поле направлено против отмеченного направле-
направления обхода контура.
§ 132. Вихревые токи
Если в переменном магнитном поле находится какой-либо
массивный проводник, то вихревое электрическое поле вызыва-
вызывает в нем индукционный ток Плотность этого тока в какой-либо
точке проводника по закону Ома равна j = АЕ. Так как линии
напряженности Е замкнуты, то и линии тока также замыкаются
внутри проводника, отчего такие токи получили название вихре-
вихревых токов.
Вихревые токи вызывают нагревание проводников. Если
внутри катушки с переменным током поместить проводящее те-
тело, например, металлический диск, ориентированный перпенди-
перпендикулярно к оси катушки, то диск можно раскалить до высокой
температуры и расплавить.
Нагревание проводников вихревыми токами применяют в ин-
индукционных металлургических печах для плавления металлов и
приготовления их сплавов Небольшие индукционные печи ши-
300
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ ХШ
роко используются в лабораторной и заводской практике для
прокаливания металлов в вакууме и для других целей.
Вихревые токи возникают также при движении массивных
проводников в магнитном поле. Взаимодействуя с магнитным
полем, вихревые токи вызывают по-
появление сил, действующих на дви-
движущееся проводящее тело, которые,
согласно закону Ленца, всегда проти-
противодействуют движению. Это тормо-
тормозящее действие позволяет также лег-
легко обнаружить вихревые токи. На
рис. 227 показан маятник в фор-
форме массивной чечевицы из красной
меди, которая при колебаниях ма-
маятника проходит между полюсами
электромагнита. При выключенном
электромагните маятник колеблется
вследствие большой массы с очень
малым затуханием, но при включе-
включении электромагнита резко останавли-
останавливается.
Если медной монете предоставить
возможность свободно падать без на-
начальной скорости между полюсами
сильного электромагнита, то она движется почти равномерно
с ничтожной скоростью порядка 1 см/с, как если бы движение
происходило в очень вязкой среде.
Если расположить медный диск вблизи
постоянного магнита и привести магнит во
вращение, то диск начинает вращаться в ту
же сторону, что и магнит (рис. 228).
Взаимодействие вихревых токов с маг-
магнитным полем подчиняется третьему закону
Ньютона. Поэтому, если в последнем опы-
опыте вращать вместо магнита диск, то магнит
приходит также во вращение.
Силы, вызываемые вихревыми токами и
действующие на движущиеся проводники
в магнитном поле, используются во многих
измерительных приборах (электрические Рис 228
счетчики, электромагнитное успокоение
Рис 227 Металлический ма-
маятник тормозится в магнит-
магнитном поле вследствие образо-
образования вихревых потоков
N
Ф
диск,
Медный
подвешенный
вблизи вращающего-
вращающегося магнита, приходит
во вращение
измерительных приборов, тахометры и др.).
В некоторых технических устройствах
вихревые токи играют вредную роль. Так,
например, в железных сердечниках трансформаторов и вращаю-
вращающихся частях электрических генераторов возникающие вихре-
§ 133
ТРАНСФОРМАТОР
301
вые токи вызывают бесполезное нагревание и снижают КПД
этих устройств Для ослабления вихревых токов такие детали
изготовляют из тонких листов, разделенных тончайшими слоя-
слоями изолятора таким образом, чтобы изолирующие прослойки
пересекали возможные линии вихревых токов. Сущность этого
приема разъясняется опы-
опытом, изображенным на
рис. 229. Подвесим кубик,
набранный из тонких ме-
металлических пластинок,
на нити, поместим его
между полюсами элек-
электромагнита и, закрутив
предварительно нить, бу- о onn ^ ,
^С ' J Рис 229 Ослабление вихревых токов в
дем наблюдать вращение ж а вихревые токи значительно сла-
кубика при раскручива- бее, чем в случае ?
нии нити Если подвесить
кубик в положение а, то изолирующие прослойки будут пересе-
пересекать линии вихревых токов (одна из них показана штриховой
линией). В этом случае вихревые токи возникают только в
пределах каждой из пластинок; их действие очень слабо,
и кубик свободно вращается с большой угловой скоростью.
Если же подвесить кубик в положение б, то прослойки будут
параллельны линиям вихревых токов и не будут мешать
образованию токов. Кубик будет вести себя так, как если бы
прослоек не было, и будет поворачиваться очень медленно из-за
тормозящего действия вихревых токов.
§ 133. Трансформатор
Трансформатор представляет собой устройство, предназна-
предназначенное для преобразования напряжения и силы переменного то-
тока. Он имеет сердечник (обычно замкнутой формы) из мягкого
железа или иного магнитно-мягкого
ферромагнетика, который несет на себе
две обмотки — первичную и вторичную
(рис. 230). Концы первичной обмотки
(вход трансформатора) подключены к
сети питающего переменного тока, а
концы вторичной обмотки (выход) —
к потребителям электрической энергии.
Рис 230 Трансформатор ЭДС электромагнитной^индукции, воз-
никающая во вторичной обмотке, про-
пропорциональна числу витков в ней, и поэтому, изменяя это число
витков, можно изменять в широких пределах напряжение на
выходе трансформатора
и, ¦:
302
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
Трансформаторы играют огромную роль в современной
электротехнике. В мощных линиях электропередачи в настоя-
настоящее время почти исключительно применяют высокие напряже-
напряжения (тысячи и десятки тысяч вольт). Это позволяет уменьшить
силу тока в линии, а значит, и сечение проводов, что приво-
приводит к сильному снижению стоимости сооружения линий элек-
электропередачи. Однако конструировать генераторы (так же как
и различные приборы, потребляющие электрическую энергию),
рассчитанные на высокие напряжения, весьма трудно, так как
необходимо обеспечить хорошую изоляцию обмоток. Поэтому
электрические генераторы строят на низкое напряжение и затем
это напряжение увеличивают при помощи повышающих транс-
трансформаторов. В местах же потребления электроэнергии ток высо-
высокого напряжения преобразуют при помощи понижающих транс-
трансформаторов в токи низкого напряжения (ПО, 220 В и др.).
Трансформаторы имеют высокий коэффициент полезного
действия, доходящий до 99%, и не содержат никаких движу-
движущихся частей, поэтому они являются весьма удобными техниче-
техническими устройствами.
Трансформатор является хорошим примером технического
использования вихревого электрического поля. Именно это поле
приводит в движение электроны во вторичной обмотке и служит
причиной возникновения в ней ЭДС. Отметим, что магнитный
поток, создаваемый первичной обмоткой, практически сосредо-
сосредоточен внутри сердечника трансформатора, в то время как вих-
вихревое электрическое поле
существует как внутри сер-
сердечника, так и снаружи По-
Поэтому ЭДС во вторичной
обмотке возникает и при на-
наличии зазора между сердеч-
сердечником и обмоткой.
Пользуясь трансформа-
трансформатором, легко проверить на
опыте, что в вихревом элек-
электрическом поле напряжение
между двумя точками зави-
зависит от формы соединяюще-
соединяющего их контура (ср. § 131).
Для этого нужно сделать
вторичную обмотку с малым числом витков (один-два) и при-
присоединить к ее концам а и б (рис. 231) вольтметр один раз так,
чтобы провода вольтметра располагались вне трансформатора
(сплошные линии), а в другой раз — проходили внутри транс-
трансформатора, охватывая его сердечник (штриховая линия). По-
Показания вольтметра в обоих случаях будут разные (во втором
Рис 231 В вихревом электрическом по-
поле трансформатора напряжение зависит
от формы контура
§ 133 ТРАНСФОРМАТОР 303
случае больше), хотя в обоих случаях вольтметр и подключен к
одним и тем же точкам а и б.
В технических трансформаторах это не проявляется, так как, во-
первых, в них обычно число витков вторичной обмотки велико, и поэто-
поэтому различие во включении вольтметра, сводящееся к добавлению одного
лишнего витка, мало сказывается Во-вторых, наличие металлического ко-
кожуха вообще не позволяет осуществить включение, показанное штриховой
линией Тем не менее указанный факт имеет принципиальное значение
Рассмотрим теперь, как связаны между собой входное на-
напряжение U\ и выходное напряжение Ui- Пусть Ф — магнитный
поток в сердечнике В случае технического переменного тока,
изменяющегося по закону синуса, и намагничивания сердечни-
сердечника, далекого от насыщения, этот магнитный поток будет также
изменяться приблизительно по синусоидальному закону: Ф =
= Фовтс^ где ш — угловая частота переменного тока (число
периодов в 2п секунд), а Фо — максимальное значение потока
(его амплитуда). В реальных трансформаторах часть линий ин-
индукции, создаваемых первичной обмоткой, выходит из сердеч-
сердечника и замыкается вне вторичной обмотки (штриховая линия на
рис. 230), образуя так называемый поток рассеяния. Однако в
хороших трансформаторах поток рассеяния мал по сравнению
с потоком внутри сердечника, и поэтому мы будем считать, что
один и тот же поток Ф пронизывает обе обмотки ЭДС, возни-
возникающая в первичной обмотке (ЭДС самоиндукции), равна
$1 = - JVi d&jdb,
а ЭДС во вторичной обмотке
где JVi и Л^2 — число витков в первичной и во вторичной об-
обмотках Применяя к обмоткам трансформатора закон Ома для
участка с ЭДС (§ 68), находим напряжение на входе трансфор-
трансформатора
U N
и напряжение на выходе
Ui = т-гЧ -%2= Ti4 + N2 d&jdt.
Здесь т\ и ri — сопротивления первичной и вторичной обмоток,
а г\ и %i — силы тока в них
Мы ограничимся только случаем разомкнутой вторичной об-
обмотки и поэтому положим 12 = 0. Далее, мы будем считать (что
обычно выполняется для всех технических трансформаторов),
что г\1\ -С Ш\. Тогда, деля почленно два последних уравнения,
находим
/ / A33.1)
304 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ. ТЕОРИЯ МАКСВЕЛЛА ГЛ. XIII
U,
Отношение К = N2/N1 называют коэффициентом трансфор-
трансформации. Он показывает, во сколько раз вторичное напряжение
больше первичного напряжения в режиме хо-
холостого хода.
Если трансформатор нагружен (вторичная
обмотка замкнута), то падением напряжения
гг нельзя пренебрегать по сравнению с ЭДС
индукции, и вместо формулы A33.1) получа-
получается более сложное соотношение.
Иногда вторичной обмоткой трансформа-
трансформатора служит часть первичной обмотки или,
наоборот, часть вторичной обмотки — первич-
первичной. В этом случае трансформатор называ-
называют автотрансформатором (рис. 232). Один из
контактов автотрансформатора часто делают
что позволяет плавно изменять выходное напря-
Рис. 232. Авто-
Автотрансформатор
передвижным
жение.
§ 134. Вытеснение переменного тока (скин-эффект)
Если в однородном проводнике с постоянным поперечным се-
сечением имеется постоянный ток, то плотность тока одинакова в
разных точках сечения проводника. Иное наблюдается при пе-
переменном токе. В этом случае плотность тока оказывается не
одинаковой по сечению: она наибольшая на поверхности и наи-
наименьшая на оси проводника. Ее неравномерность тем больше,
чем толще проводник и чем
больше частота переменного
тока, а при очень больших
частотах ток практически
существует только в тонком
поверхностном слое. Это яв-
явление получило название
скин-эффекта.
Указанное любопытное
явление также объясняется
возникновением вихревого
электрического поля электро-
электромагнитной индукции. Рассмот- р
рим проводник с перемен-
объяснение вытеснения пе-
ременного тока на поверхность про-
ным током, и пусть в данный ВОдника: а - ток нарастает; б - ток
момент времени ток г име- убывает
ет направление, указанное на
рис. 233. Этот ток создает внутри проводника магнитное по-
поле, линии индукции которого лежат в плоскости, перпендику-
перпендикулярной к оси проводника. Предположим, что ток i усиливается.
§ 134 ВЫТЕСНЕНИЕ ПЕРЕМЕННОГО ТОКА (СКИН-ЭФФЕКТ) 305
Тогда возрастающая индукция В вызовет появление вихревого
электрического поля Е (рис. 233 а), которое у поверхности про-
проводника направлено так же, как и ток г, а на оси проводника —
противоположно току. Это поле, следовательно, будет усиливать
ток на поверхности и ослаблять его на оси.
Допустим теперь, что ток г уменьшается. В этом случае осла-
ослабевающая индукция В вызовет электрическое поле Е, которое
будет направлено противоположно по сравнению с первым слу-
случаем (рис. 233 б), т.е. будет у поверхности противоположно току,
а на оси — совпадать с током. В обоих случаях и при усилении,
и при ослаблении тока, вихревое электрическое поле на оси про-
проводника препятствует, а на поверхности способствует изменени-
изменениям тока, а значит, на оси проводника переменный ток слабее, а
на поверхности сильнее.
Закон распределения плотности тока по сечению проводника особенно
прост, если проводник имеет форму плоского слоя, толщина которого ID
значительно меньше ширины (пластина). Расчет показывает, что это рас-
распределение зависит от величины
<*=,*, A34.1)
которая получила название глубины проникновения тока. Здесь /j, — маг-
магнитная проницаемость вещества проводника, цо — магнитная постоянная,
Л — удельная электрическая проводимость, w = Ikv — круговая частота
переменного тока. Выражая эти величины в единицах системы СИ, мы по-
получим d в метрах.
Если d^> D, го плотность тока практически постоянна по сечению про-
проводника. Если d<HD (сильный скин-эффект), то закон распределения при-
приблизительно имеет вид
j(tf)=jno.exp(-|), A34.2)
где j(y) — плотность тока на расстоянии у от поверхности проводника,
Зпов — плотность тока у поверхности. Из A34.2) видно, что глубина про-
проникновения d есть такое расстояние от поверхности проводника, на котором
плотность тока уменьшается в е = 2,71 раза.
Вследствие скин-эффекта электрический ток при больших
частотах течет преимущественно сквозь поверхностный слой
проводника. Это приводит к уменьшению действующего сече-
сечения проводника и, как следствие, к увеличению сопротивления
проводника. При больших частотах или толстых проводах это
увеличение сопротивления может быть значительным.
Благодаря неравномерному распределению тока в проводни-
проводнике изменяется не только его сопротивление, но и индуктивность.
Действительно, при постоянном токе магнитное поле возникает
как во внешнем пространстве, так и внутри проводника. При
наличии сильного скин-эффекта ток существует практически
306
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
только в поверхностном слое, и магнитного поля внутри про-
проводника нет. Магнитная энергия становится меньше на величи-
величину энергии поля внутри проводника, а следовательно, индуктив-
индуктивность проводника уменьшается.
Существование скин-эффекта всегда учитывают в технике
быстропеременных токов. Так как такие токи практически не
идут в глубине проводника, то линии для них собирают из полых
труб. В современной радиотехнике сверхвысоких частот многие
детали (волноводы, коаксиальные линии) покрывают тонким,
хорошо проводящим слоем серебра, так как их сопротивление
практически обусловлено только поверхностным слоем.
§ 135. Индукционный ускоритель
Вихревое электрическое поле получило замечательное при-
применение в индукционных ускорителях, или бетатронах, пред-
предназначенных для получения
пучков электронов большой
скорости.
Схема устройства индукци-
индукционного ускорителя изображена
на рис. 234. Основной его частью
является мощный электромаг-
электромагнит ММ. Создаваемое им в зазо-
зазоре магнитное поле симметрично
относительно оси 00. Это поле
имеет также плоскость симмет-
симметрии А А, проходящую в середине
зазора. Обмотка электромагни-
электромагнита питается переменным током,
частота которого имеет порядок
сотен герц. Для усиления тока в
обмотке электромагнита парал-
параллельно ей присоединяют боль-
большую батарею конденсаторов и
используют явление электричес-
электрического резонанса (см. гл. XXI).
Между полюсами электромагни-
электромагнита находится камера К в фор-
Рис 234 Схема устройства ин- ме тороида (рис. 234), откачи-
дукционного ускорителя: а - по- ваемая до высокого вакуума. В
люсы электромагнита и ускори- определенные промежутки вре-
тельная камера, б — ускорительная г> п
камера в плане мени, когда 5 « 0, в камеру по-
падает пучок электронов, полу-
получаемых при помощи термоэлектронной эмиссии в специальном
источнике, расположенном внутри камеры.
А--
§ 135 ИНДУКЦИОННЫЙ УСКОРИТЕЛЬ 307
При изменении магнитного потока в соответствии с основным
положением теории Максвелла появляется вихревое электриче-
электрическое поле Еина каждый из электронов в камере ускорения дей-
действует сила еЕ. Так как линии напряженности электрического
поля замкнуты, то направление силы будет все время совпадать
с направлением движения, и электроны, обращаясь в магнитном
поле, будут непрерывно увеличивать свою энергию.
Таким образом, индукционный ускоритель подобен транс-
трансформатору, у которого роль вторичной обмотки из одного вит-
витка играет камера. Различие заключается в том, что в проводах
обмотки обычного трансформатора электроны движутся с тре-
трением, и поэтому накапливаемая ими энергия непрерывно рас-
расходуется на выделение тепла; в индукционном же ускорителе
электроны движутся в вакууме практически без сопротивления,
и работа сил электрического поля превращается в кинетическую
энергию электронов.
На протяжении первой четверти периода магнитное поле на-
нарастает и вызывает появление электрического поля определен-
определенного направления. В это время и происходит ускорение элек-
электронов. Во второй четверти периода магнитное поле убывает, и
направление электрического поля изменяется на обратное. Для
ускорения может быть использована лишь одна четверть перио-
периода, начинающаяся при В а 0, т.е. либо первая, либо третья.
Когда энергия электронов становится близкой к максималь-
максимальной (к концу периода ускорения), электроны выводят с орбиты
ускорения и бомбардируют ими мишень, укрепленную внутри
камеры. Это осуществляют разными способами.
Один из них заключается в том, что в центре полюсных на-
наконечников электромагнита укрепляют диски д (рис. 234), изго-
изготовленные из магнитного материала, в котором при В = Вмакс
• уже достигается насыщение. Поэтому к концу периода уско-
ускорения изменяются пространственное распределение магнитного
поля и радиус электронной орбиты, а электронный пучок по-
попадает на мишень или в специальное окошко, через которое он
i выходит из камеры наружу.
Индукционные ускорители применяются главным образом
в исследованиях по ядерной физике. Они позволяют получить
потоки быстрых электронов, т.е. искусственное /3-излучение.
При бомбардировке различных мишеней этими электронами
возникает электромагнитное излучение (искусственные 7-лучи),
гораздо более проникающее, чем 7-излучение естественных ра-
радиоактивных препаратов. Небольшие ускорители начинают при-
применять для получения жестких рентгеновских лучей (возникаю-
(возникающих при бомбардировке мишеней электронами), используемых
для рентгеновской дефектоскопии в промышленности и для дру-
других целей.
308
ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ. ТЕОРИЯ МАКСВЕЛЛА ГЛ. XIII
§ 136. Ток смещения
В предыдущих параграфах мы видели, что всякое пере-
переменное магнитное поле вызывает вихревое электрическое поле.
Анализируя различные электромагнитные процессы, Максвелл
пришел к заключению, что должно существовать и обратное
явление: всякое изменение электрического поля вызывает появ-
появление вихревого магнитного поля. Это утверждение выражает
важнейшее свойство электромагнитного поля (второе основное
положение теории Максвелла).
Так как магнитное поле есть основной, обязательный при-
признак всякого тока, то Максвелл назвал переменное электриче-
электрическое поле током смещения, в отличие от тока проводимости,
обусловленного движением заряжен-
заряженных частиц (электронов и ионов).
Следует отметить, что этот термин не яв-
является удачным. Он имеет некоторое осно-
основание в случае диэлектриков, так как в них
действительно смещаются заряды в атомах и
молекулах. Однако понятие тока смещения мы
применяем и к вакууму, где никаких зарядов, а
следовательно, и никакого их «смещения» нет.
Тем не менее этот термин сохранился в силу
исторических традиций.
Понятие тока смещения можно по-
пояснить при помощи опыта, изображен-
изображенного на рис. 235. Составим контур, со-
содержащий металлический проводник,
конденсатор, батарею и переключатель.
Для суждения о токе в контуре вклю-
включим в него небольшую лампочку на-
накаливания, играющую роль демонстра-
демонстрационного амперметра. Мы имеем здесь
разомкнутый контур, который разры-
разрывается конденсатором. Как мы знаем, через такой разомкнутый
контур постоянный ток не проходит и при длительном включе-
включении батареи лампочка не обнаруживает никакого накала.
Иное будет в первые моменты после включения батареи.
Конденсатор будет заряжаться, и в металлическом проводе воз-
возникнет кратковременный зарядный ток. Если после окончания
зарядки переключить батарею при помощи переключателя, то
конденсатор перезарядится, и в процессе перезарядки в про-
проводе опять возникнет ток, но теперь обратного направления.
При каждом переключении батареи в проводе будет возни-
возникать импульс тока и лампочка будет давать кратковременную
вспышку.
Рис. 235. Изменяющийся
во времени ток проводимо-
проводимости г в металлическом про-
проводе замыкается в диэлек-
диэлектрике током смещения
§ 136 ТОК СМЕЩЕНИЯ 309
Если концы провода, присоединенные к переключателю, под-
подключить в осветительную цепь переменного тока, то перезаряд-
перезарядки конденсатора будут следовать непрерывно друг за другом с
частотой 100 раз в секунду и в контуре длительно будет суще-
существовать переменный ток. В этом случае отдельные вспышки
лампочки уже не будут заметны и она будет накаливаться рав-
равномерно.
Мы видим, что, в отличие от постоянного тока, изменяющи-
изменяющиеся или переменные токи могут существовать и в разомкнутых
контурах. При этом всякий раз, когда в разомкнутом конту-
контуре имеется ток, между его концами (обкладками конденсатора)
имеется изменяющееся во времени электрическое поле или ток
смещения. Таким образом, токи проводимости в металлическом
проводнике замыкаются токами смещения в диэлектрике.
Согласно Максвеллу электрическое поле в конденсаторе в
любой момент времени создает такое же магнитное поле, как
если бы между обкладками существовал ток проводимости с си-
силой, равной силе тока в металлических проводах. Или, иными
словами, магнитное поле нашего разомкнутого контура оказы-
оказывается таким же, как если бы контур был замкнут.
Это позволяет найти количественную связь между изменяю-
изменяющимся электрическим полем и вызываемым им магнитным по-
полем. Действительно, если электрическое смещение в конденса-
конденсаторе есть ?>, то, согласно § 41, поверхностная плотность заряда
на обкладках
a = D.
Поэтому полный заряд q на каждой из обкладок равен
q = SD,
где S — площадь обкладок. Если за время dt заряд конденсатора
изменяется на dqy то сила тока в проводе
г = dq/dt = SdD/dt.
Она однозначно связана с быстротой изменения индукции
электрического поля. Отсюда следует, что меняющееся поле кон-
конденсатора вызывает такое же магнитное поле, как ток, имеющий
силу SdD/dt или плотность
jc = dD/dt. A36.1)
Эта величина получила название плотности тока смещения.
Пользуясь этим понятием, можно выразить второе положе-
положение теории Максвелла в следующей количественной форме: пе-
переменное во времени электрическое поле вызывает такое же
магнитное поле, как и ток проводимости с плотностью jc,
определяемой формулой A36.1).
В общем случае электрическое поле может быть неоднород-
неоднородным и может зависеть не только от времени, но и от координат.
310 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ. ТЕОРИЯ МАКСВЕЛЛА ГЛ. XIII
В этом случае выражение для плотности тока смещения будет
jc = dB/dt, A36.2)
где знак частной производной указывает на то, что магнитное
поле зависит от быстроты изменения индукции во времени в
каждой точке поля.
Следует подчеркнуть, что ток смещения определяется про-
производной вектора D, но не самим этим вектором. Так, например,
в поле плоского конденсатора вектор D направлен от положи-
положительной пластины к отрицательной. Если электрическое поле
увеличивается, то dD/dt, а следовательно, и ток смещения на-
направлены так, как показано на рис. 236 а. Если же электрическое
поле убывает, то dD/dt направлено от отрицательной пластины
¦dD/dt
•dD/dt
Рис. 236. Изменяющееся во времени электрическое поле вызывает появле-
появление (вихревого) магнитного поля
к положительной, и магнитное поле противоположно по сравне-
сравнению с первым случаем (рис. 236 6').
Если в каком-либо проводнике имеется переменный ток, то
внутри проводника существует переменное электрическое поле.
Поэтому внутри проводника имеются и ток проводимости, и ток
смещения и магнитное поле проводника определяется их сум-
суммой, т.е. полным током. Плотность полного тока
A36.3)
В зависимости от электропроводности среды и быстроты изме-
изменения поля (частоты переменного тока) оба слагаемых в A36.3)
играют разную роль. В хорошо проводящих веществах (метал-
(металлах) и при низких частотах плотность тока смещения мала и им
можно пренебречь по сравнению с током проводимости. Поэто-
Поэтому, например, в явлении вытеснения переменного тока в метал-
металлах (§ 134) ток смещения не играет заметной роли. Напротив, в
плохо проводящих средах (изоляторах) и при высоких частотах
ток смещения играет основную роль.
§ 137
УРАВНЕНИЯ МАКСВЕЛЛА
311
Оба члена в формуле A36.3) могут иметь и одинаковые зна-
знаки, и противоположные. Поэтому полный ток может быть как
больше, так и меньше тока проводимости и в частном случае
может обращаться в нуль.
Такой пример приведен на рис. 237, где изображен сферический кон-
конденсатор, заполненный проводящей средой. Если заряд обкладок есть q, то
электрическое смещение D на расстоянии г от центра равно
Плотность тока смещения
4тгг* ¦
Jc — . 9 ,, i
4тгг2 dt'
а сила тока смещения
ic = 4nr2jc = dq/dt.
При разряде конденсатора этот ток направлен от внутренней обкладки
к наружной. Ток же проводимости направлен противоположно (от плюса к
минусу) и его сила есть
dq
dt'
Поэтому полный ток
Рис. 237. Движение зарядов, не
сопровождающееся магнитным
= О
и, несмотря на движение зарядов между
обкладками, магнитное поле равно нулю.
Таким образом, в общем случае
меняющихся токов магнитное поле
определяется не током проводимо-
проводимости, а полным током. Если мы име-
имеем разомкнутый контур, то на кон-
концах проводника обрывается лишь полем
ток проводимости. В диэлектрике
же между концами проводника имеется ток смещения, который
замыкает ток проводимости. Поэтому, если под электрическим
током понимать полный ток, определяемый формулой A36.3),
то окажется, что в природе все электрические токи замкнуты.
Этот важный вывод также был получен Максвеллом.
§ 137. Уравнения Максвелла
Полученный в предыдущем параграфе вывод о магнитном
поле тока смещения можно выразить в виде уравнения. Рас-
Рассмотрим проводник, в котором имеется изменяющийся ток, и
выделим внутри него произвольную площадку S, ограничен-
ограниченную контуром / (рис. 238). Применим к этому контуру теорему
о магнитном напряжении (§ 81), учитывая, однако, что в об-
общем случае изменяющегося тока магнитное поле определяется
312 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
полным током:
? Щ<11 =
l
где гПолн — сила полного тока через площадку S.
Вычислим теперь гПолн- На основании формулы A36.3) имеем
Г . ,c , Г dDn ,c
«полн = J Jndb + J -^- db.
s s
Но первое слагаемое есть сила тока проводимости i. Во втором
слагаемом можно изменить последовательность интегрирования
и дифференцирования. Это дает
Г dDn ,q _ д Г j-, <q _ dN
s s
где N — поток вектора электрического сме-
смещения сквозь площадку 5*. Поэтому
_ . dN
^полн — * "Г "дТ";
и окончательно получаем следующее соот-
соотношение:
г л ¦ , dN
Г^1 = г + Ж.
Рис. 238 В общем
случае внутри про-
водника имеются и
ток проводимости, и
ток смещения '
A37.1)
Оно является вторым основным уравнением
теории Максвелла и выражает в математи-
математической форме положение Максвелла о маг-
магнитном поле тока смещения.
Выпишем теперь основные уравнения, определяющие элек-
электрическое и магнитное поля. В § 131 мы установили одно из
уравнений Максвелла:
§
**-%¦
A37.2)
Здесь Ф — поток магнитной индукции через площадку S, огра-
ограниченную контуром I, причем, так же как и в A37.1), мы поль-
пользуемся символом частной производной по времени, так как В, а
следовательно, и Ф могут еще зависеть от координат (от поло-
положения площадки S).
К этим уравнениям нужно добавить еще два уравнения, вы-
выражающие теорему Остроградского-Гаусса для электрического
(§ 44) и магнитного полей (§ 106):
fDndS = q, A37.3)
f BndS = 0. A37.4)
§ 138 УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ 313
Наконец, следует напомнить, что различные величины, входя-
входящие в эти уравнения, не независимы и между ними существуют
следующие связи:
В = /i/u0H, D = ее0Е, A37.5)
где /i и е — магнитная и диэлектрическая проницаемости веще-
вещества. Сила же тока проводимости i в A37.1) определяется плот-
плотностью тока j, которая связана с напряженностью Е законом
Ома
j = АЕ, A37.6)
где А — удельная электрическая проводимость вещества.
Уравнения A37.1)—A37.6) составляют систему уравнений
Максвелла. Они являются наиболее общими уравнениями для
электрических и магнитных полей в покоящихся средах.
Отметим, что величины е, ц и А входят в уравнения Максвел-
Максвелла как материальные постоянные, т.е. как заданные величины,
характеризующие свойства среды.
§ 138. Уравнения Максвелла в дифференциальной
форме
Уравнения Максвелла A37.1)—A37.4) применимы к поверх-
поверхности любого размера, и поэтому входящие в них величины от-
относятся к разным точкам поля. Так, например, в левой части
уравнения A37.1) Н есть напряженность магнитного поля в точ-
точках контура, ограничивающего рассматриваемую площадку, в
то время как поток N в
правой части зависит от
значений D в точках самой
площадки.
Можно, однако, преоб-
преобразовать эти уравнения в
такую форму, чтобы все
величины относились к од-
одной и той же точке поля.
Для этого уравнения Мак-
Максвелла нужно применить к
площадкам бесконечно ма- X
лого размера.
Обратимся сначала Рис 239. Бесконечно малая площадка
к уравнению Максвелла dydz и значения составляющих магнитно-
A37.1). Введем правовин- го поля на ограничивающем ее контуре
товую прямоугольную си-
систему координат XYZ и рассмотрим прямоугольную площадку
1-2-3-4 (рис. 239) со сторонами dy и dz, параллельными осям
Y и Z. Вершину площадки 1 поместим в произвольную точ-
1
314 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
ку поля (х, у, z) и обозначим составляющие напряженности маг-
магнитного поля в этой точке через Нх, Ну и Hz. В соответствии
с правовинтовым характером координатной системы выберем,
далее, положительное направление обхода по контуру 1-2-3-4
против часовой стрелки и вычислим магнитное напряжение по
этому контуру. Оно распадается на четыре слагаемых, соответ-
соответствующих четырем отрезкам контура. Магнитное напряжение
на отрезке 1-2 равно Hydy. На отрезке 3-4 составляющая на-
напряженности поля вдоль отрезка равна [Ну + —^- dz). Направ-
Направление обхода здесь противоположно положительному направ-
направлению Ну (оси Y), и поэтому магнитное напряжение равно —
— I Ну + -тг^ dz) dy. Аналогично напряжение на отрезке 2-3
естъ [ Hz + -^- dy I dz, а на отрезке 4-1 равно -Hz dz. Поэтому
§ Hsds = Hydy + (hz + Щ?- dy} dz-
, дНу , \ , „ , (dHz дНу\ , ,
у + -аГ dz) dy ~ Hz dz = VW - ~df) dy dz-
Вычислим теперь слагаемые в правой части уравнения
A37.1). Для потока JV существенна лишь нормальная к площад-
площадке составляющая электрического смещения Dx. Поэтому поток
через dydz равен Dx dydz и, следовательно,
dN дВх
Точно так же ток проводимости через площадку определяется
лишь нормальной составляющей плотности тока jx и равен
jx dy dz.
Подставляя все эти величины в формулу A37.1) и сокращая обе
части равенства на dydz, находим
дну
. _
Jx
у
dt JJl dy dz '
Приведенные рассуждения можно применить к двум другим
площадкам dz dx и dx dy, перпендикулярным соответственно к
осям Y и Z. Поэтому вместо уравнения A37.1) мы получим три
уравнения, образующие первую группу уравнений Максвелла:
dD^ . _cmt_dHx dD^ _ dHx _ dHz
at Jx ду dz ' at
ад . =днхдн±
dt +Jz dx dy
§ 138 УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ 315
Подобным образом мы можем применить к указанным трем
площадкам второе уравнение Максвелла A37.2). Это приведет
нас ко второй группе уравнений Максвелла:
_дВ± = дЕ±_дЕ± _дВу_ = дЕ^ _дЕ± dBz _ дЕу _ дЕх
dt ду dz ' dt dz дх ' dt ~ дх ду '
A38.2)
Выражение потока вектора через замкнутую поверхность мы
уже преобразовали в дифференциальную форму в § 14. Поль-
Пользуясь полученным там результатом, можно записать уравнения
A37.3) и A37.4) в виде
Р + ^
дх ду
= о- <138-4)
Уравнения A38.1)—A38.4) совместно с уравнениями A37.5),
A37.6) и представляют собой полную систему уравнений Макс-
Максвелла в дифференциальной форме, в которых все входящие ве-
величины относятся к одной и той же точке поля.
Уравнения Максвелла можно записать в компактной век-
векторной форме, не зависящей от выбора системы координат, ес-
если воспользоваться понятием вихря вектора. Рассмотрим в по-
поле какого-либо вектора А малую площадку AS, ограниченную
контуром /, и составим отношение циркуляции вектора А вдоль
контура / к AS. Из векторного анализа известно, что предел это-
этого отношения при AS —>¦ 0 (если этот предел существует) есть
проекция нового вектора на направление нормали п к площад-
площадке. Этот вектор называется вихрем вектора А и обозначается
символом rot А (сокращение от французского rotation — враще-
вращение) или curl А (от английского curl, что соответствует русскому
«вихрь»).
Таким образом, по определению
rot пА = lim — ? Ai dl.
AS->0 ob J
Но эти величины (для трех направлений п, параллельных осям
X, Y, Z) мы как раз и вычисляли выше (для А = Н и А =
= Е); они равны правым частям уравнений A38.1) и A38.2).
Отсюда видно, что составляющие rotH в прямоугольных осях
координат равны
,H=ii, rotyH = ^^> rot,H= .
ay dz " dz дх дх ду
Такие же формулы справедливы и для rotE.
316 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
Из сказанного следует, что уравнения Максвелла A38.1) и
A38.2) в векторной форме имеют вид
^+j = rotH, A38.1а)
-25= rot E. A38.2а)
СЕ
Если среда является диэлектриком, то в первой группе урав-
уравнений Максвелла нужно положить jx = jy = jz = 0.
§ 139. Значение теории Максвелла
Теория Максвелла сыграла выдающуюся роль в развитии на-
наших знаний об электричестве. Для того чтобы лучше понять
значение этой теории, необходимо вспомнить историческую по-
последовательность основных открытий в области электричества
до работ Максвелла.
Как уже упоминалось, количественное изучение электриче-
электрических явлений началось с работ Кулона A785 г.), установившего
сначала закон взаимодействия электрических зарядов и распро-
распространившего его позднее на взаимодействие «магнитных заря-
зарядов». Однако вплоть до 1820 г. электрические и магнитные явле-
явления рассматривали как различные явления, не связанные между
собой.
Открытие Эрстедом в 1820 г. магнитного действия тока пока-
показало, что между магнитными и электрическими явлениями су-
существует связь и что магнитные действия можно получить при
помощи электрических токов. Магнитное действие токов было
детально изучено Ампером, который пришел к заключению, что
все магнитные явления в природе, в том числе и связанные с
постоянными магнитами, вызваны электрическими токами (тео-
(теория молекулярных токов Ампера).
Дальнейшими важными результатами того периода мы обя-
обязаны Фарадею. Из них особое значение имело открытие элек-
электромагнитной индукции. Фарадей исходил из основной идеи о
взаимной связи явлений природы. Он считал, что если ток спо-
способен вызывать магнитные явления, то и, обратно, при помощи
магнитов или других токов можно получить электрические то-
токи. В результате настойчивых и многочисленных попыток Фа-
Фарадей действительно открыл в 1831 г. это явление, которое еще
более укрепило представление о связи между электричеством и
магнетизмом.
Второй важнейшей идеей в работах Фарадея было признание
основной, определяющей роли промежуточной среды в электри-
электрических явлениях. Фарадей не допускал действия на расстоянии,
которое, как мы сейчас хорошо знаем, физически бессодержа-
§ 140 ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ДВИЖУЩИХСЯ ТЕЛАХ 317
тельно, и считал, что электрические и магнитные взаимодей-
взаимодействия передаются промежуточной средой и что именно в этой
среде разыгрываются основные электрические и магнитные про-
процессы.
В работах Максвелла идеи Фарадея подверглись дальнейше-
дальнейшему углублению и развитию и были превращены в строгую мате-
математическую теорию. В теории Максвелла мысль о тесной связи
электрических и магнитных явлений получила окончательное
оформление в виде двух основных положений теории, рассмо-
рассмотренных нами в§131и13б,и была в строгой форме выражена
в виде уравнений Максвелла (§ 137, 138). Поэтому теория Мак-
Максвелла явилась завершением важного этапа в развитии учения
об электричестве и привела к классическому представлению об
электромагнитном поле, содержащем в общем случае и электри-
электрическое, и магнитное поля, связанные между собой и способные
взаимно превращаться друг в друга.
Уравнения Максвелла содержат в себе все основные зако-
законы электрического и магнитного полей, включая электромаг-
электромагнитную индукцию, и поэтому являются общими уравнениями
электромагнитного поля в покоящихся средах.
Теория Максвелла не только объяснила уже известные фак-
факты, но и предсказала новые и важные явления. Совершенно
новым в этой теории явилось предположение Максвелла о маг-
магнитном поле токов смещения (§ 136). На основе этого пред-
предположения Максвелл теоретически предсказал существование
электромагнитных волн, т.е. переменного электромагнитного по-
поля, распространяющегося в пространстве с конечной скоро-
скоростью. Теоретическое исследование свойств электромагнитных
волн привело затем Максвелла к созданию электромагнитной
теории света, согласно которой свет представляет собой так-
также электромагнитные волны. В дальнейшем электромагнитные
волны действительно были получены на опыте, а еще позднее
электромагнитная теория света, а с нею и вся теория Максвел-
Максвелла, получили полное и блестящее подтверждение.
Однако мы отложим рассмотрение электромагнитных волн
до гл. XXII, так как для понимания методов их получения и ис-
исследования необходимо изучение электронных явлений и элек-
электрических колебаний.
§ 140. Электромагнитное поле в движущихся телах
До сих пор в настоящей главе мы рассматривали взаимные
превращения электрических и магнитных полей, вызванные из-
изменением полей во времени. Аналогичные явления имеют место
и при движении электромагнитного поля относительно наблю-
наблюдателя.
318 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ. ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
Рассмотрим заряд, движущийся в магнитном поле в вакуу-
вакууме. С точки зрения наблюдателя, неподвижного относительно
магнитного поля, на заряд действует сила (§ 88)
F = qvB sin (v,В). A40.1)
Здесь q — заряд, В = /^оН — индукция магнитного поля, a v —
скорость движения заряда относительно магнитного поля. На-
Направление этой силы перпендикулярно к v и В и подчиняется
правилу правого буравчика (совпадает с направлением вектор-
векторного произведения [vB]).
Представим себе теперь второго наблюдателя, движущего-
движущегося вместе с зарядом. Для этого наблюдателя заряд будет непо-
неподвижным, а между тем на заряд будет действовать та же сила F.
Но если на неподвижный заряд действует сила, пропорциональ-
пропорциональная заряду, то это значит, что имеется электрическое поле. Его
напряженность равна
Е = F/q = vB sin (v, В), A40.2)
а направление поля совпадает с направлением силы F, т.е. пер-
перпендикулярно к v и В (рис. 240).
Таким образом, электромагнитное поле зависит от системы
отсчета. Если в какой-либо системе отсчета существует одно маг-
магнитное поле, то в других системах, движущихся относительно
первой, мы имеем и магнитное поле, и электрическое.
Е
Рис. 240. При движении от-
относительно магнитного по-
поля появляется электриче-
электрическое поле
Рис. 241. Если в системе отсчета К\
имеется только магнитное поле, то в си-
системе К, движущейся относительно Ki,
появляется еще и электрическое поле
Полученные результаты можно представить в другом виде.
Пусть имеются две системы отсчета К и К\, причем К движет-
движется относительно К\ с постоянной скоростью v параллельно оси
Х\ (рис. 241). Пусть, далее, в К\ существует магнитное поле,
которое в произвольной точке а имеет составляющие Н\х, Н\у и
H\z. Тогда в той же точке, но в системе К появится вследствие
§ 140
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ДВИЖУЩИХСЯ ТЕЛАХ
319
движения электрическое поле Ех, Еу, Ez. Применяя к отдель-
отдельным составляющим поля формулу A40.2), получаем
Ех = 0, Еу = -vBlz, Ez = +vBly.
Если в системе К\ имеется еще и электрическое поле, то пол-
полное электрическое поле в системе К имеет составляющие
Ex = Elx, Ev = Ely-vBlZl Ez = Elz + vBly. A40.3)
Отметим еще раз, что v есть скорость системы К относительно
системы К\.
Совершенно аналогично при движении относительно
электрического поля появляется магнитное поле. Чтобы
определить это поле, рассмотрим заряд +q, движущийся от-
относительно наблюдателя со скоростью v. Такой заряд создает
магнитное поле (§ 86)
Я =
_ qv
4тгг2
sin(v,r),
A40.4)
где г — радиус-вектор, проведенный из заряда в данную точку.
Но в выражении A40.4) q/Dirr2) есть электрическое смещение
D = ЕоЕ, создаваемое зарядом в рассматриваемой точке а. По-
Поэтому, учитывая еще, что D направлено вдоль г, можно напи-
написать
Н = vDsm(v,D). A40.5)
Поле Н перпендикулярно к v и D (совпадает с направлением
векторного произведения [vD]).
Для наблюдателя, движущегося вместе с зарядом, существо-
существовало бы только электрическое поле. Если же это электрическое
поле движется относительно наблюдателя, то появляется еще и
магнитное поле, выражаемое формулой A40.5) (рис. 242).
Рис. 242. При движении от-
относительно электрического
поля появляется магнитное
поле Н
Рис. 243. Если в системе отсчета К\
имеется только электрическое поле, то
в системе К, движущейся относительно
К\, появляется еще и магнитное поле
320 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ ХШ
Введем, как и раньше, две системы отсчета, одна из кото-
которых К движется относительно другой К\ в направлении Х\
(рис. 243), и положим, что заряд покоится в системе К\. Следо-
Следовательно, электрическое поле этого заряда будет двигаться отно-
относительно К со скоростью —V. Тогда, применяя формулу A40.5)
к отдельным составляющим поля и изменяя в ней знак у скоро-
скорости v, получим
Нх = 0, Ну = +vDlz, Hz = -vDiy.
Если в системе К\ имеется еще и магнитнее поле
(Hix,Hiy,H\z), то полное магнитное поле в системе К имеет
составляющие
Hx = Hlx, Hy = Hly + vDlz, Hz = Hlz-vDly. A40.6)
Здесь, как и раньше, v есть скорость движения системы К (в
которой наблюдается поле Нх, Hv, Hz) относительно системы
Къ
Напомним в заключение, что формулы A40.1) и A40.4), из
которых мы исходили в наших рассуждениях, были получены в
конечном счете из опытов с магнитным взаимодействием про-
проводов с током. Но в проводах мы имеем всегда лишь медленные
движения зарядов. Поэтому и написанные выше формулы пре-
преобразования полей можно считать обоснованными только для
медленных движений (по сравнению со скоростью света). Для
быстрых движений эти формулы должны быть заменены на бо-
более общие (см. § 143).
§ 141. Для электромагнитных явлений валено
относительное движение
В предыдущем параграфе мы говорили, что скорость и,
входящая в формулы преобразования электромагнитного по-
поля, есть скорость относительного движения. Совершенно так же
опыт дает, что и для всех других электрических явлений важ-
важно только относительное движение: в явлении электромагнитной
индукции — движение провода относительно магнита, в магнит-
магнитных действиях движущихся зарядов — движение этих зарядов
относительно наблюдателя (магнитной стрелки) и т.д.
Однако вопрос о том, какая скорость входит в законы элек-
электрических явлений, не был сразу самоочевидным. Примерно с
конца XVII века для объяснения электрических и световых яв-
явлений в физике начали пользоваться зародившимся еще гораздо
раньше представлением об эфире, т.е. представлением о некото-
некоторой всепроникающей среде, заполняющей все мировое простран-
пространство. Так как физика в XVIII-XIX веках была по преимуще-
преимуществу физикой механистической, то и эфир считали также хотя
§ 141 ВАЖНОСТЬ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 321
и особой, но некоторой механической средой, а электрические
и магнитные явления рассматривали как различные процессы
деформаций и движений эфира. В соответствии с этим можно
было сделать два предположения: либо электромагнитные явле-
явления обусловлены движением относительно эфира («абсолютное»
движение), либо они определяются движением относительно на-
наблюдателя (относительное движение).
Легко видеть, что оба эти предположения приводят к со-
совсем различным следствиям. В качестве примера рассмотрим
заряженный плоский конденсатор, неподвижно установленный
на земной поверхности. Так как Земля движется по орбите со
скоростью около 30 км/с, то с такой же скоростью должно бы-
было бы двигаться и электрическое поле относительно эфира (оп-
(оптические явления, например, так называемая аберрация света,
требуют допущения, что эфир не увлекается Землей при дви-
движении). Если бы важно было движение относительно эфира,
то такой конденсатор должен был бы создавать еще и магнит-
магнитное поле, напряженность которого определилась бы формулой
A40.5). Так, например, если расстояние между пластинами рав-
равно 1 см = 10~2 м, напряжение между ними 10 кВ, а направление
поля перпендикулярно к скорости Земли (sin(v, D) = 1), то
D = е0Е = 8,85 • 10~6 Кл/м2,
Н = vD = 30 • 103 • 8,85 • 10~6 « 0,33 А/и,
что нетрудно обнаружить на опыте. Если же важно движение
относительно наблюдателя, то никакого магнитного поля быть
не должно. Поэтому, исследуя, имеется ли магнитное поле воз-
возле заряженного конденсатора, можно решить поставленный во-
вопрос.
Такие опыты были действительно произведены Рентгеном и
А.А. Эйхенвальдом Они показали, что магнитометр, располо-
расположенный вблизи конденсатора, не обнаруживает никакого маг-
магнитного поля.
Другой вариант подобного опыта был осуществлен Троутоном и Ноб-
Ноблем в 1904 г. Идея опыта заключалась в следующем. Представим себе заря-
заряженный конденсатор, напряженность электрического поля которого Е со-
составляет угол •& с направлением орбитальной скорости Земли v (рис. 244).
Если бы было важно движение относительно эфира, то внутри конденсато-
конденсатора имелось бы, кроме электрического, магнитное поле напряженности
Н = veoEsmd.
Поэтому в каждой единице объема поля заключалась бы не только энергия
электрического поля еоЕ2/2, но еще и энергия магнитного поля цоН /2 и
полная энергия конденсатора была бы равна
W = ~(ейЕ2 + моЯ2)т = WEA + eofiov2 sin2 ¦&),
322 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
где We = теоЕ2/2 — энергия электрического поля, т — объем поля. Сле-
Следовательно, энергия конденсатора зависела бы от угла •&, а значит, на кон-
конденсатор действовала бы пара сил с моментом
М = -dW/dtf - -WB?Ofio ¦ v2 sin 20.
Под действием этой пары сил конденсатор должен был бы повернуться так,
чтобы линии напряженности его электрического поля сделались параллель-
параллельными скорости v (•& = 0), причем его
энергия стала бы минимальной.
В опытах небольшой конденсатор
подвешивали на тонкой нити, заряжали
его до высокой разности потенциалов и
с помощью светового указателя наблю-
наблюдали крутильные колебания конденса-
конденсатора. Отсюда можно было определить
положение равновесия конденсатора.
Так как направление предполагаемо-
предполагаемого движения Земли относительно эфи-
эфира неизвестно, то наблюдения произ-
производили в различное время суток. При
Рис. 244. Опыт Троутона и Ноб- этом вследствие вращения Земли на-
ля правление скорости относительно эфи-
эфира должно было изменяться, а следова-
следовательно, должно было меняться и положение равновесия конденсатора. Эти
опыты не обнаружили никаких систематических отклонений конденсато-
конденсатора в течение суток Подобные опыты впоследствии повторялись с большей
точностью и также дали отрицательный результат.
Описанные опыты показывают, что магнитное поле зависит
от относительного движения электрического поля.
Попытки обнаружить абсолютное движение Земли в эфи-
эфире производились и оптическими методами, которые отличают-
отличаются особенно большой точностью. Однако все подобные опыты
неизменно давали один и тот же отрицательный результат. Так
как свет представляет собой тоже электромагнитное явление,
то, суммируя результаты всех опытов, можно заключить, что с
помощью электромагнитных явлений, так же как и с помощью
механических, невозможно обнаружить абсолютное движение.
Или иначе: для электромагнитных явлений важно только отно-
относительное движение.
Неизменные отрицательные результаты различных и много-
многочисленных опытов, имевших целью обнаружить движение от-
относительно эфира, привели также к безнадежному крушению
всех теорий эфира. В результате этих опытов в теориях эфи-
эфира возникло принципиальное и неустранимое противоречие, за-
заключающееся в том, что, с одной стороны, эфир трактовался
как механическая среда, а с другой, — эфир оказался лишен-
лишенным основного свойства всякой механической системы — свой-
свойства служить системой отсчета. Указанное, а также и другие
§ 142
ИНДУКЦИЯ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ
323
I
противоречия привели постепенно к выводу, что их причина ле-
лежит в самой исходной предпосылке теорий, т.е. что эфира вооб-
вообще не существует. Поэтому современная физика рассматривает
электрические явления как особый класс явлений природы, не
сводимый к механическим явлениям.
§ 142. Электромагнитная индукция в движущихся
проводниках
Мы знаем, что в случае неподвижных (относительно магни-
магнитов и токов) проводников причина электромагнитной индукции
заключается в возникновении вихревого электрического поля
(§ 131). Спросим себя теперь, чем обу-
обусловлено возникновение ЭДС индукции
в проводниках, движущихся в магнит-
магнитном поле?
Ответ на этот вопрос дают зако-
законы преобразования электромагнитного
поля, рассмотренные в § 140. Когда
проводник перемещается относительно
магнитного поля, то в нем (т.е. в си-
системе отсчета, связанной с проводни-
проводником) тоже появляется электрическое
поле (но не электростатическое!). Это
поле и является той сторонней силой,
которая обусловливает возникновение
ЭДС и приводит в движение электро- р
ны внутри проводника.
Объяснение
- „_„ электромагнитной индук-
Вычислим ЭДС индукции, исходя из ции при движении провод-
этих соображений. Рассмотрим отрезок Ника. Магнитная индук-
прямого провода длины /, расположен- ция В направлена от
ный в плоскости, перпендикулярной к чертежа к читателю
магнитной индукции В, и движущийся
в этой плоскости с постоянной скоростью v (рис. 245). Элек-
Электрическое поле, возникающее в проволоке вследствие движения,
определяется формулой A40.2):
E = vB.
Так как это поле в данном случае является сторонней силой,
то ЭДС равна (ср. § 69)
i
8= [Edl = vlB.
Но vl есть площадь, описываемая проводником в единицу вре-
времени, a vlB — магнитный поток через эту площадь, или, иначе,
324 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ. XIII
число пересекаемых в единицу времени линий магнитной индук-
индукции, т.е. мы получили закон электромагнитной индукции Фа-
радея (§ 91). Направление индукционного тока совпадает с на-
направлением напряженности поля Е. На рис. 245 видно, что оно
удовлетворяет закону Ленца.
Таким образом, причина электромагнитной индукции в дви-
движущихся проводниках заключается в появлении электрическо-
электрического поля при движении относительно магнитного поля.
Рассмотрим один специальный случай индукции, являющийся хорошей
иллюстрацией сказанному. Пусть имеется цилиндрический постоянный маг-
магнит, вращающийся вокруг своей оси
(рис. 246). Половина магнита включена
в электрическую цепь при помощи двух
скользящих контактов, один из которых
касается оси магнита, а другой — само-
самого магнита в нейтральной линии. Такой
опыт был осуществлен еще Фарадеем
(«униполярная индукция») и показал,
что в цепи действительно появляется ин-
индукционный ток. ЭДС индукции оказы-
оказывается такой же, как если бы магнит
находился в покое, но двигался контур
abcVa с такой же угловой скоростью, но
в обратном направлении.
Для объяснения этого опыта иногда
представляют себе, что линии индукции
магнитного поля скреплены с магнитом
наподобие жестких спиц, и рассматри-
рассматривают возникающую ЭДС как следствие
пересечения линиями магнитной индук-
индукции проволочного контура abcVa. Одна-
Однако это объяснение совершенно неверно.
Ведь линия магнитной индукции — это
введенный нами способ изображения по-
поля (а не магнита). При вращении же магнита все его положения неотли-
неотличимы, а создаваемое им поле постоянно и не зависит вовсе от скорости
вращения магнита. Поэтому и говорить о движении линий поля вместе с
магнитом нет никаких оснований.
Истинная сущность этого явления опять заключается в законах преоб-
преобразования электромагнитного поля при движении системы отсчета (§ 140).
Чтобы сделать рассуждения наиболее ясными, заменим вращательное дви-
движение поступательным и представим себе бесконечную равномерно на-
намагниченную ленту, движущуюся с постоянной скоростью v вдоль оси X
(рис. 247). В системе отсчета, связанной с магнитом (Кг), мы имеем только
магнитное поле. Но в системе отсчета (КO связанной с контуром abVa, дви-
движущейся относительно магнита со скоростью —v, появляется электрическое
поле, которое и вызывает индукционный ток.
Полагая в формулах A40 3) Е\х = E\v = EXz = 0, Bix = Biz = О,
B\y = В и заменяя в них v на —v, имеем
Рис. 246. Схема униполярной
машины Фарадея
Е = -vB.
§ 143
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
325
Следовательно, ЭДС в отрезке аЬ (с длиной I) равна
ъ
%= fEdl = -vlB.
В этой формуле vlB есть магнитный поток через площадь аЪЬ'а'а, описы-
описываемую линией аЬ в единицу времени. В случае вращательного движения
Рис. 247. К объяснению униполярной индукции
поток войдет через боковую поверхность магнита abcc'b'a (рис. 246), опи-
описываемую линией аЬс (тоже в единицу времени).
§ 143. Преобразования Лоренца
Как известно, механические явления в различных системах
отсчета, движущихся друг относительно друга прямолинейно
и равномерно, протекают одинаково. С помощью механических
измерений невозможно установить, какая из этих систем поко-
покоится, а какие — движутся, и поэтому можно лишь говорить об
относительном их движении по отношению друг к другу (прин-
(принцип относительности для механических явлений).
Совершенно то же мы имеем в электромагнитных явлениях.
В § 141 мы видели, что с помощью электромагнитных явлений,
так же как и с помощью явлений механических, нельзя полу-
получить никаких указаний о существовании абсолютного движения,
и поэтому нельзя указать никакой привилегированной системы
отсчета. Все системы отсчета, движущиеся друг относительно
друга прямолинейно и равномерно, равноправны между собой и
во всех этих системах законы электромагнитных явлений одина-
одинаковы. В этом заключается принцип относительности для элек-
электромагнитных явлений.
Вернемся теперь опять к формулам преобразования электро-
электромагнитных полей A40.3) и A40.6) и посмотрим, удовлетворяют
ли они принципу относительности. Для простоты будем считать,
что в системе отсчета К\ электрическое поле направлено вдоль
оси Y (Е\у = Е\, Е\х = E\z = 0), а магнитное поле — вдоль оси
326 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ. XIII
Z (Я12 = Я], Hix = Hiy = 0). Тогда формулы преобразования
принимают вид
E = Ei-vBu H = Hl-vDi. A43.1)
Они выражают поле в системе К, движущейся относительно
К\ со скоростью v. Но, согласно принципу относительности, мы
с таким же правом можем считать, что система К\ движется
относительно системы К со скоростью —v, и исходить в своих
рассуждениях из полей Е и Н в системе К. Мы должны были бы
получить те же формулы A43.1), только с измененным знаком
у скорости v:
Ех = Е + vB, Hi = H + vD.
Однако если мы с помощью формул A43.1) выразим Е\ и Н\
через Е я Н, то получим выражения
A - eo/W)?i =E + vB, (I - eo/W)#i =H + vD,
которые отличаются от написанных выше. Эти выражения мож-
можно представить в более удобном виде. Произведение ?оМо имеет
размерность, обратную размерности квадрата скорости. Поэто-
Поэтому
с— 1/VeoMo
есть некоторая скорость. Она равна с = 4-108 м/с, т.е. скорости
света в вакууме. Такой результат не является случайным совпа-
совпадением, а непосредственно следует из электромагнитной теории
света (ср. § 240). Учитывая это обстоятельство, последние два
соотношения можно записать в следующем виде:
где /3 = vjc есть скорость относительного движения, выражен-
выраженная в долях скорости света в вакууме.
Таким образом, формулы A43.1) не удовлетворяют принци-
принципу относительности. Хотя величина /З2 обычно весьма мала по
сравнению с единицей (даже для орбитального движения Зем-
Земли /З2 ~ Ю~8), это обстоятельство имеет принципиальное зна-
значение и указывает на то, что формулы A43.1) не вполне точны.
Они справедливы только для медленных движений, для кото-
которых /З2 <С 1 (т.е. и2 <^ с2). Однако для быстрых движений (на-
(например, для движений электронов и ионов в ускорителях, где
мы имеем /5 ~ 1) они уже неприменимы и должны быть замене-
заменены другими.
Формулы преобразования полей, пригодные для любых ско-
скоростей (вплоть до v = с), были впервые найдены Лоренцем (пре-
(преобразования Лоренца для электромагнитных полей) и имеют
§ 143
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
327
ВИД
Ех =
1 - (З2 Еу = Е1у - vBlz>
1 - Р2 Ez = Еи + vBly,
Нх — Н
A43.2)
Они позволяют найти электромагнитное поле Е и Н в системе
отсчета К, движущейся относительно другой системы К\ в на-
направлении положительной оси Х\ со скоростью v, если известно
электромагнитное поле Ei и Hi в системе отсчета К\. Позднее
эти формулы были строго обоснованы как следствие принципа
относительности в теории относительности Эйнштейна.
Легко убедиться, что преобразования Лоренца A43.2) удов-
удовлетворяют принципу относительности. Если систему A43.2) раз-
разрешить относительно полей Е\ и Н\, то получатся те же самые
выражения, с той только разницей, что знак у скорости изме-
изменится на обратный. Если /З2 <^ 1, то преобразования Лоренца
переходят в формулы A40.3) и A40.6), установленные на опыте
для медленных движений.
В качестве примера применения преобразований Лоренца ис-
исследуем, как изменяется электрическое поле заряда при движе-
движении. Для наблюдателя, относительно которого заряд покоится
(система К\), линии напряженности электрического поля расхо-
расходятся во всех направлениях с одинаковой густотой (рис. 248 а).
Для наблюдателя же, относительно которого заряд движется
Рис. 248 Электрическое поле неподвижного (о) и движущегося (б) заряда
(система К), электрическое поле заряда будет другим. Разло-
Разложим это поле на две составляющие: Et, параллельную скорости
v, и Еп, перпендикулярную к скорости. Так как в нашем случае
В1:с = Biy = Bi2 = 0, то преобразования Лоренца дают
Ex — Eix, a/1 — /32 Ey = Ely,
328 ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ПОЛЕЙ ТЕОРИЯ МАКСВЕЛЛА ГЛ XIII
Следовательно,
771 771 Г71 Г71 / TTlO I Z7I2 С /
&t — &x — &XI-, &n — \l ?<y + nz — -bin/
Для угла а, составляемого в какой-либо точке поля линий на-
напряженности с направлением скорости v, мы имеем
tna.--En_ I Eln_ I
Ub " — Et — г. Я? 17..
где а.\ — соответствующий угол наклона в случае покоящегося
заряда. Так как уч. — /З2 < 1, то а > сч, т.е. при движении заря-
заряда линии напряженности поворачиваются, стремясь стать пер-
перпендикулярно к направлению движения (рис. 248 6). Нетрудно
показать, что рис. 248 б можно получить из рис. 248 а путем
сжатия всех линейных размеров в направлении движения в от-
отношении 1/л/1 — 02.
Таким образом, при движении электрического заряда отно-
относительно наблюдателя не только появляется магнитное поле, но
и первоначальное электрическое поле также изменяется. Впро-
Впрочем, это изменение становится заметным только при очень бы-
быстрых движениях, так как оно зависит от /З2 (в то время как
магнитное поле пропорционально первой степени /3).
ЭЛЕКТРОННЫЕ И ИОННЫЕ ЯВЛЕНИЯ
ГЛАВА XIV
ПРИРОДА ЭЛЕКТРИЧЕСКОГО ТОКА В
МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ
§ 144. Измерение заряда электрона
Наиболее прямое определение заряда электрона было произ-
произведено в опытах Р. Милликена, в которых измерялись очень ма-
малые заряды, возникавшие на мелких частицах. Идея этих опы-
опытов заключалась в следующем. Согласно основным представле-
представлениям электронной теории заряд какого-либо тела возникает в
результате изменения содержащегося в нем числа электронов
(или положительных ионов, заряд которых равен или кратен
заряду электрона). Вследствие этого заряд любого тела должен
изменяться только скачкообразно и притом такими порциями,
которые содержат целое число зарядов электрона. Поэтому уста-
установив на опыте дискретный характер изменения электрического
заряда, можно получить тем самым и подтверждение существо-
существования электронов, и определить заряд одного электрона (эле-
(элементарный заряд).
Понятно, что в подобных опытах измеряемые заряды долж-
должны быть очень малыми и состоять лишь из небольшого числа
зарядов электрона. В противном случае добавление или отня-
отнятие одного электрона будет приводить только к небольшому в
процентном отношении изменению общего заряда и поэтому мо-
может легко ускользнуть от наблюдателя вследствие неизбежных
ошибок при измерении заряда.
В опытах было обнаружено, что заряд частичек действитель-
действительно изменяется скачками, причем изменения заряда всегда были
кратны определенному конечному заряду.
Схема опыта Милликена показана на рис. 249. Основной ча-
частью прибора является тщательно изготовленный плоский кон-
конденсатор, пластины которого присоединяются к источнику на-
напряжения в несколько тысяч вольт. Напряжение между пласти-
пластинами можно изменять и точно измерять. Мелкие капельки мас-
масла, получаемые с помощью специального пульверизатора, попа-
попадают через отверстие в верхней пластине в пространство между
330 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
пластинами. Движение отдельной капельки масла наблюдают в
микроскоп. Конденсатор заключен в защитный кожух, поддер-
поддерживаемый при неизменной
температуре, предохраняю-
предохраняющей капельки от конвекцион-
конвекционных токов воздуха.
Капельки масла при рас-
распылении заряжаются, и по-
поэтому на каждую действуют
две силы: результирующая
силы тяжести и выталки-
выталкивающей (архимедовой) силы
Рис 249. Схема опыта Милликена и сила, вызванная электри-
электрическим полем. Если U —
напряжение между пластинами конденсатора, ad — расстояние
между ними, то напряженность поля в конденсаторе есть
Е = U/d. Поэтому на капельку с зарядом q действует сила поля
Результирующая силы тяжести капельки и выталкивающей (ар-
(архимедовой) силы со стороны окружающего воздуха равна
где а — радиус капельки, 5 — плотность масла, 5q — плотность
воздуха при условиях опыта, g ~ ускорение свободного падения.
Подбирая должным образом знак заряда на пластинах кон-
конденсатора, можно сделать направление силы Т?е противополож-
противоположным направлению Fg. Если при этом Fe > Fg, то капелька
будет двигаться вертикально вверх. Если Fe < Fg, то капелька
будет опускаться. Изменяя напряжение на конденсаторе, можно,
очевидно, добиться и такого положения, чтобы обе силы были
равны друг другу:
^a3E-50)g=q^. A44.1)
В этом случае капелька не будет ни опускаться, ни подниматься,
а будет находиться в равновесии. Поэтому, определяя на опыте
напряжение С/, соответствующее равновесию капельки, и зная
ее радиус а, можно по формуле A44.1) найти заряд капельки.
Для определения радиуса капельки наблюдают скорость ее
движения в отсутствие электрического поля. Как известно из
механики, на шар, движущийся с малой скоростью в вязкой сре-
среде, действует сила трения, пропорциональная скорости (закон
Стокса):
FTp = &rrqav.
Здесь v — скорость движения шара, г/ — вязкость среды. При
установившемся движении шар приобретает постоянную ско-
§ 144 ИЗМЕРЕНИЕ ЗАРЯДА ЭЛЕКТРОНА 331
рость, при которой сила трения равна силе Fg:
-7га3(<5 — 5Q)g = бтгг/сш. A44.2)
О
Измеряя скорость равномерного падения капельки v (определяя
время, за которое капелька проходила расстояние между двумя
нитями, видимыми в поле зрения микроскопа), можно по фор-
формуле A44.2) определить радиус капельки а.
Практически удобнее не уравновешивать капельку, а измерять скорость
ее движения. Если при наличии поля капелька приобретает скорость v\,
направленную вверх, то
4 з
qU/d — -тга E — 6o)g = 67:7701I.
о
Скорость равномерного падения капельки v в отсутствие электрического
поля определяется уравнением A44.2). Из этих двух уравнений можно ис-
исключить радиус капельки а, и тогда для заряда q получается выражение
Поэтому, измеряя скорость равномерного движения капельки при наличии
поля (vi) и без поля (г>), можно найти ее заряд по формуле A44.3).
При точных измерениях заряда приходится еще учитывать, что для
очень малых капель (радиус которых невелик по сравнению со средним
свободным пробегом атомов газа) закон Стокса требует поправки. Более
точное выражение для силы трения имеет вид
где р — давление газа, Ь — постоянная. Если давление р измерено в см рт. ст.,
о — в см, то для воздуха Ь = 0,000617 при температуре 23 °С. Из формулы
A44.4) видно, что для введения необходимой поправки в выражение A44.3)
нужно заменить в нем вязкость п на ——.
1 + о/ар
В опытах Милликена сначала определяли заряд капельки q0,
полученный ею при распылении. Затем в пространстве между
обкладками создавались ионы, для чего воздух в конденсаторе
подвергался действию рентгеновских лучей, ультрафиолетовых
лучей или излучения радиоактивных препаратов. Ионы оседа-
оседали на капельку, ее заряд изменялся и принимал значения q\,
42 и т.д. Сравнивая найденные заряды, а также их изменения
(9i ~ Qo), ((}2 — Qi), • • •) можно определить общий наибольший де-
делитель этих количеств, который, очевидно, и является зарядом
электрона.
Наряду с рассмотренным существуют и другие методы опре-
определения заряда электрона. На основании сопоставления всех
экспериментальных данных в настоящее время считают, что
наиболее точное значение заряда электрона равно
е = 1,602189 • ИГ19 Кл.
332 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
§ 145. Природа носителей заряда в металлах
Выше мы неоднократно говорили, что электрический ток в
металлах есть движение электронов и что ионы металла не при-
принимают участия в переносе электрического заряда. Сейчас мы
рассмотрим опытные доказательства этого.
Прежде всего отметим, что если бы при электрическом токе
происходило движение ионов, то электрический ток в металлах
должен был бы обязательно сопровождаться переносом веще-
вещества металла. Чтобы проверить, имеет ли место это явление,
Рике произвел специальные опыты, в которых электрический
ток проходил в течение года через три поставленных друг на
друга цилиндра — медный, алюминиевый и медный. Несмотря
на то, что общий заряд, прошедший через цилиндры, достигал
огромного значения около 3,5 МКл, никакого проникновения ме-
металлов друг в друга обнаружено не было и масса цилиндров со-
сохранялась с погрешностью до ±0,03 мг.
Наиболее убедительное доказательство электронной приро-
природы тока в металлах было получено в опытах с инерцией элек-
электронов. Идею этих опытов разъясняет рис. 250. Представим себе
кусок незаряженного металла,
движущийся с постоянной ско-
скоростью v. Вместе с металлом
будут двигаться с той же ско-
скоростью и электроны, и поэтому
никакого движения электронов
Рис.250. Идея опытов с инерцией относительно кристаллической
электронов решетки, а следовательно, и
электрического тока не будет.
Однако электроны, помимо заряда, обладают еще и массой, и
поэтому им присуща определенная инерция. При всяком изме-
изменении скорости движения металла электроны будут либо отста-
отставать от движения решетки, либо его опережать, отчего возника-
возникает электрический ток. Это явление можно сравнить с толчками,
испытываемыми пассажирами трамвая при резкой остановке ва-
вагона или резком трогании с места.
Легко видеть, что направление этого тока зависит от знака
заряда подвижных частиц в металле. Так, например, при тормо-
торможении металла (ускорение j направлено слева направо, рис. 250)
частицы будут опережать решетку и двигаться относительно нее
справа налево. Если частицы несут положительный заряд, то и
возникающий ток i+ будет направлен также справа налево. Ес-
Если же частицы заряжены отрицательно, то направление тока
г- будет противоположно. Поэтому, исследуя на опыте направ-
направление возникающего тока, можно определить знак носителей
заряда в металлах. Измеряя же еще и значение заряда, пере-
§ 145
ПРИРОДА НОСИТЕЛЕЙ ЗАРЯДА В МЕТАЛЛАХ
333
несенного этим током, можно определить отношение заряда к
массе е/т носителей заряда, а следовательно, и установить их
природу.
Идея этого опыта была высказана в 1913 г. Л.И. Мандель-
Мандельштамом и Н.Д. Папалекси. Они произвели качественные опыты
и установили, что в катушке с проволокой, совершающей враща-
вращательные колебания вокруг своей оси, действительно возникает
переменный ток. Затем этот опыт был предложен вновь Г. Ло-
Лоренцем и осуществлен с количественными ре-
результатами Толменом и Стюартом в 1916 г.
Схема опыта Толмена и Стюарта показана
на рис. 251. Катушка с большим числом вит-
витков тонкой проволоки приводилась в быстрое
вращение вокруг своей оси. Концы обмотки бы-
были присоединены к чувствительному баллисти-
баллистическому гальванометру при помощи длинных
гибких проводов, скручивающихся при враще-
вращении катушки. После раскручивания катушки
она резко тормозилась специальным приспособ-
приспособлением. Общая длина обмотки составляла при-
примерно 500 м, а линейная скорость движения
проволоки достигала 300 м/с. При измерени-
измерениях тщательно устранялось действие магнитного
поля Земли, которое могло бы вызвать появле-
появление индукционных токов.
Опыты показали, что при торможении ка-
катушки в цепи действительно возникает кратко-
кратковременный ток, а его направление соответствует отрицательно
заряженным частицам. В этих опытах было определено отноше-
отношение заряда к массе носителей заряда е/т. При помощи простых
рассуждений легко показать, что заряд q, протекающий по цепи
За время торможения катушки, выражается формулой
? = ^, A45.1).
где vo ~ начальная линейная скорость проволоки, / — ее длина,
R — сопротивление цепи. Поэтому, измеряя заряд q баллисти-
баллистическим гальванометром и зная остальные (легко определяемые)
величины vq, l и R, можно найти значение е/т.
Зная значение элементарного заряда е, можно было найти
массу т носителей заряда в металлах. Она оказалась поряд-
порядка 10~30 кг, примерно в 2000 раз меньше массы самого легкого
атома — водорода (тпн = 1,67 • 10~27 кг). Это показало, что
носителями заряда в металлах никоим образом не могут быть
заряженные атомы (ионы). С другой стороны, найденное зна-
значение е/т близко к значению е/т для электронов, получаемо-
°пыта олмена и
334 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
му другими методами, в частности по отклонению электронов в
электрических и магнитных полях.
Формула A45.1) легко выводится следующим образом. При торможе-
торможении катушки на электроны действует сила инерции, которая и является в
данном случае сторонней силой (§ 64). При ускорении проволоки dv/dt на
один электрон действует сила
„ dv
F = -mTf
Сила, отнесенная к единице заряда, т.е. напряженность поля сторонних сил
Е*, равна
, т dv
Е =1-
Отсюда, пользуясь формулой F9.2), находим ЭДС, развивающуюся в цепи
при торможении катушки:
а, _ т dv
б — — I,
е dt
где I — длина проволоки катушки. Если R — сопротивление цепи, то сила
тока, вызываемого этой ЭДС, равна
. _ т I dv
1 ~ е R dt'
Поэтому заряд, прошедший по цепи за полное время торможения катушки,
определяется формулой
О О
/. .. то I Г , т lv0
idt = r= I dv- —.
e R J e R
§ 146. Причина электрического сопротивления
Результаты опытов, описанных в предыдущем параграфе,
показывают, что в металлах имеются электроны, способные пе-
перемещаться по металлу. Такие электроны получили название
электронов проводимости.
Так как в отсутствие тока объемных зарядов в металлах нет
(в проводнике постоянного сечения их нет и при наличии тока),
то отсюда можно заключить, что в металлах имеются еще и по-
положительные заряды, которые, однако, не принимают участия в
образовании тока. Положительные заряды металла представля-
представляют собой ионы, образующие кристаллическую решетку металла.
Электроны проводимости движутся в металлах не свобод-
свободно, но испытывают соударения с ионами решетки. В отсутствие
внешнего электрического поля электроны совершают только
беспорядочное тепловое движение — каждый электрон описы-
описывает сложную траекторию, подобную траектории атома газа
или частицы, совершающей броуновское движение (рис. 252 а).
Вследствие беспорядочности теплового движения количество
§ 146
ПРИЧИНА ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ
335
электронов, движущихся в любом направлении, в среднем все-
всегда равно числу электронов, перемещающихся в противополож-
противоположном направлении. Поэтому в отсутствие внешнего поля суммар-
суммарный заряд, переносимый электронами в любом направлении, ра-
равен нулю.
При наложении внешнего электрического поля электроны
получают дополнительное упорядоченное движение в направле-
направлении, противоположном направлению поля (так как заряд элек-
электронов отрицательный; рис. 252 6). Поэтому фактическое дви-
движение электронов представляет собой сумму беспорядочного и
упорядоченного движений,
а следовательно, появляется
преимущественное направ-
направление движения электронов
(рис. 252 е). В этом случае
число электронов, движущих-
движущихся противоположно полю, бу-
будет больше числа электронов,
перемещающихся в направле-
направлении поля, так что возникнет
перенос электрического заря-
заряда, т.е. электрический ток.
Рассмотренная картина
движения электронов при-
приводит также к объяснению
электрического сопротивления
металлов. Между двумя после-
последовательными соударениями
Рис. 252. Движение электронов в
металле: о) беспорядочное тепло-
тепловое движение в отсутствие электри-
электрического поля (отрезки пути между
столкновениями показаны для про-
простоты одинаковыми); б) составляю-
составляющая движения электронов под дей-
действием электрического поля; в) фак-
фактическое движение электронов
электроны движутся под дей-
действием поля с ускорением и
приобретают определенную
энергию. Эта энергия пере-
передается полностью или частично положительным ионам при
соударениях и превращается в энергию беспорядочного коле-
колебания ионов, т.е. в тепло. Поэтому при наличии тока металлы
нагреваются. Точно так же после исчезновения внешнего поля
упорядоченное движение электронов вследствие соударений
быстро превращается в беспорядочное тепловое движение, и
электрический ток прекращается. Таким образом, движение
электронов в металлах происходит с трением, которое вызвано
соударениями и подобно внутреннему трению в газах. Мы ви-
видим, что причина электрического сопротивления заключается
в соударениях электронов с положительными ионами решетки
металла.
Трение электронов в металлах приводит не только к выде-
выделению тепла Джоуля-Ленца, но и к обмену импульсами между
336
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ. XIV
электронами проводимости и решеткой металла. Это можно про-
продемонстрировать на опыте, изображенном на рис. 253. Метал-
Металлический диск, способный вращаться с малым трением вокруг
горизонтальной оси, помещен
между полюсами магнита.
Диск включен в электрическую
цепь, так что в нем имеется ток,
идущий между осью и краем
диска, погруженным в чашку
со ртутью. При наличии тока
диск приходит во вращение, на-
направление которого изменяется
при перемене направления то-
тока. На электроны, движущиеся
Рис. 253. Демонстрация существо- в нижней половине диска, дей-
вания трения электронов в металлах ствует сила Лоренца (§ 88), на-
направленная перпендикулярно к
току и к магнитному полю. Если бы электроны двигались без
трения, то сила Лоренца лишь искривляла бы траекторию элек-
электронов внутри металла, но диск оставался бы в покое. Вслед-
Вследствие же трения электронов получаемое ими количество движе-
движения передается диску и поэтому он приходит во вращение.
§ 147. Классическая электронная теория металлов
Объяснение различных свойств вещества существованием
и движением в нем электронов составляет содержание элек-
электронной теории. В классической электронной теории металлов
предполагается, что движение электронов подчиняется законам
классической механики Ньютона. Далее, в этой теории прене-
пренебрегают взаимодействием электронов между собой, а взаимо-
взаимодействие электронов с положительными ионами сводят только
к соударениям. Иными словами, электроны проводимости рас-
рассматривают как электронный газ, подобный идеальному атомар-
атомарному газу молекулярной физики.
Такой электронный газ должен подчиняться всем законам
идеального газа и, в частности, закону равномерного распреде-
распределения энергии по степеням свободы, согласно которому сред-
средняя кинетическая энергия теплового движения, приходящаяся
на каждую степень свободы, равна A/2)кТ (к — постоянная
Больцмана, равная 1,38 • 10~23 Дж/К, а Г — термодинамиче-
термодинамическая температура газа). Так как свободный электрон обладает
тремя степенями свободы, то средняя энергия беспорядочного
теплового движения, приходящаяся на один электрон, равна
1 9 — Зьт
A47.1)
§ 147 КЛАССИЧЕСКАЯ ЭЛЕКТРОННАЯ ТЕОРИЯ МЕТАЛЛОВ 337
где v\ — среднее значение квадрата скорости теплового движе-
движения.
Несмотря на эти допущения, которые, как мы увидим ниже,
являются только весьма приближенными, классическая элек-
электронная теория качественно объясняет многие законы электри-
электрического тока.
Объяснение закона Ома. Чтобы выяснить физическую
сущность этого объяснения и упростить расчеты, будем предпо-
предполагать, что время свободного пробега г между двумя последова-
последовательными соударениями одинаково для всех электронов. Далее
будем считать, что при каждом соударении электрон передает
решетке накопленную энергию полностью и поэтому после со-
соударения начинает движение без начальной скорости.
Вычислим плотность тока j, возникающего в металле под
действием электрического поля с напряженностью Е. Согласно
сказанному в § 53 имеем
j = nev, A47.2)
где п — концентрация электронов проводимости, е — заряд элек-
электрона, a, v —- средняя скорость упорядоченного движения элек-
электронов (скорость дрейфа).
На каждый электрон действует сила, равная еЕ, и электрон
приобретает ускорение eEjm. Поэтому к концу свободного про-
пробега скорость электрона равна
_ еЕ
г>макс — — Т.
Так как электрон между соударениями движется равноускорен-
равноускоренно, то среднее значение скорости равно половине ее максималь-
максимального значения:
еЕ
v = —-т.
2т
Скорость дрейфа оказывается пропорциональной напряжен-
напряженности поля Е. Поэтому можно положить
v = ЬЕ, A47.3)
где Ь = (е/2т)т не зависит от Е. Величина b называется по-
подвижностью электронов. Она равна скорости дрейфа в поле
с напряженностью, равной единице. Если измерять скорость в
м/с, а напряженность поля в В/м, то подвижность будет выра-
выражена в м2/(В-с).
В действительности, конечно, времена свободного пробега у различных
электронов не одинаковы. Расчет показывает, что при учете этого обстоя-
обстоятельства выражение для подвижности есть
Ь = (е/т)т, A47.4)
гдр т — среднее время свободного пробега для всей совокупности электро-
электронов.
338 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
Подставляя найденное значение v в A47.2), находим
— Е. A47.5)
1 z^
2т
Мы видим, что плотность тока j оказывается пропорцио-
пропорциональной напряженности поля Е, а это и выражается законом
Ома (§ 61). Для удельной электрической проводимости А полу-
получается выражение
А = |—т. A47.6)
Оно показывает, что электропроводность тем больше, чем боль-
больше концентрация электронов проводимости и чем больше время
свободного пробега т. Это и понятно, так как чем больше г, тем
меньшую помеху представляют соударения для упорядоченного
движения электронов.
При учете распределения времен свободного пробега удельная электри-
электрическая проводимость выражается формулой
А = — Т. A47.6а)
т
Объяснение закона Джоуля—Ленца. К концу свободного
пробега электроны приобретают под действием поля кинетиче-
кинетическую энергию
1 2 1 е2г2 „2
2 макс 2 m
Согласно сделанному предположению вся эта энергия передает-
передается решетке при соударении и переходит в тепло
В единицу времени каждый электрон испытывает 1/т соуда-
соударений, а следовательно, выделяет тепла во столько же раз боль-
больше. Так как в каждой единице объема имеется п электронов, то
количество теплоты Q\, выделяемое в единице объема металла
в 1 с, равно
!
2 т
Воспользовавшись формулой A47.6), получаем
Ql = ХЕ2 = - Е2, A47.7)
где р = 1/А — удельное сопротивление металла.
Формула A47.7) выражает закон Джоуля-Ленца в диффе-
дифференциальной форме.
Связь между теплопроводностью и электропроводностью ме-
металлов. Уже давно было замечено, что металлы, обладающие большей
электропроводностью, имеют и лучшую теплопроводность, и наоборот. Ви-
деман и Франц на основании опытных данных пришли к заключению, что
§ 147 КЛАССИЧЕСКАЯ ЭЛЕКТРОННАЯ ТЕОРИЯ МЕТАЛЛОВ 339
отношение коэффициента теплопроводности К к удельной электрической
проводимости Л для всех металлов при одинаковой температуре одинаково
и увеличивается пропорционально термодинамической температуре (закон
Видемана-Франца):
К/Х = аТ, A47.8)
где а не зависит от рода металла.
Классическая электронная теория легко объясняет и эту закономер-
закономерность Действительно, электроны проводимости, перемещаясь в металле,
переносят с собой не только свой электрический заряд, но и присущую им
энергию беспорядочного теплового движения, т.е. осуществляют перенос
тепла. В металлах концентрация электронов весьма велика (см. § 150), и
все тепло практически переносится электронами, а ионная решетка прини-
принимает лишь небольшое участие в этом процессе. Поэтому те металлы, кото-
которые хорошо проводят электричество, являются и хорошими проводниками
тепла.
Как известно из молекулярной физики, кинетическая теория газов дает
для коэффициента теплопроводности идеального одноатомного газа выра-
выражение
К = nkvrl/2, A47.9)
где п — число атомов в единице объема^ к — постоянная Больцмана, vt —
средняя скорость теплового движения, / — средняя длина свободного пути
атомов Такая же формула должна быть справедлива и для коэффициента
теплопроводности электронного газа, только в этом случае п, г>т и I должны
обозначать концентрацию, тепловую скорость и средний пробег электронов
в металле. Далее, для I можно положить I = vtt. Здесь мы пренебрегаем
скоростью дрейфа v по сравнению с тепловой скоростью пт- Это действи-
действительно можно сделать, так как, вследствие малой подвижности электронов
в металлах (см § 150), даже для очень сильных электрических полей п<Спт
Тогда из формул A47 9) и A47 6) находим
К _ пк(утJт/2 _ тпк(утJ
Т ~ (пе2/т)т/2 ~ е2
Полагая приближенно (vtJ ~ tjf- и пользуясь соотношением A47 1), полу-
получаем
К/Х = ЦкеJТ, A47 10)
т.е. закон Видемана-Франца. При этом постоянная а оказывается равной
о = Ъ(к/еJ Она определяется только универсальными постоянными к и е и
поэтому не зависит от природы металла Теоретическое значение а хорошо
согласуется с опытными данными
Таким образом, классическая электронная теория хорошо
объясняет существование электрического сопротивления метал-
металлов, законы Ома и Джоуля-Ленца, позволяет выразить удель-
удельную электрическую проводимость через атомарные постоянные
металла, позволяет понять связь между теплопроводностью и
электропроводностью.
Однако в некоторых вопросах классическая электронная тео-
теория приводит к выводам, находящимся в противоречии с опы-
опытом. Наиболее ярким примером является сверхпроводимость.
340
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
§ 148. Сверхпроводимость
Согласно классической электронной теории удельное сопро-
сопротивление металлов должно монотонно уменьшаться при охлаж-
охлаждении, оставаясь при всех температурах конечным. Такая темпе-
температурная зависимость сопротивления действительно наблюдается
на опыте при сравнительно высоких температурах. Однако если
сделать температуру достаточно низкой (несколько Кельвинов),
то эта зависимость становится совсем иной. Прежде всего ока-
оказывается, что удельное сопротивление перестает зависеть от
температуры и достигает некоторого предельного значения. Оно
различно для разных веществ и даже для разных образцов одно-
одного и того же вещества. Это остаточное сопротивление особенно
велико у сплавов, но существует и в чистых металлах. Опыт по-
показывает, что остаточное сопротивление тем меньше, чем чище
металл и чем меньше структурных дефектов содержит исследу-
исследуемый образец.
Если понижать температуру еще больше, то в некоторых
веществах наблюдается удивительное явление сверхпроводи-
сверхпроводимости, открытое Камерлинг-Оннесом в 1911 г. При некото-
некоторой определенной температуре, различной для разных веществ,
удельное сопротивление внезапно, скачком, уменьшается прак-
практически до нуля. В табл. 9 приведены температуры перехода в
сверхпроводящее состояние Ткр для некоторых веществ.
Таблица 9
Вещество
Титан
Кадмий
Цинк
Алюминий
Олово
Ткр, К
0,4
0,5
0,38
1,2
3,7
Вещество
Ртз'ть
Ванадий
Свинец
Ниобий
Nb3Sn
гкр, к
4,1
5,3
7,2
9,3
18
Сверхпроводимость наблюдается не только у элементов, но и
во многих химических соединениях и сплавах, причем сами эле-
элементы, входящие в состав сверхпроводящего соединения, могут
и не являться сверхпроводниками.
Вещества в сверхпроводящем состоянии обладают исключи-
исключительно необычными свойствами. Во-первых, в сверхпроводни-
сверхпроводниках однажды возбужденный электрический ток может длитель-
длительно существовать без источника тока. Это происходит потому,
что вследствие исчезновения сопротивления время затухания
тока Г = Ljr (ср. § 95) становится огромным. Такое явление
наблюдали в первых же опытах со сверхпроводниками: неболь-
небольшой замкнутый контур из сверхпроводника погружали в сосуд с
§ 148
СВЕРХПРОВОДИМОСТЬ
341
жидким гелием и возбуждали в контуре ток с помощью электро-
электромагнитной индукции. Этот ток обнаруживали по отклонению
магнитной стрелки, помещенной вблизи сосуда, причем стрелка
оставалась в отклоненном состоянии в течение многих суток.
На рис. 254 показана схема другого опыта со сверхпровод-
сверхпроводниками. Здесь сверхпроводник с соединен с гальванометром, но
замкнут в точках а и б проволокой, находящейся также в сверх-
сверхпроводящем состоянии. После возбуждения тока в сверхпровод-
сверхпроводнике с помощью электромагнитной индукции этот ток цирку-
циркулирует лишь по замкнутой цепи абса из сверхпроводника и не
ответвляется в гальванометр, который по-
поэтому не показывает никакого отклонения.
Если же через некоторое время разорвать
при помощи нити Н перемычку аб, то ток
устремляется по единственно возможному
пути — через гальванометр, который обна-
обнаруживает кратковременный отброс.
Второе важное свойство сверхпровод-
сверхпроводников заключается в том, что внутри
вещества в сверхпроводящем состоянии
магнитная индукция всегда равна нулю.
Положим, что какое-либо тело из сверх-
сверхпроводника мы сначала охладили и пере-
перевели в сверхпроводящее состояние, а за-
затем включили внешнее магнитное поле,
индукция которого (в отсутствие тела)
есть Ва = /ioHa. При включении маг-
магнитного поля в сверхпроводнике возникнут
индукционные токи, создающие дополни-
дополнительную индукцию Вг = /ioHj (рис. 255 й),
которая в соответствии с законом Ленца
будет компенсировать внешнюю индукцию
Ва. В обычном проводнике компенсиру-
компенсирующие индукционные токи быстро затуха-
затухают, и остается лишь поток, обусловленный
намагничивающей катушкой. В случае же
сверхпроводника компенсирующие токи не
затухают вовсе, и поэтому результирую-
результирующая индукция внутри тела все время будет В = Ва + Вг = 0.
Во внешнем же пространстве линии результирующей индукции
будут иметь вид, показанный на рис. 255 б: они выталкиваются
из тела и его огибают.
Это свойство сверхпроводящего состояния связано не толь-
только с исчезновением электрического сопротивления. Представим
себе проводник, единственное отличие которого от нормального
металла заключается лишь в том, что его сопротивление равно
1
У.~-
-7:
аб
- c~-
Л
я
7 i
N9
Рис. 254. Опыт для
обнаружения длитель-
длительного тока в сверхпро-
сверхпроводнике
342
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
нулю. Положим далее, что мы сначала создаем внешнее магнит-
магнитное поле и только потом охлаждаем проводник до исчезновения
его сопротивления. Так как при этом внешнее поле не изменяет-
изменяется, то и индукционные токи возникать не будут, а следователь-
следовательно, и после исчезновения сопротивления магнитный поток вну-
внутри проводника должен сохраниться. Опыт, однако, показывает,
что в сверхпроводниках и в этом случае магнитный поток исче-
Рис. 255 Сверхпроводящее тело в магнитном поле
зает. Равенство нулю магнитной индукции есть специфическое
свойство сверхпроводящего состояния. Напряженность же маг-
магнитного поля, определяемая лишь намагничивающей катушкой,
может и не равняться нулю. Можно сказать, что сверхпроводя-
сверхпроводящее вещество является идеальным диамагнетиком с магнитной
восприимчивостью к = — 1 и магнитной проницаемостью [i =
= 1 + х=0.
Из этого следует, что плотность тока в толще массивного
сверхпроводника равна нулю. Действительно, магнитная индук-
индукция внутри тела есть
Для каждого из полей На и Нг справедлива теорема о магнит-
магнитном напряжении, и поэтому, вычисляя интеграл от В по любому
замкнутому контуру L, мы получим
Вь dl = /iOi.
Здесь i — полная сила тока через любую поверхность, ограни-
ограниченную контуром L. Если L целиком лежит внутри сверхпро-
сверхпроводника, то интеграл по контуру равен нулю, так как в каж-
каждой точке контура В\ = 0, а значит, г = 0. В сверхпроводящем
сплошном теле ток может быть сосредоточен только в тонком
поверхностном слое.
§ 148
СВЕРХПРОВОДИМОСТЬ
343
Если тело имеет форму длинной цилиндрической проволоки,
то магнитное поле Н во внешнем пространстве не зависит от рас-
распределения тока по сечению проволоки, а определяется только
полной силой тока. Поэтому и для сверхпроводящего провода Я
выражается прежней формулой (81.5), а индукция В = /io#. У
поверхности прямого провода напряженность магнитного поля
равна
S~ 2тга'
где а — радиус провода. При переходе извне внутрь провода
В быстро (экспоненциально) уменьшается до 0. Распределение
индукции в пространстве показано на рис. 256. Расстояние d от
поверхности, на котором В умень-
уменьшается в е раз, носит название
глубины проникновения индукции.
Она различна для разных веществ
и увеличивается с повышением
температуры. Ее типичные значе-
значения имеют порядок 10~5 см.
Третья важная особенность
сверхпроводимости состоит в том,
что магнитное поле разрушает
состояние сверхпроводимости.
Чем сильнее охлажден сверх-
сверхпроводник ниже температуры
перехода в сверхпроводящее состо-
состояние, тем больше и «критическое»
магнитное поле, при котором
исчезает сверхпроводимость. При температуре перехода
сверхпроводящее состояние критическое поле равно нулю.
Магнитным полем, разрушающим сверхпроводимость, мо-
может быть и поле самого тока в сверхпроводнике. Когда сила тока
становится такой, что магнитное поле у поверхности провода до-
достигает критического значения, сверхпроводимость исчезает. Из
сказанного ясно, что эта максимальная (критическая) сила тока
при температуре перехода равна нулю, но увеличивается по мере
понижения температуры. Кроме этого, для данного вещества и
данной температуры она прямо пропорциональна диаметру про-
провода. Укажем для примера, что у олова при 1 К Якр составляет
около 2-104 А/м. Поэтому для оловянной проволоки диаметром
2а = 3 мм критическая сила тока при этой температуре равна
гкр = 2тгаЯКр = 2тг ¦ 1,5 ¦ 1(Г3 • 2 • 104 и 180 А.
Влияние магнитного поля на сверхпроводимость имеет интересную осо-
особенность Если форма тела такая, что размагничивающий фактор /3 (§ 107)
равен нулю, то при увеличении Н внутри тела выше Нкр вещество пере-
Рис 256 Магнитная индукция
прямого провода в сверхпрово-
сверхпроводящем состоянии
в
344 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
ходит в нормальное состояние сразу во всем объеме. Это имеет место, на-
например, для прямых проволок, параллельных направлению поля. Если же
/3 ф О, то при Н = Дкр тело переходит сначала в промежуточное состояние,
в котором одновременно сосуществуют малые области в сверхпроводящем
и в нормальном состояниях Промежуточное состояние существует в неко-
некотором интервале магнитных полей и только при достаточном увеличении
Н нормальная проводимость устанавливается во всем объеме.
Описанные выше магнитные свойства характерны для так
называемых сверхпроводников 1-го рода, к которым принад-
принадлежит большинство чистых металлов Однако существуют и
сверхпроводники другого типа (сверхпроводники 2-го рода), у
которых магнитные свойства более сложны.
Совокупность имеющихся данных о сверхпроводимости по-
позволяет заключить, что электроны в сверхпроводящем веществе
ведут себя подобно смеси двух жидкостей, одна из которых со-
состоит из сверхпроводящих электронов, а другая — из нормаль-
нормальных электронов.
Концентрации сверхпроводящих электронов пс и нормаль-
нормальных пн зависят от температуры. При Т ^ Ткр концентрация
пс = 0 и все электроны находятся в нормальном состоянии. При
Т —> 0 пн —> 0 и все электроны становятся сверхпроводящими.
Вещество в сверхпроводящем и нормальном состояниях с термодина-
термодинамической точки зрения можно рассматривать как разные фазы данного
вещества, а превращение сверхпроводящего вещества в нормальное — как
фазовый переход Однако, в отличие, например, от фазовых переходов пар-
жидкость или жидкость-твердое тело, скрытая теплота такого перехода в
отсутствие магнитного поля равна нулю Теплоемкость же вещества при
Т — Ткр меняется скачкообразно. Такие фазовые переходы называются пе-
переходами 2-го рода Если же переход из сверхпроводящего состояния в нор-
нормальное происходит во внешнем магнитном поле, т.е при Т < Ткр, то для
перехода при неизменной температуре необходимо подведение тепла извне
В этом случае скрытая теплота перехода уже не равна нулю, и мы имеем
фазовый переход 1-го рода
% 149. Пределы применимости классической
электронной теории металлов
Вторым примером несостоятельности классической элек-
электронной теории может служить теория теплоемкости металлов.
Согласно основному допущению классической электронной
теории (§ 147) средняя тепловая энергия каждого электрона рав-
равна C/2)&Т. Если N' есть число электронов проводимости в 1 мо-
моле металла, то тепловая энергия этих электронов должна быть
равна
W' = N' ¦ ^кТ.
Число электронов проводимости в металлах по порядку величи-
величины равно числу атомов (см. § 150), а значит, N' равно прибли-
§ 149 ПРЕДЕЛЫ ПРИМЕНИМОСТИ ЭЛЕКТРОННОЙ ТЕОРИИ МЕТАЛЛОВ 345
зительно постоянной Авогадро N — 6,02 • 1023 моль. Поэтому
W « -NkT = -RT,
где R — газовая постоянная, рассчитанная на 1 моль Отсюда
следует, что электронный газ в 1 моле металла должен иметь
теплоемкость при постоянном объеме C'v = dW'jdT « C/2)Л,
т.е. такую же, как и 1 моль идеального одноатомного газа.
Теплоемкость всего металла складывается из теплоемкости
его кристаллической решетки и теплоемкости электронного га-
газа. Согласно кинетической теории тепла молярная (т.е. рассчи-
рассчитанная на 1 моль) теплоемкость одноатомных кристаллов равна
Су = 3R. Поэтому следовало бы ожидать, что молярная тепло-
теплоемкость металлов будет близка к 4,5R. Однако опыт показывает,
что она равна приблизительно ЗД, т.е. для металлов, так же как
и для диэлектрических кристаллов, хорошо выполняется закон
Дюлонга и Пти. Таким образом, наличие электронов проводимо-
проводимости практически не сказывается на теплоемкости, что непонятно
с точки зрения классической электронной теории.
Помимо указанных, имеются и другие расхождения между
выводами классической электронной теории и опытом.
Одна из причин расхождений заключается в том, что дви-
движение электронов в металлах подчиняется не законам классиче-
классической механики, а более сложным законам квантовой механики. А
эта последняя показывает, что движение электронов в периоди-
периодическом поле потенциала решетки кристалла может существенно
отличаться от предсказываемого классической механикой.
Далее, в классической электронной теории предполагается,
что электроны проводимости подчиняются, как и атомы газа,
законам статистики Максвелла-Больцмана. В действительности
же для электронов внутри металла справедлива иная, квантовая
статистика, и они подчиняются другому закону распределения
(ср. § 155).
И, наконец, в классической электронной теории не учиты-
учитывается взаимодействие электронов друг с другом, а их взаимо-
взаимодействие с решеткой металла описывается с помощью представ-
представления о кратковременных соударениях. Между тем при очень
низких температурах взаимодействие между электронами мо-
может играть решающую роль.
Было бы, однако, ошибкой считать, что классическая элек-
электронная теория утратила свое значение вовсе. Она позволяет во
многих случаях быстро найти правильные качественные резуль-
результаты и притом в наглядной форме. Более того, оказывается, что
расхождения между теорией и опытом тем меньше, чем мень-
меньше концентрация электронов проводимости и чем выше темпе-
температура. В металлах, где концентрация электронов велика, эти
различия имеют существенное значение. В ряде же других слу-
346 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
чаев, где концентрация электронов мала (электронные явления
в газах, многие явления в полупроводниках), классическая элек-
электронная теория применима не только качественно, но и количе-
количественно.
§ 150. Концентрация и подвижность электронов
в металлах
Согласно сказанному в § 147 электропроводность металлов
зависит от концентрации электронов проводимости п и от их
подвижности Ь. Обе эти величины, являющиеся важными ха-
характеристиками металла, могут быть определены из опыта.
Для измерения концентрации электронов чаще всего поль-
пользуются эффектом Холла. Рассмотрим проводник в форме пря-
прямоугольной пластинки, в которой имеется ток с плотностью j
(рис. 257). Эквипотенциальными
поверхностями внутри такой пла-
пластинки будут плоскости, перпен-
перпендикулярные к направлению тока,
и поэтому разность потенциалов
между двумя металлическими зон-
зондами 1 и 2, лежащими в одной из
этих плоскостей, будет равна нулю.
Если, однако, создать в образце
магнитное поле, перпендикулярное
к току и к зондам, то между зон-
зондами возникает разность потенци-
Рис. 257. Эффект Холла ^ов' указывающая на то, что при
наличии магнитного поля эквипо-
эквипотенциальные плоскости в пластинке становятся наклонными. В
возникновении этой поперечной разности потенциалов и заклю-
заключается эффект Холла.
Опыт показывает, что поперечная разность потенциалов U в
слабых магнитных полях пропорциональна магнитной индукции
В; она пропорциональна также плотности тока j и расстоянию
между зондами d:
U = RdjB, A150.1)
где R — постоянная, зависящая от рода вещества. Она получила
название постоянной Холла.
Эффект Холла просто объясняется электронной теорией и
является следствием существования силы Лоренца (§ 88). Что-
Чтобы лучше выяснить физическую сущность этого явления, мы
ограничимся только упрощенной его теорией и будем прибли-
приближенно считать, что все электроны движутся с постоянной скоро-
скоростью, равной средней скорости их упорядоченного движения v.
§ 150
КОНЦЕНТРАЦИЯ ЭЛЕКТРОНОВ В МЕТАЛЛАХ
347
Тогда на каждый электрон действует сила, перпендикулярная
к направлению тока и к магнитному полю и равная evB. Под
действием этой силы электроны будут смещаться, так что одна
из граней пластинки зарядится отрицательно, а другая — по-
положительно, и внутри пластинки возникнет поперечное (к току
и к магнитному полю) электрическое поле Е. При равновесии
evB = еЕ. Поэтому поперечная разность потенциалов равна
U = Ed = vBd.
В этом уравнении среднюю скорость электронов v можно выра-
выразить через плотность тока j, так как
j = nev,
и поэтому
U = —djB.
пе
Полученное выражение совпадает с формулой A50.1). Постоян-
Постоянная Холла оказывается равной
R = 1/пе. A50.2)
Она зависит от концентрации электронов п, и поэтому, измеряя
постоянную Холла, можно определить концентрацию электро-
электронов внутри проводника.
Легко также видеть, что знак поперечной разности потенциа-
потенциалов зависит от знака заряда подвижных частиц, обусловливаю-
обусловливающих электропроводность. Действительно, пусть в проводящей
Пластинке ток течет слева направо (рис. 258 а). Если подвижные
IF б | IF
7
_ s
Рис. 258. Знак поперечной разности потенциалов в эффекте Холла зависит
От знака носителей заряда проводника
частицы в проводнике несут положительный заряд, то скорость
Этих: частиц имеет то же направление, что и ток, и при ука-
указанном направлении магнитного поля отклоняющая сила будет
Направлена снизу вверх. В этом случае верхняя грань пластин-
пластинки будет заряжаться положительно, а нижняя — отрицатель-
отрицательно. Если же частицы заряжены отрицательно, то их скорость
Направлена противоположно току (рис. 258 5). Так как откло-
отклоняющая сила зависит и от заряда частиц, и от их скорости, то
ее направление не изменится, и поэтому заряженные частицы
будут также накапливаться у верхней грани. Однако, так как
частицы заряжены отрицательно, верхняя грань в этом случае
348
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
будет заряжаться отрицательно, а нижняя — положительно, т.е.
явление Холла будет иметь обратный знак.
Измеряя постоянную Холла, можно найти концентрацию но-
носителей заряда п. Зная же электрическую проводимость А =
= enb, можно найти произведение пЬ и, следовательно, опреде-
определить концентрацию п и подвижность b порознь.
Подобные определения, однако, в действительности сложнее, чем это
может показаться на первый взгляд. Причина усложнений заключается в
том, что изложенная выше простая теория эффекта Холла основана на
классической электронной теории, имеющей ограниченную применимость
для металлов. Более того, для некоторых веществ наблюдается обратный
знак эффекта Холла, т.е соответствующий движению положительных но-
носителей заряда, в то время как в действительности и в этих металлах
носителями заряда являются отрицательные электроны. Это явление объ-
объясняется современной квантовой теорией твердых тел и связано с существо-
существованием так называемых положительных дырок (ср. § 152).
Во всяком случае измерения постоянной Холла и удельной электриче-
электрической проводимости позволяют найти порядок концентрации и подвижности,
что уже позволяет сделать важные выводы о природе проводимости.
Концентрация электронов проводимости в металлах, опреде-
определенная из значения постоянной Холла, имеет порядок 1028 м~3
и оказывается близкой к концентрации атомов.
Подвижности электронов в металлах, напротив, весьма ма-
малы. Выражая их в единицах м2/(В-с) (т.е. выражая среднюю
скорость, приобретаемую в поле 1 В/м, в м/с), мы получаем
подвижности порядка (табл. 10) 10~3 — 10~4 м2/(В-с). Низкие
значения подвижности указывают на то, что электроны испы-
испытывают большое число соударений с кристаллической решеткой.
Таблица 10
Металл
Подвижность электро-
электронов, 1(Г4 м2/(В-с)
Ag
56
Na
48
Be
44
Си
35
Аи
30
Li
19
Al
10
Cd
7,9
Zn
5,8
§ 151. Полупроводники и диэлектрики
До сих пор мы ничего не говорили о процессах, приводящих
к образованию электронов проводимости в проводниках. Для
выяснения этого вопроса большое значение имеет исследование
зависимости концентрации электронов проводимости от темпе-
температуры. Эти данные, как мы знаем (§ 150), можно получить,
измеряя, например, значение постоянной Холла при различных
температурах.
Опыт показывает, что в металлах концентрация электро-
электронов практически не зависит от температуры. Даже при самых
§ 151 ПОЛУПРОВОДНИКИ И ДИЭЛЕКТРИКИ 349
низких температурах в металлах уже имеется большое количе-
количество подвижных электронов. Это показывает, что в образова-
образовании электронов проводимости в металлах тепловое движение не
играет существенной роли.
Атомы типичных металлов характеризуются тем, что в них
имеется один или несколько электронов, связанных с ядром сла-
слабо. При сближении атомов металла такие электроны под дей-
действием сил взаимодействия с соседними атомами отщепляются
от своих атомов. Они принадлежат уже не какому-либо опреде-
определенному атому, а всему металлу в целом и движутся по металлу
в результирующем поле всех ионов и электронов. Эти отщепив-
отщепившиеся электроны и являются электронами проводимости.
Наряду с металлами мы встречаемся с проводниками и дру-
другого типа. Эти проводники являются, так же как и металлы,
электронными (проводниками 1-го рода), и в них электрический
ток не сопровождается никакими химическими изменениями.
Однако концентрация носителей заряда в таких проводниках
чрезвычайно сильно увеличивается с увеличением температуры.
Подобные проводники при низких температурах имеют весьма
большое удельное сопротивление и практически являются изо-
изоляторами, но с увеличением температуры их удельное сопротив-
сопротивление сильно уменьшается и при достаточно высоких температу-
температурах становится весьма малым. Вещества такого типа получили
название электронных полупроводников.
Полупроводниками являются многие элементы (кремний,
германий, селен и др.), закись меди Сиг О, сернистый свинец
PbS и многие другие химические соединения. Так, например,
по данным опыта можно заключить, что концентрация электро-
электронов в чистейшем кремнии при комнатных температурах долж-
должна быть меньше 1017 м~3, а его удельное сопротивление должно
быть больше 103 Ом-м; но при температуре 700 °С концентрация
электронов в нем возрастает до 1024 м~3, а удельное сопротив-
сопротивление падает до 0,001 Ом-м, т.е. больше чем в миллион раз.
Сильная зависимость концентрации носителей заряда в по-
полупроводниках от температуры показывает, что в этом случае
электроны проводимости возникают под действием теплового
движения. В полупроводниках атомное взаимодействие само по
себе еще недостаточно для отщепления электронов от атомов
и превращения их в электроны проводимости. Для этого даже
наиболее слабо связанным электронам нужно сообщить неко-
некоторую добавочную энергию, которая и заимствуется из энергии
теплового движения. Чем выше температура, тем большее число
Электронов будет существовать в полупроводнике в отщеплен-
отщепленном состоянии, т.е. в виде электронов проводимости.
Если энергия отщепления велика по сравнению со средней
энергией теплового движения (имеющей порядок кТ) при всех
350 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ. XIV
температурах в области существования данного кристалла, то
электроны проводимости в заметном количестве не образуются
и такой кристалл будет диэлектриком.
§ 152. Собственная проводимость полупроводников
Остановимся подробнее на процессе образования электронов
проводимости в полупроводниках. Для конкретности дальней-
дальнейших рассуждений рассмотрим кремний, являющийся типичным
полупроводником.
Атом кремния имеет порядковый номер в периодической си-
системе Менделеева Z = 14. Поэтому заряд ядра атома кремния
равен +14е и в состав его атома входит 14 электронов. Однако из
них только четыре слабо связаны.
Именно эти слабо связанные элек-
электроны участвуют в химических ре-
реакциях и обусловливают четыре ва-
валентности кремния, отчего они и
получили название валентных элек-
Рис. 259. Атом кремния и че- тронов. Остальные десять электро-
тыре его валентные связи нов вместе С ядром составляют
остов атома, имеющий заряд +14е —
— 10е = +4е. Он окружен четырьмя валентными электронами,
которые движутся вокруг остова и образуют облако отрицатель-
отрицательного заряда (рис. 259).
В решетке кремния расположение атомов таково, что каж-
каждый атом окружен четырьмя ближайшими соседями. Упрощен-
Упрощенная плоская схема расположения
атомов в кристалле кремния пока-
показана на рис. 260. Связь двух со-
соседних атомов обусловлена парой
электронов, образующих так назы-
лентную, связь.
Картина, изображенная на
рис. 260, соответствует чистому
кремнию (о влиянии примесей будет
сказано ниже) и очень низкой тем- Рис 260 Парно-электронные
пературе. В этом случае все валент- связи в кристалле кремния
ные электроны участвуют в образо-
образовании связей между атомами, являются структурными элемен-
элементами и не участвуют в электропроводности.
При повышении температуры кристалла тепловые колебания
решетки приводят к разрыву некоторых валентных связей. В
результате часть электронов, ранее участвовавших в образова-
образовании валентных связей, отщепляется и становится электронами
§ 152
СОБСТВЕННАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ
351
проводимости. При наличии электрического поля они переме-
перемещаются против поля и образуют электрический ток.
Однако, кроме процесса переноса заряда с помощью электро-
электронов проводимости, возможен еще и другой механизм электро-
электропроводности. Он обусловлен тем,
что всякий разрыв валентной свя-
связи приводит к появлению ва-
вакантного места с отсутствующей
связью. Такие «пустые» места
с отсутствующими электронами
связи получили название дырок
(рис. 261). Легко видеть, что воз-
возникновение дырок в кристалле
полупроводника создает дополни-
дополнительную возможность для пере-
Рис. 261. Возникновение элек-
электрона проводимости и дырки в
носа заряда. Действительно, при решетке кремния
наличии дырки какой-либо из
электронов связи может перейти на место дырки. В результа-
результате на этом месте будет восстановлена нормальная связь, но зато
появится дырка в другом месте. В новую дырку в свою очередь
сможет перейти какой-либо из других электронов связи и т.д.
Такой процесс будет происходить многократно, в результате че-
чего в образовании тока будут
принимать участие не только
электроны проводимости, но и
электроны связи, которые бу-
будут постепенно перемещаться,
так же как и электроны прово-
проводимости, против электрическо-
электрического поля. Сами же дырки будут
двигаться противоположно, в
направлении электрического
поля, т.е. так, как двигались
бы положительно заряженные
частицы (рис. 262).
сг-
сг-
Рис. 262. Схема дырочной проводи-
проводимости: черные точки — связанные
электроны, светлые кружки — ва-
вакантные места (дырки)
Рассмотренный процесс по-
получил название дырочной про-
проводимости. Следовательно, в
полупроводниках возможны
два различных процесса электропроводности: электронный, осу-
осуществляемый движением электронов проводимости, и дыроч-
дырочный, обусловленный движением дырок.
На первый взгляд может показаться, что представление об электропро-
электропроводности с помощью дырок весьма искусственно и даже неоправдано, так
как дырки, т.е. «пустые» места, естественно, не могут переносить электри-
352 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
ческий заряд, а в действительности, как мы видели, перенос заряда осу-
осуществляется перемещением электронов связи Дело, однако, заключается в
том, что движение электронов, как уже упоминалось (§ 149), подчиняется
законам не классической, а квантовой механики. А законы квантовой меха-
механики показывают, что если только концентрация дырок мала по сравнению
с концентрацией электронов связи, то простые законы движения получа-
получаются лишь для дырок, но не для электронов связи. А именно, оказывается,
что дырки в электрических и магнитных полях движутся так же, как дви-
двигались бы положительно заряженные частицы, обладающие зарядом +е и
некоторой определенной массой (вообще не равной массе электрона) По-
Поэтому и все электрические процессы при наличии дырок происходят так,
как если бы наряду с отрицательными электронами проводимости имелись
еще и положительно заряженные частицы — дырки.
Наряду с переходами электронов из связанного состояния в
свободное существуют обратные переходы, при которых элек-
электрон проводимости улавливается на одно из вакантных мест
электронов связи. Этот процесс называют рекомбинацией элек-
электрона и дырки. В состоянии равновесия устанавливается такая
концентрация электронов (и равная ей концентрация дырок),
при которой число прямых и обратных переходов в единицу вре-
времени одинаково.
Рассмотренный процесс проводимости в совершенно чистых
полупроводниках, лишенных вовсе химических примесей и дру-
других дефектов решетки, получил название собственной проводи-
проводимости.
§ 153. Примесная проводимость полупроводников
При наличии примесей электропроводность полупроводни-
полупроводников сильно изменяется. Укажем в качестве примера, что крем-
кремний с добавкой фосфора в количестве всего около 0,001 ат. %
имеет удельное сопротивление при комнатной температуре око-
около 0,006 Ом-м, т.е. его сопротивление уменьшается более чем в
100000 раз по сравнению с совершенно чистыми кристаллами.
Такое влияние примесей вполне объясняется изложенными
выше представлениями о строении полупроводников. Вернем-
Вернемся опять к конкретному примеру кремния и предположим, что
в нем имеются атомы химической примеси, замещающие неко-
некоторые атомы кремния. В качестве примеси рассмотрим сначала
какой-либо элемент пятой группы, например мышьяк. Атом мы-
мышьяка как элемент пятой группы имеет пять валентных электро-
электронов. Но для осуществления парно-электронных связей в решетке
кремния, как мы видели, необходимы всего четыре электрона.
Поэтому пятый электрон атома мышьяка оказывается связан-
связанным особенно слабо и может быть легко отщеплен при тепловых
колебаниях решетки. Тогда возникает один электрон проводимо-
проводимости, а атом мышьяка превращается в положительно заряженный
§ 153 ПРИМЕСНАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ 353
ион. Образование же дырки не происходит. Подобный процесс
схематически изображен на рис. 263 а.
Посмотрим теперь, как будет вести себя атом примеси
какого-либо элемента, стоящего левее в периодической системе,
нежели кремний; пусть это будет бор, стоящий в третьей группе.
Атом бора имеет всего три валентных электрона, в то время как
для нормальной валентной связи в решетке кремния необходи-
необходимы четыре электрона. Недостающий четвертый электрон будет
Рис. 263. Атомы мышьяка (а) и бора (б) в решетке кремния
захвачен из соседних мест кристалла, в соответствующем месте
образуется дырка, а атом бора превратится в отрицательный
ион (рис. 263 5). Таким образом, и при наличии бора в кри-
кристалле кремния окажется возможным возникновение тока, но,
в отличие от случая мышьяка, электрический ток здесь будет
обусловлен движением дырок, а не электронов.
Следовательно, электропроводность полупроводников может
быть обусловлена также примесями (примесная проводимость).
Примеси, вызывающие появление электронов проводимости (на-
(например, мышьяк в кремнии), получили название донорных при-
примесей, а примеси, вызывающие появление дырок (например, бор
в кремнии), названы акцепторными.
Резюмируя сказанное, мы видим, что полупроводники обла-
обладают той особенностью, что электропроводность в них может
быть обусловлена как подвижными электронами, так и дырками.
Если концентрация электронов в полупроводнике значительно
больше концентрации дырок, то мы говорим, что полупроводник
имеет электронную проводимость, или проводимость п-типа.
Если же значительно преобладают положительные дырки, то
электропроводность называется дырочной, или р-типа. Носите-
Носители заряда, представленные в большинстве (электроны в полу-
полупроводнике n-типа и дырки в полупроводнике р-типа), полу-
получили название основных носителей заряда, а представленные
в меньшинстве — неосновных. Если же концентрации электро-
электронов и дырок сравнимы между собой, то мы имеем смешанную
проводимость.
Так, например, кремний с примесью мышьяка при низких
температурах имеет только примесную проводимость и являет-
354
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
ся полупроводником n-типа. Основные носители заряда в нем —
электроны, а неосновные — дырки Последние возникают лишь
в результате разрыва валентных связей и их концентрация при
низких температурах мала Но при увеличении температуры
примесная проводимость, напротив, делается гораздо меньше,
нежели собственная, и концентрация дырок становится практи-
практически равной концентрации электронов.
§ 154. Понятие об энергетических зонах
Результаты § 152 и 153 можно изобразить при помощи энер-
энергетической диаграммы (рис. 264). Здесь по вертикали снизу
вверх отложены значения полной энергии электрона и отмечены
наименьшая энергия электронов проводимости Ес и наибольшая
энергия связанных электронов Ev. Возможные значения энергии
электронов проводимости за-
заполняют некоторую область или
зону энергии W ^ Ес, на-
называемую зоной проводимости.
Аналогично, энергии электро-
электронов связи образуют другую зо-
зону с W ^ Ev, которая полу-
получила название зоны валентных
электронов или просто валент-
валентной зоны. Обе эти зоны раз-
разделены энергетическим проме-
промежутком ширины Eg = Ес — Ev,
образующим зону запрещенных
энергий. В отсутствие примес-
...„ —,„г—~ Г "оГ"*' ных атомов и структурных де-
переходы зона-зона A, 2) и донор- , rjjri^
зона (ЗА) фектов решетки, стационарные
движения электронов с энерги-
энергией внутри запрещенной зоны невозможны. Разрыв химической
связи, приводящий к образованию электрона проводимости и
положительной дырки (см. рис. 261), есть электронный пере-
переход валентная зона-зона проводимости A на рис. 264). Обрат-
Обратный процесс — рекомбинация электрона проводимости и поло-
положительной дырки представляет собой электронный переход 2.
При наличии примесных атомов в запрещенной зоне возни-
возникают дискретные разрешенные уровни энергии (один из них Ed
показан на рис. 264). Они существуют не во всем объеме кри-
кристалла, а лишь в местах нахождения примесных атомов (локаль-
(локальные уровни энергии). Каждый локальный уровень дает энергию
электрона, когда он находится на примесном атоме.
Локальные уровни энергии создают возможность дополни-
дополнительных электронных переходов. Так, ионизация донора с обра-
Ed
Ev
—
н
г- -<
;
-9
h- -
h- -]
2
- -л
г- -i
3
э— -1
>-
4
— 60
Рис 264 Энергетическая диаграм-
диаграмма полупроводника и электронные
§ 154
ПОНЯТИЕ ОБ ЭНЕРГЕТИЧЕСКИХ ЗОНАХ
355
Ec
Еа
Ev
-@—
-<
-i
1
h —
s
2
Рис 265 Электронные пе-
переходы акцептор-валент-
акцептор-валентная зона
зованием электрона проводимости (см. рис. 263 а) изображается
на диаграмме рис. 264 электронным переходом 3. Обратный ему
процесс захвата электрона на атом донора есть электронный пе-
переход 4 из зоны проводимости на незаполненный уровень доно-
донора. Аналогично ионизация акцептора с образованием нарушенной
химической связи — положительной
дырки (см. рис. 263 б) — изображается
электронным переходом 1 на рис. 265.
Обратный ему переход 2 с заполнен-
заполненного акцепторного уровня в валентную
зону описывает воссоединение связан-
связанного электрона со свободной дыркой,
когда последняя при своем движении
сближается с заряженным акцептором.
Помимо рассмотренных переходов, ко-
конечно, могут происходить еще и другие.
Картина энергетических зон, к ко-
которой мы пришли из рассмотрения хи-
химических связей, в квантовой теории
существенно обобщается и уточняется.
А именно, решение задачи о движении электрона в поле пе-
периодического потенциала решетки показывает, что существует
целая система зон разрешенных энергий (рис. 266, локальные
уровни не показаны). Каждая из зон
ограничена снизу некоторой энергией
И^мин («дно* зоны) и сверху энерги-
энергией И^макг («ПОТОЛОК» ЗОНы). Эти ЗО-
ЗОНЫ отделены друг от друга полосами
запрещенных энергий. Ширина разре-
разрешенных зон энергии увеличивается по
мере возрастания энергии, и широкие
верхние зоны в некоторых случаях мо-
могут перекрывать друг друга, образуя
единую сложную зону.
Происхождение энергетических зон
имеет следующую общую причину. По-
Положим, что мы имеем N изолирован-
изолированных атомов, удаленных друг от друга
и поэтому не взаимодействующих меж-
между собой. В каждом из этих атомов
энергия электронов может изменяться
лишь скачками и поэтому характеризу-
характеризуется набором резких, дискретных уров-
уровней энергии. В рассматриваемой системе невзаимодействующих
атомов вместо каждого атомного энергетического уровня име-
имеется N совпадающих уровней энергии. Представим себе теперь,
'"З макс
мин
W,
2 макс
ш
УГ2 мин
'1 макс
Рис 266 Энергетические
зоны электрона в твердом
356 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
что мы сближаем атомы до образования кристаллической ре-
решетки. При этом возникает взаимодействие между атомами и
уровни энергии электронов изменяются. Оказывается, что в ре-
результате такого взаимодействия первоначально совпадавшие N
уровней энергии становятся различными. Эта совокупность те-
теперь уже не совпадающих уровней энергии и есть разрешенная
зона энергий. Таким образом, энергетические зоны возникают в
результате расщепления дискретных уровней энергии электрона
в атомах под влиянием взаимодействия атомов в решетке.
Число энергетических уровней в каждой зоне очень вели-
велико — порядка числа атомов в кристалле, и уровни расположены
очень близко друг к другу. Поэтому во многих случаях мож-
можно считать, что внутри каждой зоны энергия электрона, как и
в классической теории, изменяется непрерывно. Однако число
этих уровней все же конечно, что, как мы увидим ниже, имеет
принципиальное значение.
В классической механике полная энергия электрона выража-
выражается формулой
W = U+*bbl+Pl + P2z), A54.1)
где U — потенциальная энергия, а рх, ру и pz — составляющие
импульса р. Последние связаны с массой электрона т и состав-
составляющими скорости соотношениями: рх — mvx, ру — mvy, pz —
= mvz Энергия есть четная (квадратичная) функция импуль-
импульса р и при изменении знака любой его составляющей не изме-
изменяется. В квантовой механике оказывается возможным также
сохранить понятие механического импульса. Энергия и в этом
случае оказывается четной функцией р. Но в общем случае она
уже не выражается простым квадратичным законом. Однако во
многих случаях важно знать энергию электронов только в непо-
непосредственной близости от дна энергетической зоны. Если при
этом отсчитывать импульс от его значения ро, соответствующе-
соответствующего дну разрешенной зоны, т.е. понимать под р разность (р —Ро)>
то функцию W(p) можно разложить в ряд Тейлора по степе-
степеням рх, ру, pz в окрестности точки рх — ру = pz = 0. Вследствие
четности функции W(p) все нечетные степени в разложении ис-
исчезают, и поэтому, ограничиваясь первыми неисчезающими чле-
членами, получим
W = Жмин + 2^ bl+Pl+Pl)- A54-2)
Эта формула имеет тот же вид, что и формула классической
механики Однако между ними имеется и существенное отли-
отличие. В формуле A54.1) т есть истинная масса изолированного
электрона. В формуле же A54.2) через 1/2тэф мы обозначили
§ 154 ПОНЯТИЕ ОБ ЭНЕРГЕТИЧЕСКИХ ЗОНАХ 357
коэффициенты в разложении Тейлора
i(*w\ A543)
2тэф 2 V dpi Ур=0 2 ^ Op* Jp=0 2 V dpi /p=0 •
Величина тэф называется эффективной массой электрона в
кристалле (ср. § 186). При движении электрона внутри кристал-
кристалла она играет ту же роль, что и масса, однако отличается от
истинной массы электрона.
Отметим также, что в формулах A54 2) и A54 3) мы считали ггаЭф оди-
одинаковой при движении вдоль каждой из осей X, Y и Z, те. не зависящей
от направления (изотропной). В действительности же т3ф может зависеть
от направления движения. Однако мы ограничимся простейшим случаем
изотропной эффективной массы.
Задавая тройку возможных значений рх, ру и pz и опреде-
определенную ориентировку электронного спина (§ 117), мы опреде-
определяем некоторое возможное стационарное движение электрона,
или, иначе, квантовое состояние электрона. Формула A54.2)
показывает, что одна и та же энергия электрона может соот-
соответствовать различным значениям рх, Ру и pz, а, следовательно,
каждому энергетическому уровню внутри зоны соответствует
целая совокупность квантовых состояний.
При заданном состоянии кристалла электроны в нем опре-
определенным образом распределяются по различным квантовым
состояниям. Однако такое распределение всегда подчиняется
принципу Паули: в любой электронной системе — атомах, мо-
молекулах, твердых телах — в каждом квантовом состоянии не
может быть более одного электрона. Это обстоятельство при-
приводит к тому, что число электронов, энергии которых лежат в
пределах какой-либо разрешенной зоны, ограничено. Или, коро-
короче: вместимость каждой энергетической зоны конечна.
Положим, что кристалл состоит из N атомов и каждый
атом в изолированном состоянии имеет ? электронов. Темпера-
Температуру кристалла будет считать равной абсолютному нулю. Тогда
имеющиеся iV? электронов будут заполнять различные кванто-
квантовые состояния в порядке возрастания их энергий. Вследствие
конечной вместимости зон часть низкорасположенных зон энер-
энергии окажется целиком заполненной электронами, а следующая
за ними зона — либо заполненной частично, либо пустой. Более
же высокие зоны будут наверняка пустыми.
Конечная вместимость энергетических: зон существенно про-
проявляется в процессах переноса электрического заряда в элек-
электронном газе. Положим, что, желая создать электрический ток,
мы ускоряем электроны электрическим полем. При этом мы уве-
увеличиваем их энергию и переводим в новые квантовые состояния.
На энергетических диаграммах это соответствует возбуждению
358
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
электронов, т.е. переходу их с первоначальных энергетических
уровней на другие, более высокие уровни внутри зоны. Но то-
тогда из сказанного выше следует, что электроны целиком за-
заполненной зоны, хотя и находятся в движении, не могут дать
никакого вклада в электрический ток. Действительно, так как
энергия электрона есть четная функция импульса, то каждому
квантовому состоянию электрона в зоне с какой-либо составля-
составляющей импульса, скажем рх, обязательно соответствует и другое
состояние с той же самой энергией, но с составляющей импуль-
импульса —рх- Составляющие скорости этих электронов равны соот-
соответственно рх/тэф и —Рх/т и направлены в противоположные
стороны. Поэтому электроны целиком заполненной зоны можно
разбить на пары, создающие противоположно направленные то-
токи, а, следовательно, результирующий ток, создаваемый такой
совокупностью электронов, всегда равен нулю. Чтобы создать
отличный от нуля электрический ток, мы должны были бы воз-
возбудить электроны внутри зоны и перевести часть из них на бо-
более высокие уровни. Однако, так как в целиком заполненной
зоне все имеющиеся квантовые состояния заняты, то вследствие
принципа Паули это оказывается невозможным.
Таким образом, для электропроводности существенны толь-
только две энергетические зоны: та, которая при температуре абсо-
абсолютного нуля заполнена лишь частично или пуста, и лежащая
непосредственно под нею целиком заполненная зона. Последняя
может тоже участвовать в электропроводности, так как при по-
повышении температуры часть электронов, находящихся под по-
потолком этой зоны, может возбуждаться в выше расположенную
незаполненную зону, и поэтому она становится уже не целиком
заполненной. Обе эти зоны и представляют собой зону прово-
проводимости и валентную зону, введенные нами выше. Незанятые
же электронами квантовые состояния, энергии которых лежат
W[
Ev
Ее
Ev
Рис 267 Заполнение энергетических зон электронами в металле (о) и в
полупроводнике (б) при температуре абсолютного нуля
§ 155 РАСПРЕДЕЛЕНИЕ ИМПУЛЬСА И ЭНЕРГИИ У ЭЛЕКТРОНОВ 359
вблизи потолка валентной зоны, соответствуют положительным
дыркам (ср. § 152).
Из сказанного следует, что металлы суть такие кристаллы, у
которых при температуре абсолютного нуля одна из энергетиче-
энергетических зон заполнена частично. Типичными же полупроводниками
являются те кристаллы, энергетические зоны которых при абсо-
абсолютном нуле либо заполнены целиком, либо совершенно пусты
(рис. 267).
§ 155. Распределение импульса и энергии у электронов
Для понимания многих электронных явлений важно выяс-
выяснить, какое число носителей заряда dn из общей их совокупности
в единице объема щ имеют составляющие импульса в пределах
Рх и рх + dpx, py и ру-\- dpy, pz и pz + dpz. Энергия такой группы
частиц будет лежать в некотором интервале W и W + dW, опре-
определяемом зависимостью VF(p). Ответ на поставленный вопрос
опять получается разным в классической и квантовой теориях.
Мы поясним это на примере электронов в зоне проводимости.
Пусть dZ есть число состояний в единице объема тела, при-
принадлежащих рассматриваемому интервалу. Для малого интер-
интервала импульсов его можно считать пропорциональным этому
интервалу: dZ codpxdpydpz. Если, далее, / есть вероятность та-
таких состояний, то интересующее нас число электронов равно
dn = dZf. A55.1)
В классической статистике вероятность / выражается зако-
законом Больцмана
/ = Cexp{-W/kT), A55.2)
где W — энергия частицы в рассматриваемом состоянии, к —
постоянная Больцмана, Т — температура, С — постоянная. Ес-
Если рассматривать электроны как идеальный газ, то в отсутствие
внешних сил их потенциальная энергия не зависит от координат
и ее можно включить в постоянную С. Тогда W есть кинетиче-
кинетическая энергия
W = ~(pl+P2y+P2z), A55.3)
и из формул A55.1), A55.2) и A55.3) находим
dn = Aexp (-P^mi^) dPxdpydPi, A55.4)
где А — новая постоянная. Последняя формула выражает закон
Максвелла, дающий распределение импульсов в идеальном газе.
360
ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
Постоянная А определяется из условия, что полное число электронов с
любыми импульсами есть заданная концентрация по, т.е.
I dn = no-
Выполняя интегрирование и учитывая, что
оо
Г ехр(—ax2)dx = л/т:/а,
—оо
получаем
А =
A55 5)
A55 6)
A55.7)
В классической статистике величина dZ ничем не ограничи-
ограничивается (любое число электронов может иметь компоненты им-
импульса в данном интервале). В квантовой статистике компо-
компоненты импульса квантуются, и поэтому dZ имеет определенное
конечное значение
dz = 2dpxdPydPz AЪЬЯ)
Здесь h есть универсальная постоянная квантовой механики —
постоянная Планка, /г. = 6,62- 10~27 эрг- с = 6,62 ¦ 1СГ34 Дж-с
(ср. § 117) Множитель 2 учитывает то обстоятельство, что каж-
каждой тройке величин (рх, ру, pz) могут соответствовать две раз-
различные ориентировки электронного спина (ср. § 117).
Второе важное обстоятельство, учитываемое квантовой ста-
статистикой, заключается в том, что вероятность квантового со-
состояния с энергией W для электронов определяется не законом
Больцмана, а функцией Ферми-
Дирака
1
W
* = l + exP[(W-F)/kTY
Здесь F есть некоторая харак-
характерная энергия, не зависящая от
переменных W и р. Она получи-
получила название электрохимического
потенциала или уровня Ферми.
Величина F является парамет-
параметром распределения и играет ту же
роль, что и постоянная С в законе
Больцмана. Конечно, F не уни-
универсальная постоянная, а зависит
Рис. 268 Функция Ферми-Ди-
Ферми-Дирака 1 — Т = 0, 2 -Т фО
от природы вещества и его состояния. Для данного вещества
F, как и С, определяется полной концентрацией электронов и
температурой (см. ниже).
§ 155 РАСПРЕДЕЛЕНИЕ ИМПУЛЬСА И ЭНЕРГИИ У ЭЛЕКТРОНОВ
361
Графики функции Ферми-Дирака показаны на рис. 268. При
Т = О она имеет вид разрывной ступенчатой функции. Для всех
энергий W < F, f = 1, г, следовательно, все квантовые состоя-
состояния с такими энергиями заняты электронами. При W = F, / =
= 0,5, а при W > F, / = 0. В классической же статистике
(формула A55.2)) мы имели бы, что для всех энергий W Ф 0,
/ = 0 (частиц с отличной от нуля кинетической энергией нет
вовсе). При Т ф 0 функция / становится непрерывной и тем
более размытой, чем выше температура. При W, большем F на
несколько кТ, единицей в знаменателе A55.9) можно пренебречь
по сравнению с экспонентой, и тогда
F-W
-—J.
A55.10)
Следовательно, при достаточно больших энергиях («хвост»
функции распределения) распределение Ферми-Дирака перехо-
переходит в классическое распределение Больцмана.
Обратимся теперь к энергетическим диаграммам и положим,
что при Г = 0 уровень Ферми F лежит в зоне проводимости
(рис. 269 а). Тогда в зоне будут квантовые состояния с энергией
W < F, и существенно
необходимо пользоваться
распределением Ферми-
Дирака. Такой электрон-
электронный газ называется вы-
вырожденным. Этот случай
мы имеем в металлах.
Здесь все квантовые со-
состояния с энергией W <
< F целиком заполнены
электронами, а электро-
электронов с энергией W > F нет
С
'/////////////s
V77777777777/
Рис 269. Положение уровня Ферми в ме-
металле (а) и в невырожденном полупровод-
полупроводнике (б)
вовсе. Следовательно, да-
даже при Т = 0 электроны
находятся в движении, а
их максимальная кинетическая энергия равна И^)Макс = F — Ес.
Существование этой энергии при абсолютном нуле есть специ-
специфический результат квантовых законов движения электронов.
При Т ф 0 распределение Ферми размывается и появляется
небольшое число электронов с энергией W > F. Однако раз-
размытие функции Ферми охватывает лишь область энергий по-
порядка кТ в окрестности уровня Ферми F. Если F отстоит от
Ес на много кТ (что и имеет место в металлах), распределение
по энергиям для большинства электронов (с энергией W < F)
практически не меняется. Поэтому, в частности, средняя энер-
энергия электронов зависит от температуры слабо. Это объясняет,
362 ПРИРОДА ТОКА В МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ ГЛ XIV
почему электронный газ в металлах слабо влияет на их тепло-
теплоемкость (§ 149).
Если же уровень Ферми лежит в запрещенной зоне
(рис. 269 5), то для всех состояний в зоне проводимости мы
имеем W > F и для них справедливо классическое распреде-
распределение Больцмана A55.10) (невырожденный электронный газ).
При Г = 0 для всех состояний в зоне проводимости / = 0 и
электронов проводимости нет. Этот случай соответствует совер-
совершенно чистым полупроводникам, не содержащим примесей или
дефектов решетки.
Вернемся теперь к закону распределения электронов по импульсам. Из
сказанного выше следует, что вместо закона Максвелла A55.4) для элек-
электронов оно выражается формулой
, г,у 2 dpx dpy dpz MEEi-n
dn = fdZ=-l + e^[{w_F)/kT]. A55.11)
Здесь энергия W есть определенная функция рх, ру и pz, зависящая от
природы кристалла. Для состояний, энергия которых близка к энергии дна
зоны проводимости Ес, она выражается формулой A54.2). Параметр же
распределения — уровень Ферми F — можно определить, как раньше, из
условия нормировки A55.5).
Такой расчет особенно прост для невырожденных проводников. В этом
случае
2 /F — w\
dn~h? exp i кт ) dpx dfy dfz =
*¦«» *-
Подставляя это выражение в A55.5) и выполняя интегрирование с учетом
A55.6), получаем
no = Nc exp (^^) , A55.13)
где введено обозначение
p^K/\ A55.14)
Величина Nc получила название эффективной плотности состояний в
зоне проводимости.
Отметим, что в этих расчетах мы использовали для W выражение
A54.2), которое, строго говоря, справедливо лишь в окрестности дна зоны
проводимости. Кроме того, интегрирование по импульсам мы проводили не
в пределах зоны проводимости, а в бесконечных пределах. Однако это не
вносит заметной ошибки, так как экспоненциальный множитель в форму-
формуле A55.12) быстро затухает при увеличении рх, ру, pz, и поэтому значение
интеграла A55.5) определяется только состояниями, близкими к дну зоны.
Формула A55 13) устанавливает связь между положением уровня Фер-
Ферми F и полной концентрацией электронов проводимости по в невырожден-
невырожденных полупроводниках. Из этой формулы видно, что чем ближе F к краю
§ 156 ЭЛЕКТРОННАЯ ЭМИССИЯ 363
зоны Ес, тем больше и концентрация электронов в зоне. Если по задано, то
формула A55.13) определяет положение уровня Ферми относительно края
зоны Ес-
Если мы теперь выразим exp [(F — W)/kT] из формулы A55.13) и под-
подставим это значение в A55.12) для dn, то постоянная Планка h сократится,
и мы получим в точности закон распределения Максвелла, выражаемый
формулами A55.4) и A55.7). Однако при этом все же вместо массы изо-
изолированного электрона т будет входить эффективная масса электрона в
кристалле тЭф. Она и учитывает квантовые особенности движения элек-
электронов.
Таким образом, для применимости классической статистики нужно,
чтобы электронный газ был невырожденным. А это значит, что концентра-
концентрация электронов в нем должна быть не очень велика. Именно это мы имели
в виду в § 149, говоря о пределах применимости классической электронной
теории
Из формулы A55.13) видно, что для отсутствия вырождения концен-
концентрация электронов должна удовлетворять условию no<KiVc. Чтобы оценить
порядок величины Nc, положим тэф = т и примем температуру Т = 300 К.
Тогда по формуле A55.14) получаем
Nc = 2,4 ¦ 1019 см~3 = 2,4 ¦ 1025 м~3.
ГЛАВА XV
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
§ 156. Электронная эмиссия
В гл. XIV мы видели, что в металлах имеются электро-
электроны проводимости, участвующие в тепловом движении. Так как
электроны удерживаются внутри металла, то, значит, вблизи
поверхности существуют силы, действующие на электроны и
направленные внутрь металла. Они возникают вследствие при-
притяжения между электронами и положительными ионами решет-
решетки. В результате этого взаимодействия в поверхностном слое
металлов появляется электрическое поле, а потенциал при пере-
переходе из внешнего пространства внутрь металла увеличивается
на некоторую величину <р. Соответственно потенциальная энер-
энергия электрона уменьшается на е<р.
Распределение потенциальной энергии электрона для огра-
ограниченного металла показано на энергетической диаграмме
рис. 270. Здесь Wo — уровень энергии покоящегося электрона
вне металла, Ес — наименьшая энергия электронов проводи-
проводимости (дно зоны проводимости). Распределение потенциальной
энергии имеет вид потенциальной ямы. Ее глубина равна х =
= eip = И^о — Ес. Эта величина называется электронным срод-
сродством и является важной характеристикой вещества.
364
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ XV
и,
W
ж
е
Если электрон внутри металла имеет полную энергию W\,
меньшую Wo (рис. 270), то такой электрон не сможет покинуть
металл. Условие вылета электрона из металла
W > Wo. A56.1)
При комнатных температурах практически для всех электро-
электронов в металлах и полупроводниках это условие не выполняется и
электроны связаны в пределах проводника. Однако электронам
можно сообщить различ-
различными способами допол-
дополнительную энергию. В
этом случае часть элек-
электронов металла получа-
получает возможность покинуть
металл, и мы наблюдаем
явление испускания элек-
электронов, или электронной
эмиссии
В зависимости от того,
каким способом сообщена
электронам энергия, мы
различаем разные типы
электронной эмиссии. Ес-
Если электроны получают
энергию за счет тепловой
энергии тела при повы-
повышении температуры это-
этого тела, мы говорим о термоэлектронной эмиссии; при под-
подведении энергии светом мы имеем явление фотоэмиссии, или
фотоэлектрический эффект; если энергия сообщается электро-
электронам при бомбардировке извне какими-либо другими частицами
(электронами, ионами), мы наблюдаем вторичную электронную
эмиссию.
Рис. 270 Распределение потенциальной
энергии электрона U в ограниченном ме-
металле; Ф = Wo — F — термоэлектронная ра-
работа выхода (§ 158)
§ 157. Вольт-амперная характеристика вакуумного
диода
Для наблюдения термоэлектронной эмиссии может служить
пустотная лампа, содержащая два электрода: один — в виде про-
проволоки из тугоплавкого материала (вольфрам, молибден и др.),
раскаливаемой током (катод), и: другой, холодный электрод, со-
собирающий термоэлектроны (анод). Подобные лампы получили
широкое применение в современной радиотехнике для выпрям-
выпрямления переменных токов (вакуумные диоды, см. § 159). Аноду
диода чаще всего придают форму цилиндра, внутри которого
расположен накаливаемый катод.
§ 157 ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА ВАКУУМНОГО ДИОДА 365
Если составить электрическую цепь, содержащую вакуум-
вакуумный диод, источник напряжения и миллиамперметр (рис. 271),
то при холодном катоде ток в цепи не возникнет, так как сильно
разреженный газ внутри диода (вакуум) не содержит заряжен-
заряженных частиц, и потому электропроводность
диода практически равна нулю. Если же
раскалить катод диода при помощи допол-
дополнительного источника тока до высокой тем-
температуры, то миллиамперметр обнаружи-
обнаруживает появление тока.
Ток в цепи диода появляется только
в том случае, если положительный полюс
батареи соединен с анодом, а отрицатель-
отрицательный — с катодом. Если же изменить знак Рис 271. Схема для
разности потенциалов, приложенной к дио- наблюдения термо-
ду, то тока в цепи не будет, как бы сильно электронной эмиссии
мы ни раскаляли катод. Это обстоятельство показывает, что ка-
катод испускает отрицательные частицы, т.е. электроны, и что по-
положительные ионы не покидают металл в заметном количестве.
Сила термоэлектронного тока в диоде зависит от величины
потенциала анода относительно катода (мы считаем, что паде-
падение напряжения на самом катоде
достаточно мало, и поэтому не
уточняем, относительно какой точ-
точки катода измеряется анодный по-
потенциал). Кривая, изображающая
зависимость силы тока в диоде от
анодного напряжения (вольт -ампер-
-амперная характеристика), изображена
на рис. 272 (кривая ОЦ)- Когда
потенциал анода равен нулю, си-
сила тока через диод мала. При уве-
увеличении положительного потенци-
потенциала анода сила тока возрастает
в соответствии с кривой 01. При
дальнейшем возрастании анодного
напряжения сила тока достигает
некоторого максимального значения is, называемого током на-
насыщения диода, и почти перестает зависеть от анодного напря-
напряжения (участок характеристики Ц)-
При увеличении температуры катода вольт-амперная харак-
характеристика изображается кривыми 0125, 01236 и т.д. При значе-
значениях тока, меньших га, зависимость силы тока от напряжения
при всех температурах изображается одной и той же кривой
0123. Различными при разных температурах оказываются зна-
значения тока насыщения г5, которые быстро увеличиваются при
Рис. 272 Вольт-амперные ха-
характеристики диода при различ-
различной температуре катода
366
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ XV
возрастании температуры катода. При этом увеличивается и то
анодное напряжение, при котором устанавливается ток насыще-
насыщения.
Мы видим, что вольт-амперная характеристика электронной
лампы оказывается нелинейной, а, следовательно, электронная
лампа представляет собой пример проводника, не подчиняюще-
подчиняющегося закону Ома.
Зависимость тока диода от напряжения имеет простое объяс-
объяснение. При наличии термоэлектронной эмиссии в пространстве
между катодом и анодом в любой момент времени находятся
электроны, движущиеся от катода к аноду, которые образуют
облако отрицательного заряда (про-
(пространственный заряд). Этот про-
пространственный заряд изменяет рас-
распределение потенциала в диоде. Если
катод и анод представляют собой
плоские пластины, параллельные
друг другу (рис. 273), то в отсут-
отсутствие пространственного заряда (при
холодном катоде) распределение по-
потенциала между катодом и анодом,
образующими плоский конденсатор,
изображается прямой линией 1. При
наличии термоэлектронного тока (на-
Рис. 273. Пространственный каливание катода) между катодом и
анодом возникает пространственный
заряд и распределение потенциала
изменяется; оно выражается теперь
кривой 2. При этом значение потенциала в любой плоскости х
оказывается меньше, чем в отсутствие пространственного за-
заряда, а следовательно, и скорости движения электронов при
наличии пространственного заряда уменьшаются. С увеличе-
увеличением анодного напряжения концентрация электронов в облаке
пространственного заряда уменьшается. Поэтому и тормозящее
действие пространственного заряда делается меньше, и анодный
ток увеличивается.
Отметим, что распределение потенциала, изображенное кривой 2, по-
получается в том случае, когда начальные скорости вылета электронов из
катода достаточно малы, что обычно и имеет место. В тех же случаях,
когда начальными скоростями нельзя пренебрегать, распределение потен-
потенциала имеет более сложный вид
Зависимость тока диода г от потенциала анода U имеет вид
i = CU3/2, A57.1)
где С зависит от формы и размеров электродов.
заряд в диоде и вызываемое
им перераспределение потен-
потенциала
§ 158 ЗАВИСИМОСТЬ ТОКА НАСЫЩЕНИЯ ОТ ТЕМПЕРАТУРЫ 367
Для плоского диода
п 4 5 /2е ,л __ оч
где е/т — удельный заряд электрона, d — расстояние между
катодом и анодом, S — поверхность катода (равная поверхности
анода), ?о — электрическая постоянная (см. Добавление 8).
Формула A57.1) выражает уравнение кривой 0123 рис. 272.
Она носит название закона Богуславского-Лэнгмюра или «за-
«закона 3/2».
Когда потенциал анода становится настолько большим, что
все электроны, испускаемые катодом за каждую единицу време-
времени, попадают на анод, ток достигает своего максимального зна-
значения и перестает зависеть от анодного напряжения. Плотность
тока насыщения js, т.е. сила тока насыщения на каждую едини-
единицу поверхности катода, характеризует эмиссионную способность
катода, которая зависит от природы катода и его температуры.
§ 158. Зависимость тока насыщения от температуры
Число электронов в металле, способных преодолеть потенци-
потенциальный барьер на поверхности и выйти в вакуум, быстро уве-
увеличивается при повышении температуры. Поэтому и плотность
тока насыщения очень сильно зависит от температуры. Расчет
показывает (см. ниже), что эта зависимость выражается форму-
формулой
^ = АТ2ехр(-ФДТ). A58.1)
Здесь А — постоянная, которая для всех металлов с совершенно
чистой поверхностью должна иметь одно и то же значение, к —
постоянная Больцмана, Ф — величина, имеющая размерность
энергии, которая по определению называется термоэлектрон-
термоэлектронной работой выхода данного металла.
Термоэлектронная работа выхода равна разности между
энергией покоящегося электрона в вакууме Wq и уровнем Ферми
F (см. рис. 270):
Ф = Wo - F. A58.2)
Следовательно, отвлекаясь от тепловой «размазки» функции
Ферми (§ 155), можно сказать, что Ф есть работа, необходимая
для перевода электрона с наибольшей кинетической энергией из
металла в вакуум без начальной скорости. Соотношение A58.1)
называется формулой Ричардсона-Дэшмэпа.
Формулы A58.1) и A58.2) справедливы не только для ме-
металлов, но и для полупроводников. Однако в последнем случае
физический смысл работы выхода становится более сложным.
368 ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ ГЛ. XV
Формулу A58.1) можно получить следующим образом. Термоэлектрон-
Термоэлектронную эмиссию можно рассматривать как испарение электронов из металла.
Рассмотрим кусок металла, который раскален до высокой температуры и
заключен в замкнутый эвакуированный сосуд, поддерживаемый при той же
температуре. С поверхности металла будет происходить испарение электро-
электронов, и обратно, часть электронов, находящихся вне металла, при тепловом
движении будет встречать поверхность металла и конденсироваться на ней.
В состоянии термодинамического равновесия над металлом будет существо-
существовать электронный газ, подобный насыщенному пару над жидкостью; кон-
концентрация электронного газа определяется условием равенства скоростей
конденсации электронов и их испарения. Скорость конденсации электро-
электронов можно просто вычислить, а следовательно, нетрудно найти и скорость
испарения.
Чтобы получить формулу A58.1), нужно учесть квантовые свойства
электронного газа (§ 155). Равновесную концентрацию электронов над ме-
металлом можно найти по формуле A55.11), которая применима как для элек-
электронов внутри металла, так и для электронов в вакууме. Под W нужно
понимать энергию электронов в вакууме:
где т в данном случае есть не эффективная, а истинная масса электрона.
Кроме того, так как Wo больше F на много кТ, единицей в знаменателе
формулы A55.11) можно пренебречь. Поэтому для концентрации в вакууме
электронов, импульсы которых лежат в интервале dpx dpy dpz, имеем
2 f
~ h? 6XP I
W - F
(
exp{
Направим теперь ось X перпендикулярно поверхности в глубь метал-
металла. Тогда для электронов, движущихся по направлению к металлу, рх > 0.
Число электронов с данными составляющими импульса, встречающих еди-
единицу поверхности металла в единицу времени и входящих из вакуума в
металл, равно vx dn, где vx = рх/гп есть z-составляющая тепловой скорости
электронов. Число электронов, выходящих из металла в вакуум и имеющих
импульсы в вакууме в том же интервале dpx dpydpz, будет таким же, так
как металл и электроны над ним находятся в равновесии. Вклад указанной
группы электронов в плотность тока равен
dja = е — dn.
m
Полная плотность тока насыщения получается интегрированием этого вы-
выражения по всем возможным положительным значениям рх- Составляющие
же импульса ру и pz (параллельные поверхности) могут иметь любые зна-
значения. Следовательно,
J« = us — exP -
fcs m -*- V fcT
159
ЭЛЕКТРОННАЯ ЛАМПА КАК ВЫПРЯМИТЕЛЬ
369
Каждый из интегралов по ру и pz выражается формулой A55.6) и равен
фтгтпкТI/2. Интеграл же по рх вычисляется непосредственно интегриро-
интегрированием по частям и дает тпкТ. Поэтому мы получаем
А-кгпек2
Wo-F
т.е. формулу A58.1). Постоянная А оказывается равной
А = 4nmek2/h3 = 12,0 ¦ 105 А/(м2 ¦ К2) = 120 А/(см2 • К2).
Измеряя на опыте зависимость тока насыщения от темпера-
температуры, можно определить работу выхода Ф для данного металла.
Работа выхода для некоторых металлов приведена в табл. 10.
Для всех металлов она имеет величину порядка нескольких
электронвольт.
Таблица 11
Металл
Работа выхода, эВ
W
4,5
Мо
4,3
Pt
5,3
Fe
4,4
Mg
3,5
Na
2,3
Наряду с термоэлектронной эмиссией существуют и другие
явления, позволяющие определить работу выхода (фотоэлек-
(фотоэлектрический эффект, контактная разность потенциалов). Значе-
Значения работы выхода для металлов, определенные различными
методами, удовлетворительно совпадают друг с другом.
§ 159. Электронная лампа как выпрямитель
Так как раскаленный катод электронной лампы испускает
только электроны, но не положительные ионы, лампа пропус-
пропускает ток только тогда, когда ее катод соединен с отрицатель-
отрицательным полюсом источника. При перемене полярности приложен-
приложенного напряжения все термоэлектроны возвращаются в катод и
ток через лампу не проходит. Поэтому лампа обладает односто-
односторонней проводимостью.
Вентильное действие диодов широко используют для устрой-
устройства выпрямителей, предназначенных для превращения пере-
переменного тока в постоянный. Простейшая схема выпрямителя с
электронной лампой показана на рис. 274. Переменное напряже-
напряжение между точками Ли Б (входное напряжение UBX) изменяется
во времени согласно кривой а. Вследствие вентильного свойства
лампы ток в нагрузочном сопротивлении г имеется только в те
полупериоды, когда лампа пропускает ток. Поэтому выходное
напряжение 1ГВЫК на сопротивлении г изображается кривой б и
мы получаем пульсирующее напряжение одного знака.
Чтобы избавиться от пульсаций, между диодом и нагруз-
нагрузкой включают фильтры. Простейший из них представляет собой
370
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ. XV
конденсатор, включенный параллельно нагрузке. При нараста-
нарастании напряжения конденсатор быстро заряжается, но затем, при
уменьшении входного напряжения, медленно разряжается толь-
только через нагрузочное сопротивление г, так как электроны в дио-
диоде не могут идти от анода к катоду. В результате получается
выходное напряжение, изображаемое кривой в. Пульсации на-
напряжения тем меньше,
чем больше постоянная
времени цепи гС. При
увеличении г постоянная
составляющая напряже-
напряжения Щ стремится к мак-
максимальному (пиковому)
значению входного на-
напряжения.
На рис. 275 показа-
показана схема двухполупери-
одного выпрямителя. В
каждый момент времени
работает лишь одна из
ламп, а именно та, на-
напряжение на которой со-
соответствует пропускному
направлению и заряжает
-11+
-11+
Рис. 274. Выпрямитель с электронной
лампой
Рис. 275. Схема двухполу-
периодного выпрямителя
соединенный с нею конденсатор. Оба конденсатора соединены
последовательно, и поэтому выходное напряжение выпрямителя
(в отсутствие нагрузки) равно удвоенному пиковому значению
входного напряжения.
§ 160. Трехэлектродная электронная лампа (триод)
Основное техническое значение электронных ламп определя-
определяется тем, что электронным током в лампе легко управлять. Для
этого внутрь лампы вводят один или несколько дополнительных
160
ТРЕХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА (ТРИОД)
371
металлических электродов; их чаще всего делают в виде прово-
проволочных спиралей и помещают между катодом и анодом. Эти
дополнительные электроды получили название сеток.
Рассмотрим трехэлектродную лампу, или триод. Она име-
имеет накаливаемый катод, анод и единственную сетку (рис. 276).
Электронный ток в такой лампе зависит не только от потенци-
Рис. 276. Управляющее действие сетки
ала анода, но и от потенциала сетки относительно катода. Если
потенциал сетки равен нулю, то число электронов, достигаю-
достигающих анода, будет практически то же, что и в отсутствие сет-
сетки (а). При положительном потенциале сетки пространствен-
пространственный заряд в лампе уменьшится и ток анода будет больше. На-
Напротив, при отрицательном потенциале сетки пространственный
заряд увеличится; вследствие этого часть термоэлектронов бу-
будет возвращена обратно в катод и ток анода будет меньше, чем в
отсутствие сетки {б). При увеличении отрицательного потенци-
потенциала сетки анодный ток будет уменьшаться (б) и при некотором
потенциале сетки ток в лампе будет заперт вовсе (г). Этот запи-
запирающий отрицательный потенциал, очевидно, будет тем больше,
чем выше положительный потенциал анода. Из сказанного ясно,
что, изменяя потенциал сетки, мы можем изменять и ток анода,
т.е. им управлять. Так как масса электронов ничтожна, то инер-
инерция триода очень мала и его управляющее действие сохраняется
даже при очень быстрых изменениях потенциала сетки.
Рассмотрим подробнее, от чего и как зависит сила термо-
термоэлектронного тока в трехэлектродной лампе.
Картина электрического поля триода схематически пред-
представлена на рис. 277. При наличии сетки линии напряженно-
напряженности, которые заканчиваются частично на катоде, а частично на
электронах пространственного заряда, исходят не только из ано-
анода А, но и из проволок сетки С. Поэтому электрическое поле
вблизи катода, а значит, и пространственный заряд зависят как
от потенциала анода ?7а, так и от потенциала сетки Uc. Однако,
так как анод частично экранируется сеткой, влияние потенциала
372
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ XV
анода слабее, чем влияние потенциала сетки, и поэтому можно
положить, что полный ток с катода определяется некоторым ре-
результирующим или управляющим напряжением
Uy = Uc + DUa. A60.1)
Здесь D — величина, зависящая от устройства лампы, причем
D < 1. Ее значение тем меньше, чем гуще сетка и чем ближе она
расположена к катоду. Величина D
+ + + + л получила название проницаемости
сетки> а обратная ей величина
К = 1/D A60.2)
— коэффициента усиления лампы
(см. ниже). Из сказанного следует,
что ток с катода, или полный ток
лампы г, есть функция управляюще-
управляющего напряжения:
i = f(Uc + DUa). A60.3)
Часть электронного потока лам-
лампы попадает на сетку, и в цепи сетки
Рис 277 Электрическое по-
поле внутри триода (схемати-
(схематически)
возникает некоторый ток ic. Очевидно, что полный ток лампы
есть сумма токов анода и сетки:
г = га + гс. A60.4)
Отметим, что появление заметного тока сетки представляет
собой нежелательное явление, так как приводит к бесполезному
расходу мощности в цепи сетки. Однако в большинстве случаев
ток сетки мал по сравнению с током анода, и поэтому можно
положить
4^i = f{Uc + DUa). A60.5)
Свойства триода можно вполне определить, задавая кривые
зависимости анодного тока ia от напряжения сетки Uc при раз-
различных значениях напряжения на аноде Ua в качестве пара-
параметра. Такие кривые называют сеточными характеристиками
триода; они приведены на рис 278. Из этих кривых видно, что
одно и то же значение га можно получить при разных значе-
значениях напряжения Uc. Чем выше потенциал анода Ua, тем ниже
должен быть потенциал сетки Uc для получения одного и того
же тока; или, иначе, при повышении потенциала анода сеточные
характеристики смещаются в сторону уменьшения потенциала
сетки. Величина
(fek <160-6>
характеризует быстроту изменения анодного тока при измене-
изменении потенциала сетки, или крутизну характеристики. Индекс
§ 160
ТРЕХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА (ТРИОД)
373
С/а обозначает, что потенциал анода остается постоянным. Кру-
Крутизна характеристики 5 равна, очевидно, тангенсу угла наклона
сеточной характеристики в рассматриваемой точке.
Если бы мы изображали зависимость анодного тока ia от
анодного напряжения Ua при различных постоянных значениях
Uс, то получили бы семейство кривых, называемых анодными
характеристиками триода. Такие кривые для того же триода,
к которому относится рис. 278, изображены на рис. 279. При
, мА
200
U„=800 В
600
700
150
100
50
UC,B -80 -60 -40 -20
50
400
-180В
1200 Ua,B
Рис. 278. Сеточные характеристи- Рис 279. Анодные характеристики
к"хт ллптттпгп тгчтпгтя. тттпття.
ки мощного триода
триода
повышении сеточного потенциала анодные характеристики сме-
смещаются в сторону уменьшения потенциала анода.
Мы видим, что триоды, так же как и диоды, представляют
пример проводников с нелинейной вольт-амперной характери-
характеристикой, не подчиняющихся закону Ома. Однако достаточно ма-
малый отрезок характеристики можно считать отрезком прямой
линии и говорить о сопротивлении при данном значении напря-
напряжения (или тока). Поэтому проводники, не подчиняющиеся за-
закону Ома (нелинейные сопротивления), характеризуют, задавая
их дифференциальное сопротивление R = dU/di. Применяя это
понятие к триоду и обозначая его дифференциальное сопротив-
сопротивление через Rt, мы имеем, следовательно,
A60.7)
где индекс Uc указывает на то, что потенциал сетки поддержи-
поддерживается постоянным. Дифференциальное сопротивление триода
374
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ. XV
часто называют его внутренним сопротивлением. Из форму-
формулы A60.7) видно, что внутреннее сопротивление триода равно
тангенсу угла наклона анодной характеристики к оси токов в
данной точке. Оно характеризует быстроту изменения анодного
напряжения при изменении анодного тока.
Крутизна характеристики 5 и внутреннее сопротивление Ri
триода в рабочей точке, а также проницаемость сетки D явля-
являются важнейшими величинами, характеризующими триод.
Эти величины не являются независимыми. Продифференцируем обе ча-
части A60.5) по га, считая Uc = const. Получим
Но
1
диу \duj^
dUy
Поэтому
'Uc
SDR, = 1.
dia
A60.8)
I
§ 161. Усиление электрических сигналов
Управляющее действие сетки, рассмотренное в предыдущем
параграфе, позволяет использовать триоды для усиления элек-
электрических сигналов и пе-
переменных токов.
Принципиальная схе-
схема усилителя с трехэлек-
тродной лампой показана
на рис. 280. Анодная цепь
лампы содержит источ-
источник тока с ЭДС "ё и на-
нагрузочное сопротивление
Ra. Усиливаемое перемен-
переменное напряжение Uc при-
прикладывается между сет-
Схема усилителя на сопротивле- КОЙ И катодом лампы.
Изменение сеточного
напряжения ДС/С вызыва-
вызывает определенное изменение анодного тока Дга. Но напряжение
между анодом и катодом, согласно закону Ома, для участка це-
цепи с ЭДС выражается соотношением
г--
I
V
I
Рис. 280.
ниях
Поэтому изменение анодного тока Аг'а вызовет изменение анод-
анодного напряжения
AL/ = -ДаД»а, A61.1)
jj 161 УСИЛЕНИЕ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ 375
и если к сетке приложено переменное напряжение, то и на ано-
аноде лампы (на нагрузочном сопротивлении Ra) появится также
переменное напряжение.
Легко видеть, что изменение анодного напряжения AUa мо-
может быть больше, чем AUC. В самом деле, рассмотрим важ-
важный частный случай, когда нагрузочное сопротивление намного
больше внутреннего сопротивления лампы (Ra ^> R{). В этом
случае ток через лампу будет практически определяться только
сопротивлением J?a, а значит, будет оставаться постоянным. Но,
согласно A60.1), это значит, что
Uc + DUa — const.
Поэтому
AUC + DAUa = 0,
а следовательно,
AUa/AUc = -1/D = -К. A61.2)
Так как всегда проницаемость сетки D < 1, то AUa > AUC,
и мы имеем усиление напряжения. Из A61.2) видно, что отно-
отношение обоих напряжений в этом случае равно К = 1/D, чем
и объясняется название «коэффициент усиления» для величи-
величины К.
Знак минус в формуле A61.2) показывает, что увеличение
потенциала сетки (положительного) вызывает уменьшение по-
потенциала на аноде. При наличии колебательного сеточного на-
напряжения это обозначает, что колебания анодного напряжения
противоположны по фазе колебаниям напряжения на сетке.
Рассмотрим теперь второй предельный случай Да -С R%- Теперь напря-
напряжение на аноде лампы будет равно ЭДС источника W, а следовательно,
здесь, в противоположность предыдущему примеру, постоянным остается
анодное напряжение U&- Напротив, изменения анодного тока в этом случае
будут наибольшими.
Обращаясь вновь к формуле A60.5), можно написать для малых изме-
изменений тока
Но производная в правой части есть крутизна S сеточной характеристики,
и поэтому
Дга = SAUC.
Так как Д{УС = Д«с»", где Дгс — изменение тока сетки, а г — сопротивление
между сеткой и катодом, то для коэффициента усиления по току находим
Усиление по току тем больше, чем больше крутизна характеристики S.
В общем случае, когда нагрузочное сопротивление Да сравнимо с вну-
внутренним сопротивлением R,, для малого изменения анодного тока можно
376 ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ ГЛ XV
написать
Но
Кроме того, согласно A61.1),
Поэтому
ИЛИ
Отсюда находим изменение анодного напряжения
Д[/а = -Да Дга = - р ^ р Л,5 Д[/с.
Ка + Кг
Согласно A60.8) заменяем в этом выражении KiS на 1/Z3 = if и получаем
окончательно
ьил = -—^-кьис. A614)
Если бы мы имели цепь (рис. 281), содержащую генератор с ЭДС fo —
= К Д[/с и внутренним сопротивлением Кг, который замкнут на нагрузку с
сопротивлением Ка, то, согласно закону Ома,
т напряжение на нагрузочном сопротивлении
I выражалось бы как раз формулой A61-4). По-
W is I этому можно сказать, что если к сетке элек-
)ъ-К&ис ^ц тронной лампы подводится переменное на-
I l/j пряокемие Д[/с, то действие лампы в анодной
1-р' цепи подобно действию генератора перемен-
I ного тока с ЭДС & = К Д[/с ы внутренним
I сопротивлением Rt, замкнутого на внешнюю
1 т^епъ с сопротивлением Ra
Это положение является основным для по-
Рис 281 Эквивалентная нимания усилительного действия электронных
гхрмя тттоля r пржимр ламп. Рассмотренный выше первый частный
t-jtcMdi 1 риодл в режиме „ , rt ~ \
^ случаи (ка 3> Кг, усиление напряжения) со-
усиления v '
ответствует, очевидно, режиму холостого хода
генератора, а второй частный случай (Да *С Яг, усиление тока) — режиму
короткого замыкания.
Ламповые усилители. Усиление сигналов можно произво-
производить многократно. Для этого напряжение, усиленное электрон-
электронной лампой, подают на сетку второй лампы, а усиленное ею
напряжение — на сетку третьей лампы и т.д. Одна из схем уси-
усилительного каскада или многолампового усилителя изображена
на рис. 282. Здесь анодные цепи всех ламп соединены параллель-
§ 162
ЭЛЕКТРИЧЕСКИЕ ФЛУКТУАЦИИ
377
но и питаются одной и той же анодной батареей. Накаливание
катодов производится также от единственной батареи накала.
Следует обратить внимание на то, что напряжение на сетку
каждой лампы подается не непосредственно, а через раздели-
разделительный конденсатор С. Он не препятствует прохождению пе-
переменных усиливаемых сигналов, но не допускает попадания на
сетку высокого постоян-
постоянного напряжения анодной
батареи. Между сеткой и
катодом каждой лампы
включено еще сопротив-
сопротивление г (утечка сетки),
роль которого заключа-
заключается в следующем. В те
периоды времени, когда
на сетке имеется положи-
положительный потенциал, на
нее попадают электроны.
Если бы утечки сетки не
Рис. 282 Схема усилительного каскада
на сопротивлениях
было, то сетка в конце
концов зарядилась бы до
отрицательного запираю-
запирающего потенциала и ток через лампу прекратился бы. Но по
сопротивлению г отрицательные заряды непрерывно стекают
с сетки и запирания тока в лампе не происходит. Подбирая
должным образом соотношение между Сиг, можно добиться,
чтобы колебания напряжения на сетке происходили относи-
относительно небольшого отрицательного значения, при котором еще
сохраняется управляющее действие сетки, но ток на сетку
практически равен нулю.
Мы рассмотрели только одну из наиболее распространенных
схем усилителей (усилитель на сопротивлениях). Существуют
и многочисленные другие схемы усилителей, описание которых
можно найти в радиотехнической литературе.
§ 162. Электрические флуктуации
Общий коэффициент усиления лампового усилителя может
быть как угодно велик. Если, например, одна лампа дает усиле-
усиление напряжения 10, то усилитель из трех подобных ламп позво-
позволит получить усиление 10 • 10 • 10 = 103, из шести ламп — 106
и т.д. Поэтому для получения на выходе усилителя определен-
определенной амплитуды напряжения, например в 1 В, сигнал на входе
при трех лампах должен иметь амплитуду 10~3 В, при шести
лампах — только 10~6 В, а при большем количестве ламп — еще
меньшее значение.
378 ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ ГЛ. XV
Однако было бы ошибкой считать, что при достаточном уве-
увеличении числа ламп можно зарегистрировать любой, произвольно
малый сигнал. При увеличении общего коэффициента усиления
на выходе усилителя появляются быстрые и неправильные
колебания напряжения, которые затушевывают усиливаемый
сигнал. Если в качестве выходного прибора служит телефон,
то в нем возникают шумы. Указанные хаотические колебания
напряжения получили название электрических шумов.
Электрические шумы обусловлены атомарной природой
электрического заряда. Они возникают как внутри электронных
ламп, так и в тех сопротивлениях, которые входят в схему уси-
усилителя.
Остановимся сначала на шумах электронной лампы. Число
термоэлектронов, испускаемых катодом за каждую единицу вре-
времени, хотя и очень велико, однако конечно. Вследствие хаотич-
хаотичности теплового движения это число остается постоянным толь-
только в среднем. Число же электронов, вылетающих из катода за
малые промежутки времени, различно в разные моменты вре-
времени; оно то больше, то меньше среднего значения. Эта неравно-
неравномерность термоэлектронной эмиссии и является одной из при-
причин появления электрических шумов. Она получила название
дробового эффекта.
Дробовой эффект проявляется особенно сильно в том случае,
когда все термоэлектроны достигают анода, т.е. когда электрон-
электронная лампа работает в режиме насыщения (§ 157). В тех же слу-
случаях, когда ток в лампе ограничен пространственным зарядом
(что и имеет место в усилительном режиме), колебания тока,
вызываемые дробовым эффектом, сильно подавляются.
Гораздо большее значение имеют шумы, возникающие в со-
сопротивлениях. Для того чтобы понять происхождение этих шу-
шумов, представим себе металлический проводник, отключенный
от источника тока. Электроны проводимости в таком провод-
проводнике, участвуя в тепловом движении, перемещаются вследствие
диффузии. Диффузия не приводит к появлению тока, так как
при тепловом движении нет никаких преимущественных на-
направлений, и число электронов, перемещающихся в любом на-
направлении, в среднем равно числу перемещающихся в прямо
противоположном направлении. Однако равенство обоих диф-
диффузионных потоков имеет место только при достаточно боль-
большом промежутке времени. В отдельные же моменты времени
вследствие беспорядочности теплового движения в проводнике
существуют слабые токи, направление и сила которых беспо-
беспорядочно изменяются, а между концами проводника появляется
хаотически изменяющееся напряжение.
Мы видим, что электрические шумы имеют то же происхож-
происхождение, что и хаотические отступления (флуктуации) давления,
§ 163
ВТОРИЧНАЯ ЭЛЕКТРОННАЯ ЭМИССИЯ
379
плотности, температуры и других макроскопических величин от
их равновесных значений, наблюдаемые в атомарных системах и
обусловленные тепловым движением. Шумы в сопротивлениях
и дробовой эффект представляют собой электрические флукту-
флуктуации.
Электрические флуктуации можно наглядно продемонстри-
продемонстрировать, если подключить ко входу усилителя с коэффициентом
усиления 105 — 106 сопротивле-
сопротивление в несколько тысяч ом, а вы-
выход усилителя присоединить к
осциллографу (рис. 283). Тогда
на экране осциллографа вместо
ровной нулевой линии, види-
видимой при отключенном усилите-
усилителе, можно наблюдать совершен-
совершенно хаотические колебания луча,
Усилитель Осциллограф
Рис. 283. Схема для наблюдения
электрических флуктуации
вызванные флуктуациями напряжения. При нагревании сопро-
сопротивления интенсивность флуктуации увеличивается.
Из сказанного ясно, что для усиления и регистрации электри-
электрического сигнала необходимо, чтобы он превосходил уровень соб-
собственных шумов усилителя или, по крайней мере, был сравним с
ним. В современных хороших ламповых усилителях минималь-
минимальный сигнал, еще заметный на фоне шумов, может быть доведен
до 10~7 В и ниже.
§ 163. Вторичная электронная эмиссия
Эмиссия электронов из металла наблюдается также при
бомбардировке металла извне электронами. Это явление «вы-
«выбивания» электронов из металла получило название вторичной
электронной эмиссии. Его причина заключается в том, что при-
приходящие извне электроны, проникая в глубь металла, передают
электронам проводимости часть своей энергии. При этом неко-
некоторая доля электронов металла приобретает скорости, достаточ-
достаточные для преодоления поверхностного потенциального барьера,
и вылетает из металла.
Отношение числа выбитых вторичных электронов п к числу
проникающих первичных uq
7 = п/щ
называется коэффициентом вторичной эмиссии. Он зависит от
рода металла и скорости первичных электронов. С увеличением
скорости первичных электронов коэффициент вторичной эмис-
эмиссии сначала возрастает, затем достигает размытого максимума
и снова уменьшается. Энергия первичных электронов, соответ-
соответствующая максимальному 7> различна для разных металлов и
имеет порядок сотен электронвольт.
380
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ XV
Катод
Эмиттеры Коллектор
Значение 7 B максимуме для чистых металлов не превыша-
превышает 2. Гораздо более сильная вторичная эмиссия наблюдается у
многих полупроводников, для которых 7макс может достигать
10 и более. Поэтому для получения сильной вторичной эмиссии
употребляют сложные катоды (эмиттеры), состоящие из метал-
металлической подложки, на которую наносят слой полупроводника,
и подвергают его соответствующей химической обработке. Та-
Таковы, например, применяемые на практике сурьмяноцезиевые
эмиттеры, получаемые обработкой сурьмы в парах цезия; эмит-
эмиттеры из арсенида галлия, покрытого тончайшим слоем окислов
цезия, и другие.
Вторичная электронная эмиссия используется в электронных
умножителях, предназначенных для усиления слабых электрон-
электронных токов. Схема одного из типов умножителей показана на
рис. 284. Умножитель пред-
представляет собой вакуумную
трубку, в которой распо-
расположен ряд плоских кон-
конденсаторов и собирающий
электрод (коллектор). Одна
из пластин каждого конден-
конденсатора является вторично-
электронным эмиттером, а
другая служит лишь для
создания электрического
поля, ускоряющего вторичные электроны. Трубка помещается
между полюсами постоянного магнита (на рисунке не показан),
создающего магнитное поле, перпендикулярное к электрическо-
электрическому полю (перпендикулярное к плоскости чертежа).
Если из катода (например, под действием света) вышло
небольшое число электронов, то эти электроны будут ускоряться
электрическим полем. Благодаря магнитному полю траектория
электронов искривляется, как показано на рисунке, и электроны
попадут на первый эмиттер. Здесь возникнет вторичная эмис-
эмиссия, и с эмиттера выйдет электронный поток, более сильный,
чем поток с катода. Этот усиленный поток отклонится магнит-
магнитным полем ко второму эмиттеру и т.д. В результате электрон-
электронный поток, приходящий на собирающий электрод, будет гораздо
сильнее, нежели первичный поток, вышедший с катода, т.е. мы
получим усиление тока с помощью вторичной эмиссии.
Наряду с электронными умножителями с магнитным управ-
управлением применяют умножители с электрическим управлением,
не требующие постоянных магнитов. Схема устройства и вклю-
включения такого умножителя показана на рис. 285. Его действие
понятно из рисунка.
Рис. 284. Электронный умножитель с
магнитным управлением
164
МНОГОСЕТОЧНЫЕ ЛАМПЫ
381
В настоящее время электронные умножители применяются
главным образом для усиления слабых фотоэлектрических то-
токов. Они находят успеш-
успешное применение В астро- Эмиттеры
физике для регистрации р /\
слабого свечения звезд,
а также в других обла-
областях науки и техники.
Электронными умно-
умножителями токи могут
усиливаться в миллио-
миллионы раз. Однако, как и
в ламповых усилителях,
усиление нельзя сделать
произвольно большим.
Оно ограничивается те-
Рис. 285. Электронный умножитель с элек-
электрическим управлением
ми токами, которые са-
самопроизвольно возникают внутри умножителя, даже без воз-
воздействия света на фотокатод (темновые токи умножителя).
Вторичная электронная эмиссия происходит не только при
бомбардировке мишени электронами, но и при бомбардировке
ее тяжелыми частицами — положительными и отрицательны-
отрицательными ионами. Вторичная электронная эмиссия, вызываемая поло-
положительными ионами, играет важную роль в некоторых формах
газового разряда (см. гл. XVI).
§ 164. Многосеточные лампы
Наряду с трехэлектродными электронными лампами (триодами) в со-
современной радиотехнике широко применяются электронные лампы, имею-
имеющие несколько сеток. Рассмотрим кратко, в чем заключается смысл приме-
применения дополнительных сеток.
В § 161 мы видели, что усиление напряжения, даваемое триодом, тем
больше, чем меньше проницаемость сетки D, т.е. чем меньше влияние по-
потенциала анода по сравнению с потен-
потенциалом сетки. Чтобы уменьшить влияние
потенциала анода на ток лампы, между
управляющей сеткой и анодом помещают
вторую сетку, на которую накладывают по-
положительный относительно катода потен-
потенциал, несколько меньший потенциала ано-
анода Такая лампа с четырьмя электродами,
или тетрод, схематически изображена на
рис. 286. Роль дополнительной сетки тетро-
тетрода заключается в том, что она перехваты-
перехватывает часть линий напряженности поля, ко-
Рис. 286. Тетрод
торые раньше достигали анода, т.е частично экранирует анод, отсюда эта
сетка и получила название экранной сетки Экранная сетка вызывает то же
382
ЭЛЕКТРИЧЕСКИЕ ТОКИ В ВАКУУМЕ
ГЛ XV
действие, что и уменьшение проницаемости управляющей сетки, и поэто-
поэтому коэффициент усиления у тетрода при прочих равных условиях гораздо
больше, чем у триода.
Однако тетроды обладают тем недостатком, что в них может легко воз-
возникнуть вторичная электронная эмиссия с анода, вызванная бомбардиров-
бомбардировкой термоэлектронами В случае триода в обычном усилительном режиме
сетка находится под небольшим (а часто и под отрицательным) потенциа-
потенциалом, поэтому электрическое поле возле анода направлено так, что возвра-
возвращает вторичные электроны обратно в анод, и вторичная эмиссия не проис-
происходит. Она, впрочем, может возникнуть и в триоде, если на сетке имеется
положительный потенциал, более высокий, нежели на аноде.
В тетроде же возле анода имеется экранная сетка, все время заряженная
положительно, и поэтому, если потенциал анода сделается ниже потенциа-
потенциала экранной сетки (что может легко произойти при наличии колебаний
направления на аноде), в тетроде возника-
возникает вторичная эмиссия. В результате это-
этого уменьшается анодный ток лампы и
на вольт-амперной анодной характеристике
тетрода появляются провалы, ухудшающие
свойства тетрода (динатронный эффект)
Для устранения динатронного эффекта
в электронные лампы вводят еще одну сет-
сетку и располагают ее между экранной сеткой
и анодом. Эту сетку, называемую защитной
(или противодинатронной), соединяют с ка-
катодом (рис. 287), так что между защитной
Рис. 287. Пентод
сеткой и анодом образуется электрическое поле, тормозящее вторичные
электроны и устраняющие вторичную эмиссию с анода Подобные лампы с
пятью электродами, или пентоды, имеют высокий коэффициент усиления,
«гладкую» анодную характеристику и ряд других достоинств и поэтому
широко применяются в современных радиотехнических схемах.
§ 165. Автоэлектронная эмиссия
Эмиссия электронов из металлов происходит также под дей-
действием очень сильного электрического поля.
Для наблюдения этого явления может служить хорошо отка-
откачанная трубка, содержащая два металлических электрода — ка-
катод и анод (рис. 288). В качестве катода применяют электрод с
очень маленькой поверхностью (острие), а анод, напротив, де-
делают большим. В этом случае линии напряженности электри-
электрического поля сильно сгущаются возле катода, и напряженность
поля у поверхности катода, даже при умеренных напряжениях,
становится очень большой.
Поясним это на примере. Пусть анод имеет форму сферы с радиусом Ь,
а катод представляет собой маленький шарик с радиусом а, помещенный в
центре сферы. Тогда значение потенциала на расстоянии г от центра катода
(вне катода) выражается формулой B4.2), а напряженность поля в этой
точке равна
dU ?l
dr I/a - 1/6 г2
§ 166
ИОНИЗАЦИЯ ГАЗОВ
383
Полагая г = аи учитывая, что 6^>а, находим напряженность поля у самой
поверхности катода:
Ел ~ U/а.
Если, например, радиус катода а = 10~2 мм = 10~5 м, то уже при напря-
напряжении U = 1000 В у катода будет громадная напряженность поля: 108 В/м.
Если постепенно повышать напряжение между катодом и
анодом, то при напряженности поля у катода 107 — 108 В/м в
трубке возникает сла-
слабый ток, который обу-
обусловлен электронами,
испускаемыми катодом;
сила этого тока быстро
увеличивается с уве-
увеличением напряжения.
Ток возникает даже
при холодном катоде,
поэтому описанное явле-
явление получило название
холодной эмиссии (его
называют также автоэлектронной эмиссией). При дальнейшем
повышении напряжения катод начинает сильно нагреваться и
испаряться и в трубке возникает газовый разряд.
Возникновение автоэлектронной эмиссии объясняется тем,
что сильное электрическое поле у катода изменяет потенциаль-
потенциальный барьер на поверхности металла. Это изменение сводится,
во-первых, к понижению высоты барьера (уменьшению работы
выхода) и, во-вторых, к уменьшению толщины барьера. Оба эти
обстоятельства приводят к увеличению вероятности прохожде-
прохождения электронов через поверхностный потенциальный барьер. Ес-
Если деформация потенциального барьера достаточно велика, то
уже при низкой температуре заметная доля электронов прово-
проводимости оказывается в состоянии выйти из металла, и тогда воз-
возникает автоэлектронная эмиссия.
Рис. 288. Схема наблюдения автоэлектрон-
автоэлектронной эмиссии
ГЛАВА XVI
РАЗРЯДЫ В ГАЗАХ
§ 166. Ионизация газов
Газы в естественном состоянии не проводят электричества.
Если поместить в сухом атмосферном воздухе хорошо изолиро-
изолированное заряженное тело, например заряженный электрометр с
384 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
хорошей изоляцией, то заряд электрометра долгое время прак-
практически остается неизменным.
Однако, подвергая газ различным внешним воздействиям,
можно вызвать в нем электропроводность. Так, например, по-
помещая вблизи заряженного электрометра пламя горелки, мож-
можно видеть, что заряд электрометра быстро уменьшается. В дан-
данном случае мы сообщили газу электропроводность, создавая в
нем высокую температуру. Если бы вместо пламени горелки
мы поместили вблизи электрометра подходящий источник све-
света, например ртутную дуговую лампу (см. ниже), дающую мно-
много ультрафиолетовых лучей, то мы также наблюдали бы утечку
зарядов с электрометра. Такое же действие на газ оказывают
рентгеновские лучи и излучение радиоактивных препаратов.
Это показывает, что в газах под влиянием высокой темпера-
температуры и различных излучений появляются заряженные части-
частицы. Они возникают потому, что от атомов газа отщепляется
один или несколько электронов, в результате чего вместо ней-
нейтрального атома возникают положительный ион и электроны.
Часть образовавшихся электронов может быть при этом захва-
захвачена другими нейтральными атомами, и тогда появятся еще от-
отрицательные ионы.
Отрыв электрона от атома (ионизация атома) требует затра-
затраты определенной энергии — энергии ионизации. Она зависит от
строения атома и поэтому различна для разных веществ.
После прекращения действия ионизатора число ионов в газе
с течением времени уменьшается и в конце концов ионы исче-
исчезают вовсе. Исчезновение ионов объясняется тем, что ионы и
электроны участвуют в тепловом движении и поэтому соударя-
соударяются друг с другом. При столкновении положительного иона и
электрона они могут воссоединяться в нейтральный атом. Точ-
Точно так же при столкновении положительного и отрицательно-
отрицательного ионов, отрицательный ион может отдать свой избыточный
электрон положительному иону и оба иона превратятся в ней-
нейтральные атомы. Этот процесс взаимной нейтрализации ионов
называется рекомбинацией ионов.
При рекомбинации положительного иона и электрона или
двух ионов освобождается определенная энергия, равная энер-
энергии, затраченной на ионизацию. Частично она излучается в виде
света, и поэтому рекомбинация ионов сопровождается свечением
(свечение рекомбинации). Если концентрация положительных и
отрицательных ионов велика, то и число ежесекундно происхо-
происходящих актов рекомбинации также будет большим, и свечение
рекомбинации может быть очень сильным. Излучение света при
рекомбинации является одной из причин свечения многих форм
газового разряда.
§ 167
ИОНИЗАЦИЯ ЭЛЕКТРОННЫМИ УДАРАМИ
385
§ 167. Ионизация электронными ударами
В явлениях электрического разряда в газах большую роль
играет ионизация атомов электронными ударами. Этот про-
процесс заключается в том, что движущийся электрон, обладаю-
обладающий достаточной кинетической энергией, при соударении с ней-
нейтральным атомом выбивает из него один или несколько атомных
электронов, в результате чего нейтральный атом превращается
в положительный ион, а в газе появляются новые электроны.
Схема типичного опыта для изучения ионизации электрон-
электронными ударами показана на рис. 289 (опыты Джеймса Франка
и Густава Герца). Исследуемый газ при давлении порядка 0,1-
0,01 мм рт. ст. вводится в стеклянную трубку, которая сначала
откачивается до высо-
высокого вакуума (для уда-
удаления других газов).
Трубка имеет накали-
накаливаемый катод К, сетку
С и коллектор ионов
Кл. На сетку подается
положительный (отно-
(относительно катода) потен-
потенциал, который можно
изменять при помощи
делителя напряжения
Д\ и измерять вольт-
вольтметром V. На коллек-
коллектор ионов накладыва-
Рис. 289. Схема опытов Д. Франка и Г. Герца
ется отрицательный потенциал, на 0,5-1,0 В больший, чем по-
потенциал катода. Эта небольшая разность потенциалов снимает-
снимается с делителя напряжения Дг, положительный конец которого
соединен с катодом.
В подобных опытах катод обычно нагревают излучением вспомогатель-
вспомогательной спирали, помещенной внутрь катода. Этим устраняется изменение по-
потенциала вдоль катода, вызываемое током накала, и поэтому все точки та-
такого катода имеют одни и тот же потенциал (катоды косвенного нагрева,
или эквипотенциальные катоды).
Расстояние катод-сетка в таких трубках делают значительно
меньшим, чем расстояние сетка-коллектор, и подбирают давле-
давление газа так, чтобы средняя длина свободного пробега электро-
электронов в газе была больше расстояния между сеткой и катодом.
Поэтому электроны, испущенные катодом, движутся в про-
пространстве катод-сетка практически без соударений, и если раз-
разность потенциалов (выраженная в вольтах), между сеткой и ка-
катодом равна U, то каждый электрон приобретает кинетическую
386
РАЗРЯДЫ В ГАЗАХ
ГЛ XVI
энергию (выраженную в электронвольтах)
mv2f2 = eU. A67.1)
Электроны, ускоренные сеткой, испытывают затем соударения
с атомами газа в пространстве между сеткой и коллектором
Так как потенциал коллектора ниже, чем потенциал като-
катода, то в отсутствие ионизации все электроны тормозятся, не до-
долетая до коллектора, и поэтому ток через гальванометр равен
нулю Если, однако, постепенно повышать разность потенциа-
потенциалов U между сеткой и катодом, то, когда энергия электронов
сделается равной энергии ионизации, в пространстве сетка-кол-
сетка-коллектор появятся положительные ионы. Они будут двигаться к
коллектору, и гальванометр обнаружит ток. Поэтому, измеряя
наименьший потенциал сетки U, при котором впервые появля-
появляется ток коллектора, можно найти энергию ионизации атомов
исследуемого газа.
В точных измерениях приходится еще учитывать то обстоятельство, что
если катод и сетка сделаны из разных металлов, то между ними существует
электрическое поле при нулевом показании вольтметра V, а, следовательно,
на отрезке катод-сетка уже имеется некоторая разность потенциалов UKC
Это — так называемая контактная разность потенциалов, возникающая
всегда между двумя различными металлами (§ 198) Поэтому более точное
выражение для энергии электронов имеет вид
тп«2/2 = eU + el/кс A67 1а)
Контактную разность потенциалов можно всегда определить на опыте и
ввести соответствующую поправку к показаниям вольтметра
Метод Франка и Герца не является единственным методом
измерения энергии ионизации. Она может быть определена также
из исследования линейчатых спектров свечения разреженных
газов и паров и притом с очень большой точностью. Значения
энергии ионизации, найденные по спектрам, хорошо совпадают
с ее значениями, определенными методом электронных ударов.
В табл. 12 даны значения энергии ионизации некоторых ато-
атомов.
Таблица 12
Элемент
Энергия ионизации, эВ
Не
24,5
Ne
21,5
Аг
13,9
Hg
10,4
Na
5,12
К
4,32
Rb
4,68
§ 168. Движение ионов в газах
В § 146, 147 мы видели, что вследствие соударений элек-
электронов с кристаллической решеткой металла появляется опре-
определенная сила трения, пропорциональная скорости, и поэтому
скорость упорядоченного движения электронов v оказывается
§ 168
ДВИЖЕНИЕ ИОНОВ В ГАЗАХ
387
пропорциональной напряженности поля Е. Этот закон оказы-
оказывается применимым и к газовым ионам, если они испытывают
много соударений; поэтому можно считать, что
«± = Ь±Е. A68.1)
Здесь Ь± — подвижность газовых ионов, аналогичная подвиж-
подвижности электронов в металлах Она равна средней скорости, при-
приобретаемой ионами в поле с напряженностью, равной единице,
и в системе единиц СИ выражается в м2/(В-с). Индексы + и
— обозначают, что подвижности положительных и отрицатель-
отрицательных ионов различны, и поэтому скорость, приобретаемая ими в
одном и том же поле, также неодинакова.
Соотношение A68.1) справедливо в том случае, если число
соударений достаточно велико, т.е. если средняя длина свобод-
свободного пути / ионов газа значительно меньше расстояния d между
электродами. Обычно это условие выполняется, начиная с дав-
давлений газа в несколько десятых мм рт. ст. и выше. Если же / 2> d,
то мы говорим, что ионы движутся в вакууме. В этом случае
движение ионов будет происходить без сопротивления и ионы в
электрическом поле будут двигаться с ускорением.
Подвижность ионов данного типа тем больше, чем меньше
сила трения, испытываемая ими со стороны окружающих ато-
атомов газа. А сила трения тем меньше, чем меньше число соуда-
соударений, которое в свою очередь пропорционально давлению газа.
Поэтому в очень широком интервале изменения давлений по-
подвижность ионов обратно пропорциональна давлению газа, т.е.
bp = const. A68.2)
Значения подвижностей некоторых ионов при р = 700 мм рт. ст.
и Т = 18 °С приведены в табл. 13.
Таблица 13
Газ
Водород
Кислород
Азот
Подвижность ионов,
10~4 м2/(Вс)
ь+
5,91
1,29
1,27
Ъ-
8,26
1,79
1,84
Газ
Окись углерода
Хлор
Подвижность ионов,
Ю-4 м2/(Вс)
ь+
1,10
0,65
Ь-
1,14
0,51
Однако движение ионов в газах более сложно, чем движение
электронов в металлах В газовых разрядах часто наблюдает-
наблюдается неравномерное распределение ионов между электродами, при
котором градиент концентрации ионов dn/dx не равен нулю, и
поэтому возникает заметный поток диффузии ионов Заряд, пе-
переносимый положительными ионами вследствие диффузии че-
через единицу поверхности в единицу времени (плотность тока
388 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
диффузии), равен
где -D-j- — коэффициент диффузии ионов, q — заряд иона. Ко-
Количество электричества, проходящее через ту же площадку за
единицу времени вследствие упорядоченного движения ионов
под действием поля (плотность тока дрейфа), есть
qn+b+E.
Поэтому плотность тока j+ равна
J+ = qn+b+E-qD+^-. A68.3)
Аналогичное выражение получается и для плотности тока j_,
вызванного движением отрицательных ионов Нужно только
учесть, что вследствие отрицательного заряда ионов направле-
направление тока противоположно направлению потока диффузии, и по-
поэтому
]_ = qn-b-E + qD- ^=-. A68.3а)
Полная плотность тока в ионизованном газе есть
j = j++j_. A68.4)
Концентрации п+ и п_ в ионизованном газе могут быть не
равны друг другу. Поэтому, в отличие от металлов, в газовых
проводниках при наличии тока появляются объемные заряды,
которые обусловливают сложное распределение электрического
поля между электродами.
Второе обстоятельство, сильно отличающее газовые провод-
проводники от металлов, заключается в следующем В металлах кон-
концентрация электронов есть величина постоянная, не зависящая
от напряженности поля и плотности тока и определяемая толь-
только природой данного металла. В ионизованном же газе носители
заряда (ионы и электроны) могут возникать в процессе разря-
разряда, например в результате ионизации электронными ударами.
Поэтому концентрации ионов п+ и п_ могут зависеть от напря-
напряженности поля.
Указанные причины приводят к тому, что газовые проводни-
проводники, как правило, не подчиняются закону Ома.
§ 169. Несамостоятельные и самостоятельные разряды
Рассмотрим цепь, содержащую источник напряжения, газо-
газовый промежуток и переменное сопротивление г, которое можно
изменять в широких пределах (рис. 290). Цепь содержит также
токоизмерительный прибор А и вольтметр V. Предположим сна-
сначала, что на газовый промежуток воздействует какой-либо ио-
§ 169
НЕСАМОСТОЯТЕЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАЗРЯДЫ
389
Рис 290 Принципиаль-
Принципиальная схема для опреде-
определения вольт-амперной ха-
характеристики газового
промежутка
низатор, например ультрафиолетовые лучи, падающие на отри-
отрицательный электрод и освобождающие из него фотоэлектроны.
От этого газ приобретет некоторую электропроводность и в цепи
появится ток. Если плавно уменьшать
сопротивление г в цепи газового про-
промежутка, то сила тока будет сначала
увеличиваться, что связано с увеличе-
увеличением напряжения между электродами
и объясняется уменьшением простран-
пространственного заряда между ними. При
дальнейшем уменьшении сопротивле-
сопротивления напряжение на электродах достиг-
достигнет такого значения, при котором все
образующиеся ионы доходят до поло-
положительного электрода, и мы получим
ток насыщения is, сила которого зави-
зависит только от интенсивности ионизато-
ионизатора (рис. 291). Наблюдаемые при этом
токи очень малы (обычно микроампе-
микроамперы и меньше, в зависимости от интен-
интенсивности ионизатора).
Если в одном из режимов разряда, изображаемых ветвью ха-
характеристики Оа, прекратить действие ионизатора, то и разряд
прекращается. Подобные разряды,
существующие только при действии
внешнего ионизатора, получили на-
название несамостоятельных газовых
разрядов.
Если продолжать уменьшать сопро-
сопротивление цепи г, то ток через разряд-
разрядный промежуток начинает сильно воз-
возрастать, хотя напряжение повышается
сравнительно мало Это соответствует
участку характеристики аб (рис. 291).
Возрастание тока на участке характе-
характеристики аб показывает, что в газовом
промежутке появляются новые ионы.
Если еще уменьшить сопротивле-
сопротивление г, то разряд приобретает совсем
другой характер. Сила тока в разряде
резко возрастает (в сотни и тысячи раз)
и в газе появляются сильно выражен-
выраженные световые и тепловые эффекты. Ес-
Если теперь прекратить действие ионизатора, то разряд продол-
продолжается. Это значит, что ионы, необходимые для поддержания
электропроводности газа, создаются самим разрядом в резуль-
U
0
Рис 291 Вольт-амперная
характеристика несамо-
несамостоятельного газового раз-
разряда
390 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
тате процессов, происходящих в разряде. Такие газовые разря-
разряды называют самостоятельными разрядами. Напряжение, при
котором возникает самостоятельный разряд, называется напря-
напряжением пробоя газового промежутка или напряжением зажи-
зажигания газового разряда.
В зависимости от того, какие именно процессы образования
ионов в разряде играют главную роль, мы говорим о различных
формах, или типах, самостоятельных разрядов. Так, например,
мы различаем коронный, искровой, дуговой, тлеющий и другие
разряды. Эти формы разряда отличаются друг от друга свой-
свойствами и внешним видом.
§ 170. Возникновение самостоятельных разрядов
Посмотрим теперь, каким образом несамостоятельный раз-
разряд в газе может перейти в самостоятельный.
Одна из первых количественных теорий возникновения са-
самостоятельного разряда в газах была предложена Таунсендом.
Как выяснилось впоследствии, эта теория имеет ограниченную
применимость и приложима только к некоторым формам газо-
газового разряда. Однако она хорошо разъясняет саму возможность
превращения несамостоятельного разряда в самостоятельный.
Представим себе, что под действием какого-либо внешнего
ионизатора, например ультрафиолетовых лучей, из катода вы-
вылетел электрон. На длине свободного пробега он будет двигать-
двигаться в электрическом поле ускоренно и перед столкновением при-
приобретет определенную кинетическую
+ энергию. Если эта энергия равна или
' больше энергии ионизации атомов
ШШИШ11Ш газа, то при соударении атом будет
ОООООООО ионизирован, в результате чего по-
УУУУУУУУ явятся один новый электрон и один
о о о о положительный ион.
У У У У Положительные ионы будут дви-
II I I гаться по направлению к катоду,
У У а электроны — к аноду (рис. 292:
I I черные точки — электроны, свет-
светлые кружки — нейтральные атомы).
После соударения электроны будут
1 опять набирать энергию, и при еле-
дующем соударении появятся уже
четыре электрона. После третьей ио-
Рис. 292. Схема образования низации их будет восемь, после чет-
электронной лавины вертой _ шестнадцать и тд. Поэтому
общее число электронов и ионов будет возрастать лавинообраз-
лавинообразно по мере продвижения электронов к аноду. Обозначим через а
§ 170
ВОЗНИКНОВЕНИЕ САМОСТОЯТЕЛЬНЫХ РАЗРЯДОВ
391
число пар электронов и ионов, образуемых одним электроном на
единице длины пути (коэффициент объемной ионизации). Так
как энергия, приобретаемая электронами на пути свободного
пробега, тем больше, чем больше напряженность электрическо-
электрического поля Е в газе, то и коэффициент а зависит от напряженности
поля. Этот коэффициент меняется также с изменением давления
газа р, так как число актов ионизации зависит от числа соуда-
соударений, испытываемых электроном на единице длины пути, а это
последнее пропорционально давлению газа.
Путем простых теоретических рассуждений можно легко установить,
что для данного газа частное а/р есть функция отношения напряженности
поля к давлению газа, т е
a/p = f(E/p), A70.1)
где вид функции / зависит от рода газа. Эта формула хорошо согласуется с
опытом и оказывается весьма полезной, так как позволяет выразить зависи-
зависимость а от двух переменных Еир при помощи одной кривой, определяемой
уравнением A70.1).
Рассмотрим теперь столб газа, заключенный между плоски-
плоскими электродами, и найдем ионизацию в слое газа толщины dx,
находящемся на расстоянии х от ка-
катода (рис. 293). Один электрон на
пути dx создает adx пар ионов. Ес-
Если в рассматриваемый слой влетают
со стороны катода не один, а п элек-
электронов, то увеличение числа элек-
электронов на пути dx будет равно
dn = nadx. A70.2)
В дальнейшем для простоты мы
будем считать, что возникающие ио-
ионы не изменяют существенно элек-
электрическое поле, которое таким обра-
образом остается однородным и при ионизации. Поэтому и коэффи-
коэффициент а мы будем считать величиной постоянной, не зависящей
от х. Тогда, интегрируя A70.2), находим
п = Сеах,
где С — постоянная интегрирования.
При х = 0, т.е. на самом катоде, п равно числу электронов щ,
производимых внешним ионизатором. Поэтому С = щ. Полагая
х = d, где d — расстояние между катодом и анодом, мы находим
окончательно число электронов па, попадающих на анод:
na = noead. A70.3)
Легко видеть, что па может на много порядков превы-
превышать по- Пусть, например, на 1 м пути возникают 300 пар ио-
ионов (а = 300 м). Если расстояние между катодом и анодом
Рис. 293. К расчету электрон-
электронной лавины
392 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
равно 3 см = 3 • 10" м, то один первичный электрон, вылетаю-
вылетающий с катода, вызовет появление у анода е = е ~ 10
электронов, т.е. произойдет огромное размножение электронов
вследствие образования электронной лавины.
Возникновение электронных лавин в газе, однако, еще не
представляет собой самостоятельный разряд. Так, например, по-
полагая в формуле A70.3) щ = 0, мы получаем и па = 0, т.е. при
выключении внешнего ионизатора исчезает и ток анода. Чтобы
разряд был самостоятельным, нужно, чтобы электронные лави-
лавины поддерживали сами себя, т.е. чтобы в газе происходил еще и
другой процесс (или процессы), непрерывно производящий но-
новые электроны взамен ушедших на анод.
Один из важных процессов такого рода заключается в обра-
образовании вторичной электронной эмиссии с катода под действием
бомбардировки положительными ионами. Если положительный
ион при своем движении к катоду приобретает достаточную
энергию, то он может выбить из катода некоторое число элек-
электронов (ср. § 163). Этот процесс можно охарактеризовать ко-
коэффициентом вторичной эмиссии 7 (ср. § 163), который пока-
показывает, сколько вторичных электронов выбивает с катода один
положительный ион. Величина 7 зависит от скорости ионов, их
природы и материала катода.
Таунсенд показал, что одновременное существование обоих
процессов, т.е. объемной и поверхностной ионизации, может при-
привести к самостоятельному разряду. Вернемся опять к рис 293 и
предположим сначала, что между электродами имеется устано-
установившийся несамостоятельный газовый разряд. Обозначим пол-
полное число электронов, выходящих с катода за 1 с (образованных
и внешним ионизатором, и вторичной эмиссией), через п\. Со-
Согласно формуле A70.3) в результате объемной ионизации число
электронов, попадающих на анод, возрастет до величины
na = mead. A70.4)
Следовательно, число новых электронов, возникших в лавине,
равно
na-m=ni(eQrf-l).
Таким же будет и число образовавшихся в лавине положитель-
положительных ионов. Положительные ионы, обрушиваясь на катод, вы-
выбьют
вторичных электронов. Это число электронов, сложенное с чис-
числом электронов по, производимых за 1 с внешним ионизатором,
равно, очевидно, полному числу п\ электронов, вышедших с ка-
катода; поэтому
п0 +7«i(eQd- 1) — щ.
§ 170 ВОЗНИКНОВЕНИЕ САМОСТОЯТЕЛЬНЫХ РАЗРЯДОВ 393
Или, иначе
По
«1 = j _ e ±
Подставляя это выражение в A70.4), мы можем выразить
число электронов, ежесекундно приходящих на анод, в следую-
следующем виде:
Полученное выражение разъясняет возникновение самостоя-
самостоятельного разряда. Действительно, предположим, что мы посте-
постепенно увеличиваем напряженность электрического поля. При
этом будут возрастать значения а и j, и па будет непрерывно
увеличиваться. При некоторой напряженности поля будет вы-
выполнено условие
7(ead - 1) = 1, A70.6)
и знаменатель формулы A70.5) обратится в нуль. Значение па
будет неограниченно возрастать даже при любом, сколь угодно
малом, значении щ. Следовательно, внешний ионизатор здесь
уже не нужен, и мы имеем превращение несамостоятельного
разряда в самостоятельный. Условие A70.6) есть условие зажи-
зажигания газового разряда.
Отметим, что в действительности, конечно, никакого бесконечного воз-
возрастания числа электронов па не будет Так как цепь разряда имеет опреде-
определенное сопротивление, то при значительном увеличении тока разряда будет
уменьшаться напряжение на газоразрядном промежутке, а следовательно,
и электрическое поле, и поэтому в газе установится конечный ток, завися-
зависящий от ЭДС источника и сопротивления цепи
Теория Таунсенда в дальнейшем подверглась многочислен-
многочисленным дополнениям и уточнениям Так, например, выше мы пред-
предполагали, что электроны на катоде возникают только под дей-
действием положительных ионов. Между тем в разряде могут
происходить и другие процессы, приводящие к возникновению
электронов. Таким процессом может быть освобождение элек-
электронов с катода, вызванное излучением самого разряда (так
называемый фотоэлектрический эффект). Электроны, необхо-
необходимые для поддержания лавины, могут возникнуть также в объ-
объеме газа при соударении атомов с положительными ионами (это
было учтено уже самим Таунсендом) или в результате фото-
фотоионизации. Далее нужно учесть и то изменение электрического
поля, которое вызывается объемными зарядами при ионизации
газа. Эти процессы часто имеют место в газовом разряде одно-
одновременно, и поэтому точная теория самостоятельных газовых
разрядов весьма сложна.
394
РАЗРЯДЫ В ГАЗАХ
ГЛ XVI
§ 171. Тлеющий разряд
Процессы, рассмотренные выше, играют важную роль в воз-
возникновении и поддержании так называемого тлеющего разряда.
Эту форму газового разряда удобно наблюдать при понижен-
пониженном давлении газа. Если к электродам, впаянным в стеклянную
трубку длиной 30-50 см, приложить постоянное напряжение в
несколько сот вольт и затем постепенно откачивать воздух из
трубки, то наблюдаются следующие явления. При атмосферном
давлении приложенное напряжение недостаточно для пробоя га-
газа и трубка остается темной. При уменьшении давления газа в
некоторый момент в трубке возникает разряд, имеющий вид све-
светящегося шнура, соединяющего анод и катод трубки. При даль-
дальнейшем уменьшении давления этот шнур расширяется и запол-
заполняет все сечение трубки, а свечение вблизи катода ослабевает.
При давлениях газа порядка 0,1-0,01 мм рт. ст. разряд име-
имеет вид, изображенный на рис. 294. Непосредственно к катоду
прилегает тонкий светящийся слой (первое катодное свечение,
Рис 294. Основные части тлеющего разряда
или катодная пленка A)), за которым следует темный слой, по-
получивший название катодного темного пространства B). Это
темное пространство затем переходит в светящийся слой (тлею-
(тлеющее свечение C)), который имеет резкую границу со стороны
катода и постепенно исчезает со стороны анода. За тлеющим
свечением наблюдается опять темный промежуток, называемый
вторым или фарадеевым темным пространством D)- Указан-
Указанные части называются катодными частями разряда. За вторым
темным пространством лежит светящаяся область, простираю-
простирающаяся до анода, или положительный столб E). В некоторых
случаях этот столб распадается на ряд слоев, или страт.
Особое значение в тлеющем разряде имеют только две его
части — катодное темное пространство и тлеющее свечение, в ко-
которых и происходят основные процессы, поддерживающие раз-
разряд. Если в газоразрядной трубке сделать анод подвижным и
§ 171
ТЛЕЮЩИЙ РАЗРЯД
395
постепенно придвигать его к катоду (рис. 294), то все катодные
части остаются неизменными, а укорачивается только положи-
положительный столб. При дальнейшем уменьшении длины разрядно-
разрядного промежутка начинает укорачиваться второе катодное темное
пространство, и когда анод попадает в тлеющее свечение, оно
исчезает вовсе. Однако при этом разряд продолжает существо-
существовать. Когда же анод при дальнейшем уменьшении расстояния
подходит к границе между первым катодным пространством и
тлеющим свечением, разряд гаснет.
Характерным для тлеющего разряда является особое распре-
распределение потенциала по длине трубки. Его можно определить,
впаивая в трубку ряд дополнительных электродов — зондов, рас-
расположенных в различных местах трубки, и присоединяя между
катодом и соответствующим зондом вольтметр с большим со-
сопротивлением. Тогда получается кривая распределения потен-
потенциала, изображенная на рис. 295. Она показывает, что почти
все падение потенциала
в разряде приходится на
область катодного темного
пространства. Эта разность
потенциалов между като-
катодом и границей тлеющего
свечения получила назва-
название катодного падения
потенциала.
Опыт показывает, что
если сила тока в разряде
не очень велика, то катод-
катодное падение потенциала не
зависит от силы тока (нор-
(нормальное катодное падение Рис 295 распределение потенциала в
потенциала). Изменение си- ТЛ€Ющем разряде
лы тока изменяет лишь раз-
размер светящейся поверхности на катоде, которая увеличивается
с увеличением силы тока. Когда же сила тока достигает такого
значения, что катодная пленка покрывает всю поверхность ка-
катода, катодное падение потенциала начинает возрастать с увели-
увеличением силы тока (аномальное катодное падение потенциала).
Существенным для понимания процессов в тлеющем разря-
разряде является то обстоятельство, что нормальное катодное паде-
падение потенциала зависит лишь от материала катода и рода газа,
причем катодное падение потенциала оказывается пропорцио-
пропорциональным работе выхода электронов из катода.
Рассмотренные свойства тлеющего разряда приводят к сле-
следующей картине процессов, поддерживающих разряд. Положи-
Положительные ионы, образующиеся в результате ионизации электрон-
396 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
ными ударами (в тлеющем свечении и в положительном столбе),
движутся к катоду и, проходя через область катодного падения
потенциала, приобретают значительную энергию. Под действи-
действием интенсивной бомбардировки быстрыми положительными ио-
ионами (а также вследствие фотоэффекта, вызванного излучени-
излучением разряда) с катода вылетают электроны, которые движутся к
аноду. Эти электроны в области катодного падения потенциала
сильно ускоряются и при последующих соударениях с атомами
газа их ионизируют. В результате опять появляются положи-
положительные ионы, которые, снова устремляясь на катод, производят
новые электроны и т.д. Таким образом, основными процессами,
поддерживающими разряд, являются ионизация электронными
ударами в объеме и вторичная электронная эмиссия на катоде.
Существование катодного темного пространства объясняет-
объясняется тем, что электроны начинают сталкиваться с атомами газа
не сразу, а лишь на некотором расстоянии от катода. Шири-
Ширина катодного темного пространства приблизительно равна сред-
средней длине свободного пробега электронов: она увеличивается с
уменьшением давления газа. В катодном темном пространстве
электроны, следовательно, движутся практически без соударе-
соударений.
Распределение концентраций положительных ионов и элек-
электронов в различных частях разряда весьма неодинаково. Так
как положительные ионы движутся гораздо медленнее, нежели
электроны, то у катода концентрация ионов значительно боль-
больше, чем концентрация электронов. Поэтому вблизи катода воз-
возникает сильный пространственный положительный заряд, ко-
который и вызывает появление катодного падения потенциала.
Напротив, в области положительного столба концентрации по-
положительных ионов и электронов почти одинаковы и здесь про-
пространственного заряда нет. Благодаря большой концентрации
электронов положительный столб обладает хорошей электро-
электропроводностью и поэтому падение напряжения на нем весьма ма-
мало (см. рис. 295).
Так как в положительном столбе имеются и положительные
ионы, и электроны, то здесь происходит интенсивная рекомбина-
рекомбинация ионов, чем и объясняется свечение положительного столба
(свечение рекомбинации; ср. § 166).
Мы видим, что катодное падение потенциалов необходимо
для поддержания тлеющего разряда. Именно благодаря его на-
наличию положительные ионы приобретают необходимую энергию
для образования интенсивной вторичной электронной эмиссии
с катода, без которой тлеющий разряд не мог бы существовать.
Поэтому катодное падение потенциала есть наиболее характер-
характерный признак тлеющего разряда, отличающий эту форму газо-
газового разряда от всех других форм.
§ 172 ИСКРОВОЙ РАЗРЯД 397
Применения тлеющего разряда. Тлеющий разряд широ-
широко используют в качестве источника света в различных газораз-
газоразрядных трубках. В лампах дневного света излучение тлеющего
разряда поглощается слоем специальных веществ, нанесенных
на внутреннюю поверхность трубки, которые под действием по-
поглощенного излучения в свою очередь начинают светиться. Под-
Подходящим подбором этих веществ (люминофоров) испускаемое
ими излучение можно сделать близким к дневному свету. Та-
Такие трубки оказываются более экономичными, нежели обычные
лампы накаливания.
Газоразрядные трубки применяются также для рекламных
и декоративных целей, для чего им придают очертания различ-
различных фигур и букв. Наполняя трубки различными газами, можно
получить свечение разной окраски (красное у неона, синевато-
зеленое у аргона).
Пользуясь тем, что катодное падение потенциала зависит от
материала катода, можно сделать газоразрядные трубки с ма-
малым напряжением зажигания. Так, например, в неоновой лампе,
в которой электродами служат два железных листочка, покры-
покрытых слоем бария, вследствие малости работы выхода электронов
у бария, катодное падение потенциала составляет только около
70 В. Поэтому лампа зажигается уже при включении в обыч-
обычную осветительную сеть. Такие лампы употребляют для целей
сигнализации в различной аппаратуре (индикаторные лампы).
В лабораторной практике используют тлеющий разряд для
катодного распыления металлов, так как вещество катода в
тлеющем разряде постепенно переходит в парообразное состо-
состояние и оседает в виде металлического налета на стенках трубки.
Причина катодного распыления, по всей вероятности, заклю-
заключается в том, что каждый положительный ион при соударении с
катодом передает свою энергию сначала небольшой группе ато-
атомов катода. Это приводит к сильному местному повышению тем-
температуры, возникающему в отдельных микроскопических обла-
областях катода, которое и приводит к испарению металла в этих
местах. Помещая в тлеющем разряде против катода различные
предметы, оказывается возможным покрыть их равномерным и
прочным слоем металла. Этим способом, в частности, пользуют-
пользуются для изготовления металлических зеркал высокого качества.
§ 172. Искровой разряд
Если постепенно увеличивать напряжение между двумя
электродами, находящимися в атмосферном воздухе и имеющи-
имеющими такую форму, что электрическое поле между ними не слиш-
слишком сильно отличается от однородного (например, два плоских
электрода с закругленными краями или два достаточно боль-
398 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
ших шара), то при некотором напряжении возникает электри-
электрическая искра Она имеет вид ярко светящегося тонкого канала,
соединяющего оба электрода, который обычно бывает сложным
образом изогнут и разветвлен (рис 296).
Рис 296 Искровой разряд
Электрическая искра возникает в том случае, если электри-
электрическое поле в газе достигает некоторого определенного значения
Ек (критическая напряженность поля, или напряженность про-
пробоя) , которая зависит от рода газа и его состояния Для воздуха
при нормальных условиях Ек ~ 3 • 106 В/м.
Значение Е* увеличивается с увеличением давления Отношение кри-
критической напряженности поля к давлению газа р для данного газа остается
приблизительно постоянным в широкой области изменения давлений
Ек/pw const A72 1)
Этот закон, который можно обосновать в теории Таунсенда, оказывается во
многих случаях весьма полезным и позволяет определить Ек при разных
давлениях, если известно его значение при каком-либо одном давлении
Напряжение пробоя понижается при воздействии на газ
внешнего ионизатора Если приложить к газовому промежут-
промежутку напряжение, несколько меньшее пробойного, и внести в про-
пространство между электродами зажженную газовую горелку, то
возникает искра Такое же действие оказывает и освещение
отрицательного электрода ультрафиолетовым светом, а также
другие ионизаторы
Для объяснения искрового разряда вначале казалось есте-
естественным предположить, что основными процессами в искре
являются, в соответствии с теорией Таунсенда, ионизация элек-
электронными ударами в объеме и ионизация положительными ио-
ионами (в объеме или на катоде) Однако впоследствии выясни-
выяснилось, что эти процессы не могут объяснить многие особенности
образования искры Остановимся для примера на скорости раз-
развития искрового разряда. Если бы в искре существенную роль
играла ионизация положительными ионами, то время развития
искры было бы по крайней мере того же порядка, что и время
перемещения положительных ионов от анода до катода Это вре-
время легко оценить, оно оказывается порядка 10~4 —10~5 с Между
тем опыт дает, что время ее развития — 10~7с и меньше, т е на
несколько порядков меньше
§ 172 ИСКРОВОЙ РАЗРЯД 399
Объяснение большой скорости развития искры, так же как и
других особенностей этой формы разряда, дано так называемой
стример ной теорией искры, в настоящее время надежно обосно-
обоснованной прямыми экспериментальными данными Согласно этой
теории возникновению ярко светящегося канала искры пред-
предшествует появление слабо светящихся скоплений ионизованных
частиц (стримеров) Пронизывая газоразрядный промежуток,
стримеры образуют проводящие мостики, по которым в после-
последующие стадии разряда и устремляются мощные потоки элек-
электронов Причиной возникновения стримеров является не только
образование электронных лавин посредством ударной иониза-
ионизации, но еще и ионизация газа излучением, возникающим в самом
разряде (фотоионизация)
Схема развития стримера изображена на рис 297 В виде
конусов на этом рисунке показаны электронные лавины, зарож-
зарождающиеся в точках вершин конусов и распространяющиеся от
катода к аноду Существенным в этой схеме является то обстоя-
А В
I 1
С D
I 1
Рис 297 Развитие отрицательного стримера
тельство, что, помимо, первоначальной электронной лавины, за-
зародившейся непосредственно у катода, происходит образование
новых лавин в точках, расположенных далеко впереди от головы
первоначальной лавины Эти новые лавины возникают вслед-
вследствие появления электронов в объеме газа в результате фотоио-
фотоионизации излучением, исходящим из лавин, возникших ранее (на
рисунке это излучение показано схематически в виде волнистых
линий) В процессе своего развития отдельные лавины нагоня-
нагоняют друг друга и сливаются вместе, в результате чего возника-
возникает хорошо проводящий канал стримера Из приведенной схемы
ясно, что вследствие возникновения многих лавин общий путь
CD, проходимый стримером, намного больше расстояния АВ,
проходимого одной первоначальной лавиной (различие в длинах
АВ и CD в действительности намного больше, чем показано на
рис 297)
Наряду со стримерами, распространяющимися от катода к
аноду (отрицательные стримеры), существуют также стримеры,
движущиеся от анода к катоду (положительные стримеры)
400
РАЗРЯДЫ В ГАЗАХ
ГЛ XVI
§ 173. Коронный разряд
Разряд, получивший такое название, наблюдается при срав-
сравнительно высоких давлениях газа (например, при атмосферном
давлении) в сильно неоднородном поле. Для получения значи-
значительной неоднородности поля электроды должны иметь очень
неодинаковую поверхность, т.е. один электрод — очень большую
поверхность, а другой — очень малую.
Так, например, коронный разряд легко
получить, располагая тонкую проволоку
внутри металлического цилиндра, ради-
радиус которого значительно больше радиуса
проволоки (рис. 298); следует отметить,
что наличие внешнего цилиндра не обяза-
обязательно и его роль могут играть окружаю-
окружающие заземленные предметы.
Линии напряженности электрического
поля сгущаются по мере приближения к
проволоке, а, следовательно, напряжен-
напряженность поля возле проволоки имеет наи-
Рис. 298. Схема полу- большее значение. Когда она достигает
чения коронного раз- приблизительно 3- 10б В/м (при атмосфер-
РяДа ном давлении и нормальной температуре),
между проволокой и цилиндром зажигается разряд и в цепи
появляется ток. При этом возле проволоки возникает свечение,
имеющее вид оболочки или короны, окружающей проволоку, от-
откуда и произошло название разряда (рис. 299).
Рис. 299. Фотографии короны вокруг проволоки
Коронный разряд возникает как при отрицательном потен-
потенциале на проволоке (отрицательная корона, рис. 299 а), так и
§ 173 КОРОННЫЙ РАЗРЯД 401
при положительном (положительная корона, рис. 299 6), а так-
также при переменном напряжении между проволокой и цилин-
цилиндром. При увеличении напряжения между проволокой и цилин-
цилиндром растет и ток в коронном разряде. При этом увеличивается
толщина светящегося слоя короны.
Процессы внутри короны сводятся в основном к следующе-
следующему. Если проволока заряжена отрицательно, то по достижении
напряженности пробоя у поверхности проволоки зарождаются
электронные лавины, которые распространяются от проволоки
к цилиндру. Так как напряженность поля уменьшается по мере
удаления от проволоки, то на некотором расстоянии от прово-
проволоки электронные лавины обрываются. Расстояние, на которое
распространяются электронные лавины, и есть толщина коро-
короны. Следовательно, в коронном разряде электронные лавины не
пронизывают целиком слой газа, т.е. мы имеем неполный пробой
газового промежутка.
В случае положительной короны электронные лавины за-
зарождаются на внешней поверхности короны и движутся по на-
направлению к проволоке.
Таким образом, внутри короны мы имеем и положительные
и отрицательные ионы. Отрицательные ионы (при отрицатель-
отрицательной короне) движутся к аноду и выходят за пределы короны.
Положительные ионы движутся к проволоке.
Электроны, вышедшие за пределы короны, присоединяются
к нейтральным атомам газа, отчего возникают отрицательные
ионы. За пределами короны мы имеем только ионы одного зна-
знака (отрицательные при отрицательной короне и положительные
при положительной короне). В этой области разряд имеет неса-
несамостоятельный характер.
Коронный разряд может возникнуть не только возле про-
проволок, но и возле любых проводников с малой поверхностью,
каковыми являются всякого рода заострения. В частности, рас-
рассмотренные ранее в электростатике свойства острий (§ 29)
объясняются зажиганием возле них микроскопической короны.
Корона возникает также иногда в природе под влиянием атмо-
атмосферного электрического поля и появляется на верхушках дере-
деревьев, корабельных мачт и т.п.
С возможностью возникновения коронного разряда прихо-
приходится всегда считаться в технике высоких напряжений. При
зажигании короны возле проводов высоковольтных линий элек-
электропередачи окружающий воздух сильно ионизируется и появ-
появляются вредные токи утечки. Чтобы коронный разряд не мог
возникнуть, провода высоковольтных линий должны иметь до-
достаточно большой диаметр, тем больший, чем выше напряже-
напряжение линий. По этой же причине и в лабораторной практике вся
проводка высокого напряжения (к рентгеновским установкам и
402 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
другим высоковольтным устройствам) осуществляется обычно с
помощью труб достаточно большого диаметра.
§ 174. Молния
Молния представляет собой гигантскую электрическую ис-
искру. Электрическая природа молнии была впервые доказана из-
известными опытами Франклина с воздушным змеем и многочис-
многочисленными исследованиями М.В. Ломоносова и Рихмана.
Наблюдая за показаниями электроскопа, соединенного с высоким ме-
металлическим шестом, Ломоносов обнаружил, что электрическое поле у по-
поверхности земли существует и в отсутствие грозы, сильно увеличиваясь в
предгрозовые периоды Он создал первую теорию возникновения электри-
электрических зарядов в атмосфере, указав на важную роль восходящих и нис-
нисходящих потоков воздуха, и этим положил начало науке об атмосферном
электричестве
Молнии возникают либо между облаками, либо между обла-
облаком и землей. Сила тока в молнии огромна и колеблется обычно
от 10 до 1000 к А, а напряжение между облаком и землей пе-
перед возникновением молнии достигает 108 —109 В. Длительность
отдельного разряда молнии очень мала, порядка микросекунды.
Поэтому общий заряд, переносимый отдельной молнией, обычно
невелик @,1-10 Кл).
Очень часто молния представляет собой ряд искровых раз-
разрядов, следующих друг за другом по одному пути (кратные мол-
молнии). Число таких разрядов может достигать нескольких десят-
десятков, а общая длительность молнии — 1 с.
Особенно интересные результаты получаются при фотогра-
фотографировании молнии камерой с вращающимся объективом. По-
Подобные фотографии позволяют проследить за последователь-
последовательными стадиями развития молнии. Они показывают, что молнии
предшествует развитие слабо светящегося канала — лидера, рас-
распространяющегося обычно от облака к земле и аналогичного
стримеру (§ 172) в коротких лабораторных искрах. Когда ли-
лидер достигает земли, по пути, пробитому лидером, устремля-
устремляются большие заряды и развивается ярко светящийся главный
канал молнии, распространяющийся с огромной скоростью 107 —
—108 м/с от земли к облаку. При этом происходит сильное разо-
разогревание воздуха в главном канале и возникает ударная звуко-
звуковая волна — гром.
Хотя основные процессы в молнии, по-видимому, такие же,
как в коротких лабораторных искрах, особенности развития обо-
обоих типов разрядов все же несколько различны. Это видно, на-
например, из следующего любопытного факта. Как говорилось
выше (§ 172), искровой разряд (короткий) в воздухе при нор-
§ 175 ДУГОВОЙ РАЗРЯД 403
мальных условиях возникает при напряженности поля Ек «
и 3000 кВ/м. Многочисленные же измерения напряженности
поля в атмосфере показывают, что даже во время грозы она
значительно меньше и не превышает 200-400 кВ/м. Такое сни-
снижение пробойной напряженности поля наблюдается и в очень
длинных лабораторных искрах (длиной до 10 м). Оно объясня-
объясняется, по-видимому, тем, что в очень длинных разрядных проме-
промежутках могут возникать случайные большие местные усиления
электрического поля, в которых и зарождаются стримеры ис-
искрового разряда.
Кроме обычных молний, наблюдаются, хотя и редко, так на-
называемые шаровые молнии. Они имеют вид светящихся шаров
диаметром 10—20 см, которые либо медленно движутся, либо
прикрепляются к неподвижным предметам. Шаровые молнии
зарождаются обычно при ударе очень сильных молний и через
несколько секунд, а иногда и минут, исчезают с сильным взры-
взрывом. Сущность этого явления окончательно еще не понята.
§ 175. Дуговой разряд
Если после зажигания искрового разряда постепенно умень-
уменьшать сопротивление цепи, то сила тока в искре будет увели-
увеличиваться. Когда сопротивление цепи станет достаточно малым,
возникает новая форма газового разряда, называемая дуговым
разрядом. При этом сила тока резко увеличивается, достигая де-
десятков и сотен ампер, а напряжение на разрядном промежутке
уменьшается до нескольких десятков вольт. Это показывает, что
в разряде возникают новые процессы, сообщающие газу очень
большую проводимость.
Дуговой разряд можно получить, минуя стадию искры Профессор фи-
физики Петербургской медико-хирургической академии В В Петров, открыв-
открывший в 1802 г эту важную форму газового разряда, получил электрическую
дугу, раздвигая два кусочка древесного угля, предварительно приведенные
в соприкосновение и присоединенные к мощной батарее гальванических эле-
элементов Он обнаружил, что при этом между концами углей возникает ярко
светящийся столб газа, а сами угли раскаляются до ослепительного свечения
В настоящее время электрическую дугу, горящую при ат-
атмосферном давлении, чаще всего получают между специальны-
специальными угольными электродами, изготовленными прессованием по-
порошкообразного графита и связующих веществ (дуговые угли).
Фотография подобной дуги приведена на рис. 300. Наиболее го-
горячим местом дуги является углубление, образующееся на по-
положительном электроде и называемое кратером дуги. Его тем-
температура при атмосферном давлении равна около 4000 К, а при
давлении в 20 атм превышает 7000 К, т.е. больше температуры
внешней поверхности Солнца (примерно 6000 К).
404
РАЗРЯДЫ В ГАЗАХ
ГЛ XVI
Что же является основной причиной большой электропро-
электропроводности газа в дуговом разряде? Установлено, что хорошая
электропроводность дуги поддерживается за счет высокой тем-
температуры отрицательного электрода из-за интенсивной термо-
термоэлектронной эмиссии. Это хорошо подтверждается тем фактом,
что во многих случаях устойчивую дугу можно получить только
при условии, что катод имеет высокую температуру, температу-
температура же анода не имеет существенного значения. Так, например,
если одним из электродов
дуги сделать угольный стер-
стержень, а другим — массив-
массивную, хорошо охлаждающуюся
медную пластину и пере-
перемещать угольный стержень
возле пластины (чтобы она
не могла разогреться), то
устойчивая дуга возникает
только при отрицательном
угле. Если же отрицатель-
отрицательным полюсом служит пла-
пластина, то дуга периодически
зажигается и снова гаснет, а
получить ее устойчивое горе-
горение нельзя.
Дуговой разряд возника-
возникает во всех случаях, когда
вследствие разогревания ка-
катода основной причиной ио-
ионизации газа становится тер-
Рис 300 Фотография дугового разря-
моэлектронная эмиссия. Так,
например, в тлеющем раз-
да между угольными электродами при
атмосферном давлении
ряде положительные ионы,
бомбардирующие катод, не только вызывают вторичную эмис-
эмиссию электронов, но и нагревают катод Поэтому если увели-
увеличивать силу тока в тлеющем разряде, то температура катода
увеличивается, и когда она достигает такой величины, что на-
начинается заметная термоэлектронная эмиссия, тлеющий разряд
переходит в дуговой. При этом исчезает и катодное падение по-
потенциала. Дуговой разряд мы получим и в том случае, если вве-
введем в разреженный газ в качестве катода металлическую спи-
спираль, раскаливаемую током.
Наряду с рассмотренными выше термоэлектронными дуга-
дугами наблюдаются и дуговые разряды другого типа. Примером
может служить дуговой разряд в так называемой ртутной ду-
дуговой лампе, изображенной на рис. 301. Такая лампа предва-
предварительно откачивается и электрическая дуга в ней возникает в
175
ДУГОВОЙ РАЗРЯД
405
Hg
ртутном паре. Электродами же являются столбики жидкой рту-
ртути. Так как температура электродов в этом случае не превышает
немногих сотен градусов, то и термоэлектронная эмиссия здесь
не может играть заметной роли.
Отметим, что дуга, горящая в ртутном паре, является мощ-
мощным источником ультрафиолетовых лучей. Поэтому ртутные
лампы широко применяются в медицине
(«искусственное горное солнце») и в научных
исследованиях, а баллоны таких ламп дела-
делают из кварца или специальных сортов стек-
стекла, хорошо пропускающих ультрафиолетовое
излучение.
Многочисленные исследования электри-
электрических дуг с холодными электродами показы-
показывают, что источником мощной электронной
эмиссии с катода является небольшое, ярко
светящееся и непрерывно движущееся пят-
пятнышко на катоде, всегда возникающее в по-
подобных дугах (катодное пятно). Плотность
тока в катодном пятне огромна и может
достигать 1010 — 1011 А/и2. Причина образо-
образования катодного пятна заключается в силь-
сильном увеличении концентрации положитель-
положительных ионов у катода, которое создает очень
сильное местное электрическое поле, вызы-
вызывающее мощную автоэлектронную эмиссию
(§ 165). Поэтому электрические дуги с хо- дуговой лампы
лодными катодами иногда называются авто-
автоэлектронными дугами. Катодное пятно может возникнуть не
только у поверхности ртути, но и у любого металлического твер-
твердого электрода
Применения дугового разряда. Электрическая дуга яв-
является мощным источником света и широко применяется в про-
проекционных (кино), прожекторных и других установках. Расхо-
Расходуемая ею удельная мощность меньше, чем у ламп накаливания.
В качестве источников света употребляют также дуговые
лампы высокого давления Дуговой разряд в этих лампах проис-
происходит в парах ртути или же в инертном газе при высоком дав-
давлении (десятки атмосфер). Зажигание дуги производится раз-
разрядом от источника высокого напряжения с помощью третьего
электрода.
Вследствие высокой температуры дуги ее применяют для
сварки и резания металлов.
Высокую температуру дуги используют также при устрой-
устройстве дуговых электрических печей, играющих важную роль в
современной электрометаллургии
Hg
Рис 301 Схема
устройства ртутной
406
РАЗРЯДЫ В ГАЗАХ
ГЛ XVI
Автоэлектронные дуги с ртутным катодом применяют для
выпрямления переменного электрического тока. Схема устрой-
устройства ртутного выпрямителя и его включение показаны на
рис. 302. Он состоит
из большого стеклян-
стеклянного (а иногда ме-
металлического) сосуда,
заполненного ртут-
ртутным паром, и содер-
содержит ртутный катод
К и три анода А, А\
и Лг (число анодов
часто бывает боль-
больше). Аноды А\ и Лг
(«дежурные» аноды)
питаются от вспо-
вспомогательного транс-
трансформатора Т\ таким
образом, что один из
них в любой полу-
полупериод положителен
относительно като-
катода. Роль анодов А\ и
i О
*¦ о
Рис. 302. Схема ртутного выпрямителя
Ai заключается в непрерывном поддержании катодного пятна.
Анод А («главный» анод) и катод входят в цепь вторичной
обмотки силового трансформатора Т, содержащую также
сопротивление нагрузки R. Так как ток на главный анод А
существует только в те полупериоды, когда анод положителен
относительно катода, то в нагрузке R появляется пульсирую-
пульсирующий ток одинакового направления, соответствующий движению
электронов от катодного пятна к главному аноду.
Если напряжение между анодом и катодом сделается слиш-
слишком большим, то катодное пятно может возникнуть и на аноде
(«обратное зажигание» ртутных выпрямителей), нарушая пра-
правильную работу выпрямителя.
§ 176. Устойчивость электрических разрядов
Как уже говорилось выше, многие формы электрических
разрядов не подчиняются закону Ома и поэтому обладают нели-
нелинейной вольт-амперной характеристикой (электрические токи в
вакууме, разряды в газах и другие). Может даже оказаться, что
увеличение силы тока через проводник сопровождается умень-
уменьшением падения напряжения на нем, т.е. в этих случаях вольт-
амперная характеристика имеет падающий участок (рис. 303).
Такую характеристику имеет, например, участок цепи, содержа-
§ 176
УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ РАЗРЯДОВ
407
щий электрическую дугу и последовательное постоянное сопро-
сопротивление. Если по вертикальной оси откладывать не напряже-
напряжение, а ток, а по горизонтальной оси — напряжение (как это часто
делают), то кривая зависимости г от U будет подобна букве S,
и поэтому характеристики такого типа называют характеристи-
характеристиками S-типа.
Сопротивлением любого проводника мы называем отноше-
отношение напряжения между концами проводника к силе тока в нем:
U/i. Для проводников, подчиняющихся закону Ома, это отно-
отношение не зависит от силы тока (и напряжения), и поэтому их
вольт-амперная характеристика
прямолинейна. В случае нели-
нелинейной вольт-амперной характе-
характеристики мы можем рассматри-
рассматривать каждый малый ее участок
как отрезок прямой линии и
ввести дифференциальное сопро-
сопротивление в данной точке харак-
характеристики
Ri = dU/di.
Если характеристика имеет
падающий участок, то на этом
участке R% отрицательно.
Конечно, это не значит, что
в проводниках с отрицательным
дифференциальным сопротив-
сопротивлением не происходит выделе-
выделения (а имеется, наоборот, погло-
поглощение) тепла Джоуля-Ленца.
Тепловой эффект тока опре-
определяется не дифференциальным, а полным сопротивлением
проводника U/i, которое-всегда положительно.
Каждая точка вольт-амперной характеристики соответству-
соответствует определенному состоянию электрического разряда, а вся кри-
кривая изображает совокупность возможных состояний разряда в
данном проводнике. Однако если проводник имеет отрицатель-
отрицательное дифференциальное сопротивление, то может оказаться, что
не все эти состояния разряда можно получить в действительно-
действительности.
Рассмотрим простую цепь, содержащую проводник и источ-
источник тока с ЭДС & (рис. 304). Обозначим через г сопротивление
всей остальной части цепи, через i — ток в цепи и через U —
напряжение на проводнике. Тогда, согласно закону Ома, для
участка цепи с ЭДС (§68)
U = ?-ir. A76.1)
Рис 303. Вольт-амперная харак-
характеристика S-типа
408 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
С другой стороны, [/иг связаны уравнением характеристики
U = /(г), где / — функция, зависящая от свойств проводника.
Поэтому при данных & и г в проводнике окажутся возможными
только те состояния разряда, при которых [/иг одновременно
удовлетворяют обоим уравнениям.
Нахождение возможных состояний разряда удобно произ-
производить графически. Для этого на графике вольт-амперной ха-
характеристики проведем прямую, уравнение которой есть A76.1)
(«линия нагрузки»). Она отсекает на оси U отрезок, равный
ЭДС источника 8", и наклонена к оси г на угол а = arctgr. Тогда
возможные при этих условиях состоя-
R ния разряда будут определяться точ-
~l I i ками пересечения характеристики и
линии нагрузки.
Положим, что состояние разря-
разряда характеризуется точкой характери-
характеристики а (см. рис 303). Если теперь
увеличивать ЭДС источника, то линия
нагрузки будет перемещаться вверх,
Рис 304 К вопросу об оставаясь параллельной самой себе, и
устойчивости электриче- разряд будет плавно менять свое со-
ских разрядов стояние в соответствии с участком ха-
характеристики аб. Если после достиже-
достижения точки б увеличивать ЭДС еще больше, то разряд скачком
перейдет в новое состояние, описываемое точкой в. При этом на-
напряжение на проводнике уменьшится, а сила тока увеличится.
Если же мы захотим поддерживать то же напряжение, которое
было в точке б, то нам придется еще увеличить ЭДС источни-
источника. При этом будем передвигаться по ветви характеристики вг
вверх, и сила тока увеличится еще больше. Если исходить из пра-
правой ветви характеристики, например из точки г, и постепенно
уменьшать ЭДС источника, то мы пройдем все состояния раз-
разряда, изображаемые ветвью гее. При этом будут существовать
и состояния, соответствующие отрезку ее, которые нельзя было
получить при увеличении ЭДС При достижении точки е про-
произойдет опять скачкообразное изменение разряда, и он перейдет
в новое устойчивое состояние а. При этом сила тока скачкооб-
скачкообразно уменьшится, а напряжение возрастет. Если же мы захо-
захотим сохранить напряжение таким, каким оно было в точке е, то
мы должны будем уменьшить ЭДС источника. Таким образом,
наблюдаемая на опыте зависимость г от U не будет воспроизво-
воспроизводить истинную вольт-амперную характеристику, а будет иметь
вид петлеобразной кривой, показанной в верхнем правом углу
рис. 303 (гистерезис разряда). При некотором значении напря-
напряжения, разном при прямом и обратном ходе, сила тока будет
делаться неустойчивой и скачком изменять свою величину.
§ 176
УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ РАЗРЯДОВ
409
Из сказанного ясно, что для устойчивости тока нужно, что-
чтобы линия нагрузки при любом значении ЭДС пересекла вольт-
амперную характеристику только один раз, а это значит, что
она должна идти более круто, чем характеристика (штриховая
линия на рис. 303). Или, иначе, внешнее сопротивление г долж-
должно быть больше модуля дифференциального сопротивления R%
в любой точке характеристики:
г > |Д,| (S-тип). A76.2)
Наряду с характеристиками S-типа существуют и характе-
характеристики другого типа, показанного на рис 305 (характеристики
N-типа). Примером провод-
проводника с характеристикой N-
типа может служить тун-
туннельный полупроводниковый
диод (§ 203). Она может так-
также возникнуть в вакуумных
лампах вследствие динатрон-
ного эффекта (§ 164).
Если проводник имеет
вольт-амперную характерис-
характеристику N-типа, то при посте-
постепенном увеличении ЭДС
мы сначала будем двигаться
по участку характеристики
аб (рис. 305). В точке б
произойдет скачкообразное
изменение разряда. Однако
в данном случае увеличится
не ток, а напряжение, а сила
тока станет меньше. Для
поддержания тока неизмен-
неизменным необходимо сместиться вдоль ветви характеристики вг,
отчего скачок напряжения сделается еще больше. При обратном
уменьшении тока мы сумеем дойти до состояния разряда е, по-
после чего опять произойдет скачок, и т.д. Поэтому наблюдаемая
на опыте зависимость U от г может иметь вид, показанный в
правом верхнем углу рис. 305. Отличие от предыдущего случая
S-характеристики заключается в том, что здесь неустойчивым
может оказаться напряжение, а не ток. Для устойчивости
разряда необходимо, чтобы линия нагрузки проходила бо-
более полого, чем вольт-амперная характеристика, т.е. чтобы
выполнялось условие
г<|Дг| (N-тип). A76.3)
Из сказанного также ясно, что если вольт-амперная харак-
характеристика не имеет падающего участка (т.е. Rt всюду положи-
Рис 305 Вольт-амперная характери-
характеристика iV-типа
410 РАЗРЯДЫ В ГАЗАХ ГЛ XVI
тельно), то линия нагрузки при любом значении г пересекает
характеристику только один раз, и поэтому разряд в таком про-
проводнике будет всегда устойчив.
В предыдущих рассуждениях мы не учитывали емкость и
индуктивность цепи. Поэтому формулы A76.2) и A76.3) выра-
выражают условие устойчивости для постоянного тока. Оно необ-
необходимо, но может оказаться недостаточным. Чтобы разряд в
данном состоянии был устойчивым, нужно еще, чтобы при слу-
случайных малых изменениях тока и напряжения в цепи возникали
такие процессы, которые препятствовали бы этим изменениям,
для чего необходимо выполнение дополнительных условий, рас-
рассмотренных в Добавлении 9 (его следует читать после гл. XX).
§ 177. Плазма
В различных формах газового разряда иногда образуется
сильно ионизованный газ, в котором концентрация электро-
электронов приблизительно равна концентрации положительных ио-
ионов. Такая система из электронов и положительных ионов, рас-
распределенных с одинаковой концентрацией, получила название
электронно-ионной плазмы или просто плазмы.
Плазму мы имеем в положительном столбе тлеющего разря-
разряда. Она образуется также в главном канале искрового разряда.
Так как концентрация электронов и ионов в плазме одинако-
одинакова, то объемный заряд в ней, как и в металлах, равен нулю. Кро-
Кроме того, при значительной ионизации газа электропроводность
плазмы может быть очень большой. Поэтому по характеру своей
электропроводности ионная плазма приближается к металлам
Если плазма находится в электрическом поле, то в ней возни-
возникает электрический ток и выделяется тепло. При этом энергию
в поле получают сначала электроны как более подвижные ча-
частицы, которые затем передают энергию ионам при соударени-
соударениях. Однако при соударениях, вследствие большой разницы масс
обеих частиц, электрон передает иону не всю энергию, а только
ее часть. При низких давлениях, когда число соударений отно-
относительно мало, это приводит к тому, что средняя кинетическая
энергия электронов оказывается больше средней кинетической
энергии ионов. Или, иными словами, температура электронного
газа в плазме выше температуры ионного газа (неизотерми-
(неизотермическая плазма). Эти температуры можно измерить косвен-
косвенными методами, причем оказывается, что, например, в поло-
положительном столбе тлеющего разряда при давлениях порядка
0,1 мм рт ст. температура электронов может достигать 105 К и
выше, в то время как температура ионов не превышает несколь-
нескольких сотен градусов.
§ 177 ПЛАЗМА 411
При повышении давления увеличивается число соударений
и улучшается теплообмен между электронным и ионным газа-
газами, отчего разность между их температурами уменьшается. При
достаточно высоком давлении электроны и ионы имеют одина-
одинаковую температуру (изотермическая плазма). Изотермическую
плазму мы имеем всегда при ионизации с помощью высокой тем-
температуры, например, в искровом канале.
В лабораторных условиях плазма получается не только в га-
газовых разрядах. В электропроводящих твердых телах (металлы,
полупроводники) мы имеем подвижные электроны проводимо-
проводимости и неподвижные положительные ионы с общим объемным
зарядом, равным нулю, т.е. тоже электронно-ионную плазму.
Однако наиболее часто плазма встречается в космических те-
телах. Основная масса вещества космоса практически полностью
ионизирована вследствие высокой температуры и действия раз-
различных излучений и находится в состоянии сильно ионизован-
ионизованной плазмы. В частности, Солнце полностью состоит из плазмы.
Верхние ионизованные слои атмосферы Земли (ионосфера) то-
тоже представляют собой плазму.
Плазма как сильно ионизованный газ имеет некоторое сход-
сходство с обычными газами и подчиняется многим газовым зако-
законам. Однако между плазмой и обычными газами имеются и
радикальные отличия. Они особенно резко проявляются тогда,
когда имеется магнитное поле. В этом случае на частицы плаз-
плазмы (ионы и электроны) действуют большие силы (силы Лорен-
Лоренца), не существующие в газе нейтральных атомов. При движе-
движении частиц вдоль магнитного поля эти силы равны нулю. При
движении же поперек магнитного поля они максимальны и пре-
препятствуют этому движению. Второе отличие заключается в том,
что ионы и электроны в плазме сильно взаимодействуют меж-
между собой с помощью кулоновских сил. Оба обстоятельства в со-
сочетании с большой электропроводностью сильно ионизованной
плазмы приводят к тому, что свойства плазмы и уравнения ее
движения при наличии электрических и магнитных полей ока-
оказываются резко отличающимися от таковых для обычных газов
и жидкостей. Изучение законов движения плазмы, рассматри-
рассматриваемой как особого рода жидкость с большой электропроводно-
электропроводностью, составляет предмет магнитной гидродинамики плазмы и
имеет большое значение для понимания многих астрофизиче-
астрофизических процессов.
Исследование свойств плазмы имеет исключительное прак-
практическое значение, так как с помощью использования плаз-
плазмы открывается принципиальная возможность осуществления
управляемых термоядерных реакций.
412
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ XVII
ГЛАВА XVII
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В
ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ
Явления электронной эмиссии (гл. XV) и газовых разрядов
(гл. XVI) позволяют получить потоки электронов и ионов, дви-
движущихся в вакууме практически без соударений. Попадая в
электрические и магнитные поля, эти частицы оказываются под
действием определенных сил и изменяют свое первоначальное
движение.
Изучая движение различных заряженных частиц в электри-
электрических и магнитных полях, оказывается возможным определить
отношение их заряда к массе е/т и отсюда получить ценные све-
сведения о природе этих частиц и о тех процессах, в которых они
возникают. Воздействуя на потоки электронов и ионов электри-
электрическими и магнитными полями, можно управлять этими потока-
потоками, т.е. изменять их силу и направление движения; это лежит в
основе действия различных важных электронных приборов (ос-
(осциллографов, электронных микроскопов, ускорителей заряжен-
заряженных частиц, телевизионных трубок и др ).
§ 178. Движение заряженных частиц в однородном
электрическом поле
Если частица, обладающая зарядом q, движется в простран-
пространстве, где имеется электрическое поле с напряженностью Е, и
магнитное поле с индукцией В, то на нее действует сила Лорен-
Лоренца (§ 88) Поэтому, согласно второму закону Ньютона, уравнение
движения частицы имеет
вид
т — = qE+ <jr[vB]. A78.1)
Написанное векторное
уравнение распадается на
три скалярных, каждое
из которых описывает
движение вдоль соответ-
соответствующей координатной
оси.
Рис 306 Движение заряженной частицы В Дальнейшем мы бу-
в однородном электрическом поле Дем интересоваться толь-
только некоторыми частными
случаями движения. Предположим, что заряженные частицы,
двигавшиеся первоначально вдоль оси X (рис. 306) со скоро-
§ 179 ЗАРЯЖЕННЫЕ ЧАСТИЦЫ В МАГНИТНОМ ПОЛЕ 413
стью vq, попадают в электрическое поле плоского конденсатора.
Если зазор между пластинами мал по сравнению с их длиной /,
то краевыми эффектами можно пренебречь и считать электри-
электрическое поле между пластинами однородным. Направляя ось Y
параллельно полю, мы имеем: Ех = Ez = О, Еу = Е. Так как
магнитного поля нет, то Вх = Ву = Bz = 0.
В рассматриваемом случае на заряженные частицы действу-
действует только сила со стороны электрического поля, которая при
выбранном направлении координатных осей целиком направле-
направлена по оси Y. Поэтому траектория движения частиц лежит в
плоскости XY и уравнения движения принимают вид
*ь = 0, ** = i-Я. A78.2)
dt dt m v
Движение частиц в этом случае происходит под действием по-
постоянной силы и подобно движению горизонтально брошенного
тела в поле тяжести. Поэтому ясно без дальнейших расчетов,
что частицы будут двигаться по параболам.
Вычислим угол в (рис. 306), на который отклонится пучок
частиц после прохождения через конденсатор. Интегрируя пер-
первое из уравнений A78.2), находим
vx = dx/dt = const = vq. A78.3)
Интегрирование второго уравнения дает
vy = {q/m)Et + С,
где t = l/vo есть время нахождения частицы в электрическом
поле, а, С — постоянная интегрирования. Так как при t = 0
(момент вступления частицы в конденсатор) vy = 0, то С = 0, и
vy = % = ^-E1-. A78.4)
у dt m ад
Отсюда получаем для угла отклонения в
t Я = ? = ?Z* i. №. A78.5)
dx dx/dt m Vq
Отклонение пучка существенно зависит от удельного заряда
частиц qjm.
§ 179. Движение заряженных частиц в однородном
магнитном поле
Рассмотрим теперь другой частный случай, когда нет
электрического поля, но имеется магнитное поле. Предположим,
что частица, обладающая начальной скоростью vo, попадает в
магнитное поле с индукцией В. Это поле мы будем считать
однородным и направленным перпендикулярно к скорости vo
(рис. 307).
414
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
Основные особенности движения в этом случае можно вы-
выяснить, не прибегая к полному решению уравнений движения.
Прежде всего отметим, что действующая
на частицу сила всегда перпендикулярна
к скорости движения частицы. Это зна-
значит, что работа силы всегда равна ну-
нулю; следовательно, абсолютное значение
скорости движения частицы, а значит, и
энергия частицы остаются постоянными
при движении. Так как скорость частицы
v не изменяется, то модуль силы
Рис. 307. Движение за-
заряженной частицы в
однородном магнитном
поле
остается постоянным. Эта сила, будучи
перпендикулярной к направлению движе-
движения, является центростремительной си-
силой. Но движение под действием посто-
постоянной по модулю центростремительной
силы есть движение по окружности. Радиус г этой окружности
определяется условием
mv
откуда
(q/m)
A79Л)
Если энергия электрона выражена в электронвольтах и равна
U, то
\™2 = Ф, v=B±u)ll\
и поэтому
г = [ -L-) У—. A79.1а)
q/mj В v '
Так, например, если электрон с энергией 100 эВ движется в магнитном
поле с индукцией 0,01 Тл, то он описывает окружность с радиусом около
3,4 • 10~3 м = 3,4 мм. Если бы вместо электрона с той же энергией и в том
же поле двигался ион атомного водорода, масса которого М = 1837т, то
радиус соответствующей окружности был бы в \jMjm раз больше, т.е. был
бы равен 3,4\/1837 = 147 мм.
Кругообразное движение заряженных частиц в магнитном
поле обладает важной особенностью: период обращения не за-
зависит от энергии частицы. Действительно, период обращения
равен
Г = 2nr/v.
§ 179
ЗАРЯЖЕННЫЕ ЧАСТИЦЫ В МАГНИТНОМ ПОЛЕ
415
Подставляя сюда вместо г его выражение A79.1), имеем
A79-2)
(я/т) В
Частота же (число оборотов за 2тг с) оказывается равной
шс = 2тг/Г = (q/m)B A79.2а)
и называется циклотронной частотой1).
Для данного типа частиц и период, и частота зависят только
от индукции магнитного поля.
Выше мы предполагали, что направление начальной скоро-
скорости перпендикулярно к направлению магнитного поля. Нетруд-
Нетрудно сообразить, какой характер будет иметь движение, если на-
начальная скорость частицы
составляет некоторый угол
а с направлением поля
(рис. 308). В этом случае
удобно разложить скорость
vo на две составляющие,
одна из которых vt = vo cos a
параллельна полю, а другая
vn = Щ sin а перпендику-
перпендикулярна к полю. На частицу
действует сила Лоренца,
Рис. 308. Движение частицы по ци-
цилиндрической спирали (начальная ско-
скорость заряженной частицы направлена
под углом к магнитному полю)
обусловленная составляю-
составляющей vn, и частица движется
по окружности, лежащей
в плоскости, перпендику-
перпендикулярной к полю. Составляющая Vt не вызывает появления
добавочной силы, так как сила Лоренца при движении парал-
параллельно полю равна нулю. Поэтому в направлении поля частица
движется по инерции, равномерно, со скоростью vt = vq cos а. В
результате сложения обоих движений частица будет двигаться
по цилиндрической спирали, изображенной на рис. 308. Шаг
винта этой спирали равен
A79.3)
/ = vtT = vqT cos a.
Подставляя вместо Т его выражение A79.2), имеем
л _ 27ruocosa 1
7 "" (q/m) T
х) Циклотронной (или гиромагнитной) называется частота обращения за-
заряженных частиц в постоянном магнитном поле в плоскости, перпендику-
перпендикулярной к полю. {Примеч. ред.)
416
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ XVII
§ 180. Циклотрон
Независимость частоты обращения в магнитном поле (§ 179)
от энергии частиц используют для устройства ускорителя за-
заряженных частиц — циклотрона. Он предназначен для ускоре-
ускорения тяжелых частиц (ионов) без применения высокого напря-
напряжения.
Принцип действия циклотрона схематически изображен на
рис. 309. Ускорение ионов происходит между двумя полукруг-
полукруглыми полыми металлическими электродами Д, имеющими вид
коробок и называе-
называемыми дуантами. К
дуантам приложено
переменное напря-
напряжение в несколько
десятков киловольт,
создаваемое мощным
ламповым генерато-
генератором. Поэтому в ще-
щели между дуантами
возникает электри-
электрическое поле, уско-
ускоряющее ионы. Сами
ионы получаются в
газовом разряде низ-
низкого давления в спе-
специальном источнике ионов И и вводятся в центре щели между
дуантами. Дуанты находятся внутри вакуумной камеры, кото-
которая помещается между полюсами большого электромагнита.
В циклотроне происходит ступенчатое ускорение ионов.
Каждый ион, попавший в щель между дуантами, ускоряет-
ускоряется электрическим полем и вступает внутрь одного из дуантов.
Здесь под действием магнитного поля он описывает полуокруж-
полуокружность и через время, равное половине времени обращения, вновь
попадает в щель между дуантами. Если частота генератора ш
равна циклотронной частоте и>с (§ 179), то к этому времени элек-
электрическое поле изменит направление на обратное и ион полу-
получит повторное ускорение и во втором дуанте будет двигаться по
окружности большего радиуса. Так как время обращения иона
по окружности не зависит от его энергии, то при следующем
прохождении щели фаза напряжения опять изменится на тг и
опять произойдет ускорение иона, и т.д. Поэтому ион будет дви-
двигаться по раскручивающейся спирали, непрерывно увеличивая
свою энергию. В периферической части магнитного поля либо
помещают мишень, подлежащую бомбардировке, либо отклоня-
отклоняют пучок с помощью дополнительного электрода, имеющего от-
Рис. 309. Принцип действия циклотрона. Маг-
Магнитное поле перпендикулярно к плоскости чер-
чертежа
§ 180 ЦИКЛОТРОН 4Г7
рицательный потенциал, и выпускают пучок из камеры через
специальное окошко, закрытое тонкой металлической фольгой.
Из сказанного ясно, что условие ускорения ионов в цикло-
циклотроне есть
и = ис=1.В. A80.1)
т
Если амплитуда переменного напряжения (выраженная в воль-
вольтах) между дуантами равна U$, а число прохождений ионов че-
через щель равно п, то максимальная энергия, приобретаемая ио-
ионами, есть hUq (выраженная в электронвольтах).
Максимальная энергия частиц зависит от магнитной индук-
индукции В и максимально возможного радиуса орбиты, т.е. от ра-
радиуса магнита R. Полагая в формуле A79.1) г = R, находим,
что максимальная энергия ионов, которую можно получить в
далном циклотроне, равна
ь'макс — 2^-П л ¦
Так, например, если ускоряются ионы водорода, то qjm =
= 0,96 • 108 Кл/кг. Для типичного циклотрона средних размеров
можно принять В^\ Тл, Д^0,5 м. Это дает [/макс = 12-106эВ =
= 12 МэВ.
Такой циклотрон представляет собой большую и сложную установку.
Масса его магнита равна сотням тонн. Общая мощность питания (высо-
(высокочастотного генератора, магнита и вакуумных насосов) составляет сотни
киловатт. Сила тока в пучке ускоренных ионов имеет порядок миллиампер.
Отметим еще, что при практическом осуществлении ускорения необхо-
необходимо обеспечить хорошую фокусировку пучка ионов, т.е. удержание пучка
вблизи центральной плоскости дуантов и предотвращение его попадания
на крышки дуантов. Это достигается главным образом тем, что магнитное
поле магнита делают слабо неоднородным, уменьшающимся от центра маг-
магнита к его периферии. Возникающая при этом радиальная составляющая
магнитной индукции вызывает появление дополнительных сил Лоренца (по
сравнению с однородным полем), отклоняющих расходящийся пучок ионов
обратно к центральной плоскости
Однако, увеличивая радиус магнита, нельзя увеличить
неограниченно максимальную энергию ионов. Предел ускоре-
ускорению кладет зависимость массы частиц от их скорости (ср. § 183).
При достаточном увеличении энергии ионов их масса увеличи-
увеличивается и циклотронная частота и>с уменьшается. Поэтому усло-
условие резонанса A80.1) нарушается и ускорение в конце концов
прекращается.
Отношение массы движущейся частицы к ее массе покоя
m/rno зависит от отношения v/c — скорости частицы, выражен-
выраженной в долях скорости света в вакууме (ср. § 183). С другой сто-
стороны, при данной энергии частиц их скорости обратно пропор-
пропорциональны фп. Вследствие этого эффект изменения массы для
418
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ XVII
легких частиц (электронов) проявляется при значительно мень-
меньших энергиях, нежели для тяжелых частиц (ионов), и поэтому
циклотроны практически непригодны для ускорения электро-
электронов.
§ 181. Определение удельного заряда электронов
методом магнитной фокусировки
В § 178, 179 мы видели, что отклонение, испытываемое заря-
заряженными частицами в электрическом и магнитном полях, суще-
существенно зависит от удельного заряда частиц. Поэтому, измеряя
это отклонение, можно определить удельный заряд частиц q/m.
В зависимости от того, известна или неизвестна скорость ча-
частиц, приходится поступать по-разному. Если скорость частиц
известна или может быть определенным образом задана в экс-
эксперименте, то достаточно измерить лишь одно из отклонений —
либо в магнитном, либо в электрическом поле. Если же неизвест-
неизвестны и удельный заряд частиц q/m, и их скорость v, то требуется
измерение и электрического,
и магнитного отклонений, так
как для определения двух неиз-
неизвестных необходимы два соот-
соотношения.
Примером методов первой
группы может служить метод
магнитной фокусировки для
определения удельного заряда
термоэлектронов. Схема опы-
опыта показана на рис. 310. Элек-
Электроны вылетают из накален-
накаленной проволоки К и ускоряются
электрическим полем, создан-
созданным между проволокой и диа-
диафрагмой D\. Диафрагма ?>2
имеет кольцевую щель, при-
причем центр соответствующей ей
окружности лежит на оси пучка. Эта диафрагма пропускает
только те электроны, которые движутся по образующим конуса
с углом раскрытия 2а. За диафрагмой D\ электроны движутся
в пространстве, свободном от электрического поля, и попадают
на люминесцирующий экран Э. Все указанные части заключе-
заключены внутрь цилиндрической стеклянной трубки, из которой тща-
тщательно выкачан воздух. На трубку надевается снаружи длинная
катушка (соленоид), создающая внутри трубки однородное маг-
магнитное поле с известной индукцией В, направленное параллель-
параллельно оси электронного пучка.
Рис. 310 Определение е/т для тер-
термоэлектронов методом магнитной
фокусировки
§ 182 МАГНЕТРОН 419
В § 179 мы видели, что в этом случае электроны движут-
движутся по цилиндрическим спиралям. Поэтому все электроны, вы-
вышедшие из диафрагмы D\ под одним и тем же углом а, вновь
пересекут ось пучка на расстояниях /, 2/ и т.д., где / — шаг
винта спирали. В этих точках сечение пучка будет наименьшим,
т.е. в них электронный пучок будет фокусироваться. Следова-
Следовательно, если изменять магнитное поле или скорость электронов,
то первоначально размытое изображение пучка на экране будет
периодически стягиваться в ярко светящееся пятнышко. Бели
расстояние / между D\ и экраном Э равно /, то пучок будет
таким, как показано на рис. 310 а. При I = 2/ пучок имеет вид,
изображенный на рис. 310 б, и т.д.
Условие фокусировки пучка на экране есть
l = nf,
где п = 1,2,3,... Подставляя вместо / выражение A79.3), имеем
, 2?rt;ocosa
/ = 7^Р~
Но скорость электронов vq определяется напряжением U, при-
приложенным между катодом К и диафрагмой D\, так как
mvl/2 = eU.
Выражая отсюда vq и подставляя ее в формулу A81.1), находим
окончательно
/ о 2 2 г г C°S2 a
Поэтому, измеряя значения U и В, при которых происходит фо-
фокусировка пучка на экране, можно определить е/т.
§ 182. Магнетрон
Важный случай движения электронов мы имеем при нали-
наличии двух полей — магнитного и электрического, перпендикуляр-
перпендикулярных друг к другу. Это осуществляется в специальных вакуум-
вакуумных трубках — магнетронах, которые можно использовать для
определения удельного заряда электронов.
Магнетрон представляет собой аналог двухэлектродной лам-
лампы (диода), содержащий накаливаемый катод и холодный анод и
помещаемый во внешнее магнитное поле. Это поле создается ли-
либо катушками с током, либо электромагнитом, между полюсами
которого помещается магнетрон.
Рассмотрим сначала плоский магнетрон, катод и анод ко-
которого ограничены плоскостями, параллельными между собой
(рис. 311). В этом случае в центральной части магнетрона элек-
электрическое поле Е однородно. Магнитное поле В, которое мы бу-
будем считать также однородным, направлено перпендикулярно к
электрическому.
420
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ XVII
Если бы магнитного поля не было, то электроны, вылетаю-
вылетающие из катода практически без начальной скорости, двигались
бы в электрическом поле вдоль прямых линий, перпендикуляр-
перпендикулярных к катоду, и все попадали бы на анод. При наличии маг-
магнитного поля траектории электронов искривляются силой Ло-
Лоренца и имеют вид циклоиды, описываемой точкой, лежащей
на окружности круга, равномерно катящегося вдоль катода в
направлении, перпендикулярном к Е и В. Если магнитное по-
поле достаточно велико, то траектории электронов не пересекают
плоскости анода и имеют вид, изображенный на рис. 311. В этом
случае ни один электрон не достигает анода.
Рис. 311. Движение электрона, вылетающего с катода с нулевой начальной
скоростью, в плоском магнетроне
В магнетроне траектории электронов уже не являются
окружностями, как в случае отсутствия электрического поля
(§ 179), а изображаются линиями с меняющейся кривизной. Это
происходит потому, что электрон при своем движении попадает
на различные эквипотенциальные поверхности электрического
поля, и поэтому модуль его скорости изменяется. Вследствие
этого изменяется модуль силы Лоренца, а следовательно, и вы-
вызываемое ею искривление траектории.
Из сказанного ясно, что для каждого данного напряжения U
между катодом и анодом существует некоторое критическое зна-
значение магнитной индукции Вк, при котором траектории элек-
электронов как раз касаются поверхности анода. Если В < Вк, то
все электроны доходят до анода и ток через магнетрон имеет то
же значение, что и без магнитного поля. Если же В > Вк, то ни
один электрон не достигает анода и ток через лампу равен ну-
нулю. Расчет показывает, что это критическое значение индукции
выражается формулой
A82.1)
jj
где d — расстояние между катодом и анодом. Поэтому, измеряя
§ 182
МАГНЕТРОН
421
на опыте f?K, начиная с которого запирается ток в магнетроне,
можно определить удельный заряд электронов е/т.
Легко показать, что траектория электрона в плоском магнетроне есть
циклоида (рис 311), Действительно, для нашего случая уравнения движе-
движения электрона принимают вид
dvx dvy moo on
m-dt=eVvB> m^f=eE-evxB. A82.2)
Если электрон вылетел в начале координат (расположенном в плоскости
катода) с нулевой начальной скоростью, то в качестве начальных условий
задачи имеем
t = 0; х = у = 0; vx = vy ~ 0.
A82 3)
Нетрудно убедиться непосредственной подстановкой, что решение уравне-
уравнений движения, удовлетворяющее этим начальным условиям, есть
х = vt - psinwj, у = р{\ -cosu>ct), A82.4)
что и представляет уравнение циклоиды в параметрической форме. Здесь
wc — циклотронная частота, определяемая формулой A79.2а), a v и р равны
соответственно
v = Е/В,
Анод
р = v/шс
A82.5)
При В = Вк циклоида каса-
касается анода, а следовательно,
2р = d. A82.6)
Подставляя для р и v их зна-
значения A82.5), учитывая вы-
выражение A79.2а) для шс и за-
заменяя Е на U/d, получаем
для Вк соотношение A82.1),
приведенное выше.
На практике приме-
применяют цилиндрические
магнетроны. Их анод
представляет собой ме-
металлический цилиндр,
а катод имеет также
цилиндрическую форму
и расположен на оси
анода. Пути электронов
в цилиндрическом магнетроне имеют более сложную форму;
они изображены на рис. 312. Соответствующий расчет по-
показывает, что критическое значение магнитной индукции в
цилиндрическом магнетроне определяется выражением
где а — радиус катода, Ъ — радиус анода. Отметим так же, что
- значение Вк не изменяется под действием пространственного за-
Рис. 312 Пути электронов в цилиндричес-
цилиндрическом магнетроне
422
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ XVII
ряда и имеет одно и то же значение как в режиме тока насыще-
насыщения, так и в режиме пространственного заряда.
Подобные измерения приводят к тем же значениям е/т для
термоэлектронов, что и найденные по методу магнитной фоку-
фокусировки (§ 181), а также другими способами.
Отметим, что магнетроны представляют интерес не толь-
только для определения удельного заряда электронов. Магнетроны
(правда, несколько измененного устройства) используют для ге-
генерации мощных электрических колебаний высокой частоты, и
поэтому они играют выдающуюся роль в современной радиотех-
радиотехнике сверхвысоких частот.
§ 183. Определение удельного заряда /3-частиц
Многие вещества, называемые радиоактивными, самопроиз-
самопроизвольно испускают из недр своих атомов (атомных ядер) различ-
различные излучения. Еще в конце XIX в. было установлено, что среди
радиоактивных излучений имеются так называемые @-частицы,
представляющие собой поток
отрицательно заряженных ча-
частиц, движущихся с большой
скоростью. Изучение отклоне-
отклонения /3-частиц в электрических
и магнитных нолях позволило
окончательно установить их
природу.
Схема одного из таких
опытов показана на рис. 313:
/3-частицы, испускаемые ра-
радиоактивным препаратом РП,
движутся в вакууме в уз-
узком зазоре между пластинами
плоского конденсатора и попа-
попадают на фотографическую пластинку Ф. Весь прибор помещает-
помещается в сильное магнитное поле, перпендикулярное к направлению
электрического поля и к направлению движения частиц.
Частицы, движущиеся между пластинами конденсатора, на-
находятся под действием электрического и магнитного полей. Си-
Сила, действующая на частицу в электрическом поле конденсато-
конденсатора, есть еЕ, а сила, вызываемая магнитным полем, равна —evB.
Чтобы частица могла пройти через конденсатор, она не должна
отклоняться, а значит, полная сила, действующая на частицу,
должна равняться нулю. Отсюда находим
v = Е/В. A83.1)
Рис. 313. Определение удельного за-
заряда /3-частиц
§ 183
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА /3-ЧАСТИЦ
423
Частицы же, имеющие другие скорости, попадают на пласти-
пластины и выбывают из пучка, так что за конденсатором получается
пучок /9-частиц с одинаковой скоростью. За пределами конден-
конденсатора на пучок действует только магнитное поле, и пучок из-
изгибается по окружности. Радиус этой окружности определяется
формулой A79.1) или, если выразить v через Е и В,
Если изменить направления обоих полей Е и Н на противо-
противоположные, то пучок будет искривлен в другую сторону.
Радиус окружности г можно определить, измеряя смещение
пучка z\ на фотопластинке и зная расстояние х\ от края конден-
конденсатора до пластинки. Действительно, пусть начало координат-
координатных осей X, Z находится в точке О (рис 313). Тогда уравнение
круговой траектории частиц есть
{z-rf + х2 -г'1.
Полагая х = х\, z = z\ и выражая из этой формулы г, имеем
r = (x{ + zl)/2z1. A83.3)
Таким образом, зная Е и В, а также расстояние х\ до фотопла-
фотопластинки и измеряя отклонение пучка z\, можно найти е/т.
Применяя в качестве источника /3-частиц различные ра-
радиоактивные препараты, можно получать разные скорости /3-
частиц. Эти скорости очень велики (близки к скорости света).
Оказалось, что значения е/т для /3-частиц, обладающих раз-
разными скоростями, не одинаковы и тем меньше, чем больше ско-
скорость частиц (табл. 14).
Таблица 14
v/c
0,3173
0,3787
0,4281
е/т,
10" Кл/кг
1,661
1,630
1,590
е/то,
10" Кл/кг
1,752
1,761
1,760
v/c
0,5154
0,6870
е/т,
1011 Кл/кг
1,511
1,283
е/то,
1011 Кл/кг
1,763
1,767
В настоящее время нет никаких оснований считать, что за-
заряд частицы может зависеть от скорости ее движения. С другой
стороны, согласно теории относительности, масса всякого дви-
движущегося тела должна зависеть от скорости тела, причем эта
зависимость выражается формулой
т = , то . A83.4)
/1 2/с2
Здесь т — масса, определяемая наблюдателем, относитель-
относительно которого тело имеет скорость щ, то — масса покоя, т.е. масса
424 ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ ГЛ XVII
того же тела, покоящегося относительно наблюдателя Поэтому
с точки зрения теории относительности для разных /9-частиц,
движущихся с разными скоростями, постоянной должна оста-
оставаться не измеренная величина е/т, а величина е/то, т.е. удель-
удельный заряд для покоящихся частиц, равный
_?_ = е/т A83.5)
Результаты опытов хорошо подтвердили это заключение. В вы-
вышеприведенной таблице даны значения е/то, полученные по
формуле A83.5) из измеренных значений е/т. Как видно из та-
таблицы, отношение е/то действительно остается постоянным и
не зависит от скорости частиц Поэтому описанные опыты явля-
являются одним из прямых экспериментальных подтверждений вы-
вывода теории относительности о зависимости массы от скорости.
К этому вопросу мы вернемся еще в гл. XXIII.
Значение е/то Для $-частиц показало, что они представляют
собой поток электронов, движущихся со скоростями, близкими
к скорости света.
§ 184. Результаты измерений удельного заряда
электронов
Помимо методов, рассмотренных выше, имеются и другие
способы определения удельного заряда электронов Однако мы
ограничимся приведенными примерами и остановимся на основ-
основных результатах.
Прежде всего отметим, что опыты по измерению е/т за-
заряженных частиц привели к открытию самого существования
электронов. А именно, Дж.Дж. Томсон в 1897 г., исследуя от-
отклонение в электрических и магнитных полях отрицательно за-
заряженных частиц, исходящих из катода в тлеющем разряде (ка-
(катодных лучей), получил впервые совершенно неожиданные в то
время результаты. Оказалось, что отношение е/т в катодных
лучах вовсе не зависит от природы газа в разрядной трубке.
Оно не зависит также от материала катода и давления газа. Но
самое удивительное заключалось в том, что значение е/т для
частиц катодных лучей оказалось намного больше, нежели это
отношение для самого легкого иона водорода, которое было най-
найдено из опытов с электролизом.
Результаты Томсона показали, что частицы в катодных лу-
лучах (природа которых в то время была еще неизвестна) не мо-
могут быть заряженными атомами газа или материала электродов
и впервые привели к заключению, что эти частицы являются
элементарными заряженными частицами, общими для всех ве-
веществ, свободно существующими в катодных лучах независимо
§ 185 ЦИКЛОТРОННЫЙ (ДИАМАГНИТНЫЙ) РЕЗОНАНС 425
от атомов и обладающими гораздо меньшей массой, нежели ато-
атомы.
Дальнейшие опыты по измерению отношения е/т подтвер-
подтвердили этот вывод. Они установили, что такое же значение е/т,
как и для частиц катодных лучей, имеют /9-частицы, отрица-
отрицательные частицы, возникающие при термоэлектронной эмиссии,
фотоэлектрическом эффекте, автоэлектронной эмиссии, а так-
также те частицы, которые обусловливают электрический ток в ме-
металлах. Это показало, что все электроны тождественны между
собой и что они являются составной частью атомов всех веществ.
Удельный заряд электронов можно определить не только из
электрических измерений, но и из оптических Совокупность
всех результатов по определению е/т для электронов приводит
к следующему значению:
е/т0 = 1,759 • 1011 Кл/кг.
Так как заряд электрона е известен из независимых измере-
измерений (§ 144), то отсюда можно найти массу электрона:
то = 9,109 ¦ 1(Г31 кг,
что составляет 1/1836 массы протона. Приведенное значение
есть масса покоящегося электрона.
Укажем в заключение, что по отклонению в электрических и
магнитных полях можно найти удельный заряд не только элек-
электронов, но и ионов. Зная же удельный заряд ионов, можно най-
найти и массу атомов исследуемого вещества, и притом с большой
точностью Поэтому измерение е/М для газовых ионов является
важным и точным методом определения атомных масс и широко
применяется в современной физике. Для этой цели разрабо-
разработаны различные приборы, получившие общее название масс-
спектрографов (если положение пучков определяют фотографи-
фотографическим способом) или масс-спектрометров (при регистрации
пучков электрическими методами).
§ 185. Циклотронный (диамагнитный) резонанс
Современная электроника располагает еще одним замеча-
замечательным методом определения удельного заряда электронов.
Особое достоинство этого метода заключается в том, что он при-
применим не только к электронам в вакууме или в разреженных
газах, но и к электронам проводимости в твердых телах. Обра-
Образец исследуемого вещества помещают в постоянное магнитное
поле и одновременно подвергают его воздействию переменного
электрического поля, перпендикулярного к магнитному полю.
При этом происходит явление, аналогичное процессу ускорения
ионов в циклотроне (§ 181), но в данном случае ускоряемыми ча-
426
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
стицами являются электроны проводимости и роль ускоряюще-
ускоряющего электрического поля между дуантами играет электрическое
поле электромагнитной волны.
Рассмотрим качественно поведение свободного электрона в
этих условиях. В постоянном магнитном поле (индукцию кото-
которого обозначим через Во)
электрон движется по ок-
окружности, лежащей в плос-
плоскости П (рис. 314), перпен-
перпендикулярной к магнитному
полю, с циклотронной ча-
частотой обращения (§ 179)
ис = {е/т)В0. A85.1)
Его круговое движение
можно разложить на два
взаимно перпендикулярных
гармонических колебания в
плоскости П и рассматри-
Рис. 314. К объяснению циклотронного вать электрон в постоянном
резонанса магнитном поле как два гар-
гармонических осциллятора, колеблющиеся вдоль осей X и Y с оди-
одинаковой частотой oic и с постоянной разностью фаз, равной п/2.
Положим теперь, что на электрон действует еще электриче-
электрическое поле Е электромагнитной волны, лежащее в плоскости П и
изменяющееся с частотой о> (длина волны намного больше ра-
радиуса орбиты, так что мгновенное значение Е одинаково во всех
точках орбиты). Тогда на каждый из указанных осцилляторов
будет действовать периодическая внешняя сила с частотой ш, и
поэтому они будут совершать вынужденные колебания с той же
частотой ш. Но из механики известно, что при условии
ш = ис A85.2)
возникает явление резонанса, при котором амплитуда колебаний
осциллятора и его энергия достигают наибольшего значения, а
в случае отсутствия затухания (сил трения) неограниченно уве-
увеличиваются с течением времени. Поэтому свободный электрон
при резонансе будет набирать энергию за счет энергии электро-
электромагнитной волны и двигаться по раскручивающейся траектории
(рис. 314), а электромагнитная волна при резонансе будет погло-
поглощаться (см. Добавление 10).
В действительности же электроны испытывают соударения.
При соударениях они передают накопленную энергию кристал-
кристаллической решетке твердого тела, после чего процесс ускоре-
ускорения электронов начинается снова. Поэтому поглощение энергии
электромагнитной волны происходит и в отсутствие резонанса.
При резонансе же поглощение достигает максимума.
§ 186 ЭФФЕКТИВНАЯ МАССА 427
Описанное явление получило название циклотронного резо-
резонанса или, иначе, диамагнитного резонанса (так как его проис-
происхождение тесно связано с искривлением траектории электронов
силой Лоренца, т.е. с тем же эффектом, который обусловливает
диамагнитные свойства, ср. § 118).
Резонансное поглощение выражено тем сильнее, чем большее число пол-
полных обращений успеет совершить электрон за среднее время свободного
пробега т, т.е. чем больше произведение шт по сравнению с единицей. Чтобы
оно вообще было заметно, необходимо по крайней мере выполнение условия
и/т ~ 1. Обычно это имеет место при частотах ш ~ 10 Гц, что соответству-
соответствует радиоволнам сантиметрового диапазона. Кроме того, выгодно увеличи-
увеличивать т, для чего исследуемое вещество в некоторых случаях охлаждают до
низких температур.
Для наблюдения циклотронного резонанса исследуемое ве-
вещество (например, небольшой кристалл) помещают внутрь резо-
резонансной полости, в которой создают стоячую электромагнитную
волну (§ 241). Резонатор с образцом помещают между полюсами
электромагнита, создающего постоянное однородное магнитное
поле, и измеряют поглощение электромагнитной энергии в за-
зависимости от отношения oj/ujc. При этом оказывается удобным
поддерживать неизменной частоту генератора ш, а изменять шс
изменением индукции Bq. На опыте определяют частоту шс, со-
соответствующую резонансу. Тогда по формуле A85.1) можно най-
найти удельный заряд е/тп, а зная еще заряд частиц, можно опре-
определить их массу.
§ 186. Эффективная масса
Исследование циклотронного резонанса в различных кри-
кристаллах показало, что получаемая из этих опытов масса элек-
электронов проводимости не равна массе свободного электрона в ва-
вакууме т. Эта — так называемая эффективная масса может быть
как больше, так и меньше т.
На рис. 315 в качестве примера приведены эксперименталь-
экспериментальные кривые циклотронного поглощения для кристаллов герма-
германия n-типа. По горизонтальной оси отложено отношение ojc/uj,
где и>с вычислено для тоэф = т. Из рисунка видно, что макси-
максимумы поглощения лежат при значениях шс/ш, не равных 1, а
значительно меньших, что соответствует тэф < т.
Далее оказалось, что значение эффективной массы зависит
от направления Во (рис. 315). Так как в этих опытах направле-
направление электрического поля всегда перпендикулярно к Во, то это
значит, что эффективная масса зависит от направления дей-
действующей силы (анизотропия эффективной массы). Так, напри-
например, в германии для силы, параллельной кристаллографическому
направлению [111] (пространственная диагональ куба), эффек-
428
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
[001]
В0Я [ПО]
0 0,08 0,16 0,24
сос/ш
тивная масса электронов равна тэф « 1,6т, а для силы, дей-
действующей в перпендикулярной плоскости, тэф ~ 0,08т.
И, наконец, число различ-
различных резонансных частот оказы-
оказывается в ряде случаев больше,
нежели ожидаемое теоре-
теоретически для частиц с одним
определенным значением тэф.
Так, например, в кристаллах
германия р-типа наблюдаются
резонансы, соответствующие
двум различным типам поло-
положительных дырок с сильно
различающимися эффектив-
эффективными массами («тяжелые» и
«легкие» дырки).
С понятием эффективной
массы мы уже встречались
в § 154, рассматривая зави-
зависимость энергии электронов
проводимости от их импуль-
импульса. Опыты по циклотронному
резонансу показывают, что и
движение электронов в кри-
кристаллах под действием внеш-
внешних сил (электрического и магнитного полей) определяется не
истинной массой электронов, а их эффективной массой.
Эти результаты, кажущиеся сначала очень удивительными,
имеют простое объяснение. Общая их причина заключается в
том, что электроны проводимости находятся все время под дей-
действием периодического в пространстве электрического поля кри-
кристалла и их движение определяется не только внешними полями,
но и полем самого кристалла. Поэтому, пытаясь описать движе-
движение электронов и учитывая только внешние силы, мы получаем
в законах движения вместо истинной массы электрона m неко-
некоторую другую, гораздо более сложную величину (эффективную
массу). Если же учесть и внутреннее поле самого кристалла и
воспользоваться квантовыми законами движения электронов, то
оказывается возможным объяснить все важнейшие эксперимен-
экспериментальные результаты, и притом не только качественно, но и ко-
количественно.
Исследование эффективных масс в различных кристаллах
играет важную роль в современной физике твердого тела и по-
позволяет получить ценные сведения об особенностях движения
электронов внутри кристаллов.
Рис. 315. Циклотронное поглощение
в германии п-то типа при двух раз-
различных направлениях магнитного по-
поля относительно осей кристалла. Тем-
Температура 4,2 К. Частота 8,9 ГГц
§ 187
ЭЛЕКТРОННАЯ И ИОННАЯ ОПТИКА
429
i_v -s-\
§ 187. Отражение и преломление электронных пучков.
Электронная и ионная оптика
Предположим, что пучок электронов, движущихся в одном
направлении, попадает в однородное электрическое поле плос-
плоского конденсатора, входя через одну из его пластин (рис. 316).
Это можно осуществить,
если пластины конден-
конденсатора сделать из ме-
металлических сеток или
из тончайших слоев ме-
металла, прозрачных для
электронов.
Пусть, далее, направ-
направление электрического
поля в конденсаторе та-
таково, что оно тормозит
электроны. Тогда нор-
нормальная к эквипотен-
эквипотенциальным поверхностям
составляющая скорости
электронов vn будет
уменьшаться, составля-
составляющая же vt, параллель-
параллельная эквипотенциальным
поверхностям, изме-
изменяться не будет. Если
электрическое поле дос-
достаточно сильно, то в
некоторой точке в сос-
составляющая vn обратится в нуль, а затем изменит свое направ-
направление. Электроны, вошедшие в электрическое поле в точке а,
будут двигаться по изогнутой траектории авб и выйдут из поля
в точке б. Так как при движении от в к б они проходят ту
же разность потенциалов, что и между айв (но в обратном
направлении), то модуль скорости vn в точке б будет тот
же, что и в точке а, а следовательно, электроны выйдут из
конденсатора под тем же углом i, под которым они вошли в
конденсатор.
Мы получим отражение электронного пучка, подобное отра-
отражению света от плоского зеркала, причем и здесь будет спра-
справедлив закон отражения: угол отражения равен углу падения, а
направления падающего пучка, отраженного пучка и нормали к
эквипотенциальным поверхностям поля лежат в одной плоскости.
Если разность потенциалов между пластинами недостаточна
для того, чтобы обратить в нуль скорость vn, то пучок электро-
б
Рис. 316. Электроны в поле плоского кон-
конденсатора (а) и его оптическая аналогия (б)
430
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
нов выйдет из поля через другую пластину (рис. 317). Однако
направление выходящего пучка будет отличаться от направле-
направления входящего, и мы получим преломление электронного пуч-
пучка, причем опять направления падающего и выходящего пучков
будут лежать в одной плоскости с нормалью к эквипотенциаль-
эквипотенциальным поверхностям. Если электроны движутся от более высокого
потенциала к более низкому (тормозящее электрическое поле),
то угол преломления г будет больше угла падения i, и явле-
явление будет аналогично преломлению света, распространяющего-
распространяющегося из среды с большим показателем преломления п\ в среду с
меньшим показателем преломления п-i (например, из стекла в
воздух, рис. 317 а). Если же электроны движутся от низшего
потенциала к высшему, то угол преломления г будет меньше
угла падения i и преломление электронных пучков будет соот-
соответствовать преломлению света при условии ni > n\ (например,
при переходе из воздуха в стекло, рис. 317 6).
a UX>U2
V,
т
Рис. 317. Преломление электронных пучков
Нетрудно найти и количественную связь между преломлением элек-
электронных пучков и изменением потенциала. Показателем преломления сре-
среды п называют отношение
п = sin г/ sin r.
Переходя к электронам и обращаясь к рис. 317, мы видим, что
sini = vt/vi, sinr = vt/v2, n = sini/sinr = г>2/1>1-
Здесь vi — полная скорость электронов до вступления в электрическое по-
поле (в «среде» 1), V2 — полная их скорость после выхода из поля (в «сре-
«среде» 2), причем учтено, что касательная составляющая скорости vt остается
§ 187
ЭЛЕКТРОННАЯ И ИОННАЯ ОПТИКА
431
постоянной. Если энергия электронов, выраженная в электронвольтах, в
пространстве 1 есть V, то
mvi/2 = eV.
Если, далее, при переходе из пространства 1 (в котором потенциал постоя-
постоянен) в пространство 2 (тоже с постоянным потенциалом) потенциал изме-
изменяется на U, то
Деля оба последних равенства друг на друга и подставляя выражение
в формулу для показателя преломления, находим
A87.1)
Так же как и в оптике, п не зависит от угла падения и определяется только
изменением потенциала пространства и начальной энергией электронов V.
Таким образом, изменение потенциала пространства оказы-
оказывает на электронные пучки такое же влияние, как изменение по-
показателя преломления среды на лучи света. Создавая подходяще
подобранные электрические поля, можно осуществить системы,
которые действуют на электроны подобно тому, как действуют
оптические линзы на лучи света, и позволяют получать изобра-
изображения объектов.
Один из способов осуществления электростатической линзы показан на
рис. 318. Линза состоит из двух отделенных узкой щелью коаксиальных ци-
цилиндров, к которым приложена разность потенциалов. Эквипотенциальные
поверхности электрического поля вблизи щели изображены на рисунке. На-
Рис. 318. Электростатическая линза в виде двух коаксиальных цилиндров
пряженность электрического поля перпендикулярна к эквипотенциальным
поверхностям и имеет составляющую Et, параллельную оси линзы, и со-
составляющую Ег, перпендикулярную к оси. Электроны, вышедшие из неко-
некоторой точки Р и попавшие в линзу, в левой половине электрического поля
отклоняются полем Ет к оси линзы, и поэтому расходящийся пучок превра-
превращается в сходящийся. В правой половине поля направление Ег изменяется
на противоположное и на электроны действует сила, направленная от оси
наружу. Однако электроны, достигнув центральной плоскости (щели), про-
прошли ускоряющую разность потенциалов U/2 (U — разность потенциалов
между цилиндрами) и увеличили свою скорость. Поэтому электронный пу-
пучок во второй части линзы, хотя и уменьшает свою сходимость, остается все
432
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
же сходящимся и пересекает ось в некоторой точке Pi, которая и является
изображением точки Р.
Для электростатической линзы, так же как и для оптической, суще-
существует определенная точка F\ на оси линзы (рис. 319 а), которая отличается
тем, что расходящийся электронный пучок, выходящий из этой точки, после
преломления в линзе превращается в параллельный. Эта точка называется
главным фокусом линзы, а ее расстояние от центра линзы (центра щели) —
главным фокусным расстоянием. С другой стороны линзы расположен ее
Рис. 319. Фокусы электростатической линзы
второй главный фокус (рис. 319 б). Легко сообразить, что для рассматри-
рассматриваемой электростатической линзы оба фокусных расстояния неодинаковы.
Отметим, что такое же положение вещей мы имеем и для оптических линз,
если показатели преломления окружающей среды с обеих сторон линзы
неодинаковы.
На рис. 320 изображена электростатическая линза, для которой оба фо-
фокусных расстояния одинаковы. Она состоит из двух диафрагм D\ и Z>2,
соединенных вместе и находящихся при одинаковом потенциале, и третьей
Рис. 320. Однопотенциальная электростатическая линза
диафрагмы ?>з, помещенной между ними. Если внутренняя диафрагма име-
имеет отрицательный потенциал относительно крайних диафрагм, то линза яв-
является для электронов собирающей. Так как потенциал пространства слева
и справа от рассматриваемой линзы одинаков, то она соответствует оптиче-
оптической линзе, с обеих сторон которой находится одна и та же среда (рис. 320).
Линзам для электронов, так же как и оптическим линзам, присущи
различные ошибки, или аберрации, не позволяющие получить абсолютно
резкое изображение, при котором каждая точка объекта отображалась бы
также точкой в плоскости изображения. Эти аберрации можно лишь умень-
уменьшить, но не устранить совсем.
188
ЭЛЕКТРОННЫЙ ОСЦИЛЛОГРАФ
433
Линзы для электронов можно получить и с помощью маг-
магнитных полей (магнитные линзы).
Исследование условий получения изображений с помощью
электронных и ионных пучков и способов практического постро-
построения таких систем составляет содержание электронной и ионной
оптики.
И
Я,
§ 188. Электронный осциллограф
В качестве примера применения электронной оптики рас-
рассмотрим устройство электронного осциллографа, который пред-
предназначен для наблюдения быстрых электрических процессов.
Основной его частью является электронно-лучевая трубка, схе-
схематически изображенная на рис. 321. Источник электронов И с
накаленным катодом
создает узкий пучок
электронов (электрон-
(электронный луч), сходящий-
сходящийся в очень маленькое
пятнышко п на люми-
несцирующем экране
Э, нанесенном изну-
изнутри на стенке труб-
трубки. Трубка откачана
до высокого вакуума. Рис 321. Осциллографическая электронно-
Между источником и лучевая трубка
экраном расположены
две пары металлических пластин П\ и Я2, которые отклоняют
электронный пучок в двух взаимно перпендикулярных направ-
направлениях. На одну из пар пластин, например 77j, накладывает-
накладывается электрическое напряжение, изменяющееся во времени, как
показано на рис. 322 («пило-
(«пилообразное» напряжение), созда-
создаваемое специальным генера-
генератором внутри осциллографа.
Это напряжение вызывает
равномерное движение пятна
на экране в горизонтальном
Рис. 322. Пилообразное напряжение, направлении (развертка во
накладываемое на пластины времени времени). На вторую пару
осциллографа пластин накладывают ис-
исследуемое напряжение. Под
действием обоих электрических полей, создаваемых пластинами
771 и 772, пятно на экране вычерчивает кривую, изображающую
зависимость исследуемого напряжения от времени.
434
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
ГЛ. XVII
Отклонение электронного луча в осциллографе пропорцио-
пропорционально приложенному напряжению, и поэтому электронный ос-
осциллограф представляет собой быстродействующий вольтметр.
Так как электроны имеют ничтожную массу, то электронный
луч практически не обладает никакой инерцией даже для очень
быстро изменяющихся напряжений, в чем и заключается основ-
основное достоинство электронных осциллографов.
В некоторых типах электронно-лучевых трубок отклонение
электронного пучка производится магнитным полем. В этом слу-
случае вместо отклоняющих пластин применяют проволочные ка-
катушки, расположенные вне трубки, в непосредственной близо-
близости к ней.
Развитие быстродействующей осциллографии и телевидения потребо-
потребовало создания таких источников электронов, которые позволили бы полу-
получить на экране возможно меньшее пятно с максимальной интенсивностью.
Это осуществляют с помощью специальных электронно-оптических систем,
получивших название электронных пушек.
Второй анод
Рис. 323. Типичная электронная пушка (а) и ее оптическая аналогия (б).
Показатели преломления т < П2 < "з < «4 < пь
Устройство типичной электронной пушки изображено на рис. 323 а. Она
имеет накаливаемый катод и три коаксиальных цилиндра: управляющий
электрод, первый анод и второй анод. Управляющий электрод имеет от-
отрицательный потенциал относительно катода и сжимает выходящий из ка-
катода электронный пучок. Изменяя этот потенциал, можно изменять число
электронов, проходящих через диафрагмы первого анода, а следовательно,
регулировать интенсивность пятна на экране. Потенциал первого анода по-
положителен относительно катода, а потенциал второго анода положителен
§ 189
435
относительно первого анода. Управляющий электрод и первый анод и соот-
соответственно первый и второй аноды образуют две электрические линзы. Их
эквипотенциальные поверхности изображены на рисунке. Регулируя потен-
потенциалы анодов, можно изменять сходимость электронного пучка и добиться
наилучшей фокусировки пятна на экране. Потенциал второго анода отно-
относительно катода определяет также конечную скорость электронов в пучке.
В типовых электронно-лучевых трубках потенциал первого анода делают
равным Ui = +B50 — 500) В, а потенциал второго анода доводят до t/г =
= +A000 - 2000) В.
На рис. 323 б изображена также оптическая система из двух линз, при-
приблизительно соответствующая рассматриваемой электронно-оптической си-
системе.
ГЛАВА XVIir
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
§ 189. Законы электролиза Фарадея
В настоящей главе мы рассмотрим особенности электричес-
электрического тока в проводниках 2-го рода — электролитах.
В § 55 мы уже говорили, что электрический ток в электро-
электролитах всегда сопровождается выделением на электродах хими-
химических составных частей электролита. Это явление было тща-
тщательно исследовано Фарадеем, который установил на опыте два
основных закона электролиза. Согласно первому закону Фара-
Фарадея, масса т вещества, выделившаяся на каком-либо из элек-
электродов, пропорциональна заряду (количеству электричества) q,
прошедшему через электролит:
m = Kq. A89.1)
Здесь К — электрохимический эквивалент, различный для раз-
разных веществ. Он равен массе данного вещества, выделяемой при
электролизе зарядом q = 1.
Обычно К выражают в граммах (или килограммах) на ку-
кулон. Значения электрохимических эквивалентов для некоторых
веществ приведены в табл. 15.
Таблица 15
Вещество
Серебро
Медь
Водород
Кислород
Хлор
Молярная масса М,
10~3 кг/моль
107,9
63,57
1,008
16,000
35,46
Валентность Z
1
2
1
2
1
Электрохимический
эквивалент К,
10 кг/Кл
11,18
3,294
0,1045
0,8293
3,674
436 ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ ГЛ ХУШ
Второй закон Фарадея касается величины электрохими-
электрохимического эквивалента. Фарадей обратил внимание на то, что
электрохимические эквиваленты К различных веществ всегда
пропорциональны молярной массе вещества М и обратно про-
пропорциональны валентности Z вещества. Отношение M/Z назы-
называется в химии химическим эквивалентом вещества. Второй за-
закон Фарадея утверждает, что электрохимический эквивалент
прямо пропорционален химическому эквиваленту данного ве-
вещества:
К = CM/Z. A89.2)
В этой формуле коэффициент пропорциональности С имеет од-
одно и то же значение для всех веществ.
Оба закона Фарадея можно выразить одной формулой. Под-
Подставляя выражение A89.2) для К в A89.1) и обозначая 1/С = F,
находим
™ = #f A89.3)
Величина F получила название постоянной Фарадея.
Полагая в A89.3) q = F, имеем т = M/Z — количество
вещества, масса которого равна химическому эквиваленту.
Следовательно, если через любой электролит проходит за-
заряд, равный постоянной Фарадея F, то на каждом из электродов
выделяется \jZ молей вещества.
Опыт показывает, что
F = 96,4845 ¦ 103 Кл/моль яз 96,5 Кл/моль.
Явление электролиза показывает, что молекулы растворен-
растворенного вещества в электролитах существуют в виде положительно
и отрицательно заряженных частей, ио-
ионов, которые под действием электри-
электрического поля движутся в противопо-
противоположные стороны: положительные ионы
— к катоду, а отрицательные ионы —
к аноду (рис. 324). Достигая анода, от-
отрицательный ион передает аноду свой
отрицательный заряд, отчего один или
несколько электронов (в зависимости
Рис. 324. Схема ионной от заряда иона) проходят по внешней
проводимости цепи, и ион превращается в нейтраль-
нейтральный атом или молекулу, выделяющую-
выделяющуюся на аноде. Положительный ион, напротив, заимствует от като-
катода один или несколько электронов и, нейтрализуясь, выделяется
на катоде.
Ионы, выделяющиеся на аноде, т.е. несущие отрицательный
заряд, Фарадей назвал анионами, а выделяющиеся на катоде
§ 189 ЗАКОНЫ ЭЛЕКТРОЛИЗА ФАРАДЕЯ 437
(положительно заряженные) — катионами. В § 55 мы видели,
что при электролизе раствора КВг на катоде выделяется К, а на
аноде — Вг. Следовательно, ионы Вг~ являются анионами, а ио-
ионы К+ — катионами. Так как все металлы и водород выделяются
всегда на катоде, т.е. являются катионами, то отсюда можно за-
заключить, что в электролитах ионы металлов и водорода всегда
заряжены положительно.
Представление об ионной проводимости электролитов позво-
позволяет не только качественно понять явление электролиза, но и
объяснить законы Фарадея. Действительно, пусть число ионов,
выделившихся на каком-либо электроде в процессе электролиза,
равно v, а заряд каждого иона есть q\. Тогда полный заряд q,
прошедший через электролит, есть q = q\v. Если масса одно-
одного иона равна mi, то масса, выделившаяся на электроде, есть
т = m\v. Исключая из этих равенств г/, находим
т = ^<7, A89.4)
т.е. первый закон Фарадея.
Из A89.4) следует, что электрохимический эквивалент К =
= rni/qi или (если умножить числитель и знаменатель на чис-
число частиц в 1 моле вещества, т.е. постоянную Авогадро N —
— 6,02 ¦ 1023 моль) К = M/q\N. С другой стороны, согласно
A89.3), К — M/(ZF). Сравнивая оба выражения для К, полу-
получаем
r?i = ZF/N. A89.5)
Следовательно, заряд электролитического иона пропорционален
валентности Z вещества, т.е. ионы двухвалентных веществ име-
имеют вдвое больший заряд, нежели одновалентные ионы, ионы
трехвалентных веществ — втрое больший и т.д.
Полученный результат показывает, что заряды ионов кратны
между собой. Наименьший заряд е имеют ионы одновалентных
веществ, заряд двухвалентного иона равен 2е, Z-валентных —
Ze, но дробные части е не наблюдаются. Отсюда Гельмгольц и
Стоней, независимо друг от друга, в 1881 г. впервые сделали
заключение, что электрические заряды имеют атомарную при-
природу, т.е. разделены на определенные элементарные количества.
Значение элементарного заряда получается из A89.5) при Z = 1:
Это значение прекрасно согласуется со значением заряда
электрона, полученным позднее другими методами.
438 ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ ГЛ XVIII
§ 190. Электролитическая диссоциация
Рассмотрим теперь, каким образом возникают ионы в элек-
электролитах. На первый взгляд можно было бы предположить, что
ионы образуются в электролитах под действием самого тока,
подобно тому как это происходит в самостоятельных газовых
разрядах. Однако если бы это было действительно так, то на
расщепление молекул на ионы должна была бы затрачивать-
затрачиваться определенная энергия. Между тем опыт показывает, что для
электролитов хорошо выполняется закон Джоуля-Ленца и вся
работа электрического тока целиком превращается в тепло. По-
Поэтому остается единственная возможность предположить, что
ионы возникают независимо от электрического тока, т.е. раство-
растворенные молекулы в электролитах распадаются (диссоциируют)
на заряженные части даже в отсутствие тока, под влиянием про-
процессов, происходящих в самом электролите. Это представление
лежит в основе теории электролитической диссоциации, зало-
заложенной Клаузиусом и Аррениусом A887) и позволившей объяс-
объяснить не только явление электролиза, но и многие другие свой-
свойства растворов.
Наиболее убедительное доказательство существования электролитиче-
электролитической диссоциации дает исследование осмотического давления растворов.
Согласно закону Вант-Гоффа при малой концентрации растворов осмоти-
осмотическое давление подчиняется тем же законам, что и давление идеального
газа А именно, если тц есть концентрация частиц растворенного вещества,
а Г — абсолютная температура раствора, то осмотическое давление р равно
р = ткТ, A90 1)
где к — постоянная Больцмана. Поэтому, измеряя осмотическое давление,
можно определить и число частиц в каждом кубическом сантиметре рас-
раствора. Представим себе теперь, что мы растворяем m граммов вещества с
молярной массой М. Это количество вещества содержит (m/M)N молекул
и, следовательно, концентрация молекул равна
-5 7- <ш-2>
где V — объем раствора. Опыт показывает, что если мы имеем дело с рас-
растворами, которые не являются электролитами (не проводят электричества),
например с раствором сахара в воде, то концентрация частиц ni, опреде-
определенная из измерений осмотического давления, всегда равна концентрации
молекул п, вычисленной по A90.2), и, следовательно, в непроводящих рас-
растворах молекулы не диссоциируют. Напротив, для электролитов опыт все-
всегда дает, что число частиц п\ больше числа растворенных молекул п, что
и доказывает диссоциацию молекул в электролитах.
Молекулы различных веществ диссоциируют по-разному и
могут распадаться на два или большее число ионов. Характер
диссоциации тесно связан с химическими свойствами вещества.
Все кислоты характеризуются тем, что в водном растворе да-
дают положительные ионы водорода Н+. Так, например, серная
§ 190
ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ
439
кислота диссоциирует по уравнению
соляная кислота
НС1 ^ Н+ + СГ
и т.д.
Для оснований или щелочей характерно образование ионов
гидроксила ОН~. Примером может служить диссоциация едкого
натра
NaOH «=i Na+ + OFT
или нашатырного спирта
Растворы, в которых концентрации ионов водорода и ионов
гидроксила одинаковы, называются нейтральными. Нейтраль-
Нейтральна химически чистая вода, диссоциирующая на положительные
ионы водорода Н+ и отрицательные ионы гидроксила ОН~. Од-
Однако концентрация ионов в ней весьма мала: при комнатной тем-
температуре в тонне воды диссоциировано только около 1,4 мг.
Коэффициент диссоциации. Процесс диссоциации моле-
молекул можно представить себе следующим образом. Пусть какое-
либо вещество, обладающее полярными молекулами (т.е. моле-
молекулами, построенными из ионов, например NaCl), растворено в
воде. Молекулы воды, обладающие большим дипольным момен-
моментом, будут ориентироваться в электрическом поле растворенной
молекулы таким образом,
что их положительная сто-
сторона (ионы Н+) окажется
преимущественно обращен-
обращенной к иону С1~, а отрица-
отрицательная сторона (ион О2~~) —
к иону Na+ (как показано
схематически на рис. 325).
Это приведет к ослаблению
связи ионов Na+ и С1~ в мо-
молекуле. Рассуждая прибли-
приближенно, можно сказать, что сила взаимного притяжения ионов
Na+ и С1~ уменьшится в е раз, где е — диэлектрическая про-
проницаемость растворителя. Но молекулы, участвуя в тепловом
движении, испытывают непрерывные соударения. Поэтому при
встрече с достаточно быстрой молекулой растворителя (или дру-
другой молекулой растворенного вещества) молекула NaCl может
распасться (диссоциировать) на ионы Na+ и С1~.
Наряду с рассмотренными актами диссоциации возможны и
обратные процессы, когда при соударении двух разноименных
Н+
Рис. 325. Молекула хлористого натрия
в воде (схематически)
440 ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ ГЛ XVIII
ионов Na+ и С1~ они воссоединяются в нейтральную молекулу
NaCl (рекомбинация ионов). В электролитах мы имеем подвиж-
подвижное (динамическое) равновесие, при котором число элементар-
элементарных актов диссоциации в каждую единицу времени равно числу
актов рекомбинации. В любой момент оказывается диссоцииро-
диссоциированной только часть всех молекул, а часть молекул находится в
недиссоциированном состоянии.
Пусть в каждой единице объема раствора имеется п моле-
молекул растворенного вещества, из которых an диссоциированы, а
A — а)п не диссоциированы. Коэффициент а называется коэф-
коэффициентом диссоциации; он показывает, какая доля всех моле-
молекул распалась на ионы.
Коэффициент диссоциации зависит от концентрации раство-
раствора. Общий характер этой зависимости можно найти из следую-
следующих простых соображений. Число элементарных актов диссоци-
диссоциации в 1 с в единице объема тем больше, чем больше имеется в
наличии нерасщепленных молекул, и поэтому можно положить,
что оно равно
А(\ -а)п,
где А — некоторый коэффициент, зависящий от природы элек-
электролита и его температуры. Число обратных актов рекомбина-
рекомбинации пропорционально числу соударений разноименных ионов, а
это последнее пропорционально как концентрации положитель-
положительных ионов па, так и концентрации отрицательных ионов, рав-
равной также па (в предположении, что молекула распадается на
две части), т.е. пропорционально (паJ. Поэтому число воссое-
воссоединяющихся молекул равно
В(паJ,
где В — некоторый коэффициент. В состоянии равновесия
АA-а)п = В{паJ,
откуда
1 -а В п
Полученная формула выражает закон Оствальда, показы-
показывающий, как зависит коэффициент диссоциации а от концентра-
концентрации раствора п. Хотя этот закон и не очень точен, он правильно
передает общий характер зависимости а от п. Мы видим, что
чем меньше концентрация раствора п, тем ближе а к единице,
и для очень разбавленных электролитов (п —>¦ 0) а —)¦ 1. В этом
случае все молекулы практически диссоциированы.
Из изложенных представлений также следует, что чем боль-
больше диэлектрическая проницаемость е растворителя, тем сильнее
ослабляются связи ионов в молекулах растворенного вещества
и, следовательно, тем больше диссоциация при прочих равных
§ 191
ДВИЖЕНИЕ ИОНОВ В ЭЛЕКТРОЛИТАХ
441
условиях. Это заключение также соответствует данным опыта.
Так, например, соляная кислота НС1 при растворении в воде
(е = 81) дает электролит с хорошей электропроводностью, тогда
как ее раствор в этиловом эфире (е = 4,3) проводит электриче-
электричество очень плохо. Различные вещества хорошо диссоциируют в
воде потому, что она имеет большую диэлектрическую проница-
проницаемость.
NaNO
§ 191. Движение ионов в электролитах
Электролитическая диссоциация происходит не только в рас-
растворах, но и во многих чистых жидкостях. Так, электролитами
являются в расплавленном состоянии многие соли, кристаллы
которых построены из ионов. Сюда отно-
относятся поваренная соль NaCl, KC1, AgCl,
AgBr, NaNC-з и многие другие.
Стекло является сильно переохлаж-
переохлажденной жидкостью с очень большой вяз-
вязкостью. Оно представляет собой так-
также электролит, в котором ионы Na~*"
обладают заметной подвижностью. На
рис. 326 показан опыт, доказывающий
ионную проводимость стекла. В тигле
находится расплавленная чилийская се-
селитра NaNC, в которую погружен стек-
стеклянный баллон лампы накаливания. Для
опыта необходимо брать лампу пустот-
пустотную, а не наполненную инертным га-
газом. Нить лампы раскаляется постоян-
постоянным током, а второй электрод а (из
угля), погруженный в расплав, присое-
присоединяется к положительному концу нити. При этом раскаленная
середина нити оказывается при отрицательном потенциале отно-
относительно расплава. При накаливании нити лампы амперметр А
показывает наличие тока в цепи. NaNCb диссоциирует на ионы
Na+ и N0^". Ионы Na+ движутся от анода а к стеклу лампы и
проходят сквозь стекло. Внутри лампы имеется чисто электрон-
электронный ток термоэлектронной эмиссии. Термоэлектроны нейтрали-
нейтрализуют заряд Na+, отчего эти ионы превращаются в нейтральные
атомы Na, выделяющиеся на стенке баллона внутри лампы. Под
влиянием высокой температуры этот натрий затем перегоняется
на более холодные части баллона, где образуется ясно видимый
зеркальный слой натрия.
Ионы в электролитах испытывают многочисленные соударе-
соударения с другими молекулами, и поэтому их движение происходит
с трением, которое имеет то же происхождение, что и трение
Рис. 326. Прохождение
ионов Na+ сквозь стекло
442
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ XVIII
при движении больших макроскопических тел, движущихся в
газе или жидкости.
Как известно, сила трения, испытываемая телами при дви-
движении в жидкостях и газах, при малой скорости движения про-
пропорциональна скорости. Аналогично сила трения иона пропор-
пропорциональна скорости v его упорядоченного движения и равна
—fv, где / — коэффициент трения, различный для разных ионов
и зависящий от рода растворителя и температуры. При наличии
электрического поля ион приобретает та-
такую скорость установившегося движения,
при которой сумма силы трения и силы еЕ
со стороны поля равна нулю:
еЕ- fv = 0.
Обозначая e/f через Ь, имеем
v = ЬЕ. A91.1)
Таким образом, электролитический ион
движется равномерно, со скоростью, про-
пропорциональной напряженности поля. Ве-
Величина Ь (так же, как для ионов в газах
и электронов в металлах) называется по-
подвижностью ионов. Она равна скорости
иона в поле с напряженностью, равной еди-
единице.
Пользуясь тем, что некоторые ионы
сообщают раствору определенную окрас-
окраску, можно сделать видимым движение ио-
ионов и непосредственно измерить их ско-
скорость. Прибор для наблюдения движения
таких «окрашенных» ионов изображен на
рис. 327. К U-образной трубке А припаяна
Рис 327 Прибор для СНИЗУ изогнутая тонкая трубка Б, закан-
наблюдения движения чивающаяся сверху воронкой и снабжен-
окрашенных ионов ная краном. В трубку А сначала наливают
при закрытом кране водный раствор азот-
азотнокислого калия KNO3, который диссоциирует на катионы К+
и анионы N0^, а трубку Б заполняют через воронку водным
раствором марганцовокислого калия КМ11О4, диссоциирующего
на ионы К+ и МпО^. Затем, осторожно открывая кран, впус-
впускают в трубку А раствор КМпО4- При тщательном выполнении
этой операции в трубке А видна резкая граница между фиолето-
фиолетовым раствором КМпО4 и бесцветным KNO3- При пропускании
тока ионы К+ в обоих растворах движутся от анода к катоду.
Однако, так как ионы К+ не сообщают раствору окраски, за
их движением следить нельзя. Ионы МпО^" движутся от като-
§ 192 ПРОВОДИМОСТЬ ЭЛЕКТРОЛИТОВ 443
да к аноду и вместе с ними перемещается фиолетовая окраска.
Поэтому в том колене, где находится катод, видимая граница
раздела жидкостей понижается, а в другом колене повышается.
Скорость перемещения этой границы равна скорости движения
ионов v.
Для успеха подобных опытов нужно, чтобы плотность тока была не
слишком велика, тал как в противном случае будет происходить заметное
нагревание растворов и граница раздела будет размываться вследствие кон-
конвекции и диффузии.
§ 192. Проводимость электролитов
Электрический ток в электролитах имеет много сходных
черт с током в металлах. В электролитах и металлах, в отличие
от газов, носители заряда образуются независимо от электричес-
электрического тока. Далее, заряд положительных ионов в каждом объеме
электролита равен заряду отрицательных ионов, и поэтому объ-
объемный заряд в электролитах, так же как и в металлах, равен
нулю. Наконец, вдали от электродов концентрация ионов (поло-
(положительных и отрицательных), как правило, одинакова в разных
точках электролита. Вследствие этого градиент концентрации
ионов внутри электролитов равен нулю и диффузия ионов не
играет роли в образовании тока.
Плотность тока, создаваемая дрейфом положительных ио-
ионов, равна
3+ = n+ev+,
где п_|- — концентрация положительных ионов, е — заряд иона,
г;+ — дрейфовая скорость положительных ионов. Аналогично
для плотности тока отрицательных ионов можно написать
Полная плотность тока
j = j+ + j- = n+ev+ + n-ev-.
Как уже говорилось, концентрации положительных и отри-
отрицательных ионов в электролитах одинаковы (мы везде предпо-
предполагаем, что молекулы диссоциируют на два иона), и поэтому
п_(- = га_ = an,
где а — коэффициент диссоциации, an — число молекул в еди-
единице объема электролита. Далее скорости ионов можно выра-
выразить через их подвижности и напряженность электрического по-
поля в электролите:
г;+ = Ь+Е, V- = Ъ-Е.
Поэтому
{+ + Ъ_)Е. A92.1)
444
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ. XVIII
Плотность тока оказывается пропорциональной напряженности
поля, а следовательно, для электролитов, так же как и для ме-
металлов, справедлив закон Ома. Удельная электрическая прово-
проводимость электролита равна
Л = пеаF+ + 6_). A92.2)
Она тем больше, чем выше коэффициент диссоциации а (чем
больше концентрация ионов па) и чем больше подвижности ио-
ионов 6+ и 6_.
Входящая в эту формулу концентрация молекул п известна,
а коэффициент диссоциации а можно определить из независи-
независимых измерений, например из опытов с осмотическим давлени-
давлением. Поэтому, измеряя удельную электрическую проводимость Л
электролитов, можно определить сумму подвижностей ионов.
В § 55 мы уже говорили, что сопротивление электролитов
при нагревании уменьшается, т.е. электролиты имеют отрица-
отрицательный температурный коэффициент сопротивления. Это про-
происходит по двум причинам: во-первых, при увеличении темпе-
температуры увеличивается коэффициент диссоциации а; во-вторых,
при нагревании вязкость жидкостей уменьшается и поэтому по-
подвижность ионов увеличивается.
§ 193. Числа переноса. Подвижности ионов
в электролитах
При электролизе положительные ионы (катионы) уходят от анода к ка-
катоду, а отрицательные ионы (анионы) удаляются от катода. Поэтому кон-
концентрация электролига в приэлектродных областях изменяется. Гитторф
еще в середине прош-
а б
I !
I I
©©©©!©©;©©©©
0000|00|0000
лого века показал, что,
определяя эти измене-
изменения концентрации, мож-
можно найти отношение
подвижностей ионов
обоих знаков.
Рассмотрим сначала
это явление качествен-
качественно, для чего обратимся
к схеме рис. 328. До
электролиза концентра-
концентрация анионов и катионов
одинакова во всех частях
электролита (рис. 328,
вверху). Между анодом
Рис. 328 Объяснение изменения концентрации и линией а имеется че-
электролита у электродов тыре пары ионов (че-
(четыре молекулы), между
б и катодом — такое же число, а в средней части между а и б — две
молекулы. При электролизе положительные ионы движутся слева направо,
1 i i
i i
! I
©!©с±^©©©©|©©©
©еюоооШо©
I
I
193
ЧИСЛА ПЕРЕНОСА. ПОДВИЖНОСТИ ИОНОВ
445
а отрицательные — справа налево. Положим, что скорость движения
катионов v+ в полтора раза больше скорости анионов и_ и что за время
электролиза три положительных иона встретили катод и выделились на
нем (рис. 328, внизу). Тогда за то же время анод встретят два отрица-
отрицательных иона. Кроме того, у катода вследствие движения отрицательных
ионов окажутся непарными два положительных иона, которые также
выделятся у катода. Поэтому всего у катода выделится 3 + 2 = 5 ионов.
У анода вследствие движения положительных ионов окажутся непарными
три отрицательных иона, а следовательно, у анода будет выделено всего
2 + 3 = 5 ионов, т.е. такое же число, как у катода.
В средней части электролита (между а и б) концентрация электролита
не изменилась. Так же как и до электролиза, здесь имеются две пары ионов
или две молекулы. В пространстве же у катода (справа от б) было четы-
четыре молекулы, а после электролиза осталось только две. У анода (слева от
а) вместо четырех первоначальных осталась лишь одна молекула. Мы ви-
видим, что у электродов происходит уменьшение концентрации электролита
и притом в неодинаковой степени. Изменение концентрации больше у того
электрода (в нашем случае — у анода), от которого уходят более быстрые
ионы (на рис. 328 — положительные катионы).
К сказанному необходимо сделать следующее замечание. В схеме
рис. 328 мы предполагали, что каждый ион выделяется при электролизе, т.е.
никаких вторичных химических реакций нет. В этом случае концентрация
у каждого из электродов уменьшалась пропорционально скорости уходяще-
уходящего иона. В действительности же судьба выде-
выделяющегося иона может быть весьма различной; + —
она зависит от материала электродов, плотно-
плотности тока и т.д. Чтобы получить окончательные
изменения концентрации, эти дальнейшие пре-
превращения выделяющихся ионов необходимо все-
всегда учитывать. Ниже мы предполагаем, что вто-
вторичные химические реакции у электродов не
происходят.
Рассмотрим теперь явление количественно.
Пусть два сосуда А и К (рис. 329), содержа-
содержащие анод и катод, соединены трубкой с попе-
поперечным сечением S. Обозначим концентрацию
ионов каждого сорта до электролиза через п, а
скорости движения ионов в трубке — через «+
и v-. Тогда за время t в сосуд К войдут nv+St
положительных ионов. За то же время из сосуда К выйдут nv_St отри-
отрицательных ионов и столько же освободится ионов положительных. Полное
число освободившихся положительных ионов в сосуде К будет равно
v = n(v+ + v-)St.
Эти ионы и выделятся у катода. Такое же точно число ионов будет выделено
и у анода.
Найдем теперь изменение концентрации в обоих сосудах А и К. Из со-
сосуда А ушло Аи — nv+St положительных ионов. Напротив, в него вошло
nv-St отрицательных ионов, но в то же время выделилось у анода, как
мы видели выше, v — n(v+ +v-)St этих ионов. Поэтому уменьшение числа
отрицательных ионов в сосуде А есть
n(v+ + v~)St — nv-St = nv+St =
±
A---S---V
--A-
T
-к--
Рис. 329. Наблюдение
изменения концентрации
электролита у электродов
446
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ. XVIII
Мы видим, что число положительных и отрицательных ионов уменьшается
на одну и ту же величину Дг^л, которая, следовательно, есть уменьшение
числа молекул растворенного вещества в сосуде А.
Таким образом,
Дг/д/г/ = v+/(v+ + V-).
Но скорости ионов ii+ и t>_ пропорциональны их подвижностям 6+ и 6_.
Поэтому
Дг/А/г/= &+/(&++6_).
Отношение
v-) = b+/(b++b-) A93.1)
Гитторф назвал числом переноса катионов. Оно показывает, какая до-
доля полного заряда переносится положительными ионами (катионами). Из
A93.1) видно, что это число определяет также и относительное изменение
числа молекул в электролите вблизи анода.
Аналогично можно найти изменение числа молекул у катода. В сосуде
К выделилось у катода n(v+ -f v-)St положительных ионов, но вошло в
сосуд nv+St этих ионов. Следовательно, убыль положительных ионов в К
равна
Avk — n(v+ + v-)St — nv+St = nv-St.
Убыль отрицательных ионов равна числу ионов, ушедших из К через труб-
трубку, т.е. nv-St. И здесь убыль отрицательных ионов равна убыли положи-
положительных, и, следовательно, Дг/х есть уменьшение числа молекул в сосуде
К. Из сказанного следует, что
AvK/v = v-/(v+ + v-) = 6-/F+ + 6_) = ра, A93.2)
где ра — число переноса анионов. Из A93.1) и A93.2) также видно, что
Ра+Рк = 1,
т.е. сумма чисел переноса анионов и катионов всегда равна единице.
Рассмотренное явление важно в том отношении, что, измеряя на опыте
изменения концентрации электролита у анода и катода, можно определить
отношение подвижностей обоих ионов. Измеряя же удельную электриче-
электрическую проводимость, можно найти сумму этих подвижностей. Зная же сум-
сумму и отношение подвижностей, можно определить и каждую из подвижно-
подвижностей аниона и катиона порознь.
В табл. 16 приведены подвижности некоторых ионов, найденные этим
способом для водных растворов малой концентрации при комнатной темпе-
температуре. С увеличением концентрации раствора подвижности ионов умень-
уменьшаются, хотя и не очень сильно.
Таблица 16
Ион
Н+
к+
Na+
Li+
Подвижность,
ю-7 м2/(в-с)
3,263
0,669
0,450
0,346
Ион
он-
сг
NO3-
Вг-
Подвижность,
Ю-7 м2/(В-с)
1,802
0,677
0,639
0,694
Малые значения подвижности ионов в электролитах указывают на то,
что силы трения, действующие на ионы, весьма велики. Для приближенной
§ 194 ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ 447
оценки коэффициента трения / ионов уподобим ион маленькому шарику
радиусом г и применим к нему закон Стокса, согласно которому / = бтгг/г,
где 77 — вязкость растворителя. Отсюда можно заключить, что подвижность
ионов, равная Ъ — е//, будет тем меньше, чем больше вязкость раствори-
растворителя, что согласуется с опытом. Так, например, увеличивая температуру
электролита, мы уменьшаем его вязкость; опыт показывает, что при этом
подвижность ионов увеличивается. Далее измерения показывают, что по-
подвижность ионов тем больше, чем меньше вязкость растворителя.
Однако если по значениям подвижностей вычислить ридиусы ионов г,
то получаются величины, не согласующиеся со значениями, определенны-
определенными другими методами. Это расхождение легко понять, если учесть, что
ионы вследствие электростатического взаимодействия притягивают к себе
окружающие молекулы растворителя. В результате ионы в электролитах
оказываются окруженными оболочкой из молекул растворителя, которая
движется вместе с ионами. Подобные группы молекул получили название
сольватов, а в случае водных растворов — гидратов. Явление сольватации
приводит к тому, что размер движущегося иона как бы возрастает, а его
подвижность вследствие этого уменьшается.
§ 194. Электродные потенциалы
Если какой-либо проводник 1-го рода, например металл, со-
соприкасается с электролитом, то на металле и электролите по-
появляются заряды противоположного знака. При этом металл
приобретает относительно электролита определенный электри-
электрический потенциал, который получил название электродного по-
потенциала.
Возникновение электродных потенциалов объясняется сле-
следующим образом. Рассмотрим простой случай металла, погру-
погруженного в водный раствор своей собственной соли. Будем далее
считать, что процессы, происходящие у электрода, обратимы.
Это значит, что если при данном направлении тока на электро-
электроде происходит определенная химическая реакция, то при про-
пропускании тока в противоположном направлении на электроде
происходит реакция обратная. В отсутствие же тока никаких
реакций на электроде нет.
Примером, приближенно удовлетворяющим этим условиям,
может служить цинк, находящийся в водном растворе серно-
сернокислого цинка ZnSC>4- Посмотрим подробнее, что происходит у
границы цинк-раствор. Ионы SO2~, находящиеся в растворе,
вступают в химическую реакцию с ионами Zn2+ металла, об-
образуя Z11SO4, который, растворяясь в воде, вновь диссоциирует
на ионы Zn2+ и SO^". В результате этого процесса ионы Zn2+
непрерывно переходят с электрода в раствор. Каждый перешед-
перешедший ион цинка переносит в раствор положительный заряд +2е
и освобождает в металле отрицательный заряд —2е.
Наряду с растворением цинка происходит и обратный ему
процесс: ионы Zn2+, находящиеся в растворе, при тепловом дви-
448
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ. XVIII
Металл Раствор
Металл Раствор
жении встречают цинковый электрод и на нем высаживаются.
При этом электрод получает положительный заряд, а в растворе
остаются некомпенсированные ионы SO2.".
Если поток ионов Zn2+ из электрода в раствор больше пото-
потока тех же ионов из раствора на электрод, то металл будет за-
заряжаться отрицательно, а раствор —- положительно. Вследствие
взаимного притяжения разноименных зарядов избыточные ио-
ионы Zn2+ в растворе будут
сосредоточены в тонком
слое вблизи границы раз-
раздела, отчего возникает
двойной электрический
слой (рис. 330 о). Элек-
Электрическое поле внутри
двойного слоя будет
противодействовать пе-
переходу ионов цинка в
раствор и способствовать
обратному переходу их
из раствора на электрод.
Если поток ионов
Zn2+ из электрода в
раствор меньше обрат-
обратного потока ионов, то
электрод будет заряжаться положительно, а раствор — отрица-
отрицательно, и появится двойной электрический слой, показанный на
рис. 330 б. И в этом случае электрическое поле двойного слоя
будет стремиться выровнять оба потока ионов Zn2+.
При некотором потенциале электрода относительно раствора
оба потока ионов становятся равными друг другу и между элек-
электродом и раствором устанавливается электрохимическое рав-
равновесие. Этот равновесный потенциал и есть электродный по-
потенциал металла (в нашем случае цинка) относительно данного
раствора.
Очевидно, что для каждого вещества в растворе своей со-
соли существует и такая концентрация раствора со, при которой
двойной электрический слой не возникает. Она называется кон-
концентрацией нулевого заряда.
В рассмотренном примере (Zn в растворе ZnSO,i) электрод и
раствор обмениваются положительными ионами металла (кати-
(катионами). В других комбинациях электродов с растворами может
происходить и обмен анионами (см. ниже табл. 17). Оба эти слу-
случая принципиально не отличаются друг от друга.
Из сказанного ясно, что электродный потенциал зависит от
концентрации раствора. Если выбирать концентрацию ионов в
Рис. 330. Двойной электрический слой на
границе металла с электролитом: а — кон-
концентрация ионов металла с в растворе
меньше концентрации нулевого заряда со;
б— о со
§ 194
ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
449
г - coz~
?37=
=
+
'+ZS—
растворе, участвующих в обмене, всегда одной и той же, то элек-
электродный потенциал будет зависеть только от вещества электро-
электрода и будет характеризовать его способность посылать ионы в
раствор. Для этого можно выбирать растворы нормальной кон-
концентрации, т.е. содержащие 1 кмоль ионов в 1 м3 раствора (или,
что то же, 1 моль в 1 л). Потенциал рав-
равновесия в таком растворе называют аб-
абсолютным нормальным электродным по-
потенциалом. Зная абсолютный нормальный
потенциал какого-либо электрода, мож-
можно вычислить его потенциал относительно
раствора любой концентрации.
Чтобы найти зависимость электродного потен-
потенциала от концентрации раствора, представим се-
себе два раствора одного и того же вещества, но с
разной концентрацией, разделенных полупронипа-
емой перегородкой (рис. 331). Пусть растворы со-
содержат катионы металла Me (Z — кратность за-
заряда ионов) и какие-либо анионы. Будем считать,
что перегородка свободно пропускает ионы Mez ,
но совершенно не пропускает анионы. Положим,
далее, что концентрация ионов Mez в одном из
растворов равна концентрации нулевого заряда со металла, а в другом рас-
растворе имеет произвольное значение с. Так как потоки ионов Mez через
перегородку из обоих растворов различны, то при равновесии между рас-
растворами появится разность потенциалов tpo — <р. Но раствор с концентрацией
со, по определению, обладает такой же способностью посылать ионы Mez ,
как и металлический электрод. Поэтому можно считать, что разность ifio — 'p
равна электродному потенциалу V рассматриваемого металла в растворе с
концентрацией с.
С другой стороны, частицы растворенного вещества ведут себя подобно
атомам газа. Поэтому, согласно закону Больцмана, имеем
с/со = exp [-Ze{<p - <po)/kT\.
Здесь Ze(tp — <ро) — —ZeV есть приращение потенциальной энергии иона
Me при переходе из раствора с концентрацией со в раствор с концентра-
концентрацией с. Отсюда находим
Рис. 331. Два раство-
раствора с различной кон-
концентрацией, разделен-
разделенные полупроницаемой
перегородкой. Кон-
Концентрация пропускае-
пропускаемых ионов с < со
В этом соотношении второе слагаемое зависит только от природы металла.
Обозначая его через Vjv, получаем окончательно
V = V}v + {kT/Ze) In с. A94.1)
В этих формулах концентрации с и Со можно выражать в любых (но
одинаковых) единицах. Если концентрации выражать числом молей ионов
металла в литре раствора (молярно-объемная концентрация), то в растворе
с нормальной концентрацией (с = 1) V = Vjv, а следовательно, V/v есть
абсолютный нормальный электродный потенциал. Формула A94.1) была
впервые получена Нернстом.
450
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ XVIII
Абсолютные электродные потенциалы определить из опы-
опыта очень трудно. А именно, чтобы присоединить к металлу и
электролиту вольтметр, мы должны ввести в электролит второй
электрод, а этот последний приобретет в свою очередь некото-
некоторый электродный потенциал. Поэтому мы измерим лишь раз-
разность потенциалов V — V', где V' — электродный потенциал
второго электрода. Однако для целей практики как раз и нужно
знать только разность потенциалов двух каких-либо электродов.
Но эта разность не зависит от того, относительно какого тела
измерены потенциалы каждого из электродов. Поэтому при из-
измерении электродных потенциалов условились применять в ка-
качестве второго электрода определенный стандартный электрод,
отличающийся постоянством своих свойств. Обычно используют
водородный электрод, состоящий из платины, насыщенной во-
водородом и находящейся в растворе, содержащем ионы водорода
(например, в растворе серной кислоты) с определенной концен-
концентрацией. Для таких измерений разработана специальная мето-
методика.
Электродный потенциал вещества в водном растворе его со-
соли с нормальной концентрацией ионов, измеренный относитель-
относительно водородного электрода, называют нормальным электродным
потенциалом. Значения нормальных электродных потенциалов
для некоторых веществ при комнатной температуре приведены
в табл. 17. В ней указаны также ионы, участвующие в обмене
между электродом и раствором.
Таблица 17
Электрод
Li
Na
Mg
Al
Zn
Cd
Pb
Пл+
Na+
Mg2+
A13+
Zn2+
Cd2+
Pb2+
Потенциал, В
-3,0
-2,7
-2,4
-1,7
-0,76
-0,40
-0,13
Электрод
н2
Си
Ag
Hg
Br2
сь
F2
Cu2+
Ag+
Hg2+
Br-
cr
F~
Потенциал, В
0
+0,34
+0,80
+0,85
+1,0
+ 1,3
+2,6
Формула Нернста A94.1) является приближенной При ее получении мы
предполагали, что при переходе иона между двумя растворами его потенци-
потенциальная энергия изменяется только вследствие скачка потенциала в двойном
электрическом слое. Однако между ионами в каждом из растворов суще-
существует электростатическое взаимодействие. Поэтому потенциальная энер-
энергия ионов в растворе зависит от среднего расстояния между ними, т.е. от
концентрации раствора. При переходе иона из одного раствора в другой его
потенциальная энергия изменяется не только вследствие скачка потенциала
на границе, но еще и из-за изменения концентрации ионов Это обстоятель-
обстоятельство не учитывается формулой Нернста, и поэтому она справедлива лишь
для очень разбавленных растворов
§195
ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА
451
В электрохимии взаимодействие между ионами формально учитывают
при помощи понятия активности ионов. В частности, в формулу Нернста
вводят поправочный коэффициент, а именно вместо концентрации с пишут
/с. Множитель / называется коэффициентом активности ионов, а про-
произведение /с — активностью ионов в данном растворе. Значение / само
зависит от концентрации и должно быть определено из дополнительных
данных.
Таким образом, более точная запись формулы Нернста имеет вид
V = Vo + (kT/Ze) In a, A94 2)
где а = /с — активность ионов, a Vo — потенциал электрода относительно
раствора с активностью ионов, равной единице
Потенциалы Vo, измеренные относительно водородного электрода, на-
называются стандартными электродными потенциалами и приводятся во
всех руководствах по электрохимии.
§ 195. Химические источники тока
Составляя электрическую цепь из двух (или нескольких)
проводников 1-го рода (электродов) и электролитов, мы получа-
получаем гальванические элементы, или, иначе, химические источники
тока. В таких устройствах сторонние силы (ср. § 64) возникают в
результате химических реакций на
электродах, а энергия, освобождае-
освобождаемая в реакциях, превращается в
работу тока.
Электродвижущая сила.
ЭДС можно просто вычислить
только для обратимых источников
тока. Именно для таких источни-
источников при отборе бесконечно слабого
тока (квазистатический режим)
работа тока равна максималь-
максимальной работе химических реакций
(ср. § 55).
Примером обратимого источни-
источника может служить элемент, по-
показанный на рис. 332 (элемент
Даниэля-Якоби). Он имеет цинко-
цинковый электрод, погруженный в рас-
Рис. 332.
Якоби
Элемент Даниэля-
твор цинкового купороса ZnSC>4, и медный электрод в растворе
медного купороса CuSO4- Оба раствора отделены друг от друга
пористым стаканом, который не препятствует движению ионов,
но предохраняет растворы от быстрого перемешивания. Поло-
Положительным электродом является медь, отрицательным — цинк.
Если замкнуть электроды элемента, то электроны с цинка
будут переходить по внешней цепи на медь и цинк станет ме-
менее отрицательным, чем нужно для электрохимического равно-
452 ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ ГЛ XVIII
весия. Вследствие этого ионы Zn2+ будут входить в раствор и
двигаться от цинка. С другой стороны, электроны, приходящие
на медный электрод, будут уменьшать его положительный по-
потенциал, и поэтому ионы Си2+ из раствора будут выделяться на
медном электроде. Таким образом, в замкнутом элементе поло-
положительные ионы движутся от катода к аноду (противоположно
движению ионов при электролизе), а отрицательные ионы — в
обратном направлении. Если же присоединить элемент к внеш-
внешнему источнику тока так, чтобы медный электрод был соединен
с положительным полюсом источника, а цинк — с отрицатель-
отрицательным, то внутри элемента будет происходить электролиз и поло-
положительные ионы будут двигаться от меди к цинку. На цинко-
цинковом электроде будет выделяться цинк, а медный электрод будет
растворяться, т.е. процессы будут обратными по сравнению с
первым случаем. В действительности этот элемент не является
точно обратимым, так как оба раствора постепенно перемеши-
перемешиваются.
Примером необратимого элемента является элемент Вольты
(цинк и медь в растворе серной кислоты).
ЭДС, т.е. разность потенциалов между электродами разомк-
разомкнутого элемента, есть сумма скачков потенциала на границах
веществ, его составляющих. Так, для медно-цинкового элемента
с двумя жидкостями (рис. 332) мы имеем цепь:
(—)Zn | раствор Z11SO4 11 раствор C11SO4 | Cu(+).
Если (p2i = </?2 — <?>1 есть разность потенциалов между вещества-
веществами 2 и 1, <р32 = (рз — ц>2 и ?>43 = Щ — V3) т0 ЭДС всего элемента
равна
$= V21 + ?>32 + V43-
Но (/521 = —V(Zn), а </?43 = V(Cu), где V — абсолютные элек-
электродные потенциалы. Поэтому, пренебрегая малым скачком по-
потенциала (рз2 на границе двух растворов, имеем
Так как сюда входит только разность потенциалов, то под V
можно подразумевать и потенциалы, измеренные с водородным
электродом (ср. § 194). Если концентрация обоих растворов нор-
нормальная, то, согласно предыдущей таблице, получаем
8 = 0,34-(-0,76) = 1,10 В.
Отметим, что для измерения этой разности потенциалов мы
должны включить в цепь соединительные провода, ведущие к
вольтметру. Но на границе двух различных металлов тоже воз-
возникают скачки потенциала (гл. XIX). Поэтому, если оба провода
сделаны, например, из меди, то появится еще скачок потенциала
§ 195 ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА 453
на границе Zn|Cu. Этот скачок потенциала мы не включаем в
ЭДС, хотя он и может давать вклад в показания вольтметра.
В § 67 мы видели, что ЭДС гальванического элемента можно выразить
через максимальную работу химических реакций, рассчитанную на едини-
единицу заряда. Конечно, оба способа расчета ЭДС дают один и тот же результат.
Положим для приближенной оценки, что максимальная работа равна пол-
полной энергии, освобождаемой при химических реакциях. Тогда
A95.1)
Здесь pi и Р2 — тепловые эффекты реакции на обоих электродах (рассчи-
(рассчитанные на 1 кг вещества электродов), а Ку и А"г — электрохимические эк-
эквиваленты вещества электродов. Представим это выражение в несколько
ином виде Пусть Q\ и Q2 — тепловые эффекты реакций на 1 кмоль. Тогда
р1 = Qi/Mi, р2 — Q2/M2 {Mi и Мг — атомные массы материалов электро-
электродов) Далее, в соответствии с § 189, К\ = Mi/ZiF, K2 — M2/Z2F {Z\ и
Zi — валентности, F — постоянная Фарадея). Поэтому
Согласно термохимическим измерениям при образовании ZnSCu выде-
выделяется количество теплоты Q\ = 4,55-108 Дж на 1 кмоль цинка, а выделение
меди из раствора сопровождается поглощением тепла <Эг = —2,33 • 108 Дж
на 1 кмоль меди Валентности цинка и меди равны Z\ = Z2 = 2. Поэтому
„ „D,55- 2,33) -Ю'-.р
8~ 2-9,65 W 1'1513'
что близко к величине, рассчитанной по электродным потенциалам, и к
значению, наблюдаемому на опыте.
Поляризация электродов. Приведенные выше значения
электродных потенциалов относятся к электрохимическому рав-
равновесию, т.е. к случаю отсутствия тока. При замыкании элемен-
элемента химический состав электродов может изменяться вследствие
выделения на них веществ электролита. Кроме того, может из-
изменяться и концентрация электролита у электродов. Поэтому
при наличии тока электродные потенциалы, а значит, и ЭДС
всего элемента могут отличаться от их равновесных значений.
Так, если замкнуть простой элемент Вольты на внешнюю
цепь, то сила тока в цепи будет уменьшаться с течением вре-
времени. Причина этого явления заключается в том, что при ра-
работе элемента положительные ионы водорода движутся внутри
элемента от цинка к меди и выделяются на медном электроде.
Выделяющийся водород, подобно металлам, обладает способно-
способностью посылать свои ионы обратно в раствор, отчего возникает
дополнительная ЭДС, направленная противоположно ЭДС эле-
элемента. Можно сказать, что если до замыкания элемента мы име-
имеем электроды из цинка и меди, то после длительной его работы
электродами являются цинк и водород. Но электродный потен-
потенциал водорода на 0,34 В ниже потенциала меди (см. табл. 17),
454
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ XVIII
г_- МпО2
- —Zn
поэтому ЭДС элемента по мере его работы снижается от началь-
начального значения около 1,1 В приблизительно до 0,8 В.
Изменение электродных потенциалов при наличии тока на-
называется поляризацией электродов.
Вредное влияние поляризации можно предотвратить, подби-
подбирая должным образом состав электродов и электролитов. Непо-
ляризующиеся электроды мы имеем в рассмотренном выше эле-
элементе, в котором положительный электрод из меди находится
в растворе CuSO4- На медном электроде происходит выделение
той же меди, и поляризация не возникает. Цинковый же элек-
электрод (находящийся в растворе Z11SO4) при работе элемента по-
постепенно растворяется, и его со-
состав также не меняется.
Если поляризация происходит
вследствие выделения водорода
на положительном электроде, то
ее можно устранить, применяя
электроды, являющиеся сильны-
сильными окислителями (химическая
деполяризация). Широко рас-
распространенный элемент с хими-
химической деполяризацией показан
на рис. 333. Его отрицательным
электродом является цинк, а
положительный электрод состо-
состоит иэ угольного стержня, окру-
окруженного спрессованной смесью
перекиси марганца МпО2 с гра-
графитом (для увеличения электрической проводимости). Электро-
Электролитом служит паста, содержащая водный раствор хлористого
аммония NH4CI. ЭДС такого элемента несколько меньше 1,5 В.
Перекись марганца является сильным окислителем и поэтому
одновременно служит деполяризатором. Выделяющийся водо-
водород вступает в реакцию, в результате которой образуются моле-
молекулы воды:
2Н + МпО2 ->¦ Н2О + МпО,
а водород в свободном состоянии не выделяется.
Топливные элементы. В гальванических элементах энергия, выде-
выделяемая в химических реакциях, непосредственно превращается в энергию
электрического тока Этот процесс обладает гораздо большим коэффициен-
коэффициентом полезного действия, нежели применяемый в обычных электростанциях,
где теплота реакции (горение топлива) сначала превращается (с большими
потерями) в механическую работу двигателя, а уже работа двигателя пре-
преобразуется в электрическую энергию.
Однако стоимость электрической энергии, получаемой от гальваниче-
гальванических элементов, значительно выше стоимости энергии от электростанций,
Смола
N.
NH4C1
_
I
1
i
i
1
1
4s.
_ _
>>
- -
Рис 333. Гальванический элемент
с химической деполяризацией
§ 196 НАПРЯЖЕНИЕ РАЗЛОЖЕНИЯ ЭЛЕКТРОЛИТА 455
так как в элементах расходуется не дешевое топливо (например, уголь), а
дорогостоящие вещества (например, цинк).
Неоднократно предпринимались попытки использовать в гальваниче-
гальванических элементах реакцию горения угля 2С + 02 = 2С0. Эта реакция сопро-
сопровождается выделением тепла Q = 3,87 • 108 Дж/кмоль и может дать ЭДС
(для углерода Z = 4)
у,, Q _ 3,87- 108
~ ZF 9,65 ¦ 1ОГ ¦ 4 ~
Такие попытки не привели к удовлетворительным результатам, так как
уголь при обычных температурах обладает малой химической активностью.
Поэтому приходится строить элементы, работающие при высоких темпера-
температурах C00-1000 °С) и содержащие в качестве электролита различные рас-
расплавленные соли. На поддержание же высокой температуры нужно затра-
затрачивать большую энергию, и такие элементы оказываются в конечном счете
невыгодными.
Однако, используя другие виды топлива, это можно сделать при нор-
нормальной (или слегка повышенной) температуре. Устройства, в которых
энергия химической реакции между топливом и окислителем непосред-
непосредственно превращается в электрическую энергию, получили название топ-
топливных элементов. Они отличаются от гальванических элементов тем, что
реагирующие вещества хранятся не внутри устройства, а подаются в него
извне во время работы.
Примером электрохимического генератора может служить водородно-
кислородный генератор Он имеет пористые угольные или никелевые элек-
электроды, находящиеся в растворе КОН, через которые вводятся газообразные
водород и кислород. На отрицательном (водородном) электроде протекает
реакция
2Н2 + 4ОН~ -> 4Н2О + 4е~,
а на положительном (кислородном) электроде — реакция
О2 + 2Н2О + 4е^ -> 4ОН~.
Суммарная реакция есть
2Н2 + О2 -> 2Н2О,
т.е. реакция сжигания водорода. ЭДС одного элемента такого генератора
равна 1,23 В.
Электрохимические генераторы как безмашинные устройства с высо-
высоким КПД представляют большой принципиальный интерес. Однако они
находятся еще в стадии разработки и применяются пока для специальных
целей.
§ 196. Напряжение разложения электролита
Поляризация электродов происходит не только в гальвани-
гальванических элементах, но и при всяком электролизе, если выделяю-
выделяющиеся вещества отличны от материала электродов.
Поляризацию при электролизе можно наблюдать при раз-
разложении серной кислоты. Если через электролитическую ван-
456
ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
ГЛ XVIII
ну, содержащую раствор H2SO4 и два платиновых электрода
(рис. 334 а), пропускать в течение некоторого времени ток, то
на электроде, соединенном с отрицательным полюсом источни-
источника, будет осаждаться водород, а на другом электроде — кисло-
кислород. По мере накопления этих газов их парциальное давление
будет возрастать, и когда
оно сделается равным ат-
атмосферному давлению, на-
начнется выделение газов в
виде пузырьков. Если те-
теперь отключить источник
тока, то оба электрода ока-
окажутся покрытыми газами,
и мы получим гальваниче-
гальванический элемент, у которого
один из электродов состо-
состоит из водорода, а другой —
из кислорода. ЭДС такого
элемента равна 1,23 В. Если
теперь замкнуть электроды,
то в цепи появится ток, на-
H2SO
Рис. 334. Поляризация при электролизе
правление которого будет противоположно направлению тока
при электролизе (рис. 334 5), а водород и кислород будут пе-
переходить обратно в раствор в виде ионов. Когда израсходуется
накопленный запас обоих газов, ЭДС снова станет равной нулю
и ток в цепи прекратится.
ЭДС поляризации влияет на процесс электролиза. Положим,
например, что мы производим разложение раствора соляной
кислоты НС1 и пользуемся платиновыми электродами. Тогда на
электродах будут выделяться газы Kb и CI2 и появится соответ-
соответствующая им ЭДС поляризации. Если приложенное напряжение
невелико, то, когда ЭДС поляризации станет равной внешнему
напряжению, ток в цепи прекратится и электролиз приостано-
приостановится. Если постепенно повышать напряжение, то будет увели-
увеличиваться и парциальное давление газов на электродах, а вместе
с ним и ЭДС поляризации. Когда парциальное давление газов
достигнет атмосферного, начнется их выделение в виде пузырь-
пузырьков, после чего количество газов на электродах уже не будет
изменяться и ЭДС поляризации достигнет своего максимально-
максимального значения. Оно равно потенциалу хлора относительно водо-
водорода; согласно табл. 17 это составит +1,3 В. После достижения
этого напряжения в электролите появится ток, который будет
увеличиваться с увеличением напряжения, и начнется выделе-
выделение веществ на электродах.
По указанным причинам зависимость силы тока через элек-
электролит от приложенного к электродам напряжения приблизи-
§ 197 АККУМУЛЯТОРЫ 457
тельно имеет вид, изображенный на рис. 335, и выражается фор-
формулой
г = ^р-, A96.1)
где г — сопротивление столба электролита. Пороговое значе-
значение напряжения V, начиная с которого происходит выделение
веществ на электродах, называется напряжением разложения
электролита.
В рассмотренном примере с НС1 напряжение разложения
равно ЭДС поляризации. Однако в некоторых случаях напря-
напряжение разложения может превышать ЭДС поляризации. Это
явление получило название перенапря-
перенапряжения при электролизе. Так, например,
разложение раствора серной кислоты
(см. рис. 334) начинается не с напряже-
напряжения 1,23 В, а с напряжения 1,64 В.
Явление перенапряжения объясняет-
объясняется особенностями процессов нейтрализа-
нейтрализации электролитических ионов на элек- 0 г~^л JJ
тродах. Однако мы на этом не будем —*-! !-*—
останавливаться.
Таким образом, чтобы выделить ио- Рис- 335' Зависимость
ны определенного сорта из раство- силы тока чеРез элек>
ра, необходимо приложить напряжение, политическую ванну от
„ напряжения между элек-
компенсирующее их стремление перейти » (схемат1?ески)
обратно с электрода в раствор. Для раз-
разных ионов это напряжение неодинаково, что позволяет отделять
различные вещества друг от друга. Так, например, из табл. 17
видно, что ионы меди имеют меньшее стремление перейти в рас-
раствор, нежели ионы цинка. Поэтому, если в растворе имеются и
ионы меди, и ионы цинка, то выделение меди начнется при мень-
меньшем напряжении. Чтобы выделить цинк после удаления меди
из раствора, необходимо дополнительно увеличить напряжение
на электролитической ванне. Этим обстоятельством пользуются
при электролитической очистке металлов.
§ 197. Аккумуляторы
Электролитическая поляризация получила важное техни-
техническое применение в аккумуляторах, или, иначе, вторичных
элементах. Аккумуляторы представляют собой гальванические
элементы, у которых после их разрядки возможен обратный
процесс зарядки с преобразованием электрической энергии в хи-
химическую, т.е. аккумуляторы пропускают в течение определен-
определенного времени ток от постороннего источника (зарядка аккуму-
аккумулятора) .
458 ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ ГЛ XVIII
Наибольшее распространение получил свинцовый, или кис-
кислотный, аккумулятор- В простейшем виде он состоит из двух
свинцовых электродов, находящихся в растворе серной кисло-
кислоты. При погружении электродов в кислоту на них образуется
сернокислый свинец PbSC>4 и раствор насыщается той же со-
солью При зарядке аккумулятора на его электроде, соединенном
с положительным полюсом источника, свинец окисляется в пе-
перекись РЬО2, а второй электрод превращается в чистый свинец,
в результате чего получается элемент
(-)РЬ
раствор H2SO4,
насыщенный PbSC>4
РЬО2(+).
При разрядке аккумулятора его положительный полюс по-
постепенно раскисляется и на нем происходит вновь образование
PbSO4, который появляется также и на отрицательном элек-
электроде. Суммарная реакция, выражающая конечные продукты
химических превращений в аккумуляторе, имеет вид
разрядка
РЬО2 + Pb + 2H2SO4t=±2PbSO4 + 2Н2О.
^ зарядка
При зарядке аккумулятора появляются дополнительные моле-
молекулы кислоты, поэтому концентрация кислоты увеличивается.
При разрядке концентрация кислоты уменьшается.
ЭДС свинцового аккумулятора в самом конце зарядки до-
достигает 2,7 В. При разрядке она уменьшается сначала быстро,
до значения около 2,2 В, а затем очень медленно, приблизитель-
приблизительно до 1,85 В. Дальнейшую разрядку аккумулятора производить
нельзя, так как при этом его электроды покрываются толстым
слоем трудно растворимого PbSC>4 и аккумулятор портится.
Аккумуляторы характеризуются, помимо ЭДС, емкостью,
т.е. величиной заряда, отдаваемого при разрядке. Она измеря-
измеряется в ампер-часах и, очевидно, тем больше, чем больше поверх-
поверхность электродов.
Для увеличения емкости электроды аккумуляторов отлива-
отливают в виде пластин с многочисленными ячейками наподобие пче-
пчелиных сот и в ячейки запрессовывают окислы свинца. Затем
вновь изготовленные аккумуляторы подвергают нескольким за-
зарядкам и разрядкам (формовка аккумуляторов), отчего поверх-
поверхность электродов разрыхляется. После зарядки отрицательный
электрод восстанавливается до металлического свинца, а поло-
положительный электрод окисляется до РЬО2.
Наряду со свинцовыми аккумуляторами в настоящее время
применяют еще железо-никелевые, или щелочные, аккумулято-
аккумуляторы, которые отличаются меньшим весом при равной емкости.
Они имеют один электрод из железа, а другой — из никеля, а
электролитом служит раствор едкого калия КОН. В заряженном
§ 198
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
459
состоянии анодом у этих аккумуляторов служит гидрат окиси
никеля №(ОН)з, а катодом — железо. Их ЭДС — около 1,3 В
Существуют и другие типы аккумуляторов.
ГЛАВА XIX
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
При соприкосновении двух проводников электроны вслед-
вследствие теплового движения переходят из одного проводника в
другой. Если соприкасающиеся проводники различны или ес-
если их гемпература в разных точках неодинакова, то оба пото-
потока диффузии электронов неодинаковы и один из проводников
заряжается положительно, а другой — отрицательно. Поэтому
внутри проводников и во внешнем пространстве между провод-
проводниками появляется электрическое поле. В состоянии равновесия
внутри проводников устанавливается такое поле, которое как
раз компенсирует разность потоков диффузии Существованием
этих электрических полей обусловлен ряд электрических явле-
явлений в контактах, которые рассматриваются в настоящей главе
§ 198. Контактная разность потенциалов
Рассмотрим два различных проводника 1 и 2, находящих-
находящихся в электрическом контакте (рис. 336). Температуру провод-
проводников будем считать сначала оди-
одинаковой Согласно сказанному вы-
выше на обоих проводниках появляют-
появляются электрические заряды, а между
свободными их концами возникает
электрическое поле. Разность потен-
потенциалов между любыми двумя точ-
точками а и б (рис. 336), находящимися
вне проводников, но расположенны-
расположенными в непосредственной близости от
их поверхностей, называется внеш-
внешней контактной разностью потен- Рис 336
циалов или просто контактной
разностью потенциалов. В даль-
дальнейшем мы будем ее обозначать че- является электрическое поле, а
рез UU = U}-U2, где Ui - потенциал на поверхности металлов воз-
вблизи проводника 1 (в точке а), а никают заряды
С/г — вблизи проводника 2 (в точке б). Так как в отсутствие тока
поверхность каждого проводника является эквипотенциальной,
то эта разность потенциалов, конечно, не зависит от положения
При соприкоснове-
соприкосновении двух различных металлов
во внешнем пространстве по-
460
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ XIX
точек а и б, пока одна из них находится у поверхности провод-
проводника 1, а другая — у поверхности проводника 2.
Обратимся теперь к электрическому полю внутри контакти-
РЗ'ющих проводников. Если температура в каждой точке про-
проводника одинакова, то по закону Ома плотность тока j внутри
однородного проводника есть j — ХЕ. Так как наша цепь разо-
разомкнута (j = 0), то и электрическое поле в любой точке в толще
каждого проводника равно нулю, а потенциал внутри него по-
постоянен. Отсюда следует, что электрическое поле внутри провод-
проводников может существовать только в тонких пограничных слоях
на границах проводник 1 -проводник 2 и проводник 1 (или 2)-
вакуум. Потенциал же на этих границах должен испытывать
скачкообразное изменение. Разность потенциалов Щ2 = </?i — </?2,
где </?i — потенциал внутри проводника 1, a tp2 — внутри провод-
проводника 2, мы будем называть внутренней контактной разностью
потенциалов или контактным
скачком потенциала.
Рассмотрим теперь цепь, состо-
состоящую не из двух, а из нескольких
металлов 1, 2, 3, 4 (рис. 337). Если
бы мы ее разрезали по аа, то меж-
между свободными концами металлов
1 и 2 была бы контактная разность
и12 = щ- и2.
Аналогично между разрезами аа и
бб была бы разность потенциалов
и23 = и2- и3,
а у последней пары металлов
ии = и3- щ.
Так как в плоскостях аа, бб и т.д.
соприкасаются одинаковые метал-
металлы, то дополнительные разности потенциалов здесь не возника-
возникают; поэтому контактная разность всей цепи равна
'б
Рис 337. При соединении не-
нескольких проводников A, 2, 3, 4)
электрическое поле между сво-
свободными концами цепи опреде-
определяется только крайними провод-
проводниками A и 4)
= (C/i - U2) + (U2 - U3) + (С/3 - Щ) = их-Щ = Uu,
т.е. она такая же, как в отсутствие промежуточных металлов 2
и 3. Контактная разность определяется только крайними метал-
металлами цепи.
Для измерения контактной разности потенциалов употребля-
употребляют компенсационные схемы. Одна из них показана на рис. 338.
Две небольшие пластинки из исследуемых веществ располагают
параллельно друг другу, одну из пластинок закрепляют неио-
198
198 КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
461
движно, а другую с помощью простого механического устрой-
устройства заставляют колебаться в направлении нормали с небольшой
амплитудой (доли миллиметра) и частотой в несколько десят-
десятков герц. Если контактная разность равна U, а расстояние меж-
между пластинами есть d, то напряженность поля между пластина-
пластинами равна U/d, а, следовательно, на каждой единице внутренней
поверхности пластин имеется заряд e^U/d. При периодическом
изменении d заряд пластин тоже изменяется периодически. По-
Поэтому во внешней цепи появляется переменный ток, а на нагру-
нагрузочном сопротивлении г развивается переменное напряжение.
Последнее можно усилить усилителем У и зарегистрировать ос-
Рис 338 Измерение контактной разности потенциалов
циллографом О. Если теперь приложить к пластинам внешнюю
разность потенциалов от батареи Б, обратную по знаку контакт-
контактной разности, и изменять ее с помощью делителя напряжения,
то можно добиться, чтобы ток во внешней цепи обратился в
нуль. В этом случае приложенное внешнее напряжение, очевид-
очевидно, как раз равно контактной разности, которая определяется
непосредственно по показанию вольтметра V.
Контактная разность потенциалов непосредственно связана с
термоэлектронными работами выхода Ф\ и Фг контактирующих
тел (см. ниже), а именно
е?/12 = Ф2-Ф1- A98.1)
Это соотношение справедливо как для металлов, так и для по-
полупроводников. Поэтому, если работа выхода одного из провод-
проводников уже известна (например, из опытов с термоэлектронной
эмиссией), то, измеряя U\2, можно найти работу выхода другого
проводника. Этот способ широко используют для определения
работы выхода веществ с низкой температурой плавления, для
которых непосредственные измерения термоэлектронной эмис-
эмиссии невозможны.
462
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ XIX
Контактная разность потенциалов, так же как работа вы-
выхода электронов, сильно изменяется даже при ничтожных за-
загрязнениях поверхностей, их окислении и т.п. Поэтому для по-
получения верных значений контактной разности исследуемые
вещества необходимо тщательно очищать и измерения вести в
вакууме.
Происхождение контактной разности потенциалов и связь ее с работами
выхода становятся ясными при рассмотрении энергетических диаграмм
обоих проводников. Особенно прост случай двух металлов, находящихся
при температуре абсолютного нуля. Их энергетические диаграммы до
соприкосновения изображены на рис. 339 а. На нем Wo, как и раньше, есть
Рис. 339. Энергетическая диаграмма двух металлов: а ¦
контакт есть, но нет равновесия; е — равновесие
¦ контакта нет; б —
энергия покоящегося электрона в вакууме. Так как оба металла не заряже-
заряжены, то электрического поля между ними нет и Wo постоянно; Eci и Е& —
энергии дна зоны проводимости; xi = Wo — Ес\ и хг = Wo — Есч — глубина
потенциальных ям, она получила название электронного сродства данного
вещества; Fi и F? — уровни Ферми в каждом из металлов. Все энергии здесь
можно отсчитывать от любого постоянного, но одинакового для обоих ме-
металлов уровня. Разность F — Ес = ? называется химическим потенциалом
электронов. В металлах при Т = 0 он равен максимальной кинетической
энергии электронов (ср. § 155). На рис. 339 показаны также термоэлектрон-
термоэлектронные работы выхода обоих металлов:
<f>i=Wo-Fi=xi-?i, *2 = JV0-.F2 = Хг- 6
(ср. формулу A58.2)).
После соприкосновения металлов потенциальный барьер, создававший-
создававшийся вакуумным промежутком, исчезает и распределение энергий должно бы-
было бы иметь вид, показанный на рис. 339 б Однако при этом электронные
газы в обоих металлах не будут находиться в равновесии друг с другом, так
как электроны из металла 2 начнут «переливаться» в металл 1; последний
будет заряжаться отрицательно, а металл 2 — положительно. Поэтому в
металле 1 потенциальная энергия электронов, т.е. дно зоны проводимости,
будет повышаться, а в металле 2 — понижаться Так как величины \ и
? характеризуют вещества и не зависят от того, заряжено ли тело или не
заряжено, то и уровни энергии F и Wo для металла 2 будут понижаться от-
относительно их значений для металла 1. Электрический ток прекратится то-
тогда, когда уровни Ферми Fi и Рг в обоих металлах окажутся равными друг
другу (рис 339 s). Это заключение, имеющее простой наглядный смысл
§ 199
ТЕРМОЭЛЕКТРИЧЕСТВО
463
для двух металлов при Г = 0, справедливо и в общем случае любой тем-
температуры как для металлов, так и для полупроводников. При равновесии
проводников, способных обмениваться электронами, и находящихся при
одинаковой температуре, уровни Ферми в этих проводниках одинаковы.
При установившемся электронном равновесии края обеих потенциаль-
потенциальных ям уже не находятся на одинаковом уровне, а значит, потенциальная
энергия электрона —eUi у поверхности металла 1 (точка а) не равна —еС/г
у поверхности металла 2 (точка б) (рис. 339 в). Их разность есть
-eUi - (-eU2) = (xi - 6) " (Х2 - Ь) = *i - Фа-
Так как (Ui — U2) есть контактная разность потенциалов Ui2, то отсюда
получается формула A98.1).
Из рис. 339 в видно также, что в равновесии днища потенциальных ям
Ес\ и ЕС2 находятся на разных уровнях. Это показывает, что при переходе
через контактный слой внутри металлов потенциальная энергия электрона
—etp тоже изменяется. Контактный скачок потенциала U\i выражается так:
eU\2 = e{Vi-^2)=^-b- A98.2)
Он определяется разностью химических потенциалов электронов в контак-
контактирующих телах.
§ 199. Термоэлектричество
В § 198 мы видели, что на границе соприкосновения двух
различных проводников имеются контактные скачки потенциа-
потенциала U1, которые существуют и при разомкнутой цепи. Это значит,
что в приконтактном слое возникает электродвижущая сила.
Сторонние силы (§ 64) появляются в данном случае в резуль-
результате давления электронного газа, которое различно в разных
проводниках. Однако если температура всей цепи одинакова, то
результирующая ЭДС равна нулю.
Рассмотрим в качестве примера цепь, показанную на рис. 340
и состоящую из двух разных проводников 1 и 2. Будем считать
для простоты, что соединительные провода, ведущие к вольт-
вольтметру, сделаны также
из проводника 1, так A BCD
что скачки потенциа-
потенциала в контактах А и D
не возникают. Тогда
распределение потен-
потенциала в цепи будет
иметь вид, показан-
показанный на рис. 341 а.
Скачки потенциа-
потенциала в контактах В и С
111
т
'mm.
—(vV
Ш
ш
шр
т
i
Рис. 340. Термоэлектрическая цепь
равны по модулю, но противоположны по знаку, и поэтому
вольтметр, присоединенный к концам цепи А и D, не покажет
напряжения. Это справедливо для любого числа проводников:
464
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ. XIX
электродвижущая сила цепи, составленной из какого угодно чис-
числа электронных проводников (проводников 1-го рода), находя-
находящихся при одинаковой температуре, равна нулю.
Однако если температура контактов неодинакова, то полная
ЭДС цепи уже не равна нулю, и при замыкании цепи в ней по-
появляется ток. Это явление получило название термоэлектриче-
термоэлектричества, а возникающая ЭДС называется термоэлектродвижущей
силой (термо-ЭДС).
Ф1
ГЧ1
'"It
в
с
D
Рис. 341. Распределение потенциала в цепи, изображенной на рис. 340, при
Ti = Т (а) и при Т\ > Т (б)
Чтобы пояснить причины возникновения термо-ЭДС вернем-
вернемся опять к простой цепи из двух проводников (см. рис. 340) и
положим, что температура 2\ контакта В больше температуры
Г контакта С. Будем также считать для простоты, что темпе-
температура разомкнутых концов цепи А и D одинакова и тоже рав-
равна Т. Так как тепловые скорости электронов вблизи контакта В
больше, чем вблизи контакта С, то в проводнике 2 возникнет
поток диффузии электронов, направленный от В к С. В случае
полупроводников, в которых концентрация электронов увели-
увеличивается при повышении температуры, появится еще и допол-
дополнительный поток диффузии того же направления, вызванный
различием концентраций электронов в горячем и холодном кон-
концах проводника. Поэтому в проводнике 2 (на его поверхности)
возникнут электрические заряды и внутри проводника образует-
образуется электрическое поле такой величины, чтобы в установившемся
состоянии вызываемый этим полем ток дрейфа компенсировал
ток диффузии. Следовательно, при наличии в проводнике гра-
градиента температуры в нем возникает и градиент электрического
потенциала. Сказанное полностью относится и к проводнику 1.
Однако термо-ЭДС обусловлена не только возникновением
диффузии в объеме, но еще и контактными скачками потенци-
потенциала U\2 и U\\- Так как они зависят от температуры, то сумма
их уже не равна нулю. Распределение потенциала в цепи при
§ 199
ТЕРМОЭЛЕКТРИЧЕСТВО
465
неравенстве температур контактов показано на рис. 341 б. На-
Напряжение V, регистрируемое вольтметром и равное термо-ЭДС,
складывается из падения напряжения в объеме проводников и
скачков потенциала в контактах.
Термоэлектричество было открыто Зеебеком еще в двадца-
двадцатых годах прошлого века. Для его наблюдения достаточно при-
присоединить к милливольтметру два куска медной проволоки и
замкнуть их куском проволоки из другого материала, напри-
например железа. Пока температура обоих спаев одинакова, милли-
милливольтметр не обнаруживает никакой ЭДС. Но при нагревании
одного из спаев в цепи появляется термо-ЭДС и стрелка милли-
милливольтметра отклоняется. Если нагретый спай охладить и затем
нагреть другой спай, то знак термо-ЭДС изменяется и стрелка
милливольтметра отклоняется в другую сторону.
В табл. 18 приведены значения термо-ЭДС в милливольтах
для некоторых особенно употребительных пар металлов (темпе-
(температура холодного спая О °С).
Таблица 18
Темпера-
Температура
горячего
спая, °С
100
200
300
400
500
Платина,
платина
+ 10%
родия
0,64
1,44
2,32
3,25
4,22
Железо,
констан-
тан
F0% Си,
40 % Ni)
5
11
16
22
27
Медь,
канстан-
тан
4
9
15
21
—
Темпера-
Температура
горячего
спая, С
600
700
800
1000
1500
Платина,
платина
+ 10%
родия
5,22
6,26
7,33
9,57
15,50
Железо,
констан-
тан
F0% Си,
40 % Ni)
33
39
45
—
—
Медь,
констан-
тан
—
—
—
—
—
Термо-ЭДС цепи, составленной из двух различных провод-
проводников 1 и 8, при малой разности температур АГ между обоими
спаями выражается формулой
Д? = К - а2)АТ, A99.1)
где а\ зависит от природы проводника 1, а а.2 — от природы про-
проводника 2. Эти величины зависят также от температуры, и по-
поэтому AT в приведенной формуле должно быть мало. Формула
A99.1) показывает, что термо-ЭДС цепи есть разность термо-
ЭДС каждого из плеч цепи, и что в каждом из проводников
возникает термо-ЭДС Д#, = с^ДТ (г = 1,2). Величина
а = d&/dt A99.2)
называется дифференциальной термо-ЭДС данного вещества.
Она равна термо-ЭДС, развивающейся в данном проводнике при
разности температур между его концами в 1 К.
466
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ XIX
При немалой разности температур обоих спаев термо-ЭДС
равна
т2
Щ= / («1 - а2) dT, A99.3)
Ti
где Т\ — температура холодного спая, а Т^ — горячего. Если в
данном температурном интервале (Т2 — Т\) величины а\ и с*2
изменяются слабо, то вместо формулы A99.3) получаем
-Т1). A99.4)
Здесь а.\ и a.i — средние значения дифференциальных термо-
ЭДС в данном температурном интервале.
Чтобы определить не только величину, но и направление тер-
термоэлектрического тока, дифференциальной термо-ЭДС припи-
приписывают определенный знак. Величина а считается положи-
положительной, если возникающий в проводнике термоток течет от
горячего конца к холодному. Или, другими словами, в замкнутой
цепи термоток течет в горячем спае от проводника с меньшим
а (алгебраически) к проводнику с большим а.
В табл. 19 в качестве примера даны средние значения а в
микровольтах на градус кельвина в температурном интервале
0-100 °С для некоторых металлов, измеренные относительно
платины.
Таблица 19
Металл
Висмут
Константан
Никель
Палладий
а — apt, мкВ/К
-65,0
-34,4
-16,4
-5,60
Металл
Серебро
Медь
Железо
Сурьма
а — apt, мкВ/К
+7,10
+7,40
+16,0
+47,0
Абсолютные значения а получаются из приведенных в табли-
таблице прибавлением apt = —4,4 мкВ/К L). Так, для сурьмы имеем:
asb = +47,0 - 4,4 = 42,6 « 43 мкВ/К.
Рассмотрим, например, термопару железо-константан. Диф-
Дифференциальная термо-ЭДС этой цепи равна +16,0 — (—34,4)= +
+50,4 мкВ/К. При разности температур спаев Тг — 7\ = 100 К
термо-ЭДС этой пары будет +50,4-100 мкВ = 5,04 мВ. Ток в го-
горячем спае будет течь от константана (—34,4) к железу (+16,0).
Из приведенных таблиц видно, что термо-ЭДС у металлов
мала. Однако для полупроводников она намного больше и силь-
сильно зависит от содержащихся в них примесей. Для некоторых
полупроводниковых соединений дифференциальная термо-ЭДС
Значение apt получено при Т = 0 °С
§ 200
ЭФФЕКТ ПЕЛЬТЬЕ
467
к
может достигать значений 1000 мкВ/К и даже больше. Поэтому
в цепи, составленной из полупроводника и металла, термо-ЭДС
цепи очень слабо зависит от рода металла и определяется прак-
практически только полупроводником.
§ 200. Эффект Пельтье
Опыт показывает, что кроме тепла Джоуля-Ленца, выделяе-
выделяемого током в объеме проводника, наблюдаются тепловые яв-
явления в контакте двух различных проводников, даже если эти
проводники первоначально находятся при одинаковой темпера-
температуре. В контакте, через который проходит ток, происходит, в
зависимости от направления тока,
выделение или поглощение тепла,
и контакт либо нагревается, либо
охлаждается. Это явление получи-
получило название эффекта Пелътъе.
Для демонстрации эффекта
Пельтье может служить опыт,
изображенный на рис. 342. Здесь 1
и 2 — два стержня из различных
проводников, соединенные между
собой. Стержни герметически
укреплены при помощи замазки
внутри стеклянного баллона, снаб-
снабженного горизонтальной трубкой
Т, в которой находится капля во-
воды В. Стеклянный баллон может
соединяться с атмосферой или
отъединяться от нее при помощи
крана К и служит в качестве
газового термометра. При нагревании спая давление внутри
баллона увеличивается и капля перемещается вправо; при
охлаждении спая капля движется в обратном направлении.
Для опыта удобно выбрать стержни из сурьмы (Sb) и висмута
(Bi). При направлении тока от Sb к Bi спай нагревается.
Тепло Пельтье Qu, выделенное или поглощенное в спае, про-
пропорционально полному заряду </, прошедшему через спай, или
произведению силы тока i на время t:
Qn = Uq = Hit. B00.1)
Коэффициент П зависит от рода соприкасающихся проводников
и от их температуры и называется коэффициентом Пелътъе.
В дальнейшем мы будем считать тепло Qn положительным,
если оно выделяется в спае. Чтобы учесть в формуле B00.1) на-
направление тока, мы будем обозначать там, где это потребуется,
Рис 342
Пельтье
Наблюдение эффекта
468 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ. XIX
коэффициент Пельтье через П12, если ток течет от проводника
1 к проводнику 2, и через П21, если ток имеет противоположное
направление. Так как в обоих случаях количество тепла Пельтье
одинаково, но только изменяется его знак, то П12 = —Пгь
Отметим, что между явлением Пельтье и выделением теп-
тепла Джоуля-Ленца имеются существенные различия. Тепло
Джоуля-Ленца пропорционально квадрату силы тока и не за-
зависит от направления тока. Тепло же Пельтье пропорционально
первой степени силы тока и меняет знак при перемене направ-
направления тока. Далее, тепло Джоуля-Ленца зависит от сопротив-
сопротивления проводника, тогда как тепло Пельтье от него не зависит.
Если в B00.1) измерить Qn в джоулях, a q — в кулонах, то ко-
коэффициент Пельтье П будет выражен в джоулях на кулон или в
вольтах. Опыт показывает, что для большинства различных пар
металлов коэффициент Пельтье имеет величину порядка 10~2 —
— 10~3 В. Для полупроводников коэффициент Пельтье, так же
как и термо-ЭДС, на несколько порядков больше.
В обычных условиях тепло Пельтье мало по сравнению с
теплом Джоуля-Ленца. Поэтому, чтобы последнее не затуше-
затушевывало тепло Пельтье, нужно по возможности уменьшить теп-
тепло Джоуля-Ленца, а для этого следует применять достаточно
толстые проводники, обладающие малым сопротивлением.
Происхождение тепла Пельтье объясняется следующим об-
образом. Каждый электрон при своем движении переносит не
только свой заряд, но и присущую ему энергию. Поэтому при
наличии электрического тока в проводнике возникает опреде-
определенный поток энергии. Он существует и в том случае, когда
температура во всех точках проводника одинакова и переноса
энергии вследствие теплопроводности нет. Направление пото-
потока энергии совпадает с направлением движения электронов, т.е.
противоположно направлению плотности тока j.
При одной и той же плотности тока потоки энергии в разных
проводниках различны. Поэтому энергия, приходящая к кон-
контактной плоскости в проводнике i, не равна энергии, уходящей
от контактной плоскости в проводнике 2. Разность этих энергий
и есть тепло Пельтье.
Число электронов, проходящих через единичную площадку, перпенди-
перпендикулярную к направлению тока, в единицу времени, равно N = j/e. Энергия
каждого электрона складывается из его кинетической энергии W* и потен-
потенциальной энергии — е<р. Если WK есть средняя кинетическая энергия для
рассматриваемой группы N электронов, то поток энергии равен
Р =-I (WK - eip). B00.2)
е
Подчеркнем, что WK не равно просто средней кинетической энер-
энергии равновесного электронного газа, которая в классической теории есть
§ 200
ЭФФЕКТ ПЕЛЬТЬЕ
469
C/2)fcT. Это объясняется тем, что в общем случае вырожденного элек-
электронного газа не все электроны могут ускоряться электрическим полем
(ср. § 154). Однако явное выражение для WK в дальнейшем нам не по-
понадобится.
Рассмотрим теперь два контактирующих проводника 1 и 2, находящих-
находящихся при одинаковой температуре. К каждой единице поверхности контакта
в проводнике 1 подводится в единицу времени энергия Pi, а отводится в
проводнике 2 — энергия Рг. Значения потенциала ip\ и ip2 с обеих сторон
контактной плоскости различны. Кроме того, WKi и Wta в обоих провод-
проводниках в общем случае не равны друг другу. Поэтому разность (Pi — Pi) не
равна нулю. Следовательно, для поддержания температуры контакта неиз-
неизменной с каждой единицы его поверхности в единицу времени нужно отво-
отводить энергию (Pi — Рг) (или подводить ее, если эта разность отрицательна).
Это и означает, что выделяется (или поглощается) тепло Пельтье.
Если S есть площадь контакта, то тепло Пельтье равно
<Эп = (Pi - P2)St = ^ [(Wk2 - WKi) + е(<р1 - ip2)]it,
где i — jS — сила тока. Сравнивая полученное выражение с формулой
B00.1), находим для коэффициента Пельтье
Так как мы интересуемся теплом в контакте (и не рассматриваем тепло
Джоуля-Ленца в объеме), то в этой формуле под Pi и Pi нужно понимать их
значения у самой контактной плоскости. Поэтому (<pi — <рг) есть контактный
скачок потенциала [/{2 (§ 198).
Если электронный газ в проводниках невырожден, то ускоряться элек-
электрическим полем могут все электроны. Распределение импульсов электро-
электронов выражается законом Максвелла (§ 155); оно зависит только от темпера-
температуры и поэтому одинаково в обоих проводниках. Тогда расчет показывает,
что WkI = Wk2, а следовательно,
IIi2 = 0,01 - ?>г) = U\2. B00.3а)
В этом случае коэффициент Пель-
Пельтье есть просто контактный скачок
потенциала, а тепло Пельтье рав-
равняется работе, совершаемой током
вследствие перепада напряжения в
контакте.
Другой крайний случай — кон-
контакт двух металлов при темпера-
температуре абсолютного нуля (сильно вы-
вырожденный электронный газ). Ему
соответствует энергетическая диа-
диаграмма рис. 343. Здесь все кванто-
квантовые состояния в зоне проводимости
с энергией, меньшей уровня Ферми
Рис' 343' К определению тепла Пель-
тье Для ДВУХ металлов при Г = 0
F, полностью заняты электронами и ускоряться электрическим полем могут
только электроны с энергией, равной F. Поэтому под WKi и Wk2 в формуле
B00.3) следует понимать максимальные кинетические энергии электронов
и положить
Wxl=F-Ecl=ti, W*2 = F - ЕС2 = &¦
470
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ XIX
С другой стороны, согласно формуле A98.2), e(ipi — <^г) = ?i —?2- Поэтому
формула B00.3) дает
При Т = О коэффициент Пельтье равен нулю Если же Т ф 0, то оба
слагаемых в формуле B00.3) уже не компенсируют друг друга, и коэффи-
коэффициент Пельтье отличен от нуля.
§ 201. Эффект Томсона
Исследуя термоэлектрические явления, В. Томсон пришел
к заключению, что даже в однородном проводнике, если этот
проводник нагрет неравномерно, при наличии тока происходит
выделение или поглощение тепла, которое либо добавляется к
теплу Джоуля-Ленца, либо вычитается из него. Это явление,
получившее название эффекта Томсона, строго говоря, не от-
относится непосредственно к контактным явлениям. Однако его
происхождение тесно связано с причинами возникновения яв-
явлений в контактах, и поэтому мы рассмотрим его в настоящей
главе.
Для наблюдения эффекта Томсона может служить опыт, изо-
изображенный на рис. 344. Два одинаковых стержня 1 и 2 из одного
и того же материала включены в цепь тока, а концы стержней
поддерживаются при
различной темпера-
температуре (например, 100
и 0°С). В стержнях
возникает градиент
температуры dT/dx
и появляются потоки
°б 1%%3 ^ тепла. В одном из
стержней направле-
направления тока и градиента
-dT/dx
Рис. 344. Наблюдение эффекта Томсона
температуры оди-
наковЫ) в другом _
противоположны. В опыте измеряют разность температур для
двух точек а и б, выбираемых таким образом, чтобы в отсут-
отсутствие тока температура в них была одинакова. Для измерения
разности температур в точки а и б помещают спаи термопары
(§ 202). При наличии тока температуры точек а и б делаются
различными; это указывает на то, что в одном из стержней
дополнительно к теплу Джоуля-Ленца выделяется некоторое
количество тепла (тепло Томсона), а в другом стержне —
поглощается.
Знак эффекта Томсона различен для различных проводни-
проводников. Так, например, в висмуте и цинке наблюдается выделение
§ 201 ЭФФЕКТ ТОМСОНА 471
тепла, если направление потока тепла и направление тока совпа-
совпадают. Но в железе, платине, сурьме при тех же условиях проис-
происходит поглощение тепла. При изменении направления тока (или
направления потока тепла) у всех проводников наблюдается из-
изменение знака эффекта, т.е. вместо выделения тепла происходит
его поглощение и наоборот.
Эффект Томсона объясняется изменением свойств проводни-
проводника при его нагревании. Первоначально однородный проводник
при неравномерном нагревании становится неоднородным, и по-
поэтому явление Томсона представляет собой в сущности своеоб-
своеобразное явление Пельтье с той только разницей, что в данном
случае неоднородность вызвана не различием химического со-
состава проводника, а различием температур.
Пусть Qt есть тепло Томсона, выделившееся за время t в
объеме проводника т. Тогда Qt/t^ представляет собой количе-
количество теплоты, выделяющееся в единице объема за единицу вре-
времени. Эта величина оказывается пропорциональной градиенту
температуры dT/dx и плотности тока, и, следовательно,
%?= а~ j. B01.1)
Коэффициент пропорциональности а называется коэффициен-
коэффициентом Томсона. Он зависит от рода проводника и от его состоя-
состояния, в частности от температуры проводника.
Формулу B01.1) (дифференциальную форму закона) можно
представить в ином виде, если применить ее к отрезку провод-
проводника с длиной Ах и сечением S, концы которого имеют малую
разность температур ДТ (чтобы не учитывать зависимость а от
температуры). Тогда т = S Ax, jS = i есть полная сила тока, а
(dT/dx)Ax = AT, и мы находим
Qt = aATit. B01.2)
Эта формула представляет собой интегральную форму закона и
дает полное количество теплоты Томсона, выделенной во всем
рассматриваемом отрезке проводника.
Так же как и в эффекте Пельтье, мы будем считать тепло по-
положительным, если оно выделяется. За положительное направ-
направление тока примем направление от холодного конца проводника
к горячему (направление градиента температуры).
Значение коэффициента Томсона мало. Так, например, для
висмута при комнатной температуре а ~ 10~5 В/К.
Эффект Томсона, как и эффект Пельтье, возникает потому, что в про-
проводнике с током существует поток энергии Р, пропорциональный плотности
тока ] и выражаемый формулой B00.2). Конечно, при наличии градиента
температуры в проводнике имеется еще и поток энергии, обусловленный
теплопроводностью. Однако последний поток не зависит от тока, и поэто-
поэтому мы не будем его учитывать.
472
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ. XIX
T+dT
Рассмотрим в однородном проводнике бесконечно тонкий слой с пло-
площадью 1, ограниченный плоскостями х = const и х + dx = const и имеющий
объем dx (рис. 345). Положим, что электроны движутся вдоль оси X и обо-
обозначим температуру на выбранных плоскостях че-
через Г и Т + dT, а потоки энергии — через Р и Р +
+ dP. Тогда за каждую единицу времени в рассма-
рассматриваемый объем будет входить энергия Р, а вы-
выходить из него — энергия Р + dP. Следовательно,
в единице объема будет выделяться энергия
От _ Р(х) - Р(х + dx) = dP(x)
rt dx dx
Подставив теперь в эту формулу вместо Р его вы-
выражение B00.2), получим
rt
X
x x + dx
Рис. 345. К объясне-
объяснению тепла Томсона
= 3-
е
dx
3 dx'
Здесь —dtp/dx = Е есть напряженность электри-
электрического поля в проводнике. Величина же WK —
функция температуры и изменяется в пространстве потому, что изменяет-
изменяется температура Поэтому можно написать
dWK _ dWK dT
dx ~ dT dx'
Следовательно,
dT
dx +3
rt Je dT
В этой формуле второе слагаемое jE есть тепло Джоуля-Ленца, рассчитан-
рассчитанное на единицу объема и единицу времени. Первое же слагаемое показывает,
что выделяется еще и дополнительная энергия, пропорциональная j dT/dx.
Это и есть тепло Томсона.
§ 202. Применения термоэлектричества
Термоэлектричество широко используют для измерения тем-
температур. Для этого служат термоэлементы (термопары). При-
Пример технической термопары схематически показан на рис. 346.
Она содержит две проволоки из различных металлов 1 и 2,
концы которых сварены (спай I). Обе проволоки заключены в
фарфоровую трубку Т для предохранения спая от химических
воздействий. Второй спай (II) поддерживается при неизменной
температуре. Концы цепи а и б присоединяют к милливольт-
милливольтметру или (при очень точных измерениях) к потенциометру
для измерения термо-ЭДС компенсационным методом. Термо-
Термопары обладают тем преимуществом, что позволяют измерять
как очень высокие, так и очень низкие температуры, что невоз-
невозможно сделать с помощью обычных жидкостных термометров.
Для увеличения ЭДС термоэлементы соединяют последова-
последовательно в термобатареи, как показано на рис. 347. При этом все
четные спаи поддерживают при одной температуре, а все нечет-
§ 203
P-N ПЕРЕХОДЫ В ПОЛУПРОВОДНИКАХ
473
ные — при другой. ЭДС такой батареи равна сумме ЭДС от-
отдельных элементов.
Миниатюрные термобатареи, составленные из тончайших по-
полосок двух различных металлов, с успехом применяют для из-
измерения интенсивности света (как видимого, так и невидимого).
Подобные термоэлектрические приемники излучения в соедине-
соединении с чувствительным гальваномет-
ром обладают огромной чувстви-
чувствительностью. Они обнаруживают,
например, невидимое тепловое излу-
чение человеческой руки, удаленной
на расстояние многих метров; такое
излучение вызывает разность тем-
температур спаев порядка всего лишь
миллионной доли градуса.
Термобатареи представляют ин-
интерес и как маломощные генераторы
Рис. 346. Схема устройства
и включения термопары
Рис. 347. Схема термобатареи
электрического тока. По сравнению с теплосиловыми установ-
установками они исключительно просты и не содержат никаких вра-
вращающихся частей. Для устройства термогенераторов в настоя-
настоящее время применяют исключительно полупроводники, так как
термо-ЭДС у полупроводников гораздо больше, чем у металлов.
Кроме того, теплопроводность у полупроводников меньше,
чем у металлов, и поэтому бесполезный переход тепла от горя-
горячих спаев к холодным уменьшается.
Эффект Пельтье в контактах полупроводников успешно ис-
используют для устройства термоэлектрических холодильников.
§ 203. Электронно-дырочные переходы
в полупроводниках
Контакты металл-полупроводник и полупроводник-полу-
полупроводник-полупроводник не подчиняются закону Ома. Сопротивление контак-
474 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ XIX
тов зависит от приложенного напряжения, а при одном и том же
его значении может сильно изменяться при перемене направле-
направления тока.
Электронные процессы в контактах полупроводник-металл
отличаются от процессов в контактах двух полупроводников.
Мы, однако, ограничимся рассмотрением только контактов двух
полупроводников, которые находят особенно важные техниче-
технические применения.
В § 152 мы видели, что по характеру своей проводимости
полупроводники могут быть электронными (n-тип) и дырочны-
дырочными (р-тип). В полупроводниках n-типа основными подвижны-
подвижными носителями заряда являются отрицательные электроны, а
в полупроводниках р-типа — положительные дырки. В случае
контакта двух полупроводников электроны и дырки получают
возможность переходить из одного полупроводника в другой, и
поэтому между полупроводниками, так же как и между метал-
металлами, возникает контактная разность потенциалов, а в тонком
пограничном слое появляется контактное электрическое поле.
Если в контакте находятся два полупроводника одного и того
же типа (оба электронные или оба дырочные), то оба полупро-
полупроводника обмениваются одинаковыми частицами: либо электро-
электронами, либо дырками, и явления в этом случае имеют большое
сходство с явлениями в двух соприкасающихся металлах. По-
Поэтому мы остановимся только на том случае, когда один из
полупроводников имеет электронную проводимость (n-тип), а
другой — дырочную (р-тип). Такие контакты называют элек-
тропно-дырочпъши переходами пли р — п-переходами.
Отметим, что такой контакт в чистом виде нельзя получить,
прижимая друг к другу два полупроводника, так как вследствие
шероховатости поверхности соприкосновение будет происходить
лишь в немногих точках; между ними будут воздушные зазоры,
в которых образуются пленки окислов, и контакт будет иметь
сложное строение. Поэтому для получения р — n-перехода обыч-
обычно в пластинку чистого полупроводника (например, германия
или кремния) вводят две примеси — одну донорную (т.е. сооб-
сообщающую электронную проводимость), а другую акцепторную
(сообщающую дырочную проводимость), и распределяют их та-
таким образом, чтобы в одном конце имелся избыток одной из
примесей, а в другом конце — избыток другой. Тогда в одной
половине пластинки возникает электронная проводимость, а в
другой — дырочная, причем между обеими областями будет рас-
расположен тонкий переходный слой, в котором обе примеси ком-
компенсируют друг друга.
Рассмотрим сначала р — n-переход в отсутствие тока. Вслед-
Вследствие теплового движения электроны из n-области будут пере-
переходить вр-область (и там рекомбинировать с дырками), а дырки
203
P-N ПЕРЕХОДЫ В ПОЛУПРОВОДНИКАХ
475
из р-области — в n-область (и рекомбинировать с электронами).
Поэтому в n-области, вблизи границы раздела, появится поло-
положительный объемный заряд, а в р-области — отрицательный
объемный заряд; n-область приобретет положительный потен-
потенциал и энергия электрона в ней станет меньше (так как заряд
электрона отрицателен), а потенциал р-области сделается отри-
отрицательным и энергия электрона в ней увеличится. Кривая рас-
распределения потенциальной энергии электронов W3 будет иметь
вид, показанный на рис. 348 а сплошной кривой. Напротив, энер-
энергия положительных дырок WA будет больше в n-области и мень-
меньше в р-области (штриховая кривая).
n +
- p
n
p
n +
- p
'н-
lo«0,i«iH
Рис. 348. Электрический ток вр- п-переходе
В состоянии равновесия полный ток через контакт равен ну-
нулю. Этот ток в отличие от металлов, где носителями заряда яв-
являются только электроны, складывается как из движения элек-
электронов, так и из движения дырок. Остановимся на этом вопросе
подробнее.
Прежде всего напомним, что в любом полупроводнике, поми-
помимо основных носителей заряда (представленных в большинстве),
всегда имеется еще и некоторое число неосновных носителей за-
заряда (ср. § 152). Поэтому в электронном полупроводнике наряду
с электронами проводимости (основные носители заряда) име-
имеется еще небольшое число дырок (неосновные носители заряда),
а в дырочном полупроводнике, кроме дырок, еще и некоторое
число электронов. Число неосновных носителей обычно мало по
сравнению с числом основных.
Обратимся опять к рис. 348. Мы видим, что контактное поле
способствует движению неосновных носителей, которые «скаты-
«скатываются» с потенциального уступа. Поэтому все неосновные но-
носители, генерируемые в приконтактной области, движутся через
476 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ XIX
р —n-переход и образуют некоторый ток силы гН; направленный
отпкр. Сила этого тока практически не зависит от разности по-
потенциалов между п- и р-полупроводниками и определяется толь-
только числом неосновных носителей, образующихся в приконтакт-
ной области в единицу времени. Основные же носители (дырки,
движущиеся справа налево, и электроны, движущиеся слева на-
направо) образуют ток i0, направленный противоположно, т.е. от
р к п. Из рис. 348 а видно, что контактное поле препятствует
движению основных носителей, которые должны преодолевать
потенциальный барьер. В состоянии равновесия устанавливает-
устанавливается такая высота потенциального барьера, при которой полный
ток
i = i0 — iH = 0.
Посмотрим теперь, что будет происходить при наличии то-
тока через контакт. Предположим, что мы приложили к контакту
напряжение такого знака, что на n-области имеется отрицатель-
отрицательный потенциал и на р-области — положительный (рис. 348 6).
Тогда энергия электронов в n-области увеличится, а в р-области
уменьшится, а, следовательно, высота потенциального барьера
станет меньше. При этом ток неосновных носителей гн, как гово-
говорилось выше, не изменится. Ток же основных носителей г0 уве-
увеличится, так как теперь больше электронов сможет преодолеть
потенциальный барьер и перейти слева направо и больше ды-
дырок — перейти в противоположном направлении. В результате
через контакт будет идти ток г = г0 — гн, направленный от р к п;
сила тока будет быстро нарастать с увеличением приложенного
напряжения.
Иное будет происходить, если к n-области присоединен поло-
положительный полюс источника тока, а к р-области — отрицатель-
отрицательный (рис. 348 е). В этом
случае высота потенциаль-
потенциального барьера увеличится и
ток основных носителей i0
уменьшится. Уже при напря-
напряжениях порядка 1 В этот ток
практически будет равен ну-
_^_ лю, и поэтому через кон-
U такт будет течь только ток
неосновных носителей, гн, ко-
который весьма мал.
Рис 349. Вольт-амперная характерно- В СИЛУ изложенного
тикар-п-перехода вольт-амперная характери-
характеристика р — n-перехода имеет
вид, изображенный на рис. 349. Когда ток направлен от р-
к n-области, сила тока велика и быстро увеличивается с на-
§203
P-N ПЕРЕХОДЫ В ПОЛУПРОВОДНИКАХ
477
пряжением, а, следовательно, контакт для этого направления
тока (проходное направление тока) имеет малое сопротивление.
Если же ток направлен от п- к р-области, сила тока весьма
мала и почти не зависит от напряжения (ток насыщения). Для
этого направления тока (запорное направление) контакт имеет
большое сопротивление. Таким образом, р — n-переход обладает
односторонней проводимостью, или вентильным свойством,
и имеет нелинейную вольт-амперную характеристику. При
включении в цепь переменного тока такие контакты действу-
действуют как выпрямители. Такие вольт-амперные характеристики
наблюдаются и в некоторых контактах полупроводников с
металлами.
Когда приложенное обратное напряжение становится доста-
достаточно большим, в контакте происходит ряд дополнительных яв-
явлений, вызванных разогреванием контакта и действием силь-
сильного электрического поля в переходном слое. Это приводит к
быстрому увеличению обратных токов, разрушающих выпрям-
выпрямляющий переход («пробой»).
Из сказанного следует, что электрический ток в контактах
принципиально не отличается от электронной эмиссии (гл. XV).
Различие заключается в том, что при обычной эмиссии элек-
электроны выходят из металла в вакуум, в случае же контактов
электроны (и дырки) переходят из одного проводника в другой.
Так как высота потенциального барьера в контакте значитель-
значительно меньше высоты барьера на границе полупроводник-вакуум,
то сильная эмиссия наблюдается уже при комнатных темпера-
температурах. Прикладывая к кон-
контакту разность потенциа- ',
лов, мы изменяем высоту
потенциального барьера и
этим управляем силой тока
эмиссии.
Если изготовить элек-
электронно-дырочный переход
из кристалла полупровод-
полупроводника, например германия,
содержащего очень большое
число доноров или акцепто-
акцепторов (~ 1024 м~3 и выше), то
в таком сильно легирован-
легированном кристалле ширина р—п-
перехода становится очень
малой (~ 10~8 м). При этом
возникают новые явления и начальная часть прямой ветви
вольт-амперной характеристики приобретает вид, показанный
на рис. 350. В некоторой области напряжений характеристика
0
0,1 0,2 0,3 0,4 U, В
Рис. 350 Вольт-амперная характерис-
характеристика очень тонкого электронно-дыроч-
электронно-дырочного перехода (туннельного диода)
478 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ XIX
становится падающей, т.е. сила тока уменьшается при увеличе-
увеличении напряжения. Такая необычная зависимость силы тока от
напряжения хорошо объясняется современной квантовой теори-
теорией твердого тела и связана, с одной стороны, с особенностями
энергетического спектра электронов в кристаллах, а с другой —
с существованием так называемого квантовомеханического тун-
туннельного эффекта.
§ 204. Полупроводниковые диоды
Одностороннюю проводимость контактов двух полупровод-
полупроводников (или полупроводников с металлами) используют для
устройства полупроводниковых вы-
„_Ое прямителей, предназначенных для
выпрямления и преобразования пере-
переменных токов.
На рис. 351 показано устройство
одного из типов германиевого вы-
выпрямителя. Он состоит из пластинки
германия с электронной проводимо-
проводимостью, в которую с одной стороны вва-
/ . рен шарик индия, сообщающего гер-
германию дырочную проводимость, а с
Рис.351 Схема германиево- ДРУГ0Й ~ Ш&РИК °Л0Ва" ПРИ „"агре-
го выпрямителя ^ании в пР°чессе сварки индии диф-
диффундирует в германий на некоторую
глубину, так что вблизи индиевого электрода возникает дыроч-
дырочная проводимость, а на некоторой глубине образуется выпрям-
выпрямляющий р — n-переход. Оловянный электрод служит только для
включения выпрямителя в цепь тока.
Для предохранения от внешних влияний выпрямитель заклю-
заключают в герметический патрон или запрессовывают в подходя-
подходящее изолирующее вещество (на рисунке не показано). Подобные
выпрямители при площади контакта около 1 мм2 и напряжении
+1 В дают проходные токи больше 1 А, а обратные токи обычно
не превышают нескольких микроампер. При площади контакта
в несколько квадратных сантиметров германиевые и кремние-
кремниевые выпрямители способны пропускать токи в несколько сотен
ампер, хотя их размеры настолько малы, что они легко умеща-
умещаются на ладони руки. Их пробойные напряжения могут дости-
достигать многих сотен и даже нескольких тысяч вольт. На рис. 352
изображено устройство широко распространенного селенового
выпрямителя. Основным выпрямляющим элементом в нем яв-
является селеновая шайба. Она состоит из железного никелиро-
никелированного диска, на который нанесен тонкий слой полупроводни-
205
НЕРАВНОВЕСНЫЕ ЭЛЕКТРОНЫ И ДЫРКИ
479
ка — селена. Селен покрыт вторым металлическим электродом,
состав которого различен (например, сплав Bi-Cd-Sn).
В результате специальной термической и электрической об-
обработки в селене вблизи поверхности второго электрода обра-
образуется запирающий слой (р — n-переход), возникающий вслед-
вследствие диффузии вещества электродов в селен. Так как селен
обладает дырочной проводимостью, то проходное направление
тока есть направление от селена к вентильному электроду. От-
Отдельные шайбы соединяются в выпрямителе последовательно.
С селеновых выпрямителей снимают прямые токи 30-50 мА на
1 см2 поверхности, а допустимые обратные напряжения равны
25-50 В на каждую шайбу.
\
У//////////ЛУ/////Л
У//////У///////////Л
I
Рис. 352. Селеновая шайба: 1 — железная шайба, 2 — слой никеля (кон-
(контактный переход), 3 — слой селена, 4 — слой сплава Bi-Cd-Sn (вентильный
электрод), 5 — запирающий слой, возникающий на границе вентильного
электрода и селена
Полупроводниковые выпрямители применяются в радиотех-
радиотехнике для выпрямления и преобразования электрических колеба-
колебаний высокой частоты (кристаллические детекторы). Они имеют
кристаллик кремния или германия, к которому прижимается
тонкое металлическое острие (диаметром в несколько микрон).
Такие детекторы позволяют выпрямлять быстропеременные то-
токи, частота которых превышает 10u периодов в секунду, что
невозможно сделать с помощью электронных ламп.
Очень тонкие р—n-переходы используют для устройства тун-
туннельных диодов, вольт-амперная характеристика которых уже
была приведена на рис. 350. Такие диоды могут служить в ка-
качестве элементов с отрицательным дифференциальным сопро-
сопротивлением для усиления и генерации электрических колебаний
(см. § 213). Их применяют также и как быстродействующие пе-
переключатели.
§ 205. Неравновесные электроны и дырки в
полупроводниках
Рассмотрим опять контакт двух полупроводников р- и п-типа
и предположим, что через него идет ток в проходном направле-
направлении (рис. 353). Дырки в р-области движутся к р — n-переходу и,
480
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ
ГЛ XIX
проходя через него, вступают в n-область в качестве неосновных
носителей заряда, где и рекомбинируют с электронами. То же
относится и к электро-
электронам в n-области, кото-
которые, переходя границу
раздела, попадают в
р-область и рекомбини-
рекомбинируют с дырками. Однако
эта рекомбинация про-
происходит не мгновенно,
и поэтому в п-области
окажется избыточная
концентрация дырок пд,
а в р-области — избы-
избыточная концентрация
электронов пэ. При этом
избыточные дырки в
n-области будут притя-
притягивать к себе электроны,
так что увеличится и
концентрация электро-
Рис. 353. Инжекция электронов и дырок в
р — п-переходе
нов; объемный заряд, как и в отсутствие тока, не образуется.
То же будет происходить и в р-области, где увеличение концен-
концентрации электронов повлечет за собой увеличение концентрации
дырок.
Таким образом, при наличии электрического тока через
р — n-переход состояние электронов и дырок в полупроводнике
становится неравновесным. Их концентрация делается больше
ее равновесного значения, происходит как бы «впрыскивание»
дырок в n-область и электронов в р-область. Описанное явление
получило название инжекции электронов и дырок.
Отметим, что нарушение равновесного состояния электронов
и дырок можно также получить под действием освещения полу-
полупроводника, даже если последний и однороден. В этом случае
изменение концентрации электронов и дырок приводит к изме-
изменению электропроводности полупроводника под действием света
(явление фотопроводимости).
По мере движения избыточные дырки и электроны будут ре-
комбинировать и их концентрация будет уменьшаться. Поэтому
распределение концентраций избыточных электронов и дырок в
кристалле существенно зависит от скорости их рекомбинации.
Остановимся на этом вопросе подробнее.
Положим, что в полупроводнике каким-либо способом (ин-
жекцией, освещением или другим способом) была создана кон-
концентрация избыточных электронов и дырок, одинаковая во всех
местах кристалла, и что эти избыточные носители заряда ис-
§ 205 НЕРАВНОВЕСНЫЕ ЭЛЕКТРОНЫ И ДЫРКИ 481
чезают вследствие рекомбинации. Уменьшение концентрации
электронов или дырок —dn за время dt пропорционально их
избыточной концентрации п и времени: —dn = r~lndt. Здесь
г — коэффициент пропорциональности, определяющий веро-
вероятность рекомбинации, а величина т получила название средне-
среднего времени жизни избыточных (или неравновесных) носителей
заряда. Она зависит от рода и качества материала, от его со-
состояния и от содержащихся в нем примесей.
Интегрируя написанное уравнение, находим
п = n@)exp I — ) ,
где п@) — начальная концентрация избыточных носителей. От-
Отсюда видно, что т есть время, через которое концентрация
неравновесных носителей вследствие рекомбинации уменьшает-
уменьшается в е = 2,71 раза.
Пользуясь понятием времени жизни, мы можем сейчас вер-
вернуться к распределению электронов и дырок в пространстве
(рис. 353). Для этого рассмотрим в правой части кристалла
(п-области) бесконечно тонкий слой, ограниченный плоскостя-
плоскостями, параллельными р — n-переходу и удаленными от него на
расстояния х и x + dx. При малом приложенном напряжении то-
током дрейфа в электрическом поле вблизи перехода можно прене-
пренебречь по сравнению с током диффузии. Через каждую единицу
поверхности плоскости х в единицу времени вследствие диффу-
диффузии внутрь слоя будет входить число дырок —DAdnA/dx\x, где
ИД — коэффициент диффузии дырок в n-области. Через плос-
плоскость x + dx будет выходить из слоя число дырок
dx
x+dx
dx
д
dx2
Поэтому полное приращение числа дырок в единицу време-
времени вследствие диффузии, отнесенное к единице объема, рав-
равно +DAd2nAjdx1. Кроме того, внутри слоя будет происходить
уменьшение числа дырок вследствие рекомбинации. Согласно
сказанному выше число исчезающих дырок в единицу времени,
также отнесенное к единице объема, есть пД/тД. В стационар-
стационарном состоянии число поступающих дырок вследствие диффузии
должно быть равно числу дырок, исчезающих вследствие ре-
рекомбинации. Поэтому для определения пространственного рас-
распределения концентрации избыточных дырок (и равной ей кон-
концентрации избыточных электронов) в n-области мы получаем
уравнение
dx2 LI ~ U>
482 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ XIX
где введено обозначение Ьд= ^/7?дгд. Граничные условия задачи
имеют следующий вид. При х = 0 пд = пдо, где пдо — концентра-
концентрация избыточных дырок на границе n-области. Кроме того, при
х -> оо пд -> 0, так как на достаточно большом расстоянии
от перехода все избыточные дырки успевают рекомбинировать
с электронами.
Решение написанного уравнения, удовлетворяющее гранич-
граничным условиям, имеет вид
\ ЬА
Оно показывает, что концентрация инжектированных дырок
уменьшается с увеличением расстояния от перехода по экспонен-
экспоненциальному закону. Введенная нами характеристическая длина
LA есть расстояние, на котором концентрация избыточных ды-
дырок уменьшается в е = 2,71 раза. Величина LA носит название
длины диффузионного смещения или, короче, длины диффузии
дырок.
Совершенно аналогично концентрация инжектированных
электронов в р-области будет тоже уменьшаться по экспоненци-
экспоненциальному закону, но будет определяться длиной диффузии элек-
электронов Ьэ = \/Цэтэ, где D3 — коэффициент диффузии электро-
электронов, атэ — время жизни электронов в р-области.
Значения L и г в различных полупроводниках изменяются
в очень широких пределах. Укажем для примера, что в очень
чистом германии при комнатных температурах т может состав-
составлять около 1 с, что соответствует длине диффузии L в несколько
сантиметров. При наличии примесей (или иных структурных
дефектов) т и L могут уменьшаться на много порядков.
§ 206. Полупроводниковые усилители
С помощью полупроводников можно производить не только
выпрямление, но и усиление электрических колебаний (а значит,
и генерацию колебаний, если в схему ввести обратную связь).
Употребляемые для этого полупроводниковые приборы имеют
не два электрода (как в выпрямителях), а три (и больше) и
действуют подобно вакуумным электронным лампам с сетками.
Они получили общее название транзисторов.
Для разъяснения принципа усиления электрических сигна-
сигналов с помощью полупроводников мы рассмотрим только один
из типов транзисторов, так называемый биполярный диффузи-
диффузионный триод р — п — р-типа, схематически изображенный на
рис. 354 а. Он представляет собой кристалл полупроводника
(обычно германия или кремния), в котором при помощи соответ-
соответствующего распределения двух примесей созданы три области с
206
ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
483
чередующимися типами проводимости: дырочной-электронной-
дырочной, между которыми находятся два р — n-перехода. На
эти области нанесены металлические электроды, с помощью ко-
которых триод включают в схему. Одна из возможных схем вклю-
включения показана на рис. 354 а.
Как видно из рисунка, один из р — n-переходов (левый), рас-
рассматриваемый как выпрямитель, работает в проходном направ-
направлении, тогда как другой переход (правый) — в запорном. Око-
Оконечная часть кристалла, прилегающая к первому из переходов,
получила название эмиттера, а вторая, оконечная часть — кол-
коллектора. Промежуточная область называется основанием или
базой триода Ее ширина всегда мала по сравнению с длиной
диффузии неосновных носите-
носителей заряда и измеряется де-
десятками (или даже единица-
единицами) микрометров. Источник
усиливаемых колебаний при-
присоединяют между эмиттером
и базой, а усиленные ко-
колебания возникают в цепи
коллектора. Показанная схема
включения триода называется
схемой с общей базой.
Рассмотрим теперь, что
происходит внутри триода.
Основная доля электричес-
электрического тока внутри эмиттера
представляет собой движе-
движение дырок, которые являются
основными носителями заря-
заряда. Эти дырки инжектируют-
инжектируются в область основания и в ка-
качестве неосновных носителей
заряда движутся к коллекто-
Рис 354 Сравнение работы би-
биполярного диффузионного триода
р — п — р-типа (а) с трехэлектродной
лампой (б)
ру. Если длина диффузии ды-
дырок в области базы больше толщины базы, то значительная
часть инжектированных дырок достигнет коллектора. Здесь по-
положительные дырки захватываются полем, действующим вну-
внутри перехода (притягиваются к отрицательно заряженному кол-
коллектору), и, вступая внутрь коллектора в качестве основных
носителей, изменяют ток коллектора. Таким образом, всякое из-
изменение тока в цепи эмиттера будет вызывать изменение тока
в цепи коллектора То же будет справедливо и для напряжении
на эмиттере и коллекторе.
Оказывается, что изменение напряжения, возникающее на
нагрузочном сопротивлении г в цепи коллектора, можно сделать
484 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ В КОНТАКТАХ ГЛ. XIX
гораздо больше, нежели вызвавшее его изменение напряжения в
цепи эмиттера, т.е. получить усиление напряжения. Приклады-
Прикладывая между эмиттером и базой переменное напряжение, мы полу-
получим в цепи коллектора переменный ток, а на нагрузочном сопро-
сопротивлении — переменное напряжение. При этом мощность пере-
переменного тока, выделяемая в нагрузочном сопротивлении, может
быть сделана больше мощности, расходуемой в цепи эмиттера,
т.е. получится усиление мощности.
Из сказанного видно, что действие полупроводниковых три-
триодов напоминает действие вакуумных трехэлектродных ламп
(рис. 354 б). При этом роль катода играет эмиттер, роль анода —
коллектор, а в качестве сетки служит база. Изменяя напряже-
напряжение между сеткой и катодом в вакуумном триоде, мы изменяем
электронный поток в лампе и получаем изменение тока в цепи
анода. Аналогично, изменяя напряжение между эмиттером и ба-
базой, мы меняем поток неосновных носителей, инжектированных
в область базы, и этим изменяем ток в цепи коллектора.
Помимо рассмотренного полупроводникового триода, суще-
существуют и другие типы транзисторов, так же как и иные схемы
включения. Транзисторы обладают рядом преимуществ по срав-
сравнению с электронными лампами. Они не имеют накаливаемого
катода и поэтому потребляют меньшую мощность. Так как, кро-
кроме того, они не требуют вакуума (который может ухудшаться
при работе лампы), то их надежность и срок службы больше,
чем у электронных ламп. Транзисторы имеют также гораздо
меньшие размеры. Поэтому полупроводниковые приборы широ-
широко применяют вместо электронных ламп во многих радиотехни-
радиотехнических схемах и счетно-решающих устройствах.
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
И ВОЛНЫ
Среди различных механических движений особо важное зна-
значение имеют колебания — движения или процессы, обладающие
той или иной периодичностью во времени. Такие движения мы
встречаем в небесной механике (движение планет), в различных
механических машинах; они лежат в основе измерения времени
(часы). Механическими колебаниями объясняются также звуко-
звуковые явления.
Подобно этому, среди различных электрических явлений осо-
особое место занимают электромагнитные колебания, при которых
электрические величины (заряды, токи, электрические и маг-
магнитные поля) изменяются периодически. Электромагнитные ко-
колебания используют в различных важных технических устрой-
устройствах и применяют для целей связи (телефонная, телеграфная
и радиосвязь). Технические переменные токи также являются
электрическими колебаниями. Укажем, наконец, что световые
явления представляют собой не что иное, как электромагнит-
электромагнитные колебания.
ГЛАВА XX
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
§ 207. Собственные электрические колебания
Простейшей колебательной системой в механике являет-
является груз, подвешенный на пружине, движущийся без трения
(рис. 355). При этом мы предполагаем, что массой пружины
можно пренебречь по сравнению с массой груза и что вся упру-
упругость заключена в пружине (система с сосредоточенными мас-
массой и упругостью). Из механики известно, что груз, выведенный
из положения равновесия, совершает гармонические колебания,
при которых смещение из положения равновесия изменяется со
временем по синусоидальному закону.
Когда груз находится в крайних положениях (айв рис. 355),
кинетическая энергия груза равна нулю, но потенциальная энер-
486
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
t = T/2 / = 3774
гия пружины достигает максимума. При прохождении грузом
положений равновесия (б и г, рис. 355), напротив, кинетическая
энергия груза имеет наиболь-
наибольшее значение, а потенциальная
энергия пружины, которая в
этом положении ни сжата, ни
растянута, равна нулю. Поэто-
Поэтому при рассматриваемых ме-
механических колебаниях энергия
системы периодически превра-
превращается из кинетической в по-
потенциальную и обратно.
Аналогичные процессы мы
имеем при электрических коле-
колебаниях. Простейший электри-
электрический колебательный контур
состоит из конденсатора и ка-
катушки индуктивности, соеди-
соединенных между собой (рис. 356).
Мы будем считать, что емкость между витками катушки весьма
мала по сравнению с емкостью конденсатора, а индуктивность
конденсатора и соединительных проводников мала сравнитель-
сравнительно с индуктивностью катушки (контур с сосредоточенными ем-
емкостью и индуктивностью или закрытый колебательный кон-
контур)-
= 3774
О
Рис. 355. Механические колебания
с сосредоточенными массой и упру-
упругостью
Рис. 356. Электрические колебания с сосредоточенными индуктивностью
и емкостью
Предположим, что мы, разомкнув контур, зарядили конден-
конденсатор. Между пластинами конденсатора появится электричес-
электрическое поле, которое будет заключать в себе определенную энергию
(рис. 356 а). Замкнем теперь конденсатор на катушку индуктив-
индуктивности. Конденсатор начнет разряжаться, и его электрическое
поле будет уменьшаться. При этом в контуре возникнет элек-
§ 207 СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ 487
трический ток разряда конденсатора, отчего в катушке индук-
индуктивности появится магнитное поле. Через некоторое время, рав-
равное четверти периода колебания, конденсатор разрядится пол-
полностью и электрическое поле исчезнет совсем. Но магнитное
поле при этом достигнет максимума, а, следовательно, энергия
электрического поля превратится в энергию магнитного поля
(рис. 356 5).
В дальнейшие моменты времени магнитное поле будет исче-
исчезать, так как нет токов, его поддерживающих. Исчезающее поле
вызовет экстраток самоиндукции, который в соответствии с за-
законом Ленца будет стремиться поддержать ток разряда конден-
конденсатора и будет направлен так же, как и этот последний. Поэтому
конденсатор будет перезаряжаться и между его пластинами по-
появится электрическое поле противоположного направления. Че-
Через время, равное половине периода колебания, магнитное поле
исчезнет совсем, а электрическое поле достигнет максимума, и
энергия магнитного поля вновь превратится в энергию электри-
электрического поля (рис. 356 в). В дальнейшем конденсатор будет сно-
снова разряжаться и в контуре возникнет ток, направленный про-
противоположно току в предыдущей стадии процесса. Через время
C/4)Г конденсатор вновь окажется разряженным, а энергия
электрического поля снова превратится в энергию магнитного
поля (рис. 356 г), и т.д. Через промежутки времени, равные пол-
полному периоду колебания Т, электрическое состояние контура бу-
будет таким же, как и в начале колебаний (рис. 356 а).
Если сопротивление контура равно нулю, то указанный про-
процесс периодического превращения электрической энергии в маг-
магнитную и обратно будет продолжаться неограниченно долго, и
мы получим незатухающие электрические колебания.
Механические колебания, возникающие под действием сил,
развивающихся в самой колебательной системе, называют соб-
собственными колебаниями. Они возникают при всяком наруше-
нарушении равновесия колебательной системы. Подобно этому, элек-
электрические колебания, происходящие под действием процессов в
самом колебательном контуре, получили название собственных
электрических колебаний. Рассмотренные выше колебания яв-
являются, очевидно, собственными.
Пользуясь аналогией между механическими и электрически-
электрическими колебаниями, можно просто вычислить период электриче-
электрических колебаний, не прибегая к точной теории. Из механики из-
известно, что период колебаний груза на пружине выражается
формулой
Г = 2<к^/гп/к, B07.1)
где т — масса груза, а к — упругость пружины. В случае элек-
электрических колебаний роль массы играет индуктивность L, а
488
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
роль упругости — величина, обратная емкости, т.е. 1/С (§ 96).
Заменяя в B07.1) т на L, а к на 1/С, находим
Г = 2-ку/ЬС. B07.2)
Частота незатухающих электрических колебаний (число колеба-
колебаний в 1 с) равна
а круговая частота (число колебаний в 2п с)
ш = 2kv = y/l/LC. B07.26)
Если в B07.2) L выражать в генри, а С — в фарадах, то период
Т будет выражен в секундах.
§ 208. Затухание колебаний
Для исследования электрических колебаний может служить
схема, изображенная на рис. 357. Колебательный контур состо-
состоит из конденсатора емкости С, катушки
индуктивности L и реостата с перемен-
переменным сопротивлением г. Когда переклю-
переключатель К поставлен в положение 1, кон-
конденсатор заряжается от батареи Б. При
перебрасывании переключателя в поло-
положение 2 колебательный контур замы-
замыкается и в нем возникают колебания.
Напряжение между пластинами конден-
конденсатора подается на одну из пар пластин
электронного осциллографа О (§ 188),
к другой паре пластин приложено пи-
пилообразное напряжение от специально-
специального генератора ГР, осуществляющее раз-
развертку во времени. Тогда электронный
луч прочерчивает на экране осциллогра-
осциллографа кривую, дающую зависимость напря-
напряжения от времени, U = f(t). Так как
это напряжение равно U = qjC, где q —
мгновенное значение заряда конденсато-
Рис. 357. Схема для на-
наблюдения электрических
колебаний с помощью ос-
осциллографа
ра, то получаемая кривая выражает одновременно в некотором
масштабе и изменение во времени заряда конденсатора.
В подобных схемах удобно производить переключение конденсатора пе-
периодически много раз в секунду; для этого в качестве переключателя К
можно использовать добавочную схему с электронными лампами. При этом
переключатель связывают электрически с генератором развертки ГР так,
208
ЗАТУХАНИЕ КОЛЕБАНИЙ
489
чтобы запуск генератора производился всякий раз одновременно с замыка-
замыканием колебательного контура. Тогда на экране осциллографа появляются
быстро следующие друг за другом тождественно расположенные кривые,
которые для глаза сливаются в единую яркую кривую U — /(?), неподвиж-
неподвижно расположенную на экране.
Если бы сопротивление контура было равно нулю, то мы име-
имели бы назатухающие электрические колебания. Изменение заря-
заряда конденсатора с течением
времени выражалось бы кри-
кривой а рис. 358, которая, как
мы увидим в § 209, есть сину-
синусоида. По такому закону из-
изменялось бы и напряжение
на конденсаторе и сила тока
в контуре — колебания были
бы гармоническими.
В действительности же
сопротивление контура всегда
не равно нулю. Вследствие
этого энергия, первоначаль-
первоначально запасенная в контуре,
непрерывно расходуется на
выделение тепла Джоуля-
Ленца, так что интенсивность
электрических колебаний
постепенно уменьшается, и
в конце концов колебания
прекращаются вовсе. Поэтому на экране осциллографа мы
видим кривую типа б рис. 358 (затухающие электрические ко-
колебания). Если увеличить сопротивление контура, то затухание
колебаний увеличивается (кривая в рис. 358).
В связи с изложенным отметим, что периодическими мы на-
называем такие процессы, в которых изменяющиеся физические
величины (например, электрический заряд q) через определен-
определенные промежутки времени (период колебания Т) принимают оди-
одинаковые значения:
q(t+T)=q(t). B08.1)
Так, например, гармонические колебания, изображаемые кривой
а рис. 358, есть периодический процесс, имеющий совершенно
определенный конечный период Т. Напротив, затухающие коле-
колебания, изображаемые кривыми бив рис. 358, не имеют конеч-
конечного периода (Т = оо) и поэтому, строго говоря, не являются
периодическим процессом. Тем не менее, если затухание мало,
небольшие отрезки кривых бив можно приближенно рассма-
рассматривать как отрезки соответствующей синусоиды и говорить о
Рис. 358. Затухание электрических ко-
колебаний
490 СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ ГЛ XX
затухающих колебаниях как о гармонических колебаниях, ам-
амплитуда которых постепенно уменьшается.
Для количественной характеристики затухания пользуют-
пользуются тем, что отношение двух последовательных амплитуд qn и
Qn+i (рис. 358 б) остается постоянным в течение всего процесса
(§ 210). Натуральный логарифм этого отношения
6 = In -2=- B08.2)
принимают за меру затухания колебаний и называют логариф-
логарифмическим декрементом затухания.
Если постепенно увеличивать сопротивление контура г, то
затухание колебаний увеличивается и логарифмический декре-
декремент растет. Когда сопротивление превышает некоторое опре-
определенное для данного контура значение гк, колебания не возни-
возникают вовсе. При достаточном увеличении сопротивления заряд
конденсатора уменьшается монотонно и асимптотически стре-
стремится к нулю (рис. 358 г).
Сопротивление гк называется критическим сопротивлением
контура. Оно зависит от емкости и индуктивности контура. Для
возникновения электрических колебаний, следовательно, необ-
необходимо, чтобы сопротивление контура г было меньше критиче-
критического сопротивления. При г > гк происходит апериодический
разряд.
Отметим, что рассмотренные особенности разряда в электри-
электрическом колебательном контуре совершенно аналогичны особен-
особенностям механической колебательной системы, обладающей тре-
трением.
§ 209. Уравнение собственных электрических
колебаний. Колебания в отсутствие затухания
Рассмотрим теперь количественно собственные колебания в
контуре с сосредоточенными постоянными.
В дальнейшем мы будем считать, что электрические процес-
процессы в контуре квазистационарны (§ 73). Это значит, что мгновен-
мгновенное значение силы тока i одно и то же
в любом месте контура и к мгновен-
мгновенным значениям электрических вели-
величин можно применять законы Кирх-
Кирхгофа.
Условимся считать заряд конден-
конденсатора q положительным, если зна-
Рис. 359 К выводу уравне- ки зарядов на обкладках совпадают с
ния электрических колеба- показанными на рис. 359, а силу то-
ний в контуре с сосредото- ка — положительной, если ток направ-
ченными постоянными лен против часовой стрелки. Согласно
§ 209 УРАВНЕНИЕ СОБСТВЕННЫХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ 491
второму закону Кирхгофа сумма падений напряжения в контуре
равна сумме действующих в нем ЭДС. В нашем случае имеются
два падения напряжения: на сопротивлении г, равное ri, и на
конденсаторе Uc, которое противоположно по знаку падению
ri. Кроме того, имеется ЭДС самоиндукции, равная —Ldijdt.
Поэтому
ri-Uc = -Ldi/dt. B09.1)
Далее, напряжение на конденсаторе равно
Uc = д/С, B09.2)
а сила тока связана с зарядом конденсатора соотношением
i = -dq/dt. B09.3)
Знак минус в последнем соотношении стоит потому, что вы-
выбранное положительное направление i соответствует уменьше-
уменьшению (положительного) заряда конденсатора.
Из этих трех уравнений можно исключить две из трех ве-
величин q, i, U и получить дифференциальное уравнение, свя-
связывающее лишь одну из них и время t. Подставляя, например,
выражения B09.2) и B09.3) в B09.1), находим уравнение для
заряда конденсатора в виде
Lcfq_ dq a Q
ь dt*+r dt + с u-
Разделим обе части этого уравнения на L и введем следующие
обозначения:
Тогда окончательно имеем
g |g 0. B09.5)
Мы получили линейное дифференциальное уравнение второ-
второго порядка с обыкновенными производными и с постоянными
коэффициентами. Такое же точно уравнение мы получили бы
для напряжения U и для силы тока %. Отметим, что колеба-
колебания, описываемые линейными дифференциальными уравнени-
уравнениями, называются линейными колебаниями, а соответствующие
колебательные системы — линейными системами.
Для того чтобы задача была определенной, необходимо еще
задать начальные условия, которых, как известно, для уравне-
уравнения второго порядка должно быть два. Положим, что мы начи-
начинаем отсчет времени с момента замыкания контура и обозначим
начальную величину заряда конденсатора через qo. Так как в
начальный момент сила тока равна нулю, то начальные условия
задачи таковы:
t = Q: q = q0, dq/dt = 0. B09.6)
492 СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ ГЛ XX
Положим сначала, что сопротивление контура г = 0. Тогда
уравнение колебаний B09.5) принимает более простой вид
^| + wjfe = 0. B09.7)
Общее решение этого уравнения есть гармоническое колебание
q — A cos (coot + <р), B09.8)
где постоянные А и у (амплитуда и начальная фаза) могут
иметь произвольные значения. В справедливости этого можно
убедиться, подставляя написанное решение в B09.7). Следова-
Следовательно, мы имеем гармоническое колебание с частотой шо =
= y/l/LC. Этот результат мы уже получили в § 207 при помощи
менее строгих рассуждений.
Постоянные А и (р определяются начальными условиями
B09.6). Подставляя решение B09.8) в B09.6), имеем
A cos <р = go) Ado sin <p — 0.
Это дает
Ч> = 0, А = q0,
после чего решение B09.8) принимает следующий окончатель-
окончательный вид:
q = qo coswo^. B09.9)
Графическое изображение этого решения есть косинусоида, по-
показанная на рис. 358 а.
Напряжение на конденсаторе изменяется по закону:
Uс — q/C = Щ cos wo*,
где Uq — qo/C есть амплитуда напряжения, равная начальному
напряжению на конденсаторе.
Сила тока в контуре равна
где io = 9owo — амплитуда тока. Сила тока, также как и заряд,
изменяется по гармоническому закону; однако если заряд изме-
изменяется по закону ко-
косинуса, то сила то-
тока — но закону сину-
синуса. Так как sinwo^ =
= cos (toot — 7г/2), то
это значит, что меж-
между колебаниями заря-
заряда и силы тока су-
существует разность фаз
7г/2, причем колебания
Рис. 360. Кривые колебаний заряда конденса- силы тока отстают по
тора и силы тока без затуханий фазе (рис. 360).
§ 210 КОЛЕБАНИЯ ПРИ НАЛИЧИИ ЗАТУХАНИЯ 493
§ 210. Колебания при наличии затухания
Рассмотрим теперь реальный контур, сопротивление которо-
которого не равно нулю. В этом случае колебания описываются пол-
полным дифференциальным уравнением B09.5). Его решение имеет
различный вид в зависимости от соотношения между коэффи-
коэффициентами. Положим сначала, что
ш§ > a2. B10.1)
Тогда решение есть
q = Ae~at cos (ш« + <р). B10.2)
Здесь А и <р — по-прежнему постоянные, значения которых опре-
определяются начальными условиями, величина же и равна
и = yjwl - a2. B10.3)
В том, что B10.2) совместно с B10.3) действительно является
решением уравнения B09.5), проще всего убедиться, подставляя
B10.2) в B09.5).
Полученное решение есть аналитическое выражение кривых
затухающих колебаний бив рис. 358. Кривая в соответствует
большему значению коэффициента or. С теми оговорками, кото-
которые были сделаны в § 208, формулу B10.2) можно истолковать
как гармоническое колебание с круговой частотой ш и с ампли-
амплитудой
У = Ае~ы,
которая не остается постоянной, а непрерывно уменьшается с те-
течением времени. Показатель а называется коэффициентом за-
затухания колебаний.
Исследуем подробнее решение B10.2) и найдем прежде всего
те моменты времени, в которые заряд q достигает максимумов
и минимумов. Для этого, согласно правилу нахождения экстре-
экстремумов, продифференцируем B10.2) и приравняем первую про-
производную нулю:
§ = -Aae~Qt cos {ut + <р) - Awe~at sin {ut + у) = 0,
или
tg (wt + ip) = -а/ш.
Пусть t = t\ есть какое-либо решение этого уравнения. Тогда
его решениями будут также
..., h-2T, tj-T, ti+T, h+2T,...
..., ti-C/2)r, ii-(l/2)T, <,+(l/2)T, t! + C/2)r,...,
где
T = 2it/uj. B10.4)
494 СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ ГЛ. XX
Легко убедиться, что если при t = t\ мы имеем максимум q,
то все значения t, стоящие в верхней строчке, соответствуют
также максимуму (cPq/dt2 < 0), а все значения нижней строч-
строчки — минимуму q. Таким образом, хотя затухающие колебания
не являются периодическим процессом в строгом смысле слова,
этот процесс обладает все же определенной повторяемостью в
том смысле, что максимальные и минимальные значения заря-
заряда (а также тока и напряжения) достигаются через одинаковые
промежутки времени Т. То же относится и к значениям заря-
заряда (силы тока и напряжения), равным нулю. Этот промежуток
времени Т мы и называем периодом затухающих колебаний.
Пусть qn и qn+\ — максимальные значения заряда конден-
конденсатора (см. рис. 358 б) в двух последовательных максимумах с
номерами пи (п +1). Они достигаются в моменты времени tn и
*п+1, причем tn+i = tn+T. Согласно B10.2) и B10.4) имеем
qn = Аехтр {-atn) cos {utn + f),
qn+i = Aexp [—a(tn + T)] cos [w(in + 2-к/ш) + <p] =
= A exp [-a(tn + T)] cos (wtn + <p).
Деля почленно оба эти равенства, находим
Мы видим, что отношение двух последовательных максималь-
максимальных значений заряда не зависит от номера максимумов. Вве-
Введенный нами в § 208 логарифмический декремент затухания 5,
следовательно, имеет значение
S = \n{qJqn+l)=aT; B10.5)
он равен произведению коэффициента затухания на период ко-
колебаний.
Логарифмический декремент затухания 5 можно определить
еще иначе. Обозначим через *i время, в течение которого ампли-
амплитуда колебаний уменьшается в е раз. Тогда
е~^ = 1/е,
а, следовательно,
aii = 1.
Деля почленно B10.5) на полученное соотношение, имеем
T/ii = 1/N = 5.
Здесь N — число полных колебаний, происходящих за время
ii. Таким образом, логарифмический декремент есть величи-
величина, обратная числу колебаний, по истечении которых амплитуда
уменьшается в е раз.
Для характеристики затухания колебательных контуров часто
пользуются (особенно в радиотехнике) еще другой величиной,
называемой добротностью контура и обозначаемой обычно Q.
§ 210 КОЛЕБАНИЯ ПРИ НАЛИЧИИ ЗАТУХАНИЯ 495
Она связана с логарифмическим декрементом соотношением
Q = п/6. B10.6)
Так как 5 = 1/N, то
Q = nN. B10.6а)
Добротность контура есть умноженное на 7Г число полных коле-
колебаний, по истечении которых амплитуда уменьшается в е раз.
Добротность контура, следовательно, тем выше, чем меньше за-
затухание колебании в нем.
Формула B10.3) показывает, что частота электрических ко-
колебаний ш зависит от коэффициента затухания а и не равна
частоте колебаний щ того же контура при сопротивлении г =
= 0 (а — 0). С увеличением сопротивления контура частота ш
уменьшается, а период колебаний Т увеличивается. Предполо-
Предположим теперь, что сопротивление контура велико, так что
w2. < а2.
Тогда частота ш, выражаемая формулой B10.3), будет мнимой.
Это значит, что решение B10.2) уже несправедливо, а, следо-
следовательно электрических колебаний в контуре не будет. В таком
случае решение основного уравнения B09.5) имеет вид
q = Ai exp {-kit) + А2 exp (~k2t), B10.7)
где
к\ — а+ J а2 — ш%, к2 — a— J а2 — w2,,
а А\ и Лг — произвольные постоянные. Подставляя B10.7) в
B09.5), можно убедиться, что уравнение при этом удовлетворя-
удовлетворяется тождественно, а, следовательно, B10.7) есть действительно
искомое решение. Так как Ц, < а2, то к\ и ki вещественны и по-
положительны.
Значения постоянных А\ и Ai определяются начальными
условиями задачи. Если таковыми являются условия B09.6), то
g|t=o = А\ + А2 = qo, dq/dt\t=o = -Axki - А2к2 = 0.
Это дает
А\ = -qofo/ih - к2), А2 = qoh/(ki - k2),
после чего решение B10.7) принимает вид
q = kiq%2 ih ехР (-^2*) ~ к2 exp (-kit)).
Если сопротивление контура очень велико, так что а2 ^§> ш2,
то к\ 3> к2, и в последнем выражении можно пренебречь вторым
слагаемым по сравнению с первым, а в знаменателе — к2 по
сравнению с к\. Тогда
<7 = qoexp(-k2t).
Этот случай соответствует рис. 358 г.
496
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
Из сказанного видно, что для возникновения электрических
колебаний необходимо, чтобы выполнялось условие B10.1). Под-
Подставляя вместо а и ц их значения B09.4), находим это условие
в виде
1
W
B10.8)
§ 211. Поддержание колебаний. Искровой контур
Всякий реальный колебательный контур обладает всегда
некоторым сопротивлением. Поэтому возникшие в нем электри-
электрические колебания затухают и через некоторое время, зависящее
от добротности контура, прекращаются совсем. Но для техниче-
технического использования электрических колебаний необходимо, что-
чтобы они существовали как можно дольше, а для этого необходимо
их поддерживать.
Простейший и наиболее старый способ поддержания коле-
колебаний заключается в применении искрового контура, изобра-
изображенного на рис. 361. Он состоит из конденсатора С, катушки
индуктивности L и искро-
вого разрядника, соеди-
соединенных последовательно.
К обкладкам конденсато-
конденсатора присоединен источник
постоянного высокого на-
напряжения.
После включения ис-
источника напряжения кон-
конденсатор заряжается и
напряжение между его
обкладками увеличивает-
увеличивается. Когда оно достигает
напряжения пробоя ис-
Рис. 361. Искровой колебательный контур крового разрядника, че-
через разрядник проскаки-
проскакивает искра, замыкающая колебательный контур, и в контуре
возникает цуг затухающих колебаний. Эти колебания продол-
продолжаются до тех пор, пока амплитуда напряжения на конденсато-
конденсаторе не сделается равной напряжению гашения искры, после чего
искровой разряд прекращается и колебания обрываются. Затем
конденсатор начинает опять заряжаться, его напряжение увели-
увеличивается, и через некоторое время искровой промежуток опять
пробивается, отчего в контуре возникает новый цуг затухающих
колебаний и т.д. Чтобы возникающие колебания не закорачива-
закорачивались на источник тока, последний присоединен к конденсатору
через катушки самоиндукции (дроссели) Д. Они представляют
§ 212 АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ 497
собой большое сопротивление для быстропеременных токов, но
не препятствуют прохождению более медленно меняющегося то-
тока от источника.
Основное достоинство искрового контура заключается в его
исключительной простоте. Его недостатками являются сильный
шум, издаваемый искрой, обгорание электродов разрядника и,
самое главное, существенное отличие получаемых колебаний от
синусоидальных (гармонических). Поэтому искровые контуры в
настоящее время применяются редко.
§ 212. Автоколебательные системы
Для получения длительно существующих электрических (и
механических) колебаний большое значение имеют так называ-
называемые автоколебательные системы. Устройства, объединяемые
под этим общим названием, характеризуются следующими от-
отличительными свойствами.
Автоколебательные системы способны генерировать незату-
незатухающие колебания. Эти колебания могут быть гармонически-
гармоническими (синусоидальными) или более сложной формы, но они могут
продолжаться неограниченно долго, до тех пор, пока не вышли
из строя элементы, образующие систему.
Автоколебательные системы отличаются от рассмотренного
в § 207 колебательного контура с сопротивлением, равным ну-
нулю. Такой контур представляет собой предельный случай, недо-
недостижимый на практике. Автоколебательные же системы суть
реальные устройства, сопротивление которых не равно нулю.
В автоколебательных системах незатухающие колебания воз-
возникают под влиянием процессов, происходящих внутри системы,
и для их поддержания не требуется никаких внешних воздей-
воздействий. В этом отношении автоколебания радикально отличаются
от вынужденных колебаний, которые также могут быть незату-
незатухающими, но для своего существования требуют периодических
внешних воздействий (в механике — внешних сил, в электриче-
электричестве — приложенных извне напряжений).
В состав автоколебательных систем входит источник энергии
(в случае механических колебаний — сжатая пружина, поднятый
груз и т.д., в случае электрических — батарея или иной источник
тока). Этот источник периодически включается самой системой
и вводит в нее определенную энергию, компенсирующую поте-
потери на выделение тепла Джоуля-Ленца, что и делает колебания
незатухающими.
Так как колебания в автоколебательных системах устанав-
устанавливаются под влиянием процессов, происходящих внутри систе-
системы, то они возникают самопроизвольно (самовозбуждение), под
действием случайных малых воздействий, выводящих систему
498
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
из равновесия (флуктуации). Возникшие малые колебания са-
самопроизвольно нарастают, и в конце концов в системе образу-
образуются установившиеся колебания, свойства которых (частота, ин-
интенсивность, форма) определяются параметрами системы и не
зависят от начальных условий.
Хорошим примером автоколебательной системы в механике
могут служить известные всем часы, в которых незатухающие
колебания маятника поддерживаются с помощью анкера.
Процессы в любой автоколебательной системе описывают-
описываются обязательно нелинейными дифференциальными уравнения-
уравнениями. Так как теория нелинейных колебаний значительно более
сложна, нежели теория колебаний линейных, рассмотренных в
§ 209, 210, мы ограничимся в дальнейшем только разъяснением
принципов действия некоторых электрических автоколебатель-
автоколебательных систем.
§ 213. Использование отрицательных сопротивлений
Мы уже говорили, что некоторые проводники обладают па-
падающей вольт-амперной характеристикой (напряжение умень-
уменьшается при возрастании тока), и поэтому дифференциальное
сопротивление R\ = dU/di таких проводников отрицательно
(§ 176).
Если ввести в колебательный контур, обладающий сопро-
сопротивлением г, проводник с падающей вольт-амперной характери-
характеристикой, то затухание контура уменьшается. При определенном
соотношении между параметрами контура и включенным отри-
отрицательным сопротивлени-
сопротивлением затухание может ис-
исчезнуть совсем, и тогда в
таком контуре возникают
незатухающие колебания.
На рис. 362 изображе-
изображена автоколебательная сис-
система, в которой отрица-
отрицательным сопротивлением
служит дуговой разряд.
Постоянное напряжение от
источника тока подводит-
подводится к электродам дуги через
дроссели Д. Если емкость
С и индуктивность L подобраны так, что частота колебаний
попадает в область звукового спектра, то появление колебаний
приводит к звучанию дуги; описанная схема получила поэто-
поэтому название поющей дуги. Появление звука объясняется тем,
что через дугу протекает переменный ток электрических коле-
Рис. 362. Получение незатухающих коле-
колебаний с помощью отрицательного сопро-
сопротивления
§ 213 ИСПОЛЬЗОВАНИЕ ОТРИЦАТЕЛЬНЫХ СОПРОТИВЛЕНИЙ 499
баний, который вызывает переменное нагревание дуги и вслед-
вследствие этого ее пульсацию, так что в окружающем воздухе воз-
возникает звуковая волна. Этот звук можно значительно усилить,
если вблизи катушки индуктивности L расположить вторую ка-
катушку К, соединенную с громкоговорителем Т. Тогда в катушке
К будет наводиться вследствие электромагнитной индукции пе-
переменный ток и громкоговоритель будет издавать звук, высота
которого будет соответствовать частоте колебаний в контуре.
Изменяя емкость и индуктивность, можно убедиться, что при
увеличении L или С высота звука понижается, т.е. частота ко-
колебаний уменьшается.
В этой схеме вместо дуги мы могли бы использовать тун-
туннельный диод. Однако падающий участок его характеристики
расположен в области малых напряжений и токов (ср. рис. 350),
и, следовательно, амплитуда колебаний в этом случае была бы
слабее.
Рассмотрим теперь подробнее, каким образом здесь возника-
возникают автоколебания. Припишем току и напряжению определенные
знаки и будем считать ток контура положительным, если он
направлен по часовой стрелке (см. рис. 362), а напряжение U
между точками 1 к 2 положительным в том случае, если по-
потенциал точки 1 выше потенциала точки 2. Следовательно, по-
положительное напряжение между 1 и ? вызывает в контуре ток
положительного направления. Обозначим через го постоянный
ток, существующий в дуге в отсутствие колебаний, и предполо-
предположим, что вследствие каких-либо случайных причин в контуре
возникли колебания и появился переменный ток г. Этот ток
будет проходить и через дугу и алгебраически складываться с то-
током iq. Так как положительное направление тока i противопо-
противоположно направлению го (см. рис. 362), то колебания полного тока
дуги будут изображаться кривой / = г'о + i, минимумы которой
совпадают с максимумами кривой г(?), и наоборот (рис. 363 5).
Колебания тока / вызовут переменное напряжение и меж-
между точками 1 и 2, которое можно найти из вольт-амперной ха-
характеристики дуги (рис. 363 а). Это напряжение изображается
кривой U (рис. 363 в), которая имеет постоянную составляющую
Uq и переменную составляющую и. Сравним теперь переменные
составляющие тока (г) и напряжения (и). Из рис. 363 б, в вид-
видно, что они находятся в фазе, т.е. положительные значения и
соответствуют положительным значениям г и наоборот. Но это
значит, что переменное напряжение способствует переменному
току, его «подталкивает», или, иными словами, что в контур
вводится определенная энергия за счет источника тока. Если
эта энергия больше расходуемой на выделение тепла Джоуля-
Ленца, то амплитуда колебаний будет нарастать. При этом бу-
будут расти и потери энергии в контуре, и когда они станут равны
500
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ XX
энергии, вводимой в контур, установятся незатухающие колеба-
колебания постоянной амплитуды.
= /„+/
V ! V
Al A
/\
V V V
А! А
U0+u
-Un
Рис. 363- Возникновение незатухающих колебаний в контуре с отрицатель-
отрицательным сопротивлением
Условия самовозбуждения колебаний в цепи, содержащей
проводник с отрицательным дифференциальным сопротивлени-
сопротивлением, рассмотрены в Добавлении 9.
§ 214. Ламповые генераторы. Обратная связь
В настоящее время почти исключительно применяют автоко-
автоколебательные схемы с электронными лампами или полупроводни-
полупроводниковыми приборами. Они обладают большой надежностью в ра-
работе и позволяют широко варьировать частоту, интенсивность и
форму колебаний.
Мы рассмотрим принцип работы таких устройств на при-
примере лампового генератора, одна из простейших схем которого
изображена на рис. 364. Колебательный контур, содержащий ем-
емкость С и индуктивность L, включен в цепь сетки электронной
лампы. В цепи анода, кроме питающей батареи, имеется еще ка-
катушка К, расположенная в непосредственной близости к катуш-
катушке L, так что между обеими катушками существует индуктивная
связь.
Принцип действия генератора заключается в следующем.
Когда в колебательном контуре возникают колебания (при
§214
ЛАМПОВЫЕ ГЕНЕРАТОРЫ ОБРАТНАЯ СВЯЗЬ
501
включении батареи или под влиянием каких-либо случайных
причин), то между обкладками конденсатора появляется пере-
переменное напряжение. Такое же напряжение возникает между сет-
сеткой и катодом лампы, так как они присоединены к обкладкам
конденсатора. Вследствие этого в цепи анода появляется пере-
переменный ток га. Но катушки К и L индуктивно связаны меж-
между собой, и поэтому переменный ток га вызывает в катушке L
переменную ЭДС взаимной ин-
индукции Ш = —М dia/dt (M — ко-
коэффициент взаимной индуктив-
индуктивности). Эта ЭДС, в зависимости
от взаимного направления вит-
витков катушек К и L, может либо
препятствовать колебаниям тока
в контуре, либо способствовать
им. Очевидно, что, пересоединяя
в случае необходимости концы
катушки К, можно всегда до-
добиться того, чтобы возникающая
ЭДС 8 была того же знака, что Рис. 364. Ламповый генератор с
И ток г в контуре. Тогда работа колебательным контуром в цепи
этой ЭДС будет положительна, сетки
и колебательный контур будет получать энергию за счет источ-
источника тока, так что затухание контура уменьшится. Если связь
между катушками достаточно велика, получаемая энергия мо-
может стать больше той, которая затрачивается в контуре. В этом
случае амплитуда колебаний будет нарастать до тех пор, пока
получаемая энергия не сделается равной потерям, после чего
установятся незатухающие колебания.
Рисунок 365 более детально разъясняет сказанное. Будем
считать заряд конденсатора положительным, если на сетке воз-
возникает положительный потенциал относительно катода, а за по-
положительное направление тока контура г (и ЭДС Щ примем
направление, указанное на рис. 364. Тогда, если сеточное напря-
напряжение ис изменяется в соответствии с кривой рис. 365 б, то ток
контура г изображается кривой в. Переменный ток га в цепи ано-
анода, вызываемый колебаниями сеточного напряжения ис, можно
найти при помощи сеточной характеристики триода (рис. 365 а).
Ее «рабочая точка» А выбрана в средней части, где характери-
характеристика близка к линейной. Так как положительный потенциал
сетки вызывает положительный ток ia, то изменения га изобра-
изображаются кривой г. Кривые д и е дают изменения ЭДС взаимной
индукции $ при двух возможных направлениях витков катуш-
катушки К. Сравнивая эти кривые с кривой в, мы видим, что в случае
кривой е колебания ЭДС и тока находятся в противофазе: при
положительном токе г возникает отрицательная ЭДС %>2 и нао-
502
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
борот. В последнем случае ЭДС взаимоиндукции препятствует
колебаниям, и затухание контура увеличится. В случае д, на-
напротив, колебания ЭДС и тока находятся в фазе и ЭДС способ-
способствует колебаниям тока, отчего затухание контура уменьшится.
При достаточно сильной связи в этом случае в контуре возни-
возникают незатухающие колебания.
а га1
>
X
с
t
'а2.
"^ис1 цс
uc=q/C
I I I
i = -dqldt
¦+¦
\I/
i i
I I I
i i
/Т\ I
Л\
¦g'2=+Mdia/dt
/Т\
i
i
i
Рис. 365. Возникновение незатухающих колебаний в ламповом генераторе
Наиболее характерной особенностью рассмотренной схемы
лампового генератора является то, что колебательный контур
воздействует на другую цепь, содержащую источник тока (в на-
нашем случае — на анодную цепь лампы), а эта последняя ока-
оказывает обратное действие на колебательный контур, которое и
поддерживает колебания. Такой прием получил название обрат-
обратной связи и широко применяется в различных механических и
электрических автоколебательных системах.
Так, например, обратную связь мы имеем в часах. Если бы в часах не
было анкера и ходового колеса, то закрученная пружина (или гиря) дей-
действовала бы на маятник с постоянной силой и сообщала бы ему односто-
одностороннее движение. Подобно этому, если в ламповом генераторе устранить
катушку обратной связи К и лампу и замкнуть контур непосредственно на
батарею, то в контуре будет лишь постоянный ток. В часах колеблющийся
маятник с помощью анкера и ходового колеса управляет силой, действую-
действующей на него самого, и превращает постоянную силу пружины в периоди-
периодические толчки В ламповом генераторе колебательный контур с помощью
лампы и катушки обратной связи управляет ЭДС взаимной индукции, дей-
действующей в нем самом, и делает эту ЭДС периодической.
215
УСЛОВИЕ САМОВОЗБУЖДЕНИЯ
503
Помимо разобранной, известны многочисленные другие ав-
автоколебательные схемы с электронными лампами. Мы ограни-
ограничимся только еще одним примером, показанным на рис. 366. В
этой схеме колебатель-
колебательный контур находится
в цепи анода, а катушка
обратной связи — в цепи
сетки. Анодная батарея
включена параллельно
лампе (на рисунке не
показана), а не последо-
последовательно с ней, как на ¦ ¦ ц у к -JL—^- С
рис. 364. Чтобы батарея
не закорачивалась на
индуктивность L, в
анодную цепь введен
разделительный конден- Рис- 366- Ламповый генератор с колеба-
сатор Ср, который не тельным контуром в цепи анода
препятствует прохож-
прохождению быстропеременного тока электрических колебаний, но
не пропускает постоянный ток батареи. Для того чтобы, с
другой стороны, токи электрических колебаний не уходили
в батарею, последняя подключена через дроссели Д. В схеме
показаны также сеточный конденсатор Сс и утечка сетки гс (не
изображенные на рис. 364), которые позволяют поддерживать
на сетке небольшой отрицательный потенциал и тем самым
устранять бесполезный ток сетки. Принцип действия этой
схемы — такой же, как и разобранный выше.
§ 215. Условие самовозбуждения
Посмотрим теперь, какому количественному условию должны удовле-
удовлетворять параметры лампового генератора (сопротивление контура г, коэф-
коэффициент взаимной индуктивности М и т.д.) для того, чтобы были возмож-
возможны автоколебания.
Обратимся опять к схеме рис 364. Колебательный контур генерато-
генератора можно изобразить эквивалентной схемой (рис. 367), в которой действие
обратной связи представлено некоторым генератором с переменной ЭДС
$ = — М di&/dt. Применяя к этому контуру второй закон Кирхгофа и рас-
рассуждая так же, как и в § 209, получим
причем, как и прежде,
Uc = q/C, i = -dq/dt.
Исключая из этих уравнений Uc и г, находим
d2q dq
' 1^ + г Tt
q_
с
~dt
= 0.
504
СОБСТВЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. XX
Здесь анодный ток га есть функция сеточного напряжения ис (выражаемая
сеточной характеристикой лампы), которое в свою очередь зависит от заря-
заряда q. Но сеточная характеристика лампы нелиней-
нелинейна. Поэтому и написанное уравнение есть нели-
нелинейное уравнение, а, следовательно, автоколебания
являются нелинейными колебаниями.
Однако для решения поставленного вопроса за-
задачу можно упростить. Положим, что мы имеем ма-
малые колебания и что рабочая точка выбрана в сред-
средней части характеристики (как на рис. 365). Тогда
малый отрезок характеристики можно считать от-
отрезком прямой линии и уравнение колебаний сдела-
сделается линейным. Кроме того, будем считать для про-
простоты, что проницаемость сетки лампы очень мала,
так что га зависит практически только от потенци-
потенциала сетки wc (но не от потенциала анода и&). Тогда
Рис. 367. Эквива-
Эквивалентная схема гене-
генератора, изображен-
изображенного на рис. 364
= А + Suc = А + — q,
где S — крутизна сеточной характеристики. Поэтому
dia. S dq
~dt ~ C~dl'
Подставляя это выражение в уравнение колебаний и деля обе части его на
L, находим
d2q (r SM\ dq \ . , N
J+{L--Lc)i+LCq = °- B151)
Это уравнение имеет тот же вид, что и B09.5), и его решение есть
q = Ae~fit cos (ut + tp). B15.2)
Но в данном случае коэффициент затухания /3 равен
B15.3)
LC
Он меньше, чем коэффициент затухания в отсутствие обратной связи: а =
= r/2L, и поэтому можно сказать, что действие обратной связи эквива-
эквивалентно введению в контур отрицательного сопротивления (при этом везде
предполагается, что направление витков в катушке обратной связи соответ-
соответствует кривой д рис. 365).
Из B15.3) видно, что при известных условиях коэффициент затухания 0
может сделаться равным нулю или даже отрицательным, что соответствует
возникновению автоколебаний. Это будет в случае
SM/C > г.
B15.4)
Написанное условие есть условие самовозбуждения лампового генератора.
Если выполняется условие B15.4), то /3 < 0, и решение B15.2) выража-
выражает нарастающие колебания, амплитуда которых увеличивается с течением
времени до бесконечности. Причина этого странного результата заключает-
заключается в том, что мы заменили нелинейное уравнение колебаний приближенным
линеаризованным уравнением B15.1), которое пригодно только для малых
колебаний (начальной стадии процесса), но не для описания всех свойств
§216
РЕЛАКСАЦИОННЫЕ КОЛЕБАНИЯ
505
генератора. В действительности же, после самовозбуждения, амплитуда на-
нарастающих колебаний будет стремиться к некоторому конечному пределу,
определяемому свойствами генератора и не зависящему от начальных усло-
условий.
§ 216. Релаксационные колебания
В рассмотренных автоколебательных схемах существенной
частью был колебательный контур, содержавший индуктив-
индуктивность и емкость. Такие генераторы (LC-генераторы) подобны
механическим колебательным системам, в которых колебания
возникают вследствие наличия массы (индуктивность) и упру-
упругости (емкость).
Однако одновременное наличие индуктивности и емкости не
обязательно для получения колебаний. На рис. 368 а показана
колебательная схема, в которой индуктивность не играет ника-
никакой роли. Здесь конденсатор С, параллельно которому присо-
присоединена неоновая лампа НЛ, заряжается от источника посто-
постоянного тока через большое сопротивление г. Если бы неоновой
лампы не было, то напряжение конденсатора Uc увеличивалось
Рис. 368- Релаксационные электрические колебания
бы с течением времени согласно штриховой кривой (рис. 368 б)
и стремилось бы асимптотически к ЭДС источника &. Уравне-
Уравнение этой кривой выражается формулой G4.1), а ее начальную
часть приближенно можно представить прямой линией:
При наличии неоновой лампы происходит иное. Когда напряже-
напряжение Uc достигает напряжения зажигания С/3, в лампе возника-
возникает газовый разряд и конденсатор начинает быстро разряжать-
разряжаться (так как сопротивление неоновой лампы значительно меньше
сопротивления г). Когда напряжекие Uc уменьшается до напря-
506 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
жения гашения разряда UT, разряд в лампе обрывается и конден-
конденсатор начинает опять заряжаться, отчего его напряжение вновь
увеличивается. Затем в определенный момент времени в лам-
лампе снова зажигается разряд и описанные процессы повторяются
периодически. В результате возникают колебания напряжения
Uc, выражаемые пилообразной сплошной кривой (рис. 368 6).
По такому же закону изменяется и заряд конденсатора.
Предположим для простоты, что время разрядки конденса-
конденсатора весьма мало по сравнению со временем зарядки. Тогда пе-
период колебаний есть время, в течение которого напряжение по-
повышается от значения Ur до значения U3. Он равен
Мы видим, что в рассматриваемом случае электрические коле-
колебания возникают потому, что существует определенное время
релаксации контура (§ 73) т = гС, причем период колебаний
определяется этим временем. Поэтому колебания рассмотрен-
рассмотренного типа получили название релаксационных колебаний.
Напомним, что с релаксационными колебаниями мы встре-
встречаемся часто и в механике. Механическими релаксационными
колебаниями объясняются вибрация тормозов трамвая, звуча-
звучание струн в смычковых музыкальных инструментах и другие
явления.
В рассмотренной выше схеме (см. рис. 368) колебания напря-
напряжения изображаются пилообразной кривой и сильно отличают-
отличаются от синусоидальных (гармонических) колебаний. Однако это
не значит, что нельзя получить релаксационные колебания сину-
синусоидальной формы в других схемах. Оказывается, что, комбини-
комбинируя несколько конденсаторов и сопротивлений с электронными
лампами, можно создать практически гармонические релакса-
релаксационные колебания. Такие ДС-генераторы получили широкое
распространение в радиотехнике и применяются в различных
измерительных устройствах. Они особенно удобны для измене-
изменения частоты в широких пределах (от нескольких герц до мно-
многих килогерц) и не требуют громоздких катушек индуктивности,
необходимых для получения низких частот в LC-генераторах.
ГЛАВА XXI
ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ
КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ
Рассмотрим теперь электрические колебания, возникающие
в том случае, если в цепи имеется генератор, электродвижущая
§ 217 СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 507
сила которого изменяется периодически. Они подобны механи-
механическим колебаниям тела, вызываемым периодической внешней
силой.
В настоящей главе мы ограничимся только цепями с сосредо-
сосредоточенными емкостями и индуктивностями и будем считать пе-
переменные токи, как и в гл. XX, квазистационарными. Иными
словами, мы будем предполагать, что время т, в течение кото-
которого электрические величины принимают установившиеся зна-
значения, мало по сравнению с периодом колебаний Т, и поэтому
будем применять к мгновенным значениям всех электрических
величин законы постоянного тока.
Далее, мы будем рассматривать только такие токи, сила ко-
которых меняется по синусоидальному закону
г = го sin(w? + </>).
Это объясняется несколькими причинами. Во-первых, как мы
знаем (гл. XII), все технические генераторы переменного тока
имеют ЭДС, изменяющуюся по закону, очень близкому к сину-
синусоидальному, и потому создаваемые ими токи практически яв-
являются синусоидальными. Во-вторых, теория синусоидальных
токов особенно проста, и поэтому на примере таких токов мож-
можно легко выяснить основные особенности электрических колеба-
колебаний.
Правда, в некоторых случаях на практике приходится встре-
встречаться и с колебаниями более сложной формы. Однако легко по-
показать, что всякое несинусоидальное колебание можно предста-
представить в виде суммы синусоидальных, гармонических, колебаний
(теорема Фурье), и поэтому исследование более сложных колеба-
колебаний можно свести к исследованию колебаний синусоидальных.
Таким образом, синусоидальные, или гармонические, колебания
являются одновременно и самым важным, и самым простым ти-
типом колебаний.
Наконец, везде в дальнейшем мы будем считать, что колеба-
колебания являются установившимися. Иными словами, будем пред-
предполагать что с момента начала колебаний прошло достаточно
большое время, так что амплитуды тока и напряжения уже до-
достигли постоянного значения (ср. § 222).
§ 217. Сопротивление в цепи переменного тока
Рассмотрим сначала частный случай, когда генератор пере-
переменного тока замкнут на внешнюю цепь, имеющую настолько
малые индуктивность и емкость, что ими можно пренебречь.
Положим, что в цепи имеется переменный ток
г = го
508
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ ГЛ XXI
и найдем, по какому закону изменяется напряжение между кон-
концами цепи а и б (рис. 369). Применяя к участку агб закон Ома,
имеем
U = ir =
Таким образом, напряжение на концах участка изменяется так-
также по закону синуса, причем разность фаз между колебаниями
тока и напряжения равна нулю. Напряжение и ток одновремен-
г
1
1
ч /
т
1
1
1
г
А
ц
Рис. 369. Сопротивление
в цепи переменного тока
Рис. 370. Колебания тока и напряжения на
сопротивлении
но достигают максимальных значений и одновременно обраща-
обращаются в нуль (рис. 370). Максимальное значение напряжения есть
Щ = ior.
В § 129 мы показали, что гармонически изменяющиеся величины
можно наглядно изображать при помощи векторных диаграмм.
Применим этот способ к нашему слу-
Uo=ior чаю. Выберем ось диаграммы таким
образом, чтобы вектор, изображающий
колебания тока, был направлен вдоль
Рис. 371. Векторная диа- этой оси- В Дальнейшем мы будем на-
наТ
0
Ось токов
грамма напряжения на со-
сопротивлении
у
зывать ее осью токов. Тогда вектор,
изображающий колебания напряжения,
будет направлен вдоль оси токов, так
как разность фаз между током и напряжением равна нулю
(рис. 371). Длина этого вектора равна амплитуде напряже-
напряжения ior.
§ 218. Емкость в цепи переменного тока
Положим теперь, что участок цепи содержит конденсатор
емкости С, причем сопротивлением и индуктивностью участка
можно пренебречь, и посмотрим, по какому закону будет изме-
изменяться напряжение на концах участка в этом случае. Обозначим
разность потенциалов точек а и б (рис. 372) через U = Ua — Uq
и будем считать заряд конденсатора q и силу тока i положи-
218
ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
509
тельными, если они соответствуют рис. 372. Тогда U = q/C. Но
г = dq/dt, и, следовательно,
q = f idt.
Если сила тока в цепи изменяется по закону
i — iosinwi, B18.1)
то заряд конденсатора равен
=——costjt
Постоянная интегрирования qo здесь обозначает произвольный
постоянный заряд конденсатора, не связанный с колебаниями
тока, и поэтому мы положим qo = 0. Следовательно,
B18.2)
Сравнивая B18.1) и B18.2), мы видим, что при синусоидальных
колебаниях тока в цепи напряжение на конденсаторе изменяет-
изменяется также по закону синуса, однако коле-
колебания напряжения на конденсаторе от-
отстают по фазе от колебаний тока на тг/2.
Изменения тока и напряжения во време-
времени изображены графически на рис. 373.
Полученный результат имеет простой
физический смысл. Напряжение на кон-
какой-либо момент
U
денсаторе в какои-лиоо момент време-
времени определяется существующим зарядом
конденсатора. Но этот заряд был образо-
образован током, протекавшим предваритель-
предварительно в более ранней стадии колебаний. По-
Поэтому и колебания напряжения запаздывают относительно ко-
колебаний тока. Так, например, когда в момент времени t — 0 си-
Рис. 372. Конденсатор в
цепи переменного тока
Рис. 373. Колебания тока в цепи напряжения на конденсаторе
ла тока равна нулю (рис. 373), то на конденсаторе еще имеется
отрицательный заряд, перенесенный током в предыдущий пе-
период времени, и напряжение не равно нулю. Для обращения в
510 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
нуль этого заряда нужно, чтобы некоторое время t\ проходил
ток положительного направления, и поэтому, когда заряд кон-
конденсатора (а значит, и напряжение) станет равным нулю, сила
тока уже не будет равна нулю.
Формула B18.2) показывает, что амплитуда напряжения на
конденсаторе равна
Щ = io/ojC.
Сравнивая это выражение с законом Ома для участка цепи с
постоянным током (U = ir), мы видим, что величина
гс = 1/шС B18.3)
играет роль сопротивления участка цепи. Поэтому она получила
название кажущегося сопротивления емкости.
Если в B18.3) выражать С в фарадах, а ш — в секундах в
минус первой степени, то tq получится в омах.
Найденные результаты можно представить в виде векторной
диаграммы (рис. 374). Здесь вектор, изображающий колебания
напряжения, уже не совпадает с осью то-
/-л/2 (!) ков. Он повернут в отрицательном на-
направлении (по часовой стрелке) на угол
7г/2. Длина этого вектора равна ампли-
. туде напряжения io/шС.
и0=10/озС Из формулы B18.3) видно, что со-
сопротивление емкости гс зависит также
Рис. 374. Векторная от частоты ш. Поэтому при очень высо-
диаграмма напряжения КЮ[ частотах даже малые емкости мо-
на конденсаторе ГуТ ПредСтавлять совсем небольшое со-
сопротивление для переменного тока. Этим объясняются многие
весьма неожиданные на первый взгляд явления.
На рис. 375 изображена схема опыта, иллюстрирующего
влияние малых емкостей при больших частотах. Эксперимента-
Экспериментатор стоит на изолирующей скамейке со стеклянными ножками и
держит лампочку накаливания, касаясь рукой ее нарезного цо-
цоколя. Второй контакт лампочки касается одного из выводов вы-
высоковольтного источника переменного напряжения с частотой в
несколько миллионов колебаний в секунду; второй вывод ис-
источника заземлен (в качестве источника можно использовать,
например, резонансный трансформатор, описанный в § 236).
Следовательно, цепь разомкнута для постоянного тока (она раз-
разрывается изолирующей скамейкой). Тем не менее в цепи прохо-
проходит ток силой в несколько ампер и нить лампочки ярко накаля-
накаляется. Это объясняется тем, что тело экспериментатора и Земля
образуют обкладки конденсатора, а конденсаторы, как мы ви-
видели, пропускают переменные токи. Поэтому цепь, разомкнутая
для постоянного тока, оказывается замкнутой для быстропере-
менного тока: токи проводимости в металлических проводах за-
§219
ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
511
мыкаются токами смещения (§ 136) внутри конденсатора. Так
как частота ш очень велика, то уже при ничтожной емкости
конденсатора (десятки пикофарад) сопротивление гс становит-
становится настолько малым, что в цепи появляются сильные токи.
У////////////////////////,
Рис. 375. Схема опыта для демонстрации тока смещения при большой
частоте
Этот опыт хорошо демонстрирует также существование
скин-эффекта, или вытеснение переменных токов на поверх-
поверхность проводника (§ 134). Через тело экспериментатора прохо-
проходят токи силой в несколько ампер, которые в случае постоянного
тока вызывали бы сильное физиологическое действие и были бы
очень опасны для жизни. Однако в описанном опыте экспери-
экспериментатор не ощущает эти токи, так как они протекают только в
тонком поверхностном слое и не заходят в глубь тела.
§ 219. Индуктивность в цепи переменного тока
Рассмотрим, наконец, третий частный случай, когда участок
цепи содержит только индуктивность. Обозначим по-прежнему
через U = Ua — Us разность потенциалов точек а и б (рис. 376)
и будем считать ток i положительным, если он направлен от а к
б. При наличии переменного тока в катушке индуктивности воз-
возникнет ЭДС самоиндукции, и поэтому мы должны применить
закон Ома для участка цепи с ЭДС (§ 68):
U = ir-S.
В нашем случае г = 0, а ЭДС самоиндукции
<§ = -L di/dt.
Поэтому
U = Ldi/dt.
512
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ
ГЛ XXI
г
U
-Чб
i
Рис. 376. Индуктивность в цепи
переменного тока
Если сила тока в цепи изменяется по закону
i = г'о sinwi, B19.1)
то
U = ii)UiLcosuit = iQUiLsm(Ljt + ж/2). B19.2)
Сравнивая B19.1) и B19.2), мы видим, что колебания напря-
напряжения на индуктивности опережают по фазе колебания тока на
7г/2. Когда сила тока, возрастая, проходит через нуль, напря-
напряжение уже достигает максимума,
после чего начинает уменьшать-
уменьшаться; когда сила тока становится
максимальной, напряжение про-
проходит через нуль, и т.д. (рис. 377).
Физическая причина возник-
возникновения этой разности фаз за-
заключается в следующем. Если со-
сопротивление участка равно нулю,
то приложенное напряжение в
точности уравновешивает ЭДС
самоиндукции и поэтому равно ЭДС самоиндукции с обратным
знаком. Но эта последняя пропорциональна не мгновенному зна-
значению тока, а быстроте его изменения, которая будет наиболь-
наибольшей в те моменты, когда сила тока проходит через нуль. По-
Поэтому максимумы
напряжения совпа-
совпадают с нулями тока
и наоборот.
Из B19.2) сле-
следует, что ампли-
амплитуда напряжения
равна
С/о = io^L,
и, следовательно,
Рис. 377. Колебания тока и напряжения на индук-
Г? = UlL B19.3) тивности
играет ту же роль, что и сопротивление участка. Поэтому ri
называют кажущимся сопротивлением индуктивности.
Если в формуле B19.3) L выражено в генри, аш-в секундах
в минус первой степени, то г^ будет выражено в омах.
Так же, как и выше, найденные результаты можно предста-
представить векторной диаграммой. Она показана на рис. 378. Вектор,
изображающий колебания напряжения, повернут относительно
оси токов в положительном направлении (против часовой стрел-
стрелки) на угол 7г/2, а его длина, равная амплитуде напряжения,
есть
U
§ 219
ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
513
Кажущееся сопротивление индуктивности используют для
устройства дросселей. Они представляют собой проволочные ка-
катушки (с железом или без него), вводи-
вводимые в цепи переменного тока для ре-
регулирования силы тока. По сравнению
с реостатом дроссели имеют то важное
преимущество, что увеличение сопро-
сопротивления цепи с их помощью не сопро-
сопровождается увеличением тепла Джоуля-
Ленца, а следовательно, не приводит к
бесполезной затрате энергии. Кроме то-
того, так как индуктивное сопротивление
существует только для переменных то-
токов, дроссели позволяют разделять по-
постоянные и переменные токи. Примеры
Uo = i(
к/2
О
(О
Рис. 378. Векторная диа-
диаграмма напряжения на
индуктивности
такого применения дросселей мы уже имели в схемах, изобра-
изображенных на рисунках 361, 362 и 366.
Формула B19.3) показывает, что индуктивное сопротивле-
сопротивление Г? пропорционально частоте переменного тока ш, и поэтому
при очень больших частотах
даже малые индуктивности
могут представлять значи-
значительное сопротивление для
переменных токов. Это мож-
можно продемонстрировать при
помощи эффектного опыта,
изображенного на рис. 379.
Толстый медный стержень
(диаметром около 5 мм) изо-
изогнут в виде дуги абвгд дли-
длиной около 1 м и его концы
присоединены к источнику
быстропеременного тока с
частотой в несколько мил-
миллионов колебаний в секун-
секунду (как в опыте, показанном
на рис. 375). Параллельно
участку дуги бег присоеди-
Рис. 379. Влияние индуктивности при йена обычная лампа накали-
большой частоте вания. Сопротивление дуги
(для постоянного тока) рав-
равно около 0,001 Ом, а сопротивление лампы — около 100 Ом.
Если бы к концам дуги был присоединен источник постоянного
тока, то дуга осуществляла бы короткое замыкание и практиче-
практически весь ток устремился бы в дугу, не заходя в лампу. Однако
для быстропеременного тока наблюдается совсем другое. Так
514
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ
ГЛ. XXI
как дуга обладает некоторой, хотя и малой, индуктивностью,
она имеет еще индуктивное сопротивление. При указанных усло-
условиях последнее становится настолько большим, что, напротив,
ток практически не ответвляется в дугу, а целиком проходит
через лампу, отчего ее нить ярко накаляется.
§ 220. Закон Ома для переменных токов
Пользуясь результатами, полученными в § 217-219, можно
найти соотношение между колебаниями тока и напряжения в
любой цепи.
Рассмотрим сначала последо-
последовательное соединение сопротив-
сопротивления, емкости и индуктивности
(рис. 380). Положим по-прежне-
по-прежнему, что ток в цепи изменяется по
закону
i—
i
ф
i
i = го smut,
B20.1)
и вычислим напряжение между
Рис. 380. Последовательное сое- концами цепи. Так как при по-
динение сопротивления, емкости следрвательном соединении про-
и индуктивности водников складываются напряже-
напряжения, то искомое напряжение и
есть сумма трех напряжений: на сопротивлении, на емкости и
на индуктивности, причем каждое из этих напряжений, как мы
видели в § 217-219, изменяется
во времени по закону синуса.
Для сложения этих трех
гармонических колебаний мы
воспользуемся векторной диа-
диаграммой напряжений (рис. 381).
Колебания напряжения на
сопротивлении изображаются
на ней вектором, направ-
направленным вдоль оси токов и
имеющим длину U& = ior,
колебания же напряжения на ^ „оп „
^ Рис. 381. Векторная диаграмма на-
индуктивности и емкости - пряжений для цепИ; изображенной
векторами, перпендикуляр- на рис 380
ными к оси токов, с длинами
iqujL и iq/ojC. Складывая два последних колебания, мы полу-
получим одно гармоническое колебание, изображаемое вектором,
перпендикулярным к оси токов и имеющим длину
U = /0(ш1-1/шС)
§ 220 ЗАКОН ОМА ДЛЯ ПЕРЕМЕННЫХ ТОКОВ 515
Таким образом, полное напряжение между концами цепи а
и б можно рассматривать как сумму двух гармонических ко-
колебаний: напряжения С/а, совпадающего по фазе с током, и на-
напряжения Up, отличающегося по фазе на тг/2. Первое из них
(С/а) получило название активной составляющей напряжения,
а второе (С/р) — реактивной составляющей. Оба эти колебания,
складываясь, дают также гармоническое колебание
U = С/о sin [ut + <p). B20.2)
Согласно сказанному в § 129 оно изображается векторной сум-
суммой, причем длина результирующего вектора равна амплитуде
напряжения С/о, а угол, образованный результирующим векто-
вектором с осью токов, — сдвигу фазы (р. Из треугольника напряже-
напряжений на рис. 381 получаем
Щ = гол/г2 + (ljL-1/ljCJ. B20.3)
Далее из рис. 381 видно, что
uLy)C B20.4)
Формула B20.3) имеет сходство с законом Ома в том смысле,
что амплитуда напряжения С/о пропорциональна амплитуде то-
тока го- Поэтому формулу B20.3) иногда называют законом Ома
для переменного тока. Однако нужно помнить, что эта формула
относится только к амплитудам, но не к мгновенным значениям
U яг.
В случае постоянного тока отношение напряжения к силе
тока называют сопротивлением проводника. Подобно этому при
переменном токе отношение амплитуды полного напряжения к
амплитуде тока
R = С/оДо = Vr2 + (wL - 1/wCJ B20.5)
называют сопротивлением цепи для переменного тока.
Аналогично отношение амплитуды активной составляющей
напряжения С/а к амплитуде тока iq
X = UJi0
называется активным сопротивлением цепи. В рассмотренной
цепи оно равно сопротивлению для постоянного тока. Актив-
Активное сопротивление всегда приводит к выделению тепла Джоуля-
Ленца.
Отношение же
Y = С/рДо = шЬ- 1/шС
есть реактивное сопротивление цепи. Для данного случая оно
равно разности кажущихся сопротивлений индуктивности и ем-
емкости. Наличие реактивного сопротивления не сопровождается
516 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ ГЛ XXI
выделением тепла (ср. § 223). Из B20.5) видно, что активное и
реактивное сопротивления цепи складываются геометрически.
Во всех приведенных выше рассуждениях мы рассматрива-
рассматривали участок цепи и понимали под U напряжение, приложенное к
концам участка а и б (рис. 380). Однако все полученные фор-
формулы можно применять и к замкнутой цепи (агСЬба, рис. 380),
включающей в себя генератор. Действительно, для всех наших
рассуждений было безразлично, в каком именно месте цепи со-
сосредоточены емкость, индуктивность и сопротивление. Поэтому
в замкнутой цепи рис. 380 мы можем считать, что г представ-
представляет собой суммарное активное сопротивление цепи, включая и
внутреннее сопротивление генератора, а С и L — емкость и ин-
индуктивность цепи, и заменить реальный генератор воображае-
воображаемым, у которого внутреннее сопротивление равно нулю. При
этом напряжение U между точками а и б будет равно ЭДС ге-
генератора & Отсюда следует, что формулы B20.1)-B20.5) спра-
справедливы и для замкнутой цепи переменного тока, если под г,
С и L понимать их значения для всей цепи и заменить во всех
формулах U на ЭДС генератора <§.
§ 221. Резонанс напряжений
Положим, что в цепи, содержащей последовательно соеди-
соединенные емкость С и индуктивность L и обладающей активным
сопротивлением г, действует переменная ЭДС, изменяющаяся
по закону
Тогда, согласно сказанному в § 220, в цепи будет протекать пе-
переменный ток
i = го sin(w? — ср),
амплитуда которого го связана с амплитудой ЭДС &q законом
Ома для переменного тока
го = «o/R. B21.1)
Здесь R есть сопротивление всей цепи:
R = \/г2 + (шЬ - 1/шСJ, B21.2)
а фазовый угол <р, на который колебания тока отстают от коле-
колебаний напряжения, определяется формулой
X гB21.3)
Допустим теперь, что мы изменяем частоту колебаний ш.
Как показывают формулы B21 1)—B21.3), это вызовет измене-
изменение и амплитуды тока г'о, и сдвига фазы ср.
§221
РЕЗОНАНС НАПРЯЖЕНИЙ
517
Остановимся сначала на изменениях амплитуды тока. Если
из = 0, то 1/изС = оо. Тогда сопротивление R обращается в бес-
бесконечность, a iq равно нулю. Это и понятно, так как при из = О
мы имеем постоянный ток, а постоянный ток не проходит через
конденсатор. При увеличении из квадрат реактивного сопротив-
сопротивления (изЬ~ 1/изСJ сначала уменьшается. Поэтому и сопротив-
сопротивление R уменьшается, а г'о увеличивается. При частоте из — изо,
определяемой условием
w§ = 1/LC, B21.4)
реактивное сопротивление (изЬ — \/изС) обращается в нуль, а
сопротивление цепи R становится наименьшим, равным актив-
активному сопротивлению цепи:
1
Сила тока достигает при этом максимума. При из > изо квадрат
реактивного сопротивления (изЬ — Х/изСI снова не равен нулю и
увеличивается с возрастанием из. В соответствии с этим сопро-
сопротивление R увеличивается, а амплитуда тока го уменьшается,
асимптотически приближаясь к нулю при увеличении из.
Зависимость г'о от из, выражаемая формулами B21.1) и
B21.2), графически изображена на рис. 382, где показаны три
кривые, соответствующие трем различным значениям активно-
активного сопротивления г. Чем меньше г (т.е. чем меньше декремент
затухания 5 или чем боль-
больше добротность контура
Q), тем больше при про-
прочих равных условиях г'о
и тем острее максимумы
кривых.
Обратимся теперь к
сдвигу фаз ср между то-
током и ЭДС Из B21.3)
видно, что при очень ма-
малых частотах, когда изЬ <§С
<§С 1/wC, tg</> очень велик
и отрицателен, а, следова-
следовательно, If Ri —7г/2. В ЭТОМ
случае ток опережает на-
напряжение и цепь имеет
емкостной характер. При
(О
Рис 382 Резонансные кривые
возрастании частоты из реактивное сопротивление (изЬ — 1/изС),
оставаясь отрицательным, уменьшается по абсолютной вели-
величине и разность фаз (р уменьшается. Когда из = изо, формула
B21.3) дает tg<p = 0, а значит, уз = 0. При дальнейшем увели-
увеличении из реактивное сопротивление становится положительным
518
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ
ГЛ XXI
и увеличивается с возрастанием ш. Поэтому 0 < tg</> < +00 и
О < <р < +тг/2. Следовательно, при и > uiq ток отстает от напря-
напряжения и цепь приобретает индуктивный характер, причем угол
</? асимптотически стремится к предельному значению +7г/2 ри
увеличении частоты ш.
Зависимость сдвига фаз ср от частоты колебаний изображе-
изображена графически на рис. 383. Так же как и г'о, <р зависит еще от
активного сопротивления контура г. Чем меньше г, тем быстрее
изменяется <р вблизи oj = cjq,
и в предельном случае г = О
изменение фазы приобретает
скачкообразный характер.
Резюмируя сказанное, мы
видим, что особый интерес
представляет случай, когда
частота ЭДС генератора (или
приложенного внешнего на-
напряжения) и) равна частоте
щ. При этом амплитуда то-
тока достигает максимального
значения, а сдвиг фаз между
током и напряжением равен
нулю, или, иными словами,
ш0
Рис. 383. Изменение сдвига фазы ко-
колебаний тока при изменении частоты
внешнего напряжения
контур действует как чисто
активное сопротивление. Этот
важный случай вынужденных колебаний называется резонан-
резонансом напряжений.
Отметим, что частота wo, при которой наступает резонанс, не
равна частоте собственных колебаний контура \/шо — а2 (фор-
мулаB10.3)). Однако в подавляющем большинстве практиче-
практических случаев a2 <§Cwq> и потому с хорошим приближением этим
различием можно пренебречь.
Выше мы предполагали, что изменяется частота ЭДС ш, а
параметры контура остаются неизменными. Однако ясно, что
для получения резонанса можно поступать и иначе: изменять у
контура индуктивность или емкость (т.е. изменять шо), оставляя
частоту ш постоянной.
Найдем теперь, чему равны амплитуды напряжения на кон-
конденсаторе и на катушке индуктивности при резонансе. Ампли-
Амплитуда тока при резонансе достигает максимума:
го = 8о/г.
Поэтому амплитуда напряжения на конденсаторе
Uoc =
§221
РЕЗОНАНС НАПРЯЖЕНИЙ
519
Полученное выражение можно преобразовать иначе. Учитывая
B21.4), имеем
1 1 ГЕ тг
(r/2LJTrVW
Но r/2L есть коэффициент затухания а (§ 209), 2n\/LC — пе-
период колебания Т, соответствующий резонансу, а значит, знаме-
знаменатель написанной формулы есть логарифмический декремент
затухания S = аТ. Поэтому (см. формулу B10.6))
где Q — добротность контура. Следовательно,
Uoc = $oQ. B21.5)
Аналогично амплитуда напряжения на индуктивности есть
B21.6)
Таким образом, колебания напряжения на конденсаторе и
на индуктивности при резонансе имеют одинаковые амплиту-
амплитуды. Однако одно из них (Uc) отстает от колебаний тока на 7г/2,
а другое (?//,) опережает их на 7г/2, так что оба колебания име-
имеют разность фаз п. Поэтому их сумма равна нулю, и остаются
только колебания напряжения на активном сопротивлении. Со-
Соотношение между тремя колебаниями напряжения Ur, Uc и Ui
при резонансе изображено при помощи векторной диаграммы
на рис. 384. Так как добротность обычных колебательных кон-
контуров больше единицы, то амплитуды напряжения Щс и U
больше амплитуды напряжения на концах всей цепи.
j Uoc = «об
Рис. 384. Векторная диаграмма
напряжений при резонансе
Рис. 385. Входной контур радио-
радиоприемника (схематически)
Резонанс напряжений широко применяют в радиотехнике и
используют в тех случаях, когда нужно усилить колебания на-
520 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
пряжения какой-либо определенной частоты. В качестве при-
примера укажем на устройство входной части радиоприемника
(рис. 385). В ней имеется колебательный контур LC с высокой
добротностью, а напряжение с конденсатора контура подается
на вход первой лампы усилителя. Приходящие радиосигналы
вызывают в антенне А быстропеременный ток, который наводит
в катушке L ЭДС взаимной индукции с некоторой амплитудой
&q. Вследствие резонанса на конденсаторе, а значит, и на входе
лампы возникает напряжение с амплитудой WiqQ, которая значи-
значительно больше амплитуды ЭДС <?о- Это усиление напряжения
имеет место только для узкого интервала частот вблизи резо-
резонансной частоты контура щ, что позволяет выделить из многих
сигналов различных радиостанций только одно колебание опре-
определенной частоты («настроиться» на определенную станцию).
§ 222. Установление колебаний
Вынужденные колебания устанавливаются не сразу, а лишь
по прошествии некоторого времени после включения внешней
ЭДС. Выясним подробнее, в чем заключается процесс установ-
установления колебаний.
Положим, что ЭДС генератора изменяется по-прежнему по
закону
П=
и будем следить за колебаниями заряда q конденсатора. Вынуж-
Вынужденные колебания заряда, как мы знаем, имеют вид
qB = Csm(u)t + (f),
где амплитуда С и начальная фаза ср зависят от параметров
контура (емкости, индуктивности и сопротивления).
Однако при замыкании цепи в ней возникнут еще и собствен-
собственные колебания, отчего на конденсаторе появится дополнитель-
дополнительный заряд, который, согласно формуле B10.2), будет изменять-
изменяться по закону
qc = Ae~~at sin (ojit + ф).
Здесь а есть коэффициент затухания контура, а и)\ =
= \/шо — ос2 — собственная частота колебаний контура. (В этой
формуле вместо cos (как в § 210) мы пишем sin, что, однако,
не играет никакой роли, так как начальная фаза ф нами пока
еще не определена.) Поэтому в первые моменты времени после
замыкания цепи будут возбуждаться колебания сложной фор-
формы, представляющие собой сумму собственных и вынужденных
колебаний, происходящих с различными частотами ш и wi.
С течением времени собственные колебания будут затухать,
и когда они практически прекратятся вовсе, мы получим устано-
§222
УСТАНОВЛЕНИЕ КОЛЕБАНИЙ
521
вившиеся вынужденные колебания. Таким образом, время уста-
установления колебаний есть время, в течение которого затухают
собственные колебания контура. Оно тем больше, чем меньше
коэффициент затухания а.
Остановимся теперь специально на случае резонанса, когда частота ге-
генератора w — uio- Будем считать, что затухание контура невелико, так что
можно положить частоту собственных колебаний uii йуо- Тогда колебания
заряда будут иметь вид
q = qc + qB = Ae~at sin (uot + ф) + С sin (u>ot + ip). B22.1)
В этой формуле амплитуда собственных колебаний А и начальная фаза
ф зависят от начальных условий процесса (ср. § 210). Положим, что мы
замыкаем цепь в момент времени t — 0, причем до замыкания заряда на
конденсаторе не было. Тогда начальные условия будут
t = 0: g = 0, i = dq/dt - 0. B22.2)
Подставляя первое из начальных условий в B22.1), имеем
AsinV> + Csin</> = 0. B22.3)
Второе начальное условие дает
—Аа sin ф + Ашо cos ф + Cuq cos tp = 0.
Если, как было предположено выше, аСц, то первым членом в этом
уравнении можно пренебречь по сравнению со вторым членом, и поэтому
AcosV + Ccosv3 = 0. B22.4)
Из уравнений B22.3) и B22,4) получаем
А = С, 1р = <р + ж.
Подставляя эти значения Аи ф в B22.1), находим закон временного изме-
изменения заряда конденсатора после замыкания цепи в виде
9 = C(l-e~a')sin(<Jo* + ?>)- B22.5)
Эта зависимость изображена графически на рис. 386. При резонансе в кон-
контуре возникают колебания с возрастающей амплитудой, которая асимпто-
асимптотически приближается к установившемуся значению. Время, в течение ко-
которого практически достигается это зна-
значение, тем больше, чем меньше коэффи-
коэффициент затухания а контура. Аналогичные
кривые мы получили бы, рассматривая
напряжение на конденсаторе и на индук-
индуктивности или силу тока в контуре.
В § 221 мы видели, что при резонансе
напряжений амплитуда установившихся
колебаний тока равна го = $о/г. Отсюда
получается, что если активное сопротив-
сопротивление цепи г —» 0, то го ~> оо. Физический
смысл этого, на первый взгляд, странно-
странного результата заключается в следующем. Рис 386. Установление колеба-
Когда сопротивление контура неограни- ний ре3онансе
ченно уменьшается, то и затухание кон-
контура стремится к нулю, а, следовательно, время установления колебаний
неограниченно увеличивается. Поэтому в действительности в контуре бу-
будут колебания конечной амплитуды, которая, однако, будет непрерывно
возрастать в процессе колебаний.
522
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ
ГЛ XXI
§ 223. Работа и мощность переменного тока
Рассмотрим теперь, чему равна работа, совершаемая в цепи
при наличии в ней переменного тока.
Положим сначала, что цепь имеет только активное сопротив-
сопротивление. В этом случае вся работа тока целиком превращается в
тепло.
Пусть напряжение на концах цепи (а и б на рис. 369) есть
U = С/о sin uit.
Так как в случае активного сопротивления сдвига фаз между
током и напряжением нет, то сила тока изменяется по закону
J
0
в
u/
1
Y/yy
f
7
Ф
it
\
\
= 90°
Рис. 387 Колебания мгновенной мощности
переменного тока
В течение малого про-
промежутка времени пе-
переменный ток можно
рассматривать как ток
постоянный, и поэтому
мгновенная мощность
переменного тока
Pt = Щ = jo[/o sin2 uit.
Изменение мгновенной
мощности с течением
времени в случае чисто
активного сопротив-
сопротивления изображено на
рис. 387 а. Здесь же
даны кривые колебаний
тока г и напряжения U
тоже для случая актив-
активного сопротивления.
Обычно необходимо
знать не мгновенное
значение мощности, а
ее среднее значение за
большой период време-
времени, охватывающий мно-
много периодов колебаний.
Так как мы имеем дело
с периодическим процес-
процессом, то для нахождения
этого среднего значения достаточно, очевидно, вычислить сред-
среднее значение мощности за один полный период. Работа перемен-
переменного тока за малое время dt есть
Pt dt =
sin2 u>t dt,
§ 225 РАБОТА И МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА 523
а, следовательно, работа Ат за время полного периода колебаний
Т выражается формулой
т
Ат = гоЩ f sin2 uit dt.
о
Но
т т
J sin2utdt = ± f (l- cos jrt) dt=\T-
о о
Поэтому
AT = ioUoT/2.
Отсюда Для средней мощности получается
Р = АТ(Т = гоС/о/2-
Так как Uq =? Но, то можно также написать
Р = i0U0 = ril = C/02/2r.
Обозначим через ie и Ue силу и напряжение постоянного то-
тока, который в{ыделяет в сопротивлении г то же количество теп-
теплоты, что и данный переменный ток. Тогда
Р = ieUe = ri2e = Ul/r. B23.1)
Сравнивая эти выражения с выражениями для мощности пере-
переменного тока, имеем
ге = го/\/2, Ue = U0/V2. B23.2)
Сила тока ге называется эффективной силой переменного тока,
a Ue — эффективным напряжением. Пользуясь эффективными
значениями, можно выразить среднюю мощность переменного
тока теми же формулами B23.1), что и мощность постоянного
тока.
Перейдем теперь к общему случаю, когда цепь содержит не
только активное сопротивление, но и реактивное. Теперь меж-
между током и напряжением существует разность фаз, и это суще-
существенно меняет дело. Обратимся к рис. 387 6^, где изображены
кривые колебаний тока г и напряжения U при сдвиге фаз (р =
= 60°, а также кривая изменения мгновенной мощности Р< = Ш.
В течение времени от 0 до Т/6 ток и напряжение имеют разные
знаки и их произведение ill отрицательно. В последующий про-
промежуток времени, от Т/6 до Т/2, i и U имеют одинаковые зна-
знаки и мгновенная мощность положительна. Начиная с момента
Т/2, мощность снова становится отрицательной, и т.д. Мы име-
имеем, следовательно, колебания мгновенной мощности с переменой
знака.
524 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
Изменение знака мгновенной мощности имеет простой физи-
физический смысл. В § 125 мы видели, что, когда генератор посылает
ток во внешнюю цепь, в его обмотке развиваются электродина-
электродинамические силы, тормозящие вращение ротора. Для их преодоле-
преодоления двигатель, вращающий генератор, производит определенную
работу, и именно за счет этой работы двигателя во внешней
цепи совершается работа тока. Данный случай соответствует
положительной мгновенной мощности — происходит передача
энергии от генератора во внешнюю цепь. Напротив, когда мгно-
мгновенная мощность отрицательна, ток имеет противоположное на-
направление, и электродинамические силы в генераторе способ-
способствуют вращению ротора. В эти промежутки времени мы могли
бы отсоединить двигатель от генератора, причем вращение по-
последнего поддерживалось бы самим током. При этом энергия
из внешней цепи (запасенная в электрическом поле конденсато-
конденсатора и в магнитном поле катушек) переходит в генератор. Таким
образом, периодическое изменение знака мгновенной мощности
означает, что часть энергии колеблется между генератором и
внешней цепью, а, следовательно, среднее значение мощности в
этом случае уменьшается.
Вычислим среднюю мощность переменного тока при наличии
разности фаз. Работа, совершенная во внешней цепи за время dt,
равна
Напряжение U, согласно сказанному в § 220 (см. рис. 381), мы
можем разложить на две составляющие: активную
Ua = Щ cos <p sin ujt,
колеблющуюся в фазе с током, и реактивную
Up = Uq sinip sin (uit ± 7г/2),
смещенную по фазе относительно тока на ±7г/2. Соответствен-
Соответственно этому при вычислении работы за полный период Т получим
тоже два слагаемых. Одно из них, обусловленное реактивной со-
составляющей напряжения, равно нулю, так как
т т
Г sin uit sin (uit ± 7г/2) dt = ± Г sin uit cos uitdt = 0.
о о
Следовательно, полная работа за период определяется только
активной составляющей напряжения:
т
Ат = ioUo cos<p f sin2 uitdt = - IqUqTcos tp.
J 2
§ 224 РАЗВЕТВЛЕНИЕ ПЕРЕМЕННЫХ ТОКОВ 525
Поэтому средняя мощность есть
Р = Ат/Т = г0С/о cos (р/2.
Вводя сюда эффективные значения ге и Ue, находим окончатель-
окончательно
Р = ieUe cos (p. B23.3)
Полученная формула отличается от B23.1) наличием дополни-
дополнительного множителя cos <p, который в электротехнике называют
коэффициентом мощности. Она показывает, что в общем слу-
случае выделяемая в цепи мощность зависит не только от силы то-
тока и напряжения, но еще и от сдвига фаз между напряжением
и током.
Если сдвиг фаз между напряжением и током <р = 90°, то
cosy = 0 и средняя мощность равна нулю, как бы ни были ве-
велики ток и напряжение. В этом случае энергия, передаваемая
за четверть периода от генератора во внешнюю цепь, в точно-
точности равна энергии, передаваемой из внешней цепи в генератор в
течение следующей четверти периода, и вся энергия колеблется
между генератором и внешней цепью (рис. 387в).
Зависимость мощности от cos ip всегда учитывают при про-
проектировании линий электропередачи на переменном токе. Когда
питаемые нагрузки имеют большое реактивное сопротивление
(например, моторы, обладающие большой индуктивностью), то
(р ф 0 и cosy? может быть заметно меньше единицы. В этих слу-
случаях для передачи нужной мощности (при данном напряжении
генератора) необходимо увеличивать силу тока ie, что либо при-
приводит к возрастанию бесполезного тепла Джоуля-Ленца, выде-
выделяемого в линии, либо требует увеличения сечения проводов (а
следовательно, и веса дорогостоящей меди), что повышает стои-
стоимость сооружения линии. Поэтому на практике всегда стремят-
стремятся распределить нагрузки (лампы, моторы, печи и т.д.) таким
образом, чтобы cos (p был по возможности близок к единице.
Формула B23.3) позволяет также полнее понять явление
электрического резонанса (§ 221). Мы видели, что при вынуж-
вынужденных электрических колебаниях сила тока и cos <p зависят от
частоты генератора ш. При резонансе (ш = щ) сила тока до-
достигает максимума, a cosip имеет также наибольшее значение,
равное единице. Следовательно, резонанс характеризуется еще
и тем, что энергия, передаваемая в контур от генератора, имеет
наибольшее значение.
§ 224. Разветвление переменных токов
Выше (§ 220, 221) мы рассматривали цепь, в которой актив-
активные и реактивные сопротивления были соединены последова-
последовательно. Посмотрим теперь, каким образом можно найти соотно-
526
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПЕРЕМЕННЫЕ ТОКИ
ГЛ XXI
шение между напряжением и током в цепи, состоящей из ветвей,
соединенных параллельно, в которой, следовательно, происхо-
происходит разветвление переменного тока.
Пусть цепь состоит из двух ветвей (рис. 388), одна из кото-
которых содержит конденсатор емкости С, а другая — катушку ин-
индуктивности L. Так как проволочные катушки всегда обладают
некоторым сопротивлением, то в этой последней ветви мы будем
еще учитывать наличие активного сопротивления г. К концам
цепи а и б приложено переменное напряжение, изменяющееся
по закону
U = UQsmut. B24.1)
Требуется определить колебания силы полного тока в цепи (т.е.
тока, обнаруживаемого амперметром Ai, включенным в подво-
подводящие провода).
В случае простой неразветвленной цепи общей для всех эле-
элементов цепи (L, С, г) была сила тока и задача сводилась к
сложению колебаний напряжения на индуктивности, емкости
и сопротивлении. Для этой цели мы пользовались векторными
диаграммами напряжения. В рассматриваемом случае, напро-
напротив, общим является напряжение между точками а и б, а. сила
тока в ветвях ic и ii различна. Полная сила тока равна
i = iL + ic, B24.2)
и поэтому задача сводится к сложению колебаний тока. Исполь-
Используя и здесь метод векторных диаграмм, мы должны будем стро-
строить векторные диаграммы токов.
Рис. 388. Разветвление переменных токов
Рис. 389. Векторная диа-
диаграмма токов для цепи, по-
показанной на рис. 388
Пусть колебания напряжения между точками а и б изобра-
изображаются вектором, направленным вдоль линии U (рис. 389, ось
напряжении). Тогда колебания тока в катушке индуктивности
изображаются вектором, длина которого (амплитуда тока), со-
§ 225 РЕЗОНАНС ТОКОВ 527
гласно формуле B20.3), в которой нужно положить С — оо,
равна
i0L = Vr2l°u2L2- B24.3)
Этот вектор повернут относительно оси напряжений на угол (pi
в отрицательном направлении (так как ток в катушке отстает
по фазе от напряжения), причем (см. B20.4))
tg <pL = ujL/r. B24.4)
Колебания тока в конденсаторе изображаются вектором, по-
повернутым относительно оси напряжении на угол -Иг/2; его дли-
длина (амплитуда тока) равна (см. B20.3), L = г = 0)
ioc = U0loC. B24.5)
Колебания полного тока определяются векторной суммой
обоих этих векторов. Его длина есть амплитуда полного тока,
а угол (р, образованный с осью напряжений, — угол, на кото-
который колебания тока опережают по фазе колебания напряжения.
Таким образом, колебания полного тока выражаются формулой
i = iosin(wt + <p). B24.6)
Так как амплитуды токов г'оь и г^с и угол </? определены форму-
формулами B24.3)-B24.5), то из треугольника рис. 389 можно найти
«о и </?, а следовательно, определить и колебания полного тока в
цепи.
§ 225. Резонанс токов
Если в цепи, изображенной на рис. 388, изменять L и С или
частоту генератора ш, то изменяются и амплитуда полного то-
тока, и сдвиг фаз между током и напряжением. При некотором
соотношении между L, С и ш сдвиг фаз (р
становится равным нулю и, следовательно,
контур ведет себя как чисто активное со-
сопротивление. Этот частный случай выну-
вынужденных колебаний в разветвленной цепи
называется резонансом токов. Векторная г- ^
диаграмма токов, соответствующая резо-
резонансу, изображена на рис. 390.
Обычно в катушках индуктивности
ujL ^> г, и угол (pi очень близок к —7г/2.
Так как ток гс в другой ветви опережает ис' '
. /с с ¦ диаграмма токов при
напряжение на угол +тг/2, т0 °ба тока %ь езОнансе
и ic обладают разностью фаз, близкой к
71", т.е. находятся в противофазах. Поэтому полный ток i равен
приблизительно разности токов %i и %с- При резонансе полный
528 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
ток становится наименьшим (ср. рисунки 389 и 390), а следо-
следовательно, сопротивление контура достигает наибольшего значе-
значения. Это сопротивление, однако, в отличие от случая резонан-
резонанса напряжений (§ 221), не равно активному сопротивлению г,
включенному в контур, и зависит еще от L и С (см. ниже).
Если бы сопротивление г было равно нулю, то разность фаз
между токами гь и ic была бы точно равна тг и оба тока при
резонансе точно компенсировали бы друг друга. В этом случае
ток в подводящих проводах был бы равен нулю, хотя каждый из
токов ii и ic мог бы иметь весьма большие значения. Сопротив-
Сопротивление же контура при резонансе было бы равно бесконечности.
Для наблюдения резонанса токов можно воспользоваться
схемой, изображенной на рис. 388, если включить в нее, помимо
амперметра Ai, измеряющего полный ток, еще амперметры Аг
и Аз в каждую из ветвей. Источником переменного напряжения
может служить осветительная сеть переменного тока. В каче-
качестве индуктивности удобно взять дроссель с подвижным желез-
железным сердечником, причем максимальная индуктивность дроссе-
дросселя должна быть больше той, которая необходима для резонанса.
Тогда можно наблюдать следующее. Вначале ток il (показания
амперметра Аз) значительно меньше тока ic (показаний Аг) и
амперметр Ai указывает на существование полного тока i за-
заметной силы (это соответствует рис. 389). При уменьшении ин-
индуктивности дросселя ток г^ увеличивается (ток ic остается по-
прежнему постоянным), а полный ток г, равный приблизительно
разности ic — ib, уменьшается. При некотором значении индук-
индуктивности ток i становится наименьшим (резонанс). При этом ам-
амперметры Аг и Аз дают мало отличающиеся показания, которые
намного больше показаний амперметра Ах. Отсюда следует, что
оба тока ic и гь почти противоположны по фазам. При дальней-
дальнейшем уменьшении индуктивности ток %l становится больше тока
%с и полный ток % начинает снова увеличиваться.
Найдем условие, при котором наступает резонанс токов. Из рис. 390
видно, что при резонансе
ioc = гоь sin i/??. B25.1)
Но из B24.4) следует, что
smipi, = uL/y/r2 + u2L2, cos (рь — r/y/r2 +u'2L'z.
Амплитуды же токов ioc и ioL имеют значения
iQL = U0/y/r2+cj*L2, ioc = UQuC.
Подставляя эти выражения в B25.1) и считая, что u2L2^$>r2, находим усло-
условие резонанса токов:
и) = 1/\/ZC = cjo- B25.2)
Таким образом, для резонанса токов, так же как и для резонанса напряже-
напряжений, частота колебаний со внешнего напряжения должна совпадать с часто-
частотой uio собственных колебаний контура в отсутствие затухания.
§ 225
РЕЗОНАНС ТОКОВ
529
Вычислим теперь амплитуду го полного тока при резонансе. Из рис. 390
следует, что
«о = ioL cos ipL. B25.3)
В том же приближении, что и выше (ш2Ь2 3> г2), имеем
го =
Uo
'Uo-
rC
L
Поэтому при резонансе
R=^ = -^. B25.4)
го тС
Если г —> 0, то R —> оо. Этот результат уже был получен выше с помощью
качественных рассуждений.
Отношение резонансного сопротивления R контура к его активному со-
сопротивлению г равно квадрату добротности Q контура (ср. выражение для
добротности в § 221):
'Выход
Так как на радиочастотах легко добиться добротности порядка 102, то от-
отношение R/r можно сделать порядка 104 и выше.
Таким образом, для переменного тока с частотой ujq (точнее,
для узкой полосы частот вблизи шо, тем более узкой, чем вы-
выше добротность контура) колебательный контур представляет
большое сопротивление, тогда как для всех других частот его
сопротивление мало. Это позволяет использовать резонанс то-
токов для выделения одного определенного колебания из сигнала
сложной формы, чем и пользуют-
пользуются широко на практике. В качестве
примера укажем на устройство ре-
резонансного усилителя, одна из схем
которого (в упрощенном виде) по-
показана на рис. 391. В анодной це-
цепи имеется колебательный контур,
настраиваемый на частоту сигна-
сигнала, который нужно усилить. Для
резонансной частоты контур пред- Рис- 391- Резонансный усили-
ставляет большое сопротивление, и тель
колебания анодного тока лампы вызывают на его концах появ-
появление переменного напряжения Для этой частоты (точнее, для
узкой полосы частот) резонансный усилитель действует так же,
как и усилитель на сопротивлениях, рассмотренный в § 161, при-
причем роль анодного сопротивления играет колебательный кон-
контур. Для всех же других частот, заметно отличающихся от
резонансной, контур практически осуществляет короткое замы-
замыкание анодной цепи, и поэтому напряжение получается близким
к нулю.
Вход
530
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ
ГЛ XXI
Как уже разъяснялось, при резонансе токов силу токов в
обеих ветвях контура можно сделать намного больше силы тока
в подводящих проводах. Это обстоятель-
обстоятельство используют при устройстве индук-
индукционных печей, в которых нагревание
металлов производится вихревыми тока-
токами (§ 132). А именно, параллельно на-
нагревающей катушке К (рис. 392) присо-
присоединяют конденсатор С и подбирают его
емкость таким образом, чтобы получить
на частоте питающего генератора резо-
резонанс токов. Тогда через генератор и под-
подводящие провода протекает только раз-
с, который может быть намного меньше
Рис. 392. Схема нагре-
нагревающего контура индук-
индукционной цепи
ностный ток i ~ %к —
тока гк в нагревательной катушке.
§ 226. Параметрический резонанс
При изучении электрического резонанса (напряжений и
токов) мы рассматривали действие периодической ЭДС
генератора на колебательный контур. Однако оказывается, что
аналогичные явления наблюдаются и при внешних воздействиях
других типов, причем возникающие колебания, так же как и при
действии ЭДС, существенно за-
зависят от частоты воздействий
на контур. Поэтому понятие ре-
резонанса можно обобщить и рас-
распространить на более широкий
класс явлений.
Положим, что внешнее воз-
воздействие изменяет один из
параметров колебательной си-
системы, и рассмотрим сначала
простой механический пример.
Пусть имеется маятник, дли-
длину которого можно изменять
(рис. 393), подтягивая конец
нити, перекинутой через блок,
или, наоборот, его отпуская. Будем периодически изменять дли-
длину маятника, подтягивая нить (уменьшая длину) всякий раз,
когда маятник будет находиться вблизи положения равновесия
@), и отпуская нить (увеличивая длину) при крайних положени-
положениях маятника A и 2), т.е. с частотой, равной удвоенной частоте
собственных колебаний маятника. Мы найдем, что маятник нач-
начнет совершать колебания с возрастающей амплитудой, которая
Рис. 393. Параметрический
нанс в механике
резо-
§ 226 ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС 531
будет увеличиваться до тех пор, пока нить не соскочит с блока.
Это будет наблюдаться и в том случае, если частота изменения
длины не равна удвоенной собственной частоте, но близка к ней.
В этом опыте мы имеем нарастающие колебания, как и в
случае резонанса под действием периодической внешней силы,
однако они возникают в результате периодического изменения
одного из параметров системы (длины). Поэтому описанное яв-
явление получило название параметрического резонанса.
Причину нарастания колебаний можно объяснить, исходя из
энергетических соображений. Когда мы укорачиваем нить в по-
положении 0 (рис. 393), то внешняя сила (сила руки) совершает ра-
работу не только против силы тяжести, но и против центробежной
силы, так как, проходя через положения равновесия 0, маятник
имеет наибольшую скорость. При удлинении нити работу совер-
совершает маятник. Однако эта работа производится только за счет
силы тяжести, так как в положениях 1 и 2 центробежная си-
сила равна нулю (скорость равна нулю), и поэтому она меньше
работы при укорочении нити. Таким образом, в колебательную
систему (маятник) непрерывно вводится энергия за счет работы
внешней силы, что и приводит к нарастанию колебаний.
Аналогичные явления параметрического резонанса наблю-
наблюдаются и в электрических колебательных контурах, если па-
параметры контура (емкость или индуктивность) изменяются пе-
периодически. Рассмотрим, например, колебательный контур LC
(рис. 394), имеющий конденсатор с по-
подвижной пластиной, которую можно
периодически приближать ко второй
пластине или удалять от нее. Положим,
далее, что в контуре в силу каких-либо
случайных причин возникли колебания
и что в момент времени, когда заряд
конденсатора проходит через нуль, мы
сближаем пластины. Это не будет СОпрО- Рис. 394. Колебательный
вождаться никакой работой, так как за- контур с изменяемой ем-
ряд конденсатора равен нулю, а значит, костью
и сила притяжения между пластинами также равна нулю. Че-
Через время, равное четверти периода собственных колебаний Т/4,
заряд конденсатора будет наибольшим. Если в этот момент раз-
раздвинуть пластины, то внешние силы совершат работу, затра-
затрачиваемую на преодоление взаимного притяжения пластин. То-
Тогда емкость конденсатора уменьшится, а напряжение между его
обкладками возрастет, способствуя колебаниям в контуре. Если
затем опять через время Т/4 сблизить пластины, то энергия кон-
контура не изменится, так как заряд конденсатора в этот момент
снова равен нулю. При последующем разведении пластин в кон-
контур снова будет введена определенная энергия, и т.д. Поэтому,
532 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
изменяя достаточно сильно емкость конденсатора с частотой,
равной удвоенной частоте собственных колебаний (или близкой
к ней), мы получим в контуре электрические колебания с возра-
возрастающей амплитудой, которая будет увеличиваться до тех пор,
пока конденсатор не будет пробит.
Отметим, что начальные малые колебания и в механиче-
механических, и в электрических системах всегда возникают под влияни-
влиянием случайных внешних воздействий, или флуктуации. Поэтому
при достаточно сильном периодическом изменении параметров
наблюдается самовозбуждение колебаний. Правильное соотно-
соотношение между фазой колебаний и фазой изменения параметра
осуществляется при этом автоматически, так как усиливаются
только те колебания, которые имеют нужную начальную фазу.
Описанный опыт с электрическим параметрическим ре-
резонансом был впервые осуществлен Л.И. Мандельштамом и
Н.Д. Папалекси в 1933 г. Построенная ими емкостная парамет-
параметрическая машина имела вращающийся конденсатор, содержа-
содержащий две системы пластин, снабженных радиальными выреза-
вырезами, одна из которых была неподвижна, а другая приводилась
во вращение с помощью электромотора. Такая машина развива-
развивала напряжения до многих тысяч вольт.
Явление параметрического резонанса можно использовать
для технического получения переменных токов.
§ 227. Комплексные величины
Для сложения колебаний тока и напряжения в различных се-
сетях переменного тока особенно удобно пользоваться символиче-
символическим методом, в котором гармонические колебания разных фи-
физических величин представляют в виде комплексных величин.
Этот метод значительно упрощает все вычисления, и поэтому
его широко применяют не только в теории переменных токов,
но и при исследовании любых механических и электрических
колебаний.
Известно, что
exp {ja) — cos a 4- j sin a.
Здесь а — вещественное число, a j' = у/-Л. Поэтому всякое ком-
комплексное число
z = х 4- ЗУ
можно представить в показательной форме
z = pexp(ja).
При этом вещественную и мнимую части х ж у комплексного
числа z можно выразить через р и а:
х = pcosat, у = psina,
§ 227 КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ 533
и, наоборот, р и а можно выразить через х и у:
р = \Л2 + ?А tg a = у/х.
Напомним, что р называется модулем комплексного числа z, a
а — его аргументом.
Положим теперь, что а изменяется со временем по закону
а = Lot 4- <р-
Тогда хну будут представлять два гармонических колебания:
х = р cos (uit 4- <р) 1 у = р sin (uit + f), B27.1)
происходящих с круговой частотой и и имеющих амплитуду р
и начальную фазу (р. Согласно сказанному выше, оба эти коле-
колебания можно выразить при помощи одного комплексного выра-
выражения
z = /эехр [j(wt 4- v?)] = pexp (jip) exp (jut). B27.2)
Если мы условимся заранее брать только вещественную часть
комплексного выражения B27.2), то мы получим первое из ко-
колебаний B27.1); если же мы будем употреблять только мнимую
его часть, то получим второе колебание.
Таким образом, гармонические колебания можно описывать
либо с помощью тригонометрических функций cos и sin, либо
с помощью комплексных выражений. Последний способ имеет,
однако, большое преимущество в тех случаях, когда приходит-
приходится складывать несколько колебаний, так как правила сложения
комплексных чисел гораздо проще, нежели правила сложения
тригонометрических функций.
Если частота ш одинакова для всех рассматриваемых коле-
колебаний, то множитель exp (jut) можно не выписывать. В этих
случаях мы вполне определим гар-
гармоническое колебание, если зада-
зададим лишь величину ". | zJz.x_^ 1У
s = pexp(j(p), B27.3)
которая называется комплексной
амплитудой. Ее модуль р дает
фактическую амплитуду гармони-
гармонического колебания, а аргумент ср —
начальную фазу колебания.
Представление колебаний с по-
помощью комплексных выражений Рис. 395. Изображение комп-
тесно связано с векторными диа- лексного числа при помощи век-
граммами. Действительно, если на тора
плоскости (рис. 395) ввести две взаимно перпендикулярные оси
и по одной из них (X) откладывать вещественную часть х ком-
комплексного числа z, а по другой (Y) — мнимую часть jy, то чис-
число z будет изображаться на этой плоскости некоторым вектором.
534 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ XXI
Длина этого вектора р = ^/х2 + у2 есть модуль комплексного
числа z, а угол <р = arctg (у/ж), составленный с вещественной
осью X, равен аргументу z. Поэтому, задавая комплексную ам-
амплитуду колебания s (формула B27.3)), мы определяем вектор,
длина которого равна амплитуде колебаний, а угол поворота —
начальной фазе, т.е. поступаем так же, как и при построении
векторной диаграммы колебаний. Различие заключается лишь
в том, что в случае векторной диаграммы мы изображаем этот
вектор графически, а пользуясь комплексным выражением, за-
задаем его аналитически.
Вернемся теперь к переменным токам и положим, что сила
тока в цепи равна г = го sincc^^. Пользуясь комплексными вели-
величинами, это колебание можно записать в виде
i = io exp (jixit).
Тогда колебания напряжения на чисто активном сопротивлении
(§ 217) будут выражаться формулой
Ur = iqt exp (juit).
Комплексная амплитуда в данном частном случае оказывается
вещественной:
UOr = tor, B27.4)
что, согласно сказанному выше, обозначает отсутствие сдвига
фаз между напряжением и током.
Колебания напряжения на индуктивности (§ 219) опережают
по фазе колебания тока на тт/2, и поэтому
Ul = iowL exp \j{uit + тг/2)].
Комплексная амплитуда этих колебаний
Uql = «o^Lexp (jtt/2).
Входящий сюда множитель exp (jtt/2) изображается на ком-
комплексной плоскости (см. рис. 395) вектором, имеющим длину 1
и направленным вдоль мнимой оси jY. Поэтому exp (jtt/2) = j
и, следовательно,
Uol = iojuiL. B27.5)
Наконец, для колебаний напряжения на конденсаторе, кото-
которые отстают от колебаний тока на тт/2 (§ 218), получим
Uc = (io/шС) exp [j(uit - тт/2)}.
Комплексная амплитуда напряжения на конденсаторе равна
или, так как ехр (—jir/2) = — j = 1/j,
Uoc = ^. B27.6)
§ 227 КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ 535
Рассмотрим теперь, как можно производить сложение коле-
колебаний, пользуясь комплексными выражениями. При этом мы
везде предполагаем, что речь идет о колебаниях скалярных ве-
величин (каковыми являются сила тока, заряд конденсатора, на-
напряжение и т.д.).
Суммой комплексных чисел
zi=xi+ jy1} z2 = x2 + jy2,. ¦ ¦,
по определению, называют комплексное число
у которого вещественная (X) и мнимая (Y) части суть суммы
соответственно вещественных и мнимых частей слагаемых:
X - xi + х2 + х3 + ..., Y = ух + 2/2 + 2/3 + ¦ • ¦
Если z\, z2, ... — комплексные выражения гармонических
колебаний, то величины х\, х2, хз, ... и соответственно j/i, y2,
2/з, • ¦ • представляют собой гармонические колебания (одно из
которых описывается функцией cos, а другое — sin). Поэтому
комплексное выражение Z будет соответствовать сумме скла-
складываемых колебаний. Если по-прежнему все колебания имеют
одинаковую частоту ш, то и здесь общий множитель exp (jut)
можно не выписывать, а достаточно сложить лишь комплекс-
комплексные амплитуды суммируемых колебаний.
Таким образом, мы приходим к следующему правилу: для
сложения нескольких колебаний одинаковой частоты доста-
достаточно сложить комплексные амплитуды этих колебаний. Мо-
Модуль полученного комплексного выражения дает фактическую
амплитуду результирующего колебания, а его аргумент — на-
начальную фазу.
Отметим, что на комплексной плоскости (X, jY) сложе-
сложение комплексных чисел изображается суммированием векторов,
представляющих эти комплексные числа, а комплексное число
Z, выражающее искомую сумму, является замыкающим векто-
вектором (векторной суммой). Поэтому данное выше правило в точ-
точности соответствует построению векторной диаграммы резуль-
результирующего колебания.
Поясним сказанное на примере. Рассмотрим опять цепь, со-
содержащую последовательно соединенное сопротивление, индук-
индуктивность и емкость, и найдем напряжение на концах этой цепи.
Оно представляет собой сумму трех напряжений, комплексные
амплитуды которых выражаются формулами B27.4)-B27.6).
Поэтому комплексная амплитуда полного напряжения есть
ior + iojuL + j^ = чг + toj (шЬ - ^
536 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
Отсюда получаем выражения для фактической амплитуды на-
напряжения (модуль) и для начальной фазы напряжения (аргу-
(аргумент):
С/о = гО\/г2+(ыЬ-1/шСJ,
, ыЬ- 1/шС
ip = arctg ———-—,
что совпадает с формулами B20.3), B20.4).
§ 228. Комплексные сопротивления
Применение комплексных величин для расчетов цепей переменного то-
тока можно еще значительно упростить, если ввести понятие о комплексном
сопротивлении. Пусть го есть амплитуда силы тока в каком-либо участке
цепи, а % — комплексная амплитуда напряжения. Тогда комплексное со-
сопротивление z этого участка определяется соотношением
uQ = zi0. B28.1)
Таким образом, комплексное сопротивление участка есть отношение ком-
комплексной амплитуды напряжения к амплитуде силы тока.
Если мы умножим обе части формулы B28.1) на exp(juit), то слева
мы получим мгновенное значение напряжения и = ио exp (juit), справа же
вместо г'о войдет г = го exp (juit), т.е. мгновенная сила тока. Поэтому для
мгновенных значений напряжения и тока справедлива формула, аналогич-
аналогичная B28.1):
и = zi. B28.2)
Найдем, чему равны комплексные сопротивления в различных частных
случаях. Пусть участок цепи имеет только активное сопротивление г. Тогда,
если амплитуда тока есть го, то амплитуда напряжения (см. B27.4)) равна
Uor — *0f И
zr = г. B28.3)
В этом частном случае комплексное сопротивление не имеет мнимой части
и равно активному сопротивлению участка.
Если участок цепи содержит только катушку индуктивности L, то, со-
согласно B27.5), uol = iojuiL, поэтому
zL = juiz. B28 4)
Совершенно так же находим, что в случае конденсатора (формула
B27-6)) комплексное сопротивление равно
zc = -L B28.5)
Представим себе теперь, что мы имеем какую-нибудь цепь переменного
тока, которая может быть сколь угодно сложной. Так как мы рассматрива-
рассматриваем только квазистационарные токи, то для мгновенных значений электри-
электрических величин справедливы те же законы Кирхгофа, что и для постоян-
постоянных токов. Поэтому для любого замкнутого контура (например, контура
1-2-3-4-5, рис. 396) мы имеем (второе правило Кирхгофа)
exp (jut) = ^2 eOfc exp (juit),
к
§ 228
КОМПЛЕКСНЫЕ СОПРОТИВЛЕНИЯ
537
где еолг — комплексные амплитуды ЭДС генераторов. Сокращая обе части
на exp (juit), получим соответствующее уравнение для амплитуд
= y>ofc. B28.6)
Точно так же для любой точки разветвления цепи справедливо первое пра-
правило Кирхгофа, которое после сокращения на общий множитель exp {jut)
имеет вид
Y, гор = 0. B28.7)
р
Таким образом, мы видим, что законы постоянного тока применимы
не к обычным фактическим амплитудам тока, напряжения и ЭДС, но к
комплексным амплитудам этих величин, причем под сопротивлениями от-
отдельных участков цепи нужно понимать их комплексные сопротивления.
Поэтому решение задачи о любой це-
цепи переменного тока можно получить \
из соответствующего решения для
постоянного тока, если силу тока,
напряжение и ЭДС заменить их ком-
комплексными амплитудами, а сопро-
сопротивление участков — их комплексны-
комплексными сопротивлениями.
Отсюда, в частности, получается
следующее простое правило для вы-
вычисления сопротивления цепей: что-
чтобы найти сопротивление цепи для
переменного тока, нужно в этой
цепи мысленно заменить каждую
индуктивностпь L на ее комплекс-
ное сопротивление jwiy, кажоую ем-
емкость С — на l/(ju>C), а все активные сопротивления оставить без из-
изменений. Затем с указанными комплексными сопротивлениями нужно
произвести те же операции, что и при вычислении сопротивления для
постоянного тока, складывая при последовательном соединении сопротив-
сопротивления, а при параллельном — им обратные величины {проводимости). По-
Полученная в результате этого комплексная величина Z — X + jY и будет
представлять собой полное комплексное сопротивление цепи Эта вели-
величина получила название импеданса цепи. Ее вещественная часть X есть
активное сопротивление цепи, а мнимая часть У — реактивное сопротивле-
сопротивление. Модуль импеданса R = у/Х2 + У2 дает сопротивление цепи для пере-
переменного тока и определяет амплитуду силы тока при заданной амплитуде
напряжения на концах цепи:
го = Uo/R.
Аргумент импеданса дает угол ip, на который напряжение опережает ток в
цепи:
D one -о
Рис. 396. Разветвленная цепь пере-
менного тока
Рассмотренный метод комплексных сопротивлений весьма удобен для
практических расчетов и поэтому широко применяется в электротехнике.
Он исключительно прост и не требует вычисления сдвигов фаз (что необ-
необходимо при построении векторных диаграмм), так как они уже учтены в
538
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ ГЛ. XXI
комплексных сопротивлениях. По сравнению с векторными диаграммами
этот метод обладает еще и тем преимуществом, что позволяет вести рас-
расчеты с какой угодно точностью, тогда как векторные диаграммы, как и
всякий графический метод, отличаются большей наглядностью, но не обес-
обеспечивают точности.
Для иллюстрации метода комплексных сопротивлений рассмотрим
некоторые простейшие примеры.
Пример 1. Цепь содержит последовательно соединенные активное
сопротивление г и индуктивность L (рис. 397 о).
Рис. 397. Примеры простых цепей
Так как при последовательном соединении складываются сопротивле-
сопротивления, то импеданс цепи есть
Z = г
Поэтому сопротивление всей цепи равно
а напряжение опережает ток по фазе на угол
ip = arctg (cjL/г).
Пример 2. Цепь состоит из конденсатора емкостью С, параллельно
которому присоединено активное сопротивление г (конденсатор с утечкой,
рис. 397 б).
При параллельном соединении складываются проводимости участков.
Поэтому, если Z есть импеданс цепи, то
1/Z = 1/r + ju)C.
Отсюда
1/r + juC
Чтобы привести это выражение к виду Z = X + JY, умножим и разделим
правую часть на 1/r — jwC. Тогда
r-jur2C
Z = 1/r" j
Сопротивление цепи равно
R =
= X+jY.
+ Y2 = г/д/Г+w2r2C2,
а напряжение опережает ток по фазе на угол
ip = arctg (Y/X) = - arctg {uirC).
§228
КОМПЛЕКСНЫЕ СОПРОТИВЛЕНИЯ
539
В данном случае угол у? оказывается отрицательным, а, значит, напряжение
отстает по фазе от тока (как и должно быть при емкостном характере цепи).
Пример 3. Рассмотрим цепь, которая обсуждалась при изучении
резонанса токов (рис. 397 в).
В этом случае мы должны найти сначала импеданс Z\ ветви, содержа-
содержащей индуктивность. Так как г и L соединены здесь последовательно, то
Z\ — т + juiL.
Обе же ветви цепи соединены между собой параллельно. Поэтому для им-
импеданса Z всей цепи имеем
1 1
Выражая отсюда Z и уничтожая мнимость в знаменателе, находим после
несложных преобразований, что
г + jcj[L(l - uP-LC) - О2]
Найдем условие, при котором мнимая часть импеданса (реактивное со-
сопротивление) обращается в нуль. Этот случай вынужденных колебаний, как
мы знаем (§ 225), называется резонансом токов. Искомое условие есть
Ц1 - ui2LC) - Сг2 = 0.
Считая, как и раньше, lj2L2 3> г2, находим, что
резонанс токов наступит при частоте шо, равной
Подставляя это значение в выражение для Z и
учитывая, что A — ш^ЬС) = 0, получаем резо-
резонансное сопротивление контура
2рез = Ь/Сг.
Приведенные выше результаты мы уже получили
раньше (§ 225) другим способом. п „по .,
Пример 4. Для измерения емкости кон- Рис' 398' Мост для из"
денсаторов употребляют мостовую схему, рабо- меРения емкости
тающую на переменном токе (рис. 398). Она подобна схеме моста на посто-
постоянном токе, но отличается от нее тем, что в два плеча схемы включены кон-
конденсаторы вместо сопротивлений. К двум противоположным точкам схемы
(например, к а и б, рис. 398) присоединен миниатюрный генератор пере-
переменной ЭДС (зуммер), а к двум другим (виг) — индикатор переменного
тока (например, телефон Г). Процесс измерения заключается в том, что,
меняя сопротивления двух других плеч Гз и г 4, добиваются такого положе-
положения, чтобы между точками виг колебания напряжения были равны нулю
(равновесие моста), т.е. в телефоне не было слышно звука. Найдем условие
равновесия моста.
Если бы мы имели ток постоянный, а вместо конденсаторов С\ и Сг
были включены сопротивления п и гг, то при равновесии мы имели бы
Tl/r2 = Гз/Г4-
540
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЕ ТОКИ
ГЛ. XXI
В случае переменного тока, как мы знаем, нужно пользоваться комплекс-
комплексными сопротивлениями, т.е. заменить п на l/{juCi), а гг — на /iC)
Поэтому условие равновесия моста на переменном токе есть
Измеряя на опыте отношение гз/г4, необходимое для равновесия моста, и
зная емкость одного из конденсаторов, отсюда можно определить неизвест-
неизвестную емкость другого конденсатора.
Отметим, что при расчетах мы предполагали, что активные сопротив-
сопротивления плеч моста, содержащих конденсаторы, малы по сравнению с емкост-
емкостными сопротивлениями, что обычно и имеет место на практике.
Пример 5. При помощи схемы моста на переменном токе можно
измерять не только емкости, но и индуктивности. Однако так как катушки
индуктивности обычно обладают заметным сопротивлением, то здесь уже
нельзя пренебрегать активным сопротивлением плеч моста, содержащих ка-
катушки, по сравнению с их индуктивным сопро-
в тивлением.
Схема моста для измерения индуктивностей
изображена на рис. 399. Она содержит четыре
переменных (безындукционных) сопротивления
fi, г2, гз и Г4, причем под г\ и г2 мы будем по-
понимать в дальнейшем полные активные сопро-
сопротивления плеч 1 и 2, включая и сопротивления
катушек.
Комплексное сопротивление плеча 1 (ср.
пример 1) есть п + juiLi, а для плеча Z оно со-
соответственно равно г2 + ju>L2- Поэтому условие
равновесия моста на переменном токе есть
(П + JL)Ll)j{r2 + jUlL2) — Г3/Г4,
или иначе
П + jcuLi = (гз/г4)(г2 + juL2)-
Но для равенства двух комплексных выражений необходимо, чтобы были
равны их вещественные и мнимые части порознь. Поэтому мы получаем
два условия
П/г2 = Г3/Г4, LxjL'i = Г3/Г4.
Наличие двух условий соответствует тому физическому обстоятельству, что
для равновесия моста необходимо, чтобы колебания потенциала в точках а и
б (рис. 399) имели не только одинаковые амплитуды, но и одинаковые фазы,
ибо только в этом случае можно добиться того, чтобы разность потенциалов
точек виг была равна нулю в любой момент времени, что необходимо для
исчезновения звука в телефоне.
Первое условие есть условие равновесия моста при постоянном токе.
Следовательно, равновесие при переменном токе возможно только в том
случае, если одновременно мост уравновешен и для постоянного тока.
В соответствии с этим при измерении индуктивностей к точкам а и б
мостовой схемы (рис. 399) прикладывают попеременно либо постоянное на-
напряжение (заменяя при этом телефон Г на гальванометр), либо переменное
напряжение и, изменяя все четыре сопротивления r\, rj, гз и г 4, добивают-
добиваются, чтобы мост был в равновесии в обоих случаях. Тогда из второго условия
равновесия можно определить отношение индуктивностей, а если одна из
индуктивностей известна, то можно найти и значение второй неизвестной
индуктивности.
Рис. 399. Мост для изме-
измерения индуктивностей
§229
РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ
541
ГЛАВА XXII
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ
ПРОВОДОВ
§ 229. Распределенные системы
До сих пор мы имели дело с простыми колебательными кон-
контурами, в которых емкость практически была сосредоточена в
одном определенном
месте контура (кон- а гу-у-^^
денсаторе), а индук- _?_ |
т I
тивность — в другом
(катушке). Рассмот-
Рассмотрим теперь системы,
в которых емкость и
индуктивность распре-
распределены непрерывно.
Такие распреде-
распределенные системы мож-
можно рассматривать как
предельный случай
систем с сосредото-
сосредоточенными постоянны-
постоянными. Простому контуру
(рис. 400 а) соответ-
соответствует в механике
материальная точка,
движущаяся в опреде-
определенном направлении
под действием упру-
упругой силы. Она имеет
единственную степень
свободы и может со-
совершать собственные колебания с одной определенной частотой.
Подобно этому простой электрический контур характеризуется
единственной собственной частотой щ.
Рассмотрим теперь два простых контура, связанных между
собой общей емкостью (рис. 400 б). Соответствующая механи-
механическая система состоит из двух материальных точек и обладает
двумя степенями свободы. В ней возможны два разных типа соб-
собственных колебаний, происходящих с различной частотой. Ана-
Аналогично в двух связанных электрических контурах возможны
два различных собственных электрических колебания с двумя
частотами: wni и
Рис. 400- Колебания с одной (а), двумя (б) и
тремя (в) степенями свободы
542 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ ГЛ. XXII
В случае контура, изображенного на рис. 400 в, мы имеем де-
дело с тремя степенями свободы, и здесь возможны три различных
колебания с тремя частотами: шоь ш02 и шоз-
Представим себе теперь, что в контуре, изображенном на
рис. 400, мы неограниченно увеличиваем число звеньев и соот-
соответственно уменьшаем индуктивности и емкости каждого зве-
звена. Тогда в пределе мы получим двухпроводную линию, в кото-
которой индуктивность и емкость непрерывно распределены по всей
длине. В механике ей соответствует резиновый шнур или стру-
струна с непрерывно распределенными массой и упругостью. Число
степеней свободы струны равно бесконечности и поэтому в ней
возможно бесконечное число собственных колебаний. То же мы
имеем и в электрических распределенных системах: число раз-
различных собственных колебаний в таких системах равно беско-
бесконечности.
Из механики известно, что колебательные движения струны
(как и всякой механической распределенной системы) представ-
представляют собой механические волны. Различные собственные коле-
колебания ограниченной струны суть не что иное, как возможные
в струне стоячие волны. Аналогично электрические колебания
в распределенных электрических системах представляют собой
электромагнитные волны, к рассмотрению которых мы и обра-
обратимся.
§ 230. Электромагнитный импульс вдоль проводов
Рассмотрим двухпроводную линию, неограниченно прости-
простирающуюся в обе стороны, и положим, что источник переменного
тока создает в какой-либо точке О линии (рис. 401 а) электри-
электрическое поле Е. Опыт показывает, что электрическое поле распро-
распространяется вдоль линии. Поставим теперь вопрос: посредством
каких процессов происходит это распространение поля?
Один из способов передачи электрического поля нам уже из-
известен — он заключается в возникновении токов проводимости.
При этом электроны в проводах перемещаются вдоль линии и
при движении переносят свой электрический заряд, а вместе с
ним и электрическое поле.
Однако наряду с этим существует и другой процесс передачи
поля, который в очень многих явлениях играет главную роль.
Он был открыт Максвеллом и состоит в распространении элек-
электромагнитных волн.
Рассмотрим сначала это явление качественно. Положим, что
в данный момент времени электрическое поле Е увеличивает-
увеличивается. Согласно основному положению теории Максвелла (§ 136)
изменяющееся электрическое поле, т.е. ток смещения, вызывает
появление магнитного поля. Модуль и направление этого маг-
230
ЭЛЕКТРОМАГНИТНЫЙ ИМПУЛЬС ВДОЛЬ ПРОВОДОВ
543
нитного поля соответствуют току с плотностью j = dD/dt =
= EodEi/dt (мы будем предполагать, что линия находится в ва-
вакууме или же, что практически то же, в атмосферном воздухе).
Так как поле Е увеличивается, то d~E/dt > 0 и направление то-
тока смещения j совпадает с направлением Е. Применяя правило
правого буравчика, мы находим, что магнитное поле Н направ-
направлено так, как показано на рис. 401 а.
t'^t1
1
X
4 J
т
1
Е
^*-
+
Е,
Н
Е,'
^
+
ч
—^
н.
о
-к
1
и
/ 1
Н х^+ |
- ,
/
Е
—*> v
О
Рис. 401. Распространение электромагнитного импульса вдоль проводов
Но согласно второму основному положению теории Максвел-
Максвелла (§ 131) изменяющееся магнитное поле вызывает появление ви-
вихревого электрического поля. Поэтому в последующий момент
времени возникнет электрическое поле Е^ Оно будет направ-
направлено так же, как и индукционный ток, который возник бы в
замкнутом проводнике под действием возрастающего поля Н
(рис. 401 а).
Если бы проводов линии не было, то линии поля содержа-
содержали бы участки, отмеченные на рисунке штрихом. При наличии
проводов в них возникнет ток проводимости г (рис. 401 а). Если
провода сделаны из хорошо проводящего материала (металл),
544 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ ГЛ XXII
то напряженность электрического поля в них будет весьма мала
и штриховых участков линий напряженности поля практически
не будет.
Возрастающее электрическое поле Ei представляет собой ток
смещения, который вызовет появление магнитного поля Hi. Из
рис. 401 а видно, что поле Ei в точке О направлено противопо-
противоположно полю Е, а следовательно, будет уничтожать это послед-
последнее, а поле Hi будет уничтожать поле Н. Поэтому первоначаль-
первоначальное поле Е и вызванное им поле Н исчезнут, но зато появятся
поля Ei и Hi в соседней точке линии 1 (рис. 401 б).
В последующие моменты времени явления будут происхо-
происходить аналогично. Возрастающее поле Hi вызовет появление ви-
вихревого электрического поля Ег, а это последнее, увеличиваясь,
приведет к возникновению магнитного поля Н2. Поля Ег и Н2
уничтожат поля Ei и Hi в точке 1 и проявятся в соседней точке
2, еще более удаленной от места первоначального возмущения
(рис. 401 б). Поэтому электрические и магнитные поля, взаимно
превращаясь и поддерживая друг друга, будут распространять-
распространяться вдоль линии (рис. 401 б). Этот процесс вполне подобен рас-
распространению механического импульса вдоль резинового шнура
или струны и может быть назван распространением электро-
электромагнитного импульса.
Для правильного понимания описанных явлений нужно
иметь в виду, что точки О, 1, 2 к т.д. (см. рис. 401) находят-
находятся бесконечно близко друг к другу. Поэтому поля Е и Н, Ei и
Hi и т.д. относятся к одной и той же точке. Следовательно, там,
где электрическое поле Е имеет максимум, там имеет максимум
и магнитное поле Н; в тех же точках, где поле Е равно нулю,
нет и поля Н. Это обстоятельство нам придется неоднократно
учитывать в дальнейшем.
Из рис. 401 видно, что направления полей Е и Н перпен-
перпендикулярны друг другу и в свою очередь перпендикулярны к
скорости распространения v:
Е JlH Jl v.
Эти три вектора связаны правилом буравчика: направление
v совпадает с направлением поступательного движения бурав-
буравчика с правой нарезкой, если его рукоятка вращается в направ-
направлении от Е к Н.
Отметим, наконец, что выше мы рассматривали только по-
половину линии, находящуюся справа от точки О. Очевидно, что
такие же явления будут происходить и в левой части линии, и
поэтому поля будут распространяться в обе стороны от места
первоначального возмущения.
Таким образом, существуют два различных процесса пере-
передачи поля: с помощью токов проводимости и при помощи то-
§231
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
545
ков смещения (электромагнитных волн). Если быстрота изме-
изменения полей мала (малые частоты), то токами смещения можно
пренебречь по сравнению с токами проводимости и последние
играют основную роль. В этом случае электрические явления
существенно зависят от сопротивления линии и, следовательно,
от материала проводов. Если же поля изменяются быстро (боль-
(большие частоты), то основную роль играют токи смещения и элек-
электрические явления определяются электромагнитными волнами.
При этом, как мы видели, основные процессы происходят меж-
между проводами, в окружающей среде, и электрические явления
практически не зависят от свойств материала проводов.
§ 231. Электромагнитные волны
Положим теперь, что в точке О (рис. 402) безграничной ли-
линии электрическое поле изменяется по гармоническому закону
Е = Eq sin wi.
Электромагнитное поле будет распространяться вдоль линии, и,
следовательно, в какой-либо точке линии, удаленной нарасстоя-
Н
Рис. 402. Распределение электрического и магнитного полей в распростра-
распространяющейся волне
ние х от точки О, также возникнут гармонические колебания
поля. Однако распространение поля происходит с конечной ско-
скоростью v, так что колебания в точке х будут запаздывать от-
относительно колебаний в О на время распространения импульса
546 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ ГЛ XXII
т = x/v. Следовательно, колебания электрического поля в точке
х запишутся в виде
E = EQsm[u(t-x/v)]. B31.1)
В § 230 мы видели, что максимумы электрического поля при рас-
распространении электромагнитного импульса совпадают с макси-
максимумами магнитного поля. Поэтому колебания магнитного поля
в точке О будут Н = Hq smojt, а в точке х
H = Hosm[u}(t-x/v)]. B31.1а)
Формулы B31.1) и B31.1а) выражают закон изменения
электрического и магнитного полей в волне, распространяющей-
распространяющейся в одном определенном направлении, а именно в направле-
направлении положительной оси X. Они называются уравнением волны.
Если волна распространяется в противоположном направлении
(вдоль отрицательной оси X), то уравнение волны будет
Е = Eosm[w(t + x/v)], H = Hosm[u>(t + x/v)}. B31.2)
Мгновенное распределение электрических и магнитных по-
полей в электромагнитной волне изображено на рис. 402. Для дан-
данного момента времени электрическое и магнитное поля достига-
достигают максимума в одних и тех же точках и в одних и тех же точках
проходят через нуль. Если же следить за изменениями полей в
какой-либо определенной точке линии, то оба поля Е и Н будут
одновременно проходить через максимумы и одновременно че-
через нулевые значения. Или иначе: в распространяющейся элек-
электромагнитной волне колебания электрического и магнитного
полей находятся в фазе. Отметим, что аналогичные фазовые
соотношения мы имеем и в механических волнах, где колебания
деформации и скорости (потенциальной и кинетической энер-
энергии) также находятся в фазе.
Расстояние между двумя точками, в которых колебания от-
отличаются по фазе на 27Г (например, между двумя соседними
максимумами, рис. 402), есть длина электромагнитной волны А.
Она равна расстоянию, на которое распространяется волна за
время одного периода колебания Т. Если v — скорость распро-
распространения электромагнитных волн (скорость распространения
фазы колебаний), то
А = vT. B31.3)
Пользуясь соотношением B31.3) и учитывая, что ш = 2тг/Т,
уравнения волны B31.1) и B31.2) можно записать и в следую-
следующем виде:
Е = Е0 sin[27r(?/T ^ х/Х)] = Ео sin (ш* ^ кх), B31.4)
где к = 2тг/А — волновое число. Такая же формула справедлива
и для магнитного поля.
§ 232 СТОЯЧИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 547
Уравнение волны в комплексной форме имеет вид
Е = Ео exp \j{u)t =р кх)}.
Следовательно, комплексная амплитуда колебаний в волне рав-
равна
Eoexp{^jkx). B31.5)
В предыдущих формулах мы считали, что амплитуды коле-
колебаний электрического и магнитного полей Ео и Но постоянны,
т.е. волна распространяется без затухания. Однако при наличии
электромагнитной волны в линии появляются токи проводимо-
проводимости (см. рис. 401). Так как сопротивление реальной линии не
равно нулю, то в ней развивается тепло Джоуля-Ленца, которое
выделяется за счет энергии электромагнитного поля. Поэтому
в действительности амплитуды Ео и Но по мере продвижения
электромагнитной волны постепенно уменьшаются. Написанные
формулы справедливы точно при условии, что сопротивление
линии равно нулю. Их можно приближенно применять и для
реальной линии, если рассматривать лишь участок линии такой
длины, что затухание волны на нем невелико.
§ 232. Стоячие электромагнитные волны
Распространяющиеся электромагнитные волны возникают в
очень длинных линиях, которые практически можно рассма-
рассматривать как неограниченные. Во многих случаях, однако, при-
приходится иметь дело с короткими линиями, на длине которых
укладывается сравнительно небольшое число длин волн. В этих
случаях существенную роль играет отражение электромагнит-
электромагнитных волн от концов линии. Отраженные волны складываются
между собой и с первоначальной волной, в результате чего воз-
возникают более сложные фор-
формы электромагнитных коле- '
баний — стоячие электро-
электромагнитные волны, подобные 1~
стоячим механическим вол- ^Л
нам в упругом шнуре или ч-ту
струне. i
Для выяснения основных
особенностей стоячих элек- а ' »-
тромагнитных волн доста- х X
ТОЧНО рассмотреть только Рис. 403. Ограниченная двухпровод-
две волны: первичную и од- ная линия
ну отраженную от конца ли-
линии. Введем координатную ось X, направленную вдоль линии
(рис. 403), и положим, что колебания электрического поля пер-
548 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ ГЛ XXII
вичной волны в точке линии О имеют вид
Е\ = Easmut. B32.1)
Тогда колебания в точке линии х будут
Е\ = Ео sin (u>t - kx). B32.2)
Считая, что волна отражается полностью, колебания поля отра-
отраженной волны в той же точке х можно представить формулой
Е2 = Ео sin (wt + kx-ip). B32.3)
Здесь знак 4- у слагаемого кх выражает то, что отраженная
волна распространяется в отрицательном направлении оси X
(справа налево, рис. 403). Угол же (р имеет следующий смысл.
Полагая в формуле B32.3) х = 0 и сравнивая ее с B32.1), мы
видим, что <? есть запаздывание по фазе колебаний поля отра-
отраженной волны в точке О по сравнению с колебаниями первичной
волны в той же точке. Это запаздывание имеет две причины.
Во-первых, до возвращения в точку О волна должна дважды
пройти всю длину линии I, отчего возникает отставание по фазе
27Г - 21/\. Во-вторых, как мы увидим ниже, возможно изменение
фазы колебаний при самом отражении. Для учета этих обоих
явлений мы и ввели в B32.3) угол (р, точное значение которого
для нас пока не важно.
Складываясь, обе волны дают результирующее поле
Е = Е\ 4- Е2 = EQ[sm (uit — кх) + sin (uit + кх — (р)].
Применяя известную формулу тригонометрии о сумме сину-
синусов и учитывая еще, что cos (—a) = cos а, находим
Е = 2Е0 cos (кх - <р/2) sin (uit - (р/2). {232 А)
Формула B32.4) показывает, что в линии будут происходить гар-
гармонические колебания поля с частотой первичной волны ш и с
начальной фазой —у/2. Однако амплитуда этих колебаний
Еь = 2Еа cos (кх - ip 12) B32.5)
оказывается зависящей от координаты х и потому различна в
разных точках линии. В определенных точках Еа, достигает мак-
максимума. Эти точки называются пучностями электрического по-
поля. Их координаты хП определяются условием
кхп — ip/2 = 0,7Г, 27Г,... , пп.
Для расстояния Ах между двумя соседними пучностями имеем
к Ах = 7г.
Так как к = 2тт\, то
Ах = А/2. B32.6)
В точках, называемых узлами электрического поля, ампли-
амплитуда Eg. обращается в нуль. Координаты узлов ху можно найти
§232
СТОЯЧИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
549
из условия
кху - (р/2 = 7г/2, Зтг/2, ...,
1)тг/2.
Пучность
Х/2
X
Следовательно, два соседних узла отстоят друг от друга на рас-
расстояние
Ах = тг /к = А/2.
Расстояние между соседними узлами и пучностями одинаково и
равно половине длины волны А/2.
Рисунок 404 поясняет характер колебаний поля в стоячей
электромагнитной волне; вдоль горизонтальной оси отложены
перемещения х вдоль линии, а по вертикальной оси — ампли-
амплитуда колебаний поля Е&. Во всех точках между двумя соседни-
соседними узлами @-1, 1-2 и т.д.) колебания происходят с одинаковой
начальной фазой, так что Е во всех точках одновременно до-
достигает максимума и одновременно обращается в нуль (в соот-
соответствии с формулой B32.4)). Но
при переходе через каждый узел
cos (kx — ip/2) изменяет знак, что
соответствует изменению фазы ко-
колебаний на 7Г.
Выше мы рассматривали толь-
только колебания электрического по-
поля. Обратимся теперь к магнитно-
магнитному полю.
В § 231 мы видели, что в рас-
распространяющейся волне колебания
электрического и магнитного по-
полей (Е И Н) находятся В фазе. Рис 404. Колебания электри-
В стоячей электромагнитной волне ческого поля в стоячей волне
это уже не имеет места, и между
колебаниями Е и Н существует разность фаз, а пучности элек-
электрического поля не совпадают с пучностями магнитного поля.
Причина этого различия заключается в том, что при отра-
отражении электромагнитной волны от конца линии происходит из-
изменение фазы колебаний. Необходимость этого явления ясна из
следующих рассуждений. Мы знаем (§ 230), что направления
векторов Е и Н связаны с направлением скорости распростра-
распространения v правилом правого буравчика. Положим, что волна (пер-
(первичная) движется слева направо и что расположение векторов Е
и Н в волне в конце линии такое, как показано на рис. 405 а. Что-
Чтобы скорость волны изменилась на противоположную, нужно,
чтобы один из векторов, Е или Н, изменил знак (рис. 405 б я в).
Но изменение знака поля обозначает изменение фазы колебаний
на 7г. Поэтому при отражении фаза колебаний одного из полей
должна обязательно изменяться скачкообразно на 7Г. При этом
если изменяется фаза электрического поля, то фаза магнитно-
550 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ ГЛ XXII
го поля остается без изменений, и наоборот, если скачок фазы
испытывает магнитное поле, то фаза электрического ноля не из-
изменяется.
Явление изменения фазы при отражении можно строго обос-
обосновать при помощи уравнений Максвелла, которые позволяют
также определить, какое именно из полей, Е или Н, меняет фазу
при данных условиях на
конце линии. Однако мы
ограничимся более просты-
простыми качественными рассуж-
• *v" ^" у"* Л дениями.
У >/ Положим, что линия на
•Т Н^ конце разомкнута. В этом
случае переменные токи,
возникающие в проволоках,
Рис 405. Взаимная ориентировка g вызывать на конце
электрического и магнитного векторов наибольшие колеба-
До (а) и после (о и в) отражения ,-.
электромагнитной волны ния зарядов. Здесь, следо-
следовательно, будет расположе-
расположена одна из пучностей электрического поля (напряжения). Это
значит, что электрическое поле в отраженной волне направлено
так же, как и в падающей, т.е. оно не изменяет фазы. Но при тех
же условиях, так как проволоки граничат с диэлектриком, ам-
амплитуда тока на конце линии будет равна нулю. Здесь будет узел
тока, а значит, и узел магнитного поля. Следовательно, магнит-
магнитное поле в отраженной волне направлено противоположно полю
падающей волны, т.е. оно изменяет фазу на 7г.
Если линия замкнута на конце проводящим мостиком, то бу-
будет происходить обратное. Так как концы проводов замкнуты,
то напряжение между ними всегда равно нулю и на конце ли-
линии будет расположен узел напряжения и электрического поля.
Напротив, амплитуда тока в проводящем мостике будет наи-
наибольшая и на конце линии образуется пучность тока. Здесь же
находится и пучность магнитного поля.
Таким образом, в стоячей электромагнитной волне узлы
электрического поля (напряжения) совпадают с пучностями
магнитного поля (тока) и наоборот. Распределение амплитуд
колебаний электрического и магнитного полей в стоячей волне
изображено на рис. 406.
Отметим в заключение, что указанные свойства электро-
электромагнитных волн аналогичны свойствам механических волн. Во
всякой механической волне (например, в струне) имеются ко-
колебания двух видов энергии: потенциальной, обусловленной де-
деформациями, и кинетической, связанной со скоростью отдель-
отдельных элементов среды; подобно этому, в электромагнитной волне
мы имеем колебания электрической и магнитной энергии. В рас-
233
СОБСТВЕННЫЕ КОЛЕБАНИЯ ДВУХПРОВОДНОЙ ЛИНИИ
551
пространяющейся механической волне колебания деформации
и скорости находятся в фазе; в распространяющейся электро-
электромагнитной волне фазы колебаний электрического и магнитного
полей также совпадают. Наконец, в стоячей механической волне
Рис. 406 Пространственное распределение амплитуд электрического и
магнитного полей в стоячей воде
узлы деформации совпадают с пучностями скорости и наоборот;
аналогично в стоячей электромагнитной волне узлы электричес-
электрического поля совпадают с пучностями магнитного поля и обратно.
§ 233. Собственные колебания двухпроводной линии
Для того чтобы в двухпроводной линии могли возникнуть
стоячие волны, длина электромагнитной волны должна иметь
определенные значения, зависящие от длины линии. Рассмо-
Рассмотрим линию длины I и положим, что она разомкнута на обоих
концах. Мы знаем (§ 232), что на концах такой линии всегда
должны быть расположены пучности напряжения (электричес-
(электрического поля) и узлы тока (магнитного поля). Поэтому в линии бу-
будут возможны только такие стоячие волны, которые удовлетво-
удовлетворяют этим условиям на границе. А тогда, очевидно, необходимо,
чтобы длина волны А удовлетворяла соотношению
1 = Хп/2, п= 1,2,3,... B33.1)
На рис. 407 изображены две возможные стоячие волны, со-
соответствующие п = 1 и п — 2. Первая из них A), называемая
основным колебанием, имеет один узел напряжения U и одну
пучность тока г, расположенные на середине линии. Вторая B)
имеет два узла напряжения и две пучности тока. В обоих слу-
случаях на концах линии находятся пучности напряжения и узлы
тока в соответствии с граничными условиями. Помимо указан-
указанных двух стоячих волн, возможно еще бесконечное количество
других, которые соответствуют п — 3,4,...
552
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ
ГЛ XXII
Так как длина волны А, частота колебаний v и скорость элек-
электромагнитной волны v связаны между собой соотношением
v = v\,
то из B33.1) можно найти частоты ип различных стоячих волн:
i/n = (v/2l)n, n = 1,2,3,... B33.2)
Очевидно, что формулы B33.1) и B33.2) мы получим и то-
тогда, когда оба конца линии будут замкнуты проводящим мости-
мостиком. Различие будет заключаться лишь в том, что во втором
случае на концах линии будут находиться узлы напряжения (а
не пучности) и пучности тока (вместо узлов).
Рис. 407. Два первых собствен-
собственных колебания двухпроводной ли-
линии, разомкнутой на концах
Рис 408. Два первых собственных
колебания двухпроводной линии, за-
замкнутой на одном конце проводя-
проводящим мостиком
Положим теперь, что линия замкнута проводящим мостиком
на одном из концов (рис. 408). В этом случае на разомкнутом
конце линии всегда будет находиться пучность напряжения (и
узел тока), а на замкнутом — узел напряжения (и пучность то-
тока). Поэтому в линии будут возможны волны только такого ти-
типа, как показано на рис. 408. Их длина удовлетворяет условиям
/ = А/4 (кривая 1, основное колебание), / = ЗА/4 (кривая 2),
/ = 5А/4 и вообще
/ = Bп-1)А/4, п= 1,2,3,... B33.3)
Так как А = v/v, то частота этих стоячих волн равна
ип = (v/4i)Bn - 1), п = 1,2,3,... B33.4)
§ 234 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ СТОЯЧИХ ВОЛН 553
Сравнивая B33.2) и B33.4), мы видим, что частоты колеба-
колебаний в обоих случаях получаются различными. Частота основно-
основного колебания (п — 1) в первом случае (оба конца разомкнуты)
равна щ = v/2l, а во втором (один конец разомкнут) v\ = v/4l,
т.е. при замыкании одного из концов частота основного колеба-
колебания уменьшается вдвое.
Таким образом, в ограниченной двухпроводной линии воз-
возможны только определенные стоячие волны, которые удовле-
удовлетворяют условиям на границах линии. Эти стоячие волны суть
собственные колебания линии. Формулы B33.2) и B33.4) по-
показывают, что собственные колебания имеют разрывный (дис-
(дискретный) набор частот (спектр частот). Число различных соб-
собственных колебаний линии равно бесконечности в соответствии
с тем, что линия как распределенная система обладает беско-
бесконечно большим числом степеней свободы.
Чтобы возбудить в линии одно из собственных колебаний,
генератор, питающий линию, должен иметь частоту, совпадаю-
совпадающую с одной из собственных частот линии vn. Если же это усло-
условие не будет выполнено, то различные волны, отраженные от
концов линии, складываясь друг с другом (интерферируя), да-
дадут изменяющиеся и сложные колебания, а устойчивой стоячей
волны не получится.
Разумеется, в линии можно одновременно возбудить не толь-
только одно из собственных колебаний, но и какое угодно их число.
При этом разные стоячие волны, накладываюсь друг на друга,
образуют колебания более сложной формы. И обратно, можно
показать, что любое сложное колебание линии можно предста-
представить в виде суммы различных собственных колебаний с опре-
определенным образом подобранными амплитудами и начальными
фазами.
§ 234. Экспериментальное исследование
стоячих электромагнитных волн
Стоячие электромагнитные волны в линии легко получить на
опыте. Один из способов их возбуждения показан на рис. 409.
Выход генератора соединен с провода-
проводами линии через конденсаторы (емкостная +11^
связь). При работе генератора между про- Г~ "
водами появляются колебания напряже- (~)
ния, а следовательно, и электрического по- L___||
ля, и в линии возникает электромагнитная -''+
волна.
Связь между линией и генератором Рис- 409. Емкостная
можно сделать также индуктивной Для связь двухпроводной
этого конец линии замыкают небольшим линии с генератором
554
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ
ГЛ XXII
связь двухпроводной
линии с генератором
числом витков проволоки (один-два) и помещают их вблизи ка-
катушки колебательного контура генератора (рис 410). Возникаю-
Возникающая в витках линии ЭДС взаимной индукции вызывает на конце
линии колебания тока (и магнитного по-
поля), которые, так же как и колебания на-
напряжения (электрического поля), дают на-
начало электромагнитной волне.
Для того чтобы судить об интенсив-
Рис 410 Индуктивная ности колебаний тока в разных точках
линии, в линию можно включить лампы
накаливания (рис. 411). Такой прием осо-
особенно удобен для демонстрационных це-
целей Для обнаружения колебаний напряжения можно пользо-
пользоваться газоразрядной трубкой, включенной между проводами.
В подобных опытах можно убедиться, что стоячие волны в
линии возникают только при определенных частотах генерато-
генератора, совпадающих с частотами
собственных колебаний линии.
Исследуя на опыте стоячие
волны, можно определить ско-
скорость распространения элек-
~ тромагнитных волн. Действи-
Действительно, измеряя расстояние Ах
между двумя соседними узла-
узлами или пучностями в стоячей
_ волне, мы определяем половину
длины электромагнитной вол-
*Ы
С
стороны,
Щ)^ ™У р,
А = «/"¦ Поэтому, измеряя еще
Рис 411 Обнаружение колебаний
токае помощью лампы накаливания
(Л) и колебаний напряжения с по- частоту генератора v, можно
мощью газоразрядной трубки (Т) найти скорость распростране-
распространения v. Такие измерения дают
для скорости электромагнитных волн величину, совпадающую
со скоростью распространения света, которая для воздуха
округленно равна 3 ¦ 108 м/с.
Еще до того, как электромагнитные волны были впервые по-
получены на опыте, Максвелл, исходя из своей теории электромаг-
электромагнитного поля (гл. XIII), вычислил их скорость. Скорость элек-
электромагнитных волн в вакууме выражается формулой
с =
108 м/с
B34.1)
(эта формула будет получена в § 240). Здесь ео = 1/D7г • 9 х
х 109) Ф/м — электрическая постоянная, а цо = 47Г-10~7 Гн/м —
магнитная постоянная. Таким образом, теория Максвелла пред-
предсказала, что скорость распространения электромагнитных волн
§ 235
ОТКРЫТЫЙ ВИБРАТОР
555
должна равняться скорости света, а факт совпадения обеих ско-
скоростей явился одним из первых указаний на то, что свет имеет
электромагнитную природу.
В § 230 мы видели, что основные процессы при распростра-
распространении волн вдоль проводов происходят не в самих проводах, а в
окружающей их среде. Поэтому при изменении среды, окружаю-
окружающей провода, скорость электромагнитных волн изменяется, а
длина волны при той же частоте генератора становится другой.
Из теории Максвелла следует (§ 240), что скорость (фазовая)
электромагнитной волны в какой-либо среде равна
v = с/у/Щ1,
B34.2)
где с — скорость в вакууме, а е и fi — относительные диэлектри-
диэлектрическая и магнитная проницаемости среды. В этом легко убедить-
убедиться на опыте, если часть двухпроводной линии, которая раньше
находилась в воздухе, погрузить в воду. Так как для воды \i и
и 1, а е > 1, то скорость электромагнитных волн в воде меньше,
чем в воздухе, и поэтому расстояние между соседними узлами
(или пучностями) уменьшается. Отметим, что е и fj, зависят от
частоты. Поэтому при вычислении v по формуле B34.2) нужно
брать их значения, соответствующие частоте колебаний в дан-
данной электромагнитной волне.
§ 235. Открытый вибратор
Представим себе двухпроводную линию, замкнутую на од-
одном из концов, и раздвинем свободные концы проволок. Тогда в
Рис 412 Переход от двухпроводной линии к открытому вибратору
пределе мы получим отрезок прямой проволоки, или открытый
вибратор (рис 412).
Длина возможных в нем стоячих электромагнитных волн
определяется длиной вибратора I и условиями на концах. Ее-
556
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ВДОЛЬ ПРОВОДОВ
ГЛ XXII
ли оба конца вибратора граничат с диэлектриком, то на них
должны быть расположены узлы тока и пучности напряжений.
Поэтому возможные длины вол-
волны А определяются условием
1 =
п = 1,2,3,... B35.1)
Частота колебаний и в различных
стоячих волнах равна
B35.2)
Стоячая волна, соответствующая
п = 1, называется основным ко-
колебанием вибратора. Распределе-
Распределение амплитуд напряжения и тока
в ней показано на рис. 413 а.
Если один из концов вибрато-
вибратора заземлить, то на этом конце бу-
будет расположен узел напряжения
и, следовательно, пучность тока. Поэтому основное колебание
заземленного вибратора имеет вид, изображенный на рис. 413 б.
Из рисунка видно, что при заземлении вибратора длина волны
его основного колебания увеличивается, а частота уменьшается
в два раза.
У////////////А
а б
Рис. 413. Основные колебания
незаземленного (а) и заземленно-
заземленного (б) вибратора
§ 236. Стоячие волны в катушках
Проволочные катушки, как и двухпроводные линии, облада-
обладают определенными индуктивностью и емкостью на каждую еди-
единицу длины, т.е. представляют
собой электрические распреде-
распределенные системы. Поэтому в них
возможны также стоячие элек-
электромагнитные волны.
Тесла использовал стоячие
волны в катушках для устрой-
устройства "резонансного трансформа-
трансформатора. Его первичная обмотка
L\ (рис. 414) имеет небольшое
число витков и входит в со-
состав колебательного контура,
например искрового контура,
содержащего конденсатор С и
искровой промежуток П. Вторичной обмоткой служит прово-
проволочная катушка Ь%.
Рис. 414.
Теслы
Схема трансформатора
§ 237 ОБРАЗОВАНИЕ СВОБОДНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 557
Когда в первичной цепи возникают электрические колеба-
колебания, то внутри катушки L\ появляется переменное магнитное
поле и во вторичной катушке Li наводится переменная ЭДС.
Если подобрать частоту колебаний в первичной цепи так, что-
чтобы она совпала с частотой одного из собственных колебаний
(стоячих волн) катушки L2 (обычно — основного колебания),
то вследствие резонанса в этой последней возникнет интенсив-
интенсивная стоячая волна и между концами катушки появится высокое
переменное напряжение. При резонансе из концов вторичной ка-
катушки можно извлекать длинные искры, а электрическое поле
вблизи катушки настолько сильно, что вызывает свечение газо-
газоразрядных трубок даже на значительном расстоянии от уста-
установки.
Если расположить катушку L2 рядом с катушкой L\, то мож-
можно исследовать распределение напряжения вдоль катушки и убе-
убедиться, что действительно в ней возникает стоячая волна. Из-
Извлекая, например, из разных мест катушки искры с помощью
заземленного металлического стержня, можно видеть, что наи-
наиболее длинные искры получаются у концов катушки (пучности
напряжения), а вблизи середины катушки искры не возникают
вовсе (узел напряжения).
Высокочастотные резонансные трансформаторы применя-
применяются иногда в лабораторной практике там, где нужно получить
очень высокие напряжения при малой мощности.
ГЛАВА XXIII
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
§ 237. Образование свободных электромагнитных волн
Мы знаем, что основные процессы в электромагнитных вол-
волнах, распространяющихся вдоль проводов, происходят в среде,
окружающей провода (§ 230). Сами же провода играют вспомо-
вспомогательную роль, задавая лишь определенное направление рас-
распространения волн. Поэтому электромагнитные волны могут су-
существовать и без всяких проводов (свободные электромагнитные
волны).
Происходящие при этом процессы по существу такие же, как
и в случае волн, распространяющихся вдоль проводов. Пред-
Представим себе, что в некоторой точке О (рис. 415) внутри без-
безграничной непроводящей среды создано каким-либо способом
электрическое поле Е. Если нет электрических зарядов, под-
поддерживающих это поле, то оно будет исчезать. Но убывающее
поле Е, согласно Максвеллу, вызывает магнитное поле Н. Так
558
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
ГЛ XXIII
t t
J
Рис. 415. Свободные
нитные волны
J
как поле Е убывает, то плотность тока смещения j = t
направлена противоположно Е и линии индукции магнитного
поля направлены по часовой стрелке (вид сверху, рис. 415).
Так как в среде нет постоянных
токов, поддерживающих поле
Н, то последнее в свою оче-
очередь будет исчезать и вызо-
вызовет вихревое электрическое по-
поле Ei. Линии напряженности
этого поля будут направлены
против часовой стрелки, как
показано на рис. 415. Поле Ei
уничтожит первоначальное по-
поле Е в точке 0, но зато проявит-
проявится в соседней точке 1. Исчезая в
! точке 1, электрическое поле Ei
приведет к появлению магнит-
магнитного поля Hi, которое будет
направлено, как и поле Н, по
часовой стрелке. Поле Hi унич-
уничтожит поле Н и обнаружится
электромаг- в более удаленной точке. Исче-
Исчезая, оно вызовет вихревое элек-
электрическое поле Е2, которое уничтожит поле Ei в точке 1, но про-
проявится в точке 2, и т.д. Таким образом, вместо первоначального
поля Е мы получим и электрическое и магнитное поля, взаимно
связанные друг с другом и распространяющиеся в пространстве,
т.е. электромагнитную волну.
Из рис. 415 также видно, что Е перпендикулярно к Н, при-
причем оба они перпендикулярны к скорости распространения вол-
волны v. Все три вектора связаны между собой правилом правого
буравчика: если вращать буравчик с правой нарезкой так, что-
чтобы его рукоятка перемещалась от вектора Е к вектору Н, то
направление поступательного движения буравчика будет совпа-
совпадать с направлением v.
Выше мы рассматривали электромагнитные волны каче-
качественно. Однако теория Максвелла не только предсказала су-
существование электромагнитных волн, но и позволила в точной,
количественной форме установить все основные их свойства.
Обратимся сейчас к более строгому исследованию этих явлений.
§ 238. Волновое уравнение
Положим, что некоторая физическая величина s распростра-
распространяется в направлении X со скоростью v. Величина s может обо-
обозначать смещение или скорость отрезков резинового шнура при
§ 238 ВОЛНОВОЕ УРАВНЕНИЕ 559
наличии в нем механической волны. В случае электромагнитных
волн под s можно подразумевать напряженность электрического
или магнитного поля и т.д. Нетрудно видеть, что общая форма
записи этого процесса есть
s = f{t-x/v). B38.1)
Здесь t обозначает время, х — координату рассматриваемой точ-
точки, а / — символ произвольной функции. Иными словами, любая
произвольная функция, если только она зависит от аргумента
(t — x/v), выражает волнообразный процесс.
Чтобы убедиться в этом, предположим, что наблюдатель
движется в положительном направлении оси X со скоростью v.
Тогда для него х = xo + vt. Подставляя это выражение в B38.1),
находим
т.е. s не зависит от времени. Такой движущийся наблюдатель,
следовательно, будет находить возле себя одно и то же значе-
значение величины s, а это и значит, что 5 распространяется со ско-
скоростью V.
Подобным же образом можно убедиться, что соотношение
s = f(t + x/v) B38.2)
выражает то обстоятельство, что величина s распространяется
в отрицательном направлении оси X.
Полагая в B38.1) или B38.2) t = 0, мы получим
s = f(Tx/v).
Это выражение представляет распределение s в момент време-
времени t = 0. Если s обозначает смещение точек резинового шну-
шнура, то написанная формула дает начальную деформацию шнура
(его изгиб). Если s есть напряженность электрического поля в
электромагнитной волне, то последняя формула выражает рас-
распределение поля в пространстве в начальный момент времени.
Следовательно, вид функции / зависит от начальных условий
процесса. В частности, если / обозначает sin или cos, то B38.1)
переходит в уже знакомое нам уравнение гармонической волны
B31.1). Таким образом, формулы B38.1) и B38.2) представляют
собой общее выражение волны, распространяющейся в направ-
направлении оси X.
Функция s удовлетворяет простому дифференциальному
уравнению. Чтобы найти его, продифференцируем формулы
B38.1) и B38.2) (которые мы объединим, вводя двойной знак
=f) два раза по координате:
d
2s
_ 1 ,„
560 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ ХХШ
где штрихами обозначено дифференцирование по всему аргу-
аргументу (t :p x/v). Вторая же частная производная по времени
равна
д?я_ _ ,ц
д& J '
Сравнивая эти выражения, мы видим, что искомое дифферен-
дифференциальное уравнение есть
w = vw- B38-3)
Оно называется волновым уравнением.
Мы предполагали, что волна распространяется в одном опре-
определенном направлении, которое считали совпадающим с направ-
направлением оси X (или ему противоположным). Если волна распро-
распространяется во всех направлениях, то волновое уравнение имеет
вид
Таким образом, если какая-либо физическая величина рас-
распространяется волнообразно, то она удовлетворяет волновому
уравнению. И обратно, если удается показать, что рассматри-
рассматриваемая величина подчиняется волновому уравнению, то можно
утверждать, что возможно ее распространение в виде волны.
При этом непосредственно получается и скорость распростране-
распространения волны, которая равна квадратному корню из коэффициента
при d2s/dx2.
§ 239. Плоские электромагнитные волны
Обратимся теперь к уравнениям Максвелла (§ 138). Будем
считать, что среда представляет собой однородный диэлектрик.
Тогда в уравнениях A38.1) нужно положить jx = jy = jz = 0.
Далее мы ограничимся особенно простым случаем электро-
электромагнитного поля, когда ЕиН зависят от одной координаты (х)
и от времени (одномерная задача). Это значит, что все простран-
пространство можно разбить на бесконечно тонкие плоские слои, внутри
которых ЕиН имеют одно и то же значение во всех точках
(рис. 416).
У всяких волн (и механических, и электромагнитных) по-
поверхность, во всех точках которой колебания имеют одинако-
одинаковую фазу, называют фронтом волны. В зависимости от того,
какую форму имеет волновой фронт, мы говорим о плоских вол-
волнах (волновой фронт плоский), сферических, цилиндрических и
т.д. Рассматриваемая одномерная задача соответствует, очевид-
очевидно, плоским электромагнитным волнам.
§239
ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
561
Для одномерного случая уравнения Максвелла сильно упро-
упрощаются. Так как все производные по у и z равны нулю, то
прежде всего из первого уравнения группы A38.1) следует, что
dDxjdt = 0, а из первого уравнения
группы A38.2) - что dBx/dt = 0. Это
значит, что составляющие полей Dx и Вх
не зависят от времени. Далее из A38.3)
и A38.4) получается, что dDx/dx = 0 и
дВх/дх = 0, а значит, Dx и Вх не зави-
зависят также и от координаты. Поэтому
JDX = const, Вх — const.
Остающиеся уравнения группы Дд
A38.1) теперь принимают вид
дРу _ _дН± dD^ _ дНу^
dt ~ дх ' dt ~ дх '
а уравнения группы A38.2) — вид
X
dBv
dEz
дх '
dBz
dt
dEv
Рис. 416. Плоская элек-
электромагнитная волна
а другая —
составляющие
dDy _
dt
dHz
дх '
2-составляющие
магнитного поля
dDz
dt
dHy
dx '
dBz
dt
dEy
dx '
Электр ического
dBy
dt
dEz
dx "
dt dx ' dt dx'
Эти четыре уравнения можно сгруппировать в две независимые
группы, одна из которых связывает у-составляющие электри-
электрического поля и ^-составляющие магнитного поля
поля и у-
Отсюда следует, что меняющееся во времени электрическое поле
Еу вызывает появление только магнитного поля Hz, направлен-
направленного вдоль оси Z, а переменное во времени магнитное поле Hz
влечет появление электрического поля Еу, целиком направлен-
направленного вдоль оси У. Или, иначе, в электромагнитном поле электри-
электрическое и магнитное поля перпендикулярны друг к другу. Такой
же вывод вытекает и из второй пары уравнений.
Найденный результат позволяет положить без нарушения
общности, что все электрическое поле направлено вдоль одной
из осей, например вдоль оси У, а магнитное поле — вдоль оси
Z (рис. 416). Поэтому в последних уравнениях можно положить
Еу =
Е, Ez = 0, Hz = Н, Ну = 0, и мы находим окончатель-
окончательно уравнения Максвелла для одномерного случая в следующем
простом виде:
B39.1)
dD
dt
дН_
' дх'
dJB
dt
dE
дх
562 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ XXIII
§ 240. Свойства электромагнитных волн
Покажем теперь, исходя из уравнений Максвелла, необходи-
необходимость существования электромагнитных волн и выясним неко-
некоторые важные их свойства.
Исключим из уравнений Максвелла B39.1) магнитное по-
поле Н. Для этого умножим первое из уравнений на /io/i и про-
продифференцируем обе его части по t:
д2Е д2Н
Второе уравнение продифференцируем по х:
д2Е д2Н
Так как правые части этих уравнений одинаковы, то, следова-
следовательно, равны и левые части, т.е.
дР еоецоц дх*"
Такое же уравнение мы получили бы и для Н, если бы из B39.1)
исключили электрическое поле Е.
Уравнение B40.1) есть волновое уравнение, рассмотренное в
§ 238. Отсюда следует, что поля ЕиН могут распространяться в
пространстве, т.е. могут существовать электромагнитные волны.
Поэтому можно положить
E = <p{tTx/v), H = ^{tTx/v), B40.2)
где v — скорость распространения электромагнитной волны.
Далее, согласно сказанному в § 238, коэффициент при
д2Е/дх2 в B40.1) есть квадрат скорости распространения волн:
v = —L= -1==* B40.3)
где с есть скорость распространения при е = /л = 1, т.е. в ва-
вакууме. Мы получили, таким образом, выражение для скорости
распространения электромагнитных волн (закон Максвелла), о
котором мы уже говорили в § 234 и которое, как мы видели,
соответствует опыту.
Как уже упоминалось (§ 237), электрическое и магнитное по-
поля в электромагнитной волне взаимно связаны друг с другом.
Поэтому между мгновенными значениями Е и Н в любой точ-
точке существует определенное соотношение, которое также можно
найти из уравнений Максвелла. Для этого мы воспользуемся
общими выражениями B40.2) для ЕиН (выбирая в них какой-
либо определенный знак, скажем минус) и подставим их в одно
из уравнений Максвелла B39.1), например в первое. Так как
дЕ , дН 1 ,,
§ 241 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ 563
(где по-прежнему штрих обозначает дифференцирование по все-
всему аргументу), то указанная подстановка дает
= - ф1.
Переходя от производных к самим функциям, получим
-ф + С,
где С обозначает постоянную интегрирования. Так как нас инте-
интересуют электромагнитные волны, т.е. только переменные поля,
то С, которое выражает произвольное постоянное поле, можно
не учитывать. Заменяя еще v его выражением B40.3), находим
окончательно
V^i-Б = ^fmxH. B40.4)
Эта формула показывает, что в распространяющейся электро-
электромагнитной волне Е и Н пропорциональны друг другу.
Из B40.4) следует, что Е и Н одновременно достигают макси-
максимума и одновременно обращаются в нуль, т.е. находятся в фазе.
Тот же результат мы получили уже в § 231 при помощи каче-
качественных рассуждений.
§ 241. Экспериментальное исследование
электромагнитных волн
Для образования электромагнитных волн необходимо создать
в пространстве достаточно быстро изменяющееся электрическое
поле (ток смещения) или соответственно быстро изменяющееся
магнитное поле. Очевидно, что для этой цели непригодны элек-
электрические колебательные контуры с сосредоточенными емко-
емкостью и индуктивностью (закрытые контуры), рассмотренные в
гл. XX. В таких контурах все электрическое поле сосредоточено
в узком зазоре конденсатора, а все магнитное поле — внутри ин-
индуктивности, а в окружающем пространстве электрическое поле
практически равно нулю.
Иное мы имеем для открытого вибратора, или электрическо-
электрического диполя (§ 235). В этом случае линии электрического и магнит-
магнитного полей выходят далеко за пределы вибратора (см. рис. 412), и
поэтому последний хорошо излучает электромагнитные волны.
Свободные электромагнитные волны были впервые получе-
получены на опыте Генрихом Герцем в 1888 г. Для изучения электро-
электромагнитных волн Герц использовал собственные электрические
колебания открытого вибратора, который состоял из двух оди-
одинаковых металлических стержней ВВ (рис. 417), разделенных
искровым промежутком. Обе половины вибратора заряжались
от источника высокого напряжения. Когда разность потенциа-
потенциалов достигала пробойного значения, в разряднике проскакивала
564
СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
ГЛ XXIII
Излучающий
вибратор
д
д
Приемный
вибратор
В
О
Q
В
Рис 417. Опыт Г Герца
искра, замыкавшая обе половины вибратора, и в нем возникали
затухающие электрические колебания высокой частоты. Чтобы
быстропеременные токи не ухо-
уходили из вибратора в источник
напряжения, между вибратором
и источником были включены
дроссели Д.
Для обнаружения электро-
электромагнитных волн Герц приме-
применял вибраторы различной фор-
формы. Наиболее простым является
прямой открытый вибратор, то-
тождественный по форме и раз-
размерам с излучающим вибрато-
вибратором (рис. 417). Под действием
переменного электрического по-
поля проходящей электромагнит-
электромагнитной волны электроны внутри
вибратора начинают совершать
вынужденные колебания, отчего
в вибраторе появляется быстропеременный ток, а между обеими
половинами вибратора — переменное напряжение Если длина
приемного вибратора равна длине излучающего, то собственные
частоты обоих диполей совпадают и электрические колебания в
приемном диполе усиливаются вследствие резонанса Появление
переменного напряжения Герц обнаруживал по возникновению
электрической искорки в микроскопи-
микроскопическом зазоре в середине вибратора или
по свечению миниатюрной газоразряд-
газоразрядной трубки Т, включенной между обе-
обеими половинами вибратора
В настоящее время для генериро-
генерирования электромагнитных волн пользу-
пользуются почти исключительно ламповыми
генераторами, которые позволяют по-
получать электрические колебания прак-
практически любой мощности и притом пра-
пильной синусоидальной формы. Для Рис 41g Возб ениеди.
возбуждения колебании в вибраторе ПОЛя при помощи лампово-
можно между обеими его половинами го генератора
ВВ включить один или несколько вит-
витков связи (рис. 418) и расположить их вблизи катушки индук-
индуктивности К лампового генератора Г (магнитная связь). Суще-
Существуют и другие способы связи между вибраторами и генерато-
генератором. Чтобы усилить колебания в вибраторе, используют явление
резонанса, для чего частоту генератора делают равной одной из
241
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
565
В
Л
собственных частот вибратора, обычно частоте основного его
колебания.
Для обнаружения электрических колебаний в приемном ви-
вибраторе можно пользоваться небольшой электрической лампой
Л (рис. 419 а), включенной в его середине ВВ (в пучности тока).
Этот способ удобен для демонстрационных целей, когда расстоя-
расстояние между приемным и излучающим вибраторами невелико, и
поэтому колебания в приемном вибраторе достаточно сильны.
В случае более слабых колебаний в вибратор можно включить
кристаллический детектор D (рис. 419 б) и к его концам присо-
присоединить гальванометр постоянного тока. Так как сопротивление
детектора зависит от направления тока (§ 203), то напряжение
на детекторе различно в
разные полупериоды коле-
колебаний: оно велико, если ток
течет в запорном направ-
направлении, и мало при токе
противоположного направ-
направления. Поэтому появляется
постоянная составляющая
напряжения на детекторе и
в гальванометре возникает
постоянный ток.
Если поместить прием-
приемный вибратор (диполь), на-
например изображенный на
рис. 419 а, вблизи излучаю-
излучающего диполя, то можно ви-
видеть, что лампа сильнее
всего накаливается в том
случае, когда оба диполя па-
параллельны. Если же прием-
приемный диполь ориентирован
перпендикулярно к излучающему, то лампа не накаливается со-
совсем. Так как электрические колебания в приемном диполе мо-
могут появиться только в том случае, если электрическое поле
электромагнитной волны имеет составляющую вдоль диполя,
то такой опыт показывает, что электрическое поле в электро-
электромагнитной волне параллельно оси диполя. Это справедливо для
всех точек плоскости, перпендикулярной к оси диполя и прохо-
проходящей через его середину. Отметим, что волны (механические
и электрические), в которых колебания происходят параллель-
параллельно какому-либо определенному направлению, называют линейно
поляризованными.
Встречая на своем пути достаточно большие (по сравнению
с длиной волны) проводящие поверхности, электромагнитные
В
Рис 419 Приемный диполь для обна-
обнаружения электромагнитных волн инди-
индикатором является лампа накаливания
(а), кристаллический детектор с гальва-
гальванометром (б)
566 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ XXIII
волны отражаются от них. Пользуясь этим, можно получить на-
направленные электромагнитные волны, подобные параллельному
пучку света. Это можно сделать, например, помещая небольшой
излучающий диполь в фокус металлического параболического
зеркала.
Встречая границу двух различных диэлектриков, электро-
электромагнитные волны, подобно свету, преломляются. Закон прелом-
преломления электромагнитных волн имеет такой же вид, как и для
света. Если волна, распространяющаяся в вакууме (практиче-
(практически — в воздухе), встречает поверхность диэлектрика под углом
падения г, то
sini/sinr = п,
где г — угол преломления, п — показатель преломления диэлек-
диэлектрика, не зависящий от углов гиг. При этом направления па-
падающей и преломленной волн и направление нормали к границе
лежат в одной плоскости.
Нетрудно получить на опыте свободные стоячие электромаг-
электромагнитные волны, подобные рассмотренным в § 232, но существу-
существующие без направляющих проводов. Если направить электро-
электромагнитную волну из параболического рефлектора нормально на
металлический лист, то между листом и рефлектором появятся
падающая и отраженная волны, распространяющиеся в проти-
противоположных направлениях. Эти волны, складываясь, образуют
стоячую волну с равноотстоящими друг от друга пучностями
и узлами. Для обнаружения пучностей и узлов электрического
поля может служить диполь, расположенный параллельно из-
излучающему диполю и имеющий ту же длину, что и последний.
Перемещая его вдоль нормали к зеркалу, можно видеть, что от-
отклонения гальванометра, соединенного с детектором, периоди-
периодически достигают максимума (пучности электрического поля) и
минимума (узлы электрического поля), причем у поверхности
металлического листа находится узел электрического поля. Из-
Измеряя расстояние Ах между соседними узлами или пучностями,
можно определить длину волны Л, а отсюда, зная частоту коле-
колебаний генератора, найти и скорость распространения свободных
электромагнитных волн (ср. § 234).
Указанные свойства электромагнитных волн были установлены еще
Герцем. Дальнейшие опыты показали, что электромагнитным волнам при-
присущи не только эти, но и все другие свойства света. Особое место среди
этих исследований занимают опыты П Н Лебедева A895 г) по распростра-
распространению электромагнитных волн в анизотропных кристаллах (сера), диэлек-
диэлектрическая проницаемость которых зависит от направления электрического
поля Так как большие кристаллы получить трудно, а размеры кристаллов
должны быть велики по сравнению с длиной волны, то Лебедев разработал
способ получения весьма коротких электромагнитных волн с длиной все-
всего около 6 мм, которые излучались миниатюрным искровым вибратором
§ 242 ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 567
В этих опытах Лебедев получил двойное преломление электромагнитных
волн и воспроизвел все основные явления, наблюдаемые при прохождении
света сквозь кристаллы.
§ 242. Энергия электромагнитных волн
Мы видели (§ 241), что электромагнитные волны способны
производить различные действия: они накаливают нить лампы,
включенной в диполь, вызывают отклонение стрелки гальвано-
гальванометра, соединенного с детектором, и т.п. Это показывает, что
электромагнитные волны переносят определенную энергию.
Рассмотрим в поле электромагнитной волны произвольную
площадку S (рис. 420) и вычислим энергию AW, переносимую
электромагнитной волной через эту площадку за малое вре-
vAt
Рис. 420. К вычислению потока энергии электромагнитных волн
мя At. Для этого построим на площадке S, как на основании,
параллелепипед, ребра которого параллельны скорости распро-
распространения волны v и имеют длину vAt. Объем этого паралле-
параллелепипеда равен
Ат — SvAt cos a,
где а — угол между нормалью п к площадке S и скоростью v.
Так как за время At волна проходит расстояние v At, то очевид-
очевидно, что через нашу площадку пройдет энергия AW, заключен-
заключенная внутри указанного параллелепипеда. Поэтому, если и есть
энергия единицы объема поля (объемная плотность энергии), то
AW = иАт = uSvAt cos a.
Объемная плотность энергии электромагнитной волны скла-
складывается из энергии электрического поля eeqE2/2 и энергии
магнитного поля 2
и = {e€qE + hjj,qH )/2.
рома
[оэто
и = ее^Е2 = h[j,qH2 = у/Щ1<
Напряженности Е и Н в электромагнитной волне связаны соот-
соотношением у/ёёо Е = у/ЦЦо Н. Поэтому можно также написать
568 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ XXIII
Учитывая еще, что v = l/y/EJly'eo/io, имеем
AW = EHS cos a -At.
Следовательно, энергия, проходящая через площадку S в еди-
единицу времени, или dW/dt, равна
dW/dt = EHScosa.
Полученный результат можно представить в более удобной
форме. Введем вектор потока электромагнитной энергии, опре-
определяемый следующим образом:
Р = [ЕН]. B42.1)
В электромагнитной волне Е и Н перпендикулярны друг к дру-
другу, и поэтому поток электромагнитной энергии Р = ЕН. На-
Направление же вектора Р перпендикулярно к Е и Н, т.е. совпа-
совпадает с направлением скорости распространения волны v. Тогда
B42.1) можно представить в виде
dW/dt = PnS. B42.2)
Здесь Рп = Pcosa есть проекция вектора Р на направление
нормали п к площадке S.
Таким образом, движение энергии в электромагнитном поле
можно вполне охарактеризовать при помощи потока энергии Р.
Его направление дает направление движения энергии. Модуль
же потока энергии равен энергии, проходящей за единицу вре-
времени через поверхность с площадью, равной единице, перпенди-
перпендикулярную к направлению движения энергии.
Понятие вектора потока энергии было введено Н.А. Умовым
в работах о движении энергии в различных средах, а выражение
B42.1) для специального случая электромагнитного поля было
получено Пойнтингом. Поэтому вектор потока электромагнит-
электромагнитной энергии Р называют вектором Умова-Пойнтинга или век-
вектором Пойптинга.
Если мы представим себе линии, касательные к которым в
каждой точке совпадают с направлением вектора Р (линии век-
вектора потока энергии), то эти линии укажут нам пути, вдоль
которых распространяется энергия электромагнитного поля. С
другой стороны, линии, вдоль которых движется энергия све-
света, в оптике называют лучами. Так как свет представляет собой
также электромагнитные волны, то лучи света суть не что иное,
как линии вектора потока энергии световых электромагнитных
волн.
Приведенный вывод выражения B42.2) не строг, так как
мы везде предполагали, что фазовая скорость распростране-
распространения волн v совпадает со скоростью движения энергии. Одна-
Однако в общем случае это заведомо не так. Тем не менее выра-
выражение B42.2), полученное нами путем нестрогих рассуждений,
242
ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
569
оказывается справедливым для всех случаев. Исходя из уравне-
уравнений Максвелла, можно совершенно строго доказать следующую
важную теорему о движении энергии в электромагнитном по-
поле (теорема Пойнтинга). Выделим внутри произвольной среды
некоторый объем т, ограниченный поверх-
поверхностью S (рис. 421). Обозначим далее пол-
полную энергию, заключенную внутри объема
т, через W. Тогда
9W _ С
— - J
B42.3)
Рис. 421. К формули-
формулировке теоремы Пойн-
Пойнтинга
Здесь Рп — нормальная к поверхности со-
составляющая вектора Умова-Пойнтинга, вы-
выражаемого формулой B42.1), а интегри-
интегрирование производится по всей замкнутой
поверхности S. При этом положительным
считается направление внешней нормали п
(рис. 421), т.е. поток J PndS считается по-
s
ложительным, если линии потока энергии Р выходят изнутри
объема наружу.
Величина —dW/dt есть уменьшение полной энергии внутри
объема т за единицу времени. Согласно закону сохранения энер-
энергии она должна равняться той энергии, которая выходит через
поверхность S за единицу времени наружу. Отсюда следует, что
энергия, выходящая через поверхность S за единицу времени,
выражается потоком вектора Р через замкнутую поверхность
S, ограничивающую рассматриваемый объем. Величину же Рп
можно истолковать как энергию, которая проходит через еди-
единицу поверхности в единицу времени.
Рассмотрим некоторые примеры вычисления потока электро-
электромагнитной энергии.
Пример 1. Распространяющаяся электромагнитная волна. Пусть
имеется плоская электромагнитная волна, распространяющаяся в вакууме
вдоль оси X. Тогда напряженности полей Е и Н в какой-либо точке х вы-
выражаются формулами (§ 231)
Е = Ео sin (ut — kx), Н = Но sin (w? — kx),
где к — 2тг/А. Поэтому мгновенное значение вектора Умова-Пойнтинга рав-
равно
Р = ЕоНо sin2(wi - kx).
Однако на опыте мы имеем дело не с мгновенным значением потока
энергии, а со средним его значением во времени Р. Так как среднее значение
sin2 а = 1/2 и, кроме того, для вакуума (е = fi = 1) ,/ео Ео = y/JIo Но, то
570 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ ХХШ
Это есть средняя энергия, проходящая через единицу поверхности в едини-
единицу времени, или интенсивность волны. Полученный результат показывает,
что энергия, переносимая электромагнитной волной, пропорциональна ква-
квадрату амплитуды колебаний.
Пример 2. Стоячая электромагнитная волна. Вычислим теперь
вектор Умова-Пойнтинга для стоячей волны. Согласно сказанному в § 232,
колебания полей Е и Н в стоячей волне можно представить формулами
Е = 2Е0 cos (fcx - ре/2) sin {uit - ч>е/2),
Я = 2ff0 cos (fcx - рн/2) sin (uit - <рн/2).
В этих выражениях ipE и ipn обозначают запаздывания по фазе отраженной
волны электрического и магнитного полей:
<рв = 2тг • 21/X + ф, ipH - 2тг ¦ 21/Х + г].
Здесь ф и г] — изменения фазы при отражении, равные либо тг, либо ну-
нулю, а I — длина линии (в случае свободных волн I есть расстояние между
излучателем и отражающей поверхностью). Введем обозначения
2Е0 cos {kx - <ре/2) - Е\,
2Н0 cos (fcx - ч>н/2) = Hi;
тогда колебания в какой-либо данной точке можно записать короче:
Е = Е\ sin (ujt - <Pe/2),
Н = #isin(wi
где Ei и Hi не зависят от времени. Но в § 232 мы видели, что если ф = тг,
то tp = 0 и наоборот. Полагая, например, ф = тг, имеем
Е = Ei cos (ui - 2nl/X), H = Hi sin (wi - 2nl/X).
Поэтому для потока электромагнитной энергии получаем
Р = ?i#i sin {uit - 2тгг/А) cos (ui - 2тг1/Х) = (EiHi/2) sin Buit - Ш/Х).
В этом случае значение Р колеблется с частотой 2ш и периодически изме-
изменяет знак. Поэтому среднее по времени
Р = 0,
а следовательно, в стоячей волне течения энергии нет (чем и объясняется
название этого типа колебаний). Периодические изменения знака Р пока-
показывают, что направление движе-
движения энергии периодически изме-
изменяется. Энергия лишь колеблется
между пучностями электрического
и пучностями магнитного полей.
Этот процесс напоминает колеба-
колебания энергии между индуктивно-
индуктивностью и емкостью в закрытом ко-
колебательном контуре.
Рис. 422. Движение энергии в случае П р и м е р 3. Провод с посто-
янным током. Рассмотрим цилин-
проводника с током дрический проводник радиуса г, в
котором имеется постоянный ток с плотностью j (рис. 422). Электрическое
поле Е и магнитное поле Н у поверхности проводника направлены так, как
§ 243 ЭЛЕМЕНТАРНЫЙ ДИПОЛЬ 571
показано на рис. 422, и поэтому вектор Умова-Пойнтинга направлен внутрь
проводника, перпендикулярно к его боковой поверхности. Это показывает,
что энергия непрерывно втекает в проводник из окружающего простран-
пространства.
Вычислим эту энергию. Если р — удельное сопротивление вещества про-
проводника, то, согласно закону Ома,
Е = рз-
Напряженность магнитного поля у поверхности равна
Я = г/Bтгг) = jr/2.
Поэтому
Р = ЕН = prj2f2.
Энергия, втекающая через всю боковую поверхность отрезка проводника
длиной I за 1 с, получается равной
W/t = Р ¦ 2nrl = pj2nr2l.
Но pj2, согласно закону Джоуля-Ленца (в дифференциальной форме), есть
количество теплоты, выделяющейся в единице объема за единицу времени,
а тгг21 — объем проводника. Поэтому мы находим, что энергия, втекаю-
втекающая в проводник, равна количеству теплоты Джоуля-Ленца, как и должно
быть по закону сохранения энергии. Приведенный пример показывает, что
электромагнитная энергия, за счет которой выделяется тепло, входит в про-
проводник через его боковую поверхность, а не вдоль его оси, как это кажется
на первый взгляд.
§ 243. Элементарный диполь
Среди различных электрических систем, излучающих элек-
электромагнитные волны, особо важное значение имеет электриче-
электрический диполь. В § 237 мы уже встречались с применением диполя
для излучения электромагнитных волн. Однако там мы говори-
говорили о так называемом полуволновом диполе,
длина которого равна половине длины волны.
Сейчас же мы рассмотрим диполь, длина кото-
которого мала по сравнению с длиной волны (эле- °-
0
ментарный диполь).
Простейшим примером элементарного ди-
диполя являются два металлических шара, за-
заряжаемые от какого-либо генератора элек-
электрических колебаний, если расстояние между
шарами I-С А (рис. 423). Момент такого диполя
есть р = ql. Если генератор создает гармони-
ческие колебания, то q = qo sinwt и момент диполя изменяется
со временем также по гармоническому закону
р = posinut. B43.1)
Здесь ро = lot есть амплитуда электрического момента диполя.
Ее можно выразить также через амплитуду силы тока iq. Дей-
Действительно, сила тока в диполе равна i — dq/dt = q^io cos wt, a
572 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ XXIII
амплитуда тока го = qoio. Поэтому qo = го/ш, а следовательно,
Ро = -*о- B43.2)
С элементарными диполями нам приходится встречаться
весьма часто. Самым важным примером элементарных диполей
являются электроны внутри атомов. Круговое (и эллиптичес-
эллиптическое) движение электронов, обращающихся вокруг положитель-
положительного ядра, можно разложить на два прямолинейных гармони-
гармонических колебания. Но электрон, совершающий прямолинейные
гармонические колебания, совместно с положительным ядром
(не принимающим участия в излучении) представляет собой
диполь, момент которого изменяется согласно формуле B43.1)
Так как длины волн, излучаемых атомом (для видимого света
округленно 5 • 10~5 см), намного больше размеров атомов
(~ 10~8 см), то рассматриваемые диполи можно считать с
большой точностью элементарными.
Излучение элементарного диполя. Рассмотрим теперь,
какой характер имеют электромагнитные волны, излучаемые
элементарным диполем Мы не будем приводить строгий вывод
выражений для электромагнитного поля из уравнений Максвел-
Максвелла, а ограничимся лишь качественными результатами.
Характер электромагнитного поля диполя существенно зави-
зависит от того, на каком расстоянии расположена рассматриваемая
точка. Если расстояние г от центра диполя до этой точки ма-
мало по сравнению с длиной волны (г С А), то справедливы те
же формулы, что и для постоянных электрического и магнит-
магнитного полей. Электрическое поле диполя выражается формулами
B5.5) и B5.6) и убывает с расстоянием пропорционально 1/г3
Магнитное же поле диполя выражается той же формулой G9.2),
что и поле элемента тока, и пропорционально 1/г2
На больших расстояниях от диполя (г 3> А) закон изменения
полей становится совсем другим Эта так называемая волновая
область представляет основной интерес, и поэтому мы остано-
остановимся на ней подробнее. Выясним, какой вид имеет волновой
фронт электромагнитной волны диполя. Так как электромаг-
электромагнитное возмущение распространяется во все стороны от диполя
с одинаковой скоростью с (мы предполагаем, что диполь нахо-
находится в вакууме), то время прохождения волны до всех точек,
удаленных от диполя на одно и то же расстояние г, одинако-
одинаково. Поэтому во всех точках сферы, центр которой совпадает с
центром диполя, фаза колебаний одинакова, т.е. мы имеем сфе-
сферический волновой фронт, и, следовательно, волна, излучаемая
диполем, есть сферическая волна.
Так как электрическое поле Е в волне перпендикулярно к
направлению распространения, то вектор Е в различных точках
§ 243
ЭЛЕМЕНТАРНЫЙ ДИПОЛЬ
573
перпендикулярен к радиус-векторам (рис. 424 а) Это поле пе-
периодически изменяется, и поэтому, перемещаясь вдоль радиус-
вектора, мы будем находить поля взаимно противоположного
Рис 424 Форма линий напряженности поля излучающего диполя
Рис 425 Линии напряженности (а) и индукции (б) в шаровой электромаг-
электромагнитной волне диполя
574 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ XXIII
направления (рис. 424 5). Соединяя на рис. 424 5 стрелки штри-
штриховой линией, мы получим одну из линий напряженности
(рис. 424 в). Полная картина линий напряженности в электро-
электромагнитной волне диполя показана на рис. 425 а. Линии напря-
напряженности представляют собой замкнутые кривые в соответствии
с вихревым характером электрического поля.
Направление магнитного поля Н в каждой точке перпенди-
перпендикулярно к Е и к направлению распространения. Поэтому линии
индукции представляют собой концентрические окружности, ле-
лежащие в плоскостях, перпендикулярных к диполю, и имеющие
центр на оси диполя (рис. 425 5; подробнее см. Добавление 11).
§ 244. Давление электромагнитных волн
Электромагнитные волны, встречая на своем пути какие-
либо тела, оказывают на них давление.
Легко понять происхождение этого давления. Положим, что
электромагнитная волна падает на плоскую поверхность тела
перпендикулярно к этой поверхности
\,Е ч^ (рис. 426). Электрическое поле Е вол-
*rv ^"Л. ны параллельно поверхности, и по-
jil ^| -^ тому оно не вызывает сил давления
—-И J- L^ (в рассматриваемом случае нормаль-
нормального падения). Однако это поле со-
создает внутри тела токи плотностью j.
Так как в волне, кроме электричес-
электрического, имеется еще и магнитное поле
Н, то на токи будет действовать си-
Рис. 426. Возникновение ла f, перпендикулярная к j и Н, т.е. в
давления электромагнит- направлении распространения волны,
ных волн Среднее значение этой силы, отнесен-
отнесенное к единице поверхности тела, и есть давление электромаг-
электромагнитной волны.
Максвелл, впервые вычисливший давление электромагнит-
электромагнитных волн, нашел, что если тело полностью поглощает падающую
на него энергию, то давление равно
р = п, B44.1)
где п — среднее значение объемной плотности энергии в падаю-
падающей электромагнитной волне (см. Добавление 12). Если же те-
тело частично отражает волну, то, кроме поля падающей волны,
будет присутствовать еще поле отраженной волны, и давление
будет равно
р = A + к)п, B44.2)
где к — коэффициент отражения (интенсивности). Следователь-
Следовательно, для абсолютно отражающего (к = 1) тела р = 2п.
§ 245 ИМПУЛЬС И МАССА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 575
Давление электромагнитной волны можно выразить также
через ее интенсивность / (среднее значение вектора потока энер-
энергии). Так как / = пс, то вместо B44.2) можно написать
р=~{1 + к). B44.3)
Наконец, если волна падает на поверхность тела наклонно,
под углом "в к нормали, то
р= 1^1A +к). B44.4)
Так как свет представляет собой электромагнитные волны,
то он оказывает давления на тела, поставленные на пути его
распространения. Световое давление очень мало. Оценим это
давление для лучей солнечного света. Интенсивность солнечного
излучения примерно равна 103 Вт/м2. Поэтому для давления
солнечных лучей на абсолютно отражающее зеркало (к = 1)
имеем
Несмотря на ничтожное световое давление, эксперименталь-
экспериментальное доказательство существования давления электромагнитных
волн было впервые получено именно на волнах света в класси-
классических опытах П.Н. Лебедева, который в 1900 г. доказал суще-
существование светового давления на твердые тела, а в 1910 г. — и
на газы. Световое давление оказалось соответствующим форму-
формуле Максвелла B44.4).
§ 245. Импульс и масса электромагнитного поля
Факт существования давления электромагнитных волн с
необходимостью приводит к выводу, что электромагнитному по-
полю присущ определенный механический импульс.
Действительно, представим себе, что на плоскую поверх-
поверхность S абсолютно поглощающего тела падает электромагнит-
электромагнитная волна. Вследствие существования давления электромагнит-
электромагнитной волны на тело действует сила F = uS. Но, согласно второму
закону Ньютона, сила равна импульсу, полученному телом за
единицу времени. Отсюда можно заключить, что излучение пе-
переносит с собой определенный импульс.
Найдем, чему равен импульс электромагнитного поля. За
единицу времени тело получает импульс поля, заключенный в
параллелепипеде с основанием S и высотой, равной скорости
распространения поля с. Если g есть импульс единицы объема
поля (плотность импульса), то импульс, получаемый телом, ра-
равен gSc Поэтому gSc — uS, а следовательно, g = и/с. Выражая
и через поток электромагнитной энергии Р по формуле Р — ис и
576 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ. XXIII
учитывая еще, что плотность импульса есть вектор, мы находим
окончательно
g = Р/с2. B45.1)
Полный импульс всего электромагнитного поля Gn есть инте-
интеграл от плотности импульса по всему объему, занятому полем:
Gn= J^dr. B45.2)
В 1899 г. А.А. Садовский предсказал, что электромагнитные волны, ес-
если они поляризованы по кругу, должны обладать еще и моментом импуль-
импульса, т.е. по механическим свойствам электромагнитные волны могут быть в
известной степени подобны вращающимся телам. Это явление было дей-
действительно обнаружено на волнах света и на радиоволнах сантиметрового
диапазона.
Полученные важные результаты позволяют обобщить зако-
законы механики Ньютона на электромагнитные явления. Они по-
показывают, что, кроме импульса GT, связанного с движущимися
телами, существует импульс Gn электромагнитного поля. Вто-
Второй закон Ньютона
dG/dt - F
относится, строго говоря, не к импульсу тел GT, но к полному
импульсу G:
G = GT + Gn. B45.3)
Если в системе тел действуют только внутренние силы, т.е.
система изолирована, то полный импульс системы остается по-
постоянным. Закон сохранения импульса можно записать в сле-
следующей общей форме, охватывающей не только механические,
но и электромагнитные явления:
G = GT + Gn = const. B45.4)
Отсюда следует, что если какое-либо первоначально покоив-
покоившееся тело испускает в определенном направлении электромаг-
электромагнитные волны, то это тело получает импульс GT — — Gn, на-
направленный в сторону, противоположную излучению, и равный
импульсу, унесенному излучением. Это явление подобно «отда-
«отдаче» ружья при выстреле.
Импульс (количество движения) какого-либо тела есть про-
произведение массы этого тела на его скорость. Или, иначе, масса
тела равна его импульсу, деленному на скорость. Так как элек-
электромагнитное поле имеет импульс и распространяется с конеч-
конечной скоростью, то отсюда можно заключить, что ему присуща
также определенная масса.
§ 245 ИМПУЛЬС И МАССА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 577
Пусть d есть масса единицы объема, т.е. плотность электро-
электромагнитного поля. Тогда импульс единицы объема поля есть g =
= cd. С другой стороны, согласно формуле B45.1), та же плот-
плотность импульса равна g = Pj<?. Следовательно,
cd = P/c2.
Но поток электромагнитной энергии Р можно выразить через
объемную плотность энергии и:
Р = ис.
Отсюда получаем соотношение
и = c2d,
которое выражает плотность электромагнитного поля d через
объемную плотность энергии и. Это соотношение между массой
и энергией справедливо, очевидно, не только для единицы объ-
объема, но и для какого угодно объема поля. Если т — масса поля,
a W — его энергия, то
W = тс2, B45.5)
где с — скорость света в вакууме.
Так как скорость света очень велика, то даже весьма значи-
значительной энергии поля соответствует очень малая масса. Однако
принципиальное значение соотношения B45.5) от этого, разуме-
разумеется, нисколько не уменьшается.
Рассмотрим пример: вычислим массу, соответствующую
энергии, излученной очень мощной радиостанцией мощностью
500 кВт = 5 • Ю5 Вт в течение 1 часа.
Имеем
W = 5 • 105 • 3,6 ¦ 103 = 18 • 108 Дж,
и из B45.5) находим
Приведем другой вывод соотношения меж- Рис. 427. К выводу соот-
ду массой и энергией электромагнитного поля, ношения между массой и
Представим себе, что тело А (рис. 427), нахо- энергией электромагнит-
дящееся в первоначально неподвижном ящи- ного поля
ке, испускает очень короткий цуг электромаг-
электромагнитных волн с энергией W, которые падают на второе тело Б и полностью
в нем поглощаются. Во время излучения тело А испытывает отдачу и по-
получает импульс gSct, направленный справа налево (S — поверхность тела,
t — время излучения). Так как g = Р/с2, то этот импульс равен также W/c,
где W = PSt есть излученная энергия. Под действием импульса отдачи
ящик приобретет некоторую скорость v и будет двигаться справа налево
до тех пор, пока излучение не достигнет тела Б. При поглощении излуче-
излучения ящик получит импульс, направленный слева направо, и остановится,
578 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ ХХШ
так что в результате произойдет перемещение центра массы ящика О на
некоторое расстояние х. Но это противоречит закону сохранения импульса,
согласно которому при действии только внутренних сил центр массы дол-
должен оставаться неизменным Для устранения этого противоречия имеется
только единственный выход, а именно — заключить, что увеличение энер-
энергии тела Б сопровождается увеличением его массы и притом как раз таким,
что положение центра массы О остается неизменным.
Отсюда нетрудно найти соотношение между массой и энергией в коли-
количественной форме. Предполагая для упрощения расчетов, что масса излу-
излучения т весьма мала по сравнению с массой ящика М, имеем
Mv = W/c, v = W/Mc.
За время t = l/с, в течение которого излучение доходит от А до Б, ящик
передвинется на расстояние
Так как масса М перемещается на расстояние х, а масса излучения т — на
расстояние I, то для неизменности центра масс необходимо, чтобы выпол-
выполнялось соотношение
Мх = ml.
Подставляя сюда вместо х его выражение, мы находим
W = mc2. B45.6)
Мы вывели соотношение B45.5) для электромагнитного по-
поля. Однако, согласно специальной теории относительности Эйн-
Эйнштейна, оно имеет совершенно общее значение и справедливо
для любых тел независимо от их внутреннего строения и со-
состояния. Оно выражает то обстоятельство, что всякое изменение
энергии AW любого тела или системы тел всегда связано с из-
изменением массы Am = AW/с2 независимо от того, какие имен-
именно превращения энергии происходят в данном теле или систе-
системе тел. Поэтому результаты, полученные в данном параграфе,
можно рассматривать как частный случай применения общего
соотношения к электромагнитному полю.
Мы уже отмечали, что вследствие весьма большой величи-
величины с даже очень большие изменения энергии сопровождаются
лишь ничтожными изменениями массы. Однако существуют и
такие явления, в которых изменением массы пренебрегать никак
нельзя. Наиболее важными из них являются различные процес-
процессы расщепления и превращения атомных ядер, в которых выде-
выделяются огромные энергии, и поэтому соответствующие измене-
изменения массы частиц, участвующих в этих процессах, оказываются
вполне ощутимыми и доступными для очень точных измерений.
Это позволило проверить соотношение между массой и энерги-
энергией на большом числе различных ядерных реакций и убедиться,
что оно действительно очень хорошо оправдывается на опыте.
§ 246 ЭЛЕКТРОМАГНИТНАЯ МАССА ДВИЖУЩЕГОСЯ ЗАРЯДА 579
§ 246. Электромагнитная масса движущегося заряда
Рассмотрим движущийся электрический заряд. Он создает в
окружающем пространстве не только электрическое поле Е, но и
магнитное поле Н, т.е. вокруг заряда образуется электромагнит-
электромагнитное поле. Это поле обладает определенным импульсом (§ 245).
Поэтому полный импульс движущегося заряженного тела, а сле-
следовательно, и масса тела будут больше, чем в отсутствие заряда.
Эта дополнительная масса, связанная с электромагнитным по-
полем, называется электромагнитной массой тела.
Электромагнитная масса зависит от скорости движения за-
заряженного тела, увеличиваясь с увеличением скорости. Что-
Чтобы найти эту зависимость, воспользуемся соотношением B45.5).
Положим, что скорость тела увеличилась на dv, отчего энергия
тела возросла на dW, а масса — на dm. Тогда, согласно B45.5),
dW = c2dm. B46.1)
По второму закону Ньютона (в форме, учитывающей зависи-
зависимость массы от скорости)
d{mv)=Fdt B46.2)
или, иначе,
mdv + v dm = F dt.
Наконец, по определению энергии
dW = F dx + Fv dt. B46.3)
Поэтому
mdv + v dm — dW/v = c2 dm/v,
или
dm _ 1 d(v2/c2)
m ~~ 2 l-v2/c2'
Интегрируя это уравнение, получаем
т = т° B46.4)
у/1 - «2/с2
где через то обозначена постоянная интегрирования. При
v2/c2 -> 0, т -> то, т.е. то имеет смысл покоящейся электро-
электромагнитной массы. При очень быстрых движениях (v2/c2 ~ 1)
электромагнитная масса увеличивается с возрастанием скоро-
скорости и как раз по тому закону, который получается из опытов с
быстрыми электронами (ср., например, § 183).
Необходимость существования электромагнитной массы,
следующая из классической электродинамики Максвелла, при-
привела Дж.Дж. Томсона еще в конце прошлого века к предполо-
предположению, что вся масса электрона имеет электромагнитное про-
происхождение, т.е. что инерция электрона обусловлена инерцией
создаваемого им поля.
580 СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ГЛ. XXIII
Впоследствии теории электромагнитной массы электрона
развивались рядом крупных физиков. В качестве одного из важ-
важных аргументов в пользу правильности гипотезы об электромаг-
электромагнитной природе массы электрона рассматривали зависимость
массы от скорости B46.4), хорошо оправдывающуюся на опы-
опыте. Однако в действительности этот аргумент совершенно не
доказателен, так как формула B46.4) получается в теории от-
относительности как универсальное соотношение, не зависящее от
физической природы массы.
Далее, следует помнить, что у нас не имеется никаких осно-
оснований отождествлять то в формуле B46.4) с массой электрона.
Ведь при выводе этого выражения мы исходим из соотношения
B45.5), полученного нами для электромагнитного поля, и поэто-
поэтому то есть масса поля покоящегося электрона, которая совсем
не обязательно равняется массе самого электрона.
В принципе проверка гипотезы об электромагнитной природе
массы электрона могла бы состоять в том, чтобы найти энергию
поля электрона W и вычислить т с помощью соотношения W =
— тс2. Сравнивая затем найденное теоретическое значение т с
экспериментально найденной массой электрона, мы могли бы
определить, составляет ли электромагнитная масса всю массу
электрона или только ее часть. К сожалению, такую проверку
сделать нельзя.
В связи со сказанным выше остановимся еще на одном во-
вопросе. Предположим, что вся масса электрона имеет электро-
электромагнитное происхождение, и будем представлять себе электрон
в виде шарика с радиусом а, находящегося в вакууме и имеюще-
имеющего заряд е, распределенный равномерно по поверхности. Тогда
электрическое поле отлично от нуля только вне шарика. Будем
считать, что электрон покоится (магнитного поля нет), и най-
найдем полную энергию W электрического поля, создаваемого ша-
шариком. Учитывая, что объемная плотность энергии поля (§ 37)
есть и = eqE*/2, где напряженность поля Е = е/^тгеог2), и вы-
выбирая (вследствие сферической симметрии поля) элемент объ-
объема в виде dr = 47гг2 dr, получаем
W= fudT = -^-f~ = -^-. B46.5)
J 8тг?о J г2 8тг?Оа
Приравнивая эту энергию тос2, получаем связь между то и а:
т0 = 5-А-. B46.6)
8тг?ос2а ч '
Отметим, что полученный результат слабо зависит от харак-
характера распределения заряда шарика. Так, например, если бы за-
заряд был распределен равномерно по объему шарика, то в форму-
§ 246 ЭЛЕКТРОМАГНИТНАЯ МАССА ДВИЖУЩЕГОСЯ ЗАРЯДА 581
лах B46.5) и B46.6) появился бы только дополнительный мно-
множитель 6/5, близкий к единице.
В системе СГС вместо формулы B46.6) мы имеем
mo = lfa- B46.6а)
Из полученных соотношений между то и а нельзя опреде-
определить массу покоящегося электрона, так как неизвестно, какое
значение а нужно брать в нашей «модели» электрона в виде
шарика. Однако можно поступить наоборот. А именно, из фор-
формул B46.6) или B46.6а) можно найти, какой радиус а должен
иметь заряженный шарик, чтобы его электромагнитная масса
была равна массе покоящегося электрона. Так как здесь речь
идет только об определении порядка величины, то множитель
1/2 в формуле B46.6а) принято опускать. Тогда в системе СГС
получается
^ B46.7)
В системе СИ выражение для а имеет вид
^^ B46.7а)
а
4тгео
Величина а получила название классического радиуса электро-
электрона. Подставляя в последнюю формулу е = 1,60 ¦ 10~19 Кл, то =
= 9,11 • Ю-31 кг, с = 3,00 ¦ 108 м/с и е0 = D?г ¦ 9 • 109) Ф/м,
находим а = 2,82 • 10~15 м ~ 103 см.
Классический радиус электрона, конечно, никоим образом
нельзя рассматривать как некоторую величину, характеризую-
характеризующую «размеры» электрона. Его смысл заключается в том, что
он дает некоторую характерную длину, определяющую порядок
величины нижнего предела области применимости классической
электродинамики. Так как то есть максимальное возможное
значение электромагнитной массы электрона (вся масса элек-
электрона равна его электромагнитной массе), то а есть минималь-
минимальная длина. На расстояниях, меньших этой длины, классическая
электродинамика принципиально не может быть справедлива.
Напряженность электрического поля электрона на расстоянии
классического радиуса равна
Е = -НЧ = 4тгео^ = 1,8 • 1020 В/м ~ 1020 В/м.
Это и есть максимальное поле, при котором может быть приме-
применима классическая электродинамика.
Однако на самом деле область применимости классической
электродинамики меньше, чем показывают приведенные оцен-
оценки, так как при больших энергиях заряженных частиц возника-
возникают различные квантовые явления. Их рассмотрение выходит за
582 ПРИНЦИП РАДИОСВЯЗИ ГЛ XXIV
пределы настоящей книги. Поэтому мы только укажем, что учет
квантовых явлений увеличивает указанную выше характерную
длину на два порядка по сравнению с классическим радиусом
электрона Предельная напряженность электрического поля Е
при этом уменьшается тоже примерно на два порядка.
ГЛАВА XXIV
ПРИМЕНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
ДЛЯ ЦЕЛЕЙ СВЯЗИ
§ 247. Принцип радиосвязи
Одним из самых замечательных технических применений
электромагнитных волн является их использование для целей
связи. Изобретением радио мы обязаны преподавателю физики
офицерских минных классов в Кронштадте, а впоследствии —
профессору физики Петербургского электротехнического ин-
института А.С. Попову, который в 1895 г. продемонстрировал на
заседании Русского физико-химического общества передачу и
прием сигналов с помощью электромагнитных волн и создан-
созданный им радиоприемник. Начатые около того же времени опы-
опыты итальянского инженера Маркони, поставленные в широком
промышленном масштабе, положили начало внедрению радио в
практику. В последующий период времени радиотехника была
превращена трудами многих выдающихся ученых и инженеров
в чрезвычайно широкую и разностороннюю область техники.
Как мы знаем, для излучения мощных электромагнитных
волн необходимо создать достаточно сильные токи смещения,
т.е. быстро изменяющееся электрическое поле. Поэтому в ра-
радиотехнике применяют электрические колебания высокой часто-
частоты. Частоты колебаний, используемые для радиовещания, ле-
лежат примерно в пределах от 105 до 108 Гц, что соответствует
длинам волн от 3 км до 3 м. Для решения специальных задач,
где существенно получение остро направленного излучения (на-
(например, в радиолокации), применяют дециметровые и сантимет-
сантиметровые волны; для этого оказывается необходимым генерировать
колебания с громадной частотой, вплоть до 1010 Гц и выше.
Схема радиосвязи изображена на рис. 428. На передающей
станции имеется генератор электрических колебаний, который
возбуждает в антенне (металлических проводах, подвешенных
высоко над землей) интенсивные вынужденные колебания. Для
усиления этих колебаний используют явление резонанса: часто-
частоту генератора делают равной одной из собственных частот ан-
§ 248 МОДУЛЯЦИЯ КОЛЕБАНИЙ 583
тенны (обычно — частоте основного колебания). Так как антенна
представляет собой открытый вибратор, то она излучает элек-
электромагнитные волны, которые, распространяясь, достигают ан-
антенны приемной станции. Под действием переменного электри-
электрического поля волны электроны в приемной антенне приходят в
колебательное движение, т.е. в ней
появляется электрический ток вы-
сокой частоты. Для усиления этих
вынужденных колебаний прием-
приемная антенна также настраивается
в резонанс с приходящими колеба-
колебаниями. Отметим, что для настрой-
настройки антенны можно включать кон-
конденсатор последовательно с ней.
В этом случае общая емкость ан-
антенного контура (как при вся-
всяком последовательном соединении Рис 428 Схема радиосвязи
емкостей) уменьшается, благодаря
чему собственная частота антенны увеличивается, а длина
волны уменьшается. В случае же параллельного соединения
(рис. 428) общая емкость увеличивается, а следовательно, длина
волны, соответствующая резонансу, становится больше.
Таким образом, принцип радиосвязи заключается в том, что
токи проводимости передатчика сначала превращаются в токи
смещения, не требующие для своего распространения провод-
проводников, а затем эти токи смещения снова преобразуются в токи
проводимости в приемнике.
§ 248. Модуляция колебаний
Схема, изображенная на рис. 428, еще недостаточна для пе-
передачи сигналов. Для этого необходимо желаемым образом из-
изменять колебания в соответствии с частотой и силой сигнала.
На первый взгляд может показаться, что для передачи сиг-
сигнала достаточно превратить его в электрические колебания и
создать в антенне переменный ток с частотой и силой, соответ-
соответствующими сигналу. Так, например, желая передать речь или
музыку, мы можем с помощью микрофона получить изменяю-
изменяющийся ток и после надлежащего его усиления послать в антен-
антенну. Однако в действительности этим способом передать сигналы
нельзя. Дело в том, что все сигналы, с которыми приходится
иметь дело на практике, представляют собой колебания низкой
частоты. При передаче речи и музыки — это частоты примерно
от 100 до 10 Гц, при передаче телеграфных знаков — еще значи-
значительно ниже. Для излучения же радиоволн необходимы высокие
584
ПРИНЦИП РАДИОСВЯЗИ
ГЛ XXIV
частоты, так как только с быстрыми колебаниями можно полу-
получить сильные токи смещения. Поэтому, направляя токи сигнала
непосредственно в антенну, мы не получим практически никакой
излученной мощности.
Это противоречие устраняется в радиотехнике весьма остро-
остроумным способом, состоящим в том, что для передачи энергии
употребляют высокочастотные колебания, а колебания низкой
частоты сигнала используют лишь для изменения высокоча-
высокочастотных колебаний, или, как принято говорить, для их модуля-
модуляции. На приемной станции из этих сложных колебаний с помо-
помощью специальных методов вновь выделяют колебаний низкой
частоты сигнала, которые после усиления используют по на-
назначению (в громкоговорителе, в телеграфном аппарате и т.п.).
Этот процесс восстановления сигнала называется демодуляцией.
Модуляцию колебаний можно производить, изменяя их ам-
амплитуду, частоту или фазу. Мы остановимся только на ампли-
амплитудной модуляции, применяемой наиболее часто.
Когда из студии радиостанции не производится передача,
немодулированные колебания тока в антенне имеют вид
i = iosinu)t. B48.1)
Они изображены графически на рис. 429 а. При наличии сигна-
сигнала (речь и музыка перед микрофоном) эти колебания с помощью
Рис. 429. Амплитудная модуляция колебания
приемов, описываемых в § 249, превращаются в более сложные:
» = »оA+ /(*)) smart, B48.2)
где /(?) — «модулирующая функция», зависящая от типа сиг-
сигнала, причем |/(?)| < 1.
§ 248 МОДУЛЯЦИЯ КОЛЕБАНИЙ 585
Простейший тип модуляции мы имеем при передаче чистого
музыкального тона (камертон перед микрофоном). В этом слу-
случае ток в цепи микрофона изменяется по гармоническому закону
и модулирующая функция (рис. 429 б) имеет вид
/(*) = к smut.
Колебания же тока в антенне описываются формулой
i = io(l + ksmUt)sinwt. B48.3)
(Мы полагаем везде начальную фазу равной нулю, что не имеет
принципиального значения.) Так как частота модуляции Q<?u,
то это колебание можно приближенно рассматривать как гар-
гармоническое, имеющее амплитуду гоA + ks'mQt), периодически
изменяющуюся во времени (рис. 429 б). Ее максимальное и ми-
минимальное значения: /макс — *оA + &)> *мин = io(l — k). Величина
г, **макс ^мин
-*макс 1 ^мин
называется глубиной модуляции. Пользуясь известной форму-
формулой:
+ /3 р -а
cos а — cos р = 2 sin —r-^- sin
легко убедиться, что
i = гоA + fesinJli) sinwt =
= го smut + - Ыо cos [и — U)t — - ki0 cos (lj + u)t.
Следовательно, модулированное колебание B48.3), выражаясь
точно, представляет собой три гармонических колебания, про-
происходящих с частотами ш, (ш + Q) и
(и) — $7) (рис. 430 б). Основная часто-
частота передатчика ш называется в радио-
радиотехнике несущей частотой, а допол-
дополнительные частоты (ш + Q) и (и — Q),
возникающие при модуляции, — верх-
верхней и соответственно нижней боковы-
боковыми частотами.
Если сигнал представляет собой
не гармоническое колебание, но име-
имеет более сложную форму, то вместо
одной определенной частоты модуля-
модуляции Q мы будем иметь много частот.
Поэтому и вместо двух боковых ча- Рис. 430. Спектры колебаний
стот мы получим целую совокупность
частот, лежащих слева и справа от несущей частоты и образую-
образующих боковые полосы частот (рис. 430 б).
Если наконец, мы передаем телеграфные знаки по азбуке
Морзе, то амплитуда колебаний изменяется так, как показано на
со
1
-П
Illlllll
со
1
со
1
1
со+П
Illilill
586
ПРИНЦИП РАДИОСВЯЗИ
ГЛ XXIV
(о) и модулированное колебание (б)
при телеграфной передаче
рис. 431 а. Она постоянна, когда телеграфный ключ замкнут, и
равна нулю при разомкнутом ключе. Колебания тока в антенне
при этом имеют вид прерывис-
прерывистых цугов различной длитель-
длительности (рис. 431(?); короткие
цуги соответствуют точкам,
длинные — тире.
Таким образом, модулируя
колебания, мы при помощи низ-
низкочастотного сигнала превраща-
превращаем одно-единственное гармони-
Рис. 431. Модулирующая функция ческое колебание передатчика в
несколько гармонических коле-
колебаний, которые, однако, все яв-
являются высокочастотными (так как П<ш)и поэтому пригодны
для излучения радиоволн. В этом и заключается основная идея
модуляции колебаний в радиотехнике.
Чтобы при демодуляции получить опять сигнал неискажен-
неискаженной формы, необходимо, очевидно, чтобы в приемник попали
колебания всех частот, возникших при модуляции. А для этого
нужно, чтобы настройка приемника хотя и была очень острой,
но все же такой, чтобы ширина резонансной кривой охватывала,
по возможности, все боковые частоты.
§ 249. Радиопередатчик
Для осуществления модуляции колебаний в радиотехнике
разработаны различные приемы. Так, например, переменное на-
напряжение сигнала можно подать на сетку генераторной лампы
(«модуляция на сетку»). Тогда при изменении сеточного напря-
напряжения будет изменяться амплитуда колебаний, и мы получим
колебания генератора, модулированные в соответствии с напря-
напряжением сигнала.
Простейшая схема радиотелефонного передатчика с моду-
модуляцией на сетку показана на рис. 432. Часть схемы, обозна-
обозначенная цифрой I, есть уже знакомый нам ламповый генератор
(см. рис. 364). Модулирующее напряжение возникает в части
схемы П. Оно появляется в цепи микрофона М и усиливает-
усиливается трансформатором Т. Отметим, что сеточный конденсатор Сс
представляет малое сопротивление для переменных токов вы-
высокой частоты генератора, а вторичная обмотка трансформато-
трансформатора вследствие ее индуктивности — большое сопротивление. По-
Поэтому эти переменные токи не ответвляются в микрофонную
цепь и генератор практически работает так же, как и в отсут-
отсутствие модулирующей цепи П. Для микрофонных же токов низ-
низкой частоты конденсатор Сс обладает большим сопротивлением,
§249
РАДИОПЕРЕДАТЧИК
587
и поэтому напряжение трансформатора Т оказывается целиком
приложенным между сеткой и катодом лампы. Модулированные
Рис. 432. Модуляция на сетку
колебания передаются в антенный контур с помощью катушки,
связанной индуктивно с катушкой L колебательного контура ге-
генератора.
Модулирующее напряжение молено прикладывать и к аноду
генераторной лампы («модуляция на анод»). Схема такого пере-
II
Рис. 433. Модуляция на анод
датчика (также в одном из простейших вариантов) изображена
на рис. 433. Колебания напряжения, возникающие в цепи микро-
микрофона М, подаются через трансформатор Г на сетку лампы Л\ и
усиленные затем прикладываются между анодом и катодом лам-
588
ПРИНЦИП РАДИОСВЯЗИ
ГЛ XXIV
пы Л генераторного контура I. Разделение низкочастотных ко-
колебаний (модулирующих) и высокочастотных (модулируемых)
производится дросселями Д\ (без железа). Их индуктивность
подбирается такой, что они свободно пропускают низкочастот-
низкочастотные колебания из цепи II в генератор I, но не пропускают обрат-
обратно высокочастотные токи. Дроссели же Д (с железом) препят-
препятствуют низкочастотным токам цепи II закоротиться на источник
питания.
В приведенных выше схемах модуляция осуществлялась в
той же самой лампе (Л), которая служила для генерации ко-
колебаний. В мощных передатчиках модуляцию колебаний произ-
производят в специальной ча-
Jcth схемы (называемой
модулируемым блоком).
Общая схема (блок-схе-
(блок-схема) радиопередатчика
приведена на рис. 434.
Отметим в заключе-
заключение, что для модуляции
колебаний электронная
лампа должна обяза-
обязательно работать в таком
режиме, чтобы ее вольт-
амперная характеристи-
характеристика была нелинейной. Действительно, анодный ток лампы г есть
функция двух переменных напряжений: высокочастотного U\ и
модулирующего U2'-
i = f{Ui,U2). B49.1)
Разлагая эту функцию в ряд Тейлора и ограничиваясь только
степенями не выше второй, имеем
Генератор
о—
Микрофон
Модул ир
блок
Усили-
Усилитель
Мощный
усили-
усилитель
Рис 434. Блок-схема радиопередатчика
г = а +
cU2
+
+ hUiU2) + ... B49.2)
Если бы характеристика была линейной, то члены, заключенные
в скобки, отсутствовали бы и мы получили бы сумму обоих ко-
колебаний. Модулированное же колебание (формула B48.3)) есть
произведение двух колебаний. Оно выражается членом разло-
разложения hUiU2, который появляется только при нелинейной ха-
характеристике.
§ 250. Демодуляция колебаний. Радиоприемник
Под действием электромагнитной волны передатчика в ан-
антенне приемника возникают модулированные токи высокой ча-
частоты, тождественные с токами в антенне передатчика, но толь-
только гораздо более слабые.
§ 250 ДЕМОДУЛЯЦИЯ КОЛЕБАНИЙ РАДИОПРИЕМНИК 589
Однако эти токи еще не пригодны для непосредственного
получения сигнала. Если, скажем, при радиотелефонной пере-
передаче мы направим их, даже после предварительного усиления, в
громкоговоритель, то мы не услышим никакого зЪука. Это про-
происходит, во-первых, потому, что телефонная мембрана обладает
большой инерционностью и поэтому не может совершать такие
быстрые колебания с заметной амплитудой. Во-вторых, и это
самое главное, если бы мы и воспользовались малоинерцион-
малоинерционным телефоном (что можно сделать), то получили бы воздуш-
воздушные волны с радиотехнической частотой A05 —108 Гц), тогда как
наше ухо слышит звуки только при частоте, не превышающей
примерно 2 • 104 Гц.
Поэтому высокочастотные колебания в приемнике снова пре-
превращаются в колебания низкой частоты, соответствующие сиг-
сигналу. Эта демодуляция колебаний (или детектирование) осу-
осуществляется тем, что модулирован-
модулированные колебания выпрямляются с по-
помощью какого-нибудь нелинейного
устройства (кристаллический де-
детектор, электронная лампа) и затем
сглаживаются цепью, обладающей
подходящей постоянной времени.
Поясним сказанное более по- рис. 435. Демодулятор с крис-
дробно. Рассмотрим простейший де- таллическим детектором
модулятор (рис. 435), состоящий из
кристаллического детектора Д и конденсатора С, шунтирован-
шунтированного сопротивлением г. Положим, что на входе демодулятора
имеется модулированное напряжение {7ВХ, соответствующее пря-
прямоугольным телеграфным сигналам (рис. 436 а). Если бы кон-
конденсатора не было, то вследствие выпрямительного действия
детектора на сопротивлении г появилось бы пульсирующее на-
напряжение одного знака (рис. 436 6). При наличии конденсатора
этот последний будет заряжаться. Если постоянная времени г =
= Сг велика по сравнению с периодом Т несущего колебания,
то за время между двумя последовательными пиками напряже-
напряжения конденсатор не будет заметно разряжаться, его напряжение
будет увеличиваться, пока не достигнет некоторого постоянного
значения, пропорционального амплитуде входного напряжения.
После прекращения колебаний конденсатор будет разряжаться
через сопротивление г и, если г = Сг значительно меньше ин-
интервала t\ между двумя последовательными сигналами, успеет
полностью разрядиться задолго до прихода следующего сигна-
сигнала. Если при этом г еще намного меньше длительности ?г са-
самого сигнала, то на выходе демодулятора мы получим напря-
напряжение ?7Вых в виде импульсов, очень близких к прямоугольным.
590
ПРИНЦИП РАДИОСВЯЗИ
ГЛ. XXIV
иг
4ыхА
гл г~\
Они изображаются огибающей кривой рис. 436 б и воспроизво-
воспроизводят сигнал передающей радиостанции (рис. 436 б).
Из сказанного ясно, что для получения неискаженного сиг-
сигнала при демодуляции нужно, чтобы постоянная времени де-
демодулятора г была велика
по сравнению с периодом
несущего колебания, но ма-
мала сравнительно с периодом
самого сигнала.
Совершенно то же мы
имеем при демодуляции ра-
радиотелефонных сигналов.
Колебания напряжения на
входе демодулятора в этом
случае можно рассматри-
рассматривать как совокупность им-
импульсов, непрерывно пере-
переходящих один в другой и
изменяющих свою высоту.
Поэтому и здесь на выходе
демодулятора получится
напряжение, изображаемое огибающей модулированного коле-
колебания, т.е. низкочастотный сигнал передатчика.
Для выпрямления колебаний при демодуляции вместо кри-
кристаллического детектора можно использовать вакуумный диод,
включаемый в схему рис. 435. Однако чаще всего для демоду-
демодуляции применяют трехэлектродную лампу, которая одновремен-
одновременно и усиливает колебания. Со-
Соответствующая схема показана
на рис. 437 («сеточная демоду-
демодуляция»). Для того чтобы лам-
лампа в этой схеме обладала выпря-
выпрямительным свойством, нужно,
очевидно, чтобы рабочая точка
лежала в нелинейной части ее ха-
характеристики, например у ниж-
нижнего излома характеристики.
Изложенное позволяет по-
понять действие радиоприемни-
радиоприемника. Высокочастотные колебания,
Рис. 436. Демодуляция радиотелеграф-
радиотелеграфных сигналов
I—«И-
Рис. 437. Демодулятор с трехэлек-
тродной лампой
возникающие в антенне приемника, попадают сначала в лампо-
ламповый усилитель высокой частоты. Входной контур этого усили-
усилителя делают настраиваемым (ср. рис. 385), чтобы можно было
выделить волну какой-либо радиостанции. Усиленные колебания
высокой частоты попадают затем в демодулятор, где превраща-
превращаются в колебания низкой частоты сигнала. Эти колебания снова
§ 252
СУПЕРГЕТЕРОДИННЫЙ ПРИЕМ
591
усиливаются и подаются в соответствующий индикатор, напри-
например в громкоговоритель. Приемник, работающий по этому прин-
принципу, называют при-
приемником прямого уси-
усиления. Его блок-схема
показана на рис. 438.
Однако радиовещатель-
радиовещательные приемники чаще
всего строят по не-
несколько иной схеме (су-
(супергетеродинные при-
приемники, § 252).
Усили-
Усилитель
высокой
частоты
Демоду-
Демодулятор
Усили-
Усилитель
низкой
частоты
Ю
Телефон
Рис. 438. Блок-схема радиоприемника пря-
прямого усиления
§ 251. Гетеродинный прием
Телеграфные сигналы — тире и точки — часто принимают
с помощью телефона на слух. Для этой цели импульсы высо-
высокочастотных токов не подвергают демодуляции, а превращают
их в колебания звуковой частоты, отчего в телефоне появляется
свист. Короткий свисток обозначает точку, а длинный — тире.
Это преобразование частоты сигнала осуществляется сле-
следующим образом. На одну из ламп приемника подают два пере-
переменных напряжения: высокочастотное напряжение сигнала U —
= asmuit и переменное напряжение U\ = ais'mtJit от местного
маломощного генератора, имеющегося в приемнике (так назы-
называемого гетеродина). В § 249 мы видели, что если лампа ра-
работает в нелинейном режиме, то в ее анодной цепи появляются
комбинационные колебания и, в частности, колебание, пропор-
пропорциональное произведению UU\. Но
UU\ = аа\ sinwtsinu)\t = -cmi[cos (w — u)\)t — cos {uj + u)i)i\
и, следовательно, в приемнике появляются колебания с разност-
разностной (ш — u)i) и суммарной (и) + о^) частотами. Частоту гетероди-
гетеродина и)\ делают близкой к несущей частоте ш, но с таким расчетом,
чтобы разность (uj — u>i) лежала в пределах звуковых частот.
Тогда колебание с разностной частотой (ш — u)i) вызывает в те-
телефоне появление звука и телеграфные сигналы становятся слы-
слышимыми.
§ 252. Супергетеродинный приемник
Приемник прямого усиления, описанный в § 250, имеет тот
недостаток, что при очень высоких частотах (коротких вол-
волнах) не позволяет получать большое усиление сигнала. Одна
из причин, затрудняющих усиление, заключается в неизбеж-
неизбежных паразитных емкостях приемника (емкость электродов ламп,
емкость соединительных проводов и т.п.), которые при очень
592
ПРИНЦИП РАДИОСВЯЗИ
ГЛ. XXIV
высоких частотах представляют малые сопротивления, шунти-
шунтирующие лампы. Кроме того, имеются и другие причины, связан-
связанные с процессами внутри самих ламп. Применить же демодуля-
демодуляцию в первой лампе приемника, отказавшись вовсе от усиления
высокой частоты, невозможно, так как в этом случае вместе с
сигналом будут усиливаться также неизбежные помехи, которые
особенно велики на низких частотах.
От указанного недостатка в значительной степени свободен
супергетеродинный приемник, являющийся в настоящее время
Смеси-
Смеситель
Усили-
Усилитель
промежу-
промежуточной
частоты
Демоду-
Демодулятор
Усили-
Усилитель
низкой
частоты
КО
Телефон
Гетеродин
Рис. 439. Болк-схема супергетеродиниого приемника
самым распространенным. Его блок-схема показана на рис. 439.
Модулированные колебания высокой частоты
U = а[1 + /(<)] sinwi
из антенны попадают в этом приемнике на один из электродов
специальной лампы, а на другой электрод этой лампы действует
напряжение местного гетеродина
В результате, так же как и в гетеродинном приемнике, на выхо-
выходе лампы возникает колебание разностной частоты, пропорцио-
пропорциональное
[1 + /(*)] cos (u-ui)i,
модулированное той же функцией [1 + /(*)], что и первоначаль-
первоначальное колебание в антенне. Этот процесс преобразования частоты
в радиотехнике называется смешиванием частот, а лампа, слу-
служащая для этой цели, — смесительной лампой. Однако, в от-
отличие от простого гетеродинного приемника, частоту {w — и)\)
(так называемую промежуточную частоту) делают достаточно
высокой (неслышимой). Колебания промежуточной частоты за-
затем выделяют и усиливают резонансным усилителем и подверга-
подвергают демодуляции обычным способом. Полученный таким образом
сигнал, уже звуковой частоты, еще дополнительно усиливают и
подают в громкоговоритель.
§ 253 ПОЛУСВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 593
В таких приемниках при настройке на разные станции од-
одновременно с изменением емкости входного контура изменяется
и емкость колебательного контура гетеродина, так что проме-
промежуточная частота (w — wi) при перестройке приемника остается
постоянной. Для этого подвижные пластины обоих конденсато-
конденсаторов (входного контура и гетеродина) насаживают на обшую ось.
Выше мы говорили о демодуляции колебаний и смешивании
частот с помощью сеточных электронных ламп. Очевидно, что
то же можно сделать, используя вместо вакуумных ламп тран-
транзисторы.
§ 253. Полусвободные электромагнитные волны
До сих пор мы рассматривали электромагнитные волны двух
типов: волны вдоль проводов и свободные электромагнитные
волны. В первом случае линии напряженности заканчивались на
проводах линии (замыкались ими, см. рис. 401), а во втором — за-
замыкались в диэлектрике (см. рис. 415). В радиотехнике мы встре-
встречаемся еще с электромагнитными волнами промежуточного типа.
Свободные волны возникают в том случае, если излучающий
диполь находится целиком в диэлектрике (в воздухе) и достаточ-
достаточно удален от всех окружающих предметов. Это имеет место при
излучении коротких волн (несколько метров и меньше), когда
размеры диполя малы и он высоко приподнят над поверхностью
земли. Для излучения длинных волн (сотни и тысячи метров),
напротив, всегда применяют антенны, заземленные на одном
конце, отчего характер электромагнитной волны изменяется.
В § 235 мы видели, что при заземлении вибратора (дипо-
(диполя) его длина волны увеличивается в два раза, а картина рас-
распределения тока и напряже-
напряжения представляет собой поло-
половину картины соответствующего
распределения для незаземлен-
ного диполя (см. рис. 413 а). По-
Поэтому и картина распределения
поля в волне заземленной ан-
тенны изображается верхней по- рис ш Пол бодные ад
ловинои рис. 425, лежащей над магнитные в0/ны
плоскостью симметрии А А. Уна
показана на рис. 440. Линии напряженности электрического
поля в этом случае замыкаются в воздухе только с одной сто-
стороны, а с другой стороны замыкаются через Землю. Такие вол-
волны можно назвать полусвободными. Распространяясь, полусво-
полусвободные волны следуют за кривизной Земли, подобно тому как
волны вдоль проводов следуют за изгибами линии, и огибают
земную поверхность.
594 ПРИНЦИП РАДИОСВЯЗИ ГЛ XXIV
Явление огибания волнами различных препятствий, т.е.
дифракция волн, играет огромную роль в радиосвязи. Именно
вследствие дифракции радиоволн возможна устойчивая радио-
радиосвязь между удаленными пунктами, разделенными между со-
собой выпуклостью Земли, несмотря на то что сама Земля, срав-
сравнительно хорошо проводящая электричество, непрозрачна для
электромагнитных волн (рис. 441).
Однако дифракция сильно зависит от длины волны и выра-
выражена тем сильнее, чем больше длина волны. Поэтому способ-
способностью хорошо огибать земную поверхность обладают только
длинные волны (сотни и тысячи метров). Такие волны можно
заставить обойти вокруг земного шара и можно принять их в
_ том же пункте, из которого они
^ /~\( \ были отправлены. Время, необ-
/~^И ->xv '-\\w~V ходимое для этого электромаг-
ЧЛчЛПУ' i\'! нитным волнам, примерно равно
^4^^ 40000/300 000 = 0,13 с.
Напротив, очень короткие волны
^ „ (несколько метров и меньше) почти
Рис 441. Огибание земной по- ^ огибают 3емлЮ) и поэтому устой-
верхности длинными электро- J J
магнитными волнами чивая связь на коротких волнах воз-
возможна только на небольших рассто-
расстояниях, немногим больших пределов прямой видимости. Этот
случай мы имеем, в частности, в телевидении, где необходимо
применять короткие волны (не длиннее нескольких метров).
Исследования распространения коротких волн обнаруживают
другие интересные явления. Попадая в верхние сильно иони-
ионизованные слои атмосферы (в так называемую ионосферу), ра-
радиоволны отражаются этими проводящими слоями, действую-
действующими подобно металлическим зеркалам, и возвращаются опять
на Землю. Поэтому и короткие волны могут достигать очень
удаленных пунктов земной поверхности. Однако радиосвязь на
коротких волнах гораздо менее устойчива, нежели на длинных.
Изучение особенностей распространения радиоволн позволяет
получить ценные сведения о строении верхних слоев атмосферы.
Укажем в заключение, что в настоящее время электромаг-
электромагнитные волны применяются для обнаружения и точного опре-
определения положения предметов (самолетов в воздухе, кораблей в
море и т.п.) (радиолокация), для передачи неподвижных и дви-
движущихся изображений (фототелеграфия, телевидение), для во-
вождения кораблей и самолетов (радионавигация), для точного
измерения расстояний на земной поверхности (радиогеодезия),
в астрофизике для исследования радиоизлучения небесных тел
(радиоастрономия); радиотехника лежит в основе устройства
электронных счетных машин.
ДОБАВЛЕНИЯ
1. Теория опытов Кавендиша и Максвелла (к § 28)
Максвелл рассчитал, каким образом распределились бы заряды между
сферами, расположенными так, как описано в опытах § 28, если бы суще-
существовало отклонение от закона Кулона, и показал, как можно вычислить
по данным опыта возможное значение этого отклонения.
Предположим, что закон Кулона несправедлив и напряженность поля
Е точечного заряда q выражается формулой
Е = q/rn,
где п отлично от 2. Мы не выписываем справа постоянный множитель
1/Dтг?о), который все равно выпадает из окончательного результата (фор-
(формула (9)). Тогда потенциал в поле
точечного заряда будет
г, 1
U =
Вычислим теперь потенциал
Ui, создаваемый равномерно
заряженной сферой в какой-либо
точке С, находящейся внутри
сферы на расстоянии ? от ее
центра (рис. 442). Пусть о —
радиус сферы, а — поверхностная
плотность заряда на ней, a q =
= 4тга2<7 — полный заряд сферы.
Тогда
2тга2 sin j? d»9
Рис. 442. К вычислению потенциала,
создаваемого равномерно заряженной
сферой
где 27го2 sin $ <Ш = dS — элемент поверхности сферы в сферических коор-
координатах. Так как
г2 = а2 + ?2 - 2а? cos ¦&,
то
sintfd»?
596 ДОБАВЛЕНИЯ ГЛ XXIV
Вводя новую переменную х = cos»?, получаем
2
-l
-1
(n — l)(n — 3) 2a?
¦t -t
Здесь гМин = я — ? есть минимальное расстояние рассматриваемой точки до
сферы, а гмакс = a + ? — максимальное расстояние.
Если точка, где разыскивают потенциал, находится вне сферы на рас-
расстоянии ? > а от ее центра, то гми„ = ? — а, гмакс = ? + а. Поэтому потенциал
Ua(?) во внешней точке есть
Положим теперь п = 2 — й (где <5 может быть как положительным, так и
отрицательным). Величина й характеризует отклонение от закона Кулона,
а при 5 = 0 мы получаем закон Кулона точно. Из опытов Кулона можно
заключить, что 5 если и не равно нулю, то очень мало. Поэтому положим
й <? 1, разложим полученные выражения для потенциала в ряд Тейлора по
степеням 5 и ограничимся только членами первого порядка малости. Тогда
U = Un-2 — I -у- | О.
\dnJn-2
Это дает
J^ « + O], A)
|^ U + a)]. B)
Полагая в найденных выражениях ? = а и раскрывая получающиеся
неопределенности, мы получим значение потенциала на самой сфере в виде
U(a) = 17,(a) = Ua(a) = ^ + <5^ In2a C)
о a
После этих подготовительных расчетов перейдем к опытам Кавендиша
и Максвелла. Пусть А — радиус внутренней сферы, В — радиус внешней
сферы, gi — заряд внутренней сферы, q2 — заряд внешней сферы. Тогда
потенциал Ui внутренней сферы (А) есть
D)
Для потенциала Ui внешней сферы аналогично имеем
[{В - А)ЩВ -А)- (В + А)Ы(В + А)].
E)
§ 1 1 ТЕОРИЯ ОПЫТОВ КАВЕНДИША И МАКСВЕЛЛА 597
Когда мы соединяем обе сферы металлической проволокой, то их потенциа-
потенциалы принимают одинаковое значение Uq, которое измеряют на опыте (потен-
(потенциал, до которого заряжают первоначально обе соединенные друг с другом
сферы). Поэтому
i/i = U2 = О
Подставляя сюда выражения для U\ и Ui из D) и E), получаем два урав-
уравнения
где введены обозначения:
f[x) - - + -
хх F)
Ф = I " 2AB [{В ~ А) 1П {В ~ А) " {В + А) Ы {В + А)]-
Из этих уравнений мы можем исключить заряд qi внешней сферы и выра-
выразить заряд gi внутренней сферы через известный из опыта первоначальный
общий потенциал сфер Uo- Это дает
Полученное выражение показывает, что если только S ф 0, то gi ф 0, т.е на
внутренней сфере будет некоторый заряд. И, наоборот, если S — 0 (закон
Кулона точно выполняется), то из F) имеем: f(B) = l/В, Ф = 1/В, откуда
qi =0.
Однако, присоединяя к внутренней сфере электрометр, мы измеряем не
ее заряд, а потенциал. Поэтому вычислим еще потенциал внутренней сферы
после того, как внешняя сфера будет удалена В этом случае потенциал U
внутренней сферы (А) создается только зарядом gi, находящимся на самой
этой сфере. Поэтому, согласно формулам C) и G), имеем
н (8)
Подставляя сюда вместо / и Ф их выражения F) и ограничиваясь только
членами со степенями S не выше первой, для числителя формулы (8) имеем
« Un2B+[(BA)\n(BA)(B + A)ln(B + A
Так как эта величина уже имеет порядок 5, то знаменатель в формуле (8)
можно взять при <5 = 0
Подставляя эти выражения в (8) и выполняя несложные преобразования,
получаем окончательно
Зная, до какого потенциала Uq были заряжены первоначально обе сферы,
и подставляя для U наименьшее значение потенциала, которое еще может
обнаружить электрометр, по этой формуле можно определить наибольшее
возможное значение 5. Таким образом и был получен верхний предел для
S, приведенный в § 28.
598 ДОБАВЛЕНИЯ ГЛ. XXIV
2. Ориентировка полярных молекул в электрическом
поле (к § 48)
Для вычисления поляризации, создаваемой в электрическом поле моле-
молекулами с постоянным дипольным моментом, будем пользоваться полярны-
полярными координатами. Рассмотрим сферу произвольного радиуса R и направим
через центр этой сферы полярную ось, параллельно электрическому полю
Е . Построим, далее, два конуса с вершинами в центре сферы, оси которых
совпадают с направлением поля, а образующие составляют с ним углы а
и соответственно а + da. Эти конусы вырежут на сфере круговую полоску
шириной Rda, с площадью dS — 2тгД8та. Rda = 2тгЯ sinada. Телес-
Телесный угол, ограниченный этими конусами, есть dQ = dS/R2 = 2тг sin a da.
В отсутствие электрического поля направления электрических моментов
молекул р распределены хаотично. Поэтому число молекул an в единице
объема, моменты которых лежат в интервале углов а и а + da, пропорци-
пропорционально телесному углу dQ,, а следовательно,
dn = A sin a da. A)
Здесь А — некоторая постоянная.
Для получения распределения диполей по направлениям в электриче-
электрическом поле нужно воспользоваться теоремой Больцмана классической ста-
статистики (см. «Молекулярную физику»), согласно которой закон распреде-
распределения молекул в состоянии термодинамического равновесия при наличии
силового поля можно получить из закона их распределения в отсутствие
поля, умножая это распределение на exp (—W/kT), где W — потенциальная
энергия молекулы в данном поле, Т — термодинамическая температура, а
к — постоянная Больцмана. Потенциальная энергия диполя в электриче-
электрическом поле (§ 15) равна W = —роЕ' cos a. Поэтому вместо распределения A)
мы получаем
dn = А ехр (о cos a) sin a da, а = роЕ'/кТ. B)
Легко видеть, что при обычных условиях а<1. Действительно, пола-
полагая ро ~ 10~3° Клм (ср. § 49), Т = 300 К и учитывая значение к = 1,38 х
х 10~23 Дж/К, находим, что даже в сильном электрическом поле Е' ~
~ 104 В/см = 106 В/м величина а ~ 10~3 <? 1. Тогда экспоненту в формуле
B) можно разложить в ряд и ограничиться первыми двумя членами раз-
разложения:
dn = АA + о cos a) sinada. C)
Значение постоянной А определяется условием, что сумма всех молекул с
любым значением угла d равна полному числу молекул п в единице объема
диэлектрика1
A J A + a cos a) sinada = п. D)
о
Написанный интеграл вычисляется непосредственно и равен 2, а следова-
следовательно, А = п/2.
Найдем теперь поляризованность Р (дипольный момент единицы объ-
объема диэлектрика). Она равна
7Г
Р = J dnpo cos a = -~ J A + a cos a) cos a sin a da. E)
о
§ 4 3 ЛИНИИ НАПРЯЖЕННОСТИ И ЛИНИИ ТОКА 599
Входящий сюда интеграл распадается на два интеграла. Первый из них
равен нулю. Второй вычисляется тоже элементарно и дает
2о _ 2р0Е'
? ~ 3fcr ¦
Поэтому поляризованность равна
Р - nplE' F)
Следовательно, среднее значение проекции дипольного момента молекул на
направление поля есть
Ре ~ п
п ~ ЪкТ
что совпадает с формулой D8.1).
3. Линии напряженности и линии тока (к § 61)
Согласно уравнению непрерывности (§ 54)
дх ду dz df ( '
Если мы имеем постоянный ток, то все электрические величины не за-
зависят от времени и dp/dt = 0. В этом случае
^ + |^ + |i = 0. B)
дх ду dz
Но для однородной проводящей среды, согласно закону Ома,
jx = \Ex, jy = \Ey, jz=\Ez,
где Л постоянно. Поэтому из формулы B) следует, что
дЕх [ ЭЕУ [ дЕ, = Q
дх ду dz
Мы видим, что поле Е в проводящей среде удовлетворяет тому же уравне-
уравнению (ср. § 14), что и электростатическое поле Ест в вакууме в отсутствие
объемных зарядов (р = 0)
Однако чтобы показать совпадение Е и Ест, нужно еще доказать, что
для обоих полей одинаковы условия на границе электродов. В общем слу-
случае эти граничные условия различны, так как Ест всегда перпендикулярно
к поверхности проводника, а поле Е этому условию может и не удовле-
удовлетворять. Но для электродов многих форм поле Е также перпендикулярно
к поверхности электродов. Примерами могут служить сферический и ци-
цилиндрический конденсаторы, для которых это очевидно из соображений
симметрии. Поле будет также всегда перпендикулярно к поверхности элек-
электродов любой формы, если удельная электропроводность среды намного
меньше электропроводности вещества электродов, так как в этом случае по-
потенциал во всех точках каждого электрода будет практически одинаковым.
А это и есть обычно наиболее интересные случаи. Поэтому можно принять,
что оба поля Е и Ест не только удовлетворяют одинаковому дифференци-
дифференциальному уравнению, но и одинаковым граничным условиям, а значит, оба
поля совпадают.
600
ДОБАВЛЕНИЯ
ГЛ XXIV
4. Метод контурных токов (к § 70)
Для уменьшения числа уравнений системы, к которой приводят прави-
правила Кирхгофа, пользуются различными вспомогательными приемами. Рас-
Рассмотрим один из них, известный под названием
метода контурных токов.
Пусть в какой-либо точке разветвления о
(рис. 443) сложной цепи сходятся п участков
цепи 1, 2, 3 и т.д., образующих стороны про-
простых контуров I, II, III и т.д. (т.е. таких, кото-
которые не имеют разветвлений). Охарактеризуем
каждый из простых контуров определенным то-
током постоянной силы вдоль всего контура. Эти
токи будем называть контурными токами и
припишем им определенное положительное на-
направление, например будем их считать направ-
направленными по часовой стрелке в каждом контуре.
Силу контурных токов определим таким обра-
Рис. 443. К методу кон- зом, чтобы сила тока в любом участке была рав-
равна разности двух соседних контурных токов. Ес-
Если обозначить контурные токи через 7i, 7г, ...,
1п, а фактические токи в участках цепи 1, 2, ... — через ii, гг, ..., in, то
это значит, что мы полагаем (рис. 443)
III
IV
турных токов
«1 = In — II, 12 = II — h, ¦ ¦ ¦ , in = In-1 — In-
Складывая почленно эти равенства, находим
A)
Это будет справедливым для каждой точки разветвления. Мы видим, что
введение контурных токов, согласно формуле A), приводит автоматически
к удовлетворению первой системы уравнений
Кирхгофа. Поэтому остается решить только
вторую систему уравнений, написанную для
контурных токов. Найдя же контурные то-
токи, мы можем определить по формулам A)
и фактические токи во всех участках цепи.
Этот метод позволяет снизить число урав-
уравнений системы на столько единиц, сколько
независимых уравнений дает первое правило
Кирхгофа.
Поясним применение метода на примере
схемы моста. Эту схему мы уже рассматри-
рассматривали в § 58, однако ограничились частным
случаем уравновешенного моста Теперь мы
рассмотрим общий случай. Рис. 444. Введение контур-
Выделим в схеме моста (рис. 444) три НЫх токов в схему моста
простых контура: I A, 3, 5), II B, 4, 5) и III
(??, 5, 4), на которые распадается эта схема, и введем контурные токи /i,
Ii и /3, направленные по часовой стрелке. Тогда вторая система уравнений
§ 5
5 МАКСВЕЛЛОВСКОЕ ВРЕМЯ РЕЛАКСАЦИИ
601
Кирхгофа, записанная для контурных токов, будет
rih + r5(h - h) + гз(/х - h) = 0,
rih 4- n{h - h) 4- rs(h - /i) = 0,
rh + r3{h - h) 4- г4(/з - h) = $.
Или
(n 4- r3 4- r5)/i - г5/г - гз-Гз = 0,
+ (Г2 + Г4 + Г5)/2 - Г4/з == 0,
Отметим, что мы получили всего три уравнения, тогда как непосредствен-
непосредственное применение обоих правил Кирхгофа привело бы нас к шести уравнени-
уравнениям, соответственно шести участкам схемы моста. Определитель этой систе-
системы равен
Г1 +ГЗ+ Гь
— ГЪ
—ГЗ
Г1 + Г4 +
— Г4
—гз
-Г4
г 4- гз 4- Г4
Найдем контурные токи. Пользуясь обычным правилом решения систе-
системы алгебраических линейных уравнений, имеем
Гъ)
4" Г3 4" Г5)
, /2 = g
г v (п 4- гз 4-г5)(г2 4-Г4 4-г5) 4-г|
/з = ? д .
Ток в ветви гальванометра
гъ = 1\ — h =
Если мост уравновешен, то is = 0. Это дает
Г2ГЗ — Г1Г4 = 0, ИЛИ ri/гг = Гз/Г4,
что совпадает с результатом § 58.
Величину Д можно найти по правилу вычисления определителя тре-
третьего порядка
Д = г5[(г1 4- гг 4- гз 4- гл)г 4- (п 4- г2)(г3 4- г4)] 4-
4- г(г2 4- г4)(п 4- гз) 4- Г1Г2(гз + г4) 4- r3r4(ri 4- г2).
5. Максвелловское время релаксации (к § 73)
Пусть объемная плотность возникшего заряда в какой-либо точке среды
равна р; тогда вызванное им электрическое поле Е определяется уравнени-
уравнением Пуассона A4.1). Полагая в нем D = еоеЕ и учитывая, что в однородной
среде е не зависит от координат, имеем
ду
дг
ЕОе
602
ДОБАВЛЕНИЯ
ГЛ. XXIV
Это поле вызывает электрические токи, плотность j которых по закону Ома
равна
j = АЕ. B)
Появляющиеся токи уменьшают заряд р. Быстрота уменьшения заряда вы-
выражается уравнением непрерывности E4.2). Подставляя в него для j вы-
выражение B) и учитывая, что в однородной среде А, как и е, постоянно,
получаем
дЕх дЕу дЕг 1 др
1V ~ ~&r~ + ~by~ + ~dz~ ~ ~A ~di' ^ '
Так как левые части уравнений A) и C) одинаковы, то равны и правые
их части. Поэтому для любой фиксированной точки среды справедливо
уравнение
др _ А ,л.
Интегрируя это уравнение при начальных условиях t = 0, р = ро, находим
р = poex-p(-t/TM), E)
где
еое
тм =
есть максвелловское время релаксации.
F)
6. Взаимная энергия двух токов (произвольные контуры)
(к § 99)
Пусть имеются два произвольных контура 1 и 2 (рис. 445) и в контуре
2 установился ток ii, создаваемый источником тока с ЭДС <#2- Замкнем
теперь контур 1 на источник тока с ЭДС <?i.
В контуре начнет устанавливаться ток »'i. Если
бы ток г'г оставался постоянным, то в контуре 1
возникла бы дополнительно только ЭДС самоин-
самоиндукции. Работа источника %\ против этой ЭДС и
есть вычисленная нами в § 96 собственная энер-
энергия тока 1, равная L\i\/2.
Однако вследствие магнитной связи в конту-
контуре 2 возникнет еще ЭДС взаимной индукции —
Li2 dii/dt. Чтобы сделать ток гг постоянным, мы
должны были бы включить в контур 2 компен-
компенсирующую переменную ЭДС
Рис. 445. К вычисле-
вычислению взаимной энергии
двух токов
dt
Она совершила бы за время установления тока
ii определенную работу, которая возникает толь-
только потому, что между обоими контурами имеется магнитная связь. Работа
ЭДС $2 и равна взаимной энергии обоих контуров.
Отсюда получается, что увеличение взаимной энергии за время dt
dW\i —
dt =
—^- ii dt =
dt
7 ТЕОРЕМА ЛАРМОРА 603
(где i2 = const), а полная взаимная энергия
W12 = L12I2 J di\ =
Мы получили формулу (99.2) для случая произвольных контуров.
Если бы мы предположили, что сначала имеется установившийся ток ii
и в присутствии этого тока создается ток гг, то в нашем мысленном опыте
потребовалось бы включение в контур 1 компенсирующей переменной ЭДС
и мы получили бы
W12 = Z/2lilZ*2-
Но совершенная работа в обоих случаях должна быть одинакова, так как в
результате мы получаем одно и то же магнитное поле. Отсюда следует, что
Li2 = L21.
В учении о магнетизме часто пользуются представлением о постоянных
магнитах. Примером постоянного магнита может служить намагниченный
кусок стали. Абсолютно жестким постоянным магнитом называют такое
намагниченное тело, которое создает неизменное магнитное поле, не зави-
зависящее от воздействия других окружающих магнитов или токов. Легко ви-
видеть, что взаимная энергия абсолютно жесткого магнита и контура с током
равна нулю. Действительно, если в контуре в присутствии магнита устанав-
устанавливается ток, то никакого индукционного воздействия контура на магнит
не будет. Поэтому магнитное поле, создаваемое магнитом, будет оставать-
оставаться неизменным и не потребуется включения компенсирующей переменной
ЭДС, работа которой и представляет взаимную энергию.
7. Теорема Лармора (к § 115)
Рассмотрим доказательство теоремы Лармора. Пусть в отсутствие маг-
магнитного поля на заряженную частицу действует центральная сила F(r).
Тогда уравнение движения частицы есть
™g=F(r). A)
Предположим теперь, что мы включили внешнее магнитное поле с индук-
индукцией В и ввели новую систему координат, которая равномерно вращается
с угловой скоростью П, параллельной направлению В. Уравнение движе-
движения частицы изменится. На нее, во-первых, будет действовать благодаря
магнитному полю сила (§ 88)
Г = q[vB].
Во-вторых, во вращающейся системе координат мы должны ввести еще до-
дополнительные силы инерции, а именно силу Кориолиса
Fk = 2m[vJ7]
и центробежную силу
F4 = тП2г.
Для достаточно малого О, центробежной силой (пропорциональной Q2)
можно пренебречь по сравнению с силой Кориолиса (пропорциональной Q).
Так как по условию В и П параллельны, то при должном выборе величины
О, можно сумму F + Fk сделать равной нулю. Это будет, если
qvB sin (v, В) + 2mvQ sin (v, В) = 0,
fi = -qB/2m.
604 ДОБАВЛЕНИЯ ГЛ. XXIV
Таким образом, в рассматриваемой вращающейся системе координат урав-
уравнение движения частицы будет иметь прежний вид A), а следовательно,
действие магнитного поля в первом приближении (пока можно пренебречь
центробежной силой) сводится к наложению дополнительного равномерно-
равномерного вращения с угловой скоростью Q. Если движущаяся частица есть элек-
электрон, то q — —е, и мы получаем формулу A15.2).
8. Закон Богуславского-Лэнгмюра (к § 157)
Рассмотрим вывод закона Богуславского-Лэнгмюра для случая плоско-
плоского диода. Распределение потенциала между катодом и анодом при наличии
пространственного заряда можно найти из уравнения Пуассона (§ 26)
^?.--?- = — A)
dx2 ?о ?о
Здесь U — значение потенциала в произвольной точке на расстоянии х от
катода, р — объемная плотность пространственного заряда в той же точке,
п — концентрация электронов, е — абсолютное значение заряда электрона,
ео — электрическая постоянная.
Далее, плотность тока j через диод равна
3 = nev, B)
где v — скорость электрона.
Наконец, скорость электронов v в любой точке определяется значением
потенциала U в этой точке. Действительно, так как в диоде имеется высо-
высокий вакуум, то электроны движутся без соударений, и поэтому их кинети-
кинетическая энергия равна работе сил поля. Если начальная скорость электронов
мала по сравнению со скоростью, приобретаемой под действием поля, то ею
можно пренебречь, и тогда
^f=eU. C)
Исключая из этих трех уравнений концентрацию п и скорость v, мы прихо-
приходим к следующему уравнению, определяющему распределение потенциала:
где введено обозначение
D)
?о\/2е/т
Так как мы отсчитываем потенциалы от потенциала катода, то
[7 = 0 при х = 0. E)
Это условие представляет собой первое граничное условие задачи. Чтобы
сформулировать второе граничное условие, будем считать, что во всем ин-
интервале изменения потенциала ток ограничивается только пространствен-
пространственным зарядом, т.е. что эмиссионная способность катода бесконечно велика.
Чтобы при этом условии плотность тока через диод была конечной, нужно,
чтобы напряженность поля —dUjdx у катода была бесконечно малой. Это
дает второе граничное условие в виде
^ = 0 при х = 0. F)
dx
9. УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ РАЗРЯДОВ
605
Решение уравнения D), удовлетворяющее граничным условиям, имеет вид
U = ax0, G)
где а и /3 — постоянные.
Значения а и /3 можно определить, подставляя выражение G) в урав-
уравнение D). Это дает
Приравнивая между собой показатели степени и коэффициенты в обеих
частях равенства, находим
Р = 4/3, а = (9а/4J/3.
Таким образом, распределение потенциала выражается формулой
U = (9a/4J/V/3. (8)
При значении х — d потенциал равен потенциалу анода С/а. Поэтому
Цл = (9a/4J/V/3. (9)
Подставляя в это выражение вместо а его значение и разрешая полученное
уравнение относительно плотности тока j, находим окончательно
3/2, (ю)
что совпадает с формулами A57.1) и A57.2), приведенными в тексте.
9. Устойчивость электрических разрядов (к § 176, 213)
Рассмотрим электрическую цепь, показанную на рис. 446 а, содержа-
содержащую источник постоянной ЭДС Ш, нагрузочное сопротивление г (включаю-
(включающее и внутреннее сопротивление источника), емкость С, индуктивность L
Рис. 446. К вопросу устойчивости электрических зарядов
и проводник Д с нелинейной вольт-амперной характеристикой U = /(г).
Выберем положительные направления токов так, как показано на рисунке,
и применим к нашей цепи правила Кирхгофа. Тогда для контура %С$
получаем
rl = —и + iS,
606 ДОБАВЛЕНИЯ ГЛ. XXIV
где и — напряжение на конденсаторе, а для контура CRLC
^l' ~U di'
Кроме того, имеем
/ + гс = г, и — q/C, ic = —dq/dt,
где q — мгновенное значение заряда конденсатора. Исключая из написан-
написанных уравнений I nic, получаем два дифференциальных уравнения первого
порядка относительно гаи:
dl~U~ ^'' ~dl ~ ~rl *¦ '
Эти уравнения нелинейны, так как для проводников, не подчиняющихся
закону Ома, функция f(i) нелинейна.
В стационарном состоянии разряда di/dt = du/dt = 0, и поэтому стацио-
стационарные значения тока г'о и напряжения ио определяются соотношениями
ио = /(го), ио = Ш - Но, B)
которые мы уже получили и обсудили в § 176.
Чтобы выяснить, является ли данное состояние разряда устойчивым,
поступим в соответствии с общим методом исследования устойчивости дви-
движений, разработанным Ляпуновым, а именно, предположим, что стацио-
стационарные значения тока и напряжения изменились на малые величины х и у
так, что
i = io + х, и = ио + у.
Далее, для малых изменений тока и напряжения малый участок вольт-
амперной характеристики можно заменить отрезком прямой линии и поло-
положить
/(г) = f(io)+Rtx,
где Rt — дифференциальное сопротивление проводника в рассматриваемой
точке характеристики. Подставляя это в уравнения A) и принимая во вни-
внимание условия стационарности B), мы получаем для хну два линейных
уравнения:
йх__Д, 1_ fty__l _ _i_
которые допускают уже простое исследование.
Исключая из уравнений C) переменную у, получаем линейное диффе-
дифференциальное уравнение второго порядка
где
Такое же точно уравнение получается и для у. С уравнением D) мы уже
встречались в § 210 при исследовании собственных электрических колеба-
колебаний. Мы видели, что при uil > а2 оно описывает затухающие колебания
с коэффициентом затухания а. При иJ, < а2 получается апериодический
процесс
^' + Ase-*2', F)
§ 9 9. УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ РАЗРЯДОВ 607
где
ki — а + уа2 -ш^, к2 = а - tja2 - wg. G)
Чтобы случайные отклонения х и у затухали с течением времени, т.е.
чтобы состояние разряда было устойчивым, очевидно, необходимо, чтобы
либо было а. > 0 (если ljq > а2), либо fci и к? были оба положительны (если
cjo < а2). Если же хотя бы одна из величин, к\ или к^, будет отрицательна,
то случайные изменения тока и напряжения будут нарастать с течением
времени и состояние разряда будет неустойчивым.
Если Ri > 0, то все величины в E) положительны и а > 0, шо > 0.
При этом а > у/а2 — ш2 и, следовательно, ki и fc2 всегда положительны.
Отсюда видно, что в проводниках с положительным дифференциальным
сопротивлением стационарные состояния разряда всегда устойчивы.
Положим теперь, что дифференциальное сопротивление R% < 0. Тогда
где \Rt\ — абсолютное значение дифференциального сопротивления. Чтобы
и в этом случае ki и кг были оба положительны, необходимо, чтобы было
по-прежнему а > 0 и шо > 0. А для этого необходимо выполнение двух
условий:
г>|Д,|, L>\Rt\rC, (9)
которые и есть условия устойчивости разряда.
Если в схему рис. 446 а включена электрическая дуга (или другой про-
проводник с характеристикой S-типа), то первое из условий (9), как мы знаем
(§ 176), означает, что при любом значении ЭДС Ш имеется только одно
стационарное состояние разряда, а следовательно, не будет скачков тока.
Если цепь содержит еще достаточно большую индуктивность, так что
выполняется и второе условие (9), то все состояния разряда будут устойчи-
устойчивы, и мы сумеем получить на опыте всю вольт-амперную характеристику.
Напротив, для получения незатухающих колебаний (§ 213) необходимо,
чтобы при данных ЭДС <? и параметрах схемы существовало тоже только
одно стационарное состояние, однако это состояние должно быть неустойчи-
неустойчивым. Поэтому при выполнении первого из условий (9) и нарушения второго
условия (9) цепь рис. 446 а, содержащая электрическую дугу, будет само-
самовозбуждаться и в ней установятся незатухающие колебания.
Условия устойчивости разряда зависят, конечно, от типа схемы, в ко-
которую входит проводник с отрицательным дифференциальным сопротив-
сопротивлением. Поэтому в качестве второго практически интересного примера мы
рассмотрим еще схему, показанную на рис. 446 б, в которой R есть нелиней-
нелинейный проводник с характеристикой iV-типа, например туннельный диод (§
203). Применяя к этой схеме правила Кирхгофа, мы получим два диффе-
дифференциальных уравнения первого порядка
L% = «-rI-u, C%=I-i, A0)
где ток t через диод связан с напряжением и и на диоде заданным уравнени-
уравнением вольт-амперной характеристики i = ф{и). Поступая дальше в точности
так же, как и в первом примере, легко найти, что условия устойчивости
разряда для схемы рис. 446 б имеют вид
г<|Лг|, Ь<\ЩгС. A1)
608 ДОБАВЛЕНИЯ ГЛ. XXIV
Первое из этих условий для туннельного диода (и любого проводника с
характеристикой iV-типа) совпадает с условием единственности стационар-
стационарного состояния (ср. § 176). Поэтому при нарушении этого условия будут на-
наблюдаться скачки напряжения. Если же первое условие будет выполнено, но
нарушено второе условие A1), в схеме будет единственное, но неустойчивое
стационарное состояние, и схема будет самовозбуждаться.
10. К объяснению циклотронного резонанса (к § 185)
Количественная теория циклотронного резонанса имеет особенно про-
простой вид для свободных электронов, движущихся без соударений. В этом
случае уравнение движения электрона есть
dv
т— =eE + e[vB0]. A)
Направим координатную ось X параллельно электрическому полю Е, а ось
Z — параллельно магнитной индукции Во (см. рис. 314). Тогда Ех — Е,
Еу — Ez = 0, Bz = Во, Вх — Ву = 0, и написанное векторное уравнение
распадается на два скалярных уравнения
dvx _ e dvy _ . .
Здесь по-прежнему шс обозначает циклотронную частоту, определяемую
формулой A85.1). Исключим из этих двух уравнений скорость vy, для че-
чего продифференцируем первое уравнение один раз по времени, умножим
второе уравнение на шс и сложим оба уравнения почленно. Тогда получим
d2vx _ е_ <Ш_ _ 2 ,о\
dt2 ~ m dt UJcVx' l ^
Аналогично, исключая из обоих уравнений vx, найдем
j2_.
Положим теперь, что электрическое поле изменяется по синусоидальному
закону
Е = Eosiauit, E)
и будем искать установившиеся вынужденные колебания электрона. Так как
вынужденные колебания гармонического осциллятора происходят с той же
частотой, что и колебания внешней силы, то мы будем искать решения в
виде
vx = Vxosin(ut + a), vy = vyo sin (wt +0), F)
где а и /3 — пока неизвестные разности фаз между колебаниями составляю-
составляющих скорости и колебаниями электрического поля. Подставляя выражения
E) и F) в уравнения C) и D), выражая из этих последних скорости элек-
электрона vx и vy и приравнивая коэффициенты при sina;? и coswi, получаем
четыре уравнения для определения u^o, vvq, а и /3. Это дает a = —тг/2,
/9 = 0,
vx = — а Ш , Ей sin (ut - ^ ) , vy = — Шс Eosinwt. G)
m ш2 - ш| V 2 / т ш2 -ш2
Вследствие вынужденных колебаний электронов в электронном газе возни-
возникают переменные токи, плотность которых равна
jx = envx, jy — envy, (8)
§ 10 10. К ОБЪЯСНЕНИЮ ЦИКЛОТРОННОГО РЕЗОНАНСА 609
где п — концентрация электронов. Электрическое поле совершает над дви-
движущимися электронами определенную работу, которая совершается за счет
уменьшения энергии электромагнитной волны.
Мгновенная мощность, выделяемая в единице объема, есть
g sin w? sin lust ) .
^ 2 /
В рассматриваемом случае отсутствия столкновений эта мощность оказы-
оказывается знакопеременной, а среднее ее значение за период колебани w — 0,
так как
sin w? sin (wt — тг/2) = 0.
При условии ш ф шс электроны при установившихся вынужденных колеба-
колебаниях не поглощают энергию электромагнитной волны.
При резонансе (и> = и>с), как видно из формул G), амплитуды колебаний
скорости стремятся к бесконечности. Это значит, что электроны все время
будут двигаться по неустановившейся траектории, непрерывно увеличивая
свою энергию, а электромагнитная волна будет поглощаться.
В реальном газе электронов, движущихся со столкновениями, поглоще-
поглощение электромагнитной волны происходит и при ш ф шс, но при некоторой
частоте имеет максимум.
Положим, что при каждом столкновении электрона он целиком переда-
передает решетке кристалла свой импульс rav. Если г есть среднее время свобод-
свободного пробега электрона, то за единицу времени он будет испытывать 1/т
столкновений и передавать импульс mv/т. Но приращение механического
импульса тела за единицу времени есть сила, действующая на это тело. По-
Поэтому влияние столкновений можно описать как действие некоторой силы
трения
FTp = -mv/т. (9)
Соответственно вместо уравнений B) мы получим уравнения движения
!Ь. = ±Е + Ые9,-±, <b- = -ucVx-V-^>. A0)
dt m " т dt т
Чтобы найти интересующую нас составляющую скорости vx в направ-
направлении электрического поля, мы воспользуемся представлением колебаний в
виде комплексных чисел (§ 227), так как это чрезвычайно упростит после-
последующие расчеты. А именно, мы положим
Е = Ео exp (iuit), vx = vxo exp (iwi), vy = vyo exp (iuit), A1)
где i = y/—T, а Ео, как и раньше, будем считать вещественным. Амплиту-
Амплитуды же vxo и vyo могут быть комплексными, так как между колебаниями
скорости и поля может быть разность фаз.
Подставляя выражения A1) в уравнения движения A0), мы получаем
два алгебраических уравнения
iojvx = — Е + uicVy -, iuiVy — —uicvx -. A2)
тп т т
Исключая из этой системы скорость vy, находим
v.=bEnJ+ZZ ,,. A3)
A + гштJ + ш?т2 v
Здесь Ь = (е/тп)т есть подвижность электронов (ср. формулу A47.4)). Осво-
Освобождаясь, далее, от мнимой величины в знаменателе и вычисляя плотность
610 ДОБАВЛЕНИЯ ГЛ. XXIV
тока jx = envx, мы находим, что jx состоит из двух слагаемых — веществен-
вещественного Re jx и чисто мнимого г Im jx:
jx = Re jx + i Im jx. A4)
При этом
Im Jy - -XoE [x + (^rJ _ (шгJ]2 + 4(шгJ, A6)
a Ao = erab есть удельная электрическая проводимость для постоянного тока
(и = 0) и без магнитного поля (шс = 0).
Так как г = exp (in/2), то чисто мнимая составляющая описывает коле-
колебания тока, смещенные по фазе на тг/2 относительно колебаний поля. По-
Поэтому среднее значение мощности, обусловленной этой составляющей, рав-
равно нулю. Следовательно, средняя мощность, выделяемая в единице объема,
равна
w = Re jx ¦ Е. A7)
Возвратимся теперь к вещественной записи колебаний. Полагая Е =
= Eosinwt, используя для Re jx выражение A5) и учитывая еще, что
sin2 uit = 1/2, находим окончательно
1 2 1 + КгJ + (ЫТJ
W ~ 2 ХоЕ° [1 + Кт)= - (Wr)T + Ч"тУ ¦
Полученный результат показывает, что вследствие столкновений элек-
электронов с решеткой кристалла поглощение электромагнитной волны отлично
от нуля при любой частоте и>. Это происходит потому, что электроны, уско-
ускоряющиеся полем между двумя последовательными столкновениями, пере-
передают затем накопленную энергию решетке при столкновениях, и поэтому
все время происходит перекачка энергии из волны в решетку. Далее, иссле-
исследование выражения A8), на котором мы не останавливаемся, показывает,
что w достигает при некоторой частоте и>ылкс максимума. Однако этот мак-
максимум имеет заметную величину только при условии шт > 1, и он тем резче,
чем больше и>т по сравнению с единицей. Это и понятно, так как для ре-
резонанса необходимо, чтобы электронный газ обладал характерной для него
частотой колебаний, а для этого нужно, чтобы за время г электрон успел
совершить хотя бы несколько полных оборотов в магнитном поле. При усло-
условии шт 3> 1 максимум поглощения лежит при частоте шмакс ~ шс.
11. Электромагнитное поле диполя (к § 243)
Рассмотрим подробнее, какой вид имеет электромагнитное поле диполя
в волновой области.
Мы знаем, что заряд, движущийся с постоянной скоростью, вызывает
только постоянное магнитное поле Н. С другой стороны, согласно основно-
основному положению теории Максвелла, для появления вихревого электрического
поля необходимо, чтобы dH/dt было отлично от нуля. Поэтому для излуче-
излучения нужно, чтобы заряд двигался с определенным ускорением v = x (точка
обозначает дифференцирование по времени) или, иначе, чтобы вторая про-
производная по времени от момента диполя р = qx была не равна нулю. В
11
11 ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ДИПОЛЯ
611
соответствии с этим точный расчет показывает, что электрическое поле Е
волны (а следовательно, и магнитное поле Н; ср. B40.4)) пропорционально
p(t — г /с). Аргумент (t — г/с) показывает, что колебания поля в точке, уда-
удаленной на расстояние г от диполя, запаздывают относительно колебаний
р на время г /с, так что E(t) и H{t) в рассматриваемой точке в момент t
определяются значением р в более ранний момент времени (t — г/с).
Легко сообразить, как зависят оба поля Е и Н от расстояния г. Энергия,
проходящая через каждую единицу поверхности в поле электромагнитной
волны, пропорциональна Е2 или соответственно Н2. Поэтому поток энер-
энергии, проходящий сквозь поверхность сферы радиусом г, окружающей ди-
диполь, пропорционален поверхности этой сферы 4тгг2 и Е2, т.е. пропорциона-
пропорционален Е2г2. Так как эта энергия не зависит от г (вакуум, поглощение энергии
не происходит), то отсюда следует что Е и Н пропорциональны 1/г.
Значения полей Е и Н зависят еще от направления излучения, т.е. от
угла $, составленного радиус-вектором г с осью диполя (рис. 447). Мы уже
говорили что вблизи диполя его магнитное по-
поле выражается той же формулой, что и для
элемента тока. Это магнитное поле пропорпио-
нально sin$ и равно нулю в любой точке, ле-
лежащей на продолжении оси диполя. Совершен-
Совершенно так же и напряженности полей Е и Н в
волновой зоне пропорциональны sin $. Точный
расчет приводит к следующему результату:
д= JLPft-rAQrintf Н= (ё±Е. A)
4тгео с1 г У (J-o
Здесь с = 3 • 108 м/с — скорость распростране-
распространения электромагнитных волн в вакууме, а все
величины предполагаются измеренными в си-
системе СИ. Оба поля Е и Н направлены перпен-
перпендикулярно к направлению распространения,
т.е. к направлению г, и связаны с ним прави-
правилом правого буравчика (рис. 447). Формула A)
справедлива лишь для таких движений зарядов, скорость которых v мала
по сравнению со скоростью света с (нерелятивистскийслучай, /3 = и/с<С1).
В частном случае, когдар изменяется по гармоническому закону B43.1),
имеем
p(t — г/с) = — рош2 sin [ui(t — г /с)] = — рои sin (ujt — кг),
и первое соотношение выражения A) принимает вид
_ 1 po^2sini9 . , . . ,
Е = sin(wf-fcr). B)
4тгео сгг
Энергия, излучаемая диполем. Модуль вектора потока энергии в
какой-либо точке с координатами г, д есть
Рис. 447. Электромагнит-
Электромагнитное поле в шаровой волне,
излучаемой диполем
4 sin2,
sin2 (uit — кг).
16тг2?Ос3г2
Интерес представляет не мгновенное значение Р, а его среднее значение Р
за период колебаний, т.е. интенсивность излучения. Так как sm2(wt — кг) =
= 1/2, то
W sin2 ti
г2 ' У '
612
ДОБАВЛЕНИЯ
ГЛ. XXIV
Интенсивность излучения пропорциональна четвертой степени частоты ко-
колебаний и*. Она зависит также от направления излучения (пропорциональ-
(пропорциональна sin2i9). Зависимость интенсив-
интенсивности излучения диполя от на-
направления изображена на рис. 448
(диаграмма направленности излу-
излучения). Таким образом, в направ-
направлении своей оси диполь ничего
не излучает. Напротив, в направ-
направлениях, перпендикулярных к оси
диполя, интенсивность излучения
наибольшая.
Вычислим, наконец, полную
энергию w, излучаемую диполем
по всем направлениям в единицу времени. Так как Р есть энергия, про-
проходящая через единицу поверхности в 1 секунду, то
Рис. 448. Диаграмма направленности
излучения элементарного диполя
где интегрирование нужно производить по произвольной поверхности S,
охватывающей диполь. Выбирая в качестве таковой сферу с радиусом г с
центром в точке нахождения диполя и пользуясь сферическими координа-
координатами г и д (рис. 447), имеем
dS - 2тп
Интегрируя это выражение по
PndS =
sin д dd.
16тг?Ос3
в пределах от 0 до тг, находим
12тг
D)
Написанное выражение можно представить в другом виде. Для этого
выразим амплитуду колебаний момента ро через амплитуду тока г'о в дипо-
диполе, согласно B43.2). Тогда
12тг
где I — длина диполя. Это выражение подобно выражению для мощности,
выделяемой переменным током в контуре с сопротивлением г:
w = г»о/2.
Поэтому величину
Гязл = 7. Т F)
бтг е0с3
называют сопротивлением излучения диполя. Это понятие часто применя-
применяют в радиотехнике к излучающим антеннам передающих радиостанций.
12. Давление электромагнитных волн (к § 244)
Давление электромагнитной волны для простейшего случая нормально-
нормального падения можно вычислить из уравнений Максвелла следующим образом.
§ 12 12. ДАВЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 613
Если j есть плотность тока, вызываемого в теле электрическим полем вол-
волны Е (см. рис. 426), а Н — магнитное поле волны, то сила /, действующая
на единицу объема тела, есть
/ =jB = ццозН.
Поэтому давление волны равно
оо
р = fjdx.
О
Здесь / обозначает среднее по времени от силы /.
Обратимся теперь к уравнениям Максвелла, которые для плоской вол-
волны имеют вид
dt + J ~ дх" dt вх'
Умножая первое из уравнений на (ЩоН, а второе — на ееоЕ и складывая
их, имеем
I дх \ 2 + 2
где выражение в круглых скобках в правой части есть объемная плотность
энергии и электромагнитной волны в рассматриваемой точке.
Усредним теперь полученное соотношение по времени. Так как Р и В
суть периодические функции времени, то d(PB)/dt есть знакопеременная
функция времени. Так, например, для синусоидальных волн D и В изме-
изменяются как sin(uii — кх). Следовательно, РВ ~ sia2(ijt— kx), a d{PB)jdt ~
~ sin (uit — кх) cos (uit — кх) и четыре раза за период колебания изменяет
знак. Поэтому d(PB)/dt = 0, а значит,
1 d -
i = ~TxU-
Подставляя это выражение в формулу для давления волны р, имеем
оо
р = — I — dx = гг(О) — гг(оо).
J ах
о
В этом выражении гг(О) есть полная объемная плотность энергии сум-
суммарного электромагнитного поля у поверхности тела, а гг(оо) = 0. Если
коэффициент отражения тела равен нулю, то у поверхности будет только
падающая волна и п@) равно объемной плотности энергии п в падающей
волне (формула B44.1)). Если коэффициент отражения равен единице (аб-
(абсолютное зеркало), то перед зеркалом будут присутствовать и падающая, и
отраженная волны, и п@) равно 2п. В промежуточном случае мы получим
формулу B44.2).
Если волна падает на тело наклонно, то появляется нормальная к по-
поверхности составляющая электрического поля волны Еп. Это значит, что на
поверхности возникают электрические заряды с поверхностной плотностью
а = ЕоЕп и появляется еще электрическая сила, равная <гЕп на каждую
единицу поверхности тела. Ее направление противоположно направлению
магнитной силы, найденной выше, и поэтому она уменьшает давление вол-
волны. Расчет показывает, что разность обеих этих сил, магнитной и электри-
электрической, выражается формулой B44.4).
614 ДОБАВЛЕНИЯ ГЛ. XXIV
13. Система единиц Гаусса
Мы видели, что для электрических и магнитных величин можно по-
построить две различные системы единиц СГС: абсолютную электростатиче-
электростатическую систему СГСЭ (§ 3) и абсолютную электромагнитную систему СГСМ
(§ 77). Принципиально вполне возможно пользоваться только одной из этих
систем, безразлично какой, так как все магнитные величины можно выра-
выразить в электростатических единицах, а все электрические величины — в
электромагнитных единицах.
Рассмотрим сначала, как будет выглядеть основной закон электроста-
электростатики — закон Кулона в системе СГСМ. Представим себе, что в среде, ди-
диэлектрическая проницаемость которой в системе СГСЭ есть е, имеется то-
точечный заряд <з>13 (измеренный в единицах системы СГСЭ), действующий
на второй точечный заряд q2S, помещенный в узкой полости, параллельной
линиям поля. Тогда сила взаимодействия в системе СГСЭ (нерационализо-
ванной) равна
где F выражено в динах, а г — в сантиметрах. При этом е есть безразмерная
величина, а ее значение для вакуума равно единице. Если измерять заряды
в единицах системы СГСМ, то ди — cqiM, дг» = сд2м, и та же сила будет
выражаться формулой
р _ <?_ <?1м1?2м
? Г» '
где Риг по-прежнему измеряются в динах и сантиметрах. Отсюда видно,
что диэлектрическая проницаемость в системе единиц СГСМ есть ем =
= е/с . Она оказывается теперь уже не безразмерной, а имеет размерность,
обратную размерности квадрата скорости.
Посмотрим теперь, какой вид будет иметь закон магнитного взаимодей-
взаимодействия токов в системе единиц СГСЭ. Для этого рассмотрим пример взаимо-
взаимодействия двух бесконечно длинных параллельных токов. Сила, действую-
действующая на отрезок длины I каждого из проводов в вакууме, в системе единиц
СГСМ выражается формулой (83.2). В среде с магнитной проницаемостью
/J, она равна
Здесь ц есть безразмерная величина, а ее значение для вакуума равно еди-
единице. Если ii3 и 12э — силы тех же токов, измеренные в единицах системы
СГСЭ, то iiM = iis/c, г~2м = *2э/с, и поэтому предыдущая формула в системе
единиц СГСЭ принимает вид
М 2n3t23 ,
Таким образом, в системе единиц СГСЭ магнитная проницаемость есть раз-
размерная постоянная: цэ = fi/c2.
Резюмируя сказанное, мы видим, что в каждой из двух абсолютных
систем (СГСЭ и СГСМ) диэлектрическая и магнитная проницаемости е и fi
играют неравноправные роли. Если е имеет нулевую размерность (система
единиц СГСЭ), то /г оказывается размерной постоянной и, наоборот, если
/г безразмерна (система единиц СГСМ), то е имеет размерность. При этом
§ 13 13 СИСТЕМА ЕДИНИЦ ГАУССА 615
оказываются различными и их значения ео и цо для вакуума:
система единиц СГСЭ: ео = 1, ^о = 20 с2/см2,
система единиц СГСМ: ео = -—гтг^ с2/см2, цо = 1-
Чтобы обойти это неудобство и сделать обе характеристики вещества
е и (J. равноправными величинами нулевой размерности, была разработа-
разработана так называемая абсолютная симметричная система электрических и
магнитных единиц, которая является сочетанием систем СГСЭ и СГСМ.
Принцип ее построения был указан в работах Гаусса и Вебера, а сама си-
система получила название системы единиц Гаусса. В этой системе единицы
всех электрических величин (заряда, напряженности электрического поля,
разности потенциалов, электрического смещения, емкости, силы тока, со-
сопротивления, проводимости и ЭДС) совпадают с единицами системы СГСЭ;
диэлектрическая проницаемость е есть безразмерная величина, равная для
вакуума единице. Единицы же всех магнитных величин (напряженности
магнитного поля, магнитной индукции, магнитного потока, индуктивности,
магнитного напряжения и «магнитных зарядов») совпадают с единицами
системы СГСМ. Магнитная проницаемость ц считается безразмерной вели-
величиной, равной для вакуума единице.
Однако в § 77 мы видели, что для обращения в единицу коэффициента
пропорциональности в законах магнитного взаимодействия токов силу тока
нужно измерять в единицах системы СГСМ. Поэтому при переходе к си-
системе единиц Гаусса во всех законах магнитного поля появится размерная
постоянная, а именно электродинамическая постоянная с.
Система единиц Гаусса употребляется в нерационализованной форме,
т.е. в нее не вводят множитель 1/4тг в законы электрического и магнитного
взаимодействий.
Из сказанного следует, что основной закон электростатики — закон Ку-
Кулона в системе единиц Гаусса — имеет тот же вид, что и в системе единиц
СГСЭ:
Основные же законы магнитного взаимодействия токов в система единиц
СГСМ принимают иной вид. Сила, действующая на элемент тока в магнит-
магнитном поле, теперь выражается формулой
dF=-fdlB]. B)
с
Индукция cffi, создаваемая каким-либо элементом тока в точке г, равна
й^ш^/М. (з)
с гл
Закон электромагнитной индукции имеет вид
где ЭДС & измеряется в единицах системы СГСЭ, а магнитный поток Ф —
в единицах системы СГСМ.
Исходя из этих основных законов, легко найти и все другие формулы
электромагнетизма в системе единиц Гаусса (см. табл. 20).
616
ДОБАВЛЕНИЯ
ГЛ. XXIV
Законы постоянных и квазистационарных токов (гл. VI, VII, XX, XXI)
не зависят явно от формы записи основных законов электрического и маг-
магнитного взаимодействий и поэтому выражаются одинаково в системах еди-
единиц СИ и Гаусса.
Таблица 20
Некоторые формулы в системе единиц Гаусса *)
Напряженность поля точечного заряда (§ 9)
Электрическое смещение точечного заряда (§ 13)
Напряженность поля внутри плоского конденса-
конденсатора (§ 13)
Уравнение Пуассона (§ 14)
Потенциал в поле точечного заряда (§ 24)
Электрическое поле элементарного диполя (§ 25)
Емкость плоского конденсатора (§ 32)
Емкость шарового конденсатора (§ 32)
Емкость цилиндрического конденсатора на еди-
единицу длины (§ 32)
Объемная плотность энергии электрического
поля (§ 37)
Поляризованность диэлектрика (§ 39)
Электрическое смещение (§ 41)
Диэлектрическая восприимчивость (§ 42)
D и Е в изотропных диэлектриках (§ 42)
Теорема Остроградского-Гаусса (§ 44)
Поле, действующее на молекулу внутри диэлек-
диэлектрика (внутреннее поле) (§ 47)
г3
Е = А-ка/е
div D = 4тгр
U = q/er
_ 2р cos a
Е'~ гз >
_ р sin а
Е°- гз
4vd
с- Е
1/о - l/b
С, - е
2 In (Ь/о)
еЕ2
Р = 12Рг/т
г
D = Е + 4тгР
Р = аЕ
D = eE,
е = 1 + 4тга
§DndS = 4tt<j
s
Е' = Е+^Р
О
1) Здесь помещены только формулы, написание которых в системах еди-
единиц СИ и Гаусса различны. (Примеч. ред.)
13
13. СИСТЕМА ЕДИНИЦ ГАУССА
617
Продолжение таблицы 20
Формулу Клаузиуса-Моссоти (§ 47)
Диэлектрическая проницаемость полярных
диэлектриков (§ 48)
Максвелловское время релаксации (§ 73)
Сила, действующая на элемент тока в магнит-
магнитном поле (§ 76)
Напряженность магнитного поля, создаваемая
элементом тока (§ 79)
Циркуляция напряженности магнитного поля
(§81)
Напряженность магнитного поля внутри соле-
соленоида (§ 81)
Магнитный момент контура с током (§ 82)
Напряженность магнитного поля элементарно-
элементарного тока в произвольной точке (§82)
Взаимодействие двух параллельных проводни-
проводников с током в вакууме (§ 83)
Напряженность магнитного поля движущего-
движущегося заряда (§ 86)
Сила Лоренца (§ 88)
ЭДС электромагнитной индукции (§ 91)
Магнитный поток, пронизывающий катушку
индуктивности L (§ 93)
Индуктивность соленоида (§ 93)
Энергия магнитного поля контура с током
(§96)
Объемная плотность энергии магнитного поля
(§97)
е-1 4тг
е + 2 3 П/3
е — 1 4л- pin
е + 2 9 кТ
е
ты = -.—г
4я-А
<Ш = -[<пВ]
с
с г3
г 4тгг
ф Hsds =
J с
п 4irni
с
рт = - iSn
с
и 2pm cos a
рт sin а
Г3
с2 R
н 9[vr]
сг3
F = qE + ^ [vB]
a, 1 d$
G = —
с dt
с
Г A N*S
L = A-KfJ,—:—
W - — Li1
W ~ 2C2 Lt
цН2
и = —^—
8тг
618
ДОБАВЛЕНИЯ
ГЛ. XXIV
Продолжение таблицы 20
Магнитная индукция (§ 105)
В и Н в изотропных магнетиках (§ 105)
Работа при намагничивании единицы объе-
объема магнетика (§ 111)
Частота ларморовой прецессии (§ 115J
Магнитная восприимчивость парамагне-
парамагнетика (§ 118)
Магнитодвижущая сила (§ 120)
Подъемная сила электромагнита (§ 121)
Плотность тока смещения (§ 136)
Уравнения Максвелла (§ 138)
Преобразования Лоренца (§ 143)
Постоянная Холла (§ 150)
Циклотронная частота (§ 180)
Фазовая скорость электромагнитных волн
(§ 240)
Соотношение Е и Н в распространяющейся
электромагнитной волне (§ 240)
Поток энергии электромагнитного поля
(§ 242)
Энергия излучения диполя в единицу вре-
времени (Добавление 11)
В = Н + 4тг1
В = ^Н, р = 1 + 47ГИ:
dw = ^-HdB
4тг
2тс
,, - пР™
ЗкТ
С
8тг
1 3D
Jc ~ 4тг dt
сШ
—— +4ttj = crotH
ot
§ = -crotE
at
Ex = Eix,
Hx = H\x,
^/l-/32Ey=Ely-/3Hu,
^l-P2Hy=Hly+i3Elz,
^/l-P2Ez = Elz+l3Hly,
y/l^Hz=Hlz-pEly.
R = 1/crae
ljc = eB/mc
v = с/у/Щ
v^E = v^H
p = h[EH]
1 9 4 1 i*) 9 .9
Таблица 21
Электрические и магнитные единицы
В таблице приведены наиболее важные электрические и магнитные единицы в системах СИ и Гаусса. Размерности
производных единиц выражены через основные единицы длины (L), массы (М), времени (Т) и силы тока (/) в
системе СИ и L, М и Т — в системе Гаусса.
В последнем столбце таблицы приведены также переводные множители для пересчета значений электрических и
магнитных величин при переходе от системы Гаусса к системе СИ.
Величина
Электрический заряд
Напряженность электри-
электрического ПОЛЯ
Электрическая постоян-
постоянная
Поток электрического .
смещения
Электрическое смещение
Разность потенциалов,
напряжение, ЭДС
Обозна-
Обозначения
q
Е
?о
N
D
и, &
Система единиц СИ
Наименование
кулон (Кл)
вольт на метр
(В/м)
фарад на метр
(Ф/м)
кулон (Кл)
кулон на
квадратный
метр (Кл/м2)
вольт (В)
Размерность
TI
ЬМТ-3!-1
L-3M-lT4j2
TI
LTI
L2MT-3j-i
Система единиц Гаусса
Наимено-
Наименование
СГСЭ,
СГСЭв
СГСЭС0
СГСЭлг
СГСЭд
СГСЭ^
Размерность
L3/2M1/2T-1
L-1/2M1/2T-1
равна 1
(безразмерна)
L3/2M1/2T-1
L-1/2M1/2T-1
L1/2M1/2T-1
Соотношение с
единицей СИ
з-ю* Кл
3 • 104 В/м
8,85 • Ю-12 Ф/м
1 Кл
4.-3.10» КЛ
^ I/./..2
47г • 3 ¦ 105
300 В
Продолснсение таблицы 21
Величина
Емкость
Сила тока
Электрическое сопротив-
сопротивление
Напряженность магнит-
магнитного поля
Магнитная постоянная
Поток магнитной индук-
индукции
Магнитная индукция
Индуктивность
Магнитодвижущая сила
(магнитное напряжение
по замкнутому контуру)
Обозна-
Обозначения
С
i
R,r
Н
цо
Ф
В
L
Система единиц СИ
Наименование
фарад (Ф)
ампер (А)
ом (Ом)
ампер на метр
(А/м)
генри на метр
(Г/м)
вебер (Вб)
тесла (Тл)
генри (Гн)
ампер (А)
Размерность
L-2M-lT4/2
I
L2MTr2
ЬМТ-2Г2
I^MT-2!-1
MT^r1
L2MT~2r2
I
Система единиц Гаусса
Наимено-
Наименование
сантиметр
(см)
СГСЭ,
СГСЭн
эрстед (Э)
сгсмй0
максвелл
(Мкс)
гаусс (Гс)
сантиметр
(см)
гильберт
(Гб)
Размерность
L
L3/2Ml/2T-2
L-1T
L-1/2M1/2T-1
безразмерна,
равна 1
L3/2M1/2T-1
L-1/2M1/2T-1
L
L1/2M1/2T-1
Соотношение с
единицей СИ
1 Ф
9 10"
1 А
3 109
9 • 1011 Ом
103 л/
— А/м
47Г
4тг- 10~7 Гн/м
10'8 Вб
Ю-4 Тл
10~9 Гн
47Г
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 497
—, условия самовозбуждения 503
Анионы 436
Анод 19, 120, 364
Антиферромагнетики 269
Вектор Пойнтинга 568
Взаимодействие магнитное 164
— электрическое 13
Волна электромагнитная 545
, длина 546
свободная 557, 560
, скорость распространения 554
стоячая 547-557
Восприимчивость диэлектрическая
88
— магнитная 227
Время жизни неравновесных носите-
носителей заряда 481
— релаксации максвелловское 158,
506, 602
Гальванометр баллистический 122
Генератор ламповый 500
— переменного тока 278
— постоянного тока 280
— электростатический 61
Гиромагнитное отношение 256, 260
Гистерезис диэлектрический 101
— магнитный 240, 241, 271
—, петля 241
— разряда 408
Давление Фарадея-Максвелла 221
Диаграммы векторные 290-293, 508,
510, 513, 514, 519, 526, 527, 533
Диамагнетизм 236
Диамагнетикн 236
Диод вакуумный 364
— вентильное действие 369
— вольт-амперная характеристика
365
Диполь 38
—, момент 38
— элементарный 55, 180, 571
Диэлектрик 11, 77
Диэлектрик анизотропный 88
— изотропный 88
Добротность 494
Единица емкости 63
— заряда 15, 17
— индуктивности 202
— индукции магнитной 198
— напряжения 137
— напряженности магнитного поля
172-173
— — электрического поля 45
— потока магнитного 184
— смещения 31
— силы тока 116, 182
электромагнитная абсолют-
абсолютная 168
— сопротивления 124
Емкость 63-66
Закон Био-Савара-Лапласа 167
— Богуславского-Лэнгмюра 367, 604
— Видемана-Франца 339
— Джоуля-Ленца 137, 338
— Дюлонга и Пти 345
— Кулона 12-15
в диэлектриках 91
для магнитных зарядов 248
— Кюри 241, 263
— Кюри-Вейсса 242
— Ленца 194, 197
— Ома 123, 337
в дифференциальной форме 129
для замкнутой цепи 140
участка с ЭДС 143
электролитов 444
— распределения скоростей Макс-
Максвелла 359
Законы электролиза Фарадея 435,
436
Заряд индуцированный 20
—, плотность 24, 25
— поляризационный 79
-, плотность 81
— пробный 22
— пространственный 366
—, распределение на проводнике 60
— свободный 84
— точечный 12
Зоны 354
622
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Импеданс 537
Индуктивность 202
Индукция взаимная 213
— магнитная 165
— электрическая — см. смещение
электрическое
— электромагнитная 192
в движущихся проводниках
, основной закон 196
Катионы 437
Катод 19, 120, 364
Катодное падение потенциала 395
— пространство темное 394
второе 394
— свечение 394
Колебания 445
—, амплитуда комплексная 533
— вынужденные 506, 507, 520
—, затухание 489
—, —, коэффициент 493
—, —, логарифмический декремент
490, 494
— затухающие 493
— линейные 491
— незатухающие 497
— релаксационные 506
— собственные 487
линии 553
, уравнение 491
—, установление 520
Конденсатор 63
—, емкость 63, 64
— плоский 28, 52, 65
— сложный 72-74
— цилиндрический 35, 53, 66
— шаровой 34, 52, 65
Контур электрический 486
, добротность 494
искровой 496
Коэффициент пьезоэлектрический
107, 108
Кристаллы, ось оптическая 105
—, — пьезоэлектрическая 105
Линии индукции магнитного поля
173, 194
, преломление 232
— напряженности электрического
поля 26
, преломление 89, 90
— тока 115
— эквипотенциальные 46, 47
— электрического смещения 29-31
Магнетики 222
— анизотропные 227
— изотропные 227
Магнетон 261
Магнетрон 419
Магнитострикция 268
Метод зеркальных изображений 68
— электролитической ванны 132
Момент тока магнитный 179-181,
223
Намагниченность 223
Намагничивание 222-224
Напряжение линейное 286
— магнитное 175
, измерение 200
— электрическое 41
, составляющая активная 515
, — реактивная 515
— фазное 285
Напряженность поля магнитного
171
внутри магнетика 224
электрического 22, 23
внутри диэлектрика 83
Натяжение Фарадея-Максвелла 221
Носители заряда 353
Обратная связь 502
Оптика ионная 431-432
— электронная 431-432
Парамагнетизм 236, 261-265
Парамагнетики 236, 264
Переходы электронно-дырочные 474
Плазма 410-411
Поверхности эквипотенциальные 46
Подвижности ионов 387, 442
— электронов 337
Поле вихревое 298
— магнитное 164
, напряженность 171
размагничивающее 230
, энергия 210
— электрическое 21
— — микроскопическое 83
, напряженность 22
, принцип суперпозиции 24
, энергия 74-77
— электромагнитное 297
, импульс 575
, масса 577
Полупроводники дырочные 353, 474
— магнитные 247
— электронные 349, 474
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
623
Поляризация 77
—, вектор — см. поляризованность
— дипольная 95
— диэлектриков 79
— ионная 96
— однородная 81
— смещения электронная 95
— электродов 453
Поляризованиость 80
Поляризуемость 95
Постоянная баллистическая 122
— времени 161, 207
— магнитная 170, 204
— Планка 360
— Фарадея 436
— Холла 346
— электрическая 18, 67
— электродинамическая 169
Потенциал химический 462
— электродный 447
нормальный 450
абсолютный 449
стандартный 451
Поток магнитный 183
Правило Кирхгофа второе 147, 536,
601
первое 146, 536, 601
— правого буравчика 167
Преобразование Лоренца 326
Прецессия вынужденная 258
— ларморова 257, 264
Принцип относительности 325
— Паули 357
Проводимость 124
— дырочная 351, 353
— примесная 353
— смешанная 353
— собственная 352
— электронная 336, 353
Проницаемость диэлектрика непо-
неполярного 96
полярного 98
— диэлектрическая 64, 89
— магнитная 205, 227
Работа выхода 364, 367, 461
Разность потенциалов — см. напря-
напряжение электрическое
контактная 459-462
Разряд 384
— дуговой 403
— искровой 397
— коронный 400
— несамостоятельный 389
— самостоятельный 390
Разряд самостоятельный, напряже-
напряжение пробоя 390
— тлеющий 394
—, устойчивость 406
Резонанс напряжений 518
— параметрический 530
— токов 527
— циклотронный 425-427
Самоиндукция 201
—, экстратоки 201, 210
Сверхпроводимость 128, 340-344
Сегнетоэлектрики 101—104
Сила Лоренца 191
— магнитодвижущая 273
— пондеромоторная 154, 218
Сила сторонняя 136, 298
— термоэлектродвижущая (термо-
ЭДС) 464
дифференциальная 465
— электродвижущая (ЭДС) 140
индукции 195, 297, 323
самоиндукции 201
Системы единиц 15, 16, 168, 169
Скачок потенциала контактный 460
Скин-эффект 304-306
Смещение электрическое 29, 31, 227
в вакууме 29
в диэлектриках 85-88
, вектор 29
, —, поток 29
Сопротивление 124
— активное 515
— дифференциальное 373, 407
отрицательное 407, 498
— комплексное 536
— магнитное 273
— реактивное 515
—, температурный коэффициент 127
— удельное 126
Сродство электронное 363, 462
Стримеры 399
Температура Кюри 102, 242, 269
— Нееля 269
Теорема Лармора 257
— Остроградского-Гаусса 31, 92, 312
для магнитного поля 229, 312
— Пойнтинга 569
Теория Максвелла 297
Тепло Джоуля-Ленца 139, 155, 209,
468
— Пельтье 467
— Томсона 471
Термопара 472
624
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Ток вихревой 293, 299-301
— двухфазный 285
—, действие магнитное 118
—, — тепловое 120
—, — химическое 119
— индукционный 193
—, источники 136
— квазистационарный 157
— контурный 600
— линейный 286
— молекулярный 222, 247, 255
— насыщения 365
—, плотность 115
— полный 310
— проводимости 310
—, сила 115
— смещения 308, 309
— трехфазный 287
— фазный 285
Триод 371
— диффузионный 482
, база 483
, коллектор 483
, эмиттер 483
— коэффициент усиления 372
— сетка 371
—, проницаемость 372
—, характеристика анодная 373
—, сеточная 372
Уравнение волновое 560
— Лапласа 56
— Максвелла 312, 562
— — в дифференциальной форме
313-316
— непрерывности 117
— Пуассона 37
Уровень Ферми 360, 367
Усилитель ламповый 377
— полупроводниковый 482
Ускоритель заряженных частиц 416
— индукционный 306
Фактор размагничивающий 230
Ферриты 246
Ферромагнетизм 238, 265
Ферромагнетики 238, 265
—, домены 266-271
—, коэрцитивная сила 241
—, намагничивание 238
, анизотропия 239
, кривая 238, 270
спонтанное 266
—, температура Кюри 241, 266
Флуктуации электрические 377
Формула Клаузиуса-Моссоти 97
— Ричардсона-Дэшмэна 367
Фотопроводимость 480
Фотоэмиссия 364
Фотоэффект 393
Функция Ферми-Дирака 360
Цепи магнитные 271
Циклотрон 416
Частота циклотронная 415, 416, 426
Числа переноса 444
Число волновое 546
Шумы 378
Электролиты 120
—, диссоциация 438
—, —, коэффициент 439, 443
—, напряжение разложения 457
—, проводимость 443
Электрометр 47
Электрон 20
—, заряд удельный 256
—, , измерение 329, 418, 424
—, масса эффективная 357, 427
—, момент магнитный 259
—, — механический 259
—, подвижность 337, 346
— проводимости 334
— связи 351
Электропроводность — см. проводи-
проводимость
Электрострикция 84, 94
Электрохимический эквивалент 436
Элемент Вольты 19, 138,
— гальванический 18, 138,
, ЭДС 138-141
— нормальный 49
— топливный 455
Эмиссия автоэлектронная 383
— электронная 363-364
вторичная 364, 379-381, 392
, коэффициент 379, 391
— термоэлектронная 364
Эффект дробовой 378
— Пельтье 467
— пьезоэлектрический 104-110
обратный 110-114
поперечный 106
продольный 105
— Томсона 470
— Холла 346-348
Явление магнитомеханическое 258
— механомагнитное 259