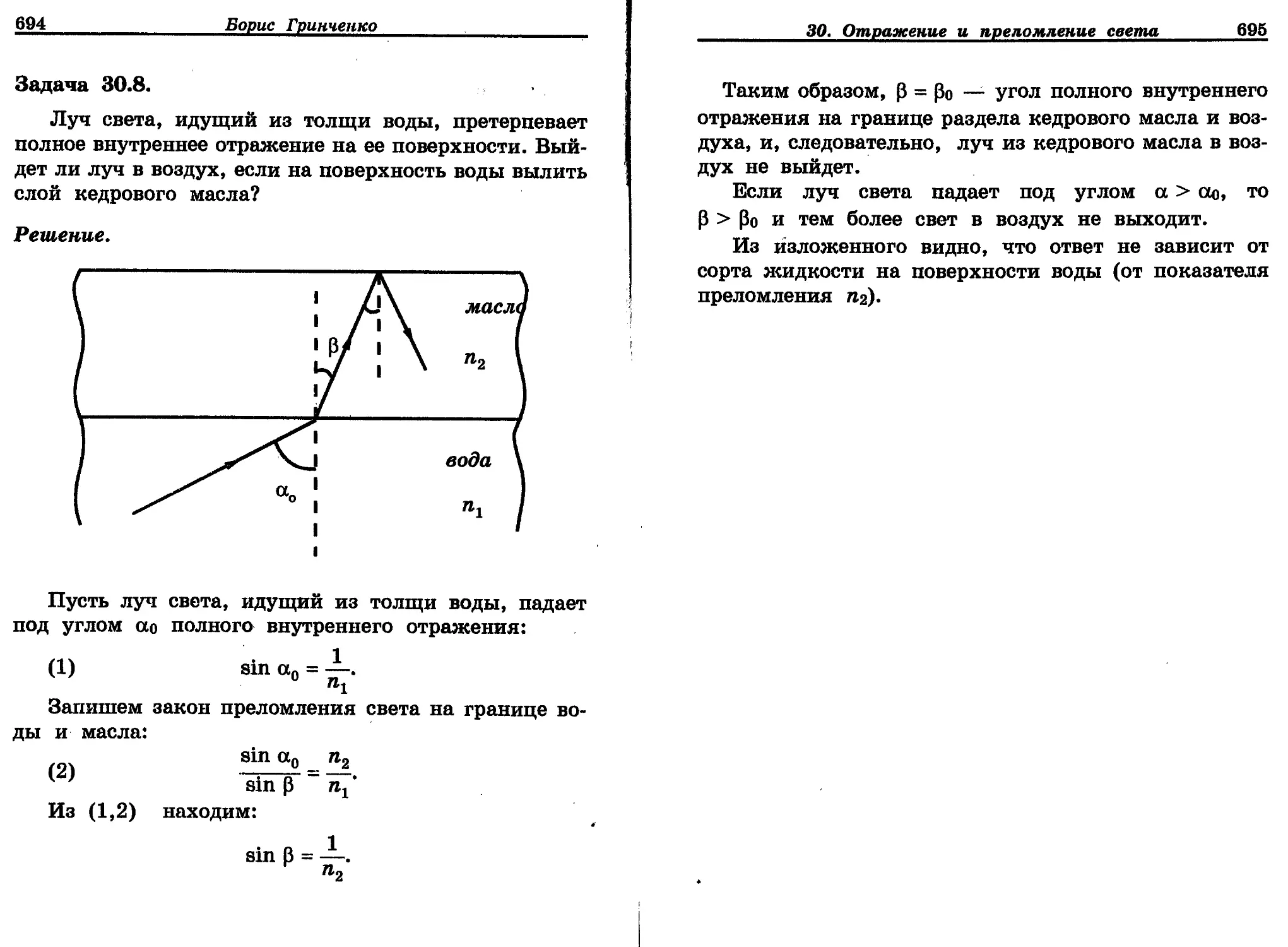
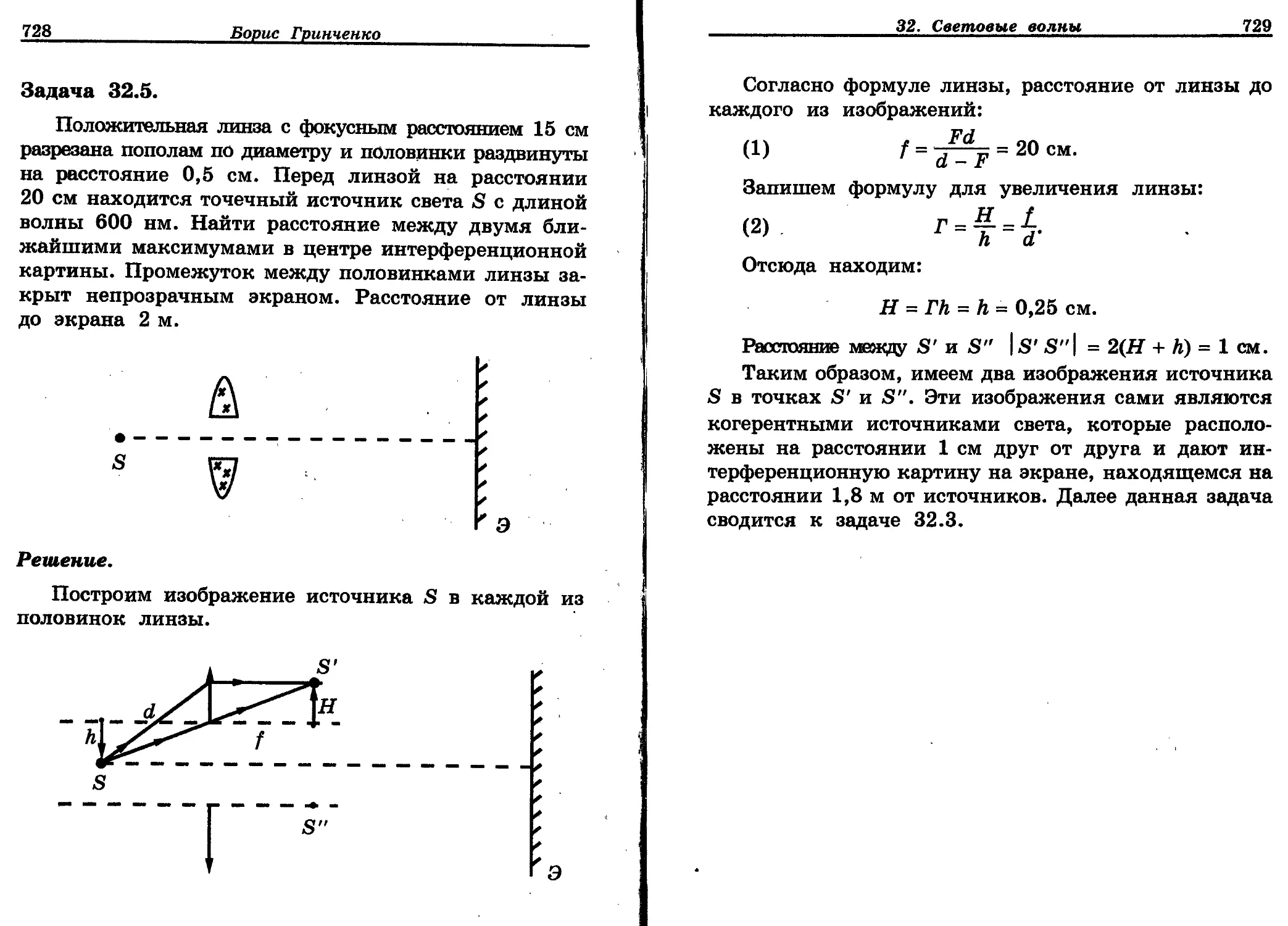
Автор: Гринченко Б.И.
Теги: физика задачи механика электромагнетизм оптика теплотехника молекулярная физика курс физики
ISBN: 5-87-503-026-Х
Год: 1998
Текст
МИР ЕМЬЛ
ДомН17 "Интерлайн, Мир и Семья - 95' Тел.: 350-17-74
Это и другие издания серии "Магист|| Вы сможете приобрести по нашему адрес О.О.О. "ИНТЕРЛАИН”, 199155, Санкт-Петербур
Уральская ул., 1
]инченк& - доцент^ *
культета есггтественно-рическдго, образования, \ций лабораторией обратных стандартов
та повышения кв ал и-_--
\(г. Москва), член феде-i экспертного совета ty образованию
рства образования РФ.
<тель жюри московских >/х физических олимпиад юв
или курс физию н задачах для школьников 1 и абитуриентов |
ГИЮ №
Г 1
Серия учебной литературы
«МАГИСТР»
Борис ГРИНЧЕНКО
Как решать задачи по физике
Школьный курс физики в задачах и решениях
Издание 2-е, дополненное и исправленное
НПО «Мир и Семья — 95» Санкт-Петербург
1998 г.
Серия учебной литературы «МАГИСТР»
Серия «Магистр» обобщает опыт ведущих преподавателей Санкт-Петербурга и Москвы
Г23 Гринченко Б. И. Как решать задачи по физике (Школьный курс физики в задачах). — Санкт-Петербург, НПО «Мир и семья-95», 1998. — 784 с., илл.
ISBN 5-87-503-026-Х
В книге с единой точки зрения рассмотрены общие подходы и методы решения задач по фундаментальным разделам школьного курса физики: механике, теплоте и молекулярной физике, электромагнетизму, оптике.
В решениях специально отобранных по каждой теме серий задач отражены основные идеи и приемы, которые используются в экзаменационных и олимпиадных заданиях.
Книга адресована широкому кругу читателей: от старшеклассников, ориентированных на изучение точных наук, до школьных учителей и преподавателей вузов. Может быть использована как в качестве пособия при работе в классе, так и в качестве самоучителя (особенно это касается лиц, не имеющих возможности заниматься с педагогами высокой квалификации).
Книга публикуется в авторской редакции.
ISBN 5-87-503-026-Х
© ЗЛО НПО «Мир и ссмья-95», текст, оригинал-макет, иллюстрации, 1998 г.
ПРЕДИСЛОВИЕ
Э. Ферми принадлежит высказывание, с которым согласится, по-видимому, каждый профессиональный физик: «Знать физику — означает уметь решать задачи». Другими словами, уровень подготовки по физике определяется уровнем трудности задач, которые ученик может решить.
Хорошо известно, что единственный способ научиться решать задачи — пытаться самостоятельно их решать. Отсюда вытекает диалектичность процесса обучения: знание теории приобретается одновременно с ее использованием для решения задач. Абстрактные поначалу законы, основные уравнения теории, определения понятий и физических величин (эта абстрактность и является главным «камнем преткновения» при изучении физики) в процессе их практического применения для описания конкретных физических явлений (то есть в процессе решения физических задач) начинают постепенно наполняться конкретным содержанием, и только тогда приходит «понимание» теории.
Высказанная точка зрения определяет концепцию настоящей книги, основывающуюся на принципе, согласно которому решение задач является одновременно и целью и средством обучения физике. В ней рассмотрены общие подходы и методы решения физических задач. С единых позиций обсуждаются при-емы и методы решения задач по фундаментальным разделам школьного курса физики. Особое внимание уделяется «трудным» вопросам школьной физики.
4 Борис Гринченко
Основное содержание посвящено решению специально отобранных по каждой теме серий задач. В решениях отражены, в частности, основные идеи и приемы, которые встречаются в задачах приемных экзаменов в вузы с повышенными требованиями по физике и физических олимпиадах. По замыслу автора, учащиеся, проработавшие книгу в соответствии с высказанными рекомендациями, не испытают затруднений па вступительных экзаменах и при дальнейшем изучении физики в вузе.
ВВЕДЕНИЕ
Первые принципы
При решении задач будем исходить исключительно из первых принципов, под которыми ниже понимаются:
1) общие формулировки законов физики (например, закон сохранения энергии, закон Кулона);
2) основные уравнения теории (например, уравнение Менделеева—Клапейрона, уравнение гармонических колебаний);
3) определения физических величин (например, определение плотности, определение электроемкости).
Нередко учащиеся при решении задач пытаются использовать формулы или факты, которые сами являются следствиями первых принципов, полученные при тех или иных условиях. Это, с одной стороны, может привести и часто приводит к ошибкам, поскольку полученные при каких-то условиях формулы или факты могут оказаться неприменимыми для данной конкретной задачи, а с другой, такое решение нельзя не признать корректным: правомерность взятой откуда-то формулы для решения данной конкретной задачи необходимо обосновать (доказать).
Хотелось бы особо обратить внимание на сказанное, поскольку во многих случаях приходится сталкиваться с ситуацией, когда учащимся рекомендуется заучивать наизусть сводки формул и фактов, не яв
6
Борис Гринченко
ляющихся первыми принципами, для последующего использования при решении задач. Это запутывает и дезориентирует школьников, создавая, в частности, представление о физике, как о нагромождении формул и фактов, что не соответствует действительности. Ничего, кроме вреда, и с практической точки зрения такое «обучение» не дает.
Общий подход (схема) решения физических задач
Основная ошибка, которую допускают, приступая к решению задач, заключается в том, что, заострив внимание на искомой величине, учащиеся сразу пытаются ее отыскать. Для этого выписывают формулы, где искомая величина выражается через другие физические величины. Поскольку, как правило, таких формул несколько и этих величин в условии задачи нет, пытаются отыскать очередные формулы для их вычисления и т. д. В результате появляется большое количество формул, и решение заходит в тупик. Такой подход к решению задач называют «формульным».
Правильный подход состоит в том, чтобы текстовое условие задачи записать в виде математических соотношений, используя, в первую очередь, первые принципы. Это является ключевым моментом решения задачи, который вызывает наибольшие трудности у начинающих. Затем следует попытаться ответить на вопрос задачи, используя полученную систему уравнений. Обычно оказывается, что искомая величина непосредственно входит в систему уравнений. Решая последнюю, эту величину находят. Если решить задачу не удается, необходимо еще раз проана-
_____________________Введение ____. „ X лизировать условие задачи и написать недостающие уравнения. Ниже мы остановимся на этих вопросах более подробно.
Таким образом, процесс решения задачи можно разделить на два основных этапа:
1) сведение текстовой задачи к системе математических соотношений, отражающих ее содержание;
2) использование полученной системы для ответа на вопрос задачи.
Первый этап обычно называют физическим, второй — математическим.
Приступая к решению, необходимо в первую очередь стремиться к тому, чтобы описать рассматриваемое в задаче явление с помощью первых принципов. Иными словами, думать надо не над тем, как решать задачу, а над тем, как записать первые принципы применительно к условиям задачи, а также другую текстовую информацию на языке математических формул. Так, например, решая задачу по механике, следует записать закон Ньютона и (или) законы сохранения импульса и энергии. Чтобы это сделать, необходимо выполнить чертеж, изобразить силы и т. д., то есть разворачивается ясная программа действий. На физическом этапе решения задачи чаще всего по--лез но вообще «забыть» о том, что спрашивается в условии.
Физический и математический этапы решения задачи должны быть по возможности четко разделены. В частности, на физическом этапе, как правило, не следует выполнять математические преобразования.
Решение задачи должно быть получено в общем раде (те есть ответ необходимо представить в буквенном виде). И только затем подставляются численные значения параметров.
8
Борис Гринченко
Как пользоваться книгой
Целесообразно начинать работу с первого параграфа и затем двигаться последовательно. Задачи следует решать также последовательно, начиная с первой. Дело в том, что изложение каждого последующего раздела и последующей задачи внутри раздела в той или иной мере предполагает проработку предыдущих.
Сначала следует внимательно прочитать введение к книге, затем введение к изучаемому разделу. Необходимо учитывать, что введение к разделу не заменяет учебника: в нем изложены основные факты теории (первые принципы) и особенности их применения для решения задач.
После этого приступают к самостоятельному решению задач, не пользуясь решениями, приведенными в книге. В принципе, одну-две задачи можно проработать по тексту книги.
В случае возникающих при самостоятельном решении затруднений следует вновь обратиться к общему введению и введению к разделу. Если после нескольких попыток существенного продвижения нет, необходимо частично воспользоваться текстом решения. При этом важно разобраться в причине неуспеха.
Если задачу удалось решить самостоятельно, полезно сопоставить собственное решение с решением, приведенным в книге.
1. Кинематика равнопеременного движения
Движение материальной точки всегда рассматривается в какой-либо системе отсчета. Положение точки можно определить, если задать ее радиус-вектор Г или, что эквивалентно, три координаты: х, у, г — проекции радиус-вектора на оси. Движение математически полностью описано, если известен радиус-вектор как функция от времени г*(£), то есть известны три скалярные функции: x(t), y(t), z(t).
равномерного движения
——- — — . eft2 Г (f) = Г = rQ + vQ t + -тр
где вектор FJ соответствует положению точки в начальный момент времени t = 0, щ — скорость точки в начальный момент времени, а* — постоянное ускорение.
Скорость точки получается дифференцированием г' по времени:
o'(t) = Цо +
При решении задач обычно пользуются не векторными уравнениями, а их проекциями на оси. Если движение материальной точки происходит в плоскос-* ти, вместо векторных уравнений для г~ и v* можем написать:
10
Борис Гринченко
Cl t
X (£) = ХО + Voxt + —, d) $
, Clyt
У (О = £/о + Voyt +
лдч , Vx = vox + axt,
' ’ 1 Vy ~ Voy -I ayt;
где vOx и vOy — проекции вектора на оси х и у соответственно, ах и ау — то же для вектора о?
Соотношения (1) и (2) являются основными уравнениями теории (первыми принципами) данного раздела, и их использования достаточно, чтобы решить любую задачу кинематики равнопеременного движения.
Основной подход к решению задач кинематики равнопеременного движения сводится к записи (1, 2) применительно к условиям конкретной задачи, а также содержащейся в тексте информации с помощью математических соотношений.
Рекомендуется следующая последовательность действий:
1. Сделать рисунок, иллюстрирующий описанное в условии задачи явление, в частности, изобразить траекторию движения, и выбрать систему координат. Систему координат чаще всего удобно выбирать так, чтобы ее начало совпало с положением точки (тела) в начальный (t = 0) момент времени, а одна из осей совпадала с направлением ускорения движущейся точки. При таком выборе из (1, 2) следует, что хо = у о = 0 и одна из проекций ускорения (ах или ау) равна нулю, то есть запись уравнений (1, 2) упрощается.
2. Записать уравнения (1, 2) применительно к условиям данной задачи в общем виде, то есть для про-
1. Кинематика равнопеременного движения 11
и——i mill...«Js«-;-№-^'«>.-«1mc.ww*i
извольпого момента времени. В некоторых случаях может оказаться, что для решения задачи достаточно использовать либо (1), либо (2), в других — необходимо использовать оба соотношения (1, 2).
3. Ввести (обозначить) моменты времени (£i, tz, и т. д.), о которых содержится информация в условии задачи, обозначить и нанести на рисунок соответствующие им координаты (Xi, Хг, yi, yz и т. д.) и проекции скоростей (Щх, viy, ...).
4. Уравнения (1, 2) записать для характерных моментов времени (ti, tz и т. д.).
5. Установить связь между введенными параметрами (моментами времени, координатами, проекциями скоростей) и данными условий задачи.
6. Записать содержащуюся в тексте задачи информацию на языке математических уравнений.
7. Решить полученную систему уравнений.
При решении задач этого и других разделов будем полагать по определению:
|Г| = &,
где Ъ — произвольный вектор. Отсюда следует, что всегда b > 0. Проекция же вектора Ь, например, на ось х, обозначается bx (bx = b eos а, где а — угол между направлением оси х и вектора Ь) и может быть как положительной, так и отрицательной. В частности, если вектор Ь и ось х параллельны и направлены в разные стороны, то Ъх = - Ь, где сама величина Ь>0.
12
Борис Гринченко
Задача 1.1.
При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь. Ускорение автомобиля считать постоянным.
Решение.
Начало системы координат 0 помещаем в точку начала торможения автомобиля. Точка с координатой Xi соответствует моменту остановки, ti — время, прошедшее с момента начала торможения до остановки.
Запишем основные уравнения теории (vqx = vq, ах = - а) для момента времени tr.
at\
(1) Xj = votx — g ,
(2) vlx = v0 - att = 0.
Очевидно, что Xi — тормозной путь, a vix = 0, поскольку в момент времени ti автомобиль останавливается.
Имеем систему из двух уравнений (1) и (2) с двумя неизвестными Xi и а. Выражая а из (2) и подставляя его в (1), находим:
х1=-^1=50(м).
1. Кинематика равнопеременного движения
13
Задача 1.2.
Уклон длиной 100 м лыжник прошел за 20 с, двигаясь с ускорением 0,3 м/с2. Какова скорость лыжника в начале и в конце пути?
Решение.
vo * 1
0 хг х
* Начало системы отсчета 0 помещаем в начало пути лыжника. Точка с координатой Х\ соответствует концу пути.
Запишем основные уравнения теории (ах = а) для момента времени ti = 20 с:
at?
(1) xl = vo^i + 2 ’
(2') »1Х = v0 + atx,
где хг = 100 м, v0 — начальная скорость (в начале пути), — скорость лыжника в момент времени (в конце пути).
Подставляя ио = 2 м/с из (1) в (2), находим щ = 8 м/с.
14
Борис Гринченко
Задача 1.3.
Во сколько раз скорость пули в середине ствола ружья меньше, чем при вылете из ствола? Движение пули в стволе считать равноускоренным.
Решение.
О
Начало системы координат 0 помещаем в точку старта пули, точка С — середина ствола, А — конец ствола, ti и t2 — время, через которое пуля после старта оказывается в точках С и А соответственно.
Запишем основные уравнения теории, учитывая, что начальная скорость пули равна нулю:
(1) х = -у,
(2) vx = at,
для моментов времени t. и f2:
2
at.
(3) *1 = -/’
2
at9
(4) х2 = - gi,
(5) »1Х = atY =
(6)
V2x = at2 = V2-
Кроме того, по условию задачи:
1, Кинематика равнопеременного движения 15
АО х?
<7>
Разделив (4) и (3) с учетом (7), находим:
1—
Г = ^
Разделив (6) и (5) с учетом предыдущего соотношения, окончательно получаем:
— = — = V2 ui *i
Таким образом, скорость пули в середине ствола в V2 раз меньше, чем на выходе ствола.
16
Борис Гринченко
Задача 1.4.
Тело брошено вертикально вверх с высоты 20 м с начальной скоростью 3 м/с. На какой высоте тело окажется через 2 с после начала движения? Сопротивлением воздуха при движении пренебречь.
Решение.
Начало системы координат 0 выберем на поверхности Земли.
Запишем основное уравнение теории для момента времени ti = 2 с, учитывая, что vOx = v0, уо = Н = 20 м, ах = - g'.
gt\
у1=Н + vQtx - — = 6 (м).
Удобство выбора именно такого начала системы координат заключается в том, что у\ совпадает с высотой, на которой находится тело.
1. Кинематика равнопеременного движения
17
Задача 1.5.
В последнюю секунду свободного падения с нулевой начальной скоростью тело прошло путь вдвое больший, чем в предыдущую секунду. С какой высоты упало тело?
Решение.
Обозначим через 0 ту точку, из которой тело начало движение. Начало системы координат помещаем в точку О. Так как тело движется вниз, ось у целесообразно направить также вниз (в этом случае значения координат тела по оси у будут положительными). Движение одномерное вдоль оси у, и оси х на рисунке нет (в любой момент времени координата тела по оси х равна нулю).
Отмечаем на рисунке положение тела в те моменты времени, о которых в задаче идет речь. Таких моментов времени четыре:
18
Борис Гринченко
1) начальный момент времени t = 0 — ему соответствует точка 0;
2) начало предыдущей секунды ti (ti — время, которое показывает секундомер, включенный в момент t = 0, в тот момент, когда началась предыдущая секунда);
3) конец предыдущей — начало последней секунды t2;
4) конец последней секунды (касание тела с поверхностью земли) ts.
Запишем основное уравнение теории:
а/2
У = У о + voyt + 2 ’ применительно к условиям настоящей задачи. При этом учтем, что у0 = 0 в силу выбора начала системы отсчета; vOy = 0 по условию задачи (у0 = 0); ау = g, поскольку ось у направлена вниз. Таким образом, получаем:
(1) V =
Уравнение (1) записываем для всех тех моментов времени, о которых идет речь в условии задачи:
(2) », =
(3) У 2 =
(4) ys = -j-;
где через ylf у2, у3 обозначены соответствующие данным моментам времени координаты.
1. Кинематика равнопеременного движения
19
Следующий шаг: информацию, содержащуюся в условии задачи в виде текста, следует записать с помощью математических соотношений.
В условии сказано, что пути, пройденные телом в последнюю и предыдущую секунды отличаются в два раза. Из рисунка видно, что путь за предыдущую секунду равен у2 - yi, а за последнюю — уз - у?.-
Следовательно:
(5) Уз - У2 = 2 (Уг ~ У1)’
Кроме того, согласно тексту условия задачи:
(6) t? - = At
(7) t3 — t2 = At,
где At = 1 c.
На этом заканчивается «физический» этап решения. Переходим к «математическому» этапу. В задаче требуется найти высоту, с которой упало тело. Обращаясь к чертежу, видим, что эта высота есть уз — величина, которая непосредственно входит в систему уравнений.
Анализируем ситуацию: имеем систему из 6 уравнений (2—7) с 6-ю неизвестными yi, у2, уз, ti, t2, t2, из которой, следовательно, можно вычислить уз.
Подставим yi, у2, и уз из (2, 3, 4) в (5) и воспользуемся разложением разности квадратов двух чисел:
(8) "2 &з + С^з ~ ~ "2 ^2 + ^1) (^2 ~ ^1)'
С учетом (6) и (7), из (8) находим
t3 + f2 ~ 2 (*i + $?) или - ^2 = 2*г
20
Борис Гринченко
С учетом (7), отсюда получаем:
*1 =~2* з
t2 = tx + At = gAt, §
t3 = t2 + At = ~cjAt'
Наконец, окончательно находим:
g(|4t)2 10(|)2
У3 =---1= 31,25 м.
1. Кинематика равнопеременного движения 21
Задача 1.6.
Тело бросают вертикально вверх. Промежуток времени между двумя моментами, когда тело проходит точку, находящуюся на высоте Н, равен to. Найти начальную скорость и время движения.
Решение.
Поскольку все события разыгрываются вверху, ось у направляем вверх. Начало системы отсчета совпадает с положением тела в начальный момент времени. Движение одномерное, поэтому ограничимся одной осью координат. Характерные моменты времени, о котором упоминается в условии задачи: t = О — начало движения; t\ — момент времени, когда тело первый раз оказалось на высоте Н; tz — момент времени, когда тело второй раз оказалось на высоте Щ t$ — ‘момент времени, когда тело коснулось земли. Напомним, что в момент времени t = 0 включается секун
22
Борис Гринченко
домер и затем по нему фиксируется время. Соответствующие данным моментам времени координаты тела обозначены на рисунке.
Основное уравнение теории: a tz
У = У о + уо/ +
запишем для условий задачи. При этом учтем, что в силу выбора начала системы координат у0 = О, иОу = ио» ау = - S- Получаем:
(1) У = М “ ^2"-
Уравнение (1) записываем для конкретных моментов времени ti, tz я tz’.
(2) z/i = — gtir
gtz
(3) У2 = y0^2 2~ ’
gta2
(4) Уз ~ уо^з 2~’
По условию задачи, с учетом обозначений на чертеже имеем:
(5) у. = Н,
(6) У2 = Н,
(7) у3 = 0.
Кроме того, согласно условию,
(8) t2 — fx = ^0*
«Физический» этап решения завершен. Подставив
1. Кинематика равнопеременного движения_____23
(5, 6, 7) в (2, 3, 4), получаем систему из 4 уравнений (2, 3, 4, 8) с четырьмя неизвестными ti, tz, ta, Vq.
Вычитая из (3) уравнение (2), после сокращения
2и
получим <2 + £1 = —С учетом (8) находим:
*2 " 2 V g +to) '
Подставляя t2 в (3), получим квадратичное уравнение относительно 1>о- Выбираем положительный ко
рень:
, , 8Н
ио ~ 2 V0 + в '
& 5 s
Наконец, из (4):
24
Борис Гринченко
Задача 1.7.
Реактивный самолет летит со скоростью i>o- С некоторого момента времени самолет движется с постоянным ускорением в течение времени to и в последнюю секунду проходит путь S. Определите ускорение и конечную скорость самолета.
Начало системы отсчета выбираем в той точке пространства, в которой самолет начал двигаться с ускорением, время отсчитываем с того же момента, то есть одновременно с включением ускорения включается секундомер. Характерные моменты времени: й — начало последней секунды и tz — конец последней секунды.
Уравнение координаты самолета: a t2
(1) X = UqZ + р .
Поскольку знак проекции ускорения самолета на ось х не известен (то есть, ускоряется самолет или тормозится), величина проекции может быть как положительной, так и отрицательной.
Запишем (1) для моментов времени ti и t2'
(2)
(3)
2
Xi ~~ У(А + 2
2
х2 = 2 *
1. Кинематика равнопеременного движения
26
По условию задачи:
(4) t2 =
(5) t2 - tj = At
(6) x2-xt = S,
где At = 1 c.
Поскольку в условии задачи идет речь о скорости в разные моменты времени, основное уравнение теории vx = vox + axt запишем для момента времени tz’
(7) v2x = v0 + axt2.
«Физический» этап задачи завершен. Величины ах и V2, которые требуется найти, непосредственно входят в систему уравнений (2—7). Подставим (2, 3) в (6) и воспользуемся (4,5). Получим:
2u0 At - 2S
а* = At (2t0 - At)"
Подставляя найденное значение ускорения в (7), имеем:
2v0 At - 2S
V2x = V°+ At (2t0 - At) to'
2fl
Борис Гринченко
Задача 1.8.
Тело начинает прямолинейное движение из точки А и движется сначала равноускоренно в течение времени to, затем с тем же по модулю ускорением — равнозамедленно. Через какое время от начала движения тело вернется в точку А?
Решение.
2
-► х
Здесь мы сталкиваемся с ситуацией, когда записать в едином виде основные уравнения теории невозможно — в разные моменты времени ускорение различно. В таких случаях следует записать соответствующие уравнения движения для каждого этапа с постоянным ускорением.
Начало системы координат выбираем в точке А, точка В соответствует моменту времени to — изменению знака ускорения на противоположный.
Основные уравнения теории на этапе движения АВ для момента времени to имеют вид:
at* 1 2
(1) х0=АВ = -^,
(2) v0 = at0.
Далее задачу ставим так: в момент времени t = 0 из точки В с начальной скоростью v0 и ускорением ах = - а начинает двигаться точка и через время ti попадает в А. Уравнение движе-
1. Кинематика равнопеременного движения 27
ния для второго этапа запишем для момента времени ti:
ат.
(3) хг = х0 + — g = 0.
Подставляя (1,2) в (3) и решая получившееся квадратное уравнение, находим:
= (1 + <) t0,
t0 + *i = (2 + V2) t0.
Отрицательный корень
ii = (1 — V2) t0
отбрасываем.
28
Борис Гринченко
Задача 1.9.
Пикирующий бомбардировщик сбрасывает бомбу с высоты Н, находясь на расстоянии L от цели по горизонтали. Найти скорость бомбардировщика, если угол пикирования а.
Решение.
Начало системы координат 0 выбираем в той точке, где происходит отрыв бомбы от самолета. В этот момент, естественно, скорость бомбы совпадает со скоростью самолета и равна vq. Поскольку все события происходят внизу, ось у направляем вниз.
Обозначим через ti время свободного полета бомбы, то есть в момент ti бомба касается збмли.
Уравнение движения бомбы для момента времени tr.
(1)
xt = v0cos a
1. Кинематика равнопеременного движения 29
(2) = Vo sin at1 + -у.
При этом мы учли, что
v0x = vocos a; v0y = uosin а; ах = °iay = S-
По условию задачи:
(3) хг=Ь
(4) = Н.
Подставляя (3,4) в (1,2), получаем систему из двух уравнений с двумя неизвестными ti и vq. Поставив h из (1) в (2) и решив квадратное уравнение относительно vq, находим:
р = ----- А / 4^
0 cos а V 2 (Н - L tg а) *
30
Борис Гринченко
Задача 1.10.
Спортсмен прыгает с 10-метровой вышки и погружается в воду, пролетев по горизонтали 3 м, через 2 с. Найти скорость спортсмена в момент прыжка и в момент начала погружения в воду.
Решение.
Введем обозначения Н = 10 м, L = 3 м, ti = 2 с. Запишем основные уравнения для момента времени tit
(1) xt = u0cos a tt
gt*
(2) yt = - o0sin a tl + -у.
В уравнении (2) учтено, что проекция начальной скорости vo на ось у voy = - Vq sin а и ау = g. Очевидно, что в (1,2) следует подставить Х\ = L и У1 =/Н.
1. Кинематика равнопеременного движения
31
Запишем также уравнения для проекций скоростей спортсмена в момент времени ti:
(3) vlx = v0 cos a
(4) vly = - vQ sin a + gtlf
причем скорость спортсмена в момент времени tr равна
(5) vt = ^L + %-
Полученная система уравнений (1—5) позволяет ответить на вопросы задачи. Для этого перепишем (1), (2) в виде:
L v0cos a = —
Н uosm a = .
Возведя правые и левые части обоих равенств в квадрат и складывая их, получим:
32
Борис Гринченко
Задача 1.11.
С какой скоростью в момент старта ракеты нужно выстрелить из пушки, чтобы поразить ракету, стартующую вертикально вверх с ускорением н? Расстояние от пушки до места старта ракеты L, пушка стреляет под углом а к горизонту.
Решение.
В задаче идет речь о двух телах, поэтому уравнения движения следует записать для каждого из них. Обозначим через ti время, прошедшее с момента старта и выстрела до попадания снаряда в ракету. Координаты снаряда в момент времени ti:
(1)
(2)
Хс ~ uoCOS а
gt\ ус = uosm а - —
1. Кинематика равнопеременного движения
33
Координаты ракеты в момент времени tr.
(3) хр = L
at2.
(4) Ур =
Поскольку в момент времени ti снаряд коснулся ракеты, то есть координаты совпали, то
(5) хс = хр
(6) Уе=Ур‘
Из системы уравнений (1—6) получаем:
(7) L = u0cos a
at\ gt2
(8) ~2~ = vo sin a ij -
два уравнения с двумя неизвестными и0 и tv Подставляя ij из (7) в (8), окончательно находим:
„ _ J + g) L 0 sin 2а
34
Борис Гринченко
Задача 1.12.
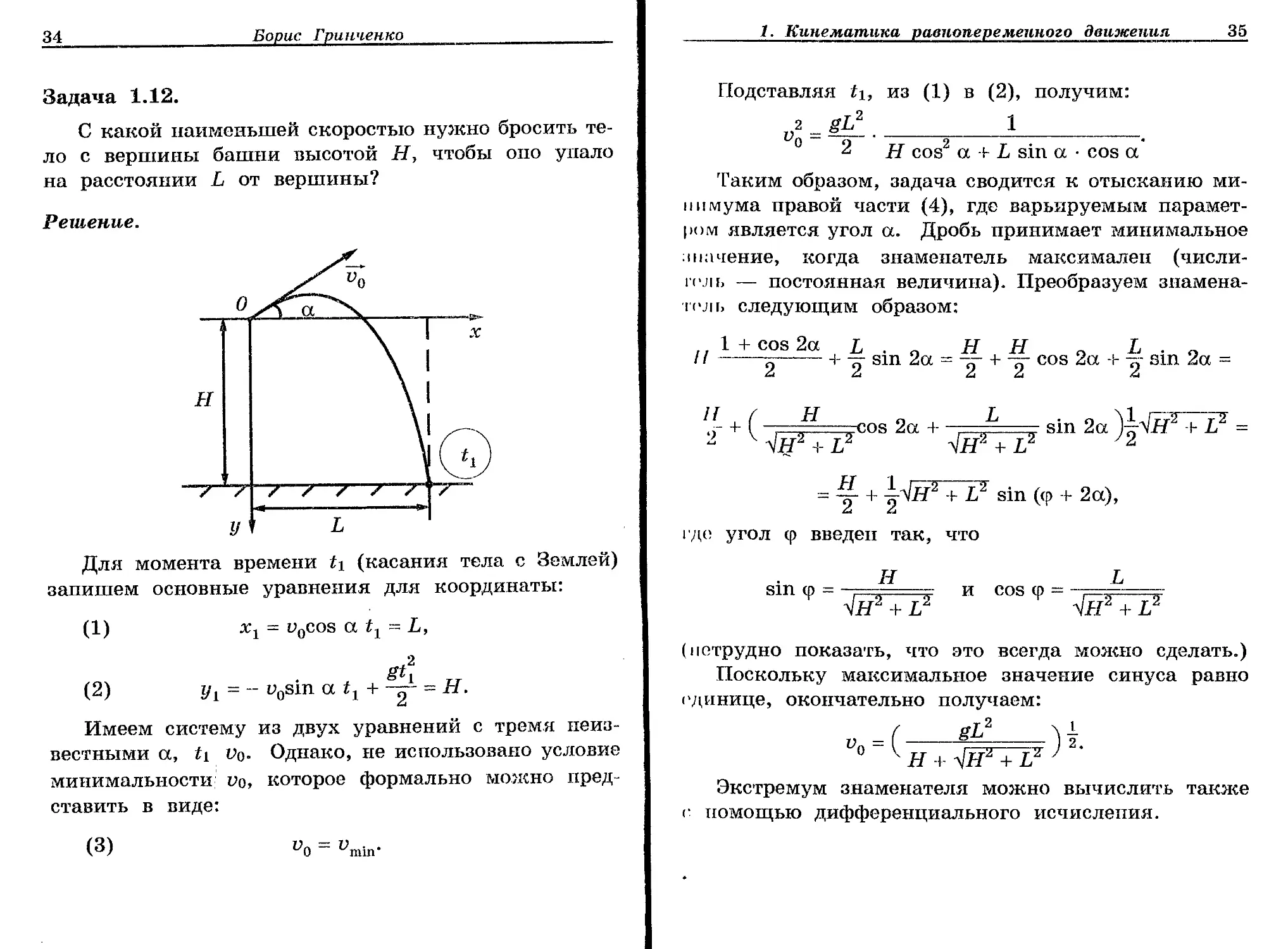
С какой наименьшей скоростью нужно бросить тело с вершины башни высотой Н, чтобы оно упало на расстоянии L от вершины?
Решение.
Для момента времени /| (касания тела с Землей) запишем основные уравнения для координаты:
(1) хг = l>0cos at1~L,
(2) = -- L>osin a ix + - H.
Имеем систему из двух уравнений с тремя неизвестными a, ti Vq. Однако, не использовано условие минимальности ио, которое формально можно пред ставить в виде:
(8) U0 — ^пшГ
1. Кинематика равнопеременного движения
35
Подставляя fi, из (1) в (2), получим:
„2 gLz 1
и0 ~ 9 " ' 77 2“ Т ~~
z Н cos а + L sin а • cos а
Таким образом, задача сводится к отысканию минимума правой части (4), где варьируемым параметром является угол а. Дробь принимает минимальное значение, когда знаменатель максимален (числитель — постоянная величина). Преобразуем знамена-кии, следующим образом:
,, 1 + cos 2а L . НН п L . о
//-----------+ — sin 2а = + -х- cos 2а + „ sin 2а =
2 2 2 2
2
< + (—=^~===^cos 2а + —7sin 2а =
J + L2 2
= + i^H2 + L? sin (ф + 2 а),
di л
где угол ф введен так, что
Н L
sin ф = -==—== и cos ф = -====
\Н2 + L2 HI2 + L2
(нетрудно показать, что это всегда можно сделать.) Поскольку максимальное значение синуса равно единице, окончательно получаем:
v =f____gb!V
Экстремум знаменателя можно вычислить также с помощью дифференциального исчисления.
36
Борис Гринченко
Задача 1.13.
Под углом а к горизонту было брошено тело с начальной скоростью ио- Через сколько времени оно будет двигаться под углом Р к горизонту? Как зависит от времени радиус кривизны траектории?
Решение.
Поскольку в условии речь идет о скоростях, запишем уравнения для проекции скоростей:
(1)
(2)
Vx = U0COS
= uosin а - gt.
Пусть в момент времени t тело находится А и угол между направлением скорости и равен р. Из рисунка видно, что
в точке осью ±
(3)
в = = posin a~gt
ё u0cos а
Отсюда получаем ответ на первый вопрос задачи:
1. Кинематика равнопеременного движения 37
uosin а - tg Р и0 cos а
7 — *
g
Для ответа на второй вопрос задачи воспользуемся известным фактом из кинематики вращательного движения:
где ап — центростремительное ускорение (проекция полного ускорения тела на ось, нормальную к касательной к траектории), R — радиус вращения. Применим соотношение (4) для наших условий. Ускорение, которое испытывает тело в любой момент времени свободного полета-(полное ускорение), равно g. Чтобы получить центростремительное ускорение, необходимо взять проекцию g* на мгновенную ось вращения АО (О — мгновенный центр вращения), то есть:
(5) ап = g cos р.
Скорость тела и выразим через проекции vx и vv
( 2 , 2
V = I Vx + Uy Л'
Из отношений (1, 2, 4, 5, 6) с учетом
cos р = — r v
окончательно получаем:
2 2 £
[(u0cos а) + (o0sin а - gt) ]2
Ugg cos а
38
Борис Гринченко
Задача 1.14.
Начальная скорость камня ио, а спустя время ti, скорость камня vi. На какую максимальную высоту над начальным уровнем поднимется камень?
Решение.
В условии упоминается о двух характерных моментах времени: h и tz — достижение камнем верхней точки траектории. Воспользуемся уравнениями для проекций скоростей в моменты времени ti и tz'.
(1) г?1ж = v0cos а,
(2) vXy = Uosin а - gtv
(3) I v2x = v0cos a,
(4) % = uosin a - St2 = 0.
Свяжем также модуль вектора v\ с его проекциями:
2 2 2
(5) = vix +
1. Кинематика равнопеременного движения
39
Максимальная высота, на которую поднимается камень, равна координате камня по оси у в момент времени tz'.
g£
(6) у2 = v0 sina t2 - -у.
Система уравнений (1, 2, 4, 5, 6) позволяет ответить на вопрос задачи. Для этого необходимо подставить (1) и (2) в (5) и вычислить vosin а. Затем из (4) выразить tz и подставить все это в (6):
2. Кинематика относительного движения.
Вращательное движение. Движение со связями
Пусть имеются две системы отсчета: «неподвижная» и «движущаяся». Движение материальной точки можно рассматривать как относительно первой системы отсчета, так и второй. Характер этого движения в разных системах отсчета может существенно отличаться.
Введем обозначения, как показано на рисунке: О — начало «неподвижной» системы отсчета, О' — «движущейся», А — движущаяся точка. Все радиус-векторы являются функциями времени (зависят от времени). Имеет место очевидное соотношение:
(1) R = Rl+R.
2. Кинематика, относительного движения
41
Из (1) можно получить:
(2) v = vr + v',
где и* — скорость точки А относительно «неподвижной» системы отсчета, — скорость «подвижной» системы' отсчета относительно «неподвижной» и v' — скорость тела относительно «движущейся» («подвижной») системы отсчета* (2) называют формулой сложения скоростей.
Если «подвижная» система отсчета движется поступательно (не вращается), то для ускорения точки Л справедливы соотношения, аналогичные (2):
(3) а = at + а'.
Соотношения (2) и (3) являются основными уравнениями кинематики относительного движения.
Решение задач по кинематике относительного движения сводится к записи основных уравнений теории (2,3) применительно к условиям данной задачи, проецировании полученных векторных уравнений на выбранные оси и записи текстовых условий задачи в ни де математических соотношений. Прежде чем воспользоваться (2,3) необходимо:
1. Выбрать системы отсчета. В качестве «неподвижной» системы отсчета, как правило, удобно выбрать систему отсчета, связанную с Землей, в качестве «подвижной» — такую, движение точки (тела) относительно которой выглядит наиболее просто.
2. Выбрать точки (тела), для которых следует применить основные уравнения теории (2,3). Как правило, это те точки, о характере движения которых * что-то известно, либо спрашивается в условии задачи.
Другими словами, (2,3) записывают для тех точек,
42
Борис Гринченко
которые в условии задачи каким-то образом упоминаются.
В случае вращательного движения линейная и угловая скорости точки связаны соотношением:
(4) v = (oR.
Полное ускорение вращающейся точки можно представить в виде:
(5) а = + ~ап,
где тангециальное (касательное) ускорение ах изменяет скорость точки по модулю, а нормальное (центростремительное) ускорение ап — по направлению. Для модулей этих ускорений справедливы соотношения:
у2 2
(7) ап = = Ю2Л.
При равномерном движении по окружности полное ускорение точки совпадает с центростремительным ускорением.
2. Кинематика относительного движения
43
Задача 2.1.
Поезд движется со скоростью 60 км/ч. Найти скорость Земли относительно поезда.
Решение.
Под скоростью Земли понимается скорость малого участка грунта или, например, лежащего на поверхности Земли камня. В качестве неподвижной системы отсчета выбираем Землю, в качестве подвижной — поезд. В качестве точки, для которой запишем формулу сложения скоростей, выбираем лежащий на земле камень:
(1) v = + v',
где в нашем случае скорость камня относительно Земли 1Г-- 0, скорость подвижной системы отсчета (поезд) относительно неподвижной (Земля) vx = 60 км/ч и v ’ — искомая скорость камня (Земли) относительно поезда.
Из (1) находим:
(2) v ' = - Ор
так что и' = l>1 = 60 км/ч, причем скорость Земли относительно поезда, согласно (2), направлена в сторону, противоположную скорости поезда.
44
Борис Гринченко
Задача 2.2.
Два поезда движутся навстречу друг другу со скоростями ui = 50 км/ч и иг = 80 км/ч. Найти скорость первого поезда относительно второго.
Решение.
----------;>
X
В качестве неподвижной системы отсчета выбираем Землю, в качестве движущейся — второй поезд, формулу сложения скоростей запишем для первого поезда:
(1) ”1 = v2 + и/,
где vt' — скорость первого поезда относительно подвижной системы отсчета (относительно второго поезда). Из (1) находим:
(2) и/ = v2-vv
Согласно правилу сложения векторов, получаем:
и/ = v2 + vr = 130 (км/ч).
Этот же результат можно получить, проецируя (1) или (2), например, на ось х.
2. Кинематика относительного движения
45
Задача 2.3.
Автомобили движутся по дорогам, угол между которыми а = 60°. Скорость первого автомобиля 01 = 10 м/с, второго — 02 = 20 м/с. Найти скорость первого автомобиля относительно второго.
Решение.
Воспользуемся результатом предыдущей задачи: о/ = о2 - ор
где и/ — скорость первого автомобиля относительно второго.
Согласно теореме косинусов:
u i = vi + у2 ~ 2o1o2cos а.
Отсюда находим: ui'«17 м/с.
46
Борис Гринченко
Задача 2.4.
Стенка движется с постоянной скоростью Vi. Навстречу стенке со скоростью ио движется шар. Считая удар абсолютно упругим, найти скорость шара после столкновения.
Примечание: удар считается абсолютно упругим, если в системе отсчета, связанной со стенкой, модуль скорости шара до и после столкновения одинаков.
Решение.
В условии задачи рассмотрены две ситуации. В первой — система стенка—шар до столкновения. Вторая ситуация соответствует системе стенка—шар после удара.
Записываем основное уравнение теории для первой ситуации:
(1) <>о = + V,
2. Кинематика относительного движения
47
где v' — скорость тела в системе отсчета, связанной со стенкой (движущаяся система отсчета). В качестве неподвижной системы отсчета удобно выбрать систему отсчета, связанную с Землей.
Основное уравнение теории для описания второй ситуации имеет вид:
(2) v = vt + v ".
По условию задачи (удар абсолютно упругий):
(3) v~" =-if.
В (2,3) v " — скорость шара относительно стенки после удара.
Решая систему уравнений (1—3), находим:
(4) v = 2vx - и0.
Проецируем векторное равенство (4) на ось х:
v = 2иг + v0.
В качестве упражнения полезно рассмотреть случай, когда скорость шара vo направлена под некоторым углом а к нормали к стенке.
48
Борис Гринченко
Задача 2.5.
С каким минимальным ускорением необходимо двигать клин по горизонтальной плоскости (см. рис.), чтобы тело, первоначально на нем покоящееся, падало свободно? Угол а известен.
Решение.
Прежде всего отметим, что условие минимальности ускорения клина в процессе движения означает, что тело и клин находятся на грани соприкосновения. Действительно, если между телом и клином образуется заметный зазор, это означает, что ускорение клина может быть уменьшено без нарушения условия свободного падения тела. В качестве «движущейся» системы отсчета естественно выбрать клин, «неподвижной» — Землю.
Записываем основное уравнение теории,
а = аг + а', для конкретных условий задачи: o’ - g~ — ускоре
2. Кинематика относительного движения
49
ние тела относительно Земли, обозначения аг в основном уравнении теории и в задаче совпадают, для а' сохраняем обозначение ускорения тела относительно клина:
(1) . g = + а'.
Поскольку относительно наблюдателя, находящегося на клине, тело движется вдоль его поверхности, направление ускорения а' так же направлено вдоль поверхности.
Спроецируем (1) на оси х и у соответственно:
(2) 0 = а* — a'cos а,
(3) - g = 0 - a'sin а.
Из (2,3) окончательно получаем:
= gctg a.
50
Борис Гринченко
Задача 2.6.
Найти скорость оси и угловую скорость вращения катушки с нитками. Катушка катится без проскальзывания, заданы скорость ио, с которой тянут нить, внешний R и внутренний г радиуса катушки.
Решение.
X
ив
Обозначим через щ скорость оси катушки, ю —
угловую скорость вращения катушки относительно ее оси. В условии задачи имеется информация о скорости двух точек катушки: vA = vQ и Vb = 0 (условие отсутствия проскальзывания).
Именно для этих двух точек естественно попытаться применить основное уравнение теории (2). В качестве «неподвижной» системы отсчета удобно выбрать Землю, в качестве «движущейся» — ось катушки. При таком выборе движение катушки в подвижной системе отсчета представляет собой вращение вокруг оси О.
2. Кинематика относительного движения
51
(1) vA = + и/,
(2) vB = vt + vB.
Направления скоростей точек Ак В относительно ♦движущейся» системы отсчета указаны на рисунке. Модули этих скоростей определяются соотношениями:
(3) и/ = юг,
(4) vB = <oR
(движение катушки относительно оси («движущейся» системы отсчета) представляет собой простое вращение).
Проецируя векторные равенства (1—2) на ось х и подставляя соотношения (3—4), находим:
и0 = Uj - юг,
V! - &R = 0.
Решение этой системы уравнений имеет вид:
R vi vo R _ r-
Нередко у школьников возникают затруднения при ответе на вопрос о величине ускорения различных точек катушки.
Воспользуемся основным уравнением теории:
а = аг + а'.
Поскольку в нашем случаем си = 0 (скорость оси постоянна), имеем:
52
Борис Гринченко
а = а'.
То есть ускорение любой точки катушки относительно Земли совпадет с ускорением этой точки относительно оси. Из кинематики вращательного движения известно, что ускорение равномерно вращающейся по окружности точки направлено к центру вращения и равно по модулю а' = о2х (х — расстояние от точки до центра вращения). Так, например, ускорение точки С показано на рисунке.
Для самостоятельного решения полезно рассмотреть случай, когда нить тянут со скоростью ио, которая направлена под углом а к горизонту. При этом целесообразно воспользоваться результатом решения следующей задачи 2.7.
2. Кинематика относительного движения
53
Задача 2.7.
Жесткий стержень движется в плоскости так, что скорость точки А стержня равна цд и направлена под углом а к оси стержня, скорость точки В направлена под углом р. Найти скорость точки В.
Решение.
В качестве «движущейся» системы отсчета выберем точку А. Основное уравнение теории запишем для точки В:
(1) VB = ^A+ vb-
Отметим, что движение стержня в движущейся системе отсчета представляет собой^ вращение вокруг точки А. Следовательно, скорость vb направлена перпендикулярно оси стержня ВА. По этой причине векторное равенство (1) целесообразно проецировать на ось х, направленную вдоль оси стержня.
В результате получаем:
(2} VBx = VAx или
' ' vBcos Р = uAcos а
54
Борис Гринченко
или, окончательно, ЦдСова VP “ cosp Соотношение (2) носит общий характер и нередко применяется при решении задач на движение протяжных тел. В качестве примера рассмотрим задачу.
Лодка движется с постоянной скоростью и0, образуя в некоторый момент времени угол а между направлением и отрезком веревки, находящимся между столбом и лодкой. С какой скоростью v*нужно тянуть в этот момент свободный конец веревки?
Решение.
Запишем для точек А и В веревки соотношение
(2):
v = v0cos а, где учтено, что скорость точки А веревки равна v и направлена вдоль отрезка АВ.
2. Кинематика относительного движения
55
Задача 2.8.
Эскалатор метро спускает идущего по нему человека за 1 мин. Если человек будет идти вдвое быстрее, то спустится за 45 с. Сколько времени спускается человек, стоящий на эскалаторе?
Решение.
В качестве неподвижной системы отсчета выбираем Землю, в качестве подвижной — ступени эскалатора. Запишем основное уравнение теории для движения человека в трех, описанных в условии задачи, ситуациях в проекции на ось, параллельную скорости ступенек эскалатора:
(1) Vj = Vj + V,
(2) vn = + 2v',
(3) иш = vt,
где слева стоят скорости человека относительно Земли, ь>г — скорость ступенек эскалатора, v' — скорость человека относительно ступенек эскалатора (движущейся системы отсчета).
Уравнение движения для человека в неподвижной системе отсчета в каждом из трех случаев запишем в виде:
(4) I = Vjtv
(5) I =
(6) I = vmtm,
где I — длина эскалатора, = 60 с, tn = 45 с и время •tni спуска неподвижно стоящего на эскалаторе человека необходимо найти.
56
Борис Гринченко
Полученная система уравнений (1—6) позволяет ответить на вопрос задачи:
. _ *i' *п
Ш 2*п “ h
Отметим, что формально полученная система уравнений содержит 7 неизвестных и решена быть не может (то есть невозможно найти все неизвестные). Однако этого по условию задачи и не требуется.
2. Кинематика относительного движения
57
Задача 2.9.
Из точки А свободно падает тело. Одновременно из точки В под углом а к горизонту бросают другое тело так, чтобы тела столкнулись в воздухе. Величины Н и L известны. Найти угол а.
Решение.
Выберем свободно падающее из точки А тело в качестве движущейся системы отсчета, в качестве неподвижной — Землю. Скорость каждого тела относительно Земли представим в векторном виде:
(1)
vA=gt
(2)
vB = v0 + gt.
Воспользуемся основным уравнением теории для тела В:
(3)
VB=VA+ VB VB =VB ~ »А’
58
Борис Гринченко
где vB' — скорость тела В относительно движущейся системы отсчета.
Из (3), с учетом (1,2), находим:
= К‘
Отсюда видно, что скорость тела В относительно движущейся системы отсчета постоянна. Поскольку само тело А относительно движущейся системы отсчета покоится, то, очевидно, для того, чтобы тела столкнулись, скорость vB = v0 должна быть направлена в точку А.
Это позволяет дать ответ на вопрос задачи: н tg а = ~у vljoil а = arctg -у.
Отметим, что результат не зависит от величины ио.
Приведем решение задачи, не использующее теорию относительного движения.
Обозначив через ti время встречи тел, запишем уравнения движения ддя каждого из них в этот момент времени:
(1) хв = v0 cos a = L,
gt2
(2) У в = v0 sin а
(3) xA = L,
gt2
(4) Ул = Н-^.
В момент столкновения координаты тел совпадают: Хв = Ха и ул = ув- Отсюда, после простых вычислений, получаем:
2. Кинематика относительного движения
59
tg а = у.
Сопоставляя этот результат с рисунком, делаем вывод о том, что вектор vq направлен в точку В.
60
Борис Гринченко
Задача 2.10.
Скорость монеты, соскальзывающей с клина, изображена на рисунке (о). Графическим построением найдите скорость клина.
Решение.
В качестве неподвижной системы выбираем Землю, подвижной — клин.
Запишем основное уравнение теории для монеты:
(1) v = + v',
где — скорость клина относительно Земли, v ' — скорость монеты относительно клина. Очевидно, что v ' направлена вдоль поверхности клина. Из (1) видно, что v — диагональ параллелограмма, сторонами которого являются Vj и v Отсюда вытекает способ построения: из начал вектора v проводим прямые ли нии по векторам и v Затем из конца вектора
2. Кинематика относительного движения
61
v также проводим прямые, параллельные векторам и v Пересечения построенных прямых дают искомый вектор а также скорость монеты относи
тельно клина v
62
Борис Гринченко
Задача 2.11.
Концы стержня А и В скользят по сторонам прямого угла. Как зависит от угла а ускорение середины стержня С, если конец В движется с постоянной скоростью ui? Длина стержня I.
Решение.
В качестве «движущейся» системы отсчета выбираем точку В. В задаче, кроме точки В,, имеется информация о движении точки А (скорость точки А направлена вдоль направляющей АО). Поэтому основные уравнения теории запишем именно для этой точки:
(1) vA = V1 +
(2) аА = аА
(учтено, что ах = 0 поскольку = const). Отметим, что в движущейся системе отсчета движение стержня представляет собой простое вращение (неравномерное!)
2. Кинематика относительного движения
63
вокруг точки В, и, следовательно, скорость и/ направлена перпендикулярно оси стержня АВ.
Проецируем векторное равенство (1) на ось х:
(1г) 0 = i?i - u/sin а.
Из кинематики вращательного движения: f 2
(3) «Ап' = •
С другой стороны, проецируя (2) па ось АВ, получим:
(4) аАп = а/sin а.
Из (1х, 3, 4) находим:
2
У . 1 . 1 =
А А V sin а' I sin а /sin3a’
АВ
Поскольку ВС = -г-, учитывая формулы (6, 7) вве-Л
дения, получаем:
64
Борис Гринченко
, 1 у1 с с 2 А 2Zsin3a
Представленное решение полезно сравнить с решением этой задачи в книге И. Ш. Слободецкого и Л. Г. Асламазова «Задачи по физике» (Задача № 7).
2. Кинематика относительного движения
65
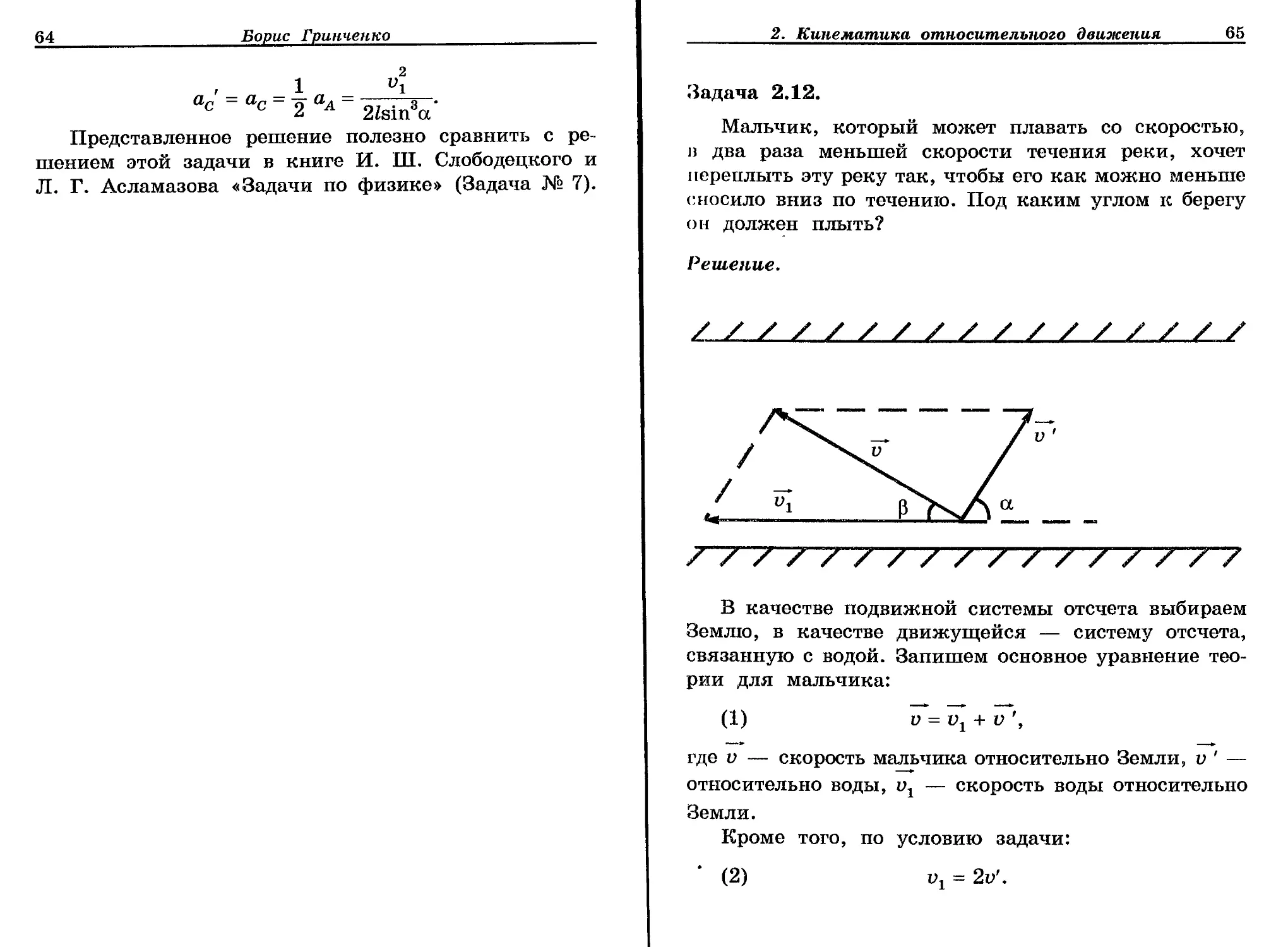
Задача 2.12.
Мальчик, который может плавать со скоростью, в два раза меньшей скорости течения реки, хочет переплыть эту реку так, чтобы его как можно меньше сносило вниз по течению. Под каким углом к берегу он должен плыть?
Решение.
В качестве подвижной системы отсчета выбираем Землю, в качестве движущейся — систему отсчета, связанную с водой. Запишем основное уравнение теории для мальчика:
(1) v = v1 + vf,
где v — скорость мальчика относительно Земли, v ' — относительно воды, — скорость воды относительно Земли.
Кроме того, по условию задачи:
(2) Vj = 2v'.
66
Борис Гринченко
При изменении угла а от 0 до л конец вектора v описывает дугу верхней полуокружности радиуса v'. Чтобы мальчика снесло как можно меньше, не
обходимо, чтобы угол Р был максимален. Именно этот случай и изображен на рисунке. Треугольник со сторонами v, Vi и v' — прямоугольный, поэтому для искомого угла 0 получаем:
. о V 1
8Ш р = — = 2
71
Мб
3. Динамика прямолинейного движения
В инерциальной системе отсчета справедлив закон Ньютона (второй закон Ньютона):
(1) АР = F • At,
где АР = Р2 - Рх изменение импульса тела за время At, F = Fx + F2 + ... — сумма всех сил, действующих на тело. Произведение F • At называют импульсом силы.
Если масса тела остается постоянной, закоц Ньютона приобретает вид:
(2) F = та.
Третий закон Ньютона:
(3) Л = - F2,
где Ft — сила, действующая со стороны первого тела на второе, F2 — со стороны второго тела на первое.
Решение задач на динамику тела (материальной точки) основывается на использовании законов Ньютона (1—3) с последующим проецированием на выбранные оси. Этим определяется последовательность действий:
1. Выполняют чертеж, на котором изображают силы, действующие на тело (тела), и направление ускорения (ускорений). Если направление ускорения неизвестно, его выбирают произвольно, и только решение задачи дает ответ о правильности выбора.
68
Борис Гринченко
2. Записывают законы Ньютона в векторном виде.
3. Выбирают оси. Обычно одну из осей удобно направить вдоль направления ускорения тела, вторую — перпендикулярно ускорению. Выбор осей определяется соображениями удобства: так, чтобы выражения для проекций законов Ньютона имели бы наиболее простой вид.
4. Полученные в проекциях на оси уравнения (1—3) дополняют соотношениями, вытекающими из текста условий задачи. Например, законом Гука, Архимеда, уравнениями кинематической связи, определениями физических величин и т. д.
5. Используя полученную систему уравнений, пытаются дать ответ на вопрос задачи. Если этого сделать не удается, вновь возвращаются к условию задачи и чертежу, с тем чтобы записать недостающее уравнение.
Несколько замечаний, которые могут быть полезными при решении задач:
1. Принцип эквивалентности сил инерции и гравитации (Эйнштейна).
Для использования принципа эквивалентности переходят в движущуюся поступательно систему отсчета, причем ускорение свободного падения тел в этой системе отсчета, согласно разделу 2, определяется уравнением:
(4) g' = g - а,
где g ' — ускорение свободного падения тел в движущейся системе отсчета, g — ускорение свободного падения тел вблизи поверхности Земли, а* — ускорение подвижной системы отсчета относительно Земли. Далее решают задачу по обычной схеме в
3. Динамика прямолинейного движения
69
движущейся системе отсчета, считая ее инерциальной и полагая, что ускорение свободного падения тел в этой системе отсчета вызвано гравитационным притяжением некоторого космического тела (например, планеты), вблизи которого происходит описанное в условии задачи явление. Другими словами, решая задачу в движущейся системе отсчета, мы вправе применять первые принципы и другие факты, которые обычно используют при решении задач в системе отсчета, связанной с Землей, заменив только ускорение g на g
Поясним сказанное решением следующей задачи:
В какую сторону и под каким углом отклонено пламя свечи в движущемся равноускоренно вагоне поезда?
Перейдем в систему отсчета, связанную с вагоном. Для наблюдателя внутри вагона ускорение свободного падения тел g ' определяется соотношением (4).
Наблюдатель в вагоне вправе считать, что он находится вблизи поверхности некоторой планеты, которая сообщает телам ускорение свободного падения g Для условий Земли известен факт: пламя свечи устанавливается вертикально, то есть по направлению ускорения свободного падения. Следовательно, в вагоне пламя свечи установится вдоль направления g причем угол отклонения пламени от вертикали
70
Борис Гринченко
определяется из соотношения: tg а = S где а — ускорение поезда.
2. Трение.
Пусть со стороны поверхности на тело действует сила F. Представим силу F в виде суммы (суперпозиции) двух сил, одна из которых направлена вдоль, а другая по нормали (перпендикулярно) к поверхности. Составляющую, направленную вдоль (по касательной) к поверхности, назовем силой трения FTp, по нормали — силой нормального давления (силой реакции) N. Таким образом:
(5) F = F~Tp + N.
Для силы трения имеем соотношение:
(6) FTP < |iN,
где ц — коэффициент трения.
Будем считать, что в случае проскальзывания сила трения скольжения равна максимальной силе трения покоя:
(7) 1гск = ^Тртах =
3. Динамика прямолинейного движения
71
В случае проскальзывания сила трения направлена против относительного движения соприкасающихся поверхностей. Направление же силы трения покоя в некоторых случаях удается определить только после решения задачи. На первом (физическом) этапе решения задачи силу трения направляют на чертеже произвольно (возможно, учитывая те или иные соображения), а уже на втором (математическом) этапе выясняется, насколько верно выбрано направление силы трения.
Нередко условия задач сформулированы таким образом, что тело находится в «экстремальных» условиях (на грани проскальзывания). В таких случаях для определения силы трения покоя полагают, что проскальзывание уже имеет место, так что направление силы трения и ее величина (7) определены, а затем, возвращаясь к условию задачи, заменяют силу трения покоя уже известной силой трения скольжения.
3. Закон Гука. Силы, упругости.
Для определения понятия силы упругости (натя-
___________I_jl_______
f-------
-----------1---------- ।
жения, сжатия) стержня (троса, пружины, нити и т. д.) в данном сечении, мысленно разрежем стержень этим сечением на две части. Сила Т, с которой правая часть стержня действует на левую, называется силой упругости (натяжения, сжатия) стержня в сечении S. Приложена эта сила к поверхности сечения S левой ‘части стержня.
72
Борис Гринченко
В соответствии с третьим законом Ньютона, с такой же по модулю силой Т, но противоположно направленной, левая часть стержня в сечении S действует на правую.
В случае, когда сечением стержня (троса, пружины, нити и т. д.) является его конец, силой упругости назовем силу, с которой стержень действует на соприкасающееся с его концом тело. Очевидно, что с такой же по модулю, но противоположно направленной силой поверхность тела действует на стержень.
Согласно закону Гука:
(8) F = k |Z-Z0| =k |az|,
где F — сила упругости, Zo, Z — длина тела в не-деформированном и деформированном состоянии соответственно, AZ — величина деформации, k — коэффициент жесткости (упругости).
Направление силы упругости определяется с учетом условий конкретной задачи.
Следует обратить внимание, что в записи закона Гука в форме:
(9) Fx = - kx
предполагается определенный выбор оси х, и по этой причине форма записи (9) не является общей.
Для коэффициента жесткости справедливо соотношение:
(10) k = ~
где S — площадь сечения, Е — модуль Юнга.
3. Динамика прямолинейного движения
73
Задача 3.1.
В лифте, движущемся вверх с ускорением а, на весах лежит груз массы т. Найти показания весов.
Решение.
Рассмотрим все силы, действующие на груз. Вверх действует сила реакции опоры со стороны подставки весов 2V, вниз — сила, с которой Земля притягивает груз (сила тяжести), равная mg'. Ускорение груза совпадает с ускорением лифта.
Записываем основное уравнение динамики для груза:
(1) N + mg = та.
Поскольку нас интересует вес груза, то есть сила, с которой груз давит на опору, воспользуемся третьим законом Ньютона:
(2) N = - Р,
где Р — вес груза.
74
Борис Гринченко
Спроецируем векторные равенства (1,2) на ось х:
(1') N - mg = та
(2') # = Р
(заметим, что (2') можно получить также, взяв обе части (2) по модулю).
Решая систему из последних двух уравнений, получим:
Р = т (g + а).
Второй вариант решения задачи основан на использовании принципа эквивалентности: в системе отсчета, связанной с лифтом, ускорение свободного падения тел:
(3) g ' = g - а.
Проецируя (3) на вертикальную ось, имеем:
g'=g + a.
Отсюда получаем ответ задачи:
Р = mg'= т (g + а).
3. Динамика прямолинейного движения
76
Задача 3.2.
Стержень длиной I тянут за один из концов, при кладывая вдоль оси стержня силу F. Найти силу натяжения стержня на расстоянии х от точки приложения силы. Другие силы не учитывать.
Решение.
(1) F = та
и для «хвоста» длиной I - х:
(2) Т = Ата,
где т — масса стержня, Атп — масса «хвоста», Т — сила натяжения.
Обозначим через т массу стержня, приходящуюся на единицу его длины. Эту величину можно назвать линейной плотностью.
Тогда получим:
(3)
т = 1л
76 Борис Гринченко
(4) Am = (I - х) т.
Решая систему уравнений (1—4), находим:
3. Динамика прямолинейного движения
77
Задача 3.3.
С каким ускорением должна двигаться обезьяна массой т, чтобы груз массой М оставался в покое (см. рисунок)? Трос считать невесомым, нерастяжимым, массой блока и трением пренебречь.
Решение.
На груз действует сила натяжения (упругости) троса Тх и сила тяжести Mg". На обезьяну действует сила натяжения троса 7*2 и сила тяжести Поскольку трос невесом и силой трения пренебрегается, сила натяжения троса в любом его сечении постоянна, в частности,
(1) Тх = Г2 = т.
Доказательство этого утверждения приведем ниже.
Направление ускорения обезьяны, очевидно, зависит от соотношения масс т и М. Для определенности ‘направим его вверх.
Записываем закон Ньютона для груза:
78
Борис Гринченко
(2) Тх + Mg = О
и для обезьяны:
(3) Т2 + mg = ma.
Спроецируем векторные равенства (2,3) на ось х:
(2) Т - Mg = О
(3) Т - mg = ma,
где учтено (1).
Решая систему уравнений (2) и (3), окончательно находим:
Видно, что если М - m > 0, то и а > 0 и, следовательно, выбор направления ускорения верен. Если М - m < 0, то а < 0, что невозможно (а = | а |). Следовательно, при выполнении второго условия ускорение обезьяны направлено вниз.
Доказательство соотношения (1) представляет собой задачу на динамику. “Л В соответствии с этим запишем закон
Ньютона для участка троса справа или слева от блока:
" — (4) А + /2 + = Атпа,
" Л
где Д?п — масса мысленно выделенного нами участка троса, fi и f2 — силы, действующие со стороны соединяющих участков троса, непосредственно примыкающих к выделенному. Поскольку по условию трос невесом, мы
3. Динамика прямолинейного движения
79
вправе положить А?п - 0, и, следовательно, силы натяжения троса в точках 1 и 2 равны по модулю: Л ~ tv Таким образом, сила натяжения прямолинейных участков троса во всех точках одинакова.
Рассмотрим участок троса, соприкасающийся с блоком. Длину его возьмем настолько малой, чтобы считать прямым отрезком. Кроме учтенных ранее сил в соотношении (4), войдет сила реакции опоры со стороны блока 7V, а сила трения со стороны блока, действующая на трос, по условию равна нулю.
Записываем закон Ньютона
(5) + f2 + Azng + N = Атпа
в проекции на ось х, направленную перпендикулярно вектору N, и, с учетом Атп = 0, вновь получаем Л = f2-
В итоге делаем вывод, что сила натяжения троса по всей длине от груза до обезьяны одинакова.
80
Борис Гринченко
Задача 3.4.
К концам нити, перекинутой через блок, прикреплены одинаковые грузы массой т. На один из грузов кладут грузик массой т\, в результате чего система приходит в движение. Найти силу давления грузика на груз. Нить считать невесомой и нерастяжимой, массой блока и трением пренебречь.
Решение.
Обозначим на рисунке силы, действующие на тела,
и запишем для каждого из них закон Ньютона в проекции на вертикальную ось:
(1) Т - mg = та (левый груз)
(2) mg - Т + Р = та (правый груз)
(3) mtg - N = mta (грузик)
и третий закон Ньютона:
3. Динамика прямолинейного движения, 81
(4) Р = N,
где Р — сила, с которой грузик давит на груз, N — сила, с которой груз давит на грузик.
Решая систему уравнений (1—4), находим:
(5) , P = N = —).
v 2m + т1'
82
Борис Гринченко
Задача 3.5.
С каким ускорением следует двигать брусок вдоль горизонтальной поверхности, чтобы лежащее на нем тело начало соскальзывать? Коэффициент трения между бруском и телом равен ц.
Решение.
На тело действуют три силы: сила тяжести, сила нормального давления и сила трения.
Запишем основное уравнение динамики для тела, считая, что ускорение бруска невелико, так что тело не соскальзывает (ускорение тела и бруска совпадают):
N + mg + FTp = та.
Спроецируем это векторное равенство на оси:
(1)
= та
(2)
N - mg = 0.
Кроме того, согласно определению коэффициента трения имеем:
3. Динамика прямолинейного движения
83
(3) F = U.N.
' ' тр max
Из системы (1—3) можно сделать вывод, что максимальное ускорение, которое может испытывать тело,
= = “ = W-
тах т т
Очевидно, что если ускорение бруска больше, чем величина де, тело начнет соскальзывать.
Нередко при выборе направления силы трения указывают на то, что «сила трения направлена против направления движения». Это утверждение, конечно, ошибочно. Кроме случая, рассмотренного в задаче, можно привести много примеров, когда именно сила трения сообщает телам ускорение в направлении движения: набирающий скорость автомобиль или спортсмен и т. д.
84
Борис Гринченко
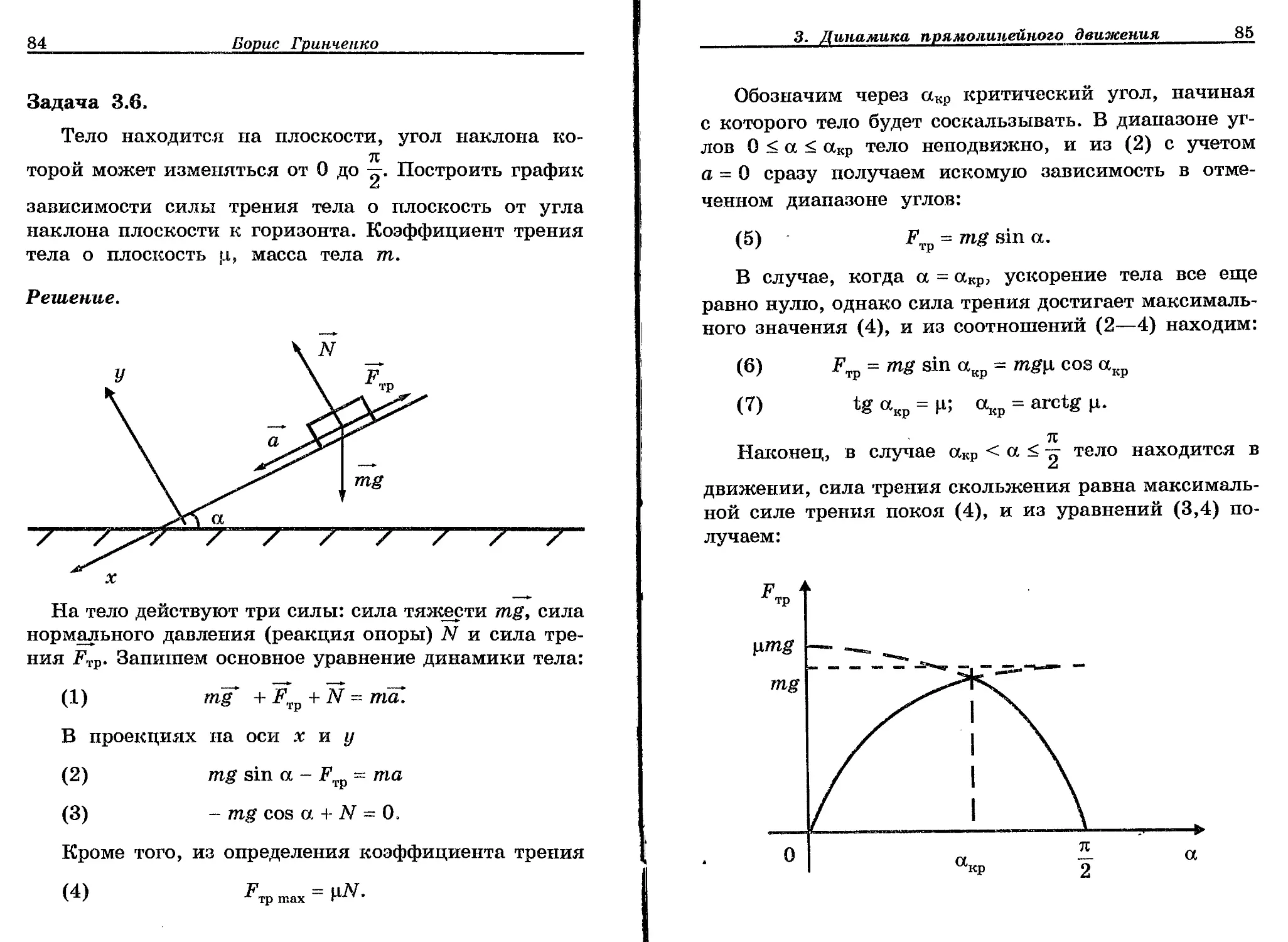
Задача 3.6.
Тело находится на плоскости, угол наклона ко-„ _ л _.
торой может изменяться от 0 до (у. Построить график 2л
зависимости силы трения тела о плоскость от угла наклона плоскости к горизонта. Коэффициент трения тела о плоскость ц, масса тела т.
Решение.
На тело действуют три силы: сила тяжести mg, сила нормального давления (реакция опоры) N и сила трения FTp. Запишем основное уравнение динамики тела:
(1) mg л-F^ + N = та.
В проекциях на оси х и у
(2) mg sin а - FTp = та
(3) - mg cos а + N = 0.
Кроме того, из определения коэффициента трения «) ^Тртах = ^.
3. Динамика прямолинейного движения
85
Обозначим через акр критический угол, начиная с которого тело будет соскальзывать. В диапазоне углов 0 < а < акр тело неподвижно, и из (2) с учетом а = 0 сразу получаем искомую зависимость в отмеченном диапазоне углов:
(5) FTp = mg sin а.
В случае, когда а = акр, ускорение тела все еще равно нулю, однако сила трения достигает максимального значения (4), и из соотношений (2—4) находим:
(6) F = mg sin а = mg^L cos а
(7) tg акр = pi; о^р = arctg pi.
т л
Наконец, в случае акр < а < ~ тело находится в движении, сила трения скольжения равна максимальной силе трения покоя (4), и из уравнений (3,4) получаем:
86
Борис Гринченко
(8) - nmg cos a.
Соотношения (5, 6, 8) позволяют построить искомый график.
3. Динамика прямолинейного движения
87
Задача 3.7.
На гладкой плоскости, наклоненной под углом а к горизонту, лежит доска массой М. Куда и с каким ускорением должен бежать по доске мальчик массой т, чтобы доска оставалась в покое?
Решение.
В задаче идет речь о двух телах, поэтому следует рассмотреть все силы, действующие на каждое из тел, и записать для каждого закон Ньютона.
Гтр 2 — сила трения, с которой ступни мальчика действуют на доску; F^j — сила трения, с которой доска действует на ступни мальчика. На рисунке не изображены силы, параллельные у: силы нормального давления (реакции опоры) со стороны плоскости на доску, нормального давления со стороны ступней мальчика на доску и нормального давления со стороны доски на ступни мальчика. Разумеется, в подобных ситуациях догадаться сразу, что учет этих
88
Борис Гринченко
сил не является существенным, не всегда удается. Поэтому, решая задачу по обычному плану, следовало бы эти силы ввести и учесть, и уже дальнейшее решение задачи выявит их несущественность. Дело в том, что для решения данной задачи оказывается достаточным спроецировать основные уравнения динамики для каждого из тел лишь на ось х — при этом силы нормального давления, перпендикулярные оси х, в полученные уравнения не войдут.
Закон Ньютона для мальчика
FTpl + mg + N = та,
где N — сила нормального давления со стороны доски, в проекции на ось х дает:
(1) F^x + mgsin а = та.
Закон Ньютона для доски
FTp 2 4- Mg + N2 + N3 = О,
где N2 — сила нормального давления на доску со стороны плоскости, JV3 — то же со стороны ступней мальчика, в проекции на ось х:
(2) Mg sin а - F^ 2 = О
(учтено, что доска по условию задачи находится в покое).
Кроме* того,*воспользуемся третьим законом Ньютона: - FTp 1 = FTp 2 или, для модулей этих величин:
(3) F-гр 1 = ^Тр 2"
Система уравнений (1, 2, 3) позволяет решить задачу:
3. Динамика прямолинейного движения 89
т + М а =------g sm а.
т
Направление ускорения мальчика показано на рисунке. Что же касается направления движения (скорости) мальчика, то оно может быть произвольным и зависит от начальных условий. Так, если в начальный момент мальчик покоился относительно доски, то его дальнейшее движение направлено по ускорению (вниз вдоль плоскости). Если же мальчик снизу вбегает на доску, то, очевидно, скорость мальчика некоторое время будет направлена против ускорения, при этом движение в отличие от первого случая является равнозамедленным. Если доска достаточно большой длины, то мальчик в какой-то момент времени остановится и затем начнет двигаться вниз вдоль плоскости (по направлению ускорения).
90
Борис Гринченко
Задача 3.8.
Воздушный шар массой М поднимается вверх с постоянной скоростью. Какую массу балласта необходимо прикрепить к шару, чтобы он стал двигаться с той же скоростью вниз? Подъемная сила шара равна Р.
*L X
В задаче описаны две ситуации, для каждой из которой следует записать закон Ньютона.
В первом случае (шар движется вверх) сила сопротивления воздуха FC1 направлена вниз. Записывая закон Ньютона
P + Fcl + M~g = 0
в проекции на ось х, учтем, что ускорение шара равно нулю (шар движется с постоянной скоростью):
(1) Р - Fcl - Mg = О
Во втором случае (шар движется вниз) сила сопротивления направлена вверх и закон Ньютона
х (М + т) g + Fc2 + Р = О
3. Динамика прямолинейного движения
91
в проекции на ось х имеет вид:
(2) (M + m)g-Fc2-P = Q,
где т — масса балласта, прикрепленного к шару.
Поскольку скорости шара в первом и втором случае равны по модулю, а, как известно, сила сопротивления зависит только от скорости (при прочих равных параметрах), то
(3) FC1 = Fc2.
Имеем систему из трех уравнений с тремя неизвестными: т, Fci, FC2. Вычитая из (2) выражение (1) и учитывая (3), находим:
2Р «и/ т ----2М.
g
92
Борис Гринченко
Задача 3.9.
Под каким углом к горизонту нужно тянуть за веревку тяжелый груз, чтобы с наименьшим усилием передвигать его волоком по горизонтальной поверхности? Коэффициент трения между грузом и поверхностью ц.
Решение.
На груз действуют четыре силы, указанные на рисунке. Поскольку речь идет о минимальной силе, ускорение груза в законе Ньютона следует положить равным нулю. Действительно, представим себе сначала, что приложенная сила F (сила натяжения веревки) недостаточна для того, чтобы сдвинуть груз. Будем постепенно увеличивать эту силу. В какой-то момент (критический момент) сила окажется такой, что еще «чуть-чуть» прибавить — и груз сдвинется. Очевидно, именно это значение силы и есть минимальная сила. Груз в этот момент покоится, однако находится па грани проскальзывания, то есть сила трения достигает своего максимального значения
3. Динамика прямолинейного движения
93
(1) ^тр = цлг.
Закон Ньютона для груза в критический момент:
(2) FTp + N + mg + F = О
запишем в проекциях на оси:
(2х) - FTp + F cos а = О
(2i/) N - mg + F cos а = 0.
Из уравнений (1, 2х, 2у) находим силу F:
(3) F = ^mg . .
cos а + р sm а
Воспользуемся еще раз условием минимальности. Из последнего соотношения видно, что сила F будет минимальна при таком угле а, при котором знаменатель (3) принимает максимальное значение.
Выполним тождественные преобразования знаменателя, аналогично тому, как это было сделано в задаче 1.12:
(4) cos а + р sin а = л/1 + р2 sin (а + <р)
( . 1 Н )
lsm<p = ^T7; COS<P = 7T77/
Следовательно, максимальное значение знаменателя равно у/1 4- р2 (максимальное значение синуса равно 1). Подставляя его в (3), окончательно получаем:
Т, М-
^1 + р2'
Использование условий минимальности силы F:
sin (а + <р) = 1
94
Борис Гринченко
позволяет вычислить сам угол а, при котором требуется минимальная сила:
71 х 1
а = - arctg д
, л , sin (р 1.
(учтено, что а + <р = £; tg ср = = д).
3. Динамика прямолинейного движения
95
Задача 3.10.
Горизонтальная доска имеет ступеньку высотой Н, в которую упирается свободно лежащий па доске однородный цилиндр радиуса R > Н. Доску двигают горизонтально с ускорением а. Определить максимально возможное ускорение а, при котором цилиндр еще не будет подниматься на ступеньку.
Решение.
В системе отсчета, движущейся вместе с доской (в системе отсчета доски), ускорение свободного падения тел
(1) g ' = F - "а.
Воспользуемся принципом эквивалентности сил гравитации и инерции (Эйнштейна): будем считать, что ускорение свободного падения g ' телам сообщает планета, на поверхности которой мы находимся. Оче-* видно, что условие неустойчивого равновесия цилинд
96
Борис Гринченко
ра будет в случае, когда центр масс цилиндра 0 лежит на одной вертикали с точкой опоры А (при этом сила реакции со стороны точки В равна нулю). Другими словами, отрезок АО параллелен вектору g
Из (1) и геометрии задачи находим:
(2) tg а = £
с*>
, R-H R-H
ёа~ № -(R-H)2 ~ (2R- Н)’
и окончательно:
а = g
(2R - Н) R-H
3. Динамика прямолинейного движения
97
Задача 3.11.
С какой силой змея массой М и длиной I действует иа землю, поднимаясь вертикально вверх с постоянной скоростью У?
Решение.
На змею действуют две силы: сила тяжести Mg* и сила реакции опоры со стороны земли N. Запишем второй закон Ньютона для змеи в виде:
ДР — —
(1) — =N + Mg
или в проекции на ось х:
(2) 77 = N - Mg.
В этих соотношениях ДР — изменение импульса змеи за время Ы.
За время At змея приобретает дополнительный импульс
ДР = Ату,
98
Борис Гринченко
где Ат — вовлеченная в движение за время At масса змеи. Введя массу змеи на единицу длины
М I
находим:
j. , j. .4 Mv ..
Mn - p (vAt) = —r- At.
(4)
Подставляя (3) и (4) в (2), получаем:
,г Mv2
N = Mg + —j—. lr
Согласно третьему закону Ньютона, сила давления змеи на землю
F = N = Mg +
£
3. Динамика прямолинейного движения
99
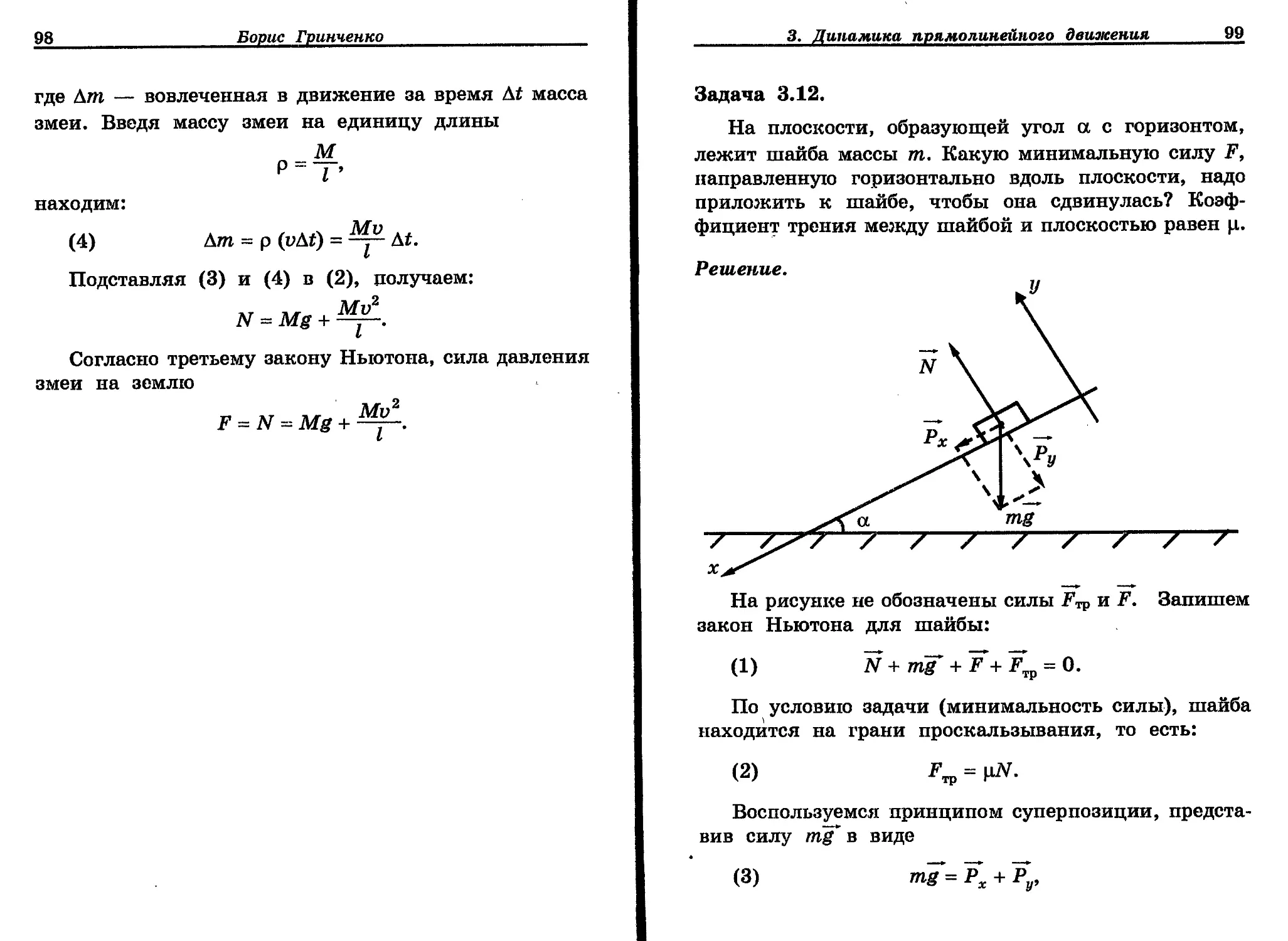
Задача 3.12.
На плоскости, образующей угол а с горизонтом, лежит шайба массы т. Какую минимальную силу F, направленную горизонтально вдоль плоскости, надо приложить к шайбе, чтобы она сдвинулась? Коэффициент трения между шайбой и плоскостью равен ц.
На рисунке не обозначены силы F^ и F. Запишем закон Ньютона для шайбы:
(1) N + nig + F + FTp = 0.
По условию задачи (минимальность силы), шайба находится на грани проскальзывания, то есть:
(2) F^ = [iN.
Воспользуемся принципом суперпозиции, представив силу nig' в виде
(3) W = Рх + Ру,
100
Борис Гринченко
где Рх = mg sin а; Ру = mg cos а. Перепишем (1) с учетом (3):
(4) N + Px + Py + lF + F^O.
Спроецируем (4) на ось у:
(5) N - mg cos а = 0.
Из последнего соотношения видно, что N = - Ру, и, следовательно, из (4) получаем
(6) Px + F + ^ = 0.
Поскольку силы Рх и F перпендикулярны друг ДРУГУ, воспользуемся теоремой Пифагора:
F2 = Р2 + F2. тр Х X '
С учетом (2) и (5), из последнего соотношения находим:
Fmin = mg'Jn2 cos2 а - sin2 а.
Предполагается, разумеется, что |л > tg а, так что
под знаком радикала неот-
(иначе шайба будет
рицательное выражение соскальзывать и при F = 0).
3. Динамика прямолинейного движения
101
Задача 3.13.
Доска массой М движется по гладкой горизонтальной поверхности со скоростью v. Сверху на доску осторожно кладут кирпич массой т. Коэффициент трения между доской и кирпичом равен ц. Какое расстояние пройдет кирпич по доске (то есть, относительно доски) за время проскальзывания?
Решение.
На рисунке введены обозначения: ai — ускорение доски, <Г — ускорение кирпича, — сила трения, действующая на кирпич со стороны доски, FTpl — сила трения, действующая на доску со стороны кирпича. Силы, действующие на доску вдоль оси у на рисунке не указаны.
Записываем закон Ньютона для кирпича:
N + mg + Frp = та в проекции на оси х и у'.
102
Борис Гринченко
(1) N - mg = О
(2) F^ = та.
Закон Ньютона для доски в проекции на ось х:
(3) ^pi=Mar
Согласно третьему закону Ньютона:
F = - F , тр тр 1’ получаем:
(4) F =F
Vх/ тр тр 1
В режиме проскальзывания:
(5) F^ = цЛГ.
Система уравнений (1—5) позволяет решить динамическую задачу — рассчитать ускорения а и аг
(6) а = pg;
Переходим к решению кинематической задачи. Для этого удобно перейти в систему отсчета, связанную с доской. Обозначив через а ' ускорение кирпича относительно доски, воспользуемся основным уравнением теории раздела «Кинематика относительного движения»:
сГ = а[ + а~'
в проекции на ось х:
- а = аг + ах, или, с учетом соотношения а' | ах |,
3. Динамика прямолинейного движения
103
(7) а' = а + аГ
Таким образом, имеем следующую задачу: кирпич, имея в начальный момент времени скорость v (относительно доски), движется относительно доски равнозамедленно с ускорением а'. Необходимо вычислить путь, пройденный кирпичом до полной остановки.
Простые вычисления дают следующий результат:
Подставляя сюда а' из (7), с учетом соотношений (6) окончательно получаем:
Представим также другое решение задачи, используя законы сохранения.
Закон сохранения импульса в проекции на ось х дает:
(8) Mv = (М + т)
где — скорость доски вместе с кирпичом в момент времени, когда движение кирпича относительно доски прекратилось.
Согласно закону сохранения энергии: Mv2 М + т 2
(9) -у = —2— U1 + PmgS’
где учтены соотношения (1) и (5). Последнее слагаемое в (9) — тепло, выделившееся за счет работы силы трения на пути S.
Из (8, 9) после несложных преобразований получим ответ, совпадающий с приведенным выше. Воз
104 Борис Гринченко
можен и третий вариант решения, связанный с переходом в систему отсчета, в которой кирпич покоится, то есть в систему отсчета кирпича. В таком варианте решения практически все выкладки первого варианта решения остаются в силе.
Наконец, четвертый вариант решения может быть выполнен в системе отсчета, связанной с Землей. Для этого необходимо после решения динамической части задачи и расчета ускорений (см. выше) рассмотреть как перемещение самого кирпича за время проскальзывания, так и той точки доски, которой кирпич коснулся в первый момент. Сумма этих путей и даст искомую величину.
3. Динамика прямолинейного движения
105
Задача 3.14.
Шайба налетает на неподвижную стенку под углом а к нормали. Коэффициент трения между стенкой и шайбой Ц. Под каким углом шайба отлетит от стенки? Движение шайбы считать поступательным, потери модуля нормальной компоненты скорости шайбы после удара не происходит.
Решение.
Закон Ньютона запишем в форме:
(1) AP = FAf; F = ^ + 2V,
где АР — изменение импульса шайбы за время At взаимодействия (удара) со стенкой, F — средняя сила, действующая на шайбу со стороны стенки.
Спроецируем (1) на оси х и у:
(1х) АРХ = - Гтр At,
106
Борис Гринченко
(М ДРу = NM,
где
(2) ДРЖ = Р2х - Р1Х = mu2sin р - znujsin а,
(3) ДРу = Р2у - Р1у = mu2cos р + ?nu1cos а, т — масса шайбы.
Кроме того, по условию задачи (отсутствие потери модуля нормальной компоненты скорости):
(4) cos а = v2 cos р.
Будем считать сначала, что во время удара шайба проскальзывает вдоль стенки, то есть угол отскока шайбы р * 0. В этом случае сила трения скольжения дается соотношением:
(5) FTp = »N.
Разделив почленно (1х) на (1г/) и воспользовавшись (2—5), после несложных вычислений получим:
tg р = tg а - 2|i или р = arctg (tg а - 2|i).
Эта формула справедлива при ц tg а. Если |i>-^tga, тор = 0. Доказательство этого утверждения предоставим читателю.
Возникает вопрос о корректности введенного понятия средней силы. Можно показать, что в данном случае ^ведение такого понятия не приводит к ошибке. Действительно, строгое использование закона Ньютона дает:
3. Динамика прямолинейного движения
107
(6)
At
АР = \l?dt о
или, в проекциях на оси:
At
(7) ДР,-{р„Л
О
At
(8) &Py=\Ndt.
о
Подставим в (7) Frp из (5) и, вынося постоянную |i за знак интеграла, получим:
At
(9) APx = pJwdt.
о
Разделив (9) на (8), приходим к тому же результату, что и в приведенном выше решении.
108
Борис Гринченко
Задача 3.15.
Ракета массы М неподвижно зависла вблизи поверхности Земли. Массовый расход двигателя ракеты равен ц. Найти скорость истечения газа.
Решение.
Закон Ньютона для ракеты в проекции на вертикальную ось:
(1) Mg = F,
где F — действующая на ракету вверх реактивная сила.
Запишем также (в проекции на ось х) закон Ньютона для массы газа Дтп, которая за время Д4 проходит через сопло ракеты:
(2) Дтпп = F^t,
где слева импульс, который приобретает газ за время Дг (поскольку начальный импульс газа равен нулю, эта величина есть изменение импульса), справа — импульс силы (Fx — сила, действующая на газ со стороны передней стенки камеры сгорания).
Согласно третьему закону Ньютона:
(3) F = Fv
Учитывая определение величины массового расхода:
3. Динамика прямолинейного движения
109
(4)
Дтп
ц = -дГ’
из (2) находим выражение для величины реактивной силы:
F = рм.
Подставив последнее соотношение в (1), окончательно имеем:
Отметим, что найденное выражение для реактивной силы является общим.
110
Борис Гринченко
Задача 3.16.
Найти ускорение груза, к которому приложена сила F. Каждый из грузов имеет массу т, нить и блок невесомы,
трения и других внешних сил нет.
Решение.
Обозначим силы, действующие на тела, и их ускорения, как показано на рисунке, и запишем закон Ньютона для каждого из тел в проекции на ось х:
(1)
(2)
(3)
F - Т = та±
Т = та2
2Т = та.
Для того, чтобы использовать условие нерастяжи-мости нити (это условие всегда предполагается выполненным), перейдем в систему отсчета груза, неподвижно связанного с блоком (то^есть в систему отсчета, движущуюся с ускорением а ). Запишем вы
3. Динамика прямолинейного движения
111
ражения для ускорения других грузов в этой системе отсчета:
(4) а/ = а± - а
(5) а2' = а2 + а.
Условие нерастяжимости, очевидно, имеет вид:
(6) а/ = а2'-
Решая систему уравнений (1—6), находим:
5 F
1 о т
При записи (3) предполагалось, что сила, действующая на груз с блоком со стороны нити, равна 2Т. Докажем это. Запишем закон Ньютона для части нити, соприкасающейся с блоком, учитывая ее невесомость:
(7) 2Т - Nj = О,
и третий закон Ньютона для взаимодействия блока с нитью:
(8) N = Nlt
где 2Т — сила, действующая со стороны оставшейся части нити, — сила, действующая, на нить со стороны блока, N — сила, действующая на блок со стороны нити.
Из (7, 8) получаем N = 2Т, что и требовалось доказать.
4. Динамика вращательного движения
Наряду с изложенным в предыдущем разделе (Динамика прямолинейного движения), при решении задач данного раздела следует использовать два факта из кинематики вращательного движения:
1. При равномерном вращении по окружности ускорение тела направлено к центру вращения (центростремительное ускорение).
2. Модуль этого ускорения определяется формулой
(1) а = =
,гС
где v — линейная скорость тела, R — расстояние от тела до центра вращения, ® — угловая скорость.
В случае неравномерного вращения составляющая полного ускорения, направленная к центру вращения, также дается формулой (1) (см. введение к разделу 2).
В качестве одной из осей координат, на которые проецируют векторное уравнение второго закона Ньютона, целесообразно выбрать ось, направленную по центростремительному ускорению (эта ось, разумеется, вращается), то есть ось, проходящую через тело и центр вращения. При таком выборе проекция полного ускорения при неравномерном вращении определяется формулой (1):
V2 2п
«»= в=®в-
4. Динамика вращательного движения
113
Величину ап называют нормальной составляющей полного ускорения. При равномерном вращении, очевидно, а - ап.
Нередко употребляется выражение «центростремительная сила». Следует иметь в виду, что «центростремительной силы», как силы особой природы, не существует. На тело могут действовать несколько реальных сил (например, сила тяжести, сила упругости и т. д.), при этом составляющую суммы всех этих реальных сил, направленную к центру вращения, иногда называют «центростремительной силой». Утверждения типа «На тело действуют сила тяжести, сила натяжения нити и центростремительная сила», очевидно, бессмысленны.
Согласно закону всемирного тяготения:
где F — сила, с которой одно из тел действует на тт 2 Л _ Il £1 • М
другое, G = 6,7 • 10 ——— — гравитационная
постоянная, R — расстояние между точечными массами тг и т2. Закон (2) справедлив также для тел со сферически симметричным распределением массы, например, для сплошных однородных шаров и тонких однородных оболочек. В частности, (2) справедлив для взаимодействия небольших (по сравнению с радиусом Земли) тел, находящихся вблизи поверхности Земли, с самой Землей. При этом в качестве расстояния R следует брать расстояние между центрами масс взаимодействующих тел.
114
Борис Гринченко
Задача 4.1.
К краю диска радиуса R, на нити длины I, подвешен груз. Найти угловую скорость вращения диска, если угол между нитью и вертикалью а.
Решение.
, На груз действуют две силы: сила натяжения нити Т и сила тяжести mg.
Поскольку тело вращается по окружности радиуса R + I sin а, его ускорение равно
(1) а = со2 (R + I sin а)
и направлено к центру вращения (точка О). Записываем Закон Ньютона для груза:
Т + nig = ma
в проекциях на оси х:
(2) 7’sin а = та
и у’.
4. Динамика вращательного движения 115
(3) Т cos а - mg = О
(ах = а; ау = 0).
Решая полученную систему уравнений (1—3) относительно о, находим:
«, = о*» .
R + I sm а
Следует заметить, что, с формальной точки зрения, система из трех уравнений (1—3) содержит четыре неизвестные величины: Т, <о, m и а. Решить такую систему в общем виде, то есть отыскать все неизвестные величины, невозможно. Однако этого в вопросе задачи и не требуется. Вычислить же величину о оказывается возможным. При этом масса в ответ не вошла и, следовательно, ответ задачи от массы груза не зависит.
Борис Гринченко
116
+
Задача 4.2.
Пружину с прикрепленным грузом раскрутили До угловой скорости со. Найти расстояние от центра вращения до груза. Длина недеформировапной пружины 1о, ее жесткость k, масса груза т. Внешними силами пренебречь.
Решение.
На груз со стороны пружины действует сила упругости F.
Ускорение груза направлено к центру вращения и равно
(1) а = Л
Второй закон Ньютона для груза
F = та запишем в проекции на ось х:
(2) F = та.
Воспользуемся также законом Гука:
(3) F = k ( / - Zo).
4. Динамика вращательного движения
117
Из уравнений (1—3) находим:
k
Это выражение имеет физический смысл при условии:
1 /и 2 л
1 - -г- со > 0 k
или
со < т
В противном случае (со > равновесие груза невозможно. В реальных условиях следует учесть, что закон Гука (3) справедлив при небольших деформациях I - 1о (обычно I - 1о « /о).
118
Борис Гринченко
Задача 4.3.
Найти массу Солнца по постоянной тяготения G, периоду обращения Земли вокруг Солнца Т и расстоянию L от Земли до Солнца.
Решение.
Будем считать, что орбита Земли — окружность (это подразумевается в условии заданием L) и Солнце неподвижно (масса Солнца много больше массы Земли). Запишем основное уравнение динамики для Земли в проекции на ось х:
(1) F = та,
где т — масса Земли, а центростремительное ускорение а, согласно кинематике вращательного движения:
(2)
а = со 2L.
Угловая скорость связана с периодом обращения соотношением:
4. Динамика вращательного движения 119
(3) 2л ®
Согласно закону всемирного тяготения:
(4) „ GMm F= Ll ’
где М — масса Солнца.
Решая полученную систему уравнений (1—4), находим:
., 1 г з ( 2л \2
M=GL М’
120
Борис Гринченко
Задача 4.4.
Какова первая космическая скорость для планеты с той же плотностью, что и Земля, но с вдвое меньшим радиусом? Первая космическая скорость Земли равна Vi.
Решение.
vi
Запишем основное уравнение динамики для спутника произвольной планеты массой М, вращающегося по круговой орбите радиуса R (близкой к радиусу планеты) со скоростью v, по аналогии с предыдущей задачей:
(1)
F = та,
где т — масса спутника, F — сила, действующая на спутник со стороны планеты, а — центростремительное ускорение.
(2) F = “V",
4. Динамика вращательного движения
121
(3) « = -#"•
It
Свяжем массу планеты с ее плотностью:
(4) М = |гсК3р,
где — объем планеты, р — ее плотность.
О
Кроме того, согласно условию задачи,
(5) Rx = 2Я2,
где и Л2 — радиусы Земли и планеты соответственно.
Далее следует выразить v из (1—4), записать полученное выражение дважды для Земли и для планеты, поделить одно на другое и воспользоваться (5). В результате получаем:
122
Борис Гринченко
Задача 4.5
При взвешивании тела массой т на пружинных весах, их показания на полюсе и экваторе планеты отличаются на ДР. Радиус планеты R. Определить угловую скорость вращения планеты вокруг своей оси.
Решение.
В условии описаны две ситуации, следовательно необходимо дважды записать закон Ньютона.
В случае взвешивания тела на экваторе в проекции на ось х получаем:
(1) F0-Na = та,
где Р8 — сила притяжения массы планетой на экваторе, N9 — сила реакции опоры со стороны подставки весов, ускорение тела
(2) а = (o2R.
4. Динамика вращательного движения
123
Аналогичное соотношение запишем для случая взвешивания тела на полюсе, учитывая, что ускорение центра масс тела здесь равно 0:
(3) ^"^ = 0.
Согласно третьему закону Ньютона:
(4) Л = Na,
(5) Ра = Nn,
где Рэ — вес тела (сила, с которой тело действует на подставку весов) на экваторе, Рп — на полюсе.
Очевидно, что на основании закона всемирного тяготения:
(6)
(в принципе, следовало бы дважды записать закон всемирного тяготения для Fg и Рп).
По условию задачи
(7) РЭ-РП = ДР.
Итак, имеем систему из 7 уравнений с 7 неизвестными. Ее решение не представляет затруднений:
со
mR'
124
Борис Гринченко
Задача 4.6.
Космический корабль движется по круговой орбите радиуса R вокруг Земли со скоростью v, вдвое большей скорости свободного движения по той же орбите. Какую силу тяги развивает двигатель корабля, если его масса /и?
Решение.
Запишем закон Ньютона для космического корабля в двух описанных в задаче ситуациях: свободное вращение по орбите радиуса R со скоростью щ и вращение по той же орбите с включенным двигателем,
развивающим силу тяги F, со скоростью о:
(1) FT = та[
(2) +
где FT — сила притяжения Земли, одинаковая в обеих ситуациях, и
4. Динамика вращательного движения 125
У?
(3) а, =
(Л\ v 2
(4) а2 = -д.
__Из ^ (2^ видно, что направление силы тяги F = та - F-r совпадает с направлением центростремительного ускорения ai. Проецируя (1, 2) на ось, направленную по ускорению, получим:
(Г) FT = та,
(2') FT + F = та.
Учитывая, что согласно условию:
(5) v = 2vv
из (1', 2', 3, 4) находим:
р 3 mv2
F=4_R“-
126
Борис Гринченко
Задача 4.7.
Найти максимальную и минимальную перегрузку, которую испытывает летчик, выполняя «мертвую петлю» радиуса R. Скорость самолета v.
Решение.
На летчика действуют сила реакции со стороны кресла N и сила притяжения Земли mg'(т — масса летчика).
Пусть в произвольный момент времени угол между вертикалью и осью х равен а (см. рис.).
Запишем основное уравнение динамики для летчика:
(1)
N + mg = та
в проекции на ось х:
(2) N cos р - mg cos а = та
и на ось у:
(3)
N sin р - mg sin а = О,
4. Динамика вращательного движения
127
где р — угол между направлениями оси х и вектором N.
Ускорение летчика
v2 а = “vr
R
и направлено к центру вращения О.
По определению, величина перегрузки дается соотношением:
(5) п = —
' mg
Из системы уравнений (2—4) выразим N. Для этого выполним преобразования:
2
(N cos Р)2 = ( + mg cos a Y
4 XI 7
(N sin Р)2 = (mg sin а)2.
Подставим полученное значение 2 1
N = [ ( + mg cos а ) 2 + (mg sin а) 2] 2
в (5):
п
= + 2^соза + !•
Отсюда видно, что максимальное значение п принимает при а = 0 (в нижней точке траектории):
Лтах Rg
Минимальное значение п достигает при а = л
(верхняя точка полета) nmin Rg
128
Борис Гринченко
Задача 4.8.
Тонкое резиновое кольцо массой т и радиуса Во раскрутили до угловой скорости со. Найти новый радиус кольца, если жесткость резины k. Внешние силы не учитывать.
Решение.
Как мы уже отмечали, в задачах на динамику следует стремиться, в первую очередь, к тому, чтобы записать Закон Ньютона. Для всего кольца это сделать невозможно, поскольку различные фрагменты кольца имеют различные (по направлению) ускорения. Поэтому, видимо, следует попытаться записать закон Ньютона для небольшого (с длиной, в пределе стремящейся к нулю) фрагмента, для всех элементов которого можно с хорошей точностью считать ускорение одинаковым.
Пусть мысленно выбранный фрагмент кольца опирается на угол 2а. _
Обозначим через и Т% силы упругости, действующие на фрагмент со стороны соседних элементов
4. Динамика вращательного движения
129
кольца. Записываем закон Ньютона для выделенного фрагмента кольца
+ Т2 = ^ina
в проекции на ось х:
(1) Тх sin а + Т2 sin а ® Атпа,
где A пг — масса фрагмента. Знак приближенного равенства связан с тем, что различные точки фрагмента имеют отличающиеся по направлению ускорения.
В силу симметрии (кольцо растянуто равномерно):
(2) Л = т2 = Т-
Из кинематики вращательного движения имеем:
(3) а = ®2Я.
Запишем закон Гука для кольца:
(4) Т = k (2nR - 2tlR0).
Чтобы обосновать соотношение (4), следует разбить все кольцо на п равных (для простоты) частей, причем при больших п каждый из фрагментов длиной Ах/ можно считать прямолинейным. Затем применить для каждого фрагмента закон Гука в обычной форме:
Г = kn (Axz - Ахг 0), где kn -kn — жесткость фрагмента кольца
Складывая п соотношений для закона Гука, приходим к равенству (4).
130
Борис Гринченко
Нетрудно убедиться, что полученных уравнений недостаточно, чтобы получить решение задачи. Для нахождения связи между а и Дтп удобно ввести физическую величину р — массу кольца, приходящуюся на единицу угла (1 радиан). Очевидно, что т п
р = =—, где 27t угол, на который опирается вся масса кольца т.
Масса Дтп, приходящаяся на угол 2а, равна:
(5) Дтп = р2а = 2а.
Учитывая, что для малых углов:
(6)
sm а « а
получаем:
2"
из системы уравнений (1—5) окончательно 4тс/г.Йп R =------------------------—
. . та ink- —
Выражение для R теряет смысл, когда знаменатель обращается в нуль или становится отрицательным,
то есть при cd > V = (Do- Физический смысл этого
ограничения (со < V------) обсуждался в задаче 4.2 —
771>
стационарное вращение при со > соо невозможно, радиус кольца увеличивается.
4. Динамика вращательного движения
131
Задача 4.9.
Две звезды образуют двойную систему с неизменным расстоянием между ними R. Сумма масс обеих звезд равна М. Чему равен период обращения звезд вокруг общей точки вращения?
Гравитационная постоянная равна G.
Решение.
Записываем закон Ньютона для каждой из звезд в проекции на ось х:
(1) Ft =
(2) Г2 = Л12а2’
и закон всемирного тяготения для каждой из звезд:
Gm.m,
(3) Л =
хг
Gm.m9
(4) F2 =
XI
где через и т2 обозначены массы звезд, так что:
132
Борис Гринченко
(5) т1 + т2 = М.
Ускорения звезд:
(6) аг = х-^2
(7) = #2® »
где х1 и х2 — расстояние от каждой звезды до центра вращения, со — угловая скорость вращения каждой звезды вокруг общего центра вращения, причем:
(8) хг + х2 = R
Подставляя (3, 4) и (6, 7) в (1, 2), после несложных преобразований с учетом (5,8) получаем:
Т = 2л V -----Д3—= 2Л л/~
G (т1 + т?) GM
4. Динамика вращательного движения
133
Задача 4.10.
С какой минимальной угловой скоростью нужно вращать ведро в вертикальной плоскости, чтобы из него не выливалась вода?
Расстояние от дна ведра до центра вращения I.
Решение.
Пусть в произвольный момент времени угол между вертикалью и осью ОА оказался равен а. На воду действует сила тяжести nig, силы реакции со стороны боковых стенок ведра, направленные перпендикулярно оси х (сумму этих последних сил обозначим через
0 ) и сила реакции N со стороны дна.
Записываем закон Ньютона для воды в ведре:
mg + N + 0 = та
в проекции на ось х (при этом 0Х = 0):
(1) N + mg cos ос = та.
Из кинематики вращательного движения имеем:
(2) а = o2Z,
134
Борис Гринченко
и, кроме того, ускорение воды направлено к центру вращения (см. рис.).
Вода не выливается до тех пор, пока ость взаимодействие с дном ведра, то есть:
(3) N > О,
причем N = 0 соответствует критической ситуации — вода и дно находятся на грани соприкосновения.
Из системы (1—3) находим:
N = - mg cos а + /nZ®2 > О или
л/£ COS а
(4) со > \-----j---.
V
Поскольку соотношение (4) должно быть справедливо для всех а, окончательно получаем:
<0 • шш1п ’ I •
Наиболее «опасный» участок движения соответствует а = 0, то есть моменту времени, когда ведро находится в высшей точке своей траектории. При вращении с угловой скоростью о = ©min в высшей точке N = 0 (во всех других N > 0), однако вода проходит это состояние (с а = 0) мгновенно и поэтому не успевает оторваться от дна (то есть вылиться).
Приведенное решение является приближенным, так как предполагалось, что все фрагменты воды имеют одинаковые ускорения. Иными словами, мы считали, что расстояние от поверхности воды до дна и диаметр дна много меньше I.
4. Динамика вращательного движения
136
Задача 4.11.
Тонкое резиновое кольцо массы т надето на горизонтально расположенный диск радиуса R. Сила, с которой растянуто кольцо, Т. Коэффициент трения между кольцом и диском ц. При какой угловой скорости ю вращения диска кольцо с него начнет спадать?
Решение.
Запишем закон Ньютона для малого фрагмента кольца, опирающегося на угол 2а:
(1) Тг + Т2 + tong + FTp + N = tona, причем:
(2) Tt = T2 = T
136
Борис Гринченко
У
а = g)2R.
(3)
Спроецируем (1) на оси х и у.
(lx) 2Т sin а - N = Ьтпа
(1г/) - Ftp + mg = О
В критический момент, когда кольцо находится на грани проскальзывания:
(4)
FTP =
Учитывая, что
(5) Дтп = ~ • 2а
и sin а ~ а, из последних пяти соотношений находим: - л /ЗлТ g Ю° V mR цВ ’
Отметим, что сила, с которой растянуто кольцо, постоянна до тех пор, пока кольцо не деформируется, то есть его радиус не изменится (закон Гука).
Таким образом, при со > соо кольцо соскользнет с диска.
4. Динамика вращательного движения
137
Задача 4.12.
На горизонтально расположенном диске находится тело массой т = 1 кг, прикрепленное к штырю, который проходит через вертикальную ось диска. В начальный момент пружина несколько растянута, действуя на тело с силой Fo = 4 Н. Коэффициент трения между телом и поверхностью диска ц=1, расстояние от штыря до тела R = 1 м. Диск начинают медленно раскручивать вокруг оси. Построить график зависимости силы трения FTp, действующей на тело, от угловой скорости со вращения диска.
Решение.
Запишем закон Ньютона для тела, полагая, что оно покоится относительно диска:
(1)
_F0 + W + ?ия + -Гтр = та
и соотношение
(2)
а = g)* 2R.
Спроецируем (1) на ось х, совпадающую с направ-• лением центростремительного ускорения и вертикальную ось у:
138
Борис Гринченко
(1Х)
(12/)
FTpx = Fo ~ т N = mg.
Согласно определению коэффициента трения:
(3)
При
При
построении графика учтем, что = | F^ х |.
А / Fo п - 1 е-
соо = Д/—б = 2 с сила трения обращается в ’’ Пп
нуль, а
- kimg + F0 _ i
при coi = \/---=— = 3,7 с достигает мак-
’ mtt
симального значения \irng = 10 Н.
Отметим, что при 0 <в < <во сила трения направлена от центра вращения, а при too < ® coi — к центру. При о > coi тело начинает скользить относительно диска, при этом FTp = FTp max = ц mg = 10 Н.
5. Статика
Пусть в пространстве имеется система тел с массами mi, m2... Выберем произвольную точку О в качестве начала системы отсчета _и соединим ее с каждым из тел радиус-векторами JRi, -Й2-.., считая тела материальными точками.
Введем понятие центра масс системы масс (центра инерции) соотношением:
(1)
— A m,R, д- —
L rnt
так что конец вектора R назовем центром масс (центром инерции). Спроецировав равенство (1) на какую-либо ось, например, ось х, получим:
(2)
S mtxi
X ---------
Е mi
140
Борис Гринченко
Именно последним соотношением и приходится обычно пользоваться при решении задач.
Возникает вопрос, корректно ли определение (1), иными словами, не изменится ли положение центра масс, если в качестве начала системы отсчета выбрать ДРУГУЮ точку О'? Простым вычислением нетрудно показать, что данное определение корректно.
Докажем несколько утверждений, которые используются при решении задач статики и других разделов механики.
1. Центр масс однородного симметричного тела совпадает с его центром симметрии.
Поместим точку О в центр симметрии тела. Разобьем все тело на очень малые фрагменты, которые можно, следовательно, считать точечными массами. Попутно отметим, что массу можно считать точечной, если ее размер намного меньше длины соответствующего радиус-вектора. Для каждого фрагмента с массой nit, найдется другой такой же фрагмент с той же массой, обозначим ее пц', симметричный фрагменту mi относительно точки О, причем, очевидно, соответствующие этим фрагментам радиус-векторы связаны соотношением:
(3) X = - Ч
Из (3) вытекает, что
(4) R = —= 0,
2^
поскольку равен нулю числитель дроби (4). А это означает, что точка О является центром масс системы тел.
5. Статика
141
2. При подсчете центра масс двух тел можно поступить следующим образом. Сначала вычислить центры масс каждого из тел, а затем заменить данные тела точечными массами (равными массам соответствующих тел), сосредоточенными в центрах масс соответствующих тел.
Центр масс всей системы, состоящей из двух тел, согласно определению (1) дается соотношением:
(5)
Ицм
+ £т/В/ 2Х + ^т(
где штрихованные параметры относятся к правому телу, нештрихованные — к левому.
Центры масс каждого из тел, согласно тому же определению (1):
(6)
(7)
Я =
IX
гС =----•
142
Борис Гринченко
Нам, следовательно, необходимо доказать, что
(8)
-- _ mR -I- m'R' цм~ т -I- т' ’
где обозначено т = и т' =
Подставляя R4M, R, R' из (5, 6, 7) в (8), получаем тождественное равенство. Таким образом, утверждение доказано. Данное доказательство может быть обобщено на систему из нескольких (более двух) тел.
3. Потенциальная энергия тела в однородном, поле тяжести равна потенциальной энергии материальной точки с массой, равной массе данного тела, помещенной в центр масс этого тела.
Разобьем тело на малые фрагменты, которые будем считать точечными массами, и запишем потенциальную энергию тела в поле тяжести:
яп = = —-— т,
Ilk
где обозначено т =
5. Статика
143
Учитывая, что, согласно определению:
Хцм ~
т ’
получаем:
Еп = т§хцм,, что и требовалось доказать.
4. Момент силы тяжести действующий на тело произвольной формы относительно произвольной точки равен моменту силы тяжести, действующей на материальную точку с массой, равной массе данного тела и помещенной в центр масс данного тела относительно той же точки. Иными словами, при подсчете момента сил тяжести протяженного тела массой М, мы вправе заменить это тело точечной массой М, помещенной в центр масс данного тела.
Разобьем тело на малые фрагменты и запишем выражение для суммарного момента сил тяжести, действующих на тело относительно точки О:
144
Борис Гринченко
М = 2JWi = 2^rnlgxi = —-— т. fit/
Воспользовавшись определением:
Х«м “ т ’ окончательно получаем:
М = mgx . цм
Сформулируем основные уравнения статики твердого тела. Для того, чтобы тело находилось в состоянии равновесия, необходимо и достаточно выполнение двух условий:
(9) 2Х=0
(10) ZX = О,
где ^Ft — сумма всех сил, действующих на тело, — сумма моментов всех сил, действующих на тело относительно произвольной точки пространства.
Моментом силы М относительно точки О называется величина М = F • I, где плечо силы I равно расстоянию от точки О до линии действия силы F, то есть равно длине перпендикуляра, опущенного из точки О на прямую, проходящую по вектору F. Обычно моменты сил, закручивающие тело по часовой стрелке, считают положительными, против — отрицательными.
Выбор точки О, относительно которой подсчитывают суммарный момент действующих на тело сил, определяется соображениями удобства. Точку О удоб
5. Статика
145
но выбирать так, чтобы через нее проходило как можно больше линий действия сил, либо неизвестные силы: в этом случае запись (10) упрощается.
Нередко при решении задач достаточно использовать одно из условий равновесия (9) или (10). Так, при решении задач с телами, имеющими ось вращения, иногда достаточно записать условие (10), выбрав в качестве О точку, лежащую на оси вращения.
146
Борис Гринченко
Задача 5.1.
Вычислить центр масс фигуры, состоящей из двух точечных масс т\ и тг, на расстоянии I друг от друга.
Решение.
Выберем начало системы отсчета в центре масс одного из тел и направим ось х, как показано на рисунке.
Согласно определению, шххх + т2х2 т21 х =---------------------—---------.
тх + т2 тх + т2 поскольку хх = 0, х2 = I.
Аналогично для координат центра масс по осям у и г находим:
Уцм ~ 0
гцм ~ 0
(Ух = У2 = 0; zx = г2 = 0).
Таким образом, центр масс данной системы тел тпг/
расположен на расстоянии --------- от тела массой
7П1 + ТП2
mi на линии, соединяющей массы.
5. Статика
147
Задача 5.2.
Вычислить центр масс фигуры (см. рис.).
т 2т Зт 4т
Решение.
Выберем систему координат, как показано на рисунке, и воспользуемся определением понятия центра масс
_ mtXi _ _2m£+_3w2£+_4m3Z хцм у, т + 2т + Зт + 4т
Для координат центра масс по осям у и г имеем:
Уцм ~ О
2=0 цм
Следовательно, центр масс расположен на расстоянии 21 от массы т на линии, проходящей через центры масс.
148
Борис Гринченко
Задача 5.3.
Определить центр масс плоского однородного диска с вырезанным отверстием (см. рис.). Величины R, г и d известны.
Решение.
При решении задач данного типа удобно применять следующий прием. Мысленно вырежем еще одно отверстие в диске, симметричное имеющемуся относительно точки О. Получившаяся фигура (диск без двух отверстий) обладает центром симметрии О и, следовательно, ее центр масс также расположен в точке О.
Центр масс мысленно вырезанного круга находится в его центре.
Будем отыскивать центр масс искомой фигуры, полагая, что она состоит из двух тел: круга и диска с двумя отверстиями. Согласно полученным во введении к разделу результатам, эта задача эквивалентна нахождению центра масс двух точечных масс, сосредоточенных в точках О и О'.
Выберем систему координат с началом в точке О.
5. Статика
149
Согласно определению центра масс: md х«м “ М + т
Обозначим через р массу диска, приходящуюся на единицу его площади. Тогда масса круга равна:
(2) т = рлг2,
а масса диска с двумя отверстиями:
(3) М = рл (В2 - 2г2).
Подставляя (2, 3) в (1) и сокращая на рл, окончательно получаем:
г2 х =—------- d.
цм
Таким образом, центр масс искомой фигуры расположен на отрезке ОО’ на расстоянии хцм от точки О.
160
Борис Гринченко
Задача 5.4.
Доказать, что центр масс плоского треугольника находится в точке пересечения медиан.
Решение.
Докажем сначала, что центр масс треугольника лежит па медиане ВМ. Для этого разобьем треугольник на тонкие полоски, параллельные основанию АС. Поскольку можем считать полоски сколь угодно тонкими, то со сколь угодно большей точностью можем считать каждую полоску прямоугольником, центр масс которого находится в его центре симметрии, то есть посередине полоски в точке К, которая, как нетрудно показать, принадлежит медиане ВМ.
Чтобы найти положение центра масс всего треугольника, мы должны, согласно доказанному во введении утверждению, собрать массу каждой полоски в ее центре и вычислить центр масс расположенных на прямой ВМ точечных масс. Очевидно (см. определение понятия центра масс и решение задач 5.1.
5. Статика
151
и 5.2.), что центр масс точечных масс, расположенных на одной прямой, сам принадлежит этой прямой.
Проводя аналогичные рассуждения для двух других медиан, получаем тот же результат.
Единственная точка, которая одновременно принадлежит всем трем медианам треугольника, — это точка их пересечения. Таким образом, утверждение задачи доказано.
152
Борис Гринченко
Задача 5.5.
На каком расстоянии от дна находится центр масс тонкостенного цилиндрического стакана, имеющего высоту Л = 12 см и радиус R = 4 см, если толщина дна в два раза больше толщины стенок?
Решение.
Будем рассматривать стакан как тело, состоящее из двух симметричных тел: боковых стенок и дна с центрами симметрии (центрами масс) Oi и О2 соответственно.
Масса первого тела:
(1) тг = 2-n.Rdhp
и второго:
(2) т2 = лг22йр,
где d — толщина стенки стакана, р — плотность материала стакана.
5. Статика
153
Выбирая ось х с началом в точке Ог, как показано на рисунке, согласно определению центра масс, получаем: ь
V —__________
чл* mr + zn2"
Подставляя (1), (2) в (3), находим:
Л 2 Хим =-----2 =4,5 см.
ЦМ *
1 + ж
Таким образом, центр масс стакана находится на расстоянии 4,5 см от его дна.
154
Борис Гринченко
Задача 5.6.
Цепочка массы М подвешена так, что вблизи точек подвеса образует с горизонталью угол а. Определить силу натяжения цепочки в нижней точке и точке подвеса.
На рисунке изображены силы, действующие на правую половину цепочки. Т\ — сила, действующая со стороны левой половины цепочки на правую; 7'2 —
Mg* сила, действующая со стороны потолка, —— рав-
недействующая сил тяжести. Запишем первое условие равновесия:
т,+ T2 + ^z=o
в проекциях на оси х и у:
(1)
(2)
- + Т2 cos а = О
Т2 sin а - -х- g = 0. А
5. Статика
155
Имеем систему из двух уравнений с двумя неизвестными Ti и Т2. Решая ее, находим:
ГГ, Mg rr, М ,
Т? = О •. и Т1 = -о" я ctg а.
2 2sm а 1 2
Следует отметить, что, изображая силу Т2, мы не доказали, что она направлена по касательной к цепочке в точке касания с потолком, как показано на рисунке. Для доказательства этого утверждения (предоставляется читателю) следует рассмотреть равновесие малого фрагмента цепочки, непосредственно прилегающего к потолку.
156
Борис Гринченко
Задача 5.7.
Тяжелый стержень согнут посередине под прямым углом и подвешен свободно за один из концов. Какой угол с вертикалью образует верхняя половина стержня?
Решение.
Запишем условие равновесия стержня относительно точки подвеса О:
(1) Ем( = о.
Сила со стороны опоры подвеса дает нулевой момент относительно О, так как проходит через эту точку.
Остается момент, создаваемый силой тяжести, который в силу (1) так же должен быть равен нулю.
5. Статика
157
Согласно доказанному во введении к разделу утверждению 4, при подсчете момента силы тяжести мы вправе приложить эту силу к центру масс стержня Чтобы момент силы тяжести был равен нулю, необходимо, чтобы продолжение линии действия силы тяжести проходило через центр масс стержня А (только в этом случае плечо силы, а вместе с ним и момент силы равны нулю). Следовательно, центр масс и точка подвеса должны находиться на одной вертикали. Этот результат, очевидно, справедлив для тела любой формы и нередко используется для решения задач статики.
Чтобы найти центр масс согнутого стержня, воспользуемся утверждениями 1 и 2 введения к разделу, рассматривая фигуру как два одинаковых стержня, соединенных под прямым углом. Нетрудно убедиться, что центр масс лежит на середине средней линии треугольника СК.
Поскольку ОВ = 2 АВ , tg р = откуда:
Л
л « 1 « = 4 - arctg .
Еще раз обратим внимание на полученный в задаче общий результат. Он справедлив не только для тела произвольной формы, подвешенного в одной точке, но и тела, стоящего, например, на подставке и касающегося ее в одной точке («Ванька-встанька» и т. п.).
Отметим, наконец, что указанное в задаче условие свободного подвеса означает: других сил, создающих момент относительно точки подвеса, нет.
158
Борис Гринченко
Задача 5.8.
На рисунке изображена балка, на которой находятся два одинаковых груза массами т каждый. Расстояния I и а заданы. Найти силу давления балки на опоры. Массой балки пренебречь.
Решение.
Запишем условие равновесия балки относительно точки А:
(1) aFx + (а + I) F2- INB = О,
где Fr и F2 — силы, действующие на балку со стороны грузов, NB — сила реакции на балку со стороны опоры В.
Воспользовавшись условием равновесия для каждого из грузов (2 закон Ньютона) и 3 законом Ньютона для взаимодействия балки с каждым грузом, получим:
(2)
Л = F2 = mg.
5. Статика
159
Из (1) с учетом (2) находим: 2а + I ”в = ~Т-
Условие равновесия балки дает:
mg.
относительно точки В
(3)
(/ - а),
mg.
NAl + F2a =
откуда, с учетом (2):
I — 2а ”л = —
Таким образом, найдены силы Nb и Na, действующие на балку со стороны опор. Согласно третьему закону Ньютона, с такими же по модулхо силами балка действует на соответствующие опоры.
160
Борис Гринченко
Задача 5.9.
Лестница опирается на вертикальную стену и пол. При каких значениях угла между лестницей и полом она может стоять, если коэффициенты трения лестницы о пол и о стену равны щ и Цг соответственно?
Решение.
Воспользуемся первым условием равновесия: сумма всех сил, действующих на лестницу, равна нулю. В проекциях на оси это даст:
(1) F2 + Nx - mg = 0
(2) N2 - = 0.
Запишем второе условие равновесия: равенство нулю суммы моментов всех сил относительно, например, точки О:
(3) cos а I - Fx I sin а - mg^cos а = 0.
5. Статика
161
Будем считать, что мы рассматриваем критический момент, то есть лестница находится на грани проскальзывания. При этом, очевидно, угол а минимален, а сила трения достигает своего максимального значения:
(4) Л =
(6) Л =
Решая систему уравнений (1—5), находим:
откуда окончательно:
. +« 1 — ^*1^2
а > arctg —=----.
Разумеется, результат не изменился бы, если бы в качестве точки О мы взяли любую другую точку. Как отмечалось во введении к разделу, выбор точки О определяется лишь соображениями удобства: максимально простой записью условия равенства суммы моментов сил нулю.
162
Борис Гринченко
Задача 5.10.
Между двумя одинаковыми досками массы М каждая, шарнирно закрепленными в точке О, удерживается шар массы тп. Точка касания доски и шара находится посередине доски. Угол между досками равен 2а. При каком минимальном значении коэффициента трения ц это возможно?
Решение.
На шар действуют силы трения Fi и Fy, силы реакции опоры Ny и Ny и сила тяжести mg.
Условие равновесия шара
+ Ff -i- N\ + -i- 0,
где в силу симметрии:
I<\ = Ff и
5. Статика
163
Проецируя второе равенство на ось х, получаем:
(1) 2FX cos а - 22V\sin а - mg = О
Запишем условие равновесия доски относительно точки О’. Силы, дающие ненулевой момент относительно точки О' — сила тяжести Mg и сила реакции опоры ТУз. Моменты двух других сил — силы трения со стороны шара и шарнира равны нулю. Итак, имеем:
(2) Mg~ sin а - ~ N2 = 0.
В силу третьего закона Ньютона:
= N9. Л А
Поскольку речь идет о минимальном коэффициенте трения, полагем, что шар и доски находятся на грани проскальзывания, то есть:
(4) Л =
Решая совместно систему уравнений (1—4), получим:
т 1,1
М sin 2а cos а
В заключение обратим внимание на то, что мы не проецировали первое условие равновесия шара, записанное в векторном виде, на ось у (и даже не изобразили эту ось на рисунке), а также не использовали первого условия равновесия (сумма всех сил, действующих на тело, равна нулю) для доски. Разумеется, запись соответствующих уравнений ничего нового к .решению задачи не добавила бы.
164
Борис Гринченко
Задача 5.11.
На горизонтальном столе находится лист бумаги, прижатый однородным стержнем массы т, верхний конец которого шарнирно закреплен.
Какую минимальную горизонтальную силу необходимо приложить к листу, чтобы его вытащить? Угол между стержнем и листом равен а, коэффициент трения между ними ц. Трением между столом и бумагой пренебречь. Рассмотреть два случая: сила направлена влево и вправо (см. рис.).
Решение.
Пусть сила F, которую необходимо приложить, направлена влево. Fx — сила трения со стороны листа на стержень, F2 — сила трения, действующая со сто роны стержня на лист, У, — сила реакции опоры со стороны листа на стержень. На рисунке не указаны: сила, действующая на стержень со стороны шарнира, и силы давления на лист со стороны стержня и стола.
5. Статика
165
Запишем условие равновесия стержня относительно точки О:
(1) Nj/cosoc + FjZsina - mg^ cosa = О, через l обозначена длина стержня.
Условие равновесия сил для листа бумаги в проекции на ось х:
(2) F - Р2 - О.
Поскольку мы рассматриваем экстремальный случай (минимальность силы F означает то, что бумага находится на грани проскальзывания):
(3) Л = ц Nv
Согласно третьему закону Ньютона:
(4) F. = F2.
Решая совместно систему уравнений (1—4), находим:
Рассмотрим второй случай — сила F направлена вправо. При этом силы Fi и Fz изменят направления на противоположные и уравнение (1) примет вид:
(1') N^lcos а - F^sin a - mg~ cos a = О,
а уравнения (2—4) остаются в силе. Решая эту систему, находим:
(6) F = ----.
2 (ц - tg ос)
166
Борис Гринченко
Проанализируем полученное выражение. При
7? - tg а - 0 знаменатель обращается в нуль. Это оз-Р-
начает, что для того, чтобы сдвинуть, лист необходимо приложить бесконечно большую силу F.
При < tga знаменатель отрицателен, то есть сис-тема уравнений (1', 2, 3, 4) не имеет решений, удовлетворяющих физическому смыслу. Следовательно, соотношение (3) выполняться не может, то есть сила трения не может достигнуть своего максимально возможного значения pTVi и при всех значениях F, согласно (2), F% = F.
Рассмотренный случай отвечает так называемому «заклиниванию». Причину этого явления можно усмотреть из (1'):
Nt = Ft tg a +
Видно, что с увеличением Fi линейно растет и Ni и, следовательно, растет максимально возможная сила трения pJVi. При этом соотношение (3) не может быть достигнуто.
5. Статика
167
Задача 5.12.
На горизонтальной поверхности стоит куб массы т. С какой минимальной силой и под каким углом к горизонту надо тянуть куб за верхнее ребро, чтобы он начал опрокидываться без проскальзывания, если коэффициент трения куба о плоскость равен ц?
На рисунке изображен куб в экстремальной ситуации, когда F = В этот момент сила реакции опоры со стороны поверхности приложена к кубу к ребру А ( вся остальная нижняя грань куба находится на грани отрыва от поверхности).
Запишем условие равновесия куба
FTp + mg + N +F = О в проекции на оси х и у:
(1)
- FTp + Feos а = О
(2) - mg + N - Fsin а = О
168
Борис Гринченко
и условие равновесия относительно точки О
(3) aFTp-^a = O,
где а — длина ребра куба. Моменты сил N и F относительно точки О равны нулю.
По определению коэффициента трения,
(4)
F^ [1N.
Решая систему уравнений (1—3) вместе с неравенством (4), находим:
(5) F =
2cos а
(6) Ц (2 + tg а) > 1.
Очевидно, возможны две ситуации. Если при
а = 0 (6) справедливо, то
1 есть Ц>-2»
2 ’
Если же ц < то в (5) мы должны взять мак-симально возможный знаменатель, то есть максимальное значение cos а, которое можно найти, решив
неравенство (6): . -
cos а < А/--1----5---,
\(ц-‘-2)2 +1
и взять, естественно, знак равенства. Таким образом, если ц < 4, то
F = ^- {(и’1 - 2)2 + 1}1,
169
_________________ 5. Статика ___________
причем из (2) tg а - - 2.
Запишем ответ задачи в компактном виде: F = при ц>-|
F = {(Н-1 - 2)2 + 1}1, приц<|.
170
Борис Гринченко
Задача 5.13.
Мотоциклист со скоростью v движется по круговой траектории радиуса R по горизонтальной поверхности. Коэффициент трения между колесами мотоцикла и поверхностью ц. Найти угол наклона мотоциклиста к горизонту. При какой скорости такое движение возможно? Считать, что размеры человека и мотоцикла намного меньше R.
В соответствии с условием малости размеров человека и мотоцикла будем полагать, что все их точки испытывают одно и тоже ускорение а~. Запишем закон Ньютона:
(1) тТ+ N + FTp = та,
где т — масса мотоциклиста с мотоциклом, и определение коэффициента трения:
(2) FTp <
Спроецируем (1) на оси х и у'.
(lx) = та
171
5. Статика
__________________________________I________|____IL1J I_1_1_1IILLI.—UIU..LIIH .4—Ц--ПИ1 . .T' — ‘-------------------— J.' -'Sb
(li/) N = mg.
С учетом
(3) a =
из (lx, ly, 2) находим:
v < 'ly.gR.
При скоростях, превышающих 'Ip.gR, движение по круговой траектории радиуса R невозможно — силы трения “не хватает”, чтобы сообщить телу центростре-v2 мительное ускорение
Л
Перейдем в систему отсчета, движущуюся вместе с мотоциклом, и воспользуемся принципом эквивалентности Эйнштейна: будем полагать, что ускорение свободного падения тел g ’ в этой системе отсчета обусловлено действием силы тяжести (гравитации) некоторой планеты. Поскольку мотоциклист с мотоциклом в движущейся системе отсчета покоятся, воспользуемся одним из условий равновесия — равенства нулю момента сил относительно какой-либо точки. Поскольку согласно доказанному во введении утверждению 4 момент силы тяжести относительно центра масс равен пулю, именно относительно центра масс А системы мотоцикл - мотоциклист и запишем условие равен
ства пулю моментов сил:
(4) FTp I sin а - Nl cos а = О (I = АВ).
С учетом (1х, 1у, 3) из (4) находим:
tga = —а = arctg — v v
6. Законы сохранения импульса и энергии
Пусть имеется система из нескольких тел. Эти тела могут взаимодействовать друг с другом, например, за счет магнитных, электрических, механических и других сил. При этом, в частности, может выделяться тепло. Если внешние силы на тела не действуют или сумма всех внешних сил, действующих на тела системы, равна нулю, справедлив закон сохранения импульса:
Р = ХЛ = const,
где Р — импульс системы тел, Pt = — импульс
тела массой mlf движущегося со скоростью vt. Иными словами, сумма импульсов системы тел в любой момент времени имеет одно и то же постоянное значение. При этом в результате взаимодействий тел друг с другом могут меняться скорости тел, их число и т.д.
Может оказаться, что на тела системы внешние силы действуют, однако проекция суммы этих сил на какую-либо ось равна нулю. В таком случае справедлив закон сохранения импульса в проекции на данную ось х:
рх = Хр/х = const-
В некоторых задачах на тела системы действуют внешние силы, однако, тем не менее, закон сохра
6. Законы сохранения импульса и энергии
173
нения импульса приближенно может быть справедлив. Это возможно, когда промежуток времени, в течение которого система тел переходит из одного (начального) состояния в другое (конечное) достаточно мал, например, речь идет о столкновении или распаде тел в поле тяжести. Докажем это, ограничившись для простоты двумя телами. Запишем закон Ньютона для взаимодействующих тел:
А' - А = (А2 + Ави) *
— А = (Ai+ Авн)
где Рг и — импульс первого тела до и после взаимодействия, Р2 и Р2 — то же для второго тела, Р12 — сила, с которой второе тело действует на первое, Р21 — сила, с которой первое тело действует на второе, Ai — время взаимодействия (время перехода из начального состояния в конечное).
Складывая полученные соотношения с учетом третьего закона Ньютона:
А2 = - Ар
получаем:
^-?=(^1вн + Авн)^
где через Р = Рг + Р2 мы обозначим импульс системы до взаимодействия, Р’ = Рг' + Р2 — после взаимодействия, Р1вп и Р2вн — внешние силы, действующие на первое и второе тела соответственно.
Поскольку внешние силы в рассматриваемых задачах конечны (например, силы тяжести), то при ма
174
Борис Гринченко
лых Ai (At — 0) из последнего равенства имеем закон сохранения импульса в приближенном виде:
Р*' = К
Приступая к решению задачи, необходимо определить, для переходов из каких состояний системы в какие можно применить закон сохранения импульса. Каждое такое состояние следует четко изобразить на рисунке. Затем записать закон сохранения импульса, выбрать оси и спроецировать векторное равенство на оси. В некоторых задачах оказывается удобным использование векторных уравнений.
Для закона сохранения энергии удобно использовать три формулировки:
1. Если нет переходов механической энергии в другие виды энергии и работа внешних сил равна нулю, полная механическая энергия системы сохраняется:
Е = Ек + Е = const,
где Е — полная механическая энергия системы тел, которая включает в себя суммарную кинетическую энергию Ек и потенциальную Еп.
2. Если в результате каких-либо процессов в системе имеет место превращение механической энергии в другие виды, то закон сохранения энергии можно записать в виде:
Еу ~ ^2 ~ Q’
где Ег и Е2 — полная механическая энергия системы в начальном и конечном состоянии соответственно, Q — часть первоначальной механической энергии,
6. Законы сохранения импульса и энергии
175
перешедшая в другие виды энергии (например, в тепло при трении).
3. Если внешние силы совершают над системой работу А и переходов механической энергии в другие виды энергии нет, то
Еу - Е, = А. ел Л
В случае, если сила F, действующая на тело, постоянна, то работа этой силы определяется соотношением:
А = F • S • cos а,
где а — угол между направлением силы F и вектора перемещения S. В зависимости от характера задачи используется одна из приведенных формулировок закона сохранения энергии.
В школьном курсе механики рассматривается потенциальная энергия упругой пружины:
„ kx2
и потенциальная энергия в поле тяжести:
Еп = mgh.
Во втором случае возникает вопрос о выборе начала отсчета потенциальной энергии. Как правило, целесообразно за нулевой отсчет выбрать то положение системы, в котором потенциальная энергия минимальна, независимо от того, начальное это положение, промежуточное или конечное.
В случае, когда размеры тела играют существен-* ную роль, следует использовать утверждение, доказанное в разделе «Статика»: потенциальная энергия
176
Борис Гринченко
протяженного тела в поле тяжести равна потенциальной энергии материальной точки, расположенной в центре масс (центр инерции) данного тела, с массой, равной массе тела.
По определению, кинетическая энергия тела массы т, движущегося поступательно со скоростью и,
Кинетическая энергия системы тел, массы которых mi, m2, ... и скорости Vi, иг, ... соответственно, определяется соотношением:
m2v2 v mtv2 ь ~~2“ —2“ " 2 ’
При решении некоторых задач удобно использовать понятие центра масс. В связи с этим докажем три полезных утверждения.
1. В системе отсчета, движущейся со скоростью центра масс V (в системе центра масс) суммарный импульс системы тел равен нулю.
Из определения центра масс системы тел (введение к 5 разделу) следует:
— Z mivi — —
V = -=---- или mV = /. т^,
где т = X тг
Используя формулу сложения скоростей из раздела 2:
(ог' — скорость массы mt относительно движущейся системы центра масс), получаем:
6. Законы сохранения импульса и энергии
177
Е "Щ' = Е ml(oi - V ) = Е mlvi - mV =0.
Таким образом, утверждение доказано:
Е т^' = 0.
2. Центр масс системы тел движется как материальная точка с массой, равной суммарной массе всей системы, под действием силы, равной сумме всех внешних сил, действующих на систему (теорема о движении центра масс).
Для ускорения центра масс а можно получить:
— Е
где at — ускорение массы тпг. С учетом закона Ньютона Ft = miai (Ft — сумма всех сил, действующих на массу тпг) получаем:
F = та (т = mj), где F = Е Ft равна сумме всех внешних сил, поскольку вследствие третьего закона Ньютона все внутренние силы взаимодействия тел системы друг с другом в сумме Ft взаимно сокращаются.
Из данного утверждения вытекает следствие, которое может использоваться для решения ряда задач: если сумма внешних сил, действующих на систему масс, равна нулю (или внешние силы отсутствуют) и в какой-то момент времени относительно • некоторой системы отсчета центр масс покоился, то и в последующие моменты времени положение
178
Борис Гринченко
центра масс не изменяется. При этом массы могут взаимодействовать друг с другом, а их положение друг, относительно друга может меняться.
В случае, если равна нулю проекция суммы всех внешних сил на какую-либо ось, то остается неизменной координата центра масс по этой оси.
3. Кинетическая энергия системы тел равна кинетической энергии материальной точки с массой, равной суммарной массе системы, движущейся со скоростью центра масс, плюс кинетическая энергия системы тел относительно поступательно движущейся системы центра масс. Это утверждение называют теоремой Кёнига:
„ mV2 „,
Ек=~2~ + Ек‘
Согласно определению кинетической энергии системы масс:
_ у _ у т;(У +и/)2 _
Zu 2 2
= Z^ + 2F; + = < +
где учтены формула сложения скоростей vt = V + у/ и доказанное ранее утверждение о равенстве нулю суммарного импульса в системе отсчета центра масс: Е пщ' = 0.
Начиная решение задачи, необходимо убедиться в возможности применить законы сохранения при переходе системы из начального состояния в конечное. Нередко целесообразно ввести промежуточные состояния.
Для решения некоторых задач вместе с законами сохранения необходимо использовать законы Ньюто
6. Законы сохранения импульса и энергии 179
на, соотношения из кинематики, а также доказанные выше утверждения.
Последовательность действий при решении задач с применением законов сохранения может быть следующий:
1. Выбирают тела, включаемые в физическую систему.
2. Выбирают те состояния системы, для которых предполагается применить законы сохранения. Это не всегда начальное и конечное состояния, указанные в условии задачи (см. ниже).
3. Обосновывают возможность применения законов сохранения при переходе из одного состояния в другое.
4. Записывают импульс или полную энергию системы в одном состоянии, затем в другом и применяют законы сохранения.
180
Борис Гринченко
Задача 6.1.
На неподвижное тело массы m2 налетает со скоростью v тело массы mi. Найти скорость тел после неупругого столкновения (тела слипаются) и долю первоначальной кинетической энергии, перешедшей в тепло (другие виды энергии). Внешними силами пренебречь.
Решение.
т2
т1 -I- т2
V
Запишем законы сохранения импульса и энергии, выбрав в качестве начального состояние системы тела до столкновения, а в качестве конечного — после столкновения:
mtv = (тх + т^ V mxv2 (ml + т2) V2
2 2 Н
(1)
(2)
Проецируя (1) на ось х, параллельную вектору и, получим:
(3)
mxv = (тг + тп2) V.
6. Законы сохранения импульса и энергии
181
Доля энергии, перешедшей в тепло (другие виды энергии), по определению, равна:
(4) 8 = _Я_. mxv2 2
Из системы уравнений (2,3,4) находим:
(5) V = 1—v + mz m9
(6) 8 = ?— m1 + m2
Отметим, что величина 5 не зависит от начальной скорости V.
182
Борис Гринченко
Задача 6.2.
Два тела массами mi и m2 перед столкновением имеют скорости Vi и V2, направленные под углом а друг к другу. Вычислить скорость движения слипшихся масс после неупругого удара. Внешними силами пренебречь.
Решение.
тг
т1 + т2
m2v2
Поскольку внешних сил нет, мы вправо воспользоваться законом сохранения импульса. За начальное состояние системы примем тела до удара, при этом импульс системы равен:
6. Законы сохранения импульса и энергии 183
Рг = mlv1 4- m2v2.
Импульс системы в конечном состоянии (после Удара):
Р2 = (тг -I-
Согласно закону сохранения импульса Pi = Рг, имеем:
(1) = (т1 4- т^)гГ
или
I 4- т^Г2 | v ~ т1 4- т2
Модуль вектора 4- тп^2 найдем, воспользовавшись теоремой косинусов:
I 4- ?и2й£ |2 = (m1v1)2 4- (m2v^2 4- 2mxv1m2v2 cos а.
Итак, окончательно находим:
_ ^(т^)2 4- (tn2v^)2 4- 2?и1о17П2 v2 cos а
~ тг 4- т2 ’
Если бы речь шла о столкновении тел, например, в поле тяжести Земли (наличие внешних сил), то, согласно замечанию во введении к разделу, закон сохранения импульса справедлив в приближенном виде. Причем за начальное состояние системы следовало бы взять тела непосредственно перед столкновением, а в качестве конечного — сразу после столкновения.
Направление скорости слипшихся масс можно определить из треугольника со сторонами mivi, ‘UI2V2 и (ин 4- /П2)п, воспользовавшись теоремой косинусов.
184
Борис Гринченко
Задача 6.3.
Из пушки стреляют под углом а к горизонту. Масса пушки М, масса снаряда т, его скорость V. Найти скорость пушки после выстрела. Пушка может свободно перемещаться вдоль горизонтальной поверхности.
Рассмотреть случай, когда вместо скорости снаряда v относительно Земли задана скорость снаряда относительно пушки в первый момент после выстрела.
Решение.
В качестве системы тел, для которой будем применять закон сохранения импульса, естественно выбрать снаряд и пушку. Согласно условию задачи, силы, действующие на систему вдоль горизонтальной плоскости, в частности, вдоль оси х, лежащей в плоскости полета снаряда, отсутствуют. Поэтому импульс системы в проекции на ось х не меняется. В качестве начального выбираем состояние системы до выстрела. Поскольку оба тела покоятся, импульс системы в начальном состоянии равен нулю:
6. Законы сохранения импульса и энергии
185
Р1х = О-
В конечном состоянии системы (сразу после выстрела) проекция импульса пушки на ось х равна Рпх = - Mvi, а проекция импульса снаряда Рсх = mv cos а. Таким образом, проекция импульса системы на ось х в конечном состоянии
Р2х = - Mvr + mv cos а.
Согласно закону сохранения импульса Pix = Pzx, имеем:
0 = — Mvt + mv cos а.
Откуда получаем ответ на первый вариант задачи: mv cos а
У1 = М ’
Чтобы получить решение задачи во втором варианте, воспользуемся основным уравнением теории относительного движения (раздел 2):
(1) v = + и'
в проекции на ось х:
(lx) vx = - v1 + v' cos a
Закон сохранения импульса записываем относительно инерциальной системы отсчета (Земли):
(2) 0 = - Mvt + т(— vt + v' cos a).
В уравнениях (1—2) v — скорость снаряда относительно Земли, Vi — скорость пушки после выстрела.
186
Борис Гринченко
Из (2) получаем ответ второго варианта задачи: mv' cos а и. = —г?--------------------•
1 М + т
Отметим, что в первом варианте задачи угол наклона ствола пушки к горизонту (в системе отсчета, связанной с Землей) отличается от угла а, под которым вылетел снаряд.
6. Законы сохранения импульса и энергии
187
Задача 6.4.
Человек массы т переходит с одного конца лодки массой М на другой. Длина лодки равна I. На сколько при этом переместится лодка? Сопротивлением воды движению лодки пренебречь.
Решение.
Пусть скорость человека относительно Земли постоянна и равна v, а скорость лодки V. Запишем закон сохранения импульса в проекции на ось х, вдоль которой по условию задачи на систему человек-лодка внешние силы не действуют:
(1) 0 = mv - MV,
поскольку в начальный момент человек и лодка покоились.
Обозначим через t время, через которое человек окажется на другом конце лодки. За это время флаг пройдет путь Vt, а человек — vt. В начальный момент времени человек и другой конец лодки находились *на расстоянии I друг от друга, следовательно:
188
Борис Гринченко
(2) I = vt + Vt.
Из (1,2) находим путь, который прошла лодка:
Другой вариант решения задачи основан на использовании формулы сложения скоростей (§ 2) с выбором лодки в качестве подвижной системы отсчета:
v = vx + v' или v' = Vj + v,
где v' — скорость человека относительно лодки, — скорость лодки относительно Земли. Следовательно, время, за которое человек переходит на другой конец лодки, t = р-. За это время лодка проходит путь Vyt. Воспользовавшись законом сохранения импульса (1), получаем тот же ответ.
Третий вариант решения задачи, основанный на использовании утверждения из введения к разделу о неизменности положения центра масс системы человек-лодка в процессе их относительного движения, предлагается читателю.
6. Законы сохранения импульса и энергии
189
Задача 6.5.
Цепочка длиной I лежит на гладком горизонтальном столе, свешиваясь ровно наполовину. Цепочку без толчка отпускают. Найти скорость цепочки в момент времени, когда ее верхний конец соскользнет со стола.
Решение.
В физическую систему включаем цепочку, находящуюся в поле тяжести Земли. Из условия задачи следует, что полная механическая энергия системы сохраняется (трение отсутствует).
В качестве начального состояния выбираем цепочку в начальный момент времени, конечного — в момент, когда ее верхний конец соскользнет со стола. Потенциальную энергию цепочки в конечном состоянии примем равной нулю, то есть будем отсчитывать потенциальную энергию от центра масс цепочки в конечном состоянии.
190
Борис Гринченко
Полная механическая энергия цепочки в начальном положении:
1 " 2 g 2 2^4’
где мы учли, что кинетическая энергия равна нулю, а потенциальную энергию для удобства записи представили как сумму потенциальных энергий двух половинок цепочки, т — масса всей цепочки. Кроме того, воспользовались доказанным в разделе 5 утверждением о том, что потенциальная энергия протяженного тела в однородном поле тяжести определяется положением его центра масс.
Полная механическая энергия цепочки в конечном состоянии:
7? - mv2
Ь2 - 2 *
Воспользовавшись законом сохранения энергии -Е1 = Е2, находим:
V =
6. Законы сохранения импульса и энергии
191
Задача 6.6.
Тело массы т толкнули вверх по наклонной плоскости, после чего оно двигалось с начальной скоростью Vo и затем остановилось, поднявшись на высоту Н. Какое количество тепла выделилось при этом?
Выбирая за нулевую точку отсчета потенциальной энергии начальное положение тела (в момент времени, когда оно имеет скорость Vo), запишем закон сохранения энергии в виде:
-- Е2 — Q, где полная механическая энергия тела в конечном состоянии (в момент остановки)
Е2 = mgH, в начальном
Q — количество выделившегося тепла. Отсюда находим:
тип
Q = "V2 - mgH,
192
Борис Гринченко
Задача 6.7.
На покоящийся гладкий шар налетает другой такой же шар. Удар абсолютно упругий, нецентральный. Найти угол разлета шаров. Внешними силами пренебречь.
Решение.
Запишем закон сохранения импульса для системы из двух шаров в начальном состоянии (до удара) и конечном (после удара):
(1) mv~0 = mv[ + mv~2,
где обозначения указаны на рисунке. Запишем также закон сохранения полной механической энергии для тех же начального и конечного состояний системы
2 2 2
mvn mvi mvt
Умножим уравнение (1) скаляр но само на себя (или, что то же самое, возведем обе части (1) в квад
6. Законы сохранения импульса и энергии
193
рат) и вычтем из получившегося равенства (2), предварительно сократив (1) на т, а (2) на Получим:
2V} • v2 • cos а = 0.
Поскольку Vi и V2 по условию задачи не равны
71 нулю (удар нецентральный), то cos а = 0 или а = -х,
А то есть шары разлетаются под прямым углом.
Полученный результат остается в силе, если рассмотреть столкновение шаров на гладкой горизонтальной поверхности. Действительно, в этом случае сила тяжести и сила реакции со стороны поверхности, действующие на каждый шар, друг друга компенсируют (движения шаров по вертикали нет). Следовательно, (1, 2) имеют место.
194
Борис Гринченко
Задача 6.8.
Определить отношение масс соударяющихся тел, одно из которых до столкновения покоилось, если после центрального упругого удара шары разлетаются с одинаковыми скоростями.
Решение.
На рисунке изображена система тел до удара (начальное состояние) и после удара (конечное состояние). Поскольку удар центральный, скорости тел могут быть направлены только вдоль оси, соединяющей центры шаров. Запишем закон сохранения импульса в проекции на ось х:
(1) miuo ~ ~ + m2P2
и закон сохранения энергии:
mivi "Vi
2 " 2 + 2 •
Кроме того, по условию задачи:
6. Законы сохранения импульса и энергии 195
(3) Vi = v2 = v.
Подставив v вместо Vi и в (1) и (2), возведем (1) в квадрат и поделим полученное равенство на (2). После несложных вычислений получим:
тп2 = Зт1.
196
Борис Гринченко
Задача 6.9.
Протон, пролетая мимо первоначально покоивше
гося ядра неизвестного химического элемента, отклонился на угол а, потеряв 10 % своей скорости. Найти массовое число химического элемента, если
4 cos а = vv-
15
Решение.
Запишем законы сохранения импульса и энергии для начального и конечного состояний системы:
(1) = mivi + m2v2
(2)
^1^0 mlVl m2V2
2 ~ 2 2 •
Кроме того, по условию задачи:
(3)
Uj — O,9vo —
6. Законы сохранения импульса и энергии
197
где мы обозначили 0 = 0,9.
Полученная система уравнений позволяет дать ответ на вопрос задачи.
Векторное равенство (1) перепишем, воспользуясь теоремой косинусов:
(4) (?n2v2)2 = (тп^)2 + (mjVj)2 - 2m1v0m1v1 cos a.
Подставив (3) в (2), получим:
(5) v22 = (1 - 0>2.
т2
Наконец, подставляя (3) и (5) в (4), после несложных вычислений находим:
тп2 = 7тГ
Следовательно, протон налетел на ядро лития (массовое число лития « 7).
198
Борис Гринченко
Задача 6.10.
На длинной нити висит деревянный шар массы М. Горизонтально летящая со скоростью Vo пуля массой т пробивает шар по центру так, что скорость пули после вылета из шара уменьшается в п раз. На какую высоту поднимется шар?
Решение.
В физическую систему включим шар и пулю в поле тяжести Земли. Выбирая в качестве начального состояния положение I, а конечного III (пробитый шар отклонился на максимально возможный угол и в этот момент покоится), мы не можем воспользоваться ни законом сохранения импульса (нет оси, вдоль которой не действовали бы внешние силы, в том числе натяжения нити), ни законом сохранения полной механической энергии (пробивая шар, пуля, как и шар, нагревается). Поэтому введем промежуточное состояние II: пуля только вышла из шара, причем сам шар
6. Законы сохранения импульса и энергии
199
практически не успел сдвинуться с места, хотя приобрел скорость V2.
Для состояний I и II мы вправе применить закон сохранения проекции импульса системы на ось х (вдоль этой оси внешние силы (силы тяжести и сила и втяжения нити) не действуют):
(1) mv0 = mvY + Mv2.
Далее, для перехода шара из состояния II в III применяем закон сохранения полной механической энергии:
(2) —= m2gH.
Кроме того, по условию задачи:
(< ) vi п •
Решая систему уравнений (1—3), получим:
При решении задачи не учитывалась вращательная энергия шара. Можно показать, что если длина нити много больше радиуса шара, это допущение корректно. Мы сделали также допущение о том, что скорость пули много больше скорости шара в положении II, то есть за время полета пули внутри шара последний практически не сдвигается. Не был также учтен возможный выброс дерева из шара.
200
Борис Гринченко
Задача 6.11.
На неподвижную систему, состоящую из двух одинаковых шаров массой т каждый, соединенных пружиной жесткостью k, со скоростью Vo налетает другой такой же шар. Удар упругий, центральный. Все три шара находятся на одной прямой. Найти максимальное сжатие пружины. Внешними силами пренебречь.
©fiQQQQQ©
2 3
► , х
vi ,
@ *~О ©66OS6U©
12 3
@ © ©8SS835©—
12 3
Включим в рассмотрение три состояния системы: I — начальное; II — в момент времени сразу после удара, когда соединенные пружиной шары практически не успели сдвинуться; III — конечное, в момент времени, когда пружина максимально сжата.
Запишем законы сохранения импульса (в проекции на ось х) и энергии для состояний I и II. При этом предполагаем, что время удара весьма мало, так что смещением шара 2 можно пренебречь и, следовательно, пружина недеформирована, а шар 3 остается
6. Законы, сохранения импульса и энергии
201
в покое. Иными словами, наличие пружины и шара 3 можно не учитывать.
(1) mv0 = mvi - mv'
mv20 mv2 mv'2 ~2~ = ~2~ + 2 '
Сократив (1) на m, a (2) на возведем обе части XU
(1) в квадрат и вычтем из получившегося равенства уравнение (2). Получим: 2oio'= 0. Поскольку | | / 0, имеем v' = 0, то есть налетающий шар после удара останавливается и, согласно (2) или (1), шар 2 сразу после удара приобретает скорость vq: 'И <Л).
Запишем законы сохранения импульса и энергии для состояний II и III. При этом, согласно условию максимального сжатия пружины, скорости шаров 2 и 3 равны. Действительно, в момент наибольшего сжатия шары друг относительно друга перестают двигаться (в противном случае происходило бы • досжатие» пружины), то есть движутся как одно тело. Введем обозначение V2 = Уз = и. Получаем:
(3) mv0 = 2mv
, mv22 о mv2 kx2
fix2
гдс - - — потенциальная энергия сжатой пружины, < величина максимальной деформации (сжатия).
Из (3, 4) находим:
202
Борис Гринченко
Следует обратить внимание на полученный промежуточный результат: при упругом лобовом ударе двух шаров, один из которых до удара покоился, шары обмениваются скоростями — налетающий останавливается, а покоящийся приобретает скорость налетающего. Можно показать, что и в случае, когда оба шара движутся, после лобового упругого удара они обмениваются скоростями (при расчете удобно перейти в систему отсчета, связанную с одним из шаров).
Второй вариант решения основан на записи закона сохранения энергии при переходе из состояния I в II и из II в III в системе отсчета, которая движется со скоростью (в системе центра масс шаров).
В первом случае имеем два шара, движущиеся на-vo vo
встречу друг другу со скоростями ~ и — —, которые после удара обмениваются скоростями. При обратном переходе в систему отсчета Земли получаем и' = 0 и
щ = v0.
Во втором случае в движущейся системе отсчета имеем два шара, скрепленные пружиной, которые в
Vo
начальный момент также имеют скорости —, направ-
ленные навстречу друг другу. При этом максимальном сжатии шары останавливаются, и закон сохранения энергии / и ч 2
о
2 2 2
приводит к прежнему результату:
6. Законы сохранения импульса и энергии
203
Задача 6.12.
Цирковой гимнаст падает с высоты Н на туго натянутую упругую сетку. Каково будет максимальное провисание гимнаста в сетке, если в случае спокойно лежащего в сетке гимнаста провисание равно Z? Какова максимальная скорость гимнаста при падении?
Решение.
В физическую систему включаем гимнаста в поле тяжести Земли и сетку. Рассмотрим четыре состояния системы: I — начальное (гимнаст на высоте Н над сеткой, сотка нерастянута); II — гимнаст имеет максимальную скорость, при этом сетка растянута на некоторую величину хо; III — гимнаст в сетке в момент времени, когда она максимально растянута (при этом, очевидно, скорость гимнаста равна нулю); IV — гимнаст спокойно лежит в сетке.
Запишем закон сохранения полной механической анергии для состояний I и. II:
mif kXn
(L) mg(H + х0)
204
Борис Гринченко
По условию, скорость гимнаста в состоянии II максимальна. Рассмотрим, как меняется скорость гимнаста в процессе падения. Скорость будет возрастать до тех пор, пока суммарная сила, действующая на гимнаста, направлена вниз. На гимнаста действуют две силы: сила тяжести и сила упругости сетки. Таким образом, пока
mg - kx > 0,
скорость гимнаста возрастает. В момент времени, когда
(2) kxQ -mg = 0,
скорость достигает максимального значения.
Закон сохранения полной механической энергии для состояний I и III:
bv2
(3) mg (Н + х^) =
Для состояния IV запишем закон Ньютона в проекции на вертикальную ось:
(4) kl = mg.
Система уравнений (1—4) позволяет ответить на вопросы задачи: решая квадратное относительно х уравнение (3) с учетом (4), имеем:
хх = I + + 21 Н
(отрицательный корень отбрасываем); из уравнения (1) с учетом (2, 4), получаем:
v = 2g (Н+1)-^-.
£
6. Законы сохранения импульса и энергии 205
Из (2) и (4) видно, что хо = I.
Отметим, что при решении задачи мы, в соответствии с условием, дважды воспользовались законом Гука и выражением для энергии деформированной пружины.
206
Борис Гринченко
Задача 6.13.
На подставку массой М, подвешенную на пружине жесткости k, с высоты Н падает тело массы т и прилипает к ней. Определить максимальное растяжение пружины. Массой пружины и нитей подвеса пренебречь.
Решение.
О
Рассмотрим четыре состояния системы: I — начальное (тело на высоте Н, подставка покоится); II — тело на грани соприкосновения с подставкой, сама подставка еще покоится; III — удар тела о подставку уже произошел, однако подставка практически еще не успела сдвинуться (в момент времени сразу после налипания тела), при этом скорость подставки вместе с телом обозначим через vr, IV — конечное состояние — подставка вместе с телом достигает нижнего положения (с нулевой скоростью).
в. Законы сохранения импульса и энергии
207
Закон сохранения энергии при переходе из состояния I в II:
„,,2
(1) = mgH,
где v0 — скорость тела непосредственно перед ударом о подставку.
Для состояния I закон Ньютона для подставки в проекции на вертикальную ось:
(2)
kx0 = Mg,
где х0 — деформация пружины.
Закон сохранения импульса для состояний II и III в проекции на вертикальную ось мы вправе применить, учитывая замечание во введении к разделу и полагая время прилипания (время относительного движения тела и подставки в процессе удара) малым:
(3) mv0 = (М + m)vr
Закон сохранения энергии для состояний III и IV:
(4)
+ (М + m)gH =
k(x + х0)2 2
2
(М + m)vl
справедлив, поскольку при переходе из III в IV переходы механической энергии в другие виды энергии отсутствуют. В (4) х — дополнительное удлинение пружины, так что х + х0 — полная деформация пру
жины в конечном состоянии.
Подставляя vo и Хо из (1—3) в (4), получаем квадратичное уравнение относительно х. Его решение:
х = "a (i + . ).
k (М + m)g '
208
Борис Гринченко
Итак, окончательно:
х + х _ + Г1 +
х + хо- k Ь к <1+ N(M + m)g>
Следует обратить внимание на то, что в данной
.задаче, как и в других, где есть переходы механической энергии в другие виды энергии, записывать закон сохранения энергии для начального и конечного состояний практически бесполезно — в уравнение войдет величина Q — количество перешедшей, например, в тепло энергии, связать которую с другими параметрами задачи обычно не удается. Если же это сделать возможно, запись закона сохранения энергии может иметь смысл. В качестве примера рассмотрим задачу 6.14.
6. Законы сохранения импульса и энергии
209
Задача 6.14.
После сообщения шайбе некоторой начальной скорости она начинает скользить по горизонтальной поверхности льда. Пройдя расстояние h в области с коэффициентом трения шайба попадает в область с коэффициентом трения р.2 и, пройдя в ней расстояние /г, останавливается. Найти отношение начальной скорости шайбы к ее скорости на границе раздела этих областей.
Решение.
Запишем закон сохранения энергии для начального и конечного состояний системы. Полная механическая / mvo \ ,
энергия 2~) в начальном состоянии (потенциальную энергию шайбы в поле тяжести полагаем равной нулю) полностью переходит в тепловую энергию Q (шайба останавливается). Тепловая энергия равна работе сил трения:
Q = [i^mgly + p.2mgl2,
где учтено = pJV = \img. Итак, имеем: _,„2
(1) -g- = ^mgli + n2mgl2.
Закон сохранения энергии для состояния в момент пересечения шайбой границы раздела и конечного состояния:
__2
TTlUi
(2) 2 =
д’де обозначено: — скорость шайбы в момент пере-
сечения границы.
210
Борис Гринченко
Разделив (1) на (2) и извлекая корень квадратный из обеих частей, получаем ответ задачи:
Ц) _ + М-2^2
и1 М-2^2
Рассматривая движение шайбы, можно было бы рассуждать иным образом. А именно, считать, что над шайбой совершает работу внешняя сила (сила трения). Соответствующие уравнения по форме совпадают с написанным выше. Так, например, для перехода из состояния со скоростью Vo (начального) в конечное (v = 0) имеем:
•®2 ~ -®i = mvl
где Е2 = 0, Ег= —g—, А = - (в послед-
нем соотношении учтено, что работа сил трения отрицательна — перемещение и сила трения направлены в противоположные стороны).
6. Законы сохранения импульса и энергии
211
Задача 6.15.
На горизонтальной поверхности находятся два тела массами mi и тпг, скрепленные легкой недефор-мированной пружиной. Коэффициент трения между поверхностью и каждым из тел равен Ц.
Какую минимальную постоянную силу необходимо приложить к телу массы mi, чтобы сдвинулось тело массы m2?
Решение.
’1
т2Г
Если приложенная сила меньше максимальной силы трения покоя первого тела, то есть F < то первое тело вообще не сдвинется. Пусть F превышает p.mig на малую величину. В этом случае первое тело начнет движение, а затем остановится из-за действия силы упругости пружины, пройдя некоторое расстояние х. Будем увеличивать силу F до такой величины Fo, чтобы после остановки выполнилось условие:
(1) kxQ =
При этом второе тело хотя и не сдвинется, но будет находится в состоянии неустойчивого равнове
212
Борис Гринченко
сия (на грани проскальзывания). Очевидно, что при F > Fo второе тело сдвинется.
Полагая, что приложенная сила F - Fo, запишем закон сохранения энергии в третьей формулировке введения, выбирая в качестве начального состояния систему (два тела скрепленных пружиной) в момент приложения силы Fo, а в качестве конечного — в момент остановки первого тела (при этом второе также покоится):
(2) Е2-Е1=А,
где
Е. = О kXQ (4)
(5) А = Fox - nm^gx.
В последнем соотношении учтено, что работа силы Fo положительна, а работа силы трения скольжения [imig — отрицательна.
Из (1—5) находим:
Ео = + —2^-.
Таким образом, если приложенная сила F > Fo, второе тело сдвинется.
6. Законы сохранения импульса и энергии
213
Задача 6.16.
На покоящуюся частицу массы zni налетает частица массы m2. Какова максимальная доля 8 кинетической энергии налетающей частицы, которая может перейти во внутреннюю энергию частиц при неупругом ударе?
Решение.
Воспользуемся теоремой Кёнинга для системы из двух частиц:
^,,.2
~2~ где скорость V центра нием (см. введение):
(1)
mV2 + F ’
' ~2~ + * ’
масс определяется соотноше-
(2)
^2V0 т1 + т2
(т = т1 + тп2),
vQ — скорость налетающей частицы, Ек’ — кинетическая энергия частиц относительно системы центра
тт т^2
масс. Поскольку величина —до и после столкно-Л
вения не меняется (теорема о движении центра масс с учетом отсутствия внешних сил), максимальная величина кинетической энергии, которая может перейти во внутреннюю, равна, очевидно, _ЕК'. Это соответствует случаю так называемого «слипания» частиц или абсолютно неупругого удара, когда скорости частиц после столкновения равны друг другу и в системе центра масс равны нулю (что возможно, поскольку .суммарный импульс частиц в системе центра масс равен нулю).
214
Борис Гринченко
Из (1, 2) получаем:
mV2
5 = Q = = 2 2 = mi
m2v^ m2v2Q m2v>Q + m2
2 2 2
6. Законы сохранения импульса и анергии
215
Задача 6.17.
Найти энергетический порог реакции возбуждения атома электроном, если масса атома т, а энергия возбуждения равна Ео.
Примечание: энергетическим порогом реакции называется минимальная кинетическая энергия налетающей частицы, при которой возможно протекание реакции.
Решение.
Согласно результату задачи 6.16., электрон отдает максимальную энергию при абсолютно неупругом ударе:
где те — масса электрона, Епор — его кинетическая энергия, равная энергетическому порогу реакции. Из (1) находим:
Учитывая, что те « т, с хорошей точностью получаем: Ецор = Ео.
216
Борис Гринченко
Задача 6.18.
Найти энергетический порог возбуждения атома гелия атомом водорода. Энергия возбуждения атома гелия равна Ео- Масса гелия в четыре раза больше массы атома водорода.
Решение.
По аналогии с решением предыдущей задачи 6.17. получаем:
_mHe + mH 4 + 1 5„
£по₽ ” Е° ~ Т~Е° ~ 4Е°-
Таким образом, для протекания реакции возбуждения атома гелия атомом водорода кинетическая энергия налетающего атома водорода должна как минимум на 25% превышать энергию возбуждения.
6. Законы сохранения импульса, и энергии
217
Задача 6.19.
Небольшой обруч скатывается без проскальзывания с нулевой начальной скоростью с горки высотой Н. Пренебрегая сопротивлением движению, найти скорость центра обруча у подножия горки.
Решение.
Воспользуемся результатом решения задачи 2.6., согласно которому движение обруча без проскальзывания можно представить как движение его центра с некоторой скоростью V и вращение вокруг центра с той же скоростью V.
Для вычисления кинетической энергии обруча воспользуемся теоремой Кёнинга (центр обруча совпадает с его центром масс):
(1) Е = = mV2.
Запишем закон сохранения энергии для обруча на высоте Н и у подножия горки:
(2) mgH = mV2.
Отсюда получаем: V = ^gH.
При решении задачи не учитывался (ввиду малости по сравнению с Н) размер обруча.
В качестве полезного упражнения читателю предлагается найти ускорение центра обруча при его скатывании, если угол наклона горки к горизонту а известен.
218
Борис Гринченко
Задача 6.20.
На гладкой горизонтальной поверхности лежит кольцо радиуса R и массы М, на котором сидит жук массы т. С некоторого момента времени жук начинает ползти по кольцу. Описать траекторию движения жука относительно Земли.
Решение.
Воспользуемся утверждением из введения к разделу о том, что центр масс системы кольцо—жук остается неподвижным. Поскольку в процессе движения расстояние между жуком и центром кольца постоянно и равно R, расстояние от жука до центра масс г также постоянно, причем:
М D г =----ггл.
т + М Отсюда заключаем, что жук движется по окружности М о л
радиуса-----гул с центром А, расположенным в цент-
т + JVL
ре масс системы кольцо—жук. Очевидно, что и центр кольца (центр масс кольца) движется по окружности т
радиуса +~~ с тем же центром.
7. Гидростатика. Закон Архимеда
Основной закон гидростатики — закон Паскаля, согласно которому в состоянии равновесия давление жидкости (или газа) в данной точке не зависит от ориентации площадки, на которую она действует.
Решение задач гидростатики основывается на использовании законов Ньютона и законов сохранения импульса и энергии. При этом следует иметь в виду, что идеальная жидкость (а именно такая жидкость рассматривается в школьном курсе физики) действует на тела только по направлению к нормали к их поверхностям.
В качестве объемов жидкости, для которых применяется закон Ньютона, обычно выбирают прямые круговые цилиндры. Их правильный выбор обычно представляет наиболее трудный момент при решении задач гидростатики.
Использование закона Паскаля заключается в том, что, если выбранные для решения задачи цилиндры упираются своими основаниями в одну точку, то давления на эти основания полагают равными независимо от ориентации осей цилиндров.
Для иллюстрации получим формулу, связывающую давление с глубиной погружения в жидкость, применяемую при решении задач гидростатики.
. Рассмотрим условие равновесия мысленно выделенного из всего объема жидкости прямого кругового
220
Борис Гринченко
цилиндра (столба) высотой h и сечением S, изображенного на рисунке. Вниз на столб жидкости действует сила атмосферного давления PqS (Ро — атмосферное давление) и сила тяжести mg, где масса жидкости
т = Shp,
р — плотность жидкости.
Вверх на столб действует сила давления на нижнее основание со стороны прилегающей жидкости PS (Р — давление жидкости на глубине Л). Силы давления со стороны жидкости на боковую поверхность столба направлены перпендикулярно вертикальной оси столба, и, следовательно, их проекция на вертикальную ось равна нулю.
Условие равновесия (закон Ньютона) для столба жидкости в проекции на вертикальную ось имеет, следовательно, вид:
PS - P0S - mg = 0.
7. Гидростатика. Закон Архимеда
221
После несложных вычислений получаем искомую формулу:
Р = Р0 + pgh.
Закон Архимеда.
Выделим мысленно из жидкости произвольный объем, ограниченный замкнутой поверхностью S. Если жидкость находится в механическом равновесии, то, разумеется, должен находиться в равновесии и выделенный объем. Поэтому должны обращаться в нуль равнодействующая и момент всех внешних сил, действующих на рассматриваемый объем жидкости (см. раздел «Статика»). Внешние силы — это вес Mg выделенного объема жидкости (М — его масса) и сила давления на поверхность S со стороны окружающей жидкости. Значит, равнодействующая Fa сил гидростатического давления, действующих на поверхность S, должна равняться Mg — весу жидкости в объеме, ограниченном поверхностью S. Равнодействующая Fa должна быть направлена вверх и проходить через центр масс О выделенного объема
222
Борис Гринченко
жидкости, чтобы полный момент внешних сил, действующих на него, был равен нулю. Допустим теперь, что жидкость из выделенного нами объема удалена, и на ее место помещено любое твердое тело. Если это тело удерживается в равновесии, то в состоянии окружающей жидкости никаких изменений не произойдет. Не изменится и давление, оказываемое жидкостью на поверхность S. В результате мы приходим к закону Архимеда:
«Если тело, погруженное в жидкость, удерживается в механическом равновесии, то со стороны окружающей жидкости оно подвергается выталкивающей силе гидростатического давления, численно равной весу жидкости в объеме, вытесненном телом. Эта выталкивающая сила направлена вверх и проходит через центр масс О жидкости, вытесненной телом».
Точку О называют центром плавучести тела. Ее положением, как можно показать, определяются равновесие и устойчивость плавающего тела: в случае, если центр масс плавающего тела расположен ниже центра плавучести, равновесие тела устойчиво; в противном случае равновесие неустойчиво. Доказательство этого утверждения предоставляется читателю.
Таким образом, закон Архимеда можно записать в виде:
Fa = pVg,
где V — объем тела или его части, погруженной в жидкость, р — плотность жидкости, g — ускорение свободного падения. Учтено, что М = рУ.
Следует иметь в виду, что при выводе закона Архимеда мы предполагали, что либо тело полностью окружено жидкостью, либо какая-то его часть выступает
7. Гидростатика. Закон Архимеда
223
над жидкостью и окружена, например, воздухом. В последнем случае выражение для выталкивающей силы должно включать в себя вес вытесненного телом воздуха (или другого газа, или жидкости, если тело плавает на границе раздела двух жидкостей). Этот случай рассмотрен в решении задачи 7.10.
Если же указанные условия не выполняются (например, в случае тела, лежащего на дне водоема, под которое не подтекает вода), то закон Архимеда в приведенной формулировке не выполняется (см. решение задачи 7.12). Более того, сила гидростатического давления может быть вообще направлена вниз.
При изложении введения к данному разделу использовался «Общий курс физики» под ред. Д. В. Си-
вухина.
224
Борис Гринченко
Задача 7.1.
Доказать, что в однородной жидкости на одной горизонтали давление одинаково.
Решение.
Рассмотрим для определенности сосуд, изображенный на рисунке. В левом колене может, например, находиться еще какая-либо жидкость, в правом что-то плавать и т.п. Наша задача доказать, что Ра = Рв-
Для этого докажем сначала, что давления в точках 1 и 2, расположенных на одной горизонтали, равны.
Мысленно выделим прямой круговой цилиндр, основаниями упирающийся в точки 1 и 2. Запишем для него условие равновесия сил (второй закон Ньютона) в проекции на ось х:
(1)
PAS - P2S = 0.
где PAS — сила, действующая на левое основание цилиндра, P.,S — на правое. Силы, действующие на боковую поверхность цилиндра, направлены по нормали
7. Гидростатика. Закон Архимеда
225
к оси х и вклада в (1) не дают. Из (1) находим, что Р} = Р2.
Рассмотрим вертикальный столб жидкости, основания которого упираются в точки 1 и А, и запишем для него условие равновесия в проекции на ось у:
(2) -PAS-mg + PtS = О,
где т — масса столба.
Для такого же столба справа аналогично получаем:
(3) - PBS - mg + P2S = 0.
Сравнивая (2) и (3), с учетом (1), получаем: Рл = Рв, что и требовалось доказать.
Приведенные рассуждения нетрудно распространить па сосуд любой другой формы.
226
Борис Гринченко
Задача 7.2.
В сообщающиеся сосуды налита ртуть, плотность которой рр. Сечения сосудов Si и S2. В первый сосуд наливают воду, плотностью рв. Высота столба воды Н. На какую высоту поднимется уровень ртути во втором сосуде?
Пунктиром на рисунке обозначен первоначальный уровень ртути, xi и хг — смещения уровней ртути после того, как налили воду.
Выбрав точки А и В, как показано на рисунке, и воспользовавшись полученным в предыдущей задаче результатом, получим:
(1) РА = Рв-
Рассмотрим условия равновесия мысленно выделенных столбов жидкости так, как это было сделано ранее и предположим, что площади столбов равны
7. Гидростатика. Закон Архимеда
227
площадям сосудов, т. е. Sa = Si, Sb = S2. Тогда для столба жидкости в левом сосуде:
(2) POSX + - PASr = О,
для столба в правом сосуде:
(3) P0S2 + mpg - PBS2 = О,
где тв = HSjpg и тр = (х1 + x2)S2pp — массы соответствующих выделенных столбов.
Из полученной системы уравнений находим:
(4) Нрв = (хх + х2)рр,
одно уравнение с двумя неизвестными. Необходимо, следовательно, попытаться отыскать еще одно уравнение, связывающее величины х1 и х2. Это уравнение, очевидно, может быть получено из условия несжимаемости жидкости (или, что то же самое, из условия сохранения неизменным объема жидкости) — сколько ртути было вытеснено водой из левого сосуда, точно на такой ясе объем увеличилось количество ртути в правом сосуде:
(5) x2S2 = x1S1.
Решая совместно систему уравнений (4—5), находим:
х - НР* &'2
1 "рр S1 + S,'
228
Борис Гринченко
Задача 7.3.
Гидравлический пресс, заполненный водой, имеет легкие поршни сечений Si и S%. На поршень Si положили груз массой т. На какую величину поднимется после этого второй поршень?
Решение.
Выберем лежащие на одной горизонтали точки А и В, как показано на рисунке, и воспользуемся полученным ранее результатом:
(1) Ра = Рв-
Давление в точке А равно
(2) РА = Р0 + pg (xt + Хг).
Запишем условие равновесия груза вместе с поршнем в правом колене:
(3) P0Sl + mg-PgS^O.
7. Гидростатика. Закон Архимеда 229
Условие несжимаемости воды дает:
(4) x1S1 = x2S2.
Решая совместно систему уравнений (1—4), находим:
_ т 1
2 " Р« ’ («! + «2)’
230
Борис Гринченко
Задача 7.4.
Куб, наполовину наполненный водой, двигают горизонтально с ускорением а. Определить форму поверхности воды в кубе.
Решение.
Рассмотрим вертикальный заштрихованный столб жидкости и запишем для него закон Ньютона в проекции на ось у.
(1) PAS - P0S - mxg = 0; тх = pSy, где — масса столба воды, Ро — атмосферное давление.
Сила атмосферного давления на верхнюю поверх-
S
ность столба воды равна Ро----- и направлена под
COS Ct
углом а к оси у. Проекция этой силы на ось у равна PoS.
Рассмотрим теперь другой мысленно выделенный столб воды с горизонтальной осью ОА. Запишем для него основное уравнение динамики в проекции на
7. Гидростатика. Закон Архимеда
231
ось х:
(2) - PAS + P0S = - т2а,
где т2 = Sxp — масса столба воды, Ро — давление на столб вблизи точки О, равное атмосферному давлению.
Складывая (1) и (2) с учетом соотношений для масс столбов, найдем:
(3) У = %х.
б
Отсюда заключаем, что поверхность жидкости ж а
— плоскость, составляющая угол а = arctg — с го-О
ризонтом.
Второй вариант решения задачи, основан на использовании принципа эквивалентности Эйнштейна.
В системе отсчета куба ускорение свободного падения тел g' определяется соотношением:
g ' = F- а.
Для условий Земли известно, что поверхность жидкости в состоянии равновесия образует горизонтальную плоскость, то есть перпендикулярна вектору ускорения свободного падения. Отсюда, после неслож-, а ных выкладок приходим к соотношению tg а = —.
О
Третий вариант решения задачи основан на использовании второго закона Ньютона для мысленно выделенного малого объема жидкости, прилегающего к ее поверхности (см. рис.):
(4) N + mg = та
232
Борис Гринченко
Проецируя (4) на оси х и у после несложных пре
образований получаем: а = arctg ~ и не зависит от
в
положения малого объема жидкости.
7, Гидростатика. Закон Архимеда
283
Задача 7.5.
Найдите форму поверхности жидкости в вертикально расположенном цилиндрическом стакане, который вращается вместе с жидкостью вокруг своей оси с угловой скоростью со.
Решение.
Вертикальный и горизонтальный столбы жидкости, для которых запишем закон Ньютона, удобно выбрать так, как показано на рисунке.
Для вертикального столба в проекции на ось у имеем:
(1) PAS - Sypg - P0S = О,
где Syp — масса столба жидкости, P0S — вертикальная составляющая силы атмосферного давления (см. выше).
Записать закон Ньютона для всего горизонтального столба ОА невозможно, так как находящиеся на раз-
* личном расстоянии от точки О фрагменты столба име-
234
Борис Гринченко
ют разные ускорения. Мы можем только сделать это для малого фрагмента столба; пусть координаты концов этого фрагмента равны Xi и Xi + 1.
х
-►
Ускорение центра фрагмента определяется формулой из кинематики вращательного движения:
Xl + 1 + Х1 2 at +1 ~ “ ~2 ® ’
а закон Ньютона для фрагмента в проекции на ось х имеет вид:
(2)
(3) Pi + 1S + PtS - ai + i ' +
где Pt+1S — сила давления со стороны прилегающей к фрагменту жидкости, направленная к центру вращения, PtS — сила, направленная пт центра,
7ni+i = -s(xi+i "xi) Р-
Из (2,3) получаем:
И) Л +
Разобьем весь столб жидкости на большое число N фрагментов, запишем д5тя каждого из них (4) и сложим получившиеся равенства почленно. После сокращений получим:
(5) PN — PQ - g (xn ~ xo)«
7. Гидростатика. Закон Архимеда
236
Поскольку
Рjif — -Рд! х^ — х и Xq — О,
из (5) находим:
(6) РА - Ро =
С учетом (1) окончательно имеем:
®2 2 у =---X
2g
Уравнение поверхности жидкости представляет собой, следовательно, параболу. Отметим, что (5) может
быть получено интегрированием.
236
Борис Гринченко
Задача 7.6.
Вес однородного тела в воде в п раз меньше, чем в воздухе. Чему равна плотность материала тела? Выталкивающей силой воздуха пренебречь. Плотность воды р.
Решение.
В задаче описаны две ситуации: взвешивание тела в воде и воздухе. Следовательно, следует дважды записать закон Ньютона (в данном случае, условие равновесия).
При взвешивании в воде в проекции на «ось х:
(1) Л + fa - т& = о,
где Рг — сила, действующая на тело со стороны подвеса, Fa — Архимедова сила, mg — сила тяжести.
Согласно закону Архимеда:
(2)
Fa = pvg,
7. Гидростатика. Закон Архимеда
237
где V — объем тела. Масса тела:
(3) т = Vpv
При взвешивании в воздухе аналогично находим:
(4) Р2 = mg.
Согласно третьему закону Ньютона, сила, с которой подвес действует на тело, равна по модулю силе, с которой тело действует на подвес, то есть весу тела. Таким образом, Л и Рг — веса тела при первом и втором взвешивании. По условию задачи:
Р2
(5) h
Решая полученную систему уравнений, находим:
п
Р1 " лГТ р’ где р! — искомая плотность.
238
Борис Гринченко
Задача 7.7.
На границе раздела двух жидкостей с плотностями pi и pa плавает шайба из материала плотности р, причем pi < р < pa. Высота шайбы h. Определить глубину погружения во вторую жидкость.
Решение.
На шайбу действуют две силы: выталкивающая сила (Архимеда) и сила тяжести. В равновесии в проекции на вертикальную ось закон Ньютона для шайбы:
(1) Fa = т$-
Силу Архимеда Fa определим, используя соображения, приведенные при выводе закона Архимеда во введении к разделу. Если мысленно заменить часть объема шайбы, погруженную в жидкость плотностью pi, самой этой жидкостью, и то же самое проделать с другой частью шайбы, то, очевидно, жидкость будет находиться в равновесии. Следовательно, мы вправе записать:
(2) Fa = {Sh1p1 + S/i2p2) g,
7. Гидростатика. Закон Архимеда
239
где S — площадь сечения шайбы, р2й2<8 — масса жидкости, заменяющая нижнюю часть шайбы, p17z1S — верхнюю, правая часть (2) — вес жидкости, вытесненной телом (шайбой).
Запишем также очевидные соотношения:
(3) h = + h2
(4) т = pSh.
Решая полученную систему уравнений (1—4), находим:
Решить задачу можно и другим способом. Обозначим давление жидкости на верхнюю поверхность шайбы через Ро, на нижнюю — Р. Запишем условие равновесия мысленно выделенного столба жидкости (см. рис.) и, после несложных преобразований, получим:
Р = Ро + (Pi^i "* Ра^а)
Сила Архимеда равна:
Fa = PS - PQS = (p^i + p2 h2) Sg, где PS — модуль силы, действующей на шайбу вверх, P0S — вниз. Силы со стороны жидкостей на боковую поверхность шайбы вклада в силу Архимеда не дают.
Далее решение аналогично первому способу.
240
Борис Гринченко
Задача 7.8.
В сообщающиеся сосуды диаметрами di и dz налита жидкость плотности р. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы М из материала, плотность которого меньше р?
Решение.
н
При решении задач такого типа удобно вновь воспользоваться соображениями, изложенными во вве- ] дении к разделу. Заменим тело жидкостью в объеме той его части, которая погружена в жидкость. Такая j замена, очевидно, не повлечет изменения состояния | равновесия жидкости в сосудах. Следовательно, по- j мещение тела в один из сосудов эквивалентно помещению воды объемом У, который можно найти, ; записав условие равновесия тела:
(1) FA = pVg
241
7. Гидростатика. Закон Архимеда
и закон Архимеда:
(2) Fa - mg = 0.
Обозначим через h высоту, на которую поднимется жидкость в обоих сосудах. Получаем:
(3) h df + h J d22 = V.
Решая систему (1—3), находим:
Л = 4т яр ( d{ +'d* )’
242
Борис Гринченко
Задача 7.9.
На дне водоема находится тело массой т со средней плотностью р, полностью погруженное в воду. Плоская часть поверхности тела площадью S плотно прилегает ко дну так, что вода не подтекает. С какой силой тело давит на дно? Глубина водоема h.
Решение.
Запишем условие равновесия тела в проекции на вертикальную ось:
(1)
F + N - mg = О,
где F — выталкивающая сила гидростатического давления, N — сила реакции со стороны дна.
Если бы вода подтекала под тело, то F = Fa- На самом деле, сила F меньше Fa па величину PS, где
Р = Р0 + ptgh
7. Гидростатика. Закон Архимеда
243
Действительно, если бы вода подтекала, то силу Архимеда можно представить как сумму двух сил гидростатического давления — на площадку S и на остальную поверхность тела. Если же вода не подтекает, то остается лишь вторая составляющая силы гидростатического давления. Следовательно:
(2) F = Fa-S (Ро + Р1£й).
Из последнего соотношения видно, что сила F может быть направлена как вверх (изображено на рисунке), так и вниз.
Из (1,2) получаем:
N =mg- ™ptg + S (Ро + p^h),
где учтено выражение для силы Архимеда:
„ т
FA = ~p Pl*
244
Борис Гринченко
Задача 7.10.
Определите натяжение нижней лески у поплавка, изображенного на рисунке, если поплавок погружен в воду на 2/3 своей длины. Масса поплавка М.
Решение.
Силы, действующие на поплавок, изображены на рисунке. Согласно закону Архимеда, сила Архимеда приложена к центру О погруженной в воду части поплавка.
Условие равенства моментов сил относительно точки О дает:
(1) mg I sin а - Т sin а = 0,
где мы использовали доказанное в разделе «Статика» утверждение относительно момента сил тяжести протяженных тел.
Из (1) находим искомую величину натяжения лески:
7. Гидростатика. Закон Архимеда
245
Отметим, что для решения задачи оказалось достаточно использовать лишь одно из условий равновесия поплавка — равенство моментов сил, причем точку О мы выбрали потому, что в этом случае исчезает необходимость подсчета силы Архимеда.
Первое условие равновесия — равенство нулю суммы всех сил, действующих на поплавок, — не понадобилось.
Напомним, что в правой части (1) первый член
—— I sm а — момент силы тяжести относительно точ-6
ки О, закручивающий поплавок по часовой стрелке, взят со знаком «плюс». Второй член Т — sin а — мо-3
мент, который создает сила натяжения лески, закручивает поплавок против часовой стрелки, взят со знаком «минус».
246
Борис Гринченко
Задача 7.11.
Какую работу А надо совершить, чтобы вдвинуть пробку на длину I? Известны: радиус цилиндрического стакана R, плотность жидкости р, радиус пробки г, величина h (см. рис.).
Решение.
О
Первый способ решения задачи основан на использовании закона сохранения энергии.
Запишем закон сохранения энергии при переходе системы из начального состояния (до вдвижения пробки) в конечное (пробка вдвинута):
(1) Е2 - Е, = А,
полагая, что переходов механической энергии в другие виды энергии пет. Для этого необходимо вдвигать пробку очень медленно, в пределе с бесконечно малой скоростью.
7. Гидростатика. Закон Архимеда
247
Поскольку кинетическая энергия системы в начальном и конечном состоянии не изменилась (равна нулю), изменение полной механической энергии системы Е2 - Ei сводится к изменению потенциальной энергии в поле тяжести. Потенциальная энергия пробки в поле тяжести не меняется (центр масс пробки остается на одном уровне). Чтобы подсчитать изменение потенциальной энергии воды, заметим, что начальное состояние воды отличается от конечного тем, что объем ABCD перемещается в положение А' В' С D'. Потенциальная энергия остальной жидкости, как и ее положение, не изменилась. Воспользуемся доказанным в разделе «Статика» утверждением о расчете потенциальной энергии протяженных тел в поле тяжести:
(2) ЛЕ = Е2 - Ег = (h + А К) mg,
где 2А h — изменение уровня воды в стакане, т — масса воды в объеме АВ CD или А'В'CD':
(3) т = iti^lp = itR2 • 2 Айр.
Из (1—3) получаем:
(4) А = (й + j I m*lpg.
Второй способ решения задачи основан на прямом вычислении работы: i
(5) A=$Fdx,
о
где F — сила, действующая на пробку вдоль ее оси и совершающая работу А. Поскольку мы считаем, что пробка из начального положения в конечное •перемещается с бесконечно малой скоростью, сопротивление воды учитывать не будем. Положим также
248
Борис Гринченко
ускорение пробки равным нулю. Кроме силы F, на пробку действуют силы давления воды и воздуха. Запишем основное уравнение динамики для пробки в проекции на ось х:
(6)
F + P0S - PS = О,
где PS — сила давления со стороны жидкости, P0S — со стороны воздуха.
Пусть в некоторый текущий момент вдвижения пробки расстояние, на которое она продвинута, равно х, а расстояние между осью пробки и поверхностью жидкости в стакане у. Тогда имеем:
(7)
P = pgy + Ро,
С учетом соотношения, аналогичного (3) (условие сохранения объема жидкости), находим:
(8)
г2
у = h + х —-.
R2
Из уравнений (6—8) получаем:
Г г2
F = pgnr2 [h + х—ъ
(9)
Подставляя (9) в (5) и интегрируя от 0 до I, получаем формулу (4).
Отметим, что при подсчете силы, действующей со стороны жидкости на пробку, мы взяли в качестве среднего давления на торец пробки давление в ее центре. Доказательство правомерности этого допущения предоставляется читателю.
Энергетический подход к решению физических задач (в данном случае первый способ решения задачи) часто бывает весьма эффективен и приводит к быстрому результату.
7. Гидростатика. Закон Архимеда
249
Задача 7.12.
Внутри тонкостененного сферического баллона радиуса R находится газ под давлением Р. Разрежем мысленно баллон плоскостью на две равные части. С какой силой F одна половина оболочки баллона удерживает другую? Рассмотреть два случая: 1) внешнее давление отсутствует и 2) внешнее давление равно Ро-
Решение.
1. Рассмотрим условие равновесия газа в верхней половине баллона. Со стороны газа нижней половины вверх на него действует сила itR1 2P, со стороны внутренней поверхности баллона сила Fi, уравновешивающая силу kR2P и направленная вниз:
(1)
nR2P = Fv
Согласно третьему закону Ньютона:
(2)
Л = ^2 1 Z
250
Борис Гринченко
где F2 — сила, с которой газ давит на поверхность верхней половины баллона.
Условие равновесия оболочки верхней половины баллона:
(3)
F2 = F,
где F — сила, действующая со стороны нижней половины оболочки на верхнюю.
Из (1—3) находим: F = кВ^Р.
2. При наличии внешнего давления Ро условие равновесия верхней половины оболочки баллона принимает вид:
(4)
F2 = F + Г3,
где Fa — сила внешнего давления на поверхность верхней половины баллона.
Для нахождения F2 рассмотрим условие равновесия объема воздуха, примыкающего к верхней поверхности оболочки баллона. Действующую вниз силу
7. Гидростатика. Закон Архимеда
251
HR 2Р0 со стороны воздуха на выделенный объем уравновешивает сила со стороны поверхности баллона F4 (силой тяжести, действующей па воздух, пренебрегаем):
(5) тсЯ2Р0 = Г4.
С учетом третьего закона Ньютона:
(6) Р3 = Р4,
из (4,5) получаем:
F = nR2 (Р - Ро).
В качестве упражнения, полезно решить задачу при условии, когда плоскость разрезает шар на две неравные части (ответ: F - itr2 (Р - Ро), г — радиус сечения шара плоскостью).
252
Борис Гринченко
Задача 7.13.
В полусферический колокол, плотно лежащий на столе, наливают через маленькое отверстие наверху жидкость. Когда жидкость доходит до отверстия, она приподнимает колокол и начинает вытекать снизу. Найти массу колокола, если его внутренний диаметр Р, а плотность жидкости р.
Запишем закон Ньютона для колокола с жидкостью, рассматривая их как одно тело. Для этого рассмотрим все действующие силы на них: Ni — сила реакции опоры со стороны земли на колокол, N2 — то же на воду, Fo — сила давления воздуха на колокол, Mg — сила тяжести на колокол и mg — сила тяжести на жидкость. Поскольку система колокол-жидкость находится в покое, сумма всех сил, действующих на эту систему, равна нулю:
(1) Nr + N2 + Fo + Mg'+ mg~= 0.
7. Гидростатика. Закон Архимеда
253
Формула (1) справедлива при любых уровнях жидкости. В момент, когда жидкость доходит до отверстия, согласно условию задачи, Ni = 0. С учетом этого условия перепишем векторное равенство (1) в проекции на ось у:
(2) N2 - (т + М) g - Fo = 0
где, учтено, что Fo = PonR2 (см. решение задачи 7.12.). Масса воды под колоколом
(3) т = р — ttjR3
3
Имеем одно уравнение с двумя неизвестными ЛГг и М.
Рассматривая условие равновесия столба жидкости (см. рис.), найдем давление в точке О:
(4) Р = Ро + pgR.
Поскольку давление жидкости на одном уровне постоянно, такое же давление оказывает жидкость на землю и во всех других точках под колоколом. Следовательно, сила давления жидкости на землю равна:
(5) N = PnR2.
Согласно третьему закону Ньютона:
(6) N = N2.
Из (2—6) окончательно получаем:
М = |лЯ3р.
О
254
Борис Гринченко
Задача 7.14.
Почему сосиска при варении лопается вдоль, а не поперек?
Решение.
А
d
Разрежем мысленно сосиску вдоль пополам так, как показано на первом рисунке. А — толщина пленки, I — длина сосиски, d — ее диаметр. Будем считать, что
I, d » А , I » d.
На пленку одной из половинок действуют две силы — сила давления со стороны съедобной части сосиски (собственно, сосиски) и сила со стороны другой половинки пленки (этой силой и разрывается пленка — сосиска лопается). Поскольку пленка первой половинки находится в состоянии механического равновесия, то есть покоится, эти силы равны по модулю и противоположно направлены.
Используя результат задачи 7.4, нетрудно вычислить силу давления на половинку пленки со стороны сосиски:
(1)
» IdP,
7. Гидродинамика. Закон Архимеда.
255
где Р — величина давления сосиски на пленку, Id — приближенно равно площади сечения разреза сосиски. Напряжение, испытываемое пленкой на разрыв
вдоль:
рп „ _Fi_ _ ЫР ~ dP
(л) О 1 — — — 9
St (21 +2d) А (21 + 2d) А 2А
где Sj ~ (21 + 2d) А — площадь разреза пленки (приближенно), на которую приходится сила Fv
Разрежем теперь сосиску поперек, как показано на втором рисунке. Рассуждая аналогично, находим
напряжение на разрыв поперек сосиски:
dP
TtdA 4А
F —р (3)а2 = -г = -А-<=»2
Отношение напряжений:
Таким образом, при варении сосиски напряжение пленки на разрыв вдоль вдвое превышает напряжение на разрыв поперек. Поскольку мы, естественно, полагаем свойства пленки, в частности, на разрыв, изотропными, то получаем ответ на вопрос задачи.
При решении задачи предполагалось, что давление сосиски на пленку равномерно — на боковую поверхность и поверхность торца одинаково. В реальной ситуации давление на торцовую часть пленки обычно отсутствует, и в этом случае напряжения на разрыв пленки поперек сосиски вообще не возникает.
8. Гидродинамика
Рассматривается стационарное течение, когда количество несжимаемой жидкости, протекающей в единицу времени через любое поперечное сечение потока, постоянно. Объем жидкости, протекающей за единицу времени через сечение S, равен:
q = vS, где скорость жидкости и предполагается постоянной ! в любой точке сечения потока. Следовательно, условие стационарности можно записать в виде q = const, или для двух сечений:
= V2^2’
Для идеальной жидкости справедливо уравнение Бернулли:
рр2
Р + pgh + !~п~ = const, являющееся следствием закона сохранения энергии (см. решение задачи 8.1).
Нередко при решении задач школьной физики достаточно использовать частный случай уравнения Бернулли — формулу Торичелли:
1> = л/2£Й,
8. Гидродинамика
257
где v — скорость жидкости, вытекающей из узкого отверстия в широком сосуде, Н — расстояние от поверхности жидкости до отверстия.
При решении задач гидродинамики, как и гидростатики и динамики, используются основные законы механики — законы Ньютона, сохранения импульса и энергии, соотношения из кинематики, которые применяются для выделенных объемов жидкости.
258
Борис Гринченко
Задача 8.1.
Получить уравнение Бернулли.
Решение.
Пусть, для определенности, имеется стационарное течение жидкости по трубе переменного сечения в поле тяжести Земли. Пусть за малый промежуток времени объем жидкости ABCD переходит в новое положение AB'C'D'. Будем считать, что в малом объеме АВА В' скорость жидкости i>i, давление Pi и плотность pi постоянны.
То же относится к скорости V2, давлению Рг и плотности р2 в объеме CDCD'.
При указанном переходе полная механическая энергия жидкости изменилась. Поскольку это изменение не коснулось жидкости в объеме А В'CD (условие стационарности течения), то все сводится к изменению полной механической энергии объемов АВА В' и CDCD':
8. Гидродинамика
259
mv9
(1) Е2 - Ег = АЕ = + mgh2 -
2 2
то, ~2~ + mgh-L где т — масса жидкости в объеме АВА'В' (или в объеме CDCD') и потенциальная энергия отсчитывается от О.
Поскольку переходами механической энергии в другие виды энергии пренебрегаем (в частности, внутреннее трение в жидкости равно нулю), по закону сохранения энергии изменение механической энергии равно работе внешних сил, которыми в данном случае являются силы давления на жидкость в объеме ABCD, переходящей в объем А'В'CD'.
Работа сил, действующих на сечение АВ положительна и равна
(2)
То же для сил, действующих на сечение CD,
(3) А2 = — P2S2x2
(в этом случае направление действия силы на рассматриваемый объем жидкости и перемещение этого объема противоположны).
Итак, имеем:
(4) АЕ=А1+А2 = РА*! - P2S2x2.
Из условия сохранения массы жидкости:
(5) PjSjX-j = P2S2X2*
Из (1,4,5) получаем уравнение Бернулли: p.p? p9v9
Pi + р^ + -Цр = Р2 + p2gh.2 +
260
Борис Гринченко
Полагая в уравнении Бернулли
Pi = Р2 = Ро> Pi = Р2 = Р и Ai - Л2 = Я, = О, приходим к формуле Торичелли:
v2 = о = ^2gH.
8. Гидродинамика
261
Задача 8.2.
Из крана выливается вода. Начиная с некоторого места диаметр струи уменьшается на протяжении h от b до с.
Сколько воды вытечет из крана за время t?
Решение.
Воспользуемся основными уравнениями данного раздела. Из условия стационарности течения несжимаемой жидкости: ,2 2
по ПС
(1) п17р=п2“р
Из уравнения Бернулли с учетом Pi = Рг (свободно падающая жидкость) и pi = рг получаем:
(2) -± + gh = -£.
Объем воды, вытекающей за время t:
(3) V = Vj-j-t.
262
Борис Гринченко
Причем, очевидно, в (3) можно также взять нижнее сечение или любое другое.
Выражая из (1,2) скорость
2gh
1 2
и подставляя ее в (3), получаем ответ задачи:
2gh
д 2
t.
8. Гидродинамика
263
Задача 8.3.
Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности р. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха Ро-
Решение.
Давление жидкости в широком сосуде (О < х < Н - Л) дается обычной формулой
(1) Р = Ро + Pgx,
поскольку из условий задачи следует, что жидкость в широком сосуде практически неподвижна, то есть находится в равновесии.
Из условия несжимаемости жидкости внутри трубки:
(2)
vS = const,
264
Борис Гринченко
то есть скорость жидкости в трубке постоянна по всей длине трубки в каждый момент времени. Разумеется, с течением времени скорость меняется (уменьшается).
Воспользуемся уравнением Бернулли в точке х = Н на выходе из трубки, где давление жидкости равно атмосферному давлению Ро, и в произвольной точке х внутри трубки, обозначив давление в этой точке через Р:
2 2
(3) ро + ^- = р + (я-х)гр + ^-.
Уровень отсчета высоты берется от нижнего конца трубки. Отсюда получаем формулу для давления в тонкой трубке:
(4) Р = Ро + (х - Н) gp.
Формулы (1) и (4) дают ответ на вопрос задачи.
Интересно отметить, что формулы (1) и (4) дают различные значения давления в точке А. Это можно объяснить тем, что вблизи А состояние жидкости нельзя считать равновесным — в этой области происходит ускорение жидкости, что приводит к скачку давления.
8. Гидродинамика
265
Задача 8.4.
Сосуд с водой подвешен к потолку. Высота воды в сосуде Н. На сколько изменится натяжение веревки, если в днище сосуда открыть маленькое отверстие сечения S, из которого вытекает вода?
Решение.
Будем считать, в соответствии с условием задачи, что скорость воды в сосуде равна нулю, а скорость воды на выходе из отверстия найдем из формулы Торичелли:
(1) v =
За время At масса воды
(2) Am = pv<S At
приобретает скорость v.
Для этой массы воды запишем закон Ньютона в 'виде:
266
Борис Гринченко
где ДР = Дтпи — изменение импульса массы Лиг за время At, F — действующая на Ат сила. Если пренебречь изменением импульса за счет силы тяжести (см. раздел «Законы сохранения импульса и энергии»), то F — сила, действующая на данную массу со стороны жидкости в сосуде.
Подставляя Дтп из (2) в (3) и воспользовавшись (1), имеем:
(4) F = 2pgHS.
В соответствии с третьим законом Ньютона, сила, действующая на воду в сосуде со стороны вытекающей струи, равна F и направлена вверх. Воспользуемся законом Ньютона (условия равновесия) для воды с сосудом при закрытом отверстии:
(5) mg = То
и открытом:
(6) mg = ТХ + F,
где m — масса воды с сосудом, То и Тх — силы натяжения веревки.
Из (5, 6) находим:
TQ - Тх = F = 2pgHS.
8. Гидродинамика
267
Задача 8.5.
Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда Si, сечение струи S2. Уровень воды в сосуде перемещается с постоянным ускорением. Найдите это ускорение.
Решение.
Воспользуемся условием несжимаемости жидкости. В каждый момент времени имеем соотношение:
(1) &1V1 =
где vx — скорость воды в сосуде, v2 — в струе непосредственно вблизи дна сосуда.
При выходе из сосуда вода начинает свободно падать, так что ее ускорение равно ускорению свободного падения: аг = g.
Продифференцируем равенство (1) по времени:
(2) SitVi? = S2(v^' или = S2a2.
Окончательно получаем:
S2
g-
268
Борис Гринченко
Задача 8.6.
Насос должен подавать ежесекундно объем воды Q на высоту Н по трубе постоянного сечения S. Какова должна быть мощность насоса? КПД насоса Л, плотность воды р.
Решение.
Воспользуемся законом сохранения энергии: изменение полной механической энергии воды ЛЕ за время At равно полезной работе Ап насоса за это время:
(1) ЛЕ=Ап.
За время At насос подает массу воды
(2) Атп = QAtp,
~ „ Amu2
сообщая ей кинетическую энергию —-— и потенци-Zu
альную ЛтпёН, то есть
. „ Amu2 АЕ = —_--»• Лт§Н.
и
Кроме того,
(3)
Q = vS.
Учитывая определение мощности Nn = и опрег деление КПД: Nn = i}N, окончательно находим:
№ (rft+
П П v 2S?J
8. Гидродинамика
269
Задача 8.7.
По трубе сечением S, изогнутой под прямым углом, течет вода со скоростью v. Плотность воды р.
Чему равна сила бокового давления в месте закругления трубы?
Решение.
Воспользуемся законом Ньютона для массы воды А т:
(1) Am = pSv At,
протекающей по трубе за время Ai:
(2) = F,
_ Л*
где F — сила со стороны стенки закругления трубы, действующая на воду, АР — изменение импульса массы Ат воды за время At:
(3) АР = Amv^ - Attw{ = Am (v^ - uj).
Поскольку скорости воды щ и иг до прохождения закругления и после перпендикулярны друг другу, из (3) получаем:
(4) АР = у/2 v Am (vt = v2 = v).
Из (1,2,4) имеем:
F = 'l2v2pS.
Согласно третьему закону Ньютона, с такой же силой вода действует на стенку трубы в месте закругления.
9. Механические колебания
Решение уравнений гармонических колебаний:
(1) х” + А = О
(2) иж2 + Л2 = const
((1) получается из (2) дифференцированием по времени) имеет вид:
(3) х = хт cos cot или х = хт sin cot.
В (1—3) х — координата, их = х’ — скорость, х” = ах — ускорение тела (точки), хт — амплитуда, со — циклическая частота колебаний. Последняя связана с периодом колебаний соотношением:
(4) Т = —.
' со
Уравнения (1,2) будем ниже называть уравнениями стандартного вида.
Частота колебаний:
Задачи на механические колебания условно можно разделить на две основные группы: 1) задачи на расчет периода (циклической частоты) колебаний некоторой системы, когда основной целью является получение уравнений типа (1),(2) и 2) задачи на ки
9. Механические колебания
271
нематику колебательных процессов, когда характер движения точки (тела) заранее известен (3).
Для решения задач первой группы применяют два подхода: динамический, основанный на использовании законов Ньютона, и энергетический — с использованием закона сохранения энергии. Применяя первый или второй подход, пытаются получить уравнения (1) или (2) соответственно, решения которых известны.
Для решения задач второй группы используются приемы, аналогичные тем, что применяются при решении задач кинематики.
272
Борис Гринченко
Задача 9.1.
Вычислить период (циклическую частоту) колебаний тела массой т на пружине жесткости k (см. рис.). Трением тела о плоскость пренебречь.
Решение.
Выберем ось х с началом отсчета в точке О — положении тела в состоянии равновесия (пружина не-деформирована). Пусть в произвольный момент времени после выведения тела из положения равновесия координата тела равна х.
1. Применим динамический подход, записав закон Ньютона в проекции на ось х:
(1)
Fr = та, X X'
где, согласно закону Гука:
(2) Fx = - kx.
Справедливость соотношения (2) проверяем непосредственно: действительно, при положительных х на
9. Механические колебания
273
правление силы упругости противоположно оси х, и, следовательно, (2) верно. Аналогично убеждаемся, что при отрицательных х соотношение (2) так же справедливо.
Подставляя (2) в (1) и учитывая обозначение ах= х", получаем:
(3) х" + —х = 0.
т
Сравнивая (3) с уравнением стандартного вида (1) из введения, находим: ___
Л/ k rr, о А/ т а = ; Т = 2 л Д/ .
” т ” к
2. Решая задачу с помощью энергетического подхода, запишем полную механическую энергию системы в произвольный момент времени после выведения системы (тела) из положения равновесия:
Полагая, что в процессе движения механическая энергия Е сохраняется, получаем
v2 + — х2 = const х т
уравнение стандартного вида. Следовательно:
<о = дГ^; Т = 2лдД|\
N т N k
274
Борис Гринченко
Задача 9.2.
Вычислить период малых колебаний небольшого тела, подвешенного на нити длиной I (математический маятник). Потерями энергии при колебаниях пренебречь.
Решение.
Направим ось х горизонтально, выбрав в качестве начала системы отсчета О равновесное положение тела.
Применяя энергетический подход, запишем выра1 жение для полной механической энергии тела в произвольный момент времени после начала движения.' 2 2
(1) + = K
Потенциальная энергия в поле (тяжести отсчитывается от точки О, высота тела ОА найдена из геометрических соображений с учетом малости х (угла а): ОА = 1-АО' = I (1 - cos а) = I • 2sin2 £ = 12( -£)2 =
9. Механические колебания
276
где учтено, что since = у ® а. V
Принимая во внимание, что для малых колебаний v = vx = х’, приходим к уравнению стандартного вида:
(2) v2 + & х2 = const.
Откуда находим:
со = Vf; Т = 2л Vy.
I 8
276
Борис Гринченко
Задача 9.3.
Вычислить период колебаний груза массы т, подвешенного на пружине жесткости k.
Решение.
mg х
Пусть 1о — длина недеформированной пружины, точка О соответствует положению груза, находящегося в состоянии равновесия, х — координата тела в произвольный момент времени после того, как тело вывели из положения равновесия. Применим динамический подход и запишем закон Ньютона (условие равновесия) для покоящегося груза:
(1) kx0 = mg,
а затем для произвольного момента времени:
(2)
- k (х + х0) + mg = тах,
9. Механические колебания
277
где х0 — модуль деформации пружины в положении равновесия.
Подставляя (1) в (2), получаем: (ах = х")
(3) х" + — х = О,
' ' т
так что, как и в случае тела на горизонтальной плоскости (задача 9.1), период колебаний
Т =
Полученный результат показывает, что наличие постоянной силы, действующей на тело, не влияет на величину со (Т).
Применяя энергетический подход, запишем полную энергию системы:
(4) Е = . * (*о +
Из (4) с учетом (1) получаем:
Ч . kx2 2'2
)
2 - mgx.
kx%
+ -х- = Е —= const, JU
которое легко приводится к уравнению стандартного вида:
о2 + — х2 = const.
х т
278
Борис Гринченко
Задача 9.4.
Найти период колебаний жидкости в U-образном сосуде, постоянного сечения. Общая длина сосуда, занятого жидкостью I.
Решение.
За начало отсчета выбираем уровень жидкости в состоянии равновесия и будем следить, для определенности, за уровнем поверхности жидкости в левом колене сосуда в процессе колебаний.
Применим энергетический подход, выбирая в качестве нулевого уровня потенциальной энергии равновесное положение жидкости. /
Запишем полную механическую энергию системы (жидкости в сосуде):
(1) JE — Ек +
„ mv2 ,
где Ек = —(полагаем, что модуль скорости жид-кости одинаков во всех частях сосуда), а чтобы под
9. Механические колебания
279
считать потенциальную энергию Еп, заметим, что состояние жидкости на рисунке отличается от равновесного перемещением объема Sx из правого колена сосуда в левый. С учетом доказанных в разделе «Статика» утверждений № 1 и 3, находим:
(2) ' Еп = Sxpg х = Spx2g.
Учитывая, что
(3) SI • р = т,
из (1) и (2) находим: (
(4) v2 + х2 = ~~ = const,
I op то есть имеем уравнение стандартного вида при
Таким образом,
280
Борис Гринченко
Задача 9.5.
Найти период колебаний математического маятника длиной I в лифте, движущемся горизонтально с ускорением а.
Решение.
Перейдем в систему отсчета, связанную с лифтом, и воспользуемся принципом эквивалентности Эйнштейна.
Ускорение свободного падения тел относительно лифта:
(1) g1 = g - «•
Из (1) находим:
(2) £ = + а2.
Окончательно получаем:
Т = 2л -4 = 2л \ .
N у g2 + а2
9. Механические колебания
281
Задача 9.6.
Вычислить период малых колебаний кубика льда с ребром I в воде.
Решение.
О
Пусть точка О соответствует положению верхней грани кубика в положении равновесия, х — коор- ' дината верхней грани в произвольный момент времени в процессе колебаний.
Запишем закон Ньютона для кубика в проекции на ось х в условиях равновесия:
(1) mg = рв • V g
и в процессе колебаний:
(2) - mg + ( V - xl* 1 2 ) рв • g = тах,
где в (1) peVg — сила Архимеда (V — объем погруженной в воду части кубика, рв — плотность воды).
Согласно определению плотности масса льда
282 Борис Гринченко
(3) /п = рЛ г.
Из (2) с учетом (1,3) находим: х" + ^ f • х = 0. Рл 1
Отсюда: Т = 2и Peg
9. Механические колебания
283
Задача 9.7.
Найти период малых колебаний маятника, представляющего собой груз массы т на легком стержне длины I, к которому прикреплена горизонтально пружина жесткости k. Расстояние от точки подвеса
I гг стержня до места крепления пружины равно При
О вертикальном положении стержня пружина не деформирована.
Решение.
Запишем полную механическую энергию системы:
(1) Е = Ек + Еп,
где кинетическая энергия:
(2) Ек =
а потенциальная энергия системы включает в себя потенциальную энергию деформированной пружины
284
Борис Гринченко
ky2
и потенциальную энергию тела в поле тяжести
mgh. В качестве нуля отсчета потенциальной энергии в поле тяжести принимаем точку О, (положение груза при вертикальном положении стержня)
(3) Еп = + mgh.
Пусть х — координата тела в произвольный момент времени. Вводя угол а так, что sina = у из гео-метрических соображений учетом малости угла a (sina = а), находим:
(4) h = I - I cos a = I (1 - cos a) = 12 sin2 =
(5)
x
y~ 3’
Из (1—5) после несложных преобразований получаем уравнение стандартного вида:
у2 (£ + Л-Л х2= 2Е
Vx + < 1+ 9т'Х т
для гармонических колебаний.
Таким образом:
T = 2л
1
g + _k_
I 9m
9. Механические колебания
285
Задача 9.8.
Найти период малых колебаний маятника массы т на нити длиной I, установленного на тележке массой М. Тележка находится на гладкой горизонтальной поверхности.
Решение.
Обозначим через О положение маятника в момент прохождения положения равновесия. Пусть через некоторое время после прохождения равновесия маятник переместился на расстояние х; за это же время тележка переместилась в противоположную сторону на расстояние у.
Запишем полную механическую энергию сйстемы:
(1) Е = + mgh,
где
v » vx и V — скорости маятника и тележки соответственно. При получении (2) учтено х + у « I.
Согласно закону сохранения импульса (предполагается, что в начальный момент импульс системы тележка-маятник равен нулю):
(3)
mvx = MV.
Воспользуемся утверждением о том, что координата центра масс по оси х системы в процессе дви-
286
Борис Гринченко
жения не меняется (внешних сил, действующих на систему вдоль этой оси, нет), и определением центра масс (разделы 5 и 6):
(4) тх - Му = 0.
(отметим, что (3) и (4) эквивалентны, например, из (3) следует (4) и наоборот).
Из (1—4) после несложных преобразований получаем:
v2 + - (1 + -^г) х2 = —-----— = const,
x I v M' m .. m
1 + M
уравнение стандартного вида для гармонических колебаний.
Т = 2л -----. * '
9. Механические колебания
287
Задача 9.9.
Тело массы т находится на гладкой горизонтальной поверхности. Пружиной жесткости k тело прикреплено к стенке. Описать движение тела после того, как на него начала действовать постоянная сила F.
Решение.
Воспользуемся результатом решения задачи 9.3, где колебания так же совершаются при действии на тело постоянной силы (в 9.3 — силы тяжести); причем величина циклической частоты колебаний не зависит от наличия постоянной силы:
(1)
Для вычисления амплитуды колебаний воспользуемся законом сохранения энергии, выбрав начальное состояние системы (тело и пружина) в момент начала действия силы F, а конечное — в момент наибольшего растяжения пружины. Как в начальном, так
288
Борис Гринченко
и в конечном состоянии скорость (кинетическая энергия) тела равна нулю.
(2) тп = F • а,
где а — деформация пружины, Fa — работа силы.
Учитывая, что амплитуда колебаний хт = тр из (2)
получаем:
F
Хт = V" т k
Таким образом, тело совершает гармонические колебания с циклической частотой и амплитудой т
F k
вокруг положения равновесия, находящегося на
расстоянии -г от конца недеформированной пружины..
В качестве упражнения полезно получить решение задачи прямым вычислением, выбирая в качестве начала отсчета положение равновесия тела, определя
емого условием равенства силы упругости пружины и силы F.
9. Механические колебания
289
Задача 9.10.
Неподвижный груз, подвешенный на пружине, растягивает ее, находясь в положении равновесия на длину Д I. Каков период вертикальных колебаний груза?
Решение-.
Запишем условие равновесия груза на пружине:
(1) mg = k&L
Воспользуемся также результатом задачи 9.3, согласно которому:
(2) со - Т = 2п VT-171 ’ к
Подставляя -г- = —, из (1) и (2) находим: « 8
Т = 2п
290
Борис Гринченко
Задача 9.11.
Вагон движется на пружинный упор со скоростью v. В момент, когда скорость вагона обратилась в нуль, пружина сжалась на величину I. Определить, за какое время это произошло.
Решение.
С момента касания пружины вагон движется по гармоническому закону с периодом колебаний:
(1) Т = 2л
где пг — масса вагона, k — жесткость пружины.
Искомое время
(2) г = f.
Запишем закон сохранения энергии, выбрав начальное состояние в момент касания вагона с пружиной, а в качестве конечного — момент обращения скорости вагона в нуль (момент наибольшего сжатия пружины):
-«-,2 li2
(3) -у- =
Выражая из (3) т = -^ и подставляя это соотно-« и*
шение в (1) с учетом (2), окончательно находим:
9. Механическиекопебания
291
Задача 9.12.
На сколько отстанут маятниковые часы, поднятые на высоту Эвереста — Н = 8,9 км?
Решение.
Обозначим через То период колебаний маятника вблизи поверхности земли (на уровне моря), через Ti — на высоте Н.
За время суток т = 24 ч маятник, поднятый на высоту Н совершит:
(1) п =
колебаний. Поскольку за каждое колебание стрелка часов передвигается на время То, (так как часы проградуированы на уровне моря), показания часов через сутки будут:
Т
(2) = tiTq = т тр-.
Отставание часов за сутки
(3) Лт = т - = т ( 1 - ).
Запишем дважды выражения для периода колебаний вблизи поверхности земли и на высоте На
(4) Го = 2я
»0
(б) = 2тг
»1
и, соответственно, для ускорений свободного падения:
292
Борис Гринченко
(7)
GM gl (R + H)2’ где R радиус Земли.
Из (1—7) после несложных вычислений с учетом Я « R находим:
дт _ т _ 2 мин.
9. Механические колебания
293
Задача 9.13.
Сквозь Землю по диаметру прорыли сквозную шахту. Пренебрегая вращением Земли и сопротивлением, определить характер движения тела, брошенного в шахту.
Решение.
Запишем закон Ньютона для тела в шахте на расстоянии х от центра Земли:
(1) F = та.
Можно показать, что сила со стороны внешнего шарового слоя толщиной R - х равна нулю. Таким образом, сила, действующая на тело со стороны Земли: „ GMm
(2)
где
(3)
М = in | х 13 0
Мо inrf 0
294
Борис Гринченко
М — масса Земли, сосредоточенная в шаре радиуса | х |
Мо (плотность Земли р = ------).
О
Из (2, 3) с учетом g = находим:
(4) F = ^|«|.
Спроецируем (1) на ось х:
(5) Fx = тпах.
Непосредственно убеждаемся, что
(6) г,=-
правильно описывает выражение для проекции силы F на ось х (из рисунка видно, что при х > О Fx < 0, а при х < О Fx > 0).
Подставляя ах = х" и (6) в (5), получаем:
х" + = 0.
Это уравнение для гармонических колебаний с периодом
(7) Т = 2л\.
" о
Таким образом, движение тела в шахте — гармонические колебания с периодом Т из (7).
Докажем, что гравитационная сила, действующая на тело внутри тонкой сферической оболочки, равна нулю.
Каждому малому фрагменту оболочки площадью S соответствует фрагмент площадью S'. Из геометрических соображений следует:
9. Механические колебания
295
где гиг'— расстояния от тела до фрагментов S и S' соответственно. Обозначим массу на единицу поверхности оболочки через о и запишем закон всемирного тяготения для взаимодействия тела с фрагментами S и S':
/пч р _ GoSm. _ GaS'/n
(9) F = —, F = —-r-
(m — масса тела).
С учетом (8) из соотношений (9) находим: F = F'. Отсюда получаем искомое утверждение.
Поскольку шаровой слой можно представить как набор тонких сферических оболочек, приходим к утверждению о том, что сила со стороны шарового слоя, действующая на тело внутри его, равна нулю.
296
Борис Гринченко
Задача 9.14.
Воздушный шарик радиуса R и массой т при слабом ударе о стенку деформируется, как показано на рисунке. При этом деформация шарика х « R. Считая избыточное давление ДР воздуха в шарике (ДР = Р - Ро, где Р — давление внутри шарика, Ро — внешнее давление) постоянным и пренебрегая упругостью оболочки, найти время соударения со стенкой.
Решение.
Из теоремы Пифагора следует:
(1) г2 = Я2 - - (R - х)2,
где г — радиус круга оболочки шарика, соприкасающийся со стенкой. Учитывая, что х « R, для площади круга имеем:
(2) S - ~ 2nRx.
Сила, действующая на шарик со стороны стенки,
9. Механические колебания
297
(3)
F = АР • S.
Запишем закон Ньютона для шарика в проекции на ось х:
(4)
- F = тх".
Из (2—4) получаем
х +---—х = О
т
уравнение для гармонических колебаний с периодом
Т = —
1 ^NZkRAP
m
2лЛДР ’
Т
Искомое время т = = тс
ЛЛ
Примечание', для доказательства соотношения (3) необходимо воспользоваться законом Ньютона для фрагмента оболочки шарика, соприкасающегося со стенкой:
F - APS = О, где учтено, что ускорение фрагмента пленки равно нулю и пренебрегается упругостью оболочки.
10. Уравнение теплового баланса. Фазовые переходы
Постановка задач данного раздела обычно заключается в следующем. Задаются параметры системы, находящейся в термодинамически неравновесном состоянии (начальное состояние системы). Затем, в результате процессов теплообмена между отдельными частями, система переходит в состояние термодинамического равновесия (конечное состояние). Требуется определить параметры этого конечного состояния. Теплообменом с окружающей средой, как правило, пренебрегают.
Закон сохранения энергии при решении таких задач удобно формулировать в форме:
Q = Q . ^отд * пол’ где — количество теплоты, которое отдают части системы при переходе из начального состояния в конечное, (?пол — количество теплоты, полученное другими частями системы в процессе перехода. Существенно, что все слагаемые, входящие как в выражение для Qirv!t, так и (Эп, положительные вели-чины. Уравнение (1) называется уравнением теплового баланса.
Следует иметь в виду, что параметры конечного состояния системы не зависят от того, каким именно путем происходит переход из начального состояния
10. Уравнение теплового баланса
299
в конечное. Важно только, чтобы полная внутренняя энергия системы не изменилась. Это означает, что либо теплообмен с окружающей средой отсутствует, либо в процессе перехода могло быть подведено извне некоторое количество теплоты, которое должно быть равно отведенному в этом же процессе количеству теплоты.
Таким образом, при решении задач путь перехода системы из начального состояния в конечное можно выбирать, исходя из соображений удобства. Как правило, эти соображения сводятся к тому, чтобы основное уравнение теории (закон сохранения энергии) имел наиболее простую форму, а входящие в него константы (теплоемкости, удельные теплоты плавления и парообразования) были известны.
Приступая к решению задачи, целесообразно изобразить на рисунке систему в начальном и конечном состояниях, четко выделяя те части системы, которые претерпевают изменения (температуры, фазовые переходы). Затем устанавливают, какие части системы тепло отдают, а какие получают. После этого записывают уравнение теплового баланса. Если возникают затруднения, необходимо попытаться найти (выбрать) другой процесс перехода из начального состояния в конечное, вводя, например, промежуточные состояния.
Далее записывают (если они имеются) другие текстовые условия в виде математических соотношений и используют полученную систему уравнений для ответа на вопрос задачи.
В некоторых задачах соотношение фаз в конечном состоянии системы заранее не известно (например, мо-*жет оказаться либо одна вода, либо вода и лед и
300
Борис Гринченко
т.п.). В таких случаях либо применяют метод оценок (см. ниже), либо выбирают состав фаз интуитивно. Если полученное в результате решение не противоречит физическому смыслу (например, окажется, что температура льда + 20°С ), конечное состояние угадано верно. Если нет, необходимо выбрать другой вариант соотношения фаз в конечном состоянии.
Удельную теплоту плавления вещества будем обозначать 1, удельную теплоту парообразования — г, удельную теплоемкость — с.
Для количества теплоты, необходимого для нагрева, плавления и превращения в пар массы т вещества, справедливы соотношения:
Q = ст (t2 - tj)
Q = km
Q = rm.
В ряде случаев (задачи 10.5 и 10.6) вместо уравнения теплового баланса, основанйого на подсчете отданных и полученных частями системы теплот, целесообразно воспользоваться законом сохранения энергии в иной форме.
10. Уравнение теплового баланса
301
Задача 10.1.
В чашке находится 500 г льда при температуре 0°С. В нее вливают 200 г воды, нагретой до 80°С. Какова будет установившаяся температура и что будет в чашке? Теплообменом с окружающей средой пренебречь^
Решение.
Первый способ решения задачи основан на методе оценок. Выясним, хватит ли тепла, запасенного в горячей воде, чтобы растопить весь лед. Максимальное количество тепла вода может отдать, охладившись до 0°С: (?макс = 4,2 • 103 • 80 • 0,2 Дж. Количество тепла, которое необходимо, чтобы растопить лед — фпл = 3,4 • 10s • 0,5 Дж. Сравнивая эти теплоты, видим, что (?Маке < Qmi, то есть даже если вода отдаст максимально возможное количество теплоты, расто-* пить весь лед невозможно. Отсюда заключаем, что в конечном состоянии в чашке находится вода и лед
302
Борис Гринченко
при температуре 0°С (температура, при которой в нормальных условиях сосуществуют в равновесии вода и лед), как показано на рисунке.
Записываем уравнение теплового баланса с учетом результата оценки:
твсв80 = Airik,
где Дтп — количество растаявшего льда.
Ответ: Дтп = 0,2 кг. Следовательно, в чашке находится 400 г воды и 300 г льда при температуре 0°С.
Второй способ решения задачи основан на предположении относительно соотношения фаз в конечном состоянии. Если предположение высказано верно, то есть предполагается сосуществование воды и льда, составленное уравнение теплового баланса дает решение задачи.
Если бы было высказано ошибочное предположение (например, в чашке находится только вода), уравнение теплового баланса:
тпвсв (80 - tj) = тлк + тлсв^
дает значение температуры воды < 0, что противоречит физическому смыслу, а, следовательно, высказанному предположению.
10. Уравнение теплового баланса
303
Задача 10.2.
В сосуде находится лед массой 1 кг при температуре tji = - 10°С. В сосуд впускают 0,2 кг пара при температуре tn - 110°С. Какая температура установится в калориметре?
Решение.
Первый вопрос, который возникает, — о фазовом составе конечного состояния. Оценка показывает, что пар при 100°С, конденсируясь в воду при 100°С отдает количество тепла « 4 • 10б Дж, которого хватает на то, чтобы нагреть лед до 0°С (® 2 • 104 Дж) и растопить его (« 3,4 • 10° Дж). Отсюда заключаем, что в конечном состоянии, по-видимому, находится вода, температуру которой обозначим ti.
Запишем уравнение теплового баланса. В процессе перехода из начального состояния в конечное тепло отдавал пар, в итоге обратившись в воду при температуре ti. Сначала пар отдает тепло, охлаждаясь до температуры 100°С (тпп сп (110- 100)). Затем пар при температуре 100°С, конденсируясь в воду, отдает количество тепла тп г. Наконец, образовавшаяся при 100°С вода отдает тепло тв св (100 - ti), охлаждаясь до конечной температуры ti. Итак,
(!) = тпсп10 + тпг + тпсв (10° - *1)-
В процессе перехода в равновесное состояние тепло получал лед, сначала нагревшись до 0°С, затем превратившись в воду при той же температуре. Наконец,
304
Борис Гринченко
вода при 0°С получила тепло, нагревшись до конечной температуры ti. Следовательно:
(2) «пол = тлсл(° “ Q + + тлсв^.
Решение уравнения теплового баланса
(3) «отд ~ «пол
дает ответ задачи: tx = 40°С.
10. Уравнение теплового баланса,
305
Задача 10.3.
В колбе находилась вода при 0°С. Откачиванием пара всю воду в колбе заморозили. Какая часть воды испарилась?
Решение.
В процессе перехода из начального состояния в конечное тепло отдавала та часть воды т - Ат, которая превратилась в лед (т — первоначальная масса воды, Ат — масса воды, превратившаяся в пар):
(1) Фотд = (т- кт) %.
Получала тепло масса воды Ат, превращаясь в пар:
(2) Qnon = Amr.
Из уравнения теплового баланса
(3) Q = Q
' ' ^отд ^пол
с учетом (1,2) находим:
Am 1 1
---—-------« —. т г ..-----7
Х+ 1
306
Борис Гринченко
Задача 10.4.
С какой скоростью должны лететь навстречу друг другу две одинаковые льдинки с температурой - 10°С, чтобы после абсолютно неупругого удара обратиться в пар при 100°С?
Решение.
После неупругого удара вся кинетическая энергия mv1 2
льдинок 2 —х— переходит во внутреннюю (тепловую). Л
Действительно, суммарный импульс двух льдинок равен нулю и, следовательно, после удара (слипания) импульс (а вместе с ним и кинетическая энергия) каждой из льдинок также обратится в нуль.
Подсчитаем количество тепла, необходимое для превращения двух льдинок при температуре - 10’С в пар при 100°С.
На нагревание льда до 0°С необходимо 2сл?п 10 Дж тепла. Чтобы растопить лед при 0°С в воду при 0°С, необходимо 2тпХ Дж. Чтобы нагреть воду до 100°С - 2тпсв 100 Дж. Для испарения воды следует сообщить количество теплоты 2тиг Дж.
Запишем закон сохранения энергии:
(1) 2 ~ = 2тсл 10 + 2тпХ +
4Ы
+ 2тсв 100 + 2тг, откуда находим:
v = 2 (10сл + X + 100св ч -г ) « 2,2 • 103 (м/с).
В принципе, можно было бы выбрать и другой путь перехода, например, сначала испарить лед при
10. Уравнение теплового баланса
307
- 10°С (2тгл), а затем образовавшийся пар при - 10°С пар нагреть до 100°С (2тплсп 110). В этом случае вместо (1) можно записать:
(2) 2 = 2тгл + 2тсп 110,
Л
откуда
v = ^2гл + сп 110,
и вопрос заключается в том, чтобы отыскать в справочниках удельную теплоту парообразования льда при температуре - 10°С гл и удельную теплоемкость пара в диапазоне температур - 10 - 100°С сп. Если входящие в (1) константы можно взять, например, из школьного задачника по физике, то константы из (2) отыскать не всегда удается.
308
Борис Гринченко
Задача 10.5.
Сколько льда может образоваться из переохлажденной до - 10°С воды массой 1 кг? Теплоемкости переохлажденной и обычной воды считать одинаковыми. Теплообменом с окружающей средой пренебречь.
Решение.
Попытаемся найти такой путь (процесс) перехода в конечное состояние, для которого запись закона сохранения энергии выглядела бы достаточно просто.
Будем медленно нагревать переохлажденную воду до (ГС, сообщив при этом количество теплоты:
(1) Qx - mceLQ.
Затем, чтобы суммарный тепловой эффект процесса стал равен нулю, будем медленно охлаждать систему, забрав от нее в итоге количество тепла Q2 = Qi- Поскольку при этом часть воды Azn превратится в лед, мы вправе записать:
10. Уравнение теплового баланса
309
(2)
Q2 = А/иХ.
Так как получившееся конечное состояние равновесно (вода и лед при 0°С) и внутренняя энергия системы не изменилась, мы вправе заключить, что данное конечное состояние то же самое, что и полученное любым другим путем (разумеется, при условии равенства нулю теплового эффекта процесса), например, в результате самопроизвольного перехода.
Итак, получаем:
тсь10 = Атк
или, окончательно, Атп = 0,13 кг.
Приведем другой вариант решения задачи.
В процессе перехода в равновесное состояние тепло отдавала масса воды Ат, превратившаяся в лед. Переход этой массы воды при - 10°С в лед при 0°С проведем в два этапа. Сначала нагреем воду до 0°С, сообщив теплоту свАт 10, затем обратим в лед при 0°С, при этом выделяется теплота Атк. Следовательно:
Фотд = к Ат - свАт 10.
Получала тепло масса воды т - А т, нагреваясь от - 10°С до 0°С:
Фпол = св(т - 10-
Из уравнения теплового баланса (?отд = фПол находим:
тса 10
Ат = -—г-----= 0,13 (кг).
А
310
Борис Гринченко
Задача 10.6.
На сколько изменяется удельная теплота плавления вещества при понижении температуры плавления на At, если удельные теплоемкости вещества в жидкой и твердой фазе равны соответственно ci и сг?
Решение.
Чтобы решить задачу, естественно попытаться записать уравнение теплового баланса (закон сохранения энергии). Однако ни о каком процессе в условии задачи не говорится. Поэтому разумно придумать такой процесс, причем в соответствующее уравнение баланса должны войти упомятутые в условии константы.
Можно выбрать, например, следующий процесс. В качестве начального состояния возьмем массу М вещества в твердой фазе в обычном состоянии с температурой плавления to- Расплавим вещество, передав системе теплоту ММ. Затем охладим жидкость на At градусов, доводя ее температуру до to - At — пониженной температуры плавления (при этом, конечно, жидкость подвергается какому-то воздействию, например, добавлению других веществ, изменению давления).
Количество тепла, которое система отдает при таком охлаждении, равно ciMAt. Далее будем отбирать от системы тепло до тех пор, пока жидкость полностью не замерзнет — ММ. Наконец, нагреем твердую фазу от температуры to - At до to, сообщив системе теплоту C2MAt, и тем самым вернем систему в исходное состояние.
10. Уравнение теплового баланса
311
Очевидно, что тепловой эффект всего процесса равен нулю, поскольку внутренняя энергия системы не изменилась. Иными словами, сколько тепла было подведено системе, столько же и отведено.
Итак, согласно изложенному, имеем:
кхМ + CgAfAt = Х2 М + CjAfAt.
Отсюда, после сокращения на М, получаем ответ на вопрос задачи:
1 2 ~ (ci C^JAt.
312
Борис Гринченко
Задача 10.7.
Какая часть затраченной на парообразование энергии идет на совершение работы?
Расчеты провести для температуры 100°С, при которой удельная теплота парообразования равна 2,3 • 106 Дж/кг.
Решение.
Прежде всего отметим, что давление насыщенного пара при 100°С равно 1 атм или 105 Па.
Пусть, для определенности, мы имеем систему, изображенную на рисунке: под подвижным невесомым поршнем находится насыщенный пар и вода при температуре 100°С.
Сообщим системе количество теплоты Q. При этом, согласно определению величины удельной теплоты парообразования, испарится масса воды
(1) Лт =
10. Уравнение теплового баланса
313
Воспользовавшись дважды уравнением Менделеева—Клапейрона для начального и конечного состояния пара с учетом постоянства давления, получим:
(2) РДУ=^ЭТ.
С другой стороны, работа, которую совершает пар (при учете постоянства давления), преодолевая силу атмосферного давления, равна:
(3)
А = РЬУ.
Из уравнений (1—3) находим:
A RT
Q Mr
« 0,08.
11. Идеальный газ
Идеальными называются газы, подчиняющиеся уравнению Менделеева—Клапейрона (далее М-К):
(1) РГ = ^ЯТ.
(1) называют также уравнением состояния идеального газа.
Если ввести плотность газа р = (1) можно
переписать в виде:
(2) Р = Й:ДГ-
Еще одна форма записи уравнения М-К:
(3) Р = nkT.
В зависимости от условий конкретной задачи используют наиболее удобную форму записи уравнения М-К.
Если масса газа постоянна, из (1) следует: PV
(4) = const.
идеальных газов справедлив закон Дальтона:
(5) р=л+^2+
где Р — дхвлевяе смеси газа, Рг — парциальное давление газа i-того рода, входящего в смесь.
11. Идеальный газ
315
Умножая обе части (5) на V и учитывая, что для каждой компоненты газа справедливо уравнение М-К:
PiV=viRT,
где
т, Vi =
— число молей данной компоненты, по-
лучаем:
(6) PV=vRT,
(v = 2 vz). Уравнение состояния смеси идеальных газов, таким образом, имеет тот же вид, что и уравнение состояния химически однородного идеального газа.
Следует отметить, что, записывая уравнение М-К для i-той компоненты газа, мы пренебрегали наличием других газов. В этой связи иногда говорят, что идеальный газ — газ невзаимодействующих молекул.
316
Борис Гринченко
Задача 11.1.
При нагревании газа при постоянном объеме на АТ = 1 К давление увеличилось на ср = 0,2%. При какой начальной температуре находился газ?
Решение.
В условии речь идет о двух состояниях газа: до и после нагревания. Для каждого из них записываем уравнение М-К:
(D
(2)
где учтено, что =
По условию задачи:
(3) Т2 - Т1 = АТ
(4) Р2 = Р1 + IQQ% PV
Поделив почленно уравнение (2) на уравнение (1), получим:
£2_£2
Р1 т/
р2
Подставим Т2 из (3) и у из (4) в последнее соотношение. После несложных вычислений находим:
Г1 = АТ100%=500(К)
11. Идеальный газ
317
Задача 11.2.
Азот массой т - 10 г поместили в сосуд объемом V = 1 л и нагрели до температуры t = 1500°С, при которой а = молекул азота диссоциировала на атомы. О
Найти давление в сосуде.
Решение.
После нагревания в сосуде находится смесь двух разных газов — атомарного азота массой
(1) mN = ат
и молекулярного азота массой
(2) mN = т - ат = (1 - а) т.
Записываем уравнение М-К для каждой компоненты смеси:
(3) PNV = ^PT
т^
где Т = 273 + 1500 = 1773 К.*
Согласно закону Дальтона:
(5) Р = PN + PN/
Система уравнений (1—5) позволяет получить ответ на вопрос задачи. Подставляя тпу и т^г из (1) и (2) в (3) и (4), и выражая из них Ру и Ру2, из (5) окончательно получаем:
Р = ) « 40 (МПа).
V < Мм '
318
Борис Гринченко
Задача 11.3.
За сколько качаний поршневым насосом с рабочим объемом V можно откачать сосуд объемом V6 от давления Ро до Р?
Решение.
Рассмотрим изменение давления газа в рабочем объеме в результате первого качка.
Имеется два состояния газа: поршень в положении 1 (при этом давление газа Ро, объем Vo) и поршень в положении 2 (при этом давление газа Pi, объем Vo + V)-
Поскольку температура газа предполагается постоянной, воспользуемся законом Бойля—Мариотта:
Vo = W + V)
или
(1)
о
Л - -^о у
11. Идеальный газ
319
После выброса объема газа V в окружающее пространство и возвращения поршня в исходное положение 1 (для этого в насосе предусмотрено специальное устройство), повторяя в точности предыдущие выкладки, получим давление в рабочем объеме после второго качка:
Vo
(2)
или с учетом (1):
(3) Р2 = Р0(^)2.
После п качаний давление в сосуде будет, очевидно, равно:
(4) рп = ро(уо + у)П-
Полагая, что именно после п качаний давление в сосуде станет равным Р, то есть Рп = Р, из (4) находим:
Отсюда, по определению логарифма:
1 Гро\
n = 10g уо+у -р ) ,
Vo + V Г
——— — основание логарифма.
320
Борис Гринченко
Задача 11.4.
Сосуд длиной 3Z разделен легкими подвижными поршнями на три равные части. Левый поршень про ницаем для Не и для Н%, правый — только для Ну.. В начальный момент в левой части сосуда находится Ня, в центре — Не, в правой части — N?., причем давление гелия в три раза больше, чем давление водорода и азота. Найти расстояние, на которое сместится правый поршень после установления равновесия.
Решение.
Н2 Не n2
X
После установления равновесия водород займет весь объем сосуда (перегородок для него не существует), гелий — пространство в сосуде слева от правого поршня, азот — справа от правого поршня (который для пего является непроницаемой перегородкой). Обозначим через х смещение правого поршня, предположив, что он сдвинется вправо (если в результате решения задачи окажется, что х — отрицательная величина, эго будет означать, что мы не угадали на
11. Идеальный газ
321
правление смещения и на самом деле поршень сдвинется влево).
Воспользуемся законом Ньютона (условием равновесия) для правого поршня:
(1) + рп8 = PNS + P„S,
где S — площадь сечения поршня; в левой части (1) — сила, действующая на поршень вправо, в правой — влево. После сокращений:
(!') РНе = Pn2-
В задаче фигурируют два состояния каждого из трех различных газов. Поскольку предполагается, что температура газа постоянна, воспользуемся законом Бойля—Мариотта для гелия:
(2) Р°е SI = РНе (2 I + х) S
и для азота:
(3) P°N Sl = PNS(l-x),
2 2
где Р£е — начальное давление гелия и Р£ — на-2V2
чалыгое давление азота, согласно условию задачи, связаны соотношением:
(4) Р£е =3PS2.
Полученная система уравнений позволяет решить задачу. Разделив соотношение (3) на (2) и воспользовавшись (1,4), получим:
322
Борис Гринченко
Задача 11.5.
При расширении идеального газа его давление Р - aV, где а — постоянная величина. Во сколько раз изменится объем газа при увеличении температуры от 200 до 400 К?
Решение.
Наряду с условием задачи:
(1) Р = aV,
для идеального газа справедливо уравнение М-К:
(2) PV=vRT.
Подставляя Р из (1) в (2), находим связь между Т и V:
9 vJR
(3) ^ = -£ГГ-
Запишем (3) для двух состояний газа:
И) =
(6)
Поделив (5) на (4) и извлекая квадратный корень из обеих частей, получаем:
11. Идеальный, газ
323
Задача 11.6.
В земной атмосфере на высоте h\ = 120 км температура воздуха + 59°С. Вблизи этой высоты при подъеме на 1 км давление падает на фр = 7%, а плотность на фр = 12%. Определить температуру воздуха на высоте hz = 121 км.
Решение.
В условии задачи говорится о двух состояниях воздуха: на высоте 120 км и на высоте 121 км. Записываем для каждого из этих состояний уравнение М-К:
(1)
(2) Рг = § KT2,
предполагая, что молярная масса воздуха на обеих высотах одинакова.
Согласно тексту задачи:
(8) Р2 = Р1--^Р1
%
р2 ~ Р1 ТОО Р1’
(4)
Для нахождения Тъ разделим уравнение (2) на (1):
рг _ Рг 2k.
Л р1' Л
р2 . ф» Рг 1 Фр ZQS
и подставим сюда “ = 1 - ^qq и = 1 - Yqq из (3) и (4):
324
Борис Гринченко
100 к 100 > Т1
Из последнего соотношения температура на высоте 121 км по Кельвину:
Т2 = Т1-----= 380 (К).
100
По шкале Цельсия *2 = 77°С.
11. Идеальный газ
325
Задача 11.7.
В стальном баллоне находятся mi = 0,2 г водорода и mz = 3,2 г кислорода при температуре 27°С. Водород соединяется с кислородом и, после окончания реакции, давление в баллоне увеличивается в 3 раза. Какая при этом установится температура?
Решение.
Согласно химической реакции:
2Н2 + О, = 2Н2О, а А А '
с каждой молекулой кислорода соединяются две молекулы водорода или, что то же самое, один моль кислорода реагирует с двумя молями водорода.
Число молей кислорода и водорода до начала реакции:
Из сказанного выше следует, что в реакцию вступит весь водород и 0,05 моль кислорода, а оставшиеся 0,05 моль кислорода не прореагируют. Итак, в смеси после окончания реакции будут присутствовать 0,1 моль воды и 0,05 моль кислорода.
Записываем уравнение М-К и Дальтона для начального состояния:
(3)
(4)
(5)
326
Борис Гринченко
и для конечного:
(6) PoV=vO2RT2
(7) V = Vr*
(8) ^2 ~ ^о2 + Л/Зо*
Кроме того, согласно условию задачи:
(9) Р2 = ЗРГ
Система уравнений (1—9) позволяет получить ответ на вопрос задачи:
Т2 = 1200 К.
11. Идеальный газ
327
Задача 11.8.
На V— Т диаграмме изображен замкнутый цикл 1231, который совершает некоторая масса азота. Известно, что минимальное давление газа в этом процессе Pmin = 3 • 10е Па.
Определить массу газа и его давление в точке 1.
Решение.
Попытаемся определить точку на диаграмме, соответствующую минимальному давлению. Для этого используем следующий прием. Проведем произвольную изобару ОА. Она описывается уравнением М-К:
(1) г-^т,
из которого видно, что, чем большему давлению Р = const соответствует изобара, тем ниже наклонена она к оси Т. Переходя плавно от изобары ОА к изо
328
Борис Гринченко
барам с большим давлением, мы сначала коснемся диаграммы процесса в точке 2. Очевидно, что в точке 2 давление минимально, так как изобары, проходящие через другие точки графика цикла, соответствуют бблыпим давлениям. В частности, максимальное давление газа в цикле достигается в точке 3.
Таким образом, давление в точке 2 Р2 = Pmin = 3 • 10б Па. Запишем для состояния газа в этой точке уравнение М-К:
(2) Р, V2 = R Т2,
где V2 = 22,4 дм3, Т2 = 409,5 К. (2) позволяет получить ответ на первый вопрос задачи:
(3)----------------m =-------------- 1 Т2 « 4 • 10- 2 (кг).
Уравнение М-К для состояния газа в точке 1:
Ю вт,>
а х>
где = 11,2 дм , Тх = 273 К, позволяет определить давление в точке 1:
Отметим, что прием, который мы использовали для определения минимального давления, является общим. Так, например, для нахождения минимальных (максимальных) значений объема или температуры в диаграммах процессов, используют соответственно изохоры и изотермы.
11. Идеальный газ
329
Задача 11.9.
В вертикально расположенном цилиндре сечения S под поршнем массы М находится воздух. На поршне лежит груз. Определить массу этого груза, если известно, что после того, как его убрали, объем газа под поршнем вдвое возрос, а температура вдвое уменьшилась. Атмосферное давление Ро.
Решение.
Наряду с использованием уравнения М-К для начального и конечного состояний системы:
(1) P.V. = vRT.
(2) P2V2 = vRT2,
воспользуемся основным уравнением динамики (законом Ньютона) для поршня с грузом в первом случае и для поршня во втором (условие равновесия):
(3) P.S = (М + m)g + P0S,
где Рг S — сила, действующая со стороны воздуха под поршнем и направленная вверх, (М + ni) g — сила тяжести и Ро S — сила атмосферного давления, направленные вниз;
(4) P2S = Mg + P0S,
где P2S — сила давления на поршень в конечном состоянии.
Отметим, что при записи (3) мы рассматривали поршень и груз как единое тело и величина силы • атмосферного давления на поршень с грузом не зависит от формы груза (см. задачу 7.12).
330
Борис Гринченко
Из текста условия задачи следует:
(5) ^=2
Г. 1
<«> 7^4
Полученная система уравнений (1—6) исчерпывает информацию, содержащуюся в условии задачи.
Поделим уравнение (2) на (1), а также (4) на (3). Получаем:
P2V2 тг
mg р Р2 "3" + Р° Р7 " М + т
§ g+P0
Отсюда с учетом (5) и (6) имеем:
mg + P0S 1
(М + m)g + P0S “ 4’ или, окончательно:
т = ЗМ + ^-. S
Заметим, что вместо (1,2) можно было воспользоваться уравнением Клапейрона:
Л Т2 •
11. Идеальный газ
831
Задача 11.10.
Один моль газа участвует в процессе, график которого изображен на Р-V диаграмме. Кривые 1-4 и 2-3 — изотермы. Нарисуйте график этого процесса на Т-V диаграмме. Найдите объем Vs, если известны объемы Vi, Vz и К*.
О
V
332
Борис Гринченко
Точку 1 на Т-V диаграмме наносим произвольно. Чтобы изобразить участок 1-2, воспользуемся аналитической связью между Р и V, вытекающей из рисунка из условия задачи:
(1) Р = axV,
где cq — некоторая постоянная. Кроме того, газ подчиняется уравнению М-К:
(2) PV = RT.
Мы стремимся к тому, чтобы найти связь между Г и У. Подставляя Р из (1) в (2), находим:
а, 9
(3) т = -ЛЛ
Л
Таким образом, участок 1-2 в координатах Т-V является частью параболы (3), причем, чтобы нанести точку 2, необходимо пойти вверх по параболе (согласно рисунку условия задачи, объем на участке 1-2 возрастает). Точку 2 наносим, с учетом сказанного, произвольно.
Участок 2-3, согласно условию задачи, изотерма, график которой в координатах T-V — прямая, параллельная оси V. Чтобы нанести точку 3, следует двигаться вправо от 2, так как объем на этом участке возрастает.
Построение участка 3-4 аналогично участку 1-2; связь между Г и У имеет вид:
(Xq п
(4) Г =
причем для нанесения точки 4 следует идти вниз по параболе, так как объем на участке 3-4 уменьшается.
Участок 4-1 аналогичен участку 2-3.
11. Идеальный газ
333
Для ответа на второй вопрос задачи запишем уравнение (3) для состояний газа в точках 1 и 2:
(5) =
(«) Г2 = ^^>
а уравнение (4) для точек 3 и 4:
(8) Tt = 4
Учитывая, что Ti = Т4 и Тя = Тз, из (5-8) находим:
Полезно еще раз обратить внимание на прием, который использовался при построении графика процесса, известного в одних координатах, в других координатах. Для этого следует представить в аналитическом виде связь между параметрами газа на участке, которая вытекает из известного графика и, кроме того, воспользоваться уравнением Клапейрона, а затем с помощью двух полученных соотношений найти интересующую связь между двумя параметрами газа, соответствующими координатам искомого графика, исключив третий.
334
Борис Гринченко
Задача 11.11.
Во сколько раз изменится подъемная сила воздушного шара, если наполняющий его гелий заменить водородом? Весом оболочки шара пренебречь. Молярная масса воздуха 29 • 10"3 кг/моль.
Решение.
По определению, подъемная сила — результирующая всех сил, действующих на шар с газом. Поскольку, согласно условию, весом оболочки можно пренебречь, следует учесть две силы: силу Архимеда рК? (V — объем шара, р — плотность вытесненного шаром воздуха) и силу тяжести mg (т — масса газа в шаре), направленные в разные стороны. Итак, подъемная сила шара, наполненного гелием, равна:
(1)
-Pi = Vpg - mxg.
Подъемная сила шара в случае заполнения родом:
(2) Р2 = VPS ~ m^g.
Воспользуемся уравнением М-К для гелия дорода в шаре, учитывая, что давление газа в равно атмосферному Ро:
P0VM.
т Р^Т m2-~R~T
и уравнением М-К для воздуха в виде (см. формулу (2) введения к данному разделу):
(б) Р- RT •
водо-
и во-шаре
(3)
(4)
11. Идеальный газ
335
Воспользуемся полученными соотношениями (1—-5) для нахождения искомой величины отношения подъемных сил:
Л м,-мг 27
Рг М,-Мг-25‘
При получении ответа мы учли, что молярная масса гелия Mi - 4 • 10" 3 кг/моль, водорода Мг = 2 • 10" 3 кг/моль.
336
Борис Гринченко
Задача 11.12.
Герметически закрытый бак заполнен жидкостью так, что на дне его имеется пузырек воздуха. Давление на дчр бака Ро. Каким оно станет, если пузырек воздуха всплывет?
Высота бака Н, плотность жидкости р.
Решение.
Давление воздуха в пузырьке равно давлению жидкости вблизи дна бака Ро. Для доказательства этого утверждения достаточно рассмотреть условие равновесия небольшого слоя жидкости, непосредственно примыкающего к воздуху пузырька.
После того, как пузырек всплывет, его объем практически не изменится (считаем, что жидкость практически несжимаема), температуру воздуха в пузырьке так же считаем постоянной. Применяя для воздуха в пузырьке уравнение М-К в двух состояниях, убеждаемся, что давление воздуха в пузырьке не изменилось. Отсюда заключаем, что давление жидкости
11. Идеальный газ
337
вблизи крышки бака, у которой оказывается пузырек после всплытия, равно Pq.
Давление у дна бака, следовательно, равно:
Р = Р0 + pgH.
12. Насыщенный и ненасыщенный пар. Влажность
Пар, находящийся в равновесии с жидкостью, называют насыщенным. Для водяного пара вводится понятие относительной влажности:
(1) <р = /-100%,
“и
где Р — давление водяного пара при данной температуре, Рн — давление насыщенного пара при этой же температуре. Для насыщенного пара, очевидно, <р = 100%.
Эквивалентное (1) определение относительной влажности имеет вид:
(2) Ф = # Ю0%
Рн
где р — плотность водяного пара при данной температуре, рн — плотность насыщенного пара при этой же температуре.
Зависимость давления или плотности водяного пара от температуры может быть представлена либо в виде таблиц, либо графически.
Поскольку пар (молекулы воды) ведет себя как идеальный газ, для него справедливо уравнение Менделеева—Клапейрона.
В случае, если ср >100%, пар называют перенасыщенным. Такое состояние пара не является устойчивым — часть его конденсируется в жидкость до
12. Насыщенный и ненасыщенный пар
339
тех пор, пока не установится равновесие между процессами испарения и конденсации, то есть пока пар не станет насыщенным.
Нередко при решении задач используется понятие точки росы. Для определения этого понятия обратимся к графику зависимости плотности насыщенного пара от температуры. Пусть имеется воздух с относительной влажностью меньше 100% (ненасыщенный пар) при температуре и плотности рл- Будем постепенно понижать температуру, при этом относительная влажность увеличивается. При некоторой температуре tp, называемой точкой росы, плотность пара станет равна плотности насыщенного пара. При дальнейшем понижении температуры пар становится перенасыщенным, что и приводит к конденсации, в частности, к выпадению росы. Если понижение температуры происходит достаточно медленно, то в каждый момент пар является насыщенным.
340 Борис Гринченко
Кипение жидкости происходит при условии равенства давления насыщенного пара и гидростатического давления внутри жидкости. В обычных условиях гидростатическое давление практически совпадает с внешним (атмосферным) давлением. Так, например, из того факта, что вода при нормальном давлении (10б Па) кипит при температуре 100°С, следует, что давление насыщенного пара при 100°С равно 10б Па.
12. Насыщенный и ненасыщенный пар
341
Задача 12.1.
Давление водяного пара Р при 14°С равно 1 кПа. Является ли этот пар насыщенным?
Решение.
Из таблицы находим, что давление насыщенного пара при 14°С равно Рн = 1,6 кПа, то есть больше давления, данного в условии задачи. Отсюда заключаем, что пар не является насыщенным. При этом относительная влажность:
(1) <? = -£- Ю0% = 62,5%
меньше 100%.
Если бы в условии задачи вместо давления 1 кПа была бы указана величина, превышающая 1,6 кПа, например, 3,2 кПа, то мы бы имели ф = 200%, то есть перенасыщенный пар. Как отмечалось во введении, такое состояние пара неустойчиво: при переходе в устойчивое состояние часть его конденсируется. Создать перенасыщенный пар можно, например, за счет быстрого сжатия ненасыщенного или насыщенного пара.
342
Борис Гринченко
Задача 12.2.
Найти относительную влажность при 18°С, если при 10°С образуется роса.
Решение.
Согласно определению, относительная влажность при 18°С
(1) Ф = £-100%,
Рн
где плотность насыщенного пара при 18°С согласно табличным данным равна ря (18) = 15,4 г/м3? ар — плотность пара при 18°С. Поскольку с понижением температуры плотность паров не изменяется (до тех пор, пока не начался процесс конденсации), находим:
(2) р = рн (Ю) = 9,4 7М8
(согласно табличным данным плотность насыщенного пара при 10°С равно 9,4 г/м8).
Подставляя найденные значения р и ря в (1), получим:
Ф = 100% * 60%.
г 15,4
12. Насыщенный и ненасыщенный пар
343
Задача 12.3.
В запаянном сосуде объемом 0,4 л находится водяной пар при температуре 423 К и давлении 8,5 кПа. Сколько росы выпадет на стенках сосуда при понижении температуры до 295 К? Давление насыщенного пара пр? 295 К равно 2,6 кПа.
Решение.
Запишем уравнение М-К для двух состояний пара: т.
(»
(2) P,(V - SV) = ВТ2,
где тх — масса пара в начальном состоянии, т2 — в конечном, ДУ — объем образовавшейся в сосуде воды (росы):
(3) ДУ = —.
Ре
Масса образовавшейся воды:
(4)
Дтп = т1- т2.
Учитывая малость ДУ по сравнению с У, из (1—4) получаем:
428-^^)1810~8.3410"^0-^-
108
344
Борис Гринченко
Задача 12.4.
Смешали объем У1 воздуха с относительной влажностью (pi и объем Уг с относительной влажностью ф2. Смесь занимает объем Уз. Определить относительную влажность смеси. Температура поддерживается постоянной.
Решение.
Запишем определение относительной влажности для трех описанных в условии задачи состояний:
(1)
Ф1 = 100%
1 Рн
(2) <Р2 = § 100%
(3) <Р3 = £ 100%
и условие сохранения массы пара:
(4) Р1 yt + р2 У2 = р3 У8.
Из (1—4) находим:
Ф1 V\ + ф2 У2 Фз-------v '
з
12. Насыщенный и ненасыщенный пар
345
Задача 12.5.
В откачанном герметически закрытом сосуде объемом 10 л находится открытая колбочка, содержащая 10 г воды. Сосуд прогревают до 100’С. Какая масса воды испарится?
Решение.
Сделаем предположение, что не вся вода испарится. Тогда пар в сосуде будет насыщенным. Запишем уравнение М-К для пара в сосуде:
где Т = 373 К, V = 10" 2 м3, М = 18 • 10“ 3 кг/моль, давление насыщенного пара при 100°С (373 К) Р = 10б Па. Из (1) находим массу пара в сосуде:
,Q4 PVM R
(2) m = = 6 г.
Полученный ответ подтверждает сделанное при решении задачи предположение.
Примечание. Если бы оказалось, что полученная из (2) масса пара превышает массу воды в колбочке, то следовало бы сделать вывод, что вся вода испарилась.
346
Борис Гринченко
Задача 12.6.
На рисунке изображена изотерма влажного воздуха. Определить относительную влажность воздуха в точках А, В, С. В точке В изотерма имеет излом.
Решение.
При достаточно больших объемах V пар является ненасыщенным. С уменьшением объема при достижении точки В излом кривой означает, что пар стал насыщенным и при дальнейшем уменьшении объема начинается конденсация и пар остается насыщенным. Таким образом, относительная влажность
(1) фЛ = срв=1ОО%.
Чтобы определить относительную влажность в точке С, воспользуемся определением:
(2) Фе = -&• Ю0%
ГН
12. Насыщенный и ненасыщенный пар 347
и законом Бойля—Мариотта для состояний пара В и С:
(3) PBVB = PCVC.
Учитывая, что Рн = Рв, из (2) и (3) находим:
Фс = — 100% = 100% = 67%.
vc
348
Борис Гринченко
Задача 12.7.
При изотермическом сжатии 9 г водяного пара при температуре Т - 373 К его объем уменьшился в 3 раза, а давление возросло вдвое. Найти начальный объем пара.
Решение.
Из условия задачи можно заключить, что в процессе сжатия масса пара меняется: если бы она была постоянна, то в соответствии с законом Бойля—Мариотта при уменьшении объема в 3 раза давление увеличилось бы так же в 3 раза. Таким образом, в какой-то момент пар становится насыщенным и при дальнейшем сжатии давление остается постоянным и вдвое большим начального.
Запишем закон Бойля—Мариотта для начального состояния пара и состояния пара в тот момент, когда он стал насыщенным:
(1) = ^2
и уравнение М-К, например, для второго состояния (в момент, когда пар стал насыщенным):
(2) -РЛ = >
Учитывая, что, согласно условию задачи:
(3) Р2 = 2 Рг
и давление насыщенного пара при температуре 373 К (100°С) Р2 = 105 Па, из (1—3) находим:
mRT2
= 2 = 30 Л'
12. Насыщенный и ненасыщенный пар
349
Задача 12.8.
На какую максимальную высоту можно поднять воду при медленном поднятии поршня?
Температура воды и окружающей среды равна Т. Поршень плотно прилегает к стенкам трубы.
Решение.
Пусть столб воды достиг максимальной высоты, так что дальнейшее поднятие поршня к увеличению высоты столба воды не приводит (см. рис.)
Согласно утверждению из раздела «Гидростатика», давление однородной жидкости на одной горизонтали одинаково, то есть давления в точках А и В равны:
(!) Рл = Рв-
С другой стороны:
(2) РА = Ро,
где Ро — внешнее (атмосферное) давление, а
350
Борис Гринченко
(3) Рв = Рн + pgPI,
где Рн — давление насыщенного пара в пространстве между водой и поршнем (предполагается, что воздуха в этом пространстве нет).
Из (1—3) получаем:
Ро-Рн
(4) Н = —------
4 ' pg
Например, при температуре воды и окружающей среды 0° С, когда давление насыщенного пара Рн = 0,6 103 Па примерно в 200 раз меньше атмосферного и им можно практически пренебречь, из (4) находим Н = 10,3 м. Это и будет максимальной высотой подъема воды. При температуре 100°С (давление насыщенного пара равно атмосферному) воду с помощью поршневого насоса вообще поднять нельзя (формула (4)). Разумеется, речь идет о медленном движении поршня, когда пар над поршнем можно считать насыщенным.
12. Насыщенный, и ненасыщенный пар
351
Задача 12.9.
В замкнутом цилиндрическом сосуде сечением S = 1см2 находится водяной пар массой т = 10 г при давлении Р = 103 Па. С каким ускорением а необходимо двигать сосуд, чтобы началась конденсация? Температура сосуда и водяного пара поддерживается равной 100° С, силой тяжести пренебречь.
Решение.
Чтобы началась конденсация, необходимо, чтобы давление пара стало равно давлению насыщенного пара при температуре 100° С, то есть Ро = Юб Па.
Запишем закон Ньютона для массы пара т, полагая, что давление у задней стенки равно Ро, и учитывая, что давление у передней стенки пренебрежимо мало по сравнению с Ро (доказательство предоставляется читателю):
P0<S - та.
Отсюда находим:
а = £»? = ю8 м/с2.
т
13. Первый закон термодинамики
Первый закон термодинамики, или закон сохранения энергии в термодинамике обычно формулируют в виде:
(1) Q = АС7 + А,
где Q — количество тепла, переданное системе, AU — изменение внутренней энергии системы, А — работа, которую совершает система над внешними телами.
Как правило, в задачах школьной физики системой является идеальный одноатомный газ. Внутренняя энергия идеального одноатомного газа дается соотношением:
о о
(2) U = ~vRT или AU = ^vRAT.
Если газ не одноатомный, его внутренняя энергия может быть представлена в виде:
(3) U = СТ,
где С — теплоемкость данной массы газа. Существенно, что внутренняя энергия любого идеального газа определяется только температурой и не зависит от других параметров газа (давление, объем).
В случаях процессов с постоянным давлением работа, совершенная газом, равна:
(4) А = PAV.
13. Первый закон термодинамики
353
Эта работа может быть как положительной (изменение объема ДУ > 0), так и отрицательной (ДУ < 0). В последнем случае положительную работу совершают над системой другие тела.
Если в ходе процесса давление газа меняется, то работа, совершенная газом, может быть представлена в виде площади криволинейной трапеции под графиком процесса в координатах P-У, как это изложено в школьном учебнике. В аналитическом виде:
v я
(5) A=$PdV,
v 1
где V\ и У2 — начальный и конечный объемы газа.
Общий подход к решению задач данного раздела основывается на применении (1—5) к процессам, описанным в условии задачи. Нередко используется уравнение М-К. В некоторых задачах целесообразно использовать закон сохранения энергии с учетом механической энергии, законы динамики и т.д.
Начинать решение задачи целесообразно с построения графика процесса в координатах P-У. Это позволяет отчетливо представить себе особенности описанного в условии задачи процесса и правильно записать основные уравнения теории.
Одним из фундаментальных понятий в термодинамике является понятие теплоемкости. По определению, теплоемкость данной массы (количества) газа:
С-^ ~ &Тг где AQ — количество теплоты, которое надо сообщить газу, чтобы нагреть его на АТ градусов.
354
Борис Гринченко
Различают удельную теплоемкость (теплоемкость одного кг газа) с и молярную теплоемкость (теплоемкость одного моля газа) cv. Эти теплоемкости связаны соотношением:
(7) cv = Мс,
где М — молярная масса данного газа. Соотношение (7) можно получить, записав дважды определение теплоемкости:
AQ = тпсАТ; AQ = vcvAT; v =
Теплоемкость газа определяется характером процесса, в котором газ участвует. Поскольку таких процессов можно представить себе и осуществить сколь угодно много, то и соответствующих теплоемкостей так же бесконечно много. Так, например, если процесс идет при постоянном объеме, то соответствующая теплоемкость обозначается с„ — теплоемкость при постоянном объеме — причем эта величина носит фундаментальный характер, поскольку непосредственно связана с внутренней энергией газа:
(8) MJ = cvmAT
(при постоянном объеме работа газа А = 0 и, следовательно, AQ = АС7.
Нередко встречается величина ср — теплоемкость при постоянном давлении.
Теплоемкость газа в адиабатическом процессе (AQ = 0), очевидно, равна нулю и т.д.
13. Первый закон термодинамики
355
Задача 13.1.
В некотором процессе объем и давление идеального одноатомного газа возросли вдвое. Во сколько раз возросла внутренняя энергия газа?
Решение.
Речь идет о двух состояниях идеального газа, поэтому запишем дважды выражение для внутренней энергии:
(1) и. =
(2) Р2 = |vBT2.
Воспользуемся также уравнением М-К для начального и конечного состояний:
(3) PJSX = vPT,
(4) Р2^2 = vBT2.
Согласно условию задачи:
(5) Р2 = 2РХ
(6) V2 = 2УГ
Поделив (2) и (1) и воспользовавшись (3—6), находим:
356
Борис Гринченко
Задача 13.2.
В сосуде объемом Vi находится идеальный одноатомный газ при давлении Pi и температуре Тъ а в сосуде объемом Уг — одноатомный газ при давлении Рг и температуре Т2. Какие давление и температура установятся в этих сосудах после их соединения? Сосуды теплоизолированы.
Решение.
Запишем дважды уравнение М-К для начальных состояний каждого из газов:
(1) P.V^v.RT.
(2) P2V2 = у^Т2
и для конечных:
(3) Р/^! + VJ = V.RT
(4) Р2’(Уг + У2) = v2PT,
где Vj и v2 — количество молей первого и второго газа соответственно.
Согласно закону Дальтона:
(5) Р = Р1'+Р2\
где Р/ и Р2 — парциальные давления газов в смеси.
Поскольку по условию задачи сосуды теплоизолированы, мы вправе записать закон сохранения энергии для начального и конечного состояний, который, очевидно, сводится к сохранению внутренней энергии газа:
(6) fvjBT, +
13. Первый закон термодинамики 367
Полученная система уравнений позволяет дать ответы на вопросы задачи. Из (1,2,6) после несложных преобразований получаем:
т + ?2V2 т т
+ Р2У2Г, г-
Складывая уравнения (3) и (4) и воспользовавшись (1,2,5,6), находим:
_ P.V. + P2V2
V1 + V2 ’
358
Борис Гринченко
Задача 13.3.
Вычислить работу, которую совершают v молей идеального газа при постоянном давлении, если его температура повысилась на АТ градусов.
Решение.
Работа при постоянном давлении:
(1) А = РАУ = P(V2 - Уг) = Р2У2 - Р^,
где и У2 — начальный и конечный объемы газа, Рг и Р2 — начальное и конечное давление, причем
Запишем уравнение М-К для начального и конечного состояний:
(2) РгУу = vRTy
(3) P2V2 - vRT2.
Подставив (2,3) в (1) и учитывая, что
Т2--Т2 = АТ, получим:
А = vRAT.
Этот результат справедлив для любого идеального газа (одно- и многоатомного) и часто используется при решении задач данного раздела.
13. Первый закон термодинамики
359
Задача 13.4.
Давление v молей идеального газа связано с температурой соотношением Т = аР2, где а — известная постоянная. Вычислить работу, совершенную газом, при увеличении объема от Vi и V%. Поглощается или выделяется тепло в таком процессе?
Решение.
Для вычисления работы полезно построить график процесса в координатах Р-V. Для этого наряду с условием задачи:
(1) Т = аР2,
воспользуемся уравнением М-К:
(2) PV = vRT.
Исключая из (1,2) температуру (то есть подставляя (1) в (2)), имеем:
360
Борис Гринченко
Таким образом, в координатах Р-V график процесса представляет собой прямую линию, проходящую через начало координат. Работа, совершенная газом, равна площади криволинейной трапеции 1 - 2 - V2 - Vi (произведению полусуммы оснований на высоту):
(4) А = ff2 (V2 - Vj),
где Р{ и Р2, давления в точках 1 и 2, согласно формуле (3), равны:
Подставляя (5) в (4), находим:
Чтобы ответить на второй вопрос задачи, воспользуемся первым законом термодинамики:
Q = АН + А.
Поскольку температура газа возросла (согласно рисунку и (1)), ACZ > 0. Подсчитанная нами работа А > 0. Следовательно, Q > 0. Газ получал тепло.
13. Первый закон термодинамики
361
Задача 13.5.
В тепловом процессе моль идеального одноатомного газа переводят из начального состояния 1 в конечное 4, как показано на рисунке. Какое количество тепла подведено газу, если разность конечной и начальной температур А7'= 100 К?
362
Борис Гринченко
Изобразим график процесса в координатах P-V. Штриховыми линиями обозначены изотермы.
Воспользуемся первым законом термодинамики для перехода из 1 и 4:
(1) Q = Д17 + А,
где
(2) ДЕ7 = jvfl (Г4 - TJ = ^vRAT. ЛА ЛА
Работа, совершенная газом в процессе перехода из состояния 1 в 4, равна:
(3) А = А^4 = А4_2 + -4-2-3 "* 4-3-4 •
Поскольку Al-г = Аз-4 = 0 (на этих участках изменение объема ДУ = 0), а работа на участке 2-3 совершается при постоянном давлении и для нее справедлива полученная в задаче 11.3 формула:
(4) А, з = vR (Та - ТА.
С учетом того, что Тз - Т% = Ti - Т± = - АГ, из (1—4) получаем:
Q = ~vR^T - vRAT = «415 Дж.
А
13. Первый закон термодинамики
363
Задача 13.6.
Моль идеального одноатомного газа совершает замкнутый цикл, состоящий из трех процессов: адиабатического расширения 1-2, изотермического сжатия 2-3 и изохорического нагревания 3-1 (см. рисунок). Какая работа была совершена газом в адиабатическом процессе, если в процессе изохорного нагревания газу подведено тепло (?з1 = 10 кДж?
Решение.
Мы стремимся к тому, чтобы воспользоваться законом сохранения энергии:
(1)
Q — &U + А.
Вопрос заключается в том, для каких этапов цикла его применить. Сделаем это, например, для всего цикла 1-2-3-1.
Учитывая, что в этом случае ДС7 = 0 ДД17 = Ui - Ui = 0), перепишем (1) в виде:
364
Борис Гринченко
(2) Qx_2 + Q2-3 + Фз-1 “ А-2 + ^2-з + ^з-1 •
Применим теперь (1) для каждого из этапов цикла:
(3) Q12 = О,
поскольку процесс 1-2 адиабатический (теплообмена нет);
(^) ^2-3 = “^2-3’
поскольку в изотермическом процессе 2-3 - з = О’
(5) Qa-i = 10 кДж,
согласно условию задачи.
Кроме того, поскольку дУз -1 = 0,
(6) = 0.
Из (2) с учетом (3—6) окончательно получаем:
А-2 = #з-1 = 10 кДж.
Возможны и другие варианты решения задачи, основанные на записи (1) для различных этапов цикла.
13. Первый закон термодинамики
366
Задача 13.7.
Моль идеального газа охлаждается при постоянном объеме, а затем при постоянном давлении приводится в состояние с температурой, равной начальной То = 300 К. В итоге газ получил тепло Q = 1500 Дж. Во сколько раз конечное давление отличается от начального?
Решение.
Построим график процесса в координатах Р-V и воспользуемся первым законом термодинамики:
(1)
Q = AU + А
для перехода из начального состояния газа 1 в конечное 3.
По условию задачи Ту = Тз = То, следовательно:
(2)
ДП = 0.
Работа, совершенная газом на участке 1-3, складывается из работ на участках 1-2 и 2-3:
(3) -^1-3 = А = -^-1-2 +
где А1-2 = 0 (ДУ = 0), а работа Л2_3 (при постоянном давлении) может быть вычислена согласно формуле задачи 11.3:
(4)
-4-2-3 — (Г3
р2
В задаче требуется вычислить отношение поэ-Pi
тому воспользуемся уравнением М-К для состояний ♦в точках 1 и 2:
366
Борис Гринченко
(5) P1V=vET0
(6) P2y=vBT2(V1 = V2 = y)
Полученная система уравнений позволяет решить задачу. Разделив (6) на (5) получим:
Р9 То
(° Pi Т2'
Из (1—4) находим:
(8)
Q = vR (То - Т2).
Выражая Т2 из (8) и подставляя в (7), окончательно получаем: q
1 о
При решении задачи мы воспользовались тем, что Р2 = Рз, так что искомое отношение давлений Рз _ Р2 Pi-Л’
13. Первый закон термодинамики
367
Задача 13.8.
Цикл, совершаемый некоторой массой идеального одноатомного газа, состоит из двух изохор и двух изобар. Известно, что наибольшее давление в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего в данном процессе. Найти КПД цикла.
Решение.
Изобразим график циклического процесса в координатах P-V.
По определению, КПД цикла:
где Qj — подведенное к газу в течение цикла тепло, А — совершенная газом работа в течение цикла. Согласно первому закону термодинамики:
• (2) = ДИ + А.
368
Борис Гринченко
Применяя последнее соотношение для каждого из участков 1-2, 2-3, 3-4, 4-1, убеждаемся, что газ получал тепло от нагревателя только на участках 1-2 и 2-3. Действительно, на участке 1-2 температура газа в 2 раза возросла и стала равна 2 То в соответствии с уравнением М-К (начальную температуру газа мы обозначили через То) и, следовательно, внутренняя энергия увеличилась. Работа на этом участке равна 3
нулю. Таким образом, Q1-2 - • RvTo > 0.
На участке 2-3 объем газа при постоянном давлении возрос в 4 раза и, согласно уравнению М-К, во столько же раз возросла температура (Тз = 8 То). При этом внутренняя энергия возросла на величину з
t/2-з = • vR 6То. Работу газа на участке 2-3 можно 2 р
подсчитать,и воспользовавшись результатом задачи 11.3: Аг-з = vR 6То. Таким образом,
^2-3 ~ Д^2-3 + -^2-3 ~ vl?T0.
Рассуждая аналогично, заключаем, что на участках 3-4 и 4-1 газ тепло отдавал, то есть Q3-4 < 0 и Q4-1 < 0. Следовательно:
(3) Qi = Q12 + Q2_3 = 16,5 • vRT0.
Работа, которую совершил газ в цикле, складывается из работы на участке 2-3 А2-3 = vR 6Т0 (см. выше) и работы на участке 4-1 А41 = - v2?To 3 (см. решение задачи 11.3.) Таким образом,
А = Ау ч + Ад. - v 32? То.
Z—o 4— JI U
13. Первый закон термодинамики
369
Подставляя полученное значение работы А и теплоты Qi из (3) в (1), получаем ответ задачи:
Полезно обратить внимание на тот факт, что работа, совершенная газом в замкнутом процессе (цикле), равна площади, ограниченной графиком этого цикла в координатах Р-V. В данной задаче эта работа равна площади прямоугольника 1234, то есть Ро ЗУ или 3vl?To, что согласуется с полученным в задаче результатом.
370
Борис Гринченко
Задача 13.9.
Поршень массы М, замыкающий объем Vb идеального одноатомного газа при давлении Ро и температуре То, движется со скоростью и. Определить температуру газа при максимальном сжатии. Теплообменом пренебречь.
Решение.
Согласно первому закону термодинамики для газа под поршнем:
(1)
Q = MJ +А = 0,
так как теплоотводом от газа пренебрегаем.
Для изменения внутренней энергии идеального одноатомного газа имеем:
(2) № = ~vR ДТ = | vR (Tj - Т„),
где Т1 — температура газа в конечном состоянии, когда поршень останавливается (в этот момент сжатие максимально).
13. Первый закон термодинамики
371
Запишем также закон сохранения энергии для поршня, который в данном случае формулируется так (см. раздел 5): изменение полной механической энергии поршня равно работе внешних сил (в условиях задачи это А): Еъ - Ei = А или, поскольку потенциальная энергия поршня не меняется (мы вправе по-
Mv2
дожить ее равной нулю), Ei = Е2 = О,
mJ
2 *
Уравнение М-К для газа в начальном состоянии:
(3)
(4)
^ого — v/ZTq.
Система уравнений (1—4) позволяет дать ответ на вопрос задачи. Подставляя MJ и А из (2,3) в (1) с учетом (4) получаем:
Т — Т Г1 +
1 1 3P0v/
Можно было бы дать и более короткое решение задачи, а именно, воспользоваться законом сохранения энергии в следующей трактовке: изменение внутренней энергии системы равно изменению ее механической энергии (так как полная энергия системы газ—поршень сохраняется — теплообмена нет). Иными словами, кинетическая энергия поршня переходит во внутреннюю энергию газа:
(5) Д<7=^; =
Последние соотношения вместе с (4) так же дают решение задачи.
872
Борис Гринченко
Задача 13.10.
В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем массы М, находится моль идеального одноатомного газа. Газ нагревают. Поршень, двигаясь равноускоренно, приобретает скорость v. Сколько тепла подведено газу? Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь.
Решение.
Воспользуемся первым законом термодинамики для газа под поршнем:
(1) Q = AU + A, где
(2) Д17 = |v2? AT.
Работа, совершенная газом, затрачена на увеличение кинетической анергии поршня:
(3) А = ^2-.
(см. решение предыдущей задачи).
Согласно закону Ньютона для поршня F = Ма и
по условию задачи (ускорение постоянно), заключаем, что сила F, действующая на поршень со стороны газа,
F постоянна. Следовательно, давление газа Р = так
же постоянно. Работа газа при постоянном давлении была вычислена в задаче 11.3:
(4)
А = vR АГ.
Система уравнений (1—4) позволяет найти Q:
„ _ 5 Mv2
2 ‘ 2 '
13. Первый закон термодинамики
873
Задача 13.11.
Моль газа участвует в циклическом процессе, график которого состоит из двух изохор и двух изобар (см. рис.) Температуры газа в точках 1 и 3 равны соответственно Ti и Тз- Определить работу, совершенную газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме.
Решение.
На участках 1-2 и 3-4 газ работы не совершает. Работа газа на участке 2-3 равна
^2-з — (Т3
(см. решение задачи 11.3).
Аналогично для участка 4-1:
= R (7\ - TJ.
Работа газа за весь цикл складывается из работ на «всех четырех участках А = А2_з + Ал-i + А\2 + Аз~4'
874
Борис Гринченко
(1) A = R(T1 + T3-T2-T^ = R(T1 + T3-2T)> где обозначено Т2 = Т4 = Т и учтено А1-2 = А3„4 = О.
Воспользуемся уравнением М-К. Например, записав его для состояний газа в точках 2 и 3, в конечном счете получим:
(2) / = /•
1 3 к3
Аналогично для точек 4 и 1:
( ’ Л Vi
Поскольку по условию задачи Уг = Уз и Vi = Уг, из (2,3) получаем:
(4) Т = л/7\ • Т3.
Подставляя Т из (4) в (1), находим:
А = R (Т1 + Т3 - 2<г7Тз) = R 0^1 “ ^з)2-
Вычисления в задаче можно было бы сделать, учитывая, что работа газа за цикл равна площади, ограниченной графиком цикла в координатах P-У, и записывая уравнение Клапейрона для состояний газа в точках 1, 2, 3, 4.
13, Первый закон термодинамики
876
Задача 13.12.
Найти теплоемкость системы, состоящей из перекрытого поршнем сосуда с одноатомным газом (параметры Ро, Vo, То). Поршень удерживается пружиной. Слева от поршня вакуум. Если газ откачать, поршень соприкоснется с правой стенкой сосуда, а пружина будет недеформироваиа. Теплоемкостями сосуда, поршня и пружины пренебречь.
Решение.
• •• о •• • • * •/Л Р« • •••• • ь • • •• • • • • • • • * ;.:.Ло ”%**.:*
W033335
По определению теплоемкости: ДО
(i) С = ^,
где, согласно первому закону термодинамики:
(2) ДО = Д17 + А,
Изменение внутренней энергии: (3) ДС7 = vR АТ.
376
Борис Гринченко
Записывая уравнения (1—3), полагаем, что газ переходит из начального состояния с параметрами Ро, Vo, То в конечное с параметрами Ро + АР, Vo + AV, То + А Т. При этом газу сообщается количество тепла AQ, его внутренняя энергия увеличивается на ДС7 и он совершает работу А = Р АК Предполагаем, что величина АТ, а вместе с ней и все другие приращения AV, АР, AU, AQ и А весьма малы, в пределе стремятся к нулю. Поэтому, в частности, записывая выражение для совершенной газом работы А = Р ДР", считаем, что в процессе перехода газа из начального состояния в конечное давление практически не меняется.
Воспользуемся уравнением М-К для обоих состояний газа:
(4) P0V0 = vRT0
(5) (Ро + ДР) (Vo + ДР) = vR (То + ДТ).
Согласно закону Ньютона (условие равновесия поршня):
(6) kx0 = P0S
(7) А(х0 + Дх) = (Ро + AP)S,
где введены обозначения: х0 — расстояние от правой стенки до поршня в начальном состоянии, Дх -I- х0 — в конечном, S — площадь сечения поршня.
Кроме того, очевидно, что
(8) ДУ = S Дх.
13. Первый закон термодинамики
377
Работа А = Pq A V, которую совершает газ, идет,
согласно закону сохранения энергии, на увеличение
(9)
потенциальной энергии сжатой пружины: р лт/ + Лх)2 - 9 2 ’
2
где первое слагаемое в правой части — потенциальная энергия пружины в конечном состоянии, второе — в начальном.
Воспользуемся полученной системой уравнений для решения задачи. Вычитая уравнение (4) из (5) и воспользовавшись малостью произведения -АР АУ по
сравнению с другими членами, получим:
(10) Ро АУ + V AV = vR АГ.
Вычитая уравнение (8) из (7), находим:
(11) /г Ах = APS.
_ „ k Ах2
Пренебрегая в (9) величиной —=— по сравнению А
с другими, имеем:
(12) Р0АУ = Лх0 Ах.
Умножая (11) на хо и учитывая (8) и (12), получим:
(13) Р0АУ=У0АР,
так что (10) принимает вид:
(14) 2Р0 АУ = vR АГ
или
Ро АУ = -Х-АТ.
378
Борис Гринченко
Подставляя в (2) Ро АИ из (14), а затем полученное
AQ в (1), и воспользовавшись vR = из (4), окон-1 о чательно находим:
с - 2
1 о
Полезно рассмотреть другой вариант решения задачи. Будем охлаждать газ, переводя его из начального состояния (Ро, Vo, То) в конечное с температурой, стремящейся в пределе к нулю. То есть будем считать, что в конечном состоянии температура газа практически равна нулю. При этом газ не производит давления на поршень (согласно основным представлениям молекулярно-кинетической теории) и, следовательно, поршень займет крайне правое положение, практически касаясь стенки сосуда. Весьма малый объем, остающийся между поршнем и стенкой, соответствует объему плотно упакованных молекул (атомов), и мы будем им пренебрегать.
Считая полученное состояние газа начальным, подведем к нему некоторое количество тепла Q. Согласно первому закону термодинамики:
(1) Q = AC7 + A,
где Д(7 — приращение внутренней энергии —совпадает с самой внутренней энергией, поскольку внутренняя энергия газа в начальном состоянии равна нулю:
о
(2) ДП = U = ~vRT,
а работа, совершенная газом, равна потенциальной энергии сжавшейся пружины (в начальном состоянии
13. Первый закон термодинамики
379
пружина, согласно условию задачи, не напряжена и, следовательно, потенциальной энергией не обладает):
/>г2
(3) Л =
£
Запишем уравнение М-К для газа, после сообщения ему, энергии Q:
(4) PV = vRT
и закон Ньютона (условие равновесия поршня):
(5) kx = PS,
где х — расстояние от правой стенки до поршня, причем, очевидно:
(6) V = xS.
Из (1—6) после несложных вычислений (умножая
X
обе части (5) на и т.д.) получаем:
А
(7)
Q = 2vRT.
Записывая (7) для различных Qi и Q2 и вычитая одно уравнение из другого, находим:
=
Величину vR определим из уравнения М-К для состояния газа с заданными в условии задачи параметрами:
vR = -1-°. 1 о
Итак, окончательно,
с~~гГ
380
Борис Гринченко
Задача 13.13.
Из небольшого отверстия в баллоне со сжатым гелием вытекает струя газа со скоростью v. Найти разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне при расчетах пренебречь.
Сформулируем закон сохранения энергии для массы гелия т, который в баллоне занимал объем V, а в струе — Уо-
Оставшимся в баллоне гелием при вытеснении массы т совершена работа:
(1) А = PV.
Эта работа затрачена на совершение работы Ао против давления наружного газа:
(2) А = Р0У0,
13. Первый закон термодинамики 381
придание массе гелия т кинетической энергии и на изменение внутренней энергии АС7 массы т гелия:
(3) ди = | ~Я (Т„ - Г).
Таким образом:
(4) JV=P0V0+^ + |-^R(T0-T).
Учитывая уравнения М-К для массы т гелия в баллоне и в струе:
(б) РИ=^ВТ
(в) P„V„ = ^вт„
из (4) получаем:
14. Поверхностное натяжение
На молекулу жидкости действуют силы притяжения со стороны окружающих молекул. Если молекула находится внутри жидкости, то эти силы в среднем уравновешиваются. Если же молекула находится на поверхности, то появляется результирующая сила, направленная внутрь жидкости. Поэтому для извлечения молекулы из внутренних частей жидкости на ее поверхность требуется затрата работы. Работа, которую надо затратить, чтобы увеличить поверхность жидкости на единицу площади при сохранении ее объема неизменным, называется поверхностным натяжением жидкости. Таким образом,
(1)
А = oS,
где величина о называется поверхностным натяжением, или коэффициентом поверхностного натяжения.
Для ответа на вопрос, почему о называют поверхностным натяжением, рассмотрим следующий опыт. Возьмем проволочный каркас, имеющий форму прямоугольника. Сторона CD каркаса может свободно скользить вдоль направляющих проволок АС и BD. Затянем площадь ABCD мыльной пленкой. Пленка эта, подобно листу бумаги, имеет две стороны — переднюю и заднюю — и состоит из двух одинаковых простых пленок, между которыми находится жидкость. Опыт показывает, что пленка стремится сократиться, и перемычка CD приходит в движение
14. Поверхностное натяжение
383
вверх. Для удержания в равновесии к CD надо приложить определенную силу. Так как пленка состоит из двух простых пленок, то модуль этой силы удобно обозначить посредством 2F, считая, что на каждую простую пленку действует сила F. Найдем F. Увеличим F на малую величину. Тогда перемычка CD начнет медленно перемещаться вниз. При перемещении перемычки на расстояние Ах над пленкой будет совершена работа АА = 2FАх. При этом площадь поверхности пленки увеличится на 21Ах = 2CDAx, где I — длина перемычки CD. По определению поверхностного натяжения работа АА может быть представлена в виде АА = 2gS = 2d Ах. Приравнивая оба выражения для работы, получим:
(2)
F = cl.
Отсюда видно, что пленка находится в состоянии натяжения. Разрежем мысленно пленку вдоль отрезка прямой линии. Тогда каждая из половин разрезанной пленки будет действовать на линию разреза с определенной силой, имеющей характер натяжения, ка
384
Борис Гринченко
сательной к пленке и перпендикулярной линии разреза. Сила, отнесенная к единице длины линии разреза, и есть поверхностное натяжение о.
Таким образом, жидкость ведет себя так, как если бы она была помещена в эластичную (например, резиновую) пленку. В отличие, однако, от резиновой пленки, когда сила натяжения зависит от величины растяжения, сила поверхностного натяжения жидкостей не зависит от величины площади ее поверхности.
Поверхностное натяжение жидкости зависит от свойств среды, с которой она граничит. В таблицах обычно приводят значения поверхностного натяжения жидкостейэ на границе с воздухом или ее насыщенным паром. Так, поверхностное натяжение воды при мН
0°С на границе с воздухом равно 75,7 -, а па гра-
м
нице с насыщенным паром 73,2 Можно говорить м
также о поверхностном натяжении на границе раздела двух песмешивающихся жидкостей или на границе раздела жидкости и твердого тела.
Для описания явлений, связанных с поверхностным натяжением, вводятся понятия смачивания, не-смачивания и краевого угла. Капля жидкости на твердой поверхности может вести себя по разному.
Л
Угол 0 называется краевым углом. Если 0 < 0 < -», то говорят, что имеет место частичное смачивание по-л
верхности жидкостью; если < 0 < л, то имеет место
частичное несмачивание. Угол 0 = 0 соответствует случаю полного смачивания (при этом капля растекается по поверхности, покрывая ее тонкой пленкой (напри-
14. Поверхностное натяжение
385
мер, керосин на поверхности жести или стекла)). Угол 0 = л отвечает случаю полного несмачивания (например, капля ртути на поверхности стекла или капля воды на поверхности парафина). При этом жидкость стягивается в шаровую каплю, несколько сплюснутую силой тяжести.
Явление краевого угла наблюдается у стенок сосудов, когда в них налита жидкость.
Соотношения (1,2) являются основными уравнениями теории данного раздела. Они, как было показано выше, эквивалентны. В зависимости от конкретных условий задачи используют либо (1), либо (2).
В целом, задачи, где поверхностное натяжение играет существенную роль, являются задачами на применение законов механики: законов Ньютона и законов сохранения энергии. Подходы и методы решения таких задач обсуждались ранее в разделах 3—8. В случае, когда для решения задачи применяются законы Ньютона, целесообразно использовать выражение для силы (1). В случае применения закона сохранения энергии — соотношение (2).
При решении задач полезно пользоваться представлениями о поверхностном слое жидкости как тонкой
386
Борис Гринченко
эластичной пленке, с теми оговорками, о которых упоминалось выше.
Существенно, что в результате эффектов, связанных с явлением поверхностного натяжения, при соприкосновении жидкости, например, с твердым телом, сила, действующая со стороны поверхности тела на жидкость, может быть направлена как в сторону поверхности твердого тела (полное или частичное смачивание), так и в сторону жидкости (полное или частичное несмачивание).
При изложении основных понятий данного раздела мы следовали книге Д. В. Сивухина «Общий курс физики», т.2, 1990.
В ряде случаев может оказаться полезным введение понятия поверхностной энергии на основе соотношения (1):
(3) Еп = aS,
где S — полная поверхность жидкости. Увеличивая поверхность жидкости, мы совершаем работу А (1), которая идет на увеличение поверхностной энергии:
А = Е„ - Еп = cS2 - aS. = a AS,
П2 пх й 1
где Si и S2 — поверхности жидкости в начальном и конечном состояниях соответственно.
14. Поверхностное натяжение
387
Задача 14.1.
Какую работу надо совершить, чтобы каплю жидкости объемом V с поверхностным натяжением о растянуть в пленку, толщина которой d мала по сравнению с первоначальным радиусом капли?
Решение.
Воспользуемся основным уравнением теории:
(1) А = ctAS = ст (S2 - SJ,
где — площадь поверхности капли, S2 — пленки. Пренебрегая площадью поверхности пленки на ее торцах, будем считать, что S2 = 2S, где S — площадь поверхности одной стороны пленки.
Объем пленки запишем в виде:
(2) V = Sd или <8 = ^-
Из условия сохранения объема жидкости:
^kR? = S d
О получаем:
4л/?2 за 2S~S2~2R‘
Поскольку по условию d < < R, мы можем пренебречь величиной Si по сравнению с 5г-
С учетом изложенного получаем окончательно:
А - 2ст d
388
Борис Гринченко
Задача 14.2.
Найти поверхностное натяжение жидкости, если петля из резиновой нити длины 1о и жесткости k, положенная на пленку этой жидкости, растянулась до окружности радиуса R после прокола пленки внутри петли.
Решение.
Рассмотрим три варианта решения. Первый вариант основан на применении второго закона Ньютона (условия равновесия) к весьма малому фрагменту резиновой нити длиной AI, опирающейся на угол 2а:
(1) Ту + Т2 + F = О,
где Ту и Т2 — силы натяжения со стороны прилегающих частей нити, причем, в силу симметрии, очевидно, Ту = Т2 = Т. Модуль силы поверхностного натяжения F равен:
14. Поверхностное натяжение
389
(2) F = 2oAi
(двойка учитывает наличие двух поверхностей пленки).
Согласно закону Гука:
(3) Т = k (2nR - /q).
Спроецируем (1) на ось х:
(4) 2Т sin а - F = 0.
Учитывая, что при малых a sin а » а, из (2—4) находим:
k (2nR -
— — ————— _
Второй вариант решения задачи основан на применении второго закона к полукольцу резиновой нити:
(1) т1 + т2 + ЕХ = «-
390
Борис Гринченко
Мы разбили полукольцо на очень малые фрагменты с длинами д Ц, и силу поверхностного натяжения, действующую на полукольцо со стороны пленки, представили в виде последнего слагаемого в правой части (1):
(2) Ft = 2Д1р.
Согласно закону Гука:
(3) Т = (2nR - l0) k
(учтено, что Tr = Т2 = Т).
Спроецируем (1) на ось х:
(4) 2Т = £ Fix,
где S Ftx = 2ctAZz cos az = 2о Alt cos az =
= 2o AZOi = 2a • 2R.
Из (2—4) получаем ответ задачи.
Третий вариант решения основан на энергетическом подходе.
Представим себе, что в результате каких-то причин радиус нити возрос на величину Ай, которую будем считать очень малой AR < < R. Это может произойти, например, через длительное время вследствие текучести резины.
При таком увеличении длины резиновой нити силы поверхностного натяжения совершают работу:
(1) А = 2лАЯТ,
где 2лАй — величина удлинения нити.
14. Поверхностное натяжение 391
С другой стороны, поверхностная энергия пленки уменьшилась на величину:
(2) ЛЕП = о28,
где S = 2kRAjR — уменьшение поверхности одной стороны гренки.
Согласно закону сохранения энергии:
(3) &Еа = А.
Из (1—3), с учетом закона Гука, получаем ответ задачи:
k (2те R - Zq)
а= 2Ё ’
392
Борис Гринченко
Задача 14.3.
Железный кубик, смазанный парафином, плавает в воде так, что его верхняя грань находится на уровне воды. Вода не смачивает парафин. Найти длину ребра кубика.
Решение.
На кубик действуют три силы: сила тяжести mg, сила Архимеда Fa = lspg (р — плотность воды) и сила поверхностного натяжения, направленная вертикально вверх:
(1) Fa = o4Z,
где 41 — периметр кубика, I — длина его ребра.
Запишем условие равновесия кубика в проекции на вертикальную ось:
(2) FA + Fn-mg = O.
Учитывая, что т = Z3pi (pi — плотность железа), из (1—2) получаем:
/ 4о л 1
I _ ( ---— ] 2 « 2,1 (мм).
ЧР1-Р)£У
14. Поверхностное натяжение
393
Задача 14.4.
Определить толщину слоя жидкости, разлитой па горизонтальной плоскости. Краевой угол 0, плотность жидкости р, поверхностное натяжение ст.
Решение.
Рассмотрим условие равновесия мысленно выделенного тонкого слоя жидкости, разрез которого на рисунке заштрихован. Толщину слоя (в направлении, перпендикулярном рисунку) обозначим через I. Для краткости атмосферное давление не учитываем.
Кроме изображенных на рисунке сил поверхностного натяжения Fi и F2 и силы давления N со стороны соседних частей жидкости, на выделенный объем действуют силы давления, перпендикулярные плоскости рисунка, а также сила давления со стороны горизонтальной поверхности. Эти последние силы направлены перпендикулярно оси х, так что их проекции ‘на ось х равны нулю.
394
Борис Гринченко
Запишем условие равновесия выделенного объема в проекции на ось х:
(1) - cos 0 + F2 - N = О.
Для сил поверхностного патяжения имеем:
(2)
F. = F9 = al. А л
Силу давления N на площадь I • Н можно рассчитать, используя зависимость давления в жидкости от глубины h от верхней поверхности жидкости Р = pgh. Поскольку зависимость линейная,
(3) N = | • pgH • Hl
(“ pgH — среднее давление). &
Подставляя (2,3) в (1), после несложных преобразований получим:
ст (1 — cos 0)
„ . 0
= 2sin g
Видно, что при 0 = 0 (полное смачивание) Н = 0, то есть жидкость растечется по поверхности. При 0 = л (полное несмачивание) Н максимальна.
Учет атмосферного давления сводится к тому, что на выделенный объем справа налево и слева направо будут действовать одинаковые силы Ро I Н (Ро — атмосферное давление), друг друга компенсирующие. Таким образом, проведенное решение остается в силе. В этой связи полезно возвратиться к решению задачи 7.12.
14. Поверхностное натяжение
395
Задача 14.5.
Вычислить давление жидкости под ее сферической поверхностью радиуса R, вызванного силами поверхностного натяжения. Коэффициент о известен.
Решение.
Воспользуемся приемом, аналогичным примененному в задаче 7.12.
Разрежем мысленно сферу на две равные части. На жидкость верхней полусферы действуют две силы: вверх — сила давления со стороны жидкости нижней полусферы РкР2 (Р — давление в жидкости) и вниз — сила поверхностного натяжения 2nRa. Поскольку жидкость верхней полусферы находится в состоянии равновесия, имеем:
PitR2 = 2hRg, откуда окончательно получаем: р=— R ’
Этот же результат можно получить, рассматривая, .например, условие равновесия маленькой квадратной или круглой площадки на поверхности сферы.
396
Борис Гринченко
Задача 14.6.
Вычислить давление внутри мыльного пузыря радиуса R. Коэффициент поверхностного натяжения о, внешнее давление отсутствует.
Решение.
Согласно результату предыдущей задачи, каждая 2ст m поверхность мыльной пленки создает давление —. Та-R ким образом, давление внутри мыльного пузыря равно 4ст
R ’
Если внешнее давление имеет место, то для равновесия пленки необходимо создать дополнительное давление внутри пузыря, равное атмосферному. То „ „ 4ст „
есть Р = Ро + -д-, где Ро — внешнее давление.
Получим этот же результат другим способом. Рассмотрим условие равновесия воздуха, занимающего объем верхней полусферы пузыря. Вверх на него действует сила давления со стороны воздуха нижней полусферы PitR2 и вниз — сила давления со стороны верхней полусферы пленки. Поскольку воздух находится в состоянии равновесия, то последняя сила также равна PitR2 (сравнить с результатом задачи 7.13). По третьему закону Ньютона, с такой же силой PitR2 газ действует на верхнюю полусферу пленки. Вниз на верхнюю полусферу пленки действует сила поверхностного натяжения (со стороны нижней части пленки), равная 2с2яК (учтено, что у пленки две поверхности и что пленка тонкая). Из условия равновесия верхней полусферы пленки имеем:
14. Поверхностное натяжение
397
PitR2 = 2ст2л7?
или
Третий вариант решения задачи основан на применении закона сохранения энергии. Представим себе, что в силу каких-либо причин объем пузыря крайне незначительно увеличился (например, из-за нагревания воздуха в пузыре). Пусть при этом радиус пузыря увеличился от /? до /? + АВ. Считая АВ очень малым (<ЛВ < < В ) и, следовательно, давление в процессе увеличения объема постоянным, для работы, совершенной газом, получаем:
А = PAV = Р | it {(В + АВ)3 - В3 } - Р4лВ2АВ, где мы пренебрегли в силу малости членами, пропорциональными АВ2 и АВ3. Эта работа идет на увеличение поверхностной энергии пленки:
А = АЕП = 2 • 4л {(В + АВ)2 - В2 } - 16лКАЯст.
Отсюда вновь получаем известный результат.
Еще один вариант расчета основан на использовании условия равновесия для мысленно выделенного малого фрагмента пленки, например, в виде квадрата.
Как отмечалось выше, при наличии внешнего давления все рассуждения остаются в силе, однако для того, чтобы уравновесить внешнее давление, необходимо создать внутри пузыря дополнительное давление, равное внешнему (при условии малости толщины . пленки).
398
Борис Гринченко
Задача 14.7.
Найти радиус кривизны капли в ее верхней точке А. Масса капли М, ее высота Н, радиус соприкосновения капли с горизонтальной плоскостью, на которой она находится, равен г. Плотность жидкости р, поверхностное натяжение с. Плоскость не смачивается жидкостью.
Решение.
Для простоты вычислений будем полагать внешнее давление равным нулю.
Давление жидкости вблизи точки А, согласно результатам задачи 12.5 и 12.6, определяется формулой Лапласа:
(1) рл=
где R — радиус кривизны капли в точке А (в силу симметрии капли относительно вертикальной оси, проходящей через А, введение понятия радиуса кривизны в этой точке корректно). Рассматривая рав
14. Поверхностное натяжение
399
новесие соответствующего столба жидкости (см. раздел 7), получим:
(2) Рв = РА + pgH,
где Рв — давление в жидкости вблизи точки В.
Во всех точках жидкости вблизи горизонтальной плоскости давление так же равно Рв (см. раздел 7: давление в однородной жидкости на одной горизонтали одинаково).
Согласно третьему закону Ньютона, сила Рвлг2, с которой жидкость давит на поверхность, равна силе, с которой поверхность давит на жидкость. Записывая закон Ньютона (условие равновесия капли) в проекции на вертикальную ось, получим:
(3) Рллг2 = Mg.
Из (1—3) после несложных вычислений получим:
R = 2о • ( - pgH ) - \
4 лг у
Следует иметь в виду, что мы существенно использовали условие несмачивания поверхности жидкостью, то есть равенство 0 = л. В противном случае появилась бы дополнительная сила со стороны поверхности, имеющая вертикальную составляющую.
Учет внешнего давления, как можно показать, не изменяет ответ, найденный выше. Действительно, внешнее давление, с одной стороны, приведет к появлению дополнительной силы, действующей на свободную поверхность капли и равной Рол/12. С другой стороны, на такую же величину внешнего давления ‘Ро возрастет давление в капле, и, следовательно, в конечном итоге появится дополнительная сила со сто
400 Борис Гринченко
роны поверхности, так же равная Рокг2. Таким образом, условие равновесия (3) остается в силе: обе силы друг друга уравновешивают.
14. Поверхностное натяжение
401
Задача 14.8.
Капля ртути массы т - 1 г помещена между двумя параллельными стеклянными пластинками. Какую силу надо приложить к верхней пластинке, чтобы ртуть имела форму круглой лепешки радиуса R = 5 см? По-' ** н
верхностное натяжение ртути о = 0,465 —. Ртуть не смачивает стекло.
Решение.
Сила, которую надо приложить к верхней пластинке, равна:
(1) F = PS,
где Р — давление в ртути, S — площадь соприкосновения пластинки с ртутью. Рассмотрим задачу без учета внешнего давления, а затем покажем, что его учет не меняет полученный результат.
Если пренебречь действием силы тяжести, давление в ртути вызвано только силами поверхностного
402
Борис Гринченко
натяжения, причем давление во всех точках внутри капли одинаково. Отсюда мы заключаем, что радиус кривизны свободной поверхности ртути, от которого зависит давление в капле, постоянен. На основании этого, в свою очередь, мы вправе считать, что радиус кривизны капли в разрезе, показанном на рисунке, d л
равен г = где а — расстояние между пластинками Л
(учтено, что ртуть не смачивает стекло — краевой угол 0 = тс).
Воспользоваться полученной ранее формулой Лапласа для сферической поверхности жидкости „ 2ст
Р = ~ мы, однако, не имеем права, поскольку в раз-
резе капли, параллельном пластинкам, ее радиус во много раз больше г: г « R, то есть поверхность ртути не является сферической.
Для того, чтобы вычислить давление в капле, рассмотрим условие равновесия массы половины капли, полученной разрезом вертикальной плоскостью.
На половину капли со стороны другой половины действует сила давления Р (2Rd + тег2) (в скобках стоит площадь сечения разреза капли) и уравновешивающая ее сила поверхностного натяжения, равная ст (4J? + 2лг) (в скобках — периметр разреза капли). Других сил, действующих на каплю в горизонтальном направлении, нет. Итак, имеем:
Р (2R 2г + яг2) = ст (4R + 2лг).
Учитывая, что г « R, из последнего соотношения находим:
ст г
14. Поверхностное натяжение
403
Подставляя (2) в (1), получаем:
F = PS = улЙ2, где г можно найти из условия сохранения объема капли V = —:
§
V = -7- ® лй2 • 2г или г = — Р 2лЯ2р
(учли, что г « R).
Итак, окончательно:
р = СТ7Е2д4р = 780 н> т
В случае учета внешнего (атмосферного) давления, давление в капле возрастет на величину Ро, однако на такую же величину возрастет давление на пластинку, поэтому сила, которую необходимо приложить к пластинке, останется той же.
Чтобы оценить влияние сил тяжести на давление внутри капли, следует сравнить максимальное гидростатическое давление pgd с давлением за счет сил 2сг поверхностного натяжения
pgd 2сг _ pgd2 d ~ 2ст 1ф
Как видно, предположение о малости сил гидростатического давления выполняется.
Давление внутри капли можно было бы получить, рассматривая условие равновесия поверхностного слоя ртути на свободной поверхности капли (сила давления на этот слой уравновешивается силами поверхностного натяжения).
404
Борис Гринченко
Мы могли бы рассмотреть условие равновесия половины капли, полученной разрезом горизонтальной плоскостью. В этом случае условие равновесия имеет вид:
PnR2 + 2лВо « Р • л (R + г)2,
где слева стоят сила давления со стороны пластинки и сила поверхностного натяжения, справа — сила давления на площадь поверхности разреза со стороны жидкости другой половины капли. В результате вновь приходим к соотношению (2).
Если бы жидкость полностью смачивала пластинки, то они притягивались бы с силой, вычисленной нами в данной задаче. Различие при этом состоит в том, что давление в жидкости было бы меньше о
атмосферного на величину —. При отсутствии послед-
него это давление является отрицательным (то есть жидкость не сжата, а растянута).
14. Поверхностное натяжение
405
Задача 14.9.
В вакууме в чашку с маслом, имеющим весьма низкую упругость пара и полностью смачивающим стекло, погружена стеклянная капиллярная трубка н радиуса г. Найти давление в масле на высоте -д- над уровнем масла в чашке, где Н — высота, на которую поднимется масло в капилляре. Поверхностное натяжение масла равно о.
Решение.
Будем полагать (см. решение предыдущей задачи), что поверхность жидкости в капилляре сферическая. Давление в жидкости вблизи поверхности масла в капилляре меньше внешнего на величину, даваемую формулой Лапласа:
2о г ' Поскольку, по условию задачи, внешним давлением можно пренебречь, давление в масле в указанной ‘области отрицательно и определяется формулой (1). Это означает, что жидкость не сжата, а растянута.
406
Борис Гринченко
Вблизи поверхности масла в чашке давление равно внешнему и равно нулю. Равно нулю на этом же уровне и давление масла в капилляре (см. раздел 7).
Рассмотрим условие равновесия столба масла в капилляре высотой, практически равной Н и сечением S. Сила тяжести mg = HSpg уравновешивается силой 2п
у S со стороны масла вблизи верхней поверхности. Приравнивая эти силы, находим:
pgr
Этот же результат можно было бы получить обычным способом, приравнивая силу тяжести, действующую на столб масла в капилляре, силе поверхностного натяжения, действующую на этот столб со стороны внутренней поверхности капилляра:
TU^Hpg = 2лга.
(2)
Рассмотрим теперь условие равновесия столба мас-« Н л
ла в капилляре высотой -5-. Аналогичные рассуждения
<5
дают в результате:
О _ Л _ 20
Р pg‘3 Зг'
Отметим (об этом упоминалось во введении к разделу), что из-за того, что давление в капилляре отрицательное (жидкость растянута), сила, действующая со стороны стенки капилляра на жидкость, направлена к стенке капилляра. С такой же силой (согласно третьему закону Ньютона) масло «тянет» на себя стенку капилляра.
15. Закон Кулона
Сила взаимодействия двух точечных зарядов qi и <?2, находящихся в вакууме на расстоянии г друг от друга, определяется законом Кулона:
m v_k kJ k2lkJ k2l
(1) г------ g-,
Г 4 П Eo r
Hm^
где k = 9 • 109 -— электрическая постоянная,
Кл
1 Кл2
sn = тт - 8,85 • 10 12 -7 — диэлектрическая про-
Н•м
ницаемость вакуума. Заряды называют точечными, если размеры тел, на которых они размещены, много меньше расстояния между ними. Закон Кулона (1) справедлив также для равномерно заряженных сферических оболочек и, следовательно, для любых тел со сферически симметричным распределением заряда, если в качестве г выбрать расстояние между центрами сфер. Задачи на взаимодействие зарядов, как правило, сводятся к задачам на применение законов Ньютона с учетом электростатического характера взаимодействия. В случае точечных зарядов сила взаимодействия между ними определяется из (1) непосредственно. В задачах, где взаимодействуют тела с пространствен-•ным распределением заряда, не являющегося точечным, необходимо рассматривать этот заряд как
408
Борис Гринченко
систему точечных зарядов и для них применять закон Кулона.
Ниже под обозначением q понимается алгебраическая величина заряда, то есть величина q может быть как положительной, так и отрицательной.
15. Закон, Кулона
409
Задача 15.1.
Три точечных заряда q, 2q и 4q соединены двумя одинаковыми непроводящими нитями длиной I каждая. С какой силой растянуты нити?
Решение. 5 Л । » .......
2q
♦—
т, 4<г
А
I
ч-х
Запишем условие равновесия заряда (закон Ньютона) в проекции на ось х с учетом электростатического характера взаимодействия (закон Кулона):
г 0
I2 (21)2 1
и то же самое для заряда 4q:
(2) т2 _ “242 _ *242 , о.
2 I2 (2г>2
Из (1—2) находим:
т _ 3^92. т _
410
Борис Гринченко
Задача 15.2.
Два одинаково заряженных маленьких шарика массы т каждый подвешены в одной точке на нитях одинаковой длины I. Нити разошлись так, что угол между ними равен а. Определить заряды шариков.
Решение.
У
Запишем закон Ньютона (условие равновесия) для одного из шариков в проекции на оси х и у:
CL
(1) FA-Tsin7 = 0
(2) mg - Tcos = 0,
где Fk — кулоновская сила, действующая со стороны левого шарика на правый:
Т — сила натяжения нити.
15. Закон Кулона
411
Из (1—3) находим:
412
Борис Гринченко
Задача 15.3.
Четыре положительных заряда Q, q, Q, q связаны нитями одинаковой длины. Найти угол между нитями при заряде Q.
Решение.
Запишем закон Ньютона для 'зарядов Q и q в проекции на оси х и у соответственно:
(1) ———2 + cos а - 2Tcos а = О
(2Zcos а)2 * * I2
(2) —^2—2 + s *in а ~ 2Tsin а = О,
(2Zsin а)2 I2
где 2а — искомый угол, Т — сила натяжения нитей,
I — их длины.
Разделив (1) на cos а, а (2) на sin а, получим:
kQ2
л /2ЛЛ 3
41 cos а
+ - 2Т = О
I2
___
4Z2sin8 а
- 2Т = 0.
I2
15. Закон Кулона
413
Отсюда находим:
; =>tea = f-flL^
4Z2cos8 a 4Z2 sin8 a ®
2a = 2arctg ( J®.
414
Борис Гринченко
Задача 15.4.
Вокруг заряда q по круговой орбите радиуса R вращаются две частицы массой т и зарядом - q каждая. Найти угловую скорость вращения частиц.
Решение.
ся зарядов правлением
в проекции на ось, совпадающую с на-центростремительного ускорения:
о о /»t't*
J?2 (2К)
(1)
и формулу для центростремительного ускорения:
(2)
а - co2jR.
Из (1,2) находим:
со
15. Закон Кулона
415
Задача 15.5.
Доказать, что если два одинаковых металлических шарика, заряженных одноименными неравными зарядами, привести в соприкосновение и затем раздвинуть на прежнее расстояние, то сила взаимодействия между ними увеличится.
Решение.
Запишем зак<
Кулона для начального состояния: „ fe9i92
После соприкосновения происходит перераспределение зарядов, причем в силу симметрии заряды шариков станут одинаковыми. Согласно закону сохранения заряда:
(2) 91 + 92 = 2g,
где q — заряд каждого из шариков после соприкосновения.
Закон Кулона после раздвижения шариков на прежнее расстояние:
(3) f2 =
Разделив (2) на (1) и учитывая непосредственно проверяемое неравенство:
(4) (9i + 92)2 - 4qxq2,
получаем:
F2 _ (9i + 92)2 .
Л 491д2 " Ъ что и требовалось доказать.
416
Борис Гринченко
Задача 15.6.
В одной из моделей иона Ня электрон движете^ по круговой орбите, лежащей в плоскости симметрии иона (то есть в плоскости, перпендикулярной линии, соединяющей протоны и делящей расстояние между ними пополам). Расстояние между протонами R. Найти скорость, с которой электрон движется по орбите радиуса г.
Решение.
Запишем закон Ньютона для электрона в проекции на ось, направленную вдоль вектора центростремительного ускорения:
(1)
Fx = та,
(2)
где ускорение электрона v2 а = — г
Для силы Fx находим:
15. Закон Кулона
417
418
Борис Гринченко
Задача 15.7.
В центре кольца радиуса R с равномерно распределенным по нему зарядом Q, находится точечный заряд q. С какой силой растянуто кольцо? Взаимодействием зарядов кольца друг с другом пренебречь.
Решение.
Запишем закон Ньютона для участка кольца, опирающегося на угол 2 а:
(1) T. + T^i-F^O,
где Тг = Т2 = Т — сила, с которой растянуто кольцо, Fk — суммарная кулоновская сила, действующая на заряды участка кольца со стороны заряда q.
Проецируя (1) на ось х, получаем:
(2) 2Tsin а - Fk = 0.
15. Закон Кулона
419
Полагая угол а малым, так что заряд AQ участка кольца можно считать точечным, для кулоновской силы имеем: —
(3) Fk = “эп-
Чтобы связать одним соотношением а и A Q, введем угловую плотность заряда (то есть заряд, приходящийся на угол в один радиан):
(4) т = £.
Тогда имеем:
(5) AQ = т • 2а = -Я 2а,
Учитывая, что при малых a sin а « а, из (1—5) получаем:
г= kqQ 27СВ2’
Другой вариант решения основан на использовании закона Ньютона (условия равновесия) полукольца (предоставляется выполнить читателю). Этот подход аналогичен второму варианту решений задач 14.2. и 25.3.
420
Борис Гринченко
Задача 15.8.
Бусинка, имеющая заряд q и массу т, может скользить без трения вдоль вертикально расположенной непроводящей спицы, в нижней части которой закреплен точечный заряд Q. Найти период малых колебаний бусинки вокруг положения равновесия.
Решение.
Запишем закон Ньютона для бусинки, находящейся в равновесии:
(1) = хо где х0 — равновесное расстояние между зарядами. Направим ось х вертикально вниз и в качестве начала отсчета выберем равновесное положение бусинки. Пусть в процессе колебаний бусинка сместилась на расстояние х вверх от положения равновесия (х < 0). Запишем закон Ньютона для этого момента
времени:
(2)
тг - эд = тХ"
mg (х0-х)2
15. Закон Кулона
421
Очевидно, что в случае смещения бусинки вниз закон Ньютона сохраняет вид (2).
Подставим mg из (1) в (2) и, с учетом х « хо, получаем:
^-х = 0 хо
уравнение для гармонических колебаний стандартного
вида с периодом
А/ хп
Т = 2п N тгг = 2п
. X
'mg ' 2g'
422
Борис Гринченко
Задача 15.9.
Имеется сфера с внутренним радиусом R и гладкой внутренней поверхностью. Какой минимальный заряд Q надо закрепить в нижней точке поверхности сферы, чтобы небольшое тело массы т с зарядом <?, помещенное в верхнюю точку поверхности сферы, находилось в состоянии устойчивого равновесия? Сфера выполнена из непроводящего материала.
Решение.
Пусть тело выведено из положения В равновесия в точку С так, что дуга ВС опирается на угол 2а. Запишем закон Ньютона для тела в точке С:
(1) mg + N + Fk = та \
и спроецируем его на ось х и у.
(2) N + mgcos 2а - Fkcos а = тах
(3) Fk sin а - mgsin 2а = тау.
15. Закон Кулона
423
В соответствии с определением устойчивого равновесия необходимо, чтобы:
(4) N> 0
(5) ajr > 0,
то есть тело должно быть прижато к сфере (не падать) и ускорение должно быть направлено к положению равновесия. Выполнение (4) означает:
(6) ax = 0.
Учитывая закон Кулона:
(7) J? - k<lQ
и тот факт, находим: (2Я)2 что при малых a sin а = а, из (2—7)
(8) ms (2JR)2 g
(9) > 2mg. (2JR)2
Поскольку при выполнении (9) соотношение (8) выполняется автоматически, окончательно получаем: q>8^ kq
16. Напряженность и потенциал электрического поля
Напряженность Е электрического поля в данной точке пространства определяется соотношением:
где F — сила, действующая на помещенный в данную точку заряд qQ.
Напряженность электрического поля удовлетворяет принципу суперпозиции:
(2) Е — Е1 + Е2 + + Et +...+ Еп — Ер
где Ег, Е2, — напряженности, создаваемые заряда-
ми qt, q2, в данной точке пространства по отдельности, Е — напряженность электрического поля, создаваемая системой зарядов qlt q2,...
Напряженность электрического поля Е, создаваемая зарядом q на расстоянии г от него, дается соотношением:
(3) E = ^f.
г
Напряженность электрического поля тонкой равномерно заряженной зарядом Q сферической оболочки радиуса R на расстоянии г от ее центра равна:
(4)
(5)
Е = О, при г < R
Е = при г > R.
16. Напряженность и потенциал
электрического поля
425
Таким образом, напряженность равна нулю внутри сферической оболочки и совпадает с полем точечного заряда Q, помещенного в центр сферы, снаружи.
Разность потенциалов между двумя точками 1 и
2 определяется соотношением:
•А, 9
(6) Ф1 “ Фй = ~7~’
Уо
где Л12 — работа, которую совершают над положительным зарядом (?0 электрические силы при его перемещении из точки 1 в 2. Введение понятия потенциала основано на фундаментальном свойстве электростатических полей: работа А12 не зависит от формы траектории, по которой заряд перемещался из 1 в 2 (свойство потенциальности электрических полей).
Если в качестве потенциала точки 2 выбрать потенциал, равный нулю (в таком случае часто говорят о потенциале бесконечно удаленной точки), то можно ввести понятие потенциала электрического поля в данной точке соотношением:
где А — работа, которую совершают электростатические силы при переносе положительного заряда из точки с нулевым потенциалом (бесконечно удаленной точки) в данную точку пространства.
Потенциал точки, находящейся на расстоянии г от точечного заряда q:
(8) <р =
Потенциал электрического поля подчиняется принципу суперпозиции:
(9) Ф = Z Фг =
' i
426
Борис Гринченко
где срг — потенциал, создаваемый зарядом qt на расстоянии гг от него, ф — потенциал электрического поля, создаваемый системой зарядов qv q2,...
Потенциал тонкой равномерно заряженной зарядом Q сферы радиуса R:
(10) Ф = при г < R
\\ лС
(11) Ф = •“, при r> R,
то есть постоянен внутри сферы и на ее поверхности, а снаружи совпадает с потенциалом, создаваемым точечным зарядом Q, помещенным в центр сферы.
В случае однородного электрического поля связь между разностью потенциалов и напряженностью определяется соотношением:
(12)
где точки 1 и 2 расположены на одной силовой линии. В случае неоднородного поля соотношение (12) может применяться для близколежащих точек пространства.
Поверхность, все точки которой имеют один и тот же потенциал, называются эквипотенциальной поверхностью. Так, например, в однородном электрическом поле эквипотенциальной поверхностью (эквипотенциалью) является плоскость, перпендикулярная силовым линиям электрического__поля (перпендикулярная вектору напряженности Е).
Напряженность электрического поля, создаваемая бесконечной равномерно заряженной плоскостью:
Е =: 2л& о = -J.—.
2е0
где о — поверхностная плотность заряда плоскости.
(13)
16. Напряженность и потенциал
электрического поля 427
Задача 16.1.
Найти напряженность и потенциал электрического поля заряда 36 нКл на расстоянии 9 см от него.
Решение.
Воспользуемся формулами для напряженности и потенциала электрического поля точечного заряда:
m р fey 9 • ю9 • 36 • ю~9
Ш (9-Ю-2)2 "
= 4 • 104- = 40 — м м
(2) Ч> = ^ = 3,6 кВ.
428 Борис Гринченко
Задача 16.2.
Два одноименных заряда q и 4q расположены на расстоянии 1 м друг от друга. На каком расстоянии от заряда q напряженность электрического поля равна нулю?
Решение.
Е2 Е1
I >- —" < Н----►
9 х 4q х
ч 1м *
\
Обозначим точку, в которой напряженность электрического поля равна нулю, через А и воспользуемся принципом суперпозиции для нахождения поля в этой точке:
(1)
Еа - Et + Е2 = О,
где Ег и Е2 — поля, создаваемые зарядами q и 4q соответственно в точке А. Из (1) следует, что Ег= - Е2, то есть точка А лежит на прямой, соединяющей заряды.
Спроецируем (1) на ось х и воспользуемся выражением для напряженности поля точечных зарядов:
(2) ^--^ = 0, .
v ’ х2 (Z-x)2
где I = 1 м — расстояние между зарядами, х — расстояние между зарядом q и точкой А.
Из последнего соотношения находим:
х = = 0,33 м. О
16. Напряженность и потенциал
электрического поля
429
Задача 16.3.
Два заряда — q и +2q расположены на расстоянии I друг от друга. В каких точках пространства потенциал равен нулю?
Воспользуемся принципом суперпозиции:
(1) Ф = <Р1 + Ф2 = °-
Подставляя в (1) epi = - и
2kq фг = получаем:
(2) - = О или г2 = 2гг
'1 г2
Таким образом, потенциал равен нулю в точках, удовлетворяющих условию г2 = 2п. Можно доказать, что геометрическое место точек, удовлетворяющих этому условию, образует сферу радиуса 2^ с центром „ 1 О, расположенным на расстоянии тг от заряда — q О на прямой, проходящей через заряды.
_*2 + 24г = оиля...
Z1 Z2
480 Борис Гринченко
Задача 16.4.
Два одинаковых заряда по 16 нКл каждый находится на расстоянии 4 м друг от друга. Найти напряженность и потенциал электрического поля в точке А, удаленной на 4 м от каждого из зарядов.
Решение.
Точка А и оба заряда образуют конфигурацию равностороннего треугольника.
Воспользуемся принципом суперпозиции:
(1) +
и выражением для напряженности поля точечного заряда:
(2) = Е2 =
где I = 4м.
После несложных вычислений находим:
Еа = а/3 = 15,3
A j2 М
16. Напряженность и потенциал
электрического поля
431
Для вычисления потенциала в точке А восполь
зуемся принципом суперпозиции:
(3) = ч>! + <р2 = = 72 В
(Ч>1 = Ч>2 = ^)-
432______________Борис Гринченко _______________
Задача 16.3.
Найти разность потенциалов (напряжение) между точками А и В, если АВ = 3 см, а = 30°, Е = 50 кВ/м. Электрическое поле однородно.
Решение.
---1----------------►
А' /'в
___J_________
। Е
-А '
Проведем эквипотенциаль А А' через точку А. Очевидно, ЧТО фд - фв = фд’ - фв-
Отсюда находим:
Фа “ Фв = Фа " Фв = Е ' '(А' В) = Е • (A Bcos а) = 3,5 кВ.
16. Напряженность и потенциал
электрического поля.433
Задача 16.6.
В некоторых двух точках поля точечного заряда напряженность поля различается в четыре раза. Во сколько раз различаются потенциалы в этих точках?
Решение:
Обозначим расстояние от заряда до точек через И и Г2 соответственно и воспользуемся формулами для напряженности и потенциала точечного заряда:
(1) я,-*4
ri
(2) Е2 = ±4
Г2
(4) <P2 = U
Г2
По условию задачи: "
Из (1—5) находим:
434
Борис Гринченко
Задача 16.7.
Найти напряженность и потенциал электрического поля на оси равномерно заряженного тонкого кольца радиуса R, на расстоянии х от его центра. Заряд кольца Q.
Решение.
Разобьем кольцо на малые, равные (для удобства подсчета) фрагменты, такие, что заряды на этих участках можно считать точечными, и воспользуемся принципом суперпозиции:
(1) в = Se,.
где Et — напряженность в точке А, отстоящей на расстояние х от центра О, Ег — напряженность электрического поля, создаваемая в точке А зарядом /то фрагмента. ,
Вектор Е направлен вдоль оси кольца. Это утверждение следует либо из соображений симметрии, либо из рассмотрения правой части (1). Действительно, на
16. Напряженность и потенциал
электрического поля
435
каждый i-ый участок кольца найдется симметричный ему участок. Таким образом, разбивается на пары векторов, сумма которых направлена вдоль оси. Следовательно, ^Ei так же направлена вдоль оси.
Спроецируем (1) на ось:
(2) Е = JjElx = IXcos а =
= cos а ^Et = cos а
___х___k____V Ал_ kxQ
= Vr* + x2 'я^х2^^ (Д* + x2)F
Аналогично находим потенциал в точке А:
(3) <,^9,=!.-^=-
ft Z AQ] вд Чй2 4-х2 Чк2 + х2 ’
436 Борис Гринченко
Задача 16.8.
Доказать, что потенциал точечного заряда в точке, находящейся на расстоянии г от него дается соот-
ношением: ср =
Решение.
Выберем две близкие точки 1 и 2, лежащие на одном радиусе, а, следовательно, на одной силовой линии. Обозначим расстояние между точками d, а расстояние между точкой 1 и зарядом q — через г. Предположим, что искомое соотношение справедливо. Тогда разность потенциалов А ср между точками 1 и 2 равна:
(1) Аср = срг - ср2 = =
_ kqd ~ kqd
(г + d)r
(с учетом d « г).
16. Напряженность и потенциал
электрического поля
437
Принимая во внимание, что из-за малости d электрическое поле вблизи точек 1 и 2 можно считать однородным, воспользуемся связью между напряженностью и потенциалом электрического поля:
(2)
то есть приходим к правильному выражению для напряженности электрического поля, создаваемого то
чечным зарядом.
Доказательство соотношения ф = —х можно провес
ти непосредственно, используя интегральное исчисление. Согласно определению потенциала:
(3) ч> = -#’
Уо
где А — работа, совершенная электростатическим полем заряда q над зарядом д0 при перемещении последнего из бесконечно удаленной точки в данную точку пространства. Заряд д0 будем перемещать вдоль радиуса: г г
(4) Jr '
<30 00 *
Подставляя (4) в (3), получаем требуемое утверждение.
438 Борис Гринченко________________
Ъър&ча 16.9.
Найти плотность электрических зарядов в атмосфере, если известно, что напряженность электрического поля вблизи поверхности Земли равна
В в
Ui = 100 —, а на высоте 1,5 км — Еъ = 25 —. Считать, м м
что плотность зарядов атмосферы постоянна, Земля имеет форму шара, а атмосфера — шарового слоя.
Решение.
Воспользуемся принципом суперпозиции для вычисления поля вблизи поверхности Земли:
(1) Ех = Егз + Ехат,
где jEj3 — поле, создаваемое зарядами на поверхности Земли, Е^ат — зарядами атмосферы. Обозначая заряд и радиус Земли через Q и R соответственно, имеем:
(2) ^13 = у
Для вычисления Е1&т разобьем атмосферу на тонкие шаровые слои. Поскольку поле зарядов слоя внутри его равно нулю,
16. Напряженность и потенциал
электрического поля
439
(3)
(3) £\ат = 0.
Принцип суперпозиции в точке 2 дает:
(4)
Е2 = Е2з + £2ат.
Поле Е2З, создаваемое зарядами Земли в точке 2 равно:
Для вычисления £гат разобьем атмосферу на тонкие слои. При этом вклад шаровых слоев, лежащих выше точки 2, равен нулю (см. выше), а вклад сло-
« kq
ев, лежащих ниже точки 2, равен ---2—где q —
(R + h)
заряд шарового слоя между точками 1 и 2. Таким образом:
Запишем определение плотности зарядов для шарового слоя между 1 и 2:
где объем V шарового слоя:
(8)
V = (R + ti)3 - « &TcR2h
О О
(учтено, что h « R).
Проецируя (1) и (4) на радиальную ось, совпадающую с направлениями векторов Ei и Е-г, и используя другие полученные соотношения, находим:
X 440
Борис Гринченко
Задача 16.10.
Металлический шар радиуса Ri, заряженный до потенциала <р, окружают концентрической проводящей оболочкой радиуса jfo. Чему станет равен потенциал шара, если заземлить оболочку?
Решение.
Обозначив заряд ние для потенциала ки:
(1)
Обозначим заряд через Q2. Согласно тенциал оболочки
шара Qi, запишем выраже-шара до заземления оболоч-
оболочки после заземления принципу суперпозиции, по-
(2)
*2
где
— потенциал, создаваемый зарядами шара
Qi на расстоянии R2 от центра (в области нахождения
16. Напряженность и потенциал
электрического поля
441
aq2
оболочки), -=---потенциал, создаваемый зарядами
Л2
Q2 оболочки на самой оболочке.
Запишем выражение для
заземления оболочки:
потенциала шара после
(3)
ftQi
Л2
ftQ2 я2
ft Qi „
где —=— — потенциал, создаваемый зарядами шара л.
ft
на самом шаре, —ь — потенциал, создаваемый за-Л2
рядами оболочки в области нахождения шара.
Из (1—3) находим:
442
Борис Гринченко
Задача 16.11.
Металлический диск вращается вокруг своей оси с угловой скоростью ®. Найти напряженность электрического поля на расстоянии х от оси вращения.
Решение.
Запишем закон Ньютона для мости, находящегося на расстоянии х от оси диска:
электрона проводи-
(1)
F = та,
где
(2) ~F = Ee,
действующая на электрон сила, е — заряд и т — масса электрона.
Центростремительное ускорение
(3) а - со2 • х.
Подставив F из (2) в (1) и проецируя его на направление ускорения, с учетом (3) находим:
„ тп<о2х
Е =------.
е
17. Теорема Гаусса
Введем определение потока Ф вектора напряженности электрического поля Е через площадку S соотношением:
(1) Ф = ES cos а,
где а — угол между направлением вектора Е и нормалью п к поверхности площадки S. В (1) электрическое поле считается однородным.
Теорема Гаусса формулируется следующим образом:
(2) Ф = J- Z<Z„
где Ф — поток вектора Е через произвольную замкнутую поверхность.
— алгебраическая сумма всех зарядов, находящихся внутри этой замкнутой поверхности. При вычислении потока Ф предполагается, что нормаль п* направлена наружу по отношению к пространству внутри замкнутой поверхности. Теорема Гаусса основывается на законе Кулона и определении вектора напряженности Е.
Теорема Гаусса является эффективным инструментом для решения многих задач электростатики, особенно это касается задач, где удается использовать соображения симметрии для расчета потока Ф. По
444
Борис Гринченко
скольку основная трудность как раз и связана с расчетом потока Ф, существенным моментом является удобный выбор замкнутой поверхности.
17. Теорема Гаусса
445
Задача 17.1.
Найти напряженность электрического поля, создаваемого равномерно заряженной бесконечной плоскостью. Поверхностная плотность заряда о.
Решение.
п
а
Из_соображений симметрии можно заключить, что поле Е однородно и направлено перпендикулярно плоскости. Выделим мысленно в пространстве куб с площадью грани а, который заряженная плоскость разрезает на две равные части. Верхняя и нижняя грани куба параллельны плоскости. Поток вектора Е через поверхность куба складывается из потока через верхнюю а2 и нижнюю а2Е грани куба. Поток через боте
ковые грани равен нулю (а = ^). Заряд, заключенный
О внутри объема куба, равен ста . Согласно теореме Гаусса:
(1) 2а2Е = ста2,
so
откуда находим:
ст
Е = ъ— = 2тейст.
2е0
446
Борис Гринченко
Задача 17.2.
Найти напряженность электрического поля, создаваемого равномерно заряженной сферой радиуса R. Суммарный заряд сферы Q.
Решение.
В силу симметрии вектор Е направлен вдоль радиуса, проведенного из центра сферы. В качестве замкнутой поверхности выберем сферическую оболочку радиуса г > R. Для вычисления потока Ф разобьем поверхность оболочки на малые фрагменты ASj. Вблизи площадки AS/ поле Е можно считать однородным, так что поток вектора Е через AjSz равен E^Si (а = 0). Полный поток:
(1) ф = Е ASt = Е &St = Е 4лг2.
Согласно теореме Гаусса:
(2) 4лг2 Е = Q
ео
или окончательно:
17. Теорема Гаусса
447
(3)
1 Q _ kQ * жё; ’ 7 ~
Таким образом, поле снаружи равномерно заряженной сферы совпадает с полем точечного заряда, по величине равного заряду сферы, помещенного в центр этой сферы.
Выбирая в качестве замкнутой поверхности оболочку радиуса г«R и применяя для нее теорему Гаусса, получим:
(4)
4лЛЕ = 0.
Правая часть (4) равна нулю, поскольку заряд внутри оболочки отсутствует. Отсюда заключаем, что напряженность электрического поля внутри равномерно заряженной сферы равна нулю.
448
Борис Гринченко
Задача 17.3.
Вычислить напряженность электрического поля, создаваемого равномерно заряженным шаром радиуса R. Плотность заряда р.
Решение.
Воспользуемся теоремой Гаусса, выбирая в качестве замкнутой поверхности сферу радиуса г с центром, совпадающим с центром шара. В силу симметрии очевидно, что напряженность электрического поля направлена вдоль радиуса, исходящего из центра шара. При г <R получаем: 4 _
тг ПГ р
(1) ±пг1 2Е = ----
ьо
или
При г> R
(2) 4пг2Е = | лВ3 4 ст
ь0 О
или
1
Зе., 7’
то есть • напряженость поля
4 „
Q = -п лВр, помещенного в центр О
точечного заряда
сферы.
17. Теорема Гаусса
449
Задача 17.4.
Вычислить напряженность электрического поля, создаваемого тонкой, равномерно заряженной бесконечной прямолинейной нитью. Линейная плотность заряда (заряд, приходящийся на 1 м длины нити) равна т.
Решение.
В качестве замкнутой поверхности выбираем поверхность прямого кругового цилиндра высотой I и радиуса г, ось которого совпадает с нитью. Из соображений симметрии ясно, что вектор напряженности электрического поля Е направлен вдоль луча, проходящего через нить перпендикулярно ей. Поток Ф складывается из потока через боковую поверхность 2пг1Е и потока через основания цилиндра, равного нулю (а = л/з). Согласно теореме Гаусса:
(1) 2nrlE = ±-1х
ьо
иди, окончательно:
т 2ле0
1 _ 2fer г г
460
Борис Гринченко
Задача 17.5.
Доказать, что система свободных зарядов не может находиться с состоянии устойчивого равновесия. (Теорема Ирншоу.)
Решение.
Предположим противное, то есть какой-либо из зарядов, для определенности положительный, находится в состоянии устойчивого равновесия. По определению устойчивого равновесия, при выведении заряда из этого положения в любом направлении на сколь угодно малую величину, возникает сила, направленная к положению равновесия.
Окружим заряд замкнутой поверхностью, например, сферой, так, чтобы внутрь ее не попадали другие заряды. Очевидно, что для устойчивости необходимо, чтобы поле, создаваемое всеми прочими зарядами кроме рассматриваемого, на поверхности сферы было направлено к положению равновесия (только в этом случае возникает сила, возвращающая заряд в положение равновесия). Отсюда находим, что поток вектора Е через замкнутую поверхность отрицателен.
17. Теорема Гаусса
451
Но это противоречит теореме Гаусса, согласно которой данный поток, создаваемый зарядами вне сферы, равен нулю. Таким образом, теорема доказана.
452
Борис Гринченко
Задача 17.6.
С какой силой расталкиваются равномерно заряженные грани куба? Поверхностная плотность заряда о, длина ребра куба I.
Решение.
Для определенности рассмотрим силу, действующую на верхнюю грань куба. Разобьем эту грань на малые площадки ASt и представим силу, действующую на грань, как сумму Ft сил, действующих на каждую площадку AS/:
(1)
Обозначим через Et напряженность электрического поля, создаваемого в области нахождения площадки AS{ зарядами всех^граней, кроме самой верхней грани. Проекция силы Ft на нормаль к грани и* равна:
17. Теорема Гаусса
453
(2) Fin = E't ASt о • cosap
а суммарная сила, действующая на верхнюю грань вдоль нормали и* :
(3) Fn = = <&E'i соеаг = ст Ф'
cosaz = Ф' — поток вектора E через верхнюю грань куба, создаваемый зарядами всех других граней).
В качестве замкнутой поверхности для применения теоремы Гаусса выберем куб, размеры которого на бесконечно малую величину превышают размеры рассматриваемого куба, то есть их грани практически совпадают. Тогда поток через верхнюю грань куба внешнего куба равен:
(4) Ф = Ф' + 2itk<yl2,
где 2nkal2 — поток, создаваемый заряженной верхней гранью куба.
Воспользуемся теоремой Гаусса для всего куба:
(5) Фо = 6Ф = = 4л/?6/2ст.
и ео
Учитывая, что согласно (3):
(6) Fn = ст Ф'
и выражая Ф' из (4, 5)
(7) Ф' = 4л/?/2 ст - 2nkl2 ст = 2лйст/2, окончательно находим:
* Fn = 2nka2 I2.
454
Борис Гринченко
Задача 17.7.
В равномерно заряженном шаре с плотностью заряда р вырезали сферическую полость. Расстояние между центром шара и центром полости d. Доказать, что электрическое поле внутри полости однородно, и найти его напряженность.
Решение.
Для нахождения поля Е в некоторой точке А внутри полости предположим, что полость отсутствует и воспользуемся принципом суперпозиции:
(1) ЕЛ = Е + Е’,
где Е — напряженность, создаваемая в точке А всеми зарядами шара, кроме зарядов полости, Е' — поле, создаваемое зарядами полости.
Представим результаты задачи 17.3 в виде:
(2) ЕА = а • Г ( Г = ОА)
455
17. Теорема Гаусса____
(3) F' = а - Г' ( г*' = СУД ), где а = i
о 6q
Подставляя (2) и (3) в (1), находим:
Е = ЕА - Е' = а ( г - f ) = ad, где d = О О ' тюслюяня&я величина.
Для модуля Е получаем:
18. Проводники в электрическом поле
Задача 18.1.
Доказать, что электрическое поле внутри неподвижного проводника, помещенного в электростатическое поле, равно нулю, а электрические заряды могут находиться только на поверхности проводника (плотность электрических зарядов в любой точке внутри проводника равна нулю).
Решение.
Если бы внутри проводника существовало электрическое поле, то оно привело бы в движение свободные заряды, которые всегда есть в проводнике. В проводнике возник бы электрический ток, и, следовательно, равновесное распределение зарядов было бы невозможным.
Для доказательства отсутствия зарядов внутри проводника воспользуемся теоремой Гаусса. Поскольку поток вектора напряженности электрического поля через любую замкнутую поверхность внутри проводника равен нулю (так как поле внутри проводника отсутствует), то и заряд внутри объема, ограниченного этой поверхностью, так же равен нулю.
Отметим, что доказанные утверждения справедливы как для в целом электрически нейтрального проводника, так и для проводника, несущего нескомпенсированный заряд.
18. Проводники в электрическом поле
457
Задача 18.2.
Доказать, что внутри тонкой проводящей оболочки произвольной формы, помещенной в электростатическое поле, напряженность электрического поля равна нулю (так называемая электростатическая защита). Оболочка неподвижна и может быть в целом заряжена.
Решение.
Предположим сначала, что внутренность оболочки полностью заполнена проводником. Из результатов предыдущей задачи следует, что напряженность электрического поля и плотность электрических зарядов в проводнике равны нулю. Удалим из тела электрически нейтральный проводник. Очевидно, что поле из-за этого нигде не изменится и равновесие зарядов не нарушится. Отсюда вытекает справедливость данного утверждения.
468 Борис Гринченко
Задача 18.3.
В проводнике имеется полость, внутри которой находится заряд q. Найти заряд, индуцируемый на внутренней поверхности проводника.
Решение.
Окружим полость оболочкой, проходящей внутри проводника и воспользуемся теоремой Гаусса. Поскольку поле и заряды внутри проводника отсутствуют, получаем:
Таким образом, индуцируемый на внутренней поверхности проводника заряд q' = - q.
18. Проводники в электрическом попе
459
Задача 18.4.
Тонкая пластина из проводящего материала расположена в однородноМ-Электрическом поле так, что вектор напряженности Е перпендикулярен ее поверхности. Найти плотность поверхностных зарядов о на пластине.
Решение.
Воспользуемся принципом суперпозиции для поля в точке А внутри пластины
(1) Ел = Е+ + Е_ + Ео ж О,
где Е+ и Е_ — поля, создаваемые в точке А зарядами па правой и левой поверхностях пластины соответственно.
В (1) учтено, что поле внутри проводника равно нулю. Согласно условию задачи, расстояние от точки А до каждой из поверхностей пластины намного мень
460
Борис Гринченко
ше, чем размеры пластины в направлениях, перпендикулярных электрическому полю. Следовательно,
(2) Е+ = Е_ = 2nko.
Проецируя (1) на ось х, с учетом (2), находим:
(3) - 2тс/гсг - 2тс/?о + Ео = 0.
Откуда Еа а - . . - SqE.
18. Проводники в электрическом поле
461
Задача 18.5.
Внутри заземленной сферы радиуса R расположен точечный заряд q. Найти заряд, индуцируемый на внутренней поверхности сферы, и поле вне сферы.
Решение.
Заряд, индуцируемый на внутренней поверхности сферы, вычислен в задаче 18.3:
Ч' = - Q-
При этом условие заземленности сферы не используется. Принято считать, что это условие эквивалентно отсутствию зарядов на внешней поверхности сферы или предположению, что заземление сферы эквивалентно заполнению пространства вне сферы проводником с нулевым потенциалом. Таким образом, предполагается, что поле вне заземленной сферы равно нулю. Иногда о рассмотренном • в условии задачи случае говорят как об электро
462
Борис Гринченко
статической защите, когда все вывернуто «наизнанку» — в окружающем пространстве поля от заряда + q нет, оно компенсируется индуцированными на внутренней поверхности зарядами - q.
1 18. Проводники в электрическом поле 468
Задача 18.6.
Тонкая проводящая пластина площадью S помещена неоднородное электрическое, поле напряженностью Е так, что вектор Е перпендикулярен поверхности пластины. Какой заряд Q необходимо сообщить первоначально незаряженной пластине, чтобы одна из поверхностей оказалась незаряженной?
Решение.
Воспользуемся принципом суперпозиции для поля в точке А внутри пластины:
(1) Еа = Е+ + Ео,
где Е+ — поле, создаваемое поверхностными зарядами на правой (для определенности) поверхности пластины:
(2)
_Е+ = 2itkc.
464
Борис Гринченко
Полный заряд пластины:
(3) Q = aS.
Проецируя (1) на ось х, с учетом (2,
E0S
«=2S=*V
3) находим:
18. Проводники е электрическом поле
465
Задача 18.7.
Доказать, что вблизи поверхности проводника вектор напряженности электрического поля Е направлен перпендикулярно поверхности проводника, причем
Решение.
Будем перемещать пробный заряд вдоль контура, представляющего собой прямоугольник, близко прилегающий к поверхности проводника. Работа электростатических сил на участке АВ равна нулю, поскольку поле внутри проводника отсутствует. Работой на участках AD и ВС можно пренебречь, выбирая длину этих участков сколь угодно малой. В силу свойства потенциальности электростатических полей (работа вдоль замкнутого контура равна нулю) заключаем, что работа на участке CD так же должна быть равна нулю. Последнее возможно только при условии, что сила, действующая на пробный заряд, перпендику
466
Борис Гринченко
лярна перемещению, то есть вектор Е перпендикулярен CD и поверхности проводника (CD параллелен поверхности проводника).
Для доказательства второго утверждения применим теорему Гаусса для замкнутой поверхности, профиль которой ABCD. Учитывая, что внутри проводника поле равно нулю, а вблизи перпендикулярно его поверхности, находим:
ES = тг оЗ
или, окончательно
18. Проводники в электрическом поле
467
Задача 18.8.
Между двумя заземленными металлическими пластинами находится такая же по размерам тонкая пластина с поверхностной плотностью заряда +о. Расстояния а и Ъ много меньше линейных размеров пластин. Найти поверхностную плотность зарядов на верхней и нижней пластинах.
Решение.
Воспользуемся теоремой Гаусса для замкнутой поверхности ABCD, проходящей внутри пластин ВС и AD. Учитывая малость потока вектора напряженности через боковую поверхность АВ и CD и тот факт, что поле внутри проводника равно нулю, получаем:
(1) ох S + g2 S + oS = О,
где ох и о2 — поверхностные плотности зарядов на верхней и нижней пластинах соответственно, S — Площадь каждой из пластин.
468
Борис Гринченко
Разность потенциалов между точками 1 и 3:
(2) <Pi - Фз = Ф1 “ Ф2 + Ф2 “ Фз = ° по условию задачи.
Запишем связь между разностью потенциалов и напряженностью:
(3) Ф2 - Ф! = Еа а
(4) Ф2 “ Фз = Еъ ь
и принцип суперпозиции для полей между пластинами:
(5) Еа = Ятс/го! + 2л/го - 2л/го2
(6) Еь = 2л/го + 2л/го2 ~
(учтено, что поле в каждой точке пространства между пластинами создается зарядами трех пластин).
Решая систему уравнений (1—6), находим:
F _ ст ь
а ео а + Ъ „ о а Еь~ ео а + Ь
°1 = “ а — 1 а + Ь
а — С _ •
2 а + Ь
18. Проводники в электрическом поле
469
Задача 18.9.
На расстоянии I от центра проводящей сферы радиуса R, имеющей заряд Q, расположен точечный заряд q. Найти потенциал сферы. Рассмотреть случаи I > R и I < R.
Решение.
1. 1>R
Воспользуемся принципом суперпозиции для вычисления потенциала центра сферы:
(1) Фо = i +2 R ’
kg ™el
— потенциал, создаваемый зарядом q в цент-
k AQt
ре сферы О, —-— — потенциал, создаваемый точеч-XL
ным зарядом в точке О.
Учитывая, что AQi = Q, из (1) находим:
(2) Фо = ^ + ^,
470
Борис Гринченко
Поскольку все точки внутри сферы (в том числе и точка О) имеют одинаковый потенциал, равный потенциалу самой сферы (задачи 18.1, 18.2), выражение (2) дает потенциал сферы.
2. 1<R
Сконструируем распределение зарядов на сфере таким образом, чтобы напряженность электрического поля внутри материала сферы равнялась нулю. Для этого возьмем распределение зарядов на внутренней поверхности сферы таким же, как в случае заземленной сферы в задач 18.5 (такое распределение зарядов дает равную нулю напряженность электрического поля в проводящем материале сферы и снаружи) и равномерное распределение заряда Q + q на внешней поверхности сферы. Сконструированное распределение обеспечивает отсутствие поля внутри материала сферы и, в силу теоремы о единственности (доказательство которой выходит за рамки школьного курса физики), единственно возможное равновесное распределение.
18. Проводники в электрическом поле
471
Таким образом, поле вне сферы совпадает с полем, создаваемым равномерно распределенным по поверхности сферы радиуса R зарядом Q + q. Потенциал такой сферы равен:
fe (Q + g) Р R ’
Расположение заряда q внутри сферы не влияет на поле вне сферы и ее потенциал (при этом, разумеется, поле внутри сферы определяется местом расположения заряда g).
Последнее утверждение справедливо для произвольной проводящей оболочки с заключенными внутри нее зарядами, и составляет часть так называемой теоремы Фарадея. Согласно этой теореме, замкнутая проводящая оболочка разделяет все пространство на внутреннюю и внешнюю части, в электрическом отношении совершенно не зависящие друг от друга. Например, при любом перемещении зарядов внутри оболочки, поле во внешнем пространстве остается неизменным и наоборот. В частности, если все внутренние заряды привести в соприкосновение со стенками оболочки, то произойдет их нейтрализация индуцированными зарядами на внутренней поверхности оболочки. При этом внутреннее поле исчезнет, но наружное поле и распределение заряда на наружной поверхности останутся неизменными (Д. В. Сивухин. Общий курс физики, т. 3).
472
Борис Гринченко
Задача 18.10.
Найти заряд, индуцируемый на поверхности заземленного металлического шара радиуса R точечным зарядом 4- q, расположенным на расстоянии I от центра шара.
Решение. с
Воспользуемся принципом суперпозиции для вычисления потенциала в центре шара:
(1) Фо - + Zu ~ О,
где ^-9- — потенциал, создаваемый зарядом q в точке &
О. Заряд Q, индуцируемый на поверхности сферы, представлен в виде системы точечных зарядов AQt, причем =
(2) Q = S AQj
18. Проводники в электрическом поле 473
ь
Вынося в (1) Н шись (2), находим:
за знак суммы и воспользовав-
474
Борис Гринченко
Задача 18.11.
Незаряженный проводник помещен в однородное электрическое поле. Изменится ли поверхностная плотность зарядов, если все размеры проводника увеличить в п раз?
Решение.
Распределение зарядов по поверхности проводника осуществляется таким образом, чтобы напряженность электрического поля в произвольной точке А внутри проводника обращалась в нуль:
(I) Ё+1д = о,
где Et — напряженность электрического поля, создаваемая в точке А зарядами, сосредоточенными на малой площадке поверхности проводника:
kcJS, _
18. Проводники в электрическом поле
476
В (2) cstSi — заряд на площадке Si, nt = — — еди-П ничный вектор, совпадающий с направлением вектора Ei.
После увеличения линейных размеров проводника в п раз площадка Si увеличится до размера Si' = и2 • Si, fi = пп, направление вектора Ei останется неизменным ( щ ' = гц ). Напряженность электричес-
кого поля, создаваемая зарядами площадки Si' в точке
А:
(3)
— kat' 3,'п,' ka,'n2S, kat'St _ г? ~ r?n2 П‘~ r? ”r
Чтобы (1) оставалось в силе (внешнее поле оставалось скомпенсированным индуцированными зарядами), необходимо, чтобы:
(4) Et = E't,
откуда с учетом (2, 3) получаем:
ot = П'р
то есть поверхностная плотность зарядов не изменится.
476
Борис Гринченко
Задача 18.12.
Вычислить поле, создаваемое зарядом + q и полупространством, заполненным проводником. Найти силу, действующую на заряд. Расстояние от поверхности проводника до заряда d.
Решение.
Поле в произвольной точке А внутри проводника (в левом полупространстве) создается зарядом + q (Еа) и индуцированными на поверхности проводника зарядами (Ед) (принцип суперпозиции):
(1) Еа + Е'а = О.
В правом полупространстве в точке Ар симметричной точке А относительно плоскости поверхности проводника, отрицательные заряды, индуцируемые на поверхности проводника, создают поле Е', причем в силу симметрии задачи векторы Е’А и Е' симметричны относительно плоскости поверхности проводника.
18. Проводники в электрическом поле
477
С другой стороны, точно такое же поле в точке А' создавало бы заряд - q, расположенный симметрично заряду + q. Таким образом, электрическое поле, создаваемое индуцированными на поверхности проводника зарядами в правом полупространстве, можно заменить полем заряда - q, расположенного симметрично заряду + q.
Следовательно, поле в правой части полупространства в любой его точке можно рассматривать как суперпозицию полей, создаваемых точечными зарядами + <7 и - <7. В частности, для силы взаимодействия получаем:
W
Заряд - q называют изображением заряда + q.
При решении некоторых задач электростатики используется прием, называемый методом электрических изображений. Суть этого приема заключается в следующем.
Пусть в пространстве имеется проводник и несколько точечных зарядов q, <72 и т. д. Поверхность проводника представляет собой поверхность одинакового потенциала (эквипотенциаль).
Представим себе, что, удалив проводник, нам удалось так подобрать и расположить некоторые заряды q'i, q'2 и т. д., что они вместе с зарядами <71, qz и т. д. образуют ту же самую эквипотенциаль. В этом случае можно доказать, что поле, создаваемое зарядами <7'1, <7'2 и т. д. вне проводника совпадает с полем, создаваемым зарядами, индуцированными на поверхности проводника зарядами <71, <72 и т. д.
478 Борис Гринченко
Поясним метод электрических изображений на примере данной задачи. Эквипотенциалыо в ней является плоскость поверхности проводника. Поместим заряд - q симметрично заряду + q. Нетрудно убедиться, что заряды + q и - q на поверхности проводника создают нулевой потенциал (каждая точка поверхности равноудалена от зарядов + q и - q). Отсюда заключаем, что поле, создаваемое наведенными на проводнике зарядами в правом полупространстве, совпадает с полем заряда - q — изображения заряда + q.
Отметим, что тот же результат получится при замене проводника, заполняющего полупространство, проводником в виде бесконечной проводящей пластины.
18. Проводники в электрическом поле
479
Задача 18.13.
Две бесконечные проводящие полуплоскости образуют прямой угол. Заряд + q расположен на расстоянии di от одной из них и на расстоянии dz от другой. Найти электрическое поле в пространстве.
Решение.
1
+ q — ——• —- — -™ _ q
Разместим заряды - q, - q и + q, как показано на рисунке. Можно убедиться, что четыре заряда образуют эквипотенциали в месте нахождения полуплоскостей. Используя метод электрических изображений заключаем, что поле, создаваемое в «четвертьпрос-транстве» I зарядом + q и зарядами, наведенными на поверхностях полуплоскостей, совпадает с полем изображенных на рисунке четырех зарядов и может быть вычислено в любой точке с использованием принципа суперпозиции.
19о Диэлектрики в электрическом иоле
иш—ниш и ini 111111||Щ|||1111ивжимми1»!кии»нииимяи8ав—MEWMagrrjwiMiiMaMEagBuujmMi w»wbi—— inminw^wiiBkHiMTmianw1 iimiiima
Согласно определению, диэлектрическая проницаемость среды дается соотношением:
Ео
(1) Е -
где Eq — электрическое поле в данной точке пространства в отсутствие диэлектрика, Е — поле при наличии диэлектрика. Следует иметь в виду, что (1) справедливо при условии, когда однородный изотропный диэлектрик полностью заполняет пространство между двумя эквипотенциальными поверхностями. В противном случае (1), вообще говоря, не выполняется (задачи 19.2. и 19.3.). Таким образом, величина 8 > 1 показывает, во сколько раз уменьшается электрическое поле в данной точке пространства при заполнении диэлектриком пространства между двумя эквипотенциалями. Очевидно, что диэлектрическая проницаемость вакуума равна единице.
При решении задач школьного курса физики предполагается, что диэлектрик является однородным и изотропным (то есть его свойства не зависят от направления в пространстве) и влияние диэлектрика на формирование электрического поля обусловлено возникновением на поверхности диэлектрика так называемых связанных зарядов, а плотность зарядов внутри диэлектрика равна нулю. Таким^об-разом, напряженность электрического поля Е в
19. Диэлектрики в электрическом поле 481
любой точке пространства (как внутри, так и вне диэлектрика) может быть представлена в виде (принцип суперпозиции):
(2) E = EQ + E\
где Ео — поле, создаваемое внешними зарядами (внешнее поле), Е' — поле, создаваемое связанными зарядами на поверхности диэлектрика.
482
Борис Гринченко
Задача 19.1.
Тонкая пластина из диэлектрика с диэлектрической проницаемостью 8 помещена в однородное электрическое поле напряженностью Eq так, что направление вектора Eq перпендикулярно плоскости пластины. Найти напряженность электрического поля внутри диэлектрика и поверхностную плотность зарядов o'.
Решение.
Обе поверхности пластины представляют собой эк-випотенциали (в силу перпендикулярности вектору Ео) и хотя диэлектрик полностью не заполняет все пространство между эквипотенциалями, тем не менее с достаточной точностью можно считать, что практически во всем объеме диэлектрика за исключением области вблизи краев выполняется:
Ео
(1)
С»
10. Диэлектрики в электрическом поле 483
С другой стороны, напряженность электрического поля Е внутри диэлектрика:
(2) Е = Е0 + Е'.
Поле Е обусловленное возникновением связанных зарядов на поверхности диэлектрика (поляризацией диэлектрика), направлено в_~ сторону, противоположную направлению вектора Ео и равно:
(3) Е' = 4-М =
ьо
Проецируя (2) на ось х, с учетом (1, 3), получаем:
£
В частности, при 8 — со (что соответствует случаю проводника), имеем:
<У = Eq -^*0’
то есть полученный ранее результат.
484
Борис Гринченко
Задача 19.2.
Тонкий длинный стержень из диэлектрика расположен в однородном электрическом поле так, что его ось совпадает с направлением силовых линий. Найти напряженность электрического поля внутри диэлектрика на достаточно большом расстоянии от его концов. Напряженность внешнего поля Eq, диэлектрическая проницаемость 8.
Решение.
Ео
-------------------------
X
Поле в точке А создается полем Ео и индуцированным на поверхности торцов стержня зарядами:
(1) еа = е0 + ё\
Полем Е'а индуцированных на торцах стержня зарядов вследствие их удаленности можно пренебречь, так что:
и поле внутри диэлектрика практически совпадает с внешним полем.
19. Диэлектрики в электрическом поле
485
Задача 19.3.
Тонкая пластина из диэлектрика с диэлектрической проницаемостью 8 помещена в однородное электрическое поле так, что нормаль к ее поверхности составляет угол а с напряженностью Ео. Найти напряженность электрического поля внутри диэлектрика.
Решение.
Представим внешнее поле Ео в виде суперпозиции двух полей:
(1) Ео = ЕОп + ЕОт,
(где ЕОп = Ео cos а ; ЕОт = Ео sin а), действующих независимо друг от друга. Если бы не было составляющей ЕОп, то, согласно результату задачи 19.2, поле в пластине вдали от краев (то есть на расстояниях, намного превышающих толщину пластины) совпадало бы с полем Е^. Наоборот, в отсутствие составляющей
486
Борис Гринченко
ЕОх, в соответствии с результатом задачи 19.1, поле внутри диэлектрика ослабляется в е раз, то есть:
F = ^Оп Еп е •
Таким образом, результирующее поле внутри диэлектрика: .
(3)
Согласно теореме Пифагора:
У
(4)
откуда
E0cos а ё
+ (Eosin а)2,
„ „С cos а , о \ 1 Е = Eq { —— + since ) г.
19. Диэлектрики, в электрическом поле
487
Задача 19.4.
Равномерно заряженная сфера радиуса R1 окружена слоем диэлектрика, внешний радиус которого R2. Заряд сферы равен + Q, диэлектрическая проницаемость материала слоя Е. Нарисовать график зависимости напряженности и потенциала электрического поля от расстояния до центра сферы и вычислить поверхностную плотность зарядов диэлектрика.
Решение.
Обозначим заряд, индуцируемый на внутренней поверхности шарового слоя -д', на внешней — + д'. Поскольку диэлектрик полностью заполняет пространство между двумя эквипотенциалями, напряженность электрического поля в произвольной точке А внутри диэлектрика:
Ео
(1) Е = -f,
kQ
где Ео = -j- (г = ОА) — электрическое поле в отсутствие диэлектрика.
488
Борис Гринченко
Согласно принципу суперпозиции:
(2)
г
(учтено, что вклад зарядов +</' в поле внутри диэлектрика равен нулю).
Из (1, 2) получаем:
(3) <r = 5-^Q.
О
При г > /?2 напряженность и потенциал электрического поля совпадают с напряженностью и потенциалом, создаваемыми зарядами сферы в отсутствие диэлектрика (поля отрицательных - д' и положительных + q' зарядов на поверхностях диэлектрика взаимно компенсируются):
(4) В =
(5) ФЛ
При Ri < г < R%, то есть внутри слоя диэлектрика, напряженность электрического поля, создаваемая зарядами + д', равна нулю, то есть
(6) Е =
а потенциал, согласно принципу суперпозиции, складывается из потенциала зарядов + Q, равного и потенциала, создаваемого зарядами + д' и - д', рав-kq' kg'
ных соответственно и - —:
В2 г
<7\ m k(Q- д') kg' щ Цъ- 1)Q
19. Диэлектрики в электрическом поле
489
При г < .R1 с учетом изложенного, имеем:
(8) Е = О
гач „.‘«-«Л-*?’6'11’
(9) <р - + В2 ей, sRj
Соответствующие графики представлены на рисунках.
20. Электроемкость. Конденсаторы
Пусть в пространстве находятся два проводника. Поместим на один из них заряд + q, на другой — - q. Обозначим возникающую при этом разность потенциалов между проводниками epi - фг = U > 0. Тогда, по определению, величина:
(1) С = —2— =
Ф1-Ф2 U называется электроемкостью двух проводников.
Электроемкость уединенного проводника, по определению, равна:
<2) С = |.
где q — положительный заряд, помещенный на проводник, <р — потенциал проводника (разность потенциалов между поверхностью проводника и бесконечно удаленной точкой, потенциал которой принимается равным нулю).
При решении задач данного раздела наряду с определениями (1,2) используются «первые принципы» предыдущих разделов, а также формулы для последовательного и параллельного соединения конденсаторов:
111
<з> ачч
(4) С = с1 + с2
20. Электроемкость. Конденсаторы
491
Задача 20.1.
Найти электроемкость плоского конденсатора, заполненного диэлектриком с диэлектрической проницаемостью е. Площадь пластин конденсатора S, расстояние между пластинами d.
Решение.
Поместим на верхнюю пластину заряд + q, на нижнюю — - q. Согласно определению:
(1) с = Д
В отсутствие диэлектрика напряженность электрического поля между пластинами конденсаторов:
(2)
° - е0 - s„S-
При наличии диэлектрика напряженность электрического поля
. (3)
£=тг-
492
Борис Гринченко
Учитывая связь между разностью потенциалов (напряжением) и напряженностью электрического поля:
(4) Л U = Ed,
из (1—3) находим: с _ е go d
20. Электроемкость. Конденсаторы
493
Задача 20.2.
Найти электроемкость сферического конденсатора, образованного двумя проводящими концентрическими сферами радиусами jRi и Rz. Рассмотреть также случай, когда пространство между сферами заполнено диэлектриком с диэлектрической проницаемос-
тью е.
Решение.
Поместим на внешнюю — - q. кости:
внутреннюю сферу заряд + q, на Согласно определению электроем-
(1)
V - (Г - тт>
Фа ~ Фв U
где U = <р° - фд — разность потенциалов (напряжение) между сферами. Потенциал сферы Rx фд, согласно принципу суперпозиции, складывается из потенциала,
494 Борис Гринченко I
)
Л Qx L
создаваемого зарядами + q (-g3-) и зарядами - q
- k q
(—5—) в области нахождения сферы Я,: л2
о _ kq _ kq
( J Фл" Rr R2‘
Аналогично, потенциал сферы Rz (рв равен:
(3) ’в = ^-^ = °-
Из (1—3) находим:
С = Q 1 feg feg k___________k_"
^1 -^2 -^1 -^2
В случае заполнения конденсатора диэлектриком, напряженность электрического поля в каждой точке между сферами уменьшается в 8 раз. Докажем, что
и разность потенциалов так же уменьшается в 8 раз. Для этого разобьем отрезок радиуса АВ на малые отрезки, такие, что поле на протяжении каждого из них можно считать практически однородным и воспользуемся связью между напряженностью и разностью потенциалов:
(4) Ф<-ф<+1 = -^2Ц,
где — — напряженность электрического поля на участке Adp Et — напряженность в отсутствие диэлектрика. Суммируя (4) по всем Adp находим:
(5) <рА - (рв = | ТА = | (ф! “ Фв)-
20. Электроемкость. Конденсаторы
496
I Подставляя (5) в определение электроемкости (1), получаем:
_ 8 _ 4л 80 8
А_А~ J_______L
Rx R2 R1 R2 6 _ 8 ^1Д2
C~A_ A~* (Я1 - Яг)’ Я1 я2
Другой способ вычисления разности потенциалов между сферами при наличии диэлектрика основан на применении результата задачи 19.4 с учетом того, что наличие на внешней сфере заряда - q' дает одинаковую добавку как к потенциалу внешней сферы, так и внутренней. Таким образом, разность потенциалов, вычисленную с учетом 19.4, следует подставить в определение (1).
496
Борис Гринченко
Задача 20.3. /
Найти электроемкость конденсатора, заполненного двумя слоями диэлектриков с проницаемостями 81 й 82, параллельными пластинам конденсатора. Площадь пластин конденсатора S, толщины слоев диэлектрика равны соответственно di и </2.
Решение.
В соответствии с определением электроемкости, поместим на верхнюю пластину заряд + q, на нижнюю — - q. Для удобства расчета введем точку С и представим разность потенциалов (напряжение) между пластинами фл - фв в виде:
(1) Фа ~ Фв = Фа - Фс + Фс - Фв-
Учитывая связь между напряженностью и разностью потенциалов, находим:
(2) Фа - Фс = Ei di
(3) фс — Фв = Е2 d2.
20. Электроемкость. Конденсаторы
497
! Обозначим через Ео напряженность электрического прля, создаваемого зарядами + q и - q в пространстве между пластинами:
<4> e° = -£s
(то есть напряженность электрического поля в отсутствие диэлектрика). Тогда, согласно определению диэлектрической проницаемости:
(б) Е1=
(в) е2=
При записи (5,6) учтено, что наличие верхнего слоя диэлектрика не влияет на поле внутри нижнего диэлектрика и наоборот.
Подставляя разность потенциалов из (1—6) в определение электроемкости:
(7)
С = Ц Фа ~ Фв’
С = —
Ео(
окончательно получаем:
q________ so &
^1 ^2 А ^2
е, ' ) е, ео
498 Борис Гринченко'
Задача 20.4. [
Как изменится емкость плоского конденсатора, если поместить его в металлическую коробку? Расстояние между обкладками конденсатора равно расстоянию от обкладок до стенок коробки.
Решение.
До помещения конденсатора в коробку его емкость
Сообщим пластинам конденсатора заряды + q и - q. Электроемкость конденсатора после помещения в коробку по определению равна:
С =—1. Фв Фс
Выбирая точки А, В, С и D, как показано на рисунке, запишем:
(3) <рЛ - Фр = фА - Фв + Фв - Фс + Фс - <?D = О,
поскольку йотенциалы точек А и D, как и всех других точек проводящей коробки, совпадают.
I
20. Электроемкость. Конденсаторы
499
I Учитывая, что электрическое поле в зазорах между сменками коробки и пластинами конденсатора практически однородно, воспользуемся связью между напряжением и напряженностью электрического поля:
(4) Фв ~ Фа = Ei d
(5) Фв — фс = Е2 d
(6) Фв - Фс = Ез d-
Обозначим через ст' поверхностную плотность зарядов на верхней и нижней стенками коробки. Полярность зарядов нетрудно предсказать без вычислений. Действительно, если бы на верхней стенке был положительный заряд, то напряженность электрического поля везде между А и D была бы направлена в одну сторону и (3) не выполнялось бы.
Воспользуемся принципом суперпозиции, учитывая связь между величиной поверхностного заряда и напряженностью электрического поля:
ст = -g находим:
. Таким образом, кость конденсатора
(9) Ea = fQ.
После несложных вычислений из (2—9) с учетом
3 6q S 2d' после помещения в коробку ем-возрастет в полтора раза.
500
Борис Гринченко
Задача 20.5.
Найти емкость между точками А и В.
Решение.
Из симметрии видно, что потенциалы точек Е и К равны. Следовательно, конденсатор в центре схемы не заряжен и влияния на распределение электрических полей не оказывает. С учетом этого, эквивалентная схема выглядит следующим образом:
то есть представляет собой два конденсатора с емкостями
20. Электроемкость. Конденсаторы
501
4 " V С + 2 С '
соединенные параллельно.
Окончательно находим емкость схемы между точками А и В:
С = — С ''АВ 3
Первоначальная схема может быть сведена также к эквивалентной с учетом равенства потенциалов точек А и В:
То есть к двум последовательно соединенным кон-С
денсаторам емкостями и С. Как и при расчете по первому варианту, емкость между точками А и В рав-
502
Борис Гринченко
Задача 20.6.
Найти емкость между точками А и В.
Решение.
Данная схема не может быть сведена, как в ранее рассмотренном случае, к простой эквивалентной схеме за счет использования формул для параллельно и последовательно соединенных конденсаторов и соображений симметрии.
В таких задачах вычисление электроемкости следует проводить непосредственно с использованием определения электроемкости: в точку А помещаем заряд + q, в точку В — - q. Тогда по определению:
С =
. Фа “ Фв‘
Обозначим через Qi и заряды на пластинах конденсаторов Cad и Сак соответственно. Поскольку зарядами на проводниках в задачах такого рода можно пренебречь, имеем:
20. Электроемкость. Конденсаторы
503
(2) q = 9i + 92-
В силу симметрии схемы заряд — - q, помещенный в точку В, перераспределится между конденсаторами Cbd и Свк аналогичным образом: на конденсаторе Свк — заряд -91, на конденсаторе Cbd------92. Полярность пластин конденсатора Cdk вы-
бираем произвольно.
Часть схемы, содержащая три проводника, исходящие из точки К, с присоединенными к ним пластинами конденсаторов изолирована и, следовательно, в целом электронейтральна:
(3) - 91 + 92 “ = °-
Запишем очевидные соотношения:
92 91
(4) Фа _ Фв = Фа ~ Фх + Фх ~ Фв = 2С + ~С
(5) Фа “ Фа = Фа - Фн + Фп " Фк + Фк “ Фа =
21 9з 2г _
~ С С 2С
Из системы уравнений (2,3,5) вырази 91 и 92 через 9:
(6) 91 = | 9
(7) 92 = | 2
и подставим их в (4), а затем в (1):
С----------2---------1 С
~ 4 q 3 п~5С-7 • 2С + 7 ’ С
Отметим, что выбор полярности пластин конденсатора Свк оказался верным. В противном случае сис
504
Борис Гринченко
тема уравнений не имела бы решений, удовлетворяющих физическому смыслу; в частности, для модуля заряда на этом конденсаторе получилась бы отрицательная величина.
Примечание.
При решении задачи была использована симметрия схемы относительно двух поворотов на 180° вокруг горизонтальной и вертикальной осей. В принципе, решая задачу «в лоб», то есть без использования соображений симметрии, мы пришли бы к тому же результату, однако с более сложными математическими выкладками.
20. Электроемкость. Конденсаторы
505
Задача 20.7.
Найти электроемкость между точками А и В бесконечной цепи конденсаторов.
Решение.
Обозначим емкость системы конденсаторов через С Ав- Учитывая, что цепь бесконечна, и удалив из схемы первую ячейку из двух конденсаторов, получим ту же самую схему: емкость между точками А и В равна емкости между точками А' В'. Таким образом, приходим к эквивалентной схеме:
С
. В о
В'
506
Борис Гринченко
Расчет дает:
(1) С = С + С + С ’
'•'АВ + ''АВ
Решая квадратное уравнение относительно Сав, находим:
= I (V5 - 1)С.
21. Взаимодействие зарядов.
Энергия электрического поля
Работа электрического поля при перемещении точечного заряда q из точки А с потенциалом срл в точку В с потенциалом фв равна:
(1) ^ = (Фа-Фв)9
и не зависит от траектории перемещения.
Потенциальная энергия точечного заряда д, помещенного в точку А пространства, с точностью до константы определяется соотношением:
(2) W=g-<pA.
Энергия взаимодействия точечных зарядов qi, q2 и т.д. может быть представлена в виде:
(3) ^ = ±£д,ф„
где ф, — потенциал, создаваемый всеми зарядами, кроме заряда qit в точке нахождения этого заряда. В частности, для системы из двух зарядов, находящихся на расстоянии г, формула (3) принимает вид:
(4) W = | (ф^ + д2ф2) =
1 / kq^ кд2дг х kqrq2 ~2 V г + г ' г ’
. Если заряды qi и q% одного знака, W > 0, в противном случае - W < 0. В первом случае энергия W > 0 равна
508
Борис Гринченко
работе, которую совершают силы электрического отталкивания при удалении зарядов на бесконечно большое расстояние (например, при свободном разлете вначале неподвижных зарядов W равна кинетической энергии разлетевшихся частиц). Во втором случае энергия W < 0 равна (с обратным знаком) работе, которую необходимо совершить, чтобы развести вначале неподвижные заряды на бесконечно большое расстояние.
Связь между работой электростатических сил и потенциальной энергией при переходе системы из состояния 1 в состояние 2 дается общим соотношением:
(5) A = W1-W2 = -AW (AW = W2-W1), которое является определением потенциальной энергии.
Энергия заряженного конденсатора:
Энергия однородного электрического поля напряженностью Е, занимающего объем V, равна:
ее-Е2
(7) W = V.
Энергия W уединенной сферы радиуса R, равномерно заряженной зарядом Q (см. решение задачи 21.1):
(8) W =
21. Взаимодействие зарядов
509
Задача 21.1.
Найти энергию уединенной сферы радиуса R, равномерно заряженной зарядом Q.
Решение.
Представим заряд Q в виде системы точечных зарядов qt (то есть разобъем заряд Q на малые заряды qi) и воспользуемся выражением для энергии системы точечных зарядов:
T,z 1 V J V JQ J V „ _ 1
W - 2 <№t 2 R 2 R ^Qi 2 R ’
где учтено, что потенциал в области нахождения любого заряда равен потенциалу поверхности сферы:
Второй вариант расчета основан на определении потенциальной энергии (5).
Разобъем заряд Q на большое число N малых зарядов
Работа An электростатических сил при удалении очередного га-го заряда с поверхности шара на бесконечность
(1)
Энергия зарядов сферы W, согласно (5), определяется суммой Ai + Аг + + An:
N 9
п = 1
610
Борис Гринченко
В (2) использовано выражение для суммы арифметической прогрессии:
, n ' N (N +1)
1 + 2 + +N = —Н;-----~
лл
и учтено, что N + 1 - N (N » 1).
21. Взаимодействие зарядов
511
Задача 21.2.
Найти электростатическое давление на поверхность тонкой проводящей пластины, находящейся в однородном __ электрическом поле напряженностью Ео. Вектор Ео перпендикулярен плоскости пластины.
Решение. —
Электростатическое давление, испытываемое, например, правой (положительно заряженной) поверхностью пластины, по определению равно:
Л
(1)
где
(2) F+ = qE,
Напряженность Е электрического поля в области нахождения положительных зарядов + q (на правой поверхности пластины) создается внешним полем Ео и полем Е_ зарядов - q на левой стороне пластины:
612
Борис Гринченко
(3) Е = Ео + Е .
Условие равенства нулю поля внутри пластины дает:
(4) Е_ + Е+ = Ео.
Спроецируем (3) на направление вектора Е-.
(5) Е = Ео- Е_
_ _ о а
и, учитывая, что Е = Е+ = ~— и ст = ze0 о
окончательно находим: п
2 *
Другой вариант расчета электростатического давления основан на применении закона сохранения энергии. Для этого заменим сплошную пластину двумя тонкими проводящими пластинами, соединенными проводником:
Очевидно, что распределение зарядов на пластинах, а вместо с ними и электростатическое давление
21. Взаимодействие зарядов
513
совпадают со случаем сплошной пластины. Обозначим через F+ силу, действующую, например, на правую пластину. Чтобы удержать правую пластину в состоянии равновесия, необходимо приложить к ней силу F (внешнюю силу), равную F+ и противоположно ей направленную.
Увеличив эту внешнюю силу на очень малую (в пределе стремящуюся к нулю) величину, переместим правую пластину влево на расстояние d. При этом будет совершена работа А = F • d. В результате в пространстве появится объем <S • d, заполненный электрическим полем и, следовательно, энергия электрического поля возрастет на величину
(6)
s0 Еп AW = Sd.
Согласно закону сохранения энергии:
(7)
А = А1У = Fd.
Из (6,7), с учетом определения давления (1), приходим к ранее полученному результату.
514
Борис Гринченко
Задача 21.3.
Найти электрическое давление, которое испытывает поверхность равномерно заряженной сферы радиуса R. Заряд сферы Q.
Решение.
Первый вариант решения основан на законе сохранения энергии. Для удобства расчета представим себе, что сфера выполнена из абсолютно эластичного (неупругого) материала, а электрическое давление уравновешивается, например, давлением окружающего газа (внутри сферы газ отсутствует). Пусть в результате медленного и очень малого уменьшения давления газа радиус сферы увеличился на малую величину AR (ЛК « R). При этом над газом совершена работа:
(1) А = PAV = P4nR2AR,
где AV = 4tiR2AR — изменение объема газа.
21. Взаимодействие зарядов
515
Работа над газом совершена за счет уменьшения электростатической энергии сферы:
(2) AW = W1-W2 = Щ-R -
kQ2 kQ2 A R
" 2(R + AB) 2B2 ’
Согласно закону сохранения энергии:
(3)
A = bW.
Из (1—3) находим:
Р=
8лВ4'
Величину AW можно было найти также, восполь
зовавшись выражением для энергии электрического поля. Действительно, после расширения сферы объем, занимаемый электрическим полем, уменьшился на величину шарового слоя толщиной АЛ: АУ = 4лВ2 АВ. Электрическое поле до расширения в этом слое
В = учитывая малость АВ , можно считать однородным, а после расширения Е = 0.
Отсюда находим:
(4) = =
2 2В2
что совпадает с (2).
Второй вариант решения задачи основан на прямом расчете давления.
Рассмотрим малую площадку ASj на поверхности сферы, поверхностная плотность зарядов которой:
(5)
4ЛВ2’
516
Борис Гринченко
JS&BJiewiie Р, испытываемое площадкой, по определению, равно:
(в> р=ь
где F — сила, действующая со стороны зарядов сферы на заряд AQ = а&8 площадки:
(7) F = Е • AQ = EcAS.
Напряженность электрического поля Е, создаваемая всеми зарядами сферы за исключением заряда AQ, найдем из следующих соображений. Рассмотрим две близкие к поверхности сферы точки А и- В: одна внутри сферы, другая — снаружи. Воспользуемся принципом суперпозиции для вычисления поля в точке В:
(8) Ев = Е + 2лЛст =
R
где 2nka — поле, создаваемое зарядом AQ в точке В. Аналогично, для поля в точке А:
(9)
Еа = Е - 2лй<т = 0.
21. Взаимодействие зарядов
517
Из (8,9) имеем:
После несложных вычислений получаем, как и прежде:
р= *3* влВ4’
В качестве упражнения полезно вернуться к решению задачи 15.7, применив энергетический подход, аналогичный использованному в первом варианте решения данной задачи.
518
Борис Гринченко
Задача 21.4.
Найти силу электростатического взаимодействия пластин плоского конденсатора, заполненного диэлектриком с проницаемостью е. Площадь пластин конденсатора S, заряд -Q.
Решение.
+++++ +++++++++++ +Q
----------------------------Q
Сила F, действующая, например, на нижнюю пластину конденсатора, равна:
(1) F = EQ,
где Е — напряженность электрического поля, создаваемая зарядами на верхней пластине конденсатора, и зарядами, индуцируемыми на поверхности диэлектрика:
(2)
Е = Е + Е ' + Е ' = Е,, -т +• —
г _ ° Q где Е‘ ~ 2е0 " 2e0S
поле, создаваемое зарядами
верхней пластины в области нахождения нижней. По
21. Взаимодействие зарядов
519
ля Е+' и Е ' индуцированных на поверхности диэлектрика зарядов в области нахождения нижней пластины друг друга компенсируют.
Из (1,2) получаем:
<3>
так что сила F не зависит от наличия диэлектрика. В частности, в случае отсутствия диэлектрика между пластинами конденсатора выражение для силы (3) остается справедливым.
При решении данной и других подобных задач нередко допускают следующую ошибку: в (1) вместо напряженности поля Е подставляют напряженность электрического поля, создаваемую обеими пластинами конденсатора, то есть напряженность электрического поля между пластинами конденсатора. В результате получают ошибочный ответ, вдвое превышающий правильный (3). Дело в том, что поле, создаваемое зарядами, например, нижней пластины, вклада в силу F из (1) не дает. Чтобы убедиться в этом, достаточно убрать верхнюю пластину. Тогда, очевидно, F = 0.
Второй вариант решения задачи, основанный на законе сохранения энергии, предоставляется выполнить читателю самостоятельно.
520
Борис Гринченко
Задача 21.5.
Какое количество тепла выделится при замыкании пластин конденсатора, находящегося в однородном электрическом поле с напряженностью Ео? Площадь пластин_конденсатора S, расстояние между ними d. Вектор Ео перпендикулярен плоскости пластин конденсатора.
Решение.
До замыкания пластин электрическое поле Ео заполняло все пространство, включая пространство между пластинами. После замыкания пластин конденсатора проводником поле внутри него исчезает. Действительно, соединенные проводником пластины имеют одинаковый потенциал, и, следовательно, напряженность электрического поля между пластинами равна нулю (электростатическая защита).
Воспользуемся законом сохранения энергии: энергия электрического поля между пластинами конденсатора перешла в тепловую энергию (за счет джоулева тепла, выделяющегося при прохождении токов по пластинам и проводнику в процессе установления равновесного распределения зарядов:
2 где Sd — объем пространства между пластинами конденсатора, Q — количество выделившегося тепла.
21. Взаимодействие зарядов
521
Задача 21.6.
Какую минимальную работу необходимо совершить, чтобы заряд q, находящийся в центре неподвижного проводящего шарового слоя с внутренним и внешним радиусами Ri и Яг, удалить через тонкое отверстие на бесконечно большое расстояние?
Решение.
Начальное и конечное состояние системы различаются тем, что в первом случае электрическое поле области пространства, занимаемого шаровым слоем, отсутствует, а во втором электрическое поле вокруг заряда существует во всем пространстве.
Таким образом, согласно закону сохранения энергии, появление дополнительной области пространства с электрическим полем осуществляется за счет совершенной работы:
(1)
А = AW,
522
Борис Гринченко
где AW — энергия электрического поля в области пространства шарового слоя при отсутствии в нем проводника.
Расчет величины AW может быть выполнен либо прямым интегрированием, либо с использованием формулы для энергии уединенной равномерно заряженной сферы. Энергия поля вне сферы радиуса R\ точечного заряда q совпадает с энергией поля, создаваемого равномерно заряженной зарядом q сферы радиуса Ri (поскольку совпадают поля):
(2) =
Аналогично для сферы R%:
<3)
Из (1—3) находим:
А = Ж, - W2 = Д1Г = - J-).
^*1 •П'2
Отметим, что речь идет о минимальной работе. На самом деле, при перемещении заряда q происходит перераспределение зарядов на сфере (то есть протекают токи) и выделяется джоулево топливо. Можно показать, однако, что в пределе при медленном перемещении заряда величина этого джоулева тепла стремится к нулю (предоставляем читателю).
21. Взаимодействие зарядов
523
Задача 21.7.
С какой силой втягивается диэлектрическая пластина в плоский конденсатор с зарядом Q, когда она входит в пространство между обкладками на длину х? Диэлектрическая проницаемость пластины е, ее толщина немного меньше расстояния между обкладками d. Размеры обкладок, как и пластин, а х Ь.
Решение.
Обозначим через F силу, с которой пластина втягивается в конденсатор, через Fi — внешнюю силу, удерживающую пластину в равновесии (Fi = F).
Воспользуемся энергетическим подходом и медленно переместим пластину вправо на малую величину Лх, добавив к силе Fi очень малую величину. При этом внешняя сила совершает работу:
(1)
А = FtAx = F/\x,
(работа электростатических сил при этом равна - А), а энергия электрического поля конденсатора увеличивается на величину:
524
Борис Гринченко
(2) AW = W9 - W..
Согласно закону сохранения энергии:
(3) А = AW.
При подсчете энергии электрического поля конденсатора удобно представить его как два параллельно соединенных конденсатора, один из которых (Ci) заполнен диэлектриком:
а в другом (С2) диэлектрик отсутствует:
(6)
причем их электроемкость:
(6) С = Сг + С2,
а заряд, в соответствии с условием задачи, равен Q.
Энергия конденсатора с учетом (4-6)
(7) w = О- = QjL. ——--
ш 2С 2е0& (е - 1) х + а
Применяя (7) для расстояния х и х - Ах, с учетом (1—6) и малости Ах (Ах « х), получаем:
f - Q2d . 6-1
2е0 Ь ' [а + х (е - l)f'
Этот же результат можно получить из вытекающего из (1,2) соотношения:
(8) F = W'
путем дифференцирования W по х.
21. Взаимодействие зарядов
625
Задача 21.8.
Какую минимальную кинетическую энергию необходимо сообщить покоящемуся электрону, чтобы он мог удалиться от поверхности равномерно заряженной сферы радиуса R на бесконечно большое расстояние? Заряд сферы + Q.
Решение.
Запишем закон сохранения энергии для двух состояний электрона:
(1) Ег = Я2,
где Е1 — полная энергия электрона в начальном состоянии (электрон находится на поверхности сферы и имеет кинетическую энергию £):
(2) Е1=Ек + ^-
и в конечном:
(3) Е2 = О,
поскольку в силу условия минимальности кинетическая энергия электрона на бесконечности равна нулю, так же как и потенциальная энергия.
Из (1—3) находим:
где е = - 1,6 • 10 19 Кл — заряд электрона.
526
Борис Гринченко
Задача 21.9.
Вокруг тяжелого ядра с зарядом Ze на расстоянии г по круговой орбите вращается электрон. Какую минимальную энергию необходимо сообщить электрону, чтобы он оторвался от ядра (удалился на бесконечное расстояние)?
Решение.
Запишем закон Ньютона для вращающегося вокруг ядра электрона, учитывая кулоновский характер взаимодействия:
где т — масса электрона,
— его центростреми-
тельное ускорение.
Сразу после того, как электрону сообщили добавочную кинетическую энергию Ек, его полная энергия стала равной:
(2) Е1=^ + Ек-^-.
Потенциальная энергия электрона на бесконечно большом расстоянии равна нулю, кинетическая энергия, в силу условия минимальности, так же равна нулю, так что полная энергия электрона:
<3) Е2 = 0.
Согласно закону сохранения энергии:
(4) Ех = Е2.
Из (1—4) находим:
21. Взаимодействие зарядов 527
„ kZe2
Отметим, что по условию задачи (тяжелое ядро) предполагалось, что ядро остается неподвижным.
528
Борис Гринченко
Задача 21.10.
На покоящийся протон налетает другой протон, имевший на большом расстоянии скорость v$. Вектор скорости протона лежит на прямой, соединяющей протоны. Найти наименьшее расстояние между протонами в процессе сближения.
Решение.
Запишем законы сохранения импульса и энергии для начального (налетающий протон на большом расстоянии имеет скорость уо, второй протон покоится) и конечного (в момент наибольшего сближения) состояний системы:
(1) mv0 = mv. + mv. 2 2 2 9
(2) му0 mvx mv2 fog2 2 - 2 1 2 + г ’
где последнее слагаемое в правой части (2) — энергия электрического взаимодействия протонов в момент максимального сближения до расстояния г между ними.
Чтобы записать условие минимальности Уо, перейдем в систему отсчета, например, налетающего протона. Тогда, очевидно, скорость вначале покоящегося протона относительно налетающего в момент максимального сближения равна нулю. Другими словами, в момент наибольшего сближения относительная скорость протонов равна нулю. Отсюда нетрудно заключить, что относительно неподвижной системы отсчета (земли) скорости протонов в момент максимального сближения равны:
(3) у^ = Г2.
21. Взаимодействие зарядов
629
Проецируя (1) на направление вектора Ро и учитывая (2,3), имеем:
(4)
4^ mv2
Другой вариант решения задачи основан на переходе в систему отсчета, движущуюся со скоростью
В этой системе отсчета (центра масс) в начальный
момент два протона движутся навстречу друг другу ио т»
с одинаковыми скоростями -z-. В момент максималь-&
ного сближения (конечное состояние) их скорости равны нулю (в следующие моменты времени протоны начинают разлетаться в разные стороны). Согласно закону сохранения энергии:
т \ 2 J ka2
(5) 2----
откуда сразу получаем (4).
530
Борис Гринченко
Задача 21.11.
В точках А и В на расстоянии I друг от друга закреплены заряды + 9q и - q. Вдоль прямой АВ к ним движется частица с зарядом + q. Какую наименьшую кинетическую энергию должна иметь эта частица на большом расстоянии, чтобы достигнуть точки В?
Решение.
(1)
Запишем выражение для напряженности электрического поля в зависимости от расстояния х от точки В в проекции на ось х:
„ 9kq kq
Из (1) видно, что на больших расстояниях имеет место отталкивание, а при малых х отталкивание сменяется на притяжение заряда +q. В некоторой точке С напряженность электрического поля равна нулю. Очевидно, что в случае достижения точки С с практически нулевой скоростью заряд достигнет и точки В, поскольку после прохождения С отталкивание сме
няется притяжением.
Воспользуемся законом сохранения энергии, выбрав в качестве начального состояния положение заряда +q на большом расстоянии от точек А и В (потенциальная энергия равна нулю) с кинетической
21. Взаимодействие зарядов
531
энергией Ек, а в качестве конечного — момент достижения частицей + q точки С с нулевой кинетической энергией:
<2> = ^ = вс>’
где правая часть представляет собой потенциальную энергию заряда + q в точке С.
С учетом Е = 0 в точке С, из (1) находим:
(3) х0 =
Подставляя (3) в (2), получаем ответ задачи:
532
Борис Гринченко
Задача 21.12.
Частица массы т с зарядом +q приближается с большого расстояния к равномерно заряженному незакрепленному кольцу, двигаясь по его оси. Радиус кольца R, заряд + Q, масса т. Вначале кольцо покоится. Найти минимальную скорость частицы vq на большом расстоянии от кольца, при которой она достигнет центра кольца.
Решение.
Покажем, что условие минимальности скорости означает, что в момент достижения центра кольца скорость частицы совпадает со скоростью кольца (то есть их относительная скорость равна нулю). Действительно, если скорость частицы превышает скорость кольца, то начальная скорость не является минимальной и может быть уменьшена. Ситуация, когда скорость кольца превышает скорость частицы в момент достижения последней центра кольца, невозможна.
21. Взаимодействие зарядов
538
Запишем закон сохранения энергии, выбирая в качестве начального состояния частицу со скоростью vq на большом расстоянии от кольца (потенциальная энергия равна нулю) и неподвижное состояние кольца, а в качестве конечного — момент достижения частицей центра кольца. В конечном состоянии потенциальная энергия электростатического взаимодействия зарядов кольца с частицей равна (см. fl решение задачи 16.7).
m mvo mv2 mv2 kQq
1L) 2 ~ 2 + 2 + R *
Согласно закону сохранения импульса:
(2)
mvQ = 2mv.
Решение системы уравнений (1,2) дает:
534
Борис Гринченко
Задача 21.13.
Внутри гладкой непроводящей сферы массы М и радиуса R находятся две одинаковые бусинки массы т, имеющие заряд q. Расстояние между бусинками I. Найти максимальную скорость сферы, если бусинки отпустить. Внешними силами пренебречь.
Решение.
Скорость сферы будет максимальна в момент, когда бусинки окажутся на одном диаметре. Действительно, до этого момента сила реакции N, действующая со стороны бусинок на сферу, совпадает с направлением скорости сферы (скорость сферы увеличивается). Затем сила меняет знак, и скорость сферы уменьшается.
Запишем законы сохранения импульса и энергии для состояний системы в начальном (сфера и бусинки покоятся) и конечном (сфера имеет скорость V, бусинки — v и лежат на одном диаметре) состоянии:
(1)
О = MV - 2mv
21. Взаимодействие зарядов
535
kQI 2 MV?‘ . 9 mv2 д. kQ2
(2) 1=~Г + 2~Г+2Н'
Решая систему уравнений (1,2), находим:
I___2R
М М2 к 2 + 4m
636
Борис Гринченко
Задача 21.14.
Какую минимальную энергию необходимо затратить, чтобы вставить один плоский конденсатор в другой. Пластины конденсаторов имеют одинаковые размеры и заряды, запасенная в них энергия равна соответственно 2Q и Q.
**фв ""t" ""t" ""t"
+++++++
Решение.
Из условий задачи, а также из выражения для энергии электрического поля:
е-Е2
(1) W--—-V
следует, что напряженности электрических полей в конденсаторах равны, а расстояние между пластинами первого из них с энергией 2Q вдвое больше, чем второго (доказательство представляется читателю).
После вдвижения второго конденсатора напряженность электрического поля между его пластинами увеличится в два раза (энергия возрастет в четыре раза), а в остальном пространстве между пластинами первого конденсатора не изменится.
Учитывая (1), найдем энергию системы после вдвижения:
(2) W2 = 4Q + Q = 5Q.
Энергия конденсаторов до вдвижения:
21. Взаимодействие зарядов
537
(3) Wx = 2Q + Q = 3Q.
Согласно закону сохранения энергии, искомая энергия:
AW = W2 - Wx = 2Q.
<&
538
Борис Гринченко
Задача 21.15.
Атом позитрония представляет собой электрон и позитрон, вращающиеся вокруг общего центра масс по окружности радиуса г. Массы электрона и позитрона т совпадают, заряд позитрона равен +е, где - е — заряд электрона. Какую минимальную дополнительную скорость необходимо сообщить электрону вдоль направления его движения, чтобы позитроний распался?
Решение.
Запишем закон Ньютона для электрона в позит-
ронии:
(1)
fee2 (2г)2
= т—. г
Пусть электрон получил дополнительную скорость
v так, что его скорость стала равна v0 + v.
Для удобства расчетов перейдем в систему центра
масс:
(2) 2mV = m(v0 + и) - mv0; V = %.
21. Взаимодействие зарядов
539
В системе центра масс сразу после получения дополнительной скорости электроном скорости электрона и позитрона равны друг другу и направлены в разные стороны:
(3) ve’ = vp' = v0 +
Запишем закон сохранения энергии для начального состояния (сразу после получения электроном дополнительной скорости) и конечного — электрон и позитрон находятся на бесконечно большом расстоянии с практически нулевыми скоростями:
т(Ро + ke2
(4) 2----^-^-=0.
Отсюда с учетом (1) находим:
L / fee2 v = 2 Д/-^-\ ” 2гт
fee2 4гт
[be2 г—
— (>/2 - 1).
гт4 7
,«э
22. Движение заряженных частиц в электрическом поле
Задача 22.1.
Частица массы т с зарядом q влетает в плоский конденсатор длины I под углом а к плоскости пластин, а вылетает под углом р. Найти первоначальную кинетическую энергию частицы Eq, если напряженность электрического поля внутри конденсатора Е.
Решение.
Начало системы отсчета выберем в точке входа частицы в поле конденсатора. Из закона Ньютона для частицы:
(1) qE = та
22. Движение заряженных частиц
641
находим:
(2)
(3)
ах •= О
Запишем основные уравнения кинематики равнопеременного движения для момента времени вы
хода частицы из поля конденсатора:
(4) хх = v0cos а • tx = I
(5) vlx = v0cos а
(6) vly = vosin а - atv
Кроме того,
(7) tgB = ^=U°8ina~“t‘
vlx Vq cos a
2
(8) Eo =
Решение системы (3—8) дает:
E =________QEl________
0 2 cos2 a £tg a + tg P)’
Движение в однородном электрическом поле заряженной частицы аналогично движению тела в поле тяжести Земли (и в том и в другом случае это движение с постоянным ускорением). В частности, траектория частицы представляет собой параболу.
542
Борис Гринченко
Задача 22.2.
Найти период малых колебаний легкой гантели длины I с шариками массы т, расположенной вдоль однородного электрического поля напряженностью Е. Заряды шариков + q и - q.
Решение.
Задача сводится к колебаниям вокруг точки О ма-I
тематического маятника длины с ускорением сво-бодного падения:
(1)
(см. предыдущую задачу).
Согласно формуле для периода колебаний математического маятника:
Т = 2л V?" =
“2 g y2qE
22. Движение заряженных частиц
543
Задача 22.3.
Электрон, двигаясь прямолинейно, попадает в электрическое поле, потенциал которого имеет вид, показанный на рисунке. В точке А электрон влетает в область электрического поля, в точке В — покидает эту область. Изменится ли скорость частицы в точке В и время пролета расстояния АВ, если вместо электрона полетит позитрон?
Заряд позитрона равен + е (~е — заряд электрона), массы электрона и позитрона равны.
Решение.
На участке АС имеет место ускорение электрона, на участке СВ — замедление. Поскольку работа сил электрического поля на участке АВ равна нулю:
Алв = ?(Фа ~ Фв) = 0
(как видно из рисунка, фд = <рв), скорости электрона в точках А и В равны. В случае позитрона на участке АС происходит замедление, а на участке СВ — ус-
544
Борис Гринченко
корение. Если начальной кинетической энергии позитрона Eq достаточно, чтобы преодолеть замедляющий потенциал <р0, он достигнет точки С, а затем и В:
Ео > q Ф0
(в случае точного равенства позитрон достигает точки С с нулевой скоростью и остается в состоянии неустойчивого равновесия).
___________22. Движение заряженных частиц______ 545
Если Ео < q «ро» позитрон не достигает точек С и В, отразившись, как говорят, от потенциального барьера.
Разбив участок АВ на малые участки, из графиков зависимости скоростей от координаты электрона видим, что на каждом из таких участков скорость электрона превышает скорость позитрона. Следовательно, время прохождения электроном каждого участка меньше соответствующего времени для позитрона. Отсюда заключаем, что электрон проходит участок АВ быстрее позитрона (если последний вообще преодолевает барьер).
546
Борис Гринченко
Два равномерно заряженных зарядом +Q шара радиуса Я каждый находятся на расстоянии I друг ст друга. Какую минимальную скорость Vo, направленную вдоль АВ, необходимо сообщить электрону, находящемуся в точке А, чтобы он мог достичь второго шара (точки В).
Решение.
На участке АС электрическое поле направлено вправо и тормозит движение электрона. На участке СВ поле направлено влево и ускоряет движение электрона в направлении точки В (в точке СЕ = 0). Следовательно, минимальная скорость (а вместе с ней и кинетическая энергия) определяется условием достижения электроном точки С с практически нулевой скоростью (если скорость электрона в точке С окажется равной нулю, он будет находиться в состоянии неустойчивого равновесия).
22. Движение заряженных частиц
547
Запишем закон сохранения энергии для состояния электрона в точке Айв точке С:
(1) Ех = Е2,
где
(2)
2
_ mv0
1 ~~2~
еФл =
2 Г mvo , J k Q
2 1 R
(e = - 1,6 • 10 19 Кл — заряд электрона, т — его мас-
са).
Из (1—3) находим:
/ 2keQ (2R - V? vo~ У mlR (I - R) •
В качестве упражнения полезно доказать, что полученный результат справедлив для задачи в более общей постановке: направление скорости 5о не оговаривается.
548
Борис Гринченко
Задача 22.5.
Электроны, обладающие на бесконечности скоростью у, падают на металлический шар радиуса R. На сколько градусов повысится температура шара через достаточно большое время, если его теплоемкость равна С?
Решение.
Из закона сохранения энергии следует, что электроны будут достигать поверхности шара до тех пор,
пока 2
(1) mv . 2
где
(2) kQ
потенциал шара, (е — модуль заряда электрона).
Количество электронов 7V, достигших шара к моменту насыщения (когда в (1) имеет место знак равенства):
(3) N = Я
е
Запишем закон сохранения энергии:
(4) ' W + С ДТ,
22 22/1
л г W02
где N — энергия электронов, достигших шара, Л
которая затрачена на создание энергии электричес-ЛО2
кого поля шара - и его нагрев С &Т.
Из (1—4) находим:
лт - (/nt?2)2 Д
А ~ 4/ге С ’
22. Движение заряженных частиц
549
Задача 22.6.
На две параллельные сетки, между которыми приложена разность потенциалов U, под углом а падает пучок отрицательных ионов. При каких энергиях частицы смогут пройти через сетки, если заряд иона д?
Решение.
Будем считать поле между сетками, однородными с вектором напряженности, направленным перпендикулярно сеткам. При этом сила, действующая на ион вдоль сетки равна нулю, а следовательно, соответствующая составляющая скорости иона vo cos а в процессе его движения между сетками остается постоянной.
Пусть Vo — критическая скорость, при которой ион едва достигает отрицательной сетки (при меньших скоростях электрон отражается, при больших — проходит сквозь сетку). В этом случае скорость иона в момент достижения сетки направлена вдоль сетки и * равна vo cos а.
550
Борис Гринченко
Запишем закон сохранения энергии для иона, выбрав в качестве начального состояния ион при входе в область электрического поля (вблизи положительной сетки), конечного — вблизи отрицательной сетки:
(1) = Е2
(2) 2 m vn Е‘= 2
(3) Д2 = ^о,«°за)2_д[/
(потенциал положительной сетки принят равным нулю).
Из (1—3) находим:
(4) f • 1>5(1 - сов2 а) = - ди.
Учитывая, что кинетическая энергия иона равна 2
„ mvo
Е = —х—, окончательно получаем:
Е> &
Zj вс — А- • sin а
23. Электрический ток
По определению, сила тока дается соотношением:
где Ад — заряд, прошедший через поперечное сечение проводника за время Af. За направление тока принимается направление движения положительных зарядов.
Плотностью тока j называется величина:
(2)
где S — площадь поперечного сечения проводника. С учетом (1,2) можно показать, что
(3) j = nqv,
где п — концентрация заряженных частиц, образующих ток, q — заряд одной частицы, v — скорость упорядоченного движения (средняя скорость) заряженных частиц.
Связь между напряжением на концах проводника и силой тока в нем определяется законом Ома:
U
R’
Величина R называется сопротивлением проводника:
(4)
(5)
R-P s,
552
Борис Гринченко
где р — удельное сопротивление, I — длина проводника, S — площадь поперечного сечения.
Из (1—5), с учетом соотношения U = Е • I, можно получить закон Ома в дифференциальной форме:
(6)
j = хе ,
1
где X = р- — удельная проводимость проводника, Е — напряженность электрического поля в нем.
23. Электрический ток
553
Задача 23.1.
Сколько электронов проходит через поперечное сечение проводника за 1 нс при силе тока 32 мкА?
Решение.
Воспользуемся определением силы тока:
(1) / = ^£
1 } At
и соотношением для количества электронов, суммарный заряд которых равен Ад:
(2) =
где е = 1,6 • 10“19 Кл — заряд электрона.
Из (1,2) получаем:
w /At 32-10-®. IO’® _ 1пб
JV =---=----------тп— =210.
е 1,6 • 10“19
654
Борис Гринченко
Задача 23.2.
Медный и алюминиевый проводники имеют одинаковые массы и сопротивления. Какой проводник длиннее и во сколько раз?
Решение.
Запишем соотношения для сопротивления проводников:
(1) В, = Pi
(2) В2 = Р24>
где Pi = 1,7 • 10"8 Ом • м и р2 = 2,8 • 10~8 Ом • м — удельные сопротивления меди и алюминия соответственно (табличные данные).
Условие равенства масс дает:
(3) = Z2p2'S2 ,
где р/ = 8,9 • 103 К1/м3 и р2' = 2,7 • 103 — плотнос-
ти меди и алюминия соответственно.
Из (1—3) после несложных преобразований находим отношение длин проводника из алюминия I2 и меди h:
£==г-4-
Ч Р2 Р2
23. Электрический ток
555
Задача 23.3.
Если предположить, что число электронов проводимости в металле равно числу атомов, то какой будет средняя скорость электронов проводимости в серебряной проволоке диаметром 1 мм, по которой течет ток 30 А?
Решение.
Воспользуемся основными уравнениями теории:
tn >4
(2) j = nev .
Масса одного моля серебра М = 108 • 10 3 кг содержит число атомов Na = 6 • 1023. Массе одного моля серебра соответствует объем:
(3)
где р = 10,5 • 103 кг/м3 — плотность серебра. Учитывая, что, согласно определению, концентрация
(4) п =
из (1—3) находим:
v = = °>4 • 10“ 2 м/с .
556 Борис Гринченко
Задача 23.4.
Плотность тока в пучке электронов /, скорость электронов v. Найти плотность заряда в пучке.
Решение.
Воспользуемся соотношением:
(1) j = nev
из введения к параграфу. Учитывая, что
(2) р = пе ,
находим:
р = .
v
23. Электрический ток
557
Задача 23.5.
В протонный пучок с плотностью тока j = 1 мкА/см2 поместили металлический шар радиуса г = 10 см. За какое время т шар зарядится до потенциала ср = 220 В? Действием поля шара на пучок пренебречь.
Решение.
Для определенности будем считать, что шар мгновенно помещен в пучок, так что в начальный момент шар поглощает протоны всей поверхностью полусферы, обращенной навстречу пучку.
Нетрудно показать (предоставляется читателю), что ток на шар
(1)
I = far*.
За время т на шаре окажется заряд:
(2)
q = It .
568
Борис Гринченко
Согласно условию задачи:
(3) <Р = ^.
Из (1—3) находим:
^ = 8,1°4с-
Т =
23. Электрический ток
559
Задача 23.6.
Плоский конденсатор емкостью С заполнен диэлектриком с проницаемостью е и обладает малой проводимостью 1. Найти ток утечки при напряжении на конденсаторе U.
Решение.
(1)
Емкость плоского конденсатора: г
С = d ’ сопротивление диэлектрика между пластинами конденсатора:
(2) "x'f •
Согласно закону Ома:
(3) / =
Из (1—3) получаем:
UM еоеПХ
S " С ’
560
Борис Гринченко
Задача 23.7.
В центре проводящего шара с удельным сопротивлением р оказался избыточный заряд Q. Найти ток, текущий из центра шара к его поверхности.
Решение.
Выделим мысленно сферу радиуса г внутри шара с центром в центре шара. Напряженность электрического поля на поверхности сферы:
(1) £ = 7г>
плотность тока через поверхность сферы:
(2) j = ХЕ = .
Сила тока через поверхность сферы, площадь которой 4лг2, с учетом (1,2) равна:
(3) / = = =
4itkQ Q ~~
и не зависит от г. Следовательно, I из (3) совпадает с током, текущим к поверхности шара.
23. Электрический ток
561
Задача 23.8.
Плотность тока j перпендикулярна плоскости раздела двух сред с удельными проводимостями Xi и А,г. Найти поверхностную плотность зарядов на этой поверхности.
Решение.
2
Е'
Обозначим напряженность электрического поля, создаваемого зарядами на внешней поверхности проводников вблизи плоскости раздела через Eq. Поле, создаваемое зарядами на поверхности раздела проводников,
(1)
О'
2е0
Направление поля Е' выбираем в предположении,
что заряд на поверхности раздела сред положителен.
Воспользуемся законом Ома в дифференциальной форме для точек 1 и 2
(2)
j = (Eo- E’)kv
662 Борис Гринченко
(3) j = (Ео + Е') Хг,
где Ео-Е'— электрическое поле слева от границы раздела, Ео+Е' — справа.
Из (1—3) находим:
.fl 1 \
°-еоЛх2 xj-
Полученный ответ справедлив, если Хг < Xi. В противном случае заряд на поверхности раздела сред отрицателен
24. Электрические цепи постоянного тока
При решении задач на расчет электрических цепей используются закон Ома для участка цепи:
(1) Ф1 - <Р2 = U = IR-,
определение электроемкости конденсатора:
(2) Ф1 - <р2 = U =
формулы для последовательного и параллельного соединения сопротивлений и емкостей (конденсаторов); энергии заряженного конденсатора:
ГТ72 л2
(3) w = =
мощности, выделяемой на участке цепи с напряжением U, по которому течет ток I:
(4)
P=UI.
Если этот участок представляет собой сопротивление
R, то с учетом (1) получаем закон Джоуля—Ленца: гт2
(5) Р=/№=—,
где Р — тепловая мощность, выделяемая на сопротивлении R.
Электродвижущая сила (ЭДС) источника вводится согласно определению:
(6)
564
Борис Гринченко
где Аст — работа, совершенная сторонними (не электростатическими) силами при перемещении положительного заряда q от отрицательной клеммы источника к положительной.
Согласно закону Ома для полной цепи:
где г и R — внутреннее и внешнее сопротивления, I — ток в цепи. Если в цепь последовательно включены несколько источников, то в качестве £ в (7) следует брать алгебраическую сумму ЭДС этих источников.
Нередко при решении задач на расчет электрических цепей использование закона Ома (7) может вызвать затруднения. По этой причине целесообразно применение общего уравнения теории (задача 24.1.):
(8) Ф+ - ф. = £ + 1г,
где ф, — потенциал «положительной» клеммы источника, ф_ — «отрицательной». Знаки «плюс» и «минус» относятся именно к клеммам источника, так что в некоторых задачах возможно ф+ < ф_. Знак «минус» в правой части (8) берется при естественном направлении тока внутри источника (от «отрицательной» клеммы к «положительной»), знак «плюс» — в противоположном (в таких случаях говорят, что ток течет навстречу ЭДС). Последняя ситуация реализуется, например, при зарядке аккумулятора.
При расчете электрических цепей, имеющих точки разветвления (узлы), используется условие стационарности: сумма токов, втекающих в точку разветвления
24. Электрические цепи постоянного тока
565
(узел), равно сумме вытекающих из этой точки токов (первое правило Киргофа).
В некоторых случаях заранее невозможно определить направление тока на том или ином участке ели полярность пластин конденсатора. В таких ситуациях направление токов и полярностей выбирают произвольно, а уже решение задачи дает ответ о правильности выбора. Так, например, если рассчитанный гок оказался отрицательным, то истинное направление тока на данном участке противоположно выбранному. Или, если в результате расчета заряд конденсатора получился отрицательным, это означает, что истинная полярность пластин противоположна выбранной.
Принято считать (если не оговорено противное), что сопротивлением проводов в электрических схемах можно пренебречь. Отсюда вытекает, что каждый провод, не прерываемый каким-либо элементом цепи, находится под одним потенциалом. Это утверждение следует из закона Ома для участка цепи с учетом равного нулю сопротивления участка.
При использовании соотношений (1) и (2) следует иметь в виду, что все величины U, I, R, С, q — с ущественно положительные. Поэтому, записывая, например, закон Ома для участка цепи при подстановке напряжения U, необходимо из большего потенциала вычитать меныпий.
666
Борис Гринченко
Задача 24.1.
Через источник с ЭДС, равной £, с внутренним сопротивлением г течет ток I. Найти разность потенциалов (напряжение) между положительной и отрицательной клеммами источника.
Решение.
8, г
н-
Рассмотрим первый случай: ток направлен «по ЭДС», то есть в направлении действия сторонних сил.
Запишем закон сохранения энергии для положительного заряда
(1)
Дд = /At ,
который за время At переместился от отрицательной клеммы к положительной:
(2)
А>л + Ат - Ф ’
где Аэл и — работы электростатических (кулоновских) и сторонних сил, совершенных над зарядом Д?, Q — количество джоулева тепла, выделившегося на сопротивлении г за время At:
(3)
(4)
(5)
Ал = (ф_ - <р+) А(?
Ат= £^1 Q = г I2At = Ir&q .
24. Электрические цепи постоянного тока
567
Закон сохранения энергии (2) сформулирован в предположении, что кинетическая энергия заряженных частиц в процессе перехода от отрицательной клеммы к положительной практически не изменяется.
Подставляя (3,4,5) в (2), получаем:
(6) <р+- <?_=£- 1г.
Второй случай — ток внутри источника направлен «навстречу» ЭДС, то есть в направлении, противоположном направлению действия сторонних сил. При этом соотношения (1,2,5) остаются в силе, а (3) и (4) принимают вид:
(3')
Ал = (<р+ - Ф-)А(?
8, г
(4') A^^-SLq.
в соответствии с определением ЭДС и разности потенциалов.
Из (2, 3', 4', 5) получаем:
(7) <р+ - <р_ = £ + 1г .
Обобщая (6) и (7), приходим к основному уравнению теории:
Ф+ - Ф_ = £ * 1г .
568
Борис Гринченко
Задача 24.2.
Получить закон Ома для полной цепи.
Воспользуемся основными уравнениями теории для двух элементов цепи: ЭДС и сопротивления:
(1) фз-ф^Я-Ь-
(2) Ф2 - Ф! = П?.
Из (1,2) находим:
24. Электрические цепи постоянного тока
569
Задача 24.3.
Вычислить разность потенциалов на клеммах верхней батарейки. £ i, и, £2, г2 заданы.
Выбираем направление тока, например, против часовой стрелки, и расставляем точки одинакового потенциала.
Запишем основное уравнение теории для каждого из элементов цепи:
(1) ф2 — Ф1 = £ 1 — Ii\
(2) ф2-фх = ^2 + 1г2 .
Из (1,2) находим:
1 £ 2
1 = —------ .
Г1+ Г2
Видно, что (3) и выбранное направление тока спра-• ведливо, если £ i - £ 2 > О. В противном случае ток
570
Борис Гринченко
направлен по часовой стрелке, и в (3) следует поменять местами £i и £2.
Разность потенциалов (напряжение) на клеммах верхней (как и нижней) батарейки получаем, подставив ток из (3) в (1):
„ _ „ _ р _ gl ~ g 2 _ g 1Г2 + g 2Г1
Ф2 Ф1 1 Г1+Гз Г1 + Гз
Нетрудно убедиться, что подстановка (3) в (2) приводит к тому же результату.
24. Электрические цепи постоянного тока
571
Задача 24.4.
В конце зарядки аккумулятора через него течет ток Ii = 4 А, при этом напряжение на клеммах Ui = 12,8 В. При разрядке того же аккумулятора при силе тока 6 А напряжение на его клеммах Uz = 11,1 В. Найти ток короткого замыкания.
Решение.
При зарядке аккумулятора ток течет «навстречу» ЭДС:
(1)
1 - ° т -Ч' •
При разрядке ток направлен по ЭДС:
(2) U2 = S-I2r.
Согласно закону Ома ток короткого замыкания:
(3) I = - .
' ' КЗ у*
Из системы уравнений (1—3) находим:
UJ. + U.K Т __2_1-----1_2 = 71 А
кз их-и2
572
Борис Гринченко
При каком соотношении между Параметрами цепи, указанными па рисунке, ток через сопротивление .R1 равен нулю?
Решение.
При расстановке точек одинакового потенциала сразу учтем, что ток через сопротивление R] равен нулю.
Запишем основные уравнения теории для элементов цепи:
(1) Фг — Фз = & 2 “ ^r2 s
(2) ф2 - Ф1 = П?2
(3) Ф1 _ Фз = Л?з
(4) Ф! - Фз = £ I •
Умножая (1) на минус единицу и складывая (1,2,3) почленно, получим:
24. Электрические цепи постоянного тока 573
(5) I = —- ь
Г2 + -^2 + «3
(закон Ома для цепи 1231).
Из (3,4) имеем:
(6)
Подставляя (5) в (6), окончательно получаем: £ 2 _ лз £ £ Г2 + 1^2 + *3
574
Борис Гринченко
Задача 24.6.
Найти силу тока через перемычку ab. ЭДС источника S, его внутреннее сопротивление пренебрежимо мало. Величина г известна.
Решение.
Запишем условие стационарности тока (первое правило Киргофа) для узла а:
(1) /2 *' = •
Учитывая малость сопротивления перемычки и, следовательно, равенство потенциалов точек а и Ь, заменим представленную схему эквивалентной.
Сопротивление между точками А и В: „ г 2 7
U) Rab-2 + 3 г ~ 6Г '
Согласно закону Ома:
24. Электрические цепи постоянного тока
575
Далее, очевидно:
(4) Л = А = |
(5) Дг = 1.2г или Д = 21. .
Для узла В:
(6) Д + Д = I .
Из (1—5) находим:
576
Борис Гринченко
Задача 24.7.
Найти разность потенциалов между точками а и Ь. Все указанные на схеме параметры цепи считать известными.
Решение. *
Сопротивление между точками 1 и 2: I
(1) я12 = |'-.
Согласно закону Ома:
(2) I - ——— = — • — । J
1 3 L 5 г 1
2Г + Г ’
С учетом условия стационарности: |
(3) <
Для расчета разности потенциалов <рв - гр* используем часто применяющийся прием:
24. Электрические цепи постоянного тока 577
(4) Фа - Фь = Фа - Ф1 + Ф1 - Фь =
= - 1г2г + 12г = - ~1г, поскольку, согласно закону Ома для участка цепи:
Ф1 - Фа = А2?*; Ф1 - Фь = V-
С учетом (2) из (4) получаем:
8
Фа ~ Фе = ~ б •
578
Борис Гринченко
Задача 24.8.
Сопротивления Bi, R2 и R3 и ток 13, протекающий через сопротивление В3, известны. Определить токи через сопротивления J?i и Бг и напряжение на клеммах батареи.
Решение.
Сопротивление между точками 1 и 3:
(1) Лм = В1 + ^А_.
Падение напряжения на клеммах батареи:
(2) <Pj — <р3 = £7 = Zj • -Rj_3 . ’
Условие стационарности для узла 2:
(3) Л =
Условие равенства напряжений на сопротивлениях Вг и В3:
(4) -^2^2 = Iз^з •
24. Электрические цепи постоянного тока 679
Из системы уравнений (1—4) находим:
680
Борис Гринченко
Задача 24.9.
После замыкания ключа заряд конденсатора уменьшился в 1,5 раза. Найти внутреннее сопротивление элемента, если R = 10 Ом.
Решение.
В условии задачи описаны две ситуации. В первой из них при разомкнутом ключе ток отсутствует, и, следовательно:
о.
(1) — Ф2 = 6 — "q” •
Во втором случае при замкнутом ключе:
(3) =
По условию задачи:
(4) 91 « 1,6 • д2 .
24. Электрические цепи постоянного тока 681
Формально имеем систему из 4-х уравнений с 6-ю неизвестными: £, С, г, I, qx, qz. Однако, согласно условию задачи, необходимо найти лишь внутреннее сопротивление г, что оказывается возможным.
Чх ЕС _ r + R _
q2 = ERC~ R ~ ’ ’
r + R
г = 5 Ом.
582
Борис Гринченко
Задача 24.10.
Найти заряд конденсатора в схеме на рисунке. Величины С, R и 8 считать известными, внутренним сопротивлением источников пренебречь.
Решение.
Расставим точки одинакового потенциала, выберем направление тока и полярности зарядов на конденсаторе.
Для контура 12451 запишем закон Ома:
(1) I = 2 - ~ £ = —
17 2R + R 3R
(непосредственное применение основных уравнений . теории для каждого из элементов контура 12451 показывает, что (1) справедливо).
Для контура 12351 имеем:
(2) Ф1 - <₽! = <Р1 - Ф2 + Ф2 - Фз + Фз ~
- Ф5 + Фб " Ф1 = °-
24. Электрические цепи постоянного тока 583
Учитывая, что:
Ф1 — Ф2 ~ ~ Фг — Фз ~ Фз ~ Фб = & ’ Фб ~ Ф1 ~ ~ & •
Из (1,2) находим:
(3) q = IRC =
Таким образом, оказалось, что q > 0, и, следовательно, полярность конденсатора выбрана верно.
584
Борис Гринченко
Задача 24.11.
Найти зависимость мощности, выделяемой во внешней цепи, КПД батареи в зависимости от величины внешней нагрузки R и построить графики. ЭДС 6 и внутреннее сопротивление г заданы.
Решение.
Используя закон Ома, для мощности во внешней цепи находим:
(1) P = UI = RI2 ^r(~-—}2 = 62—^-2. ^R + r' (R + f)2
График зависимости Р от R имеет вид, представленный на рисунке. Максимальное значение мощности определяется из экстремума функции P(R)i
(2) Л,акс » V
и достигается при R = г.
КПД батареи, по определению, равен:
(3) П=-/-.
^ПОЛН
24. Электрические цепи постоянного тока
585
где полная мощность, выделяемая в цепи: с 2
(4)
Из (3,4) находим:
„ Д
В + г ’
586
Борис Гринченко
Задача 24.12.
Какой заряд протечет через гальванометр после замыкания ключа? Какое количество теплоты выделится на сопротивлении? Величины 8 и С известны, внутренним сопротивлением батареи пренебречь.
До замыкания ключа простой расчет дает:
где qr — заряд каждого из конденсаторов.
После замыкания ключа с установлением равновесного распределения зарядов (прекращения тока в цепи) нижний конденсатор не заряжен, а заряд верхнего определяется из уравнения:
(2)
Чтобы определить заряд, прошедший через гальванометр, мысленно выделим часть схемы, обозначен
24. Электрические цепи постоянного тока
587
ную пунктиром. До замыкания ключа суммарный заряд этой части схемы равен нулю, после замыкания — заряду положительной обкладки верхнего конденсатора (/2- Таким образом, через гальванометр прошел заряд q2 = 8 С.
Для вычисления выделившейся на сопротивлении теплоты воспользуемся законом сохранения энергии. До замыкания ключа энергия двух конденсаторов:
8 2 С
(3) Ж1 = 2.«к = Л_С.
После замыкания ключа энергия схемы за исключением батареи равна:
<4) >г2=^+е=^ + е,
где Q — количество теплоты, выделившейся на сопротивлении.
Согласно закону сохранения энергии, изменение энергии W2 - Wi равно работе сторонних сил батарей:
(5)
с учетом равенства нулю величины внутреннего сопротивления батареи.
Величина заряда Ад, прошедшего через батарею, равно изменению заряда на левой обкладке верхнего конденсатора:
(6) q2 ~ 91 - Л? = С8 - ~С8 = jc8 .
Подставляя (3), (4) и (6) в (5), находим:
сб 2
588
Борис Гринченко
Задача 24.13.
Какую химическую энергию приобретет аккумулятор после замыкания ключа? Какое количество теплоты выделится при этом? Величины С, U и С заданы.
Решение.
После замыкания ключа и установления равновесного распределения зарядов:
(1) U^E.
Запишем закон сохранения энергии:
си2 си^
(2) “=A,' + Q,
где А! — работа против сторонних сил аккумулятора равна увеличению его химической энергии:
(3) Аот' = £Д<7,
24. Электрические цепи постоянного тока
689
Q — выделившееся в схеме тепло.
Учитывая, что заряд, прошедший через аккумулятор,
(4) \q = CU-CUx = C(U- £) , из (2,3) находим:
AJ = C£ (U - £); Q = ±C(U-£)2,
Из выражения для видно, что аккумулятор приобретает энергию при U > £ и расходует ее при обратном соотношении.
590
Борис Гринченко
Задача 24.14. J
При разомкнутом ключе вольтметр Vi показывает 0,9£. Что покажут вольтметры при замкнутом ключе, если сопротивление вольтметра Vz вдвое меньше сопротивления вольтметра Vi?
Решение.
Обозначим сопротивление вольтметра Vz через R, тогда сопротивление вольтметра Vi равно 2R.
При разомкнутом ключе с учетом закона Ома:
получаем, согласно условию задачи:
(2)
При замкнутом ключе сопротивление внешней цепи, состоящей из двух параллельно соединенных со-
24. Электрические цепи постоянного тока
591
2R противлений R и 2R, равно -j-, а напряжение на
О
нольтметрах с учетом закона Ома:
S 2р „.2 '3й-
1 + 3R
аг=7г.|в =
(3)
1
0,9 ’
Перепишем (2) в виде:
(4) 1 + ife
2R
Подставляя г = -q- из (4) в (2), получаем:
692
Борис Гринченко
Задача 24.15. !
Найти сопротивление между точками А и В и рассчитать токи, текущие через сопротивления. Величины г и U известны.
Решение.
Заменим данную схему эквивалентной. Для этого заметим, что последние два сопротивления справа 2г и 2г соединены параллельно и могут быть заменены одним сопротивлением г. Это сопротивление, в свою очередь, последовательно соединено с сопротивлением Зг — они вместе дают сопротивление 4г. Последнее сопротивление 4г соединено параллельно с сопротив-
4 о лением Заменяя их эквивалентным, получаем со-
противление г и т.д. В результате находим, что сопротивление между точками А и В равно г, а пол-
„ т U
ный ток в цепи I = —.
24. Электрические цепи постоянного тока 693
Для расчета токов следует действовать в обратном направлении: ток I в точке 1 разветвляется поровну на £ и 77. Поступающий в узел 2 ток разветвляется обратно пропорционально сопротивлениям 4^ и 4г, то есть на и 4-, причем ток поступает в узел
О О о
3, где делится пополам между сопротивлениями 2г n2r(i).
594
Борис Гринченко
Задача 24.16. I
Вычислить мощность, потребляемую лампочкой в схеме, изображенной на рисунке. Вольтамперная характеристика лампочки представлена сплошной линией на другом рисунке, ЭДС элемента £ = 4JB, его внутренним сопротивлением пренебречь, R = 10 Ом.
Решение.
Из соотношения:
Ф1 - Фз = Ф1 - Ф2 + Фг - Фз с учетом равенства нулю внутреннего сопротивления (Ф1 - Фз = 8), Ф1 - Фг = и и Фг - Фз = IR » находим:
(1)
е = U + IR.
Формально связь между током и напряжением на лампочке можно записать в виде:
(2)
U = /(I).
Таким образом, имеем систему из двух уравнений (1,2) с двумя неизвестными U и I, которую удобно решить графически, переписав (1) в виде:
24. Электрические цепи постоянного тока 595
(1')
V = е - IR.
График (1’) в координатах InU представляет собой прямую линию, точка пересечения которой с графиком U = f(I) (то есть вольтамперной характеристикой) дает значения тока I = 0,25 А и напряжения U = 1,5 В.
Потребляемая мощность:
Р = U • I = 1,5 • 0,25 « 0,38 Вт.
25. Электрический ток в жидкостях
Согласно закону Фарадея:
(1) т = ftZAt,
где т — масса вещества, выделившегося на электроде за время At, I — сила тока, k — электрохимический эквивалент данного вещества:
(2) Л = -Цг = #•
М — молярная масса, п — валентность, е — заряд электрона. Величину sNa = F = 9,65 • 104 К л/моль называют постоянной Фарадея.
25. Электрический ток в жидкостях
597
Задача 25.1.
Сколько времени длилось никелирование, если на электроде выделилось 3,6 г никеля при силе тока 4 А?
Решение.
Поскольку в условии задачи валентность никеля не указана, следует обратиться к табличным данным, согласно которым никель имеет валентность 2 и электрохимический эквивалент k = 3 • 10' 7 кг/Кл.
Воспользовавшись законом Фарадея
(1) т = kl&t,
находим:
At = -ту = 3 • 108 с = 50 мин. kl
598
Борис Гринченко
Задача 25.2.
При никелировании изделия за время 1 ч отложился слой никеля толщиной 0,03 мм. Найти плотность тока при электролизе. Плотность никеля 8,9 • 103 кг/м3.
Решение.
Запишем закон Фарадея:
(1) т = kl&t,
определение плотности:
/п\ т т
(2) Р " V ~ Sd’
где объем никеля V = Sd, S — площадь покрытой никелем поверхности, d = 0,03 мм — толщина слоя никеля, и определение плотности тока:
(3) > =
Из (1—3) получаем:
>=й=62А/м2-
25. Электрический ток в жидкостях
599
Задача 25.3.
При электролизе раствора серной кислоты (H2SO4) расходуется мощность 37 Вт. Найти сопротивление электролита, если за время 50 мин выделяется масса водорода 0,3 г.
Решение.
Воспользуемя законом Фарадея:
(1) т = ~1М
nF и выражением для мощности:
(2) N = I2R.
Из (1,2) находим:
R = N = 0,4 Ом [ znraF [
(га = 1, М = 10 3 кг/моль).
600
Борис Гринченко
Задача 25.4.
Сравнить затраты электроэнергии на получение электролитическим путем одинаковых масс алюминия и меди, если по нормам напряжение на ванне при получении алюминия в 14 раз больше, чем при рафинировании меди.
Решение.
Воспользуемся дважды законом Фарадея: М
(1) t ДА*.
1 nxF 1 1 М2
(2) пг2 - 12^2
и выражением для мощности:
(3) W\ ~ Л^А^ = UJiAti
(4) W2 = N2M2 = U^t2,
vjifi W\ и W2 — затраты электроэнергии (индекс 1 относится к алюминию, 2 — к меди).
Согласно условию задачи:
(5) Щ = 14 U2
(6) т1 = т2.
Разделив (3) на (4) с учетом (1,2,5,6), получаем:
W. U.M2n.
W2 UJd,n2 Л и к л
(пг = 3, п2 - 2, Мх = 27 • 10“ 3 кг/моль, М2 = 64 • 10" 3 кг/моль).
25. Электрический ток в жидкостях
601
Задача 25.5.
Сколько электроэнергии надо затратить для получения 2,5 л водорода при температуре 25°С и давлении 100 кПа, если электролиз ведется при напряжении 5 В и КПД установки 75% ?
Решение.
Запишем закон Фарадея для выделившегося водорода:
(1) тп = ^1Д*,
nF выражения для полезной мощности:
(2) = UI
и КПД установки:
N
(3) п N .
Количество затраченной энергии:
(4) W = N&t.
Согласно уравнению Менделеева-Клапейрона для образовавшегося водорода:
(5) РГ=^-ЯТ.
^2
Из системы уравнений (1—5) находим:
UnFPVM„
W =----™ -вт 2 = !>3 • 10& Дж
(n = 1, т] = 0,75, Мн = 10“ 3 кг/моль,
•Мн = 2 • 10 3 кг/моль).
26. Магнитное поле
Сила, действующая на проводник в магнитном поле с индукцией В, определяется законом Ампера:
(1) FA = 11 В sin а ,
где I — сила тока, текущего по прямолинейному проводнику длиной I, а — угол между вектором В и направлением тока. Направление силы Ампера определяется с помощью правила левой руки.
Из (1) и определения силы тока следует выражение для силы, действующей на движущийся заряд в магнитном поле (силы Лоренца):
(2) Гл = si*1 ос ,
где а — угол между вектором скорости v" и индукцией В, q — величина заряда. Направление силы Лоренца определяется аналогично силе Ампера.
Поскольку сила Лоренца направлена перпендикулярно скорости частицы, работа этой силы равна нулю. Следовательно, кинетическая энергия частицы в магнитном поле, а вместе с ней модуль скорости остаются постоянными (если других сил, действующих на частицу, нет).
Движение частицы массой т с зарядом q, скорость которой v направлена перпендикулярно индукции В однородного магнитного поля, представляет собой вращение по круговой орбите с ларморовским радиусом:
26. Магнитное поле
603
(3)
и периодом:
(4)
mv
Г~ qB
Т^. (ю=ав
qB v т
Задача 26.1.
На линейный проводник длиной 20 см, расположенный под углом 60° к вектору индукции магнитного поля, действует сила 15 Н. Сила тока в проводнике 0,15 А. Найти величину индукции магнитного поля.
Решение.
Согласно закону Ампера:
(1)
F = ВИ sin а .
15
Из (1) находим:
В = -=~— = —---« 580 Тл .
Пэта о,15-О,2-А
2
604
Борис Гринченко
Задача 26.2.
В однородное магнитное поле поместили прямоугольную рамку, по которой течет ток I. Индукция магнитного поля В параллельна плоскости рамкц. Площадь рамки S. Найти момент сил, действующих на рамку.
Решение.
Согласно закону Ампера, сила, действующая на участки провода AD и ВС:
(1) F = I • I • В sin а ,
(а = 0), а на участки АВ и CD:
(2) Fx = F2 = F = ПВ
и направлена перпендикулярно плоскости рамки.
Момент сил Fi и F2 относительно оси 0’0 равен:
26. Магнитное поле
605
(3) Мо = F1a1 + F2 а2 = ПВ (ах + а2 ) =
/
= IBS = BM,
где S = Z(a1 + a2) — площадь рамки, а величина М = IS называется магнитным моментом.
606
Борис Гринченко
Задача 26.3.
Доказать, что формула Mo = ВМ (см. предыдущую задачу) справедлива для плоской рамки произвольной формы.
Решение.
Разобьем проводник на малые (практически прямолинейные) участки U и представим момент сил Мо, действующих на рамку, в виде:
(1) Мо = Af0/ = Ftxt >
где M0l = Ft xt — момент силы Ft относительно оси O'O, создаваемый участком lt.
Согласно закону Ампера:
(2) Ft = IlfB sin at .
Подставляя (2) в (1), получаем:
(3) = sin az xt - bi 11 I fa sin az.
26. Магнитное поле
607
Очевидно, что величина Ц xt sin aj практически равна площади криво линейной трапеции abed и, следовательно,
(4) £ lt xt sin af = S .
Подставляя (4) в (3), окончательно получаем:
Мо = BIS = ВМ .
Из решения задачи видно, что момент Мо не зависит от положения оси 0'0, лежащей в плоскости рамки. Доказательство того, что (4) справедливо для любой оси, параллельной плоскости рамки, предоставляется читателю в качестве несложного упражнения.
608
Борис Гринченко
Задача 26.4.
Катушка, по виткам которой течет ток I, стоит вертикально на горизонтальной плоскости. Масса катушки т, число витков п. При какой индукции В однородного магнитного поля, направленного горизонтально, катушка опрокинется?
Решение.
Запишем условие равновесия катушки относительно оси О'О, лежащей перпендикулярно плоскости рисунка и проходящей через точку А, в критический момент, когда все точки донышка за исключением точки А (на оси 0'0), вокруг которой катушка опрокидывается, оторвались от горизонтальней поверхности на очень малое расстояние:
(1) mgR = nBnR2!,
где mgR — момент силы тяжести относительно оси 0'0, BnF? I — момент силы Ампера, действующий на один виток (см. предыдущую задачу). Сила реак
26. Магнитное поле
609
ции со стороны поверхности проходит через точку А на оси О'О, и ее момент относительно 0'0 равен нулю.
Из (1) получаем:
nnRI
610
Борис Гринченко
Задача 26.5.
Кольцо радиуса R, по которому циркулирует ток I, поместили в однородное магнитное поле с индукцией В, перпендикулярное плоскости кольца. С какой силой растянуто кольцо? Действием на кольцо магнитного поля, создаваемого током кольца, пренебречь.
Решение.
Запишем закон Ньютона (условие равновесия) для малого элемента кольца длиной Z, опирающегося на угол 2а:
(1) + т2 + = о,
где Тх = Т2 = Т — сила, с которой растянуто кольцо,
(2) Fa = ВП
сила Ампера, действующая на элемент кольца I, по которому течет ток I (учтено, что угол между вектором В и направлением тока I равен 90°).
Проецируя (1) на ось х:
26. Магнитное поле
611
2Т sin а = РА
и учитывая, что I = R 2а и для малых a sina « а, получаем:
Т = BIR .
Примечание.
При рассмотренном в данной задаче взаимном расположении кольца с током и индукции магнитного поля В, кольцо находится в состоянии устойчивого равновесия. При изменении направления вектора В или изменении направления тока в кольце равновесие кольца становится неустойчивым: кольцо уже не растягивается магнитным полем, а сжимается.
Другой вариант решения задачи основан на использовании закона Ньютона (условия равновесия) полукольца (аналогично второму варианту решения задачи 14.2.).
, Разобьем полукольцо на малые фрагменты Ц. Силу F, действующую на полукольцо со стороны магнитного поля, представим в виде
(3) г = Е F„
612
Борис Гринченко
где Ft = В I lt. Спроецируем (3) на ось х: (Зх) F = 2 Fix = S BIltsin at =
= BI% Z,sin a, = Bl£ l0l = BI2R.
Условие равновесия полукольца
(4) 2T - F.
Из (Зх, 4) находим Т = BIR.
26. Магнитное поле
613
Задача 26.6.
Во сколько различаются радиусы траекторий двух протонов, скорости которых направлены перпендикулярно индукщщ магнитного поля, если кинетические энергии протонов равны Ал и КъЧ
Решение.
Воспользуемся выражением для ларморовского радиуса:
(1) mv. Г1 ~ qB
(2) mv9 2 qB
и определением кинетической энергии: mv?
(3) = 2 2
(4) *2 = 2 •
Из (1—4) после несложных преобразований нахо-
дим: II a n
614
Борис Гринченко
Задача 26.7.
Электрон со скоростью v = 107 м/с влетает в область однородного магнитного поля с индукцией —3
В = 10 Тл. Направление скорости перпендикулярно вектору индукции В. На какую максимальную глубину h электрон проникнет в магнитное поле, если угол падения электрона на границу поля а = 30°?
Решение.
по
При попадании в область трон начинает двигаться ларморовским радиусом:
магнитного поля элек-круговой траектории с
т.п еВ ’ те = 9,1 • 10-31 кг, заряд
г =
(1)
где масса электрона
е = 1,6 • 10"19 Кл.
С помощью несложных вычислений (см. рис.) находим:
h = г - г sin а = (1 - sin а ) = 2,8 10 2м .
qB v 7
26. Магнитноеполе
615
Задача 26.8.
На рисунке изображена схема простейшего масс-спектрометра, индукция магнитного поля в котором В = 0,1 Тл. В ионизаторе А образуются ионы, которые ускоряются напряжением 17 = 10 кВ. После поворота в магнитном поле ионы попадают на фотопластинку и вызывают ее почернение. На каком расстоянии от щели будет находиться полоса ионов 4Не+ г
Решение.
© в
Воспользуемся законом сохранения энергии при прохождении ионом разности потенциалов (напряжения) U: работа сил электрического поля qU равна приращению кинетической энергии. Полагая, что кинетическая энергия ионов в ионизаторе пренебрежимо мала, получаем:
(1) = qU,
А
где q = 2е = 3,2 • 1(Г19 Кл — заряд ядра гелия, т = 6,7 • 10-27 кг — его масса.
616
Борис Гринченко
Расстояние от щели, из которой ионы влетают в магнитное поле, до полосы:
(2) Z = 2B=2-^g.
Из (1—2) находим:
, 2>/2mt7 ОЛ
I я - 20 см.
Л В
26. Магнитное поле
617
Задача 2в.9.
В однородном магнитном поле с индукцией В движется со скоростью v частица массы т с зарядом q, причем угол между векторами В и v равен а. Найти радиус и шаг спирали, по которой движется частица.
> 9
Решение.
(1) О=Р|| + Р±,
где о[| и Б2 — компоненты скорости, параллельные и перпендикулярные индукции В, причем:
(2) О| । = v cos а
(3) = v sin а ,
Движения со скоростями оц и о± независимы (это следует из записи выражения для силы Лоренца в * векторном виде, что выходит за рамки школьного
618
Борис Гринченко
курса). В частности, если скорость vjl = 0 (а = 0), то частица двигалась бы прямолинейно равномерно со скоростью v| |. Если, наоборот, = 0 (а = 90°), то движение частицы представляло бы собой равномерное вращение с ларморовским радиусом:
mv
Г ~--
дБ
(4)
и периодом:
„ 2лТП
Т =----.
qB
(5)
Таким образом, в общем случае в результате не-, зависимого сложения обоих движений имеем движение по спирали радиуса г, ось которой параллельна индукции магнитного поля. Шаг спирали h определяется величиной смещения частицы вдоль оси спирали за время полного оборота частицы Г:
... , m 2nmv cos а
(6) h = v„-T =----.
Очевидно, что в системе отсчета, движущейся со скоростью ин , движение частицы представляет собой простое вращение.
26. Магнитное поле
619
Задача 26.10.
Пластины плоского конденсатора с шириной зазора между ними d расположены перпендикулярно магнитному полю с индукцией В. На отрицательной пластине расположен источник А медленных электронов (катод), вылетающих в разных направлениях. При каком напряжении на конденсаторе электроны будут фокусироваться на положительной пластине?
Решение.
Рассмотрим движение электрона, вылетевшего из катода со скоростью ро, направленной под углом а к линиям магнитной индукции.
Согласно закону Ньютона:
(1) <л + K = rna,
где сила со стороны электрического поля:
(2) Рал = еЕ
620
Борис Гринченко
направлена в сторону, противоположную вектору напряженности Е, сила Лоренца:
(3) Ея = qvB sin а .
Как и в предыдущей задаче, представим скорость электрона в виде:
(4) Г=й[| + и2-
На составляющую скорости vjl электрическое поле не влияет, следовательно при О| । = 0 движение электрона представляло бы равномерное вращение с ларморовским радиусом и периодом:
(5) Т = —_&
еВ
На составляющую оц, наоборот, не влияет магнитное поле, так что при щ = 0 движение электрона представляло бы равноускоренное движение с ускорением еЕ
а = —; при этом смещение электрона по оси х:
/лч . at2 а?
(6) х = uocos а • t + ns" «
с учетом малости начальной скорости о0.
Обозначив время движения электрона до положительной пластины через т, перепишем (6) в виде:
2
Таким образом, движение электрона представляет собой движение по спирали ларморовского радиуса с увеличивающимся после каждого витка шагом.
Условие фокусировки сводится к тому, чтобы, долетев до положительной пластины, электрон сделал полное число оборотов п, то есть
26. Магнитное поле
621
(8) т = ПТ .
При этом, очевидно, точка вылета электрона А и точка фокусировки С лежат на одном перпендикуляре к поверхности пластин конденсатора.
С учетом связи между напряженностью электрического поля и напряжением:
(9) U = Ed ,
окончательно получаем:
2 n2 j2
“ = где п = 1,2,3,...
2л тп
622
Борис Гринченко
Задача 26.11.
В скрещенных электрическом и магнитном полях (угол между векторами Е и В равен 90°) частица «дрейфует» поперек обоих полей. Чему равна дрейфовая скорость частицы?
Решение.
Е
(2)
Представим скорость частицы в виде:
(1) 7= н7 + ^ ,
причем скорость выберем таким образом, чтобы связанная с ней сила Лоренца qvB компенсировала силу со стороны электрического поля qE:
qvB = qE .
В системе отсчета, движущейся со скоростью Одр, электрическое поле Е оказывается скомпенсированным и частица в этой системе отсчета движется в однородном магнитном поле В, то есть по спирали (см. задачу 25.9.). Следовательно, движение частицы в скрещенных полях представляет собой движение по спирали, ось которой (параллельная вектору В ) сама движется со скоростью
_ Е
V№ В ’
27. Электромагнитная индукция
Магнитный поток Ф, пронизывающий контур площадью S, находящийся в однородном магнитном поле с индукцией В, по определению, равен:
(1) Ф = BS cos а ,
где а — угол между направлением нормали к поверхности контура и вектором В. Единицей измерения магнитного потока является Вб = Тл-м2.
Согласно закону электромагнитной индукции (закону Фарадея),
где £ t — возникающая в контуре ЭДС индукции, АФ — изменение магнитного потока, пронизывающего контур, за время At.
При поступательном движении проводника длиной I в однородном магнитном поле с индукцией В со скоростью о, направленной под углом а к вектору В, в нем возникает ЭДС индукции:
(3) £ t = Bvl sin а,
если прямолинейный провод расположен перпендикулярно вектору В.
Индуктивность контура L определяется соотноше-* нием:
624
Борис Гринченко
(4) Ф = LI,
где Ф — магнитный поток, пронизывающий контур, который создается текущим по контуру током I. Единица измерения индуктивности — 1 Гн = Вб/А.
При изменении тока в контуре возникает ЭДС самоиндукции:
। । iATi । ।
(5) |/?tel=L 1^1 =L|r|,
если индуктивность контура L — постоянная величина.
Для определения направления возникающего в контуре индукционного тока (направление ЭДС индукции) используется правило Ленца: возникающий в контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым этот ток вызван.
Энергия магнитного поля, созданного током I, протекающего по контуру индуктивностью L, равна:
Г Г2
(6) W =
27. Электромагнитная индукция
625
Задача 27.1.
Проводник движется поступательно в однородном магнитном поле так, что его постоянная скорость и" составляет угол а с направлением вектора индукции В. Найти электрическое поле Е внутри проводника.
Решение.
Запишем закон Ньютона для электрона проводимости в проводнике:
(1) ^л + ^л = О,
где FgjI = Ее — сила со стороны электрического поля, действующая на электрон, Fn - е и В sin а — сила Лоренца.
Из (1) получаем:
Е = vB sin а .
Этот результат справедлив, очевидно, для проводника произвольной формы.
626
Борис Гринченко
Задача 27.2.
Тонкая металлическая пластина толщиной d движется в магнитном поле с индукцией В, как показано на рисунке. Плоскость поверхностей пластины параллельна векторам В и В ± «7
Найти разность потенциалов между поверхностями пластины и величину поверхностного заряда на них.
Согласно результату предыдущей задачи, напряженность электрического поля внутри пластин:
(1) Е = vB.
Разность потенциалов между поверхностями пластин с учетом (1):
(2) U = Ed = vBd.
Плотность поверхностного заряда, создающего поле Et
(3) о = EqE (Е = 4nkcs = ^).
27. Электромагнитная индукция 627
Этот Ясе результат молено получить, воспользовавшись соотношением:
(4) £ t = vBd ,
если учесть, что ток через проводник отсутствует:
(5) U = £ t~Ir= £ t = vBd.
628
Борис Гринченко
Задача 27.3.
Самолет летит горизонтально, со скоростью 800 км/ч. Найти разность потенциалов, возникающую на концах крыльев, если вертикальная составляющая индукции магнитного поля Земли равна б • 10~б Тл. Размах крыльев самолета 20 м. Найти максимальную ЭДС, которая может возникнуть при полете самолета, если горизонтальная составляющая индукции магнитного поля Земли равна 2 • 10-в Тл.
Решение.
Воспользуемся основным уравнением теории:
(1) £ t = BIV sin а .
Согласно результату раздела 24:
(2) ф+ — Ф_ = £ f + Ir— £ i ,
поскольку ток отсутствует.
По условию задачи, вертикальная составляющая магнитного поля Земли:
(3) В = В sin а = б • 10 е Тл .
Подставляя (1) и (3) в (2), получим:
ф+ - ф_ = Bylv = 0,22 В .
Максимальная ЭДС индукции (при заданной скорости самолета), согласно (1), достигается при а = 90°, то есть при наклонном движении самолета. Учитывая, что по теореме Пифагора:
(4) В2 = В* + В*
•* а
27. Электромагнитная индукция
629
где В = 2 • 10 6 Тл, В = 5 • 10 6 Тл, из (1) находим: х у
£. = >№Х + В* Zu = 0,24 В. » х у
680
Борис Гринченко
Задача 27.4.
В простейшей схеме магнитного гидродинамического генератора между пластинами плоского конденсатора течет проводящая жидкость (газ, плазма). Конденсатор находится в магнитном поле, причем вектор индукции В параллелен плоскости пластин конденсатора, а скорость жидкости if— перпендикулярна В и направлена вдоль пластин. Найти силу тока во внешней цепи, если площадь пластин конденсатора S, расстояние между ними d, удельная проводимость жидкости 1, внешнее сопротивление R.
Решение.
© ©
v
0
d
R
© © в
ЭДС индукции, возникающая между пластинами конденсатора:
(1)
£ i = vBd .
Сопротивление между пластинами конденсатора: did
(2) '• = Ps=Xs'
27. Электромагнитная индукция 631
Согласно закону Ома для полной цепи:
Подставляя (1, 2) в (3), находим: г _ уВс?
Ъ S + R
632
Борис Гринченко
Задача 27.5.
Проводящий диск радиусом г = 0,05 м вращается с угловой скоростью со = 2л 50 рад/с в однородном магнитном поле с индукцией В = 1 Тл, причем направление вектора индукции перпендикулярно плоскости диска. Найти ток через сопротивление R. Сопротивлением току, текущему через диск, пренебречь.
Решение.
Вычислим ЭДС индукции между центром диска О и скользящим контактом А, воспользовавшись определением ЭДС:
д
(1)
где Ат — работа сторонних сил (в данном случае это сила Лоренца) при перемещении положительного заряда из точки А в точку О. Обозначим через х — расстояние от заряда q до центра О. Сила Лоренца, действующая на заряд:
27. Электромагнитная индукция
633
(2) Гл = qvB = qcoxB (a = 90°).
Работа Ат силы Лоренца:
Г г
(3) Аст = f Fadx = J qcoxBdx =
0 0
г.
= qmB J xdx = ^qmr^B о
может быть вычислена так же элементарно с помощью разбиения отрезка АО на малые участк Ах; = xi + 1- xt, вычисления работы на каждом участке
xt + 1 + xt
At = qoB----=---(х( + j - х() и суммирования:
x2 -x2 1
Подставляя (3) в (1), получаем:
(4) £t = |(oBA
Согласно закону Ома для полной цепи:
£ t соВг2
1 “ R ~ 2R'
Борис Гринченко
ш__________
Задача 27.6.
Два диска радиусами п и Г2 вращаются с угловой скоростью со в однородном магнитном поле с индукцией В. Центры дисков присоединены к обкладкам конденсатора с емкостью С1, ободы — через скользящие контакты — к Сг. Направление вектора В перпендикулярно плоскости дисков. Найти заряды на конденсаторах.
Решение.
Воспользуемся результатом предыдущей задачи для расчета. ЭДС индукции в дисках:
(1)
(оВг?
соВг|
(2) ег = ~2^
Для наглядности вычислений воспользуемся экви-валентной схемой, представленной на рисунке. Рас-
27. Электромагнитная индукция
636
ставим точки одинакового потенциала и запишем основные уравнения теории для расчета электрических цепей:
^2
Ф1 “ Ф4 = 5 1 q Ф2“Ф1 = ^-
С2
Фг ~ Фз ~ & 2 q
Ф4 “ Фз =
(3)
(4)
(5)
(6)
В (4, 6) учтено, что Qi - Q2 = q. Умножая (5) на минус единицу и складывая (3—6), находим:
С,С2
(7) q — (£ 2 ~ & 1) Z* . А”»
'-'1 + ^2
где Б х и определяются соотношениями (1, 2).
Выбранная на рисунке полярность пластин конденсатора и полученное решение (7) соответствуют
636
Борис Гринченко
случаю £2- £1> О или Га > и. Если Гг < и, полярность пластин изменится на противоположную, а (7) примет вид:
С. С2
<7’>
(предлагается для самостоятельного решения).
27. Электромагнитная индикция
637
Задача 27.7.
Схема двигателя постоянного тока представлена на рисунке. Найти установившуюся угловую скорость перемычки ОА, ток в цепи и развиваемую двигателем мощность, если сила трения в подвижном контакте А равна F. Величины £, I, R, В заданы, внутренним сопротивлением батареи и сопротивлением перемычки пренебречь.
Решение.
Условие постоянства угловой скорости означает, что суммарный момент сил, действующих на перемычку, равен нулю:
i
(1) Fl = f IBx dx = jfBl2,
о
где Fl — момент силы трения, i IB12 — момент силы а
.Ампера относительно точки О. Элементарное вычис-
638
Борис Гринченко
ление момента силы Ампера может быть выполнено по аналогии с задачей 27.5.
Согласно закону Ома:
£-£t
~ R ’
в движущейся перемычке вы-задаче 27.5:
£1 = —В(о21 АЛ
и направлена навстречу ЭДС £ батареи.
Из (1—3) находим:
(4) 7 = Ц
(2) 1
где ЭДС индукции £ t числяется аналогично
(3)
,кч 2£ 4FR
( ' Ю В? В2? ’
Мощность, развиваема^ двигателем:
(6) Р = UI = £lI = FUa .
Соотношения (4—6) справедливы при © > О или:
2FR
В1 *
(7)
В противном случае со = О, Р - О,
£
R
27. Электромагнитная индукция 639
Задача 27.8.
Индукция однородного магнитного поля внутри цилиндра радиусом г = 0,1 м линейно возрастает со временем В = pt ( р = 10 3 Тл/с ) и направлена вдоль оси цилиндра. Найти напряженность вихревого электрического поля на расстоянии I = 0,2 м от оси цилиндра и ЭДС индукции в проводнике, концы которого А и В образуют угол АОВ = а (см. рис.).
Решение.
Согласно определению:
Ат
где в данном случае работа сторонних сил есть работа силы Eq, действующей на заряд q со стороны вихревого электрического поля Е по замкнутой окружности радиусом I:
(2)
Аст = Eq2nl
640
Борис Гринченко
(учтено, что в каждый момент времени угол между направлением силы и скорости равен нулю).
Учитывая закон электромагнитной индукции:
(3) 81 = Ф' = (пйВ)' = лг2р ,
из (1, 2) получаем:
(4) B = ^ = 2,510~=f.
Проводя аналогичные вычисления для ЭДС индукции £а'&, возникающей между точками А’ и В' (см. рис.), получим:
(5)
Запишем закон электромагнитной индукции для контура А'А В В'А':
(®) ^А'АВВ'А' ~ 0
(магнитный поток через контур ААВВ’А’ отсутствует).
Поскольку на участках А'А и В’В ЭДС индукции равна нулю (вихревое поле Е, а вместе с ним сторонняя сила на этих участках перпендикулярна перемещению), имеем:
(7) ^А'АВВ'А' ~ ^А'В’ + *
Таким образом, окончательно находим:
£ав = Ряг2 2л •
27. Электромагнитная индукция
641
Задача 27.9.
Круглое кольцо составлено из двух проводников одинаковой длины: один сопротивлением R, другой — 2R. Внутри кольца проходит концентрическая цилиндрическая трубка радиуса г, в которой создается направленное вдоль оси цилиндра переменное магнитное поле, скорость возрастания которого постоянна и равна ДВ/At = К.
Определить заряды на обкладках конденсатора, емкость которого равна С.
Решение.
Воспользуемся результатом задачи 27.8 и для наглядности расчета изобразим эквивалентную схему для данной системы. Согласно закону Фарадея:
(1) £ х = Ф' = (BS)' = Кп А
Запишем закон Ома:
642
Борис Гринченко
и соотношение для разности потенциалов на клеммах батареи с внутренним сопротивлением R:
е.
(3) ч>, - <р2 = у - IR .
С другой стороны:
£ л G
(4) Ф1 - Ф2 = Ф1 - Фз + Фз - Ф2 = ~2 + с ’
Из (1—4) находим: etc КпРс 9~ 3 " 3 ‘
Следовательно, полярность зарядов на пластинах конденсатора соответствует выбранной на рисунке.
27. Электромагнитная индукция
648
Задача 27.10.
Контур в виде окружности, содержащий два конденсатора с емкостями Ci и Сг, соединяют по диаметру проводником ab. Найти заряды на обкладках конденсаторов, если скорость изменения магнитного
Решение.
С учетом результатов решения задачи 27.8, заменим данный контур эквивалентной схемой. Запишем основные уравнения теории для расчета электрических цепей:
<л 1 О л
(!) Фв - Фь = Фв " Фа + Фа - Фь = у " -у = °-
Согласно закону Фарадея:
(2) 6-, = Ф' = р.
Из (1, 2) находим:
644
Борис Гринченко
а - — С “ 2 г Аналогично для заряда на конденсаторе Сг:
а - — С
4.2 ~ 2
27. Электромагнитная индукция
645
Задача 27.11.
Металлическое кольцо радиусом I с сопротивлением R помещено в однородное электрическое поле с индукцией В, направленной перпендикулярно плоскости кольца. Поле выключают. Какой заряд протечет через поперечное сечение кольца?
Решение.
Запишем закон Фарадея:
(1)
Si-
АФ
At
и закон Ома:
(2)
St
R •
Заряд Ад, прошедший через поперечное сечение кольца за время At, равен:
(3) Ag = I At
или, с учетом (1, 2),
(4)
АФ
Д? = -д-.
АФ
Полный заряд g получается суммированием
из (4):
Ф
q=R
{q-Ъ Ад ; Ф = Z АФ ).
646
Борис Гринченко
Задача 27.12.
Доказать, что магнитный поток, пронизывающий замкнутый контур из сверхпроводника, сохраняется.
Решение.
Запишем законы Ома и Фарадея для контура:
(1) 1=^
ЛЬ
ДФ
(2) ₽,= дГ
Из (1) следует: £i = I’R = I- Q = 0. С учетом этого , из (2) получаем: ДФ = 0, и утверждение доказано.
Таким образом, возможное изменение магнитного потока через контур за счет изменения внешних условий компенсируется магнитным потоком, создаваемым возникающим (или изменившимся) в сверхпроводнике током.
27. Электромагнитная индукция
647
Задача 27.13.
Сверхпроводящее кольцо индуктивности L, в котором течет ток /о, вносят в однородное магнитное поле с индукцией Во. Найти ток в кольце, если нормаль к плоскости кольца составляет с направлением вектора Во угол а. Радиус кольца R.
Решение.
Согласно результату задачи 27.12, магнитный поток через кольцо, равный вначале Фо = Lio, не изменяется после внесения кольца в магнитное поле:
(1) Фо = Ф + BnR2 cos а ,
где Ф~Ы — магнитный поток через кольцо, создаваемый током после внесения кольца в поле. Отсюда получаем:
(2) Z = z0-^^cosa.
648
Борис Гринченко
Полученный ответ соответствует случаю направления тока, изображенному на рисунке. В противоположном случае аналогичный расчет дает:
r r 7tR2B cos а
1 = 'о +-----г-----•
27. Электромагнитная индукция 649
Задача 27.14.
Во сколько раз изменится ток в двух одинаковых, удаленных друг от друга, тонких сверхпроводящих кольцах при их совмещении? В начальный момент по кольцам протекали одинаковые токи I.
Решение.
Поскольку магнитный поток через кольцо сохраняется, то единственно возможное совмещение соответствует ситуации, когда в каждом из проводников течет ток При этом суммарный ток I через оба Л кольца создает тот же магнитный поток, что и ток I в каждом из колец по отдельности.
650
Борис Гринченко
Задача 27.15.
Непроводящее кольцо массой т и радиусом R с равномерно распределенным по нему зарядом Q может свободно вращаться вокруг своей оси. Индукция однородного магнитного поля В внутри кольца направлена перпендикулярно плоскости кольца. Найти скорость, которую приобретает кольцо после выключения магнитного поля, если в начальный момент оно покоилось.
Решение.
При уменьшении магнитного поля в области нахождения зарядов кольца возникает вихревое электрическое поле Е (см. задачу 27.8):
1 ДФ
2nR bt ’
которое действует на элемент кольца с зарядом Qt с силой:
(1)
(2) F = Eqt.
Запишем закон Ньютона для этого элемента кольца:
(3) mi Ди = F • М
Из (1—3) с учетом очевидного соотношения:
(4)
mt т
находим:
(5)
Ди =
ДФ
2itR *
т
Таким образом, при изменении потока через кольцо на величину ДФ, скорость кольца возрастает на
27. Электромагнитная индукция
651
величину Ди. Суммируя равенства (5), окончательно получаем:
2nRm (ЕДу = у; ЕдФ = Ф).
Применение интегрального исчисления несколько упрощает выкладки.
652
Борис Гринченко
Задача 27.16.
Какую максимальную мощность может развить электромотор, включенный в сеть постоянного тока с напряжением 120 В, если полное сопротивление цепи 20 Ом?
Решение.
Согласно закону сохранения энергии, мощность источника UI расходуется на мощность электродвига-теля Р и джоулева нагрева RI :
(1) UI = Р + RI2.
Отсюда находим:
(2) Р = - RI2 + Ш.
Последнее выражение имеет экстремум (наиболь-ч т U
шее значение) при силе тока I = и равно:
и2
Л.акс = = 180 ВТ.
Примечание. ЭДС индукции St, возникающая в обмотках электромотора, дается соотношением:
(3) £t = U-IR,
так что с учетом (2) мощность электромотора может быть представлена в виде:
P = I£t.
28. Нестационарные токи. Электромагнитные колебания
Рассматриваются так называемые квазистационар-иые, то есть медленно меняющиеся во времени токи. Условие квазистационарности означает, что в каждом сечении последовательно соединенных проводников и элементов цепи, не имеющих разветвлений, в данный момент времени течет один и тот же ток. Ранее сформулированные (§ 24) соотношения для расчета электрических цепей постоянного тока для данного раздела остаются в силе. Кроме того, добавляется уравнение для разности потенциалов (напряжения) на катушке индуктивности L:
(1) Ф1 ~ Ф2 = ul = Li’’
где ток I течет из точки 1 в точку 2 (1 и 2 — начало и конец катушки).
Решение уравнения:
(2)
q" + LCq~°’
описывающего свободные колебания в контуре, содержащем катушку индуктивности L и конденсатор емкости С (активное (омическое) сопротивление контура равно нулю), имеет вид:
(3)
<1 = <lm cos (q = qm sin at),
664
Борис Гринченко
где q — заряд конденсатора, со = — циклическая
частота гармонических колебаний.
Период свободных гармонических колебаний: 2л г——
(3) Г = -^=2Я1ЕС
(формула Томсона).
28. Нестационарные токи
655
Задача 28.1.
К источнику с ЭДС £ и равным нулю внутренним сопротивлением присоединили катушку индуктивности L. Найти зависимость тока в цепи от времени. Активным (омическим) сопротивлением катушки и подводящих проводов пренебречь.
Решение.
Учитывая условия задачи, запишем условие равенства напряжений на катушке (epi - фг = Li') и клеммах источника (ф1 - фг = £ ):
(1) £=Li'.
Интегрируя (1), находим: £ (2) i = ,
то есть ток линейно возрастает со временем.
656
Борис Гринченко
Нетрудно убедиться в том, что совершенная сторонними силами источника за время t работа:
8^8 t
(3) = --2= 2£
t
f £ t2
(g = } ldt = j—— — заряд, прошедший через источ-о
ник за время t), равна энергии магнитного поля ка-
Li2
тушки -S-:
Li2 L^Lt^ £2t2
2 ~ 2 “ 2L ’
28. Нестационарные токи
667
Задача 28.2.
Найти максимальный ток в цепи и максимальный заряд конденсатора после замыкания ключа. Величины 8, L и С заданы, внутренним сопротивлением источника пренебречь. В начальный момент конденсатор не заряжен.
Решение.
Учитывая, что внутреннее сопротивление источника равно нулю, имеем:
(1) 8=1л' + %
(ф1 - фз = Ф1 - фз = Ф1 - ф2 + ф2 - фз = Li’ + ^).
В момент времени, когда ток максимален, производная тока по времени равна нулю (условие экстремума функции). Следовательно, (1) принимает •вид:
658
Борис Гринченко
(2)
V/ где q — заряд конденсатора в момент времени, когда ток достиг максимального значения.
Запишем закон сохранения энергии: работа сторонних сил источника затрачена на энергию заряженного конденсатора и катушки с током:
т г2 Л2
(3) Act=£A« = ^- + ^.
Очевидно, что прошедший через источник заряд A q равен заряду пластины конденсатора:
(4)
bq = q.
Из (2 —4) получаем:
г
I~G L'
В момент времени, когда заряд максимален, ток в цепи равен нулю и закон сохранения энергии принимает вид: 2
(5) Ж”59"’
откуда получаем:
ди = 2£С.
При этом напряжение на конденсаторе вдвое превышает ЭДС источника.
Второй вариант решения задачи основан на отыскании общей зависимости заряда на конденсаторе и тока от времени. Для этого запишем закон сохранения энергии для произвольного момента времени:
Ti2 п2
<6> =Т + 1с = е«-
28. Нестационарные токи
669
Продифференцировав (6) по времени и учитывая, что д* — I и q" = V, получим после сокращения на q’ = i:
(7) q" + А = р
2 - 1
где о
Можно показать (предоставляется читателю), что решением уравнения (7) является функция:
(8) q = СЕ (1 - cos cot).
Продифференцировав (8), находим:
(9) I = СЕ —— sin cot.
да
Взяв в (8) и (9) максимальные значения, приходим к ответам первого варианта решения.
660
Борис Гринченко
Задача 28.3.
В схеме на рисунке заряд конденсатора равен qo. Найти максимальный заряд на конденсаторе после замыкания ключа. 8, С и L известны, внутреннее сопротивление источника равно нулю, диод идеальный.
Решение.
Рассмотрим два возможных случая. В первом случае ф1 < фг и ток через диод не течет:
(1) Ф1 - Ф2 = <Р1 - Фз + Фз - Ф2 = Е~ 0.
Таким образом, при 8 < после замыкания ключа С/
заряд конденсатора не меняется.
Во втором случае (ф1 > ф2 или 8 > после за-С» мыкания ключа ток сначала нарастает, затем уменьшается до нуля и из-за наличия диода в дальнейшем отсутствует.
661
28. Нестационарные токи
Запишем закон сохранения энергии:
(2)
где учтено, что заряд, прошедший через равен q - q0.
Из (2) находим:
q = 2Е С — Qo.
источник,
662
Борис Гринченко
Задача 28.4.
Электрическая цепь имеет пренебрежимо малое активное сопротивление. Левый конденсатор зарядили до напряжения Uq и. затем замкнули ключ. Найти зависимость от времени напряжений на конденсаторах. Величины L и С заданы.
Решение.
Запишем закон сохранения энергии с учетом пренебрежения активным сопротивлением цепи (выделением джоулева тепла):
2 о
(1) — = ~ (а = CU )
1 ' 2С 2С 2С 2 °7’
где учтен закон сохранения заряда: если заряд правого конденсатора равен q, то заряд левого — 9о “
28. Нестационарные токи
663
После дифференцирования и несложных преобразований получаем:
+ LC q = LC ’
По аналогии с решением задачи 27.2. получаем:
U = С = (1 f cos
где со = N777 и знак «плюс» соответствует левому кон-денсатору, а знак «минус» — правому.
664
Борис Гринченко
Задача 28.5.
В начальный момент напряжение на конденсаторе равно Uq. Найти количество терла, выделившегося после замыкания ключа к моменту времени, когда ток в цепи достиг максимального значения, равного I. Величины С, L и R известны.
Решение.
В момент времени, когда ток максимален, напряжение на катушке равно нулю (задача 28.2.). Следовательно в этот момент времени напряжение R на конденсаторе равно напряжению на сопротивлении:
(1) U = IR .
Запишем закон сохранения энергии для начального момента времени (до замыкания ключа) и конечного (в момент достижения максимального тока):
28. Нестационарные токи
665
(2)
CU20
2
+ + Q
где Q — количество выделившегося тепла.
Из (1—2) получаем:
Q 2 2 2 ’
Отметим, что в момент достижения максимального тока напряжение на конденсаторе, а, следовательно, и заряд, отличны от нуля (1).
666
Борис Гринченко
Сколько тепла выделится на каждом из сопротивлений Ri и Rz через большой промежуток времени после замыкания ключа? В начальный момент напряжение на одном из конденсаторов емкости С равно Uo, а другой конденсатор не заряжен.
Решение.
Через достаточно длительное время (после того, как ток прекратился) напряжения U на конденсаторах, а следовательно, и заряды на них равны. С учетом закона сохранения заряда имеем:
(1) CU0 = 2CU,
где CU0 — начальный заряд конденсатора, CU — заряды конденсаторов после прекращения тока.
Запишем закон сохранения энергии:
28. Нестационарные токи
667
(2) £Е° = 2 .^ + Q1 + Q2,
где Qx и Q2 — количества теплоты, выделившейся на сопротивлениях R1 и R2 соответственно.
Для теплот Qi и Q2 получаем:
00 00
(3) Qi = / R^dt = J i2dt
О о
00 00
(4) Q2 = J R2izdt = R2 J i2dt
о 0
Разделив (3) на (4) с учетом (1, 2), находим:
о __А_
R{ + R2 ' 4 *
п Д2 CU2 Rt + R2 4
Задача может быть решена без применения интегрирования, если записать выражения:
(5) AQB = Rjf Atz
(6) sAQ2i = R2if Atz
для количества теплоты, выделившейся за время Atz на сопротивлениях R1 и R2 соответственно, а затем просуммировать (5) и (6), вынося Rx и R2 за знак суммы.
668
Борис Гринченко
Задача 28.7.
Какой заряд протечет через резистор после замыкания ключа? Активным сопротивлением катушки пренебречь. Параметры £, г, L и R заданы.
Решение.
Напряжение на катушке равно напряжению на Сопротивлении:
(1) LiL = ipR .
Через достаточно большое время ток в цепи определяется законом Ома:
£
(2) 1 = ~
(ток через сопротивление R равен нулю, поскольку активное (омическое) сопротивление катушки равно нулю).
Проинтегрируем обе части (1) по времени в пределах от нуля до бесконечности:
28. Нестационарные токи
669
(3)
или
JLi'L dt = Ji^dt о о
QO 00
L \i[dt = R f о о
где iL и iR — токи через катушку и сопротивление соответственно. Учитывая, что i£(0) = 0 и iL(oo) = I, СО
q = J irfit — заряд, прошедший через сопротивление, о
из (2,3) находим:
LI L£ q~ R Rf
Задача может быть решена без применения интегрирования. Перепишем (1) в виде:
<4)
или
(5) L Ai = Aq R .
Суммируя (5) по всем промежуткам времени с учетом (2), приходим к полученному выше ответу.
670
Борис Гринченко
Задача 28.8.
R
Найти установившиеся в катушках индуктивности Li и L2 токи после замыкания ключа. Параметры £, г и R известны, омическим сопротивлением катушки пренебречь.
Решение.
Запишем условие равенства напряжений на катушках Li и L2:
(1) bj • = L2 • i2 .
В установившемся (стационарном) режиме, согласно закону Ома:
(3) Л +12 = I,
где I — ток через сопротивление R, и /2 — токи через катушки.
28. Нестационарные токи
671
Интегрируя обе части (1) по времени от нуля до бесконечности и учитывая, что ii(oo) = Ii и ia(°o) = I2, h(0) = гг(О) = 0, находим:
(4) Л = L2 I2.
Решая систему уравнений (2—4), получаем:
т _ £ ^2 ,
1 г + R Ьг+Ь2
г _ £ £1
2 r + R L.+L2
Другой вариант решения основан на использовании результата задачи 27.12.: магнитный поток, пронизывающий замкнутый контур из сверхпроводника, в котором отсутствует ЭДС, сохраняется. Поскольку предполагается, что до замыкания ключа токи в цепи и магнитное поле отсутствовали, нулевой магнитный поток через замкнутый контур, состоящий из двух индуктивностей Li и 1г остается нулевым после замыкания ключа. Отсюда сразу вытекает соотношение (4), решение которого совместно с (2) и (3) дает ответ задачи.
672
Борис Гринченко
Задача 28.9.
В цепи, состоящей из заряженного конденсатора и индуктивности L, замыкают ключ. Как в зависимости от времени должна изменяться емкость конденсатора, чтобы ток в цепи нарастал прямо пропорционально времени? Начальная емкость конденсатора Со.
Решение.
Согласно условию задачи:
(1)
i = at,
где а — некоторая постоянная величина. Заряд на конденсаторе:
t t
f f af2
(2) q = <Z0 “ J idt = ~ J atdt = 9o “ ~2~’ о о
Напряжение на катушке:
(3)
UT = Li' = La
Lt
28. Нестационарные токи
673
равно напряжению на конденсаторе:
(4) и«~с’
то есть:
(5) ia = £.
Учитывая, что в начальный момент:
(6) La = Д,
со из (2,5) находим:
29. Электрические цепи переменного тока
При протекании тока
(1) i = Im sin <ot
через сопротивление R, конденсатор емкостью С п катушку индуктивности L напряжения на этих элементах определяются соотношениями:
(2) UR = Шт sin <ot
л 1
(3) Uc = XJm*vb(at-^Xc = -^
Tt
(4) C7£ = X£Zmsin(tDt-l--);X£ = (oL.
При подаче напряжения
(5) U = Um cos at
на перечисленные элементы ток через них равен:
ит
(6) iR = cos at
и' it
(7) ic = cos (at +
С
U л
(8) iL = cos (at - 2).
L
29. Электрические цепи переменного тока 676
Из приведенных соотношений следует, что в случае активного сопротивления ток и напряжение совпадают по фазе, емкостного — ток опережает л напряжение на индуктивного — ток запаздывает 4» , я по фазе на а
676
Борис Гринченко
Задача 29.1.
Генератор переменного тока подключен к последовательно соединенным сопротивлению В, емкости С и индуктивности L. По цепи течет ток i - Im sin art. Найти напряжение на генераторе, сопротивление цепи и сдвиг фаз между током и напряжением.
Решение.
Напряжение на генераторе представим в виде:
(1) и = и„ + uL + ис. I
Подставив в (1) соответствующие формулы из введения и проводя преобразования, получаем:
(2) U = R Im sin cot + XLImcos ot -
- XcIm cos ot = RIm sin art + (XL - Xc) Im cos art.
Введя угол ф таким образом, что:
R cos ф = .... -...... ;
XL-XC
sm ф = -..=---....
1/Я2+(Хь-Хс)2
Х,-Хс
tgq>= Lr °.
преобразуем (2) к виду:
(3) и = Im "V Я 2 + (Хй - Хс ) 2 sin (<в t + ч> ).
29. Электрические цепи, переменного тока 677
Величину
(4) Z = Б* + (Х£ -
называют импедансом (сопротивлением) цепи, ф — сдвиг фаз между током и напряжением.
678
Борис Гринченко
Задача 29.2.
Найти ток, сопротивление и сдвиг фаз между током и напряжением в цепи, состоящей из параллельно соединенных сопротивления В, емкости С и индуктивности L, подсоединенных к генератору напряжения U = Um cos (at.
Решение.
Полный ток в цепи:
(1)
i = iR + ic + iL.
Подставляя в (1) соответствующие формулы из введения, получим после преобразований, аналогичных предыдущей задаче:
(2)
i = cos (cot + <р),
29. Электрические цепи переменного тока
679
где
680
Борис Гринченко
Задача 29.3.
Конденсатор, катушка и резистор соединены между собой последовательно. Действующие напряжения на них равны соответственно Uc, Ul и Ur. Найти действующее напряжение на всем участке.
Решение.
Воспользуемся результатом решения задачи 29.1, подставляя вместо амплитуды тока его действующее значение:
и = Л/Я 2 + (XL - Хс) 2 =
= )2 + (ixL - ix) * = V о* +
29. Электрические цепи переменного тока
681
Задача 29.4.
Лампу мощностью W = 60 Вт, рассчитанную на напряжение Ui = 120 В, нужно включить в сеть переменного тока с напряжением Us = 220 В. Конденсатор какой емкости (или катушку какой индуктивности) следует-включить последовательно с лампой, чтобы она горела в нормальном режиме?
Решение.
Лампа рассчитана на силу тока
W
U)
Ток в цепи, состоящей из последовательно соединенных лампы и конденсатора (см. решение задачи 29.1):
(2)
^2
^Ir2 + (
Учитывая, что
(3)
из (1,2) находим:
сопротивление лампы:
U.
W
С = ^Uz-Uz U.o А Л А
= 8,6 мкФ.
Аналогично, L = 1,2 Гн.
682
Борис Гринченко
Задача 29.5.
Участок цепи состоит из резистора сопротивлением R = 60 Ом и катушки индуктивности с сопротивлением Xl = 80 Ом, соединенных параллельно. К участку подведено синусоидальное напряжение. Чему равно сопротивление участка?
Решение.
Воспользуемся результатом решения задачи 29.2: И = Г-4 + ДгУ’ = 480м.
29. Электрические цепи переменного тока
683
R = 10 Ом и катушку индуктивности L = 0,01 Гн течет переменный ток с циклической частотой со = 103 с\ Амперметр А1 показывает силу тока h = 2А. Найти показания амперметра А2. Сопротивлением амперметра А1 пренебречь.
Решение.
Обозначим через Uq действующее напряжение
между точками а и Ь. Тогда, согласно решению задачи 29.2, находим:
(1)
684
Борис Гринченко
(2)
_ °
1 Leo
Из (1, 2) получаем:
/2 = ЛЬ1> -S/^jf + CjL)2 да 2,8 А.
30. Отражение и преломление света
При падении света на отражающую поверхность угол падения равен углу отражения:
(1) а = Y,
причем луч падающий, отраженный и перпендикуляр к поверхности, восстановленный в точке падения, лежат в одной плоскости.
Абсолютным показателем преломления среды называется величина:
(2) « =
где с = 3-10® — —скорость света в вакууме, v — ско-С
рость света в данной среде.
Относительный показатель преломления одной среды относительно другой определяется соотношением:
п9
(3) п = -Д
где пг и п2 — абсолютные показатели преломления сред.
Согласно закону преломления света:
(4)
sin а _ п2 sin р -
где а — угол падения, р — угол преломления.
686
Борис Гринченко
Если при переходе из оптически более плотной среды в оптически менее плотную угол падения луча на поверхность раздела сред а > ао, где угол удовлетворяет соотношению:
(5) sin ао =
Г*'
(п — относительный показатель преломления двух сред), то имеет место явление полного внутреннего отражения. Другими словами, преломленный луч отсутствует.
30. Отражение и преломление света
687
Задача 30.1.
Построить изображение источника света S в плоском зеркале.
Решение.
Рассмотрим два луча, идущие от источника: один, направленный по нормали к поверхности зеркала, другой — произвольный. Нетрудно видеть, что продолжения отраженных лучей в область за зеркалом пересекаются в одной точке, причем эта точка S' симметрична источнику S относительно плоскости зеркала. Для наблюдателя, в глаз которого попадают отраженные от зеркала лучи, создается впечатление, что они испущены источником, расположенным в тючке S'. По этой причине S' называют изображением S в зеркале.
688
Борис Гринченко
Задача 30.2. л
Какой минимальной высоты нужно взять зеркало, чтобы человек высотой Н мог бы увидеть себя во весь рост?
Решение.
На рисунке представлены человек (справа) и его изображение в зеркале (слева). Лучи, попадающие в глаз человека и дающие изображение в полный рост, — это лучи, отраженные от участка зеркала н АВ, длина которого равна -х-.
30. Отражение и преломление света
689
Задача 30.3.
Построить изображение источника S в двухгранном зеркале с углом 90° при вершине.
S’ — изображение источника в нижнем зеркале. S" — искомое изображение S' в верхнем (вертикальном) Зеркале. Очевидно, что этот же результат будет получен, если сначала построить изображение S в вертикальном зеркале, а затем изображение изображения в нижнем.
690
Борис Гринченко
Задача 30.4.
Определить фокусное расстояние сферического зеркала радиусом R.
Решение.
На рисунке изображен луч, направленный параллельно главной оптической оси 0'0, где О — центр сферы 0'0 = R.
Поскольку треугольник AOF — равнобедренный (Z OAF = Z AOF ), AF = FO. Полагая, что расстояние от падающего луча до главной оптической оси d « R, приходим к соотношению:
O'F = FO = %.
Таким образом, тонкий пучок света, параллельный главной оптической оси, фокусируется на расстоянии R
от центра зеркала О’.
30. Отражение и преломление света
691
Задача 30.5.
Источник S находится на расстоянии d от центра О' сферического зеркала. На каком расстоянии f от точки О' находится изображение источника? (формула сферического зеркала).
Решение.
Рассмотрим два исходящих от источника луча: один направим параллельно главной оптической оси, другой проходит через центр сферы О. Из подобия треугольников ASS' и FOS' имеем:
m AS_AS^_
17 FO FS''
Учитывая, что AS' = О'В и FS = FB, получаем:
(2)
или
FO FB
1 1 F d
692
Борис Гринченко
Задача 30.6.
Солнечные лучи падают на горизонтальное дно озера под углом а = 30°. Под каким углом 0 солнечные лучи падают на поверхность воды? Показатель преломления воды п = 1,33.
Решение.
Запишем закон преломления: sin В —---------------------= п.
sin а
Подставляя численные значения, находим:
sin 0 = 0,67; 0 « 42°.
30. Отражение и преломление света
693
Задача 30.7.
Под каким углом свет падает на плоскую поверхность стекла, если отраженный и преломленный лучи образуют между собой прямой угол? Скорость света в стекле v = 2 • 108 м/с.
Решение.
(1)
Запишем закон преломления: sin а с
Sin Р V
Учитывая, что
(2)
Р = |-а
Из (1) находим:
sin а sin р
= tg а =
1,5
с v
а = arctg 1,5 * 56°.
694
Борис Гринченко
Задача 30.8.
Луч света, идущий из толщи воды, претерпевает полное внутреннее отражение на ее поверхности. Выйдет ли луч в воздух, если на поверхность воды вылить слой кедрового масла?
Решение.
Пусть луч света, идущий из толщи воды, падает под углом ао полного внутреннего отражения:
1
sin ап = —.
0 пг
Запишем закон преломления света на границе воды и масла:
(1)
(2)
sin а0 п2 sin р ~ п/
Из (1,2) находим:
• о 1 sm В = —, п2
30. Отражение и преломление света 695
Таким образом, Р = Ро — угол полного внутреннего отражения на границе раздела кедрового масла и воздуха, и, следовательно, луч из кедрового масла в воздух не выйдет.
Если луч света падает под углом а > ао, то Р > ро и тем более свет в воздух не выходит.
Из изложенного видно, что ответ не зависит от сорта жидкости на поверхности воды (от показателя преломления Пг).
696
Борис Гринченко
Задача 30.9.
На дне водоема, глубина которого I = 13 м, лежит предмет S. На каком расстоянии от поверхности воды видит предмет человек, если луч зрения перпендикулярен поверхности воды? Показатель преломления воды п = 1,3.
Решение.
Рассмотрим два луча, исходящие от предмета S: один перпендикулярен поверхности воды, другой падает на поверхность воды под малым углом a (sina « а). Согласно закону преломления:
m sin Р _ „ Р
) sin a ~ a’
Из треугольников AS'B и AS'B с учетом малости углов аир, находим:
(2)
АВ = BS' • р = BSa = а-1.
.30. Отражение и преломление света 697
Из (1,2) получаем:
BS' = - = 10 м. п
Таким образом, изображение предмета находится на расстоянии 10 м поверхности воды.
698
Борис Гринченко
Задача 30.10.
Найти положение изображения S' источника S, расположенного на расстоянии I = 4 см от передней поверхности плоскопараллельной стеклянной пластинки толщиной d = 1 см, посеребренной с задней Стороны. Показатель преломления пластинки п = 1,5. Изображение рассматривается перпендикулярно к поверхности пластинки.
Решение.
Для построения изображения S' один луч направим перпендикулярно поверхности пластины, а другой под малым углом а:
С учетом малости углов а и Р (sin а«а и sin р « р), из треугольников SOA, АВС и S'OB имеем:
(1) ОА = SO • а = 1а
(2) AB=AC-2p«d2p
30. Отражение и преломление света 699
OB = OS' • а.
(3)
Согласно закону преломления:
(4) а =
Поскольку (5)
из (1—4) находим:
ОВ = ОА+АВ,
d2a
OS' • a =--+ al
n
OS' = I + — = см. n 3
700
Борис Гринченко
Задача 30.11.
Тонкий пучок света, проходящий через центр стеклянного шара радиуса R, фокусируется на расстоянии 2R от его центра. Найти показатель преломления стекла.
Решение.
Запишем соотношения между углами:
(1)
(2)
а = 2у
а + у = 20
и закон преломления с учетом малости углов:
(3)
а = п • 0.
Отсюда находим:
30. Отражение и преломление света
701
Задача 30.12.
Если смотреть на капиллярную трубку сбоку, то видимый внутренний радиус будет равен г'. Каков истинный внутренний радиус? Показатель преломления стекла п.
Решение.
Построим изображение А' точки А и воспользуемся законом преломления с учетом малости углов а и 0.
(1) Р = ап.
Из геометрических соображений, с учетом малости углов аир, имеем:
(2) г' = Ret
(3) г = Яр,
где R — внешний радиус капилляра.
Разделив (2) на (3) с учетом (1), находим:
. г'
702
Борис Гринченко
Задача 30.13.
На дне сосуда, наполненного водой до высоты Н, находится точечный источник света S. На поверхности воды плавает диск так, что его центр О находится под точечным источником света. При каком минимальном радиусе диска ни один луч не выйдет через поверхность воды? Показатель преломления воды п.
Решение.
На рисунке построен луч, падающий на поверхность воды под углом полного внутреннего отражения:
(1) sin а,, = |.
ft
Очевидно, что при а > ао лучи испытывают полное внутреннее отражение, а при а < ао выходят на по- , верхность. Таким образом, при радиусе, равном или большем величины
30. Отражение и преломление света 703
(2) R = ОА = h tg а0,
ни один луч не выйдет из воды. После несложных преобразований находим:
д = _ .
- 1
704
Борис Гринченко
Задача 30.14.
Показатель преломления атмосферы некоторой планеты меняется с высотой h над ее поверхностью
по закону: п = по - ah при h « На какой высоте тонкий пучок света, выпущенный горизонтально, будет обходить планету, оставаясь все время на этой высоте? Радиус планеты R.
Решение.
Поскольку скорость распространения световой волны перпендикулярна ее фронту, время прохождения двумя лучами светового пучка полного оборота вокруг планеты одинаково:
2тг/?,
где и Я2 — расстояния от лучей до центра планеты, Vj и и2 — скорости света на расстояниях
Rx и R2 от центра планеты соответственно:
(2)
(3) v2 = ^.
Полагая, что
(4) = R + h
(5) R2 = R + h-\- Ah,
и учитывая условие задачи:
(6) h = h0- ah,
30. Отражение и преломление света
705
после несложных вычислений находим:
(учтено АЛ < < ti).
31. Линзы
Рассматриваются так называемые тонкие линзы, то есть линзы, толщина которых мала по сравнению с радиусами кривизны ее поверхностей. Для тонкой собирающей (положительной) линзы формула линзы имеет вид:
(1) 7 = | + 7 при d>F’
(2) j - у при d < F,
где d — расстояние от линзы до предмета, f — расстояние от линзы до изображения предмета, F — фокусное расстояние.
Формула линзы для рассеивающей (отрицательной) линзы:
Величины F и f предполагаются положительными. Увеличение Г линзы определяется соотношением:
где h и Н — высота предмета и его изображения соответственно.
Оптической силой линзы называется величина: D = -K
(5)
31. Линзы
707
Изображение S' источника (предмета) S называется действительным, если лучи, исходящие из источника S, после прохождения через линзу действительно пересекаются в пространстве, формируя изображение.
Собирающая линза дает действительное изображение, если предмет расположен на расстоянии от линзы, превышающем фокусное. Рассеивающая линза всегда дает мнимое изображение.
Для построения изображения в линзе обычно пользуются тремя лучами: 1) лучом, проходящим через оптический центр линзы и не преломляющимся в ней; 2) лучом, параллельным главной оптической оси (после преломления проходит через фокус в случае собирающей линзы, а в случае рассеивающей через фокус проходит продолжение преломленного в линзе луча); 3) лучом, проходящим через фокус в случае собирающей линзы (после преломления луч проходит параллельно главной оптической оси).
708
Борис Гринченко
Задача 31.1.
Найти фокусное расстояние тонкой собирающей линзы, одна из поверхностей которых плоскость, а другая — сфера радиусом R. Показатель преломления вещества линзы п.
Построим ход луча, параллельного главной оптической оси и воспользуемся законом преломления, который с учетом малости углов аир (sin а«а и sin Р « Р) имеет вид:
(1) Р = па .
Поскольку линза тонкая, полагаем, что точки А и А' практически совпадают. Из треугольников О'А'О и A'OF, с учетом малости углов, находим:
(2)
А'О = aR
(3) А'О = F (Р - а).
31. Линзы 709
Из (1—3) получаем:
п - 1’
В случае, если линза находится в среде, п =----
относительный показатель преломления на границе среда — лйнза.
В случае падения луча справа налево, аналогичный расчет дает такое же выражение для фокусного расстояния.
710
Борис Гринченко
Задача 31.2.
Найти фокусное расстояние f линзы, составленной из двух собирающих линз с фокусными расстояниями Ft и Рг, прижатых вплотную одна к другой так, что главные оптические оси липз совпадают.
Поместим источник S в фокус первой линзы. Тогда его изображение попадает в фокус второй линзы Г2.
Согласно формуле линзы:
(1) 4 = 4- + 4-
f Fi F2
(Fr и F2 —расстояние от линзы до источника и его изображение соответственно).
31. Линзы
711
Задача 31.3.
Найти фокусное расстояние тонкой собирающей линзы, поверхностями которой являются сферы радиусов и 1?2. Показатель преломления вещества линзы п.
Решение.
Воспользуемся результатами решения двух предыдущих задач, представив данную линзу, как составленную из двух сложенных вместе линз, одна из поверхностей которых плоскость, а другая — сфера радиусов Ri и Лг соответственно:
712
Борис Гринченко
Задача 31.4.
Найти фокусное расстояние двояковыпуклой линзы с радиусом кривизны поверхностей 30 см, изготовленной из стекла с показателем преломления п = 1,6.
Решение.
Воспользуемся результатом решения предыдущей задачи:
F =------7-j--Г7 = 0,25 м.
<п_1)(я + я)
31. Линзы
713
Задача 31.5.
На каком расстоянии от линзы расположен предмет, если расстояние между предметом и его действительным изображением минимально? Фокусное расстояние линзы F.
Решение. -
Запишем формулу линзы:
Согласно условию задачи, необходимо найти минимальное значение величины:
. л л Fd d2
(2) d f~d + d-F~d~F'
Дифференцируя последнее выражение по d и приравнивая производную нулю, найдем условие экстремума функции d + /:
d2 - 2dF Л
------5- = 0.
(d - F)2
Отсюда находим:
d = 2F.
714
Борис Гринченко
Задача 31.6.
Расстояние от заднего фокуса собирающей линзы до изображения в девять раз больше расстояния от переднего фокуса до предмета. Найти увеличение линзы.
(1)
Решение.
Запишем формулу линзы: 1 =1+1 F d f
и соотношение для увеличения:
(2) T = f = |
Согласно условию задачи:
(3) 9 (d - F) = f - F.
Решая систему уравнений (1—3), находим:
Г= 3.
31. Линзы
716
Задача 31.7.
Плоская поверхность плосковыпуклой линзы, фокусное расстояние которой F, посеребрена. Найти фокусное расстояние F' получившегося зеркала.
Решение.
Направим на линзу пучок лучей, параллельных главной оптической оси. Сразу после отражения от зеркала луч направлен в точку F, однако после второго прохождения линзы, преломляясь, попадает в точку F', которая, по определению, является фокусным расстоянием системы линза—зеркало.
Чтобы вычислить F', воспользуемся следующим приемом. Поместим в точку F' источник. Нетрудно видеть, что F является мнимым изображением точки F' в линзе (принцип обратимости световых лучей). Согласно формуле линзы:
F F' F’
откуда находим:
716
Борис Гринченко
Задача 31.8.
Две линзы с фокусными расстояниями F = 30 см находятся на расстоянии Z = 15 см друг от друга. При каких положениях предмета система дает действительное изображение предмета?
Рассмотрим предельный случай положения предмета S, при котором система линз дает его изображение на бесконечности. При этом исходящие из него лучи после прохождения двух линз идут параллельно главной оптической оси. Очевидно, что при положении предмета левее S лучи после прохождения двух линз фокусируются в одной точке, то есть дают действительное изображение источника, а при положении правее — расходятся, давая мнимое изображение.
Для определения расстояния OS удобно воспользоваться приемом предыдущей задачи. Для этого заметим, что продолжение луча ВА влево пересекает главную оптическую ось в точке S', которая совпадает
31. Линзы,
717
с фокусом линзы В. С другой стороны, как видно из рисунка, S' является изображением источника S в линзе А. Запишем формулу линзы для источника и его изображения в левой (А) линзе, учитывая, что изображение мнимое:
Из (1), учитывая, что OS' = F - I, получаем:
F OS = 4 = 10 см.
О
718
Борис Гринченко
Задача 31.9.
Объектив состоит из двух линз: собирающей с фокусным расстоянием F = 15 см и рассеивающей с тем же фокусным расстоянием. Линзы расположены на расстоянии I = 10 см друг от друга. Определить положение главных фокусов объектива.
Решение.
нахождения правого главного фокуса рассмотрим ход луча, параллельного главной оптической оси. Расстояние d от рассеивающей линзы до пересечения луча с главной оптической осью S дает положение правого главного фокуса объектива. Помещаем, как и при решении предыдущей задачи, источник в точку S и, пользуясь принципом обратимости световых лучей, убеждаемся, что изображение источника S в рассеивающей линзе попадает в точку F правого фокуса собирающей линзы. Запишем формулу линзы для источника S его изображения в точке F в рассеивающей линзе:
11 1
F d F-Г
31. Линзы
719
откуда находим:
. (F - I ) F „ s d =----— =7,5 см.
V
Rnn нахождения левого главного фокуса объектива рассмотрим ход луча, падающего параллельно главной оптической оси справа налево. Продолжение этого луча (обозначено штриховой линией) попадает в фокус F рассеивающей линзы. Помещая источник в точку F и удалив рассеивающую линзу, запишем формулу линзы для изображения источника в точке S', даваемой собирающей линзой:
Отсюда находим:
, (F + Z) F „ f ---------= 37,5 см.
Расстояние / от левой линзы дает положение главного левого фокуса системы линз.
720
Борис Гринченко
Задача 31.10.
Предмет в виде отрезка длиной I расположен вдоль оптической оси собирающей линзы с фокусным расстоянием F, дающей действительное изображение всех его точек. Середина отрезка расположена на расстоянии d от линзы. Найти продольное увеличение предмета.
Запишем формулу линзы для концов отрезка А и В:
(1) 1 11 1л
(2) + — |сч l-l 1 тз II
По определению, продольное увеличение:
(3) Г =
С
Из (1—3) находим:
F 2
(4)
7 2’
32. Световые волны
Зависимость показателя преломления вещества от длины волны X (частоты) света называется дисперсией. С уменьшением длины волны величина показателя преломления увеличивается.
При переходе из одной среды в другую частота света v не меняется. Учитывая связь между длиной волны и частотой:
(1)
v = X v
(Г = y — период колебаний световой волны), где v — скорость распространения света в данной среде, и определение показателя преломления:
(2)
с
п = —
V
(с = 3 • 108 м/с — скорость света в вакууме), приходим
к выводу о том, что при переходе из оптически менее плотной среды 1 в оптически более плотную среду 2
(пг < п2) длина волны X = уменьшается (Хо —
длина волны в вакууме).
В случае наличия двух когерентных источников света в пространстве возникает постоянное во времени , распределение амплитуд колебаний световых волн, называемое интерференцией. Условие максимума ин
722
Борис Гринченко
терференции (максимума амплитуды колебаний) в точке А имеет вид:
(3) Ad = *X (* = 0,1,2,...),
где Ad = | dx - d21 — разность хода, dr и d2 — расстояние от точки А до каждого из источников.
Условие минимума интерференции:
2k + 1
(4) Ad =—д—X (* = 0, .1, 2, ...).
Таким образом, если на разности хода Ad укладывается целое число волн, имеет место максимум интерференционной картины, если же нечетное число полуволн — минимум.
Если лучи распространяются в разных средах, в (3) необходимо учитывать зависимость длины волны
Хо „
от показателя преломления среды: X = —. В частнос-п
ти, если лучи 1 и 2 распространяются в средах с показателями преломления щ и т соответственно, а длина света в вакууме равна Хо, выражение для раз-ности хода принимает вид: Ad = | nidi - mdz I, причем <
в формулах (3, 4) вместо X следует брать Хо. |
При нормальном (перпендикулярно поверхности решетки) падении света на дифракционную решетку < максимумы интерференции будут наблюдаться под уг- | лами ср, удовлетворяющими условию: 1
(5) d sin ф = k X (k = 0, ± 1, ± 2, ...), I
где величина d = а + Ъ называется периодом дифрак- | ционной решетки (а и b — ширины прозрачной и непрозрачной полос).
32. Световые волны
723
Задача 32.1.
Найти скорость света в воде, если при частоте 4,4 • 1014 Гц длина световой волны в воде равна 0,5 мкм.
Решение.
Воспользуемся соотношением между частотой и длиной световой волны:
v = X v = 4,4 • 1014 • 0,5 • 10~ 6 = 2,2 • 108 м/с.
724 Борис Гринченко
Задача 32.2.
Длина волны света в воде 0,46 мкм. Найти длину света в воздухе.
Решение.
Хо
Воспользовавшись формулой X = — из введения
п
для воздуха (Xi) и воды (Ха):
(1)
(2)
получим:
(3) X. = -2-Л
Поскольку в условиях, близких к нормальным, показатель преломления воздуха щ » 1, из (3) находим:
Хх = Х2 п2 = 0,46 • 1,3 = 0,6 мкм, где учтено, что п2 = 1,3.
32. Световые волны
725
Задача 32.3.
Два когерентных источника Si и S2 испускают монохроматический свет с длиной волны 600 нм. Определить, на каком расстоянии от точки О на экране будет первый максимум освещенности, если | ОС | = 4 м и IS1S2I— 1 мм.
Решение.
Условие максимума интерференции:
(1)
Ad = /?Х
в точке В, ближайшей (/? = 1) к точке нулевого максимума О (k = 0, Ad = 0) принимает вид:
(2)
Ad = X,
где
(3) Ad = dx - d2 = a/Z2 + (a + x)2 - 'll2 + (a - x)2 =
726
Борис Гринченко
_ (V/2 + (а + х)2 - л/z2 + (а - х)2) ^Z2 + (а + х)2 + ^Z2 + (а - х)2
• (л/Z2 + (а + х)2 + л//2 + (а - х)2) =
Z2 + (а + х)2 - (Z2 + (а - х)2) 4ах , п . .
-------------2Z-----------~^Г (а = 0’5мм>-
В (3) учтено: а «I, х « I. Окончательно полу-чаем: х = -х— « 2,4 мм.
2а
32. Световые волны
727
Задача 32.4.
Точечный источник света находится на расстоянии 1 мм от плоского зеркала и на расстоянии 2 м от экрана, расположенного перпендикулярно зеркалу. Найти расстояние от точки О до ближайшего максимума на экране. Длина волны источника 600 нм.
Решение.
Интерференцию на экране создают световые волны, идущие к экрану непосредственно от источника, и волны, отраженные от зеркала. Вклад последних можно учесть, заменив зеркало точечным источником S', помещенным в место изображения источника S. Таким образом, приходим к условиям предыдущей задачи 32.3.: два когерентных источника Sh S', расположенных на расстоянии 2 мм, создают на экране интерференционную картину.
728
Борис Гринченко
Задача 32.5.
Положительная линза с фокусным расстоянием 15 см разрезана пополам по диаметру и половинки раздвинуты на расстояние 0,5 см. Перед линзой на расстоянии 20 см находится точечный источник света S с длиной волны 600 нм. Найти расстояние между двумя ближайшими максимумами в центре интерференционной картины. Промежуток между половинками линзы закрыт непрозрачным экраном. Расстояние от линзы до экрана 2 м.
Решение.
Построим изображение источника S в каждой из половинок линзы.
32. Световые волны
729
Согласно формуле линзы, расстояние от линзы до каждого из изображений:
(1) / = ^р = 20см.
Запишем формулу для увеличения линзы:
Отсюда находим:
Н = Th = h = 0,25 см.
Расстояние между S' и S" |S’ S"| = 2(Н + h) = 1 см.
Таким образом, имеем два изображения источника «8 в точках S' и S". Эти изображения сами являются когерентными источниками света, которые расположены на расстоянии 1 см друг от друга и дают интерференционную картину на экране, находящемся на расстоянии 1,8 м от источников. Далее данная задача сводится к задаче 32.3.
730
Борис Гринченко
Задача 32.6.
Для уменьшения доли отраженного света на поверхность стекла нанесли тонкую пленку с показателем преломления п = и толщиной d = 0,6 мкм.
О
Пучок белого света в диапазоне волн от 0,4 до 0,7 мкм падает нормально к поверхности стекла. На каких длинах волн отраженный свет максимально ослабляется?
1 — луч, отраженный от поверхности пленки,
2 — луч, отраженный от поверхности стекла.
Решение.
Запишем условие минимума интерференции для лучей, отраженных от поверхности пленки и поверхности стекла:
(1) Ad = 2dn = ^2 *
Нетрудно убедиться, что только Х,2 = 0,64 мкм и Х,з = 0,457 мкм, удовлетворяющих условию (1), попадают в диапазон 0,4 - 0,7 мкм.
32. Световые волны
731
Задача 32.7.
На какой угол отклонятся лучи зеленого (0,54 мкм) света в спектре первого порядка, если период дифракционной решетки равен 0,02 мм?
Решение.
Согласно формуле дифракционной рещетки (/г = 1):
d sin = X.
Отсюда находим:
X
sm m. = —.
T1 d
Учитывая, что для ф « 1 sin ф * ф (в радианной мере), получаем: фх = 2,7 • 10~2. В градусах фх = 1,5°.
732
Борис Гринченко
Задача 32.8.
Найти ширину спектра первого порядка с длинами волн в диапазоне от Хф = 0,38 мкм до Хкр = 0,76 мкм, полученного на экране с помощью линзы с фокусным расстоянием F = 3 м. Дифракционная решетка имеет 100 штрихов на 1 мм.
Решение.
Прошедший через дифракционную решетку свет разлагается на параллельные пучки, которые направлены под углами, определяемыми формулой дифракционной решетки. Как известно, параллельный пучок света, падающий на собирающую линзу, фокусируется в ее фокальной плоскости (то есть в плоскости, перпендикулярной главной оптической оси и проходящей через фокус линзы). Следовательно, для
получения четкого изображения спектра необходимо расположить экран в фокальной плоскости линзы (расстояние между линзой и экраном равно фокусному расстоянию линзы). Для спектра первого (й = 1) порядка имеем картину, представленную на рисунке.
32. Световые волны
733
Запишем формулу дифракционной решетки для спектра первого порядка для длин волн Хф и Хкр:
(1) d sin <ркр = Хкр
(2) d sin фф = Хф.
Из геометрических соображений ширина спектра I определяется соотношением:
(3) I = F (tg фкр - tg фф).
Учитывая, что для малых ф sin ф « tg ф « ф, из (3) находим:
i=5 (ч, - м -п (<>“)•
734
Борис Гринченко
Задача 32.9.
На дифракционную решетку с периодом d = 4 мкм нормально падает свет в диапазоне длин волн от X,i = 500 нм до Х,2 = 550 нм. Будут ли спектры разных порядков перекрываться друг с другом?
Решение.
На рисунке изображены неперекрывающиеся спектры k и k + 1 порядков. Видно, что условие того, что спектры не перекрываются, имеет вид:
(!) Фл,2~Фй + 1,1
или, что то же самое, для синусов:
(2) Sil1 Ф*,2 Sin Ф*+1,1
Запишем формулу дифракционной решетки:
32. Световые волны
735
(3) d sin фА12 = k Х2,
(4) d sin cpA + li х = (k + 1) Xj.
Из (2—4) получаем:
(5) k < = 10.
Л2 Л-1
Максимальный порядок спектра ко определим из условия:
kn к
(6) sin ф *о =-—р < 1,
поскольку эп1ф<1. Из (6) получаем k0 = = 8.
Таким образом, для всех возможных порядков спектров от 0 до 8 (5) условие выполняется и, следовательно, спектры не перекрываются.
33. Кванты. Физика атома
Энергия Е светового кванта (фотона): he
(1) Е = hv =
Л
где h = 6,6 • 10-34 Дж • с (с — постоянная Планка, v — частота, X — длина волны).
Импульс р фотона:
(2) р " с Т
скорость света в вакууме с = 3 • 108 м/с.
Длина волны, скорость и частота связаны соотношением:
с = X.V.
(3)
Уравнение Эйнштейна (закон сохранения энергии) для фотоэффекта:
, . , mv
hv=A + -у-,
(4)
л а THl?
А — работа выхода электрона из вещества, —х— — & кинетическая энергия вылетевшего электрона. Работа выхода обычно измеряется в эВ (электронвольтах) (1 эВ = 1,6 • 10~19 Дж — энергия, которую приобретает электрон при прохождении разности потенциалов 1 В).
33. Кванты. Физика атома
737
Красной границей фотоэффекта называют длину волны:
(5)
. he
А’
начиная с которой наступает явление фотоэффекта. При больших длинах волн X > Хгр (меньших энергиях фотона) фотоэффект отсутствует.
Энергия стационарного состояния атома водорода определяется соотношением:
(6) Еп = -
Величину Ei =----г—— = 13,6 эВ называют энер-
гией (потенциалом) ионизации атома водорода в нор-h
мальном (невозбужденном) состоянии (-^—).
Энергия атома водорода равна сумме потенциальной и кинетической энергий электрона:
1«л2 г 2
С7\ F "в ।
(7) £ = __+ _
При излучательном переходе из состояния п в состояние k (п> k) атом водорода испускает фотон с энергией:
(8) hvnk = Еп~ Ek‘
738 Борис Гринченко
Задача 33.1.
Определить энергию фотонов, соответствующих наиболее длинным (М = 0,75 мкм) и наиболее коротким (Хг = 0,4 мкм) волнам видимой части спектра.
Решение.
Подставляя в выражение для энергии фотона:
Е = Л
соответствующие длины волн, получим:
Et = 2,6 • 10“19 Дж, Е2 = 5 • 10“19 Дж.
33. Кванты. Физика атома
739
Задача 33.2.
Источник света мощностью 100 Вт испускает 5 • 1О20 фотонов за 1 с. Найти среднюю длину волны излучения.
Решение.
Энергия W испущенных за время At = 1 с фотонов:
(1) W = NAt,
где N = 100 Вт — мощность источника.
С другой стороны,
(2) W = пЕ,
где п = 5 • 1О20 фотонов, испущенных за 1 с, he
(3)-----------Е = -т-----энергия одного фотона.
Л
Из (1—3) находим:
. nhc п -
Л = ТглТ = 0,1 мкм.
NAi
740
Борис Гринченко
Задача 33.3.
Какой длины волны свет следует направить на поверхность цезия, чтобы максимальная скорость фотоэлектронов была равна 2000 км/с? Красная граница фотоэффекта для цезия 690 нм.
Решение.
Воспользуемся определением красной границы фотоэффекта:
С учетом v =
Л.
he
Из (1,2) с
и уравнением Эйнштейна:
(9\ Ьл> = А +
находим:
2 = 94 нм.
he mv
ч, 2
33. Кванты. Физика атома
741
Задача 33.4.
Мощность точечного источника света Ро = 10 Вт, длина волны А, = 500 нм. На каком максимальном расстоянии I этот источник сможет заметить человек, если глаз реагирует на световой поток в п > 60 фотонов в секунду? Диаметр зрачка d = 0,5 см.
Решение.
Обозначим через I плотность потока (интенсивность) излучения на расстоянии I от источника, то есть количество световой энергии, которая за 1 с проходит через площадку в 1 м2:
(!) I =
где 4л/2 — площадь поверхности сферы радиуса I.
Количество фотонов, проходящих за 1 с через 1 м2:
(2) / —~ —
( “ he ~ he’
где hv — энергия одного фотона (доказательство предоставляется читателю).
Согласно условию задачи: лс?2 7td2
(3) - п (~2~ — площадь зрачка).
Из (1—3) находим:
Л/ Р0Ы2
V IQhcn
= 106 м.
742
Борис Гринченко
Задача 33.5.
При каком запирающем напряжении Ua фотоэлектроны, вырванные из вольфрамового электрода, не смогут достичь другого электрода? Длина волны ультрафиолетового излучения X = 0,1 мкм, работа выхода электронов из вольфрама А = 4,5 эВ.
Решение.
(1)
Воспользуемся уравнением Эйнштейна: , . , mv2
hv =А +
и законом сохранения энергии для электрона, вырванного из вольфрама и достигшего другого электрода с нулевой скоростью (нулевой кинетической энергией):
H^ = eU
2 3
В (2) eU3 — работа электростатических сил (приращение потенциальной энергии электрона). Очевидно, что при U > U3 электроны не достигнут другого электрода.
Из (1,2) получаем:
Лс
X ~
е
(2)
иа
= 7,9 В
(е = 1,6 • 10"19 Кл).
33. Кванты. Физикаатома
743
Задача 33.6.
Возникнет ли фотоэффект в цинке под действием излучения с длиной волны 0,45 мкм?
Решение.
Красная граница фотоэффекта для цинка (работа выхода 4,2 эВ)
Л he 6,6 • 10"34 -З Ю8 пп гр“ А ~ 4,2 • 1,6 • 10“19 “ ’
мкм.
Поскольку X > Хгр, фотоэффект не возникнет.
744
Борис Гринченко
Задача 33.7.
В рентгеновской трубке напряжение между анодом и катодом, которым ускоряются электроны, равно U. Найти минимальную длину волны рентгеновского излучения.
Решение.
Полагая, что вся кинетическая энергия электрона
mv2 тг я .he
—77- = eU преобразуется в энергию фотона -г—, нахо-
2 Ло
дим: тт Лс eU = -т-. Ло Отсюда получаем: . he 1,23 xo = Zt7'“~tF
(Хо — в нанометрах, U — в киловольтах).
1
33. Кванты. Физика атома
746
Задача 33.8.
Вычислить давление света, падающего нормально к поверхности. Рассмотреть случаи полностью поглощающей (абсолютно черной) и полностью отражающей (зеркальной) поверхностей. Интенсивность излучения I.
Решение.
Пусть S — площадь поверхности, на которую падает излучение.
Рассмотрим первый случай (поглощающая поверхность). За время количество световой энергии, поглощенной поверхностью,
(1) ДЕ = IS At.
При этом переданный поверхности импульс:
ДЕ
(2) Др = —
Согласно второму закону Ньютона:
(3) FAt = Др
и определению давления:
F
(4) P-f.
Из (1—4) находим: Р = ~-
В случае зеркального отражения переданный поверхности импульс:
ДЕ
(2' ) Др = 2—.
Решение системы (1, 2', 3, 4) дает:
с
746
Борис Гринченко
Задача 33.9.
Определить длину волны фотона, испущенного атомом водорода при переходе из состояния п = 4 в состояние k = 2.
Решение.
Воспользуемся соотношениями:
(1) -~- = En-Eh
^nk
(2) Е“ = ~^
Е.
(3) Е* = ~~£-
К
Отсюда находим:
33. Кванты. Физика атома
747
Задача 33.10
Найти энергию ионизации атома водорода в возбужденном состоянии, если известно, что радиус орбиты электрона равен г.
Решение.
Энергией ионизации называется минимальная энергия, которую необходимо сообщить электрону атома для удаления его на бесконечно большое расстояние от ядра. Условие минимальности сводится к тому, что скорость электрона на бесконечности равна нулю. При этом полная энергия электрона:
/1 \ г _ mvZ ke2
(1) Е 2 г
(г — <х>, v — 0) также равна нулю = 0).
Энергия ионизации:
(2) Ег = Ex - Е = - Е.
Запишем закон Ньютона для электрона в атоме
водорода:
(3)
Из (1—3)
fee2 _ mv2 т* ~ г
находим:
748
Борис Гринченко
Задача 33.11.
Найти энергию ионизации водорода в состояний п.
Решение.
В соответствии с решением задачи 33.10:
£, = £.-£, = -Я» = 4-п
Задача 33.12.
Вычислить радиус орбиты электрона в n-ом состоянии атома водорода.
Решение.
Учитывая результаты задач 33.10. и 33.11.» имеем: fee2 Е.
(1)
Из (1) находим:
Гп = Ы^_ = Г1л2, п kme2 1
f—т
\2tU _ Л_ л
где величина г. = -—-к = 5-10 м соответствует ра-
feme
диусу орбиты электрона в атоме водорода в нормаль-
ном (п = 1) состоянии.
33. Кванты. Физика атома
749
Задача 33.13.
Найти энергетический порог реакции ионизации неподвижного атома массы М частицей массы т. Энергия ионизации Ео.
Решение.
Воспользуемся результатом решения задачи 6.16.: частица отдает максимальную энергию атому в случае абсолютно неупругого удара:
С1) Е0 = М + тп^пор-
Отсюда находим:
(2) = (1 + Ж
Из (2) видно, что, например, при ионизации атома электроном (М » т), пороговая энергия практически совпадает с энергией ионизации. Можно показать, что это же относится к ионизации атома фотонами (предоставляется читателю).
34. Физика атомного ядра
Атомное ядро состоит из нейтронов и протонов, взаимодействие между которыми описывается так называемыми ядерными силами. Число протонов в ядре обозначают Z, число нейтронов — А. Суммарное число нуклонов (протонов и нейтронов) А в ядре называют массовым числом:
(1) A = Z + N.
Обозначение ядра /X показывает, что ядро имеет массовое число А и число протонов (заряд ядра) Z. Так, например, ядро 2Не (а — частица) состоит из двух протонов и двух нейтронов.
Дефект массы ядра ДМ определяется как разность между суммой масс покоя составляющих ядро нуклонов и массой покоя ядра:
(2) ДМ = + Nmn - Мя,
где тр = 1,00728 — масса протона, тп = 1,00865 — масса нейтрона (в атомных единицах массы), Мя — масса ядра. В практических расчетах с использованием (2) удобно вместо массы протона брать массу нейтрального атома водорода, а вместо массы ядра — массу соответствующего нейтрального атома данного элемента. При этом (2) остается справедливым, так как массы электронов сокращаются.
34. Физика атомного ядра
751
Энергия связи Есъ ядра определяется соотношением:
(3) Есъ = ДМ с\
с = 3 • 108 м/с — скорость света в вакууме. Энергия связи равна минимальной энергии, которую необходимо затратить, чтобы расщепить ядро, находящееся в нормальном (невозбужденном) состоянии, на отдельные нуклоны (протоны и нейтроны). Или, что то же самое, энергия связи ядра равна энергии, которая выделяется при слиянии нуклонов в ядро в нормальном состоянии.
Удельной энергией связи ядра называют величину:
И)
то есть энергию связи, приходящуюся на один нуклон. При протекании я дер ной реакции, в ходе которой выделяется (поглощается) энергия Q:
(5) А + В — С + D + Q,
справедлив закон сохранения энергии:
(6) Q = [МА + Мв - (Мс + Мр) } с2,
А и В — ядра, вступающие в реакцию (реагенты), С и D — образовавшиеся в результате реакции продукты (продукты реакции). Число продуктов (ядер и других частиц) может быть отличным от двух.
Закон сохранения энергии (6) в более общем виде:
(7) Q - (М„„ - Мород) с2,
где Мреаг — масса ядер, вступающих в реакцию,. Л^прод — масса ядер и других частиц, образовавшихся в результате реакции.
752
Борис Гринченко
Предполагается, что выделившаяся (поглощенная) в ходе ядерной реакции энергия Q связана только с увеличением (уменьшением) кинетической энергии ядер. Если реакция экзотермическая (выделение энергии, Q > 0), кинетическая энергия продуктов Е11рОд превышает кинетическую энергию реагентов Ереаг:
(8) ^прод ~ ^реаг = Q’
В случае эндотермической реакции (поглощение энергии, Q < 0) кинетическая энергия реагентов превышает кинетическую энергию продуктов в соответствии с (8). В частности, если кинетической энергией реагентов можно пренебречь, Q равно суммарной кинетической энергии продуктов.
Наряду с законом сохранения энергии, в ядерных реакциях сохраняется число нуклонов (число нуклонов, содержащихся в реагентах, равно числу нуклонов в продуктах), а также справедлив закон сохранения заряда.
При испускании электрона (р — распад) заряд ядра увеличивается на единицу (можно рассматривать как распад одного из нейтронов ядра на протон и электрон).
Для удобства расчетов полезно иметь в виду, что одной атомной единице массы (равной массы нейтрального атома углерода) соответствует энергия покоя 931,5 МэВ:
1 а.е.м. с2 = 931,5 МэВ.
Так, например, дефект массы ядра гелия зНе составляет:
34. Физика атомного ядра
763
Ш = 2 • 1,00783 + 2 • 1,00865 - 4,0026 = 0,03036 , а энергия связи ядра гелия:
Есв = ДМс2 = 0,03036 • с2 = 0,03036 • 931,5 =
= 28,29 МэВ.
Закон радиоактивного распада:
(9) N = N02"t
No — число нераспавшихся ядер в момент времени t = 0, N — число нераспавшихся ядер к моменту времени t, Т — период полураспада ядер данного сорта (вида).
754
Борис Гринченко
Задача 34.1.
При захвате ядра бора (“В ) а -частицей (аНе ) образуется нейтрон. Написать уравнение реакции.
Решение.
(1) l61B +2Не — ZX +
Согласно законам сохранения числа нуклонов и заряда» получаем:
(2) 11+4=А+1,
(3) 5 + 2 == Z + О.
Следовательно, А = 14, Z = 7. Из таблицы Менделеева находим, что заряду ядра (порядковому номеру элемента) Z = 1 соответствует ядро азота (X = N). Таким образом, уравнение реакции имеет вид:
“В +‘Не + \п.
34. Физика атомного ядра.
755
Задача 34.2.
При бомбардировке железа («Fe) нейтронами образуется 0 — радиоактивный изотоп марганца с атомной массой 56. Написать реакцию получения искусственного радиоактивного марганца и реакцию происходящего с ним 0-распада.
Решение.
Учитывая (таблица Менделеева), что заряд ядра (порядковый номер) марганца равен 25, запишем:
(1) “Fe + >-“ Мп + £Х.
По аналогии с решением задачи 34.1. находим: А = 3, Z = 1, то есть:
(Г) “Fe +'п — “Мп + ®Н. .
Реакция 0-распада марганца:
“Мп — “Fe + °е.
ZO ZO — 1
756
Борис Гринченко
Задача 34.3.
При бомбардировке изотопа бора^В а-частицами образуется изотоп азота ”N. Какая при этом выбрасывается частица? Изотоп азота является радиоактивным, дающим позитронный распад. Написать реакцию.
Решение.
(1) 108B+£ie-,87N + *X.
Используя законы сохранения числа нуклонов и заряда, получаем: Z = О, А = 1. Следовательно:
< 1ОбВ+4Не — 18N +Jn.
V- ' < .. !’
Реакция позитронного распада:
(С — ядро атома углерода).
34. Физика атомного ядра
757
Задача 34.4.
Найти энергию связи и удельную энергию связи ядра алюминия fjAl.
Решение.
Учитывая, что ядро алюминия fjAl состоит из 13 протонов и 14 нейтронов, находим:
Еов = ДМ с2 = (13 • 1,00783 + 14 • 1,00865 -
- 26,98146) с2 = 0,24143 • 931,5 « 225 МэВ, где вместо массы протона мы, воспользовавшись табличными (справочными) данными, подставили массу нейтрального атома водорода, а вместо массы ядра алюминия — массу нейтрального атома алюминия (см. введение).
Удельная энергия связи:
Е
Е = -т* « 8,3
УД 21
МэВ нуклон*
758 Борис Гринченко,
Задача 34.5.
Поглощается или выделяется энергия в реакции:
;ы + ;не - \“в + ‘п + е?
Решение.
Согласно формулам (5,6) введения и табличным данным о массах нейтральных атомов зЫ, гНе,™В и нейтрона, равных соответственно: 7,01601; 4,0026; 10,01294 и 1,00865, получаем:
Q = {7,01601 + 4,0026 - (10,01294+ 1,00865)} с2 =
= - 0,00298 • с2 = - 0,00298 • 931,5 = - 2,78 МэВ.
Так как Q = - 2,78 МэВ < 0, реакция эндотермическая (идет с поглощением энергии).
Задача 34.6.
Какая энергия выделяется в термоядерной реакции:
2Н + *Н — *Не + >?
Решение.
По аналогии с решением задачи 34.5. находим:
Q = {2,01410 + 3,01605 - (4,0026 + 1,00865)} с2 =
= 17,6 МэВ.
34. Физика атомного ядра
759
Задача 34.7.
Какая энергия выделяется при синтезе 0,4 г дейтерия (1Н) и 0,6 г трития (?Н)?
Решение.
Согласно результату предыдущей задачи 34.6., на один акт реакции дейтерия с тритием выделяется энергия 17,6 МэВ. В 0,4 г дейтерия содержится число атомов:
(1) N = Na = 91^ .10 . 6 • Ю23 « D MD А 2 • 10“ 3
« 1,2 • 1023.
Аналогично в 0,6 г трития содержится число атомов трития:
(2) = = °з6 i^ 6'1023 * 1>2 ’1о28-
Отсюда заключаем, что в реакцию вступают все ядра дейтерия и трития. Для выделившейся в 12 • 1022 актах реакций энергии получаем:
W = 17,6 • 106эВ • 1,2 • 1023 = 3,5 • 10“ Дж
(1эВ = 1,6 • 10“19 Дж).
760
Борис Гринченко
Задача 34.8.
В реакции^Н + ?Н — гНе + у образующийся у-квант имеет энергию 19,7 МэВ. Найти скорость а-частицы, если кинетической энергией ядер дейтерия (?Н) можно пренебречь.
Решение.
В реакции выделяется энергия:
(1) Q = (2 • 2,01410 - 4,00260) с2 =
= 0,025 • 931,5 = 23,3 МэВ, в которую входят энергия у-кванта и кинетическая энергия а-частицы. На долю кинетической энергии а-частицы, следовательно, приходится:
(2) Е = 23,3 - 19,7 = 3,6 МэВ= 5,76 10"18 Дж.
Учитывая, что
(3) Е-—Х- или v = -,
z т
где массу т а-частицы можно определить, например, из соотношениям
(4) т = = 0,67 • 10- и кг,
окончательно получаем:
v = 13 • 10е м/с.
34. Физика атомного ядра
761
Задача 34.9.
Какой минимальной кинетической энергией должна обладать а-частица для протекания реакции:
:ы+:не
Ядро лития в начальный момент покоится.
Решение.
Согласно результату задачи 34.6., для протекания реакции необходима энергия Q = 2,8 МэВ.
Учитывая результаты решения задач 6.16. - 6.18., получаем:
или mfi + т„ 7 + 4
Е = —Q = —у—Q = 4,4 МэВ. ^Li 7
Таким образом, минимальная кинетическая энер-
гия (энергетический порог реакции) Е = 4,4 МэВ.
762
Борис Гринченко
Задача 34.10.
Какую долю полной энергии, выделяющейся при распаде ядра радона 2ee2Rn, уносит а-частица?
Решение.
Запишем закон сохранения импульса для реакции:
222Rn — 2’®Ро + ‘Не ОО 04 Z
(1) O = MV-mv,
где М — масса образовавшегося в результате распада ядра полония 2™Ро, V — его скорость, т и и — масса и скорость а-частицы.
Учитывая, что выделившаяся полная энергия:
(2) Q =
для доли 5 находим:
2 2 2
mv ти ти
е _ 2 2.2 _ 1 л QQ
Q mv2 МУ2 тл? Мт2у2 i , ЛЬ
2 2 2 2М2 м
(т = 4, М = 218).
Таким образом, а-частица уносит около 98% выделившейся в реакции энергии.
34. Физика атомного ядра
763
Задача 34.11.
Найти наименьшую энергию у-кванта Еу, необходимую для протекания реакции:
> :н + у-;н + х
Решение.
Энергия связи ядра дейтерия ?Н, то есть энергия, необходимая для расщепления его на протон 1Н и нейтрон In, определяется соотношением:
(1) Есв = (1,00783 + 1,00865 -
- 2,01410) с2 = 2,2 МэВ.
Запишем законы сохранения энергии и импульса для рассматриваемой реакции:
(2) Еу = £св + Екин,
(3) Ру = (тр + mJ V,
Еу
где Ру = -у- — импульс у-кванта, V — скорость ядра дейтерия сразу после поглощения у-кванта,
... г МУ2
(4) ^КИН 2 ’
Учитывая (3) и (4), получаем:
£кин = ЕУ
При подстановке численных значений величин (предоставляется читателю) нетрудно убедиться, что:
_5_ =_______212___
2Мс2 2 • 2 • 931,5
764
Борис Гринченко
то есть £кин « Есв и, следовательно,
Еу = Есз = 2,2 МэВ.
Этот же результат можно получить, воспользовавшись результатами задачи 6.16. и тем фактом, что
Ev
масса у-кванта —4 много меньше массы ядра дейтерия, с
так что практически вся энергия у-кванта преобразуется во внутреннюю энергию ядра дейтерия (ядро при этом переходит в возбужденное состояние с возможным последующим распадом на протон и нейтрон).
34. Физика атомного ядра
765
Задача 34.12.
Какова электрическая мощность Р атомной электростанции, расходующей в сутки т = 220 г изотопа 2®®U и имеющей КПД 25% ?
При делении ядра урана выделяется энергия Q = 200 МэВ.
Решение.
Количество распавшихся за сутки (т = 24 • 3600 с) ядер 2e’U найдем из соотношения:
(1) N =
где М — молярная масса *£U.
Количество выделившейся за сутки энергии:
(2) Е - NQ.
Согласно определению КПД и мощности:
(3) 11=-/--
•^затр
D _ Е где * ааТр •
Из (1-3) находим:
р = пт^е = 53Мвт.
М т
766
Борис Гринченко
Задача 34.13.
Активность радиоактивного элемента уменьшилась в 8 раз за 3 дня. Найти период полураспада.
Решение.
Поскольку активность пропорциональна числу не-распавшихся ядер, количество последних также уменьшилось в 8 раз за 3 дня.
Запишем закон полураспада
(1) N = AT0.2’t
где t = 3 дня.
С учетом условия задачи:
X 1
X 8’ получаем:
2'* = 2-’; -| = ~3.
Таким образом, Т = 1 день.
ОГЛАВЛЕНИЕ
Предисловие.................................. 3
Введение .................................... б
1. Кинематика равнопеременного движения........ 9
2. Кинематика относительного движения.
; Вращательное движение. Движение со связями........................ 40
3. Динамика прямолинейного движения........... 67
4. Динамика вращательного движения............112
5. Статика . . ..................... . . ъ -.139
в. Закон сохранения импульса и энергии....................................172
7. Гидростатика. Закон Архимеда............. 219
,8. Гидродинамика..............................256
9. Механические колебания..................... 270
10. Уравнение теплового баланса. Фазовые переходы ..............................298
11. Идеальный газ..............................314
12. Насыщенный и ненасыщенный пар. Влажность......................................338
13. Первый закон термодинамики ................352
14. Поверхностное натяжение....................382
15. Закон Кулона...............................407
16. Напряженность и потенциал электрического поля ...........................424
17. Теорема Гаусса.............................443
18. Проводники в электрическом поле............456
768
Борис Гринченко
19. Диэлектрики в электрическом поле...........480
20. Электроемкость. Конденсаторы .............. 490
21. Взаимодействие зарядов. Энергия электрического поля.................... 507
22. Движение заряженных частиц в электрическом поле........................... 540
23. Электрический ток.......................... 551
24. Электрические цепи постоянного тока........ 563
25. Электрический ток в жидкостях.............. 596
26. Магнитное поле............................. 602
27. Электромагнитная индукция.................. 623
28. Нестационарные токи. Электромагнитные колебания..................... 653
29. Электрические цепи переменного тока........ 674
30. Отражение и преломление света.............. 685
31. Линзы...................................... 706
32. Световые волны............................. 721
33. Кванты. Физика атома....................... 736
34. Физика атомного ядра....................... 750
Серия учебной литературы «МАГИСТР»
ГРИНЧЕНКО Борис Исакович
Как решать задачи по физике
Книга издается в авторской редакции
Издание 2-е, дополненное и исправленное
Ответственный за подготовку издания: Александр ПОЛУДА
Компьютерный набор, верстка и графика: Ольга ЛУНЕВА, Ирина МЕЖЕБУРСКАЯ, Наталья КОРОБОВА, Галина БЕЛОВА.
Корректоры: Наталия ФЛЕЙШМАН Нина АТАМАНЕНКО
ЛР № 062918 от 09.08.93.
Издание подготовлено в НПО «Мир и семья-96» Санкт-Петербург, ул. Уральская, 17, тел. (812) 350-17-74.
Отпечатано с диапозитивов в ГПП «Печатный Двор» Государственного комитета РФ по печати.
197110, Санкт-Петербург, Чкаловский пр., 15.
Подписано в печать 23.02.98. Формат 60X90/16. Объем 49 печ. л.
Бумага офсетная № 1. Тираж 10 000 экз. Заказ № 1307.
Книга напечатана на бумаге производства
Каменогорской фабрики офсетных бумаг, г. Каменогорск, Ленинградская область, Ленинградское шоссе, д. 54.
Представительство в С.-Петербурге т/ф: (812) 278-84-59, 278-84-60