Автор: Карлин С.
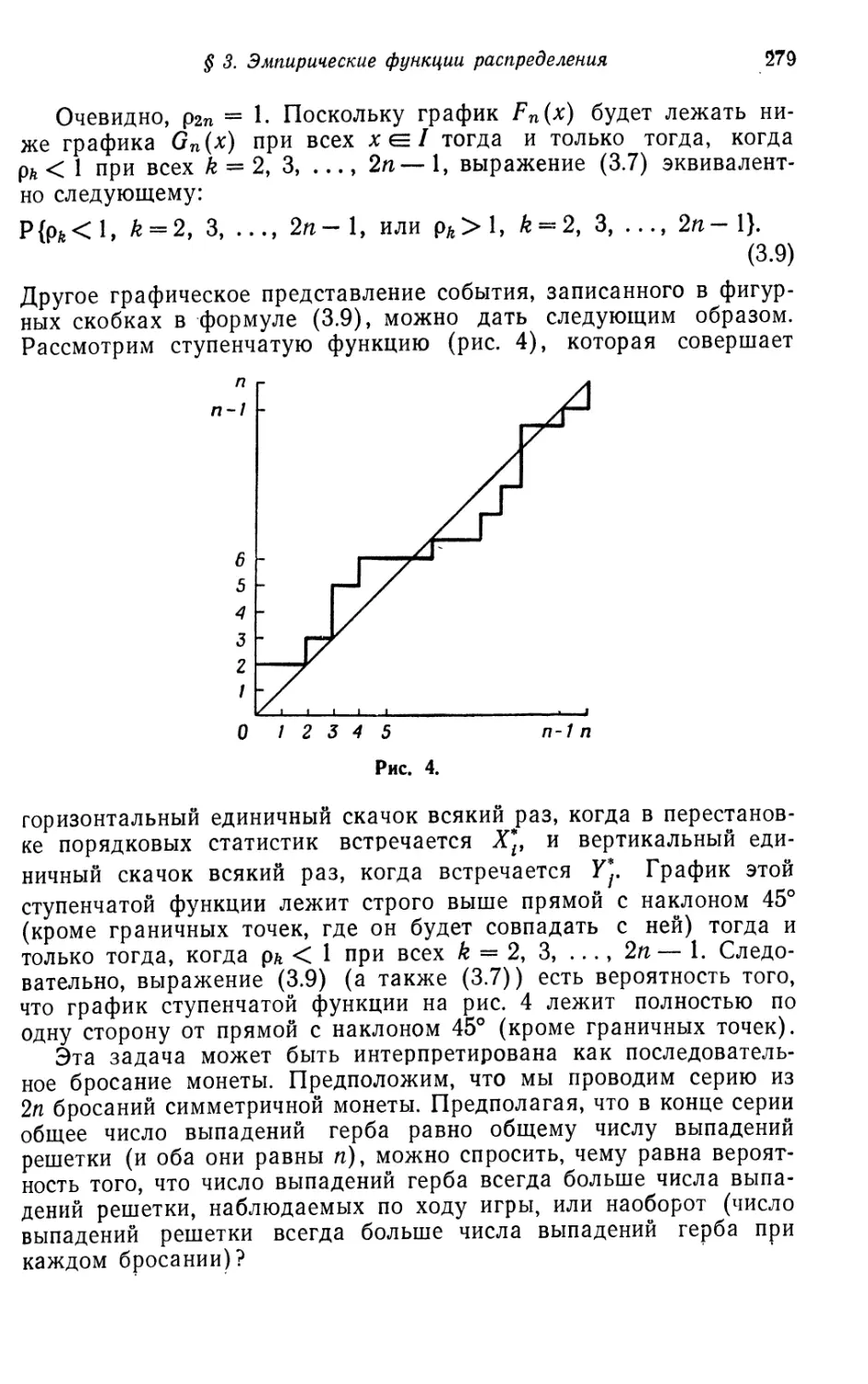
Теги: математика физика математическая физика переводная литература издательство мир
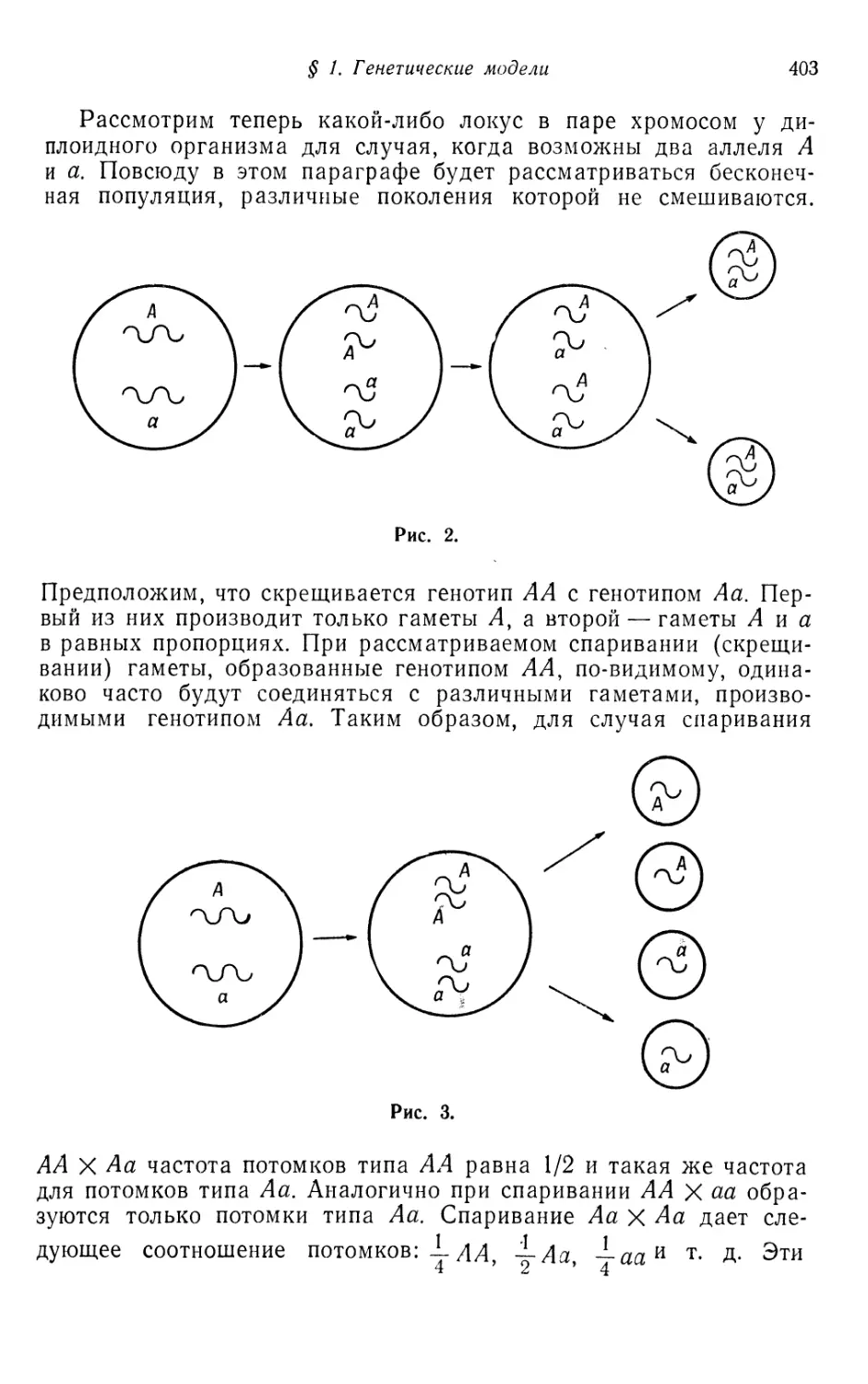
Год: 1971
Текст
С. КА РАИН
ОСНОВЫ
ТЕОРИИ
СЛУЧАЙНЫХ
ПРОЦЕССОВ
A FIRST COURSE
IN STOCHASTIC
PROCESSES
Samuel Karlin
Department of Mathematics
Stanford University
Stanford, California
ACADEMIC PRESS
New York and London
1968
С. «АРЛИН
ОСНОВЫ ТЕОРИИ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Перевод с английского
В. В. КАЛАШНИКОВА
Под редакцией
И. Н. КОВАЛЕНКО
ИЗДАТЕЛЬСТВО «МИР»
Москва ? 1971
УДК 51Я2
Книга С. Карлина является связующим звеном между элемен-
тарным курсом теории вероятностей и специальными курсами теории
случайных процессов, которые используют сложный аппарат совре-
менной математики. Для чтения книги практически достаточно зна-
ния математики в объеме стандартного курса высших учебных за-
ведений. Наряду с изложением математического аппарата книга
содержит прекрасный набор приложений к биологии, задачам мас-
сового обслуживания и др. вопросам.
Книга представляет интерес как для математиков, интересую-
щихся приложениями, так и для биологов, инженеров и специали-
стов других областей науки, в которых математика находит свое
применение.
Редакция литературы, по математическим наукам
Инд. 2-2-3
27-71
С. Карлин
ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Редакторы В. Ф. Пахомов и Л. Б. Штейнпресс Художник Г. И. Мануйлов
Художественный редактор В. И. Шаповалов Технический редактор Г. Б. Алюлина
Корректор Г. И, Секачева
Сдано в набор 13/1 1971 г. Подписано к печати 9/VIII 1971 г. Бумага № 1 60Х90716=
= 16,75 бум. л.; печ. л. 33,5; уч.-и%д. л. 31,61. Изд. № 1/5825- Цена 2 р. 52 к. Зак. 939.
ИЗДАТЕЛЬСТВО «МИР> Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени Ленинградская типография №2 им. Евгении Соколовой
Главполиграфпрома Комитета по печати при Совете Министров СССР,
Измайловский проспект, 29,
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Теория случайных процессов, возникшая в результате построе-
ния математических моделей реальных физических процессов, в на-
стоящее время представляет собой наиболее содержательную и бо-
лее всего используемую в приложениях часть теории вероятностей.
Классическим разделом теории случайных процессов является тео-
рия стационарных (в широком смысле) процессов, которая дает
основу решения многих прикладных задач. Задачи современной
науки и техники выдвинули на первый план проблемы, связанные
с исследованием случайных процессов, порождаемых последова-
тельностями независимых случайных величин. Это цепи Маркова,
марковские процессы со счетным множеством состояний, процессы
восстановления, полумарковские процессы. Их роль объясняется
в значительной степени тем, что реальные процессы, изучаемые
с помощью вероятностных методов, по самой своей природе свя-
заны с чередованием событий случайной продолжительности (на-
пример, процесс функционирования резервированной системы
с заменой отказавших элементов). Интересно отметить, что и те
физические процессы, которые ранее изучались в терминах мате-
матического ожидания и корреляционной функции, например флук-
туационные процессы в радиотехнических устройствах, теперь
в соответствии с новыми задачами рассматриваются с точки зре-
ния случайных последовательностей, отражающих определенные
изменения состояний процесса. Из такого рода задач возникает
теория потоков однородных событий, порождаемых случайными
процессами.
Книга известного ученого С. Карлина, предлагаемая вниманию
читателя, посвящена основам теории марковских процессов и про-
цессов, связанных со случайными блужданиями, а также примене-
ниям этих процессов к задачам генетики, экологии и массового об-
служивания. Наиболее ценное в книге — изложение основных ана-
литических методов исследования соответствующих процессов. Чи-
татель, стремящийся изучить теорию случайных процессов, найдет
здесь аппарат, повседневно применяемый специалистами, а не
только собрание готовых результатов. Вместе с тем следует отме-
тить, что рассматриваемые автором классы процессов все же яв-
ляются достаточно частными: не только в теоретических, но и
6
Предисловие редактора перевода
в прикладных работах исследуются более общие классы (напри-
мер, классы процессов, описывающих функционирование систем
массового обслуживания). Однако это не является недостатком
книги: методы, действие которых продемонстрировано на простых
примерах, могут служить читателю и в более сложной ситуации;
большую же часть интересующих сейчас прикладников математи-
ческих задач можно решать и в пределах тех моделей, которые
даются в книге.
В конце каждой главы автор поместил задачи; читателю, есте-
ственно, следует их решать.
Книга С. Карлина может быть рекомендована математикам,
физикам, специалистам по исследованию операций, биологам и
вообще всем, желающим войти в проблематику теории случайных
процессов и овладеть методами этой теории. При переводе и ре-
дактировании устранены некоторые погрешности оригинального из-
дания.
И. Н. Коваленко
ПРЕДИСЛОВИЕ
Теория случайных процессов изучает последовательности собы-
тий, управляемых вероятностными законами. Она находит много-
численные приложения в физике, технике, биологии, медицине,
психологии и других дисциплинах, а также в различных разделах
математики. Назначение этой книги — дать введение многочислен-
ным специальным руководствам по случайным процессам. При ее
написании я преследовал три цели: во-первых, дать систематиче-
ское вводное изложение некоторых основных разделов теории слу-
чайных процессов, во-вторых, привлечь внимание тех, кто зани-
мается чистой математикой, к богатому многообразию приложе-
ний теории случайных процессов и, в-третьих, для читателя, инте-
ресующегося приложениями, подчеркнуть важность «математиче-
ских тонкостей», показать, что они зачастую связаны с самой при-
родой вероятностных процессов.
Примеры в этой книге в основном заимствованы из биологии
и техники; вместе с тем везде делается акцент на тех вероятност-
ных аспектах, которые важны или представляют математический
интерес для более чем одной дисциплины. В книге обсуждается и
иллюстрируется ряд понятий и проблем, привлекающих в настоя-
щее время внимание исследователей.
Поскольку в элементарной книге невозможно охватить все
основные разделы теории случайных процессов, нам пришлось опу-
стить некоторые важные темы и среди них такие, как стационар-
ные случайные процессы и мартингалы. Не предполагалось, что
эта книга будет служить исчерпывающим руководством по вопро-
сам, затронутым в ней. Напротив, она должна рассматриваться
прежде всего как промежуточное звено между элементарными кур-
сами теории вероятностей и многими превосходными работами по
случайным процессам, высокий математический уровень которых
делает их недоступными для читателей, знакомых лишь с осно-
вами теории вероятностей.
У читателей предполагается знакомство с началами теории ве-
роятностей в объеме первого тома ставшей уже классической
книги Феллера «Введение в теорию вероятностей и ее приложения».
В § 1 гл. 1 мы даем сводку основных свойств случайных величин
и функций распределения, а также вводим важнейшие термины.
8
Предисловие
Материал, набранный мелким шрифтом, при первом чтении моЖнО
опустить. В конце каждой главы приводятся задачи, цель кото-
рых — разъяснить, а во многих случаях и развить изложенную
теорию.
Книгу можно использовать для полугодового или годового
курса в зависимости от потребностей. Логическая взаимозависи-
мость глав отражена на схеме, приведенной ниже.
При написании книги я пользовался обширной литературой по
случайным процессам. Каждая глава завершается списком работ,
в которых читатель найдет дальнейшую информацию и библиогра-
фию.
Я благодарен коллегам: профессору Чжун Кай-лаю и профес-
сору Дж. Мак-Грегору (Станфордский университет) за советы и
полезные комментарии, профессору Дж. Ламперти (Дартмусский
университет), профессору Дж. Киферу (Корнеллский университет)
и профессору П. Нею (Висконсинский университет) за конструк-
тивную критику, доктору А. Файнстейну за тщательную проверку
значительной части рукописи, а также моим студентам П. Милчу,
Б. Сигеру, М. Фелдману и Б. Кришнамурти за их полезные советы
и помощь при выборе и составлении задач.
Сэмюэл Карлин
Станфорд, Калифорния
ЛОГИЧЕСКАЯ ЗАВИСИМОСТЬ ГЛАВ
§ 1 гл. 1 можно читать, не вдаваясь в детали. Глава 12 почти
не зависит от гл. 11. Первая половина гл. 6 не зависит от гл. 5.
Для понимания глав 4—14 не являются необходимыми § 5 и § 6
гл. 3.
/
Для полугодового курса рекомендуется следующий вариант:
§ 2 и § 3 гл. 1с предшествующим кратким изложением материала
§ 1; гл. 2 полностью; гл. 3, исключая § 5 и, быть может, § 6; гл. 7
без § 3 и, возможно, § 7. Содержание последней части курса со-
ставляется по усмотрению лектора, при этом можно использовать
гл. 9—12, полностью или частично.
Глава 1
ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
§ 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ
ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
В этом параграфе приводятся основные термины и элементар-
ные понятия теории вероятностей. В последующих главах мы бу-
дем пользоваться ими без каких-либо дальнейших ссылок на ли-
тературу. Читателю настоятельно рекомендуется обратиться к уп-
ражнениям, помещенным в конце главы; эти упражнения помогут
ему вспомнить и закрепить предварительный материал. Детальное
изложение этих вопросов можно найти в книгах Феллера, Гнеденко
и Парзена (см. литературу в конце этой главы).
Предполагается, что читатель знаком со следующими поня-
тиями:
(1) действительная случайная величина Х\
(2) функция распределения F случайной величины X (определяе-
мая как F(X) = Р {X X}) и ее элементарные свойства1);
(3) события, связанные со значениями случайной величины X, и их
вероятности;
(4) математическое ожидание М{Л} случайной величины X и мо-
менты высших порядков М{ХП};
(5) формула полной вероятности и формула Байеса.
Вместо слов «действительная случайная величина» мы будем
часто пользоваться сокращением «д. с. в.» 2).
Д. с. в. X называется дискретной, если существует конечное или
счетное множество различных чисел Xi, Хг, ..., такое, что =
= Р {X = XJ > 0, Z=l,2,... и S at = 1. Если Р {X = X} = 0 для
i
любого значения X, д. с. в. X называется непрерывно распределен-
ной. Если существует неотрицательная функция p(t), определенная
на всей оси — оо < t < оо и такая, что функцию распределения F
*) В отечественной литературе функция распределения, как правило, пони-
мается в смысле Р{Х < X}. Очевидно Р {X Л}« lim Р {X < X + е}, Р {X < X} =
е4<0
= lim Р {X Л — е}, так что между обоими определениями существует простое
е^О
соответствие. — Прим. ред.
2) Иногда будет использоваться сокращение «с, в.» —- «случайная величи-
на». — Прим, перев,
12 Гл. 1. Элементы teopuu случайных процессов
д. с. в. X можно представить в виде
к
F(A)= J p(f)dt,
— оо
то будем говорить, что р является плотностью распределения ве-
роятностей (или короче — плотностью вероятности) случайной ве-
личины X. Если д. с. в. X имеет плотность вероятности, то она с не-
обходимостью непрерывно распределена; однако известны примеры
непрерывно распределенных случайных величин, не обладающих
плотностью вероятности *)•
Если X — дискретная д. с. в., то ее m-й момент (или момент
порядка ш) определяется так:
м [xm] = 5 %Тр {х = л j
i
(где kj имеют тот же смысл, что и выше) при условии, что ряд
сходится абсолютно.
Если X — непрерывно распределенная случайная величина с
плотностью вероятности р(-), то ее m-й момент определяется со-
отношением
М[Г"]= J xmp(x)dx
— оо
при условии, что интеграл сходится абсолютно.
Первый момент (или среднее значение) д. с. в. X будем обозна-
чать через шх или m-й центральный момент д. с. в. X опреде-
ляется как m-й момент д. с. в. X — mXl если тх существует. Пер-
вый центральный момент, очевидно, всегда равен нулю; второй
центральный момент называется дисперсией в2х А- с- в- Медиа-
ной д. с. в. X по определению является любое число v, обладаю-
щее тем свойством, что Р {X > v} >7г и Р {X v} > 7г-
А. Совместные функции распределения
Пусть (X, У) — пара случайных величин; их совместная функ-
ция распределения является функцией двух действительных пере-
менных и определяется как
F (Ль Л2) = Fxy (Ль Л2) - Р {X < Ль У < Л2).
(Индексы X и У обычно опускаются, если нет опасности возникно-
вения путаницы.)
’) В отечественной литературе принято называть случайную величину не-
прерывной именно в случае существования плотности. — Прим, ред.
§ 1. Сводка основных терминов
13
Функция F(K{, + оо) = lim F(Ab А2) является функцией
Л,2 “> °О
распределения и ее называют частной (или маргинальной) функ-
цией распределения д. с. в. X. Аналогично функция F(+ оо, А2) на-
зывается частным распределением д. с. в. У. Если случится так, что
Г(АЬ + оо)-5(+ оо, А2) = Е(АЬ А2) для любой пары значений па-
раметров Ai и А2, то случайные величины X и У называются неза-
висимыми. Говорят, что совместная функция распределения FXy
имеет (совместную) плотность вероятности, если существует функ-
ция Pxy^s, t) двух действительных переменных, такая, что
Х2 М
Лхк(^ь ^2) ~ j J Pxr(5> t) ds dt
—00 —00
для всех X], Если X и У — независимые д. с. в., то Pxy(s, t)
с необходимостью представима произведением px(s)pY(t), где рх
и ру — плотности вероятности частных распределений д. с. в. X и
У соответственно.
Совместная функция распределения любого конечного набора
Хь ..., Хп д. с. в. определяется как
^(Аь • kn) = Fxv ..., хп (Aq, ..An) == Р Ри < Ab ...»
Функция распределения
1 Л/ X.->oo, i^ivik
называется частной функцией распределения случайных величин
Xh, .... xlk.
Если F(Ab An) = /?(Ai)/?(A2) ... F(Kn) для всех значений
Ai, А2, ..., Ап, то д. с. в. Хь ..., Хп называются независимыми.
Говорят, что совместная функция распределения F(Ab Ап)
имеет плотность вероятности, если существует неотрицательная
функция p(t\y ..., tn) от п переменных, такая, что
^1
F(M, ..., Л„)= J ... J р(/ь .... tn)dtx ...dtn
— 00 —00
для всех действительных Аь ..., Ап.
Б. Условные распределения и плотности
Пусть X и У — д. с. в., принимающие счетные множества значе-
ний, скажем 1,2, ... . Условная вероятность Р{Х = i| У = /} опре-
деляется соотношением
14 Гл. 1. Элементы теории случайных процессов
Здесь предполагается, что Р {У = /} > 0; в противном случае зна-
чение Р{А = г| У = /} произвольно (скажем, равно нулю).
Условные вероятности могут быть определены и для случайных
величин других типов. Мы рассмотрим только случай, когда X и
У имеют совместную плотность вероятности Pxy(s, t). Тогда услов-
ное распределение
Р{Х<а\У - Ь}
определяется формулой
а
P{X<xi\Y = b} = (ру (Ь) Г1 J рХУ (s, b) ds,
— оо
если Ру(^)>0, и произвольно в противном случае. Из определе-
ния pY (b) следует, что
lim Р {X < а | Y - b} = 1
а->оо
для всех 6, таких, что ру(Ь) >0. Таким образом, F{r=^(a) =
= Р {X а | У = Ь} представляет собой функцию распределения
в случае ру(&) > 0. Легко видеть, что эта функция распределения
имеет плотность, а именно таковой является функция
Pxr(fl, Ь)1ру(Ь), Последняя называется условной плотностью ве-
роятности случайной величины X при условии, что У = Ь, и часто
обозначается рх|Г(а; Ь).
Условное математическое ожидание д. с. в. X при условии, что
У = у, определяется формулой
оо
М [X IУ = у] = J хрх! у (х, у) dx
— оо
для всех у, таких, что Ру(у)> 0. Аналогичное определение услов-
ного математического ожидания можно дать и для дискретного
случая. Нетрудно видеть, что М (X | У) является случайной вели-
чиной.
Следующее соотношение является очень важным свойством
условного математического ожидания:
М[М[X | У] ] = М [А].
В. Бесконечные семейства случайных величин
При рассмотрении бесконечных семейств случайных величин не-
посредственное обобщение предыдущих определений сопряжено
с существенными трудностями. Поэтому мы воспользуемся не-
сколько другим подходом.
Рассмотрим счетное семейство Х2, ... случайных величин.
Будем считать их статистические свойства заданными, если для
§ 1. Сводка основных терминов
15
каждого целого числа п>1и любого набора и, in из п раз-
личных положительных целых чисел задана совместная функция
распределения случайных величин Xi{, Xin. Разу-
меется, при этом на бесконечное семейство [Fx,,.... х. ) должны
быть наложены условия согласованности, состоящие в том, что
%.....•••> Л/-ь Л/+1’ •••’ =
= lim Fx ... г. (Ль Лу-ь Л/, Л/+1, Ага),
Ху->оо '1 ‘п
и в требовании инвариантности функции
Тх,, х,...х{ (Ль Л2, •••, Л„)
Ч 1'2 1п
относительно перестановки любой пары индексов iv и и соответ-
ствующих им Xv и Последнее просто означает, что способ ну-
мерации д. с. в. Хь Х2, ... не имеет значения.
Совместные распределения х.) называются конечно-
'• ч in)
мерными распределениями семейства случайных величин {ХД'Д.
В принципе все важные вероятностные свойства этих величин мо-
гут быть выражены через конечномерные распределения.
Г. Характеристические функции
С каждой функцией распределения F связана важная функ-
ция ср(О> где —оо, оо), называемая характеристической. По
определению имеем1)
<₽(/) = | e^dFp), /2=-1. (1.1)
— оо
Пока читатель может интерпретировать запись интеграла в пра-
вой части как символическую. Если F имеет плотность вероят-
ности р, то характеристическая функция представима в виде
(£(0= J ешр(Л)я!Л.
— оо
Если F — распределение д. с. в. X со счетным множеством воз-
можных значений и Р{X = kk} == ak (& = 0, 1,...), то
!) Интеграл в правой части (1.1) является интегралом Лебега — Стильтьеса.
У читателей не предполагается знания интегралов этого типа.
16
Гл. 1 Элементы теории случайных, процессов
правая часть (1.1) сводится к ряду
оо
fe=0
Весьма полезным фактом является следующее легко доказы-
ваемое утверждение: если {Xi, Хп} — семейство независимых
д. с. в., то характеристическая функция их суммы представляет со-
бой произведение характеристических функций этих д. с. в.
Соответствие между функциями распределения и характеристическими функ-
циями—взаимно однозначное. Представление функции распределения через ее
характеристическую функцию известно как формула обращения Леви. Поскольку
она нам в дальнейшем не понадобится, мы рекомендуем интересующемуся чита-
телю обратиться к литературе, где эти вопросы рассматриваются подробно.
Взаимно однозначное соответствие между функциями распределения и ха-
рактеристическими функциями сохраняется и при различных предельных перехо-
дах. В частности, если F, Fb F2, ... — функции распределения, такие, что
lim Fn (%) == F (Л) для всех X, где F непрерывна, и срп (/)—характеристиче-
П-»оо
ские функции членов последовательности {Fn}, то
оо оо
<Р«(0= J eitKdFn(V-+<f(t)= ^eltKdF(X)
— ОО —оо
равномерно по t в каждом конечном интервале. Обратно, если (pi, ср2, ... — ха-
рактеристические функции членов некоторой последовательности A, F2, ... функ-
ций распределения и lim срп (t) = ср (/) для любого /, а ф(/) непрерывна в
П->оо
точке t — 0, то (р(/) является характеристической функцией функции распреде-
ления F и -lim Fn (Л) — F (Л) для любого X, где F непрерывна. Этот результат
П->оо
известен под названием критерия сходимости Леви.
Д. Производящие функции
Для случайных величин, которые могут принимать только неот-
рицательные целочисленные значения, вместо характеристической
функции используется функция
оо
g («) = 5 PkSk, Pk = p {X = k},
л=о
называемая производящей. Так как по предположению и
оо
функция g(s) определена по крайней мере для s, та-
&=о
ких, что |s| 1 (s— комплексная переменная), и бесконечно диф-
ференцируема при | s | < 1.
Отметим следующие элементарные свойства производящих
функций.
(а) Если У = Ху + Х2, где д. с. в. Х\ и Х2 независимы и могут
принимать лишь неотрицательные целочисленные значения, то про-
§ 1. Сводка основных терминов
17
изводящая функция д. с. в. У1) является произведением произво-
дящих функций слагаемых.
(б) Пусть Azi, Х2, ... — независимые и одинаково распределен-
ные неотрицательные целочисленные случайные величины, и пусть
N — неотрицательная целочисленная д. с. в., не зависящая от Х^
Мы хотим найти производящую функцию д. с. в. R = Х{ + ... + XN
(суммы случайного числа слагаемых, каждое из которых является
д. с. в.). Пусть g\v(s)—производящая функция д. с. в. N, a g(s) —
производящая функция, общая для всех Xi. Тогда
gR («) = gN (g (») )•
Имеет место следующее обобщение предыдущего результата.
Пусть Xi, Х2, ... — произвольные независимые одинаково распре-
деленные случайные величины (необязательно целочисленные),
а д. с. в. N, как и ранее, неотрицательная целочисленная и не за-
висящая от Xi. Тогда
<Рд (0 = gN (<Р (0 ),
где фд и gN — характеристическая и производящая функции д. с. в.
R = Xi + ... + XN и д. с. в. N соответственно, а ср — общая харак-
теристическая функция Д. С. в. Xi.
Рассматривая неотрицательные д. с. в., полезно заменить харак-
теристические функции преобразованиями Лапласа функций рас-
пределения. Если распределение Fx имеет плотность р, преобразо-
вание Лапласа определяется формулой
оо
Фх ($) = [ e~sxp (х) dx.
о
Интеграл в правой части существует для значений комплексной
переменной s = о + *7, таких, что о > 0. Для s чисто мнимых фх(^)
сводится к характеристической функции фх(—/)• Для дискретных
неотрицательных д. с. в. преобразование Лапласа определяется по
формуле
оо
Фх («) = 2 e~sKnan.
п — 0
Как и для характеристических функций, если Хи Х2, ..., Хп —
неотрицательные независимые д. с. в., то
'Фх,+ ... +Xrt(s)= П Фх (в).
1 п fc=l
*) В дальнейшем для краткости мы будем пользоваться термином «произво-
дящая функция случайной величины», хотя более правильно было бы говорить
«производящая функция распределения д. с. в.». В оригинале часто используется
термин «probability generation function», т. е. «вероятностная производящая
функция». — Прим, перев.
18
Гл. 1. Элементы теории случайных процессов
В случае общих функций распределения для преобразования
Лапласа имеем формулу
оо
Фх (*)=.[ e~*dFx®.
О
Как и характеристическая функция, преобразование Лапласа
однозначно определяет функцию распределения.
Е. Примеры функций распределения
Мы предполагаем известными элементарные свойства функций
распределения, которые приведены в таблицах I и II.
Следующие два многомерных распределения имеют принципи-
альное значение.
(а) Многомерное нормальное распределение
Пусть llaijll, /= 1,2 — симметрическая положительно опреде-
ленная матрица порядка 2 X 2 (т. е. а12 = а21 и аи>0, ана22 —
— ^2>0) и mi, mz — любые действительные постоянные. Тогда
/4*1» х2) =^-ехр
2
-у 2 bukXi-m^Xj-tnj)
где ll&fjl — матрица, обратная к ||агД и В = det является
плотностью распределения, называемого невырожденным двумер-
ным нормальным распределением. Если Xit Х2— д. с. в., совмест-
ная функция распределения которых равна
Аг Xi
F(%i, Л2)= J J f (xb х2) dx\ dx2,
то М(Х,) = o2(X,-) = ац при i = 1, 2 и М(Х1Х2) — гпхт2 — а12,
Переход к случаю n-мерного нормального распределения оче-
виден.
(б) Полиномиальное распределение
Совместное дискретное распределение г величин, принимаю-
щих только неотрицательные целочисленные значения 0, ..., п,
называется полиномиальным. Оно определяется выражением
P(^ = ^, ..., Xr = kr) =
n! k, kr , , , ,
= . Pr’ если ^+---+^ = n,
О в противном случае,
г
где р/>0, i=l, ..., г и 2 Pi = 1.
i=i
Таблица I
Непрерывная функция распределения Плотность Допустимые значения параметров Характеристическая функция Среднее Дисперсия
Нормальное распределе- ние с пара- метрами т и о2 1 Г (х — т)21 - — ехр — — у 2л о L 2о2 J ДЛЯ — ОО < X < ОО m — любое действительное число сг> 0 Г °2/2 . • л ехр г imt m О2
Гамма-распре- деление 9 с парамет- рами а, X I 1 для х > 0, ( 0 для х < 0 Л>0 а> 0 Ла (Л - И)а а т а Л2
Бета-распре- деление с параметра- ми р, q 2) ( г (p+_£Lxp-i (1 | Г (р) Г (?) * 11 х) для 0 < х < 1, 0 в противном случае о о Л Л Си 1 г(р + р) f еч*хр~' X Г (р) Г (?) .1 0 X (1 р p-rQ др (р + р)2 (р + <7 + 1)
’) Гамма-распределение при а== 1 называется экспоненциальным; параметр X называется масштабным.
2) Бета-распределение с параметрами р = д = 1 обычно называется равномерным распределением в (0,1).
20
Гл. 1. Элементы теории случайных процессов
Таблица II
Дискретная функция распределения Возможные значения случайных величин Вероятность состояния Производящая функция Среднее Дис- Персия
Пуассоновское распределение с параметром Z>0 п = 0, 1, 2, ... е~кКп п\ g—k-Vks X X
Биномиальное распределение с параметра- ми и р (N — целое по- ложительное, <7 = 1 -Р я = 0, 1 е 1 Sr е Ci. st (1 -р +ps)N Np Npq
Отрицательное биномиальное распределение (Паскаля) 9 с параметра- ми а>0, 0<р< 1 п = 0, 1, 2, ... ( а + п —1 \ а И ( п )pq a со т ' — aq Р aq р2
’) Геометрическое распределение является важным частным случаем распределения
Паскаля, получающимся при а=Н.
ж. Предельные теоремы
Многие из основных результатов теории вероятностей имеют
вид предельных теорем. (Мы не будем формулировать эти резуль-
таты при наиболее слабых предположениях.) Из них упомянем
следующие.
Закон больших чисел (слабый). Пусть Хь Х2, ... — независимые
одинаково распределенные случайные величины со средним m и
конечной дисперсией. Тогда для любого е > О
1. ул f I X J -f- . . . -1- Хц I 1
lim P < —----------- — m < e > = 1.
,4-11 n I i
Усиленный закон больших чисел. Пусть случайные величины
Xi, Х2, ... те же, что и выше, и пусть Sn = (Xi + ... + Хп)1п\ тогда
для любых е, б > 0 существует целое число N(е, б), такое, что
Р {| Sn — ш | 8 для всех п N (е, б)} < б х).
*) Оба последних утверждения остаются в силе и при отсутствии конечной
дисперсии у случайных величин Хп. — Прим. ред.
§ 2. Два простых примера случайных процессов
21
Центральная предельная теорема. Пусть случайные величины
Xi, Х2, ... те же, что и выше; тогда
lim Р< а
П->оо I
X1 + ... + Хп — ш
оУп
/ exp (- у-) dx,
а
где о2 — общая дисперсия величин
Лемма Бореля — Кантелли. Пусть Ль А2,... — бесконечная по-
следовательность независимых событий. Тогда событие Лоо, кото-
рое означает осуществление бесконечного числа событий из Ль
Л2, ..., имеет вид
оо оо
Ао=П и л
/г=1 i = k
Лемма Бореля — Кантелли устанавливает, что вероятность собы-
оо
тия Аоо равна нулю или единице, если соответственно S Р (А/)< оо
оо i = l
или S Р (Лг) = оо.
i = 1
§ 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
Данная книга может служить введением в различные направле-
ния случайных процессов. Теория случайных процессов имеет дело
с исследованием структуры семейств случайных величин Xt, где
t — параметр, принадлежащий соответствующему множеству Т.
Иногда, когда это не приводит к недоразумениям, мы будем пи-
сать X(t) вместо X/.
Реализацией, или выборочной функцией, случайного процесса
{Xt, t е Т} является функция, ставящая в соответствие каждому
t е Т одно из возможных значений Xt. Множество параметров Т
может быть дискретным, т. е. Т = {0, 1,2,3,...}, а {X/} может при
этом представлять исходы последовательных испытаний, таких, как
результаты бросаний монеты, последовательные реакции объекта
на изучающий эксперимент или последовательные наблюдения не-
которой характеристики популяции и т. д.
Величина Xt может быть одномерной, двумерной, ^-мерной или
иметь более общую природу. В случае, когда Хп является исходом
п-го бросания кости, возможные ее значения образуют множество
{1, 2, 3, 4, 5, 6}, а одной из типичных реализаций процесса является
последовательность 5, 1, 3, 2, 2, 4, 1, 6, 3, 6, ... . Она показана на
рис. 1, где ординатой при t = п является значение Хп. В этом при-
мере случайные величины Хп взаимно независимы, но в общем
случае величины Хп являются зависимыми.
Случайные процессы, у которых Т = [О, оо), особенно важны
в приложениях. В этом случае t обычно интерпретируется как
время,
22
Гл. 1. Элементы теории случайных процессов
Здесь мы ограничимся весьма кратким обсуждением некоторых
понятий, относящихся к случайным процессам, и двумя примерами.
Рис. 1,
В конце главы дана сводка различных типов случайных процессов.
Некоторые из них будут подробно изучаться в последующих гла-
вах.
Пример 1. Весьма важным примером является известный
процесс броуновского движения. Этот процесс характеризуется сле-
дующими свойствами:
(а) Пусть < /1 < ... < tn. Тогда приращения Xtx — Х/о, ...
Xtn — Xtn_x — независимые в совокупности д. с. в. Го-
ворят, что процесс, обладающий таким свойством, являет-
ся процессом с независимыми приращениями, выражая
тем самым тот факт, что изменения Xt на неперекрываю-
щихся интервалах времени являются независимыми д. с. в.
(б) Вероятностное распределение величин — если
/2>/ь зависит только от t2—ti (и не зависит, например,
от 6).
х
(в) J
В — положительная постоянная.
Пусть XQ = 0. Заметим, что M(XZ) = 0, o2(Xt) = Bt, где В —
фиксированное положительное число. Можно доказать, что если
0 < t\ < t2 < ... <tn < t, то условное вероятностное распределе-
ние величины Xt при известных значениях Xtn равно
(см. гл. 10)
Р pG х I Хц = • • • > Xtn “ Хп] в
х~хп
= [2лВ (t - tn}\~'12 j exp [ - 2д (< _ tn) ] du.
§ 2. Два простых примера случайных процессов 23
История возникновения этого случайного процесса началась с на-
блюдений Р. Броуна в 1827 г., заметившего, что маленькие ча-
стицы, помещенные в жидкость, совершают непрерывное беспоря-
дочное движение. В 1905 г. А. Эйнштейн объяснил это явление тем,
что наблюдаемые частицы подвержены непрерывным соударениям
с молекулами окружающей среды. Выведенные Эйнштейном ана-
литические результаты были позднее проверены экспериментально
и обобщены другими физиками и математиками.
Пусть Xt — расстояние броуновской частицы от начальной точки
в момент t. Смещение Xt — Х8 за интервал времени (s, t) можно
рассматривать как сумму большого числа малых смещений. В этой
ситуации применима центральная предельная теорема, поэтому
естественно ожидать, что Xt — Xs имеет нормальное распределение.
Аналогично естественно предположить, что распределения величин
Xt — Xs и Xt+h — Xs+h совпадают при любом h > 0, если среда на-
ходится в равновесии. Наконец, интуитивно ясно, что смещение
Xt — Xs должно зависеть только от Z— s, а не от момента начала
наблюдения.
Процесс броуновского движения (называемый также винеров-
ским процессом) играет фундаментальную роль при изучении мно-
жества случайных процессов других типов. Одномерный процесс
броуновского движения будет более полно изучен в гл. 10.
Пример 2. Другим важным примером случайного процесса,
непрерывного по времени (Т = [0, оо)), является пуассоновский
процесс. Его выборочная функция Xt представляет собой число ре-
гистрации наступления некоторого события за период от 0 до теку-
щего момента времени t. Очевидно, всякая возможная реализа-
ция Xt есть неубывающая ступенчатая функция.
Реализация, изображенная на рис. 2, соответствует первому на-
ступлению события в момент Zi, второму — в момент Z2, третьему —
в момент Z3 и т. д. Общее число наступлений события возрастает
только единичными скачками, а Хо — 0. Конкретными примерами
наблюдаемых величин, образующих подобного рода процессы, яв-
ляются: число фотонов, испускаемых веществом при радиоактив-
ном распаде, число телефонных вызовов из данного района, число
происшествий на данном перекрестке, число ошибок на странице
машинописного текста, число выходов из строя некоторого меха-
низма и число поступивших заявок на обслуживание.
Рассмотрение этих процессов как пуассоновских основывается
на законе редких событий. Представим себе большое число испы-
таний Бернулли с малой вероятностью успеха (наступления собы-
тия) и постоянным средним числом успехов. При этих условиях
известная теорема утверждает, что число наступлений события
подчиняется закону Пуассона. В случае радиоактивного распада
пуассоновское приближение дает превосходное согласие с экспери-
Гл. 1. Элементы теории случайных процессов
ментом, если время наблюдения много меньше периода полурас-
пада радиоактивного вещества.
Мы постулируем, что число наступлений события в некотором
интервале не зависит от числа наступлений этого события в любом
Рис. 2.
другом не пересекающемся с ним интервале (см. свойство (а) пре-
дыдущего примера). Предположим также, что с. в. XtQ+t — Xto за-
висит только от t и не зависит от i0 или от значения Сформу-
лируем дальнейшие постулаты, согласующиеся с интуитивным опи-
санием, данным выше:
I. Вероятность того, что за период времени продолжительно-
сти h произойдет по меньшей мере одно событие, есть
р (Л) = ah + о (й), й->0, а>0
[£•(/) = о (t) при t —* 0 означает, что lim g(t)Ц = 0].
II. Вероятность того, что за время h произойдет два или более
события, есть o(h).
Постулат II равнозначен исключению возможности более чем
однократного одновременного наступления события. В приведен-
ных нами физических процессах это условие обычно выполняется.
Пусть Pm(t) обозначает вероятность того, что за время t про-
изойдет ровно m событий, т. е.
Pm(/) = P{^ = 4 m-0, 1, 2, ...
Условие II можно записать в виде
2Р„(Л) = 0(Л),
m=2
и, очевидно,
P(h)=pl(h)+P2(h)+....
§ 2. Два простых примера случайных процессов
25
В силу предположения о независимости имеем
Ро (t + h) = Ро (/) Ро (й) = Рй (/) (1 - Р (й))
и поэтому
Ро (/ + h) - Ро (/) _ р p(h)
h ~ ™ ~Г *
Из постулата I следует, что p(h)/h—* а. Поэтому вероятность Ро(О
того, что событие не наступит в интервале (0, /), удовлетворяет
дифференциальному уравнению
Ро(/)=-аРо(С,
общее решение которого имеет вид Ро(О = ce~at. Константа с опре-
деляется из начального условия Ро(О) = К из которого следует, что
с = 1. Итак, Ро(О = e~ai-
Найдем теперь Рт(/) для любого т. Легко видеть, что
Рт (t + h) = Рт (/) Ро (й) + Рт-х (t) Р, (й) + 2 Pm-i (0 Pi (Й). (2.1)
1 = 2
По определению Р0(Л)= 1—p(h). Из постулата I следует, что
Р1(й) = р(Л) + о(Л),
т т (2 2)
2 Pm-i (О Pi (Л) < 2 Pt (й) = о (й),
1=2 1=2
поскольку, очевидно, Р&(0^1- С помощью (2.2) мы можем пере-
писать (2. 1) в виде
рт (t + h)- рт (о - рт (t) [Ро (й) - 1 ] + Рт.х (/) Р} (й) +
+ 2 Pm-i (0 Pi (й) = - Рт (/) р (Й) + рт_, (/) р( (й) +
i=2
+ 1 Pm-i (/) Pi (Й) = - аРт (О й + аРт_. (/) й + 0(h).
Отсюда следует, что
рт (t + h)- Рт (0„ _ аРт (/) + аРт_} (/) при Л_>0
или, формально,
Р'т (/) = - аРт (/) + аРт-! (О, /и = 1, 2, ..., (2.3)
при начальных условиях
Рт(0) = 0, /п=1, 2........
26
Гл. 1. Элементы теории случайных процессов
Для решения уравнений (2.3) введем функции
Qm^ = Pm^eat, m = 0, 1, 2.......
Подставляя Qm(t) в (2.3), получаем
Qm(0 = «Qm-l(0, m=l, 2, (2.4)
где Qo(/)== 1; начальные условия остаются теми же: Qm (0) = 0,
m = 1, 2, ... . Последовательно решая уравнения (2.4), получаем
Q'i (/) = а, или Qi (/) = at + с, так что (/) = at;
Q2(0 = -^- + c, так что Q2(0 = -^p;
Q
Следовательно, имеем
Другими словами, при каждом t с. в. Xt подчиняется распределе-
нию Пуассона с параметром at. В частности, среднее число на-
ступлений события за время t равно at.
Часто пуассоновский процесс возникает в форме, где временной
параметр заменяется соответствующим пространственным пара-
метром. Следующий формальный пример иллюстрирует эту ситуа-
цию. Рассмотрим систему точек, распределенных в пространстве Е
(Е обозначает евклидово пространство размерности d 1). Пусть
Nr обозначает число точек, содержащихся в области R простран-
ства Е. Предположим, что NR является случайной величиной. Со-
вокупность случайных величин {NR}, где область изменения ин-
декса R состоит из всех возможных подмножеств пространства Е,
представляет собой однородный пуассоновский процесс, если удо-
влетворяются следующие условия:
(i) количества точек в неперекрывающихся областях являются
независимыми с. в.;
(ii) для любой области R конечного объема с. в. NR подчи-
няется распределению Пуассона со средним AV(E), где V(R) —
объем области R. Параметр Л фиксирован и в некотором смысле
служит мерой интенсивности распределения, не зависящей от раз-
мера и формы.
Пространственные пуассоновские процессы возникают при рас-
смотрении распределений звезд или галактик, распределений рас-
тений и животных, бактерий на предметном стекле и т. д. Мы вер-
немся к этим вопросам в гл. 12 для более глубокого их изучения.
§ 3. Классификация общих случайных процессов
27
§3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Основные признаки, по которым различаются случайные про-
цессы, касаются природы пространства состояний S, временного
параметра Т и отношений зависимости между случайными величи-
нами Xt.
Пространство состояний S
Это пространство, которому принадлежат все возможные зна-
чения, принимаемые всеми с. в. Xt. В случае, если S=(0, 1,2, ...),
мы относим процесс к классу целочисленных процессов, или про-
цессов с дискретным пространством состояний. Если S совпадает
со всей действительной осью (—оо, оо), то мы называем процесс
действительным случайным процессом. Если S — евклидово
6-мерное пространство, то говорят, что процесс {XJ является 6-мер-
ным.
Как и в случае отдельной с. в., выбор пространства состояний
не определяется однозначно описываемым физическим процессом,
хотя во многих случаях выбор наиболее подходящего пространства
состояний очевиден.
Временной параметр Т
Если Г = (0, 1,...), то мы будем говорить, что {Xz} является
случайным процессом с дискретным временем. В этом случае мы
будем часто писать Хп вместо Xt. Если Т = [0, оо), то случайный
процесс {Xf} будем называть процессом с непрерывным временем.
Мы уже приводили примеры временного параметра Т более
чем одного измерения (пространственные пуассоновские процессы).
Другим примером могут служить волны в океане. Географические
долготу и широту можно рассматривать как /, а высоту волны
в данном месте — как Xt.
Отношения зависимости
Важной чертой случайного процесса {А\} является зависимость
между случайными величинами Xti t Т.
Характер этой зависимости определяется заданием совместных
функций распределения для каждого конечного семейства Xtli...
...,XZn с. в. процесса. Как мы увидим из примеров (а) и (б), при-
водимых ниже, совместные функции распределения часто могут
быть выражены через другие распределения, связанные с процес-
сом.
Для целей настоящей книги случайный процесс можно считать
полностью заданным, если определены его пространство состоя-
28
Гл. 1. Элементы теории случайных процессов
ний, временной параметр и семейство конечномерных распределе-
ний. Однако при рассмотрении случайных процессов с непрерыв-
ным параметром возникают некоторые трудности, которые мы ил-
люстрируем на следующем примере.
Пусть U — с. в., равномерно распределенная на [0, 1]; опреде-
лим Xt и Yt следующим образом:
( 1 при U = t,
Xt = _ Г,а=0 (*>0).
I 0 в противном случае;
Непосредственным вычислением легко убедиться, что {Х(} и {У;}
имеют одинаковые конечномерные распределения. Вместе с тем
Р | Xt у при всех 0 t 1 j = 0,
а
при всех 0 11= 1
— положение вещей просто обескураживающее. Чтобы объяснить,
чем вызваны эти затруднения, рассмотрим следующий пример.
Предположим, что {Х(, 0 t оо} является случайным процес-
сом с непрерывным временем. Наша задача — найти Р{Х( >0,
0 С t < 1}.
Рассмотрим последовательность сужающихся событий:
Л„={^>0, ti = il<2n, Z = 0, 1, ..., 2"}, n= 1, 2, ....
Вероятность каждого события Ап можно выразить через совмест-
ную функцию распределения соответствующих с. в. Xt{, i — 0, ...
..., 2". На первый взгляд кажется естественным положить Р {Xt
^0, 1}равным значению предела lim Р{Л„}.Однако не все,
П->оо
что кажется естественным, свободно от противоречий. В такой же
степени естественно считать, что Pft>0, 0</<1}= lim Р{л'},
где А'п = {Xti 0, tt = 113", / = 0, 1, ...» 3”}, но отнюдь не оче-
видно, что пределы НтР{Л„}и НтР{Л„} равны между собой.
П->оо П->оо
Более того, без дополнительных ограничений, касающихся глад-
кости выборочных функций процесса, эти пределы, вообще го-
воря, могут иметь различные числовые значения. Известны различ-
ные достаточные условия их равенства; одно из этих условий со-
стоит в том, что lim Р{| Xt — Хх |>е} = 0 для всех е>0 и всех t.
В этом случае можно показать, что никаких противоречий не возни-
кает, если определить Р{Хг>-0, 0^/<С1) как общее значение
указанных пределов. Более того, если /j, /2, ... — любое множе-
§ 3. Классификация общих случайных процессов 29
ство точек, всюду плотное в интервале (0, 1), то Р {Xt О,
- lim Р [АД>0, z=l, 2, п].
П->оо 1 1
Суть дела состоит в следующем: в то время как формула пол-
ной вероятности позволяет вычислять вероятности событий, вклю-
чающих последовательности с. в., через вероятности событий, свя-
занных с любым конечным, а следовательно, и счетным подмноже-
ством этой последовательности, событие {А^ > О, О t 1} зави-
сит от несчетного числа с. в. Мы не можем подробно исследовать
этот вопрос в нашей книге и рекомендуем читателю обратиться
к монографии Дж. Дуба [4]. Некоторые вопросы, касающиеся осно-
ваний теории случайных процессов, мы затронем в гл. 8.
Опишем теперь некоторые классические типы случайных про-
цессов, характеризующиеся различными видами зависимости ме-
жду Xt- В этих примерах мы будем считать, если не оговаривается
противное, что Т = [О, оо). Для простоты изложения мы предпо-
лагаем, что с. в. Xt — действительные.
(а) Процесс с независимыми приращениями
Если с. в.
Xt -Xt, Xt -Xt , Xt -Xt
l2 *1’ *3 П-1
независимы для всех Л, ..., tn, таких, что
/1 ^2 < ^3 < • • • <
то мы будем говорить, что {АД является процессом с независимыми
приращениями. Если множество индексов содержит наименьший
индекс /о, то предполагается также, что
^0- ^-^0- •••> Ч-Ч-,
независимы. Если Т = (0, 1, ...), то процесс с независимыми при-
ращениями сводится к последовательности независимых с. в.
Zo = Ао, Z2 = Xi — (z = 1, 2, 3, ...) в том смысле, что, зная
распределения с. в. Zo, Zb ..., мы можем определить (и это должно
быть ясно читателю) совместное распределение любого конечного
множества с. в. Х^ В самом деле,
X} — Zq-h Xi ... + Zz, z = 0, 1, 2, ....
(б) Мартингалы
Пусть {АД — действительный случайный процесс с дискретным
или непрерывным пространством индексов. Мы назовем {AJ мар-
тингалом, если для любых t\ < /2 < • • • < ^n+i математическое
ожидание М(А^+11 АД = ..., АД = равно ап для всех допу-
стимых значений ..., ап. Мартингалы можно рассматривать как
модели безобидных игр. В самом деле, если Xt описывает состоя-
ние капитала игрока в момент t, то по определению мартингала
30
Гл. I, Элементы теории случайных процессов
средняя величина его капитала в момент fn+i при условии, что
в момент tn он располагал капиталом ап, равна ап независимо от
того, каков был его капитал в предшествующие моменты времени.
Легко убедиться в том, что процесс Хп = Z\ + ... +Zn, n =
= 1,2,..., является мартингалом (с дискретным временем), если
с. в. Zi — независимые, с нулевыми средними значениями. Анало-
гично если процесс {Xt, 0^/<оо} имеет независимые прираще-
ния, средние значения которых равны нулю, то {Xt] является мар-
тингалом с непрерывным временем (см. упр. 18).
(в) Марковские процессы
Марковский процесс — это процесс, обладающий тем свойством,
что если известно значение с. в. Xt, то значения Xs, s > t, не зави-
сят от Хи, и <t\ другими словами, вероятность любого события,
связанного с будущим поведением процесса, при условии, что его
настоящее состояние точно известно, не изменится, если учесть до-
полнительную информацию относительно прошлого этого процесса.
Подчеркнем однако, что если наше знание настоящего состояния
процесса не точно, то вероятность будущего поведения процесса
будет, вообще говоря, зависеть от того, что мы знаем о прошлом
процесса. Формально, процесс является марковским, если
Р [а < Xt < b | Xtx = Xi, Xt2 = х2, ..., Xtn = =
= P{a<Xt^b\Xtn~xn} (3.1)
при t[ < t2 < ... < tn < t- Пусть A — интервал на действительной
оси. Функция
P(x,s;/, A) = P{XteiA\Xs~x}, t > s, (3.2)
называется функцией переходных вероятностей. Эта функция
играет важную роль при изучении марковских процессов. Условие
(3.1) можно выразить следующим образом:
Р {а < Xt < b | Xt{ = xi, Xt2 == х2, ..., Xtn = хп}~Р (xn, tn\ /, Д), (3.3)
где А = < g Ь}. Можно доказать, что распределение набора
х‘.....х'.)
можно выразить через функцию переходных вероятностей (3.2) и
распределение начальной с. в. Xtl. Мы остановимся подробнее на
этих понятиях при рассмотрении дискретных во времени и про-
странстве марковских процессов (гл. 2).
(г) Стационарные процессы
Случайный процесс {Xt, t <= Г} [здесь Т может быть одним из
следующих множеств: (— оо, оо), [0, оо), множество всех целых
Задачи
31
чисел, множество положительных чисел] называется стационарным
в узком смысле, если совместные распределения семейств с. в.
(X.tx+h, Xt2+h, Xtn+h) И (Xte Xt2, Xtn)
одинаковы при всех h > 0 и всех t\, , tn из Т. Это условие
означает, по существу, что процесс находится в вероятностном рав-
новесии и момент начала нашего наблюдения не имеет значения.
В частности, распределение с. в. Xt одно и то же при всех t.
Случайный процесс {Xt, t Т} называется стационарным в ши-
роком смысле, или ковариационно стационарным, если он обладает
конечными вторыми моментами и cov(Xf, Xt+h) — N[(XtXt+h)—
— М(Х/)М(Х/+/г) зависит только от h при всех t^.T.
Стационарные процессы служат для описания многих явлений
в теории связи, астрономии, биологии, а иногда и экономики.
Говорят, что марковский процесс имеет стационарные переход-
ные вероятности, если P(s, х; t, А), определенная формулой (3.2),
является функцией лишь разности t — s1). Вспомним, что
P(s, х; t, Л) есть условная вероятность — настоящее состояние
процесса считается известным. Поэтому нет никаких оснований
ожидать, что марковский процесс со стационарными переходными
вероятностями является стационарным процессом, что и соответ-
ствует действительному положению вещей.
ЗАДАЧИ
1. Пусть а, b и с — независимые с. в., равномерно распределенные в (0,1).
Какова вероятность того, что уравнение ах2 + Ьх + с = 0 имеет действительные
корни?
Ответ: (5 + 3 In 4)/36.
2. Пусть при каждом фиксированном X > 0 с. в. X имеет пуассоновское рас-
пределение с параметром к. Предположим, что сам параметр Л является с. в.,
подчиняющейся гамма-распределению (т. е. имеющей плотность распределения
0, Л < 0,
где п — фиксированная положительная константа). Показать, что
n r(fe + n) ь-п 1
РЦ-*} г (п) Г (6 + 1) \2/ ’ k °’ ......
Когда п —целое, эта формула есть не что иное, как отрицательное биномиальное
распределение с р « 1/2.
3. Пусть при каждом заданном р с. в. X имеет биномиальное распределение
с параметрами р и N. Предположим, что параметр N сам подчиняется бино-
миальному распределению с параметрами q и М, причем М N.
*) Такой процесс называется также однородным марковским процессом, —
Прим, ред.
32
Гл. 1. Элементы теории случайных процессов
(а) Показать аналитически, что X имеет биномиальное распределение с па-
раметрами pq и М.
(б) Дать вероятностное обоснование этому результату.
4. Пусть с. в. X при каждом заданном р имеет биномиальное распределение
с параметрами р и N. Предположим, что р само подчиняется бета-распределению
с параметрами г и $. Найти результирующее распределение с. в. X. Когда это
распределение является равномерным на множестве {0, 1, ..., N}?
Ответ:
р Г V = м = ( N \ Г (г + s) Г (fe + г) Г (n — fe + s) .
1 ** \k) Г (г) Г (s) Г (У + г + s)
Р {I = Ч = 1 /(N + 1), когда г = s — 1.
5. Проводится следующий эксперимент. Наблюдается с. в. X, подчиняющаяся
пуассоновскому распределению с параметром X. Затем проводится X испытаний
Бернулли с вероятностью успеха р. Какойо распределение числа успехов о?
Ответ: пуассоновское с параметром Кр.
6. (а) Предположим, что с. в. X подчиняется пуассоновскому распределению
с параметром X Параметр X сам является с. в. с экспоненциальным распределе-
нием и средним, равным 1/с. Найти распределение с. в. X.
(б) То же для случая, когда X подчиняется гамма-распределению порядка а
с масштабным параметром с, т. е. плотность распределения с. в. X равна
Л+1 Л
Г(а+1)
при X > 0 и равна 0 при X 0.
Ответ: (а) Р (X = k} = ^*+1 <
<“> р’*-61’тгНтг(|
*+“+> са+1
7. Число происшествий за неделю на некотором производстве является с. в.
со средним ц и дисперсией х2. Количества травм, полученных в результате раз-
личных происшествий, представляют собой независимые с. в. с одинаковыми
средними v и дисперсиями т2. Найти среднее и дисперсию числа травм за
неделю.
Указание: Выразить производящую функцию распределения числа травм за
неделю через производящие функции распределений числа происшествий за не-
делю и числа травм за одно происшествие.
Ответ: среднее число травм за неделю равно p/v; дисперсия числа травм за
неделю равна v2x2 + рт2.
8. Предположим, что имеется N фишек, помеченных числами 1, 2, ..., N
соответственно. Выберем без возвращений и случайным образом 2n + 1 фишек.
Пусть Y — медиана полученной случайной выборки. Показать, что Y имеет рас-
пределение
р- 1 \ -&\
P{F ==&}=*------———~------- при & = п+1, п + 2, .N — n.
\ 2п + 1 )
Проверить, что
&
(ЛГ —2ft—1) (У+1)
8п + 12
& Ю =
Задачи
33
9. Предположим, что имеется N фишек, занумерованных числами 1, 2, N.
Извлекается без возвращений случайная выборка объема п. Пусть X — наиболь-
ший номер в случайной выборке. Показать, что X имеет распределение
Р{Х = £} =
ik - 1 \
\ п — 1 )
(«)
при k — n, п+ 1, ..N
и что
10. Предположим, что в урне находится п фишек, занумерованных числами
1, 2, ..., п. Производится последовательное извлечение фишек до тех пор, пока
одна и та же фишка не появится дважды подряд. Пусть X — число извлечений
до наступления этого события. Найти распределение вероятностей с. в. X.
Ответ: р (k) = (k — 1)! ( П \
\ k - 1 / п*
при k = 2, 3, ..п 4-1.
11 (продолжение). Показать, что среднее значение с. в. X есть
М(Х) = 2+(1--) + (1--)(1-—)+ ... + (1-Д (1-—) ... (1-^=4V.
v \ а) \ п) \ п / \ п / \ п / \ /г /
12. Пусть Xi и Х2— независимые с. в., равномерно распределенные на от-
резке [0—1/2, 0+1/2]. Показать, что разность Xi — Х2 имеет распределение,
не зависящее от 0, и найти ее плотность вероятности.
Ответ:
fx^X2 “
1+^,
1 ~~ У>
0,
-1 < У <0,
0 < у < 1,
Ы>1.
* 13. С. в. X и Y обладают следующими свойствами: X положительна, т. е.
Р{Х>0}== 1, и имеет непрерывную плотность вероятности /(х); У при фиксиро-
ванном X имеет равномерное распределение в (0, X). Доказать, что если У и
X — У независимы, то
f (х) = а2хе~ах, х>0, а>0.
* 14. Пусть с. в. U подчиняется гамма-распределению порядка р, и пуст#
с. в. V подчиняется бета-распределению с параметрами q и р--q (fi<q<p).
Предположим, что U и V независимы. Показать, что UV имеет гамма-распреде-
ление с параметром q.
Указание.
Р|г/г
0'0 /
Перейти в этом соотношении к преобразованию Лапласа, изменить порядок ин*
тегрирования и разложить найденное выражение в ряд вида
&=о
2 Зак. 939
34
Гл. 1. Элементы теории случайных процессов
* 15. Пусть X и У — независимые одинаково распределенные положительные
с. в. с непрерывной плотностью распределения f(x). Предположим, далее, что
U = X — Y и V = min(X, У) являются независимыми с. в. Показать, что
f(x)=!Xe~Kx п₽и*>0'
[О в противном случае,
при некотором X > 0.
Указание. Показать сначала, что совместная плотность вероятности с. в. U
и V имеет вид
fu. V^U’ v) = f f (v + I “ I )•
Затехм показать, что частные распределения с. в. U и V равны соответственно
оо
М“) = J hv(v) = 2[\-F(v)]f(v),
max (0, и)
v
где F (и) « J f (g) d%. Приравнивая произведение частных распределений сов-
о
местному распределению, получить .соотношение
f (» + 1 и I) = f (| и I) [1 — F (»)]
и с его помощью вывести требуемый результат.
16. С. в. Хп принимает значения k/n, k = 1, 2, ..., п, каждое с вероятностью
1/и. Найти ее характеристическую функцию и предел последней при п->оо.
Каков вид с. в., которой соответствует предельная характеристическая функция?
Ответ: (а) ср„ (f) = (1 — elt) -7—г—гд—г,
4 'п ехр (— in~[t) — 1
(б) равномерно распределенная на (0, 1).
17. Применив центральную предельную теорему к соответствующим пуассо-
новским с. в., показать, что
18. Показать, что суммы Sn == Xi + . • • + Хп независимых с. в. с нулевыми
средними образуют мартингал.
19. Показать, что всякий случайный процесс с независимыми приращениями
является марковским процессом.
20. Пусть Ao, Ai, ..., Аг — исходы некоторого эксперимента. Пусть рг- —
вероятность исхода Аг (i = 0, 1, 2, ..., г). Предположим, что эксперимент по-
вторяется до тех пор, пока исход До не будет отмечен k раз. Пусть Xt— число
Задачи
35
появлений исхода А;. Показать, что
21. Показать, что производящая функция отрицательного полиномиального
распределения (I) с параметрами ро, р\, рг) имеет вид
<P(Z1......'rWoH ~ 2 hPi
\ i * I t
22. Рассмотрим векторную случайную величину {Хо, Х\, ..., Хг), подчиняю-
щуюся полиномиальному распределению с параметрами (ц; ро, р\, ..., рг), и
предположим, что п является случайной величиной с отрицательным биномиаль-
ным распределением с параметрами (k; р). Показать, что распределение вектора
{Xi, Х2, ..., Хг} при условии Хо = k является отрицательным полиномиальным
распределением с параметрами (k\ р0(1 —р), Pi(l —р)> •••> Рг(1 — р))
(О < р < 1).
23. Предположим, что некоторая совокупность состоит из т, п{, ..., пг
предметов, принадлежащих нулевому, первому, ..., r-му классам соответственно.
Предметы извлекаются один за другим без возвращения до тех пор, пока не бу-
дет извлечено k предметов нулевого класса. Показать, что совместное распреде-
ление частот Х}, ..., Хг первого, ..., r-го классов имеет вид
где
m — (k — 1)
tn + n-(k + y— 1) ’
^xi и ft= 2 ni-
z = ! /-=!
24 (продолжение). Показать, что если m-+oo и п->оо таким образом, что
т/(т + ц)->Ро и п,/(т + п)-> i = 1, 2, ..., г, то это распределение стре-
мится к отрицательному полиномиальному.
ЗАМЕЧАНИЯ
Колоритное и богатое разнообразным материалом введение
в теорию вероятностей и ее приложения читатель найдет в книге
Феллера [1]. В этой книге автор ограничивается изложением диск-
ретных распределений ]).
*) Распределениям общего вида посвящен второй том «Введения в теорию
вероятностей и ее приложения» В. Феллера, переведенный на русский язык. —
Прим. ред.
2*
36 Гл. 1. Элементы теории случайных процессов
Прекрасным введением может служить учебник Гнеденко [2].
Другим полезным элементарным учебником является книга
Парзена [3].
Классической монографией, посвященной теории случайных
процессов, является книга Дуба [4]. Ее можно считать обязатель-
ной для всех, занимающихся случайными процессами.
Другой выдающейся монографией по теории случайных процес-
сов является книга Дынкина [5].
ЛИТЕРАТУРА
1. Феллер В., Введение в теорию вероятностей и ее приложения, т. 1, «Мир»,
М, 1964.
2. Гнеденко Б. В., Курс теории вероятностей, Физматгиз, М., 1961.
3. Р а г z е п Е., Modern Probability Theory and Its Applications, Wiley, New York,
1960.
4. Д у б Дж. Л., Вероятностные процессы, ИЛ, М., 1956.
5. Дынкин Е. Б., Марковские процессы, Физматгиз, М., 1963.
Глава 2
МАРКОВСКИЕ ЦЕПИ
§ 1. ОПРЕДЕЛЕНИЯ
Дискретная марковская цепь {Хп} представляет собой марков-
ский случайный процесс, пространство состояний которого счетно
или конечно, а множество индексов Т = (0, 1, 2,...). Мы можем го-
ворить об Хп как об исходе n-го испытания.
Часто пространство состояний процесса удобно отождествить
с множеством неотрицательных целых чисел (0,1,2,...) и гово-
рить, что Хп находится в состоянии Z, если Хп = i.
Вероятность с. в. Хп+1 попасть в состояние /, если известно,
что Хп находится в состоянии i (называемая одношаговой переход-
ной вероятностью), обозначается Рпцп+\ т. е.
P?/n+1 = P{Xrt+1=/| (1.1)
В таком обозначении подчеркивается, что в общем случае пере-
ходные вероятности зависят не только от начального и конечного
состояний, но и от момента осуществления перехода. Когда одно-
шаговые переходные вероятности не зависят от временной пере-
менной (т. е. от значения п), мы говорим, что марковский про-
цесс обладает стационарными переходными вероятностями (см.
§ 3 гл. 1). Именно на этом классе марковских цепей мы и сосре-
доточим свое внимание.
Итак, отметим, что Рц rt+1 == Рц не зависит от п и есть ве-
роятность перехода из состояния i в состояние / за одно испыта-
ние. Обычно вероятности Рц объединяют в матрицу
Pqq рт Р 02 Р 03
Р10 Рц Р12 Р13
Р 20 Р21 Р‘22 Р 23
р = PiO Рц Р12 Pi3
которую называют марковской матрицей, или матрицей переход-
ных вероятностей марковской цепи,
38
Гл. 2. Марковские цепи
В матрице Р (i + 1)-я строка представляет собой распределе-
ние вероятностей с. в. Xn+i при условии, что Хп = i. Если число
состояний конечно, то Р — конечная квадратная матрица, порядок
которой (число строк) равен числу состояний. Очевидно, вероят-
ности Рц удовлетворяют следующим двум, условиям:
Pf/>0, Z, / = 0, 1, 2, ..., (1.2)
2 ро=1, 1 = о, 1,2,.... (1.3)
/=0
Условие (1.3) отражает тот факт, что каждое испытание вызывает
некоторый переход из состояний в состояние. (Для удобства мы
говорим о переходе и в том случае, когда состояние остается не-
изменным.)
Процесс полностью определен, коль скоро заданы вероятности
(1.1) и состояние (или, более общо, распределение вероятностей)
с. в. XQ. Докажем это утверждение.
Пусть Р{Ло = i} = pi. Достаточно показать, как вычисляются
вероятности
Р{Хо == *о> = Х2 ” hi •••» Xn = in] (1-4)
для любого конечного п, так как по формуле полной вероятности
любые другие вероятности, касающиеся с. в. Xjt, ... , Xjk,
ji < /2 < • • • < Л, могут быть получены суммированием членов ви-
да (1.4).
По определению условной вероятности имеем
Р {Хо Zg, Х\ = Zi, Х2 = Z2, • • •, Хп — in}
— Р {Хп = in\ Xq~ hi Xy — i^ ..., Xn-.i=Z„_i}X
X P {Xo — Zo, Xj = Zi, ..., Xn-i ~ Z„-i}. (1.5)
Но по определению марковского процесса имеем
Р I Xq Zq, X] Zj, . •., Xп— । h— 1}
= P {Xn itl I Xn-x == Zn_J = Pin_v in, (1.6)
Подстановка (1.6) в (1.5) дает
P {Xo = Zo, = i], ..., Xn = in} —
= Pin_v /nP{%0 = Z0, XI==Zb X^Z^J. (1.7)
Продолжая по индукции, получаем
P{Xo = i0, JV| = it, xn = in} = Pin_v inPin_2, 1п^ • • • Pia, tlPi0. (1.8)
§ 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
Большое число физических, биологических и экономических яв-
лений описываются марковскими цепями. Ниже приводится не-
сколько примеров.
$ 2. Примеры марковских цепей
39
А. Пространственно однородные марковские цепи
Пусть дискретная с. в. g принимает неотрицательные целочис-
оо
ленные значения, причем P{g = /} = ^, и 2#z==l- Пусть
i = l
gb ?2, • • ., ?п, • • • представляют результаты независимых наблю-
дений с. в. g.
Мы опишем две различные.марковские цепи, связанные с после-
довательностью {gj. В обоих случаях пространство состояний сов-
падает с множеством неотрицательных целых чисел.
(I) Определим процесс {Хп, п = 0, 1,2, ..положив Хп = gn
(начальное значение Хо = go задано). Матрица переходных веро-
ятностей этого процесса имеет вид
а0 «1 а3 ...
^0 #1 #2 • • •
Р = а0 ai а2 а3 ...
Тот факт, что у матрицы Р все строки одинаковы, означает, что
с. в. Xn+i не зависит от с. в. Хп-
(II) Другой важный класс марковских цепей возникает при
рассмотрении последовательных частичных сумм т]п с. в. gf, т. е.
% = + Ь+ • • • + п== 1, 2, ... .
Считаем по определению, что цо = 0. Процесс {Хп = Цп}, как не-
трудно видеть, является марковским. Легко найти его матрицу пе-
реходных вероятностей; именно:
P{xrt+i = /|Xn = o = P{?i+ ... +gn+1 = /|g1+ ... +g„ = 0 =
P {£n + l 1 l} I 0> < L
Здесь мы, очевидно, воспользовались независимостью g2-. В дан-
ном случае матрица Р имеет вид
ад а{ а2 а3 а4 ...
0 Цд @2 @3 * • •
Р = 0 0 а0 а, а2 ... • (2.1)
Если с. в. g может принимать как положительные, так и отри-
цательные целочисленные значения, то возможные значения для
каждого п содержатся в множестве всех целых чисел. В данном
40
Гл. 2. Марковские цепи
случае пространство состояний удобнее отождествить со всеми
целыми числами (а не преобразовывать в множество неотрица-
тельных чисел), так как тогда матрица переходных вероятностей
имеет более симметричную форму
... а-! а0 6Z1 а2 ^3
р = . . . $—2 «1 а2
... а-з 0-2 ах
• • • •
оо
где Р {£ = k} — ak, k = Q, ±1, ±2, ..и ak 0, 3 а* = 1-
k~ “ОО
Б. Одномерные случайные блуждания
При рассмотрении случайных блужданий состояние системы
для наглядности интерпретируют как положение движущейся
«частицы».
Одномерное случайное блуждание представляет собой мар-
ковскую цепь, пространство состояний которой состоит из конеч-
ного или бесконечного множества целых чисел; если частица на-
ходится в состоянии /, то за один шаг она может либо перейти
в одно из своих соседних состояний (/— 1 или i + 1), либо остать-
ся в состоянии i. Если пространством состояний служит множе-
ство неотрицательных целых чисел, то матрица переходных веро-
ятностей случайного блуждания имеет вид
Го Ро о 0 ...
q\ pt о ...
О <72 Г 2 р2 ...
Р = , (2.2)
о <7/ r{ Pi О
где Pi>0, qi>0, и QtX-г= 7=1,2,... (7> 1),
Ро^гО, ro^O, ro + Po~ 1- Числа qh ph rt имеют следующий смысл:
если Хп — 7, то при i 1
Р {%n+i — i + 1 I Хп = 0 — Рь Р {Хя+1 = 7 — 11 Хп = 7} = <7г;
Р {^п+1 ~ Л Хп — I} — г
изменения для 7 = 0 очевидны.
§ 2, Примеры марковских цепей
41
В пользу названия «случайное блуждание» для процесса та-
кого типа говорит тот факт, что его реализация описывает путь
«абсолютно пьяного» человека, делающего случайным образом
шаг вперед или шаг назад.
Капитал игрока, участвующего в серии партий азартной игры,
часто описывают процессом случайного блуждания. Предположим,
что игрок А, имеющий капитал k, играет с бесконечно богатым
партнером, при этом вероятность того, что он выиграет партию
и увеличит свой капитал на единицу, равна pht а вероятность того,
что он проиграет и тем самым уменьшит свой капитал на единицу,
равна qh = 1—pk(k^l). Зависимость вероятностей выигрыша и
проигрыша от k отражает возможную зависимость условий игры
от капитала. Так, можно условиться, что, оказавшись в состоянии О
(соответствующем разорению игрока А), процесс остается в этом со-
стоянии, т. е. /'о = 1. Процесс {Хп}, где Хп — размер капитала игро-
ка А после п партий, является процессом случайного блуждания.
Этот процесс известен под названием «задачи о разорении игрока».
Случайное блуждание с pk = Р, qk = 1 — р = q (k 1) и г0 = 1
соответствует одинаковым повторяющимся партиям; если р> q,
то в каждой партии шансы игрока А явно предпочтительнее.
В гл. 3 мы покажем, что в этом случае с вероятностью (qp)x\
где %о — его начальный капитал, игрок А разоряется (теряет свой
капитал) и с вероятностью 1 — (q!p)x* его капитал будет беспре-
дельно возрастать. Если же р < q, то игра явно выгодна хозяевам
игорного заведения, и почти наверное (с вероятностью 1) игрок А
разорится, если будет играть достаточно долго. Игрок А обречен
на разорение (с вероятностью 1) и в том случае, когда игра без-
обидна, т. е. когда ph = qk = Vs-
Если партнер, игрок Б, тоже начинает игру, располагая огра-
ниченным капиталом у, то капитал игрока А снова описывается
марковской цепью {Хп}. Однако эта цепь имеет конечное множе-
ство состояний 0, 1, ..., а, где а = х + у, хну — начальные со-
стояния игроков А и Б соответственно. Разность а — Хп интерпре-
тируется как капитал игрока Б после п партий. Если среди исхо-
дов каждой партии допускается ничья, то матрица переходных ве-
роятностей цепи {Хп} имеет вид
1 0 0 0 ............
q\ р{ о ............................
о q2 г2 р2 .........................
Уа — \ га~\ Ра-\
0 .............0 0 1
(2.3)
42
Гл. 2. Марковские цепи
Как и ранее, рг(рг), i = 1, 2, а—1, есть вероятность того,
что игрок А, имея капитал /, увеличит (уменьшит) его на единицу
в следующей партии. Отметим, что в соответствии с матрицей пе-
реходных вероятностей (2.3) капитал игрока А (состояние процес-
са), достигнув величины а или обратившись в 0, остается в этих
состояниях навсегда. Мы говорим, что игрок А разорен, если про-
цесс достиг состояния 0; если же процесс попадает в состояние а,
то мы говорим, что разорен игрок Б.
Случайные блуждания оказываются полезными не только для
описания игровых ситуаций, но и служат неплохими моделями фи-
зических процессов, в частности диффузии частиц. Если частица
претерпевает случайные столкновения, то ее положение подверже-
но случайным флуктуациям, хотя описываемая ею траектория не-
прерывна. Если будущее положение (точнее, его распределение ве-
роятностей) частицы зависит только от ее настоящего положения,
то процесс {XJ, где Xt — положение частицы в момент t, являет-
ся марковским. Дискретная аппроксимация такого непрерывного
движения соответствует случайному блужданию. Симметричное
случайное блуждание представляет собой классический дискретный
аналог броуновского движения (см. § 2 гл. 1). Под симметричным
случайным блужданием на множестве всех целых чисел подразу-
мевается марковская цепь с пространством состояний, являющимся
множеством всех целых чисел, с элементами матрицы переходных
вероятностей вида
р, если j = i + 1,
р, если j = i— 1,
Рц= I . .
1 г, если j = i,
0 во всех остальных случаях,
где р > 0, г > 0, 2р + г = 1 и /, / = 0, ±1, ±2, ... . Обычно сим-
метричным случайным блужданием называют марковскую цепь
с г = 0 и р = V2.
Исследование некоторых физических моделей приводит нас
к рассмотрению случайных блужданий на множестве неотрица-
тельных целых чисел. Можно дать классификацию таких процес-
сов на основе свойств нулевого состояния. Пусть случайное блуж-
дание описывается матрицей (2.2). Если р0 = 1 (а значит, и
го = 0), то нулевое состояние обладает свойствами отражающего
экрана. Всякий раз, когда частица достигает нулевого состояния,
в результате следующего перехода она оказывается в состоянии 1.
Это соответствует ситуации, когда в нуле находится упругая
стенка и частица отскакивает от нее без каких-либо остаточных
явлений.
Если ро = 0 и Го = 1, то нулевое состояние ведет себя как по-
глощающий экран. Попав в нулевое состояние, частица остается
§ 2. Примеры марковских цепей
43
в нем навсегда. Если ро > 0 и г0 > О, то нулевое состояние яв-
ляется частично отражающим экраном.
Если случайное блуждание ограничено конечным числом со-
стояний, скажем 0, 1, 2, ..., а, оба крайних состояния 0 и а не-
зависимо и в любой комбинации могут быть отражающими, погло-
щающими или частично отражающими экранами. Мы уже имели
дело со случаем, когда состояния 0 и а были поглощающими
[см. (2.3)].
Классическую модель диффузии через мембрану представляет
собой модель Эренфестов. Модель описывается как процесс слу-
чайного блуждания с конечным числом состояний (/ = —а,
—а + 1, ..., —1, 0, 1, ...,«), причем крайние состояния — а и а
являются отражающими экранами. Матрица переходных вероят-
ностей задается следующим образом:
а — i
2а
а + i
2а
О
если / = / + 1,
если j = i~ 1,
в остальных случаях.
Физическая интерпретация этой модели такова. Имеется две
урны А и Б, содержащие вместе 2 а шаров. Предположим, что
урна А содержит k шаров. При каждом испытании случайным об-
разом выбирается один шар и перекладывается в другую урну; при
этом каждый из шаров имеет равную со всеми остальными вероят-
ность быть переложенным независимо от того, в какой урне он
находится. Каждое испытание приводит к изменению состояния *)
системы. Характерным для перемещения шаров будет преимуще-
ственное направление от урны с большей концентрацией к урне
с меньшей концентрацией. Модель Эренфестов в некоторых слу-
чаях можно использовать для исследования физических систем,
находящихся под действием восстанавливающих сил, величина
которых пропорциональна расстоянию от положения равновесия.
Классическое симметричное n-мерное случайное блуждание
определяется следующим образом. ПространствОхМ состояний про-
цесса является целочисленная решетка в Еп (n-мерном евклидо-
вом пространстве), точки которой суть наборы из п целых чисел
вида к = (^1, k2,..., kn). Переходные вероятности определяются
следующим образом:
п
Pki= 2Л> если
О в противном случае.
’) Состоянием здесь является величина разности между числом шаров в
урне А и урне Б с учетом знака. — Прим, персе.
44
Гл. 2. Марковские цепи
Аналогично одномерному случаю n-мерное симметричное случай-
ное блуждание представляет собой дискретный аналог п-мерного
броуновского движения.
В. Дискретная марковская цепь, описывающая очередь
Заявки поступают к месту обслуживания и становятся в оче-
редь. Допустим, что обслуживание одной заявки занимает фикси-
рованное время (период), продолжительность которого принимает-
ся за единицу. Если к моменту окончания обслуживания заявки
очередь отсутствует, в следующий период обслуживания не про-
исходит. (Можно представить себе, например, стоянку такси, на
которую через одинаковые промежутки времени прибывают маши-
ны одна за другой. Если в очереди нет пассажиров, машина сразу
же уезжает.) Во время обслуживания некоторой заявки могут по-
ступить новые заявки. Предположим, что число заявок gn, посту-
пающих в течение n-го периода, является случайной величиной,
функция распределения которой не зависит от номера периода и
имеет вид
Р{за один период поступило k заявок} = P{£n = k} = ak, (2.4)
оо
fe = 0, 1,..., ak>0, 5^=1.
k=o
Мы предположим также, что с. в. независимы. Состояние си-
стемы в n-й момент времени определяется как число заявок, жду-
щих обслуживания к началу n-го периода. Если система находит-
ся в состоянии Z, то по прошествии одного периода она перейдет
в состояние
[ Z— 1 + L если /^1,
| I, если 1 = 0, (2-5)
где % — число поступивших за этот период заявок. В терминах
значений случайного процесса мы можем выразить (2.5) так:
X„+1 = (X„-1)+ + U (2.6)
где У+ = max (У, 0). В силу (2.4) И (2.5) матрица переходных ве-
роятностеи имеет вид
а0 «1 а2 «3 а4 ...
aQ «1 п2 «3 «4 •••
0 а0 а. а2 «з •••
1НМ = 0 0 а0 ai а2 ... (2.7)
0 0 0 а0 а, ...
£ 2, Примеры марковских цепей
45
Интуитивно ясно, что если среднее число новых заявок S kakt
k—Q
прибывающих за период, превышает единицу, то со временем оче-
редь будет беспредельно увеличиваться.
С другой стороны, если l^kak<l, то, как мы увидим, распре-
деление длины очереди приближается к некоторому равновесному
(стационарному) распределению. Если то возникает
существенно неустойчивая ситуация. Все эти утверждения будут
строго доказаны после того, как будет изложена теория рекуррент-
ных событий (см. § 5 гл. 3).
Г. Модель из теории запасов
Рассмотрим систему, в которой запасается некоторый товар
с целью удовлетворения постоянного спроса. Предположим, что
восполнение запаса осуществляется в моменты времени /2, .. .,
а суммарный спрос на товар в интервале tn) представ-
ляет собой случайную величину с распределением
P£n = k} = ak, £-0, 1, 2, (2.8)
одинаковым для всех интервалов, причем как обычно, 0 и
оо
2 а. = 1. Уровень запаса фиксируется в начале каждого периода.
Стратегия запасания такова: если имеющееся количество товара
не превышает некоторого критического уровня s, то производится
немедленное пополнение запаса до уровня S > s. Если же имею-
щееся количество товара больше $, то пополнения не производит-
ся. Пусть Хп обозначает уровень наличного запаса непосредствен-
но перед моментом tn. Пространство состояний процесса {Хп}
складывается из возможных значений уровня запаса
S, S — 1, ..., +1, 0, - 1, —2, ...,
где отрицательные значения интерпретируются как неудовлетво-
ренный спрос (эти заказы подлежат немедленному исполнению
при пополнении запаса). Согласно описанной стратегии, уровни
запаса двух последовательных периодов связаны соотношением
f если s<Xn^S,
Х„+1 = q / у (2-9)
lS-Un> если Xn<s, 7
где In — суммарный спрос за n-й период с распределением вероят-
ностей (2.8). Если предположить, что с. в. gn независимы, то уровни
запаса XQ, Х2, ... образуют марковскую цепь, матрицу пе-
реходных вероятностей которой можно вычислить, отправляясь
от соотношения (2.9).
46
Г л. 2. Марковские цепи
Д. Серии успехов
Рассмотрим марковскую цепь с неотрицательными целыми зна-
чениями и матрицей переходных вероятностей вида
Рй <7о 0 0 ...
Р1 0 0 ...
II Рц 11 = Р-2 0 0 q2 ... (2.10)
Pi 0 0 0 . . .
где qi > 0, pi > 0 и qi + pi = 1, i = 0, 1,2, ... . Нулевое состоя-
ние отличается от других тем, что оно может быть достигнуто из
всех остальных за один переход, тогда как состояние i + 1 дости-
жимо только из состояния
Этот пример очень прост с вычислительной точки зрения, и мы
будем часто к нему обращаться для иллюстрации вводимых поня-
тий и получаемых результатов.
Частный случай матрицы переходных вероятностей (2.10) опи-
сывает серию повторяющихся испытаний, имеющих два возмож-
ных исхода — успех (У) и неудача (Н). В каждом испытании ве-
роятность успеха равна а, а вероятность неудачи р=1 — а. Мы
будем говорить, что на n-м испытании реализовалась серия успе-
хов длины г, если последние г + 1 испытаний, включая п-е,
имели своими исходами последовательность НУУ...У. Мы будем
отмечать состояние процесса длиной серии успехов, реализовав-
шейся на последнем испытании. В частности, если исходом по-
следнего испытания была неудача, то процесс находится в нуле-
вом состоянии. Если же исходы предшествующих г + I испытаний
дали последовательность НУУ...У, то переменная состояния будет
помечена индексом л Такой процесс, очевидно, является марков-
ским (поскольку каждое испытание было независимо от всех
остальных), а его матрица переходных вероятностей имеет
вид (2.10), где
= n = 0, I, 2, ....
Е. Ветвящиеся процессы
Предположим, что организм в конце своего времени жизни
производит случайное число I потомков согласно распределению
вероятностей
P{l = k} = ak, k = 0, 1,2............. (2.11)
оо
где, как обычно,ak^Q и2^ = 1- В свою очередь потомки не-
k=0
зависимо друг от друга в конце своего времени жизни (для про-
§ 2. Примеры марковских цепей
47
стоты продолжительность жизни предполагается одинаковой для
всех организмов) производят потомство, каждый в соответствии
с распределением (2.11), продолжая таким образом свой биологи-
ческий вид. Процесс {Хп}, где Хп— численность популяции в п-м
поколении, представляет собой марковскую цепь.
В самом деле, в конечномерном распределении случайных ве-
личин ХП{, ХП2, ..., ХПг, Хп, п}<п2< ... <пг<п, существенны
лишь данные последней переписи популяции, поскольку число по-
томков является функцией числа непосредственных предков и
только. Матрица переходных вероятностей, очевидно, определяет-
ся соотношением
Ри-Р{Хп+г-ПХп~1} = Р{Ъ+ ... +^ = /}, (2.12)
где |1, ..., li — независимые наблюдения с. в., имеющей распре-
деление (2.11). Формулу (2.12) можно объяснить следующим об-
разом. Независимо друг от друга i индивидуумов, составляющих
ti-е поколение популяции, производят потомство (/-й — в коли-
честве gi). Следовательно, общее число потомков равно gi + +
+ ... + |г-
Мы знаем, что производящая функция суммы + Ь + • .. +
равна [?($)]*, где g — производящая функция распределения ве-
роятностей с. в. (Мы опираемся здесь на свойство композиции
производящих функций для случая суммы независимых с. в. См.
§ 1 гл. 1.) Следовательно, Pij является коэффициентом при /-й
степени в степенном разложении функции [£($)]*.
Ж. Марковские цепи в генетике
Следующая идеализированная генетическая модель была
предложена С. Райтом для исследования флуктуаций частот ге-
нотипов под влиянием мутаций и отбора. Начнем с так называемой
простой гаплоидной модели случайного воспроизведения, в которой
не учитываются действие мутационного процесса и силы отбора.
Предположим, что мы имеем дело с популяцией фиксированного
объема, состоящей из 2N индивидуумов типов а и А. Состав сле-
дующего поколения определяется результатом 2N испытаний Бер-
нулли; а именно: если родительская популяция состоит из j генов
типа а и 2N—j генов типа Л, то вероятности появления гена а
или гена А при каждом испытании соответственно равны
^=2ЛГ’ = 1 ~ 2N ’
что эквивалентно случайному выбору с возвращением. Эта про-
цедура описывается марковской цепью {Хп}, где Хп — число я-ге-
нов в n-м поколении популяции, размер которой остается неизмен-
ным от поколения к поколению. Пространством состояний цепи
48
Гл. 2. Марковские цепи
является набор из 2N + 1 чисел {0, 1, 2, ..., 2N}. Элементы
матрицы переходных вероятностей вычисляются в соответствии
с биномиальным распределением:
P{Xn+l = k\Xn = j} = Plk^^)p^-\ j, fe = 0, 1, .... 2N. (2.13)
Биологическое обоснование этой модели обсуждается в книге
Р. Фишера 9 (см. также гл. 13).
Отметим, что состояния 0 и 2N являются поглощающими в том
смысле, что если Хп = 0 или 2N, то и Хп+ь = 0 или 2N соответ-
ственно для всех & >0. Один из интересующих нас вопросов —
это определение вероятности того, что популяция в каком-либо
поколении, а значит и во всех последующих, будет целиком со-
стоять из индивидуумов одного типа (произойдет «фиксация») а
или А при условии, что Хо = i. Представляет интерес также ско-
рость приближения к такому состоянию. Эти и связанные с ними
вопросы будут изучены при общем анализе вероятностей погло-
щения.
Более реалистичная модель учитывает мутационное давление.
Предположим, что прежде, чем будет образовано новое поколе-
ние, каждый ген имеет возможность мутировать, т. е. превра-
титься в ген другого типа. Точнее, мы предположим, что для всех
генов типа а вероятность мутации а-* А равна аь а для генов
типа А вероятность мутации А -> а равна аг. Как и ранее, будем
считать, что состав каждого следующего поколения определяется
результатом 2N испытаний Бернулли. В том случае, когда роди-
тельская популяция содержит / генов типа а, соответствующие ве-
личины pi и qi имеют вид:
Pi^ --ai)4-(l “ 2дг)а2,
/ / / \ (2.14)
2N 1 2N /
Суть дела состоит в следующем: согласно этой модели, сперва дей-
ствует мутационный процесс, после чего тип каждого гена сле-
дующего поколения определяется случайным выбором (с возвра-
щением) из родительской популяции. Вероятность выбора я-гена
из популяции, подвергшейся действию мутационного процесса, рав-
на числу a-генов в этой популяции, умноженному на V2Af; поэтому
средняя вероятность (усредненная по возможным мутациям) есть
произведение среднего числа a-генов после мутаций на V2N. Но
это число, очевидно, равно /(1—ai) + (2N — /)а2, что и приводит
к (2.14).
!) R. A. Fischer, The Genetical Theory of Natural Selection, Oxford (Claren-
don) Press, London New York, 1962.
§ 2. Примеры марковских, цепей
49
Переходные вероятности соответствующей марковской цепи вы-
числяются по формулам (2.13) с использованием величин pj и qj
из (2.14). Если ось аг > 0, то система не фиксируется ни в одном
из состояний. При п —> оо распределение вероятностей с. в. Хп
стремится к распределению некоторой случайной величины g:
2N
P{% — k} = nk, k = 0, 1, .2N, S nk = 1, л/е>0.
&=0
Это распределение называется стационарным распределением ча-
стот генотипа в популяции.
Рассмотрим простую модель случайного скрещивания и введем
понятие силы отбора, действующей, скажем, в пользу «-генотипа.
Предположим, что мы хотим определить селективное преимуще-
ство «-гена над Л-геном так, чтобы математические ожидания от-
носительного числа потомков были пропорциональны 1 + s и 1
соответственно. Заменим величины pj = j/2N и qj = 1 — j!2N на
(1 + s) j <
Pi =: •" и Qi ~ 1 ~ Pi
2N + sj 77
и определим состав следующего поколения, как и прежде, с по-
мощью испытаний Бернулли. Если родительская популяция со-
держала / генов типа «, то в следующем поколении средние зна-
чения числа генов типа а и числа генов типа А равны соответ-
ственно
2Л/ и 2N ^~i) .
2N + sj 2N + sj
Отношение среднего числа «-генов к среднему числу /4-генов
в (п 4- 1)-м поколении равно
1 4- s /’ _ / 1 + s \ / число fl-генов в /г-м поколении
1 2N — j \ 1 ) \ число Д-генов в n-м поколении
Это соотношение поясняет сущность действия отбора.
3. Генетическая модель II
Ген состоит из некоторого числа, скажем, N элементарных еди-
ниц. Прежде чем клетка, содержащая ген, начнет делиться, каж-
дая из этих единиц удваивается, и каждая из двух «дочерних»
клеток получает ген, состоящий из того же количества элементар-
ных единиц, что и ген «материнской» клетки. Одна или несколько
единиц могут быть в мутантной форме. Предполагается, что в про-
цессе удвоения гена каждая мутантная единица превращается
в две мутантные единицы, а каждая немутантная единица — в две
немутантные. Кроме того, мы предполагаем, что после удвоения
50
Гл. 2. Марковские цепи
эти единицы распределяются между двумя новыми генами случай-
ным образом, как если бы они извлекались из урны. Мы будем
следить за судьбой потомков только по одной линии, а не за всей
популяцией. Чтобы описать генетическую историю этой линии, рас-
смотрим марковскую цепь, пространство состояний которой обра-
зовано числами 0, 1, .. . , N. Мы будем говорить, что ген нахо-
дится в состоянии Z, если он содержит i мутантных и N — i нему-
тантных единиц. Переходные вероятности цепи вычисляются по
формуле
/ 2i \ ( 2N - 2Z \
Это выражение для Рц получено следующим образом. Предполо-
жим, что родительский ген находится в состоянии тогда после
удвоения мы получим набор из 21 мутантных и 2N — 21 немутант-
ных единиц. Для того чтобы образовать дочерний ген, из этого на-
бора извлекаются N произвольных единиц. В соответствии с ги-
пергеометрическим распределением вероятность того, что дочерний
ген окажется в состоянии /, определяется формулой (2.15).
Состояния j = 1,2, ..., N—1 называются смешанными, а со-
стояния 0 и N — чистыми. Состояние N интересно тем, что ген, все
элементарные единицы которого мутантны, может принести смерть
своему обладателю, в то время как ген, находящийся в состоянии
0, при делении не порождает мутантных генов. Позже мы вычис-
лим в явном виде вероятности того, что ген из состояния i попа-
дает в состояние 0 или N.
§ 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
Марковская цепь полностью определяется своей матрицей од-
ношаговых переходных вероятностей и заданием распределения
вероятностей состояния процесса в момент времени 0. Анализ мар-
ковской цепи связан главным образом с вычислением вероятно-
стей возможных ее реализаций, важнейшей характеристикой кото-
рых является матрица вероятностей переходов за п шагов
Р(п) = || ||. обозначает вероятность того, что процесс перей-
дет из состояния i в состояние / за п переходов, или, в принятых
ранее обозначениях,
Р"; = Р{Хл + т = j\Xm=i}. (3.1)
Заметим, что мы имеем дело только с процессами, однородными
во времени, т. е. с процессами, имеющими стационарные переход-
ные вероятности; в противном случае правая часть в (3.1) зави-
села бы от fn.
$ 3. Матрицы переходных вероятностей
51
Марковское свойство процесса позволяет выразить (3.1) непо-
средственно через ИЛЛ, как это видно из следующей теоремы.
Теорема 3.1. Если Р = || Pi3 II — матрица одношаговых пере-
ходных вероятностей марковской цепи, то
рпа = 2 PrikPki
/г —О
(3.2)
для любой фиксированной пары неотрицательных целых чисел г
и s, такой, что г 4- s = п; при этом по определению
p'ii =
1,
о,
если i = /,
если i¥=j-
В формуле (3.2) нетрудно узнать формулу умножения матриц
(см. приложение). Отсюда следует, что Р<п) = Рп; другими сло-
вами, вероятности Pq можно рассматривать как элементы мат-
рицы Рп — п-и степени матрицы Р.
Доказательство. Рассуждения проведем для случая
п = 2. Событие, состоящее в переходе из состояния i в состояние
/ за 2 шага, может произойти любым из следующих взаимно ис-
ключающих друг друга путей: на первом шаге — переход в неко-
торое промежуточное состояние k (k — 0, 1, 2, ...), затем, на вто-
ром шаге, переход из состояния k в состояние /.
Так как процесс марковский, то вероятность второго перехода
равна Pkj, а первого — Рц{. Воспользовавшись формулой полной
вероятности, приходим к (3.2). Рассуждения в общем случае точно
такие же.
Если вероятность того, что процесс в начальный момент нахо-
дится в состоянии /, равна pj, то вероятность оказаться в состоя-
нии k в момент п равна
й-’-ДрЛ-РИ.-Ч- м
Помимо определения совместных распределений вероятностей
процесса для всех моментов времени, что, кстати, обычно является
очень трудной задачей, часто интерес представляет выяснение
асимптотического поведения вероятностей Рц при п—* оо. Можно
ожидать, что влияние начального состояния со временем умень-
шается, а, следовательно, Л/ стремится при п -> оо к пределу,
52
Гл. 2. Марковские цепи
не зависящему от i. Для того чтобы дать точный анализ асимпто-
тического поведения марковской цепи, мы введем классификацию
ее состояний.
§4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
Говорят, что состояние j достижимо из состояния г, если Р?/>0
для некоторого целого числа п 0, т. е. вероятность того, что
процесс за конечное число шагов попадает в состояние /, отправ-
ляясь из состояния /, положительна. Состояния i и /, достижимые
друг из друга, называют сообщающимися; этот факт обозначают
i <-> /. Если два состояния i и / не сообщаются, то либо Рпц = О
для всех п 0, либо Рпц = 0 для всех п 0, либо оба условия
выполняются одновременно. Свойство сообщаемости представляет
собой отношение эквивалентности. Действительно:
(i) / / (рефлексивность), так как по определению имеем
о ( 1, Z = /
р" = Чо,
(ii) если i <-> j, то / i (симметричность), согласно определе-
нию сообщающихся состояний;
(iii) если i / и / fe, то i <-> k (транзитивность).
Транзитивность доказывается следующим образом. Из i / и
/ k следует, что существует пара неотрицательных целых чисел
пит, таких, что Р?;>0 и Р^>0. Следовательно, в силу (3.2) и
неотрицательности всех Р*Г8 имеем
оо
г=0
Аналогично показывается существование целого числа v, такого,
что Рь->0.
Из этого следует, что все множество состояний можно разбить
на классы эквивалентности. Состояния объединяются в один класс,
если они сообщаются друг с другом. Возможно, что, отправляясь
из состояния, принадлежащего одному классу, мы с положитель-
ной вероятностью попадаем в другой класс, но тогда, очевидно,
возврат в исходный класс уже невозможен, так как иначе оба
упомянутых класса входили бы в один класс эквивалентности. Мы
будем говорить, что марковская цепь неприводима, если введен-
ное нами соотношение эквивалентности порождает только один
класс состояний. Другими словами, процесс неприводим, если все
его состояния сообщаются друг с другом.
§ 4. Классификация состояний марковской цепи
53
Для иллюстрации стей вида рассмотрим матрицу переходных вероятно-
1 2 1 2 0 0 0
1 4 _3 4 0 0 0 р' 0II
Р =•• 0 0 0 1 0 0 Р2|г
0 0 1 2 0 1 2
0 0 0 1 0
Состояния марковской цепи, имеющей такую матрицу переходных
вероятностей, распадаются на два класса сообщающихся состоя-
ний: {1, 2} и {3, 4, 5}. В зависимости от начального состояния про-
цесс развертывается либо только в первом классе состояний и его
переходы описываются подматрицей Рь либо только во втором
классе и его переходы описываются подматрицей Р2.
В марковской цепи процесса случайного блуждания с матри-
цей переходных вероятностей
состояния
1 0 0 0 ... О О О О
q 0 р 0 ... О 0 0 1
О <7 0 р ... О 0 0 2
О ...............q 0 р а — 1
О.................0 0 1 а
мы имеем три класса состояний: {0}, {1, 2, ..., а— 1} и {а}. Оче-
видно, что из второго класса можно попасть и в первый и в тре-
тий классы, но возвратиться из них во второй класс невозможно.
Марковская цепь, описывающая процесс образования очереди
в примере В из § 2, неприводима, если ak > 0 при всех k. Легко
проверить, что при этом же условии неприводима и марковская
цепь из примера Г. Если qi > 0, Pi > 0 (i = 0, 1, ...), то марков-
ская цепь серий успехов (пример Д) также неприводима.
Периодичность марковской цепи
Определим период состояния /, далее обозначаемый d(z), как
наибольший общий делитель (н.о.д.) всех целых чисел /г>1, для
которых Рпц>$. (Если Р"/==0 при всех то по определению
54
Г л. 2. Марковские цепи
d(i) = 0.) Если в матрице переходных вероятностей (2.2) случай-
ного блуждания все = 0, то период каждого из состояний цепи
равен двум. Если же хотя бы для одного состояния iQ величина rio
больше нуля, то все состояния цепи имеют период 1, так как неза-
висимо от начального состояния / система может попасть в состоя-
ние iQ и оставаться в нем в течение произвольного времени прежде,
чем вернуться в состояние /.
В конечной марковской цепи с п состояниями и матрицей пере-
ходных вероятностей
0 1 о о ... о
0 0 1 о ... о
0 0 .... 1
1 о о ... о
каждое состояние имеет период п.
Приведем без доказательства три основных свойства периода
состояния (см. задачи 5—7 в конце главы).
Теорема 4.1. Если i /, то d(i) = d(j).
Это утверждение определяет период как характеристику класса
сообщающихся состояний.
Теорема 4.2. Если состояние i имеет период d(i), то суще-
ствует целое число N, зависящее от I, такое, что для всех целых чи-
сел n>N вероятность
Этим утверждается, что возвращение в состояние i может про-
исходить во все достаточно далекие моменты времени, кратные
периоду d(i).
Следствие 4.1. Если Р™>0, то p™+ndW>o дЛЯ всех до-
статочно больших положительных целых чисел п.
Марковская цепь, каждое состояние которой имеет период 1,
называется непериодической. Большинство марковских цепей, рас-
сматриваемых нами, относятся к классу непериодических. Резуль-
таты будут в основном доказываться именно для этого случая;
для общего же случая мы обычно будем ограничиваться их фор-
мулировками. Трудолюбивый читатель сможет легко провести до-
казательство самостоятельно
§ 5. Возвратность
55
§ 5. ВОЗВРАТНОСТЬ
Рассмотрим произвольное, но фиксированное состояние с По-
ложим для каждого целого числа п 1
X^i, v-1, 2, ... n-qx.-i).
Другими словами, есть вероятность того, что, отправляясь из
состояния I, система впервые возвратится в это состояние через п
переходов. Ясно, что }Н=РН, a можно вычислить рекуррент-
но в соответствии с формулой
р",~«я. (5.1)
где, согласно определению, /?. = 0 для всех i. Соотношение (5.1)
выводится следующим образом. Рассмотрим все возможные реа-
лизации процесса, для которых Хо = i, Хп = ц а первое возвраще-
ние в состояние i происходит на fe-м шаге. Обозначим это событие
символом Eh. События Ek (fe = 1, 2, ..., и), очевидно, являются
несовместными. Вероятность события, состоящего в том, что пер-
вое возвращение происходит на k-м шаге, есть, согласно опреде-
лению, fku. Рассмотрим теперь те реализации, которые в течение
оставшихся п — k шагов ведут себя так, что Хп = I. Используя
марковское свойство, имеем
P{Ek} = Р {первое возвращение происходит на k-м шаге | Хо -= /} X
хри.
(напомним, что Р°ц=1). Следовательно,
п п п
р - -к - <) = s р (е.) - 2 /?,р"г*=М
г2 == 1 k *" 1 Л О
поскольку по определению /9. = 0.
Введем теперь производящие функции.
Определение. Производящая функция Л?($) последователь-
ности {Pih п = 0, 1, 2, ...} задается формулой
P,/(s)= 2 P?/sn, |s|<l. (5.2)
n — Q
Аналогично определяется производящая функция последователь-
ности п — 0, 1, 2, ...} (определение вероятностей f", для
56
Г л. 2. Марковские цепи
случая, когда i 4= h следует ниже непосредственно за формулой
(5.9)):
|s|<l. (5.3)
Мы уже приводили (см. стр. 16 гл. I)1) следующее свойство
производящих функций:
если
A ($) = 2 aksk и В ($) = 2 bis1, (5.4)
k=Q Z=0
TO
A (s) В (s) = C (s) = S crsr, |s|<l, (5.5)
r=0
где
cr = a^br + axbr_x + ... +агЬц. (5.6)
Если ak положить равными fka, a bt равными P'u, то из (5.1) и
(5.6) следует, что
Fzz(s)Pzz(s) = Pzz(s)-l, |s|<1, (5.7)
или
= |S|<1. (5.8)
В (5.7) единица вычитается потому, что (5.1) не выполняется
при п — 0.
Точно так же, как мы получили соотношение (5.1), приходим
к соотношению
п
Р'^ЖР^, п>0, (5.9)
fe=0
гДе fkij есть вероятность того, что процесс впервые достигнет со-
стояния / из состояния i на й-м шаге. Как и ранее, полагаем
= 0 для всех i и /. Из (5.9) и (5.5) получаем
Pz/(s) = Fz/(s)Pz/(s), | s |< 1. (5.10)
9 A (s) В ($) =[ 2 aks л 2 £/)==
\/г=0 / \/=0 /
= aQbQ + (ajbo + Ь^о) s + (л260 + а^ - а0^2) $2 + . • • “
$ 5. Возвратность
57
ОО
Будем называть состояние i возвратным, если 2f^=r=l- Это
означает, что состояние i является возвратным тогда и только
тогда, когда вероятность вернуться в исходное состояние i после
оо
некоторого конечного числа шагов равна единице. Если 2 Гц < 1,
п = 1
то состояние i будем называть невозвратным. Ниже мы докажем
теорему, связывающую свойство возвратности состояния с поведе-
нием гг-шаговых переходных вероятностей Рр> Для доказатель-
ства этой теоремы нам понадобится следующая
Л е м м а 5.1 (Абель).
оо
(а) Если ряд 2 CLk сходится, то
£=0
Нт 2 aksk = ^ak~a (5.11)
fe=o k—0
(lim означает, что s стремится к 1 слева, т. е. по значе-
1
ниям, меньшим 1).
оо
(б) Если ak^0 и lim 2 aksk = а<оо, то
s>M /г=0
ОО N
2 ак = lim 5 ak = а.
&=() у-»со ьо
Доказательство, (а) Мы покажем, что
lim
оо
3 ak (sk- 1)
£==0
= 0.
(5.12)
Поскольку ряд 2 CLk
fc=0
N'
N (в), такое, что 2
k—N
Далее,
сходится, то для
ak <&/4 всех
любого е>0 можно найти
Выберем такое N.
оо
3 «*(«* “ О
&=0
N
2 ak(sk- 1)
/г«0
2 ak(sk- 1) .
k^N+1
(5.13)
+
58
Гл. 2. Марковские цепи
Для 0 ^з< 1
N
2 aft(sft- 1)
/г=0
< W|s*- 1 |,
(5.14)
где Л4= max | ak |< оо, так что для $, достаточно
0</2<tf
близких к 1,
имеем
л/
S ak(sk- 1)
£=0
<е/2.
оо
Для оценки 2 ^($*—1) просуммируем по частям:
fe=W+l
2 a*(sfe-l)
k=N + l
S (Л-Л+Ж-1) =
&=ЛГ+1
= ^v + 1(s"+1-l)- 2 Ak(sk — sk+1) , (5.15)
k—N+2
где Ak=^ar. Легко видеть, что для (5.15) имеет место оценка
Г = /2
||(з"+1-1)| + |з"+1<|.
Вместе с предыдущей оценкой это дает
5 ak(sk- 1)
/2 = 0
< е
при условии, что <$ достаточно близко к 1.
оо оо
(б) Поскольку 2 aksk^ 2 для 0<s< 1, случай а = оо оче-
/г=0 /2=0
виден. Если а<оо, то в силу исходного предположения имеем
оо
aksk < а < <х> rjih. 0<$<1,
/2=0
а значит, и
оо
/2=0
для всех п.
п
Кроме того, У ак является монотонно возрастающей функцией п.
к=0
оо
Таким образом, ряд 2 сходится. Пусть сумма ряда равна а',
/2=0
Обращаясь к первой части леммы, получаем, что af = а, В
£ 5. Возвратность
59
С помощью этой леммы легко доказывается
Теорема 5.1. Состояние i является возвратным тогда и
только тогда, когда
оо
2 РПц--= оо.
Доказательство. Пусть z — возвратное состояние, т. е.
оо
2/7.= 1- В силу леммы 5.1(a) имеем
п=0 “
ОО
lim 2 Гц5п = lim F.. (s) = 1;
n=0
тогда из (5.8) следует, что
lim Рц (s) = lim 2 РиЗп — оо.
Обращаясь к лемме 5.1(6), заключаем, что
ОО
2 Ph =
п—0
Чтобы доказать достаточность, предположим, что состояние i не-
оо
возвратное, т. е. Используя лемму 5.1(a) и соотноше-
п~ 1
ние (5.8), получаем
lim PH(s)< оо.
1
оо
Отсюда в силу леммы 5.1(6) следует, что 2^и<°°-
п — 1
Из теоремы 5.1 непосредственно вытекает
Следствие 5.1. Если ij и i — возвратное состояние, то
состояние j также является возвратным.
Доказательство. Так как то существуют такие
целые числа tn, п 1, что
Р?/>0 и Р^>0.
Пусть v — положительное целое число. С помощью аргументов,
к которым мы уже прибегали (см. стр. 52), нетрудно получить не-
равенство
PH+n+v > PTiPlPh.
60
Гл. 2. Марковские цепи
Суммирование по v дает
оо оо оо
2 2 pmpv^^ = рпг.р^ 2 pv .
v=u v=0 v=0
оо
Таким образом, если 2 Ри расходится, то расходится и
v=0
оо
2 р1,-
V = 0
Доказав это следствие, мы установили, что возвратность, как
и периодичность, является свойством класса эквивалентности, т. е.
все состояния в классе эквивалентности либо возвратны, либо
невозвратны одновременно.
§ 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
Пример 1. Рассмотрим одномерное случайное блуждание
по одномерной целочисленной решетке. За каждый переход ча-
стица с вероятностью р перемещается на единицу вправо и с ве-
роятностью q — на единицу влево (р + q = 1); следовательно,
имеем
Роо =0, Роо = п )Р q ==:'^гР q , я = 0, 1, 2, .. .. (6.1)
Воспользуемся формулой Стирлинга
п\ ~ 2е~п У2л (6.2)
и запишем (6.1) в виде
Р2п ~ (4Р^п
00 У ЛП У' лп
Легко проверить, что р(1—р) = pq <Л/4, причем равенство имеет
место тогда и только тогда, когда р = q = V2. Следовательно,
оо
S Роо= 00 тогда и только тогда, когда р ~ х)2. Таким образом, од-
номерное случайное блуждание возвратно тогда и только тогда,
когда р = q = V2. (Вспомним, что возвратность является свойством
класса!) Интуитивно ясно, что если рфц, то положительна ве-
роятность того, что частица, отправляясь из начала координат,
будет смещаться к + оо, если р > q (к — оо, если р < q), ни разу
не возвращаясь в исходное состояние.
Пример 2. Обратимся теперь к двумерному случайному
блужданию по двумерной целочисленной решетке. Пусть вероят-
ности смещения на единицу влево, вправо, вверх, вниз — все рав-
§ 6. Примеры возвратных марковских цепей
61
ны 1/4. Как и ранее, будем исследовать возвратность состояния,
представляемого началом координат. Рассмотрим все траектории,
состоящие из I перемещений вправо, i перемещений влево, / пере-
мещений вниз и / перемещений вверх, 2i + 2/ = 2п. Легко убе-
диться, воспользовавшись полиномиальным распределением, что
___ V (М! Ш2П
00 a a ji ji \ 4 J ’
г. /. i + j=n
п=1, 2, 3, ..
м = 0, 1, 2, ....
(6.3)
Умножая числитель и знаменатель в правой части (6.3) на (я!)2,
получаем
п
г = 0
но
Следовательно,
п
(п\( п \
\ i ) \ п — i) \ п
i = Q
Формула Стирлинга (6.2) дает
Таким образом, 2^оо=°°и состояние, представляемое началом
координат, является возвратным.
Пример 3. Рассмотрим теперь симметричное случайное блу-
ждание по трем измерениям. Аналогично предыдущему легко убе-
диться, что Роо+1 = О, п = 0, 1, 2, ...,
о ьэ О» II :М (2ч)! ( П2« (6-4) /!/!/!/! (п — i — j)l (п — i — j)! \ 6 / ’ ’ ’
i, I, Q<i + j^n
Умножая числитель и знаменатель на (я!)2 и выделяя сомножи-
тель (!/2)2п, получаем
•2п - 1 12п\ V Г I2 (±\2п
00 ~ 22п ( п / . [/! /! (n — i — j) I J Ь/
F°° С п 22п (я / Зп ’
(6.5)
(6.6)
62
Гл. 2. Марковские цепи
где
Г п\
шах -7Г-77-7------------:---7ГТ
i, j, 0<Z + /<nL *! j! (n — I — /)!
Здесь мы воспользовались тем фактом, что
у _____________________пЛ___________
П /! (п ~ i — /)! \3/
i, Г
(6.7)
(6.8)
Для больших п значение сп достигается при i = j ~ п/3. Действи-
тельно, пусть /о и /о — те значения i и /, на которых достигается
максимум выражения
____п!___
i\ j! (n — i— /)!
при 0<л + / ^ ft. Сразу же можно выписать следующие четыре
неравенства:
п\<nl.
/о! Go “ 1)! (п - /о - io + 1)! /о! 'о! (п ~ /о - «о)! ’
rt!<п!.
jo! (г'о + О! (п — /о ~ io 1)! ]о- *о! (п /о ~ й>)1 ’
п! <п!е
(/о-1)1'о1(л-/о~<о+1)! /о! V (« ~ /о ~ io)! ’
________п!______________п!________________
(/о+ 1)1 «о! («-/о ~'о - О! '''• /о! i0! (п- j0- /0)!
Эти неравенства сводятся к следующим двум:
п —10 — 1 «С 2/0 «С п — i0 + 1,
« - /о “ 1 < 2io < п - /о + 1.
Следовательно, io ~ »/3 и /о ~ и/3 при больших п. Подставляя
в (6.7), преобразуем (6.6) к виду
р2п <______________п!___________/2п\
00 (п/3)! (п/3)! (п/3)! 22пЗп \ и /
(6.9)
Воспользовавшись- формулой Стирлинга, для правой части (6.9)
получаем следующее асимптотическое выражение:
3/3
2nV ’
Суммируя такие члены, получаем
3/3
2Л%
ОО.
$ 6. Примеры возвратных марковских цепей
63
Следовательно, 2 Роо<°°, и в силу теоремы 5.1 состояние, пред-
ставляемое началом координат, является невозвратным. Поскольку
возвратность — свойство класса, а все состояния сообщаются, ча-
стица, совершающая одно- или двумерное симметричное случай-
ное блуждание, с достоверностью вернется во всякое состояние,
в котором она когда-либо пребывала. В трехмерном симметрич-
ном случайном блуждании частица, покинув состояние, с положи-
тельной вероятностью не вернется в него никогда.
Пример 4. Рассмотрим марковскую цепь, описывающую се-
рии успехов при биномиальных испытаниях. Матрица переходных
вероятностей этой цепи имеет вид
Po 1 “Po 0 0
Pl 0 1 - Pi 0
P'2 0 0 1 -p2
(0<р»<1).
Рг 0 .......................
1 - Рг 0 . . .
Состояния цепи образуют единственный класс эквивалентности
(всякое состояние цепи можно достичь из любого другого состоя-
ния). Поэтому в силу следствия 5.1 нам достаточно исследовать
возвратность одного состояния, например нулевого. Имеем
/оо Ро 1 О Ро)>
(п — 2 \
П (1 ~ Pi) I Рп-1,
i—О /
П> 1.
(6.10)
Уравнения (6.10) можно переписать в виде
С=П(1 -(1 ~P„-i)L »>!•
^оо = (1 - Ро)(1 - Pl) ... (1 - р„-2)-(1 — Ро)(1— р{).. .(1 - pn-i), п> 1.
Положим
( (1 -Ро)(1 - Pl) ••• (1 -Рп), »>0,
Un~[ 1, и= - 1.
Теперь если мы просуммируем вероятности то получим
m+1 m+l
2 /оо = 2 (ип—2 Щп — l) (1 «о) “Ь («0 ^1) “F • • • “F (Um-1 ^m)>
n=l n = l
64
Гл. 2. Марковские цепи
или
т+1
(6.11)
П = 1
Для завершения наших рассуждений полезной окажется сле-
дующая
т
Лемма 6.1. Если 0<р{< 1 (/ = 0, 1, 2,...), то ит = Ц(1 -Р/)->0
1=0
оо
при т~>оо тогда и только тогда, когда 2р/ = о°-
Доказательство. Предположим, что 2р/ = °°. Так как
;=о
степенное разложение • функции ехр(— Р/) представляет собой
знакопеременный ряд с уменьшающимися по абсолютной величине
членами, то справедливо неравенство
2 3
l_p.<l_p. + Zl_ Zl+ ... — exp(—pi), / = 0,1,2,... (6.12)
m / m \
Так как (6.12) выполняется при всех I, то Ц (1 — pz)<exp( — 2 Pt/•
Z=0 \ z=0 /
m
Но по предположению lim 2р( = °°; следовательно,
m->oo z=0
m
lim П(1-р<) = 0.
m->oo j=0
Для доказательства необходимости воспользуемся следующим
легко выводимым неравенством:
m
П(1 -Pi)>(j -Pj-Pi+i- ... -pm),
i /
справедливым при всех j и m = / + l, / + 2, .... Предположим
оо оо
теперь, что 2р/<°°; тогда 0<2р{-<1 при некотором /. От-
i—i i=j
сюда следует, что
m f m \
lim П (1 - Pi)> Um 1 - 5 Pt >0.
m->oo i=j m~^oo\ i = j /
Это противоречит предположению о том, что И
Возвращаясь к (6.11) и применяя лемму 6.1, заключаем, что
оо оо
2/оо = 1 тогда и только тогда, когда 2 °°> или, что то же
n=l i=o
§ 7. Еще о возвратности
65
самое, состояние 0 возвратно тогда и только тогда, когда ряд
оо
S pi расходится.
/=0
Заметим попутно, что для любого набора положительных чи-
оо
сел {6Zi, а2, такого, что az>0, S 1, можно построить
марковскую цепь только что рассмотренного вида, причем вели-
чины Pi будут такими, что %о~ап. Действительно, положим
foo ~ Ро~ а1> /оо = 0 ~ Ро) Pi “ а2>
откуда получаем
Пусть
/оо= 0 ~ Ро) 0 - Pi) Pi ж
тогда
—•
I — а{ — а2
Продолжая аналогичным образом, мы получим явные выражения
для величин рг-, причем 0 < Pi < 1.
§ 7. ЕЩЕ О ВОЗВРАТНОСТИ
Теорема, которую мы сейчас докажем, утверждает, что если
некоторое состояние возвратно, то это состояние с вероятностью 1
встречается в процессе бесконечное число раз. Пусть
__р( частица, отправляясь из состояния /, 1
возвращается в него бесконечно часто J*
Теорема 7.1. Состояние i возвратно или невозвратно в зави-
симости от того, Qu = 1 или Qu = 0.
Доказательство. Положим
— частица, отправляясь из состояния Z, 1
возвращается в него по крайней мере N раз /•
Имеет место соотношение
оо оо
где =
Я=1 k—i
в справедливости которого нетрудно убедиться, представляя собы-
тие, фигурирующее в правой части предыдущего соотношения,
з Зак. 939
66
Г л. 2. Марковские цепи
в виде суммы несовместных событий, определяемых временем пер-
вого возвращения. Последовательно применяя последнюю фор-
мулу, получаем
QJ-W-(CT«?r2=
Но, очевидно, Q\. = /*.; следовательно,
эд -
Поскольку lim = Qi{, то Ql{ = 1 или 0 при f*{{ = 1 или < 1 со-
#->оо
ответственно, или, что эквивалентно, в зависимости от того, яв-
ляется ли состояние i возвратным или невозвратным.
Теорема 7.2. Если i / и оба состояния принадлежат воз-
вратному классу, то
Мы опускаем простое доказательство этого факта.
Пусть
п частица, отправляясь из состояния Z, будет 1
бесконечное число раз находиться в состоянии / J
Из теоремы 7.2 непосредственно вытекает
Следствие 7.1. Если i j и оба состояния принадлежат
возвратному классу, то = 1.
Доказательство. Нетрудно видеть, что
Поскольку состояние / возвратно, то Qjj = 1 по теореме 7.1. По
теореме 7.2 имеем = 1, следовательно, Qij == 1.
ЗАДАЧИ
1. Найти матрицы переходных вероятностей для марковских цепей, описы-
вающих следующие процессы.
(а) Рассмотрим серию бросаний монеты с вероятностью выпадения решетки,
равной р. Состояние процесса после п переходов (бросаний монеты) определим
как разность между числом выпадений решетки и числом выпадений герба.
(б) В двух урнах размещены N черных и W белых шаров так, что каждая
содержит по N шаров. Состоянием системы является число белых шаров в пер-
вой урне.
Задачи
67
(в) Белую крысу помещают в лабиринт, изображенный на рисунке. Крыса
передвигается из ячейки в ячейку случайным образом, т. е. если ячейка имеет
k выходов, то крыса выбирает каждый из них с вероятностью \/k. В каждый
момент времени крыса обязательно переходит в одну из соседних ячеек. Состоя-
ние системы — номер ячейки, в которой находится крыса.
(г) Рассмотрим производственную линию, где каждая единица выпускаемой
продукции с вероятностью р идет в брак. Качество каждого отдельного изделия
(годно или дефектно) предполагается не зависимым от качества других изделий.
Процедура контроля качества изделий состоит в следующем. Сначала прове-
ряется каждое выпускаемое изделие. Так продолжается до тех пор, пока не
появятся i небракованных изделий подряд. В этом случае из каждых г после-
дующих изделий для проверки равновероятно выбирается лишь одно. Если те-
перь будет обнаружено бракованное изделие, то процедура предписывает воз-
вращение к исходному правилу: проверять каждое изделие впредь до появления г
небракованных изделий подряд и т. д.
Состояние Eh (k « 0, 1, ..., i) означает, что при проверке согласно первой
части процедуры контроля (проверяется каждое выпускаемое изделие) последо-
вательно появились k небракованных изделий. Состояние же Ei+\ означает, что
проверка осуществляется согласно второй части процедуры (проверяется одно
изделие из г) и появилось одно, или более, небракованное изделие. (Предпола-
гается, что время т отсчитывается вместе с появлением каждого изделия при
проверке по первому правилу и с появлением серии из г изделий — по второму.)
Ответы:
(а)
{разность между числом выпадений решетки и числом
выпадений герба = k после п + 1 бросаний | эта раз-
ность = / после п бросаний
| р, если k ~ j + 1,
= { 1 — р, если k — j — 1.
| 0 во всех остальных случаях.
Pjk не зависит от п.
68
Гл. 2. Марковские цепи
(б)
Р = р { белых шаров в первой урне после п + 1 перекладываний
i I / белых шаров в первой урне после п перекладываний
Pjk не зависит от п.
(, если k = / — 1, j = 1, 2, ..., N,
\N ) J
)’ если й = /’ / = °> 1.
-----м7) » если k—j+l, j = 0, 1......М~1,
\ N)
О во всех остальных случаях.
(г)
Pjk = P{
пребывание в состоянии Ek после т + 1 проверок | пре-
бывание в состоянии Е] после т проверок
р, если k — О, / = 0, 1.........Z, /4-1,
= 1 — р, если k = j 4- 1, j — О, или k — j = i 4- 1,
О во всех остальных случаях
при всех т.
2. (а) шаров размещены в двух урнах А и Б. В момент времени t
(f = 1, 2, ...) из общего числа N шаров случайно (все выборы равновероятны)
выбирается один шар и помещается с вероятностью р в урну А и с вероятностью
q в урну Б. Состояние системы при каждом испытании представляется числом
шаров в урне А. Определить матрицу переходных вероятностей марковской цепи,
описывающей серию таких испытаний.
(б) Предположим, что в момент t в урне А лежит k шаров. В момент
t 4- 1 с вероятностью, пропорциональной числу содержащихся в ней шаров, вы-
бирается одна из урн [т. е. урна А выбирается с вероятностью k/N, а урна Б —
с вероятностью (N — k)/N]. В выбранную урну кладется шар, который предвари-
тельно извлекается из урны А или из урны Б с вероятностями р и q (р 4- q =* 1)
соответственно. Определить матрицу переходных вероятностей этой марковской
цепи.
(в) Предположим теперь, что урна, из которой извлекается шар, также
выбирается с вероятностью, пропорциональной числу содержащихся в ней шаров
[т. е. шар извлекается из урны А с вероятностью k/N или из урны Б с вероят-
ностью (N — k)/N и возвращается в урну А с вероятностью k]N или в урну Б
с вероятностью (А/-~£)/А/]. Найти матрицу переходных вероятностей марковской
цепи, состояния которой соответствуют числу шаров в урне А.
(г) Определить классы эквивалентности (классы сообщающихся состояний)
в (а), (б) и (в).
Ответы:
(а)
N-i к
—г;— р, если k = 14-1.
N г
I N —- I
I ~дГр+ ..q, если k = i, 0,1, 2, ..., N)
Pik “ /v /v
-jy q, если « = i - 1,
0 во всех остальных случаях,
Один класс эквивалентности: {0, 1, 2, ..., N}.
Задачи
69
(б)
t t. • । i
— q, если k == i + 1,
N
~ p 4- q, если k == i, (i — 1, 2.........У — 1)
p«=l ЛИ w
N-i , . -
—-r— p, если k — i — 1,
N
О во всех остальных случаях,
Pa = 1, если i = 0 и i — N. Классы эквивалентности: {0}, {N}, {1, 2, N — 1}.
(в)
i2 , 0V“02 t .
ДГ2 + ДГ2 » еСЛИ k — I,
?lk~ если ^ = /+1 и k-=i — 1,
N2
0 во всех остальных случаях.
Классы эквивалентности: {0}, {!, 2, ..., N — 1}, {N}.
3. (а) В серии психологических экспериментов испытуемый реагирует на
воздействия Si, S2, ...» S.v одним из двух возможных способов, Ai или А2.
Каждое воздействие вызывает одну из этих реакций. В каждом эксперименте
испытуемый подвергается случайно выбираемому воздействию (все воздействия
имеют одинаковую вероятность быть выбранными) и реагирует на него в зави-
симости от того, с какой реакцией (Ai или А2) данное воздействие связано в
настоящий момент. После проявления реакции испытуемый с вероятностью л
(0<л<1) получает поощрение независимо от предшествующей части опыта.
Если поощрение реализовалось, то воздействие остается связанным с той же
реакцией, в противном случае это воздействие вызовет у испытуемого другую
реакцию в следующий раз, когда оно будет выбрано. Рассмотреть марковскую
цепь, состояния которой отождествляются с числом воздействий, связанных в
данный момент с реакцией Ai, и найти ее матрицу переходных вероятностей.
(б) Испытуемый S реагирует одним из трех возможных способов: Ао, А\
или Аг- Реакция Aq соответствует состоянию, в котором может произойти смена
реакции. За реакцию Ai испытуемый получает поощрение с вероятностью Ль
Если поощрение реализуется, то в следующем эксперименте S реагирует тем же
способом. В противном случае (его вероятность равна 1 — Л1) S переходит в
состояние смены реакции. Аналогично вероятность получить поощрение за реак-
цию А2 равна л2; S остается в том же состоянии (реагирует прежним образом),
если он получает поощрение, и переходит в состояние смены реакции в против-
ном случае. Находясь в состоянии смены реакции, испытуемый остается в нем
до следующего эксперимента с вероятностью 1—с или реагирует способами Ai
или А2 с одинаковыми вероятностями, равными с/2. Рассмотреть марковскую
цепь, состояниями которой являются состояния испытуемого, и определить ее
матрицу переходных вероятностей.
Ответы'.
(а ) Рц = Щ = Р/,« (W) (1 - л), Р/7=~0 во
всех остальных случаях (г, /= 1, 2, .... Af).
(б ) Роо = 1 - с, Pqi =*= Р02 - о/2; Piq = 1 - ль Рц^ л}; Р20 == 1 - Р22 = я2,
Р12-Р21=*®'
4. Каждой стохастической матрице соответствует марковская цепь, для ко-
торой она является матрицей рдвошагрвш переходаш вероятностей. (Под
70
Гл. 2. Марковские цепи
«стохастической матрицей» мы понимаем матрицу Р == ||Лjll, элементы которой
удовлетворяют условиям 1 и У Pij= 1.) Однако не всякая стохастиче-
/
ская матрица может служить в качестве матрицы двухшаговых переходных
вероятностей марковской цепи. В частности, показать, что стохастическая матри-
ца второго порядка является матрицей двухшаговых переходных вероятностей
тогда и только тогда, когда сумма ее диагональных элементов больше или равнй
единице.
5. Пусть П1, п2, . • •, nk — положительные целые числа, наибольший общий
делитель которых равен d. Показать, что существует такое положительное целое
число М, для которого из неравенства т М следует существование неотрица-
тельных целых чисел таких, что
k
md = С]П>.
/=1
(Этот результат потребуется ниже в задаче 7.)
Указание'. Пусть
Л == {п | п = Cj/tj + ... + cknk, {cj — неотрицательные целые},
Ь{п{ + ... + Ь.п. | nv п2...п. е А и Ь{.....Ь.
суть положительные или отрицательные целые
Пусть df — наименьшее положительное целое число в множестве В. Показать,
что df является общим делителем всех чисел множества А. Затем показать, что
d' является наибольшим общим делителем чисел множества А. Следовательно,
d' = d. Перенумеруем слагаемые в представлении d = ахпх + . .. так,
чтобы’ члены с положительными коэффициентами были записаны сначала. Тогда
d = Ni — N2, где Ni е А и N2^ А. Пусть М = N2/d. Каждое целое число т М
может быть записано в виде т — М + k — N^/d + (^в®, 1, •••), причем
k == dN2/d + b, где 0 < b < N2/d и 6 = /*, если /(Ma/d) k < (/ + V)N2/d
(j = 0, 1, 2, ...). Таким образом, md = N2 + (d#2/^ + &) d — N2(#2 + $ — &) + bN{
6. Доказать теорему 4.1.
Указание: Пусть PsH>0, P^s+m Р".Р5цР™-> 0 для некоторых т>0 и
п>0. Поскольку Р2ц> 0, имеем Pyy+2^+zn>0; таким образом, d (/) является
делителем числа (п + 2s + т) — (п + s + т) = s.
7. Доказать теорему 4.2 и следствие 4.1.
Указание: В задаче 5 мы видели, что существует такое N, что если п N, то
nd{i) = (схпх+ ... +cknk)
ГЦ ~ i i
8. Доказать, что для непериодической неприводимой конечной цепи Маркова
все элементы матрицы Рп положительны для некоторого п.
9. Доказать, что если / — невозвратное состояние, то для всех i имеем
2 ^-<00.
п= 1
Указание: Использовать соотношение (5.9).
Некоторые элементарные задачи
71
10. Пусть марковская цепь имеет г состояний. Показать, что
(а) если состояние k достижимо из состояния /, то оно может быть достиг-
нуто меньше чем за г шагов;
(б) если /— возвратное состояние, то существует число а (0<а<1), та-
кое, что для п > г вероятность того, что первое возвращение в состояние j про-
изойдет после п переходов, меньше или равна ап.
11. Рассмотрим последовательность испытаний Бернулли, исходы которых
описываются случайными величинами Ai, Х2, А3, ..., где Хп = 1 или 0. Пред-
положим, что
Р {Ап = 1 |АЬ Х2, .... Ап_!}>а>0, п=1, 2.
Доказать, что
(а) Р{ХИ=1 для некоторого п} = 1,
(б) Р{А\=! бесконечно много раз}=1.
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
1. Для марковских neneii с матрицами переходных вероятностей
0 0 1 0 0 1 0 0
1 0 0 0 0 0 0 1
J_ 2 1 2 0 0 и 0 1 0 0
3 £ 3 3 0 1 3 0 2 3 0
определить классы эквивалентности и периодичность различных состояний.
2 . Рассмотрим случайное блуждание по одномерной целочисленной решетке,
где Pi, f+1 = p, Pi, i-i = q для всех целых i (0 < р < 1, р + <?=!). Опреде-
лить Р$.
Ответ: Р$ = ( ) pmqm-, P§m+" = 0.
3 (продолжение). Найти производящую функцию вероятностей ип = Р”о,
оо
т. е. определить Р (х) == 2 ипХп-
п = 0
Указание. Использовать тождество ( j = (— \)п I 2 } 22п, где
\ п /
( а\ а (а - 1) ... (а - п + 1)
=-------------j--------— для всех действительных а.
Ответ:
Р (х) = (1 — 4pqx2)~\
4 (продолжение). Определить производящую функцию времени возвращения
для состояния 0. __________‘
Ответ: F (х) = 1 — У(1 — 4pqx2).
5 (продолжение). Какова вероятность когда-нибудь возвратиться в начало
координат?
72
Гл. 2. Марковские цепи
6 . Рассмотрим повторяющиеся независимые испытания, для каждого из ко-
торых возможны два исхода, У (успех) или Н (неудача). Определить распре-
деление числа испытаний, требуемых для наступления события УН (т. е.
успех и следующая за ним неудача). То же самое для событий УУН и УНУ.
7 . Предположим, что две правильные различимые монеты бросаются одно-
временно и многократно. Ведется счет числу выпадений герба и решетки для
каждой монеты. Рассмотрим событие Еп, заключающееся в том, что при
п-м бросании суммарное число выпадений герба у одной монеты равно суммар-
ному числу выпадений герба у другой. Установить связь между событием Еп
и временем возвращения в заданное состояние при симметричном случайном
блуждании на целочисленной решетке.
ЗАМЕЧАНИЯ
Некоторые аспекты теории марковских цепей освещены в книге
Феллера [1].
Книга Кемени и Снелла [2] содержит много увлекательных
примеров марковских цепей, встречающихся в психологии, социо-
логии, экономике, биологии и других областях.
Наиболее полное и глубокое рассмотрение марковских цепей
дано в книге Чжун Кай-лая [3].
ЛИТЕРАТУРА
1. Феллер В., Введение в теорию вероятностей и ее приложения, т. 1, «Мир»,
М., 1964.
2. Kemeny J. G., Snell J. L., Finite Markov Chains, Princeton, New Jersey,
1960.
3. Ч ж у н К а й - л а й, Однородные цепи Маркова, «Мир», М., 1964.
Глава 3
ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
§ 1. ДИСКРЕТНОЕ УРАВНЕНИЕ ВОССТАНОВЛЕНИЯ
Ключевым в анализе марковских цепей является результат,
формулируемый в следующей теореме:
Теорема 1.1. Пусть {#4, {uk}, {bk} — числовые последователь-
ности с индексом k, принимающим значения 0, ±1, ±2, ... . Пред-
положим, что ak^0, l^ak=?A, ^kak>G, 2l^l<
< оо и что наибольший общий делитель индексов k, для кото-
рых, ah > 0, равен 1. Если уравнение восстановления
оо
ип- 2 = П = О, ±1, ±2,
fe= —оо
имеет своим решением ограниченную последовательность {ип} дей-
ствительных чисел, то пределы lim ип и lim ип существуют. Бо-
П->оо п-> — оо
лее того, если
оо
2
lim ип = 0, то lim ип = — °°—. (1.1)
Я-»—оо Я-»оо XI ,
XJ kak
fe=—ОО
оо
В случае, если S kak = <x>, предельное соотношение остается
k = —ОО
справедливым, если положить
— = о.
оо
2 kak
k= — оо
Доказательство этой теоремы в том общем виде, в каком она
сформулирована выше, выходит за рамки этой книги. Нам пона-
добится ее частный случай для последовательностей {ak}, {ик}, {bk},
обращающихся в нуль при отрицательных значениях k, и > 0.
Доказательство теоремы для этого случая мы дадим в § 2.
74 Гл. 3. Основные предельные теоремы для марковских цепей
Замечание 1.1. В случае, когда a-h = 0, b_k = 0 и и~л = 0
для k > 0, уравнение восстановления принимает вид
п
Un~ 2 ^n—k^k “ tt = 0, 1,2,....
£=0
Замечание 1.2. (Довод в пользу названия «уравнение вос-
становления».)
Пусть «время жизни» электрической лампочки представляет
собой случайную величину g и измеряется в дискретных единицах,
причем
оо
Pfe = 6) = afe, 6 = 0, 1, 2... Saft = l.
Как только лампочка перегорает, ее сразу же заменяют новой.
Пусть первая лампочка перегорает в момент gi, вторая — в мо-
п
мент gi + ga и и-я— в момент 2 где &— взаимно независи-
z=i
мые, одинаково распределенные случайные величины (распреде-
ление каждой из них совпадает с распределением с. в. g). Пусть
ип обозначает среднее число замен, произведенных к моменту п.
Если первая замена имела место в момент k, то среднее число за-
мен в оставшееся до момента п время есть un~h. Суммируя по
всем возможным значениям k, получаем
П оо
ж 2 О "Ь k№k “Ь о * 2 =
6=0 fe=n+l
п п п
2 ^n—k^k "1" 2 = 2 "Ь (1*2)
/г=0 /г=0 &=0
где
п
2 ~
k—Q
Обоснование соотношения (1.2) таково. Величина 1 +' ип-ъ пред-
ставляет собой среднее число замен за время п при условии, что
первая лампочка перегорела в момент k вероятность
этого события равна ah. Вторая сумма есть вероятность того, что
первая лампочка будет служить более чем п единиц времени.
Учитывая повторяющийся характер процесса, мы получаем выра-
жение для ип с помощью разложения возможных реализаций по
моменту первой замены.
Следующая теорема, так называемая «эргодическая» теорема
для данного частного случая, описывает предельное поведение ве-
роятностей Рпц при п —> оо для всех i и j для непериодической
возвратной марковской цепи.
§ 1. Дискретное уравнение восстановления
75
Теорема 1.2. (Основная предельная теорема для марковских
цепей.)
(а) Рассмотрим возвратную неприводимую непериодическую
марковскую цепь. Пусть Рпц есть вероятность оказаться в i-м со-
стоянии на п-м шаге, п = 0, 1, 2, .. . , при условии, что Х(0) = i
(т. е. состояние i — начальное). Пусть, как и ранее, Рц = 1. Пусть
п. есть вероятность впервые возвратиться в состояние i на п-м
шаге, причем = По доказанному ранее [см. формулу (5.1)
гл. 2], имеем
„ b ь fh ecAU n^=Q,
рп __ V — {
il il I 0, если ц>0.
В этом случае справедливо равенство
lim Рпн = -^—.
2 nfh
п=0
(б) При этих же условиях lim Рц = lim Р^,
П->оо П-><х>
Доказательство, (а) Положим
ип = Pit, п^О; ип — 0, п<0;
an = 4i’ ап = 0, ге<0;
( 1, п = О,
Ьп[ 0, п=£0.
Воспользовавшись теперь теоремой 1.1, получаем доказываемый
результат.
(б) Пусть
п
Уп ~ —
k=0
где
оо
О, S«m=l> limxft = c.
m = 0 fe-»oo
Докажем, что при этих условиях lim уп = с. В самом деле, имеем
П->оо
П П оо
Уп С ^n—k^k С ^tn ^n~k^k С S ^tn*
k=Q m=0 zn==n + l
76 Гл. 3. Основные предельные теоремы для марковских цепей
Для любого заданного е>0 существует Д'(в), такое, что
— с |< в/3 для всех Следовательно,
К (е) п оо
Уп С 2 ttn—k (xk 4“ S ^n—k С 2 ^ГПУ
fe=0 т=л + 1
откуда
К (е) п оо
I Уп С 1 ^n~k 4 .^aJ ^n—h 4" I £ I ^my
&=0 h=K(z)+\. m—n+1
где
M = max | xk — c |.
fc>0
oo
Выберем теперь N (s), такое, что | с | ~S ат<&/3 и
m=n + l
К (е) п
^an-k= Т а«<‘з7Г для «>^(8):
k~Q т—п—К (е)
МЫ ВИДИМ, ЧТО
|г/»-сК4 + 4 + 4 = е для я>ЛЦе).
ООО
Воспользуемся теперь ранее доказанным нами соотношением (см.
формулу (5.9) гл. 2)
п
Полагая
Уп~Рц> an=sfiP Xn~?ii>
получаем доказываемый результат.
Замечание 1.3. Пусть С — возвратный класс. Тогда Р?/ = 0
при i е С и j ф С для всех п. Следовательно, попав в С, выйти
из него невозможно. Таким образом, подматрица iy 1 Су
является матрицей переходных вероятностей, а соответствующая
марковская цепь неприводима и возвратна. Это означает, что
предельная теорема справедлива дословно для любого непериоди-
ческого возвратного класса.
Замечание 1.4. Если ап->а при /г->оо, то, как легко пока-
зать, выполняется равенство
п
Пт ak = а. (1.3)
§ 1. Дискретное уравнение восстановления
77
Значит, если состояние i входит в возвратный непериодический
класс, то
п
п = 0
где trti — среднее время возвращения.
Если состояние i входит в возвратный периодический класс, то,
как можно показать (см. задачу 7 гл. 2), Р™ = 0, если m не кратно
периоду d (т. е. если m 4= nd для какого-либо п), и
Эти два последних результата вместе с (1.3) показывают, что со-
отношение (1.4) справедливо и для периодического случая.
Если lim Рц =л/>0 для некоторого состояния i из непе-
П->оо
риодического возвратного класса, то Л; > 0 для всех j из этого
класса. (Доказательство этого факта аналогично доказательству
следствия 5.1, и мы его опускаем.) В этом случае мы называем
класс возвратным положительным* или сильно эргодическим. Если
все Tti = 0 и класс возвратный, то будем говорить, что класс воз-
вратный нулевой* или слабо эргодический.
Теорема 1.3. Для непериодического возвратного положи-
тельного класса с состояниями j = 0, 1,2,...
lim Р”; = л/ = 2 щРц, 2 Щ ==• 1,
п->оо /=0 i=0
и величины {лг} однозначно определяются условиями
оо оо
п^О* Яи — ^щРц. (1.5)
i=0 i = 0
Набор {лг}, удовлетворяющий условиям (1.5), называется стацио-
нарным распределением марковской цепи. Подробнее об этом речь
пойдет в гл. 5.
Доказательство. Для любых п и М
оо М
1 = 2 Р"ц> 2 Ph.
j^O /=0
Устремляя п—> оо и используя теорему 1.2, получаем
/«=0
78
Гл. 3, Основные предельные теоремы для марковских цепей
м м
для любого М, откуда Далее, Р"при
/=0 *=0
м
п->оо это дает nkPki. Поскольку левая часть этого не-
k=0
равенства не зависит от М, при М -> оо получаем
оо
(1.6)
fe=0
Умножая обе части (1.6) на Р/г- и суммируя по /, получаем не-
ос
равенство 2 nk?kr Точно так же убеждаемся, что это нера-
оо
венство справедливо для любого п: nkP^r Предположим,
что для некоторого /0 имеет место строгое неравенство. Суммируя
по /, имеем
оо оо оо оо оо оо
2 л/> 2 2 ftkPkj == 2 nk 2 Pkt = 2
/ = 0 /=0 /г=0 fe=0 /=0 /г=0
оо
таким образом, л, = 2 ЛйР?/ для всех п. Поскольку ряд 5 л*
k=Q
сходится, а Рц равномерно ограничены, при /г—>оо
оо оо
Л/ = 2 Mm Pkj = Л/ 2 Я/г ДЛЯ ВСеХ /•
fe=0 п->оо /г^О
В силу того что класс возвратный положительный, имеем л/ > О,
оо
и поэтому 2 nk = 1-
fe=0
Предположим теперь, что последовательность х = {хп} удовле-
творяет соотношениям (1.5), тогда
оо оо
xk ~ xjPjk == 2
/ = 0 /И
откуда, устремляя п —>оо, получаем
оо оо
xk = 2 х/ lim Р"ь = лк 2 х> =
i-о
§ 1. Дискретное уравнение восстановления
79
Пример. Рассмотрим класс процессов случайного блужда-
ния, матрицы переходных вероятностей которых имеют вид
P = IIPOII =
10...
0 pi . . .
<?2 0 р2 ...
О
(см. пример Б гл. 2).
Мы исследуем существование стационарного распределения,
т. е. найдем положительное решение уравнений
оо
Xi = 2 XjPjl = + + J = 0, 1,..., (1.7)
/=0
при условии «нормировки»
оо
5 1,
где р-i = 0 и ро = 1, а значит, х0 — (hx\- Уравнение (1.7) при i = 1
позволяет выразить х2 через х0, при i = 2 выразить х3 через Хо
и т. д. Легко проверить, что
1
удовлетворяют (1.7), причем х0 еще
пользуя условие нормировки, получаем
надлежит определить. Ис-
1 =Хо + 2хо1Т-^-,
. 1 "k+l
или
х0 =
Таким образом, х0 > 0 тогда и только тогда, когда
Pk
^k+i
< ОО.
80
Гл. 3. Основные предельные теоремы для марковских цепей
В частности, если Рл = р и = ? = 1 — р при k > 1, ряд
сходится, только когда р < q.
§ 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
Мы докажем теорему 1.1 при следующих дополнительных пред-
положениях: при k < 0 все члены последовательностей {ak}, {bk},
{uk} равны нулю; bk 0 и а\ > 0. Уравнение восстановления
в этом случае принимает вид
п
^n—k^k “ /1 — 0, 1, 2, . . .,
fc=0
или, что то же самое,
п
ип 2 ^k^n—k= /1 — 0, 1,2,.... (2.1)
/г=0
Применяя индукцию (рассматривая уравнения последовательно),
легко убедиться, что uk > 0 при всех k. Поскольку, согласно пред-
положению, {ип} — ограниченная последовательность, величина
Л= lim ип конечна. Пусть такая подпоследовательность, что
lim z/rt.==X. Используя условие а\ > 0, мы докажем, что
/->оо J
lim z/rt._[ = Z. Предположим противное; тогда из определения Л
/ ->оо J
следует, что существует такое V < Л, что для бесконеч-
ного числа значений индекса /. Положим 8 = [ai(Z— Л')]/4 и
М = sup ип и найдем N, такое, что
л>0
если
(2.2)
Пусть / настолько велико, что rij N и
и
ttfij X е, Unj—\ X X, 0 Ьц. 8
мп<Л + е для всех n^tij — N. (2.3)
Такое / существует по определению Л и ЛЛ
§ 2. Доказательство теоремы 1.1
81
Из (2.1), (2.2) и (2.3) имеем
ni /V п1
akUni-k + e<^ akuni k + М з ак + г<
k=0 k=Q ! fe^.V+l
N
< 3 ОА«П;-й + 28<
ьо 7
<С (&о Ч~ #2 Ч“ Ч~ • • • Ч~ aN) (А> Ч~ в) Ч~ ci\)J + 2е
(1 — &i) (X Ч- с) 4 ct[h' Ч- 2е < А, Ч- Зе — ci[ (Л — А/) = Л — е.
Но это противоречит первому из неравенств (2.3), и, следова-
тельно, lim wrt.-i = А,. Повторением предыдущих рассуждений убе-
/ ОО 7
ждаемся, что для любого целого числа d > 0
lim un -d = ^ (2.4)
/->оо J
оо оо
Далее, положим rn = art+1 + ап+2+ ..очевидно, 3 kak— 3 гп.
k=0 п-0
^Заметим, что сходимости ряда ^гп не требуется.^ Подставляя
ai = rQ — гъ а2 = г{ — г2, ... в (2.1), получаем
rotfn + riun-.l+ ... +гпи^гоипЧ Ч-Г]^_2Ч- ... 4-rrt_iW04- bn
(п = 1, 2, ...).
Полагая An = rQun+ ... +rnuOi мы можем записать последнее
равенство в виде
Ац ==s An—i Ч~ Ьп, /1=1, 2, ...,
п
где Д0 = г0м0 —(1 — ао)ио —^о- Отсюда следует, что Д„=2&г-
»=0
Так как гп^0 и м„^0 при всех п, то для любых фиксированных
7V > 0 и />0 имеет место неравенство
nJ
roun, + r\Un,-i+ ... +rNun -ы^Ап -= ^Ьп.
11 11 п=о
оо
Устремляя /->оо, получаем неравенство (г0Ч- ... Ч-г^)А,^2 Ьп,
п = 0
оо / N \“ 1
которое можно записать в виде А,^ Ж 3rd . Поскольку
о \ о /
N>0 произвольно, отсюда следует неравенство
ОО •
3^
(2.5)
82
Гл. 3. Основные предельные теоремы для марковских цепей
Так как uk^0 при всех k, из неравенства (2.5) следует утвер-
оо
ждение теоремы для случая, когда 2гд==°°, поскольку [как это
п=0
следует из (2.5)] Л = lim ип == 0.
П->оо
оо
Если положим ц = Птмп. Те же рассуждения, что
д->оо
и для верхнего предела, показывают, что если lim ип, = \^ то
/->ОО '
оо
lim ип.-й = ^ Для любого целого числа d^O. Положим S гп =
' n^N+l
= g (N)‘, ясно, что lim g (N) = 0 и
2V->oo
п/
S + ••• + rtilltii-N + ё (Ю
n~0 * J 1
Устремляя /->oo, получаем
oo
2&n<(r0+ ••• +Глг)ц + я(Л1)М.
n=0
Переходя теперь к пределу при Af-> оо, получаем неравенство
оо
оо оо Ъп
или —• (2.6)
«-° п=о 2 г«
п==0
Из (2.5) и (2.6) следует, что ц > X. С другой стороны, по
самому их смыслу. Следовательно, р = X, что означает, что пре-
дел lim ип существует и, более того,
П ->оо
Нт ип = ^—.
П оо
21 ГП
г2=0
Для случая, когда а\ — 0, но наибольший общий делитель целых
чисел т, для которых ат > 0, равен 1, теорему 1.1 можно дока-
зать аналогичным способом, воспользовавшись при этом след-
ствием 4.1 гл. 2.
§ 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
Ранее мы установили (см. задачу 9 гл. 2), что если состояние j
невозвратное, то Р?/->0, и что если состояния i и / принадлежат
одному и тому же непериодическому возвратному классу, то
§ 3. Вероятности поглощения
83
Если состояния i и j входят в один и тот же возврат-
ный периодический класс, то последнее утверждение сохраняет
п
силу, если Рпц заменить в нем на п~х S Рц. Для того, чтобы
m= 1
завершить рассмотрение предельного поведения вероятностей
остается рассмотреть случай, когда состояние i невозвратное, а со-
стояние / возвратное.
Пусть Т — множество всех невозвратных состояний; введем ве-
личины х? с помощью следующей рекуррентной формулы:
где i <= Т и п >2. Заметим, что х" есть вероятность того, что, от-
правившись из состояния Z, процесс не выйдет из класса Т в тече-
ние следующих п шагов. Покажем с помощью индукции, что по-
следовательность {х", п=1, 2, является невозрастающей.
Действительно, так как хП^ 1 при всех и, то
^=2 рг.х}< 2 = 4
j^T1 1 j^T 1
Предположим теперь, что х^^.х^~х при всех j^T, тогда
Это означает, что ограниченная последовательность {х*, п =
= 1, 2, ...] не возрастает и, следовательно, стремится к некоторому
пределу xit причем
Xj-~ 2 PijXh (3.1)
Таким образом, если единственным ограниченным решением урав-
нений (3.1) является нулевой вектор (0, 0, ...), то, отправляясь
из любого невозвратного состояния, процесс с вероятностью 1 бу-
дет поглощен некоторым классом возвратных состояний. В самом
деле, Xi (i <= Т) есть вероятность никогда не попасть в возврат-
ный класс, если i было начальным состоянием процесса. Посколь-
ку {хг, i^T} является ограниченным решением уравнений (3.1),
то Xi = 0 при всех i.
Замечание 3.1. Если марковская цепь имеет лишь конечное
число состояний, скажем М, то среди них нет возвратных нулевых
84 Гл. 3. Основные предельные теоремы для марковских цепей
состояний, а все состояния не могут быть невозвратными. Дей-
М-1
ствительно, так как S Рпц = 1 для всех п, то lim Р?/ = 0 не для
/ = 0 П->оо
всех j. По этой же причине отсутствуют нулевые возвратные со-
стояния. Пусть С, Сь С2, ... — возвратные классы. Определим
лг(С) как вероятность того, что, отправляясь из невозвратного со-
стояния /, процесс рано или поздно войдет в класс С. (Вспомним,
что, однажды попав в возвратный класс, процесс уже никогда его
не покидает.)
Пусть л" (С) есть вероятность того, что процесс достигнет
класса С и, следовательно, будет им поглощен, впервые на п-м
шаге, при условии, что начальным состоянием было /еГ; тогда
оо
Я/(С)=
(3,2)
Л?(С)= 5 ЛХ-ЦС), п>2. (3.3)
Используя (3.3), (3.2) можно переписать в виде
(С) = л\ (С) + 2л« (С) = л' (С) + 2 з PtM~' (Q =
п=2 1 п = 2 4 1
= л’(С)+ 2
1 j^T 4 п—2 7
л, (С) = л! (С) + 2 РцлЛС), 1<е=Т. (3.4)
/еГ 7 7
Если предположить, что единственным ограниченным решением
однородной системы уравнений
Wi = 2 i Т,
j^T
является тривиальное решение (нулевой вектор), то {л2(С)}
является единственным ограниченным решением системы уравне-
ний (3.4). Более того, либо л! (С)>0 для некоторого /е Г, либо
л2(С) = 0 для всех i^T и, следовательно, л"(С) = 0 для всех п.
Теорема 3.1. Пусть j^C (С — непериодический возврат-
ный класс), тогда для i е Т имеем
lim Р"/==лДС) lim Р// = л/(С)л/.
§ 3. Вероятности поглощения
85
Доказательство. Легко видеть, что л"(С) = S 7tnik(C),
где л^(С) есть вероятность того, что, отправляясь из состояния
i^T, процесс на n-м шаге войдет в класс С через состояние k.
Имеем
лдс) = 2 2л^(с)<1.
v=l k^c
Следовательно, для любого в>0 существуют конечное число со-
стояний С7 czC и целое число N (е), такие, что
Hi (С) -2 2 *д(с)
v=l k^C'
т. е.
<8
< е»
(3.5)
для всех n>N(e). (Здесь мы пишем л^ вместо л^(С).)
Для je^C рассмотрим разность
р"/ - 2 2
v==l k^C' 7
С помощью знакомых нам рассуждений получаем
р?/=2 2 nikpnk7v, i^r, j<=c.
v = l k^C
Опираясь на эти соотношения, получаем неравенство
рп. _
г и
2
k^C'
Л/
п п
AeC' v-1 k^c, к<£с'
2 2
v=l k^C'
+
2 2Ж'->,)+2 2 ЛР1Г-
v=W+l £е=С' v=l f,(=Ci k^C'
Но Ру v ^1, |Pyv — Л/1 <2 и lim Ру v = л/, если С — непериоди-
П->оо
ческий класс и Поэтому существует такое N'>N, что при
n>N'имеем | Pk^N — л/|<е так что при п> N' выпол-
няется неравенство
Р?/-(2 2
\v=l k^C' /
п
<е + 2 2
у=^+!
k
86
Гл. 3. Основные предельные теоремы для марковских цепей
Однако выбор N и С' гарантирует нам, что правая часть послед-
него неравенства не больше, чем 4е. Отсюда, воспользовавшись
(3.5), получаем
| Р?/--Лу (С) Лу | 4е + ел, при n>N' (е)
и, следовательно,
lim Pfj = (С) л/.
П->оо
Если С — периодический класс и /'еС, то точно так же можно
показать, что
п
Пт 4- У Pjj = лу (С) лу.
П-»оо "
т — \
В заключение заметим, что если i — невозвратное состояние,
a j ~ возвратное, то предельное значение вероятности зависит от
обоих состояний i и /. В этом состоит существенное отличие от
случая, когда i и / принадлежат одному и тому же возвратному
классу.
Пример. (Задача о разорении игрока, играющего с партне-
ром, капитал которого ограничен.)
Как мы видели, марковская цепь, описывающая игру, имеет ко-
нечное число состояний, скажем п + 1, а ее матрица переходных
вероятностей имеет вид
1 0 0 0 ...
q 0 р 0 ...
О q 0 р ...
... q 0 р
... О 0 1
Мы найдем Ut = лг(С0) и и, = лу(Сп) —вероятности, отправляясь
из состояния г, рано или поздно попасть в поглощающие (и, следо-
вательно, возвратные) состояния 0 и п соответственно. Система
уравнений (3.4) для рассматриваемой задачи имеет вид
щ = q + риъ
ul = qui-{ + pui+l
(2 < i < п -2),
(3.6)
qun—2*
§ 3. Вероятности поглощения
87
Система состоит из п—1 неоднородных уравнений с п—1 неиз-
вестными. Будем искать решение в виде иг = хг. Подставляя это
выражение в средние из уравнений (3.6), получаем
рх2 + q = х.
Последнее уравнение имеет два решения, х = 1 и х — q/p. Таким
образом, величины ur = А + B(q/p)r, г = 2, 3, ..., п — 1, удовле-
творяют средним уравнениям из (3.6) при любых значениях А
и В. Определим А и В так, чтобы первое и последнее уравнения
также удовлетворялись. (Если q = р, то решение х = 1 является
двукратным корнем уравнения рх2 + q = х, в этом случае (q!p)r
следует заменить на г.) Подставляя соответствующие выражения
в первое уравнение, получаем
А д- В ~ q р^А + В
или, упрощая,
А - 1 - В.
Последнее уравнение дает
/ л \п~{ / / л \п“2\
Л + в(^-) ~q{A + B\±) ), или pnA + qnB = 0.
Отсюда пп — пп Д — Ч D __ Р - qn_pn, D - qn_ рп
и _ (q/p)n-(q/p)r ± . Ur (ч/р)п-1 ’ если Р *'
Если q = р, что то точно так же находим, что А — 1, В = —1/п, так иг ~ ~п~ ’ если Р Р'
Аналогичные выкладки показывают, что
Vi = 1 - иь
чего и следовало ожидать, поскольку поглощение одним из клас-
сов Со или Сп есть событие достоверное.
Рассмотрим теперь игру с бесконечно богатым партнером.
Уравнения для вероятности разорения игрока (поглощение состоя-
нием 0) имеют вид
Щ = q + ри2, (3.7)
Ui^qui^ + pui+i, i^2.
Так же как и раньше, находим, что
Ui = А + В (q/p)1 (q^p) и щ = А + Bi (q = р = '/2).
88 Гл. 3. Основные предельные теоремы для марковских цепей
Если р, то из условия ограниченности щ следует, что В = О,
а из первого из уравнений (3.7) следует, что Если q < р,
то мы находим, что щ = (q!p)\ для чего нужно лишь перейти
к пределу при /woo в решении предыдущей задачи — задачи
о разорении с конечным числом состояний.
§ 4. КРИТЕРИИ ВОЗВРАТНОСТИ
Мы докажем две теоремы, которые окажутся полезными при
определении возвратности или невозвратности марковских цепей,
а затем применим их к нескольким примерам.
Теорема 4.1. Пусть — неприводимая марковская цепь, со-
стояния которой отождествлены с неотрицательными целыми чис-
лами, Для того чтобы цепь ф была невозвратна, необходимо и до-
статочно, чтобы система уравнений
2° РцУ1 = Уь i о/ (4.1)
имела ограниченное решение, отличное от yi = const.
Доказательство. Пусть
Л)Э Л)1 • • •
— матрица переходных вероятностей цепи Сопоставим ей мат-
рицу переходных вероятностей
которая обращает нулевое состояние в поглощающий экран, остав-
ляя вероятности переходов между другими состояниями без из-
менения. Обозначим марковскую цепь, матрица переходных ве-
роятностей которой имеет вид (4.2), символом
Для доказательства необходимости предположим, что процесс
невозвратный, а затем покажем, что в этом случае система (4.1)
имеет ограниченное решение, отличное от константы.
Пусть f*iQ есть вероятность рано или поздно попасть в состоя-
ние 0, выйдя из состояния I. Поскольку процесс $ невозвратен, то
fjo< 1 Для некоторого j 0, так как в противном случае состоя-
ние было бы возвратным. (Докажите это! Напомним, что состоя-
ния неприводимой марковской цепц либр все одновременно воз-
§ 4. Критерии возвратности
89
вратны, либо невозвратны.) Для процесса очевидно, имеем
«о (Со) = 1, nj (Со) = f‘o <1 для некоторого j 0 и (Со) =
оо оо
= S (Со) для всех L Следовательно, nz (Со) = S (Со)
/=о /=о
для i 0; таким образом, ///==л/(С0) (/— 0, 1, 2, ...) есть иско-
мое ограниченное решение, отличное от константы.
Предположим теперь, что система (4.1) имеет ограниченное
отличное or константы решение {//J. Поскольку постоянный вектор1)
является решением системы (4.1), то Zi = ayi 4- b также есть ре-
шение этой системы, которое при подходящем выборе а и b будет
удовлетворять условиям г0 = 1, 0 Zi 2. Поэтому можно пред-
оо
положить, что 0 4^/i42 и = 1; в таком случае ^Рцу^у1
для всех i 0 и, значит, для всех п 1 имеем
оо
2р^/ = //р />о.
Поскольку цепь ф неприводима, Р?о>О для любого I и некоторого
и, поэтому каждое из состояний j = 1, 2, ... должно быть невоз-
вратным в цепи ф, так что Рпц—>0 для /#=0 и по теореме 3.1
имеем Р?о~>2Т/(Со), где (Со) — вероятность (относительно ф),
отправившись из состояния /, быть поглощенным состоянием 0.
Следовательно, так как при всех 1^0 выполняется неравенство
оо
7=0
то, устремляя н~>оо, мы приходим к неравенству ftz(C0)<Jz/z.
Возможны два случая: либо существует такое ^(^¥"0),что
yh < 1, либо такое, что yh > 1 (&¥=()). В первом случае /^0 =
= (Со) < 1, откуда следует, что цепь ф невозвратна, так
как состояние k достижимо из состояния 0 по предположению,
в то время как вероятность возвращения меньше, чем 1. Во вто-
ром случае эти же рассуждения следует применить к решению
Zi = 2 — yi системы (4.1), что даст неравенство л^(С0) ^zk< 1,
откуда опять же следует, что цепь ф невозвратна.
Теорема 4.2. Для того чтобы неприводимая марковская цепь
была возвратной, достаточно, чтобы существовала последователь-
ность {у^, такая, что
оо
5 РцУ1 < Уь i о, yt -> ОО. (4.3)
/=-0
4 Здесь и далее под «постоянным вектором» понимается вектор с одина-
ковыми компонентами. — Прим. ред.
90
Гл. 3. Основные предельные теоремы для марковских цепей
Доказательство. Используя обозначения предыдущей тео-
ремы, имеем
оо
2 для всех i.
Поскольку Zi — tji + b удовлетворяет неравенствам (4.3), мы мо-
жем предположить, что Уг > 0 для всех i 0. Из предыдущего
неравенства получаем
2
Пусть задано 8 > 0. Мы можем выбрать такое Л4(е), что l/z/i<^8
для i М (е). Далее, имеем
М- 1 ОО
7=0 4 1 }—М 1 1
откуда
М— 1 оо ~
2 РцУ, + min (z/J % P”<yt,
и поскольку
2^=1,
Н 4
то
М-1 ~ \
2 Р™У) + min {z/r} 1 - 2 Р?/) < У
/«о 4 1 г>м 1 } \ 7
Как было отмечено в доказательстве предыдущей теоремы,
lim Рпц = 0 при j ф 0.
Переходя к пределу при т—*оо, получаем для каждого фиксиро-
ванного i
(Q) Уо + min {z/r} (1 - Hi (Со)) < yh
или
1 ~ (Co) < (У1 ~ (Co) Уо) < eK,
где
К~У1- ла (Со) у0.
£ 5. Пример из теории очередей
91
Поскольку 8 произвольно, а Л;(С0)^1, то ftf(C0)=I для каждого
i, что и означает возвратность исходной марковской цепи.
§ 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
Рассмотрим модель процесса обслуживания из гл. 2 (при-
мер В). Матрица переходных вероятностей соответствующей мар-
ковской цепи имеет вид
aj a, Я1 «2 a2 ^3 ^3
WPii 11 = 0 ^0 «1 a2
0 0 ^0
оо
> где at>0 и 2at=l-
ьо
(На самом деле при дальнейшем анализе нам потребуются только
два условия: 0 < aQ < 1 и а0 + < 1, обеспечивающие неприво-
оо
димость марковской цепи.) Мы покажем, что если S kak>\, то
k—0
оо
система уравнений 2 РцУ1 = Уь имеет ограниченное ре-
/=о
шение, отличное от константы, что, согласно теореме 4.1, означает
невозвратность процесса. Положим у$ = тогда упомянутая си-
стема уравнений принимает вид
оо оо
i=Q
или
ОО оо
/ = Z-1 k=Q
оо
Так как f(O) = ao>O и f(l)=ZjaA=l, то из условия /'(!) =
k=0
оо
== ^kak>l следует, что существует точка £0, 0<£0< I, такая,
fc=0
что f(^o) = ^o- Это легко видеть на рис. 1. Вектор у^Ц, / = 0,
1, ..., и представляет собой искомое ограниченное решение, оче-
видно, не являющееся постоянным.
Пусть теперь 2 kak^l. Тогда, полагая yj^j, имеем
ОО ОО оо
2Л//= 2 а/-<+1/= 2 0/-ж(Н+1)Н-1 =
/-0 l — i—l /=<-1
оо
= s kak - 14 i с i (i ¥= 0).
k=0
92 Гл. 3. Основные предельные теоремы для марковских цепей
Таким образом, в силу теоремы 4.2 процесс является возврат-
ным, если
Прежде чем обратиться к вопросу о том, является ли процесс ф
возвратным нулевым или возвратным положительным, рассмотрим
следующую вспомогательную задачу, представляющую самостоя-
тельный интерес.
Рис. 1.
Пусть Х2, Аз, • • • — последовательность независимых, одина-
ково распределенных случайных величин, принимающих значе-
ния — 1, 0, 1, 2, ... с вероятностями
P{Xi = k} = bk, k= -1, 0, 1, 2, ..., б^Х),
и пусть Sn = Xi + Х2 + ...'+ Хп. Определим Z как значение пара-
метра гг, для которого Sn впервые становится отрицательным, и
пусть
P{Z = k} = yk, 2, 3, .... (5.1)
Пусть
оо
и (s) = 2 VkSh (Yo = о) (5.2)
ЬО
есть производящая функция распределения (5.1). Пусть Тп’ есть
случайная величина, равная первому значению параметра п, для
которого Т{п<0, где T(n—r + Sn (г — неотрицательное целое
число). Поскольку каждая из с. в. Х{ >—1, нетрудно убедиться
в том, что /(г) = Zj + Z2 + ... + Zr+l, где с, в. Z, — независимые и
§ 5. Пример из теории очередей
93
одинаково распределенные в соответствии с (5.1). Производящая
функция с. в. Z<r\ очевидно, равна [U (s)]r+1. Пусть у^+1 есть
коэффициент при Sm в разложении функции [U (s)]r+1. Наконец,
положим
G(s) = -^- + &o + ^iS + 62s2+ ••••
Наша цель — выразить U(s) через G(s). Для этого запишем сле-
дующие соотношения типа уравнений восстановления:
оо
V) = b_v = S 6 ¥</+'>, k > 2. (5.3)
/ = 0
Первое из этих соотношений очевидно. Что касается второго, то
событие {Sn > О, п = 1, ..., k — 1; Sk = — 1} представляет собой
объединение следующих несовместных событий: {Х{ = j; Х2 +
+ ... + Хп + j' > 0, п = 2, ..., k — 1; Х2 + ... + Хь + j = —1},
j = 0, 1, .... Так как с. в. Хг- независимы и одинаково распреде-
лены, вероятности этих событий, как легко видеть, равны
Формула полных вероятностей дает (5.3). Переходя к производя-
щим функциям, с помощью (5.3) получаем
оо / оо \
и (S) = 6_IS + s Здак”’
п=2 \/=0 7 п /
== b-ts + s 2 ь, ( S ) =
/=0 7 \п=2 /
= 6_,s + s s bt [U (s)]/+1 =
/=0
= b_,s + sU (s) [ G (U (s)) - 4^- ] =
= sU (s) G (t/(s)), 0<s^l.
Далее, U (s) непрерывна и строго возрастает при s е [0, 1], при-
чем U (0) = 0. Следовательно, U (s) удовлетворяет уравнению
G(t7(s)) = 1/s при 0 < s 1. Но
G" (s) = ~^-~{-2b2 + 6b3s + I2b4s2 + ...>0 при s>0,
так что функция G(s) является выпуклой; к тому же, по опреде-
лению G (s), lim G(s)= 4-оо и G(l)=l. Из рис. 2 легко заклю-
чить, что уравнение G(x) = 1/s может иметь самое большее два
положительных решения при каждом фиксированном Ц
94
Гл. 3. Основные предельные теоремы для марковских цепей
Поскольку lim U ($) = 0 и U($) строго возрастает на интервале
[О, 1], то U(s) должно быть меньшим из двух решений уравнения
G(x) = 1/s, если таковых два.
оо
Исследуем теперь условия, при которых Ул — 1 или <1-
Возникают следующие две возможности:
Рис. 2.
Случай 1. G'(l) >0. Условие Gz(l) >0 эквивалентно тому, что
оо оо
b^<^nbn. Из рис. 2 видно, что U (1) = S Yfe — £о< 1- Следова-
п«0 &=0
тельно, вероятность события {Sn > 0 при всех п} строго положи-
тельна.
Случай 2. G'(l) -^0. Условие G'(l) -<0 эквивалентно тому, что
оо оо
&-i 2 и в этом случае мы имеем 2 уА= (7(1)= 1. Далее,
д=0 k—Q
G'(U($))U'(s) = —1/s2 при 0<s-<l, так что в рассматриваемом
случае G(s)->1 при s->l (рис. 3). Отсюда следует, что если
G'(l) < 0, т. е. если
оо
b-i> 5 пьп,
п = 0
ТО
оо
М (Z) = 2 пуп = U' (1) = < 00,
лв0
§ 5. Пример из теории очередей
95
а если G'(1) = 0, т. е.
оо
b-i = 2 nbn,
п = 0
ТО
оо
M(Z)=SMY„=t/'(l)=°o.
п = 0
Возвращаясь к процессу обслуживания, поставим в соответ-
ствие распределению {bk} распределение {ak} количества посту-
пающих заявок за период следующим образом: Опреде-
лим Zij как число переходов (время), требующееся для того, что-
бы впервые попасть в состояние / < i из состояния I. Нетрудно
видеть, что Z2) i-i есть в точности с. в. Z, производящую функцию
U(s) которой мы только что рассматривали. Так как
оо
S az= 1,
х=0
то мы имеем
96
Гл, 3. Основные предельные теоремы для марковских цепей
и, аналогично,
оо \ / оо \ / оо
Ь-1 = 5 nbn «-> а0= s tian+l 1 = 2 пап
n~Q / \ п=0 / \ п=0
оо
Следовательно, М(Zit = ц< оо, если ^пап<1, и M(Z/U_1) =
п=0
= |х=оо, если ^пап=1. Ясно, что
%i, / i-l + ^i-1, i-2 + ••• +^/ + 1,/> /<Л
и поэтому M(Z^j) = (i — /)ц; в частности, M(Z2>0) ='ф,.
Рассмотрим теперь среднее время возвращения в состояние 0.
Отметим прежде всего, что вероятность времени возвращения быть
равным 1 есть просто #о, т. е. вероятность перехода Роо- Далее,
траектории, которые выходят из состояния 0 и возвращаются в это
состояние впервые за два или более переходов, могут быть раз-
биты на группы в зависимости от состояния Z, занимаемого после
первого перехода. Такое разложение в совокупности с марков-
ским свойством процесса позволяет получить для среднего вре-
мени возвращения следующее выражение:
оо
2 nf"0 = М (время возвращения) =
п~0
оо оо
= #о + 5 <МЕ (Zit о) + 1] = 1 + 5 fljE (Zit
i=l
оо оо
= 1 + 2 “ 1 + Н 2 tap
(-1 1=0
Таким образом,
оо
м< оо, если ц< оо„
п»0
т. е. при условии
оо
2 < 1,
i=0
и
оо
2<3=°°> если н = о°»
п=»0
или, что то же, если
оо
2 lai — 1.
1=0
$ 6. Еще один пример из теории очередей 97
Резюмируя полученные результаты, имеем
S пап< 1 ==>возвратный положительный,
/1 = 0
оо
2 пап 1 =^> возвратный нулевой (5.4)
п = 0
И
оо
2 пап > 1 невозвратный.
п=0
Эти результаты представляются довольно естественными. Вира-
оо
жение S пап есть среднее число требований, прибывающих за
/1=0
оо
один период обслуживания. Тогда если ^пап>1, то в среднем
п=0
больше заявок поступает, чем обслуживается за каждый период.
Следовательно, можно ожидать, что очередь будет расти беспре-
оо
дельно. С другой стороны, если ^nan<lt то процесс стремится
п=0
к некоторому стационарному состоянию. Нахождение стационар-
ного распределения связано со значительными трудностями (см.
гл. 14).
§ 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
Состоянием процесса, как и ранее, является длина очереди;
за каждую единицу времени прибывает одна заявка, а обслужи-
вается k заявок в соответствии с распределением {ah > 0, k =
= 0, 1,2,...}, если в очереди столько заявок окажется. Матрица
переходных вероятностей, как нетрудно убедиться, в этом случае
имеет вид
«о 0 0 ...
а{ aQ 0 ...
#2 «0
4 Зак. 939
эа
Г л. 3. Основные предельные теоремы для марковских цепей
Мы покажем, что если то существует стационарное
распределение, так что в этом случае процесс возвратный положи-
тельный. Так как 2 kak есть среднее число обслуживаемых за
период заявок, тогда как за это же время поступает только одна
заявка, то существование стационарного распределения при ука-
занном условии не является неожиданным,
оо
Рассмотрим уравнения = и положим £г = ^. Тогда
1=0
оо оо
при />1, т. е. ig<_/+1af-/+i = £,
откуда заменой индекса суммирования получаем
Zj = £•
А=0
Если (0 < | < 1) удовлетворяет этому уравнению, то для j = О
получаем
ОО ОО / ОО \
oo k—l
= 22 <^г —
A=1 j=0
k—l \ Л=1 '
= TZTf (1 - «о - (£ - ао)) = 1,
т. е. уравнение удовлетворяется и для /' = 0.
оо
Рассмотрим производящую функцию f (g) — S ak^k. Так как
k=0
оо
f(O) = ao>O и f(l)=l, то при условии f'(1)= S kak> 1 суще-
&=0
ствует точка go, 0 < go< I, такая, что f (go) = go (см. рис. 4). Вели-
чины jiz = (1 — go)go> /в0, 1, 2, ..., сумма которых равна 1, пред-
ставляют собой стационарное распределение вероятностей иссле-
дуемой марковской цепи. В частности, финальная вероятность
отсутствия очереди равна 1—go.
оо
Система уравнений = £/, / =/= 0, совпадает с системой
оо
У Pfjlj — h, i ф 0, из предыдущего примера. Как мы видели,
§ 6. Еще один пример из теории очередей 99
оо
P-процесс является возвратным, если В этом случае
k^Q
последняя система не имеет ограниченного непостоянного реше-
оо
ния. Следовательно, если S kak^A, то система S ViPij = Г|у
7=о
не имеет ограниченного непостоянного решения, и поэтому,
в частности, не существует стационарного распределения и про-
цесс является либо возвратным нулевым, либо невозвратным. Мы
докажем сейчас, что система
оо
2 РцУ) = Уь «=0=0, (6.1)
/=»0
имеет непостоянное ограниченное решение тогда и только тогда,
когда ^kak<l. Следовательно, процесс является невозвратным
тогда и только тогда, когда ^kak<\f и возвратным нулевым,
оо
когда ^kak=\. Так как любая последовательность с одинако-
во
выми членами удовлетворяет системе (6.1), мы можем считать,
что yQ = 0. Тогда (6.1) сводится к уравнениям
«2i/0 + «li/1 + «0i/2 = У\,
ЯзУо + «2^1 + а{у2 + aQy3 = у2,
ап+1Ув + апУ1+ ••• +^уп + аоуп+1=уп,
Умножая f-e уравнение на si+1, суммируя и пользуясь формулой
для преобразования свертки, получаем
Y (s) A (s) - saoyi = (s), или Y ($) = , (6.2)
4'
100
Гл. 3. Основные предельные теоремы для марковских, цепей
при условии, что Л(з)=£з. В (6.2) мы положили
Г(з)=2^з\ Л(5)=Ь/
4=0 А=0
Так как Л(О) = ао и Л(1)= 1, то Л(з)=з для некоторого з, та-
оо
кого, что 0 < s < 1, если Л'(1) = S kak > 1. Следовательно, У(з) не
k=0
может иметь ограниченных коэффициентов в этом случае, так как
это означало бы, что У(з) сходится для каждого $е[0, 1]. Таким
оо
образом, если У kak>\, то процесс возвратен.
*=0
Из строгой выпуклости функции Л(з), т. е. из того факта, что
Л"(з)>0, следует, что Л(з)¥= з при 0<s< 1, если Л'(1) =
оо
= S kak^. 1 (см. рис. 5). При условии 1 имеем:
£=•0
Л (s) — s = (1 — s)p
1 - A (s) 1
1 — s J
= (1-з) 1—(Л(1) —Л(з»2-з* =
- fe=0 -
оо
= (l-s)[l-F(3)], Г(з) = 2 wnsn,
м=0
где
оо
Wn= 2 af>0
i=n + l
И
оо оо / оо \ оо
2 а,-
n=0 n=0 \i=n+l / /г=0
§ 6. Еще один пример из теории очередей
101
Тогда
= ^-(l + ^(s) + (^(s))2+ •••) =
оо оо
= saayi^-^-, где и„>0, U (s) = unsn = [ W (з)]\
п=0 ^а0
П оо
Y (s) = saayiV (s), где vn = uk, V (з) = vnsn,
т. е.
y(s) = £l£L.
Далее, следующие условия эквивалентны:
(оо \ / оо \
r(i) = t/(i) = 2 uk<oo ,
4=0 / \ 4 = 0 /
так как (7(1) = 1 + №(1) + (№(1))2+ ... есть сходящийся ряд
типа геометрической прогрессии. Ясно, что t»i < v2 < ...—>(7(1),
так что Y(s) = saoyiV(s), будучи разложенной в степенной ряд,
имеет ограниченные коэффициенты тогда и только тогда, когда
2 kak < 1. Поэтому если 2 &Й4 < 1, можно взять yi¥=0, yk = a(sylVk-i
и получить ограниченное непостоянное решение уравнений (6.1),
102
Гл. 3. Основные предельные теоремы для марковских цепей
последовательно возвращаясь к уравнению (6.2) и приравнивая
коэффициенты. Это означает, что процесс невозвратный. Если
S kak = 1, любое решение системы (6.1) с необходимостью неогра-
ничено, откуда следует, что в этом случае процесс возвратен.
Итак,
процесс невозвратный, если
процесс возвратный нулевой, если ^ikak — \,
процесс возвратный положительный, если ^jkak>\.
§ 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
Мы приложим теперь критерии возвратности из § 4 к исследо-
ванию процесса случайного блуждания с матрицей переходных
вероятностей /"о Ро 0 0
<71 И Pi 0
II Рц 11 = 0 <72 Г2 Р2
Пусть
__ 1 РоР1 • • • Рп-1
Ла — 1, лп ~ 777--------—
Я1Я2 • • • Яп
Для случая, когда г, s 0, было показано (см. пример в § 1), что
процесс случайного блуждания обладает стационарным распреде-
оо
лением тогда и только тогда, когда 2ял<°°- Рассмотрим си-
п»0
стему уравнений
оо
г‘¥=0,
или
<71Ро + + рху2 = уъ
УпУп-l + ГпУп + рпУп+х = уп,
Легко видеть, что решения этой системы образуют двумерное ли-
нейное пространство. Мы можем задать уо и ух произвольно, и
тогда все остальные у, определяются из системы. Очевидно, yi=l
П—1
является решением. Покажем, что у0 — 0, уп= S Х/р^х, 1,
<-о
$ 7. Случайное блуждание
103
также является решением. Для первого уравнения имеем
«» + r,s, + Р,у, - Ш + Р1 <77 + " 77 " »'
Проверяя выполнение ft-го уравнения, мы должны показать, что
Поскольку рп + rn + qn = 1, достаточно убедиться в том, что
п—2 п п—1
Qn JtaL Л Л • РП ЛТГ/ = “Ь Qn) n ,-r. •
лшя лил piTii лея pi^ii
i —0 i — Q i—0
Но левая часть этого равенства есть не что иное, как
п—1
, . \V 1 1 , 1
(<7п + Рп) 2i 1Гл-У* ~Ь---л----Рп п л ’
Pini Pn-lnn-l рппп
1 - 1 - 1
Рп-1%-1 “ ~ Лп
по определению величин пп- Этим проверка и завершается. По-
п—1
скольку два решения yt 1 и r/n=21/Pi^i линейно независи-
оо
мы, общее решение системы l^PijZi=zb i^=0, имеет вид гп — а +
/=0
+ рг/п, и ограниченное непостоянное решение существует у этой
системы тогда и только тогда, когда ограничены уп, т. е. когда
оо
S 1/р/Л/<оо. Итак, мы установили, что
/-0
процесс возвратный, если
1
Pini
процесс возвратный нулевой,
оо оо
если V —— = оо и V П; = оо,
Pinl
1 1 f==0
оо ос
процесс возвратный положительный, если 2j------= 00 и л/ < °°>
/-о Pi 1 1=0
процесс невозвратный, если —Т-
104
Гл. 3. Основные предельные теоремы для марковских цепей
ЗАДАЧИ
1. Рассмотреть процесс случайного блуждания, где
Pl,i+1-P- 0<р<1,
Рц ® q — 1 — q при /=1, 2, ...» г—1,
Го, о ~ ГTt т = I,
и найти d(k) = М [время до поглощения состояниями 0 или г | начальным со-
стоянием является £].
Ответ'.
d(k) =
k______г (J — (q/p)k)
q-p q-p \-(q!p)T ’
если P ¥= -g,
k (r — k), если p = y.
2. Матрица P= || Pi] 117/==! называется стохастической, если
(i) Pij^Q при всех i, j = 1, 2, ...
oo
(ii) 2 Гу=1 при всех /=1, 2..........
/-1
Матрица Р называется двояко стохастической, если помимо условий (i) и (ii)
выполняется следующее условие:
оо
2 Pij~ 1 при всех /=1, 2, ....
Доказать, что если матрица переходных вероятностей конечной неприводимой
марковской цепи двояко стохастическая, то все стационарные вероятности равны
между собой.
3. Пусть || Гц ||^ ув1 —матрица переходных вероятностей неприводимой
марковской цепи с конечным числом состояний, и пусть {л— стационарное рас-
пределение этой цепи. Пусть, далее, <р(х)—выпуклая функция, определенная на
положительной полуоси х 0, || pffl || — матрица вероятностей переходов за
п шагов и
N
Ет =» 2 Я/<Р I ФиксиРовано*
/-1
Доказать, что Ет является неубывающей функцией аргумента т, т. е.
£m+i > Ет при всех т > 1.
4. Пусть Р = ИЛЛ — матрица переходных вероятностей неприводимой мар-
ковской цепи. Доказать, что если матрица Р идемпотентна (т. е. Р2==Р), то
Рц = pj} для всех i и / и марковская цепь непериодична.
п
Указание: Использовать теорему 1.2 для средних (1/т) 2 Р™*
т—1
5. Предположим, что состояние 0 — возвратное положительное, и обозначим
через {1ь} (п =Л, 2, ...) последовательные времена возвращения в состояние 0.
Очевидно, с. в. {ТГП}— независимые, одинаково распределенные, с конечным сред-
оо
ним. Пусть F (0 = *2 « Л} (I /1 < 1) — производящая функция их общего
Задачи
105
распределения. Определим Уп как момент последнего пребывания в состоянии 0
перед моментом п. Показать, что
оо п
{Yn = j} —
п=0
(l-P(t))
Указание: Доказать и воспользоваться соотношением Р {Yn ~ /} = Р + ...
...+IFV где qi = P{l^i > i} и Nn—число «визитов» в состояние0
за первые п испытаний.
6. Рассмотрим марковскую цепь SO? с конечным числом состояний и матрицей
переходных вероятностей Р ~ || Pij ||^ у=0, порождающей три класса: {0},
{1, 2, ..., N — 1} и {N}. Пусть первый и третий из названных классов поглощаю-
щие, а второй — невозвратный, и пусть состояние k принадлежит второму классу.
Определим вспомогательный процесс ЭЛ, называемый «процессом возвращения»,
изменив первую и последнюю строки матрицы Р таким образом, что Роа —
= РNk = 1, оставив все другие строки без изменения. Очевидно, что процесс
возвращения неприводим. Доказать, что среднее время uk до того момента, когда
процесс ЭЛ будет поглощен состояниями 0 или N, отправившись из состояния k,
равно 1/(ло 4- Ядт) — 1, где До + есть стационарная вероятность быть в со-
стоянии 0 или N для процесса ЭЛ.
Указание: Воспользоваться соотношением между стационарными вероятно-
стями и средними временами возвращения для состояний.
7. Рассмотрим марковскую цепь с состояниями 0, 1, N и матрицей пере-
ходных вероятностей с элементами
Ц.,
Р,7= / = г + 1- - = 0 [...у.
1 j = i,
о,
Предположим, что ц0 — ~ р-л = Kn~0, а все остальные Цг и Хг положительны.
Пусть k — начальное состояние процесса. Определить вероятности поглощения
для состояний 0 и N.
Ответ:
Р {поглощение в состоянии 0} == 1 — Р {поглощение в состоянии А/} =
JV-1
i=k
2 Pi
М
где
_ И1ц2 ... ц.
р0 l’ pi ...Л/
*8. В предыдущем упражнении определить среднее время до поглощения.
Указание: Использовать метод процесса возвращения, описанный в задаче 6.
Показать, что система уравнений для стационарных вероятностей {л/}^=0 сво-
дится к уравнениям
k+\<i^N,
106
Гл. 3. Основные предельные теоремы для марковских цепей
Ответ'. Среднее время до поглощения - 2 где
i-1
0<-
W-l \ \ /ГЛГ—1 'I
5 р/ 2 Р/ n 2 p/HtPz-i r Ze 2................
J-jfe ) \/—о //1/-0 J
'fc-1 \ /ЛГ-1 \ If N-l ’I
2 Р/ 2 Р/ n 2 p/HiPz-i i^k+\...................w-i.
J»o / \/ = i //l/=o J
9. Рассмотрим марковскую цепь с состояниями 0, 1, ...» W и матрицей пере-
ходных вероятностей с элементами
где
1 _e~ZailN
Щ'----°>0-
Отметим, что состояния 0 и N — поглощающие. Проверить, что ехр(—2аХ()
является мартингалом, т. е. М(ехр(—2a?G+i) | %/) == ехр(—2aXt), где Xt—со-
стояние процесса в момент t (t = 0, 1, 2, ...). Используя это свойство, показать,
что вероятность Px(k) поглощения состоянием N равна
1 - e~2ak
где k — начальное состояние.
Указание: Использовать тот факт, что поглощение одним из состояний 0
или происходит с достоверностью; доказать соотношение
М (exp (- 2aXJ) = М (exp (- 2аХп)) = PN (k) exp (- 2аМ) +(1-PN (*))
и воспользоваться им.
10. Рассмотрим следующий процесс роста конечной популяции (фиксирован-
ного размера N), состоящей из индивидуумов двух типов А и а. В моменты
времени t\ < t2 < /3 •. • один индивидуум умирает и заменяется другим одного
из возможных двух типов. Если непосредственно перед моментом замены tn
популяция состоит из / индивидуумов типа А и W — j индивидуумов типа а, то
вероятность того, что умрет индивидуум типа А, равна и того, что умрет
индивидуум типа а, равна (W — j)ц2/Вь где Bj = Ц1/ + p,2(W —-/). Логическая
основа этой модели такова. Вообще говоря, вероятность смерти в момент tn
* равна Ц1/(Ц1 + ц2) для индивидуума типа А и р2/(Ц1 + ц2) для индивидуума
типа а (gi/цг можно интерпретировать как преимущество при отборе типа А
над типом а). Принимая во внимание состав популяции, естественно приписать
вероятность событию, состоящему в том, что будет заменен индивидуум
типа А, и вероятность p2(AZ —-/)/Bj — замене индивидуума типа а. Предположим,
что характер рождения одинаков для обоих типов: вероятность того, что будет
рожден индивидуум типа А, равна //У, и типа а—(W — j)/N. Рассмотреть мар-
ковскую цепь {Хп}, где Хп есть число индивидуумов типа А в момент tn (п =» 1,
2, .с вероятностями перехода
В^' Р' /и------------BjN’
Задачи
107
Найти вероятность того, что популяция рано или поздно будет состоять только
из индивидуумов типа а, при условии, что в начале популяция состояла из k
индивидуумов типа А и (N — k) индивидуумов типа а.
Указание'. Показать, что уравнения, определяющие вероятности поглощения,
могут быть сведены к соответствующей системе уравнений для вероятностей
поглощения в задаче о разорении игрока, где используется представление про-
цессом случайного блуждания.
Ответ'.
Р {популяция состоит только из индивидуумов типа а} =
(Н1/Нг)Й
= (Hi/gz)'V - 1
\-k!N
Ц1У=Ц2.
U1 = ц2.
*11. Пусть А—конечная марковская цепь и 8 —множество всех возможных
предельных матриц для подпоследовательностей последовательности {Ak, k ~
== 1, 2, ...}. Доказать, что £ обладает следующим свойством: если Гр Г2е^,
то и е? (при условии, что Г^"1 существует).
12. Пусть Р — марковская матрица третьего порядка и ц (Р) = max —
й, i2, / b
— Pi2 •]. Показать, что ц(Р) = 1 тогда и только тогда, когда Р имеет вид
1 0 0
0 Р Я
г s t
(р, p + q—l*t г, s, г + s + t = 1)
либо получена из этой матрицы перестановкой местами строк и/или столбцов.
*13. Пусть Pi, Р2, ...» Р/< — матрицы переходных вероятностей неприводи-
мых непериодических марковских цепей, каждая из которых имеет по три со-
стояния, и пусть ц (Р) ~ max у — у). Предположим, что для каждого
Л. it, i
m
ci. (1 а. k), i == 1, 2, ..., матрица Ц Ра/ также
набора целых чисел
представляет собой матрицу переходных вероятностей неприводимой непериоди-
ческой марковской цепи. Доказать, что для любого е> 0 существует Л4(в) такое,
что при m > М
(т \
II <8 для люб°го набора ах- (1 а{. С k), i= 1, 2, ..., m.
i3»! /
Указание: Воспользоваться интерпретацией матриц Ра как линейных отобра-
жений симплекса А, задаваемого условиями Xi + Хг + Хз = 1, 1 х* 0, в себя.
(Показать, что такая интерпретация имеет смысл.) Показать, что
(а) ц(АВ) ц(А)ц(В) для любой пары стохастических матриц А и В;
(б) если А — стохастическая матрица, то ц(А) = 1 тогда и только тогда,
когда А преобразует некоторую вершину симплекса А в одну из других
вершин, а вторую вершину в точку на ребре, противоположном образу
108 Гл. 3. Основные предельные теоремы для марковских цепей
первой вершины, или когда А преобразует одну из вершин в вершину,
а противоположное ей ребро в ребро (или на ребро), противоположное
образу этой вершины. Показать, что последний случай невозможен в
условиях теоремы;
(в) показать, что Н (PaiPa2Pa3) < 1 для любых ai, «2, аз, для чего убедиться
в том, что если это неравенство не выполняется, то ребро отображается
на себя произведением матриц Ра, что противоречит исходному предпо-
ложению.
14. Если i — возвратное состояние, а Xk представляет состояние марковской
цепи в момент k, то показать, что
lim Р {Xk =/= I при п + 1 < k < п + N | Хо == 0 = 0-
ЛГ->оо
Показать, что если i — возвратное положительное состояние, то стремление к
пределу равномерно по п.
15. Обобщенная урновая схема Пойа. Из урны, содержащей а белых и b
черных шаров, случайно извлекается шар. Если шар оказывается белым, то его
возвращают, добавив еще а белых и р черных шаров, а если извлеченный шар
оказывается черным, его возвращают, добавив у белых и б черных шаров, при-
чем a 4- Р = у 4- б. Процесс многократно повторяется. Пусть л п — число извле-
чений белого шара после первых п испытаний.
п
(i) Если Рп, k = Р {Хп == k} и (х) = 2 рп, kxkt то показать, что имеет
место соотношение
/ \ (а — у) (х2 — х) / , . ,
ф/iW (П_1)(а + р) + а + 6 q>rt-iW +
{х[(п-1)у + а] + г> + (п-1)а}
(га- 1) (а + Р) + а + ь Фп-! W-
Й Показать, что М(Хп/я) -> у/(Р 4- У) при п~* со.
гзание: Показать, что
, , Ф*-10) ,v a + (£—1)у
<₽п Ш У> ^4 (k-1) (a + $) + a + b + ^4 (k-l) (a + p) + a + Z> '
fe=l
и отсюда вывести предельное соотношение фд (1)/п -> у/(Р 4- у).
16. В условиях предыдущей задачи показать, что
П-»оо 1\ п ) J \ Р + у ) Е
Указание* Найти рекуррентное соотношение для ф„(1), подобно тому как
это делается в (ii).
17. При тех же условиях показать, что Хп[п у/(Р 4- У) по вероятности
при п оо.
Литература
109
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
1. Марковская цепь на состояниях {0, 1, 2, 3, 4, 5} имеет матрицу переходных
вероятностей вида
1 3 _2 3 0 0 0 0 1 0 0 0 0 0
2 3 1 3 0 0 0 0 0 _3 4 4 0 0 0
0 0 A 2 A 0 0 0 _1_ Q 2 Q 0 0 0
(a) 1 A . (b) 1 О 1 О 1 3
0 0 1 "5 ‘t "5 0 0 1 1 1 T 0 1 ¥ 1 J 1 0
1 T 0 1 T 0 1 T i "4 1 0 1 6" 1 ”6 1 “3 0
_i_ 1 1 _1_ 0 0 0 0 0 1
6 6 6 6 6 6
Выделить классы состояний и найти предельные вероятности lim Р£ t для
П->оо '
i = 0, 1, 2, 3, 4, 5.
2. Рассмотреть задачу о разорении с начальными капиталами aw b (а > 10,
b > 10) у игрока I и игрока II соответственно. Пусть р(1—р) есть вероятность
игроку I выиграть (проиграть) единицу у игрока II в каждой партии. Какова
вероятность того, что размер капитала игрока I достигнет величины а + b — 3
раньше, чем уменьшится до 5.
ЗАМЕЧАНИЯ
Содержание § 1—4 является стандартным аппаратом марков-
ских цепей и имеется в большинстве руководств по этому пред-
мету.
Примеры из § 5 являются классическими для теории очередей.
Последовательное изложение теории читатель найдет, например,
в книге Такача [1].
ЛИТЕРАТУРА
1. Takacs L., Introduction to the Theory of Queues, Oxford Univ. Press, London
and New York, 1962.
Глава 4
АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
МАРКОВСКИХ ЦЕПЕЙ
Алгебраические методы либо их сочетание с вероятностными
позволяют получить многие важные результаты теории марков-
ских цепей. Мы остановимся на ряде таких методов в настоящей
главе. Для того чтобы не уходить далеко от основного предмета,
мы дадим лишь краткую сводку основных результатов из теории
матриц, которые потребуются нам в дальнейшем. Более полное
изложение этих результатов читатель найдет в приложении.
§ 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
При рассмотрении марковских цепей вычисление вероятностей
перехода за п шагов занимает очень важное место. Для этой цели
мы разовьем специальный аппарат, основывающийся на теории
собственных значений и собственных векторов1). (Специальные
методы для исследования марковских цепей, описывающих про-
цессы случайного блуждания, будут изложены в § 4—6.)
(а) Спектральное представление
Пусть А — квадратная матрица порядка п. Ненулевой вектор х,
удовлетворяющий соотношению Ах = Хх для некоторого комплекс-
ного числа %, называется правым собственным вектором матрицы
А, принадлежащим (или соответствующим) собственному значе-
нию X. Если хА == Хх, то мы назовем вектор х левым собственным
вектором матрицы А. Если правые (или же левые) собственные
векторы образуют базис в n-мерном линейном пространстве, то
существуют линейно независимое семейство ..., ф(п) правых
собственных векторов и линейно независимое семейство .
.левых собственных векторов матрицы А, являющиеся
биортогональными системами. Это значит, что
п
/ (]\\ _ ( 0, если ij,
“ lti ( l, если t = j,
*) Читателю, не знакомому с основами теории собственных значений и собч
ственных векторов матриц, рекомендуем обратиться к приложению.
§ 1. Предварительные сведения
111
ГДе ф(й = (ф.ь ..., фгп), фб‘) = (фл, .tyjn) и ф^ — число, ком-
плексно сопряженное числу ф^. В этом случае говорят, что матри-
ца А диагонализируемая. Пусть
Ф11 ... Фп1
Фи ••• Ф1П
%! О
О Я>2
фш • • • фпп
Фш ••• Фшг
о
о
О 0 . •. Кц
где Хь ..., — собственные числа (не обязательно различные)
матрицы А, а фб), .. ., ф(п) — соответствующие им собственные
векторы. (Отметим, что нумерация элементов матрицы Ф отли-
чается от обычной.) Тогда матрица А обладает представлением,
называемым спектральным, в виде произведения трех специаль-
ных матриц:
А -= ФЛФ*.
Используя соотношение (фб), ф(Л) = можно непосредственно
убедиться, что ТФ = ФЧ1* = I (I — единичная матрица). Отсюда
А2 = ФЛЧ'ФАЧ'* = ФА2Т, и вообще
Аот = ФА^Г,
(1.1)
где, очевидно,
В случае если А — марковская матрица, формула (1.1) дает удоб-
ное представление матрицы m-шаговых переходных вероятностей.
Правда, его эффективное использование требует вычисления всех
левых и правых собственных векторов.
(б) Положительные матрицы
Пусть А — действительная матрица, которая имеет по крайней
мере один положительный элемент, но не имеет ни одного отри-
цательного элемента. В этом случае мы будем писать А > 0 и на-
зывать матрицу А положительной. Если все элементы матрицы А
положительны, то мы будем писать А » 0 и называть матрицу А
строго положительной. Нам понадобятся следующие результаты
(их доказательства вынесены в приложение).
Каждой матрице А>0 соответствует число г(А)^0, называе-
мое спектральным радиусом матрицы А, которое равно нулю то-
гда и только тогда, когда Aw = 0 для некоторого целого числа
112 Гл. 4. Алгебраические методы исследования марковских цепей
m > 0. Если А > 0, то существуют положительные векторы f, х>0,
такие, что Ax = r(A)x, fA = r(A)f. Если Л — любое собственное
значение матрицы А, то |Л|О(А); если |^| = /'(А), то ц = V^(A)
есть корень из единицы, т. е. = 1 для некоторого положитель-
ного целого числа k, и r]mr(A) является собственным значением
матрицы А при m = 1, 2, .... Наконец, предположим, что Aw 0
для некоторого tn > 0; тогда векторы х и f строго положительны
и определены однозначно с точностью до постоянного скалярного
множителя. Более того, если X — собственное значение матрицы А,
отличное от г (А), то |Х| <г(А).
§ 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ
ВОЗВРАТНЫХ СОСТОЯНИЙ
Предыдущие результаты имеют непосредственные приложения
в теории марковских цепей с конечным числом состояний.
Пусть Р = ИЛЛ, / = 1» • ••, — матрица переходных веро-
ятностей. Очевидно, Р > 0. Пусть х — произвольный вектор, удов-
п
летворяющий условию 2*/=Ь Тогда
(п п п \
2 XiPn, £ XtPi2, . . ., 5 XtPin] .
i=l 1=1 i=I /
Далее,
п / tl \ n n n
SpWo (2.1)
7-1 \f-l / l-l 7=1
Мы утверждаем, что неравенство хР > Кх не может выполняться
для вектора х > 0 при любом Л > 1 (откуда следует, что
г(Р)<1). В самом деле, суммируя компоненты в обеих частях
п п
соотношения хР>Хх и учитывая (2.1), получаем
/=1 i=i
п
Так как 2 xi > 0, то отсюда следует, что Z
z=i
С другой стороны, вектор (1, ..., 1), как легко видеть, яв-
ляется собственным вектором матрицы Р, принадлежащим соб-
ственному значению 1. Таким образом, r(P) = 1.
То, что 1—собственное значение любой конечной марковской
матрицы и ему соответствует положительный левый собственный
вектор, можно также вывести из теоремы 1.3 гл. 3. Действитель-
но, мы знаем, что в конечной марковской цепи по крайней мере
одно состояние (а следовательно, по крайней мере один класс)
является возвратным положительным. Перенумеровав состояния,
если это необходимо, мы може^м считать, что состояния
i = 1, ...» г составляют возвратный положительный класс. Сле-
§ 2. Собственные значения и классы возвратных состояний 113
довательно, Рц = 0 для всякой пары состояний /,/, такой, что
i е {1, .... г}, a j е {г + 1, ..., п}. Таким образом, Р имеет вид
II Pi 011
Р-|в с|' <2'2>
где Pi — марковская матрица порядка г X л В силу основной пре-
дельной теоремы для марковских цепей (см. теорему 1.3 гл. 3) су-
ществуют положительные числа ль ..., лг, такие, что
5^/ = ^, г,
И
S Л/ = 1.
Z = 1
Пусть х° = (ль ..., Лг, 0, ..., 0); опираясь на специальную
структуру (2.2) матрицы Р, легко проверить, что х°Р = х°. Не-
сколько более подробный анализ показывает, что справедлива сле-
дующая
Теорема 2.1. Если Р — матрица переходных вероятностей
марковской цепи с конечным числом состояний, то кратность соб-
ственного значения 1 равняется числу возвратных классов в цепи.
Доказательство. Мы видели, что если — возвратный
класс состояний, то существует левый собственный вектор х<!) > 0,
отвечающий собственному значению 1, такой, что = 0 при
1фС\. Точно так же для каждого возвратного класса Ch, h =
= 2,3, ..., существует положительный собственный вектор x<h\
/г = 2,3, ..., отвечающий собственному значению 1, такой, что
х(.А) = 0 при i ф. Так как различные классы не пересекаются, то
векторы х^1), х<2\ ... линейно независимы. Отсюда следует, что
кратность собственного значения 1 не меньше, чем число различ-
ных возвратных классов. Покажем теперь, что она и не больше
этого числа. Пусть хР = х, тогда хРт = х при m = 1, 2, ..., т. е.
^x^^xh m==l, 2, ....
z=-i
Но если /— невозвратное состояние, то, как мы знаем, lim Р^^О
т->оо
для всех i. Отсюда следует, что х$ — 0 для каждого невозврат-
ного состояния /, так что мы можем написать
г г
S S XiPii = xh j е= □ ch,
t^ch ы
114 Гл. 4. Алгебраические методы исследования марковских цепей
где Ci, Сг — возвратные классы. Так как = О, если i и /
принадлежат разным возвратным классам, то
5 XiPu^Xt, i^ch, h-\, г.
Если Xi #= О для некоторого i е Сл, то по теореме 1.3 гл. 3 су-
ществует константа cth, такая, что
Xi = ahx{i1^ i е
Таким образом,
X = 2 аЛх(Л),
/1=1
откуда заключаем, что векторы х^ образуют базис в подпростран-
стве левых собственных векторов, соответствующих собственному
значению 1.
Вероятностная интерпретация собственных значений и собственных
векторов
Рассмотрим подпространство правых собственных векторов
матрицы Р, отвечающих собственному значению 1. Оказывается,
в этом подпространстве существует базис, имеющий очень про-
стую вероятностную интерпретацию.
Пусть Ci, ..., Сг — возвратные классы марковской цепи с мат-
рицей переходных вероятностей Р. Определим р^ как вероятность
рано или поздно попасть в класс Ch из состояния /, т, е.
pW = Р Ch для некоторого =
Ясно, что
( 1 при i е С7,
'Но при ™
так как возвратный класс покинуть невозможно. Пусть р(Л) =
= (р(1Л), • ••, h = 1, ..., г, тогда из (2.3) следует, что векто-
ры р(1), ..., р(г) линейно независимы. Кроме того, вероятности
удовлетворяют уравнениям
p\h} = Р1, ..., я; h = 1, ..., г
(см. уравнения (3.1) гл. 3), из которых следует, что pW, pw
являются правыми собственными векторами матрицы Р, соответ-
ствующими собственному значению I. Так как этих векторов г и
они линейно независимы, то в правом собственном подпростран-
§ 2. Собственные значения и классы возвратных состояний 115
стве, отвечающем собственному значению 1, векторы р<4
образуют базис. Непосредственной проверкой нетрудно убедиться
в том, что
( 1, если, i = /,
(Х(П, р(/))= ’ '
г ( 0, если z=/=J,
где — левые собственные векторы, отвечающие собственному
значению 1 (см. доказательство предыдущей теоремы).
Предположим теперь, что матрица Р обладает спектральным
представлением и что собственные значения Z2, ..., зану-
мерованы так, что 1 == Zi = ... = ^>|Z,r+i ... и Xr+i 4= 1. Мы
можем положить = р(1), ..., <р(г) = р(г) и = х<!), ..., ф(г> =
= (см. приложение). Из представления
рт = ФЛШЧГ
получаем
р™ = 2 ФЛлЭл/ = + • • • + . 2, флХ%-
П = 1 ’ П — Г+1
Предположим, что матрица Р не имеет собственных значений, от-
личных от 1, модуль которых был бы равен 1. Тогда |Хл| < 1,
h = г + 1, ..., /г, и при /л —> оо
2 флХ%-^°>
Л=г + 1
причем скорость сходимости имеет порядок самое меньшее
|Xr+i|m. Скоро будет показано, что < 1, h = г + 1, ..., /г,
тогда и только тогда, когда Р не имеет периодических возвратных
классов (см. теорему 3.1 следующего параграфа). Предполагая,
что Р не имеет таких классов, и вспоминая, что = tyh., h =
= 1, 2, .. ,fr, / = 1, ... ,п, отлично от нуля тогда и только тогда,
когда / е Ch, мы видим, что
= Фг/'Фз/ = ••• = ФггФг/ = 0 для невозвратных состояний /.
Таким образом, если состояние / невозвратно, то Р™~
п
= S и эта величина стремится к нулю со скоростью
| Vh |т при т —► оо. Если же j,i е Ch, то среди первых г слагае-
мых в выражении для Рц отлично от нуля только ф/ифл/, но ф^г =
= 1 (вспомним, что фЛ/ = Р/Л)) и ~ lim Р™ Мы видим,
т-»оо
что вообще для всех состояний / разность Л/ — Р™ стремится
к нулю при т -* оо со скоростью самое меньшее |2ir+i|m.
116
Г л. 4. Алгебраические методы исследования марковских, цепей
Теперь предположим, что, кроме |Vh|< 1, имеет место еще и
неравенство |Xr+2| < |%r+i |. Пусть, как обычно, Т обозначает мно-
жество всех невозвратных состояний, i, j е Т\ мы хотим найти
следующий предел:
lim P{Xm = i\XQ = i, Xm^T},
т. e. предельное значение (при m-*oo) вероятности того, что, ис-
ходя из i е Г, процесс будет находиться в невозвратном состоянии
/ в момент т. Имеем
Как мы
п
2
1 h~r+l
видели, для
Так как | | > 11г+г|, то
невозвратного состояния j вероятность
llm =
т-»оо 2 PTj 2 Фг+1, + /
^г + 1, /
2 %+!,/
/еГ
при условии, что знаменатель не равен нулю. Если же знаменатель
равен нулю, то нам придется исследовать члены в сумме
п
2 ФлЛл'Фй/’ содержащие Лг+2 и другие собственные значения,
Л=г+1 7
модуль которых равен |Хг+2|, и т. д. (См. § 8 гл. 13, где эти идеи
развиваются далее.)
§ 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
В этом параграфе мы дадим более полное описание структуры
периодической цепи. Простейший пример периодического класса
с периодом d дает цепь с d состояниями 1, ..., d и матрицей пе-
реходных вероятностей
О
Р12 — Ргз —
~ Pd-\,d~ Рdl — 1>
1 0 ... О
О 1 ... О
о о ... О
Менее тривиальный пример возникает, если каждое из состояний
1, ..., d заменить группой состояний, причем группы состояний
.... Cd не пересекаются, а Рц определить таким образом, что
§ 3. Периодические классы
117
Pij =р 0 только тогда, когда i е Сь / е С2, или i <= С2, j <= С3, ...
.или i е Cd, j^C[. Матрица Р принимает в этом случае вид
О
О
Pi
О
о
pd 0 о
При этом мы можем определить Pij так, чтобы любые два состоя-
ния сообщались. Мы покажем сейчас, что всякий периодический
класс имеет такую структуру. Пусть d — период класса состояний
W, которые помечены целыми числами 1, ..., М. Обозначим через
Ci множество всех состояний, достижимых из состояния 1 за какое-
либо число шагов, кратное d, т. е. / Сх тогда и только тогда,
когда Р"/>0 для некоторого целого п > 0. Далее, для каж-
дого r= 1, d—1 определим Cr+i как множество тех состоя-
ний, которые могут быть достигнуты из состояния 1 за г плюс
кратное d число шагов, т. е. / е Cr+i тогда и только тогда, когда
Р?/+г>0 для некоторого целого п > 0.
Покажем сначала, что если / G, то из Рр > 0 следует, что
h = md для некоторого целого т > 0. Действительно, так как
j (?= Ci, то P\f>0 для некоторого п > 0. Следовательно, так как
pnd+h^ р^р™* >о (см. следствие 4.1 гл. 2), то по определению
периода nd + h должно делиться на J, а потому и h делится на d.
Теперь мы покажем, что если i е Ci и / <= Cr+i, то из Рц>0 сле-
дует, что h = nd + г для некоторого целого п>0. В самом деле,
пустьР//>0 для некоторого s>0, Рц > 0 для некоторого q>Q
и p^f+r >0 для некоторого т 0; тогда если w = s + dq +
+ md + г, то Pn>Pijd+rP/iP?iZ> 0, и, значит, w кратно d; следова-
тельно, s + г кратно d. Но P//+s PSjiPhu>®> так что h + s делится
на d. Эти два результата позволяют утверждать, что h — г делится
на d, т. е. h = nd + г для некоторого п > 0.
Мы оставляем читателю проверить, что из доказанного сле-
дует, что множества ..., Cd не пересекаются и непусты, что
d
(JCt=IF и что i Сг гарантирует равенство Рц == 0 для каж-
дого / ф Cr+i, где Cd+i = Сь Проанализировав матрицу периодиче-
ского класса, мы можем теперь доказать ранее высказанное ут-
верждение относительно появления собственных значений, модуль
которых равен 1, у матрицы переходных вероятностей марковской
цепи.
118 Гл. 4. Алгебраические методы исследования марковских цепей
Теорема 3.1. Ес.м Р — матрица переходных вероятностей
конечной неприводимой периодической марковской цепи с перио-
дом df то корни d-й степени из 1 являются собственными значе-
ниями матрицы Р, кратность каждого из них равна единице, и не
существует других собственных значений, модуль которых равен 1.
Доказательство Пусть Z)f, ..., Dd — «циклические клас-
сы» процесса в том смысле, в каком мы их только что определили,
т. е. из i е Dr следует, что Pij == 0 для каждого / ф DT^ Не теряя
общности, предположим, что Di = {1, . .., nJ, Ь2 = {ni + 1, ...
..., ni + п2}, ,.,, Dd = {М — nd + 1, ...» М}. Из определения
циклических классов следует, что
А] 0 ... О
О А2 ... О
О 0 ... А,
где Аг- — марковская пг- X ni-матрица. Кроме того, для каждого i
существует целое число пг > 0, такое, что АГ О (см. упр. 8
гл. 2). Следовательно, Аг- имеет строго положительный левый соб-
ственный вектор принадлежащий собственному значению 1
алгебраической кратности 1. Благодаря структуре матрицы Pd мы
можем, дописав нужное количество нулей к цЯ, получить линейно
независимые векторы xW ..., x(d\ такие, что
x(i) = x(i)pd, /=1, d.
Рассмотрим векторы у(1) = х(1), у(2) = х(1)Р, ..., y{d} = x(I)PJ"1. Един-
ственные отличные от нуля компоненты вектора х^1) — это те, что
имеют индексы 1,2, ..., п^ вероятность Р{$ отлична от нуля толь-
ко в том случае, если класс, которому принадлежит состояние /,
переходит за h шагов в циклический класс, которому принад-
лежит состояние k. Таким образом, ненулевые компоненты вектора
имеют индексы щ + ... + + 1, ..., ni + ... + п». Это
значит, что векторы 1, ..., d) линейно независимы. Кроме
того,
yU)pd х(пр 1 prf = x(1)pdpf‘“I = == у(П.
Следовательно, если мы ограничимся рассмотрением пг-мерного
линейного пространства, включающего только те компоненты век-
тора у<*>, что лежат в Di, то получим левый собственный вектор
матрицы Ai, соответствующий собственному значению 1.
Так как собственное значение 1 матрицы А/ простое (имеет
кратность 1), то каждый у^') совпадает с х<*) с точностью до ска.
§ 3. Периодические классы
119
лярного множителя. На самом деле, если нормировать векторы
п
х<4 x<d> условием /г=1, d, то получим, что
i=i
у(Л) = h ~ 1, ..., d. Соответственно мы можем теперь запи-
сать х^2) = хП)Р, х<3) = х(2)Р, ..., х<!) = х«*Ф.
Пусть со = e2ni!d', тогда с помощью последних соотношений по-
лучаем
(х(1) + х(2) + х(3) + ... + XW) р ях(1) + х(2) + ... + XW,
+ СОХ^) 4- б)2х(3) 4- ... 4. х(^)) Р = G)-l + (дх^ + ... +
+ ©2х^2) + ®4х(3) + ... + со2 (d—l)x(d)) р = (о"“2 (х(1) Ю2Х(2) 4. ,., 4. ю2 (d — 1)х(^)),
(ха)+©^“Ох(2)4.02(б?-1)х(3)4. ... 4. (о(^~02х(^)) р =0)-(^-1) (x(D+®^-l)x(2)+...+0^“I)2XR.
Линейная независимость векторов х<*> гарантирует, что ни один из
векторов в этих соотношениях не равен нулю. Кроме того, послед-
ние соотношения означают, что все корни d-й степени из 1 яв-
ляются собственными значениями матрицы Р.
Предположим далее, что хР = Ах для некоторого ненулевого
вектора х. Тогда xPd = Adx. Разбивая этот вектор на векторы z6) =
= (хр .... хпу z® = (xni+I> .... x„i+„2).......
мы видим, что
z(Z)At-= Vz(z), Z= 1, d.
Поскольку по крайней мере один из z^ не равен нулю, а для каж-
дой матрицы Аг существует целое число т, такое, что АГ > 0, то
либо № = 1, либо |V|< 1. Если № = 1, то существуют константы
си ..., Cd, такие, что
z(Z) = с^\ i = 1, ..d,
а следовательно, x = CiX^ + ... + cdx(dX
Итак,
Ax = xP = f jX(2) + c2x(3) + . •. + QX(1),
или
ACjX(1) + . . . + hcdX{d} = CdX{i} + C1X(2) + . . . + Q_jX(J).
Так как векторы х<г’) линейно независимы, то
ZCj ~ Cdi hC'2 ^1, • • •, hcd = Cd — i,
или
Cj—i = ^cd = (л ) cdi
Cd-2 “ Cd = (л ) cdi ..., cx = Kd cd — k cdi
поскольку V = 1. Это означает, что х с точностью до скалярного
множителя совпадает с одним из уже построенных собственных
векторов матрицы Р.
120 Гл. 4. Алгебраические методы исследования марковских цепей
Перейдем к случаю произвольной марковской матрицы.
Теорема 3.2. Если Р — матрица переходных вероятностей
конечной марковской цепи, то все ее собственные значения, по мо-
дулю равные 1, являются корнями из 1. Корни d-й степени
из 1 являются собственными значениями матрицы Р тогда и толь-
ко тогда, когда множество состояний марковской цепи, которой
соответствует Р, включает возвратный периодический класс пе-
риода d. Кратность каждого корня d-й степени совпадает с чис-
лом возвратных классов периода d.
Доказательство этой теоремы по существу идентично доказа-
тельству теоремы 3.1. Поскольку из соотношения Ах = хР сле-
дует, что
Л - хРт,
или, в координатной форме,
Л/=5х/РГ/,
/ —1
то, переходя к пределу при m —► оо, мы видим, что х$ = 0, если
состояние / невозвратно. Таким образом, мы можем рассматри-
вать только возвратные состояния, что немедленно сводит рассмат-
риваемый общий случай к предыдущей теореме.
§ 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ
ЦЕПЕЙ
Пусть Р — матрица переходных вероятностей случайного блуж-
дания по неотрицательным целым числам, вероятность перехода в
одно из соседних состояний из состояния &(&> 1) равна V2, а ну-
левое состояние является отражающим экраном, т. е.
0 1 00...
Чтобы найти вероятность перехода из состояния k в состояние I
за п шагов, мы могли бы получить n-ю степень матрицы Р и вы-
делить элемент Ры- Этот путь, однако, слишком громоздок.
Другой возможный путь — это попытаться обобщить метод
собственных значений и собственных векторов, развитый в § 2.
В случае бесконечных матриц это не всегда можно сделать,
§ 4. Специальные вычислительные методы 121
Однако для матриц только что описанного вида и, более того, для
матриц переходных вероятностей, соответствующих процессам слу-
чайного блуждания, имеет место бесконечномерный аналог пред-
ставления (1.1).
Мы сейчас получим выражение для Pki способом, который ил-
люстрирует общий подход, применимый к произвольным процес-
сам случайного блуждания.
Складывая два тригонометрических тождества
cos (а ± Р) = cos а cos Р Т sin а sin р,
приходим к следующему тождеству:
cos а cos р = у cos (а + Р) + -у cos (а — Р). (*)
Пусть а = 0, а р = &0(& = 1,2, ...); в этом случае имеем
cos 0 cos kQ = у cos (k + 1) 0 + — cos (6 — 1) 0. (4.1)
Так как элементы k-n строки матрицы Р имеют вид
==0, Pkfk-.2~®) Pk,k-\ — ^ Pk.k^^i
P k, k + i у» = •••, ^ = 2, 3,
/’1,0 = 4. ph> = o. /’.,2=4’ Plt3 = 0,...,
Po,o = O, P0,i = l> P0>2 = 0,
тождества (4.1) можно записать как
cos 0 cos &0 = 2 Pkr cos rO, k = 0, 1, .... (4.2)
r = 0
Умножая обе части (4.2) на cos 0, получаем
cos2 0 cos £0 = 2 Pkr cos 0 cos r0. (4.3)
r=»0
Представим произведение cos 0 cos r0 с помощью (4.2) в виде
cos 0 cos r0 == 2 Prs cos S0.
s=0
122
Гл. 4, Алгебраические методы исследования марковских цепей
Подставляя это в (4.3), получаем
оо / оо '
COS2 6 COS kB = 2 ( Pkr 2 Prs COS $0
r«0 \ s==0 t
oo / oo '
= 2 (cos «e 5 PkrPrs
s=0 \ r=0 /
oo
= 2 pIs cos $e.
s=0
Отметим, что суммирование от 0 до oo введено лишь для упроще-
ния обозначений; на самом деле лишь конечное число слагаемых
отлично от нуля. После п — 1 повторений процедуры, состоящей
в умножении на cos0 и изменении порядка суммирования, полу-
чаем
оо
cos" 0 cos £9=2 Pkr cos r0. (4.4)
r=0
Умножим обе части этого уравнения на coss0 и проинтегрируем
по 0 от 0 до 2л:
2л
J cos" 0 cos £0 cos s0 dB
о
2Л oo
= J 2 P^r cos r0 cos ~
0 r=*0
oo 2л
= j cos r0 cos $0 dQ. (4.5)
r=0 0
Используя тождество (*) с a = r0 и p — s0, легко показать, что
2л
J cos г0 cos s0 dB =
о
О при r=/=s,
л при r = s^l,
2л при г = s = О,
(4.6)
Из (4.5) и (4.6) сразу же получаем
2л
2 f cos" 0 cos £0 cos s0 dB
•П J
0
2л
4- f cos" 9 cos £0 dB
ZJT J
0
при s=£0,
при s = 0.
Эти интегралы легко вычислить для любых заданных п, £ и $.
Общий же метод, частным случаем которого мы только что
воспользовались, состоит в следующем.
§ 4. Специальные вычислительные методы
123
Пусть нам задан процесс случайного блуждания на множестве
неотрицательных целых чисел с матрицей одмдшагобых переход-
ных вероятностей вида
Р =
''о
<h
О
Ро О
П Pi
?2 Г2
О ...
О ...
Р'2 ••• >
(4.8)
где q„ + rn + рп = 1, qn > 0, рп >0, гп > 0 при п = 1, 2, ... и
Го + Ро = I, Ро > 0, Го 0. (Отметим для будущих ссылок, что ни
один из результатов, которые мы получим ниже в этом параграфе,
не зависит от условий qn + гп + рп = 1, п = 1, 2, ..., и Го + ро =
= 1.) Рассмотрим следующую систему уравнений:
xQk W - qkQk-i W + rkQk (x) + pkQk+i (x), k - 1, 2, ..(4.9)
с начальными условиями Qo(x) = 1 и Qi(x) = (x — rQ)lpQ. По-
скольку pn > 0 при всех n = 0,1,2, ..., ясно, что Qn(x), n >2,
последовательно определяются из формулы (4.9) и что Qn(x) яв-
ляется полиномом от х степени в точности п. Далее мы восполь-
зуемся теоремой, доказательство которой выходит за рамки этой
книги и которая устанавливает следующий факт. Существует не-
убывающая и непостоянная функция о(х), определенная на отрезке
[—1, 1], такая, что
г ( =0 при &=/=<$,
h k==0> 2> ••• • (4Л°)
J I > 0 при к = s,
О функциях Qfe(x), k = 0, 1, ..., обладающих свойством (4.10), го-
ворят, что они являются ортогональными полиномами относитель-
но распределения о(х) на отрезке [—1, 1]. Функция о(х) един-
ственна с точностью до аддитивной постоянной. Эта общая теорема
позволяет получить явные выражения для вероятностей PJL. В са-
мом деле, учитывая то, как мы задали Q0(x) и Qi(x), уравнения
(4.9) можно переписать в виде
оо
xQk(x)=^PkrQr(x), k = 0, 1............... (4.11)
г = 0
Умножая обе части на х и подставляя это в (4.11), получаем
оо ОО оо
xX^x) = %Pkr%PrsQs(x)=%PlsQs(x), 6 = 0,1,.... (4.12)
Ги0 S—0 s="0
124
Гл. 4. Алгебраические методы исследования марковских цепей
Продолжая таким же образом, переходим к соотношениям
x"Qft(x)=SPftrQr(x), £ = 0,1,..., п=1, 2, .... (4.13)
г=0
Умножая обе части на Qs(x) и интегрируя на интервале [—1, 1] по
do(x), мы находим, воспользовавшись соотношением ортогональ-
ности (4.10), что
1 оо 1 1
J xnQk (*) Qs (х) da (х) = Pnkr J Qr (х) Qs (х) da (х) = Pnks J Q; (x) da (x),
-1 r=0 -1 -1
откуда следует доказываемая формула
j xnQk (x) Qs (x) da (x)
Pks = ——i----------------. (4.14)
J Qs (x) da (x)
-1
Как мы уже отмечали, приведенная процедура напоминает
метод диагонализации из § 1. Действительно, соотношения (4.9)
просто означают, что для каждого х бесконечномерный вектор
(QoW, Qi(*), ...) является, формально, собственным вектором
матрицы (4.8), соответствующим собственному значению х. По-
скольку мы имеем дело с континуумом собственных значений, есте-
ственно предположить, что представление Рц дискретной суммой,
аналогичное полученному в § 1, 2, не имеет места. Оказывается,
однако, что соответствующее обобщение спектрального представ-
ления (1.1) дается формулой (4.14). В его основе лежит существо-
вание «непрерывного спектра» в дополнение к дискретному (воз-
можно, пустому), что является характерным для бесконечных мат-
риц. Строгое математическое рассмотрение этих вопросов выходит
за рамки настоящей книги. Тем не менее мы рассмотрим еще не-
сколько иллюстративных примеров, связанных с этой теорией.
Может показаться, что изложенный метод, сколь ни элегантна
его теория, не имеет практической ценности. Действительно, чтобы
найти Pks, необходимо определить полиномы {ФИх))Г==о и распре-
деление ог(х), относительно которого нами установлен до сих пор
лишь факт существования. В действительности же положение дел
много лучше, чем это намечается указанными трудностями.
Прежде всего мы располагаем хорошо разработанной теорией ор-
тогональных полиномов, которая позволяет получить важные тео-
ретические результаты, касающиеся поведения вероятностей и
в частности их отношений, при п —> оо,
§ 5. Примеры
125
С другой стороны, процессы случайного блуждания, возникаю-
щие в конкретных задачах, имеют матрицы переходных вероятно-
стей более специального вида, чем (4.8). Например, может быть,
что ро = pi = р2 = ..., qo = qi = •.., или же рп = pn±i = . ..,
qn = qn±x = ... для некоторого п. В этих случаях, как впрочем
и в других, можно показать, что полиномы Qn(^) являются ком-
бинациями различных классических систем полиномов, теория ко-
торых хорошо развита.
§ 5. ПРИМЕРЫ
(а) Симметричное случайное блуждание с отражающим экра-
ном. Для того чтобы подвести вычисления, проведенные в § 4, под
общую схему, основывающуюся на ортогональных полиномах, до-
статочно положить
Qk (*) — cos k (arc cos x), k = 0, I,....1)
Полиномы Qk(x) ортогональны на отрезке [—1, 1] по отношению
к распределению do (х) = р (х) dx, где р (х) = (!/2 л) (1 — х2)~1/2, так
как
1 л
J Qk W Qi (х) Р (х) dx = С J cos kB cos /0 dB = 0, если k =£ I,
-1 о
в чем убеждаемся заменой переменной х == cos 0.
(б) Еще один процесс случайного блуждания с отражающим
экраном. Рассмотрим случайное блуждание во множестве неотри-
цательных целых чисел матрицей переходных вероятностей вида
О
О
О
1 о
о р
q о
q
о
Р =
Р
о ...
о ...
о ...
где q, р > 0, q + р = 1. ___ _____
Умножая обе части тождества (4.1) на 2 Уpq (Vp/q) , по-
лучаем
2 ]/ pq cos 0 (/q/pt cos kB^ pWq/pt^ cos (k + 1)0 +
+ q(Vqlp)k 1cos(^— 1)0, k= 1, 2, ... . (5.1)
Таким образом, полиномы
Qfe(x)==(]/67/p)fecos^0, 2 у pq cos 0 = x, k = 0, 1,2,...,
*) Qa(x) называются полиномами Чебышева. — Прим, ped,
126 Гл. 4. Алгебраические методы исследования марковских цепей
удовлетворяют системе уравнений (4.9), соответствующей рас-
сматриваемой матрице Р, за исключением уравнения для k = 0.
Здесь мы имеем Qo(x) — 1 и Qi(x) = х/2р, тогда как нам нужны
начальные условия Qo(l)= 1> Qi(x)=x.
Чтобы исправить положение, начнем с тождества
cos 0 sin (k + 1) 0 = у sin 60 + ysin (k + 2) 0, k = 0, 1,2. (5.2)
Умножив обе его части на 2 У pq (Уq/pf и разделив на sin 0, пе-
репишем (5.2) в виде
= *-1,2.......
Пусть
4-0,1,...;
тогда
ZO(0)^1 и Zr(0)=/^-^,
и при этом
2 Ум (cos 0) Zk (0) = qZk_v (0) 4- pZft+1 (0), k = 1, 2.
Пусть __
Rk (x) = Zk (0); x = 2 Уpq cos 0.
Отметим, что Ro(x) = 1 и /?i(x) = x/p, тогда как
xRk (x) = qRk-i (x) + pRk+i (x), /г = 1, 2, .. . ,
причем Rk(x) является полиномом k-и степени. Наконец, положим
Ph(x) = (2р —l)Rh(x) + (2 — 2p)Qk(x), k = Q, 1,2,...; тогда
Po(x) = 1, Л(х) — X и
xPft (х) = qPk-i (х) 4- pPk+i (х), k = 1, 2, ... ,
так как (х) и <2й(х) удовлетворяют одним и тем же соотноше-
ниям. Таким образом, полиномы Рн(х) отвечают матрице переход-
ных вероятностей Р.
Детальная процедура -нахождения распределения <т(х), орто-
гонализирующего полиномы Рл(х) на отрезке [—1, 1], нами не
рассматривается. Мы просто приведем соответствующее распреде-
ление, оставив читателю проверить, что оно обладает всеми нуж-
ными свойствами.
§ 5. Примеры
127
Если р>7г, то о(х) постоянна вне [— У4pq, y4pq], а в са-
мом интервале
, / к cy$pq — x2 ,
da W = —\LX2-----dx.
Если p < 72,__to or(x) сохраняет свой вид внутри отрезка
[- У 4pq, У 4pq I, a в точках —1 и 4-1 появляются скачки вели-
чины 7г (1 —2р)/д. Константа С служит в качестве .нормирующего
множителя, обеспечивающего равенство единице интеграла
1
J da(x).
— 1
(в) Случайное блуждание с поглощающим экраном. В каче-
стве следующего примера мы рассмотрим процесс случайного
блуждания по целым числам —1,0, 1, 2, 3, ... с вероятностью пе-
рехода в одно из соседних состояний из состояния й(й>0), рав-
ной 7г, и с поглощающим экраном, расположенным в состоянии
— 1. Матрица переходных вероятностей этого процесса имеет вид
1000...
Хотя эта матрица и отличается от тех, для которых был развит
общий метод, мы будем следовать, по существу, процедуре, изло-
женной в § 4.
Ключевым в нашем анализе будет тождество
cos 0 sin (k + 1) 0 = у sin sin (k + 2) 0, k = 0, 1,2,.... (5.3)
Так как k-я строка матрицы Р состоит из элементов
^.-1 = 0) Pk, о = О, ..., — у, Р^,^ = 0, Pk,k+\—^)
Pk,k+2 = 0, . •k = 1, 2, ... ,
A), ~i = у> Р о, о = О, PQt i —у> Л), 2 = 0, ...,
соотношение (5.3) можно записать для k = 0, 1, ... в виде
cos 0 sin (k + 1) 0 = S Pkr sin (r + 1) 0*
r=-l
128 Гл. 4. Алгебраические методы исследования марковских цепей
Умножая обе части на cos0 и подставляя
cos 0 sin (г + 1)0= 2 Prssin(s+1)0
s=-l
в правую часть получающегося соотношения, имеем
cos2 0 sin (k + 1) 0 = 5 Pkr 2 Prs sin (s 4-1) 0 =
r~ — 1 s = —1
= 5 sin (s+ 1)0 2 PkrPrs —
s = —1 Г = —1
= 2 Pls sin (s+ 1)0.
s= — 1
Повторив эти действия n — 1 раз, приходим к формуле
cos" 0 sin (k + 1) 0 = 2 Pkr sin (r + 1) 0.
г= —1
Умножим обе ее части на sin(s+ 1)0 и проинтегрируем по 0 на
отрезке [0, 2л]:
2л
J cos" 0 sin (k + 1)0 sin (s + 1) 0 dQ =
о
= j Pkr sin(r + 1) 0 sin(s + 1) 0 dQ =
0 r=--l
= Pkr J sin(r + 1)0sin(s + 1)0dQ (s = 0, 1,...). (5.4)
r=—1 0
Легко показать, используя элементарные тригонометрические тож-
дества, что
2л
Г sin (г + 1) 0 sin (s + 1) 0 dQ = | еСЛИ r^=s' (5.5)
J I л, если г = s,
г, s = 0, 1, 2, ... .
Из (5.4) и (5.5) следует, что вероятности перехода за п шагов вы-
ражаются формулой
2Л
PnkJ = 1 j* cos" 0 sin (k + 1) 0 sin (s + 1) 0 dQ, (5.6)
0
k, s =*= 0, 1, 2, .. ♦ , n«0, 1, ....
§ 5. Примеры
129
До сих пор все, что мы сделали, — это получили применение об-
щего метода к матрице
p = 0 4 0 0 ... у ° | ° ... 0 4 0 у ••• >
получаемой вычеркиванием первой строки и первого столбца из
матрицы
1 000...
± о | о ...
2 2
Р = „ 1 Л 1
0 у 0 у • • •
Возможность такого сведения при вычислении вероятностей Pks
перехода за п шагов для k, s = 0, 1, ... основывается на том фак-
те, что нам нет необходимости рассматривать те траектории, кото-
рые ведут в состояние —1, так как эти траектории не могут выйти
из него.
Ортогональные полиномы в рассматриваемом случае таковы:
Qft(x) = -si-n(fe±^, £ = 0, 1, 2, ....
где х = cos 0 и, как это легко проверить, полиномы Qk(x) ортого-
нальны по отношению к do (х) =* л-1 (1 — х2)+1/г dx на интервале
[-1, 1].
Как приложение полученного результата вычислим вероят-
ность события, состоящего в том, что поглощение состоянием —1
произойдет точно на n-м шаге, если исходным состоянием было
состояние k. Поглощение состоянием —1 на n-м шаге может про-
изойти, очевидно, только в том случае, если на (и—1)-м шаге про-
цесс пребывал в состоянии 0. Но вероятность попасть в состоя-
ние 0 на (п—1)-м шаге, отправляясь из состояния k, задается
формулой (5.6), т. е.
2л
Рьь' = ~ [ cos'1”1 0 sin (k + 1) 0 sin 0 dd>
о
5 Зак.. 939
130 Гл. 4. Алгебраические методы исследования марковских цепей
а вероятность Ро,-1у. Следовательно, вероятность поглощения
состоянием —1 на п-м шаге при начальном состоянии k есть
2л
Ак = i f cos'1"1 е sin (k + 1) 0 sin 0 dQ. (5.7)
ZJX J
0
§ 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
Рассмотренные процессы случайного, блуждания связаны с за-
дачами о бросании монеты. Предположим, что два игрока дого-
вариваются провести серию бросаний симметричной монеты на
следующих условиях: если выпадает герб, то игрок I выигрывает
единицу у игрока II, в противном случае он проигрывает единицу
игроку II. Пусть
( +1, если игрок I выигрывает,
1 (—1, если игрок I проигрывает
при Лм бросании монеты. Тогда Р{Хг- = + 1} = Р{Хг- = — 1} = !/2
п
и Sn= % (п^ 1)есть суммарный выигрыш игрока I после п бро-
саний монеты. Положим также So = 0. Один из самых простых
вопросов, касающихся этой игры, таков: какова вероятность того,
что после п бросаний монеты суммарный выигрыш игрока I будет
равен нулю? Очевидно, что выигрыш игрока I не может быть
равным нулю, если п нечетно. Пусть п = 2m, тогда если выигрыш
равен нулю после 2m бросаний, то игрок I выиграл m партий
и столько же проиграл. Искомая вероятность, очевидно, равна
Р2т = 2 , m=l, 2........
Далее, чему равна вероятность того, что после п = 2m бросаний
выигрыш игрока I будет равняться нулю в первый раз? Очевид-
но, Sn описывают симметричное случайное блуждание на множе-
стве всех целых чисел. Поэтому наш вопрос может быть сформули-
рован так: чему равна вероятность /о, о первого возвращения в со-
стояние 0 на n-м шаге? Первый переход из состояния 0 может
произойти в одно из двух состояний —1 или +1 с одинаковыми
вероятностями обоих исходов, равными 7г- В силу очевидной сим-
метрии относительно нулевого состояния вероятность первого до-
стижения состояния 0 из состояния +1 должна равняться вероят-
ности первого достижения состояния 0 из состояния —1, поэтому
мы ответим на вопрос, если найдем вероятность первого достиже-
ния состояния 0 из состояния +1 за 2m — 1 шагов. Но эта вероят-
§ 6. Приложения к бросаниям монеты
131
ность равна вероятности первого достижения состояния —1 из со-
стояния 0 в силу однородного характера процесса. Последняя же
вероятность равна вероятности поглощения состоянием —1
за 2m— 1 шагов при условии, что исходным состоянием, было со-
стояние 0, в процессе случайного блуждания на множестве целых
чисел {—1, 0, 1, 2, ...} с поглощающим экраном, расположенным
в состоянии —1. Из формулы (5.7) при k = 0 и п = 2m— 1 по-
лучаем
2Л Л
Ло”1-1 = J- [ cos2"1-2 0 sin2 0 dQ = f cos2m~2 0 sin2 0 dQ.
2л J Л J
о 0
В последнем интеграле сделаем замену х = cos 0; тогда
1 1 1 з 1
Aom~' = 1 [ x2m~2 (1 - х2)2 dx = - • -J- [ (х2)'"~ (1 - х2)2 2xdx.
Л J Л 2 J
-1 о
Еще одна замена t = х2 дает
1 3 3
= f Г-2 (1-/)2^ = 1в(т-1, 4), (6.1)
о
где
1
в (а, ₽)= J
о
есть бета-функция,
цию:
которую можно выразить через гамма-функ-
в (а, ₽) =
Г (а) Г (р)
Г(а + ₽) •
Воспользовавшись известными свойствами гамма-функции, полу-
чаем
Г [т - — Г
1 1 \____2 /
Л° “ л Г(т+1)
1.1г
2 2
л
tn (tn — 1) • ... -2-1
Так как мы находим, что вероятность равенства нулю
суммарного выигрыша игрока I после 2m бросаний монеты
5*
132
Гл. 4. Алгебраические методы исследования марковских цепей
задается формулой
=
'0, о =
_1_
2
(2/72-3) (2m-5) • ... -3-1
2m • ml
при m=l,
при m^2.
(6.2)
Простой подсчет приводит к следующему интересному резуль-
тату:
^0 = H2zn-2 Н2т» m = 1 ’ 2, • • • ,
где по определению ц0 = 1. Далее,
оо оо
^0 = [^2^-2 ““ ^2&] ” ^2/П ^2п ~
Л—гп+1 £=т+1 п °9
= ц2 — lim 2-2" (2”) = ц2т, (6.3)
П->оо \ /
а это значит, что
H2/n = P{52m = 0}= P{SI у= 0, S2y=0, S2/rt¥=0}. (6.4)
Чему равна вероятность того, что выигрыш игрока I обратится
в нуль в k-й раз (k > 1) после 2т-го бросания монеты? Мы отве-
тим на этот вопрос, сформулировав его в терминах процесса слу-
чайного блуждания: «какова вероятность того, что k-e возвращение
в нулевое состояние произойдет на 2т-м шаге?» Как и ранее, мож-
но считать, что из состояния 0 на первом шаге процесс попадает
в состояние +1, и, более того, это же происходит после каждого
из k — 1 первых возвращений в состояние 0. Далее, поскольку
наше случайное блуждание однородно, мы можем «менять места-
ми» во времени промежуточные шаги, не изменяя при этом вероят-
ности достижения одного состояния из другого. Так, мы можем
считать, что непосредственно за первым шагом «вправо» (в со-
стояние + 1) происходят все переходы в состояние +1, следующие
за каждым из k— 1 первых возвращений в состояние 0, и, таким
образом, за первые k шагов процесс оказывается в состоянии k.
Тогда искомая вероятность равна вероятности достижения состоя-
ния 0 в первый раз за 2m— k шагов при начальном состоянии А,
или, что то же, вероятности достижения состояния —1 из состоя-
ния k - 1 в первый раз за 2m — k шагов. Последняя же вероят-
ность есть вероятность поглощения состоянием —1 на
(2m— fe)-M шаге при начальном состоянии k— 1 в процессе слу-
чайного блуждания по множеству целых чисел {—1, 0, I, 2, ...}
§ 6. Приложения к бросаниям монеты
133
с поглощающим экраном, расположенным в состоянии —1. Фор-
мула (5.7) дает
Ak^\k = — [ cos<?'n~*~I 0 sin £0 sin 0 <70. (6.5)
6
Значение этого интеграла,
в конце главы), таково:
как можно подсчитать (см. задачу 7
1 / 2т — k \ k /с с\
m )2rn-k' W*V'
Рассмотрим теперь последовательность Sb S2, ...» S2w. Нас
будет интересовать следующий вопрос: чему равна вероятность
того, что ровно k членов этой последовательности обращаются
в нуль. Это соответствует вероятности Zk, 2m того, что за 2m бро-
саний монеты выигрыш игрока I обратится в нуль ровно k раз.
В силу (6.4) имеем z0,2m = Ц2т- Вычислим теперь ?i, 2m- Пусть
Br — событие, состоящее в том, что среди Sb S2m только S2r
равно нулю. Тогда для г < m
В г = {S} 0, ..., S2r -1 =7^= 0, S2r = о, S2r +1 =/= 0, ..., 52т =И= 0} —
=И=0, • • •> 52г_1У=0, *S2r == 0} П {S2r+i — S2r =/=0, ..., S2rn — S2ry=0}.
Ясно, что события {S} =# 0, ..., S2r-i =£ 0, S2r = 0} и {S2r+i — S2r
=# 0, . .., S2m— S2r =# 0} независимы и вероятность последнего
есть просто ц2т~2г. Тогда
Р 0^0, 2m-2r’ 1 г
где по определению Zo,p = 1- Таким образом,
m m
Z\, 2m ~ I P e 2 /ofo^O, 2m-2r* (®.7)
r=l r=1
Однако Ц2т-2г есть вероятность того, что выигрыш игрока I будет
равен нулю после 2m — 2г бросаний монеты; эта вероятность, как
мы уже отмечали, равна вероятности Р {S2m — S2r = 0}. События
{S( ф о, ..., S2r-t =# 0, S2r = 0} и {S2m — S2r = 0} также незави-
симы, и, таким образом, мы получаем соотношение
Р {^r} = Р {*^1 0, • • • > ^2г-1 §2г ~ 0» ^2т §2г ~
События в правой части этого соотношения несовместны, а их
объединение состарляет событие {S2m = 0}; следовательно,
2 Р {Вг} = Р {S2w = 0} = Ц2т.
г=»1
134 Гл. 4. Алгебраические методы исследования марковских цепей
Таким образом, zl:2m = цгт = Zo,2m при m^l. Точно так же
можно показать, что
m—1
Zk,2m~ 2 $)fo2£-l, 2т-2г» /П^1. (6.8)
г=1
Сравнивая (6.8) и (6.7) и используя равенство Zi>2m = z0,2m, а так-
же тот факт, что = p.2m_2 - ц2т = z0 2m_2 - z,. 2m, получаем
Z2, 2m ~ Zl, 2m~ h™0~ %Zl, 2m ~ Z0, 2m-2’ ГП^2.
Подставляя это в (6.8), индукцией получаем следующее рекуррент-
ное соотношение:
^k, 2m = 2z& —it 2m ^k-2,2m~2* (6.9)
Если положить в нем ^,2™== 2*~2та^2т, то оно сведется к соот-
ношению
2m = ^kt 2m 4" ^k —2, 2m~2* (6.10)
Этому рекуррентному соотношению удовлетворяют величины
(6.11)
Итак, нам известны z0,2m и Zi, 2m, а прямая подстановка показы-
вает, что aQ> 2m и ait2m задаются формулой (6.11). Очевидно, соот-
ношение (6.10) однозначно определяет ak,2m при £>2; следова-
тельно, формула (6.11) дает нам выражение для величин 2т, и
поэтому
^,2rn = 2k-2m(2m~k). (6.12)
С тем чтобы ответить на следующий вопрос, касающийся по-
следовательности 51, ..., S2n, определим понятие перемены знака
в последовательности. Мы скажем, что в момент k произошла пе-
ремена знака, если S&,= 0 и S/t-iS/t+i = —1. Вопрос же состоит
в следующем. Чему равна вероятность того, что в последователь-
ности Si, ..., S2n имеется ровно г перемен знака? Событие, о ко-
тором идет речь, произойдет, если среди S2, S4, ..., S2n_2 имеется
ровно k нулей (k — г, г + 1, ..., п — 1) и ровно в г из них про-
цесс меняет направление1). Пусть
п-1
С*2л= 5 Р{среди S2, S4........S2„_2 ровно k нулей}X
k=r
ХР {находясь в нуле k раз, процесс меняет направление г раз}.
*) Под сменой направления следует понимать, переход на другую полуось.
Прим, перев.
Задачи
135
Но
Р {среди S2) S4, ..., S2n~2 ровно k нулей}=
= Р {среди Sb S2, S3, S4, S2ft_2 ровно k нулей} ==
___ Qfe-2ft+2 / 2n — k — 2 \
\ П-1 Г
как это следует из формулы (6.12). Далее, смена направления
в нуле происходит с вероятностью !/2. Следовательно,
Р {находясь в нуле k раз, процесс меняет направление г раз} =
_ / k\ 1 1 _[ k\%-k
\r ] 2r 2k~r \r j 9
откуда
Cr, 2n
ft—1
_ 2k~~2n+2
k-r
2n — k — 2\( k \
n-i 1\гГ
== 22-2n
2n — r — j — 2
n — 1
ft—г—1
,2—2n V Z2n-r-/-2\/r + j\
\ji-r-j-i )\ i г
Используя равенства
a + i — 1
i
И
s
/ a \ / b \_fa + 6\
\ Z / \ s — Z / ~ \ s / 1
t=0
получаем
ft — r-l
/=»0
__ 22~2«/ / - (n + r + l)\ 22~^2п ( 2rt —1 \
' \ n — r—l / \n —r—1/*
ЗАДАЧИ
1. Пусть
II 1 — a a ||
P== a i a ’ 0<a, Z><1.
II b 1 — b ||
Доказать, что
pn = l_p all , (1 - a-fe)n II a —all
a + b И 6 a|| a 4- b || — b 6||
106 Гл. 4, Алгебраические методы исследования марковских цепей
2. Рассмотреть конечное случайное блуждание по множеству чисел О, I,
2, .,,, Nt матрица одношаговых переходных вероятностей которого имеет вид
0 10 0...
1 О
Найти формулу для вероятностей перехода за г шагов с помощью метода орто-
гональных полиномов.
Ответ: Тригонометрические полиномы
Qn (х) — cos пО, х « cos 0,
удовлетворяют рекуррентным соотношениям
xQnW-^-Qn-t (*)+у Qn+i (х) при л-1, 2............JV-1.
Кроме того,
*Qo W - Qi (х).
Для того чтобы удовлетворялось уравнение
xQN
должно выполняться равенство
cos 6 cos AfO « cos (N — 1) 0,
т, e.
sin WO sin 0«* 0.
Это означает, что 0 — kn/N, k • 0, 1, 2, ...» 2W—-1. Итак, при 0 = kn/N мы
имеем
N
xQn W e ?nmQm W»
m—0
' Я
где P llPnmll. Из этого уравнения также следует, что при 0 = Лл/W
W ““ 2 Pnnfim W» (*)
m»0
Задачи
137
где Рг —1[ Р^т [|. Покажем, что Qn(x) образуют ортогональную систему на ко-
нечном множестве xk = cos kn/N} k = 0, 1, 2, ...» 2N — 1. Действительно,
2ЛГ—1 2У-1
V л / \ л / \ V «bt
2d Qn(xk)Qm(xk)~ 2d
jfe-0 k~Q
2Ar
IVf (n — tn) kn , (n, + tn)kft"\
= 2 24COS +C0S N J"
^=0
2ЛГ-!
1 _ Г f (n — m)kni ) , ( (n + m)kni )1 / . —r\
- ~2 2d exp] ~-------n------> + expj----------->1= (здесь j-V-1)
6=0
, 1 ReJ l“°- если n m.
2(1 — exp [(n — tn) nt/N] 1 — [exp (n -f- tn) ni/N] J
Кроме того,
2/C- 1 27V— 1
V1 ^2'/ \ I Л . 2nkn \ ..
Zj Qn(^)-y L ^+cos-y-J~tf.
fe=»0 6-0
Умножая обе части соотношения (♦) на Qm<i (х), суммируя по множеству
хА = cos/гл/jV, k = 0, 1, 2N—1, и используя соотношения ортогональности,
получаем
2/V- 1
S x'kQn (xk) Qtrh (хо) e Рпт9 ’
k~Q
откуда, опустив нуль в индексе, имеем
2JV—1
,г) IV1 г nkn, tnfal Л ,
Ъ C0S lTC0S“ArC0ST'’ п* maSlQt L N-
k^O
3. Рассмотреть процесс, описанный в предыдущем упражнении, но отличаю-
щийся от последнего тем, что состояния 0 и N являются поглощающими экра-
нами. В этом случае (N — 1) X (Л^ — 1)-матрица одношаговых переходных веро-
ятностей, соответствующая невозвратным состояниям, имеет вид
0 2 0 0 . .. 0 0
2 0 2 2 0 . .. 0 0
0 • 2 0 1 2 * .. 0 0
0 0 0 0 . '* 2 0
Найти формулы вероятностей перехода за г шагов при условии, что поглощение
не имело места,
138
Гл. 4. Алгебраические методы исследования марковских цепей
Указание: В качестве ортогональных полиномов взять Qn (х) = sin nQ,
х — cos 0, где 0 пробегает значения 0 =* knjN, /? = О, 1, ..., 27V — 1.
Ответ'.
2N-1
?пт “ IB [cos kii/N]r sin nkft/N sin mkn/N (n, m = 1, 2, t..N — 1).
4. Рассмотреть случайное блуждание на окружности, имеющее W + 1 состоя-
ний, симметрично, расположенных на этой окружности. Матрица одношаговых
переходных вероятностей процесса имеет вид
» 4 0 0 ... 0 0 1 2
4 ° 1 2 0 ... 0 0 0
» 4 0 2 ... 0 0 0
р = • • •
0 0 0 0 2 ••• 2 0 2 2
4 ° 0 0 , ... 0 2 2 0
Найти выражение для r-шаговых переходных вероятностей.
и
Q„(e)=e‘ne,
Задачи
139
Эти величины удовлетворяют рекуррентному соотношению
Z(0)Qn(0) = yQ«+i (0) + у<2«-1(0) при п=1, 2........ЛГ-1.
И
Кроме этого, требуется выполнение еще двух соотношений:
Z(0)Qu(0) = y Q, (0)+yQw(6)
Л0)<2„ (0) = |Q,,_I(0) + y<?o(0)-
Они выполняются при одном лишь условии
! =еН^+1)0
т. е. при
Q 2nk
0 = Т+Г’
6 = 0, 1............№.
Итак, при 0 = 2л&/(М + 1)
N
Z (0) Qn (0) = 5 PnmQm (0). п, т = 0. 1..N.
т~0
откуда получаем
zr (0) Q„ (0) = 2 PnmQm (0), 0 = (*)
w= О
Далее, функции Q?J(0) образуют ортогональную систему на конечном множестве
0А = 2nkl(N +1) (k = 0, 1, ..., Af; п = 0, 1, ..., N), так как при п=^=т
N N
V-л п /Ёп V 1 1 - exp [2ш (п - т)]
2j Qn (0) Qm (9) " 2- ехР L-ЛГИ---J - 1—ехр [2ш(п- т)Ж + 1П " °’
fe-=0 ьо
Кроме того,
Sl<?" (0*) 12 = ^ +1-
k~0
Умножая обе части соотношения (*) на Qmo (0), суммируя по всем
0А = 2rik/(N + 1), k = 0, 1, N, и пользуясь свойством ортогональности, по-
лучаем
2 Zr (0А) Qn (0*) Qm, (0ft) - OV +1) p^,
откуда
?пт 1 С0^Г
Л-0
2itk
W-i-1
[2nk (п — т) /1
}
п, 1, 2, ...» N*
140
Гл. 4. Алгебраические методы исследования марковских цепей
5. Рассмотреть случайное блуждание на окружности (см. задачу 4) с ма-
трицей одношаговых переходных вероятностей вида
О р 0 ... О q
q 0 р ... О О
О q 0 ... О О
6 6 о ... О р
р О 0 ... q О
Найти выражение для r-шаговых переходных вероятностей.
Указание: В решении к задаче 4 положить Z (0) = ге* ° + qe~ie.
Ответ:
N
nir\ 1 W ( , ( 2nik \ \г Г 2nik(n — m) 1
рЛщ - дг + 1 г ехр (т+т) + q ехр ( w + i))exp[. J’
/к-0
п, m — 0, 1. 2, ..., N.
6. Доказать, что
2л
— f cos'7 0 cos £0 cos/0 d0 =
Л J
о
{17 п \ . ( п 1 , , , .
L\(« + £ —/)/2 / + 1(я + А + /)/2Л 2л+1 ’ еСЛИ n + k + l четно
О в противном случае.
(Этот интеграл есть выражение для ПРИ /=#0 из формулы (4.7).) Найти
предел lim У п Р^.
П-*оо
Указание: Пусть k — неотрицательное целое число. Доказать, что
2л
-J— f cos'1 0 cos kB dB ~
2л J
о
0,
2~Л ( (n -+\)/2 )
если n + k нечетно,
в противном случае.
Для этого воспользоваться тождеством
cos'7*1 0 cos (k — 1) 0 = cos'7 0 cos kB 4- cos'7 0 sin (k — 1)0 sin 0,
проинтегрировать по частям и получить рекуррентное соотношение
J cos'7 0 cos kB dB =* ~ J cos'7*1 0 cos (k — 1) 0 dB.
Ответ: j/2/л.
7, Найти значение интеграла
2л
=т /cos" °sin +6 sin + 0 dQ-
о
Задачи
141
Указание-. Воспользоваться решением задачи 6.
Ответ:
п — П—\ [7 п п
[\ (п — k + Г)/2 ) \(n + k + l + 2)/2 )]'
8. Пусть Р ~ llPijll обозначает матрицу переходных вероятностей конечной
марковской цепи {Хл}^°, имеющей три класса состояний {0}, {1, 2, ....,#—1} и
{-У}, из которых 0 и N — поглощающие состояния, а остальные — невозвратные
состояния. Введем семейство матриц
р (0) = || PijeQ (/ “ ^ || = || (0) || (0 — любое действительное число)
и производящую функцию моментов Л4^)(0 | k) по формуле
Mw (0 I X = k) = М [ехр (0 (X, - Хо) ) | Хо = *] = е' Pz (0) е » £ Pfkj (0).
/==0
где обозначает вектор-строку (0, 1, 0, 0) с единицей на &-м месте,
е обозначает N + 1-мерный вектор-столбец, все элементы которого равны еди-
нице, и Р‘(0) - t-ю степень матрицы Р(0). Пусть л^о ило = 1 —Лй0 (1 k
N—1) обозначают вероятности поглощения состояниями 0 и N соответствен-
но при начальном состоянии k. Доказать, что
lim (0|£) == nkQe~kQ +
t-+OO
9. В условиях предыдущей задачи предположить, что существуют действи-
тельные числа а и Ь, такие, что
M(a\k)<A^M(b\k) (k= 1, 2, .... АГ —1), (4-)
где М (0 | k) = (0 | k). Доказать, что
ekb - 1 eka - 1
eNb _ j eNa _ ! •
Указание: Показать, что M^(a | k) 1 М<^(Ь | k) (6=1, 2, N—1),
и затем воспользоваться результатом предыдущей задачи.
10. Рассмотреть марковскую цепь с состояниями (0, 1, N) и переход-
ными вероятностями
г» ( N \ i /1 \N—i (1 + О') / Л .
pil-\i ]PiO-Pi) ’ где Pi- N + ai............> 0<а<1
(см. пример Ж из § 2 гл. 2). Показать, что
ЛК0|й) = е-“(р^9+1-р^
(определение A4(0/Z?) см. в задаче 8).
11. Для марковской цепи из предыдущей задачи показать, что числа
удовлетворяют условию ( + ) задачи 9, и затем получить оценки
((1 -р)/(1 -1 <л < 1/(1 +<?)*-!
[(1 — а)/(1+a)]w — 1 1/(1+0^-1 *
142
Гл. 4. Алгебраические методы исследования марковских цепей
12. Рассмотреть конечную марковскую цепь {Хп}, п == О, 1, с двумя
классами состояний, один из которых представляет собой поглощающее состоя-
ние. Для определенности пусть поглощающий экран расположен в нуле,
a i = 1, 2, TV представляют состояния другого класса. Пусть собственные
значения матрицы переходных вероятностей занумерованы в порядке убывания
их абсолютных значений: Хо = 1 > | Х2 I > I Х3| | . (Подчеркнем, что мы
предполагаем условие 1 > I Х2 I > I Х31.) Пусть bj — предельная вероятность пре-
бывания в состоянии / при условиях, что поглощения состоянием 0 не произошло,
а начальным состоянием было i, т. е. bj « lim Р {X (n) e j | X (п) #= О, X (0) ® £}.
П-» ОО
(См. стр. 116.) Оценить скорость сходимости к нулю величин
....* 0>1).
1 “ гх0
Ответ'. Скорость сходимости имеет порядок | Х3/Х21 п.
13. Некоторые соотношения для бросаний монеты. Пусть с. в. {XJ, 1 i < оо,
независимы, одинаково распределены и
Р{Х; = 1} = Р{Хг=-1}=1/2.
п
Пусть Sn — 2 ПРИ 1 < п < °° и
Р (m, п) « Р {S2j = 0 для некоторого /, tn < j < т 4- п}.
Доказать, что Р(т, п) 4- P(nt т) = 1 при т 1, п 1.
Указание: Воспользоваться равенством P{S2n ~ 0} — P{Sj =£0, S2 =£0,...
.... S2n =0} и, предположив, что доказываемый результат справедлив при m=k
и произвольном п 1, обосновать следующие равенства:
I — Р (k 4- 1, п) — Р {S2y #= 0 при k j <k 4- п 4- 1} 4-
4- Р {S2k = 0 и S2j =# 0 при k+l^j<k + n+l}=*
= Р {S2j ¥= 0 при k^j<k + n+ 1} 4-
+ Р {S2fc = 0} Р {S2j О при 1 </<п 4-1} ~
«= Р {S2j = 0 при некотором /, п4-1</<£4-п4-1}4-
4-P{S2/=/=0 при I</<Hl)P{S2n«0) =
= Р {S2y = 0 при некотором /, п 4- 1 j < k 4- п 4-1} 4-
4” Р {S2/i == 0 и S2j 0 при п 4* 1 j k 4- п 4~ 1} =®
= Р (п, k + 1).
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
1. Проверить утверждение теоремы 2.1 на марковской матрице р * II,
II q 1 — q ||
где 0 р 1 и 0 q 1. При каких значениях р и q марковская цепь с двумя
состояниями, которой соответствует эта матрица, имеет ровно один возвратный
класс?
2. Пусть Р и Q — конечные матрицы переходных вероятностей порядка п,
такие, что PQ = I — QP. Показать, что матрицы Р и Q являются матрицами
перестановок, т. е. матрицами с одним отличным от нуля элементом в каждом
столбце и каждой строке.
Литература
143
3. Пусть {Хп,п 0}— марковская цепь с двумя состояниями 0 и I, причем
р00 = 1 __ а, Р01 = а, Рп = 1 — р, Рю= (3(0 < а, р < 1). Пусть N есть значение
индекса п 1, для которого Xn-i = Хп ж 0, и пусть d0 = М(Л;Ц0 = 0). Пока-
зать, что
а 1 +Р
rf0=i + a^—р—
Указание'. Установить связь между dQ и d\ = M(V | Хо = 1).
ЗАМЕЧАНИЯ
Алгебраическим методам исследования марковских цепей по-
священа гл. 16 книги Феллера [1]. Эти же вопросы освещены
в книге Кемени и Снелла [2].
ЛИТЕРАТУРА
1. Феллер В., Введение в теорию вероятностей и ее приложения, т. 1, «Мир»,
1964.
2. Kemeny J. G., Snell J. L., Finite Markov Chains, Van Nostrand, Princeton,
New Jersey, 1960.
Глава 5
ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ
ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
§ 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
В возвратной нулевой неприводимой марковской цепи среднее
п— 1
1 X? т
переходных вероятностей — 2j Рц стремится к нулю при стрем-
лении п к оо. Но и при этом возвращение в любое данное состоя-
ние происходит с достоверностью. Другими словами, относитель-
ная частота посещений любого данного состояния стремится
к нулю с ростом времени, но тем не менее процесс находится
в каждом состоянии бесконечное число раз с вероятностью 1.
Имеет смысл рассмотреть число пребываний в данном состоянии i
в отношении к числу пребываний в некотором другом состоянии j
при бесконечном возрастании числа переходов. Для этой цели по-
лезно ввести «вероятности перехода с запрещением»:
kPtj = Р{Хп = j, Xv=£k, v= 1, 2, п — 1 |Хо = О ПРИ &#=/, 1-
Здесь в правой части стоит событие, состоящее в том, что процесс
перейдет из состояния i в состояние / за п шагов, ни разу не по-
пав при переходе в состояние k. Состояние k в этом смысле назы-
вают запрещенным. Аналогично при & =# /, n > 1 определим
Л = РПп = Ь Xv^k, v = l, 2, .... n — 1 |У0= Z),
вероятность того, что процесс, исходя из состояния г, на n-м шаге
впервые достигнет состояния /, не попав при переходе в состоя-
ние k. Для удобства положим при k 4= i
0 JO, если i j,
( 1, если i = /,
и
/^ = 0 для всех i, j.
Далее, при iV / н л>0 имеет место следующая важная формула:
§ 1. Вероятности перехода с запрещением
145
основывающаяся на разложении события, состоящего в первом
достижении состояния i из состояния / на п-м шаге, на п несов-
местных событий, состоящих в возвращении в состояние i на v-m
шаге при запрещенном состоянии / и последующем первом дости-
жении состояния j за п — v шагов при запрещенном состоянии Z,
v = 0, 1,..., п — 1.
При выводе (1.1) ключевую роль играет классификация траек-
торий по последнему моменту нахождения процесса в состоянии
предшествующему моменту п. Упомянем здесь, что при выводе
формулы (5.1) гл. 2 траектории подразделялись по моменту пер-
вого наступления этого события.
Вообще соотношения, связанные с запрещенными состояниями,
чаще всего устанавливаются с помощью рассмотрения первого или
последнего появления некоторого события. Эта двойственность ме-
жду первым и последним играет важную роль во многих разделах
теории вероятностей. Наиболее яркой иллюстрацией этого служит
теория сумм независимых одинаково распределенных случайных
величин, где имеет место полная эквивалентность между поня-
тием первого и понятием последнего момента.
Соотношение (1.1) можно заменить эквивалентным ему урав-
нением для производящих функций. Последнее можно вывести ме-
тодом, аналогичным примененному нами при выводе соотношения
(5.10) из соотношения (5.9). Итак, сначала определим производя-
щие функции:
П=«1
!Pn(s)=ilp^sn.
Затем, так как соотношение (1.1) является сверткой, при i 4= j мы
получаем
M(s) = /Pn(s)^/(s). (1.2)
Поскольку
оо оо
Ж«1 и 2Л<|.
Й=1
в силу части (а) леммы Абеля (лемма 5.1 гл. 2) имеют место сле-
дующие соотношения:
ОО оо
lim (s) = 5 р lim / .(s) = 2 Л-
s->l — n=l S->1~ n = l
Если состояния i и / сообщаются, то существует такое целое число
1, что ^>0, и тогда в силу (1.1)
^”^>0 для некоторого v = 0, 1, n—I.
146
Гл. 5. Теоремы об отношениях переходных вероятностей
Последнее неравенство позволяет утверждать, что
оо
2 Л>о,
п-=1
а следовательно, и
оо
2ft
lim ----<оо.
2 Л/
Наконец, в силу части (б) леммы Абеля имеем
оо
jP'a = 2 /Pit = lim jPa (s) < oo.
n=0 s~>l —
§ 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
Для доказательства двух теорем этого параграфа
бится следующая
Лемма 2.1. Пусть
с„=2лп-^\, n = 0, 1, 2,...,
где 0 ап К (К — положительная константа)
Тогда если предел lim bn = b конечен, то
нам понадо-
2 ап = оо.
п-0
a
lim =Ь.
хп
2
п
Zj ^n-v
n
Доказательство. Заметим, что
2j «v
v=»0
Следо-
вательно,
п
2 an-v (bv Ь)
Сп
п
2 аУ
Ь
п
2 an—vby
---------ь =
п--------п
22 an—v
Поскольку Ьп стремятся к конечному пределу Ь, существует такое
М > 0, что |йп| <М при всех «>0. Выберем теперь такое N «
?= N(e), что
\bn — b \<е для всех
§ 2. Теоремы об отношениях
147
Тогда при п> N имеем
Сп
п
2 av
v=0
N-l
2 an-V (by — b)
v=0
n
v=0
n
2 an-v(bv — b)
v=0
w-i
2 an-V
v=0
n
atl — v
n
2«v
V = 0
<2Ж
n
v=0
+ 8.
Так как e > 0 произвольно, то, устремляя п к оо, мы получаем до-
казываемый результат.
Приведем теперь три соотношения, подобных соотношению
(1-1):
п
р?) - 2 Ри ,Р’Г". (2.2)
v=0
п
P’l^^riIPll'' (2-3)
при k =# /, i =£ i и п 0. Последнее соотношение совпадает с соот-
ношением (5.9) гл. 2. Вывод их аналогичен выводу соотношения
(1-1).
Теорема 2.1. Пусть i и j — произвольные состояния, причем
состояние j — возвратное; тогда
где
(2.4)
Доказательство. Из (2.3) имеем
m m п m п m оо
2' "и - 2 2 f’,py - 2 2 "р; - 2 2 f“/p“,
п=»о 1 n«0v=0 1 11 п=0ц = 0 4 11 п«0ц«0 7 77
поскольку = 0 при р > п (по определению).
148 Гл. 5. Теоремы об отношениях переходных вероятностей
Поскольку на самом деле обе суммы конечны, порядок сумми-
рования можно поменять:
/г-ц
И
Положим
пг
р7г%Тц при ™ = °, 1,2, ...
И
F?/ = 0 при 1, — 2,
тогда
пг оо пг пг
^pI,-^ ртгрЪ “ 2 FT'P'ti - 2 Pu-'Fh-
П-0 ц =0 ц=0 V=o
Применим теперь лемму 2.1, положив
пг
av = P]h b^Fvu и с^=2Р?/.
п-0
Условия леммы выполнены, так как
о<рУ/<1
И S P'li — оо;
v=0
последнее в силу того, что состояние j — возвратное. Поскольку
lim bm
- пт ft,-2
zn~>oo r—0
то в силу леммы имеем
m
Zj p"i
m->o° ул DV
Zi f//
V-0
и теорема доказана.
Перепишем теперь соотношение (2.1) для k = i =!= j:
п
^Zf^pr, n>0.
(2.5)
Переходя к соответствующим производящим функциям, получаем
Л/(5) = Л/(5)1Л/(5).
§ 2. Теоремы об отношениях
149
оо
Ранее мы уже показали, что — S iPn < 00, если состояния
/2 = 0
i и j — сообщающиеся. Поэтому по лемме Абеля
lim iPu(s)= lim Л/(Ф Hm !?//(«)<<»
s->l — s -> 1 — S->1~
и окончательно имеем
оо
,Р,/ = 2 iP"i = lim [Pa (s) < oo.
/2 = 0 S~>1 —
(2-6)
Теорема 2.2. Если i и j принадлежат одному и тому же воз-
вратному классу состояний, то
lim
m->oo
m
м — 0
m
^Рп„
/2=0
= iPib
Замечание. Для i =/= j
введем случайные величины:
1,
если процесс, исходя из состояния Z, за п ша-
гов попадет в состояние /, при переходе не
возвратившись в состояние Z;
в противном случае.
Тогда М(£/„)=Л и
\/2 = 1 / /2=1
Таким образом, в условиях теоремы 2.2 вероятность есть сред-
нее число попаданий в состояние / между последовательными воз-
вращениями в состояние i.
Доказательство. В силу соотношения (2.2) имеем
m m п tn оо
2 р"и -22 р1, ,р,Г -22 р"„ ,р!Г.
/2 = 0 п = 0 v = 0 n = 0v = 0
так как iPTb 6 при v > п. Меняя порядок суммирования, по-
лучаем
m оо m оо
2 p"i = 2 Pl, 2 ,/V = 3 Ри iPTr,
V = 0 /2 = 0 V —0
150
Гл. 5. Теоремы об отношениях переходных вероятностей
где
m
iPTi^HiPn, « = 0,1,2,...
v=0
И
iPTj = 0, m = — 1, —2...
Тогда
mm m
2 Ри=%Ра1Р^=%РТГ\Ри.
n=0 v=0 v=0
Теперь мы можем применить лемму 2.1, положив av = Рц, bv=
m оо
и Сщ= 2 Рпц, так как | Рц | 1 и 2 Рн = 00 (состояние i возврат-
n=0 v=0
ное). Но
оо
lim bm = lim jP™ = 2 tPvtJ = {Рц,
m-^oo m-^oo v=0
а, следовательно, в силу леммы 2.1 имеет место равенство
lim
m->oo
Теорема доказана.
Если состояния i и / — сообщающиеся, то мы можем записать
lim
m-»oo
m
n=Q
m
2^
n=0
lim
m
Zpti
n=0
m
H
n=0
m
так как S Р?/>0 для достаточно больших m. Далее, если оба со-
п=0
стояния i и / возвратны и принадлежат одному и тому же классу,
то, согласно последним двум теоремам, первое отношение в правой
части стремится к 1/^=1, а второе отношение —к .Р*у; следо-
вательно,
m
%РИ
lim
m->oo
m
2^
n-0
iPib
§ 3. Существование обобщенных стационарных распределений 151
Из (1.1) и (2.5) получаем соответственно
fa (s) == jPii (s) if а («),
Л/(*)==Л/(*)Л/(4
Отсюда, воспользовавшись леммой Абеля, получаем тождества
р* р* р*
' И = га й ip
р*__________________________р* р*
г и i'arir
Если i и / принадлежат одному и тому же классу возвратных со-
стояний, то = 1, откуда
§ 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ
РАСПРЕДЕЛЕНИЙ
В случае неприводимого возвратного положительного класса
стационарное распределение представляет собой сходящееся
оо X
(такое, что 2 ^i<°° положительное решение системы уравнений
i=0 /
2 XiPii^Xj, i = 0, 1,2,....
Z=0
Это утверждение доказывается в теореме 1.3 гл. 3. В следующей
теореме доказывается, что это свойство является достаточным
условием для положительной возвратности.
Теорема 3.1. Предположим, что марковская цепь неприво-
дима. Если система уравнений
оо
^XiPji^Xi, / = 0,1,2,..., (3.1)
/«о
имеет решение, у которого
2 \Х/ I < оо,
/-0
причем не все Xj равны нулю, то марковская цепь является воз-
вратной положительной.
Доказательство. Из (3.1) последовательно получаем
2x/P// = *f, М>1,
/=о
152
Гл. 5. Теоремы об отношениях переходных вероятностей
Пусть Рц — UM) 2 Pli"> тогда
п-1
ОО
2 Х/Рц = Х{.
1-0
Перейдем теперь к пределу при т->оо. Так как
21 xiPh\< 21 xi I < °°>
/=0 /-0
мы можем перейти к пределу в каждом слагаемом (т. е. поменять
местами суммирование и переход к пределу); тогда
xt = lim 2 XjPft = 2 xi lim
m-^oo j=Q i=0 m->oo
Ho
m
lim Рц = lim У Рпц = л,- > 0.
m-»oo m->oo
n^O
Следовательно,
oo
Xi == Щ 2 Xi.
/=»0
oo
Так как 2 I К 00 и> согласно условию, существует /, такое, что
/-о
Xi Ф 0, то последнее равенство гарантирует, что для некоторого i
=/= 0, а значит, Лг > 0 для всех i = 0, 1,2, ... .
Сейчас мы докажем теорему, обратную к только что доказан-
ной, в усиленном варианте, опирающемся на систему неравенств.
Теорема 3.2. Если неприводимая марковская цепь — воз-
вратная положительная и {Xj > 0, / = 0, 1,2,...} есть решение си-
стемы неравенств
2 XfPji^Xi, z = 0, 1, 2, ...,
/-о
то
оо
2 Xj < оо.
1-0
Доказательство. Так же как и в предыдущем доказа-
тельстве, мы имеем
оо
2 х,рц < х{, га>1,
/-о
$ 3. Существование обобщенных стационарных распределений 153
а при m 1
оо tn — 1
Sx/^Схь где =
/=0 п=0
Л1
Так как х/>0и то S XjP™Xi при любом М>0.
j^Q
Переходя к пределу при гп —> оо, получаем
м м
lim S Х}Рц~ ni S Xj ^x£.
m->oo /=o /==0
M
Так как я, > 0, частичные суммы 2 х/ равномерно ограничены
/“0
при всех М > 0; следовательно, имеет место
оо
У Xj < ОО .
/»0
Согласно теореме 3.1, в случае неприводимой возвратной нуле-
вой марковской цепи система (3.1) не может иметь нетривиаль-
ного сходящегося решения. Вместе с тем существуют положитель-
ные решения, представляющие значительный интерес; о них пойдет
речь в следующей теореме.
Теорема 3.3. Если марковская цепь неприводима и возврат-
на, то положительная последовательность
*0=1, *, = 0^ /=1,2,...,
является решением системы уравнений
vi=^iVjPji, / = 0, 1, 2,... (3.2)
/-о
(определение 0Р’. дается в формуле (2.6)).
Доказательство. По определению йР*й1 имеем
оо оо оо оо
2 VjPji = 2 + Рм == Poi +22 oPnjPji»
/“0 /=1 л=«1
Поскольку oPq/< оо {), повторный ряд в правой части, все члены
которого неотрицательны, сходится, и поэтому порядок суммиро-
вания можно изменить, что дает нам
оо оо оо
^viPii^POi+'Sl ^oPoiPii.
п==1 /=*1
i) Это условие требует пояснения. Мы можем формально изменить порядок
суммирования, и если получающийся ряд сходится абсолютно, то сходится и
исходный ряд, причем суммы обоих рядов одинаковы, — Прим, перев.
154
Гл. 5. Теоремы об отношениях переходных вероятностей
Но
2 oPojPji =
/-1
если i О,
если i — 0.
рп + 1
rn + l
100 >
Следовательно, при i ¥= 0 имеем
5 viPji — Poi + 2 о/’оГ' = ^4 оРоГ = oPfli = Vi,
f=0 п — 1 п=0
так как
Pol = oPoi при i О-
При i = О
оо оо оо
2 "Л» ~ р»+ 2 С - 2 С
/=0 п=1 п=0
чем и завершается доказательство теоремы.
Теорема 3.4. Для неприводимой возвратной марковской цепи
система
Vt^iiV/Pfi, 2,..., (3.3)
/•о
t>o=l, /=1, 2, ..., (3.4)
имеет единственное решение.
Доказательство. В силу предыдущей теоремы последова-
тельность v0«l, vi==oPoii * = 1,2,..., является решением си-
стемы уравнений (3.3), удовлетворяющим условиям (3.4). Мы до-
кажем нашу теорему, если покажем, что не существует никакого
другого решения системы (3.3), которое удовлетворяло бы усло-
виям (3.4).
Пусть {аг} — последовательность, удовлетворяющая (3.3) и
(3.4), тогда
at = 2 счРц, i~0, 1, 2, ....
/м
Умножая обе части последнего равенства на Pih и суммируя по Z,
получаем
оо оо оо
5=5 2 &iPik 2l P ik 2j ^jPji =
t=0 t=0 /=0
oo oo oo
2 2 PjiPik = 2
i=Q /=0
§ 3. Существование обобщенных стационарных распределений
155
Изменение порядка суммирования правомерно, так как все члены
ряда неотрицательны. Повторяя эту процедуру, получаем для лю-
бого п 1
1 = 0, 1, 2, ... .
Л=0
Так как рассматриваемая марковская цепь неприводима и воз-
вратна, для каждого i существует такое, что Рог^О. Сле-
довательно,
cti = 2 UqPqi > 0,
/=о
так как а0 > 0. Итак, сц > 0 при всех i.
Введем в рассмотрение следующие величины:
$ц=~±Рц- (3.5)
Очевидно,
Таким образом, мы можем рассматривать величины как эле-
менты матрицы переходных вероятностей некоторой марковской
цепи Q. Соответствующие вероятности перехода за два шага за-
даются формулой
оо оо оо
- £ QlkQki = X ? т- р^ = рЛ = у- р/‘-
Ь0 6=0 1 * 1 Ы 1
Вероятности перехода за п шагов имеют вид
Поэтому
и Qij являются переходными вероятностями возвратной марков-
ской цепи. Воспользуемся теперь теоремами об отношениях. В силу
теоремы 2.1 имеем
lim
/П->оо
2%
2 Qoo
П=0
156
Гл. 5. Теоремы об отношениях переходных вероятностей
f*iQ(Q) определена по отношению к цепи Q обычным образом.
Ее значение равно 1, так как Q — возвратная неприводимая мар-
ковская цепь. Но в силу теоремы 2.2
lim -
m'°° М
п=»0
m
— Нт =
ai m->«> v п at
Zi roo
n«0
Поскольку fl0 = 1, то тем самым мы показали, что
= Z=l, 2, ....
Единственность доказана.
§4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ
РАСПРЕДЕЛЕНИЙ
Марковскую цепь с матрицей переходных вероятностей ||Qtj||,
связанной с матрицей по формуле (3.5) через некоторое по-
ложительное решение системы (3.3), называют обратной марков-
ской цепью к цепи Р. В возвратном положительном случае, когда
Vi = ст^г (с — константа), можно интерпретировать следующим
образом. Предположим, что начальное распределение совпадает
с {nJ, т. е. марковская цепь X (п) в начальный момент находится
в состоянии i с вероятностью лг-. Вычислим условную вероятность
того, что начальным состоянием было /, если известно, что после
одного перехода процесс находился в состоянии L По формуле
Байеса имеем
- Р (Х(0) - /( X (1) = /) = . (4.[;
Так как процесс стационарен, то
Р{Х(1) = /} = P{X(0) = /} = ttz
и (4.1) принимает вид
Q,, - (4.2)
Последовательное применение соотношения (4.2) приводит, по су-
ществу, к «обращению» времени. Легко видеть, что если с. в. Х(0)
имеет своим распределением {nJ, то
Q?/ = P{X(0) = /|X(n) = j}.
Название «обратный процесс», данное марковской цепи с матрицей
переходных вероятностей JJQi/ll, таким образом, отражает сущ-
ность дела,
§ 4. Интерпретация обобщенных стационарных распределений 157
Метод введения обратного процесса применим всякий раз, когда
имеется положительное (не обязательно сходящееся) решение си-
стемы (3.3). Этим приемом мы воспользуемся ниже в теореме 5.2.
Как следует из теоремы 3.1, решение системы (3.3) расходится
в случае возвратного нулевого класса и сходится в случае возврат-
ного положительного класса. Интересную интерпретацию можно
дать как сходящемуся, так и расходящемуся решениям системы
(3.3). Для возвратного положительного класса значения
пропорциональны стационарным вероятностям пребывания в соот-
ветствующих состояниях. В общем случае значения можно ин-
терпретировать как стационарное среднее число частиц, находя-
щихся в состоянии i при соответствующих условиях равновесия.
Точный смысл имеющегося в виду равновесия выявляется в сле-
дующей теореме:
Теорема 4.1. Предположим, что счетное число частиц неза-
висимо подчиняются марковскому процессу, заданному матрицей
Р = Пусть д.с.в. Ai(ri) представляет число частиц, находя-
щихся в состоянии i в момент п. Если ЛДО), i = 1, 2,..., являются
независимыми д. с. в., подчиняющимися распределению Пуассона
со средними Vi соответственно, где ^vkPki = vh t)z>0, то А^п),
k
i = 1,2,..., также являются независимыми д. с. в. с теми же рас-
пределениями, что и соответствующие ДДО), i = 1,2, ....
Замечание. Когда мы говорим о бесконечном числе слу-
чайных величин, что они независимы и подчиняются распределе-
нию Пуассона, то это означает, что любая их конечная совокуп-
ность обладает этим свойством.
Доказательство. Пусть Ah(n-, i) есть число частиц, нахо-
дящихся в состоянии k в момент п, из общего числа частиц, пребы-
вавших в состоянии i в момент п— 1. Определим векторы А(п) и
А(п; 0 следующим образом:
А (л) == (Л, («), А2(п), ...), А (и; 1) = (АЦп-, г), А2(п; г), ...),
тогда A (n) = S А (п; /). Доказательство теоремы проведем по ин-
i
дукции. В силу индуктивного предположения (что д. с. в. А^п— 1)
независимы), а также потому, что частицы ведут себя независимо
друг от друга, д.с.в. Ah(n\ i), i = 1,2,..., независимы при каж-
дом фиксированном k. Мы покажем, что компоненты Ak(n; i),
k = 1,2,..., каждого вектора А(лг; Г) также являются независи-
мыми д.с.в., откуда следует, чтоЛ^(ц) = Ak (n;i), k = 1,2, ... ? —~
i
независимые д. с. в.
158
Гл. б. Теоремы об отношениях переходных вероятностей
Для любого конечного числа компонент вектора А(м; i) и це-
лых чисел «1, а2, ..., аг имеем
Р {ДА] (п; i) = а{, Aki (tv, I) = а2, Akr (п; I) = аг] =
оо
= 2 Р{Л( (п — 1) = а}Р (Akl (п; i) = ah ..Ак(п; i) — ar | Дг (п — 1) = а].
(4.3)
По предположению индукции первый сомножитель общего члена
суммы равен
v?
ехР(~ ^)^г- (4.4)
Ввиду обусловленности и независимого характера поведения ча-
стиц второй сомножитель представляет собой полиномиальное рас-
пределение, т. е.
р [Л, («; 0 = .......Akf (tv, i) = аг | А/ (п - 1) = а) =
Это выражение полагается равным нулю, если av> а. Под-
V-I
ставляя (4.4) и (4.5) в (4.3), получаем
Р {>Ц («; 0 = ah А^ (п; i) = а2, ..., Акг (п-, i) = аг] =
= S П • - am! еХР (- V^m) X
г т=!
а“ 2 , av
V=1 v
§ 5. Регулярные последовательности марковских цепей 159
Но данная сумма равна 1 (достаточно положить а = п* 4- а и про-
суммировать по а), так как она является суммой вероятностей
частных значений для пуассоновского распределения с пара-
метром
6-
\ m=l т/
Полученное в формуле (4.6) разложение показывает, что
Ah(n\ i), &= 1,2, являются независимыми с. в., подчиняющи-
мися распределению Пуассона со средними {ViPik} соответственно.
оо
Следовательно, Ak (п) = 2 Ak (п; /^ — независимые с. в. с пуас-
i=o
оо
соновским распределением и средними 2 щРцъ = Vk соответственно.
/=о
Поскольку по условию ДДО), i = 1,2,..., независимы и имеют
пуассоновское распределение со средними vif то тем самым дока-
зательство по индукции закончено.
§ 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
Мы уже познакомились с несколькими критериями для опреде-
ления возвратности, невозвратности и положительной возвратности
марковской цепи (см. теоремы 4.1—4.2 гл. 3) и применили их при
изучении некоторых моделей из теории очередей. Условия этих
критериев связаны с характером решений системы уравнений
оо
= £ = 0,1, 2, .... (5.1)
i-0
либо системы уравнений
3 = г = 0, 1, 2, ... .
fe=0
Современный подход к этой проблеме состоит в применении тео-
рии регулярных, суперрегулярных и субрегулярных последователь-
ностей. Мы остановимся на наиболее простых аспектах этой эле-
гантной теории, которая основывается на теории потенциала мар-
ковских матричных операторов. Классическая теория потенциала
привлекается при рассмотрении этих же идей в исследовании броу-
новского движения. Такое взаимопроникновение теории потенциала
и теории вероятностей чрезвычайно плодотворно и в последнее
время привлекло внимание исследователей,
160 Гл. 5. Теоремы об отношениях переходных вероятностей
Пусть Р — заданная матрица переходных вероятностей. Будем
говорить, что неотрицательный вектор (неотрицательная последо-
вательность) и = {ы (/)}°^_0 является по отношению к Р
правым регулярным (сокращенно г-регулярным),
если 2 Рц-и (/) = и (I),
!
правым суперрегулярным (г-суперрегулярным),
если и (0,
/
правым субрегулярным (г-субрегулярным),
если 2 Рц-и (/) > и (fy
i
Правую суперрегулярную последовательность {u(i)} будем назы-
вать минимальной, если из условия 0<С|(/)-^«(/) (/^0), где
l(i)—регулярная последовательность, следует, что l(i)= cu(i) при
некоторой константе с. Неотрицательный вектор (и (i))“L0 будем
называть
левым регулярным (/-регулярным),
если S v (/) Рп = v (j),
i
левым суперрегулярным (/-суперрегулярным),
если S v (/) Pu^v (/),
левым субрегулярным (/-субрегулярным),
если S v (/)Ph>v(/).
i
Сначала мы докажем теорему о представлении правых регу*
лярных последовательностей минимальными регулярными после-
довательностями.
Теорема 5.1. Пусть и есть r-суперрегулярный вектор по от*
ношению к Р. Тогда предел
a(i)= lim ^P^u(j)
j
существует для всех, i и вектор а является r-регулярным вектором
по отношению к Р. Более того, если b есть r-регулярный вектор по
отношению к Р и b(i)<u(i) при всех i, то b(i)^.a(i) для всех L
Если мы представим компоненты вектора и в виде
и {Г) — а (Z) + с (/), / 0, (5.2)
где
с (/) — и (/) — а (I),
то c(i) образуют минимальный r-суперрегулярный вектор.
§ 5. Регулярные последовательности марковских цепей 161
Доказательство. По определению г-суперрегулярного
вектора имеем
2 Рни (/) = 22 р%~i}pklu (/) - 2 р%~1) 2 pkiu (/) < 2 р{“Л {k).
j i k k j k
В векторно-матричных обозначениях мы можем записать это со-
отношение в виде P^u^P^u, подразумевая под этим покомпо-
нентные неравенства.
Итак, для каждого i
и (Г) > 2 Рци (/) > 2 PfjU (!)>
j i
Поскольку все члены этой цепочки неравенств неотрицательны, то
a(i) существует и a(i)4u(i) при всех i. Далее,
2p</2p%^) = 2p&+1W).
/ k k
В пределе при / z —> оо выражение в правой части сходится к a(i),
тогда как левая часть, если формально перейти к пределу под зна-
ком суммы, стремится к 2 Pna(j), т. е.
7
2 Рца (/) = a (i).
7
Для доказательства правомерности предельного перехода под зна-
ком суммы зафиксируем некоторое значение индекса L Для лю-
бого s > 0 существует N(&), такое, что
2 Рци(])^&;
i> N (е)
тогда
2 Рц 2 Р{$и (k) < 2 при всех п.
j> N (е) k f>N (е)
Далее, воспользуемся представлением
2 Л/2/>$«(*) = 2 Рц2 Pn^p^u{k).
j k /<AZ(e) k j > N (e) k
Как мы уже видели, при п —+ оо левая часть стремится к a(i). Так
как первый член в правой части является конечной суммой по /,
то его предел есть просто
2 Л7«(/).
/<ZV(e)
Величина второго члена не превышает 8. Итак, имеем
«(«)= 2 Pua(j) + d(i), где 0<(/(0<е,
j < N (е)
6 Зак. 939
162
Гл. 5. Теоремы об отношениях переходных вероятностей
откуда следует, что a(z) = 2^z/a(/)> т. е. a = {a(z)} является
r-регулярным вектором по отношению к Р.
Предположим, наконец, что
b (z) = И^РцЬ (/) ^и(Г) при всех i.
i
Тогда с помощью индукции получаем
b (z) = 2 Р{$Ь (/) < 2 P(ffu (/) при всех п и I.
/ /
Следовательно,
fe(z)^h‘m 2 P{ij^ (]) == ci (z) при всех z.
П-»оо j
He составляет никакого труда проверить, что последовательность
c(z) = zz(z)—а(Г) является r-суперрегулярной. Остается только
установить минимальность последовательности c(z’). Предположим,
что
0<&(z)<c(z), z>0, (5.3)
где {£(0} есть r-регулярная последовательность. Применяя п раз
Р к обеим частям (5.3), получаем
Ь Р'К Р"с.
Но из определения вектора с следует, что Pnc = Pnu — Рпа =
= Pnu — а стремится к нулевому вектору. Этим завершается до-
казательство минимальности вектора с.
Представление (5.2) в случае броуновского движения является
не чем иным, как классическим представлением Рисса, связанным
с гармоническими, супергармоническими и потенциальными функ-
циями. Изложение этой элегантной теории выходит за рамки на-
шей книги.
Для невозвратных марковских цепей очень легко построить
r-суперрегулярные последовательности. Напомним, что в невоз-
оо
вратном случае 2^<°° при всех z, &>0. Мы утверждаем,
п=0
что при фиксированном
оо
1 = 0,1,..., (5.4)
п=0
является r-суперрегулярной последовательностью. Действительно,
оо оо
(5.5)
/=0 п«0
Приведенное построение позволяет сделать вывод о том, что су-
ществует достаточно обширное множество непостоянных положи-
£ 5. Регулярные последовательности марковских цепей 163
тельных r-суперрегулярных векторов. То, что последовательности
вида (5.4) не являются постоянными, следует из соотношения
(5.5), которое при i = kQ является строгим неравенством. Совер-
шенно иная картина имеет место в возвратном случае. Следующая
теорема утверждает, что единственной r-суперрегулярной последо-
вательностью является постоянный вектор. Она обобщает крите-
рий, полученный в теореме 4.1 гл. 3.
Теорема 5.2. Неприводимая марковская цепь с матрицей пе-
реходных вероятностей Р возвратна тогда и только тогда, когда
всякий неотрицательный вектор v, r-суперрегулярный по отноше-
нию к Р, у которого хотя бы одна компонента положительна, яв-
ляется постоянным.
Доказательство. Пусть марковская цепь возвратна. Рас-
смотрим систему неравенств
Ui^^PiiUi, Ui^O, / = 0, 1, ....
Мы покажем сначала, что если UjQ > 0 для некоторого /0, то и$ > О
при всех /. В самом деле, для любых заданных /0 и k существует
такое п, что Р$3>0. Тогда, как и в предыдущей теореме, имеем
7
Таким образом, если и 0, то щ > 0 при всех i. Пусть теперь k
произвольно, но фиксировано и положим = Ui/uk. Тогда
= 2 Piili + Pik- (5.6)
7 7 * k
Итерируя это неравенство, получаем
Si 3 Рц Г Jj P/sSs + Pjk \ + Pik ==
i =?*= k Ls k J
= 2 PijP/s^>s+ 2 РцРjk + Pfk —
i.s^k i^k
/, s =И= k
где последние два члена по ранее данному определению являются
вероятностями первого достижения. Опять подставляя (5.6) в по-
лученное неравенство, получаем
S, > 2 pt,p„ f 2 РЛ ++ fg + f’g =
/, s Ф k Lr k J
= 2 PiiPlsPsrir+ 2 PaP^sk + m+f^^
J, S, Г k s 1 s
= 2 р(!Р1ЛЛг + № + ^ + №
/, s, r =/= k
6!
164 Гл. 5. Теоремы об отношениях переходных вероятностей
Продолжая таким же образом, приходим к неравенству
m
справедливому при любом т. Отсюда следует, что
« = 1
так как цепь возвратна и неприводима.
Таким образом, 1, или щ^и^ Но I и k произ-
вольны, значит, щ = uh при всех г, k.
Докажем теперь достаточность. Пусть марковская цепь невоз-
вратна. Положим
( f\k> если i=£k,
Ui =)
I 1, если Z = &,
где k произвольно, но фиксировано. (Напомним, что f*ik есть ве-
роятность попасть в состояние k за конечное число шагов, исходя
из состояния i.) Отсюда следует
ui ~fik~ ^kP^ + P^ Pauj> если
и
uk hk 2 Pkjf + Pkk 2 Pkjur
/ Т*= ft J
Таким образом, вектор и является r-суперрегулярным. Но если
FJk = 1 при / =/= k, то
i;,- 2 pj',t+ри - S р„+ра - 2 р„ -1,
/ 'Г® к ! 7“ п> J
что противоречит предположению о невозвратности цепи. Следо-
вательно, и — непостоянный ограниченный r-суперрегулярный век-
тор. 9
С помощью теоремы 5.2 легко доказать усиленный вариант тео-
ремы 3.4, допускающий неравенства.
Теорема 5.3. Для возвратной неприводимой марковской цепи
система
2 ViPib / = О, 1, ..
/=S° (5.7)
о0 = 1, Z== 1, 2, ..
имеет единственное решение.
§ 5. Регулярные последовательности марковских цепей
165
Метод, принятый в доказательстве теоремы 3.4, состоит в пере-
ходе к обратному процессу, что позволяет свести рассмотрение
/-суперрегулярных векторных последовательностей к рассмотре-
нию г-суперрегулярных числовых последовательностей. Этот прием
сведения задач о левых регулярных объектах к задачам о правых
регулярных объектах с помощью обратного процесса является до-
вольно распространенным и продуктивным.
Доказательство. Как мы уже видели, у0=1,
является решением системы (5.7). Действительно, эта последова-
тельность удовлетворяет условиям
если в них заменить знак знаком
Vi > 0 при всех I. Полагая
2 VjPfh / == О, 1, ...,
/»о
равенства, и, кроме того,
Qa = -^> / = °> i, •••
мы получаем некоторую матрицу переходных вероятностей Q =
= IlQijIL поскольку и
оо оо
/==0 Z /=0
V.
_L=1
v.
К тому же, как и в теореме 3.4,
Q{ink==^-Pki
vi
и неприводимость матрицы Q следует из неприводимости матрицы
Р. Далее, если
оо 2 * = 0, !,•••> /=о
и
с0=1, £/^>0, /=1, 2, ...,
то
оо оо
/=0 z * /=0 1
т. е. вектор {Cj/v}} является r-суперрегулярным по отношению к ма-
трице Q. Но в силу предыдущей теоремы {Cj/Vj} должен быть по-
стоянным вектором. Так как cQ = vQ = 1, то Ci = vit i = 0, 1..
Теорема доказана.
166
Гл. 5. Теоремы об отношениях переходных вероятностей
ЗАДАЧИ
1. Рассмотрим неприводимую возвратную положительную марковскую цепь,
начальное состояние которой Хо в Пусть Nn(i) —число возвращений в состоя-
ние i за первые п переходов. Доказать, что
оо
где Цг — среднее время возвращения в состояние /, т. е. = 2 п^1*
п—1
2 (продолжение). Пусть Tm(i) обозначает число переходов до m-го возвра-
щения в состояние i (Хо = /). Показать, что
P{Tm(i)>n}~P{Nn(i) <m},
оо
*3 (продолжение). Предположим, что 2 n2fii <00• Лп (*) является сум-
П=1
мой пг независимых одинаково распределенных с. в. со средним цг- и диспер-
сией О/. С помощью центральной предельной теоремы и соотношения, получен-
ного в предыдущей задаче, найти предельное распределение с. в. Afn(O, долж-
ным образом нормированной, т. е. найти такие ап > 0 и Ьп > 0, что
(Nn(i)—оп)/Ьп имеет предельное нормальное распределение.
4. Пусть {Хп,п 0} — неприводимая возвратная марковская цепь с матри-
цей переходных вероятностей Р « || Pij || и обобщенной инвариантной мерой
{OJ, т. е. 2 viP Цу>0, / —0, 1, .... Определим вложенный процесс
{Уп,«^0}. Он определяется предыдущим, если рассматривать только те мо-
менты времени, когда Хп — 0 или 1 (т. е. Уо = Хпо, где п0— момент первого
достижения состояний 0 или 1; Уот = ХПт, где пт— момент /n-го возвращения
в состояния 0 или 1). Процесс {Уп, п >0} является неприводимой возвратной
марковской цепью. Пусть wo, Wi обозначают стационарные вероятности вложен-
ной марковской цепи. Показать, что wi/wo == vJvq.
Указание: Воспользоваться интерпретацией сч, данной в теоремах 3.3 и 3.4.
5. Пусть Р = |] Рц\\ и Рп — \\Рг j (п) ||, п = 1, 2, ..., — матрицы переходных ве-
роятностей неприводимых марковских цепей, и пусть {yj и ««I. 2, .
соответствующие инвариантные меры, нормированные таким образом, что
уо = иоП)=я^ ПРИ всех п- Доказать, что если Рц(п)-+Рц для всех i и j при
п -> оо, то -> vi для всех i.
Указание: Доказать, что lim — существует и удовлетворяет системе
П->°° ' 7
оо
/==0, 1.2, ... сг)0=1.
i=o
Затем воспользоваться свойством единственности, установленным в теореме 5.3.
6. Доказать, что для неприводимой марковской цепи любая неотрицательная
r-суперрегулярная последовательность {u(i)} обладает следующим свойством:
« (Z) fiku (k) при всех i и k,
г*
где fik — вероятность достижения состояния k из состояния L
Указание: См. доказательство теоремы 5.2.
Задачи
167
7. Пусть {u(i)}— конечная неотрицательная r-суперрегулярная последова-
тельность. Положим
w (/) = и (i) - 2 piJu (/)•
I
Показать, что множество А всех состояний /, для которых w (i) > 0, совпадает
с множеством невозвратных состояний.
Указание'. Обобщить результат задачи 6 на рассматриваемый случай; точнее,
получить строгие неравенства и воспользоваться ими.
8. В неприводимой марковской цепи зафиксируем некоторое состояние, обо-
значим его 0. Показать, что если f/0^a>0 для всех f=£0, то цепь возвратна.
Указание'. Показать, что вероятность возвратиться в состояние 0 лишь ко-
нечное число раз равна нулю (см. теоремы 7.1 и 7.2 гл. 2).
9. Доказать, что неприводимая марковская цепь невозвратна тогда и толь-
ко тогда, когда существует ограниченная /-суперрегулярная последовательность
(ц(/)}, такая, что
(и (k) > 2 И (0 ?ik для некоторого состояния k.
i
Указание-. Воспользоваться теоремами 5.3, 3.3 и 3.4 (достаточность); вос-
пользоваться соотношением (5.5) (необходимость).
*10. Доказать следующие тождества для тройки состояний из одного и того
же положительного возвратного класса (/=^=^):
(а) т1к + тк1-тЦ = /ц(.т!к + mkj)’
и
mkk kfkl
i-де mik = 2 nfjk-
11. Пусть для неприводимой, но не обязательно возвратной марковской цепи
ороо 1 и оЛ)/ <00 Показать, что последовательность QPQi является
/-суперрегулярной.
12. Рассмотрим электрическую цепь с т граничными и п внутренними кон-
тактами; всего п 4- т контактов. Пусть Тц™ ток, текущий от контакта i к кон-
такту /, и — сопротивление между этими контактами, причем i и j не яв-
ляются граничными контактами одновременно. Пусть V j — потенциал контакта /.
Предположим, что сопротивления известны и заданы потенциалы в граничных
контактах. Согласно закону Ома, имеем
(О Kz-Ky = /?,7r,7.
а по первому закону Кирхгофа
(и) 2 =°-
/
168
Гл. 5. Теоремы об отношениях переходных вероятностей
С помощью (ij и (ii) показать, что Vi удовлетворяет соотношениям
(Hi)
Дать интерпретацию (ш), согласно которой мы можем рассмотреть случайное
блуждание по контактам электрической цепи, считая граничные контакты погло-
щающими состояниями и определив переходные вероятности в виде соответ-
ствующих выражений для
13 (продолжение). Занумеруем состояния процесса случайного блуждания
так, что состояния 1, 2, ..., m соответствуют граничным контактам, а состоя-
ния m + 1, пг + 2, m + п — внутренним контактам. Показать, что потенциал
внутреннего контакта Д/ можно представить в виде
m
Vm+i^^bikVk при 1=1,2............
fe-1
где — вероятность поглощения граничным контактом Bh при начальном со-
стоянии, соответствующем внутреннему контакту Ah.
14. Пусть {С7/}у^0— действительное решение системы уравнений
2 PijUj-Ui-l, 1 = 0, 1,2.........
/-о
и пусть | Хо ==/) обозначает среднее значение с. в. Ux при начальном
условии XQ == i. Доказать, что
к(их 1*о = 0
Пт ( Л»1 0 ^=1.
П->00 п
оо
Указание-. Воспользоваться соотношением P^Uf-Ui-n, 1 = 0, 1.........
/-о
15 (продолжение). Доказать, что Ux — п является мартингалом.
16. Пусть HPijII — матрица переходных вероятностей возвратной нулевой или
невозвратной марковской цепи, и пусть {и,} — /-регулярный положительный век-
Литература
169
тор, а А — некоторое множество состояний. Введем обозначение Р$ — 2
je=A
Показать, что если р, (Л) = 2 ut < °0’ то ^/А ПРИ п °0-
i s а
Указание: Пусть В — конечное подмножество Л, такое, что ц^<е.
i <= А-В
Показать, что Р^а-в^^11^ и воспользоваться этим фактом. (Л—В обозначает
множество состояний, входящих в Л и не входящих в В.)
17. Рассмотреть задачу о разорении игрока с W + 1 состояниями и матрицей
переходных вероятностей, приведенной в гл. 3. Найти /--регулярные векторы от-
носительно этой матрицы.
Ответ: u(i) ~ aiii(co) +Ьл{(сп), где а и b — произвольные числа (обозна-
чения см. в гл. 3).
18. Пусть HPijII—матрица переходных вероятностей марковской цепи с бес-
конечным числом состояний. Предположим, что Pij = 0 при j > i + 1 и Pij+i > О
при всех i. Зададим систему полиномов Qi(z\ рекуррентными соотношениями
Qo
i
zQi(z) = Pi,i+iQl+l(z)+'^1PijQj(z), z = 0, 1,2........
/=0
Пусть Tj — время первого достижения состояния j + 1 из состояния /, и пусть
оо
fy (г) = 2 Р {Г/ = гП ~ производящая функция с. в. Tj. Показать, что
Указание: Получить рекуррентную формулу для Р{7\ = /г}, рассматривая воз-
можные исходы первого перехода, затем перейти к производящим функциям.
ЗАМЕЧАНИЯ
Материал этой главы почерпнут в основном из книги Чжун
Кай-лая [1].
Наше изложение представляет собой лишь введение в эту важ-
ную и развивающуюся область теории вероятностей.
Готовящаяся к изданию книга Кемени и Снелла [2] содержит
подробное изложение теории потенциалов для марковских цепей.
ЛИТЕРАТУРА
1. Чжун К а й - л а й, Однородные цепи Маркова, «Мир», М., 1964.
2. Kemeny J. G., Snell J. L., Potential Theory for Markov Chains (готовится
к печати).
Глава 6
ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
§ 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН
Пусть Xi, Х2, . . . — последовательность целочисленных незави-
симых одинаково распределенных случайных величин. Положим
Sn = Х1 + Х2 + ... + Хп, п = 1,2,.... Для полноты будем счи-
тать, что So = 6.
В этой главе мы остановимся на некоторых свойствах сумм
Sn, п == 0, 1, 2,..., независимых случайных величин. Сами суммы
мы будем рассматривать как последовательные значения марков-
ской цепи специальной структуры с дискретным пространством со-
стояний. В пределах нашего элементарного изложения мы лишь
поверхностно коснемся теории сумм независимых случайных вели-
чин. Полное и элегантное изложение этой богатой и красивой тео-
рии читатель найдет в книге Спицера [1].
В примере А § 1 гл. 2 мы упоминали о последовательности Sn
(где Х{ были неотрицательными целочисленными случайными ве-
личинами) как о примере марковской цепи. В этой главе простран-
ство состояний соответствующей марковской цепи состоит из всех
целых чисел: положительных, отрицательных и нуля. Так как мы
положили So 0, начальным состоянием является нуль. Характер-
ной чертой марковской цепи {Sn} является пространственная одно-
родность, т. е. ее одношаговые переходные вероятности обладают
следующим свойством: Р {Sn = / | Sn_} =• 1} = Рц = Ро, = Pt^h 0.
Простой индукцией легко убедиться, что этим же свойством обла-
дают /г-шаговые переходные вероятности:
Pli == Рп0> о = Р {Sn+k = /1 S* = /}, n > 1.
В этой главе мы будем предполагать, что случайная величи-
на Х[ «неприводима». Под этим подразумевается, что марков-
ская цепь с матрицей переходных вероятностей Рц = Р {Sn =
= /|Sn_i = 1} неприводима. Ниже мы дадим простой критерий не-
приводимости для рассматриваемого случая.
Условимся с самого начала, чтобы не повторять это каждый
раз, что с. в. Xi является невырожденной, т. е. она может прини-
мать по крайней мере два значения с положительными вероятно-
стями.
Перейдем теперь к условиям возвратности и невозвратности
марковской цепи, порожденной последовательностью {Sn}. Для
§ 1, Свойства возвратности сумм
171
того чтобы получить эти условия, введем следующие величины:
П оо
G?,- 2 PTh вц — 2 Рц<<*>,
определенные для всех z, j и п — 0, 1, 2, ... , Величина Gzj является
аналогом функции Грина и связана с элементами теории потен-
циала, о которой мы упоминали в гл. 5.
Лемма 1.1.
G?y<G?0, n = 0, 1, 2, ..., (1.1)
для всех целых чисел i и j. В частности, при п-+ оо
Gz/<G00 (1.2)
для всех целых чисел i и j.
Доказательство. В силу пространственной однородности
процесса G"j = G?_/,0. Поэтому достаточно показать, 4toG"o^Goo
при всех i = 0, ±1, ±2, ... и п = 0, 1, 2,.... Но
п пт п п п п—1
Ч - 2 Ч - 2 2 СЧ. ~ 2 Pi, 2 /г' - 2 р‘„ 2 fi„
т=0 т=0 Z=0 Z=0 m—l Z==0 r=0
где friQ есть вероятность достичь 0 из i в первый раз на r-м шаге.
п—I
Так как 2 т0
г=0
п
G”o S ^оо — Gqo- Н
z=o
Изящный и полезный критерий возвратности составляет содер-
жание следующей теоремы.
Теорема 1.1. Если
оо
M|XJ = M|X1|= 2 |/1Л)/<°о> 6 = 2,3,..., (1.3)
/==~ОО
и
оо
ц = М(Х*) = М(Х,) = 2 /А/ = 0, (1.4)
/=-оо
то марковская цепь {Sn} является возвратной.
Замечание. Поскольку M(Xi)=0 и Xi— невырожденная
случайная величина, то она принимает как положительные, так и
отрицательные значения с положительными вероятностями. Усло-
вие неприводимости гарантирует, что-марковская цепь, порождае-
мая последовательностью {Sn, п = 0,1,2, ...}, неприводима (со-
стоит из одного класса). Пространство состояний цепи состоит из
172
Гл. 6. Последовательность сумм независимых величин
всех целых чисел: положительных, отрицательных и нуля. Нако-
нец, в соответствии со следствием 5 гл. 2 для доказательства воз-
вратности рассматриваемой цепи достаточно установить возврат-
ность хотя бы одного (скажем, нулевого) состояния.
Доказательство. В силу леммы 1.1 Go/Goo при всех
целых /. Это неравенство сохраняется и при осреднении:
м
о-5)
Но
М п п п
2 Go/= S 2 Poj~ 5 2 Ро/^2 2 Pqj> (1«6)
j=*—M m=Q m=0
последнее неравенство имеет место просто потому, что т^п.
Сравнив (1.5) и (1.6), мы видим, что
п
°»>иг+т2 2 ч- с-7)
т=0 | j/MKM/n
Далее, по определению
Po/ = P{Sm = /|So = O}. (1.8)
Поскольку Sk представляет собой сумму k независимых одина-
ково распределенных случайных величин с конечным средним
р, = M(Xi) =M(Sfe) = 0, можно применить закон больших чисел
(см. § 1 гл. 1, стр. 20), согласно которому для любого 8> 0
Р11 ~ тН. [ е | — р | j | е |1 ПрИ m~>oo. (1.9)
Из (1.8) находим
P{|Sm|Cme}= 2 P"i-
I / К [me]
(Здесь [h] обозначает наибольшее целое число, не превышающее Л;
поэтому h—l<[h]^h.) Предельное соотношение (1.9) можно
представить в следующем эквивалентном ему виде:
Нт(г) = 2 Ро/~>1 при m->oo. (1.Ю)
I / К [те]
Положим теперь в (1.7) М = [ns], где 8 > 0. Тогда
п
00 2 [ne] + 1 2 Р°>
та0 I / К т [пг]/п
1
2 [не] + 1
т=0 | / |< [те]
(1.11)
§ 1, Свойства возвратности сумм
173
Из (1.10) следует, что
п
2 Н>п (е) “* 1 прига-»оо.
т=0
Кроме того,
«. п 4- 1 1 • /г + 1 1
lim -777—г—г = Ит -—— = —
п->оо 2 [ne] + 1 п^оо2пе+1 28
Из (1Л1) и (1.12) заключаем, что
lim Goo^'oT*
n->oo
(1.12)
Так как е > 0 может быть выбрано сколь угодно малым, то из по-
следнего соотношения следует, что
оо
3?оо = lim G?o=oo.
k~ 0 n->oo
Наконец, обращаясь к теореме 5.1 гл. 2, вспоминаем, что равен-
ство Goo = °° эквивалентно утверждению, что нулевое состояние
возвратно.
Отметим, что мы не использовали всей силы предположения
о том, что Xi имеет конечное среднее значение. Нам понадобился
лишь слабый закон больших чисел, выполнение которого в форме
соотношения (1.9) достаточно для справедливости утверждения
теоремы.
В следующей теореме, являющейся частичным обращением тео-
ремы 1.1, существование конечного среднего играет более важную
роль.
Теорема 1.2. Если
М(Ш)== i |/1Л)/<оо, z = l,2,..., (1.13)
I == — оо
и
оо
H = M(XZ)= 2 /Ро/^О,
/ = -оо
то марковская цепь {Sn} является невозвратной.
Доказательство. Пусть А обозначает событие {Sn = 0}.
Воспроизведем известный нам критерий возвратности (см. тео-
рему 7.1 гл. 2) в форме
1 тогда и только тогда,
когда марковская цепь
р(Лп наступает при беско-1 {SJ возвратна,
I нечно многих п J 0 тогда и только тогда,
когда марковская цепь
{Sn} невозвратна.
174 Гл. 6. Последовательность сумм независимых, величин
Усиленный закон больших чисел утверждает, что
р{ lim= (1.15)
’ га->оо п '
Поскольку 0, рассмотрим события
c„={|4l-h|>V}> п==1’2...............
Пусть С — событие, состоящее в том, что Сп наступает при беско-
нечно многих п. найдем вероятность Р {С}. Всякая реализация
процесса, для которой lim Srt/n = p, очевидно, не может принадле-
П->ОО
жать событию С, Но, согласно (1.15), реализации процесса, для
которых lim Snln = ja, имеют вероятность 1. Следовательно, ве-
роятность события, дополнительного к С, равна 1, или Р {Сп про-
исходит при бесконечно многих п} = 0. Ясно, что наступление со-
бытия Ап влечет наступление события Сп, т. е. An cz Сп. Поэтому
Р{ЯП наступает при бесконечно многих п}^Р{С} = 0.
Принимая во внимание критерий (1.14), заключаем, что марков-
ская цепь {Sn} невозвратна.
§ 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Заметим, что если марковская цепь {Sn} возвратна, то она мо-
жет быть только возвратной нулевой. Это так, потому что в силу
пространственной однородности
sii = lim Рц = lim Poo = Ло при всех i.
оо
Если же л0>0, то 2 Л/ = оо, что невозможно. Следовательно,
Tti = 0 при всех i.
Итак, марковская цепь {Sn} является либо возвратной нулевой,
либо невозвратной; следовательно, при всех j
Pqi~>Q при /г->оо.
Представляет интерес оценка скорости сходимости к нулю. Резуль-
тат подобного рода относится к так называемым «локальным пре-
дельным теоремам». Приступая к этой задаче, введем характери-
стическую функцию
^хь(0)== 2 Р0^ехР(^9) = М[ехр(/Х^9)], k = 1, 2, . .., — л<0<л,
V» —• оо
§ 2. Локальные предельные теоремы
175
где ряд сходится абсолютно и равномерно. Мы утверждаем, что
оо
[*/*(0)]" = 2 -Povexp(tv0), — л^0<л.
V® — оо
(2.2)
Действительно, Xk, k = 1,2.....п, — независимые одинаково рас-
пределенные случайные величины, так что
Ро/ = Р{5Л = /},
2 Povехр(Zv0) = M[ехр(z‘S„0)] = M[ехр[/0(^1 + ... + ЙСЛ)]] =
V=- оо
= ft М [ехр (Z0XJ] = п [Фхк (0)] = (0)]"
(см. стр. 15). Отметим, далее, что
___ __i_
здесь 1=У — 1. Таким образом, функции (2л) 2 eiie (/ — любое
целое) образуют ортонормированную систему. Поэтому, умножив
обе части (2.2) на (2n)~1e"tS9 и проинтегрировав по 0 на отрезке
[—л, л], получим
Л
Р$ = (2л)"1 / е~™ [ф (0)]” dQ, (2.4)
— Л
так как в правой части остается лишь член, соответствующий
v = k.
Прежде чем сформулировать и доказать результат, касаю-
щийся скорости сходимости Ро/ к нулю при п —> оо, введем некото-
рые понятия, которые нам понадобятся для этого, и обсудим их
свойства. Будем говорить, что X является периодической случай-
ной величиной, если все значения, которые X может принимать
с положительной вероятностью, содержатся в множестве
X = ® + rc, г = 0, ±1, ±2, ...,
где со и с — целые и |с| =£ 1.
Отметим, что из утверждения «марковская цепь {Sn} является
периодической» следует, что Xh — периодические случайные вели-
чины, но не обратно. (Доказать это.) Напомним еще, что если мар-
ковская цепь {Sn} — непериодическая, то наименьшая аддитивная
группа, порождаемая целыми числами /, для которых P{%i = /}>0,
есть группа всех целых чисел.
176
Гл. 6. Последовательность сумм независимых величин
Случайная величина
f + 1 с вероятностью р,
k I — 1 с вероятностью q
дает пример периодической случайной величины. В самом деле, ее
возможные значения можно представить в виде
X=l+2r, r = 0, ± 1, ±2, ....
(Здесь с = 2, со = 1.)
Лемма 2.1. Случайные величины Xh являются периодическими
тогда и только тогда, когда их характеристическая функция ^>(0)
обладает следующим свойством-
1Яе0)1=1 (2.5)
для некоторого 0о ¥= 0, —л 0о «С л.
Доказательство. Предположим, что при 0О — h =/= О
(—л h л)
|^(Л)1=1.
Тогда существует такое действительное число w, что <f>(h) = eiwh,
а следовательно,
1 = (ft) = У pojei(i-w)h=:
j--00
оо оо
= 2 Pqi cos (/ — w) h + i 5 Рщ sin (/ — w) h.
J = — OO j = — OO
Отсюда
OO
1 = 2 Poj cos (/ - w) h.
Так как | cos x | 1 при всех x, то для всех состояний /, достижи-
мых из нулевого, т. е. для тех /, для которых Р^ > 0, с необходи-
мостью
cos (/ ~ гел) h = 1.
Решения последнего уравнения задаются формулой
(/ — ш)h = 2лг, г==0, ±1, ±2,....
Это означает, что всякое /, достижимое из нуля, можно предста-
вить в виде / = w + (2л/h) г, г = 0, ±1, ±2, ..., где, очевидно,
|с| = \2л/И\=/= 1. Ясно, что Xk может принимать только эти значе-
ния /, т. е. Xh — периодическая случайная величина.
§ 2. Локальные предельные теоремы
177
Докажем теперь необходимость. Если все возможные значения
содержатся в множестве
Xk = ® + rc, г = 0, ±1,...
(со и с — целые, | с 14= 1), то
r= —оо
И
оо
5 Pq, <&+ГС ~
Положим 0о = (2л/с). Так как с — целое и |с|¥= 1, то 0о ¥= 0,
— л 0о л и
о, (2я,с)е12пг = е1а<2я/с> р0> о+„ = eie>
Г=в—СО f= —ОО
Таким образом, (2.5) выполняется для 0О = (2л/с) ¥= 0,
0о < л.
Далее мы будем предполагать, если не оговорено противное,
что Xk является непериодической случайной величиной.
Лемма 2.2. Существует константа Х> 0, такая, что
1 -Re^(0)>Z02, - л<0<л. (2.6)
Доказательство. Заметим, что
оо оо
1 —Re^(0)=l — 3 Po/COS/0= 2 (1 - cos/0) Ро/-
j = — оо J из — ОО
Нам понадобится тождество
1 — cos а = 2 sin2-у,
имеющее место при любом действительном а. С помощью этого
тождества приходим к неравенству
оо L
1 — Re^(0) = 2 2 (sin2 4)^о/>2 £ (sin2 4) POI, (2.7)
/»-оо / = -£
справедливому для любого положительного L.
Мы воспользуемся хорошо известным неравенством
I • I \ А Л
sin X —!—L
1 1 -- ТГ
(2.8)
2
178
Гл. 6. Последовательность сумм независимых величин
Доказать это неравенство можно, например, так. Функция
(sinx)/x является убывающей при 0<^х^л/2. Действительно,
d / sin х \ __ х cos х — sin х
dx \ х / х2
Но l^sec2x, и интегрирование обеих частей этого неравенства от
О до х дает x-^tgx. Так как cos х > 0 при 0<О<л/2, то
(d/dx)[(sin х)/х] < 0; значит, (sin х)/х убывает при 0 х л/2.
Следовательно, при 0^х<-^-
sin х sin (л/2) __ _2_
х л/2 л ’
ИЛИ
2
sinx^ — X.
л
Поскольку обе части последнего неравенства являются нечетными
функциями, ясно, что (2.8) выполняется.
Учитывая (2.8), из неравенства (2.7) получаем
1-Re #((>)> 2 2 У рры. (2.9)
1/1<Д |/1<Д
Это неравенство справедливо для значений 0, таких, что |/0|<л.
Но если |/|^L, то неравенство |/0|-Сл будет выполнено, если
|6|<^. (2.10)
При достаточно большом L должно существовать по крайней мере
одно /, |/| L, для которого Poj > 0. Выбирая L именно таким,
имеем
с = 2л-2 2 i2Pol>o
\I\<L
и
1 - Re <j> (0) > С02
(2.U)
при всех |0|<^n/L.
До сих пор мы не пользовались непериодичностью случайной
величины Хк. Это допущение нам потребуется для оценки
1 — Re 0(0) при |0| > n/L. Мы знаем, что непериодичность Xh эк-
вивалентна тому, что равенство ] 0 (0) | = 1 выполняется на отрезке
[—л, л] только при 0 = 0 (лемма 2.1). Но J0(0) |<С 1 при всех 0,
как характеристическая функция. Следовательно,
1-Re0(0)> 10(0)|>О (2.12)
при 0 =# 0, —л 0 л. Так как разность 1 — Re0(O) является
непрерывной функцией аргумента 0 на отрезке [—л, л], то
m — min {1—Re 0(0)}
л > I е । > л/д
§ 2. Локальные предельные теоремы
179
существует и в силу (2.12) положителен. По самому смыслу вели-
чины m неравенство
1 — Re </>(0) /п — (2.13)
выполняется при всех 0, таких, что л>|0|>njL. Положим теперь
Л = min (С, т/л2).
Тогда (2.6) выполняется при всех |0|-Сл.
Мы подготовили все, что требуется для того, чтобы сформули-
ровать и доказать теорему об оценке скорости сходимости вероят-
ностей Р"/ к нулю при п -♦ ОО.
Теорема 2.1. Если случайные величины {Ха} непериодические,
то при некоторой константе А > 0 (не зависящей от j и п)
(2.14)
У и
для всех целых j и 1.
Доказательство. Из (2.4) следует, что
Р^<(2л)-1 / | ф (0) \2п dB. (2.15)
— Л
Покажем, что |^(0) |2 является характеристической функцией не-
которой целочисленной случайной величины. В самом деле, так как
Ф(0) = М[ехр(iXft0)] для любого &=1, 2, ...
и _________
^(0) = М[ехр(—ZXz0)] для любого 1=1, 2, ...,
то при k =/= I
I £ (0) I2 = Ф (0) £70) = М [ехр (ZXft0)] М [ехр (- ZXz0)] =
= M[exp(Z(XA-Xz)0)],
так что |^(0) |2 является характеристической функцией целочислен-
ной случайной величины (Xh — ЛД, где Xk и Xt — независимые и
одинаково распределенные случайные величины. Непериодичность
Хк эквивалентна непериодичности разности Xh — Xt. Это является
непосредственным следствием леммы 2.1. Пусть ф(0) = |^(0)|2.
Применим теперь результат леммы 2.2 к действительной характе-
ристической функции ф(0). Это даст неравенство 1—ф(0)->Х02,
справедливое при всех 0 из отрезка [—л, л] и некотором X > 0. Пе-
репишем это соотношение в виде
ф (0)< 1 - А02 < ехр (- Л02), (2.16)
180 Гл. 6. Последовательность сумм независимых величин
где последнее неравенство следует из соотношения 1—у~^е~У,
которое в свою очередь следует из тривиального неравен-
ства как результат интегрирования последнего в пределах
от 0 до у.
Из (2.16) интегрированием получаем
j ф (0)" d& J ехр (— пЛ02) d& = J ехр (— Ла2) da <
-л V П -nVn
(]//Г) 1 j ехр (—Ла2) da.
(2.17)
Сравнение соотношений (2.15) и (2.17) дает
оо
Р*^'±- Г ехр(-Ла2)б?а=-ф-, (2.18)
у п 2л J у 2п
где
Л! = 1^2 (2л) 1 J ехр ( — Ла2) da.
Поскольку |^(0) |<1, мы также получаем
л л
P20k+i <(2л)"1 [ | ф(0) |2n+IdB<(2л)-1 [ | </>(0) I2"dB =
—л —л
л = (2 л)-1 / (0)Г dB < S —л ' У2Л‘... (2.19) /2и+ I
Положим теперь А = Y2At; (2.18) и (2.19) совместно дают (2.14),
что и требовалось, и
Нужно подчеркнуть, что оценка (2.14) справедлива как для воз-
вратной марковской цепи {Sn}, так и для случая, когда эта цепь не-
возвратна. В этой связи полезно еще раз обратиться к классиче-
ской вероятностной модели бросаний монеты. В этой модели
1
- 1
Xk =
с вероятностью р,
с вероятностью q,
§ 2. Локальные предельные теоремы
181
а последовательность {Sn} представляет собой марковскую цепь
с переходными вероятностями специального вида 9:
р, если j = i + 1,
Pif = - q, если j = i — 1,
О в остальных случаях.
Как мы видели (формулы (6.1) —(6.2) в гл. 2),
n2n ( 2fl \ п п
а асимптотическая формула для Роо имеет вид
(2.20)
У пл
Из (2.20) видно, что если р#=у, то Роо экспоненциально (со ско-
ростью геометрической прогрессии) стремится к нулю. Формула
(2.14) дает точную оценку, если p = q= -%-
Приведенный нами пример является типичным для общей си-
туации. Имеются значительные уточнения оценки (2.14) при до-
полнительных ограничениях М(Х1)< оо и M(X^) = p = 0. В этом
случае, согласно теореме 1.1, марковская цепь {Sn} является воз-
оо
вратной, а точнее, возвратной нулевой. Следовательно, S Роо =
п= 0
= оо, а Ро/~>О. С помощью центральной предельной теоремы дока-
зывается, что _
lim Vn P“t = B, (2.21)
П->оо
где В — конечная положительная константа, не зависящая от /.
Доказательство этого результата выходит за рамки нашей книги.
Мы отсылаем читателя к монографиям [1, 2], где подробно изла-
гаются результаты этого характера. Если М(Л1) = оо и M(|XJ1+6) <
< оо при 0 < d < 1, но |1+?) = оо при £ > 6, то часто
(2.21) заменяется другой точной асимптотической формулой
lim п1/(1+б)Ро" =В. (2.22)
П->оо
Последний результат справедлив в случае, когда центральная пре-
дельная теорема неприменима, но имеет место притяжение к соот-
ветствующему устойчивому закону. Теория устойчивых законов
!) Заметим, что здесь Xh — периодическая случайная величина. — Прим, перев.
182 Гл. 6. Последовательность сумм независимых величин
представляет собой довольно сложную область теории вероятно-
стей, играющую важную роль в приложениях к физике и астроно-
мии. Элементарный характер нашей книги не позволяет нам даже
поверхностно затронуть эти вопросы. Мы ограничимся лишь кон-
статацией существования этой теории и рекомендуем читателю об-
ратиться к ней при дальнейшем изучении теории вероятностей.
§ 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ
ЦЕПЕЙ
Для специальных классов марковских цепей обычно удается
получить более сильные результаты, касающиеся свойства возврат-
ности, задач о времени пребывания, нахождения законов распре-
деления различных функционалов от процессов и др. В этом пара-
графе мы получим уточнение свойств правых регулярных последо-
вательностей (теорема 5.2 гл. 5) для марковской цепи {Sn}.
Если марковская цепь является неприводимой и возвратной, то
единственным правым регулярным вектором является постоянный
вектор (теорема 5.2 гл. 5). Если же марковская цепь описывает
последовательность сумм независимых случайных величин, то этот
результат можно распространить на непериодический невозврат-
ный случай, если мы потребуем, чтобы правый регулярный вектор
был ограниченным. Более точно, мы докажем следующее.
Теорема 3.1. Если марковская цепь {Sn} с матрицей переход-
ных вероятностей Р неприводима, и если последовательность {у^}—
правая регулярная, т. е. {у;} удовлетворяет условиям
у^09 /-0, ±1, ±2, (3.1)
и
оо
2 РцУ1~Уь / = 0, ± 1, ±2, .... (3.2)
/=~оо
причем {yj} ограничена, то у$ const при всех j.
Доказательство. Пусть ограниченная последовательность
{Уз} удовлетворяет условиям (3.1) и (3.2). Пусть й0 — любое со-
стояние, отличное от нулевого и достижимое из него. Тогда суще-
ствует такое п, что Рой0>0- Зафиксируем kQ и положим
г^У^У^, / = 0, ±1, ±2......
Используя пространственную однородность процесса, мы можем
написать
оо оо оо
i, 1У]~ko . Р^кь+кУк. 2 Рi—kq, кУк У i—ktf
] — — оо k=~ ОО fe= —оо
§ 3. Правые регулярные последовательности
183
т. е. последовательность также удовлетворяет
(3.2).. Следовательно, {Zj} удовлетворяет условиям (3.2). Очевид-
но, {Zj} ограничена, поскольку ограничена {yj}. Пусть
Af = sup<z/<oo и sup 1г; | = М'. (3.3)
1 1
Так как {Zj} ограничена, мы можем выбрать последовательность
целых чисел {гп}, для которой
lim zr = М. (3.4)
п->оо п
Опять же в силу ограниченности {Zj} из последовательности {гп}
можно выбрать подпоследовательность такую, что суще-
ствует lim z (1). В свою очередь из можно выбрать подпосле-
довательность для которой существует предел lim z tJ_ (-п.
1 П 1 П->оо ~1+Гп
Затем из выбираем подпоследовательность такую,
что существует lim z Продолжая таким образом, мы полу-
П->оо 2 + Г«
чим ряд последовательностей {ПГ3)}’ • • каждая
из которых является подпоследовательностью предыдущей. Суще-
ствует последовательность, а именно == которая является
подпоследовательностью каждой из последовательностей
{'•„}. к1). W-"). ('-?’)• К”). ('-!.”) (<-”)..
начиная с некоторого члена. Действительно, {sn} является подпо-
следовательностью последовательности начиная по крайней
мере с п | р |. (Построение последовательности {sn} носит назва-
ние процесса диагонализации.) В силу этого свойства {sn} и факта
существования соответствующих пределов мы можем утверждать,
что
X[™zi^,Tz'i (3-5)
П->оо П
существует для каждого /.
По построению {гп} (см. (3.4)) имеем
z*=limzs=Af, (3.6)
П->оо П
а в силу (3.3)
= lim z-, с j = 0, ±1, ± 2, ....
1 rt_>oo
Как мы уже видели,
оо
+ 8 f Zj + s *
/«-оо J l±Sn
184
Гл. 6. Последовательность сумм независимых величин
Переходя к пределу в обеих частях при п —> оо, получаем
оо оо
lim z,._ - lim 2 Р..„ .г,— lim 2 P> > * z,- =
V • l + 11 3 l> l"~sn 1
ft->oo tl и->оо / = ~ оо П П->оо / = —oo П
oo
= lira 2 P„z (3.7)
fZ-> oo / = —oo П
Мы сейчас покажем, что в правой части соотношения (3.7) можно
перейти к пределу под знаком суммы. Для этого нам нужно пока-
зать, что для любого заданного е > 0 существует целое число
п(е), такое, что
при условии, что /г>п(е). Выберем L настолько большим, что
V р <_Л_
4М' ’
Затем выберем п0 таким, что
\zi+sn~zi |<’2
при —L / и всех п п0. Тогда при п ;> па(е)
Установив правомерность перехода к пределу под знаком сум-
мы, из (3.7) получаем
оо
*1= 2 pazt, (з.8)
Z=~OO
т. е. 2*. удовлетворяет условию (3.2), хотя не обязательно усло-
вию (3.1). Последовательно применяя соотношение (3.8), полу-
чаем
оо
Z*.— 2 Рц*] ПРИ всех
Обращаясь к (3.6), мы видим, что предыдущее соотношение при
i = 0 дает
2 ^; = Z0 = M при всех /г^О. (3.9)
§ 3. Правые регулярные последовательности
185
Левая часть в (3.9) представляет собой взвешенное среднее чисел,
каждое из которых М. Поэтому равенство (3.9) может иметь
место только в том случае, если для всех /, таких, что Ро/> 0 при
некотором /г>0, величина zj равна М. В частности, по определе-
нию kQ
z\ = М, г* = М. ..., г* =я ...
«о 9 ’ the >
для любого положительного целого t. В силу (3.5) п можно
выбрать таким, чтобы все неравенства
выполнялись одновременно. Складывая эти неравенства, получаем
t (М - 8) < Zko+Sn + Z2ka+Sn + ... +ztko+sn =
=(Ч^,г"Ч) + (Ч^„-Ч+^ +
+~ + • • • + Vs»)=
= У*ко+!!п “ Узп
Так как yj ограничены, то существует такое К > 0, что у} < К для
всех /. Тогда, очевидно,
t (AI - е) < 2К.
Поскольку это неравенство должно выполняться при любом целом
t > 0 и любом е > О, М с необходимостью должно быть отрица-
тельным либо равным нулю. Таким образом, yj — у^_^ — Zj^O, или
(ЗЛ°)
для всех / и любого k0, достижимого из нуля.
До сих пор мы нигде не использовали условия (3.1), т. е. того
факта, что z/j 0. Нам потребовалось только, чтобы |z/j| были ог-
раничены. Следовательно, мы можем провести все предыдущие
рассуждения для последовательности [z/yj, у которой z/< = — yf.
Разумеется, [z/<] остается ограниченной и удовлетворяет (3.2).
В этом случае
У^У^Ь (З.П)
186
Гл. 6. Последовательность сумм независимых величин
для всех j и всех состояний k$, достижимых из нулевого состояния.
Сравнивая (3.10) и (3.11), получаем
У^У^ы
для всех / и всех состояний kQ, достижимых из нулевого состоя-
ния. В частности,
(3-12)
для всех состояний достижимых из нулевого состояния. Теперь
мы впервые за все доказательство воспользуемся предположением
о неприводимости марковской цепи. Это предположение гаранти-
рует, что все состояния достижимы из нулевого состояния. Сле-
довательно, (3.12) выполняется для всех kQ = 0, ±1, ±2, ... и
все члены последовательности {yj} равны константе yQ. Н
В заключение этой главы мы применим теорему 3.1 для доказательства обоб-
щенной теоремы восстановления для сумм независимых одинаково распределен-
ных целочисленных случайных величин. Мы будем далее предполагать, что сум-
мы Sn являются непериодическими д.с.в., т. е. что наименьшая аддитивная груп-
па, порождаемая целыми числами /, для которых P{?G = i} > 0, есть группа
всех целых чисел.
Мы дадим прямое доказательство теоремы восстановления; однако несколько
вспомогательных результатов, получаемых попутно, представляют самостоятель-
ный интерес, а методы их доказательства типичны для задач о флуктуациях
в теории сумм независимых д. с. в.
Теорема 3.2. Если Sn = Х\ 4- Х2 + .. • + Хп являются непериодическими
д. с. в. и М(|Х1|) < оо, a M(Xi) > 0, то
оо
«</ - Дт. S /-< т® • <3-'3>
п==0
Пт G;/ = 0. (3.14)
/->-оо 4
Для удобства разобьем доказательство на несколько этапов. Для любой ве-
личины а положим а+ = шах (а, 0) и а~ = min (а, 0). Пусть
== min (Sb S2, ..., Sn)-
Поскольку последовательность Мп не возрастает, предел
lim Mrt = inf(Sb S2, ...) = Л4
П->оо
существует, хотя возможно, что М = —оо. Однако, поскольку М(Л\)>0, усилен-
ный закон больших чисел гарантирует нам, что
Р {М = — оо} Р {£п 0 при бесконечно многих п} = 0*
Следовательно, М конечно с вероятностью 1.
Далее,
M(A4n)«M{min(Sb ..., Sn)}-
= М {Xj + min (0, X 2, Х2 + Х3, ..., Х2+...+Хп)} =
= M(X1) + M{min(0, Х2, У2 + У3...Х2+ ... +Х„)}. (3.15)
§ 3. Правые регулярные последовательности
187
Так как Xi независимы и одинаково распределены, то последнее слагаемое есть
не что иное, как
Устремляя п к оо, получаем
М (М) = М (ХО + М (ЛГ). (3.16)
(Читателю рекомендуется доказать возможность перехода к пределу под знаком
математического ожидания.) Очевидно,
М (М) = М (М+) + М (ЛГ),
откуда с учетом (3.16) получаем
М(М+) = М(Х!). (3.17)
Наши рассуждения имеют одно слабое место: мы не знаем a priori, что
М(М“)>—оо, а только в этом случае соотношение (3.16) имеет смысл.
Чтобы восполнить этот пробел, нам понадобится следующая теорема, имею-
щая и самостоятельный интерес.
Теорема 3.3. Пусть Z — неотрицательная целочисленная с. в., т. е.
оо
P{Z — п} =» рП1 п = 0,1,..., 2 Рп^ Ь « ф(0) — бе характеристическая функ-
п=*о
оо
ция. Предположим, что [ср (0) — 1]/Z9 = (1/Z0) 2 Рп(ем — 1) сходится к
оо
а (0 < а < оо) при 0 ф 0. Тогда М (Z) = 2 пРп — а-
гг=>0
Доказательство. Выделяя действительную и мнимую части выраже-
ния (<р(0) — 1)/Z0, мы заключаем, что
1. V (1—cosnO) Л .. V sinnO /п1о.
hm У Рп--------д---= 0 и lim У рп —х— = а. (3.18)
тг=О тг=О
Для любого фиксированного 0>О найдем наибольшее целое число £ = &(0),
удовлетворяющее условию л/2^£0>О.
оо
В силу (3.18) сумма 2 Рп (sin н0)/0 равномерно ограничена при достаточ-
но
но малых 6. Представим эту сумму в виде
ОО k ОО
Ssin н0 V sin п0 , V sinnO zn 1ПЧ
р" ~е— Рп -Q- + р«-0-- <3J9>
72 = 0 72=0 72 = 8+1
Оценим снизу (sin ц0)/0л используя тот факт, что (sin 0)/0 является убываю-
щей функцией при 0 0 < л/2 (см. стр. 178):
sin 6 sin л/2 2 Q л
л/2 ~Т' °<0<Т‘
Из определения h следует, что 0 < п0 л/2 при 0 п Тогда предыдущее
неравенство дает
Ssin /20 2 V
'’“ТПрп-
п=0 71=0
188
Гл. 6. Последовательность сумм независимых величин
С другой стороны, для второй суммы в (3.19) имеем
sin лгО
Рп—0—
/2 = Д+1
Рп-
п=Н1
Но 1 — (sin nO)/nO > 1 — (1/п9) > 1 — 2/л — b > 0 для всех п, таких,
что п9 > л/2. Следовательно,
оо оо
1 V 1 V Л sin п$ \ _
е 2а Рп^ ьв 2а Рп\1 п&
оо 0
“То S p4f(i-cos^)«
п = Ж о
оо 0
1 V _ f 1 — COS ng
be 2j Рп J g
п=й+1 О
0 оо
Г V Г 1 “* cos ng I .
2j Pn\------z—- dg < (перемена местами суммирования
о n~E+i * и интегрирования возможна, так
как все члены неотрицательны)
0 оо
. 1 f V 1 ~ COS ng
сТо J 1 Рп—I—rfs“
О п=0
0
1 f Tm Г <*> ~ 1 Ъ?
“То J ImL /g П-
О
Но Im([cp(gy — 1]/Zg) ->0 при gJrO в соответствии с (3.18), и поэтому ее сред-
нее значение стремится к нулю:
0
lim
©Что
] dl = 0.
(Читателю следует доказать это.)
Из полученных оценок следует, что вторая сумма в (3.19) стремится к нулю
при 0 ф 0. Поэтому сумма
^прп (k^k(G))
п = 0
равномерно ограничена при 9 > 0. Очевидно, k = k(Q) возрастает до бесконеч-
оо
яости при 0 ф 0, а отсюда и следует сходимость ряда 2 npn = M(Z). Чтобы
§ 3. Правые регулярные последовательности
189
завершить доказательство теоремы 3.3, мы должны показать, что
оо
S прп = Ф (?е~1 • (3-20)
п«0
оо
Для этого зададим е>0 и выберем N(z) таким, что 2 прп<ъ12. Послед-
оо
нее возможно, поскольку, как мы уже показали, ряд 2 пРп сходится. Далее,
/1=0
ПРп.
Так как
Отсюда
— 1)/Z0| п, то вторая и третья суммы ограничены величиной е/2.
lim I
e^ol
Ф (0) — 1
/0
— M(Z)
— п
+ е.
При фиксированном N сумма в правой части стремится к нулю, так как каждое
ее слагаемое стремится к нулю. Поэтому
Шй| ф(е)~1--М(7)|<е.
0^01 w I
Выражение в левой части представляет собой фиксированное неотрицательное
число; 8 > 0 можно выбрать произвольно малым. Отсюда вытекает справедли*-
вость соотношения (3.20). Я
Теперь мы можем дать строгое доказательство соотношения (3.17). Введем
характеристические функции случайных величин Х[ и
ФД4 (6)“ 3 ?ft0P{Mn = 4
П k==-oo
оо
Фх,(0)“ 2
k~ — оо
И
о
<р„ - (°)= 5 eMP{M-_^k}.
Mfl-1 /г = -оо
Отметим, что случайная величина может принимать только неотрицатель-
ные целые значения. Очевидно, с. в. Хх и JW“_1 = min(0, Х2, Х2 + Х3, Х2 4-
-Ь Л73 -Ь ... +Х^ независимы. Кроме Toro,Af~__j и одинаково распреде-
лены, так как Af~_j определяется через Х2, Х3,..., Хп точно так же, как AfJJLi
определяется через Х1} ..,, Хл-ь
190
Гл. 6. Последовательность сумм независимых величин
Так как Мп == (это соотношение неявно фигурирует в (3.15)),то
Ф„ (0) = Ф„ (9)Ф~_ (в)-
Мп Xi мп-1
Из определений следует, что Мп->М и при п->оо (сходимость
понимается как сходимость в смысле распределений). В силу критерия сходи-
мости П. Леви (стр. 16) имеем
<р (0) = ф (0)ф (0). (3.21)
М А1 М
Но
оо
Фм(6) = 3 eM0P{Af = fe} =
/г= —оо
оо — 1
= 2 e'ft6p {M+ = й} + 2 еМр {м- = 6} + р {М = 0).
&=1 k= — ОО
Так как
р [М = 0}= р (М > 0} + р {М СО}- 1 -
= р {м~ = 0} + р {м+ = о}- 1,
мы можем записать предыдущее соотношение в виде
Фм О) - 2J emP {М+ - k} + 2 e,fe9p {АГ = k} - 1 =
/г=0 —oo
-фл1+<в) + ч.л,-(е>-|.
Подставляя это соотношение в (3.21), получаем
ФЛ1+(О)-1 = ФЛ1_(0)(ФХ1(е)-1)- (3.22)
Поделив обе части на Z0 и устремив 0->О, получаем
фу, (0) - 1
------------= М(У0,
е->о ж
так как M(|Xil)<oo. (Формальное доказательство этого предельного соотноше-
ния проводится так же, как и доказательство соотношения (3.20) в теореме 3.3.)
Очевидно, Нт <р . (6) = 1, и из (3.22) следует, что
0->о М
фм+ (0) -1
О < lim м ~5-------= М (Х1) < ОО.
0-»О W
(3.23)
Так как М+ — неотрицательная д. с. в., мы можем воспользоваться теоре-
мой 3.3, из которой следует, что предел в (3.23) равен М(М+) и, таким образом,
M(M+)= M(Xi).
Нам потребуется следующая лемма.
Лемма 3.1. Пусть ei (i 0) есть вероятность того, что процесс {Sn}, от-
правляясь из состояния i, на первом шаге окажется в одном из положительных
§ 3. Правые регулярные последовательности
191
состояний и после этого никогда не окажется ни в одном отрицательном состоя-
нии. При i > 0 вероятности вг полагаются равными нулю. Тогда
о
/ = — оо
Доказательство. Из самого определения вероятностей et следует, что
f P{inf(Sb S2, ...)> —z} = Р {zW+> —z'}, i<0,
0, 1>0.
Далее,
0 0 оо
2 2 р<Л1+>-4= 2 р{м+>/}=
/= —ОО /= — оо / =0
= 2 S р{м+ = б}= 2 р{м+ = /г)2 1=м(м+)=м(х,).
/=0&=/+1 &=о /=0
Лемма доказана.
Пусть
V (/) = Р {Srt > 0 для некоторого n > 1 | So = i},
т. е. V(i) есть вероятность, отправляясь из состояния Z, оказаться на положи-
тельной оси.
Рассмотрим те реализации процесса, которые выходят из состояния i и вклю-
чают в себя неположительные состояния. По условию теоремы 3.2 M(Xj) == ц > 0;
поэтому в силу закона больших чисел такая реализация с вероятностью 1 мо-
жет быть в неположительных состояниях лишь конечное число раз. Вероятность
того, что процесс в последний раз находился в неположительном состоянии на
0 оо
n-м шаге, равна ~ S последнее равенство следует из опреде-
&= — оо —• оо
ления 6k для k > 0. Перебирая все возможности, связанные с последним момен-
том пребывания в неположительных состояниях, получаем важное соотношение:
оо оо оо / оо \
по =2 2 р^Ч= 3 2 р« =
/1=1 fe=x~oo k= — ОО \пе»1 /
ОО / оо \ оо
= 2 MS = 2 Oikek-et (3.24)
&=—ОО \М==0 / —ОО
— символ Кронекера). Теперь мы можем доказать теорему восстановления.
Доказательство теоремы 3.2. Из определения Оц следует, что
оо оо
2 PikPkj = 2 Pik 2 - 2 p(i!+X} = О И - Ъа- (3-25)
k k n=0 п=0
Так как Иц Gqq (лемма 1.1), то с помощью диагонализации (см. доказатель-
ство теоремы 3.1) мы можем выделить подпоследовательность {/ш}, такую, что
предел
существует для каждого L
192
Гл. 6. Последовательность сумм независимых величин
В соотношении (3.25) перейдем к пределу при j, стремящемся к бесконеч-
ности по значениям подпоследовательности это даст
2 Л-л=<₽г (з-26)
k——OO
причем {(pi) — ограниченная последовательность. (Читателю рекомендуется само-
стоятельно убедиться в возможности предельного перехода под знаком суммы.)
В силу теоремы 3.1 ограниченная регулярная последовательность {cpj является
постоянной; пусть все ее члены равны константе а. Из (3.24) имеем
Так как и ряд ek сходится, то
оо
lim — = а eh=z aM(Xj) (в силу леммы 3.1).
-> оо • оо
Но, очевидно, lim V(—fm)~l. Следовательно, а = l/M(Xi). Если имеется
/П-»оо
другая последовательность /т->оо, обладающая тем свойством, что G ~
Gm
сходится при всех /, то точно так же можно показать, что предел lim G ~ ==
m->oo llm
==(М(У])~1). Таким образом, мы установили справедливость соотношения (3.13).
Предельное соотношение (3.14) доказывается аналогичным образом.
ЗАДАЧИ
1. Рассмотрим выборочное пространство, состоящее Из п циклических пере-
становок набора («1, «2, •.., Яп); вероятность каждой перестановки равна 1/п.
Для каждой точки х—(яй, аь+\, .... ak+n-i), где по определению an+i = су,
I — 1, ..., и — 1, пусть N(x) обозначает число частичных сумм среди {ak, ak+ak+i,
ak + ak+i 4- ak+2, ..., 4- ... 4- aft+n}, равных нулю, а Л1(х) —число различ-
п
ных частичных сумм. Показать, что если 2 ^. = 0, то М(1/Л,7(х)) = Л1(х)/п.
г = 1
2. Пусть Xi, X2f ..., Хп, ... — независимые случайные величины, равномерно
распределенные на отрезке [0, 1]. Показать, что при 0 а п
1а]
Р(Х,+
/=0
[а] обозначает, как обычно, наибольшее целое число, меньшее или равное а.
Указание: Применить индукцию по и.
3 (продолжение). Пусть г — такой индекс, что Xi 4- ... +Xr-i a, Xi 4- ...
t.. 4- Хг > а. Показать, что
1VI _
M(r)=S(~i)7 еа~‘-
i-o
Задачи
193
Указание', Доказать соотношение М (г) = Р {г >п} «= P{Xi+ ... +
П“0 п=0
4- Хп и] и затем воспользоваться результатом задачи 2.
4. Пусть Xj, X2i ... — последовательность независимых одинаково распреде-
ленных целочисленных случайных величин, а Sft==Xi + Х2 + ... + Xh, 6=1, 2,..
— частичные суммы. Как обычно, So = 0. Индекс п>1 назовем лестничным,
если Sn > Sj при j — 0, 1, ..., п — 1. Событие, состоящее в том, что п является
лестничным индексом, обозначим через Определим YN как момент (т. е. ин-
декс) последнего наступления события где N — номер текущего испытания.
Пусть W — момент первого наступления Предположим, что & происходит на
n-м испытании. Показать, что число испытаний до следующего наступления (5 не
зависит от п и распределено, как W.
5 (продолжение). Доказать соотношение
оо
п»0
1
l-F(xO ’
где = S P{W=n}tn.
* Указание: Использовать соотношение
Р {Yn - k} = Р {П = k} Р {Yn_k = 0}.
6 (продолжение). Пусть U(t) — 1/(1 — F(Щ. Показать, что U(t) можно
представить в виде
U (/) = ехр
£ Л{М(К*)-М(У*_,)}
Указание: С помощью результата предыдущего упражнения вывести диффе-
ренциальное уравнение
оо
и решить его.
7. Пусть Хь Х2, ... — независимые одинаково распределенные целочислен-
ные с. в. Положим
So==0 и S& = + <¥2 + ... + Xk при &==1, 2, ....
Пусть fn — вероятность того, что процесс {S/J впервые вернется в нулевое со-
стояние на n-м шаге. Пусть уп — вероятность того, что на n-м шаге процесс бу-
дет занимать новое состояние, т. е. Yn e P{Sn ^So, Sn=#Si, Sn^S2,...
. .., Sn =# Sn-i}. Доказать, что
yn « Р {Sj #= 0, S2 #= 0. ..., =/= 0}.
Выразить yn через Для случая, когда М(|Л\|) <оои М(Л\) =0,
7 Зак. 939
194
Гл. 6. Последовательность сумм независимых величин
8 (продолжение). Пусть Rn—число различных состояний, которые процесс
(5&}~в0 занимал за первые п шагов. Выразить среднее значение д. с. в. Rn че-
рез {уА}.
Ответ: М (Rn) = jjj] уг
9 (продолжение). Показать, что
j. мш
lim ---------
П -> оо П
- 1 ~/оо>
где
foo - S foo-
10 (продолжение). Пусть Ln = j тогда и только тогда, когда Sj > Si при
0<i</ и Sj^Si при j < i п, т. е. Ln есть первый индекс, на котором
достигается max S/. Доказать соотношение
P{Ln^j}^P{Lj = j}P[Ln4^Q}.
11. Определим процесс {Xti t = 0, 1, 2, ...}, где Xt—действительные числа,
следующим образом: Хо = 0,
Х/-1 + с веР0ЯТН0СТЬ10
у 1
^/-1 с вероятностью
Показать, что в пределе при распределение с. в. Xt стремится к равномер-
ному распределению на интервале (-—1, 1).
Указание-. Распределение с. в. Xt стремится к распределению с. в. К =
°° k
= Yk , где Yk — одинаково и независимо распределенные с. в. со зна-
&=1
оо
чениями ±1, принимаемыми равновероятно. Пусть f (s) =» JJ cos s/2k't f(s) удо-
1
влетворяет функциональному уравнению
f (2s) = (cos s) f (s).
Показать, что единственным непрерывным решением этого уравнения, удовле-
творяющим условию f(0) = 1, является функция (sins)/s, т. е. характеристиче-
ская функция равномерного распределения на интервале (—1, 1).
12. Рассмотрим двумерное случайное блуждание по целочисленной решетке
В положительном квадранте. Если на некотором шаге процесс находится в со-
стоянии (пг, п), то на следующем шаге процесс с одинаковой вероятностью V2 пе-
рейдет либо в состояние (/п+1,п), либо в (пг, я + 1). Пусть Г —ломаная,
соединяющая соседние точки решетки (и простирающаяся от оси Y до оси X)
в положительном квадранте. Показать, что М(У1)=М(У2) где У1 и У2 обо-
Задачи
195
значают число шагов вправо и число шагов вверх соответственно перед попада-
нием на границу Г. Предполагается, что процесс выходит из начального со-
стояния (0, 0). Пример ломаной Г приведен на рисунке.
Г
Указание: (а) Сначала рассмотреть случай, когда ломаная Г состоит из
двух сегментов АВ и ВС. АВ — горизонтальный отрезок, соединяющий точки
(0,1) и (N, 1), а ВС — вертикальный отрезок, соединяющий точки (N, 1) и (N, 0).
Показать, что для этого случая
М(Г2)=| +
k*=l
и эти величины равны между собой.
(б) Всякую область, ограниченную осями X и У и ломаной Г, можно раз-
бить на блоки вида, описанного в (а). Использовать соответствующее правило
сложения средних и результат пункта (а) настоящего указания.
Задачи 13—18 основаны на следующей модели.
Рассмотрим случайное блуждание Хп = (Ап,Вп) на плоскости, возможными
состояниями которого являются все точки с целочисленными координатами в дву-
мерном пространстве. Предположим, что вероятность перехода в любое из четы-
рех соседних состояний равна V4. Пусть Т — время первого попадания случайного
блуждания, начинающегося из начала координат, на биссектрису положительного
квадранта, а Хт — точка на биссектрисе, в которую попадает случайное блу-
ждание. Пусть
Qo/ = P{^r=(j. /)|Хо = (О; 0)}.
Этим соотношением определяется переходная вероятность одномерного случай-
ного блуждания, порождаемого исходным двумерным случайным блужданием,
наблюдаемым лишь в моменты его попадания на биссектрису. Определим харак-
теристическую функцию указанного одномерного случайного блуждания:
ф (0) - S QomellnQ. - 00 < 0 < ОО.
m=-oo
13. Положим Uq = Vo = 0 и ип—АпА-Вп, Vn—An — Bn> л =1,2,....
Показать, что последовательность с. в. {Un} не зависит от последовательно-
сти {Уп}. (Переход к переменным {Un, Уп) соответствует замене исходной
7*
196
Гл. 6. Последовательность сумм независимых величин
системы иоординат на систему, в которой одной из осей является биссектриса
положительного квадранта.)
Указание', (а) Показать сначала, что
P{t7m-t7m_I = ±r|f7o = Vo = O} =
О, 1г|^1;
и
P{^-F„_1 = ±s|t/o=lzo = O} =
(пг = 1, 2, ...)
(я== I, 2, ...).
у. |s|-l.
О, |s |¥=0;
(б) Далее показать, что
1. P„-V„_1 = ± l|t/o=Po = O) = l
Р {Um - Um-, = г, Vn - Vn_, = s | (70 = Vo = 0} > 0,
если | r | =£ 1 либо | s | =^= 1 (n, m = 1, 2, ...).
Воспользоваться формулами пунктов (а) и (б) и показать, что последова-
тельность {Um — £/w-i} не зависит от последовательности {Vn — Vп_вывести
отсюда, что {Um} не зависит от {Гп}
14. Доказать, что с. в. Т не зависит от последовательности {Ип}.
15. Убедившись предварительно, что из Т =?= k следует, что Vh = 0, устано-
вить формулу
оо оо
ф (6) = 5 р {Г = £1*0 = (О, 0)) 2 еМр Wk = 211 XQ = (0. 0)}.
1— — ОО
16. На основе того факта, что {Un} описывает одномерное случайное блу-
ждание, показать, что
Ф (е) = 2 р {Г = й | Хо = (0. 0)} (cos 0/2)*.
k-1
17. Доказать, что производящая функция с. в. Т имеет вид
М (sT) - 1 - .
18. Доказать формулу
ф (0) — 1 — | sin 0/2 |, — оо < 0 < оо.
ЗАМЕЧАНИЯ
В значительной степени источником материала этой главы по-
служила элегантная книга Спицера [1]. Превосходными руковод-
ствами по теории вероятностей, содержащими изложение предель-
ных теорем для сумм независимых случайных величин на значи-
тельно более высоком уровне, являются монографии Гнеденко и
Литература 197
Колмогорова [2], Лоэва [3] и Реньи [4]. Современное полное изло-
жение предельных теорем теории вероятностей в различных аспек-
тах читатель найдет во втором томе книги Феллера [б].
ЛИТЕРАТУРА
1. Спицер Ф., Принципы случайного блуждания, «Мир», М., 1968*
2. Г н е д е н к о Б: В., Колмогоров А. Н., Предельные распределения для
сумм независимых случайных величин, Гостехиздат, М., 1949.
3. Л о э в М., Теория вероятностей, ИЛ, М., 1962.
4. R ё п у i A., Wahrscheinlichkeitsrechnung, mit einem Anhang fiber Informations-
theorie. Deutscher Verlag der Wissenschaften, Berlin, 1962.
5. Феллер В., Введение в теорию вероятностей и ее приложения, т. 2, «Мир»,
1967.
Глава 7
КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
§ 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ)
И ПУАССОНОВСКИЕ ПРОЦЕССЫ
В предыдущих главах были введены основные понятия и рас-
смотрены методы анализа цепей Маркова с дискретным временем.
В этой главе дается краткое обсуждение некоторых важных при-
меров марковских процессов с дискретным множеством состояний
и непрерывным временем.
Точнее, здесь мы будем иметь дело с семейством случайных
величин {%(/), О^/^оо}, принимающих неотрицательные цело-
численные значения. Мы ограничимся случаем, когда {%(/)}—
марковский процесс со стационарными переходными вероятностя-
ми. Таким образом, переходная вероятностная функция при t > О
PZ7(/) = P{X(/ + u) = /|X(u) = z}, /,/ = 0, 1,2,..., (1.1)
не зависит от и >0.
Обычно при исследовании частных вероятностных моделей фи-
зических явлений более естественно описать так называемые ин-
финитезимальные вероятности, связанные с процессом, а затем
вывести из них точное выражение для переходной функции.
В рассматриваемом случае мы будем постулировать вид Pij(h)
для малых h и, используя марковское свойство, выведем систему
дифференциальных уравнений, которой удовлетворяют Pij(t) при
всех t > 0. Pij(t) являются решением этих уравнений при соот-
ветствующих начальных условиях. Напомним, что пуассоновский
процесс, введенный в § 2 гл. 1, рассматривался именно таким об-
разом.
Перед тем как перейти к общему процессу чистого рождения,
напомним кратко аксиомы, характеризующие пуассоновский про-
цесс.
А. Постулаты пуассоновского процесса
Пуассоновский процесс был рассмотрен в § 2 гл. 1, где было
показано, что его можно определить с помощью нескольких про-
стых постулатов. Для того чтобы определить более общие процес-
сы подобного рода, укажем на некоторые свойства, которыми об-
ладает пуассоновский процесс. Пуассоновский процесс — это мар-
§ 1. Процессы чистого рождения и пуассоновские процессы
199
ковский процесс, принимающий неотрицательные целочисленные
значения и обладающий следующими свойствами:
(1) Р {X (t + А) - X(t) = 11 X(t) = х} = ЛА + o(h) при /ЦО
(х = 0, 1, 2, .)
Свойство (1) можно записать еще так:
Нт-^РЦ (t + h)-X(t)= 1|Х(0 = х} = Л.
h^o п
Символ o(h) обозначает такую величину, которая, будучи делен-
ной на А, стремится к 0 при h 0. Заметим, что правая часть не
зависит от х.
(2) р{х(t + h)-х(о = о|х(о = *}= 1 -ла + o(h) при а;о.
(3) Х(0)-0.
Эти свойства легко проверить непосредственным вычислением,
поскольку имеются точные формулы для всех рассматриваемых
вероятностей.
Б. Примеры пуассоновских процессов
(а) Можно проиллюстрировать пуассоновский процесс на при-
мере процесса ловли рыбы. Пусть случайная величина X(t) обо-
значает число пойманных рыб за временной интервал [0, /]. Пред-
положим, что общее число рыбы, имеющейся в наличии, весьма ве-
лико, так что «завзятые» рыбаки имеют не больше шансов поймать
рыбу, чем все остальные, и что интенсивность клева не зависит от
времени. При этих «идеальных» условиях процесс {%(/), />0}
можно считать пуассоновским. Этот пример поясняет марковское
свойство (вероятность поймать рыбу не зависит от числа уже пой-
манных) и свойство независимости от времени ожидания1), ко-
торое является наиболее характерным свойством пуассоновского
процесса; оно означает, что рыболов, только что прибывший на
рыбалку, имеет такой же шанс поймать рыбу за определенный от-
резок времени, как и тот, который уже просидел четыре часа
безуспешно.
(б) Менее искусственный пример связан с задачами, возни-
кающими в теории счетчиков. Если X(t) —число радиоактивных
частиц, зарегистрированных счетчиком Гейгера за временной интер-
вал [0, /], то этот процесс является пуассоновским при /, много
меньших полупериода распада вещества. Отсюда получается, что
вероятность распада за единицу времени можно считать не ме-
няющейся с течением времени.
!) В оригинале «по premium for waiting property», т. e. дословно «свойство
отсутствия поощрения за ожидание». — Прим, перев.
200 Гл. 7. Классические примеры цепей Маркова
(в) Пуассоновские процессы естественным образом возникают
во многих моделях образования очередей (массового обслужива-
ния). В этих примерах наибольшее внимание уделяется моментам
времени, когда X(t) (длина очереди в момент t) изменяется, а не
самим значениям /(/) !). Процесс ловли рыбы (см. пример (а))
является, конечно, частным случаем подобных моделей.
В. Процесс чистого рождения
Естественное обобщение пуассоновского процесса получим, до-
пустив зависимость вероятности осуществления события в данный
момент времени от числа событий, которые уже произошли;
примером такого явления может служить воспроизведение живых
организмов (отсюда и название процесса), когда при соответ-
ствующих условиях — избытке пищи, отсутствии смертности, от-
сутствии миграции и т. д. — вероятность рождения в данный мо-
мент прямо пропорциональна размеру популяции. Этот пример из-
вестен как процесс Юла.
Рассмотрим последовательность положительных чисел {X/J.
Определим процесс чистого рождения как марковский процесс,
удовлетворяющий постулатам:
(1) Р{Х(/ +Л)-%(/)= 1 \ X(t) = k} —kkh +oitk(h), /ЦО,
(2) Р {X (/ + h) - X (t) =* 01 X (/) = &} = 1 - lkh + о2, k (Л),
(3) Х(0) = 0,
(4) P{X(t + h)-X(t)<Q\X(f} = k} = Q, /?>0.
Постулат (3) введен только для удобства. В нем под X(t) под-
разумевается не размер популяции, а число рождений в интервале
[0, /].
Заметим, что левые части (1) и (2) равны /\А+1(Л) и /\*(/г)
соответственно (вследствие -стационарности), так что Oi, &(А) и
02, kW не зависят от t.
Определим Pn(t) = Р{Х(/) =
Точно так же, как и для пуассоновского процесса* 2), можно
вывести систему дифференциальных уравнений относительно Pn(t)
при I 0 вида
РИ0=-МШ
с начальными условиями
Ро(О)=1, Р„(0) = 0, м>0.
Для пуассоновского процесса такие моменты времени образуют пуассо*
новский поток. — Прим, перев.
2) См. гл. 1, § 2. — Прим, перев.
1. Процессы чистого рождения и пуассоновские процессы
201
В самом деле, если h > 0, п>1, то, используя формулу полной
вероятности, марковское свойство и постулат (4), получим
Pn(t + h) = 2 Pk(t) P{X(t + h) —n\X (t) = k} =
k—0
= % Pk(t)P{X(t + h)- X(t)*=n-k\ X(t) = k} =
k=Q
= 2 Pk(t)P{X(t + h)-X(t) = n-k\X(t)~k}.
k=0
Далее, при £ = 0, 1, ..., n — 2 имеем
P {X (i + h) - X (t) = n - k | X (t) = k} <
^P{X(t + h)-X(i)^2\X(t)=‘k} = olik(h) + o2,k(h),
или
P{X (t + h) — X (i) = n~ k\X (t) = k} = o3,n, k(h), k = 0, ..., n —2.
Таким образом,
Pn(t + h)=:Pn(t)[l- %nh + O2, „ (Л)] +
n—2
+ Pn-i (0\Ki-ih + Oi, n-i (Л)] + 2 Pk (О °з, n, k (h),
k^Q
ИЛИ
Pn (t + h)- Pn (t) = Pn (0 [ - Knh + o2, „ (A)] +
+ Pn-i (f) + °i, л-i (^)] + on (h), (1.3)
где, очевидно, limo„ (h)/h = 0 равномерно no / > 0, поскольку
/i^-О
n-2
on(h) ограничена конечной суммой 2 o3> n,kW> не зависящей
от t.
Деля на h и переходя к пределу при /Ц 0, получим соотноше-
ние (1.2), в котором, если быть точным, в левой части нужно пи-
сать правостороннюю производную. Однако, используя несколько
более тонкие рассуждения, можно вывести такое же соотношение
для левосторонней производной. В самом деле, из (1.3) сразу сле-
дует, что Pn(t) —непрерывная функция t. Заменяя в соотношении
(1.3) t на t — ht деля на h и переходя к пределу при h | 0, най-
дем, что каждая функция Pn(t) имеет левостороннюю производ-
ную, которая также удовлетворяет уравнению (1J2).
Первое уравнение в (1.2) можно решить сразу и получить
Р0(/) = ехр(- М)>°-
202 Гл. 7. Классические примеры цепей Маркова
Обозначим через Ть время между &-м и (k + 1)-м рожде-
ниями. Тогда
р„(0 = рГз'л<^<2 т{}
I i=0 i-0 J
и
£-1
Sfe = S Tt — время k-то рождения.
i =0
Мы уже видели, что PQ(t) = ехр {—М}. Следовательно,
Р {То С г} = 1 - Р {X (г) - 0} = 1 - ехр{ — Лог},
т. е. То имеет экспоненциальное распределение с параметром Хо.
Из постулатов (1) — (4) можно вывести, что величины Tki k > 0,
также имеют экспоненциальные распределения с параметрами X/?
и что они взаимно независимы (см. § 3 гл. 8, где дано формальное
доказательство этого факта). Следовательно, характеристическая
функция величины Sn равна
п — 1 п—1
<р„ (ш) = М {ехр (Z®Sn)} = JJ М {ехр (iwTk)} = JJ (7“^г) U -4)
/г=0 k~0
В случае пуассоновского процесса, когда Кн = X при всех k, из
(1.4) видно, что величина Sn распределена в соответствии с гам-
ма-распределением порядка п со средним п/Х.
При конкретных значениях > 0 можно последовательно про-
интегрировать уравнения (1.2):
t
Pk(i) = hk-i ехр(- W) J exp(Xftx)/Vi (x)dx, k= 1, 2, ..
о
откуда ясно, что все Рь(Т) 0.
Но еще остается возможность того, что
оо
2 ?„(/)< 1.
п = 0
Чтобы гарантировать регулярность процесса, т. е. дать критерий
оо
того, что будет 2^>п(^)==1 для всех мы должны ограничить
п=0
Z/j условием
оо оо
(1-5>
д=0 п=0
$ 1. Процессы чистого рождения и пуассоновские процессы 203
Доказательство этого дано в книге Феллера 9 и здесь не приво-
дится. Интуитивные соображения в пользу этого результата сле-
дующие. Время Tk между последовательными рождениями, как
показано ниже, распределено экспоненциально с параметром
V 1 1
Следовательно, величина У равна среднему времени до того
Ли
п
оо
момента, когда популяция станет бесконечной. Но 1—2 ЛИО
п=0
есть вероятность того, что X(t) = оо.
Если то среднее время, за которое популяция
становится бесконечной, конечно. Поэтому правдоподобно, что при
этом для всех t > 0 вероятность того, что Х(/) = оо, положительна.
Г. Процесс Юла
Процесс Юла является примером процесса чистого рождения,
который возникает в физике и биологии. Предположим, что ка-
ждый член популяции в интервале времени длины h с вероят-
ностью рЛ + о(/г) порождает нового члена (|3>0). Кроме того
предположим, что в момент 0 в популяции имеется N членов.
Предполагая независимость и отсутствие взаимодействия между
членами популяции, получим в силу биномиального закона
Р {X (t + h) - X (f) - 11 X (f) = n} =
= (n |N ) [р/г + о (/г)] [ 1 - р/г + о (h)]n+N~' =
= (n + N) fih + o„ (/i),
т. e. в этом примере Xn=(« + A^)p. Система уравнений (1.2)
в случае, когда N = 1, принимает вид
« = 0, 1,...
с начальными условиями
Ро(О)=1, Р„(0) = 0, п=1, 2, ....
Ее решение равно
что можно проверить непосредственно.
9 Феллер В., Введение в теорию вероятностей и ее приложения, 2-е изд.,
т. 1, «Мир», М., 1964.
204
Гл. 7. Классические примеры цепей Маркова
§ 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ
ПРОЦЕССАХ
В предыдущем параграфе мы определили пуассоновский про-
цесс системой допущений (постулатов), которые довольно хорошо
описывают многие реальные ситуации. Этот процесс часто назы-
вают абсолютно случайным процессом1), так как он «распреде-
ляет» точки «случайным образом» на прямой [0, оо) совершенно
аналогично тому, как распределяются точки при равномерном
распределении на конечном интервале. В частности, вероятность
наступления события в некотором интервале является функцией
лишь его длины, а количества событий, происходящих в двух не-
пересекающихся интервалах, являются независимыми случайными
величинами.
Рассмотрим теперь пуассоновский процесс более подробно.
А. Характеристическая функция и длительности пребывания 2)
Характеристическую функцию пуассоновского процесса X(t)
можно записать в виде
(®) = М («} = 2 е-м eiwn = ехр [М (eiw - 1)].
zz=~O
Таким образом,
M(I(f)) = W, o2(X(f)) = Xf.
При обсуждении процесса чистого рождения мы показали, что
P{7’o<z}= 1 — ехр( — V),
и упомянули, что Th имеет экспоненциальное распределение с па-
раметром Ха и все Th независимы. Для пуассоновского процесса
Ха = X при всех k, так что справедлива
Теорема 2.1. Длительности пребывания 7\— независимые
и одинаково распределенные случайные величины, имеющие экспо-
ненциальное распределение с параметром X.
Строгое доказательство этой теоремы будет следовать из более
общих рассмотрений § 4 гл. 8.
Из определения процесса следует большее, нежели утвержде-
ние этой теоремы. Так, время до ближайшего изменения Х(/)
имеет точно такое же распределение, если его отсчитывать от
любого момента, а не только от момента предыдущего скачка.
Иначе говоря,
Р {X (/0 + т) - X (/0) > 0} = 1 - е~Кх,
’) Принят также .термин «чисто случайный процесс». — Прим. ред.
2) В оригинале Awaiting timei (длительность ожидания). — Прим. перев.
§ 2. Дополнительные сведения о пуассоновских процессах 205
что было получено в § 1. Это свойство можно получить и непо-
средственно. Пусть F(x) — P{X(Z0 + х)—Х(4)>0}, где /0— неко-
торый момент времени, зависящий, возможно, от истории про-
цесса до этого момента, значение которого не изменяет данной
вероятности1). Тогда
F(x + y)^P{X(t() + x + y)-X(tQ)>0}^
^=Р {X (tQ +у) — X 0}+ Р {X (tQ +у) — X = 0} X
X Р{X(t0 +х + у) — X(tQ +у)>0\X(td +у) — X(tQ) = 0}
Из определения F(x), независимости приращений пуассоновского
процесса и того факта (который является исходным предположе-
нием при определении пуассоновского процесса), что
Р {X (/0 4-х)--X (/0) > 0}
не зависит от /0, получаем функциональное уравнение
F (х + у) = F (у) + [1 - F (t/)] F (х).
То, что это уравнение определяет экспоненциальное распреде-
ление, доказывается в следующей теореме.
Теорема 2.2. Если F(x) — такое распределение, что F(0) = О
и F(x)< 1 при некотором х > 0, то F (х) является экспоненциаль-
ным тогда и только тогда, когда
F(x-+ у) — F (у) ~ F(х)[1 — F(у)] (*)
ри всех х, у 0.
Доказательство. То, что экспоненциальное распределе-
ние удовлетворяет условиям теоремы, проверяется непосредствен-
но. Чтобы доказать обратное утверждение, положим G(x) =
= 1—F(x). Тогда условие (*) примет вид
G(x+z/)=G(x)G(//). (2.1)
Очевидно, G(0)= 1, G(x)—невозрастающая функция и О(х)>0
при некотором х > 0. Предположим, что G(xo) = O при некотором
хо > 0. Из (2.1) следует, что G(x0) = [g Для всякого целого
п>0. Следовательно, G^^-^ = 0. Но тогда из (2.1) следует, что
G(x) = 0 при х>-~~. Так как п произвольно, то G(x) = 0 при
всех х > 0, что противоречит сделанному предположению. Таким
!) Смысл этой кажущейся неясной фразы будет пояснен при обсуждении по*
нятия «марковское время». См. § 4, гл. 8.
206 Гл. 7. Классические примеры цепей Маркова
образом, G(x)>0 при всех % > 0. Далее, для любых целых
/ т
tn,n>Q из (2.1) легко вывести, что G\~-1 = [G (1)]п . Так как
G(%) и [G(l)]x— невозрастающие функции, совпадающие при всех
рациональных х, и [G(1)]х непрерывна, то отсюда следует, что
G(x) = [G(l)r = exp(xlnG(l))
при всех х > 0. Но F(x)— функция распределения, поэтому
lim G (%) = 1 — lim F (%) = 0,
х->оо х-»оо
откуда G(l)< 1. Следовательно, G (х) = е~Кх, где
Л = - In G (1) > 0.
Другое доказательство в предположении, что G дифференци-
руема, следующее. Заметим, что из (2.1) получается
G' U + У) = G (х + У) = G' (х) G (у),
G(x) G' (y) = -^G(x + y)=G'(x + y)
и, следовательно,
G'(x) = aG(x), (2.2)
где G,(z/o)[GQ/o)l'"1 при некотором yQ, таком, что G(r/o)¥=O.
Решением уравнения (2.2) является G(x) = /4eax, и А = 1, по-
скольку G(0) = 1—F(0)=l. Параметр а отрицателен, так как
G(x) < 1 при некотором х > 0.
Б. Равномерное распределение
Класс распределений, связанных с пуассоновским процессом,
не ограничивается пуассоновским и экспоненциальным распределе-
ниями. Мы покажем сейчас, что возникают также равномерное
и биномиальное распределения.
Рассмотрим моменты времени {SJ, когда происходят изменения
Х(0, т. е.
fc=0
Имеем следующий результат.
Теорема 2.3. Для любых чисел Si, 0><Si . -^sn
S1 sn-1 sn
P{S(<S(,i=l........n|X(0 = n}=^-J ... J jdxn...dxlt
о xn-2 Xn-l
§ 2. Дополнительные сведения о пуассоновских процессах
207
что является распределением порядковых статистик из выборки
объема п, взятой из равномерного распределения на [0, Z]1 * * *).
Доказательство. Доказательство является простым след-
ствием теоремы 2.1. Действительно,
P{Si<sb ^2> •••» X(f) — n} =
= Р{Г0^£1, TQ + То + ... + Tn~i^.sn, TQ+ ... + Tn>t}=
S1 S *2~?l + itl-1) 00
= J J / ... f / Лп+,е-х(/>+-+/«+>)<+1...Л1 =
ooo о +y
~^+1j J J ... J
0 0 0 0
oo
X [-^exp(-Mrt+1)] d/„...d/i =
si 82~*1 5з“(*1+/г) sn”(*i++*л-1)
= XVWJ J J ... J
0 0 0 0
Если ввести новые переменные
un = t\ + ... 4* tn,
un-l = Л + ... + ^л-1,
И] = #Ь
то последнее выражение примет вид
Но
S1 S2 S3 Sn
Kne~M J J j ... j dun ... dUl.
° “1 u2 иП-\
Р{Х(0 = и} = е-«в-.
l) Это означает следующее. Возьмем п независимых наблюдений (реали-
заций) случайной величины, которая равномерно распределена на отрезке [0, /].
Пусть У1 У2 Уп — наблюдения, упорядоченные по величине. Тогда
совместное распределение величин У1, ..., Уп в точности совпадает с выраже-
нием, приведенным в теореме. Доказательство этого факта весьма простое, но
(5рлее подробное обсуждение дано в гл. 9.
208
Гл. 7. Классические примеры цепей Маркова
Следовательно,
P{Sj *^2 *$2, sn Sn ! X (f) — tl} =
S1 52 Sn
— Р ♦ ч Sfl^Sfb X (t) = п} __ п\ С Г { rh/ rfn
~ P{X(i)^n] tn J J J аип---ащ-
° U1 Un-l
В. Биномиальное распределение
Из свойств пуассоновского процесса следует, что при и < t
и k<n
Р{Х (w) = A?|X(/) = n} =
= Р{X(u) = k, X (f) — X (и) = п — k}[P {X (f) = «}]“’= (2.3)
Xu Uk K (t-u) (t-u)n~k
__ kl (n — k)\ _M \ uk (t — u)n k
6 n\
Второй пример, в котором играет роль биномиальное распре-
деление, можно получить, рассматривая два независимых пуассо-
новских процесса Л\(/) и Xz(t) с параметрами М и Хг. Именно:
р (%, w - k । %.«)+х, ю -«} - =
ехр (- Л.,/) ехр (- М) г- . Л х n_ft
__ KI \П — R)l _ I П \ I \ ( A>2 I
ехр[- (Л,+Л2) /]“U/U.+A.J U.+A.J
§ 3. МОДЕЛЬ СЧЕТЧИКА
Интересным применением пуассоновского процесса является
следующая задача. Электрические импульсы случайной ампли-
туды Xi поступают в случайные моменты времени t{ (образуя
пуассоновский поток) на детектор, реакция которого на каждый
отдельный импульс в момент t выражается функцией
Хгехр[-а(/-М]+ = | ° ПрИ t<tb
( Хгехр[— a(t — /г)] при
То есть в момент подачи импульса значение выходного сигнала
равно амплитуде подаваемого импульса, а затем оно убывает по
экспоненциальному закону. Детектор является линейным (т. е.
§ 3. Модель счетчика
209
аддитивным). Так, если за интервал (0, I) поступит Nt импульсов,
то значение выхода в момент t равно
Nt
П (0 = 2 Х{ ехр [ - а (/ - /,)]+.
i-i
Типичная реализация этого процесса имеет вид, показанный
на рис. 1. Мы хотели бы знать функцию распределения т] (/) для
каждого t или, что эквивалентно, ее характеристическую функцию
<p((w).
Предположим, что X, — независимые и одинаково распределен-
ные случайные величины с плотностью й(х) и характеристической
функцией
оо
ф (s) = J e’sxh (х) dx.
о
Положим
оо
R(v; /) = Р{т1(/)<а}-2Р{п(0<У|^ = п}Р{М/ = «}. (3.1)
П“0
Конечно, Р {Nt = п} — е~',л , где X — интенсивность пуас-
соновского потока, задающего моменты поступления импульсов.
Из теоремы 2.3 известно, что tt распределены, как упорядоченные
наблюдения из равномерного распределения на (0, /), при усло-
вии, что Nt — n (т. е. на интервале (0,/) поступило п импульсов).
Пусть ц (i = 1, 2, ..., Nt)— независимые одинаково распределен-
ные на (0, t) случайные величины, упорядочение которых по при-
нимаемым значениям приводит к величинам tj.
210 Гл. 7. Классические примеры цепей Маркова
Далее, пусть Z4, Zn— независимые случайные величины,
распределения которых совпадают с распределением Xi и кото-
рые также не зависят от {тг}. Рассмотрим сумму
п
2 Z,ехр[-а(/-?,)]+.
/==1
Определим новые случайные величины Z{, Zfn следующими
равенствами:
Zi = Z/, если тп) = /ь
Z2' = Z/, если т/ = t2 — второй по величине член из {rj,
Zn = Z/, если т/ = тах(т1, ..., тп) = /д.
Неопределенность, которая возникает в случае равенства не-
которых из величин Тг, не причиняет беспокойства, поскольку ве-
роятность этого события равна нулю. Тогда
2 Z<exp[- a(/-rz)]+ = 2 Z/exp[- a(t - /г)] ,
z = l i=l
поскольку эти две суммы отличаются лишь порядком слагаемых.
Далее, так как случайные величины Zi являются независимыми,
одинаково распределенными и также не зависящими от тг-, то
легко проверить, что и Z\—независимые случайные величины,
их функция распределения совпадает с общей функцией распре-
деления величин Zj, и они также не зависят от т;. Будучи незави-
симыми от Тг, семейства {ZJ и {zQ, очевидно, не зависят от
Поскольку Z'i обладают всеми свойствами величин Х^
можно записать
П(0 = S Z'zexp[-a(/-/z)] = 2 Ziexp[-a(f-
i=l i=l
Положим
Уt (i) = Zi exp [ - a (t - TZ)]+.
Очевидно, при фиксированном t с. в. Ъ(0, i — 1, ...» п, неза-
висимы и одинаково распределены. Определим теперь характери-
стическую функцию величины Yt(k):
оо
6/(s)= j elsygt(y, k)dy,
о
J 3. Модель счетчика
211
где gt(y\ k)—плотность величины Yt(k), Поскольку Xk равномерно
распределена на (О, t) и Хь и Zk независимы, то
у
j gt (и, k) du = P {Yt (k) < у} = Р [Zk ехр [- а (/ - тй)]+ < у] =
О
t
= J Р [Zftexp[ — a(t — тй)]+ <z/| rft = и}-^- =
О
t t
= P{Zk^yea^} j- i Н№du> (3.2)
0 0
где H — функция распределения, соответствующая плотности h.
Дифференцируя (3.2), получаем
t
gt(y\ k)==~ j h(yea{t^u))ea{t‘'u') du.
о
Следовательно,
oo t f oo \
6; (s) == j* elsygt (y\ k)dy = Y§ ea^~u) ( J eisyh (yea dy \ du =
0 0'0
(при замене переменных уеа^~и} = z)
t oo
= y J du j exp[zs(e-a(/-u)2)]A(z) dz = (в силу определения ф)
о о
t t
= у j ф (se~afeau) du = (положим v = t — u) = у J ф (se~av) dv.
о о
Отсюда если r(x; t) — плотность распределения R(x, t), то
(fl^)= / eiWxr (х; t) dx =
о
ОО / оо \
= 2 / e‘wx р {п (о < х । ^=«} dx |е-« =
п=0 '0 7
(в силу независимости величин Yt(k) при фиксированном Nt)
оо ft \П
'Kt 7Г Г = S е~и 4" (Л / 'l’ (дае~аи) dv / =
п=0 '0 /
— Л J [1 — 'ф(ше~аи)]^ 1.
• о J
(в силу (3.1))
= ехр
212
Гл. 7. Классические примеры цепей Маркова
Дифференцируя по w, можно вычислить моменты rj(O- На-
пример,
м h (/)] = (- /) cpz (w) = Л (- I) 4' (0) j е~а* dv =
1 -e~at
§ 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
Одно из очевидных обобщений процессов чистого рождения,
обсужденных в § 1, состоит в том, чтобы позволить процессу X(t)
как возрастать, так и убывать, например, из-за гибели членов по-
пуляции. Таким образом, если в момент t процесс находится в со-
стоянии /г, он может через некоторый случайный отрезок времени
перейти в любое из соседних состояний п + 1 или п—1. Возни-
кающие при этом «процессы рождения и гибели» могут рассма-
триваться как процессы с непрерывным временем, служащие ана-
логами случайных блужданий (см. пример Б, § 2 гл. 2).
А. Постулаты
Мы предположим, что, как и в случае процессов чистого
рождения, X(t) является марковским процессом с состояниями
0, 1, 2, ... и что его вероятности перехода стационарны, т. е.
ро(/) = Р{Х(/ + 5) = /|Х(5) = 0.
Кроме того, предположим, что РцЦ) удовлетворяет посту-
латам:
I- Л,1+|(^) = М + о(А) при h | 0, г^О.
2. Pit z_] (/г) = \i-th + о (Ji) при h | 0, 1~^\.
3. Рц (/г) = 1 — pi + р.г) h + о (/г) при h | 0, г^О.
4. Pi7(o) = dz/.
5. jij = 0, , 0, p.z, Xz 0,
В каждом из этих случаев член о (Л) может зависеть от i. Мат-
рица
- Ao Ло 0 0
Pi — Ui + Pi) М о
А = 0 Н2 (^2 4" Иг) ^2 • • • (4 1)
0 0 Цз — (Л3 + р.3) ...
§ 4. Процессы рождения и гибели
213
называется инфинитезимальной матрицей процесса1)- Параметры
Лг и рг называются инфинитезимальными интенсивностями ро-
ждения и гибели соответственно. В постулатах 1 и 2 предпола-
гается, что если процесс находится в состоянии /, то за малый
интервал времени вероятность того, что размер популяции увели-
чится или уменьшится на 1, пропорциональна длине этого интер-
вала. Иногда рассматривают случай, когда нулевое состояние
является поглощающим, т. е. Ло == 0 (см. § 7).
Поскольку Pij(t)—вероятности, то Рц(Г)^0 и
оо
2 Рп (/)=!. (4.2)
/-о
Используя марковское свойство процесса, можно получить урав-
нение Колмогорова — Чэпмена
(4.3)
ьо
Смысл этого уравнения следующий: для того чтобы перейти из
состояния i в состояние j за время t + s, процесс X(t) в момент t
должен принять некоторое значение k, а затем перейти из этого
состояния в / за оставшееся время $. Это аналог формулы (3.2)
гл. 2 для непрерывного времени.
До сих пор рассматривались лишь вероятности перехода Рц(Г).
Для того чтобы найти вероятность события {X (/) = и}, нужно знать,
в каком состоянии процесс находился в начальный момент вре-
мени, или, в более общем случае, — распределение начального со-
стояния, Тогда
j =»0
где
P{X(0) = Z}.
Б. Длительности пребывания
Используя принятые допущения, можно найти распределение
случайной величины 7\, которая является длительностью пребы-
вания процесса X(t) в состоянии L То есть мы найдем распределе-
ние времени 7\ до первого выхода процесса из состояния i при
условии, что вначале процесс находился в состоянии i. Обозначая
Р{Т, >0=^(0,
1) В оригинале «infinitesimal generator of the process». — Прим, перев.
214 Гл. 7. Классические примеры цепей Маркова
получим в силу марковского свойства, что при h | О
Gi (t + h) = Gt (/) Gt (ft) = Gt (t) (Ptl (ft) + о (ft)) =
= Сг(/)[1-(Лг + Иг) ft] + о (ft),
или
Gi (t + h) — Gi (t) \ r (+\ i zn
--------------------h-----= - (Zt- + pj Gi (/) + О (1),
и поэтому
G/(0.=+ (4.4)
Если использовать условие Gj(O) = 1, то найдем
Gz(/) = exp[ — (ШМ
т. е. 1\ имеет экспоненциальное распределение со средним
(Лг- + Иг)-1. Приведенное доказательство не вполне корректно, по-
скольку было использовано соотношение
Gz(ft) = Pn(ft) + o(ft)
без формального доказательства .этого факта. Строгое доказатель-
ство справедливости (4.4) будет дано в § 4 гл. 8.
В соответствии с постулатами 1 и 2 в течение временного ин-
тервала длины h переход из состояния i в i + 1 происходит с ве-
роятностью + о(Л), а в состояние i—1—с вероятностью
р^ + о(Л). Интуитивно ясно, что при условии осуществления пе-
рехода в момент t вероятность того, что процесс перейдет при этом
в состояние i + 1, равна Лг(цг + а вероятность перехода в со-
стояние i—1 равна цг(цг + Лг)”1. Строгое доказательство этого
утверждения выходит за рамки данной книги, однако обсуждение
его и связанных с ним тонкостей будет дано ниже (см. гл. 8).
Развитие процесса X(t) можно описать следующим образом.
Процесс проводит в данном состоянии I случайное время, функция
распределения которого является экспоненциальной с параметром
ki + Цг. Из состояния i процесс переходит в состояния i + 1 либо
i— 1с вероятностями лг(цг- + М"”1 и + М”1 соответственно.
Динамика аналогична случайному блужданию, за исключением
того, что переходы осуществляются в случайные моменты времени,
а не в фиксированные !).
Традиционная процедура построения реализаций процессов ро-
ждения и гибели состоит в задании параметров рождения и гибели
{Xz, и построении выборочных траекторий следующим об-
разом. Предположим, что X(0)=i\ частица проводит случайное
время (экспоненциально распределенное с параметром Xt + цО
9 Весьма подробно эта аналогия рассмотрена в книге Дынкина Е. Б. и
Юшкевича А. А. «Теоремы и задачи о процессах Маркова», «Наука», 1967. —
Прим, перев.
§ 4. Процессы рождения и гибели
215
в состоянии /, а затем переходит с вероятностью Мп* + М-1 в со-
стояние i + 1, а с вероятностью цДцг + М-1— в состояние i ~~ 1.
Затем частица проводит случайное время в новом состоянии и
вновь переходит в одно из соседних состояний и т. д. Более точно,
мы выбираем значение t\ из экспоненциального распределения
с параметром + Zi), которое фиксирует время пребывания в со-
стоянии L Затем бросается монета, у которой вероятность выпаде-
ния герба равна pi — (цг- + Zi)'1. Если выпадает герб (решетка),
мы переводим частицу в положение /4-1 (i—1). В состоянии
i + 1 выбирается значение /2 из экспоненциального распределения
с параметром (ni-ы + Zi+i), которое фиксирует время пребывания
во втором по счету состоянии. Если частица при первом переходе
попала в состояние i— 1, то следующее время пребывания t2 вы-
бирается из экспоненциального распределения с параметром
(pti-i + Zi-i). После этого вновь проводится биномиальное испыта-
ние, выбирающее следующее состояние, и т. д.
Исход этой процедуры выборок определяет реализацию про-
цесса. Она может иметь вид
Х(/) =
i,
i 4- 1,
i,
0</</b
t\ t < t[ +
+ ^2 + ^2 + <3,
Таким образом, делая выборки из экспоненциального и биноми-
ального распределений соответственно, мы строим реализации про-
цесса. Далее, возможно ввести на этом множестве реализаций
(траекторий процесса) вероятностную меру таким образом, чтобы
определяемые ей вероятности Pij(t) удовлетворяли соотношениям
(4.2) и (4.3) и инфинитезимальным соотношениям (см. стр. 212).
Этот результат довольно глубокий, и его строгое обсуждение
лежит за пределами настоящей книги. Процесс, полученный та-
ким образом, называется минимальным процессом, связанным
с матрицей А.
Приведенная выше конструкция минимального процесса яв-
ляется фундаментальной, поскольку инфинитезимальные пара-
метры не определяют, вообще говоря, единственный вероятност-
ный процесс, удовлетворяющий (4.2), (4.3) и постулатам, при-
веденным на стр. 212. На самом деле может быть несколько
марковских процессов, обладающих одной и той же матрицей
инфинитезимальных переходных вероятностей. Вопрос этот до-
вольно сложен, и читатель может найти его в книге Чжун Кай-
лая1). В частном случае процессов рождения и гибели достаточ-
’) Чжун Кай-лай, Однородные цепи Маркова, «Мир», М., 1964.
216
Гл. 7. Классические примеры цепей Маркова
ним условием, при котором существует единственный марковский
процесс с переходными вероятностями удовлетворяющими
инфинитезимальным соотношениям (4.2) и (4.3), является
где
1,
. ♦ • ^П—1
1, 2, ....
(4.5)
В большинстве реальных примеров процессов рождения и ги-
бели выполняется условие (4.5), и процесс, удовлетворяющий этому
условию, определен единственным образом.
§ 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ
РОЖДЕНИЯ И ГИБЕЛИ
Так же как в случае процесса чистого рождения и пуассонов-
ского процесса, в данном случае переходные вероятности Pij(t)
удовлетворяют системе дифференциальных уравнений, известных
как обратные дифференциальные уравнения Колмогорова. Они
имеют вид
Ро/(О= — А/о/^о/ (/) + Ло/^i/(^),
Р'ц (О = нЛ-,.! (О - (А, + |Х<) р17 (0 + АД+1, , (/), i > 1. (b-1}
Начальное условие: Ро(0) =
Чтобы вывести их, запишем (4.3) в виде
= Pit (А) Р^, / (0 + Ра (h) Ра (/) + PL i+1 (/г) P(+I.) (/) +
+ l>'Pik(h)Pkl(i), (5.2)
k
где последняя сумма берется по всем k =£ i— 1, i + 1. Используя
постулаты 1, 2 и 3 (§4), получаем
2' Pik (A) Pkl (0 < S' р1к (А) = 1 — [Рн (А) + Р{, (А) + Р i, г+1(А)] =
= 1 — [1 — (Az + цг) h + о (А) + ц(А + о (А) + АгА + о (А)] = о (А)>
так что
Р{/ (^ + А) = HihPi-i, j (/) + (1 — (Az + цг) А) Рц (t) + KthPi+i, j(t) + o (Ji).
§ 5. Уравнения для процессов рождения и гибели 217
Перенося член ЛДО в левую часть, деля полученное равен-
ство на h и переходя к пределу при h | 0, получим
Р'ц (t) = / (0 - + Их) P(l (О + М\+1, / (0.
Проведенные выкладки являются частным случаем вывода
обратных дифференциальных уравнений, который дается в
гл. 8, § 2.
Обратные уравнения выводятся с помощью разбиения времен-
ного интервала (0, Z-f-A), где h положительно и мало, на два:
(0, h) и (A, t + А) и отдельного рассмотрения переходов процесса
на каждом из них.
В уравнениях (5.1) начальное состояние является переменным,
а конечное — фиксированным параметром.
Другая ситуация возникает при разделении интервала
(0, t + h) на (0, t) и (/, t + h) и применении предыдущего ана-
лиза. В этом случае при более жестких условиях можно вывести
следующую систему дифференциальных уравнений:
Р'о(О=-+
^/(0 = ^_A/-iW-(S + H/)p//W + H/+A/+IW, />1. (,3)
с тем же самым начальным условием Рц(0) = ()ц. Они известны
как прямые дифференциальные уравнения Колмогорова. Чтобы
проделать это, поменяем местами t и h в (5.2) и при дополнитель-
ных предположениях (кроме постулатов 1, 2, 3) можно показать,
что последний член снова равен o(h). Остальное дословно повто-
ряет предыдущий вывод. Полезность этих дифференциальных
уравнений станет очевидной из примеров, которые будут разо-
браны ниже.
Достаточным условием для справедливости (5.3) является ра-
венство — Pfc/(Л) = о(1) при А =#/,/—I, /+ I, где член о(1)
(кроме того, что он стремится к 0) равномерно ограничен по k при
фиксированном / при А~>0. В этом случае нетрудно показать, что
S' Pik(t) Pkl (h)~o(h).
k
Прежде чем переходить к примерам, обсудим кратко поведе-
ние АД/) при больших t. Можно доказать, что пределы
lim Рг/(/) = /?/ (5.4)
<->ОО
существуют, не зависят от начального состояния I и удовлетво-
ряют уравнениям
-AoPo + PiPi = 0.
“ U/ + Р/) Pj + Р7+1Р/+1 = 0» /^1- (5-5)
218
Гл, 7. Классические примеры цепей Маркова
Эти уравнения получаются из (5.3), если приравнять нулю ле-
вую часть. Сходимость 2р/ следует из того, что 2^>и(0=1-
/ /
Если 2Р/” Сто последовательность {pj} называется стационар-
ным распределением. Причиной для этого служит то, что р$ удо-
влетворяют уравнению
оо
(5.6)
г = 0
если процесс начинается из состояния i
в любой последующий фиксированный мо-
которое говорит, что
с вероятностью р7-, то и
мент времени он будет находиться в состоянии i с вероятностью рг*.
Доказательство (5.6) следует из (4.3) и (5.4), если устремить
оо
t f оо и использовать то, что 2рг<°°- Решение уравнений (5.5)
z=o
получается по индукции. Полагая
... Л,- 1
Ло = 1, Л; =---------— / 1,
получим Pj = Хоц~ ]р0 = Предполагая, что pk = nkpQ при
k =1, ..., /, получаем
М7+1Р/+1 = (X/ + Н/) Л/Ро ~ -1JT/ _ 1 ро =
= ‘hjTtjPQ + (ЦуЛу Ху _ 1Лу_j) Pq = hjTCiPo
и, наконец,
Р/ + 1 == л/ + 1Ро-
Для того чтобы последовательность {рД являлась распределе-
нием, нужно, чтобы Spj = 1. Если 2л/г < оо, то в этом случае
Л/
ъ nk
Если 2л/г = оо, то с необходимостью ро = 0 и все р, равны нулю.
Следовательно, не существует предельного стационарного распре-
деления.
§ 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
Пример 1. Линейный рост с иммиграцией. Процесс рожде-
ния и гибели называется процессом с линейным ростом, если
Хп = Хп + а, цп — ци, где X > 0, ц > 0, а > 0. Такие процессы воз-
никают при изучении биологического воспроизведения и роста
популяций. Если состояние п описывает текущий размер популя-
ции, то средняя мгновенная интенсивность роста равна Кп + а.
§ 6. Примеры процессов рождения и гибели
219
Аналогично вероятность того, что состояние процесса уменьшится
на 1 за малый промежуток времени, равна ц/2/ + о(/).
Коэффициент Хп соответствует естественному приросту попу-
ляции размера н, в то время как второй коэффициент а можно
интерпретировать как инфинитезимальную интенсивность роста
популяции за счет внешнего источника, такого, как иммиграция.
Коэффициент цн, который равен средней инфинитезимальной ин-
тенсивности гибели в популяции размера и, имеет очевидную
интерпретацию.
Если подставить эти значения Хп и в (5.3), то получим
Р'п (0 = ~ аР/о (0 + (^),
= (М/ — + /-1 (/) — ((X + ц)/ + а) Рц (t) +
+ Н (/ + О Pi, Ж 1-
Если теперь умножить /-е уравнение на j и просуммировать
уравнения, получим, что среднее
м[Х(0] = м(0 = 2/Рг/(0
удовлетворяет дифференциальному уравнению
Л4'(/) = а + (Л-ц)М(0
с начальным условием M(0) = z, если = Решение этого
уравнения имеет вид
М (f) = at + z, если X = ц,
М (0 = х-р f ~ 1} если X =^= ц.
Второй момент или дисперсия могут быть найдены аналогично.
Интересно заметить, что Л4(/)->оо при I—>оо, если X ц, в то
время как при X < ц средний размер популяции при больших t
примерно равен
а
ц — X *
Пример 2. Образование очереди. Процесс образования оче-
реди является процессом, в котором клиенты прибывают в не-
которое определенное место (обслуживающий прибор), где им-
оказываются услуги какого-либо рода, например окно кассира
в банке или место около кассира в магазине самообслуживания.
Предполагается, что интервалы между прибытиями клиентов (по-
ступлениями требований) и время, которое проведено данным
клиентом на обслуживании, управляются вероятностными законами.
220 Гл. 7. Классические примеры цепей Маркова
Длину очереди в данный момент времени t обозначим через
Если в описании общего процесса рождения и гибели поло-
жить Хг = X для всех z, то получим простой частный случай про-
цесса обслуживания с непрерывным временем. Состояние системы
при этом интерпретируется как длина очереди, в которую посту-
пают клиенты через независимые друг от друга интервалы, имею-
щие экспоненциальное распределение с параметром X, и для кото-
рой продолжительность времени обслуживания очередного клиен-
та является случайной величиной, имеющей экспоненциальное рас-
пределение с параметром цп, который может зависеть от длины
очереди. После завершения каждого акта обслуживания длина оче-
реди убывает на 1, а при каждом поступлении очередь увеличи-
вается на 1. Классический случай одноканальной системы (системы
с одним обслуживающим прибором) соответствует ц* = ц, * 1,
т. е. каждое время обслуживания имеет одно и то же экспонен-
циальное распределение с параметром ц, не зависящим от длины
очереди.
Классическая модель телефонного узла может быть сформу-
лирована как система обслуживания, описываемая процессом
рождения и гибели, с бесконечным числом обслуживающих при-
боров, каждый из которых имеет экспоненциально распределен-
ное время обслуживания с одним и тем же параметром ц, так что
Рг = ф, Это обосновывается следующим образом. Предпо-
ложим, что очередь состоит из i клиентов, тогда, поскольку число
обслуживающих приборов неограничено, все клиенты одновремен-
но обслуживаются. Далее, времена обслуживания каждого из них
независимы и экспоненциально распределены с параметром ц. От-
сюда следует, что вероятностное распределение времени до того
момента, пока по крайней мере один из клиентов закончит обслу-
живаться (т. е. времени до момента уменьшения очереди на 1),
также является экспоненциальным, но с параметром ф (читатель
должен доказать это).
Кроме двух рассмотренных частных случаев, можно рассмо-
треть другие многочисленные модели обслуживания, выбирая со-
ответствующим образом параметры Например, система с п
обслуживающими приборами, каждый из которых имеет экспонен-
циально распределенное время обслуживания с одним и тем же
параметром ц, соответствовала бы случаю |м = £р при
щ = /ф при i п.
Для случая одного обслуживающего прибора при X < ц ста-
ционарное распределение легко находится. Действительно, в этом
*) Под «очередью» здесь и ниже понимается число клиентов, находящихся
в системе обслуживания, т. е. суммарное число обслуживаемых и ожидающих
обслуживания клиентов. — Прим, перев.
§ 6. Примеры процессов рождения и гибели
221
случае
откуда
ZpAq . . , Л/г— 1
Н1Ц2 • • • Цп
g-л /лГ
Ц \ 1J ’
ЛГ
н/
п^О,
т. е. получили геометрическое распределение со средним Л(ц— Л)"1.
Для модели телефонного узла Лп = X, Цп = пц и легко полу-
чить, что
Т-r Ъ
Получили известное пуассоновское распределение со средним .
н
Как и в примере 1, легко показать, что
оо
jPi! (/)
/=о
удовлетворяет уравнению
М' (/) = Л - цЛ1 (/),
решение которого имеет вид
м (/) = -(! -
н
Л
Если положить /—>оо, то Л1 (/)-> — , которое равно среднему зна*
чению стационарного распределения, приведенному выше.
Пример 3. Некоторые генетические модели. Рассмотрим по-
пуляцию, состоящую из N индивидуумов, которые имеют либо
гены а, либо гены А. Под состоянием процесса Х(/) будем пони-
мать число индивидуумов с генами а в момент t. Предположим,
что вероятность того, что состояние изменится за интервал вре-
мени (/, / + й), равна kh + o(h) и не зависит от Х(/), а вероят-
ность двух или более изменений за время h равна o(h).
Изменения в составе популяции происходят следующим обра-
зом. Индивидуум, который должен быть заменен другим, выби-
рается из популяции случайным образом. То есть если Х(/) = /,
то индивидуум с геном а отбирается для замены с вероятностью
j/H, а индивидуум с геном А — с вероятностью 1 — j/N. Мы будем
называть данную замену «гибелью». Далее, «рождение» происхо-
дит по следующему правилу. Из популяции делается еще один
случайный выбор, с тем чтобы определить тип нового индивиду-
ума, который займет место погибшего. В модели вводится мута-
ционное давление, которое создает возможность того, что тип
222 Гл. 7. Классические примеры цепей Маркова
нового индивидуума может измениться после рождения. Именно:
пусть Yi — вероятность того, что ген а мутирует в ген А, и у2 — ве-
роятность того, что ген А мутирует в ген а.
Вероятность того, что новый индивидуум, добавленный к попу-
ляции, имеет ген а, равна
id - Yi) + (1 - i) Y2. (6.1)
Эта формула получена следующим образом. Вероятность того,
что будет выбран ген а и не произойдет мутации, равна -jj- (1 — Yi).
Кроме того, новый ген индивидуума может иметь ген а, если будет
выбран ген А, который затем мутирует в ген а. Вероятность этого
события равна (1—Комбинация этих двух возможностей
дает формулу (6.1).
Мы утверждаем, что вероятность события X(t+)— X(t)=l
при условии, что в момент t имело место изменение состояния,
равна
(1 “iHi^1 - Yi) + (1 -iM. где X(t) = j. (6.2)
В самом деле, число индивидуумов с геном а увеличивается
только в случае гибели (замены) индивидуума с геном А. Вероят-
ность этого равна (1 — . Второй сомножитель есть вероятность
того, что новый индивидуум имеет ген а (см. (6.1)).
Аналогично вероятность того, что X(t + )— X(t) = —1 при усло-
вии, что в момент t произошло изменение состояния, равна
i[(* ~i)(1 ”Y2) + iYi], где X(/) = /.
Описанный вероятностный процесс является, таким образом,
процессом рождения и гибели с конечным числом состояний1),
инфинитезимальные интенсивности рождения и гибели которого
равны
Л, = Л ^1 — (1 — Yi) + (1 ~ ‘yyj Y2] >
+ — дг) О ~ Y2)]
соответственно при числе индивидуумов с геном а, равном /,
Определение процессов рождения и гибели было дано для случая беско-
нечного числа состояний. Случай конечного числа состояний более прост, и не-
обходимые изменения в определениях и анализе предлагается сделать читателю.
§ 6. Примеры процессов рождения и гибели
223
Хотя эти параметры кажутся довольно сложными, интересно
посмотреть, что произойдет со стационарным распределением
{^}^=о ПРИ N °о и вероятностях мутации для отдельных инди-
видуумов у1 и у2, стремящихся к нулю так, что yiN—>xi, >Х2,
где 0 < Xi, Х2 < оо. Одновременно мы будем считать состояние
процесса изменяющимся на отрезке [0, 1], принимая в качестве
него -jj-, т. е. долю индивидуумов с геном а в популяции. Чтобы
найти плотность состояния %, 0<х< 1, оценим Пп при k -> оо, где
k = [xN], a [xN]— наибольшее целое число, не превышающее xN.
Имея это в виду, запишем
— Yi — Т2>/(1 + у), где ,
H/ = TFA(1-Y1-Y2)/(1 + yzy)> где ь =
Тогда
k-i k k-\
In 4 == S In In Н/ = In (1 + y) -
/=0 / = 1 / = 1
k-\
- S ln (1 + дД-) + 1пЛ/а - k) k (1 + .
/«1
Используя разложение
in(i+ x)=x-~4'+4"““ • ••> ixi<i>
Z о
можно записать
fc-1 fe-1
ln(l + j-) = a^-j + ck,
M /=1
где Ck имеет конечный предел при &->оо. Следовательно, исполь-
зуя соотношение
k-\
£j~ln£ при Й->оо,
имеем
k-\
In + 4) ~ ln£a + ck при &~>оо.
7=1
224
Гл. 7. Классические примеры цепей Маркова
Аналогично можно получить
А—1 ь
Sin f 1 Ч-—'l ~ In —N + dk при k —> oo,
\ N-jl (N~k)b k
где dk имеет конечный предел при k -> оо. Используя выписанные
соотношения, имеем
. . /„ ka(N — k)bNa\ ,
1пль~1п(Сь—;----------- при 6—>оо, (6.3)
ft й Nb (К - k) k I r
где In Ck = Ck + dh и Ch —► С < oo при k —> oo. Заметим, что a —»x2
и b — xi, при AT —> oo. Поскольку k — [ЛГх], то при AT —► oo имеем
nk ~ Сп2^2~'х*г~' (1 - x)x*"1.
Далее, из (6.3) имеем
Следовательно,
JV-l У-I , . ,
(‘-ж •
/М fe=0
Поскольку Сй-»С при k-+<x>, то в правой части стоит аппрокси-
мация суммы Римана для интеграла
х2С J хКг~' (1 - х)*1"1 dx.
О
Таким образом,
N 1
лг ~ ЛГХгх2С J хХг“' (1 - x)Xl-1 dx,
i-o о
так что плотность в (0,1) равна
пь 1 х*2-1 (1 — х)*>-1 х*2-1 (1 — х)Х|-1 dx
уГ" ЛГ = ’
1 J Xх’"1 (1 — x)x,-Idx J Xй’-1 (1 —х)я ~* dx
о о
поскольку dx ~ -jj-. Получили бета-распределение с параметра-
ми Х1 И Х2.
Пример 4. Логистический процесс. Предположим, что мы
рассматриваем популяцию, размер которой X(t) изменяется в пре-
делах от Ni до N2 (Nit Ni — целые, Ni<Ni) при всех t. Пусть
§ 7. Процессы с поглощающими состояниями
интенсивности рождения и гибели для каждого индивидуума в мо-
мент t равны
Л = «(ЛГ2-Х(0), ц = ₽(*(/)-Л^),
а отдельные индивидуумы в популяции развиваются независимо
друг от друга. Результирующие интенсивности рождения и гибели
для всей популяции равны
= ап (W2 - я), = ₽n (n - N\).
Чтобы показать это, заметим, что если размер популяции А’(7)
равен п, то каждый из п индивидуумов имеет инфинитезимальную
интенсивность рождения А, так что кп = an(N2 — п). Такое же
обоснование можно предложить и для интерпретации цп.
В этих предположениях естественно ожидать, что процесс из-
меняется между двумя уровнями Ni и Л^2, поскольку если, скажем,
X(t) близок к Л^2, то интенсивность гибели высока, а интенсив-
ность рождения низка и, следовательно, X(t) стремится к Ац. В ре-
зультате процесс должен флуктуировать стационарным образом
между двумя уровнями A/i и М2-
Стационарное распределение в этом случае равно
п __ С ( N2 “ \ / a \m Л 1 О АТ АТ
РN<+m ~Гт i I I I ТГ I , П2 — » 2, * • ’ ? A/А N1,
/vi-rm Ni+m \ m /\Р/ 2
V _ 1
где с — константа, определяемая из условия Чтобы
показать это, заметим, что
п == '** —
М+^1 И1ц2 ... Цт
amNv (Лб + 1) ... М + m - 1) (П2 - Л7) ... (#2 - Лб - Ж 1)
Р™ (ЛА,-Ь 1) ... (Ni+mjml
== / П2 - \ /а\т
Ni + m \ т М₽/
§ 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ
состояниями
Представляет интерес рассмотреть такие процессы рождения
и гибели, у которых Ао = 0. Это предположение делает нулевое
состояние поглощающим. Если переход осуществляется из состоя-
ния 1, частица перемещается в состояние 2 с вероятностью
А1(Ц1 + А1)-1 или попадает в состояние 0 (и остается там в даль-
нейшем) с вероятностью цДц! + М)”1. Важным примером процесса
рождения и гибели, где состояние 0 поглощающее, является про-
цесс линейного роста без иммиграции (ср. с примером 1 § 6).
8 Зак. 939
226
Г л, 7, Классические примеры цепей Маркова
В этом случае Лп = /гЛ и цп = гщ* Поскольку рост популяции обя-
зан исключительно существованию популяции, ясно, что когда раз-
мер популяции становится равным 0, он остается равным нулю и
после этого, т. е. О является поглощающим состоянием.
А. Вероятность поглощения в состоянии О
Представляет интерес нахождение вероятности поглощения
в состоянии 0 при начальном состоянии i (i 1). Такое поглоще-
ние не является априори достоверным событием, поскольку воз-
можно, что частица (т. е. переменная, характеризующая состоя-
ние) будет все время блуждать по состояниям 1, 2, ... или, быть
может, уходить в бесконечность.
Пусть щ (i = 1, 2, ...)—вероятность поглощения в состоянии
О из начального состояния L Можно написать рекуррентное соот-
ношение для цг-, рассматривая возможные состояния после первого
перехода. Мы знаем, что при первом скачке осуществляются сле-
дующие переходы:
с вероятностью (pz + Л/)"1,
1 с вероятностью +
Непосредственно получаем
%. ц.
ц + Л ц +z ui~b (7.1)
г1/ ' г/
где «о= 1. Другой метод получения (7.1) состоит в рассмотрении
«вложенного случайного блуждания», связанного с процессом
рождения и гибели. Именно рассмотрим процесс рождения и ги-
бели только в моменты переходов. Цепь Маркова с дискретным
временем, получающуюся при этом, обозначим через {Кп}“=0, где
Yo = Xt> — начальное состояние, a Yn (n^sl) — состояние после
п-го перехода. Очевидно, матрица переходных вероятностей имеет
вид
р = 1 0 0 0... ?! 0 Pi 0 ... 0 ?2 0 р2 ... >
где
И/ +
Вероятность поглощения в состоянии 0 для вложенного слу-
чайного блуждания совпадает с аналогичной вероятностью для
§ 7. Процессы с поглощающими состояниями 227
процесса рождения и гибели, поскольку оба процесса совершают
одни и те же переходы.
Обратимся к задаче решения (7.1) при условиях, что uQ = 1
и 0 щ 1 (i 1). Перепишем (7.1):
(иг+1-нг) = -^-(иг-иг-1), г>1.
Введем переменную Vi = ui+i — щ. Получим
Итерируя последнее соотношение, найдем
«<+1-«/ = ог = | «>!•
\/=i /
Суммируя эти уравнения от I = 1 до i = tn, получим
m / i \
^zn+i (^i 0I j> I• (7*2)
Поскольку um в силу определения ограничена числом I, мы видим,
что если
s(iU)=~. р-з)
то с необходимостью щ = 1 и ит = 1 при всех tn 2. Другими
словами, если выполнено равенство (7.3), то из любого начального
состояния происходит поглощение в 0 с вероятностью 1.
Пусть 0 < щ < 1. Тогда, конечно,
°° / i \
S IR <“
i=l \м /
Очевидно, ит не возрастает с ростом т, поскольку при перехо-
де из состояния т в состояние 0 процесс попадает во все промежу-
точные состояния1)- Более того, мы утверждаем, что wm->0 при
т ► оо.
Если предположить противное, т. е. wm>a>0 (m^l), то
простые вероятностные рассуждения показывают, что ит = 1
!) Иначе говоря, событие, заключающееся в том, что за время t произошел
переход т->0, содержится в событии «за время t произошел переход
где k <tn, at — любое положительное число. — Прим, персе,
3*
228
Г л. 7. Классические примеры цепей Маркова
1). (Читатель должен уметь доказать это формально.) Да-
лее, устремляя т —> оо в (7.2), найдем
и кроме того имеем
В частном случае процесса рождения и гибели с линейным рос-
том, где |l?i пр и Кп = пЪ непосредственное вычисление пока-
зывает, что
(ц\т
> если ц<Л,
ит^\, если
Б. Среднее время до поглощения
Рассмотрим задачу нахождения среднего времени до поглоще-
ния, начиная из состояния т.
Предположим, что условие (7.3) выполнено, так что поглоще-
ние происходит с вероятностью 1. Заметим, что в данном случае
задачу нельзя свести к изучению вложенного случайного блужда-
ния, поскольку действительное время, проводимое процессом
в каждом состоянии, существенно для нахождения среднего вре-
мени до поглощения.
Пусть сщ — среднее время (быть может, бесконечное) до по-
глощения при начальном состоянии L Рассматривая возможные
состояния, следующие за первым переходом, и вспоминая тот
факт, что среднее время пребывания в состоянии i равно
(щ- Ч- Xi)"1 (это время имеет экспоненциальное распределение
с параметром ц; + 2ч), получим рекуррентное соотношение
1 Л. ц.
II , 4-1 + U +Я. Ю* + '+ и 4-1 в»*-!» (7-4)
где по условию соо = 0- Полагая = сог- — coi+i и комбинируя чле-
ны в (7.4), получим
Ж+Ы- i>1- (7-5’
§ 7. Процессы с поглощающими состояниями
229
Итерируя это соотношение, найдем
у ______________ 1 । Р’т 1 ।
Я ' Я 1 1 Ъ . ^гп—2
л tn л tn—l
и, наконец,
m m / tn \
/=1 j-i+l \i-l /
(tn \
Произведение полагается равным l.j Иначе
m+1 ' /
m m m
®m-®m+i = Sz7 П V_C01l-Il7’ m>L (7-6)
/-1 j~i+i /-I
Более удобно записать
m tn tn tn
S^IU-IRSp-. <”)
/ = 1 /М + 1 /-1 M
где
_ ^1^2 * • • ^i-1
P/
Затем, используя (7.7), соотношение (7.6) перепишем в виде
(tn - \ tn
ПтгН®'п“®'п+|) = 2р«“®1- м
7-1 Z/ Z-1
оо
Заметим, что если 2 Pi = 00, то из (7.8) следует, что с необходи-
i-i
мостью <01 = оо1). В самом деле, из вероятностных соображений
очевидно, что <om < com+i для всех tn, а это свойство было бы на*
рушено для больших tn, если бы мы предположили, что <oi < оо.
оо
Предположим теперь, что 2р/<°°. Тогда, полагая /п~>оо
i — 1
в (7.8), получим
®1 = Ур/- lim (ТТ-^-I (®m-®m+l).
1) И, следовательно, - qp, m \.—Прим. перев,
230
Гл. 7. Классические примеры цепей Маркова
Можно показать, хотя и достаточно сложно, что
lim
m-»oo
— <om+1) = O.
Тогда, очевидно,
оо
= 5 Pi-
z—1
Подведем итоги этого параграфа в виде следующей теоремы.
Теорема 7.1. Рассмотрим процесс рождения и гибели с па-
раметрами Кп и рп, и 1, Хо = 0, так что 0 является поглощаю-
щим состоянием.
Вероятность поглощения в состоянии 0 при начальном состоя-
нии пг равна
Среднее время до поглощения равно
оо, если S Р/ = °°,
i=i
ОО т — 1 ✓ Г \ оо оо (7-10)
Spi+ SIll'S/ Sр/* если 2р«<оо>
Z-l r=l \ Ы / /-r+1 i-1
где pt- = (XiX2.. - Xi-i)/(piH2... gi).
В случае процесса рождения и гибели с линейным ростом
(Xn = пК, Цп = пц, р > X) среднее время coj до поглощения из со-
стояния 1 равно
о
§ 8. Цепи Маркова с конечным числом состояний
231
§ 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ
И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Марковская цепь с непрерывным временем Xt (t > 0) является
марковским процессом с состояниями 0, 1, 2, ... . Предположим,
как обычно, что переходные вероятности стационарны, т. е.
Pf/(0 = P{Xz+s = /|Js = 0. (8.1)
В этом параграфе мы рассмотрим лишь случай, когда простран-
ство состояний S конечно, S = {0, 1, 2, ..., 2V}. Некоторые про-
блемы, касающиеся цепей Маркова с бесконечным числом состоя-
ний и непрерывным временем, рассмотрены в следующей главе.
Марковское свойство требует, чтобы Рц(1) удовлетворяли усло-
виям:
(a) PiZ(0>0,
(б) 5Рг/(/)=1,
/=о
N
(в) Pik(s + f) = S Pt/(s) /,$>0 (уравнение Колмого-
рова — Чэпмена),
и мы требуем, кроме того, чтобы выполнялось условие
( 1, i = j,
(г) limP(/(l)= n .,.
/->0+ I <J,
Если обозначить через P(/) матрицу ||P/Z (t) ll^/=0, то условие
(в) можно записать более компактно в матричных обозначениях
P(/ + s) = P(0P(s), t, s>0. (8.2)
Условие (г) говорит о непрерывности Р(/) при t = 0, поскольку
из (8.2) следует, что Р(0) — I (I — единичная матрица). Из (8.2)
вытекает, что Р(/) непрерывна при всех t > 0. В самом деле, если
s = й > 0 в (8.2), то в силу (г) имеем
lim P(f + й) = Р(/) lim Р (й) = Р(/)! = P(f). (8.3)
Л-»0+ Л->0
С другой стороны, при / > 0 и 0 < й < t запишем (8.2) в виде
Р (/) = Р (/ — й) Р (й). (8.4)
Но Р(й) при достаточно малых й близка к единичной матрице.
Поэтому (Р(й))-1 (обратная матрица к Р(й)) существует и также
близка к I. Следовательно,
Р (t) = Р (0 lim (Р (й))“’ = lim Р (/ - й). (8.5)
Л->0+ Л->0+
232
Гл. 7. Классические примеры цепей Маркова
Предельные соотношения (8.3) и (8.5) показывают, что Р(/) не-
прерывна.
В теоремах 1.1 и 1.2 гл. 8 доказано, что в общем случае для
цепей Маркова с бесконечным (счетным) числом состояний и не-
прерывным временем существуют пределы
1. l-Pii(h)
hm ----=
Л->0+ П
<8-6’
где 0 < qa < оо (/=#/) и 0 оо, т. е. q^ (i 4= j) всегда ко-
нечны, a qi определены, но могут принимать бесконечные значения.
Возможность qi = оо не может осуществиться в случае марков-
ской цепи с конечным числом состояний и непрерывным временем.
Действительно, запишем соотношение
2 РМ
7=0, / =/= i
разделим его на Л и устремим ЛфО, получим
qi= 2 Уф
откуда следует конечность q^
Предполагая справедливым (8.6), найдем точное выражение
для Pij(t) через инфинитезимальную матрицу
~ <7о <7oi • • • <7одг
?ю ~ <71 • • • <7iw
<7уо <7ли • • • ~ Qn
Предельные соотношения (8.6) запишем в матричном виде
lim £<V-A-
h->0+ Л
С помощью этой формулы и равенства (8.2) находим
Р(/ + Л)-Р(0 __ Р (Q [Р(Л) -1] _ Р (Л) — I
h ~ h ~ h г
(8.7)
(8.8)
Предел правой части существует, и, таким образом, получаются
матричные дифференциальные уравнения
Р'(/)== Р(0 А = АР (0, (8.9)
где Р'(/) — матрица с элементами Р//(/).
Существование Pz/(/) является очевидным следствием (8.7)
и (8.8).
Задачи
233
Уравнения (8.9) можно решать при начальном условии
Р(0) = I стандартными методами теории обыкновенных диффе-
ренциальных уравнений1)- Получим
Р (t) = еА*
у AM
+ А! ’
(8.10)
Практически мы находим собственные значения Хо, %i, ..., Kn
матрицы А и полную систему соответствующих им правых соб-
ственных векторов и<°), ..., nW, если это возможно (см. прило-
жение в конце данной книги). Затем мы пользуемся представле-
нием
Р (/) = UA (0 и-1, (8.11)
где U — матрица, столбцами которой являются соответственно век-
торы u(0), и(1), u(yv), а Л (f) —диагональная матрица
ехр (Я,о/) 0 0
0 ехр (Я,!/) 0
А(0 = * • • •
0 0 ехр(Л^)
Строки матрицы U-1 можно рассматривать как полную систему
левых собственных векторов, биортогональных к {u(Z)}/L0 •
Применения формул (8.10) или (8.11) рассматриваются в за-
дачах 18, 20 и 21 к данной главе.
ЗАДАЧИ
1. Рассмотрим пуассоновский процесс с параметром X. При условии что за
время t произошло п событий, найти плотность вероятности времени осуществле-
ния r-го события (г < п).
Ответ:
Р(х)~
п\ хг 1 Л х\п г
(Г-1)!(П-г)! /г V t)
0 < х <t,
0
в противном случае.
2. Предположим, что прибор отказывает после воздействия k возмущений
Пусть возмущения случаются в моменты, образующие пуассоновский поток с па-
раметром X. Найти плотность времени жизни Т прибора.
Ответ:
ykik—ia—Xt
Л f___е-___ t > о
Г (k) 9 > °’
о, /<0.
f(0 =
1) Коддингтон Э. А., Левинсон Н., Теория обыкновенных дифферен-
циальных уравнений, гл. 3, ИЛ, 1958 (см. также Гант махер Ф. Р., Теория
Матриц, гл. V, «Наука», 1967. — Перев.).
234
Гл. 7. Классические примеры цепей Маркова
3. Пусть (%(/), У(/))—вероятностный процесс в двумерном пространстве,
где X(t) — пуассоновский процесс с параметром %i, а У(/) —пуассоновский про-
цесс с параметром Х2, не зависящий от X(t). При условии что процесс нахо-
дится в состоянии (хо, уо) в момент t = 0, Хо + уо < z, найти вероятность пере-
сечения процессом прямой х + у = г в точке (х,у).
Ответ:
(Z-X9-y9\ I %! ( %2 \У~У>
\ X — Хо / \ + %2 / \ М + ^2 /
при х>х0, у^у0,
О
в противном случае.
4. Рассмотрим пуассоновский процесс с параметром %. Пусть Т — время до
наступления первого события, a N(T/k) —число событий в следующие T/k еди-
ниц времени. Найти первые два момента величины N Т.
Ответ:
5. Пусть {%(/), / > 0} — пуассоновский процесс с параметром X. Предполо-
жим, что каждое событие «регистрируется» с вероятностью р независимо от
остальных событий. Пусть {У(/),/^0} — процесс, скачки которого происходят
лишь в моменты наступления «зарегистрированных» событий. Доказать, что
У(/) —пуассоновский процесс с параметром Кр.
6. Рассмотрим п независимо действующих объектов (таких, как электриче-
ские лампочки), время безотказной работы (т. е. время жизни) которых являет-
ся случайной величиной, экспоненциально распределенной с плотностью
[ О-1 ехр (— х 0,
f(x. 6) = ] F\ 6/
I О, х < 0,
0 — положительный параметр. Действительные длительности реализации без-
отказной работы становятся известными в порядке отказов объектов. Пусть
— длительности времен жизни первых г отказавших объектов. Найти совместную
плотность величин i = 1, 2, ..., г.
Ответ:
/<«.. X,...
7. В предыдущей задаче введем
Уш =
Yin в Хщ — п> 2</^ г.
Доказать, что Уг’п независимы в совокупности, и найти функцию распределения
каждой из них.
Ответ:
Р {Yin < у} = 1 - ехр (- ! уj.
8. Пусть {%(/),/ 0} и {У(/),/^0} — два независимых пуассоновских про-
цесса с параметрами и Х2 соответственно. Введем процесс
2(0«Х(0-У(0, />о.
Задачи
235
Пространство состояний этого процесса состоит из всех целых чисел (положи-
тельных, отрицательных и нуля). Пусть
Рп (/) = р {Z (/) « п}, п = 0, ±1, ±2..
Доказать формулу
оо
Рп(0 2л = ехр(-(%1+Л2)0ехр^,г/ + -^-ф |z|^=0.
И же — оо
Найти M(Z(/)) и M(Z2(/)),
Ответ:
М (Z2 (0 ) = (Xj + Х2) t + (Xj - Х2)2t2.
9. Рассмотрим два независимых пуассоновских процесса X(t) и У(/), где
M(X(f))=Xf, а М(У(/)) = рЛ Пусть два последовательных события процесса
X(t) поисходят в моменты Т и Т' > Г, так что Х(/)=Х(Г) при T — t<T' и
Х(Т') = Х(Т) 4- 1. Пусть N = Y(T') — У(Т) —число событий процесса У(/), про-
исшедших на интервале (?,?')• Найти распределение N,
Ответ:
P(tf = m} = —A—j"1, m = 0, 1, 2.............
1 А + ц \ Л + ц/
10. Пусть X(t) —марковский процесс чистого рождения с непрерывным вре-
менем. Предположим, что
Р {событие наступит в (f, t 4- Л)| X(t) нечетно} « X\h 4- о (Л) ,
Р {событие наступит в (/, t 4- h) \ X(t) четно} = Х2Л 4- о(Л)\
где -5—0 при h ф 0. Примем Х(0) = 0. Найти следующие вероятности:
Р\ (0 = Р {X (/) нечетно}, Р2(0 = Р{Х(/) четно}.
Указание: Вывести дифференциальные уравнения
(/н-х^ (/)4-х2р2ю,
P^HAjPj (/)-Х2Р2 (/)
и решить их.
Ответ:
р1 W = гтг ~ ехР + Л2) t}
Aj тА2
р, ®=тли-+~rh~ ехР <- Ы/}-
Л1 Т л2 Aj Т Л2
11. В условиях задачи 10 найти М(Х(/)).
Ответ:
М (X (0) = t + [ехр {- (Л, + Л2) 0 - 1].
Aj 4“ А2 (Aj 4“ А2)
12. Пусть g(t)—условная интенсивность исчезновения частицы в момент t
при условии, что она не исчезла до /, т. е. Р {исчезновение произошло в
(/,/4-Л)| исчезновения не было до момента /}= g(/)A + o(h) при ЛфО. Пред-
положим, что g(t) положительна и непрерывна на (0, оо). Найти выражение для
F(t) = Р{исчезновение произошло в некоторый момент т </} через g(-).
236
Гл. 7. Классические примеры цепей Маркова
Указание'. Вывести дифференциальное уравнение для Г(/).
Ответ'. F (f) = 1 — ехр
- j g (0 dr
О
13. Рассмотрим пуассоновский процесс с переменной интенсивностью, т. е.
вероятность осуществления события Е в интервале (/, t + h) не зависит от
предыстории процесса и равна X(t)h + o(h) (/z->0). (Заметим, что X может
теперь зависеть от /.)
(а) Доказать, что вероятность неосуществления события Е на отрезке [0, s]
равна
ехр | - J A(g)dgj.
\ о J
(б) Доказать, что вероятность наступления k событий на отрезке [0, $] равна
/ $ \ k Is \
Jj-I J МБИИ ехр I - J МБНи.
\о / \ о /
14. Рассмотрим процесс чистой гибели, в котором рп = пр, п = 1, 2, ..., т. е.
Р {X(t + h) = j | X(t) = k] = 0 при / > k, t > 0, k > 0. Предположим, что началь-
ный размер популяции равен i. Найти Рп (/) =Р{^(/) =п}, M(X(t)) и а2(Х(/)).
Ответ:
М (X (0 ) = ie~^.
15. Рассмотрим процесс Юла с параметром 0 и начальным состоянием
N — 1. Предположим, что первый индивидуум может погибнуть, причем вероят-
ность гибели в интервале (/, t + h) при условии, что индивидуум не погиб до
момента /, равна рЛ + o(h). Найти распределение общего числа потомков всех
поколений единственного индивидуума в момент гибели «родоначальника».
Ответ: Вероятность того, что общее число потомков всех поколений в момент
гибели «родоначальника» равна и, выражается формулой
j р
о
г(-й- + 1)г(п + 1)
r(n + f + 2)
16. Телефонный узел имеет m каналов. Моменты поступления вызовов обра-
зуют пуассоновский поток с параметром X. Они принимаются (обслуживаются),
если имеется свободный канал. В противном случае они теряются. Продолжи-
тельность каждого разговора — д. с. в. с экспоненциальным распределением,
имеющим параметр р,. Длительности отдельных разговоров — независимые слу-
чайные величины. Найти стационарное распределение * числа занятых каналов.
Ответ:
(-Г-
Рп = -^------—> n = 0, 1. 2.т.
v
\ pj k\
ЬО
Задачи
237
17. Найти стационарное распределение для процесса рождения и гибели с
линейным ростом при X < р (см. пример 1 § 6).
Ответ',
18. Цепь Маркова с непрерывным временем имеет два состояния: 0 и 1.
Время пребывания в состоянии 0 распределено экспоненциально с Параметром
X > 0. Время пребывания в состоянии 1 распределено экспоненциально с пара-
метром р > 0. Найти вероятность Роо(О нахождения процесса в состоянии 0
в момент /, если в момент 0 он находится в состоянии 0.
Ответ:
V) = ТТУ + ТТТ е"(Л+и) z
Л + р Л + р
19. Пусть в задаче 18 X = р, a N (/) —число моментов изменения состояний
процесса за время /7^0. Найти вероятностное распределение N(f).
Ответ:
P{N(t) = n} = e~M-^-.
20. Имеется два трансатлантических кабеля, каждый из которых может пере-
давать одновременно только одно телеграфное сообщение. Время до отказа каж-
дого из них имеет одно и то же экспоненциальное распределение с параметром X.
Время ремонта каждого кабеля имеет одно и то же экспоненциальное распре-
деление с параметром р. При условии, что в момент 0 оба кабеля находятся
в рабочем состоянии, найти вероятность того, что если в момент t одновременно
поступают два сообщения, то они найдут оба кабеля исправными.
Указание: Рассматриваемый процесс является цепью Маркова с тремя со-
стояниями и непрерывным временем.
Ответ:
Р2 , (Л+(Х) t
(Х + ц)2 Ц + М2 (*+ц)2
21. Предположим, что некоторый механизм подвержен отказам двух типов.
Пусть вероятность отказа первого типа в интервале (/,/ + /?) равна Xi/? + o(A),
а вероятность отказа второго типа в том же интервале равна X2/? + o(/i). В состоя-
нии очказа производится ремонт, длительность которого экспоненциально рас-
пределена с параметром, зависящим от типа отказа. Пусть pi и р2— значения
этих параметров. Найти вероятность того, что механизм работает в момент t.
Ответ:
— (Xj 4- Х2)
Hi
1*2
X] Х2
-Hl 0
о ~р2
Р (/) = еЧ
где Q =
22. Система состоит из W идентичных компонент, каждая из которых рабо-
тает независимо от других случайное время до отказа. Предположим, что время
до отказа имеет экспоненциальное распределение с параметром X. Когда какая-
либо компонента отказывает, она ремонтируется. Время ремонта случайно с
экспоненциальной функцией распределения, имеющей параметр р. Говорят, чю
система находится в состоянии п в момент /, если в этот момент ровно п ком-
понент находится в ремонте. Этот процесс является процессом рождения и ги-
бели. Найти его инфинитезимальные параметры.
238
Гл. 7. Классические примеры цепей Маркова
23. В задаче 22 предположим, что вначале все N компонент работают.
Найти распределение F(t) до первого момента, когда имеются две неработающие
компоненты.
Ответ: Преобразование Лапласа <p(s) функции F (t) равно
ЛЧЛГ-1)Я,2
s2 + s [(2.V — 1) Л + ц] +/V (/V — 1) V '
В случае X = р
1 - F (0 = (^-1) {ехр [(- N + /ЛО М - ехр [(- ЛГ-/лГ) X/]}.
24. Рассмотрим следующий непрерывный аналог модели Эренфестов (см.
гл. 2, стр. 43). Имеется 2N шаров, занумерованных от 1 до 2N. В момент О
каждый шар с равной вероятностью может быть помещен в одну из двух урн.
В дальнейшем шары независимым образом перемещаются в случайные моменты
времени из одной урны в другую в соответствии со следующими правилами.
Шар с вероятностью h 4- о (h) попадает из одной урны в другую в течение
интервала (/, / 4-Л) и с вероятностью 1--^- + o(h) остается в той же урне в
этом интервале. Перемещения на непересекающихся интервалах времени незави-
симы. Пусть X(t) — число шаров в урне 1 в момент t. Обозначим
PJk (0 = Р {X (/) = k | X (0) = /}, м == 0, 1.2ЛГ.
Доказать формулу
2N
g {t. s) = 2 Pjk (0 = 2-2ЛГ [ 1 - + (1 + e-() s]' [1 + е~* + (1 - е~<) s]™4.
fc=0
Указание: Ввести случайные величины
{1, если /-й шар находится в урне 1 в момент Л
О в противном случае.
2N
Тогда X (t) = 2 (0- Показать, что
/«1
1 4- е~*
P{Xz(/) = XH0)} = -^y—, z=l, 2,..., 2N.
25. Рассмотрим процесс X(t) рождения и гибели с линейным ростом с па-
раметрами X, р, и а = 0. Предположим, что Х(0)=1, Найти распределение
числа живущих индивидуумов в момент первой гибели.
Ответ:
Р {число рождений до первой гибели равно &} =—-г-—-т-) .
ц 4~ л \ р, 4- Л /
26. Для процесса X(t) рождения и гибели с линейным ростом при X =» р,
(см. пример 1 § 6) доказать, что
и(0 = Р{Х(/) = 0|Х(0) = 1}
Задачи
239
удовлетворяет интегральному уравнению
t t
u(t) = -^ J 2Хе~2Ал dx 4-~ j* 2he~2Kx [u (t — t)]2 dx.
о о
Указание: Заметить, что время до наступления первого события (рождения
или гибели) распределено экспоненциально с параметром 2Х.
27 (продолжение). Показать, что «(/) удовлетворяет дифференциальному
уравнению Рикатти:
и' (/) + 2Хи (0 - К + Хи2 (0, и (0) « о.
28 (продолжение). Найти «(/).
Ответ:
и®~ 1+21/ *
29 (продолжение). Найти Р {%(/) = 01 Х(0) « 1, Х(Т) = 0} при 0 < t < Т.
30. Рассмотрим процесс рождения и гибели с инфинитезимальными парамет-
рами Хп, Рп. Показать, что среднее время достижения состояния г + 1 из со-
стояния 0 равно
г п
п-0 /г-0
где лп определяется в (4.5).
Указание: Пусть Тп — время первого достижения состояния п + 1 из
состояния п. Вывести рекуррентное соотношение для М (Г*).
31. Начнем наблюдать радиоактивный атом в момент 0. Он распадается
и перестает быть радиоактивным в момент /, t > 0, определяемый распределе-
нием
( 0, т<0, ]
Рассмотрим состояние атома в момент / как случайную величину
{0, если атом радиоактивен в момент
1, если атом не радиоактивен в момент г.
Переменная {г J образует случайный процесс.
Предположим, что в момент 0 мы начинаем наблюдать N независимых ра-
диоактивных атомов, которые описываются, как показано выше, величинами
N
Хр Z® 1, 2, ...» N. Пусть Xt — 2 xt* Тогда {XJ —также случайный про-
/-1
цесс. Показать, что при t {i мало по сравнению с yj и достаточно боль-
шом N процесс {Xt} хорошо аппроксимируется пуассоновским процессом У(/)
с параметром ХЛ/7.
240
Гл. 7. Классические примеры цепей Маркова
32. Предположим, что в задаче 31 нельзя считать t V1.
(1) Является ли процесс процессом с независимыми приращениями?
(2) Является ли он стационарным?
(3) Имеет ли он стационарные переходные вероятности?
(4) Является ли он марковским?
Ответ: (1) да, (2) нет, (3) да, (4) да.
33. Пусть W — процесс рождения и гибели с непрерывным временем, где
= 7 > 0, п 0, jig — 0, Нп > 0, п 1. Пусть л ~ лп< оо, где лп —
п
Л.
” Х,г (Пь Ц2.. • Ип)’1, так что “—стационарное распределение процесса. Пред-
положим, что начальное состояние — д. с. в, распределение которой совпадает со
стационарным распределением процесса. Доказать, что число случаев гибели на
отрезке [0, ZJ имеет распределение Пуассона с параметром X/.
Указание-. Пусть ak(J)—вероятность того, что число случаев гибели за
время t равно /?. Получить дифференциальное уравнение
ak (0 = “ (0 + Xak_1 (t), k > 1.
34. Следующее построение является одним из способов задания многомер-
ною пуассоновского процесса для случая двух измерений. Пусть (Х(/), У(/)) —
пара, где X(i) = а(/) + у(/), Y(t) == 0(/) + у(/), а(/), 0(/), у(/) — три неза-
висимых пуассоновских процесса с параметрами Xi, Аг и Аз соответственно. Найти
производящую функцию распределения (X(t), У(/)).
Ответ-.
yj Р {X (/) = /, Y (о = /} х1у’ » ехр (/ (Л,х + %2у + К7ху Л3)}-
35. Рассмотрим процесс Юла {Nt, t 0} с интенсивностью рождения X и
начальным размером популяции 1. Найти функцию распределения величины
ЛМх), равной числу членов популяции возраста не большего х в момент t.
Ответ-.
Р {N t (х) = k} =
36. Пусть {АД/), t 0}, i = 1, 2, — два независимых процесса Юла с одним
и тем же параметром А. Пусть АДО) = пг-, /= 1, 2. Найти распределение вели-
чины АД/) при условии, что АД/) 4- Аг(/) = N (N ti\ + п2).
Ответ:
Р{ХЯ (/) = /г | X, (t)+X2 (t)=N} =
/ k-l \(N-k-l \
\ «1 ~ 1 / \ П2~1 /
/ ЛГ-1 \
\ Н] + п2 — 1 /
37 (продолжение). Доказать предельное соотношение
Щ.....
•Щ ' I Y, (!) + Х2(1)
1. (n,+n2- 1)!
J ynt 1 (1 -у)Пг 1
о
dy.
Некоторые элементарные задачи
241
Указание: Пусть N -> оо и &->оо, так что (0<^<1). Тогда с
помощью формулы Стирлинга установить предельное соотношение
/k-\\(N~k-\\
\П1-1Д «2-1 /_ («1+«2- 1)1 „«!-!,< ,лП2-1
* П”->оо-----( N-l~\---------(/i'l — 1)! («2 — 1)! •
N k ->оо \ П\ + П2 1 /
Использовать его для доказательства равенства
!. Р f „ *1(0 < „ , h К (п2 + п^\)\
hyn' 1
(1 - i/)”2"1 + о (й).
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
1. Пусть {%(/), / 0} и {У(/), / 0} — независимые пуассоновские процессы
с параметрами М и Х2 соответственно. Пусть Z\ (/) =/(/)+ У(/), Z2(t) «
= Х(/)— У(/), Z^t) = X(t) + k, где k — положительное целое число. Опреде-
лить, который из перечисленных выше процессов является пуассоновским, и найти
его параметр.
2. Телеграммы поступают на телеграф в соответствии с пуассоновским про-
цессом, в среднем 3 телеграммы за час.
(а) Какова вероятность того, что за утро (от 8 до 12) не поступит ни одной
телеграммы?
(б) Каково распределение момента поступления первой дневной телеграммы?
3. Пусть X(t)—однородный пуассоновский процесс с параметром X. Найти
ковариацию между X(t) и Х(/ + т), /, т > 0, т. е. определить
М[(Х(/) -М(Х(/)))(Х(/ + т) -М(Х(/ + т)))].
4. В молекулярной биологии возникает следующая задача. Предполагается,
что поверхность бактерии содержит несколько точек, где могут закрепляться мо-
лекулы, пришедшие извне, если они имеют правильное строение. Молекулы,
имеющие такое строение, будем называть допустимыми. Рассмотрим фиксиро-
ванную точку и примем, что молекулы прибывают в эту точку в соответствии
с пуассоновским процессом, имеющим параметр |л. Долю р этих молекул со-
ставляют допустимые. Недопустимые молекулы остаются в точке экспоненциаль-
но (с параметром X) распределенное время. Пока они находятся в рассматривае-
мой точке, они препятствуют другим молекулам. Допустимые молекулы зани-
мают это место навечно, также препятствуя в этом другим молекулам. Какова
вероятность того, что рассматриваемая точка свободна в момент /?
Указание: Свести задачу к изучению цепи Маркова с непрерывным време-
нем и 3 состояниями.
Ответ:
_₽н_Г(1+Х)в^_(1
$2 S1 L \ $1 / \ $2 /
где Si, s2 — корни уравнения s2 + s(% + ц) + цр% « 0.
ЗАМЕЧАНИЯ
Пуассоновские процессы и процессы рождения и гибели играют
фундаментальную роль в теории и приложениях, охватывающих
модели создания запасов и массового обслуживания, рост популя-
242
Гл. 7. Классические примеры цепей Маркова
ций, технические системы и т. д. Элементарные обсуждения пуас-
соновских и родственных им процессов можно найти в любом учеб-
нике по случайным процессам.
ЛИТЕРАТУРА
1. Феллер В., Введение в теорию вероятностей и ее приложения, т. 1, «Мир»,
М., 1967.
2. Bailey N. Т., The Elements of Stochastic Processes with Applications to the
Natural Sciences, Wiley, New York, 1964.
3. Blanc-Lapierre A,, Fortet R.. Theorie des Fonctions Aletoire, Masson,
Paris, 1953.
Глава 8
ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Цель этой главы состоит в том, чтобы познакомить читателя
с некоторыми из наиболее изученных вопросов и понятий, возни-
кающих при исследовании цепей Маркова с непрерывным пара-
метром (временем). Как и прежде, мы будем рассматривать лишь
однородный случай.
§ 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ
ВЕРОЯТНОСТЕЙ
Пусть Xt — марковский процесс с дискретным множеством со-
стояний и непрерывным временем, матрица переходных вероятно-
стей которого IIР*/(О С/-о* Таким образом,
P{X(/ + s) = /|X(s) = z} = Pl/(/).
Кроме обычных ограничений, накладываемых на переходную мат-
рицу II Рц(Г) II, т. е.
(a) P/z(0>0, />0,
(б)2Р//(0=1, *>0,
(в) 5 Ptk (t) Pkl (Л) = Ptl (t + h), t,h>0,
k
предположим, что Pu(t) непрерывны при t > 0 и что
(г) limP//(0 = { 1’
I О,
если i = /,
если i =/= /
(см. также задачу 3). Такую переходную матрицу часто называют
«стандартной». Оказывается, что из условий (а) — (г) можно по-
лучить гораздо больше следствий, чем можно было бы ожидать.
Одним из таких результатов является дифференцируемость Рц(1)
при всех / >0. Мы докажем лишь гораздо более простое утвержде-
ние, что функции Pn(t) дифференцируемы (т. е. имеют правосто-
ронние производные) при t = 0, Рассмотрим сначала Рц(Г).
244 Гл. 8. Цепи Маркова с непрерывным временем
Теорема 1.1. При каждом i предел
— Pn(0) = lim
t-+0 1
существует, но может быть бесконечным.
Доказательство. Покажем сначала, что Pa(t) > 0 при
всех t > 0. Действительно, в силу (г)1) для любого i существует
число 8 > 0, такое, что Р^(/)>0 при 0<J<^8. Далее, путем по-
следовательного применения (в) можно получить
Рц (tx+ ...tn) = 3 Piki (Л) Pkik2 (t2) ... Pkn_v i (tn). (1.1)
h h 1 1 2 n 1
£1...n
Полагая ... =/n = ~, i = j и беря в правой части лишь
члены, соответствующие ki = . = &n-i = i, получим
г / / \ПЛ
• (1.2)
При достаточно больших п, очевидно, е. Следовательно,
Рц >0, таким образом, Рц(Р) >0. Пусть —In Рц(Р) = <р(/).
Это определение корректно, поскольку Рц(Р) > 0. Так же как и
(1,2), можно доказать справедливость неравенства
Pii(t + s)>Pil(t)Pil(S).
Беря логарифм от обеих частей, получаем неравенство полуадди-
тивности для ф(/):
Ф (t + $)< <р (t) + <р (s).
Поскольку 0 < Pu(t) 1, то ф(/) 0, Положим
<р (/)
^ = sup-^-.
t>0 1
Тогда 0"С<7г ^оо, так как ф(/)^0 при t > 0. Если q{ < оо, то
существует to > 0, для которого qt — е. Для любого t
величину to можно представить в виде to = nt + б, где п > 0,
0 б < t. Тогда
фМ<ф(п/) + ф(б)<ф((л- 1)0 + <₽(О + ф(6)< •••
... < п<р (t) + ф (б)
и, таким образом,
г о) <- л<Р (О + ф (б) _ п/ <р (0 . ф (б)
еч= t0 t0 ta t 'r t0 *
9 И непрерывности Pn(t), t > 0. — Прим, перев.
£ 1. Свойства дифференцируемости переходных вероятностей
245
Следовательно,
nt ф (/) J ф
to t +
tit
-->1 и <р(б)-»О (поскольку P,i(6)->-l при
Го
Но при /->0 имеем —
Го
б -» 0). Отсюда
ПтГ«£Ф10 + Ф^1 = ИтФ10.
t . t0 J — t
Далее, из определения qi
Пт-^С qt.
/->0 '
Комбинируя последние три неравенства, получаем
qt — е < lim lim < q/.
Поскольку е произвольно, имеем
lim -^7^- = lim = q{.
t+o ‘
Если qi — оо, то можно вместо — е написать сколь угодно боль-
шое число М и затем получить, что M=CIim-^-^-. Таким образом,
<->о
оо = lim . В любом случае
7^>о
lim -2-^- = qt.
t->Q 1
Далее,
lim
/->0
Теорема 1.2.
t
1_е-Ф(0 ф(/)
11т---= Я1-
Для любых i и j, i Ф j, предел
P$/(0) = lim-^-
f-хЛ *
существует и конечен.
Доказательство. Для любого
||Ро(Л)|| является матрицей переходных
кова {Xnh}- Очевидно, Рц (Л) = Рц (nh).
Л(Л)=1 и
фиксированного h > О
вероятностей цепи Мар-
Введем вероятности
246
Гл. 8. Цепи Маркова с непрерывным временем
Тогда
п—1
Рц (nh) > 2 № (h) Рц (Й) Pn ((n-v-1) h),
v=0
(1.3)
поскольку каждое слагаемое в правой части соответствует неко-
торому возможному пути, ведущему из состояния i в состояние /
за п шагов (относительно шага длины Л); эти пути несовместны,
но, вообще говоря, не исчерпывают всех путей. Член jPva(h) Рц(И)
является вероятностью события, заключающегося в том, что по-
следнее попадание в i перед попаданием в / происходит на v-м ша-
ге. (Соотношение (1.3) также появлялось при обсуждении теорем
для отношений в гл. 5.)
Далее, аналогичным образом получаем
и-1
Pli(vh)=.P\.(h) + s ^(й)РЛ((о-т)й).
т=1
Первое слагаемое есть вероятность достижения состояния i на
v-м шаге без попадания до этого в состояние /. Члены, стоящие
под знаком суммы, учитывают достижение состояния j в некото-
рый промежуточный момент. Поскольку
и —I
3/” (Л)<1,
/71 = 1
то
jPu (й) Рц (vh) — max Pn((v — m)h). (1.4)
1 </7t < v
Далее, из условия (г) *) следует, что для любого е>0 и любых
фиксированных г, j (i =# /) существует число /о, такое, что
max РЛ(/)<8, min P/z (£) > 1 — в, min Pn(t)>l— 8.
Следовательно, если nh<te и то из (1.4) получаем
iPl (h) >1—28.
Подставляя эту оценку в (1.3), находим
м-1
Рц (nh) >(1 - 2е) 5 Рц(й)(1 - е) >(1 - Зе)пРц (h),
о=0
или
Pij(nh) Q .хк.
——h— X1 - Зе) ——, если nh < tQ. (1.5)
9 И непрерывности Рц(1).— Прим, перев.
§ 1. Свойства дифференцируемости переходных вероятностей
247
Положим
.. Piid)
q{l = hm ——.
t-»o 1
Тогда из (1.5) следует, что < оо. Действительно, если бы
qti = 00, то можно было бы найти сколько угодно малое h, для ко-
РцМ п х / а
торого —— сколь угодно велико. Выбирая п так, чтобы
z° zi х Pi] (n'h)
-^-<п'п<1о, из (1.5) мы бы получили, что —— можно
сделать сколь угодно большим, но в то же самое время
Ру (n'h) е 2е
n'h < n'h < t0
Полученное противоречие доказывает, что qy < 00. Оставшаяся
часть доказательства носит чисто аналитический характер и яв-
ляется следствием из (1.5). В силу определения qy существует
k < to, такое, что
Поскольку Py(t) непрерывна, можно найти настолько малое ho,
что
—+ е при f е Z = [/! —/г0, Л + Ло1- (1-6)
Далее, для любого h < h0 определим целое число «л, такое, что
nhh&I. Тогда, используя (1.5) и (1.6), найдем
ч РjAh) Pn(tihh\
(1 - Зе) ъ < —д < ql} + е, h < h0,
п.
откуда заключаем, что
(1 — Зе) lim ^А'и + е.
л->о "
В силу произвольности е получаем
тт- Pi] (А)
lim—т—
Утверждение теоремы следует теперь из определения qy.
Если взять в качестве примера процессы рождения и гибели, то
= X/ +
9;/-
Л./, j — i + 1,
О, / ¥= i— 1, i + 1, I,
ixz, / = «-1.
Z = 0, 1, ....
248
Гл. 8. Цепи Маркова с непрерывным временем
В общем случае
У qa^qi при всех I.
1 Ф i
Действительно, поскольку
i * i
то для любого конечного N
N
/»1, i * i
Деля на ft и устремляя h —► 0, получим неравенство
лг
Поскольку W произвольно, а все слагаемые неотрицательны,
получаем требуемое утверждение.
§ 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Говорят, что цепь Маркова с непрерывным временем «консер-
вативна», если
2 при всех L
Заметим, что процесс рождения и гибели консервативен. Дока-
жем теперь, что для консервативной цепи Маркова все Pij(i) не
только дифференцируемы, если < оо (/>0), но и удовлетво-
ряют системе дифференциальных уравнений, известных как обрат-
ные уравнения Колмогорова. (Частный случай процесса рождения
и гибели рассмотрен в гл. 7, § 5.) Напомним, однако, читателю, что
дифференцируемость Рц(1) следует непосредственно из условий
(а) — (г). Предположение о консервативности делает доказатель-
ство чрезвычайно простым. В самом деле,
Рц (s + n- Р(! (/) = 3 Pik (S) Pkl (0 - ри (/) =
k
= 2 Р1к(8)Рк1(1) + [Рц(5)-1]Ри(1).
k=£ i
Деля на s и устремляя s->0+, формально получаем обратные
уравнения
P'n(t)= S qikPkj (0 - qiPii (0 для всех i, (2.1)
А ¥= I
§ 2. Консервативные процессы
249
Чтобы строго вывести эти уравнения, следует показать, что
lirn | 2 р.И«)^/(0 = 2 ЯиМЪ-
s-*0+ k7i
Далее,
N N
Hmj ^РгИ«)^/(0>Пт| 2 pik(s)Pkl(t)= 4ikPkid)
s->0 k^i s->0 fe=l, k^i k~\,k=£i
для любого N, и поэтому
limy 2 pids)Pki(t)> 2 (2.2)
s“>° k Ф i k^i
С другой стороны, при N > i
N oo
2 Pik(s)Pkl(t)< 3 Pik(s)Pkj(t)+ 3 Pz*(s) =
k=fi i Ы, k i k=N+\
N N
= 2 Pik(s)Pki(.t)+\-Pu(s)- 2 P«(s).
6=1, k Ф I 6=1, k i
Деля на s и беря lim от обеих частей, получаем
$->о+
N N
йту 2 p«(s)p*/(0< S qikPki(t) + qi- 2
k =/* i k=*\, i 6=1, k i
Устремляя N -> оо и используя консервативность процесса, мы
видим, что
пж у 2 pik(s)pkl(tx 2 ^Л(о-
S">0+ k^i k^i
Сравнивая это неравенство с (2.2), заключаем, что предел
Пт| 2 Pik(s)Pkl(t)
s-*° k^i
существует и равен
^qikPkjtf}.
Аналогичным образом можно формально вывести систему так
называемых прямых уравнений. Запишем
Ру (s +1) - Pti (s) = 2 Pik (s) Pki (/) - P(l (s) = 2 Pik (s) [Pk] (0 -
k k
250
Гл. 8. Цепи Маркова с непрерывным временем
Деля на t и переходя к пределу при t -* 0, формально получаем
прямые уравнения
P'ij(s)= 2 Pik(s)qkl~Pil(s)ql для всех i, j. (2.3)
k =/® /
Вопрос о справедливости этих уравнений существенно более сло-
жен, чем для обратных уравнений, и мы его затрагивать не будем.
Обе системы уравнений в матричных обозначениях принимают
весьма простой вид. В самом деле, рассмотрим бесконечную мат-
рицу А = || ||, элементы которой равны
( я a, i^i,
aii I -qt, i = i,
и которая называется инфинитезимальной матрицей процесса.
Обратные уравнения могут быть компактно записаны в виде сле-
дующего матричного дифференциального уравнения:
Р'(/) = АР(/),
а прямые уравнения —
Р'(0 = Р(/)А,
где
р (0 = 11 Ра (ОН.
§ 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
Интересным и важным вопросом в теории цепей Маркова с не-
прерывным параметром является следующий. Предположим, что
дано множество неотрицательных чисел {q^}, обладающих свой-
ством
2 Ян^Ян для всех I.
(В целях единства обозначений мы иногда пишем qu вместо qi,
как это сделано выше.) Существует ли цепь Маркова, т. е. стан-
дартная матрица переходных вероятностей || Рц(Р)\\, для которой
Р'и (°) = Яц> i !>
РцМ^-Яи ?
Задача становится более определенной, если предположить, что
S Яц — Ян < 00 Для всех I,
§ 3. Построение цепи с помощью инфинитезимальных параметров 251
так как в этом случае известно, что любая цепь Маркова, связан-
ная с {^г;}, должна удовлетворять по крайней мере обратным урав-
нениям.
Практическая важность этих вопросов покоится на том факте
(как мы уже видели, в частности, для процессов рождения и ги-
бели, см. гл. 7), что довольно часто цепь Маркова с непрерывным
временем определена таким образом, что мы вынуждены выво-
дить обратные уравнения. Затем следует попытка решить эти
уравнения для того, чтобы вычислить полную функцию перехода
процесса.
В настоящее время для общего случая не получены определен-
ные результаты. Известно, что при условии
2 Яц = с!и Для всех i
/ ¥= i
существует по крайней мере одна отвечающая этим параметрам
переходная матрица Р(/), и если их существует более одной, то су-
ществует и бесконечно много. Конечно, больше известно о частных
видах матрицы А = 11^11, например в случае процесса рождения
и гибели. В этом частном случае известна полная классификация
всех процессов, отвечающих заданной инфинитезимальной матри-
це. Эти процессы в основном отличаются поведением на границе,
т. е. видом выборочных функций в оо. Напомним читателю, что
в частном случае процесса рождения и гибели матрица А должна
удовлетворять условию (4.5) гл. 7 для того, чтобы процесс опре-
делялся единственным образом.
Для общего случая цепей Маркова с непрерывным временем
задача классификации инфинитезимальной матрицы А и отвечаю-
щих ей процессов достаточно сложна, и мы лишь отошлем интере-
сующегося читателя к соответствующей литературе (см. ссылки
в конце данной главы).
Пусть для состояния i выполняется условие 0 < qi < оо. Да-
дим теперь некоторую интерпретацию элементам матрицы А, ана-
логичную интерпретации, данной в случае процессов рождения и
гибели величинам 1/ + щ и Pi = Mr + М"1- Напомним, что
в этом случае мы формально доказали, что (1< + Цг)~4 — среднее
время пребывания в состоянии /, a Mr + М”1 — вероятность пе-
рехода в состояние i + 1 из состояния i при условии совершения
какого-либо перехода. Результаты для случая общей цепи Марко-
ва с непрерывным временем аналогичные.
Пусть t > 0 фиксировано, а п > 0 — произвольное положитель-
ное целое число. Предположим, что процесс начинается из со-
стояния I. Тогда рассмотрим
p{lW-< при т = 0, i....................'НМЯГ-
252
Гл. 8. Цепи Маркова с непрерывным временем
Поскольку
1-Рн = (о(1)->0 ПрИ /_>0+),
то
/ t [ t\\n /Г tq.
11 --<7г + о l-l I =explnln 1 — —L + o
\ ' \ / Р / / \ I !v
Используя разложение логарифма вида 1п(1—х) =—х +
+ 0(х)х2, верное при |х|<-^- и |0|< 1, где я = ~^' + °(4)» и
затем переходя к пределу при п —> оо, получим
п'™[р',ШГ"ехр("'7‘')-
Но (см. гл. 1, стр. 18) вероятность
Р{Х(т) = /,
совпадает с
lim p(x(t) = Z, т = 0, —......^-t, /}
(при этом неявно предполагается, что процесс является сепара-
бельным), откуда видно, что вероятность пребывания в состоянии
i в течение отрезка времени, не меньшего /, равна ехр(—^/).
Другими словами, время пребывания процесса в состоянии i
имеет экспоненциальное распределение с параметром Это яв-
ляется строгим доказательством (в общем случае цепей Маркова
с непрерывным временем) того, что было эвристически показано
для частного случая процессов рождения и гибели (см. стр. 214).
Состояние Z, для которого < оо, называется устойчивым.
Оно называется поглощающим, если qt = 0; очевидно, если про-
цесс перешел в такое состояние Z, то он останется там навсегда.
Конечно, в этом случае
P{X(T) = Z, 0<т</Щ0) = /}==ехр(-^)== 1
для всех t. С другой стороны, если > 0, то время пребывания
в состоянии i является случайной величиной, функция распреде-
ления которой есть «настоящая» экспонента, и, следовательно, вы-
ход из состояния i осуществляется за конечное время.
Состояние Z, для которого ?г= оо, называется мгновенным.
Среднее время пребывания в таком состоянии равно нулю. Наи-
менование «мгновенное» обязано тому факту, что время пребы-
§ 3. Построение цепи с помощью инфинитезимальных параметров 253
вания процесса в состоянии i равно нулю, т. е., попадая в это со-
стояние, процесс мгновенно его покидает1).
Теория цепей Маркова с непрерывным временем, имеющих
мгновенные состояния, крайне сложна, особенно при рассмотре-
нии выборочных траекторий процесса. Дело усложняется еще тем,
что марковские цепи могут состоять только из мгновенных состоя-
ний. Имеет смысл найти технические задачи, отвечающие таким
примерам. Но в то же самое время утешительно сознавать, что
почти все цепи Маркова с непрерывным временем, возникающие
в приложениях, имеют только устойчивые состояния. Действитель-
но, в большинстве случаев, представляющих интерес, изучаемый
процесс обычно определяется инфинитезимальными характеристи-
ками как известными данными. Чтобы завершить теорию, необхо-
димо установить существование процесса (т. е. определить выбо-
рочные траектории и их вероятностные законы), обладающего за-
данной инфинитезимальной матрицей.
Наиболее элементарные учебники и обсуждения цепей Марко-
ва с непрерывным временем избегают этого аспекта задачи (так
же поступим и мы), делая упор преимущественно на нахождение
функций распределения процесса и вычисление различных вероят-
ностных характеристик, представляющих интерес. Вычисление пе-
реходной функции для всех t традиционно сопровождается выво-
дом обратных дифференциальных уравнений и, в лучшем случае,
их решением. Такой подход был основой нашего рассмотрения
процессов рождения и гибели (см. гл. 7).
В оставшейся части главы мы будем рассматривать цепи Мар-
кова с непрерывным временем, имеющие лишь устойчивые состоя-
ния. Наша следующая задача — придать физический смысл пара-
метрам qij. Действительно, если процесс консервативен, то
<h
можно интерпретировать как условные вероятности того, что
произойдет переход из состояния i в состояние /. Чтобы показать
это, рассмотрим
RiJ(h)=P{X(h) = j\X(0)~i, X(h)^i},
9 На первый взгляд кажется, что если i—мгновенное состояние, то Рц(1)
не является непрерывной функцией в нуле. Однако это не так. Если Х(0) = /,
то, хотя процесс и покинет сразу это состояние, он будет «достаточно часто» в
него возвращаться. Именно если обозначить через Qi(t) общее время пребыва-
ния процесса в состоянии i на отрезке [0, /], то оказывается, что
Р I lim 4 0f (/) = 11 X (0) =»)=!.
[/->0 t J
Это обеспечивает непрерывность функции Рц(1), когда i— мгновенное состояние
(см., например, Прохоров Ю. В., Розанов Ю. А., Теория вероятностей,
«Наука», 1967, гл. V, § \). — Прим. иерее,
254
Гл. 8. Цепи Маркова с непрерывным временем
и найдем lim R^ (й). Он равен вероятности перехода из состоя-
h 4" О
ния i в состояние j при условии, что переход осуществляется. Да-
лее, в силу определения Rij(h) имеем
Pt1 (h)
Деля числитель и знаменатель на h, устремляя h | 0 и используя
результаты теорем 1.1 и 1.2, получаем искомую формулу
= , j=£i.
Если взять сумму от правой части (по /), то она будет равна 1,
так как процесс консервативный.
Мы отметили выше, что для любых инфинитезимальных пара-
метров (i=£j) и qi (0<дг <оо) (/>0), удовлетворяю-
щих qt S qih может существовать одна или бесконечно много
цепей Маркова с непрерывным временем, имеющих одну и ту же
инфинитезимальную матрицу А. В случае консервативной инфи-
нитезимальной матрицы (т. е. qi = при всех /) существует
один специальный процесс (минимальный процесс), для которого
можно просто описать выборочные траектории. Построение мини-
мального процесса для случая процессов рождения и гибели было
показано в гл. 7, § 4. В общем случае метод остается тем же. Опи-
шем кратко основные идеи этого построения для общего случая.
Типичная реализация, начинающаяся из некоторого состояния,
скажем /, имеет следующий вид. Возьмем выборку из экспонен-
циального распределения с параметром q^ Она определяет время
пребывания в состоянии I. В конце этого интервала частица пере-
q if
мещается в состояние / с вероятностью —- (j I). В новом со-
Vi
стоянии, скажем jf, она пребывает случайное время (экспонен-
циально распределенное с параметром qy). По окончании вре-
мени пребывания в состоянии /' она переходит в новое состояние
/ с вероятностью (/¥=/); там частиНа проводит случайное
время с соответствующим экспоненциальным законом распреде-
ления, затем снова совершает переход и т. д. С помощью этой
последовательной процедуры мы строим все возможные реализа-
ции процесса. Используя довольно глубокие методы теории меры,
можно найти переходную функцию IIAj(/)ll, имеющую заданную
инфинитезимальную матрицу.
Другой путь описания минимального процесса состоит в сле-
дующем. Переходная матрица НАДО II определяется через матри-
§ 3. Построение цепи с помощью инфинитезимальных параметров 255
цы вероятностей различных переходов, совершаемых только за
конечное число скачков. Более определенно: мы вводим в рассмо-
трение вероятность Рц (/; N) перехода из состояния i в состояние j
за время t и за число переходов, не превосходящее АЛ В частности,
в соответствии со смыслом инфинитезимальных параметров
i = i>
i =£ j,
и можно выписать рекуррентное соотношение, связывающее
N) с Рц(Р, N — 1) следующим образом.
Рассмотрим сначала Pa(t;N). В соответствии с тем, произошел
переход до момента t или нет, возникают две возможности. Время
пребывания в состоянии i распределено экспоненциально с пара-
метром qu так что с вероятностью ехр(—qd) перехода не проис-
ходит. Предположим, что первый переход произошел в интервале
от т до т + dx (вероятность этого события равна ^ехр(—qtx)dx)
и что при этом состояние приняло значение / #= i.
этого последнего события равна
Вероятность
(Вероятность
возвратиться
в состояние i в оставшееся время t — х не более чем за N— 1 пе-
реходов равна Pn(t — x\N—1). В силу формулы полной вероят-
ности имеем
t
Рц (/; N) = ехр (- qit) + 2 V’ / Р a (! - т; N - 1) q{ ехр (- ^т) dr.
I^i 1 о
С помощью аналогичного перечисления различных возможностей
получим равенство
t
Pu(t; N)=> JI Qik J N-l)exp( —qrfdr, i=£j.
k I 0
Можно показать, что
lim Рц(1-, N) = Pt](t)
N-><x>
(см. ссылки в конце главы).
Здесь мы вынуждены принести извинения перед читателем за
то, что ввели множество понятий, важных в теории марковских
процессов, и почти не изучали чих. Эти понятия содержат в себе
много тонкостей и патологий, изучение которых далеко выходит за
рамки этого учебника. Можно лишь надеяться, что читатель про-
должит изучение этих вопросов по другим отличным книгам, рас-
сматривающим данный предмет.
§ 4. Строго марковское свойство
257
если при 04t4s, то Уг ==/ и заведомо a(K/)^a(XJ.
Следовательно, в силу симметрии о(Х/) = о(У/). Такая случайная
величина а называется временем первого достижения состояния L
Аналогично марковским моментом является время первого дости-
жения любого конечного множества состояний С, не содержащего
Х(0) = /о и определяемого следующим образом:
a(X,binf{T|XTeC}.
Доказательство этого повторяет предыдущие рассуждения. Три-
виальным марковским моментом является о =э const. Читатель без
труда должен построить другие примеры марковских моментов.
Если ограничиться интуитивным уровнем, то марковское свой-
ство однородных марковских процессов утверждает следующее.
Если известны значения X(S{) при 0 Si < S2 <... < sn = to
(to > 0 фиксировано), то вероятностное распределение величин
Xtfo + 'i), Х(/0 + /2), X(tQ + tk) (0<Л</2< ... <tk) (4.1)
зависит только от значения X(tQ). Более точно, вероятностное рас-
пределение величин (4.1) при условии, что известны значения
X(s) в моменты $i < s2 < . •. < sn = to [или даже, в более об-
щем случае, вся история процесса X(s) вплоть до момента to
(0-^s^.io)], совпадает с вероятностным распределением величин
X(t{\ Х(/2), X(tk) при известном X (0).
Другими словами, можно найти вероятностный закон для ве-
личин (4.1), перемещая шкалу времени так, чтобы to = 0, и беря
в качестве начального состояния значение X(tQ).
Интуитивно кажется правдоподобным, что то же самое соотно-
шение должно выполняться, если заменить фиксированное значе-
ние to на «марковский момент» о. Более точно, предположим, что
мы хотим найти вероятностное распределение величины
Х(о + т) при известном Х(с) = х, (4.2)
т. е. вероятностное распределение Х(т), где т>0 — время, про-
шедшее с момента о, при известном значении X в момент а. В слу-
чайной величине о «учитывается» поведение процесса только до
момента о включительно, но не далее, хотя само значение о не
обязательно фиксировано и может изменяться от одной реализа-
ции к другой. Другими словами, это случайный момент.
Кажется естественной возможность считать, что марковское
свойство справедливо для случайного момента о. Отсюда тогда
следовало бы, что вероятностное распределение величины (4.2)
совпадает с законом распределения величины
X(t) при условии, что Х(0) = х. (4.3)
9 Зак. 939
258 Гл. 8. Цепи Маркова с непрерывным временем
Этот факт не является прямым следствием марковского свойства,
поскольку в первоначальной формулировке говорилось о фикси-
рованных моментах. Утверждение, что (4.2) и (4.3) «управляются»
одним и тем же вероятностным законом, и выражает строго мар-
ковское свойство. Более точно, если для любого марковского мо-
мента о вероятностное распределение величин
Х(Л + а), X(t2 + o\ ..., X(tk + v), t{<t2< ... <tk, (4.4)
при известных X(s), s^or, и X(o) =x совпадает с вероятностным
распределением величин
*Ю, хю, ..., хю (^< ... <tk)
при известном Х(0) = х, то говорят, что процесс Маркова обладает
строго марковским свойством. Существуют примеры марковских
процессов, не являющихся строго марковскими.
Результат такого рода, который следует из (4.4), крайне важен
для вычисления различных представляющих интерес вероятност-
ных характеристик. Действительно, один из основных приемов ана-
лиза случайных процессов и вычисления вероятностных характе-
ристик состоит в получении рекуррентных соотношений, исполь-
зующих обычно первые или последние моменты осуществления
определенных событий. Рассмотрим пример. Предположим, что мы
хотим найти РгДО» представляя рассматриваемое событие через
момент первого достижения состояния /. Пусть вц — момент пер-
вого достижения состояния /, начиная из состояния i. Выше было
указано, что моменты первого достижения конечного множества
состояний являются марковскими, в частности вц — марковский
момент. Пусть
Л/ (s) = P{a//<s}.
Разумеется, начиная с момента вц, когда частица попадает в со-
стояние /, вероятностное распределение ее будущей истории такое
же, как если бы оц — 0, а начальное состояние цепи было бы j и
цепь Маркова «управлялась» бы матрицей ||Р^(/)|| обычным обра-
зом. Это положение справедливо лишь при условии выполнения
строго марковского свойства. Тогда верно соотношение
t
(4-5)
О
которое является непрерывным аналогом формулы (5.9) гл. 2. Чи-
татель может интерпретировать dFij(s) как функцию плотности
fa(s)ds величины от/;, когда эта плотность существует. Формула
(4.5) следует из формулы полной вероятности, где dFa(s)—ве-
роятность того, что s бц + ds, a Pjj(t — s) — переходная
вероятность, т. е. вероятность того, что если момент сщ начальный
Задачи
259
(частица тогда с необходимостью находится в состоянии /), то
t — s единиц времени спустя процесс будет снова в состоянии /.
Можно выписать множество других соотношений типа восстано-
вления, подобных (4.5) (родственных формулам (2.1), (2.2) и (2.3)
гл. 5). Мы еще раз подчеркнем, что такие соотношения справедли-
вы в общем случае лишь при выполнении строго марковского свой-
ства.
Тот факт, что длительности последовательных пребываний
в данном состоянии (или в двух фиксированных состояниях) яв-
ляются независимыми случайными величинами, есть непосред-
ственное следствие строго марковского свойства. (Читатель дол-
жен уметь обосновать это формально.)
Поскольку строго марковское свойство играет фундаменталь-
ную роль при анализе марковских процессов, мы в заключение
приведем наиболее приятный результат. Любая консервативная
цепь Маркова с непрерывным временем, имеющая лишь устойчи-
вые состояния, — строго марковский процесс. Или, в более общей
формулировке, марковское свойство выполняется для любого мар-
ковского момента а, такого, что Х(ц)#= оо с вероятностью 1.
С практической точки зрения это означает, что почти все соот-
ношения типа восстановления для таких процессов вполне коррект-
ны и могут использоваться безбоязненно. Доказательство приве-
денного выше результата, более подробное обсуждение строго мар-
ковского свойства для цепей Маркова с непрерывным временем и
другие фундаментальные вопросы можно найти в книге
Чжун Кай-лая [1].
ЗАДАЧИ
1. Пусть Р (/) = || Ру (/) ||^ /яж0 — матрица переходных
Маркова с конечным множеством состояний и непрерывным
что det [Р (/)] > 0 при всех t > 0.
2. Пусть Р — стохастическая матрица размера 2X2, т.
вероятностей цепи
временем. Показать,
II а р||
е. р = J ’ гДе
IIY б ||
а, Р» У» д 0, а + р = 1, у+ 6=1. Доказать, что тогда и только тогда суще-
ствует непрерывное семейство Р(/), t > 0, стохастических матриц 2X2, таких,
что Р (1) = Р, когда
det Р = ад — уР > 0 и a + d > 1.
Указание-. Использовать
вить в виде еА, где А имеет
тот факт, что по предположению Р можно предста-
1| — a a
вид А = , I (а, b > 0).
— b |
— а
b
3. Показать, что если Р (t) ~ || Ру (/) ||“/я0 удовлетворяет постулатам
(а) — (г) § 1, то Р(/) непрерывна при всех t > 0.
Указание: См. гл. 7, § 8.
4. Рассмотрим неприводимую цепь Маркова с непрерывным временем и ко-
нечным числом состояний 1, 2, ..., N. Пусть qy, i, j — 1, ..., N,— инфинитези-
мальные параметры процесса. Предположим, что qij^qa для всех /, j«l,
9*
260
Гл. 8. Цепи Маркова с непрерывным временем
2, ..., N. Пусть Pi(t)—вероятность того, что процесс находится в момент t
в состоянии i. Введем функцию
£(0 = - In Pi (t).
t=l
где x In x = 0 при x — 0.
Доказать, что E(t) —неубывающая функция t 0.
Указание'. Доказать сначала, что
N
р'ЛП-^Чц Р/ (О--Р/СО]-
/=1
Используя эту формулу, доказать затем, что
N
5. Пусть Xt (t > 0)—консервативная цепь Маркова с непрерывным време-
нем, у которой все состояния устойчивы, т. е. S Предположим, что
j =/= i
>0, i =# j, и 0 < qt < oo. Показать, что процесс Xt возвратен, если существует
последовательность z = (z0, *2,.. .), такая, что (1) zn -> оо при п -> оо,
(2) -Я& + 2 1>1. (Возвратность означает, что в каждое со-
/ Ф i
стояние процесс возвращается бесконечное число раз, или, что то же, суммарное
время пребывания в каждом состоянии бесконечно.)
Указание'. Использовать вложенную цепь Маркова {Уп}, п — 0, 1, 2, со
стационарной матрицей переходных вероятностей Р = || Рц ||, где
Рц = Ъ.
Вложенная цепь Маркова {Уп} попросту фиксирует последовательность со-
стояний, через которые проходит процесс Xt безотносительно к длительностям
пребывания в различных состояниях. Использовать теорему 4.2 гл. 3.
6. В предположениях задачи 5 показать, что Xt невозвратен, если существует
ограниченная непостоянная последовательность z = (z0, zlf z2,...), такая, что
-Zi<?i + 2 ‘Zi/Z/”0- I>1-
/ =/= i
Указание: См. гл. 3, § 4.
7. Показать, что сумма двух независимых пуассоновских процессов — снова
пуассоновский процесс.
8. Процесс восстановления является целочисленным случайным процессом,
который равен числу точек (событий) в интервале (0,/), если интервалы между
наступлениями событий — независимые одинаково распределенные случайные ве-
личины с общей функцией распределения F(x), х^0 (F (х) =0, х < 0); F не-
прерывна при х = 0. Общим процессом восстановления назовем такой процесс,
у которого общая функция распределения F (х) имеет скачок величины q в нуле.
Показать, что общий процесс восстановления эквивалентен обычному, у кото-
Литература
261
рого число одновременно наступаемых событий в момент 0 и в другие «вызываю-
щие» моменты — независимые одинаково распределенные случайные величины
Ро, Pi, /?2, ... с распределением
P{^ = n} = p<7« _ « = 0, 1, 2, ...
для всех i = 0, 1,2, ..., где р = 1 — q.
9. Доказать, что если сумма двух независимых процессов восстановления
есть пуассоновский процесс, то оба процесса восстановления — пуассоновские.
10. Показать, что для неприводимой непериодической возвратной цепи Мар-
кова
lim (роо)'/П= 1-
П->оо
Указание: Использовать полуаддитивные функции, введенные в процессе до-
казательства теоремы 1.1.
11. Рассмотрим цепь Маркова с непрерывным временем и конечным (ска-
жем, равным N) числом состояний. Пусть А — инфинитезимальная матрица. По-
казать, что А имеет ранг N— 1.
12. Рассмотрим консервативную цепь Маркова с непрерывным временем и
двумя состояниями. Пусть
АРи «12|
II #21 а22 II
инфинитезимальная матрица процесса. Показать, что в этом случае обратные
уравнения имеют вид
(0 - (Sp A) P'if (0 + (det А) Рц (/) = 0, /, / = 1, 2 ’).
|| - 1 11
Решить эти уравнения для А = |.
ЗАМЕЧАНИЯ
Эта глава содержит лишь малую часть материала обстоятель-
ной книги Чжун Кай-лая [1]. Основные идеи этой главы, развитые
для случая общих марковских процессов, можно найти в книгах
Дынкина [2] и Дуба [3].
ЛИТЕРАТУРА
1. Чжун Кай-лай, Однородные цепи Маркова, гл. 3 и 4, «Мир», 1964.
2. ДЙнкин В. Б., Марковские процессы, Физматгиз, 1963.
3. Дуб Дж. Л., Вероятностные процессы, ИЛ, 1956.
Если А= || a.j ||, то Sp A= ац~ след матрицы А. — Прим, перев,
Глава 9
ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ
ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
В этой главе приводятся различные специальные приложения
некоторых методов, связанных с пуассоновскими процессами и
суммами независимых случайных величин.
§ 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ
ПРОЦЕССАМИ
Пусть Уь Уг, ..., Уп суть п независимых одинаково распреде-
ленных случайных величин, имеющих непрерывную строго возра-
стающую функцию распределения F(y). Определим случайные ве-
личины У*, ..., У* следующим образом:
У”, есть г-я в порядке возрастания величина среди Уь У2, ..., Уп ’)•
В частности,
y; = min{yp У2, ..., Уп] и У* = max (Ур У2, ..., Уп).
Очевидно,
у;<у;<...<у;.
У\ называется i-й порядковой статистикой выборки (Уь ...
.... Уп), а набор (Ур ..., У*)— множеством порядковых стати-
стик объема п, соответствующих выборке (Уь ..., Уп).
В этой главе рассматриваются распределения порядковых ста-
тистик выборок, их связь с пуассоновскими процессами и другие
приложения. Сначала, однако, сделаем существенное упрощение
без потери общности.
Положим
X^FiYiY i=\,...,n,
и найдем распределение величины X,:
Р < х} = Р {F (Уг) < х} = Р {yz < У7"1 (х)} =
= f(f_i(x)) = x, 0<х<1, i = 1, .... га, (1.1)
9 В случае равенства делается произвольный выбор среди равных по вели-
чине Yi. В действительности событие, состоящее в том, что по крайней мере два
значения Уг- будут равны, имеет вероятность 0, и его можно не принимать во
внимание.
£ 1. Порядковые статистики
263
где Г-1— функция, обратная к F,— определена единственным об-
разом в силу сделанных предположений относительно F. Далее,
поскольку 0 F (у) 1, то
1 о,
Р{Хг<х} = | ъ
если
если
х<0,
х> 1,
i — 1.......п.
(1.2)
Таким образом, в силу (1.1) и (1.2) Xi распределена равномер-
но на [0, 1] при всех i = 1, ..., п независимо от вида непрерывной
строго возрастающей функции F. Заметим, что отношение поряд-
ка среди {К,} сохраняется при преобразовании Xt = F(Yi). Это
означает, что вместо исследования порядковых статистик (У’},
соответствующих выборке общего вида (Уь ..., Уп), можно изу-
чать порядковые статистики (X^j для равномерного на отрезке,
[О, 1] распределения.
Поэтому в дальнейшем мы ограничимся изучением порядковых
статистик
х;<х;<...<х; а.з)
для выборки независимых равномерно распределенных на отрезке
[0,1] случайных величин
Хь Х2, .... Х„.
Тот факт, что для случайных величин X’, X*, ..., X* выполня-
ется (1.3), ясно указывает, то они не являются независимыми. Мы
сначала найдем совместное распределение порядковых статистик
X*, ..., X* или, вернее, его функцию плотности, которую'обозна-
чим через f* (Xi, ..., хп). Ее существование будет очевидно из
доказательства. Выбирая 0 < Xi < х2 < ... < хп < 1 и достаточно
малые приращения hi, h2, ..., hn так, чтобы интервалы
(хь Xi + hi), (х2, х2 + h2), ..., (хп, хп + hn) не пересекались, полу-
чаем
*П+ЛП *1+*1
/ J О-i» • • • > хп) dXi ... dxn =
*п Х1
= Р{х/<Х;<х/ + /1/, 1 = 1, 2, .... п} =
= S Р {xt X!g < xt + hh i=l, 2, ..., n} =
по всем перестановкам
о из (1, 2, ...» п)
п
= 2 П Р {xi Х/а < Xi + h^ = (в силу независимости величин X»)
а 1-1
•= 2 П ht = n\hih2 ... hn\ (1.4)
a i-i
264
Гл. 9. Порядковые статистики и пуассоновские процессы
здесь использовались независимость, равномерное распределение
величин Xi (i — 1, ..., п) и тот факт, что число всевозможных
перестановок индексов 1,2, ..., п равно п\.
Из (1.4) следует, что совместная плотность порядковых ста-
тистик X*, X* равна
{п\, 0 1,
О в противном случае.
Такое же доказательство показывает, что если бы величины
Xi, ..., Хп были взяты из равномерного распределения на от-
резке [а, 6], то соответствующая совместная плотность порядковых
статистик равнялась бы
Г(ХЬ х„) =
п!
(Ь-а)п'
О
а х{ х2 ... хп b,
в противном случае.
(1.6)
Мы уже сталкивались с плотностью (1.5) при обсуждении
пуассоновских процессов (см. стр. 206). Именно: пусть
{У(/),0<^/<Л}— пуассоновский процесс, в частности, при каж-
дом t е [0, 1] пусть У (/) будет дискретной случайной величиной с
распределением
е-М№
е k\
0
Pk (t) =
k = 0, 1, 2...
в противном случае,
где %—фиксированный действительный параметр.
Предположим, что У(0) =0. Тогда при условии, что У(1) = п
'(целое число), на отрезке [0, 1] будет ровно п временных точек,
в которых Y(t) совершает «скачок». Точное положение этих точек
зависит от случая и определяется случайными величинами
Гь Т2, ..., Тп (Т{<Т2< ... <Тп)
со значениями из отрезка [0, 1].
Утверждается следующее. При условии
У(1) = п
случайные величины Л, 7г, ..., Тп распределены как множество
порядковых статистик объема /г, взятых из равномерного распре-
деления на отрезке [0, 1].
Доказательство этого положения непосредственно вытекает из
уже полученных результатов. Действительно, вывод условной
плотности распределения величин 7\, Г2, ..., Тп при условии, что
У(1) = п, был дан в теореме 2.3 гл. 7. Сравнение с (1.5) показы-
вает, что эти формулы совпадают, и утверждение, таким образом,
доказано.
§ 1. Порядковые статистики
265
Соответствие между порядковыми статистиками и условными
моментами наступления событий пуассоновских процессов упро-
щает вывод других свойств порядковых статистик.
Например, пусть, как и ранее, X*, X*, ..., X* — порядковые ста-
тистики выборки объема п из равномерного распределения. Мы
утверждаем, что совместное распределение величин Х\, Х*2, ...
.X*k__x при условии, что X*k = ck, ..X* = сп, совпадает с распре-
делением порядковых статистик для выборки Х^ ..., Xk-i, где
каждая д. с. в. равномерно распределена на [0, Съ\. Чтобы прове-
рить этот факт, переформулируем задачу в терминах событий
пуассоновского процесса.
Пусть — моменты наступления со-
бытий пуассоновского процесса Y(t) при условии, что У(1) = п.
Предположим, что налагаются дополнительные условия Tk =
Tk+i = cfe+1, ..., Тп = сп и требуется определить совместное рас-
пределение величин Г1, Г2, ..., Ffe-i. Так как Y(t)—процесс с не-
зависимыми приращениями, то очевидно, что если сделано пред-
положение Th = или, что эквивалентно, Y (ck— в) = £— 1 (где
8>0 и достаточно мало), то вся информация, относящаяся к
величинам 7\ Т2, Тк-\, содержится в этом предположении. Но
при этом условии Л, ..., Tk-\ распределены как порядковые ста-
тистики выборки объема k—1 из равномерного распределения на
отрезке [0, Таким образом, условное совместное распределение
величин X*, Х*9 ..., X*k_x при условии X*k=ck, ...,Х*п = сп совпадает
с совместным распределением порядковых статистик объема k— 1,
взятых из равномерного распределения на отрезке [0, cj. Соответ-
ствующая условная плотность равна
f’(xb ..|cft.с„) =
(fe-l)l
Jb-l
ck
О
в противном случае. (1.7)
В точности таким же образом можно доказать, что условная
плотность величин Х^+1, ..., Х*п при условии, что значения пер-
вых k порядковых статистик равны
Х\ = с{, .... X*k = ck,
совпадает с совместной плотностью п — k порядковых статистик
выборки из п — k независимых случайных величин, распределен-
ных на отрезке [cfe, 1]:
f (Xk + b • • • > %n I ^1 > • • • >
(» — fe) I
V-'kr
0
в противном случае.
(1-8)
266
Гл. 9. Порядковые статистики и пуассоновские процессы
Формулы (1.7) и (1.8) показывают, что эти совместные услов-
ные плотности зависят лишь от Ck и не зависят от Ci, i =
= k + 1, ..., п и 1 = 1, 2, ..., k — 1 соответственно. Это озна-
чает, что совместные плотности величин А], ..., X*k_l и!’+|, ...
..., Х*п при одном и том же единственном условии X*k = ck имеют
соответственно вид
Г(х,, ..., xk.t \ck) =
(fe-1)!
_fe-l
ck
о
0<х, < ... <сА,
(1-9)
в противном случае
и
Г(хй+1, ..., xn\ck) =
(n-k)l
О
Ск ^^5 Xff 1 ,
+ (1.10)
в противном случае.
Формулы (1.7) и (1.8) совместно с (1.9) и (1.10) также пока-
зывают, что множества величин Хр Х*_, и X* р X*
(условно) независимы при условии, что X*k = ck.
Более того, два множества случайных величин X*, ..., X*
и Х*+1, X* (i<k) условно независимы при известных значе-
ниях остальных величин Х*+р X*.
Пользуясь этим, можно получить совместную плотность для
любого числа последовательных порядковых статистик. Так, совме-
стная плотность величин X*, ..X*, Х*+1, ..X* (i<k) при усло-
вии, что Х*+1 = х/+1, .X* = xk, равна
Г(хь ..., х/( xft+1, ..., x„|x/+b ..., Xfe)= <1,П)
С другой стороны, в силу вышеприведенного утверждения о не-
зависимости левая часть равна
f(xb .... xz|xz+I, ..., xk)f*(xk+l, ..., xn |xi+i, ..., х4) =
= Г(Х,......хг|х/+1)Г(хй+1, ..., xjxfe)= f
xi+l (1-4)
Отсюда, а также из (1.11) и (1.5) получаем для 0 4u < k
f (jp+b • • • > Xk)
... П' mi ~xX~k' О^х,.. < ... <xfe< 1,
il(n —й)! г+1\ в/ • <+1 я ц |2)
0 в противном случае.
§ 1. Порядковые статистики
267
В частности, (1.12) при i + 1 = k дает маргинальную (част-
ную) плотность величины X*k
Г(хк) =
------щ------Xk~41 - х \п~к
(k -!)!(«-*)! V ХН ’
О
(1.13)
в противном случае,
о С х. < 1,
которая является плотностью бета-распределения.
Порядковые статистики Хр X*, X* делят интервал (0, 1)
на п + 1 непересекающихся интервалов, имеющих длины
u^x\, t/2=x;-x;,..., £/„ = х;-х;_р t/„+1 = i-x;.
Очевидно, Ult Uz, ..., Un, Un+l не являются независимыми слу-
п+1
чайными величинами, поскольку Записывая преобра-
зование переменных (хр ..., х*) в (и{, ..., мп)
«1 = xv
и2= — х’ + х’, (1.14)
и
~xn-l + xn
и вычисляя якобиан этого преобразования, который в данном слу-
чае равен тождественно 1, можно найти совместную плотность
g(ui.....мп) случайных величин {t/i, .... Un}. Именно
g(Mb ..., «„) =
п
п\, щ 0 (г = 1, ..., п), 2 м> 1>
i=i
(1.15)
О в противном случае.
Таким образом, можно сказать, что случайные величины
{Ult ..., Un} распределены равномерно в области
п
1=1, .... n, Swf’Cl.
i-i
268 Гл. 9. Порядковые статистики и пуассоновские процессы
Это также определяет распределение случайных величин {Ui, ...
ип, ип+\} в области
п+1
иг^0, г=1........п, п+1, 3«z=l.
Покажем теперь, что совместное распределение величин
{(71, ..., Un+i} совпадает с распределением величин
У1/5, YJS, Yn+dS,
где S = Ki + ... + Yn + Kn+i, а Уг-, i = 1, .,., n, п + 1, — независи-
мые экспоненциально распределенные случайные величины (с па-
раметром X). Этот результат может быть доказан с помощью вве-
дения пуассоновского процесса и анализа задачи в новых терми-
нах. Для разнообразия дадим прямое доказательство. Для этого
запишем совместную плотность величин (Уь Уп+1)
НУ1, , Уп+1)~
yt 0, i = 1, ..., п + 1,
о
в противном случае
и сделаем преобразование
1 У{ + • • • + //п+1
v У2
2 У1+ ••• + Уп+1 ’
V п
vn:=-7—L----+Т----’
У1+ ••• +Уп+1
vn+l ~У\ + • • Уп+1-
Обратное преобразование имеет вид
У1 ~ V\Vn+i,
y2 = v2vn+i,
yn = vnvn+l,
yn+i = vn+i[\ ~(t>i+ ... +v„)].
§ 1. Порядковые статистики
269
Отсюда можно найти якобиан
Vn+1 0 0 ... 0 »1
0 V„+1 0 ... 0 »2
0 0 vn+i ... 0 O3
J = •
0 о о ... vn+t O„
^n+1 “ »n+l »n+l • • • ®n+l 1 Vi-V2- ... -u,
on+i о 0 ... 0 u.
0 vn+I 0 ... 0 v2
0 0 vn+l ... 0 t>3
— . . . . = 0" .. n+I
Vn+l vn
0 0 0 ... 0 1
Следовательно, совместная плотность величин
YJS, YJS, Yn/S, S
равна
f(vh Vn, t»n+i) =
n+1
Лл+1 exp (—Л0ц+1)Уп+ь Of >0, i= 1, ..n+1,
= /-i
0
в противном случае.
Отсюда следует, что S и случайный вектор (Yt/S, Yn/S) не-
зависимы и имеют следующие маргинальные плотности:
f(O„+l) =
j^n +1
—— ехр ( — о",, с» ,1^0,
Ц\ г \ п + 1/ п + Р п+1 ’
о
в противном случае
и
/(»!......
п
п\, V/^О, г=1...... So/^1, (j jg)
О в противном случае.
Поскольку (1.16) согласуется с (1.15) и поскольку
s + s + ••• + s + s - i.
270
Гл. 9. Порядковые статистики и пуассоновские процессы
утверждение о равенстве распределений величин
ОЛ, t/n+f) и (^/3, У„+1/3)
доказано.
§ 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
Теперь мы хотим показать некоторые применения пуассонов-
ских процессов и соответствующих порядковых статистик к ана-
лизу различных случайных величин, связанных с эмпирическими
функциями распределения. Для этого мы сначала получим некото-
рые результаты, известные под названием задачи о баллотировке,
которые представляют значительный интерес и ценность сами по
себе.
Задача о баллотировке может быть сформулирована следую-
щим образом.
При баллотировке (выборах) и общем количестве избирате-
лей с кандидаты А и В получают а и b голосов соответственно,
а + b = с. В течение подсчета голосов лидерство кандидатов мо-
жет все время меняться. Задача о баллотировке (в ее простейшем
варианте) состоит в следующем: предполагая, что я > &, найти
вероятность того, что кандидат А при подсчете голосов будет все-
гда впереди (хотя бы на один голос).
Непосредственное решение задачи о баллотировке следующее.
Рассмотрим фиксированное размещение а символов А и b симво-
лов В на окружности. Для данного размещения определим число
начальных позиций, при отсчете от которых, скажем по часовой
стрелке, символы А всегда будут лидировать в счете.
Чтобы найти эти позиции, исключим последовательно все со-
седние пары АВ, проходя для этого окружность, возможно,
несколько раз. В результате останется а — & символов Л. Легко по-
нять, что оставшиеся места и являются теми исходными пози-
циями, при отсчете от которых символы А всегда лидируют. Отсю-
да следует, что вероятность того, что А всегда лидирует (возмож-
ное наблюдение является описанным размещением или одной из
его циклических перестановок), равна (а — Ь)/{а + &). Эта веро-
ятность не зависит от выбора исходной последовательности. Отсю-
да вероятность того, что кандидат А всегда лидирует при подсчете
голосов, равна {а — &)/(а+&).
Проведенный анализ весьма элегантен. Однако, поскольку мы
имеем в виду другие обобщения, сформулируем теперь задачу
о баллотировке в терминах более общей «урновой схемы» и про-
анализируем ее структуру.
В урне а карт, на которых написан нуль, и b карт, на которых
написана двойка, а + b = с, а^Ь. Карты вынимаются из урны
одна за другой случайным образом без возвращения до тех пор,
§ 2. Задача о баллотировке
271
пока не будет вынута последняя карта. Пусть — случайная ве-
личина, равная числу, написанному на i-й карте, i = 1, ...» с.
Тогда задача о баллотировке будет решена, если найти
P{vi + v2+ ... +vr<r, r=l, 2, ..., с}. (2.1)
Это утверждение следует из того факта, что если среди первых
г чисел имеется а нулей и 0 двоек (а + р = г), то условие
vi + ... + vr < г означает, что а«0 + р«2<а + р, или р < а.
Очевидно, (2.1) является вероятностью того, что это неравенство
(Р < а) выполняется для г = 1, 2, ..., с.
Чтобы найти вероятность (2.1), заметим сначала, что
(vi, V2, ...» vc) является набором из а нулей и b двоек и все из
с!/(а!&!) возможных перестановок равновероятны. Это означает,
что для любого г (г = 1, ..., с) и любого множества и, ..., ir
различных чисел из набора {1, ..., с} совместное распределение
vf2, ..., v/r) совпадает с распределением (vi, V2, ..., vr).
Говорят, что случайные величины vi, ..., vr, обладающие таким
свойством, перестановочны. (Независимые одинаково распределен-
ные случайные величины являются перестановочными.) Тогда,
поскольку
Vi + V2"Т ••• +'V£.==6z,0 + 6’2 = 2b, (2.2)
имеем
SM{vJ = M{vi+v2+ ... + vc} = 2b.
i = l
Поскольку д.с.в. vi,V2, ..., vn перестановочны, все тг- имеют одно
и то же маргинальное распределение и, следовательно,
cM{vJ = 26, или M{vi} = 2b/(a +b), f=l, 2, ..., с. (2.3)
Используя этот факт, докажем теперь по индукции относительно
с, что
P{vj + ... + vr<r, r==l, ..., с |vj + v2 + ... +v£. = 26}-=
= 1 - 2b/c = (a — b)/(a + b). (2.4)
Покажем сначала, что (2.4) справедливо для с = 1. Но из того,
что с = 1, следует, что а = 1, b = 0, поскольку неравенство
а > b 0 предполагалось в постановке задачи. Тогда, очевидно,
P{v1<l}==P{v1 = 0}==I.
Утверждение (2.4) тривиально для 2Ь = с, поскольку в этом слу-
чае vi + ... + vc = 26 = с.
Предположим теперь, что (2.4) выполнено для всех с^п—1
и 0-<26<с. Мы хотим доказать, что (2.4) справедливо также
для с = п и 0 4^ 26 < п,
272
Гл. 9. Порядковые статистики и пуассоновские процессы
Пусть Ь' — целое число, такое, что 0 Ь' Ь. Тогда
P{vi + ... + vr<r, r=l, ..., с I Vi + ... +v2& = 2&,} =
= P{vi+ ... +vr<r, r=l, ..., 2b |vj + ... +V2£> = 2&'}, (2.5)
так как неравенство vi + ... +vr<r всегда выполнено при г =
= 2b + 1, ..., с в силу условия (2.2). Но правая часть (2.5) яв-
ляется выражением того же типа, что и левая часть (2.4) при ус-
ловии вида (2.2). Действительно, в (2.4) заменены лишь с на
2Ь и 2Ь на 2Ь', Используя гипотезу индукции, где с и b заменены
соответственно на 2Ь и Ь', получаем
P{vi+ ... 4-vr<r, r=l, ..., 2b |Vj + ... + v2* = 2&'} =
= 1 -2b'12b. (2.6)
Чтобы завершить доказательство, запишем
P{vi+ ... +vr<r, r=l, ..., n} =
b
= 2 P{V1 + ... +vr<r, Г=1, ..., ... +V2ft = 2&,}X
d' = 0
b
XP{v,+ ... + v2, = 2&'} = 2(1 — 2b'/2b) P{V1+ ... + v2b = 2b'}
b' =0
(2.7)
в силу (2.6). Но
b
226'P{vi+ ... + v2^ = 2/?,} = M{vi + ••• + v2b} = 2b • 2b/n
b'=0
в силу (2.1). Следовательно, из (2.7) вытекает, что
P{vi + ... + vr < г, r=l, ..., =
b b
= SP<V'+ ••• +^ь*=Ы}-~ ^2&'РЬ+ ... +v26 = 2y} =
&' = 0 &'=0
= 1—— = 1— —.
2b n n
Таким образом, (2.4) выполняется для с = п и 0 2Ь < п. Это
завершает доказательство.
Обобщение задачи о баллотировке состоит в предположении
о наличии урны с с картами, на которых написаны числа
&i, ..., kc, такие, что
ki — неотрицательные целые числа, i = 1, ..., с,
+ ... +kc = k9 O^k^c.
Если Vi снова означает число на i-й по счету карте, вынутой из
урны без возвращения, то (2.4) для общего случая примет вид
P{vi + ... + vr <г, г = 1, ..с} — 1 — k/c. (2.8)
§ 2. Задача о баллотировке
2П
Доказательство этого более общего утверждения можно про-
вести, почти дословно повторяя доказательство (2.4). Мы опускаем
детали. (Читателю предлагается провести доказательство само-
стоятельно.)
Дальнейшее обобщение ведет к следующей задаче. Пусть
Vi, ...., vn — неотрицательные перестановочные случайные вели-
чины и
Vi + ... +vn--y (фиксированное число). (2.9)
Пусть ть ..., Тп — порядковые статистики для п независимых
наблюдений случайной величины, равномерно распределенной на
отрезке [0, t\. Предположим далее, что случайные величины
ViO’= 1, ..., п) не зависят от величин тД/= 1, ..., и).
Введем в рассмотрение ступенчатую функцию (рис. 1)
О,
Vi-F- ... + vr, тг^х<тг+1, r=l, ..., п— 1,
Vj + ... +v„, тп<х</,
и поставим вопрос, чему равна вероятность того, что график /(х)
не пересечет прямой у = х (рис. 1). Аналитическая формулировка
и решение этой задачи таковы:
( \ — y/t,
P{vj+ ... +vr<Tr, r= 1, ... n} = | Q (2.10)
274
Гл. 9. Порядковые статистики и пуассоновские процессы
Докажем (2.10) по индукции. При п = 1
( 1 ~ УЧ
P{vi<r1} = ( * _
y>t,
поскольку vi = у, a ti распределена равномерно на [0, t\.
Предположим теперь, что (2.10) выполняется для п—1. На-
кладывая условия
v1 + ... +
(0 < z < у)
и
(2.П)
найдем условную вероятность
P{vj + ... + уг <тг, г = I, ..., п I Vi + ... + = z, xn = u}. (2.12)
Предположим сначала, что Тогда в силу (2.9) нера-
венство
V1 + ... + Уп
будет заведомо выполнено при условии (2.11). Следовательно, ве-
роятность (2.12) равна
P{vj + ... + yr ^тг, г = 1, ..., п — 1 I Vj + ... + Vn-1 =*z, хп = u} =
( I — z/u, 0^.z
I 0, z>u,
в силу гипотезы индукции, поскольку (п, . . . , tn-1) при условии
(2.11) являются порядковыми статистиками для п — 1 независи-
мых случайных величин, равномерно распределенных на [0, и].
Далее, помня, что Уг не зависит от тп при всех i = I, ..., п,
рассмотрим плотность
P{V! + ... +vn_! <z}.
Тогда для у <1 и t
P{vj + ... + vr<Tr, r=l, ..., п\тп = и} =
У
= J P{vi + ... + yr <tr, r = 1, ..., n I Vi + ... + Vn-1 = 2, xn = u}X
0
У У
X Ф (z) dz= J (1 — Ф (z) dz = I — — J гф (г) dz =
о о
= 1._±M(V1+ ... +Vn_1)==i-±£rJ_^ (2.13)
14 14 ip
§ 3. Эмпирические функции распределения
275
так как из (2.9) и перестановочности vi, ..., vn следует, что
M{vJ = yln, i= 1, 2, п.
При и < у, однако,
P{vi+ ... +vr<Tr, r=l, ..., n|v„ = «} = 0, (2.14)
поскольку при условии (2.11) неравенство
V1 + ... +vn<T„
выполнено быть не может. Далее, в силу (1.13) плотность вели-
чины Тп равна
1/г(«//)"“'(I/O-
ф (и) = ) Л
7 ( 0 в противном случае.
Тогда в силу (2.13) и (2.14) при O^y-^t
P{Vi + ... +vr<Tr, г = 1, ..., n} =
t
= J P {vi + ... + vr тг, r = I, ..., n | %n — и} ip (u) du ==
о
t f
П1 l n — I \ (и \n 1 du 1 у
>-? —w) T-= 7'
У
При y>t, очевидно,
P {V| + ... + vr тг, r — 1, ..., n} = 0.
Это доказывает равенство (2.10).
Мы теперь в состоянии дать некоторые приложения упомянутых
идей к порядковым статистикам.
§ 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ
СТАТИСТИКИ
Важный класс задач, связанных с порядковыми статистиками,
касается эмпирических функций распределения случайных вели-
чин. Если X — случайная величина с функцией распределения F(x)
и
(х;, х'2>..., х^
— множество порядковых статистик, соответствующих выборке
размера п из F(x), то эмпирическая функция распределения
276
Г л. 9. Порядковые статистики и пуассоновские процессы
Fn(x) величины X является случайной величиной, определяемой
следующим образом:
О, если х<Хр
k/n,
1,
если
если х Х*п.
k= 1,
•, п-1, (3.1)
Пусть X — случайная величина с непрерывной строго возрастаю-
щей функцией распределения F(х) и эмпирической функцией рас-
пределения Fn(x). Мы хотим найти вероятность
Р {Fn (х) < yF (х), - оо < х < оо}. (3.2)
Как мы уже видели в начале этой главы, без потери общности
можно считать, что X равномерно распределена на отрезке [0, 1].
В самом деле, заменим X на величину F(X), соответствующие на-
блюдения которой равны F(Xi), F(X2), ..., F(Xn). Тогда (3.2)
сведется к
P{Fn(x)<yx, 0<х<1}, (3.3)
где Fn(x) —теперь эмпирическая функция распределения, связан-
ная с равномерным распределением.
На рис. 2 показана типичная реализация Fn(x) для равномер-
ного распределения.
§ 3. Эмпирические функции распределения
277
Докажем, что
Р (Fn (х) < ух, 0 < х < 1} =
О , если у < 1,
1 — 1/у, если у> 1.
(3.4)
Если у^1, то равенство (3.4) очевидно, поскольку не выполнено
условие Fn(l) < у. Результат для случая у> 1 является след-
ствием равенства (2.10). Необходимо лишь сделать подстановку
t = 1, у = 1/у. В самом деле, ясно (рис. 2), что событие
Fn (х) < ух,
0<х< 1,
произойдет тогда и только тогда, когда
X\>k!(ny\ 6= I, 2, ..., /г, (3.5)
где X*k (k == 1, 2, ..п) —порядковые статистики объема /г, соот-
ветствующие равномерному распределению на отрезке [0, 1]. Слу-
чайные величины vi,V2, ,vn (см. (2.10)) в данном случае являют-
ся фиксированными числами Vi = 1/(пу) 0 = Ь •••» п)> которые,
несомненно, перестановочны. Тогда (3.5) можно записать в виде
Vj + v2+ ... +vft<x’,
k= 1, 2.п,
где vi + V2 + ... + vn = 1/у = У-
Равенство (3.4) теперь следует из (2.10). Заметим, что правая
часть (3.4) не зависит от п.
Следующая задача, относящаяся к бросанию монеты, также
включает в себя эмпирическую функцию распределения. Пусть
X — случайная величина с непрерывной строго возрастающей
функцией распределения F(x). Пусть (Хь ..., Хп) и (У1, ...
.Yn) —две независимые случайные выборки объема п из рас-
пределения величины X. Пусть (X*, ..., Х*п) и (Ур ..., Уп)~
соответствующие порядковые статистики. Образуем эмпирические
функции распределения:
0, если х <
F„(x) = k[n, если ;x<rfe+1
1, если X
0, если У<
G„G/) = l]n, если гу<г1+и
1, если У>
&= I, ..n— 1,
(3.6)
/= 1, ..., п- 1,
Можно снова предположить, что Г(х) —равномерное распределе-
ние на отрезке [0,1]. Как показывает рис. 3, Fn (х) — Gn (х) = 0
при х < min (XJ, У[) и Fn(x) = Gn(x) = 1 при х max (X*, У*).
278
Гл. 9. Порядковые статистики и пуассоновские процессы
В интервале / = У*), шах(Х*, У*)) один из двух гра-
фиков может лежать полностью ниже другого или, как на рис. 3,
они могут пересекаться. Перейдем к определению вероятности пер-
вого из двух упомянутых событий, т. е. найдем
P{Frt(x)#= Grt(x) в любом подинтервале в /}. (3.7)
Эта вероятность может быть интерпретирована следующим
образом. Будем рассматривать (А\, ..., Хп, Уь ..., Уп) как од-
ну выборку и образуем соответствующие порядковые статистики.
Возможный вид их может быть следующим (рис. 3):
/V* V* V* V* V* V”* V* V* V* V* Y* Y* V*\
(Гр I 2, Ар Л2, 13, Л3, Г4, Г5, 16, Л4, Л5, ..., Лп, I
Так как обе выборки взяты из одного распределения, все та-
кие перестановки равновероятны. Обозначим порядковые статисти-
ки вектором
(ZJ, 4 .... z;„), (3.8)
где половина величин Z*k является статистиками X*, а другая по-
ловина — статистиками Y*. Для каждого k можно найти отношение
число величин X*t<ZZ*b
Рл =--------------^7^-
число величин Y < Zk
§ 3. Эмпирические функции распределения
279
Очевидно, ргп = 1. Поскольку график Fn(x) будет лежать ни-
же графика Gn(x) при всех хе/ тогда и только тогда, когда
< 1 при всех k == 2, 3, ...» 2п— 1, выражение (3.7) эквивалент-
но следующему:
Р{р&< 1, 6 = 2, 3, ..2n— 1, или рА> 1, 6 = 2, 3, ..., 2n — 1}.
(3.9)
Другое графическое представление события, записанного в фигур-
ных скобках в формуле (3.9), можно дать следующим образом.
Рассмотрим ступенчатую функцию (рис. 4), которая совершает
горизонтальный единичный скачок всякий раз, когда в перестанов-
ке порядковых статистик встречается X*, и вертикальный еди-
ничный скачок всякий раз, когда встречается KJ. График этой
ступенчатой функции лежит строго выше прямой с наклоном 45°
(кроме граничных точек, где он будет совпадать с ней) тогда и
только тогда, когда < 1 при всех k = 2, 3, ..., 2п— 1. Следо-
вательно, выражение (3.9) (а также (3.7)) есть вероятность того,
что график ступенчатой функции на рис. 4 лежит полностью по
одну сторону от прямой с наклоном 45° (кроме граничных точек).
Эта задача может быть интерпретирована как последователь-
ное бросание монеты. Предположим, что мы проводим серию из
2п бросаний симметричной монеты. Предполагая, что в конце серии
общее число выпадений герба равно общему числу выпадений
решетки (и оба они равны и), можно спросить, чему равна вероят-
ность того, что число выпадений герба всегда больше числа выпа-
дений решетки, наблюдаемых по ходу игры, или наоборот (число
выпадений решетки всегда больше числа выпадений герба при
каждом бросании)?
280 Гл. 9. Порядковые статистики и пуассоновские процессы
Если сопоставить горизонтальным скачкам события, состоящие
в выпадении герба, а вертикальным скачкам — в выпадении ре-
шетки, то таким образом каждой серии ставится в соответствие
ступенчатая функция типа показанной на рис. 4. Следовательно,
вероятность того, что число выпадений герба превышает число вы-
падений решетки (или наоборот) в течение всей серии из 2п бро-
саний при условии, что они равны в конце, равна вероятности
(3.9).
Перейдем теперь к вычислению этой вероятности, для которой
было дано несколько интерпретаций. Для этой цели мы ради удоб-
ства будем ссылаться на типичные случайные ступенчатые функ-
ции вида функции, представленной на рис. 4. Графики этих сту-
пенчатых функций идут из точки (0, 0) в точку (п, п) за 2п скач-
ков, п из которых должны быть вертикальными. Очевидно, об-
(2/2 \
п I. Чтобы сосчитать те из
них, графики которых не имеют общих точек (кроме граничных)
с прямой, имеющей наклон 45°, достаточно в силу симметрии со-
считать те ступенчатые функции, графики которых проходят ниже
указанной прямой, и удвоить это число. Однако график любой сту-
пенчатой функции, лежащий ниже прямой с наклоном 45°, прохо-
дит на первом шаге через точку (1,0) и затем идет к точке (п, п).
/ 2п — 1 \
Очевидно, существует! п Iступенчатых функций, графики кото-
рых ведут из точки (1,0) в точку (п, п).
Мы хотим сосчитать лишь те из них, которые лежат ниже прямой
с наклоном 45°. Чтобы найти это число, мы сосчитаем число сту-
пенчатых функций, графики которых ведут из точки (1, 0) в точку
(п, п) и имеют по крайней мере одну общую точку с прямой
с наклоном 45°, а затем вычтем это число из . Покажем сна-
чала, что любая ступенчатая функция, график которой ведет из
(1,0) в (п, п), имеет хотя бы одну общую точку с прямой с на-
клоном 45° и заканчивается вертикальным скачком (рис. 5), соот-
ветствует ступенчатой функции, график которой ведет из (1, 0) в
(п, п), пересекает прямую с наклоном 45° и заканчивается гори-
зонтальным скачком. Чтобы показать это, возьмем ступенчатую
функцию, график которой соприкасается с прямой с наклоном
45° и заканчивается вертикальным скачком; пусть (k, k) —точка
их последнего соприкосновения перед достижением (п, п). Отра-
зим часть графика между точками (k, k) и (п, п) ж симметрично
относительно указанной прямой (см. пунктирную линию на
рис. 5). Очевидно, такой процесс устанавливает взаимно одно-
значное соответствие между двумя видами графиков ступенча-
тых функций — касающихся прямой с наклоном 45° и заканчиваю-
щихся вертикальным скачком и оканчивающихся горизонтальным
$ 3. Эмпирические функции распределения
281
скачком после соприкосновения с прямой с наклоном 45°. Таким
образом, нужно лишь подсчитать ступенчатые функции, графики
которых ведут из (1, 0) в (/г, /г), пересекают прямую с наклоном
45° и оканчиваются горизонтальным скачком. Но, очевидно, гра-
фик любой ступенчатой функции, ведущий из (1, 0) в (п, п) и
оканчивающийся горизонтальным скачком, должен проходить че-
/ 1 \ л, ( 2п — 2\
рез точку (п— 1, п), а таких графиков существует ровно I I.
В силу принципа отражения мы знаем, что число ступенчатых
функций, графики которых ведут из (1, 0) в (п, п), пересекают
прямую с наклоном 45° или касаются ее и оканчиваются верти-
(2п-2\ ~
кальным скачком, также равно! I. Тогда число ступенчатых
функций, графики которых ведут из (1, 0) в (п, п) и всегда
остаются ниже прямой с наклоном 45° (кроме точки (п, п)),
равно
/2п — — 2\__ 1 / 2п — 2\
\ п / \ п / п — 1 \ п ) *
Это также равно числу ступенчатых функций, графики которых
ведут из (0, 0) в (п, п) и остаются ниже прямой с наклоном 45°
(кроме граничных точек).
Следовательно, вероятность того, что график ступенчатой функ-
ции (рис. 4), выбранной случайным образом, не будет иметь об-
щих точек, кроме граничных, с прямой с наклоном 45°, равна
2^r(2";2)/(2")"W^r- (з-ц»
282 Гл. 9. Порядковые статистики и пуассоновские процессы
Это также вероятность, задаваемая формулами (3.7) и (3.9). Ре-
зультат (3.10) также может быть выведен с помощью непосред-
ственного приложения теоремы о баллотировке.
Наконец, результат (3.10) можно получить из результатов, ка-
сающихся бросания монеты и полученных в гл. 4. Соответствую-
щим примером была первая из цепей Маркова, рассматривавшая-
ся в гл. 4, § 4. В нашей формулировке искомая вероятность яв-
ляется в точности вероятностью того, что первый переход из
состояния 1 в состояние 0 произойдет при (2п—1)-м испытании
при условии, что общее число выпадений герба равно общему
числу выпадений решетки за 2п испытаний.
Безусловная вероятность того, что первый переход из состоя-
ния 1 в состояние 0 произойдет при (2п—1)-м испытании, вычис-
лена в гл. 4, § 6. Было показано, что она равна -^=у2“2п^2^.
Следовательно, условная вероятность такого первого перехода
равна в точности --/оо=“о----г, как и должно быть.
Ргп — 1
§ 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ
ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
Следующая лемма представляет интерес сама по себе и будет
использована при нахождении предельного распределения для
эмпирических функций распределения.
Лемма 4.1. Пусть х — (хь ..., хп)—вектор в п-мерном
евклидовом пространстве. Предположим, что
X) + Х2 + . . . + Хп = 0
/
и что S xk =£ 0 для 1 i j п.
k=i + \
Пусть Xk+n = Xh, и пусть x(k) = (xh, Xk+1, ..., Хп, ..., Xn+fe-1) —
циклическая перестановка компонент вектора х, k = 1, 2, ..., п.
Тогда для любого г = 0, 1, ..., п—1 существует ровно один из
векторов x(fe), k= 1, ..., п, такой, что среди частичных сумм его
компонент (взятых по порядку, начиная с первой) в точности г
сумм положительны.
Доказательство. Пусть sk — х\ + х2 + ... + xk, k = 1, ..:
..., п, и So = 0, Sk±n = Sfe, k = 0, 1, ..., п. Тогда все sh, k = 1,2, ...
..., п, различны, поскольку если
Sz = Sy для 1 ^п,
ТО Xi + . . . + Xi — Х{ + . . • + Xi + Xi+i + . . . 4~Xj, т. e. Хг+I + . . .
.,. + x,= 0, что противоречит сделанным предположениям. Оче-
§ 4. Некоторые предельные распределения
283
видно, частичные суммы взятых по порядку (начиная с первой)
компонент вектора х(&) равны
Sk Sn <$£-4, •••, $k+n-l $k-l*
(4.1)
Эта последовательность статистически эквивалентна следующей:
Sk~sk-^ sk+\~~ •••> sn~~sk-i> Si“-5fc-b •••» Sjfe-i — Sfc-i- (4.2)
Пусть теперь
s* s* ..s*
I7 2’ ’ П
— единственная перестановка $<, s2, sn, для которой
♦ *
Sj >S2> ... >Sn.
Такая перестановка действительно существует (и единственна),
поскольку все Sk (k = 1, п) различны.
Число положительных членов в последовательности (4.2) (или,
что то же, в последовательности (4.1)) совпадает с числом поло-
жительных членов в последовательности
S2~~Sk~V $n~~Sk-l> (4.3)
поскольку это попросту перестановка (4.2). Далее, для любого
г = О, 1, ..., п—1 будет существовать ровно одно число k (1<<
^k^n), такое, что в точности г членов в (4.3) (а следовательно,
и в (4.1)) будут положительны. Чтобы показать это, достаточно
выбрать k так, чтобы
Sk-\ = Sr + T
Тогда «j —sjfe_I>0, s’ —$^>0, .... -s^ —sfe_j>0, a s;+1-sft_, = 0,
Sr+2 — < 0, Sn- Sfe_i<0.
Эта лемма имеет геометрическую интерпретацию. Отвлечемся
от предположения sn = 0. Отметим точки (0, 0), (1, $i), ..., (/г, sn)
на плоскости в декартовой системе координат. Соединим соседние
точки отрезками прямых, как показано на рис. 6. Получившаяся
ломаная называется суммарным полигоном вектора х = (хь ...
..., хп). Точно таким же образом можно получить суммарные
полигоны векторов х(й), компоненты которых являются цикличе-
скими перестановками компонент вектора х. Отрезок прямой, со-
единяющий точки (0,0) и (и, sn), называется хордой суммарного
полигона. Рассмотрим точку пересечения Р этой хорды с верти-
кальной прямой, проходящей через точку (&,$&).. Из элементарных
геометрических соображений ясно, что ордината Р равна (k/n)sn.
Следовательно, расстояние по вертикали от точки (k, sk) до хор-
ды полигона равно Sk— (k/n)sn.
284 Гл. 9. Порядковые статистики и пуассоновские процессы
Далее, вектор с компонентами
Ui - sn/n, х2 - sn/n, ..., хп - sn/n),
очевидно, удовлетворяет условиям леммы, включая и требование
того, чтобы n-я частичная сумма была равна нулю. Лемма утвер-
ждает, что среди суммарных полигонов, соответствующих п цик-
лическим перестановкам вектора х, для любого г = 0, 1, ..., п~ 1
существует ровно один, у которого в точности г вершин находятся
Рис. 6.
выше хорды. В частности, для случая г = 0 нужно взять цикличе-
скую перестановку, начинающуюся с номера 1 + £0, где kQ — ин-
декс, при котором достигается max (s* — (k/n) sn). Случай
г = п—1 соответствует номеру 1 + Ai, где ki — индекс, при кото-
ром достигается min (sk — (k/n) sn), и т. д.
В заключение главы укажем на применение леммы 4.1 к ана-
лизу некоторых д. с. в., связанных с эмпирическими функциями
распределения. Пусть, как обычно, Fn (х)— эмпирическая функция
распределения, построенная по выборке объема п из равномерного
распределения на [0, 1]. Введем две случайные величины Un и 17п.
Положим
Un = {общая длина всех интервалов на оси х,
на которых Fn(x)t>x} (4.4)
(рис. 7). Для реализации, показанной на рисунке, Un равна сум-
ме длин всех отрезков, отмеченных жирной линией.
Определим
7^ = inf {х |/^(х)-х = max [Fn (х) - х]}. (4.5)
§ 4. Некоторые предельные распределения 285
Величина max [Fn(x) — х] = , обычно называемая односто-
0 <1
ронней статистикой Колмогорова — Смирнова, является важной
характеристикой наблюдения, используемой в статистических те-
стах при решении, принадлежит ли исследуемая выборка задан-
ному равномерному распределению.
Наша цель в данном параграфе — определить закон распреде-
ления величин Un и Ип. Замечательным результатом является то,
что при любом п любая из этих величин распределена равномерно
на отрезке [0, 1].
Чтобы доказать это утверждение, рассмотрим пуассоновский
процесс Х(/), с параметром 1/Далее, разделим интер-
вал (0, 1) на г + 1 частей:
(О О 11____________Л
Г’ г+1 г \г + 1 ’ г+1 Г ’ ’’ \г + 1 ’
где г + 1 — простое число, большее п. (Причина этому будет ясна
из дальнейшего.) Приращения
(—гтК .... М
\г+1 / \г+1/ \г+1 /’ ’ \г+1/
— независимые и одинаково распределенные по закону Пуассона
случайные величины. Обозначим эти приращения через W2l ...
286 Гл. 9. Порядковые статистики и пуассоновские процессы
..., Wr+i соответственно и определим случайные величины
у i=l, ..., г+1,
которые, очевидно, независимы и одинаково распределены. Обра-
зуем последовательность частичных сумм
5* = ^ + ... + УЪ £=1, 2, ..., г+1,
и заметим, что
р{Sz = 0} = 0, г = 1, 2, ..., г. (4.6)
В самом деле, из равенства Si = 0 следует, что (г + 1)Х =
= ш. Но этого не может быть в силу предположения о том, что
г + 1 больше /г, i и не делится ни на /г, ни на /, поскольку г + 1 —
простое число1). Следовательно, равенство (4.6) доказано.
Аналогично можно показать, что P{Sj— Si = 0} — 0 для лю-
бых / > i. Это означает, что с вероятностью 1 никакая из частич-
ных сумм Sj — Si (0 i < j < г + 1, So = 0) не равна нулю.
Пусть
Nr — число положительных членов в последовательности Sb
S2, ..., Sr,
Lr — наименьший индекс /, для которого Sj = max (0, Sb ..., Sr).
Для последовательности Xt = Si — Si-i, i = 1, ..., г, выпол-
нены гипотезы леммы 4.1, если Sj — Si =# 0 (/> 0 и Sr+i^O. Но
указанные события имеют вероятность 1. В соответствии с леммой
P{Lf = m|Sr+1 = 0} = P{JVr = /«|Sr+I=0} = 7^T (m = 0, 1, .... г).
(4.7)
Если Х(1) = /г, то X(t)!n распределена по закону Fn(0, 1.
(Это следует из результатов § 1.) Следовательно, можно опреде-
X (t)
лить величины Un, Vn для , 0 t 1, при условии, что
Х(1) = п. Утверждается, что
|о»-^т|<т4г- К - 7ТТ |<7ТГ' <4-8»
где постоянные А и В зависят от и, но не от г.
Первое из неравенств (4.8) доказывается следующим'образом.
Если
!) Следует напомнить, что i г < г +1, а случайная величина X может
принимать лишь целочисленные неотрицательные значения. — Прим, перев.
Задачи
М>7
v/y\ / Лг Лг +1 \
и если л(/) не имеет скачка в интервале I{ I, то при
4 k j k + 1
любом /,
X(t) — ni>0. (4.9)
Поскольку X(t) имеет ровно п скачков (при условии Х(1) = /г),
то существует самое большее п интервалов длиной не более
1/(г -Т 1) каждый, для которых из условия Si > 0 не следует
справедливость неравенства
X(t) — nt>Q, //(r+l)</<f+l(r+l).
Но величина Mr/(r + 1) равна числу положительных Si, умножен-
ному на длину 1/(г 4- 1). Учитывая сказанное выше, можно за-
ключить, что Л/г/(г+ 1) может отличаться от Un не более чем на
п/(г+1). Таким образом, А^п. Аналогично можно получить
второе соотношение (4.8). Таким образом, при условии Х(1) = п
обе абсолютные величины в (4.8) стремятся по вероятности
к нулю при г-хю1). Так как Nr/(r + 1) и Lr)(r+ 1) распреде-
лены асимптотически равномерно на отрезке [0, 1] при г-*оо
(г + 1 стремится к оо, принимая лишь простые значения), это за-
вершает доказательство следующей теоремы.
Теорема 4.1. Пусть Fn(x) — эмпирическая функция распре-
деления, построенная по выборке объема п из равномерного рас-
пределения на отрезке [0, 1]. Рассмотрим случайные величины Un
и Vn, определенные формулами (4.4) и (4.5). Тогда
P{Un^x}=P{Vn^x}^ х, 0<х<1.
ЗАДАЧИ
1. Пусть Xi, Хг, ...» Хп — независимые одинаково распределенные случайные
величины с непрерывной функцией распределения, F(x). Обозначим k-e по вели-
чине из чисел
Х2....Хп
через Xnk\ таким образом,
Xfii Хп2 ^ ... ^ Xntp
Найти функцию распределения величины Хпь-
Ответ:
п
Pnk W “ S ( " ) [^ (Я)]' [1 - Р Ю]П~1'
l~kх
9 Из (4.8) следует, что указанные величины стремятся к 0 с вероятно-
стью 1. — Прим, перев.
288
Гл. 9. Порядковые статистики и пуассоновские процессы
2. При обозначениях задачи 1 показать, что
1
Fnk (х) = k ( nk j j tn~k(\-t)k~'dt.
l-F(x)
Указание'. Взять интеграл по частям.
3. При обозначениях задачи 1 найти
P{Xnk>y. Xn+i,k<x} для х^у.
Ответ:
«Р [1 -Р(У)]п~к+1.
4. Пусть Хр Z=l, 2, п, — порядковые статистики для равномерного
на отрезке [0,1] распределения. Показать, что 1пХ£ имеет такое же распреде-
п
ление, как и — 0///, где 0> — независимые случайные величины е экспонен-
i=k
циальным распределением с параметром 1.
Указание: Использовать соответствие между пуассоновскими процессами и
порядковыми статистиками для равномерного распределения.
5. Доказать, что(Х^Х^+1)\ /=1, 2, п, где по определению Х* + 1 = 1,—
независимые равномерно распределенные на [0, 1] случайные величины. Здесь
Хр Хп— порядковые статистики, соответствующие выборке объема п из
равномерного распределения.
6. Пусть Xi, Х2, ..., Хп — независимые выборки из равномерного на от-
п
резке [0, 1] распределения. Найти распределение случайной величины Р = JJ X/.
i — 1
Указание: Либо вычислить непосредственно, либо ввести новые переменные
X/ = ехр (— Yi), i =1, 2, .... п.
Ответ:
pill Р
Р{Р<р}=( [ [... f = J t(lni)“dt.
J J J J Ь2ЬЗ • • • ЪП П-1 J
° * Ч? %П-1 °
7. Пусть Xi, Х2, ..., Xh — независимые одинаково распределенные случай-
ные величины с функцией распределения F(x) и плотностью f(%). Пусть
X*^Х2^ ... ^Xfe—соответствующие порядковые статистики. Пусть Уь
У2, ... — независимые одинаково распределенные случайные величины с распре-
делением F(x), Определим целочисленную случайную величину N соотношением
yz<X*, ? Z= 1, 2, N- 1,
но YN>X*k. Аналогично определим М как случайную величину, для которой
Y^X^V i = 1,2, ..., М-1,
Задачи
289
но
Ум>4-1-
Найти распределения случайных величин N и М.
Ответ;
ь
P{N = n}= , -п *
(п 4- k) (п 4- k — 1)
2k(k-\)
+ (n + k- 1) (n + k-2) ’
Задачи 8—15 имеют дело со следующими объектами.
Пусть Xj, Хп-\— независимые случайные величины, каждая из которых
равномерно распределена на отрезке [0, 1]. Пусть
♦ * *
... <хп_,
— упорядоченные значения величин Xi. Эти порядковые статистики разбивают
единичный отрезок на п непересекающихся интервалов, имеющих длины
и^х\, и2 = х2-х\.......ип=\-Х*п_х.
— упорядоченные значения величин Ui.
В тексте этой главы установлены следующие результаты.
(А) Случайный вектор
K2/Sn, .... Kn/Sn)
(где У г — независимые экспоненциально распределенные д. с. в. с параметром 1)
и д. с. в. Sa = Yi 4- ... + Yn независимы.
(Б) Случайные векторы (Z7i, ..., Un) и
(Xi/Sn, Y2/Sn, ..., Yn/Sn)
одинаково распределены.
(В) Если S— случайная величина, распределенная, как Sn, и независимая
от вектора (£Л, U^ ..., Un), то случайные векторы (SUi, SU2,..., SUn) и
(Уь ..., Yn) распределены одинаково.
8. Найти М (и\Ш22 ... ^Л), где /1,12, • • •', in—неотрицательные целые
числа.
Ответ:
п\ ... inl
(п 4- z‘i 4- ... 4- Zn)!
9. Доказать, что
.....<./1
— независимые случайные величины.
Указание; См. задачу 5.
10. Пусть Зь = У1 4- ... 4- Yk. Показать, что
Si/S2, S2/S3, Sn_i/Sn
— независимые случайные величины.
1Q Зак. 939
290
Гл. 9. Порядковые статистики и пуассдновские процессы
11. Если Z, /, k и I — различные индексы, то показать, что
VilUh Uk/Ui
независимые случайные величины.
12. Найти распределение величины
[/1 + ... + Ur
U г+1 + ... + U r+s
Ответ: Отношение двух независимых д. с. в., каждая из которых имеет
гамма-распределение.
13. Показать, что
FUi. ..., /n)==P{t/i>/i, U2>t2, .... Un>tn}-
1, если /<0,
= (1 — t)n, если
0, если /> 1,
где t «== t\, + ... + tn*
14. Пусть Y\ ^2 < • • • < —упорядоченные значения величин Уь ...
..., Yn* Найти совместное распределение величин
гх - «у; z2=(П -1) (у; - у;),.... zn=(у; -
Указание: См. задачу 5.
Ответ: Независимые экспоненциально (с параметром 1) распределенные слу-
чайные величины.
15. Показать, что векторы (£Л, U2, ...» Un) и (nU*i9 (n — 1) (t/g ^1)» •••
...» £/д —£/^-1) имеют ОДНО и то же совместное распределение.
16. Пусть п точек выбраны на отрезке прямой длины L «случайным обра-
зом» (т. е. в соответствии с равномерным распределением). Показать, что если
0 < d < L/(n—1), то вероятность того, что никакие две точки не будут распо-
ложены ближе друг к Другу, чем на расстояние d, равна ([Л—(п — l)d]/L)n,
Указание: Установить и интерпретировать соотношение
L xrTd xrd x3~d x2~d
pr j dxn J dxn-i... J dx3 J dx2 J dxx = .
(n—2)d 2d d 0
*17. Предположим, что n точек выбраны независимо друг от друга в соот-
ветствии с равномерным распределением на окружности. Показать, что вероят-
ность того, что длины фиксированных j дуг (из образованных с4 помощью ука-
занных точек п дуг) будут больше а, фавна
( (1 — /а/0п~1, если 0</а</,
л/ = >
7 I 0 в противном случае.
где t — длина окружности.
Указание: В силу круговой симметрии выбрать любую из п точек за начало
отсчета и предположить, что остальные п — 1 точек были выбраны случайным
образом на отрезке [0,1] независимо друг от друга. Пусть
...
Задачи
291
— порядковые статистики, отмечающие расстояния от начала отсчета до первой,
второй, ..., (п—1)-й точки соответственно. Использовать результаты задачи 16.
*18. В задаче 17 показать, что вероятность того, что в точности k из п дуг
между соседними точками будут иметь длины, превышающие а, равна
^/«1 л-1
Указание: Пусть Vk — вероятность того, что из фиксированных k дуг каждая
длиннее а, а оставшиеся п — k дуг короче а. Заметить, что
У*. * = 0,1.....п.
Затем установить формулу
/ \n — k) k
где вероятность зт; определена в задаче 17. Показать, что, решив эти уравне-
ния, получим
« v ' \ п — / / J
t-k
^Напомним, что « 0 при r>n.j
19. Пусть п импульсов поступают на счетчик в моменты t\..........tn, где
6, /г, .. •, tn распределены как порядковые статистики для равномерного рас-
пределения на отрезке [0, 1]. Всякий раз после того, как счетчик зарегистрирует
импульс, у него имеется «мертвый период» длительности т, в который он не
регистрирует импульсы, даже если они на него и поступают. Интервал (0, т)
также считается «мертвым периодом». Найти вероятность того, что счетчик за-
регистрирует первые k импульсов, которые на него поступают (т. е. ti — ti-\ т,
г = 1, 2, ..., k, /о = О).
Указание: Использовать метод решения задачи 16.
Ответ:
( (1 — kx)n, если /гг<1,
[ 0, если kx > 1.
20 (продолжение). В задаче 19 найти плотность f(z/) д.с.в. У, которая равна
моменту поступления n-го импульса, при условии, что счетчик регистрирует пер-
вые k поступивших импульсов (п > k).
Ответ:
21. Используя обозначения задачи 1, скажем, что ранг величины Xj в мно-
жестве Xi, Х2......Хп равен г, если Xj ~ Хпг (см. задачу 1). Далее, пусть
Rj — ранг величины Xj в множестве Xi, Х2, ..., Xj. Показать, что случайные
величины /?1, /?2, . • •, Rn независимы и
= 1/4 r= 1, 2........п.
10*
292 Гл. 9. Порядковые статистики и пуассоновские процессы
Указание'. Доказать, что
Р{^1 =гь = ...» Rn = rn}= {/п\,
Г1 = 1; г2 = L 2; г3 = 1, 2, 3; . ..; rn = 1, 2, ..., п.
22. Пусть X], Х2, ... — независимые одинаково распределенные положитель-
ные случайные величины с непрерывной функцией распределения F(x). Доказать,
что
Р{Х*>тах (Хь Х2, ...» Xk-!)}=i/k.
23. Пусть Xj, Х<2, ... — независимые одинаково распределенные д. с. в.; опре-
делим
Мп= max (Хь Х2, .... Хп).
Пусть Пп (^, ц) (0 < X < ц) —число членов в последовательности
^[/гЛ] + 1’ ^[/гЛ]+2’
таких, что Xi = Mi. Здесь, как обычно, символ [•] означает взятие целой части.
Показать, что вероятностная производящая функция величины АМА,, р») равна
Указание. Ввести д. с. в.
г f 1. если XZ = MZ,
[О в противном случае.
Используя задачу 21, показать, что С(г)—независимые случайные величины, и
затем найти
П М(гс<г>).
I = [ггЛ]
24 (продолжение). Показать, что предельное распределение величины
Л7П(Х, ц) при п -> оо является пуассоновским с параметром 1п(рД).
25. Пусть Wi, Пн — индекс последнего максимального члена последовательно-
1
сти Xi, Х2, ..., Х|Д|Л]. Доказать, что величина имеет предельное при
п -> оо распределение, являющееся равномерным на отрезке [0, 1].
26. Пусть I^i, 1F2, ... — независимые и равномерно распределенные на [0,1]
i
д. с. в. Пусть N— число индексов /, удовлетворяющих соотношению/< JflT/<l,
7=1
где / — фиксированное число, 0 < t < 1. Найти функцию распределения вели-
чины N.
Ответ-. N имеет пуассоновское распределение с параметром —In t.
27. Пусть Xi, Х2, ..., Хп суть п наблюдений случайной величины с непре-
рывной функцией распределения F(x). Пусть Nn—число индексов k, для кото-
рых Xk > max (Xj, Х2, ..., Xft_i)^ где k — 1, 2, ..., п. Показать, что произво-
дящая функция для Nn равна
Задачи
293
28. В предыдущей задаче установить соотношение
lim
П->оо
М(2УП)
In п
29. Пусть Zi = (Xi, Yi), i = 1.n, суть n пар действительных случайных
величин, причем все из них независимы и одинаково распределены с непрерыв-
ной функцией распределения F(x). Говорят, что вектор Zi = (Xit Уг)—допусти-
мый, если не существует другого Zj = (Xj, Yj), у которого Xj Xit Yj > У,.
Пусть In—число допустимых векторов в последовательности Z], Z2, Zn.
Без потери общности предположим, что Zi перенумерованы в таком поряд-
ке, что
... <Хп,
Доказать, что
п
/п=3 Ui.
i = 1
где Ui — независимые случайные величины, определяемые равенством
(1, если ранг Уг- в множестве Yi, Zj+1, .... Yn равен п — г + 1,
1 I 0 в противном случае.
Указание. Использовать результат задачи 21.
30. При условиях задачи 29 найти вероятностную производящую функции
g(t) величины In (см. задачу 27).
Ответ:
81 ’ п\ Г(0
31. Пусть Xi, Х2, ...— последовательность независимых одинаково распре-
деленных случайных величин с функцией распределения F (х) и плотностью f(x).
Пусть Hi—целочисленная случайная величина, равная наименьшему индексу,
такому, что X >XV Далее, пусть п2 — наименьший индекс (>п{), такой, что
Хп>Хп, и во°бще пусть пг — наименьший индекс (>nr_i), для которого
>ХП . Найти функцию распределения величины Хп .
Указание: Накладывая условие на значения величин Хп , Хп , ..., Хп ,
доказать формулу
р(Ч«:гГ
Z хг хг—\ ’ Х1
f fz - . f f(xr-t) dxr-i С f (xr_2) dxr_2 f f (x0) dx„
\Hxear J 1-F(xr_,) J 1-F(xr_2) J t-F(x0)-
— oo — oo —oo —oo
Затем упростить ее. Другой путь решения — использование индукции по г.
Ответ: Плотность величины Хп равна
. . . [-In (1 - F (г) )]г ... . п
fxn (?) = ---- г,. - Z>0.
32. Пусть Х\, Х2, ... — последовательность независимых одинаково распре-
деленных случайных величин с функцией распределения F (х) и плотностью f(x).
Пусть n,i—д. с, в., определенные в задаче 31. Найти распределение случайной
величины пг — пг-р
294
Гл. 9. Порядковые статистики и пуассоновские процессы
Ответ:
i-1
Р{«г-«г-1 = (}=^ (-1) ' ( k ) (й +2)г
6=0
Задачи 33—37 являются вариантами задачи о баллотировке.
33. В качестве модификации задачи о баллотировке, приведенной в тексте,
найти вероятность того, что А никогда не будет отставать при подсчете голосов.
Указание: Рассмотрим более общую урновую схему, когда в урне имеется
с карт, на которых написаны числа k\, k2, ..., kc. Пусть nQ, n2, ... — коли-
чество нулей, единиц, двоек, ... среди k\, k2, ..., kc. Предположим, что
k[ + ... +kc = k (0 k с). Пусть Vi (f = 1, 2, ..., c) — д. с. в., значение ко-
торой равно числу на i-й вынутой карте. За один раз вынимается одна карта;
обратно в урну она не возвращается. Обозначим
Pj (ct k; п0, ..) ~ Р {vi + ... + vr <r + /, г = 1, 2, ..., с}.
Поместив в урну дополнительную карту с числом 0, получим рекуррентную фор-
мулу
Pj-i (с 4- 1, k\ nQ + 1, п2, ...) = n°.jl,-Py (с> k\ tlQ, nb ...) +
J c + 1
/-1
VI n.
+ 2jT+TP/-i(C’k~i:n0+Lnt...................ni-l- ni~1' ni + V •••)•
i = l
С помощью метода, использованного в тексте (где nQ = а, п2 = b, а 4- b = с),
показать, что вероятность того, что А никогда не будет отставать при подсчете
голосов, равна
Р {vi 4- ... 4- vr <Г + 1, Г = 1, 2, ..., с}.
Ответ: (а — b 4- !)/(«+ 1).
34. Рассмотрим урну, содержащую а белых и b черных шаров (а > Ь).
Последовательно вынимаются все шары случайным образом без возвращения.
Одновременно производится случайное блуждание по неотрицательным целым
числам, которое начинается с 1. Направление шага (вправо или влево на 1)
зависит соответственно от того, белый или черный очередной шар вынут из
урны. Чему равна вероятность того, что за а + b шагов хотя бы один раз будет
достигнута точка 0?
Ответ:
Ь/(а+1).
35. Пусть а и b — положительные целые числа, а > Ь. Доказать следующие
равенства:
(о -4т+
а 4- о
ь-\
, у n-i/2fe+l\ а(а—1) ... (a- k+ 1)6 (b - 1) ... (b - k) _ 6
k ) (a + b) (a + b-1) ... (a + 6 —2/г) a + 1’
fe=l
b
ц- Д (a — 1) ... (a — r 4- 1) 6 (6 — 1) ... (6 — r + 1) / 2r \ a — b _ b
(a 4- b) (a 4- b — 1) ... (a 4- b — 2r 4- 1) \ r / a 4- b — 2r a 4-1 ’
r=l
Задачи
295
Указание'. (1) Рассмотреть ситуацию задачи 34. Выразить событие, заклю-
чающееся в достижении начала координат, через момент первого достижения
начала координат.
(2) Это равенство получается при рассмотрении последнего момента, в кото-
рый количества вынутых белых и черных шаров равны.
Должны быть использованы результаты задачи о баллотировке, задачи 34
и вывод формулы (6.12) в гл. 4.
36. При условиях задачи 34 доказать, что вероятность достижения начала
координат равна
, . b(b-~\) ... (6-n-M)
Рп^а' (а+ 1) (а+ 2) ... (а+«) ’
если случайное блуждание начинается в точке п. Здесь п — положительное целое
число, п Ь.
Указание: Найти рекуррентную формулу для рп(а,Ь). Затем использовать
индукцию по п совместно с результатом задачи 34, т. е. равенством pi (а, Ь) =»
— b/(a + 1).
37. Пусть Fn(x) —эмпирическая функция распределения, соответствующая
п наблюдениям из равномерного распределения на [0, 1]. Найти вероятность
Рп (а* V) =“ Р {Fn (х)<а + ух при всех 0<х<1),
где (п — 1)/п а 1, у > 0, у 4- а > 1.
Ответ: 1—[(1—а)/у]п.
38. Пусть а < (и— 1)/п, а все остальные условия — те же, что и в задаче 37.
Доказать, что
1
(l-a)ly
Указание: Наложить условие на максимальное значение реализации случай-
ной величины и использовать формулу полной вероятности.
39. Пусть
п а\п~1(. (ti — i а\(у + а — 1 \
с»-Uhr-у) I’-Hf-v)) гНН'
Показать, что
k
Рп (а, у) = 1 - 2 Сл (а’ V- 0.
/==0
где целое число k определяется соотношением
Указание: Рассмотрим вспомогательное событие, заключающееся в том, что
Fn (х) а + ух при некотором х. Оно происходит тогда и только тогда, когда
„ ( п — г а\^п — г ,
---V/^—п— ПРИ некотоРом г==1’ 2........k.
296
Г л. 9. Порядковые статистики и пуассоновские процессы
Введем событие Аг, заключающееся в том, что минимальный индекс г, для
которого выполняется неравенство
„ / п — г а \ п — г
р---------->-------
\ пу У / п
k
равен i (Z = О, 1, k). Найти Р {А/}.
М
Другим методом решения является использование результата задачи 37 и
проведение индукции по п.
ЗАМЕЧАНИЯ
В этой главе мы придерживаемся точки зрения Реньи [1] на
порядковые статистики и пуассоновские процессы.
Комбинаторные методы, примененные во второй половине
главы, в основном базируются на работе Такача, которая пока
еще не вышла в виде книги1).
Подробное обсуждение порядковых статистик с точки зрения
классической статистики можно найти в книге Уилкса [2]. См.
также приводимые там ссылки.
ЛИТЕРАТУРА
1. Renyi A., Wahrscheinlichkeitsrechnung, mit emem Anhang fiber Informations-
theorie, Deutscher Verlag der Wissenschaften, Berlin, 1962.
2. Уилкс С., Математическая статистика, «Наука», M., 1967.
') Монография Л. Такача «Комбинаторные методы в теории случайных про-
цессов» вышла в оригинале практически одновременно с книгой Карлина; рус-
ский ее перевод вышел в 1971 г. (изд-во «Мир»), — Прим. ред._
Глава 10
БРОУНОВСКОЕ ДВИЖЕНИЕ
§ 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Математический анализ некоторых специальных классов слу-
чайных процессов развит весьма детально. Наиболее известен
процесс броуновского движения, который исторически был пер-
вым среди досконально исследованных процессов. Мы лишь слегка
коснемся некоторых из наиболее интересных его особенностей и
надеемся вызвать у читателя интерес к элегантной и совершенной
теории этого процесса.
Броуновское движение как физическое явление было открыто
английским ботаником Броуном в 1827 году. Математическое опи-
сание этого явления было выведено из законов физики Эйнштей-
ном в 1905 году. С тех пор в этой области отмечен значительный
прогресс. Физическая теория была далее усовершенствована Смо-
луховским, Фоккером, Планком, Бюргером, Ферсом, Орнштейном,
Уленбеком, Чандрасекаром, Крамерсом и другими. Математиче-
ская теория развивалась медленнее, потому что точное математи-
ческое описание модели связано с рядом трудностей, тогда как
некоторые из вопросов, на которые физики получили ответы из
данной модели, были весьма простыми и интуитивно ясными. Мно-
гие из ответов были получены эвристическим путем Башелье
в его книге (1912 г.), тогда как первое математически четкое по-
строение теории было дано Винером в его диссертации (1918 г.)
и более поздних работах (см. ссылки в конце данной главы).
В терминах нашей общей классификации случайных процессов
процесс броуновского движения является примером марковского
процесса с непрерывным временем и непрерывным пространством
состояний. Мы обсудим только одномерный случай.
Пусть X(t)—положение частицы (как функция времени)
в броуновском движении (см. стр. 22). Пусть х0— положение ча-
стицы в момент /о, т. е. X(to) — Xot а р(х, /|х0) — условная плот-
ность вероятности величины X(t + t0) при условии, что X(Iq) = Xq.
Мы постулируем, что вероятностный закон, «управляющий» пере-
ходами, стационарен во времени (поскольку р(х, /|х0) не зависит
от начального момента /0).
Поскольку p(x,t\xo)—плотность вероятности, то
оо
р (х, 11 X(j) 0, J р(х, 11 х0) dx = 1. (1.1)
298
Гл. 10. Броуновское движение
Далее, предположим, что X(t + /0) при малых t с большой вероят-
ностью находится вблизи точки Х(/о) = *о. Это достигается усло-
вием
lim р (х, 11 xQ) = 0 при х#=х0. (1.2)
Исходя из физических законов, Эйнштейн показал, что функ-
ция р(х,/|х0) должна удовлетворять уравнению в частных произ-
водных
(1-з)
di дх2 ’ х 7
которое называется уравнением диффузии; D является коэффици-
ентом диффузии. Малые частицы совершают броуновское движе-
ние благодаря столкновениям с молекулами окружающих их газа
или жидкости. Величина D находится из формулы D = 2RT/Nf,
где R— газовая постоянная, Т — температура, N— число Авогад-
ро, f — коэффициент трения. Выбирая соответствующий масштаб,
можно получить D = 1/2. Тогда непосредственной проверкой уста-
навливаем, что функция
р (х, /1 х0) =
у==г ехр [- (х - х0)2/2/]
(1.4)
является решением уравнения (1.3), точнее единственным его
решением, удовлетворяющим условиям (1.1) и (1.2). (Вопрос о
единственности решения уравнения (1.3) должен быть сформули-
рован строго, а его анализ требует большой аккуратности и выхо-
дит за рамки данной книги. Прилежный читатель может обра-
титься к книге Ито и Маккина, упомянутой в ссылках в конце
главы.)
Другим подходом к (1.3) является аппроксимация с помощью
дискретного случайного блуждания1). Рассмотрим симметричное
случайное блуждание на целочисленной решетке (см. пример Б,
гл. 2, § 2). Пусть Pk(n)—вероятность того, что частица при слу-
чайном блуждании в момент п оказывается на расстоянии k спра-
ва от исходной точки (—оо<й<оо). Уравнение Колмогорова —
Чэпмена (формула (3.2) гл. 2) принимает в этом случае вид
рИ«+ 1) = уРй+1(«) + уРй-1(«),
или
Pk («+ О - Pk («) = у fpfe+i («) - 2Pk («) + Pk-i(«)]• (1.5)
Слева стоит дискретный аналог производной по времени, а спра-
ва— с коэффициентом 1/2 — дискретный аналог второй производ-
!) Подробности можно найти в книге Е. Б. Дынкина и А. А. Юшкевича
«Теоремы и задачи о процессах Маркова», «Наука», 1967. — Прим, перее.
§ 2. Совместные вероятности
299
ной по пространственной переменной. Переходя соответствующим
образом к пределу при одновременном стремлении времени между
переходами и величины шага к нулю, можно получить (1.3) из
(1-5).
В частности, пусть интервал времени между переходами равен
А, а величина каждого шага равна т]. Тогда аналог соотношения
(1.5) имеет вид
р411((п+1)Д)-ри(пЛ) (1/2)[р(й+01)(пЛ)-2рАт)(пД) + р(А 1)т)(/гД)]
Д Д •
Пусть теперь Лит] стремятся к 0 так, что сохраняется соотноше-
ние Л = т]2, и в то же самое время пусть п и k стремятся к оо так,
чтобы £т]->%, а лгД —► Л Тогда pk^ (/гД) -н> р (х, ZjO) и соотношение
(1.6) формально переходит в (1.3).
Мы не будем пытаться проводить эту процедуру более строго.
Это просто по существу, но требует довольно тонкого анализа.
При другом способе перехода к пределу используется цен-
тральная предельная теорема. Имеем
рА(п) = Р{Х1 + Х2+ ... +Xn = k},
где {XJ — последовательность исходов бросания симметричной
монеты (т. е. Xi = 1, если выпал герб, и Xi = —1, если выпала ре-
шетка, причем вероятность каждого исхода равна 1/2). По цен-
тральной предельной теореме (см. гл. 1, § 1)
V п х х
1
К2л
Предельное соотношение (1.6) и равенство (1.7) в сущности экви-
валентны и связаны друг с другом «принципом инвариантности
для случайных процессов». Приведенные эвристические выводы
могут быть сделаны строгими, но это выходит за пределы данной
книги.
§ 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
Переходная плотность (1.4) дает вероятностное распределение
только для величины X(t) — Х(0). Полное описание процесса броу-
новского движения дается следующим определением.
Определение 2.1. Броуновское движение является случай-
ным процессом {Х(/); t^O} со следующими свойствами:
(а) любое приращение X(t + s)—X(s) нормально распреде-
лено со средним значением 0 и дисперсией ct] с > 0 — фиксирован-
ный постоянный параметра
lim У рДга)
4
j ехр (— и212) du. (1.7)
300
Гл. 10. Броуновское движение
(б) для любых двух непересекающихся интервалов (/ь/2),
(/3,/4), t\ <4^4 приращения X(t4)— Х(/3) и X(t2)— X(t{) —
независимые случайные величины с распределениями, указанными
в пункте (а); аналогичное свойство имеет место и для п непересе-
кающихся интервалов, где п — произвольное положительное целое
число.
Таким образом, мы постулируем, что смещение X(t + s) — X(s)
не зависит от прошлого, или, другими словами, если известно
X(s)-=x0, то никакая дополнительная информация о поведении
Х(т) при т < 5 не влияет на наше знание вероятностного закона,
«управляющего» приращением Х(/ + $)—X(s). Формально это
означает, что при t > tQ > ti > ... > tn
Р{Х(О<х|Х(/о) = хоД(/1) = х1) ..., X (/„) = %„} =
= P{X(O<x|X(fo) = xo}. (2.1)
Это говорит о марковском характере процесса. Подчеркнем, одна-
ко, что предположение (б) о независимости приращений на самом
деле более ограничительно, чем марковское свойство. В силу
пункта (а) определения при с = 1 имеем
Р{Х(О<х|Х(/о) = хо}=Р{Х(О-Х(/о)<х-хо} =
х-х0
= -7=J== [ ехр Г--------~---1 da. (2.2)
/2л(/-/0) Ч 2(/-/0) J
Согласованность пункта (б) определения с пунктом (а) сле-
дует из известных свойств нормального распределения, например
если ti t2 t3, то
X (/3) - X (/0 = [X (f3) - X (t2)] + [X (t2) - X (/3)].
Слагаемые справа являются независимыми случайными величи-
нами со средними 0 и дисперсиями t3—t2 и t2—ti соответственно.
Следовательно, их сумма распределена нормально со средним 0
и дисперсией t3 — tit как и должно быть.
Используя (2.1) и (2.2), нетрудно найти совместную плотность
величин X(ti), X(t2), ..., X(tn) (0 </1 </2 < ... < tn) при усло-
вии, что X(0) = 0. В самом деле, для этого нам необходимо лишь
знать плотность вероятности того, что Х{ =-Х(Л) = хь Х2— Х{ —
= х2—Xi и т. д. и, наконец, Хп — Xn~i = xn — хп-ь В силу пункта
(б) определения сразу получаем следующее выражение для функ-
ции плотности:
/(*)....Xn) = p(xb ti)p{x2-Xi, ti-ti) ... р(хп-X^-i, tn-tn^),
(2.3)
где
р (х, t) = ехр I - —).
/2л/ \ 2/ /
§ 2. Совместные вероятности
301
Имея формулу (2.3), можно в принципе найти любые интере-
сующие нас условные вероятности.
Из марковского свойства следует, что если < /2 < /3, то услов-
ная плотность величины Х(/3) при известных X(/i) и Х(/2) совпа-
дает с условной плотностью величины Х(/3) при известной вели-
чине Х(/2).
Однако плотность величины Х(/2) при известных X(ti) и X(t3)
также представляет интерес. Предположим для определенности,
что = Х(/3) = 0 и /1 = 0, /з = 1, а /2 = t (0 < / < 1).
В силу (2.3) совместная плотность Х(/) и Х(1) равна
Отсюда следует, что условная плотность величины %(/) при усло-
вии X(0) = X (1) = 0, которую мы обозначим через f/(x|X(0) =
= Х(1) = 0), равна
В частности, Мс(Х(/)) = 0, а МС(Х2(/)) =/(1 — /), где Мс озна-
чает математическое ожидание, взятое при условии Х(0) = Х(1) =
= 0. Такими же методами можно получить более общий интерпо-
ляционный результат.
Теорема 2.1. Условная плотность величины Х(/), /1 < / < Z2,
при условии, что X{ti)-=A, а Х^)=^В, является нормальной со
средним
и дисперсией
(t-td
/2 —1\
Это можно свести к разобранному случаю следующим образом.
Рассматриваемая условная случайная величина Х(/), т. е. д. с. в.
X(t) при условии, что Х(/1) = А и Х(/2)= В, имеет такую же плот-
ность, как и случайная величина Л+Л'(/ —/4) при условии, что
Л (0) = 0, X(Z2—/1) = В — Л, которая в свою очередь имеет такую
же плотность, как и случайная величина
при условии, что Лг(0) = 0 и Х(/2 — Л) == 0.
302
Гл. 10. Броуновское движение
§ 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ
ЗНАЧЕНИЯ
Броуновское движение — физический процесс, и это наводит
на мысль, что возможные реализации X(t) как графики изменения
положения частицы (т. е. выборочные траектории), движения ко-
торой определяются непрерывными столкновениями с молекулами
окружающей среды, являются непрерывными функциями времени.
Этот факт является верным, но его строгое доказательство тре-
бует довольно тонкого анализа. Выборочные траектории Х(/),
хотя и непрерывны, но весьма причудливы, и у них ни в одной
точке не существует производной. Этот факт является довольно
глубоким. Исчерпывающее описание структуры выборочных тра-
екторий процесса броуновского движения можно найти у П. Леви,
а также у Ито и Маккина (см. ссылки в конце этой главы).
Используя свойство непрерывности траекторий, покажем, как
вычислить различные интересные вероятностные характеристики
броуновского движения. Первый пример иллюстрирует использо-
вание так называемого принципа отражения.
Имея в виду непрерывность X(t), рассмотрим множество тра-
екторий Х(/), Х(0) = 0, обладающих тем свойством, что
а (я>0). Поскольку X(t) непрерывна и Х(0) = 0, суще-
ствует момент т (который сам является случайной величиной, за-
висящей от рассматриваемой выборочной траектории), в который
Л(/) впервые достигает значения а.
При t > т построим отражение X(t) относительно прямой х = а
и обозначим
j X (t) цяя. t <
I а — [X(/) — а] для t>x
(рис. 1). Заметим, что Х(Т)<а, поскольку Х(Т)>а. Так как ве-
роятностный закон развития процесса при t > т при условии, что
Х(т) = а, симметричен по отношению к значениям х > а и х < а
и не зависит от предыстории процесса до момента т, операция от-
ражения ставит в соответствие каждой выборочной траектории
сХ(7’)>й две равновероятные выборочные траектории X(t) и
Х(0> такие, что
max X (и) а и max X (и) а.
Обратно, в силу самой природы этого соответствия каждая траек-
тория Х(/), для которой maxX(u)^#, является одной из двух
равновероятных выборочных траекторий, одна из которых такова,
что Х(Т}> а, если Х(Т)4=а. Но Р{Х(71) = а} =0. Таким образом,
§ 3. Непрерывность траекторий
303
можно заключить, что если X (0) = 0, то
оо
Р{ max Х(и)>а} = 2Р{Х(Г)>а} = -7= [exp(-^-)dx. (3.1)
о<и<т У2лГ J \ 2Т /
Приведенное выше рассуждение нельзя считать исчерпываю-
щим, хотя этот метод и типичен для многих задач анализа слу-
чайных процессов с непрерывными траекториями. (Такие процес-
сы называются диффузионными.) Строгое обоснование включало
Рис. 1,
бы использование строго марковского свойства для марковского
времени (см. гл. 8, § 4), соответствующего первому прохождению
уровня а.
С помощью этого же «принципа отражения» можно теперь
решить следующую задачу: найти
А(х, y) = P{X(t)>y, min X(u)>0 |X(0) = х} (3.2)
для х > 0 и г/> 0. Чтобы найти (3.2), запишем очевидное соотно-
шение
Р{Х(/)></|Х(0) = х} =
= Л(х, у) + Р{Х(/)>«/, min Х(м)<0|Х(0) = х} (3.3)
и применим принцип отражения к последнему члену.
Рис. 2 поясняет рассуждение. Можно заключить, что
Р{X (/)>у, min X (ц)< 01X (0) = х} =
= Р{X(/)< — у,. min X(и) <0 |X (0) = х} =
= Р{Х(0< -у|Х(0) = х}. (3.4)
304
Г л. 10. Броуновское движение
Обосновать (3.4) можно следующим образом. Рассмотрим
траекторию, начинающуюся в точке х > 0, удовлетворяющую усло-
вию X(t)> у и достигающую значения 0 в некоторый промежуточ'
ный момент т. Отражая такую траекторию относительно нуля
после момента т, получаем траекторию, начинающуюся из х и до-
стигающую значения, меньшего, чем —у, в момент t. Отсюда по-
лучается первое равенство в соотношении (3.4). Второе равенство
очевидно, поскольку условие min X(z/)^O излишне при выпол-
нении неравенства %(/)<— у (г/>0)1)- Подставляя (3.4) в (3.3),
получаем
°° ~и
А (х, у) = f ехр [ — ———1 du-------l=r f exp Г — 1 du.
J 4 2/ /2л/ J 2/ I
У -oo
С помощью соотношения (3.4) можно определить распределе-
ние момента первого достижения уровня а > 0 при условии, что
J) Т. е. {X (/) < — у (r/>0)}cz{ min .V (//) < 0} и, следовательно, Р fV (/) <
<~у(у>^У mitl (и) < 0} = Р {X (0 < — у (у > 0)}. — Прим, перев,
§ 3. Непрерывность траекторий
305
/(0)^-0. Пусть Та — момент первого достижения траекторией
Х(0 значения а, где Х(0) = 0. Тогда, очевидно,
Р{ГЙ<О=Р{ max Х(и)>а|Х(0) = 0}. (3.5)
Но в соответствии с (3.1)
Р{ max X (u) > а | X (0) - 0} = 2Р {X (/) > а} =
и поэтому
exp[-44].l.v.
а
Делая замену переменной х = уУ t, получаем
__1 оо
Р{7’й<0 = ]/| / ехр[-4]^- (3.6)
aJVT
Функция плотности случайной величины Та получается дифферен-
цированием (3.6) по t. Таким образом,
fTa (t | X (0) = 0) dt = Г3/г exp [ - 4] dt. (3.7)
у 2,71 L J
В силу симметрии и пространственной однородности процесса
броуновского движения мы заключаем, что
Р{ min X (и) 0 | X (0) = а} = (в силу симметрии)
= Р{ max X (и) 0 | .Y(O) = — а} = (в силу однородности)
= Р{ max Х(и)>а|Х(0) = 0}=Р{7’я<0= (в силу (3.7))
О с и с t
t
= __А_ J u-3/2exp dzz, а>0. (3.8)
Другой способ получения результата (3.8) состоит в следую-
щем. Если Х(/0) = я, то вероятность Р(а) того, что X(t) имеет
хотя бы один нуль между to и равна
Р (а) --= ]' ехР £ ~ “j U~V‘ du. (3.9)
306
Гл. 10. Броуновское движение
С помощью этой формулы можно найти вероятность а того,
что если Х(0) = 0, то Х(/) обращается в нуль хотя бы один раз
на интервале (/о, ti)-
В действительности мы налагаем условие на возможные зна-
чения %(/о). Так, если X(t0) = a, то вероятность того, что X(i)
обращается в нуль на интервале (/о, ti) хотя бы раз, равна Р(а).
В силу формулы полной вероятности1)
а = j' P(a)P{|X(/o)|==a|X(O) = O}rfa =
о
___ оо
<3-9 10>
о
Подставляя в (3.10) выражение (3.9) и меняя затем порядок ин-
тегрирования, получим
___ОО /Л-^0 \
а — 1/Г— f ехр Г——1 Л— I f ехр Г——1 и~,,г du I da =
> nt0 J L 2<0 J /2л \ J r L 2u J J
— —f и~я/1 f f°a exp [—— f— + — 'll da | du. (3.11)
n\t0 J [J HL 2 \u tj\ )
Внутренний интеграл может быть взят, и после упрощения по-
лучаем
h-h
а = ^to f du - .
л J (to + и) У и
После замены переменных и = iov2 получим выражение
do 2 , Г ti —t{
которое можно записать с помощью стандартных тригонометри-
ческих соотношений в виде
ла
-COS —,
или
2
а = —arc cos
JT
В результате получаем следующую теорему.
9 В первом интеграле сомножитель Р {| A’(/0)l=« I А’(О) =0} является услов-
ной плотностью вероятности величины Х(/о), а не условной вероятностью, т. е.
здесь Р {| Х(/о)I = а | Х(0) = 0} = р(а, tQ | 0) + р(-а, tQ | 0) = 2р(п, tQ | 0), а > 0. -
Прим, перев.
Задачи
307
Теорема 3.1. Вероятность того, что X(t) имеет по крайней
мере один нуль в интервале (/0, /1) при условии, что Х(0) = 0,
равна ___
2 ->/Ч
а = — arccos 1/ ~~ .
Л г н
Проведенные вычисления и обсуждения являются лишь введе-
нием в сложную структуру процесса броуновского движения. Су-
ществует множество фундаментальных связей между процессами
броуновского движения и различными типами случайных процес-
сов, возникающих в физике, биологии и экономике. Мы отсылаем
читателя к специальным книгам, посвященным этой теме.
ЗАДАЧИ
Следующие задачи имеют дело с броуновским движением, определенным на
стр. 299, с=\ (т. е. о2(X(/))=/ и Х(0) = 0). Они дополняют предыдущий
текст и раскрывают другие интересные свойства обычного процесса броуновского
движения.
1. Доказать, что
Р{ max X (и) <1, (/) ^x + dx}~
0<u<t
If / Х2\ /
~ ( ехр |---— ехр —
/2л/ I \ 2// \
(2|-х)2
2/
для g > х, g > 0.
Указание'. Использовать принцип отражения или продифференцировать соот-
ветствующим образом переписанную формулу для А(х, у) (см. формулу (3.3)).
2. Определить совместную плотность для М (/) = max X (и) и X (/).
Ответ'.
2 (2g — х)
tY2nt
(2g-x)2\
2t /
0,
l<x.
3. Доказать, что P {Л1 (/) > g | X (/) = M (/)} » exp (—g2/2f).
Указание'. Пусть Y (/) = M(t)—X(t). Найти условное распределение для
M(t) при условии, что У(0 = 0.
4. Пусть Tq — максимальный нуль функции Х(т), не превышающий t. Дока-
зать формулу
9 у---
Р {То < М = — arcsin у tjt .
Указание'. Использовать теорему 3.1.
5. Пусть Т1 — минимальный нуль функции Х(т), превышающий t. Показать,
что
(а) Р {Тх <h} = ~ arccos/7ДГ,
(б) Р{7'0</0. Л > Л) = arcsin Vtjti.
л
308
Гл. 10. Броуновское движение
6. Доказать, что |АД/)|— марковский процесс с непрерывным временем.
(Использовать симметрию Х(/) относительно начала координат.)
7. Доказать, что У(/)=Л4(/)—Х(/) —марковский процесс с непрерывным
временем.
Указание-. Учесть, что для t' <t
Y (/) = max { max (X (и) - X (f) ), Y (Г)} - (X (/) - X (f)).
8. Показать, что случайные процессы Y(/) = M(t)—X(t) и | X(/) | эквива-
лентны. (Говорят, что два процесса эквивалентны, если у них совпадают все
конечномерные распределения.)
Указание-. Поскольку |Х(/)| и У(/)—марковские процессы, достаточно до-
казать, что плотности функций распределения
Р{Г (0<//|Г (/о) = //оДо</} и Р{|Х(0|<^| \X(i0)\^y0, t0<t}
совпадают.
Для вычисления первого члена использовать задачу 2 и представление У(/),
данное в задаче 7.
9. Доказать, что вероятность того, что У(/) обратится хотя бы один раз в О
на интервале (/оЛ1), равна (2/л) arccos Ytjt\ •
10. Пусть т\ (г’)- минимальный (максимальный) нуль функции У(т) =
= Л1(т)—Х(т), превышающий (не превышающий) t. Показать, что и
обладают теми же распределениями, что Pi величины Т$ и Ti соответственно,
определенные в задачах 4 и 5.
11. Доказать, что _________
9 /~ и — f
Р{Х (т)У=0, 0<Д<т<и< 1 | X (0) = X (1) = 0} = arccos "I/ —~~~ .
л I и (1 — I)
Указание: Вычислить
оо 1
2 J J Р {X (/) = a, T(a) = x — t, X (1 - т) = 01 X (0) = 0} X
а=0
X [Р {X (1) = 0 I X (0) = 0)1 da dx,
где Т(а)—время первого достижения броуновским процессом уровня 0, если
АДО) =а (см. формулу (3.7)). Тогда равенство
_ _ _2 _________1______________1___________t =
я /1 -(„-/)/«(! -О ’ ’ 2 1/1_f_LK2 ~
V \ и)
К t 1
л «^(1 — и) (и — /)
доказывает искомый результат.
12. Пусть Г(Х)—время первого прохождения уровня А > 0, если АДО) = 0.
Доказать, что распределение величины 4- А2) совпадает с распределением
суммы Т(Л1) и Т(%2), где Т(Ai) и Т(А2) рассматриваются как независимые слу-
чайные величины, Xi, Х2 > 0.
Задачи
3(J9
13. Найти условную вероятность того, что X(t) не обращается в нуль на
интервале (W2) при условии, что X(t) и.е обращается в нуль на интервале
(Mi), 0 < tQ /1 С f2.
Ответ: ___
arcsin Vta!4
arcsin Уt0/tt
14. Показать, что вероятность того, что X(t) не обращается в 0 на интер-
вале (0,/2) при условии, что X(t) не обращается в 0 на интервале (0, t\),
О < t\ < /2, равна Vtxlt2.
Указание: Найти
Р{Х (/)У=0, 0</0</</2|Х(/) ¥=0, 0</0
а затем положить fo~>O.
15. Показать, что вероятность события |Х(6)—X(f0)l>£ при условии, что
X(t) принимает какое-то экстремальное значение (X(t) имеет два экстремаль-
ных значения) на интервале (/0, fi) либо в точке f0, либо в fb равна
ехр(—g2/2(fi — f0)), /о>О.
Указание: Доказать следующие утверждения.
(1) Событие, упомянутое в задаче, может произойти лишь при осуществле-
нии одной из четырех возможностей: (А) Х(/о) является минимумом, (В) X(f0)
является максимумом, (С) Х(Л) является минимумом, (D) X(t\) является ма-
ксимумом.
(2) Условная вероятность осуществления какого-либо одного из событий
(А), (В), (С), (D) при условии, что имеет место любое другое из этих событий,
равна нулю.
(3) Р {| X (fj — X (t0) I > g I (А) или (В), или (С), или (D) имеют место} =
= Р {I X (fi) — X (tQ) | > g I а} Р {а | (А) или (В), или (С), или (D)
а=(А), (В), (С), (D)
имеют место} = ехр {—g2/2(fi— f0)} (использовать задачу 3 и принцип отраже-
ния).
16. Доказать, что
Р {X (т) 0. т е= (ОЛ) | X (0) = а, X (t) = b, ab > 0} = 1 - e~2ablt.
Указание: Использовать функцию А(х, у).
17. Проверить, что M(AZ(f)X(s)| X(0) — 0) = min (f, s).
18. Доказать, что следующие пары случайных величин имеют одни и те же
распределения при всех t > 0:
(а) Х(сЧ)!с, с>0 и X(t),
(б) tX(Vt) и X(t).
19. Доказать равенство
1
Р {Л1 (1)< х | X (1) < 0} = — [ Р {Л1 («)< х I X (и) = 0} . L — du.
я 0J Уи(1-и)
Указание: Рассмотреть последний момент времени (меньший 1), когда X(t)
обращается в 0, при условии, что Х(1) 0. Использовать также тот факт, чю
условие Х(1)^ 0 эквивалентно условию —оо < Х(1) < оо в силу принципа отра-
жения.
310 Гл. 10. Броуновское движение
20. Доказать, что Р {X(1) х | Х(и) 0, 0 и 1} = 1 — ехр(—х2/2).
Указание-. Использовать пространственную однородность броуновского дви»
жения. Тогда
Р{Х(1)<х|Х («)>0, 1} =
= Р {X (1)< х | X (и)^ X (1), 0 < и < 1} = 1 - ехр (- х2/2)
(см. задачу 3).
21. Доказать, что для а, 0 > 0
Р {X (и) <аи + р, 0< и < 1 |Х (0) = Х (1) = 0}= 1-е“2Р(Р+а).
Указание: Использовать теорему 2.1 для доказательства равенства
P{X(a)<au + 0, 1 |Х(0) = Х (1) = 0} =
^Р{Х(ц)<0, 0<и<1 |Х(0)= - 0, Х(1)= - 0-а}.
а затем использовать задачу 16.
22. Рассмотрим семейство случайных величин W(t) = Показать, что
{№(/), t 0} является мартингалом, т. е.
М (Г (/) IГ (Л), Г (/2), ..Г (tk)) = W (/j),
где t > Zi > t2 > ... > tk > 0.
23. Пусть О = /о</”<^2< ••• </^ = 1 — последовательность точек разбие-
ния единичного отрезка, таких, что
max [/? —при п->оо.
J
Пусть
«=‘-2......
z=o
(а) Доказать, что M(t/n) = 1 для всех п.
(б) Доказать, что lim M(t/^)=1.
П->ОО
24. Доказать, что плотность
р (/, х, у) = —4^- ехр [- (х - z/)72/]
у 2л/
удовлетворяет уравнению теплопроводности
др 1 д2р
'дТ~'2~дх2‘
25. Какова вероятность того, что частица, находившаяся сначала в 0 и со-
вершающая броуновское движение, достигает уровня b прежде, чем уровня —с
(Ь>0, с>0)?
Указание: Пусть и(х) (—с < х < Ь)—вероятность того, что броуновская
частица достигает из точки х уровня b прежде, чем —с. Доказать, что и(х)
удовлетворяет уравнению
Ъ
u(x) = —=L=r [ ехр[— (x-y)i/2t]u(y)dy + o(tr), Z->0„
У 2л/ J
Литература
311
при любом г > 0. Затем доказать, полагая /->0, что и(х) удовлетворяет диффе-
ренциальному уравнению и"(х) = 0 и граничному условию
и (— с) = 0, и (Ь) = 1.
Ответ:
и (х) = (х + с)/(Ь + с).
Двумерным процессом броуновского движения X(t) = (Xi(t), X2(t)) является
процесс с независимыми приращениями (см. гл. 1), такой, что Xi (0) = Х2(0) = 0
и совместная плотность X(t) равна
1 Г 4- 1 1 / \ 1 / \
1 Л^2 I * I । 1 / Л-2 |
f(xi, х2) =---ехр--------------- 7=т~ехр--------:______ - ехр — .
2л/ L 2t J /2л/ \ 2// /2л/ \ 2//
26. Пусть X(f)—двумерный процесс броуновского движения. Пусть
ЖО-Vx? (/) + %1(/).
Доказать, что R(t)—марковский процесс с непрерывным временем, простран
ство состояний которого есть (0, оо).
ЗАМЕЧАНИЯ
Содержание этой главы полностью основывается на классиче-
ской работе Леви [1], в особенности на ее гл. 6.
Мы рекомендуем также блестящую монографию Каца [2], где
можно найти приложения броуновского движения к статистиче-
ской механике и математическому анализу.
Выдающейся работой по диффузионным процессам, которая
завершает и глубоко обобщает работу Леви, является книга Ито
и Маккина [3].
ЛИТЕРАТУРА
1. Levy Р., Processus stochastiques et mouvement Brownian, Gauthier-Villars,
Paris, 1948.
2. К а ц M., Вероятность и смежные вопросы в физике, М., «Мир», 1965.
3. Ито К., Маккин Г., Диффузионные процессы и их траектории, М., «Мир»,
1968.
Глава 11
ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
§ 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
Ветвящиеся процессы были введены в качестве примеров це-
пей Маркова в гл. 2, § 2. Существуют многочисленные примеры
марковских ветвящихся процессов, которые возникают естествен-
ным образом в различных научных дисциплинах. Перечислим не-
которые из наиболее интересных процессов.
(а) Электронные умножители. Электронный умножитель яв-
ляется устройством, усиливающим слабый поток электронов. На
пути электронов, испускаемых источником, устанавливается ряд
пластин. Каждый электрон, ударяясь о первую пластину, поро-
ждает случайное число новых электронов, которые в свою очередь
ударяются о следующую пластину и в свою очередь порождают
электроны и т. д. Пусть XQ — число исходных электронов, Xi —
число электронов, испущенных первой пластиной благодаря со-
ударению с Хо исходными электронами. Вообще пусть Хп — число
электронов, эмиттированных п-й пластиной благодаря столкнове-
нию с электронами, испущенными (п—1)-й пластиной. Последо-
вательность случайных величин Хо, Х\, Х2, Хп образует ветвя-
щийся процесс.
(б) Нейтронная цепная реакция. При случайном столкновении
с нейтроном ядро расщепляется. В результате деления испускается
случайное число новых нейтронов. Каждый из этих вторичных ней-
тронов может бомбардировать другие ядра, производя случайное
число новых нейтронов, и т. д. В этом случае первоначальное чис-
ло нейтронов равно Хо= 1. Первое поколение нейтронов включает
все произведенные при делении, вызванном исходным нейтроном.
Размер первого поколения является случайной велшшной Х{.
В общем случае размер м-го поколения Хп складывается из слу-
чайного количества нейтронов, произведенных при бомбардировках
ядер Xn-i нейтронами (п— 1)-го поколения.
(в) Выживание фамилий. Фамилию наследуют только сыновья.
Предположим, что каждый индивидуум с вероятностью р& имеет
k потомков мужского пола. Далее, каждый индивидуум порождает
1-е, 2-е, ..., /г-е, ... поколения потомков. Можно исследовать
распределение такой случайной величины, как число потомков
§ 2. Соотношения для производящей функции 313
В п-м поколении, или определить вероятность того, что фамилия
исчезнет. Такие вопросы будут изучаться в данной главе при об-'
щем анализе ветвящихся процессов.
(г) Выживание мутантных генов. Каждый отдельный ген имеет
возможность породить k «потомков», k = 1, 2, ..., которые яв-
ляются генами того же типа. Однако любой отдельный ген также
может трансформироваться в другой тип, называемый мутантным
геном, который может стать первым в последовательности поко-
лений мутантных генов. Представляет интерес вероятность выжи-
вания мутантных генов в популяции исходных генов.
Все приведенные выше примеры имеют следующую структуру.
Пусть Хо— размер исходной популяции. Каждый индивидуум не-
зависимо от других порождает k новых индивидуумов с вероят-
ностью ph, где
оо
й = 0, 1, 2, .... 2pt=l. (1.1)
6=0
Общее количество всех прямых потомков индивидуумов исход-
ной популяции образует первое поколение, размер которого мы
обозначим через Хь Каждый индивидуум первого поколения вновь
независимым образом порождает потомство в соответствии с рас-
пределением (1.1). Общее количество всех потомков образует вто-
рое поколение размера Х2. Вообще п-е поколение складывается
из потомков (п— 1)-го поколения, каждый из членов которого не-
зависимо порождает k потомков с вероятностью рь, k = 0, 1, 2, ...
Размер популяции n-го поколения обозначается через Хп. Величи-
ны Хп образуют последовательность целочисленных случайных
величин, связанных в цепь Маркова.
§ 2. СООТНОШЕНИЯ для ПРОИЗВОДЯЩЕЙ ФУНКЦИИ,
ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
Получим некоторые соотношения для производящих функций
распределений величин Хп. Предположим, что исходная популя-
ция состоит из одного индивидуума, т. е. Хо = 1. Очевидно, для
любого п = 0, 1, 2, ... можно записать
Хп
Г=1
где |r (г^1)—независимые одинаково распределенные случай-
ные величины с распределением
PM=ftl ^ = 0,1.2...........
314
Гл. 11. Ветвящиеся процессы
Введем производящие функции
оо
Ф (s) = 2 pksk
/г»0
И
Ф„(«) = 2 P{Xn^k}sk, ra = 0, 1, 2....
fc=0
Ясно, что
Фо (s) = s, а ф(- (s) = <Р (s).
Далее,
оо
фп+. («) = 2 PPUi = k}sk =
fe=0
oo oo
= 2 2ph„+1 = A!|x„ = /}p{x„=/}? =
/?=0 /=0
oo oo
= S?2pg„=/}P{al+ ... +&/ = £} =
£=0 /=0
= 2р{хй=Л2р{&1+ ••• +^ = ^}Л (2.1)
/=0 fc=0
Поскольку (г — 1, 2, /)— независимые одинаково распреде-
ленные случайные величины с общей производящей функцией
<p(s), сумма |i + ... + gj имеет производящую функцию [qp(s)p.
Таким образом,
оо
Фп+1(«)=2р{^ = /}[ф(«)]/.
/=0
Но правая часть этого равенства равна производящей функции
фп(-) с аргументом ф($). Таким образом,
Фп+ i(s) = <p„(<p(s)). (2.2)
Итерируя это соотношение, получаем
фп+1 (s) = Фп (ф («)) = Фп-1 (ф (ф (s))) = ф„-1 (ф2 («)) =
= Фп-2 (ф2 (ф («))) = фп—2 (фз («))•
По индукции получаем, что для любого k = 0, 1, ..., п
Фп+1 ($) = Ф/г-fe (Ф& + 1 ($))>
в частности, при k — п— 1
Фп+1(«) = ф(Фп(«)). (2.3)
§ 2. Соотношения для производящей функции
315
Если вместо условия Хо = 1 рассмотреть более общее условие
Хо = (о, где /о — любое постоянное число, то
Фо ($) = «'% а ф1(«) = [ф(«)]4
потому что
= 2 !/•
м
Равенство
Фп+1($) = Фп (ф (5))
сохраняется, но соотношение (2.3) не выполняется1).
С помощью (2.2) можно теперь вычислить математическое
ожидание и дисперсию величины Хп. Далее всюду будет предпо-
лагаться (если не оговорено противное), что ^0=1. Предполо-
жим, что
т = М(Х1) и ст2 = о2(А'1) = М(Х?)-(М(Х1))2
существуют и конечны.
Очевидно, М(Хп) = ф' (1). Дифференцируя (2.2) и полагая
s=l, получаем (поскольку ф(1)=1), что ф'+1(1) = ф' (1)<р'(1),
или по индукции
Ф;+1(1) = Ф'(1)ф'(1) = [ф'(1)]2Ф;_1(1) = [ф,(1)]3Ф;_2(1).
По индукции получаем
ф;+1(1) = [ф'(1)Гф;(1) = [ф'(1)Г+1.
Но ф'(1) = ф| (1) = М pQ = т. Таким образом,
ЩХп+^т^. (2.4)
Чтобы найти a2(Xn+i), заметим сначала, что
<р" (1) = 2 k (k -1) р {хп = k}=м (х2) - м (хп)=м (х2) - ф' (1)
и отсюда
!) Вместо (2.3) выполняется равенство
ф«+1 (s) = Ф1 (фп («)) = [ф (фп («))] 1“-
В общем случае если XQ — случайная величина с производящей функцией
оо
ф(в) = 2 P{Xo = £}sfe, то эквивалентом соотношения (2.3) будет
6 = 0
фп+1 (s) = [ф (фп («»]•
Соотношение (2.2) сохраняется и в этом общем случае. — Прим, перев.
316
Гл. 11. Ветвящиеся процессы
Дифференцируя (2.3) дважды и полагая $ = 1, получаем
<р"+1 (1) = ф"(1)[ф'(1)]ч-ф'(1)ф;д1).
Поскольку ф' (1) = ш, а ф" (1) = М (X2) — М (Xi) = o'2 + гп — т, имеем
= Lm2n + ту" (1\
где L = о2 + т2— т. По индукции
ф"+1 (1) - L {т2п + m2"”1} + (1) = ...
... = L {т2п + т2п~' + ... + тп}.
Таким образом,
o2(Xn+i) == (o'2 + tn2 — m){m2n + т2п~х + ... 4~ тп} + тп+{ — т2п+2 =
~ $2{т2п + m2n~i + ... + тп} = в2тп > если т =/= 1.
Если т = 1, то
(Ж+1МН 1)о2.
Мы получили формулы М(ХП) = тп и
Г 9 пг11 — 1 , .
I в2тп 1----г-, если m^=i,
a2(X„) = j w-’
I мог2, если /м=1.
Таким образом, дисперсия увеличивается (уменьшается) со ско-
ростью прогрессии, если мг > 1 (мг<1), и изменяется линейно,
если т = 1. Такое поведение лежит в основе многих результатов
для ветвящихся процессов.
§ 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
Мы хотим найти вероятность того, что популяция выродится,
т. е. Р{ХП = 0 для некоторого п}. Очевидно, если Хп = 0, то
Xk = 0 при всех k > п.
Заметим сначала, что вырождения никогда не произойдет, если
вероятность того, что индивидуум не порождает ни одного потом-
ка, равна нулю, т. е. если р0 = 0. Таким образом, при исследовании
вероятности вырождения предположим, что 0<р0<1. Пусть
qn = р {хп = 0} = <р„ (0).
В силу формулы (2.3)
qn+i = <рп+! (0) = ф (фп (0)) = ф (</„). (3.1)
Так как ф(«) — строго возрастающая функция (степенной ряд с не-
отрицательными коэффициентами и р0<1) и q\ = ф1(0) =
= ро > 0, то = ф(70 >ф(0) =7г Предположим, что qn > qn4.
§ 3. Вероятности вырождения
317
Тогда б/п+1 = >ф(7п-1) = qn- Этим доказано, что q\, q2, ...
.qn, ... — монотонно возрастающая последовательность, огра-
ниченная единицей. Следовательно, существует
л = lim qn
и 0 < л С 1. Поскольку <p(s) непрерывна при 0 s < 1 (непре-
рывность в точке s = 1 следует из леммы Абеля, см. гл. 2, лем-
ма 5.1), полагая п —> оо в (3.1), получаем
л = ф (л). (3.2)
Поскольку qn — вероятность вырождения популяции не позже,
чем за п поколений, то л — вероятность вырождения популяции,
и из (3.2) следует, что л — корень уравнения
ф(х)^5. (3.3)
Покажем теперь, что л — наименьший положительный корень
уравнения (3.3). Пусть s0 — положительный корень уравнения
(3.3). Тогда qi = ф(0) < <p(s0) = $о- Предположим, что qn < -$о.
Тогда в силу (3.1) qn+i = ф(<7п) < ф(-$о) = $о. Таким образом, по
индукции показано, что qn < <$о для всех п. Отсюда следует, что
л= lim qn^.sQ, т. е. л — наименьший положительный корень урав-
П->оо
нения (3.3).
Теперь предположим, что ро + pi < 1. Тогда ф(х) —выпуклая
функция при 0 < s < 1, поскольку ф"С?) = 2 k (k — 1) pksk~2> 0.
k = '2
Следовательно, график функции <p(s) может пересекать прямую
с наклоном 45°, идущую из начала координат, самое большее
в двух точках. Мы знаем, что <р (1) = 1, и поэтому пересечение
определенно имеет место в точке (1,1). Очевидно, может иметь
место один из двух случаев, представленных на рис. 1 и 2. Если
т = Ф'(1) > 1, то тангенс угла наклона касательной к графику
ф($) в точке s = 1 больше 1 и имеет место случай, представлен-
ный на рис. 1. В этом случае 0<л<1. Если т = ф'(1)<<1, то
тангенс угла наклона касательной в точке s = 1 меньше или ра-
вен 1 и имеет место ситуация, представленная на рис. 2. Тогда
с необходимостью л = 1. Таким образом, мы доказали, что ве-
роятность вырождения равна 1, если т^,1, и меньше 1, если
m > 1. Другими словами, вырождение определенно имеет место
тогда и только тогда, когда среднее число потомков от одного ин-
дивидуума не превышает 1.
Далее, заметим, что ф(х)<ф(л) при 0 < s < л (рис. 2).
По индукции имеем <pn(s) л (0 s л) для всех п.
Рис, 1.
Рис. 2.
§ 3. Вероятности вырождения 319
Но cpn(s) >фп(0) = qn, и, таким образом, qn^qn(s) < л. Пусть
п -* оо. Тогда.
lim срп ($)=*= л при О^з^л.
П->оо
В случае пг > 1, когда л < s < 1, имеем л < cp(s)< s < 1
(рис. 1). По индукции
Л<ф„(«)<ф„_1(5)< ... (л<$<1).
Отсюда
lim ф„ (s) л. (3.4)
П->оо
Предел в (3.4) должен равняться л, так как если бы lim<pn(s) =
/2->оо
= а>л, то ф(а)<а, и указанная в (3.4) сходимость была бы
невозможна в силу соотношения 11тфд+1(з) = Пшф(фп(5)), Таким
п->оо п->оо
образом,
Нтфп(«) = л при 0^s<l.
П->оо
Из того факта, что фп(з) сходится к постоянной л при 0^s< 1,
следует, что в разложении
Ф«(«)=5р{Хп = *}**
&=0
первый коэффициент Р(ХП = 0} сходится к л при п~*оо, а все
остальные коэффициенты Р{Хп = &} сходятся к 0 при п -> оо,
k = 1, 2, ... .
Следовательно, при любом значении пг = M(Xi)> 1 вероятность
того, что n-е поколение будет состоять из любого положитель-
ного конечного числа индивидуумов, стремится к 0 при п —> оо,
в то время как вероятность вырождения стремится к л. В этом слу-
чае мы скажем, что Хп —► оо при п оо с вероятностью 1 — л.
Этот результат является также следствием общей теории цепей
Маркова, поскольку марковская цепь, определяемая последова-
тельностью Хо, Xi, Х2, ..., имеет единственное поглощающее со-
стояние {0}, и поэтому limPf/ = 0, l^Z,/<оо, так как i и j
являются автоматически переходными (невозвратными) состоя-
ниями.
В заключение параграфа отметим интересное свойство, состоя-
щее в том, что условное математическое ожидание величины
Хп+г (г — положительное целое число) при условии, что известно
Хп, равно пггХп, т. е. M(Xn+r|Xn) — пггХп, Чтобы доказать это,
рассмотрим сначала случай г = 1:
МН„+1|Х„}=М) з
Х„М(^) = тХ„.
320
Гл. 11. Ветвящиеся процессы
Предположим теперь, что соотношение установлено для числа г,
и докажем его для /*4-1. Имеем
M{X„+f+I|X„} = M{M[X„+r+I|X„+r,X„+r_I> .... хп]\хп}-
= 1Л(М[Хп+г+Ц Хп+Г]\ Хп},
где использована марковская природа последовательности {Хп}.
Но M[Xn+r+i |Хл+г] = Хп+г, и в силу индукции M[mXn+r|Xn] =
= mr+iXn. Таким образом,
M{Xn+r\Xn} = Xnmr для г-0,1,2,..., п - 0, 1, 2, . . . . (3.5)
Рассмотрим теперь случайные величины
Wn = —« = 0, 1, 2, .. ..
п mn ’
Тогда в силу (3.5) имеем
м {Г„+г | Гп} = М{Хп+Г | Хп} = —Xnmr ~ \Vn.
Можно записать, что для г, п — 0, 1,2, ...
М{Гп+г| wn, .... r„ r0}=rn, (3.6)
откуда следует, что последовательность {lFn}~e0 является мартин-
галом.
§ 4. ПРИМЕРЫ
(1) Пусть (p(s) = ро 4- p\S, 0 < ро < 1. Соответствующий вет-
вящийся процесс является процессом чистой гибели. В любой пе-
риод времени каждый отдельный индивидуум погибает с вероят-
ностью ро и остается жить с вероятностью pi — 1 — ро.
(2) Пусть <p(s) - ро 4- pis2 (0 < ро < 1, ро 4- р2 = 1). Такая
производящая функция соответствует ветвящемуся процессу, в ко-
тором в каждом поколении отдельный индивидуум либо погибает,
либо порождает двух потомков.
(3) Рассмотрим пример, где каждый индивидуум порождает N
или 0 прямых потомков с вероятностями р и q соответственно. Та-
ким образом, ро = q, Pn = р и pk = 0 для k 4= 0, N. Тогда
ср (s) - q 4- psN. (4.1)
(4) Каждый индивидуум может иметь k потомков, где k — слу-
чайная величина с биномиальным распределением вероятностей
с параметрами' N и р. Тогда
<р (s) = (<7 + ps)N. (4.2).
§ 4. Примеры
321
(5) В связи с примером (г), описанным в начале этой главы,
часто предполагается, что случайное число k (k = 0, 1, 2, ...)
прямых «потомков» мутантного гена имеет пуассоновское распре-
деление со средним X = 1. Тогда qp(s) = es~l и л= 1.
Основания для выбора именно этого распределения следующие.
Во многих популяциях производится большое число зигот (опло-
дотворенных яиц), и лишь малая доля их доживает до зрелости.
События, состоящие в оплодотворении и выживании до зрелости,
подчиняются закону независимых биномиальных испытаний. Чис-
ло испытаний (т. е. число зигот) настолько велико, что действи-
тельное число зрелых потомков следует пуассоновскому распреде-
лению. Именно следствие закона редких событий оправдывает при-
менение пуассоновского приближения. Оно кажется вполне при-
емлемым в модели роста популяции редких мутантных генов.
Если мутантный ген обладает некоторым благоприятствующим
(или неблагоприятствующим) биологическим признаком, то бе-
рется пуассоновское распределение со средним К > 1 (или X < 1).
В этом случае
qp (s) = ем$-1) (43)
и 0 < л < 1 тогда и только тогда, когда К > 1.
В случае гетерогенной (неоднородной) популяции мутантных
генов можно предположить, что вероятностное распределение чис-
ла потомков является пуассоновским, но со случайным средним.
Например, можно представить большую географическую об-
ласть, в каждой подобласти которой ветвящийся процесс характе-
ризуется производящей функцией пуассоновского распределения
с параметром X. Предположим далее, что значение К изменяется
в зависимости от подобласти и распределение значения X во всей
области является гамма-распределением. Формально постулирует-
ся, что вероятность того, что мутантный ген имеет в точности k
прямых «потомков», равна
pk = e~^, £ = 0,1,2,...,
где X — случайная величина, имеющая гамма-распределение
с плотностью
Г (a) (р) Л<Х 'ехр( р Л)’
0
в противном случае;
здесь q, р, а — положительные постоянные, q + р = 1. Если усред-
нить по параметру X, то получим вероятность того, что индивидуум
имеет k потомков:
р {£ = £} = J Р£=k\VHVdK.
о
11 Зак. 939
322
Гл. 11. Ветвящиеся процессы
Производящая функция равна
оо
<p(s) = £PMs‘ =
ьо
оо оо
= j ехр(— Л)-^- Tk W(f) ехр(~Ч) s*^ =
k~0 о
оо / оо \
= / ехр(-Л) К ехр (- у- лН (>.s)ft j dK =
о \&=о /
оо
= I* expl —(—4- 1 -sh |-г-гт(-Г^а-' =
J Ч \Р J J Г (а) \ р J
о
= ( q!P Г_ f q \а
\ (q/p) +1 - s / \ i ~ ps J
Мы получили производящую функцию отрицательного биномиаль-
ного распределения.
(6) В примерах (2) — (4) неизвестно выражение для произво-
дящей функции <рп($) в замкнутой форме. Пример, рассматривае-
мый ниже, допускает достаточно полный анализ. Найдем, в част-
ности, производящую функцию для n-го поколения. Пусть
pk = bck~\ k == 1, 2, ..
и
оо
Ро = 1 - 5 pk,
/г=1
где &, с > О и 6 + с < 1. Тогда
оо
fe=l
а соответствующая производящая функция равна
оо
Ф (s) = 1 - yr? + bs S • <4-4)
k^\
Заметим, что cp(s) имеет вид функции дробно-линейного преобра-
зования
= «6-₽Y^0. (4.5)
Выпишем несколько элементарных свойств дробно-линейных
преобразований, необходимых для дальнейшего.
§ 4. Примеры
323
(i) Итерации дробно-линейных преобразований вновь являются
дробно-линейными преобразованиями, так как если f(s) задается
соотношением (4.5), то из элементарных выкладок следует, что
е ze z _ а (у + р) + (ад 4- р2) s
/ V ~ y2 + д (у + Р) s •
(и) Всегда существует два конечных (возможно, совпадающих)
решения уравнения f(s) = s. Эти решения называются неподвиж-
ными точками [(•). Если f(s) —производящая функция, то одна
из неподвижных точек Si = 1, и мы увидим, что другая неподвиж-
ная точка So меньше 1, равна 1 или больше 1 в соответствии с тем,
будет ли значение f'(l) больше, равно или меньше 1.
Для производящей функции (4.4) можно непосредственно про-
верить, что вторая неподвижная точка при с > О, b + с < 1 равна
1 — Ь — с
s° ~~ с (1 — с)
(iii) Для любых двух точек s2-, i = 0, 1, легко показать, что
f(s)-f (sf) __ ур-ад .
s - s. ~ (у 4- ds) (у 4- dsz) ’
следовательно,
f(s)-f(s0) __ / y4-dst \ / s — s0 \
f(s)-f(si) \Y + ds0/U-sJ'
Если теперь принять, что So и Si— две (несовпадающие) не-
подвижные точки f(-), и обозначить w = f(s), то равенство (4.6)
примет вид
(4.7)
W — Si S — Si ' '
где % можно найти из (4.6) или, что проще, из (4.5), полагая s = 0.
Используя (4.7), нетрудно получить итерации fn(s) = wn
функции f(s):
„ wt~so -„L
W2 — Si U>1 — Si \ s — S, I
и вообще
Wn - So = %n S-Sp . , 4 8)
Wn — Si S-S1 ’ '
Для производящей функции геометрического распределения,
задаваемой формулой (4.4), замечая, что неподвижные точки рав-
ны So = (1 — b — с)/с(1 — с) и Si = 1, получаем
И*
324
Гл. 11. Ветвящиеся процессы
где tn — среднее геометрического распределения. Для m =А 1 две
неподвижные точки $0 и 1 различны. Следовательно, решая (4.8)
относительно wn, находим
70] - So~(i/^)[(s--So)/(s~l)] }
Wn~' l-(l//n")[(s-s0)/(s-l)] ,
(4.9)
ИЛИ
ГР М - 1 - rnn ( \ ! тП^Х s
-1 i-[(m«-l)/(m«-s0)]s-
Вероятность вырождения за п поколений равна
Р {Хп - 0} = фга (0) = 1 - тп (4^-) •
Заметим, что это выражение сходится к $0 при п—> оо, если
и к 1, если Вероятностное распределение размера попу-
ляции в n-м поколении Р{Хп = k}, k = 1,2, ..., можно найти
разложением (4.10) в степенной ряд по $. Если определить время
до вырождения Т как наименьший индекс п, для которого Хп = 0,
т. е. время первого попадания в состояние 0, то
Р {Т < п} = Р {Хп = 0} = ф„ (0),
Р{Т = п} = Р {Т < п} - Р {Т < п - 1} = ф„(0) - фп_, (0).
В случае m > 1 имеем
Р{Г = п} = 1 - тп - 1 + тп~' (=
\ тп — s0 / \ тп — sj
(пг- 1) (1 -s0)
l-s0)(mtt'“1-s0) ’
Если tn = 1, то b = (1 — с)2; в этом случае уравнение ср(s) = s
имеет двойной корень s = 1 и не имеет других корней. Таким об-
разом,
(4.10)
= mn~1s0
( х . (1 “ с)2 S с — (2g - 1) s
Ф ($) = С -Ь ---------— = —4--------------—
Х 7 1 — gS 1 ~ gs
Тогда
Фг («) = Ф (ф («)) = 1 — с ((с — (2с — 1) s)/(l — cs)]
g — (2g — 1) [(g — (2g — 1) s)/( 1 — gs)] _ 2g — (3g — 1) s
1 — g [(g — (2g — 1) s)/( 1 — gs)] ~ 1 + g2cs
и по индукции
z ч nc- [(/г + 1) g- 1] s
j + (n- i) c ~ tics ’
Вероятности вырождения для случая tn = 1 равны
Р{Х„ = 0} = ф„(0) = -ГП^гТ)7> п==1’2.........
Время до вырождения Т имеет распределение
Р г у __ ________((£______0 . . ______£)_____________
rv -П)~ 1+(/г_1)с 1 + (п_2)с - [! + («- 1)с] [!+(«- 2) сГ
(4.И)
§ 5. Ветвящиеся процессы с двумя типами частиц
325
§ 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
Обобщим развитую выше теорию на случай двух измерений.
Рассмотрим популяцию организмов или объектов, в которой раз-
личаются два типа этих объектов. Индивидуумы каждого типа
могут в общем случае порождать потомков обоих типов независи-
мо от других индивидуумов. Пусть Un и Vn — число индивидуумов
типов I и II соответственно в п-м поколении. Можно записать
v„+1=2\<l)+2^),
/»1 1 /=1 7
где (£'/', C/Z)) — независимые одинаково распределенные случай-
ные векторы с распределением
Р {£</> = k, = 1} = Pi (k, /), k, I = 0, 1, 2, ..
/=1, 2, Z=l, 2.
Здесь pi(k, Z)>0, S pi(k, Z)=l, Z=l, 2.
k, /=о
Другими словами, p\ (k, l) и p2(k,l) — вероятности того, что ин-
дивидуум типа I или II соответственно порождает k + I прямых
потомков, из которых k имеют тип I и I — тип II.
Предположим, что процесс начинается, когда имеется один
индивидуум, т. е. предположим, что
t/o=l, Vo = O (5.1)
или
f7o = O, V0=l. (5.2)
Введем две двумерные производящие функции
<p(«(s, /)= 2 Pi{k, l)sktl, z= 1, 2,
k, M
t. e.
/)= 2 P{un~k, iz„ = /|t/0=i, ivo}?/1,
kt '=-0
ф<2)($, 0= 2 P{un = k, iz„ = /|t/o = o, Vo=i}s¥.
k, 1-0
Производящая функция распределения (5.1) имеет вид
ф’1' ($, t) вэ S,
а распределения (5.2) —
326
Гл. 11. Ветвящиеся процессы
Кроме того,
<P(if) О, * L 2.
Обобщая метод, примененный для одномерного случая, можно по-
казать, что
Ф<%(8, /) = Ф»>(Ф*‘>(s, О, Ф<2,(*. 0), <= 1, 2, п, m = 0, 1, 2, .... (5.3)
Это двумерный аналог формулы (2.3).
Чтобы обобщить формулу (3.5), введем следующие обозначе-
ния. Пусть Xn = (Un, Vn) — двумерный вектор с компонентами
Un и Vn. Положим
= Уо = О} = М(|(')),
m12 = M{71|t/0=l, 70 = 0} = М(£'>),
щ21 = М{{7, | Uo = 0, Vo = 1} = М (£<2>),
щ22 = М {V! | Uo = 0, /0=1} = М(^)
и введем матрицу математических ожиданий
II Шц II
М =
II ^21 ^22 II
Таким образом, ти и mi2— средние количества потомков типов
I и II соответственно, порожденных единственным родителем ти-
па I. Тогда обобщением (3.5) является матричное равенство
M[Xrt+r|Xrt] = X„Mr, г, п = 0, 1, 2........... (5.4)
Доказательство его для г = 1 проводится непосредственно:
М[Х„+Г|Х„] =
/ ^’п
= (м 2 + 2 | щп, vn) > м
ип Vn 1\
тп
= 4" ^21 ^12^« 4* Bl22^п) “ (^n, ^n) m
II /П21
т22
т22
= хпм.
Предположим теперь, что соотношение (5.4) выполняется для г,
и докажем его для г + 1. В силу того что последовательность
{Хп} образует цепь Маркова, имеем
XJ|XJ =
= М {М [Хп+г+11 Х„+г] | Xп} = М {ХП+ГМI Хп}»
s= М {Хп+Г | Х„} • М = (по индукции) = XnMr+I.
§ 5. Ветвящиеся процессы с двумя типами частиц
327
Тем самым (5.4) доказано.
Введем следующие вероятности поглощения для двумерного
ветвящегося процесса:
л0) = Р{^п = Vn = 0 при некотором n\U0=l, Vo = O},
л(2) =, р= уп = о ПрИ некотором п\ UQ~ О, Ио=1}.
«Одномерная» теория распространяется на этот случай с той
лишь разницей, что роль математического ожидания m здесь иг-
рает наибольшее собственное значение р матрицы М.
Мы отсылаем читателя к приложению и, в частности, к теоре-
ме Фробениуса относительно матриц с неотрицательными элемен-
тами. Там доказано, что если М — матрица с положительными
элементами (что условимся обозначать М^>0), то собственное
значение, максимальное по модулю, является положительным
и, следовательно, действительным. Это собственное значение бу-
дет обозначаться через р(М) == р.
Удобно ввести следующие векторные обозначения:
u = (s, /),
ф(и) = (<p(1)(s, t), <p(2)(s, 0)»
‘РП(«) = (Ф^(5, О, С (S, t)),
Л = (лО, Л<2>),
1=(1, 1).
Теперь можно доказать такую теорему.
Теорема 5.1. Предположим, что компоненты вектора ф(и)
не являются линейными функциями s и t и что М » 0 (все эле-
менты матрицы М положительны). Тогда л = 1, если максималь-
ное собственное значение р матрицы М не превышает 1, п л<1,
если р > 1. (Обозначение u<v (u<v) означает, что вектор
v — и имеет положительные (неотрицательные) компоненты.)
В случае р> 1 л — наименьшее неотрицательное решение уравне-
ния
и = ср (и), и<1. (5.5)
Доказательство. Рассмотрим случай р<И. В соответ-
ствии с общей теорией цепей Маркова мы знаем, что если цепь
имеет единственное поглощающее состояние, то все состояния, из
которых оно может быть достигнуто, — переходные (невозврат-
ные). Двумерный процесс Xn = (Un> Vn) является как раз таким
процессом: начало координат является единственным поглощаю-
щим состоянием, и оно может быть достигнуто из любого дру-
гого. Это является следствием того факта, что ф(и) не имеет ли-
нейных компонент и р<1. Таким образом, все состояния, за
328
Гл. И. Ветвящиеся процессы
исключением начала координат, невозвратны. Следовательно, есл
I Х„ I = ип + Ип, ТО
Р{0 < |Хп| < N для бесконечно многих п} = О
для любого положительного N (см. теорему 7.1 гл. 2). Это озна-
чает, что
P{|XJ->0} + P{|XJ->oo}=l.
Из формулы (5.4) имеем
М[ХП | Хо] = ХОМЛ. Но из теоремы 2.3
приложения следует, что
п—>оо. Следовательно, в
рт-М" сходится покомпонентно при
случае р 1 компоненты векторов
М[ХП|ХО] остаются ограниченными при п -> оо. Отсюда следует,
что событие |ХП|—»оо происходит с вероятностью 0. Следователь-
но, Р{|ХП|->0} = 1, или, что то же, Un^-0 и Уп->0 при /г->оо
с вероятностью 1. Таким образом, если р1, то
Я(1) = Л(2)= 1.
Рассмотрим теперь случай р > 1. Из формулы (5.3) при
Ф<Д.х (0, 0) = ф(Д<р<„1>(0, 0), <р(2»(0, 0)), i= 1, 2. (5.6)
Пусть
<?(0 = ф(1)(0, О) = Р{С/я = У„ = О|С/о=1, Ио=О),
?<2) = Ф<2)(0, О) = Р([7п^Рге = О|(/о = О, Ио= 1].
Тогда (5.6) можно переписать в виде
е1 = Ф(,')(СЛ- г=1, 2. (5.7)
Поскольку <р<г’> (s, t) является возрастающей функцией s и t (при-
чем если увеличиваются обе эти переменные одновременно, то —
строго возрастающей) и поскольку q\i} == qff (0, 0)>0, i = 1, 2, то
имеем, очевидно,
q^ = q/z) g(i2))> qp(f) (0, 0) = ?(Д z=l, 2.
Тогда по индукции
с, -ф(,,(е «!?)>»'"(«.. e.w,?. *=1,2-
Следовательно, qU\ п — 1, 2..... при любом i = 1, 2 — монотон-
но возрастающая последовательность, ограниченная сверху чис-
лом 1, и
§ 5. Ветвящиеся процессы с двумя типами частиц
329
Пусть в соотношении (5.7) п->оо. Тогда
п(0 = фи)(п(1), л<2>), /= 1, 2,
или, в векторных обозначениях, л = ф(л). Докажем теперь, что
л < 1 и что это — единственное решение уравнения (5.5) при ука-
занных условиях. Раскладывая Ф^( • , •) по формуле Тейлора
в окрестности точки (1, 1), получаем выражение
/ (s, t)
= !) + (- *nds -
Is +
s«/=l/
! / О
“Ц dt
р + о(| s I + U |), (5.8)
3 = /=1/
которое справедливо при 11 — s| 1, 11 — 11 1 и достаточно ма-
лых s и t. Символ о(-) означает, что [о(|s| + |/|)]/(|s| +
при |s| + |/| -> 0. Очевидно,
ЛлД) (s i)
= М[(/Jf/0=l, Уо=01==т<«>,
ds s=t=i l ш О ’0 J 11’
I,.,., = M [ГМ " 1 “ °l - <•
= м КI - 0. - 1] - <
Перепишем (5.8) в векторной форме
Ф„(1 -u)=l — M(n)u + о (| s |+ |/I),
(5.9)
где
M(ra) =
II
Il ^21
m<12) ||
mW I
и | u | < e. Из соотношения M[Xn | Xo] = X0Mn следует, что M<n> =»
= Mn. Пусть норма вектора v = (ub v2) определяется как сум-
ма абсолютных значений его координат: ]v| = |t>i| + |г»2|- Дока-
жем теперь, что для достаточно больших п
|M"u|>2|u|, u = (s, /), (5.10)
при условии, что и > 0. Действительно, в соответствии с теоремой
2.3 приложения
х0^
х2у\
х^°||
Мли = р”
и -I- О (р”) U,
330
Гл. 11. Ветвящиеся процессы
где р — максимальное собственное значение М, ах(0) = (4 х%),
y0 = (f/p У2) —отвечающие ему единственные (с точностью до
постоянного множителя) соответственно левый и правый собствен-
ные векторы, нормированные таким образом, что xfy® + x®yQ2 = 1.
Обозначение о(рп) является обобщением общепринятого. Именно
о(рп)/рп — вектор, каждый элемент которого стремится к 0 при
п->оо. Множитель о(рп) не зависит от и. Он равен разности меж-
ду-^- Мп и его предельным (при п—>оо) значением. Перепишем
вышеприведенное выражение в виде
M^u = рп (y®s + y"f) х° + о (рп) и, и ~ ($, /).
Если и 0, то получим очевидную оценку
| М"и | > рп [х? + х®] min (^, z/О) | u Н о (pn) | и |.
Поскольку р> 1, то при достаточно большом п получим неравен-
ство (5.10). Комбинируя (5.9) и (5.10), получаем
|1— Фп(1— u)|>2|u|
при условии, что |u| достаточно мал, а п достаточно
велико, скажем Пусть v = 1 —и. Тогда
| 1 - Фп(у) |>2 11 - v | (5.11)
при всех 0 v 1, удовлетворяющих условию |1—v | < е, и
п > п0. Используем (5.11) для того, чтобы доказать, что
Предположим, что л= 1, т. е. = 1 для 1 = 1,2. Тогда величи-
на (0) 0 стремится к 1 при п~>оо. Из (5.3) следует,
что
ф„+л, (0) = ф„ (фд, (0)).
Используя (5.11), где v = ф^(0), имеем
I 1 - Фл+уу (0) I = I 1 - Фп (фуу (0)) | > 21 1 - ф,у (0) |, (5.12)
если |1—Флт(0)| < е, а этого можно добиться, выбрав N доста-
точно большим. Однако соотношение (5.12) противоречит предпо-
ложению о том, что Ф^(0)->1 при и—>оо. Таким образом, равен-
ство = л(2) = 1 невозможно. Предположим теперь, что < 1
и л<2) = 1. Тогда
Л(1) «= ф(1) (л(1), 1)
и
l==n(2) = (p(2)(n(l)>
Таким образом, имеем
ф<241, 1)=1, <p<2>(jt<1>, 1) = 1,
§ 5. Ветвящиеся процессы с двумя типами частиц
331
где л(1) < 1. Поскольку q/2>(s,/) монотонна по s, q/2)(s, 1) должна
быть постоянной на отрезке 1:
d<P(2)(s. О = о
ds
и, следовательно,
т(2) = _^Ь...о =01
21 ds s~t~l
что противоречит сделанному предположению о том, что М 0.
Аналогичным образом можно доказать, что случай nW = 1,
лЯ < 1 невозможен. Таким образом, установлено, что л С 1. Про-
верка того, что л меньше любой другой положительной неподвиж-
ной точки, производится следующим образом. Пусть вектор л* > 0
удовлетворяет уравнению ф(л*) = л*. В силу монотонности имеем
л* = <р(л*) >ф1(0,0). Итерируя, получаем л*>фп(0,0) и, пере-
ходя к пределу, находим, что л* > л.
Мы можем усилить результат теоремы 5.1 следующим образом.
Теорема 5.2. В предположениях теоремы 5.1 для любого
вектора q из единичного квадрата, отличного от 1,
lim <p„(q) = л.
П-»оо
Доказательство. Предположим сначала, что
\i = 1, 2). Если N— положительное целое число, то разложение
Тейлора функции Ф^п(я) имеет вид
| |х«|“ Ор»" ' 1'«=0) +
+ 3 Р(Х„-хЦ/,= 1. и,-0)(?"|)”(?и)’’ +
О < | X | < АГ
+ 2 Р{Хга = х |£/0= 1, =
I X | > N
Последняя сумма ограничена величиной
(max(?(4 q^))NP{\Xn\> N} < (тах(^), q^))N,
которая при /V —► оо стремится к 0, поскольку max(^1), q&) <1.
Каждый коэффициент первой суммы стремится к нулю при
п->оо, поскольку | Хп | стремится либо к 0, либо к оо. Этот факт
базируется на том, что все конечные состояния, не совпадающие
с (0,0), невозвратны. Отсюда следует, что при фиксированном М
и п —> оо первая сумма стремится к 0. Следовательно,
lim <р«) (q) = lim Р {| X J = 0 | Uo = 1, Vo = 0) = lim <р<» (0) = л*1»,
П->оо П->со П->°°
как и утверждается в теореме. Аналогично
lim (q) = л,2).
332
Гл. И. Ветвящиеся процессы
Если одна из величин (i = 1,2) равна 1, но не обе одно-
временно, то (pi (q) = (<p(I)(q), cp(2)(q)) является положительным век-
тором, каждая компонента которого строго меньше 1. Применяя
предыдущие рассуждения к q>i (q), получаем
lim fp„ (q>, (q)) = л = lim ф„+1 (q).
n->oo n->oo
Следствие 5.1. Единственными решениями уравнения (5.5)
являются 1 и л.
§ 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
Обобщение теории, развитой в предыдущем параграфе, на случай большего
количества типов повторяет дословно все, сделанное для случая двух типов.
Доказательства не содержат новых идей или приемов. Мы приведем лишь сами
результаты. Прилежный читатель должен провести полностью все доказательства.
Мы рассмотрим ветвящийся процесс для р типов частиц. Различные типы
могут отвечать реальным различным мутантным формам некоторого организма
или могут соответствовать одному организму, где отдельный тип отвечает воз-
расту или другому подобному свойству. То, что рассматривается лишь конечное
число типов, можно интерпретировать, например, как установление конечного
набора возрастных классификаций.
В случае излучения фотонов, возникающего в электронном ливне космиче-
ских лучей, тип может соответствовать уровню энергии фотона.
Типу i соответствует производящая функция
где ...» гр) — вероятность того, что один объект типа i породит гц объ-
ектов типа 1, Г2 объектов типа 2, ... , гр объектов типа р. Введем вектор
s = (sb ..., sp).
Пусть f^(s) — производящая функция числа индивидуумов в п-м поколении
при условии, что первоначально был лишь один индивидуум типа /. Аналогично
(5.3) имеем
= n = 0. 1...., г=1.....р.
Пусть Zn = (Z„\ ..—вектор, представляющий размер популяции, состоя-
щей из р типов в п-м поколении. Аналог соотношения (5.4) имеет вид
М (Zn+m I Zn) = ZnM™,
где М= [|° — матрица первых моментов:
....'>. ,.;=|........р.
1
а е/ — вектор, у которого f-я компонента равна 1, а остальные — 0.
Приведем теперь аналог теоремы 5.1 для р типов. Предположим, что
тц > 0 для всех /. (Достаточно потребовать, чтобы > 0 для некоторого п
§ 7. Ветвящиеся процессы с непрерывным временем
333
и всех i, j.) Пусть — вероятность вырождения, если первоначально имеется
лишь один объект типа i (i = 1, ..., р), т. е.
jx^ = P{Zn==0 для некоторого п [ Zo = ej.
Вектор (л(...» л/?)) обозначим через л и введем вектор 1 = (1, 1,..., 1).
Теорема 6.1. Пусть тц>®, *,/= 1, ..., р, и пусть р — максимальное
собственное значение матрицы М. Если р 1, то л == 1. Если р > 1, то
0^ л < 1 и л удовлетворяет уравнению
л(1) == f(t) (л), i== 1, ..р,
§ 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Для ветвящихся процессов, изучавшихся в § 1—6, время су-
ществования одного поколения было фиксировано. Хотя некоторые
явления, в особенности экспериментальные испытания, удовлетво-
ряют этому условию, более естественным представляется процесс
с непрерывным временем. Поэтому описание ветвящихся процес-
сов с непрерывным временем представляет несомненный интерес.
В данном параграфе мы исследуем структуру однородных по
времени марковских ветвящихся процессов; в § 11 предположение
о том, что процесс является марковским, будет снято. Определим
марковский ветвящийся процесс с непрерывным временем, имею-
щий в качестве состояния X(t) число частиц в момент t при усло-
вии, что Х(0) = 1, через инфинитезимальные параметры процес-
са. Пусть
+ Ukh Ч- о (h), & = О, 1,2,... (7.1)
(см. § 4 гл. 7 и § 3 гл. 8) — вероятность того, что одна частица по-
родит k частиц (или объектов) за малый интервал (/, t + h) дли-
тельности h. В (7.1) 61й обозначает, как обычно, символ Кронеке-
ра. Предположим, что ах Q, ak 0 для k = 0, 2, 3, ... и
оо
2«fe = 0. (7.2)
fe=0
Далее, постулируем, что отдельные частицы действуют незави-
симо друг от друга и всегда «управляются» инфинитезимальными
параметрами (7.1). Заметим, что при этом предполагается одно-
родность по времени, поскольку не зависят от моментов пре-
вращения (или расщепления) частиц.
Другим способом выражения инфинитезимальных переходов
является разбиение времени на участки, где не происходит пре-
вращений, и рассмотрение различных вариантов превращений.
Так, каждый объект живет случайное экспоненциально распреде-
ленное время со средним значением V1, X = aQ + а2 + а3 +... .
334
Гл. 11. Ветвящиеся процессы
По завершении времени жизни он порождает случайное число D
потомков, представляющих из себя такие же объекты. Вероятно-
стное распределение D имеет вид
Р{£) = А!}=—, k = 0, 2, 3, ....
1 J aQ + а2 + а3 + ... ’
Время жизни и число потомков для отдельных индивидуумов — не-
зависимые случайные величины, и их распределения не меняются
от индивидуума к индивидууму. Принимая во внимание предполо-
жения о независимости, в особенности то свойство, что отдельные
индивидуумы действуют независимо друг от друга, можно (7.1)
представить как инфинитезимальные переходные вероятности:
Р {X (t + h) = п +k — 1 \X(t)~n} = nak!i + o(h), (7.3)
Р {X (/ + Л) = и | X (/) = п} = \-па{1г + о(К), (7.4)
где о (Л) lh~+Q при h —> 0 +.
Мы уже имели дело с примером ветвящегося процесса с непре-
рывным временем, когда рассматривали процесс рождения и гибе-
ли. Действительно, если положить аг = X, aQ = ц, = — (X + р),
ak = 0, k =/= 0, 1, 2, то величину (Z, + ц)"1 можно интерпретировать
как интенсивность наступления событий рождения и гибели;
Х/(% 4-ц) (ц/(% + ц)) — вероятность рождения (гибели) при усло-
вии, что какое-то из этих событий произошло. Так определенный
случайный процесс, состоянием которого является размер популя-
ции, есть не что иное, как процесс рождения и гибели с линейным
ростом (см. гл. 7, § 6).
Как указано в гл. 8, задача построения марковского процесса,
соответствующего заданной инфинитезимальной матрице, не яв-
ляется легкой. Еще более трудная задача — проверить, что по-
строенный процесс имеет реализации, соответствующие предполо-
жениям для ветвящегося процесса, т. е. отдельные частицы по-
рождают независимые семейства, потомки действуют независимо
друг от друга и т. д. Мы не будем касаться анализа этого построе-
ния, так как он выходит за рамки данной книги. Более подготов-
ленный читатель может эти вопросы найти в книге Харриса (см.
литературу в конце данной главы); мы же сошлемся на § 3 гл. 8,
где обсуждаются связи между марковскими процессами и инфи-
нитезимальными матрицами.
Пусть Pn(t) (предположим, что всюду далее она определена
корректно) — вероятность того, что размер популяции в момент t
равен / при условии, что в момент 0 он был равен г, или ЛДО =
= Р{Х(/ + s) = j\X(s) = i}. Как показывает обозначение, эта ве-
роятность зависит лишь от прошедшего времени, т. е. процесс
§ 7. Ветвящиеся процессы с непрерывным временем 335
имеет стационарные переходные вероятности. Введем производя-
щую функцию
4>(/; s)= 2^/(0*'. (7.5)
/=0
Поскольку индивидуумы развиваются независимо, имеем основное
соотношение (ср. со стр. 315)
оо
= < (7.6)
/=о
Формула (7.6) характеризует ветвящиеся процессы и выделяет их
среди других цепей Л1аркова с непрерывным временем. Она вы-
ражает то свойство, что различные индивидуумы (частицы) по-
рождают независимые реализации процесса, где потомство одних
индивидуумов не влияет на потомство других. Другими словами,
популяция Xпорожденная i объектами, статистически совпа-
дает в момент t с суммой i независимых популяций, каждая из ко-
торых порождена одним объектом.
В силу однородности по времени уравнения Колмогорова —
Чэпмена имеют вид
оо
Роа + т)=ЗР«(0^/(г). (7.7)
k=0
С помощью (7.5), (7.6) и (7.7) получим
оо оо оо
[Ф (t + т; з)]г = 2 Pt! (/ + т) s' = 2 2 Ptk (0 Pkt (т) s' =
/=»0 /=0/^=0
оо оо оо
= 2P«(/)2Pfe/(r)s'=2P«(0^(r; s)]ft = [^; Ф(ъ s))]'
fe=o /=о /г=о
и, в частности,
^>(/ + т; s) ==<£(/; ^(т; s)). (7.8)
Соотношение (7.8) является непрерывным аналогом итера-
ционной формулы, введенной в § 2, которая является основной для
ветвящихся процессов с дискретным временем. Введем произво-
дящую функцию инфинитезимальных параметров (7.1). Именно
пусть
и (s) = 2 aksk.
/?=0
336
Гл. И. Ветвящиеся процессы
Проводимый ниже анализ является формальным. Рассмотрим
(Л; $) = 2 P\j (h) sJ = 2 (61/ + ajh + o(h)) sJ =
j=0 /=o
= s + h 2 ctjSJ + o(h) = s + hit (s) + о (A). (7.9)
/»o
Из (7.8) при т = h имеем
ф (t + h\ s) = ф (/; Ф (h; s)) = Ф (t\ s + hu (5) + о (h))
и, разлагая правую часть по второй переменной по формуле Тей-
лора, получаем
ф (t + /г, s) = Ф (/; s) + hu (s) + о (/г).
Тогда
Ф (t + h\ s) — Ф (t; s) __ дФ (/; s) ,, 0 (h)
h ~~ ds U + h '
Устремив h к 0, получим
Это уравнение в частных производных относительно функции
двух переменных ^(/; $), удовлетворяющей начальному условию
^(0; s)s= 2 Pll(Q)sJ^s. (7.11)
/ = 0
Если известна u(s), то уравнение (7.10) с начальным условием
(7.11) можно решить относительно ^(/; $).
Дифференциальное уравнение (7.10) является формой прямых
дифференциальных уравнений Колмогорова, которые были сверну-
ты в уравнение относительно производящей функции исходных
переходных вероятностей.
Можно вывести второе дифференциальное уравнение относи-
тельно ф, которое соответствует обратным уравнениям Колмогоро-
ва. Для этого положим в (7.8) t = h. Получим
^(Л + т; s) = ^(/z; <^>(т; s)).
Вновь используем (7.9) и разложение Тейлора. Тогда
Ф (h + т; 5) = Ф (т; s) + hu (ф (т; s)) + о (Л).
Это выражение можно переписать в виде
Ф(т + Л; s)-0(t; s) = (т; > j о(Л) _ J2)
§ 8. Вероятности вырождения для ветвящихся процессов
337
Устремляя Л —> 0 + и заменяя т на /, получаем
= s) ).
(7.13)
Это обыкновенное дифференциальное уравнение. Начальное усло-
вие для него вновь (7.11). Позже будет показано, как можно эф-
фективно решить уравнение (7.13).
§ 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Решим сначала более легкую задачу нахождения среднего зна-
чения Х(/). Для этого продифференцируем (7.10) по s и изменим
порядок дифференцирования в левой части. Получим
dt ds ds2 ' ' ds ' 7 7
Положим s = 1. Тогда, поскольку z/(l) = 0 (условие (7.2)), имеем
dm (t)
(8.2)
где
tn (/) = M(X(0) =
дФ (t\ s) I
ds |.
Решение уравнения (8.2) имеет вид
m(t) = ехр [u'(l) f],
(8.3)
поскольку m(0) = 1, если предположить, что /(0) = 1.
Займемся теперь задачей о вырождении. Для этого всюду да-
лее в этом параграфе будем предполагать, что ац > 0, так как
в противном случае вырождение невозможно. Достаточно рассмот-
реть случай, когда в момент 0 имеется один индивидуум. Дей-
ствительно, из (7.6) известно, что
оо Г оо "V
W L/ = 0 J
следовательно,
Ло(О = Р1о«
Но Pio(i)—вероятность того, что популяция, имеющая в началь-
ный момент размер f, выродится к моменту t. Интуитивно очевид-
но, что Рг-о(О — неубывающая функция t. Докажем это формально,
используя (7.8). В самом деле,
Р10 (/ + Т) = [ф (/ + т; 0)]z = [ф (Р,Ф (т, 0) )f > [М 0)V = Р(о (/),
338
Гл. И. Ветвящиеся процессы
где использован тот факт, что ф(1, s) является степенным рядом по
s с неотрицательными коэффициентами и, следовательно, возра-
стающей функцией s.
Вероятность вырождения можно определить как вероятность
того, что популяция, порожденная одним индивидуумом, исчезнет,
т. е.
q= lim P,o(O-
f->oo
Используя теорию ветвящихся процессов с дискретным временем
(§ 3), легко найти вероятность вырождения в случае непрерывного
времени. Пусть /о — любое фиксированное положительное число;
рассмотрим процесс с дискретным временем
Х(0), X(U X (2/0), ..., Х«), ...,
где X(f) —размер популяции в момент t, соответствующий исход-
ному ветвящемуся процессу с непрерывным временем, Х(0) = 1.
Поскольку по предположению X (/)—марковский процесс, про-
цесс с дискретным временем, то Yn=X(nto) образует, очевидно,
цепь Маркова. Более того, он является ветвящимся процессом с
дискретным временем. В самом деле, в силу гипотезы об однород-
ности процесса Х(/) и в силу (7.6) получим
оо
2р{к„+1 = ^1К„ = /}? = м[Л+-|у„ = г-! =
fe=0
= М [s* < <*+о | X (nQ - /] = М [sx I X (0) - /] =
- 1Ф < = {М (X (0) = 1 J}z = {М | Уо - 1 ]}*.
Отсюда следует, что {Уп} является ветвящимся процессом. Про-
изводящая функция числа потомков одного индивидуума для
этого процесса равна ^(/0, s). Следовательно, вероятность вырож-
дения процесса {Ул} является наименьшим неотрицательным кор-
нем уравнения
Ж: S) = s, (8.4)
как это показано в § 3. Но
Р{К„ = 0 при некотором п}= lim Р {Yn = 0} =
П->оо
= lim P{X(nfo) = O}= lim Р{Х (/) = 0} = q.
Следовательно, вероятность вырождения q ветвящегося процесса
X(t) с непрерывным временем является наименьшим неотрица-
тельным корнем уравнения (8.4), где tQ— любое< положительное
число.
Поскольку q — корень уравнения (8.4) при любом /0, следует
ожидать, что вероятность q можно найти из уравнения, не содер-
§ 8 Вероятности вырождения для ветвящихся процессов
339
жащего этого параметра. Это в действительности так и утвер-
ждается следующей теоремой.
Теорема 8.1. Вероятность вырождения q является наимень-
шим неотрицательным корнем уравнения
и (s)= 0. (8.5)
Следовательно, q = 1 тогда и только тогда, когда ы'(1)-*С0.
оо
(Вспомним, ЧТО u(s) = S akSk als + [Яо + а2^ + . . • ] = UlS + g ($).)
Рис. 3
Доказательство. Поскольку q удовлетворяет уравнению
(8.4) при любом /о, из (7.12) следует, что
0 = и (q) + о (h)/h при любом Л > 0.
Устремляя h к 0 + , получаем и(#) = 0.
оо
Поскольку u"(s) = 2\akk (k — 1) sk~2^0, функция u(s) вы-
пукла на отрезке [0, 1]. Так как и (1) =0, а ы(0) = а0 > 0, то u(s)
340
Гл. 11. Ветвящиеся процессы
может иметь самое большее один нуль в интервале (0, 1). Слу-
чаи 40 и г/(1) >0 представлены на рис. 3 и 4 соответ-
ственно. Заметим, что М(Х(/0)) = М(У1) > 1 тогда и только тогда,
когда ur (1) > 0 1). Это означает, что для ветвящегося процесса
с дискретным временем X(nt0), п = 0,1,.-. (^о > 0 и фиксиро-
вано), вырождение в этом случае происходит с вероятностью <1
и, следовательно, это же справедливо и для процесса Х(/). Вероят-
ность вырождения q в этом случае с необходимостью является наи-
меньшим нулем функции u(s) на [0, 1]. Аналогичным образом по-
казывается, что если ц'(1) то q = 1. В любом из этих слу-
чаев q — наименьший неотрицательный корень уравнения (8.5).
§ 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Вернемся к задаче решения обыкновенного дифференциального
уравнения (7.13), анализу и интерпретации его свойств при
t —* оо. Поскольку exp[w'(l)Z] — среднее число частиц в момент /,
мы будем различать тип поведения в зависимости от того, какое из
условий и'(1) <0, ц'(1) =0 или ц'(1) >0 выполняется. Мы об-
судим лишь случай и'(1) <0 при дополнительном предположе-
нии и"(1)<оо. Сначала докажем, что функция
В (<$) = —тг--Г7ТГ7---п
4 7 и (s) и (1) ($ — 1)
ограничена и, следовательно, интегрируема при 0 4Cs< 1. В самом
деле, разлагая u(s) в окрестности точки s = 1, получаем формулу
u(s) = ^(1) + и' (l)(s — 1) + 7? (s) (s — l)2, $<1,
где
lim R(s)==y~^-<<x>. (9.1)
S~>1 —
Вспоминая, что u(q') = ц(1) = 0, получаем
1 1 1 1
u(s) “ n'(l) (s- 1) 4-Ze (s) (s- I)2 ~ и' (1) (s - i) 1 + [/? (s) (s -\)/uf (1)]
__ 1 f 1 _ 1
Uf (1) (s- 1) I l + [/?(s)(s-l)/u'(l)] J’
Следовательно,
D / _____________________(s)l[u' (I)]2 (9 2)
и как следствие (9.1) получаем, что B(s) ограничена в окрестности
точки s=l —. Функция B(s) заведомо ограничена при всех s, не
9 См. формулу (8.3). — Прим, перев.
§ 9. Предельные теоремы
341
принадлежащих окрестности точки 5=1, т. е. О s 1 —6; это
следует из определения, поскольку в исследуемом случае (и'(/)<0)
w(s) = O только при s=l. Таким образом, B(s) ограничена при
О5 < 1 при условии, что и,,(1)<оо и и'(1) < 0. В силу этого
можно ввести функцию
,9-3)
1
поскольку интеграл существует и конечен. Заметим, что
/</^==7W>0 при °<s<1
снова в силу предположения z/'(l) <0. Это означает, что K(s) —
строго возрастающая непрерывная функция. Следовательно, ото-
бражение
w = К (5) (9.4)
имеет обратное, которое является непрерывной строго возрастаю-
щей функцией
s = = £(/<($)) = $, (9.5)
обладающей тем свойством, что при изменении $ на интервале
[0, 1) функция w изменяется на интервале |7С(0), оо), /С(0) < 0.
Теперь у нас есть все необходимое, чтобы найти искомое решение
(7.13) при начальном условии (7.11). Разделяя в (7.13) перемен-
ные и интегрируя, получаем точную формулу относительно
Фа-, s)
[
J и (х) '
s
Совершая очевидные преобразования и используя определение
/((•), находим
Ф Ц; 5) Ф (t; s)
, Г dx f Г 1 1 1л । 1 1 /1
t = ~ГТ = ~~ГГ--------------ГТГП----ГТ dx J--F7TV In (1 — x) =
J u(x) J Lu(x) и (l)(x- 1)J «'(1) x 7|5
s s
Ф s)
= J [vtxT “ «'(l)(x-l)] dX + «' (1) 1П^ “ ~
1
s
- f Г—ГТ--Т7К7------= s))-K(s).
J Lu (x) u' (I) (x- 1) J U' (1) v 77 V 7
1
Отсюда
Ш s)) = * + X(s).
342
Гл. 11, Ветвящиеся процессы
Поскольку существует обратная функция, то
з) = /С'(/ + /<(з)), 0<s<l, />0. (9.6)
В предположениях «'(1) <0 и и"(1) < оо можно также получить
некоторые асимптотические результаты относительно вероятности
вырождения к моменту i Так как B(s) ограничена при
0<О < 1 и lim В (s) существует, можно записать (см. (9.3))
s-> 1 —
^) = ^^ + C.(l-s) + 0(l-s). (9.7)
Здесь С — отрицательная постоянная. В самом деле,
Нт Г_!__________। 1_г »"0)
X4!i-L«(x) u-i)«z(i)J 2[z/'(i)]2*
Перепишем равенство (9.7) в виде
In(1 — s) = и'(l)K(s) -Си'(1)(1 -з) + о(1 — s),
откуда
1 — s — ехр [и' (1) К (s)] ехр [ — Си' (1) (1 — s)] ехр [о (1 — s)].
Но
ехр [о (1 — з)] = 1 + о (1 — s),
а
ехр[ — Сп'(1)(1 -*)]= 1 — C«'(I)(1 -s) + o(l -s).
Отсюда
1 -з = ехр[н'(1)/<(з)][1 — Crz'(l)(1 -s) + o(l -s)]. (9.8)
Следовательно,
Д.Т- exp [и' (1) К (s)] — 1 ‘
С помощью этого предельного соотношения можно записать (9.8)
в виде
1-5 =
= {ехр [и' (1) К ($)]} { 1 - Си' (I) ехр [и' (1) К («)] + о (ехр [и' (1) (з)])}.
Заменяя з на (см. (9.5)), получаем
1 — (да) = ехр [м'(1)да]{1 — См'(1) ехр [м'(1) да] + о (ехр [м'(1) да])};
(9.9)
при этом соотношение з —» 1— эквивалентно да —»оо. Теперь с по-
мощью равенств (9.6) и (9.9) можно найти вероятность того, что
вырождение не произойдет к моменту /:
1 - Р10 (0 = 1 - /> (/; 0) = 1 -K~}(i + K (0)) =
= {exр [и' (1) (К (0) + 0]} {1 - Си' (1) ехр [н' (1) (К (0) + /)] +
+ о (ехр [и' (1) (/((0) + /)])} =
— ехр {и' (1) К (0)} ехр {и' (1) t} -I- О (ехр {2 м' (1) /}) + о (ехр [м' (1) t]),
§ 9. Предельные теоремы
343
ИЛИ
1 — Pio(0 = exp[«/(l)/<(0)]/n(0 + o(exp[u/(l)H)- (9.10)
Другой асимптотический результат (при t —> оо) можно полу-
чить следующим образом. Условная производящая функция вели-
чины X (/) при условии, что X (/) Ф 0, определена равенством
оо
g(z, 0=2р{^(0 = ^1^Ю^0}Д
fe=0
0<z< 1.
Но
ph(0 = k | x(0 0} = p{X(LV,yoj- =
o,
p (X (0 = k}
i —P{X(0 = 0) ’
если k = 0,
если k #= 0.
Таким образом,
„, л _ V P I* (0 ° 7k = »(/; ?)-*(/; Q) =
1-Р{Х(/)=0} ~ 1-ф(/;0)
fe=l
_ K~l Ц + К(г))-К-' (< + X(0)) .
1-X-’ (/ + X(0))
.. [1 — K"1 (Z + X(O))]-[l -X~' (t + K(z))]
(t + KiO)) ’
где использована формула (9.6) для ^(/; s).
Подставляя выражение для /С-1(ш) (формула (9.9)), получаем
g(z-, i) =
ea'(l) (t+K (0)) [ I + О (e«' <1) «+К (0)))] _ eu' (1) (i+K (z)) [ [ + о (eu' W(i+K (z)))]
e eu- (1) U+X <°)) [1 + о (s«' (О «+Х (0)))] =
I +0 (Ри’(1)а+К(г))\
= 1 _eu'(l)[X(z)-X(0)| 1 +(J -----------L
1+о(е“'(1)Ц+Х(0)))-
Пусть теперь t —»oo. Тогда отношение, стоящее в правой части,
стремится к 1, если ы7(1) <0. Следовательно,
lim g{z-, t) = g(z)= 1 -exp{«'(l)[K(z)-7<(0)]).
/->oo
В силу (9.3), однако,
z
X (z) - К (0) = [Г -4т - -Z7TT7-ni dx + -"Т7Л£)- =
х х J 4 ’ J L«W u (l)(x- 1) J ы'(1)
0
z z
f dx — *n P ~ Г I 1 n (1 ~ ?) _ Г dx
J «W ~ «'(1) In “'(1) “J «М ’
0 0 0
344
Гл. 11. Ветвящиеся процессы
Следовательно, при * оо предельная производящая функция
равна
g (г) = 1 - ехр
= У lim Р{Х(0 = Ш(0=^0}г*.
Подведем итоги предыдущему обсуждению в виде следующей
теоремы.
Теорема 9.1. Рассмотрим ветвящийся процесс X(t) с непре-
рывным временем, определяемый инфинитезимальной производя-
щей функцией
оо
w(s)=2a4?, (9.11)
fe=0
где интерпретация последовательности {ak} дана в (7.1) и выпол-
няется условие (7.2). Предположим, что и"(\)< оо. Предположим,
далее, что и' (1) <0, так что вероятность вырождения q равна еди-
нице (см. теорему 8.1). Тогда
оо
Ф (Л s) = 2 Р {X (t) = k | X (0) = 1} sk =
fe=0
= K~'(t + X(s)), |s|<l,
(9.12)
где функция K(s) определена соотношением (9.3). Вероятность
того, что до момента t не произойдет вырождения, стремится к 0
как экспонента в соответствии с соотношением
г __________1 -Р10(/) = 1
ехр [w' (D # (0)] ехр [и' (1) t]
Кроме того, случайная величина X (t) (при условии, что X (t) >
> 0) имеет предельное распределение с производящей функцией
(9.13)
Мы приведем без доказательства следующую предельную тео-
рему для случаев и'(1) =0 и и'(1) >0. Ее доказательство более
сложно, хотя и аналогично предыдущему по существу.
§ 10. Процесс с непрерывным временем и двумя типами частиц 345
Теорема 9.2. (1) Предположим, что «'(1) = 0 и и'”(1) < оо.
Тогда
P{X(/)>0|X(0)=l}~-^-J-, /->оо,
и
lim Р{1?7ТП->^1Х(/)>0} = е-\ Л>0.
t->oo I “ v? ‘ J
(2) Если «'(!)> О и «"(!)< оо, то случайная величина
Z(t) =
X(t)
ехр [и' (1) t]
имеет предельное распределение при ^->оо!).
§ Ю. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ
ТИПАМИ ЧАСТИЦ
Рассмотрим два различных типа частиц, которые мы будем на-
зывать частицами типов 1 и 2 соответственно. Ветвящийся мар-
ковский процесс с непрерывным временем будет определяться со-
ответствующими инфинитезимальными параметрами. Именно мы
постулируем, что каждая частица типа i (i = 1, 2) может в тече-
ние интервала (/, t + Л) независимо от прошлого и независимо от
истории или текущего состояния любой другой частицы любого
типа превратиться в kx частиц типа 1 и k2 частиц типа 2 с вероят-
ностями
для »=1’
бЛ+<'^+о(Л) лля /=2-
где й1, ^2 = 0, 1, 2, ..., a (из— символ Кронекера. Заметим, что
мы снова постулируем однородность по времени для процесса, по-
скольку постоянные не зависят от времени. Введенные па-
раметры подчиняются следующим ограничениям:
для всех kv k2 — 0, 1,2,..., кроме ^=1, k2 = 0;
aki Для всех = 1, 2, кроме k{ = 0, й2=1;
2 г‘=1-2-
9 Более конкретно, случайная величина Z(/) сходится при f->oo к случай-
ной величине W с вероятностью 1. Для величины W можно найти вид произво-
дящей функции (см. книгу Т. Харриса, упоминаемую в списке литературы в кон-
це главы). — Прим, перев.
346
Гл. 11. Ветвящиеся процессы
Введем две производящие функции
оо
(Sl> S2) = А S=o < kSk^, /=1,2 (I s, I < 1, I s21 < 1).
Пусть Pklfk2; h, J2U) —вероятность того, что в момент t популяция
состоит из /1 объектов типа 1 и /2 объектов типа 2 при условии, что
в момент 0 было k[ объектов типа 1 и k2 объектов типа 2. По-
скольку инфинитезимальные параметры не зависят от вре-
мени, переходные вероятности с необходимостью стационарны.
Определим производящие функции
оо
^>(7; s„ s2)= 2 Л, 0; л. а (0
/1. /2=0
ОО
sp s2) = 2 Po>I;/i>a(OsN2.
/1» /2=0
Тогда аналогично одномерному случаю получим
оо *
, JL0 Pk" кл h S‘'S22 =
= slt s2)]k' [?» (/; s„ s2)]fe, kh k2=\, 2, ... . (10.1)
Фактически соотношение (10.1) можно считать определяющим
для ветвящихся процессов с двумя типами частиц и непрерывным
временем. Другими словами, можно сказать, что любая переход-
ная функция, удовлетворяющая (10.1), порождает марковский вет-
вящийся процесс с двумя типами частиц и непрерывным временем.
Марковский характер процесса выражается уравнениями Колмо-
горова — Чэпмена
Pkh k2; h, /2 (^ + т) = 5 Р^, fe; h (t) Ph, h; /„ h (T)- (10.2)
h, /2=0
Из (10.1) и (10.2) следует
(t + v, S2)= 2 Р1,0;/ь/г(/ + т)5{'5Л =
/1. /2 = 0
oo 00
= J-o /„?=oP1-0: h ’<• » =
00 00
- 2 ₽>.«>,.<,(W"(t; s„ si, s,)]'1-
h, /2=0
= sb s2), </>(2)(r; sb s2)).
§ 10. Процесс с непрерывным временем и двумя типами частиц 347
Аналогичное соотношение выполняется и для функции
^<2)(/; sb s2). Таким образом,
^(Z)(/ + t; sb s2) = (t; ^(1)(т; sb s2), ^(2)(т; 8b s2)), i= 1,2. (10.3)
Кроме того,
^(,) (ft; sp s2) = 2 Plt 0. /b h (ft) s{^ =
/1. /2“v
= S [6b 60/2 + fl/'.’ jh + о (ft)] s{>s/= — s, + hu(1} (sp s2) + о (h);
fl, /2=0 L
аналогичное равенство имеет место для ^<2>(Л; sb s2). Таким обра-
зом,
^(Z) (ft; sb s2) = sf + ftu(Z) (sb 82) + o(ft), Z== 1, 2. (10.4)
Получим теперь уравнения в частных производных, которым удо-
влетворяют функции ^(i)(/; Si, s2) (i = l, 2), аналогичные уравне-
ниям (7.10) и (7.13). Для этого положим сначала т = Л и подста-
вим (10.4) в (10.3). Используя формулу Тейлора, получаем
^(Z) (t + ft; sb s2) —
= (/; Si + ft«(1) (sb s2) + о (ft), s2 + ftu<2) (sb s2) + 0 (ft)) =
~ (t-, 81, s2) = hu^ (81, S2) +
USi
+ d^^Lhu(24 S2) + o{h).
0S2
Разделив обе части на ft и положив ft -* 0, формально получим
дифференциальные уравнения
(/; Si, s2) _ <?4>(Z) (/; Si, s2) <i(n 4 ,
di dSi (Sb
+ дФ™ (i’’ S1, St) u™ (sh S2), / = 1,2. (10.5)
OS2
Обратимся вновь к равенству (10.3) и положим на этот раз t = ft.
Используя (10.4), получаем формулу-
^(Z)(ft + r, sb s2) = ^<<>(ft; ^(1) (т; sb s2), (t; sb s2)) =
= </>(,) (t; sb s2) +/ш(() (^>(1) (t; sb s2), </>(2) (t; sb s2)) + o(ft).
Разделив на ft, положив ft—>0 и заменив т на t, получим вторую
систему дифференциальных уравнений
М = (^>0) (/; S1, s2), </>(2) (/; S1) s2))( г= 1, 2. (10.6)
Начальные условия для уравнений (10.5) и (10.6) таковы:
^<Z) (0; sb 8г) = 8г, 1=1, 2.
348
Гл. 1L Ветвящиеся процессы
С помощью (10.5) и (10.6) можно получить системы обыкновен-
ных дифференциальных уравнений, которым удовлетворяют мо-
менты искомых случайных величин. Здесь мы не будем входить
в детали этих вычислений.
Дадим теперь несколько применений и примеров ветвящихся
процессов с двумя типами частиц и непрерывным временем.
Пример 1. В первом примере рассматривается ветвящийся
процесс с иммиграцией. Рассмотрим одномерный ветвящийся про-
цесс с непрерывным временем и обобщим его, допустив, кроме
ветвления, миграцию частиц в систему. Напомним, что
+ akh + o(h\ fe = 0, 1, 2,
— вероятность того, что какая-либо частица превратится в k ча-
стиц за малый интервал (/, i + h) независимо от предыстории про-
цесса. Включим процесс иммиграции в популяцию следующим об-
разом. Пусть
60й + bkh + o(h), k = 0, 1, 2,
— вероятность того, что (независимо от предыстории процесса) k
частиц того же типа добавятся к популяции за временной интервал
(/, t + h). Заметим, что параметры ак так же, как и параметры bh<>
по предположению не зависят от времени; иначе говоря, соответ-
ствующие переходные вероятности стационарны. Величины ah и
подчиняются условиям
Я1<0,
для fe = 0, 2, 3,
bk^Q для k = 1, 2, 3, ..
оо оо
2 ak bk= о.
k=Q
Пусть
Pk (f) = P {размер популяции в момент t равен k\ в момент 1 — 0
размер популяции =0} =
= Р{Х(/) = /г Щ0) = 0}, £ = 0, 1, 2, (10.7)
и пусть
оо
<НР s)^%Pk(t)Sk. (10.8)
k-0
Наша цель —найти вероятности РкЦ) или —если это невозмож-
но— получить некоторые их свойства.
Введем производящие функции
оо оо
и (s) = 5 aksk, v(s)= ksk.
Л-Q
§ 10. Процесс с непрерывным временем и двумя типами частиц 349
Можно представить одномерный ветвящийся процесс с непрерыв-
ным временем и иммиграцией в виде ветвящегося процесса с двумя
типами частиц.
Идея, лежащая в основе упомянутого представления, заклю-
чается в следующем. Имеются два типа частиц: частицы типа 1 —
реальные, в то время как частицы типа 2 — фиктивные. Реальная
частица по окончании своего времени жизни (которое является
экспоненциально распределенной случайной величиной с парамет-
ром X = + а2 + «з + ...) порождает k новых реальных частиц
с вероятностью h~xak (k = Q, 2, 3, ...). Фиктивная частица также
живет случайный отрезок времени (экспоненциально распределен-
ный с параметром Х = Ь\ + Ь2 + ...) ив конце его порождает I
реальных частиц и одну фиктивную с вероятностью \~xbt (I ==
оо
= 1, 2, 3, ...). Заметим, что 2л Потомство фиктивных
z=i
частиц соответствует иммиграции. Таким образом,
если k2 = О,
если k2 =/= О,
если k2 = 1,
если 62#=1.
Тогда в соответствии с обозначениями, введенными в начале этого
параграфа, имеем
«(1)(sb s2)= S Ч? k2Sl'S2 = S ak,Sl'>
К Ь 2/ ki, fc2=0 b 2 ^=о 1
«(2)(sp s2)= s a® S^ = s2 s bksb.
v 1 27 k,=0 ft” й ' A,=0 *' 1
Таким образом,
u(1) ($ь «г) = u (si). u<2) ($!> S2) = S2V (si)-
В рассматриваемом частном случае дифференциальное уравнение
(10.5) принимает вид
= *.?>. и (S1) + S2V (Sj)> (Ю.9)
z = 1, 2,
350
Гл. И. Ветвящиеся процессы
а дифференциальное уравнение (10.6) —
= и (^>(1) (t- Si> s2)), 00.10)
—^'S2) =№2)(t; s2')]v(^(t- Sl, s2)). (10.11)
Установим теперь соответствие между вероятностями Род/ь/2(0>
введенными для процесса с двумя типами частиц, и вероятностями,
определяемыми соотношением (10.7). В соответствии с введенными
обозначениями начальное состояние (0, 1) для процесса с двумя
типами частиц означает, что в момент 0 реальные частицы отсут-
ствуют, а имеется лишь фиктивная частица — «потенциальные им-
мигранты», В силу определения очевидно, что
п ... / Pi At), если /2 = 1,
’ 1 1 ( 0, если /2=И= 1,
и, следовательно,
^(2)(^; <$ь S2) = s2^>(/; Sj). (10.12)
Тогда из (10.9) получаем
= u(s) + ^(/; s)v(s)> (I013)
где вместо мы написали $. Начальное условие имеет вид
</>(0; s) = 1. (10.14)
Вместо того чтобы решать это дифференциальное уравнение,
решим систему уравнений (10.10) и (10.11), что легче. Уравнение
(10.10) можно рассмотреть методами, примененными для анализа
уравнения (7.13). Решение уравнения (10.10) можно представить
в виде, аналогичном (9.6). Обозначим его через f(/; s); здесь вме-
сто Si и s2 записано сокращенно s. В силу (10.12) уравнение
(10.11) принимает вид
= s))
(10.15)
с начальным условием (10.14). Решение уравнения (10.15) равно
Ф (/; $) = ехр
v (f (т; s)) ch
Пример 2. В заключение параграфа опишем простой немар-
ковский одномерный ветвящийся процесс (бинарного деления)
с непрерывным временем, который можно свести к марковскому
§ 10. Процесс с непрерывным временем и двумя типами частиц 351
ветвящемуся процессу с двумя типами частиц. Предположим, что
частица имеет распределение времени жизни с плотностью
It-te-M (10.16)
(гамма-распределение порядка 2). По истечении времени жизни
частица заменяется на две частицы такого же типа, каждая из ко-
торых независима от другой и исходной частицы и имеет плот-
ность (10.16) времени жизни.
Марковские процессы в общем случае характеризуются тем
свойством, что время пребывания в любом состоянии распределено
экспоненциально. В данной главе время пребывания в данном со-
стоянии определяется временем жизни частицы. Если оно распре-
делено экспоненциально, то процесс роста популяции этих частиц
является марковским. В рассматриваемом случае время жизни
распределено не по экспоненте, а по свертке двух экспонент.
Пусть Х(/)—число частиц в момент /; предположим, что
Х(0) — 1. Поскольку (10.16) —плотность суммы двух независимых
экспоненциально (с параметром Z) распределенных д. с. в., можно
считать, что каждая частица как бы проходит две фазы развития,
каждая из которых имеет экспоненциально распределенную с па-
раметром % длительность. Такой процесс нетрудно свести к мар-
ковскому ветвящемуся процессу с двумя типами частиц. Вместо
того чтобы говорить о двух фазах жизни одной и той же частицы,
будем говорить о двух типах частиц. Частица типа 1 имеет экспо-
ненциально распределенное с параметром X время жизни и по
окончании его превращается в частицу типа 2. Частица типа 2
имеет экспоненциально распределенное с параметром X время
жизни и по окончании его превращается в две частицы типа 1. Та-
ким образом, в обозначениях данного параграфа имеем
’ -1, если k{ = 1, k2 — 0,
л(1) = ukit k2 + 1, если kx = 0, *2=1,
. 0 в противном случае,
+ 1 > если ^1=2, /t’j = 0,
aW = k2 -1, если ki = 0, 62 = 1,
. 0 в противном случае,
где для простоты предполагается, что Z — 1. Тогда
и
«(1) («1> s2) = - «1 + s2
u(2)(sp s2) = sf-s2.
352
Гл. И. Ветвящиеся процессы
Соотношения (10.5) и (10.6) примут соответствующий частный вид.
Производящая функция величины X (/) при условии X (0) = 1 мо-
жет быть получена из ^6)(/; sb s2) при si = s2 = s.
§ II. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
В этом параграфе мы рассмотрим модель ветвящегося про-
цесса, где каждый объект (или частица, или индивидуум) имеет
случайное время жизни с произвольным распределением, а по
окончании его порождает своих потомков. Этот процесс следует
сравнить с ветвящимися процессами, у которых время жизни од-
ного объекта фиксировано или экспоненциально распределено.
Предположим, что отдельный объект имеет время жизни случай-
ной длительности Т с плотностью /(/), т. е. вероятность того, что
время жизни объекта лежит в интервале (/, t + dt), равна f(t)dt.
Предположим далее, что по окончании времени жизни объект по-
рождает два новых объекта такого же типа, времена жизни кото-
рых будут независимыми случайными величинами с той же плот-
ностью f(t). По окончании своего времени жизни каждый объект
снова породит два новых объекта того же типа, и этот процесс
продолжается бесконечно долго. Пусть N (/)—число объектов
в момент /; обозначим его вероятностное распределение через
pk(t) = Р {N (t) ~ k}, k = Q, 1, 2, ... .
Очевидно, Ро(О == 0 при всех t 0, поскольку в наличии всегда бу-
дет по крайней мере один объект. Действительно, до первого «раз-
двоения» будет в точности один объект, а после него — по крайней
мере 2 объекта. Таким образом,
Pt (0 = Р {N (/) = 1} = Р {Т > /} = 1 - F (/),
где
t
f(/)-P{7’</} = j f (х) dx
о
— функция распределения величины Т.
Пусть G(s, t) —производящая функция величины N(t), т. е.
оо оо
G (S, /) = 2 Pk (0 sfe = 2 Pk (0 sk.
6=0 k=l
Получим интегральное уравнение относительно G(s, t). Вероят-
ность pk(t) того, что в момент t имеется ровно k объектов, можно
выразить следующим образом. Предположим, что первое ветвле-
ние происходит на интервале (т, т + dr), вероятность
чего равна f(x)dx, и за оставшееся время / — т оба новых незави-
симо развивающихся объекта породят в сумме k потомков. Есте-
§11. Ветвящиеся процессы, зависящие от возраста 353
ственно, что момент первого ветвления т может принимать любые
значения из отрезка [0, /]. Таким образом, из формулы полной
вероятности следует, что
t k
Р* (0 = J k~2, 3,
О /=1
Pl(t) = \ — F (t).
В силу определения G(s, /) имеем
оо t оо
G(s, /) = [! - F (/)] s + sk J dxf (x)^pt(t - х) pk^(t - х)
k=2 0 1=1
оо t k
= [1 -F(/)]s + ^sft J dxf (x)^pt(t - х) pk^i(t - х).
k = 0 0 1 = 0
Поскольку все входящие под знак суммирования величины неот-
рицательны, знаки суммирования и интегрирования можно поме-
нять местами. Тогда
t ОО k
о k=0 1=0
Двойная сумма в правой части является производящей функцией
двукратной свертки последовательности {pk(t — т)}. Таким обра-
зом,
t
G(s, t)= J [G(s, Z-T)]2/(T)dT + [l-F(0]s. (11.1)
0
К сожалению, в общем случае данное интегральное уравнение
не решается. Решим его для частного случая, когда Т имеет экспо-
ненциальное распределение с плотностью
= (И.2)
Процесс, соответствующий данному частному случаю, является
процессом чистого рождения Юла. Действительно, если вначале
имеется п объектов, то время до первого ветвления является слу-
чайной величиной Z = min (Хь Х2, Хп), где Xi независимы и
имеют плотность (11.2). Распределение величины Z является экс-
поненциальным с параметром пк. Следовательно, вероятность того,
что ветвление произойдет на интервале длины h, равна nhh +,o(h).
Когда это случается, популяция увеличивается до размера
12 Зак. 939
354
Гл. 11. Ветвящиеся процессы
и временной интервал до следующего ветвления будет распреде-
лен экспоненциально с параметром (п + 1)Х и т. д. Анализ этого
примера с точки зрения процессов чистого рождения был дан
в гл. 7, § 1. Другой метод, излагаемый ниже, имеет самостоятель-
ный интерес.
Если 1—F(/) = е~2Л, то уравнение (11.1) примет вид
t
G(s, = K J [G(s, /-T)]2e?-«-T'</r + s.
0
Произведем замену переменных и = t — т и получим
t
G(s, t)eKt = X J [G(s, и)]2 eKu du +s.
о
Продифференцируем полученное равенство no t:
eKtG'(s, /) + KeKtG (s, /) = A[G(s, t)]2eu,
где
G'(s, /) = -^-G(s, 0-
Разделив обе части на eKt, получим дифференциальное уравнение
Бернулли
Gz(s, 0 - Z[G(s, t)]2 — kG(s, f). (11.3)
Чтобы решить это дифференциальное уравнение, можно разделить
переменные:
dG (s. О_____.
G (s, t)[G(s. /) — 1]
Тогда решение имеет вид
G (s, t) ^\s)e ,
или
<1L4>
где C(s) не зависит от t, но, быть может, зависит от s. Чтобы
найти C(s), положим в (11.4) t = 0. Поскольку
( 0, если k 1, !
Рк (0) — I 1 «. 1 s == G (s, 0) = —/гт-г ,
7 [1, если k = 1, v ’ l-C(s)’
мы имеем
C(S) = (S-1)/S.
§11. Ветвящиеся процессы, зависящие от возраста 355
Таким образом, решение уравнения (11.3), а также уравнения
(11.1) в случае экспоненциального времени жизни равно
GU, U1.S)
Чтобы найти точный вид Рй(/), разложим (11.5) в ряд по степе-
ням s:
G (s, /) = e~Ms 2(1- e~Kt)k sk.
Очевидно, что
pk(t) = e~Kt (I — е~м)к~1, k = 1,2...
Хотя мы не можем в общем случае решить интегральное уравне-
ние (П.1), можно получить из него уравнение относительно сред-
него m(/) = М (?/(/)). Вспомним, что
сю
° I = S kPk =m w-
S=1 fe-1
Дифференцируя (11.1) nos, получаем
^Л- = 2 J G(s, f-т) dG(^~T) Z(T)rfr+l-F(0.
о
Положим теперь s = 1 и учтем, что
G(l, /-т)=2 Pk(t— т)=1;
/г-1
тогда
t
m(t) = 2 J tn (t — т) f (t) dx + 1 — F (t).
о
Это интегральное уравнение является примером так называе-
мого уравнения восстановления. Его характерной особенностью яв-
ляется наличие неизвестной функции под знаком интеграла в виде
свертки. Существует множество методов, которые описывают асим-
птотические свойства решения m(t) уравнения восстановления.
Очевидным обобщением описанной модели является допущение
о том, что объект по истечении его времени жизни порождает
ровно г новых объектов того же типа, где г — фиксированное це-
лое число, г>2. Легко видеть, что интегральное уравнение (11.1)
заменяется тогда следующим:
t
G(s, t)= J [G(s, /-T)]7(T)dT + [l-F(/)]s.
Q
12*
356
Гл. 11. Ветвящиеся процессы
Дальнейшее обобщение этой модели состоит в допущении того,
что любой объект по истечении своего времени жизни может поро-
дить случайное число новых объектов того же типа, например
можно предположить, что объект порождает I новых объектов
с вероятностью qb I = 0, 1,2,.... Пусть
оо
h (s) = 2 qtsl
/ = 0
— соответствующая производящая функция. При этом интеграль-
ное уравнение можно получить следующим образом. Предполо-
жим, что первое ветвление произошло в интервале (т, т + б?т),
О т t, и при этом образовалось I новых объектов. Это событие
имеет вероятность qi]{x)dx. Тогда в течение оставшегося времени
t — т каждый из I объектов может породить любое число новых
объектов, но так, чтобы их суммарное число в момент t равня-
лось k. В силу формулы полной вероятности имеем
t оо
Pk (О = f drf (т) У qt У pk (t - т) pk (t - т) ... pk (t - т),
V 12 I
О / = 0 •••
k = 2, 3, . ..,
Pj (/) = [1 — F (/)] +
t oo
+ J drf^^qi У} p^ (t~ x)pk^t-x) . .. PkiU~ t)1).
Тогда производящая функция равна
G (s, t) = [l -F(t)]s +
oo t oo
+ S s>t J dxf w Ц <7/ pkl T) • • • Pkt ~ T) =
/2 = 0 0 /=0 kr + ... +^z = /2
t oo oo
= [1 — F (/)]$ + f Л/(т) 7/ S5* pfti(/-r) ... pki(t-x).
0 Z=0 /г = 0 k}+ ... +k^ = k
Но сумма
lj Sk 2 Pk (t - t) ... pk (t - r)
fe=0 + ... -Vk^ — k 1
!) Отличие от первоначально рассмотренного случая бинарного деления в
выражении для pi(/) проистекает от того, что если в момент t размер популяции
равен 1, то это означает, что либо до момента t не произошло ни одного ветвле-
ния (вероятность чего равна 1—Г(t)), либо ветвление произошло до момента t
и к моменту t размер популяции вновь стал равным 1 (вероятность этого со-
бытия выражается вторым слагаемым). — Прим, перев.
Задачи
357
является производящей функцией /-кратной свертки последователь-
ности {/?/?(/ — т)} (читатель должен это проверить). Таким обра-
зом, эта сумма равна /-й степени производящей функции
оо
3 skpk (t — r)=G(s, t- г),
k~0
т. е. величине [G(s, t — т)Р, и поэтому
t оо
G (s, t) = [1 - F (/)] s + / q, [G (s, t - r)]z.
О /=0
Но сумма под интегралом равна производящей функции А(*)
в точке G(s, t —т), и окончательно интегральное уравнение при-
нимает вид
t
G(s, t)= J h(G(s, / — т))/(т) dr + [1 -F(/)]s.
0
ЗАДАЧИ
1. Пусть Xn — ветвящийся процесс, XQ = 1. Для произвольного, но фиксиро-
ванного положительного целого k определим последовательность
Yr = Xrk, r = 0, 1, 2....
Показать, чго последовательность {Уг, г = 0, 1, 2, ...} образует ветвящийся про-
цесс. Кроме того, доказать, что если (p(s)—производящая функция числа пря-
мых потомков одного индивидуума для процесса {Хп}, а <рп(*)—-ее n-я итера-
ция, то <Pfe (s)—производящая функция числа прямых потомков одного инди-
видуума для процесса {Уг}.
2. Пусть f (s) = 1 — р (1 — s) Р, где р и р — постоянные, 0 < р < 1, 0 < Р < 1.
Доказать, что f(s)—производящая функция и ее итерации имеют вид
fn (s) = 1 - pl+₽+--- +3”~' (1 -s)3” n= 1, 2...
3. Предположим, что f(s)—производящая функция, a h(s)—функция, та-
кая, что
?(5) = /!-1[НЛ (S) )]
— производящая функция. Проверить, что
(*) = /"’[М* (s))]
— производящая функция, где fn и gn — функциональные итерации функций f
и g соответственно.
4. В качестве иллюстрации к задаче 3 возьмем
f (s) =--—тт—, т > 1.
т — (tn — 1) s
и /i(s) = k > О — целое число.
358
Гл. 11. Ветвящиеся процессы
Доказать, что g'(s) — h~lf(h(s)) — производящая функция и что n-я итера-
ция функции g равна
П (mn — (тп - 1) sk)i/k
(оо \
2 ) = т/(1 — т), если m = М(Л'1) < 1, Хо == 1, а
п==1 /
{Хп} — ветвящийся процесс.
6. В момент 0 в культуре клеток крови имеется один эритроцит. Через ми-
нуту эритроцит погибает и заменяется одной из следующих комбинаций с соот-
ветствующей вероятностью (показана справа):
2 эритроцита 7ь
1 эритроцит, 1 лейкоцит 2/3,
2 лейкоцита 712-
Каждый эритроцит живет одну минуту и «порождает потомство» указанным
образом. Каждый лейкоцит живет одну минуту и погибает, не оставляя никакого
потомства. Предположим, что клетки развиваются независимо.
(а ) Чему равна вероятность того, что к моменту п Ч- 1/2 не появилось ни
одного лейкоцита?
(б ) Чему равна вероятность того, что культура клеток крови погибает?
Ответ: (а) (‘Л)2"+ (б) '/з-
7. Пусть f(s) = as2 + bs + с, где а, Ь, с > 0 и f(l) = 1. Предположим, что
вероятность вырождения равна d (0 < d < 1). Доказать, что d = da.
8. Предположим, что в ветвящемся процессе число потомков исходной ча-
стицы имеет распределение с производящей функцией f(s). Каждый член первого
поколения порождает случайное число потомков, функция распределения кото-
рого имеет производящую функцию g(s). Следующее поколение вновь имеет
производящую функцию f, затем g и т. д.
Исходя из общих принципов (т. е. не используя какие-либо общие резуль-
таты, полученные в § 2 для процессов с несколькими типами частиц), найти
вероятность вырождения процесса и среднее число частиц в n-м поколении (на-
пример, для четных п). Изменятся ли эти величины, если поменять f и g ме-
стами?
9. Рассмотрим ветвящийся процесс с дискретным временем {Хп}, где Хо = 1.
Доказать простое неравенство Р {Хп > L при некотором 0 п m | Хт = 0}
[Р{ХШ = 0}]ь.
10. Для исследования некоторого урологического процесса была введена
следующая модель. Предположим, что бактерии растут в соответствии с процес-
сом Юла с параметром Л (см. § 1 гл. 7). В каждую единицу времени каждая
бактерия уничтожается с вероятностью р. Чему равна производящая функция
числа бактерий, существующих в момент п?
Указание: Эта производящая функция является n-й итерацией производящей
функции, характеризующей некоторый ветвящийся процесс.
Ответ: fn (s) является n-й итерацией функции
f(s) =—fhp+vl—.
1—(1—е x)(p + ?s)
11. (а) «Зрелые» индивидуумы порождают потомство в соответствии с про-
изводящей функцией f(s). Предположим, что имеется популяция, состоящая из
k «незрелых» индивидуумов, каждый из которых с вероятностью р достигает
Задачи
359
зрелости и затем размножается независимо от других индивидуумов. Найти про-
изводящую функцию числа (незрелых) индивидуумов в следующем поколении.
(б) Найти производящую функцию числа «зрелых» индивидуумов в сле-
дующем поколении при условии, что в родительском поколении имеется k «зре-
лых» индивидуумов.
Ответ: (а) (1 р + pf(s))h-, (б) (f(1 — р + ps))h.
12. Показать, что распределения (а) и (б) в задаче 11 имеют одно и то же
среднее, но в общем случае разные дисперсии.
13. Рассмотрим ветвящийся процесс {Хп} с дискретным временем и произво-
дящей функцией
. 1-(6 + с) bs а .
Ф =я------------L ------- 0<£<6 + С<1,
1 — с I — CS
где (1—b — с)/с(\—с) > 1. Предположим, что Хо — 1. Найти условное пре-
дельное распределение
lim Р {Хп — k \ Хп>0}.
П->оо
Ответ:
/ _i-b-c
\ So / \ So / ’ s° с (1 - с)
14. Предположим, что в предыдущей задаче 1— Ь — с — с(1—с). Опреде-
лить Р {Хп > 0}.
Ответ: (1 — с)/[1 + (п— 1) с].
15. При условиях задачи 14 доказать, что Р{Хп^пх \ Хп > 0} сходится
при л-> оо к экспоненциальному распределению.
Указание: Найти преобразование Лапласа распределения величины Хп1п при
условии Хп > 0 и найти его предел при оо.
Ответ: Экспоненциальное распределение с параметром (1—с)/с.
16. Рассмотрим ветвящийся процесс с начальным размером популяции X и
производящей функцией
Ф (s) = q + ps, q, p> 0, q + p = 1.
Найти распределение времени T вырождения популяции.
Ответ: Р {Т == п} = (1 — pn + l) N — (1 — pn)N.
17. Пусть {Хп,п^0} — ветвящийся процесс с соответствующей производя-
щей функцией <p(s). Пусть Уп— суммарное число индивидуумов в первых п по-
колениях, т. е.
У^Хо + Х^ ... +Хп, n = 0, 1, 2, ..., X0=l.
Пусть Fn (х) — производящая функция величины Уп- Доказать функциональное
соотношение
Fn+1 (s) = sqp (Fn (s)), n = 0, 1, 2, ... .
18. Пусть <p(s) — производящая функция числа потомков одного индиви-
дуума в ветвящемся процессе, в котором в момент 0 имеется один индивидуум.
Пусть <pn(s)—его n-я итерация. Предположим, кроме того, что имеется имми-
грация в популяцию. Размер иммиграции за время одного поколения описы-
вается производящей функцией h(s). Рассмотрим ветвящийся процесс с иммигра-
цией, переходная матрица которого задается соотношением
оо
2 Рц^=[ч (s)]z h(s).
/-0
360
Гл. И. Ветвящиеся процессы
Доказать, что матрица переходных вероятностей за п шагов определяется соот-
ношением
оо
У Рц*1 = [ф„ (-S)]1’ h (Ф„_1 (s)) h (ф„_2 (s)) ... h (ф (s)) h (s).
/=0
19. Предположим, что в ветвящемся процессе с иммиграцией (см. задачу 18)
q/(l) = m < 1. Доказать, что соответствующая цепь Маркова имеет стационарное
оо
распределение с производящей функцией л (s) ~ ^rsr, удовлетворяющей
г=о
функциональному уравнению
л (ф (s)) h (s) = зт (s).
20. В предположениях задачи 19 для частного случая ф($) = q + ps(fi <
<р<1,^4-р=1) и h(s) = es-1 найти стационарное распределение.
21. Найти о2(Х(/)), где X(t)—ветвящийся процесс с непрерывным време-
нем и Х(0) = 1.
Ответ:
о2 (* (0 ) =
и'(1) J
если и' (1) =# 0,
если ц'(1) = 0.
22. Найти производящую функцию ф(/;$) для ветвящегося процесса с не-
прерывным временем и производящей функцией
и (s) = sk — s (k 2 — целое число).
Указание: Решить уравнение
s)- = и (ф (/; s)), Ф (0; s) = s.
Ответ:
Ф (/; s) = s к*-'>г - (^-[)' - 1)
23. Найти производящую функцию ф(/;«) для ветвящегося процесса с не-
прерывным временем и производящей функцией инфинитезимальных параметров
и (s) = 1 — S — V1 — S.
Ответ:
Ф(С s) = i-[i_e-^ + e-z/2/r^]2.
24. Рассмотрим ветвящийся процесс с непрерывным временем и начальным
размером популяции N. Обозначим размер популяции в момент t через XN(t).
Пусть Kkh 4- о (h), k = 0, 2, 3, — вероятность того, что индивидуум породит k ин-
дивидуумов в интервале (/, t + h). Предположим, что о(/г) —>0 при Л->0 рав-
номерно по k и t. Пусть 1—Mi 4- o(h)—вероятность того, что в интервале
(Z, t 4- h) ветвления нет = Ло 4- Х2 4- Хз + ...). Предположим, что ^k2Xh < оо.
Предположим также, что индивидуумы развиваются независимо. Пусть У(/)
число моментов ветвления на отрезке [0, /].
Показать, что
Р {У (< + Т) - Y (/) = 01 XN (0 = п} = е~пкТ.
Задачи
351
25. Рассмотрим процесс Юла, в котором каждый член популяции с вероят-
ностью p/i + o(h) порождает k новых членов, а с вероятностью 1 — |3/г + o(h)
не происходит рождений на интервале длины /г(Р > 0, k — положительное целое
число). Предположим, что в момент 0 имеется W членов популяции.
(а) Пусть X(f)—число моментов ветвления до момента t. Найти характер
роста М(Х(О).
(б) Пусть тп — момент n-го ветвления. Найти плотность величины тп.
Указание: Учесть, что
/ l-exp{-[(n-l)^ + 2V]P(/~g)},
Р Пй » I гп~1 == SJ — |
и получить рекуррентную формулу для плотности величины тп через плотность
величины Тп—1-
Ответ: (a) e~k^ М (X (/))-> N при t -> оо;
(б) плотность величины тп равна
f _ w (W + 6) • •• [ЛГ + (га- 1) Л 0-k^t\n~l
(га-1)1 б"-1 Ц”е ’ ’
*26. Рассмотрим простой процесс рождения и гибели (линейный рост без им-
миграции), т. е. = Хп и Нп = где X > О, ц > О и р, > Л. Пусть Z(t)—
размер популяции в момент t. С помощью подходящей интерпретации показать,
что период занятости для процесса обслуживания с бесконечным числом обслу-
живающих устройств, где интервалы между поступающими требованиями рас-
пределены по закону 1 — е~м, а функция распределения времени обслуживания
оо
равна 1 — имеет такое же распределение, что и величина J Z (f) dtt где
о
Z(0) = 1.
27. Пусть {Хп} — ветвящийся процесс с соответствующей производящей
оо
функцией cp(s), и пусть <prt(s) = P{^n = Предположим, что <р'(1) > 1.
/г—о
Пусть Хп — число всех частиц в n-м поколении, имеющих бесконечное число по-
колений потомков. ~
Показать, что производящая функция величины Хп равна
оо
Р [Хп = k I Хо =» Хо = 1} = ^ (^ О-Д+
ьо
где q — вероятность вырождения.
Указание: Заметить, что при k 1
Р{^ = ^|Х0=1, Уо = 1} =
оо
2 Р{Хп = £, Л-„ = /|Х0=1)
l~k____________________
Р{Х0=1|У0=1}
28. Популяция состоит из двух типов индивидуумов — мужских и женских
особей. Предположим, что все женские особи могут производить потомство в со-
ответствии с производящей функцией f(x) при условии, что в популяции имеется
362
Гл. 11. Ветвящиеся процессы
по крайней мере одна мужская особь. Если в потомстве с вероятностью а по-
являются женские особи, то чему равна производящая функция числа родив-
шихся женских особей при условии рождения хотя бы одной мужской особи.
Ответ- ^as + <-1
°ТвеТ- 1-/(а)
ЗАМЕЧАНИЯ
Материал этой главы следует книге Т. Харриса [1] по ветвя-
щимся процессам, в которой также содержится обширная библио-
графия по данному предмету и его приложениям.
ЛИТЕРАТУРА
1. Харрис Т., Теория ветвящихся случайных процессов, изд-во «Мир», 1966.
Глава 12
СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
В этой главе будет рассмотрен ряд отдельных вероятностных
моделей, имеющих отношение к приложениям в астрономии, био-
логии, технике и физике. Эти процессы имеют своими составными
частями различные классические процессы, включая пуассоновские,
ветвящиеся и процессы роста диффузионного типа. Во всех слу-
чаях подчиненный процесс определяется через основной, и его ис-
следуют, изучая распределения состояний основного процесса.
В § 1 будут рассмотрены многомерные пуассоновские процессы, а
в следующем параграфе будет дано их приложение к астрономии.
Понятие многомерного пуассоновского процесса будет играть важ-
ную роль при определении каскадных, или составных, случайных
процессов. Некоторые из них будут изучены в последующих пара-
графах этой главы (см., например, § 2).
В § 3 будет исследована вероятностная модель роста и имми-
грации. В § 4 будет определен случайный процесс роста двух ти-
пов индивидуумов — нормального и мутантного. Популяция «ди-
ких» (т. е. нормальных, немутантных) типов растет детерминиро-
ванным образом, в то время как популяция мутантных типов
растет в соответствии с законами марковского ветвящегося процес-
са. Кроме того, каждый индивидуум нормального типа в момент
гибели (время его жизни распределено экспоненциально) превра-
щается в мутантный тип, а затем развивается подобно другим ин-
дивидуумам мутантного типа.
В § 5 и 6 рассматриваются вероятностные модели роста, учи-
тывающие фактор географического распределения и распростра-
нения популяции, а также и процесс естественного роста.
Исследуемые случайные процессы типичны для широкого клас-
са общих каскадных процессов. Цель настоящей главы — познако-
мить читателя с задачами, связанными с комбинациями случай-
ных процессов, имеющими множество приложений и требующими
для своего анализа большого искусства.
В § 7 дан обзор некоторых детерминированных моделей роста
популяций, учитывающих их возрастную структуру.
364
Гл. 12. Составные случайные процессы
§ 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУАССОНОВСКИЕ ПРОЦЕССЫ
Пуассоновские процессы были введены в гл. 7; при этом пара-
метр процесса являлся действительным положительным числом
/ > 0 и обычно считался временем. Введем теперь вариант пуас-
соновского процесса, у которого значение параметра определяется
мерой множества на плоскости, в трехмерном пространстве или
в пространствах более общего вида. Цель данного параграфа —
определить некоторые варианты многомерных пуассоновских про-
цессов и описать некоторые примеры этих процессов и их при-
ложения.
В гл. 7 пуассоновский процесс X(t), был введен аксио-
матически. Было доказано, что X(t) имеет вероятностное распре-
деление
Р {X (t) — k} = е~и £ = 0,1,2,...,
где к— положительная постоянная, интерпретируемая как сред-
няя интенсивность наступления событий. В данном параграфе мы
введем постулаты, характеризующие однородный пространствен-
ный пуассоновский процесс АЦ5), где параметр S является про-
извольной областью плоскости или пространства, имеющей конеч-
ную меру, a X(S) обладает вероятностным распределением
Р{X (S) = £} = е~хл (S) , £ = 0,1,2,.... (1.1)
Здесь к— положительная постоянная, называемая интенсив-
ностью (или параметром) процесса, а Л(5) —площадь или объем
области S в зависимости от того, является ли область S частью
плоскости или пространства. Введем следующие постулаты:
(1) X(S) принимает лишь неотрицательные целочисленные зна-
чения и 0 < Pf¥ (S) = 0} < 1, если A (S) > 0.
(2) Вероятностное распределение величины X(S) зависит
только от Л(5), и, кроме того, если Л(5)->0, то Р{Х (S) > 1} -> 0.
(3) Если Si, S2, . ..,Sn (п 1) — непересекающиеся области,
то X(Si), ..., X(Sn)—независимые в совокупности случайные
величины и
... USn) = X(S1)+ ... +X(S„).
(4) Выполняется требование
Р{Х (S) = D Е
Прежде чем переходить к описательному обсуждению этих ак-
сиом, полезно привести некоторые примеры.
(а) В трехмерном пространстве X(S) может представлять со-
бой число звезд, расположенных в области S.
§ 1. Многомерные однородные пуассоновские процессы 365
(б) На плоскости X(S) может представлять собой число бак-
терий определенного вида, содержащихся в области S.
Объяснение и интерпретация введенных аксиом вполне оче-
видны. Постулат (2) утверждает, что X(S) зависит не от вида об-
ласти S, а только от ее площади или объема. Такое предположе-
ние представляется разумным (см. примеры (а) и (б)). В соответ-
ствии с постулатом (3), если использовать терминологию примера
(а), количества звезд, содержащихся в непересекающихся обла-
стях, являются независимыми случайными величинами, а значе-
ние X(S) для суммарной области является суммой значений Х(-)
для составляющих областей. По-видимому, предположение о не-
зависимости является разумным приближением к реальной ситуа-
ции распределения звезд. Постулат (4) достаточно понятен интуи-
тивно и не требует объяснений.
Основной целью этого параграфа является доказательство сле-
дующей теоремы:
Теорема 1.1. Если случайный процесс X(S), определенный
относительно областей S евклидова пространства размерности п,
удовлетворяет постулатам (1) — (4), то X(S) имеет распределе-
ние (1.1).
Доказательство. Рассмотрим произвольную область S,
такую, что 0< Л(5) < оо. Разобьем S на непересекающиеся об-
ласти Si, S2, ..., Sn равной площади (объема), т. е.
5jU52U ... =
SiAS/ = 0, /¥=/ (0 — пустое множество),
A (SJ = ~ A (S) для всех /=1, 2, п.
Тогда в силу постулата (3)
P(X(S) = 0} = P{X(S1U ... U5n) = 0} =
= P{Jf(S1)+ ... +X(Sj=0}.
n
Но из постулата (1) следует, что событие S A (St«) = О может
произойти тогда и только тогда, когда ^(Sf) = 0 при всех 1=1,
2, п; тогда, используя независимость величин X(£г), Z=l,
2....п (постулат (3)), получим
P{X(S) = 0}=P{X(Si) = 0, 1=1, 2, ..., п} = П Р{X(Si) = 0}.
Из постулата (2) следует, что Р{.¥(5г) = 0} зависит только от
/1 (S^ = -Г A (S). Следовательно,
P{X(S1) = 0}=P{X(S2) = 0}= ... =P{*(S„) = 0}.
366
Гл. 12. Составные случайные процессы
Таким образом, получаем
P{I(S) = 0} = [P{I(SJ = 0}]".
Я jjpp
Р{Х($„) = 0}=1-Р{Х($„)>1}.
(1.2)
Взяв логарифм от обеих частей (1.2), что допустимо в силу посту-
лата (1), получаем
- In Р {X (S) = 0} = - n In [1 - P{X(SJ> 1}] =
= n[p{X(SJ>l} + |(P{X(Sn)>l})2+ ...], (1.3)
где использовано разложение
— In (1 — х) = х 4- 4- х2 + 4 х3 4- ... ,
Z о
справедливое при —1. Очевидно, что 0 P(X(Sn)> 1} < 1,
поскольку в противном случае было бы P{X(Sn) = 0} =0, откуда
P{X(S) = 0} = 0. Это, однако, невозможно в силу постулата (1),
поскольку по предположению Л(£)>0. Формулу (1.3) можно
переписать в виде
— In Р {X (S) = 0} =
= пР{Х (Sn) =
1 > [|{{X(t)=~TT(1 + 0 (Р {Х (SJ > )] • (1 -4)
Символ O(P{X(Sn)^ 1}) имеет обычный смысл, т. е. величина
О (Р {X (Sn) > 1})
Р{Х (S„)>1}
ограничена при п—>оо. Заметим, что в силу постулата (2) имеем
P{X(Sn) > 1} —>0 при п-»оо,
поскольку при этом A (Sn) = 4 A(S)->0. Далее, из постулата (4)
следует, что
lim
п->оо
Р {X (Sn) > 1} ,
Р {X (Sn) = 1}
Следовательно, из (1.4) при п->оо получаем
- In Р {X (S) = 0} = limnP {X(S„)= 1}. (1.5)
П->оо
В силу постулата (1) левая часть равенства с необходимостью
должна быть положительной и конечной.
§ 1. Многомерные однородные пуассоновские процессы 367
Рассмотрим производящие функции величин Х(3)‘ и X(Sn):
g (s) = М (s* <s>) = 2 P {X (S) = k} sfc,
gn (s) = M (/ (s«)) = 2 P {X (S„) = k} sk.
fe=0
В силу постулатов (2) и (3)
g (S) = M (/(S)) = M (/ (s>)+ • • • +x (s«)) = fl M (/ = [M (/ (s»))]n,
£(*) = [£„(<• (1.6)
Можно записать gn(s) в виде
gn (s) = P {X (S„) = 0} + P {X (S„) = 1} s + P {X (Sn) > 1} 6 (s),
где | 0 (s) К 1, но
P {X (Sn) = 0} = 1 - P {X (S„) = 1} - P {X (Sn) > 1).
Следовательно, подставляя вместо P{X(Sn) =0} это выражение,
получим
gn (s) = 1 + (s - 1) P {X (S„) = 1} + (0 (s) - 1) P {X (S„) >1}. (1.7)
Используем теперь постулат (4), который утверждает, что
P{X(In!Si]-"0 при П->ОО. (1.8)
Кроме того, выполняется условие P{X(Sn) = 1}-»0 при п-»оо.
В самом деле, мы выше установили (см. (1.6)), что
или, что то же самое,
[g(s)]^=2P{X(S„W}?, 0<з<1.
fe=0
В силу гипотезы (1) имеем g(0) = P{X(S) = 0} > 0 и, следова-
тельно,
Р{Х (3„) -114 Is L - 7 ти- <s)l41. -
“ » “'° ПРИ
368
Гл. 12. Составные случайные процессы
Далее, пользуясь разложением
1п(1 + г) = z - -у- + -у - ••• =г + о(г), | z | -> 0,
из формул (1.6), (1.7) и (1.8) получим
lng(s) = nlng„(s)==n[(s- 1)P{X(S„)= 1} +
+ (0 (s) - 1) Р {X (S„) > 1} + о (Р {X (Sn) = 1})].
Взяв предел при /г-*оо от обеих частей равенства и вновь ис-
пользовав постулат (4) (в виде соотношения (1.8)), получим
In £($) = ($- 1) lim пР{Х (Sn) = 1}. (1.9)
П-> ОО
Из (1.5) и (1.9) следует, что
lng(s) = -(s- l)ln P{X(S) = 0},
или
g (s) = exp [(s - 1) (- In P {% (S) = 0})]. (1.10)
Это выражение является производящей функцией пуассоновско-
го распределения с математическим ожиданием
A4(X(S)) = ^(1)= - lnP{X(S) = 0}.
Но математическое ожидание является неотрицательной аддитив-
ной функцией, зависящей лишь от Л(3), откуда получаем
- In Р{Х (S) = 0} = Ы (S). (1.11)
Формально последнее утверждение доказывается следующим обра-
зом. Пусть f — функция, удовлетворяющая равенству
M(*(S)WH(S)),
которое следует из постулата (2). Докажем теперь, что f — линей-
ная функция. Пусть Si и S2 — два непересекающихся множества,
таких, что Д(51), X(S2) < оо; тогда
M(X(S1US2)) = /.H(S1) + ^(S2))
в силу аддитивности Д(3). С другой стороны, в силу постулата
(3) имеем
M(X(S1US2)) = M(X(S1)) + M(X(S2)) = fM(S1)) + fH (S2)).
Поскольку Л(5) может изменяться от 0 до оо, то
f (x + y) = f (x) + f (у) Для любых %, у^О. (1-12)
Кроме того, в силу определения f(x) >0 и, очевидно, /(0) = 0.
Единственным решением (1.12), обладающим указанными свой-
§ 1. Многомерные однородные пуассоновские процессы 369
ствами, является линейная функция f(x) = Кх с некоторой по-
стоянной X (см. стр. 205) !). Равенство (1.11) доказано.
Из замечания после формулы (1.5) следует, что Z — действи-
тельный параметр. Подставляя в (1.10) равенство (1.11), полу-
чаем
g(s) = eM
или, что то же самое,
оо
g(s) = e~KA ««J
Очевидно, это доказывает равенство (1.1), утверждающее, что
вероятностное распределение величины X(S) является пуассонов-
ским. Доказательство теоремы 1.1 завершено.
Исследуем дальнейшие свойства распределения случайного
процесса, характеризуемого постулатами (1) — (4). Удобно гово-
рить, что событие {X(S) = k} состоит в том, что «в области S су-
ществуют в точности k точек».
Покажем теперь, что если процесс X(S) удовлетворяет посту-
латам (1)—(4),т. е. является пуассоновским процессом на плоскости
или в пространстве, то при условии, что в области S положитель-
ной площади существует в точности одна точка (т. е. X(S)= 1,
Д(5)>0), местоположение этой точки является случайным с рав-
номерным распределением в S. В самом деле, пусть S = SiUS2,
где Si и S2 не пересекаются. Тогда в силу постулата (3)
р ц (S,) = 11 х (S) = 1} = =
= Р {X (S,) = 1, X (S2) = 0} Р (X (S,) = 1} Р {X (S2) = 0}
Р (X (S) = 1) P{X(S)=1}
ехр [- ЛЛ (S|)] ХА (S,) ехр [- ХА (S2)J
ехр [ — ХА (S)] ХА (S)
Поскольку Si и S2 не пересекаются и Si U S2 = S, то 4(S) =
= A (Si) + A (S2) и ехр [—2.Д (Si)] ехр [—7.Д (S2)] = ехр [—7.Д (S)].
Таким образом, имеем
PU(S,) = I |X(S)= 1} = 4§г
’) Цитированное здесь доказательство опирается на факт монотонности f(x).
Указанное свойство, очевидно, выполняется: если х, у > 0, то можно выбрать
Si, S2 так, что х = A (Si), у — A (S2) ; отсюда
X (S1) < X (St и s2); f М = М (X (S1)) < М (X (Si и S2)) (X + у),
что и требовалось доказать. — Прим, ред.
370
Гл. 12. Составные случайные процессы
а это и выражает тот факт, что местоположение точки в S имеет
равномерное распределение.
Этот результат можно обобщить следующим образом.
Теорема 1.2. Если X(S) удовлетворяет постулатам (1) —
(4), то при условии X(S) = k, где /4(5) >0, местоположения
этих k точек являются независимыми случайными величинами,
равномерно распределенными в S.
Замечание. Утверждение о том, что k точек в S независи-
мы и равномерно распределены, будет означать, что для любых п
п
непересекающихся областей Sb S2, Sn, (JS^S, и ЛК)бых
i=i
п
целых чисел k{, k2, kn, = выполняется условие
i=i
Р{&1 точек лежит в Si; k2 точек лежит в S2; ..,; kn точек ле-
жит в Sn IX(S) = k] =
k! Г Л (S|) Г Л (S2) 1%2
6J k2! ... kn\ L A (S) J L A (S) J
A (Sn)
A (S) J '
Доказательство. Пусть
S = S,US2U ... U s„,
где Si, S2, ..., Sn — непересекающиеся области; тогда для любых
неотрицательных целых чисел ki, k2, ..., kn, ki + k2 + ... + kn =
= k,
P{X(S1) = Ai1; X(S2) = fc2; ...; X (S„) = kn | X (S) = k} =
P{X(S,) = fe,; X{S2) = k2-, ; X(Sn) = kn} _
P {X (S) = k}
P {X (S,) = fe,} P {X (S2) = Ц ... P{X (Sn) = kn} 7
P{X(S) = 6}
e-KA (S.) 1 (S1)]\-M(32) 1 (Sn) > [ЛЛ (Sn)]*n
__________fej!____________K21______________ Kfil____________
e~KA (s)lr^A
k\ Г Л(51)ЛЛ:1 ГЛ(52)]42 Г Л (Sn)
- 61! k2\ ... kn\ L A (S) J L л (S) J • • I A (S) J ’
поскольку /4 (Si) 4- A (S2) + ... + /4 (Sn) = A (S).
§ 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ
В АСТРОНОМИИ
Рассмотрим звезды, распределенные в пространстве в соответ-
ствии с трехмерным пуассоновским процессом /V(S), описанным
в § 1. Пусть х и у — трехмерные векторы. Предположим, что ин-
тенсивность света, создаваемая в точке х звездой, находящейся
§ 2. Применение в астрономии
371
в точке у, равна f(x, у, а). Здесь а — действительный случайный
параметр, зависящий от яркости звезды, находящейся в точке у.
Предположим, что параметры а, соответствующие различным звез-
дам, являются независимыми одинаково распределенными случай-
ными величинами с общей плотностью распределения £(•). Пред-
положим также, что общая интенсивность света, создаваемая в
точке х световыми сигналами от различных звезд, является суммой
составляющих интенсивностей. Пусть У(х, S)—общая интенсив-
ность света, создаваемая в точке х всеми звездами, локализован-
ными в области S, т. е.
Г (х, S) = s f(x, уг, аг).
Заметим, что данная сумма содержит случайное (но конечное с ве-
роятностью 1) число членов. Мы желаем найти распределение ве-
личины У(х, S). Задача будет решена, если будет найдено преобра-
зование Лапласа g(z;x, S) этого распределения, т. е.
оо
g (z; х, S) = М (е~г¥ <х- s>) = j e~*h (£; x, S) d^, Re z > 0,
0
где Л(-;х, S)— плотность распределения величины У(х, S).
Конечно, в принципе, зная преобразование Лапласа, можно
найти стандартным образом моменты величины У(х, S), и вооб-
ще по формуле обращения можно определить функцию h через g.
Вычисления по этой формуле в рассматриваемом случае довольно
громоздкие, и поэтому мы не будем здесь их проводить.
По формуле полной вероятности имеем
g (г; х, S) = М (е~г¥ <*• s>) = 2 М [е~*¥ | X (S) = k] Р {X (S) = k}.
fe=0
Но из теоремы 1.2 известно, что при условии X(S) = k эти k то-
чек распределены равномерно как k независимых случайных ве-
личин в области S. Следовательно,
М s>| X (S) = k] = (М [е~г¥ <х> * | X (S) = 1 ] )к.
Чтобы найти M[e~zy<x’s>| X (S) = 1], заметим, что У(х, S) =
= f(x,y,a) при условии X(S) = 1, где у — местоположение един-
ственной звезды в S, а а — соответствующий случайный параметр,
отражающий ее яркость. Далее, поскольку положение этой звез-
ды распределено в S равномерно, имеем
М[е~гУ<х- S)|X(S)=1] =
H(S)
j* e-zf (X, у, a) £ (a) Jy,
372
Гл. 12. Составные случайные процессы
где интеграл по переменной у понимается как тройной интеграл
по области S. С помощью выведенных выше соотношений оче-
видным образом получаем
g (z; х, S) =
оо Г ос
= 2 WrJ J ^k(a)da
k = Q S сю
J g-zf (X, y, a) k
}R.
exp[ —ЛЛ (S)] =
= exp
e-zf (x, y, a) £ __
1 dy
так как [ dy ~ A (S). Мы определили g(z;x,S) через f(x, у, a),
5
k(a) и S, которые можно считать известными или получаемыми
на основе других данных.
§ 3. ИММИГРАЦИЯ и РОСТ ПОПУЛЯЦИЙ
Модель, изучаемая в данном параграфе, описывает однотип-
ную популяцию, развивающуюся из исходной популяции, а про-
цесс роста этой популяции соответствует марковскому ветвящему-
ся процессу. Кроме того, в дополнение к самопроизвольному росту
популяции имеется приток иммигрантов того же типа, которые
в дальнейшем развиваются, как и остальные члены популяции.
Процесс поступления иммигрантов в общем случае является слу-
чайным. Для определенности опишем процесс, являющийся мо-
делью роста популяций бактерий.
Рассмотрим колонию бактерий, состоящую из п0 индивидуумов.
Предположим, что каждая бактерия независимо от остальных по-
рождает поколение потомков, которые в свою очередь производят
следующее поколение потомков и т. д. Рост популяции, развиваю-
щейся из одной бактерии, описывается марковским ветвящимся
процессом с непрерывным временем. Пусть F(s,t)—вероятност-
ная производящая функция размера в момент t популяции, раз-
вившейся из одной бактерии. Очевидно, размер популяции, раз-
вившейся из колонии, имевшей в момент 0 размер п0, является
случайной величиной с производящей функцией [F(s, f)]n\ Предпо-
ложим далее, что иммиграция новых бактерий происходит в мо-
менты tj, j = 1,2, ..., N. Каждый иммигрант порождает потом-
ство таким же образом, как и исходные nQ бактерий, независимо от
них и от других бактерий. Размер в момент t популяции, порож-
§ 3. Иммиграция и рост популяций
373
денной иммигрантом, прибывшим в момент tj, имеет производящую
функцию F(s,t— tj). Общий размер популяции в момент t имеет
производящую функцию
N
[F(s, ОГПЛз, /-/Д
/ = 1
поскольку каждая бактерия развивается независимо от других.
Предположим теперь, что иммиграция происходит не в фиксиро-
ванные моменты fj, а в моменты, образующие пуассоновский по-
ток с параметром г. Наша задача — выразить производящую функ-
цию общего размера популяции через F(s, /) и г.
Моменты иммиграции tj являются случайными величинами, и
их число за отрезок времени [0,/] — также случайная вели-
чина с пуассоновским распределением, имеющим параметр rt.
Пусть Yj(t,tj)—размер популяции к моменту t, развившейся из
одного иммигранта, поступившего в колонию в момент tj, j =
= 1,2, ..., Af (/); тогда
N(t)
tj)
/=1
есть число всех бактерий в момент /, «предками» которых были
иммигранты, поступившие за отрезок времени [0, /].
Производящая функция величины Y(/) может быть получена
стандартным образом с помощью наложения условия на N(t) и
формулы полной вероятности:
M[sr(Z)] = ^M[sYV\N{t) = k]P{N(t)==k}. (3.1)
k=Q
Из результатов § 2 гл. 7 известно, что совместное распределе-
ние на [0, /] моментов поступления tj, / = 1, 2, ..., N(t), при из-
вестном их числе N(t) = k совпадает с распределением порядко-
вых статистик k независимых равномерно распределенных на [0, t\
случайных величин. Поэтому
[k
l" ° fk-i
г k
= -Lf dtx\ dt2...
0 0 0
поскольку интегрируемая функция симметрична относительно
t\, t2) ..., t^ Далее, поскольку различные иммигранты создают
374
Гл. 12. Составные случайные процессы
независимо развивающиеся популяции, имеем
Следовательно,
t t i k
M[s™IN(t) = k] = ± J dttj dt2 ... J dtk JJf(s, =
0 0 0 /=»!
kt ft \ k
= -^11 J F(s> - 0)^0 = ("Г J F(s, t-x)dx\
/ — 10 \ 0 /
Подставляя эту формулу в (3.1) и учитывая, что N(t) яв-
ляется пуассоновским процессом, получим
(3.2)
Следовательно, производящая функция общего размера популя-
ции в момент t равна
G (s, t) = [F (s, 0Г exp I г Г [F (s, t - т) - 1] dx [. (3.3)
l о J
Пример. В качестве примера предположим, что каждая от-
дельная бактерия развивается в соответствии с процессом Юла
Х(/) с параметром р > 0 (см. § 2 гл. 7); и размер популяции в мо-
мент /, развившейся из одной бактерии, имевшейся в момент
t = 0, имеет распределение
рцо = р(Х(О = *|*(О)=1},
где
Лг(0 = е~₽/(1 £=1, 2, ...
Производящая функция для процесса Юла равна
F(s, 0 = ^ =
§ 4. Вероятностные модели мутации и роста 375
В соответствии с (3.2) производящая функция размера популя-
ции, развившейся из иммигрантов, имеет вид
М [$г <«] = expl г / t dx-rt ~
== ехр| — у In [1 — s + — rt j =
= e~r£ (1 - s + = e~rt [1 - (1 - e^) s]"T
Если учесть исходную популяцию бактерий, то в соответствии
с (3.3) производящая функция общего размера популяции в мо-
мент t имеет вид
G(s, t) = ехр [ — (г + pn0) t] [1 — (1 — е~&) s] (Пй+
Средний размер популяции в момент t равен /)|5=а1, или
(rto + f)(^- 1).
Моменты более высоких порядков можно найти, последователь-
но дифференцируя производящую функцию в точке s = 1.
§ 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
Часто в микробиологических популяциях, первоначально одно-
родных, один или более индивидуумов изменяются в мутантную
форму и затем эта форма размножается. Мутация может соответ-
ствовать, например, иммунитету от вируса, который сохраняется
в потомстве, или в общем случае некоторому свойству, отличающе-
му мутантную форму от исходной (от индивидуумов «дикого ти-
па»). Исследуем теперь модель, описывающую случайные флуктуа-
ции мутантного роста. Предположим, что материнская, или роди-
тельская колония состоит в момент t = 0 из N индивидуумов и
растет детерминированным образом так, что ее размер в момент t
равен Ne*. Далее, предположим, что каждый индивидуум дикого
типа с вероятностью р/г + o(h) изменяется в мутантную форму
за отрезок времени [/, t + /г]. Поскольку родительская популяция
в момент t имеет размер Ne\ а индивидуумы развиваются незави-
симо, вероятность образования некоторого мутанта на отрезке
[/, t + h] равна
+ о (h).
Кроме того, мы постулируем, что вероятность двух или более мута-
ций на отрезке [/, t + h\ есть o(h). Из приведенной формулировки
376 Гл. 12. Составные случайные процессы
следует, что число индивидуумов мутантного вида, как функ-
ция времени, описывается неоднородным пуассоновским процес-
сом с функцией интенсивности r(Z) = pNef (см. задачу 12 гл. 7).
Используя решение задач 12 и 13 гл. 7, можно показать, что
вероятностная производящая функция числа событий, произо-
шедших за отрезок времени [0, /], для неоднородного пуассонов-
ского процесса с параметром r(t) равна
ср (Z, s) = (*) G-s),
где
t
m(f) = г (т) dx — pN (е* — 1).
о
Таким образом, в нашем частном случае выполняется равенство
ф(/, s) = exp{pAf(ef-~ l)(s—1)}. (4.1)
Предположим теперь, что каждый мутант порождает свой собст-
венный процесс роста, и пусть F(s,t) — вероятностная производя-
щая функция числа потомков одного мутанта спустя время t
после его возникновения. В данной модели мы предположим, что
в мутантной популяции не происходит гибели, т. е. /ДО, /) = 0.
Пусть H(s, /; /V)—вероятностная производящая функция чис-
ла мутантов в момент t при условии, что родительская колония
состояла из N индивидуумов в момент t = 0 и в этот момент в ней
не было ни одного мутантного индивидуума. Наша цель — найти
через F(s,t) и параметры р и 7V, которые в рассматри-
ваемой задаче считаются известными. Для этого введем вероят-
ности
/Д(/) = Р{в момент t существует ровно k потомков одного
мутантного индивидуума, возникшего в момент Z = 0},
Afe(Z; Л9 = Р{в момент t существует ровно k мутантов при усло-
вии, что родительская популяция в момент t = 0 имела
размер N и не содержала ни одного мутанта}.
В таком случае
оо
р (s, t) = 2 Pk(t) sk, (4.2)
/2=1
поскольку по предположению Po(t)==O и
Н ($, /; N)^ 5 hk (/; N) sk. (4.3)
/2 = 0
Из (4.1) следует, что
Ао(/; /V) = Р {первая мутация происходит позже /} =
= ф (t, 0) = ехр [ - рЛГ (е' - 1)] = 1 - Ц-, N), (4.4)
§ 4. Вероятностные модели мутации и роста 377
где K(t-, N) —функция распределения момента рождения первого
мутанта при исходной популяции, состоящей из N индивидуумов.
Ее плотность равна
_ dh^.N) = ехр (_ 1Я
Событие, состоящее в том, что в момент t имеется ровно k 4- 1 му-
тантных индивидуумов (k = 0, 1, 2, ...), произойдет, если первая
мутация случится в момент т (О^т<С/) и появившийся мутант
и родительская популяция (в данном случае размера AteT) вместе
породят k мутантов за оставшееся время t — т. Вероятность того,
что до момента т не произойдет ни одной мутации, равна
ехр{—p2V(eT—1)}. В интервале (т, т + dx) мутация произойдет
с вероятностью pNexdx + o(dx). Наконец, вероятность того, что
мутантный организм и родительская колония размера Nex породят
в точности k мутантов за время t — т, равна
k
%Pk-i(t-x)ht(t-x-, Nex)
1=0
(напомним, что Ро(1)==О). Но момент т может быть любым
между 0 и /, поэтому в силу формулы полной вероятности полу-
чаем
t
hk (t\ N) = j exp [ - pyV (eT - I)] pNex dx X
о
(fe \
IS pk-i (* ~ T) hi (t - t; Nex) j, k = 1, 2, ....
i=o /
Теперь можно записать соответствующую производящую функ-
цию. Получим формулу
оо t
H(s, t; Af) = exp[ — pN (e* - l)] + ^sft J exp[- pN {ex — 1)] X
fe=l о
(fr \
Pk~i (/ — t) ht (t — t; Nex) j dx =
1=0 /
t
= exp[— pAf(e'~ 1)] 4- J exp [~ рУУ(ет- 1)] X
о
f oo oo \
X pNex hl 0 - V, Nex) sl (t - r) sk~l dx,
4-0 k=l /
378
Гл. 12. Составные случайные процессы
где мы использовали гипотезу /%(/) = 0. В силу (4.2) и (4.3)
это соотношение можно переписать в более простом виде
H(s, t; Af) = exp[—рЛЦе*—1)] +
t
+ pW J eyexp[ — p7V(ey- l)]F(s, t-y)H(s, t - y, Ney)dy. (4.5)
0
Это интегральное уравнение относительно довольно
сложное. Однако его можно решить, используя следующий прием.
Пусть g(/; Я)— число мутантов в момент t при условии, что в мо-
мент t = 0 родительская популяция состоит из N индивидуумов.
Поскольку мутации происходят в соответствии с неоднородным
пуассоновским процессом и индивидуумы развиваются независимо,
отсюда следует, что величина N) удовлетворяет функциональ-
ному уравнению
U/; ^) + g(Z; N2) = l(t; Я, + Я2). (4.6)
В силу независимости g(/; Ni) и N2) и определения
Я(я, /; Я) = М($^ ^)
заключаем, что
Н (s, t\ t\ N2)-H(sf t\ N{iN2)
для всех неотрицательных целых чисел N2 ..... Отсюда, оче-
видно, следует, что
Я(х, /; Я) = [Я(5, t\ 1)]^
т. е.
Я(я, /; Я) = eNL z), (4.7)
где L(s, t) = 1пЯ($, /; 1). Нам осталось найти функцию L(s. t).
Для этого подставим формулу (4.7) в (4.5) и разделим обе части
на Я:
-i-{exp[WL(s, /)] —ехр[—рЛЦе*—1)]} =
t
= р J еу ехр [ — рЯ (еу — 1)] F (s, t — у) ехр [NeyL (s, t — z/)] dy. (4.8)
о
Равенство (4.8) справедливо лишь при неотрицательных целых
Я. Однако мы будем оперировать с ним, как если бы оно было
справедливым при всех Я > 0. (Это можно сделать, соответ-
ствующим образом изменяя р. Мы не будем входить в детали дан-
ного вопроса, который является достаточно тонким.)
§ 4. Вероятностные модели мутации и роста 379
Положим теперь Af->0 в (4.8), тогда правая часть устремится
к пределу
р j eyF (s, t - у) dy.
О
В левой части имеем
lim 44ехР[Л^ ($, 0] ~ехр[—pjV(^ — 1)]} =
= lim М[ехр(иЛ(«, t))~ 1] + |[1 -ехр(- ри(е‘- 1))]} =
w->0 <• и и I
= ехр [uL (s, 0] |и_0 - ехр [ - р« (^ - 1)] |и=о =
= L(s, /) + p(ez — 1).
Следовательно, формально получается
t
L(s, f)~ - р(е'-l) + p J exF(s, t-x)dx (4.9)
0
и функция H(s, t\ N) определяется равенством (4.7).
Чтобы найти среднее число мутантов в момент /, положим
V(Z)==^O| . (410)
us ‘S«"l
v(Z) равно среднему числу потомков одного мутанта спустя вре-
мя t после его рождения. Из (4.7) и (4.10) имеем
ма(/; Ю) = I = eNL(11 ()N dL(^ t) | t
os ’s-1 os 's=1
HO
t
A(l, /)=-pG?'-l) + p fexdr = O,
0
поскольку
F(l, /-т)=2Р»(<-т)=1.
s=o
Из (4.9) и (4.10)
380
Гл. 12. Составные случайные процессы
Следовательно,
t
М (£ (/; N)) == рЛГ J eTv (t - т) dx. (4.11)
о
Если для не слишком больших t можно приближенно записать
V (/) ~ (пд = const),
то из (4.11) следует, что M(g(/; Af)) ~ pNtibte*.
§ 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
Другой пример экспоненциального роста популяций дает опи-
сываемая ниже модель. Ядерные частицы расположены на беско-
нечной прямой. При их расщеплении «потомки» рассеиваются в со-
ответствии с некоторым вероятностным законом. Более опреде-
ленно, предположим, что «потомок» частицы, расположенной
в точке %, будет находиться в точке х + у с плотностью вероят-
ности f(y),
оо
-оо<г/<оо, J/(z/)dz/=l.
— оо
Заметим, что f(z/) зависит только от расстояния у между «роди-
тельской» частицей и «потомком» и не зависит от местонахожде-
ния «родительской» частицы. Для простоты предположим сначала,
что каждая частица делится в точности на две новые. Если в мо-
мент 0 имеется одна частица в точке х = 0, то ее «потомство» на-
зовем первым поколением; «потомство» первого поколения обра-
зует второе поколение и т. д.
Введем случайную величину Zn(x\ 0), равную числу частиц
л-го поколения, расположенных на полуинтервале (— оо, х], если
нулевое поколение состояло из одной частицы, расположенной
в точке х = 0. Положим
p<">(x) = P{Z„(x; 0) = k}.
Предположим, что мы поместили исходную частицу в точку и. Пусть
Zn(x;w)—число частиц n-го поколения, расположенных в (—оо,х],
при условии, что нулевое поколение состояло из одной частицы,
расположенной в точке и. В силу пространственной однородности
закона распределения разброса потомков интуитивно ясно, что
Р {Zn (х; и) = k} = Р {Zn (х - /г, 0) = 6} = р™ (х - ц). (5.1)
Формальное доказательство этого читателю предлагается провести
самостоятельно.
§ 5. Экспоненциальный рост одномерной популяции 381
Введем производящую функцию
оо
gn (s; X) = s pf (х) sk (5.2)
и среднее
оо
еп (х) = М (Z„ (х; 0)) = 2 kpf (х) = g'n (1; х), (5.3)
где штрихом обозначена производная по s.
Событие, заключающееся в том, что в (п 4- 1)-м поколении на
полуинтервале (— оо, %] будет в точности k частиц, произойдет,
если два «потомка» исходной частицы, расположенной в точке
х = 0, будут локализованы в интервалах (w, и 4- du) и (о, v 4- dv)
соответственно, где — оо < uf v < оо, и каждая из новых частиц
будет иметь через п поколений в (— оо, %] такое число «потомков»,
что в сумме они составят k. Вероятность того, что две частицы пер-
вого поколения будут расположены в интервалах (w, и 4- du) и
(у, v 4- dv) соответственно, равна
f(u)f(v) du dv.
Вероятность того, что эти две частицы через п поколений дадут
в сумме k «потомков», находящихся в полуинтервале (— оо, х],
равна
k
(х-и) p^tx-v)
(см. (5.1)). Далее, величины и и v могут принимать любые зна-
чения на действительной прямой независимо друг от друга. Сле-
довательно,
ОО ОО k
pU+1) (v) = j J du dvf (и) f (v) V (x - и) p^_t (x - v),
— OO —OO Z = 0
k = 0, 1,2.....
Переходя к производящей функции, находим:
ОО 00 оо k
gn+i (s; *) = 2sk J J f f (°) 2 P{in) (x ~ “) Pk-i (x -w)du dv =
k = 0 —oo —oo Z = o
oo oo oo oo
= J J f («) f(v) J} p<ra) (X - u) sl p<«2z (x - u) sk~‘ du dv =
— oo —oo (=0 k — l
oo oo
= J J gn(s; x-u)gn(s-, x — v) f(u)f (v) du dv =
— oo — oo
oo oo
= Jgn(«; x-u)f(u)du J gn(s; x—v)f(v)dv,
382
Гл. 12. Составные случайные процессы
Т. е.
(со |2
gn+i (s; х) = < [ gn (s; х - и) f (и) du
(5.4)
Если в качестве обобщения предположить, что каждая частица
порождает г новых частиц, где г > 0 — целое число, то вместо (5.4)
получим формулу
g„+i(s; х) = < f gn(s-, x-u)f(u)du\ .
I
Если в качестве дальнейшего обобщения предположить, что
каждая частица порождает г новых частиц с вероятностью аг, то
точно таким же образом получим формулу
g-,l+1(s; х)=-Л1 J g„(s; x-u)f(u)du j,
где
оо
Л (г) = 2 arz'
г=*0
есть производящая функция числа новых частиц, производимых
при каждом расщеплении.
Математическое ожидание Mn+i (х) числа частиц в (п + 1)-м
поколении можно найти обычным путем:
M„+iW=^+i(i; *) =
/ оо \ оо
= 4'1 J* §•„(!; х-u)f(u)du\ J х- u)f(u)du. (5.5)
Из (5.1) следует, что
оо
g„(l; х-и)= 2 Р^'1 (х)= 1,
k = Q
И
оо
A' (1) = 2 гаг = m
м
есть среднее число новых частиц, производимых при каждом рас-
щеплении. Формула (5.5) приобретает вид
Mn+i(x) = m J М„(х — и) f (и) du. (5.6)
"»ОО
§ 6. Модель роста популяции в пространстве и времени
383
Это рекуррентное соотношение можно легко решить. Будем рас-
сматривать исходную частицу, находящуюся в точке х = 0, как ну-
левое поколение; тогда, очевидно,
( 0, если х<0,
М0(х) = 1
[1, если х^О.
Из (5.6) получаем
X
(х) = m J f (и) du = mF (х),
— оо
где F(x) есть функция распределения, соответствующая плотности
/(%). Далее,
М2 (х) = m2 J F (х — и) f (и) du = m2F(2) (х),
— оо
где Я2)(х)—двукратная свертка функции F(x). По индукции
с очевидностью получаем
Мп(х) = тпЛп)(х), (5.7)
где Лп>(х) есть n-кратная свертка функции F(x).
Если плотность f(y) имеет дисперсию о2 и среднее ц, то в силу
центральной предельной теоремы
(иц + Уп ) —> Ф (£), п —> оо,
где Ф(£) —стандартная нормальная функция распределения, т. е.
£
— оо
Отсюда получаем асимптотическую формулу для Мп(х), а именно
при П->оо,
которая представляет некоторый самостоятельный интерес.
§ 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ
И ВРЕМЕНИ
Предположим, что некоторые растения распределены в про-
странстве в соответствии с двумерным распределением Пуассона,
имеющим интенсивность X. (Мы рассматриваем модель распреде-
ления растений в двумерном пространстве, но все рассуждения без
изменений могут быть перенесены на трехмерный случай.) Пред-
положим, что каждое родительское растение, чье местоположение
384
Гл. 12. Составные случайные процессы
описывается двумерным вектором г0, порождает независимо от дру-
гих растений случайное число потомков с производящей функцией
Н ($), т. е.
оо
/г=0
где hh — вероятность того, что родительское растение породит k
потомков. Предположим также, что потомство одного родителя,
расположенного в точке г0, распределяется независимым образом
вокруг точки г0 в соответствии с двумерной плотностью f(г — г0),
зависящей лишь от вектора г — г0, например можно взять двумер-
ную нормальную плотность
f (г - г0) = ехр { - -В- [(х - х0)2 + (у - //0)2] 1.
\ у 2ла2 /12а2 )
Таким образом, вероятность того, что данный потомок родителя,
находящегося в точке г0, будет находиться в области R, равна
р= J f(r-r0)dr. (6.1)
R
Если родительское растение, находящееся в точке г0, имеет в точ-
ности п потомков, то число потомков этого родителя, находящихся
в области /?, имеет биномиальное распределение с параметрами р
и п, где р задается равенством (6.1). Общее число потомков одного
родителя является случайной величиной с вероятностной произво-
дящей функцией H(s). С помощью обычного метода использова-
ния формулы полной вероятности можно показать, что производя-
щая функция числа потомков одного родительского растения, рас-
положенного в точке г0, которые находятся в области R, равна
//[1 + p(s—1)], где р задается равенством (6.1). Наша цель —
найти производящую функцию числа потомков в области R, по-
рожденных всеми родителями из области S. Для этой цели введем
следующие обозначения.
Пусть X(S) — число родительских растений в области S;
Y (г0, 7?)—число потомков одного родительского растения,
находящегося в точке г0, которые расположены
в области R\
Y (S, R) — суммарное число потомков в области R, которые
порождены всеми родителями из области S.
Тогда в этих обозначениях имеем
у (S, R) = 2 г (г0, R).
Если S имеет конечную площадь, то сумма справа с вероятностью 1
содержит конечное число членов, поскольку число родителей в S
§ 6. Модель роста популяции в пространстве и времени 385
имеет пуассоновское распределение с параметром \А (S) (Л (S) —
площадь S). Далее, величина X(S) описывается двумерным пуас-
соновским процессом с интенсивностью X. Производящую функцию
величины У(5, R) можно найти с помощью формулы полной ве-
роятности, налагая условие на значения X(S). Таким образом, по-
лучаем
g (s) = М (sy (s> S)) = 2М[51'(5.й|Х($) = ^]РЦ($) = ^}. (6.2)
6 = 0
Поскольку родительские растения развиваются независимо, то
М [sy <s' » \X(S) = k] = {М [$у <5- ® | X (S) = 1]}\ (6.3)
Кроме того, из теории пространственных пуассоновских процессов
известно, что при условии X(S) = 1 выполняется равенство
Y(S, /?) = У(г0, /?),
где вектор г0 распределен равномерно в S. В таком случае имеем
М [sy (S’ R) | X (S) = 1]=M [sy<r0, ю |Го равномерно распределен в S] =
= WrM[1 + /’(s-1)]rfr°’ (6,4)
7 s
где p определяется равенством (6.1). Последнее равенство выпол-
няется, так как было доказано, что Н [1 + p(s — 1)] является про-
изводящей функцией числа потомков в R, порожденных одним ро-
дителем, расположенным в точке г0. Здесь, однако, вектор г0 рав-
номерно распределен в S, и поэтому мы получили равенство (6.4).
Из (6.2), (6.3) и (6.4) следует
8 = S (TW J Н [ 1 + р (s " 1)] е~КА <S> ’
s J
поскольку X(S) имеет пуассоновское распределение с параметром
A/1(S). Последнюю формулу можно переписать в более простом
виде:
g(s) = ехрIЛ j (Я[1 + p(s- 1)]- 1)dr0|, (6.5)
I s J
где
P = / f(r-r0)dr.
R
В выражении (6.5) часто в качестве S берут все двумерное про-
странство.
Формула (6.5) остается в силе, если растения распределены
в пространстве в соответствии с трехмерным пуассоновским рас-
пределением, а г, г0, R, S означают трехмерные векторы и области
13 Зак. 939
386
Гл. 12. Составные случайные процессы
соответственно. В любом (дву- или трехмерном) случае, если
область R достаточно мала, вероятность р приближенно равна
f(r -Го) А (Я).
В качестве г можно взять любой вектор из области R, г <= R. Тогда
равенство (6.5) перепишется в виде
g-(s) ~ ехр/Л| (Я[1+/(г_г0)Л(/?)(5- 1)]- 1)г/г01.
I s J
Если S — все, пространство (дву- или трехмерное), то можно за-
писать
g(s)~exp{z + (6.6)
где интеграл (двойной или тройной) берется по всему простран-
ству.
Для примера рассмотрим в качестве f нормальное распределе-
ние на плоскости:
/(«) = 2^ехР[~ ^<Л'2 + /О], где и = (х, у).
Пусть вероятностное распределение числа потомков одного роди-
теля равно
/гА = иД1-и), fc = 0, 1, 2.....
оо
где ц — постоянная, 0 < р. < I. Тогда Н(s) = /Е p?sfe(l — р) =
k = 0
= (1 — |i)/(l —p.s). Подставляя в (6.6) и упрощая, получим при
малых Д(/?) приближенное равенство
g (s) ~ ехр
р.Д (R) (s — 1) ехр [— (2а2) 1 (х2 + у2)] dx dy
2яа2 (1 — р.) — цД (R) (s — 1) ехр [— (2о'2)— 1 (х2 + у2)]
После перехода к полярным координатам гиб выражение для
g(s) примет вид
ё (s) ~ ехр
оо
о
______рЛ (7?) (s — 1) г ехр (—(2а2) !г2) г/г I
2ла2 (1 - р) - рЛ (R) (s - 1) ехр [- (2о2)~1 г2] I
= ехр
1
2лЛ J
о
рЛ (R) (s — 1) g2 dz_____
2ла2 (1 — р) - рЛ (R) (s - 1) z
= ехр! — 2лЛсг21 п Г1 — 1 =
L 2ла2 (1 - р) j J
§ 7. Детерминированный рост популяции
387
где
Р = ..., k = 2л%(т2.
г 2лог2 (1 - ц) ’
Таким образом g(s) есть производящая функция отрицательного
биномиального распределения.
§ 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ
ПО ВОЗРАСТАМ
В этом параграфе обсуждаются некоторые простые детермини-
рованные модели роста популяций, учитывающие возрастную
структуру популяции. Вероятностный вариант этих процессов ро-
ста весьма сложен и выходит за рамки данной книги.
А. Простая модель роста
Рассмотрим сначала однородную популяцию. Пусть
N (/) — размер популяции в момент /,
число потомков, порождаемых каждым индивидуумом за
«малый» интервал (/, t + dl). Более точно, число потом-
ков, порожденных индивидуумом за интервал (/, t + /г),
равно v(i)h 4- o(h).
В этих обозначениях имеем
N [t + h) = N (/) + N(t) v (/) h + о (/г),
«(> + ^«h=v(<)a,w + £m.
Переходя к пределу при /г —> 0 в обеих частях равенства получим
-^==v(0W)- (7.1)
Решение этого уравнения равно
/ t \
N (/) == N (0) ехр Н v (т) dx , (7.2)
t
где Af(O) —начальный размер популяции. Если интеграл ]\(т)б/т
о
расходится при Z—>оо, то размер популяции увеличивается до
бесконечности1). Если v(r) = v постоянна, то N (t) = N(0)evt и по-
пуляция увеличивается экспоненциальным образом с интенсивно-
стью V.
!) Особо следует оговорить случай, когда J v (т) dx -> оо при t -> tQ < оо.
о
В этом случае решение (7.2) определено лишь при t < /0. — Прим, перев.
13*
388
Гл. 12. Составные случайные процессы
Б. Модель, в которой размер популяции влияет на рост
В рассмотренной выше модели увеличение размера популяции
не влияло на ее рост. Учтем теперь это влияние, допустив зависи-
мость v(0 от N(t). В частности, предположим, что
v(/) =
0(1 - ) при
О в противном случае,
где а и |3 — положительные числа. Заметим, что размер популяции
не может быть больше а. В этом случае уравнение (7.1) примет
вид
= = (7.3)
(Л I \ V4 ]
Решая уравнение методом разделения переменных, получим
Л/ <л\ = aN (°) e&t =_____________a# (0)___ /7Л)
' a + ЛГ (0) [e^—1] ae_|3i + W (0) - ЛГ(О) '
Анализ решения показывает, что N (/) —>a при / —»oo.
В. Влияние возрастной структуры
Рассмотрим теперь влияние возрастной структуры на процесс
роста популяции.
Введем следующие обозначения:
р(и, /) — функция частоты индивидуумов возраста и в популяции
в момент /, т. е. функция p(z/, t) обладает тем свойством,
«2
что J р (ц, /) du — доля индивидуумов в популяции в мо-
мент t, возраст которых лежит в интервале (их, и2). Ре-
альное число индивидуумов такого возраста равно, есте-
«2
ственно, N (/) J р (и, t) du\ (7.5)
и,
й (/)—интенсивность рождения новых индивидуумов в популя-
ции в момент /. Более точно, J b(t)dt — число новых ин-
дивидуумов, рожденных в интервале времени (/ь /2);
(7.6)
§ 7. Детерминированный рост популяции
389
dt — среднее число потомков одного индивидуума возраста и
в dt единиц времени;
(7.7)
/(w)— вероятность того, что время жизни индивидуума превы-
шает и\
(7.8)
с (и) — инфинитезимальная интенсивность гибели, т. е. вероят-
ность того, что индивидуум возраста и погибнет в сле-
дующие h единиц времени, равна c(u)h + o(h).
(7.9)
Соотношение между /(•) и f(-) может быть получено следую-
щим образом. При известных «, /г > О время жизни индивидуума
превышает и -4- h тогда и только тогда, когда он является живым
в момент и (отсчитываемый от рождения) и не погибает в следую-
щие h единиц времени. Таким образом, получаем
I (и + h) = I (и) [1 — с (и) h\ + о (h)
и
Z (ц + Л) — / (и)_I (и) с (и) h +о (Л)
h ~~ h '
Переходя к пределу при 1г -» 0, получаем
4м=_/(М)с(И).
Решая уравнение, находим
I (и) = I (0) ехр
(7.Ю)
поскольку Z(0) — 1.
При рассмотрении влияния возрастной структуры на растущую
популяцию мы будем интересоваться функцией b(t), т. е. функ-
ции Х(и), /(«) и с (и) будут считаться известными, а задача будет
состоять в нахождении Ь(и). Интенсивность рождения новых ин-
дивидуумов в популяции в момент t имеет две составляющие. Одна
составляющая, скажем b0(t), является интенсивностью воспроиз-
водства для тех индивидуумов в популяции в момент t, которые
уже существовали в момент 0. Плотность индивидуумов возраста и
в популяции в момент 0 равна р(и, 0). Вероятность того, что инди-
видуум, имеющий в момент 0 возраст и,- будет жить в момент t
(в это время его возраст будет равен и + t), равна • Сле-
довательно, доля тех индивидуумов, которые имеют в момент 0
390
Гл. 12. Составные случайные процессы
возраст и и которые доживут до момента /, равна [/(/ +
+ и)fl(и)} р(«, 0). Интенсивность воспроизводства для индивидуу-
мов возраста t + и равна Z(/ + и). Усредняя по всевозможным
возрастам, получаем
оо
М0 = #(0) [л(/ + «)-^£г-р(«. 0)rf«. (7.11)
J L \U)
о
Другой составляющей b(t) является интенсивность воспроизвод-
ства новых индивидуумов в момент t для тех индивидуумов в по-
пуляции, которые родились после момента 0. Интенсивность рожде-
ния новых индивидуумов в популяции в момент т равна Ь(х). При
0<т^/ вероятность того, что индивидуум, рожденный в мо-
мент т, будет жить в момент t (в это время его возраст будет ра-
вен t — т), равна l(t— т). Интенсивность воспроизводства для
индивидуумов возраста t — т равна — т). Отсюда получаем
t
b(t) = b0(t) + J Л(/— т)/(/— т)6 (r)dr, (7.12)
о
где функция bQ(t) дается формулой (7.11).
Соотношение (7.12) является непрерывной формой уравнения
восстановления (см. § 1 гл. 3). Его решение можно найти с по-
мощью метода последовательных приближений.
Пример. Предположим, что как интенсивность рождения, так
и инфинитезимальная интенсивность гибели являются постоян-
ными, не зависящими от возраста, т. е. Л (и) = Л, с (и) = с. Тогда
в силу (7.10) вероятность того, что индивидуум доживет до воз-
раста и, равна
1(и) = е-си. (7.13)
Предположим, что в момент 0 рождается первый индивидуум,
тогда
оо
ЛЦО) J р(м, 0)du = 1. (7.14)
о
В действительности возрастная плотность p(w, 0) является дельта-
функцией, соответствующей вырожденному распределению, скон-
центрированному в точке и = 0. Из (7.11), (7.13) и (7.14) заклю-
чаем, что
&о(О = ^-< (7.15)
Следовательно, в силу (7.13) и (7.15) уравнение (7.12) приобре-
тает вид
t
Ь (/) = \e~ct + X J е~с (?) dr. (7.16)
О
§ 7. Детерминированный рост популяции
391
Решим уравнение (7.16) относительно функции Ь(-). Умножим обе
части уравнения на ect, получим
t
ectb (t) •= Л + Л J ecxb (t) dx
о
и обозначим
/(т) = ^&(т). (7.17)
Уравнение относительно / (•) имеет вид
t
/(/) = Л + Л J f(x)dx.
О
Очевидно, f(0) = Л. При дифференцировании обеих частей по t
получаем /7(/) =Zf(/). Таким образом, f(t) = \е7Л и, подставляя
это выражение в (7.17), получаем
b(t)^te^t. (7.18)
Определив в этом примере &(/), используем этот результат для
нахождения возрастной структуры, которая задается величиной
A^(/)p(zz, /). Поскольку мы предположили при выводе (7.18), что
в момент 0 рождается первый индивидуум, нам нужно рассмотреть
лишь случай и-^t. Индивидуум в момент t имеет возраст и в том
и только том случае, если он родился в момент t — и. Интенсив-
ность рождения новых индивидуумов в популяции в момент t — и
равна b (t — и) = Вероятность того, что индивидуум до-
живет до возраста и, равна е~си в силу (7.13). Отсюда
N (/) р („, t) = e~c“b (t -и), и < t. (7.19)
Подставляя (7.18) в (7.19), получаем
W (/) р (zz, /) = (7.20)
Обратимся теперь к исходной формулировке, сохраняя лишь
предположение о том, что в момент 0 рождается первый индиви-
дуум; тогда вывод равенства (7.19) сохранится, и в общем случае
при имеем
W)p(zz, t) — b(t - (7.21)
Здесь 6(/) определяется как решение уравнения восстановления
(7.12) при условии &о(О = 0, поскольку в момент t = 0 не было
живущих индивидуумов. Таким образом,
t t
b(t) = J Л(/-т)/(/-т)6(т)Л= j b (t — и)к(и)Ци) du.
0 0
392
Гл. 12. Составные случайные процессы
Пусть ф(и) = Z(w)/(w), тогда уравнение примет вид
t
b(t) = J b (t — и) ф (и) du. (7.22)
О
В качестве пробного решения уравнения (7.22) выберем
b (t) - eyt (7.23)
(у = const), где постоянную у следует выбрать так, чтобы урав-
нение (7.22) выполнялось при больших t. Подставляя (7.23)
в (7.22), получим условие
t t
eyt = J ey (w) = eyt J е-чиф (w)
о 0
или
t
j e~^(u)du^l. (7.24)
0
Мы интересуемся предельным поведением (при / —► оо) возрастной
структуры популяции. Устремим в (7.24) t к оо, получим
R (у) = J е~^ф (и) du—1. (7.25)
О
В силу определения /?(у) является строго убывающей функцией
по у. Следовательно, уравнение (7.25) имеет максимум один поло-
жительный корень. Пусть
оо оо
R = J ф (и) du = J Л, (и) I (и) du.
о о
Величина R называется репродуктивным числом индивидуума и
равна среднему числу потомков, порожденных индивидуумом за
время жизни. Иногда R называют мальтусовской интенсивностью.
Если R > 1, то R(y) имеет вид, показанный на рис. 1, и реше-
ние уо > 0 уравнения (7.25) существует.
В этом случае b(t) асимптотически пропорциональна ехр(у0/)
и рост популяции — экспоненциальный. Если R < 1, то /?(у) имеет
вид, показанный на рис. 2, и уравнение (7.25) имеет решение
уо < 0. В этом случае b(t) асимптотически пропорциональна
ехр(уоО, а популяция вымирает с экспоненциальной скоростью.
Если R = 1, то задача должна исследоваться вероятностными
методами.
§ 7. Детерминированный рост популяции
393
Полученные выше результаты найдены эвристическим путем.
Предположения и анализ, необходимые для того, чтобы придать
строгий смысл решению, выходят за рамки данной книги. Основ-
ной вывод, который получен, — тот, что при соответствующих усло-
Рис. 1.
виях популяция растет экспоненциальным образом. Еще одно под-
тверждение этого явления мы получим, рассматривая ниже ди-
скретную модель (§8).
Продолжим теперь эвристические рассуждения. В случае R > 1
найдем асимптотическую возрастную структуру, задаваемую плот-
ностью p(zz, t), В силу (7.21)
/ b (t —и) I (и) .
р (z/, t) N (t) ’ u^.t.
Далее, b(t — и) асимптотически пропорциональна ехр[у0(^ —
Следовательно, N(/) асимптотически пропорциональна ехр(уоО>
394
Гл. 12. Составные случайные процессы
поэтому р(и,/) асимптотически пропорциональна
ехр [у0 (t - ц)] I (и)
ехр (уоО
= ехр(- уом)/(м).
Коэффициент пропорциональности можно найти, используя тот
факт, что плотность является вероятностным распределением. Сле-
довательно, возрастная структура популяции при больших t за-
дается асимптотической функцией плотности
р(«, t}-----
J ехр (— уох) I (х) dx
О
§ 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
Рассмотрим теперь строгий подход к задаче, изучавшейся в пре-
дыдущем параграфе, в случае дискретного времени. Пусть t —
= 0, 1, 2, ..., и пусть
— число индивидуумов возраста х в момент /;
Рх — доля индивидуумов возраста х, доживающих до возраста
х + 1;
F х — число индивидуумов, рождающихся от каждого родителя воз-
раста х в следующий момент времени.
Предполагается, что и Рх не зависят от t и Рх > 0, х = 0, ...
..., m—1, Fx > 0, х = 0,1,2, ..., m. Предположим, что возраст
любого индивидуума ограничен числом т, т. е. положим Рт = 0;
тогда переходные соотношения для возрастной структуры между
моментами t = 0 и t = 1 имеют вид
т
х=0
nV = Р'ПЮ,
я(1) _ р „(0)
нт гт-1Пт-1
Запишем эти соотношения в матричном виде
П(1> = Мп<°>,
(8.1)
Задачи
395
где n(0) = (n<j0), п^\ ..., n^), п(1) == (дО), п\'\ ..., nW) и матрица М
записывается в виде
м = F. F, F2 ... Ро 0 0 Pt ... Fm ... 0 ... 0 (8-2)
ООО... Лп-1 0
М является матрицей с неотрицательными элементами. Свойства
таких матриц даны в § 2 приложения. Поскольку Рх и Fx не зави-
сят от времени, точно такие же переходные соотношения справед-
ливы для любых двух последовательных моментов времени. Таким
образом, применяя последовательно формулу (8.1), получим
nW - МЧ nW = (nW nW, ..., nW), /=1,2,3,..., (8.3)
где мы обозначили х= 1, 2, ..., m.
При достаточно больших t все элементы матрицы М* строго
положительны. Кроме того, существует собственное значение Хо>О,
которое по абсолютной величине строго превосходит другие соб-
ственные значения (теорема 2.2 приложения). Для любого век-
тора п вектор М'п асимптотически равен Xoz, где z пропорциона-
лен правому собственному вектору матрицы М, отвечающему соб-
ственному значению Хо. Асимптотически при /—>оо соотношение
(8.3) принимает вид
nW = jvfn ~ Xoz = [ехр (/ In Хо)] z
и величина In Хо соответствует критическому значению уо, введен-
ному при эвристическом рассмотрении варианта с непрерывным
временем. Популяция растет экспоненциально, если Хо > 1, и вы-
мирает экспоненциально быстро, если Хо < 1.
ЗАДАЧИ
1. Предположим, что некоторый объект имеет целочисленные размеры и что
за время h объект с вероятностью h + o(h) вырастает на одну единицу неза-
висимо от предыстории роста и от текущего размера. При условии, что объект
первоначально имеет размер 1, найти вероятности того, что за время t он вы-
растет до размера п.
Указание: Рост объекта образует процесс Юла; см. § 1 гл. 7.
Ответ: e~f (1 — е~*)П .
2. N бактерий распределены равномерно и независимо на слайде микро-
скопа площади А. Для наблюдения произвольным образом выбирается область
площади а. Найти вероятность того, что на этой площади имеются k бактерий.
396
Гл. 12. Составные случайные процессы
Ответ:
±\N~k
А)
3. Показать, что при Af оо и а -> 0 так, что I -~т-12V -> с (0 < с < оо),
ck
pW->e-^.
*4. Предположим, что между бактериями происходит реакция, если две или
более бактерий отстоят друг от друга меньше, чем на расстояние г. Найти функ-
цию распределения числа реакций в области А при r->0, N -+ оо и nr2N2 -»
Л, 0<Л < оо.
Ответ: р (Г) = е ц»
5. Рассмотрим двумерное пуассоновское распределение (с интенсивностью v)
частиц на плоскости. Найти функцию распределения FD(x) расстояния между
произвольной частицей и ее ближайшим соседом. Найти среднее расстояние.
Ответ:
Fd (х) = 1 - ехр (- шг); М (D)
6. Решить задачу 5 в трехмерном случае.
Ответ:
Г j
(х) - 1 ~ ехр ( — v — ; М (D) ==------- 3 ir.
D k 3 / (36vjt)/з
7. Предположим, что прибор подвержен влиянию одного из k возможных
воздействий Е\, Е2,..., Ek, которые могут иметь место с соответствующими ве-
2 ci ~ 1 ) • При каждом воздействии опасные пики
/=1 /
нагрузки происходят в соответствии с пуассоновским потоком с параметром Л;,
/= 1,2, ...,£. Условная вероятность того, что прибор выйдет из строя при пи-
ковой нагрузке воздействия Ej, равна pj. Найти вероятность того, что прибор
выйдег из строя за время t.
Ответ:
k
Р {Т< 0 = 1 - 2 С/ ехр (- hfPjt).
8. Группа из п инженеров работает над проектом. Время безошибочной ра-
боты инженера имеет функцию распределения F(t). Если ошибка сделана, то
с вероятностью р это ошибка типа I, а с вероятностью 1—р — типа II. Ошибка
типа I настолько серьезна, что если кто-либо допустит ее в любой момент вре-
мени, то весь проект наверняка обречен на неудачу. Ошибка же типа II на-
столько незначительна, что опа может испортить весь проект, только если все
инженеры независимо друг от друга допустят ее. Найти вероятность того, что
в момент I проект еще не обречен на неудачу.
Задачи
397
Указание'. Найти вероятность того, что в точности k инженеров сделали
ошибки типа 11, а остальные не допустили ошибок к моменту t. Показать, что
эта вероятность равна ) [(1 — р) F (/)]fe [1 — F (/)]п“*.
Ответ. [l-pF(/)],:~-[(l-p)F(/)P.
9. Рассмотрим схему, состоящую из m параллельных подсистем. Каждая
подсистема состоит из п одинаковых элементов, включенных последовательно.
Предположим, что время безотказной работы каждого элемента имеет функцию
распределения F(t). Показать, что вероятность того, что схема будет работать
в момент t, равна 1 —[1 — (1 —F(t))n]m.
10. Рассмотрим электрические элементы i = 1,2, ...,m сложной системы S.
Пусть Fi(t) — функция распределения времени безотказной работы f-ro элемента.
Пусть 1 — Pi — условная вероятность того, что если i-й элемент выходит из
строя, то вся система перестает работать.
(i) Говорят, что система элементов является полупараллелыюй, если она
отказывает либо (с вероятностью 1) при отказе всех элементов, либо (с вероят-
ностью 1 —рг) при отказе одного элемента (скажем, i-го).
(ii) Говорят, что система элементов является последовательной, если она
отказывает при отказе любого элемента.
Надежностью системы в момент I называется вероятность того, что си-
стема S работает.
(1) Предположим, что Fi (t) — F(t), Pi ~ р (t = 1, 2,..., m) и рассмотрим
полупараллельную систему. Доказать, что надежность системы в момент t равна
[l-F(0+ pF(t)]™-[pF(t)]™.
(2) Пусть выполнены условия пункта (1). Предположим, что F(t) = 1 —
—е~^(А>0). Доказать, что среднее время безотказной работы системы равно
Указание для пункта (2): Пусть ит — среднее время безотказной работы по-
лупараллельной системы, Состоящий из т компонент. Вывести рекуррентную фор-
мулу
Um = ТпК + pUm~b
*11. Предположим, что новые мутантные виды возникают в соответствии с
пуассоновским потоком с параметром V. Популяция, порожденная каждым новым
мутантом, развивается в соответствии с процессом рождения и гибели, имеющим
параметры Кп = п\, рп = пр, где Ц > К. Различные мутанты порождают неза-
висимо развивающиеся популяции. (Напомним, что поскольку Ц > К, каждая та-
кая популяция вырождается за конечное время с вероятностью 1, см. § 7 гл. 7.)
Показать, что число мутантных популяций Lt, существующих в момент /, имеет
пуассоновское распределение.
Ответ: Пусть Й(£)—функция распределения времени вырождения линейного
процесса рождения и гибели (Хп = пк, = п,и) с единичным начальным усло-
вием. Параметр пуассоновского распределения равен
t
V j [1 — Q (£)] dl.
о
398
Гл. 12. Составные случайные процессы
12 (продолжение). Найти предельное распределение величины Lt при t -> оо.
Ответ: Пуассоновское распределение с параметром
vj [l-Qft)J4 = v g-(-In (1 - £-) ).
О
13. Рассмотрим множество кругов на плоскости, центры которых распре-
делены в соответствии с пространственным пуассоновским процессом с па-
раметром Х|Л|, где |Л| — площадь множества А. (Таким образом, число центров
£(Л), расположенных в множестве А, имеет распределение Р{£(Л) = £} =
= е~^ ।А 1 (Л | Л | Радиус каждого круга по предположению является
случайной величиной, независимой от местоположения центра круга, с плотно-
стью /(г) и конечным вторым моментом. Показать, что семейство случайных
величин С (г)—число кругов, покрывающих начало координат, центр которых
отстоит от начала па расстояние, меньшее г, — является пуассоновским процес-
сом с непрерывным параметром г (см. задачу 13 гл. 7).
Указание: Доказать, что
(1) вероятность того, что существует круг с центром, лежащим в кольце
с внутренним и внешним радиусами г и г + dr соответственно, покрывающий
начало координат, равна
Л2лг dr J f (р) dp + о (dr);
г
(2) события, определяемые непересекающимися кольцами, независимы. По-
казать, что С (г) является неоднородным пуассоновским процессом с параметром
Л (г) = 2лЛг J / (р) dp.
г
14. Показать, что число кругов, покрывающих начало координат (см. зада-
чу 13), является пуассоновской случайной величиной с параметром
Л J лг2/ (г) dr.
о
15. Рассмотрим сферы в трехмерном пространстве, центры которых распре-
делены по пуассоновскому закону с параметром Х|Л|, где |Л|— объем множе-
ства Л. Радиусы всех сфер распределены по закону F (г) с плотностью /(г),
имеющему конечный третий момент. Показать, что число сфер, содержащих вну,
три себя точку t, является пуассоновской случайной величиной с параметром
оо
у Ял / r3f (г) dr .
о
16. Предположим, что частицы прибывают в соответствии с пуассоновским
потоком, имеющим параметр X. По прибытии частица принимает одно из г (г^1)
состояний с вероятностями р\, ръ,..., рг соответственно. После этого состояние
каждой частицы изменяется в соответствии с законами однородного по времени
марковского процесса с переходными вероятностями Рц (/) = Р {состояние в мо-
мент t равно j | состояние в момент 0 было z}, i, j = 1, ..., г. Пусть Y(/)= {X{(t)y
...,Xr(t); t 0} — векторный случайный процесс, где (/)—число частиц,
находящихся в состоянии i в момент t. Доказать, что {Y(/); t 0} — однородный
Задачи
399
по времени марковский процесс. (Состояния можно интерпретировать как различ-
ные стадии некоторой болезни.)
17 (продолжение). Рассмотрим одну частицу типа i в момент 0. Пусть
f 1, если в момент t эта частица находится в состоянии j;
д/ / (/) = s п
( 0 в противном случае.
Доказать соотношение
.. ( 6- (t) 6, (t) «, (/)! J,
м (z,n Z212 ...Zr,r j = ZjPiftt).
/=1
18 (продолжение). Доказать, что производящая функция вектора {Xi(/),...
..., Хг (/)} равна
/ М1Х1^Х2^ хг^\
<p(ZpZ2....гг;/) = М(г11 г22 ...г/ } =
{ Ц г t |
=ехрр2^2(г*_1)1 pik^dx ь
I i«l k=\ о )
Указание (см. анализ § 3).
1. Наложить условие на число частиц, прибывших до момента /, и восполь-
зоваться формулой полной вероятности.
2. Использовать тот факт, что в пуассоновском процессе при известном
числе событий, происшедших до момента t, моменты наступления событий рас-
пределены независимо и равномерно в (0,/).
3. Использовать тот факт, что отдельные частицы развиваются независимо
друг от друга.
19. Рассмотрим следующую модель роста популяции, состоящей из двух
типов частиц — нормального и мутантного. Продолжительность жизни частиц
нормального типа имеет экспоненциальное распределение со средним значе-
нием V1. По окончании времени жизни нормальная частица с вероятностью р
порождает две нормальные частицы, а с вероятностью q = 1 —р — одну нормаль-
ную и одну мутантную. Все потомки нормального типа развиваются так же, как
родители. Частица мутантного типа живет случайное время, имеющее экспо-
ненциальное распределение со средним значением ц"1, и затем порождает две
мутантные частицы, развивающиеся таким же образом, как их родитель. Пред-
положим, что все частицы развиваются независимо. В начале имеется одна
частица нормального типа. Пусть {X(t), Y(/)} — число частиц нормального и му-
тантного типов в момент t соответственно. Найти производящие функции
ф}(г, 0 иф2(г,/) = M(zy<*)).
Указание: (а) Показать, что {Х(/)}— процесс Юла с параметром Хр.
(б) Вывести следующее интегральное уравнение относительно ф = ф2, нала-
гая условие на время первого деления и пользуясь формулой полной вероят-
ности:
t
ф (г, t) = е~м + j* [рф2 (г, i — т) + <?ф (z, t — т) g (z, t — т)] dx,
о
где
g (z, t) = [1 — г(1 ~
Произвести под интегралом замену переменных t — т = и и, продифференцировав
затем уравнение по /, получить
+м> (рф+Qgf-
400
Гл. 12. Составные случайные процессы
Пусть <р =
1
— ; тогда
= Л<р - Кр - Kqg<p.
Решив это уравнение, найти, что
j F (и, /) du
о
Л<7
где F (г, t) — е“^[1 *" z (1 “ ц • В частном случае Л = ц показать, что
4- = 1 + {1 - (1 - z + ze-»*')4}.
*ф Z
20. Пусть {Х[ (t), t 0}?el — независимые пуассоновские процессы с па-
раметром X. Найти функцию распределения времени до того момента, пока во
всех процессах не произойдет хотя бы одно событие.
Ответ: Р {Т < t} = (1 - е~м)П-
21. Некоторый эксперимент имеет N возможных исходов, f-й из которых
N
происходит с вероятностью р., 2 Pi^ Пусть Т — число испытаний, необходи-
i — 1
мое для того, чтобы осуществились все различные исходы. Показать, что
оо Г П
М(П= J td .
о Lf=i
Указание'. Отождествить проведение эксперимента с моментом наступления
события пуассоновского процесса с параметром 1=1. Использовать результат
задачи 41 (стр. 527).
ЗАМЕЧАНИЯ
Источником материала для данной главы послужили книги
Бартлетта [1] и Харриса [2].
Дальнейшее обсуждение составных случайных процессов с ак-
центом на их приложениях содержится в книге Бартлетта [3].
Обширная библиография до 1960 г. собрана в книге Баруча-
Рида [4].
ЛИТЕРАТУРА
1. Bartlett М. S., Stochastic Population Models in Ecology and Epidemiology,
Wiley, New York, 1960.
2. X a p p и с T. E., Теория ветвящихся случайных процессов, «Мир», М., 1966.
3. Бартлетт М. С., Введение в теорию случайных процессов, ИЛ, М., 1958.
4. Б а р у ч а - Р и д А. Т., Элементы теории марковских процессов и их прило-
жения, «Наука», М., 1969.
Глава 13
ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ
И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
Одной из главных областей применения вероятностных идей
являются системы, изучаемые в генетике. В § 1 мы приведем ка-
чественное описание основных понятий, лежащих в основе генети-
ческого механизма, а в следующих двух параграфах сконцентри-
руем наше внимание на некоторых классических детерминирован-
ных моделях. В § 4 будет рассмотрено несколько вероятностных
моделей генетических систем, а также будет обсуждена их взаимо-
связь с ветвящимися процессами. Представленный ниже материал
следует расценивать как введение в богатый и чрезвычайно инте-
ресный раздел генетики популяции, связанный с ее внутренней ве-
роятностной структурой.
§ 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО
МЕХАНИЗМА
В ядре клетки (рис. 1) находятся хромосомы, которые «ответ-
ственны» за наследственные характеристики организма. Их число
различно для различных организмов ]).
Единица, контролирующая полностью или частично наследова-
ние некоторого признака, называется геном. Место, которое ген
занимает в хромосоме, называется локусом.
Набор хромосом может содержать по одной хромосоме каждого
типа (гаплоиды'), как у некоторых грибов, по паре хромосом (ди-
плоиды), как у млекопитающих, или группы большего размера
(триплоиды, тетраплоиды и в общем случае полиплоиды), как
у многих растений.
В каждом локусе гены могут принадлежать к различным кон-
трастирующим типам, которые называются аллелями* 2). Различ-
ные возможные комбинации аллелей в соответствующих локусах
разных хромосом называются генотипами. При диплоидии, если
имеются аллели А и а, возможны следующие генотипы: ЛД, Аа,
9 У большинства видов организмов число хромосом в клетке колеблется от
10 до 50. В клетках человека и многих животных содержится по 46 хромосом. —-
Прим, перев.
2) Так, некоторый ген, «отвечающий», например, за карий цвет глаз, являет-
ся аллелем гена, «отвечающего» за голубой цвет глаз. — Прим, перев.
492
Гл. 13. Генетические и экологические процессы
аа. Генотипы АА и аа называются гомозиготными, а генотип Аа—
гетерозиготным.
Фенотипами называются различные внешние проявления ал-
лельных комбинаций. Например, если А доминирует над а, то раз-
ные генотипы АА и Аа будут определять один и тот же фенотип,
а комбинация аа определяет другой фенотип.
А. Размножение и закон Харди — Вейнберга
Существует два способа клеточного деления. Более распростра-
ненным из них является митоз (рис. 2). При этом способе каждая
хромосома делится на две и, когда клетка расщепляется на две
дочерние клетки, каждая из вновь образованных клеток получает
по одной хромосоме из каждой пары. Таким образом, каждая но-
вая клетка имеет полный набор хромосом.
Процесс второго типа — мейоз (рис. 3) — происходит при поло-
вом размножении диплоидных клеток. Каждая хромосома при
этом удваивается. Затем образуются четыре новые клетки, каждая
из которых содержит одну хромосому. Таким образом, каждая из
четырех новых клеток содержит половину нормального набора хро-
мосом. Такая клетка называется гаметой. Когда две гаметы соеди-
няются, образуется оплодотворенная клетка — зигота, которая
имеет полный набор хромосом.
§ 1, Генетические модели
403
Рассмотрим теперь какой-либо локус в паре хромосом у ди-
плоидного организма для случая, когда возможны два аллеля А
и а. Повсюду в этом параграфе будет рассматриваться бесконеч-
ная популяция, различные поколения которой не смешиваются.
Рис. 2.
Предположим, что скрещивается генотип АА с генотипом Аа. Пер-
вый из них производит только гаметы Д, а второй — гаметы А и а
в равных пропорциях. При рассматриваемом спаривании (скрещи-
вании) гаметы, образованные генотипом ДД, по-видимому, одина-
ково часто будут соединяться с различными гаметами, произво-
димыми генотипом Аа. Таким образом, для случая спаривания
Рис. 3.
АА X Аа частота потомков типа АА равна 1/2 и такая же частота
для потомков типа Аа. Аналогично при спаривании АА X аа обра-
зуются только потомки типа Аа. Спаривание Аа X Аа дает сле-
потомков: 1 дд ±да> 1ади т. д. Эти
дующее соотношение
404
Гл. 13. Генетические и экологические процессы
пропорции исходов различных возможных спариваний известны под
названием отношения при расщеплении.
Рассмотрим некоторую раздельнополую популяцию с тремя ге-
нотипами АА, Аа, аа, в которой осуществляется случайное спари-
вание. Пусть исходное соотношение генотипов следующее: доля АА
равна //, доля Аа равна v и доля аа равна w, и + v + w = 1,
В табл. I показаны результаты случайного спаривания.
Таблица I
Скрещивание Типы потомков Частота данного типа скрещивания
АА X АА АА У АА + ~ Аа W2
АА X Аа 2uv
АА X аа Аа -Г АА + ± Аа + -Г аа 2uw
Аа X Аа V2
Аа X аа 1 . , 1 Аа + ~2 аа 2vw
аа X аа аа w2
Следовательно, в следующем поколении эти три генотипа бу-
дут представлены в отношении
АА Аа аа
U2 + £W + y^2 + VW + UV v2 W2+wvA~~^V2
Положим p=u-\--^t q=w-\--^, тогда эти пропорции примут вид
АА Аа аа
р2 2qp q2
и р + q = 1. Точно таким же образом мы найдем, что после сле-
дующего спаривания генотипы распределяются в отношении
АА Аа аа
(р2 + pq)2 = р2 2 (р2 + pq) (q2 + pq) = 2pq (q2 + pq)2 = q2
Таким образом, начиная co второго поколения, соотношение
между генотипами не меняется, т. е. устойчивое состояние дости-
гается за одно поколение. Этот результат известен, как закон Хар-
ди — Вейнберга.
Можно получить этот же результат следующим образом. Рас-
смотрим популяцию гамет: если начальное соотношение между ге-
нотипами то же, что и выше, то соответствующая доля гамет А
§ 1. Генетические модели
405
, v । v
в популяции равна и+~^ = р, а гамет а равна ш + у = так
что в следующем поколении генотипы представлены в отношении
АА Аа аа
р- р = р2 2pq qq = q2
Рассматривая совокупность гамет в новой популяции, найдем:
доля (Л) = р2 + pq = р (р 4- q) = р,
доля (а) = <72 + pq = q (р + q) = q,
что указывает на достигнутую устойчивость. Факт совпадения ре-
зультатов, полученных обоими методами, известен в виде следую-
щего предложения: «случайное слияние гамет» эквивалентно слу-
чайному спариванию. (Вероятностная интерпретация этой теоремы
содержится в задаче 17.)
Теперь мы рассмотрим, как три фактора — мутация, миграция
и отбор — влияют на популяцию генотипов в предположении
о случайном спаривании.
Б. Мутация
1. Рассмотрим гаплоидную популяцию генов А и а. Предполо-
жим, что в промежутке между любыми двумя последующими по-
колениями доля ц генов а мутирует (изменяется) в форму А.
Если рп — доля генов а в n-м поколении, то 1 — рп — доля ге-
нов А в n-м поколении. Тогда pn+i = pn(l — p) = pn_i(l— ц)2 и
окончательно рп = р0(1 — ц)п, т. е. если 0 < ц < 1, то рп—>0 по
геометрической прогрессии со знаменателем 1 — ц.
2. Пусть теперь между двумя последующими поколениями на-
ряду с рассмотренной мутацией доля v > 0 генов А мутирует
в форму а. Тогда
Pn+l = Pn(l -g) + v(l-p„) = p„(l-|l-v) + v,
что эквивалентно соотношению
P„+i-7Tv = ^--7+vJ(l-H-v).
По индукции получаем
Ря+1 —= (ря-1 - jrv) (1 -H-v)2= ... =(ро--J—) (1 -H-v)n.
Снова сходимость имеет геометрический характер. Заметим, что
если ц + v > 1, 1 — ц —• v < 0, то будет сходиться к пределу
немонотонно, если же ц + v<Cl, то сходимость монотонная1).
9 Заметим, что поскольку ц, v < 1, то в любом случае |1 — ц — v| < 1 и,
„ V
следовательно, сходимость действительно имеет место: рп->--.—
rt-»oo Ц-f-v
Прим, перев.
406
Гл. 13. Генетические и экологические процессы
В. Миграция
Предположим, что мы имеем 2 популяции, составленные из ге-
нов А и а, — внутреннюю популяцию, в которой частоты этих генов
равны рп и qn соответственно (и их мы хотим найти), и внешнюю
«большую» популяцию, в которой гены Ама имеют постоянные
частоты Р и Q. «Миграция» означает, что доля / всей внутренней
популяции за время одного поколения замещается таким же коли-
чеством индивидуумов, взятых из внешней популяции.
Тогда pn+i = рп(Д —I) + PI. Поскольку величина Р постоянна,
полученное рекуррентное соотношение совпадает, очевидно, с опи-
сывающим процесс мутации, если взять v = PI, p = (1 —Р)1. От-
сюда следует, что рп сходятся к величине —= Р.
+ V
Г. Отбор
Существует 2 вида отбора — гаметический, который отражает
относительные преимущества некоторых гамет над другими, и зи-
готный, который отражает преимущества некоторых генотипов над
другими. Такие преимущества могут соответствовать различным
смертностям, относительной плодовитости и т. д.
(а) Гаметический отбор
Пусть 1 и 1 — s (0 < s < 1) — меры относительного селектив-
ного преимущества гаметы А по сравнению с гаметой а. Пусть
рп и qn означают их частоты в популяции в п-м поколении. Эти
данные сведены в таблицу II.
Таблица II
Гамета А Гамета а
Частота Относительное преимущество Рп 1 Яп 1 — S Рп + <1п=1
<7n+) = (l -5)7„[p„ + (l -$)?„] ’.
является нормирующим. Имеем
_ (1 -s) qn
C'n+l l-QnS *
Сформируем следующее поколение гамет А и а, приписывая
имеющимся частотам гамет веса 1 и 1 — s соответственно. Полу-
чим
рп+\ ~ Рп [Рп "F* (1 s) qn] >
Сомножитель [рп + (1 — s) gj-1
о = Рп •
Pn+i 1 -qns ’
§ 1. Генетические модели
№7
Отсюда
-^^- = (1—5) — = ... = (1 — s)rt+l ——>0 при п->00.
^п+1 Рп Ро
Следовательно, qn —► 0 и рп->1, т. е. популяция генов а вырож-
дается.
(б) Зиготный отбор. Общий случай
Рассмотрим диплоидную популяцию, в которой каждый генотип
характеризуется индексом а, отражающим его преимущество или
недостаток по сравнению с другими типами. Предположим, что
относительное преимущество не зависит от времени и частот га-
мет в n-м поколении.
Таблица III
АА Аа аа
Частота в n-м поколении Относительное преимущество 2 Рп 01 2РпРп о2 Рп Оз
Пусть рп и qn — частоты А и а соответственно в n-м поколении
(см. таблицу III).
Зиготные частоты АА, Аа и аа в (az+1)-m поколении равны
соответственно
°lP2n ^2рпдп <3^
W ’ W ’ W ’
где величина w == o[pl + 2a2pnqn + a3q2n называется функцией при-
способленности и w'1 играет роль нормирующего множителя. Сле-
довательно, частоты гамет А и а равны соответственно
_ ° 1 Рп + а2РпРп _ <h<?n + °2Рп<1п ,. п
Pn+1 w > w •
Таким образом,
Лг> __ Г) п — п П “ а2) Рп + (<?2 — (Уз) Яп 119'1
&Рп — Рп+\ Рп — Рп<7п ~ • U
Равновесной частотой является любая величина р (0 р 1), та-
кая, что из равенства рп = р следует pn+i = Д Она называется
устойчивой, если для значений рп, близких к р, переменная pn+k
при й —* оо стремится к р. Равновесная частота, не являющаяся
устойчивой, называется неустойчивой. Определим полиморфизм
как такое устойчивое равновесное состояние, в котором представлен
408
Гл. 13. Генетические и экологические процессы
каждый генотип. Такая ситуация имеет место, когда гетерози-
готный индивидуум имеет селективное преимущество перед каж-
дым гомозиготным индивидуумом, как, например, при наследова-
нии признака серповидноклеточной анемии.
Пример полиморфизма'. 02 > 04, 02 > Оз- Такая ситуация обыч-
но называется гетерозиготным преимуществом, или доминирова-
нием. Рассмотрим случаи, когда /±рп равна нулю.
(а) рп = 1. Это равновесное состояние. Однако если рп близко
к 1, то Дрп < 0 и переменная рп удаляется от 1. Это неустойчивое
равновесие.
(б) рп = 0. Это состояние также неустойчивое, поскольку
\рп > 0 при малых рп-
(в) а == гг / ’ или’ чт0 т0 же’ Рп = Р , где
Пусть р = р* + б. Тогда Др ~ [(р*7*)/(МР*) )](<Я + 0з — 202)6
имеет знак, обратный знаку 6, так как оц + о3 — 2о2 < 0. Отсюда
следует, что положение равновесия устойчивое. Чуть более под-
робный анализ показывает, что процесс (1.1) сходится к равно-
весному состоянию р* при любом начальном состоянии р, таком,
что р(1 — р) ¥= 0.
Д. Модели двуполых популяций
Рассмотрим теперь популяцию, состоящую из мужских ш жен-
ских особей, спаривание при этом происходит только между пред-
ставителями различных полов. Если ограничиться рассмотрением
лишь генов, локализованных на аутосомных (неполовых) хромосо-
мах (как это было в предыдущем случае), то процесс случайного
спаривания можно описать точно таким же образом, как и выше.
Предположим, что частоты генотипов внутри мужской и женской
популяций равны:
Мужская популяция
АА Аа аа
r{ 2sj t{
Женская популяция
АА Аа аа
и{ 2Vi Wf
Гаметы имеют следующие частоты:
Мужская популяция
А а
Женская популяция
А а
p{ = r{ + sx + Р\^Щ + и{ q{ = v{ + w{
Для случайного спаривания, которое эквивалентно случайному
выбору из мужских и женских совокупностей гамет, мы найдем,
§ 1. Генетические модели
409
что частоты генотипов в обеих мужской и женской популяциях во
втором поколении равны p\q\ + p\Q\, q\q\ для АА, Аа и аа
соответственно. Как и в случае самооплодотворения, устойчивое
распределение достигается за одно поколение.
Однако, если рассмотреть половые хромосомы, ситуация резко
изменится. Причина этого состоит в том, что в некоторых диплоид-
ных клетках могут находиться два различных типа хромосом X
и Y. У млекопитающих женские особи характеризуются наличием
двух гомологичных 9 Х-хромосом, в то время как у мужских осо-
бей спарены хромосомы X и Y. Более того, многие, если не все, ге-
ны из Х-хромосомы не имеют комплементов на Y-хромосоме. В рас-
сматриваемом случае генотип мужской особи полностью опреде-
ляется аллелями, локализованными на Х-хромосоме. Такие гены
и контролируемые ими признаки называются сцепленными с по-
лом.
Рассмотрим распределение сцепленного с полом гена в после-
довательных поколениях. Предположим, что начальные частоты
генотипов у мужских и женских особей равны
Женские особи (XX) Мужские особи (XY)
АА Аа аа А а
Го 2s0 /0 /70 qQ
Заметим, что генотип у мужской особи определяется только
одним символом гена, поскольку Y-хромосома не содержит ни
одного гена, содержащегося в Х-хромосоме.
Частоты гамет у женских особей равны
А а
П) + s0 s0 + tQ
В предположении о случайном спаривании, или, что то же,
о случайном выборе из совокупности гамет, частоты генотипов
в следующем поколении равны у женских особей:
АА Аа аа
r( = (ro + so)po 2«! =(r0 + s0)<7o + (so + ^o)Po Л = (So + to) <7о
и у мужских особей
А а
Pi = r0 + s0 <71 == s0 + to
Каждая вновь образованная мужская зигота получает Y-xpo-
мосому из мужской популяции и Х-хромосому из женской. Следо-
вательно, доля генов А в мужской популяции в точности равна
доле генов А в предыдущем поколении женской популяции.
*) Гомологичными называются хромосомы, образующие пару (в диплоидном
случае). Все неполовые гомологичные хромосомы тождественны.—Прим, перев.
410
Гл. 13. Генетические и экологические процессы
В общем случае если рп— частота аллеля А в совокупности
женских гамет в п-м поколении, то pn-i — частота аллеля А в муж-
ской популяции в п-м поколении. Следовательно, (п + 1)-е поколе-
ние женских генотипов имеет состав
АА Аа аа
РпРп-1 РпЯп-1 + ЯпРп-1 ЯпЧп-1
Отсюда можно вывести рекуррентное соотношение
Рп+1 = PnPn-l+-j(pnQn-l + ЯпРп-ll
которое сводится к следующему:
2[pn+l-p„]= -(pn-Pn-l),
или 2Дп = —Ап-i, где Дп — pn+i— Рп. По индукции получаем
/ j \п
^п ~ у Д(Ъ
ИЛИ
/ 1 \п
Рп+1 ” Рп у ‘2‘j До*
Отсюда
Л
/ 1 \п /1 \rt”1 I \ ~2)
Рп+1 \ 2"; До + До+ • • • + До+Ро==Ро+До ----зу2---/•
В пределе
а = lim рЛ = р0 + у (pi - р0) = -j- Pl + у pu;
получили выражение для предельной частоты генов А в мужской
популяции. В женской популяции предельные частоты генотипов
имеют вид
АА Аа аа
а2 2а (1—а) (1—а)2
Это, конечно, в точности соответствует частотам Харди—Вейнберга.
§ 2. ИНБРИДИНГ1)
Существует два типа неслучайного спаривания. Первый из них,
называемый ассортативным спариванием, подразумевает обязатель-
ность спаривания подобных (или неподобных) генотипов (или фе-
’) Инбридингом в биологии называется спаривание двух близкородственных
индивидуумов. — Прим, перев.
§ 2. Инбридинг
411
нотипов). Очевидным примером является спаривание генотипов XX
и XY при половом размножении. Вторым типом неслучайного спа-
ривания является спаривание близкородственных индивидуумов.
А. Самооплодотворение
Первая модель инбридинга, которую мы рассмотрим, относится
к самооплодотворению. Каждый индивидуум при этом обладает
обеими гаметами. Допускаются только спаривания типов АА X
ХЛЛ, аа X аа, Аа X Аа, т. е. спариваться могут только индиви-
дуумы, имеющие один и тот же генотип. Например, у цветов пыль-
ник выделяет пыльцу (мужские гаметы), а в пестике развиваются
семяпочки (женские гаметы) и при этом часто происходит своего
рода инбридинг.
Если начальные частоты зигот АА, Аа и аа равны соответствен-
но «о, Vo и Wo, то аналогичные частоты для следующего поколения
равны
। 1 . 1 ,1
Щ ==^0+7^0, ^1=у^ Wi = W0+jV0,
поскольку при спаривании Аа X Аа производятся потомки в отно-
шении А А, ~ Аа, -- аа. С каждым последующим поколением
частота гетерозигот Аа уменьшается в 2 раза. В п-м поколении ча-
стоты равны
1 Г 1 /1 \n~l 1 1 Г /1
Un = Wo + j Vo L 1 + Y + • • • + (yy J = Wo + у Vo p — (yj J ,
f 1 \n
^=(y) vo,
1 Г 1 /1 1 Г /1 \nl
wn=w} + Tt»o[l + 2-+ ... + (y) ] = ®0 + yt»o[l-(y) ]•
Предельные частоты при n->oo равны: и = м04--у > v = 0, w —
I У0
= ^+-f
Б. Спаривание сибсов
В следующей модели рассматривается спаривание потомков од-
них и тех же родителей1), или спаривание сибсов. Опять целью яв-
ляется определение предельных частот различных генотипов, участ-
вующих в спаривании. Однако вместо непосредственного рассмот-
рения частот генотипов мы проследим за флуктуациями частот
спаривающихся особей в последовательных поколениях.
Если ограничиться рассмотрением двух аллелей А и а, то суще-
ствуют три возможных генотипа для каждого родителя и шесть
*) В оригинале «brother — sister mating». — Прим. перевъ
412
Гл. 13. Генетические и экологические процессы
возможных вариантов сочетания, или скрещивания генотипов, т. е.
существует шесть различных вариантов спаривания: АА X АА,
аа Хаа, АА X Аа, аа X Аа, Аа X Аа, АА X аа. Предположим, что
частоты каждого из этих вариантов известны. Мы хотим вычислить
эти частоты для следующего поколения. Для того чтобы сделать
это, мы сейчас найдем распределение генотипов потомков, а затем,
предполагая, что спариваться могут только сибсы, определим ча-
стоту получаемых при этом различных видов спаривания потомков.
Например, все дети, получаемые при спаривании АА X АА,
имеют тип АА, и поэтому среди сибсов допустимым является лишь
спаривание вида АА X АА. При спаривании АА X Аа производятся
потомки в отношении — Л/1, ~Аа. Частоты различных вариантов
спаривания среди сибсов, очевидно, равны X АА, ~ АА X Аа,
~ Аа X Аа. Аналогичным образом можно рассмотреть и другие
возможности. Так, при спаривании Аа х Аа потомки производятся
в отношении -^-ЛА, у Ля, ~ аа. Частоты различных вариантов спа-
ривания среди сибсов можно легко вычислить. Они равны
АА X АА, 4^ аа X аа, 4 АаХ Аа,
1о 1о 4
4 АА X аа, 4- АА X Аа, 4 аа X Аа.
о 4 4
Другие сочетания исследуются аналогичным образом.
Можно проанализировать изменения частот спаривающихся ти
пов от поколения к поколению с помощью цепей Маркова. Для
этого рассмотрим цепь Маркова с шестью состояниями, соответст-
вующими шести вариантам спаривания:
состояние 1 —АА X АА, состояние 2 — АА X Аа, состояние 3 —
АА X аа, состояние 4 — Аа X Аа, состояние 5 — Аа X аа, состояние
6 — аа X аа.
Эта цепь Маркова имеет следующую матрицу перехода:
1 0 0 0 0 0
1 4 _1_ 2 0 1 4 0 0
0 0 0 1 0 0
А = 1 1 1 1 1 1
— -- -
16 4 8 4 4 16
0 0 0 £ 4 _1_ 2 1 4
0 0 0 0 0 1
§ 2. Инбридинг
413
В строках матрицы записаны частоты различных вариантов спа-
ривания среди сибсов, родившихся в результате соответствующего
номеру строки варианта спаривания. Имеются два поглощающих
состояния: 1 и 6.
Из теории марковских цепей известно, что в конце концов про-
изойдет поглощение в одном из этих двух состояний. Вероятность
поглощения из переходных состояний (состояний 2 — 5) представ-
ляет интерес, поскольку она, очевидно, соответствует той интенсив-
ности, с которой исчезают гетерозиготные генотипы. Эта интенсив-
ность равна, конечно, наибольшему собственному значению мат-
0
О
2 >
4
2
2
которая получится при исключении первого и шестого состояний.
Поскольку последствия вариантов спаривания АА X Аа и аа X Аа
симметричны, можно должным образом объединить первую и чет-
вертую строки матрицы В. При этом получим матрицу
о . о
2 2
2 8
С =
2
4
1
4
Собственные значения С являются корнями уравнения
а именно
, 1 , _ 1-/5 , 1 + /5
“ ~4 > ---4 ’ Лз “--4
Следовательно, скорость приближения к гомозиготному состоянию
(фиксации) равна
Лз=4(1+т
т. е. с каждым поколением частота вариантов спаривания различ-
ных генотипов уменьшается в Аз раз.
Теперь не представляет труда вычислить при любых начальных
частотах (щ, вариантов спаривания финальную частоту
414 Гл. 13. Генетические и экологические процессы
поглощения, или фиксации в состояниях 1 (АА X АА) или 6 (аа X
X аа). Точно так же мы определим частоту фиксации двух гомози-
готных генотипов.
Вероятность Хг фиксации в состоянии 1 (спаривание АА X АА)
при начальном состоянии /, i = 1, 2, ..6, является решением урав-
нения
6
2 = *z,
/=1
где полагается Xi = 1, Хв = 0 и А = ||а^-||. Нетрудно найти, что
-А -1 , -± -1
х2 " 4 » хз ~~ 2 > ^4 “ 2 * ^5 “ 4 •
Если начальные частоты различных состояний равны (wi, и2,..., w6),
то вероятность фиксации в состоянии 1, очевидно, равна
6
V । 3 । 1 । 1 । 1
2j UiXi + Т ^2 + ~2 Г/3 + V Z/4 + 4" ^5-
i ~ 1
В. Гены, идентичные по происхождению
Еще одно определение степени инбридинга в популяции дается
через понятие коэффициента инбридинга. Коэффициент инбридинга
индивидуума X определяется как вероятность того, что два гена
в одном локусе у индивидуума X идентичны по происхождению. Под
этим мы понимаем, что два гена являются «копиями» одного и того
же гена некоторого индивидуума из предшествующего поколения.
Рассмотрим теперь конечную популяцию, состоящую из N инди-
видуумов, воспроизводящихся бесполым путем, т. е. каждый инди-
видуум «поставляет» бесконечное число копий своих двух генов
в совокупность гамет, в которой затем происходит случайное спа-
ривание с целью образования новых /V индивидуумов1)- Пусть
Fn — коэффициент инбридинга в п-м поколении популяции, т. е.
Fn — вероятность того, что два гена, выбранные случайным обра-
зом, идентичны по происхождению.
В совокупности гамет происходит их спаривание с целью обра-
зования W новых индивидуумов. Предположим, что выбрана неко-
торая гамета и нужно (случайным образом) выбрать вторую га-
мету с тем, чтобы спарить с первой. Вероятность того, что ген, со-
держащийся во второй гамете, будет копией того же самого гена,
что и в первой, равна так как каждый из 2N типов гамет, про-
изведенных М индивидуумами, равновероятен. При этом два спа-
Точнее, каждый индивидуум поставляет одно и то же число генов k и
рассматривается предельный случай /г->оо. При этом понятие частоты не теряет
смысла. — Прим, перев.
§ 2. Инбридинг
415
репных гена являются, конечно, идентичными по происхождению.
Теперь, если два спаренных гена не являются копиями одного и
того же гена (вероятность чего равна вероятность того,
что они идентичны по происхождению, равна Fn. Следовательно,
Р 1 I 2N~[ р
Гп+\ 2N ' 2N
/ 1 \ / I \2 / 1 \П
/7„=1-F„= (1-2^)(1-2^) Я„_2= ... =(1-2^) Но.
Таким образом, вероятность того, что некоторый индивидуум в п-м
поколении — гетерозигот, стремится к 0 при п -> оо со скоростью
/ 1 \п
11—. Поскольку было сделано предположение о большом
размере популяции, эта скорость весьма низка. Значение проведен-
ного анализа состоит в получении качественного результата о том,
что конечность популяции влечет за собой (в какой-то мере) ин-
бридинг.
Г. Бесконечная диплоидная популяция
и коэффициент инбридинга
Предположим, что имеется бесконечная диплоидная популяция,
у которой в одном локусе ген А может находиться с частотой р,
а ген а — с частотой q = 1 —р. Предположим, что популяция имеет
постоянный коэффициент инбридинга F, который имеет тот же
смысл, что и в предыдущем параграфе. Доля F популяции состоит
из гомозигот, у которых гены идентичны по происхождению. Оче-
видно, доли гомозигот АА и аа с генами, идентичными по проис-
хождению, равны соответственно Fp и Fq, Доля всех зигот, в кото-
рых гены не идентичны по происхождению, равна 1—F. Следова-
тельно, доли типов АА, Аа и аа соответственно равны (1—F)/?2,
(1 — F)2pq и (1 —F)q2, Поэтому если и, v и w — частоты генотипов
АА, Аа и аа соответственно, то
и = (1 — F) р2 + Fp = р2 + Fpq,
v = — F) • 2pq, (2.1)
w == (1 — F) q2 + Fq = q2 + Fpq.
Очевидно, и + v + w — 1, как и следовало ожидать. Эти частоты
являются модификациями частот Харди — Вейнберга. Заметим, что
частота гена А равна w + y v == р2 + pq = р и остается постоянной,
если F = const. Значение коэффициента F становится ясным, если
заметить, что при F = 0 и, v, w являются частотами Харди — Вейн-
берга, описывающими популяцию без инбридинга, в то время как
при F = 1 частота гетерозиготных индивидуумов равна нулю, т е.
популяция достигает состояния максимального инбридинга.
416
Гл. 13. Генетические и экологические процессы
Д. Популяция с самооплодотворением и случайным
спариванием
Предположим, что доля s популяции воспроизводится самоопло-
дотворением, в то время как в другой ее части имеет место случай-
ное спаривание. Соответствующие схемы размножения показаны
в табл. IV, где р = и v, q 1 — р w + у v.
Таблица IV
АА Аа аа
Частоты Потомство от само- оплодотворения Потомство от случай- ного спаривания и su (АА) (1- S) Р2 (АА) V sv (Ц- ЛЛ + 4- Ла 4- ~ аа\ \ 4 2 4 / (1 -$) 2pq (Аа) W sw (аа) (l-s)q2 (аа)
Частоты генотипов во втором поколении равны
и' = (1 — s) р2 + sw + tj sv,
vz = 2(1 - s)pq + ±-sv,
w' = (1 — s) q2 + sw + — sv.
Кроме того,
p' = u' + ~v' = (1 - s)p + s (u +y vj = (1 - s)p + sp = p.
Таким образом, p остается постоянным от поколения к поколению,
как и следовало, конечно, ожидать, поскольку мы не рассматри-
ваем какие-либо факторы, могущие влиять на частоту гена.
Следовательно, можно записать
Ул+1 —2(1 —s) pq + ~svn =
I 1 / 1 \2 /1 \п\ ( 1 \n+1
= 2 (1 - s) pq (^1 + -j s + (у sj + ... + (у sj ) + (у s) =
4(1 -s)
“ 2 —s
Г, (i \n+1] , (i \n+1
Wp"V2S) J+M y0’
§ 3. Полиплоиды
417
/ i \ / ।
ип = (1 -s) p2 + s J v„-i] = (поскольку Vn-i = р
= (1 -S)p2 + s[p — Д- v„_,) = р? + pqs + ^svn-i =
= Р2 + 7S 42~~- р<7[ 1 - (4 s) ]~4S(IS)
= Р2 + Р?з[1 “Й'(1 “(15Г )]~Ts(Is) °0,
Следовательно, предельное значение и при /г->оо равно
Р2+Р^у4г = Р2 + Р^^7-
Аналогично предельные значения v и w равны соответственно
2рД1 —-93—) и <?2 -И р? ( . 1 ) • Таким образом, обращаясь к (2.1),
\ £ S J \ 1 /
27 5
мы видим, что в равновесном состоянии г имеет значение yzry*
Чем больше s, тем медленнее достигается равновесное состояние,
и наоборот.
В частности, при s = 0, т. е. при полностью случайном спарива-
нии, коэффициент F равен нулю и инбридинга нет. Если s = 1 или
происходит только самооплодотворение, то F = 1 ив равновесном
состоянии популяция полностью гомозиготна.
§ 3. полиплоиды
Многие организмы, в особенности растения, являются полиплои-
дами, т. е. гомологичные хромосомы встречаются группами раз-
мера более чем 2. Рассмотрим 2/г-плоидную популяцию (т. е. на-
боры гомологичных хромосом имеют размер 2/г), у которой в каж-
дом рассматриваемом локусе имеется лишь два аллеля. Будем
обозначать комбинации зигот (генотипы) через Asa2n~s (5 = 0,
1, ..., 2/г), где s — число хромосом, несущих ген Д, а остальные
2/г— s хромосом несут ген а. Возможные гаметические комбинации
имеют вид
Aran~r, r = 0, 1, п.
Расщепление гамет в полиплоиде более сложное, нежели в случае
диплоидных организмов. Это объясняется тем фактом, что в тече-
ние мейотического цикла происходит процесс удвоения, когда каж-
дая хромосома расщепляется вдоль своей длины на две одинаковые
хроматиды, которые, однако, остаются соединенными в пары с по-
мощью центрального стерженька — центромера. Между хромати-
дами гомологичных хромосом имеет место некоторый обмен генети-
ческим материалом. (Это называют явлением кроссинеовера, или
14 Зак. 939
418
Г л. 13. Генетические и экологические процессы
перекреста.) Природа расщепления гамет зависит от расстояния
рассматриваемого локуса от центромера. Два наиболее распро-
страненных способа расщепления — хромосомное и хроматидное.
В случае хромосомного расщепления родитель Asa2n~s будет
Производить гаметы Агап~г с частотой
1 ( s \ ( 2п — s\ п ,
vk—г , г = 0, 1, ..., s,
1 2п \ \г ) \ п — г ) * ’ ’ ’ ’
\ п )
а в случае хроматидного расщепления — с частотой
В случае п = 1 эти выражения совпадают.
Получим аналог закона Харди — Вейнберга для локуса при
хромосомном расщеплении. Если в популяции из 2п 4- 1 гамет, в ко-
торой частота генов А равна р, а частота генов а равна q, происхо-
дит случайное слияние гамет, то частота особей Asa2tl~s в следую-
щем поколении равна psq2n~s- Соответствующие гаметы Агап~г
имеют частоту
2п -I
= У______W 2"! D^n-S =
г! ($ — /-)! (п — /-)! + г — s)! 2/г! (2^ —s)!s!
s
~= ----—___ Пгпп~г _____—________ ns-rnn-s+r ~
г\(п — г)\ Ч (s — г)! (п — s + г)!
S
= (") РГЧП~Г 2 (s - Г) ps~rqn~s+r =
= [nr)prqn-r(p + q)n = (nr)prqn-r-
Таким образом, ген А, например, имеет частоту
2 И?
Г
Можно сформулировать следующее утверждение о сходимости:
пусть pk (Aran~r), r = 0, I........n, — частота гаметы Aran~r в k-м по-
§ 3. Полиплоиды
419
колении. Рассмотрим случайное спаривание и хромосомное расщеп-
ление. Тогда
lim pk(Aran~r) = (")/( 1 -p)n~r,
где p — начальная частота аллеля А в популяции. Сходимость
имеет скорость геометрической прогрессии со знаменателем ,
т. е.
]fAav-9-(?)/(1 -рГ'|«да‘, , = !. 2..............п,
для всех k, где % = (п — 1) / (2п — 1).
Мы не будем доказывать эту теорему. Ее можно пояснить с по-
мощью следующих эвристических рассуждений;
Пусть Br = tlr j pr (1 — р)п~г» Для образования гаметы выберем
п хромосом из совокупности размера 2п. Если п хромосом взять от
различных предков, то имеет место хромосомное расщепление ну-
левого поколения популяции, и рассматриваемые частоты являются
биномиальными, т. е. pk (Aran~r) = Вг. Мы определенно ожидаем,
что при больших п это соответствует действительности.
Нс предположим теперь, что п — 2 хромосомы получены от раз-
личных предков, а две — от одного и того же предка (другие воз-
можности можно не учитывать, поскольку они гораздо менее ве-
роятны) .
Пусть 1 — p<ft)—вероятность того, что все п генов в гамете &-го
поколения получены от различных предков нулевого поколения.
Тогда pk(Ar ап~г) ==--(1 — Br + p{k}Cr, где Cr не зависит от и,
а зависит лишь от числа «родственных» хромосом в гамете. Следо-
вательно,
pk(.Aran~r) = Br +p(kl (Сг —Вг).
Для того чтобы получить рекуррентное соотношение относительно
р(М-ц, заметим, что р(М-1) зависит от вероятности спаривания между
гаметой, имеющей хромосомы, пришедшие от различных предков,
и гаметой, у которой имеется хотя бы две «родственные» хромо-
сомы. Но мы можем распорядиться произвольным образом лишь
(п — 2) хромосомами — две «родственные» должны остаться в паре.
Мы пренебрегаем случаем, когда имеется большее число «род-
ственных» хромосом. Тогда
( 2 \ / 2п - 2 \
p^»=2Pw(i-p^v2^2;-2 \
к П )
14*
420
Гл. 13. Генетические и экологические процессы
Пренебрегая в правой части членом, содержащим [р(/г)]2, получим1)
/ 2 \ / 2п - 2 \
0(fe + l) 20(/г) 2.П~2_1 = — п~— = п(® .ПГ 1
Р Zp /2п\ Р 2 2/1-1 Р 2/г - 1 ‘
\ п )
Таким образом, pk{Aran"r} = Br + p(fe) [Cr — Br] сходится к Вг, посколь-
ку p(fe)->0 геометрически с параметром (п—1)/(2п—1).
§ 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ
ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
Существует тесная связь между теорией ветвящихся процессов
и некоторыми вероятностными моделями частот, используемыми
в генетике и экологии популяций. Мы введем в рассмотрение класс
конечных цепей Маркова специального вида, который включает
в себя как частные случаи цепи, рассмотренные в § 2 гл. 2 в каче-
стве примеров приложения к генетике,
оо оо
Пусть /(«)= 5 ansn, 2а„=1,ая>0. Тогда марковский ветвя-
п = 0 п = 0
щийся процесс определяется как цепь Маркова, для которой эле-
мент матрицы переходных вероятностей Рц определяется, как ко-
эффициент при sj в разложении p'(s) (см. гл. 11). Вероятностное
распределение, определяемое последовательностью {«rj, называется
распределением числа потомков для одного индивидуума, a p(s)—
вероятностной производящей функцией для числа независимо по-
рожденных потомков i индивидуумов. Аналогично процесс {Хп} яв-
i
ляется ветвящимся, если Хп+х = 2 Ik = /, где Хп i — число инди-
6=1
видуумов в текущем поколении, — число потомков й-го индиви-
дуума в текущем поколении, a j — число индивидуумов в после-
дующем поколении. Случайные величины g2, • • •, It являются
независимо распределенными с общей вероятностной производящей
функцией f(s).
]) Заметим, что поскольку
p(fe+l)<2p(ft)
то действительные значения не превышают решения «линеаризованной» си-
стемы. В частности, если решение линеаризованной системы сходится к 0 при
^->оо, то это же справедливо и для исходной системы. — Прим, перев.
§ 4. Марковские процессы, порождаемые ветвящимися процессами 421
Рассмотрим теперь две популяции типов А и а, каждая из кото-
рых независимым образом размножается, как ветвящийся процесс.
Это — двумерный процесс, развертывающийся как последователь-
ность пар случайных величин Zn-=^ (Хп\ Yn)b где Хп и Yn— соот-
ветственно числа типов А и а в п-м поколении. Состояние процесса
описывается парой (*,/), г>0, />0, где i и j — текущие значения
числа типов А и а соответственно. В такой формулировке компо-
ненты Хп и Yn образуют независимые ветвящиеся процессы. По-
этому можно назвать Zn прямым произведением ветвящихся про-
цессов {XJ и {Yn}.
Пусть /(г)—производящая функция распределения числа по-
томков индивидуумов типа Л, a g(w) —производящая функция рас-
пределения числа потомков индивидуумов типа а. Если индиви-
дуумы развиваются независимо друг от друга, то компоненты мат-
рицы переходных вероятностей вычисляются по формуле
ррг(О-/,. гм-у-у,,.
= коэффициент при zf'wh в разложении fh (г) gt2 (w).
Можно сформулировать марковскую модель частот, связанную
с ветвящимся процессом для двух типов индивидуумов, в которой
размер популяции постоянен во времени. Имея это в виду, найдем
сначала вероятность того, что в поколении потомков имеется j ин-
дивидуумов типа А при условии, что общее число потомков равно
М и текущее поколение состоит из i индивидуумов типа А и N — i
индивидуумов типа а:
Р{Х(1) = / |X(O) = Z, Y(0) = N — i, X(l) + Y (1)-7И} =
Р{Х(1) = /, Y (1) = М-/|У(0) = /, Г (0) = —/} =
Р{Х(1) + У (1) — А11 X (0) = f, Y (0) — N — i}
__ коэффициент при в разложении Р (z) g^ (w) (4 1)
коэффициент при в разложении f* (/) g^ * (/)
Здесь использован тот факт, что fl (/) gN~l (0 — производящая
функция общего числа потомков, не различаемых по типам. Если
N = М, то можно считать выражение (4.1) определяющим матрицу
переходных вероятностей Рц(М) конечной цепи Маркова с про-
странством состояний {0, 1,2, ..., N}.
Отношение номера состояния к числу N можно интерпретиро-
вать как частоту типа А во всей популяции. Построенная цепь
Маркова, следовательно, является дискретной вероятностной мо-
делью, которая описывает изменения частот типов в популяции по-
стоянного размера, состоящей из двух типов индивидуумов. Изме-
нения частоты в каждом из поколений определяются видом мат-
рицы переходных вероятностей цепи Маркова.
422
Гл. 13. Генетические и экологические процессы,
Размер популяции N является параметром, который часто для
упрощения обозначений будет опускаться. Таким образом,
Л7 = Р{Х(1) = /|Х(1) + У(1) = ^, Х(0) = /, У(0) = 7У —=
__ коэффициент при Z^'w^ в разложении (z) g^ * (w) qk
, , /А? ft (/\ cfN — i ы\ * V * /
коэффициент при l в разложении / (?) g (?)
Марковскую цепь, характеризуемую матрицей переходных ве-
роятностей (4.2), иногда называют цепью Маркова, порожденной
прямым произведением марковских ветвящихся процессов.
Мы проиллюстрируем возможности данного класса цепей Мар-
кова на трех простейших примерах и укажем их место в приклад-
ных задачах.
(1) В качестве первого примера рассмотрим прямое произведе-
ние пуассоновских ветвящихся процессов, когда
= g(w) = Л, ц>0.
При этом
, , J „tk (z— 1)
р ___ коэффициент при Z в разложении С
~ .. tN _(А + (А7—Z) ц) (/ —1) *
коэффициент при ? в разложении £
X [коэффициент при в разложении
e-(ZX+(y-Z) ц) | + _ z) |
= nkj-rl'[ р; z .=0) 1)2>...)У.
\ / ) L th + (УУ -- i) ц J L tK + (N — t) ц J ’ J ’
(4.3)
Если Л = ц, то получаем выражение
'«-(ТКЖ'-т)'"'. ‘-i-0-1....................Л' (4Л)
не зависящее от X. Это в точности совпадает с вероятностной мо-
делью биномиального выбора (пример Ж § 2 гл. 2), предложенной
С. Райтом для изучения флуктуаций частоты гена в гаплоидной по-
пуляции при воздействии случайного дрейфа. Если то (4.3)
сводится к модели отбора Райта, в которой — = 1+а, а о — коэф-
и
фициент отбора, выражающий преимущество индивидуумов типа
А над индивидуумами типа а.
В общем случае, соответствующем формуле (4.1), мы скажем,
что отбор имеет место, если /(г) =0=g(z), т. е. если вероятностные
производящие функции числа потомков двух типов различны.
(2) Пусть f(г) = g(г) = (q + рг)2, #==1— р, 0<р<1. Порожден-
§ 4. Марковские процессы, порождаемые ветвящимися процессами 423
ная цепь Маркова (4.2) в данном случае принимает вид
л,--=[(™)Г*(2/1>/=0’ь 2>••••(4-5)
Интерпретация этой цепи Маркова как модели полисомного на-
следования дана в примере 3 § 2 гл. 2.
(3) Пусгь
/(*) = •,, q „ , g(z} = ^-р-, q=l — p, 0<р<1, а, Р>0.
(l“pz) (1-рг)р
Тогда, используя разложение
1 _ V / у + я-1\ п п
£0\ п I
мы видим, что порожденная цепь Маркова имеет следующие пере-
ходные вероятности
d __ 17 Za + (^“ 0 ₽ + N- 1 \Г! / za + /- 1 \ ( (N — i) р + N -i- 1 \ ,,
N )\ \ j )\ N-j г { }
i, /-0, 1, N.
Эта цепь Маркова может интерпретироваться как модель роста ге-
терозиготной популяции (см. стр. 321).
Явления миграции и мутации могут быть учтены в частотной
модели, представляемой порожденной марковской цепью, следую-
щим образом. Сначала рассмотрим явление иммиграции. Предпо-
ложим, что кроме размножения происходит процесс иммиграции
в систему независимо от текущего размера популяции. Пусть h(s)
и k(s) —вероятностные производящие функции числа иммигрантов
типов А и а, поступающих в систему за время одного поколения
соответственно. Совместная производящая функция U (г, w) =
оо
= Zj ип, вероятностей числа индивидуумов типов
п, т=0
А и а в популяции в следующем поколении равна [/(г, w) =
= /z(z) h(z) gN~l (w) k(w). Здесь
un,m=P{X(l) = n, У (1) = m | X (0) = Z, Y(0) = N — i}.
Для того чтобы построить порожденную цепь Маркова, введем ус-
ловие Х(1) + У(1) = N. Порожденная марковская цепь имеет пе-
реходные вероятности
Р/у= Р{Х(1) = /|Х(0) = Л Y(0) = N — i, Х(1)-ЬУ (1) = ЛГ} =
___ коэффициент при в разложении (z) h (г) (ш) k (w) (4 7)
коэффициент при в разложении /г (/) h (t) i (/j (/j
Z, / = 0, 1, N.
424
Гл. 13. Генетические и эко югические процессы
Явление мутации можно учесть в порожденной цепи Маркова
двумя способами. Предположим, что каждый индивидуум типа Л
может мутировать в индивидуум типа а с вероятностью (0
al 1) и каждый индивидуум типа а может мутировать в ин-
дивидуум типа А с вероятностью а2 (О се? 1). По отношению
к мутации индивидуумы являются независимыми. Для того чтобы
образовать следующее поколение, мы можем постулировать, что
процесс мутации следует за процессом роста (ветвящегося размно-
жения) или наоборот. Эти два постулата приводят к различным
цепям Маркова.
Наиболее просто описать функционирование модели мутации
непосредственно в терминах соответствующих вероятностных про-
изводящих функций. Рассмотрим сначала случай, когда мутация
происходит после воспроизведения. Пусть f(z) и g(w), как и преж-
де,— производящие функции числа потомков одного родителя ти-
пов А и а соответственно. Предположим, что при следующем про-
цессе воспроизведения каждый потомок индивидуума типа А (типа
а) может производить индивидуумы обоих видов с производящей
функцией Л(г, w) (В (г, w)). Другими словами, мы постулируем
две фазы процесса воспроизведения: первая соответствует обыч-
ному процессу размножения, в котором потомки являются копиями
родителей, в то время как вторая фаза соответствует своего рода
процессу трансформации и роста, когда один индивидуум одного
типа может превращаться в индивидуумов другого типа, т. е. ко-
эффициент ат,п в разложении A(z,w) является вероятностью того,
что на второй фазе потомок типа А произведет tn индивидуумов
типа А и п индивидуумов типа а. Производящая функция, описы-
вающая вид популяции потомков одного индивидуума типа Л (типа
а) после обеих фаз воспроизводства, равна f(A(z, w))(g(B(z, w))).
Механизм мутации получается при следующем ограничении:
Л (г, w) = (1 — а}) г 4- а] w, В (г, w) ~ a2z + (1 ~ а2) w. (4.8)
При этом вторая фаза воспроизводства сводится к процессу
трансформации С вероятностью 1—потомок типа Л сохраняет
свой тип, а с вероятностью ai мутирует в тип а. Аналогичную ин-
терпретацию имеет и производящая функция B(z,w) = a2z +
+ (1 — С62) tsp.
В результате производящая функция популяции потомков, по-
лученных при размножении одного индивидуума типа Л и подвер-
женных затем мутационному давлению, равна
/(г, йу)==П(1 -аОг + агоу]. (4.9)
Аналогичным образом можно описать популяцию потомков одного
родителя типа а, учитывая мутационное давление, с помощью про-
изводящей функции
g (z, w) = g [a,z + (1 - a>) да].
(4.10) j
§ 4. Марковские процессы, порождаемые ветвящимися процессами 425
С другой стороны, если мутационные превращения происходят до
воспроизводства, производящие функции принимают вид
Г (г, w) = (1 - aj) f (г) + atg (а>),
g‘ (z, w) = a J (2) + (1 - a2) g (ш).
Проведенное выше обсуждение приводит к следующей более об-
щей конструкции.
Мы постулируем, что каждый индивидуум типа А может произ-
водить потомков обоих типов. Обозначим вероятностную произво-
дящую функцию размера популяции потомков через /(г, w). Ана-
логично предположим, что индивидуум типа а может производить
индивидуумов обоих типов, и пусть g(z, w) —производящая функ-
ция популяции его потомков. Пусть li(z, w) — производящая функ-
ция числа индивидуумов типов А и а, иммигрирующих в систему
в течение каждого периода. Пусть (Х(л), У(п)) = Z(n), п = О,
1, ..., — результирующий двумерный ветвящийся процесс. Вероят-
ностная производящая функция величины Z(l) при начальных ус-
ловиях Х(0) = z, У(0) = k равна
[f(z, йУ)Г[£(г, w)]kh(z, w). (4.11)
Матрица переходных вероятностей порожденной цепи Маркова при
условии, что размер популяции фиксирован числом N, вычисляется
обычным образом. Получим
Р{Х(1) = / |X(O) = z, r(O)==/V-z, X(l)4-r(l) = ^} = Pz/ =
_ коэффициент при Z^ в разложении (z, w) gN ?> (z, w) h (z, w}
коэффициент при в разложении fi (t, t) g^ (t, t) h (t, t)
В частности, если
f (г, ipj) = е~к exp {Z[(l — c^) z + a^]},
g (г, w) = e~v exp {ц [а2г + (1 — a2) w]},
/г (г, w) == exp {[я (z — 1) + b (w — 1)]},
то переходные вероятности (4.12) порожденной цепи Маркова
равны
р = ( N \ К1 + GV-О Иг + а]7 [а^/Ч-ц (N-i) (1 •~a2) + ^]Af"/
\j) + ц (N-i) + a + b]N ’
Z, / = 0, 1, N,
Эта конечная цепь Маркова была предложена С. Райтом для изу-
чения флуктуаций частоты гена при учете отбора, мутации, миг-
рации и генетического отбора.
426
Гл. 13. Генетические и экологические процессы
§ 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ
ТИПАМИ ИНДИВИДУУМОВ
Теория, развитая выше, непосредственно обобщается на случай
произвольного числа типов. Рассмотрим многомерный ветвящийся
процесс для р типов индивидуумов, обозначенных через А{, А2, ...
..., Ар. Предположим, что индивидуум типа Ak за одно поколение
порождает потомство всех типов в соответствии с производящей
функцией
s2, ..., sp)= 2 _ v . «у, k= 1, 2, p, (5.1)
V^>0 1’ 2’ ’ p M
где —вероятность того, что индивидуум типа Ak произ-
Vl’V2’--*’Vp
ведет потомство, состоящее из Vi индивидуумов типа Ai, v2 индиви-
дуумов типа Д2 и т. д. Предполагается, что индивидуумы действуют
независимо.
Пусть (Xi(n), Х2(п),..., Хр(п)) означает соответствующий вет-
вящийся процесс, где Xk(n) является числом индивидуумов типа
Ak в начале zz-го поколения. Вероятностная производящая функция
числа потомков за одно поколение равна
fi1 (sP • • •, sp)f22 (sr • • •» sp) • • - fpP (si> • • • ’ sp) ^(si> • • •, sp)> (5-2)
где Xk(0) = ik (k = 1,2,..., p), a h(Si,...,sp)—производящая
функция числа иммигрантов различных типов.
Как и в случае двух типов, цепь Маркова, порождаемая путем
фиксации размера популяции, может интерпретироваться как час-
тотная модель. Мы опишем ее точную структуру. Пространство
состояний будет содержать все совокупности к = (k\, k2, ..., kp)
неотрицательных целых чисел, удовлетворяющих ограничению
р
2 kv = N. Матрица переходных вероятностей строится с помощью
v=l
ветвящегося процесса следующим образом. Пусть к = (k{, k2,. ..
... ,kp), 1 = (Zi, /2,. .. ,/p). Тогда
Pki =
*i(l) = /i,*2(l) = /2,...,
Xv(0) = £v, v = l, p,
2xv(0M, ixv(iw
V=1 v=l
коэффициент при S •• • S^P в разложении ft (s) № (s) . . . fkP (S) h (s)
-----------------—--------p---------------1-----?---------p--------- (5.3)
коэффициент при в разложении (t) (t) ... f?P (t)
где s = (sb .... sp), t = (/b ..., tp).
§ 5. Популяции с несколькими типами индивидуумов
427
В частном случае
г / р \
fl (s) = ехр I Хг 2 atvsv — 1 (> *=1,2, (5.4)
I \v=l / J
14, 1
A(s) = exp( 2j cv(sv— 1) L (5.5)
V V=1 J
где
p
aZv>0, Saiv==l, Zz>0, v, /=!, p,
V=1
cv>0, v=l, p;
переходные вероятности (5.3) равны
Ui, /2. .... Ip) W ... lPl ‘
Параметры, встречающиеся в выражении (5.6), должны быть ин-
терпретированы следующим образом: aiv является вероятностью
того, что индивидуум типа А< после рождения будет мутировать
в тип Av, Xi представляет собой относительный коэффициент от-
бора (т. е. приспособленности) типа Аг-, а Ct является средней ин-
тенсивностью, с которой индивидуумы типа Аг- иммигрируют в по-
пуляцию. Переходные вероятности (5.6) являются точным много-
мерным аналогом марковской модели Райта частоты гена при учете
мутации, миграции и отбора.
Вероятностная модель самооплодотворения при диплоидии
Вероятностная модель самооплодотворения может быть по-
строена аналогично (5.3) следующим образом. Рассмотрим случай
трех генотипов АА, Аа и аа. Каждый индивидуум спаривается с ин-
дивидуумом такого .же типа. Пусть fi(n) —вероятностная произво-
дящая функция числа потомков, получающихся от одного спарива-
ния вида АА X АА. Все потомки, конечно, имеют вновь тип АА.
Пусть /з(^)—вероятностная производящая функция числа потом-
ков, производимых от одного спаривания аа X аа. Наконец, пусть
Ы^)—вероятностная производящая функция числа потомков, по-
рождаемых при спаривании Аа X Аа. В последнем случае каждый
потомок имеет генотип АА, Аа или аа с вероятностями 4 ’ 4 ’ 4
соответственно.
428
Гл. 13. Генетические и экологические процессы
Пусть число индивидуумов типов АА, Аа и аа в начальном по-
колении равнялось fi, /2 и 1з соответственно. Флуктуации популяции
из-за самооплодотворения и роста описываются марковским вет-
вящимся процессом, у которого совместная производящая функция
общего числа потомков в следующем поколении равна
КччгА (5-7)
при начальном состоянии (fi,/2, г’з). Коэффициенты при степенях и,
v и w в разложении (5.7) являются соответственно вероятностями
того или иного числа потомков АА, Аа и аа.
Сформулируем теперь частотную модель, порождаемую фикси-
рованием размера популяции ветвящегося процесса (5.7). При
этом подобно (5.3) можно найти, что
коэффициент при в разложении fp (w) f^2 | — U + — V + — до] /з'(^)
. =________________________________, , Z, 4 ,
коэффициент при t в разложении (/) (/) /33 (/)
(5.8)
где 1 = (г,, i2, 1Я), j = О’,, /2, /з),
/i + h + /з~ Ч + h + h = К, iv^Q,
Переходные вероятности (5.8) являются частным случаем (5.3).
Эту конечную цепь Маркова можно рассматривать как вероят-
ностный аналог детерминированного процесса самооплодотворения,
сформулированного в § 1. Если взять в качестве рассматриваемых
производящих функций пуассоновские, то цепь Маркова с переход-
ными вероятностями (5.8) будет описывать процесс самооплодо-
творения с биномиальным выбором.
§ 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ
ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
В предыдущих двух параграфах мы рассмотрели несколько це-
пей Маркова, связанных с ветвящимися процессами. В настоящем
параграфе мы изучим некоторые вопросы, относящиеся к структуре
этих цепей. Более точно, будет найдено все множество собственных
значений и описаны некоторые свойства соответствующих векторов.
В § 8 мы укажем на различные применения и интерпретации этих
результатов.
Пусть задана производящая функция
оо оо
/(я)=Х««Л (6.1)
и ~ । > ц = О
§ 6. Собственные значения цепей Маркова
429
Рассмотрим порожденную цепь Маркова с матрицей переходных
вероятностей Р = llPjjll, где
D ____ коэффициент при в разложении М (s) fN~l У
* а ,, /,ч\
коэффициент при о) в разложении / (СО)
__ коэффициент при S^CO^ в разложении (sco) (со) /<• qx
коэффициент при СО в разложении / (СО)
z, / = 0, 1, N.
Для того чтобы найти собственные значения матрицы Р,
анализируем производящую функцию вероятностей {Рц}:
р \ __ V' р j ___ коэффициент при СО^ в разложении fi (sco) i ((О)
/V r/V / \ *
коэффициент при СО в разложении / (СО)
про-
(6.3)
/=0
Дифференцируя G (s) по s, получим
G' (s) == S p4isl~' =
/ = 0
__ коэффициент при СО^ в разложении * (SCO) f (sco) ? (co) _
коэффициент при CO в разложении f (co)
__ коэффициент при CO^ * в разложении if * (sco) f (sco) (co)
коэффициент при CO2^ в разложении (co)
Полагая 1, имеем
ДГ ?
Gz / <\ n ; • I коэффициент при CO в разложении f (co) f (co)
(1) = 7, = I {--------------------v-----------пгт—------
(6.4)
ДГ гЛГ / \
коэффициент при СО в разложении / (СО)
—
(6.5)
где
л __ коэффициент при СО^ * в разложении * (со) f' (ой
N sN / \
коэффициент при СО в разложении / (СО)
Таким образом, если мы будем трактовать Р как матрицу, за-
дающую линейное преобразование в линейном пространстве раз-
мерности N + 1, то из соотношения (6.5) следует, что Pv = Xtv,
где v= (0,1,2, ..., N). Таким образом, (0,1,2, N) является
собственным вектором матрицы Р, соответствующим собственному
значению Хь Очевидно, Ре = 1-е, где е=(1, 1, 1), поскольку
ПРИ всех Эти два результата являются частным про-
/
явлением формулы
2 P//Qr (/) = №(/), i = 0, 1......N, (6.6)
j
430 Гл. 13. Генетические и экологические процессы
где Qr(-) является полиномом степени г. При г0, 1 имеем
Q0(x) = 1 и Qi (х) = х.
Наша цель теперь — доказать формулу (6.6) для всех г. Для
этого продифференцируем (6.4) еще раз по s:
у
G" («)=•• 2^/ [/(/-1)] ^-2 =
7=0
жж
коэффициент при СО в разложении
_ _________{t (t- 1) f‘~2 (sco) (f' (sco) )2 afN~‘ (co) + Z/‘~' (sco) f" (sco) (co)}
коэффициент при оД в разложении (co)
Положим s=l, тогда
G"(D = S Л/[/(/-!)] =
7“0
коэффициент при СО^ 2 в разложении [/ (/ — 1) 2 (со) (f' (со) )2 + 1 (со) (со)]
== N \
коэффициент при СО в разложении / (СО)
Пусть
а____коэффициент при со^ 2 в разложении % (со) (f' (со) )2
^2 дг n/у , ч
коэффициент при СО в разложении / (СО)
Тогда
w
2 Рц [j(i- 1)] = A2[Z(Z — 1)] + Z82j Z = 0, 1, .... N,
f-o
где
„ __ коэффициент при СО^ 2 в разложении * (со) j" (со)
е2 N (N / \
коэффициент при СО в разложении / (СО)
Таким образом,
N
2 р„Г- = Л2/2 + (полином степени по /)»
/=о
Следовательно, нами установлена формула
N
2 Рц!г = (z), z = 0, 1, N,
i=o
где zzr_i(*)—полином степени r—1, по крайней мере для
г = 0, I, 2. В действительности же справедлив следующий более
общий результат.
§ 6. Собственные значения цепей Маркова 431
Теорема 6.1. Пусть Zo = 1,
л коэффициент при to^ г в разложении fN Г (to) [f (to)]r /~
Zr 77 iN f \ > X™»*)
коэффициент при to в разложении / (to)
г=1, 2, N.
Тогда
^Ptljr=-krir + ur^, (6.8)
/=0
где ur-i(i) — полином степени г — 1 по i, г = 0, 1, ..., N. (Усло-
вимся^ что полином степени —1 есть тождественный нуль.)
Доказательство. Если продифференцировать (6.3) k раз,
левая часть примет вид
GM (S) = 2 Pi! [/(/- 1) ... (/ - k + 1)] S!~k -
/=0
(6.9)
/-0
где —полином степени ^.k—1. Если продифференциро-
вать (scd)/24^* (со) в правой части k раз по $, то получим
[Л (3(0) fN~l (®)J = f""' (<о) £ [f' ($«>)] =
dsK dsR
= [Z(Z - 1) ... (Z - k + 1)1 fl~k (soy) (f' (say) )k fN~l (ay) ayk +
+ остальные члены. (6.10)
Первый член появляется при последовательном дифференци-
ровании f* (sco) k раз. Оставшиеся члены возникают при дифферен-
цировании других сомножителей, таких, как f'(sco), f,z(sen) и т. д.,
которые появляются в процессе дифференцирования исходного вы-
ражения. Степени этих возникающих сомножителей не зависят от /.
Это означает, что результат указанных операций дифференцирова-
ния есть линейная комбинация различных степеней f, коэффи-
циенты которой содержат в качестве сомножителей максимум
k — 1 из чисел f, i — 1, i — 2, ..., i — k + 1, т. e. коэффициенты
являются полиномами степени не выше k -— 1 по отношению к пе-
ременной I. Каждое слагаемое второго члена выражения (6.10)
зависит от f через выражение вида
ft-1 (say) fN~l (оу) (f' (say) f If" (s«>)]v* .. .
при некотором 0 4 / 4^ и т. д.
432
Гл. 13. Генетические и экологические процессы
Группируя члены в равенстве (6.10), получим
•уу [Л (sg>) fN~l (со)] = 1кР~к (so) [Л (SCO)]6 p-i (со) COfe + Uk-i (Z; f), (6.1 1)
dsR
где f) —полином от переменной i степени не выше k— 1
при s = 1. Фактически при $ = 1 степени члена (so))fN~i(со)
складываются, и зависимость от i сохраняется лишь в коэффициен-
тах При .
Предположим, что равенство (6.8) доказано для всех степе-
ней —1. Тогда в силу гипотезы индукции
GW(l)=2Pj/+i/’^r-i(/)=3Pf/+Vr-i(0, (6.12)
/=о 7=0 7=о
где flr-i(-) и гг_1(-) —полиномы степеней не выше г — 1. В силу
(6.11)
Gw(l)
коэффициент при СО в разложении
/^ (<>)]
N (N ( \
коэффициент при СО в разложении / (СО)
— irhr + иг_1(/). (6.13)
Сравнивая (6.12) и (6.13), видим, что утверждение индукции вы-
полняется и для г. Это завершает доказательство формулы (6.8). в
Докажем теперь основную теорему данного параграфа, кото-
рая раскрывает природу собственных значений матрицы Р.
Теорема 6.2. (1) Собственными значениями матрицы Р яв-
ляются числа Хо, Xi, ..., Х^, определяемые равенством (6.7). Более
того,
(2) числа Хг удовлетворяют соотношению 1 = Хо = Xi > Хг > ...
... > XN > 0, если a0aia2 > 0, где f(s)= S ansn,
п — 0
Доказательство. (1) Введем базис из N + 1 векторов раз-
мерности N + 1 : лг = (лг (0), пг (1), ... , лг (AZ)), г = 0, 1, . .. , N,
где лг(л) = хг. Эти векторы, очевидно, линейно независимы, по-
скольку в противном случае мы могли бы построить полином Л;-й
степени, имеющий N + 1 корней, что невозможно.
Найдем теперь вид матрицы Р в специально выбранном базисе
{ло, ль ..., лдф. Понятно, что i-й столбец матрицы Р состоит из
коэффициентов вектора Рл^ который представлен в виде линейной
комбинации векторов {л^}у¥=0.
§ 6. Собственные значения цепей Маркова 433
Из соотношения (6.8) следует, что матрица Р в новом базисе
имеет вид
j 1 0 * *
О * *
О Хо *
. О О Х3
. . О 0 \
0 0 0 0
где элементы, обозначенные *, соответствуют полиному иг_\ в (6 8).
Таким образом, матрица Р, представленная в новом базисе, яв-
ляется треугольной и ее собственные значения, очевидно, равны
1 = Хо, Xi, ..., Xn. Поскольку собственные значения инвариантны
относительно выбора базиса, доказательство пункта (1) закон-
чено.
(2) Заметим, что для любого степенного ряда л(со) = 2 cm®m
tn~Q
коэффициент при сом. очевидно, равен р-1 [коэффициент при orv~l
в разложении л/(со)]. Полагая М — N — г и л (со) — fN~r(®)
получим
коэффициент при со¥~г в разложении {Р~г (со) (Г (со))7} =
= [коэффициент при cov~r~1 в разложении
{(N - г) fN~r~' (®) (Г (®) )г+1 + (®) (Г (со) Г’ f" («)}] ~
= коэффициент при co'v-r“1 в разложении
{ f v’r"1 (®) (/' (®) )r+I + fN~r («О (Г (®) Г’ f" (®) }.
Если разделить обе части на коэффициент при соу в разложении
fN(co), то, вспоминая определение Хг, получим соотношение
коэффициент при г 1 в разложении Г(©) (f'(co))r 7" (со) |
Лг = Xr+i н — N ' ,
коэффициент при ® в разложении / (СО}
1. (6.14)
При г = 0 второе слагаемое в правой части, очевидно, равно 0,
таким образом, 1 = Хо = Хь
Поскольку f (со) —вероятностная производящая функция, то ее
коэффициенты неотрицательны. Следовательно, коэффициент при
в разложении (ci))fN~r(со) [/'(со)]г-1 неотрицателен, так что
434
Г л. 13. Г енетические и экологические процессы
всегда Хг>Хг+ь Из предположения о том, что а0ащ2 > 0, непосред-
ственно вытекает, что второе слагаемое в (6.14) положительно при
г > 0. (На самом деле достаточны гораздо более слабые предпо-
ложения.) Поэтому > Vn (г^1), что и требовалось дока-
зать.
Из теоремы 6.2 известны все собственные значения матрицы
(6.2). В предположениях пункта (2), т. е. > 0, где
оо
f (s) = S ansn,
п = 0
собственные значения kr < 1, г == 2, 3, ..., N, все различны. Обра-
тимся теперь к задаче описания собственных векторов, соответ-
ствующих этим собственным значениям.
Мы уже показали, что собственному значению 1 = Zo = М соот-
ветствует пара правых собственных векторов е = (1, 1, 1, ..., 1)
и и = (0, 1, 2, ..., N). Интуитивно более привлекательна пара
векторов, являющихся линейной комбинацией указанных, а именно
Л 2V-1 1 n\ и /п 1 2 1 и п
\1 ’ АГ ’ • • • ’ ЛГ ’ °) е ‘ уу 11 дг ’ дг ’ • • • > 1 N ) 'JV • Для
компонент векторов, представленных в такой форме, можно дать
вероятностную интерпретацию (см. § 2 гл. 4).
Анализ выражения для показывает, что матрица Р имеет
вид
1 0 0 ... 0
откуда с очевидностью следует, что 0 и N — поглощающие состоя-
ния. Более того, из предположения о том, что 0 < aQ < 1, следует,
что 0 и N достижимы за один переход из каждого состояния
{1, 2, ..., N—1} с положительной вероятностью. Следовательно,
0 и N — единственные поглощающие состояния.
Следующая теорема характеризует правые собственные векто-
ры, соответствующие собственным значениям Хг (г = 2, 3, ..., AZ).
Теорема 6.3. Существуют полиномы Qr(%) степени г, для ко-
торых
PQr = XrQr.
(Вектор Qr равен (Qr(0), Qr(1), ..., Qr(/V)).)
£ 6, Собственные значения цепей Маркова 435
Доказательство. Теорема уже доказана при г = О, L
Если г > 1, мы знаем, что
/=0
где —полином степени О—1. Выберем Qr+i(/) в виде
Qr+i (/)== /r+1 + ajr 4- a2jr *4- ... +ar+i (/ = 0, 1, ..., N),
где постоянные ai, а% ..., ar+i нужно подобрать. Необходимо вы-
брать {аг] так, чтобы соотношение
5 РцО.г+\ (/) = Ur+/+I + Нг (/)) 4- а{ (krir 4- Яг_! (/)) 4-
/=о
4-^2(лг_1/г 1 4- Нг-2 (Z)) 4- ... = Zr+1Qr+I (/) =
= Ar+i (zr+1 4- ci\ir 4- ... 4-ar+i) (6.15)
выполнялось при всех i. Приравнивая коэффициенты при ir в обеих
частях равенства, получим условие
= a{kr 4- известная часть Hr(i). (6.16)
Поскольку Лг+1 < kr при r> 1, можно найти такое число aif чтобы
равенство (6.16) удовлетворялось. Затем, приравнивая коэффи-
циенты при Л1-1 в обеих частях (6.15) и используя то обстоятель-
ство, что а\ известно, получим соотношение вида
a2kr-\ + известный член = а2Лг+ь (6.17)
Найдем а<2 из (6.17). Это возможно, поскольку Xr+i < %r_i. Про-
должая процедуру таким же образом, можно вычислить последо-
вательно все коэффициенты я3, а4, аг+\ так, чтобы (6.15) вы-
полнялось тождественно по i.
Вышеприведенное построение доказывает существование пол-
ного базиса из собственных векторов специального вида (т. е. по-
лученных с помощью полиномов). Из теории матриц (см. стр. 505)
следует, что существует полная система левых собственных векто-
ров. Предположим, что мы записали правые собственные векторы
в следующем порядке:
/12 \
ф0 = р, 1 - др 1 --ц , ..0J для Хо= 1,
•••’ 0 для х>=1’ (6Л8)
fPr = (Qr(O), Qr(l), • • •, Qr(N)) для Лг, r = 2, N,
где Qr(x) — полином, определенный в теореме 6.3,
436
Г л. 13. Генетические и экологические процессы
Обозначим биортогональную
торов через
ipo= (1, 0, 0, О, 0)
ф, = (О, О, О, . . О, 1)
систему левых собственных век-
дл я Л/)= 1,
для (6.19)
Фд = (фг (0), ФгО), • ••, фг(Лг)) для Лг, г = 2, V.
По-видимому, довольно трудно выразить <рг и фг в замкнутом виде.
Тем не менее срг может быть в принципе вычислен рекуррентно
(фактически с помощью того же метода, который использовался
при доказательстве теоремы 6.3).
Для вычисления фг также можно предложить рекуррентный ме-
тод. Можно доказать, что компоненты вектора фг имеют вид
= RN-r(i), 1, 2, .... N,
\ I /
где /?т(-) —полином степени т, который можно найти рекуррент-
ным образом.
Мы завершим параграф несколькими конкретными примерами.
Примеры. (A) f(со) = еМю-п. Тогда при г>1
л __ коэффициент при СО^ Г в разложении Г (со) (Г (со) )Г _
коэффициент при 0) в разложении / (СО)
, , ,uV-r Л (N-r) (со- Do г„гк (0-1)
__ коэффициент при со в разложении в л, е _
“ 77 Tn an (о-1)
коэффициент при СО в разложении в
_ 7.r\{/.N]N~rl<N - п\} _JVI__L
“ [(M^/Nl] ~ (N-rY. Nr '
(Б) f(s) = (1 — р + ps)\ у—целое число >1,
__ коэффициент при <0^ Г в разложении (1 — р + рйр [уР (1 Р рСоЦ '] _
коэффициент при <й^ в разложении (1 — р + рсо)'^
- vH tfv-op'yr1
' \ N - г Д N J •
(В) f(s) = [(l-p)/(l-ps)]a, a>0,
, , ,'N-~r
коэффициент при <0 в разложении
А =_____________________[(1 - р)/(1 - рй)]а w~r' [(ap (1 - р)а)/(1 - рю)а4 Т =
коэффициент при (0^ в разложении [(1 — р)/(1
__ (1 --р)0^ (схр)г • {коэффициент при <0^ Г в разложении [1/(1 — pco)]a^ + r} __
(1 —- p)aN «{коэффициент при 0)^ в разложении [1/(1 — р(о)]а^}
1xr r(~aN-r\(-aN \”1 r (aN + N - 1\ /cuV + N - 1 \~1
“(-О « ( Л7-г )( TV ) =а ( У-р )( Л7 ) ’
£ 7. Собственные значения для модели мутации
437
Значение К2 для этих частных случаев представляет интерес,
поскольку оно характеризует скорость приближения системы к по-
глощающему состоянию или, в генетической терминологии, ско-
рость приближения к гомозиготному состоянию. Для примера (А)
. = Nl J_ = 1 _±
Д2 (N— 2)1 N2 1 N ’
Для примера (Б)
, =v2(^~2\INv\-1 угУ (У — 1) у (У — 1). ( п_______1
Л2 v\N-2)\n) Wy(/Vv--1) Ay-1 VY 'Ay-l*
следовательно, асимптотически no N
Аналогично для случая (В)
, _ 2 f ~ I \ — Ц-1 aW^-!) ; /, , ' 1_
Л2 У-2 Д У ) аУ(аУ+1) 1 U + ’ 1 + аУ ’
так что асимптотически
Л2~1 --E+L ’
2 a N
Заметим, что в пуассоновском случае значение к2 (для больших А)
является промежуточным между соответствующими значениями
для биномиального распределения потомков и отрицательного би-
номиального распределения.
§ 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ
С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
В предыдущем параграфе мы нашли вид собственных значений
и собственных векторов матрицы перехода порожденной цепи Мар-
кова (6.2). В этом параграфе мы будем изучать порожденную
марковскую цепь для р типов (р > 2) индивидуумов при общих
предположениях относительно мутации. В частности, будет найден
вид собственных значений и собственных векторов цепи Маркова
с переходными вероятностями
kl k2 kD ТТ i
коэффициент при S2 ... в разложении I I f v
Pi, к ~ N e/V , ч
коэффициент при S в разложении / (S)
Р Р
где i (<|, г2, • • • > iP), k = (kh k2, kp), 2 Ч = 5 zv^0
v=l V=1
и kv^Q при всех v. Р{,к задают условные (при условии, что
' р \
(7.1)
438 Гл. 13. Генетические и экологические процессы
общее число потомков равно N) частоты р типов индивидуумов,
когда v-й тип производит потомство с производящей функцией f(s),
после чего каждый из потомков мутирует в тип Aj с вероятностью
«VJ (/ = 1, 2, . . . , р).
В силу определения матрица Г = || aV(X ||р Ц=1 является стохасти-
р
ческой, т. е. avgi>0, 2 1, v=l, Мы предположим,
Ц=1
что матрица Г диагонализируема (см. приложение). Это означает,
что ее р собственным значениям соответствуют р линейно незави-
симых собственных векторов. Пусть и^1), и<2\ ..., — полное се-
мейство правых собственных векторов, причем можно взять и^1) =
= (I, 1, 1, ..., 1), поскольку сумма элементов любой строки ма-
трицы Г равна 1.
Выражение (7.1) можно переписать в следующем виде:
fin ТТ 7
коэффициент при $р*1 1% ••• в разложении Jj / S Zi I
р —----------------------------------------!--------------L (7 о)
ri, k .. Л cN /„X • V"6/
коэффициент при S в разложении /
Производящая функция, соответствующая вероятностям Pi, к,
равна
G(o •••> ^)=2ддХ2
к
Р { / Р \
коэффициент при 8^ в разложении II f >2 I
=---------------------„-----" УД1----------(7.3)
коэффициент при S в разложении /
Прежде чем находить все собственные значения матрицы
Р = l|Pi, к II, мы рассмотрим два частных случая, которые помогут
пояснить общий метод нахождения собственных значений матрицы
(7.1).
Случай 1. Дифференцируя уравнение (7.3) по и полагая за-
тем /1 = /2 = • • • — = 1, получим
— G(/b /р) lf t . =t =1 == 2 к ==
A* 1 z p
к
— коэффициент при sN в разложении
f (s)f(s) + s/2a2jLJyV“1 (s)f (s)+ ... +sipaPjXfN"i(s)l'(s) 1
I ЖД. f/V / \ (
к коэффициент при S в разложении / vS; )
/ P \
( 2 ) [коэффициент при 8^ 1 в разложении * (s) (s)]
N tN t \
коэффициент при S в разложении / \S)
§ 7. Собственные значения для модели мутации 439
Равенство (7.4) выполнено при всех i. Положим
л __ коэффициент при 1 в разложении 1 (s) Г (s)
Л1 JV cN
коэффициент при S в разложении / (S;
Тогда равенство (7.4) можно записать в виде (справедливом
при всех i)
р
2 k = Х1 2 iv«vn> и=1, 2, р. (7.5)
к v=l
Далее, умножим обе части равенства (7.5) на и просумми-
руем по ц, где u^ = (u\Q\ и^\ ..., ^) — </-й собственный вектор
матрицы r = ||aVMJ|, <7 = 1, 2, ..., р. Получим
р
2 2 Р, к£ц = Л,, 2 «ц * 2 iv«vn’
К V I
или, меняя порядок суммирования,
/ р \ р р
2 Pi, к 2 u^k ) = Л] 2 Ц 2 a «<"> для всех i.
к \ц = 1 ц ц/ 1 v-l v ц-1 11 ц
Так как ufa) — собственный вектор матрицы ||ауЦ||, соответствую-
щий собственному значению уд, то
р
^av^) = y4Uv}-
(1 = 1
Отсюда
(р \ р
2 «'«Sj-1,V, 2 (7.6)
Для дальнейшего удобно ввести вектор Lq, k-я компонента кото-
рого равна
р
2 -L, W-
(Заметим, что Lq(k) —линейная функция от к, в частности (к) =
р
= 2 Равенство (7.6) примет вид
Ц = 1
' 2 Pi, kLq(k)~= hi\qLq(i), 2, ..., p для всех i, (7.7)
к
откуда следует, что является собственным значением матрицы
Р, a Lq(i) — соответствующим ему собственным вектором.
Заметим, что Li (i) = N (константа, не зависящая от i). Мы
будем в какой-то мере выделять вектор Aj(i) из остальных векторов
440
Гл. 13. Генетические и экологические процессы
Lg(i), 7 — 2, р, которые являются (не постоянными) линей-
ными функциями от L Собственные векторы /^(i), соответствую-
щие собственным значениям XiyQ (? = 1, 2, р), линейно неза-
висимы. Это следствие линейной независимости собственных век-
торов матрицы |iavPJ|. В самом деле, если бы векторы Lq(i)
были линейно зависимы, то для некоторых действительных по-
р
стоянных ап, не всех равных нулю, было бы S anLn (i) = 0. Но
тогда
Так как это выполняется при всех /, то отсюда следует
2
П = 1
v = 1, 2, ..., р,
что противоречит линейной независимости векторов и^/).
Поскольку Lj(i), L2(i), . .., Z>p(i) линейно независимы, то легко
показать, что любая линейная функция Я (i) может быть предста-
влена в виде линейной комбинации векторов {Lq т. е. суще-
ствуют постоянные Z?i, ..., bp, такие, что
р
£(i)=2 bvLv(i) для всех L (7.8)
V=1
Из (7.7) и (7.8) вытекает, что матрица Р переводит линейные
функции в линейные, т. е. если 2 (i) линейна, то функция
2 A. j2 (j) = V (i) (7.9)
j
также линейна по i. Мы используем это свойство ниже.
Случай 2. Он аналогичен случаю 1, но требует для своего до-
казательства несколько более сложных выкладок и в некотором
смысле более общих рассуждений.
Дифференцируя равенство (7.3) по любым двум аргументам
(они могут и совпадать) и полагая затем t\ = t2 == ... = tp = 1,
получим в левой части равенства
-эЛт- О (<»••• С) I = У Л, k (kmkn + Vm, „ (к)), (7.10)
oln \f = / = ... = f =1 -*"
'1 J к
in, n = 1, 2, ..., p,
где
( km,
*m, n (k) = } Q
если т = п,
в противном случае.
§ 7. Собственные значения для модели Мутации
441
После дифференцирования правой части равенства (7.3) получим
выражение
( / р \ / р \
коэффициент при в разложении \ S I j iyCtym ]fN~2 (s) P'(s)]2
I \v = l / \V=1 /
ДГ № ( \
коэффициент при S в разложении /
4-линейная функция от переменных (z'j, z2, ip). (7.11)
Введем в соответствии с предыдущим величину
ДГ—2 f/V—2 / \ г { \i2
__ коэффициент при S в разложении / [/
^2 — ДГ ,ДГ , ч
коэффициент при S в разложении /
Далее, умножим выражение (7.10) на z/^zz^') (7, q'1, 2, р)
и просуммируем по всем m и п. Получим
3 3 «^2A.k(Mn + Sm.n(k)),
m~ 1 п = 1 к
или, меняя порядок суммирования,
ЗД, кЩ(к)^(к) + 2’(к)]. (7.12)
к
Выполняя аналогичные операции над выражением (7.11),
получим
~ р р а г р р чрр
2 SsX? ДДм?1 + 2, 2 . « <7-i3)
_v=l m = l JLV = 1 n = l J m = l n = l
где Lm, n(i) при всех tn и n —линейная функция от i. Мы снова
р
воспользуемся тем фактом, что S avmzz^} -= по определению
m— 1
собственных векторов матрицы Г == || aVLl ||. Выражение (7.13) тогда
примет вид
(р \/р \ р р
3 11 з \ + з 3 п (i) =
v«i / \v=l / n = i m = l
p p
где Г(1)=3 3 u^mun’ Lm n (0 есть линейная функция от i =
/72 = 1 72 = 1
‘ G*1, ^2, • • • , ^*p)’
Результатом этих вычислений является равенство 3 *
3 Pt, k [Lq (k) Z.4'(k) + 2* (k)] = Z2Y</Y<z'i<? (i) + L* (i) при всех i,
k
442
Гл. 13. Генетические и экологические процессы
Перенося 2 Pi к^*(к) в правую часть, получим
к
5 Л, kLq (к) Lq’ (к) = (i) Pq' О) + & (i), (7.14)
к
где S (i) = L* (i) — 2 A, k8* (к) — линейная функция от i (в силу (7.9)).
к
Для простоты предположим (на самом деле это не суще-
ственно), что 0 #= ZiYtf Iz4q4q' =/= Опри всех q, q' (2 q, q' р).
Мы не будем рассматривать случай q = 1, так что £Дк)А^(к) —
квадратичные функции переменных (&ь k2, ..., kp).
Если бы в равенстве (7.14) не было линейного члена £(i), то
это было бы соотношение, определяющее собственное значение.
Мы утверждаем, что ЛгУ^У^'— собственное значение матрицы
(7.1). Покажем, как построить собственный вектор, соответствую-
щий значению ЛгУ^у^.
Предположим, что существует собственный вектор следующего
вида:
ciqq'^b i2, .... Zp)=-LJi) A^(i) + /C(i),
где форма K(i) линейна no i и пока произвольна. Вектор aqq' — не-
тривиальный, поскольку квадратичный член не может быть тожде-
ственно равным линейному члену. Представим 7<(i) в виде
р
2^(0» что может быть сделано, поскольку Lh(i) (/г — 1,2, ...
/г=1
..., р) образуют полную систему линейно независимых линейных
собственных векторов (см. также (7.8)).
Следующий метод построения собственных векторов аналогичен
методу, использованному при нахождении собственных векторов
матрицы перехода для модели с двумя типами индивидуумов при
отсутствии мутации (см. § 6). В вышеприведенное выражение для
собственных векторов входят неизвестные коэффициенты bk. Для
того чтобы aqq'(i) был собственным вектором, нужно, чтобы удо-
влетворялось равенство
{р
MkHHk)+S Шк)
V-1
q
Lq(i)Lq^i)+^bkLk(i)
k~\
Из равенств (7.7) и (7.14) следует, что левая
для всех i. (7.15)
часть (7.15) равна
~ р
faVqVq'Lq (0 Lq' (») + 2 (1) + Л1 5 Ь^кЬк (1).
k—1
§ 7. Собственные значения для модели мутации 443
Приравняем это выражение правой части (7.15). Приведя подоб-
ные члены, получим
~ р р
$(i) + M s bkykLk(i) = K2yqyQ's bkLk(i) для всех i. (7.16)
k=i fe=l
Так как й (i) линейна по i, можно записать
р
k=l
где коэффициенты ck определяются единственным образом из вида
Й (i) и являются известными величинами. Таким образом,
р
2 + Ck~ Lk (i) = 0;
поскольку L/j(i), k = 1, ..., p, линейно независимы, то
UbkVk + Ck-^<tfq'bk = Q, fe=l, 2, p,
откуда
^ = 1-----—у-----> k=1,2,...,p.
Собственный вектор может быть теперь записан в виде
»«. (о - «) (о+i p-i’>
где q, q' -2, 3, ..., p.
Мы доказали, что каждому собственному значению со~
ответствует собственный вектор aqq> (i). Все собственные векторы
л^'(1) линейно независимы, поскольку квадратичные части
L^(i) Lq> (i), очевидно, линейно независимы.
Общий случай. Рассмотрим теперь общий случай. Дифференци-
руя равенство (7.3) ц раз по ti (i = 1, 2, ..., р) и полагая затем
tx = /2 ==... = tp = 1, получим
2 Pi, k (k\)ri (k2)r2 • • • (kp)rp =
Ip \ri / p \r2 / p \rp
= 2 Wu j 2 ifon I •. • I 2 / +
\/=i / \z=i / \z=i /
+ полином от (fb ..., ip) степени < R, (7.18)
где R= 2 rit
z=i
a ___ коэффициент при % в разложении (s) [f' (s)]^
. N UV >
коэффициент при s в разложении / \S)
414
Гл. 13. Генешческие о экологические процессы
a (kt)m определяется так:
(kt\n = kt (kt - 1) ... (kt- m+ 1).
Первый член в правой части равенства (7.18) является одно-
родным полиномом от (zb i2, . . . , ip) степени R. Он получен при
однократном дифференцировании правой части (7.3). Как только
при дифференцировании появляется член f/z(s), степень коэффи-
циента при нем относительно i обязана быть меньше R, поскольку
для того, чтобы получить /"($), нужно продифференцировать fz(s),
a f'(s) не возведено в степень iv (v = 1, 2, . . . , р). Используя ра-
венство (7.18), можно найти собственные значения матрицы пере-
ходных вероятностей (7.1).
Первое собственное значение равно 1 и соответствующий ему
собственный вектор имеет равные между собой компоненты. При-
чиной этому служит то, что сумма элементов строк матрицы пере-
ходных вероятностей равна 1. При R = 1 мы имеем случай 1, а при
R = 2 — случай 2, рассмотренные выше. В случае 1 мы получили
линейно независимых собственных векторов. Член
^~2j = l отвечает собственному значению 1. Член(Р1 1 j р — 1
отвечает собственным значениям yq, q = 2, 3, . . . , р. В случае 2
было ~ линейно независимых собственных векторов, соответствую-
щих у р(р— 1)собственным значениям вида k2yqyq', q, q' = 2, .. ., р.
Процедура, аналогичная использованной в случаях 1 и 2, мо-
жет быть применена для построения ( r I линейно независи-
мых собственных векторов, которые являются полиномами сте-
пени г от переменных
/ р \ р
z2(i)=2^v,
\v==l / v = l
р р
Lq (i) = S u(vq}iv, • • • > K-, (i) = 2 ЧР)Ц.
и соответствуют собственным значениям
• • • Yv 2<<7!<<72< ... (7.19)
Точное выражение для собственных векторов имеет вид
Clq^ ct2, qr kt, •••> ip) — (0) 3"
+ полином от (fb ..., ip) степени < r. (7.20)
<$ 7. Собственные значения для модели мутации
445
Число собственных значений вида kryq yq ... yq , #v = 2, ...
..., p, можно найти, рассматривая соответствующую задачу о раз-
мещении, где k шаров нужно разместить в п ячеек. В нашем слу-
чае k равно степени г соответствующего собственного вектора,
а п равно числу различных чисел yq (7 = 2, ..., р), т. е. р—1.
При такой интерпретации число различных собственных значений
равно числу сочетаний из г 4- р — 2 по г. Поэтому число различ-
ных собственных векторов вида
. Y?r. ^ = 2.......р, (7.21)
(г + р — 2\ (г + р — 2\
Равно ( г Н р-2 )•
Общее число линейно независимых собственных векторов равно
ГоХЛ'Мк - +гп+ -
_(N + p-\\
\ N Г
что в точности совпадает с числом состояний цепи Маркова (7.1).
Подытожим полученные результаты в следующей теореме.
Теорема 7.1. Пусть Г —1|aVM,||^ ц=в1 — стохастическая матрица
(т. е. aVJLl>0, 2aVJLX== 1, v = 1, 2, ..., р\, соответствующая не-
\ ц > /
приводимой цепи Маркова. Пусть yi = 1, уг, • • •, Yp — ее собствен-
ные значения, и предположим, что u<1), и<2\ ..., и*?) образуют пол-
ное семейство соответствующих им собственных векторов, т. е. Г
диагонализируема. Более того, предположим, что Л v у ... у„ =/=
q\ q2 Чг
W/V ••• V/ , для любых у и у - (2^qk, q'k<p), 1,
1 Xf < *i 1 rV n>
где
;N—r
—
коэффициент при S в разложении / (S)
, , „N—г
а коэффициент при S в разложении /
Д = ------------------------------------
(s) (Г (s))‘
(7.22)
Рассмотрим цепь Маркова для р типов индивидуумов с матри-
цей переходных вероятностей, задаваемой равенством (7.1). При
r> 1 существует ^г + рг 2 j линейно независимых собственных век-
торов, которые получаются из полиномов степени г от переменных
р
Lq (i) = 2 7 = 2, р.
V=1
Вид собственных значений дается формулой (7.21), а правые соб-
ственные векторы имеют вид (7.20). На эти собственные векторы
446
Гл. 13. Генетические и экологические процессы
и постоянный вектор натянуто пространство размерности^ +
равной порядку матрицы ||/Д к ||.
В качестве примера применим теорему 7.1 к случаю, когда Г —
единичная матрица. Другими словами, нет мутационного давления.
В этом случае цепь Маркова (7.1) является непосредственным об-
общением модели с двумя типами индивидуумов на случай р ти-
пов Л1, Л2, .. ., Ар. Каждый из них размножается независимо в со-
ответствии с законами развития ветвящегося процесса, характери-
зуемого вероятностной производящей функцией f(s). Порожденная
цепь Маркова имеет следующие вероятности перехода:
коэффициент при <$j!S22 • . . Spp в разложении f v (<Sv)
Л, j =----------------------й---------. (7.23)
коэффициент при ? в разложении / \1)
В этом случае yj = у2 = • • • = у? = 1. Пусть константа опреде-
лена равенством (7.22). Теорема 7.1 утверждает, что Кг является
собственным значением кратности + Р (г = 0, 1, 2, ..., N),
т. е. существуют I ? I линейно независимых собственных век-
торов, соответствующих собственному значению Гг. Кратность воз-
никает из-за того, что Kryqiyq2 ... yq и не зависит от выбора
= yq2 = ... =:у^г=1. Правые собственные векторы, соответ-
ствующие Хг, являются полиномами степени г от переменных
Lq (i) = 2 = iq (<7 = 2,3,..., p),
v 4
поскольку можно выбрать = .
§ 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
Мы можем теперь, используя теорему 7.1, дать вероятностную
трактовку собственным значениям
л _ 1 а ____ коэффициент при 8^ г в разложении Г (s) [fz (s)]r /Q 1X
л0 — 1, rr — yy— N (6.1)
коэффициент при S в разложении / (S)
и соответствующим собственным векторам матрицы переходных
вероятностей (7.1), которая описывает процесс размножения р ти-
пов индивидуумов в отсутствие мутации. Напомним, что в этом
случае собственное значение К имеет кратность I I.
Начнем обсуждение со случая р = 2. В этом случае все соб-
ственные значения, отличные от Ло = М = 1, имеют кратность 1.
$ 8. Вероятностный смысл собственных значений 44?
Из теоремы 6.3 мы знаем, что матрица (7.1) диагонализируема.
Используя множество попарно ортогональных собственных векто-
ров, можно записать
N
^=2Д'фг(0Фг(/), (8.2)
где <рг — r-й правый собственный вектор, а — r-й левый соб-
ственный вектор, упоминаемые в теореме 6.3. (Здесь t — неотрица-
тельное целое число, а <рг и попарно ортогональны.) Целесооб-
разно выделить два члена в (8.2), соответствующих Хо = Xi = 1.
Получим
N
pt{/ = Фо (0 Фо (/) + Ф1 (О Ф1 (/) + 5 АХ (г) % (/)• (8.3)
Г=2
Из соотношений (6.18) и (6.19) имеем
Фо (/) = 6о/. Ф1 (/) = bivh
Фо (0 = » Ф1 (0 = (8.4)
Сумма в правой части (8.3) стремится к нулю при / —> оо, как
X2f (Х2<1). Более того, из выражений для гро (/’) и гр1 (/') следует,
что при 0 < j < N первые два члена в правой части (8.3) равны
нулю. Отсюда
’ О,
N — i
lim Р</ = Ф0 (/)ф0(/) + Ф1 (0Ф1 (/)= N
f-> ОО
/¥=0, N,
j = °> (8.5)
j = N,
и имеет место экспоненциальная сходимость (с параметром Хг)1),
т. е. Х2— «скорость приближения к гомозиготному состоянию». Ана-
логично вероятность того, что система не находится в гомозиготном
состоянии (0 или N), имеет порядок Х2 при * оо. Далее, так как
Хз Х2, то
pt
Ит =- <р2 (/) ф2 (/), I, j #= 0, Н. (8.6)
t ->оо ^2
Легко показать, что фг(0^0 при 0 < t < М В самом деле,
в противном случае было бы ф2(;) = 0 ПРИ Q <i < N. Но всегда
ф2 (0) = 0 = ф2 (N), поскольку ф2 ортогонален ф0 и фь Таким об-
разом, ф2(0 = 0 при 0^.i^.N, что невозможно, поскольку ф2 —
собственный вектор, соответствующий значению Z,2.
’) То есть I Pl(j - <р0 (г) ф0 (/) + <р! (/) Ф! (/) I ~ A-2-“ Прим, перев.
448
Гл. 13. Генетические и экологические процессы
Нормализуя ф2 так, чтобы ф2(*0)>0 при некотором i°, мы за-
ключаем, используя (8.6), что ^2(/)^0, 0 < j < М Мы утверж-
даем, что гр2(/) =А 0, 0 < / < N. Доказательство аналогично уже ис-
пользованному при выводе утверждения, что ф2(0 0. Мы дока-
/v-i
залп, что S Можно показать, что -фгС/) >0, 0 < j < М
/ =1
В самом деле, поскольку 0 < aQaia2 (где f (s) = S ansn\ то
переходные состояния Т = {1, 2, . .., N—1} все сообщающиеся,
т. е. начиная из любого состояния из Т возможно (с положитель-
ной вероятностью) достичь любого другого состояния из Т. Ог-
сюда следует, что показатель, с которым Рц стремится к нулю
(при t —> оо, ц j Т), не зависит от выбора i и j в Т. (Читателю
предлагается строго доказать это.)
Мы уже доказали, что при некоторых i = io и / = /0
ф2 (^о) (/о) > 0. НО
Р‘ц ~ Л2<₽2 (0 ^2 (/)’ Z‘> 1 G T-
Следовательно, ф2(*)ф2(/) >0 при всех Г откуда полу-
чается, что ф2(0 не меняет знака при /е Т. Это же справедливо
для ф2(/), j Мы условились, что после нормализации ^2(/)> 0
при всех / е Т.
Заметим, что ф2(0)<0 и гр2(М)<0, поскольку вектор ф2 орто-
гонален фо и ф1. Из соотношения (8.6) можно теперь получить,
что предельное условное распределение состояния j при условии.,
что j 4= 0, N, равно
/V-1 •
2 ^2 (/)
/=1
Обратимся теперь к вероятностной интерпретации собственных
значений и векторов в случае цепи Маркова для трех типов инди-
видуумов, матрица переходных вероятностей которой задается со-
отношением (7.23) при р = 3. Обозначим симплекс в пространстве
состояний через Д3, а его ребра — через Е\, Е2 и Е3, т. е.
Д3 = {i = (А, *2, Ч) I h > °, h > 0, i3 0, Z2 + i2 + i3 - /V,
iv— целые числа}»
a Ek состоит из всевозможных векторов i е Л3, для которых ih = 0
(& = 1, 2, 3). Кратность собственного значения Тг равна
Запишем соответствующие правые и ле-
вые собственные векторы в виде
<*rk^Urk(h, h, hl h, hl & = 0, 1, r, (8.8)
§ 8. Вероятностный смысл собственных значений 449
где (/1, *з)—компоненты векторов; здесь всюду i2i
h + *2 + h = N. Векторы (8.8) в силу построения попарно ортого-
нальны.
Заметим, что собственное значение 1 == Zo = М имеет крат-
ность 3 (Zo — однократный корень и Zi — двукратный), как и сле-
довало ожидать, поскольку существует три поглощающих состоя-
ния (/V, 0, 0), (0, N, 0) и (0, 0, N). Левые собственные векторы,
соответствующие этим собственным значениям, совпадают соответ-
ственно со стационарными распределениями каждого из возврат-
ных классов и, следовательно, имеют вид
( 1, если = М
Ро°'' I 0 в противном случае,
( 1, если i2=*N,
Р10^ (О в противном случае,
( 1, если i3 = W,
₽n(i)= л
( 0 в противном случае.
Соответствующие правые собственные векторы (они являются
линейными функциями от i), которые попарно ортогональны
с {Poo, Pio, ₽ii}, равны соответственно
а<ю(0 = 7Р aio(i) = -y> ац(1) = -^-.
О левых собственных векторах можно сказать больше. Заме-
тим, что если начальное состояние цепи Маркова принадлежит
ребру £i, то все последующие состояния также принадлежат Е{.
Интуитивно это очевидно, поскольку принадлежность начального
состояния ребру означает, что индивидуумы типа 1 отсутствуют
и не могут быть произведены с помощью индивидуумов типа 2 и 3.
Непосредственной проверкой нетрудно найти, что в матрице пере-
ходных вероятностей (7.23)
Л, j = 0, если ie£h ]фЕг. (8.9)
Более того, если и i и j принадлежат то матрица НА, j|| сво-
дится к матрице цепи Маркова для индивидуумов двух типов
2 и 3.
Рассмотрим теперь вектор с компонентами
( W4), i^Elf
₽2о(’) = ( оу (8.10)
где i|?2 — второй левый собственный вектор матрицы (6.2). По
определению *ф2 имеем
5 ^(4) (8.Н)
15 Зак. 939
450
Гл. 13. Генетические и экологические процессы
где i = Gi, *2, *з), j = (/ь /2, /з). Принимая во внимание (8.9) и
(8.11), получим
?20 (0 j “ ^2^20 (j),
i
где |?2o(i) определяется равенством (8.10).
Аналогично пусть
₽21 (0 ~ 1 ^2(0, 1. 0, i е £2, i<££2,
' фгО’З, ie Е3,
р22 (0 = | . о, 1фЕ3.
(8.12)
Это также левые собственные векторы, соответствующие соб-
ственному значению ^2- Соотношения (8.10) и (8.12) показывают,
что нулевые значения векторов Р20, Р21 и Р23 сосредоточены в раз-
личных ребрах £1, Е2 и £3 соответственно, и поэтому они, очевидно,
линейно независимы.
Вообще для каждого левого собственного вектора (см.
(6.19)) цепи Маркова в случае двух типов можно построить три
левых собственных вектора матрицы (7.23), соответствующих соб-
ственному значению Z&. Аналогично построениям (8.10) и (8.12)
можно взять
Рйо = на £1 и 0 в противном случае,
Р/li = 4‘/i на £2 и 0 в противном случае, (8.13)
р/12 = i|)/i на £3 и 0 в противном случае.
Эти векторы линейно независимы, поскольку их ненулевые зна-
чения сосредоточены в различных ребрах А3.
Из общей теории следует, что собственному значению Хз соот-
ветствует четыре собственных вектора. Векторы р30, Рзь Рз2, зада-
ваемые равенством (8.13), — три из них, и все они равны нулю при
ieАз (А?—внутренность Д3). Мы утверждаем, что (Ззз(0 не мо-
жет тождественно равняться нулю в A3.
Формальное доказательство этого следующее. Каждый соб-
ственный вектор (для случая двух типов) (г = 2, . . . , N) опре-
деляет собственный вектор (для случая трех типов), ненулевые
компоненты которого соответствуют точкам на £ь Аналогично
мы получаем М—1 линейно независимых собственных векторов,
ненулевые компоненты которых сосредоточены в £2, а также N— 1
собственных векторов, соответствующих £3. Наконец, мы имеем
векторы Роо, рю и р1Ь ненулевые значения которых сосредоточены
в вершинах Аз- В целом это дает З/V линейно независимых векто-
ров, ненулевые компоненты которых соответствуют границе Д3.
Обозначим множество этих собственных векторов через V
§ 8. Вероятностный смысл собственных значений
451
На границе А3 имеется ровно 3N состояний. Следовательно, на
перечисленные собственные векторы натянуто линейное простран-
ство всех векторов, имеющих ненулевые координаты только на
границе А3.
Далее, вектор р33 не равняется (при некотором г), поскольку
он соответствует собственному значению %3, а мы уже установили
соответствие между (Рзо, Рзь Рзг) и ф3. Если бы Рзз(])= 0 при
j^A°, то Р33 линейно зависел бы от перечисленных векторов. Но
это невозможно, поскольку р3з по построению не зависит от р30, p3i
и р32 и, очевидно, не зависит от остальных векторов из V, так как
они соответствуют собственным значениям, отличным от Z3.
Выше доказано, что РззО) Ф 0 при j <= Д3. Аналогично ссзз (О Ф О
при i Аз. Действительно, предположим противное, что a33(i) = 0
при i^A3. Тогда, поскольку вектор а33 ортогонален любому век-
тору из 1/, получаем, что а33 = 0. То есть a33(i)Efl при isA3, что
противоречит определению а3з- В самрм деле, отсюда следует, что
значения а3з(0 с необходимостью равны нулю на границе Д3.
Матрицу перехода можно представить в виде
N г
р[ j = 2 2 ^rk (j)» * = G’b z*2, h)> j ~ (/b /2, /з)« (8.14)
r=0 &=0
Перепишем (8.14), выделяя члены, включающие первые три соб-
ственных значения:
П, i = Иоо (О Poo О) + “10 0) Рю (j) + «11 (i) Рп (j) +
N / г \
+ Ц [«20 (’) P20 0) + a21 (0 P210) + a22 (0 P22 0)] + 5 4 ( 2 ark (i) Prfe (j) I •
r=3 \fe=0 /
(8.15)
Можно дать теперь обещанную ранее вероятностную интерпре-
тацию собственных значений и собственных векторов, используя
при этом специальный вид векторов |3Оо, ₽ю, ₽оь ₽2о, Э21, Р22.
(а) Скорость поглощения (или фиксации, или приближения
к гомозиготному состоянию) в вершинах равна Хг, поскольку для
j, не совпадающих с вершиной А3, выражение для P\t j в (8.15)
сводится к сумме от г = 2 и далее.
Распределение для больших t при условии, что фиксация не
происходит и что первый тип не исчезает из популяции, пропорцио-
нально |?2o(j), где |?2o(j)—собственный вектор с ненулевыми ком-
понентами, сосредоточенными в ребре, отвечающем только второму
и третьему типам. Собственные векторы 02i (j) и P22G) имеют ана-
логичную интерпретацию. Доказательство этого повторяет по су-
ществу доказательство (8.7)
15*
452
Гл. 13. Генетические и экологические процессы
(б) Скорость поглощения в ребрах (т. е. скорость, с которой
один из типов, все равно какой, выбывает из популяции) равна
Хз. Фактически при i, j е Дз (внутренность Д3)
W /г
A, j — ( 2 ark (0 0)
r==3 \fc=0
членом является первый, поскольку коэффи-
Доминирующим
циенты при в частности схзз (0 Рзз (j), отличны от нуля в неко-
торых точках пД®, в то время как все ненулевые компоненты век-
торов p3o(j), ₽3i(j), fWj) сосредоточены на границе Д3. В действи-
тельности же ссзз (0 Рзз (j) > 0 при всех i, ]’еДз. В самом деле, мы
знаем, что все состояния из Дз являются сообщающимися. Более
того, уже доказано, что а33 (i0)Р33(j0) ¥= 0 при некоторых i0, Д°,
и поскольку
О Р\ . ~ Z|P33(j)a33(i) при / —> оо для всех i, j е Д°,
то азз0’о)₽зз0’о)^ 0. Но скорость сходимости к нулю с необходи-
мостью одна и та же для всех состояний i, j е Д3, поскольку они
сообщаются. Следовательно,
аззО) Рзз О’) > °> Ь Iе Аз-
Это означает, что Рзз(1) и ссзз(1) не меняют знака при i, j е Д3-
Мы можем, следовательно, без потери общности выбрать РззО) > 0
и ссзз (i) > 0 при всех i е Дз, j е Д3,
Предполагая эти свойства выполненными для р33 и а33, можно
утверждать, что условное распределение вектора состояния j при
больших t при условии, что все типы индивидуумов имеются в на-
личии, асимптотически равно
рзз (j) • ,— Л о
^7)7’ )е41'
)-*S
Вероятностный смысл правых собственных векторов очевиден. Так,
а00 (i) — вероятность поглощения в вершине (М, 0, 0) при началь-
ном состоянии i,
«10 (i) — вероятность поглощения в вершине (0, N, 0) при на-
чальном состоянии i,
an (i) — вероятность поглощения в вершине (0,0, N) при на-
чальном состоянии i.
Аналогичным образом можно дать интерпретацию и для векто-
ров <Z2o(i), cc2i(i) и a22(i)- Для этой цели рассмотрим предельную
условную вероятность того, что поглощения в вершине не про-
§ 8. Вероятностный смысл собственных значений 453
изойдет. Очевидно, отсюда можно получить распределение на реб-
рах Д3. При векторе j, не являющемся вершиной, но лежащем на
ребре Дз, очевидно,
J ~ [«20 (0 020 О) + ₽21 0) «21 (’) + «22 0) 022 0)]« * - (8.16)
Напомним, что
( t|?2 (j), j €= Е[,
Р2°ш { о в противном случае
и аналогичные равенства имеют место и для других величин. Из
(8.7) заключаем, что x|?2(j) >0 всюду, кроме вершин. Следова-
тельно,
2 ₽2о0)= 2 ₽2i(j)= 2 ₽22(1) = 2ф2(0>0.
i, |т4=вершине 1, j=/= вершине i, j ^вершине I
Поскольку 02о, 021 и 022 — неотрицательные векторы, каждый из
которых принимает ненулевые значения всюду, кроме вершин,
принадлежащих различным ребрам, то aso(i), «21 (i) и аггО) также
неотрицательны при всех i, не являющихся вершинами, а по край-
ней мерё один из этих векторов положителен. Предельное условное
распределение Р{ j (/->00) для j, не являющихся вершинами,
Ь °
«20 О) Р20 (j) + <*21 (0 Р21 (j) + «22 (0 Р22 (j) Zg J y\
Ф2 (0^ [<*20 (0 + «21 (D + «22 (i)]
Заметим, что для каждой пары i и j только одно слагаемое в чис-
лителе положительно, поскольку произведение любых двух
₽2o(j)₽2i(j) = 0 при j, не являющемся вершиной. Вероятность того,
что при начальном состоянии i поглощение произойдет на грани
£ь а не на Е2 или £3 (вершины автоматически исключаются), по-
лучается суммированием выражения (8.17) по всевозможным ин-
дексам j е £1, не соответствующим вершинам. Поскольку p2i(j) =
= 022 (j) = 0 при j е £1, то отсюда следует, что .
Р {поглощение произойдет в £ь а не в £211£з1 ^о==О==
= _______________«20 0)_
«20 (0 + «21 (0 + «22 (0
Аналогично,
Р {поглощение произойдет в £2, а не в Ех U £31 Ло = О =
= _______________«21 0)_
«20 (0 + «21 О) + «22 (0
И, наконец,
Р {поглощение произойдет в £3, а не в Е{ U £21 ^0 = 1} =
=________________«$2 G)_
«20 (0 + «21 (0 + «22 (0
454 Гл. 13. Генетические и экологические процессы
Это показывает, что а20 (0, «21(0 и а22 (0 положительны при
всех i eEE До, a20(i) = 0 при i g= EQ2 U «21(0 = 0 при и
a22(i) = 0 при i *= Е° U Е?2 (верхний индекс 0 определяет внутрен-
ность рассматриваемого множества).
Все приведенные рассмотрения распространяются на общий
случай нескольких типов. Мы приведем соответствующие резуль-
таты без доказательства. Доказательство их получается путем
обобщения примененных выше методов.
Теорема 8.1. Пусть Р — матрица переходных вероятностей
(7.23) порожденной цепи Маркова для р типов в отсутствие мута-
ций. Собственные значения Р не зависят от числа типов и равны
Ло = 1,
__ коэффициент при Г в разложении [f ($)]^ Г [/z (s)]f /- -- ] 2 N
коэффициент при в разложении [f (s)]^
Собственное значение Тг имеет кратность + 2j. Пусть Дп —
симплекс состояний цепи Маркова, т. е. Ap=|i|i = (Zb z2, zp),
0 — целые числа, S iv ~ N I.
V J
Вероятностная интерпретация собственных значений следую-
щая:
(1) Скорость поглощения приближения, к гомозиготному со-
стоянию равна Z2, т. е. если i и j не совпадают с вершинами, то
Р\ t ~ с. .Ц (t -> оо), где с. . — постоянная, зависящая от i и j, но
не зависящая от t.
(2) Скорость, с которой в популяции вырождаются все, кроме
k типов (k^p) (все равно, каких именно), равна Kk, т. е. вероят-
ность того, что популяция в t-м поколении содержит по крайней
мере k типов, имеет порядок Дь- Другой способ выражения этого
же свойства — это сказать, что скорость, с которой происходит по-
глощение в (k—1) -мерной границе множества Др, равна Kk.
Более определенно, если i и j принадлежат либо внутренности
множества Др, либо внутренности его границы, имеющей размер-
ность k, то
р{ j ~ z->oo,
где с' j — постоянная, зависящая от i и j и не зависящая от t.
В частности, вероятность того, что популяция содержит все типы
индивидуумов в t-м поколении, стремится к нулю со скоростью
кр,т. е. Pi,)~Citikp при i, ]’еДр (внутренность Др), данное со-
отношение асимптотически точно при t оо,
Задачи
455
Перечисленные выше результаты были детально доказаны для
случая /7 = 3. Интересующийся читатель может распространить
доказательство на общий случай.
ЗАДАЧИ
1. Рассмотрим популяцию, изменяющуюся непрерывно во времени, с часто-
тами генотипов P(t) для АА, Q(/) для Аа и R(t) для аа. Предположим, что
в любом интервале времени длины h(h мало) доля Мг (% > 0 и фиксировано)
популяции, выбранная случайным образом, заменяется на популяцию такого же
размера, которая получается путем случайного спаривания выбранной доли по-
пуляции. Показать, что при /->оо Р(/)->а2, (?(/)->2сф, /?(/)->|32 для не-
которых а, Р, где а + р = 1 (а > О, Р > 0) и сходимость при этом экспоненци-
альная (~ е"^)-
2. Рассмотрим диплоидную популяцию с коэффициентами отбора 1, 1 и 1—$
для генотипов АА, Аа и аа соответственно. Предположим также, что в каждом
поколении доля р генов А мутирует в гены а. Пусть s и р достаточно малы
так, чтобы влияния отбора и мутации были аддитивны. Показать, что стацио-
нарная устойчивая частота гена равна q ~ и достигается при условии,
что р < s, и при достаточно малой величине s.
3. Рассмотрим гаплоидную популяцию с коэффициентами отбора 1—s и 1
для генов а и А соответственно. Предположим, что доля р генов А мутирует
в гены а в каждом поколении. Предположим также, что s и р достаточно малы,
. Г-Г Ц
так что влияния отбора и мутации аддитивны. Показать, что q ~ ~ —
устойчивая стационарная частота гена и достигается при условии р < s и до-
статочно малой величине <$.
4. Для локуса, сцепленного с полом, с двумя аллелями А и а допустимые
виды спаривания приведены в таблице. (Y означает мужскую половую хромо-
сому, которая не содержит генов.)
Женские особи Мужские особи
АА X ЛУ
аа X «У
АА X «У
аа X ЛУ
Аа X аУ или ЛУ
Показать, что в случае спаривания сибсов матрица имеет вид
1 0 0
0 0 1
111
4 4 2
где типы спаривания очевидным образом объединены в три группы. Найти соб-
ственные значения, собственные векторы и частоты различных типов спаривания
в n-м поколении, получившемся в результате инбридинга при произвольном на-
чальном типе спаривания.
456
Гл. 13. Генетические и экологические процессы
5. Для задачи 4 определить предельные относительные частоты типов спари-
вания АА X AY и аа X aY, когда начальный тип спаривания был Аа X aY.
6. Пусть тетраплоидная популяция при отсутствии преимуществ при отборе
Является объектом для хроматидного расщепления. Обозначим генотипы {Л4, А3а,
А2а2, Аа3, а4}. Пусть начальные доли гамет равны
АА Аа аа
х 2у z
Показать, что соответствующие доли в следующем поколении равны
Xl = x2 +^'4ху +18 (4у2 + 2хг^ + ^У^'
= f (х, у, z).
= g (х, у, г),
и найти f (х, у, z) и g (х, у, z).
7. В условиях задачи 6 показать, что частоты X\,y\,Zi можно записать
в виде
о 4 1
Х1=уХ + у р2 + ур.
2 4
= у (2г/)+у (2р<?).
2 4 1
= + q,
Где р = Х +у и q = у + Z.
8. Используя результат задачи 7, доказать, что частоты гамет в ft-м поко-
2
лении сходятся показательно с параметром у, и наити предельные (равновес-
ные) доли гамет
9. Рассмотрим тетраплоидную популяцию с двумя генами А и а при хромо-
сомном расщеплении. Предположим, что осуществляется инбридинг в форме са-
мооплодотворения. Доказать, что сходимость к гомозиготному состоянию пока-
5
зательная с параметром у.
10. Рассмотрим тетраплоидную популяцию с двумя генами при хромосомном
расщеплении с возможными зиготами (генотипами) Л4, А3а, А2а2, Аа3, а4. Свя-
жем с каждой из них величины (коэффициенты отбора) а, 0, у, 0, а соответ-
ственно.
(1) Доказать, что множество частот 1,0,0,0, 0 зигот Л4, А3а,.,., а4 соответ-
ственно устойчиво тогда и только тогда, когда а> — и 0 < а.
О
(2) Показать, что частоты (u,v, w, v, и) являются равновесными тогда и
только тогда, когда или и = w, или v2 + 2иш — 6auw.
11. В самостерильных популяциях, встречающихся у некоторых диплоидных
растений, пыльца не оплодотворяет растения, имеющие гены того же типа, что
и содержащиеся в пыльце. Следовательно, при этом невозможно формирование
гомозиготных индивидуумов. Пусть рп—частота какого-либо аллеля в трех-
аллельной системе1). Найти рекуррентное соотношение для рп в случае беско-
В п-м поколении. — Прим, перев.
Задачи
457
нечной популяции и определить предельное значение для рп(п->оо). Показать,
что задача сводится к исследованию двухаллельной не самостерильной системы
с очень большим (-► оо) коэффициентом мутации.
12. Рассмотрим популяцию из N индивидуумов, воспроизводящихся бесполым
путем. Написать рекуррентное соотношение для коэффициента инбридинга Fn
(см. стр. 414), если предполагается, что с вероятностью и произвольный аллель
за время одного поколения мутирует в аллель другого типа. Чему равно равно-
весное значение для Fn?
Ответ: F = 2N — (27V — 1) (1 — w)2-
13. Рассмотрим диплоидную популяцию, в которой потомки спариваются со
своими родителями и затем считаются родителями для следующего поколения.
Найти матрицу переходных вероятностей для частот различных типов спариваний.
Указание: Различные типы спариваний приведены в следующей таблице.
Потомки Родители
1 Аа АА
2 Аа аа
3 АА Аа
4 аа Аа
5 Аа Аа
6 АА аа
7 аа АА
8 АА АА
9 аа аа
Случаи 6 и 7 не реализуются после первого поколения, поскольку в результате
могут производиться лишь гетерозиготные потомки. В силу симметрии случаи 1
и 2 могут быть сгруппированы так же, как и случаи 3 и 4.
14. В условиях задачи 13__показать, что сходимость к финальному распреде-
лению имеет скорость (1 +}/Г5)/4.
15. (Самооплодотворение при тетраплоидии) Предположим, что в тетрапло-
идной популяции в каждом локусе может находиться четыре различных гена.
Обозначим их через a, b, с, d. Один из способов воспроизведения тетраплоидов
заключается в том, что от каждого родителя случайным образом берутся по два
гена и комбинируются, чтобы получить требуемую комбинацию генов для по-
томка. Рассмотрим популяцию, в которой все потомки получаются путем само-
оплодотворения, т. е. одни и те же индивидуумы выступают одновременно в роли
родителей мужского и женского родов. Например, индивидуум типа aaab после
самооплодотворения производит потомка одного из следующих типов: аааа,
aaab, aabb в отношении -i-, -j-. Обозначим индивидуума, содержащего лишь
однотипные гены (аааа, ЬЪЪЪ и т. д.), через 6?4, индивидуума, у которого три
гена одного типа, а четвертый — другого, — через 6?3i (aaab, bbbd и т. д.);
индивидуума, у которого два гена одного типа, а другие два гена также имеют
одинаковый тип, но отличный от первого, — через G22 (aabb, аасс и т. д.), инди-
видуума, у которого два гена одного типа, а другие два — различных типов, —
через 6?2ц (aabc, ddca и т. д.) и индивидуума типа abed — через 6?цп. Пусть
р£\ р[п\ р[п\ р[п}— доли типов 6?4, 6?34, 6?22, 6?2и, Стин соответственно в и-м
поколении. Определить матрицу перехода этой цепи Маркова.
458
Гл. 13. Генетические и экологические процессы
Ответ:
О О
2 2
4 2
J_ 2
6 3
О
О
О
О
£
6
16. В задаче 15 проанализировать Р с тем, чтобы найти ее собственные
значения, а также скорость сходимости к состоянию G±.
Ответ: Собственные значения равны
£ 2 ± ±
6 ’ 2 ’ 6 ’ 6 ‘
17. Случайное спаривание генотипов. Рассмотрим простейший случай, когда
имеются лишь две возможные гаметы (альтернирующих генов), обозначенные че-
рез А и а. При этом возможны генотипы АА, Аа и аа.
В модели случайного спаривания W детей производится от W родителей в
соответствии со следующим вероятностным механизмом. Два родителя выби-
раются случайным образом (с замещением) из родительской популяции, содер-
жащей i генотипов АА, j генотипов Аа и k генотипов аа (i + j + k = N). От
каждого родителя гамета берется случайным образом. Эта процедура повто-
ряется N раз.
Случайное слияние гамет. В этой модели рассматриваются сами гаметы, а
не генотипы. Родительская популяция состоит из 2N гамет; i из них имеют
тип A, a j — тип а. Следующее поколение состоит из 2N гамет, выбранных бино-
миальным образом из родительской популяции (с замещением).
Если в каком-либо фиксированном поколении необходимо построить популя-
цию генотипов, это делается путем случайного выбора N пар (без замещения)
гамет из популяции, состоящей из 2N гамет.
Доказать следующую теорему.
Теорема. Если родительская популяция состоит из i, j и k генотипов АА,
А а, аа соответственно, то вероятность того, что следующее поколение имеет I, пг,
п соответствующих генотипов, одинакова для модели случайного спаривания ге-
нотипов и модели случайного слияния зигот (i + j + k = I + m + п = N).
18. Выписать точный вид матрицы переходных вероятностей (5.8) для част-
ного случая, когда
М'О = 00 =/з И =еа(“-!>. а>0.
19. В предыдущей задаче найти собственные значения матрицы переходных
вероятностей.
20. Рассмотрим марковскую цепь Райта (4.13) при X = р, и а — b = 0. Чему
равны собственные значения этой матрицы?
Ответ:
....
Литература 459
21. Рассмотрим марковскую модель, учитывающую мутационное давление,
описанную в задаче 20. Пусть л = {л --стационарное распределение про-
цесса. Найти его первый и второй моменты.
Указание: Использовать тот факт, что 2 ?1}1 линейна по I, а 2 Fiji2 —
/«о /=о
квадратичная функция i. См. также стр. 430.
ЛИТЕРАТУРА
1. Moran Р. А. Р., The Statistical Processes of Evolutionary Theory, Oxford
Univ. Press (Clarendon), London and New York, 1962.
2. Fisher R. A., The Genetical Theory of Natural Selection, Oxford Univ. Press
(Clarendon), London and New York, 1930.
3. Malecot G., Les mathematiques de I’heredite, Masson, Paris, 1948.
4. Li С. C., Population Genetics, McGraw-Hill, New York, 1956.
Глава 14
ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ1)
§ 1. ОБЩЕЕ ОПИСАНИЕ
В гл. 3 мы обсудили два простых примера процессов массо-
вого обслуживания с дискретным временем. В этой главе мы более
подробно рассмотрим идеи и методы, используемые при анализе
некоторых процессов массового обслуживания с непрерывным вре-
менем. Общая модель обслуживания имеет следующую структуру.
На некоторое устройство в случайные моменты времени поступают
требования2) и требуют какого-либо рода обслуживания. Про-
цессы массового обслуживания классифицируются по следующим
признакам.
(1) Входящий поток требований, для задания которого необ-
ходимо знать распределение моментов поступления требований,
или, в более частном случае, распределение интервалов между мо-
ментами поступления.
(2) Распределение времени обслуживания требования.
(3) Дисциплина обслуживания (очереди), число обслуживаю-
щих приборов и организация очереди и процесса обслуживания.
В большинстве моделей принята дисциплина «первый пришел —
первый обслужен» — прямой порядок обслуживания, когда обслу-
живание требования начинается, как только оно достигает начала
очереди. Все модели, которые будут рассмотрены в этой главе,
такого типа. (Другие типы дисциплин обслуживания рассматри-
ваются в задачах 2—4 настоящей главы.)
Мы повсюду будем предполагать, что входящий поток требо-
ваний не зависит от размера очереди и что интервалы между по-
следовательными моментами поступления требований являются
независимыми одинаково распределенными положительными слу-
!) В оригинале «queueing processes», т. е. «процессы образования очередей».
При переводе мы используем принятый в отечественной литературе термин «про-
цессы массового обслуживания», который был введен А. Я. Хинчиным и более
полно отражает существо рассматриваемых задач. — Прим, перев.
2) Под термином «требования» можно понимать, например, клиентов, тре-
бующих обслуживания, корабли, входящие в порт, поток сообщений в некоторую
контору, неисправные машины, ожидающие ремонта, и т. д. (Вместо термина
«требование» используют также термины «клиент», «вызов», «заявка», а вместо
термина «обслуживающее устройство» — «прибор», «линия», «канал». Употребле-
ние того или иного термина часто определяется характером решаемой приклад-
ной задачи. — Перев.)
§ 2. Простейшие процессы обслуживания 461
чайными величинами. Такие потоки иногда называют рекуррент-
ными, или потоками восстановления.
Термин «простейший поток» используется иногда в случае,
когда моменты поступления требований образуют пуассоновский
поток, т. е. когда интервалы между моментами поступления рас-
пределены экспоненциально.
Будет также предполагаться, что длительности обслуживания
отдельных требований — независимые одинаково распределенные
случайные величины, не зависящие от входящего потока.
§ 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)1)
Наиболее простыми и наиболее полно изученными являются
процессы обслуживания с пуассоновским входящим потоком и
экспоненциальным распределением времени обслуживания. Эти
процессы уже были описаны и было показано, что процесс изме-
нения длины очереди является процессом рождения и гибели (см.
пример 2, § 6 гл. 7) 2).
Вновь рассмотрим случай одного обслуживающего прибора.
Функция распределения интервалов между моментами поступле-
ния равна
F(/)== 1 Л>0,
а функция распределения длительности обслуживания
G(/)=l-r^, ц>0.
В силу «отсутствия последействия» (теорема 2.2 гл. 7) у экспо-
ненциального распределения очевидно, что процесс X(t) (длина
очереди в момент /) — однородный по времени марковский процесс
рождения и гибели. Пусть ЛД/)—его переходная вероятностная
функция. Тогда Pit w (/г) — вероятность того, что за время h по-
ступит одно новое требование и не закончится обслуживание ни
одного требования. При малых h
Pi, i+i W — +о (Л), i 0.
*) Для обозначения простых процессов обслуживания в литературе широко
используются стандартные сокращения. Дадим для справки сокращенные обозна-
чения процессов, которые будут изучаться ниже. В записи (A/BIc) с —число
обслуживающих приборов, а А и В указывают типы распределений интервалов
между моментами поступлений требований и длительностей обслуживания соот-
ветственно. На первых двух местах используются следующие символы: G или
6/, когда относительно распределений не делается никаких частных предположе-
ний; М, когда соответствующее распределение экспоненциальное; Ek, когда со-
ответствующие интервалы имеют гамма-распределение порядка k (эрланговское
распределение) (так что Е{ = Al); D (детерминированное), когда указанные ин-
тервалы имеют фиксированные длительности.
2) Под «длиной очереди» здесь и далее понимается общее число требований,
находящихся на обслуживании и ждущих его. — Прим, перев.
462
Гл. 14. Процессы массового обслуживания
Аналогично находим
Л, z-i W = + o (/г), i 1,
и
Рц W = 1 — (X + н) h + о (h\ i 1,
P0Q (Л) = 1 -- Х/г + о (Л).
Инфинитезимальная матрица равна
- Л к 0 0
н — (Л + р) к 0
А = 0 н — (Л + р) к
В § 6 гл. 7 показано, что
( /XW Л х\ _
— 1 — — > Х< ц,
lim Pij(t) = pj= ' !Л;' и'
/_>о° I 0, Х^ц.
Отсюда получаем ответ на многие вопросы, включая стационар-
ность. Если процесс развивался достаточно долгое время и X < ц,
го вероятность того, что поступившее требование начнет немед-
ленно обслуживаться (обслуживающий прибор свободен, т. е. дли-
на очереди равна нулю), равна
В случае X < ц можно также найти распределение времени
ожидания в стационарном режиме. Если поступающее требование
застает очередь длины п, то его время Т пребывания в системе
складывается из длительностей обслуживания его самого и тре-
бований, стоящих перед ним. Все эти величины распределены экс-
поненциально с параметром ц, и, поскольку длительности обслу-
живания не зависят от размера очереди, Т имеет гамма-распреде-
ление порядка п + 1 с масштабным параметром ц:
Р{Г^/| длина очереди равна п}— J г + j ~ dx, (2.1)
о
В силу формулы полной вероятности имеем
оо
Р {Т -С 0 = У] Р {Т 11 длина очереди равна «)(—) (1—-у),
«=о
§ 3. Модели обслуживания одним прибором
463
/ \ п /
поскольку (^1 — — j — вероятность того, что в стационарном ре-
жиме поступающее требование застанет очередь длины п. Учиты-
вая (2.1), находим
р <г < '> - 2 J ттгпт (Ж1 ~ Ж -
п=0 О
t оо
= J г(»+1) T't^c?T =
О /г==0
= /(1-|)нехр{-т|г(1 -|)рт =
О
= 1 -ехр[-ф(1
Вновь получили экспоненциальное распределение.
Если мы хотим исследовать неустановившийся режим, следует
прежде найти Pij(t) для всех t. Это существенно более сложная
задача, но она решена. Подробности этого решения выходят за
рамки данной книги, и мы отсылаем интересующегося читателя
к любой из специальных книг по теории массового обслуживания,
перечисленных в конце главы.
Если имеются два обслуживающих прибора, то для тех же за-
конов поступления требований и обслуживания, когда в очереди
имеется не меньше двух требований, среднее время ц”1 до за-
вершения очередного акта обслуживания вдвое меньше, чем при
одном приборе. Таким образом, цп = 2ц, п^2. Если же п = 1, то
один прибор пустует, и щ == ц. Инфинитезимальная матрица этого
процесса рождения и гибели имеет вид
-XX О о
ц — (X + ц) X 0 ...
А= 0 2ц —-(Х + 2ц) X
О 0 2ц _(х + 2ц)... ’
§ 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ
ОДНИМ ПРИБОРОМ
Обсудим некоторые аспекты трех методов анализа частных ви-
дов системы обслуживания (G//G/1). Первый метод, известный под
названием метода интегрального уравнения, сводит задачу нахо-
ждения предельного распределения времени ожидания начала
464
Гл. 14. Процессы массового обслуживания
обслуживания гг-м требованием (п->оо) к задаче решения инте-
грального уравнения типа Винера — Хопфа.
Если входящий поток является пуассоновским, то при втором
методе исследования рассматривается длина очереди в моменты
окончания актов обслуживания. Можно показать, что этот вложен-
ный процесс является цепью Маркова (см. ниже § 4). Если рас-
пределение времени обслуживания является экспоненциальным,
а входящий поток определяется общим распределением, то вло-
женная цепь Маркова получается при рассмотрении длины очере-
ди в моменты новых поступлений. Результирующий процесс яв-
ляется цепью Маркова специального вида.
С помощью третьего метода исследуются свойства случайной
величины равной времени до начала обслуживания, которое
пришлось бы ожидать требованию, если бы оно поступило в мо-
мент t независимо от того, поступило оно на самом деле в этот
момент или нет. Эта величина называется виртуальным временем
ожидания в момент t.
Рассмотрим сначала метод интегрального уравнения, а затем
перейдем к моделям более частного вида, к которым применим ме-
тод вложенных цепей Маркова1). Некоторые вопросы, относя-
щиеся к третьему методу, обсуждаются в § 8.
А. Метод интегрального уравнения 2)
Введем величины
Wr — время ожидания r-м поступившим требованием начала обслуживания,
Sr — длительность обслуживания r-го требования,
ТГ — длительность интервала между поступлением r-го и (г+1)-го требо-
ваний,
где 1Го = So = То = 0. Условие Ж; = 0 означает, что первое поступающее требо-
вание застает обслуживающий прибор свободным. Предположим, что оно посту-
пает в момент t = 0.
Очевидно, Wr + Sr — время пребывания r-го требования в системе. Следова-
тельно, если Tr > Wr 4- Sr, то (г -Г 1)-е требование застанет обслуживающий
прибор свободным, т. е. в этом случае Wr+i = 0. Если Tr Wr + Sr, то дли-
тельность времени ожидания (г + 1)-го требования равна, очевидно,
Wr + Sr — Тг. Следовательно,
( Wr + Sr-Tr, если WT + Sr-Tr^Q,
r+1 “ t 0, если WT + ST-Tr< 0.
Обозначим
Ur = Sr-Tr.
!) Заметим, что при выводе интегрального уравнения типа Винера — Хопфа
также сначала строится вложенная цепь Маркова (см. ниже), у кото-
рой пространством состояний является полупрямая [0, оо). Поэтому отличие пер-
вого метода от второго относится по существу к типам вложенных цепей Мар-
кова и, следовательно, к методам их анализа. — Прим, перев.
2) При первом чтении оставшуюся часть материала данного параграфа мож-
но опустить.
§ 3. Модели обслуживания одним прибором
465
при х >0,
при х < 0,
— оо <х < ОО.
(X - у) - Fr (х - у)] g (у) dy.
Тогда, очевидно, —последовательность независимых одинаково распреде-
ленных д. с. в. *)• Пусть Fr(x)—функция распределения величины Wr, а
g(x)=G'(x)—плотность величины Ur, которая по предположению одинакова
для всех г2). Поскольку WT и Ur независимы, то при х О
Fr+1 (х) == Р {Wr+i < *} == Р {max (Wr + Ur, 0) <х} = Р {Wr + Ur^x}~
~ ^P{Wf + Ur<x\Ur~y}g(y)dy = J Fr(x —у) g (у) dy (г>1). (3.1)
-oo
Далее, поскольку первое требование поступает в момент t = 0 и застает
обслуживающий прибор свободным, то
и так как при х<0 все Fi (х) — 0, то
Fi (х) - F2 (х) 0,
Но
FrM-Fr+iW = J [F,_,
У<х
и отсюда по индукции следует, что при любом г
Fr (х) — Fr+i (х)>0, —оо<х<оо.
Следовательно, при каждом х функция Гг(х) убывает с ростом г.
Поскольку Fr(x)^0, то отсюда следует, что Fr (х) сходится, скажем,
к функции F (х). Переходя к пределу при г -> оо в равенстве (3.1), получим
F(x) = J F (х —у) g (у) dy *),
У
или, если положить г==х — у,
оо
F (х) = j F (z) g(x-z) dz.
о
Теперь нужно исследовать вопрос о том, когда предел F(x) является соб-
ственным распределением. Очевидно, что F(x)—неубывающая функция, но мо-
жет оказаться, что lim F (х) < 1, а не lim F (х) = 1. Первый случай можно
X -> ОО х->оо
интерпретировать как возможность того, что время ожидания n-го требования
(п-+<х>) стремится к оо с положительной вероятностью (или длина очереди
стремится к оо с положительной вероятностью).
9 Заметим, что множество значений д. с. в. Ur, г = 1, 2, ..., — вся действи-
тельная прямая (—оо, оо). — Прим, перев.
2) Ограничение, что 6(х) имеет плотность, наложено для простоты рассмо-
трения и не существенно для последующих рассуждений.
3) Обоснование возможности перехода к пределу под знаком интеграла
требует знания теории интеграла Лебега. Если читатель еще не знаком с ней, то
ему следует принять соответствующее утверждение на веру.
466
Гл. 14. Процессы массового обслуживания
Получим сначала другое выражение для Г(х). Поскольку
flW = (a
х О,
х < О,
то F2 (х) = J g (и) du — Р {Ux х), х^О. Далее,
и <х
g («2) g («1) du2 dui =
tl2^X, U1+U2^X
= P{£72<x, Ui + U2^x}==P{Ui <x, +
где использован тот факт, что Ui и /72 — независимые одинаково распределен-
ные д. с. в. По индукции непосредственно получаем, что
Fr+1(x) = P{C7r<x, Ur + Ur^x,
Ur + ... +£71<х} =
= P{(7j<x, Щ+U^x........Ux+ ... +Ur^x),
поскольку /71, /72, ..., Пг одинаково распределены. Таким образом, если
йг = 2 Ui, то
/ = 1
Fn-\-\ М = Р {U Г х, г=1, ..., п}, х^О.
Очевидно, Fn(x) монотонно убывает с ростом п (это было также доказано
выше), и поэтому
F (х) = Р {Uг х при всех г}, х 0.
Если х < 0, то Гг-(х) = 0, и тривиальным образом получаем F(х) =-0, х < 0.
Используя полученный результат, можно определить, когда F(х) является
собственным распределением. Предположим, что M(S)<oo и М(Т)<оо, т. е.
д. с. в. S и Т имеют конечные математические ожидания. Тогда справедлива сле-
дующая
Теорема 3.1. (1) Если М (/7) J>- 0, то F (х) == 0. (2) Если М (U) < 0, то
lim F (х) = 1.
Х->оо
Интуитивно этот результат очевиден. Он утверждает, что если средняя дли-
тельность интервала между моментами поступления меньше средней длительно-
сти обслуживания, то очередь растет бесконечно и lFr->oo с вероятностью 1.
Доказательство разбивается на три части.
Доказательство.
(1) М(/7)>0.
В силу усиленного закона больших чисел
lim ^=М(/7) с вероятностью 1,
П->оо П
§ 3. Модели обслуживания одним прибором
457
следовательно, для почти всех реализаций последовательности £7Ь U2> U^ ...»
т. е. с вероятностью 1 имеем
(/„>-£ М(£/)
(3.2)
при достаточно больших п, где выбор п зависит от реализации. Событие [Ur х
при всех г} является частью события, дополнительного к событию (3.2). Следо-
вательно, его вероятность равна нулю.
(2) M(t/)<0.
Вновь в силу усиленного закона больших чисел для любых е > 0 и б > О
существует целое Ne, такое, что при п N&, §
Р { | Un — М (С7) | < е при всех п > N&, ъ | > 1 — 6.
Выберем е таким малым, что M(t/)4-8<0. Тогда для любого 6>0 суще-
ствует Л;б, такое, что
1 — 6 < Р {Un < n (М (U) + е) при всех п N^} <
Р {Un < 0 при всех п Л^}.
Далее, поскольку (7(х)—собственное распределение, для указанных 6 и Мб
можно выбрать достаточно большое х, такое, что
Р {В} = Р {Ur х при всех 1 г Мб -- 1} 1 — 6.
Смысл события В очевиден из приведенного равенства.
Пусть А = {Un 0 при всех п N^}. Событие {Ur х при всех г}
содержит пересечение двух событий А и В и его вероятность не меньше
Р {Д П В} = Р {Д} + Р {В} — Р {A (J В} > 2 — 26 — 1 = 1 — 26. Следовательно,
F(x) 1 — 26 при достаточно больших х, или
lim F(x)>l-26.
Х~>оо
Но, поскольку б произвольно, это означает, что lim F (х) = 1.
Х->оо
(3) М (U) = 0.
В этом случае утверждение следует из довольно глубокой теоремы, относя-
щейся к возвратности сумм независимых случайных величин, которая лежит за
пределами данной книги1)- Дискретным аналогом теоремы является тео-
рема 3.3 гл. 6.
Б. Возвратность собып^я, заключающегося в том, что время ожидания
поступающего требования равно нулю
При анализе случайной последовательности с пространством состоя-
ний [0, оо) возникает вопрос о возвратности события А, заключающегося в том,
что некоторое требование застанет систему свободной. Формально скажем, что
событие А наступило на n-м шаге, если Wn — 0. Предложение «событие А про-
исходит» будет в дальнейшем означать, что оно происходит на некотором конеч-
ном шаге. Заметим, что, если событие А происходит, процесс начинается с оче-
редного значения W, равного нулю.
!) См. Спицер Ф., Принципы случайного блуждания, «Мир», М., 1968.
468
Гл. 14. Процессы массового обслуживания
Теорема 3.2. (1) Если М(^7)>0, то событие А — невозвратное (т. е. ве-
роятность события А меньше 1).
(2) Если М((/) 0, то событие А — возвратное (т. е. Р {Л} = 1).
(3) Если М((7) < О, то событие А — положительное возвратное (т. е. сред-
нее время до наступления А конечно).
Доказательство.
(1) Используя те же обозначения, что и прежде, заметим, что
Wn+x>Un.
(Напомним, что Оп = . + Un = Si + ... + Sn — T\ — ... — Гп — разность
между суммарным временем обслуживания первых п требований и временем
поступления (п + 1)-го требования.) При этом равенство выполняется лишь в том
случае, если обслуживающий прибор был все это время занят (т. е. до момента
поступления (л + 1)-го требования не было перерыва в его работе).
Таким образом, если все Un > 0, то событие А не наступает. В силу усилен-
ного закона больших чисел для любых е, 6 > 0 существует число N, такое, что
Р 11 — М ((/) | ^ 8 при всех п> N | 1 — д.
Таким образом, если М(£/)>0 и выбрать достаточно малое е (e<M(Z7)), то
существует число N, такое, что
Р {Un> 0 при всех n^N}>(k
Это означает, что с положительной вероятностью А может происходить лишь
конечное число раз, т. е. событие {lFr = 0 лишь для конечного набора индек-
сов г) имеет положительную вероятность. Но событие является возвратным тогда
и только тогда, когда вероятность его осуществления бесконечное число раз
равна 1 (см. теорему 7.1 гл. 2). Следовательно, если М(£/) > 0, то А невоз-
вратно.
(2) Если М((/) <0, то для произвольных е, 6 > 0 существует число N, та-
кое, что
Р1— М (U) | < е для всех п N | 1 — д.
Отсюда, если е достаточно мало, получаем
Р {Un С 0 при всех п N} 1 — д
и в силу произвольности 6, усиливая неравенство, имеем
Р{£7п^0 при некотором п} = 1.
Но если Un 0, то некоторая величина Wi == 0; в частности, если Uk — первая
из последовательности {Un} величина, которая 0, то Wk = 0. Поэтому если
М(£/)< 0, то А — возвратное событие.
Если М(£/)==0, то соответствующее доказательство является довольно тон-
ким и мы не будем его проводить, а отошлем читателя к цитируемой в конце
главы литературе.
(3) Если М(£7)<0, мы утверждаем, что событие А является возвратным
положительным. Доказательство этого мы опускаем.
$ 4. Метод вложенных цепей Маркова
469
§ 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО
К МОДЕЛИ ОБСЛУЖИВАНИЯ (Af/G/l)
Рассмотрим частный случай одноканальной системы с пуас-
соновским входящим потоком (с параметром X). Предположим,
что длительность обслуживания V является положительной случай-
ной величиной с произвольным распределением В (у), для которого
M(V)<oo. Для простоты изложения предположим, что B(v)
имеет плотность b(v). Исследуем этот процесс с помощью вложен-
ной цепи Маркова, определяемой следующим образом.
Пусть Z(t)— число требований в очереди в момент t
Предположим, что процесс Z(t) наблюдается в моменты окончаний
операций обслуживания1)- При этом получается последователь-
ность целых чисел
ZGO, Z(/2), Z(f3), ..., (4.1)
где /i, Zs, ^з, - — последовательные моменты окончаний операций
обслуживания. Последовательность {Z(tn)} образует процесс с ди-
скретным временем
Хо = О, X„ = Z(frt), п=1, 2, ....2) (4.2)
Ниже будет показано, что в силу «пуассоновости» входящего
потока последовательность (4.2) является цепью Маркова.
Дадим несколько более интуитивное описание данного процесса
с дискретным временем. Его переходы происходят только в те
моменты времени, когда заканчиваются операции обслуживания
требований. Состоянием процесса является число требований в оче-
реди (включая и требование, которое начало обслуживаться, если
таковое имеется), оставшееся после того, как обслуженное требо-
вание покинуло систему.
Легко видеть, что этот процесс является марковским, посколь-
ку если Хп — состояние системы в момент п, то
_(Хп-1+Л/,
Ал+1 | ДГ>
если Хп 1,
если Хп = О,
(4.3)
где jV —число требований, поступающих за время V обслужива-
ния (и + 1)-го требования. Но случайная величина V по предпо-
ложению не зависит от предыдущих длительностей операций обслу-
живания и длины очереди. В силу стационарного характера пуас-
соновского потока число поступлений N за время обслуживания
!) Именно если операция обслуживания оканчивается в момент /, то си-
стема наблюдается в момент t + 0 (после ухода обслуженного требования).—
Прим, перев
2) Условие Хо = 0 говорит о том, что рассматривается система, в которой в
момент / = 0 отсутствуют требования. — Прим. перев.
470
Гл. 14. Процессы массового обслуживания
зависит только от V и не зависит ни от длины очереди, ни от
момента начала обслуживания. Отсюда следует, что {Хп} — цепь
Маркова.
Вероятностное распределение величины N можно найти, нала-
гая условие на значение V и применяя формулу полной вероятно-
сти
Р(Д/ = п}= j P{tf = n|7 = c>}&(v)dt,.
о
Далее, число требований, поступающих за время v, является
случайной величиной с пуассоновским распределением, имеющим
параметр ко. Следовательно,
р {N = п | V = v} = ~ (Av)n,
поэтому
Pii - Р {*„+! = /I Хп = i] = Р {N = j - i + 1} =
= f Р {N = j — i + 1 | V = t>) b (v) dv = f , .-ст b (t>) dv,
J J \J l “Г 11
0 0
1 (/>1),
Po = 0, j<i—l (/>1).
Если требование покидает систему, оставляя ее свободной, то
ее состояние остается нулевым до тех пор, пока не поступит и не
начнет обслуживаться очередное требование. Таким образом, ну-
левое и первое состояния эквивалентны относительно переходов
в другие состояния.
Если обозначить
kr= j e~Kvb (v) dv, r = 0, 1, 2, ...
о
(kr— вероятность того, что за время обслуживания одного требо-
вания поступит г требований), то
kQ kr k2 ...
kQ kx k2 ...
0 kQ kx ...
0 0 k0 ...
(4.4)
§ 4. Метод вложенных цепей Маркова
471
Детальный анализ цепи Маркова (4.4) уже был проведен в § 5
гл. 3. Там было доказано, что цепь является возвратной положи-
тельной, возвратной нулевой или невозвратной в зависимости от
того, р < 1, р = 1 или р > 1 соответственно, где
оо оо оо
P = Sr^= J
r=0 0 r=0
= % [ а6(у)</о = ЛМ(Г).
6
Величина
__ _____среднее время обслуживания одного требования__
Р средний интервал между моментами поступления требования
называется нагрузкой системы. Найдем теперь предельное рас-
пределение для данной цепи Маркова в случае р< 1.
А. Стационарное распределение вложенной цепи Маркова
Найдем вектор
«гс (л0, «п>। j • • •), «п>£ 0, 1,
/=0
такой, что
оо
3 л{Рц = Л/, / = о, 1,2,...,
/=0
где матрица \\Рц\\ = Р определена равенством (4.4). Если выра-
зить эти уравнения через величины kiy то они примут вид
Z + 1
Л^ — Л0Йi ~TCfk£ —/• -j-1, I 0, 1, 2, • • • •
r=l
Найдем производящую функцию
л (s) = 5
i=0
через функцию
оо
K(s)=%kiSl.
1=0
Умножая записанное выше равенство на s\ получим
f + 1 z
5'лг = ла^г + |2лЛ-г+1«г+1--°-у—/ = 0, 1, 2............
Г—0
472
Гл. 14. Процессы массового обслуживания
i +1
Суммируя по i и учитывая, что является сверткой, по-
г-0
лучим
оо
2 л^‘ = л (s) = л0/( ($) + 4 [Д’ («) Л ($) - л0/г0] - -у- [К ($) - &0].
/-0
Отсюда
Эта формула определяет производящую функцию стационарного
распределения с точностью до постоянного множителя л0. По-
скольку
оо
/с(1)=2^=1,
>=0
то дробь
s-K(s) s — 1 1 - K(s)
s — 1 S — 1 1 — s ’
стоящая в знаменателе выражения для rrc(s), стремится при s-
к величине 1 — К' (1).
Найдем /С(1)—среднее число требований, поступающих за
время обслуживания одного требования:
/С(1) = ^rkr = ЛМ(Ю = -^ = Р
Г=1
(р, очевидно, является нагрузкой системы), где -у = М(Л)--сред-
няя длительность интервала между моментами поступления. По-
скольку р< 1, стационарное распределение существует и, следова-
тельно, я(1)= 1. Но из полученной формулы следует
^0) = ^’
поэтому
~ 1 — р.
Таким образом производящая функция стационарного распре-
деления равна
Величина 1—р является стационарной вероятностью того, что си-
стема свободна.
!) Данное выражение для л($) называют формулой Полячека — Хинчина.—
Прим, перев.
§ 4. Метод вложенных цепей Маркова 473
Б. Средняя длина очереди для системы (M/G/1)
в стационарном режиме
В заключение данного параграфа найдем среднюю длину оче-
реди и среднее время ожидания поступившим требованием начала
обслуживания для системы, находящейся в стационарном режиме.
Дифференцируя л($), нелегко непосредственно получить вы-
ражение для М(д), где q — состояние вложенной цепи Маркова,
находящейся в стационарном режиме. Изберем для получения
М(^) другой метод.
Если q — число требований в очереди после ухода некоторого
требования, a qr — число требований в очереди после следующего
ухода, то
q' *= q — 1 + б + N,
где N — число поступивших за время обслуживания требований, а
f 1, если я —О,
б = А \ Л
I 0, если #>0.
В стационарном режиме величина q' имеет такое же распреде-
ление, что и q. Таким образом, М(^')= М(<?) и
М(б)=» 1 -M(AQ~ 1 ~р. (4.5)
Из этого же выражения, поскольку б2 = б, имеем
/ = + б + 1)2 + 2<7d 4- 26СМ — 1) + — 1).
Так как ^6 = 0 (см. определение б), то
/ = <72 + 6 + ^(^- l) + (l-JV) + 2d(2V- I) + 29^- 1).
Но величина N (число требований, поступивших за время обслу-
живания) не зависит от q и, следовательно, от б.
Усредняя полученное равенство и учитывая (4.5), получаем
М (/) = М (<72) + 1-р + М[ЛЧЛГ-1)] +
+ 1 — р + 2(1 — р) (р — 1) + 2М(</)(р—1).
Поскольку М (/2) = М (</2) в силу предположения о стационарно-
сти, то
„М[ЛГ(ЛГ-1)]
2(р-1) •
Далее,
К (s) — 2 ^nS" ~ / e~Kv (а)
n=«0 0
М [ЛГ (N - 1)] = S П (п - 1) kn = /<"(!)
n=Q
474
Гл. 14. Процессы массового обслуживания
И
оо
К" (<$) = ^2 J (у) dv.
о
Следовательно,
М [2V (N - 1)] = Л2 J v2b (v) dv - Л2 {о2 (Г) + [М (Г)]2} = о2 (ЛУ) + р2,
о
поскольку
Таким образом
р = ЛМ(У).
(4.6)
В. Среднее время ожидания
В условиях стационарности можно найти среднее время ожи-
дания требования. Предположим, что требование ожидает время
W начала своего обслуживания, которое продолжается время V.
Предположим, что, когда требование покидает систему, в очереди
остается q требований. Это означает, что за время W + V посту-
пило q требований пуассоновского потока. В силу стационарности
сумма
(среднее время ожидания) + (среднее время обслуживания
требования) = M(IF) + М( V)
должна равняться среднему числу требований, поступивших за
этот период, умноженному на среднюю длительность интервала
между требованиями, т. е. величине уМ(^). Но поскольку рас-
сматривается стационарный режим, то в силу (4.6)
М (IF) + М (У) - V [р + "2 НГ) Р)р2 ] •
Деля на рг1 =M(V) и вспоминая, что — = р, из последнего соот-
Н
ношения получим
М (Г) = а2(Л7) + р2
M(V) “ 2р (1-р) ’
или
М(Ю = Р--2((^р7 M(V)- (4J)
Из формул (4.6) и (4.7) следует один несколько неожиданный
факт. Именно: при заданных средних интервалах между поступ-
лениями и длительностях обслуживания можно уменьшить сред-
§ 5. Экспоненциально распределенное время обслуживания
475
ние длину очереди и время ожидания, уменьшая дисперсию вре-
мени обслуживания. Очевидно, что наилучшим в этом отношении
случаем является постоянное время обслуживания.
Г. Распределение времени ожидания
В тех же предположениях, что и выше, найдем преобразование
Лапласа распределения времени ожидания. Пусть {л?} — равновес-
ные вероятности, производящая функция которых n(s) была най-
дена выше. Если требование ожидает время W начала обслужива-
ния и обслуживается время V, то вероятность того, что после его
ухода останется q требований, равная совпадает с вероятно-
стью поступления q требований за время W + V. Поскольку входя-
щий поток — пуассоновский с параметром Z, то
о
где C(t) — функция распределения величины W + V. Отсюда
л (s) = J] = f e-MO-^dC(0 = C(X(l -s)),
<7=0 6
где C(s) — преобразование Лапласа функции C(t) !). Но C(t)—
функция распределения суммы независимых случайных величин
W и V, функции распределения которых равны W(t) и B(t) соот-
ветственно. Преобразование Лапласа для суммы W и V равно
произведению соответствующих преобразований. Следовательно,
n(s)==IF(Z(l-s))B(Z(l-s)\
или
IЛ — и \
п —Т“
= ---L л 7 ,
в (и) •
§ 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ
(G/M/1)
Другой моделью, которая может быть изучена с помощью ме-
тода вложенных цепей Маркова, является модель с произвольным
распределением Н(и) интервалов между моментами поступлений
и экспоненциально распределенным (с параметром ц) временем
обслуживания.
9 Такое преобразование часто называют преобразованием Лапласа — Стиль-
тьеса. — Прим, перев.
476 Гл. 14 Процессы массового обслуживания
В этом случае примем, что переходы вложенной цепи Маркова
определяются моментами поступления новых требований, а ее
состояние до следующего перехода — длина очереди перед вновь
поступившим требованием.
Если q — состояние системы после некоторого момента поступ-
ления, a qf — состояние после следующего момента поступления, то
q' = q+l~N, (5.1)
где iV —число обслуженных требований за рассматриваемый отре-
зок времени. В силу свойства «отсутствия последействия» у экспо-
ненциального распределения (см. теорему 2.2 гл. 7) число N тре-
бований, обслуженных за время между моментами поступлений,
зависит только от длины этого интервала и величины q и не за-
висит от времени, в течение которого уже обслуживалось очеред-
ное требование. Интервалы между моментами поступлений яв-
ляются, конечно, независимыми случайными величинами. В силу
указанных фактов заключаем, что соотношение (5.1) определяет
цепь Маркова. Вычислим ее матрицу перехода ||Л?11-
Поскольку N > 0, то Рг?- = 0 при j > i 4- 1. Если f 4- 1 > / > 1,
то i 4- 1 — j требований было обслужено до поступления очеред-
ного требования. Обозначим вероятность этого события через
j. Очевидно, если i 4- 1 1, то Pij =
Целесообразно найти выражение для ak через распределение
интервалов между моментами поступления и распределение вре-
мени обслуживания. Для этого заметим, что если длина интер-
вала между моментами поступления равна g, то вероятность того,
что завершится обслуживание в точности k требований, равна
F(ft)(|)-^(ft+l,(^ (5.2)
где F(g) = 1—— распределение времени обслуживания, а
FW(g)—^-кратная свертка F(%). Действительно, пусть Ej, Е2, ...
..., Ег, ... — длительности первой, второй и т. д. операций об-
служивания. Величины Ег- независимы и одинаково распределены
по закону ^(g). Вероятность того, что за время g закончатся по
меньшей мере k операций обслуживания, совпадает с вероятностью
того, что временной интервал до окончания k-ro акта обслужива-
ния не превышает g, т, е.
Р{3, + 32+ ... +sfe<£W(fe)(£).
Следовательно, вероятность завершения за время g в точности
k операций обслуживания равна Р {время, необходимое для завер-
шения по крайней мере k операций обслуживания <^g} — Р {время,
необходимое для завершения по крайней мере k 4- 1 операций об-
§ 5. Экспоненциально распределенное время обслуживания 477
служивания Отсюда следует формула (5.2). Точное выраже-
ние для следующее:
О
Интегрируя соответствующую формулу для по частям,
получим
В силу формулы полной вероятности имеем
dH®>
J * \к Г А /
О
где Н(1) — функция распределения интервалов между моментами
поступления. Формула для ak может быть выведена непосредствен-
ным образом. Однако метод, приведенный выше, имеет самостоя-
тельную ценность и может использоваться при решении других
задач.
Наконец, величина Рю— вероятность того, что все имевшиеся i
требований были обслужены, равна вероятности того, что при
наличии более чем i требований по крайней мере i из них были бы
оо
обслужены. Лучше всего записать Pi0 = 1 — 2 Рц\ тогда
/“1
г0 а0 0 0 0 ...
Г1 aQ 0 0 ...
р = r2 а2 а{ aQ 0 ... , (5.3)
• • • • • • • • • •
где rt = 1 - а0 - «1 ~ • • • - «/•
Цепь Маркова с матрицей переходных вероятностей (5.3) была
рассмотрена в § 6 гл. 3 и там был проведен довольно подробный
анализ, касающийся таких свойств, как положительная возврат-
ность и невозвратность. В частности, было доказано, что если
kak> 1,
ьо
то цепь Маркова является возвратной положительной и предель-
ное распределение имеет вид
;=<>. 1,2.....
478
Гл. 14. Процессы массового обслуживания
где — единственное решение уравнения f (g0) = ^о(О < £о < 1), а
Н&)=2 а£к.
В силу определения ak имеем
Р/п_ V _ средняя длина интервала между моментами поступления _ 1
' ' ' k среднее время обслуживания р
/г-0
Следовательно, процесс является возвратным положительным то-
гда и только тогда, когда р < 1.
Время ожидания
Если (1)> 1 и функция распределения длины очереди яв-
ляется стационарной, найдем функцию распределения времени
ожидания W начала обслуживания.
Вероятность того, что требование не будет ожидать в очереди,
равна
“ 1 ~ So-
Если требование поступает и застает впереди себя п 1 тре-
бований, то оно должно ожидать время, равное сумме п независи-
мых одинаково (экспоненциально) распределенных длительностей
обслуживания, прежде чем поступит на обслуживающий прибор.
Эта сумма обладает гамма-распределением порядка п с парамет-
ром ц. Таким образом,
п п~\ _цТ
|длина очереди равна n}== j (п)-------dr, 1.
о
Следовательно, в силу того, что
Р {длина очереди равна п} == лп = (1 —
имеем
оо
W (/) = Р {W t} = 2 Р {W /| длина очереди равна п} X
п — \
X Р {длина очереди равна д} + л0 =
t «<ОО
"(‘ "У.[ 2 -Е.)-
О и = 1
= (1 -£о) + ёо(1 - ехр[-1*/(1 -у]).
§ 6. Гамма-распределение интервалов
479
Это распределение является комбинацией экспоненциального
с параметром ц(1—go) и вырожденного (сосредоточенного в точ-
ке 0). Последнее имеет вес 1 — go, который равен вероятности того,
что поступившее требование не будет ожидать начала обслужива-
ния. Условная функция распределения времени ожидания при ус-
ловии занятости обслуживающего устройства равна при этом
2(0= 1 - ехр[- |i/(l -Ы].
§ 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ
ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ек/М/1)
Это частный случай предыдущей модели, который может быть
исследован с помощью изящного приема, широко применяемого
также и в других задачах1)- Рассмотрим одноканальную систему
с экспоненциально (с параметром р) распределенным временем
обслуживания и с интервалами между моментами поступления,
имеющими гамма-распределение Н (и) порядка k с плотностью
Г (k) л и
h (и) =
и>0,
и
<0.
Функцию распределения Н(и) можно считать распределением
суммы k независимых случайных величин, каждая из которых рас-
пределена экспоненциально с параметром X. Следовательно, мож-
но свести задачу к анализу марковского процесса, считая, что
каждое поступление состоит из k фаз 0, 1, ..., k— 1, в каждой из
которых требование проводит экспоненциально (с параметром X)
распределенное время, а затем переходит к следующей фазе. Дей-
ствительное поступление требования в систему соответствует его
достижению &-й фазы. В любой момент времени лишь одно требо-
вание находится в одной из фаз 0, 1, ..., k— 1, причем новое тре-
бование поступает на фазу 0 в момент, когда предшествующее тре-
бование покидает фазу k— 1.
Состояние системы определяется как сумма соответствующих
всем требованиям фаз. Таким образом, если система находится
в состоянии nk + /, I < k, это означает, что п требований нахо-
дится либо в очереди, либо на обслуживании (что соответствует
й-й фазе), а еще одно требование находится на «/-й фазе поступ-
ления». Когда какое-либо требование заканчивает обслуживаться,
состояние системы убывает на k.
!) Излагаемый ниже прием получил название метода фиктивных фаз Эр-
ланга. — Прим, перев.
480
Гл. 14. Процессы Массового обслуживания
Тем самым определена цепь Маркова с непрерывным временем,
инфинитезимальная матрица которой равна
А =
__________k_________
-к к о о....... о о о о 0 ...
О —Л Л о....... о о о о 0...
О О -Z Z....... о о о о 0...
0 0 0 . . . ... 0 — А к 0 0 0
н 0 0 ... ... 0 0 — (ц+А) А 0 0
0 н 0 ... ... 0 0 0 — (ц+А) Л 0
0 0 р.... ... 0 0 0 0 — (ц+А) А
Можно найти равновесные свойства данной цепи Маркова с не-
прерывным временем. Мы не будем этим заниматься, поскольку,
как упомянуто выше, рассматриваемый пример является частным
случаем системы (G/Af/l), которая рассматривалась в § 5. Преиму-
щество описанного приема состоит в том, что, используя марков-
ский характер процесса, можно найти его переходные характери-
стики. Обсуждение этого вопроса выходит за рамки данной книги.
А. Гамма-распределение времени обслуживания и произвольный (рекуррентный)
входящий поток ’)
Можно использовать приемы, изложенные в последних нескольких парагра-
фах, для нахождения стационарных характеристик процесса обслуживания с од-
ним обслуживающим прибором с произвольным распределением H(v) интерва-
лов между моментами поступления и гамма-распределением порядка k с пара-
метром р времени обслуживания.
Будем считать, что обслуживание состоит из k фаз 1, 2, ..., kt в каждой из
которых требование проводит экспоненциально (с параметром ц) распределенное
случайное время. После того как обслуживание на &-й фазе завершилось, тре-
бование покидает систему.
Построим вложенную цепь Маркова, переходы которой обусловлены поступ-
лением требований. Пусть состояние цепи между моментами поступления равно
kq— р+ 1, где q— число требований в системе, а р — номер фазы обслужива-
ния, на которой находилось в момент последнего поступления обслуживаемое
требование. Поскольку k — р 4- 1 — число фаз, которое осталось пройти обслу-
живаемому требованию, то состояние системы kq — р 4- 1 = k(q—1) 4-
!) При первом чтении текст, напечатанный петитом, можно опустить без
потери целостности изложения.
f 6. Гамма-распределение интервалов
48!
4-(& — р+ 1) можно интерпретировать как число экспоненциально распределен-
ных интервалов времени, которые должны завершиться прежде, чем вновь по-
ступившее требование начнет обслуживаться. Если q = 0, то состояние системы
полагается равным 0.
Вероятности перехода за один шаг для данной цепи имеют следующий вид.
При всех i
(1) если j>i + k, то =
(2) если j i + k, j ф 0, то в одном интервале между моментами поступ-
ления содержится i 4- k — j экспоненциально распределенных отрезков и
= 7j-(U»)re dH (о),
о
где г =s i 4- k — j. Вывод этого равенства идентичен выводу выражения для Дл
на стр. 477,
(3) наконец, Рщ есть вероятность того, что сумма i + k экспоненциаль-
но распределенных отрезков времени не превышает длину интервала между мо-
ментами поступления:
оо оо V
Pio-J P{Si+fe<v}dtf(t>) = j J
0 0 0
(i4-£-l)l
d£dff(v).
Б. Стационарные вероятности
Если нагрузка системы
_ М (время обслуживания) __
Р ~ М. (время между моментами поступления)
____________________k_____________________
цМ (время между моментами поступления)
меньше 1, то мы ожидаем, что вероятностное распределение состояний системы
стремится к предельному. Такое стационарное распределение пропорционально
неотрицательной сходящейся последовательности х= (хо, *i, ...), удовлетворяю-
щей равенству
Х = хР. (6.1)
По аналогии с предыдущими моделями выберем пробное решение в виде
Xi = V,
где % — некоторое действительное число. При j>k из (6.1) получаем
оо оо оо оо
= (6.2)
t=0 i^j—k r=»0 r=0
ИЛИ
Kk = F{X),
где
oo oo
= J (y).
r-o о
>/,16 Зак. «о»
482
Гл. 14. Процессы массового обслуживания
С помощью теоремы Руше можно доказать, что функция V — Г (%) при
|Л| < 1 имеет k корней (считая и кратные).
В частности, теорема Руше утверждает, что если f(z) и g(z)—аналитические
функции в области D и | f(z)| > | g(z)| при значениях г, принадлежащих гра-
нице D, то функции /(г) и /(г) + g(z) имеют в D одинаковое количество нулей.
(Доказательство этой теоремы можно найти в любом учебнике по теории функ-
ций комплексного переменного.) Применим теперь теорему Руше для случая
D = {z||z|5^1 — б, б > 0}, f(z) = zh, g(z) =—F(z). В самом деле, при
I z | = 1—6 имеем | zh | = (1—б)Л = 1—kb 4- о (б). Далее, при |z| = 1—б
|E(z)|^F(l—б) (поскольку F(z)—степенной ряд с неотрицательными коэф-
фициентами). Но при б~>0
F (1 - б) = F (1) - 6F (1) + о (б).
Кроме того, непосредственный подсчет показывает, что
оо
F'(l) = n f vdH (v) = — >k,
J p
0
поскольку по предположению р < 1. Отсюда следует, что при достаточно ма-
лых б | zk | > | F (z) I, | z | = 1 — б. В силу теоремы Руше заключаем, что функции
zh и zk — F(z) имеют в области {z | |z| 1 —6} одинаковое количество нулей.
Если обозначить k корней через Ль Лг, ...» Лл, то последовательность
{хп = Л"}^°=0 будет удовлетворять уравнению (6.2) при любом г (r= 1,2,..., Л).
Можно попытаться найти линейную комбинацию
k
яп = а1Х" + а2Л2 + ••• +afeZfe> Sar = I’
r=l
такую, что система уравнений х = хР удовлетворяется при хп — лп, п — 0, 1,....
оо
Действительно, уравнения Xj = XiPij (j = G, 1, ...) при j k удовлетворя-
i=0
ются при любом выборе коэффициентов ar, поскольку любая последовательность
{Л^}, г — 1, k, является решением и их линейная комбинация вновь является
решением. Остается найти постоянные ai, аг, ..., а&, такие, чтобы первые k
уравнений системы х = хР также удовлетворялись. В случае если все Лг различ-
ны, совершая некоторые алгебраические преобразования, получим точное решение
/ ОО \
I в котором произведена нормировка 2 Пп = 1 I
\ гс=0 /
k
Пп = ~k a ’
Saz z=i
1 -Ki
z=i
где
/-1
Изменения, которые необходимо внести в случае кратных корней, а также
соответствующие подробности утомительны и будут опущены.
§ 7. Экспоненциальное обслуживание s приборов
483
В. Время ожидания
Выше было указано, что состояние системы определялось как число экспо-
ненциально (с параметром ц) распределенных отрезков времени, которые состав-
ляют время ожидания вновь поступившего требования. Следовательно, если со-
стояние системы равно п > 0, то время ожидания только что поступившего тре-
бования имеет гамма-распределение порядка п с параметром ц. Если п = О,
время ожидания равно 0. Следовательно,
£ оо
u7 (I) = р < а = / 2 77^7)1 ’^-'e-^dw + л0.
0 /=1 и
В случае различных корней можно подставить выражение для лу, приведен
ное выше, и получить
S k
1 + J VdV&i ехр [-|w (1 - X/)] dw
о /=1
k
+ S 7гЧл - exP (1 - Ml)
“ (1 — A/J
Zel
exp [-gB (1 -X/)]
1-Xf
§ 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ 5 ПРИБОРОВ (GI/M/s)
Обобщим рассмотренные выше для случая одного обслужи-
вающего прибора приемы на случай системы, состоящей из $
приборов, в которую требования поступают через интервалы,
имеющие распределение а распределение времени обслужи-
вания экспоненциально с параметром ц. Предположим, что рас-
пределения длительностей обслуживания для всех приборов сов-
падают.
Как и прежде, процесс обслуживания не является марковским,
но можно построить вложенную цепь Маркова. Пусть переходы
484 Гл. 14. Процессы массового обслуживания
цепи определяются моментами поступления новых требований, и
пусть q, состояние системы, есть число требований, ожидающих
или обслуживаемых, которые находились в системе в момент по-
ступления последнего требования.
Вероятность Рц можно найти следующим образом:
(1) Если j > i + 1, то Рц = 0 при всех / = 0,1,2, ... .
(2) Если + 1 то все требования находились на обслу-
живании и до следующего момента поступления закончилось
i — /+ 1 актов обслуживания Вероятность того, что за время t
фиксированное требование обслужится, равна 1—е~^. Таким об-
разом,
оо
Рц~ J Р {/+ 1 — / актов обслуживания закончится за время /|
о
в момент 0 в системе было i+ 1 требований}d// (/) =
= / (г + 1)(1(7.1)
о
Подинтегральная функция является вероятностью из биномиаль-
ного распределения, соответствующей i + 1 — j успехам (завер-
шениям актов обслуживания до следующего момента поступления).
(3) Если i 4- 1 >j>s и s, то все приборы до следующего
момента поступления заняты обслуживанием. Следовательно,
Рц == Р{окончилось /+ 1 — / актов обслуживания} =
оо
= J Р{за время / окончилось i + 1 — j актов обслуживания}dH(f) =
о
оо
= J 7ГГТЯ<№(*)
о
(Вывод последнего равенства совпадает с выводом, приведен-
ным после формулы (5.2). В нашем случае функция распределения
времени до завершения очередного акта обслуживания является
экспоненциальной с параметром sp, поскольку в рассматриваемом
случае заняты все s приборов.)
(4) Если то в начале рассматриваемого интер-
вала т = i — s + 1 требований будут ожидать, a s требований об-
служиваться. В конце интервала будет п = s — j свободных прибо-
ров. Пусть v — время до того момента, когда не останется ожи-
дающих требований, т. е. время до окончания обслуживания т
требований всеми s работающими приборами. Поскольку интер-
валы между моментами окончаний актов обслуживания распре-
§ 7. Экспоненциальное обслуживание s приборов
485
делены экспоненциально с параметром sjx, то величина v имеет
гамма-распределение порядка т с параметром sjx. Предположим,
что оставшиеся п требований обслуживаются время и — V, где
и — длительность интервала между соседними моментами поступ-
ления. Тогда
оо
Рц= J Р{за время и обслужилось т + п требований} dH (и) =
о
оо оо
₽ j [ J Р{эа время u—v обслужилось п требований} X
о о
X \т - l)l' e~S>i0 dv]. dH (u) =
oo U
- I J vtn-ie-siiv (1 ~ e~^u~v})n dv dH (a),
о о
где последнее равенство получено с помощью биномиального рас-
пределения, аналогично равенству (7.1).
А. Стационарные вероятности
Естественно ожидать, что если нагрузка системы <1, т. е.
М (длина интервала между окончаниями актов обслуживания,
________________когда все приборы заняты)__________
М (длина интервала между моментами поступлений)
----------------------1--------------------< 1
SJ1M (длина интервала между моментами поступлений) *
то спустя достаточно долгое время вероятности пребывания в ка-
ждом состоянии должны стабилизироваться. Найдем положитель-
ный вектор х = (%о, Xi, %2, • •.), удовлетворяющий соотношениям
< оо и х = хР. Сравнивая с рассмотренным ранее частным
случаем одноканальной системы, приходим к рассмотрению проб-
ного решения вида
х = (₽о, Р1, Ps-2, 1, а, а2, ...).
В системе х = хР /-е (/ > s) уравнение имеет вид
оо оо оо
х ai-s+i==^xр = з Х.Р = з ai-s+ip
/а0 Z=/-l Z=/-l
= a/-sJ e-*su"-a}dH(ti).
0
16 Зак. 939
486
/л. 14, Процессы массового обслуживания
Это уравнение вида а = F(a), где
F(a)= j
О
— выпуклая возрастающая на (0, 1) функция, F(0)>0 и F(l) = 1.
Выпуклость функции F можно проверить двойным дифференциро-
ванием. Следовательно, решение а в (0, 1) существует тогда и
только тогда, когда /?/(1)> 1. Поскольку
F' (1) == ps J и dH («),
о
то это условие как раз совпадает с условием р<1. Найдя а,
можно найти и остальные компоненты ps_2, р5-з, ..., Ро из рекур-
рентных соотношений
S —2 оо
Р/= 2 + 2 а^+!Л/, / = 0, 1, .... S-2,
i=s—\
или
Р/-1 = U’f-l, /)
2 а‘~з+'Рц
= S— 1
/=1, 2, . ..,5-1,
где ps_i = l. Нормализуя, получим финальные вероятности
XJ
П1~ 7—2 •
(1 - a)"1 + ₽,•
i=0
Б. Время ожидания в стационарном режиме
Вероятность того, что поступившее требование не будет ожи-
дать начала обслуживания, совпадает с вероятностью того, что
в момент поступления по крайней мере один прибор свободен, И
равна
s—1
W (0) = P{?<s- 1} = 2 = --------i=0 s_-2
(1-а)-‘+2;₽г '-°
i-0
где
₽s-i=l.
§ 8. Виртуальное время ожидания и период занятости 487
Если состояние системы равно /г > s, то вновь поступившее
требование должно ожидать начала обслуживания до тех пор,
пока не обслужатся п — s + 1 требований, стоящих перед ним. Но
поскольку работают все $ приборов, интервалы между окончания-
ми актов обслуживания распределены экспоненциально с парамет-
ром Таким образом, время ожидания такого требования имеет
гамма-распределение порядка п — s + 1 с параметром jxs, и
£ оо
р= w(|) = W (0) + Л ГУ , 1 =
v леи П — S) I
0 n«s
! -ns5(l-a)
3—2
1 + (1 -а)^ ₽<
i~0
§ 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
В этом параграфе рассматривается другой подход к задаче
о времени ожидания для одноканальной системы обслуживания
с пуассоновским входящим потоком и произвольным распределе-
нием времени обслуживания (М/G/l). Будут также получены не-
которые результаты, относящиеся к периоду занятости данной си-
стемы. Для этой цели будет использован материал гл. 9, § 3.
Поскольку процесс обслуживания в целом является немарков-
ским, мы выше рассматривали вложенную цепь Маркова и ана-
лизировали времена ожидания требований, используя ее. Однако
если рассмотреть величину тД/) (л (6 иногда называют виртуаль-
ным временем ожидания), которая равна времени, в течение кото-
рого должно было бы ожидать требование, если бы оно поступило
в момент /, то л(^) определяет марковский процесс с непрерывным
временем. Так, если tn и оп — момент поступления и время обслу-
живания n-го требования соответственно, то при tn < t < Zn+1
имеем
п (0 = bi (*«+)-a-Uk1)
и
Л (tn 4*) = Л (tn ) 4” vrt,
6] (^4-) = lim л (/ 4-е), т](/-) = lim т](/ - е)\
V е->0 е->0 J
’) Символ [х]+ определяется равенством
г д.1 _ I ’ ’
+ 10, если х < 0.
16*
488
Гл. 14. Процессы массового обслуживания
Обозначим через X параметр входящего потока (который по
предположению пуассоновский), а через Я (с')—распределение
времени обслуживания. Типичная реализация процесса т](/) пока-
зана на рис. 1. Очевидно, что будущее поведение траектории тДО
не зависит от ее предыстории до попадания в текущее состояние.
В самом деле, поскольку значения tj являются моментами наступ-
ления событий пуассоновского потока, то время для следующего
поступления требования не зависит от того, когда поступило пре-
дыдущее требование.
Можно дать величине г](/) другую интерпретацию как времени,
необходимому для завершения обслуживания всех требований,
q(t)
Рис. 1.
имеющихся в системе в момент t. Действительное время ожидания
n-го требования равно v\(tn) = r)(/n—). Обозначим
F(f, х) = Р{т](0<4
Можно вывести интегро-дифференциальное уравнение, которому
удовлетворяет F(t,x). Это уравнение может быть проанализиро-
вано с целью нахождения свойств функции F(t, х), В § 3 было
доказано, что функция распределения времени ожидания гг-го тре-
бования
F (tni х)
сходится к предельному распределению при п—>оо. С помощью
соответствующих теорем восстановления можно доказать также
сходимость функции F(/,x) и показать, что ее предел совпадает
с пределом функций Fn(x) *). Дальнейшие подробности выходят
за рамки данной книги (см. литературу в конце данной главы).
’) Заметим, что последний факт не является очевидным в силу того, что
моменты tn случайны и совпадают с моментами скачков процесса г](/), т. е. по-
следовательность {/п} и функция т](/) не являются независимыми, — Прим, перев,
§ 8. Виртуальное время ожидания и период занятости 489
В оставшейся части главы будут рассмотрены различные пред-
ставляющие интерес случайные величины, связанные с системой
(M/G/1).
Заметим, что если г) (/) > 0, то обслуживающий прибор в мо-
мент t занят, а если rj (/) = 0, то свободен. Пусть
ро(О = р{п(О = о},
т. е. Po{t) —вероятность того, что прибор в момент t свободен.
Период занятости определяется как такой временной интервал,-
в течение которого прибор постоянно занят. Если т) (0) > 0, т. е.
обслуживающий прибор в момент t = 0 занят, то существует на-
чальный период занятости, который заканчивается, когда т|(/)
в первый раз обращается в 0. Обозначим через G(x) вероятность
того, что длительность начального периода занятости х. Следую-
щие за начальным периодом занятости (если таковой имеется)
периоды незанятости и занятости чередуются. Длительности перио-
дов занятости, следующих за начальным, являются независимыми
одинаково распределенными случайными величинами, поскольку
каждый последующий период занятости начинается в одних и тех
же условиях. Обозначим через G(x) вероятность того, что дли-
тельность периода занятости (отличного от начального) х. Пе-
риоды незанятости также являются независимыми одинаково рас-
пределенными случайными величинами, функция распределения
которых экспоненциальна с параметром Z.
Нашей первоочередной задачей является доказательство тео-
ремы 8.1, сформулированной ниже. Это доказательство опирается
на один результат, полученный в гл. 9, § 2, который мы для удоб-
ства приведем здесь в виде леммы 8.1.
Лемма 8.1. Пусть хь Х2, ..., Хп— неотрицательные переста-
новочные, случайные величины с суммой Xi + Х2 + • ♦ • + Хп = У,
пусть Ti, Т2, ...» Тп — координаты {расположенные в порядке воз-
растания) п точек, распределенных равномерно и независимо друг
от друга на интервале (0,/). Если {%h} и {т^}—независимые после-
довательности, то
{1 — ~, если 0 у t,
0, если y>t.
(8.1)
Доказательство леммы 8.1 и ее применения даны в гл. 9 (см.,
в частности, § 2). Приведем еще одну лемму.
Лемма 8.2. Пусть хь хг, . • •, Хп — неотрицательные переста-
новочные случайные величины с суммой xi + %2 + ... +хп = t, и
пусть ть тг, ...» Тп—1 — координаты {расположенные в порядке
490
Рл. 14. Процессы массового обслуживания
возрастания) п — 1 точек, распределенных равномерно и незави-
симо друг от друга на интервале (0,/). Если {/д} и {тд}— незави-
симые последовательности, то
Р{х> + ... + Х*<тъ fe=l, 2, ..., «-1} = у. (8.2)
Доказательство. В силу леммы 8.1
P{Xi + • • +Xfe<^> k= 1, 2, ..., п- 1 |Х1 + • • • +Хп-1 = у} =
1 --у, если
. 0, если y>t.
Далее, в силу формулы полной вероятности
Р{Х1+ +Xfe<Tft, й=1, 2, п~ 1} =
t
= J P{Xi+---+X*<Tft, k= 1, 2, ..., п- 1 |Xi + • • • +Xn-i=Z/}X
о
X dP {Xi + • • • +Хл-1 <у} =
t
= J (1 - f)dP{x1 + ... +Xn-i < */}= 1 -уМОс! + ... +Xn-i) =
0
= 1- 1(^1/),
t \ n )
поскольку Xn перестановочны и их сумма равна t. Отсюда,
очевидно, получаем
Р{Х1+ ••• +x*<Tft, /г=1, 2, ..., га-1} = у.
Теорема 8.1. Если т](())=--•£ (с — постоянная), то вероятность
того, что начальный период занятости имеет длительность х,
равна
J е~^с+у\су)п~х dH п(у), если х^с,
n = Q 0
G (х) = 0, если х<с, (8.3)
где Н п(у) — п-кратная свертка функции Н (у) (HQ (у) — распределе-
ние, имеющее единичный скачок в точке 0).
Доказательство. Проведем вычисления, налагая условие
на число поступивших требований. Число поступлений за началь-
ный период занятости может принимать значения п = 0, 1, 2, ....
Если п = 0, то начальный период занятости имеет длительность с,
§ 8. Виртуальное время ожидания и период занятости
491
а вероятность того, что за время (0, с) не поступит ни одного
требования, равна е~Кс. Таким образом, получен первый член
(п = 0) суммы (8.3). Если п>1, то обозначим через ть тг, ...» тп
моменты поступлений требований, а через хь Х2, •••> Хп — дли-
тельности их обслуживания, Эти величины должны удовлетворять
условиям
Т/<Х1 + • • +Х/-1 + с, /=1,2,..., п, (8.4)
где сумма по пустому множеству индексов полагается равной нулю.
Действительно, ' соотношение (8.4) утверждает, что суммарное
время обслуживания / — 1 требований, поступивших после момента
0, и требований, имевшихся в системе в момент 0, превышает мо-
мент поступления /-го требования, j = 1, 2, ..., п. Это условие,
очевидно, гарантирует, что обслуживающий прибор занят по край-
ней мере до завершения обслуживания n-го поступившего требо-
вания. Конечно, P{xi + Х2 + • • • +Хп -^4 = Нп(х).
Если Xi + .. • + Хп = У, то длительность начального периода за-
нятости равна с + у, а вероятность того, что в интервале (0, с + у)
поступит в точности п требований, равна-—- [Л(с + у)]п e~^{c+y\ Мо-
менты поступления можно считать координатами (расположенны-
ми в возрастающем порядке) п точек, распределенных равномер-
но и независимо друг от друга в интервале (0, с + у) (см. стр. 206,
гл. 7). Далее, хь Хг, •••> Хп — неотрицательные перестановочные
случайные величины.
Вычитая неравенства (8.4) из у + с, получим эквивалентные
соотношения
г/ + с-т/>^-Х1-Х2- ••• -Х/-ь /=1, 2, .... п. (8.5)
Пусть = у + с — т/; и, поскольку Xi + • • • + Хп = У, неравен-
ства (8.5) можно переписать в виде
%„ + %„_!+ ... +Х/, /=1, 2....п. (8.6)
Но величины т* + 1_р /= 1, п, очевидно, вновь распределены
как п порядковых статистик равномерного распределения на
(0, с + у). Чтобы убедиться в этом, достаточно посмотреть на зна-
чения tj в обратном порядке, проходя интервал от точки с + у
к точке 0. Требуемое утверждение получается из соображений
симметрии. Кроме того, величины Хп, Хп-ь • • •, Xn+i-j имеют сов-
местное распределение, такое же, что и величины Хь Хг, •••, X;»
в силу перестановочности. Следовательно, событие (8.6) имеет ту
же вероятность, что и событие
Xi + Хг + • • • + X/» /= 1, 2, .... п. (8.7)
492
Гл. 14. Процессы массового обслуживания
Обращаясь к лемме 8.1, мы заключаем, что вероятность события
(8.7) равна
1 У с
с + у с + у*
Учитывая все приведенные факты, с помощью формулы полной
вероятности получаем
оо X — С
G (х) = J Р {начальный период занятости х|т) (0) = С, П требований,
п=0 0
поступивших за это время, имеют суммарное время обслужи-
вания у} х Р {за период занятости поступило П требований
| Т] (0) = С, суммарное время обслуживания п требований рав-
но у} dHn (у) =
оо X — С
<7 О | у I С к
п=0 0
оо X — С
= £сж ! е~К^С+у} (с + y)n~l dHп(у).
п = 0 0
В следующей теореме выводится функция распределения пе-
риода занятости, отличного от начального.
Теорема 8.2. Вероятность того, что период занятости, отлич-
ный от начального, имеет длительность ^.х, равна
00 / —1 х
G w=S / e~Kvyn~'dH- х > °- <8-8>
/2=1 0
Доказательство. Если предположить, что период занято-
сти состоит из п, п = 1, 2, ..., актов обслуживания, то его дли-
тельность равна Xi + %2 + • •. + Хп, где %i, Х2, •••> Хп —независи-
мые одинаково распределенные случайные величины с функцией
распределения P{xi ^х} = Н(х), i = 1, 2, ..., п. В этом случае
за период занятости поступит в точности п—1 требований. Будем
отсчитывать время от начала периода занятости и обозначим через
Ti, тг, ..., тп-1 моменты поступлений. Они должны удовлетворять
условиям
т/<Х1+ ••• +Х/, / = 1, 2, ..п- 1. (8.9)
Если xi + • • • +/» = У, то период занятости имеет длительность у,
а моменты поступлений можно считать расположенными в порядке
возрастания координатами п точек, равномерно и независимо друг
от друга распределенных в интервале (0, у). Далее, %i, ..., —
неотрицательные перестановочные случайные величины. Если
Задачи
493
Xi + • • •+х™ ~ то событие (8.9) имеет ту же вероятность, что
и событие
х,+ ... 6=1,2........../г-1, (8.10)
поскольку в (8.9) можно заменить %,- на Хп-й-j и т,- на у — rn-j,
j = 1, 2, ..., п— 1, не изменяя вероятности события. По лемме 8.2
вероятность события (8.9) (и (8.10)) равна Поскольку
Р{Х1 + ••• + %«у} — Нп{у), а вероятность того, что за интервал
времени (0,у) поступит в точности п—1 требований, равна
(га11)! (A.j/)”~'e~Xy, т0> применяя формулу полной вероятности, по-
лучим
(8Л1)
п = 1 О
что и требовалось доказать.
ЗАДАЧИ
1. Показать, что стационарное распределение длины очереди {рп, и = 0, 1,
2, ...} для системы (M/M/s) равно
D
р0 Bl
S'5
РоР^,
1 п S,
S < П < оо,
гдер = —<1. Пусть Q = max(n — s, 0)
обслуживаемых требований. Показать, что
(п = 0, 1, 2, ...) —длина очереди без
у =
(1)
1 s ;
Up)'
i — о
(2) M(Q)=-^r|
2. Сравнить системы типа (Af/Af/l) с прямым и обратным порядками обслу-
живания (обратный порядок возникает, скажем, когда статьи из стопки берутся
сверху). Насколько отличаются (если это отличие есть) распределения длин оче-
редей, времен ожидания и периодов занятости?
Ответ: Распределения длин очередей и периодов занятости не отличаются.
Отличаются распределения времен ожидания. Почему это так?
3. Рассмотрим систему с обратным порядком обслуживания. Пусть
X(t) —длина очереди в момент t. Показать, что процесс {%(/), t 0} является
процессом рождения и гибели, и найти его параметры.
Ответ: Хп = X, цп — ц.
494
Г л. 14. Процессы массового обслуживания
4. Рассмотрим систему с бесконечным числом обслуживающих приборов и
экспоненциально (параметр ц) распределенным временем обслуживания. Предпо-
ложим, что требования поступают группами, а интервалы между моментами
поступлений распределены экспоненциально с параметром X. Число требований
в каждой группе случайно и имеет геометрическое распределение с параметром р
(О < р < 1), т. е. Р {число требований в группе равно k} = р*-1 (1 — р) (k =
“ 1, 2, ...).
Представить этот процесс в виде цепи Маркова с непрерывным временем и
найти ее инфинитезимальную матрицу.
Ответ: Q = || ||ч где
qi, i-i = Ф, К
^V = Zp/"'/“1 (1 -р), />/,
qij = Q, j<i- 1,
qa = ~~ qij'
5 (продолжение). Найти производящую функцию n(s) равновесного распре-
деления процесса.
Ответ:
_______________________________________________
3i(s) = p + t £ р (1 -s)j ₽Ц.
6. (Система с ограничениями) !). Требования поступают в систему по пуассо-
новскому потоку с параметром X. Длительности их обслуживания — независимые
одинаково распределенные д. с. в. с распределением Н(х). Требование, которое
застает прибор занятым, присоединяется к очереди с вероятностью р (0 < р < 1).
Найти переходные вероятности вложенной цепи Маркова, построенной по мо-
ментам ухода требований из системы. Найти предельное распределение длины
очереди.
Ответ:
Ро Pi Pz • • •
Ро Pi Pz • • •
оо
-« °' z.:.
о
oo
H
где
оо
р = Zap < 1, a = j* х dH (x) < oo.
6
7. Рассмотрим систему, описанную в задаче 6. Пусть 77 (х) = 1 Опи-
сать эту модель как случайный процесс рождения и гибели.
1) В оригинале «queueing with balking», т. е. дословно «процесс образования
очереди с препятствиями». — Прим. перевь
Задачи
495
Ответ'
г Л, п — 0, f О, п = О,
(кр, п>0, (р, п>0.
8. Следующие два процесса рождения и гибели (см. § 4 гл. 7) можно ин-
терпретировать как модели обслуживания с ограничениями.
(а) = 0 < q < 1, Л>0, п = 0, 1,2..
Н>0.
Но = 0;
(б) = = «= 1. 2....
Цо = О-
Для каждого случая найти стационарное распределение.
Ответ:
(а) Рт~Ро (— I <7 2 . «>о,
/ X \т ] - —
(б) рт = р<ц— J «>о, р0 = е »*.
9. Рассмотрим задачу о пешеходах, желающих перейти улицу с односторон-
ним движением в заданной точке. Предположим, что автомобили (нулевой дли-
ны), которые движутся без остановок, проезжают мимо данной точки в моменты,
образующие пуассоновский поток с параметром ц. Все ожидающие пешеходы
перейдут дорогу, как только временное «окно» между автомобилями составит по
крайней мере Т секунд. Чему равны (1) распределение времени ожидания пеше-
хода, который подошел к дороге в произвольный (не зависящий от движения
автомобилей) момент времени, (2) распределение времени между моментом
окончания перехода улицы некоторым пешеходом и следующим моментом начала
возможного перехода? Ответ дать в терминах преобразований Лапласа. Найти
среднее время ожидания пешехода.
Ответ: Распределения (1) и (2) имеют одно и то же преобразование Лап-
ласа
L ($) “[(н + «) е~цГ/($ +Це~(ц+5)Г)];
е^-О+цТ)
среднее время ожидания -------------.
Ц
10. (Система (Л4/6/оо)). Предположим, что имеется бесконечное число об-
служивающих приборов и, следовательно, требования не ждут в очереди. Мы
интересуемся числом занятых приборов. Моменты поступления требований обра-
зуют пуассоновский поток с параметром X. Длительности обслуживания требова-
ний независимы и одинаково распределены по закону Н(х).
Найти
(1) Pk (/) = Р {в момент t обслуживается ровно k требований},
(2) lim Pk (0 = Pk при условии, что в начальный момент в системе нет тре-
/~>оо
оо
бований и а = J х dH (х) < оо.
о
496
Гл. 14. Процессы массового обслуживания
Указание'. Использовать формулу полной вероятности и тот факт, что при
условии поступления п требований за время t моменты поступления распреде-
лены как порядковые статистики размера п для равномерного распределения в
(о, О-
Ответ:
(t
-X J (1 -H(x))dx
о
t X k
Л J (1 -Н (x))dx
о J
оо
(2) Pk = e-Ka-T^k' “ = f х dH (х).
! J
о
11. В системе (M/G/oo) моменты поступления требований образуют пуассо-
новский поток с параметром К, а функция распределения времени обслуживания
равна Н(х). В начальный момент в системе нет ни одного требования. Пока-
зать, что вероятность того, что за время t будет обслужено п требований, равна
1
п\
t X tl
Z Н (и) du I ехр
б J
- Л
du
12. Рассмотрим процесс, описанный в задаче 11. Показать, что вероятность
ф(/, Т) того, что в интервале (/, t + Т) ни одно требование не покинет систему,
удовлетворяет рекуррентному соотношению
t
<р (Л Т) = J [Н (т) + 1 - Н (т + Г)] Ф (т, Т) dr +
О
/+т
+ j Ле“Хт[1-Я(7' + /-т)]ф(0, T + t-T)dr + e~W+T}. (*)
t
Указание: Рассмотреть возможности, возникающие в момент поступления
первого требования.
13. Используя результат задачи 12, доказать, что
(t+T X
t /
Указание: Вывести дифференциальное уравнение первого порядка (по пере-
менной t) относительно функции ф(/, Т) и решить его.
14 (продолжение). Пусть фп(/, Г) — вероятность того, что в интервале
(/, t + T) п требований покинули систему. Получить интегральное соотношение
типа (*) между фп и фп-ь Затем показать, что
t+T X п
zj dU ехр
t j
t+T
-л / H(l)dl
t
15. В задаче 10 рассматривалась система с бесконечным числом обслужи
вающих приборов и пуассоновским входящим потоком. Рассмотрим «двойствен-
ную» систему (GI/M/oo), у которой интервалы между моментами поступления не-
Задачи
497
зависимы и одинаково распределены с плотностью h(x), а длительности обслужи-
вания независимы и распределены по экспоненте с параметром ц. Число обслу-
живающих приборов бесконечно. Найти матрицу переходных вероятностей вло-
женной цепи Маркова, состояние которой цп в момент п есть число занятых
приборов в момент n-го поступления.
Oreei:
оо
р frln+i = 11 = 0 = РИ = ( 1 +] 1 ) / e-/li* о - e~MJC)Z+1-/ h (х) dx.
О
* 16. Рассмотрим систему (A4/G/I). Пусть Вь В2, ... — последовательность
независимых одинаково распределенных случайных величин с функцией распре-
деления В(х), которая равна функции распределения периода занятости системы.
Предположим, что длительность обслуживания первого (за период занятости)
требования равна X (с функцией распределения Н(х) « Р {X х} и средним
а < оо) и что за время его обслуживания поступают п других требований. По-
казать, что
В (х) = Р{Х + В1 + В2+ ... +Вп<х}.
Отсюда получить, что преобразование Лапласа
оо
В (0)= j e~QxdB(x)
О
удовлетворяет функциональному уравнению
В(О) = ф(О + Л(1-В(0))),
где
оо
i|> (0) = J e~9xdH(x).
О
Использовать этот результат для нахождения средней продолжительности перио-
да занятости.
Указание'. Период занятости не зависит от порядка обслуживания. Предпо-
ложим (поскольку случай п = 0 тривиален), что за время первого акта обслужи-
вания поступают п > 0 требований. Обслуживанием первого из этих требований
начнем новый период занятости. По завершении его вернемся ко второму из
указанных требований и начнем другой период занятости и т. д. п раз.
Ответ:
а
Средняя продолжительность периода занятости ® >
оо
а= J xdH (х).
х-0
* 17. В условиях задачи 3 при X < ц рассмотрим систему в момент поступле-
ния требования. Найти вероятность того, что за время ожидания этого требо-
вания обслужатся в точности п требований при условии, что поступившее требо-
вание не застает систему свободной.
У казание: Применить метод решения задачи 16 для доказательства того, что
вероятностная производящая функция g(s) числа требований, обслуженных за
период занятости, удовлетворяет функциональному уравнению
g(s) = gs (g + A.-A.g(s))-1.
498
Гл. 14. Процессы массового обслуживания
Ответ:
я(*) = 2Д J(-1)
Г в1
18. Рассмотрим систему обслуживания, в которой требования поступают ре-
гулярно в моменты n = 0, 1, 2, .... Предположим, что время обслуживания
Xj j-vo требования распределено экспоненциально с параметром ц. Пусть X > ц.
Найти вероятность того, что прибор никогда не освободится, если в момент О
в системе имеется одно требование.
Указание: Показать, что искомая вероятность равна
Р {У^ 4- Г2 4- ... +rz>Z, /«1,2, ...},
где Yi — независимые д. с. в., имеющие экспоненциальное распределение с пара-
X
метром -jj- (использовать лемму 8.1).
Ответ: 1 —
Л
19. (Очередь с абсолютными приоритетами.) Рассмотрим одноканальную
систему, в которую поступают пуассоновские потоки двух типов требований
(приоритетных и неприоритетных) с параметрами Xi и Х2 (Xi 4- Х2 = 1). Дли-
тельности обслуживания требований этих типов распределены экспоненциально
с параметрами jii и ц2 соответственно. Внутри требований одного типа поддер-
живается прямой порядок обслуживания и процесс обслуживания приоритетных
требований никогда не прерывается. Если приоритетное требование поступает во
время обслуживания неприоритетного требования, то обслуживание последнего
немедленно прерывается и начинает обслуживаться приоритетное требование.
Требование, процесс обслуживания которого был прерван, вновь поступает на
прибор, когда в системе не остается приоритетных требований. Пусть рт, п —
стационарная вероятность того, что в системе имеется m приоритетных и п не-
приоритетных требований. Стационарный режим существует при pi + р2 < 1
/ Xj Х2 \ г»
Pj = —р2 = — .Доказать, что величины рт, п удовлетворяют системе
\ Р-1 Р-2 /
уравнений
{X] 4- Х2 4- p-i (1 — бш0) 4- Рг (1 ~ &по) &то] Рт, п в
e XiP/n-i, п 4-Х2Рш, п-1 + PiPm + 1, п + 1 (w, Я « 0, 1,2, ...),
где — символ Кронекера и где принимается, что величина р с отрицательным
индексом есть 0. Используя это уравнение, показать, что среднее число непри-
оритетных требований равно
оо оо
V и п — Р2 f 1 , Р2Р1 1
2j 2j прт-п 1 - р, - Р2 г + И1 и - р,) /•
т=0 п=0
20. Показать, что для системы (Л4/Л1/1), находящейся в стационарном режиме,
распределение времени между последовательными моментами ухода требований
из системы совпадает с (экспоненциальным) распределением времени между мо-
ментами поступления (см. также задачу 33 гл. 7).
21. Требования поступают в систему в соответствии с произвольным рекур-
рентным потоком. Проанализировать структуру очереди в моменты регенерации
для следующих двух систем:
Задачи
499
(1) Имеется s приборов с одинаковым экспоненциальным распределением
времени обслуживания на каждом из них.
(2) Имеется один прибор с эрланговским распределением времени обслужи-
вания.
22. Рассмотрим следующее обобщение системы обслуживания (G//G/1) с
распределениями Л(/) интервала между моментами поступления и B(t) времени
обслуживания, имеющими средние а и b соответственно. Требование, поступаю-
щее и застающее прибор свободным, ожидает случайное время с функцией
распределения V(t), а затем начинает обслуживаться.
Пусть Fn(x)—функция распределения времени ожидания n-го требования.
Показать, что предел F (х) = lim Fn (х) существует и
д->оо
(1) если b — а > 0, то F (х) == О,
(2) если Ь — а<0, то F (х) — собственная функция распределения.
*23. Обобщим идею задачи 9 на случай двух односторонних движений по
пересекающимся дорогам А и В. Движение по дороге А имеет абсолютный при-
оритет. На дороге В имеется останавливающий движение сигнал. Как и прежде,
автомобили, движущиеся по дороге Л, проезжают перекресток в моменты, обра-
зующие пуассоновский поток с параметром у,. Автомобили, движущиеся по до-
роге В, подъезжают к перекрестку в моменты, образующие пуассоновский поток
с параметром X, и выстраиваются в очередь, ожидая возможности пересечь его.
Когда автомобиль (на дороге В) становится первым в очереди, он ожидает, пока
между автомобилями, движущимися по дороге Л, не образуется временное
«окно» длительностью по крайней мере Т, и тогда пересекает перекресток за
время Т. Другие автомобили из очереди не начинают движения, пока он не пере-
сечет перекрестка. Длина автомобиля равна нулю. Найти производящую функ-
цию распределения числа автомобилей в очереди на дороге В в стационарном
режиме и среднюю длину очереди.
Указание: Это пример системы (Af/G/l), и достаточно найти распределение
«времени обслуживания» автомобилей на дороге В.
Ответ:
n(s)~ (1~^)(у~АИ(Д) , K(s)-B(b-bs).
S — Д (S)
7? лп ин <г\ _ ^ + е) в-^+9) т
В (0) = J е dH (х)-----——
ЗАМЕЧАНИЯ
Литература по теории массового обслуживания обширна. Пре-
красной монографией, в которой дается обзор этой теории с при-
ложениями, является книга Кокса и Смита [1].
Мы также рекомендуем читателю более сложные книги Така-
ча [2] и Риордана [3]. Многие результаты по теории массового об-
служивания приведены в книге Саати [4]. В ней также имеется
большая библиография.
Применения к транспортным задачам и задачам телефонии
можно найти в книге Сиски [5].
500
Гл. 14. Процессы массового обслуживания
В монографии Бенеша [6] развиты некоторые специальные
математические вопросы теории массового обслуживания.
ЛИТЕРАТУРА
1. Кокс Д. Р., Смит В. Л., Теория очередей, «Мир», М., 1966.
2. Takacs L., Introduction to the Theory of Queues, Oxford Univ. Press, London
and New York, 1962.
3. Риордан Дж., Вероятностные системы обслуживания, «Сов. радио», М.,
1966.
4. С а а т и Т. Л., Элементы теории массового обслуживания с применениями,
«Сов. радио», М., 1965.
5. S у s кд Е., Congestion Theory, Wiley, New York, 1960.
6. В e n e s V. E., General Stochastic Processes in the Theory of Queues, Addison
Wesley, Reading, Massachusetts, 1963,
ПРИЛОЖЕНИЕ
§ 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
А. Вводные понятия, линейная независимость и базис1)
Множество всех n-векторов х = (хь ..., хп), где хг-— ком-
плексные числа, образует n-мерное векторное пространство. Сум-
ма двух векторов х = (хь ..., хп) и у = (r/ь , уп) определяется
как х 4- у = (xi + ух, ..., хп + уп), а произведение вектора х на
комплексное число X по формуле Хх = (Ххь ..., Ххп).
Векторы хб), ..., х<г> называются линейно независимыми, если
из равенства
CiX(1) + с2х(2) 4- ... 4- сгх(г) = О
следует, что Сх = с2 = • . • = Ст = 0; в противном случае эти векторы
называются линейно зависимыми. Например, векторы (1,0,...,0),
(0,1, 0, ..., 0), ..., (0, ..., 0, 1) являются, очевидно, линейно
независимыми. В n-мерном векторном пространстве не может быть
более, чем п линейнр независимых векторов, или другими сло-
вами, любое множество, состоящее более чем из п векторов, ли-
нейно зависимо.
Пусть фь ..., фг, г < п,— линейно зависимые векторы. Тогда
существует вектор фг+1,не являющийся линейной комбинацией век-
торов фь ..., фг, или, что то же самое, не представимый в виде
С1ф1 4- ... + сгфг. Это означает, как легко видеть, что фЬ ..., фг+1
линейно независимы. Рассуждая далее точно так же, мы получим
множество фь ..., фп из п линейно независимых векторов, по-
строенное пополнением множества векторов фь ..., фг векторами
фг+1, ..., фп. Поскольку никакое линейно независимое множество
не может состоять более чем из п векторов, для каждого вектора у
и любого линейно независимого множества векторов фЬ ..., фп
мы можем определить (и притом единственным образом) констан-
ты сх, ..., сп, такие, что ^1ф1 4- ... 4- сп(рп = у.
Аналогичные результаты имеют место для любого линейного
подпространства 3D?, т. е. для любого множества векторов 3D?, та-
кого, что если х, у е 3D?, то ах 4- by е 3D? для любых комплексных
чисел а и Ь. Каждое линейное подпространство характеризуется
целым числом пг, 0^т^,п, называемым размерностью подпро-
Некоторые утверждения приводятся нами без доказательства; читателю
будет полезно провести их самостоятельно.
502
Приложение
странства, которое равно максимальному числу векторов, все еще
образующих линейно независимое множество. Если фь ..., фг,
г < т,— линейно независимые векторы из ЗИ, то существует век-
тор фг+1 е Зй, который нельзя представить в виде линейной ком-
бинации векторов фь фг. Как и ранее, легко показать, что
существуют векторы фг+1, ..., фт, такие, что фЬ ..., фт образуют
линейно независимое множество векторов. Более того, для любого
вектора уе® существуют (и единственны) константы С\, ..., ст,
такие, что С1ф1 + ... + стфт = у. Заметим, что если размерность
подпространства Зй равна нулю (бппЗЙ = 0), то это означает,
что Зй состоит лишь из нулевого элемента; если же dim ЯЛ = п,
то ЗЙ совпадает с исходным векторным пространством. Если
dim = т, то любое линейно независимое множество из m век-
торов, принадлежащих ЗЛ, называется базисом подпространства ЗЙ.
Мы будем пользоваться термином «базис» (без указания подпро-
странства) для обозначения любого множества из п линейно не-
зависимых векторов.
Б. Скалярное произведение
Скалярное произведение двух векторов х и у определяется
формулой
(х, у) = 5 х,у{,
t==l
где yi — числа, комплексно сопряженные с Отметим следую-
щие легко доказываемые свойства скалярного произведения:
(i) (х, х)^0, причем равенство имеет место тогда и только
тогда, когда х = (0, 0) = 0;
(ii) (Zx, у) = Z(x, у), где X — комплексное число;
(iii) (х, у) = (у^х).
Из последнего соотношения следует, что (хДу) = Х(х, у).
Говорят, что векторы х и у ортогональны, если (х, у) = 0.
Норма ||х|| вектора х определяется как ||х|| = (х, х)’/2.
Набор {ац}, i, j = 1, ..., я, комплексных чисел образует (квад-
ратную) матрицу порядка п, обычно обозначаемую А = ||а^-||,
г, j = 1, ..., п. Квадратная матрица порядка п определяет пре-
образование (или оператор) в /г-мерном пространстве, ставящее
в соответствие вектору х из этого пространства вектор у = Ах, где
п п
yi = S atfXj, i = 1, .... п, либо вектор z = хА, где Zj = S х(ац,
j = 1, ..., п.
Из этого определения непосредственно следует, что
А (ах + Ру) = аАх + рАу, (ах + ру) А = ахА + РуА
£ /. Спектральная теорема
S03
для любых векторов х_и у и любых констант аир. Кроме того,
(х, Ау) = (хА, у), где А — квадратная матрица порядка п с эле-
ментами dij.
В. Собственные значения и собственные векторы
Комплексное число X называется собственным значением (или
характеристическим числом) матрицы А, если существует такой
вектор х<%) =# 0, что Ах<М = Хх<4 Пусть X — собственное значение
матрицы А; множество состоящее из всех векторов х, таких,
что Ах = Хх, называется правым собственным подпространством
матрицы А, соответствующим собственному значению X. Элементы
подпространства называют при этом правыми собственными
(или характеристическими) векторами, соответствующими (отве-
чающими или принадлежащими) собственному значению X. Оче-
видно, что из у, z е следует, что ау 4- bz е ЗЭТх для любых
констант а и Ь. Размерность называют кратностью собствен-
ного значения X.
Если 1, ..., Ш1г — собственные подпространства оператора А,
соответствующие различным собственным значениям, то ненуле-
вые векторы фь ..., фг, принадлежащие подпространствам
соответственно, линейно независимы. В самом деле,
предположив противное, обозначим через m наименьшее целое
число, для которого существуют векторы ф^ е ШЦ, ...,
и константы с\, ст, такие, что + ... +cw<P/OT = O, где не
все Ci равны 0 и все ij, различны. Очевидно, т>2.
Применяя А к обеим частям предыдущего равенства, получаем
Л^ф/ + ... + Х^С/пФ/^ = 0. Если хотя бы одно из' собственных
значений равно нулю, то т — 1 векторов ф^. линейно зависимы,
что противоречит определению числа т. Если же все отличны
от нуля, то, умножая равенство . + cm4im == 0, например,
на и вычитая из результата равенство Л^Ф^ + ... + =
= 0, получаем
(Х2 — Л1) С2Ф/2 + • • • + Um — ^1) cm^im = 0.
Последнее также противоречит определению т.
Пусть ф(°, ..., ф^ —базис собственного подпространства ЭК.,
i=l, ..., г; легко видеть, что векторы
ф(л • • •. , ф(л • • •. • • • - <’> • • • • ф(;’г
линейно независимы. Из вышесказанного следует, что А Может
иметь лишь конечное число собственных значений и собственных
подпространств. В том важном случае, когда сумма размерностей
504
Приложение
собственных подпространств равна /г, в n-мерном векторном про-
странстве существует базис из собственных векторов матрицы А.
Матрица А, обладающая этим свойством, называется приводимой
к диагональной форме (или диагонализируемой).
Точно так же, как в предыдущих рассуждениях мы отправля-
лись от уравнения Ах = Хх, за основу можно принять уравнение
хА = Хх. Оказывается, что значения X, при которых уравнение
хА = Хх имеет ненулевое решение, суть собственные значения
матрицы А, определенные ранее. Размерность подпространства,
образуемого векторами, удовлетворяющими уравнению хА = Хх
(левыми собственными векторами), равна кратности собственного
значения X. (Читателю следует убедиться в этом самостоятельно.)
Как и в предыдущем случае, левые собственные векторы, отве-
чающие различным собственным значениям, линейно независимы.
Отметим, что собственные значения матрицы А являются кор-
нями алгебраического уравнения /г-й степени det||A — Х1||=0,
где I — единичная матрица. Отсюда следует, что если
II Ai О
А “ I В А2 ’
где А], А2 — квадратные матрицы, то X является собственным зна-
чением матрицы А тогда и только тогда, когда X — собственное
значение по крайней мере одной из матриц Ai или А2. Действи-
тельно, так как
det || А — XI || = det || А1 -- XI || det || А2 - XI ||,
где через I обозначены единичные матрицы соответствующих по-
рядков, то утверждение очевидно.
(а) Спектральное представление
В этом пункте мы будем предполагать, что матрица А действи-
тельная, т. е. что ее элементы — действительные числа. Пусть
матрица А такова, что ее правые собственные векторы образуют
базис в /г-мерном векторном пространстве. В этом случае, как
легко убедиться, левые собственные векторы также образуют ба-
зис. Если элементы матрицы А действительны, указанные базисы
можно сделать биортогональными. Покажем это. Пусть <рь ..., <рп
и -ф], ..., фи — базисы из правых и левых собственных векторов
соответственно. Биортогональность базисов означает, что
( 1, если i = j,
(фь %) | q, если /у.у.
Прежде всего отметим, что если Ах^ = Крц и у^А = ц;у;, то
Н/(У/> xt)==(|i/y/, xz) = (yzA, х/) = (у/, Ах/) = (у/, lixi)^Ki(yh xz).
§ /. Спектральная теорема So5
Таким образом, если ц; = то (у>, хг) = 0. Далее, из Ах = лх
следует, что Ах = Хх, где х = (xi,... ,хп). Это означает, что X
является собственным значением матрицы А той же кратности,
что и Л. Пусть
Zq, Л}, Z/2, ^2> • • • , +1 > ^г+2> • • • >
— собственные значения матрицы А, причем Xi, ..., — комп-
лексные, a Xr+i, — действительные. Обозначим соответствую-
щие правые собственные подпространства через ЭЙЬ 2ЙГ,
. . .,_9Ит, а левые собственные подпространства через
9 9 9 9 9 9
М’ V}, • • • , Л,г, • • • ,
Как мы уже показали, каждый вектор из 21 ортогонален лю-
бому правому собственному вектору, за исключением принадле-
жащих подпространству 2Ri. Наша задача теперь состоит в выборе
базиса *ф1, ..., подпространства 21 и базиса <pi, ..., <pd
(d — кратность собственного значения %i) подпространства 2)?ь
векторы которых обладают тем свойством, что (4ч, ф;) = d?-j. Чтобы
решить эту задачу, предположим, что фь ..., ф^— произвольный
базис в 2)?ь а уь ..., у^— произвольный базис в Нам нужно
найти такие константы Ci, ..., cd, что 4i = Cjyi + ... + cdyd и
(4'1’ фг) = 61г, i = 1, 2, . . . , d, Т' е.
С| (У1, <Р1) + сг(Уг, Ч>1) -I- • • • + cd(yd, Ф1) = 1,
С1 (У1, Фг) + с2(у2, Фг) + • • + cd(yd, Фг) = 0,
Ci (Уь Ф<г) + с2 (Уг, Ф</> + • • • + cd (yd, <fd) = 0.
Если эта система линейных уравнений относительно •••, cd не
имеет решения, то вектор (1,0,..., 0) не представим в виде ли-
нейной комбинации векторов
/1 = ((У1, Ф1), •••, (У1, фй)), Ь = ((У</, Ф1), •••, (У<г> Фа))-
Отсюда следует, что эти векторы линейно зависимы, т. е. суще-
ствуют константы <7ь ..., ad, не все равные нулю, такие, что
«if 1 + ... + «dfd == 0- Но это значит, что
(a,yi + ... +adyd, Ф,) = 0, d.
Ранее нами было доказано, что векторы уь ..., yd (а следова-
тельно, и любая их линейная комбинация) ортогональны любому
правому собственному подпространству, за исключением ЯНь Те-
перь мы видим, что aiyi + ... + adyd ортогонален всем правым
собственным векторам и, разумеется, любой их линейной комби-
нации. По предположению правые собственные векторы образуют
17 Зак. 939
506
Приложение
базис. Поэтому вектор «iyi + ... + «dYd ортогонален самому себе
и, следовательно, равен нулю. Это противоречит линейной неза-
висимости векторов уь yd. Таким образом, искомый вектор ф1
существует. Остальные векторы, ф2, • • •, фй, строятся точно так же.
Остается показать, что векторы фь ..., ф^ линейно независимы.
Предположим, что + ... + adtyd = 0; тогда
0 = (Я1Ф1 + ... + adqd, (pj =
0 = (а1ф1 + ... + ad^d, ф2) = а2,
0==(а1ф1 + ... + q)d) = ad,
а это и означает, что векторы ф^ линейно независимы.
Итак, мы показали, что действительная диагонализируемая
матрица имеет базис из правых собственных векторов фЬ ..., фп
и базис из левых собственных векторов фь ..., фп, векторы кото-
рых биортогональны, т. е. (фг-, ф;) = бг;. Мы воспользуемся этим
результатом при построении канонического представления мат-
рицы А, называемого спектральным. Пусть Аь ..., Ап— собствен-
ные значения матрицы А, а фь ..., фп и фь ..., фп — соответ-
ствующие им правые и левые собственные векторы. Пусть
<р,- = (<рг1, ..., фг„), ifi = (Фл. • • • > Фгп),
Фп • • • Фгг1
• • • Фгггг
• • • tynn
о
о ... о
а2 ... о
0 Ап
Из биортогональности базисов фь ..., фп и фь ..., фп сразу же
следует, что ЧГФ = I, где I — единичная матрица. Кроме того, не-
посредственным вычислением легко установить, что ФАТф; = А^фь
i = 1, ..., п. Поскольку Афг- = Агфь i = 1, ..., п, и векторы фя
образуют базис во всем пространстве, то
А = ФАгГ и ФТ = 1,
§ 2. Теория Фробениуса
507
Легко видеть, что Аш = ФА'ГФАТ ... ФАТ = ФЛтТ. Так как
ЛГ 0 ... 0
О Л? ... О
Aw« . • • ,
О 0 ... Кп
то Ат относительно легко вычисляется, если известно спектраль-
ное представление матрицы А.
(б) Сходимость
Нам понадобится понятие сходимости для последовательностей
векторов и матриц.
Говорят, что последовательность xW, х<2>, ... векторов п-мер-
ного векторного пространства сходится к вектору х<°), если
Ит хр = х(,0), i = 1, ...» ti.
1
Точно так же последовательность квадратных матриц AW AW, ...
порядка п сходится к матрице AW, если
lim ар) = i. / = 1, ...» п.
Из этих определений сразу же следует, что если lim A(ft) == А<0)
и lim х<;> — х<°>, то lim A(ft)x(ft) = А(0)х(0). Более того, если [А^'} —
/->ОО Л->ОО
« А (0)
последовательность матриц, для которой существует матрица А'
и базис х<'>, ..., х(,!), такие, что
lim А(Л>х(г) = А<0)х(0, /= 1, п,
h-> оо
то lim А(/г) = А<0>. Действительно, в этом случае lim А(Ыу = А<0)у
/l->oo /l->oo
для любого у, так как х(1), ..., х(п) образуют базис, а, следова-
тельно, у == CiX(I) + ... + cnx^\
§ 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
Теория положительных матриц, развитая Фробениусом, играет
важную роль во многих разделах теории вероятностей, в частности
в анализе матриц переходных вероятностей цепей Маркова.
Предварительные замечания
Если каждый элемент ац некоторой квадратной матрицы
А = ||aj|, /, / = я, неотрицателен, то мы будем писать
17:
508
П риложение
А>0; если А>0 и по крайней мере один элемент > 0, то мы
будем писать А > 0 и называть А положительной матрицей. Если
все > 0, то этот факт мы будем обозначать А >> 0. Такими же
обозначениями мы будем пользоваться и для векторов. Именно
если х = (%i, ...» хп), то х >0 означает, чго > 0 для всех
i= 1, п; х>0 означает, что х>0 и Xi > 0 хотя бы для од-
ного г, и, наконец, х>$> 0 означает, что Xi > 0 для всех i = 1, ..., п.
Мы также будем писать х>у, если х — у>0, и т. п. Ясно, что
из А^-0 и х>у следует, что Ах>Ау, аизА»0их>у сле-
дует, что Ах ,^> Ау.
Пусть А>0; рассмотрим множество Л всех действительных
чисел %, каждому из которых соответствует вектор х = (хь ..., хп),
такой, что
п
3 Х{= 1,
1=1
х > 0, Ах Хх.
Пусть Zo = БирдХ; легко показать, что Хо конечно, а в случае
когда А >> 0, еще и положительно. В самом деле, если
п
М = max aih то из условий 2^=1 и х > 0 следует, что
1 i, i = 1
n П
S а^Х] 7И X/ == Af, i = 1, ..., n, а также что Xj 1/n хотя
/=1 /=i
бы для одного /. Отсюда получаем неравенство ?,0^пМ. Если
А»0и 0 < S-- min aih то это означает, что чис-
к«,/<п /
ло (Ему соответствует вектор х = (1/п,..., 1/п).)
Предположим теперь, что л0 = 0 для матрицы А > 0. Для
х^> 0 соотношение Ах 0 невозможно, так как Ло = 0. С другой
стороны, из равенства Ах = 0 для некоторого х 0 следует, что
А = 0. Таким образом, существует вектор х 0, такой, что Ах>0.
Пусть Ci — множество индексов положительных элементов век-
тора Ах; очевидно, С\ не зависит от выбора вектора х Х>> 0. Пусть
вектор у = (z/i,..., Уп) > 0 таков, что yt > 0, если i е Сь и уг = 0,
если 1фС\. Определим С2 как множество индексов положитель-
ных координат вектора Ау; это множество не зависит от выбора
вектора у и, кроме того, C2^Ci. Поскольку Хо = 0, то С2 =/= Сь
Рассуждая точно так же, легко убедиться, что
С] ZD С2 ~ ~' 0?
причем здесь все включения являются строгими. Теперь уже не
составляет труда показать, что А™ = 0. Действительно, А™х = 0
для х^>0, но так как любой вектор может быть представлен как
разность двух строго положительных векторов, то Amz = 0 для
любого z, что эквивалентно равенству нулю матрицы Aw.
§ 2. Теория Фробениуса
509
Первая теорема Фробениуса
Теорема 2.1. Если А >> 0, то (а) существует вектор х°и$>0,
такой, что Ах° = Хох°; (б) | X| < Хо для всех собственных значе-
ний К матрицы А, отличных от Хо*, (в) правые собственные век-
торы матрицы А, соответствующие Хо, образуют одномерное под-
пространство, т. е. dim == 1.
Доказательство, (а) По определению Хо существует после-
довательность yi, у2, ...-~>Хо и векторы хб), х<2), ..., такие, что
х(/)>0, Ах(/) yfx(f), х(/}+ ... +х^=1. (П.2.1)
Так как значения компонент всех векторов хб’> принадлежат от-
резку [0, 1], то с помощью процесса диагонализации мы можем
построить последовательность положительных целых чисел
П\ <П2 <п^ , такую, что
lim х^ -+х°, г = 1, п, (П.2.2)
где [0, 1], г=1,2, ..., п. Из (2.1) следует, что х^ + ... + = 1
и х° = (ху, ..., х^)>0. Кроме того, если мы заменим в неравен-
стве АхО') > yzx(0 индекс i на п$ и устремим j к оо, то придем
к неравенству Ах° > Хох°. Мы покажем, что на самом деле
Ах° = Хох0. Действительно, если это не так, то Ах° > Хох°. Умно-
жая обе части этого неравенства слева на А, получаем неравен-
ство Ау° Хоу°, где у° = Ах°££>0. Это неравенство сохранится и
тогда, когда мы прибавим к Хо достаточно малое положительное
число е: Ау° >> (Хо + е)у°. Нормируя вектор у0 так, чтобы сумма
его координат равнялась единице, мы убеждаемся в том, что
Хо + е принадлежит множеству Л. Но последнее противоречит
определению Хо. Таким образом, Ах° = Хох0. Поскольку х° > 0,
а А:^ 0, то Хох° >> 0, т. е. х° 0. Этим завершается доказатель-
ство утверждения (а).
(б) Пусть Х=#Хо и Az = Xz, где z=#0. Координатная запись
равенства Az == Xz имеет вид
п
2 aZ/Zy = Лгг, г=1, п.
Отсюда для абсолютных величин имеем
п
2 ан | Zj |
I А. | | Zj |,
i = 1, ...» п,
т. е.
A|z|>|Z||z|, где | z | = (| Zj |, ..., |z„|).
Нормируя вектор |z| так, чтобы сумма его координат равнялась
единице (напомним, что z¥=0), мы видим, что принадле-
жит Л. Тогда по определению /,0 имеем |Х|^ГХО. Чтобы показать,
510
П риложение
что |Х| < Хо, введем матрицу А6 = А — 61, где I — единичная мат-
рица, а 6 — положительное число, малое настолько, что Аб^> 0.
Поскольку Хо — наибольшее по абсолютной величине положитель-
ное собственное значение матрицы А, то X — 6 является таковым
для матрицы Аб. Повторяя те же рассуждения, что и при дока-
зательстве неравенства |Х| -<Х0, для матрицы Аб и ее собствен-
ного значения X — 6, получаем неравенство |Х — 6|^Х0—6. Но,
с другой стороны,
| X | = I X — 6 + 6|<| X- 6| + 6<Х0,
так что из |Х| == Хо следует |Х| = |Х — 6| + 6. Последнее означает,
что X действительно и положительно. Таким образом, имеет место
равенство Х = |Х| = Х0, что противоречит исходному предположе-
нию (X =#Хо).
(в) Предположим, что Ау = Хоу и не существует такой кон-
станты с, что у = сх°. Поскольку А — действительная матрица,
векторы и и v, координатами которых служат соответственно дей-
ствительные и мнимые части координат вектора у, являются соб-
ственными векторами матрицы А, соответствующими Хо. По-
скольку у =# сх° для всех констант с, то по крайней мере один
из векторов и или v не представим в виде сх°. Поэтому мы
можем считать вектор у действительным. Так как х° 0, можно
выбрать такое число р, что х° — ру > 0, но не ^>0; при этом
| р |= min 1х®1\ у. | 1. Отсюда А(х° — ру) = Хо(х° — ру), и, как и
1 11 1 1 J
в доказательстве утверждения (а), с необходимостью получаем:
(х°— ру) >> 0. Это противоречит выбору р. Б
Отметим попутно несколько простых фактов. Если А^+0, то
можно утверждать, что существует вектор f° 0, такой, что
f°A = Xof°, а подпространство левых собственных векторов, соот-
ветствующих Хо, одномерно. Следуя доказательству теоремы 2.1,
положим Xх = зирл'Х, где Л' = {Х| fA > Xf для некоторого f > 0}.
Легко убедиться в существовании вектора f° >> 0, такого, что
f°A = Xxf°, в одномерности подпространства левых собственных
векторов, отвечающих Xх, а также в том, что если X — любое соб-
ственное значение матрицы А, не равное Xх, то | X | < Xх. Но от-
сюда следует, что | Хо | < Xх, если Хо ¥= Xх, тогда как по теореме 2.1
| Xх | < Хо, если собственное значение Xх отлично от Хо. Следова-
тельно, Xх = Хо.
Теорема 2.2. Если матрица А>0 такова, что Aw^>0 для
некоторого целого числа т> 0, то для нее остаются справедли-
выми утверждения предыдущей теоремы.
Доказательство. Как и в доказательстве теоремы 2.1,
мы можем найти вектор х° > 0, такой, что Ах° > Хох°. Если
§ 2. Теория Фробениуса
511
Ах° = Хох0, то Ах° > Хох0. Умножая обе части этого неравенства
слева на Aw, приходим к соотношению Ay CgXoy, где у = Awx° 'Э? 0.
Это противоречит определению Ло (см. доказательство теоре-
мы 2.1); следовательно, Ах° = %ох°. Отсюда получаем соотношение
Атх° = Хогх°. Так как Д'" >0 и х°>0, то Л?‘х°» 0, т. е. х° > 0.
Для доказательства неравенства |Х| в пункте (б) тео-
ремы 2.1 нам было бы достаточно положительности (не строгой)
матрицы А. Поэтому это неравенство выполняется и в условиях
настоящей теоремы. Предположим, что |%| =%0 И Az = %z для
некоторого вектора z =# 0. Тогда A z = Л z, А х = Ло х и
| Кт | = Ло- Если мы покажем, что Хо* является наибольшим по мо-
дулю положительным собственным значением матрицы Аш, то
теорема 2.1 сразу же приведет нас к противоречию. Так как
Ат 0, то Ат имеет наибольшее по модулю положительное соб-
ственное значение по теореме 2.1, которому соответствует соб-
ственный вектор с положительными компонентами. В таком слу-
чае, если Хо* не является наибольшим по модулю положительным
собственным значением матрицы А™, то матрица Аш имеет по
крайней мере два положительных собственных значения > %2,
которым соответствуют собственные векторы х1,х2^>0. Но это
невозможно; действительно, пусть ц>0 таково, что х2— pxi > 0,
но не >> 0. Тогда Ат(х2— pxi)^ 0. С другой стороны,
А™(х2 — pxj = Х2х2 — pZiXi = Х2(х2 — р,хх) — (Л1 — Л2)рхь Поскольку
вектор (х2 — pxi) имеет по крайней мере одну нулевую компо-
ненту, в то время как все компоненты вектора Xi положительны,
мы приходим к противоречию.
Тот факт, что все собственные векторы матрицы А являются
собственными векторами матрицы Aw, сводит доказательство
утверждения (в) к повторению доказательства утверждения (в)
теоремы 2.1.
Продолжая изучение матриц А >0, для которых Ат > 0 при
некотором целом т > 0, введем матрицу ранга 1 по формуле
р=1Ю1.
где х° — правый собственный вектор, введенный в доказательстве
теоремы 2.1, a f0 0 — левый собственный вектор, принадлежа-
п
щий Хо и нормированный условием Такая матрица
обладает следующими свойствами:
(I) Рх = (х, f°)x°, fP = (f, x°)f° для любых векторов х и f и,
в частности, Рх° = х°, f°P = f°;
(И) Р2 = Р;
(III) АР = РА = Л0Р.
512
/7 риложение
Первые два свойства проверяются непосредственно; что же ка-
сается третьего, то заметим, что для любого вектора х имеем
АРх = А (х, f°) х° = (х, f°) Ах° = (х, f°) Хох° = Х0Рх,
так что АР = ХоР; аналогично fPA = fX0P, т. е. РА = Х0Р.
Приведем без доказательства следующий факт. Пусть В —
квадратная матрица; положим
г == lim Vmax | |,
П->оо /, /
где — элементы матрицы В^. Матрица В имеет собственное
значение X*, такое, что |Х*| = г; для всех других собственных
значений X матрицы В имеет место неравенство | X | < г.
г часто называют спектральным радиусом матрицы. Мы вос-
пользуемся этим понятием при доказательстве следующей тео-
ремы.
Теорема 2.3. Если А > 0 и Атх>0 для некоторого целого
m > О, то
где Хо и Р имеют прежний смысл.
Док а з ат е ль ст в о. Покажем сначала, что если X является
собственным значением матрицы В = А — Х0Р, то | X | < Хо. Дей-
ствительно, предположим, что Bz = Xz при некотором z =# 0; тогда
XPz - PBz = Р (А - X0P)z = (Х0Р - X0P2)z = Х0(Р - Р) z = 0,
откуда следует, что всякое собственное значение матрицы В яв-
ляется собственным значением матрицы А; то же можно сказать
о собственных векторах. Из теоремы 2.2 следует, что либо X = Хо,
либо | X| < Хо. Предположим, что X = Хо, тогда в силу одномерно-
сти собственного подпространства, соответствующего Хо, мат-
рицы А, а следовательно, и матрицы В имеет место соотношение
Вх° = Хох°. С другой стороны, Вх° = (А — Х0Р)х° = Ах° — Х0Рх° =
= Хох° — ХоХ° = 0. Получаем противоречие. Значит, спектральный
радиус г матрицы В удовлетворяет неравенству г < Хо. Пусть р —
положительное число, такое, что г < р < Хо; поскольку
г — lim V^maxl&^l <р,
n->oo i, j
то max | Ь(ц | <on для достаточно больших и. Используя свой-
к /
ства (II) и (III) матрицы Р, получаем
= Ат - Хо"Р,
§ 2. Теория Фробениуса
513
или
Так как тах|&//)|<рч для достаточно больших п, то
i. I
а следовательно, В”1/Ло’->0.
Вторая теорема Фробениуса
Теорема 2.4. Пусть А > О, а Хо имеет тот же смысл, что и
в теореме 2.1; тогда-, (а) Хо является собственным значением ма-
трицы А и ему соответствует собственный вектор х° > 0; (б) если
X— любое другое собственное значение матрицы А, то |Х| -<Хо;
(в) среднее
сходится, если х°^г>0; (г) если "к— собственное значение мат-
рицы А и |Х| = Хо, то т) = Х/Хо является корнем из единицы,
а т)тХо, гп = 0, 1, 2, ..., суть собственные значения матрицы А.
Доказательство, (а) Пусть Е — матрица, все элементы
которой равны единице; тогда А + бЕ.^0 при любом б > 0.
Пусть 0 < 61 < 62. Выберем х = (хь .... хп) > 0 таким, что
2 Xt = 1, тогда из (А + 6iE)x>Xx следует, что
(А + 62Е) х = (А + 6(E) х + (62 — 6J Ex [X + (б2 — 6])] х.
Таким образом, если Хо(6) — значение Хо, соответствующее матрице
А + 6Е, то Хо(б) является возрастающей функцией аргумента 6.
Заметим, что Хо(О) есть значение Хо, соответствующее самой мат-
рице А. По теореме 2.1 существует вектор х(6)>5>0, нормирован-
ный условием 2 *<(б)= 1, такой, что
1 = 1
(А + 6Е) х (6) == (6) х (6).
Пусть 61 > S2 > • • • — последовательность положительных чисел,
сходящаяся к нулю. Как и при доказательстве теоремы 2.1, мы
514
Приложение
можем выделить последовательность целых чисел П\, п2, .та-
п
кую, что lim х .) -> х°, где вектор х° > 0 и 2 = 1. Ясно, что А +
/ -> оо 1 1 = 1
+ 6^Е—>А И Хо (6/гу) К Хо- Поскольку
(А + SrtyE) X (бПу) = Хо (б/гу) X (б/гу),
в пределе при /~^оо получаем равенство Ах° = Х'х°. Но из дока-
зательства пункта (б) теоремы 2.1 следует, что Хо^Х'; значит,
Хо = XX
Доказательство утверждения (б) совпадает с доказательством
для случая А 1^> 0.
Доказывая утверждения (в) и (г), мы можем предположить
без потери общности, что Хо = 1, так как если Хо =# 1, то можно
разделить каждый элемент матрицы А на Хо-
(в) Так как Ах0 = х0, то Ажх0 = х0. Записав это соотношение
в координатной форме, мы сразу же найдем, что
max х®
Таким образом, элементы матриц Aw равномерно ограничены.
Пусть L = {х: Ах = х} и К = {у: у = (I — А)х для некото-
рого х}, т. е. L есть линейное пространство неподвижных точек
матрицы А, а К — линейное пространство, совпадающее с об-
ластью значений матрицы I — А. Положим еще
ч = А + А2+ ••• + A™
т
Ясно, что L является замкнутым линейным пространством, таким,
что для каждого х из L
и следовательно, lim Smx = x. Мы покажем также, что Smx схо-
т-» оо
дится для каждого х из К и что м-мерное векторное пространство
можно представить в виде прямой суммы пространств L и К.
Этим мы докажем утверждение (в).
Покажем сначала, что lim Smy = O для всякого уеК. Ho-
rn-»^
скольку у = (I —А)х при некотором х,
Ч — Ау + • • • + АтУ __ Ах — Ат + 1х
т-У т т
стремится к 0 при т-*оо в силу того, что элементы матриц А™
равномерно ограничены.
§ 2. Теория Фробениуса
515
Чтобы показать, что каждый вектор х можно представить в
виде суммы вектора из L и вектора из К, разложим х в сумму
вида
х = (х Smx) + Smx = ут + zm.
Так как элементы матриц Aw равномерно ограничены, то ограни-
чены и компоненты векторов ут и zm. Поэтому существует после-
довательность положительных целых чисел т\ < m2 < ... и век-
тор z°, такие, что
lim zm = z0.
i->oo
Поскольку
a-a'”/+1
zm. - Azm =-----------------—-----x —> О при г -> oo,
I 11^1
TO
z0 = lim zm.= lim kzm. = A lim zm. = Az0,
i->oo 1 i-+<X> 1 1
t. e. Zo L.
Кроме того,
ym = x - Smx = -T [(x - Ax) + (x - A2x) + ... + (x - Amx)] =
— л д\Г x 1 (I + A)x 1 (I+A + A2)x ,
' ' L fn fn *" m i~ • • •
, (i+A + A2+ ... +A'”~1)x]
• • • ” m J >
откуда следует, что ymeK. Так как К — замкнутое линейное
пространство и элементы векторов ут равномерно ограничены, то
ym. х — z0 е К при i -> оо. Итак, х = (х — z0) + z0, где х — z0^К,
zoe L, и доказательство утверждения (в) закончено.
(г) Мы знаем, что существует вектор f° > 0, такой, что f°A=f°.
Предположим сначала, что f°£^>0. Пусть теперь Х=#1, |Л| = 1 и
Ах = Хх при некотором х 4= 0; тогда
п
У atjXj = Xxlt I = 1, 2, . . . , п,
и, таким образом,
п
3 ац\ Х/\ xt!, или А|х|>|х|.
Но если А|х|>|х|, то (f°, |х|) < (f°, А|х|) = (f°A, |х|) = (f°, |х|).
Итак, А|х| = |х|; следовательно,
п
3 Иц\ Xj 1 = 1 Xi 1 =
п
i = 1, 2, ..п.
Г16 Приложение
Это означает, что существуют такие константы =
что
a^Xj = а^\ Xj |pz при всех i и /. (*)
Обозначим через х-у вектор (xjz/i, хпуп). Умножая соотно-
шение (*) на и суммируя по /, получаем
А (х • gr) = ц • А (| х | • iiг).
В то же время суммирование по i приводит к равенству
Ах == ц • А | х |,
откуда следует, что
Хх = ц • | х |.
Далее,
А (х • gr) = g • А (Лх • jV"1) = Лц • А (х • Цг-1), г = 1, 2, ...,
откуда следует, что А(х-р/) = АЛм(цг-х). Итак, Хг является соб-
ственным значением матрицы А при г = 1, 2, ... . Поскольку чис-
ло собственных значений матрицы А конечно, % должно быть
корнем из единицы.
Пусть теперь f° > 0, но не >>-0. Проведя в случае надобности
перенумерацию строк и столбцов матрицы А, мы можем считать,
что f° = (f°, 0, 0), где f?>0, /=1, г. Так как
А > 0, то из соотношения f°A = f° вытекает, что
II Ai 0
А = | В А2 ’
где порядки квадратных матриц А] и А2 равны соответственно г
и п — г. Вектор ..., является левым собственным векто-
ром матрицы Аь Пусть %— собственное значение матрицы А;
тогда, если X является собственным значением матрицы Аь то за-
дача сводится к рассмотренному выше случаю. Если же л не
является собственным значением матрицы Аь то оно должно быть
собственным значением матрицы А2. Но собственные значения
матрицы Аг являются собственными значениями матрицы А п по-
этому не превышают по модулю единицы. В то же время, так как
А2 > 0, то она имеет наибольшее положительное собственное зна-
чение, являющееся верхней границей для абсолютных величин
всех остальных ее собственных значений. Так как |%|= 1, то наи-
большее собственное значение матрицы А2 равно единице. Теперь
предыдущие рассуждения применимы к матрице Л2, именно: ли-
бо А2 имеет левый собственный вектор со всеми положительными
координатами, соответствующий собственному значению 1, либо А2
§ 2. Теория Фробениуса
517
имеет вид (после соответствующей перенумерации строк и столб-
цов)
А |А3 0 II
Нв, а4Г
Продолжая таким образом, мы придем за конечное число шагов
к ситуации, когда существует левый собственный вектор О,
соответствующий собственному значению 1.
Приводимые ниже следствия содержат полезную информацию
относительно спектрального радиуса Z0(A) положительной мат-
рицы А. Первое из них представляет собой другую формулировку
утверждений (а) и (б) теоремы 2.4.
Следствие 2.1. Если А > О, то наибольшее по абсолютной
величине собственное значение Хо = МА) является действитель-
ным неотрицательным и может быть охарактеризовано как
Ло = max X, где
д
Л = {Л,| Ах>Лх, х>0}.
Следствие 2.2. Если А>0 и существует вектор 0, та-
кой, что Ах°^цх0, то ц является верхней границей для Х0(А).
Доказательство. Умножая слева на А обе части нера-
венства Ах° рх°, получаем А2х° < цАх° ц2х°. Легко видеть,
что и в общем случае
Алх°<|Л0, п==1, 2, ...,
откуда сразу же следует неравенство
ч
max x°j
i_____
min x®
Это неравенство приводит к оценке
Л0(А)== lim Утах I I < pi. В
П->оо i, J 11 1
Следствие 2.3. Если А^В^О, то Хо(В)^Хо(А).
Доказательство. Так как из А В > 0 следует, что
Ап > Вп > 0, п = 1, 2, ..., то
Л0(А) = lim ymaxa^^ lim УтахМ'р = ЛП(В). В
л->оо i, j 1 it j 7
РАЗЛИЧНЫЕ ЗАДАЧИ
1 . Рассмотрим популяцию из п пар, в которой у i-и пары с вероятностью pt
рождается мальчик, а среднее число детей в семье равно с. Предположим, что
вероятности pi остаются постоянными во времени для всех пар, при каждых
родах рождается не более одного ребенка, а пол рожденного ребенка не зависит
от пола детей, рожденных ранее и тех, что появятся на свет после него. Введем
характеристику распределения детей по полу
S =
среднее число мальчиков, рожденных в популяции из п пар
среднее число детей, рожденных в популяции из п пар
Найти S для этой популяции.
/ \ f
Ответ: S 8^= ( pj \ п.
\ ™ 1 Г
2 (продолжение). Показать, что если все пары
тех пор, пока не будет рожден мальчик, после чего
решают рождать детей до
детей больше не имеют, то
So.
3 (продолжение). Предположим, что все пары в зависимости от того, маль-
чик или девочка их первый ребенок, продолжают рождать детей, пока не будет
рождена девочка или, во втором случае, мальчик, после чего детей больше не
имеют. Найти S для этого случая.
Ответ:
{П п 1
д=г>2 = _^--------<,. = 1-^.
SfMil
х = 1
4 (продолжение). Пусть все пары, если их первый ребенок —- мальчик, про-
должают рождать детей, пока не родится девочка. Если же первый ребенок —
девочка, то пары ограничиваются одним ребенком. Найти S.
Ответ:
п
i — 1
5 (продолжение). Показать, что в
жет быть как S2 > So, так и S2 So.
зависимости от значений pi}
.., рп мо--
Различные задачи
519
6 (продолжение), а) Предположим, что вероятность осложнений при родах
для i-й пары равна р;, t = 1, п, а наступление осложнений приводит к тому,
что пара решает больше детей не иметь. Пусть s — число детей в отдельно взя-
той семье при условии отсутствия родов с осложнениями, и вероятность родов
с осложнениями pi не изменяется во времени. Показать, что
11-<71
среднее число родов с осложнениями __ j-i_______
1 среднее число рожденных детей " .
5 V-qSi)lPi
б) Предположим, что пара решает больше не иметь детей после двух (а не
одних, как ранее) родов с осложнениями. Показать, что в этом случае
^ = “7^---------------------•
7. Пусть X и У — пара независимых неотрицательных целочисленных с. в.,
обладающих тем свойством, что
для всех неотрицательных целых чисел х и у (пг и п — заданные положительные
целые числа). Предположим, что вероятности Р {X = 0} и Р {У = 0} строго поло-
жительны. Показать, что как X, так и У распределены по биномиальному закону
с одним и тем же параметром р, причем другими параметрами служат tn и п
соответственно.
8. (а) Пусть X и У — независимые случайные величины, такие, что Р {X = /}=
оо оо
= P{l^W(0, где /(0>0 и
2,... . Пусть, кроме того,
Sf(/)=Sg(0 = l>
i*e0 2=0
f = 0, 1,
P{X = k\X + Y~l)
( I
\ £
о,
k>l.
) pk (1 - p)l~k,
Доказать, что
f (i) = e-e“ g(i)=-e-e-^, a = 0. 1. 2......
где a = p/(l-p) и 0>O
(б) Показать, что p
произвольно.
определяется из уравнения
G (s) - У, g (г)
520
Различные задачи
Указание'. Сначала установить соотношение
F (и) F (v) = F (vp + (1 — р) и) G (vp -г (I — р) и),
где F (s) = У f (г) s'.
9. Пусть X — неотрицательная целочисленная с. в. с производящей функцией
f (s) = 2 anSn> Предположим, что после наблюдения с в. X проводится X бино-
п=0
миальных испытаний с вероятностью успеха, равной р. Пусть У обозначает ре-
зультирующее число успехов.
(а) Найти производящую функцию с. в. У.
(б) Найти производящую функцию условного распределения X при условии,
что X биномиальных испытаний закончились успехом.
Ответ: (a) f(l—p + qs); (б) f(ps)/f(p).
10 (продолжение). Предположим, что при каждом р (0<р< 1) производя-
щие функции вероятностей (а) и (б) совпадают. Доказать, что в этом случае
с. в. X распределена по закону Пуассона, т. е. f(s) с некоторым па-
раметром А > 0.
11 . Рассмотрим последовательность Xi, Х2, ... независимых одинаково рас-
пределенных с. в., функция распределения которых F(x) непрерывна. Значение
Хк называется «рекордным», если
Xk > max (Хь .Yg, • • •, Х^—i).
(По определению значение X] является рекордным.)
Пусть Nn есть число рекордных значений в последовательности Хь Х2,..., Хп,
a Vk—индекс &-го рекордного значения (см. задачи 21—28 гл. 9). Доказать со-
отношение
Р{П>«)=Р{^<Н1).
12 (продолжение). Доказать формулу
p(iv =Г| = 1 У ________________________!__________L—______________L—
{ п 1 п U. (n-kr-i) (n-kr-2) (n-ki)'
1 < fej < k2< ... < kr_ t < n
13. Пусть Xi, X'2, ..., Xm и Уь У2, ..., Уп — выборки соответственно из tn
и n случайных величин с одной и той же непрерывной функцией распределения
вероятностей F (х). Пусть N — число значений в выборке из второго набора, не
превышающих Xk, k-n порядковой статистики первого набора. Показать, что
распределение с. в. N имеет вид
I пг \ / п \
р О'=«= 11 _yL для /=0> ।.........
( m + п\ k +1
\ k + l /
Указание: Воспользоваться результатом задачи 7 гл. 9.
14. Рассмотрим выборку объема п из популяции с функцией плотности ве-
роятностей f(x). Из этой же популяции берется другая выборка того же объема,
не зависящая от первой. Пусть £/" — число значений во второй выборке, превы-
шающих r-е наименьшее значение в первой выборке, aVj - число значений во
Различные задачи
521
второй выборке, больших s-ro наибольшего значения в первой выборке. Дока-
зать, что
Р \ипг = х)
п — х+г—1\/п— г + х \ ( п — 1 \ ( И \
г — 1 / \ X / _ 1 \ Г — 1 / \ х /
/ 2п \ 2 / 2п — 1 \
\ п ) \п—г+х/
х = 0, 1..п, и, кроме того, что
Р = х] = Р [уп = х], где s — n — r.
Указание: Воспользоваться результатом задачи 7 гл. 9.
15. Пусть Xi, Х2, Хт и У1, У2, Yn—независимые наблюдения над
случайными величинами с распределениями F(x) и G(y) соответственно. Пред-
положим, что F и G — непрерывные функции и
Г=Об, д>0.
Пусть
Xf, tn^ Х2, •••
и
У1, п < У2, п ••• Уд, п
суть порядковые статистики соответствующих выборок. Найти
Р {X/n—i, п< X/n—i + ], т I ^п, п ж
Ответ:
(7) (°
16 (продолжение). Найти вероятность того, что ровно i значений из первой
выборки больше всех значений из второй выборки.
Ответ:
/ tn\ п Г ((n/d) + m — i) Г (i + 1)
Г ((п/6) Л-m + 1)
17 (продолжение). Найти вероятность того, что ровно i значений из первой
выборки меньше всех значений из второй выборки.
Ответ:
тп— i
. ) п! (-!)r ( r ) [6(z + r) + i]Id(z + r) + 2]. ... .[d(t + r)+n] •
r«0
18. Пусть Xi, Х2, ..., Xm и Уь У2, ..., Уп — независимые случайные вы-
борки для распределений F (х) и G(y) соответственно. Предположим, что F(x)
и G(y) —непрерывные строго возрастающие функции, и положим
р = Р{У<Х},
где X и У — независимые с. в. с распределениями F и G соответственно. По-
ложим
U = число пар (X/, У у), для которых Уу<Х/.
Показать, что
М (U) = тпр.
Указание: Представить U в виде
т, п
2 ич>
где
( 1, если
[ 0, если
Yj < Xi,
Yj>Xi.
522
Различные задачи
19 (продолжение). Показать, что
a2 (U) = тп {(т — 1) а 4- (п — 1) р — (т + п — 1) р2 + (2т — 1) р ~ (т — 1)},
где
1 1
а= J L[(t)]2dt, р= 1 —2 j iL (t) dt,
О о
L(t) = F(G~} (t)) и G~'— функция, обратная к G.
20. Пусть gi, g2, ...» — совокупность из n независимых равномерно рас-
пределенных на [0, /] с. в. Найти среднее и дисперсию их минимума.
Ответ: Среднее равно t/n + 1; дисперсия равна nt2/[(n + 1 )2(п + 2)].
21. Пусть Xi, Х2, . Хп—независимые с. в. с плотностями fi(x), f2(x), ...
.fn(x) и распределениями Fi(x), Fzix), ..., Fn(x) соответственно. Положим
Z = min(Xi, Х2, .Хп) и N — первый индекс, при котором достигается
min(X], Х2, ..., Хп). Пусть
Доказать, что
Hk(z) = P{N~k, Z<?}.
/Г JI {(1-Г/W)}] М(0
dt.
— оо L/ =5^ k
22. Группа из 2П игроков, в равной степени искусных, принимает участие в
следующей незамысловатой игре. Игроки разбиваются на пары случайным обра-
зом и проводят партию; вероятность выигрыша для каждого из них равна 1/2.
В следующей партии 2п~1 победителей опять разбиваются на пары случайным
образом и т. д. Игра продолжается до тех пор, пока не останется один победи-
тель. Пусть игрок А и игрок Б принимают участие в игре; какова вероятность
этим игрокам когда-нибудь оказаться противниками?
Ответ:
р.=(4Г.
23. Игроки А и Б договариваются провести N бросаний правильной монеты
на условиях, соответствующих безобидной игре. Какова вероятность pN того,
что во время игры они ни разу не окажутся при своих интересах?
Ответ:
( /У-П 1
I п ] 2N - \ ' если ЛГ = 2/г+1>
PN I (п)/2^ еСЛИ ЛГ = 2/г-
24. Пусть X], Х2, ... — последовательность с. в., такая, что Хд равномерно
распределена в интервале (Хд_1, 1) и Хо^О. Доказать, что
оо оо
i — 1 i — 1
Различные задачи
523
вид
Указание". По индукции доказать, что плотность вероятностей с. в. Хг- имеет
(- In (1-х) И"1
(г-1)!
п
25 (продолжение). Показать, что — М (In У/) ограничены равномерно
i = i
по п.
Указание-. Показать, что
П оо П — 1 , оо оо
-^M(lnXz) = - j J ln(l-e-“)d<o = 2-^-
4 = 1 0 i=0 0 fc=l
26 (продолжение). Показать, что
(oo \
= B | = e5-1.
i =*k /
(oo \
JJ Xi | Xk-\ « £ j. (Почему ср не зависит
i=k /
от k?) Воспользоваться результатом предыдущего упражнения для того, чтобы
показать, что ср(£) #=0 при О g < 1. Затем вывести функциональное уравнение
1
4>W = TZ7 <р0) = 1>
X
и найти его решения. Это уравнение имеет два решения, одно из которых непре-
рывно в точке 1, а другое разрывно. Показать, что решение (р(£) = 0 (0 < 1),
q-(l) = 1 не является искомым.
/ оо \ оо
27 (продолжение). Показать, что М I Ц X/1 =/= JJ М (Х/)> и указать, ка-
V-1 / i-1
кая из этих величин больше.
Ответ:
(оо \ оо
П*г >Пм®.
1 / 1
28. Урна содержит п различных занумерованных шаров. Нам ничего не из-
вестно о том, каковы эти номера. Мы извлекаем шары один за одним и оста-
навливаемся тогда, когда так или иначе приходим к заключению, что номер
последнего извлеченного шара является наибольшим среди номеров всех п шаров.
Наша цель — максимизировать вероятность того, что это заключение справед-
ливо.
(а) Рассмотрим следующие стратегии остановки: сначала извлечь ш шаров;
продолжать извлечение до тех пор, пока номер последнего извлеченного шара не
будет больше номеров первых пг шаров. Какова вероятность того, что номер
последнего извлеченного шара наибольший среди всех?
(б) Выберем р между 0 и 1 и пусть m = [пр] (наибольшее целое число,
меньшее, чем пр). Каково значение р, асимптотически (при п->оо) наилучшее
в смысле максимизации указанной вероятности?
524
Раз.шчиые задачи
Решение, (а) После извлечения шара, номер которого мы считаем наиболь-
шим среди номеров всех п шаров, продолжим извлечение и выясним, какой же
на самом деле наибольший номер. Тогда
Р {выбранный номер наибольший) =
п-1
Sp f (k + 1)-й является наибольшим во всей совокупности и 1
( наибольший среди первых k содержится среди первых т J
k=m
п — 1
, 1Ч „ ... n f наибольший среди первых k )
Р Hl-и номер наиоольшии} • Р< г
1 г ( содержится среди первых т J
k~m
п — 1 n —1
_ 1 т __ т V* 1
п k п k ‘
k=m k=>m
Другое доказательство состоит в следующем. Предположим, что номера на
шарах представляют собой выборку объема п при некотором известном нам не-
прерывном распределении F. Покажем, что результат не зависит от F. Действи-
тельно,
Р {выбранный номер наибольший} —
П~ 1 оо
= j Р {max (Хт+и Хт+2, .... Xk) < х) X
k=>m —оо
X р {А'й +1 = max {Xk+b Xk+2, .... Хп) > х) Р {max (ЛГ,. ..., Хт) > х}.
В силу независимости правая часть этого выражения равна
11 — 1 °о
j Fk~m (х)-^-^[\~Fn~k(x)\mFm~l (x)dF(x) =
k^m —оо
п— 1 1 п— 1 п —1
- S-Гт 2 4.
k=m 0 k — tn k—m
здесь I = F (x).
(б) Воспользовавшись найденным решением, получаем
п— 1 п-1 п
m v 1 УчЛ V 1 Г 1 1
— — /, -г~р — dx=-plnp.
п м k п k J X
k=--m k=[npl пр
d!dp[—pin p] = 1 — In p является убывающей функцией p при 0 < р 1. Макси-
мум достигается при 1п р = —1, т. е. при р = е~'.
29. Задача Банаха о спичечных коробках формулируется следующим обра-
зом. Некто носит с собой две коробки спичек А и Б, в которых первоначально
было М и N спичек соответственно. Когда ему нужна спичка, он берет ее из
коробки А с вероятностью р (0 < р < 1) или из коробки Б с вероятностью 1 — р.
Найти вероятность иг того, что в момент, когда одна из коробок окажется пу-
стой, в другой будет г спичек.
Различные задачи
525
Ответ'.
( M + N-г \ м+1 v_r / M + N -г \ м-r N+\
Ur \ М !Р q \N )Р Я '
30 (продолжение). Предположим, что всякий раз, когда выбор падает на
коробку А, из нее извлекают две спички, а когда выбор падает на коробку Б,
из нее по-прежнему извлекают одну спичку. Найти иг.
Ответ:
[ЛГ/2] )Р Я +\ N )Р 4 г>
{1, если М — г четно,
0, если М — г нечетно.
31. Пусть {%{(/); t 0}, i= 1, 2, — независимые пуассоновские процессы с
параметрами М и Лг соответственно. Предположим, что Xi(0) « m, Хг(0) = N — 1
и m < N. (а) Найти вероятность того, что процесс Хг достигнет состояния W
раньше, чем процесс Xi. (б) Решить эту же задачу для случая, когда Х2 (0) — п,
n<N.
Ответ:
N—m—1
V ( N-n + r-l\ r„N-n
(б) 1 ( г )pq • /’“TTW
r=0
32. Проводятся последовательные независимые наблюдения случайной ве-
личины, плотность вероятностей которой имеет вид •
( хе~х, х>0,
,V>-[ о, л < 0.
Наблюдения проводятся до тех пор, пока сумма наблюденных значений не пре-
высит числа t. Пусть N + 1 — число требующихся для этого наблюдений. По-
казать, что
Г.1М i Z2ra+1e-/ , t2ne~(
Р Г (2га + 2) + Г (2n + 1) •
33. Рассмотрим процесс восстановления с функцией распределения F(x) (см.
задачи 8—9 гл. 8). Предположим, что каждое событие с вероятностью 1—q не
регистрируется («стирается»). Изменим масштаб времени на множитель 1/q. По-
казать, что результирующая последовательность событий представляет собой
процесс восстановления с функцией распределения интервала времени между
двумя последующими событиями вида
оо
где как обычно, обозначает n-кратную свертку распределения F.
34 (продолжение). Пусть ф($) — преобразование Лапласа функции F(x),
Найти преобразование Лапласа функции Fq(x).
Ответ:
<0 ы - w W
Ф<? 1-(1-?)ф(«9) ‘
526
Различные задачи
35 (продолжение). Если распределение F имеет два первых конечных мо-
мента, то показать, что
^^Т+77
при q —> 0 4- для всех s, Re s О,
где Л 1 = j xdF (х),
о
36 (продолжение). С помощью теоремы о сходимости из § 1 гл. 1 показать,
Fq(x)->l~e при + .
37. Рассмотрим симметричное случайное блуждание в пространстве г измере-
нии (см. стр. 43). Пусть есть число траекторий, состоящих из и переходов
и не содержащих ни одного состояния дважды. Доказать простое неравенство
7аг+т УМт
и с его помощью показать, что предел limn _> оо/1/” существует.
Указание-. Воспользоваться тем фактом, что функция фп == In является
полуаддитивной, т. е. фп+т фп 4- фт; см. также стр. 244.
38. Рассмотрим дискретный во времени марковский процесс, пространством
состояний которого служит единичный интервал. Если процесс в настоящий мо-
мент находится в состоянии р (0<р<1), то с вероятностью р в следующий
момент он перейдет в состояние а 4- $р и с вероятностью 1 — р в состояние рр;
здесь а, р > 0 и а + р = 1, Таким образом, процесс описывается соотношением
f а + $Хп
Хп+1“\
с вероятностью Хп,
с вероятностью 1 — Хп.
Показать, что этот процесс является мартингалом.
*39. Задача о баллотировке. Кандидат А получил а голосов, а кандидат Б —
6 голосов (а > Ь). Предположим, что голоса подсчитывались один за другим, и
пусть аг и рг представляют число голосов, поданных за кандидата А и за канди-
дата Б соответственно в момент, когда было рассмотрено г избирательных бюл-
летеней. Пусть Ха, ь—число раз, когда кандидат А лидировал при подсчете
голосов, т. е. Хо, ъ —число индексов г, при которых cir > рг (г 1, 2, ..., а 4- Ь).
Через Ха ь обозначим число индексов, для которых аг рг (г=1,2,..., а 4- Ь).
Показать, что
Й72] /26-2m \ / а-Ь-2+2т
b — т /\ т
1 / я 4- 6
Р{Ч»,& = а- 6 + г} = { а
тп««0
(6 — т 4- 1) (а — b + т — 1) ’
а> b 4-1,
26 4-1 ’
а = 6 4-1,
Различные задачи
527
р{да, j = a-&+'•}=
Кг-Р/г! /2Ь—2т — 2\(а-Ь + 2т\
a — b + 1 \ 6 — m — 1 / \ т )
(a + b\ / \ (Ь — т)(а — Ь + пг + 1)
\ а / т=о
а — b + \
а 4- 1
О
г = 1, 2, ...» 26-1,
г = 26,
во всех остальных
случаях.
Следующая группа задач связана с преобразованиями пуассоновских процес-
сов.
40. Пусть 0 = То < ti < т2... — последовательность времен наступления со-
бытий пуассоновского процесса с параметром Л. Предположим, что наступление
событий (независимо от моментов других наступлений) фиксируется с вероят-
ностью р и не фиксируется с вероятностью 1—р. Показать, что Xi(t), число
зарегистрированных наступлений, и число незарегистрированных наступле-
ний, представляют собой пуассоновские процессы с параметрами Хр и Х(1—р)
соответственно.
Указание: Рассмотреть производящую функцию совместных вероятностей, а
именно:
f(zt, z2) = M(zf' =
= М [М [zf1 (t)z^2 (/) | Xt (0 + X2 (/)}] -
= M (pZj + qz2)x' (Z)+X*(Z) =
(так как при заданной сумме Х^ (t) + X2(f) величина Х{ (/)
подчиняется биномиальному распределению)
= (pZi + qz2-V) e ekpt (Zi- l)eKqt (z2-V).
41 (продолжение). Пусть каждое событие, независимо от других, объяв-
ляется принадлежащим одной из k категорий с вероятностью р^ i = 1, 2, ..., k,
k
2 p. = 1, и пусть Xi(t) —число событий, попавших в i-ю категорию за время t.
i~i 1
Показать, что Xi(/), Хг(0, •••» Xh(t) являются пуассоновскими процессами с
параметрами Лрг-, i — 1, 2, ..., k, соответственно.
42 . Рассмотрим пуассоновский процесс с параметром X на положительной
полуоси (0, оо). Предположим, что событие, наступившее в момент /, относится
k
к одной из k категорий с вероятностями р- (/)> / = 1, 2, ..., &, pf (/) = 1.
Вероятности pi(t} будем считать непрерывными функциями времени. Пусть ХДО
обозначает число событий, наступивших за время t и отнесенных к категории i.
Показать, что при каждом i процесс {Xi(t)\ / 0} является нестационарным
пуассоновским (см. задачу 13 гл. 7).
Указание: Показать, что Р {событие категории i наступает в интервале
(/, t + h)} = Хрг(/)6 + o(h) и что событие в левой части этого равенства не за-
висит от значений Хг(т) при т < t.
528
Различные задачи
43 (продолжение). Показать, что процессы PG(/); t 0}, i = 1, 2, . s, k,
независимы.
Указание: Пусть (aiybi)f i — 1, 2, ..., k, — произвольные k интервалов на
полуоси [0, оо). Положим Yi = Xi (bi) — Xi (а{). Показать, что Уц Уг, Yk —
независимые с. в. Для этого обозначим через N (Т) число событий всех катего-
рий, наступивших в интервале (0, Г), где Г = max bi Если значение N(T)
1 < k
задано, то моменты наступления событий всех категорий в интервале (0, Т)
можно представить как п независимых наблюдений случайной величины, равно-
мерно распределенной на (0,7'). При условии N(Т) п совокупность
Уь У2, •••» У&, п ~ 2 подчиняется полиномиальному распределению с ве-
i = i /
роятностями
Ь1
Рг = 4 / Pi4)dt, i=l. 2, .... k,
ai
k
Pk+t~l~ 2 Pi-
i = l
Следовательно,
M (zj ‘Z22 . . . I N (O " ”) “ (PiZl + Р2г2 + + Pkzn + 1 - Pi - • • • ~Pk)n‘
Ho N(T) распределена по закону Пуассона со средним XT, поэтому
где
bl
\ “kJ Pi <0 dt.
ai
Эти же доводы справедливы и в том случае, если каждый интервал (ai, Ьу) за-
менить любым конечным объединением интервалов.
44 (продолжение). Пусть J pt (t) dt < оо при Г — 1, 2, ..., г, где г < k — 1.
0
Доказать, что совместное распределение набора с. з. (X\(t), Xr(t)) стре-
мится в пределе при ^->оо к совместному распределению г независимых е. в.,
о®
распределенных по закону Пуассона со средними Л J p^(/)J/<og, /«1,
0
2, ..., г.
45. Пусть 0 = То < Ti < Тг... — моменты наступления событий пуассонов-
ского процесса с параметром Л. В момент / « 0 частица начинает совершать
броуновское движение (о2 = 1) из начального положения т$. Событие, наступив-
шее в момент тг-, не регистрируется, если броуновская частица, отправившаяся
из состояния т/, находится слева от —а(а > 0) в момент /о; в противном случае
Различные задачи
629
это событие регистрируется. Показать, что зарегистрированные и незарегистриро-
ванные события образуют пуассоновские процессы с параметрами соответственно
л[1-ф((/+а)//^)] и ЛФ ((/ + а)/уто), где Ф — функция нормального распре-
деления.
46. Пусть 0 = То < Tj < ... — моменты наступления событий пуассоновского
процесса с параметром %. Пусть ср(х,у)—действительная функция, х^О; рассмот-
рим последовательность т* = ф(тг-, где {£(/); t 0} — случайный процесс,
не зависящий от исходного процесса, такой, что для любого п и любых t\, t2, ...
..., tn с. в. £(Л), ..., независимы. Положим F(x, t) = Р{ф(£, g(0) < х}.
Для каждого t > 0 и любых г непересекающихся интервалов (аг-, bi), i = 1, 2, ...
..., г, на оси (—оо, +оо) положим Xi(t) равным числу моментов на интервале
(0,/), таких, что ai < f, < bi. Показать, что {Xi(t); t 0), i = 1, 2, ..., г, яв-
ляются независимыми неоднородными пуассоновскими процессами. Показать,
что М( Xi (0) - Л J [F (b., u)-F (at, «)] du, предполагая, что при каждом х
о
функция F(x,u) интегрируема по и на любом конечном интервале.
Указание: Воспользоваться результатами и методами доказательства задач
42 и 43.
оо
47. В предыдущей задаче предположить, что J F (х, и) du<?o при каждом х.
0
Показать, что функция распределения с. в. Xi (/) стремится при оо к функции
распределения пуассоновской с. в. Показать также, что {N(a); —оо < а < оо},
где N(a2)—N(ai) есть число величин Tj в интервале (ai,a2), является процес-
сом с независимыми, но не обязательно стационарными приращениями.
48. В предыдущей задаче предположить, что существует функция h(x), та-
кая, что для любых Xi < Х2
— Xi
J F (х2, и) du — F (хь и) du=* J h (t) dt.
0 Q xt
Показать, что процесс {N(a); —оо < а < оо} является пуассоновским процессом,
не обязательно однородным, с параметром 'kh(t).
49. В предыдущей задаче положить h(t) ® ц. Показать, что {Ща);
—оо < а < оо} является одномерным пространственным пуассоновским процессом
с параметром Хц.
50. Пусть процесс {£(/);/> 0}, определенный в задаче 46, таков, что при
любом п и любых /1, /2, ..., /п > 0 случайные величины §(6), •••, Wn) поло-
жительны, независимы и обладают общим распределением 6(х). Получить ре-
зультаты задач 46—49 для следующих частных случаев:
(а) Ф (*,*/) = ху-
(б) Ф(х,г/) - х + у.
ОО
В (а) предположить, что 1/ш = J (dG (v)/u) < оо.
о
51. Из результата задачи 50 (б) вывести, что для процесса обслуживания
(М/(7/оо) (см. задачу 10 гл. 14) со стационарным пуассоновским входящим по-
током и произвольным распределением времени обслуживания G(x) выходной
530
Различные задачи
поток {U(/), t 0} (т. е. число обслуженных заявок к моменту t) является не-
стационарным пуассоновским потоком при условии, что в момент t = 0 система
свободна от заявок. Параметром этого процесса служит %(?(/).
52. Предположим, что в моменты 0 = То < Ti < Тг < ... промежутки между
которыми распределены по закону Пуассона с параметром X, на магистраль с
одного ее конца въезжают автомобили и движутся в положительном направле-
нии. Автомобиль, въезжающий на магистраль в момент т&, приобретает скорость
Vk и сохраняет эту скорость неизменной. Предположим, что скорости vk яв-
ляются независимыми с. в. с общим распределением F(x). Показать, что в ста-
ционарном случае, т. е. по прошествии бесконечного времени, пространственное
распределение автомобилей на магистрали будет описываться однородным
оо
пуассоновским процессом при условии, что \/w = J dF (v)/v < оо. Найти пара-
о
метр процесса.
Указание: Пусть (ai, и (аг, Ь2)—два непересекающихся интервала на
полуоси (0, оо). Представим себе ось времени, простирающуюся от настоящего
момента времени к бесконечному прошлому, и будем теперь отмерять положение
автомобилей от въезда на магистраль. Моменты въезда автомобилей на маги-
страль образуют пуассоновский процесс на этой временной оси. Будем относить
Xi к категории 1, если а\ Ti??i Ь\, к категории 2, если а2 XiVi Ь2, и к
категории 3 во всех остальных случаях. Тогда, в обозначениях задачи 43, имеем
Магистраль
----------►
------1-------1------н-------------------------
^2 Г/
Pl(t) = F(b,/t)- F(aj/t)
pz(t)^F(b./t)- F(a2/t)
Рз(*) = 1 ~Р1(Ч~Рг(1)
OO
Воспользоваться теперь результатами задач 42—44. Отметим, что J F(x/t)dt =
о
оо
= х/ш, где w"1 — J dF (v)/v. Подобные же доводы применимы и для случая
о
любого конечного числа неперекрывающихся интервалов.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абеля лемма 57, 145, 146, 149, 151, 317
Аллели 401
Байеса формула 11, 156
Бернулли испытания (биномиальные ис-
пытания) 23, 48, 49, 63
Бета-распределение 19
Биномиальный выбор 422, 428
Биортогональность 504
Бореля — Кантелли лемма 21
Бросание монеты 130, 180, 279, 282
Броуновское движение 22, 42, 159, 162, 297
Вероятности перехода с запрещением 144
---стационарные 31, 37, 50
— поглощения 82
Вероятностные модели мутации и роста 375
Ветвящиеся процессы 46, 312
----с двумя типами частиц 325
----непрерывным временем 333, 344
----несколькими типами частиц 332
Временной параметр 27
Время марковское 205
— ожидания 467
— — виртуальное 464, 487
— первого достижения 257
— пребывания (длительность пребывания)
204, 213
Возвратный класс (состояние) 57, 59, 60,
66, 76
----непериодический 76, 82, 84
— — нулевой 77, 92, 97, 102
•---положительный 77, 92, 97, 102, 152
Выборочная функция (реализация) 21
Гамета 402
Гамма-распределение 19
----времени обслуживания 480
----интервалов между поступлениями 479
Гаплоиды 401
Ген 401
— мутантный 313, 321
Генотипы 401
— гетерозиготные 402
— гомозиготные 402
Грина функция 171
Диагонализация 183
Диплоиды 401
Дисперсия 12
Длина очереди 461
Дробно-линейное преобразование 322
Задача о баллотировке 270
Закон больших чисел (слабый) 20, 173
----усиленный 20, 174, 466
— устойчивый 181
— Харди — Вейнберга 404
Занятости период 487, 489
Зигота 321, 402
Идентичность по происхождению 414
Инбридинг 410
Инбридинга коэффициент 414
Инфинитезимальная матрица 213, 232, 250.
253, 480
•— —- консервативная 254
Инфинитезимальные интенсивности рожде-
ния и гибели 222
— параметры 215, 255, 333, 345, 346
Ковариационно стационарный 31
Колмогорова дифференциальные уравнения
обратные 216, 248, 336
-----прямые 217, 249, 336
Критерий сходимости Леви 16, 190
Кроссинговер 417
Лапласа преобразование 17
Мальтусовская интенсивность 392
Маргинальная (частная) функция распреде-
ления 13
Марковская цепь 37, 38
*--в генетике 47
— —• вложенная 464, 469, 480, 483
— — консервативная 248, 259
— — непериодическая 54
---неприводимая 52, 88, 89, 152, 170
---пространственно однородная 39
Марковский момент 256, 257
Мартингал 29
Медиана 12
Миграция 406
Модели обслуживания одним прибором 463
Модель мутации с несколькими типами ин-
дивидуумов 437
— счетчика 208
— телефонного узла 220
Мутационное давление 48, 221
Мутация 405
Нагрузка системы 471
Невозвратный класс (состояние) 57, 97, 102
Нейтронная цепная реакция 312
Непрерывность траекторий 302
Образование очереди 44, 219
Обслуживание s приборов 483
Обслуживания дисциплина 460
— порядок обратный 493
• — — прямой 460, 467
Ортогональные полиномы 123, 125
Отбор 49
— гаметический 406
* — зиготный 406
Отношения при расщеплении 404
Очередь с абсолютными приоритетами 498
Перекрест 418
Периодические классы 116
Периодичность марковской цепи 53
Плотности функция 263
Полиморфизм 407
Полиплоиды 401
Положительные матрицы 111
Полуаддитивности неравенство 244
Порядковые статистики 207, 262, 373
Последовательности регулярные 159, 182
— субрегулярные 159
— суперрегулярные 159
Потенциала теория 171
Поток восстановления 461
— входящий 460
532
Предметный указатель
Поток входящий произвольный 480
--- пуассоновский 469
— простейший 461
Представление Рисса 162
— спектральное ПО, 124, 504
Принцип инвариантности для случайных
процессов 299
— отражения 302, 303
Производящая функция 16
Пространственная однородность 171
Пространство состояний 27
Процесс винеровский 23
---восстановления 260
---общий 260
— диффузионный 303
— логистический 224
— марковский 30
— минимальный 215, 254
— обратный 156
— пуассоновский 23, 262
---неоднородный 376, 378
--- однородный 26
------многомерный 364
------пространственный 26, 364
— рождения и гибели 212, 247
— — с линейным ростом 218, 228, 230.
334
— с независимыми приращениями 29, 265
— стационарный 30
— чистого рождения 200, 212
— Юла 200, 203, 236, 240, 374
Прямое произведение ветвящихся процес-
сов 422
Разорение игрока 41, 86, 87
Распределение биномиальное 20, 208
--- отрицательное 20
— времени обслуживания 461
— геометрическое 20
— конечномерное 15
- - нормальное 19
многомерное 18
— Паскаля 20
— по возрастам 387
— полиномиальное 18
отрицательное 35
— пуассоновское 20
— равномерное 19
— стационарное 77, 218
---обобщенное 151, 156
— условное 13
— экспоненциальное 19, 202
— эрланговское 461, 499
Расщепление хроматидное 418
— хромосомное 418
Рост популяции 372
— — детерминированный 387
Самооплодотворение 411
— вероятностная модель 427
Серии успехов 46, 63
Система с бесконечным числом обслужи-
вающих приборов 220, 494
---ограничениями 494
---одним обслуживающим прибором 220
Скорость приближения к гомозиготному со-
стоянию 447
Случайное слияние гамет 405, 418
Случайные блуждания 120, 123, 130, 214
----вложенные 226, 228
----одномерные 40, 60
----симметричные 42, 43, 61, 298
— — с отражающим экраном 125
------поглощающим экраном 127
— величины невырожденные 171
----независимые 13, 16
----перестановочные 271, 273, 489
---- периодические 175
Совместные функции распределения 12
Сообщающиеся состояния 52, 54
Состояние мгновенное 252
— устойчивое 252, 259
Спаривание ассортативное 410
— неслучайное 410
— сибсов 411
— случайное 404
Спектр непрерывный 124
Спектральный радиус 111
Среднее время возвращения 77
— значение 12
Статистика Колмогорова — Смирнова 285
Строго марковское свойство 256
Супергармонические функции 162
Теорема восстановления 488
----обобщенная 186
— Руше 482
— спектральная 501
Теоремы об отношениях 146, 155
Упорядоченные наблюдения из равномерного
распределения 209
Уравнение восстановления 73, 74, 80, 390
— диффузии 298
— Колмогорова — Чэпмена 213, 231, 298, 335,
346
Условная вероятность 13
— плотность 13
Условно независимые множества 266
Условное математическое ожидание 14
Формула полной вероятности 11, 29, 255,
353, 492
Фробениуса теория положительных матриц
507
Характеристические функции 15
Центральная предельная теорема 21, 23, 181,
299, 383
Центромер 417
Электронные умножители 312
Эмпирические функции распределения 270,
275
Эргодическая теорема 74
Эренфестов модель 43, 238
ОГЛАВЛЕНИЕ
Предисловие редактора перевода ....................................... 5
Предисловие .......................................................... 7
Логическая зависимость глав............................................9
Глава 1. Элементы теории случайных процессов......................... 11
§ 1. Сводка основных терминов и свойств случайных величин и функ-
ций распределения............................................... 11
§ 2. Два простых примера случайных процессов....................21
§ 3. Классификация общих случайных процессов....................27
Задачи ..........................................................31
Замечания........................................................35
Литература.......................................................36
Г лава 2. Марковские цепи.............................................37
§ 1. Определения ...............................................37
§ 2. Примеры марковских цепей...................................38
§ 3. Матрицы переходных вероятностей марковской цепи............50
§ 4. Классификация состояний марковской цепи . .................52
§ 5. Возвратность ..............................................55
§ 6. Примеры возвратных марковских цепей...................... 60
§ 7. Еще о возвратности . . . ..............,...................65
Задачи ..........................................................66
Некоторые элементарные задачи....................................71
Замечания........................................................72
Литература.......................................................72
Глава 3. Основные предельные теоремы для марковских цепей и их прило-
жения .................................................................73
§ 1. Дискретное уравнение восстановления.........................73
§ 2. Доказательство теоремы 1.1 80
§ 3. Вероятности поглощения......................................82
§ 4. Критерии возвратности ......................................88
§ 5. Пример из теории очередей . ................................91
§ 6. Еще один пример из теории очередей..........................97
§ 7. Случайное блуждание........................................102
Задачи .........................................................104
Некоторые элементарные задачи...................................109
Замечания.......................................................109
Литература......................................................109
Глава 4. Алгебраические методы исследования марковских цепей . . . .110
§ 1. Предварительные сведения................................ . ПО
§ 2. Связь между собственными значениями и классами возвратных
состояний......................................................112
§ 3. Периодические классы..................................... 116
§ 4. Специальные вычислительные методы для марковских цепей . .120
§ 5. Примеры....................................................125
534
Оглавление
§ 6. Приложения к бросаниям монеты.............................130
Задачи ...........................................................135
Некоторые элементарные задачи..................................142
Замечания......................................................143
Литература.....................................................143
Глава 5. Теоремы об отношениях переходных вероятностей и их приложения 144
§ 1. Вероятности перехода с запрещением ..........................144
§ 2. Теоремы об отношениях.....................................146
§ 3. Существование обобщенных стационарных распределений . . .151
§ 4. Интерпретация обобщенных стационарных распределений . . .156
§ 5. Регулярные, суперрегулярные и субрегулярные последовательности
марковских цепей ............................................. 159
Задачи ...........................................................166
Замечания......................................................169
Литература.....................................................169
Глава 6. Последовательность сумм независимых случайных величин как
марковская цепь ................................................. . 170
§ 1. Свойства возвратности сумм независимых случайных величин . . 170
§ 2. Локальные предельные теоремы.................................174
§ 3. Правые регулярные последовательности марковских цепей . . . 182
Задачи ...........................................................192
Замечания.........................................................196
Литература........................................................197
Глава 7. Классические примеры цепей Маркова с непрерывным временем 198
§ 1. Общие процессы чистого рождения (размножения) и пуассонов-
ские процессы..................................................198
§ 2. Дополнительные сведения о пуассоновских процессах.........204
§ 3. Модель счетчика...........................................208
§ 4. Процессы рождения и гибели................................212
§ 5. Дифференциальные уравнения для процессов рождения и гибели 216
§ 6. Примеры процессов рождения и гибели.......................218
§ 7. Процессы рождения и гибели с поглощающими состояниями . . 225
§ 8. Цепи Маркова с конечным числом состояний и непрерывным вре-
менем .........................................................231
Задачи ...........................................................233
Некоторые элементарные задачи.....................................241
Замечания.........................................................241
Литература........................................................242
Глава 8. Цепи Маркова с непрерывным временем............................243
§ 1. Свойства дифференцируемости переходных вероятностей . . . 243
§ 2. Консервативные процессы. Прямые и обратные дифференциаль-
ные уравнения. . ..............................................248
§ 3. Построение цепи Маркова с непрерывным временем с помощью
ее инфинитезимальных параметров............................... 250
§ 4. Строго марковское свойство...................................256
Задачи ...........................................................259
Замечания .'...........-..........................................261
Литература........................................................261
Глава 9. Порядковые статистики, пуассоновские процессы и их приложения 262
§ 1. Порядковые статистики и их связь с пуассоновскими процессами 262
§ 2. Задача о баллотировке...................................... 270
§ 3. Эмпирические функции распределения и порядковые статистики 275
Оглавление
535
§ 4. Некоторые предельные распределения для эмпирических функций
распределения ................................................ 282
Задачи ................................................................287
Замечания............................................................. 296
Литература..............................................................296
Глава 10. Броуновское движение............................................ 297
§ 1. Предварительные сведения..........................................297
§ 2. Совместные вероятности для броуновского движения..................299
§ 3. Непрерывность траекторий и их максимальные значения .... 302
Задачи .................................................................307
Замечания...............................................................311
Литература..............................................................311
Г лава 11. Ветвящиеся процессы.................................... . 312
§ 1. Ветвящиеся процессы с дискретным временем.......312
§ 2. Соотношения для производящей функции, описывающей ветвя-
щийся процесс.................................................313
§ 3. Вероятности вырождения......................316
§ 4. Примеры ...................................................320
§ 5. Ветвящиеся процессы с двумя типами частиц.......325
§ 6. Ветвящиеся процессы с несколькими типами частиц.332
§ 7. Ветвящиеся процессы с непрерывным временем......333
§ 8. Вероятности вырождения для ветвящихся процессов с непрерыв-
ным временем...................................................337
§ 9. Предельные теоремы для ветвящихся процессов с непрерывным
временем .....................................................340
§ 10. Ветвящийся процесс с непрерывным временем и двумя типами
частиц ..................................................... 345
§ 11. Ветвящиеся процессы, зависящие от возраста.......................352
Задачи .................................................................357
Замечания...............................................................362
Литература..............................................................362
Глава 12. Составные случайные процессы..................................... 363
§ 1. Многомерные однородные пуассоновские процессы....................364
§ 2. Применение многомерных пуассоновских процессов в астрономии 370
§ 3. Иммиграция и рост популяций.......................................372
§ 4. Вероятностные модели мутации и роста..............................375
§ 5. Экспоненциальный рост одномерной популяции........................380
§ 6. Вероятностная модель роста популяции в пространстве и времени 383
§ 7. Детерминированный рост популяции с распределением по возра-
стам .........................................................387
§ 8. Дискретная возрастная модель.................................... 394
Задачи .................................................................395
Замечания...............................................................400
Литература..............................................................400
Глава 13. Детерминированные и случайные генетические и экологические
процессы ............................................................401
§ 1. Генетические модели. Описание генетического механизма . . .401
§ 2. Инбридинг ...................................................
§ 3. Полиплоиды .......................................................417
§ 4. Марковские процессы, порождаемые прямым произведением вет-
вящихся процессов............................................. 420
§ 5. Модели роста популяций с несколькими типами индивидуумов . 426
536
Оглавление
§ 6. Собственные значения цепей Маркова, порожденных прямым про-
изведением ветвящихся процессов............................... 428
§ 7. Собственные значения для модели мутации с несколькими типами
индивидуумов ................................................. 437
§ 8. Вероятностный смысл собственных значений . .............446
Задачи ........................................................455
Литература.....................................................45°
Глава 14. Процессы массового обслуживания............................460
§ 1. Общее описание............................................460
§ 2. Простейшие процессы обслуживания (Л4/Л4/1) . .............461
§ 3. Некоторые общие модели обслуживания одним прибором . . . 463
§ 4. Метод вложенных цепей Маркова применительно к модели об-
служивания (M/G/1) 469
§ 5. Экспоненциально распределенное время обслуживания (G/M/1). 475
§ 6. Гамма-распределение интервалов между поступлениями и обоб-
щения (Е\/М/1).................................................479
§ 7. Экспоненциальное обслуживание $ приборов (GI/M/s).........483
§ 8. Виртуальное время ожидания и период занятости........... 487
Задачи ........................................................493
Замечания .....................................................499
Литература.....................................................500
Приложение ..........................................................501
§ 1. Спектральная теорема......................................501
§ 2. Теория Фробениуса положительных матриц ................. 507
Различные задачи.....................................................518
Предметный указатель.................................................531
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформле-
нии, качестве перевода и другие просим присылать по
адресу: 129820, Москва, И-110, ГСП, 1-й Рижский пер.,
д. 2, издательство «Мир».