Автор: Грудев А.П.
Теги: технология обработки без снятия стружки в целом: процессы, инструмент, оборудование и приспособления металлургия
ISBN: 5-229-00102-х
Год: 1988
Текст
i
гм *’
АЛГрудсз
ТЕОРИЯ
ПРОКАТКИ
A. 11. ГРУДЕВ
ТЕОРИЯ ПРОКАТКИ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебника для студентов вузов,
обучающихся по специальности
«Обработка металлов давлением»
&
МОСКВА «МЕТАЛЛУРГИЯ» 1988
УЧЕБНИК ДЛЯ ВУЗОВ
Александр Петрович Грудев
ТЕОРИЯ ПРОКАТКИ
Редактор издательства Т. А. Дьяконова
Художественный редактор Ю. И. Смурыгин
Технический редактор Г. Б. Жарова
Корректор Ю. И. Королева
ИБ № 3018
Сдано в набор 16.09.87. Подписано в печать 23.02.88. Т-06256. Формат бумаг?
84Х108’/з2. Бумага типографская № 1. Гарнитура литературная. Печать высо-
кая. Усл. печ. л. 12,60. Усл. кр.-отт. 12,60. Уч.-изд. л. 12,71. Тираж 7000 экз.
Заказ 947. Цена 75 коп. Изд. № 1317
Ордена Трудового Красного Знамени издательство «Металлургия»,
119857 ГСП, Москва, Г-34, 2-й Обыденский пер., д. 14
Владимирская типография Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и книжной торговли
600000, г. Владимир, Октябрьский проспект, д. 7
УДК 621.771
Рецензенты: кафедра обработки металлов давлением Магни-
тогорского горно-металлургического ин-та им. Г. И. Носова; проф.
докт. техн, наук В. Т. Жадан
УДК 621.771
Теория прокатки: Учебник для вузов./Грудев А. П. — М.: Метал-
лургия, 1988, 240 с»
Изложены основы современной теории продольной прокатки. Рас-
смотрены геометрия и кинематика очага деформации, условия захва-
та полосы прокатными валками, особенности напряженно-деформи-
рованного состояния металла, закономерности поперечной деформа-
ции (уширения), методы определения контактных напряжений, уси-
лий, крутящих моментов и мощности. Наряду с анализом простого
процесса прокатки приведены основы теории сложных случаев про-
катки. Приведены сведения по математическому моделированию
и расчету параметров прокатки на ЭВМ.
Учебник предназначен для студентов вузов, изучающих прокатное
производство, а также может быть полезен инженерно-техническим
работникам прокатных цехов, заводских лабораторий, научно-иссле-
довательских, конструкторских и проектных организаций. Ил. 139.
Табл. 16. Библиогр. список: 16 назв.
2704030000—087
аллургия», 1988
{ПЛАВЛЕНИЕ
Предисловие............................................... 6
Глава I. Определение и классификация процессов прокатки 9
I. Определение процесса—прокатки.......................... 9
2. Классификация процессов прокатки.......................10
3. Основные задачи теории прокатки........................13
Глава II. Геометрия очага деформации......................15
I. Очаг деформации и его геометрические характеристики . 15
2. Показатели величины. деформации........................16
3. Формулы для расчета углов захвата......................20
4. Определение длины очага деформации.....................22
5. Внеконтактная деформация ..............................23
(>. Сплющивание валков....................................26
7. Площадь контактнойповерхности..........................30
Глава III. Условия захвата полосы валками .... 33
I. Условие свободного начального,—захвата.................33
2. Принудительный захват-.................................35
3. Динамический захват....................................39
4. Условие захвата при установившемся процессе прокатки . 46
5. Сравнение условий захвата в начальный момент прокатки
и при установившемся процессе.............................48
6. Способы повышения захватывающей способности валков . 50
Глава IV. Кинематика очага деформации.....................52
1. Стадии процесса прокатки................................52
2. Соотношение скоростей металла и валков в очаге дефор-
маций . ... ..................................54
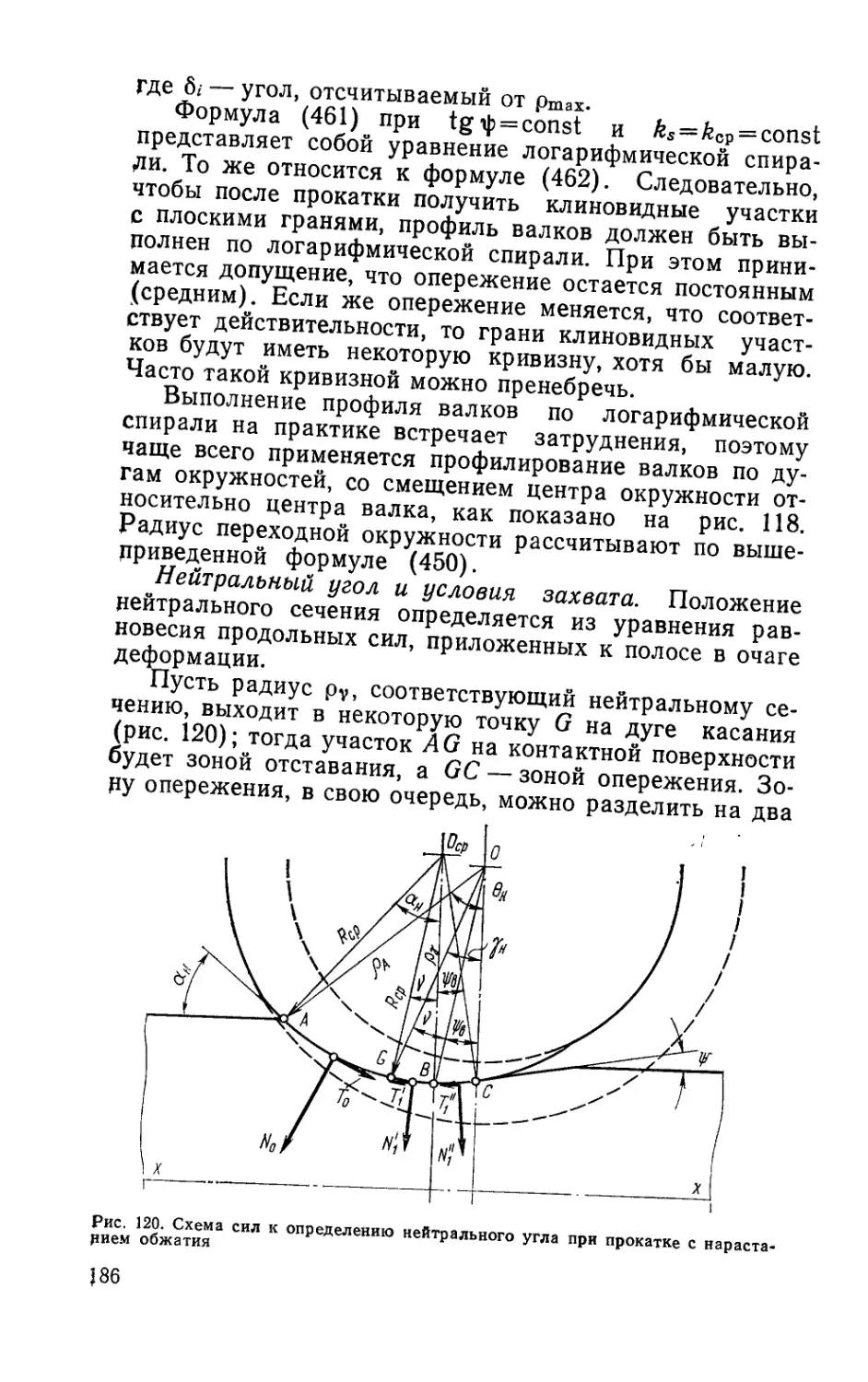
3. Определение положения нейтрального сечения ... 59
4. Влияние -натяжения концов полосы на положение нейт-
рального сечения...........................................63
-*5. Определение нейтрального сечения с учетом неравномер-
ного распределения давлений по дуге контакта ... 65
6. Опережение и отставание концов полосы...................69
7. Экспериментальное определение опережения .... 70
8. Теоретическое определение опережения....................72
9. Зависимость опережения от факторов прокатки ... 74
К). Опережение при прокатке в калибрах......................77
11. Опре,целение средней скорости деформации .... 79
Глава V. Напряженно-деформированное состояние и фор-
моизменение полосы..........................................82
I. Общая характеристика напряженного и деформированно-
го состояния металла ' ................................. 82
I 1 3
2. .Распределение деформаций по высоте полосы .... 86
3. Определение напряженного состояния полосы методом по-
строения линий скольжения..................................89
4. Поперечная деформация (уширение)----------,-------- . 93
5. Влияние факторов-прокатки на уширение.....................95
6. Теоретическое определение уширения........................98
Глава VI. Силы трения......................................105
1. Распределение сил, трения пп-дуЕе-контяктя _ . . . . 105
2. Соотношение коэффициентов трения при захвате и при уста-
новившемся процессе прокатки.......................109
3. Методы экспериментального определения коэффициента тре-
ния ......................................................111
4. Влияние факторов прокатки на коэффициент трения . . 115
5. Расчетное определение коэффициента трения . . . . 119
Глава VII. Усилие прокатки..........................121
1. Распределение давлений по контактной поверхности . . 121
2. Среднее контактное давление и усилие прокатки . . . 123
3. Влияние факторов прокатки на среднее контактное давление 124
4. Определение среднего предела текучести металла в очаге
деформации.........................................127
5. Дифференциальное уравнение равновесия продольных сил 135
6. Теоретическое определение давления по А. И. Целикову . 138
7. Теоретическое определение давления по А. П. Чекмареву . 142
8. Давление при прокатке в калибрах................145
9. Особенности определения давления прн прокатке высоких
полос.....................................................146
Глава VIII. Крутящие моменты, работа и мощность про-
катки .......................................................148
1. Определение крутящих моментов по удельным силам трения 148
2. Определение крутящет-мпмента по усилию прокатки . . 149
3. Определение крутящего момента при прокатке с натяжением 152
4. Теоретическое определение работы и мощности прокатки . 154
5. Экспериментальные данные по определению работы про-
катки ....................................................155
6. Мощность.двигателяпрокатного стана.......................156
Глава IX. Сложные случаи прокатки............................158
1. Прокатка в валках неравного диаметра.....................158
2. Прокатка с одним приводным валком........................170
3. Прокатка при разных условиях трения на валках . . . 177
4. Периодическая прокатка...................................181
Глава X. Моделирование и расчет параметров прокатки
с помощью ЭВМ................................................194
1. Особенности использования различных ЭВМ для расчетов
в области теории прокатки ............................... 194
4
Этапы подготовки задач к решению на ЭВМ .... 198
3. Алгоритмизация задач расчета параметров прокатки . . 200
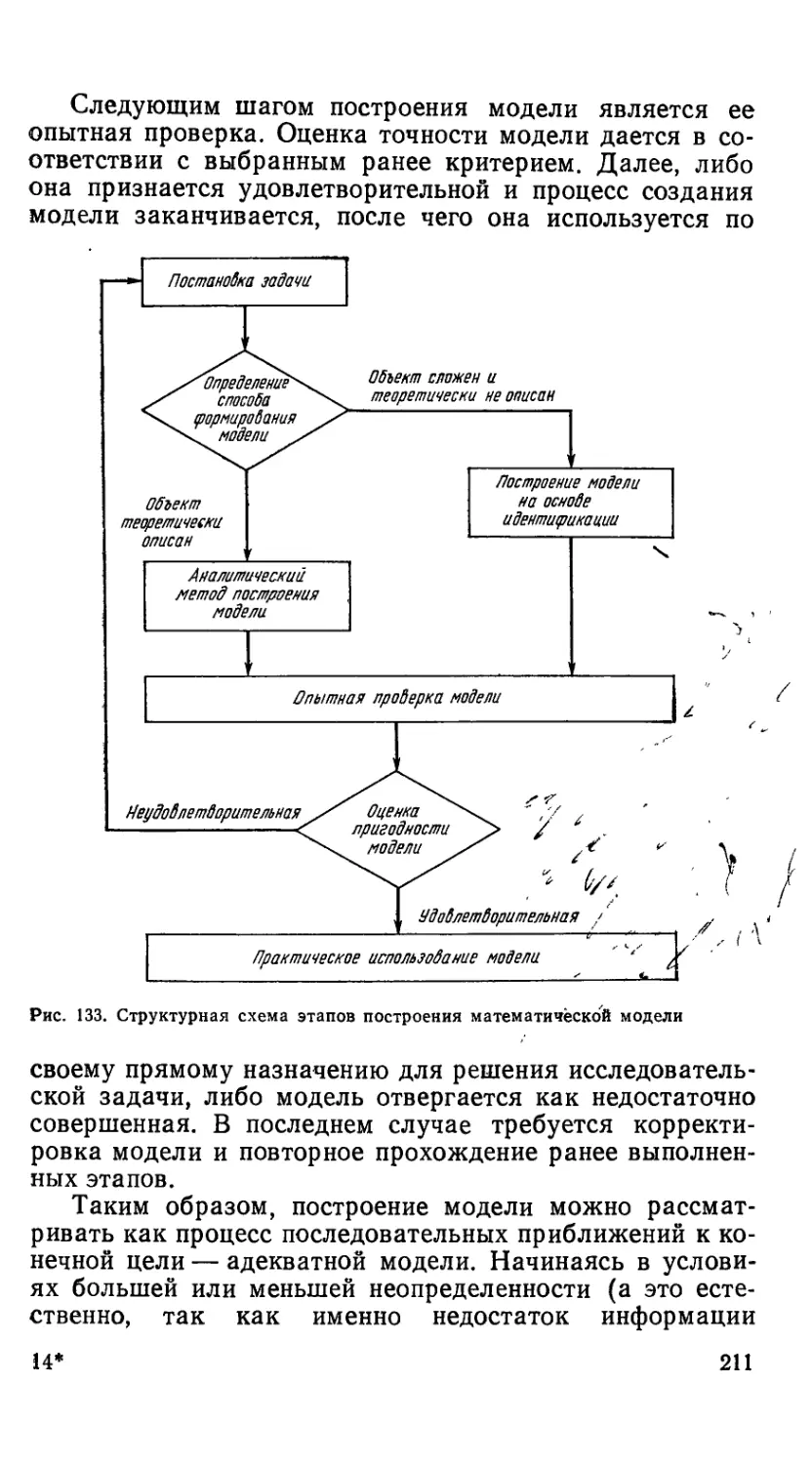
-I. Общая характеристика методов моделирования . . . 206
!">. Основные принципы построения математических моделей 210
(>. Примеры построения и использования математических мо-
делей в теории прокатки ................................ 214
Контрольные вопросы.......................................223
I (рпложение I. Коэффициент трения при прокатке свинца . 232
Приложение II. Зависимость коэффициента трения от темпе-
ратуры деформации.........................................234
Рекомендательный библиографический список .... 236
Предметный указатель......................................237
ПРЕДИСЛОВИЕ
Прокат является основным видом металлургической про-
дукции. Примерно 90 % всей выплавляемой стали обра-
батывается в прокатных цехах. В Основных направлени-
ях экономического и социального развития СССР на
1986—1990 годы и на период до 2000 года к концу XII
пятилетки запланирован выпуск готового проката в на-
шей стране в объеме 116—119 млн. т/год.
Снижение себестоимости проката, улучшение его ка-
чества и расширение сортамента существенно влияют па
эффективность производства в металлопотребляющих
отраслях народного хозяйства. Имеются все основания
утверждать, что от уровня развития прокатного произ-
водства зависит ускорение научно-технического прогрес-
са в народном хозяйстве в целом.
Совершенствование существующих процессов про-
катки, разработка и внедрение новых прокатных станов
и новых прогрессивных технологий — все это требует до-
статочно глубоких знаний в области теории прокатки.
В настоящем учебнике изложены основы теории про-
дольной прокатки. Основное внимание уделено анализу
простого процесса прокатки, но рассмотрены также и не-
которые распространенные сложные случаи прокатки.
Приведены сведения по математическому моделированию
и расчету параметров прокатки с применением ЭВМ.
В основу учебника положены наиболее устоявшиеся,
экспериментально подтвержденные теоретические поло-
жения и выводы; новые разработки приведены в ограни-
ченном объеме. Главное требование, которому стремил-
ся удовлетворить автор — ясное, логически завершенное
и доходчивое изложение материала.
Содержание учебника отражает многолетний опыт
чтения лекций по дисциплине «Теория прокатки»
в Днепропетровском металлургическом институте
им. Л. И. Брежнева.
Автор благодарен рецензентам — кафедре ОМД Маг-
нитогорского горно-металлургического института им.
Г. И. Носова и профессору докт. техн, наук В. Т. Жада-
ну, замечания которых были учтены при доработке тек-
ста рукописи.
Автор будет признателен за пожелания и предложе-
ния по улучшению содержания учебника.
6
Основные условные обозначения:
h, Ь, I—толщина (высота), ширина, длина полосы;
Ло, Ьо, 10— то же, до прокатки;
hi, blt — то же, после прокатки;
ftcP— средняя толщина полосы в очаге деформа-
ции;
Aft — абсолютное обжатие;
&—&hlhQ— относительное обжатие;
АЬ— абсолютное уширение;
Fo и F±—площадь поперечного сечения полосы до
и после прокатки;
Л— коэффициент вытяжки;
R и D— радиус и диаметр валков;
а—угол контакта (угол захвата при установив-
шемся процессе прокатки);
а3 — начальный угол захвата;
ld— длина очага деформации;
FH—площадь контактной поверхности;
ив — окружная скорость валков;
ц0 и Vi— скорость заднего и переднего концов полосы;
S — опережение;
S0T— отставание;
у — нейтральный (критический) угол;
и— скорость деформации;
цср — средняя скорость деформации;
от— предел текучести металла;
о*—вынужденный предел текучести (при плоской
деформации о*' = 1,15 от);
Отср — средний предел текучести в очаге деформа-
ции;
N— нормальная сила;
Р—усилие прокатки;
р— контактное нормальное давление;
рсР— среднее контактное давление;
Т— сила трения;
t—удельная сила трения (напряжение трения);
^ср— средняя удельная сила трения;
f и р— коэффициент и угол трения;
f3 и Рз — то же, при захвате;
fy и ру— то же, при установившемся процессе прокат-
ки;
/а — показатель силы трения;
Q — продольная сила, приложенная к полосе;
7
и Я1 — удельные силы заднего и переднего
ния;
Л4пР— крутящий момент на бочке валка;
ЛпР—работа прокатки (деформации);
Р7пр—мощность прокатки (деформации).
Глава I
ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ
ПРОЦЕССОВ ПРОКАТКИ
1. Определение процесса прокатки
Прокаткой называется процесс пластического деформи-
рования тел между вращающимися приводными валка’-
ми. В этом определении следует обратить внимание на
слова «приводными валками». Они означают, что энер-
гия для осуществления деформации передается через
валки, соединенные с двигателем прокатного стана. Де-
формируемое тело можно протягивать через непривод-
ные (холостые) валки, но это будет не процесс прокат-
ки, а процесс волочения.
Простейшая и основная схема процесса прокатки по-
казана на рис. 1. Обрабатываемое тело, в общем случае'
называемое полосой, пропускает-
ся между валками, вращающими-
ся в противоположные стороны.
Полоса втягивается в валки за
счет действия сил трения на кон-
такте. При прохождении между
валками толщина полосы умень-
шается, а длина и ширина увели-
чиваются.
Прокатка относится к числу
основных способов обработки ме-
таллов давлением. Методом про-
катки получают изделия самой
разнообразной формы: тонкие
и толстые листы, профили квад-
ратного и круглого сечений,
Рис. 1. Схема процесса про-
дольной прокатки:
1 — валки; 2 — полоса
уголки, швеллеры, двутавровые
балки, рельсы, трубы и многие
другие. При прокатке изделий типа листов применя-
ются валки, рабочая часть (бочка) которых имеет
форму круглого цилиндра без каких-либо вырезов и вы-
ступов (рис. 2, а). Прокатку в таких валках часто назы-
вают прокаткой «на гладкой бочке». При производстве
более сложных (сортовых) профилей применяются ка-
либрованные валки, и деформация полосы осуществля-
ется в калибрах (рис. 2,6).
Как и другие способы обработки давлением, прокатка
бывает горячей и холодной. Горячая прокатка распрост-
ранена шире, чем холодная. Нагретый металл при высо-
ких температурах обладает пониженным сопротивлени-
ем деформации и повышенной пластичностью. Холодная
прокатка применяется для получения относительно тон-
ких изделий с высококачественной поверхностью, на-
пример тонких листов или тонкостенных труб. Иногда
находит применение обработка в области промежуточ-
ных температур — так называемая теплая прокатка.
Рис. 2. Валки с гладкой бочкой (а) и калиброванные валки (б)
Следует отметить, что прокатка служит не только
для получения изделий определенной формы, но и в зна-
чительной степени способствует повышению механичес-
ких свойств металла.
2. Классификация процессов прокатки
..Процессы прокатки многообразны и классифицировать
их можно по разным признакам. Сначала рассмотрим
классификацию по взаимному расположению осей обра-
батываемого тела и валков. По этому признаку разли-
чают прокатку продольную, поперечную и косую (вин-
товую). Если ось прокатываемой полосы перпендикуляр-
на оси валков, то прокатку называют продольной (рис.
1р При таком способе прокатки полоса перемещается
только вперед,.т. е. совершает только поступательное
движение. Продольная прокатка является наиболее рас-
пространенной. ’
Поперечная прокатка отличается тем, что ось обра-
батываемого тела параллельна оси валков (рис. 3). Оба
валка вращаются в одну и ту же сторону. Они постепен-
Ю
Рис. 3. Схема поперечной:
прокатки:
1 — валки; 2 — ролики; 3 —
изделие
но сближаются, в результате чего уменьшается диаметр
изделия, которое также вращается, но в сторону, проти-
воположную вращению валков. В продольном направле-
нии обрабатываемое тело не перемещается (если нет
специальных тянущих устройств). Боковые ролики, по-
казанные на рис. 3, выполняют вспомогательную функ-
цию: они удерживают изделие между валками.
^Поперечная прокатка исполь-
зуется в металлургии и машино-
строении для изготовления валов,
осей, втулок, шестерен и других
изделий типа тел вращения.'
ГКосая прокатка, называемая
талоне винтовой, занимает проме-
жуточное положение между попе-
речной и продольной. В этом слу-
чае оси валков располагаются
под углом друг к другу и к оси
прокаты_ваемой круглой заготовки
(рис. 4) 4 Благодаря такому рас-
положению валков заготовка
в процессе прокатки совершает
не только вращательное, но и по-
ступательное движение. Точки на
поверхности заготовки движутся
по винтовой линии.^'Поскольку
угол наклона валков по отноше-
нию к оси обрабатываемого тела
обычно невелик (до 12—18°), ко-
сая прокатка по своему характеру
чем к продольной. .1
^Процесс косой прокатки широко применяется при
производстве бесшовных труб, в частности на прошив-
ных станах, где из сплошной круглой заготовки получа-
ют черновую трубу — гильзу? Именно такой процесс схе-
матично показан на рис. 4. Для образования в заготов-
ке отверстия правильной формы между валками / уста-
навливается оправка 2, закрепленная на стержне. Ли-
нейки 3 служат для удержания заготовки в валках.
"^Особым видом прокатки является так называемая
периодическая прокатка. Она отличается тем, что в про-
цессе деформации высота зазора между валками пери-
одически изменяется. Чаще всего это достигается путем
придания валкам специальной некруглой формы (рис.
бД Таким способом получают периодические профили
ближе к поперечной,.
проката, форма сечения которых периодически изменя-
ется по длине полосы.
Далее, процессы прокатки подразделяют на симмет-
ричные и несимметричные. Симметричной прокаткой на-
зывают такой процесс, при котором воздействие каждо-
Рис. 4. Схема косой прокатки на прошивном стане:
1 — валки; 2 — оправка; 3 — линейки; 4 — заготовка; 5—черновая труба (гиль-
за)
го из валков на обрабатываемое тело является совер-
шенно одинаковым, идентичным. Если это условие
нарушается, то прокатка характеризуется как несиммет-
ричная. К числу несиммет-
ричных процессов относятся:
прокатка в валках неравно-
го диаметра, прокатка с од-
ним приводным валком, про-
катка при разных окружных
скоростях валков, прокатка
при неравномерном (несим-
метричном) распределении
механических свойств по вы-
соте полосы, прокатка при
различных условиях трения
Рис. 5. Схема периодической прокатки ВЭЛКЭХ И Др.
Важным условием про-
цесса прокатки является на-
личие или отсутствие внешних сил, приложенных к кон-.
цам полосы. По этому признаку различают свободную
и несвободную прокатку. Свободной называют прокатку
тогда, когда на полосу действуют силы только со сторо-
12
ны валков. Несвободная прокатка осуществляется с на-
тяжением или подпором концов полосы (рис. 6). Силы
натяжения или подпора создаются смежными прокатны-
ми клетями, намоточно-натяжными барабанами или дру-
гими устройствами.
Рис. 6. Силы натяжения (а) и подпора (б) при прокатке:
/ — заднее натяжение; 2 — переднее натяжение; 3 — задний
подпор; 4 — передний подпор
В теории прокатки часто применяется термин простой
процесс прокатки или простой случай прокатки. Под
этим термином подразумевается процесс свободной сим-
метричной продольной прокатки, причем чаще всего име-
ется в виду прокатка полосы прямоугольного сечения
в цилиндрических валках. Теория простого процесса про-
катки служит той основой, на которой базируется ана-
лиз других, более сложных случаев прокатки.
3. Основные задачи теории прокатки
Разработка основ теории прокатки начата в середине
XIX века, более 100 лет назад*. Большой вклад в раз-
витие и становление этой дисциплины внесен трудами
отечественных ученых: И. А. Тиме, Р. Р. Тонкова, Н. С.
Верещагина, А. Ф. Родзевича-Белевича, С. Н. Петрова,
В. Е. Грум-Гржимайло, А. Ф. Головина, А. П. Виногра-
дова, И. М. Павлова, С. И. Губкина, А. И. Целикова,
* Первой крупной теоретической работой, не потерявшей своего
значения до настоящего времени, явилась статья С. Финка «Теория
работы прокатки», опубликованная в 1874 г. (S. Fink, Theorie der
Walzen—Arbeit. «Zeitschrift fur das Berg—Hiitten und Salinenwesen
in Preussischen Staate», B.22, 1874).
13
А. Я. Хейна, А. П. Чекмарева, В. С. Смирнова, И. Я. Тар-
новского, П. И. Полухина и многих других. Получили
признание исследования зарубежных ученых: С. Финка,
К. Кодрона, В. Тафеля, Э. Зибеля, Т. Кармана, С. Эке-
лунда, В. Тринкса, В. Люега, А. Помпа, А. Надаи,
Э. Ороуона, Г. Форда, Р. Симса, М. Стоуна, А. Гелей,
3. Вусатовского и других.
Какие же основные вопросы рассматриваются в тео-
рии прокатки? Среди них в первую очередь надо наз-
вать следующие:
изучение и формулировка условий захвата полосы
прокатными валками;
определение скорости относительного взаимного пе-
ремещения точек полосы и валков, а также других ки-
нематических параметров процесса прокатки;
исследование соотношения между продольной и по-
перечной деформациями при заданной высотной дефор-
мации полосы;
анализ распределения напряжений и деформаций во
всем объеме деформируемого тела;
определение энергосиловых параметров процесса:
усилия прокатки, крутящих моментов на валках, расхо-
да работы и мощности.
В процессе прокатки особую роль играют силы внеш-
него (контактного) трения. Как уже отмечалось, полоса
втягивается в валки за счет действия именно этих сил.
От величины сил трения зависят почти все кинематиче-
ские и энергосиловые параметры процесса, поэтому
важной частью теории прокатки является изучение сил
трения, действующих на контактных поверхностях в зо-
не деформации.
Современная теория прокатки интенсивно развива-
ется, опираясь на достижения математики, физики, ме-
ханики сплошной среды, металловедения и других фун-
даментальных наук. Для решения численных задач
и математического моделирования все более широко
применяются электронные вычислительные машины
(ЭВМ). Выводы теории прокатки используются при раз-
работке оптимальных режимов деформации, конструи-
ровании оборудования и проектировании прокатных це-
хов.
V
Глава II
ГЕОМЕТРИЯ ОЧАГА ДЕФОРМАЦИИ
1. Очаг деформации
и его геометрические характеристики
Очагом деформации называется часть полосы, которая
в данный момент времени подвергается пластической
деформации. Посмотрим на рис. 7. При упрощенном опи-
сании процесса прокатки за очаг деформации принимают
область, ограниченную сече-
ниями АА', ВВ' и дугами
окружностей валков АВ,
А'В'. Это так называемый
геометрический (идеализи-
рованный) очаг деформа-
ции.
Экспериментальные ис-
следования показывают, что
действительные границы
очага деформации могут не
совпадать с сечениями АА'
и ВВ'. Например, пластиче-
ская деформация может на-
чинаться на линии М, а за-
канчиваться на линии N. Об-
ласть, заключенная между
линиями М и N — это фи-
зический (действительный)
очаг деформации. Протяжен-
ность физического очага де-
формации больше, чем гео-
метрического. Части поло-
сы, примыкающие к очагу
деформации, но не деформи-
руемые в данный момент
времени, называются внеш,- Рис. 7. Очаг деформации
ними зонами или жесткими
концами.
Познакомимся с основными понятиями, относящимися
к геометрическому очагу деформации. Дугу АВ (также
А'В') называют дугой контакта или дугой захвата, а со-
ответствующий ей центральный угол а — углом контак-
та или углом захвата. Горизонтальную проекцию дуги
контакта (отрезок ДС) принимают за длину очага де-
15
формации Id. В нижней части рис. 7 штриховкой показа-
на горизонтальная проекция поверхности касания поло-
сы с валками — контактная поверхность FK.
Важнейшей характеристикой геометрических условий
деформации является отношение длины очага деформа-
ции к средней толщине полосы: ld/hCp. Этот показатель,
называемый иногда коэффициентом формы, (или факто-
ром формы) широко используется при анализе процес-
сов прокатки. •
Среднюю толщину полосы в очаге деформации обыч-
но определяют как среднеарифметическую
Лср = (h0 + Ai)/2. (1)
Выражение (1) является наиболее простым, но не
совсем точным, так как толщина полосы изменяется на
протяжении очага деформации не прямолинейно (не по
хордам АВ и А'В'), а по окружности. Истинная средняя
толщина полосы в очаге деформации несколько меньше,
чем вычисляемая по формуле (1). Если дугу окружно-
сти заменить параболой, что вполне допустимо, то полу-
чается формула
Лср = (Ло + 2А1)/3. (2)
Также достаточно точное значение hcp дает формула
Лер — /Ло 1ц. (3)
Параметр ldlhcp характеризует геометрические условия
в продольном сечении очага деформации. Для характе-
ристики формы очага деформации в плане служит отно-
шение ЬсрЩ, где ЬСр — средняя ширина полосы в очаге
деформации; иногда используется отношение
При прокатке в калибрах геометрические условия
деформации зависят, естественно, от формы калибра.
2. Показатели величины деформации '
В процессе прокатки изменяются линейные размеры по-
лосы — высота (толщина), ширина и длина. Рассмотрим
систему показателей, которые характеризуют величину
деформации в каждом из этих направлений.
Высотная деформация
Изменение высоты (толщины) полосы характеризуется
величиной абсолютного и относительного обжатия.
Абсолютное обжатие составляет
Ah = hQ — 1ц. Г'. 'У- ' (4)
16
Относительное обжатие может быть определено
с различной степенью точности. Истинное относительное-
обжатие определяется по формуле
eh = \n(h0/ht). $ (5}
Вычисление величины ен несколько неудобно, так как
требует логарифмирования. Поэтому часто пользуются-
величиной условного относительного обжатия
6 = (й0 —^i)//i0 = ЛШ0. с
В более редких случаях условное относительное об-
жатие определяют в виде
в' = (Ло — h^lht = ДШр (7)
Рис. 8. Сравнение показателей, характеризующих отно-
сительное обжатие:
hi h0 hi h0+hi Vhohi
Надо отметить, что относительное обжатие, вычисля-
емое по формуле (6), меньше истинного ен, а вычисляе-
мое по формуле (7) — больше его. Это видно из графика
на рис. 8. Хорошее приближение к величине в/г получа-
ется, если условное относительное обжатие рассчиты-
вать по формуле
БИБЛИОТЕКА ,|
БПРОПЕТШВСКОГО [
ТАЛЛУРГИЧЕСКОГО |
1дХЛГ',гГТ1г>’л,Г|П А
(8)
17
причем наиболее точный результат достигается при вы-
числении ЛСр по формулам (2) или (3).
Относительное обжатие определяют в долях единицы
или в процентах; в последнем случае результаты расче-
тов по формулам (5) — (8) умножают на 100.
Помимо величин ДЛ, вй, е показателем высотной де-
формации служит коэффициент обжатия
х\ == Га/'о (9)
Поскольку т] меньше единицы, в расчетах иногда удобно
пользоваться обратной величиной 1/'П==^о/Л1.
Поперечная деформация
Изменение поперечных размеров полосы называется
уширением. Показатели уширения по смыслу аналогич-
ны показателям высотной деформации.
Абсолютное уширение составляет
ДЛ = Л1 — Ьо. (Ю)
Истинное относительное уширение
^ = 1п(ЬА). (Н)
Условное относительное уширение
С = (Ь1-Л0)/Л0 = ДЛ/Л0. (12)
Коэффициент уширения
? = W (13)
Величину поперечной деформации также характери-
зуют отношением абсолютного уширения к абсолютно-
му обжатию
а = ДЬ/ДЛ. (14)
Эту величину называют показателем уширения.
Продольная деформация
Абсолютное удлинение полосы составляет
Д/ = /1 —10. (15)
Истинное относительное удлинение
e, = ln(W. < « (16)
Условное относительное удлинение
в = (4-/о)//о = Д///о- (17)
Следует отметить, что величины Д/, в/, 0 редко при-
меняются на практике для характеристики продольной
18
деформации. Вместе с тем очень широко используется
показатель, называемый коэффициентом вытяжки
К = 1Х/1О.
Коэффициент вытяжки характеризует не только из-
менение длины полосы, но и изменение площади попе-
речного сечения ее. Действительно, из условия постоян-
ства объема имеем FqIo=FiIi, откуда следует Zi//0 =
=/?o/F1.
Таким образом, коэффициент вытяжки можно опре-
делить также по соотношению площадей поперечного се-
чения полосы до и после прокатки
Л = FJF,. (19>
Если технологический процесс включает несколько,
проходов полосы через валки, что бывает почти всегда,,
то различают частные коэффициенты вытяжки (в каж-
дом проходе) и общий коэффициент вытяжки.
В соответствии с формулами (18) и (19) общий ко-
эффициент вытяжки составляет
^ОбЩ -
(20>
где 1п и Fn — соответственно длина и площадь попереч-
ного сечения полосы после n-ного прохода.
Нетрудно доказать, что общий коэффициент вытяж-
ки равен произведению частных коэффициентов вытяж-
ки:
^общ = ^2 ^3 ••• ^П- (21)f
Допустим, прокатка ведется в три прохода. Произве-
дение частных коэффициентов вытяжки Х1Х2Хз= (Zi/Z0) X
X (Z2/Z1) • (Z3/Z2) ==/з/^о =А«общ-
Последнее выражение доказывает справедливость
формулы (21).
Существует еще понятие о среднем коэффициенте
вытяжки Хер в нескольких проходах. Под величиной
Хер подразумевают такой коэффициент вытяжки, кото-
рый был бы в том случае, если бы коэффициенты вытяж-
ки во всех проходах были одинаковыми. Исходя из этого
определения можно написать:
^общ = ^ср^срХср ... Хср = Хср, (22)
где п — число проходов.
2* 19
Из формулы (22) находим величину среднего коэф-
фициента вытяжки
^СР ~ У^общ • (23)
На основании формулы (22) можно решить и другую
задачу: определить необходимое число проходов п при
прокатке данного профиля, если известны значения
Лобщ и Лер
л = lg ^o6nj/lg Лср. (24)
Формула (24) часто применяется в технологических
расчетах при разработке режимов деформации.
Взаимосвязь деформаций
Коэффициенты деформации в трех основных направле-
ниях связаны между собой условием постоянства объема
металла. Так, для прямоугольной полосы имеем
/1оМо=^1Ыь откуда следует
(Mo)(Wo)=^=l- (25)
Таким образом, произведение коэффициентов обжа-
тия, уширения и вытяжки должно быть равно единице.
В противном случае нарушается условие постоянства
объема.
Логарифмируя выражение (25), получим
In + In (bjbo) + In (IJIq) = 0
или
— In (h0/h^ + In (bjbo) + In (/х//0) = 0. (26)
Сумма истинных относительных деформаций потрем
основным направлениям (с учетом знака) равна нулю.
Знаки перед членами формулы (26) показывают, что по
высоте полосы происходит уменьшение, а по другим на-
правлениям — увеличение размеров.
3. Формулы для расчета углов захвата
Выведем формулу для определения угла контакта (угла
захвата) а, пользуясь схемой на рис. 9. Из прямоуголь-
ного треугольника АОС получаем
cos а = ОС/ОА, (27)
Имеем ОС=ОВ—CB=R—ДА/2; OA=R.
20
Подставляя значения отрезков ОС и ОА в формулу
(27), после несложных преобразований получим
•coscc = 1 — (Д/г/2Д) = 1 — (Д/i/D). (28)
Можно придать иной вид формуле (28), если исполь-
зовать известное тригонометрическое равенство
1 — cos а = 2 sin2 (ос/2).
Тогда из формулы (28)
следует 2 sin2 (ct/2) =kh!D,
откуда находим
-sin(a/2) = у \h/(2D) . (29)
Формулы (28) и (29) по
существу одинаковы и взаи-
мозаменяемы. Однако по
этим формулам угол а оп-
ределяется в виде тригоно-
метрической функции. Если
принять допущение sin (а/
/2)«а/2, то получим приб-
лиженную, но простую и
удобную формулу для рас-
чета угла контакта .
в радианах
Рис. 9. К определению геометриче-
ских параметров очага деформации
a = (30)
в градусах
a = (180/я) V&MR « 57,3 /Дй/Я.
(31)
Точность приближенной формулы (30) вполне доста-
точна. Сравнительные расчеты по формулам (28) и (30)
показывают, что даже при очень больших величинах уг-
лов контакта (до 30—35°) погрешность вычислений по
формуле (30) не превышает 1,0—1,5 %.
В технологических расчетах часто возникает необхо-
димость определения абсолютного обжатия Д/i по за-
данным значениям а и D. Тогда формулы (28) и (30)
можно преобразовать и использовать в виде
Д/i = D (1 — cos а); (32)
Д/г = 7?а2. (33)
Формулы (28) — (31) служат для расчета угла кон-
такта при установившемся процессе прокатки. Вместе
21
определению начального
с учетом пружины стана
Рис. 10. К
угла захвата
с тем для правильной оценки захватывающей способно-
сти прокатных валков необходимо знать тот угол захва-
та ос3, который соответствует моменту начального каса-
ния полосы с валками (рис. 10). Угол ос3 по своей вели-
чине больше угла а, вычисляемого по формулам (28) —
(31). Это объясняется тем,
что при подводе полосы
к валкам зазор между
ними h меньше толщины
выходящего конца поло-
сы h\. По мере осуществ-
ления захвата валки не-
сколько раздвигаются, так
как происходит упругая
деформация деталей ста-
на, а также выбираются
люфты в сочленениях де-
талей рабочей клети. Уве-
личение зазора при входе
полосы в валки условно
называют пружиной ра-
бочей клети прокатного
стана. Величина пружины
составляет 6 = fti—h.
Для определения на-
угла захвата а3 могут быть использованы фор-
чального
мулы (28) — (30), но при этом вместо обжатия ho—hi
в них надо ввести разность hQ—h. Учитывая, что hQ—h =
=Д/г-|-б, можно написать
cosa3 = 1 — (h0 — h)/D = 1 — (Д/г + 6)/D;
sin (<Хз/2) = —/i)/(2D) = /(Aft + 6)/(2D) ;
»3 = —= K(A/i + 6)/R.
Из сравнения формул (34) — (36) с формулами (28) —
(30) видно, что различие между углами ос3 и а зависит
от соотношения величин 6 и Д/г. Если пружина 6 мала
по сравнению с обжатием Д/г, то значения углов а3 и а
близки. Если же величина 6 вполне соизмерима с Д/г»
а тем более в случаях, когда 6>Д/г (что встречается, на-
пример, при тонколистовой прокатке), тогда различие
между углами а3и а существенно.
4. Определение длины очага деформации
Обратимся к схеме на рис. 9. В задачу настоящего пара-
графа входит определение длины отрезка AC=ld. Из
22
(34>
(35>
(36)
треугольника АОС находим
ld = R sin а. (37)
С некоторым приближением можно принять
4 = Яа. (38)
Однако формулы (37) и (38) не совсем удобны, так
как для определения 1& требуется предварительно рас-
считать угол а. Поэтому в теории прокатки чаще приме-
няется другая формула, позволяющая определить длину
очага деформации непосредственно по значениям Д/г
и/?. Вновь обращаясь к треугольнику АОС (рис.9), на-
пишем
ld = АС = V(OA)* — (OCr = К Я2— (Я —Д/г/2)2.
После возведения в квадрат выражения в скобках
и простых преобразований получим
ld = V RAh — Ah2/4. (39)
Расчеты по формуле (39) свидетельствуют о том, что
величина второго члена под радикалом мала по сравне-
нию с первым членом. На этом основании членом Д/г2/4
можно пренебречь, придав формуле для определения дли-
ны очага деформации более простой вид
ld = VRKh. (40)
Несложный геометрический анализ показывает, что
переход от формулы (39) к формуле (40) по существу
означает замену полухорды АС хордой АВ (рис. 9). По-
скольку углы захвата обычно невелики, такая замена
вполне допустима.
5. Внеконтактная деформация
Рассмотренные в предыдущих параграфах геометриче-
ские зависимости относятся к идеализированному (гео-
метрическому) очагу деформации. Вместе с тем ранее от-
мечено, что границы действительного (физического)
очага деформации могут выходить за пределы геометри-
ческого. Наглядным проявлением этого служит внекон-
тактная высотная утяжка заднего конца полосы перед
входом в валки.
Многочисленные измерения образцов-недокатов1 сви-
1 Образцы, прокатанные не полностью (не по всей длине) и из-
влеченные из валков.
23
детельствуют о том, что в процессе прокатки высота по-
лосы начинает уменьшаться еще до входа в контактную*
зону очага деформации (рис. 11). Внеконтактная высот-
ная утяжка распределяется по ширине полосы неравно-
мерно: вблизи боковых кромок она больше, чем посере-
Рис. 11. Внеконтактная высотная утяж-
ка заднего конца полосы
дине (за исключением
очень узких полос, у
которых наблюдается
обратная картина: мак-
симальная утяжка на-
ходится на продольной
оси образца).
Величину высотной
утяжки можно характе-
ризовать показателем:
v = ДЯВН/ДЬ, (41).
Проведенные исследования
где АЛвн — абсолютное
обжатие во внеконтакт-
ной области.
показывают, что величи-
на показателя высотной утяжки v зависит главным обра-
зом от геометрических условий
Рис. 12. Зависимость внеконтактной
высотной утяжки от параметра ^^ср:
I — свинец; II — сталь; 1 — у кромки;
2 — посередине образца
деформации. Особенно-
большое влияние ока-
зывает фактор формы
ld/hCp, с уменьшением
которого внеконтакт-
ная деформация возра-
стает.
В качестве примера
на рис. 12 приведены
результаты измерений
внеконтактной утяжки
при прокатке свинцо-
вых и стальных (Ст. 3'
при 1000 °C) образцов
сечением /zoXbo=3OX
Х50 мм на валках ди-
аметром 194 мм. Из
графиков видно, что
в диапазоне ld/hcp<i(},5
менее
величина внеконтактного обжатия составляет не
15—25 % от полного обжатия.
Очевидно, что внеконтактная высотная утяжка вызы-
вает уменьшение дуги контакта и угла а (рис. 11). Если
24
известен показатель v, то можно определить истинные
параметры контактного очага деформации. Величина
фактического обжатия в контактной области будет Д/i—
—A/ibh. Учитывая это, находим
где ldK — длина контактного очага деформации с учетом
высотной утяжки.
Вводя показатель v, получим
ldK= /RAft(l-v) = ld (42)
Аналогично находим
ак = ]/(Д/г — Д/гвн)/7?
или
zxK = K(A/i/7?)(l — v) = а К1 — v, (43)
где ак — угол контакта с учетом высотной утяжки.
На рис. 13 приведен график, характеризующий умень-
шение длины контактного очага деформации и угла кон-
Рис. 13. Влияние высотной утяжки
на геометрические параметры кон-
тактного очага деформации
Рис. 14. Зависимость длины вне-
контактного очага деформации от
параметра /^/ЛСр
такта в зависимости от величины фактора формы Id/h^.
График построен с помощью выражений (42) и (43) по
экспериментальным данным на рис. 12; при этом значе-
ния v принимались средними по ширине полосы. Таким
образом, уменьшение угла контакта и длины контактной
зоны деформации из-за высотной утяжки составляет при
/й/Лср=1,0 приблизительно 6 %, а при /й/^ср<0,5 — бо-
лее 10 %.
Измерения образцов-недокатов также позволяют оп-
ределить фактическую границу начала пластической де-
25
формации, т. е. длину внеконтактного очага деформации
/йвн (рис. 11). Соответствующие экспериментальные дан-
ные приведены на рис. 14 (значения /йвн усреднены по
ширине полосы). Анализ их приводит к выводу, что при
ld/hcp<0,5 имеет место соотношение ^вн^^к-
Некоторая внеконтактная деформация может наблю-
даться и за плоскостью выхода полосы из валков, но
она проявляется в гораздо меньшей степени, чем на
входе.
6. Сплющивание валков
При холодной прокатке стали и других высокопрочных
металлов, а в некоторых случаях и при горячей прокатке,
в очаге деформации возникают очень большие контакт-
Рис. 15. Схема сплющивания валков
ные давления, под действи-
ем которых валки претерпе-
вают значительную местную
упругую деформацию—ра-
диальное сжатие. Это явле-
Рис. 16. К выводу формулы для опре-
деления длины сплющенной дуги кон-
такта
ние называется сплющиванием валков.
В результате сплющивания увеличивается длина оча-
га деформации, уменьшается обжатие, изменяются дру-
гие геометрические параметры (рис. 15). Точная форма
контактной поверхности при значительном сплющивании
валков пока не выяснена. В порядке допущения при ана-,
лизе геометрических условий прокатки принимают, что
26
в зоне контакта с металлом валки сохраняют круглую
форму, но их радиус увеличивается до значения Rc,
а центры кривизны смещаются в точки Ос.
Имеется ряд теоретических работ, посвященных оп-
ределению длины очага деформации с учетом сплющи-
вания валков. Наибольшей известностью пользуется фор-
мула Хичкова (J. Н. Hithcook), вывод которой приведен
ниже.
Представим полную длину очага деформации ldc в ви-
де суммы отрезков /0 и Ц (рис. 16). Обозначим упругое
радиальное сжатие валка по линии ОВ через е (BF—e).
Приближенно принимая, что точки F и К лежат на одной
горизонтали, в соответствии с формулой (40) можно
написать
4 = 1 R(bh + 2e).
Аналогично находим длину отрезка /1
4 = / R2e.
(44)
(45)
Таким образом, полная длина очага деформации будет
<-с = /« (ДЛ + 2г) + = //?ДЛ +/[ +k- (46)
Главная задача заключается в определении величи-
ны е. С этой целью Хичкок использовал известную в тео-
рии упругости формулу Герца
для расчета упругой деформа-
ции цилиндра при сжатии его
с плоскостью (рис. 17)
A/? = 2pnor(l-^)/(3i£), (47)
где /?пог — давление па едини-
цу длины цилиндра; ц и Е —
соответственно коэффициент
Пуассона и модуль упругости
материала цилиндра.
Проводя аналогию между
схемами деформации цилинд-
ра (рис. 17) и валка при про-
катке (рис. 16), Хичкок принял
Рис. 17. Сжатие цилиндра с
плоскостью (задача Герца)
e=&R и /1 = 6. В соот-
ветствии с этим допущением расчетное давление на ва-
лок составляет
РпОГ -- 2/хРср,
(48)
27
где Pep — среднее давление на контактной поверхности:
в очаге деформации.
Тогда с помощью формулы (47) находим
е = 4 lr рср (1 — ц2)/(л£). (49>
Совместное решение формул (45) и (49) позволяет
определить длину отрезка /ь т. е. приращение длины оча-
га деформации за линией центров недеформированных
валков
h = [8 (1 - р2)/(л£)] /?рср. (50>
Подставляя это значение Zi в уравнение (46), полу-
чим формулу для определения полной длины очага де-
формации с учетом сплющивания валков
1„с = 1/RM. + [ ? + 8(1Rp0P. (51)
у [ л£ J лЕ
Если ввести обозначение 8(1—|12)/(л£) =т, то фор-
мулы (50) и (51) соответственно принимают вид
h = mRp™, (52)
ldc = V №h + (m^cp)2 + mRPcy (53)
Величина коэффициента m зависит только от механи-
ческих свойств материала валков и может быть рассчи-
тана заранее. Она составляет:
для стальных валков (£ = 2,06-105 МПа; р, = 0,3) т=
= 1,12-IO"5 1/МПа;
для чугунных отбеленных валков (£=1,26-105 МПа;
ц=0,25) т=1,9-10-5 1/МПа;
для карбидвольфрамовых валков (£ = 6,51 • 105 МПа;
ц=0,3) т=0,36-10-5 1/МПа.
Из сравнения величин т видно, что лучше всего про-
тивостоят сплющиванию валки из карбида вольфрама,
а наиболее слабыми в этом отношении являются чугун-
ные валки.
Следует подчеркнуть, что формулы (52) и (53) выве-
дены на основании приближенной аналогии между сжа-
тием цилиндра с плоскостью и деформацией валка в кон-
такте с полосой. В первом случае схема деформации яв-
ляется симметричной (относительно вертикальной оси),
а во втором — несимметричной, значительно более слож-
ной, поэтому формулы (52) и (53) могут рассматривать-
ся только как приближенные.
Действительно, экспериментальные исследования по-
28
называют, что фактическое приращение длины дуги кон-
такта в результате сплющивания больше, чем рассчитан-
ное по формуле (52). Для согласования теоретических
данных с опытными в формулу (52) вводится поправоч-
ный коэффициент с, величина которого больше единицы
4 = cmRpcv. (54)
По рекомендации А. И. Целикова и А. И. Гришкова
коэффициент с принимается в пределах с= 1,2ч-1,5,.
в среднем с—1,375.
В соответствии с выражением (54) полная длина оча-
га деформации определяется по формуле
4с = V RM + (cmRpcpy + cmRpcp. (55)
В некоторых случаях приходится рассчитывать сплю-
щивание валков не по величине среднего контактного
давления рСр, а по усилию прокатки Р. Для этого преоб-
разуем формулу (55), учитывая, что
Рср = Р/(^Ьср). (56)
Подставим выражение (56) в формулу (55)
1 PNh -4-1 cmRP V _u cmRP
Решая это уравнение относительно ldc, после неслож-
ных преобразований получим
ldc = V + %cmRP/bcV . (57)
Если известна длина дуги контакта, то, пользуясь
схемой на рис. 15, можно определить радиус кривизны
сплющенной поверхности валков Rc и соответствующий
угол контакта ас. По аналогии с формулой (40) напишем
(58)
Приравнивая правые части формул (57) и (58), на-
ходим
Rc = R [ 1 + 2cmP/(A/i6cp)]. (59)
Угол контакта с учетом сплющивания валков будет
“с = = /awFo • (60)
Сравнивая формулы (30) и (60), можно сделать вы-
вод, что сплющивание валков приводит к уменьшению
угла контакта, поскольку Rcz>R.
29
7. Площадь контактной поверхности
При прокатке полос прямоугольного сечения в цилиндри-
ческих валках определение площади контактной поверх-
ности не представляет затруднений. В этом случае форма
поверхности касания в плане может быть принята за тра-
пецию с основаниями Ьо и bi и высотой Ц (рис. 7). Сле-
довательно, площадь контактной поверхности определя-
ется по формуле
FK = 0,5 (b0 + bt) ld = &ср ld. (61)
Если уширение очень мало, т. е. Ь0^Ь\^Ь, то фор-
мула (61) еще более упрощается
FK = bld = b]ARbh. (62)
При необходимости учета внеконтактной высотной
утяжки полосы или сплющивания валков в приведенные
формулы вместо ld следует подставлять значения ldK
или ldc.
Более сложно определяется площадь контактной по-
верхности при прокатке в калибрах, когда обжатие по
ширине полосы распределяется неравномерно. Эта зада-
ча решается графическим, графоаналитическим или ана-
литическим способами.
При графическом определении FK калибр вместе
с прокатываемой полосой вычерчивают в трех проекциях,
причем горизонтальная проекция является искомой
и строится с помощью двух других (рис. 18). Через про-
филь входящей в калибр полосы проводят несколько вер-
тикальных сечений: 1, 2, 3, 4 и т. д. В каждом сечении
графически определяются величина обжатия, радиус вал-
ков и длина очага деформации. Например, рассмотрим
сечение 2. Здесь обжатие составляет kh2=2(AB). Про-
ведя из точки В горизонтальную линию до пересечения
с осевой линией валков, находим соответствующий ката-
ющий радиус Далее из точки А проводим горизон-
тальную линию до пересечения с окружностью радиуса
#2, в результате получаем точку С. Проектируя точку С
на горизонтальную плоскость, находим точку Е. Анало-
гичные операции выполняются для других сечений, что
позволяет построить по точкам искомую границу кон-
тактной поверхности. Площадь в пределах этой границы
(на рис. 18 заштрихована) планиметрируется.
Графическим методом можно определить площадь
контактной поверхности при прокатке в калибрах даже
30
Очень сложной формы, однако этот метод не лишен не-
достатков. Во-первых, графическое построение является
Трудоемкой операцией, причем всегда вносится некоторая
Погрешность, связанная с вычерчиванием. Для получения
более точных результатов рекомендуется вести построе-
ние в увеличенном масштабе. Во-вторых, приходится при-
ближенно учитывать влияние уширения полосы на пло-
щадь контактной поверхности. Если пренебречь уширени-
ем, то граница контактной поверхности на рис. 18 будет
Рис. 18. Графическое определение площади контактной поверх-
ности
соответствовать пунктирным линиям, выходящим в точ-
ки М. Вместе с тем очевидно, что ширина контактной
поверхности в плоскости выхода равна или почти равна
конечной ширине полосы Ь\. Поэтому для более правиль-
ного определения FK в плоскости выхода проставляются
точки N, которые плавными (касательными) линиями со-
единяются с -основной контурной линией проекции.
В-третьих, не учитывается внеконтактная высотная утяж-
ка полосы, которая при прокатке в калибрах может быть
значительной. В целом погрешность в определении FK
графическим методом составляет 5—6 %.
Графоаналитический метод, разработанный А. А. Дин-
ником, близок к графическому. Также необходимо по-
31
строить в совмещенном виде профили калибра и прока-
тываемой полосы, а затем провести ряд вертикальных се-
чений, в которых определяются значения АЛ и R. Однако
длина очага деформации в каждом сечении находится
не графическим построением, а расчетом по формуле
(40).
Аналитический метод определения FK заключается
в использовании формул, полученных с помощью уравне-
ний аналитической геометрии. Для ряда простых калиб-
ров такие формулы разработаны В. Г. Дроздом:
а) для прокатки ромбической полосы в квадратном
или ромбическом калибре (рис. 18)
= 0,67^ И#вД/гв ; (63)
б) для прокатки квадратной полосы в овальном ка-
либре (рис. 19, а)
F„ ~ 0,54 (Ьо + 6,) ; (64)
в) для прокатки овальной полосы в квадратном (рис.
19, б), круглом (рис. 19, в) или овальном калибре
Fx = O,75b1VrR^. (65)
Рис. 19. Схемы прокатки в калибрах:
/ — овала из квадрата; II— квадрата из овала; III— круга или овала
из овала
При прокатке в калибрах других форм площадь кон-
тактной поверхности можно приближенно определить
аналитически, применив формулу (61) в виде
Р к = ^ср V ^ср А/гСр* .(66)
Величины 7?ср и Д&Ср определяются методом приведен-
ной полосы. Сущность этого метода состоит в том, что ка-
либр и полоса любой формы условно приводятся к пря-
моугольному профилю (той же ширины). С помощью та-
32
КОГО приема находим:
АЛор = Лоер - Чр = - Ft/bt- (67)
Я«р = Ri - М2 = F^ <68>
Где и Л1ср — средняя высота полосы соответственно
: ДО и после прокатки; Я; — идеальный радиус, равный по-
ловине расстояния между осями валков.
В литературе отмечается, что площадь контактной по-
верхности, рассчитанная по методу приведенной полосы,
Получается завышенной на 7—18 %.
Глава III
УСЛОВИЯ ЗАХВАТА ПОЛОСЫ ВАЛКАМИ
1. Условие свободного начального захвата
Пусть полоса подведена к вращающимся валкам и кос-
нулась их своими кромками (рис. 20). Произойдет ли за-
хват полосы валками? Чтобы ответить на этот вопрос, на-
до сформулировать условие
захвата. Если заталкиваю-
щая сила Q, с помощью ко-
торой полоса подводится
к валкам, мала и не вызыва-
ет значительного смятия
кромок, то захват называет-
ся свободным или естествен-
ным. Такой захват чаще все-
го встречается на практике.
В точках касания А со
стороны валков на полосу
действуют силы нормально-
го давления N и силы тре-
ния Т (рис. 20). Силы тре-
ния стремятся втянуть поло-
Рис. 20. Схема сил в начальный
момент касания полосы с валками
су в зев валков, а силы нор-
мального давления препятствуют этому. Очевидно воз-
можность захвата зависит от соотношения втягивающих
и отталкивающих сил. Для осуществления захвата необ-
ходимо, чтобы горизонтальные составляющие сил трения
Тх были больше горизонтальных составляющих сил нор-
мального давления Nx или равны им. Математически
3 А. п. Грудев
33
это условие можно представить в следующем виде
NX<TX. (69)
Из схемы сил на рис. 20 находим
NX = N sin а3; (70)
7\ = Tcosa3. (71)
Используем закон трения Амонтона
T = faNt (72)
где f3 — коэффициент трения при скольжении кромок по-
лосы по валкам, называемый в дальнейшем коэффициен-
том трения при захвате.
Тогда получим
T’a = f8Vcosa3. (73)
Подставим найденные значения горизонтальных сил
Nx и Тх в исходное условие (69)
N sin a8 fa N cos a8.
Разделив левую и правую части этого выражения на
N cos аз, получим
tga8<f8. (74>
Формула (74) представляет условие свободного на-
чального захвата. Словесная формулировка этого усло-
вия такова: чтобы произошел захват полосы валками,,
тангенс угла захвата должен быть меньше коэффициента
трения при захвате или, по крайней мере, равен ему.
Очень часто условие захвата выражают в несколько'
ином, еще более простом виде. Учитывая, что f3=tgp3^
где р3 — угол трения при захвате, вместо' формулы (74)
можно написать tg a3^tg р3;
следовательно
аз 'С Рз- у (75)'
Таким образом, чтобы произошел захват полосы вал-
ками, угол захвата должен быть меньше угла трения или,,
по крайней мере, равен ему. Из формул (74) и (75) вид-
но, что предельная величина угла захвата всецело зави-
сит от величины коэффициента трения f3. Чем больше
коэффициент трения, тем выше захватывающая способ-
ность валков.
Как будет показано в дальнейшем (см. гл. VI), вели-
чина коэффициента трения зависит от многих факторов:
состояния поверхности и материала валков, скорости
34
Прокатки, температуры металла и др. Все эти факторы
совокупности и предопределяют максимальные углы
Мхвата, достигаемые на практике.
При прокатке в калибрах в большинстве случаев ус-
ловия захвата лучше, чем на гладкой бочке, так как бо-
ковые (наклонные) стенки калибра способствуют защем-
лению полосы.
/ Практические значения максимальных углов захвата
’Аля прокатных станов разного назначения приведены
• табл. 1.
Таблица 1. Максимальные углы захвата
Станы, условия прокатки Валки Максималь- ный угол захвата “зтах’ г₽ад
Блюминги, черновые клети аготовочных и сортовых Станов Стальные с затрубленной поверхностью (насечен- ные, рифленые) Стальные обточенные 26—34
Сортовые станы 22—24
Листовые станы горячей прокатки Стальные или чугунные, во многих случаях шли- фованные 15—22
Листовые станы холодной Прокатки (применяется технологичес- кая смазка) Стальные шлифованные или полированные 4—10
' 2. Принудительный захват
Теперь рассмотрим случай, когда заталкивающая сила Q
(рис. 20) велика и способна осуществить значительное
вдавливание металла в валки. Такой захват называется
принудительным или искусственным. При наличии доста-
точной заталкивающей силы захват может произойти при
условии а3> 0з.
Сила Q, как и силы трения Т, направлена по ходу
Прокатки (рис. 20). Однако роль этих сил в осуществле-
нии захвата очень различна. Остановимся на этом под-
робнее.
Составим уравнение равновесия продольных сил,
действующих на полосу, с учетом силы Q
itf. = 2Tx + Q. Z
Подставляя в это уравнение значения сил Nx и Тх
Согласно формулам (70) и (73), после несложных пре-
35
образований находим
Q = 2N cos a, (tg а, — f a)
И
N = Q/12 cos а8 (tg а8—/8)].
(76)
(77)
Выражение (77) позволяет утверждать, что всякое
увеличение заталкивающей силы Q вызывает ответный
рост отталкивающих сил N. Таким образом, сила Q са-
ма по себе не может создать перевеса втягивающих сил
над отталкивающими.
Сила Q способствует осуществлению захвата кос-
венно. Под действием ее сминаются передние кромки
полосы, в результате чего точка приложения сил N и Т
смещается в глубь зева валков (рис. 21). Происходит
Рис. 21. Принудительный захват — смятие кромок поло-
сы под действием силы Q
поворот сил, благоприятный в отношении захвата. Ког-
да угол ф, определяющий наклон сил N и Т, уменьшится
до величины угла трения, возникает истинный захват
полосы валками. Кроме того, в результате действия за-
талкивающей силы выбирается часть пружины рабочей
клети стана, т. е. валки несколько раздвигаются, что
также способствует осуществлению захвата.
Заметим, что по условию статического равновесия
сил заталкивающая сила вообще может существовать
(иметь положительное значение) только в том случае,
когда угол захвата больше угла трения: аэ>₽3. Это вид-
36
I NO ИЗ формулы (76), левая часть которой обращается
Г В Нуль при tga3=f3 и становится отрицательной при
[ tgChC/V Последнее означает, что в случае tga3<Ja
[ ВВЛКИ даже способны преодолеть некоторое тормозящее
К усилие, приложенное к полосе.
К । Основной вопрос теории принудительного захвата
Можно сформулировать так: какую величину должна
| *меть заталкивающая сила, чтобы произошел захват
ЕВри заданной разности углов а3 и р3? Ниже приводится
I Вывод соответствующей формулы.
| Допустим, под действием силы Q полоса начала
| Вжиматься в зев валков. В некоторый промежуточный
Момент передняя грань полосы будет находиться под
f углом <р, а точка приложения сил N и Т — под углом ф
I (рис. 21). Для этого момента в соответствии с формулой
[ (76) можно написать:
| - 2W cos ф (tg ф — /), (78)
|К*де f — коэффициент трения на площадках смятия кро-
мок.
Преобразуем формулу (78):
Q9 = 2N (sin ф — cos ф ""у j ~ (si п ф cos р —
* — cos ф sin р) = sin (ф — Р), (79)
cos р
Где р — угол трения, соответствующий коэффициенту
трения f.
Ввиду малой величины разности углов ф и р примем
8in(<p—р)=ф—р.
Если допустить, что точка приложения сил N и Т нахо-
дится посередине площадки смятия, то ф=(а3+<р)/2«
Следовательно, формуле (79) можно придать такой вид;
«,“^г(“. + ч>-2₽). <80’
т cos р
Выразим силу N через среднее контактное давление
Дер на площадках смятия
N " Pop Рк = Pep bR (a3 — <р), (8Р
^де FK — площадь контактной площадки.
f Подставляя это значение силы N в формулу (80),
Получим:
L - (“а--(>)(«,+ ф-2₽). (82)
37
По выражению (82) можно судить, как изменяется
величина необходимой заталкивающей силы Q<p по мере
продвижения переднего торца полосы через зев валков.
В начальный момент касания имеем <р = а3 и Qq> =0. Да-
лее, по мере уменьшения угла <р сила Qq> сначала воз-
растает, а затем снижается. Когда угол ф уменьшится
до значения ф=20—а3, сила фф вновь становится рав-
ной нулю. Это означает, что валки захватили полосу
и дальше процесс может идти без заталкивающей силы.
Определим то значение угла ф, при котором величина
необходимой силы Q максимальна. Для этого решаем
обычную математическую задачу на отыскание макси-
мума: продифференцируем функцию (82) и первую про-
изводную приравняем нулю:
_ Рср^ (_ 2(р 20) = о, откуда ф = 0.
4ф cos р
Таким образом, заталкивающая сила максимальна,
когда угол ф равен углу трения 0. Найдем значение за-
талкивающей силы в этот момент, заменив в формуле
(82) угол ф на 0. В результате получим
е1М1 = -г££^-(«з-₽)2. (83)
cos р
Вывод формулы (83) содержится в трудах А. П. Чек-
марева и других ученых. Если формулу (83) решить от-
носительно угла а3, то она принимает вид, аналогичный
условию свободного захвата (75), а именно
«3 < 0 + / QmaxCOS0/(pcpbtf) . (84)
Формулу (84) можно назвать условием принудитель-
ного захвата. Из формулы (84) видно, что в случае при-
нудительного захвата предельная величина угла а3 за-
висит не только от коэффициента (угла) трения, но и от
величины заталкивающей силы, контактного давления
(а следовательно, и от механических свойств металла),
ширины полосы и радиуса валков. Все эти факторы ока-
зывают влияние на степень смятия кромок полосы под
действием заталкивающей силы.
Обратим внимание на то, что правая часть формулы
(85) сохраняет определенное положительное значение
даже при 0 = 0. Однако отсюда не следует, что при на-
личии достаточной заталкивающей силы захват полосы
валками будет осуществляться даже в отсутствие сил
внешнего трения. Без трения может происходить про-
38
ДВВЛИВание металла через валки, но подлинный захват
N прокатка невозможны.
Для расчетов по формулам (83) и (84) надо знать
Вреднее контактное давление рСр и коэффициент трения
На площадках смятия. Приближенно можно принять
Яср"3 (1.2 ч-1,5) от, где от—предел текучести деформи-
руемого металла. Коэффициент трения f может быть
Принят как средний между коэффициентом трения в на-
чальный момент захвата и при установившемся процес-
се* прокатки: /=0,5(/зН"/у)«
Методика определения коэффициентов трения fs
Я /у приведена в гл. VI.
I. Динамический захват
При выводе условий захвата (75) и (84) исключены из
рассмотрения инерционные силы, возникающие при за-
медлении или ускорении движения захватываемой по-
Йосы, т. е. задача решалась в статической постановке.
Между тем, захват по своему существу является дина-
мическим процессом, в котором всегда участвуют инер-
ционные силы.
Как известно из механики, при изменении скорости
Движения тела сила инерции составляет
Син =* та ~т (dv/dx), (85)
Где т — масса тела; a=dvldx — ускорение; dv — изме-
нение скорости тела за время dx.
Напишем уравнение равновесия продольных сил,
приложенных к полосе, с учетом силы инерции (при от-
сутствии статической заталкивающей силы Q)
2NK ± т (dv/dx)«- ± 2ТХ.
(86)
Инерционный член m{dv!dx) может быть положи-
тельным или отрицательным в зависимости от того,
ускоряется или замедляется движение полосы при входе
В валки. Действительный знак перед этим членом выяв-
ляется при вычислении производной dvfdx. Вид знака
ред силой Тх зависит от соотношения скоростей поло-
hl и валков в процессе осуществления захвата.
Анализируя влияние инерционных сил на процесс
ВХВата, рассмотрим несколько конкретных вариантов
рокатки.
Вариант первый: а3<₽з; vo<^b, где — скорость
39
подвода полосы к валкам; vB — окружная скорость вал-
ков1.
В этом случае сила Тх положительна и NX<TX. Следо-
вательно, с первого момента касания на полосу будет
действовать статически неуравновешенная втягивающая
сила 2(7\—Nx). Под действием этой силы полоса входит
в валки с ускорением. Последнее будет нарастать
вплоть до момента, когда скорость передней грани по-
лосы сравняется с окружной скоростью валков; после
этого ускорение начнет падать и процесс прокатки ста-
билизируется.
Из приведенного рассуждения как будто бы следу-
ет, что при а3<р3 инерционная сила, имеющая знак
плюс в уравнении (86), не оказывает существенного
влияния на процесс захвата. Действительно, если угол
захвата а3 значительно меньше угла трения fJ3, то за-
хват осуществляется очень четко, мгновенно. Если же
угол а3 близок к 03 и к тому же инерционная сила вели-
ка (большая масса полосы, большая разность скоростей
ав—По), то характер захвата становится неустойчивым.
В этом случае относительно малая втягивающая сила
2(ТЖ—Nx) с трудом преодолевает силу инерции. На
практике это проявляется в том, что полоса входит
в валки с предварительными подергиваниями и рывка-
ми. Следовательно, при прокатке с большими углами
захвата желательно добиваться того, чтобы разность
скоростей vB—t’o была как можно меньше.
Второй вариант: а3<03; ^о>^в. В этом случае при
соприкосновении полосы с валками происходит удар.
В начальный момент сила инерции направлена по ходу
прокатки, а силы трения Тх отрицательны. На этой
стадии полоса движется с замедлением. Период тормо-
жения длится до тех пор, пока скорость металла вблизи
сечения входа не станет ниже окружной скорости вал-
ков; после того на соответствующей части контакт-
ной поверхности силы трения начинают осуществлять
втягивание полосы. Наступает стадия установившейся
прокатки. Таким образом, захват осуществляется на-
дежно.
Третий вариант: а3>р3; t>0<uB. При заданных усло-
виях в начальный момент касания силы трения Тх по-
1 Скорость подвода полосы у0 надо сравнивать не с окружной
скоростью валков vB, а с ее продольной проекцией в точках касания,
которая составляет vB cos а3. Но с целью упрощения анализа допус-
тимо пользоваться и величиной ув.
40
.никительны, но TX<NX, поэтому разность Тх—Nx от-*
рнцатсльна. Это значит, что валки не могут захватить
полосу. Соприкоснувшись с валками, полоса должна
пыла бы остановиться, но за счет ее кинетической энер-
। пи (если ио#=О) произойдет некоторое смятие кромок.
При этом угол гр, характеризующий наклон сил N и /
(рис. 21), станет меньше угла а3. Если в результате
смятия кромок будет выполнено условие гр^р, то воз-»
никнет захват и скорость полосы начнет возрастать
(аналогично варианту а3<р3). Но если до полной оста-
нивки полосы сохранится соотношение гр>р, захват не
• •существится.
Можно определить теоретически ту разность углов
и, р3, которая допустима при заданной скорости под-
вода полосы v0. Также можно решить обратную задачу.'
пинги ту скорость vq, которая требуется_ для осуществ-*
1Г1И1Я захвата при заданной разности углов а3—р3. Один
и । методов решения таких задач освещен ниже.
Четвертый вариант: а3>р3; и0>ив.
Это наиболее сложный случай захвата. Поскольку
полоса входит в валки с ударом (ио>^в), в начальный
момент касания силы трения Тх отрицательны. Инерци-
онные силы направлены по ходу прокатки, так как поло^
• ;i тормозится. Естественно, происходит смятие кромок.
В пекоropi.iii момент скорость полосы падает до окруж-
ном скорости валков; после этого силы трения Тх меняют
• ное направленно па противоположное — становятся
втягивающими. Если к моменту выравнивания скоро-
••ceii полосы и валков будет достигнуто соотношение
Ф (рис. 21), то полоса будет захвачена. Однако воз-
можна и другая ситуация: в момент достижения равен-
«1Н.1 Со (»„ сохранится соотношение и захват не?
нро11.1опде1'; югди скорость полосы будет продолжать
пади । ь. ()с гшппаяся кинетическая энергия полосы рас-
ходуется на дополни!елыюе смятие кромок. Если до
пол поп остановки полосы условие г|хр все же будет до-
• гпгпуто, то возникнет захват с последующим некоторым
\ нслпчением скорости полосы до стабилизации процесса
прокатки. В противном случае (гр>Р) захват полосы
палками так и не состоится.
Рассмотрим теоретическое решение задачи о воз-»
можном увеличении угла захвата за счет использования
пверционных сил, разработанное В. М. Полещуком
• ' сотрудниками;
Кинетическая энергия, отдаваемая при торможении
41
полосы в процессе захвата, составляет
^E = m(vo — v)/2, (87)
где т — масса полосы; v — скорость полосы в данное
мгновение (текущая скорость).
Отдаваемая кинетическая энергия расходуется на
.смятие кромок полосы и на преодоление сил трения.
Следовательно, можно написать
ДЕ = An + Лт, (88)
где Лдг — работа сил нормального давления; АТ — рабо-
та сил трения.
Определим величину слагаемых An и Дт при продви-
жении передней грани полосы через валковую щель на
Рис. 22. К определению работы
смятия кромок при динамическом
захвате
некоторое расстояние I
(рис. 22). Работа давя-
щей нормальной силы N
на пути I с учетом смятия
кромок равна
/
An = 2 J Ndl cos (Л\ г),
о
(89)
где cos (N, x) — косинус
угла между радиально на-
правленной силой N и
продольной осью х.
Для упрощения вывода заменим дугу контакта АВ от-
резком касательной АС. Тогда cos (N, х) будет величи-
ной постоянной: cos (N, x)=cos (90°—a3)=sina3.
Силу N можно представить в виде:
N = Рср & ИВ) « Pep b (AC) ж рсР bl/cos a3.
Подставляя значение силы W в выражение (89) и про-
ведя интегрирование, находим:
i
AN = 2Рср b аз f = Pcp b tg a312• (90)
6
Работа сил трения будет:
i
,ЛТ = 2 j7V/Zcos(7\ х), (91)
42
। 'it' ( <>s(7\ x) — косинус угла между тангенциальной ей"
'll «li /' п продольной ОСЬЮ X.
<учетом T=fN=fpcpbl/cos а3; cos (Т, х) =cos а3 оп-
...ел нем работу сил трения
1, |2/РсрЬрЛ=+)рор6Р. (92)
О
Величина Ат берется со знаком минус или плюс в за-
висимости от того, как направлена сила трения. Если
• '11.11;! Т направлена по ходу прокатки, т. е. способствует1
• мятпю кромок, то составляющая Ат входит в равенство
(НН> (‘о знаком минус, в противном случае — со знаком
плюс.
Подставим в равенство (88) значения Af, А-у и Ат:
hi (।v')/2 = рср bf (tg а3 + f). (93}
Уравнение (93) и является той основой, на которой
с । роится решение задач по возможному увеличению угла
и хвата за счет действия сил инерции полосы в различ-
ных случаях прокатки.
('начала найдем решение для более простого случая
встречи полосы с валками: а3>₽:ъ Уо<^в. Очевидно, за-
пас кинетической энергии полосы будет израсходован
полностью при падении ее скорости до нуля. Следова-
тельно, решая уравнение (93), надо принять и=0. При
условии Vo<vH силы трепня направлены по ходу прокат-
ин, поэтому перед членом f берем знак минус. С учетом
сказанного из уравнения (93) находим
/ | //Wo/[2p(.pb(tgaa —/)!• (94)
Гакона длина учасн<а полосы, который войдет в вал-
ки ы счет )i,eiic।ння инерционных сил (рис. 22). Найдем
ci к > । не тс тн у и угол ip. С учетом R (а. -ip) ~ //cos аз
па ходим
«I» ocu l/(R cosocB). (95)
Подставим в формулу (95) значение / из выражения
('»I):
* 2рСр bR2 (tg а3 — /) cos2 а3
Путем тригонометрических преобразований можно
показать справедливость равенства
(11.’. /) C()S2 а-л ~ SIH («з — Р) COS cc3/cos р.
43
Введем допущения: sin (а3—Р) =а3—р; cos a3/cos 0 =
s=l; тогда вместо формулы (96) получим
Ф = а3 — Уmv20/[2pcp bR2 (а3 — р) ] . (97)
Вспомним, что для осуществления захвата на проме-
жуточной стадии входа полосы должно быть выполнено
условие (рис. 21)
ф = (а3 + ф)/2 < 0
или
Ф < 2р — а3. (98)
Используем формулу (97)
---------------2р — а3.
2рСр bR2 (аз - Р)
После простых преобразований получим условие за-
хвата
«з < Р + Y mvl/ (8рсР bR2). (99)
Из выражения (99) нетрудно определить ту мини-
мальную скорость подвода полосы к валкам, которая не-
обходима для осуществления захвата при заданной раз-
ности углов а3—р:
v„ = /8рсрда(аз-Р)3/т. (100)
Далее рассмотрим более сложный случай захвата:
а3>р3; Уо>^в. Как отмечалось, в этом случае процесс
входа полосы в валки может быть разбит на несколько
стадий. На первой стадии скорость полосы падает от vq
до ив; в этот период силы трения направлены против
хода прокатки, и в уравнении (93) перед коэффициен-
том трения f должен быть взят знак плюс.
Определим расстояние 1\, на которое продвинется по-
лоса в зеве валков на первой стадии захвата. Используя
уравнение (93), получим
т (ио — ь’в)/2 = рсР bR (tg a3 + f),
откуда
li = ]/rtn(v20 — vl)/[2pclib(tga3-\-f)] . (101)
Вторая стадия захвата начинается в момент ио = ^в
и продолжается при соотношении ио<^в. В пределе ско-
44
рость полосы падает до нуля. Поскольку на этой стадии
<нлы трения направлены по ходу прокатки, в уравнении
(93) перед f должен стоять знак минус. При определе-
нии работАниАт по формулам (90) и (92) интегрирова-
ние надо проводить в пределах от до /г, где 12— длина
и жатого конца полосы в момент завершения второй ста-
дии захвата. Тогда из уравнения (93) получим:
= рср b (g — li) (tgОз — f).
Определим длину 12:
С = /11 + mt£/[2pcP Ь (tg а, — /)] (102)
Подставим в формулу (102) значение Ц из (101):
/.
„,„2
mo-
2рСр b (tg (М- f) “Г 2pcp b (tg a3 — f)
°0-°в
(ЮЗ)
' »2pcpb Ltga3 + f tga3 — f J*
По формуле (95) определяем угол ц>2, соответствую-
щий расстоянию 12:
! 1г f
<1>2 — сс3 . — а3
/?cosa3 в
р0“~рв
» 2pcpb£?cosa3 |_tga34-f tga3 — f .
Введем допущения:
(Ю4)
cos’- (tg а„ — f) ~ (а„ — Р).
После ото го формула (104) принимает вид:
*1':! : —
”1
a3 —P )
Л «з —P
tn / po • - v'j
2Pcp bRi \ a3 + P
/п Г/ 2
„ +t>. . (105)
2pcpbR2(a3 — P) L a3 + P J
Обозначим (uo—d!) a3~~j? + d =a2 и получим
a3 + P
Я’л аз — V fna2l[2pcv bR* (a3 — p)].
аа —
(106)
В соответствии с формулой (98) находим условие за-
т
т
"2
45
хвата:
а3 — Vzna2/[2pcp bR2 (a3 — p)] < 2p — a3
или
з r-----------------
«3 < 0 + у /na2/(8pcp bR2). j
(107)
Следует отметить, что расчеты по формуле (107) тре-
буют применения метода последовательных приближе-
ний, поскольку искомый угол захвата а3 входит в пара-
метр а. Определим минимальную скорость подвода поло-
сы к валкам, при которой произойдет захват. Для
упрощения решения задачи примем, что захват должен
быть обеспечен уже на первой стадии заполнения зева
валков металлом, т. е. при падении скорости полосы от
до Vb. Используем условие захвата (98). Угол <р в соот-
ветствии с принятым допущением равен
<р — а3------*---« а3 — I/ ------------------. (1U6)
v /?cosa3 ' 2рср bR2 (а3 + 0)
Следовательно, можно написать
a3 — Yт ( ио — vв )/[2рср bR2 (a3 + р)] = 2р — а3.
После преобразования получим
«о = К «2 + [8р0р 6R2 (а, - ₽ )2 (a, + ₽)/т] (109)
Действительная минимальная скорость подвода поло-
сы будет несколько ниже рассчитанной по формуле (109),
так как па второй стадии захвата происходит дополни-
тельное смятие кромок полосы.
4. Условие захвата
при установившемся процессе прокатки
Допустим, начальный захват полосы произошел и воз-
ник устойчивый процесс прокатки. Теперь будем сбли-
жать валки, постепенно увеличивая обжатие и угол кон-
такта. Спрашивается, до какого предельного значения
можно довести угол контакта, пока не начнется буксова-
ние валков по металлу. Рассмотрим силы, приложенные
к полосе на стадии установившейся прокатки. В каждой
точке контактной поверхности на полосу действует эле-
ментарная сила нормального давления; суммирование
этих сил дает равнодействующую АГ, направленную под
46
Рис. 23. Схема сил в предельный
момент установившегося процесса
прокатки
некоторым углом ф <рис. 23). По всей контактной по-
верхности действуют также элементарные силы трения;
пн равнодействующая— это сила Т.
11о поводу суммирования элементарных сил трения
надо сделать следующее замечание. В дальнейшем будет
показано, что в обычном (непредельном) процессе про-
ка гки на контактной поверх-
ности существуют две зоны
• кольжения, причем в одной
юно силы трения направле-
ны по ходу прокатки, а в
крутой — против хода. Одна-
ко при выводе условия за-
мыта рассматривается тот
предельный момент прокат-
ки, когда все силы трения
полностью используются как
н оп ивающие. В этом случае
на контактной поверхности
• у шествует только одна зо-
на скольжения и все силы
<рсиия приводятся к одной
(па каждом валке) равно-
и.спствующей Т, направлен-Xj
поп перпендикулярно к силе N.
Процесс прокатки не будет нарушен до тех пор, пока
втягивающие силы будут достаточными для того, чтобы
преодолеть отталкивающие силы. По аналогии с форму-
лой (69) условие захвата можно написать в виде NX^TX.
Из рис. 23 видно, что
Л/, WsiiM|r, (ПО)
/\ 7’созф Л//у гояф, (111)
где /у ко и|н|н|цп(‘пг трепня при установившемся про-
цессе прокатки.
11одставляя значение сил Nx и Тх в исходное условие
ia хвата, получим N sin ф^сЛ^у cos ф, откуда следует
’Г.Ф fy (112)
Поскольку /y=tg ру, где ру— угол трения при уста-
новившемся процессе прокатки, условие захвата можно
представить в виде
'I' Пу- (113)
11епосрсдственное использование формул (112)
47
формулы (112) и (113)
tg(a/2)<fy;
клиновидно-
Рис. 24. Прокатка
го образца
и (113) встречает трудности, так как требуется предва-
рительное определение угла ф, характеризующего точку
приложения равнодействующих N нТ (рис. 23). В поряд-
ке первого приближения принимают, что силы N и Т при-
ложены посередине дуги контакта, т. е. ф=а/2. Тогда
' ' ) приводятся к расчетному виду:
(П4)
(115)
Последняя формула исполь-
зуется наиболее часто. Именно
эту формулу обычно называют
условием захвата при устано-
вившемся процессе прокатки.
Как видим, максимальный
угол захвата (контакта) при
установившемся процессе не
может быть больше удвоенной
величины угла трения. Делая
такой вывод, надо помнить,
что формулы (114) и (115) яв-
ляются в некоторой мере при-
ближенными.
При экспериментальном оп-
ределении максимального уг-
ла контакта часто применяет-
ся метод прокатки клиновид-
ных образцов (рис. 24). По ме-
ре прокатки такого образца,
валки тонким концом, обжатие непрерыв-
вплоть до момента, когда возникает про-
входную толщину образца
задаваемого в
но возрастает,
буксовка валков. Измерив
в том месте, где началась пробуксовка, и его конечную
толщину, по формуле (28) рассчитывают максимальный
угол контакта.
5. Сравнение условий захвата
в начальный момент прокатки
и при установившемся процессе
Из условия свободного захвата в начальный момент ка-
сания полосы с валками (75) следует
“зта1=Рз- (116)
Аналогично из условия захвата при установившемся
48
процессе прокатки (115) находим
атах = 2Ру. (Н?У
Сравним значения углов а3тах и атах, имея своей це-
лью определить, на какой стадии процесса прокатки за-
хватывающая способность валков выше.
Сначала допустим, что коэффициенты (углы) трения
при захвате и при установившемся процессе одинаковы,
т. е. рз= ру = 0. В этом случае имеем
(>18>
“max = 2₽. (119)
Из сравнения формул (118) и (119) видно, что макси-
мальный угол контакта при установившемся процессе
может быть вдвое больше, чем начальный угол захвата:
атак —2а3тах. Отсюда вытекает вывод, что наиболее
трудным в смысле осуществления захвата является на-
чальный момент прокатки. Если начальный захват поло-
сы совершился, то в дальнейшем появляется возможность
значительного, минимум двукратного увеличения угла
контакта.
Однако надо подчеркнуть, что такое заключение спра-
ведливо только при условии fa—fy. Вместе с тем многие
исследования показывают, что в действительности коэф-
фициенты трения и [у часто различаются по величине,
причем в большинстве случаев коэффициент fy бывает
меньше, чем коэффициент /3:|:. Это существенно меняет
оценку захватывающей способности валков. Если допу-
стим, коэффициент (угол) трения при установившемся
процессе прокатки вдвое меньше коэффициента трения
при захвате (ру=0,5 03), то из формул (116) и (117) сле-
дует осиьи т. с. захватывающая способность вал-
ков при установившемся процессе снижается до уровня
начального захвата. Если же имеет место соотношение
ру <0,5 03, то получим amax<a3max. Последнее означает,
что захватывающая способность валков на стадии уста-
новившейся прокатки становится ниже, чем в начальный
момент касания полосы с валками. При этом наблюдает-
ся такая картина: сначала происходит захват полосы,
а затем процесс прокатки прерывается из-за возникно-
вения пробуксовок. Такие случаи действительно иногда
* Физические причины различия коэффициентов трения f3 и /у
подробно рассматриваются в гл. VI.
d А. П. Грудев 49
встречаются на практике, когда имеются причины, вы-
зывающие резкое падение коэффициента трения при за-
полнении зева валков металлом.
Подводя итог изложенному в настоящем параграфе,
надо все же отметить, что на практике в большинстве
случаев коэффициент трения хотя и снижается после на-
чального захвата, но не вдвое, а в меньшей степени; по-
этому сохраняется соотношение amax>a3max. Таким об-
разом, захватывающая способность валков при устано-
вившемся процессе прокатки, как правило, оказывается
более высокой, чем в начальный момент касания полосы
с валками.
6. Способы повышения
захватывающей способности валков
На многих прокатных станах величина обжатия за про-
ход ограничивается именно условиями захвата. Это на-
блюдается на обжимных станах, прокатывающих круп-
ные слитки, в черновых проходах на сортовых и листовых
станах, на некоторых трубных станах и т. д. Используя
выводы теории прокатки, можно указать пути повышения
захватывающей способности валков.
Проанализируем условие начального захвата (75),
имея в виду выявление возможностей увеличения обжа-
тия за проход. Поставленная цель может быть достигну-
та двумя путями: либо повышением коэффициента тре-
ния, либо увеличением обжатия при сохранении заданной
(ограниченной) величины угла а3.
Что касается коэффициента трения, то на его величи-
ну влияют многие факторы (см. гл. VI). Этими факто-
рами можно управлять, изменяя коэффициент трения
в соответствующем направлении. Известно, что при про-
катке на стальных валках коэффициент трения выше, чем
на чугунных валках. Поэтому в тех случаях, когда об-
жатие лимитируется условиями захвата, целесообразно
применять стальные валки.
Величина коэффициента трения зависит от шерохова-
тости поверхности валков. С целью повышения коэффи-
циента трения, когда это необходимо, применяется искус-
ственное загрубление поверхности валков: накатка зуб-
чатым роликом, насечка и др. Многими исследованиями
установлена зависимость коэффициента трения от скоро-
сти прокатки: с ростом скорости коэффициент трения сни-
жается. Поэтому на тех прокатных станах, где установ-
50
левы двигатели с регулируемым числом оборотов, реко-
мендуется осуществлять захват на малой скорости,,
и затем ее можно повысить.
Далее рассмотрим те пути, которые позволяют уве-
личить обжатие при заданном предельном значении угла
•а хвата а3. Из формулы
... /(дл + в)//?
видно, что обжатие АЛ может быть увеличено (при неиз-
менном значении а3), если соответственно увеличить ра-
»| нус валков jR. Таким образом, применение валков повы-
шенного диаметра выгодно с точки зрения использования
и\ захватывающей способности.
Из вышеприведенной формулы также видно, что об-
жатис Л// может быть увеличено за счет уменьшения пру-
Miiii.i стана 6. Следовательно, применение жестких про-
к;..... клетей, наряду с другими преимуществами, спо-
«•«»(><твует улучшению условий захвата.
Отметим распространенный способ облегчения началь-
ного захвата при прокатке с большими обжатиями, ко-
торый заключается в том, что переднему концу полосы
придается клиновидная форма. При задаче такой полосы
в нал к и начальный угол захвата мал, т. е. выполняется
условие (75), .з за тем угол захвата (контакта) возраста-
ет, но по допустимо, конечно, до тех нор, пока не будет
па рушено условие зачпата при установившемся процессе’
(115).
Волее полное использование захватывающей способ-
.. тп валков также может быть достигнуто посредством;
применения принудительного или динамического захвата.
• iii.ii.iko надо учитывать, что для осуществления прину--
пп re.ui.кого la хвата требуется создание достаточно мощ-
ны ч in тал к 11 на 1ош,н \ ус гровстп, а подвод волосы к вал-
ким с ударом вызывает дополнительные динамические
ii.irpy.iKii па прока тную клеть.
Вее вышеуказанные рекомендации основаны на пред-
ho.iio/Kciihii, что величина возможного обжатия лимити-
руется условием начального захвата. Это справедлива
и (1ол1,пн1нстве случаев прокатки. В отдельных случаях,
। ан отмечалось в предыдущем параграфе, наблюдается
но шнкповепие пробуксовок при установившемся процес-
• прокатки, что связано с резким снижением коэффици-
<|ц.| трепня после начального захвата. Такие ситуации
ш 1.елателы1Ы. При горячей прокатке причиной падения
• >ффпн,пента трения прц установившемся процессе мо-
51
жет быть присутствие относительно толстого слоя раз-
мягченной окалины на поверхности металла. Для обес-
печения устойчивого процесса прокатки необходимо
сбивать такую окалину с поверхности слитков и заготовок
перед задачей их в валки. Попутно заметим, что удале-
ние окалины также целесообразно с точки зрения умень-
шения износа валков и улучшения качества поверхности
продукции.
Глава IV
КИНЕМАТИКА ОЧАГА ДЕФОРМАЦИИ
1. Стадии процесса прокатки
Процесс прокатки можно разделить на три стадии:
захват, установившийся процесс и выброс. На каждой из
этих стадий закономерности деформации имеют свои осо-
бенности.
В период захвата происходит заполнение зева валков
металлом (рис. 25, а). По мере продвижения переднего
Рис. 25. Стадии прокатки:
а — захват; б — установившийся процесс; в — выброс
торца полосы через валковую щель изменяются коэффи-
циенты деформации, площадь контактной поверхности,
давление на валки и другие параметры. Процесс прокат-
ки имеет явно неустановившийся характер. Важно отме-
тить, что на стадии захвата отсутствует передняя внеш-
няя зона. Только после того, как передний конец полосы
52
»||.11(дст из валков на некоторое расстояние /п (рис. 25, а),
процесс прокатки стабилизируется.
Также неустановившийся характер имеет процесс вы-
проси полосы из валков (рис. 25, в). Как только длина
ыцпего конца полосы сократится до некоторого размера
/.. начинают изменяться деформационные, кинематиче-
ские и энергосиловые параметры прокатки. Это связано
। ослаблением влияния задней внешней зоны, которая
новее исчезает, когда задний
горец полосы входит в валко- х*"
ную щель. / \
Основная стадия прокат- 1____________________1
кв — установившийся процесс /
(рис. 25,6). На этой стадии ।---------у
нес параметры прокатки во \ у —т
времени не изменяются. Де- ----4-
формация осуществляется при / ----*
наличии передней и задней '-----------у Л.
внешних зон \
При установившемся про- Т Т
цессе прокатки через любое \ J
поперечное сечение очага де- х^
формации в единицу времени
ПРОХОДИТ ОДИНаКОВОе КОЛИЧе- Рис- 26- К выводу условия по-
1 ~ стоянства секундных объемов
<чво металла. Это условие
в теории прокатки называется
условием постоянства секундных объемов. Оно широко
используется в различных выводах, поэтому выразим его
в математической форме.
Объем металла, проходящий через любое поперечное
сечение очага деформации в единицу времени (секунду),
‘•‘•сзвляет Z^,,
где* /'ф площадь поперечного сечения полосы под про-
извольным углом ср (рис. 26); /фт — продольное переме-
щение полосы через выбранное сечение за время hr; —
скорость полосы в данном сечении.
Следовательно, условие постоянства секундных объ-
емов можно сформулировать в следующем виде:
Г|)уф = const. (120)
Для трех сечений — входного, любого промежуточного
1 В некоторых случаях основная часть полосы прокатывается
< переменным обжатием (периодическая прокатка и др.); тогда и
• •л стадия прокатки является неустановившейся.
53
и выходного можно написать
^0*0 = V<₽ = Fivv (121>
Формула (121) позволяет определить соотношение
скоростей движения переднего и заднего концов полосы
при установившемся процессе прокатки
= = (122>
Таким образом, отношение скорости переднего конца
полосы к скорости заднего конца равно коэффициенту
вытяжки. Если известен закон изменения площади попе-
речного сечения полосы на протяжении очага деформа-
ции, то с помощью формулы (121) можно определить»
скорость металла в любом промежуточном сечении.
2. Соотношение скоростей металла и валков
в очаге деформации
Одна из основных кинематических задач теории прокат-
ки заключается в определении скорости перемещения
деформируемого металла относительно поверхности вал-
ков. Исследования пока-
Рис. 27. Зоны отставания и опережения
в очаге деформации:
1 — зона отставания; 2 — зона опере-
жения; 3 — нейтральное сечеиие
зывают, что при устано-
вившемся процессе про-
катки скорость выхода пе-
реднего конца полосы ив.
валков больше окружной
скорости валков, а ско-
рость входа заднего кон-
ца — меньше окружной
скорости. Рассмотрим, по-
чему так получается.
При обжатии полосы
по высоте частицы метал
ла вынуждены переме-
щаться в продольном на
правлении. При этом не
которое количество метал
ла выжимается вперед, по ходу прокатки; скорость этих
частиц, полученная в результате деформации, суммиру-
ется с окружной скоростью валков. Другая часть сме-
щенного объема металла отжимается назад, против хода
прокатки; скорость этих частиц вычитается из окружной
скорости валков? Таким образом, в очаге деформации об-
разуются две области: зона опережения, где скорость
54
полосы больше окружной скорости валков, и зона отста-
вания, где соотношение скоростей обратное (рис. 27). ‘
Очевидно, между зонами опережения и отставания
и.олжпо быть сечение, где скорости валков и полосы оди-
наковы. Это так называемое нейтральное или критиче-
ское сечение. Его положение в очаге деформации харак-
теризуется величиной
нейтрального или кри-
тического угла у. 1
Построим диаграм-
му, отражающую соот-
ношение скоростей вал-
шш к металла на всем
протяжении очага де-
формации (рис. 28).
Горизонтальная про-
екция окружной скоро-
сти валков Ubx в любой
точке дуги контакта со-
етаиляет
"..х = uBcos<p, (123)
Рис. 28. Соотношение скоростей валков и
металла в очаге деформации:
/ — горизонтальная составляющая окруж-
ной скорости валков; 2 — скорость металла
где <р — текущий центральный угол.
Таким образом, на протяжении дуги контакта гори-
зонтальная проекция скорости валков изменяется от
г’м cos а (в сечении входа) до (в сечении выхода, где
<р -0 и cos(p=l). Это изменение показано на рис. 28
линией 1.
Закон изменения скорости полосы на протяжении оча-
га деформации может быть выведен из условия постоян-
ства секундных объемов (121). Полосе прямоугольной
формы соответствуют следующие равенства
КК”», (124)
Если допустить, что уширение отсутствует, т. е. Ьо =
— Ь\, то получим
= = (125)
Из условия (125) находим
(126)
Текущую высоту полосы hq, в любой точке дуги кон-
такта можно определить с помощью формулы (32), на-
55
писав ее в виде
Лф = hi + = hi + D 0 — cos Ф)- (127}
j-При входе в очаг деформации имеем <р=а, Дйф=Дй,
/гф =А0 и, следовательно, иф = и0. По мере продвижения
металла от плоскости входа к плоскости выхода скорость
его возрастает, так как уменьшается Лф. В сечении выхо-
да имеем ф=0, h$=hx и Уф=иь причем j
На рис. 28 изменение скорости металла на протяже-
нии очага деформации показано линией 2. Точка пересе-
чения линий 1 и 2 соответствует нейтральному сечению.
1 При анализе кинематических условий процесса про-
катки часто принимается гипотеза плоских сечений, со-
гласно которой продольные скорости в любом поперечном
сечении по высоте полосы распределяются равномерно^
"СПри таком поле скоростей кривая 2 на рис. 28 характе-
ризует не только изменение средней (по сечению) ско-
рости полосы на протяжении очага деформации, но и ско-
рость контактных слоев металла. Тогда можно сделать
вывод, что ординаты, заключенные между кривыми
1 и 2, показывают распределение скорости скольжения по
дуге контакта^
Г Однако гипотеза плоских сечений может быть приня-
та не во всех случаях прокатки. Она наиболее справед-
лива при прокатке тонких полос. При прокатке же тол-
стых полос, когда существует значительная неравномер-
ность в распределении деформаций по высоте тела,,
гипотеза плоских сечений не соответствует истинной кар-
тине течения металла..)
Возможность и даже неизбежность неравномерного
распределения продольных скоростей в вертикальных се-
чениях очага деформации доказывается тем фактом, что
при определенных условиях прокатки на дуге контакта
возникает целый участок (а не одна точка!), где скорости
металла и валков совпадают. Этот участок получил
название зона прилипания. Следует подчеркнуть, что тер-
мин «зона прилипания» используется в чисто кинемати-
ческом смысле; он выражает только отсутствие скольже-
ния, а не какое-либо физическое схватывание поверхно-
стей полосы и валков.
При рассмотрении рис. 29 допустим, что зона прили-
пания занимает на контактной поверхности участок ab.
На протяжении всего этого участка скорость приконтакт-
ного слоя металла совпадает с окружной скоростью вал-
ков. Возьмем три поперечных сечения в зоне прилипания:
56
I, II и HI. Пусть в сечении II скорость металла по всей
высоте полосы равна горизонтальной составляющей ско-
рости валков (нейтральное сечение). Тогда можно дока-
зать, что в сечениях I и III распределение скоростей по
высоте полосы обязательно будет неравномерным^
Г Действительно, горизонтальные скорости приконтакт-
пых частиц металла в сечениях /, II и III почти одинако-
1’ис. 29. К анализу распределения скоростей по высоте
полосы II очаге деформации при наличия зоны прилипа-
нии
вы, так как cos <p/«cos <р// «cos уш. Вместе с тем сред-
ине продольные скорости металла в этих сечениях могут
различаться существенно, в соответствии с условием по-
стоянства секундных объемов (уширением пренебрегаем)
В час гноетн, для сечення I находим
‘'пМ'',- 1
Таким образом, имеем t’icp <Цц. Однако как может
быть выполнено это соотношение, если скорости прикон-
тактного слоя металла в сечениях I и II одинаковы?
Только за счет пониженной скорости движения средин-
ных слоев металла в сечении I. Следовательно, эпюра
продольных скоростей в сечении I должна иметь вогну-
।ын вид (рис. 29).
Аналогичный анализ можно провести для сечения III;
при ном нетрудно сделать вывод, что для выполнения
условия <чпс, >fn необходимо, чтобы скорость средин-
57
ных слоев металла в этом сечении была больше скоро-
сти поверхностных слоев, т. е. эпюра продольных скоро-
стей должна иметь выпуклый вид.
Изменение продольных скоростей валков и металла
на протяжении всего очага деформации в том случае,
когда на контактной поверхности имеется зона прилила
Рис. 30. Соотношение скоростей валков и
металла при наличии зоны прилипания:
Z — горизонтальная составляющая окруж-
ной скорости валков; 2 — скорость прикон-
тактиого слоя металла (ab — зона прили-
пания) ; 3 — скорость срединного слоя ме-
талла; 4 — средняя скорость полосы
ния, графически пред-
ставлено на рис. 30.
Расхождение между
линиями 2 и 3 харак-
теризует степень нерав-
номерности распреде-
ления продольных ско-
ростей по высоте поло-
сы в каждом сечении.
График на рис. 30 по-
строен без учета вне-
контактной деформа-
ции. При наличии вне-
контактной высотной
утяжки уже во вход-
ном сечении надо бы-
ло бы показать некото-
рое расхождение меж-
ду линиями 2 и 3.
Если на контактной поверхности существует зона при-
липания, то более сложным становится понятие о ней-
тральном угле. Ведь на протяжении всего участка ab
(рис. 29, 30) скорости приконтактных слоев металла
и валков равны. В этом случае за нейтральный угол при-
нимают:
либо угол (обозначим его ук), соответствующий точке
на дуге контакта, где силы внешнего трения меняют свой
знак (подробнее см. гл. VI);
либо угол (ус), отвечающий тому сечению, где сред-
няя (по высоте) скорость полосы равна горизонтальной
составляющей скорости валков.
При анализе кинематических условий в тех случаях
прокатки, когда имеет место значительная неравномер-
ность распределения деформаций по высоте полосы, обя-
зательно следует учитывать различие между углами ук
и ус.
Остановимся кратко на вопросе о причинах возникно-
вения зоны прилипания на контактной поверхности. Про-
дольное перемещение частиц металла, обусловленное вы-
58
»сотной деформацией, может осуществляться либо путем
равномерной вытяжки всех слоев полосы со скольжением
по поверхности валков, либо путем внутренних сдвигов
при отсутствии скольжения на контакте. В действитель-
ности процесс идет в соответствии с законом минималь-
ного расхода энергии. Если условия прокатки таковы,
что затраты энергии на внутренние сдвиги меньше, чем
на внешнее скольжение, то на контактной поверхности
-образуется зона прилипания.
Все те факторы, которые затрудняют контактное
скольжение и облегчают формоизменение за счет вну-
тренних сдвигов, способствуют возникновению зоны при-
липания. Например, этому способствует повышение ко-
эффициента внешнего трения и увеличение толщины
прокатываемой полосы. Последнее объясняется тем, что
с увеличением толщины полосы легче осуществляются
внутренние межслойные сдвиги. По ориентировочным
данным А. И. Целикова длина зоны прилипания /Пр со-
ставляет:
— при горячей прокатке
U = (0,5 2,0) Лср; (128)
—при холодной прокатке
4р = (0,3-^-1,0)Лср. (129)
Как видно, предполагаемая длина зоны прилипания
при горячей прокатке больше, чем при холодной. Это ес-
тественно, поскольку при горячей деформации металла
меньше сопротивление внутренним сдвигам и, как пра-
вило, выше коэффициент трения.
3. Определение положения нейтрального сечения
Предположим, что гипотеза плоских сечеппй справедли-
ва п па дуге контакта имеется лишь одна точка, где ско-
рости металла и валков равны. Определим положение
этой точки, т. е. величину нейтрального угла у.
Для решения поставленной задачи используем условие
равновесия горизонтальных сил, приложенных к полосе
при установившемся процессе прокатки.
Па деформируемый металл со стороны валков дейст-
вуют, как уже отмечалось, нормальные напряжения (дав-
ления) р, направленные по радиусу, и напряжения тре-
пня /, направленные по касательной к поверхности валка
(рис. 31). Надо обратить внимание на направление эле-
59
ментарных сил трения t на разных участках дуги кон-
такта. В зоне отставания, где валки обгоняют металлои-
ды трения направлены по ходу прокатки, а в зоне опере-
жения, где скорость валков меньше скорости металла, эти
силы действуют в противоположном направлении. Гори-
зонтальные составляющие нормальных напряжений р
также направлены против хода прокатки. Таким образом,
из всех рассмотренных
внешних сил, приложен-
ных к металлу в очаге де-
формации, только силы
трения в зоне отставания
являются втягивающи-
ми; именно они обеспечи-
вают захват полосы и не-
прерывное продвижение
ее между валками.
Поскольку при уста-
новившемся процессе про-
катки концы полосы дви-
жутся с постоянной ско-
Рис. 31. Элементарные силы на дуге
контакта при установившемся процес-
се прокатки
ростью, сумма всех приложенных к полосе продольных
сил (втягивающих и отталкивающих) должна быть рав-
на нулю. Если бы это условие не выполнялось, то полоса
двигалась бы с непрерывным ускорением или замедлени-
ем (при постоянной скорости вращения валков!), что
противоречит действительному ходу процесса.
Составим уравнение равновесия продольных сил, при-
ложенных к полосе.
Выделим на контактной поверхности элементарную
площадку длиной Rdcp и шириной b (рис. 31). На этой
площадке действуют силы нормального давления dN=
=pbRdq и трения dT=tbRdq. »
Определим горизонтальные составляющие этих сил:
dNx — pbRdcp sin tp; dTx = tbRdcp cos tp.
Теперь, суммируя все элементарные продольные силы,
напишем общее уравнение равновесия
а V а
J tbR cos cpdcp — j tbR cos cpdq) — J pbR sin tpdcp = 0. (130)
V о 0
При решении уравнения (130) примем следующие до-
пущения:
силы (напряжения) нормального давления и трения
распределяются по дуге контакта равномерно;
60
справедлив закон трения Амонтона t-=fyp\
ширина полосы на протяжении очага деформации не
изменяется, т. е. прокатка идет без уширения.
При указанных допущениях величины р и Ь, а также
R, во всех слагаемых уравнения (130) могут быть выне-
сены за знаки интегралов и сокращены. Тогда уравнение
равновесия принимает вид:
а V а
j cos (prftp — j /у cos фс?ф — J sin фб/ф = 0. (131)
v 6 6
Проведем интегрирование
fy | sin ф |® —/у | Sin ф | — COS ф |“ = 0.
I (осле подстановки пределов и несложных преобразо-
ваний находим
.•tin у = (sin а)/2 — (1 — cos а)/(2/у). (132)
Обычно формулу (132) упрощают, принимая siny«
-у; sin а~а; 1—cos а=2 sin2 (а/2)~а2/2; fy=tgpy«
Тогда получим
у (а/2)(1 —а/2ру). (133)
По формуле (133) можно определить величину ней-
трального угла при заданных значениях угла контакта
и коэффициента (угла) трения. По имени ученых, впер-
вые осуществивших вывод этой формулы, ее называют
формулой Экелунда — Павлова. Поскольку она связыва-
ет три характерных угла (а, ру и у) и больше никаких
переменных не включает, ее называют также «формулой
альфа — бэта — гамма».
помощью формулы (133) исследуем зависимость
нейтрального угла от величины угла контакта. При а=О
имеем у 0. С увеличением угла а, как показывают ра-
счеты по формуле (133), угол у сначала растет, достига-
ет некоторого максимального значения, а затем умень-
шается. При а=2ру вновь имеем у=0. Это означает, что
возможность дальнейшего увеличения обжатия исчерпа-
на; последнее вполне согласуется с условием захвата
при установившемся процессе прокатки (115).
Определим то значение угла а, при котором угол у
максимален. Для этого продифференцируем по а функ-
цию (133) и первую производную приравняем нулю:
НуIda = 0,5 (1 — а/ру) = 0.
6t
Отсюда находим 1—а/ру=0;
и
а = Ру (134)
Таким образом, угол у достигает максимального зна-
чения, когда угол контакта становится равным углу тре-
ния. Подставив в формулу (133) вместо а угол трения
Ру, получим:
Ymax = (135)
Следовательно, приходим к выводу, что максималь-
ная абсолютная величина нейтрального угла составляет
одну четвертую часть угла трения.
Рис. 32. Изменение величины нейт- Рис. 33. Изменение отношения у/а в
рального угла в зависимости от уг- зависимости от угла контакта (Ру =
ла контакта (0 =0,2) *=0,2) *
Зависимость нейтрального угла от угла контакта ил-
люстрирует график на рис. 32 (при его построении при-
нято ру = 0,2).
Далее исследуем, как изменяется отношение углов
у/a при увеличении угла а от 0 до его предельного зна-
чения а=2ру. С этой целью перепишем формулу (133)
так:
у/а = 0,5(1 — а/2ру).
Таким образом, между отношением у/а и углом а
существует прямолинейная зависимость. При а = 0 име-
ем у/а=1/2- С увеличением угла а отношение у/а умень-
шается (рис. 33). При а = 2ру находим у/а = 0.
Установленный характер зависимости отношения у/а
от угла а имеет вполне определенный физический смысл.
Чем больше угол контакта, тем выше силы нормального
давления, стремящиеся вытолкнуть металл из зева вал-
ков, поэтому для осуществления процесса прокатки тре-
буется увеличение втягивающих сил. Такими силами яв-
62
горизонтальной составляю-
щей
0,15
0,10
0,05
Рис. 34. Зависимость величины
нейтрального угла от угла трени»
(а=0,4)
/7,4 0,5/Зу, рад.
О
0,1 0,2 0,3
ляются силы трения в зоне отставания. Необходимое по
условию равновесия увеличение втягивающих сил как
раз и достигается за счет роста зоны отставания и соот-
ветствующего сокращения зоны опережения, т. е. за счет
уменьшения отношения у /а.
При очень малых значениях угла а силы нормально-
го давления почти не дают
щей. Следовательно, в этом
случае силы трения в зонах
отставания и опережения
должны быть почти полно-
стью взаимно уравновешен-
ными. Для этого требуется,
чтобы угол у делил дугу
контакта почти пополам;
при а=0 получаем у/а=’/2-
Рассмотрим зависимость
величины нейтрального уг-
ла от коэффициента (угла)
i рения. В соответствии с фор-
мулой (133) и рис. 34 при увеличении коэффициента тре-
пня угол у растет. Объясняется это тем, что при увели-
чении коэффициента трения на контактной поверхности
появляются дополнительные, избыточные втягивающие
силы, которые вызывают ускорение полосы. Однако при
этом растет длина зоны опережения и соответственно
увеличиваются силы трепня отрицательного знака. В ко-
нечном итоге равновесие втягивающих и отталкивающих
сил восстанавливается, но при новом, повышенном зна-
чении угла у.
Из всего сказанного следует, что нейтральный угол
является своеобразным регулятором равновесия продоль-
ных сил при прокатке.
4. Влияние натяжения концов полосы
па положение нейтрального сечения
Нели к концам прокатываемой полосы приложены силы
натяжения или подпора, то они входят составляющими
и общий баланс продольных сил и, следовательно, ока-
зывают влияние на положение нейтрального сечения
в очаге деформации. Пусть в процессе прокатки действу-
ют силы заднего Qo и переднего Qi натяжения (рис.
(»,а). Тогда уравнение равновесия (130) должно иметь
63
следующий вид:
а V
j* tbR cos qxicp — J tbR cos cpdcp —
v 0
J pbR sin tpdcp--------y- + = 0.
о
(136)
Силы Qo и Qi взяты с коэффициентом V2 потому, что
уравнение (136) составлено для одного валка. Разделим
все члены этого уравнения на произведение pbR-.
a V a
J cos cpdcp — J cos cpdcp — J sin tpdtp +
v 0 0
После интегрирования получим
fу (sin a — sin у) — fy sin у + cos a — 1 +
Отсюда находим
cin ,, — sinK 1 — cos a ; Qi —Qo
2 !2fy WyPbR
Q1-Q0 = Q (137)
2pbR '
Qi Qo _ q
2pbR
(138)
Формулу (138) можно упростить путем замены три-
гонометрических функций углами, по аналогии с упро-
щением формулы (132); в результате получим:
у = — {1-----—_1_ Qi.r.Qo . (139)
2 \ 2Ру / 4pypW?
Вместо полных сил Qo и Qi в формулу (139) могут
быть введены удельные натяжения — заднее qQ и перед-
нее qi.
С учетом того, что
Qo = Qo Pq — Qo ^0 &о‘> Qi = Qi
после соответствующих подстановок, получим
У = 11___a \ I 41^1—qoho (140)
2 \ 2₽у ) 4Ру pR ’ '
Формулы (139) и (140) предложены Ю. М. Файнбер-
гом. Величина р в этих формулах представляет собой
среднее контактное давление. Из формул (139) и (140)
видно, что переднее натяжение увеличивает угол у, а зад-
нее уменьшает его. При некоторой величине заднего на-
тяжения угол у может стать равным нулю; это означает,
что процесс достиг критической стадии, после которой
-64
начинается буксование полосы в валках. Формулы спра-
ведливы не только при прокатке с натяжением, но и про-
катке с подпором концов полосы (рис. 6,6). Отличие со-
стоит лишь в том, что знак перед силами Qo и Qi меня-
ется на обратный.
5. Определение нейтрального сечения
с учетом неравномерного распределения давлений
по дуге контакта
Одно из главных допущений при выводе формулы ней-
трального угла (133), а также (140), заключается в том,
что принимается равномерное распределение давлении по
дуге контакта. Вместе
с тем многочисленные ис-
следования показывают,
что в действительности
давления распределяются
по дуге контакта нерав-
номерно (подробнее см.
гл. VII). Поэтому целесо-
образно при выводе фор-
мулы нейтрального угла
учесть этот фактор и сопо-
ставить полученный ре-
зультат с упрощенной
формулой (133).
В большинстве случаев
Рис. 35. Схематичная диаграмма рас-
пределения давления по дуге контакта
прокатки распределение
давлений по дуге контакта может быть схематично пред-
ставлено эпюрой (диаграммой), показанной на рис. 35.
Если известно давление на входе р0, на выходе pi и сред-
нее контактное давление рср, то можно определить все
необходимые для дальнейшего вывода элементы такой
эпюры.
Согласно теории пластичности, при прокатке с натя-
жением давление на входе составляет
Ро — ОтО ?0,
(141)
на выходе
Pi = ffJi —<7ь (142)
где ст*0 и (t’j —вынужденный предел текучести металла
соответственно на входе и выходе из очага деформации.
Найдем давление рт в нейтральном сечении. Из ус-
5 А. П. Грудев
65
ловия равновесия сил в вертикальной плоскости соста-
вим равенство
pcpRa = Ро + Р'" R (« - ?) + P1yPm- RV-
После простых преобразований получаем
Pm = 2Рср — К« — V) Ро + ТР11/а- (143)
Также нетрудно определить закон изменения давле-
ния р в зонах отставания и опережения. Имеем в зоне от-
ставания (рис. 35)
Р = Ро + (а —<P)#tgpo = Po (Pm —Ро); (144)
в зоне опережения
Р = Pi + «pR tg pi = рх + (<p/?)(pm — Pi)» (145)
где ср — текущий центральный угол.
По аналогии с формулой (136) напишем уравнение
равновесия продольных сил с учетом натяжения концов
полосы
а а у
I р/у cos cpdcp — f pbR sin cpdcp — C pfy bR cos cpdcp —
v v 6
— § pbRsintpdxp — -^-+-^1- =0. (146)
о
Сократим все члены этого уравнения на bR и с целью
упрощения примем sincp^cp и cos ср 1*
“ “ У У п —П
f pfy Жр — | pq>d<p — Г pfy Жр — f pcpdcp-°-—= 0.
</ J J J Zuf\
v V 0 0
(147)
Введем под интегралы функциональные значения р
согласно формулам (144) и (145)
J [₽• + - Ро> ] d<f ~~ J [Ро+~
V V
V
—Ро)] Ч**<Р — J [pi + у (рт — Р1) ] /у Жр —
__________ о L
* Применение более точной замены тригонометрических функ-
ций в виде sincp=(p—ср3/6 и cos<p=l—ср2/2, как показывают вы-
кладки, не меняет конечного результата.
66
V
j'l -I- f (РИ -Pi)]4>d<P - = 0-
После почленного интегрирования и ряда преобразо-
ваний находим
<4
I [Ро + у — Ро) ] Мф = /у (а — ууРУ-^-Рт- ;
V
I [ро + -? ~ф (pm — Ро) ] Ф^Ф = 4" [<2а2 — аТ — VI- 2) Ро 4-
J L а — У J о
v
(а2 + ау — 2у2) pj;
у
j [Pl + у (Pm — Pl)] fy ЙФ = °>5 tfy У (Рт + Р1)И
О
V , ,
Pl + — (Pm — Р1) фЖр = — I?2 (2Рт + P1)V
,)[_ У J о
Суммируем все члены уравнения равновесия
f (а — v) р0 + ?т (2а2 — а? — У2) Ро + (а2 + «т — 2у2) рт __
М YJ 2 6
_ f Pm + Pi _ У2 (2Pm + Pi) __ Po ho — <7i q
/yY 2 6 2R
Подставим в это уравнение значение рт из формулы
(143), после чего можно определить величину угла у.
В результате алгебраических преобразований получим
6/?(Р1~',°) № - 2 [3/, (2Рср + Р1 - р„) +
а
+ “ (pep — Pl>^'P1 )] V + “ (6/у Рср — ар» — 2арср) +
-|-4<?1/,*-’о/!о) = 0- <148>
Л\
Введем обозначения: &р=р{—p0-t A = 3fy(2pcp4-Ap) +]
+а[Рср— (po+Pi) /2].
Тогда уравнение (148) принимает следующий вид:
6^у — Т2 — 2Ау 4- а [6/у рср — а (р0+ 2рср)] +
а
I- (149)
К „
5*
67
При решении этого квадратного уравнения получим
искомую формулу нейтрального угла
Y = 6/Др [А~]/ Л2—6/уАр[6/у РсР — а (Ро + 2рсР) +
+ '4~(.qih1 — qoho)] !. (150)
Если прокатка ведется без натяжения, то получим
У = (А— У A2 — 6fy Лр [6/урср — а (р0 + 2рср)] 1.
Ь/у Др I J
(151)
В частном случае, когда давления в плоскости входа
и выхода из очага деформации равны (р0=р^ Др = 0),
а также отсутствует натяжение, из (149) следует
— 216/у рср + «(Pep — Ро)1 Y + а I6fy Рср — «(Ро + 2рср)] =0.
Отсюда находим
ю = а Г Рср а (^° ~1~ 2/?ср) 1 /152)
2 I 6fyPcp4-a(pcp —р0) ]*
Если принять, что давления распределяются по дуге
контакта равномерно, т. е. ро=рср, то формула (152)
превращается в формулу Экелунда — Павлова (133).
Сравним результаты расчетов нейтрального угла по формулам
(133) и (151). В качестве примера рассмотрим процесс холодной
прокатки листовой низкоуглеродистой стали при следующих исход-
ных данных: й0=4 мм; D = 400 мм; fy=0,07. Значения р\ и рСр при-
няты изменяющимися в зависимости от величины обжатия (учиты-
вая упрочнение металла и другие факторы).
Расчетные данные, приведенные в табл. 2 и на рис. 36, свиде-
тельствуют о том, что в диапазоне а<0у формулы (133) и (151)
дают очень близкие результаты. Аналогичные данные получены в рас-
четах для других условий прокатки. На этом основании можно сде-
Таблица 2. Результаты расчетов нейтрального угла
(&о=4 мм; £>=400 мм; fy=0,07; р0=20 МПа)
а, рад е. % р„ МПа Рср. МПа V по фор- муле (133), рад V по фор- муле (151), рад Расхож- дение, %
0,03 4,5 25 30 0,0118 0,0115 2,6
0,05 12,5 35 45 0,0161 0,0156 3,2
0,07 24,5 45 65 0,0175 0,0175 0
0,10 50 55 70 0,0143 0,0173 —17,3
0,12 72 60 70 0,0085 0,0150 —43,3
0,14 98 60 70 0 0,0117 —100
68
лать вывод, что при а<ру допущение о равномерном распределении
давления по дуге контакта не приводит к большим погрешностям
в определении угла у и, следовательно, возможно использование бо-
лее простой формулы (133).
В диапазоне а>₽у расхождение в расчетах по формулам (133)
и (151) становится значительным, причем оно возрастает по мере
приближения угла а к предельной величине.
6. Опережение и отставание концов полосы
Опережением называется величина, которая показывай
ет, насколько скорость выхода полосы из валков боль-*
ше окружной скорости валков.
Опережение S рассчитывают по формуле
S = -'^~Vb . (153)
«в
Часто опережение определяют в процентах:
5=._р1--°в Ю0%. (154)
*>в
В некоторых случаях опережение S является величи-
ной заданной, а требуется определить скорость выхода
полосы из валков. Тогда формулу (153) преобразуют, ре-
шая ее относительно ид
= ив (1 + S). (155)
Если опережение задано в процентах, то
У1 = vB(l + S/100). (156)
Величина, называемая отставанием, характеризует со-
отношение скоростей полосы и валков на входе в очаг
деформации. Этот термин подчеркивает, что скорость
движения заднего конца полосы меньше окружной ско-
69
рости валков (точнее, меньше горизонтальной проекции
скорости валков в сечении входа).
Отставание 50т рассчитывают по формуле:
S0T = C0S а — Ц))/(^в C0S а)- (157)
Опережение и отставание — величины взаимозависи-
мые. Зная одну из них, можно определить другую. Дей-
ствительно, используя соотношение (122), формулу (157)
можно написать так:
~ _ vBcosa —Uj/X
4->0т -
ив cos a
После подстановки в это выражение значения Vi из
(155) и несложных преобразований получим
S0T = 1 — (1 + S)/(Xcosa). (158)
В теории прокатки основное внимание уделяется ис-
следованию опережения. Это объясняется тем, что опе-
режение экспериментально и аналитически определяется
проще, чем отставание. С другой стороны, именно вели-
чина опережения необходима для решения ряда практи-
ческих задач, когда требуется достаточно точно опреде-
лить скорость выхода полосы из валков. Если же изве-
стно опережение, то отставание нетрудно рассчитать по
формуле (158).
Многочисленные исследования свидетельствуют о том,
что в большинстве случаев прокатки опережение нахо-
дится в пределах 1—10 %, т. е. его численное значение
невелико. Что же касается отставания, то оно может
быть гораздо больше, например, может составлять 20—
30 % и болсс. Покажем это па ч пел сипом примере. До-
пустим, 5 = 0,05 (5%); cosa = 0,92 (a=23°); A,= l,5;
тогда по формуле (158) 50Т=1—1,05/(1,5-0,92) =0,24,
т. е. 24 % •
Из формулы (158) видно, что величина отставания
зависит в основном от величины коэффициента вытяжки
% (сомножители 1+5 и cos а близки к единице и изме-
няются мало): чем выше коэффициент вытяжки, тем
больше отставание.
7. Экспериментальное определение опережения
Исходя из формулы (153) можно сделать вывод, что для
экспериментального определения опережения надо изме-
рить скорость переднего конца полосы и окружную ско-
рость валков. Эти измерения необходимо выполнять с до-
70
Рис. 37. Керновые отпечатки на
полосе
статочно высокой точностью, так как даже небольшая
ошибка в определении величины vi или рв (например,
порядка 1 %) может привести к существенному искаже-
нию величины 5.
При проведении опытов по определению опережения
для измерения скорости переднего конца полосы часто
применяется электроконтакт-
ный метод: выходящая из вал-
ков полоса последовательно
замыкает электрические кон-
такты, расположенные на оп-
ределенном расстоянии друг от
друга. Электроконтактный спо-
соб позволяет также достаточ-
но точно измерить число оборо-
тов валков и найти их окруж-
ную скорость (по диаметру).
Существует широко распро-
страненный метод определения
опережения, не требующий
прямого измерения скоростей полосы и валков. Это так
называемый метод керновых отпечатков или просто кер-
новый метод. Сущность его заключается в следующем.
С помощью керна или иного инструмента на поверх-
ность валка наносят две отметки (лунки, риски) на рас-
стоянии 1В одна от другой (рис. 37). После прокатки на
поверхности полосы остаются отпечатки (бугорки), рас-
стояние между которыми/п точно измеряют. Опережение
вычисляют по формуле
S = (159)
Можно показать, что формула (159) по существу
совпадает с формулой (153). Действительно, передний
конец полосы проходит путь /1Г за то же самое время т,
за которое отметка на поверхности валка проходит путь
/в. Разделив каждый член формулы (159) на т, получим
_ (/п/т) (/в Д) __ Р1
/в/т vB
Если полоса имеет достаточно большую длину, то мо-
жно ограничиться нанесением одной отметки на поверх-
ность валка. Тогда lB = nD и формула для вычисления
опережения принимает вид
S = (ln~ jiD)/(jiD). (160)
При горячей прокатке расстояние между отметками
71
на полосе измеряют, естественно, после остывания ме-
талла. Но в формулы (159) и (160) надо подставлять
истинную длину /п, соответствующую горячей полосе.
С этой целью используется следующее выражение
Zo = /Blon(l + xO. (161)
где /Пхол —расстояние между отметками на холодной
полосе; %—коэффициент теплового линейного расшире-
ния металла; t — температура металла во время про-
катки (минус температура окружающей среды).
Коэффициент линейного расширения % может быть
принят: для углеродистых сталей 13-10-6; для аустенит-
ных сталей (16—20) • 10-6.
Метод керновых отпечатков ввиду его простоты при-
меняется для исследования опережения не только в ла-
бораторных, но и в производственных условиях.
8. Теоретическое определение опережения
Напишем условие постоянства секундных объемов для
нейтрального сечения и сечения выхода полосы из вал-
ков:
, (162)
Рис. 38. К выводу теоретической формулы опережения
где hy и bv — соответственно высота и ширина полосы
в нейтральном сечении; —продольная скорость ме-
талла в том же сечении (рис. 38).
Допустим, уширение полосы в зоне опережения пре-
небрежимо мало, т. е. тогда получим
h7vv = hivv (163)
72
Равенство (163) является основой для вывода теоре-
тической формулы опережения. В соответствии с форму-
лой (32) высота полосы в нейтральном сечении состав-
ляет
= + ДЛ? = hx -{-D(l — cosy), (164)
где ДЛ?—абсолютное обжатие в зоне опережения.
Продольная скорость металла в нейтральном сечении
равна горизонтальной проекции окружной скорости вал-
ков в этом сечении
flY=flBcosy. (165)
Подставим значения hy и vv из формул (164) и (165)
в исходное равенство (163), а также используем выра-
жение (155)
Л14-2)(1 — cos у)] ив cos у = h1vB(l + S).
После сокращения левой и правой части равенства на
цв и простых преобразований получим
S = [A1 + D(1 — cos у)] cos у/Нг—1. (166)
Эта формула впервые выведена С. Финком и носит
его имя, иногда ее представляют в таком виде
S = (1 — cos у) (— cosy—1Y (167)
\ К /
Существует несколько упрощенных формул опереже-
ния, которые выводятся из формулы Финка. Например,
примем cosy^l—у2/2; 1—cosy»y2/2.
Тогда формула (167) приобретает видЗ=(у2/2)
[(D//z1)(l-y72)-l].
Пренебрегая членом у2/2 в квадратных скобках, как
величиной очень малой по сравнению с единицей, полу-
чим формулу опережения Экелунда
S = (y2/2)(D//i1—1). (168)
Во многих случаях, особенно при прокатке тонких
листов и лент, имеет место соотношение D/hC^>\. Сле-
довательно, формулу (168) можно еще более упростить
и принять
S-y2/?/^. (169)
Выражение (169)—это формула опережения Голо-
вина— Дрездена. Она наиболее проста, удобна для ана-
лиза и часто используется в расчетах._у
73
9. Зависимость опережения от факторов прокатки
Опережение является чувствительным кинематическим
показателем процесса прокатки. Изменение любого гео-
метрического или физического фактора прокатки отра-
жается на величине опережения. При анализе зависимо-
сти опережения от различных факторов (условий) про-
катки используется формула (169). При этом учитыва-
ется, что формулу (169) можно представить в виде:
S = bhy/hv (170)
так как 7?у2=Д/ц>.
Из формулы (170) следует, что опережение численно
равно относительному обжатию в зоне опережения. Пе-
рейдем к анализу влияния конкретных факторов прокат-
ки на величину опережения.
Диаметр валков. Из формулы (169) видно, что с уве-
личением диаметра валков опережение возрастает. Это
объясняется тем, что при увеличении диаметра растет
абсолютное обжатие в зоне опережения ДА7.
При первом взгляде на формулу (169) может пока-
заться, что опережение изменяется прямо пропорцио-
нально изменению диаметра валков. Однако этот вывод
не точен. Дело в том, что диаметр влияет также и на ве-
личину угла у. Действительно, подставляя в формулу
(169) значение угла у из выражения (133), получим
С/-------------\ 2
। 1 1 / А/г j (171)
2ру |/ R ) 'k
Анализ формулы (171) подтверждает, что с увеличе-
нием диаметра валков опережение растет, однако эта за-
висимость не прямолинейна. На рис. 39, а показан гра-
фик, построенный по формуле (171) для одного из кон-
кретных случаев прокатки, а на рис. 39, б приведены
экспериментальные данные, полученные И. М. Павловым
с сотрудниками.
Толщина полосы. Как видно из формулы (169), с уве-
личением конечной толщины полосы опережение умень-
шается, что является следствием падения относительно-
го обжатия в зоне опережения. Вид зависимости 5 =
=ср(А1) показан на рис. 40. Особенно резкое падение
опережения наблюдается в области малых значений h\.
Теоретическая кривая (рис. 40, а) по своему характеру
соответствует экспериментальным данным, полученным,
например, В. П. Северденко (рис. 40,6).
74
Рис. 39. Зависимость опережения от диаметра валков:
а — теоретическая кривая (принято h0=12 мм; hi = 10 ми; |Зу=О,2); б — экспе-
риментальные данные (прокатка меди на сухих, слабо полированных валках;
Ло=2.5 мм; hj = l,5 мм)
Рис. 40. Зависимость опережения от толщины полосы:
а—теоретическая кривая (принято A/ii=2 мм; /? = 200 мм; [3^=0,2); б — экспе-
риментальные данные (холодная прокатка стали; Л/г=0,3 мм; R-75 мм; 1 —
без смазки; 2 — с глицерином)
Однако надо отметить, что при прокатке особо тол-
стых полос обнаружено расхождение между теоретиче-
скими и экспериментальными данными по опережению.
Согласно формулам (167) — (169) при большой толщи-
не полосы Ai опережение должно быть очень малым, а на
практике его величина получается значительной. Этот
факт объясняют неравномерностью деформации и воз-
растающей ролью зоны прилипания, которая не только
охватывает почти всю контактную поверхность, но и рас-
пространяется в глубь полосы, вследствие чего прикон-
тактный слой металла становится как бы продолжени-
75
ем тела валка. Поскольку растет фиктивный радиус вал-
ка, это способствует увеличению опережения.
Обжатие и угол контакта. В формулу (169) угол кон-
такта в явном виде не входит, но, учитывая формулу
(133), можно сделать вывод о сильном влиянии этого<
фактора на опережение через угол у.
Характер зависимости S=cp(a) подобен зависимости
у=ф(а) (рис. 41, а, кривая /). С увеличением угла кон-
' 0 20 I/O 50 80 £,%
Рис. 41. Зависимость опережения от угла контакта и обжатия:
а — теоретические кривые (принято hi=4 мм; /?=200 мм; Ру =0,2); б — экспе-
риментальные данные (холодная прокатка стали; fto=4 мм; D—X27 мм; смаз-
ка-эмульсия минерального масла)
такта опережение сначала растет, достигает максимума
при а=0у, а затем уменьшается. При а=2ру опереже-
ние падает до нуля; дальнейшее увеличение угла кон-
такта невозможно из-за возникновения буксования вал-
ков по полосе.
График изменения опережения в функции относитель-
ного обжатия (рис. 41, а, кривая 2) несколько отличает-
ся от графика 5=ф(а), так как обжатие и угол контак-
та связаны между собой не линейной, а квадратичной
зависимостью. По этой причине кривая 3 = ф(е) не сим-
метрична относительно вертикальной оси.
Имеются экспериментальные данные, подтверждаю-
щие в основных чертах теоретическую зависимость опе-
режения от угла контакта и обжатия. На рис. 41,6 при-
ведены экспериментальные данные автора.
76
Коэффициент трения. Влияние этого фактора также
•осуществляется через угол у: чем выше коэффициент
трения, тем больше угол у и соответственно больше опе-
режение. Через коэффициент трения влияют на опереже-
ние многие другие факторы: шероховатость поверхности
валков, скорость прокат-
ки, температура металла,
вид технологической смаз-
ки и т.д.
Влияние трения на
опережение видно из рис.
40. При прокатке с при-
менением глицерина в ка-
честве технологической
смазки опережение ниже,
чем при прокатке на су-
хих валках.
Натяжение концов по-
лосы. На основании фор-
мулы (139) можно сде-
лать вывод, что переднее
натяжение и задний под-
пор увеличивают опере-
жение, а заднее натяже-
Разносшь натяжений 0,-Оо.кН
Рис. 42. Зависимость опережения от
разности переднего и заднего натяже-
ний (холодная прокатка стальной лен-
ты:
Ао=1,44 мм; Й1 = 1,15 мм; &o=15-j-2O мм)
ние и передний подпор уменьшают его. Эксперименталь-
ное исследование, выполненное Н. Н. Дружининым,
подтверждает эту зависимость (рис. 42).
10. Опережение при прокатке в калибрах
При прокаТке в калибрах опережение переменно по ши-
рине калибра. Это объясняется тем, что скорость поло-
сы на выходе во всех продольно-вертикальных сечениях
одинакова, а радиус и окружная скорость валков изме-
няются по периметру калибра. Рассмотрим, например,
случай прокатки квадратной полосы в овальном калибре
(рис. 43, а). Опережение в вершине калибра (сечение
I—I) будет:
S = = vi-vRi = ----(172)
1 UBl G)/?I ®/?1
где (о — угловая скорость валков.
В сечении II—II
g = fi—’.п = (173)
°вп ®Яц
77
Рис. 43. Распределение опе-
режения при прокатке квад-
рата в овальном калибре
Из сравнения формул (172) и (173) видно, что опе-
режение больше в тех продольных сечениях, где меньше
радиус валка. Можно отметить, что во всех калибрах,
приведенных на рис. 19, максимальное опережение соот-
ветствует вершине калибра.
Если известно опережение в каком-либо одном сече-
о определить его величину в лю-
бом другом. Из формулы (172)
и (173) находим
(SI+1)/(SII + 1)=«II/7?I,
откуда следует
SI4'?u/«I)(S„ + !)~1 <174)
или
VW(V 1)- 1. (175)
На рис. 43,6 показана типич-
ная эпюра распределения опере-
жения по ширине овального ка-
либра при прокатке квадратной
заготовки. В отдельных случаях,
например при малых значениях
коэффициента трения, опереже-
ние вблизи кромок полосы может быть отрицательным,
как показано на рис. 43, б пунктиром. На этих участках
полоса выходит из валков со скоростью меньшей, чем
окружная скорость валков.
В связи с неравномерным распределением опережения
по ширине калибра граница между зонами отставания
Рис. 44. Зоны отставания и
опережения на контактной
поверхности при прокатке
квадрата в овальном калиб-
ре (вид в плане):
1 — зона отставания; 2 —
зона опережения; 3 — нейт-
ральная линия
и опережения на контактной по-
верхности (нейтральная линия)
теряет прямолинейную форму
и становится более или менее
сложной кривой. Вид нейтральной
линии в случае прокатки квадра-
та в овальном калибре показан
на рис. 44.
Для усредненной характери-
стики скоростных условий при
прокатке в калибрах вводят по-
нятие о среднем опережении
и среднем нейтральном угле. Под
средним опережением понимают
78
его среднеинтегральное значение, которое можно опреде-
лить, например, делением площади эпюры на рис. 43, б
на ширину полосы на выходе. Зная среднее опережение,
можно перейти к скорости прокатки через средний ката-
ющий радиус 7?Ср, определяемый по формуле (68).
Для теоретического определения среднего опереже-
ния применяется формула (169), написанная в виде:
S = R th . (176)
ср ’Ср 'ср 1ср ' '
Средний нейтральный угол уСр при прокатке в калиб-
рах простой формы (квадратных, ромбических, оваль-
ных, круглых) рекомендуется определять по формуле
?ср = (аср/2)(1-аср/2ру), (177)
где
аср = р (^Оср ^1Ср)^ср- U78)
В калибрах сложной формы средний нейтральный,
угол уСр определяется по специальным формулам.
11. Определение средней скорости деформации
Скорость деформации при прокатке, как и при других
способах обработки давлением, необходимо рассчиты-
вать для правильного определения сопротивления де-
формации (предела текучести) металла. Как известно
из теории пластичности, скорость деформации состав-
ляет:
u — d&ldx, (179)
где с?е—.элементарное относительное обжатие за бес-
конечно малый промежуток времени dx.
Имеем ds = dh/h, следовательно, можно написать
и = (dh/dx) (1/h). (180)’
Заметим, что dh/dx=Vh,
где vh — скорость сжатия (скорость перемещения давя-
щего инструмента).
Учитывая это, получим
u = vhlh. (181}
При прокатке величины Vh и h изменяются на протя-
жении очага деформации. Следовательно, скорость де-
формации также является величиной переменной. Най-
дем закономерность изменения скорости деформация
вдоль дуги контакта.
79
В любом поперечном сечении очага деформации, на-
ходящемся под углом ср (рис. 45), скорость деформации
составляет:
“ф = ЧА> (182)
где — скорость сжатия в выбранном сечении (со сто-
роны одного валка).
Рис. 45. К определению средней скорости деформации
(о„ — касательная скорость металла на дуге контакта
Ф
в сечении <р)
Из рис. 45 видно, что
V..m = tg ф,
где иХф —горизонтальная скорость металла в данном
сечении (в предыдущих параграфах эту величину обо-
значили упрощенно иф).
Скорость vX(p определяем из условия постоянства се-
кундных объемов иХф =vlhi/h(p.
Таким образом, скорость сжатия в любом попереч-
ном сечении составляет:
% = °i tg Ф (183)
Подставляя это значение и0ф в исходную формулу
(182), получим
“ф = Ч hi tg ф/йф- (184)
Формула (184) выражает закон изменения скорости
деформации вдоль дуги контакта.
80
(185)
(186)
Для определения средней скорости деформации ис-
пользуем выражение
1
uCD = — «т dx.
р id J ф
о
Введем сюда значение «ф из формулы (184)
ld
„ _ 2vihi С teT Hr
“ср — । ——-их.
ld J Лф
0
Выберем в качестве основной переменной толщину
полосы и соответственно проведем интегрирование
в пределах от h\ до h0. Выделяя элементарный прямо-
угольный треугольник со сторонами dh^/2 и dx, примы-
кающий к контактной поверхности, находим:
dx tg ф = dh^!2.
Учитывая это, перепишем интеграл (186) в виде
л.
„ _ »1*1 Г dhv
“ср — j I ——- •
ld J Л2
и «ф
Интегрируем
ср Id 1 ф Id Ui л» I
После несложных преобразований получим
«cP = (^d)(AW- (187)
Формуле (187) можно придать иной вид, например
«СР = У1е//й (188)
или
Мир = ViCc/Hq. (189)
Рассмотренный вывод формулы средней скорости де-
формации при прокатке принадлежит А. И. Целикову.
В литературе встречаются и другие, близкие формулы
для расчета средней скорости деформации. Например,
широко известна формула Экелунда:
иср = = 4>а. (190)
Ло ^1 ^ср
6 А. П. Грудев
81
Характерные значения средней скорости деформации
на промышленных станах разного типа приведены
в табл. 3.
Таблица 3. Скоростные условия прокатки на станах разного
назначения
Тип стана Максимальная скорость прокат- ки »в, м/с Скорость деформации “ср’
Обжимные (блюминги, слябинги) 5—6 0,5—10
Заготовочные 5—7 0,5—30
Крупно- и среднесортные 10—15 1—50
Мелкосортные 20—25 1—250
Проволочные 60—100 До 1000
Толстолистовые 5—6 1—25
Широкополосные непрерывные (горя- чей прокатки) 20—25 До 500
Таким образом скорость деформации на современных
высокоскоростных станах может достигать значений по-
рядка 103 с-1. Для сравнения отметим, что при испыта-
нии образцов на растяжение на стандартных разрывных
машинах скорость деформации составляет 10-3—
10-2 с-1, т. е. в сотни тысяч раз меньше.
Глава V
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
И ФОРМОИЗМЕНЕНИЕ ПОЛОСЫ
1. Общая характеристика напряженного
и деформированного состояния металла
В теории прокатки, как и в теории других процессов об-
работки давлением, одним из центральных является во-
прос о распределении напряжений и деформаций в объ-
еме деформируемого тела. Сначала рассмотрим этот
вопрос в общей, качественной форме. Начнем с анализа
напряженного состояния прокатываемой полосы. Мыс-
ленно выделим в объеме очага деформации элементарный
(бесконечно малый) прямоугольный параллелепипед
и дадим характеристику напряжений, действующих на
его трех взаимно перпендикулярных гранях (рис. 46).
Расположим параллелепипед так, чтобы его оси совпа-
82
дали с основными направлениями прокатки — продоль-
ным, поперечным и вертикальным. Будем считать, что
эти направления и соответствующие площадки паралле-
лепипеда являются главными, т. е. на них отсутствуют
касательные напряжения.
При анализе схемы напряженного состояния необ-
ходимо учитывать направление действия внешних сил.
В продольном направле-
нии основные горизон-
тальные составляющие об-
разуются силами трения,
причем в зоне отставания
они направлены по ходу
прокатки, а в зоне опере-
жения — против хода (см.
рис. 31). Таким образом,
при любом продольном
перемещении частиц ме-
талла в очаге деформа-
ции (вперед или назад
к поверхности валков) они испытывают подпирающее
действие со сторрны сил трения. Отсюда следует, что
в продольном направлении на гранях выделенного эле-
мента действуют сжимающие напряжения, обозначаемые
обычно о3 (рис. 46). При поперечном перемещении частиц
металла в очаге деформации они также встречают сопро-
тивление со стороны сил трения, поэтому и в поперечном
направлении будут действовать некоторые сжимающие
напряжения <у2. Наконец, совершенно ясно, что в верти-
кальном направлении силы давления валков на металл
создают сжимающие напряжения оь
Из всего сказанного вытекает важный вывод: напря-
женное состояние полосы при прокатке характеризуется
объемной схемой с тремя сжимающими напряжениями.
Такая схема имеет место не во всех точках очага дефор-
мации, но она является основной, доминирующей.
Величина напряжений си, сг2 и <у3 изменяется по объ-
ему очага деформации. Не рассматривая пока конкрет-
ных методов количественного определения этих напря-
жений, составим суждение об их соотношении. Очевид-
но, наибольшим по абсолютной величине должно быть
вертикальное напряжение си — то, которое создается
давлением валков и обеспечивает пластическую дефор-
мацию металла. Наименьшее из трех указанных главных
напряжений может быть найдено с помощью закона на-
6*
83
именьшего сопротивления: металл течет в основном в том
направлении, где он встречает минимальное сопротивле-
ние своему перемещению. При прокатке таким направ-
лением обычно является продольное. Отсюда следует,
что наименьшую величину имеет продольное сжимающее
напряжение сг3. Что касается поперечного напряжения сг2,
то оно в большинстве случаев занимает промежуточное
положение между напряжениями си и сг3. Таким обра-
зом, для процесса прокатки характерно соотношение*:
<т 1 ><У2^> 03-
Как было отмечено выше, на некоторых участках оча-
га деформации схема напряженного состояния может от-
личаться от основной схемы трехстороннего сжатия.
Рассмотрим, например, напряженное состояние вблизи
боковых кромок полосы. Здесь частицам металла легче
перемещаться в поперечном направлении (на уширение),
чем в продольном (на вытяжку), так как поперечные
силы трения относительно малы. Однако полоса представ-
ляет собой единое целое, и все ее части (середина
и кромки) получают одинаковую вытяжку. При этом
кромки полосы принудительно вытягиваются, в них со-
здаются дополнительные напряжения растяжения. В ре-
зультате схема напряженного состояния на кромках ста-
новится разноименной с двумя сжимающими напряже-
ниями (ел и <г2) и одним растягивающим (о3). Заметим,
что на свободной боковой поверхности полосы напряжен-
ное состояние является плоским — отсутствует напряже-
ние <г2.
Своеобразная картина напряженного состояния возни-
кает в очаге деформации при прокатке с большими об-
жатиями, когда угол контакта превышает угол трения
(а>>ру). Анализируя этот случай, рассмотренный впер-
вые А. Я. Хейном, выделим на контактной поверхности
точку, находящуюся в области ф>ру (рис. 47). Сумми-
руем горизонтальные проекции элементарных сил давле-
ния р и трения t в этой точке. Из приведенного на рис.
47 построения видно, что результирующая продольная
сила гх в выделенном сечении направлена против хода
прокатки, т. е. она вызывает растяжение. Таким образом,
при прокатке-с большими углами контакта (а>ру)
в задней части очага деформации, примыкающей к се-
* В теории прокатки, в отличие от общей теории пластичности,
сжимающим напряжениям часто присваивается знак плюс, а растя-
гивающим — знак минус.
84
чению входа, возникает схема напряженного состояний
с продольным растягивающим напряжением, а в осталь-
ной части сохраняется схема с продольным сжимающим
напряжением. Теоретически (по А. Я- Хейну), в предель-
ном случае, когда а=2ру, продольные растягивающие
напряжения распространяются на весь очаг деформации.
Сильное влияние на напряженное состояние оказыва-
ет неравномерное распределение обжатия по ширине по-
Рис. 47. Схема напряженного состоя-
ния в задней части очага деформации
при а>Ру
Рис. 48. Схемы напряженного со*
стояния при неравномерном распре-
делении обжатия по ширине поло-1
сы
лосы, так как при этом неизбежно возникают дополни-
тельные напряжения. Чтобы пояснить это, рассмотрим
конкретный пример. Предположим, в цилиндрических вал-
ках прокатывается полоса, имеющая утолщение по кра-
ям (рис. 48). В этом случае обжатие на краевых уча-
стках I и III будет больше, чем на участке II. Соответ-
ственно должна была бы распределиться и продольная
деформация, однако в процессе прокатки все части по-
лосы получают единую, усредненную вытяжку. Это до-
стигается за счет принудительного сокращения вытяжки
краевых участков и растяжения средней части полосы.
На участках I и III за счет действия дополнительных
продольных напряжений схема трехстороннего сжатия
усугубляется а на участке II возникает схема с продоль-
ным растягивающим напряжением (рис. 48). Практика
показывает, что дополнительные растягивающие напря-
жения на участке II могут стать так велики, что на по-
лосе образуются поперечные надрывы.
Перейдем к анализу деформированного состояния
прокатываемой полосы. Опять выделим в объеме очага
85
деформации элементарный параллелепипед и рассмот-
рим, как изменяется длина его ребер в процессе прокатки
(рис. 49). Учитывая наличие обжатия, вытяжки и уши-
рения полосы, нетрудно сделать вывод, что в вертикаль-
ном направлении происходит укорочение (сжатие) вы-
деленного элемента, а по двум другим осям — удлинение
Рис. 49. Основная схема деформи-
рованного состояния полосы при
.прокатке v' -А
его. Таким образом, схема
деформированного состоя-
ния является объемной и ха-
рактеризуется одной дефор-
мацией укорочения и двумя
деформациями удлинения.
Существуют условия про-
катки, при которых ушире-
ние полосы практически от-
сутствует. Это наблюдается,
например, при прокатке ши-
роких листов. В таких слу-
чаях деформированное со-
стояние полосы является
плоским (е2 = 0). Из теории пластичности известно, что
поперечная деформация отсутствует тогда, когда попе-
речное сжимающее напряжение составляет
<т2 = (<*1 + аз)/2.
При прокатке в четырехвалковых калибрах, образо-
ванных горизонтальными и вертикальными валками, по-
лоса обжимается сразу в двух направлениях — в верти-
кальном и поперечном. Следовательно, в этом случае
схема деформированного состояния характеризуется дву-
мя деформациями укорочения (ei и ег) и одной дефор-
мацией удлинения (б3).
2. Распределение деформаций по высоте полосы
Для более детального анализа деформированного состо-
яния металла при прокатке представляет интерес рас-
пределение высотной деформации (обжатия) по высоте
полосы. При рассмотрении этого вопроса необходимо
учитывать, что в любой точке полосы высотная деформа-
ция связана условием постоянства объема с продоль-
ной и поперечной деформациями. Если принять, что вы-
тяжка всех слоев полосы одинакова, то приходим к вы-
воду, что распределение высотной деформации должно
соответствовать распределению поперечной деформации
(уширения). Таким образом, о распределении обжатия
86
по высоте полосы можно судить по форме ее боковые
граней. Например, если прокатанная полоса имеет вы-
пуклые боковые грани, то это свидетельствует о том, что
обжатие в средних слоях больше, чем в приконтактных
Рис. 50. Зоны затрудненной дефор-
мации (показаны дуговой штри-
ховкой)
деформируемого
относительно по-
слоях.
Имеется несколько причин неравномерного распреде-
ления обжатия по высоте полосы. Одной из главных при-
чин является действие сил
трения. Как уже отмечалось,
эти силы затрудняют пере-
мещение
металла
верхности валков в продоль-
ном и поперечном направле-
ниях. Влияние сил трения
ослабевает по мере удале-
ния от контактной поверхно-
сти. Вследствие подпираю-
щего действия сил трения
в очаге деформации образу-
ются зоны затрудненной де-
формации (рис. 50). Величи-
на обжатия в этих зонах
меньше, чем в других точках
объема полосы. Наиболее
глубоко простираются зоны
затрудненной деформации
в районе нейтрального сече-
ния, где суммарное действие подпирающих сил трения
определяется наиболее резко.
Распределение деформаций по высоте полосы сильно
зависит от геометрических факторов — от коэффициента
формы ldlhZp и отношения ширины полосы к ее толщине
Ьъ/hQ. Чем толще прокатываемая полоса (по отношению
к длине дуги контакта), тем ярче выражена неравномер-
ность деформации. При очень малых значениях фактора
формы ld/h^ (менее 0,1—0,2) пластическая деформация
вовсе не проникает в средние слои металла.
Влияние параметра ^о/^о на распределение деформа-
ций объясняется тем, что от его величины зависит ин-
тенсивность поперечного течения металла. Чем меньше
отношение bQ/h0 (т.е. чем уже прокатываемая полоса),
тем легче перемещается металл в поперечном направле-
нии (на уширение). В связи с этим возникают условия,
способствующие неравномерному распределению дефор-
87
Рис. 51. Форма поперечного сече-
ния полосы после прокатки при
различной величине параметра
^d^cp :
*-'Лр>ЗЧ; 6 “ 3^4>Zd/ftcp >
>0,6—0,8; в — 0,6-r0,8>Zd/ftcp >0,1-
.•i-0,2; г — Zd/hcp<0,l-0,2
маций. Поэтому при прокатке узких полос неравномер-
ность деформации проявляется в большей степени, чем
при прокатке широких.
Существенно влияют на распределение деформаций
внешние части полосы, находящиеся за пределами гео-
метрического очага деформации. Благодаря воздействию
внешних частей происходит принудительное выравнива-
ние вытяжек всех слоев полосы. Если бы прокатке под-
рергался очень короткий образец, длиной примерно рав-
ный длине дуги контакта, то распределение деформаций
в его объеме было бы более неравномерным, чем при
прокатке длинной полосы.
Учитывая большое влияние фактора формы ldlhz? на
распределение деформаций по высоте полосы, ряд иссле-
дователей (А. П. Чекмарев,
И. Я. Тарновский и др.)
предложили классифициро-
вать процессы прокатки по
этому параметру. Достаточ-
но обоснована следующая
классификация:
Прокатка тонких полос —
Id/> 3-i~4.
В этом случае длина ду-
ги контакта в несколько раз
превышает среднюю толщи-
ну полосы в очаге деформа-
ции. Подпирающее действие
сил трения распространяется
на всю толщину полосы.
В соответствии с этим де-
формация распределяется
по высоте тела приблизи-
тельно равномерно. Боковые
кромки полосы после про-
катки имеют очень малую
выпуклость (рис. 51, а).
Прокатка полос средней толщины — 3-+-4>ld/hCn>
>0,64-0,8.
В связи с относительным увеличением размера hc?
действие сил трения на средние (по высоте) слои метал-
ла ослабевает; эти слои деформируются наиболее интен-
сивно. В то же время в приконтактных слоях образуют-
ся зоны затрудненной деформации. Боковые кромки по-
лосы приобретают явно выпуклую форму (рис. 51, б).
38
Такой вид поперечного сечения полосы иногда называют
«одинарной бочкой».
Прокатка толстых полос — 0,64-0,8>/d//iCp>0,14-0,2,
При большой толщине полосы деформация сжатия
слабо проникает в срединные слои металла. В результа-
те после прокатки поперечное сечение полосы приобре-
тает форму «двойной бочки» (рис. 51, в). Такое распре-
деление деформаций служит причиной возникновения
продольных растягивающих напряжений в центральных
слоях полосы. Те слои металла, которые получают наи-
более интенсивное обжатие (зоны А на рис. 51, в), воз-
действуют на центральные слои, принудительно увеличи-
вая их вытяжку. Возникающие растягивающие напря-
жения даже могут вызвать поперечные надрывы внутри
полосы (так называемые «скворечники»). Вследствие
действия растягивающих напряжений иногда наблюда-
ется также уменьшение ширины полосы в средней частщ
т. е. происходит поперечная утяжка.
Прокатка особо толстых полос—ldlhcp<Z0,14-0,2.
Такие малые значения фактора формы Id/h^ на прак-
тике встречаются, например, при прокатке на ребро
плоских слитков или широких полос. Характерным при-
знаком этого типа прокатки является отсутствие вытяж-
ки полосы. Весь обжимаемый металл смещается в по-
перечном направлении, образуя боковые наплывы в при-
контактной области (рис. 51,г). На среднюю (по высо-
те) часть полосы деформация не распространяется.
Итак, согласно приведенной классификации все слу-
чаи прокатки подразделяются на четыре типа в зависи-
мости от величины фактора формы Idth^. Следует иметь
в виду, что эта классификация является приближенной,
в некоторой мере условной, потому что формоизменение
полосы, как отмечалось выше, зависит по только от па-
раметра ldlhCXb ио и от лругих факторов, в частности от
параметра balh^.
3. Определение напряженного состояния полосы
методом построения линий скольжения
Количественное определение напряжений во всем объ-
еме очага деформации относится к числу наиболее слож-
ных теоретических задач. В тех случаях прокатки, когда
деформация близка к плоской (или осесимметричной), эта
задача может быть решена методом построения линий
скольжения. Как известно, линии скольжения являются
89
траекториями главных касательных напряжений. В де-
формируемом теле линии скольжения образуют поле,
состоящее из двух семейств взаимно ортогональных ли-
ций. Если известен ход линий скольжения, то можно оп-
ределить напряженное состояние в любой точке очага
деформации.
Сугубо теоретическое построение линий скольжения
Требует решения так называемых уравнений характери-
Рис. 52. Поле линий скольже-
ния при сжатии высокой поло-
сы плоскими бойками
стик. Однако на этом пути
встречаются большие матема-
тические трудности. Поэтому
в теории обработки металлов
давлением, и в частности в тео-
рии прокатки, поля линий
скольжения обычно строят уп-
рощенными методами, исполь-
зуя геометрические свойства
линий скольжения и основные
положения механики сплош-
ных сред.
Во всех случаях должны
быть заданы граничные усло-
вия (касательные напряжения
на контакте и др.).
При разных значениях па-
раметра ld/hcv вид полей ли-
ний скольжения неодинаков,
при /Др<1 поле может быть
принято таким же, как при
сжатии высокой полосы плос-
кими бойками (рис. 52). Оно
состоит из равнобедренного
прямоугольного треугольника
ДВС1, двух веерных зон ACD
и ВСЕ и криволинейного четырехугольника CEOD. Ис-
следуя это поле линий скольжения, можно определить не
только давление на контакте, но и распределение напря-
жений по высоте тела. Рассмотрим основные шаги тако-
го исследования (по А. Д. Томленову и В. М. Луговско-
му). Выделим на вертикали /—/ некоторую точку М и
определим продольное напряжение ох, действующее
в этой точке. Для этого построим две ортогональные ли-
1 Принимается отсутствие сил трения на контактной поверх-
ности.
*90
нии скольжения FG и GM. Используя первую теорему
Генки, напишем
сг„ — = —2т а •
F G s FG’ I ц91^
<та-<гм = Ч“вм-
где of, Og, ом — средние напряжения в точках F, G и М\
aFG, лам — углы поворота линий скольжения соответст-
венно между точками F и G, G и Л4; ts — сопротивление
пластическому сдвигу.
Линия GM, как и АС, подходит к вертикали /—/ под-
углом 45° (из условия симметрии поля относительно вер-
тикальной оси). Кроме того, заметим, что луч AG явля-
ется прямым, следовательно, угол поворота линии GM
равен углу 0. Такой же угол поворота, но с обратным
знаком, имеет линия FG:
асм ~ aFG = 9"
Учитывая это, из уравнений (191) находим
°F—°м - Ч (“ал —“га) = 4ts0- (192>
Средние напряжения oF и ом можно определить из
условия пластичности. В пределах треугольника АВС
имеем
р—^ = 4; °> = (р + °«)/2’
откуда
cF = p — rs. (193)
Аналогично в пределах четырехугольника CEOD на-
ходим
°л = ах + т1- (194>
Подставляя значения oF и ом в уравнение (192), по-
лучим
од. = р-2тД1 + 20). (195)
Так распределяются продольные напряжения по вы--
соте полосы на участке ОС, т. е. в пределах z/=0-r*
-4-(/i—/)/2. На участке выше точки С продольные напря-
жения постоянны и равны
Gx = P~ 2ts. (196)
Поскольку полоса находится в равновесии, должно
91
соблюдаться условие
ft/2
J crxdz/ = O.
о
С учетом выражений (195) и (196) напишем
(p-2T5)i + Г [р-2т, (1+29)] */ = (). (197)
О
Решаем это уравнение относительно контактного
давления р:
p = 2rJl+-^-J 0dp]. (198)
О
Для вычисления интеграла в квадратных скобках на-
до знать функцию Q=q>(y). Согласно исследованиям
В. М. Луговского, эта функция может быть аппроксими-
рована зависимостью
(h — 2у)/1 = е1,6в. (199)
После логарифмирования находим
0 = 0,625 In (200)
Теперь можно проинтегрировать уравнение (198),
после чего получим давление на контактной площадке
р = 2,5т6 [In
— +— — 0,2).
I h /
(201)
В литературе отмечается, что формула (201) спра-
ведлива в пределах l,0:>Z//iXjs0,12.
Подставляя найденные значения 0 и р в уравнения
(195) и (196), можно исследовать распределение напря-
жений ох по высоте всего тела. В частности, задаваясь
различными значениями l/h, можно определить величи-
ну растягивающих напряжений, возникающих на оси
X—х, т. е. при у=0. Результаты соответствующих рас-
четов приведены ниже:
Uh. P/2ts 0, рад V2rs
1,0 1,00 0 0
0,8 1,03 0,14 —0,25
0,6 1,14 0,32 —0,50
0,4 1,40 0,57 —0,75
0,2 2,01 1,00 —1,00
Р2
При llh^\ растягивающие напряжения в средней ча-
сти полосы не возникают.
В тех случаях прокатки, когда /<//пср = 1-ьЗ, поле линий сколь-
жения имеет вид, показанный на рис. 53. Для упрощения анализа
дуги контакта заменены хордами. Принимается, что в сечениях АА'
и ВВ' продольные напряжения отсутствуют или распределены раВ'
номерно. В соответствии с этим
линии АЕ (А'Е) и BD (B'D)
показаны прямыми. Из усло-
вия симметрии все линии
скольжения должны пересекать
горизонтальную ось под углом
45°; только при этом условии
касательные напряжения на
оси х—х будут равны нулю.
Криволинейный характер тре-
угольников АОВ и А'ОВ', при-
мыкающих к контактным по-
Ряс. БЗ. Поле линий скольжения
при прокатке полос средней толщи-
ны
верхностям, свидетельствуют
о том, что напряженное состоя-
ние металла в этих объемах
неоднородно.
Численное построение ли-
ний скольжения с определением напряжений в узловых точках ве-
дут последовательно, начиная с граничных линий АЕ (А'Е) и BD
(B'D). Необходимым шагом построения является определение уг-
лов 01 и 0г. В результате можно установить распределение напря-
жений во всех сечениях очага деформации, а также получить эпюру
нормальных напряжений на контактной поверхности.
4. Поперечная деформация (уширение)
При обжатии полосы в валках металл течет не только
в продольном, но и в поперечном направлении. По мере
нарастания обжатия в очаге деформации растет и уши-
рение. Рассматривая вопрос о распределении уширения
вдоль очага деформации, многие авторы (И. Я. Тарков-
ский, В. Н. Выдрин и др.) считают, что истинное относи-
тельное уширение пропорционально истинному относи-
тельному обжатию:
ln(VM = *!ln(V4). (202)
где и /i<p — текущие значения ширины и толщины по-
лосы в очаге деформации; k — истинный показатель уши-
рения.
Величина k принимается постоянной на протяжении
всего очага деформации. Поэтому ее можно определить
по конечным размерам полосы Ь\ и hr.
k = . (203)
ln(VM 1п(1/Т|) '
93
Из формулы (202) можно найти ширину полосы
в любом поперечном сечении очага деформации:
i„ = 6o(W- (204)
Формула (204) достаточно хорошо согласуется с экс-
периментальными данными. Вместе с тем надо отметить,
что кривизна боковых кромок полосы в плане в большин-
стве случаев прокатки очень невелика. Это видно, на-
пример, из построения горизонтальной проекции очага
Рис. 54. Форма очага деформации
и плане (принято ЛоХ&о=50Х
Х50 мм; ftiX&i=30X 60 мм; D=
= 500 мм)
деформации на рис. 54, вы-
полненного для одного из
конкретных случаев прокат-
ки с применением формулы
(204). Линии бокового кон-
тура полосы почти совпада-
ют с прямыми линиями, по-
казанными пунктиром. Учи-
тывая это, в теоретических
выводах форму очага дефор-
мации в плане обычно при-
нимают за трапецию.
Для практики важно
знать полное уширение ЛЬ,
полученное полосой при прохождении через валки. Осо-
бенно важно знать эту величину при прокатке в калиб-
рах, так как неправильный учет уширения может приве-
сти либо к переполнению, либо к незаполнению калибра.
Если поперечному течению металла в очаге дефор-
мации препятствуют только силы трения на контактной
поверхности, то уширение называется свободным. Такое
уширение имеет место при прокатке в цилиндрических,
некалиброванных валках. При прокатке в калибрах по-
перечному перемещению металла препятствуют в той
или иной мере боковые стенки калибра; в этом случае
уширение является ограниченным. Существует также
понятие о вынужденном уширении, которое наблюдает-
ся в тех случаях прокатки, когда обжатие распределяет-
ся неравномерно по ширине полосы. Для пояснения этого
обратимся снова к рис. 48. Части полосы I и III, которые
претерпевают наибольшее обжатие, соответственно
стремятся получить большую вытяжку, но она сдер-
живается действием средней части полосы II. В резуль-
тате металл на участках / и /// вынужден перемещать-
ся в поперечном направлении в большей мере, чем при
свободном уширении., Таким образом, вынужденное уши-
S4
рение имеет место на тех участках полосы, которые по-
лучают повышенное обжатие.
5. Влияние факторов прокатки на уширение
Соотношение между поперечной и продольной деформа-
циями зависит от сопротивлений перемещению металла
в этих направлениях. При свободном уширении сопро-
тивления создаются действием сил трения. Если по ка-
кой-либо причине в очаге деформации возрастают про-
дольные подпирающие силы трения, то это приводит к сни-
жению вытяжки и увеличению уширения. И наоборот,
если возрастают поперечные силы трения, то уширение
уменьшается, а вытяжка увеличивается.
Исходя из этих общих соображений проанализируем
влияние отдельных факторов прокатки на уширение.
1. Обжатие. С ростом обжатия уширение увеличива-
ется (рис. 55). Это объясняется, во-первых, тем, что уве-
личивается смещаемый объем
металла как в продольном, так
и в поперечном направлении. Во-
вторых, в соответствии с форму-
лой (40), растет длина очага де-
формации, а это значит, что воз-
Рис. 55. Зависимость уширения от Рис. 56. Зависимость уширения от диа-
абсолютного обжатия (по М. Л. метра валков (по Метцу)
Зарощинскому)
растает сумма продольных подпирающих сил трения, ко-
торые затрудняют вытяжку; последнее способствует рос-
ту уширения.
2. Диаметр валков. При одном и том же обжатии
и постоянстве прочих факторов, с увеличением диаметра
валков уширение возрастает (рис. 56). Это объясняется
опять-таки увеличением длины очага деформации и со-
ответствующим ростом суммы продольных подпирающих
сил трения.
3. Ширина полосы. Чем шире прокатываемая полоса,
95
тем больше сумма поперечных подпирающих сил трения
на контактной поверхности. Следовательно, с увеличе-
нием ширины полосы уширение уменьшается (рис. 57).
Из практики хорошо известно, что при прокатке широ-
ких полос и листов уширение незначительно.
В области прокатки очень узких полос абсолютное
уширение падает при уменьшении ширины полосы (рис.
57, а), но это связано с резким сокращением смещаемо-
Рис. 57. Зависимость абсолютного (а) и относительного (б)
уширения от ширины полосы (по Ю. М. Чижикову)
го объема металла. Если построить график изменения
относительного уширения, то оно монотонно уменьшает-
ся, начиная с самых малых значений Ьо (рис. 57,6).
4. Коэффициент трения. С увеличением коэффициен-
та трения возрастают как продольные, так и поперечные
подпирающие силы трения. Однако надо учитывать, что
металл течет в основном в продольном направлении (на
вытяжку). Рост тормозящего действия сил трения в про-
дольном направлении влияет на распределение дефор-
маций более существенно, чем рост поперечных сил тре-
ния. В результате с увеличением коэффициента трения
вытяжка уменьшается, а уширение возрастает.
Через коэффициент трения влияют на уширение мно-
гие факторы: состояние поверхности валков, температу-
ра металла, скорость прокатки и др. Из практики изве-
стно, что при прокатке на изношенных валках с грубой
поверхностью заполнение калибров происходит в боль-
шей степени, чем при прокатке на новых валках с отно-
сительно гладкой поверхностью. Это подтверждается
специальными исследованиями (рис. 58).
5. Натяжение концов полосы. Если к концам полосы
приложены растягивающие силы, то они облегчают про-
дольное течение металла, т. е. способствуют вытяжке.
96
Следовательно, натяжение концов полосы должно умень-
шить уширение. Зависимость такого рода отчетливо на-
блюдается на практике (рис. 59).
В первом приближении можно считать, что ушире-
ние уменьшается пропорционально величине приложен-
ного натяжения.
Важно отметить, что заднее натяжение влияет на
уширение гораздо сильнее, чем переднее натяжение. Это
Рис. 58. Заполнение овального ка-
либра при прокатке свинцовых по-
лос сечением 20X20 мм на валках
с шероховатой (а) и гладкой (б)
поверхностью (по Зибелю и Озен-
бергу)
Рис. 59. Влияние заднего (<7о) и
переднего (<?i) натяжения концов
полосы на уширение (по А. П. Чек-
мареву и Л. Ф. Машкину)
объясняется тем, что заднее натяжение воздействует на
зону отставания, где происходит основная деформация
и почти полностью формируется ширина полосы. Перед-
нее же натяжение воздействует на зону опережения, где
обжатие мало и соответственно очень мало уширение.
Во многих случаях влиянием переднего натяжения на
уширение можно пренебречь.
Если к концам полосы приложены не силы натяже-
ния, а силы подпора, то они вызывают увеличение уши-
рения. При этом задний подпор оказывает более сильное
воздействие, чем передний.
6. Форма калибров. В большинстве случаев при про-
катке в калибрах уширение получается меньше, чем при
прокатке в цилиндрических валках (при той же высот-
ной деформации), так как боковые стенки калибра соз-
дают дополнительное сопротивление поперечному тече-
нию металла. Степень ограничения уширения зависит от
угла наклона боковых стенок калибра и от соотношения
между шириной калибра и шириной задаваемой полосы.
7 А. П. Грудев
97
6. Теоретическое определение уширения
Предложено много формул для расчета уширения. К чис-
। лу наиболее ранних относится формула Жеза
Ш = (205)
где а — показатель уширения.
Формула (205) учитывает лишь зависимость ушире-
ния от абсолютного обжатия. Влияние всех других фак-
торов скрыто в показателе а, поэтому величина а может
изменяться в широких пределах, примерно от 0,1 до 1,0.
Заранее выбрать величину а трудно. Формулу Жеза мож-
но использовать лишь тогда, когда известно значение а
для конкретных условий прокатки.
Широко известна и нередко применяется достаточно
простая формула Зибеля:
\/дЬ = С (Ah/hJ VRAh, (206)
где С — коэффициент, находящийся в пределах 0,3—0,45.
Как видим, формула Зибеля учитывает относительное
обжатие и длину очага деформации. Предложены и бо-
лее сложные формулы для расчета уширения. Среди них
можно назвать формулу Губкина и Чекмарева.
Формула Губкина имеет вид
Д& = (1 + Д/1//1о) (f7 VRAh — Ah/2) Ah/h?. (207)
Формула Чекмарева
Ab =--------------------Mhbw-------------------- , ^208)
I i. Ji I zi i J 6cp _____ftp + 1
(Л. + W [1+ (1 + «) (-jjj 2M1 + fy Ra/6cp)J
где n—показатель, зависящий от формы очага дефор-
мации в плане.
Принимают п=1 при &Ср<#а и п=2 при bCp>Ra.
Расчеты по формуле (208) показывают, что сомножи-
/in Ч- ht ,
тель -------——±-------- мало отличается от 1 и во мно-
2fti(l+fy/?a/ftCp)
гих случаях им можно пренебречь; тогда формула Чек-
марева принимает вид:
АЬ =-------------^^5--------------. (209)
(Ло + Лх) [1 + (1 +а) (&сР//?а)ге]
Практически в расчетах принимают bCp~bo или ЬСр~
~bi (последнее, в случае определения размеров полосы
против хода прокатки).
98
Все вышеприведенные формулы уширения относятся
к числу эмпирических, т. е. получены путем обработки
экспериментальных данных. Далее рассмотрим формулы
уширения, выведенные аналитическим путем.
Б. П. Бахтинов предположил, что объем металла, смещаемый на
уширение, пропорционален работе, затрачиваемой на это переме-
щение:
= A^IA^ (210)
где — объем металла, смещаемый на уширение; V —полный
смещенный объем; Ддй — работа, затрачиваемая на уширение; Дд^ —
полная работа прокатки.
Процесс прокатки Б. П. Бахтинов рассматривал как процесс
накатки валков на полосу (рис. 60). Очаг деформации делится на
Ion
Рис. 60. Схема к выводу
формулы уширения Б. П.
Бахтинова
зоны отставания (1), опережения (2) и уширения (3). При такой
схеме деления очага деформации величины, входящие в формулу
(210), определяются из выражений
Уд6 = Д№1£; (211)
УДА = ь0 Ш/Ь = (ДЛЧ) hi bi L> (212>
^ = PCP^; <213)
Ли = Рср^ <214>
7*
99
где L — путь, пройденный валками (см. рис. 60); FZj—вертикаль-
ная проекция зон уширения; Fz — полная вертикальная проекция
контактной поверхности.
Подставляя найденные значения смещенных объемов и работ
в формулу (210), после несложных преобразований находим
(215)
Площади Fz и FZa приближенно определяются так:
Fj = Fz3 — Ahlym,
где /уш — длина зоны уширения в поперечном направлении.
После подстановки значений FZa и Fz в формулу (215) по-
лучим
ЛЬ = (Д/г//г0) /Уш (fri/*cp) • (216)
Допустим, существует определенное соотношение между по-
перечным размером зоны уширения /уш и длиной зоны опереже-
ния /оп
/уш == ^/оп* (217)
Длину зоны опережения находим с помощью формулы Экелун-
да—Павлова (133)
(218)
Z \ Zpy / " \ "/у /
С учетом выражений (217) и (218) из формулы (216) получим
(219)
2fto \ 2/у / &ср
По данным Б. П. Бахтинова, коэффициент k изменяется в узких
пределах: k= 1,10ч-1,12. Величина отношения &1/&Ср лишь немного
больше 1. На этом основании произведение k(b\/bCp) заменяется од-
ним числовым коэффициентом, равным 1,15. Тогда формула (219)
принимает конечный вид
Д6-1,15-^-(УяДЬ—(220)
2Л0 \ 2fy/
Несмотря на упрощенность вывода и принятие многих допуще-
ний, формула Бахтинова правильно отражает влияние ряда основ-
ных факторов на уширение (обжатия, диаметра валков, коэффици-
ента трения). Она соответствует случаю прокатки относительно ши-
роких ПОЛОС (&ср>2/уш).
Более строгий вывод формулы уширения сделан
А. И. Целиковым, который также принял, что очаг де-
формации может быть разделен на зоны отставания, опе-
режения и уширения (рис. 61). Предполагается, что весь
объем металла, заключенный в пределах зоны ABD, при
обжатии будет перемещаться в направлении уширения.
При переходе от сечения аа' к сечению bb' равенство эле-
ментарных смещенных объемов имеет вид (см. рис. 61)
0,5/ix dx 0,5dfcx =— 0,5# dx dhx.
100
Рис. 61. Схема к выводу формулы ушире-
ния А. И. Целикова
Знак минус в правой части уравнения поставлен по-
тому, что Ьх увеличивается при уменьшении hx. Из при-
веденного уравнения находим
dbx=~2y(dhx/hx). (221)
Для решения дифференциального уравнения (221) не-
обходимо знать зависимость у от hx, т. е. положение ли-
ний AD и DB. Эта за-
висимость может быть
найдена из условия,
что на границе между
зоной уширения и зо-
нами отставания и опе-
режения поперечные
напряжения <зу равны
продольным напряже-
ниям Если же оу=
=ох, то при движении
вдоль границы каждо-
му изменению оу будет
соответствовать равное
ему изменение ох, т. е.
dGy=dox.
При перемещении
элементарного объема
металла в поперечном
направлении приращение напряжения составляет
= (2ty!hy) dy, (222)
где ty — поперечная удельная сила трения; hy — высота
сечения полосы, постоянная в поперечном направлении.
Аналогично из условия равновесия элементарного объ-
ема металла в продольном направлении выводится фор-
мула (вывод см. на стр. 137)
Л’ж = (<+ (223)
\ tg <Р / ftx
где tx — продольная удельная сила трения; ср — текущий
угол наклона контактной поверхности.
В этом выражении знак минус относится к зоне отста-
вания, знак плюс — к зоне опережения.
Приравнивая правые части уравнений (222) и (223),
находим
__ 1 / °т - tx \ dhx
ay — ~~ I 4“ I hy
2 \ ty ty tg ф/ hx
(224)
101
(225)*
(226)?
ho
(227);
Для приближенного решения этого уравнения прини-
маются допущения: ty==fvG<r и tytttx. Кроме того, дуга
контакта заменяется хордой, в результате чего угол ср
становится постоянным и tg cp=Ah/2Zd. Сделав соответ-
ствующие подстановки в уравнение (224), получим
= .
к Ufy АЛ / ’ Лх
Поскольку дуга заменена хордой, имеем
hx = h1-\- х ; dhx = dx.
Id Id
С учетом этих выражений получим
, / Aft _ « \ , dx
dy = -----+ 1 \hv----------.
\2/dfy / yfti + xAft//d
Интегрируем уравнение (226) в пределах от x=ld
до х:
У = ( + —М h
( Aft 2f7} v ht + x^h/ld
Подставим найденное значение у в уравнение (221):
dbx = — (ld + h In + . (228)
“ ЛЛ l d 2/y / " h. hx
Величины hx и hy можно сократить, так как значения
их вдоль линии AD равны.
Для интегрирования уравнения (228) опять-таки необ-
ходимо установить связь между hx и х. В данном случае-
замена дуги контакта хордой является слишком грубой,,
так как искажает картину распределения уширения вдоль
очага деформации. Поэтому принимаем
= hx 4- 27? (1 — cos ср) = 4- 47? sin2 (ср/2) « ht 4~ x2/R,
откуда находим dhx= (2x/R)dx.
Возвращаясь к уравнению (228), напишем:
dbx = А Л + In b1 + xWld
PdV 2h) Ло
Теперь можно сформулировать закон изменения ши-
рины полосы на протяжении очага деформации
, __ 4 /. _ АЛ
°х ~ vd +
ld v
Интегральное уравнение (230) решается методом под-
становки. Введем новую переменную (hiA-x^h/ld)/hQ=g.
(229>
(230}
102
Тогда имеем х= (hQg—h{) и dx== (ldhQ/&h)dg.
Соответственно уравнение (230) принимает вид
= (231)
\ Z/y / J
После интегрирования получим
6 £~ Л fog------^-g-\- 1] + С.
х Aft? \ d 2/у / S |Д 2ftj / 4й1 J
(232)
Произвольную постоянную С определяем из гранич-
ных условий: при x—ld имеем bx=b0 и g=l; после под-
становок находим
C = bQ
__Ahp^ / J _ Aft \ /
Aft? \ d + 2fy ) \
ftp \
4ftJ’
Таким образом, распределение уширения вдоль очага
деформации может быть выражено следующей форму-
лой:
Ьх —&
° Aft?
1)+g-1].
h J
(233)
Уширение в основном развивается до нейтрального се-
чения, т. е. на участке АС (см. рис. 61). Учитывая это,
можно пренебречь уширением на участке СВ и считать,
что уравнение (233) действительно на протяжении всего
очага деформации. Тогда при х=0 и g=hx/hQ получим
формулу для расчета полного уширения
ДЬ= id
— —U2 (-МЧп
2fy / L \ АЛ /
hp n |
fti Aft
(234)
А. И. Гришков показал, что
2/^? ln-^ —
\ Aft /
2-^- + 1 0,5In,
Aft fti
поэтому формулу уширения Целикова обычно приводят
в виде
ЛЬ = 0,5 (УЯДЛ — —'I In-А . V (235)
\ 2fy / fti
Формула (235) не отражает влияния ширины полосы
и натяжения ее концов на уширение. Для учета этих
факторов в формулу вводят два дополнительных коэф-
103
фициента — соответственно Сь и Са
ЬЬ = 0,5Cb Со (VRM — —) In . (236);
\ 2fy / hr
Величина коэффициента Сь, учитывающего ширину
полосы, может быть найдена с помощью графиков, при-
веденных на рис. 62. Величина коэффициента Со прибли-
женно определяется по формуле
ZCO= 1 — 2?0/от. (237).'
Влиянием переднего натяжения на уширение, как.
отмечалось выше, можно пренебречь.
Рис. 62. Графики для определения коэффициента Св в
зависимости от ширины полосы и относительного обжа-
тия
Все вышеприведенные формулы относятся к случаю»
прокатки прямоугольной полосы в цилиндрических вал-
ках. При расчете уширения в калибрах чаще всего ис-
пользуют те же формулы, но вводят в них поправочный
коэффициент, учитывающий особенности деформации
в калибрах разной формы. По данным В. И. Зюзина
поправочный коэффициент Кф составляет: для систем
ромб — квадрат, ромб — ромб, овал — круг, овал — овал
Кф=0,84-0,85; для системы квадрат — овал Кф=0,74-
4-0,74; для системы ребровой овал—плоский овал Кф =
= 1,2. Обжатие и другие геометрические параметры ре-
комендуется рассчитывать по методу приведенной по-
лосы.
Г л а в a VI
СИЛЫ ТРЕНИЯ
1. Распределение сил трения по дуге контакта
Из предыдущего материала ясно, что при прокатке силы
внешнего (контактного) трения играют исключительно
важную роль. Захват полосы валками осуществляется за
счет действия сил трения: если бы не было трения, то
процесс прокатки вообще был бы невозможен.
Ранее уже объяснялось, что от коэффициента трения
зависят опережение и уширение полосы. В дальнейшем
будет показано, что от величины сил трения также зави-
сят энергосиловые параметры — усилие прокатки и рас-
ход работы. Все это требует углубленного изучения
внешнего трения при прокатке.
В настоящее время разработано несколько методов
-исследования распределения сил трения по контактной
поверхности. К числу наиболее распространенных отно-
сятся методы наклонных точечных месдоз, универсально-
го штифта и разрезного валка.
Метод наклонных точечных месдоз заключается в том,
что в тело валка вставляются три силоизмерительных
штифта*— месдозы, причем один штифт располагается по
нормалй к поверхности (по радиусу), а два других—
с наклоном (рис. 63). Термин точечная месдоза означает,
Рис. 63. Схема установки радиальной и то- Рис. 64. Схема сил, дейст-
чечных месдоз в прокатном валке вующих на штифт наклон-
ной месдозы
что диаметр штифта, выходящего на контактную поверх-
ность, достаточно мал (практически 1,0—1,5 мм). Если
зарегистрированы усилия Mlt М2, М3, действующие вдоль
105
оси штифтов при прохождении ими очага деформации,
то можно определить продольную силу трения в любой
точке контактной поверхности.
Для вывода расчетной формулы рассмотрим схему
сил на рис. 64. Спроектируем силы N и Т на ось штифта
и составим уравнение равновесия
М = N cos ф 4- Т sin ф. (238)
Переходя к удельным силам (напряжениям), напи-
шем
та = р (alcos ф) cos ф -|-1 (al cos ф) sin ф,
где т — продольное напряжение в штифте; а — площадь
поперечного сечения штифта; р и t — соответственно нор-
мальное давление и удельная сила трения на площадке
касания.
После сокращений получим
т - - р -|-1 tg ф, (239)
удельная сила трения
t = (т — р) ctg ф. (240)
Можно определить и коэффициент трения
f — tip = (mlp — 1) ctg ф. (241)
Входящая в расчетные формулы (240) и (241) вели-
чина нормального давления р определяется из показаний
радиальной месдозы М3: p=Mz/a.
Приведенный вывод свидетельствует о том, что для
исследования удельных сил трения достаточно одной на-
клонной месдозы. Однако практически устанавливают
две наклонные месдозы, что повышает надежность изме-
рений. При этом углы ф1 и фа обычно принимаются рав-
ными.
Недостатком рассмотренного метода является то, что
штифты трех (или двух) месдоз проходят через очаг
деформации не одновременно, а последовательно; в связи
с этим показания месдоз записываются на ленту осцил-
лографа с некоторым сдвигом. Вместе с тем величины т
и р, подставляемые в формулы (240) и (241), должны
строго отвечать одной и той же точке контактной поверх-
ности. Поэтому совмещение осциллограмм при их обра-
ботке должно быть очень тщательным.
Некоторые трудности возникают также в связи с не-
обходимостью учета боковых сил трения при перемеще-
нии штифтов в каналах.
106
Метод универсального штифта основан на том, что
^измерительный штифт устанавливается в радиальном ка-
нале с небольшим кольцевым зазором, благодаря чему
он может несколько смещаться в любом поперечном на-
правлении (рис. 65). Действующие на штифт касатель-
ные силы регистрируются с помощью месдоз ЛТЬ М2, Л43
►и М4, а сила нормального давления — с помощью месдо-
зы ЛТ5. Такое измерительное устройство позволяет одно-
Рнс. 65. Схема установки универ-
сального штифта
Рис. 66. Схема прокатного валка с
силоизмерительной вставкой
временно регистрировать продольную и поперечную со-
ставляющие силы трения и нормальное давление. В этом
заключается преимущество метода универсального (ка-
чающегося) штифта.
Вместе с тем сам принцип замеров, основанный на
боковом отклонении штифта, нельзя считать безупреч-
ным. Показания такого прибора зависят не только от ве-
личины сил трения, но и от величины относительного
смещения контактирующих поверхностей. Эксперимен-
тальные данные могут быть достоверными только в слу-
чае ii|)iimciiciiii5i штифтов, обладающих очень высокой
боковой жесткостью при достаточной чувствительности.
Другим источником погрешностей может быть затека-
ние металла в кольцевой зазор между штифтом и телом
валка, поэтому величина зазора должна быть очень мала
(порядка 0,02—0,04 мм).
Л Метод разрезного валка основан на применении сило-
измерительной вставки, представляющей собой часть боч-
ки валка (рис. 66); вставка опирается на месдозы ЛТ1,
М2 и М3. По мере поворота валка и вхождения вставки
в очаг деформации растет давление на месдозу Mif обус-
ловленное действием сил трения в зоне отставания; од-*
новременно растет давление на месдозу Л43. Когда перед-
107
ний конец вставки проходит нейтральное сечение, дав-
ление на месдозу Mi начинает падать. Месдоза М2
является контрольной. Для построения эпюры распреде-
ления удельных сил трения и давлений по дуге контакта
надо продифференцировать кривые, записанные месдоза-
ми Afj, ЛТ2 и М3. Поскольку вставка располагается вдоль
всей бочки валка, значения удельных сил t и р получа-
ются усредненными по ширине полосы. Кроме того, сле-
дует иметь в виду, что этим ме-
тодом измеряются только про-
дольные составляющие сил
трения.
В настоящее время накоп-
лен большой эксперименталь-
ный материал по распределе-
нию сил трения на контактной
поверхности. Естественно, вид
эпюр сил трения зависит от ус-
ловий прокатки. Однако среди
всего многообразия опытных
данных все же можно выде-
лить эпюру сил трения наибо-
лее общего типа (рис. 67). Из
Рис. 67. Типичная эпюра рас-
пределения сил трения по дуге
контакта
нее видно, что при движении
от плоскости входа удельная
сила трения сначала растет
(участок /), а затем постепен-
но снижается вплоть до нуля в нейтральном сечении (уча-
сток II). Аналогично изменяется сила трения в зоне опе-
режения, если двигаться от плоскости выхода к ней-
тральному сечению. Эпюра сил трения в зоне опережения
показана ниже базовой линии, чтобы отразить различие
знаков сил t в зонах отставания и опережения.
На участках I сила трения t изменяется приблизи-
тельно пропорционально изменению давления р, т. е. в оп-
ределенной мере справедлив закон трения Амонтона:
t=fyp. С физической точки зрения эти участки характе-
ризуются наличием контактного скольжения.
Участки II, по современным представлениям, соответ-
ствуют зоне прилипания на контактной поверхности.
Здесь действуют статические, неполные силы трения,
и их величина зависит от тех касательных напряжений,
которые возникают в поверхностном слое металла при
деформации. Касательные напряжения можно интерпре-
тировать как стремление к сдвигу. В нейтральном сече-
108
нии на контактной поверхности стремления к сдвигу нет,
поэтому и силы трения здесь равны нулю. По мере уда-
ления от нейтрального сечения стремление к поверхно-
стному сдвигу увеличивается — соответственно растут
удельные силы трения.
В некоторых случаях на эпюрах сил трения между
участками / и II наблюдаются почти горизонтальные
площадки, как показано пунктиром на рис. 67. Обычно
считают, что такие площадки возникают тогда, когда си-
лы трения достигают предельно возможной величины (из
условия прочности металла на сдвиг).
На основе анализа эпюры сил трения уточним само
понятие коэффициент трения при установившемся про-
цессе прокатки. Отношение элементарных сил t/p в лю-
бой точке дуги контакта представляет собой коэффици-
ент трения в данной точке. Причем в пределах зон
скольжения это будет истинный, физический коэффици-
ент трения, а в пределах зоны прилипания — условный
коэффициент трения, так как на этой части дуги контак-
та действуют силы трения покоя. В теории прокатки, как
правило, используется единое, усредненное значение ко-
эффициента трения для всего очага деформации. Оно
определяется как отношение суммы элементарных сил
трения (без учета знака) к сумме нормальных давлений
или как отношение средней удельной силы трения
к среднему давлению
fy = S//Sp = /cP/pcp. (242)
В тех случаях, когда на контактной поверхности су-
ществует значительная анизотропия трения, т. е. сила
трения зависит от направления скольжения, следует раз-
личать коэффициенты продольного и поперечного трения.
2. Соотношение коэффициентов трения при захвате
и при установившемся процессе прокатки
Условия трения в начальный момент касания полосы
с валками и при установившемся процессе не одинаковы.
Следует отметить ряд существенных различий, на кото-
рые необходимо обратить внимание. Прежде всего, до
защемления металла валками трение осуществляется
между твердыми, недеформируемыми телами. Природа
и закономерности трения в этот момент должны быть та-
кими же, как при обычном (машинном) трении метал-
лических тел. Другая особенность трения в начальный
109
момент захвата заключается в своеобразии геометриче-
ских условий контактирования поверхностей. При сколь-
жении передних острых кромок полосы по валкам пло-
щадь касания поверхностей мала, что отражается на
физических условиях трения. Даже при очень кратковре-
менном скольжении и небольшом усилии задачи кромки
полосы заметно истираются. С кромок легко счищаются
окалина и другие промежуточные среды. В связи с этим
в момент захвата с валками контактирует относительно
чистая поверхность металла.
При горячей прокатке стали в области высоких темпе-
ратур окалина на поверхности металла находится в раз-
мягченном состоянии, играя роль смазки. Попадая в очаг
деформации, она значительно уменьшает коэффициент
трения при установившемся процессе прокатки. В то же
время на передних кромках полосы окалина не удержи-
вается, поэтому коэффициент трения при захвате сохра-
няется на более высоком уровне.
Геометрические условия контактирования поверхно-
стей играют особенно большую роль при прокатке с жид-
кими технологическими смазками. Малая площадь каса-
ния в начальный момент захвата не способствует обра-
зованию устойчивой разделительной смазочной пленки.
Острые кромки полосы прорезают слой смазки, в связи
с чем коэффициент трения при захвате получается выше,
чем при установившемся процессе прокатки, когда суще-
ствуют благоприятные условия для втягивания смазки
в очаг деформации.
Отметим еще некоторые особенности трения в на-
чальный момент захвата. Давления на кромках полосы,
касающейся валков, могут быть значительными, но они
все же меньше, чем среднее давление при заполненном
очаге деформации. До защемления металла валками ско-
рость скольжения равна окружной скорости валков, а при
установившемся процессе прокатки средняя скорость
скольжения на контактной поверхности намного ниже.
При прокатке нагретого металла температура кромок по-
лосы обычно бывает ниже температуры основных поверх-
ностей. Помимо отмеченных факторов, различие между
коэффициентами трения f3 и /у может быть обусловлено
«образованием зоны прилипания в очаге деформации при
установившемся процессе. Наличие зоны прилипания, где
силы трения являются неполными, приводит к снижению
величины fy.
Таким образом, анализ физических и кинематических
110
условий трения приводит к выводу, что в большинстве
случаев прокатки должно иметь место соотношение f3>
Этот вывод согласуется с экспериментальными дан-
ными (табл. 4).
Таблица 4. Результаты исследования коэффициентов трения при*
захвате и при установившемся процессе прокатки
Материал образцов Темпера- тура про- катки, °C Промежуточная среда (смазка, окалииа) ^3 fy ^з^у
Сталь Комнат- Нет 0,143 0,086 1,66
08кп ная Керосин Эмульсия*1 0,151 0,129 0,053 0,055 2,85 2,34
Сталь СтЗ*? 1150— 1200 С печной ока- линой Без печной ока- лины 0,44 0,44 0,18— 0,29 0,30— 0,35 1,5—2,4 1,2—1,4
Свинец Комнат- ная Нет Хлопковое мас- ло 0,269 0,119 0,261 0,064 1,03 1,86
** 10 %-ный водный раствор эмульсола Э-2 (Б); *2 Данные А. П. Чекма-
рева с соавторами.
Как видно из табл. 4, различие между коэффициента-
ми трения f3 и /у проявляется в наибольшей степени;
именно тогда, когда на трущихся поверхностях присут-
ствуют промежуточные среды (смазка, размягченная ока-
лина). Эти данные подтверждают большое влияние гео-
метрических условий контактирования поверхностей на.
величину коэффициента трения на разных стадиях про-
катки.
3. Методы экспериментального определения
коэффициента трения
Известно около 20 методов определения коэффициента;
трения при прокатке. Наиболее часто применяются сле-
дующие методы: максимального угла захвата, предель-
ного обжатия, принудительного торможения полосы, кру-
тящего момента, опережения и давления. Рассмотрим-
сущность этих методов и основные расчетные формулы.
Метод максимального угла захвата. Образец с неболь-
шим усилием прижимается к вращающимся валкам, за-
зор между которыми устанавливается таким, чтобы за-
хвата сначала не было. Затем валки постепенно разводят
111:
до тех пор, пока не осуществится захват. Измерив тол-
щину образца до и после прокатки, по формуле (28) рас-
считывают максимальный угол захвата а3тах. Если не-
обходимо учесть пружину стана, то применяется форму-
ла (34). Коэффициент трения определяют из условия
/з = tga3maX- (243)
Следует подчеркнуть, что рассмотренным методом на-
ходят величину коэффициента трения при захвате. Все
остальные методы служат для определения коэффициен-
та трения при установившемся процессе прокатки.
Метод предельного обжатия. В процессе прокатки тем
или иным способом постепенно повышают обжатие, а сле-
довательно, и угол контакта. Наступает момент, когда
процесс прокатки прерывается: возникает буксование
валков по металлу. Коэффициент трения определяют из
условия захвата при установившемся процессе, исполь-
зуя равенство (117). Расчетная формула имеет вид
fT = tg(amai/2). (244)
Максимальный угол контакта рассчитывают по фор-
муле (28), подставляя в нее обжатие, соответствующее
появлению первых пробуксовок.
Рис. 68. Схема сил при торможении поло-
сы в валках
Постепенное увели-
чение обжатия в про-
цессе прокатки чаще
всего достигается при-
менением образцов кли-
новидной формы, зада-
ваемых в валки тонким
концом (см. рис. 24).
Вместо клиновидных
образцов можно прока-
тывать обычные прямо-
угольные образцы с за-
остренными передними
концами при различной
установке валков.
Метод предельного обжатия нельзя считать теорети-
чески строгим, так как в основе его лежит приближенное
условие захвата (117).
Метод принудительного торможения полосы. К задне-
му концу прокатываемой полосы прикладывается тормо-
зящая сила Q, под действием которой полоса останавли-
вается в валках (рис. 68). В начальный момент буксо-
112
вания измеряют вертикальную силу Р и усилие
торможения Q. Зная эти две величины, можно определить
коэффициент трения /у.
Составим уравнение равновесия сил, приложенных
к полосе:
в горизонтальной плоскости
2Т cos ф — 2Л/ sin ф — Q = 0; (245)
в вертикальной плоскости
Р — N cos ф — Т sin ф = 0, (246)
где /V— равнодействующая нормальных давлений; Т —
равнодействующая элементарных сил трения; ф — угол,
характеризующий точку приложения сил N и Т.
Учтем, что T=fyN. Кроме того, допустим, что точка
приложения равнодействующих /V и Т находится посере-
дине дуги контакта, т. е. ф=а/2. Тогда уравнения равно-
весия принимают вид
2Nfy cos (а/2) — 2ЛГ sin (а/2) — Q = 0; (247)
Р —Ncos (а/2) — fy W sin (а/2) = 0. (248)
Найдем значение силы N из уравнения (247)
2 [fy cos (а/2) — sin (а/2)] *
Подставим это значение силы N в уравнение (248)
и, решая его, получим формулу для определения коэффи-
циента трения
f _ (Q/2P) + tg(a/2)
'У 1-(Q/2P) tg(a/2)‘ ( '
Численный анализ показывает, что член (Q/2P) tga
в знаменателе всегда очень мал по сравнению с едини-
цей, поэтому формулу (249) можно использовать в упро-
щенном виде
fy = (Q/2P) + tg(a/2). (250)
При исследовании коэффициента трения торможение
образцов осуществляется с помощью специального тор-
мозящего устройства, в котором крепится задний конец
образца. Торможение должно быть достаточно плавным,
с непрерывным изменением силы Q. Вертикальная силаР
измеряется месдозами, установленными под нажимными
винтами. Следует применять малоинерционную, самопи-
шущую аппаратуру, чтобы можно было зафиксировать
значения сил Q и Р в самый начальный момент возник-
8 А. П. Грудев ИЗ
новения буксования, точнее, в тот момент, когда опере-
жение падает до нуля, но деформация еще продолжа-
ется.
Метод крутящего момента. Сущность метода заклю-
чается в измерении «чистого» крутящего момента на боч-
ке валка Л4пр и усилия прокатки Р. Измерения проводят
при наличии сплошного однозначного скольжения на кон-
тактной поверхности (опережение равно нулю). Такие
кинематические условия создаются либо за счет заднего
натяжения полосы либо путем применения предельного
обжатия.
Крутящий момент на бочке валка составляет
Мпр = ТЯт = /удат, (251)
где Рт — плечо силы Т относительно центра валка 0 (см.
рис. 68).
Из формулы (251) находим
/у = ^пр/(^тЛ9. (252)
С достаточной точностью можно принять N&P и
~R, тогда получим
/у=^пр/^- (253)
Расчеты показывают, что расхождение между форму-
лами (252) и (253) не превышает 5—6 %. При проведе-
нии опытов основная трудность состоит в определении
«чистого» крутящего момента деформации. Обычно мо-
мент измеряют на шпинделях, передающих вращение
валкам. С этой целью на шпиндели наклеивают прово-
лочные датчики или применяют крутильные динамометры
разных типов. Для определения «чистого» крутящего мо-
мента на бочке валка следует из замеренного на шпин-
деле момента Мшп вычесть момент сил трения в подшип-
никах валков Мп: Л4пр=Л4Шп—Мп.
Момент Мп можно определить при холостом ходе ста-
на, создавая нагрузку на валки и подшипники с помощью
нажимного устройства. Для уменьшения трения между
самими валками их поверхности смазывают маслом.
Метод опережения. При установившемся процессе
прокатки методом керновых отпечатков определяют ве-
личину опережения S, далее с помощью преобразований
формулы Финка (166) находят величину нейтрального-
угла
cos у = £ilx + /£±11? _ M^+S) (254)
' 2D |/ \ 2D / D T
114
Также может быть использована упрощенная формула
опережения (169)
у = V ShJR. (255)
Значение угла у подставляют в формулу Экелунда—
Павлова (133), решенную относительно коэффициента
трения (принято |3у~/у)
= а2/[2 (а —2у)]. (256)
Многие исследования показывают, что метод опере-
жения дает достаточно надежные значения коэффициен-
та трения при прокатке тонких полос, когда /d/^cp>34-4.
Метод давления. Измеряемой величиной является уси-
лие прокатки Р. Сущность определения коэффициента
трения сводится к тому, что подбирается такое значение
fy, которое, будучи подставленным в одну из теоретиче-
ских (наиболее обоснованных) формул давления про-
катки, обеспечивает совпадение опытных и расчетных ве-
личин Р.
Достоверность полученных таким путем значений f7
зависит от точности используемой формулы давления,
а также от того, насколько правильно выбрано значение
подставляемого в нее предела текучести металла. В свя^-
зи с этим надо отметить, что все существующие формулы
давления выведены с некоторыми допущениями, т. е. не
являются совершенно точными. При прокатке тонких по-
лос, в частности при холодной прокатке, возникает не-
обходимость в учете сплющивания валков, что вносит
дополнительную погрешность. Некоторые трудности пред-
ставляет и выбор величины предела текучести металла
с учетом всех факторов (температуры, скорости и степе-
ни деформации, гидростатического давления и др.).
Таким образом, при современном состоянии теории
прокатки метод давления может быть использован толь-
ко для приближенного определения коэффициента тре-
ния.
4. Влияние факторов прокатки на коэффициент трения
Величина коэффициента трения зависит от многих фак-
торов (условий) прокатки, главные из которых приведены
ниже.
Материал валков. Прокатка ведется в стальных или
чугунных валках. Многие данные свидетельствуют о том,
что при прокатке на стальных валках коэффициент трения
«*
115
выше, чем при прокатке на чугунных. Различие составля-
ет в среднем 15—20 %. Объясняется это тем, что
в структуре чугуна большое место занимают составляю-
щие (ледебурит, цементит, графит), которые имеют от-
носительно низкую склонность к адгезионному взаимо-
действию (схватыванию) с собственно металлическими
фазами (феррит, аустенит). Из практики хорошо извест-
но, что на чугунные валки деформируемый металл нали-
пает значительно меньше, чем на стальные. Особенно
малое налипание характерно для валков из отбеленного
чугуна.
Состояние поверхности валков. Рассматривая влияние
этого фактора, надо учитывать два обстоятельства: ше-
роховатость (микрорельеф) поверхности и присутствие
на поверхности налипших частиц металла, окалины и пр.
Шероховатость поверхности валков сильно влияет на
величину коэффициента трения. С увеличением высоты
неровностей коэффициент трения растет (рис. 69). Име-
Рис. 69. Зависимость коэффициента трения
f3 от шероховатости поверхности валков
при разных температурах прокатки (по
В. С. Смирнову и Хаи Пхе Ук)
Рис. 70. Зависимость коэффи-
циента трения f3 от содержа-
ния углерода в стали (по А. П.
Чекмареву и В. А. Николаеву)
ющиеся опытные данные свидетельствуют о том, что при
изменении шероховатости поверхности валков от 6—
7 класса (по ГОСТ 2789—73) до 2—3 класса коэффици-
енты трения f3 и /у возрастают примерно в 1,5—2 раза.
В тех случаях, когда условия захвата ограничивают
возможное обжатие, прибегают к загрублению поверхно-
сти валков разными способами. Например, на дне ка-
либров вырубают канавки или производят насечку по-
верхности пневматическими зубилами. В последние годы
широкое распространение получила накатка поверхности
валков зубчатым (рифленым) роликом.
Также сильно влияет на коэффициент трения налипа-
ние (наваривание) на валки частиц деформируемого ме-
116
талла. При этом резко увеличиваются силы молекуляр-
ного сцепления на контакте. Так, при прокатке свинца на
освинцованных валках коэффициент трения f3 возраста-
ет в 3—3,5 раза, а коэффициент трения /у — в 1,4—1,8 ра-
за по сравнению с прокаткой на чистых валках. Сущест-
венное влияние налипания установлено в опытах горячей
прокатки алюминия и меди.
При горячей прокатке стали коэффициент трения зна-
чительно (в 1,5 раза и более) повышается в результате
накопления на поверхности валков частиц окалины и про-
дуктов износа. Попадая в зону трения, такие частицы
играют роль шипов, усиливая механическое зацепление
поверхностей.
Химический состав металла. При прокатке углероди-
стых сталей установлено, что коэффициент трения не-
сколько уменьшается с увеличением содержания углеро-
да в металле (рис. 70). По-видимому, это связано
с уменьшением сил адгезионного взаимодействия в обла-
сти контакта металла с валками. Те металлы, которые
Рис. 71. Типичная зависимость
коэффициента трения от темпе-
ратуры при горячей прокатке
стали
Рис. 72. Зависимость коэффициента трения'
fa от скорости прокатки (по Тафелю и
Шнейдеру):
1 — насеченные валки; 2 — гладкие валки
обладают ярко выраженной склонностью к схватыванию
и налипанию, имеют повышенные значения коэффициен-
та трения. К числу таких металлов относятся нержавею-
щая сталь (типа Х18Н9Т и др.), алюминий и его сплавы,
титан, цинк, свинец. Например, при горячей прокатке не-
ржавеющей стали коэффициент трения в 1,3—1,5 раза'
выше, чем для углеродистой стали.
Температура прокатки. С повышением температур^
металла t° коэффициент трения сначала возрастает, а за-*
тем уменьшается (рис. 71). Такая закономерность наблю-
дается при прокатке различных сталей и некоторых дру-
гих металлов, например меди. В зависимости от химиче-
117
«кого состава стали и условий нагрева максимум на
кривой может смещаться в ту или иную сторону, но чаще
всего он находится в пределах 700—1000 °C.
Указанный характер температурной зависимости ко-
эффициента трения имеет следующее объяснение. С по-
вышением температуры металла растет слой оксидов на
его поверхности. Сначала оксиды вызывают повышение
коэффициента трения, а затем прочность их падает и они
начинают играть роль смазки, способствуя снижению
сил трения.
Скорость прокатки. Многочисленные исследования
свидетельствуют о том, что с увеличением скорости про-
катки коэффициент трения понижается. Результаты од-
ного из ранних исследований этого фактора приведены на
рис. 72. Эти данные получены при прокатке низкоуглеро-
дистой стали при 1200—1250 °C.
Как видно из рис. 72, при повышении скорости при-
мерно до 2 м/с величина f3 изменяется незначительно,
в интервале 2—3 м/с происходит резкое снижение коэф-
фициента трения, а затем его величина остается почти
постоянной.
Четкие данные по влиянию скорости на коэффициент
трения получены при холодной прокатке с технологиче-
скими смазками (рис. 73). Резкое снижение коэффициен-
Рис. 73. Зависимость коэффициента
трения fy от скорости при холод-
ной прокатке с пальмовым маслом
(по Стоуну)
Рис. 74. Зависимость коэффициента
трения fy от вязкости и вида смазки
(у» — кинематическая вязкость смазки
при 50 °C):
1 — минеральные масла; 2 — раститель-
ные масла
та трения наблюдается при повышении скорости пример-
но до 5 м/с. Исследования показали, что прямой
причиной падения коэффициента трения является увели-
чение количества смазки, втягиваемой в очаг деформа-
ции.
Технологические смазки. Основное назначение техно-
логических смазок — снижение сил трения на контакт-
118
пых поверхностях в очаге деформации и уменьшение из-
носа валков. Эффективность действия смазки зависит от
двух факторов: вязкости смазки и содержания в ней по-
верхностно активных веществ (жирных кислот, их произ-
водных и др.).
С увеличением вязкости растет толщина слоя смазкй
па контактных поверхностях. Естественно, это приводит
к уменьшению коэффициента трения (рис. 74).
В качестве смазки применяются в основном минераль-
ные и растительные масла в чистом виде или в виде водо-
масляных смесей (эмульсий). Минеральные масла почти
не содержат поверхностно активных веществ и обладают
более низкой смазочной способностью, чем растительные
масла. Это видно из сравнения уровня кривых 1 и 2 на
рис. 74.
Наиболее* эффективными по степени снижения коэф-
фициента трения являются те смазки, которые имеют вы-
сокую вязкость и содержат поверхностно активные веще-
ства. Примером такой смазки может служить касторовое
масло.
5. Расчетное определение коэффициента трения
Накопленные экспериментальные данные показывают,
что в большинстве случаев горячей прокатки коэффици-
енты трения находятся в пределах: при захвате f3=0,3-г-
4-0,5; при установившемся процессе /у=0,2-?-0,4.
При выборе величины коэффициента трения в указан-
ных пределах следует учитывать конкретные условия
прокатки: материал и состояние поверхности валков, тем-
пературу металла, скорость прокатки и т. д.
Для более точного расчетного определения коэффи-
циентов трения при горячей прокатке рекомендуются
формулы*:
f3 = ka kM kD (0,84 — 0,0004/°); (257)
fy = kv (0,55 — 0,00024/°), (258)
где kn, ku, kv — коэффициенты, учитывающие соответст-
венно состояние поверхности и материал валков (kn), со-
держание углерода в стали (&м) и скорость прокатки
(kv); /° — температура металла °C.
Значения коэффициентов приведены ниже.
Коэффициент kn:
* Эти формулы получены на основе опытных данных С. Эке-
лунда, И. М. Павлова и Н. Н. Гета и других исследователей.
119
Чугунные закаленные, шлифованные ... 0,9
Чугунные................................ 1,0
Стальные................................ 1,1—1,2
Стальные с насечкой, накаткой........... 1,3—1,6
Коэффициент kM:
Содержание С в / стали, % 0,05— 0,2— 0,3— 0,5— 0,8—
0,2 0,3 0,5 0,8 1,2
। по формуле 0,8
J (257) 1,0 0,9 0,75 0,7
kM по формуле
(258) 1,3 1,2 1,1 1,0 0,9 %
Коэффициент kv:
Скорость прокатки vB, м/с . 0—1 ' Л 2,5 3 4 >5
k-U • i.o. Д 0,9 0,75 0,65 0,55 0,5
Формулы (257) и (258) действительны в области тем-
ператур выше 700 °C.
При холодной прокатке коэффициенты трения обыч-
но находятся в следующих пределах: при захвате f3=
=0,14-0,2; при установившемся процессе fy=0,03 4-0,15.
Наиболее низкие значения коэффициентов трения со-
ответствуют условиям прокатки на тонко шлифованных
'(полированных) валках с применением вязких активных
смазок. Для расчета параметров холодной прокатки в ос-
новном необходим коэффициент трения при установив-
шемся процессе /у. Его величина может быть определена
по эмпирической формуле:
f *ем[1 +(0,4 +0,01s)Rz] Г0 07 0.1^ ~[ (259)
7 14-0,25Kv^-0,005v50L * 2 (I +ив) + 3vl J ’
где kCM — коэффициент, учитывающий природу смазки;
е — относительное обжатие, %; Rz — высота неровностей
на поверхности валков, мкм; vso — кинематическая вяз-
кость смазки при 50 °C, мм2/с.
Коэффициент kCM равен 1,0 для растительных масел,
1,4 — для минеральных. Величины vso для большинства
масел указаны в соответствующих ГОСТах. При прокат-
ке с эмульсиями на основе стандартных эмульсолов типа
Э-2 (Б), ЭТ-1, Т, ОМ за расчетную величину V50 прини-
мают вязкость масла индустриального 20, для которого
V5q = 20 мм2/с.
Формула (259) действительна при прокатке на вал-
ках шероховатостью 6—9 класса (/?z=0,8-bl0 мкм).
120
Глава VII
УСИЛИЕ ПРОКАТКИ
1. Распределение давлений
по контактной поверхности
J На ранних этапах развития теории прокатки существо-'
i вали противоречивые суждения о характере распределе-
।ния давлений по дуге контакта. Одни ученые предпола-
гали, что наибольшее давление находится в плоскости
. входа металла в валки, а затем оно постепенно снижа-
I ется, вплоть до нуля; другие считали, что в плоскости
! входа давление равно нулю, а максимум его находится
на выходе из очага деформации. В настоящее время рас-
пределение давлений достаточно хорошо исследовано
ic помощью точечных месдоз. Установлено, что ъид эпюр
давления зависит от условий прокатки, и в первую оче-
редь от таких факторов, как отношение/dMcp, коэффици-
ент трения fy и угол контакта а.
При малых значениях параметра ld/hcp (примерно
Ж<0,7) давление имеет максимальную величину
вблизи плоскости входа (рис. 75, а). Это объясняется
Рис. 75. Типичные эпюры распределения давлений по
дуге контакта при прокатке толстых (а), средних (б) и
топких (в) полос
подпирающим действием заднего жесткого конца поло-'
сы. Опытами доказано, что при прокатке очень коротких
образцов, длиной примерно равных длине очага дефор-
мации, т. е^ при отсутствии задней внешней зоны, пик-
давления на входе исчезает (пунктирная линия на рис.
75, а).’
В интервале /d/^cp=0,74-1,5 давления распределяют-
ся по дуге контакта приблизительно равномерно (рис.
121
хода составляет
М' = 2 (Gn fn dJ2inY (355)
хол \ п* п п] пJ ' '
Динамический момент Л1ДИН возникает только при из-
менении числа оборотов валков; если скорость прокатки
постоянна, то динамический момент равен нулю.
Величина 7ЙдИН для каждой вращающейся
определяется по формуле
______ GD? do ___ j do
дин - ~fa ~fa '
тд$ CD2 — маховый момент (D — удвоенный
инерции); da^ldx — угловое ускорение; J — момент инер-
ции, приведенный к валу двигателя.
детали
(356)
радиус
Г л а в а IX
СЛОЖНЫЕ СЛУЧАИ ПРОКАТКИ
1. Прокатка в валках неравного диаметра
При анализе простого, симметричного процесса прокат-
ки принималось, что оба валка имеют совершенно оди-
наковый диаметр. Такой процесс прокатки является
идеализированным. На прак-
Н----------лх-----b тике диаметры валков всег-
Рис. 100. Схема прокатки в вал-
ках неравного диаметра
да различаются, хотя бы
в небольшой мере. На неко-
горых станах, например, на
листовых трехвалковых
(трио Лаута), прокатка ве-
дется между валками, диа-
метры которых различаются
очень существенно. Рассмот-
рим основные закономерно-
сти процесса прокатки в вал-
ках неравного диаметра.
Геометрия очага дефор-
мации. Пусть (рис.
100). Найдем величину об-
жатия со стороны каждого
валка. Поскольку вертикальные силы, действующие на
один и другой валок, равны (из условия равновесия
полосы в вертикальной плоскости), можно написать:
Pcpi ^cpi "j/"— Рср2 ^ср2 ^1^2
(357)
158
Неравномерность распределения давлений существу-»
ет не только в продольных, но и в поперечных сечениях
очага деформации/Типичные эпюры распределения дав-
лений по ширине полосы показаны на рис. 77. В случае’
прокатки относительно узких полос (60<5М макси-
мальное давление действует посередине полосы (рис.
77,а). К боковым кромкам давление резко падает, что'
является следствием возникновения продольных растя-
гивающих напряжений на кромках. При прокатке широ-
ких полос (6о>5 Id) наблюдаются два максимума дав-^
ления, находящиеся на некотором расстоянии от кромок
(рис. 77,6). Появление их связано с возникновением
зон продольных сжимающих напряжений, которые рас-
полагаются рядом с зонами растягивающих напряжений
(на кромках,). Во внеконтактной области растягиваю-
щие напряжения должны быть полностью уравновешены
сжимающими напряжениями.
2. Среднее контактное давление и усилие прокатки
Одним из важнейших энергосиловых показателей про-»
цесса прокатки является среднее контактное давление.
Смысл этой величины достаточно прост: это то давле-
ние, которое было бы при условии равномерного распре-
деления его по контактной по-
верхности. Среднее контактное
давление рСр можно представить
как частное от деления усилия
прокатки Р на площадь контакт-
ной поверхности FK
Рср = Р/^- (260)
Под усилием прокатки пони-
мается равнодействующая всех
элементарных сил нормального
Рис. 78. Усилие прокатки
давления и трения, приложенных
к металлу со стороны валков (рис. 78). Такая же, но1
противоположно направленная сила действует со сторо-
ны металла на валки. При установившемся процессе
прокатки равнодействующая Р, вне зависимости от ее
величины, направлена перпендикулярно к оси полосы.
В противном случае сила Р давала бы продольную со-
ставляющую, которая вызывала бы либо торможение,
либо ускорение полосы. Последнее противоречит усло-
вию движения концов полосы с постоянной скоростью,
123
т. е. условию самого существования установившегося
процесса прокатки.
При теоретическом определении усилия прокатки
формула (260) приводится к виду
/>=Рср^к- (261)
Расчет площади контактной поверхности FK в боль-
шинстве случаев не представляет особых трудностей (см.
гл. II, п. 7). Главная задача в. теории расчета усилия
прокатки заключается именно в определении среднего
контактного давления. С этой целью разработано много
математических моделей, некоторые из которых будут
рассмотрены ниже. Однако сначала необходимо уяснить
физическую сущность и причины зависимости среднего
контактного давления от различных факторов.
3. Влияние факторов прокатки
на среднее контактное давление
Величина среднего контактного давления зависит от
естественной жесткости металла (его предела текучести)
и от того напряженного состояния, в котором находится
деформируемый металл. Исходя из сказанного, можно
написать
Рср = СТХ’ (262)
где по' — коэффициент напряженного состояния.
Коэффициент по также называют коэффициентом
подпора. 11о своему физическому смыслу он показывает,,
насколько среднее контактное давление выше предела
текучести деформируемого металла: па =рСр/от. Из вы-
ражения (262) видно, что различные факторы прокатки
могут влиять на величину рср либо через предел текуче- ।
сти металла, либо через коэффициент напряженного со-
стояния.
Как известно, предел текучести зависит от химичес-
кого состава металла, а также от температуры, скоро-
сти и степени деформации. Все эти факторы соответст-
венно влияют на среднее контактное давление. Что ка-
сается коэффициента напряженного состояния, то его
величину можно представить в виде произведения трех
сомножителей
"<, = ПаП'Х> (263)
где по, п”а и па — коэффициенты, учитывающие влия-
J24
ние соответственно внешнего трения, внешних зон и на-
тяжения концов полосы.
Опираясь на эти общие положения, рассмотрим зави-
симость среднего контактного давления от отдельных
конкретных факторов прокатки.
1. Обжатие. С увеличением обжатия растет длина
очага деформации, а значит растет и сумма продольных
подпирающих сил трения.
Перемещение металла по
контактной поверхности за-
трудняется. Вследствие это-
го среднее контактное дав-
ление возрастает (рис. 79).
Следует отметить, что
при увеличении обжатия не
только усиливается подпи-
рающее действие сил тре-
ния, т. е. растет коэффици-
1 ент /г'а, но также повышает-
ся предел текучести металла
в связи с деформационным
Рис. 79. Зависимость среднего кон-
тактного давления от обжатия при
горячей прокатке образцов из ста-
ли У7А (по Л. Ф. Молоткову)
упрочнением.
2. Диаметр валков. Следует учитывать, что с увели-
чением диаметра валков, при прочих равных условиях,
растет длина очага деформации и, следовательно, уси-
ливается подпирающее действие сил трения. Это служит
причиной роста среднего контактного давления (рис. 80).
Рис. 80. Зависимость среднего контактного давления от диаметра валков при
холодной прокатке образцов из низкоуглеродистой стали (по Люегу и Помпу)
Отмеченная зависимость позволяет сделать важный прак-
тический вывод: в тех случаях прокатки, когда давление
на валки ограничивает величину возможного обжатия,
целесообразно применять валки малого диаметра.
125
3. Толщина полосы. Чем меньше толщина полосы, тем
резче проявляется тормозящее действие сил трения в оча-
ге деформации, поэтому с уменьшением толщины полосы
среднее контактное давление возрастает. Однако все это
относится только к области прокатки относительно тон-
ких полос. Рассматриваемая зависимость для толстых по-
лос имеет противоположный характер: давление растет
с увеличением толщины полосы (рис. 81). Это объясня-
Рис. 81. Принципиальный вид за-
висимости среднего контактного
давления от толщины прокатывае-
мых полос
Рис. 82. Зависимость среднего кон-
тактного давления от фактора фор-
мы при прокатке слябов (по А. П.
Чекмареву и др.)
ется тем, что при прокатке толстых полос силы трения
не оказывают заметного влияния на давление, а главную
роль в формировании напряженного состояния играют
внешние зоны, подпирающее действие которых усилива-
ется с увеличением толщины полосы (растет коэффици-
ент /г").
4. Фактор формы ld/hcp. В современной теории про-
катки данные по среднему контактному давлению часто
представляются не в функции отдельных параметров —
е, D и h0, а в обобщенном виде — в функции фактора
формы ld/hw Смысл такого представления данных за-
ключается в том, что фактор формы учитывает и длину
очага деформации, и толщину полосы. Характерный вид
Зависимости Рср=ф(/<г/Лср) показан на рис. 82. При ма-
лых значениях ld/hcp изменение давления связано с вли-
янием внешних зон, при больших ld/hcp — с действием
сил трения. Минимум давления чаще всего находится
‘ в интервале /d//icp=0,3-?-0,7.
5. Ширина полосы. Как показывают исследования, при
прокатке относительно узких полос (приблизительно
bo/ld<Z5) среднее контактное давление снижается при
уменьшении ширины полосы (рис. 83). Это объясняется
126
уменьшением поперечных подпирающих сил трения,
в связи с чем облегчается течение металла в поперечном
направлении.
При прокатке широких полос среднее контактное дав-
ление не зависит от ширины полосы.
6. Коэффициент трения. С увеличением коэффициен-
та трения давление на валки повышается, так как растут
Рис. 84. Влияние заднего (qa) и
переднего (^i) натяжения на сред-
нее контактное давление при хо-
лодной прокатке стальных полос с
обжатием 30 % (по Люегу и Шуль-
це)
Рис. 83. Зависимость среднего кон-
тактного давления от ширины по-
лосы при холодной прокатке об-
разцов из низкоуглеродистой стали
толщиной 2 мм с обжатием 20 %
(по Люегу и Помпу)
подпирающие силы трения на контактной поверхности.
Этот факт подтверждается многочисленными опытными
данными. Чем тоньше прокатываемые полосы, тем резче
проявляется влияние сил трения на давление.
7. Натяжение концов полосы. Силы натяжения облег-
чают продольное течение металла и, следовательно, спо-
собствуют снижению среднего контактного давления (ко-
эффициент //” меньше единицы). Натяжение заднего кон-
ца 11(>./к)С1.1 влияет на давление в большей степени, чем
натяжение переднего конца (рис. 84). Происходит так
потому, что заднее натяжение воздействует назову отста-
вания, которая составляет основную часть очага дефор-
мации.
11одпор концов полосы соответственно вызывает по-
вышение среднего контактного давления.
4. Определение среднего предела текучести металла
и очаге деформации
В(* все теоретические формулы для расчета контактного
давления входит величина предела текучести деформиру-
127
емого металла*. Причем в большинстве случаев в фор-
мулах используется средний предел текучести металла
в очаге деформации. Его величина определяется на осно-
вании накопленных экспериментальных данных.
Определяя предел текучести при горячей прокатке,
необходимо учитывать температуру, скорость и степень
деформации. Имеющиеся экспериментальные данные, по-
лученные в основном на специальных испытательных ма-
шинах— пластометрах, обычно представляются в виде
графиков в координатах огт—8 или ат—и. В качестве
примера на рис. 85 и 86 приведены графики из широко
Рис. 85. Предел текучести низкоуглеродистой стали (0,15 % С; 0,68% Мп) в
зависимости от обжатия при разных температурах и скоростях деформации
(по Куку)
известных работ П. М. Кука (Р. М. Соок) и А. А. Дин-
ника. При пользовании такими графиками средняя ско-
рость деформации вычисляется по формуле (187). На
графиках А. А. Динника (рис. 86) основные кривые со-
ответствуют обжатию 8=30 %; корректировка данных
на величину фактического обжатия осуществляется с по-
мощью вспомогательного графика, из которого берется
* В теории обработки металлов давлением эту величину назы-
вают также сопротивлением деформации или напряжением теку-
чести.
128
поправочный коэффициент К
СГТ -^^тзо»
(264)
где От,, — предел текучести при обжатии 30 %.
Всего в исследовании П. М. Кука приведены данные
для 12 марок сталей, в исследовании А. А. Динника —
для 15 сталей. Для удобства использования эксперимен-
тальных данных В. И. Зюзин разработал метод термо-
Рис. 86. Предел текучести стали Ст.Зсп в зависимости от скорости деформации
при разных температурах (по А. А. Диннику)
механических коэффициентов. По этому методу в каче-
стве базисной величины принимается предел текучести
Оо.д, полученный из опытов при следующих параметрах
деформации: t°—1000°C; u=10 с-1; 8 = 0,1. Средний
предел текучести в очаге деформации для конкретных
условий горячей прокатки определяется из выражения
сгт = <то.д k^ kg ku, (265)
где kt, ke и ku — термомеханические коэффициенты, учи-
тывающие соответственно температуру, степень и ско-
рость деформации.
В литературе* приведены базисные значения преде-
Теория прокатки. Справочник./Целиков А. И., Томленов А. Д.,
Зюзин В. И., Третьяков А. В., Никитин Г. С. М.: Металлургия,
1982. 335 с.
<) Л. II. Трудов
129
лов текучести оо.д для 44 марок сталей и 20 цветных ме-
таллов и сплавов. Коэффициенты kt, kR и ku определяют
из специальных графиков, построенных индивидуально
для каждого металла: например, для стали 45 базисное
значение предела текучести составляет оо.д=86 МПа,
а соответствующие графики для выбора коэффициентов
&t, kg и ku приведены на рис. 87.
Рис. 87. Термомехаиические коэффициенты для стали 45 (по
В. И. Зюзину)
Для ряда сталей разработаны эмпирические форму-
лы, позволяющие определить предел текучести при горя-
чей прокатке чисто расчетным путем. Структура формул
следующая:
<гт = Авт» , (266)
где А, гп\, т2, т3 — эмпирически определяемые величи-
ны, индивидуальные для каждого металла.
Например, для коррозионностойкой (нержавею-
щей) стали марки 12X18Н9Т рекомендуется формула,
(МПа):
ат = 31,9е0’28 и0-087 /(Ю-2 е°’0028/о).
Аналитические зависимости для определения преде-
130
ла текучести особенно необходимы в случае выполнения
расчетов на ЭВМ.
При холодной прокатке основным фактором, влияю-
щим на предел текучести, является деформационное
упрочнение (наклеп), поэтому при выборе величины от на-
до прежде всего учитывать
суммарное обжатие, получен-
ное при холодной деформации.
I (редел текучести определяется
с. помощью кривых упрочне-
ния, которые строятся по ре-
зультатам испытаний металлов
па разрывных машинах (рис.
88). В настоящее время кривые
упрочнения имеются почти для
всех металлов и сплавов, де-
формируемых в холодном со-
стоянии*.
Для определения предела
текучести расчетным путем
кривые упрочнения аппрокси-
мированы математическими
выражениями. Чаще всего при-
меняются формулы следую-
щего вида:
<тт Отисх + а&п,
Рис. 88. Кривые упрочнения ста-
лей:
1 — 08кп; 2 — ЭЗЗОА; 3 —
12Х18Н9Т
(2б7>;
где оТисх —предел текучести ненаклепанного (горячека-
таного или отожженного) металла; е — суммарное отно-
сительное обжатие, %; а и п — эмпирические коэффици-
енты, зависящие от химического состава металла.
Так, по данным А. В. Третьякова для группы низко-
углеродистых сталей (марок Ст 1, Ст 2, 08кп, 10, 20,.
09Г2) применима следующая формула (МПа):
"т = + 33,4е0’60.
В дальнейшем анализ кривых упрочнения показал,
что их можно аппроксимировать функциями более про-
стыми, чем (267). Для большинства сталей достаточно
точная аппроксимация кривых упрочнения достигается
" Третьяков А. В., Зюзин В. И. Механические свойства метал-
.пон п cii.naiioB при обработке давлением. Справочник. М.: Металлур-
I нм, 1973. 224 с.
ч
131
применением формулы
<тт = огтисх + АУ~Ъ 7268)
и лишь для некоторых сильно наклепывающихся метал-
лов (например, коррозионностойких сталей) более под-
ходит выражение
<Гт = СГтисх]+ /ё + Вб, (269)
где А и В — эмпирические коэффициенты.
Расчеты по формулам (268) и (269) удобнее и про-
ще, чем по формуле (267). Численные значения коэффи-
циентов А и В для ряда сталей приведены ниже:
Коэффициент............................... А В
Марка стали:
Ст 2, 08кп, 08Ю, 10, Юсп, 20, 50ХФА, 08X13,
23Х2НВФА, 12Х21Н5Т........................... 50—60 0
20А, 35, 10Г2, 12Г2, 12Х5МА, 25ХГСА, ЗОХГСА,
ЭЗЗО, ЭЗЗОА.................................. 60—75 0
40, 45, 50, 85ХФ, ХН78Т...................... 80—95 0
85, 65Г..................................... 110—120 0
Динамная сталь, У8А, У10А.................... 30—50 3,5
12Х18Н9, 12Х18Н9Т, 12Х18Н10Т................ 100—120 3,5
Средний предел текучести в очаге деформации при
холодной прокатке часто определяют как среднеарифме-
тический
о'Тср=;(ат„'+<гт;)/2, (270)
где От,, и о'Т1 — пределы текучести соответственно в се-
чении входа и выхода из очага деформации.
Величины сгТо и оТ1 находят по кривым упрочнения
или вычисляют по формулам (267), (268), (269). Опре-
деление среднего предела текучести по формуле (270)
не совсем точно, так как механические свойства металла
изменяются вдоль дуги контакта не прямолинейно. В на-
чале очага деформации предел текучести нарастает бо-
лее интенсивно, чем в конце.
Хорошие результаты дает определение среднего пре-
дела текучести по среднему относительному обжатию,
вычисляемому по формуле
«ср = 0,48о + 0,681, (271)
где 8о и 81 — суммарное относительное обжатие до и пос-
ле пропуска металла через валки.
Во многих случаях при холодной прокатке предел
текучести определяют только с учетом упрочнения (на-
432
клепа) металла. Вместе с тем на его величину в некото-
рой мере влияют и другие факторы. Принято считать, что
при холодной прокатке механические свойства металла
мало зависят от скорости деформации. Это утверждение
в общем справедливо, однако следует обратить внимание
па то обстоятельство, что базой для выбора вели-
чины предела текучести служат кривые упрочнения, по-
лученные на разрывных машинах при скорости деформа-
ции 10~3—10-2 г1, а при холодной прокатке на промыш-
ленных станах скорость деформации составляет 102—
103 г1, т. е. в 104—106 раз больше. Такой резкий скачок
в скорости деформации приводит к повышению предела
текучести на 30—40 %.
Кроме того, при испытании на разрывных машинах
образцы подвергаются растяжению, а при прокатке осу-
ществляется схема сжатия. Исследования свидетельству-
ют, что величина сгт при сжатии примерно на 10 % выше,
чем при растяжении.
Далее надо учесть, что в результате пластической де-
формации температура металла повышается. При интен-
сивной холодной прокатке температура металла в очаге
деформации достигает 200—250 °C и более. Разогрев ме-
талла способствует некоторому снижению предела теку-
чести.
Изменение температуры металла в процессе прокат-
ки может быть рассчитано теоретически. В очаге дефор-
мации действуют два источника тепла: диссипация энер-
гии при пластической деформации и трение на контакт-
ных поверхностях. Следовательно, полное приращение
тепла 0s составляет
вХ = 0де'ф + % (272)
где Одеф — тепло, выделяющееся при пластической де-
формации; 0тР — тепло, получаемое полосой вследствие
трения.
Величину 02 можно определить, используя, например,
формулу Финка. Учитывая коэффициент выхода тепла
при деформации т)Вых, получим
0>; ; Л ВЫХ Рср In (^о/^1)/5, (273)
где Э — механический эквивалент теплоты (3 = 1 по си-
стеме СИ).
(' другой стороны, приращение тепла 0s можно выра-
зить формулой
(/»-<«), (274)
133
где G — масса прокатываемой полосы; с — удельная те-
плоемкость металла; и — соответственно начальная,
и конечная температура металла.
Приравнивая формулы (273) и (274), после неслож-
ных преобразований находим приращение температуры
М °
СС(/»-^=11вы11р(:рУ1п(Л0/Л1)/Э;
W - Чвых Рср V In (ЛА) W), (275>
где р — плотность металла.
Средняя температура металла в очаге деформации
составляет
^р = ^ + д^2- (276>
В расчетах по формуле (275) коэффициент выхода
тепла -Цвых принимают при холодной прокатке 0,8—0,9,
при горячей прокатке 0,95—1,0.
Следует отметить, что формула (275) является при-
ближенной и не учитывает потери тепла в зоне контакта
металла с валками, а также то обстоятельство, что толь-
ко часть тепла трения воспринимается металлом. Для
определения указанных потерь необходимо привлечение
формул теории теплоотдачи.
С учетом всех отмеченных дополнительных факторов
предел текучести при холодной прокатке определяется
по формуле
ar = (JTkckuP (277>
где о' — предел текучести, найденный с учетом только
упрочнения; kc — коэффициент, учитывающий схему на-
гружения; kut — температурно-скоростной поправочный
коэффициент.
В расчетах по формуле (277) коэффициент kc может
быть принят равным 1,1. Анализ режимов деформации,
выполненный для ряда промышленных станов холодной
прокатки, показал, что коэффициент kut обычно находит-
ся в пределах 1,1—1,2. Для более точного определения
коэффициента kut необходимо использовать эксперимен-
тальные данные по температурно-скоростной зависимо-
сти предела текучести в условиях холодной деформации.
5. Дифференциальное уравнение равновесия
продольных сил
Вывод большинства теоретических формул для расчета
усилия прокатки основан на решении дифференциально-
го уравнения равновесия продольных сил, приложенных
к металлу в очаге деформацииЛПри составлении этого
уравнения выделим в очаге деформации элементарный
объем металла, заключенный между сечениями тт'
и пп', проведенными на расстоянии dx друг от друга
(рис. 89). Рассмотрим условия равновесия выделенного
Рис. 89. Схема к выводу дифференциального
уравнения равновесия
элемента тпп'т' в продольном направлении при следу-
ющих допущениях:
напряжения в любом поперечном сечении по высоте
полосы распределяются равномерно;
деформация является плоской, т. е. прокатка идет без
уширения и напряжения по ширине полосы не изменя-
ются.
Продольная сила, действующая на грань пп' выде-
ленного элемента, равна oxhxb,
где ох, hx и b — соответственно продольное напряжение,
толщина и ширина полосы в сечении пп'.
Аналогично для грани тт' находим (ox-\-dux) (ftx-F
\dhx)b.
Далее необходимо определить продольные силы, соз-
даваемые контактными напряжениями р и t на площад-
ках тп и т'п'. Предположим, что выделенный элемент
135
находится в зоне отставания, тогда элементарные силы
трения t будут направлены по ходу прокатки. Находим
горизонтальную силу от действия нормальных напряже-
ний р
р-----b sin ф = pb tg ф dx,
COS ф
где dx/созф — длина площадок тп и т'п' (по касатель-
ной).
Напряжения трения t дают горизонтальную состав-
ляющую
t —dx b cos ф = tb dx.
COS Ф
Теперь, суммируя все действующие на выделенный
элемент продольные силы, напишем условие его равно-
весия (принимаем направление прокатки за положитель-
ное):
SX= (ох + dox) (Ах + d/ix) Ь — oxhxb — 2pb tgq>dx +
+ 2tbdx = 0. (278)
Сократив все слагаемые на b, раскрыв скобки и пре-
небрегая бесконечно малыми величинами второго поряд-
ка, получим
hxdox + oxdhx — 2ptgadx + 2tdx = 0.
Учтем, что dx—dhx/(2igq) (см. рис. 89). Сделав эту
подстановку и ряд преобразований, приведем уравнение
равновесия к виду
dax-(p-gJ-^+ J =0. (279)
«X tg Ф hx
Уравнение (279) содержит три неизвестных: р, их nt.
Контактное давление р является искомой величиной.
Удельная сила трения t задается тем или иным законом
трения. Следовательно, для решения уравнения (279)
необходимо исключить из него продольное напряжение
Ох. Для этого воспользуемся уравнением пластичности
в главных осях в упрощенной форме
Oi — е3 = oj, (280)
где ci и о3 — главные напряжения, максимальное и ми-
нимальное; от = 1,15 От — вынужденный предел текуче-
сти.
Допустим, что для выделенного элемента главными
136
осями напряжений являются вертикальная и горизон-
тальная оси. Тогда напряжение oi будет равно
о, = (р -d~- bcos ф 4-1 dx ~ bsinф^ —}— = р + ^ф.
\ COS Ф COS Ф / box
Вторым слагаемым полученного выражения можно
пренебречь, поскольку оно намного меньше первого.
Следовательно, имеем и, кроме того, огз=о'«. Со-
ответственно перепишем уравнение пластичности (280)
р —сгж=ст;. (281)
Решая совместно уравнения (279) и (281), получим
———^ = 0
r h* 1§ф hx
или
dtp—<£)=(<£-----(282)
\ ’ tgf! Л«
Если бы при выводе уравнения равновесия (282)
было принято, что рассматриваемый элемент тпп'т'
находится не в зоне отставания, а в зоне опережения,
то решение осталось бы прежним, за исключением того,
что перед членом, учитывающим действие сил трения t,
знак изменился бы на противоположный. Поэтому урав-
нение равновесия можно представить в обобщенной
форме
dip — o’) = /'а* + — (283)
1 \ ' tg<P/ Л»
где знак минус относится к зоне отставания, а плюс —
к зоне опережения.
Если предел текучести нц протяжении очага дефор-
мации остается постоянным (или берется усредненным),
то da-r =0, dvx = dp и уравнение равновесия принимает
вид
dp = k+-^-)-^. / ‘ (284)
\ 1яф/ Лх *
По своему физическому смыслу уравнение (284) вы-
ражает приращение давления р при перемещении не-
которой точки вдоль дуги контакта. Входящие в это
уравнение переменные величины ф и hx являются коор-
динатами перемещаемой точки.
Дифференциальное уравнение равновесия продоль-
ных сил при прокатке выведено Т. Карманом (Th. v,
137
Karman) в 1925 г. Конкретные решения этого уравнения
могут быть разными в зависимости от выбора закона
трения, геометрических характеристик очага деформа-
ции и других условий.
6. Теоретическое определение давления
по А. И. Целикову
Для упрощения решения уравнения (284) А. И. Целиков
Принял, что толщина полосы в пределах очага деформа-
ции изменяется не по дуге АВ,
а по ее хорде (рис. 90). В со-
ответствии с этим угол наклона
контактной поверхности ф ста-
новится постоянной величиной:
tgф=tg(a/2). Силы трения
определяются по закону Амон-
тона: t=fyp.
Тогда уравнение равнове-
сия (284) приводится к виду:
dp = « + 6p)-^ , (285)
где обозначено 6=fy/tg(a/2).
Интегрируем уравнение (285), разделив переменные
dp f* dh%
J
J °Т=р
+ In (сг‘ + 6р) = 1п/1х + С,
где С — постоянная интегрирования.
После преобразований получим для зоны отставания
p=-W + °?6’ (286)
и для зоны опережения
Р =
(287)
где Со и Ci — постоянные интегрирования соответствен-
но для зон отставания и опережения.
Найдем значения постоянных Со и Сь
В плоскости входа очаг деформации hx=hQ',
р=°: - «о=°; (1 -
где £о=1—qolor —коэффициент заднего натяжения.
138
После подстановки граничных параметров в уравне-
ние (286) получим
E1)<=-c(,v+</6;
В плоскости выхода из очага деформации hx=h\,
= — = 5, а',
где — коэффициент переднего натяжения.
Из уравнения (287) находим
С, = <(?, +1/6)^.
Подставляя значения Со и Ci в
и (287), получим для зоны отставания
< 1г„ г 1ч/Ло_\в , fl
hx ) J’
(288)
Р =
для зоны опережения
р=4-Г«1в+
(289)
Формулы (288) и (289) вы-
ражают закон распределения
давлений по дуге контакта в
соответствующих зонах. Если
прокатка ведется без натяже-
ния концов полосы, то </о =
= <7i=0, £o=£i = 1 и формулы
(288) и (289) принимают сле-
дующий вид:
для зоны отставания
р^-т-fa-1) (44’+ 4
уравнения (286)
Рис. 91. Теоретические эпюры
распределения давлений по дуге
контакта по А. И. Целикову
(291)
(290)
для зоны опережения
р ‘^[(6+1)^-1].
Для иллюстрации результатов вычислений по урав-
нениям (290) и (291) на рис. 91 приведены в качестве
139
примера теоретические эпюры распределения давлений,
построенные для конкретных условий прокатки: 8 =
= 30 %; а = 5°40'; ftt/D=l,16 %; fy=0,14-0,4.
Получив уравнения распределения давлений по дуге
контакта, можно приступить к решению дальнейшей за-
дачи: определить усилие прокатки и среднее контактное
давление. Усилие прокатки можно выразить в виде ин-
тегральной суммы распределенных давлений
ld
P — b^pdx. (292)
о
В последующем решении используем уравнения
(290) и (291), которые содержат в качестве независи-
мой переменной толщину полосы hx. В связи с этим за-
меним дифференциал dx на dhx
dx = i dhx.
2 tg Ф ДЛ
Кроме того, учтем, что интегрирование необходимо
вести раздельно для зон отставания и опережения, со-
ответственно в пределах от hv до ho и от hi до hy, где
hv —толщина полосы в нейтральном сечении. Таким
образом, уравнение (292) приводится к виду
После несложных преобразований из формулы (293)
140
получим:
1>
т ДЛ 6
(294}
Исключим из выражения (294) величину h^h^. Это
можно сделать, если учесть, что в нейтральном сечении,
т.е. при hx=hN, уравнения (290) и (291) дают одно и то
же значение р. Итак, используем равенство
(« - 1) (hjhtf + 1 = (в + 1) (ЛД)« - 1, (295>
откуда находим
Подставив найденную величину ho/hy в выражение
(294), получим конечную формулу для расчета усилия
прокатки
Р = <Ы.-----------(iH/'A-V—1]. (296}
1 -< ДЛ(6-1) к Л1 / J
Формула для среднего контактного давления полу-
чается из уравнения (296) после деления его правой ча-
сти на площадь контактной поверхности FK~bld:
р =а- — (М Гт - 1]. (297)
Кср ’ДЛ(6 — 1)Ц2 ДЦ/ J
Входящая в формулы (296) и (297) величина hv/hr
определяется из равенства (295)
| 14- V 14~(6а — 1) (hp/hi)6 | (298)
Лх I 6 4-1 / ’
Для облегчения расчетов среднего контактного дав-
ления на основании формулы (297) построена диаграм-
ма (рис. 92), позволяющая определить коэффициент
напряженного состояния па =рср/&с по двум предвари-
тельно вычисленным величинам: 6=fy/tg(a/2) и е =
= Milhv, %. Определив по диаграмме численное значе-
ние па, далее находим: рСр = сгт^а = 1,15отПа.
Заканчивая вывод формулы давления по А. И. Це-
ликову, следует подчеркнуть, что в соответствии с пред-
посылками вывода и принятыми допущениями формула
(297) относится к случаю прокатки тонких широких по-
лос. В первую очередь она может быть рекомендована
для холодной прокатки, когда валки подвергаются
сплющиванию и достаточно справедлив закон трения
Лмонтопа.
141.
Формула (297) не учитывает натяжения концов поло-
сы. Если прокатка ведется с натяжением, то влияние
этого фактора учитывается с помощью дополнительной
формулы
Рср = Рср "а = Рср [1 - (?0 + P.t^Pcp] • (2")
где р'р — среднее контактное давление при прокатке
без натяжения.
Рис. 92. Диаграмма для определения коэффициента подпора п^, построен-
ная по формуле давления А. И. Целикова
В случае прокатки узких полос расчетное давление
составляет Рсрв=РсрПв» где Пв — поправочный коэффи-
циент, учитывающий ширину полосы. Для приближен-
ного определения значения пв может служить эмпири-
ческая зависимость
пъ = 0,67 + 0,15 (bcp/Zd) - 0,017 (VQ2- (300)
Выражение (300) действительно в пределах ЬСр//^=1-ь5.
7. Теоретическое определение давления
по А. П. Чекмареву1
При решении дифференциального уравнения равновесия
(284) в качестве переменной принимается текущий угол
Нижеприведенный вывод формулы давления опубликован
А. П. Чекмаревым совместно с И. А. Чекмаревым.
142
Имеем (см. рис. 89) dftx/2=R sin qxZtp; допустим, что
sin cpMgcp^tp, тогда уравнение равновесия (284) при-
водится к виду
+ (301)
Далее, для упрощения решения принимается, что
толщина полосы на протяжении очага деформации оста-
ется постоянной: Л<р =ЛСр=const. Величина hcp нахо-
дится из выражения
а
i 1 С (и । г» л и । Яа? ft0 + 2ЛХ
/icp = — (^ + R<p2) dtp = + —— = • 1 .
ОС tJ о о
о
Силы трения t определяются по условию Зибеля
где fa— показатель сил трения1.
С учетом изложенного из уравнения (301) получим
dp = <-^-(<pT/0)dq>. (302)
Лср
После интегрирования находим
р = <-^-(-у-+А,ч>) + С- (зоз>
Лер \ /
где С — постоянная интегрирования.
Решение уравнения (303) ведется раздельно для зон
отставания и опережения.
В зоне отставания
р = /Оф) + С0. (304).
«ср \ /
Определим постоянную Со, учитывая, что на входе
в очаг деформации при отсутствии заднего натяжения
Р о*. Из уравнения (304), принимая <р=а, находим.
После этого из уравнения (304) получим
/> <[’ + -Л (<Р2-2А,Ф~“2 + 2f0“)]- (305>
L "ср J
В зоне опережения действительно уравнение
Z' < + + (306)-
"г.р \ * /
1 11ок.'1затель сил трения fa связан с коэффициентом трения fy
<<»<»।ношением: fa=fyna>
143.
В плоскости выхода (ф=0) при отсутствии передне-
го натяжения р=от. Учитывая это, находим С1 = от.
Уравнение распределения давлений в зоне опережения
в конечном виде будет
Рср = <[1 + (ф2 + 2М>)]-
(307)
Теперь переходим к определению среднего контакт-
ного давления, которое можно выразить формулой
= + -^-(ф2 —^аф —“2 +2/aa)]d(P +
V ср
+ <j[1+-^(q>s + 2foq>)]d<1>}. (308)
0 ср
После интегрирования и простых преобразований по-
лучим
Рср = — 1“ + — 4"а3 + 2/aT2 + a2 Y — 2/оау)1.
(309)
Чтобы привести выражение (309) к расчетному виду,
надо определить угол у. Для этого приравняем правые
части уравнений (305) и (307), приняв Ф=у
1 + -г- (** - 2/л- + 2М =1 + ~г~ ("? + 2f°V-
“ср “ср
(310)
После сокращений и преобразований находим
(311)
Как видим, формула (311) подобна формуле Эке-
лунда — Павлова, только вместо коэффициента (угла)
трения ру в нее входит показатель сил трения fa- Под-
ставляя значение у из (311) в уравнение (309), после
преобразований получим конечную формулу для расчета
среднего контактного давления
о = <(1 + —[L — af—+ -Й-УП. (312)
т( 2/гср |/а \ 3 4fa/JJ
•144
Формула (312) достаточно проста и удобна для ана-
лиза. Как и формула А. И. Целикова (297), она отно-
сится к случаю прокатки тонких полос. Поскольку при
выводе этой формулы применен закон трения Зибеля, ;
опа может быть рекомендована для расчета давления
при горячей прокатке.
\
8. Давление при прокатке в калибрах
Величина среднего контактного давления при прокатке
в калибрах, как правило, несколько выше, чем при про-
катке прямоугольной полосы на гладкой бочке при
той же степени деформации. Можно указать две ос-
новные причины этого. Во-первых, в связи с увеличе-
нием контактной поверхности по периметру калибра
возрастает сумма продольных подпирающих сил тре-
ния. Во-вторых, при входе металла в валки обжатие
начинается не по всей ширине полосы, а на отдельных
участках, благодаря чему усиливается влияние внеш-
них зон.
Исследования показывают, что-в большинстве случа-
ев давление при прокатке в калибрах превышает тако-
вое при прокатке на гладкой бочке в 1,1—1,5 раза. Име-
ется ряд теоретических решений по определению давле-
ния при прокатке сортовых профилей.
А. П. Чекмарев и В. А. Николаев предложили при
расчете давления в калибрах увеличивать коэффициент
напряженного состояния па пропорционально увеличе-
нию периметра калибра по сравнению с прокаткой поло-
сы. В соответствии с таким подходом^давление при
прокатке в калибрах рСр.к определяется по формуле
— Л л
< ) '
(313)
где Р<а> — давление при прокатке на гладкой бочке, рас-
..та иное для приведенной полосы; Пф — коэффициент
формы калибра,
(314)
гл,о II — периметр калибра; b — ширина калибра по I
разъему. ___/
Величина коэффициента формы п$ для наиболее рас-
пространенных калибров приведена ниже:
К) А. П. Грудев
145
Коэффициент формы....................... Яф
Калибр:
квадратный........................ 1.41
ромбический с углом при вершине:
100°............................... 1.30
110°............................... 1,20
120°............................... 1,15
круглый............................. 1,40
овальный однорадиусный с 6/й:
1,5................................ 1,27
2,0................................ 1,15
3,0................................ 1,09
шестигранный........................ 1,15
угловые и зетовые:
чистовые........................ 1,41
черновые........................ 1,2—1,25
двутавровые...................... 1,7—2,2
швеллерные....................... 1,7—2,3
Многие авторы при расчете давления в калибрах ис-
ходят из выражения
РсР.К = ^кРсР, (315)
где пк — коэффициент, учитывающий особенности де-
формации в калибрах.
А. И. Целиков, Г. С. Никитин и С. Е. Рокотян пред-
ложили определять коэффициент пк по аналогии с про-
цессами ковки на вырезных и плоских бойках. Сравни-
вая соответствующие формулы давления, выведенные
Е. П. Унксовым, они получили
пк —
2, _0________ld_
3 у л Лор
3 'У ftCp
(316)
где 0 — угол охвата полосы валками.
Для квадратных, ромбических и овальных калибров
принимают 0/л=0,64-0,9, а для сложных фасонных ка-
либров 0/л=1.
9. Особенности определения давления
при прокатке высоких полос
С увеличением толщины полосы роль сил трения в фор-
мировании напряженного состояния в очаге деформации
ослабевает. При значении фактора формы ldlhCv<A силы
трения оказывают очень малое влияние на среднее кон-
тактное давление (па — 1). Поэтому применение фор-
146
мул давления А. И. Целикова, А. П. Чекмарева или дру-
гих, учитывающих только действие сил трения, в этом
случае нецелесообразно.
Как уже отмечалось, при прокатке высоких полос ос-
новным фактором, влияющим на величину давления,
являются внешние зоны (жесткие концы). Имеются тео-
ретические формулы для расчета среднего контактного
давления с учетом внешних зон. Если допустить, что при
сжатии толстой плиты с внешними зонами и прокатке
высоких полос давление примерно одинаково, то может
быть применима формула Луговского (201), которой
можно придать вид
рс = 1,25а; Г1п-^ + -^-----0,21. (317)
L М "ср J
При Zrf//icp<0,12 среднее контактное давление определя-
ется по формуле Прандтля
Рср = <(1 +л/2)^2,57<. (318)
Часто при расчете давления используются эмпириче-
ские зависимости pcp=q(ld/hCp). Широко известны опыт-
ные данные А. И. Целикова и В. В. Смирнова, аппрокси-
мированные формулой
РеР=/’;Р%=р;р('Ар)-°'4. (319)
где р"р — давление при отсутствии внешних зон.
С достаточным основанием можно принять p'cp~ol',
тогда получим расчетную формулу для определения дав-
ления
Рср = <(1Лр)-0'4- (320)
При выборе величины предела текучести в формулах
(317), (318), (320) в некоторых случаях надо учитывать
масштабный фактор. Исследования показывают, что при
прокатке слитков в первых проходах, когда металл име-
ет крупнозернистую структуру и неплотности, его сопро-
тивление деформации ниже, чем при испытании малых
образцов в лабораторных условиях. В связи с этим спра-
л....io значения от необходимо умножать на поправоч-
ный коэффициент масштабного фактора kM, величина
которого меньше единицы. По данным А. А. Динника,
при прокатке слитков в начальных проходах &M=0,7-i-
: 0,8. По мере увеличения степени деформации величи-
на /гм приближается к единице. Когда Х=3, влияние
масштабного фактора сходит на нет (&м~1).
кг
147
Глава VIH
КРУТЯЩИЕ МОМЕНТЫ, РАБОТА
И МОЩНОСТЬ прокатки
1. Определение крутящих моментов
по удельным силам трения
Определим величину крутящих моментов, которые необ-
ходимо приложить к валкам, чтобы обеспечить их вра-
щение в процессе прокатки.
Рассматривая элементарные силы, распределенные
по дуге контакта (рис. 31), нетрудно сделать вывод, что
крутящий момент создается действием касательных сил
трения t. Силы р не создают крутящего момента, так как
линии их действия проходят через центр валка.
Для элементарной площадки bRdq на бочке валка
крутящий момент будет
dMDP = Wd(p. (321)
Полный крутящий момент для одного валка с учетом
различного направления сил трения в зонах отставания
и опережения составляет
Л4пр = J tb d(p _ J tb (322)
V 0
Если допустить, что силы трения t и ширина полосы
b на протяжении очага деформации остаются постоянны-
ми, то после интегрирования получим
Л4ПР — tbR2 (а — 2у). (323)
С использованием закона трения Амонтона (t—fypCp)
получаем формулу крутящего момента, впервые предло-
женную В. Ф. Баюковым
Мпр = РеР«7у(“~2Т)- (324)
Формула (324) имеет ограниченное применение, так
как вывод ее основан на предположении о равномерном
распределении давлений и сил трения по дуге контакта.
Кроме того, расчет по формуле (324) требует достаточ-
но точного определения нейтрального угла у.
2. Определение крутящего момента
но усилию прокатки
Как было отмечено ранее, при установившемся процессе
свободной прокатки равнодействующая всех сил, прило-
женных к валку в очаге деформации, сила Р (рис. 93)
направлена вертикально.
Крутящий момент, создавае-
мый силой Р, равен
Рис. 93. К выводу формулы крутя-*
щего момента по усилию прокатки
МПР = Ра, (325)
где а — плечо равнодейст-
вующей Р относительно цен-
тра валка.
Плечо а принято опреде-
лять как некоторую часть
длины очага деформации:
a=tyld. Величину ф назы-
вают коэффициентом, пле-
ча момента или коэффициентом плеча усилия прокатки.
Таким образом, для одного валка имеем
Мпр = P^ld = Рф ИЯМ. (326)
Поскольку P=pcpldb, можно также написать
Л,пр = Рср = Рср Ц* КДЛ. (327)
Если считать, что усилие прокатки Р (или контакт-
ное давление рСр) задано, то основная проблема расчет^
крутящего момента сводится к правильному определен
пню точки приложения силы Р, т. е. к нахождению ко-
эффициента плеча момента ф.
Линия действия силы Р практически проходит через
центр тяжести эпюры контактных давлений. Следова-
к'льно, коэффициент плеча момента зависит от характе-
ра распределения давлений по дуге контакта. При
равномерном распределении давлений точка приложе-
ния силы Р находится посередине дуги контакта и ф =
0,5. Любая асимметрия в распределении давлений
приводит к отклонению величины ф от значения 0,5. При
нр<»катке толстых полос ф>0,5, так как в этом случае
максимум давления смещен к плоскости входа (рис,
/!', н). Напротив, при прокатке тонких полос ф<0,5, по*
< кильку максимум давлений смещен к плоскости выхода
(находится в нейтральном сечении, рис. 75, в).
Если установлен закон распределения давлений по
149
дуге контакта, то величина коэффициента плеча момен-
та может быть определена строго аналитически.
Н. М. Кирилин решил эту задачу, используя уравнения
А. И. Целикова (290) и (291) при допущении o*=const.
^Результаты вычислений представлены в виде диаграммы
jia рис. 94.
Рис. 94. Теоретические значения коэффициента плеча момента, вычисленные
<по уравнениям распределения давления А. И. Целикова
В большинстве случаев коэффициент плеча момента
определяют по экспериментальным данным. На рис. 95
приведены результаты исследования П. Л. Клименко,
который для нахождения зависимости xp=<p(/d//iCp) ис-
Рис. 95. Коэффициент плеча момента по экспериментальным данным
П. Л. Клименко
J50
пользовал экспериментальные эпюры распределения дав-
лений по дуге контакта, полученные при прокатке свин-
цовых и стальных (t°= 1000-j-l 100 °C) образцов.
Как видно из графика на рис. 95, максимальное зна-
чение ф=0,58 соответствует фактору формы /d//icP~0,4.
В диапазоне /d//icp= 1,04-1,5 значение ф приблизительна
равно 0,5. При /d//icp>l,5 имеем ф<0,5, причем с увели-
чением отношения а/ру коэффициент ф несколько снижа-
ется. Последнее объясняется смещением нейтрального
сечения и пика давлений к плоскости выхода.
По опытным данным Г. Валквиста при горячей про-
катке (^=800-? 1100 °C) образцов из низкоуглеродис-
той стали коэффициент плеча момента находится в пре-
делах 0,34—0,47. Более высокие значения ф получены
при прокатке относительно толстых образцов с малыми
обжатиями. Для других сталей пределы изменения ф не-
сколько шире; например, для быстрорежущей стали ф =
= 0,284-0,56.
При холодной прокатке коэффициент плеча момента
в большинстве случаев находится в пределах 0,2—0,35.
Такие результаты были получены в исследованиях
М. М. Сафьяна, Г. Форда (Н. Ford) и других ученых.
Относительно низкие значения ф при холодной прокатке
объясняются влиянием сплющивания валков. Вследст-
вие сплющивания передняя граница очага деформации
смещается за линию центров валков (рис. 15) и соответ-
ственно точка приложения равнодействующей Р прибли-
жается к линии центров, т. е. плечо а уменьшается. Чем
тоньше и тверже прокатываемые полосы, тем больше
сплющивание валков и тем ниже наблюдаемые значе-
ния ф.
Имеет значение и то обстоятельство, что по мере при-
ближения к плоскости выхода увеличивается наклеп ме-
талла, а это вызывает соответствующий рост давления.
11ри прокатке в калибрах определение крутящего момен-
та через коэффициент плеча силы Р становится затруд-
нительным, так как величина ф существенно зависит от
действия сил трения на боковых стенках калибра. Кро-
ме того, приходится учитывать сложный вид контактной
поверхности, поэтому при прокатке в калибрах более на-
дежные результаты получаются при определении крутя-
щего момента по расходу энергии, например, с помощью
нижеприведенной формулы (348).
3. Определение крутящего момента
при прокатке с натяжением
i При наличии переднего или заднего натяжения (или под-
пора) равнодействующая всех сил в очаге деформации
отклоняется от вертикального направления; соответст-
венно изменяется ее плечо относительно центра валка.
Положение равнодействующей в каждом конкретном
Рис. 96. Силы, действующие на полосу (а) и валки (б) при прокатке с зад-
дим натяжением
случае можно определить из условия равновесия всех
продольных сил, приложенных к полосе.
Допустим, прокатка ведется с задним натяжением
(рис. 96, а). При установившемся процессе прокатки
сила заднего натяжения Qo должна быть уравновешена
силами, приложенными к металлу со стороны валков,
т. е. должно соблюдаться равенство
4о = 2Рх. (328)
Именно равенство (328) предопределяет направление
действия силы Р. Переходя к силам, действующим на ва-
лок (рис. 96,6), видим, что величина крутящего момен-
та может быть найдена по формуле:
М^ = Руа + Рхс, (329)
где с — плечо составляющей Рх относительно центра
валка.
С небольшой погрешностью можно принять: РУ = Р;
с~Р. С учетом того, что и Px = Qo/2, получим
yWnp=Pxl)/d + (Q0/2)P. (330)
J52
Далее рассмотрим случай прокатки с передним натя-*
жением (рис. 97). Из условия равновесия продольных
сил, приложенных к полосе, находим
Qi = 2РХ. (331>
Величина крутящего момента будет
Mm = Pta-Pxc. (332>
Рис. 97. Силы, действующие иа полосу (а) и валки (б) при прокатке с передо
ним натяжением
По аналогии с формулой (330) получим
MBP=P^-MR. (333>
Если силы натяжения приложены к обоим концам
полосы — переднему и заднему, то положение равнодей-
ствующей зависит от разности сил Qo—Qi. В этом более
общем случае опять-таки должно соблюдаться равенства
(334?
Формула крутящего момента принимает вид
= + Q°~Q1 R- (335>
В частном случае, когда Q0 = Qi, имеем Рх=0, т. е.
равнодействующая Р направлена вертикально и форму-
ла (335) совпадает с формулой крутящего момента (326)
для свободной прокатки. Однако под воздействием сил
Qo и Qi снижается величина равнодействующей Р, а сле^
/к и laтельно, уменьшается крутящий момент.
11ри прокатке с подпором концов полосы формула
круги того момента (335) остается без изменений, на
• II.HI.I Qo и Qi надо подставлять в нее с обратным знаком^
153
4. Теоретическое определение работы
и мощности прокатки
I Если известна величина крутящих моментов, то опреде-
ление работы и мощности прокатки не представляет за-
труднений.
Работа прокатки Дпр составляет
Ар = 2МПР Ф = 2Л4ПР Zx/[( 1 + S) £], (336)
где ф — угол поворота валков за период прокатки поло-
сы длиной Zi.
Величиной опережения можно пренебречь
AJ1P = 2M^11/R. (337)
Подставляя в формулу (337) значение Мпр из выра-
жения (326), получим
Ар = 2рср фЬ ДЫх. (338)
Для определения работы прокатки может быть ис-
пользована также известная из теории обработки давле-
нием формула Финка:
Япр = Рср^1п(Ш), (339)
где V — объем прокатываемой полосы.
Между формулами (339) и (338) нет принципиаль-
ного различия. Если принять ln(/i0//ii)«ДщЛ1 и ф = 0,5,
то эти формулы будут одинаковыми.
При прокатке профилей сложного (не прямоуголь-
ного) сечения работа деформации определяется по фор-
муле
Ар = Рср V In (W = Рср V In X. (340)
Мощность, расходуемая на бочке валков, составляет:
дг = Лр_ = „2Л*пр*1 .. = 22Ипп_ (341)
пр т tf(l + S)T R в
где т — время прокатки полосы длиной 1\.
Определяя МПР по формуле Баюкова (324), находим
Гпр = 2рСР ЬРЪ (а - 2у) ив. (342)
Формулу Баюкова (342) можно преобразовать, если
подставить в нее значение угла у из выражения (133).
Такое преобразование сделал И. М. Павлов, получив
^пр = Рср^а2пв. (343)
Если использовать формулу крутящего момента
354
(327), то мощность прокатки будет:
IV11P = 2рср qb &hvB. (344)
В случае 4) = 0,5 формулы (343) и (344) совпадают
(Яа2 = ДЛ).
При определении работы прокатки по формуле (340)
получим
Ц7ПР = In % = рср F, In (345)
т
где Fi — площадь сечения выходящего конца полосы.-/
5. Экспериментальные данные
по определению работы прокатки
В литературе накоплен большой экспериментальный ма-
териал по расходу энергии на промышленных прокатных
станах разных типов. Эти данные, наряду с теоретиче-
скими расчетами, могут быть использованы для опреде-
ления величины крутящих моментов на валках и необ-
ходимой мощности привода. Использование практиче-
ских данных особенно целесообразно при прокатке
сложных профилей, когда теоретическое определение
усилия прокатки и коэффициента плеча момента встре-
чает значительные трудности.
Результаты экспериментальных исследований обыч-
но представляют в виде кривых, показывающих расход
энергии (работы) на 1 т проката в зависимости от нара-
стающего коэффициента вытяжки (рис. 98). При про-
катке листовой продукции кривые удельного расхода
энергии строят в зависимости от уменьшения толщины
полосы (рис. 99).
Допустим, удельный расход энергии до n-ного прохо-
да ('оставил а,, |, после прохода ап (рис. 98). Тогда
полный расход энергии (кВт-ч) за n-ный проход будет:
Л = (ап — an-i) G, (346)
где G — масса прокатываемого изделия, т.
Потребляемая мощность (кВт) определяется из вы-
ражения:
IV 3600 (on — an-i)G/x, (347)
। ле । время прохода, с.
Расход энергии при прокатке обычно измеряют по
нагрузке па двигатель. Поэтому экспериментальные кри-
HI.IC удельного расхода энергии включают потери на
155
трение в главной линии прокатного стана, но при по-
строении их исключается расход энергии на вращение
валков стана вхолостую. Таким образом, определяемая
по формуле (347) величина мощности W представляет
собой сумму U^np+^тр, где И7тр — расход энергии на
Рнс. 98. Типичная зависимость
удельного расхода энергии при
прокатке от общего коэффици-
ента вытяжки
Рис. 99. Удельный расход энергии при го-
рячей и холодной прокатке стальных по-
лос (по А. А. Королеву):
1 — непрерывный широкополосный стан
1700 горячей прокатки; 2 — четырехклете-
вой стан 1700 холодной прокатки
трение в механизмах главной линии стана в процессе
лрокатки.
При определении крутящих моментов на валках по
расходу энергии используются формулы (341) и (347),
из которых следует, что M=WR/vB-,
2Мир + Мтр _ 3600 (ап Дп—i) 0^ кН* м (348)
t tvb
где Л1Пр — крутящий момент на бочке одного валка;
Мгр — момент сил трения в подшипниках валков и в пе-
редаточных механизмах главной линии стана; i— пе-
редаточное число от двигателя к валкам. С помощью
формулы (348) можно определить величину Мпр.
; 6. Мощность двигателя прокатного стана
Полная мощность, расходуемая на осуществление про-
цесса прокатки, складывается из следующих частей:
' №дв = р + №тр + л ± ^дин» (349)
где Гхол — мощность холостого хода; №дин— динами-
J56
веская мощность, возникающая в результате действия
инерционных сил при изменении числа оборотов валков
(при разгоне входит со знаком плюс, при замедлении —
со знаком минус).
Составляющие уравнения (349) определяют по ве-
личине соответствующих крутящих моментов, приведен-
ных к валу двигателя:
М» - 2м;р + №„ + М'т ± . (350)
Момент прокатки на бочке одного валка Mnp, при-
веденный к валу двигателя Мпр =Mn9fi, рассчитывают
по формулам (324), (326) или (327). Мощность прокат-
ки (деформации) №Пр можно определить также непо-
средственно по формулам (342), (343), (344) или (345).
Момент сил трения Мтр, как уже отмечалось, скла-
дывается из момента сил трения в подшипниках валков
(Л4ТР1) и момента сил трения в передаточных механиз-
мах (MTPi). Момент, приведенный к валу двигателя, со-
ставляет
+ (351)
Величина МТР1 для двух валков (четырех подшип-
ников) определяется по формуле
М,Л = Р^ (352)
где fui — коэффициент трения в подшипниках валков;
dm — диаметр шеек валков.
Потери на трение в передаточных механизмах (Л^тр.)
обычно учитывают с помощью коэффициента полезного
действия передачи т]п
М,к = (14- 1) [(Л!^ + Л4ТИ)«]. (353)
Момент холостого хода Мхол представляет собой сум-
му моментов Мп, необходимых для вращения отдельных,
деталей главной линии стана при отсутствии металла
и валках МХол = ^Мп.
Для одной детали момент, приведенный к валу дви-
гателя, равен
Д', (354)
i/i.<* (>п — масса детали (нагрузка на подшипники); fn —
»ф(|шциент трения в подшипниках; dn — диаметр
п.1И(|», /п— передаточное число между двигателем и дан-
П( ш деталью.
Полная величина приведенного момента холостого
157
- 75,6). В этом случае влияние внешних зон на очаг де-
• формации становится незначительным, а силы трения
на контакте еще не оказывают заметного подпирающего
действия,/так как толщина полосы остается относитель-
1 до болыпой.
При более высоких значениях параметра ldlhcPl осо-
бенно при /d//icp>3-r-4 (тонкие полосы), на эпюрах дав-
ления появляется отчетливо выраженный пик, располо-
женный в нейтральном сечении (рис. 75, в). Такой ха-
рактер распределения давлений вдоль дуги контакта
обусловлен действием сил трения. По мере перемещения
от границ очага деформации к нейтральному сечению
растет сумма продольных подпирающих сил трения —
соответственно растут контактные давления. Максималь-
ный подпор силы трения создают в нейтральном сечении,
поэтому и давление здесь максимально. J
Таким образом, высота пика на эпюре давлений дол-
жна зависеть от величины коэффициента трения. Этот
вывод подтверждается экспериментальными данны-
ми. С увеличением коэффициента трения, при прочих
фавных условиях, пик на эпюрах давления возрас-
тает’
Эпюры давлений при прокатке с углами контакта,
превышающими угол трения, имеют седловидную форму
Рис. 76. Распределе-
ние давлений по ду-
ге контакта при а>
>₽у
Рис. 77. Эпюры распределения давлений в -по-
перечных сечениях очага деформации при
прокатке узких (а) и широких (б) полос
(рис. 76). Как отмечалось ранее (см. гл. V. п. 1), в слу-
чае а>ру в задней части очага деформации возникают
продольные растягивающие напряжения, которые и слу-
жат причиной падения давлений на этом участке (с об-
разованием «седла»).
/22
(358)
где Д/ii и ДЛ2 — удвоенное обжатие соответственно со
стороны верхнего 1 и нижнего 2 валков.
Имеем дСР1 = bCPi, тогда из уравнения (357) нахо-
дим
AAt_ _ #2 / РсР2
м2 Ri \ Pcpi
Введем коэффициент /n=pcP1/pcPi, характеризую-
щий различие контактных давлений на валках 1 и 2:
Mit 1 R2
Mi2 т2 Rr
Учтем, что
Mit/2 + Дйа/2 = ДЛ. (360)
При совместном решении уравнений (359) и (360) по-
лучаем: обжатие со стороны валка малого диаметра
Mir/2 = R* Mil(m2 Rr + #2), (361)
обжатие со стороны валка большого диаметра
Л/г2/2 = т2 Rj Мг/(т2 Rt + R2). (362)
Затем определим значения углов контакта на одном
и другом валке. На основании формулы (30) получим
ПС, = / ДйЖ = ]/2R2Aft/[Ri(ma/?, + ;?,)]; (363)
«, = / ДЛЛ = V Чт‘ Rr ДЛ/1% (т2 /?, + ед]. (364)
Если допустить, что контактные давления на валках
/ и 2 равны, т. е. рСР1 = PcPi и т=1, то вместо формул
(359), (361) — (364) получим
Л///ДЛ2 = RjRi, (365)
Ml.12 = Я2ДМЯ1 + Я2); (366)
ММ2 = Rr Мг/ЦЪ + #2); (367)
|/2R3 !/»/[«,№ +Ra)]; (368)
Гг^шкд/^ + ед]. (369)
Формулы (366) и (367) впервые выведены А. Ф. Го-
..иым. При условии рСР1 = Рср2 длина очага дефор-
....а обоих валках одинакова и составляет
/, I Л',Л77Г=! (370)
Г R1 +
159
Величина 2RiRz/(Ri’r^-Rz) =Rnp называется приве-
денным радиусом.
Условия захвата. Рассматривая втягивающие и от-
талкивающие силы, действующие в точках касания по-
лосы свалками (рис. 101), сформулируем условия началь-
Рис. 101. Схема сил при захвате
полосы валками неравного диамет-
ра
ного захвата в виде
Nx. + NX2 < ТХ1 + ТХ2 (371)
или
sin а14-Лг2 sin cos otfb
4- Т2 cos а2. (372)
Для определения сил 1\
и Т2 используем закон тре-
ния Амонтона
sin «i + ?/2 sin а2 </3 X
X cos + /з cos a2. (373)
Составим уравнение рав-
новесия сил в вертикальной
плоскости
N-L cos at + f3 N-l sin = N* cos a2 + /3 ?/2 sin a2» (374)
откуда находим
Nt = Nr (cos at 4- fa sin aj)/(cos a2 4- fa sin 02), (375)
Подставим это значение силы N% в формулу (373)
У, sin a, 4- N. + k N1 cos ai +
cos a2 4" /3 sin aa
(cos <%! 4~ fs sin ax) cos a2
cos a2 4- fa sin a2
+ АЛ1
После сокращений и тригонометрических преобразо-
ваний получим
sin (ax 4- a2) 4- 2/3 sin sin a2 < f 3 [f3 sin (oj + a2) 4-
4- 2 cos cos a2]. (376)
Сделаем ряд дополнительных преобразований
sin (04 4- a2) — f23 sin (04 4- a2) < 2Д cos (cq 4- a2);
tg(a14-a2)(l-f23)<2/3.
160
Заметим, что
2[з_ = 2 tgg3 = t (2р )
1-/2 l-tg2p3 7
Следовательно, условие начального захвата можно
привести к виду
tg («1 + а8) < tg (203) (377)
или
wi 4~ а2 'С 203. (378)
Условие захвата при установившемся процессе про-
катки выводится из выражения (рис. 102)
sin ip! 4- N2s in ip2 <- Л cos % + T2 cos ф2, (379);
которое вполне аналогично
выражению (372). Поэтому
последующие выкладки при-
водят к формуле
^ + ^<2^. (380)
Если в порядке первого
приближения принять ipi =
=ai/2 и ip2=a2/2, то по-
лучим для установившегося
процесса
«1 + «2<4Ру. (381)
Опережение и нейтраль-
ный угол. При анализе ско-
ростных условий прокатки
следует учитывать, что ок-
Рис. 102. Схема сил при установив-
шемся процессе прокатки с пре-
дельным обжатием в валках не-
равного диаметра
ружные скорости валков
пропорциональны их диаметрам. Это является очень су-
щественным фактором при определении кинематических,
показателей. Поскольку полоса выходит из валков с оди-
наковой скоростью по всему сечению (если пренебречь
<*<* изгибом), то опережение и нейтральный угол на вал-
ке меньшего диаметра всегда будет больше, чем на вал-
ке большого диаметра.
Рассмотрим изменение скоростных условий в очаге
'••формации при увеличении обжатия и углов контакта
• ч пуля до некоторых предельных значений. Как пока-
ii.iii.nor экспериментальные исследования, при очень ма-
|"м (пулевом) обжатии полоса выходит из валков со
. i.<»р«icti.io, практически равной окружной скорости валка
II А II Г|>уде«
lit
малого диаметра иВ1; при этом валок большого диамет-
ра скользит по полосе, обгоняя ее, со скоростью vBs—vBi.
С увеличением обжатия растут втягивающие силы,
и скорость полосы повышается. В результате на валке
малого диаметра появляется зона опережения, хотя на
валке большого диаметра
Рис. 103. Нейтральные углы и
у2, силы нормального давления и
трения на валках малого и боль-
шого диаметра
еще существует сплошное
проскальзывание. При до-
стижении некоторого обжа-
тия зона опережения возни-
кает и на валке большого
диаметра1. При дальнейшем
увеличении обжатия в свя-
зи с ростом отталкивающих
сил скорость полосы падает,
зона опережения исчезает
сначала на валке большого
диаметра, а затем и на вал-
ке малого диаметра. После
этого наступает полное бук-
сование.
Перейдем к количествен-
ному определению величины
нейтрального угла на одном
и другом валке. С этой
целью используем уравнение равновесия продольных сил,
приложенных к полосе при установившемся процессе
прокатки. Будем исходить из наличия в очаге деформа-
ции кинематических зон, показанных на рис. 103. По
аналогии с уравнением (131) напишем
а, V, а,
j* f7 cos (fi dq?! — J fy cos (fi dcpx — sin cpx +
Ti 0 6
аг v2 a2
4- j fy cos <p2 dq>2 — J fy cos <p2 dcp2 — sin <p2 d(p2 = 0. (382)
v2 о 6
После интегрирования получим
1 ’ COS OCi । e • fie •
y sin cq — 2fy sin Yi--------i + fy sin a2 — 2fy sin y2 —
1 - cos a2 = 0 (383)
1 Ниже будет показано, что при значительной разности в диа-
метрах валков зона опережения на валке большого диаметра может
вообще не появиться.
162
Учитывая малость углов, сделаем встречавшиеся
ранее упрощения: sinai«ai и т.д. (см. стр. 61). В ре-
зультате несложных преобразований получим
Следовательно, из уравнения равновесия продольных
сил можно найти только сумму нейтральных углов yi'+,
| 72. Для определения нейтрального угла на каждом
валке необходимо к уравнению равновесия присоеди-
нить еще одно уравнение, содержащее углы yi и у2. Та-
ким уравнением может служить зависимость между опе-
режениями на одном и другом валке.
При условии прямолинейного (без изгиба) выхода
волосы из валков должно соблюдаться равенство
п„1(1+ 50=^(14-52), (385)
где 51 и 52 — опережение соответственно на валке 1 и 2.
Поскольку Ув2 = то равенство (385) приво-
дится к виду
1 + 5i = (ад0(1 + 52). (386}
Выразим опережения 51 и S2 через соответствующие
нейтральные углы. Возьмем два поперечных сечения
в очаге деформации: выходное и находящееся под уг-
лом уь Из условия постоянства секундных объемов (при
отсутствии уширения) следует, что
^cosy^ = Мр (387)
где /iV1 — высота полосы в сечении под углом уь
Можно принять cosyi^l. Далее находим
//vt = hx + М;/2 + ДЯ'/2, (388)
где Mi'J2 и — обжатия co стороны валков 1 и 2
при переходе от сечения, расположенного под углом уь
к выходному сечению.
Имеем
А//; :у?/?1; (389)
Л'< = = + (390)
\ ^2 / ^2
। /к> ipVi — угол на валке 2 в сечении hVt.
111
163
Подставим эти значения обжатий в формулу (388)
После этого из условия (387) находим
9
Л_=1+21Л(1 +АЛ
°»Г 2Л1 \
Следовательно, опережение Si составляет
(392)
= P1 °B1
vfoi Л . Ki \
Vbi \ R% /
По аналогичной схеме определяется
на валке большого диаметра
Sa = 2^71 +
2/h \ 7
(393)
опережение S2
(394)
Вернемся к равенству (386). Подставляя в него най-
денные значения Si и S2, получим
1 + 22k (1 + 2Ц = 21. Г1 _|_ 22kh (395)
2ht \ L 2/н \ /?! /J
Это равенство и выражает кинематическую связь
между углами yi и у2. Из него находим
» = 1 [ (АЛ3 -I- —. (396)
V \R.)
y, = ]/ Hl—}3— ^^t-R^R, (397)
V \R,) (R1+R^)Rl
Теперь решаем совместно уравнения (384) и (397)
, Д)2 ( \3 2M*»-*i)*i ai + а2 а1 + а2
+ V 71 ТО “ (Rl+R^ 2 '
(398)
Введем обозначения:
«1 + «2 а1 + а2 = А. = в
2 4Ру -|- /?з
Тогда уравнение (398) принимает вид
V1 + \/ V? ('—У — В А. = А.
>' 1 \ R, I R,
164
Приведем его к канонической форме
у’—2Лт1 + Л« + В-^- = 0. (399)
При решении этого квадратного уравнения, опреде-
лим величину нейтрального угла 71 на валке малого
диаметра
Зная угол уь находим по формуле (397) величину
нейтрального угла у2 на валке большого диаметра. Как
уже отмечалось, зона опережения на большом валке су-
ществует не во всем диапазоне обжатий. Установим ту
область изменения угла аь в которой нейтральный угол
Тг имеет действительное значение.
Примем 72=0, тогда из уравнения (396) получим
2Л1 (Т?2 — ft})
(*1+*^
Формула (401) показывает, при каком значении угла
Vi возникает, а затем исчезает (при дальнейшем увели-
чении обжатия) зона опережения на большом валке.
При определении соответствующих значений угла oci ис-
пользуем уравнение равновесия (384), приняв 7г=0
к подставив в него значение угла 71 из формулы (401):
fJf Г + а1 а1 + а1 ( р )
__________________\ Аа /
~2 4ру
Решая это уравнение относительно угла аь получим
(401)
(403)
Формула (403) дает два граничных значения угла
165
си. Если в числителе формулы (403) перед радикалом-
принимается знак минус, то получаем нижнее значение-
угла ai (обозначим его оф, при котором зона опереже-
ния на большом валке только появляется. Если же пе-
ред радикалом берется знак плюс, то находим верхнее
значение угла ai (обозначим его оф, при котором зона
опережения на большом валке исчезает.
Таким образом, угол 72 имеет действительное значе-
ние при изменении угла ai в пределах от а[ до . В ди-
апазонах aiCai и ai>ai существует только угол уь
который определяется непосредственно из уравнения
равновесия (384). Последнее можно представить в виде
Vi = А. (404)
0 0,1 0,2 0,0 О,Ь 0,5 af
Рис. 104. Зависимость нейтральных уг-
лов Vt и у» от величины угла контакта
си (условия прокатки):
/?1=360 мм; /?2=400 мм; ftt=40 мм;
=0,25
Чтобы проиллюстрировать
характер изменения углов yi
и уз в зависимости от величи-
ны угла си, на рис. 104 приве-
дены результаты расчетов по
формулам (404), (400) И'
(397) для конкретных условий
прокатки: У?1 = 360 мм; /?2=
=400 мм; /ii = 40 мм; ру=0,25.
В этом случае угол у2 возника-
ет при ai = aj =0,18 и исче-
зает при ai = ai =0,34. Вели-
чина угла у2 в области его су-
ществования гораздо меньше
угла уь
Возможны и такие условия
прокатки, при которых зона
опережения на валке большого
диаметра вообще не образует-
ся, т. е. уг=0 при любых зна-
чениях угла аь Из формулы
(403) видно, что при соотно-
шении
(405)
углы и ai становятся мнимыми.
Используем приближенное равенство
ЛАф2
к Ъ /
1 +
2
Тогда условие полного отсутствия зоны опережения на валке
166
большого диаметра принимает вид
Оу <
(406) •
Рис. 105. Вид полос, прокатанных
в валках неравного диаметра с раз-
личными обжатиями (по А. П. Чек-
мареву и А. А. Нефедову)
Изгиб полосы. Важной особенностью процесса про-
катки в валках неравного диаметра является изгиб по-
лосы при выходе из валков. На первый взгяд может по-
казаться, что полоса всегда должна изгибаться в сторону
валка меньшего диаметра, что обусловлено различи-
ем окружных скоростей валков. Однако эксперименталь-
ные исследования, проведен-
ные А. П. Чекмаревым и
Л. А. Нефедовым, показали,
что выходящий конец поло-
сы, в зависимости от усло-
вий деформации, может из-
гибаться как на валок мень-
шего, так и большего диа-
метра.
Основным фактором,
влияющим на направление
изгиба и кривизну полосы,
является величина относи-
тельного обжатия. При не-
больших частных обжатиях,
примерно до 30—40 %, по-
лоса изгибается на валок
меньшего диаметра, а при
дальнейшем увеличении об-
жатия— на валок большего
диаметра. Вид полос одина-
ковой начальной толщины, прокатанных с постепенно воз-
растающим обжатием (сверхувниз), показан на рис. 105.
Некоторые количественные данные по кривизне полос
после прокатки в валках неравного диаметра приведены
па рис. 106. Опыты проводились на валках средним диа-
метром £>Ср около 200 мм, при разности диаметров Д£)
от 5 до 35 мм. На графике на оси ординат отложены зна-
чения показателя кривизны полосы риз=1/Яиз, где
А’из—радиус внутренней поверхности полосы. Условно
принято, что при изгибе полос на валок малого диамет-
ра кривизна является положительной, а при изгибе на
палок большого диаметра — отрицательной.
Опыты показали, что общий характер изменения кри-
167
визны полосы в зависимости от степени деформации со-
храняется при прокатке образцов разной толщины и при
разном соотношении диаметров валков.
При анализе причин изгиба полосы в ту или иную
сторону надо учитывать, что изгиб происходит вследствие
Рис. 106. Изменение кривизны полос в зависимости от относительного обжа-
тия при прокатке в валках неравного диаметра (по А. П. Чекмареву и А. А.
Нефедову):
/—свинец, ft0=10 мм, Д£>=35 мм; 2 — Ст.2 при 1100 “С, /io=20 мм, ДО = 12 мм
неравенства обжатий, совершаемых каждым из валков.
Соотношение обжатий, в свою очередь, зависит от соот-
ношения контактных давлений, что видно из формулы
(359).
В диапазоне малых обжатий валок большого диамет-
ра, обгоняя полосу, вызывает появление в прилегающих
к нему слоях металла растягивающих напряжений. Это
способствует снижению контактного давления рСр2. Сле-
довательно, возникают условия, при которых коэффици-
ент т в формуле (359) больше единицы (точнее больше
V R-z/Ri) и A/i2>A^b В результате полоса будет изги-
баться на валок малого диаметра.
При дальнейшем увеличении обжатия, когда на вал-
ке большого диаметра появляется зона опережения, рас-
тягивающее действие сил трения на этом валке сменя-
16»
стся подпирающим действием. Вследствие этого контакт-
ное давление рср, быстро возрастает. Одновременно
подпирающее действие сил трения навалке малого диа-
метра относительно ослабевает, т. е. контактное давление
рСрх растет менее интенсивно. Таким образом, коэффи-
циент т уменьшается и соотношение обжатий принима-
ет вид ДЛ1>>Д/12- При этом полоса будет изгибаться на
валок большого диаметра.
Усилия и крутящие моменты. В связи с различием ок-
ружных скоростей и тенденцией к возникновению растя-
гивающих напряжений на отдельных участках очага де-
формации при прокатке в валках неравного диаметра
контактные давления меньше, чем при прокатке в вал-
ках одинакового (среднего) диаметра. Снижение давле-
ния, в зависимости от соотношения диаметров, может
достигать 20—30 % и более.
Поскольку в процессе прокатки валок большого диа-
метра является тянущим, величина крутящего момента
на нем больше, чем на валке малого диаметра. В соот-
ветствии с этим определяется положение равнодействую-
щих Р) и Р2, приложенных к соответствующим валкам
(рис. 107): сила Pt отклоняется к центру валка 1, а си-
Рис. 107. Положение равнодействующих
неравного диаметра:
а — при свободном выходе конца полосы;
сил и Рг при прокатке в валках
б — при наличии проводки
ла Р2— от центра валка 2; плечо щ меньше плеча ц2.
При отсутствии внешнего изгибающего момента, прило-
женного к выходящему концу полосы, силы Pi и Р2 рас-
полагаются по одной прямой (рис. 107,а). Если же пе-
редний конец полосы опирается на проводку и возникает
169
сила Рпр, которая противодействует изгибу полосы, то
линии действия сил Pi и Р% будут параллельными, но не
совпадающими (рис. 107,6). Возникающий в зоне обжа-
тия момент Р\е уравновешивается моментом Рщ>с.
Крутящие моменты на бочке каждого из валков мо-
гут быть определены с помощью формулы Баюкова (324)
МпИ=рси6Л?Гу(а,-2Т1); (407)
Л4пи = Рер2^/у(«2-2т2). (408)
В диапазоне малых обжатий возможны случаи, когда
тогда расчетный момент Mnpi становится отри-
цательным или нулевым. Физически это означает, что
весь крутящий момент, необходимый для прокатки, пе-
редается валком большого диаметра, а малый валок яв-
ляется тормозом.
2. Прокатка с одним приводным валком
В некоторых случаях в прокатном производстве приме-
няются станы, у которых приводным является только
Рис. 108. Схема сил в началь-
ный момент захвата при прокат-
ке с одним приводным валком
один из двух валков, обычно
нижний. К числу таких станов
относятся тонколистовые ста-
ны штучной (пакетной) про-
катки. Иногда схема прокатки
с одним приводным валком
применяется в чистовых клетях
непрерывных проволочных и
полосовых станов. Во всех этих
случаях процесс прокатки име-
ет существенные особенности.
Условия захвата. При на-
чальном соприкосновении ме-
талла с валками неприводной
(холостой) валок не оказыва-
ет втягивающего действия на
полосу. Более того, непривод-
ной валок в некоторой мере
противодействует втягиванию
полосы из-за сопротивления
вращению в его опорах. С уче-
том этого схема сил в начальный момент захвата показа-
на на рис. 108 (неприводной валок верхний).
Сформулируем условие захвата в виде
+ Тнх + МПх ТПх,
(409)
170
1’де Nhx, Т„х, Nnx, tnx—горизонтальные проекции соот-
ветствующих сил.
Учитывая наклон сил, получим
sin а + Тп cos а + Nn sin а cos а- (410)
Силу трения Тп на бочке холостого валка можно оп-
ределить, если известен момент сопротивления враще-
нию в шейках этого валка МтРш. Имеем
= = (411)
где Тш — равнодействующая сил трения в шейках;
гш — радиус шейки неприводного валка; fm — коэффи-
циент трения в шейках.
Составим уравнение равновесия моментов для непри-
водного валка:
Гн R =
откуда
T„ = NwfmrJR. (412)
С учетом того, что Tn=f3Nn, подставим найденные
значения сил Тн и Тп в формулу (410)
JVH sin а 4- NH ?шГш cos а + Na sin а < f3 Nn cos а. (413)
С небольшим допущением можно принять NH=Nn.
После сокращения на Nu, деления всех членов на cos а
и простых преобразований получим
Принимая tga^a и f3~03, окончательно получим ус-
ловие начального захвата при прокатке с одним при-
водным валком
а<4(₽3-Ц^4 (415)
Перейдем к формулировке условия захвата при уста-
новившемся процессе прокатки. Исходя из схемы сил,
приведенной на рис. 109, напишем
2VH sin фн + Т„ cos фн 4- Nn sin фп < Тп cos фп. (416)
Подставим в условие (416) значения сил Тн из фор-
мулы (412) и Tn=fyA^n
2VH sin фн + cos фн 4- sin фп < Na cos фп. (417)
A
171
Выражение (417) по своей структуре подобно выра-
жению (413). Если принять 'фн=‘фп=а/2, то по анало-
гии с выводом формулы (415) получим условие захвата
при установившемся процессе прокатки
а 1 / о /ш гш \
2^2 Vy R )
ИЛИ
(418)
В результате сравнения формул (75) и (416), а так-
же (115) и (418), следует, что при прокатке с одним при-
Рис. 1С9. Схема сил к определению
условия захвата при установившем-
ся процессе прокатки с одним при-
водным валком
Рис. ПО. К определению нейтраль-
ного угла на приводном валке
водным валком условия захвата более чем в два раза
хуже, чем при симметричной прокатке.
Опережение и нейтральный угол. Рассматривая кине-
матические закономерности данного процесса прокатки,
надо учитывать то обстоятельство, что скорость враще-
ния неприводного валка задается самой прокатываемой
полосой, причем скорость вращения должна быть такой,
чтобы удовлетворялось условие отсутствия внешнего
крутящего момента на этом валке. Если бы не было со-
противления вращению в опорах, то нейтральный угол
на неприводном валке был бы равен а/2, так как силы
трения в зоне опережения должны были бы полностью
уравновешивать силы трения в зоне отставания. Прак-
тически, из-за наличия момента трения в опорах, нейт-
ральный угол на неприводном валке всегда несколько
172
больше а/2. Этим условием и определяется скорость,
вращения неприводного валка.
С другой стороны, на приводном валке зона опереже-
ния всегда должна быть значительно меньше зоны отста-
вания, иначе будет иметь место нехватка втягивающих
сил, необходимых для осуществления процесса прокат-
ки. Поэтому нейтральный угол на приводном валке всег-
да относительно невелик.
Приведенные общие рассуждения подтверждаются
математическим анализом. Сначала определим величину
нейтрального угла уп на приводном валке (рис. ПО).
Составим уравнение равновесия продольных сил, при-
ложенных к полосе при установившемся процессе про-
катки
SX = - NB sin -2- - Тя cos -2— Nm sin 2±1в +
+ Tmcos2±l£-_^sin^--7’nlcos-^-=0. (419)>
Значения сил (равнодействующих), входящих в урав-
нение (419), можно определить в виде произведения эле-
ментарных сил на площадь соответствующих зон1. Име-
ем:
Nh~ Рср Тя = Рн = Рср bafmrш>
^по ~ Рср bR (а Yn) > ^по = tbR (а уп) =
= /уРсрЬР(а — уп);
^Vni = Рср bRyn', Pni = tbR Yn = fy Рср bRyn.
Подставим эти значения сил в уравнение (419), од-
новременно сократив все слагаемые на pcpbR:
— a sin— — а cos —--(а — уп) sinа~^Уп + /у (а —
—Yn) cos — уп sin — /у Yn cos ^2- = 0. (420)
Принимая в порядке упрощения sin-^-^-—, cos-^-^
«1 ит. д. (см. стр. 61), получим
2
—<£.+^+₽уа-мп-
1 В предыдущих выводах аналогичная задача решалась путем?
интегрирования элементарных сил, см. уравнение (130).
173,
0у?п = О.
(421)
После приведения подобных и сокращений получим
— as_a^H_ + ₽ja_2₽yTn = 0.
/\
*Рис. 111. К определению ней-
трального угла на неприводном
валке
Отсюда находим величину
нейтрального угла на привод-
ном валке
ct /1 а /ш гш \
2 Ру ру/? /
(422)
Нейтральный угол на холо-
стом валке легко определяет-
ся из условия равновесия кру-
тящих моментов, приложен-
ных к этому валку. Уравнение
равновесия моментов относи-
тельно оси валка будет (рис.
111):
SM =- Тн0 R + ТИ1R - /ИтРш = 0, (423)
где Тиои Тн1 — равнодействующие сил трения в зонах
отставания и опережения.
Выразим значения равнодействующих Тио и Ли через
элементарные силы
Тн0 = ОД (а — ун) = /у рср bR (а — ун); (424)
Ли = ад?н = /у Рср bRl„. (425)
Подставим значения сил Тп0 и THi в уравнение (423),
а также используем выражение (411)
— /у Рср W (« — Тн) + /уРср bR* Т„ — Рср bRaful гш = 0. (426)
После простых преобразований получим формулу для
определения величины нейтрального угла на неприводном
валке:
(1 +
fmrm \
Ру/? Г
(427)
Для наглядного представления характера изменения
углов уп и ун в зависимости от угла а на рис. 112 приве-
.дены результаты расчетов по формулам (422) и (427)
174
при следующих условиях прокатки: /?=400 мм; гш=
=300 мм; ру=0,25; /ш=0,1. Как видим, угол уп прю
всех значениях угла а относительно невелик и изменя-
ется по обычной параболической кривой, характерной'
для приводных валков. В то же время угол ун на непри-
водном валке с увеличением угла а непрерывно, прямо-
линейно возрастает, намного превышая угол уп.
Рис. 112. Зависимость нейтральных уг-
лов уп и ун от величины угла кон-
такта а (условия прокатки:
/?=400 мм; гш=300 мм; |3 =0,25;
fln=0,l)
Рис. 113. Экспериментальные дан-
ные по опережению на приводном»
(Sn) и неприводном (SH) валках
при холодной прокатке стальных
полос толщиной /10=1,95 мм (по
А. А. Королеву)
При известной величине нейтральных углов уп и ун
нетрудно определить опережение на приводном (Sn)
и неприводном (SH) валках, используя, например, фор-
мулу (169). Разумеется, опережение на неприводном
валке всегда значительно больше, чем на приводном
(рис. 113).
С помощью формул (422) и (427) можно определить также
скорость вращения неприводного валка. Учтем, что
иин О + Зн) = ивп U + ^п), (428}>
где Овн и ивп — окружные скорости соответствующих валков.
Из равенства (428) находим
14-у2 —
1 _|_ е ' *п .
«'..и = <429>
175-
или
1+Y"^r
Л1
лвн= пвп п ’ (430)
где «вн и «вп — числа оборотов неприводного и приводного валков.
Усилия и крутящий момент. Положение равнодейст-
вующих сил, приложенных к валкам, определяется из
условий отсутствия внешнего крутящего момента на хо-
лостом валке и равновесия сил, приложенных к полосе
при установившемся процессе прокатки. Если пренебречь
моментом трения в опорах холостого валка, то следует
сделать вывод, что равнодействующая Рн проходит че-
рез ось валка (рис. 114, а). Равнодействующая Рп дол
•Рис. 114. Положение равнодействующих сил Рн и Рп при прокатке с одним
приводным валком без учета (а) и с учетом (б) сопротивления вращению
в опорах холостого валка
жна быть равна силе Рн и лежать на одной прямой с ней.
При наличии момента трения в опорах равнодейст-
вующая Рн будет направлена по касательной к кругу
трения (на рис. 114,6 р— радиус круга трения). Соот-
ветственно изменится наклон силы Рп, которая по-
прежнему будет находиться на одной прямой с си-
лой Рн.
Крутящий момент на бочке приводного валка опре-
деляется по формуле Баюкова
^пр.п — Рср fy (а 2уп).
(431)
176
Можно показать, что крутящий момент на привод-
ном валке примерно равен удвоенному крутящему мо-
менту на одном валке при симметричной прокатке.
Действительно, если принять МтРш = 0, то из формул
(431) и (422) получим
М„р.п = Pep bR* fy [а - 2 11 - -2-)] = рср Ы? f, .
L 1 \ Ру /J Ру
Для одного валка при симметричной прокатке
Мп» = Pep Wfy[a-2-2-(l-|-)] = P«pW7y^- •
Таким образом, имеем Л1Пр.п=2Л1пр.
3. Прокатка при разных условиях трения на валках
В практике прокатного производства часто наблюдаются
случаи, когда условия внешнего трения на верхнем
и нижнем валках не одинаковы. Имеется много причин,
которые вызывают это различие. Например, при про-
катке нагретых слитков и заготовок печная окалина
с их нижней поверхности легко осыпается, а на верхней
поверхности сохраняется на протяжении нескольких про-
ходов (до кантовки).
При холодной прокатке различие в коэффициентах
трения на валках часто возникает из-за различия в усло-
виях поступления технологической смазки на верхнюю
и нижнюю контактные поверхности.
В некоторых случаях специально применяются валки
с разной шероховатостью поверхностей. Это необходимо,
в частности, при производстве листов с разным микро-
рельефом двух основных поверхностей. Во всех случаях,
когда коэффициенты трения на валках различны, про-
цесс прокатки приобретает черты асимметричного про-
цесса. Это находит выражение в неравенстве обжатий
со стороны каждого валка, различии опережений и ней-
тральных углов, изгибе выходящего конца полосы, не-
равномерности распределения крутящих моментов меж-
ду валками. Такой процесс требует отдельного анализа.
Отражая различие в условиях трения, будем назы-
вать один из валков (верхний) гладким, а второй (ниж-
ний) — шероховатым.
Условия захвата при прокатке в разношероховатых
валках формулируются так же, как для простого случая
Г> А. П. Грудев
177
прокатки, однако в формулы входит средний коэффици-
ент (угол) трения для двух валков. Имеем:
для начального момента прокатки
«а (Рвг + ₽в„)/2; (432)
для установившегося процесса
а<РУг + РУш, (433)
где индексы г и ш относятся соответственно к гладкому
и шероховатому валку.
При анализе кинематических закономерностей дан-
ного процесса приходим к выводу, что возможное разли-
чие в значениях опережения на одном и другом валке
тесно связано с изгибом полосы в вертикальной плоско-
сти. Если бы полоса выходила из валков строго прямо-
линейно, то нейтральные углы и опережения на обоих
валках были бы одинаковыми (поскольку окружные
скорости валков равны). В действительности полоса вы-
ходит из валков с изгибом, а это означает, что скорости
движения ее поверхностей — верхней и нижней — раз-
личны. Отсюда и возникает различие в опережениях на
одном и другом валке.
Исследования показывают, что при прокатке относи-
тельно толстых образцов выходящий конец полосы изги-
бается в сторону гладкого валка. Это объясняется асим-
метричным действием сил трения на контактных поверх-
ностях, вследствие чего в слоях металла, примыкающих
к шероховатому валку, возникают растягивающие на-
пряжения. Последнее способствует снижению давления
и увеличению обжатия со стороны шероховатого валка.
При прокатке тонких полос картина напряженного
состояния в очаге деформации меняется. Главную роль
начинает играть подпирающее действие сил трения. На
гладком валке силы трения меньше, поэтому их подпи-
рающее действие выражено слабее. Следовательно, со-
здаются условия для повышенного обжатия со стороны
гладкого валка, и полоса изгибается на шероховатый
валок.
При изгибе полосы скорость движения ее внешней по-
верхности будет больше, чем скорость внутренней по-
верхности. В связи с этим нейтральный угол и опереже-
ние всегда больше на том валке, от которого полоса от-
гибается.
Среднее значение нейтрального угла уСр для двух
контактных поверхностей определяется из условия рав-
178
повесия продольных сил, приложенных к полосе при ус-
тановившемся процессе прокатки. Решение уравнения
равновесия по типу вывода формулы (133) приводит
к выражению
а Л а \
(434)
Нейтральный угол уСр
характеризует положение
того сечения /г?ср, где сред-
няя по высоте полосы про-
дольная скорость равна ок-
ружной скорости валков.
Зная величину угла уСр и pa- ।
диус изгиба выходящего |
конца полосы, можно опре-
делить опережение и нейт-
ральный угол на каждом из
валков.
Считая ширину полосы
неизменной, напишем усло-
вие постоянства секундных
объемов в виде
v nhv = у. h,
“ Ycp ср J
Рис. 115. К определению кинемати-
ческих зависимостей при прокатке
в разношероховатых валках
(435)
где Uicp — средняя по высоте скорость полосы на выхо-
де. В соответствии с радиусом изгиба (рис. 115)
= + (436)
где Uir и Vi —скорости поверхностей, внутренней и на-
ружной (по отношению к центру изгиба).
Находим среднюю скорость полосы на выходе
хср
' 1 L. । «. %из + ЬЛ___________
------ = ------I Vi ~г Vi ---------- =
2 2 1г /?из )
% / 2/?из -j-
2 \ ^?из
(437)
Подставим это значение uicp в равенство (435), уч-
тем также, что hVc? =hi+ylpR, тогда из выражения
(435) получим
“г 2('‘1 + <ЛКз
°п (2^?из ~Ь ^1)
(438)
12*
179
(439)
Отсюда легко определяется опережение на том вал-
ке, в сторону которого изгибается полоса
S = А_— 1 = 2(ftl+Vcpj?) ^из _ J
°в (2^?из + ^i) hi
После преобразований получим
£ _ Vcp h]
(2/?из + hy) hy
Введем понятие о среднем опережении SCp=ycp#/^i,
тогда формула (439) может быть приведена к виду
s = 2g,8Scp-\. (440)
2₽ЯЗ + Л1
Аналогично определяется опережение на втором
валке, от которого полоса отклоняется. Из формул
(436) и (437) находим
_ ш ( 2/?из + \ .
*ср 2 \ /?из hy /
В конечном итоге, используя равенство (435), по-
лучим
s = +
(441)
ИЛИ
о ___ 2 (7?из Л1) <Scp 4~ hy
“ 2flH3 + /h
При известных значениях опережений Sr и 5Ш мож-
но определить соответствующие нейтральные углы
(442)
, Г Sphy = I f WR^^-h] .
V R ? (2^из + hy) R
1 /~Зщ hy __ I f (^из ~Ь ^1) 7ср 4~
V R ? (2/?из + М^
(443)
(444)
Экспериментальные данные свидетельствуют о том,
что крутящий момент на шероховатом валке обычно бы-
вает больше, чем на гладком. Отсюда следует, что рав-
нодействующие силы Рр и Рш располагаются по отноше-
нию к оси прокатки под некоторым углом: плечо аш не-
сколько больше плеча щ (рис. 116).
Суммарный крутящий момент для двух валков мо-
180
Рис. 116. Положение
равнодействующих сил
Рг и Рш при прокатке
в разношероховатых вал-
ках
жет быть определен по формуле Баюкова (308) при
подстановке в нее усредненных значений коэффициента
трения, нейтрального угла и других параметров процес-
са прокатки:
2М„р = Pep W* (/yr + fym) (а - 2Тср). (445)
Результаты экспериментальных исследований пока-
зывают, что распределение крутящих моментов между
разношероховатыми валками при-
близительно соответствует соот-
ношению коэффициентов трения:
Л1Пр.г/Мпр.ш = /Уг//Уш. (446)
Соотношение (446) более
справедливо при прокатке с об-
жатиями выше 15—20 %.
4. Периодическая прокатка
Главной особенностью периодиче-
ской прокатки является законо-
мерное, периодическое изменение
обжатия при прохождении по-
лосы между валками. Изменение
обжатия сопровождается изме-
нением опережения, уширения,
контактных напряжений, т. е.
всех кинематических и динамиче-
ских параметров. Таким обра-
зом, процесс периодической про-
катки является неустановившим-
ся. Обжатие можно изменить пе-
ремещением (сближением или разведением) валков, од*
пако в большинстве случаев это достигается посредст-
вом применения валков некруглой формы1.
Геометрия очага деформации. В теории периодичес-
кой прокатки в качестве основных моделей рассматри-
ваются два варианта прокатки: с нарастанием и убыва-
нием обжатия (рис. 117). И в том, и в другом случае
деформация полосы осуществляется валками перемен-
ного радиуса р, но при прокатке с нарастанием обжатия
1 В настоящем разделе приводятся сведения по теории продоль-
ной периодической прокатки. Кроме того, существует процесс по-
перечно-винтовой периодической прокатки, который применяется для
производства периодических профилей круглого сечения.
185
Яри повороте валков их радиус растет (рис. 117, а),
а при процессе с убыванием обжатия — уменьшается
.(рис. 117,6). Соответственно изменяется форма полосы:
будучи клиновидной, она выходит из валков либо тол-
стым, либо тонким концом вперед.
а 5
Яис. 117. Прокатка с нарастанием (а) и убыванием (б) обжатия
Характеризуя геометрические параметры очага де-
формации, различают угол захвата (ан, ау) в сечении
©хода и угол касания (0Н, 0У), как центральный угол
между осевой линией валков и начальным радиусом рл-
Эти углы не одинаковы, так как нормаль к поверхности
валка в сечении входа NA не проходит через центр
валка.
Форма выходящего конца полосы характеризуется
углом клиновидности ф. В зависимости от профиля
валков, этот угол может быть либо постоянным, либо
переменным.
Определим значение углов касания и захвата. Най-
дем величину условного обжатия, которое было бы в том
случае, если бы вся контактная поверхность была опи-
сана радиусом ра (рис. 118)
AV=fto-2(D/2-Pz). <447)
где D — расстояние между центрами валков (идеаль-
ный диаметр).
Тогда угол касания 0 определяется по формулам
0 = arccos (1 — А/1усл /2рл) (448)
J82
или
О = VА/гусл/рА • (449)
Формулы (448) и (449) действительны при прокатке
как с нарастанием, так и с убыванием обжатия. Введем
понятие среднего радиуса контактной поверхности, ве-
личину которого будем определять по формуле
₽ср У Pmln Ртах •
(450)
5
Рис. 118. Геометрические параметры очага деформации при прокатке с нара^
гганием (а) и убыванием (б) обжатия
183
Центр соответствующей окружности Оср лежит на
нормали к поверхности валка в точке А. Из рис. 118, а
видно, что углы ЛОсрС и АОС практически равны, так
как они опираются на одну и ту же дугу АС, а радиусы
Rcp, Ра и рс различаются незначительно. Следовательно,
имеем
4~ Фв ®н>
откуда
Он = 0н — Фв- (451)
Существует доказательство того, что при отсутствии
опережения угол фв равен углу клиновидности ф. По-
этому, если пренебречь опережением и принять фв=ф,
получим
ан = 0н — Ф- (452)
Путем аналогичных рассуждений, используя схему
на рис. 118, б, для случая прокатки с убыванием обжа-
тия находим
Оу = 0у + фв (453)
или (пренебрегая опережением)
«у = 0у + ф. (454)
Длину очага деформации можно определить по сле-
дующим формулам: при нарастании обжатия (рис.
118, а)
IdM — ld-п === RCp 81П OCjj —|- Rep S1H фв =
«= Rcp (sin ссн + sin фв), (455)
при убывании обжатия (рис. 118,6)
Az-У = ^d y ld-y = Rcp SIH ОСу Rcp фв =
= RCp(sinay — sin фв). (456)
Следует подчеркнуть, что основные геометрические
характеристики очага деформации (0, a, Id и др.) явля-
ются мгновенными, т. е. они зависят от положения вал-
ков в данный момент времени.
Профиль валков и полосы. Принципиальный вопрос
калибровки валков для периодической прокатки заклю-
чается в следующем: каким должен быть профиль вал-
ков, чтобы выходящая из них клиновидная полоса име-
ла плоские грани (ф = сопз1)?
Рассмотрим формирование профиля элементарного
J84
участка полосы (рис. 119). При повороте валков на бес-
конечно малый угол d6 их радиус в выходном сечений
рс изменится на величину dpc. При этом сечение полосы
продвигается вперед на расстояние pcd6 (14-S), где S—•
мгновенное опережение. Следовательно, мгновенный
угол клиновидности полосы будет
Рис. 119. К определению клиио^
видности полосы при прокатка
в валках переменного радиуса
Рс d8 (1 + S) Pc d8ks
(457)
где &з=(14-3) — коэффици-
ент опережения.
Представим выражение
(457) в виде
Фс/рс = tg tyks d&. (458)
После интегрирования по-
лучим
In рс = tg ^ks 6 4- In С;
pc = Cete^‘\ (459)
где 6 — угол поворота валков;
С — постоянная интегрирова-
ния.
Выражение (459) может
быть также представлено в
следующих обозначениях:
р, = Сее^‘. (460)
где рг- — текущее значение ра-
диуса валка на переходном
участке; 6г — текущее значе-
ние угла, отсчитываемого от
Pmin-
Постоянную С определяем
из начального условия:
при б, = 0 имеем р« = рпнп. Отсюда находим C = pmin,
и формула (460) принимает конечный вид
tg <№ S7-
Pi = Pmine - (461>
Для случая прокатки с убыванием обжатия анало-
гичный вывод приводит к выражению
Pi = Ртах е 5 l, (462>
185»
где 6i — угол, отсчитываемый ОТ Ртах.
Формула (461) при tgip = const и ks = kcp = const
представляет собой уравнение логарифмической спира-
ли. То же относится к формуле (462). Следовательно,
чтобы после прокатки получить клиновидные участки
с плоскими гранями, профиль валков должен быть вы-
полнен по логарифмической спирали. При этом прини-
мается допущение, что опережение остается постоянным
(средним). Если же опережение меняется, что соответ-
ствует действительности, то грани клиновидных участ-
ков будут иметь некоторую кривизну, хотя бы малую.
Часто такой кривизной можно пренебречь.
Выполнение профиля валков по логарифмической
спирали на практике встречает затруднения, поэтому
чаще всего применяется профилирование валков по ду-
гам окружностей, со смещением центра окружности от-
носительно центра валка, как показано на рис. 118.
Радиус переходной окружности рассчитывают по выше-
приведенной формуле (450).
Нейтральный угол и условия захвата. Положение
нейтрального сечения определяется из уравнения рав-
новесия продольных сил, приложенных к полосе в очаге
деформации.
Пусть радиус ру, соответствующий нейтральному се-
чению, выходит в некоторую точку G на дуге касания
(рис. 120); тогда участок ДО на контактной поверхности
будет зоной отставания, a GC — зоной опережения. Зо-
ру опережения, в свою очередь, можно разделить на два
Рис. 120. Схема сил к определению нейтрального угла при прокатке с нараста-
рием обжатия
|86
участка: GB, где силы нормального давления действуют*'
против хода прокатки, и ВС, где равнодействующая
нормальных давлений дает составляющую, направлен-
ную по ходу прокатки.
В соответствии с таким делением контактной поверх-
ности на участки можно составить следующее уравнение
равновесия продольных сил (см. рис. 120):
- + Т„х - N'„ - т;х + N"lx -т;х = о. (463>
Учитывая углы наклона всех равнодействующих,
найдем значения слагаемых, входящих в уравнение
(463). Имеем
= М, sin (v -j - j = pcp W?CP (ocH v) X
X sin—H-^~v « pcP bRcv (aH — YH + фв) —; (464)
Tox = To cos (v 4- « pCp bRcv p (aH — ?H + %); (465)
Nlx = sin = pcp bRcp v sin -y « pcpZ>7? . (466)
Tlx = Т[ cos y- pcP bRcv p (?H — -фв); (467)
Nix = Ni sin -^2- = pCp bRcrt фв sin-у- « pcp ; (468)
T"x = 7\ cos « pcp bRcv рфв. (469)
После подстановки найденных значений продольных
сил в уравнение (463), сокращения всех членов на
PcpbRCp и алгебраических преобразований получим
- 2тн ₽ + ₽ (ан + фв) - -^=^- = °'
Отсюда находим (принимая фв = ф):
= ан+_Ф_ (1------\ (470j
Гн 2 \ 20 I
или
? _^н_ (1 _ , JL [ 1 + . (471)
Гн 2 \ 2р V 2 \ 2р У
Если учесть зависимость между углами ан и 0н, то
187
из формулы (470) получим
__ 6н / 1 _ \
2 \ 2₽ /
(472)
Перейдем к определению нейтрального угла при про-
катке с убыванием обжатия (рис. 121). В этом случае
На дуге касания будут только два участка: зона отста-
Рис. 121. Схема сил к определению нейтрального угла при прокатке с убыва-
нием обжатия
вания AG и зона опережения GB. Уравнение равновесия
продольных сил имеет следующий вид:
— NOx + Tqx ~~ Nlx — Tix = °- (473)
Выразим слагаемые этого уравнения в конкретной
форме:
sin (ту + Ф, + -^"7^ \ « рорbRcs(ау —
— Ту — 4>в) ( + + (474)
Т., = Т, cos (Ту + ф, + j
Рср kRcp Р (ау Yy “Фв)> (475)
Nlx = ЛГ, sin (ф, + -£-) « рср bRcp уу (ф, + (476)
Л, = Л cos (ф, + .11.) яа рср bR^ рТу. (477)
188
Подставив значение сил NOx, ТОх, Nlx и Т1х
в уравнение (473), по аналогии с выводом формул (470)
и (472) получим
= (478)
2 \ 2р /
у = _М1 — — Jk (1 —(479)
у 2 \ 2р / 2 \ 20 / v '
Ту = А_ (1 — 9у+—). (480)
Формулы (472) и (480) впервые выведены
В. К. Смирновым.
Сравнивая формулы (471) и (473) с формулой нейт-
рального угла при простом процессе прокатки (133), ви-
дим, что они имеют одинаковую структуру. Отличие
состоит в том, что в правой части формул (471) и (479)
содержится дополнительный член, который при прокат-
ке с нарастанием обжатия имеет знак плюс, а при про-
катке с убыванием обжатия — знак минус. Последнее
свидетельствует о том, что втягивающая способность
валков при прокатке с нарастанием обжатия выше, чем
при прокатке с убыванием обжатия.
Предельные значения углов захвата в обоих случаях
могут быть найдены соответственно из формул (470)
и (478), если положить у = 0. Из формулы (470) полу-
чаем
। _ ан Ф _ Q.
2₽
=2₽+(481)
Аналогично из формулы (478) находим
“ymi = 2P-*- <482)
Таким образом, максимальный угол захвата при про-
катке с убыванием радиуса валков меньше, чем при про-
катке с нарастанием радиуса: аутах<антах- Этот вывод
полностью согласуется с данными практики. При про-
катке с большими деформациями пробуксовка валков
возникает в первую очередь именно на тех участках по-
лосы, на которых обжатие падает.
Опережение. Задача состоит в том, чтобы при извест-
ном значении нейтрального угла определить величину
опережения. Следовательно, требуется вывести формулу
189
опережения типа формулы Финка (166) при переменных
параметрах периодической прокатки.
Следует подчеркнуть, что при периодической про-
катке от величины опережения зависит не только ско-
Рис. 122. к выводу формулы опе-
режения при прокатке в валках
переменного радиуса
рость выхода металла из
валков, но и длина периодов
на полосе, т. е. ее форма.
При теоретическом оп-
ределении опережения бу-
дем исходить из условия не-
сжимаемости металла, а
также примем отсутствие
уширения в зоне опереже-
ния.
Рассмотрим фигуру
GOOiGi на рис. 122, которая
охватывает зону опережения
очага деформации и секто-
ры валков GOC и GiOiCi.
Будем считать, что объем
металла, вступающий в поле
фигуры GOOiGi за время
dx, равен объему металла,
выходящему из поля этой фигуры за то же время. При
этом в понятие «объем металла» включается как тело
полосы, так и тело валков.
Исходя из сказанного, составим равенство
АУП? 4- ДУВ? = ДУП1 4- ДУВ1, (483)
где ДУп^'—объем полосы, прошедший через нейтраль-
ное сечение за время dx; ДУВу—объем валков, всту-
пивший в поле фигуры GOOiGi ^за время dx; ДУп,
и ДУВ1— величины, аналогичные ДУП1? и ДУВ?, но
относящиеся к сечению выхода из очага деформации.
Имеем (см. рис. 122):
ДУп? = 66?и?с/т; (484)
АУВ? = 26 = 6р2 &dx, (485)
где со — угловая скорость валков;
ДУП1 = bhx Uj dx; (486)
ДУВ1 = 2b f j = bp% (odx. (487)
190
Сделаем соответствующие подстановки в равенство
(483)
bhy dr 4- &р“ adr = bhx vx dr 4- bp2c wdr.
Сократим все члены этого выражения на bdr
Mv + Р? ® = Di 4- Рс (488)
С учетом того, что vv = pvcocosy и Ci = рссо (l-{-S),
получаем
hv Pv®cosy4- р2 со = /i1Pcay(l 4-S) 4- Рс®- (489)
После сокращения всех членов на со и простых пре-
образований получим искомую формулу для определе-
ния опережения
9 9
S = .Pv^cost + p.-p, _
Pclh
Ряд величин, входящих в формулу (490), требует до-
полнительного определения:
&i = £> —2рс; (491)
hv = D — 2p?cosy; (492)
Ру = Рсв±1е*1’. (493)
В последнем выражении знак плюс относится к слу-
чаю прокатки с нарастанием обжатия, знак минус —
с убыванием обжатия. При небольших значениях углов
ф и у (фу <0,15) с погрешностью менее 1 % можно при-
нять:
Pv = Рс (1 ± фу). (494)
Опережение, найденное по формуле (490), является
мгновенным: оно непрерывно изменяется по мере пово-
рота валков. Для определения общего (среднего) опере-
жения на конечном участке полосы необходимо рассчи-
тать его величину в отдельных сечениях, а затем найти
среднеинтегральное значение.
Анализ формулы (490) показывает, что при прокатке
с нарастанием обжатия опережение больше, чем при про-
катке с убыванием обжатия; в первом случае р? >рс,
а во втором pv <рс. Эта закономерность отчетливо про-
является в опытных данных.
На рис. 123 приведены результаты исследования опе-
режения при прокатке свинцовой полосы толщиной h?—
= 10 мм в валках с переменным радиусом от 7?«iax —
191
= 83,3 мм до 7?min = 80,0 мм. Толщина полосы на клино-
видных участках изменялась от hlmax =7,4 мм до
^imin =0>9 мм. Угол клиновидности составлял ‘ф = 45/.
Из рис. 123 видно, что ветвь опережения SH на участке
прокатки с нарастанием обжатия располагается выше,
чем ветвь Sy на участке прокатки с убыванием обжатия.
Общее опережение на участке /н составило 3Нобщ =
= 17,7 %, а на участке /у—3Уобщ = 12,9 %.
Усилия и крутящие моменты. При прокатке в валках
переменного радиуса контактные давления, как и дру-
гие. 123. Изменение величины опере-
жения при прокатке с нарастанием и
Убыванием обжатия (по А. П. Чекма-
ревУ и А. Ф. СмольяниновУ)
гие параметры, непрерыв-
но изменяются. В связи с
этим, а также изменени-
ем площади контактной
поверхности, непрерывно
изменяется усилие про-
катки. Обычно теоретиче-
ски рассчитывают то уси-
лие, которое соответству-
ет максимальному обжа-
тию. Для расчета могут
быть использованы фор-
мулы Целикова (285),
Чекмарева (300) и дру-
гие.
Если иметь в виду сим-
метричный процесс пери-
одической прокатки и
пренебречь инерционными
силами, возникающими
вследствие изменения ско-
рости движения концов полосы, то следует сделать вы-
вод, что равнодействующие всех сил, приложенные к
валкам, направлены вертикально, как и в простом про-
цессе прокатки (см. рис. 93).
При определении величины крутящих моментов не-
обходимо учитывать, что в данном случае элементарные
силы нормального давления не проходят через центр
вращения валка и наряду с силами трения создают часть
крутящего момента (рис. 124).
Допустим, что радиус-вектор р изменяется на протя-
жении очага деформации по закону логарифмической
спирали. Тогда угол между нормалью и радиусом р
в любой точке кривой остается постоянным (таково
192
свойство логарифмической спирали), в данном случае
равным ф. Этим определяется направление действия
элементарных сил р.
Логарифмическую спираль, как и в предыдущих вы-
водах, аппроксимируем дугой окружности среднего ра-
диуса 7?ср.
Сначала рассмотрим определение крутящего момен-
та при прокатке с нарастанием обжатия (рис. 124, а).
Рис. 124. К выводу формул крутящего момента при периодической прокатке с
нарастанием (а) и убыванием (б) обжатия
Плечо элементарной силы трения t относительно центра
валка можно принять
с = рфсоз(р«рф«Яср.
Плечо элементарной силы нормального давления р
будет
ан = РФ5М«РфФ~Пере-
учитывая деление очага деформации на зоны опе-
режения и отставания, составим уравнение крутящего
момента для одного валка
<Рн = f ^Нср dq — f /&Рср dq 4- | pbRcp Ipcfrp. (495)
Тн Ь b
Примем, что элементарные силы I и р распределя-
ются по дуге касания равномерно и прокатка идет без
уширения (b = const). При этих допущениях после ин-
тегрирования получим
<Р„ = ад2ер (0к - 2?„) + pbRip #)„ (496)
По смыслу вывода t = tCp и р = рСр. Используем закон
13 А. п. Грудев
193
трения Амонтона (/cp=fPcp« рРср), тогда формула (496)
принимает конечный вид
Л4ПРн = Pop Wop f («в - 2?н + 9н */₽) (497)
Аналогично выводится формула крутящего момента
для случая прокатки с убыванием обжатия. Пользуясь
схемой на рис. 124, б, напишем
°у vy ej
Л4пРу = J ЗДср dcp — f й/Йр d<p — J рЬР?сх> фб/ф. (498)
vy 6 о
После интегрирования и простых преобразований по-
лучим
Кр, = Pop Wep f (9у - 2?у - 9, («9)
Из сравнения формул (497) и (499) видно, что при
прочих равных условиях крутящий момент при прокат-
ке с нарастанием обжатия больше, чем при прокатке
с убыванием обжатия. Если принять ф = 0, т. е. отсутст-
вие клиновидности, то формулы (497) и (499) приобре-
тают вид ранее полученной формулы Баюкова (308) для
случая прокатки в валках постоянного радиуса.
ГлаваХ
МОДЕЛИРОВАНИЕ И РАСЧЕТ ПАРАМЕТРОВ
ПРОКАТКИ С ПОМОЩЬЮ ЭВМ1
1. Особенности использования различных ЭВМ
для расчетов в области теории прокатки
При решении задач, относящихся к теории прокатки,
а также при разработке рациональных режимов дефор-
мации приходится выполнять самые разнообразные вы-
числения. Некоторые из них достаточно просты и могут
быть выполнены без помощи ЭВМ. Другие сложны,
и без применения ЭВМ расчетная работа становится
слишком трудоемкой или даже вообще невыполнимой.
Расчеты, при проведении которых необходимо ис-
пользовать ЭВМ, можно разделить на следующие кате-
гории:
1 Глава написана совместно с канд. техн, наук Г. Ю. Макла-
ковым.
.194
простые, несложные вычисления, аналогичные выпол-
няемым вручную, но повторяющиеся многократно;
вычисления слишком громоздкие, чтобы их можно
было выполнить вручную, так как при этом потребу-
ются огромные затраты времени и не будет обеспечена
необходимая точность.
При использовании вычислительной техники следует
иметь в виду, что одна и та же задача может быть ре-
шена с помощью ЭВМ различных типов. Выбор подхо-
дящего типа ЭВМ в каждом конкретном случае зависит
от вычислительной сложности задачи, требуемой точно-
сти решения, объема исходных данных, формы выдачи
результатов, скорости получения решения, стоимости
вычислений. Правильный выбор ЭВМ позволяет не толь-
ко, получить приемлемые результаты за наиболее корот-
кое время, но и рационально использовать ресурсы вы-
сокопроизводительных ЭВМ, необходимых для решения
более сложных задач.
В зависимости от способа представления информации
и способа ее переработки принято делить ЭВМ на три
класса: цифровые вычислительные машины (ЦВМ или
ЭЦВМ), аналоговые вычислительные машины (АВМ)
и гибридные вычислительные машины (ГВМ).
В ЦВМ информация представляется дискретно в ви-
де чисел. Причем под понятием «число» подразумевается
не только какая-либо последовательность цифр, но и по-
следовательность любых символов, в частности, букв
какого-либо алфавита. Информация в ЦВМ перераба-
тывается с помощью программы-алгоритма, записанного
в форме, понятной ЭВМ. Именно программный способ
переработки информации обусловливает широкую уни-
версальность этого типа машин. К достоинствам ЦВМ,
помимо универсальности, можно отнести возможность
ввода практически неограниченного объема исходных
данных, разнообразную форму выдачи результатов (ди-
сплей, печать, графопостроитель), высокое быстродейст-
вие для большинства решаемых задач, большой объем
памяти, возможность диалоговой работы. К недостат-
кам, ограничивающим применение ЦВМ, относится не-
обходимость использования для решения задач числен-
ных методов; в некоторых случаях быстродействие ЦВМ
значительно уступает АВМ.
Для решения задач сравнительно несложных, с не-
большим объемом входных и выходных данных наиболее
целесообразно использовать программируемые микро-
13*
195
калькуляторы (ПМК). К числу таких задач относятся
расчеты опережения, уширения, энергосиловых парамет-
ров при стационарной прокатке. Получили распростра-
нение ПМК типа «Электроника БЗ-34», «Электроника
МК-54», «Электроника МК-56», «Электроника МК-61».
Их преимуществами являются простота в обращении,
низкая стоимость, малая масса и габариты, низкая
потребляемая электрическая мощность. Диапазон вы-
числений составляет 1 • 10-99^х<9,9999999-10". Некото-
рые основные характеристики указанных ПМК приведе-
ны в табл. б.
Таблица 5. Характеристика некоторых отечественных
программируемых микрокалькуляторов
Тип ПМК Число встро- енных функ- ций Регистры Число шагов программы Габариты, мм Масса, г
адресуе- мые стека предыду- щего ре- зультата
S3—34 27 14 4 1 98 100X185x46 390
МК—54 27 14 4 1 98 78X167X36 250
МК—56 27 14 4 1 98 240X205X60 3000
МК—61 43 15 4 1 105 167X78X36 250
Недостатками ПМК следует считать очень малый
объем памяти, необходимость при каждом новом вклю-
чении повторного ручного ввода программы, отсутствие
печатающего устройства. Однако при умелом програм-
мировании класс задач, решаемых на ПМК, достаточ-
но широк.
Для решения более сложных задач, например, отно-
сящихся к непрерывной прокатке, когда приходится учи-
тывать взаимодействие очагов деформации в ряде кле-
тей, целесообразно применение ЦВМ серии ЕС или СМ
(ЕС—1022, ЕС—1033, ЕС—1040, СМ—2, СМ—3, СМ—4).
В последние годы взамен этих машин начинают широко
применяться микро-ЭВМ («Электроника НЦ», «Элект-
роника—60», «Искра—226») и персональные ЭВМ типа
«Агат», «Электроника БК—0010».
Для решения особо сложных задач, требующих не
только большого объема памяти, но и значительных за-
трат времени, приходится использовать быстродейст-
вующие ЭВМ типа ЕС—1045, ЕС—1055, ЕС—1060,
БЭСМ—6.
196
В АВМ информация представляется и перерабатыва-
ется в непрерывной форме, в виде меняющихся во вре-
мени физических величин (обычно электрического тока
или напряжения). Конструктивно АВМ состоит из от-
дельных частей, называемых операционными блоками.
Каждый такой блок выполняет какую-либо математиче-
скую операцию. Для получения решения некоторой за-
дачи операционные блоки соединяют между собой в со-
ответствии с аналитическим выражением задач. При пе-
реходе от решения одной задачи к другой блоки
разъединяют и соединяют по-новому, согласно новому
аналитическому выражению. Таким образом, принци-
пиальное отличие АВМ от ЦВМ состоит в том, что
в АВМ в зависимости от содержания задачи меняется
структура самой машины. Решение задач на АВМ
сходно с экспериментом. Оно сводится к измерению зна-
чений физических величин измерительными приборами,
к регистрации изменения во времени измеряемых вели-
чин с помощью самопишущих приборов, к наблюдению
за изменением величин с помощью осциллографа. Осо-
бенностью АВМ является их узкая специализация, т. е.
они в основном предназначены для решения задач опре-
деленного класса. Находят применение АВМ типа
МН—7М и более совершенные МН—ЮМ. Для особо
сложных задач применяются машины типа ЭМУ—10,
МН—17М. Наиболее эффективно использовать АВМ
для решения дифференциальных уравнений, особенно
невысокого порядка.
ГВМ — машины, в которых используется смешанная
форма представления информации: аналоговая и цифро-
вая. В связи с этим ГВМ в некотором смысле объединя-
ют достоинства АВМ и ЦВМ. Однако надо отметить,
что ГВМ также являются в основном узкоспециализи-
рованными машинами.
Задачи, которые эффективно решаются на ГВМ,
можно разделить на следующие основные группы: мо-
делирование в реальном масштабе времени автомати-
ческих систем управления, содержащих как аналоговые,
так и цифровые устройства; статистическое моделирова-
ние; решение уравнений в частных производных; опти-
мизация систем управления.
Используя вычислительные машины для различных
расчетов, следует иметь в виду, что независимо от типа
применяемой ЭВМ всегда необходимо разрабатывать
контрольный пример. Он служит для проверки коррект-
197
ности составления алгоритма решения задачи и пра-
вильности отладки программы. Исходные данные для
контрольного примера могут быть реальными или искус-
ственно созданными числами (или функциями), но обя-
зательно должны охватывать все этапы решения по-
ставленной задачи. Только при совпадении результата
контрольного примера с результатом его решения на
ЭВМ можно сделать вывод, что задача будет решена
при любых вариациях исходных данных.
2. Этапы подготовки задач к решению на ЭВМ
Подготовку задачи к решению на вычислительной ма-
шине можно условно разделить на следующие этапы:
постановка задачи; математическое описание задачи;
подбор численного метода решения; разработка алго-
ритма; программирование; подготовка программы и ис-
ходных данных к вводу в ЭВМ; отладка программы.
Постановка задачи. На этом начальном этапе необ-
ходимо уточнить сущность задачи, определить, имеет ли
она решение и единственно ли оно. Далее, сделав пред-
положение, что задача решена, надо определить удоб-
ную форму выдачи результатов (таблица, графики,
и т. п.) и задать приемлемую точность вычислений. Сле-
дует указать перечень исходных данных и диапазон их
изменений. Все исходные данные должны быть выраже-
ны в одной системе единиц.
Математическое описание задачи. Определяется мето-
дика решения задачи, подбираются соответствующие ма-
тематические формулы. Графические функциональные
зависимости, как правило, необходимо выразить в ана-
литическом виде. Все буквенные символы в формулах
должны быть полностью и однозначно определены исход-
ными данными или рассчитанными их значениями.
Здесь же подбирается или специально разрабатыва-
ется простейший контрольный пример, решение которого
известно. Он будет использован в дальнейшем с целью
проверки алгоритма и программы.
Подбор численного метода решения. Численные мате-
матические методы приходится применять при решении
систем дифференциальных уравнений, систем линейных
и нелинейных алгебраических уравнений, трансцендент-
ных уравнений и в некоторых других случаях. При этом
вместо индивидуальной разработки метода целесообраз-
но использовать какой-либо из известных в литературе
численных методов: Гаусса, Ньютона, последовательных
198
приближений и т. д. Из всех численных методов решения
конкретной задачи выбирается тот, который наилучшим
образом удовлетворяет предъявляемым требованиям по
точности, скорости сходимости вычислений и др.
При решении задач на основе аналитических формул,
дающих результат в явном виде, применение численных
методов не требуется.
Разработка алгоритма решения задач. Алгоритм —
это система правил, определяющих содержание и поря-
док действий, которые необходимо выполнить над исход-
ными данными для получения конечного результата при
решении всех задач определенного типа. Более подробно
этот этап рассматривается в следующем параграфе на-
стоящей главы.
Программирование. Составленный алгоритм не может
быть непосредственно использован вычислительной ма-
шиной. Каждому пункту алгоритма должна соответство-
вать определенная команда для машины. Свод таких
команд и представляет собой программу решения задачи.
Для записи программ служат языки программирова-
ния. В теории программирования языком называют при-
нятую совокупность символов и правила, определяющие
способы объединения этих символов в языковые конст-
рукции. Одним из простейших языков программирования
является мнемокод. Для его характеристики рассмотрим
конкретный пример расчета на ПМК «Электроника
БЗ—34». Пусть в алгоритме указана формула (30) для
угла контакта
а = V^hlR.
Введем значение А/г в первый регистр памяти маши-
ны, R — во второй регистр, а расчетное значение а будет
находиться в третьем регистре; тогда программа на мне-
мокоде будет иметь вид, представленный в табл. 6.
Достоинством мнемокода является то, что при его
применении наилучшим образом реализуются возможно-
Таблица 6. Пример программы, записанной на мнемокоде
Номер команды Клавиши Код команды Номер команды Клавиши Код команды
00 ИП1 61 03 21
01 02 ИП2 62 13 04 05 с/п 43 50
199
сти данной ЭВМ, экономно используется память машины,
сама программа получается наиболее эффективной. Од-
нако в этом случае от программиста требуется глубокое
знание технологических особенностей вычислительной ма-
шины и системы ее команд. Поэтому наибольшее приме-
нение получили машинно-независимые языки програм-
мирования, к числу которых относятся ФОРТРАН,
БЕЙСИК, ПЛ-1, АЛГОЛ и ряд других. Программа, за-
писанная на таких языках, очень мало зависит от конст-
рукции конкретной ЭВМ. Запись формул приближается
к общепринятой математической записи, что облегчает
процесс составления программ. Например, вышеприве-
денная формула для угла контакта на языке ФОРТРАН
представляется в виде:
L = SQRT (DH/R), (500)
где L, DH и R — условные обозначения (идентификато-
ры) соответственно величин а, Д/г и R; SQRT — обозна-
чение функции взятия квадратного корня.
Подготовка программы и исходных данных к вводу
в ЭВМ. На этом этапе текст программы и исходные дан-
ные переносят на носители информации ЭВМ (перфокар-
ты, перфоленты, магнитные ленты, магнитные карты).
Отладка программы. Первоначальный вариант про-
граммы часто содержит ошибки, допущенные как при ее
составлении, так и при выполнении предыдущих этапов.
Различают синтаксические и логические ошибки. След-
ствием первых являются остановы машин или, как их ча-
ще называют, «авосты» (аварийные остановы). Вторая
категория ошибок приводит к получению неверных ре-
зультатов счета.
Поиск и устранение этих ошибок называется отлад-
кой программы. Для проверки правильности работы про-
граммы решают на ЭВМ контрольный пример. При сов-
падении результатов счета по данной программе и извест-
ного ответа, полученного другим способом, признают
программу правильной.
3. Алгоритмизация задач расчета
параметров прокатки
Для решения на ЭВМ математическое описание задачи
должно быть четко формализовано. Это достигается пу-
тем составления соответствующего алгоритма.
Чаще всего алгоритм записывается в виде графиче-
200
ской блок-схемы по ГОСТ 19.002—80 и ГОСТ 19.003—80
или в текстуальной (словесной) форме по ГОСТ
2.105—68. При словесной записи алгоритмов использу-
ются общепринятые математические символы и выраже-
ния, которые сопровождаются пояснительным текстом.
Однако такая запись трудна для восприятия и весьма
громоздка. Поэтому обычно применяют изображение ал-
горитма в виде блок-схемы.
Рассмотрим основные принципы построения блок-схемы алгорит-
ма и некоторые понятия, относящиеся к этому вопросу.
Блок-схема алгоритма — это графическое изображение в виде
геометрических фигур (блоков) последовательности функциональных
элементов. Каждый из блоков имеет определенное смысловое значе-
ние. Наиболее распространенными блоками являются: арифметиче-
ские, логические, ввода — вывода и вспомогательные («соединитель»,
«межстраничный соединитель», «пуск—останов», блок подпрограм-
мы и др.).
Линией потока называют линию, соединяющую блоки и указы-
вающую ход вычислительного процесса. Линии потока должны быть
параллельны линиям внешней рамки схемы. Линии потока, иду-
щие сверху вниз и слева направо, считаются основными и стрелкой
могут не отмечаться; в остальных случаях их заканчивают стрелкой
обязательно. При составлении блок—схемы надо стремиться к тому,
чтобы линии потока пересекались как можно меньше.
Арифметический блок («процесс») служит для записи арифме-
тического выражения (совокупности переменных, констант или функ-
ций, соединенных знаками математических операций). Блок обозна-
чается прямоугольником, в котором записывают формулу в виде
У—А, где У — переменная; А — арифметическое выражение. Запись
означает требование: присвоить вычисленное значение арифметиче-
ского выражения А переменной У.
Примеры записи арифметических выражений в блоках приведе-
ны на рис. 125. По ГОСТ 19.002—80 допускается размещение в од-
г_
р
zl/?- h0 ~hj
а-Ум/я
Рис. 125. Изображение арифметических Рис. 126. Изображение блоков:
блоков: а — логического; б — ввод-вывода
а — общее изображение; б, в — запись
последовательности арифметических!
выражений
ном блоке нескольких формул. Записи внутри блока в этом случае
должны быть представлены так, чтобы их можно было читать слева
направо и сверху вниз, независимо от направления линии потока.
Так, часть блока, изображенная на рис. 125, б, может быть записана
одним блоком (рис. 125, в).
201
Рис. 127. Изображение разрыва связей:
а — внутристраничных; б — межстра-
ничных
Логический блок («решение») служит для записи условия, в за-
висимости от выполнения которого разветвляется процесс вычисле-
ния. Он изображается ромбом, где записывают проверяемое условие
(рис. 126,а). В структурной схеме после логического блока образу-
ются самостоятельные ветви. Выходы логического блока обознача-
ют «да» — для случая выполнения условия, и «нет» — для случая
невыполнения условия. Ино-
гда вместо «да» и «нет»
пишут математические зна-
ки условий (например, если
в логическом блоке записа-
но В —С, то вместо «да»
можно писать =, а вместо
«нет»#:). Признак условий
(«да», «нет», >, =, < и
т. п.) проставляют над ли-
нией потока или справа от
нее.
Блок ввода — вывода слу-
жит для записи вводимых
в расчет исходных данных
и выводимых на внешнее
устройство ЭВМ (например,
на печатающее устройство)
окончательных или промежуточных результатов расчета. Графиче-
ское изображение блока «ввод — вывода» с записанным в него сло-
вом «Ввод» или «Вывод» и соответствующим списком величин при-
ведено на рис. 126, б.
Блоки «соединитель» и «межстраничный соединитель» применя-
ются для указания мест разрыва связей между блоками. Такие ука-
зания необходимы для устранения слишком большого числа пересе-
кающихся линий в структурной схеме или для установления связей
между блоками, расположенными на различных страницах блок-схе-
мы. Обозначение внутристраничных связей показано на рис. 127, а,
а межстраничных — на рис. 127, б. Внутри блока «соединитель» за-
Рис. 128. Изображение в структурных схемах:
а — блока «пуск-останов»; б—блока подпрограммы; в — текста ком-
ментариев
писывают номер блока, из которого идет данная связь, либо номер
блока, к которому идет данная связь. В блоке «межстраничный со-
единитель» дополнительно еще отмечают номер страницы.
Блок «пуск—останов» предназначен для указания начала и кон-
ца алгоритма или останова (прерывания) процесса вычислений. Гра-
202
фически изображается овалом, в который вписывают слова соответ-
ственно «Начало» («Пуск») и «Конец («Останов», «Стоп») (рис.
128, а).
Блок подпрограммы («предопределенный процесс») вводится для
использования в алгоритме ранее созданных и отдельно описанных
алгоритмов и программ. Его изображают прямоугольником, мень-
шие стороны которого обозначают двойными линиями (рис. 128,6).
В прямоугольнике записывают название подпрограммы. Блоки ну-
меруют по порядку. Номер блока располагают в разрыве контура
блока слева вверху.
Допускается дополнение структурной схемы необходимыми ком-
ментариями к блокам и к линиям потока. Комментарии помещают
в свободном месте и соединяют с поясняемым объектом пунктир-
ной линией (рис. 128, в).
Сущность составления алгоритма заключается в под-
боре и установлении такого порядка применения матема-
тических выражений, который обязательно приведет к ре-
шению поставленной задачи при любой комбинации ис-
ходных данных.
Составление алгоритма в общем случае включает не-
сколько этапов. Сначала составляется укрупненная
схема, которая отражает только принципиальный ход
решения задачи и блоки которой являются блоками под-
программ. Далее определяется тип вычислительного про-
цесса в каждом блоке и в целом. На конечном этапе
составляется детальная, подробная схема алгоритма,
полностью характеризующая вычислительный процесс
без каких-либо сокращений.
При определении типа вычислительного процесса на-
до учитывать, что существуют следующие его разновид-
ности:
линейный вычислительный процесс — такой процесс,
когда все расчетные операции выполняются последова-
тельно друг за другом;
разветвляющийся вычислительный процесс — ход опе-
раций на некотором этапе разветвляется в зависимости
от выполнения какого-либо условия;
циклический вычислительный процесс — это много-
кратное (циклическое) выполнение набора арифметиче-
ских или логических операций. Повторяющуюся совокуп-
ность арифметических или логических операций называ-
ют телом цикла.
Для линейного или разветвляющегося вычислитель-
ного процесса алгоритм представляет собой последова-
тельную запись функциональных элементов, расположен-
ных таким образом, чтобы результаты предыдущих
вычислений являлись исходными данными для последую-
203
щего действия. В этом случае схему изображают в виде
последовательного расположения соответствующих бло-
ков.
Простейшим примером линейного вычислительного'
процесса может служить структурная схема алгоритма
для определения площади контактной поверхности по
формуле (61) (рис. 129). В качестве исходных данных
Рис. 129. Структурная схе-
ма алгоритма расчета пло-
щади контактной поверхно-
сти
Рис. 130. Фрагмент структурной схемы
алгоритма расчета давления на валки с
разветвляющимся вычислительным процес-
сом. Следует вместо (303) читать (319), а
вместо (285) надо (297)
приняты величины h0, h\, Ь0Ь1} R. Блок-схема на рис. 129
представлена как детальная.
Разветвляющийся вычислительный процесс можно
проиллюстрировать расчетом давления на валки когда
выбор расчетной формулы зависит от величины фактора
формы ld/hcv- Как отмечалось ранее (гл. VII), при
4г/^ср>1 расчет давления ведется по формуле А. И. Це-
ликова (297) или аналогичным формулам, учитывающим
влияние сил трения на напряженное состояние металла.
204
С другой стороны, при Zd/^cp^l на первый план выходит
влияние внешних зон, и расчет ведется по формуле (319).
Во многих практических случаях, например при прокатке
толстых листов, в первых проходах имеет место соотно-
шение Zd//icp^l, а в последующих 4г//*ср>1- Это об-
стоятельство и учитывает алгоритм расчета давления,
приведенный на рис. 130 (фактор формы обозначен Ф).
Рис. 132. Фрагмент схемы алгоритма
расчета коэффициента трения по фор-
муле (259) при изменении окружной
скорости валков от yB^ до иВк с ша-
гом Аув
Рис. 131. Структурная схема алго-
ритма циклического вычислитель-
ного процесса
При составлении структурной схемы алгоритма, вклю-
чающего циклический вычислительный процесс с задан-
ным числом циклов, необходимо:
выделить тело цикла, т. е. записать выражения, кото-
рые предстоит многократно использовать в вычислениях;
добавить блок подготовки — арифметический блок,
в котором задается начальное значение переменной;
добавить блок продвижения — арифметический блок,
в котором будет происходить изменение переменной с за-
данным шагом;
добавить блок управления цикла — логический блок,
предназначенный для проверки условия окончания цикла.
Принципиальная схема построения циклического вы-
числительного процесса с заданным числом циклов по-
казана на рис. 131.
В качестве конкретного примера рассмотрим алгоритм
205
расчета коэффициента трения при холодной прокатке по
^формуле (259) в зависимости от скорости прокатки
(рис. 132). Допустим, окружная скорость валков изме-
няется от значения уВн до уВк. Примем шаг изменения
скорости Дув. Для получения численных результатов не-
обходимо проводить многократные вычисления по фор-
муле (259), переменную часть которой вводим в ариф-
метический блок тела цикла. Для вывода полученных
значений на печать включаем в тело цикла также блок
вывода. Первое значение fy вычисляется при £>в=#Вн, что
следует записать в блоке подготовки. Каждое последу-
ющее значение аргумента должно быть увеличено на Дов,
поэтому в блоке продвижения указываем ув = Ув+Лув.
Циклический процесс завершается тогда, когда будет
вычислена функция при ув = иВк, т- е- условие окончания
процесса следующее: при вычисления продол-
жать, при Ув>уВк вычисления закончить. Это условие
и отражено в логическом блоке управления цикла
(рис. 132).
Циклические вычислительные процессы применяются
также при решении задач итерационного характера. Схе-
мы построения алгоритмов таких процессов близки к вы-
числительным процессам с заданным числом циклов.
4. Общая характеристика методов моделирования
Под моделированием понимают исследование различных
объектов, процессов или явлений на моделях. Понятию
модель придается различный смысл. Но во всех случаях
подразумевается, что модель определенным образом изо-
бражает поведение объекта или процесса в натуре. Изу-
чение какого-либо явления на его модели можно рас-
сматривать как особый вид эксперимента — модельный
эксперимент. Он позволяет изучать такие объекты, пря-
мые эксперименты на которых затруднены, а иногда
и вовсе невозможны. Различают три основных метода мо-
делирования: физическое, аналоговое и математическое.
Физическое моделирование — такое моделирование,
которое состоит в замене изучения некоторого объекта
или явления экспериментальным исследованием его мо-
дели, имеющей ту же физическую природу. Необходимым
условием физического моделирования является подобие
модели и натуры: отношения величин в натуре к соответ-
ствующим величинам на модели должны быть постоян-
ное
ными, т. е. должна соблюдаться пропорциональность
между величинами на модели и в натуре. Наличие такой
пропорциональности позволяет проводить пересчет экс-
периментальных результатов, полученных на модели, на
натуру путем умножения каждой найденной величины на
постоянный множитель — коэффициент подобия. Безраз-
мерные комбинации физических величин называют кри-
териями подобия. Равенство всех критериев подобия мо-
дели и натуры является наиболее строгим условием фи-
зического моделирования. Однако в большинстве
случаев, в том числе при исследовании процессов обра-
ботки металлов давлением, одновременно выполнить все
условия подобия не удается. В связи с этим физическое
моделирование обычно является приближенным.
Аналоговое моделирование основано на аналогии яв-
лений, имеющих различную физическую природу, но опи-
сываемых одинаковыми математическими уравнениями
(дифференциальными, алгебраическими или какими-либо
другими).
Например, при исследовании сложных задач нестационарной
теплопроводности используется аналогия между теплопроводностью
и электропроводностью, которая видна из сравнения дифференци-
ального уравнения теплопроводности.
д2Т д2Т \ дТ
+ = (501)
дх2--------------ду2-а дх
и уравнения, которое описывает нестационарное распределение элек-
трического потенциала
д2 и д2 и ди
-4- = Ь ,
дх2--------------------------ду2-дх
(502)
где Т — температура; х — время; и — электрический потенциал; х, у —
координаты; а, b — константы.
Уравнения (501) и (502) полностью совпадают при равенстве
коэффициентов 1/а=&. Таким образом, между физическими закона-
ми (501) и (502) имеется прямая аналогия: сохранение заряда
в электрической схеме соответствует сохранению тепла в термиче-
ской системе. Если в электрической схеме величина тока связана
с напряжением по закону Ома, то в термической системе величина
теплового потока зависит от напряженности температурного поля
в соответствии с законом Фурье. Другими словами, закон Ома
в электрической системе является аналогом закона Фурье в термиче-
ской системе.
Аналоговое моделирование обычно реализуется с по-
мощью электрических и электронных устройств. Досто-
инство электрических моделей заключается в простоте
изменения их параметров за счет переключения элемен-
тов электрических цепей, а также в удобстве измерений
207
и регистрации величин, моделируемых в виде электри-
ческих напряжений или токов. Такой метод моделирова-
ния отличается большой физической наглядностью. Ис-
следователь сразу видит, как влияет изменение какого-
либо отдельного фактора на поведение изучаемой
системы в целом, поскольку в этом случае каждый
физический элемент имеет свое электрическое «изобра-
жение».
Основное ограничение в применении аналогового мо-
делирования состоит в том, что с его помощью нельзя
исследовать любую предложенную физическую задачу.
Для этого должна существовать соответствующая анало-
гия, ее требуется найти, и лишь затем можно построить
модель и проводить моделирование.
Математическое моделирование — это исследование
математических моделей с помощью ЭВМ. Под матема-
тической моделью подразумевают математическое выра-
жение, описывающее поведение данного физического объ-
екта. Математическая модель должна наиболее адекват-
но отражать именно те черты объекта, которые важны
для решения поставленной задачи.
Математическое моделирование является наиболее
универсальным и общим методом моделирования. Оно
может быть выполнено с помощью вычислительных ма-
шин разного типа: ЦВМ, АВМ и ГВМ. Краткая сравни-
тельная характеристика этих машин приведена в п. 1
настоящей главы. Некоторые дополнительные данные,
представляющие интерес с точки зрения моделирования,
приведены в табл. 7.
Следует подчеркнуть, что ценность аналоговых вычис-
лительных устройств определяется не столько их вычис-
лительными возможностями, сколько тем, что они помо-
гают осмыслить физическую сущность и математическое
описание исследуемого явления в процессе его изучения.
Вместе с тем нельзя недооценивать и чисто вычислитель-
ные возможности АВМ, которые достигаются благодаря
их высокому быстродействию. Преимущество АВМ перед
ЦВМ особенно начинает сказываться, когда требуется
работа вычислительной машины в реальном масштабе
времени или даже в значительно более быстром темпе,
позволяющем в малый интервал времени получить и со-
поставить между собой множество решений. В АВМ со-
став используемого оборудования находится в прямой
зависимости от сложности задачи, так как все элементы
работают одновременно и параллельно. Поэтому, в отли-
208
Таблица 7. Некоторые сравнительные характеристики АВМ
и ЦВМ
Показатель АВМ ЦВМ
Принцип перера- Параллельный (вся Последовательный (в од-
ботки информации информация перера- батывается одновре- менно во всех элемен- тах АВМ) нопроцессорных ЦВМ в каждый момент времени в работе находятся толь- ко два числа)
Быстродействие Быстрое решение диф- ференциальных урав- нений Более медленное реше- ние дифференциальных уравнений (в 10...100 раз)
Точность Порядка 0,01 % Любая необходимая точ- ность, получаемая за счет времени вычислений
Память Небольшая Большая
Программное Плохое, отсутствует Хорошее, высокий уро-
обеспечение стандартизация вень стандартизации
Метод решения за- дачи Подобия Алгоритмический
Класс решаемых задач Преимущественно дифференциальные уравнения (машины специализированы) Практически любой
Взаимодействие с исследователем Очень хорошее Слабое, но улучшается с. применением микро- ЭВМ. Очень хорошее при использовании персо- нальных ЭВМ
чие от ЦВМ, решение самых сложных задач, в принципе,
не занимает большего времени, чем решение простейших
задач.
При работе на ЦВМ следует учитывать, что между
вводом данных и выдачей результата проходит некоторый
интервал времени, необходимый для осуществления
арифметических и логических операций. На протяжении
этого интервала времени информация об исследуемом
процессе недоступна, поскольку она еще не выработана
в законченной форме.
Основные преимущества ЦВМ состоят в высокой точ-
ности получаемых результатов и в возможности исполь-
зования таких машин для решения широкого круга самых
разнообразных задач. Решение более сложных задач от-
личается от решения простых задач лишь затрачиваемым
временем; при этом состав оборудования остается при-
мерно одинаковым.
14 А. П. Грудев
209
Для моделирования в реальном масштабе времени
целесообразно использовать ГВМ, т. е. машины, вычис-
лительный процесс в которых расчленяется на отдельные
операции, выполняемые АВМ и ЦВМ в комплексе. При-
мером задачи, успешно решаемой на ГВМ, может слу-
жить моделирование системы управления прокатным
станом. В этом случае динамика процессов воспроизво-
дится на аналоговой машине, а специализированная,
управляющая станом машина моделируется на универ-
сальной ЦВМ. Вследствие кратковременности переход-
ных процессов в приводах прокатных станов полное мо-
делирование таких процессов в реальном масштабе
времени потребовало бы применения сверхбыстродейст-
вующих ЦВМ.
5. Основные принципы построения
математических моделей
Построение модели, как правило, состоит из нескольких
этапов, которые могут быть представлены графически
в форме структурной схемы (рис. 133). Первым шагом
во всех случаях является уточнение и четкая формули-
ровка исследовательской или иной задачи, конкретизация
конечных целей исследования. Указывается перечень ис-
ходных данных и при необходимости — диапазон их из-
менения. Определяется форма выдачи результатов вычис-
лений и приемлемая точность моделирования. Разраба-
тывается критерий качества модели для суждения о ее
пригодности.
Вторым шагом является выбор метода формирова-
ния модели. Если исследуемый объект (процесс) хорошо
изучен и имеет теоретическое истолкование, то целесооб-
разно избрать аналитический путь построения модели,
т. е. воспользоваться соответствующими теоретическими
формулами. Однако встречаются случаи, когда из-за сла-
бой изученности явления и отсутствия соответствующих
теоретических разработок этот путь не может быть реа-
лизован. Тогда необходимо строить модель на основе
идентификации, т. е. экспериментального определения су-
щественных для решаемой задачи свойств и характери-
стик исследуемого объекта или явления. Иначе возника-
ет необходимость в получении эмпирических зависимо-
стей. Они могут быть установлены методом
регрессионного анализа или другими методами математи-
ческой статистики.
210
Следующим шагом построения модели является ее
опытная проверка. Оценка точности модели дается в со-
ответствии с выбранным ранее критерием. Далее, либо
она признается удовлетворительной и процесс создания
модели заканчивается, после чего она используется по
Рис. 133. Структурная схема этапов построения математической модели
своему прямому назначению для решения исследователь-
ской задачи, либо модель отвергается как недостаточно
совершенная. В последнем случае требуется корректи-
ровка модели и повторное прохождение ранее выполнен-
ных этапов.
Таким образом, построение модели можно рассмат-
ривать как процесс последовательных приближений к ко-
нечной цели — адекватной модели. Начинаясь в услови-
ях большей или меньшей неопределенности (а это есте-
ственно, так как именно недостаток информации
14*
211
о свойствах объекта вызывает необходимость моделиро-
вания), построение модели неизбежно связано с введе-
нием ряда допущений и гипотез. Некоторые из них ока-
зываются правомерными, другие на последующих этапах
не подтверждаются, в связи с чем требуется возврат
к тем пунктам, где сделаны некорректные допущения.
Рассмотрим более детально структурную схему по-
строения модели на основе аналитического описания объ-
екта (рис. 134). Под аналитическим описанием подразу-
Рис. 134. Структурная схема построения модели на аналитической основе
мевается совокупность математических формул, характе-
ризующих свойства и поведение объекта при некоторых
воздействиях. Следует обратить внимание на этап, пре-
дусматривающий разработку моделирующего алгоритма.
Фактически моделирующий алгоритм представляет собой
систему алгебраических формул, по которым ведутся вы-
числения, и логических условий, позволяющих установить
212
определенную последовательность применения этих фор»
мул. Как правило, расчетные формулы группируются
в так называемые циклы, которые в общем вычислитель-
ном процессе проходят многократно. После разработки
алгоритма создаются программы для выбранной ЭВМ.
Рис. 135. Структурная схема построения модели на основе идентификации
Далее осуществляется опытная проверка модели и её
корректировка, если в последней есть необходимость.
Структурная схема построения модели на основе
идентификации представлена на рис. 135. Она отличается
от схемы на рис. 134 тем, что в нее введены блоки, от-1
ражающие этапы планирования экспериментов и обра-
ботки экспериментальных данных.
Разработка оптимального плана проведения экспери-
ментов особенно необходима тогда, когда они многочис-
ленны и многофункциональны. В общем случае входные
213
я выходные переменные носят случайный характер, по-
этому для обработки экспериментальных данных следу-
ет привлекать статистические методы. При этом конеч-
ный результат исследования может быть получен в фор-
ме вероятностно-статистических оценок.
6. Примеры построения и использования
математических моделей в теории прокатки
Математическое моделирование с применением ЭВМ
дозволяет достаточно просто и удобно исследовать влия-
ние различных факторов на те или иные параметры про-
датки. Рассмотрим некоторые примеры.
Допустим, требуется исследовать влияние абсолютно-
го обжатия Д/г и радиуса валков R на величину абсолют-
ного уширения Д6. Известен ряд формул для расчета
уширения. Следовательно, имеется возможность постро-
ения модели на основе аналитического описания формо-
изменения полосы. Построение модели будем вести в со-
ответствии со структурной схемой на рис. 134.
Постановка задачи. Принимаем следующие исходные
данные: начальная ширина полосы />о=200мм; конечная
толщина hi=20 мм; обжатие Д/г изменяется от 2 до 10 мм
£. шагом 2 мм; радиус валков R варьируем от 100 до
500 мм с шагом 100 мм. Устанавливаем точность расчета
уширения 0,1 мм.
Поскольку объем исследований является относитель-
но небольшим, считаем целесообразным выводить резуль-
таты расчетов на печатающее устройство или на дисплей
(в случае использования ЭВМ без печатающего устрой-
ства). Для оценки пригодности модели используем соот-
ветствующие экспериментальные данные.
Аналитическое описание модели. В качестве базового
математического выражения принимаем формулу ушире-
ния А. П. Чекмарева (209). При точном использовании
этой формулы расчет приходится проводить путем по-
следовательных приближений, так как величина Ьср за-
висит от искомого уширения:
*ср = -^^=6» +V- (503)
Подставив в формулу (209) выражение (503), полу-
чим уравнение, которое целесообразно решать итераци-
онным методом. При этом задается некоторое начальное
приближение Д63, определяется предварительное значе-
214
ние ЬСр и вычисляется Д6Р. Далее полученное значение
Дбр принимается в качестве ЛЬ3 для нового вычисления
ЬСр и ДЬР. Расчет необходимо продолжать до тех пор,
пока не будет выполнено условие |Д6Р—Дб3|<0,1мм
(в соответствии с принятой точностью определения уши-
рения).
Разработка моделирующего алгоритма. Исходя из не-
обходимости применения итерационного метода расчета,
Рис. 136. Блок-схема алгоритма моделирования уширения по формул»
А. П. Чекмарева
алгоритм строим на основе циклического вычислительно-
го процесса. Структурная схема алгоритма приведена на
рис. 136.
Выбор средств вычислительной техники. Учитывая
принятую относительно невысокую точность моделирова-
215-
Таблица 8. Программа расчета уширения по формуле
А. П. Чекмарева
Адрес Команда Код Адрес Команда Код Адрес Команда Код
00 5 05 24 ИП2 62 49 ИП 6 66
01 ПЗ 43 25 + 10 50 X 12
02 ИП 1 61 26 П 8 48 51 F 1/х 23
03 ИП 7 67 27 ИП С 61 52 ИП 8 68
04 + 10 28 1— И 53 X 12
05 П 0 40 29 F х<0 5[ 54 ИП 7 67
Об ИП 1 61 30 35 35 55 X 12
07 + 10 31 1 01 56 П А 4—
08 2 02 32 П 5 45 57 ИП 3 63
09 -1- 13 33 БП 51 58 1— 11
10 П6 46 34 37 37 59 F х2 22
11 12 ИП 7 ИП 4 67 64 35 36 2 П 5 02 45 60 fV 21 00
13 -i- 13 37 ИП 8 68 01 и
14 F V 21 38 ИП С 6[ 13 65 1 А 02 63 1 и— 01
15 16 пв ИП 4 41 64 оУ 40 А1 ИП 5 64 65 Fx>0 11 59
17 18 19 20 21 22 23 ИП 7 X F V п с ИП 3 2 67 12 21 41 63 02 13 42 43 44 45 46 47 48 F хУ ИП В 1 + X 1 + 24 6L 01 10 12 01 10 66 67 68 69 70 71 72 71 ИП А П 3 БП 22 ИП А с/п 71 6— 43 51 22 6— 50
дия, возможность вывода результатов вычислений на
дисплей, а также то, что алгоритм моделирования полу-
чился достаточно простым, принимаем в качестве ЭВМ
программируемый микрокалькулятор «Электроника
ВЗ-34».
Разработка программы. Для реализации алгоритма
разработана программа, представленная в табл. 8. Рас-
пределение регистров памяти указано в табл. 9.
Результаты моделирования приведены на рис. 137.
Как видно из графиков на рис. 137, а, с увеличением аб-
солютного обжатия уширение растет более интенсивно,
чем само обжатие. Это означает, что с увеличением об-
дсатия показатель уширения a=&b/\h возрастает (но не
остается постоянным). Такого рода данные получены во
многих экспериментальных исследованиях.
Из графиков на рис. 137,6 следует, что зависимость
между уширением и радиусом валков носит приблизи-
те
Таблица 9. Распределение регистров памяти в программе
расчета уширения по формуле А. П. Чекмарева
Исходные данные
Промежуточный
результат
Окончательный
результат
параметр
регистр
памяти
параметр
регистр
памяти
параметр
регистр
памяти
Д&
Ьо
hi
R
Ah
2
1
4
7
h0
hep
^ср
а
Id
Рис. 137. Зависимость уширения от обжатия (а) и радиуса валков (б) при?
моделировании по формуле А. П. Чекмарева
тельно прямолинейный характер. Это подтверждается-
экспериментальными данными Люега и Помпа, а также*
других исследователей.
В качестве второго примера рассмотрим моделирова-
ние давления на валки при холодной прокатке листовой
стали. Пусть в задачу исследования входит определение
зависимости среднего контактного давления рср от шеро-
ховатости поверхности валков Rz и относительного обжа->
тия г. Вычисления будем проводить с учетом сплющива-
ния валков.
Постановка задачи. Принимаем следующие условия^
прокатки: исходная толщина полос /г0=2, 3 и 4 мм; ма-
териал— сталь марки 10 (исходный предел текучести
ат =250 МПа); диаметр валков D = 500mm; скорость
прокатки ив = 10м/с. В качестве технологической смазки
217'
применяется эмульсия минерального масла (вязкость
масла V5o=2O сСт); &см=1,4.
Влияние обжатия на давление будем исследовать при
значениях е=10, 20, 30, 40 и 50 % и фиксированной ве-
личине шероховатости Rz—5 мкм.
Влияние шероховатости валков на давление опреде-
ляем при значениях Rz—1, 3, 5, 7 и 10 мкм и обжатии
е=25 %.
Принимаем точность моделирования 5,%. Учитывая
сравнительно небольшой объем исследований, считаем
возможным выводить результаты расчетов на дисплей.
Аналитическое описание модели. Для моделирования
используем формулу А. И. Целикова (297). Коэффици-
ент трения будем находить по формуле (259). Средний
предел текучести металла в очаге деформации определя-
ем как среднеарифметический по формуле (270). Закон
упрочнения металла при холодной деформации принима-
ем в виде (268). Тогда расчетная формула для среднего
предела текучести будет
%, = + (Л/2)Гё • (504)
Принимаем А = 60 (см. с. 132), длину очага дефор-
мации с учетом сплющивания валков ldc определяем по
формуле (55), принимая ш = 1,12* 10-51/МПа (для
стальных валков) и с = 1,375.
Разработка моделирующего алгоритма. Анализ фор-
мул (297) и (55) показывает, что для определения рср
требуется применять итерационный метод расчета, т. е.
использовать циклический вычислительный процесс. Это
объясняется тем, что контактное давление рср зависит от
длины очага деформации Z^1, а та, в свою очередь, за-
висит от Рср. Процесс итерационного вычисления рср за-
канчиваем тогда, когда ошибка в определении рср ста-
нет меньше 5%. Структурная схема алгоритма приве-
дена на рис. 138.
Следует отметить, что если бы давление рассчитыва-
лось без учета сплющивания валков, то мог бы быть ис-
пользован линейный вычислительный процесс.
Представленная на рис. 138 структурная схема алго-
ритма расчета давления предполагает, что величины fy
и <уТср являются заданными и определяются по отдель-
ным программам.
1 Через величину 6=2fyZdc/A/i.
218
Выбор средств вычислительной техники. Как и в пре-
дыдущем примере, учитывая поставленные требования
и достаточную простоту алгоритма моделирования, а так-
же возможность вывода результатов на дисплей, прини-
маем в качестве ЭВМ программируемый микрокальку-
лятор «Электроника БЗ—34».
Рис. 138. Блок-схема алгоритма моделирования среднего контактного давле*
ния при холодной прокатке по формуле А. И. Целикова. В четвертом блок#
Й1 = /г0—Д/г
Разработка программы. Проведение расчетов потре-
бовало составления трех программ: основной (табл. 10)
и двух дополнительных (табл. 12 и 14). Реализовать вы-
числительный процесс в одной объединенной программе
оказалось невозможным из-за малого объема памяти
ПМК. Распределение регистров памяти в указанных про-
граммах приведено соответственно в табл. 11, 13, 15.
Разработанные программы моделирования среднего
219
Таблица 11. Программы моделирования среднего контактного
давления по формуле А. И. Целикова с учетом сплющивания валков
Адрес Команда Код Адрес Команда Код Адрес Команда Код
00 ИП8 68 32 П6 46 64 X 12
01 ИП 2 62 33 ИП2 62 65 ИП5 65
02 X 12 34 ИП5 65 66 2 02
03 П 1 41 35 4- 13 67 X 12
04 ИП 2 62 36 F ху 24 68 X 12
05 14 37 ИП6 66 69 ИП 1 61
06 — 11 38 F х2 22 70 -4 13
07 П 5 45 39 1 01 71 ИП6 66
08 ИП 0 60 40 — 11 72 1 01
09 п в 4L 41 X 12 73 — 11
10 ИП4 64 42 1 01 74 4- 13
11 ИП 1 61 43 + 10 75 ипо 60
12 X 12 44 F 21 76 X 12
13 ИП 9 69 45 1 01 77 ИП А 6 -
14 ИП4 X 46 + 10 78 X 12
15 X 12 47 ИП6 66 79 t ОЕ
16 ИП в 61 48 1 01 80 ОЕ
17 X 12 49 + 10 81 ИП в 6L
18 ИП с 61 50 4- 13 82 — 11
19 X 12 51 ИП6 66 83 — 14
20 п д 4Г 52 F 1/х 23 84 4- 13
21 F х2 22 53 14 85 F х2 22
22 + 10 54 F ху 24 86 F \Г 21
23 F 21 55 t OL 87 ИП 7 67
24 ИП Д 6Г 56 1 01- 88 — 11
25 + 10 57 ИП6 66 89 F х< 0 5L
26 ИП 3 63 58 14 90 92 92
27 X 12 59 F ху 24 91 С/П 50
28 2 02 60 1 01 92 14
29 X 12 61 — И 93 БП 51
30 ИП 1 61 62 — 14 94 09 09
31 -г 13 63 F О 25
контактного давления пригодны не только для расчетов
на ПМ.К «Электроника БЗ—34», но также для других
ПМК с аналогичным языком программирования («Элек-
троника М.К—54», «Электроника М.К—56», «Электроника
МК—61» и др.).
Результаты, модельного исследования представлены
в виде графиков на рис. 139, из которых видно, что ше-
роховатость поверхности валков и относительное обжа-
тие существенно влияют на величину среднего контакт-
220
Таблица 11. Распределение регистров памяти в программе
моделирования среднего контактного давления по формуле
А. И. Целикова
Исходные данные Промежуточный результат Окончательный результат
параметр ’ регистр памяти параметр регистр памяти параметр регистр памяти
ho 2 АЛ 1 Рср В
fy 3 hi 5
Ъ 4 6 6
е 8 Е 7
1,15 А
0,05 7
tn 9
с С
ат 0
ср
Таблица 12. Программа расчета среднего предела текучести
Адрес Команда Код || Адрес Команда Код | Адрес Команда Код
00 ИП 8 68 04 2 02 08 П 5 45
01 02 03 fV ИП 1 X 21 61 12 05 06 07 ИП 0 + 13 60 10 09 С/П 50
Таблица 13. Распределение регистров памяти в программе
расчета предела текучести
Исходные данные Окончательный результат
параметр регистр памяти параметр регистр памяти
ат исх А е 0 1 8 ат ср 5
ного давления при холодной прокатке, причем влияние
этих факторов резко возрастает с уменьшением толщины
прокатываемых полос. Полученные зависимости в основ-
ном согласуются с экспериментальными данными.
221
Таблица 14. Программа расчета коэффициента трения
Адрес Команда Код Адрес Команда Код Адрес Команда Код
00 ИП 1 61 17 X 12 33 ИП 5 65
01 1 01 18 ИП 9 69 34 ИП 2 62
02 + 10 19 14 35 X 12
03 2 02 20 11 36 ИП 8 68
04 X 12 21 П В 41 37 + 10
05 ИП 1 61 22 ИП 4 64 38 ИП 3 63
06 07 08 09 F х2 3 X + 22 03 12 10 23 24 25 26 97 fV~ ИП 6 X 21 66 12 39 40 41 42 X 1 + ИП А 12 01 10
10 F Их 23 1 U1 10 67 64 12 11 4[ 43 X 12
11 12 13 14 ИП 1 F х2 X 0 61 22 12 00 28 29 30 ИП 7 ИП 4 X 44 45 46 47 ИП С ИП в X 61 13 6L 12
15 16 1 0— 01 О1 32 П С 48 49 п с с/п 4[ 50
Примечание. Для удобства написания программы вместо символ?
ху принято обозначение Zi.
Рнс. 139. Зависимость среднего контактного давления от шероховатости по-
верхности валков (а) и относительного обжатия (б) при моделировании по
формуле А. И. Целикова
При наличии программ (табл. 10,12 и 14) можно лег-
ко расширить диапазон изменения вышеуказанных фак-
торов, а также провести исследование влияния других
факторов.
222
Таблица 15. Распределение регистров памяти в программе
расчета коэффициента трения
Исходные данные
Промежуточный
результат
Окончательный
результат
параметр
регистр
памяти
параметр
регистр
памяти
параметр
регистр
памяти
VB
е
Rz
V60
0,01
0,25
0,005
0,4
0,07
&см
1
2
3
4
5
6
7
8
9
А
КОНТРОЛЬНЫЕ ВОПРОСЫ
к гл. I
1. Что такое прокатка?
2. За счет действия каких сил полоса втягивается в прокатные
валки?
3. Что означает термин «прокатка на гладкой бочке»?
4. Какая прокатка называется горячей? В чем ее преимущества?
5. Какая прокатка называется холодной? Когда она применяется?
6. Изменяются ли механические свойства металла при прокатке?
7. Изобразите схему продольной прокатки.
8. Изобразите схему поперечной прокатки. Для получения каких
изделий она применяется?
9. Изобразите схему косой прокатки. В каких случаях она при-
меняется?
10. Что такое периодическая прокатка?
11. Приведите примеры несимметричной прокатки.
12. Изобразите схему прокатки с задним и передним натяжением,
с задним и передним подпором.
13. Что такое простой процесс прокатки (простой случай прокатки)?
14. Назовите основные вопросы, изучаемые в теории прокатки.
15. Назовите несколько имен отечественных и зарубежных ученых,
внесших большой вклад в развитие теории прокатки.
к гл. II
1. Что называется очагом деформации?
2. В чем различие между геометрическим и физическим очагом де-
формации?
3. Покажите на схеме продольной прокатки угол контакта (угол
захвата) и дугу контакта (дугу захвата).
4. Что такое фактор формы очага деформации?
223
5. Назовите все показатели, характеризующие высотную деформа-
цию полосы.
6. Какой показатель условного относительного обжатия наиболее
близок к истинному относительному обжатию?
7. Назовите все показатели, характеризующие поперечную дефор-
мацию полосы.
8. Укажите два способа расчета коэффициента вытяжки.
9. Как определяется общий коэффициент вытяжки за несколько
проходов по частным коэффициентам вытяжки?
10. Что такое средний коэффициент вытяжки, как он рассчитывает-
ся?
11. Чему равна сумма трех истинных относительных деформаций,
взятых по трем главным осям?
12. Почему начальный угол захвата по величине отличается от уг-
ла захвата (угла контакта) при установившемся процессе про-
катки?
13. Как определяется длина геометрического очага деформации?
14. Каким показателем характеризуется внеконтактная высотная
утяжка полосы?
15. От какого фактора в основном зависит величина внеконтакт-
ной высотной утяжки полосы? Каков вид этой зависимости?
16. Как изменяются геометрические параметры очага деформации
в результате сплющивания валков?
17. Как зависит величина сплющивания валков от их диаметра?
18. Какие валки — стальные или чугунные — подвергаются сплющи-
ванию в большей мере?
19. Какой материал валков обеспечивает минимальное сплющивание?
20. Назовите основные методы определения площади контактной
поверхности при прокатке.
21. В чем заключается сущность определения площади контактной
поверхности графическим методом?
22. В чем заключается сущность определения площади контактной
поверхности графоаналитическим методом?
23. Как определяется площадь контактной поверхности методом
приведенной полосы?
к гл. 111
1. Какие силы действуют на полосу в момент начального сопри-
косновения с валками?
2. Что такое свободный или естественный захват?
3. Назовите условие начального свободного захвата.
4. Что такое принудительный захват?
5. Какие факторы влияют на величину заталкивающей силы, не-
обходимой для осуществления принудительного захвата?
6. Что такое динамический захват?
7. Как составляется условие равновесия продольных сил, действу-
ющих на полосу при динамическом захвате?
8. Объясните схему сил, принимаемую при выводе условия захва-
та в установившемся процессе прокатки.
9. Сформулируйте условие захвата при установившемся процессе
прокатки.
10. Какой способ экспериментального определения максимального
угла контакта (захвата) чаще всего применяется на практике?
11. Сравните условия захвата в начальный момент касания полосы
с валками и при установившемся процессе прокатки с учетом
возможного различия коэффициентов трения f3 и fy.
224
12. Какие меры применяются для увеличения коэффициента трения
при захвате?
13. Выгодно ли увеличивать диаметр валков с точки зрения улуч-
шения условий захвата?
14. Влияет ли жесткость прокатной клети на условия начального
захвата?
15. Какие максимальные углы захвата применяются на практике?
к гл. IV
1. Назовите три стадии процесса прокатки полосы. Поясните тер-
мин «установившийся процесс прокатки».
2. Сформулируйте условие постоянства секундных объемов.
3. Как соотносятся скорости переднего и заднего концов полосы?
4. Почему в очаге деформации возникают зоны опережения и от-
ставания?
5. Что такое нейтральное сечение и нейтральный угол в очаге де-
формации?
6. Изобразите графически соотношение скоростей металла и вал-
ков на протяжении очага деформации.
7. Что такое зона прилипания на контактной поверхности?
8. Докажите, что при наличии зоны прилипания продольные ско-
рости по высоте полосы обязательно распределяются неравно-
мерно.
9. Какое условие служит основой для вывода формулы нейтраль-
ного угла?
10. Напишите формулу нейтрального угла Экелунда—Павлова.
11. Как изменяется величина нейтрального угла при увеличении уг-
ла контакта?
12. Как изменяется отношение у/а при увеличении угла контакта?
13. Поясните зависимость нейтрального угла от коэффициента (уг-
ла) трения.
14. Как влияет на величину нейтрального угла переднее натяже-
ние, заднее натяжение?
15. Можно ли пользоваться формулой нейтрального угла Экелун-
да—Павлова в условиях прокатки при неравномерном распре-
делении давлений по дуге контакта?
16. Что выражает термин «опережение» при прокатке? Напишите
формулу опережения.
17. Что выражает термин «отставание»? Напишите формулу отста-
вания.
18. Можно ли определить величину отставания, если известно опе-
режение?
19. Объясните сущность кернового метода определения опережения.
20. Какое условие положено в основу вывода формулы Финка для
теоретического определения опережения?
21. Напишите формулу опережения Головина—Дрездена.
22. Как зависит опережение от диаметра валков?
23. Как зависит опережение от толщины прокатываемых полос?
24. Покажите графически зависимость опережения от величины уг-
ла контакта.
25. Как влияет на опережение коэффициент трения?
26. Поясните зависимость опережения от натяжения и подпора кон-
цов полосы.
27. Почему скорость деформации изменяется на протяжении дуги
контакта? Из какой формулы это следует?
15 А. п. Грудев
225-
28. Напишите формулу для расчета средней скорости деформации
при прокатке.
29. Назовите характерные скорости деформации на промышленных
прокатных станах.
к гл. V
1. Какая схема напряженного состояния металла является основ-
ной при прокатке?
2. Какие схемы напряженного состояния возможны на боковых
кромках полосы?
3. В чем особенности напряженного состояния в очаге деформации
при прокатке с углами контакта, превышающими угол трения?
4. Поясните причины возникновения дополнительных продольных
напряжений при прокатке с неравномерным распределением об-
жатий по ширине полосы. Рассмотрите какой-либо конкретный
пример, покажите изменения в схемах напряженного состояния.
5. Какая схема деформированного состояния металла характерна
для прокатки в двух валках?
6. Какая схема деформированного состояния имеет место при про-
катке в многовалковых калибрах?
7. Назовите основные причины неравномерного распределения де-
формаций по высоте полосы.
8. Приведите классификацию процессов прокатки в зависимости
от величины фактора формы.
9. Изобразите поле линий скольжения при прокатке высокой по-
лосы.
10. Как решается задача о распределении уширения по длине оча-
га деформации?
11. Что называется свободным, ограниченным и вынужденным уши-
рением?
12. Изобразите графически типовую зависимость уширения от аб-
солютного обжатия.
13. Как зависит уширение от диаметра валков?
14. Как изменяется уширение в зависимости от ширины прокаты-
ваемых полос?
15. Как зависит уширение от коэффициента трения?
16. Как влияет натяжение концов полосы на уширение? Какое на-
тяжение влияет сильнее — переднее или заднее?
17. Напишите формулу уширения Зибеля.
18. На какие зоны делится очаг деформации при выводе формулы
уширения по Бахтинову?
19. Какая энергетическая предпосылка положена в основу вывода
формулы уширения Бахтинова?
20. Из какого условия определяются границы зон продольной и по-
перечной деформации при выводе формулы уширения по Це-
ликову?
21. Как учитывается ширина полосы и натяжение в формуле уши-
рения Целикова?
к гл. VI
1. Назовите основные методы исследования распределения сил
трения на контактной поверхности в очаге деформации.
2. Поясните сущность исследования сил трения методом наклон-
ных точечных месдоз. Приведите расчетные формулы.
3. Поясните метод исследования сил трения с помощью универ-
сального (качающегося) штифта.
226
4. Как проводится исследование распределения сил трения методом
разрезного валка?
5. Изобразите типичные эпюры распределения сил трения по дуге-
контакта. Дайте физическое истолкование характерным участ-
кам на этих эпюрах.
6. Что понимается под термином «коэффициент трения при уста-
новившемся процессе прокатки»?
7. Каковы причины различия коэффициентов трения при захвате-
и при установившемся процессе прокатки?
8. Назовите основные методы экспериментального определения ко-
эффициентов трения при прокатке.
9. Опишите метод определения коэффициента трения по максималь-
ному углу захвата.
10. Как определяется коэффициент трения методом предельного
обжатия?
11. Поясните сущность определения коэффициента трения методом
принудительного торможения полосы.
12. Изложите теоретические основы определения коэффициента тре-
ния методом крутящего момента.
13. Изложите теоретические основы определения коэффициента тре-
ния по опережению.
14. В чем заключается сущность определения коэффициента тре-
ния по давлению на валки?
15. Как влияют на коэффициент трения материал валков и шеро-
ховатость их поверхности?
16. Можно ли отнести к числу сильных факторов, влияющих на тре-
ние, присутствие на поверхности валков частиц налипшего ме-
талла, окалины и других промежуточных сред?
17. Как влияет на коэффициент трения содержание углерода в ста-
ли?
18. Изобразите графически температурную зависимость коэффици-
ента трения (для стали). Укажите причины изменения коэффи-
циента трения в зависимости от температуры прокатки.
19. Как влияет скорость прокатки на коэффициент трения?
20. Какие масла — минеральные или растительные — являются бо-
лее эффективной технологической смазкой? Чем это объясняет-
ся?
21. Почему с увеличением вязкости смазки повышается ее анти-
фрикционная эффективность?
22. Назовите характерные значения коэффициента трения при го-
рячей прокатке.
23. Назовите характерные значения коэффициента трения при хо-
лодной прокатке.
к гл. VII
1. С помощью какого измерительного устройства исследуется рас-
пределение давлений по контактной поверхности?
2. Изобразите типичные эпюры распределения давлений по дуге
контакта при прокатке тонких, средних и толстых полос. Дай-
те объяснение этим эпюрам.
3. В каком случае на эпюрах контактных давлений наблюдается
провал («седло») вблизи сечения входа в очаг деформации?
4. Как распределяегёяХдавление по ширине прокатываемых полос?
5. Поясните термин «вреднее контактное давление».
6. Что подразумевается под термином «усилие (сила) прокатки»?
7. Как направлена сила прокатки при установившемся процессе
15*
227
деформации при отсутствии натяжения или подпора концов по-
лосы?
8. Что называется коэффициентом напряженного состояния (или
коэффициентом подпора)?
9. В виде каких трех сомножителей можно представить коэффи-
циент напряженного состояния?
10. Как изменяется среднее контактное давление при увеличении
обжатия? Почему?
И. Как влияет на среднее контактное давление диаметр валков?
12. Изобразите графически и объясните зависимость среднего кон-
тактного давления от толщины прокатываемых полос.
13. Изобразите графически зависимость среднего контактного дав-
ления от фактора формы.
14. Как влияет на среднее контактное давление ширина полосы?
15. Как зависит среднее контактное давление от коэффициента тре-
ния?
16. Как влияет на среднее контактное давление натяжение концов
полосы? Какое натяжение влияет сильнее — переднее или зад-
нее?
17. Какие факторы необходимо учитывать при выборе величины
предела текучести металла при горячей прокатке?
18. В каких координатах представлены экспериментальные данные
по пределу текучести в работах Кука и Динника?
19. Поясните сущность определения предела текучести при горячей
прокатке методом термомеханических коэффициентов, разрабо-
танным Зюзиным?
20. Какие факторы необходимо учитывать при определении преде-
ла текучести металла при холодной прокатке?
21. Зависимость между какими величинами показывают кривые
упрочнения (наклепа)? Изобразите типичные кривые упрочне-
ния.
22. Какими формулами можно аппроксимировать кривые упрочне-
ния?
23. Как определяется средний предел текучести в очаге деформации
при холодной прокатке?
24. Как можно рассчитать повышение температуры металла в оча-
ге деформации?
25. Изобразите схему напряжений, действующих на элемент поло-
сы, при выводе дифференциального уравнения равновесия про-
дольных сил по Карману.
26. Какие основные допущения принимаются при выводе дифферен-
циального уравнения равновесия?
27. Почему при определении функции давления из дифференциаль-
ного уравнения равновесия приходится привлекать уравнение
(условие) пластичности?
28. Какие допущения приняты А. И. Целиковым при выводе фор-
мулы давления из дифференциального уравнения равновесия?
29. Какой вид имеют эпюры контактных давлений, построенные по
теоретическим уравнениям Целикова?
30. Какой закон трения принят А. П. Чекмаревым при выводе фор-
мулы давления? Какие приняты геометрические упрощения?
31. Как можно приближенно учесть влияние натяжения концов по-
лосы на среднее контактное давление?
32. Какие существуют рекомендации по ощ^елению давления при
прокатке в калибрах?
33. По каким формулам определяется давление при прокатке тол-
стых полос, когда фактор формы меньше единицы?
228
к гл. VIII
1. Поясните возможность определения крутящих моментов, необ-
ходимых для вращения валков, по удельным силам трения (по
Баюкову).
2. Как определяется крутящий момент по усилию прокатки?
3. Что такое коэффициент плеча момента (или коэффициент пле-
ча усилия прокатки)?
4. При каких условиях прокатки коэффициент плеча момента ра-
вен 0,5?
5. Почему при прокатке толстых полос коэффициент плеча момен-
та больше 0,5?
6. Почему при холодной прокатке тонких полос коэффициент пле-
ча момента значительно меньше 0,5?
7. Как направлена равнодействующая всех сил, приложенных к
валку, при прокатке с натяжением или подпором? Из какого
условия определяется направление действия этой силы?
8. Приведите формулу для расчета крутящих моментов при про-
катке с натяжением или подпором.
9. Как определяется работа прокатки по известному крутящему
моменту?
10. Можно ли при определении работы прокатки использовать фор-
мулу Финка, полученную для определения работы осадки?
11. Как определяется мощность, расходуемая на деформацию ме-
талла при прокатке?
12. Какой вид имеют экспериментальные графики расхода энергии
при прокатке?
13. Какие слагаемые расхода энергии необходимо учитывать при
определении мощности двигателя прокатного стана?
14. Как определяются потери на трение в подшипниках прокатных
валков и передаточных механизмах главной линии прокатного
стана?
15. Что такое мощность холостого хода?
16. Всегда ли необходимо учитывать динамическую мощность при
выборе двигателя прокатного стана?
к гл. IX
1. Из какого условия находится величина обжатия со стороны
каждого валка при прокатке в валках неравного диаметра?
2. Как определяются углы контакта при прокатке в валках нерав-
ного диаметра?
3. Как определяется длина очага деформации при прокатке в вал-
ках неравного диаметра?
4. Что такое приведенный радиус? Напишите соответствующую
формулу.
5. Сформулируйте условие начального захвата при прокатке в вал-
ках неравного диаметра.
6. Сформулируйте условие захвата при установившемся процессе
прокатки в валках неравного диаметра.
7. При прокатке на валках с разными диаметрами на каком из
них больше величина опережения?
8. Может ли идти процесс прокатки в валках неравного диаметра
при полном отсутствии опережения на валке большого диамет-
ра?
9. Чем вызывается изгиб полосы в вертикальной плоскости при вы-
ходе из валков?
229
10. Может ли прокатываемая полоса изгибаться в сторону валка
большего диаметра?
11. Зависит ли направление изгиба полосы от величины обжатия?*
12. Целесообразно ли применение валков разного диаметра с точ-
ки зрения снижения усилия прокатки?
13. На каком из двух неравных по диаметру валков крутящий мо-
мент больше?
14. По какой формуле можно определить величину крутящего мо-
мента на каждом из валков неравного диаметра?
15. Сформулируйте условие начального захвата при прокатке с од-
ним приводным валком (без учета сопротивления вращению а
шейках неприводного валка).
16. Сформулируйте условие захвата при установившемся процессе-
прокатки с одним приводным валком (см. примечание к преды-
дущему пункту).
17. Чему равен нейтральный угол на неприводном валке?
18. На каком валке больше величина опережения — на приводном
или неприводном?
19. Изобразите схематично положение равнодействующих сил, при-
ложенных к приводному и неприводному валкам при устано-
вившемся процессе прокатки.
20. Чему равен крутящий момент на приводном валке по сравне-
нию с крутящими моментами на валках при симметричной про-
катке?
21. Какие причины могут вызвать различие в условиях трения на
двух валках (верхнем и нижнем)?
22. Сформулируйте условие начального захвата при прокатке а
разношероховатых валках.
23. Сформулируйте условие захвата при установившемся процессе
прокатки в разношероховатых валках.
24. Существует ли различие в значениях опережения на гладком
и шероховатом валках, если обеспечен прямолинейный выход
полосы из валков?
25. Что показывают исследования изгиба полосы при прокатке в
разношероховатых валках?
26. Приведите формулу для определения среднего нейтрального уг-
ла при прокатке в разношероховатых валках.
27. На каком из валков — гладком или шероховатом — крутящий
момент обычно бывает больше?
28. Как можно определить суммарный крутящий момент на дв'ух
разношероховатых валках с помощью формулы Баюкова?
29. Изобразите схемы продольной периодической прокатки с нара-
станием и убыванием обжатия.
30. Что называется углом захвата и углом касания в теории пе-
риодической прокатки? Как связаны между собой эти углы?
31. Как определяется средний радиус контактной поверхности при
переменном радиусе валков?
32. Какой профиль должны иметь валки, чтобы выходящая из них
полоса имела постоянный угол клиновидности?
33. Чему равен максимальный угол захвата при прокатке с нара-
станием и убыванием обжатия? Какой из этих случаев прокат-
ки является более трудным в смысле осуществления захвата?
34. Проанализируйте формулы для определения нейтрального угла
при прокатке с нарастанием и убыванием обжатия.
35. В каком случае опережение больше—при прокатке с нараста-
нием или убыванием обжатия?
230
36. Почему при периодической прокатке особенно важно поддержи-
вать постоянство условий трения?
37. Можно ли использовать при периодической прокатке формулы
давления, выведенные для простого случая прокатки?
38. В каком случае выше величина крутящего момента — при про-
катке с нарастанием или убыванием обжатия?
к гл. X
1. При проведении каких вычислений и решении каких задач це-
лесообразно применение электронных вычислительных машин?
2. Назовите три основных типа ЭВМ. Укажите их особенности,
преимущества и недостатки.
3. В каких случаях целесообразно применение программируемых
микрокалькуляторов?
4. Назовите наиболее распространенные марки программируемых
микрокалькуляторов. Каким объемом памяти они обладают?
5. Из каких этапов состоит подготовка задач к решению на ЭВМ?
Объясните сущность каждого этапа. Какие этапы не являются
обязательными?
6. Опишите простейший язык программирования — мнемокод.
7. Как проверяется правильность составления программы и рабо-
ты ЭВМ?
8. В чем достоинства построения алгоритма в виде блок — схе-
мы?
9. Назовите основные блоки, используемые при составлении блок —
схемы. Как они изображаются, нумеруются?
10. Что называется линией потока?
11. Назовите основные типы вычислительных процессов.
12. Как составляется блок — схема алгоритма, включающего цик-
лический вычислительный процесс?
13. Что такое физическое, аналоговое и математическое моделиро-
вание?
14. Укажите преимущества математического моделирования.
15. Укажите основные принципы построения математических моде-
лей.
16. Опишите структурную схему построения модели на основе ана-
литического описания объекта.
17. Опишите структурную схему построения модели на основе иден-
тификации.
18. Приведите примеры расчетов параметров прокатки с примене-
нием ПМК.
Коэффициент трения при прокатке свинца (в числителе — пределы,
Материал и твердость валков Обработка поверхности валков Класс шерохо- ватости Смазка
Закаленная хро- мистая сталь, 690 НВ Шлифовка наждачной бумагой в стане 7 Без смазки
Шлифовка на станке 7—8 Без смазки
Шлифовка наждачной бумагой в стане 7 Керосин
Шлифовка на станке 7—8 Хлопковое мас- ло
Ст5 150 НВ Шлифовка наждачной бумагой в стане 6 Без смазки
Шлифовка на станке 7 То же
Грубая обточка 4 » »
Серый чугун 190 НВ Шлифовка наждачной бумагой в стане 7 » »
Шлифовка на станке 7 » »
То же 7 Машинное мас- ло
» » 7 Хлопковое мас- ло
Поимечан и е. Скорость прокатки 0,3 м/с 1
232
Приложение I
в знаменателе — среднее значение)
Коэффициент трения
при захвате f3 при установившемся процесе fy
чистые валки освинцованные валки чистые валки освинцованные валки
0,24—0,30 0,83—0,89 0,23—0,30 0,35—0,38
0,27 0,86 0,26 0,37
0,24—0,32 — 0,28—0,29 —
0,28 — 0,28 —
0,15—0,17 0,22—0,28 0,12—0,17 0,18—0,20
0,16 0,25 0,14 0,19
0,11—0,13 0,12 Освинцевания не происходит 0,084—0,10 0,095 Освинцевания не происходит
0,29—0,36 0,89—0,95 0,29—0,32 0,55—0,57
0,32 0,93 0,31 0,56
0,25—0,34 0,26—0,29 —
0,29 0,27 —
0,57—0,62 0,98—1,01 0,56—0,63 —
0,60 1,00 0,60 —
0,25—0,29 0,95—0,98 0,27—0,32 0,41—0,46
0,27 0,96 0,29 0,43
0,24—0,28 — 0,27—0,30 —
0,26 — 0,28 —
0,086—0,103 0,098 Освинцевания не происходит 0,052—0,063 0,059 Освинцевания не происходит
0,092—0,118 0,103 То же 0,056—0,073 0,065 То же
233
Зависимость коэффициента трения от температуры деформации
Металл 8, % Темпера
20 200 250 300 350 400 «0 |
Алюминий 30 0,15 0,25 0,28 0,31 0,34 0,37 0,39
Латунь 95/5 30 0,27 0,35 0,40 — — — —
85/15 30 0,21 0,32 0,39 0,42 — — 0,44
70/30 30 0,17 0,28 — — — 0,40 —
Медь 50 0,30 0,37 0,40 — — — 0,42
Свинец 50 0,20 0,28 0,38 0,54 — — —
Магний 50 — 0,39 0,42 0,47 0,52 0,57 0,52
Никель 50 0,25 0,32 0,33 0,34 0,36 0,37 0,38
Мягкая сталь 50 0,16 0,21 — — 0,29 — —
Нержавеющая сталь 50 0,32 — — — — 0,42 —
Цинк 50 0,23 0,32 0,53 — 0,57 — —
Титан 50 — — — — — — —
Титан * 50 — — — 0,18 — 0,19 —
Титан ** 50 — — 0,15 — —
* Смазка — графит. ** Смазка — дисульфид молибдена.
234
Приложение II
М. Г. Кокрофта)
600 650 700 750 800 850 900 950
0,48 — — — — — — —
— — — — — 0,40 0,33 0,24
0,48 0,52 0,55 — — 0,57 — —
0,42 0,48 0,53 0,55 — 0,57 — —
— — 0,39 0,34 0,30 0,26 0,22 0,20
— — — — — — — —
— — — — — — — —
0,41 0,42 0,43 0,44 0,44 0,45 0,45 0,46
0,45 0,54 — 0,57 0,54 0,49 0,46 0,41
— 0,44 0,48 0,50 0,54 — 0,57 —
— — — — — — — —
0,57 — — — — — — —
0,21 0,22 0,23 0,25 0,28 0,34 0, 8 0,57
— — 0,18 0,20 0,26 0,37 0,52 0,57
235
РЕКОМЕНДАТЕЛЬНЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Выдрин В. Н., Федосиенко А. С., Крайнов В. И. Процесс непре-
рывной прокатки. М.: Металлургия, 1970. 456 с.
Грудев А. П. Внешнее трение при прокатке. М.: Металлургия»
1973. 288 с.
Гун Г. Я- Математическое моделирование процессов обработки
металлов давлением. М.: Металлургия, 1983. 352 с.
Клименко В. М., Онищенко А. М. Кинематика и динамика про-
цессов прокатки. М.: Металлургия, 1984. 232 с.
Контактное трение в процессах обработки металлов давлением
1Леванов А. Н., Колмогоров В. Л., Буркин С. П. и др.: М.: Метал-
лургия, 1976. 416 с.
Пластичность и разрушение/Коллюгорое В. Л., Богатов А. А.,
Мигачев Б. А. и др. Под ред. В. Л. Колмогорова. М.: Металлуогия»
1977. 336 с.
Полухин В. П. Математическое моделирование и расчет на ЭВМ
листовых прокатных станов. М.: Металлургия, 1972. 511 с.
Поляков М. Г., Никифоров Б. А., Гун Г. С. Деформация метал-
ла в многовалковых калибрах. М.: Металлургия, 1979. 240 с.
Смирнов В. С. Теория прокатки. М.: Металлургия, 1967. 460 с.
Смирнов В. С., Григорьев А. К- Применение ЭЦВМ для расчета
параметров прокатки. М.: Металлургия, 1970. 230 с.
Теория прокатки. Справочник/Целиков А. И., Томленое А. Д.,
Зюзин В. И. и др. Под ред. В. И. Зюзина и А. В. Третьякова. М.:
Металлургия, 1982. 335 с.
Теория прокатки крупных слитков/Чекмарев А.П., Павлов В. Л.,
Мелешко В. И., Токарев В. А. М.: Металлургия, 1968. 251 с.
Целиков А. И., Гришков А. И. Теория прокатки. М.: Металлур-
гия, 1970. 360 с.
Целиков А. И., Никитин Г. С., Рокотян С. Е. Теория продольной
прокатки. М.: Металлургия, 1980. 320 с.
Чекмарев А. П., Нефедов А. А., Николаев В. А. Теория про-
дольной прокатки. Харьков: Изд. Харьковского университета, 1965.
212 с.
Чиченов Н. А., Кудрин А. Б., Полухин П. И. Методы исследова-
ния процессов обработки металлов давлением. М.: Металлургия,
1977. 331 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Алгоритм 198, 200
Аппроксимация кривых упроч-
нения 131
Б
Бахтинова Б. П. формула 100
Баюкова В. Ф. формула 148,
170
Блок-схема алгоритма 201
В
Валки:
с гладкой бочкой 9
калиброванные 9
Выдрина В. Н. формула 93
Вычислительный процесс:
линейный 203
разветвленный 203
циклический 203
Г
Генки Г. теорема 91
Герца Г. формула 27
Головина А. Ф. формулы 73,
159
Губкина С. И. формула 98
д
Давление:
распределение по контактной
поверхности 121
среднее контактное 123
Деформация:
внеконтактная 23
неравномерная 87
показатели величины 16
Деформированное состояние
полосы 82
Диаметр валков 74, 95, 125
Динника А. А. графики 128
Дифференциальное уравнение
равновесия продольных сил
135
Длина очага деформации 15
Дрозда В. Г. формулы 32
Дуга контакта 15
Ж
Жеза Л. формула 98
3
Закон трения Амонтона 34
Захват:
динамический 32
принудительный 35
свободный, естественный 33
Зибеля Э. формулы 98, 145
Зона:
внешняя 15, 147
затрудненной деформации 8?
опережения 54, 60, 99
отставания 55, 60, 99
прилипания 56, 109
скольжения 59, 109
уширения 90
Зюзина В. И. метод 131
И
Идентификация 213
Изгиб полосы 167
К
Калибры:
квадратный 32
круглый 32
овальный 32
ромбический 32
Кармана Т. уравнение 137
Коэффициент:
вытяжки за проход 19
вытяжки общий 19
вытяжки средний 19
линейного расширения 72
напряженного состояния 124
обжатия 18
плеча момента 149
трения при захвате 34
трения при установившемся
процессе прокатки 47, 106
уширения 18
формы полосы 16
Кривые:
расхода энергии 155
упрочнения 131
Кука П. графики 128
Л
Линии:
потока 20;1
скольжения 90
Луговского В. М. формула 92,
147
237
м
Месдозы точечные 105
Метод:
аналитический 30
графический 30
графоаналитический 30
давления 115
керновый 71
крутящего момента 114
линий скольжения 89
максимального угла захвата
111
наклонных точечных месдоз
105
опережения 114
предельного обжатия 112
приведенной полосы 32
принудительного торможения
112
разрез'ного валка 107
универсального штифта 107
’Микрокалькулятор программи-
руемый 195
Моделирование:
аналоговое 207
математическое 208
физическое 206
Модельный эксперимент 206
Момент крутящий:
динамический 158
прокатки (на бочке валка)
148, 152, 157
трения 157
холостого хода 157
Мощность:
расходуемая на бочке вал-
ков 154
полная 156
Мнемокод 199
Н
Напряженное состояние поло-
сы 82
Натяжение концов полосы:
заднее 63, 66
переднее 63, 66
удельное 64
О
Обжатие:
абсолютное 16
относительное 17
Образцы-недокаты 23
Опережение 69, 70, 72, 74, 77,
161, 172
Отставание 62
Очаг деформации:
геометрический 15
физический 15
П
Павлова И. М. формулы 61,
154
Площадь контактной поверх-
ности 30
Подпор концов полосы 13, 65
Показатель:
сил трения 144
уширения 18
Предел текучести 124
Пробуксовка 48
Программирование 198
Прокатка:
в валках неравного диамет-
ра 158
в разношероховатых валках
177
горячая 10
косая 10
несвободная 10
несимметричная 12
периодическая 11
поперечная 10
продольная 10
простой процесс 13
свободная 12
симметричная 12
с одним приводным валком
170
теплая 10
холодная 10
Профиль валков 184
Пружина прокатного стана 22
Р
Работа прокатки 154
Равнодействующая сил нор-
мального давления и трения
123
Распределение деформаций 86
Расход энергии 155
С
Сечение:
входа 56
выхода 56
нейтральное 56
Сила:
заталкивающая 35
нормального давления 33
238
трения 33
инерции 39
Скорость:
валков окружная 40
деформации 79
деформации средняя 79
подвода полосы 40
прокатки 82
сжатия 80
Смещенный объем 99
Смирнова В. К- формулы 189
Соотношение скоростей метал-
ла и валков 54
Сплющивание валков 26
Стадии процесса прокатки:
выброс 52
захват 52
установившийся процесс 52
Стан прокатный 22
Т
Тарковского И. Я. классифика-
ция 88
Тело цикла 206
Температура прокатки 117
Технологические смазки 118
Третьякова А. В. формула 129
У
Угол:
захвата 15
касания 182
клиновидности полосы 182
контакта 15, 20
нейтральный (критический)
55, 59, 161, 172
трения при захвате 37
трения при установившемся
процессе прокатки 46
Удар 40
Удлинение:
абсолютное 18
относительное 18
Упрочнение деформационное
127
Уравнение:
пластичности 137
равновесия продольных сил
39, 59, 63, 162, 170
Усилие (сила) прокатки 123
Условие:
захвата при установившемся
процессе прокатки 46, 160,
170, 177, 182
начального захвата 34, 160,
170, 178
постоянства секундных объ-
емов 53
принудительного захвата 35
Утяжка внеконтактная высот-
ная 23
Уширение:
абсолютное 18
вынужденное 94
ограниченное 94
относительное 18
свободное 94
Ф
Фактор формы 16, 126
Файнберга Ю. М. формула 67
Финка С. формулы 73, 154
Формоизменение полосы 83
X
Характеристика напряженного
и деформированного состояния
82
Хейна А. Я. анализ 84
Химический состав металла 131
Хичкока Дж. формула 27
U
Целикова А. И. формулы 138-
Ч
Чекмарева А. П.
классификация 88
формулы 98, 142
Число проходов 19
Ш
Шероховатость поверхности
валков 119
Шпиндель 114
Э
ЭВМ:
аналоговые 195
гибридные 195
цифровые 195
Экелунда С. формулы 61, 73,
81
Эксперимент модельный 210
Энергия кинетическая 41
Энергосиловые параметры 14
Эпюры:
давлений 121
сил трения 108
Эффективность действия смаз-
ки 119
Я
Язык программирования 200
239