Кибернетический сборник. Новая серия. Выпуск 07 - Лупанов О.Б., Ляпунов А.А.

Автор: Лупанов О.Б. Ляпунов А.А.
Теги: математика кибернетика
Год: 1970
Похожие
Кибернетический сборник. Новая серия. Выпуск 06
Кибернетический сборник. Новая серия. Выпуск 05
Кибернетический сборник. Новая серия. Выпуск 04
Кибернетический сборник. Новая серия. Выпуск 02
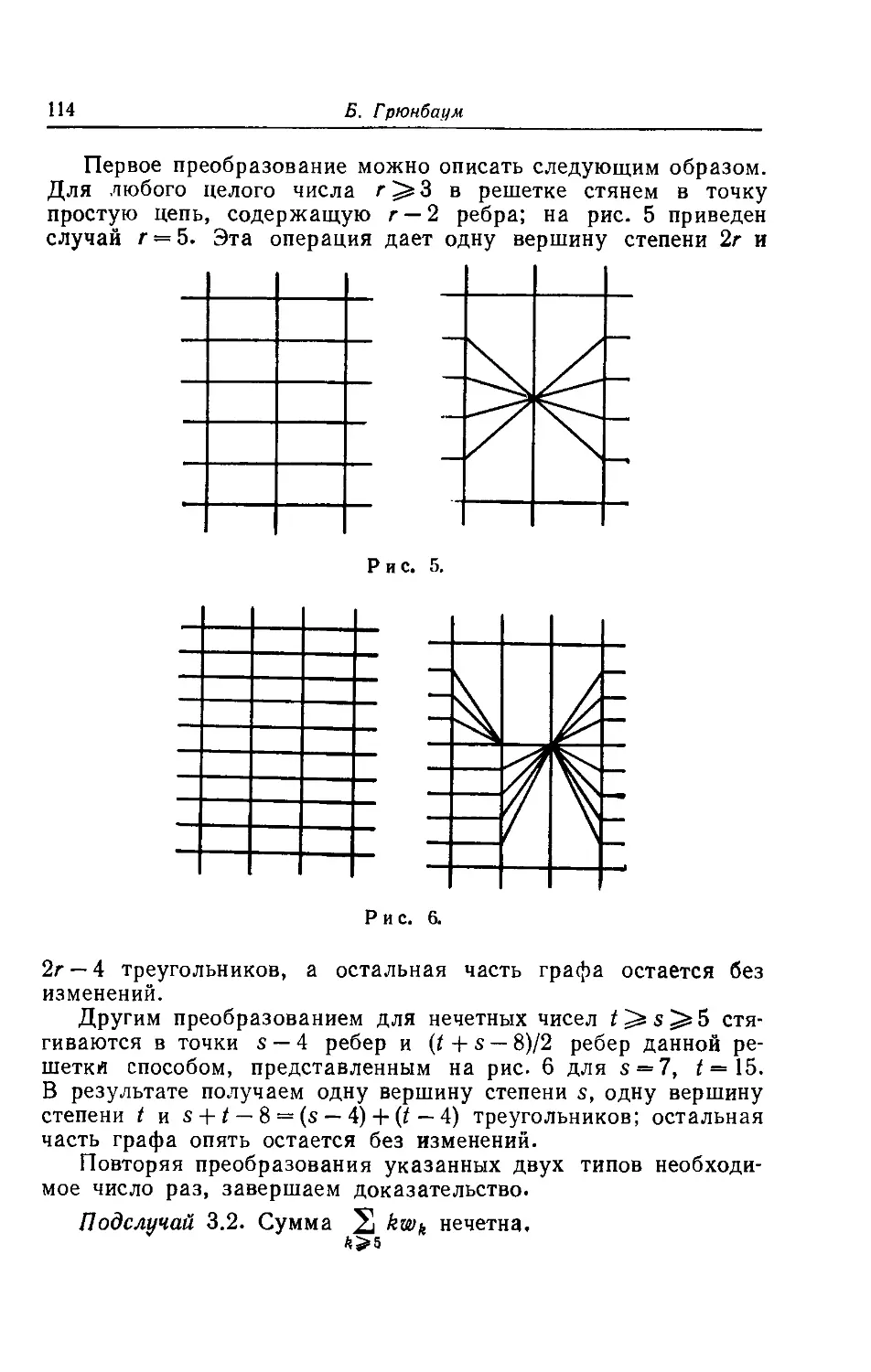
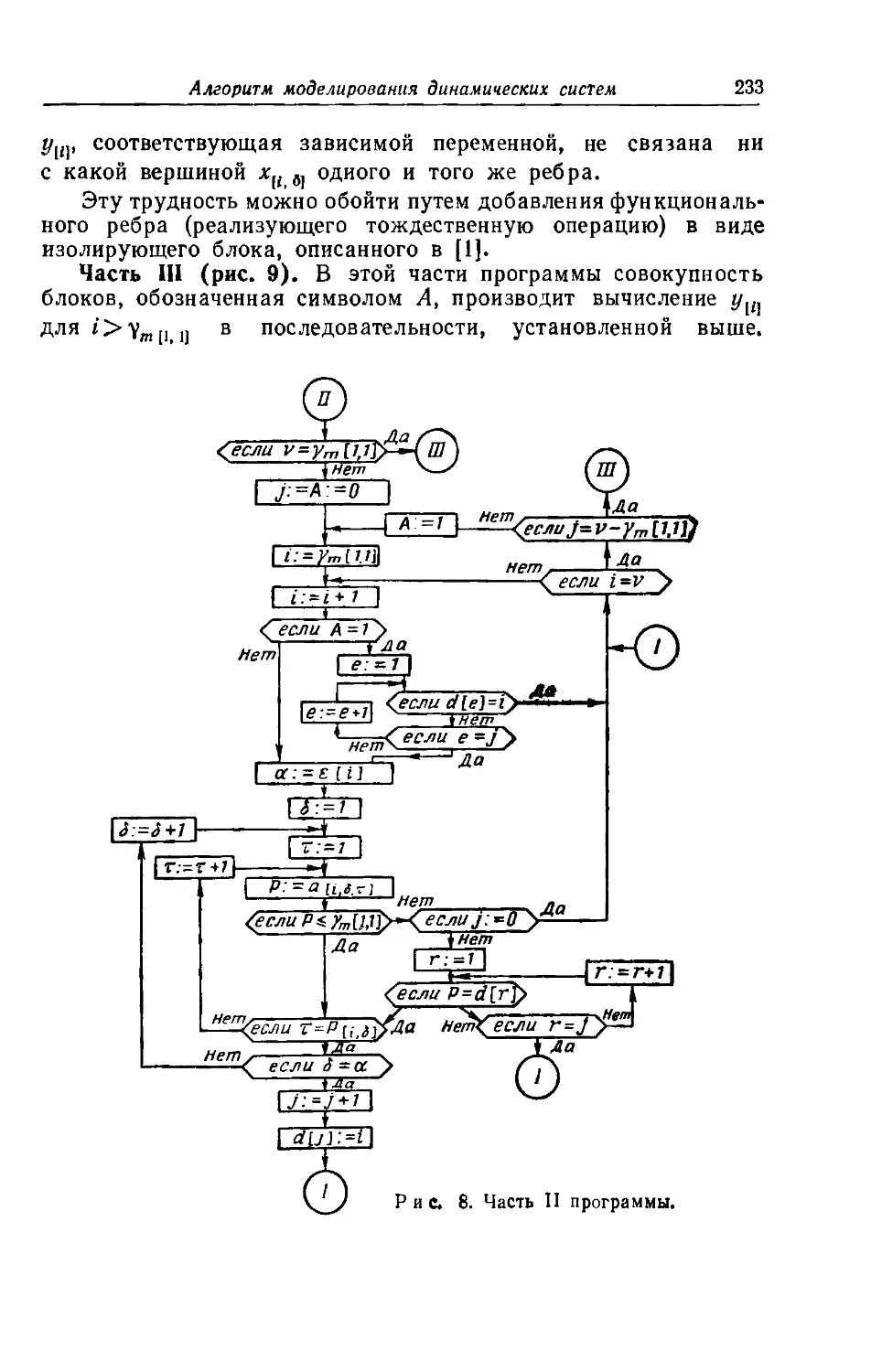
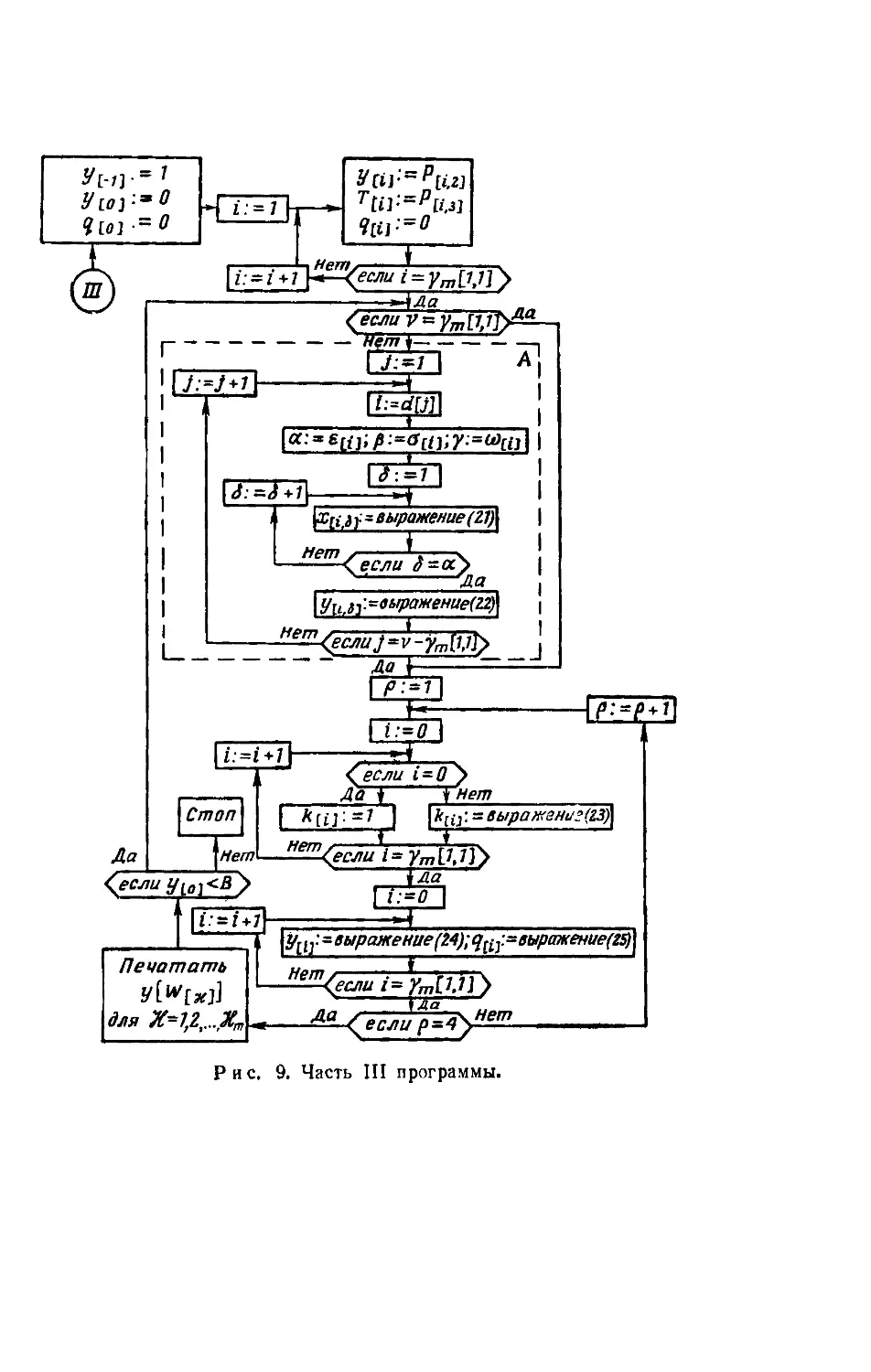
Текст
                    Кибернетический
сборник
НОВАЯ СЕРИЯ
выпуск
Сборник переводов
Под редакцией
А. А. ЛЯПУНОВА и О. Б. ЛУПАНОВА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1970

УДК 519.95
Научный совет по кибернетике
Академии на§к СС€#
Седьмой выпуск новой серии кибернетических сборников состоит из
двух разделов: математические вопросы и прикладные вопросы. В первом
разделе представлены работы по теории кодирования, синтезу логических
устройств, теории графов, а также статьи по вопросам машинного доказа-
доказательства теорем. Во втором разделе помещена статья Р. Якубовски об алго-
алгоритме моделирования динамических систем.
Сборник рассчитан на научных работников, инженеров, аспирантов и
студентов различных специальностей, занимающихся и интересующихся ки-
кибернетикой.
Редакция, маературн яо яатемагшчеашж наукам
Инд 2-2-3
5-70

Математические вопросы
Предельное распределение
для минимального расстояния
в случайном линейном коде1)
Дж. Н. Пирс
Распределение отношения минимального расстоянии к длине кода в слу-
случайном линейном коде приближается к скачкообразному распределению,
когда длина кода становится достаточно большой при фиксированной ско-
скорости. Скачок возникает прн наименьшем значении р, удовлетворяющем
соотношению
1 + р Iog2 р + A - р) log2 A - р) = kin.
ВВЕДЕНИЕ
Рассматривается следующее семейство случайных кодов.
Пусть (?i, ..., Gk есть я-разрядные двоичные последователь-
последовательности, не обязательно различные. Линейный код из 2к слов
Ао ^2ft-i формируется из этих последовательностей с по-
помощью соотношений
At=2BuGtt (la)
где суммирование осуществляется поразрядно по модулю 2,
а вектор
Bt = (Bn Bik) (lb)
есть двоичное представление индекса /.
Минимальное Кодовое расстояние определяется ЫШ
D = min Dt, Ba)
') Pierce J. N.. Limit dtotribation of the minimal dittance of
linear codes, ШДД ТттШ№т<1фМаН0П Яивф «•!!,. 1*4
595 - 599,

Дж. Н. Пирс
где
Dt равно числу ненулевых координат в А{. BЬ)
Постулируется вероятностное пространство Q, содержащее
2"'е точек, выбираемых с равными вероятностями 2~пк и соответ-
соответствующих числу способов выбора последовательностей Gu ...
..., Gk.
Рассмотрим теперь бесконечную последовательность таких
семейств случайных кодов с фиксированным отношением k/n
и обозначим через р наименьшее решение уравнения
C)
Ниже будет показано, что
P(D/n<p)-*0 при n->oo Da)
и что
P(D/n>р + в)-*0 при п->оо для любого е>0. DЬ)
Граница Варшамова —Гилберта') позволяет установить,
что имеется по крайней мере один код, для которого D/n^р;
соотношение Dа) показывает, что существует очень мало длин-
длинных кодов, для которых D/n ^p, в то время как из DЬ) сле-
следует, что существует очень мало длинных кодов, для которых
D/n превышает р на сколь угодно малую величину.
НЕКОТОРЫЕ ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Для упрощения различных выражений повсюду будет
использоваться обозначение
K = 2k-\. E)
Применение формулы Стирлинга приводит к следующему
асимптотическому выражению для биномиальных коэффициен-
коэффициентов:
при n->oo равномерно по б^а^1—6. Fa)
Здесь символ ~ означает, что отношение левой и правой
частей стремится к единице; б —произвольное положительное
число; Я (а) —функция энтропии,
Н{а)= -alog2a-(l-a)log2(l-a). Fb)
') См. Питерсон У., Коды, исправляющие ошибки, „Мнр", М., 1934,
68.

Предельное распределение для минимального расстояния в коде 7
Используя F) и простые границы для отношения соответству-
соответствующих членов, получаем следующее выражение для суммы би-
биномиальных коэффициентов:
па 1 \
2 Г )~(l-a)'l4l-2a)-1Bnna)-'h2nH{a>
при п-+°о равномерно по б<?а<!-у— б. G)
Из G) легко следует, что
м , ,
К 2 2~"->0 при п-*оо, если М^пр, (8а)
m-0 \tnj
И ЧТО
если М^п(р + &) для любого фиксированного е>0. (8Ь)
В дальнейшем понадобится аппроксимировать некоторое
число с помощью суммы, аналогичной сумме в левых частях
соотношений (8а) и (8Ь). Легко показать, что для заданных
положительных чисел х, е, и е2 существуют число jV0, две пос-
последовательности Мп и /„ и число а, такие, что
(9a)
aK<In<K, (9b)
м„
i *. \
если и ^ iV0. (9c)
ДОКАЗАТЕЛЬСТВО СООТНОШЕНИЯ Dа)
Запишем верхнюю границу для
Однако легко убедиться, что символы в каждой последова-
последовательности Ai независимы и принимают с равной вероятностью
значения 1 и 0, так что
(") A1)
и, следовательно,
j(^)-«. A2)

Дж. Н. Пирс
Используя (8а), немедленно получаем
P(D<d)->0 при п->оо, если d^np, A3)
что и завершает доказательство соотношения Dа).
ДОКАЗАТЕЛЬСТВО СООТНОШЕНИЯ DЬ)
Некоторые пояснения. Для того чтобы пояснить использо-
использованный метод доказательства, полезно доказать сначала бо-
более слабое утверждение:
lim infP(D<n(p + e))>4"- 04)
Для упрощения обозначений положим
A5а)
A5b)
Следует иметь в виду, что события St и S зависят от d. Да-
Далее, при 1^К имеем
5=(Js'rDUs" О6»)
так что
ЯE)>РШ5')" A6Ь)
Кроме того,
Us< = Ufs'.-Si, (]([] St,)) A7a)
i U \ \i,<t, II'
поэтому
Р /U 5,j = S Р (Su - Stl П ( U? s'.)) = S (P E,-,) - P (Stl П
n / U S^))) = S p (Si) - 2 p / U (s'. n s
и, следовательно,
(Написанные равенства следуют из того, что объединение мно-
множеств можно представить, как видно из A7а), в виде объеди-
объединения непересекающихся множеств, каждое из которых есть
разность между множеством и подмножеством; в последнем

Предельное распределение для минимального расстояния в коде 9
неравенстве использована обычная верхняя граница для ве-
вероятности объединения.)
Следует заметить, что для любой последовательности iu ...
..., iM имеет место
Р (St, П ... Л StM) = П р (sim) = lp (SMM> A8)
если (В{, ..., В1м) линейно независимы, где векторы Bt суть
векторы, определенные в AЬ). В частности, так как Bit и В(г
всегда линейно независимы при 1\Ф1Ь то из A6Ь) и A7Ь) по-
получаем
P(S)^Iy-I(I -1)г/2/2, A9а)
где
A9Ь)
Но, согласно (9), при достаточно больших п, некотором d из
интервала (пр, п(р + &)) и подходящем выборе / величину 1у
можно сделать как угодно близкой к единице, и, следова-
следовательно, нижнюю границу в A9а) можно сделать как угодно
близкой к 1/2, что и доказывает соотношение A4).
Естественно попытаться распространить этот подход для
доказательства DЬ), используя границу в виде знакоперемен-
знакопеременного ряда
Р (\JSi) ^О\ — (Т2 + ... — СТ2/,
где
Всего в многократной сумме содержится I .) слагаемых; если
бы события под знаком пересечения были независимы, то была
бы применима следующая оценка снизу:
Если в соответствии с (9) аппроксимировать 1у некоторым зна-
значением х, то эта нижняя граница приближается к величине
„2/
х ,
*--оГ+
2! п - " " B/)! '
которая в свою очередь равна приближенно 1 — ехр(— х), если
/ выбрано с самого начала достаточно большим,

10 Дж. Н. Пирс
Чтобы этот способ доказательства был эффективным и
в том случае, когда некоторые события в пересечениях не
являются независимыми, необходимо привести знакоперемен-
знакопеременную границу к такому виду, для которого можно было бы
получить достаточно точные оценки вероятностей зависимых
событий. Желаемый результат будет получен в следующих
леммах.
Лемма 1. Пусть 0/ есть множество j-наборов целых чи-
чисел, удовлетворяющих условиям
(/„ ...,i/)s9,4/> h>...>i,>l, B0a)
It I \ f~~ ft
[/niTh^ Bhl_x) линейно
\l hi)e °2/ ) независимы. B0b)
Пусть
o, = ^iP(Sil[\...[\Sll)t B1)
e/
и пусть
v/ = 2Ws,1n...nsi/n( U s4+l)\ B2)
e/ I V/+i«/ /Г
Тогда
2/-1
p(USi)> ^ (~ l)/+'or/-v2/-i для любого J. B3)
Доказательство леммы 1 проводится индукцией по /.
Первые два шага, согласно A7а), можно записать в виде
ai~Vi' B4).
что показывает справедливость соотношения B3) при / = 1
Далее,
-v2y-,= - 2 P(shf\ ... nSi2/_,nf U St2\). B5)
Используя разложения того же типа, которые привели к не-
неравенству A7Ь), выражение B5) можно переписать в виде
U
'2/+i < hi
Shl+\]. B6)
/J
В обеих суммах суммирование ведется по (iu ..., f2y-i) s в2^-!,
kj<i2j-\- Ограничения на числа / в суммах эквивалентны
определению множества Q2j> так что первая сумма есть просто

Предельное распределение для миниМйЛьного рассеяния в коде 11
Ojj. Вторую сумму можно ограничить снизу, отбросив доста-
достаточно много значений i2j под знаком суммы и i1J+l под зна-
знаком объединения так, чтобы набор из 27+1 чисел i удовлет-
удовлетворял ограничению (г,, .... г2У+1) <= 627+1. Таким образом, полу-
получаем, что
-v2/-i>-cx2/+ 2 P(Stir\..-r\Sl2J()([JSi2J+l)). B7)
92/+l
Каждую вероятность в сумме снова можно переписать в другом
виде, используя разложения того же типа, что и раньше.
В результате получим
92/+l
Отсюда следует, что
- vy_, >
т. е. индукция завершена.
Лемма 2.
П(U
B8)
/ ' \ 2/
Р\ [jSi >2(-0/+'tf/ <5ля любого J. B9)
w=i / /=1
Доказательство. Внося в выражении B2) все пересе-
пересечения под знак объединения и применяя обычную оценку для
вероятности объединения событий, получаем неравенство
После подстановки этого неравенства в B3) получаем требуе-
требуемый результат.
Лемма 3. Для каждого J существует положительная кон-
константа Cj, такая, что
J 2 (- l)t+l(lyyij\-cjap{ly)/l -
-cJexp(Iy)maxP(Sl2J\Sil S^X (80)
Доказательство. Число /-наборов, удовлетворяющих
условию B0а), равно

12 Дж. Н. Пирс
Число /-наборов, удовлетворяющих условию B0а) и дополни-
дополнительному ограничению, что соответствующие последовательно-
последовательности Bi линейно независимы, больше чем
Представляя каждое из этих выражений как полином от /,
можно убедиться, что для каждого j существует такое число dt,
не зависящее от /, что полное число /-наборов в 0У ограничено
сверху величиной
I'm
и снизу величиной
Кроме того, число /-наборов, которые удовлетворяют условию
B0а) и для которых соответствующее множество последова-
последовательностей Bt имеет ранг (/—1), меньше, чем разность между
полным числом /-наборов и числом /-наборов, для которых
соответствующие последовательности Bt линейно независимы,
а потому ограничено сверху величиной
В обеих оценках число ds можно заменить любым числом cJt
большим, чем все числа df при 1<!/<!2/.
Члены, соответствующие в неравенстве B9) нечетным /,
положительны, а вероятности, фигурирующие в определении
величин Gj в B1), суть вероятности пересечения независимых
событий, так что можно сразу написать оценку
Bm-\)lo9m-l^(l2m-1-cJl2m-2)y2m~l при т</. C1)
Члены, соответствующие в B9) четным /, отрицательны. Те
вероятности в B1), которые, как и ранее, определяются неза-
независимыми событиями, равны у1, а число таких членов по ука-
указанным выше причинам не превосходит Ij/j\. Оставшиеся члены
соответствуют случаю, когда первые (/—1) событий в пересе-
пересечении независимы, а последнее событие зависит от них; выше
было показано, что число таких членов не превосходит cjl1'1.
Следовательно,
Bт)! аш < (Iyfm + Cj (IyJm~l max P (Si2m | S?j S,2m_,) C2)
при m^J.
Вероятность в C2) зависит только от числа тех из преды-
предыдущих последовательностей Bt, сумма которых дает последо-
последовательность Bt ; поэтому наиболее слабые ограничения при

Предельное распределение для минимального расстояния в коде 13
максимизации имеют место для случая m — J:
(Si2/|S<1, .... Si2;_,) C3)
при т</.
Утверждение леммы будет получено, если подставить соот-
соотношения C1) — C3) в B9) и использовать для упрощения
результата слабые неравенства
2 AуJт-'1Bт)! < S (Iy)'lj! = exp (Iу).
Лемма 4. Для заданного б>0 существуют положительные
константы а{ и а2, такие, что
C4)
еслы (/ь ..., i2J) е 02/ ы если — < -j - 6.
Доказательство. Согласно условию леммы, последова-
последовательности Aiv .... .Л»2/-1 линейно независимы, а последователь-
последовательность Ai2I равна сумме по модулю 2 некоторого числа (ска-
(скажем, L) этих последовательностей. Для удобства предположим,
что ими являются первые L последовательностей, и введем
обозначения
V, = Aljt 1</<L, C5a)
Vo= 2 V/t C5b)
/>o
до (Vy) — число единиц в последовательности V/. C5с)
Теперь оценим вероятность р, определяемую следующим выра-
выражением:
p=P(w(V0)^d\w(Vl)^d, .... B»(Ki)<d). C6)
Пусть
V — множество (fj, ..., оД такое, что если
Vj^Vj для 1</<L, то ay(V0)<d. C7)
Тогда имеем
Р=2П^(^/ = «/|ш(У/)<?/). C8)
Так как все возможные последовательности Vj, удовлетворяю-
удовлетворяющие ограничению на полное число единиц, равновероятны,

14 Дж Н. Пирс
условные вероятности в C8) определятся следующим образом:
0, если w(Vi
C9a
t-Де
[ of-
L.m-0 J
Теперь рассмотрим функцию
C9Ь)
Так как функция g{t) монотонно убывает по / при —<у>
имеем g(t)z^g(d), если t^d, а потому
log2g{t)^ — nH I — I, если t^.d. D1)
Но в таком случае из G), C9b) и D1) находим
1
y для / < d, D2)
и, следовательно, р можно оценить с помощью неравенств
p<aniV<a«V. D3а)
где а —некоторая константа и
д
Но величину р* можно сразу же отождествить с вероятностью
того, что w(V0)^d при условии, что все координаты всех дру-
других последовательностей V) независимы и имеют одинаковое
распределение, причем
4
Однако при этих условиях координаты последовательности Vo
также являются независимыми случайными величинами и
-»- 1
/нечетно
Так как
для некоторого положительного е при всех L^2 и
отсюда находим (с помощью легко получаемых оценок бино-

Предельное распределение для минимального расстояния в коде 15
миального распределения), что для заданного 6>0 сущест-
существует положительное число а', такое, что
р'<ехр(-а'л), если -f^T~6> <44)
Из D3) и D4) следует утверждение леммы для некоторых ах и
а2 при а2<а'.
Лемма 5. Для последовательности (/„, dn), удовлетворяю-
удовлетворяющей условиям InP(Di^.dn)->х и /„->оо, имеет место нера-
неравенство
Iim inf P (D <</„)> 2 (-1)/+'*7Л D5)
для любого фиксированного J.
Доказательство. Подставим в соотношение C0) опре-
определения St и у; первый из остаточных членов в оценке стре-
стремится к нулю, так как /„-^-оо, второй член стремится к нулю,
согласно лемме 4.
Лемма 6. Соотношение DЬ) справедливо.
Доказательство. Нужно показать, что для заданных
е и в) и достаточно больших п имеет место неравенство
Выберем х так, чтобы
ехр(-лг)<-^-; D6а)
выберем / так, чтобы
l-exp(-*)-2(-l)/+V//!<ijS D6b)
/-о
и, следовательно, так, чтобы
S<-1)/+V//!>1-1J-. D6с)
/¦=о
В силу непрерывности можно подобрать такое е2, что
21
--^. если |л:'-х|<е2. D6d)

16 Дж. И. Пирс
Используя (9), выберем последовательность (/„, dn), причем
/„->¦<», dn<n(p + e), и число No, такое, что
\InP(Di^dn)-x\<e2, если n^N0. D6e)
Из леммы 5 следует, что
!im inf P(D <</„)> 1 -^-. D6f)
Наконец, выберем N} (JV, ^ No) так, чтобы
P(D<dn)> 1-еь если n^N{. D6g)
Этим заканчивается доказательство леммы н соотношения DЬ).
РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ НА КОДЫ СО СЛУЧАЙНЫМИ
ПРОВЕРКАМИ
Путем несложных преобразований результаты Dа) и DЬ)
можно распространить на коды со случайными проверками,
в которых первые k разрядов в кодовых словах предназначены
для информационных символов. В частности, пусть на элементы
порождающих последовательностей наложены следующие огра-
ограничения:
1, если т = /,
Gfm = 0, если тф / и т < k, D7)
О или 1 с одинаковой вероятностью, если т>k.
Число кодов в этом подмножестве пространства Q равно
2* (»-*). обозначим это подмножество Q'.
Из каждого кода в Q' можно построить семейство кодов,
используя в качестве порождающих последовательностей кодов
семейства некоторые линейные комбинации последовательно-
последовательностей G:
/2
Если матрица \, образованная величинами ytj, не сингулярна,
то упорядоченный набор кодовых слов (Ло, ..., Ак), связанный
с (Г] ГА), есть просто перестановка кодовых слов в наборе,
связанном с (G,, ..., Gk), и, конечно, имеет то же самое ми-
минимальное расстояние D. Если обозначить число различных
несингулярных матриц у через т), то легко проверить, что
n=nBft-2m-') D8)
l

Предельное распределение для минимального расстояния в коде 17
и что все л кодов, образованных из заданной точки мно-
множества й', различны.
Пусть ф(©) —набор кодов, связанных с точкой ©ей'.
Пусть Q" — подмножество Q, образованное объединением
всех таких наборов,
Й" = У ф(ш). D9)
(OSQ'
Можно доказать, что множества в объединении не пересе-
пересекаются. Отсюда сразу следует, что если Т — любое событие,
не затрагивающее порядка в списке слов, то условная вероят-
вероятность события Т одна и та же на Q' и Q":
. E0)
Далее, вероятность й" есть просто отношение числа точек
в Й" к 2"\ или
)
Бесконечное произведение сходится к некоторой положительной
константе, скажем Ь, поэтому получается оценка
РG|Й0 = Р (Т П п"IР (Й") <Р{ТIЬ. E1)
В частности, события с исчезающе малой вероятностью во
всем пространстве имеют исчезающе малую вероятность и
в подпространстве:
Р(Г)->0 при п-»оо=^РG'|й')->-0 при п-*оо. E2)
Таким образом, соотношения Dа) и DЬ) остаются справедли-
справедливыми, если ограничиться рассмотрением кодов со случайными
проверками.

Класс оптимальных нелинейных кодов
с исправлением двойных ошибок1)
Ф. #. Препарата
В этой статье представлены нелинейные блочные коды длины BП— 1)
(п четно) с исправлением двойных ошибок. Они имеют максимально воз-
возможное число кодовых слов для их длины и минимального расстояния и
образованы добавлением к определенному линейному коду (называемому
ядром) специального подмножества из его смежных классов. Ядро полу-
получается из соединения и суперпозиции кодов Боуза — Чоудхури — Хоквингема
(БЧХ кодов) длины B"—l). Представленные коды являются системати-
систематическими и сравнимы с соответствующими линейными кодами относительно
сложности операций кодирования и декодирования.
1. ВВЕДЕНИЕ
В течение последних лет в литературе появились сообще-
сообщения о некоторых примерах нелинейных двоичных кодов (Ва-
(Васильев [2], Надлер [8], Грин [6]). Особенно интересным в силу
своей структуры и общности был класс, открытый Василье-
Васильевым [2], т. е. класс совершенных групповых и негрупповых
кодов с исправлением одиночных ошибок, содержащий коды
Хемминга.
Недавно некоторый интерес к линейным кодам был возро-
возрожден открытием Нордстромом и Робинсоном [9] нелинейного
A5,8) кода с исправлением двойных ошибок. Из этого кода
путем укорачивания получаются опубликованные ранее негруп-
негрупповой A2,5) код Надлера [8] и негрупповой A3,6) код Грина [6].
Код A5,8) обладает интересными свойствами, а именно он
является систематическим и удовлетворяет верхней границе
Джонсона [7] для числа кодовых слов в коде длины 15 и
с расстоянием 5. Впоследствии A5,8) код был описан в тер-
терминах полиномиальных (т. е. линейных) кодов над полем GF B)
(Препарата [11])- Это описание оказалось полезным, так как
оно привело к формальному доказательству (Препарата [12])
некоторых метрических свойств этого кода, определенных ра-
ранее эвристически.
') Preparata F. P., A class of optimum nonlinear double-error-corree-
ting codes, Information and Control, 13. J* 4 A968), 378-400,

Класс оптимальных кодов с исправлением двойных ошибок 19
Оставался открытым вопрос, впервые поставленный Норд*
стромом и Робинсоном [9], является ли A5,8) код элементом
некоторого класса кодов. В настоящей статье на этот вопрос
дается положительный ответ. Для каждого четного л^4 су*
ществует негрупповой B" — 1, 2" — 2п) коде исправлением двой-
двойных ошибок, поэтому A5,8) код является частным случаем.
Здесь снова полиномиальное описание оказалось существенным
при построении этих кодов.
Интересные свойства этих кодов можно суммировать сле-
следующим образом: 1) они содержат удвоенное число кодовых
слов по сравнению с БЧХ кодами той же длины с исправле-
исправлением двойных ошибок, что является максимально возможным
числом кодовых слов для данной длины и расстояния, т. е.
они оптимальны; 2) их декодирование основано на вычислении
величин, сходных с синдромом, и сложность его сравнима
с соответствующими БЧХ кодами; 3) эти коды являются систе-
систематическими, и кодирование может быть выполнено очень
просто с помощью регистров сдвига за то же число тактов,
которое требуется для последовательной передачи информа-
информационных разрядов.
Следующие параграфы посвящены описанию этих кодов и
доказательству сформулированных выше свойств.
2. ОПИСАНИЕ КОДОВ1)
В дальнейшем будем считать, что все рассматриваемые по-
полиномы принадлежат алгебре Ап^1 полиномов над полем GFB)
по mod (л:2""'" + l) (п^-4). Для данных а(х)еЛ„_, и Ь (х) е
eiH пусть №[a(x)] обозначает число ненулевых коэффициен-
коэффициентов а{х), и пусть d[a{x), Ь (х)] ~ W [а (х) + Ь (х)] есть расстоя-
расстояние Хемминга между а(х) и Ь(х). Символом а(х) мы будем
также обозначать вектор-строку [a.jn-i_2, a^i-i_3, ..., Oq]. гДе
a(*) = Sa/*'.
Пусть {m{x)} есть БЧХ код длины 2" ' — 1 с исправлением
одиночных ошибок, порожденный примитивным полиномом gi (х)
степени («—1), т. е. если a — примитивный элемент поля
GFBn~l), то gi(a) = 0. Рассмотрим далее код {s{x)}, порождаю-
порождающий полином которого имеет корни а, а3 и 1. Ясно, что {s(x)}
является БЧХ кодом с минимальным весом 6 [10] и {s (x)} cz
с:{т(л:)}. Ясно также, что {s(x)} существует только тогда,
') Материал этого параграф* отчасти пересекаете» со статьей [12], по-
поскольку настоящая работа является естественным ее обобщением.

20 Ф. П. Препарата
когда 2" — 1^2(я — 1)+1, т. е. при я^4; при я = 4 поли-
полином s(x) тождественно равен 0. Наконец, обозначим через и(х)
полином (лг2"""'-' + l)j(x + 1).
При заданных полиномах а(х) и b(х) (а(*)еЛ„_,, 6(х)е
е Л„_,) и двоичном параметре / построим B — 1)-компонентные
векторы над полем GF B) вида
При заданных m (х) <= {гп (х)} и s (x) e {s (x)} и произвольном i
положим теперь а(х) = ш{х) и b{x) = m(x) + (m(l) + 0м W + SW-
Получаем
v = [т (х), г, т (х) + (т A) + i)u (х) + s (x)]. A)
Лемма 1. Векторы v, задаваемые (I), образуют некоторый
линейный код Я!>п.
Доказательство. Утверждение немедленно следует из
проверки того, что <вп является группой относительно сложе-
сложения над GFB). Действительно: 1) "<Р„ содержит аддитивную
единицу [0, 0, 0], получаемую из A) при m(x) = 0, s(x) = 0,
i — 0; 2) Фп замкнут относительно сложения, так как {ш{х)} и
{s(x)} являются групповыми кодами.
Лемма 2. Минимальное расстояние между любыми двумя
кодовыми словами из 48n равно по крайней мере 6').
Доказательство. Так как "<Р„ является линейным ко-
кодом, его минимальное расстояние совпадает с минимальным
весом W его ненулевых кодовых слов, к определению которого
мы переходим. Предположим сначала, что ш(х) = 0. Если также
г = 0, то W=W[s{x)]>6. Если г= 1, то W=\ + W[u{x)+s{x)]^
> I + W[u{x)]~max W[s(x)]. Мы знаем, что W[и(х)] = 2п~'- 1
и что max W [s{x)] равен 2"~' —6 при я>4 и равен 0 при
я = 4 (так как max W [s(x)] равен максимальному четному весу
кодовых слов БЧХ кода с исправлением двойных ошибок).
Следовательно, имеем
W > 1+ 2" - 1 - 2"~' + 6 = 6.
Предположим теперь, что ш{х)ф0. Если m (x) ф {s (x)}, то
m'{x) = m(x) + {m{\) + i)u{x) + s{x)=?0 и пС(х)е {m(х)}. От-
') В действительности минимальное расстояние между словами кода tn
равно 5. В частности, вектор A) имеет вес 5, если ш(х) есть элемент БЧХ
кода с исправлением двойных ошибок, имеющий вес 5, i = 0 и s(x)~ m(x)+
+ и (х). Однако это обстоятельство не влияет на справедливость основного
результата статьи (теорема \). — Прим. перев.

Класс оптимальных кодов с исправлением двойных ошибок 21
сюда следует, что W > W [m (х)] + W [m* (х)] > 3 + 3 = 6, так
как и т(х), и т*(х) являются ненулевыми, а {т(х)} имеет
минимальный вес 3. Если же наоборот т (х) е= {s (x)}, то
W[m{x)\~^§ и W^W[m(x)]^Q. Доказательство закончено.
Число информационных разрядов кода <вп легко получить,
если учесть, что независимо выбираемые т(х), s{x) и i дают
соответственно B" — п), Bп~1 — 2п) и 1 информационных раз-
разрядов. Следовательно, ^„ есть B" — 1, 2" —Зл+1) линейный
код с минимальным расстоянием 6.
Рассмотрим далее полином ф(*) = (я2" '-1 + l)/gi (x), т. е.
последовательность длины 2п~ — 1, являющуюся последова-
последовательностью максимальной длины. Покажем сначала, что спра-
справедлива следующая лемма.
Лемма 3. Существует число s (O^s ^.2n~x — 2), такое, что
s)J s(
Доказательство. Вычислим произведение q>(x)q>(x).
Так как ф(х) не делится на gi(x), полином Ф2(л:) не равен нулю;
кроме того, ч?(х) принадлежит коду, порожденному <р(х), т. е.
Ф2(*) = *'ф(х) B)
при некотором г, 0^г^2"-1 —2. Если умножить B) на x2s,
то получится x2sq>2{x) = xr+2sy(x), т. е. (xs<p(x)f = xsq>(x) • xr+s.
Отсюда вытекает утверждение леммы, если xr+s=l, т. е. если
r + s = 0 (mod2"~1— l), или, что эквивалентно этому, s = 2"~' —
— 1—г (mod2"~'— l). Доказательство закончено.
Положим1) f(x)Axs<p{x).
Ясно, что полином q(х) = ах1 (а = 0, 1; / = 0, 1, ..., 2"~' — 2)
при а = 1 является главным элементом смежного класса кода
{ш(х)}, имеющим наименьший вес. Построим теперь вектор а
вида
и = [?(*), О, q(x)f(x)]. C)
Справедливы следующие леммы.
Лемма 4. Полином q(x) + q (x) f (x) принадлежит {пг {х)}.
Доказательство. Утверждение немедленно следует из
леммы 3, так как
f (x) {q (х) + q{x)f (x)} = f(x)q (x) + f2 (x) q (x) = О,
<) Знаком = автор обозначает рамяство цо овределмню, - Прим. перев.

22 Ф. П. Препарата
т. е. полином q{х) + q{х)f{х), будучи ортогональным к f{x),
делится на g, (*).
Лемма 5. Сумма двух векторов и, и и2 вида C) допускает
при л^4 представление
U! + u2 = v + q + p, D)
где
v = [«'(*). О, т'(х) + т'A)и{х)], т'(х)<={т(х)}, т.е.у<=<$п,
q = [q{x),0,q{x)], E)
р = [0, 0, пг"(х)], т"(х)^{т(х)}. F)
Если q {х) — 0, то т' {х) = 0; если q (х) Ф 0, то либо т' (х) = О,
либо т'{х) является трехчленом.
Доказательство. Пусть ul = [ql{x), 0, qi(x)f(x)] и
и2=Ы*)> °. Q2(x)f(x)]. Имеем
Ui + u2 = Mjr) + 02(x), 0, (9,(jf) + <72(*))f(*)]. G)
Пусть q (х) f (х) = (<?, (дс) + <?2(х)) f (х) и т' (дг)^ 9, (дс) + q3(x)+ q (x).
Так как {q{x) +q](x) +q2{x))f{x) = O, ясно, что m' (x) e {m (л:)}.
Если <7i(*) = <72(*)> to отсюда следует, что q(x) = 0 и т'(л:) = 0.
Если qx (x) Ф q2(x), to либо q{x) = qi{x) {i=\, 2), либо поли-
полиномы q\{x), q2(x) и q{x) различны и не равны нулю; в первом
случае пг'(х) = 0, в последнем случае пг'{х) является трехчле-
трехчленом.
Это дает возможность написать
Я\ (x) + q2(x) = m'(x) + q{x)
и переписать G) следующим образом:
Ul+u2 = [m'W, 0, m'(x) + m'(l)u(x)] + [q(x), 0, q{x)] +
+ [0, 0, q{x) + q{x)f(x) + m'{x) + m'{l)u(x).
Теперь очевидно, что полином пг" {х) =. q (x) + q {x) f (x) +
+ пг (х) + пг'(\)и{х) принадлежит {пг{х)}, так как он является
суммой полиномов, принадлежащих {пг{х)}.
Лемма 6. Для любого трехчлена m(x)=xs+xl + xJe{
справедливо равенство
m (а3) = а3* (ал + а2Л),
где Л — некоторое число @</г <2"~'— l).

Класс оптимальных кодов с исправлением двойных ошибок 23
Доказательство. Пусть пг(х) = Xs + х1 + х1, где s, i и /
различны. Тогда пг (а3) = a3s + а3' + а3;. Вспоминая, что пг(а) =
= as + а' + а; = 0, имеем
а3* = (а' + а'K = а3' + а3' + а'а> (a' + а'),
что эквивалентно m(a3) = a'a-'ai = a3V~'sa^~'s. Но a/~s=l+a'~s,
следовательно, полагая / — s = h ф О, получаем утверждение
леммы.
Рассмотрим теперь матрицы
Я,-[a*"-* а, 1],
Я3 = [(а3J"-|-21 .... а3, 1],
t/-[l, .-., 1, 1].
Матрица Н = \Н\, #з, U \ является проверочной матрицей
кода {s{x)} (индекс Т обозначает операцию транспонирования).
Для заданного полинома h(x) определим h(x)HT=[^l, Рз, с]
как характеристики h(x). Для произвольного s{x)e{s{x)}
имеем
W[h(x) + s(x)]>W[k(x)],
где k (x) — элемент с минимальным весом из смежного класса
по {s (x)}, которому принадлежит h (x). Вычислим теперь харак-
характеристики некоторых полиномов, которые часто будут исполь-
использоваться в дальнейшем:
q(x) = xs, q(x)HT=[as, a3*, 1],
пг (х) s {пг (х)}, пг (х) Нт = [0, пг (а3), пг A)], (8)
ш"{х) (см. F)), пг"(х)Нт = [0, пг'(а3) + а?°, 1].
Первое соотношение очевидно. Второе следует из того, что
пг (а) = 0, так как пг (х) <= {пг (х)}. Чтобы доказать третье из
соотношений (8), вспомним, что пг" (х) = q(x) + q (x) f (x) +
+ т'{\)и{х) + т'{х) и что q (x) f (х) НТ = [as, О, 0], так как f(x)
делится на минимальную функцию gs(x) от а3 и на (*+1);
а также примем во внимание, что ш' (\)и(х)Нт = [0, 0, т'A)],
так как и(х) делится на g3(x) и минимальную функцию g, (л:)
от а.
Лемма 7. Для nt"(х) = q{х) + q{x)f{х) + т'{I)и(х) + т'(х)
и произвольного s(x)e{s(x)} справедливо
4 при четном п,
2 при нечетном п.

24 Ф. П. Препарата
Доказательство. Характеристики (пг"(х) + q(x)) суть
[а5, т'(а3), 0] (см. (8)). Далее, W [m" (х) + q (х) + s (х)] есть ми-
минимальное число столбцов Я, которые прибавляются к
[а*, т'(а3), 0]Т. Так как с = 0, это число четно. Предположим, что
имеются два элемента *, и х2 из GF^"), которые удовле-
удовлетворяют уравнениям
Учитывая, что а5 ф 0, сделаем подстановку у, (j),
Уъ — (x2las). После простых преобразований убеждаемся, что у}
и у2 являются решениями единственного уравнения
Так как либо т' (х) = 0, либо т' (х) является трехчленом
(лемма 5), то лемма 6 дает т' (а3)/а^ = аЛ + а2Л @ < h < 2" -2);
предыдущее уравнение преобразуется в уравнение
которое при z = y + ah эквивалентно уравнению
z2 + г + 1 = 0. (9)
Но решениями уравнения (9) являются первообразные корни
третьей степени из единицы, в силу чего уравнение (9) имеет
решения в GFBn~') лишь при нечетном п. Доказательство
закончено.
Построим теперь B" — 1)-компонентные векторы следую-
следующего вида:
w = [m(x) + q(x), i, m(x) + q(x)f{x) + (m(l) +i)u(x) + s(x)], A0)
где m (x), q (x), i, s (x) выбираются независимо и дают соответ-
соответственно B""' — п), (п— 1), 1, BП~'— 2и) информационных раз-
разрядов, так что общее число информационных разрядов равно
B" —2и). Векторы w образуют некоторый B"— 1, 2п~2п)
код Жп. Общий вектор w можно разложить следующим обра-
образом:
w = v + u, A1)
где v и и определены соотношениями A) и C) соответственно.
Пусть w, = v, + и, и w2 = v2 + Щ — два различных кодовых слова
из Жп. Используя соотношение D) (лемма 5), имеем
w, + w2 = (V] + va) + (u, + Us) = v, + v2 + v + q + p
или
Wj + w2 = v' + q + p, {Щ

Класс оптимальных кодов с исправлением двойных ошибок 25
где v' = v,+V2 + v. Ясно, что v' является некоторым произ-
произвольным элементом кода ^п, a q + p можно представить сле-
следующим образом:
q + p = [q(x), О, q(x)f(x) + tn'(x) + tn'(l)u(x)] =
= [q(x), О, q(x)f(x)] + [Q, О, tn'(х) + m'A) и (х)) =
= и' + [0, 0, m'{x) + m'{\)u{x)].
В случае, когда пг' (х)фО, вспомним, что m' (x) <?{s(x)} (лемма 5),
т.е. [О, 0, пг' {х) + тг {\)и{х)]ф^п. Следовательно, код Жп
яиляется нелинейным кодом. Кроме того, каждый ненулевой
вектор и в A1) определяет некоторый смежный класс кода 11?п,
так как отличный от нуля полином q(x) определяет неко-
некоторый смежный класс кода {т(х)}. Следовательно, код Жп
можно рассматривать как теоретико-множественное объедине-
объединение кода <&п и некоторого подмножества его смежных клас-
классов, мощность которого равна 2"~'— 1.
Пусть W обозначает вес суммы (w,+w2). Мы можем теперь
доказать основной результат этой статьи.
Теорема 1. При четном п^4 код Жп является нелиней-
нелинейным BП — 1, 2" — 2п) кодом с минимальным расстоянием 5.
Доказательство. Если q(х) = 0, то Wj + w2^'S'n и W^6
по лемме2'). Предположим теперь, что q {x) = x {Q<^s<^2n~{ —2).
В общем случае имеем
W = / + W [пг (х) + q (х)] + W [ш (х) + (пг A) + /) и (х) +
+ s(x) + m"(x) + q(x)]. A3)
В зависимости от значений тA) и i мы различаем три случая:
1) /пA) = 0, /= 1. Соотношение A3) преобразуется следую-
следующим образом:
W > 1 + W [ш (х) + q (х)] + W [и (х) + s (х) + т" (х)] -
- W [т [х) + q (х)] = 1 + W [и [х) + s (х) + т" {х)\.
Из соотношения (8) и и (х) НТ = [0, 0, 1] получаем
Но, согласно леммам 5 и 6, имеем ш' (а3) =*= a3i (a* + а2*),
< 2"-1 - 2. Следовательно, m' (a3) + а3* = а35 A + а* + а2*) Ф 0 в
GFBn~") при четном п. Отсюда следует, что W [и (х) + s (x) +
+ т"(х)]фО. Кроме того, W[и(х) + s(х) + т"(х)] есть четное
число, превышающее 3, так как с = 0 и р,=0 (Я, является
') См. примечание на стр 20. — Прим. перев.

26 Ф. П. Препарата
проверочной матрицей кода с исправлением одиночных ошибок).
Мы заключаем, что W^z 1+4 = 5.
2) ягA) = 0, / = 0. Если т(х)Ф0, то соотношение A3) дает
W > W [т (х)) + W[m (х) + т" (х) + s (*)] - 2W [q (*)].
Соотношения (8) дают
(га (х) + т" (х))НТ = [р,, рз, с] = [0, m (a3) + m' (а3) + а3*, 1 ],
т. е. вес W [т {х) + т" (х) + s (х)] — нечетное число (с = 1), не
меньшее 3 (р,=0). Кроме того, соотношения т(х)Ф0 и тA) = О
означают, что W[m(x)]^4, откуда й^^4 + 3 — 2 = 5. Если
т{х) = 0, то соотношение A3) преобразуется к виду
W > W [д (х)] + W [m" (x) + q(x) + s (x)).
Из леммы 7 имеем, что W \т" (х) + q (х) + s (х)] ^ 4 при четном п,
откуда W^z 1+4 = 5.
3) гаA)=1. В этом случае число W [т {х) + q (x)] четно и
не менее 2. Предположим сначала, что W [nt (x) + q (х)] = 2. Это
означает, что т (х) = Xs + х1 + х' (s, i, j различны); отсюда по
лемме 6 имеем т(а3) = а3*(аЛ + а2Л) при некотором А, 1<Л^
<2"-'-2. Соотношение A3) дает
W = i + 2 + W [т (х) + A + i) и (х) + т" (х) + q (x) + s (*)].
Для простоты положим fe(j:)=m(j:) + A +/)«(>:) + m" (д:) + <7 (*) +
+ s(j:). С помощью соотношений (8) легко получаются следую-
следующие характеристики k(x):
k (х) НТ = [р„ Рз, с] = [of, m (a3) + m' (а3), /].
Так как т' (а3) = а^ (а* + а2*) @</г<2"-'-2), отсюда следует,
что т (а3) + яг'(а3) = а35(а' + а2Г) при r = h + k. Следовательно,
() () ( ) р
по лемме 7 имеем W[k(х)]>2 при четном rt, т. е. [()]^
^4 — { (так как { есть четность tt^[/e(jc)]). Мы заключаем, что
W > / + 2 + 4 - г = 6.
Наконец, предположим, что U7 [яг (*) + <7 (*)] ^4. Так как
Р, = а\ находим W [k {х)\ > 1, откуда следует W > i + 4 + 1 =
= г + 5. Доказательство окончено.
Замечание. Интересно рассмотреть задачу расширения при-
примененного метода с целью построения кодов Жп для других
значений числа исправляемых ошибок, а именно для /=1 и
2
Имеются две различные схемы, которые кажутся перспек-
перспективными для обобщений. Рассмотрим сначала соотношение A0),

Класс оптимальных кодов с исправлением двойных ошибок 27
которое описывает код Жп с исправлением двойных оши-
ошибок, т. е.
w = [ш (х) + q (х), i, m(x) + (m(l) + i)u{x) + s{x) + q(x)f{x)].
Здесь Жп строится с помощью двух кодов {ш (х)} и {s (x)}, где
{s {х)} а {ш (х)}. В частности, если а — первообразный корень
в GFB"~'), то {пг(х)} характеризуется корнем a, a {s(*)} —
корнями 1, а, а3. Поэтому имеются два потенциальных обобще-
обобщения на случай ^-кратных ошибок.
A. {ш(х)} имеет корень a, a {s(*)} имеет корни 1, а, а3, ...
...,а2'-'.
B. {т(х)} имеет корни а, а3, ..., а2' 3, a {s(x)} имеет корни
1, а, а\ ....а2'.
При t = 1 обе схемы приемлемы и порождают, как легко
показать, одни и те же коды. В частности, т(х) в схеме В
является общим элементом Л„_,, a {s(x)} имеет (*+1) ?,(.*:)
в качестве своего порождающего полинома. Получающийся
код Ж(п состоит из векторов
wB = [т (х), i, m(x) + (m(l) + i)u (x) + s(x)). A4)
Удивительно, что код Жп является линейным кодом, как это
легко видеть из A4). Кроме того, можно показать, что ои сов-
совпадает с кодом Васильева [2]. В действительности A4) можно
выразить следующим образом:
wB=[m(Ac), i, т (х) + р (х)],
где
p(x) = (m(l) + i)u(x) + s(x).
Если теперь наложить условие, что р (х) принадлежит коду,
порожденному полиномом gl (x), то это соотношение становится
уравнением относительно неизвестных s(x) и /, которое всегда
можно разрешить, если
/ = четность W [т (х)] + четность W [р {х)].
Тем самым получается линейный код Васильева (эквивалентный
коду Хемминга).
При t>2 вопрос о том, дает ли какая-либо из двух опи-
описанных схем приемлемое обобщение, остается полностью от-
открытым.
3. ВИД ИЗБЫТОЧНЫХ ФУНКЦИЙ
Рассмотрим выражение A0) общего вектора кода Жп, т. е.
w-[т(х) + q{x), i, т(*) + (тA) + i)u(x) + s(x) + q(x)f (x)].

28 Ф. П. Препарата
Легко видеть, что Ж'„ можно кодировать как систематический
код, т. е. B" —2п) двоичных информационных разрядов можно
произвольно приписать в фиксированных позициях, а осталь-
остальные Bп—1) избыточных разрядов можно подсчитать как функ-
функции информационных разрядов. В этом параграфе мы иссле-
исследуем природу этих функций. Для удобства представим теперь w
в виде
_г/о) щ ,@) , ,о) л) 1
где буквы i и р обозначают информационные и избыточные
разряды соответственно.
Предположим сначала, что s(a:) = O. Тогда левые 2"~' раз-
разрядов [i2n-i_2, .... г] полностью определяют 2"~'— 1 правых
разрядов. Обозначим последние через [<p2n-i_2. • ••> Фо] и ПР°"
анализируем их зависимость от предыдущего множества раз-
разрядов. Пусть
c(*JU*/ f{)^f'
m(x) = ^itrijX1,
где все суммы берутся по / = 0, 1, ..., 2п~1 — 2. Если q {х) = 0, то
с/ = 0 при каждом /. Если q(x) = xs, то, согласно свойству одно-
однозначности последовательности максимальной длины [10], имеем
cs+Jc5+s_, •••cs+ft_n+2= 1 и c/+ft-" c/+J_n+2 = 0 при j=?s, где
число b таково, что fbfb-\ •"f*-n+2=l- Легко видеть, что
Я(Х) = Sc/ + b ' ' * Ci + b-n+2* , ttlf = if +Cj + b ••• Cj + b-n+2
и
<P/ = 4°* + с!+ь •' • ci+b-n+2 + i + 2(Д0> + Ck+ь • • • Ck+b-n+2) + c/
или после перегруппировки членов
Ц ch • • • сь-п+А. (is)
Вспомним теперь, что поскольку с (х) = q (x) f (х) = /(х) f (x),
то с/ = ^jfj-ki^ есть линейная функция от переменных in0), if*, .. •
.-., 4" '-2- ^ частности, так как f{x) есть последовательность
максимальной длины, то для различных г и s существует
число t, такое, что cr + cs = ct. Если q, (x) есть трехчлен, то при
s = (r + n — 1) число t удовлетворяет неравенствам г <t <г + п— 1.
Следовательно, имеем
h-\Ch ' • ш Ch-n+1 =

Класс оптимальных кодов с исправлением двойных ошибок 29
Отсюда следует, что в последнем члене выражения A5), кото-
который является суммой B"~' — 2) произведений, каждая пара по-
последовательных произведений из (и—1) множителей преобра-
преобразуется в одно произведение из (п — 2) множителей, так что по-
получается B"~2—1) произведений. В заключение мы получаем
выражение
2 Г Н2 ' Н-„ A6)
A-0 J ft-0 s=-0
которое показывает, что ф/D«-1_2 'о. t) является суммой
некоторой строго линейной функции и некоторой нелинейной
функции степени не выше (и —2). В качестве проверки заметим,
что для A5,8) кода (п = 4) последняя функция является квад-
квадратичной.
Пусть Нц — общий вход проверочной матрицы Н* кода {s(*)},
записанной в систематическом виде, т. е. Bи— I) правых столб-
столбцов Я* образуют единичную матрицу и индекс / пробегает
значения справа налево. Тогда соотношения
Р< = Ф<+ 2 М4° + Ф/) (/ = 0, 1 2я-2) A7)
/=2п-|
дают искомые избыточные функции-
Выражения A5) и A7) дают возможность предложить очень
простую схему кодирования. Действительно, ф/ является цик-
циклической функцией от своих аргументов. Следовательно, ее
можно реализовать с помощью нелинейного сверточного кодера,
состоящего из циклического регистра сдвига и комбинацион-
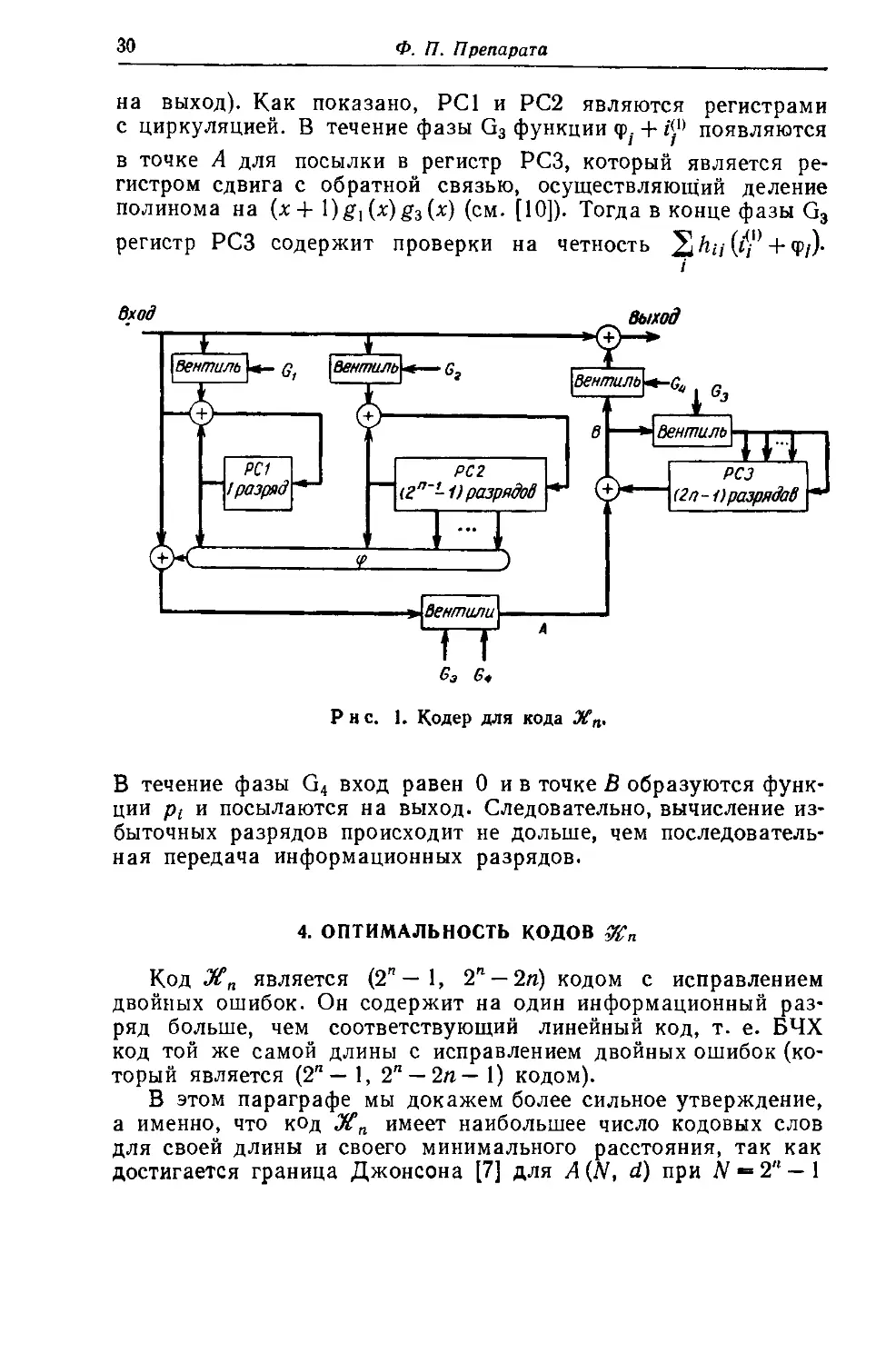
комбинационной схемы, реализующей Ф = Ф2га-|_2 (см. рис. I). Полный кодер
состоит из трех регистров сдвига PCI, PC2, РСЗ, имеющих 1,
B"-.' —1) и Bи—1) разрядов соответственно. Операция раз-
разбивается на четыре фазы G|, G2, G3, G4, продолжительность
которых равна I, B" — I), B""'— 2п) и Bп—1) тактам соот-
соответственно. Указанные вентили проводят, когда приложенные
сигналы равны 1. Все регистры первоначально заполнены ну-
нулями. Информационные разряды посылаются в виде последо-
последовательности i, 4n-i_2> •••» 40>' 4"-|-2> •••> 4n-i по одному раз-
разряду на каждый такт. Тогда в течение фазы Gi разряд / по-
посылается на РС1 и в течение фазы G2 разряды 4«-i-2> •¦•> С
посылаются на РС2 (при этом они одновременно посылаются

30
Ф. П. Препарата
на выход). Как показано, РС1 и РС2 являются регистрами
с циркуляцией. В течение фазы G3 функции ф;. + г*1* появляются
в точке А для посылки в регистр РСЗ, который является ре-
регистром сдвига с обратной связью, осуществляющий деление
полинома на (х + I)g\(x)g3{x) (см. [10]). Тогда в конце фазы G3
регистр РСЗ содержит проверки на четность 2 кц D° + Ф/)-
вход
выход
Вентиль U— q Хвентиль
Р н с. 1. Кодер для кода Жп.
В течение фазы G4 вход равен 0 и в точке В образуются функ-
функции pi и посылаются на выход. Следовательно, вычисление из-
избыточных разрядов происходит не дольше, чем последователь-
последовательная передача информационных разрядов.
4. ОПТИМАЛЬНОСТЬ КОДОВ ^Г„
Код Жп является B"—1, 2" — 2л) кодом с исправлением
двойных ошибок. Он содержит на один информационный раз-
разряд больше, чем соответствующий линейный код, т. е. БЧХ
код той же самой длины с исправлением двойных ошибок (ко-
(который является B" —1, 2" —2п—1) кодом).
В этом параграфе мы докажем более сильное утверждение,
а именно, что код Жп имеет наибольшее число кодовых слов
для своей длины и своего минимального расстояния, так^как
достигается граница Джонсона [7] для A(N, d) при А/= 2"— 1

Класс оптимальных кодов с исправлением двойных ошибок 31
(я четно) и d = 5 ')• Граница Джонсона при d = 2/ + l задается
следующим образом:
MN,d)<-r j" ^,„ _» О»)
/-о
где [а] есть целая часть числа a, a R(N, d, t) удовлетворяет
верхней оценке
При N = 2n — 1 и f = 2 соотношения A8) и A9) приобретают вид
2"-' ^l2 -1'5'
Рассмотрим соотношение B1). При четном п число B" —4)
делится на 3, так что [B" - 3)/3] = B" - 4)/3. Кроме того, B" - 4)
делится на 4. Мы должны теперь показать, что {2п — 1)BП — 2)Х
X B"~2— 1) делится на 5. Это немедленно следует из того за-
замечания, что вычеты числа 2" (п четно) по mod 5, чередуясь,
равны 1 и 4, т. е. вычеты чисел B"—I), чередуясь, равны О
и 3. Поскольку число BП-1)B"-2)Bп-2-1) содержит две
последовательные четные степени 2, имеет место неравенство
/?B"-1, 5, 2)<<2Я-1)BП-2)BП-4>,
из которого при четном п легко получить соотношение
С2" ,-C25/?Bn-l,5,2)
На основании этого мы заключаем, что при п четном имеем
02п-1
А B" - 1,5) <-r—i г т = 22"-2\
) Дж. П. Робинсон первый заметил, что /4B"- 1,5) (п четно) есть сте-
степень 2. Еще ранее автор сформулировал предложение, основанное на довольно
туманных геометрических аргументах, что нелинейные коды длины BП-1)
и с расстоянием 5, аналогичные A5,8) коду, существуют лишь при четных»
(частные сообщения, январь и март 1968 г.).

32 Ф. П. Препарата
Последнее число в точности совпадает с числом кодоцых слов
кода Ж п. Ясно, что при нечетном п отношение в B2) строго
больше, чем B"-'-1), так как [B"-3)/3] = B"-5)/3. Это
обстоятельство также показывает, что при нечетных п коды
Жп не существуют.
5. ДЕКОДИРОВАНИЕ КОДА &Сп
В этом параграфе мы покажем, что декодирование кода
Ж„ можно легко выполнить с помощью вычисления и иссле-
исследования величин, подобных синдрому.
Вектором е = [ео(л:), е, е\(х)\ мы представим общий вид
ошибки, где е/(л:)еЛ„_, и е есть двоичный параметр. Исполь-
Используя свойства расстояния кода Жп, заключаем, что ошибка е
может быть исправлена прн выполнении следующего условия:
B3)
В общем случае полученный вектор есть т = [го(х), г, Г] (лгI =
¦» w + е, где w e Ж'„¦ Вычислим теперь следующие функции:
Со = го (х) Ни
d = r + ri(x)UT.
Так как г0 {х) = m{x) + q {х) + е0 (х), a m (х) НТ\ = 0, то при
q(x)=bx* имеем а0 — bas + е0(а). Аналогично из гх (х) = m(x) +
+ (m(l) + i)u{x) + q(x)f (x) + s(*) + e,(*) и и(х)Н\ = 0, s{x)H* =
= 0, q(x)f (х) Н\ = Ьа получаем, что а, = Ьа+ех (а). Из го{х)+
+ ri(x) = q(x) + q(x)f(x) + s(x) +ео(х) + е, (х) + (т A) + i)u (x),
вспоминая, что s(a:)#3=0, f(x)Hl = 0, и(х)Нз = 0, находим,
что а= &a3s + e, (a3) + e0(a3). Наконец, так как числа W[q(x)X
Xf(x)], W[s(x)\, W[m{x) + m(\)u(x)\ четны, то d = r + i +
+ ех A) = е + е, A). Все это можно выразить следующим обра-
образом:
а0 =* bas + е0 (а),
а, = bas + e, (а),
B4)
C) C)
тора
,()
Четверку 2=(а0, аи a, d) удобно называть синдромом век-
века г.

Класс оптимальных кодов с исправлением двойных ошибок 33
Теперь мы приведем лемму, которая основана на доста-
достаточно известных результатах из теории конечных полей ').
Лемма 8. Множество в всех 0 g GF B"), для которых
уравнение у2 + у + 0 = 0 имеет решения в GF B""'), образует
векторное пространство размерности (га —2), определяемое чет-
четными линейными комбинациями элементов нормального базиса
р, р2, р4, .... Г поля GFB"-').
Доказательство. Известно (см., например, [1]), что
существуют базисы поля GFBre~'), состоящие из полных мно-
множеств сопряженных элементов (нормальные базисы). Пусть р,
Р2, ..., р2" —одно из таких множеств линейно независимых
сопряженных элементов. Тогда каждый элемент YeGFB"~l)
однозначно выражается следующим образом:
Y = сор + с,р2 + ... + С-гР2* (с, е GF B)).
Так как
Р2"" = Р,
¦имеем
Y2 + Y = <*„Р + <*,Р2 + • • • + 4-2Р2"(d, <= GF B)), B5)
где dj = С/ + С/-, (индексы вычисляются по modtt—1). Но пра-
правая часть B5) есть общий элемент в. Действительно, предпо-
предположим, что d0, du ..., dn_2 заданы. Тогда мы имеем сге_2 =
= do + co = do + dx + Сх — ... =do+ ... + dn_2 + с„_2, следова-
следовательно,
d0 + dx + ...+ dn_2 = 0,
т. е. число ненулевых dj четно. Доказательство закончено.
Эта лемма дает правило для проверки того, является ли
Y e GF B") элементом в. Фактически мы должны сначала
кайти нормальный базис р, р2, ..., р2 поля GFB't~1) (см.,
например, [4]). Пусть через у обозначен вектор-столбец пред-
представления над полем GFB) элемента YsGFB'l~l) относи-
относительно базиса 1, а, ..., ап~2, и пусть Л1 = [р, ..., р2 J —
') Рассуждения, приведенные ниже, по существу заимствованы из ра-
работы [1]. Весьма сходная теорема была доказана Берлекампом и другими
([3], теорема 1). Довольно подробное изложение рассматриваемого вопроса
имеется в статье [4], в которой содержится также обобщение этой леммы.
Так как приведенное здесь утверждение тесно связано с дальнейшими ре-
зультатами, лемма и ее доказательство приводятся полностью.
3 3dK. 560

34 Ф. П. Препарата
невырожденная (п — 1) X (п — 1) матрица. Тогда \ связан с пред-
представлением [d0, ...,dn_2] элемента y относительно базиса р,
Р2,...,Р2 следующим образом:
Y = M[d0) ...,dn.2r,
т. е. M~'Y = [rf0. •••>dn_2]T. Умножая слева обе стороны ра-
равенства на вектор-строку и = [1, 1 1], получаем условие
3, если y •= в,
I, если y не-
некоторое, если обозначить через Хг сумму строк М~1, Перехо-
Переходит в условие
хг @, если v^e,
[ 1, если y Ф- "•
Следующая лемма проливает некоторый свет на взаимосвязь
расстояний между общим вектором г и элементами w кода Жп.
Лемма 9. Для любого заданного г = [г0 (а:), г, г, (х)]
существует w е Х„, такое, что г + w = [0, е, е (х)], причем
Доказательство. Пусть {t(x)} есть БЧХ код с исправ-
исправлением двойных ошибок, порожденный полиномом g\(x)g3(x).
Разложим го(х) следующим образом: ro(x) —mo(x) +qo{x) и
образуем г\ (х) = г, (х) + пг0(х) + (пг0A) + г) и (х) + q0(x) f (x). Да-
Далее г* (а:) представим как г\ (х) = t (х) + е (х), где t (x) e {t (x)} и
е(х) есть элемент с минимальным весом смежного класса по
{?(*:)}. Известно [5], что 1^[е(л:)]<3. Легко также проверить,
что (t(x) +t(l)u(x))^{s(x)}. Образуем далее кодовое слово
Полагая t(\) = e, получаем, что г + w = [0, e, e(x)]. Доказа-
Доказательство закончено.
В дальнейшем индекс / у at или е/(х) следует рассматри-
рассматривать по mod2. Положим р = а + (o0 + ctiK и докажем следую-
следующую основную лемму.
Лемма 10. Условия р + о^ = 0 (/=0 и 1), d = 0 выполняются
тогда и только тогда, когда г е Жп, т. е. они характеризуют
код Жп.

Класс оптимальных кодов с исправлением двойных ошибок 35
Доказательство. В силу леммы 9 без ограничения
общности можно предположить, что разность между г и неко-
некоторым welB имеет вид [0, е, е(х)\, Н^[е(х)]<3. Тогда соот-
соотношения B4) приобретают вид
а0 = bas,
а, = bas + e (а),
Прямое утверждение немедленно следует, если в B7) поло-
положить е(х) = 6, е = 0. Чтобы доказать обратное утверждение,
предположим, что р + а^ = 0 (/ = 0,1). Это влечет сг^ = а^, и
в силу единственности корня третьей степени в поле GFB"~')
(число п четно) имеет место aQ = ar Из B7) следует, что
е(а) = 0. Теперь имеем р + а3 = а + о^ = е (а3) = 0. Так как
[#f, Яз] является проверочной матрицей кода с исправлением
двойных ошибок, a W[e(x)]^3 (лемма 9), из равенства
е(а) = е(а3) = 0 заключаем, что е(х) = 0. Наконец, условие d = 0
дает, что е = еA) = 0. Доказательство окончено.
Легко проверить, что условия р + а3 = 0(/ = 0, l),d = 0 экви-
эквивалентны условиям
ao = av o-o* = o\, d = 0, B8)
которые также характеризуют код.
Перейдем к доказательству трех теорем B.1, 2.2 и 2.3), ко-
которые устанавливают соответствие между множествами синд-
синдромов и множествами конфигураций исправимых ошибок.
Утверждения и соответствующие доказательства почти иден-
идентичны. Необходимое условие („тогда") доказывается путем
проверки с помощью соотношений B4) того, что конфигурация
ошибки определенного типа производит синдром определен-
определенного типа. Обращение („только тогда") доказывается следую-
следующим образом: образуется вектор „коррекции" с = [со(дс), с,
с[ (х)], который является функцией только синдрома 2 и та-
такой, что с + W [со(х)] + W [с, (х)] < 2; затем показывается, что
r + се Жп, поскольку синдром 2* = (а*, а*, а*, d'\ вычислен-
вычисленный для (г + с), т. е.
а] -с^ + с^а) (/ = 0, 1),
а' = а + Со(а3) + с,(а3), B9)
удовлетворяет условиям леммы 10 (или эквивалентным усло-
условиям B8)); наконец, благодаря свойствам расстояния кода Жп

36 Ф. П. Препарата
устанавливается, что е = с есть единственная конфигурация
исправимой ошибки, которая может произвести г. Ясно, что
каждая из этих теорем дает также декодирующее правило,
заключающееся в вычислении вектора с на основании 2.
После этих пояснений мы только наметим доказательство
каждой из следующих теорем.
Теорема 2.1. В случае исправимой ошибки е условие
р + а3 = 0 выполняется лишь для одного из значений / = О, 1
тогда и только тогда, когда W [е0 {х)\ + W [е, (х)] = 1.
Доказательство. „Тогда". Соотношения et(x) = xk,
e;+i(x) = 0 дают Oj = bas + ak, aj+l = bas, а = baZs + a3k, следова-
следовательно, р = ba3s. Отсюда имеем р + о3.+1 = 0 и
р + а3 = a3k \{bas-kJ + bas~k + 1]=?0,
так как z2 + z +1^=0 при любом значении 2gGFB""')
(я четно).
„Только тогда". Если р + а3.ф0, р + <т^+1 = О, то подсчи-
подсчитаем ao + a,=aft, а затем положим с/{х) = xh, c/+1 (х) = 0,
c = d + cx(l) и вычислим S*, т. е.
a* = a + a3h = a + (<r0 + a,K = p = a3+l = a3+l.
Итак, условия B8) выполняются, причем c+W[cQ(x)] +
Теорема 2.1 дает следующее декодирующее правило.
Правило 1. Если Ур=а/-, у р Фа1 + и то ci+l (x) = хн и
c = d + c\(l), где aft = a0 + a,.
Теорема 2.2. В случае исправимой ошибки е условия
р + а3ф0 (/ = 0, 1), d=l выполняются тогда и только тогда,
когда е = 0 и W[ej{x)]=l (/ = 0, 1).
Доказательство. „Тогда". Соотношения ei {х) = xkl,
е = 0дают al = bas + aki, a = ba3s + a34' + a3ki+l, rf=l, следова-
следовательно, p = ba3s + aklakl+l(akl + aki+1). Отсюда имеем
Я OF (8*) (я четно).

Класс оптимальных кодов с исправлением двойных ошибок 37
„Только тогда". Если d= 1, р + а^фО (/ = 0, 1), то подсчи-
подсчитываем р' = а + oQol (а0 + СТ,) и получаем а/+1 + К р' = а*'. Затем
полагаем c = [x\ 0, **¦] и вычисляем 2*, т. е.
а] = а. + а*/ = а, + ог/+1 + f ? = а*/+ь
<г* = а + а3*' + сЛ+' = а + (ог/+1 + f р7K + (а/ + 1/7K =
= (а + аЛ + 1 (а/+1 + а,) + р') + (а,. + а/+1 + )VK = of,
так как ог + а/ог/+1(ог/+1 + <г/-) = р/. Наконец, d* = d + Ci(l) = 0.
Соотношения B8) удовлетворяются, причем c = W[co(x)] +
+ W[cl(x)] = 2.
Отсюда мы имеем следующее декодирующее правило.
Правило 2. Если V р ф а0, V р ф a,, d=\, то с = 0 и
Cj {х) = xki, где а*/ = а/+1 + Кот + ог0а, (а0 + а,).
Перед формулировкой теоремы 2.3 заметим, что при усло-
условии (ао + а^ФО функции т; = (р + а/)/(а0 + aiK (/ = °> 0 свя"
заны равенством
Выражая эти элементы поля GFBn~') как вектор-столбцы отно-
относительно базиса 1, а, ..., ап~2 и умножая слева на Хг (см. B6)),
имеем
так как X7" -1 = 1 и (aoai)/(ao + aiJ e 9 [фактически, ao/((To
решает уравнение г/2 + г/ + ((то(т1/((то + (т1J) = О]. Этим доказана
следующая лемма.
Лемма 11. Если (ао + а{) Ф 0, то точно одна из двух функ-
функций tj, т/+1 принадлежит в.
Теорема 2.3. В случае исправимой ошибки е условия
р + огЗ Ф 0 (/ = 0, 1), d — 0, (а0 + а^Ф 0 выполняются тогда и
только тогда, когда е/(д;) = 0, W[e/+i(x)] = 2, е = 0.
Доказательство. „Тогда". Соотношение е = 0, в/(х) = 0,
ej+l(x) = xki + xk' дают as = bas, aJ+l = bas + eJ+l(a), a = ba3s +
+ eJ+l(a3). Отсюда (так как e/ + 1(a)=7^=0) имеем
(a)

33 Ф. П. Препарата
Вспоминая, что е3+1 (a) + e.+l (a3) = afeia*2 (a*1 + ak*), и полагая
Y = aftl/afe' ФО, г/ = аг/е.+1(а), имеем р + а3 = а3*^ A + У) Ф О,
поскольку Y Ф 1 (&i =5^= ^г)> а также имеем
р + a3+1 = а3*> A + YK (у2 + У + 1 + т^г) ^ О,
поскольку 1^6и у/О +VJe0 означают, что 1 + y A + Y2) Ф в.
Кроме того, d = 0 и a0 + a, = e;+1 (a) ^ 0.
„Только тогда". Если d = 0, р + а3 Ф 0 (/ = 0, 1), (а0 + а,) =^ 0,
то получаем а^'Д^о + ai) и a*V(^o + ai) B качестве решений урав-
уравнения
=°- C0)
(Тот факт, что уравнение C0) имеет решения в GF \2п~ ) в точ-
точности для одного из значений /, гарантируется леммой 11.)
Положим ci+l (fe) = xki + xk\ Cj{x) = O, c = 0 и вычислим 2*, т. е.
3t, , 3k,
так как (a*' + ak^)/(aQ + a,) = 1 и ak'ak-/{aQ + a,J = (p + tf3)/(a0 + or,K
являются суммой и произведением решений уравнения C0) соот-
соответственно. Соотношения B8) выполняются, причем с+ W [со(х)] +
+ W [С] (х)] = 2.
Это дает следующее декодирующее правило.
Правило 3. Если V р ф а0, Урфа1г d = 0, ao + a, Ф 0, то
положим с = 0, Cj{x) ~0 и с/+1 (а:) = л^' + л:*2, где а*1 и а*" являются
решениями уравнения г2 + (aQ + а,) г + (р + а^)/(а0 + ai) = 0-
Правила 1—3 составляют алгоритм, который производит
коррекцию всех образцов исправимых ошибок. Выясним теперь,
каково поведение этого алгоритма, когда полученный вектор г
находится на расстоянии ^3 от любого we Жп. Ответ на этот
вопрос неявно следует из предыдущих теорем, которые дают
необходимые и достаточные условия для существования кодо-

Класс оптимальных кодов с исправлением, двойных ошибок 39
вого слова, находящегося на расстоянии 2 или менее от полу-
полученного вектора г. В силу этих теорем вектор г лежит на рас-
расстоянии ^ 3 от любого кодового слова тогда и только тогда,
когда р + <т?=?О (/ = 0, 1) (теорема 2.1), d = 0 (теорема 2.2) и
ffo + а\ = 0 (теорема 2.3).
Ясно, что когда S удовлетворяет этим условиям, произвести
коррекцию нельзя. В самом деле, хотя свойства расстояния
кода Жп гарантируют, что существующий вектор коррекции с
с весом ^2 является также единственным, тем не менее в слу-
случае, когда правила 1—3 неприменимы, можно построить более
чем один вектор с с весом 3. Это показывается с помощью сле-
следующего рассуждения. Предположим, что условия у р Ф aj
(/ = 0, 1), d = 0, aQ = ai выполняются для г. Определим aft так,
что (l + (а + <To)/a3/l) е в. (Имеется 2п~2 значений Л, которые
удовлетворяют этому требованию, поскольку а3 порождает
мультипликативную группу поля GFBn~1), и при фиксирован-
фиксированном (о + °1) элемент A + (а + <T3)/a3ft) пробегает множество
{О, а, а2, .. ., а2"}, которое содержит в при четном п (лемма 8).)
Образуем затем вектор коррекции с следующим образом: с = 0,
со(х) = хн, с, (*) = /' + х\ где а*' = ао + г,а" (г = 1, 2) и г„ г2
являются решениями уравнения
Заметим, что aft] +ak- = (zl +z2)ah = ah, так как г, +z2— 1. С уче-
учетом того, что о0 = ои синдром S* дает (см. B9))
^о^о + а" = от, + а*. + а*' = от;,
а* = а + азн + а3*' + а3*- =¦ от, + aft'afe> (а*' + а*') =
= а + а" (а0 + г,а") (<т0 + г2а") = (<т0 + а*K = а'0\
т. е. г + сеХ„. Это рассмотрение доказывает, что имеется
несколько') кодовых слов на расстоянии 3 от г (но ни одного
слова на расстоянии < 3), и дает следующее правило обнару-
обнаружения ошибки.
Правило 4. Если К р Ф <т0) 1/р" Фаи d = Q, a0 + a, = 0, то по-
полученный вектор г находится на расстоянии ^3 от любого
кодового слова.
') Другой вектор коррекции с весом 3 получается по правилу 2, т. е.
с - [а*, 1, а*], где ak = а0 + $'а = а, + f"a.

40
Ф. П. Препарата
Дополнительный результат проведенного обсуждения состоит
в том, что для любого заданного г имеются кодовые слояа на
расстоянии ^3 от г. Это свойство аналогично свойству, обна-
обнаруженному в работе [5] для БЧХ кодов с исправлением двой-
двойных ошибок.
Полученное сообщение
^Вентиль
РСЗ
переклю-
переключательная
схема 2
блок
управле-
управления
блок
обращении
блок
обращения
nun |> ,
Переклю-
Переключательная
схема 1
Вычислитель
синдрома
сС
оС *
Вспомогатель-
Вспомогательных, функций
блок
решения
квадратного
уравнения
Рис. 2. Декодер для кода Sffn.
На рис. 2 мы сделали набросок возможной блок-схемы де-
декодера для кода Жп. Последовательно получаемое сообщение
запоминается в трех регистрах с циркуляцией PCI, PC2, РСЗ,
соответствующих аналогичным регистрам на рис. 1. Получаемое
сообщение посылается также на вычислитель синдрома, кото-
который после того, как прием завершен, хранит функции d, a,
а0, о,, т. е. синдром 2. Эти функции являются входными сиг-
сигналами комбинационных схем, которые мы теперь опишем (на
рисунке жирными линиями обозначены пучки из («—1) двоич-
двоичных линий).
Вычислитель вспомогательных функций (рис. 2) находит р + сх',
Р + СТЬ °0 + °1> % + ^° + «V*! К + ^l) И °1 + ^ОГ + ОГООГ, @Г0 + (Г,).

Класс оптимальных кодов с исправлением двойных ошибок 41
Первые три из них р + а^, р + о^, а0 + а1 вместе с d посылаются
в блок управления, который определяет, какое декодирующее
правило должно быть применено. Параллельно с этим вели-
величины 0 + 9%, р + сг^, (То + (Т, посылаются в блок решения квад-
квадратного уравнения, где вычисляются т0 = (р + <у1)/(о0 + а,K и
т, = (р + а3)/(а0 + а,K и проверяется принадлежность множе-
множеству в. Если Т;ев, то Txj и (I+Txj) являются решениями
уравнения у2 + у + xs = О, где Т — соответствующая квадратная
матрица (см., например, [3]); затем Ttj и A + Тх{) умножаются
в GFB"~') на (ao + ai) Для получения решений а*1 и а*2 урав-
уравнения z2 + (a0 + а,)г + (р + (Т^//(а0 + <т,) = 0 (см. правило 3). Так
как W [с0 (х)] + W [с, (*)] ^ 2, должно быть произведено испра-
исправление самое большее двух разрядов. Это выполняется сле-
следующим образом:
1) величины ог0 + (т,, а0 + Vo + or0<r, (or0 + or,), <r, +
+ Vo + aoai {aQ + ai), ak\ а*г посылаются в переключательную
схему 1; здесь сигналы из блока управления определяют выбор
двух корректирующих функций уи у2 в виде векторных пред-
представлений двух элементов поля GFB"~');
2) комбинационная схема блок обращения (см. рис. 2) вы-
вычисляет обращение элемента yj = ah/ (если yj = O, то выход
блока обращения условно считается равным 0), и а~ / вводится
в счетчик С], работающий в поле Галуа. Следует заметить,
что если предположить отсутствие задержек в комбинационных
элементах, то ввод а~ i (/= 1, 2) в С/ происходит одновременно
с выработкой d, а, о0, а,. На этом этапе содержимое регист-
регистров РС2 и РСЗ циркулирует синхронно с работой счетчиков С[
и С2. Когда в С/ регистрируется последовательность 10 ... 0,
в блоке D образуется сигнал протяженностью в один такт и
направляется через переключательную схему 2 для выполнения
требуемой коррекции содержимого регистров. Поэтому опера-
операция декодирования заканчивается через B" — l) тактов после
завершения последовательного приема сообщения.
Этим заканчивается описание метода декодирования.
ЛИТЕРАТУРА
1. Albert A. A., Fundamental concepts of higher algebra, University of
Chicago Press, Chicago.
2. Васильев Ю. Л., О негрупповых плотно упакованных кодах, Пробле-
Проблемы кибернетики, вып. 8, Физматгиз, 1962, стр. 337—339.

42 Ф. П. Препарата
3. Berlekamp E. R., Rumsey H., Solomon Q., On the solution of
algebraic equations over finite fields. Inform, and Control, 10, № 6 A967),
553—564.
4. Berlekamp E. R., Algebraic coding theory, McGraw-Hill, New York,
1968. (В издательстве «Мир» готовится русский перевод этой книги.)
5. Gorenstein D., Peterson W. W., Zierler N., Two-error correcting
Bose-Chaudhuri codes are quasi-perfect, Inform, and Control, 3, № 3 A960),
291—294. (Русский перевод: Кибернетический сборник, вып. 6, ИЛ, М.,
1963.)
6. Green M. V., Two heuristic techniques for block-code construction, IEEE
Trans, on Inform. Theory, 1T-12, № 2 A966), 273.
7. Johnson S. M., A new upper bound for error-correcting codes, IRE
Trans, on Inform. Theory, IT-8, № 3 A962), 203—207. (Русский перевод:
сб. Теория кодирования, «Мир», М., 1964.)
8. Nadler M., A 32-point я=12, d=5 code, IRE Trans, on Inform. Theory,
IT-8, № 1 A962), 58.
9. Nordstrom A. W., R о b i n s о n J. P., An optimum nonlinear code, In-
Inform, and Control, 11, № 5/6 A967), 613—616.
10. П е т е р с о н У., Коды, испраиляющие ошибки, «Мир», М., 1964.
11. Preparata F. P., An alternate description and a new decoding proce-
procedure of Nordstrom — Robinson optimum code, Proc. 2nd Princeton Conf.
on Information Sciences and Systems, 1968, pp. 131—134.
12. Preparata F. P., Weight and distance structure of Nordstrom — Robin-
Robinson quadratic code, Inform, and Control, 12, № 5/6 A968), 466—473 (см.
также: Исправление, там же, 13, № 7 A968).)

О проблеме Дедекинда:
число монотонных булевых функций1)
Д. Клеит мен
Проблема определения числа т|>(/г) элементов свободной ди-
дистрибутивной структуры с п образующими была поставлена
Дедекиндом [1] в 1897 г. Она была им решена для /г = 4.
Р. Чёрч [2] в 1940 г. и М. Уорд [3] в 1946 г. получили реше-
решения соответственно для /г = 5 и /г = 6.
В 1954 г. Э. Н. Гильберт [4] показал, что гЬ(/г) удовлетво-
удовлетворяет неравенствам
Ап/2] Лп/2]
2» < ф (л)< л " + 2,
где С1Г/21 — биномиальный коэффициент.
В. К- Коробков в нескольких статьях [5, 8*, 9*], опублико-
опубликованных в 1962—1965 гг., сумел улучшить верхнюю границу
для т|>(/г) до
^1
В 1966 г. Ж. Ансель [6] понизил верхнюю границу еще
дальше, до
В данной статье мы покажем, что log2ib(n) асимптотически
равен С[п12], а именно мы покажем, что
где о. - «-«•, Р»--^
Число \|з(п) равно числу идеалов, или антицепей, или моно-
монотонно возрастающих функций со значениями 0 и 1, определенных
') Kleitman D., On Dedekind's problem: the number of monotone Boo-
Boolean functions, Proceedings of the American Mathematical Society, 21, № 3
A969), 677-682.

44 Л. Клейтмен
на наборах длины п с элементами из Е2 = {0, I}1). Здесь
идеал —это совокупность / наборов, такая, что если ре/ и
а<{$, то а е/; антицепь — это совокупность наборов, никакие
два из которых несравнимы. Идеалу может быть однозначно
поставлена в соответствие антицепь (его максимальные эле-
элементы) и монотонная функция (которая принимает значение О
внутри и 1 вне его).
Ж. Ансель разбивал некоторым образом наборы длины п
на С\?12] цепей (вполне упорядоченных совокупностей наборов).
Затем он определял всевозможные монотонные функции на
каждой цепи по очереди. Так как оказалось, что можно не
более чем тремя способами определить функции на каждой
цепи, он получил следующий результат:
г [«/2]
КХЗ
Мы также разобьем наборы на цепи и определим монотон-
монотонные функции на них по очереди. Однако мы будем допускать
только два возможных определения на большинстве цепей
(асимптотически на всех цепях). Поскольку такая процедура
не дает всех возможных функций, повторим ее, используя п\
различных разбиений на цепи и а(п) различных упорядочений
цепей. Докажем затем, что каждая функция получается при
этом по крайней мере один раз. Таким образом, мы получим
оценку для \|з (п) в виде
Ниже дается процедура построения монотонных (со значе-
значениями 0 и 1) функций на наборах длины п. Затем доказы-
доказывается, что каждая функция получается при этом хотя бы
один раз.
Для удобства сначала построим монотонные функции на
наборах, имеющих не менее /г/2 — т и не более /г/2 + т единиц.
Такое же построение может быть применено для других интер-
интервалов числа единиц; так как каждая монотонная функция
монотонна внутри каждого интервала, общее число таких функ-
функций не может превысить произведения числа таких функций,
полученных для каждого интервала.
Рассмотрим некоторое определенное разбиение Р наборов
(с числом единиц в интервале, описанном выше) на С1? цепей.
') В оригинале „иа структуре подмножеств «-элементного множества Sn".
Здесь и в дальнейшем терминология автора заменена терминологией, упо-
употребляемой в отечественной литературе. — Прим. перее.

О проблеме Дедекинда: число монотонных булевых функций 45
Мы считаем, что каждый член цепи, кроме наименьшего, покры-
покрывает другой член1)- Согласно теоремам Дилворта и Шпернера,
такое разбиение существует, а его пример дан Анселем2). Пусть
я —любая подстановка компонент наборов. Она индуцирует
подстановку среди наборов и, следовательно, среди цепей и
среди разбиений на цепи. Процедура построения, описанная
ниже, будет применена ко всем п\ разбиениям, полученным
применением всех подстановок я к данному разбиению Р.
Эта процедура включает упорядоченные разбиения на цепи,
а именно такие разбиения, как в предыдущем абзаце, в которых
группы цепей расположены в определенном порядке. Для
каждого разбиения я(Р) мы будем рассматривать некоторое
количество различных упорядочений цепей. Зададим сначала
особое упорядочение следующим образом. Каждая цепь содержит
один набор с [п/2] единицами; мы зададим упорядочение для
них и тем самым порядок цепей. Упорядочим наборы с^,
а:, ..., artvj] с [п/2] единицами таким образом, чтобы как можно
дальше наборы а; удовлетворяли условию |а;Па? |<у —т — 1
для всех k из интервала / —/<&</3). Так как а; при таком
ограничении не может совпадать самое большее с
Т+1
2
наборами [см. п. 1 дополнений переводчика в конце статьи],
можно считать, что а; удовлетворяют данному условию для
т+1
Разобьем целые числа /*^/о на блоки длины /; целые числа
между /о и С1Г/21 будем рассматривать как отдельные блоки.
Возьмем в качестве упорядочений цепей (в упорядоченных раз-
разбиениях на цепи, используемых в построении ниже) все
Т+1
S
r-Q
') Выражение „набор д: покрывает набор у" в данной работе имеет
следующий смысл: у получается нз х заменой одной 1 на 0. Таким образом,
рассматриваются цепи без пропусков и, кроме того, они предполагаются
непересекающимися. — Прим. перев.
*) См. работу [6]. Из свойств цепей Анселя в дайной статье исполь-
используются только следующие: 1) цепи не имеют пропусков, 2) цепн не пересе-
пересекаются, 3) нх чксл:> равно С|^2'. — Прим. перев.
3) Здесь a,(]ak означает покомпонентную конъюнкцию, а | a ] - число
единиц в наборе а. — Прим. перев.

46 Д. Клейтмен
упорядочений блоков цепей, связанных с только что определен-
определенными блоками наборов а;. Для каждых пит выберем / так,
чтобы минимизировать выписанный выше факториал, мини-
минимальное значение факториала будем обозначать через а(п, т).
К каждому из п\а{п, т) упорядоченных разбиений на цеги
применим следующую процедуру. На каждой цепи по порядку
зададим значения 0 или 1 на каждом наборе любым способом
в соответствии с уже выбранными заданиями на предшествую-
предшествующих цепях так, чтобы построенная функция была монотонно
возрастающей. Однако рассматривать будем только те функции,
в процессе задания которых не более чем на t цепях встре-
встречается следующая ситуация: в множестве членов цепи, на
которых значения функции не предопределены (то есть еще не
определены по монотонности заданием функции на предшест-
предшествующих цепях), на предмаксимальном члене значение функции
положено равным 1. Число функций, построенных согласно
этому предписанию, не может превысить величины
С?[п12]Bт + 2)'2с"т-\ A)
сга
так как на всех цепях (кроме t цепей, на которых функция
на этом предмаксимальном непредопределенном наборе может
принимать значение 1) можно задать только две функции: на
наибольшем непредопределенном наборе может быть положен О
или 1.
Желаемый результат (на интервале /г/2 —т, п/2 + х) будет
получен, если мы покажем, что для некоторого t, такого, что
будут построены все монотонные функции при помощи про-
процедуры, описанной выше и примененной ко всем вышеописан-
вышеописанным упорядоченным разбиениям.
Рассмотрим монотонную функцию / на наборах, число еди-
единиц в которых заключено между [п/2] — т и [п/2] + т').
Разобьем наборы х, удовлетворяющие условию f(x)—l, на два
класса: х е Ak, если среди наборов у, покрываемых набором х,
не более чем к удовлетворяют условию f {у)— 1, и хе Bk в про-
противном случае. Если х е Ak, то не более чем в k/\ х\ всех раз-
разбиений, описанных выше, набор у, покрываемый набором х и
лежащий в цепи, содержащей х, удовлетворяет условию f(y)= 1
[см. п. 2 дополнений], тогда как по крайней мере в 1— k/\x\
') Считается, что вне этого интервала при меньшем числе единиц функ-
функция равна 0, а при большем — равна 1. —Прим. перев.

О проблеме Дедекинда: число монотонных булевых функций 47
всех разбиений для набора у, входящего в цепь с х и покры-
покрываемого набором х, будет f(y) = О1)- Последнее будет иметь
место, следовательно, по крайней мере для
цепей в неупорядоченных разбиениях. Отсюда следует, что
[см. п. 3 дополнений]
I1 ~ (п/21-тI Л*1^С«
и поэтому условие
xe=Ak, х покрывает у, f{y)=l
выполняется в среднем по всем разбиениям не более чем на
,o[rt/2] « / . k \
С" [«/21-tI1 [«/2]-tJ
цепях.
Следовательно, должно существовать разбиение на цепн,
в котором это условие выполняется не более чем на
ГШ12] k I. _ k \~l
Crt [n/2] -x V In/2] -г )
цепях. Выберем одно из таких разбиений Pf. Пусть в даль-
дальнейшем х есть наименьший член цепи из Pf, удовлетворяющий
условию x^Bk. Значение f(x) будет предопределено, если
некоторая из цепей, содержащих наборы у, покрываемые набо-
набором х и удовлетворяющие условию /(*/)= 1 (таких цепей не
менее k), появится в упорядоченном разбиении раньше, чем
цепь, содержащая х. Конструкция блоков, данная выше, обе-
обеспечивает то, что никакие два набора, покрываемые набором х,
не могут лежать в одном и том же блоке цепей, образован-
образованном при формировании упорядоченных разбиений, рассмотрен-
рассмотренном выше [см. п. 4 дополнений]. Таким образом, набор х
будет впереди k цепей, содержащих такие г/, не более чем
для l/k всех упорядочений. Следовательно, f(x) будет пред-
олределено по крайней мере для (k—l)/k всех упорядочений
разбиения Pf.
Так как имеется самое большее С«"/2! членов Bk, которые
являются наименьшими членами цепи с таким свойством, то
в среднем по всем упорядочениям число цепей, содержащих
наборы х из Вк, такие, что f{x) не предопределено, не более
') Либо х есть минимальный элемент цепи. —Прим. перев.

48 Д. Клейтмен
чем -тС[п12\ Следовательно, должно существовать упорядоче-
упорядочение О;, в котором f{x) предопределено в Bk на всех, кроме,
быть может, -rClnl2\ цепях.
Если при построении f на данной цепи предмаксимальному
непредопределенному члену приписано значение 1, то наиболь-
наибольший непредопределенный член должен:
а) либо быть в Ak и покрывать набор, удовлетворяющий
условию f{y)= 1,
б) либо быть в Bk и быть непредопределенным.
По доказанному выше, если выбрано упорядочение Of раз-
разбиения Pf, то эта альтернатива может выполняться не более
чем на
С|» \T+[nl2]-xV 1п/2]-х)
цепях. Таким образом, для
,_Г[«/2]/1 ¦
1 k I k \~'
процедура, описанная выше, должна дать все монотонные
функции на данном интервале. Оптимальное значение для k
здесь приблизительно равно ([п/2] — т)'/2, так что мы можем
выбрать
. _ ?[л/2] 2 / . „ / 1_\ \
Легко убедиться в том, что п\ и а(п, т) крайне незначительны
по сравнению с A) при т ~ /Д р<1, и что число монотонных
функций в рассмотренном интервале не может превосходить
число
Второй член в показателе появляется из выражения A) при
значении /, данном выше [см. п. 5 дополнений].
Подобные рассуждения могут быть применены к вычислению
числа монотонных функций на других интервалах числа единиц.
Выбирая подходящим образом эти интервалы, можно показать,
что рассмотрение остальных наборов дает много меньший вклад
в общее число монотонных функций, чем определяемый выше
вклад за счет второго члена в показателе [см. п. 6 дополнений].
Таким образом, имеем

О проблеме Дедекинда: число монотонных булевых функций 49
с[п/2]
Можно легко составить 2 " антицепей, рассматривая все
совокупности наборов с [п/2] единицами. Большинство таких
антицепей будет содержать приблизительно половину всех набо-
наборов с [п/2] единицами и будет содержать наборы, которые
покрываются всеми наборами, кроме приблизительно С|г"/21+1е~"/4
наборов с [п/2] + 1 единицами. Любые из оставшихся наборов
с [п/2]+ 1 единицами могут быть добавлены к антицепи. Сле-
Следовательно,
Эта нижняя оценка может быть улучшена [7].
ДОПОЛНЕНИЯ ПЕРЕВОДЧИКА
1. Число рассматриваемых наборов, имеющих [п/2] —г общих
единиц с набором ak, равно Сг1п/2]Сп_{п/2] (г единиц заменяется О
и г нулей заменяется 1). Поэтому ak запрещает ставить на
t+i
место с^ не более чем 2 С[«/2]Сп-[/г/2! наборов. А всего на место с^
t+i
нельзя ставить не более чем /^СиС^-и наборов.
2. Пусть в х' единицы соответствуют компонентам с номе-
номерами i\, ..., im, а в х — компонентам с номерами /ь ..., /т.
Если в первоначальном разбиении на цепи х' покрывает в своей
цепи у', а х' н у' различаются на г>й компоненте, то среди всех
подстановок, переводящих х' в х, ^-я компонента будет с оди-
одинаковой частотой (в силу симметрии) переходить во все компо-
компоненты с номерами /р. Поэтому звено (х\ у') будет с одинаковой
частотой переходить во все ребра (х, у), выходящие из х. Кроме
того, х? может быть минимальным в своей цепи; тогда при
подстановках, переводящих х' в х, из х не будет исходить
звено цепи. Отсюда следует нужное утверждение.
3. При любом разбиении на цепи на каждой цепи не более
чем один набор х, такой, что /(jc)=1, является минималь-
минимальным элементом цепи или покрывает в своей цепи набор у, на
котором f(y) = O. Поэтому при каждом разбиении не более
чем CjT/2! элементов из Ak покрывают в своей цепи набор у,
такой, что f(y) = 0, или ничего не покрывают. Следовательно,
откуда по сокращении на п\ и получается требуемое нера-
неравенство.
4 Зак. 560

50 Д. Клейтмен
4. Пусть х покрывает ух и у2, а цепи, проходящие через ух
и yh содержат наборы с [п/2] единицами соответственно с^ и а(..
Если | л: | > [«/2], то а^<х и ah<x. Так как |at.Ua,J =
l lJjU<|nJ ||'|;|
|;||J |J
Если |.*|<Л/г/2], то г/, и у2 покрывают один и тот же набор г.
Так как а^ Г) а,-2 > г, то | с^ П Q-h | > I z I > /г/2 — т — 1. Таким обра-
образом, в любом случае цепи, содержащие у\ и у2, лежат в раз-
разных блоках.
5. Произведем указанные вычисления:
Оценим loga(n, т). Легко получить, раскрыв факториалы в фор-
формуле СТ = (ад)|(п-ап)| п0 Формуле Стирлиига, что СТ = A + у)п,
t+i
где y-^0 при а->0. Так как т//г->0, то R = 2 С^С^-ад <
< (т + 2) (C^tUJ ~ «р A_-HY)" = A + 6)", где у -> 0_и_6 -> 0 при
-^— (^например, ^ = [|/ ~^~]/> тогДа
Отсюда
log a (л, т)< L log L <? 2 \
/" ^ /г[л/21 log Я \
так как /? = A +б)".
f t С[га/2)
Упростив A), получим Сс[п/2](т+ 1) 2 " . Имеем
ft
log(T+ l/ = Hog(x+
При a->oo и fe = o(a) находим log С* ~ b logy, что также
легко получить, используя формулу Стирлинга. Отсюда

О проблеме Дедекинда: число монотонных булевых функций 51
6. Рассмотрим все наборы с числом единиц вне интер-
вала (-2"~т> +т)- Их число не более чем 2 2 Сл<
< 2 • ([л/2] - т + 1) d*/21~T. Имеем
с[«/2|-т ([я/21-T+l). ... -[у
[f]
Так как при а<Ь имеем -~< ° , то
При х~Ф и Р>-5" находим
2
r=0
ЛИТЕРАТУРА1)
1. Dedekind R., Uber Zerlegungen von Zahlen durch ihre grossten ge-
meinsamen Teilor, Festschrift Hoch. Braunschweig u. ges. Werke, II, 1897,
S. 103—148.
2. Church R., Numerical analysis of certain free distributive structures,
Duke Math. /., 6 A940), 732—734.
3. Ward M., Note on the order of free distributive lattices, Abstract 135,
Bull. Amer. Math. Soc, 52 A946), 423.
4. Gilbert E. N., Lattice theoretic properties of frontal switching functions,
/. Math. Phyi., 33 A954), 57—67. (Русский перевод: Гильберт Э. Н.,
Теоретико-структурные свойства замыкающих переключательных функций,
Кибернетический сборник, вып. 1, ИЛ, М., 1960.)
') Работы, отмеченные звездочкой, добавлены при подготовке русского
перевода.— Прим. ред.

52 Д. Клейтмен
5. К о р о б к о в В. К., О монотонных функциях алгебры логики, сб. Пробле-
Проблемы кибернетики, вып. 13, изд-во «Наука», М., 1965, стр. 5—28.
6. Hansel G., Sur Ie nombre des fonctions booleennes monotones de я va-
variables, С R. Acad. Sci. Paris, 282 A966), 1088—1090. (Русский перевод:
А и сель Ж., О числе монотонных булевых функций я переменных, Ки-
Кибернетический сборник, новая серия, вып. 5, «Мир», М., 1968.)
7. Yamamoto K-, Logarithmic order of free distributive lattices, /. Math.
Soc. Japan, 8 A954), 343—353.
8*. К о р о б к о в В. К., К вопросу о числе монотонных функций алгебры ло-
логики, Дискретный анализ, вып. 1, 1963, сборник трудов Института мате-
математики СО АН СССР.
9*. К о р о б к о в В. К., Оценка числа монотонных функций алгебры логики
и сложности алгоритма отыскания разрешающего множества для произ-
произвольной монотонной функции алгебры логики, ДАН СССР, 150, № 4
A963), 744—747.

Время,
требующееся для умножения в группе1)
Ф. М. С пира
В работах Винограда [1, 2] было исследовано времи, требующееся для
выполнения сложения и умножения натуральных чисел и для выполнения
умножения в группе логической схемой из элементов с ограниченным чи-
числом входов и задержкой, равной 1. В даииой сгатье принята та же самаи
модель. Получена новая нижняя оценка для умножения в группе, совпа-
совпадающая для абелевых групп с оценкой Винограда, но, вообще говоря, более
сильная. Приводится также схема для выполнения умножения, которая
в отличие от схемы Винограда может использоваться и для иеабелевых
групп. В случае абелевой группы эта схема оказалась по крайней мере
столь же быстрой, как и схема Винограда. Следуя его методу применения
схемы, построенной для абелевой группы, оказывается возможным также
понизить верхнюю оценку времени, требующегося для выполнения сложении-
и умножения натуральных чисел.
1. МОДЕЛЬ
Принятая нами модель —по существу модель Винограда [1, 2].
Мы рассматриваем логические схемы, построенные из элемен-
элементов, каждый из которых имеет не более г входных линий,
одну расщепляемую выходную линию и задержку при вычи-
вычислении выхода, равную 1. По каждой линии переда отся зна-
значения из множества Zd = {0, 1, ..., d — 1}. Входные линии схемы
разбиваются на п множеств; через /Ci/ обозначается множество
всевозможных наборов значений на входах /-го множества
(/=1, 2, ..., я). Через Ос обозначается множество всевозмож-
всевозможных наборов значений на выходных линиях схемы. Такая схема
называется (d, г)-схемой.
Определение 1.1. Пусть ср: Х}ХХ2Х ... Х1„->5'-
функция, определенная на конечных множествах. Говорят, что
схема С вычисляет qp в момент времени т, если существуют
отображения gf. Xj ->/Cl j (j — 1, 2, ..., n) и взаимно однозначная
функция h: У->ОС, такие, что если С с момента времени 0 и до
момента времени т—1 получает постоянный вход [gx {xx), ...
• • •» ёЛхп)\, то ее выход в момент времени т есть h((p(x , хп)).
') Spira Ph. M., The time required for group multiplication, Journal of
the Association for Computing Machinery, 16, № 2 A969), 235-243.

54 Ф. М. С пира
2. ОСНОВНАЯ ЛЕММА
Здесь мы получим общую нижнюю оценку времени работы
{d, г)-схемы, вычисляющей заданную конечную функцию ф.
Эта оценка проясняет метод, лежащий в основе результатов
Винограда. Она зависит от свойств выходного кода h, введен-
введенного в предыдущем разделе, и использует новое понятие, ко-
которое мы здесь вводим, — понятие разделимых множеств. Сна-
Сначала необходимо дать некоторые предварительные определения.
Определение 2.1. Пусть ]х[ обозначает наименьшее
целое число, большее или равное х; пусть [jc] обозначает наи-
наибольшее целое число, меньшее или равное х; пусть | 51 обо-
обозначает мощность множества S.
Определение 2.2. В любой (d, г)-схеме всегда, когда
выходной набор значений есть h (у), через hj(y) будем обозна-
обозначать значение на /-й выходной линии.
Определение 2.3. Пусть qp: Xt X ... X Хп-> Y, и пусть
С вычисляет ф. Тогда Sslm называется ^-разделимым мно-
множеством для С в т-и аргументе ф, если для любых двух раз-
различных элементов s, и s2 из S мы можем найти хи х2, ..., дгт_,,
xm+i, ¦¦¦, хп, где Xi^Xh такие, что
Л/(ф(*1> •••> xm-i> sl> хт + и •••> хп)) ^
Фк1(ч>{х1, ..., хт-и s2, хт+{, ..., хп)).
Лемма 2.1. В (d, г)-схеме выход любого элемента в момент
времени т может зависеть не более чем от гх входных линий.
Доказательство. Достаточно рассмотреть древообразную
схему глубины т из элементов с г входными линиями'). >
Это наблюдение, сделанное сначала Виноградом, в совокуп-
совокупности с понятием разделимых множеств позволяет доказать
следующую лемму.
Лемма 2.2 (основная лемма). Пусть С есть (d, г)-схема,
вычисляющая ф в момент времени т. Тогда
т>тах{ ]logr( ]logd\ SAD\ l+ ••• + J log, I SB (У) I [ )[ },
где St (/) есть hj-разделимое множество для С в i-м аргументе ф.
Доказательство. В момент времени т /-я выходная
линия должна зависеть не менее, чем от ] logd| St{j) \[ входных
') Знак > означает конец доказательства. — Прим. перев.

Время, требующееся для умножения в группе 55
линий, определяющих ICti, так как в противном случае в S,(/)
нашлись бы два элемента, которые не были бы Ау-раздели-
мыми. Таким образом, /-й выход зависит не менее чем от
]logd| S,(/)| [+ ... +]logdi Sn{j)\ [ входных линий, а это число
не превосходит гх. >
С помощью леммы 2.2 мы раскроем ход рассуждений, ко-
который в изложении Винограда, посвященном времени сложения
и умножения, выражен не в столь явной форме. За счет этого
в оставшейся части раздела мы не только быстро получим не-
некоторые результаты Винограда, но и дадим более глубокий
анализ других понятий и исследуем значительно более широкий
класс функций впоследствии.
Следствие 2.1. Пусть ф: ZNXZN-*{0, 1} есть
, если х <: ц,
I, если х > у.
Тогда если С есть {d, г)-схема, вычисляющая ф в момент вре-
времени т, то х >] log, 2] logd N [ [.
Доказательство. Возьмем /, такое, что Ау @) ф h/(l).
Тогда ZN есть Лгразделимое множество для С в обоих — пер-
первом и втором —аргументах ф, так какеслид;>г/, тоф(д;, y)?=<f(y, у)
и ф {х, у) ф ф (х, х). >
Следствие 2.2. Пусть ф: ZNXZN->ZN есть
Тогда если С вычисляет ф в момент времени т, то
Доказательство. Возьмем /, такое, что ЛДО) ф h}\\).
Пусть m = \N *]. Тогда {1, 2, ..., ш) есть Л/-разделимое множество
для С в обоих аргументах Ф, так как для каждой пары х, у,
в которой х<у и х, у^{\, 2, ..., пг}, мы можем выбрать
w^ZN, такой, что xw<N^.yw<2N, с тем, чтобы получить
ф(л-, w) = 0, ф(г/, а))=1. В силу симметрии это утверждение
верно также и для второго аргумента. Применение леммы 2.2
завершает доказательство. >
Данный раздел мы закончим примером, который показы-
показывает, что размеры разделимых множеств могут сильно зависеть
от выходного кода схемы, вычисляющей заданную ф.
Пример 2.1. Пусть ф: Z#X Zn~>Zns есть умножение на-
натуральных чисел, причем Af = 28. Рассмотрим выходной код,

56 Ф. М. Спира
при котором всегда, когда выход равен М, /-я выходная линия
передает t-ю цифру двоичного представления М. При этом
имеется шестнадцать выходных линий. Возьмем произвольную
пару х, у, в которой хфу и х, y^ZN. Двоичные представле-
представления этих чисел отличаются хотя бы в одном разряде, скажем
в k-м. Выберем z = 28~\ Тогда Л8(ф(#> z)) ф h%(qp(д:, z)) и
^(фСг, у)) Ф hs(ф(z, x)). Таким образом, существует Л8-разде-
лнмое множество в обоих аргументах ф мощности 28.
Рассмотрим теперь ту же самую ф, но в качестве выход-
выходного кода для г возьмем набор двоичных представлений пока-
показателен степени в разложении z на простые сомножители.
Пусть первые шесть выходных линий') используются для коди-
кодирования показателя степени числа два в результате. Возьмем
х, y^ZN, такие, что х и у в разложении на простые сомно-
сомножители содержат различные степени числа два; пусть, напри-
например, показатели этих степеней при двоичном представлении
отличаются в k-м разряде. Тогда, полагая г = 23~к, получаем
Л3(ф(*. г))=И=Л3(ф(«/, г)) и Л3(ф(г, л:)) ф h3(ф(г, у)). Таким об-
образом, поскольку элементы из ZN могут иметь в разложении
на простые сомножители восемь различных степеней числа два,
существует Л3"РазДелимое множество в обоих аргументах ф
мощности 8. Поскольку число два — наименьшее простое число,
то, как нетрудно заметить, это максимальный размер раздели-
разделимого множества. Отметим, однако, что для этого выходного
кода требуется тридцать девять выходных линий.
3. ОБЗОР РЕЗУЛЬТАТОВ
Рядом авторов исследовалось время, необходимое для вы-
выполнения (d, г)-схемой сложения по модулю N. Офман [3] по-
построил схему для частного случая N = 2п. Важные результаты
получил Виноград [1, 2]. Он установил нижнюю оценку, ко-
которую мы здесь приведем, и построил (d, г)-схему с временем
работы, близким к нижней оценке. Поскольку любая конечная
абелева группа является прямым произведением циклических
групп [4, стр. 50], результаты Винограда применимы также и
к умножению в абелевой группе.
Определение 3.1. Пусть Я —группа. Говорят, что Н об-
обладает свойством Р, и пишут Р(Н)=1, если существует эле-
элемент аеЯ, причем афе, такой, что каждая нетривиальная
подгруппа группы Н содержит а. Последнее обозначается в виде
1) По-видимому, многие числщ а этом абзаце указаны автором неверно. —
Прим. перев.

Время, требующееся для умножения в группе 57
Р(а,Н)=1. Через a(G) обозначим максимальный порядок
H<=G, такой, что Р(Я)=1.
Лемма 3.1 (Виноград [1]). Если G — абелева группа, то
a(G) равно максимальному, являющемуся степенью простого
числа порядку циклической подгруппы, содержащейся в G.
Доказательство см. в работе [1]. >
Теперь мы полностью охарактеризуем a(G).
Определение 3.2. Обобщенной группой кватернионов Qn
называется группа порядка 2п с двумя порождающими элемен-
элементами а и Ь, удовлетворяющими соотношениям
Теорема 3.1. р-группа содержит единственную подгруппу
порядка р тогда и только тогда, когда она является цикличе-
циклической или обобщенной группой кватернионов. (Если р нечетно,
то она должна быть циклической.)
Доказате льство см. в работе [4, стр. 211]. >
Следствие 3.1. Пусть G — произвольная конечная группа.
Тогда a(G) равно либо порядку наибольшей циклической р-под-
группы группы G, либо порядку наибольшей обобщенной группы
кватернионов, содержащейся в G, а именно тому из них, ко-
который больше.
Доказательство. Пусть Я —произвольная подгруппа
группы G. Если Р(Н)= 1, то \ Н\ = рп для некоторого простого
числа р, так как в противном случае нашлось бы другое про-
простое число q, делящее \Н\, и, следовательно, нашлись бы эле-
элементы и и v из Н с порядками о(и) = р и o(v) = q]). Но тогда
подгруппа (и) П (и) содержала бы только единицу. Итак, при-
принимаем \Н\ = рп. В таком случае каждая нетривиальная под-
подгруппа группы Н содержит подгруппу порядка р. Таким об-
образом, Р(Н)=\ тогда и только тогда, когда Н содержит
единственную подгруппу порядка р, т. е. Н является цикличе-
циклической группой или обобщенной группой кватернионов. >
Величина a(G) играет решающую роль в нижней оценке
Винограда для времени умножения в группе. Эту оценку мы
сейчас приведем. В разд. 4 мы дадим новую нижнюю оценку,
которая, вообще говоря, выше оценки Винограда, но в случае
абелевой группы совпадает с ней.
') См., например, [4, стр. 54]. — Прим. перев.

58 Ф. М. Спира
Теорема 3.2 (Виноград [1]). Пусть G — произвольная
конечная группа. Пусть С есть (d, г)-схема, вычисляющая
ф: GXG->G, где ф(а, Ъ) = аЪ. Тогда для выполнения вычи-
вычислений схемой С требуется время т, где
T>]logr2]log,a(G)[[.
Доказательство см. в работе [1]. >
Виноград указал также способ построения схемы для вы-
выполнения умножения в абелевой группе G с временем вычи-
вычисления
т = 2 + ] 1ой(г+,)д] ] -щ- ] logda (G) [ [ [,
причем этот способ применим при г^З и d>2. Мы дадим
совершенно другой метод построения схем, который применим
при г^2 и db^i и действует независимо от того, является ли
группа абелевой или нет. Более того, для любой заданной
абелевой группы и для любых заданных d и г время вычисле-
вычисления у нас окажется меньше, чем у Винограда.
4. НИЖНЯЯ ОЦЕНКА
В этом разделе мы дадим новую нижнюю оценку времени,
требующегося для выполнения умножения в группе (d, ^-схе-
^-схемой, и сравним ее с оценкой Винограда. Пусть G— произволь-
произвольная конечная группа, q>: G X G -> G — умножение в группе и
С есть (d, г)-схема, вычисляющая <р. Обозначим через ht(g)
значение на /-й выходной линии схемы С при выходе, рав-
равном h(g).
Определение 4.1. Пусть х, y^G. Будем говорить,
что х п у являются /^-эквивалентными, если при всех geG
выполняется равенство hs{xg) = hj(yg), и будем говорить, что
они являются ^-эквивалентными, если при всех geG вы-
выполняется равенство h,(gx) = hs(gy). Ясно, что Rf и L, являются
отношениями эквивалентности. Класс, /^-эквивалентный эле-
элементу g, будем обозначать через Rt (g), а класс, /-/-эквива-
лентный элементу g, — через Lj(g).
Лемма 4.1. Классы Rj = Rj(e) и Lt = Lj(e) являются груп-
группами для всех выходных линий схемы С. Более того, для лю-
любого g e G справедливы соотношения Rj (g) = Rjg и Ls (g) —
L

Время, требующееся для умножения в группе 59
Доказательство. Допустим, что а, Ь se. Rf. Пусть с —
произвольный элемент из G. Тогда h,{ab~[c) = h,<(bb~]c) = ht (с).
Следовательно, ab~] e/?; и Rt является группой. Возьмем
теперь произвольный g^G. Тогда d^R,(g) в том и только
том случае, если /i/(dc) = hj(gc) при всех c^G. Но последнее
имеет место тогда и только тогда, когда hj (dg'lc) — hj (с), т. е.
dg~] e Rr Вторая половина леммы доказывается двойствен-
двойственным образом. >
Максимальные разделимые множества выявляются с по-
помощью следующей леммы.
Лемма 4.2. hj-разделимое множество максимальной мощ-
мощности в первом аргументе ф содержит в точности по одному
представителю из каждого правого смежного класса по под-
подгруппе Rj в G. Таким образом, его мощность равна \ G |/| Rs |.
Двойственный результат имеет место для разделимых множеств
во втором аргументе.
Доказательство следует непосредственно из леммы 4.1.
и определения разделимых множеств. >
Теперь мы имеем все необходимое для получения нижней
оценки, зависящей от выходного кода.
Лемма 4.3. Пусть С есть (d, г)-схема, предназначенная
для умножения в группе G за время т. Тогда
Доказательство непосредственно следует из лемм 2.2
и 4.2. >
Оценка по всем кодам получается путем минимизации
максимальных размеров Rf и Lt для заданной группы G.
Определение 4.2. Если G = {e), то положим б(G) = 1.
В противном случае пусть б (с) обозначает максимальный по-
порядок подгруппы G, не содержащей с. В этом случае положим
6(G)= min б (с).
в\{)
{
Поскольку мы имеем дело только с конечными группами,
величина 6(G) всегда определена и конечна. Заметим, что
если Р(а, G)=l, то б(а)=1 и, таким образом, 6(G)=1. Отме-
Отметим также, что если G— нетривиальная группа и P(G)^=l, то
всегда 6(G)>1. Впоследствии нам понадобится следующая
простая лемма.

60 Ф. М. Спира
Лемма 4.4. Пусть Я и К — подгруппы конечной группы G,
такие, что Я Л К = {е}. Тогда \H\\K\<\G\.
Доказательство. Пусть А,, А2е Я и ku &2<= К, такие,
что А,&, = A2fe2. Тогда Аг~'А, = k2k71^ Я f] ft. Следовательно, А, =
= А2 и й, = А:2. Таким образом, \{hk: АеЯ, А: е= /С}|>|Я|| К\.
Но ведь {А&: АеЯ, & е /С} также является подмножеством
группы G. >
Важнейшим для нас свойством величины 6(G) является
следующее.
Лемма 4.5. Для любой конечной группы G справедливо
соотношение a(GN(G) ^| G \.
Доказательство. Если 6(G)=1, то лемма, очевидно,
верна. Поэтому предположим, что 6(G)^1. Возьмем Н a G и
а<=Я, такие, что афе, Р(а,Я)=1 и |#| = a(G). Вы-
Выберем подгруппу К <= G, такую, что а<?К и ! /С | = б(а). Тогда,
поскольку Н()К является подгруппой группы G, не содержа-
содержащей а, имеем Н (]К = {е}. Следовательно, по лемме 4.4 и с уче-
учетом того, что 6(G)<6(a), имеем a(GN(G)<a(GN(a) =
= |Я||/с!<|с|. >
Теперь может быть установлена универсальная нижняя
оценка для произвольной (d, г)-схемы, выполняющей умноже-
умножение в конечной группе С
Теорема 4.1. Пусть G — конечная группа, q>: G X G —>G —
умножение в группе и С есть (d, г)-схема, вычисляющая ф, при-
причем d ^ 2 и г ^ 2. Тогда, если время вычисления схемы С есть
т, то
Доказательство. Допустим, что 6(G)>1, и выберем
а е G, такой, что 6(a) = 6(G). Найдется выходная линия схе-
схемы С, скажем /-я, такая, что hj{e)^hl{a). Но тогда оба
класса R/ и Li являются подгруппами группы G, не содержа-
содержащими а. Следовательно, их порядки не превосходят 6(G). Та-
Таким образом, в этом случае утверждение следует из леммы
4.3. Если б(С)=1, то либо G = {e}, либо \G\ = a(G). В первом
из этих случаев теорема устанавливается тривиально. Во вто-
втором случае выберем g^G, такой, что P(g, G)=l, и возьмем
выходную линию, скажем г-ю, такую, что АДе)=И=АД^). Тогда
/?у = ?/ = {е} и утверждение снова следует из леммы 4.3. >
Лемма 4.5 показывает, что эта нижняя оценка не слабее
результата Винограда, сформулированного в теореме 3.2;

Время, требующееся для умножения в группе 61
в действительности же, как показывает следующий пример,
эта оценка сильнее.
Пример 4.1. Пусть р — нечетное простое число. Тогда
существует группа с тремя образующими а, Ь и с и опреде-
определяющими соотношениями [4, стр. 63]
а? = Ь9 = ср = е, ab = bac, ca = ac, cb = bc,
не содержащая элементов порядка р2. Нетрудно показать, что
любая ее подгруппа порядка р2 обязана содержать с. Таким
образом, 6(G) = 6(c) = p. Но ясно, что a(G) = p. Поэтому
a(G) 6(G) <| G |. Тем не менее в одном важном случае обе
оценки совпадают.
Лемма 4.6. Пусть G — конечная абелева группа. Тогда
a(GN(G) = |G|.
Доказательство. Согласно теореме о разложении абе-
левой группы [4, стр. 50], имеем G = 2\ X ... X Zn, где каж-
каждое Zt является циклической р-группой; пусть, например,
\Zt \ — prtl. Без ограничения общности будем считать, что
Если я=1, то теорема верна, так как P{G)=\ и 6(G)=1.
Допустим, что я>1, и пусть at порождает Zt(i= 1,2, ...,«).
Теперь если мы выберем произвольный
g = (af>, .... a»,
у которого хотя бы один из показателей степени, скажем kl
отличен от 0, то окажется, что
где е( —единица группы Z{. Отсюда в силу (•) следует, что
fi Piii
1Ф1 ' /=2
Таким образом,
Однако любая подгруппа, порядок которой больше Ц р^', обя-
обязана пересекаться с Zx нетривиальным образом и поэтому

62 Ф. М. Спира
должна содержать
(а0/' ', е2, ..., еп) ф {<?,} X Z2 X ... X Zn.
Таким образом,
((ГГ'~', е2 en)) = f[prJ. >
В целях полноты изложения мы приведем здесь несколько
примеров неабелевых групп Git для каждой из которых
a(G/)fi(G,) = |G,|.
Пример 4.2. Пусть р — нечетное простое число. Пусть
G| — группа с образующими а и 6 и определяющими соотно-
соотношениями [4, стр. 63] а? — Ър = е\ b~]ab = а1+р. Тогда a(Gi) = p2
и любая подгруппа порядка р2 обязана содержать ар.
Пример 4.3. Пусть G2 —прямое произведение двух групп
А и В, таких, что а{АN(А) = \А\; а{ВN(В) = \ В |. Тогда не-
нетрудно заметить, что
a(G2) = max{a(A), а (В)}; fi(G2) = гшп{|В|6(Л), \А\Ь{В)}
и, таким образом, a(G2N(G2) = | G2|. В частности, эти свой-
свойства имеют место, если G2 неабелева, но все ее подгруппы
инвариантны [4, стр. 213].
5. СХЕМА ДЛЯ УМНОЖЕНИЯ В ГРУППЕ
В этом разделе мы дадим метод построения (d, г)-схемы
для умножения в произвольной конечной группе G, примени-
применимый при d^s2 и г ^2. Время вычисления такой схемы самое
большее на единицу превосходит только что полученную ниж-
нижнюю оценку. Если G — абелева группа и г^З, то нашу схему
можно сравнить со схемой Винограда. Можно заметить, что
время вычисления у нашей схемы меньше, чем у схемы Ви-
Винограда, и что на самом деле мы можем указать группу, для
которой разность между этими значениями времени произ-
произвольно велика.
Лемма 5.1. Пусть К — произвольная подгруппа группы G.
Тогда существует (d, г)-схема, вычисляющая qp: G X G—>{0, 1},
где
0, если ab e К,

Время, требующееся для умножения в группе 63
за время')
Доказательство. Пусть M = \G\/\Kl Для каждого
правого смежного класса по подгруппе К в группе G возьмем
по представителю vt e Kvr Тогда {у~'} будет множеством
представителей левых смежных классов, так как V7lK = vflK
тогда и только тогда, когда vtvy] е К- Возьмем отображение
2] группы G в множество ]logdM[-HHx векторов над Zd, такое,
что zl(gl) = z1(g2) тогда и только тогда, когда Kgi = Kg2- За-
Затем определим другое отображение г2 посредством равенства
Z\(g)®z2(g~1) = 0, где 0 —вектор, все координаты которого
равны 0, а 0 — операция покомпонентного сложения по мо-
модулю d. Заметим, что z2 отображает любые два элемента из
одного левого смежного класса в один и тот же вектор.
В первом ярусе схемы содержится г /oi W°e<t Щ\ однотипных
элементов. При вычислении ab каждый из этих элементов
складывает [г/2] компонент векторов z,(a) и z2(b) по модулю
d (последний сумматор складывает менее [г/2] компонент, если
[г/2] не делит М). Выход элемента равен 0, если для всех
пар входных компонент суммы сравнимы с 0 по модулю d.
В противном случае выход равен 1. Таким образом, выходы
всех элементов равны 0 тогда и только тогда, когда сущест-
существует /, такое, что a^Kv. и Ьеу~'/С. Оставшаяся часть
схемы представляет собой „дерево" из элементов с г входами.
Ее выход равен 0, если все входы равны 0, и равен 1, если
хотя бы один вход отличен от 0. Глубина этого дерева равна
|logr гг/оТ" Jl°gd M[ . Таким образом, схема вычисляет <р за
время
Следствие 5.1. Для любого оеС существует (d, г)-схема
с тем же временем вычисления, которая определяет, выпол-
выполняется ли соотношение ab^Kv
Определение 5.1. Полным множеством подгрупп груп-
группы G называется такое множество {Kt) подгрупп, для кото-
которого f\Ki = {e}.
') В первоначальной формулировке леммы было т = 1 + llogr logj L_n
J -1 I** ILL
Улучшение было указано автору Виноградом.

64 Ф. А*. Спира
Лемма 5.2. Если {КJ — полное множество подгрупп груп-
группы G, то для любого a^G знания правых смежных классов,
содержащих а, достаточно для определения а.
Доказательство. ("|(^а) =
Отметим, что полное множество подгрупп существует для
любой группы G; таким, например, является множество, со-
состоящее из единственной подгруппы {е}. Если P(G)^l, то су-
существуют также и другие полные множества.
Лемма 5.3. Пусть {Ki) — полное множество подгрупп груп-
группы G. Тогда существует {d, г)-схема, выполняющая умножение
в группе G за время
Доказательство следует из леммы 5.1, следствия 5.1 и
леммы 5.2. >
Теперь мы в состоянии доказать следующую теорему.
Теорема 5.1. Пусть G —произвольная конечная группа.
Тогда для любых d~^1 и г^2 существует (d, г)-схема, выпол-
выполняющая умножение в конечной группе G за время
Более того, время вычисления схемы превосходит нижнюю
оценку не более, чем на одну единицу времени.
Доказательство. Допустим, что 6(G)>1. Для любого
g e G, g ф е, существует подгруппа Kg порядка 6(g), не
содержащая g. Таким образом, {Kg: g e G \ {е}} есть полное
множество подгрупп, для которого min (| Kg |: g e G \ {е}} = 6(G).
Если же 6(G)=1, то мы пользуемся полным множеством,
состоящим из {е}. Второе утверждение теоремы следует из
того, что при г ^2 имеем
d x [[[< ] logr 2] logd x [[. >
Следствие 5.2. Если G — абелева группа или если 6 (Q) — 1,
то существует {d, г)-схема, выполняющая умножение в группе О
за время

Время, требующееся для умножения в группе 65
Как уже отмечалось, схема Винограда для абелевой группы G
требовала времени
Поскольку при г>3 имеем
отсюда следует, что время вычисления у нас меньше, чем
у Винограда.
Пример 5.1. Возьмем, скажем, г = 4 и ] logda(G) [ = 22
для некоторого k~^\. Тогда время вычисления у Винограда
будет равно 2 + 2fe, а у нас равно 1 + k, т. е. его схема будет
требовать вдвое большего времени. Читатель легко сможет
построить самостоятельно подобные примеры.
Виноград [2] распространил свои результаты, полученные
для группы, на сложение и умножение натуральных чисел,
заметив, что схема, выполняющая умножение в циклической
группе порядка 2W — 1, может также складывать пару чисел,
заключенных между 0 и N, и что умножение натуральных
чисел может выполняться путем сложения показателей степени
в разложениях обоих сомножителей на простые множители.
Поскольку мы сумели понизить время, необходимое для умно-
умножения в циклических группах, мы можем также соответственно
уменьшить время для сложения и умножения натуральных
чисел. Мы представим этот результат на основе определений
Винограда. Читателя, который заинтересуется подробностями
взаимосвязи между умножением в группе и двумя другими
операциями, мы отсылаем к исходной статье Винограда.
Определение 5.2. При любом целом m положим Qm —
= н. о. к. {1, 2 т) и -v(A0 = min{m: Qm^N}.
Теперь, следуя методу применения верхней оценки для
времени умножения в группе, предложенному Виноградом, мы
воспользуемся следствием 5.2 и получим теоремы 5.2 и 5.3.
Теорема 5.2. Пусть ср: ZN X ZN-> Z2N-i есть <p(a, b) =» a + b.
Тогда существует (d, г)-схема, вычисляющая <р за время
r>2,
Теорема 5.3. Пусть i|>: {1, 2, .... JV} X {1, 2, ...,#}-¦
->{1,2, ..., N2} есть ty(a, b) = ab. Тогда для любых r^s2 и
d ^ 2 существует (d, г)-схема, вычисляющая г|з за время
Зак. 560

66 Ф М. Спира
В заключение для справки отметим, что Виноград оценил
снизу тф и t^ следующим образом.
Теорема 5.4 (Виноград [2]). При любых .<f!>2 и г^2
для любой (d, г)-схемы, вычисляющей ср, требуется время хч,
где
а для любой (d, г)-схемы, вычисляющей ф, требуется время
О близости результатов, сформулированных в теоремах 5.2
и 5.3, к этим нижним оценкам говорит тот факт, что -у D*)^
< 2 + у (х).
Автор выражает глубокую признательность за помощь своему
научному консультанту проф. М. А. Арбибу, а также благо-
благодарит д-ра С. Винограда за весьма полезные обсуждения.
Л ИТЕРАТУРА
1. Winograd S., On the time required to perform addition, /. ACM, 12,
№ 2 A965), 277—285. (Русский перевод: Виноград С, О времени, тре-
требующемся для выполнения сложения, Кибернетический сборник, новая се-
серия, вып. 6, «Мир», М., 1969, стр. 41—54.)
2. W i n о g r a d S., On the time required to perform multiplication, /. ACM,
14, № 4 A967), 793—802. (Русский перевод: Виноград С, О времени,
требующемся для выполнения умножения, Кибернетический сборник, новая
серия, вып. 6, «Мир», М., 1969, стр. 55—71.)
3. О ф м а н Ю. П., Об алгоритмической сложности дискретных функций,
ДАН СССР, 145, № 1 A962). 48—51.
4. Холл М., Теория групп, ИЛ, М., 1962.

Алгоритм Гаусса не оптимален1)
В. Штрассен
1. Ниже мы приведем алгоритм для вычисления элементов
произведения двух квадратных матриц Л и В порядка п по
заданным элементам матриц А и В с числом арифметических
операций, меньшим чем 4,7 • п)°е7 (все логарифмы в этой статье
берутся по основанию 2, так что log 7 «2,8; обычный метод
требует приблизительно 2«3 арифметических операций). Этот
алгоритм индуцирует алгоритмы для обращения матрицы, для
решения системы п линейных уравнений с п неизвестными, для
вычисления детерминанта порядка п и т. д. Все они требуют
меньше чем const ¦ n)°s7 арифметических операций2).
Этот результат следует сопоставить с результатом
В. В. Клюева и Н. И. Коковкина-Щербака [1] о том, что
алгоритм Гаусса для решения систем линейных уравнений
является оптимальным, если допускаются лишь операции над
целыми строками и столбцами. Заметим также, что Виноград [2]
модифицирует обычные алгоритмы для умножения матриц,
обращения их и решения систем линейных уравнений, используя
около половины умножений по сравнению со сложениями и
вычитаниями 3).
2. Определим алгоритмы ат, ь которые перемножают матрицы
порядка пг2к, индукцией по fe:am,0—это обычный алгоритм для
умножения матриц, требующий т3 умножений и m2(m— 1)
сложений. Если amtk уже определен, то am, fc+( определим сле-
следующим образом.
•) Strassen V., Gaussian elimination is not optimal, Nutnerische
Mathematik, 13, H. 4 A969), 354—356.
2) Все результаты работы сохраняются для операций с матрицами над
произвольным (в частности, конечным) полем. — Прим. ред.
3) См. также работы: К л ос с Б. М., Оценки сложности решения систем
линейных уравнений, ДАН СССР, 171, № 4 A966), 781-783; Коноваль-
цев И. В., Об одном алгоритме решения систем линейных уравнений
в конечных полях, сб. „Проблемы кибернетики", вып. 19, 1967, стр. 269—
274. — Прим. ред.

68 В. Штрассен
Для умножения матриц А и В порядка m2fe+1 запишем их
в виде
Ап Ап\ (Вп В12\ /С„
п Л2
22
2*
где Л,р В(/, Сц — матрицы порядка т2*. Используя алгоритм amik
для умножения и обычные алгоритмы для сложения и вычита-
вычитания матриц порядка m,2k, вычислим:
11 = (A21 + A22)BU,
Ul = Au(Bn-B22),
W=A22(-BU + B2
V = (Au + Ai2)B22,
Cn = I + IV-V
C21 = II + IV,
C12=III + V,
C22 = I + III-II + VI.
Индукцией по k легко установить следующие утверждения.
Утверждение 1. Алгоритм ат_к вычисляет произведение
двух матриц порядка m2k с m37k умножениями и E + m) m27k —
— 6(m2*J сложениями и (ычитаниями чисел.
Таким образом, умножение двух матриц порядка 2* воз-
возможно с 7* умножениями и менее чем 6 • 7* сложениями и
вычитаниями.
Утверждение 2. Произведение двух матриц порядка п
можно вычислить менее чем с 4,7 • nl0«7 арифметическими опе-
операциями.
Доказательство. Положим
k = [\ogn-4], m = [tt2"fe] + l.
Тогда
Погружая матрицы порядка п в матрицы порядка m2k, сводим
нашу задачу к оценке числа операций в алгоритме ат,к.

Алгоритм Гаусса не оптимален
Из утверждения 1 следует, что это число равно
E + 2m)m27*-6(m2feJ<
< 2га3 G/8)fe + 12,03га3 G/4)* <
(здесь мы пользуемся тем, что 16 • 2* <1 п)
< B (8/7)log "-* + 12,03 D/7)'°г ""*) /г'°в т
< max B(8/7)'+12,03 D/7)')/г'°г7<
,7-^7
из соображений выпуклости.
Перейдем теперь к обращению матриц. Для приложимости
наших алгоритмов требуется предположить не только обрати-
обратимость матрицы, но и то, что появляющиеся деления имеют
смысл (аналогичное предположение необходимо, конечно, и для
алгоритма Гаусса).
Мы определим алгоритмы pm,k, которые обращают матрицы
порядка т2к, индукцией по k: pm,0 —это обычный алгоритм
Гаусса; алгоритм %,ik уже определен; теперь определим pm, k+[
следующим образом.
Если Л —матрица порядка m2*+I, для которой необходимо
найти обратную, то запишем
IА А \ IГ Г
//1ц /ii2 \ | / ^п >-12
где Ац, Ctj — матрицы порядка т2к. Используя am>k для умно-
умножения, pm,fc для обращения и обычные алгоритмы для сложе-
сложения и вычитания матриц порядка т2к, вычисляем:
1 = ЛП", С12= III • VI,
Н = Л,11, ' С21 = VI - II,
Ш = 1Л,2, VII = 111-Си,
^ = Л211П, ' Cn = I-VII,
V-IV-Ля, C22=-VI.
VI = V"',
Индукцией по k легко установить следующее утверждение.

70 В. Штрассен
Утверждение 3. Алгоритм $„ък вычисляет обратную
матрицу к матрице порядка m2k с m2k делениями, ^ I ¦=¦ ш37к — m2k )
умножениями и ^ Г ¦=- E + пг) т27к — 7 (пг2кJ1 сложениями и вы-
вычитаниями чисел.
Следующее утверждение доказывается почти так же, как
и утверждение 2.
Утверждение 4. Обращение матрицы порядка п воз-
возможно с не более чем 5,64«Iog7 арифметическими операциями.
Аналогичные результаты справедливы для решения систем
линейных уравнений и вычисления детерминанта, если исполь-
использовать равенство
Det A = (Det Au) Det (Л22 - A2iA7\A^.
ЛИТЕРАТУРА
1. Клюев В. В., Коковкин-Щербак Н. И., О минимизации числа
арифметических операций при решении линейных алгебраических систем
уравнений. Журнал вычисл. матем. и матем. физики, 5, № 1 A965), 21—23.
2. Winograd S., A new algorithm for inner product, IBM Research Report
RC-1943, Nov. 21, 1967.

Некоторые аспекты
последовательностного
построения экспериментов )
Г. Роббинс
1. ВВЕДЕНИЕ
До недавнего времени в статистической теории ограничивались
построением и анализом экспериментов, в которых количество
и способы выбора испытаний полностью определялись до на-
начала эксперимента. Причины этого частично имеют историче-
историческое происхождение и относятся ко времени, когда статистика
проводилась только после окончания эксперимента, если это
вообще было возможно, и частично связаны с математическими
трудностями, которые возникают при работе с произвольным,
но фиксированным числом независимых случайных величин.
Основной сдвиг в этом направлении, по-видимому, состоит
в создании теории последовательностного конструирования экс-
экспериментов, в которых количество и способы выбора испыта-
испытаний не фиксированы заранее, а зависят от предшествующих
испытаний.
Первое важное отступление от фиксирования количества испы-
испытаний появилось при контроле качества в промышленности
(метод контроля Доджа и Ромига, связанный с двойной вы-
выборкой [1]). В данном случае выбирается только одна сово-
совокупность изделий и вопрос заключается в том, превышает ли
количество брака в этой совокупности данный уровень. Сна-
Сначала выбирается произвольно /г, объектов из совокупности
и через х обозначается число бракованных объектов. Если х
меньше некоторого фиксированного значения а, то вся сово-
совокупность изделий принимается без дальнейшей проверки; если
х больше некоторого фиксированного значения Ь (а<Ь), то вся
совокупность бракуется; однако если а ^ х ^ Ь, то второй раз
выбирается п2 изделий из совокупности, и заключение прини-
принимать или браковать всю совокупность делается на основании
числа бракованных изделий в общем количестве выбранных
щ + «2 объектов. Таким образом, число п выбранных объектов
из совокупности есть случайная величина, принимающая два
значения щ и щ + /ц и зависящая от испытаний.
¦) Rob bins H., Some aspects of the sequential design of detriments,
Bull. Amer. Math. Soc, 58, № 5 A952), 527-535.

72 Г. Роббинс
Во время второй мировой войны было развито направление,
главным образом Вальдом, получившее в дальнейшем название
последовательностного анализа [2], в основе которого лежит
идея, обобщающая идею двойной выборки. Грубо говоря, она
состоит в том, что испытания проводятся друг за другом, и
заключение о том, принять или забраковать данную совокуп-
совокупность (или, в более общем виде, сомнительную статистическую
гипотезу), может быть сделано на любом шаге. Количество
испытаний п становится теперь случайной величиной, связан-
связанной с данной совокупностью и принимающей в принципе бес-
бесконечно много значений, хотя в большинстве практических за-
задач оно может быть ограничено. Преимущество этого метода
состоит в том, что при некоторых обстоятельствах разумный
выбор последовательности испытаний может привести к значи-
значительному уменьшению среднего числа испытаний, необходимого
для того, чтобы вероятность ошибки была минимальной. Теория
последовательностного анализа еще очень несовершенна'), и
нужно преодолеть значительные трудности, чтобы использовать
ее для решения проблем статистики.
Использование последовательностных методов при выборе
способа испытаний освобождает статистическую теорию от огра-
ограничений, связанных с фиксацией количества испытаний. Однако
не только количество испытаний характеризует эффективную
конструкцию эксперимента. Большинство статистических про-
проблем, встречающихся на практике, связано с рассмотрением
нескольких совокупностей, и нужно определить, из какой сово-
совокупности производить выборку на каждом шаге.
Следующий пример иллюстрирует сказанное. Пусть имеются
две совокупности, соответствующие случайные величины кото-
которых нормально распределены. Пусть неизвестны математические
ожидания A, и ц2 и дисперсии а] и а?2 этих случайных величин.
Требуется оценить значение разности Hi — щ- Чтобы подчерк-
подчеркнуть обсуждаемую точку зрения, предполагается, что п фикси-
ронано. Возникает вопрос, как распределить п испытаний между
двумя совокупностями. Пусть X] и х-2 суть средние арифмети-
арифметические значения случайных величин, получающихся при пх и гц
испытаниях с двумя соответствующими совокупностями, тогда
естественно считать, что хх— х2 является оценкой для ц, — ц2
с дисперсией о2 = (а2/я,) + (а2/я2). Для фиксированного п = п[ + п9_
дисперсия а2 достигает минимума при «i/n2 = a,/a2. Если aja2
известно, то сразу строится соответствующий эксперимент;
') Нужно иметь в виду, что настоящая статья была опубликована
в 1952 г. - Прим. ред.

Некоторые аспекты ппследовательностнпго построения экспериментов 73
если же это отношение неизвестно, то процесс испытаний мо-
может быть разбит на два этапа. Производится некоторое число m
испытаний с каждой совокупностью, и таким способом полу-
полученные значения случайных величин используются в качестве
оценки для CTi/a2; оставшиеся п — 2т испытаний распределяются
между двумя совокупностями в соответствии с оценкой для ах1а2.
Возникает вопрос, как лучше выбрать т. Если т мало, то по-
получается грубая оценка для aj/c^. При достаточно больших т
малость разности п — 2т не позволяет полностью использовать
полученную оценку О\1а2. (Подобная дилемма весьма характерна
для всех задач последовательностного конструирования.) Вообще
говоря, возможно рассмотрение схем, в которых испытания
проводятся одно за другим, и заключение, с какой совокуп-
совокупностью производить каждое испытание, делается на основании
предыдущих испытаний; общее количество испытаний п может
быть фиксированным или может быть случайной величиной,
зависящей от проведенных испытаний.
Несмотря на полное отсутствие теории, Махалонобис [3]
в 1938 г. первым попытался в духе последовательностных по-
построений определить в Бенгалии площади, пригодные для вы-
выращивания джута. Первоначальное исследование было прове-
проведено в малом масштабе, чтобы оценить значения определенных
параметров, знание которых было весьма существенно для
перехода к эффективным исследованиям в большом мас-
масштабе.
В последующих публикациях Махаланобис [4] обратил вни-
внимание на то, что было бы желательно иметь способ изменения
эксперимента по мере накопления новых данных.
Мы обязаны Вальду за большой вклад в теорию последо-
последовательностного анализа. В его книге [5] ставится проблема
в самом общем виде и очерчиваются методы ее решения. За-
Затронутые в этой книге вероятностные проблемы обширны, по-
поскольку вероятностные зависимости встречаются в ней во всей
их сложности, в то время как еще не найдены удовлетвори-
удовлетворительные средства для исследования практически интересных
задач. Тем не менее достаточно явно подтверждается предпо-
предположение, что дальнейшие результаты в теории последователь-
последовательностного конструирования будут весьма важны в математиче-
математической статистике и в науке в целом.
Ниже будет рассмотрено несколько простых задач последо-
последовательностного конструирования, которые теперь привлекают
внимание и которые отличаются от тех задач, которые обычно
встречаются в статистической литературе. Оптимальное реше-
решение этих задач неизвестно. Однако часто лучше иметь доста-
достаточно хорошее решение нужной задачи, чем оптимальное ре-

74 Г. Роббинс
шение ненужной. В настоящее время этот принцип с особенной
пользой применяется в проблемах последовательностного экспе-
экспериментирования.
2. ПРОБЛЕМА ВЫБОРА ИЗ ДВУХ МНОЖЕСТВ
Пусть А и В —два множества (монеты, урны, промышлен-
промышленные изделия и т.д.) с заданными на них функциями распреде-
распределения F(x) и G (х). Об этих функциях известно только, что
они принадлежат некоторому классу D. Мы будем предпола-
предполагать, что интегралы
О© ОО
а= jxdF(x), p= jxdG(x) A)
— ОО —СЮ
существуют. Возникает вопрос, как сделать выборку xltx2, ..., хп
из двух указанных множеств, чтобы сумма Sn = xt + ... +хп
достигала наибольшей возможной величины.
Например, пусть А и В —две произвольные монеты, и пред-
предположим, что мы совершаем п бросаний, причем при выпаде-
выпадении орла мы получаем выигрыш в 1 единицу, а при выпадении
решетки не получаем ничего. Если xt=l или xt = 0 соответ-
соответствуют выпадению орла или решетки при /-м бросании,
то 5„ —общая сумма, которую мы можем получить, а а и р
(О^а, Р^1) суть вероятности выпадения орла при единичном
бросании монет А и В соответственно.
Интуитивно ясно, что всякий раз, когда на основании пре-
предыдущих испытаний возникает уверенность, что одно из двух
чисел а или р больше другого, в будущем следует предпочесть
соответствующее множество. Заметим, что мы при этом не ин-
интересуемся оценкой разности а —р. Вся задача состоит в том,
какое множество А или В выбрать для i-vo испытания. Без-
Безусловно, существуют практические ситуации, в которых задача
ставится скорее в процессе эксперимента, чем до него. Факти-
Фактически проблема представляет собой в упрощенном виде общую
задачу о том, как мы учимся или как бы мы могли учиться
на основании прошлого опыта. По-видимому, решение этой
проблемы сводится к построению средствами математической
статистики конструкции, которая была названа фон Нейма-
Нейманом [6] целесообразным поведением.
Начнем с рассмотрения уже упомянутого специального слу-
случая, в котором множества А тл В суть монеты, а соответствую-
соответствующие вероятности аир выпадения орла (*,= 1) при единичном
бросании неизвестны. Возьмем, например, следующее правило
построения последовательности испытаний.

Некоторые аспекты последовательностного построения экспериментов 75
Правило Ri. Для первого бросания выбираем А или В
произвольно. Затем, если при г-м бросании выпал орел, то при
(г + 1)-м бросании используем ту же монету, что и при г-м
бросании; если же при г-м бросании выпала решетка, то для
(г+ 1)-го бросания берем другую монету; здесь i= 1, 2
Чем можно охарактеризовать правило R,? Последователь-
Последовательность бросаний можно описать простой цепью Маркова с че-
четырьмя состояниями (А, Н), (А, Т), (В, Н), (В, ГI) и с вероят-
вероятностными переходами, которые легко записываются. Например,
вероятность перехода из (А, Н) в (А, Т) равна A—а) при
(г-1)-м бросании. Пусть pt обозначает вероятность выпадения
орла при г-м бросании. Исключая тривиальный случай, будем
предполагать, что аир обе не равны 0 и обе не равны 1;
тогда |а + р—1|<1. Легко показать, что
B)
отсюда следует, что
и, следовательно,
I- а + р-2сф , б2
где
y=, a-lH^J-. E)
Используя правило R,, получаем
Mm P'+---+P" ~Y + Tg-. F)
Теперь, если известно, какое из двух чисел а или р больше,
то, используя только ту монету, у которой вероятность выпа-
выпадения орла больше, получаем
= тах(а, р) = у + й. G)
Таким образом, разность
, Я, RI)-(Y + 6)-(Y + T^) = fi(l--T47)>0 (8)
может быть принята за меру асимптотической потери при ис-
использовании правила R,, которая обусловлена незнанием истин-
истинных свойств монет. Легко видеть, что L(A, В, R,) принимает
') Здесь Я (от англ. head) — орел, Г (от англ. tail) — решетка. — Прим.
ред.

76 Г. Роббинс
свое максимальное значение AJ, = 3— (]/2~Ksg 0,172, когда а = С
и р=»2— V^2 ?^0,586, или наоборот. Таким образом, при ис-
использовании правила R, для больших п потеря при одном бро-
бросании не превышает 0,172 единицы. Возможно также исполь-
использование правила Ro, которое состоит в том, что на каждом
шаге монета выбирается произвольно (или монеты А и В бро-
бросаются поочередно). Соответствующее значение L{A, В, Ro),
как легко видеть, равно величине (у + 6) — у = 6, которая при-
принимает свое максимальное значение М0={/2 при а = 0 и Р=1,
или наоборот. Ясно, что правило R, значительно „лучше",
чем Ro.
Правило Ro таково, что выбор монеты при i-м бросании
не зависит от результатов предыдущих бросаний, в то время
как при использовании правила R, этот выбор зависит только
от (г—1)-го бросания. В более общем случае можно считать,
что правило R таково, что выбор монеты при г-м бросании
зависит от значений *, х{-{ для всех предыдущих броса-
бросаний. Для любого такого правила R пусть
La(A, В, R) = max(a, $-e(^), (9)
где Е обозначает математическое ожидание, вычисленное
на основе a, p и R, и пусть
Mn(R) = max[Ln(A, В, R)], A0)
(о, В)
. .. _ A1)
(R)
Интересно изучить поведение <р(я) и описать „минимаксное"
правило R, для которого значение ф(я) достигается.
Более простая задача: существует ли правило R, такое, что
lim Ln{A, В, R) = 0 A2)
для всяких А и В? Мы увидим в следующем разделе, что
ответ на этот вопрос положителен не только в случае монет,
но и в случае двух произвольных множеств.
Возвращаясь к общему случаю, в котором А и В —произ-
—произвольные множества, для которых значения A) существуют,
рассмотрим правило R проведения испытаний, определенное
следующим образом. Пусть
= a, <av< k.,. <а„< ..,, ,
= bi<b2< ... <bn< ... { '

Некоторые аспекты последовательностного построения экспериментов Т7
— две фиксированные несовпадающие возрастающие последо-
последовательности натуральных чисел плотности 0, т.е. такие, доля
которых в натуральном ряду стремится к 0. Правило R опре-
определим индуктивно: если / — одно из чисел ап, то соответствую-
соответствующее значение xt получается как результат испытания с А;
если г —одно из чисел Ьп, то xt получается как результат ис-
испытания с В; если i не совпадает ни с одним из чисел ап или
Ьп, то Х{ получается как результат испытания с А или В в со-
соответствии с тем, превышает или нет среднее арифметическое
всех предыдущих испытаний с А среднее арифметическое всех
предыдущих испытаний с В. Можно показать, что из усилен-
усиленного закона больших чисел следует, что с вероятностью 1
имеет место равенство
lim —- = max (a, p). A4)
Это в свою очередь означает, что
. , lim El—-I = max (а, р), A5)
П-»оо \ П /
так что
lim Ln (А, В, R) = max (a, p) - lim E (^) = 0 A6)
ДЛЯ всех А, В, для которых существуют а, р.
3. НЕКОТОРЫЕ ДРУГИЕ ПРОБЛЕМЫ
ПОСЛЕДОВАТЕЛЬНОСТНОГО КОНСТРУИРОВАНИЯ
Задачи, рассмотренные в разд. 2, могут быть обобщены
различными способами. В некоторых случаях можно считать,
что общее число испытаний п является случайной величиной,
как зависящей, так и не зависящей от предыдущих испытаний.
Например, в задаче о двух монетах предположим, что следует
платить некоторую сумму с за возможность произвести каж-
каждое бросание. В этом случае можно прекращать бросание всякий
раз, когда кажется достаточно достоверным, что max (а, р) < с;
это относится к специальному случаю задачи для трех мно-
множеств. Возможно рассмотрение случая континуума множеств.
Предположим, что мы осуществляем уход за растениями или
животными с интенсивностью 9 из некоторого интервала, и
пусть F (х, 9) —функция распределения реакций х на уход
с интенсивностью 9. Математическое ожидание
оо
а(9)= J xdF{x, 9) A7)

78 Л Роббинс
„регрессии" л: от 0 предполагается неизвестным. Пусть {0,}
обозначает произвольную последовательность значений 9, вы-
выбранных последовательно экспериментатором, и пусть {*,} обо-
обозначает соответствующую последовательность реакций, причем
каждое х{ имеет распределение
(I) Пусть а@) имеет единственный максимум в некоторой
неизвестной точке 0О. Спрашивается, каким образом экспери-
экспериментатору выбирать последовательность {0J, чтобы максими-
максимизировать математическое ожидание суммы Sn = х{ + ... + хп
и тем самым оценить значение 0О.
(II) Пусть а (э) —возрастающая функция от 0, которая при-
принимает заданное значение а0 в некоторой неизвестной точке 0О.
Спрашивается, каким образом экспериментатору выбрать по-
последовательность {0,}, для того чтобы оценить значение 0О.
Проблема (I) по существу состоит в экспериментальном опре-
определении максимума функции, когда испытания подвержены
случайным ошибкам. Проблема (II) является основной при
изучении чувствительности и в биологии.
Ясно, что в каждой из этих проблем выбор 9( может зави-
зависеть от реакций х, *,_, на предыдущие уровни 9,, ..., 9,_,
ухода. Таким образом, возникает задача последовательностного
построения эксперимента. Изучение проблемы (I), но не в тер-
терминах последовательностного построения экспериментов, было
предпринято Хотлингом [7, 8]. В то время по теории последо-
последовательностного анализа, однако, еще не было публикаций.
Проблема (II) была рассмотрена Роббинсом и Монро [9]. Они
предложили следующий метод. Пусть {ап} последовательность
положительных чисел, такая, что
2Х<°°. 2а„ = оо. A8)
Выберем произвольно 0| и положим
0„+| = 0„ + а„(ао-*„) (п=1, 2, ...)• A9)
Тогда при некоторых слабых ограничениях на F (х, 9) может
быть показано, что в вероятностном смысле имеет место соот-
соотношение
Мт9„ = 0о. B0)
Л-*оо
В этой и других задачах может быть предложена после-
довательностная конструкция с достаточно хорошими свойствами,
которая, возможно, встретит положительный отклик среди чи-
читателей. Это будет способствовать применению вероятностных

Некоторые аспекты последовательностного построения экспериментов 79
методов для нахождения эмпирических приближений путем по-
построения последовательности экспериментов, когда полное ма-
математическое решение задачи затруднено. Эмпирическое иссле-
исследование скорости сходимости в B0) было выполнено Техрое-
вым [10J.
4. ПРОБЛЕМА НЕПРЕДВИДЕННОЙ ОСТАНОВКИ
Пусть случайная величина jc имеет нормальное распределение
с неизвестным математическим ожиданием 8 и единичной дис-
дисперсией. Пусть испытываются две гипотезы: 8 = 0 (гипотеза Но)
и 8>0 (гипотеза Н,). Стандартный статистический прием, ос-
основанный на фиксированном количестве испытаний п, состоит
в следующем. Пусть Sn = *, + ... + хп. Гипотеза Но отвергается
в пользу Н] тогда и только тогда, когда
Sn>an\ B1)
где а —некоторая константа. Вероятность отвергаиия Но, если
эта гипотеза верна, равна
е(а)=1-Ф(а), B2)
где
e~llhdt' Bз)
причем выбирая величину а достаточно большой, можно вели-
величину е(а) сделать как угодно малой. Например, если а = 3,09,
то е (а) ^ 0,001.
Предположим теперь, что гипотеза Но верна, но „экспери-
„экспериментатор" желает получить некоторую статистику для того,
чтобы на ее основе отвергнуть Но. Если количество испытаний
не было оговорено заранее, то при выполнении неравенства B1)
„экспериментатор" мог бы закончить эксперимент. Закон по-
повторного логарифма в теории вероятностей означает, что с ве-
вероятностью 1 неравенство B1) будет справедливо для беско-
бесконечно большого числа значений п, если испытания продолжаются
неограниченно, вне зависимости от величины а. Следовательно,
„экспериментатор" должен стремиться достичь в конечном счете
такого п, когда B1) имеет место и, останавливая эксперимент
в этом месте, он получит нужный ему результат. Это обстоя-
обстоятельство показывает, что выполнение условия B1) не гаранти-
гарантирует проверки на истинность гипотезы Но, так как существует
некоторая вероятность того, что может иметь место непредви-
непредвиденная остановка.
Простейший способ избежать эффекта непредвиденной оста-
остановки состоит в том, чтобы количество испытаний было

Г. Роббинс
зафиксировано до начала эксперимента. Это ограничение было
бы слишком жестким для практического использования. Ста-
Статистики могли бы поэтому удовлетвориться установлением гра-
границ щ <п<п2 для числа испытаний, которые будут достаточно
гибкими, чтобы предотвратить случайности при эксперименти-
экспериментировании, и довольно строгими, чтобы устранить нежелательный
эффект непредвиденной остановки.
С этой целью статистикам было бы полезно знать значение
функции
g{nu n2, a) = Pr[Sn>an'/2] B4)
для некоторых щ ^.п^.п2, где хг есть независимая и нормально
распределенная на @, 1) случайная величина. Совсем легко
установить справедливость неравенства
где Л = -?, B5)
\ (A.-1)
которое полезно в случае, когда К не очень велико; более точ-
точные оценки также могут быть получены.
Проблема непредвиденной остановки мало освещена в ста-
статистической теории (см. тем не менее [11], особенно стр.
286 — 292). Нет нужды, однако, предполагать, что эксперимен-
экспериментатор сознательно выбирает неверную статистику, и, по мнению
автора, было бы весьма желательно создание методов стати-
статистического анализа, нечувствительных к эффекту непредвиден-
непредвиденной остановки.
ЛИТЕРАТУРА
1. Dodge H. F., Roraig Н. С, A method of sampling inspection, BSTJ,
8 A929), 613—631; Single sampling and double sampling inspection tables,
ibid., 20 A941), 1-61.
2. W a 1 d A., Sequential analysis, New York, Wiley, 1947.
3. M a h a 1 a n ob i s P. C, A sample survey of the acreage under jute in
Bengal with discussion of planning of experiments, Snakhya, 4 A940),
511—531.
4. M a h a 1 a n о b i s P. C, On large-scale sample surveys, Philos. Trans. Roy.
Soc. London, Ser. B, 231 A944). 329—451.
5. W a 1 d A., Statistical decision functions, New York, Wiley, 1950.
6. Neyman J.. First course in probability and statistics, New York, Holt, 1950.
7. Ho telling H., Experimental determination of the maximum of a func-
function, Ann. of Math. Statist., 12 A941), 20—45.
8. Friedman M., Savage L. J., Planning experiments seeking maxima,
Chap. 3 of Selected techniques of statistical analysis, New York, McGraw-
Hill, 1947.
9. Robbins H., Monro S., A stochastic approximation method, Ann of
Math. Statist., 22 A951), 400—407.
10. Teichroew D., не опубликовано.
11. Feller W., Statistical aspects of ESP, Journal of Parapsychology 4
A940), 271—298.

Построение
последовательностных экспериментов
с конечной памятью1)
Г. Роббинс
Рассматривается задача послздовательностного выбора одного из двух
возможных снобов действий, каждое из которых может привести к выигрышу
или проигрышу. Спрашивается, как при этом максимизировать количество
полученного выигрыша; выбор действий каждый раз основывается на резуль-
результатах конечного числа предыдущих испытаний.
ВВЕДЕНИЕ
Экспериментатор имеет две монеты, монету 1 и монету 2,
с соответствующими вероятностями выпадения орлов, равными
р, = 1 — ^, и р2=1 — q2, значения которых ему неизвестны. Он
хочет произвести бесконечное число бросаний, используя в каж-
каждом бросании или монету 1, или монету 2 таким образом,
чтобы получить максимально возможное число выпадения орлов.
Задача экспериментатора заключается в том, чтобы найти пра-
правило выбора монеты для бросания на каждом шаге, основан-
основанное на результатах предыдущих бросаний.
Если бы он знал вначале, какое из чисел р, или р2 больше,
то он мог бы использовать только соответствующую монету,
независимо от результатов предыдущих бросаний. В этом слу-
случае с вероятностью 1 имело бы место соотношение
,. число орлов в первых п испытаниях , , ,,,
hm v- v- = max (p,,p2). A)
В предыдущей статье2) [1] было показано, что даже для
неизвестных рх и р2 существует правило проведения бросаний,
такое, что равенство A) справедливо для любых р{ и р2. Од-
Однако любое правило, обладающее этим свойством, очевидно,
должно быть таким, чтобы решение вопроса, какую монету
использовать при n-м бросании, зависело от результатов всех
предыдущих п—\ бросаний; другими словами, правило требует
') R о b b i n s H., A sequential decision problem with a finite memory,
Proc. Nat. Acad. Scl. USA, 12 A956), 920-923.
2) См. другую статью автора в этом же сборнике иа стр. 71— Прим. ред.
f) Э»к. 5«0 71

82 Г. Роббинс
бесконечной „памяти". В этой статье мы будем интересоваться
тем, какие правила можно получить, если использовать „память"
конечной длины; будем говорить, что правило имеет тип г, если
заключение, какую монету использовать при п-м бросании за-
зависит от результатов только п—г, п — (г+1) п— 1 преды-
предыдущих бросаний. (Под „результатом" бросания мы подразу-
подразумеваем и выбор монеты, и сообщение о том, какая сторона
монеты выпала.)
Мы рассмотрим правило Яг (типа г), для которого с веро-
вероятностью 1 имеет место соотношение
число орлов в первых п испытаниях Р$1г Ptff\
lim = . B)
n 7 +g
Заметим, что при г, стремящемся к бесконечности, правая часть
равенства B), возрастая, стремится к правой части равенства A).
Интересно было бы знать, насколько наше правило Rr „лучше"
любого другого правила типа г в том смысле, что левая часть
соответствующего равенства B) для этого правила существует
для всех р, и р2, является симметрической функцией от р, и р?
и по крайней мере не больше —-—-— для всех р, и р2. Мы
не знаем, так ли это.
ОПРЕДЕЛЕНИЕ ПРАВИЛА Rr И ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Мы напомним [2], что если для единственной монеты с ве-
вероятностью q = 1 — р выпадения решетки производятся бросания
до того момента, когда впервые появится последовательность
выпавших подряд г решеток, то с вероятностью, близкой к еди-
единице, число бросаний должно быть не меньше
1-?'
Теперь предположим, что повторные бросания производятся
по следующему правилу: если при первом бросании выпала
решетка, то заканчиваем бросания, в противнэм случае про-
продолжаем бросания до первой встречи последовательности из г
следующих друг за другом решеток. Тогда предполагаемое
число бросаний с вероятностью, близкой к единице, будет не
меньше
C)
Доткем следующую теорему.

Построение последовательностных экспериментов с конечной памятью 83
Теорема. Определим правило Rr следующим образом. На-
Начинаем бросание с монеты 1. Если первое же выпадение—ре-
выпадение—решетка, то останавливаемся; в противном случае продолжаем
бросание монеты 1 до первого появления последовательности г
следующих друг за другом решеток и только тогда останавли-
останавливаемся. Таким образом, мы получим первый блок бросаний
монеты 1. После этого начинаем бросать монету 2, используя
тот же прием. Получим первый блок бросаний монеты 2. Потом
опять начинаем бросать монету 1. Получим второй блок броса-
бросаний монеты 1 и т. д. В конце концов получим бесконечную по-
последовательность блоков бросаний либо монеты 1, либо монеты 2.
Для такого определения правила R, равенство B) справед-
справедливо с вероятностью 1.
Доказательство. Пусть х{(у{) — длина i-ro блока бро-
бросаний монеты 1 B), /=1,2 В процессе бросания с веро-
вероятностью 1 генерируется бесконечная последовательность неза-
независимых случайных величин
хи уи х2, уъ ..., хп, уп D)
Тогда отношение числа бросаний монеты 1 к общему числу
бросаний в первых 2п блоках есть
*i + ¦¦¦ +хп (*i + ... + хп)/п .-.
... +yn)ln' W
Согласно усиленному закону больших чисел и равенству C),
это отношение с вероятностью 1 стремится к пределу
Через ы„ обозначим отношение числа выпавших орлов к об-
общему числу бросаний в первых 2п блоках. Тогда
ип равно отношению числа бросаний монеты 1 к общему числу
бросаний в первых 2ге блоках, умноженному на отношение числа /_.
орлов, выпавших при использовании монеты 1, к общему числу '•/
бросаний монеты 1, плюс подобное же произведение для монеты 2.
Заметим, что при этом с вероятностью 1 имеем
(8)
Для всякого п определим целое положительное число N =
() так, что
(9)
6*

84 Г. Роббинс
Пусть wn — число орлов, выпавших в первых п бросаниях.
Тогда
число орлов, выпавших в первых 2N блоках бросаний, ие
больше wn и wn не бсльше числа орлов, выпавших в первых A0)
2N + 2 блоках.
Из (9) и A0) следует, что
иы(х\ + У\+ ••• +xN + yN) < wn
n
< <
... +xN+l+yN+l ^ n ~-
1+У1+ ¦¦¦ +xN+]+yN+l)
Так как (xN+l + yN+t)/N стремится к 0 с вероятностью 1 при
возрастании п (и, следовательно, jV), то с вероятностью 1 спра-
справедливо равенство
*,+у,+ ¦¦¦ +xN+l+yN+l_
Таким образом, с вероятностью 1 из соотношений (8) и A1)
находим
lim—=hmuN=—-—-—, A2)
Л N 7 Ь 9
Л
что и требовалось доказать.
ЛИТЕРАТУРА
1. Robbins H., Some aspects of the sequential design of experiments, Bull.
Am. Math. Soc, 58 A952), 529—532. (Русский перевод см. иа стр. 71
настоящего сборника.)
2. Феллер В., Введение в теорию вероятностей и ее приложения, т. 1,
«Мир», М„ 1967.

Правильность программ')
3. Манна
В статье рассматривается соотношение между правильностью программ
и выполнимостью (или невыполнимостью) формул исчисления предикатов
первой ступени. Кроме того, в статью включены некоторые результаты
об эквивалентности программ.
ВВЕДЕНИЕ
В последнее время значительные усилия направлены на оты-
отыскание методов установления правильности (вычислительных)
программ. Программа называется правильной, если ее выпол-
выполнение заканчивается и дает желаемый окончательный результат.
В настоящей работе мы пытаемся формализовать эту про-
проблему путем сведения ее к выполнимости (или невыполнимости)
определенных формул первой ступени. Точнее говоря, мы опи-
описываем алгоритм, преобразующий любую программу Р из дан-
данного класса {Р} программ в формулы первой ступени WР и WP,
такие, что:
(i) Wр выполнима тогда и только тогда, когда Р правильна
или выполнение Р не заканчивается, и
(ii) WP невыполнима тогда и только тогда, когда Р правильна.
Подобный результат получен и для эквивалентности про-
программ. Две программы называются эквивалентными, если для
одинаковых входных величин выполнение обеих заканчивается
и обе дают одинаковый окончательный результат2). Ясно, что
проблемы правильности и эквивалентности программ связаны
между собой, ибо вместо того, чтобы непосредственно дока-
доказывать правильность программы, мы можем доказать эквива-
') М a n n a Z., The correctness of programme, Journal of Computer and
System Sciences, 3, № 2 A969), 119-127.
2) Это определение отличается от обычного определения эквивалентности:
для одинаковых входных величин либо выполнение обеих программ не
заканчивается, либо обе программы дают одинаковый окончательный ре-
результат.

86 3. Мйнна
лентность этой программы некоторой другой программе, пра-
правильность которой заранее известна.
Чтобы сократить предварительные определения, мы будем
предполагать, что читатель знаком с обычными понятиями,
рассматриваемыми в исчислении предикатов первой ступени
(см., например, Мендельсон [6]). Представленных здесь резуль-
результатов касаются также работы Флойда [2, 3], Манны [4, 5] и
Купера [1].
ОПРЕДЕЛЕНИЕ ПРОГРАММ
Программа Р состоит из:
1) (а) входного вектора х,
(b) программного вектора у,
(c) выходного вектора z,
2) (а) непустой входной области Dx,
(b) непустой программной области Dy,
(с! непустой выходной области Dz,
3) начальной функции (initial assignment function) g(x) —
всюду определенной функции, отображающей Dx в Dy, и
4) последовательности из N (N^\) предложений, где /-е пред-
предложение A<л^Л0 имеет вид
*: если pi (х, у), то [у«- /' (х, у); переходи к *',],
иначе [yW?(x, у); переходи к *2],
где:
(a) pt(x, у^ — всюду определенный предикат на DxXDy%
(b) f} (х, у) и f2t (x, у) — всюду определенные функции, ото-
отображающие Dx X Ьу в Dy, и
(c) 1<?„ i2^N.
Каждая команда типа переходи к ik: [y-<—f*(x, у); переходи
к ik], k = 1 или 2, может быть заменена стоп-командой
[z<-/**(x, у), стоп], где /г*(х, у) —всюду определенная функция,
отображающая DXX Dy в Dz.
ВЫПОЛНЕНИЕ ПРОГРАММ
Если дана программа Р и входное значение geDx для
входного вектора х, то программа может быть выполнена.
Выполнение всегда начинается с первого предложения (поме-
(помеченного цифрой 1) при начальном значении у, равном g(Q.
Вообще если достигнуто i-e предложение (l^i^JV) при
у = т], то выполнение происходит следующим образом: если
') То есть для каждой пары (|, tj) e Z>x X Dy вначением р{ (|, г\) является
либо И (истина), либо Л (ложь).

Правильность программ 87
pdl> Т1) = И, то [заменяем значение у на /}(?, ti) и переходим
к 1,-му предложению], иначе [заменяем значение у на /?(|, ti)
и переходим к 12-Щ предложению]. Если команда переходи к ik
заменена стоп-командой, то выполнение осуществляется так:
приписываем z значение Л*(?, г\) и останавливаемся.
Если выполнение заканчивается с z = ?, то мы говорим,
что Р(|) определено и Р(|) = ?. В противном случае, т. е. если
выполнение никогда не оканчивается, мы говорим, что Р (|)
не определено. Иначе говоря, программу Р можно рассматри-
рассматривать как представление частичной функции z = P(x), отобра-
отображающей Dx в Dz.
Пусть Р — программа, ф(х) —всюду определенный предикат
на Dx (называемый входным предикатом) н -ф (х> z) —всюду
определенный предикат на Dx X Dz (называемый выходным
предикатом). Мы будем говорить, что:
1) Р является правильной относительно <р и of>, если для
каждого ?, такого, что ф(|) = И, программа Р(|) определена
и фE, Р(Ш = И;
2) Р является частично правильной относительно qp и ф,
если для каждого ?, такого, что ф(|) = И и Р(|) определена,
имеет место if(|, Р(|)) = И.
Пример. Рассмотрим программу Р* (для умножения целого
числа jfj на неотрицательное целое число х2 путем повторных
сложений):
х = (*,, х2) — входной вектор,
у = (г/i, г/г) — программный вектор,
z = z — выходной вектор,
Dx = / X / — входная область (где / — множество целых
чисел),
Dy = 1 X / — программная область,
DZ = I — выходная область,
g(x) = @, x2) — начальная функция.
Единственным предложением является
1: еслм у2 = 0, то [г*-уи стоп ],
иначе [(г/,, г/2)<- (г/, + *,, г/2-1), переходи к I].
В дальнейшем мы рассмотрим правильность программы Р*
относительно входного предиката х2^0 и выходного преди-
предиката г = хххг.
АЛГОРИТМ
Если дана программа Р, входной предикат f (ж) Я выходной
предикат г|з(х, z), то можно построить формулы WP[<f>, ij)J
и IFp [ф, \|э] следующим образом:

88 3. Манна
1. Для каждого предложения вида
/: если pt(x, у), то [y<-/J(x, у), переходи к /,],
иначе [y-«-/f(x> У)> переходи к i2\
определим Wt как
Vy(<7f(x, у)=> еслм pt(x, у), го gjx, /'(х, у)),
иначе qh(x, f2t(x, у))I),
где:
a) qt — различные предикатные символы, т. е. символы,
представляющие неопределенные предикаты;
b) если команда переходи к ik заменена в Р стоп-командой,
то q{ (x, f*(x, у)) заменяется в Wt на г|з(х, Л*(х, у)).
2. Определим [Р, ф] (х) как
?,(х, ^(х))ЛГ,Л^2Л ... AWN.
3. Наконец, определим:
1^р [ф, ¦*] как Vx (Ф (х) zd [P, Ц] (х)),
Wp[y,qi\ как Зх(ф(х) Л[Р, ~i|>](x)).
Формула W вида U^P или WР называется выполнимой, если
каждому предикатному символу qh встречающемуся в ней,
мы можем приписать всюду определенный предикат на Dx X Dy,
так, что W станет истинной. Формула W называется невыпол-
невыполнимой, если она не является выполнимой.
Пример. Рассмотрим программу Р' с входным предикатом
х2^0 и выходным предикатом z = xtx2. Следуя вышеописанному
алгоритму2), мы получим, что WP'[x2^0, z = X\x^ есть
V*,V*2(*2>0 zd (q @, х2) Л
?СЛ« г/2 = 0. Го i/l = *1*2>
, z = Х\х2] есть
ОЛ^О, ^г) Л Vjf,V|fc(<7(#i, Уг) => есл« {/2 = 0,
го у, ^= лт,л:2,
иначе q(yi+xh г/2-1))).
') То есть Vy(((<7/(x, у)Лрг(х, у)) => ^ (х, /{(х, у)))л( (<7< (х, у) Л
^(х,у))=<7,г(х,/2(х,у)))).
2) Для краткости мы вместо qt (жь «2, Уи Уг) пишем q (yit у3).

Правильность программ 89
Можно легко проверить, что приписыванием предиката
j/i = *i (*а — г/г) в качестве значения символа q(yu у2) в W>
получаем истинное выражение. Таким образом, WP* выполнимо.
С другой стороны, мы покажем позднее, что можно вывести
противоречие из Wp; что означает невыполнимость Wp*.
ЛЕММА
Результаты настоящей статьи доказываются с помощью
следующих определений и леммы.
Пусть geD*. Всюду определенный предикат б (у) на Dy на-
называется:
1) характеристическим (valid) предикатом i-го предложения
для РA), если для каждого т] из Dy, такого, что в процессе
выполнения Р (%) мы достигаем г-го предложения при у = т),
имеем б (ti) = И;
2) минимальным характеристическим предикатом i-го предло-
предложения для Р (|), если для каждого г\ из Dy, такого, что в про-
процессе выполнения Р (|) мы достигаем г-го предложения при
у = т) и ни для каких других г\, имеем 6(ti) = H.
Пример. Рассмотрим программу Р* при значении входа
| = C, 4). Предикат @ < г/, < 12) Л @ < у2 <4) является харак-
характеристическим предикатом (в то время как предикат б(уи у2),
истинный только для @, 4), C, 3), F, 2), (9, 1) и A2, 0), является
минимальным характеристическим предикатом) первого пред-
предложения для Р" C, 4).
Лемма 1.
(i) P(l) не определено или
(ii) P (D определено и -ф (?, Р (|)) = И тогда и только тогда,
когда [Р, ip] (%) выполнимо.
Доказательство.-*: Для каждого предикатного символа qh
l^i^N, в [Р, гр] (|) придадим qi{%, у) значение минимального
характеристического предиката /-го предложения для Р(?). Так
как Я (|) либо не определено, либо определено и -ф(g, Р(|)) = И
(другими словами, если Р (I) определено, то $(%, Р(|) = И), то,
согласно построению [Р, г|з], значением [Р, г|з](|) при выше-
вышеуказанном значении qt является истина, т. е. [Р, i|)](?) вы-
выполнимо.
¦*- : Если [Р, г|з] (|) выполнимо, то это означает, что преди-
предикатным символам qt(%,y), l^i^N, можно приписать в качестве
значений такие всюду определенные на Dy предикаты б; (у), что
значением [Р, -ф] (g) будет истина. Согласно определению [Р, ip],
это означает, что каждое 6i( I ^i^JV, есть характеристический

90 3. Mdma
предикат i-го предложения для Р (|), и, следовательно, если
РЦ) определено, то г|з(?, Р(|)) = И.
Из леммы 1 следует, что:
1) [Р, ИЩ) всегда выполнима и
2) [Р, Л]A) выполнима тогда и только тогда, когда Р(?)
не определено.
ПРАВИЛЬНОСТЬ. ПРОГРАММ
Следующие результаты формализуют понятие правильности
программ.
Теорема 1. Программа Р является частично правильной
относительно <р и ip тогда и только тогда, когда lFP[<p, ip] вы-
выполнима.
Теорема 2. Программа Р является правильной относи-
относительно ф и г|з тогда и только тогда, когда WP [<p, г|з] невыполнима.
Теорема 1 представляет собой результат Флойда [2] и дока-
доказывается непосредственно с помощью леммы 1. Теорема 2 также
может быть доказана с помощью леммы 1, если показать, что
программа Р не является правильной относительно <р и г|з [т. е. 3|
такое, что г|з (|) = И и
(i) P(l) не определено, либо
(ii) P(l) определено и г|з(|, Р(|)) = Л] тогда и только тогда,
когда №р[<р, ф] выполнима.
Из теоремы 1 (при i|) = JI) и теоремы 2 (при г|з^И) соот-
соответственно получаем следствия.
Следствие 1. Для каждого %,, такого, что <р(|) = И, значе-
значение Р (|) не определено тогда и только тогда, когда WP [ф, Л]
выполнима.
С лед ств ие 2. Для каждого %, такого, что ф(|) = И, зна-
значение РA) определено тогда и только тогда, когда WP[(f, И]
невыполнима.
Пример. Из теоремы 2 следует, что мы можем доказать
правильность программы Р* относительно входного предиката
х2^0 и выходного предиката z = xlx2, показав, что W[^0
z — X\X2\ невыполнима. Как уже было найдено, Wp
z = ххх2\ есть
3*,3*2 (х2 > 0 Л q @, х2) Л Vi/,Vi/2 (q {yu y2) =>
если у2 = 0, то ух Ф
иначе q(yi + xt, y2-l))>

Правильность программ 91
Мы покажем, что WP*[x2^0, г = Х\Х2] невыполнима, путем
вывода противоречия, используя следующие четыре предложения:
A) х2>0,
B) q@,x2),
C) ЧуУу2((я(У1У2) Л */2>0)о </(*/,+*„ г/2-1)),
D) VyiVy2((q (Уи У2) Лу2 = 0)=>У\?= хух2).
Путем подстановки х{ (х2 — у2) вместо г/, в C) получаем:
C') Vi/2((<7 (*, (х2-у2), у2)Лу2>0) =>q(*i (х2-у2) + *,, у2-1)).
Используя принцип индукции
при Q{t)^q{xx{x2 — t), t), мы получим из A), B) и C')
Q@), т. е. q(x{x2, 0), что противоречит D).
ЭКВИВАЛЕНТНОСТЬ ПРОГРАММ
Две программы Р, и Р9 назовем сравнимыми, если они
имеют одинаковые входную переменную х, выходную перемен-
переменную z, входную область Dx и выходную область Dz.
Пусть Р, и Р2 —две сравнимые программы, и пусть <р(х) —
всюду определенный предикат на Dx (называемый входным
предикатом). Мы скажем, что Pj и Р2 эквивалентны относи-
относительно ф, если для всякого |, такого, что ф(|) = И, как Pi(|),
так и Р2(|) определены и Р, (g) = P2 (|).
Эквивалентность программ можно формализовать с помощью
формулы Wpu p, [ф], которая определяется так:
Зх(Ф(х) Л [Р„ г](х) Л [Р2, -г](х)),
где:
(a) г(х, г) — произвольный предикатный символ,
(b) символы г, ц\ (использованные при построении фор-
формулы [Р, г]) и q" (использованные при построении формулы-
[Р2, ~г]) должны быть различными.
Теорема 3. Программы Р{ и Р2 эквивалентны относи-
относительно ф тогда и только тогда, когда Wpu p, [ф] невыполнима.
Доказательство. Мы покажем, что Р, и Р2 не экви-
эквивалентны относительно ф, т. е. существует |, такое, чтоф(|)=И, и
0) Р\ (%) не определено, либо
(ii) P2(%) не определено, либо
(iii)P,(|) и Р2(\) определены, но Pi(|)?=P2(l). тогда и
только тогда, когда Wpu p, [ф] выполнима.
(i)->: Придаем г значение Л и используем лемму 1.
(ii)-»: Придаем г значение И и используем лемму I,

92 3. Мйнна
(Hi)-»: Берем в качестве г предикат б (где б(х, z) = И тогда
и только тогда, когда (х, z) = (g, Pi (?))). Согласно лемме 1
[Рь 6] (|) выполнима. Кроме того, так как Р, (|) Ф Р2(|), имеем
6(Ё, Рг(&)) = Л, т. е. ~6(|, Р2 (%)) = И. Следовательно, по лемме 1
[Р2, ~6](|) также выполнима. Это означает, что и ЙРр„ р,[ф]
выполнима.
<—: Предположим, что Н^р„ р, [ф] выполнима при %, подста-
в-ленном вместо х, и б —вместо г. Так как [Р,, 6](?) выполнима,
то из леммы 1 следует, что если Рх (|) определено,
то б(|, Р, (Е)) = И. Так как [Р2, ~6Щ) выполнима, из леммы 1 так-
также следует, что если Р2(Ю определена, то ~ 6(?, Р2(?)) = И. Это
означает, что если определены Р, (?) и Р2(Ъ), то 6(|, Р,(|)) = И,
а 6F. Р2A)) = Л, т. е. P,(g)?=P2(g).
Пример. Рассмотрим две программы Р\ и Р2 (вычисляю-
(вычисляющие *! для неотрицательных целых х), где:
1) в обеих программах
х = х, У = (у1,у2), z = z, Dx = I, Dy = /X/, Dz = I;
B) кроме того,
(a) Pi состоит из начальной функции gi(x) = (l, x) и пред-
предложения
1: если z/2 = 0> то [z*- «/t; cron],
«наче [(#,, y2)<r-{yxy2, y2~\)\ переходи к 1];
(b) P2 состоит из начальной функции ?2(*) = 0> 0) и пред-
предложения
1: если у2 = х, то [z*- г/,, сгои],
иначе [(#„ г/i) ч-(г/, (г/2 +1), г/2 + 1); переходи к 1].
* *
Ясно, что Pi и Р2 сравнимы.
Из теоремы 3 следует, что мы можем доказать эквивалент-
эквивалентность программ Pi и Р2 относительно входного предиката х^О,
показав, что W* *[*^0] невыполнима, где W • -[х^О] есть
Л ^(ж, 1, х) Л Vy,Vy2[^(x, «/,, J?2)=> если г/2 = 0, го г(х, «/,)
Л q"{x, 1, 0) Л V^V^^f7^, г/,, у2) гэ еслм г/., = х, то ~г (х, г/,),
иначе q'{ (х, ух (у2 + 1), у2 + 1)]}.
ЛИТЕРАТУРА
1. Cooper D. С., Program scheme equivalences and second order logic, Pre-
Presented at Fourth Annual Machine Intelligence Workshop, University of
Edinburg, August 1968.

Правильность программ 93
2. Floyd R. W., Assigning meaning to programms, Proceedings of Simposia
in Applied Mathematics, American Mathematical Society, v. 19, 1967,
p. 19—32.
3. Floyd R. W., The verifying compiler, Computer Science Research Review
Carnegie-Mellon University, December 1967.
4. M a n n a Z., Termination of algorithms, Ph. D. Thesis, Computer Science
Department, Carnegie-Mellon University, April 1968.
5. Manna Z., Properties of programs and the ferst-order predicate calculus,
JACM (April 1969).
6. Men del son F., Introduction to mathematical logic, Van Nostrand Com-
Company, Princeton, 1964.

О проблеме нахождения
минимальных программ для таблиц1)
Д. Пейджер
В этой статье мы накладываем очень слабое условие на „длину про-
программы" Q (z). He предполагая, что Q (г) частично рекурсивна, мы доказы-
доказываем несколько неожиданный результат: для некоторого целого числа т
существует конечный набор программ, содержащий кратчайшие программы
для множества характеристических функций, определенных на множествах
яз т элементов, и такой, что проблема отыскания по таблице функции ее
кратчайшей программы в этом наборе неразрешима.
Вопрос о сложности программ привлек внимание многих
авторов. Блюм [1] рассматривал соотношение между сложностью
программы и временем вычисления. Чейтин [2] получил оценку
сложности кратчайших программ, порождающих последователь-
последовательности данной длины 2). Радо [4] показал, что невозможно эффек-
эффективно определить для произвольного п наибольшее число,
которое может вычислить программа с п командами. Мы интере-
интересовались обратной проблемой: найти кратчайшую программу
для таблицы. Под таблицей мы понимаем конечное множество
пар: {(*,, yt): 1</<«; х, = х,-> i = /}.
Результат, который мы получили, обладает двумя несколько
неожиданными свойствами:
A) выбор кратчайшей программы для рассматриваемого мно-
множества таблиц оказывается невозможным, несмотря на то, что он
производится каждый раз из одного и того же конечного мно-
множества программ;
B) теорема верна для любого определения длины программы,
такого, что данную длину имеет только конечное множество
программ. В частности, не предполагается, что длина эффек-
эффективно вычислима 3).
') Р a g e r D., On the problem of finding minimal programs for tables,
Information and Control, 14, № 6 A969), 550-554.
!) Ранее аналогичный результат в терминах реализации функций алгебры
логики машинами Тьюринга и нормальными алгоритмами (а также конеч-
конечными автоматами) получил В. А. Кузьмин. (См. Кузьмин В. А., Реали-
Реализация функций алгебры логики автоматами, нормальными алгорифмами и
машинами Тьюринга, сб. „Проблемы кибернетики", вып. 13, 1965, стр. 75—96.) —
Прим. ред.
3) Однако предполагается, что множество всех программ данной ДЛИНЫ
Известно. - Прим. перед.

О проблеме нахождения минимальных программ для таблиц 95
Примерами невычислимой функции длины (применимой
к данной программе Z) являются:
(a) номер первой программы (в некотором упорядочении
программ), которая эквивалентна Z;
(b) номер первой таблицы вида
{(*„ Z(*,)), (х2, Z(x2)) (xz, Z(x2))},
которая встречается в некотором упорядочении множества всех
таблиц. Здесь Z(x) есть выход программы Z для входа х.
В этом и других примерах нерекурсивной функции длины
возможно, что существуют некоторые непрямые способы нахо-
нахождения кратчайшей программы для таблицы, даже если мы
не всегда можем вычислить длину произвольной программы.
Мы примем некоторую синтаксическую систему для предста-
представления алгоритмов, причем такую, что к ней применима гёде-
левская нумерация. Мы будем называть эти синтаксические
представления программами, обозначая их прописными буквами,
а их гёделевские номера будем обозначать соответствующими
строчными буквами.
Под длиной программы мы понимаем некоторую числовую
характеристику программ Q{z), обладающую следующим свой-
свойством: для любого k множество программ X, таких, что
Q(x)<k, конечно.
Длина Q(z) программы может быть некоторой мерой „объема
памяти", занимаемого программой, например числом символов,
содержащихся в Z '). Нетрудно видеть, как меры такого рода
могут быть применены к таким алгоритмическим системам,
как машины Тьюринга, вычислительные машины, системы урав-
уравнений Клини [3], U.R.M. Шефердсона и Стургиса [6] и т. д.
Под таблицей мы понимаем конечное множество записей:
а программой для этой таблицы является программа Z, такая, что
Z (*{) = t/i для 1 ^ i ^ п.
В частности, мы рассмотрим таблицы для характеристи-
характеристических функций конечной мощности, называемые разрешающими
таблицами. Такие таблицы состоят из записей вида
(х;, t{), где ti есть 0 или 1.
Будем называть такие записи характеристиками.
') Под символом мы понимаем элементарный символ. Таким образом,
составной „символ" <7u машины Тьюринга должен рассматриваться как со*
стоящий из трех символов.

9в Д. Пейджер
Теорема. Существует конечный набор программ, содержа-
содержащий кратчайшие программы для некоторого множества разре-
разрешающих таблиц одинаковой (конечной) длины и такой, что
проблема получения по таблице ее кратчайшей программы из
этого набора неразрешима.
Мы докажем эту теорему, показав, что существует конечная
разрешающая таблица Хо, такая, что проблема нахождения
кратчайшей программы для таблицы, полученной добавлением
к Яо одной характеристики, не является равномерно разрешимой ').
Заметим, что в любом случае программа может выбираться
из одного и того же конечного множества U программ длины
< max (Q(Z0), Q{ZX)),
где Zo, Zj — произвольные программы для Яо, такие, что Z0(x) = 0
и Z1(x)=l для всякого х, не принадлежащего области опре-
определения Ко.
Доказательство
Определение (Роджерс). Два непересекающихся рекур-
рекурсивно перечислимых (р. п.) множества 0{ и G2 называются
сильно неотделимыми тогда и только тогда, когда:
(i) Gi U G2 бесконечно и
(и) если А есть р. п. множество и А П G, (J G2 бесконечно,
то (AftGJf 0 и(ЛПE2)^ 0.
Пусть 6\ и G2 — сильно неотделимые множества2), и пусть
/(jc) —частично рекурсивная функция, такая, что
. О, если xeGi,
Пх>~\ 1, если xe=G2.
Любое частично рекурсивное расширение F(x) функции f(x)
определено только на конечном множестве дополнительных
элементов. Действительно, область определения функции F (х)
можно разбить на два непересекающихся рекурсивно перечис-
перечислимых множества /С,, Kz, а именно:
Ki = {x: F(x) = 0}, K2 = {x: F (х)ФО},
') То есть не существует алгоритма, который для любого такого попол-
пополнения таблицы Хо давал бы кратчайшую программу. — Прим. перев.
3) Пример пары сильно неотделимых множеств содержится в работе:
Мучник А. А., Об отделимости рекурсивно перечислимых множеств,
ДАН СССР, 109, № 1 A956), 29-32. Множества в построенном А. А. Муч-
Мучником примере неотделимы даже в более сильном смысле. — Прим. ред.

О проблеме нахождения минимальных программ для таблиц 97
так, что G[ s K\, G2 s K2- Но тогда K\ — Gx и /Сг— G2 конечны и,
следовательно, конечно множество
которое является разностью области определения F(;c) и об-
области определения /(*).
Пусть Н — конечное множество программ, вычисляющих
функцию f (x) на ее области определения с минимальной Q-ме-
рой, и пусть k есть значение Q на элементах Н. Если Ze#,
то Z(x) является расширением f(x). Пусть V является (конеч-
(конечным) объединением всех конечных множеств Dz — Df, где
Zs#, Dz — область определения Z(x), Df —область определе-
определения f(x).
Если Z есть произвольная программа, которая не вычисляет
f (х) на ее области определения, то существует х из Df, такое,
что Z{x) либо не определено, либо Z(x)=?f{x). Пусть ^ — наи-
наименьшее такое значение для программы Z, и пусть S обозна-
обозначает конечное множество {хг: Q(z)^k}.
Множество характеристик {(л:, f(x)): jeS) обозначим через
Ко. Если t ф V, то t ^ Df тогда и только тогда, когда самая
короткая программа для таблицы Xq, пополненной характери-
характеристикой {t, 0) либо характеристикой (t, 1), является элементом Н.
Если бы существовал единый метод нахождения кратчай-
кратчайшей программы для %0, пополненной одной дополнительной
характеристикой, то, так как V конечно, из последнего утвер-
утверждения следовало бы, что множество {t: t фУ и t ф. Df}, т. е.
{t: t^G1{JG2 — V}, рекурсивно перечислимо. Атак как мно-
множество V конечно, это противоречит сильной неотделимости G,
и G2. Теорема доказана.
Фактически мы получили более сильный результат, чем
утверждается в теореме: пусть U — конечное множество про-
программ, такое, что Н — его (собственное) подмножество. Пусть
? — рекурсивное множество разрешающих таблиц, состоящее
из таблиц, являющихся пополнением к0 одной характеристикой.
Тогда кратчайшая программа для каждого члена Z, принадле-
принадлежит U, но мы не можем эффективно решить, принадлежит ли
она И или U — Н.
Предположим теперь, что существует эффективное много*
однозначное отображение, которое соотносит программам Z
эквивалентные программы Z* с тем же числом команд, так, что
7 Зак. 560

Д. Пейджер
множество программ Z* с данным числом команд конечно1).
Тогда можно получить вариант теоремы, в котором слова
„кратчайшая программа" заменены словами „программа с наи-
наименьшим числом команд".
Подобный результат имеет место и по отношению к шенно-
новской мере сложности машин Тьюринга, т. е. произведению
числа состояний на число ленточных символов [5].
С другой стороны, если рассмотреть более слабый случай,
когда 1) множество кратчайших программ для рассматриваемых
таблиц бесконечно и 2) длина эффективно вычислима, то можно,
используя теорему о рекурсии, доказать: если справедливы
1) и 2) и если множество рассматриваемых таблиц рекурсивно
перечислимо, то не существует эффективного способа находить
кратчайшие программы.
ЛИТЕРАТУРА
1. Blum M., On the size of machines, Inform, and Control, И A967),
257—265. (Русский перевод: Блюм М., Об объеме машин, сб. «Проблемы
математической логики», стр. 423—431, «Мир», М., 1970.)
2. С h a i n t i n G. Т., On the length of programs for computing linite binary
sequences, /. ACM, 13 A966), 547—569.
3. Клин и С. К., Введение в метаматематику, ИЛ, М., 1957.
4. Rado Т., On noncomputable functions, Bell Sistem Techn. I. A966),
877—884.
5. Shannon С. Е., A universal Turing machine with two internal states, in
«Automata Studies», Princeton University Press, Princeton, New Jersey,
1956. (Русский перевод: см. в сб. «Автоматы», ИЛ, М., 1956, а также в
сб.: Шеннон К.-, Работы по теории информации и кибернетике, ИЛ, М.,
1963.)
6. S h e p h e r d s о п J. С, S t u г g i s H. E., Computability of recursive func-
functions, /. ACM, 10 A963), 217—225.
7. Yong P. R., Towards a theory of enumerations, IEEE Conference Record,
Symposium on Switching and Automata Theory, 1968, pp. 334—350.
') Например, оно получается с помощью замены отсылок к большим
адресам памяти в реальных вычислительных машинах или в U. R. М. отсыл-
отсылками к неиспользованным меньшим адресам либо заменой составных символов
<?j и Si в командах машнн Тьюринга символами с неиспользованными мень-
меньшими индексами.

Об арифметических выражениях
и деревьях1)
Р. Р. Реджеёвски
В работе описывается, каким образом дерево, представляющее вычисле-
вычисление арифметического выражения, можно изобразить так, что количество тре-
требуемых для счета ячеек памяти легко определяется. Это представление сво-
сводит проблему выбора наилучшего порядка вычисления к одной из задач тео-
теории графов Предлагается алгоритм решения этой задачи.
1. ВВЕДЕНИЕ
В работе [1] обсуждается алгоритм вычисления арифмети-
арифметического выражения, минимизирующий требуемое для вычисле-
вычисления количество ячеек памяти. Как показано ниже, дерево,
используемое в [1], может быть модифицировано таким обра-
образом, что требуемое количество ячеек памяти получает явное
представление. Это представление приводит к специфической
проблеме „минимальной ширины" упорядочения дерева, кото-
которая и является темой настоящей статьи.
Чтобы вычислить выражение, например
((a + b)-c-d)/(e(f-g)),
потребуется выполнить ряд арифметических операций: А = а + Ь,
B = c-d, C = f-g, D = A-B, E = e-C, F = D/?, вычисляя
таким образом промежуточные результаты А, В, ..., Е и конеч-
конечный результат F. Этот процесс может быть представлен
в виде дерева, как на рис. 1. Каждая вершина этого дерева
представляет одну операцию; дуга из вершины х в вершину у
представляет промежуточный результат, который используется
в операции х, а вычисляется операцией у.
Выбрать возможный порядок операций —значит топологически
упорядочить дерево, т. е. расположить его вершины в такой
последовательности, что вершина х предшествует вершине у,
если существует дуга из у в х. (Это условие эквивалентно
требованию, чтобы каждый промежуточный результат был вы-
вычислен раньше, чем использован.)
') Re d z i e j о w s k i R. R., On arithmetic expressions and trees, Com*
munications of the ACM, 12, № 2 A969), 81—84.

100
P. P. Реджеёвски
Результат такого упорядочения удобно представлять в виде
диаграммы, как это сделано на рис. 2. В дальнейшем мы
будем называть такую диаграмму „укладкой" дерева, изобра-
изображенного на рис. 1. Она может рассматриваться как предста-
представление вычисления на шкале времени.
Предположим, что мы имеем „моментальный снимок" вы-
вычисления в момент выполнения операции х. Такой моменталь-
моментальный снимок покажет некоторые результаты предыдущих опе-
операций, хранящиеся для дальнейшего использования и не
Рис. 1.
Рис. 2.
участвующие в операции х. Легко видеть, что на рис. 2 эти храня-
хранящиеся результаты представляются дугами, проходящими над
вершиной х. Если число этих дуг есть w, то мы должны иметь не
менее w + 1 запоминающих элементов (ячеек в оперативной
памяти или иа магнитной ленте) в нашем распоряжении в дан-
данный момент: w для результатов, уже хранящихся, и один для
результата х. Число запоминающих элементов, которые мы
должны иметь для всего вычисления, определяется, таким
образом, как максимальное число дуг, проходящих над одной
вершиной на рис. 2; мы будем называть это число „шириной"
нашей укладки. Выбор наилучшего порядка операций сводится,
таким образом, к построению укладки минимальной ширины
для дерева на рис. 1.

Об арифметических выражениях и деревьях 101
В третьем разделе предлагается алгоритм построения такой
укладки; во втором разделе даны определения.
Хотя деревья, соответствующие арифметическим выраже-
выражениям, всегда бинарны, решение задачи для общего случая не
является более сложным. Поэтому в дальнейшем рассматри-
рассматривается общий случай.
2. ОПРЕДЕЛЕНИЯ
В дальнейшем используется понятие (направленного) графа,
определенного как упорядоченная пара (X, U), состоящая из
непустого множества X вершин и множества U дуг. Дуга из
вершины hsIb вершину i/el обозначается здесь (х, у) е U.
Для х, jel, таких, что существует дуга (х, у) е U, вер-
вершину у назовем последователем х. Предполагается, что чита-
читатель знаком с элементарными понятиями пути в графе, кон-
контура и т. д.
Граф {X, U) называется деревом, если он конечен, не со-
содержит контуров и содержит вершину г, такую, что:
a) г не является концом никакой дуги и
b) каждая вершина i;el, х Ф г является концом в точ-
точности одной дуги.
Вершина г, обладающая этими свойствами, называется
корнем дерева. Вершина х^Х, не являющаяся началом ника-
никакой дуги, называется листом дерева'); любая вершина, не
являющаяся листом, называется узлом. Для дерева G = (J, U)
и его вершины х^ X мы обозначаем через G (х) поддерево,
состоящее из х и всех вершин, достижимых из х путями в G.
Укладка дерева G = (X, U) формально определяется как после-
последовательность q> = (xu х2, ..., хп) всех вершин дерева G, такая,
что для каждой дуги (xt, xt)^ U имеет место /</. В укладке
Ф = (я,, х2, ..., хп) дуга {xh Xj)^U называется проходящей
над вершиной xk^X, если j<k<i.
Для этой укладки пусть w( обозначает количество дуг, про-
проходящих над вершиной xt e X. Ширина укладки ф определяется
тогда как maxait(i = l, 2, ..., п) и обозначается W(<р).
3. АЛГОРИТМ
Укладка минимальной ширины данного дерева G может
быть получена заполнением таблицы вида, указанного на рис. 3.
Таблица имеет 3 колонки и п строк. Заполнение начинается
') В советской литературе более распространен термин „висячая вер-
вершина". - Прим. первв.

102
P. P. Реджеёвски
с перечисления в колонке 1 всех вершин дерева G. Мы запи-
записываем здесь снизу вверх сначала корень дерева G, затем
записываем всех его последователей, затем — последователей
этих последователей и т. д. Каждой вершине, таким образом,
сопоставляется строка таблицы, причем если вершина у есть
Колон-
Колонка № 1,
X
L
К
]
1
Н
G
F
Е
D
С
В
А
Колон-
Колонка ЛГ» 2,
V (X)
0
0
0
0
1
0
1
0
2
2
0
2
Колонка № 3. ф (х)
L
К
1
1
KLH
G
UF
Е
UFKLHGD
UFKLHGDEC
В
UFKLHGDECBA
К,
I,
F,
D,
L;
];
н,
Е;
G;
0. 1;
0, 1;
1, 2, 2;
2, 1;
С, В;
2, 1;
Рис. 3.
последователь вершины дг, то строка, сопоставленная х, лежит
ниже строки, сопоставленной у. Заполнив колонку 1, запол-
заполняем таблицу по строкам.
Предположим, что мы уже заполнили т^О строк и собираемся
заполнять следующую (т+\)-ю строку. Пусть вершина, соот-
соответствующая этой строке, есть х. Мы заполняем (т+1)-ю

06 арифметических выражениях и деревьях 103
строку по одному из следующих правил, в зависимости от того,
является х листом или узлом дерева G.
Правило 1. Если х является листом дерева G, то пишем 0
в колонке 2 и пишем х в колонке 3.
Правило 2. Если х есть узел дерева G, то находим в G
всех последователей х; пусть это у0, ух yk, где &1>0. На-
Находим в таблице строки, соответствующие у0, уи ..., yk; бла-
благодаря способу заполнения колонки 1, все они должны быть
среди m уже заполненных строк. Пусть v (yt) для i = 0, I, .. ., k
обозначает содержимое колонки 2 в строке, соответствующей уь
и ф(уд — содержимое колонки 3 в той же строке. Расположим
г/0, уи .. ., yk в последовательность по убыванию величины v (у^
для i = 0, 1 k. Пусть эта последовательность есть (yt , yt , ...
..., yiky, тогда и(г/со)>и(г/A)>.. .>и (г/^). Подсчитаем число
р = тах(р0, ри ..., pk), где pl = v(yijj + j для у = 0, 1, .... k.
Запишем р в (т+1)-й строке второй колонки; в колонке 3
запишем друг за другом ф(г/*0)ф («/«,) • • • ф(#<А) в таком порядке
и сзади припишем х.
Для иллюстрации применения правила 2 на рис. 3 пока-
показаны последовательности (t/i(i, yix, ..., yikj и числа ра, /?,, .. ., pk;
оии расположены справа от каждой строки, заполнявшейся
по этому правилу. Например, для x = D мы имеем г/,0 = F,
Ун = Н, yt, = G и ро=и (г/;„) + ()= 1, p, = v{yil)+\=2, p, = v(yh)+
+ 2 = 2.
Покажем теперь, что после заполнения таблицы последова-
последовательность, появившаяся в последней строке колонки 3, есть
укладка минимальной ширины дерева G.
4. ДОКАЗАТЕЛЬСТВО АЛГОРИТМА
Предположим, что таблица заполнена по вышеуказанным
правилам для дерева G = (X, U) с корнем г. Для xeJf пусть
v (х) есть число, стоящее в строке таблицы, соответствующей х,
в колонке 2; пусть <р(*) — последовательность, стоящая в той же
строке в колонке 3. Последняя строка соответствует корню г;
для этой строки мы имеем v(r) и <р(г) соответственно. Могут
быть доказаны следующие два утверждения относительно со-
содержимого таблицы.
Теорема 1. Для каждой вершины. xeJT последователь-
последовательность ф (х) есть укладка поддерева G (х), а ее ширина равна v (x).
Теорема 2. Для каждой укладки дерева G ее ширина
не меньше, чем v (r).

104
P. P. Реджеёвски
Из теоремы 1 и того факта, что G(r)=G, немедленно сле-
следует, что последовательность <р(г), стоящая в последней строке
третьей колонки, есть укладка дерева G, имеющая ширину v(r).
Теорема 2 утверждает, что эта ширина минимальна.
Доказательство теоремы 1. Чтобы доказать теорему,
достаточно показать, что A) теорема имеет место для каждого
листа дерева G, и B) если теорема верна для всех последова-
последователей узла х, то она верна и для х.
Рис. 4.
То, что утверждение A) верно, следует из правила 1. Если
X есть лист, то поддерево G (х) состоит из единственной вер-
вершины х. Последовательность (х) есть укладка такого дерева,
и ее ширина равна 0.
Справедливость утверждения B) может быть показана еле*
дующим образом. Пусть х есть узел дерева G и yi(j, ytl, ...
..., y[/t — его последователи, как в правиле 2. Предположим,
что теорема верна для всех этих последователей, т. е. ф(г/(,)
для у = 0, 1 k есть укладка поддерева G (yt Л, и ее ширина
равна v(ytl). Сочленение ф(г/(о), ф(&,), •••, 4>(ytk) и (х) в пра-
правиле 2 соответствует конструкции, показанной на рис. 4.
Имея (k+l) дерево G (г//о), G(ylt) G (yik), мы строим
дерево G (х), добавляя вершину х и (fe+1) дуг [х, y(j,
{х, ytl) (х, г/fj. Легко видеть (из рис. 4), что полученная
таким образом последовательность ф(х) должна быть уклад-
укладкой G (х). Чтобы показать, что ширина этой укладки есть v{x),

Об арифметических выражениях и деревьях
105
рассмотрим вершину у, принадлежащую дереву G{ytX где
0^/^&. Легко видеть, что число дуг, проходящих над у,
не превышает числа р/, определенного по правилу 2: имеется
j дуг (х, yio), (х, yh), ..., (х, уч_^ вне дерева G (г/(/) и ровно
v[yif) дуг в этом дереве1). Отсюда ширина <р(х) должна быть
равной тах(р0, р,, ..., pk) = v{x). Теорема, таким образом,
верна также и для х.
о
• - помеченный лист <р
шт - помеченная дуга
Рис. 5.
Числа в вершинах — значении v(x).
Доказательство теоремы 2. Теорема, очевидно, верна
в случае v(r) — 0. Пусть р(г)>0, и, предположим, существует
укладка <р дерева G, имеющая ширину W (ф)<и(г). Для ка-
каждого узла лей сделаем следующее: найдем последователь-
последовательность (yio, yi{, ..., yik) и числа р0, р,, .... pk, вычисленные во
время заполнения по правилу 2 строки, соответствующей х;
затем найдем наименьшее j, O^j^k, для которого pt = v(x),
и пометим дуги (х, yia)y {x, yh), ..., (х, yif). Например, если
на рис. 3 х = D, то /= 1, и мы пометим дуги (D, F) и (D, Н);
результат таких пометок дерева, изображенного на рис. 3,
показан на рис. 5. Легко видеть2), что A) каждый узел х есть
начало по меньшей мере одной помеченной дуги и B) для
') Точнее, ие более чем »({/^) дуг. — Прим. перев.
21 Из определения р (х). — Прим. перев.

106 P. P. Реджеёвски
каждой помеченной дуги (х, у) е U узел х есть начало по мень-
меньшей мере (q + I) помеченных дуг, где q = v (x) — v (у)').
Пометим теперь все листы дерева G, достижимые из корня г
путями, состоящими только из помеченных дуг; из утвержде-
утверждения A) следует, что существует по крайней мере один такой
лист. Пусть г е X — помеченный лист, самый правый в после-
последовательности ф; пусть ц —путь из г в г (ц. состоит только из
помеченных дуг). Возьмем дугу и = (х, у)е[/, принадлежа-
принадлежащую ц. Пусть v (х) — v (у) = q; согласно утверждению B), узел х
в этом случае является началом не менее чем (q + 1) помечен-
помеченных дуг. Пусть <7>0, и пусть тогда и,, и2, ..., uq — помечен-
помеченные дуги, начинающиеся в узле х и отличные от и. Для
Рис. 6.
/=1,2, . .., q пойдем из х по пути, состоящему целиком из поме-
помеченных дуг и начинающемуся дугой щ сколь возможно далеко
(для иллюстрации см. рис. 6). Этот путь \х, должен кончаться
в помеченном листе, т. е. слева от 2 в последовательности <р
(по выбору 2). Так как <р есть укладка дерева G, то узел х
должен быть справа от 2 в <р, т. е. путь цг должен содержать
дугу ы', проходящую над 2. Это дает q дуг, проходящих над
г: «р и'2 и'. Беря в качестве и по очереди все дуги ц,
получаем, таким образом, v (г) — v (z) = v (r) дуг, проходящих
над 2, что противоречит предположению W(q>)<v (г). (Анало-
(Аналогично можно доказать, что v (х) для каждого х е= X есть мини-
минимальная ширина всевозможных укладок поддерева G (х).)
5. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Если дерево G представляет процесс вычисления, как это
описано во введении, то объекты, обсуждавшиеся в разд. 2 — 4,
имеют следующую интерпретацию. Лист дерева G представляет
операцию, выполняемую исходя только из начальных дан-
данных, а узел дерева G — операцию, использующую по крайней
') Действительно, пусть у = yts\ поскольку дуга (х, у) помечена, tos</,
т. е. v (у1;) < v (yi$); q = v (x) - v (у) = о(^(/) + /- v (yt$) < /; но в узле х
начинается (/+1) помеченных дуг, н из q^j следует B). — Прим. перев.

06 арифметических выражениях и деревьях 107
Мере один промежуточный результат в качестве своего аргу-
аргумента. Корень дерева G представляет операцию подсчета ко-
конечного результата. Укладка ф дерева G изображает допусти-
допустимый порядок выполнения операций; она может рассматриваться
как некоторая программа для вычисления, изображаемого де-
деревом G. Ширина Ц^(ф) представляет собой уменьшенное на 1
число клеток памяти, требуемых для выполнения этой про-
программы. Для операции х поддерево G (х) изображает часть
вычисления, состоящую из х и всех операций, требуемых для
установления значений аргументов х. Теорема 1 утверждает,
что последовательность у{х)% появляющаяся в строке таблицы,
которая соответствует вершине х, есть программа для „частич-
„частичного" вычисления G (х) и что число v (x), появляющееся в той же
строке, есть уменьшенное на 1 количество клеток памяти, тре-
требуемое для выполнения этой программы. Предложенный здесь
алгоритм состоит в построении таких „частичных" программ.
Сначала мы строим наиболее элементарные „частичные" про-
программы, используя правило 1, а затем сочетаем их по пра-
правилу 2, получая все более и более сложные программы.
Последовательности ф(#ь), имеющиеся в правиле 2, пред-
представляют собой программы нахождения значений аргументов
операции х. Объединяя их в одну программу ф(х), мы упоря-
упорядочиваем их по убыванию требования количества памяти. Этот
принцип совпадает с принципом, изложенным в работе [1]; наш
алгоритм в основе такой же, как и предложенный там. Дока-
Доказательство, проведенное в разд. 4, может рассматриваться как
формальное доказательство алгоритма, приведенного в ра-
работе [1].
ЛИТЕРАТУРА
1. Nakata I., On compiling algorithms for arithmetic expressions, Comm.
ACM, 10, Mr 8 A967), 492-494.

Плоские карты с заданными степенями
вершин и граней1)
Б. Грюнбаум
1. Введение. В 3-связном графе G, уложенном на плоскости,
обозначим через vk(G) число вер-шин степени k, а через pk{G) —
число граней степени k (число fe-угольников карты, которая
определяется графом G). Рассмотрим здесь только графы без
петель и параллельных ребер, поэтому vk(G) и pk{G) опреде-
определены лишь для fe^=3. Следующее выражение получаем из
формулы Эйлера:
2D- fe)p,(G) + ЦD- fe)MG) = 8.
k k
Продолжая и обобщая различные исследования, касающиеся
теоремы Эберхарда (см. работы [1 — 5,7], а также работу [6],
в которой даны исторические замечания об этой теореме и ее
вариантах), рассмотрим следующую проблему: пусть даны по-
последовательности р — (рз рп) и v = (v3, ..., vm) неотрица-
неотрицательных целых чисел, удовлетворяющих уравнению
?D-*)/>*+2 D-*)**-8. A)
fc-3 *=3
Выясним, можно ли пару р, v реализовать, т. е. существует ли
3-связный плоский граф G, такой, что
Pn() Pk и )
для всех k ф 4.
По теореме Штейница [4, 8, 9] граф G изоморфен графу,
образованному ребрами и вершинами 3-мерного выпуклого
многогранника тогда и только тогда, когда G плоский и 3-связ-
3-связный; поэтому легко понять значение этой проблемы в комби-
комбинаторной теории выпуклых многогранников.
Так как для плоского графа G число ребер равно половине
суммы
k>3
') Grunbaum В., Planar maps with prescribed types of vertices and
laces, Mathematika, 16, № 1 A969), 28-36.

Плоские карты с заданными степенями вершин и ераней 109
то еще одним необходимым условием реализуемости пары р, v
является четность сумм
п m
2ikpk и 2 kvk. B)
k=3 k=3
Докажем следующую теорему.
Теорема. Если последовательности р = (р3, ..., рп) и
v = (v3, ..., vm) неотрицательных целых чисел удовлетворяют
условиям A) и B), то пара р, v реализуема.
2. Доказательство теоремы. Для доказательства теоремы
построим 3-связный плоский граф для каждой пары р, v, удо-
удовлетворяющей A) и B). Из построения будет видно, что все
получаемые графы плоские и 3-связные. Поэтому эти свойства
особо рассматриваться не будут, а все внимание мы сосредо-
сосредоточим на получении заданных степеней вершин и граней.
Удобно разбить доказательство теоремы на ряд случаев.
Случай 1. vk = 0 для k ф 4. Уравнение A) примет вид
()р* = 8. C)
fe>3
Мы должны построить однородный граф G степени 4, Такой,
что pk{G) = pk для всех k ф 4.
Начнем с построения специальных графов, которые будем
называть блоками. Для построения r-блока (г^4) возьмем
квадрат, на каждой из его двух смежных сторон отметим г —4
точек, которые соединим, как указано на рис. 1 (для г = 9).
Если точки выбраны соответствующим образом'), то каждый
r-блок будет содержать один r-угольник, (г — 4) треугольников
и Сг-4 четырехугольников. При этом все внутренние вершины
имеют степень 4, а на двух сторонах квадрата будет 4 вер-
вершины степени 2 и 2 (г — 4) вершины степени 3.
Пусть дана последовательность р, удовлетворяющая урав-
уравнению C). Для каждого k^5 образуем pk fe-блоков. Из этих
блоков и дополнительных четырехугольников построим большой
блок (superblock), так, как указано на рис 2. (Общий случай
мы не будем описывать ввиду очевидности построения.)
„Внешний" вид большого блока такой же, как и самого
блока. Большой блок включает необходимое число fe-угольни-
ков для всех fe^5, но для выполнения уравнения A) еще тре-
требуется 8 треугольников.
') Линии можно проводить как угодно, лишь вы выполнялось условие:
любые две лииин пересекаются в одной точке. — Прим. пврев.

Ряс. 1.
Ряс. 2.

Плоские карты с заданными степенями вершин и граней Ш
Построение теперь легко завершить способом, указанным
на рис. 3 для большого блока, представленного на рис. 2.
Так как на этом этапе добавляются только четырехугольники
и 8 треугольников, обеспечивающие всем вершинам степень 4,
мы получаем требуемый граф. Доказательство теоремы в слу-
случае 1 завершено.
Замечание. Рассмотренную выше конструкцию можно найти
в работе [4; § 13.3]. Она была приведена здесь для полноты
Рис. 3.
изложения, а также для выделения следующих этапов реше-
решения, необходимых при изучении оставшихся случаев:
(i) Два блока, заштрихованные на рис. 2, назовем верхним
и нижним. Подчеркнем здесь важность того, какие именно
fe-блоки нужно разместить в эти выделенные области. (Отме-
(Отметим, что ориентация нижнего блока отлична от ориентации
других блоков.)
(и) Произвольно большой набор четырехугольников (далее
используется термин четырехугольная решетка) можно органи-
организовать в большой блок, реализующий любую последователь-
последовательность при добавлении необходимого числа 4-блоков в кон-
конструкцию больших блоков. Чтобы в некоторых особых случаях
(таких, как pk = 0 для всех &^5) не менять эту конструкцию,

112
Б Грюнбацм
будем всегда в большой блок включать по крайней мере два
4-блока.
Случай 2.
= 4, где v3>5.
Обозначим через v' последовательность: v'3= v3 + S, v'm_] =
==om-l+1> V'm=Vm~l> ?>? = &fc ДЛЯ fc =#= 3, /П — 1, /П. ПоСЛеДО-
вательность v' удовлетворяет уравнению C) (последователь-
(последовательность v' соответствует р в случае 1). Построим, как и в слу-
случае 1, однородный граф G степени 4, имеющий vk граней
степени k. Возьмем в качестве верхнего блока (т — 1)-блок
(далее будем использовать термин „вершинная компонента"
конструкции). Теперь рассмотрим граф G', двойственный к G.
Все грани графа G' суть четырехугольники, и v'k вершии имеют
степень k (fe=#=4). Верхняя вершина К, графа G соответствует
в графе G четырехугольнику V\, который имеет 3 вершины
степени 3 и одну вершину степени (т— 1) (рис. А, а, где т = 8).
Пусть р' — последовательность, определяемая соотношениями:
Рз = Рз + 3- P»_|-Pn-i + l. Pn = Pn-1 и K = Pk Для fe=^3.
n—\,n- Эта последовательность также удовлетворяет уравне-

Плоские карты с заданными степенями вершин и граней 113
нию C), и, как в случае 1, мы можем построить однородный
граф G" степени 4 с p'k гранями степени k {k Ф 4), имеющий
в качестве верхнего блока (я — 1)-блок. Представим G" на пло-
плоскости так, как это показано на рис. 4, Ъ (на котором квадрат
соответствует жирной линии, окружающей вершину Vt на
рис. 3). Наконец, объединим графы G' и G", выбросив Fj
из G", помещая оставшуюся часть G" в четырехугольник V\
в С и соединяя ребрами четыре пары вершин, расположенные
друг против друга (рис. 4, с). Как легко проверить, полученный
граф имеет pk граней степени k и vk вершин степени k для
всех k ф 4. Этим завершается построение в случае 2.
Случай 3.
п m
2D-*)p*>4>2D-fc)t>ft для о3>5.
fc=3 А=3
Теперь начнем с выбора последовательности w целых чисел,
в которой w3 = 0, w^O, ..., wm ^ 0 и такой, что будем иметь
S D-*К = 4,
положив v'k = vk — wk ')• Дальнейшее построение зависит от чет-
четности суммы 2 kwk.
Подслучай 3.1. Сумма 2 kwk четна.
fc>5
Определим последовательность р' с помощью
р'3 = р3— 2 D-k)wk и p'k = pk Для
Легко проверить, что последовательности р', и' удовлетворяют
условиям, наложенным на р и v в случае 2. К графу, по-
построенному так, как это делается в случае 2, реализующему
р', и' и содержащему достаточно большую четырехугольную ре-
решетку, применим следующие преобразования, которые, однако,
еще не обеспечивают конструкцию треугольниками и верши-
вершинами с большими степенями.
') Существование такой последовательности можно доказать следующим
п
образом. Обозначим 2 И — k)pk = t, тогда р'3 = р3 — (t — 4) и t — 4 =
= — 2 D — k)pk. Например, можно взять w.^t — 4, o>fc =0 для б^б. Тогда
fc-5
п
Рз>0, так как иначе получаем < = р3+ 2 ^4 ~ *) Pk<Н и Р3<<~4' т* е-
fc>5
< < рз < t — 4. — Прим. перев.
8 Зак. 560

114
Б. Грюнбаум
Первое преобразование можно описать следующим образом.
Для любого целого числа г^З в решетке стянем в точку
простую цепь, содержащую г —2 ребра; на рис. 5 приведен
случай г = 5. Эта операция дает одну вершину степени 2г и
Рис. 5.
Рис. 6.
2г — 4 треугольников, а остальная часть графа остается без
изменений.
Другим преобразованием для нечетных чисел t^s^b стя-
стягиваются в точки s — A ребер и {t + s — 8)/2 ребер данной ре-
решетки способом, представленным на рис. 6 для s = 7, ^=15.
В результате получаем одну вершину степени s, одну вершину
степени t и s + t — 8 = (s — 4) + (t — 4) треугольников; остальная
часть графа опять остается без изменений.
Повторяя преобразования указанных двух типов необходи-
необходимое число раз, завершаем доказательство.
Подслучай 3.2. Сумма 2 kwk нечетна.

Плоские карты с заданными степенями вершин и граней
118
Пусть г^5 — нечетное число, такое, что wr~^\. Определим
последовательности v", р" с помощью соотношений v" = v3+ I,
= 0.-1, V't
для k фЪ, г—I,
и
p" = p3 — 2, p"k = pk для k ф 3. Эти последовательности удовле-
удовлетворяют предположениям подслучая 3.1. Пусть Я —граф, по-
Рис. 7.
строенный, как в подслучае 3.1, и реализующий р", v" таким
образом, что нижним блоком, который используется в по-
построении „вершинной компоненты", является (г— 1)-блок. Из
задания графа Н следует, что он включает подграф (изображен
на рис. 7, а), содержащий четырехугольник Кг с тремя верши-
вершинами степени 3 и одной — степени {г— 1). Проведя в Кг диаго-
диагональ (рис. 7, Ь), получаем из Я граф, реализующий данные
последовательности р, v. Этим завершается доказательство
этого подслучая.
Случай 4. 2 D-6)р*>4> 2 D — ft) oft и 0<i>3<4.
ft>3 fc>3
Заменим последовательность v новой последовательностью
v' = v'3 — v3 + Q, t»j = D5 + 6 и v'k=vk для k ф 3, 5. Последова-
Последовательности р и v' удовлетворяют предположениям случаев 2
или 3, поэтому, как и выше, можно построить реализующий
их граф G. Единственным дополнительным шагом в этом по-

116 Б. Грюнваум
строении является размещение 6 „новых" 5-блоков „вершинной
компоненты" в трех противоположных парах, вид которых
показан на рис. 8, а. Каждой такой паре в графе G соответ-
соответствует подграф, показанный на рис. 8, Ь. Каждый из трех
подграфов затем преобразуется так, как указано при переходе
от рис. 8, b к рис. 8, с. Полученный граф реализует данные
последовательности р, v.
Случай 5. 2 {A-k)pk<4< 2 D-Jfe)ok.
k>3 k>3
Доказательство в этом случае можно получить из уже рас-
рассмотренных случаев, используя переход к двойственным графам.
Таким образом, все случаи разобраны и доказательство
теоремы закончено.
Замечания. Построение, используемое при доказательстве
теоремы, приводит, вообще говоря, к очень большому числу
четырехугольников и вершин степени 4. Было бы интересно
найти нижнюю границу числа p4(G) + vA(G) в зависимости от
р и v.
Эберхард [3] получил следующий результат: пусть р3, ..., рп,
г — целые неотрицательные числа, удовлетворяющие уравнению
2 F — k)pk = 12 + 2r, тогда существует 3-связный плоский граф G,
>
такой, что Pk{G) = Pk Для всех 6=^=6 и 2 C — k)Vk{G) = — г.
*>4
Как обобщение этого результата и по аналогии с доказан-
доказанной теоремой выдвигается следующее предположение.
Предположение 1. Если р3, ..., р„; v3 vm — неот-
неотрицательные целые числа, такие, что сумма 2 kvk четна и
А>3
2 (Q-k)pk + 2 2 C-*К=12, D)
k>3
то существует 3-связный плоский граф G, у которого Pk(G) — Pk
для всех k ф 6 и vk(G) = Vk для всех k ф 3.
Если допустить кратные ребра и петли и отказаться от
3-связности, то можно выдвинуть второе предположение.
Предположение 2. Пусть рх р„; vu ..., vm-неотри-
vm-неотрицательные целые числа, такие, что сумма ^ kvk четна и
2 D-/0р*+ 2 D-/0о* = 8
(соответственно 2 F-Щpk + 2 2 C-fc) w* = 12). Тогда суще-
ствует связный плоский граф G, такой, что Pk{G) = pk «

Плоские карты е заданными степенями вершин и граней
117
j Vj для всех кф\ и \ф\ (соответственно для всех
ИфЬ и \Ф"$). Однако если р{ = V\=0, то можно предполо~
жить, что будет существовать 2-связный плоский граф G.
В частном случае, когда vk = 0 для k ф 4 (соответственно
Для k ф 3), предположение 2 было доказано Рауландом [7]').
По-видимому, доказанная теорема и приведенные выше
предположения можно обобщить на графы, которые уклады-
укладываются на 2-мерном многообразии рода g, поставив в правой
части условий A), D) и др. множитель A — g).
ЛИТЕРАТУРА
1. Barnette D., On ^-vectors of simple 3-polytopes, /. Combinat. Theory
(в печати).
2. В б 11 g e r G., H a r d e r s H., Note on a problem by S. L. Hakimi con-
concerning planar graphs without parallel elements, /. SI AM, 12 A964),
838—839.
3. E b e r h a r d V., Zur Morphologie der Polyeder, Teubner, Leipzig, 1891.
4. G г п n b a u m В., Convex polytopes, New York, 1967.
5. G r ii n b a u m В., A companion to Eberhard's theorem, Israel J. Math.
(в печати).
6. Griinbaum В., Polytopes, graphes, and complexes, Bull. Amer. Math.
Soc. (в печати).
7. R о w 1 a n d D., An extension of Eberhard's theorem, M. Sc. Thesis, Uni-
University of Washington, 1968.
8. S t e i n i t z E., Polyeder und Raumeinteilung, Enzykl. math. Wiss., v. 3
(Geometrie), Part ЗАВ 12, 1922, S. 1—139.
9. S t e i n i t z E., R a d e m а с h e r H., Vorlesungen Ober die Theorie der
Polyeder, Berlin, 1934.
10*. Chvatal V., Platiarity of graphs with given degrees of vertices, Nleuw
arch, wiskunde, 17, № 1 A969), 47—60.
') В работе [10*] было получено необходимое условие реализуемости.
Невозрастающую последовательность положительных целых чисел di,d2, ..., dn,
п~^Ъ, можно реализовать степенями п вершин плоского графа, если выпол-
выполняется неравенство
ГЦ»
I (k, П) ¦
k
2
'ft(n-l),
2« + 6ft-
3n + 3k-
16,
12,
a S (ft,
если
если
если
Для заданных k, г существует такая последовательность d,, d2 dn, до-
k
пускающая плоскую реализацию, что имеет место 2 ^<***(*i n) Ддя
п. — Прим. перев.

Вложение графов
в ориентируемые поверхности1J)
Дж. Ч. Боланд
§ 1. В работе [1] мы дали необходимые и достаточные усло-
условия вложимости графа в проективную плоскость. Возникает
вопрос, применимы ли методы, использованные в [1], для по-
получения необходимых и достаточных условий вложимости графа
в другие поверхности. В данной статье мы будем называть
замкнутое ориентируемое 2-мерное многообразие рода g ориен-
ориентируемой поверхностью и обозначать ее Tg. Можно было бы
ожидать, что, например, в случае тора Г, справедливо следую-
следующее утверждение, аналогичное теореме Маклейна для Т0[2] и
теореме в работе [1] для проективной плоскости.
Утверждение. Граф X вложим в Тх тогда и только
тогда, когда существует множество циклов С; G=1, ..., п) в X,
такое, что:
1) каждое ребро графа X принадлежит не более чем двум
циклам из этого множества;
2) циклы Ct{i= 1, ..., п) порождают подгруппу N(С,, ..., С„)
группы гомологии НХ{Х, Z), такую, что Я, (X, Z)/N(CU...
..., С„) — свободная группа ранга 2.
Однако это утверждение не имеет места, как показывает
следующий контрпример. Пусть С —меридиан тора Ти а р —
некоторая точка Ти р фС. Факторпространство Т\ = Т\/(С [}{р])
есть ориентируемое псевдомногообразие, у которого первая
группа гомологии с целыми коэффициентами Н\{Т'\) есть сво-
свободная абелева группа ранга 2.
') Во land J. Ch., Embedding of graphs into orientable surfaces, Intla-
gationes Mathematicae, XXIX, Fasc I A967), 33-44 (Proceedings Konink-
lijke Nederlandse Akademie van Wetenschappen, LXX, ser. A, № 1).
2) В статье предполагаются известными некоторые понятия и теоремы
алгебраической топологии. Для справок можно рекомендовать, например,
книги [5*, 6*]. При доказательстве основной теоремы существенно нсполь-
зуются результаты статей [2, 4], переводы которых помещены в настоящем
сборнике (стр. 133, 145). —Прим. ред.

Вложение графов в ориентируемые поверхности 119
Как показывает рис. 1, факторпространство Ti содержит два
графа Куратовского К\ и /С2» которые имеют не более одной
общей точки. Рассмотрим триангуляцию факторпространства Т\,
такую, что ее 1-остов X содержит KiUKz- Возьмем границы
2-симплексов в качестве циклов С;с1(|'=1 я); ясно, что
граф X удовлетворяет условиям высказанного утверждения.
Однако X нельзя вложить в Ти поскольку этого нельзя сде-
сделать уже с графом /Ci U /С2- Для доказательства предположим,
Рис. I.
что существует вложение /: К\\]К2~>Т1. Легко убедиться, что
компоненты из 71, \ f (Ki) = {х\х е Тх, х ^f(Ki)} суть 2-к летки.
Следовательно, /(/С2) содержится в замыкании некоторой
2-клетки Е, с границей дЕ которой f{Ki) имеет ровно одну
общую точку. Рассмотрим последовательность
в которой Е — замыкание Е в топологии Ти а ф — естественное
отображение Е на факторпространство Е/дЕ. Мы получили
гомеоморфизм ф/ графа К2 в 2-сферу Е/дЕ, что невозможно.
Отсюда следует, что высказанное нами утверждение не имеет
места, и мы не сможем получить обобщение теоремы Мак-
лейна, работая с Нх (X, Z). Однако мы добьемся успеха, если
заменим группу Я, {X, Z) фундаментальной группой л, (X).
Прежде чем формулировать основную теорему, введем сле-
следующие обозначения:
1) Fr — свободная группа ранга г,
2) А * В — свободное произведение групп А и В,
п
3) П. A-i ~ свободное произведение групп Аи ..., Ап.

120 Дж. Ч. Боланд
4) Если С,, ..., С„ — циклы графа X, то N(Ch ..., С„)—
наименьшая нормальная подгруппа в л, (X), определенная цик-
циклами С, С„.
Используя эти обозначения, сформулируем следующую тео-
теорему.
Теорема. Связный граф X вложим в поверхность Tgтогда
и только тогда, когда X содержит множество циклов С,, ..., Сп,
такое, что:
1) каждое ребро в X принадлежит не более чем двум цик-
циклам из этого множества,
2) nl(X)/N(Cl Cn) = Fgo*n.n'(r4 причем 2
В § 3 мы докажем эту теорему, а в § 2 установим леммы,
необходимые для доказательства.
§ 2. Графом мы называем конечный 1-мерный комплекс.
Связность понимается как обычно. В данной статье мы рас-
рассматриваем только связные графы.
Циклом будем называть связный граф, каждая вершина
которого принадлежит ровно двум ребрам. Если цикл С с ба-
базисной точкой с0 содержится в графе X с базисной точкой х0,
то отображение вложения /: С —*¦ X не обязательно индуцирует
гомоморфизм я, (С, с0) в щ (X, х0), поскольку С не обяза-
обязательно содержит точку х0. Мы выбираем путь г\ из х0 в с0
в графе X и определяем N (С) как наименьшую нормальную
подгруппу в л, (X, х0), содержащую все пути Л^-тр', где
I е я, (С, с0). Ясно, что подгруппа N (С) не зависит от выбора г\.
Говорят, что элемент а в щ(Х, х0) соответствует циклу С,
если а сопряжен с элементом т^тр1, где ? есть образующий
в я, (С, с0). Пусть {С,, ..., С„} — множество циклов в X. Опре-
Определим N(C\, ..., С„) как наименьшую нормальную подгруппу
в я, (X, х0), содержащую все подгруппы N(Ct) (t=l п).
Если не возникает неясности, мы будем писать Я! (X) вместо
Щ(Х, х0).
Вложение f: X-*Tg называется 2-клеточным вложением
тогда и только тогда, когда компоненты Tg \ f (X) суть 2-клетки.
Лемма 2.1. Пусть X есть связный граф, х0е X, ге Tg, и
пусть
f: (X, *0)-(Г„ z)
есть 2-клеточное вложение. Тогда индуцированный гомомор-
гомоморфизм
f.: я,(Х, Хо)-*щ{Тр г)
есть эпиморфизм.

Вложение графов в ориентируемые поверхности 121
Доказательство следует из рассмотрения точной после-
последовательности
щ(Х, хо)-+щ(Те, 2)->я,(Гг
поскольку щ(Тг, {(Х)) = щ {Tglf{X)) = nx (букет 2-сфер) = 0.
Определение. Пусть X — граф, и пусть S = {C, Сп} —
множество циклов в X. Множество S называется т-системой
в X тогда и только тогда, когда каждое ребро в X принадле-
принадлежит не более чем двум элементам из S.
Разделяющая точка связного пространства Y — это такая
точка jeF, для которой K\{i/} несвязно. Локально разде-
разделяющая точка пространства К—это точка у е Y, которая
является разделяющей для всех достаточно малых окрестно-
окрестностей у.
Далее, 2-мерное псевдомногообразие есть 2-мерный ком-
комплекс со следующими свойствами:
a) каждый 1-симплекс лежит на границе по крайней мере
одного, но не более двух 2-симплексов;
b) для любых двух 2-симплексов ? и г\ существует последо-
последовательность |lf ..., |г 2-симплексов, такая, что ?!=?, ?r = у], и
два соседних элемента этой последовательности имеют общий
1-симплекс.
Лемма 2.2. Пусть X — связный граф, и пусть S = {С,, ..., С„}
есть %-система циклов в X. Существует свободная группа F и
множество псевдомногообразий К,, ..., Yr, такие, что
Доказательство. Приклеим 2-клетку Е{ к каждому
п
из циклов Ci (i=l, ..., п). Пусть Y = X{j{jEt, и пусть ?,—
замыкание Et в Y (/=1, ..., п). В множестве 2-клеток Et
(i=l, ..., п) введем отношение эквивалентности № следующим
образом: Et9iEj (i, /=1, ..., п) выполнено тогда и только тогда,
когда существует последовательность Fk = Etk{k = l,..., s), такая,
что Fi^Ei, Fs = Ej ц FkfiFk+i содержит не меньше одного
ребра из X (k=l, ..., s—1). Пусть Я,,..., Нг — классы экви-
эквивалентности по отношению Ы, и пусть Yt= (J Ek (i= 1, ..., г).
Поскольку 5 есть т-система циклов в X, ясно, что каждое Yt

122 Дж. Ч. Боланд
(/=1, ..., г) является псевдомногообразием1)- Пусть Хо—под-
Хо—подграф в X, определенный теми ребрами, которые не вошли ни
в один цикл из S, и пусть Х{ — максимальное дерево, содержа-
содержащееся в Xf[Yi (t=l, ..., г).
г г
Пусть теперь Уо = {Jx{. Ясно, что У = (J Yt. Каждое псевдо-
1=0
многообразие У,- (i=l, ..., г) имеет в пересечении с Yo[) [jYj
ацикличное множество Xt.
Согласно теореме Ван Кампена, отсюда следует, что
Я1(Г)-П.(Я1(У|)).
Поскольку Yo — граф, щ (Уо)~ свободная группа. Обозначив
ni(Yo) = F> получим
С другой стороны, пространство Y было построено путем при-
приклеивания 2-клетки к каждому циклу С,(/= 1, .... п). Поэтому
я,(У)-я,(да(„ . n) n.
¦ 1'
Лемма 2.3. Для всякого 2-мерного псевдомногообразия Y
существуют свободная группа F и замкнутое 2-мердое многооб-
многообразие У, такие, что л, (У) = F *я, (У).
Доказательство. Если Y не имеет локально разделяю-
разделяющих точек, то ясно, что Уесть компактное 2-мерное многообра-
многообразие, быть может, с границей. Если граница У не пуста, то она
состоит из некоторого числа циклов Си ..., Сг. Пусть циклу
Сг (/= 1 г) соответствует элемент |геЛ|(У). Известно, что
в этом случае всегда найдутся такие элементы хи ..., хь, что
х, xk, ?,, ..., lr будут системой образующих для я, (У),
которые удовлетворяют только одному соотношению вида
а|, • ... • |г = е,
') Рассмотрим У. Пользуясь гомотопической эквивалентностью, можно
заменить каждую (изолированную) разделяющую точку отрезком и получить
гомотопически эквивалентное пространству Y пространство, состоящее из
букета замкнутых 2-многообразий, окружностей и 2-многообразий с границей.
Заметим, что 2-многообразие с границей гомотопически эквивалентно букету
окружностей. Окончательно получаем: пространство Y гомотопически экви-
эквивалентно букету g0 окружностей и замкнутых многообразий.

Вложение графов в ориентируемые поверхности 123
где а ==[*,, х2] • ... • [jtft-i, xk], если Y ориентируемо, и
а = х\ ... х\, если К не ориентируемо; здесь [дг(., х^ = x^^r^xj1.
Итак, в этом случае щ(У) есть свободная группа ранга
k + r—l, и достаточно положить F = nl(Y), Y = То, чтобы убе-
убедиться в справедливости леммы 2.3.
В случае, когда граница Y пуста, лемма выполняется, если
взять Y — Y и F = {e], где {е} — группа, содержащая только один
элемент. Таким образом, лемма доказана для псевдомного-
псевдомногообразий без локально разделяющих точек. Возьмем теперь
целое п и псевдомногообразие Yen локально разделяющими
точками, и пусть лемма выполняется для всех псевдомногооб-
псевдомногообразий с не более чем (п— 1) такими точками. Ясно, что для
локально разделяющей точки реК существует достаточно ма-
малая окрестность У этой точки, такая, что:
a) V — U Еи каждое Et есть 2-клетка,
b) ?|Пя"/ = {р} (/, / = 1, .--,_«),
c) каждая компонента из V \ V есть цикл или дуга
(V означает замыкание V).
Пусть Си ..., Сг — те компоненты из УЧУ, которые
являются циклами, a Lr+l, ..., Ls — остальные компоненты.
Приклеим 2-клетку Е\ к каждому из циклов С{ (/= 1, .... г) и
г
рассмотрим пространство Y' = (К Ч У) U JJ Е\, которое, очевидно,
есть псевдомногообразие с не более чем (п—1) локально раз-
разделяющими точками.
Согласно предположению индукции, имеем
Выберем теперь точки pt^Et (t=l,..., r), pj^Lj (/ = r +
+ 1, . .., s) и обозначим Р = {pj U • • • U {psl- Рассмотрим фактор-
пространство Y"—Y'/P. Известно, что jt, (Y") = Fs-i * я, (Yf).
Легко доказать, что Y" гомотопически эквивалентно первона-
первоначально взятому псевдомногообразию Y, откуда получаем
а, значит, я, (Y) = f,_, . Г . я, (Г) = F • я, (У), где F = Fs_, • F'
и Y=Y'.
Лемма 2.4. Пусть X есть связный граф, и пусть 5 —
~{С\, ..., Ся} есть х-система циклов в X. Тогда:

124 Дж. Ч. Волана
a) существуют свободная группа F и замкнутые 2-мерные
многообразия Yu ..., Y „ такие, что
щ (X)/N (С„ ..., С„) = F * щ (У,) * ... * щ (Yr); A)
b) более того, множество S определяет группу F с точностью
до изоморфизма, а многообразия У,, ..., Yr — с точностью до
гомеоморфизма.
Доказательство. Первое утверждение следует из лемм
2.2 и 2.3. Ден [3] показал, что в разложении A) сомножители
определены с точностью до изоморфизма и, значит, соответст-
соответствующие многообразия — с точностью до гомеоморфизма, что и
доказывагт второе утверждение.
Опреде ление. Пусть X есть связный граф; S = {Си .. ., Сп}
есть т-система циклов в нем; F — свободная группа ранга g0;
Yt (i = 1, ..., г) есть 2-мерное многообразие рода gt (i = 1, ..., г),
и пусть
Щ (X)/N (С, Ся) = F * щ (К,) * ... * щ {Yr).
Определим род g{S) для т-системы S как
§(S) = go + gi+ ••• +gr-
Лемма 2.5. Пусть S{ и S2 есть х-систе мы циклов связного
графа X. Если S,czS2, то g(S2)<:g(Sl).
Доказательство. Пусть Sl = {Cu..., С„}, и пусть
CeS2\Si. Рассмотрим множество S'={Ci, ..., Сп, С}-<циклов
в X. Поскольку Si cz S2, ясно, что S[ есть т-система. Доста-
Достаточно доказать, что g(Si)<[g(Si), так как отсюда по индукции
следует, что g{S2)<:g(Si).
Приклеим 2-клетку Et к циклу Ct (i — 1, ..., п) и рассмот-
г
рим пространство Y = X\J (J Е%.
i-\
Как и при доказательстве леммы 2.2, пишем
K=K0UK,U ... U Кг,
где К,, ..., YT — псевдомногообразия (быть может, с границей),
a Yo — граф, который пересекается с каждым Yt (г = 1, ..., г)
Г
по ацикличному множеству. Разумеется, л, (Y) = Ц.(я! (^г))-
Предположим сначала, что С содержится в одном из про-
пространств К, (/= 1, ..., г), например С с: К,. Согласно лемме
2.3, имеем

Вложение графов в ориентируемые поверхности 125
где Yy есть 2-мерное многообразие. Рассмотрим отображение
вложения i: C-*Yi и индуцированный им гомеоморфизм
г',: я, (С)-* я, (У,) (базисная точка в Y выбрана лежащей на С).
Ясно, что С —граничный цикл псевдомногообразия У,. Поэтому,
если | есть образующий группы jt, (С), то i, (|) e я, (К,)').
Приклеим 2-клетку ? к циклу С. Получим пространство
Y[—Y\\]E. Снова пишем п\ \Y[) = F * iti (F1). Ясно, что jti(Fi)
получается из n{(Yi) факторизацией по наименьшей нормаль-
нормальной подгруппе, содержащей г, (?J), a F' = F. Если 9[ имеет не-
непустую границу, то непустую же границу имеет и ?,. Как Jti(y'),
так и n\(Yi) в этом случае суть свободные группы, причем
ранг Jti(?0 равен рангу я\ (?i) без единицы.
Если же Y\ — замкнутое многообразие рода g, то п,(?,) —
свободная группа ранга 2g3). В обоих случаях имеем по
определению рода т-системы g(Si)^g(Si).
Пусть теперь С не содержится полностью ни в одном из
псевдомногообразий Y\ Yr. Тогда при ?= 1, ..., r Cf]Yt
есть ацикличное множество. Легко показать, что в этом случае
в X П Yi существует максимальное дерево Lh содержащее
Cf]Yi (г=1 г). Если обозначить Хй подграф в X, опреде-
определенный теми ребрами X, которые не входят ни в один цикл
г
т-системы Sb и обозначить Yq = XQ \j (J Lt, то можно записать,
что r=yoU(Jr< и чт0
П.
Ясно, что теперь С с: Ко- Снова рассмотрим г: С->Ко. Вы-
Выберем базисные точки в Y, Yo, С так, чтобы они совпадали,
тогда и (?) е пДКд) (здесь I есть образующий в jt, (С)). Оче-
') Автор пользуется здесь леммой 2.3 не в том виде, в котором она
сформулирована, а следующим утверждением, легко вытекающим из дока-
доказательства леммы 2.3: если псевдомногообразие Y имеет р локально разде-
разделяющих точек, то существует многообразие Y (возможно, с границей), та-
такое, что Я] (Y) = Я| (У) * Fp. — Прим. перев.
2) Эта подгруппа может состоять лишь, из единицы. — Прим. перев.
3) В этом случае ?i получается нз многообразия рода g вырезанием
дыры. — Прим. перев.

126 Дж. Ч. Боланд
видно, что л,(К0) изоморфно л, (KgI). Приклеим 2-клетку Е
к циклу С, тогда я, (Y\]E) = А * ДДя| (Kj)), где А получено
из пу{У'Л факторизацией по наименьшей нормальной подгруппе,
содержащей i, (|). Но rank A ^ rank л, (К^) = rank n^Y0), так что
и в этом случае g(Si)^g(Si)- Лемма 2.5 доказана.
По определению т-система S в графе X называется макси-
максимальной, если S не содержится ни в какой т-системе, отличной
от S.
§ 3. В этом параграфе мы докажем следующую теорему.
Теорема 3.1. Связный граф X может быть вложен в ориен-
ориентируемую поверхность Tg рода g тогда и только тогда, когда
в X существует т-система циклов S = {Ci, ..., Сп}, для которой
выполнены условия
1) g(S)<g,
2) nl{X)/N{Cl С„) = ^*П.Ы7^)J).
Доказательство. Сначала докажем необходимость этих
условий индукцией по g. При g = 0 поверхность Tg является
2-сферой. Пусть связный граф X вкладывается в То. В этом
случае, как утверждает теорема Маклейна, существует т-си-
т-система S = {Ci, ..., С„} циклов в X, для которой
щ(Х)/М(С„ .... С„) = 0.
Очевидно, что условия 1) и 2) при этом выполнены.
Возьмем теперь натуральное число g. Предположим, что
в каждом связном графе, который вкладывается в поверх-
поверхность Tg', 0 <! g' < g, существует т-система циклов, удовлетво-
удовлетворяющая условиям теоремы. Рассмотрим связный граф X, вкла-
вкладывающийся в поверхность Tg. Согласно Янгсу [4], в этом слу-
случае существует 2-клеточное вложение X в поверхность Tg>, где
O^g'^g. Если g'<g, то в X по предположению индукции
существует такая т-система, род которой не превосходит g',
а следовательно, не превосходит и g, причем выполнено также
условие 2). Пусть теперь g' = g, т. е. существует 2-клеточное
вложение / графа X в Tg. По лемме 2.1 индуцированное ото-
отображение f,: щ (X) -> щ (Tg) является эпиморфизмом. Поэтому
') Это следует, например, из однозначности разложения в лемме 2.3. —
Прим. перев.
2) Здесь требуется бол! ше. чем утверждает лемма 2.4, а именно, чтобы
все новерхиоств, участвующие в разложевии, были бы ориентируемыми. —
Прим. перев.

Вложение графов в ориентируемые поверхности 127
в X существует 2g циклов Du ..., D2g, таких, что для соот-
соответствующих элементов хи ..., x2g в щ (X) их образы
f,(*,), ..., ft(x2g) можно взять в качестве образующих группы
я, (Tg), связанных единственным соотношением
[yv У2\- ¦•¦ ¦ [Уга-v У2е] = е CДесь ^ = f.(xt))•
Разрезав Tg по каждому из циклов /ф») (t=l 2g), мы
получим замкнутую 2-клетку Р и непрерывное отображение
a: P->Tg, сужение которого на внутренность Р есть гомео-
гомеоморфизм.
Более того, a(dP)czf (X).
Рассмотрим множество X' = а~' (f(X)). Очевидно, что X' есть
плоский граф, поэтому в X' существует т-система циклов
S' = {Ci, ..., С'п), для которой
nx{X')IN{C\, .... Q = 0.
Согласно [4], каждый цикл С\ (/=1, ..., п) лежит на грани-
границе некоторой компоненты из Р \ X''). Каждое ребро границы дР
принадлежит ровно одному циклу С\ (t=l, ..., п). Предполо-
Предположим сначала, что а | , есть гомеоморфизм при всех i— 1, ..., п.
Ci
Положим d = f~[a{c'i) (г=1 п). Ясно, что множество
S = {C[, ..., Сп} является т-системой в X, причем N(CU ..., Сп)
есть ядро отображения ft: ni(X)^>-nl(Tg). Поскольку /, эпимор-
эпиморфизм, имеем Я[(^)/А^(С[, ..., Cn) = nl{Tg), а значит, S удовле-
удовлетворяет условиям 1) и 2) нашей теоремы.
Пусть теперь а | , не есть гомеоморфизм при некотором /,
ci
например, а | , не есть гомеоморфизм. Тогда существуют точки
ci
а и Ь на С', а ф Ь, такие, что а (а) = а (Ь). Поскольку С\ лежит
на границе некоторой компоненты из Р \ X'', существует дуга
LaP, для которой
Очевидно, D=a(L) есть цикл на Tg, причем D(]X = {p}, где
р = а(а)—а(Ь). Разрежем поверхность Tg по циклу D. Пусть
D' и D" — циклы, полученные из D при разрезании. В зависи-
зависимости от того, разделяет или нет цикл D поверхность Tg, рас-
рассмотрим два случая.
') То есть на границе некоторой 2-клетки. — Прим. пере».

128 Дж. Ч. Боланд
Пусть D разделяет поверхность Tgl). При этом мы получаем
две поверхности Tg' и Tg«, причем g' + g" = g. Поскольку цикл D
не ограничивает на поверхности Tg никакой 2-клетки2), то
g' > О и g" > О, и, следовательно, g'<g, g" < g- Пусть Х{ и Х2
означают подграфы графа X, попавшие соответственно на Tg'
и Tg". По предположению индукции существуют т-система
S^iCi Crj циклов из Х{ и т-система S2 = {Cr+u ..., Ст}
циклов из Хъ для которых
1) (S)<'
g(S2)<g",
2) n, (XJ/N (C, CT) = F{* П, (я, G^)),
т*
n, \X2)IN (Cr+1, ..., COT) = F2* 11. (Jt, [i gjj )•
Приклеим к каждому циклу С, (i=l, ..-, m) 2-клетку Et и
г m
рассмотрим Y, = Xi[}{JEi, Y2 = X2\j (J Et. Имеем
i°*l i=r+\
rj и Tti \i2) = П( {Л))/iv \L,r+i, ¦ . ., оот^.
Если отождествить теперь точку, взятую на Xt П D', с точ-
точкой, взятой на Х2 П D", то получится пространство Y, для кото-
которого nl{Y) = n,{Yl)*nl{Y2).
Рассмотрим множество S = {(?!, ..., Ст} как т-систему в X.
Ясно, чтоМХул^С, Cm) = n,(Yl)*nl(Y2), т. е. g(S)^g' +
+ g" — g- Условия нашей теоремы выполнены.
Остается случай, когда D не разделяет поверхность Tg. Раз-
Разрезание Tg no D дает ориентируемую незамкнутую поверх-
поверхность Tg-j рода g— 1, для которой D' и D" являются гранич-
граничными циклами. Разрезанию соответствует отображение
ч\: Tg-i~+Tg, каждой точке х е Tg-\ оно сопоставляет точку
r\(x)^Tg, из которой х получено при разрезании. Приклеив
к D' и D" соответственно 2-клетки Е' и Е", получим замкну-
замкнутую поверхность Гя_, = Г_, \}Е'\] Е". Рассмотрим J' = tT' (f (X)).
По предположению индукции в X' существует т-система циклов
S" = {С\ Ст), для которой
') То есть при разрезании по D поверхность Tg распадается иа две ком-
компоненты. — Прим. перев.
2) Это легко показать, всаомнив, как выбирались циклы D , Dig. —
Прим. перев.

Вложение графов в ориентируемые поверхности 129
причем g(S")^g — 1. Приклеим к каждому циклу С{ 2-клетку Et
m
(г=1, ..., m) и рассмотрим Y = X\j\jEt. Ясно, что ny{Y) =*
= я, (X')jN(С", ..., С?). Если отождествить теперь две точки
из тт'(р), получится пространство Y'', для которого щ(У) =
= Fi • «1 (К) (fi есть свободная циклическая группа). Если взять
теперь в качестве т-системы S множество циклов С(-= /~'т](с"),
i=\ m, то получим
т. е. g{S)^l+ {g—l)~ g. Таким образом, условия 1) и 2)
оказываются выполненными и здесь. Это завершает доказа-
доказательство необходимости условий нашей теоремы.
Докажем теперь достаточность. Пусть X — связный граф, и
пусть S = {Ci, ..., Сп) есть т-система циклов из X, удовлетво-
удовлетворяющая условиям 1) и 2) нашей теоремы. Мы предполагаем,
что среди всех таких т-систем S обладает минимальным ро-
родом g(S). Приклеим к каждому циклу С,- 2-клетку Et (i— I,..., п).
п
Рассмотрим Y' = X[)\J Е{.
г
В обозначениях леммы 2.2 имеем Y' = \jYh где Ко содержит,
1=0
в частности, все ребра X, не вошедшие ни в один цикл из S.
Поскольку g(S) минимально, каждое псевдомногообразие Yt
(г=1, ..., г) замкнуто1) и каждая компонента связности М,
г
графа >"\(jKi есть ДеРево 0=1 s).
Можно считать поэтому, что каждое М/ вложено в 2-сферу Yr+,
r+s
(/=1, ..., s) так, что YT+i{\Y' = Mt. Рассмотрим Y = \jYt. По
теореме Ван Кампена, имеем
я, (К) = я, (Г) = щ (X)/N (С, Сп) = Fga * Д. (я, (Tg{)) -
-П. (я, (К,)).
') Это неточно. Лемма 2.5 утверждает лишь, что при расширении т-си-
т-системы ее род не убывает, а не обязательно возрастает. Легко построить
контрпример, взяв сферу с дырой и парой тождественных точек. Заклейка
дыры в этом случае не изменяет фундаментальной группы, равной Z. Мы
можем, однако, считать, что выбранная нами т-снстема соответствующим
образом расширгна, так что все псевдомногообразия действительно замк-
замкнуты. — Прим. перев.
в Зак. 560

130 Дж. Ч. Боланд
Если вспомнить, что я, (Yi) — Fht * ях (Tg^ (г=1, ..., г + s),
r+s
ТО МЫ ПОЛУЧИМ 2й, = ?о')> ёг+\= ••• = gr+s = 0.
l
Для некоторых целых и, v, 1<л, и^г + 5, пусть Yu(] Ко=И=0.
Пусть реК„A Yv. Рассмотрим замкнутые 2-клетки Е и Е', со-
содержащиеся соответственно в Yu и К„ и такие, что ? Г) Я =
= Е' f\X = {р}. Пусть С = дЕ и С = д?' — граничные циклы этих
клеток, Ё и ?'— их внутренности, и пусть Z'= Y\{E[] Ё'),
Y'u=Yu\ Ё, Y'v = Yv\E'. Ясно, что
и
где Л —группа с образующими xt, ..., x2g , /и единственным
соотношением
[у t*|.
X,, *2j ...
а / — элемент из я, (У^), соответствующий циклу С. Точно так же
получаем
*.(n)-v*
где S —группа с образующими у., ..., г/„ , m и единственным
соотношением
am — элемент из я, GQ, соответствующий циклу С. Для 2! имеем
где О( = я,G'йг), если i ф и, v и О„ = Л, GV = B.
Приклеив 2-клетку к Z' вдоль пути / • т, мы получим про-
пространство Z. Его фундаментальная группа имеет те же обра-
образующие и соотношения, что и группа щ {Z'), и еще одно соот-
соотношение 1'т — е. Добавление этого соотношения не изменяет
групп G; при 1фи, v, но приводит к замене группы GU*GO
группой я, (T^+sJ. Отсюда получаем
r+s
я, (Z) = Fg0. П. (я, (Г,,)) * я (Tgu+gv).
( Ч4 U, О
') Здесь допушена неточность. На самом деле g0 — hn + 2 ^г> гДе ^о
равно рангу Л| (Ко). Именно так и следует понимать это в дальнейшем. —
Прим. перев.

Вложение графов в ориентируемые поверхности 131
r+s
Очевидно, что 2 gi ПРИ эт°й операции не изменяется, поэтому.
повторяя ее, мы в конце концов получим вложение X в псевдо-
псевдомногообразие Z,, для которого
Пусть ^ — локально разделяющая точка Z,; U — окрест-
окрестность q; Ux и U2 — две различные компоненты U\{q); D — цикл,
содержащий точку q и такой, что D{\Ux=fr <Z> и Ь(]С/2Ф0.
В группе Fgo этому циклу соответствует элемент |. Рассмотрим
2-клетки ? и ?', для которых ?f] * = ?' П * = {?}, ?с= ?/, Ufa},
Е' cz U2\J{q}- Удалим из Zx внутренности клеток Е и Е' и обо-
обозначим полученное пространство ZJ. Имеем nx{Z'^ = F x* A,
где Л —группа с 2А + 3 образующими хи ..., Хгл, /, пг, |, свя-
связанными единственным соотношением
[*i, ^] * • • • • [Xik-u *2ft] • I • I ¦ tn • l~l = e.
Здесь I Yi tn — элементы группы jt, (ZQ, соответствующие гра-
граничным циклам дЕ и 5?' клеток ? и ?'. Приклеив 2-клетку
к Z\ вдоль пути / • пг, мы получим пространство Z". Его фунда-
фундаментальная группа л, (Z[') отличается от группы л, (Z[) лишь
наличием одного дополнительного соотношения I • пг = 1, т. е.
имеем
где Л' задается образующими лг,, ..., х2а, |, / и единственным
соотношением
[х„ х2]- ... -[Х2Н-1, x2h]-[l, \\ = е.
Следовательно, А' = пх (Th+]). Таким образом, мы получили
вложение X в Z\, где
Повторяя описанную операцию, можно уничтожить все ло-
локально разделяющие точки и получить вложение X в Tga+h.
Поскольку go + h^ g, достаточность условий 1) и 2) доказана,
а тем самым полностью закончено доказательство теоремы 3.1.
Замечание 1. В лемме 2.4 мы доказали, что для любой
т-системы S = {CU ..., С„} связного графа X выполнено сле-
следующее равенство:
Щ (X)/N (С, С„) = F * щ (Г,) * ... * я, (Yr),

132 Дж. Ч. Боланд
где F — свободная группа, У,, ..., Y, — замкнутые многообра-
многообразия. Отсюда следует, что группа n{(X)/N{Ci, ..., Сп) опреде-
определена при помощи конечного числа образующих и конечного
числа соотношений, причем каждый из образующих появляется
в соотношениях этой группы не более двух раз. Ден [3] пока-
показал, что в таких группах проблема тождества слов алгоритми-
алгоритмически разрешима, а следовательно, и наше описание графов,
вкладывающихся в ориентируемую поверхность рода g, эффек-
эффективно.
Замечание 2. Пусть Хх и Х2 — два графа, р, —вершина в Хи
р2 — вершина в Х2. Обозначим Хх V Х2 граф, полученный ото-
отождествлением точек рх и р>. Известно, что род графа Хх V Х2
равен сумме родов графов Хх и Х2. Это можно теперь легко
доказать с помощью теоремы 3.1.
ЛИТЕРАТУРА
1. Во land J. Ch., Embeddings of graphs in the projective plane, Fund.
Math., 57 A965), 195—203.
2. MacLane S., A combinatorial condition for planar graphs, Fund. Math.,
28 A937), 271—283. (Русский перевод см. иа стр. 133 настоящего сбор-
сборника.)
3. D e h n M., Ueber unendliche diskontinuierliche Gruppen, Math. Ann., 71
A911), 116—144.
4. Y о u n g s J. W. Т., Minimal embeddings and the genus of a graph, /. of
Math, and Mech., 12, № 2 A963). (Русский перевод см. на стр. 145 на-
настоящего сборника.)
5*. X и л т о н П., У а й л и С. Теория гомологии, «Мир>, М., 1966.
6*. К р о у э л Р., Фокс Р., Введение в теорию узлов, «Мир», М., 1964.

Комбинаторное условие
для плоских графов1}
С. Маклейн
1. ВВЕДЕНИЕ
Куратовский [I]2) доказал, что топологический3) граф яв-
является плоским (т. е. может быть взаимно однозначно отображен
в плоскость) тогда и только тогда, когда он не содержит под-
подграфа одного из двух особенных видов. Уитни [2] показал, что
граф плоский тогда и только тогда, когда у него есть комби-
комбинаторный „двойник". В данной статье устанавливается еще один
критерий того, что граф плоский. Он формулируется при по-
помощи обычных комбинаторных понятий.
Теорема I. Комбинаторный граф является плоским тогда
и только тогда, когда он содержит такую полную систему циклов,
для которой никакое ребро не принадлежит более чем двум ц иклам.
Граф, расположенный на плоскости, делит ее на некоторое
число областей, каждая из которых ограничена одним или бо-
более циклами. Легко показать, что множество таких циклов
содержит полную систему, а каждое ребро графа принадлежит
ие более чем двум циклам этой системы. Отсюда следует не-
необходимость высказанных условий (разд. 5). Доказательство
достаточности носит более комбинаторный характер. Для удоб-
удобства мы сначала сводим задачу к случаю несепарабельных гра-
графов (разд. 3), ранее рассмотренных Уитни. Удалив из несепа-
рабельного графа подходящее ребро, мы получаем более простой
(и опять несепарабельный) граф. Его мы укладываем на пло-
плоскость, а затем показываем, что условия теоремы позволяют
добавить удаленное ребро уже на плоскости (разд. 4, 5).
Чисто комбинаторными рассуждениями мы показываем за-
затем эквивалентность критерия теоремы I критерию в терминах
существования двойника (разд. 6). В свою очередь последний
критерий, как известно [3], эквивалентен (в комбинаторном
смысле) условию Куратовского.
') MacLane S., A combinatorial condition for planar graphs, Funda-
menta Maihematika, 28 A937), 22-32.
2) В [I] рассматриваются не графы, а множества с более общими свой-
свойствами.
3) Терминология автора часто отличается от современной, однако изме-
изменять ее было бы нецелесообразно. Исключение сделано для термина „2-fold set",
хоторый переводится как „т-система" (см. стр. 136 и стр. 139). — Прим. ред.

134 С. Маклейн
2. ОПРЕДЕЛЕНИЯ
Комбинаторный граф G состоит из конечного множества эле-
элементов а, Ь, с, ... , называемых ребрами, и конечного мно-
множества вершин р, q, г, ... , такого, что каждое ребро b соеди-
соединяет в точности две вершины р и q (в этом случае говорят,
что р и q — „концы" ребра Ъ, или р и q лежат на Ь). Мы пред-
предполагаем, что каждая вершина лежит хотя бы на одном ребре').
Любое множество ребер вместе со всеми лежащими на них вер-
вершинами образует подграф графа G. Каждый подграф полностью
определяется своими ребрами.
Если ш>1 и если рь р2, ¦¦¦, рт~различные вершины, то
подграф С, определяемый ребрами р,р2, р.гр3, ..., рт-\рт, ртри
называется циклом, а подграф D с ребрами р,р2, •••, рт-\Рт
цепью с концами р, и рт. Цепь называется подвешенной, если
из всех ее вершин только рх и рт лежат не менее чем на трех
ребрах из G. Если А и В — подграфы, то А f[B — подграф, опре-
определенный пересечением, А + В — объединением, G — А — разно-
разностью соответствующих множеств ребер.
Если граф G имеет E(G) ребер, V (G) вершин и P(G) ком-
компонент связности, то
R(G) = V(G)-P(G), N(G) = E(G)-V(G) + P(G) A)
называются соответственно рангом и цикломагическим числом
графа G. Сумма по mod 2 циклов С) + С2 + ... +Ст — это под-
подграф, содержащий все ребра, присутствующие в нечетном числе
циклов написанной суммы. Циклы С), ..., С„ образуют полную
систему в G, если каждый цикл из G единственным образом
представляется в виде суммы mod 2 некоторых из циклов
С, С„. Каждый граф G содержит по крайней мере одну
полную систему из n — N{G) циклов.
Плоский топологический граф Н состоит из конечного числа
дуг (гомеоморфных образов отрезка) на плоскости. Две таких
дуги либо не пересекаются, либо точка их пересечения является
концом каждой из двух дуг. Дуги графа Я и их концы, оче-
очевидно, образуют комбинаторный граф Н', который тоже назы-
называется плоским.
3. НЕСЕПАРАБЕЛЬНЫЕ ГРАФЫ
Граф G называется сепарабельным, если он обладает двумя
подграфами F, и F2, такими, что Fx + F2 = G, a Fx и F2 не имеют
общих ребер и могут иметь не более одной общей вершины.
') Исключение „изолированных" вершин не влияет, очевидно, иа выводы
теоремы I.

Комбинаторное условие для плоских графов 135
Если F, и F2 не имеют общей вершины, то они не связаны '),
а если такая вершина р есть, ее называют разделяющей вер-
вершиной графа G. Про сепарабельный граф G говорят, что его
можно разделить на графы F, и F2. Граф F, либо несепара-
белен, либо его можно разделить на графы F3 и F4. To же
верно и для F2- Повторяя этот процесс разделения графа, мы
в конце концов получим подграфы G,, ..., Gm, которые будут
несепарабельными, причем, проводя разделения другим спосо-
способом, мы все равно получим те же самые графы ([2], теорема 12).
С другой стороны, два ребра а и Ъ графа G назовем цикли-
циклически связанными, если либо а = Ь, либо в G существует
цикл, содержащий как а, так и Ь. Можно доказать, что отно-
отношение „а и Ъ циклически связаны" симметрично, рефлексивно
и транзитивно и что его выполнение равносильно условию „при-
„принадлежит той же несепарабельной компоненте, что и 6" (см. [2],
теорема 7). Тем самым несепарабельность оказывается опреде-
определенной инвариантно относительно процесса разделения, что до-
доказывает единственность несепарабельных компонент графа.
Теорема 3.1. Если G — несепарабельный граф, N(G)> 1,
a R есть цикл в G, то в R существует2) цепь А, подвешенная
в G, для которой G — А есть несепарабельный граф и N (G — А) =
G)l
Доказательство заключается в построении графа G
из последовательности несепарабельных подграфов Я,с=Я2с1 .. .
...czG. Поскольку N{G)>\,b G существует ребро аи не ле-
лежащее на R. Возьмем в качестве Ht цикл, содержащий а{ и
некоторое ребро из R. Если Hm-^G уже выбрано, то Нт
строим так: возьмем ребро ат в G — #ш_,, не содержащееся
в R (если такое имеется). Поскольку граф G несепарабелен,
существует цикл D, содержащий ат и некоторое ребро из #ш_,.
Пусть теперь Ат — максимальная из цепей, лежащих на цикле D,
содержащих ат и не содержащих ребер из Яш_,. Остается по-
положить Яш = Яш_, + Лт.
Каждый подграф Нт несепарабельный; мы докажем это
по индукции. Цикл Ни очевидно, является несепарабельным
графом. Если Ят_, несепарабельный, то ребра из Ат цикли-
циклически связаны с остальными ребрами Нт, поэтому и Нт — несе-
несепарабельный граф.
Покажем теперь, что из RczHm следует Hm = G. По по-
построению Я, имеем R<?HV Возьмем наименьшее т> 1, для ко-
') В этом случае граф G называется несвязным. — Прим. перев.
2) Это утверждение включает частный случай, доказанный в работе [2],
теорема 18, в котором не фигурировало условие AczR. Теорему 3.1 можно
также вывести по индукции из теоремы Уитни.

136 С. Маклейн
торого R<^Hm. В этом случае RgtHm^i ив R существует ребро Ь,
не принадлежащее Ят_,. Обозначим через Е максимальную из
цепей, лежащих на R, содержащих Ь и не содержащих ре-
ребер из Яот_,. Поскольку /?<=ЯОТ, то и ЕаНт = Ят_, + Ат. По
построению в Е нет ребер из Нт-и поэтому Е а Ат. Но Ат
выбиралось так, что единственными вершинами Лот, общими
с Яот_,, были концы этой цепи. Тем же свойством обладает
и Е, следовательно, Е — подцепь цепи Ат с теми же концами,
что и у Ат. Отсюда Е = Ат. Если бы G — Hm-l не содержа-
содержалось в R, то Ат имело бы ребро ат, не лежащее в R,
откуда АтФЕс^к. Полученное противоречие доказывает, что
G — Ят_, a R. Но Ят содержит по построению Яот_, и по
предположению содержит R, т. е. Hm=G.
Каждое Ат представляет собой цепь, подвешенную в Яот,
поэтому N{Hm) = m. Процесс построения заканчивается при
Hn = G, так что n = ./V(G). Последняя из добавленных цепей
Л = Ап подвешена в Я„ = G и содержится в R (как показано
выше), следовательно, N(G — А) = п—1, что и завершает дока-
доказательство теоремы.
Сепарабельные графы можно также строить стандартным
способом.
Теорема 3.2. Если граф G является сепарабельным, то в G
существует такая несепарабельная компонента Я, что Я и G — Я
имеют не более одной общей вершины.
Доказательство. Возьмем любую несепарабельную ком-
компоненту Я, в G. Либо Я, обладает нужными свойствами, либо
в G — Я, существует несепарабельная компонента Я2, которая
имеет с Я, общую вершину /?,. Если Я2 также не обладает
требуемыми качествами, существует компонента Н3ФН2, у ко-
которой с Я2 имеется общая вершина р2фрг Если бы Н3 = Ни
то цепи в Я2 и Я,, соединяющие точки р, и ръ образовывали бы
цикл, не содержащийся целиком ни в одной из этих компонент,
что невозможно. Следовательно, Я,, Я2 и Я3 различны, а по-
поэтому, если Я3 нас не удовлетворит, можно взять новую ком-
компоненту Я4 и т. д., пока (в силу конечности графа) не получим
компоненту Нт с ровно одной вершиной, общей с G — Нт.
4. ПРОЦЕСС ИНДУКЦИИ
Рассмотрим комбинаторный граф G, который удовлетворяет
условиям теоремы I, т. е. предположим, что G содержит пол-
<ую систему циклов
СиС2 С„, n = JV(G), B)

Комбинаторное условие для плоских графов 137
в которую любое ребро входит не более двух раз. Такую си-
систему назовем полной х-системой. Циклы Ct независимы, а по-
поэтому сумма
R = Cl+C2 + ... +Сп (mod 2) C)
не равна нулю. Будем называть R ободом графа G. Обод об-
обладает следующим свойством.
Лемма 4.1. Если G — несепарабельный граф, то его обод
является циклом.
Доказательство. Пусть, напротив, R не есть цикл.
Тогда во всяком случае каждая вершина из R имеет четную
степень, а следовательно, R в собственном смысле содержит
некоторый цикл D. Можно написать разложение D по полной
системе циклов B), возможно изменив нумерацию,
D = C{+ ... +Cm(mod2).
Поскольку D=?R, имеем n>m. Поэтому ни один из графов
F, =- С, + ... + Cm, F2 = C+ +C
не пуст. Мы покажем, что G можно разделить на F, и F2.
Ребро b из F, П F2 должно содержаться в одном из первых m
циклов С , Ст и в одном из последних п — т циклов
COT+i, ..., С„. Поскольку B) есть полная т-система, это единст-
единственные ее щиклы, в которые входит Ь. Таким образом, b входит
в одно слагаемое в разложении D и в два слагаемых в раз-
разложении R. Мы получили, что Ь входит в D, но не в R, хотя,
с другой стороны, DaR. Это противоречие доказывает, что F, Л ^2
не содержит ни одного ребра.
Так как граф G несепарабелен, существует цикл Е, содер-
содержащий как ребро из Fu так и ребро из F2- Разложим этот
цикл по полной системе B): Е — 2'С/ + 2"^/ (mod 2) (суммиро-
(суммирование в 2' выполняется по некоторым индексам от 1 до т,
а в 2 —по некоторым из оставшихся индексов). Каждая из
сумм 2'. 2" содержит какие-то слагаемые, поскольку в Е есть
ребра как из Fu так и из F2. Таким образом, первая сумма
?' = 2'Q не равна Е. Но Е' содержится в F, так что ни одно
ребро из Е' не входит в циклы Сш+1, ..., Сп. Поэтому Е'аЕ. Мы
получили цикл Е, в котором есть не совпадающий с ним под'
цикл, что невозможно. Следовательно, R есть цикл.
В несепарабельном плоском (топологическом) графе всегда
есть цикл, который ограничивает конечную область и примыкает
к границе бесконечной области по некоторой цепи.

I3S С. Маклейн
Лемма 4.2. Если G — несепарабельный граф, N(G)>1, то
существует подвешенная цепь А, для которой
(О G-A несепарабален, N{G - А) = N(G)-\;
(ii) А содержится в R и ровно в одном из Gt, например, в Сп\
(in) С,, ..., С„_, образуют полную х-систему для G — А;
(iv) концы р и q цепи А принадлежат R', где
R' = Cl+C2 + ... +С-, (mod 2); D)
(v) R' состоит из двух цепей R — А и Сп — А, соединяющих
р и q.
Доказательство. Возьмем, как и в теореме 3.1, подве-
подвешенную цепь Ac^R. Тогда G — А несепарабелен, как и утверж-
утверждает (i). Поскольку граф G несепарабелен, каждое ребро из А,
а поэтому и вся цепь А, содержится в некотором цикле. Любой
цикл представляется суммой по mod 2 циклов С,-, так что А
содержится в некотором Ct. Изменим нумерацию, чтобы полу-
получить Лс=Сга. Так как А содержится в R и не более чем в двух
из циклов С,, ..., С„, ясно, что А не содержится ни в каком
Cj^Cn, что и утверждается в (ii). Циклы С Сп-и таким об-
образом, входят в G — А, причем они остаются там независимыми,
как и в G. В G — А существует не более п— \ = N {G — А) не-
независимых циклов, поэтому С], ..., С„_, образуют полную т-
систему, как и отмечалось в (Hi).
Покажем теперь, что A = Cnf\ R. Предположим, что сущест-
существует ребро b в Cn[\R, не входящее в А. Тогда Ь содержится
в G — А, а следовательно, и в некотором цикле D из G — А.
Согласно доказанному утверждению (Hi), цикл D можно
представить в виде суммы (mod 2) некоторых из циклов С
..., С„_,. Но b содержится в С„ и в R и не содержится ни
в каких других Ch поэтому представление цикла D в виде
гуммы по mod 2 циклов, не содержащих С„ и R, невозможно.
Полученное противоречие показывает, что всякое ребро из
Сп П R входит и в Л, а поэтому Сп П R = А.
Из D) имеем R' = R + Сп (mod 2), так что R' состоит из ре-
ребер, принадлежащих либо R, либо Сп, но не принадлежащих
RП Сп. Поскольку Rf\Cn = А, получаем, что R' состоит из ре-
ребер R — А и С„ — А. Так как R есть цикл, R — A (а также
С„ — А) есть цепь, соединяющая р и q, т. е. соединяющая концы
цепи А. Для доказательства (iv) и (v) остается заметить, что
R ¦— А лежит в R'', следовательно, концы этой цепи также ле-
лежат в R',

Комбинаторное условие для плоских графов 139
5. ДОКАЗАТЕЛЬСТВО ДОСТАТОЧНОСТИ
Теорема 5.1. Несепарабельный граф G, в котором имеется
полная х-система циклов B), можно вложить на плоскость так,
что каждый из циклов С,, ..., Сп будет ограничивать одну из
конечных областей, на которые G делит плоскость, a R будет
ограничивать внешнюю (бесконечную) область.
Доказательство будем вести индукцией по N (G). Чтобы
не привлекать не относящиеся к делу сведения из топологии,
мы покажем, что G можно вложить на плоскость так, чтобы
каждому ребру из G на плоскости соответствовала бы ломаная
линия, а циклу R — равносторонний треугольник. Сначала рас-
рассмотрим случай N(G)=\. В этом случае G представляет со-
собой цикл, так как G — несепарабельный граф (см. [2], теорема 10);
следовательно, G можно вложить на плоскость описанным об-
образом. Пусть теперь N (G)> 1. Тогда, как утверждает лемма 4.2,
в графе G имеется такая подвешенная цепь А, что G — А не-
сепарабелен, содержит полную т-систему циклов а N (G — Л) <
N{G)
{)
По предположению индукции G — А можно вложить на
замкнутую плоскую треугольную область, границей которой
является R'. Согласно лемме 4.2 (iv), концы р и q цепи А лежат
на R', а, согласно (v), цепи С„ — А на плоскости соответствует дуга,
соединяющая точки р и q. Поэтому вне треугольной области
можно так провести ломаную А*, соединяющую точки р и q,
что А* и С„ — А вместе будут образовывать границу новой ко-
конечной области. Тогда из(у) следует, что граница новой внеш-
внешней (бесконечной) области есть R = А* + (R — А). Доказательство
будет завершено, если мы покажем, что R можно сделать
равносторонним треугольником.
Для этого предположим, что G — А вложен на замкнутую
треугольную область с вершинами r, s, t. Сначала рассмотрим
случай, когда С„ — А содержит сторону треугольника с верши-
вершинами г и /.На плоскости цепь А будет представляться ломаной
puvq (рис. 1). Нам нужно сделать обод spuvqs треугольником.
Рассмотрим полуплоскость, содержащую s, край которой про-
проходит через точки р и ц, и подвергнем ее преобразованию
сдвига. Сдвигом полуплоскости мы называем такое преобразо-
преобразование, при котором точка Р, лежащая на расстоянии d от края
полуплоскости, сдвигается параллельно этому краю на расстоя-
расстояние kd (k не зависит от Р). В данном случае мы применим та-
такой сдвиг, при котором точка s перейдет в s' так, что up и ps'
будут лежать на одной прямой. Теперь применим к полупло-
полуплоскости, содержащей точку v, край которой проходит через uq,
такой сдвиг, чтобы s'q и qv оказались бы на одной прямой

140 С. Маклейн
s'qv'. Новым ободом графа будет теперь треугольник us'v'. Его
можно сделать равнобедренным при помощи подходящего сдвига
полуплоскости с краем v's', а затем и равносторонним, сжимая
его по высоте. Преобразование сдвига переводит прямые линии
в ломаные, так что мы получили вложение графа G с требуе-
требуемыми свойствами. Другие случаи, когда Сп — А содержит осталь-
остальные вершины г, s или /, можно рассмотреть аналогично.
5
Рис.
Теорема 5.2. Граф G с полной х-системой циклов можно
вложить на плоскость так, чтобы каждому ребру соответство-
соответствовала ломаная линия.
Доказательство. Если G — сепарабельный граф, его
можно разложить на несепарабельиые компоненты Я,, Я2, ¦••
..., Ят. Каждая из этих компонент, которая не является реб-
ребром, содержит некоторые циклы из системы B), например,
С], ..., Ск содержатся в Ht и образуют там полную систему,
так как, во-первых, они независимы, во-вторых, любой цикл D
в Я,- представляется в виде D = 2'C/ + 2 С/(mod 2), где пер-
первое суммирование производится но некоторым из индексов/^
<: k, а второе—по некоторым j>k. Тогда D — 2'Ct состоит из
ребер, содержащихся в Яг, и равно 2" С/, которое не содер-
содержит ребра, входящие в Ht, и поэтому равно нулю.
Мы получили, что D = 2' С/ (mod 2), а следовательно, С,, ...
..., Cfe образуют в Я, полную т-систему. По теореме 5.1 за-
заключаем, что Ht есть плоский граф. При доказательстве нашей
теоремы достаточно теперь рассматривать связные графы.

Комбинаторное условие для плоских графов 141
Доказательство будем проводить индукцией по числу ком*
понент. Выберем любую компоненту Нт. Согласно теореме 3.2, Нт
и G — Hm = F имеют одну общую вершину р. Предположение ин-
индукции будет заключаться в том, что граф F уже вложен на
плоскость. Если N (Нт) = 0, то Нт состоит из единственного
ребра, которое легко добавляется к F на плоскости. Если же
N(Hm)>0, то р принадлежит по крайней мере одному циклу С,
в компоненте Нт. Если р при этом не попадает на обод графа,
мы заменяем в выбранной полной системе цикл С/ ободом
графа Нт. Очевидно, что получится снова полная т-система, но р
уже будет лежать на новом ободе. Используя теорему 5.1, вло-
вложим Нт на плоскость так, чтобы получился топологический
граф Н*т, а вершина р перешла в точку р\ на внешней гра-
границе. Но вершине р соответствует также точка р* при вложе-
вложении на плоскость графа G — Нт. Осталось устроить такие вло-
вложения, чтобы точки р\ и р* совпали.
Для этого разделим плоскость прямой, проходящей через р\, и
применим к каждой полуплоскости такие сдвиги, чтобы в точке р*
угол а между отрезками границы Н"т стал меньше угла р между
отрезками в точке р*. Теперь сожмем Н*т до таких размеров,
чтобы его можно было поместить внутри угла 0; поместим его
туда и объединим точки р* и р\, получив, таким образом, тре-
требуемую разделяющую вершину р' для G = (G — Нт) + Нт. Все
использованные отображения переводят ломаные линии в ло-
ломаные ').
Мы установили достаточность критерия теоремы I. Остается
проверить необходимость. Если каждая несепарабельная ком-
компонента графа G имеет полную т-снстему, то объединение всех
таких систем дает полную т-снстему для G, поэтому достаточно
рассмотреть несепарабельный случай.
Теорема 5.3. Если G — несепарабельный плоский граф,
N (G) > 0, то каждая из конечных областей, на которые G делит
плоскость, имеет своей границей цикл из G; множество всех
таких циклов образует в G полную t-систему, а их сумма
по mod2 является границей внешней (бесконечной) области.
Доказательство. При N(G) = 1 это есть теорема Жор-
дана о плоских кривых. В общем случае применяем индукцию
по N (G) и теорему 3.1, а также тот факт, что разрез вну-
внутренней (внешней) области жордановой кривой делит эту
') Другие, более .топологическое" доказательство см. в работе [2], тео-
теорема 27.

142 С. Маклейн
область на две области с соответствующими границами. По*
следнее нужно для доказательства того, что каждая добав-
добавляемая дуга лежит на границе не более чем двух компонент.
6. КОМБИНАТОРНОЕ ПОСТРОЕНИЕ ДВОЙСТВЕННОГО ГРАФА
Установленный нами критерий, конечно, должен быть экви-
эквивалентен критерию Уитни, заключающемуся в требовании су-
существования комбинаторного двойника. Мы дадим вывод этой
эквивалентности при помощи комбинаторных рассуждений,
получив, таким образом, новое доказательство критериев Уитни
и Куратовского для плоских графов.
Граф G' называется двойником графа G, если существует
взаимно однозначное соответствие между ребрами этих гра-
графов, при котором для любого подграфа Н в G и его образа Н'
в G' будет выполняться равенство R (G'— Н') = R (G') — N (Н)
(разд. 1). Множество 5 ребер из G называется сечением, если
у G — S имеется либо большее, чем у G, число компонент
связности, либо меньшее, чем у G, число вершин') и если это
не выполняется ни для какого собственного подмножества в S
(см. [3], стр. 76). Граф обладает двойником тогда и только
тогда, когда двойником обладает каждая его несепарабельная
компонента ([2], теорема 23 и 25), с другой стороны, мы пока-
показали, что аналогичная ситуация возникает и при рассмотрении
полных т-систем циклов. Поэтому мы ограничимся рассмотре-
рассмотрением кесепарабельных графов.
Теорема II. Несепарабельный граф G обладает двойни-
двойником тогда и только тогда, когда в G имеется полная х-система
циклов.
Тривиальный случай, когда G состоит из одного ребра,
опустим. Пусть теперь G имеет полную т-систему B), п>0.
Обозначим обод R в C) через С„+1. Поскольку каждое ребро
принадлежит не более двум циклам полной системы, ясно,
что оно принадлежит в точности двум циклам системы
С,, С2, ..., Сп, Сга+1. Построим новый граф G' с вершинами
Pt, •¦•> /?rt+i, соответствующими циклам С,, ..., Ся + 1, и с реб-
ребрами Ь\, ..., b't, которые взаимно однозначно сопоставлены реб-
ребрам G так, что ребро b'f имеет концы рг и pk, если соответ-
соответствующее ребро bt принадлежит циклам С, и Ck. Докажем,
что этот „граф циклов" G' является двойником графа G.
') Практически второй случай означает, что граф G — S несвязен и
в качестве одной из компонент имеет изолированную вершину. Мы исклю-
исключили из рассмотрения такую ситуацию.

Комбинаторное условие для плоских графов 143
Основную роль будет играть комбинаторный аналог теоремы
Жордана о плоских кривых.
Лемма 6.1. Если D есть цикл в G, то соответствующий
подграф D' в G' является сечением.
Доказательство. Цикл D можно разложить по пол-
полной системе циклов CL. Перенумеруем эти циклы так, чтобы
в разложение для D входили только первые k циклов. Исполь-
Используя определение C), получаем
О = С, + С2+ ... +Ck = Ck+l+ ... + Crt+I(mod2). E)
Этим разложениям соответствует разбиение множества вершин
графа G' на два множества ри ..., pk и pk+\, ••-, рп+\- Со-
Согласно E), D' состоит из тех ребер, один конец которых нахо-
находится в первом, а другой — во втором из упомянутых мно-
множеств. Таким образом, в G'— D' два этих множества не свя-
связаны между собой. Однако в каждом из множеств вершины
связаны друг с другом. Для доказательства этого предполо-
предположим противное. Пусть, например, ри ..., р/ не связаны
в G'— D' никакими ребрами с вершинами Pj+i, ..., pk- Тогда
? = С| + ... + С;-(mod2) не содержит ребер, входящих в Cj+l, ...
..., Сь, но в то же время содержит только ребра из D. Полу-
Получилось, что в цикле D есть собственный подцикл Е, что не-
невозможно. Совершенно так же рассматривается множество
Pk+u •••» Pn+i- Добавление любого ребра из D' восстанавли-
восстанавливает связность. Следовательно, D' является сечением, что и
утверждалось в лемме.
Теперь, чтобы доказать1), что G' есть двойник G, доста-
достаточно убедиться ([3], теорема 2), что циклу в G соответствует
сечение в С и обратно. В одну сторону мы доказали это
в предыдущей лемме. Покажем обратное. Пусть S' — сечение
в С При доказательстве леммы мы убедились, что сечение D'
делит связный граф G' на две компоненты связности. Ясно,
что и S' поэтому разделяет G' на две компоненты связности.
Пусть первая компонента содержит (перенумерованные) вер-
вершины рх, ..., pk, вторая —вершины pk+i, ..., р„+р Соответ-
Соответствующие циклы в G образуют подграф
D = C{+ ... +Ck = Ck+l+ ... +Cn+I(mod2).
Каждое ребро D принадлежит одному из циклов Clt ..., С„ и
одному из остальных циклов, и оно соответствует, таким обра-
образом, ребру, соединяющему в графе G' первое множество
') Мы будем проводить такие же рассуждения, как и в [2], теорема 29.
Там доказывается, что плоский граф имеет двойник. Мы заменяем только
теорему Жордана ее комбинаторным анал^ом.

144 С. Маклейн
вершин со вторым. Такое ребро должно принадлежать сечению
в графе G', поэтому D cz S. Но подграф D непременно содер-
содержит цикл Dl (см. лемму 4.1). Согласно лемме 6.1, граф D\
есть сечение в G', а по определению сечения имеем D\ = S',
откуда получаем S = Z?i. Мы доказали, что каждому сечению
в графе G' соответствует цикл в графе G. Отсюда следует,
что G' — двойник G.
Пусть теперь G имеет двойник G''. Мы будем искать в G
полную т-систему. Заметим сначала, что если граф G несепа-
рабельный, то и G' несепарабельный1).
Согласно определению двойника, п = N(G) = V (G) — 1 (см. A)),
поэтому G' имеет (п+l) вершину р,, ..., рп+г Множество D't
всех ребер, инцидентных данной вершине р{, является сече-
сечением, так как, удалив его, мы получим изолированную вер-
вершину pi- Соответствующий подграф Dt является циклом в G
по цитированной выше теореме Уитни. Каждое ребро циклов
D,, ..., Dn+l содержится ровно в двух циклах, так что их
сумма (mod 2) равна нулю. Никакими другими соотношениями
по mod 2 эти циклы не связаны. Действительно, если бы
Dx + D2+ ... +Dm = 0(mod2),
то любое ребро одного из этих циклов принадлежало бы еще
ровно одному из них. Это означает, что любое ребро в G',
у которого один конец находится среди вершин ри ..., рт<
имеет среди этих вершин и второй конец; следовательно, вер-
вершины ри ..., рт не связаны с остальными вершинами. Это
противоречит несепарабельности G'. Поэтому D{, ..., Dn неза-
независимы (mod 2) и их ровно n=N(G). Мы получили полную т-си-
т-систему циклов. Теорема II доказана.
ЛИТЕРАТУРА
1. Kuratowski С, Fund. Math., 15 A930), 271—283.
2. Whitney H., Non separable and planar graphs, Trans. Amer. Math. Soc,
34 A932), 339-362.
3. Wh i 1 n e у Н., Planar graphs, Fund. Math., 21 A933), 74—83.
4. Kuratowski C, Whyburn, Sur les elements cycliques et leurs applica-
applications. Fund. Math., 16 A930), 305—331.
:) Cm. [2], теорема 26; в данном случае существенно, что графы не имеют
изолированных вершии.

Минимальные вложения и род графа1)
Дж. Янгс
1. ВВЕДЕНИЕ
1.1. Достаточно очевидно, что связный граф можно вло-
вложить в ориентируемое 2-многообразие. Однако вовсе не оче-
очевидно, существует ли для данного вложения вложение в ориен-
ориентируемое 2-многообразие меньшего рода. Если такого вложения
не существует, данное вложение называется минимальным вло-
вложением; род поверхности при таком вложении называется ро-
родом графа.
1.2. Эта статья посвящена проблеме описания минималь-
минимальных вложений и вычислению рода графа.
1.3. Важную роль будет играть вспомогательное понятие
2-клеточного вложения. Это такое вложение, при котором каж-
каждая компонента связности дополнения образа графа на поверх-
поверхности представляет собой открытую 2-клетку. Если для дан-
данного графа число компонент в дополнении графа на поверх-
поверхности при некотором вложении не меньше, чем при любом
другом, такое вложение называется максимальным.
1.4. Теорема характеризации утверждает, что вложение
минимально тогда и только тогда, когда оно максимальное
2-клеточное.
1.5. При этом значительную роль играет операция пере-
перекройки2) (имеющая, по-видимому, и самостоятельную ценность).
Эта операция позволяет при любом вложении графа так „пере-
„перекроить" компоненты его дополнения, что в результате полу-
получается 2-клеточное вложение (см. п. 3.5).
1.6. Теорема характеризации имеет интересное ответвление.
Можно ли считать, что 1-мерный остов триангуляции ориенти-
ориентируемого 2-многообразия вложен в это многообразие при помощи
минимального вложения? Для рассматриваемой тематики это
традиционный вопрос. Теорема характеризации и „вычислитель-
„вычислительный процесс" решают его утвердительно, как и ожидалось (см.
п. 5.2-5.5).
') Youngs J. W. Т., Minimal irnbeddings and the genus Df a graph,
Journal of Mathematics and Mechanics, 12, № 2 A963), 303-315.
2) В подлиннике «capping operation». — Прим. перев.
10 Зак. 560

146 Дж. Янгс
1.7. Приведенные результаты выделены потому, что они
касаются классических вопросов. В данной статье аналогичные
утверждения доказаны в более общем виде, когда 2-многообра-
зие не обязательно ориентируемо.
1.8. Статью завершает алгоритм вычисления рода графа,
использующий теорему характеризации и изящный результат
Дж. Эдмондса [1, 2J. К сожалению, этот алгоритм очень трудо-
трудоемкий, а методы сокращения перебора неизвестны. Поэтому
он мало пригоден для практических вычислений.
2. ГРАФЫ
2.1. Граф — это упорядоченная пара (G°, G1), в которой
G0 —непустое конечное множество объектов, a G1 —множество
неупорядоченных пар различных элементов из G0. Элементы
множества G0 называются вершинами, а элементы множества
G1 — ребрами графа G.
Число элементов в G1 обозначается ||G'||» i = 0, 1.
2.2. Дугой в произвольном топологическом пространстве X
называют гомеоморф замкнутого единичного отрезка. После
удаления из дуги образов концов этого отрезка получается
открытая дуга.
Пусть G — граф, у которого
G0: о,, ..., vn,
G1: а,, .... ат.
Вложением G в X называется под пространство G{X) про-
пространства X, такое, что
где:
1) Vi (X), ..., vn(X) есть п различных точек в X;
2) ах {X), ..., ат(Х) есть т попарно непересекающихся от-
открытых дуг в X;
3) at(X)()v,(X)=0, /=1, ..., п, /=1, .... т;
4) если а* = (»*,, VkX то открытая дуга uk(X) имеет о*, (X)
и vk2{X) своими концами; k=\, ..., т.
Мы нередко пользуемся сокращениями: пишем vt вместо
vt (X) и ак вместо ак (X) (i = 1, ..., п, k = 1 т) и говорим
„вложение G (X)" вместо „вложение G (X) графа G в X".
2.3. Очевидно, что два вложения G (X) и G (Y) одного и
того же графа G гомеоморфны.
Граф G связен, если для некоторого вложения подпро-
подпространство G (X) связно. Предыдущее замечание показывает, что
равносильным будет определение, в котором связность подпро-

Минимальные вложения и род графа 147
странства G {X) требуется при любом вложении. В дальнейшем
рассматриваются только связные графы.
2.4. Очевидно, что для любого графа G существует вложе-
вложение G в 3-мерное евклидово пространство ?3- На самом деле
можно добиться даже того, чтобы любая открытая дуга была бы
открытым интервалом на некоторой прямой. Очевидно также,
что для данного графа G можно найти такое (зависящее от G)
ориентируемое 2-многообразие М, что существует вложение G(M).
Например, можно взять ||С°|| различных точек 2-сферы и по-
поместить каждую дугу ak на отдельную ручку, подходящим
образом прикрепленную к 2-сфере. Род такого многообразия М
будет слишком велик, и задача нахождения многообразия М
с минимальным числом ручек весьма естественна.
2.5. Уточним сделанные замечания. Обозначим %(М) харак-
характеристику Эйлера 2-многообразия М. Напоминаем, что %(М)
является топологическим инвариантом М; для данного клеточ-
клеточного разбиения М, у которого число /-клеток равно a' (i = 0, 1, 2),
имеем
Кроме того, %{М)^2. Если М ориентируемо, то %{М) четно.
Род у{М) 2-многообразия М определяется формулой
Y (Af) = [2 - х (М)]/2.
Для каждого четного значения характеристики Эйлера, мень-
меньшего двух, имеется два 2-многообразия с этой характеристи-
характеристикой: одно ориентируемое, а другое нет. Любое ориентируемое
2-многообразие М можно представлять себе как 2-сферу с не-
некоторым числом ручек, тогда род \(М) попросту равен числу
этих ручек.
2.6. Буквами М и N мы будем обозначать 2-многообразия;
ф и N# означают ориентируемые 2-многообразия; G (М) и
G (Мф) означают вложение графа G в не обязательно ориен-
ориентируемое и ориентируемое 2-многообразие соответственно.
Используя эти обозначения, мы назовем вложение G (М) про-
простейшим, если %(M)^%(N) для любого вложения G (N). Если
G (М) — простейшее вложение, то показатель вложения ц (G)
графа G по определению равен %(М). Употребление термина
„простейшее" оправдывается тем, что с возрастанием характе-
характеристики Эйлера 2-многообразие усложняется. Если рассматри-
рассматриваются только ориентируемые 2-многообразия, то вместо про-
простейшее вложение говорят минимальное вложение. В силу 2.5
вложение G (М#) минимально, если для любого вложения
G (ЛГф) имеем у{Мф) ^ y(^#)- Р°д графа y{G) в этом случае
полагают по определению равным ^)
Ю*

148 Дж.
Если G (М) — простейшее вложение, а G (М#) — минимальное,
то х(Л1)^х(^#)- Следовательно,
Y(G)>[2-n(G)]/2.
Для примера возьмем в качестве графа G любой из двух зна-
знаменитых графов Куратовского. Его простейшим вложением
будет вложение в проективную плоскость, а минимальным —
в тор. Соответствующие характеристики Эйлера суть 1 и О,
так что приведенное неравенство выполняется.
2.7. Оказывается важным рассматривать для данного вло-
вложения компоненты связности открытого множества [М — G{M)].
Каждая такая компонента является открытым множеством,
поскольку открытым множеством является М, и ясно, что этих
компонент конечное число.
Обозначим ||G(M)|| число компонент в [М — G (М)]. Если
каждая компонента из [М — G (М)] является открытой 2-клеткой,
то G (М) называется 2-клеточным вложением.
2.8. Вложение G (М) максимально, если || G (М) || > || G (N) \\
для любого вложения G (N); оно — максимальное ориентируемое
вложение, если УИф ориентируемо и || G (М#) || ^ || G (N#) || для
любого Ыф (вспомните 2.6).
3. ОПЕРАЦИЯ ПЕРЕКРОЙКИ
3.1. Результаты этого раздела не имеют такой простой и
естественной формы, как результаты остальных разделов.
Вызвано это тем, что мы вынуждены принять меры предосто-
предосторожности, необходимость которых некоторые авторы проглядели.
Грубо говоря, мы показываем, как из произвольного вложения
получить 2-клеточное. Метод, который применяется при этом,
имеет большое значение и будет применяться в других работах.
Добиваясь предельной краткости, мы собрали все существен-
существенные результаты в одном месте, даже если некоторые из них
не находят здесь применения. Те, которые понадобятся в даль-
дальнейшем (в других работах), заключены в скобки.
Чтобы ввести основные идеи, рассмотрим некоторое вложе-
вложение G (М) и некоторую компоненту 5 из [М- G(M)]. Если S
не является 2-клеткой, можно пытаться заменить S некоторым
набором 2-клеток, изменив тем самым 2-многообразие М.
Именно здесь и необходима осторожность. Рингель [3, стр. 61],
например, рассматривает (М — S) и утверждает, что это 2-мно-
2-многообразие с краем, граничные циклы которого Ju ..., Js он
заклеивает соответствующими 2-клетками Си ..., Cs. Множе-
Множество G (М) является вложением G в 2-многообразие N s=

Минимальные вложения и род графа 149
= (М — S)U(JCb ПРИ этом мешавшая ранее компонента S
из [М — G (М)], так сказать, заменяется 2-клетками С,, .... С,
из [N-G(M)].
К сожалению, (М — S) далеко не всегда есть 2-многообразие
с краем. Оно может даже в точности совпадать с множе-
множеством G (М). Возьмем, например, в качестве графа G тре-
треугольник и уложим его на тор М так, чтобы G (М) нельзя
было стянуть в точку; [М — G (М)] здесь имеет ровно одну
компоненту S, т. е. само [М — G (М)], так что (М — S)—G{M),
a G (М), конечно, не является 2-многообразием с краем.
Исправление ошибки требует тонких дополнительных рас-
рассмотрений, в результате которых появляется лемма Робертса
и Стинрода [4]. Они показывают следующее.
Лемма (Робертса и Стинрода). Если М есть {не обязательно
ориентируемое) 2-многообразие, К есть непустой континуум,
являющийся собственным подмножеством М, a S — компонента
из (М — К), то S содержит комплекс Т, который является 2-мно-
2-многообразием с краем. Более того, если У,, ..., У2 есть жордановы
кривые, образующие границу Т, то:
1) компоненты {S — T) суть открытые цилиндры Lu ..., Ls;
2) Fr (Li), т. е. граница Liy имеет две компоненты, У,- и под-
подмножество из К, /'= 1, . • •, s.
Пусть теперь G {М) — вложение графа G в 2-многообразие М,
a S —компонента из [М— G (М)\. Множество G (М) можно
рассматривать как непустой континуум в М, причем с очень
хорошими дополнительными свойствами. Поэтому можно не
только применять лемму Робертса и Стинрода, но даже полу-
получить в этом частном случае ее доказательство, основанное
на простых комбинаторных рассмотрениях. Для доказательства
возьмем такую триангуляцию т многообразия М, чтобы G (М)
было подкомплексом ее 1-мерного остова. Возьмем также т2—ба-
т2—барицентрическое подразделение т. Рассмотрим теперь R — откры-
открытую звезду границы Fr(S) относительно т2, и пусть У,, .. ., Js —
компоненты Fr (R) Г) S.
Легко видеть, что у графа Jt каждая вершина имеет
степень 2, а значит Jt есть элементарный цикл (i=l, .... s).
Если Q — открытая звезда подкомплекса (J J( относительно т2,
то компонентами множества Q f) R являются открытые цилиндры
L,, ..., Ls. Граница Ft(Li) имеет две компоненты: У, и цикл
из G {М). В качестве 2-многообразия Т, фигурировавшего
в лемме, достаточно взять (S — (Jl^).
Совершенно очевидно, что число s в этой лемме не меньше
числа компонент границы Fr(S).

150 Дж. Инге
3.2. Пусть Т° означает внутренность Т. Ясно, что в отличие
от (М — S) пространство (М — Т°) является 2-многообразием
с краем (вспомните замечания в 3.1). Рассмотрим 2-многообра-
2-многообразие Ms, полученное из (М — Т°) заклейкой каждого граничного
цикла ]t 2-клеткой С„ i=l, ..., s, другими словами, Ms =
= (М - Т°) U (J С,-. Поскольку G (М) с (М - Т°), получаем вло-
вложение G{MS) графа G в Ms. Процесс получения Ms из М
обозначим
и назовем операцией перекройки компоненты S. Заметим, что
IIG(Afs)|!>||G(Af)||, ибо s>l (см. 2.7).
3.3. Если Ts есть 2-многообразие T[]\JCt, то элементарные
вычисления показывают, что
Напомним, что для любого 2-многообразия N имеем
причем, равенство имеет место в том и только в том случае,
когда N есть 2-сфера.
Поскольку s>l и
получаем
Равенство здесь выполняется тогда и только тогда, когда s= 1,
a Ts есть 2-сфера, другими словами, когда Т° (а следовательно,
и S) есть открытая 2-клетка. В этом случае в качестве Т можно
взять 2-клетку, которой заклеен единственный граничный цикл
в {М—Т°), причем только в этом случае MS = M.
(Соответствующие замечания можно сделать и относи-
относительно Ts; действительно,
Равенство выполнено тогда и только тогда, когда (М — Т) есть
открытая 2-клетка.)
(Докажем для использования в дальнейшем такой факт.
Если G (М) есть жорданова кривая, а среди компонент
[М— G(M)] нет открытых 2-клеток, то %(TS)>%(M). Предпо-
Предположим, что это не так, тогда %(TS) = %(M), а, следовательно,
{М — Т) есть открытая 2-клетка. Имеем G {М) cz (M — Т), сле-
следовательно, по теореме Жордана о плоских кривых в [(М—Т) —
— G (М)] существует такая компонента R, которая является

Минимальные вложения и род графа 151
открытой 2-клеткой. Но R также есть компонента из [M — G (М)],
где по предположению открытых 2-клеток нет. Мы пришли
к противоречию.)
3.4. В случае, когда М ориентируемо, ориентируемы также
Ms и Ts. Далее,
Это равенство получено из 3.3 с помощью соотношения 2у
= 2 — %. Аналогично
причем равенство выполняется в том и только в том случае,
когда S — открытая 2-клетка.
(Если G (М) — жорданова кривая, а среди компонент [M — G (M)]
нет открытых 2-клеток, то \(TS)< у (Щ.)
(В заключение этого пункта заметим, что из леммы п. 3.1
следует существование последовательности {Тп} 2-многообра-
зий Тп, каждое из которых обладает теми же свойствами,
что и Т, причем Тп(^-Т°п+1 и [jTn = S. Поэтому для любого
замкнутого подмножества F в S можно выбрать такое 2-много-
образие Т, что FcT, а, следовательно, F с: Ts.)
3.5. Пусть S,, ..., Sp — все компоненты [М — G{M)]. Рассмо-
Рассмотрим операцию перекройки М —> MSl = М1. Ясно, что G (М) с: М1,
а при перекройке изменениям подвергалось только S^ Поэтому
компонентами [М1 — G (М)] будут S2, . . ., Sp и несколько откры-
открытых 2-клеток, причем || G (M[) ||>|| G (М) || (см. 3.2).
Теперь рассмотрим М' -> М^ *s= M2. Здесь снова G(M)c:M2
и компонентами [Mr — G (М)] являются S3, ..., Sp и некоторые от-
открытые 2-клетки, причем опять || G (M2) ||^|| G (М[) ||. Повторяя
эту операцию р раз, получаем в результате 2-многообразие ЛГ,
Л4р~'-> М$~[ = М , с такими свойствами:
1) G(M)czM*. Следовательно, имеется вложение G (ЛГ)
графа G в М'; подмножество G (М) в М — это то же самое,
что G(M') в ЛГ (см. 2.2).
2) Компоненты [ЛГ — G (М')] суть открытые 2-клетки.
3) Si с: М* тогда и только тогда, когда St есть открытая
2-клетка (см. 3.3).
4) || G (ЛГ) || > || G (Л!) ||.
Композиция операций перекройки М—> М1 ... М" ' —> М
Называется операцией перекройки многообразия М; обозначим ее
Очевидно, что для любых двух нумераций компонент
[AI — G {М)\ в результате операции перекройки многообразия М

152 ДЖ. Янгс
получаются гомеоморфные 2-многообразия, т. е. эта операция
не зависит от порядка компонент.
3.6. Полезно записать некоторые свойства ЛГ.
1) Если М ориентируемо, то ориентируемо и ЛГ (см. 3.4).
2) G (ЛГ) есть 2-клеточное вложение [см. 1) и 2) в 3.5].
3) ЛГ = М тогда и только тогда, когда G (М) есть 2-клеточ-
2-клеточное вложение [см. 3.3 и 3) в 3.5].
4) Если G (Л!) не есть 2-клеточное вложение, то % (ЛГ) > % (М),
поэтому, если М ориентируемо, то у(М")<\(М) (см. 3.3 и 3.4).
5) ||G(M*)||>||G(M)|| [см. 4) в 3.5].
[6) Если F — замкнутое подмножество G (Л!) и некоторая
компонента из (М — F) есть открытая 2-клетка С, то С является
компонентой из (ЛГ — F).]
Для доказательства 6) заметим, что М = G (Af)ll(J Si;
р
i=\, ..., р. Следовательно, С = С{] М = [G (M)f]C) []\J(S{ f] С).
i
Однако, поскольку С есть компонента (М — F), a S,-есть связное
подмножество (М — F), то утверждение S, П С ф 0 эквивалентно
утверждению S, с: С. Следовательно, C = [G {М) Г) С] U (J S^,
SiCzC. Но С —открытая 2-клетка, поэтому если S, с: С, то
Sj — открытая 2-клетка, поскольку G связно. Таким образом,
согласно 3) из 3.5, имеем М* =э (J Sh S(c:C. С другой стороны,
[G (Л!) П С] с: G (Л!) с: ЛГ, согласно 1) из 3.5. Следовательно,
Ссг ЛГ. Ясно, что С с: Л4', г'= 1 р, где ЛР = ЛГ. Используя
определение операции перекройки Л1—>Л41, легко убедиться,
что С — компонента из {М — F) есть также компонента из (ЛГ — F).
Отсюда сразу же следует по индукции, что С есть компонента
(ЛГ — F), что и завершает доказательство.
4. ТЕОРЕМА ХАРАКТЕРИЗАЦИИ
4.1. Теперь легко доказать обещанную во введении теорему
характеризации.
Сначала заметим, что если G (Л!) есть 2-клеточное вложение,
то оно определяет клеточное разбиение М, для которогоа°=|| G°||,
а1 =|| G11|, <x2 = ||G(M)|| (см. 2.1, 2.5 и 2.7). Отсюда
Вели G {N) есть другое 2-клеточное вложение, то
= \\G(M)\\-\\G(N)\\.
Теорема 4.2. Вложение графа является простейшим тогда
U только тогда, когда оно максимальное 2-клеточное.

Минимальные вложения и род графа 153
Доказательство. Пусть G (М) — простейшее вложение,
a G (N) — максимальное 2-клеточное. Тогда G (М) есть 2-клеточ-
2-клеточное вложение, согласно 4) из 3.6. Используя 4.1 и условия
теоремы, получаем
Следовательно,
] = \\G(N)\\.
Отсюда следует, что G (М) есть максимальное 2-клеточное вло-
вложение, a G (JV) — простейшее.
Следствие. Если G (М) — максимальное вложение, то
в результате операции перекройки М-+М* получается простей-
простейшее вложение G (М*).
Доказательство непосредственно следует из 3.6, 2),
5) и теоремы 4.2.
Теорема 4.3. Вложение графа минимально тогда и только
тогда, когда оно есть максимальное ориентируемое 2-клеточное
вложение.
Доказательство очевидным образом получается из до-
доказательства предыдущей теоремы, надо только заметить, что
в этом случае минимальное вложение G (Af#) является 2-кле-
точным, согласно 1) и 4) из 3.6.
Следствие. Если G (Мф) — максимальное вложение, то
операция перекройки М# —*¦ М# дает минимальное вложение.
Доказательство основано на использовании 1), 2), 5) из 3.6
и теоремы 4.3.
5. ПРОБЛЕМА ТРИАНГУЛЯЦИИ
5.1. Пусть Т есть 1-мерный остов триангуляции 2-много-
образия М, т. е. совокупность 0- и 1-мерных симплексов этой
триангуляции. Очевидно, что существует граф G и вложение
G {М), такие, что T=G{M). Возникает два вопроса:
1) Является ли G (М) простейшим вложением?
2) Если М ориентируемо, является ли G (М) минимальным
вложением?
Второй вопрос стал широко известен благодаря Ауслендеру,
но во всяком случае он издавна бытовал в математическом
фольклоре, связанном с теорией графов. Ответы на оба вопроса
единодушно считались утвердительными, оставалось только
доказать эти естественные предположения. Результаты разд. 4

154 Дж. Янгс
и приводимые ниже вычисления, основным достижением которых
является формула 5.3, B), позволяют провести весьма про-
прозрачное доказательство.
5.2. Пусть G (М) есть 2-клеточное вложение графа G в 2-мно-
гообразие М. Пусть <S — совокупность компонент [М — G {М)\.
Если 5eS, a^G\ то из а (М) (] Fr (S) Ф 0 следует
а(М) czFr(S). Поскольку М есть 2-многообразие, существует
не более одного Sog3, So ф S, для которого а{М) с FrE0).
Следовательно, для SeS и оеС выполняется одно из трех
соотношений:
Случай 0. a(M)f\?r(S)=0.
Случай 1. a(Af)c:Fr(S) и а {М) с: Fr E0) для некоторого
единственного 50 е (® — 5).
Случай 2. a (Af) cr Fr (S), но а(М) с: Fr (So) не выполняется
ни при каком 50еC —5).
Для a^G1 и 5еб определим fs(a) = i, если имеет место
случай /. Заметим, что при фиксированном a^G1 имеем
а) = 2. A)
5.3. Компонента Sgo называется k-угольником, если
Пусть Sft = {5|5s3 и 5 есть й-угольник}. Введем опре-
определения
Nk = число элементов в <Sft,
7 (), в*^ 0.
Используя A), получаем прямым вычислением
2|| G1 ||=S*JVt. B)
Но
sp
Поэтому из B) следует
p||G(Af)IK2||G'IK?IIO(A«)||, C)
причем
||G(M)|| = 2||G'|l D)

Минимальные вложения и род графа 155
тогда и только тогда, когда р = q, т. е. когда в состоит исклю-
исключительно из р-угольников.
5.4. Предположим теперь, что G есть такой граф, для кото-
которого некоторое вложение G (М) является триангуляцией много-
многообразия М, т.е. каждая компонента из [M — G{M)\ есть тре-
треугольник. В силу D) имеем
3||G(Af)|| = 2||G4l. E)
Если G (N) есть 2-клеточное вложение, то в силу C) находим
/>||G(A0IK2||G4l, F)
причем равенство имеет место тогда и только тогда, когда
р = q при вложении G (N).
Мы так определили граф, что 1-угольники невозможны:
концы ребра не должны совпадать. Более того, никакие две
вершины графа не связаны двумя или более ребрами, так что
и 2-угольники невозможны, за исключением тривиального слу-
случая, когда граф состоит из единственного ребра и двух вершин.
Поскольку G(М) определяет некоторую триангуляцию М,
граф G должен иметь по крайней мере 3 ребра. Следова-
Следовательно, ни 1-, ни 2-угольников нет, и для вложения G(N) имеем
G)
Используя E) — G), получаем
(8)
причем равенство имеет место тогда и только тогда, когда
р = q = 3 для вложения G (N).
5.5. Если предполагать, что в 5.4 имеется в виду ориенти-
ориентируемое многообразие М, a G(N) — минимальное вложение, то
по теореме характеризации 4.3 имеем
|| G (N) || > || G(M) ||.
Отсюда, согласно (8), получаем
II G (N) Ц = II G(M) ||
и р = q = 3 для вложения G (N).
Следовательно, G (М) является также максимальным ориен-
ориентируемым 2-клеточным вложением, а поэтому в силу 4.3 — ми-
минимальным вложением, причем G(N) определяет триангуля-
триангуляцию многообразия N. Тем самым доказана следующая теорема.
Теорема. Если G (М) есть 1-мерный остов триангуляции
ориентируемого 2-многообразия М, то G (М) — минимальное вло-
вложение, причем если G(N) есть вложение в ориентируемое

156 Дж. Янгс
2-многообразие N того же рода, что и М, то G (N) является
1-мерным остовом триангуляции N.
5.6. Теперь не будем предполагать, что М ориентируемо.
Пусть G (М) — вложение, определяющее некоторую триангуля-
триангуляцию М, a G (N) — простейшее вложение. В силу 4.2 G (N) есть
максимальное 2-клеточное вложение и, согласно 5.4 и 5.5, имеем
|| G (N) || = || G(M) ||,
причем р = q = 3 для вложения G (N).
Аналогично 5.5 получаем теорему.
Теорема. Если G (М) есть 1-мерный остов триангуляции
2-многообразия М, то G (М) есть простейшее вложение, причем
если G (N) есть вложение в 2-многообразие N с той же харак-
характеристикой Эйлера, что и у М, то G (N) является 1-мерным
остовом триангуляции N.
Замечание. В случае, когда %(М) нечетно, a G (N) — простей-
простейшее вложение, М и N есть гомеоморфные неориентируемые
2-многообразия. Если %(М) четно, можно утверждать лишь, что
х(М) = х(Л0, так как логически имеется возможность, когда
одно из многообразий ориентируемо, а другое нет, т. е. они
не гомеоморфны. Однако вложение представляется настолько
жестко определенным, что кажется, будто такая возможность
исключена. Вначале так считал и автор этих строк. Но это
предположение не оправдалось. Пусть Кп означает полный
граф с п вершинами (т. е. К°п: v vn; Kln: (vt, и,), 1ф'и
i, j—l, ..., n). Граф К\2 вкладывается как в ориентируемое,
так и в неориентируемое 2-многообразие характеристики—10,
причем в обоих случаях он определяет некоторую триангуля-
триангуляцию (см. [3], стр. 74, 78).
6. ОПРЕДЕЛЕНИЕ РОДА ГРАФА
6.1. Теорема характеризации не дает способа нахождения
минимального вложения, т. е. не решает классической задачи
определения рода графа. Однако, если использовать эту тео-
теорему вместе с теоремой Эдмондса (см. [1,2], а также [3], где
на стр. 68 — 70 имеется подобный результат), можно построить
соответствующий алгоритм.
6.2. Обозначим вершины данного графа G = (G°, G1) не
и,, . . ., vn, а 1, . . ., п. Во избежание тривиальных случаев предпо-
предположим, что вершин степени 1 нет. Определим V (i) {i — 1,..., п) —
множество таких k, для которых (i, k) есть ребро графа, т. е.

Минимальные вложения и род графа
Число элементов в V (i) обозначим щ. Пусть
pt: V(i)^V(i)
есть циклическая перестановка множества V(i), i=\, ..., п,
т. е- взаимно однозначное преобразование с единственной орби-
орбитой длины щ.
Теорема Эдмондса утверждает, что каждый набор (рь ..., р„)
определяет 2-клеточное вложение G (М) графа G в ориентируе-
ориентируемое 2-многообразие М, для которого существует ориентация М,
индуцирующая циклическое упорядочение ребер (/, k), инцидент-
инцидентных /, причем за ребром [i, k) непосредственно следует ребро
(/, pi(k)), i=\, ..., п. Более того, для любого 2-клеточиого
вложения G (М) графа G в ориентируемое 2-многообразие М
с данной ориентацией существует набор (рь ..., р„), опре-
определяющий это вложение описанным образом.
Действительно, существует алгоритм, который по данному
(ри ..., рп) строит соответствующее вложение.
6.3. Опишем этот алгоритм. Определим W как множество
упорядоченных пар [а, Ь], для которых соответствующая неупо-
неупорядоченная пара (a, b)^Gl. Определим
Р: W->W
формулой
Р[а,Ь] = [Ь, Рь(а)].
Преобразование Р определено корректно, поскольку из (a, b)^Gl
следует aeFfd), а поэтому рь(а) имеет смысл. Легко видеть,
что преобразование Р взаимно однозначно.
Рассмотрим любую орбиту R преобразования Р и предпо-
предположим, что ее длина есть k.
Возьмем ориентируемую 2-клетку S в виде многоугольника
с k сторонами. Обозначим какую-нибудь сторону [a, b], сле-
следующую за ней в направлении ориентации, через Р [а, Ь] и т. д.
Получим такие обозначения:
[а,Ь], Р[а, Ь], .... Р*-Ча,Ь].
Если /?,, ..., RN есть совокупность различных орбит Р, то
описанный выше процесс определяет 2-клетки 5,, ..., SN. За-
Заметим, что множество /?,, ..., RN обладает таким свойством:
если [а, Ь] попадает в одну из этих орбит, то и [Ь, а] попадает,
причем каждое по одному разу. Более того, поскольку граф G
связный, никакое собственное непустое подмножество множе-
множества /?,, ..., RN этим свойством не обладает.
Теперь остается получить ориентируемое 2-многообразие при
помощи обычного склеивания, как в элементарной топологии.

158 Дж. Янгс
Из определения Р и из того, что W — U Rh следует, что стороны
2-клеток Si, .... Sv образуют 2-клеточное вложение G(M)
графа G в М, при котором компонентами [М — G (М)] являются
внутренности этих клеток. Ориентация клеток Sj, ..., S^ опре-
определяет ориентацию многообразия М. Противоположная ориен-
ориентация М повлечет за собой такое циклическое упорядочение
ребер (/, k), инцидентных i, при котором (i, k) непосредственно
предшествует (/, pi{k)), i = 1, .... п.
6.4. Получение орбит R\, ..., RN можно систематизировать
следующим образом.
Возьмем наименьшее kx в V (I) и запишем R\, орбиту, опре-
определенную [1, k{].
Найдем наименьшее k2^V A), при котором [1, k2] не содер-
содержится в /?], и запишем Rl, орбиту, определенную [1, k2]-
Возьмем наименьшее k3<^V{l), при котором [1, k3] не со-
содержится ни в Ri, ни в R2, и запишем Rl3, орбиту, определен-
определенную [1, k3].
После конечного числа таких шагов мы запишем все орбиты,
определенные парами [1, k], feey(l).
Теперь рассмотрим V B). Либо мы уже записали все орбиты,
определяемые парами [2, /], /еКB), либо существует наимень-
наименьшее /,еУB), при котором [2, j{] в записанных орбитах отсут-
отсутствует. В первом случае перейдем к V C), во втором — запишем
орбиту R\, определенную [2, jx\. Продолжая этот процесс, мы
получим все орбиты преобразования Р.
6.5. Не вдаваясь в подробности, заметим, что число N
орбит Р есть функция N = N(ри ..., рп) выбранных заранее
циклических перестановок pt: V(i)-*V{i), i=l, ..., п, а 6.4
дает способ вычисления N.
Мы отмечали в 6.3, что 2-клеточное вложение G (М), опре-
определенное набором (р,, ..., рп), таково, что [М — G (М)] имеет
N{pt, ..., рп) компонент.
Теорема Эдмондса утверждает, в частности, что для любого
2-клеточного вложения G (М) в ориентируемое 2-многообразие М
существует такой набор перестановок (рь . . ., рп), который опре-
определяет это вложение описанным образом. С другой стороны,
теорема характеризации 4.3 утверждает, что набор (pi, ..., рп),
на котором N{ри ..., рп) достигает максимума, определяет
минимальное вложение. Обозначим \\G\\ = maxN(рь ..., рп).
Существует множество одинаково утомительных эффектив-
эффективных способов выписывания всех циклических перестановок
Pi- V Ц)-+V {i), t=l, ..., п. Таким образом, мы получили ре-

Минимальные вложения и род графа 159
шение классической проблемы о вычислении рода графа y{G)
(см. 2.6). Действительно, согласно 2.5, имеем
Трудности применения этого алгоритма, конечно, возникают
из-за огромного числа [«;—1]! циклических перестановок
р(: V{i)->V(i), i=l, .-., п, причем при вычислении || G ||
(а, следовательно, и y(G)) пока не удалось изобрести ничего
существенно лучшего, чем полный перебор этих перестановок.
ЛИТЕРАТУРА
1. Edmonds, Jr., A combinational representation for polyhedral sunaces,
Amer. Math. Soc. Notices, 7 A960), 646.
2. Edmonds, Jr., Symmetric imbeddings of complete graphs, Amer. Math.
Soc. Notices, 7 A960), 948.
3. R i n g e 1 G., Farbungsprobleme auf Flachen und Graphen, Math. Mono-
graphien, v 2, VEB Deutscher Verlag der Wissenschaften, Berlin, 1959.
4. Roberts J. H.. S t e e n г о d N. E., Monotone transformations of two-di-
two-dimensional manifolds, Annals of Math., 39 A938). 851—862.

Устранение лишнего
из механических доказательств1)
М. Девис
В математике исключение опровергает правило. Следова-
Следовательно, общее утверждение арифметики (например, последнюю
теорему Ферма) можно опровергнуть явным указанием един-
единственного контрпримера. Когда каждый частный случай общего
утверждения допускает проверку с помощью единообразного
алгорифма (как это имеет место для последней теоремы Ферма),
такой контрпример, если он существует, в конце концов может
быть найден (в предположении, что нет никаких ограничений
на время или память) с помощью вычислительной машины, за-
запрограммированной для последовательного исследования всех
возможностей. Возникает вопрос, имеется ли подобная про-
процедура поиска доказательства (а не опровержения) таких общих
предложений. Если полиостью описаны аксиомы, из которых
должно исходить доказательство, то ответ на вопрос положи-
положительный. Единообразные процедуры поиска можно определить
как процедуры, которые дают возможность машине (соответ-
(соответственно запрограммированной) обнаруживать доказательство
данного предложения из данных аксиом, если такое доказатель-
доказательство существует. Такие процедуры поиска называются логиче-
логическими процедурами доказательства. В последнее время проявлен
значительный интерес к улучшению таких процедур и програм-
программированию их для вычислительных машин. Здесь мы дадим
общую схему для сравнения различных существующих в на-
настоящее время процедур доказательств, а также рассмотрим
их преимущества и недостатки. В конце будет описана новая
улучшенная процедура доказательства. Мы не будем обсуждать
работу Ван Хао, потому что она не укладывается просто в нашу
общую схему. Работа Ван Хао, а также и другая новейшая
литература по рассматриваемому вопросу, указана в конце
статьи.
') Davis M., Eliminating the irrelevant from mechanical proofs, Procee-
Proceedings of the Fifteenth Symposium in Applied Mathematics of the American
Mathemat.cal Society, v. XV, Experimental arithmetic, high speed computing
and mathematics, 19t>3, p. 15 — 30.

Устранение лишнего из механических доказательств
161
1. ЛОГИЧЕСКИЙ ЯЗЫК МАТЕМАТИКИ
В книгах или исследовательских статьях по математике
утверждения формулируются на обычном русском') (или не-
немецком, французском, английском и пр.) языке с использова-
использованием математических символов. Развитие современной симво-
символической логики позволило формулировать математические
утверждения, используя только технические символы и не
используя слов. Удивительно, насколько экономичен этот „сло-
„словарь" символической логики. Здесь мы дадим краткий логи-
логический словарь, который отвечает требованиям математики, но
никоим образом не является максимально экономичным. Мы
разбиваем логические символы на следующие группы: знаки
пунктуации, пропозициональные связки, переменные и кванторы.
Знаки пунктуации: ( ) , . Это круглые скобки и запятая.
Пропозициональные связки: ~\ V Л —> •<—*•. Эти символы
означают определенные операции над утверждениями; они
приводят к новым утверждениям. Если р и q данные утвер-
утверждения, то:
„ ~]р" обозначает утверждение: „не р," т. е. „р не имеет места".
„р Л q" обозначает утверждение: „р и q".
„р V q" обозначает утверждение: „р или q".
„p-+q" обозначает утверждение: „Если р, то q".
„р •*-> q" обозначает утверждение: "р тогда и только тогда,
когда имеет место qu.
Двусмысленность и отсутствие точности в разговорном
языке устраняется в случае пропозициональных связок сле-
следующими требованиями:
a) ~]р, р V q, p A q, p-*q a p *-*¦ q должны рассматриваться,
как вполне определенные утверждения, если таковы р и q,
независимо от того, связано содержание р с содержанием q
или нет;
b) истинность и ложность этих утверждений полностью
определяется истинностью или ложностью р и q в соответствии
с приводимой ниже „истинностной" таблицей (табл. 1).
Таблица 1
p
t
1
t
f
1)
t
t
/
/
В оригинале
заменен на термин
11
Зак
560
/
f
t
PVq
t
t
t
f
pAq
t
1
f
— „английском". Далее в тексте
„русский'
. - Прим.
nepee.
t
i
f
i
термин
t
f
f
t
.английский*

162 М. Цевис
Это требование имеет следствие, отчасти противоречащее
интуиции: мы должны считать истинным такое неудобоваримое
утверждение, как „Если 2 + 2 = 5, то снег горячий". Но это
лишь новый пример общематематической тенденции по возмож-
возможности расширять область определения операций, даже если
при этом придается смысл тому, что прежде считалось бессмыс-
бессмыслицей (вспомним, например, 2 — 5 или Y—4). Дальнейшее
обсуждение этого вопроса читатель найдет в любом учебнике
логики, см., например [1, 2, 7, 10].
Переменные. Это символы, о которых предполагается, что
они принимают произвольные значения из некоторого заранее
фиксированного множества. Здесь мы будем использовать
в качестве переменных буквы х, у, z, и, v и w с нижними
индексами или без них.
Кванторы. Выражение, образованное заключением перемен-
переменной в круглые скобки [например, (х) или (у)], называется
квантором общности. Подразумевается, что выражение (х) А
утверждает истинность А для всех значений х. Аналогично
выражение, образованное заключением в круглые скобки буквы
Е, за которой следует переменная [например, (Ех) или {Еу)\,
называется квантором существования; подразумевается, что
выражение (Ех)А утверждает истинность А по крайней мере
для одного значения х.
В дополнение к только что перечисленным логическим
символам мы должны ввести некоторые специальные математи-
математические символы. Примерами таких символов будут: 0, 1, +, =,
<, е. Какие из этих символов действительно встречаются, будет
зависеть от рассматриваемой конкретной области матема-
математики. Однако все эти символы разделяются на три категории:
символы констант, символы функций и символы отношений.
Предполагается, что каждый символ константы (обычные
примеры 0 и 1) обозиачает иекоторую определениую констаиту.
Предполагается, что каждый символ функции (например, +)
обозначает функцию от одного или более аргументов (например,
обычно предполагается, что + обозначает функцию от двух
аргументов). Символ отношения (например, =, < или е)
обозначает отношение с одним или более аргументами.
В таблице 2 дается перевод различных утверждений
из обычной математики в логический символизм.
Теперь мы можем систематически исследовать все утвер-
утверждения, которые можно записать, используя этот символизм.
Во-первых, исходя из переменных и символов констант, мы
можем образовывать термы, т. е. выражения, построенные из этих
символов с помощью различных символов функций. В част-
частности, если g — символ функции от п аргументов и уже известно,

Устранение лишнего из механических доказательств
163
Таблица 2
Утверждение
A) Существует
бесконечно много
простых чисел
B) Сложение
коммутативно
C) Множество
положительных
целых чисел, содер-
содержащее 1 и вместе с
каждым из своих
элементов содер-
содержащее следующий
за ннм элемент, со-
состоит из всех по-
положительных це-
целых чисел
D) Между п и
In всегда имеется
простое число
Перевод в
логический
символизм
(*) (Еу)
{у>хЛ
АР (у)]
(х)(у)(х +
+у=у+х)
(о){ [1еоЛ
А(х) (хеа->
-м (*)s
ео) ]->(*)
[/(*)->
->^ео]}
(х) (Еу) [у>
>хАх+х>
>УАР(У)]
Подразуме-
Подразумеваемая об-
область значе-
значений перемен-
переменных
Положи-
Положительные це-
целые числа
Элементы
некоторой
абелевой
группы
Множество
всех поло-
положительных
целых чисел
и все мно-
множества по-
ложитель-
ложительных целых
чисел
См. A)
Символы
коистаит
Нет
Нет
1
Нет
Символы
функций
Нет
+
s (сле-
(следующее
за)
+
Символы
отношений
Р (... есть
простое
число)
больше,
чем ...)
= (... рав-
равно ...)
s (...
принадле-
принадлежит ...)
/ (... по-
ложитель-
ложительное целэе
число)
>, Р
См. A)
что щ, щ, ..., ип — термы, то g(uu щ, .... «„) — также терм.
Обычно допускают небольшое изменение этой записи.
Для символа функции g от двух аргументов (вроде симво-
символа + ) пишем (ugv) вместо g(uv).
Примеры термов:
(х + у), @ + {x + y)), s(O + y).
Если R — символ отношения от п аргументов и к,, ...,
ы„ — термы, то выражение R(uu ..., «„) называется атомарной
формулой. [Введенные выше особые соглашения о записи для
символов функций от двух аргументов используются также
и для символов отношений; например, пишут (х = у) вместо
= {ху).\ Итак, утверждения, которые мы собираемся рассмат-
рассматривать — это утверждения, которые могут быть построены
П*

164 М. Девис
из атомарных формул с помощью пропозициональных связок
и кванторов. Нетрудно увидеть, что все утверждения, приве-
приведенные в табл. 2, попадают в эту категорию. Кроме того, мы
утверждаем, что все математические суждения находятся среди
утверждений, которые можно выразить таким способом. Это
утверждение иногда приводит к определенной путанице. Именно,
виды логических выражений, которые мы допустили, часто
называются выражениями „первого порядка", и утверждается,
что для математики необходимы логики „более высокого
порядка". Однако сами эти логики „более высокого порядка"
могут быть выражены описанным способом (например, с помощью
символа е из теории множеств). В частности, различные
формулировки аксиоматической теории множеств могут быть
выражены описанным способом (ср. [2]), и тогда, как известно,
для развития классического анализа может быть использована
программа Пеано — Дедекинда.
2. ЭРБРАНОВСКИЕ ДОКАЗАТЕЛЬСТВА
Пусть С — утверждение, выраженное в только что описан-
описанном символизме. В С входят логические символы (именно:
знаки пунктуации, пропозициональные связки, переменные и
кванторы) и математические символы (именно: символы кон-
констант, символы функций и символы отношений). Интерпрета-
Интерпретация утверждения С задается путем указания „смысла" мате-
математических символов. Точнее, интерпретация утверждения С
задана, если указаны:
A) непустое множество и, называемое универсумом;
B) определенный элемент из и для каждого символа кон-
константы из С;
C) функция от п переменных из и в и (т. е. отображение
из и11 в и) для каждого символа функции от п аргументов;
D) «-местное отношение на и для каждого символа отно-
отношения от п аргументов.
Когда интерпретация утверждения С указана, С становится
определенным математическим утверждением — истинным или
ложным. Например, пусть в качестве С выбрано B) из табл. 2:
(х)(у)(х + у = у + х).
Ниже приводятся три интерпретации утверждения С.
A) Универсум есть множество рациональных чисел; + есть
сложение; = есть равенство.
B) Универсум есть множество векторов в трехмерном евкли-
евклидовом пространстве; + есть векторное произведение; = есть
равенство.

Устранение лишнего из механических доказательств 165
C) Универсум есть множество положительных целых чисел;
+ есть умножение; = есть „меньше чем".
Здесь С истинно прн интерпретации A) и ложно при
интерпретациях B) и C). Интерпретация, которая делает утвер-
утверждение С истинным, называется моделью утверждения С. Под
моделью утверждений Сь С2, .... Сп мы подразумеваем мо-
модель для одного утверждения CtAC2A ... АСп; иными сло-
словами, такая модель есть интерпретация математических сим-
символов из С! С„, которая делает все эти утверждения
истинными. Например, рассмотрим следующий список утвер-
утверждений, который мы обозначим через ©^
(х)(е°х = х),
(х) (х = *),
(х)(у)[х = у-*у = х],
(*) (у) (г) [((х = у) Л (у = г)) -* (х = г)].
То, что обычно называется группой, есть просто модель
этих утверждений, в которой „ = " интерпретируется как ра-
равенство. Интерпретациями символов е, ° и / тогда будут
соответственно тождественный элемент группы, умножение
группы и функция, которая отображает каждый элемент
группы в обратный ему. В действительности эти утверждения
составляют формальную систему аксиом теории групп. В лю-
любой модели этих аксиом „ = " должно интерпретироваться как
отношение эквивалентности, сохраняющее операции, которые
являются интерпретациями символов /и о. Тогда соответ-
соответствующие классы эквивалентности будут образовывать группу.
Результат групповой операции (класс эквивалентности, содержа-
содержащий а о Ь) будет при этом естественно получаться умножением
класса эквивалентности, содержащего а, на класс, содержа-
содержащий Ь.
Другой список утверждений, который также представляет
интерес в связи с группами, это следующий список, который
мы назовем ©2:
(х) Р (е, х, х),
(х)(у)РA(х), х, е),
(х) (у) (z) (и) (v) (о;) [(Р (х, у, и) Л Р (и, z, w) Л Р (У, г, v)) -* Р (х, v,о;)],
(x)(y)(z)(u)(v)(w)[(P(y,z,v)AP(x,v,w)AP(x,y,u))-*P(u,z,w)].

166 М. Девис
Именно, если мы возьмем любую группу, то ее можно
использовать как модель для ©2, интерпретируя е как тож-
тождественный элемент, / как функцию обращения и Р{х,у,г)
как отношение (x°y) = z. Мы не будем обсуждать здесь обрат-
обратный вопрос о сопоставлении некоторой группы каждой модели
для ©2; заметим только, что любая модель для ©2, в которой
интерпретация символа Р такова, что для каждого х, у имеется
точно одно г, для которого истинно Р{х, у, z), есть группа
с операцией умножения:
х о у есть то единственное г, для которого истинно Р(х, у, z).
Теперь предположим, что мы хотим доказать некоторое
утверждение Т. В интересующей нас ситуации мы имеем ко-
конечный список аксном Ах, ..., Лт, исходя из которых мы хо-
хотели бы доказать Т. Это означает, что мы хотим показать,
что
Каждая модель для Л,, ..., Ат есть также модель для Т.
Например, предположим, что мы хотим доказать элемен-
элементарную теорему теории групп (х) (х ° I (х) = е), т.е. что посту-
постулированный левый обратный есть также и правый обратный.
Мы хотим показать, что это предложение истинно во всех
группах. Так как каждая группа есть модель для ©[, доста-
достаточно показать, что это предложение истинно в каждой мо-
модели для ©|. Или иначе, мы можем, используя обозначения
системы ®ъ записать это предложение в виде
(х)Р(х, 1(х), е)
и пытаться показать, что это последнее истинно в каждой
модели для ©2. Такая точка зрения на доказуемость из аксиом
обычно называется семантической или теоретико-модельной.
В учебниках логики обычно подчеркивается другая, синтакси-
синтаксическая точка зрения, согласно которой выводимость Т из
Л,, ..., Ат — это возможность использовать некоторый список
формальных правил вывода для получения Т из Л,, ..., Ат.
Но тогда основным результатом оказывается теорема Гёделя
о полноте, которая утверждает, что указанные правила вывода
полны в следующем смысле:
Т может быть получено из Л,, ..., Ат с помощью указан-
указанных правил вывода тогда и только тогда, когда каждая модель
для Л,, ..., Ат есть также модель для Т.
Итак, синтаксическая и семантическая точки зрения ока-
оказываются эквивалентными. Здесь мы будем пользоваться се-
семантической точкой зрения. Более подробную информацию
о теореме Гёделя можно получить в [1, 2, 7, 10],

Устранение лишнего из механических доказательств 167
При каждой интерпретации утверждение Т либо истинно,
либо ложно. Следовательно, каждая модель для Л, Ат есть
либо модель для Г, либо модель для ~]Т. Таким образом, утвер-
утверждение, что каждая модель для Аи ..., Ат есть также модель
для Г, эквивалентно утверждению, что никакая модель для
Л,, ..., Ат не есть также модель для ~]Т. Все процедуры дока-
доказательства, предложенные здесь, можно рассматривать с этой
точки зрения: т. е. мы предлагаем доказывать, что Т есть
следствие At Am, показывая, что список предложений
Л,, ..., Ат, ~]Т не имеет модели.
Мы начинаем с предварительной обработки отдельных ут-
утверждений Аи ...,Ат, ~]Т, согласно шагам 1 — 8 приводимого
ниже описания. Каждый шаг будет выполняться снова и снова
до тех пор, пока это возможно; когда данный шаг нельзя
больше применить, переходим к следующему шагу. Читатель
должен заметить, что:
A) Эти шаги могут быть легко сделаны чисто механическими
и, следовательно, приспособлены для программирования на
машине. (Практически эти предварительные шаги легко про-
проделать вручную.)
B) Наличие модели для некоторого списка утверждений
эквивалентно наличию модели для списка, получающегося из
рассматриваемого в результате одного из данных шагов.
Шаг 1. Переименование переменных. Если одна и та же
переменная встречается более чем в одном кванторе в одном
и том же утверждении, то используем новую переменную для
одного из этих кванторов. Например, (х) R (х) V (*) S (х) следует
переписать в виде {х) R (х) V {у) S {у).
Шаг 2. Исключение ->«*->. Всякий раз, когда встречаются
-> и ¦«-+, делаем замену:
Заменяем А-+В на {~\A)VB.
Заменяем Л<->В на (АЛВ)\/[(~\ А)/\AВ)].
Шаг 3. Продвижение символа ~] внутрь. Везде, где воз-
возможно, делаем замены:
Заменяем ~\(х)М на {Ех)~\М.
Заменяем ~\{Ех)М на (х)~\М.
Заменяем ~]{MAN) на {~]М)\/(~]N).
Заменяем ~](M\/N) на (~\M)/\AN).
Заменяем ~ПМ на М.
В конце концов получаются утверждения, где каждое ~| встре-
встречается непосредственно перед атомарной формулой.
Для атомарной формулы мы пишем R(Ul Um) вместо
1R(UU ..., Um); здесь R(Ult ...,Um) и R(UU ...,Um) назы-
называются литерами.

168 М. Девис
Таким образом, начав с
W{*(¦*)V l{Ey)[S(x, y)A(R(x)VU(x))]},
мы получим
(x)[R(x)V (y)[S(x, y)v(R(x)AU(x))}}.
Шаг 4. Исключение квантора существования. Вычерки-
Вычеркиваем поочередно кванторы существования. Соответствую-
Соответствующая переменная (обозначим ее через у) заменяется на
g{xx, ...,xm), где g — новый символ функции, а х{ хт —
все переменные, встречающиеся в кванторах общности, нахо-
находящихся слева от вычеркиваемого квантора существования
(у нас-(?»).
В случае, когда слева от рассматриваемого квантора су-
существования нет кванторов общности, переменная заменяется
на новый символ константы g; этот случай может быть вклю-
включен в общий, если мы будем считать, что символ константы —
это просто символ функции от О аргументов.
Чтобы доказать, что шаг 4 сохраняет свойство иметь или
не иметь модель, мы заметим, что если до использования
шага 4 рассматриваемые утверждения имели модель для лю-
любых хь ..., хт из рассматриваемого универсума, то можно
найти хотя бы одно значение у, для которого обрабатываемое
утверждение истинно. Следовательно, мы можем взять в ка-
качестве интерпретации для g такую функцию, что для любых
х, хт функция g(x{ xm) равна упомянутому значе-
значению у. (Можно избежать молчаливого использования аксиомы
выбора, но мы не будем этим заниматься.) Обратно, если
рассматриваемые утверждения имеют модель после обработки,
то y = g(x xm) обращает исходное утверждение в истину
для всех *, хт, так что первоначальное существователь-
ное условие также имеет модель.
Шаг 5. Вынесение кванторов общности. Выносим все кван-
кванторы общности влево, так что рассматриваемое утверждение
переходит в выражение стандартного вида (последовательность
кванторов общности, за которой следует бескванторное выра-
выражение).
Шаг 6. Применение (до тех пор, пока это возможно) дис-
дистрибутивности V относительно А. Иными словами, заменяем
{АЛВ)\/С на (AVC)A(BVC).
После выполнения шагов 1—6 каждое утверждение при-
принимает вид
(xi)(x2)...(xn)[BlABiA... ABk],

Устранение лишнего из механических доказательств 169
где для каждого Bt справедливо
и где каждая // есть литера. В этом выражении каждое Bt
называется простой дизъюнкцией {дизъюнктом), l]l) называется
литерой дизъюнкта Bt.
Шаг 7. Упрощение. Если дизъюнкт Bt содержит атомарную
формулу вместе с ее отрицанием, то вычеркиваем весь ди-
дизъюнкт. Если литера встречается дважды в одном и том же
дизъюнкте Bit то вычеркиваем одно из вхождений (например,
дизъюнкт /,V/2V/i следует заменить на liVl2)-
Этим заканчивается предварительная обработка дизъюнк-
дизъюнктов. Нужно подчеркнуть, что здесь не утверждается, будто
результат, получающийся после этой обработки, эквивалентен
(по смыслу) Аи .... Ат, ~\Т.
Утверждается лишь, что модель существует для одного из
этих утверждений тогда и только тогда, когда она существует
и для другого.
Мы воспользуемся преимуществами весьма простой формы,
к которой приведены теперь рассматриваемые утверждения,
чтобы ввести некоторые сокращения. Мы вычеркиваем кван-
кванторы общности. Мы также устраняем явное использование
символов Л и V- Таким образом, пишем /,/2 . . . /г вместо
l\ V h V • • • V h- Конъюнкция дизъюнктов представляется вер-
вертикальной колонкой, составленной из них. Дизъюнкты, проис-
происходящие от каждого из утверждений Аи ..., Ат, ~]Т, можно
теперь собрать в единый список дизъюнктов. Этот единый
список можно дальше упростить, используя следующий шаг.
Шаг 8. Исключение лишних дизъюнктов. Вычеркнем все
дизъюнкты, частью которых являются другие (или которые
совпадают с другими). (Действительно, конъюнкция всех дизъ-
дизъюнктов истинна тогда и только тогда, когда все дизъюнкты
истинны; но если некоторый дизъюнкт истинен, то истинен
также и любой дизъюнкт, частью которого является данный.)
Например, пусть Аи ..., Л4 есть аксиомы теории групп ©2>
и пусть Г есть (х) Р (х, I (х), е). Применяя шаги 1—8 к ©2
вместе с ~]Т, мы получим дизъюнкты:
Р(е,х,х), A)
), х,е), B)
Р (х, у, и)Р(и, z, w) Р (у, z, v) Р (х, v, w), C)
~PJy, z, v) Р (х, v, w) Р(х, у, и) Р (и, z, w), D)
Р(а,1(а),е), E)

170 М. Девис
где а —символ константы. Чтобы увидеть, как обрабатывается,
например, ~]Т, мы начинаем с  (х)Р{х, I(х), е). Шаги 1 и 2
не применимы. Шаг 3 дает
(Ех)Р(х,Цх),е).
Шаг 4 дает Р{а, 1{а), е), и оставшиеся шаги не применимы.
Объединенный список дизъюнктов С,, С2, .... Ck можно
мыслить как единое бескванторное выражение
С, Л С2 Л ... Л Ck.
Такое выражение находится в конъюнктивной нормальной
форме; это означает, что оно есть конъюнкция дизъюнктов,
к которым применено упрощение шага 7. Обычно выражение
в конъюнктивной нормальной форме (или более общо, всякое
бескванторное выражение) называется тождественно ложным,
если это выражение ложно при любом сопоставлении значений
„истина", „ложь" его атомарным формулам (это эквивалентно
требованию, чтобы его отрицание было тавтологией).
С каждым полным списком дизъюнктов, полученных из
Аи ..., Ат, ~\Т, мы связываем некоторый список Н термов,
который мы называем эрбрановским универсумом для этого
списка. Сперва определим Но как множество символов кон-
констант и переменных, встречающихся в этом списке. Далее по-
полагаем по определению, что Нпт1 состоит из элементов Нп
вместе со всеми термами, которые могут быть получены путем
применения символов функций, встречающихся в рассматри-
рассматриваемом списке дизъюнктов, к элементам из //„. Наконец, мы
полагаем
Н = []Нп.
п
Для только что рассмотренного примера (теории групп)
имеем
Но = {е, а, х, у, z, и, v, w},
Я, = {е, a,x,y,z,u,o,w,I (е), I (а), 1 (х), I (у), 1 (г), / (и), 1 (v), I (a;)}.
Все рассматриваемые нами процедуры поиска доказательств
основываются на следукгцел форме теоремы Эрбрана.
Теорема Эрбрана. Пусть Ах, ..., А,п — данные аксиомы,
и Т — предполагаемая теорема. Пусть Сь С2, .... Ck — список
дизъюнктов, полученных из Л, Ат и ~\Т с помощью
шагов 1—8, и пусть Н — результирующий эрбрановскии универ-
универсум. В этом случае Т есть следствие Аь ..., Ат тогда и только
тогда, когда существует такой список дизъюнктов Qu ..., Qn

Устранение лишнего из механических доказательств 171
каждый из которых получен из некоторого Сь i—\, 2, ..., k,
путем замены его переменных членами Н, что формула
Qi Л С?2 Л • • • Л Qr — тождественно ложная.
Эта теорема доказывается следующим образом:
1) Предположим, что Qi Л Qi Л ... Л Qr тождественно
ложно, но тем не менее Л,, ..., Ат, ~]Т имеет модель. Сле-
Следовательно, С,, ..., Ck имеют модель с универсумом U. При-
Припишем каждой переменной и каждому символу константы в Н
некоторый фиксированный элемент из U. Тогда каждому эле-
элементу множества Н будет сопоставлен единственный элемент
множества U. При этой интерпретации каждое Qt (i — 1, 2, ..., г)
истинно. Таким образом, Qi A Q2 Л ... Л Qr не может быть
тождественно ложным.
2) Обратно, предположим, что Аи ..., Am, ~] T не имеют
модели. Тогда С{ Ck не имеют модели. Пусть Q1( Q2,
Q3, ... — всевозможные дизъюнкты, полученные из Си ..., Ck
путем замены его переменных членами универсума Я. Тогда
мы утверждаем, что при любом сопоставлении истинностных
значений атомарным формулам из Qlt Q,, Q3, ..., по крайней мере
одно из Qi будет ложным. Допустив временно, что это утвер-
утверждение верно, мы закончим доказательство, так как, согласно
[10, стр. 254 — 256] („закон бесконечной конъюнкции"), мы тогда
будем иметь, что QS[ Л Qs2 Л • • • Л Qs тождественно ложно
для некоторых su s2, ..., sr. Наконец, чтобы обосновать истин-
истинность нашего утверждения, достаточно заметить, что если бы
оно было ложно, то мы могли бы построить модель для
С[, .. ., Ck с универсумом Н. Интерпретация символов констант
и функций в этой модели определяется автоматически. И если
дано сопоставление истинностных значений атомарным форму-
формулам из Q[, Q2, Q3, ..., которое делает все Qt истинными, то
мы можем интерпретировать каждый символ отношения R,
считая R(Ult ..., Um) истинным для Uu .... (/„еЯ, тогда
и только тогда, когда данное сопоставление истинностных зна-
значений делает атомарную формулу R(UU ..., Um) истинной.
Таким образом, теорема доказана.
Используя теорему Эрбрана, мы можем построить любое
число полных процедур поиска доказательств следующим спо-
способом.
Если даны аксиомы Аи ..., Ат и предполагаемая теорема Т,
то мы сперва применяем шаги 1—7 для получения списка
дизъюнктов С[, ..., Ck. Затем применяем процедуру порожде-
порождения, ксторая порождает дизъюнкты Qb Q2, ..., получаемые
из С{ Ck путем замены переменных на члены эрбранов-
ского универсума. Время от времени мы прерываем процедуру

172
М. Девис
порождения и проверяем конъюнкцию Q{ Л Q2 Л ... Л Qn
дизъюнктов, порожденных к этому моменту, на тождественную
ложность. Если эта конъюнкция тождественно ложна, то мы
Начало
1
Порождение
увеличение N 1
Проверка на Теорема
противоречивость *— доказана
Да
Рис. 1,
имеем доказательство. Если нет, порождаем новые дизъюнкты.
Эта общая схема иллюстрируется на рис. 1.
3. ПРОЦЕДУРА ГИЛЬМОРА
Процедура Гильмора [6] может быть описана (с несущест-
несущественными изменениями) следующим образом. Пусть переменные,
присутствующие в С,, .... СА,-это л:, хп. Пусть (t['\ ..., tf),
j = 1, 2, 3, ..., — некоторое определенное перечисление всех эле-
элементов универсума Н. Пусть С\п, ..., С*" есть результат замены
хп на t\n, ..., t(n] в Си ..., Ck соответственно. Формулу
CV А С? Л
л с!2) л с? л
л
л
л
л сГ> л
л
л
(*)
приводим к дизъюнктивной нормальной форме для каждого
из последовательных значений г; здесь N — некоторое данное
целое число (допустим 10).
Приведение (*) к дизъюнктивной нормальной форме озна-
означает итерирование распределения V относительно Л (т. е. за-
замену, где возможно, (А V В) Л С на (А Л С) V {В Л О) до тех
пор, пока формула не примет вид
у, vv2v ...vn,

Устранение лишнего из механических доказательств
173
где для каждого Vt справедливо
Vt = if Л ff A ... Л 1%.
Такая формула тождественно ложна тогда и только тогда,
когда в каждом Vt одна из встречающихся литер есть отри-
отрицание другой. (В противном случае можно так выбрать истин-
Полагаеп г- /
Порождение
rN nodcmaно бон
изданных
дизъюнктов
Приведениеш
конъюнкции к
дизъюнктивной
норпальной
форме
—
проверка на
протибо-
речивость
Нет
Да
Теорема
доказана
Рис. 2.
ностные значения атомарных формул, что взятое Vи и следова-
следовательно вся формула, станет истинной.)
Вся процедура может быть представлена схемой, показан-
показанной на рис. 2.
4. ПРОЦЕДУРА ДЕВИСА- ПАТНЭМА
Процедура Гильмора, которая запрограммирована на IBM*
704, не смогла дать доказательство следующего примера:
(Ex) (Еу) (z) {[F (х, у) -> (F (у, г) A F (г, г))] А
A [{F (х, y)AG (x, y))-*(G (х, г) А в (г, г))]}.
Эта теорема должна быть доказана без использования специ-
специфических аксиом, т. е. это логическая теорема. Применяя
шаги 1 — 8 к отрицанию этой теоремы (заметим, что шаг 8
исключает три дизъюнкта), мы получаем список дизъюнктов:
F {х, у),
F (у, f (х, у)) FJf (х, у), f(x,y))G_ (x, у),
F(у, f (x, y))F(f (x, у), f (х, у))G(x,f (x, y))G({(x, у), f (x, у)).
Сообщалось, что программа Гильмора испытала ровно 7 под-
подстановок, т. е. rN = 7. Легко видеть, что при этом получается
дизъюнктивная нормальная форма из 127 конъюнктивных

174 М. Девис
дизъюнктов, каждый из которых содержит 21 литер. Процедура
из работы [3] (так же, как и несколько улучшенная версия
из работы [4]) совершенно аналогична процедуре Гильмора,
но не использует сведения к дизъюнктивной нормальной форме.
Процедура проверки на противоречивость формулы в конъюнк-
конъюнктивной нормальной форме происходит по следующим правилам:
1. Правило однолитерных дизъюнктов.
(a) Если имеются однолитерные дизъюнкты р и р, то фор-
формула противоречива.
(b) Если (а) не применимо и имеется однолитерный дизъ-
дизъюнкт /, то вычеркиваются все вхождения ~\1, а также все
дизъюнкты, в которых встречается /. (Под ~]1 мы понимаем р,
если /—атомарная формула р, и понимаем р, если / есть ато-
атомарная формула р.) Если после этого совсем не остается
дизъюнктов, то формула непротиворечива.
2. Положительно-отрицательное правило. Если имеется ли-
литера /, но нет ~]1, то можно вычеркнуть все дизъюнкты, со-
содержащие /. Если после этого совсем не остается дизъюнктов,
то рассматриваемая формула непротиворечива.
3. Правило расщепления. Пусть р — атомарная формула,
такая, что имеются как р, так и р. Пусть Л, и А? получены
из исходной формулы путем вычеркивания всех дизъюнктов,
в которых встречаются соответственно р или р. Тогда исход-
исходная формула противоречива тогда и только тогда, когда Л,
и Л2 обе противоречивы.
Пример Гильмора легко выводится (даже вручную) с исполь-
использованием этой процедуры (ср. [3]); ио задача из теории групп,
рассматриваемая выше, оказывается трудной (обсуждение труд-
трудностей см. в [4]).
б. ПРОЦЕДУРА ПРАВИЦА
Недостатком процедуры Девиса — Патнэма является порожде-
порождение значительно большего числа дизъюнктов, чем нужно для
завершения доказательства. Правиц в работе [9] предлагает
алгорифм, свободный от этого дефекта.
Пусть дан список дизъюнктов Си ..., Ck, и пусть входящие
в него переменные — это хи ..., хп. Пусть теперь С1/', ..., С*'
суть соответственно результаты замены хи ..., хп новыми раз-
различными переменными Хц, ..., xnj. Снова мы выбираем целое
число N, и для последовательных значений г мы приводим
формулу (*) из разд. 3 к дизъюнктивной нормальной форме.
Затем ищем подстановки элементов эрбрановского универсума Н
вместо переменных, которые могут перевести две литеры в одном
и том же (конъюнктивном) дизъюнкте в отрицание друг друга.

Устранение лишнего из механических доказательств 175
Если не существует таких подстановок для всех дизъюнктов,
то увеличиваем г и начинаем снова.
В качестве примера [9] рассмотрим логическую теорему
(*) (У) [Р (*) V Q (у)) -> [(*) Р (х) V (у) Q (у)].
Шаги 1—8 дают список дизъюнктов:
P(x)Q(y),
Р(а),
Q(b).
В дизъюнктивной нормальной форме это переходит в формулу
\Р(х) Л Р(а) Л Q(b)\ V [Q(y) Л Р(а) Л Q(b)],
которая будет противоречивой только в случае х = а и у — Ь.
Здесь для доказательства достаточно положить rN=l.
Большим достоинством процедуры Правица является поро-
порождение только таких подстановок в Ci А С2 Л ... Л Ck, кото-
которые действительно нужны для противоречия. Но использование
дизъюнктивной нормальной формы неизбежно порождает те же
самые трудности, что и в процедуре Гильмора.
6. НОВАЯ ПРОЦЕДУРА
Мы теперь опишем новый тип процедуры, в которой попы-
попытаемся объединить достоинства процедуры Правица и процедуры
Девиса — Патнэма.
Определение. Формула в конъюнктивной нормальной
форме называется связной конъюнкцией, если для каждого
вхождения литеры I в данный дизъюнкт существует по крайней
мере одно вхождение ~\1 в какой-нибудь другой дизъюнкт.
Назовем такое вхождение ~\1 партнером для данного вхожде-
вхождения I.
Теорема. Пусть Си ..., Ck — список (дизъюнктивных) дизъ-
дизъюнктов, конъюнкция которых находится в конъюнктивной нор-
нормальной форме и является противоречием. Тогда существует
подмножество {С,, ...,Ск}, конъюнкция которого противоречива
и является связной конъюнкцией.
Предположим, что некоторый дизъюнкт содержит литеру /
и что нет другого дизъюнкта, содержащего \1. Тогда все
дизъюнкты, содержащие /, можно вычеркнуть. Действительно,
полагая / истинным, мы сделаем истинными также все дизъ-
дизъюнкты, содержащие /. Следовательно, всякое сопоставление
истинностных значений атомарным формулам должно делать

176 М. Девис
ложным некоторый дизъюнкт, не содержащий /. (Это замеча-
замечание является просто обоснованием положительно-отрицатель-
положительно-отрицательного правила.) Повторение этого процесса должно привести
к связной конъюнкции, которая также противоречива.
Эта теорема о связной конъюнкции (или, скорее, двойствен-
двойственная ей) была независимо замечена Данхэмом и Нортом [5].
Следовательно, мы можем модифицировать процедуру
Девиса — Патнэма так, чтобы искать именно связные конъюнк-
конъюнкции; проверку на противоречивость надо делать только после
получения связной конъюнкции. Найдем подходящую связную
конъюнкцию в рассматриваемой задаче теории групп.
Искомая связная конъюнкция должна содержать дизъюнкт E),
так как он— единственный след доказываемой теоремы. Под-
Подстановка в A) или B) никогда не даст E). Следовательно,
в связной конъюнкции должен присутствовать дизъюнкт, кото-
который получается подстановкой из C) или D). Попытка исполь-
использовать C) таким способом приведет в тупик, как легко может
проверить читатель. Используя D), получим:
Р(а,Ца),е),
~Р {у, I (a), v) Р(х, V, е) Р(х, у, а) Р (а, I (а), е).
При подстановке в этот список мы должны заставить первые
три литеры иметь ту же форму, что и какая-нибудь подста-
подстановка в A) или B) или в последнюю литеру из C) (или, быть
может, другая подстановка в D)). Достичь этого можно раз-
различными путями; мы выбираем подстановку у = е, v = / (а).
Тогда первая литера будет иметь вид A), и если мы далее
положим х = 1A(а)), то вторая литера будет иметь вид B).
Это приводит к списку дизъюнктов:
Р (а, I (а), е),
Р (е, I (а), 1(а))Р (/ (/ (а)), / (а), е) Р (/ (/ (а)), е, а) Р (а, I (а), е),
Р(е,/(а),1(а)),
Р(ЦЦа)),Па),е).
Но так как третья литера второго дизъюнкта не имеет себе
партнера, то это еще не есть связная конъюнкция. Дизъюнкты
A) и B) не помогают, поэтому испытаем C):
Р (/ (/ (а)), у, и) Р (и, г, а) Р (у, z, e) P (f (I (a)), е, а).
Здесь первая литера подсказывает подстановку у = / (а), и««в,
и тогда второй дизъюнкт подсказывает подстановку 2"= а.

Устранение лишнего из механических доказательств 177
Таким образом, получим связную конъюнкцию:
Па,1{а),е),
Р (е, I (а), 1{а))Р (I (I (а)), / (а), е) Р (/ (/ (а)), е, а) Р (а, I (а), е).
_
Р (/ (/ (а)), I (а), е) Р (е, а, а) Р (/ (а), а, е) Р (/ (/ (а)), е, а),
Р(е,а, а),
Нескольких применений правила однолитерного дизъюнкта доста-
достаточно, чтобы показать, что эта связная конъюнкция противо-
противоречива.
Остается предложить исчерпывающую процедуру поиска
связных конъюнкций. Мы начнем с замечания, что в связной
конъюнкции, полученной из A) — E), мы могли бы ожидать больше
дизъюнктов, происходящих от A) и B), чем от C) и D). Дело
в том, что каждое использование C) или D) требует от нас
нахождения партнеров для трех литер вида P(U, V, W).
Таким образом, мы можем предположить, что от A) и B)
происходит примерно втрое больше дизъюнктов, чем от C)
или D). Мы можем выразить это предположение в виде отно-
отношения:
3:3: 1:1:1.
Вообще, пусть даны дизъюнкты Сь С2, ..., Ck; сопоставим
им целые числа щ, пъ ..., nk, где njri/ мыслится как отно-
отношение числа ожидаемых дизъюнктов, происходящих от С{,
к числу дизъюнктов, происходящих от С/. Для каждого фикси-
фиксированного значения г, г = 1, 2, 3, ..., существует только конеч-
конечное число существенно различных связных конъюнкций, содер-
содержащих не более чем rnt дизъюнктов, происходящих от каждого
Ct, i=\, 2, ..., k. (Две связные конъюнкции несущественно
различны, если одна может быть получена из другой подходящей
заменой переменных.) Их можно систематически порождать
в процессе поиска всевозможных путей нахождения партнера
для различных литер.
Д. Мак-Илрой предложил интересную схему ллт выпол-
выполнения поиска всех связных конъюнкций для каждого фиксиро-
фиксированного значения г. Эта схема подобна некоторым игровым
алгорифмам, так как она основана на оценке „позиций" и пере-
переходе к „позиции" с наилучшей оценкой.
Список дизъюнктов оценивается следующим образом. Каж-
Каждое вхождение литеры, которое еще не имеет партнера, полу-
12 Зак. 560

178 М. Девис
чает в качестве оценки суммарное число литер из других
дизъюнктов, которые могут быть использованы в качестве
партнеров для него (после подходящей подстановки). Оценка
задачи теории групп начинается следующим образом:
б
Р(е, х, х), A)
Р (/&,*, е), B)
_ 3 _ 3 _ 3 3
Р{х, у, и)Р(и, г, w)P(y, г, v)P{x, v, w), C)
_ 3 _ 3 _ 3 3
Р{у, г, v)P{x, v, w)P{x, у, и)Р{и, z, w), D)
Р(а, Ца), е). E)
Наша стратегия состоит в нахождении партнера сначала для
литеры (или одной из литер) с наилучшей оценкой. Если, как
в нашем случае, эта наилучшая оценка больше, чем 1, то
имеется несколько возможностей. Мы испытаем их все одну за
другой (просмотром вперед) и произведем переоценку. При
этом мы сохраняем литеры с наименьшей минимальной
оценкой. В нашем случае имеются две возможности:
5
Р(е, х, х),
Р(Цх), х, е),
_ I _ 3 _ 2
Р{а, у, и)Р{и, г, е)Р(у, г, 1{а)) Р{а, 1 {а), е),
_ 3 _ 3 _ 3 4
Р{у, г, v)P{x, v, w)P(x, у, и)Р(и, г, w),
Р(а, Ца), е)
с минимальной оценкой 1 и
5
Р(е, х, х),
Р{1(х), х, е),
3 3 3 4
Р(х, у, и)Р(и, г, w)P{y, г, v)P(x, v, ш),
_ 3 _ 3 _ 2
Р{у, 1{а), v)T>(x, v, e)P(x, у, а)Р{а, /(а), е),
Р(а, 1(а), е)
с минимальной оценкой 2.
Следовательно, мы продолжи» рассяотрение первого вари-
варианта. В конце концов нам, может бить, придется вернуться

Устранение лишнего из механических доказательств 179
ко второму либо потому, что не удастся получить никакой
связной конъюнкции, либо потому, что полученная связная
конъюнкция будет непротиворечива. В рассматриваемой задаче
теории групп первой встречается связная конъюнкция, найден-
найденная выше.
Усовершенствование предложенной процедуры, которое,
возможно, обладает некоторыми практическими преимуществами,
состояло бы в попытке объединить связные конъюнкции
с помощью новых подстановок таким образом, чтобы у них
появились общие литеры. Это не является теоретически необхо-
необходимым, но на практике могло бы привести к более быстрым
доказательствам некоторых теорем.
Процедура доказательства, основанная на этих идеях,
в настоящее время программируется на вычислительной машине
IBM 7090 (Лаборатории компании Bell Telephone).
Л ИТЕРАТУР А
1. Черч А., Введение в математическую логику, т. 1, ИЛ, М., 1960.
2. Davis M., Mathematical logic, Mimeographed lecture notes, New York
Univ., Inst. Math. Sciences, New York, 1960.
3. Davis M., Putnam H., A computing procedure for quantification theory,
/. ACM, 7 A960), 201—215.
4. Davis M., Logemann G., Loveland D., A machine program for
theorem-proving, Comm. ACM, 5 A962), 394—397.
5. Dunham В., North J. H., Theorem testing by computer, Proc. Sympos.
Math. Theory Automata, 1962, Polytechnic Press, Brooklyn, N. Y. 1963,
pp. 173—177.
6. Gil more P. C, A proof method for quantification theory, IBM J. Res.
Develop., 4 (I960), 28—35.
7. Гильберт Д., Аккерман В., Основы теоретической логики, ИЛ, М.,
1947.
8 Prawitz D., An improved proof procedure, Theoria, 26 A960), 102—139.
9. Prawitz D., Prawitz H., Voghera N., A mechanical proof proce-
procedure and its realization in an electronic computer, /. ACM, 7 A960),
102-128.
10. Quine W. V. O., Methods of logic, Henry Holt, New York, 1959.
11. Robinson A., Proving a theorem (as done by man, logician or machi-
machine). Summaries of talks at Cornell Summer 1957, Institute for Symbolic
Logic, IDA, Princeton, N. J., 1960, p. 350—352.
12. W a n g H a o. Towards mechanical mathematics. IBM J. Res. Develop,
4 A960), 2—22. (Русский перевод: Бан X а о, На пути к механической
математике, Кибернетический сборник, вып. 5, ИЛ, М., 1962.)
13. W a n g H а о, Proving theorems by pattern recognition, 1, Comm. ACM, 3
A960), 220—234.
H.Wang Hao, Proving theorems by pattern recognition, II, BSTJ, 40
A961), 1—41.
12»

Формализация
и автоматическое доказательство
теорем')
Ван Хао
ОБЩИЙ ОБЗОР
Главная цель этой статьи — привести ряд новых примеров
механизации доказательств в арифметике и исчислении преди-
предикатов, которые, как мы полагаем, позволяют несколько про-
продвинуться в развитии механической математики. Прежде чем
приступить к детальному изложению, дадим в соответствии
с пожеланиями организаторов конференции краткую сводку
известных результатов.
Возможны различные пути использования вычислительных
машин при доказательстве теорем. Чрезвычайно интересная
работа Лемера [23] по доказательству теоретико-числовых тео-
теорем заключается по существу в сведении (человеком) общей
теоремы к ряду сложных численных примеров, которые прове-
проверяются на машинах. Это несомненно разумный путь примене-
применения машин, при помощи которого уже доказаны новые тео-
теоремы. Но здесь мы будем рассматривать применения иного
сорта, отличные от указанного пути, так как машина может
выполнять только численные операции.
В качестве исходных данных не обязательно брать только
аксиомы Пеано (с этим логики, по-видимому, согласятся).
В связи с этим автор рассматривает вопрос о накоплении
запаса стандартных математических результатов, а также до-
допускает возможность частого вмешательства человека. Наш
подход отличает желание применить хорошо известные способ-
способности машин к численным расчетам в области построения логи-
логических выводов.
Среди попыток осуществить такое применение различаются
две основные тенденции, которые можно назвать психоцентри-
психоцентрической и логоцентрической. В принципе различие между ними
невелико. На практике психоцентрический подход обладает
обманчивой привлекательностью, которая часто ведет к разо-
разочарованиям. Во всяком случае, лучше, по-видимому, оценивать
') Wang На о, Formalization and automatic Iheorem-proving, Proceedings
of IFIP Congress 65, v. 1, 1965, p. 51-58.

Формализация и автоматическое доказательство теорем 181
каждую индивидуальную работу по ее конкретным результатам
вместо того, чтобы вдаваться в общие рассуждения.
Известная работа Ньюэла, Шоу и Саймона [25, 26] имела
важные побочные результаты в изучении языков программиро-
программирования; что же касается доказательства теорем, она, по-види-
по-видимому, мало пригодна для этой цели. Кроме того, хотя размы-
размышления по вопросам механического моделирования, вероятно,
могут быть полезны для психолога, трудно предсказать, каким
образом результаты осуществления этих идей на вычислитель-
вычислительных машинах могли бы способствовать прогрессу в области
психологии.
Схема доказательства геометрических теорем, разработанная
Гелернтером и др. [17], дает результаты, которые сначала оза-
озадачивали. Но тщательный анализ Гильмора, по-видимому,
показывает, что достигнуто было много меньше, чем перво-
первоначально казалось. „Авторы составили обычную машинную про-
программу, в которой были реализованы совершенно определен-
определенные алгорифмы" (Гильмор [19], стр. 26).
Слегл [34] написал удачную программу для решения на
машинах проблемы интегрирования в анализе. Было бы инте-
интересно изучить более подробно всю проблему интегрирования.
Программа, которая составлена Бобровым [2] для решения на
машине задач описательной алгебры, тщательно разработана
и снабжена пояснениями. Интересно, что небольшой запас про-
простых средств дает ему возможность манипулировать достаточно
широким кругом английских предложений. Однако вопросы рас-
рассматриваемого нами типа являются побочными для его статьи.
В рамках логоцентрического подхода главное внимание пока
что уделяется исчислению предикатов. Вне исчисления преди-
предикатов некоторые авторы, в частности Коллинз [5], рассматри-
рассматривали разрешающую процедуру Штурма — Тарского для элемен-
элементарной алгебры. Робинсон предложил в несколько ином напра-
направлении систему для теории уравнений [29, 30]. Браун развил
эффективную практическую систему для алгебраических пре-
преобразований [3].
Первая серьезная попытка поставить исчисление предикатов
на машины, по-видимому, относится к лету 1958 г. [36]. Она
дала довольно обнадеживающие результаты. С того времени
было сделано много близких работ как по процедурам дока-
доказательства [4, 6 — 8, 18, 27, 28, 31, 32, 40], так и по разрешающим
процедурам [14— 16, 37] для интересных подклассов. Приятно на-
наблюдать медленный, но неуклонный прогресс по направлению
ко все более и более эффективным процедурам.
Основополагающий для обоих подходов теоретический ре-
результат восходит к творению Сколема и Эрбрана, известному под

182 Ван Хао
названием теоремы Эрбрана. Однако для того, чтобы сделать
теоретически возможные разложения ') практически пригодными,
возникает новая серия вопросов, которая требует более слож-
сложных рассмотрений.
В области разрешимых подклассов исчисления предикатов
Фридман [16] не только дает эффективную программу для
решения вопроса о том, будет ли формула вида
(дг,) ... (xm)(Eyi)(Ey2)(zt) ...(zn)M
теоремой, но также систематически рассматривает вопросы
расширения (дизъюнкты, которые сами о себе заботятся).
Непосредственные обобщения, которые желательно было бы
получить, — это включение равенства и снятие ограничения на
размерность предикатов.
Среди процедур доказательства, изученных на машинах,
наиболее полезными методами, достаточно завершенными к на-
настоящему моменту, являются, по-видимому, методы Чинлунда
и др. [4] и Робинсона [31]. Более эффективная процедура раз-
разработана Робинсоном в работе [32], подобные идеи были неза-
независимо изложены Аандера [1]. Ни один из этих методов не
был реализован на машине, хотя, по-видимому, работа Аандера
содержит больше подробностей, нужных программисту. Для
обоих методов желательно было бы включение равенства.
Ни одна из программ, законченных к настоящему времени,
не смогла вывести примеры ExQ\, ExQ2, ExQ3 (в порядке воз-
возрастания трудности), рассматриваемые ниже. Надеемся, что эти
примеры будут приняты в качестве тестов для новых программ.
Более общий' вопрос состоит в том, является ли метод
эрбрановских разверток достаточным в своей основе. Может
быть необходимо ввести специальные стратегии, которые не
имеют прямых связей с проверкой эрбрановских разверток.
Например, ниже рассматривается стратегия устранения кван-
кванторов подстановкой Fu вместо(Ех)(х = и A Fx) или (х) (х = игэ Fx).
Для механизации рассуждений в случае арифметики сде-
сделано мало. Очень вероятно, что многие пытались сделать это
и нашли задачу слишком трудной. Следующий раздел с при-
примерами из арифметики посвящается предварительному иссле-
исследованию некоторых возможностей. По-видимому, для недале-
недалекого будущего подходящей целью должна быть механизация
доказательств из работы Сколема [33]2).
') Имеются в виду эрбранэвские развертки. — Прим. ред.
2) См. также: Гудстейн Р. Л., Рекурсивная теория чисел (в cflL-*Р»«
курсивный математический анали.»», „Наука", М., 1970). — Прим. ред.

Формализация и автоматическое доказательство теорем 183
Автор в других работах [35—39] уже много рассуждал о буду-
будущем автоматического доказательства теорем и не хочет здесь
повторяться. По-видимому, необходимо подчеркнуть четыре
коротких тезиса.
Хотя формализация есть только часть решения проблемы
(так как для механизации нам нужен, кроме того, метод вы-
выбора следующего шага), весьма желательно выполнить больше
работ по формализации, имея в виду расширение набора точ-
точных приемов. Привлекательная черта этого направления работ —
возможность обойтись без машин. Следовательно, мы имеем
область, где не обязательно пачкать руки. Это помогает раз-
разделению труда.
Нереалистично с самого начала ожидать практических ме-
методов, которые были бы полностью „автоматическими", так
как цель состоит в том, чтобы расширить человеческие способ-
способности, поручив машинам наиболее утомительные шаги (см. [37],
стр. 221, а также [31]).
Поучительно сопоставить возможность механизировать не-
некоторый процесс с возможностью обучить его выполнению.
Монтаж различных методов в более широко применимую
структуру представляет много серьезных трудностей. Например,
булевы операции быстро выполнимы, но если мы введем такие
операции на многих различных стадиях, то существенно, чтобы
на каждой стадии требовалось не слишком много таких опе-
операций.
ПРИМЕРЫ ИЗ АРИФМЕТИКИ
Чтобы доказать некоторую формулу арифметики, мы допу-
допускаем, что она ложна и берем минимальный контрпример МК,
который представляется неопределенной константой. В общем
случае существовательное утверждение (Ex)Fx дает неопреде-
неопределенную константу, которая произвольна, но обладает свой-
свойством F. Кванторы общности опускаются, и используются сво-
свободные переменные. Мы будем использовать а, Ь, с, х, у, г и
т. д. в качестве переменных, m, n, k, xm, ym и т. д. — в каче-
качестве неопределенных констант. Основная стратегия состоит
в том, чтобы выводить утверждения об этих неопределенных
константах в надежде найти противоречивые. Перемен-
Переменные пробегают только положительные целые числа (исклю-
(исключая 0).
Чтобы сделать такой подход практичным, необходимо ис-
использовать некоторый запас известных математических резуль-
результатов ЗР и список TF простых пропозициональных преобразо-
преобразований.

184 Ван Хао
Следующие четыре примера предназначены просто для
иллюстрации того, какого рода преобразования можно делать.
Доказательства становятся все более и более эскизными и ме-
менее механическими. Можно обобщить методы, намеченные ниже,
и получить полную систему арифметики в том смысле, что вся-
всякая теорема обычной аксиоматической арифметической системы
теоретически может быть доказана; однако этот аспект здесь
не будет рассматриваться. Например, чтобы выполнить повтор-
повторные индукции, необходим, кроме МК, обычный выбор мини-
минимальной неопределенной константы.
Пропозициональные постулаты (включая постулаты для ра-
равенства) ограничены пока следующими:
TF1. Если А и A => В, то В.
TF2. Если А, С, (AAC)zd В, то В.
TF3. Если Az=> В и ~]В, то ПЛ.
TF4. Если A => {В V С) и ПС, то А => В.
TF5. Если Л = В и А, то В (обычно для определений).
TF6. Замена равных на равные.
TF7. Если ~]А, вычеркнуть А гэ В.
Основные инструкции (для первого уровня сложности) та-
таковы:
МК. Записать условия для минимальных контрпримеров.
НК. Сформировать неопределенные константы и подставить
их вместо свободных переменных в предыдущие строчки дока-
зат льства.
TFL. Применять TF1—TF7, пока это возможно, к получен-
полученным до сих пор строчкам доказательства, не содержащим сво-
свободных переменных.
TFG. Применять TF1 — TF7 как на основе строчек доказа-
доказательства, так и на основе ЗР, но с ограничением, что хотя бы
одна из посылок взята из доказательства и не содержит сво-
свободных переменных и что заключение не содержит функций и
предикатов, не встретившихся в доказательстве.
ИП. Искать противоречия среди уже полученных строчек
доказательства.
Вводится ряд механизируемых неявных соглашений. Напри-
Например, сложение и умножение коммутативно и ассоциативно.
Так, х^у и х 4- у для ~[х\у, ~]х<у; х<у<г для х<у/\у<г\
а = Ъ и 6 = о —все считаются совпадающими.
За начальный ЗР мы взяли произвольно следующий список
(с широкими возможностями усовершенствования):
81. а <?а\
82. (а<Ь Л.Ь<с)=>а<с;

Формализация и автоматическое доказательство теорем 18R
83. а ^ а;
84. ab — ас zd b = с;
85. х^ у^{х = у V х<у);
86. x = yV x<yV y<x;
87. a^bz^b <?а.
D1. х\х;
D2. (jc |i/ Л ?/|z)=d x|z;
D3. x\yssy = xuxy;
D4. *!/ = z:=>(*|zA 1/1z);
D5. д; I у zd x ^ y.
PI. (Яде Л ж I J/z) =з U I y V x |z);
P2.
На первом этапе предпринимаемого доказательства мы по-
поступаем следующим образом. Начало: A) МК, B) НК, C)
TFL, D) ИП, E) TFG, F) ИП, G) возвращаемся к B) и по-
повторяем. Выход: либо когда противоречие найдено на этапе ИП,
либо когда НК не дает новых подстановок. В последнем слу-
случае требуется более сложное обращение к ЗР.
Пример 1. ExNl. х>1 =>(Еу){РуА у\х).
Используя МК, получаем следующее:
пг>\, A)
PbzDb\m, B)
Ka<mzD(PyaAya\a). C)
Применяем НК:
PmzDml m, D)
l<m<m=>(PymAym\in). E)
Применение TFL и ИП ничего не дает. Прнмемем TFG.
Используя TF7 и В1, можно вычеркнуть E).
Используя D), D1 и TF3, получаем
~]Рт. F)
Далее,
А хт\ т), согласно A), Р2, TF1. G)
В силу F), G), TF5 имеем
(8)
\т. (9)

186 Ван Хао
Применение ИП не дает никакого результата. Возвращаемся
к НК:
Рхт zd xm -f m после подстановки в B) хт вместо Ь, A0)
1 < хт< т гэ (РУхт Л уХт | хт) после подстановки в C)
хт вместо а. A1)
Применяем TFL:
~]Рхт> [(9), 10), TF3], A2)
РуХа, [(8), A1), TF1], A3)
Ухя\хт, [(8), A1), TF1]. A4)
Применение ИП не дает никакого результата. Применяем TFG:
-\Рхт^(КиХт<хт А иХт\хт) в силу (8), Р2, TF1, A5)
КиХт<хт, [A2), A5), TF5], A6)
иХт\хт, [A2), A5), TF5], A7)
уХт\т, [(9), A4), D2, TF2], A8)
«,тК [(9), A7), D2, TF2]. A9)
Применение ИП не дает никакого результата. Возвращаемся
к НК:
РУхя => Ухт -Г гп, B0)
B2)
Применяем TFL:
Ухт*т, [B0), A3), TF1], B4)
1РуХ|я, [B0), A8), TF3], B5)
~]РиХт> [B1), A9), TF3]. B6)
Применяем ИП и находим, что B4) противоречит A8), а B5)
противоречит A3). Следовательно, ExN\ есть теорема арифме-
арифметики.
Для того чтобы доказать следующую теорему, мы расши-
расширяем ЗР, присоединяя:
РЗ. у>1^ПРу^(Кху<у АРХуАху\у)),
В8. {а\ЬЛа\(Ь + с))=за\с,
F1. а^ Ь=>а\Ы;
F2. 1<а!+ 1;
F3. а<а\+ 1;
F4. "jo! + 1 ^ а.

Формализация и автоматическое доказательство теорем 187
Пример 2. ExN2. Рх => {Еу) (Ру Л х< у g xl + 1).
Условие о минимальности оказывается бесполезным, и мы
для краткости его опускаем.
В силу МК:
Рт, A)
Ра => (а ^ т V т! + К а). B)
Применяем НК:
PmD(mgmVm! + Kra), C)
P(m! + l)D(m! + l^mVm! + l<m! + |). D)
Применение TFL и ИП не дает ничего, кроме
т^т\/т\+ \<т, [A), C), TF1]. E)
Применяем TFG:
P(m! + l)Dm! + l^m, [D), Bl, TF4], F)
1Р(т! + 1), [F), F4, TF3], G)
1<т! + 1, [F2 (не обосновывается ограниченным TFG)], (8)
l<jfml+i<m! + l, f(8), G), РЗ, TF1, TF5], (9)
РхтШ, A0)
jcmi+i|m! + l. A1)
Применение ИП ничего не дает. Вернемся к НК:
Рхт1+] =>(xmi+l gm\/m! + l <Arm,+i). A2)
Применяем TFL:
т\ + 1 < хт]+1 в силу (9), A3)
РХтШ^ХтШ ^ Ш, [A2), A3), TF4], A4)
хтш^т, [A4), A0), TF1]. A5)
ПрпнимшкИШ не дает никакого результата. Применяем TFG:
хтш\т\, [A5), Fl, TF1], A6)
*,„,+, |1, [A6), A1), В8, TF2], A7)
Jfmi+i ^ 1, [A7), D5, TF1], A8)
1 <СхтШ, [A8), В7, TF1]. A9)
Но A9) противоречит (9).
Следующие два примера наводят на мысль, что необходимы
более сложные стратегии, такие, как упорядочение всех встре-
встречающихся неопределенных констант, разбиение произведений,
рассмотрение отдельных случаев a = b, a<b, b<a и т. д.

188 Ван Хао
Пример 3. ExN3. Pw zd wx2 ф у2.
Применение МК неоднозначно, так как здесь не одна сво-
свободная переменная. Выбираем следующее:
Pk, A)
km2 = п2, B)
(а < т Л Ь < п) => ka2 ф б2. C)
Существуют различные пути применения НК, большей
частью с тривиальными результатами. Применение TFL срав-
сравнительно бесполезно. Перейдем к либерализованному TFG,
ведущий принцип которого — разбиение произведения. Имеем
k\n2, [D4, B), TF1], D)
т2\п2, E)
k In, [A), D), PI, TF2 (и соглашение о замене А V А на А)], F)
n = xknk, [F), D3, TF5], G)
п2 = k2 {xknf, используя а = Ь => а2 = Ь2,
так как п2 встречается выше, (8)
km2 = k2(xkj, [(8), B), TF6], (9)
m2 = k{xknf, [(9), В4, TF1], A0)
т<п, согласно B), A) и {Ра Л аЬ2 = с2) => Ь<с, A1)
xkn<n, согласно G), A) и {Ра Л ab = с) =) Ь<с. A2)
Подставляем xkn вместо ант вместо b в C):
{xkn<m Atn<n)=>k{xknJ Ф т2, A3)
к{хкп?Фт2, согласно A3), A1), A2), TF2. A4)
Но A4) противоречит A0).
Пример 4.
U = П hi = П г, Л @" ' (У( ^ г/г+i Л Рг/г Л Ру,+1) Л
Л (/)""' (г, ^ 2/+1 Л Ргг Л Рг?+|) => (и = v Л @" ^ =
Возьмем минимальный контрпример x = k. Если yx=zu то
II У1 = Г1 2/ < ft. Если t/i < 2|, то г/, П г,- < П г, и i/, делит обе
части неравенства. Отсюда г/,| (z, — г/,)Ц г,-. Так как Pz,, то
Ш ц
Vi -f B1 - г/i) и ir, |гг<... гЛ. Отсюда г/, Д ^« = (*¦ - г/,) П *г < А;.

Формализация и автоматическое доказательство теорем 189
ПРИМЕРЫ НА ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
Вместо того чтобы доказывать, что данная формула является
теоремой, мы берем ее отрицание и выводим противоречие.
Будем использовать для неопределенных констант запись, по-
подобную записи их в разделе с примерами из арифметики.
Основной пример настоящего раздела следующий:
Пример 1. ExQl. Вывести противоречие из конъюнкции:
тфп, A)
пфк, B)
кфт, C)
y = mV\Fym = (Ег) {z Ф т А г ф у A Fyz A Fzy)], D)
у = п V \Fyn= ~]{Ez) (z Ф п A z Ф у A Fyz A Fzy)], E)
y = kV[Fyk^(y = mVy = n)]. F)
Имеются еще два родственных, но более трудных примера.
Пример 2. ExQ2. Заменить B) и C) в ExQl на
(П = k V k = т) и B')
y = k). C')
Пример 3. ExQ3. Вычеркнуть B') из ExQ2.
Не будем обсуждать здесь эти довольно трудные примеры.
Для более интуитивного понимания указанных примеров сле-
следует мыслить F как отношение принадлежности е.
Существуют три до некоторой степени различных метода
решения ExQl.
Первый метод —использовать разрешающую процедуру для
специального префикса. Таким способом мы приводим конъюнк-
конъюнкцию к предваренной форме с префиксом
(Em)(En)(Ek)(y)(z)(Eu)(Ev).
Если в программе, которую дает Фридман [16], удалить
искусственные ограничения и присоединить методы обращения
с равенством, то с примером ExQ\, по-видимому, можно
справиться.
Второй метод. Подставим т, п, k вместо у в D), E), F),
т. е. действуем почти так же, как прежде с НК. Из девяти
возможных подстановок три дают тривиальные результаты
(т вместо у в D) и т. д.). М.ы рассмотрим ровно четыре из

190 -¦ Ван Хао
остальных шести и упростим их с помощью A), B), C), k = k,
п = п:
Fkm = (?2) {гфтАгфк AFkz A Fzk), k вместо у в D), G)
Fkn = ~] (?z) {гфпАгфк A Fkz A Fzk), k вместо у в E), (8)
Fmk, m вместо у в F), (9)
Fnk, n вместо у в F). A0)
Попытаемся использовать (Ez), применяя ЭЮЮЯШИЯГСность
Gw = (Ez)(z = w A Gz). Из F) получаем:
(Fyk А У Ф k А У Ф tn)zDу = п;
(Fyk АуфкАу?=п)=эу = т.
Поэтому мы можем добавить у = п к правой части G) и
у = т к правой части (8). Таким образом, исключая Ez в обоих
¦случаях, получаем:
Fkm = (пфтАпфкА Fkn A Fnk),
Fkn = ~](т Ф п А т ф k A Fkm A Fmk).
Используя A) и B), сделаем упрощения:
, ... Fkm = {FknAFnk), A1)
сп . Fkn **П Fkm VI Fmk), A2)
:... Fkn= ~\Fkm, согласно (9) и A2), A3)
.,,.,,„..,,.< Fkm^Fkn, согласно A0) и A1). A4)
Согласно A3) и A4), Fkm=~]Fkm, имеем противоречие.
Третий метод. Кванторы и = в D) и E) исключаем более
механическим способом, что дает:
V (и = mV и = у V 1 FyuV I Fuy)] A
(хуФтАХуФуАРухуЛРхуу)\, D')
v = yV IFyvV ~]Fvy)]A
A[y = nV Fyn V (ЮуФпЛЮуфу Л Fywy A Fwyy)]. E')
Задача заключается в выводе противоречия из A), B), C)
D'), E') и F). Мы записываем каждый дизъюнкт в конъюнк-
конъюнктивной нормальной форме, так что результат является конъюнк-
конъюнкцией многих дизъюнктов:
A);
B);
C);

Формализация и автоматическое докааьтельство теорем 191
D.1) y = mV ~]FymV Хуфпг;
D.2) y = mV ~[FymV хуфу;
D.3) y = mV ~]Fymy Fyxy;
D.4) у = m V 1 Fym V Fxyy;
D.5) y = mV Fym V
E.1) y = ny Fyny
E.2) y = n\J Fyn\J
E.3) y = nV FynV y
E.4) y = nV FynV Fwyy;
E.5) j/ = nV ~]FynVv = n\/v = yV lFyv\/~\Fvy;
F.1) y = k\l уфт\/ Fyk\
F.2) у = к\/уфпу Fyk;
F.3) j/ = &v y = my y = nV ~\Fyk.
Подставляем m вместо г/ в F.1), используя тфИ и т = т:
Fmk, A5)
[л вместо г/ в F.2), пфк, п = п], A6)
= nV m = kV ~]FkmV ~]Fmk,
k вместо унт вместо у в E.5), A7)
~]Fkm, используя A)-C), A5), A7), A8)
FkmV ~\Fkn, k вместо у и п вместо и в D.5),
используя A), B), C), A6), A9)
~]Fkn, используя A8), A9), B0)
хвиФп, шкф1г, Fkwk, Fwkk, k вместо у в E.1) —E.4),
используя B) и B0), B1)
wk = m, wk вместо у в F.3), используя B1), B2)
Fkm, используя B1) и B2), B3)
хкфт, хкФк, Fkxk, Fxkk, k вместо у в D.1)-E.4),
используя C) и B3) B4)
xk = п, xh вместо у в F.3), используя B1), B5)
Fkn, используя B4), B5). B6)
Отсюда видно, что B0) и B6) противоречат друг другу.
Это доказательство довольно близко по характеру к дока-
доказательству, полученному Чинлундом и др. [4]. Действительно,
если мы обобщим метод Чинлунда и др. [4], присоединив ра-
равенство и исключив лишние шаги, машина, вероятно, сможет
выдать в разумное время доказательство, более или менее по-
похожее на данное. Если оставить в стороне вопрос о равенстве,
имеется существенное теоретическое различие между методом

192 Ван Хао
Чинлунда и др. [4] и приведенным доказательством, а именно:
приведенное доказательство не использует предваренной нор-
нормальной формы. Такое усовершенствование предложено в дис-
диссертации Эрбрана (см. также [9, 20, 38]) и требует несколько
более тщательного обоснования [10], чем метод, использующий
предваренную форму.
ЛИТЕРАТУРА
1. Aanderaa S., A deterministic proof procedure (manuscript), Harvard,
May 1964.
2. Bobrow D. G., Natural language input for a computer problem-solving
system, Ph. D. thesis, MIT, September 1964.
3 Brown W. S., The ALPAK system, MM-63-1214-3, Bell Laboratories,
April 1963
4. С h i n 1 u n d Т., Davis M., Hinman P. G., Mcllroy D., Theorem-
proving by machine, Bell Laboratories, Spring 1964.
5. Collins G. E., Computational reductions in Tarski's decision method for
elementary algebra, IBM Corporation, Yorktown Heights, July 1962.
6. DavisM., Putnam H., A computing procedure for quantification theory,
/. ACM, 7 A960), 201—215.
7. Davis M., Logemann G., Loveland D., A machine program for
theorem-proving, Comm. ACM, 5 A962), 394—397.
8. Davis M., Eliminating the irrelevant from mechanical proofs, Proceedings
of Symposium in Applied Mathematics, American Mathematical Society,
v. 15, 1963. (Русский перевод: Девис М., Устранение лишнего из ме-
механических доказательств, см. настоящий сборник, стр. 160.)
9. Dreben В., Andrews P, Aanderaa S., False lemmas in Herbrand,
Bull. Am. Math Soc, 69 A963), 699—706.
10. Dreben В., Wang H., A refutation procedure and its model-theoretic
justification (manuscript), Harvard University, November 1964.
11. Dunham В., Fridshal R., Sward G. L., A nonheuristic program for
proving elementary logical theorems, Proc. of the First International Con-
Conference on Information Processing, Paris, 1959; pub. Unesco, 1960,
pp. 282—285.
12. Dunham В., Fridshal R., North J., Exploratory mathematics by
machine, Recent Development in Information and Decision Processes, Ro-
Robert E. Machol and Paul Grey (eds.), MacMillan, N. Y., 1%2. (Proceedings
of a Symposium at Purdue University, April 1961).
13. Dunham В., North J. H., Theorem testing by computer, paper presented
April 24—26, 1962, Mathematical Theory of Automata, Polytechnic Press,
Brooklyn, 1963, p. 173—177.
14. Friedman J., A semidecision procedure for the functional calculus,
/. ACM, 10 A963), 1—24.
15. Friedman J., A computer program for a solvable case of the decision
problem, /. ACM, 10 A963), 348—356.
16. Friedman J., A new decision procedure in logic and its computer reali-
realization, Ph. D. thesis, Harvard University, September 1964.
17. Gelernter H., Hanson J. R., Loveland D. W., Empirical investi-
investigations of the geometry theorem machine, Proceedings of the Western
Joint Computer Conference, San Francisco, 1960, pp. 143—149.
18. Gilmore P. C, A proof method for quantification theory — its justifica-
justification and realization, IBM Journal of Research and Development, 4 A960),
28-35.

Формализация и автоматическое доказательство теорем 193
19. Gilmore P. С, An examination of the geometry theorem machine, IBM
Corporation, Yorktowtl Heights, April 1962.
20. H e r b r a n d J., Recherches sur la theorie de la demonstration, Travaux
de la Societe des Sciences et des Lettres de Varsovie, Cl. Ill, Math. Phys.,
33 A930).
21. К anger S., A simplified proof method for elementary logic, Computer
Programming and Formal Systems, P. Braffort and D. Hirschberg (eds.),
North-Holland Publishing Co., Amsterdam, 1963, pp. 87—94. (Proceedings
of Seminars at Blaricum, Holland in 1961.)
22. К u г о d a S., An investigation of the logical structure of mathematics,
XIII, A method of programming proofs in mathematics for electronic com-
computers, Nagoya Math. J., 16 A960), 195—203.
23. Lehmer D. H., Some high speed logic, Proceedings symposium in App-
Applied Mathematics, American Mathematical Society, v. 15, 1963.
24. M с С a r t h у J., Computer programs for checking mathematical proofs,
AMS Symposium on Recursive Function Theory, New York, April 1961.
25. Newell A., Shaw J. C, Simon H. A., Empirical explorations of the
logic theory machine, Proceedings of the Western Joint Computer Confe-
Conference, 1957.
26. Newell A., Shaw J. C, A variety of intelligent learning in a general
problem solver, Self-Organizing Systems, M. С Yovits and S. Cameron
(eds.), New York, Pergamon Press, 1560, pp. 153—189. См. русский пере-
перевод в сб. «Самоорганизующиеся системы», стр. 211—261, «Мир», М., 1964.
27. Р г a w i t z D., Prawitz H., Voghera N., A mechanical proof proce-
procedure and its realization in an electronic computer /. ACM, 7 A960),
102—128.
28. P r a w i t z D., An improved proof procedure, Theoria (a Swedish Journal
of Philosophy and Psychology), 26 A960), 102—139.
29. Robinson A., On the mechanization of the theory of equations, Bulletin
of the Research council of Israel, 9F A960), 47—70.
30. Robinson A., A basis for the mechanization of the theory of equations,
Computer Programming and Formal Systems, pp. 95—99.
31. Robinson J. A., Theorem-proving on the computer, /. ACM, 10 A963),
163-174.
32. Robinson J. A., A machine-oriented logic based on the resolution prin-
principle, J. ACM, 12 A965), 23—41. (Русский перевод: Робиисои Дж. А.,
Машинио-ориентированная логика, основанная на принципе резолюции,
см. настоящий сборник, стр. 194.)
33. Skolem Th., BegrQndung der Elementaren Arithmetik, 38 pp., Oslo, 1923.
34. S 1 a g 1 e J. R., A heuristic program that solves symbolic integration pro-
problems, Ph. D. thesis, MIT, May 1961.
35. Wang H., A variant to Turings theory, /. ACM, 4 A957), 63—92.
36. Wang H., Toward mechanical mathematics, IBM Journal of Research
and Development, 4 A960), 2—22. (Русский перевод: см. [12] на стр. 179.)
37. Wang H., Proving theorems by pattern recognition, «I», Comm. ACM, 3
A960), 220—234; «II», Bell System Tech. J., 40 (I960), 1—41.
38. Wang H., Mechanical mathematics and inferential analysis. Computer
programming and Formal Systems, P. Braffort and D. Hirschberg (eds.),
North-Holland Publishing Co., Amsterdam, 1963, pp. 1—20 (Proceedings
of the seminars at Blaricum, Holland 1961.)
39. Wang H., The mechanization of mathematical arguments, Proceedings of
the Symposium in Applied Mathematics, v. 15, 1963, pp. 31—40.
.40. Wos L., Carson D., Robinson G., The unit preference strategy in
theorem proving, Proceedings Fall Joint Computer Conference, 1964,
pp. 615—621; IBM 704, Argonne National Laboratory Report ANL-6447,
1961, 46 pp.
13 Зак. 560

Машинно-ориентированная логика,
основанная на принципе резолюции1)
Дж. А. Робинсон
Исследуется возможность увеличения эффективности и расширения об-
области практической применимости машинного доказательства теорем, исполь-
использующего процедуры, базирующиеся на основополагающей теореме Эрбрана
для исчисления предикатов первого порядка. Тщательное исследование про-
процесса подстановки (термов вместо переменных) и процесса проверки резуль-
результатов таких подстановок на тавтологичность показывает, что оба процесса
могут быть соединены в один новый процесс (называемый резолюцией),
итерирование которого гораздо более эффективно, чем прежняя циклическая
процедура, состоящая в чередовании шагов подстановки и шагов проверки
на тавтологичность.
Теория резолюционного процесса представлена в виде системы логики
первого порядка, состоящей из единственного правила вывода (принципа
резолюции). Доказана полнота этой системы; простейшей процедурой поиска
доказательства, основанной на этой системе, является прямое использование
доказательства полноты. Однако эта процедура совершенно неэффективна,
и работа завершается обсуждением нескольких принципов (называемых прин-
принципами поиска), которые применимы для построения эффективных процедур
поиска доказательства, использующих резолюцию как основной логический
процесс.
1. ВВЕДЕНИЕ
В настоящей работе приведена формулировка логики пер-
первого порядка, специально предназначенная для использования
в качестве теоретического аппарата машинных программ дока-
доказательства теорем. Предшествующие программы доказательства
теорем были основаны на системах логики первого порядка,
которые первоначально предназначались для других целей.
Характерной чертой этих логических систем, которая отсут-
отсутствует у описанной в этой работе системы, является относи-
относительная простота их правил вывода.
По традиции в силу прагматических и психологических при-
') Robinson J. A., A machine-oriented logic based on the resolution
principle, Journal of the Association for Computing Machinery, 12, № 1 A965),
23-41.

МашинноориенТироваНная логика, основйнная на принципе резолюции 195
чин обычно требуют, чтобы каждый отдельный шаг в дедукции
был, вообще говоря, прост настолько, чтобы человек понял
его правильность за один интеллектуальный акт. Эта традиция,
вне сомнения, связана с желанием, чтобы каждый отдельный
шаг был неоспоримым, даже если вся дедукция состоит из
длинной цепи таких шагов. Окончательное заключение дедук-
дедукции, если она правильна, логически следует из посылок, исполь-
использованных в дедукции, но человеческий ум вполне может найти
этот скачок от посылок к заключению удивительным, а потому
(психологически) сомнительным. Отчасти поэтому логический
анализ дедуктивных рассуждений состоит в сведении сложных
выводов, которые не могут быть охвачены человеческим умом
за один шаг, к цепочкам более простых выводов, каждый из
которых может быть постигнут человеческим умом за один шаг.
Однако с теоретической точки зрения от правила вывода
требуется только, чтобы оно было корректным (т. е. позволяло
выводить лишь логические следствия посылок) и эффективным
(т. е. должно быть алгорифмически проверяемо, является ли
предполагаемое применение этого правила вывода в действи-
действительности его применением). Когда правило вывода применяет
современная вычислительная машина, традиционное ограниче-
ограничение на сложность правил вывода более не является разумным.
Становятся доступными более мощные правила, требующие,
быть может, много больше комбинаторной обработки инфор-
информации для одного применения.
В системе, описанной в этой работе, используется одно
такое правило. Оно называется принципом резолюции, и в свете
предыдущего замечания оно скорее ориентировано на машину,
чем на человека. Принцип резолюции является очень мощным
как в психологическом смысле, ибо он допускает отдельные
шаги, которые человеческий ум часто может постичь лишь
путем рассуждения, так и в теоретическом смысле, ибо он
один в качестве единственного правила вывода образует пол-
полную систему логики первого порядка. Хотя второе свойство
не очень важно, интересно отметить, что (насколько известно
автору) никакая другая полная система логики первого порядка
не состоит из единственного правила вывода, если считать пра-
правилами вывода (беспосылочными) логические аксиомы, заданные
явно или в виде схемы.
Основное преимущество принципа резолюции состоит в том,
что он позволяет избежать одного из основных комбинаторных
препятствий к достижению эффективности, которое погубило
предыдущие процедуры доказательства теорем.
В следующем разделе объясняются синтаксис и семантика
того формализма, который используется в настоящей работе.
13*

196 Дж. Робинсон
2. ПРЕДВАРИТЕЛЬНЫЕ ФОРМАЛЬНОСТИ
Формализм, используемый в настоящей работе, основан
скорее на понятиях невыполнимости и опровержения, чем иа
понятиях общезначимости и доказательства. Известно (ср. [2]
и [5]), что задачу о проверке произвольного множества вы-
высказываний на выполнимость можно свести к проверке на вы-
выполнимость конечного множества S, состоящего из высказы-
высказываний в предваренной форме без кванторов существования
в префиксе1); кроме того, можно предполагать, что матрица
каждого высказывания из S есть дизъюнкция формул, каждая
из которых или является атомарной формулой, или отрица-
отрицанием атомарной формулы. Поэтому наш синтаксис устроен
таким образом, что естественной синтаксической единицей
является конечное множество S высказываний, имеющих эту
специальную форму. Кванторный префикс в каждом высказы-
высказывании опускается, поскольку он состоит только из кванторов
общности, связывающих все переменные этого высказывания;
далее, матрица каждого высказывания рассматривается про-
просто как множество ее дизъюнктивных членов, поскольку по-
порядок и кратность членов дизъюнкции несущественны.
В соответствии с этим мы даем следующие определения
(отчасти следуя терминологии работ [2] и [5]).
2.1. Переменные. Следующие символы являются перемен-
переменными:
и, v, w, х, у, z, «,, о„ да,, хи уи z,, и2, . .. и т. д.;
порядок, в котором они перечислены, называется алфавитным.
2.2. Символы функций. Следующие символы являются сим-
символами га-местных функций для каждого га^О:
ап Ъп с" dn en fn an hn kn an hn и т и •
u,u,c,u,nti,g,n,K,ui,ol, ... и т. д.,
порядок, в котором они перечислены, называется алфавитным.
В случае га = 0 верхний индекс может быть опущен. Символы
0-местных функций являются индивидными константами.
2.3. Символы предикатов. Следующие символы являются
символами л-местных предикатов для каждого га^О:
Р", Qn, Rn, P?, Qr- #f. РЬ • • • и т. д.;
порядок, в котором они перечислены, называется алфавитным.
Верхний индекс может быть опущен при п — 0.
2.4. Символ отрицания- Следующий символ является сим-
символом отрицания: ~\.
1) См. статью М. Девиса в настоящем сборнике, стр. 160. — Прим. ред.

Машинно-ориентированная логика, основанная на принципе резолюции 197
2.5. Алфавитный порядок символов. Множество всех симво-
символов вполне упорядочено в алфавитном порядке посредством
добавления к предыдущим соглашениям о порядке следую-
следующего правила: переменные предшествуют символам функций,
символы функций предшествуют символам предикатов, сим-
символы предикатов предшествуют символу отрицания, символы
функций меньшей размерности предшествуют символам функ-
функций большей размерности, а символы предикатов меньшей
размерности предшествуют символам предикатов большей раз-
размерности.
2.6. Термы. Переменная является термом; последователь-
последовательность символов, состоящая из символа га-местной функции
(п'^0), за которым следует п термов, является термом.
2.7. Атомарные формулы. Последовательность символов,
состоящая из символа га-местного предиката (и^О), за кото-
которым следует п термов, является атомарной формулой.
2.8. Литеры. Атомарная формула является литерой; если
Л —атомарная формула, то ~~] А является литерой.
2.9. Дополнения. Если Л —атомарная формула, то две ли-
литеры Л и ~] Л называются дополнениями друг друга и обра-
образуют в любом порядке контрарную (complementary) пару.
2.10. Дизъюнкты. Конечное (быть может, пустое) множество
литер называется дизъюнктом (clause). Пустой дизъюнкт обо-
обозначается через ?•
2.11. Фундаментальные литеры. Литера, не содержащая пе-
переменных, называется фундаментальной литерой.
2.12. Фундаментальные дизъюнкты. Дизъюнкт, все члены
которого являются фундаментальными литерами, называется
фундаментальным дизъюнктом. В частности, ? является фун-
фундаментальным дизъюнктом.
2.13. Правильно построенные выражения. Термы и литеры
являются (единственными) правильно построенными выраже-
выражениями.
2.14. Лексикографический порядок правильно построенных
выражений. Множество всех правильно построенных выраже-
выражений вполне упорядочено в лексикографическом порядке посред-
посредством следующего правила: Л предшествует В только в том
случае, когда Л короче В, или Л и В имеют равную длину,
но на первом месте, где А и В имеют разные символы, в Л
стоит более ранний, согласно алфавитному порядку.
При написании правильно построенных выражений с целью
иллюстрации мы будем придерживаться более удобного для
чтения способа, заключая п термов, следующих за символом
га-местной функции или предиката, в круглые скобки и раз-
разделяя термы запятыми, если их более двух. В этом случае

198 Дж. Робинсон
мы можем опустить все верхние индексы, не вызывая недора-
недоразумений. При записи конечных множеств мы придерживаемся
обычного соглашения о заключении членов в фигурные скобки
и разделении членов запятыми, помня, что порядок записи
членов безразличен.
2.15. Эрбрановский универсум. Любому множеству S
дизъюнктов следующим образом сопоставляется множество фун-
фундаментальных термов, называемое эрбрановским универсумом
для S: пусть F — множество всех символов функций, входя-
входящих в S. Если F содержит какой-либо символ 0-местной
функции, то функциональный словарь для S совпадает с F;
в противном случае он есть множество {a}\JF. Эрбрановский
универсум для S состоит из всех фундаментальных термов,
в которых встречаются лишь символы из функционального
словаря для S.
2.16. Насыщение. Если S — множество дизъюнктов, а Р —
множество термов, то через P(S) мы обозначаем насыщение
S над Р, которое является множеством всех фундаменталь-
фундаментальных дизъюнктов, получаемых из членов S такими заменами
переменных членами Р, при которых все вхождения одной и
той же переменной в какой-либо дизъюнкт заменяются на
вхождение одного и того же терма.
2.17. Модели. Множество фундаментальных литер, не со-
содержащее контрарных пар, называется моделью. Пусть М —
модель, a S —множество фундаментальных дизъюнктов; тогда
М называется моделью для S, если каждый дизъюнкт из S
содержит некоторый член М. В общем случае, если 5 —произ-
—произвольное множество дизъюнктов, а Я —эрбрановский универсум
для S, мы говорим, что М есть модель для 5 тогда н только
тогда, когда М есть модель для H{S).
2.18. Выполнимость. Множество 5 дизъюнктов является
выполнимым, если существует модель для S; в противном
случае S невыполнимо.
Из определения выполнимости ясно, что любое множество
дизъюнктов, содержащее ?, невыполнимо и что пустое мно-
множество дизъюнктов выполнимо. Эти два обстоятельства пока-
покажутся вполне естественными в ходе развития нашей системы.
Ясно также, что в соответствии с нашими семантическими
определениями каждый непустой дизъюнкт интерпретируется
(согласно объяснению в неформальных замечаниях в начале
этого раздела) как замыкание всеобщности дизъюнкции литер,
из которых этот дизъюнкт состоит.
2.19. Фундаментальные резольвенты. Если С и D — два
фундаментальных дизъюнкта и L^C, MeD-два одночлен-
одночленных множества, элементы которых образуют контрарную пару,

Машинно-ориентированная логика, основанная на принципе резолюции 199
то фундаментальный дизъюнкт (С — L) U (О — М) называется
фундаментальной резольвентой С и D.
Ясно, что любая модель для {С, D} является также мо-
моделью для {С, D, R), где R — фундаментальная резольвента С
и D. Не все пары фундаментальных дизъюнктов имеют фун-
фундаментальные резольвенты, а некоторые имеют более одной;
однако в любом случае, как явствует из определения, два фун-
фундаментальных дизъюнкта имеют конечное число фундаменталь-
фундаментальных резольвент.
2.20. Фундаментальная резолюция. Если S — множество фун-
фундаментальных дизъюнктов, то фундаментальной резолюцией 5,
обозначаемой через 0i(S), является множество фундаменталь-
фундаментальных дизъюнктов, состоящее из всех элементов S и всех фун-
фундаментальных резольвент всех пар элементов S.
2.21. N-я фундаментальная резолюция. Если S — множество
фундаментальных дизъюнктов, то га-я фундаментальная резо-
резолюция 5, обозначаемая через Ж1 (S), определяется для каж-
каждого п^О следующим образом: $?°(S) = S; для каждого
()())
Этим завершается первая часть определений. Следующий
раздел посвящен различным формам, которые принимает тео-
теорема Эрбрана в нашей системе. Для каждой такой формы
имеется некоторый тип процедуры опровержения, которую эта
форма подсказывает и оправдывает. Основная формулировка
такова (ср. [2, 4]):
Теорема Эрбрана. Если S — произвольное конечное
множество дизъюнктов, Н — его эрбрановский универсум, то S
невыполнимо тогда и только тогда, когда некоторое конечное
подмножество эрбрановского универсума H(S) является невы-
невыполнимым.
3. ПРОЦЕДУРА НАСЫЩЕНИЯ
Как отмечено в работе [5], теорему Эрбрана можно выра-
выразить в следующей форме.
Теорема 1. Если S — произвольное конечное множество
дизъюнктов, то S невыполнимо тогда и только тогда, когда
Р (S) невыполнимо для некоторого конечного подмножества Р
эрбрановского универсума для S.
Эта формулировка теоремы Эрбрана подсказывает следую-
следующий тип процедуры опровержения, которую мы назовем про-
процедурой насыщения: по данному конечному множеству S
дизъюнктов выбирается последовательность Ро, Рх, Р2, ¦ ¦ ¦ ко-
конечных подмножеств эрбрановского универсума Н для S, та-

200 Дж. Робинсон
кая, что Pj^Pl+] для каждого /^0 и (J Р, = Н. Затем по-
/=о
очередно проверяются на выполнимость множества P0(S), P, (S),
P2(S), .... Ясно, что каково бы ни было конечное подмноже-
подмножество Р множества Я, имеем PsP/ для некоторого / и, сле-
следовательно, P(S)sPy(S). Следовательно, по теореме 1, если
S невыполнимо, то для некоторого / подмножество P,{S) не-
невыполнимо.
Конечно, любая конкретная процедура такого типа должна
осуществлять выбор Ро, Ри Р2, ... одинаково для всех ко-
конечных множеств дизъюнктов. Самым естественным методом
такого выбора является использование так называемых уров-
уровней #0, Я,, #2, ... эрбрановского универсума Я, где Яо со-
состоит из всех индивидных констант эрбрановского универсума
Я, а Я„+1 для п ^ 0 состоит из всех термов эрбрановского
универсума Я, которые входят в Нп или чьи аргументы вхо-
входят в Нп. В работе [5] мы назвали процедуру, использующую
этот метод, процедурой насыщения уровня. Там же было отме-
отмечено, что процедуры Гильмора [4] и Девиса — Патнэма [2] по
существу являются процедурами насыщения уровня.
Основным комбинаторным препятствием для достижения
эффективности процедур насыщения уровня является огромная
скорость роста конечных множеств Ht и Я,- (S) с ростом / по
крайней мере для большинства интересных множеств S. Эта
скорость роста до некоторой степени проанализирована в [5],
там же приведены примеры совсем простых невыполнимых S,
для которых первое невыполнимое Я,- (S) столь велико, что
лежит далеко за пределами достижимости.
Интересное эвристическое замечание состоит в том, что
для каждого конечного множества S дизъюнктов, которое не-
невыполнимо и для которого фактически можно построить опро-
опровержение, существует по крайней мере одно конечное подмно-
подмножество эрбрановского универсума для S, имеющее приемлемые
размеры, такое, что Р (S) невыполнимо, причем Р минимально
(в том смысле, что Q (S) выполнимо для любого собственного
подмножества Q множества Р). Такое Р было в [5] названо
доказательным множеством для S. Если бы в этих условиях
нашелся всезнающий и благосклонный демон, который мог бы
снабжать нас в приемлемое время доказательным множест-
множеством Р для каждого невыполнимого конечного множества S
дизъюнктов, которое мы рассматриваем, то мы могли бы про-
просто начать насыщать S над Р и потом извлечь подходящее
опровержение множества S нз окончательного конечного не-
невыполнимого множества P(S) фундаментальных дизъюнктов.

Машинно-ориентированная логика, основанная на принципе резолюции 201
Такова была в сущности основная схема машинной програм-
программы, описанной в [5], где роль такого демона играет в меру
своей изобретательности математик, использующий эту про-
программу. Однако в действительности хотелось бы моделировать
на машине самого „демона доказательства"; однако об этом,
казалось интуитивно, не может идти и речи.
Тем не менее ситуация здесь не такая уж безнадежная.
В частности, метод, развитый в остальных разделах этой
статьи, по-видимому, достаточно хорошо моделирует требуе-
требуемого демона посредством вычислительного процесса. В четвер-
четвертом разделе мы сделаем первый основной шаг к развитию
этого метода, доказав новые формы теоремы Эрбрана. Мы
также дадим предварительный неформальный обзор остальных
идей, откладывая строгое рассмотрение до следующих разде-
разделов.
4. ТЕОРЕМЫ О РЕЗОЛЮЦИИ И ОСНОВНАЯ ЛЕММА
Как специальный метод проверки конечных множеств фун-
фундаментальных дизъюнктов на выполнимость, метод Девиса —
Патнэма [4] вряд ли можно улучшить с точки зрения эффек-
эффективности. Тем не менее здесь мы приведем другой метод, го-
гораздо менее эффективный, который играет только теоретическую
роль в нашем построении и который формулируется много про-
проще: по данному конечному множеству S фундаментальных
дизъюнктов строятся последовательно множества S, Si{S),
0P{S), ..., пока какое-нибудь Ж1 (S) будет содержать ? или
не будет содержать ?, но будет совпадать с 0?n+1 (S). В пер-
первом случае S невыполнимо, во втором случае S выполнимо.
Рано или поздно одно из этих условий конца должно выпол-
выполниться, поскольку число различных дизъюнктов, построенных
из конечного множества тех литер, которые входят в S, ко-
конечно и, следовательно, в бесконечной последовательности вло-
вложенных множеств
4.1. S?^(S)cf(S)c...gr(S)c... не все включе-
включения являются собственными, так как резолюция не вводит
новых литер.
Ввиду того что описанный процесс рано или поздно обо-
оборвется, мы можем доказать его корректность в смысле, сформу-
сформулированном выше, в виде теоремы о фундаментальной резо-
резолюции.
Теорема о фундаментальной резолюции. Если
S. есть произвольное конечное множество фундаментальных
дизъюнктов, то S невыполнимо тогда и только тогда, когда &п (S)
для некоторого га ^ 0 содержит ?.

202 Дж. Робинсон
Доказательство. Часть „тогда" очевидна. Чтобы дока-
доказать часть „только тогда", предположим, что Т — заключитель-
заключительное множество в последовательности D.1), так что Т замкнуто
относительно фундаментальной резолюции. Нам надо лишь
показать, что если Т не содержит П, то Т выполнимо и, сле-
следовательно, S выполнимо, ибо S^T. Пусть Lu ..., Lk — все
различные атомарные формулы, которые входят в Т (быть
может, со знаком ~\). Пусть М — модель, определяемая сле-
следующим образом: Мо — пустое множество, и для каждого /,
0</<?, множество Mt есть множество Mj-x\]{Lj}, если ника-
никакой дизъюнкт из Т не состоит лишь из дополнений литер из
множества Му_,11{?Д; в про^ ном случае Mf есть множество
Mj-iUiiLj}. Наконец, М есть Mk. Если Т не содержит ?,
то М есть модель для Т. Действительно, в противном слу-
случае существует наименьшее /, 0<j^.k, такое, что некоторый
дизъюнкт (скажем, С) в Т состоит целиком из дополнений литер
множества М}. Следовательно, по определению М/ есть
Му_, U{~1 Lj}. Поэтому ввиду минимальности ;' дизъюнкт С со-
содержит Lj. Но поскольку Mj есть Af/_, (J {~~| Z-у}, существует не-
некоторый дизъюнкт (скажем, D) в Т, который состоит целиком
из дополнений литер множества М;_, (J {Z-y}. Поэтому ввиду
минимальности / дизъюнкт D содержит ~\L}. В таком случае
дизъюнкт B = (C — {Lj})[}(D — {~\Lj}) состоит целиком из допол-
дополнений литер множества Mj-U если В не есть ?. Но В —это
фундаментальная резольвента С и D, поэтому В входит в Т
и, следовательно, В отлично от D. Но это противоречит мини-
минимальности /, и теорема доказана.
Теорема о фундаментальной резолюции позволяет сформу-
сформулировать более специальную форму теоремы 1.
Теорема 2. Если S — произвольное конечное множество
дизъюнктов, то S невыполнимо тогда и только тогда, когда для
некоторого конечного подмножества Р эрбрановского универ-
универсума для S и некоторого п^Орезолюция Ж1 (Р (S)) содержит ?.
Теперь стало возможным изложить неформально основные
шаги оставшейся части построения. Мы обобщим понятия фун-
фундаментальной резольвенты и фундаментальной резолюции до
понятий резольвенты и резолюции соответственно, устранив
условие фундаментальности дизъюнктов. Любые два дизъюнкта
будут тогда иметь нуль, один или более дизъюнктов в качестве
своих резольвент, но в любом случае лишь конечное множество.
В специальном случае, когда С и D являются фундаменталь-
фундаментальными дизъюнктами, их резольвенты, если они существуют,

Машинно-ориентированная логика, основанная на принципе резолюции 203
являются в точности их фундаментальными резольвентами, со-
согласно вышеприведенному определению. Аналогично обозначе-
обозначения 31 (S), Ж1 (S) будут сохранены, но S будет произвольным
множеством дизъюнктов. Тогда $(S) будет обозначать резо-
резолюцию S, которая будет множеством, состоящим из всех эле-
элементов S и всех резольвент всех пар элементов S. Если S ока-
окажется множеством фундаментальных дизъюнктов, то &(S) будет
фундаментальной резолюцией S в смысле предыдущего опре-
определения.
Детали обобщения и формальные определения приведены
в разд. 5. Тем не менее неформальное представление об общем
понятии резолюции можно получить уже сейчас, до его точного
определения, если просто допустить, что оно обладает следую-
следующим важным свойством (это будет показано ниже): резолюция
полукоммутативна с насыщением. Более точно это свойство
сформулировано в следующей основной лемме, которая будет
доказана в разд. 5.
Лемма. Если S — произвольное множество дизъюнктов,
а Р — произвольное подмножество эрбрановского универсума
для S, то $(P(S))<=P($(S)).
В действительности, как будет показано ниже, любой фун-
фундаментальный дизъюнкт, который может быть получен в ре-
результате подстановки термов из Р в пару дизъюнктов С и О
из 5 и последующего образования фундаментальной резольвенты
получившихся дизъюнктов, может также быть получен в ре-
результате подстановки термов из Р в одну из конечного числа
резольвент С и О.
Простым следствием основной леммы является полукомму-
полукоммутативность га-н резолюции и насыщения.
Следствие. Если S — произвольное конечное множество
дизъюнктов, а Р — произвольное подмножество эрбрановского
универсума для S, то I"(PE))?P(/(S)) для всех л>0.
Доказательство проводится индукцией по п. Имеем
M°{P{S)) = P{S) = P@P{S)), так что случай п = О тривиален.
А если 3tn (Р (S)) = Р CF E)) для л>0, то имеем
())) по определению Я"+|,
n (S))) s по предположению индук-
индукции, ибо 31 сохраняет вклю-
включение,
s Р{Я{Яп'E)))=- по лемме,
1 E)) по определению 0t+l
И СЛМСТВве «оказано.

204 Дж. Робинсон
Теперь с помощью вышеприведенного следствия мы можем
непосредственно получить из теоремы 2 третью форму теоремы
Эрбрана.
Теорема 3. Если S — произвольное конечное множество
дизъюнктов, то S невыполнимо тогда и только тогда, когда для не-
некоторого конечного подмножества Р эрбрановского универсума
для S и некоторого п^О подмножество P($>"(S)) содержит ?.
Здесь изменен порядок операций насыщения н п-й резолю-
резолюции. Теперь стало возможным неожиданное упрощение тео-
теоремы 3 ввиду замечания, что подстановка термов вместо пере-
переменных не может преобразовать непустой дизъюнкт в П. Сле-
Следовательно, P{$Ln{S)) будет содержать ? тогда и только тогда,
когда Я"(S) содержит П. Из теоремы 3, следовательно, мы
немедленно получаем нашу окончательную форму теоремы Эр-
Эрбрана, которая является основным результатом этой работы.
Теорема о резолюции. Если S — произвольное конечное
множество дизъюнктов, то S невыполнимо тогда и только тогда,
когда SK1 (S) содержит ? для некоторого п^О.
Утверждение теоремы о резолюции есть в точности утвер-
утверждение теоремы о фундаментальной резолюции без какого-либо
упоминания о фундаментальности. Следовательно, за исключе-
исключением несколько более сложного способа вычисления резольвент
двух дизъюнктов (описанного в разд. 5), подсказываемый тео-
теоремой о резолюции метод проверки конечного множества S
дизъюнктов на выполнимость в точности таков, как приведен-
приведенный ранее метод для случая, когда S есть множество фунда-
фундаментальных дизъюнктов; в действительности он автоматически
сводится к этому методу, будучи применен к конечному мно-
множеству фундаментальных дизъюнктов. Однако теперь, вообще
говоря, неверно, что последовательность вложенных множеств
должна оборваться для каждого конечного S. По теореме Чёрча
это не может быть так, ибо иначе мы имели бы разрешающую
процедуру для нашей формулировки логики первого порядка.
Перейдем теперь к рассмотрению „демона доказательства",
о котором шла речь в разд. 3. Мы предположили там, что
если бы нам было дано доказательное множество Р для невы-
невыполнимого множества S дизъюнктов, то все, что нам надо
было бы делать, — это вычислять резолюции до тех пор, пока
мы не встретим первую резолюцию &"(P(S)), которая содер-
содержит П, и извлечь из нее формальное опровержение S. Но тео-
теорема о резолюции гарантирует нам, что к тому времени, когда
мы вычислили бы $"(?), если не раньше, мы встретили бы П,

Машинно-ориентированнйя логика, основанная на принципе резолюции 205
несмотря на наше незнание Р. В этом смысле теорема о резо-
резолюции делает лишней роль демона доказательства.
В пятом разделе мы введем немного более формальный
аппарат посредством второй группы определений и выполним
наш долг по определению общего понятия резолюции и доказа-
доказательству основной леммы.
5. ПОДСТАНОВКА, УНИФИКАЦИЯ И РЕЗОЛЮЦИЯ
Следующие определения касаются операции конкретизации
(т. е. подстановки термов вместо переменных в правильно по-
построенных выражениях и множествах правильно построенных
выражений) и различных вспомогательных понятий, необходи-
необходимых для определения общего понятия резолюции.
5.1. Подстановочные компоненты. Подстановочная компо-
компонента — это выражение вида T/V, где V — переменная, а Г—терм,
отличный от V, причем V называется переменной компоненты
T/V, a T — термом компоненты T/V-
5.2. Подстановки. Подстановка — это конечное (быть может,
пустое) множество подстановочных компонент с попарно раз-
различными переменными. Если Р — произвольное множество тер-
термов, а термы всех компонент подстановки 0 входят в Р, то
говорят, что 0 есть подстановка над Р. Мы записываем подста-
подстановку с компонентами TJV\, ..., TJVkV виде{Г,/^1, ..., Tk/Vk},
помня, что порядок компонент безразличен. Строчные грече-
греческие буквы используются для обозначения подстановок. В част-
частности, е есть пустая подстановка.
5.3. Конкретизация. Если Е — произвольная конечная цепочка
символов, а
е = {г,/у Tk/vk)
— подстановка, то конкретизацией Е посредством 6 называется
операция, состоящая в замене всех вхождений в Е перемен-
переменной Vit l</<&, на вхождение терма Тс. Получающаяся це-
цепочка символов, обозначаемая через ?0, называется 0-приме-
ром Е. Иными словами, если Е есть цепочка EqV i{Ei . . . V inEn,
то ?0 есть цепочка EoTi^Ei ... TinEn. Здесь ни одна из подце-
подцепочек Ej цепочки Е не содержит вхождений переменных
Vu ..., Vk, некоторые из Е/ могут быть пустыми; п, возможно,
равно 0, а каждое Vi, является вхождением одной из перемен-
переменных V\, ..., Vk- Всякая цепочка вида Ев называется приме-
примером цепочки Е. Если С — произвольное множество цепочек,
а 0 -•- подстановка, то 0-примером С является множество всех це-
цепочек вида EQ, где Е входит в С. Мы будем обозначать это
множество через С0 и говорить, что это есть пример С.

206 Дж. Робинсон
5.4. Стандартизация. Если С —конечное множество цепочек,
а V\, ..., Vь. — все попарно различные переменные, входящие
в цепочки из С, расположенные в алфавитном порядке, то
^-стандартизацией С, обозначаемой через |с, называется под-
подстановка, состоящая из всех подстановочных компонент вида
Xj/Vj, где Is^/s^fe, V/фх,-, а ^-стандартизацией С, обозна-
обозначаемой через т)с, называется подстановка, состоящая из всех
подстановочных компонент вида yj/V/, где 1 s^/s^fe, a V/ ф У].
5.5. Композиции подстановок. Если 8 = {Г1/1/,, ..., Tk/Vk) и
X — две произвольные подстановки, то множество 8' U X' (где
X' — множество всех компонент X, переменные которых не встре-
встречаются среди Vu ..., Vk, a 8' —множество всех компонент
TiklVi, \^.i^.k, таких, что TtX отлично от Vt) называется
композицией 6 и А, и обозначается через QX.
Непосредственно проверяется, что ев = ве = 8 для любой под-
подстановки 8. Кроме того, композиция подстановок ассоциативна,
@Л)\i = 8 (X\i), так что мы можем опускать скобки при записи
кратных композиций подстановок.
Сущность композиции операций подстановки состоит в том,
что если Е — произвольная цепочка, a a = QX, то цепочка Еа
есть в точности цепочка ?8А,, т. е. А,-пример ?8.
Эти свойства композиции подстановок устанавливаются
с помощью следующих предложений.
5.5.1. (Еа) X = Е(аХ) для всех цепочек Е и всех подстано-
подстановок а, X.
Доказательство. Пусть а = {Г,/1/,, ..., Tk/Vk}, X =
= {?/,/№„ ..., UJWJ, a ? = ?0F«,?i ••- VtaEn в обозначениях
пункта E.3). Тогда по определению Еа = EoTitE\ ... TinEn,
а {Еа)Х = EoTixE\ ... TirEn, где каждое fij есть TtX, а каждое
Ej есть EjX', где X' есть множество всех тех компонент X, пере-
переменные которых не встречаются среди У,, ..., Vk (поскольку
ни одна из этих переменных не входит ни в одну из этих Ej).
Но аХ = a' U X', где каждая компонента а' есть в точности
fi/Vi, если только Tt отлично от Vt- Следовательно, Е (аХ) =
= EoTi^i .. . TinEn.
5.5.2. Для любых подстановок а, X справедливо следующее:
если для каждой цепочки Е имеет место равенство Еа = ЕХ,
то а = Х.
Доказательство. Пусть Vu ..., Vk включает перемен-
переменные всех компонент а и Я,; тогда Vta = V/X для 1 ^ / ^ k,
В таком случае а к X состоят из одних и тех же компонент.

Машинно-ориентированная логика, Основанная на принципе резолюции 207
5.5-3. Для любых подстановок а, X, р справедливо (стЛ,)(х=or (
Доказательство. Пусть Е — произвольная цепочка.
Тогда по 5.5.1 имеем
Е ((аХ) ц) = (Е (аХ)) ц = ((?<т) К) ц = (Еа) (Я,ц) = Е (a (*ji)).
Отсюда по 5.5.2 (aX)\i = a(X\i).
У нас будет в дальнейшем случай использовать следующую
дистрибутивность.
5.5.4. Для любых множеств А, В цепочек и произвольной
подстановки X справедливо (А [} В) X = АХ [} ВХ.
5.6. Множества несогласованности. Если А — некоторое мно-
множество правильно построенных выражений, то множеством
несогласованности множества А называется множество всех
тех правильно построенных подвыражений элементов множе-
множества А, которые начинаются с того места, где не все правильно
построенные выражения из А имеют один и тот же символ.
Пример:
А = {Р (х, h (х, у), у), Р (х, k (у), у), Р {х, а, Ь)}.
Множество несогласованности для А есть {h (x, у), k (у), а}.
Ясно, что если А содержит более одного элемента, то мно-
множество несогласованности множества А также содержит более
одного элемента.
5.7. Унификация. Если А — множество правильно построен-
построенных выражений, а 8 — подстановка, то говорят, что 8 унифи-
унифицирует А или что 8 является унификатором А, если Л8 есть
одночленное множество. Множество правильно построенных
выражений, имеющее унификатор, называется унифицируемым.
Ясно, что если Э унифицирует А, а А содержит более одного
элемента, то 8 унифицирует множество несогласованности мно-
множества А.
5.8. Алгорифм унификации. Следующий процесс, применимый
к любому конечному непустому множеству А правильно
построенных выражений, называется алгорифмом унификации.
Шаг 1. Положить <то = е и k = 0 и перейти к шагу 2.
Шаг 2. Если Аа^ не есть одноэлементное множество, то перейти к шагу 3.
В противном случае положить вА «= ok и окончить работу.
Шаг 3. Пусть Кц —самый первый, a Uk — следующий за ним в лексико-
лексикографическом порядке элементы множества несогласованности Bk для мно-
множества АЯр Если Vk — переменная, не входящая в Uk, то положить
ok+i=ok{Uk/Vky увеличить k на I и возвратиться к шагу 2; в противном
случае окончить работу.
Это определение нуждается в доказательстве того, что опи-
описанный процесс всегда завершается. Действительно, этот про-

208 Дж. Робинсон
цесс всегда заканчивается для любого конечного непустого
множества правильно построенных выражений, в противном
случае порождалась бы бесконечная последовательность А,
Лог,, Аа2, ¦ ¦ ¦ конечных непустых .множеств правильно построен-
построенных выражений, в которой каждый последующий член содержит
на одну переменную меньше, чем предшествующий (а именно Aak
содержит Vи, a Aak+l не содержит Vk)- Но это невозможно,
поскольку А содержит лишь конечное множество переменных.
5.9. Наиболее общий унификатор. Если Л —конечное непу-
непустое множество правильно построенных выражений, для кото-
которого алгорифм унификации оканчивает работу на шаге 2, то
построенная подстановка аА называется наиболее общим уни-
унификатором Л и говорят, что Л является общеунифицируемым
множеством.
5.10. Ключевые тройки. Упорядоченная тройка {L, M, N)
конечных множеств литер называется ключевой тройкой упоря-
упорядоченной пары (С, D) дизъюнктов, если выполнены следующие
условия:
5.10.1. Множества L и М не пусты, и L s С, М ^ D.
5.10.2. Множество N есть множество всех атомарных формул,
которые входят (быть может, со знаком ~]) в множество
L?cL)Mt]d (ср. определение E.4)).
5.10.3. Множество N является общеунифицируемым множе-
множеством, aN обозначает его наиболее общий унификатор.
5.10.4. Множества Lt,caN и Mr\DaN одночленны, и их эле-
элементы образуют контрарную пару.
Ясно, что пара (С, D) дизъюнктов имеет лишь конечное
(быть может, пустое) множество ключевых троек.
5.11. Резольвенты. Резольвентой двух дизъюнктов С и D
называется любой дизъюнкт вида (С — L) lcaN U (D — М) ¦r\DaN,
где (L, M, N) есть ключевая тройка пары (С, D).
Ввиду замечания к определению 5.10 ясно, что два
дизъюнкта С и D имеют конечное число резольвент Или не
имеют их вообще.
5.12. Резолюции. Если S —множество дизъюнктов, то резо-
резолюцией S, обозначаемой через &(S), называется множество
дизъюнктов, которые являются или членами S, или резольвен-
резольвентами членов 5.
5.13. N-я резолюция. Если S —множество дизъюнктов, то
п-я резолюция S обозначается через Ж1{S) и определяется для
всех л^0 аналогично B.21).
На этом завершается наша вторая группа определений.
Определение &(S) вполне подходит для наших теоретических
целей, но при фактическом вычислении не следует включать
в M(S) одновременно резольвенты пары (С, D) и пары (D, С),

Машинно-ориентированная логика, основанная на принципе резолюции 209
поскольку они совпадают друг с другом с точностью до
переименования переменных. Если С и D — фундаментальные
дизъюнкты, то, как легко проверить, резольвенты пар (С, D)
и (D, С) в точности совпадают друг с другом и с фундамен-
фундаментальными резольвентами Си/).
Теперь осталось лишь доказать основную лемму, что и будет
сделано после того, как мы докажем следующую теорему,
устанавливающую основное свойство унификации, которое по-
потребуется нам для доказательства леммы и в дальнейшем
в нашей теории.
Теорема об унификации. Пусть А — произвольное
конечное непустое множество правильно построенных выражений.
Если А унифицируемо, то А общеунифицируемо; кроме того,
если 8 — произвольный, а аА — наиболее общий унификаторы А,
то существует такая подстановка К, что Э = аАК.
Доказательство. Достаточно доказать, что в условиях
теоремы алгорифм унификации заканчивает работу над А на
шаге 2 и если алгорифм унификации еще не окончил работу и
построена ak, fe^O, то равенство
5.14. 6 = <TftAfc
справедливо на шаге 2 для некоторой подстановки Kk. Для k = 0
это верно при Яо=6, поскольку <то = е. Допустим, что при неко-
некотором /г^О справедливо E.14) для некоторой подстановки Xk.
Тогда если Aak есть одночленное множество, то алгорифм уни-
унификации кончает работу на шаге 2, при этом aA = ak — наиболее
общий унификатор и Л = Я,& есть требуемая подстановка; в про-
противном случае алгорифм переходит к шагу 3. В последнем слу-
случае, поскольку А.? унифицирует Aak (в силу E.14), ибо Э уни-
унифицирует А), то Kk должно унифицировать множество несогла-
несогласованности Bk множества Aak. Поэтому V\ и Uk, определенные
на шаге 3 алгорифма унификации, удовлетворяют равенству
5.15. Vk\k = Uklk.
Поскольку Bk есть множество несогласованности, то пра-
правильно построенные выражения из Bk не могут все начинаться
с одного и того же символа; следовательно, не все они начи-
начинаются с символов, отличных от переменных, ибо Bk унифици-
унифицируемо. Поэтому по крайней мере одно правильно построенное
выражение в Bk начинается с переменной и потому является
переменной, ибо оно правильно построено. Так как в лексико-
лексикографическом порядке переменные предшествуют всем другим
правильно построенным выражениям, a Vk является самым
первым правильно построенным выражением в Bk, то Ffc есть
переменная. Если Vk входит в Uk, то VkKk входит в U^k, что
невозможно, ибо Vk и ?/* не тождественны друг другу и имеет
14 Зак. 560

210 Дж. Робинсон
место равенство E.15). Следовательно, Vk не входит в Uk.
Поэтому алгорифм унификации не кончает работу на шаге 3,
а возвращается к шагу 2, и при этом ok+x = ak{Uk/Vk}. Поло-
Положим Xk+l = kk-{VkXk/Vk}. Тогда
= по определению %k+l,
= no E.15),
= ибо Vk не входит в Uk,
= {Uk/Vk}Xk+i по определению E.5).
Отсюда по E.14) в = сгй+1Я,Л+1. Таким образом, равенство E.14)
выполнено для всех ak, которые строит алгорифм унификации,
и теорема доказана.
Теперь мы можем доказать основную лемму, которую для
удобства сформулируем еще раз.
Лемма. Если S — произвольное множество дизъюнктов,
а Р — произвольное подмножество эрбрановского универсума
для S, то $(P(S))sP($(.S)).
Доказательство. Пусть Ле$(РE)). Тогда либо
Ae=P{S) [в этом случае 4<=P(#(S)), ибо S <=#(?)], либо А
есть фундаментальная резольвента двух фундаментальных
дизъюнктов Са, D% где Cg5, DgS, a = {TxIVx Tk/Vk},
$ = {UX/WX, ..., Um/Wm}. Здесь Vu ..., Vk~полный список всех
переменных, входящих в С и расположенных в алфавитном
порядке, Wx Wm— полный список всех переменных, входя-
входящих в D и расположенных в алфавитном порядке, а Ти ..., Tk,
Uи ..., Um — элементы Р. В этом случае А = (С - L)a (J {D - М) {$,
где L s С, М ^ D, L и М не пусты, а La и Мр —одночленные
множества, элементы которых образуют контрарную пару. Пусть
Tk/Xk, uxiyx,.... ujyj.
Тогда A = (C-L)lcQ\J(D-M)r\DQ и ЦС6 = La,
Следовательно, Э унифицирует множество N тех атомарных
формул, которые либо входят в множество L|c U Mx\D, либо
являются дополнениями формул из этого множества. По тео-
теореме об унификации N имеет наиболее общий унификатор aN,
и существует такая подстановка Я, над Р, что Q = aNX. Отсюда
L\caNX = La, Mr\DaNX = Мр и, следовательно, L\caN и Mr\DaN
суть одночленные множества, элементы которых являются
дополнениями друг друга. Поэтому (L, M, N) является ключе-
ключевой тройкой для (С, D), а дизъюнкт

Машинно-ориентированная логика, основанная на принципе резолюции 211
является резольвентой С и D; следовательно, Bg^(S). По-
Поскольку Q=aNX, то, согласно E.5.4), А = ВХ и, следовательно,
Ле Р (ffl(S)). Доказательство завершено.
Условия леммы не влекут обратного включения P($(S))s
^$(P(S)). Рассмотрим простой пример:
S = {{Q (х, } (у) )},{1Q (g (У), х)}}, Р = {а}.
Короткие выкладки показывают, что P(&(S)) содержит ?
(ибо &{S) содержит ?), в то время как &(P(S)) не содержит ?•
Таким образом, S невыполнимо, но Р не является доказатель-
доказательным множеством для S.
в. ПРИНЦИП РЕЗОЛЮЦИИ. ОПРОВЕРЖЕНИЯ
Единственным правилом вывода в нашей логической системе,
упомянутой в разд. 1, является принцип резолюции: из любых
двух дизъюнктов С и D можно вывести резольвенту С и D.
Под опровержением множества S дизъюнктов мы понимаем
конечную последовательность дизъюнктов Ви ..., Вп, такую,
что: а) каждое Bit l^/^n, либо входит в S, либо является
резольвентой двух предшествующих дизъюнктов и Ь) Вп есть ?•
Из теоремы о резолюции немедленно следует, что конечное
множество S дизъюнктов невыполнимо тогда и только тогда,
когда существует опровержение S. Таким образом, теорема
о резолюции является теоремой о полноте нашей логической
системы.
Два примера опровержения демонстрируют работу нашей
системы.
Пример 1. Множество, состоящее из двух дизъюнктов С\
и С2, где
С1! = {Q (х, g (х), у, h (х, у), z, k (х, у, z))},
C2=>{lQ(u,v,e{v),w,f{v,w),x)},
имеет опровержение С], С2, ?• Отметим, что (С,, С2) имеет
ключевую тройку (Си С2, N), где N — множество
{Q(xit g(*i),x2, h(xux2), x3, k(xu х
Читатель легко может проверить за несколько минут вычисле-
вычислений, согласно алгорифму унификации, что oN — подстановка со
следующими компонентами:
h(yue(g(yi)))/y3,
g ЫА/2. f (g Ы. h (yu e {g Ы)) )fx3,
е (g Ы )/х2, k(yue(g (yj), / {g {yj, h (г/1( е \g Щ))) )/yit
И*

212 Дж. Робинсон
a Cl%ClaN и C2r\cjaN являются одночленными множествами, эле-
элементы которых являются дополнениями друг друга.
Этот пример показывает, как доказательное множество авто-
автоматически строится в качестве побочного результата операции
резолюции. Термы вышеприведенных подстановочных компонент
становятся термами доказательного множества для {Ci, C2}, если
переменную ух всюду заменить на какой-либо терм эрбранов-
ского универсума для {С1; С2}, например, на индивидную кон-
константу „а". Интересно отметить, что наименьшим уровнем
эрбрановского универсума, содержащим это доказательное
множество, является Нъ, который имеет порядка 1064 членов.
Следовательно, #5({С,,С2}) имеет порядка 10256 членов. Этот
пример недоступен процедуре насыщения уровней.
Пример 2. Более интересный пример был рассмотрен в ра-
работе [5]. Он возник нз следующей алгебраической проблемы.
Доказать, что в любой ассоциативной системе, в которой
имеются решения всех уравнений х ¦ а = Ь и а • у = Ь, существует
правый единичный элемент.
Чтобы формализовать эту проблему в нашей логике, мы
отрицаем предполагаемое заключение и пытаемся опровергнуть
множество, состоящее из следующих дизъюнктов (здесь Q(x, у, г)
понимается как x-y~z):
С,: HQ(x, у, и), ~]Q(y, z, v), ~]Q(x, v, w), Q(u, z, w)}, ) ассоциа-
C2: {lQ(x, y, u), ~]Q(y, z, v),-]Q(u, z, w), Q(x, v, w)}, J тивность
C3: {Q(g(x,y),x,y)},\
r> int , t ч \i f существование левого и правого решении,
С4: {Q (х, h (х, у), у)}, )
С5- {Q(x, y,f(x, у))}, замкнутость относительно умножения,
С6: {~]Q(k(x), х, k(x))} отсутствие правой единицы.
Добавляя следующие резольвенты, мы получаем опровержение:
x6, y{), Q(y2, x6, у2)},
Q: ПЯ(У» УъУх)),
С9: D.
Комментарий. Резольвента С7 — резольвента пары (Си С3)
с ключевой тройкой
{{lQ{x, у, и), ~\Q(x, v, w)}, {Q(g{x, у), х, у)}, N),
где N есть множество {Q {xit х5, х;), Q (дг4, х2, х3), Q {g {yu у2), Ун

Машинно-ориентированная логика, основанная на принципе резолюции 213
Как легко проверить, aN, вычисляемая с помощью алгорифма
унификации, такова:
{yjxu yjx2, у2/х3, g(yu y2)/xit yjx5}.
Резольвента C8 — единственная резольвента пары (С6, С7), а П —
единственная резольвента пары (С4, С8).
Этот пример показывает, что отдельный шаг опровержения,
выполняемый по правилу резолюции, может являться столь слож-
сложным, что человеческий ум не может убедиться в его правиль-
правильности за один интеллектуальный акт. Работая крупноблочно,
правило резолюции является очень компактным, если не ска-
сказать элегантным, способом рассуждений. Резольвенты С2 и С5
не были использованы в опровержении в качестве посылок, хотя
это не имеет ничего общего с правилом резолюции. Поэтому
экономным опровержением для этого примера является после-
последовательность Си С3, С4, С6, С7, С8, П.
7. ПРОЦЕДУРЫ ОПРОВЕРЖЕНИЯ; ТАКТИКИ ПОИСКА
Целью вышеизложенного было лишь установление теорети-
теоретической базы в виде специальной логической системы для пост-
построения различных программ доказательства теорем, т. е. в дан-
данном случае процедур опровержения. До сих пор не рассматривался
вопрос о нахождении эффективной процедуры опровержения;
в данном разделе мы кратко обсудим вопрос.
Если строить процедуру опровержения непосредственно по
теореме о резолюции, то получится совсем неэффективная про-
процедура. Эта процедура состоит в вычислении для данного ко-
конечного множества S дизъюнктов последовательности множеств
S,&(S), #2(S), ... до тех пор, пока не встретится $"(S), та-
такое, что оно или содержит П, или не содержит П, но совпа-
совпадает с 52n+1 (S). В первом случае опровержение S можно получить,
проследив порождение ?; во втором случае S выполнимо. В силу
теоремы Чёрча [1] мы знаем, что для некоторых множеств S
эта процедура, как и вообще все корректные процедуры опро-
опровержения, не окончит работу ни тем, ни другим способом, а бу-
будет продолжать вычисления бесконечно.
В некоторых случаях мы можем предвидеть бесконечность
процесса. Рассмотрим пример множества, состоящего из двух
дизъюнктов
С,: {Q(a)}, C2. {1Q (х),
(Это формулировка в нашей логике фрагмента аксиом Пеано
для натуральных чисел, если интерпретировать ,,Q{x)" как „х
есть натуральное число", „а" — как „О", а „/ (л:)" — как „число,

214 Дж. Робинсон
следующее за х".) Легко видеть, что описанная выше процедура
будет порождать последовательно резольвенты
и т. д. до бесконечности.
Данный пример наводит на мысль о правиле, которое по-
позволяло бы нам эффективно распознать этот специальный вид
бесконечного процесса в случае его возникновения, так, чтобы
мы могли включить это правило в процедуру опровержения,
в результате чего она окончила бы работу над S и другими
аналогичными примерами. Такое правило возможно, оно осно-
основано на понятии литеры, чистой в данном множестве S дизъ-
дизъюнктов, и мы назовем его правилом чистоты.
7.1. Чистые литеры. Если S — произвольное конечное мно-
множество дизъюнктов, С —дизъюнкт из S, а L — литера из С,
причем не существует ключевой тройки {{L}, M, N) ни для
какой пары (С, D) дизъюнктов, где D — дизъюнкт из S — {С},
то говорят, что литера L чиста в S.
Правило чистоты основано на следующей теореме.
Теорема о чистоте. Если S — произвольное множество
дизъюнктов, L^C^S, и литера L чиста в S, то S выполнимо
тогда и только тогда, когда S — {С} выполнимо.
Доказательство. Если S выполнимо, то и S — {С} вы-
выполнимо, ибо S — {C} есть подмножество S. Если S —{С} выпол-
выполнимо, то существует модель А для S — {C}, каждая литера
которой входит в некоторый дизъюнкт из Н (S), где Н — эрбра-
новский универсум для S. Пусть N— множество всех фунда-
фундаментальных литер вида Z.6, где 6 — подстановка над Н, и пусть К
состоит из дополнений всех членов N. Тогда множество Р =
= N[j(A — К) является моделью, более того, оно есть модель
для 5, поскольку каждый дизъюнкт в Н ({С}) содержит член Р
(а именно какой-либо член N) и каждый дизъюнкт из
H(S — {С}) содержит член Р, а именно некоторый член А — К.
Действительно, никакой дизъюнкт из Н(S — {С}) не содержит
членов К, ибо в противном случае если Dp был бы таким
дизъюнктом (где De(S — {С})), то нашлось бы такое М, что
М s D, а М$— одноэлементное множество, содержащее член К.
Тогда имелась бы некоторая подстановка а над Н, такая, что
{L}a и Мр —это одночленные множества, элементы которых
являются дополнениями друг друга. Рассуждая так же, как
в доказательстве основной леммы, мы нашли бы ключевую
тройку ({L}, M, N) для пары (С, D), что противоречит чистоте
литеры L в 5. Теорема доказана.

Машинно-ориентированная логика, основанная на принципе резолюции 215
Правило чистоты формулируется так: можно вычеркивать из
конечного множества S дизъюнктов любой дизъюнкт, содер-
содержащий литеру, чистую в S.
Если S —рассмотренный выше небольшой фрагмент аксиома-
аксиоматики Пеано, т. е. множество, состоящее из двух дизъюнктов
С,: {Q(a)}, C2: {~]Q(x), Q (/(*))},
то мы видим, что подчеркнутая литера чиста в S. Поэтому мы
можем вычеркнуть С2, получив множество 5 — {С2}, единствен-
единственным дизъюнктом которого является
С,: {Q(g)}.
Очевидно, что подчеркнутая литера чиста в S — {C2}. Поэтому
мы можем вычеркнуть С,, получив множество S — {С,} — {С2},
которое пусто и поэтому выполнимо. Отсюда по теореме о чи-
чистоте S выполнимо.
Таким образом, процедура опровержения, объединяющая
правило резолюции и правило чистоты, „сходится" для боль-
большего числа конечных множеств дизъюнктов, чем процедура,
основанная лишь на одном правиле резолюции. Такие правила,
как правило чистоты, мы называем тактиками поиска, чтобы
отличать их от правил вывода.
Существует другая тактика поиска, которая хотя и не уве-
увеличивает область сходимости, но полезна для увеличения ско-
скорости сходимости процедуры опровержения. Мы называем эту
тактику тактикой поглощения.
7.2. Поглощение. Если С и D— два различных непустых
дизъюнкта, то мы говорим, что С поглощает D, если сущест-
существует такая подстановка а, что Со s D.
Следующая теорема устанавливает основное свойство погло-
поглощения.
Теорема о поглощении. Если S — произвольное конеч-
конечное множество дизъюнктов, a D — дизъюнкт из S, который
поглощается некоторым дизъюнктом из S — {D}, то S выпол-
выполнимо тогда и только тогда, когда выполнимо S — {D}.
Доказательство. Достаточно показать, что если М —
модель для S — {D}, то М является также моделью для 5. Пусть
М — модель для S — {D}, и предположим, что Ce(S —{D}) по-
поглощает D. Тогда существует такая подстановка а, что CasD.
Так как DeS, то термы компонент а построены из символов
функций, входящих в функциональный словарь для 5 и, быть
может, переменных. Следовательно, каждый фундаментальный
пример Со над Н является фундаментальным примером С над Я

216 Дж. Робинсон
и потому содержит член М. Но каждый фундаментальный при-
пример DK дизъюнкта D содержит фундаментальный пример СоХ
дизъюнкта С и потому содержит член М. Таким образом, М
является моделью для S и теорема доказана.
Тактика поглощения формулируется следующим образом:
можно вычеркивать из конечного множества S дизъюнктов
любой дизъюнкт D, который поглощается некоторым дизъюнк-
дизъюнктом из S — {D}.
Для того чтобы тактику поглощения можно было включить
в процедуру опровержения, мы должны указать алгорифм рас-
распознавания того, что один дизъюнкт С поглощает другой дизъ-
дизъюнкт D. Таким алгорифмом является следующий алгорифм
поглощения:
Шаг 1. Пусть Vu ..., Vm — полный список всех переменных, входящих
в D и распол >женных в алфавитном порядке. Пусть J} Jm — различные
индивидные константы, нн одна из которых не входит ни в С, ин в D.
Пусть 6 == {/i/V| Jm/Vm}- Вычислить DQ н перейти к шагу 2.
Шаг 2. Пел жить Ао - [С], k = 0 и перейти к шагу 3.
Шаг 3. Если Ak не содержит П, то Л/s+i будет множеством, состоящим
нз всех дизъюнктов внда(/Ссгд/ - Ma N), где K^Ak, Ms К, N = MU {P}, P^DQ,
oN — нанбелге общий унификатор N; в противном случае прекратить работу.
Шаг 4. Если Ak+\ непусто, то увеличить k на 1 н вернуться к шагу 2.
В противном случае прекратить работу.
Ясно, что этот алгорифм всегда кончает работу, ибо каж-
каждый дизъюнкт в Ак+1 меньше по крайней мере на одну литеру
того дизъюнкта в Ак, из которого он был получен. Поскольку
единственный дизъюнкт в Ао содержит лишь конечное число
литер, то в последовательности Ао, Аь ... рано или поздно
встретится множество, которое либо содержит D, либо пусто.
Следующее рассуждение показывает, что алгорифм погло-
поглощения заканчивает работу на шаге 3 тогда и только тогда,
когда С поглощает D.
Если С поглощает D, то Со г D для некоторой а. Следова-
Следовательно, Сов ^ D6. Таким образом, Сц s D6 для некоторых ц.
Допустим, что для &^г0 существует К, такое, что К^Ак и
/C(i E D6 для некоторой ц. Если К непусто, то пусть Р будет,
литерой из Кц и, следовательно, из D6. Тогда существует М S
? К, такое, что N = M[){P} унифицируется ц. Построим с по-
помощью алгорифма унификации наиболее общий унификатор aN-
множества N. Дизъюнкт G=KoN — MaN входит в Ak+\. По
теореме об унификации ц = aN% для некоторой А., следовательно,
KoNX ^ D8. Поэтому G% E Ьв. Так как СеЛ0 непусто, то и
каждое Ак, k^O, либо непусто, либо содержит П. Поэтому
алгорифм поглощения оканчивает работу не на шаге 4, а на
шаге 3.

Машинно-ориентированная логика, основанная на принципе резолюции 217
Если алгорифм поглощения оканчивает работу над С и D
на шаге 3, то существует конечная последовательность дизъ-
дизъюнктов Со, С, Ся+1, такая, что CQ-=C, Cn+1 = D и для каж-
каждого /, 0^/<я, имеем Cl+x = Clal — MjOj, где Mt E СЛ a at —
наиболее общий унификатор Af7 U {Я}, где Ре?>9. Отсюда сле-
следует (поскольку MjOj не содержит переменных, 0^/<д), что
Cnf, = П = Cffoff, ... сг„ - М0ог0 - Af,ar, - ... - Мпап,
т. е. Со^ст, ... ап s (М0(г0 (J М,(г, (J ... U Alnart) ^ D8. Положим
Я = (Toff) ... (г„. Тогда СА, s ?>Э. Пусть а — подстановка, получаю-
получающаяся из Я заменой в каждой компоненте Jt на V\ для 1 ^
< i < m. Тогда Сст s ?>.
Особенно полезным применением тактики поглощения
является следующее. Предположим, что резольвента R дизъ-
дизъюнктов С и D поглощает один из них; тогда, добавив R по пра-
правилу резолюции, мы можем одновременно вычеркнуть, согласно
тактике поглощения, тот из дизъюнктов С или D, который по-
поглощается R. Эта объединенная операция сводится к замене С
или D на R; мы назовем это правило вывода правилом заме-
замещения, а соответствующую тактику — тактикой замещения.
Следующий пример, который рассмотрели Гильмор [4], Де-
вис и Патнэм [2] и Фридман [3], демонстрирует пользу этих
тактик для увеличения скорости сходимости. Пусть множество S
состоит из следующих дизъюнктов:
С,: {/>(*„ х2)},
F)
С2: {1Р(у-2, ПУь Уз)), 1РЦ(У„ У2), fiyu У*)).
(О B)
C) D)
IQiVu
E)
Мы получим множество S', имеющее лишь два члена
Q: lQ(ylt
всего за шесть шагов, которые состоят в вычеркивании под-
подчеркнутых литер и дизъюнктов в указанном порядке. Вычерки-
Вычеркивания с A) по E) проводятся согласно правилу замещения;
вычеркивание F) целого дизъюнкта проводится согласно пра-
правилу чистоты. Мы немедленно получаем, что S' невыполнимо,
ибо D — единственная резольвента С4 и С5.

218 Дж. Робинсон
Программа Гильмора на IBM 704 не окончила работу
над этим примером за 21 мин счета. Более эффективная про-
процедура Девиса и Патнэма закончила работу над этим приме-
примером за 30 мин ручного счета.
Применение одной из трех описанных тактик к конечному
множеству 5 дизъюнктов дает множество S', которое либо со-
содержит меньше дизъюнктов, либо содержит столько же
дизъюнктов, но одни или несколько из них являются более
короткими. Поэтому обычный способ использовать эти тактики
в процедуре опровержения состоит в том, чтобы добавлять но-
новый дизъюнкт по правилу резолюции лишь тогда, когда ни одна
нз этих трех тактик неприменима. Мы можем назвать такие
множества несводимыми. Если множество S выполнимо, то та-
такая процедура может кончить работу либо на пустом множе-
множестве (как в случае аксиом Пеано), либо на непустом несводи-
несводимом множестве, обладающем следующим свойством: любая
резольвента любой пары дизъюнктов из этого множества по-
поглощается одним из дизъюнктов этого множества.
Имеются и другие тактики поиска того же типа, но менее
простые, чем рассмотренные. Предполагается, что эта работа
послужит началом серии работ, в которых развитая здесь тео-
теоретическая база будет использована для дальнейшего изучения
тактик поиска и построения процедур опровержения. Этот раз-
раздел был всего лишь наброском общей картины проблемы и
кратким взглядом на возможные подходы к ней.
В заключение я хотел бы выразить свою благодарность
моим коллегам д-ру Дж. А. Робинсону и д-ру Л. Т. Восу
из Аргонской национальной лаборатории и проф. В. Давидоиу
из колледжа Хаверфорда за обсуждение статьи и критические
замечания по основным понятиям этой работы. Я благодарю
также рецензентов из АСМ и д-ра Т. Гальперина, чьи замеча-
замечания по рукописи статьи во многом способствовали написанию
окончательного варианта.
ЛИТЕРАТУРА
1. Church A., A note on the Entscheidungsproblem, /. Symb. Logic, 1 A936),
40—41.
2. Davis M., Putnam H., A computing procedure for quantification theory,
/. ACM, 7 (I960), 201—215.
3. Friedman J., A semi-decision procedure for the functional calculus.
I. ACM, 10 A963), 1-24.
1 G i 1 m о r e P. C, A proof method for quantification theory, IBM J. Res.
Develop., 4 (I960), 28—35.
5. Robinson J. A., Theorem proving on the computer, /. ACM, 10 A963),
163-174.

Прикладные вопросы
Алгоритм моделирования
динамических систем
с помощью вычислительных машин,
основанный на теории
потоковых графов1)
Р. Якубовски
1. ВВЕДЕНИЕ
Сравнительно недавно в литературе появилось много статей
о применении аналоговой техники для моделирования динами-
динамических систем с помощью вычислительных машин [1—4]. Ана-
Аналоговая техника воспроизводит ясно очерченную картину для
исследуемой задачи. В частности, это имеет место при моде-
моделировании нелинейных динамических систем. В последнее время
наблюдается также прогресс в применении потоковых графов
в программировании для аналоговых вычислительных ма-
машин [5—7]. Учитывая обе эти тенденции, в настоящей статье
мы хотим изложить метод, основанный на графах с много-
многоаргументными функциональными ребрами, который позволял бы
нам подготавливать данные для вычислительной машины; при-
причем последняя в свою очередь могла бы использовать их в само-
самоорганизующейся программе для решения системы дифферен-
дифференциальных уравнений, задаваемой графом. Из-за простоты
получающегося алгоритма он может найти широкое применение
в технических задачах и задачах обучения, связанных с моде-
моделированием динамических систем. Так как упомянутый алго-
алгоритм основан на теории потоковых графов, мы вначале опре-
определим элементы графа и сформулируем зависимости между
этими элементами.
J) Jakubowski R., An algorithm for the simulation of dynamical
systems by means of digital computers, based on signal-flow graph, Journal
of Mathematical Analysis and Applications, 22 A968). 172-187.

МО Р. Якубовски
2. ГРАФЫ И ИХ ПРИМЕНЕНИЕ В ПРОГРАММИРОВАНИИ
ДЛЯ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
В графе, который служит базой для реализации программы
работы вычислительной машины, зависимые и независимые
переменные изображаются вершинами. Умножение на постоян-
постоянный коэффициент и другие математические операции изобра-
изображаются ребрами (математические операции суммирования ассо-
ассоциируются со стоками —выходами). Мы будем различать два
типа ребер и вершин. Ребра разделяются на нефункциональные
и функциональные, а вершины —на источники и стоки. Вер-
Вершины, которые не являются ни источниками, ни стоками (эти
вершины имеют как входящие, так и выходящие ребра), здесь
не существуют. Операция, которая сопоставляется этим верши-
вершинам, изображается специальным функциональным ребром, опи-
описанным в разд. 2.3.
2.1. НЕФУНКЦИОНАЛЬНЫЕ РЕБРА
Нефункциональное ребро есть ориентированная линия с на-
направлением (указанным стрелкой), связывающая две вершины.
Это ребро характеризуется коэффициентом усиления, причем
Рис. 1. Элементы нефункциональных ребер.
коэффициент является константой и обозначается символом,
приписываемым ребру. На рис. 1, а показано нефункциональ-
нефункциональное ребро, связывающее вершины х{ и х2\ коэффициент усиле-
усиления этого ребра обозначается через /12.
Если стрелка данного ребра направлена к вершине, то мы
будем называть это ребро заходящим ребром по отношению
к данной вершине и исходящим ребром в противном случае.
Вершина, имеющая только исходящие ребра, называется ис-
источником (рис. 1,6), а вершина, имеющая только заходящие
ребра, называется стоком (рис. 1, с). Список правил для не-
нефункциональных ребер [6J приведен в табл. 1.

Алгоритм моделирования динамических систем
221
Таблица 1
A.
В.
С.
Правило
Правило
Список
правил для нефункциональных ребер
соответствия для
X,
= L. х. ~
соответствия для
Ш*14Х1Л
Дополнительнее
ХС,
С
правило:
2Х, +112 X
hi
«« ^
единственного нефункционального ребра:
— п' \а п2
нескольких нефункциональных ребер:
_ (tu*t'a)
гхг х, х2
2.2. ОДНОАРГУМЕНТНЫЕ ФУНКЦИОНАЛЬНЫЕ РЕБРА
В рассматриваемом здесь грйфе можно различить два типа
функциональных ребер: ребра с одним аргументом и ребра
со многими аргументами. Рассмотрим первый тип. Одноаргу-
ментное функциональное ребро есть ориентированная линия
(нарисованная толще, чтобы отличить от нефункциональных
ребер), связывающая две вершины. Этому ребру всегда припи-
приписана определенная операция. Пара вершин Х\ и х2 и связы-
связывающее их ребро, которому приписана операция Р, изображает
следующее соотношение (рис. 2, а):
х2 = Р(х1). A)
Вершины, связанные функциональным ребром, тем самым
определяются единственным образом; вершина xlt изображаю-

222 Р. Якубовски
щая независимую переменную, становится источником, а вер-
вершина х2, изображающая зависимую переменную,— стоком.
Рассмотрим граф, имеющий два функциональных ребра
(рис. 2, Ь). Согласно правилу (А) из табл. 1, для этого графа
имеем
Хг = Х2-
Из определения функционального ребра следует:
X2=P{Xi), X4 = N{X3).
Таким образом, в результате получаем:
Так как х2 = х3, мы можем изобразить граф на рис. 2, Ь
в упрощенной форме, показанной на рис. 2, с. В соответствии
а
с
*» (хг,х3) *«
р -ft ~
— о » о > о
/
Рис. 2. Связи между однозначными функциональными ребрами.
с принятым правилом вершина {х2, х3) в графе на рис. 2, с есть
сток для ребра N и источник для ребра Р. Таким образом,
для графа на рис. 2, d мы имеем:
2.3. МНОГОАРГУМЕНТНЫЕ ФУНКЦИОНАЛЬНЫЕ РЕБРА
Многоаргументное функциональное ребро есть ориентиро-
ориентированная геометрическая структура — „куст" (рис. 3, а), связы-
связывающая «вершин хи х2 хп-ьхп. Одна из них, хп, изобра-
изображает зависимую переменную. Этому ребру всегда приписана
определенная операция Р. Множество вершин хь х2, ..., хп и
ребро, связывающее эти вершины, изображает следующее отно-
отношение;
xn = P(xlt x2t х3, ..., *„-[). B)

Алгоритм моделирования динамических систем
223
Рис. 3. Связи между функциональными ребрами.
Подобно предыдущему, вершины, связанные с многоаргумент-
многоаргументным ребром, определены единственным образом. Вершины
хх, х2, ..., хп-и изображающие независимые переменные, ста-
становятся источниками, а вершина хп, изображающая зависимую
переменную, становится стоком.
Рассмотрим теперь граф, содержащий два функциональных
ребра (рис. 3, Ь). Согласно правилу А, из табл. 1 для этого
графа мы имеем

224 Р. Якубовски
а из определения функционального ребра получаем
х3 = Р(хи х2), xs = F(x4).
Таким образом, в результате находим
xs = F(P(xu x2)).
Этот последний граф можно изобразить также в другой форме
(рис. 3, с). При этом следует помнить, однако, что вершина
(*з, х4) является стоком для ребра Р и источником для ребра F.
Учитывая это, мы получаем для графа, показанного на рис. 3, d,
следующие связи:
В дополнение к рассмотренному выше можно отметить, что
функциональное ребро на рис. 3, е описывает подобную опе-
операцию, так как она поставлена в соответствие (в классическом
потоковом графе) вершине, которая имеет как входящие, так
и выходящие ребра.
2.4. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ФУНКЦИОНАЛЬНЫХ РЕБЕР
Как уже упоминалось, на базе графов (описывающих обыкно-
обыкновенные линейные и нелинейные функциональные уравнения)
будет разработан метод подготовки данных для ЭВМ, так что,
базируясь на этих данных и на заранее заданной программе,
с помощью ЭВМ можно решать такие уравнения.
Имея в виду указанные применения, мы ограничимся гра-
графами, характеризуемыми следующими элементами:
/. Единичный источник. Величина, изображаемая этой
вершиной, принимается постоянной и равной 1. Как и для
аналоговых ЭВМ, эта вершина будет играть роль ввода
константы.
2. Нефункциональные ребра вместе с соответствующими коэф-
коэффициентами усиления. Эти ребра будут связывать вершины,
смежные с функциональными ребрами, или же связывать вер-
вершины с единичным источником.
3. Одноаргументные и многоаргументные функциональные
ребра. Во множестве функциональных ребер, имеющих задан-
заданное число аргументов, существует несколько типов ребер.
Каждому из этих ребер приписаны различные операции.
Среди функциональных ребер одного и того же типа суще-
существует несколько видов ребер; каждому из них приписана одна
и та же операция, но описанная другими параметрами (на-

Алгоритм моделирования динамических систем 225
пример, если некоторое ребро соответствует интегрированию,
то параметрами являются константы интегрирования и началь-
начальные условия).
В общем случае операция, приписанная данному функцио-
функциональному ребру, определяется символом F[a. р, у\, где а —число
аргументов для данного ребра; р —тип функционального ребра
с а аргументами; у —вид функционального ребра, встречающе-
встречающегося в графе и принадлежащего к р-типу с данным а.
Пусть для данного функционального ребра, обозначенного
символом F[a, р, Y] (рис. 4, а), вершины, изображающие независи-
Рис. 4. Описание функциональных ребер.
мые и зависимые переменные, обозначаются следующими сим-
символами: *[OipiY,6] — вершины, изображающие независимые пере-
переменные; б —индекс вершины, он обозначается операторным
символом; у[а р Y] — вершина, изображающая зависимую пере-
переменную. Тогда, согласно B), имеем
У [а, Р. VI = F К Р. VI (Х1а. Р. V. !]• ^[о, Р, V. %' ' ' *' ХЮ, Р, V, а])- C)
При этом в частном случае, когда а=1 (рис. 4, Ь), имеем
У[1. Р. V) = F[l Р. V) (*[1, Р, V. I)I D)
В дальнейшем мы введем некоторые другие обозначения:
ат— максимальное значение для а, встречающееся в про-
программе;
Рт |а] — максимальное число ребер типа р, встречающихся
в программе (для данного а);
Ym|a р]~~ максимальное число a-аргументных ребер вида у
среди ребер типа р, встречающихся в графе;
т. д. — число параметров, необходимых для описания опе-
операции F[о, р, vl">
Р[а.Ь. v. м — параметры, описывающие операцию f[a,p, Y]. где
Я=1, 2, 3, ..., mlaW.
15 Зах. МО

226 Р. Якубовски
Предположим, что первые а параметров
Р[а, Р. V. П> Р[а. Р, V. 2]'. • • •', Р[а. 6. V. «1
определяют число функциональных и нефункциональных ребер,
входящих в вершины
*[а,Р, V. И' *|а.Р. V,2)' ••'» Х[а, р, V. о]
соответственно.
В программе, описанной ниже, числа ат, pmfa] и т[а, щ
задаются заранее, так же как и все операции. При рассмотре-
рассмотрении частного графа возможно определить числа Ym[ap) и пара-
параметры P[a,P,v.4*
Договоримся, что частные a-аргументные ребра типа р и их
частные виды y рассматриваются в следующей последова-
последовательности:
'> ри.i.2j; •••; F[I,i,Vm[!p „j; F\\,2.\\\ Л1.2.2);...; F[i.2,Vm[I2)];
[I], !]¦> f [1. Pm |1], 2]! —> F[i. Pm ID. Vra [1, Pra HI] ]'. F[2, I, I)! Fp, I. 21",
E)
Используя эту последовательность, можно единственным обра-
образом приписать каждой операции F[a, p, Y] номер, под которым
эта операция встречается в последовательности. Это соответ-
соответствует преобразованию индексов a, p, y в новый индекс i, так что
F[a.p.v]( ) = FV1(). F)
Эти операции, очевидно, действуют на одни и те же аргументы.
Зависимость i = f(a, p, у) задается формулой
Р-1 a-lPmI")
'• = Y+2Ym[a,f] + 2 S Y«[«, o]; Y»[o, 0] = pm[0] = 0. G)
Предположим, что рассматриваемые графы описываются со-
согласно вышеприведенной последовательности. Поскольку суще-
существуют и другие системы обозначения, связанные с символом
операции F\a, p, Yi> мы будем производить преобразование ин-
индексов также и в этих случаях; таким образом,
*[а, р, v. в] ~ хи, в]» (8)
»[«. Р. VI S »[!!• t9)
*.««Л*.ч- 0°)

Алгоритм моделирования динамических систем
2.5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СВЯЗЕЙ
ФУНКЦИОНАЛЬНЫХ РЕБЕР
Предварительно было установлено, что в рассматриваемых
графах вершины, изображающие независимые переменные,
связаны с вершинами, изображающими зависимые переменные,
с помощью нефункциональных ребер.
Рис. 5. Описания связей между
функциональными ребрами.
1Б»

228
Р. Якубовски
Для того чтобы дать ясное описание этих связей, введем
два члена a[t в т) и Ь.г в т). Первый из них дает индекс вершины,
изображающей зависимую переменную, которая связана с вер-
вершиной х{1 6, посредством нефункционального ребра. Второй дает
[г] ^
-г
-о
Рис. 6. Пример графа.
Таблица 2
Члены а[/( в т] и 6(i e т) для графа иа рис. 6
1,«, t
1,1
2,1
3,1
4,1
5,1
5,2
6,1
6.1
2
6,2, [
i
™" 1
1
6
3
1
3
4
5
2
bU. в, т]
-2
г
1
коэффициент усиления этой связи. Индекс т определяет пере-
переменный номер ребра, входящего в вершину х{{ в| (рис. 5, а).
Полное число таких ребер определяется, согласно предвари-
предварительному соглашению, параметром Рц.щ.
Рассмотрим ребро с а аргументами (рис. 5, о), в котором
каждая из вершин, изображающая независимые переменные,
связана посредством нефункциональных ребер с определенным
числом функциональных ребер. Согласно введенным ранее

Алгоритм моделирования динамических сиеПМ
соотношениям, для такого ребра мы имеем
(P[i, I] PU, 2]
...; 2 у[а ах]Ь J- 00
В частности, для одноаргументного ребра (рис. 5, Ь) имеем
В добавление к приведенным ранее рассуждениям укажем, что
вершину (рассматриваемый единичный источник) будем обо-
обозначать символом #[_[]. Таким образом, когда описание графа
составлено из нескольких функциональных ребер различных
типов (одноаргументных и многоаргументных) и нефункциональ-
нефункциональных ребер в форме подготовленных данных для вычислительной
машины, оно должно дать независимо от таких данных, как
v Р = Р
»т [о, Р]> г [а, р, у, Ч И, Ч'
также члены a[t 6 т| и b[{ e т]. Чтобы проиллюстрировать описа-
описание графа, выполненное заданием членов а[{ в т) и Ь[{ 6 т), рас-
рассмотрим граф, показанный на рис. 6. Члены этого графа при-
приведены в табл. 2.
2.6. ГРАФЫ С ИНТЕГРИРУЮЩИМИ РЕБРАМИ
Рассмотрим граф, состоящий из нескольких функциональных
ребер, связанных посредством нефункциональных ребер, в ко-
котором независимые и зависимые переменные, изображаемые
вершинами, суть функции переменной /, т. е.
Х\а, Р. V, »] = Х[а, р, у, в] (Oi У[а, р, Yj = У [а, р, vl (^#
Пусть, кроме того, ребра, для которых а— 1 и р= 1, реализуют
операцию интегрирования. В связи с этим можно записать
t
где Т\у\— постоянная интегрирования, связанная с операцией
F[i,\ yi и определенная соотношением
Т\у\ = P|i, I, y, з], A4)

230 Р. Якубовски
а у[и i Y) @) — начальное условие, определенное равенством
%..vl(°) = /)[...,v.2]-
После дифференцирования обеих частей A3) мы получим
Об)
отсюда после перехода к индексу „/" находим
где i= 1, 2, 3 Ym [,,,)•
Вершина х~ ,, связана посредством нефункциональных ребер
с вершинами, изображающими зависимые переменные, опреде-
определенные единственным образом структурой графа. Эти связи
определяются, как всегда устанавливалось выше, членами
а[( 6 х] и Ъ{1 в т], так что, согласно A2) и A7), можно написать,
что
~4r~ = 7^"%.i)(') = 7^ 2j ^H/,i,fl]*U.».Tj. О8)
где
1=1, 2, .... Ym[IiIJ.
Эта формула описывает систему дифференциальных урав-
уравнений типа
где
¦ 1. B0)
(Величину г/[0) можно трактовать как второй единичный источ-
источник.) Численное интегрирование системы уравнений A8) описы-
описывается в следующем разделе.
3. АЛГОРИТМ ДЛЯ РЕШЕНИЯ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ, ЗАДАВАЕМЫХ ГРАФОМ
Программа численного решения системы дифференциальных
уравнений, определяемой структурой графа, будет дана в виде
блок-схемы. Применяемая при описании этой схемы термино-
терминология аналогична использованной в работе [8].

Алгоритм моделирования динамических систем 231
Рассматриваемая программа требует подготовки данных
в следующей последовательности:
L Ym[a>P) Для всех а и р;
2. Жт — число вершин, изображающих зависимые переменные
интегрирующих ребер: значения Ж должны выдаваться на
печать;
3. W.W — индексы вершин, изображающих зависимые пере-
переменные интегрирующих ребер, которые должны выдаваться на
печать; 2в=\, 2, ..., Увт;
4. Л —шаг интегрирования;
5. Б —значение переменной t, для которой может быть вы-
выполнено интегрирование;
6. Ри „ для всех Я
для всех
„ , | для всех 6, т
Мы предполагаем, что в программе значения am, pm [а],
т[а р] задаются заранее, так же как и процедуры, соответст-
соответствующие операциям F[a, p, vl- Эти процедуры описываются пара-
параметрами
где
Л = а + 1, а + 2, ...,
так как мы знаем, что параметры с индексами от %=\ до
% = а резервируются для описания количества ребер, входящих
в соответствующую вершину, изображающую независимую
переменную данной операции. Блок-схема программы состоит
из следующих трех основных частей.
Часть I (рис. 7). В этой части программы выполняется
ввод данных, а также преобразование индексов a, p, y B един-
единственный индекс „i", согласно уравнению G). Тройка индексов
a, p, Y. соответствующая данному „Iй, хранится в ячейках
V V По-
Попасть II (рис. 8). Эта часть программы вырабатывает по-
последовательность, в которой вычисляются выражения у1{] для
<>Yra[1 и- Последующие индексы членов yw упорядочены для
того, чтобы требуемые члены были записаны в ячейках d[l]t где
/= 1, 2, 3, ..., (v — Ym [I, ii). Предполагается также, что вершина

\~Начамо |
Читать
Ут [a.fi] <**я всех а,/
Vrxj для X=Ji2...,%m
h и В
*
i:=0; a\
(если уm
Да
Л=ЦП
Читать
Нет
X
если А=/
\Аа
-\д:=д+1\
31
Читать
Нет.
Нет
если r=Pt//7~>
д =а
\Да
Нет /
\AaZZLHem
»=am >
л
с:=ос* 7
Рис 7. Часть I прогремим.

Алгоритм моделирования динамических систем
233
yw соответствующая зависимой переменной, не связана ни
с какой вершиной x.t б] одного и того же ребра.
Эту трудность можно обойти путем добавления функциональ-
функционального ребра (реализующего тождественную операцию) в виде
изолирующего блока, описанного в [1].
Часть III (рис. 9). В этой части программы совокупность
блоков, обозначенная символом А, производит вычисление у[1}
для/>ут[1I] в последовательности, установленной выше.
Рис 8. Часть II программы.

тШ:вРил
Рис. 9. Часть III программы.

Алгоритм моделирования динамических систем 235
Отношения, которые не включены в блоки этой совокупности,
имеют форму
p[i, 6]
Нужно указать, что в вычислении последнего уравнения мы
можем использовать соотношения F) и A0).
Последующие вычисления выполняются путем решения си-
системы дифференциальных уравнений, задаваемых графом, по
методу Рунге —Кутта [9], модифицированному Джиллом. Этот
метод выбран из-за его простоты; вполне возможно примене-
применение других методов.
Основной упор в этой статье был сделан не на выбор опти-
оптимального численного решения и не на оценку точности, а на
подготовку данных и на построение программы. Соотношения,
не задаваемые явно в блоках этой программы, перечислены
ниже:
ри. и
11 Т-1
Уму -
где
Y =1 ц =2 ф -1
I I
' ^[3] = *• ^[31 = * +
? --!¦ „ =2 en =1
[4] 6 ' ^[4| ^' ^[41 8 '
ЛИТЕРАТУРА
1. Steel G. H., Programming of digital computers for transient studies in
control systems, Int. J. Electr. Eng. Educ, 3 A965), 261-278.
2. В r a n n a n R. D., F a n i d у Т. D., Digital simulation, Instruments and
Control Systems, № 3 A966), 133—137.
3. Janoski R. M., Schaeffer R. L., COBLOC —a program for all-digital
simulation of a hybrid computer, IEEE Trans. Electronic Computers, EC-15,
№ 1 A966), 74—82.
4. В e r 1 e F. J., H a b e r s t о с к F., Blockorientierte Programmierung bei der
Untersuchung dynamischer Systenie, Elektronische Rechenanlagen, Heft 3
A966), 135—140.

236 Р. Якубовски
5. Becker S. M., Try signal flow graphs to simplify analog programming,
Contr. Eng., 11, № 9 A964), 109—11 [.
6. R о b i с h a u d L. P. А., В о i s v e r t M., Robert J., Graphs de fluence,
Applications a l'electrotechnique et a l'electronique. Calculateurs analogi-
ques et digitaux, Presses de I'Universite Laval, 1961.
7. С h о w Y., С a s s i g n о 1 E., Linear signal-flow graphs and applications,
Wiley, New York, 1962.
8. Burnett-Hall D. G., Dressel L. A. G., Samel P. A., Computer
programming and autocodes, The English Universities Press L. T. D., 1961.
9. Ralston A., Wilf H. S., Mathematical methods for digital computers,
Wiley, New York, 1962.

СОДЕРЖАНИЕ
Математические вопросы
Дж. Н. Пирс. Предельное распределение для минимального расстоя-
расстояния в случайном линейном коде. Перевод Э. 1Л. Габидулина ... 5
Ф. П. Препарата. Класс оптимальных нелинейных кодов с испра-
исправлением двойных ошибок. Перевод В. И. Левенштейна 18
Д. Клейтмен. О проблеме Дедекинда: число монотонных булевых
функций. Перевод В Б. Алексеева 43
Ф. М. С п и р а. Время, требующееси для умиожеияя в группе. Перевод
В. М. Храпченко 53
B. Штрассен. Алгоритм Гаусса не оптимален. Перевод Е. П. Липа-
Липатова • 67
Г. Р о б б и н с. Некоторые аспекты последовательностиого построения
экспериментов. Перевод В. А. Буевича 71
Г. Р о б б и и с. Построение последовательиостиых экспериментов с конеч-
конечной памятью. Перевод В. А. Буевича 81
3. М а и и а. Правильность программ. Перевод Ю. И. Якова 85
Д. Пейджер. О проблеме нахождения минимальных программ для
таблиц. Перевод Ю. И. Янова • 94
Р. Р. Реджеёвски. Об арифметических выражениях и деревьях.
Перевод М. А. Шейдвассера 99
Б. Грюибаум. Плоские карты с заданными степенями вершин и гра-
граней. Перевод В. П. Козырева 108
Дж. Ч. Б о л а и д. Влэжеиие графов в ориентируемые поверхности. Пе-
Перевод В. Е. Фельдмана 118
C. М а к л е й и. Комбинаторное условие для плоских графов. Перевод
В. Е. Фельдмана 133
Дж. Я н г с. Минимальные вложения и род графа. Перевод В. Е. Фельд-
Фельдмана [45
М. Девис. Устранение лишнего из механических доказательств. Пере-
Перевод А. В. Сочилиной 160
В а и X а о. Формализация и автоматическое доказательство теорем.
Перевод А. В. Сочилиной [80
Дж. Робинсон, Машинно-ориентированная логика, основанная на
принципе резолюции. Перевод Ю. В. Матиясевича 194
Прикладные вопросы
Р. Якубовскн. Алгоритм моделярованяя динамических систем с по-
помощью вычислительных машин, основанный на теории потоковых
графов. Перевод В. А. Евстигнеева . , , 219

КИБЕРНЕТИЧЕСКИЙ
СБОРНИК
Новая серия
Выпуск 7
Редактор А. С. Попов
Художник Н. К. Сапожников
Художественный редактор В. И. Шаповалов
Технический редактор И. /С. Церва
Корректор Н. И. Баранова
Сдано в производство 19/III 1970 г. Подписано
к печати 21/VIII 1970 г. Бумага тип. № I,
60 X 9О'Лб=7,5 бум. л. 15 усл. печ. л. Уч.-изд. л.
12,82. Изд. № 1/5747. Цена 1 р. 24 к. Зак. 560.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени
Ленинградская типография № 2
имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Измайловский проспект, 29

В ИЗДАТЕЛЬСТВЕ «М И Р»
готовится к печати:
Берлекэмп Э. Алгебраическая теория кодирования,
Нью-Йорк, 1968, перев. с англ., 25 л.
Книга американского ученого, освещающая основ-
основные вопросы общей теории линейных кодов, исследо-
исследования циклических (двоичных и недвоичных) кодов
для метрик Хэмминга и Ли, вычисление параметров
оптимальных кодов, а также вопросы построения ко-
кодирующих и декодирующих устройств. Теоретические
исследования сопровождаются большим количеством
примеров и задач, что делает книгу интересной и до-
доступной не только для математиков, но и для широ-
широкого круга специалистов, связанных с разработкой
систем передачи цифровой информации, а также для
аспирантов и студентов соответствующих специаль-
специальностей.
Минский М., Пейперт С. Персептроны, Нью<
Йорк, 1969, перев. с англ., 15 л.
Книга видных американских ученых посвящена
параллельным вычислительным устройствам, извест-
известным под названием персептронов. В ней подробно про-
проанализированы общие алгебраические и геометриче-
геометрические свойства подобных схем, рассмотрены вопросы,
связанные с обучением персептронов, в частности дли-
длительность процесса обучения, эффективность схемы как
адаптивного запоминающего устройства и т.п., а также
исследованы потенциальные возможности персептро-
нов как обучающихся распознающих устройств.
Книга представляет несомненный интерес для
специалистов по современной кибернетике, в частности
зарождающейся общей теории вычислений и вычис-
вычислительных схем.