СОВРЕМЕННЫЕ
ПРОБЛЕМЫ МЕХАНИКИ
ПОД ОБЩЕЙ РЕДАКЦИЕЙ
проф. А. И. ЛУРЬЕ
и проф. Ж. Г. ЖОЙЦЯНСКОГО
огиз
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
ЛЕНИНГРАД 1948 МОСКВА

В. В. НОВОЖИЛОВ
основы
НЕЛИНЕЙНОЙ ТЕОРИИ
УПРУГОСТИ
БИБЛИОТЕКА
ИНСТИТУТА
„.«.И. •- СТАЛИНА
1962 г.
огиз
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
ЛЕНИНГРАД 1948 МОСКВА
г.

12-5-4
Редактор А, И.'Чекмарев Техн. редактор К. М. Волчок
Подписано к печати 25/Х 1948 г. 13,25 печ. л. 36 676 тип. зи. в печ. л. М-19510.
Тираж 6 000 экз. Цена книги 7 р. 25 к. 12,12 уч.-изд. л. Заказ № 3175.
4-я типография им. Евг. Соколовой треста „Полиграфкнига" ОГИЗа
при Совете Министров СССР. Ленинград, Измайловский пр., 29.

ОГЛАВЛЕНИЕ
Предисловие 9
Глава I. Геометрия деформации
§ 1. Координаты 11
§ 2. Углы, определяющие направления координатных
линий 14
§ 3. Компоненты деформации • 21
§ 4. Преобразование компонентов деформации при пе-
переходе от одних, осей к другим 24
§ 5. Главные направления деформации 26 .
§ 6. Преобразование параметров е. и ш^ при переходе
от одних осей к другим 31
§ 7. Геометрический смысл параметров о^ 34
§ 8. Волокна, сохраняющие свое направление после
деформации. 39
§ 9. Инварианты деформации и поворота 41
§ 10. Общая картина деформации в окрестности про^
извольной точки тела. 43
§ 11. Изменение объема 46
§ 12. О величине удлинений и сдвигов 48
§ 13. Теория, малых деформаций 50
§ 14. Случай, когда малы не только деформации, но и
углы поворота 51
§ 15. Переход к формулам классической теории .... 56
§ 16. О переходе к криволинейным коордиватам • . . . 59
Глава II, Равновесие объемного элемента тела
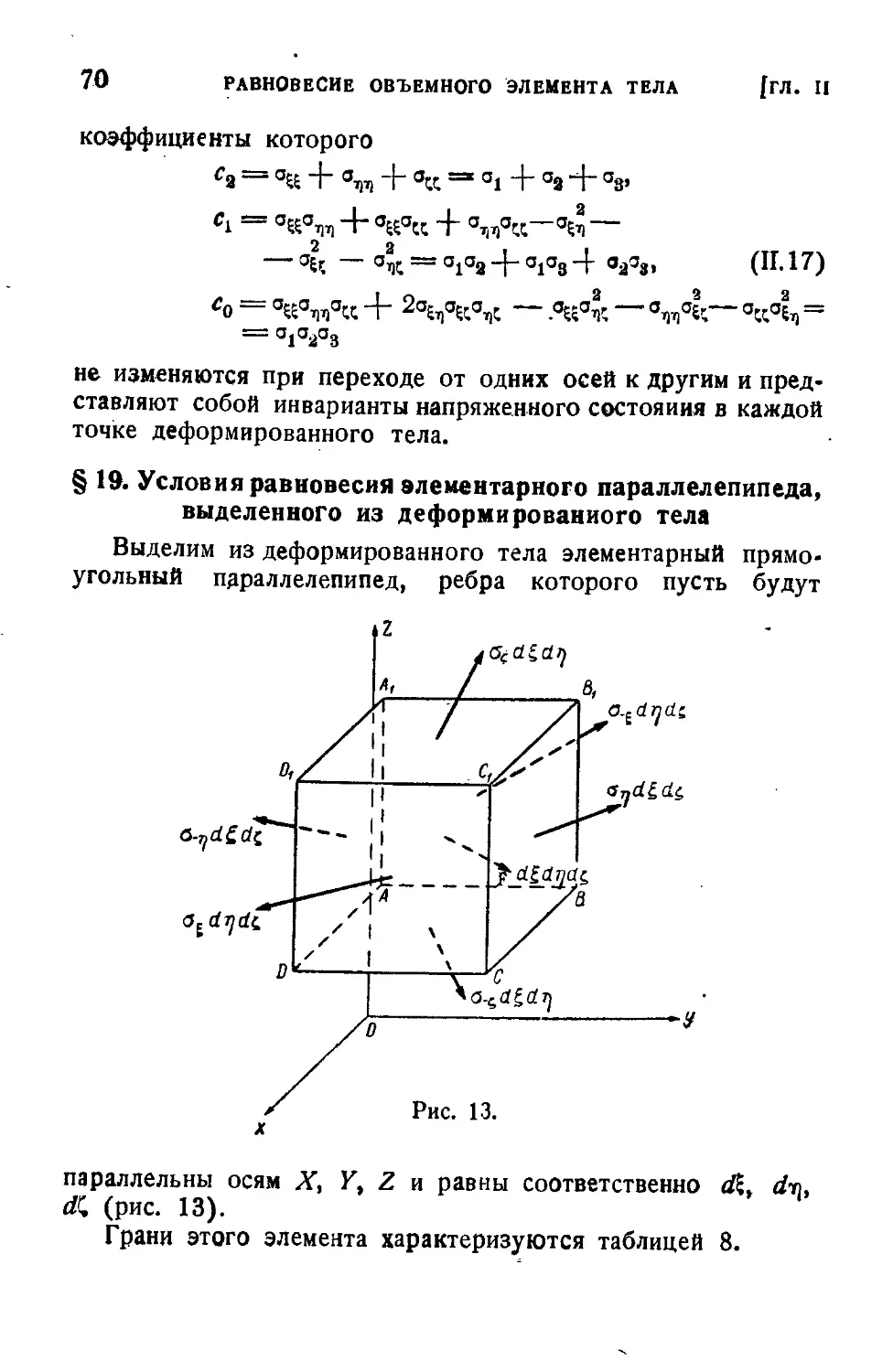
§ 17. Напряжения . 63
§ 18. Формулы для пересчета компонентов напряжения
при переходе от одной системы координат к дру-
другой 66

ОГЛАВЛЕНИЕ
§ 19. Условия равновесия элементарного параллелепи-
параллелепипеда, выделенного из деформированного тела ... 70
§ 20. Преобразование уравнений равновесия объемного
элемента к декартовым координатам точек тела до
его деформации 74
§ 21. Упрощение уравнений равновесия при малых удли-
удлинениях и сдвигах 81
§ 22. Упрощение уравнений равновесия прн малых пово-
поворотах 83
§ 23. Переход к уравнениям равновесия классической
теории упругости 84
§ 24. Переход к криволинейным координатам 86
Глава III. Работа деформации, граничные условия, упру-
упругий закон
§ 25. Работа деформации 93
§ 26. Начало возможных перемещений 96
§ 27. Вывод дифференциальных уравнений равновесия
деформированного изотропного тела из принципа
возможных перемещений 99
§ 28. Связь между напряжениями и компонентами дефор-
деформации 107
§ 29. Граничные условия 112
§ 30. Упрощение полученных формул в случае малой
деформации 113
§ 31. Закон Гука По
§ 32. О возможности применения формул (III. 38) к упру-
гопластическим деформациям • . . . 118
§ 33. О наиболее простых вариантах нелинейной связи
между напряжениями и деформациями 121
§ 34. Заключение 125
Глава IV. О постановке задач теории упругости в на-
напряжениях
§ 35. Еще две формы написания уравнений равновесия
объемного элемента 128
§ 36. Упрощение уравнений (IV. 7), (IV. 8) применитель-
применительно к малой деформации 133
§ 37. Еще одна форма граничных условий 134

ОГЛАВЛЕНИЕ
§ 38. Упрощгиие уравнений (IV. 7), (IV. 8) применительно
к случаю, когда углы поворота малы 137
§ 39. Обобщение соотношений Сен-Венана иа случай
больших поворотов и деформаций 139
§ 40. Упрощение соотношений (IV. 26; для малых дефор-
деформаций 143
§ 41. О возможности формулировки задач теории упру-
упругости в напряжениях и деформациях 145
Глава V. Проблема упругой устойчивости
§ 42. Неоднозначное гь решения задачи теории упруго-
упругости 147
§ 43. Дифференциальные уравнения для определения
критических нагрузок 149
§ 44. Краевые условия проблемы упругой устойчивости 157
§ 45. Энергетический критерий определения критиче-
критических нагрузок 162
Глава VI. О дефзрмации гибких тел
§ 46. Деформация пластин 170
§ 47. Двухмерная деформация бесконечно длинной по-
полосы ' 175
§ 48. Деформация оболочек 178
§ 49. О сущности допущений Кирхгофа . . '. 185
§ 50. Деформация стержней (первог приближение) ... 189
§ 51. Деформация стержней (второе приближение) . . , 199
§ 52. Чистое кручение 202
§ 53. Окончательные выражения для деформаций тон-
тонкого стержня 204
§ 54. Заключение 205
Библиография 207

ПРЕДИСЛОВИЕ
Эта книга написана иа основе курса лекций, прочтенных
автором в 1947 г. на Математико-механяческом факультете
Ленинградского Государственного ордена Ленина университета.
Она посвящена изложению теории упругости свободной от
предположений, ограничивающих величину удлинений, сдви-
сдвигов и углов поворота. В ней рассматривается также в общей
постановке вопрос о связи между напряжениями и деформа-
деформациями в изотропном упругом теле.
Уравнения классической (линейной) теории упругости
получаются из уравнений излагаемой ниже общей теории,,
если предположить, что
а) удлинения и сдвиги пренебрежимо малы по сравне-
сравнению с единицею;
б) квадраты углов поворота пренебрежимо малы по
сравнению с удлинениями и сдвигами;
в) связь между напряжениями и деформациями выра-
выражается законом Гука.
Будучи существенным обобщением классической теории,
нелинейная теория упругости позволяет подойти к решению
ряда важных задач, которые из первой теории, в силу ее:
ограниченности, выпадают.
Подобными задачами в частности являются:
1. Проблема устойчивости упругого равновесия.
2. Проблема деформации тел, имеющих начальные напря-
жешя.
3. Проблема сильного изгиба стержней.
4. Проблемы кручения и изгиба, осложненные наличием
осевых сил.
5. Проблемы изгиба пластин и оболочек, при прогибах
сравнимых с толщиною.

10 ПРЕДИСЛОВИЕ
6. Проблема деформации упругих тел, не следующих
закону Гука.
Наконец, в последнее время было доказано, что равно-
равновесие упруго-пластических тел (при соблюдении некоторых
'ограничений) может рассматриваться на основании общих
принципов теории упругости. Тем самым и проблема равно-
равновесия упруго-пластической среды в известной мере вклю-
включается в круг зацач нелинейной теории упругости.
Перечисленные выше задачи взсьма актуальны, чем и
объясняется все возрастающее внимание к.нелинейной теории
упругости со стороны ученых Советского Союза и других
стран (см. библиографию).
Чтобы сделать книгу доступной возможно более широ-
широкому кругу читателей, автор стремился проводить все выводы
наиболее наглядно и просто, избегая в частности тензорного
исчисления и соответствующей ему сложной символики (или,
точнее говоря, применяя их лишь в том небольшом объеме,
который присущ курсам классической теории упругости).
В заключение автор приносит благодарность проф.
А. И. Лурье, доценту ЛГУ Л. М. Качанову и редактору
книги А. И. Чекмареву за ряд ценных, высказанных ими при
чтении рукописи критических замечаний.
Ленинград,
ноябрь 1947 г.

ГЛАВА I
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
§ 1. Координаты
В этой главе будут рассмотрены основные геометриче-
геометрические свойства деформации.
Вопрос ставится так — даны положения точек тела
в первоначальном его состоянии (то есть до деформации)
и даны их положения в окончательном его состоянии
(то есть после деформации). Нужно определить изменение рас-
расстояния между двумя произвольными бесконечно близкими
точками этого тела, обусловленное переходом из первого
состояния во второе. Вопрос этот чисто геометрический
и при его рассмотрении совершенно не важны ни причины,
вызывающие деформацию, ни закон, по которому тело ей
сопротивляется.
Пусть положения точек тела в первоначальном с остояни
определяются их проекциями х, у, г на оси н екоторо
прямоугольной системы декартовых координат X, У, Z.
Пусть, далее, точки тела потучаюг перемещения с ком-
компонентами, по тем же осям и, v, w, которые будем считать
заданными функциями х, у и г. Тогда окончательное по-
положение произвольной точки тела определится де картовыми
координатами:
% = х -f и (х, у, г),
¦n = y + v(x, у, г), A.1)
С = г-j-да (я, у, г).
Функции и, v, w, а также их частные производные по х,у и г
будем считать непрерывными. Это ограничение может быть
названо условием непрерывности деформации.

12
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[ГЛ. I
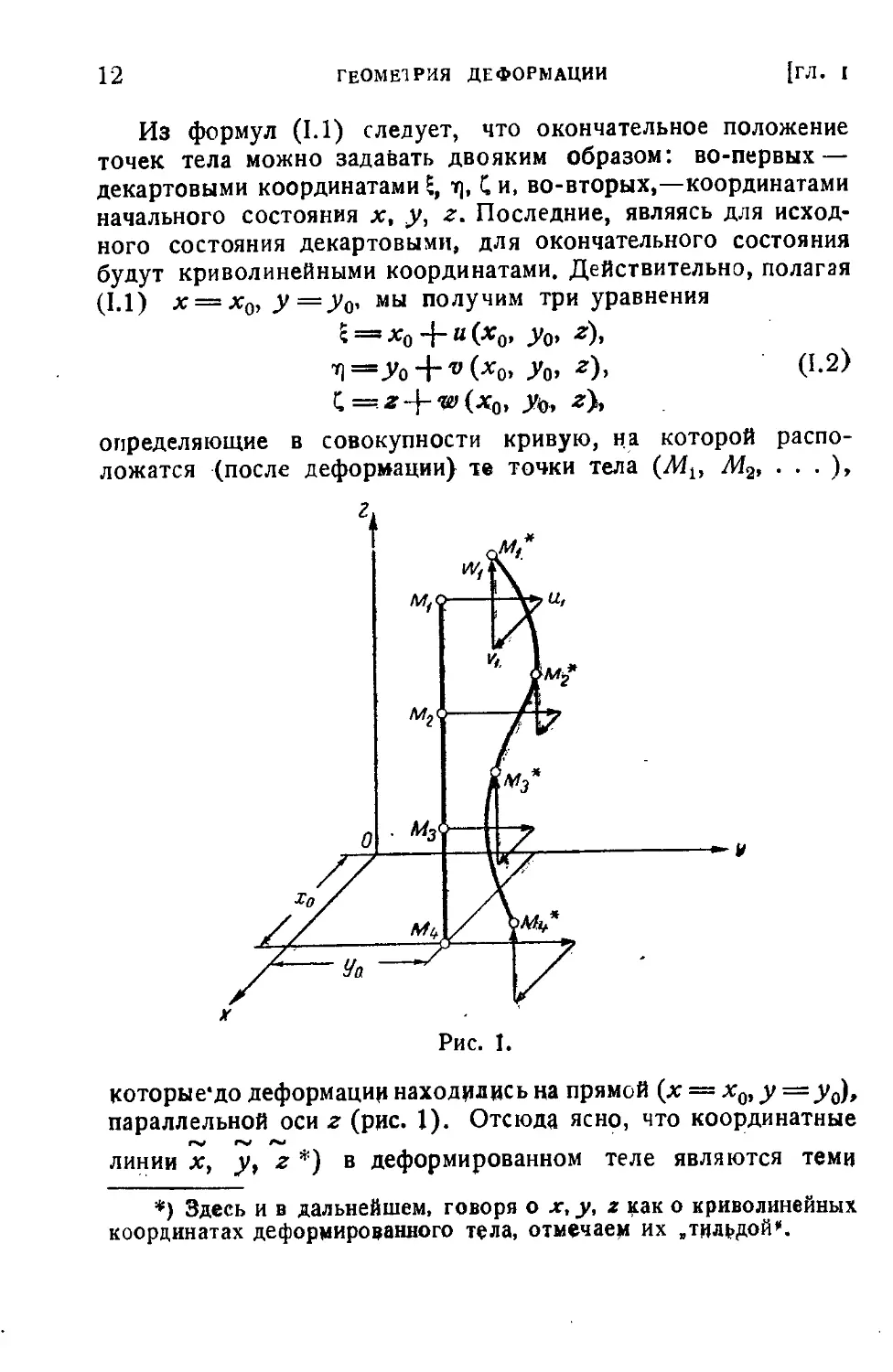
Из формул A.1) следует, что окончательное положение
точек тела можно задавать двояким образом: во-первых —
декартовыми координатами \, т), С и, во-вторых,—координатами
начального состояния х, у, г. Последние, являясь для исход-
исходного состояния декартовыми, для окончательного состояния
будут криволинейными координатами. Действительно, полагая
A.1) лг = лг0, У=Уо' мы получим три уравнения
S =¦ *о + « (*о> Уо> г)>
¦ц =Л + v (дг0) у0, z), A.2)
t=**-f-w(*o, Ж -г).
определяющие в совокупности кривую, на которой распо-
расположатся (после деформации) те точки тела (Mlt М2, . . . ),
г
Рис. I.
которые'до деформации находились на прямой (лг = хо,у=уй),
параллельной оси z (рис. 1). Отсюда ясно, что координатные
линии х, у, z *) в деформированном теле являются теми
*) Здесь и в дальнейшем, говоря о х, у, г 1сак о криволинейных
координатах деформированного тела, отмечаем их „тильдой*.

§ 1] КООРДИНАТЫ 13
(вообще говоря, кривыми) линиями, на которых размещаются
точки, бывшие до деформации на прямых параллельных соот-
соответствующим координатным осям.
Таков физический смысл преобразования координат, за-
заключающегося в формулах A.1).
Исследование деформации в окрестности произвольной
точки М (дг, у, г) сводится к изучению геометрических свойств
координат х, у, z, трактуемых как криволинейные координаты
деформированного тела.
Отметим далее, что I, т\, С,' будучи декартовыми коор-
координатами для деформированного тела, являются криво-
криволинейными координатами по отношению к телу до деформации.
В самом деле, полагая в A.1) ? = Ё0> 1Г1а='»1о' мы получим три
уравнения
S + (*. У, *),
(*, У, z)< A3)
С =г-\-w(x, у, г),
которые, после решения их относительно х, у, г, при-
принимают вид
z =Л (^о. "По. Q
и определяют в системе X, Y, Z кривую, на которой
находились до деформации точки тела, располагающиеся
после деформации на прямой I = ?0, ч\»тH, параллельной
оси Z.
гч» **J 1**»
Таким образом линии ?, ч\, С *) являются в теле до дефор-
деформации теми кривыми, которые в результате деформации пре-
превращаются в прямые, параллельные соответствующим коор-
координатным осям. Условимся в дальнейшем называть „волокном
тела" совокупность его точек, расположенных вдоль некоторой
линии, а „линейным элементом тела" —дифференциально-малый
отрезок какого-либо волокна.
*) Здесь н в дальнейшем, говоря о S, vj, С как о криволиней-
криволинейных координатах точек тела до его деформации, отмечаем их
„тильдой".

14 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Кроме того, условимся называть „слоем тела" совокуп-
совокупность его точек, располагающихся на некоторой поверхности,
а „элементарной площадкой тела" — бесконечно малый эле-
элемент какого либо слоя.
§ 2. Углы, определяющие направления координатных
линий
В результате деформации точка М (х, у, z) переместится
в положение М* с декартовыми координатами ?, t\, С, а бес-
бесконечно близкая к ней точка N(x-\-dx, y-\-dy, z~\-dz) —
в положение N* с координатами ?-f- dl, т) -j-d% C-j-dC,.
Вектор M*N* (с проекциями dl, dr\, dt.) определяет
величину и направление линейного элемента тела, величина
и направление которого до деформации были заданы век-
вектором MN (с проекциями dx, dy, dz).
Применив формулы A.1) к точке (X-}-dx, y-\-dy, z-\-dz)
и разлагая их правые части и ряды Тэйлора в точке х, у, z
(при сохранении малых только первого порядка), будем иметь:
,t /, . ди\ . , ди , , ди ,
., dw „__ , dw
"¦¦• — ЗТГ
Выражения A.5) определяют проекции произвольного
линейного элемента тела после деформации, через его проек-
проекции до деформации.
Если ввести обозначения:
da dv dw
еха>~д~х' еУУ ~ ду ' вйг~дг'
дгг , dv ди .dw dv.dw n R,
e*v~~ду~*~дх> xz ~~дг<~дх ' V» ~ дг~т~ду ^л>
dw dv _ ди dw n dv ди
Н= 2в>

§ 2] НАПРАВЛЕНИЕ КООРДИНАТНЫХ ЛИНИЙ 1а
то формулы A.5) могут быть записаны в виде:
d\ = A + ехх) dx+ (| ещ — шг) dy + (i е„ -f шу) dz,
д ^~ »«)<**. 0-8)
Пусть линейный элемент до деформации параллелен оси Х^
имея проекции (MN)^ == dx, (MN)^ = 0, (ЛШ)г = 0. Тогда
согласно A.8) его проекции после деформации будут равны
<Й=A + О <**, rft) = (-g- еед -f
A \
^«ш.—»») dx,
а его длина после деформации
j еху + шгJ+ A ^ - ш,J • dx =
= A+?„,)«/*, A.10)
A-11)
есть относительное удлинение элемента dx при деформации..
Отсюда косинусы углов, образуемых вектором M*N*
с осями X, Y, Z (в том частном случае, когда MN парал-
параллелен оси X), определяются формулами
cos (MN, X) = i±Sg., cos (Af^V, Г) =
Z)= 2 . • A.12)
Линейный элемент </д: в результате деформации превра-
превращается в элемент дуги линии х в деформированном теле..
Ввиду этого формулы A.12) дают направляющие косинусы
касательной к этой линии в точке М*. Путем аналогичных
рассуждений, но применяя их к линейным элементам dy и

16
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[ГЛ. I
dz, можно вывести выражения и для направляющих коси-
косинусов касательных к линиям у и г в той же точке. Обо-
Обозначим единичные векторы, направленные по вышеуказанным
м
X
Рис. 2.
/Г
трем касательным, через i,, i2, i3 (рис. 2). Тогда, в соот-
соответствии с полученными выше результатами, можно составить
следующую таблицу проекций данных векторов на оси X, У, Z.
Таблица 1
X
У
z
1
1
h
1 +exx
l+Ex
еХу+*г
i+Ex
exz ~ фу
i*
1
\+Ev
l+Ey
\ + Ey
1
2
1
h
eXz + <»y
i+e7

§ 2] Направление координатных линий 17
Здесь, кроме уже введенных обозначений:
Таблица 1, как ясно из вышеизложенного, определяет
направляющие косинусы касательных к линиям х, у и z
в тОчке М*.
Решая далее A.8 или 1.5) относительно dx, dy, dz,
находим:
dx — р
A-14)
=~ (<x3ldl + a
где
, dw\ dv dw
dw\du
dv dw (л . dw\ dv A \ /1 \
aai = & g; — \} + ^ J at = ^2" ev~ **) \Je«* — *») —
-~е%, + 4, A.15)
2 Зак. 3804. В. Новожилов.

18 ГЕОМЕТРИЯ ДЕФОРМАЦИИ
du dv Л , du\dv /1 , \/1
1 __ \
1
32 dy dx ~\
dv dw Л . dv\ dw /1
аз' = бх dj, - {1 + Ту)Ш = (Т
1 .а
{гл. I
0tt л | OV 0*3
~Ъ~х ' ' dy ' я*
dx ' dy '
ate»
IF
"T" exx> ~2 ещ юг> ~2
A.16)
Формулы A.14) выражают проекции произвольного линей-
линейного элемента тела до деформации, через его же проекции
после деформации."
Рассмотрим теперь линейный элемент d\, то есть линей-
линейный элемент, параллельный после деформации оси X.
Согласно A.14) его проекции до деформации равны:
< = Щ-йЬ, dz = ~$rdlt A.17)
\MN\
а его длина до деформации
¦Д1.18)
* Определитель D, между прочим, в рассматриваемой задаче
всегда отличен от нуля, поскольку равенство его нулю означало бы
бесконечное уплотнение тела в соответствующей точке (§ 11).

2]
НАПРАВЛЕНИЕ КООРДИНАТНЫХ ЛИНИЙ
19
где
_ \M*N*\ — \MN\_
~ \MN\ "~
D
-1 A.19)
И21"Г а31
есть относительное удлинение элемента MN, параллельного
после деформации оси X. ^
Отсюда косинусы углов, образуемых вектором MN, будут
в рассматриваемом случае равны
cos (MN, X) = -Ц^- ап, cos (MN, Y) = li^- «21,
cos (MN, Z) = -i±^i-a8l.
Эти косинусы определяют направление (до деформации) того
линейного элемента, проходящего через точку М, который
Рис. 3.
в результате деформации становится параллелен оси X, или„
иначе говоря, они определяют направление касательной
к линии 5 в точке М (см. предыдущий параграф).
2*

20
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[ГЛ. I
Путем аналогичных рассуждений, но, применяя их к линей-
линейным элементам d-ц и dC, можно получить и косинусы углов,
задающих направления касательных к линиям tj и С в точке М.
Обозначим единичные векторы, направленные по выше-
вышеуказанным трем касательным, через \[, \'%, U (рис. 3). Тогда,
для проекций этих единичных векторов, на основании выше
изложенного, может быть составлена таблица.
Таблица 2
X
Y
Z
.1
4
D
1+Щ
D
D
an
...
«ai
D "**
—5-^032
1
1
1
i
D
~D~
D
1
- a13
-«28
L«33
в ней, кроме уже введенных обозначений:
с. D , D
:— 1.
— 1, ?г
Таблица 2, определяет направляющие косинусы касательных
к линиям!, к), С в точ-
точке /W (дг, д/, г) или,
иначе говоря, опре-
определяет направляющие
косинусы тех воло-
волокон, проходящих через
точку М, которые пос-
после деформации стано-
становятся параллельными
осям X, Y-, Z.
В дальнейшем мы
будем рассматривать
встречающиеся тензо-
ы
/
с
/
iy
/
N
/{
dz
ix
/
и
У*
w
u
/
V
А
Рис.
ры и векторы либо в декартовой системе X, Y, Z, либо
в неортогональной криволинейной системе х, у, z, локаль-

§ 3] КОМПОНЕНТЫ ДЕФОРМАЦИИ 21
ными ортами которой являются ily I3, 13. При этом усло-
условимся в первом случае отмечать составляющие индексами
I, т), С, а во втором — х, у, z (без „тильдочек" — во избе-
избежание пестроты формул).
§ 3. Компоненты деформации
Квадрат расстояния между точками М н N (рис. 4) равен
до деформации
ds*
после деформации
Составляя разность этих квадратов и подставляя при
этом во вторую из формул (I. 20) вместо dt, dt\, dZ их
значения согласно формулам A.5 или 1.8), будем иметь:
}eyydy\^dz}
\ xy dy + sxgdx dz -f- zdydz)
Здесь
dx lv;
[4 (y ^ 4- <
du , dv . du to , dt/ &• , ga; dw
— ¦ф7"т7 i 17^"гаг 15Г г-^л^г —
-5-^ — ^) J;

22 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ I
ди I dw I ди ди , до до ¦ dw dw
г™ —дТ "г ~Ш "г Их ЪТ "г ~дх~ Л "г" "дГ "дТ ~"
Введем обозначение:
• ¦**&*- О'23)
— есть увеличение расстояния между точками М и N
(обусловленное деформацией), отнесенное к расстоянию между
ними до деформации. Данную величину назовем относитель-
относительным удлинением в точке М в направлении точки N.
При использовании обозначения A.23) формула A.21)
приводится к виду:
Емц A + 4" Е*я) rfs2 = exxdx* -f e^dy» + г^г* +
+ ew</jcdy + eeedjc«te-f-t|Bfl[y<fe A.24)
или еще
4 ^'+Vv' 0-25-)
где X, |x и v — суть косинусы, определяющие направление
вектора MN (то есть направление линейного элемента до
деформации)
, dx dy dz ,-, „?..
Из формулы A.25) видно, что для вычисления относи-
относительного удлинения в произвольной точке М в любом на-
направлении (X, [л, v) достаточно знать шесть величин е^,

§ 3] - КОМПОНЕНТЫ ДЕФОРМАЦИИ 23
syy, *гг> sxw е»г. вг/г- выражающихся через перемещения фор-
формулами A.22). Данные шесть величин, будучи известными
в каждой точке тела, полностью характеризуют его дефор-
деформацию. Равенство их нулю во всех точках тела означает не-
неизменность расстояний между любыми его двумя точками,
что равносильно отсутствию деформации. Отсюда ясно, что
перемещения и, v, w, удовлетворяющие уравнениям
ex:B = sw — **> = *яу:="*х*=: V=0> 0-27)
могут быть лишь перемещениями тела как абсолютно твердого
целого.
Выясним физическое значение параметров s^, гуу, егг,
еху, s^g, &yz, которые в дальнейшем будем называть .компо-
.компонентами деформации.
Полагая в формуле A.25) |* = 0, v = 0, к — 1, то есть
считая, что до деформации рассматриваемый элемент паралле-
параллелен оси X, будем иметь:
= .„,. • О-28)
Откуда
Л,—1, A.29)
где Ех— относительное удлинение в точке М в направлении
оси X.
Аналогично
??„ = /! +23^-1.
1
где Еу, Ez—суть относительные удлинения в точке М
в направлениях осей Y и Z.
Таким образом компоненты деформации е^, е№, г^ ха-
характеризуют удлинения тех линейных элементов, которые до
деформации параллельны координатным осям.
Для выяснения физического смысла компонентов дефор-
деформации е^, гхх> ayz найдем косинусы углов, образуемых век-
векторами ij, i.2, is друг с другом (то есть косинусы углов
гч* ew /w
между касательными к линиям х, у, г, проходящим через
точку /И*).

24 ГЕОМЕТРИЯ ДЕФОРМАЦИИ • [ГЛ. I
По известной формуле аналитической геометрии
cos (llf i2) = cos A1Э X) cos (i2, АО ¦+¦ cos (i,, Y) cos (ia, Y)-\-
+ cos(i1>Z)cos(J2Z). A.30)
Подставляя сюда значения косинусов из таблицы 1, полу-
получаем:
До деформации угол между линейными элементами dx, dy
является прямым. Обозначим его уменьшение, обусловлен-
обусловленное деформацией, через «р^. Тогда:
cos A„ 12) = cos (д — ^ =
l' (L32)
Обозначив, далее, уменьшения углов между линейными эле-
элементами dx', dz и dy, dz (получающиеся при деформации)
через <рхг, ср^, можно написать еще две формулы (по ана-
аналогии с предыдущей)
Углы <вху, yxz, фуг назовем сдвигами.
Из вышеизложенного следует, что компоненты деформа-
деформации sxyf ъх„ syz характеризуют сдвиги, и если эти три
компонента деформации равны нулю, то углы между линей-
линейными элементами dx, dy, dz остаются прямыми и после де-
деформации.
§ 4. Преобразование компонентов деформации
при переходе от одних осей к другим
Одна и та же деформация может быть рассмотрена в раз-
различных системах декартовых координат. Во всех случаях
она будет полностью характеризоваться установленными выше

§ 4]
ПРЕОБРАЗОВАНИЕ КОМПОНЕНТОВ ДЕФОРМАЦИИ
25
шестью компонентами деформац'ии, значение которых, однако,
будет зависеть от выбора направления координатных осей.
Таблица 3
Дадим формулы пересчета
этих параметров, при пере-
переходе от одной системы коор-
координат к другой. Рассмотрим
для этого, наряду с основ-
основной нашей системой X, Y, Z,
другую систему X', Y', Z',
направления осей которой по
отношению к осям первой си-
системы пусть задаются сле-
следующей таблицей косинусов
(табл. 3).
Так как обе системы являются прямоугольными, то между
этими косинусами существуют зависимости:
X'
г
Z'
X
h
h
h
У
Нч
1^2
Z
ч
ч_
V3 =
,= 0, A.33)
1,
или, записанные в другом виде,
2,2 ,
Проекции на оси первой системы линейного элемента,
имеющего по осям второй системы компоненты dx', dy',
dz', будут равны:
dx = X^dx'x -\- \2dy'
dy^^dx' + ^
dz = vxdx' -f- v2d/ -{- 4.Adz'.
A.34)
Возвратимся к формуле (I. 21). В левой ее части стоит
изменение квадрата расстояния между точками М и N, обу-
обусловленное деформацией. Поскольку выбор этих точек не
зависит от выбора системы координат, постольку левая часть

26 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
t
формулы (I. 21) также от него не зависит, оставаясь инва-
инвариантной при переходе от одних осей к другим.
Подставляя в правую часть формулы A.24) вместо dx,
dy, dz их выражения через проекции вектора МЫ на новые
оси координат, то есть через dx', dy', dz' [см. формулы
A. 34)] будем иметь:
Ems U 4" \
4- е^(йг-')а 4-4/ dx'dy'-\-
1 4- 4i dx' dz' 4- e'y, dy'dz', A.35)
где
h 4~ eW H-l 4" s*z 4 4" eas» КЪ 4" &xz XjVj -|- S
*2 4" SJ/J/ И-2 4" e*3v<! 4~ в^ ^г^Э 4" 8«г ^2V2 4~
4-e!/sI12ve. C1-36)
^3 4" &yy 1*3 4" в«г V3 4~ sxy ^sH 4~ ea» ^3V8 4" eJ/« Ii3v3>
4" 8*s (^1V2 4- X2Vl) 4- SV* (H-1V2 4"
вхг == 2 (exx Xj X3 4- eyy ^1*3 4- вгг V
4- ео,г (V3 4- VO 4"
s^ = 2 (exx X2X8 4- ewIi2IJ.s 4" 8«г v2v3) 4~ еЖ2/(^2^з "Г КЫ 4"
4" s^ (^2vs 4" ^2"» 4- V (^2^ 4" !Va)-
Формула (I. 35) имеет вид, подобный формуле (I. 24) и
очевидно, что входящие в нее коэффициенты ехх, &уу,
в^ имеют по отношению к системе осей X' У, Z' тот же
смысл, какой имеют коэфициенты гхх,еУу, , svz по
отношению к системе X, Y, Z.
Отсюда ясно, что формулы (I. 36) дают искомый закон
преобразования компонентов деформации при переходе от
одной системы координат к другой,

§ 5J ГЛАВНЫЕ НАПРАВЛЕНИЯ ДЕФОРМАЦИИ 27
§ 5. Главные направления деформации
Будем искать такое направление, в котором относи-
относительное удлинение Emn принимает экстремальное значение.
Если взять ось X1 параллельной этому направлению, то,
согласно формуле A.35), будем иметь:
Ся'М "Г ~2^^')== sxx A.37)
ИЛИ
Из этого выражения видно, что вопрос отыскания экстре-
экстремума удлинения Е& сводится к отысканию экстремума компо-
компонента деформации ехя., то есть к определению таких значе-
значений *„ ]1. и Vj, при которых первое из выражений A.36)
становится экстремальным. При этом речь идет об относитель-
относительном экстремуме, поскольку между к{, JJ.J, Vj существует связь
[—1=0. A.38)
Составляя функцию
L = e'xx — e(^-|-^-fv? — 1), A.39)
где е — лагранжев постоянный множитель и, приравнивая
нулю ее частные производные по \lt j^ и vlf получим сле-
следующие три линейных однородных уравнения:
s-cy^i Ч~ 2 (&уу — е) ji, -f- еуг vt = О, A.40)
®ам ^l -f" &yz V-l -\~ 2 (ваг s) V, = 0.
Нулевое решение этой системы нас не устраивает в силу
существования условия (I. 38), и следовательно определитель,
составленный из ее коэффициентов, должен быть равен нулю
2/ \
\ хх )) ®а?2/) °хх
&ху, 2{svy — s), syz =0. A.41)
exs, *у*, 2(агг —е)
Данное уравнение является кубическим по отношению к мно-
множителю Лагранжа и, следовательно, оно имеет, по крайней
мере, один вещественный корень, который обозначим через е}.

28 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Заметим, что формула для &хх может быть приведена к виду:
&хх = (sxx *1 ~Ь 2" &ХУ 1*1 ~\~ 2 Sx* vi^i "Ь (г &хУ ^1 ~Ь ВУУ 1*1 4"
4(X +4j. A.42)
Подставляя сюда вместо выражений, стоящих в скобках, их
значения согласно A.40) и- учитывая (I. 38), находим, что
параметр е, равен экстремальному значению ехл,
ej = Extr. гхх. A.43)
Обратим далее внимание на то, что компоненты- деформации
&ху, &ха могут быть представлены в форме:
+
l ] 0-44)
5" в
Подставив сюда вместо выражений, стоящих в круглых скоб-
скобках, их значения согласно A.40), будем иметь:
viva). " J
но тогда, ввиду соотношений A.33), &ху — 8ла = 0. Таким
образом, если удлинение по оси X' является экстремаль-
экстремальным, то компоненты деформации еху, ехз равны нулю, то
есть деформация происходит без изменения прямых углов
между направлениями X', У и X', Z'.
Рассмотрим теперь еще одну систему осей X", У\ Z",
отличающуюся от X', Y', Z' поворотом вокруг оси X' на
угол 6.
Таблица косинусов углов между осями этих двух систем
имеет вид, ясный из рис. 5.

§ 5]
ГЛАВНЫЕ НАПРАВЛЕНИЯ ДЕфоРМАЦИИ
29
Тогда, в силу формул перехода (U6), а также установ-
установленных выше следствий, вытекающих из предположения,
2 Таблица 4
X"
У"
Z"
X'
1
0.
0
г
0
cos 0
— sin 8
Z'
0
sin 0
cos 8
Рис. 5.
что ось X' является экстремальным направлением для компо-
компонента деформации е'^, будем иметь:
= *'тsin3 9
If
— *ху ~ 0,
/acos о sin и,
— &m cos 9 sin 9, A-43)
s;^(s;s-v)s'n29+vc°s39-
Определим угол 8 так, чтобы удлинение г" было
экстремальным, условие чего получим, дифференцируя е" по 8
и приравнивая производную нулю. Эта операция дает:
1 V
A.47)
УУ
Отсюда следует, что каковы бы ни были значения
e'ys, e^, e'zs, всегда можно найти такой угол 9, при котором
е" будет экстремальным. Для этого же угла экстремальным
будет и г"гз, что легко установить, повторив применительно
к нему описанные выше действия. Подставляя далее резуль-
результат A.47) в последнюю из формул A.46), мы видим, что
при выборе направлений Y", Z" из условия экстремальности гуу,
ssg, компонент деформации syz получается равным нулю.

36 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. t
Вышеизложенным доказано, что для всякой точки тела
можно выдрать такие три взаимно перпендикулярных напра-
направления X", Y", Z", для которых компоненты деформации
е" в" , в" (а следовательно, и относительные удлинения
Ех; Еу» Ez-) будут иметь экстремальные значения, а компо-
компоненты деформации е^, s^, &" (а следовательно, и сдвиги
?*«/> <Р**> %,»} будУг равны НУЛЮ-
Отсюда вытекает, что какова бы ни была деформация
тела во всякой его точке, можно указать такие три прохо-
проходящие через нее в<Улокна, которые, будучи взаимно перпен-
перпендикулярны до деформации, остаются таковыми и после нее.
Эти три направления назовем главными направлениями
деформации в точке М (*, у, г) и обозначим соответствующие
им экстремальные значения компонентов деформации s^,
8wi еет чеРез 81- 82> Ч-
Таким образом, отправляясь от несомненного факта
существования одного экстремального направления, который
является следствием наличия у кубического уравнения A.41)
хотя бы одного вещественного корня, мы доказали затем
существование трех таких направлений. Тем самым доказано,
что все три корня уравнения A.41) всегда вещественны.
Единичные векторы, соответствующие главным направлениям
деформации, будем обозначать через sv sa, s3.
Удлинения волокон, имеющих до деформации эти напра-
направления, будут равны:
?a==i/l-|-2ea—I, (I.48)
Косинусы углов, образуемых вектором Sj с осями X, Y, Z,
(Хр 1*и Vj), могут быть определены из уравнений:
(sxx— Sj) Xj -{- _8aw|il -f y*xz*1 = °.
2 s.r^i + 2"VH
и равенства ,2.2,2 ,
Xi -J— i*i -f-vi — 1.

§ 6] ПРЕОБРАЗОВАНИЕ ПАРАМЕТРОВ 31
Аналогично определяются и направляющие косинусы в к-
торов е2, е3 (Ха, |х2, va и Х8, |is, v8).
Так как в результате деформации волокна, направленные
по Sj, е2, е3, оставаясь взаимно перпендикулярными, могут
получить некоторый поворот, то нужно различать главные
направления деформации для исходного и для окончательного
положения тела.
Единичные векторы главных направлений после дефор-
деформации (то есть направления, которые будут иметь после
деформации волокна, имеющие до деформации направления
si» е2» 8з) будем обозначать г\, г\, г\.
Углы между взаимно пеупендикулярными векторами elt
е2, е8 и взаимно перпендикулярными векторами г*, s*, г*3
характеризуют поворот, который в результате деформации
получает бесконечно малый элемент тела, выделенный вокруг
точки М. Несколько ниже этот вопрос будет освещен более
подробно.
§ 6. Преобразование параметров е^, еуу, ees, e^, exz, eyz
и сиж, шу, ш2 при переходе от одних координатных осей
к другим
Установим закон преобразования параметров (I. 6) и
(I. 7) при переходе от системы X, У, Z к другой декарто-
декартовой системе X1, Y', Z', направление осей которой, по отно-
отношению к осям первой системы, задано таблицею 3 (§ 4).
Составляющие перемещения произвольной точки тела по
новым осям будут выражаться через его составляющие по
старым осям очевидными формулами:
w' = M
Подставляя первую из них в выражение
ди' да' дх , ди' ду , да' дг т
и учитывая, что согласно A.34)
дх i
k
С1-52)

32 _ Геометрия деФэрмации [гл. i
будем иметь:
ехх ~ ехх}л -j- еуу\н ~\- еггч\ -j- exyk1\x1 -|-
H-^Vi + V^iV A-53)
Выполняя аналогичные выкладки по отношению к осталь-
остальным параметрам A.6), приходим к заключению, что данные
параметры (ехх, еуу, ezz, еху, exz, evz) преобразуются при
переходе от одних декартовых координат к другим по такому
же закону, по какому преобразуются компоненты деформации.
Этот результат позволяет доказать, что в каждой точке
тела существуют такие три взаимно перпендикулярных волок-
волокна, дли которых параметры ехх, еуу, ezz, принимают экстре-
экстремальные значения, а параметры еху, exz, eyz равны нулю.
Позволим себе, однако, не останавливаться на этом во-
вопросе, поскольку ход рассуждений в данном случае ничем не
отличается от рассуждений, изложенных в предыдущем пара-
параграфе. Существенно только отметить, что три волокна, обла-
обладающие указанным свойством, вообще говоря, не будут со-
совпадать с главными направлениями деформации в рассма-
рассматриваемой точке и, следователвно, углы между ними не будут
после деформации оставаться прямыми.
Параметры ехх, ет ezz имеют простой геометрический
смысл, для выяснения которого рассмотрим линейный элемент
тела dx, параллельный (до деформации) оси х. Проекция этого
элемента (после деформации) на ту же ось, согласно первой
из. формул A.8), будет равна:
Отсюда
то есть ехх' есть относительное удлинение проекции на ось X
линейного элемента, направление которого до деформации
было параллельно этой оси.
Аналогичный геометрический смысл имеют и параметры
еуу, ezz (но для элементов dy, dz). Что касается еху, exz, eyz,
то в общем случае произвольно большой деформации они
наглядного геометрического смысла, повидимому, не имеют.
Остановимся в заключение параграфа на формулах пересчета
шх, шу, о)г при переходе от одних координатных осей к другим.

§ 6) ПРЕОБРАЗОВАНИЕ ПАРАМЕТРОВ 33
В системе X', У', Z' параметр шхг будет определяться
формулой:
* (L55>
Подставляя сюда вместо w' и v' их значения, согласно
формулам A.50), и, переходя от дифференцирования по / и г'
к дифференцированию по х, у, г, что можно сделать на
основании формул A.34), будем иметь:
По аналогии с этим результатом
) + » (t* A — Уъх\л A 57)
)
V = о>х{ЧН — »Ve) + my(hvs — xsvi) + »* (t* A —
Полученные три формулы могут быть упрощены, если
учесть, что единичные векторы, определяющие направления
X', У', Z', связаны между собою (ввиду ортогональности
осей) равенствами
i'B = 4xC, i» = CxU C=i*Xiy, 0-58)
где символ X означает операцию векторного умножения.
Проектируя A.58) на направления X, Y, Z и принимая
при этом во внимание таблицу косинусов 3, находим:
Это — известные соотношения между направляющими ко-
косинусами двух систем декартовых прямоугольных координат,
написанные в предположении, что обе системы имеют одина-
одинаковую ориентацию осей. Если бы одна система была правой,
а другая левой, то в формулах A.59) нужно было бы пере-
переставить члены, стоящие в их правых частях.
На основании A.59) и сделанного выше замечания, фор-
формулы A.56, 1.57) принимают вид:
3 Зак. 3801. В. Новожилов.

34
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[ГЛ. 1
причем верхний знак должен быть взят, если системы X, У, Z
и X', Yf, Z имеют одинаковую ориентацию, а нижний — если
их ориентация различна.
Отсюда видно, что параметры шх, ту, шг при переходе
от одних осей к другим преобразовываются как проекции
аксиального вектора to, длина которого равна
' = У
Ш1
а направление задается косинусами:
cos(w,*)=-J, cos(«0,10 = ^. cos(«>,Z)
A.61)
.(I.62)
§ 7. Геометрический смысл параметров шх, шр, wz.
Совместим мысленно точку М с точкой М* и перенесем
начало координат системы X, У, Z в эту общую точку (не
изменяя направления осей). При
z дЛ этом векторы MN, M* N* будут
исходить из начала координат,
имея проекции:
MN —dx, dy, dz.
¦ M*N*~dl, d-q, dL
Такое изображение (рис. 6)
устраняет несущественное посту-
пательное перемещение окрест-
окрестности точки М, позволяя сосре-
сосредоточить внимание на сравнении
величины и направлении векто-
ров MN и M*N*, характеризую-
характеризующих относительное расположение
точек М и N до и после деформации.
Величины, определяющие изменение размеров линейных
элементов тела и изменение углов между ними, обусловлен-
обусловленные деформацией, уже были изучены в предыдущих парагра-
параграфах. Однако при деформации меняются не только относи-
относительные, но и абсолютные направления волокон, ввиду чего
бесконечно малый объемный элемент, выделенный из тела
Рис. 6.

§ 7]
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПАРАМЕТРОВ
35
в исходном его положении, получает в окончательном поло-
положении кроме деформаций также и некоторый поворот. Употре-
Употребляя этот термин применительно к элементу объема, изменяю-
изменяющему в процессе перемещения не только положение, но также
размеры и форму, будем подразумевать под ним среднее
значение поворота, получаемого всем множеством линейных
элементов, принадлежащих данному объемному элементу.
При этом условимся называть углом поворота волокна
вокруг оси 2, к которой оно до деформации перпендикулярно,
угол ty между этим волокном (в положении до деформации)
и его проекцией (после деформации) на плоскость, перпенди-
перпендикулярную указанной оси (рис. 7).
м,м*<
Рис. 7.
Чтобы выяснить величины, характеризующие поворот, по-
получаемый окрестностью точки М в результате перемещений
я, v, w, обратимся к формулам A.8) и применим их к част-
частному случаю, когда линейный элемент -MN перпендикуля[ ен
оси Z. Тогда & = 0 и формулы A.8) принимают вид:
(I.63)
т '•* + ».) dx. + A + е„) dy,
-J e
v*
На рис. 8 показана плоскость X, Y, причем отрезок MN
представляет собою линейный элемент до деформации (в на*
3*

36 ГЕОМЕТРИЯ ДЕФОРМАЦИЙ (гЛ. 1
туральную его величину), а отрезок MNt* — проекцию M*N*
на рассматриваемую плоскость.
Как ясно из рисунка
<*» = &. *е*-ЗК A-64)
Вводя во вторую из этих формул значения d\ и dt\, согласно
A.63), будем иметь:
?(* + ) сод 8+ A+ви,) sin 8
tgb* = ^ '- п г . A.65)
A + ехх) cos 6 + (¦!¦ exy - a,,) sin 6
Рассмотрим угол
«k = e*— 6, A.66)
то есть угол поворота волокна MN вокруг оси Z, получаю-
получающийся в результате деформации. Согласно формулам A.65)
и A.66)
' >
Откуда
<¦>*+ -о-^ cos 26 ^- н-(fiyy-e^) sin 26
i
sin?6 + -^exy sin 26
Среднее значение tgtye в интервале от 9 = 0 до в = 2тс (то
есть среднее его значение для всех волокон, перпендикуляр-
перпендикулярных до деформации оси Z) определяется выражением:
2л
Ij + V 0.69)

§ 7} ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПАРАМЕТРОВ
Зд»сь
2*
1 2п J .
37
о 1 + е„ cos'6 + em sin2» + ^еху sin 29 '
2*
4 о 1 + «яа, co's'9 + eyy sin?6 4- -5 exy sin 26
Интеграл 12 может быть взят путем подстановки
которая дает
9 = 2*
9 = 2*
9=0
о-
а.72)
Что касается интеграла 1Х, то он приводится к виду:
2*
(О /* '"^
¦¦[ 2 + в.
е„
»„ sin B6 + р)
2и J
A.73)
*»
sin т
где
р = arcsin / _faM> g«* N
= arccos
Отсюда
( -r _
X!
arctg
2n. /
У 1+*«
B + ^+^)tgi
X
e*t/
A.74)
A.75)
„2
21/ 1
2

38 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Ввиду многозначности функции arctg ( ) полученный ре-
результат неопределен.
Однако эта неопределенность может быть раскрыта, если
учесть, что при стремлении exai, еуу, е^у к нулю, интеграл /,
(а следовательно и tgtyz), как видно из формулы A.73), дол-
должен стремиться к шг.
На этом основании в формуле A.75) надо положить:
& + '<*, + *„)%¦?¦
arctg -
ехх ет—
1 2
xy
что приводит к следующему выражению для
= 2я, A.76)
0-77)
По аналогии с полученным результатом можно написать
еще две формулы:
-ш / /ч I л \/1 I _\ *-2
A.77)
определяющие средние значения тангенсов углов поворота
вокруг осей X и Y линейных элементов тела, перпендику-
перпендикулярных до деформации этим осям.
Три параметра tg ^я, tg tyy> tg ^ характеризуют поворот
бесконечно малого объема, окружающего точку М. Они про-
пропорциональны Юд,, шу и шг и равны нулю, коль скоро равны
нулю эти последние параметры.
Но, как ясно из формул A.60), если т^, ть, шг равны
нулю в какой-либо системе координат X, Y, Z, то они бу-
будут равны нулю и в любой другой системе координат..
Отсюда следует, что при существовании в какой-либо
точке тела равенств
ю„ = ш,= ш,= 0, A.78)

§ 8} ВОЛОКНА, СОХРАНЯЮЩИЕ СВОЕ НАПРАВЛЕНИЕ 39
линейные элементы, проходящие через эту точку, в среднем
не будет получать поворота, относительно любой, прохбдя-
щей через эту точку, оси.
Таким образом равенства A.78) являются условиями от-
отсутствия поворота произвольного бесконечно малого объем-
объемного элемента тела, окружающего точку М.
§ 8. Волокна, сохраняющие свое направление
после деформаций
Подойдем теперь иным путем к выяснению условий отсут-
отсутствия поворота, установив попутно принципиально интерес-
интересный факт существования в каждой точке тела по крайней
мере одного волокна, сохраняющего свое направление при
деформации. Для такого волокна векторы MN и M*N*
(рис. 6) будут одинаковы по направлению, в силу чего их
проекции должны подчиняться соотношениям:
S = g-§ = X = coMt., 0-79)
причем
где Е'—удлинение в направлении MN.
Подставляя в A.79) значения <Д, dt[, dC, согласно фор-
формулам A.8), приходим к следующей линейной алгебраиче-
алгебраической системе:
+ (\еу, — «.) v = 0, A.
%) (у») V + («- -?') ^ = О,
ч
в которой
1 dx 11^ у—
суть направляющие косинусы искомого, не поворачивающегося
при деформации, волокна.

40
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
(гл.
Так как эти косинусы подчиняются равенству
*-ai-v3+v9=1. (Im83)
то нулевое решение системы A.81) не будет решением за-
задачи. Поэтому нужно приравнять нулю определитель, соста-
составленный из коэффициентов системы A.81), что приводит
к уравнению:
- е Ч-ш
2 еху'
1
1
«V 2
= 0.
A.84)
ем
Как доказывается в высшей алгебре, достаточным услови
вещественности всех трех корней уравнений вида A.84)
является симметрия элементов определителя относительно его
главной диагонали. Именно это обеспечивало вещественность
корней уравнения A.41).
В отличие от A.41), определитель A.84) не симметричен,
ввиду чего уравнение A.84) будет иметь в общем случае
всего один вещественный корень Е\. Подставив этот корень
в уравнения A.81) и присовокупив к ним соотношение A.83),
можно определить \и ja1s vt — косинусы, задающие направле-
направление не поворачивающегося волокна.
При соблюдении некоторых соотношений между элемен-
элементами определителя, уравнение A.84) может иметь и три
вещественных корня. Не вдаваясь в подробное исследование
данного вопроса, укажем (в качестве приблизительной оценки),
что это может иметь место только, если максимальные пово-
повороты не превосходят максимальных сдвигов.
Коль скоро поворот в некоторой точке тела удовлетво-
удовлетворяет этому ограничению, то в этой точке могут иметься три
волокна, не повертывающиеся при деформации, причем, в об-
общем случае, они не будут взаимно перпендикулярны. Их на-
направления определяются из уравнений A.81) и соотношений
вида A.83), подобно тому, как это было изложено выше.
Остановимся в заключении на частном случае, когда
<°а;= ши= <°г= °- A.85)

§ 9]
ИНВАРИАНТЫ ДВФОРМАЦИИ И ПОВОРОТА
41
При этом определитель A.84) становится еимметричен и
все три его корня — вещественны. Аналогия, существующая
в данном случае между уравнениями A.41) и A.84), а также
установленная в § 6 тождественность закона преобразования
параметров е^, еда , е^ с законом преобразования
компонентов деформации, позволяет утверждать, что если
в рассматриваемой точке тела имеют место равенства A.85),
то в ней существуют три и притом взаимно перпендику-
перпендикулярных волокна, не изменяющих своего направления при
деформации. Поскольку эти волокна остаются взаимно пер-
перпендикулярными и после деформации, то они неизбежно
должны совпадать с главными направлениями деформации
в рассматриваемой точке.
В свою очередь векторы sv e2, е3 (совпадая с направле-
направлениями не повертывающихся волокон) будут равны векто-
векторам е*, е*, е*, то есть главные направления в деформированном
теле будут совпадать в данном случае с главными направле-
направлениями в теле до деформации.
Мы пришли таким образом еще раз к заключению, что
равенства A.85) являются условиями отсутствия поворота
в окрестности той точки, где они соблюдаются. Деформацию
без поворота принято называть чистой деформацией. При
такой деформации волокна, направленные по векторам г1( ea, e3,
удлиняются, сохраняя свое первоначальное направление.
§ 9. Инварианты деформации и поворота
Развёртывая определитель A.41) в строку, приходим
к уравнению &3 _ a^
в котором
«2 — еаке + ег,2/ + егг'
_UQ== Q>
«0 =
1
2 °xyi
1
О SSZt
st,y<
1
2 s»*
2sye
(L86)
A.87)
-f ггге^ —

42
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[гл. i
Так как корни этого уравнения (et, е2, е8) не зависят
от выбора направлений X, Y, Z, то не должны зависеть от
этого выбора и коэффициенты а0, аи а2, являющиеся, следо-
следовательно, инвариантами деформации.
В силу известных соотношений, существующих между
коэффициентами и корнями алгебраических уравнений, данные
коэффициенты будут равны:
A.88)
а0 == е1е2г8'
Развертывая, далее, в строку уравнение (Т.84), будем
иметь:
- Ь% (?"J + ЬХЕ' — bo = O, (I.89)
где
еххеуу
"Т 4"
еххе
1.90)
~Г
+ Ша-СОув^ -j-
Эти величины, так же как и величины A.87), остаются
неизменными при преобразовании координат. Вспомнив анало-
аналогию, существующую между законом преобразования компо-
компонентов деформации и законом преобразования параметров

§ 10] ДЕФОРУ.АЦИЯ В ОКРЕСТНОСТИ ПРОИЗВОЛЬНОЙ ТОЧКИ 43
ехх, еуу еуг, можно утверждать, что эти последние па-
параметры должны иметь инварианты:
Ь'2=Ь%== ехх + еуу -j- ezz,
— ? (е%у + 4, + 4*) »
1 / 2 2 A.91)
ехз> еуу + е.х еяг + еуу
еуу
.)¦
но тогда инвариантами должны быть и выражения
По отношению к первому из них это было уже доказано
в (§ 6).
§ 10. Общая картина деформации в окрестности
произвольной точки тела
Из формул A.8) следует, что проекции вектора At* N*
(то есть проекции произвольного линейного элемента тела
после деформации) связаны с проекциями вектора MN (то
есть с проекциями того же элемента до деформации) ли-
линейными зависимостями. В соответствии с этим и обратные
зависимости, выражаемые формулами A.14), также будут
линейными. Коэффициенты формул A.8) и A.14) нужно счи-
считать постоянными и равными их значениями в точке М, так
как учет их изменяем с сти равносилен учету в формулах A.8)
и A.14) малых высшего порядка.
Таким образом деформация бесконечно малой области,
окружающей точку М, описывается линейным преобразова-
преобразованием с постоянными коэффициентами.
Но при таком преобразовании, как известно из аналити-
аналитической геометрии, прямые превращаются в прямые, а пло-
плоскости — в плоскости*, при сохранении параллельности тех и
других, если таковая имела место до преобразования.

44
ГЕОМЕТРИЯ ДЕФОРМАЦИИ
[ГЛ. I
Кроме того, при таком преобразовании поверхности вто-
второго порядка превращаются в другие поверхности второго
порядка—в частности сфера превращается в эллипсоид
(вообще говоря, трехосный).
Отсюда следует, что всякий бесконечно малый параллеле-
параллелепипед, выделенный в теле до деформации, превращается
в результате деформации в параллелепипед с другими (вообще
говоря) размерами ребер и углами между ребрами.
В частности, прямоугольный параллелепипед с ребрами
dx, dy, dz, параллельными координатным осям, [после дефор-
— У
Рис. 9.
Рис. Ю.
ними |—-
мации превращается в косоугольный параллелепипед с ребрами
A-\-Еу) dy, (l-\-Ez)dz и с углами между
|^ ?• — <fxt, \ — V (Рис- 9). Параллелепипед,
ребра которого до деформации совпадают с главными направле-
направлениями в рассматриваемой точке, после деформации остается пря-
прямоугольным, имея ребра A -\-Ел) da, A -\-Е2) db, (I -\-Es)dc,
где da, db, dc — размеры ребер до деформации.
Точки, расположенные до деформации на сфере радиуса
ds, в результате деформации размещаются на эллипсоиде
с полуосями A -J-ZTj) ds, A -J- E2) ds, A -j- Es) ds, причем
направления осей эюго эллипсоида будут совпадать с »lt
Sji Sj, то есть с главными направлениями в деформированном

§ 10] ДЕФОРМАЦИЯ В ОКРЕСТНОСТИ ПРОИЗВОЛЬНОЙ ТОЧКИ 4§
теле. Последнее ясно из того, что полуосям эллипсоида бу-
будут, очевидно, соответствовать экстремальные значения удли-
удлинений (рис. 10).
Вышеизложенное дает некоторое представление о характере
деформации бесконечно малой области, окружающей точку М.
Можно сказать, что эта область при деформации, во-пер-
во-первых, получает поступательное перемещение, в результате ко-
которого точка М совмещается с точкой М*, во-вторых,
получает поворот, при котором волокна, направленные
по Sj, е2, е3, становятся направленными по Sj, e2, 5з> и, нако-
наконец, получает чистую деформацию, при которой волокна,
имеющие направления е1( е2, е3, получают удлинения Еи Е2, Еъ.
В предыдущих параграфах были изложены все сведения,
необходимые для фактического определения (по заданным
перемещениям и, v, w) перечисленных выше трех факто-
факторов, определяющих окончательное положение и форму беско-
бесконечно малого объемного элемента, мысленно выделенного из
тела.
Заметим, что поступательное перемещение и поворот
объемного элемента не являются характеристиками его де-
деформации. Последняя будет определяться только компонен-
компонентами вдл,,, Вуу, вет, г^у, е^, еуХ.
Однако, если говорить о деформации тела в целом, то
более характерными будут именно перемещения его точек и
углы поворота его волокон.
Так, например, говоря о деформации балки, обычно под-
подразумевают под этим термином стрелку ее прогиба (то есть
перемещение), а говоря о деформации вала — подразумевают
закручивание одного его торца относительно другого (то
есть угол поворота).
С этой точки зрения перемещения и повороты могут быть
названы характеристиками деформации тела в целом, а удли-
удлинения и сдвиги — характеристиками деформации бесконечно
малого объемного элемента тела.
Отмеченная двойственность понятия деформации, заклю-
заключающаяся в необходимости различать ее микро- и макро-ха-
макро-характеристики, приводит к возможности двух различных тол-
толкований термина „малая деформация". Под ним, согласно
вышеизложенному, можно понимать либо малость удлинений

46 ' ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
и сдвигов (по сравнению с единицею), либо малость пере-
перемещений (по сравнению с линейными размерами тела) и уг-
углов поворота (по сравнению с единицею).
Упомянутые два определения нельзя смешивать. Между
тем, некоторые курсы теории упругости дают к этому повод.
Дело в том, что классическая теория малых деформаций
фактически покоится на допущении, что перемещения а по-
повороты малы. Однако это обстоятельство реако оговари-
оговаривают с должной четкостью, ввиду чего у читателя, привык-
привыкшего ассоциировать понятие деформации с ее компонентами,
легко создается впечатление, что речь идет о малости удли-
удлинений и сдвигов. Следует подчеркнуть, что предположение
о малости перемещений и поворотов в большей степени
ограничивает общность рассуждений, нежели предположение
о малости компонентов деформации, причем первое предпо-
предположение влечет за собою, как следствие, соблюдение и вто-
второго, тогда как обратное утверждение несправедливо. По-
Подробнее это выяснится из дальнейшего. Следует далее от-
отметить, что в тех случаях, когда необходимость малости
перемещений указывается, обычно, не оговаривают по срав-
сравнению с чем должны быть они малы. Между тем, такая
оговорка совершенно необходима, так как перемещения
суть размерные величины.
Для выхода из положения некоторые авторы прибегают
к понятию бесконечно малого перемещения, полагая его в
основу рассуждений. Однако это решение вопроса пред-
представляется неудовлетворительным, так как совершенно не-
неясно, в каких же пределах можно пользоваться теорией
упругости, покоящейся на таком чисто формальном осно-
основании.
Перечисленные методологические неточности (свойствен-
(свойственные многим курсам теории упругости) заслуживают быть
отмеченными, поскольку они касаются основ рассматриваемой
дисциплины.
Со свсей стороны, употребляя в дальнейшем термин „ма-
„малая дефо'рмация", мы будем под ним всегда подразумевать
малость удлинений и сдвигов по сравнению с единицею.
Если, кроме того, в рассматриваемых задачах будут так же
малы перемещения и повороты, то это всегда будет специально
оговорено.

§ 11]
ИЗМЕНЕНИЕ ОБЪЁМА
§ 11. Изменение объема
Бесконечно мал ли параллелепипед с ребрами dx, dy, dz
после деформации превращается в косоугольный параллеле-
параллелепипед, проекции ребер которого на оси X, У, Z будут
в силу формул A.5) равны:
на ось* Л ¦ a"V' ди ' ди
на ось У
на ось Z
dw
dw
dv
dw
Отсюда, воспользовавшись известной формулой аналити-
аналитической геометрии, находим
л | (/?/ C/W C/t*
' ~dx ' ~dy ' dz
dx ' ' dy '
dw_ dw_ . .
dv
~dz~
dw
dxdydz = Ddxdydz, A.93)
где V* — объем элемента после деформации.
Разделив V* на V = dxdydz (то есть на объем элемента
до деформации) и обозначив через Д относительное прира-
приращение объема, обусловленное деформацией, будем иметь:
, ди ди да
д» , г д» dv
1 -\ —
dx ' ' dy dz
dw dw ч i dw
t— , -3—. 1 + -3—
dx ' dy ' ' «
A.91)
Чтобы выразить Д через компоненты деформации, возве-
возведем полученный результат в квадрат. Тогда, учитывая пра-
правило перемножения определителей, а также формулы A.22),
получим:
2*
'УУ>
¦2в«
A.95)

48 Геометрия деформации {гл. t
Отсюда, после раскрытия определителя, имеем:
») =
где а0, ах, а2 суть инварианты A.87).
Таким образом окончательно
Д = V
-1 . A.97)
где Еи Eg, Ei — суть главные удлинения в той точке, где
вычисляется приращение объема.
Заметим, что полученный результат не зависит от того,
какой формы элемент выделяется из тела. В этом можно
убедиться, рассмотрев сферу радиуса dS. После деформа-
деформации данная сфера превратится в эллипсоид с полуосями
(l-^-EjdS, (I -{-E^)dS, (l-\~E^)dS. Вычтя из объема этого
эллипсоида объем сферы и разделив разность на объем эле-
элемента до деформации (то есть на объем сферы), будем иметь:
4-M(l + ?i)<
Д = * _
= A+/?1)A+?2)О+?а)-1 A-98)
Полученный результат идентичен A.97).
§ 12. О величине удлинений и сдвигов
До сих пор мы не налагали никаких ограничений на ве-
величину удлинений и сдвигов. Однако такая общность рас-
рассуждений в теории упругости, как правило, не нужна, ибо
только немногие материалы (как например резина) сохра-
сохраняют свои упругие свойства при значительных относительных
деформациях. Подавляющее большинство применяемых в тех-
технике материалов (как, например, все металлы и их сплавы)
упруги только при весьма малых (по сравнению с единицею)
удлинениях и сдвигах.
В качестве характерного примера рассмотрим сталь — наи-
наиболее употребительный в настоящее время материал, идущий

§ 12]
О ВЕЛИЧИНЕ УДЛИНЕНИЙ И СДВИГОВ
49
на изготовление конструкций, подвергающихся значительным
нагрузкам. На рис. 11 приводятся результаты испытания на
растяжение образца, изготовленного из стали одной из марок,
применяемых в судостроении. По оси абсцисс, как обычно, отло-
отложены относительные удлинения, а по оси ординат—напряжения.
На этом графике участок ОВ соответствует упругой ста-
стадии работы стали, участок ВС— пластической стадии (пло-
50
30
го
<о
h—
—
D
5S 1С Z
7 8 9
Рис. 11.
10 II 12 13 Ш 15 IS 17%l
щадка текучести) и наиболее длинный участок CD — стадии
упрочнения. Длина упругого участка в данном частном слу-
случае равна 1,15-Ю-3, длина площадки текучести 10-2, а
длина участка упрочнения (до максимума кривой) 0,17 *.
Эти цифры достаточно типичны и можно сказать, что для
сталей вообще область упругих деформаций ограничивается
относительными удлинениями, имеющими величину порядка
10-3~f- 5 • 10-а. Аналогичный порядок имеет для стали и
предельная величина упругих сдвигов.
Для цветных металлов (и их сплавов) цифры будут не-
несколько иными, однако и для них область упругих деформа-
деформаций ограничивается весьма малыми удлинениями и сдвигами.
Из вышеизложенного следует, что, применяя теорию уп-
упругости к металлическим конструкциям, естественно и разумно
упрощать формулы путем пренебрежения удлинениями и
сдвигами по сравнению с единицею. Отсюда» наибольший
практический интерес представляет теория малых деформа-
деформаций, к рассмотрению которой мы и переходим.
*) Фактически длина участка упрочнения еще больше ввиду
образования на образце шейки. Мы не вдаемся здесь, однако,
в эти детали, поскольку для дальнейшего они не нужны.
4 Зак. 3804. В. Нввожилов.

50 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [гл. 1
§ 13. Теория малых деформаций
Упростим выведенные ранее формулы, исходя из допусти-
допустимости пренебрежения удлинениями и сдвигами по сравнению
с единицею. Вводя это упрощение в формулы A.29), находим
р е р ~ р р П QQ-V
*-х — вдаг> '-'у— УУ •— 22" \i*wj
Пренебрегая далее Ех, Еу, Ez по сравнению с единицею
в формулах A.32) и считая, что сдвиги <pxy, <ржг. ?yzt малы,
получаем:
фр^е «Дйе »!=t!s. (I.100)
Таким образом при малых относительных деформациях
компоненты гхх, syv, szz могут быть отождествлены с соот-
соответствующими удлинениями, а компоненты еху, ехг, syz —
с соответствующими сдвигами.
Формула для изменения объема A.97), посла пренебре-
пренебрежения в ней произведениями удлинений по сравнению с их
первыми степенями, принимает вид
Aajfj + fj-ffi,, A-101)
или, если учесть A.99)ч
Д^г1+е2 + е3 = а2 = ежа.+ е^ + ггг- A.102)
Отсюда следует, что при малых деформациях инвариант
а2 можно отождествлять с объемным расширением. И, нако-
наконец, вводя аналогичные упрощения в табл.1 1 и 2, будем
иметь табл. 5 и 6.
Таблица 5
X
У
Z
h
1+ехХ
1
-rf exy + «>г
1
~2 ехг — шу
Ч
 еху — °>*
1
~2 ev> + и>х
h
~2 pxz + <°у
1
2 еуе фя>
1 + е.

СЛУЧАЙ, КОГДА МАЛЫ УГЛЫ ПОВОРОТА
51
X
У
Z
h
°11
«21
«л
«2
«12
О?2
.'з
«13
«3J
В последней из них величины а^- определяются формулами
A.15). Возможность замены при малых деформациях табли-
таблицы B) таблицею F) следует из того, что параметры Е^ ?Г|, Бс
являются величинами одного порядка с удлинениями, а опре-
определитель D, согласно формулам A.94) и (98), равен:
то есть равен единице, коль Таблица 6
скоро удлинения по сравне-
сравнению с единицей можно от-
отбрасывать.
Из вышеизложенного яс-
ясно, что таблицы E) и F)
определяют косинусы углов
между ib i2, i3 (I,', \'A, Q
и осями X, У, Z с погреш-
погрешностью, которая может быть
оценена путем сравнения
компонентов деформации с
единицею; с этой степенью точности диагональные члены
таблиц 5 и 6 могут единицу превышать.
Заметим, что если повороты велики, а сдвиги малы, то,
при определении направлений волокон тела после деформации,
вторыми можно пренебрегать по сравнению с первыми (ра-
(разумеется это не означает возможности пренебрежения в дан-
данном .случае сдвигами вообще; в тех формулах, куда они будут
входить не наряду с поворотами, их надо будет учитывать).
Примерами такого упрощенного подхода к опредению напра-
направления волокон деформированного тела являются гипотезы
плоских сечений в теории балок и гипотезы Кирхгофа в
теории пластин. И в том и в другом случае суть допуще-
допущений заключается в пренебрежении сдвигами по сравнению
с поворотами.
§ 14. Случай, когда малы ие только деформации,
но и углы поворота
Пусть малы по сравнению с единицею не только ком-
компоненты деформации, но и углы поворота. При этом напра-
направления векторов ij, i9, i8 и lu i3, is будут, очевидно, мало
4*

52 ГЕОМЕТРИЯ ДЕФОРМАЦИИ {гл. I
отличаться от направлений X, Y и Z, в соответствии с чем
диагональные члены таблиц 1 и 2 будут отличаться от еди-
единицы только величинами второго порядка, а остальные члены
этих таблиц будут величинами первого порядка (если считать
величиной первого порядка малости максимальное значение
угла поворота).
Рассмотрим формулу A.77), дающую среднее значение
тангенса угла поворота элементарного объема тела вокруг
оси Z. Эта формула, если учесть последнее из выражений
A.15), может быть приведена к виду:
откуда
A.104)
a
Но согласно табл. 6 при малой деформации а33 ^ cos D> Z)
и, следовательно,
5мГ.»,7=^т=- О-106)
У cos (/s. Zj
Выше было отмечено, что косинус угла между осью Z и
вектором 1з в рассматриваемом случае отличается от единицы
только на величину второго порядка малости. Кроме того,
поскольку поворот мал, фг будет отличаться or sin <!/г только
величинами третьего порядка. Отсюда, пренебрегая в фор-
формуле A.106^ квадратами угла поворота по сравнению с еди-
единицею, получаем:
? A.107)
По аналогии с этим' результатом можно написать еще две
формулы:
Таким образом пренебрежение квадратами углов поворота
по сравнению с единицею приводит к отождествлению пара-
параметров шх, а>у, <ог со средними поворотами элементарного
объема вокруг направлений X, Y, Z.

§ 14] СЛУЧАЙ, КОГДА МАЛЫ УГЛЫ ПОВОРОТА 53
А так как малые повороты суммируются как векторы,
то можно сказать,- что в данном случае объемный элемент
поворачивается на угол <о вокруг оси, направление которой
определяется косинусами A.62).
Исследуем далее возможности упрощения формул для
компонентов деформации, вытекающие из предположения, что
углы поворота и деформации малы по сравнению с единицей.
Первая из формул A.22) может быть приведена к виду
откуда следует, что она тождественно удовлетворяется, если
положить:
- е 4-ш
A.109)
Аналогично, вторая и третья из формул A.22) тождественно
удовлетворяются подстановкой:
1
Yl+2*yy
1
о
+уу
= Sin CPo Sin Yo, . = COS
f* Л21 Yl+2
A.109)
= cos ср.,
но, согласно табл. 2, ^, является углом между \х и осью А",
Фа — между ia и осью Y, ф8 — между i3 и осью Z.

54 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Все эти углы имеют величину порядка угла поворота и,
следовательно, в рассматриваемом случае, будут малы. На
Этом основании можем написать:
1 + eW _ i ?2
1 РГ~ >
VT+^j 2
^«1--^. A.110)
Отсюда, поскольку компоненты деформации предполагаются
малыми, имеем:
Ч>1
2
Из этих формул следует, что в рассматриваемом случае
ехх, еуу, ezz будут отличаться от соответствующих компо-
компонентов деформации только на величины порядка квадратов
углов поворота.
Подставляя затем A.109) в три последних выражения из
формул A.22), будем иметь:
= cos <?! sin (fa sin xa 4"
-\- cos cpa sin cpj cos x.i —j— sin <рх sin <pa sin ул cos Xa,
*== cos g>. sin % cosv3-[- A-П2)
-f cos <ps sin <fj sin Xi + sin yt sin % cos Xi sin /s,
— = cos «9 sin Ф, sin y4 +
2t)(l+24) '2 Т3 /ЗП^
-|- cos (f8 sin <fa cos Xa 4- s'n Та s'n Ts s'n 7.a cos ^з*
Пренебрежем здесь компонентами деформации по сравне-
сравнению с единицей и отбросим все члены, содержащие <?> выше
чем во второй степепи.

§ 14] СЛУЧАЙ, КОГДА МАЛЫ УГЛЫ ПОВОРОТА 55
Тогда получим:
«*, ~ Ъ sin Ъ + ?i cos Xi + <?i?2 sin Xi cos x2,
¦ «i» ~ ?в sin Xs + ?a cos Xa + ?a?e sln Xa cos Xs-
Производя аналогичные упрощения в формулах A.109),
находим:
^¦«aw + a)«{!si(PiC0SXi. -г
Y^ + ^
2" е*г 4" ш* ^ <Р 2 C0SX2. ~2 V — ma» ^ % sin Xs«
Используя эти приближенные выражения, можно привести
формулы A.113) к виду:
еад — еху «<Pi% sin xi cos x2,
nXs. A.115)
sin Xa cos Xs»
откуда вытекает, что параметры езд, е^, eyz отличаются
от соответствующих компонентов деформаций только вели-
величинами порядка квадратов углов поворота.
Полученные результаты позволяют перейти к непосред-
непосредственной цели исследования—упрощению формул для ком-
компонентов деформации. В основу упрощения положим при
этом возможность пренебрежения углами поворота и компо-
компонентами деформации по сравнению с единицей.
Рассматривая первую из формул A.22)
видим, что в ней можно отбросить квадраты параметров ехх,
еху, ехт так как, согласно доказанному выше, учет этих чле-
членов равносилен. удержанию в формуле наряду с первыми
степенями деформаций и вторыми степенями поворотов так
же вторых степеней деформаций и четвертых степеней пово-
поворотов, что находилось бы в противоречии с намеченной си-
системой упрощений.

56 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Отбрасывая указанные члены, приходим к формуле:
[«0» Зо+<4 + <°2] О-117).
Если подставить сюда вместо еху, exz их выражения' через
компоненты деформации и углы поворота, то появятся квад-
квадраты деформаций и кубы поворотов, из чего следует, что
первые два члена квадратной скобки формулы A.117) суще-
существенно меньше двух последних ее членов. Это позволяет
написать:
Аналогичным образом могут быть упрощены и остальные
из формул A.22). В итоге получатся следующие приближен-
приближенные выражения для компонентов деформации
у
^
еху —
гУУ ^ еУУ + 2"^* + ш* ) ' . еа« ~ «аи — ШЛ' (I-119)
szz « e^ +  ("^ + ш» )> ег/г *=« V ~~ Ш*Шг'
справедливые с точностью до пренебрежения углами пово-
поворота и компонентами деформации по сравнению с единицей.
Следует отметить, что в частных случаях эти формулы
могут поддаваться дальнейшим упрощениям. Так, например,
может оказаться, что из составляющих угла поворота одна
или две будут весьма малы. Тогда их можно будет отбро-
отбросить, сохраняя лишь ту (или те) составляющие поворота,
которые существенны.
В заключение подчеркнем как важный момент вышеизло-
вышеизложенных рассуждений, что из малости поворотов и деформа-
деформаций по сравнению с единицею отнюдь еще не следует, что
они являются величинами одного порядка. Именно поэтому
в формулах A.119), наряду с членами, содержащими пара-
параметры ета>, ...,eyz в первой степени, приходится удержи-
удерживать также члены, содержащие повороты во второй сте-
степени.

§ 15] ПЕРЕХОД К ФОРМУЛАМ КЛАССИЧЕСКОЙ ТЕОРИИ 57
§ 15. Переход к формулам классической теории
Предположим теперь, что квадратами и произведениями уг-
углов поворота в формулах A.119) можно пренебречь.
В этом частном случае мы приходим к следующим вы-
выражениям для компонентов деформации.
~ ЕЕ. ~ он . dv
exx~exw*n= qx > гху~еяу dy ' dx '
dv ди | dw ,. 1пг.ч
dw dv , dw
то-есть приходим к формулам классической теории упругости.
Из содержания двух предыдущих параграфов видно, что
использование линейных выражений для компонентов дефор-
мации [формул A.120)] возможно лишь при соблюдении сле-
следующих двух условий:
а) удлинения, сдвиги и углы поворота должны быть малы
по сравнению с единицею,
б) квадратичные комбинации углов поворота, входящие
в формулы A.119), должны быть малы по сравнению с соот-
соответствующими компонентами деформации.
Последнее условие, грубо говоря, может быть сформу-
сформулировано как требование, чтобы квадраты углов поворота
были пренебрежимо малы по сравнению с удлинениями и сдви-
сдвигами. Если тело массивно, то-есть имеет одинакового порядка
протяженность во всех своих трех измерениях, то соблюде-
соблюдение условия а влечет за собою и соблюдение условия б.
Иначе будет, если тело является гибким, то-есть имеет
в одном или двух направлениях существенно малые размеры
(стержень, пластина, оболочка). В этом последнем случае
углы поворота могут значительно превосходить удлинения
и сдвиги, и применение формул A.120) становится, вообще
говоря, необоснованным.
Из вышеизложенного следует, что областью применения
линейных формул A.120) является по преимуществу дефор«
мация массивных тел, а областью применения нелинейных
формул A.22 и 1.119) — деформация гибких тел.
Однако, формулы A.120) применимы и к некоторым за-
задачам о деформации гибких тел. В частности ими можно

58 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
пользоваться при рассмотрении изгиба и кручения тонких
стержней (при условии, что стержень не подвергается одно-
одновременному действию осевых сил, а углы поворота его сече-
сечений, хотя и велики по сравнению с деформациями, но малы
по сравнению с единицею).
Нетрудно объяснить, почему, например, кручение остается
задачей классической теории упругости. Дело в том, что
в этой задаче большим по сравнению со сдвигами является
только один из углов поворота (шх — если считать, что
ось X направлена вдоль стержня), два же других угла по-
поворота— суть величины одного порядка с деформациями.
В то же время существенную роль в кручении играют лишь
два компонента деформации:
причем последние члены в данных выражениях могут быть
отброшены (несмотря на то, что тх значительно превосхо-
превосходит еху и ехг), поскольку, как было выше отмечено, ту и
шг—весьма малы.
Этот пример показывает, что определение круга приме-
применимости формул A.120) требованием, чтобы квадраты углов
поворота были пренебрежимо малы по сравнению с дефор-
деформациями, как уже указывалось, не всегда является точным.
Фактически область применения линейных формул оказы-
оказывается несколько более широкой.
В заключение параграфа следует обратить особое вни-
внимание на установившуюся в большинстве курсов теории
упругости традицию называть формулы A.22) „компонентами
конечной деформации". Тем самым неизбежно (даже если
это явно и не говорится) выражения классической теории
упругости A.120) воспринимаются как „компоненты беско-
бесконечно малой деформации".
Между тем, из содержания этой главы совершенно ясно,
что степень малости удлинений и сдвигов по сравнению
с единицею вовсе не является достаточным критерием для
перехода от формул A.22) или A.119) к формулам A.120).
Существенную роль при решении данного вопроса играет
так же и величина углов поворота.
В некоторых задачах определение деформаций линейными

§ 16] О ПЕРЕХОДЕ К КРИВОЛИНЕЙНЫМ КООРДИНАТАМ 59
формулами оказывается недопустимым даже при весьма малых
удлинениях и сдвигах (сжатие тонкого стержня, изгиб тонкой
пластины). В других задачах эти формулы будут пригодны
при гораздо более значительных удлинениях и сдвигах (рас-
(растяжение стержня, изгиб толстой пластины).
Таким образом и нелинейная теория упругости и класси-
классическая теория упругости занимаются конечными деформаци-
деформациями и притом, как правило, деформациями одного порядка
малости.
Будь иначе — классическая теория упругости не имела бы
никакого практического значения.
Разница между подходом этих двух теорий к определению
деформаций заключается лишь в том, что линейная теория
пренебрегает влиянием поворотов на удлинения и сдвиги, а
нелинейная теория его учитывает, в соответствии с чем не-
нелинейная теория охватывает все задачи о деформации тел,
а линейная—только определенный круг задач.
Последними словами мы отнюдь не хотим умалить значение
классической теории, которая дает вполне согласующиеся с
истиной решения многих практически важных проблем. Ес-
Естественно, что нет никакой нужды трактовать эти проблемы,
как нелинейные.
Оцнако, в. то же время далеко не все задачи о деформа-
деформации тел охватываются классической теорией: ряд проблем
из нее выпадает (см. предисловие) и должны рассматриваться
в духе нелинейной теории.
Сказанное представляется достаточным для отказа от
наименования нелинейной теории деформаций теорией конеч-
конечных деформаций.
§ 16. О переходе к криволинейным координатам
До сих пор предполагалось, что положения точек тела
задаются в декартовой системе координат XYZ. Иногда, при
решении конкретных задач, выгоднее пользоваться для этой
цели криволинейными координатами. В связи с этим выясним
правила преобразования выведенных выше формул к произ-
произвольным ортогональным криволинейным координатам.
Пусть криволинейные координаты связаны с декартовыми
посредством формул
* = /i(ai»aa>as)> У = /а(а1»аа'ав)> г = /з(а1> аа> *з)- 0-121)

60 ГЕОМЕТРИЯ ДЕФОРМАЦИИ [ГЛ. I
Данные формулы определяют три семейства кривых —
координатные линии а,, а2, и а3, причем каждой точке про-
пространства соответствует пересечение трех линий, принадлежа-
принадлежащих различным семействам.
Обозначим единичные векторы, касательные к- координат-
координатным линиям, соответственно через к1( ка, к3. В силу пред-
предполагаемой ортогональности криволинейных координат, эти
векторы будут взаимно перпендикулярными и будут обра-
образовывать в каждой точке триедр локальных координатных
осей (локальными их называем потому, что их направления,
в отличие от декартовых осей, изменяются при переходе от
одной точки к другой).
Проекции перемещения какой-либо точки тела на напра-
направления ки ka, k3, построенные в той же точке, будем обоз-
обозначать через и, v, те>»
Как доказывается в курсах линейной теории упругости
(см., например [м] или [*3]), параметрам еха;, еуу, ею, е^, еае,
еуя соответствуют в ортогональных криволинейных коорди-
координатах выражения
1 ди , 1 d#! , I dHt
е 'vi w
+в + ^
//i д fv\ , Ht д (a
//! д (u\ , На д /w\
где #м H2, Hs — суть коэффициенты Ляме.
"¦=/(?)'+(?)'+(?)'¦

§ 1б] О ПЕРЕХОДЕ К КРИВОЛИНЕЙНЫМ КООРДИНАТАМ ' 61
Соответственно параметры ш,,, ту, шг, будучи отнесены
к произвольным ортогональным криволинейным координатам,
выражаются формулами
AЛ24)
которые представляют собою известные формулы для ком-
компонентов вихря.
В линейной теории упругости, основанной на предполо-
предположении, что деформации и повороты малы и сравнимы по ве-
величине, параметры еп, «аа, e3S будут удлинениями линейных
элементов, имеющих направления ко к2, к3, параметры е12, е13>
е23 — будут сдвигами между этими элементами, а ш,, ш2, ш3—
углами поворота объемного элемента тела вокруг ку к2, к3.
В общем случае при произвольной деформации перечис-
перечисленные параметры не будут уже иметь столь простого гео-
геометрического смысла и не могут быть отождествляемы
с компонентами деформации и углами поворота. Для ком-
компонентов деформации мы вывели (в декартовой системе коор-
координат) формулы A.22). Данные формулы конструируются
из параметров «им, правила преобразования которых выше
были выяснены.
Это позволяет сразу же написать следующие общие вы-
выражения для компонентов деформации в произвольной орто-
ортогональной системе координат:
{/ + ( e+) +("g-ei8 — W2J J.
S83 = езз + 
e12 = ell + e
И + ( 6is J Ш2) + ( ev ~~

62 ГЕОМЕТРИЯ ДЕФОРМАЦИИ fГЛ. I
8K = *13 + еи (у
е23
Здесь параметры е и <о определяются формулами A.122) и
A.124).
Относительные удлинения линейных элементов, имеющих
до деформации направления к,, к2, к3, будут равны
Соответственно сдвиги между теми же линейными элемен-
элементами определяются формулами:
?12
При малых удлинениях и сдвигах эти формулы могут
быть упрощены подобно тому, как это было сделано (§ 13).
Соответственно, к этим формулам применимы и другие упро-
щэния из числа тех, которые рассматривались в предыдущих
параграфах.

ГЛАВА II
РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА
§ 17. Напряжения
В этой главе будут исследованы условия равновесия произ-
произвольного, бесконечно малого объемного элемента деформи-
деформированного тела.
Выделяя мысленно такой элемент, нужно приложить к нему
силы, распределенные по ограничивающей его поверхности,
которые будут представлять собой воздействие на объем-
объемный элемент окружающей его среды. Рассмотрим на данной
поверхности элементарную площадку dQ. Ее ориентация
может быть задана единичным вектором нормали п, который
будем считать положительным, если он направлен во внеш-
внешнюю сторону по отношению к выделенному объему. При-
Приходящуюся на рассматриваемую площадку силу обозначим
через adQ. Вектор а является интенсивностью поверхност-
поверхностной нагрузки на площадке dQ. Его величина и направление
будут зависеть как от положения площадки (которое может
быть задано координатами ее центра тяжести ?, yj, С), так
и от ориентации Площадки (то есть от п). Но совокупность
Ё, к), С определяет радиус-вектор г, проведенный из начала
координат к центру тяжести площадки, в соответствии с чем
<r = ff(r, п). (II. 1)
Таким образом интенсивность поверхностной нагрузки
является функцией двух векторов. Заметим, что по отноше-
отношению к п эта функция будет нечетной
а (г, n) = — <j(r, — п\ (II.2)
Последнее обусловлено тем, что действие среды на пло-
площадку dQ объемного элемента должно быть равно по ве-

64 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
личине и обратно по направлению действию этой площадки
иа прилегающую к ней площадку среды, ориентация которой
определяется единичным вектором — п.
Вектор 5 будем называть напряжением, отмечая его
в дальнейшем нижним индексом, указывающим направление
нормали к той площадке, на которой оно действует.
Покажем, что достаточно знать значения напряжения на
трех взаимно перпендикулярных площадках, проходящих
через точку М* деформированного тела, чтобы иметь воз-
возможность найти его значения и на любой другой площадке,
проходящей через ту же точку.
С этой целью рассмотрим объемный элемент, предста-
представляющий собою тетраэдр, три ребра которого пусть будут
параллельны координатным осям XYZ и равны соответ-
соответственно d\<, df\, dX.
Для того, чтобы данный элемент находился в равновесии,
необходимо, прежде всего, чтобы сумма всех сил, на него
действующих, была равна нулю. Следует помнить при этом,
что, кроме поверхностных сил, на элемент будут действо-
действовать также и массовые силы, распределенные по его объему
(например силы веса или инерционные силы), значение ко-
которых ввиду малости элемента можно считать постоянным
во всех его точках.
С учетом этого замечания условие равенства нулю суммы
всех сил, действующих на тетраэдр, запишется следующим
образом:
4 , dgdC , йЫч , F dWvK _ 0
-I —2~ "г а~п ~J~ т "-<¦ ~Т~т~ F 6
(И.З)
Здесь
dQ —площадь наклонной грани тетраэдра;
п —единичный вектор ее внешней нормали
. F —среднее значение удельной объемной силы, прихо-
приходящейся на тетраэдр (например среднее значение
удельного веса или среднее значение инерционной
силы, отнесенной к единице объема);
ff-5 — напряжение на площадке, перпендикулярной оси X;
а_.Г1 — напряжение на площадке, перпендикулярной оси У";
в_с — напряжение на площадке, перпендикулярной оси Z.

§ 17)
НАПРЯЖЕНИЯ
65
Индексы трех последних напряжений отрицательны, по-
потому что внешние нормали к соответствующим площадкам об-
ратны по направлению координатным осям (рис. 12).
Рис. 12.
Разделив (П.З) на dQ и принимая во внимание формулу
(II. 2), будем иметь:
^ = cos(n,*), !g^cos(n,y),
но —k—, » , —у-* суть проекции наклонной грани те-
тетраэдра на плоскости YZ, XZ и XY, в соответствии с чем:
= cos (n, Z).
(II.5)
Кроме того, дробь—J1*' представляет собою отношение
объема тетраэдра к площади его наклонной грани и, следо-
следовательно, будет величиною порядка линейного размера те-
тетраэдра (то есть бесконечно малой величиной). Отсюда вы-
вытекает, что последний член формулы (II.4) будет так же
бесконечно мал и может быть отброшен^ поскольку осталь-
5 Зак. 3801. В. Новожилов,

66
РАвновейие Объемного элемента тблА
{гл. 1!
ные члены формулы конечны. В результате вышеизложенного
приходим к векторному равенству
<jn = <jj:cos(n, ^-r-s^costn, Y) -\- <jc cos (n, Z), A1.6)
выражающему напряжение в точке М* на площадке, внеш-
внешняя нормаль которой задана единичным вектором л, через
три напряжения на площадках, перпендикулярных коорди-
координатным осям.
Таким образом напряженное состояние тела в окрестно-
окрестности произвольной точки М* полностью характеризуется
векторами а^, ап, а^, величины и направления которых, ра-
разумеется, зависят от выбора направлений осей X, Y, Z.
§ 18. Формулы для пересчета компонентов напряжения
при переходе от одной системы координат к другой
Обозначим через
оц, oErj, о^ — проекции 5^ на X, Y, Z,
<3ф ящ, очг — проекции ап на X, Y, Z,
°«» °Ст)> °« — проекции 5С на X, Y, Z.
Совокупность девяти величин о^ назовем компонентами на-
напряженного состояния в системе
Таблица .7 х, Y, Z.
Выясним, как будут выра-
выражаться эти величины, если вместо
системы X, Y, Z взять другую
прямоугольную систему X', Y, Z',
'направления осей которой по
отношению к осям предыдущей
системы задаются таблицей ко-
косинусов G).
Косинусами нормали к пло-
площадке, параллельной плоско;ти
Z' У, будут, очевидно, 1и ти пх
(поскольку нормалью к этой плоскости является X').
Отсюда, согласно формуле A1,6),
("•7)
X'
г
Z
X
к
к
к
Y
тх
тг
Щ
Z
«1
«2
«3

§ 18] ЙЕРЕЙЧЕТ КОМпбнЕНТОВ НАПРЯЖЕНИЯ 61
проектируя это выракение на оси X1, Y', Z', будем иметь:
но проекции векторов 5г, »ч, 5С на оси X', У, Z' могут
быть выражены через их проекции на оси X, Y, Z, а именно:
(<ft)f - ой с°з (X, Хг) + ое„ cos (Y, X') +
4- <Jfc cos (Z, X') = ou
(П.9)
+ °К Л8»
(*ч)с' = Ч h + °Чг, Щ + "гц «в,
(<J Jc, = ок /8 -f «Си «8 + °К «8-
Подставляя эти выражения в (II.8), находим:
»« = ^е = °tt ;i + вчч "•" + "« я* + (^ 4" <
hni 4" о« ^а«1 4"
4- ок /хяв +ок/sft84. о^ Я1,я,4-"сч «1отз-
Теперь по аналогии могут быть написаны и выражения
для остальных компонентов напряжения. Заметим при этом,
что, как будет показано в одном из следующих параграфов,
в любой системе координат:
<»« = <> (И-П)
то-есть при перестановке индексов величина компонента
напряжения не изменяется.
5»

68
РАВНОВЕСИЕ ОВЪЕМНОГО ЭЛЕМЕНТА ТЕЛА
[ГЛ.
Учитывая этот доказываемый в дальнейшем факт, будем
окончательно иметь:
Л»
я"
l + 2 V- OTl"l'
A1.12)
"к
+ hnx) 4 o^ (т,я2 4
•« — 4
Сопоставляя формулы A1.12) с формулами A.36), видим,
что компоненты напряжения преобразовываются при переходе
от одних осей к другим, подобно тому, как преобразовы-
преобразовываются величины
— 8 -8
1
8#JfJ» Л
уу* 2 У"
(8)
На основании этого ряд положений, доказанных в пре-
предыдущей главе применительно к компонентам деформации,
могут быть немедленно высказаны и для компонентов напря-
напряжения. В частности, можно утверждать, что в каждой точке
деформированного тела существует три таких взаимно пер-
перпендикулярных направления, для которых о^, <з^, о^ будут
равны нулю.

§ 18] ПЕРЕСЧЕТ КОМПОНЕНТОВ НАПРЯЖЕНИЯ 69
Косинусы /, т, п, определяющие одно из этих направле-
направлений, могут быть найдены из уравнений:
(ок— о)/4- <з^т-{-^п = 0,
— о)« + очСя = 0, A1.13)
и равенства
/а + я»94-яг=1, A1.14)
причем входящий в систему A1.13) параметр о является одним
из трех корней кубического уравнения
:0. (П.15)
Ввиду того, что элементы этого определителя симметричны
относительно его главной диагонали, все корни уравне-
уравнения A1.15) будут вещественными, в соответствии с чем можно
написать три системы вида A1.13) и найти из них затем все
три направления, соответствующие экстремальным значе-
значениям <j??, <зщ, о,., и нулевым значениям о^, о^, о^. При этом
экстремальные значения о^, о^, ок (обозначаемые
в дальнейшем о1} о2, о8) будут равны корням уравнения A1.15).
Условимся называть о№, Qw ^ нормальными напряжения-
напряжениями на площадках, перпендикулярных координатным осям,
a <j?v o^r, очС — касательными напряжениями на тех же
площадках.
Соответственно экстремальные •' значения нормальных
напряжений в точке М *': oj, o2, <з3 будем называть главными
нормальными напряжениями в этой точке, а направления
нормалей -к тем площадкам, на коих они действуют, будем
называть главными направлениями напряженного состояния.
Формулы A1.13), A1.14) и A1.15) позволяют определить
в каждой точке тела величину главных напряжений и ориен-
ориентацию площадок, на которых они действуют, коль скоро
известны во всех этих точках компоненты напряжения, от-
отнесенные к произвольной системе осей X, У, Z.
Развертывая' определитель A1.15) в строку, приходим
к уравнению
* s+ 0 (Н16)

70 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
коэффициенты которого
fa = °« + ат + °к =» °i + °а + °8>
Ч1 Й
— %, — Овд = °108 + °1°8 4 °аа8. (U-17)
2 2 2
со —
не изменяются при переходе от одних осей к другим и пред-
представляют собой инварианты напряженного состояиия в каждой
точке деформированного тела.
§ 19. Условия равновесия элементарного параллелепипеда,
выделенного из деформированного тела
Выделим из деформированного тела элементарный прямо-
прямоугольный параллелепипед, ребра которого пусть будут
Рис. 13.
параллельны осям X, Y, Z и равны соответственно <#, di\,
rfC (рис. 13).
Грани этого элемента характеризуются таблицей 8.

§ 19]
РАВНОВЕСИЕ ЭЛЕМЕНТАРНОГО ПАРАЛЛЕЛЕПИПЕДА
71
Таблица 8
Наименование
грани
AAxBfi
DD,AtA
BBXCVC
ADCB
AyD.C.B,
Координаты центра тя-
тяжести ее площади
«.! + ?. С+?
б+Л.-4 + f. С + §
t . d? . . «, ¦ dC
«+ 2"' *i + dYi> ^ + -2"
Площадь
грани
d-qd^
dt\(K.
dldX,
dUt,
dbl-n
. dUn
Ориен-
Ориентация
грани
— »e
+ i*
-4
+ «r
— I,
В соответствии с этим на них будут действовать сле-
следующие поверхностные силы (которые определяем с точностью
до величин третьего порядка малости)
- 4- у Л) rf№ =
"
с,с
j, с 4-j
, (II. 18)

72 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
ADCB ~*-(S + « 4 +
Кроме поверхностных сил, на элемент будут действовать
также объемные силы. Их равнодействующая f.ipn той же
точности ее определения, какая принята в формулах (II. 18)]
будет равна:
F* F 4- у d\, ij + -j flTYj,C + j Л)
(II. 19)
где F* E, iq, С) —удельная объемная сила в точке М* (?, yj, С).
Суммируя все поверхностные и объемные силы и прирав-
приравнивая результат нулю, приходим (после сокращения на общий
множитель d\df\d^) к соотношению
являющемуся условием равенства нулю главного вектора всех
сил, действующих на выделенный из деформированного тела
объемный элемент.
Векторное уравнение (П. 20) эквивалентно трем скаляр-
скалярным:
Для полного решения вопроса 6 равновесии паралле-
параллелепипеда нужно дополнить уравнения (II. 21) условиями ра-

§ 19] РАВНОВЕСИЕ ЭЛЕМЕНТАРНОГО ПАРАЛЛЕЛЕПИПЕДА 73
венства нулю главного момента всех сил, действующих на
параллелепипед.
Относительно прямой, параллельной оси X и проходящей
через центр объема параллелепипеда, эти силы будут давать
момент
^ = Il(yiZi — ziYi), (II. 22)
где Z{ и Y4— проекции какой-либо силы на направления
Z и Y, а у{ и zi плечи этой силы относительно указанной
выше оси.
Применяя данную формулу ко всем силам (II. 18) и (II. 19)
и сохраняя при этом только величины до третьего порядка
малости (включительно), будем иметь:
(П. 23)
Приравнивая этот момент нулю, приходим к равенству:
Подобным же образом, но исходя из рассмотрения мо-
моментов сил относительно осей, параллельных Y и Z, могут
быть получены еще два аналогичных равенства:
%> = °Ф <te'—°«- (»• 25)
Таким образом условие равенства нулю главного мо-
момента сил, действующих на элементарный параллелепипед,
сводятся к требованию, чтобы касательные напряжения до-
допускали перестановку индексов. При этом данное условие
должно соблюдаться независимо от выбора направления
осей X, Y, Z, то-есть им должны обладать компоненты
напряжений в любой системе ' декартовых координат. Не-
Несколько забегая вперед (§ 18), мы уже пользовались этим
свойством- компонентов напряжения.
Результаты (II. 21) и (П. 25) по виду не отличаются от
условий равновесия параллелепипеда, выводимых в класси-
классической линейной теории упругости. По существу, однако,
они от них отличны, так как в линейной теории упругости
при выводе формул (II. 21, II. 25) отождествляют 5, ij, С
с х, у и г, пренебрегая, следовательно, при проектировании
сил изменениями положения точек тела, обусловленными erq
деформацией.

74 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
Отсюда в линейной теории не делают различия межлу
величиною и положением до и после деформации тех пло-
площадок, на коих действуют напряжения, или, иначе говоря,
пренебрегают, при проектировании сил, тем поворотом, ко-
который получает объемный элемент тела в результате де-
деформации. Однако, это допустимо далеко не во всех зада-
задачах и в общем случае надо считать, что в уравнениях (II. 21)
дифференцирование выполняется не по X, у, г (координатам
точек до деформации), а по ?, t\, С (координатам оконча-
окончательного положения точек).
Хотя, как уже было отмечено, по внешнему виду урав-
уравнения (II. 21) не сложнее аналогичных уравнений линейной
теории, тем не менее фактически они значительно более
сложны. Дело в том, что в задачу теории упругости входит
определение напряжений и перемещений по заданной на-
нагрузке на тело и условиям его закрепления.
Между тем [согласно формулам A.1)] и, v, <w входят
в Е, т], С и следовательно дифференцирование в уравнениях
(II. 21) выполняется по параметрам, зависящим от искомых
функций, в отличие от уравнений равновесия элемента в ли-
линейной теории упругости, в которых дифференцирование вы-
выполняется по параметрам, не содержащим неизвестных ве-
величин. В связи с вышеизложенным целесообразно преобра-
преобразовать уравнение (II. 21) таким образом, чтобы выявить
наружу все скрытые в них неизвестные функции.
Иначе говоря, целесообразнб перейти в этих уравнениях
от дифференцирования по ?, ч\, С к дифференцированию по
х, у, г, что и будет выполнено (§ 20).
§ 20. Преобразование уравнений равновесия объемного
элемента к декартовым координатам точек тела до его
деформации
Переходя в уравнении (II. 20) от дифференцирования по
5, т), С к дифференцированию по х, у, г, будем иметь
да; дх ¦ да^ ду ¦ да; _д? , да^ дх , да^ ду_
дх д- ~г ду д$ "Г дг д? ' дх <?>] ' ~ду ~д~ч
•• <"-26>

§1 20] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ 75
Входящие сюда частные производные -~г, -гт- опре-
определяются формулами A.14), согласно которым:
дх Он ал: dig дх а)з
Ж 5~> ~Щ ~D г Ж 7Г*
ду tf^ ду _aj2_ ду_
аа 5"' й1) ~ /) • ас=
а* вд а^ ^^ дг_ __ ^з
"аТ== ~d^ ' rfij /> ' ас d '
Подставляя эти выражения A1.26), находим:
;э~ ;э~ л« Яд
1 1 ~
Данное уравнение может быть записано также в виде
щвл) a C2ige + аю°т) + ап°д ,
дх г ду "т"
«г- (IL29)
| дх ' ду ' йг j ч
Но, как нетрудно убедиться, путем замены параметров a{j
их выражениями через м, г>, да [согласно формулам (I.l5)J,
величины, заключенные в квадратные скобки A1.29), тожде-
тождественно равны нулю.
На этом основании
1Явд a (aglg; -f "Mg + аЯяд
дх ~1~ ду
Входящие сюда, заключенные в круглые скобки, комби-
комбинации напряжений имеют определенный физический смысл,
который может быть выяснен путем следующих рассуждений.

76 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
Предположим, что в теле до деформации выделена прямо-
прямоугольная площадка, перпендикулярная оси Z и имеющая сто-
стороны dx, dy. В результате деформации эта площадка пре-
превратится в параллелограм, направления сторон которого будут
определяться единичными векторами iu i2 (§ 2). Отсюда
вектор единичной нормали к данной площадке может быть
найден из равенства
n8sin(llt 12) = 11Х'2» A1.31)
проектируя которое на оси X, Y, Z, будем иметь:
cos (X, n3) = sjn ^ k) [ cos (Г, it) cos (Z, i2) —
— cos(Z,I1)cos(K, у],
cos (Y, n3) = -^—^ [cos (Z, ix) cos (X, г2) —
— cos(,Y, ycos (Z, i2)l, A1.32)
cos (Z, n3) == . cos (X, ii) cos (K, i2) —
— cos(r, I,) cos (A, I,)],
но, согласно A.32) и A.29),
1
^Xl-f^)-»^, (И-33)
а косинусы, входящие в квадратные скобки формул A1.32),
даются таблицею 1 (стр. 16).
На этом основании получаем:
cos (X, щ) = * X
УA+2)A}2О4
A1.34)

§ 20] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ 11
cos (Y n ">
roc G п,Л —
\,\Jb \l~. Ilg^
Vd-
V(H
Of 32
f2ea!a!)(l+2
«иЗ
-2^) A+2.
Подобным же образом можно
COS (llj
cos (n
cos (X,
cos (Г,
cos (Z.
i. 2) =
л 1
i J
n-1 —
. n^ -
Vd +2е,г
/A4-2%.:
/A+2егг
У{1+2««
Vd+2w
установить,
) A + 2^)-
«12
«18
)(! + *»)-
«21
)A+2ега)-
a22
)A+2еи)-
что
•4.
i1
•г.'
A1.35)
где Ui и п2—суть векторы единичных нормалей к тем пло-
площадкам деформированного тела, которые по деформации были
перпендикулярны оси X и оси Y.
Заметим далее, что поскольку площадка dxdy в резуль-
результате деформации превращается в параллелограм со сторо-
сторонами ij (I -\-Ex) dx, i2 (I -f-?y) dy, то отношение ее пло-
площади после деформации к ее площади до деформации будет
равно:
-|? = A +ЕХ) ;A +Еу) sin A„ у =
= УA+2ежа,)A+2еу,)-е2у, A1.36)
аналогично
A1.37)

?8 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. И
Таким образом корни, входящие в знаменатели формул
A1.34, 11.35), равны отношениям площадей элементарных пло-
площадок тела, перпендикулярных до деформации осям X, Y, Z,
к их площадям после деформации.
Что касается определителя D, то он, в силу фор-
формулы A.94) представляет собою отношение объема элемента
тела после деформации к его объему до деформации
?> = -?-. A1.38)
Учитывая тепгрь все полученные результаты, а также
формулу (II. 6), определяющую напряжение на произвольной
площадке через напряжения на площадках, перпендикулярных
координатным осям, можем записать уравнение A1.30) в сле-
следующей окончательной форме:
Такой вид принимает уравнение A1.20), если определять
положение точек деформированного тела не декартовыми
*"Ч/ *"Ч/ *"Ч/
координатами S, t\, С, а криволинейными координатами х, у, г
(которые являются декартовыми координатами для тела
в исходном его положении).
Величина и направление удельной объемной силы в общем
случае могут зависеть от перемещений и, v, <w, так что
F* = F* (x, у, г, и, v, w). (II.40)
Действительно, если, например, объемные силы имеют
инерционный характер, происходя, скажем, от вращения
тела вокруг некоторой оси, то величина их явно должна
более или менее существенно изменяться вследствие дефор-
деформации.
Разложим вектора ffm, <зт, <зПг по направ:ениям i1( i2, ia
и примем следующие обозначения для их составляющих:

§ 20J ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ РАВНОВЕСИЙ f$
Тогда уравнение (II. 39) может быть записано в форме
"F F* = °-
Проектируя последнее векторное равенство на оси X, Y, Z
и учитывая при этом, что проекции ортов ilt i2, i3 на указан-
указанные оси даются табл. 1 предыдущей главы, будем иметь:
[О
(H.43)
y V-0,

80 Равновесие объемного элемента тела {гл. п
где приняты обозначения:"
Ъ9, Уя * *-*9, а" . _ «„ »«* /T| лл\
Три уравнения (П. 43) эквивалентны векторному уравне-
уравнению (II. 39) и являются скалярной формой его написания.
Величины <зу, определяемые формулами (П. 44), не бу-
будут напряжениями в точном смысле этого слова. Их можно
назвать напряжениями, отнесенными к размерам объемного
элемента не после, а до деформации.
Если деформации малы, то отношения
(II. 45)
и <hj можно отождествлять с о^. —то-есть с составляющими
напряжений по направлениям ll3 i2, i3. Таким образом разница
между ау и atj проявляет себя только при больших дефор-
деформациях — когда сдвигами и удлинениями нельзя пренебрегать
по сравнению с единицею.
В следующей главе будет доказано, что
то есть, что индексы при а* допускают перестановку. Но
тогда, как ясно из формул (II. 44), напряжения а у такой
перестановки допускать в общем случае (при больших де-
деформациях) не будут. Это не находится в противоречии
с доказанным в предыдущем параграфе свойством симметрии
матрицы напряжений, ибо данное свойство было там доказано
только для напряжений на трех взаимно перпендикулярных
площадках, разложенных по направлениям нормалей к этим
площадкам.

§ 21] Упрощение уравнений равновесия 81
§ 21. Упрощение уравнений равновесия при малых
удлинениях и сдвигах
s* s* s* V*
Отношения ~ , ^ , ^г , ~у. отличаются от единицы
Од. Оу О?
только на величины одного порядка с удлинениями и сдви-
сдвигами. Отсюда, при малой деформации их можно полагать равны-
равными единице, после чего уравнение (II. 39) принимает вид:
Выполняя это упрощение также в скалярных уравне-
уравнениях A1.43) и пренебрегая в них сверх того относительными
удлинениями Ех, Еу, Е3 по сравнению с единицею, будем иметь:
= О,
+ (y V - «*) «.] + ^ == 0, A1.48)
»)Оа;г J +
ж [(j'«""¦ шу) °га!+(т
6 Зак. 3804. В. Новожилов.

8U РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [гл. Ц
Поясним рисунком геометрическую сущность упрощений,
с помощью которых эти уравнения были получены. Выделим
из тела до его деформации прямоугольный параллелеципед
с ребрами dx, dy, dz, параллельными осям X, Y, Z (рис. 14).
В результате деформации этот прямоугольный параллеле-
параллелепипед превратится в косоугольный с ребрами (l-f-Дв) dx,
A-\-Еу) dy, (l-\-Ez) dz и углами между ними -g-—^ху,
Если, однако, углы поворота велики по сравнению со
сдвигами срау, фжг, ууг, то (как было отмечено еще в § 13
I главы) при проектировании сил можно пренебрегать вто-
вторыми по сравнению с первыми. Последнее равносильно тому,
что можно изобразить рассматриваемый параллелепипед прямо-
прямоугольным и после деформации (рис. 14). Кроме того, малость
удлинений и сдвигов позволяет (при рассмотрении равно-
равновесия параллелепипеда) не делать различия между его разме-
размерами до и после деформации, относя напряжения и объем-
объемные силы соответственно к первоначальным размерам пло-
площадок и первоначальному объему элемента. Это позволяет
изобразить параллелепипед после деформации равным парал-
параллелепипеду до деформации и отличающимся от него (гео-
(геометрически) только своим положением в пространстве
(рис. 14).
На основании сделанных замечаний единичные векторы
lj, i2, i3 следует считать взаимоперпендикулярными (рис. 14).
Их совокупность образует (при принятой точности рассу-
рассуждений) триедр декартовых осей, повернутый по отношению
к осям X, Y, Z в соответствии с поворотом, получаемым
в результате деформации окрестностью рассматриваемой
точки тела.
Физический закон, о котором будет идти речь в следую-
следующей главе, устанавливает связь между деформациями и соста-
составляющими напряжений по направлениям it, i2, V
Учитывая это, изобразим напряжения разложенными по
этим направлениям (рис. 14), после чего данный рисунок
будет в точности соответствовать системе A1.48).
Подводя итог вышеприведенным рассуждениям, можно
сказать, что данная система выведена в предположении, что

§ 22) УПРОЩЕНИЕ УРАВНЕНИЙ ПРИ МАЛЫХ ПОВОРОТАХ 83
при рассмотрении условий равновесия бесконечно малого
элемента, выделенного из тела, допустимо пренебрегать де-
деформацией элемента, учитывая только его поворот. В соот-
Рис. 14.
ветствии с этим система (II. 48) может быть названа усло-
условием равновесия бесконечно малого элемента, справедливым
при малых относительных деформациях и произвольных
поворотах.
§ 22. Упрощение уравнений равновесия при малых
поворотах
Если углы поворота малы по сравнению с единицей, то,
как было показано (§ 14), параметры е^, ..., егх будут
отличаться от компонентов деформации только на величины
порядка квадратов углов поворота. Это позволяет упростить
в данном частном случае систему (II. 48), пренебрегая в ней
деформациями и квадратами углов поворота по сравнению
с первыми степенями последних.
В результате такого упрощения получим уравнения:
¦gj
V»
-gj
«А,

84 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [гл. II
V Г ¦ Т I О г I
ду г усе уу не
' = 0, A1.49)
В данных уравнениях а>х, в>у и а>г можно считать углами
поворота элемента тела вокруг осей X, Y и Z.
С учетом этого замечания систему (II. 49) нетрудно вы-
вывести независимо от предыдущих рассуждений, воспользо-
воспользовавшись для этой цели рис. 14 и проектируя все действую-
действующие на параллелепипед, выделенный из деформированного
тела, поверхностные и объемные силы на направле-
направления X, Y, Z.
§ 23. Переход к уравнениям равновесия
классической теории упругости
Следующий шаг в направлении упрощения уравнений
равновесия элемента может быть сделан, если предположить,
что все углы поворота настолько малы, что в системе A1.49)
можно отбросить члены, которые на них умножены, по срав-
сравнению с членами, которые их не содержат.
После этого упрощения уравнения A1.49) принимают вид:
^f.+ .^+^fl + ^ = O,
дх ' ду ' дг > ' '
д*„
Очевидно, что написание уравнений равновесия в такой
форме равносильно пренебрежению поворотом объемного
элемента при проектировании всех сил, на него действующих,
то-есть равносильно отождествлению направлений i,, f8, J8
с направлениями X, Y, Z. Но если так, то исчезает разница

§ 23] ПЕРЕХОД К УРАВНЕНИЯМ КЛАССИЧЕСКОЙ ТЕОРИИ 85
между <зХЯ!, ..., ayz и offi, ..., о^, то-есть разница между
компонентами напряжения по направлениям локального три-
едра криволинейной системы координат lu ia, i8 и компо-
компонентами напряжения по направлениям декартовых осей X, Y, Z.
Отсюда система A1.50) может быть записана также
в форме:
д d dag | р о
Три уравнения A1.51) могут быть заменены одним век-
векторным
которое в совокупности с равенствами вида
является формулировкою условий равновесия элемента клас-
классической теории упругости. Уравнение A1.52) получается из
уравнения A1.20), если в последнем дифференцирование по
\, т),'С заменить дифференцированием по х, у, г.
Мы пришли к уравнению A1.52) путем цепи последо-
последовательных упрощений точного уравнения (II. 39). Из характера
этих упрощений видно, что критерием их допустимости является
малость удлинений и сдвигов и малость углов поворота.
Существенно обратить внимание на то обстоятельство, что
встречаются задачи, в которых даже при малых по сравне-
сравнению с единицею поворотах переход от уравнений (II.i9)
к уравнениям A1.50) оказывается невозможен. Чтобы это
показать, рассмотрим, например, выражения
входящие в третье из уравнений A1.49).

86 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
Очевидно, что возможность пренебрежения в этих выра-
выражениях нелинейными членами зависит не только от величины
a>j, но и от сравнительной величины stj.
Достаточно предположить, что напряжения amtt оуг> агх
значительно меньше напряжений ахх, <зуя!, ауу, чтобы
линеализация формул A1.53) была поставлена под сомне-
сомнение, несмотря на малость всех о>^ по сравнению с еди-
единицею.
Тем самым становится невозможной и линеализация третьего
из уравнений системы A1.49).
Таким образом малость углов поворота по сравнению
с единицею еще не является достаточным критерием для ли-
неализации уравнений равновесия элемента, выделенного из
деформированного тела. При выполнении данного упроще-
упрощения существенно обращать внимание на то, не являются ли
напряжения, умножаемые на повороты, большими по срав-
сравнению с теми напряжениями, которые входят в уравнения
линейно. Проблемы упругой устойчивости, изгиба тонких
пластин и др. являются примерами, когда указанное выше
обстоятельство играет существенную роль.
§ 24. Переход к криволинейным координатам
Предыдущие рассуждения соответствовали случаю, когда
положения точек тела задавалось в декартовой системе коор-
координат. Данная система удобна для тел, ограниченных взаимно
перпендикулярными плоскостями, и гораздо менее удобна
для тел, ограниченных кривыми поверхностями, так как,
если в первом случае уравнения границ тела записываются
в декартовых координатах весьма просто, то во втором
случае они будут более сложны, чем затрудняется подчине-
подчинение решения краевым условиям.
Поэтому во многих случаях вместо декартовых целесооб-
целесообразней пользоваться криволинейными координатами, причем
всегда надо стремиться выбирать их такими, чтобы поверх-
поверхности, ограничивающие тело, принадлежали к числу коорди-
координатных поверхностей, поскольку именно тогда краевые ус-
условия формулируются особенно просто. В связи с вышеиз-
вышеизложенным дополним полученные в настоящей главе резуль-
результаты рассмотрением условий равновесия элемента тела, точки

§ 24J ПЕРЕХОД К КРИВОЛИНЕЙНЫМ КООРДИНАТАМ 87
которого заданы в произвольной ортогональной системе
криволинейных координат а1э a2, ag.
Для сокращения связанных с этим преобразованием выкла-
выкладок уместно воспользоваться тем, что уравнения равновесия
элемента тела в нелинейной теории, как уже отмечалось,
сходны по виду с соответствующими уравнениями класси-
классической теории упругости.
Именно —в нелинейной теории условия равновесия эле-
элемента, при использовании декартовых координат, сводятся
к уравнению
5 S S у*
-^=о. (н.54)
которое в линейной теории принимает вид
+ F*^0 (И.55)
дх ' ду ' дз
ду
и получается при замене в уравнении A1.54) векторов
Sx Sy Sz
с- ап,. -с- а» . "с-«», векторами
Отсюда ясно, что если преобразование уравнения A1.55)
к произвольным ортогональным криволинейным координатам
известно, то соответствующее преобразование уравнения
A1.54) может быть написано по аналогии.
Коль скоро положение точек тела задается- криволиней-
криволинейными координатами (§ 16, I глава), то и бесконечно малый
объемный элемент нужно выделить, ограничивая его шестью
координатными поверхностями избранной криволинейной си-
системы. В итоге деформации этот элемент изменит свое по-
положение в пространстве .(за счет смещения и поворота) и,
кроме того, изменит свои размеры и форму (рис. 15). Его
ребра, первоначально равные: k1H1dctl, k2f/2^ag> k8//3fi?a3,
станут р«вны:
%) daa, k^3A + Ea>) d H,
где под ki, кг, »з подразумеваются единичные векторы, со-
соответствующие направлению линейных элементов, совпадавших

88
РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА
[ГЛ. II
до деформации с векторами ки k2, ks. Косинусы углов
между ортами kt, ka, k8 и ортами kj, кг, кз даются табли-
таблицею 1 (I глава), в которой под параметрами е и о> надо
понимать их вначения согласно формулам A.122), rf (I.124).
Напряжения, действующие на грани выделенного указан-
указанным образом элемента, будем разлагать по направлениям
Рис. 15.
ki, kg, кз, что аналогично разложению по направлениям
h> U* h-> которым мы пользовались, применяя декартовы
координаты.
В курсах классической теории упругости (см. напри-
например .Математическую теорию упругости" А. Лява, стр. 101)
доказывается, что при использовании ортогональных криво-
криволинейных координат, уравнение A1.55) заменится следую-
следующими тремя "скалярными уравнениями:
¦щщг
3 да3
^^
Htfia

§ 24J ПЕРЕХОД К КРИВОЛИНЕЙНЫМ КООРДИНАТАМ 89
Здесь: #ц Я9, Я8 — коффициенты Ляме (§ 16, I глава);
/%,,, Fw^a, — проекции удельной объемной силы на
направления ах, а2, а3;
^^ ^^ ^-^
а^и а,аа, а,а8 — составляющие напряжения аа% по ki, k2, k3;
«2а,, а9а2, а2а8—составляющие напряжения аа% по k^ k2, k8;
a3aj,a3a2, a8a8—составляющие напряжения авг по kj, k2, к8;
вп-> '«I» 5«3 — напряжения на площадках, перпендикуляр-
перпендикулярных ортам [кз, кз], [1ц, ki], [kj, kj],
причем в линейной теории упругости не делают различия
между klf к2) к8 и к[, кз, кз.
Переходя к нелинейной теории упругости и принимая во
внимание сходство уравнений A1.54) и A1.55), можно заклю-
заключить, что в координатах av a2, «8 уравнению (И.54) будут
соответствовать уравнения, идентичные по виду системе A1.56),
причем, однако, в этих уравнениях под
alali ala2» aIaS'
a3al> a2a2> a8a2)
a3a,, a2a8, a3a3
*
надо будет подразумевать составляющие векторов -я- <зт,
* *
If'"»'§'••»' где Ib==[k»- *>'• П2 = fкз, к'], п8= fki.ki]

90 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. II
по направлениям осей локального триедра ки ка, к3. При
нимая для составляющих <зп%, <зщ, <зПз по направлениям kt, k2,
k3 обозначения
«н> oi2> «13— Для составляющих <sni,
a21, a,2, a28— для составляющих апг,
азг» aa2> a88 — для составляющих <зПз,
можем написать:
If "«— SI
|5 сг §j
§j (aa.kl+a^k^ + a^k;), (H.57)
Учитывая далее сказанное выше, а также' правило про-
проектирования ортов ki, k2, кз на направления kv k3, к8, вы-
выражаемое таблицею 1 (I глава), приходим к заключению, что
скалярная система уравнений, соответствующая векторному
уравнению A1.54), при отнесении его к криволинейным орто-
ортогональным координатам <Xj, aa, as может быть получена при
замене в системе A1.56) ct1ct1>. . .,a8a8 следующими выраже-
выражениями:
а1<*1 "= 0+
= ( е
12 + У (
( ) *2 + A +езз)
B
«22 + (f e»8 ~
«82
A1.58)

§ 24] ПЕРЕХОД К КРИВОЛИНЕЙНЫМ КООРДИНАТАМ 91
» О + ен) °31 + (д е1% — »,
(г б12 + <°з) °31 + A + е22> °32 + (f е2
азаз = B ei3 — та) °« + (г е23 + «>i) а32 + С1 + езз) азз,
где а1Ь ..., а3з связаны с ап, .. .,а33 формулами вида A1.44),
причем в данном случае:
^=l/(l+2ea2)(l
s:
¦2slt)(l +2e88)~-s23, A1.59)
s;
3
а параметры еи, . .. ,0)^ .. . ,еи, .. . выражаются через
составляющие перемещений по направлениям kj, kj, kg (и, f, w)
формулами A.122), A.124), A.125).
Кроме указанной замены напряжений, для превращения
уравнений A1.56) в уравнения нелинейной теории нужно
подставить в них вместо Fai, Fnt Ftz соответственно
у* * v* р* v* р* р* р* р*
у ' «1» у *«i» у '*tIs> ГДе ' «1» ' «s> ' «з
проекции на kls ka, k3 удельных объемных сил, отнесенных
к деформированному телу, а
где Д—объемное расширение (§11, I глава).
Рассмотренные выше правила преобразования системы
(П.43) к ортогональным криволинейным координатам были
установлены без пренебрежения какими-либо членами, так
что система A1.56), после подстановки в нее формул A1.58),
будет точно соответствовать системе A1.43).

92 РАВНОВЕСИЕ ОБЪЕМНОГО ЭЛЕМЕНТА ТЕЛА [ГЛ. И
Если удлинения и сдвиги пренебрежимо малы по сравне-
сравнению с единицею, то формулы A1.58) могут быть упрощены
путем отождествления в них зц, о12, ....,033 с составляю-
составляющими напряжения <з1и о12, , <з33 (§ 21).
Если, кроме того, малы по сравнению с единицею углы
поворота, то эти формулы допускают дальнейшее упрощение
и могут быть заменены выражениями:
= °12 + Ю8°11
Ю2°23.
<*2а2 = °22 + Ю3°21 — Ю1°23.
а2ач = °23 + Ш1°22 — Ma°31t
«8а1
= °81 Ю8°32 +
«8а2 = °82 + ^"Bl — M1°8S.
а3а3 = o3s -f- oijOga —
И, наконец, если углы поворота являются малыми вели-
величинами одного порядка с компонентами деформации, то
в формулах A1.61) можно пренебречь произведениями напря-
напряжений на углы поворота, что приводит к равенствам:
= °82. «2«8=О25 О1-62)
аЗа1 = °31> аЗа2 = °82' а8а8 ^ °33-
При этом уравнения A1.56) становятся идентичными урав-
уравнениям равновв1ия линейной теории упругости, отнесенным
к ортогональным криволинейным координатам aj, a2, a8.

ГЛАВА III
РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ,
УПРУГИЙ ЗАКОН
§ 25. Работа деформации
Полученная в предыдущей главе система дифференциаль-
дифференциальных уравнений, выражающая условия равновесия объемного
элемента, выделенного из деформированного твердого тела,
содержит более неизвестных, чем в ней имеется уравнений.
Именно — налицо шесть уравнений A1.43 и 11.46), содержа-
содержащих двенадцать неизвестных (девять составляющих напряже-
напряжения и три компонента перемещения).
Ввиду этого задача о равновесии деформированного твер-
твердого тела остается неопределенной до тех пор, пока не
установлено еще шесть дополнительных соотношений, связы-
связывающих составляющие напряжения с компонентами переме-
перемещения и выражающих тот закон, по которому материал
рассматриваемого тела сопротивляется всевозможным видам
деформации. Теоретическое выяснение этого закона неизбежно
требует проникновения в природу междумолекулярных сил,
стремящихся удержать частицы твердого тела на определен-
определенных расстояних друг от друга, причем на современном этапе
развития науки данная тр 'дная задача не может быть доста-
достаточно достоверно решена. Поэтому в настоящее время связь
между деформациями и напряжениями (которая не одинакова
для различных материалов) устанавливается главным образом
экспериментальным путем. Однако, некоторые общие свойства,
присущие этой связи, могут быть выяснены и теоретически.
Будем исходить из предположений, что процесс деформа-
деформации изотермичен и что работа, затрачиваемая на изменение
объема и формы произвольного бесконечно малого прямо-

1L рАботА деформации, граничные условия [гл. in
угольного параллелепипеда, выделенного из тела, не зависит
от того, каким путем осуществляется переход от начального
положения этого элемента в деформированное.
Иначе говоря, будем считать, что роль диссиппативных
сил, в процессе взаимодействия частиц тела при его дефор-
деформации, пренебрежимо мала по сравнению с ролью консерва-
консервативных сил.
Тело, удовлетворяющее данному предположению, после
снятия с него нагрузки должно возвращаться к исходным
своим размерам и форме, в соответствии с чем оно может
быть названо идеально упругим.
Работа, необходимая для деформации элементарного па-
параллелепипеда, выделенного нз упругого тела, может быть
представлена в виде
A4 = 3(soa>, 6W, егг, sxy, sX3, еу„) dxdydz, (Ш.1)
то-есть будет равна произведению первоначального объема
параллелепипеда на некоторую функцию шести компонентов
деформации, вид каковой зависит от физических свойств
рассматриваемого материала (и не зависит от размеров и
формы тела). Но компоненты деформации могут быть всегда
выражены через три главных компонента деформации ех, s2, s3
и косинусы углов между главными направлениями деформации
*\> е2> ез и осями X, Y, Z (§ 4, 5, I глава). При этом
последние косинусы можно рассматривать как функции трех
независимых величин — например эйлеровых углов 0, ср, и ф,
определяющих ориентацию триедра 8lt e2, е3 по отношению
к триедру X, Y, Z.
Отсюда формула (Ш.1) может быть записана также сле-
следующим образом:
*4 = 3(si, Н> Ч, е> <Р. Ъ) dxdydz. (III.2)
Данный вид формулы (Ш.1) подчеркивает зависимость
работы, затрачиваемой на деформацию элементарного парал-
параллелепипеда как от величины главных компонентов деформа-
деформации, так и от направления волокон тела, получающих эти
деформации.
Таким образом формула (Ш.2), как и эквивалентная ей
формула (Ш.1), предполагает, что тело неодинаково реаги-

§ йБ) работа Деформаций §5
рует на деформацию в различных направлениях, или, иначе
говоря, эта формула предполагает материал тела анизотроп-
анизотропным. Если физические свойства тела одинаковы во всех
направлениях, то элементарная работа деформации не может
зависеть от величин, изменяющихся с поворотом координатных
осей, и должна быть функцией только инвариантных величин.
Поэтому для изотропного тела:
A4=*3(s,, ea, ea)dxdydz. (III.3)
Три независимых инварианта е,, е2, s3 хороши в том
отношении, что имеют простой физический смысл (особенно
при малой деформации). Математически они, однако, не-
неудобны, так как выражение их через компоненты дефор-
деформации связано с необходимостью решения кубического урав-
уравнения A.86).
Ввиду этого целесообразнее рассматривать работу дефор-
деформации элемента изотропного тела не как функцию корней
уравнения A.86), а как функцию его трех коэффициентов:
= Ч + S
2
al = sxxeyy ~\~ exxesz ~\~ Byyezz 4
^ ~^~ Вхг ~^~
8> О11-4)
_ s s e — l fe e2 -J- s s2 -4-
которые имеют перед е,, е2, s3 то преимущество, что являются
рациональными функциями компонентов деформации.
В соответствии с этим замечанием работу, необходимую
для деформации элементарного параллелепипеда, выделенного
из изотропного тела, удобнее всего записывать в следующем
общем виде:
??Л = Ф(а2, йц ao)dxdydz. (III.5)
Отсюда работа, затраченная на деформацию тела в целом,
будет равна
///(«2. «1. ao)dxdydz,

96 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [гЛ. III
где интегрирование должно быть распространено по всему
объему тела до его деформации (поскольку dxdydz есть
объем элементарного параллелепипеда, выделенного из тела
в исходном его положении).
Функцию Ф (а2> в и %) можно назвать работою деформа-
деформации, отнесенной к единице объема недеформированного тела,
или короче — удельной работой деформации.
§ 26* Начало возможных перемещений
Применим начало возможных перемещений к деформиро-
деформированному телу, находящемуся в равновесии. Для этого со-
сообщим перемещениям и(х, у, г), v(x, у, г), w(x, у, г)
виртуальные приращения Ьи, bv, bw, которые будем считать
произвольными непрерывными функциями х, у, г, равными
нулю в тех точках, где значения перемещений заданы.
Тогда работа деформации получит приращение ЬА, кото-
которое должно быть равно работе на указанных виртуальных
перемещениях всех внешних сил, приложенных к телу.
Отсюда приходим к равенству
(III. 7)
где о#, — приращение работы.объемных сил, ЬЦ2 — прираще-
приращение работы поверхностных сил.
Приращение работы объемных сил будет равно
8/?1 = Jf J [F|8« -f- F^v -f FJ8w] Ddxdydz, (III.8)
где (как и раньше) F* F*, F* суть компоненты по напра-
направлениям X, Y, Z силы, отнесенной к единице объема дефор-
деформированного тела, dxdydz — объем элемента, выделенного
V*
из тела до его деформации, Ddxdydz = -~ dxdydz — объем
соответствующего элемента деформированного тела.
При этом, принимая за независимые переменные х, у, z,
интегрирование в формуле (III. 8; нужно распространить по
первоначальному объему тела.
Что касается приращения работы поверхностных сил, то
оно определяется выражением:
, = J J {ДЬи -f/J8t> -\-fibw] dQ',

§ 26] НАЧАЛ О ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 97
где Д, /J, /?—составляющие (по осям X, Y, Z) силы дей-
действующей на единицу площади поверхности деформирован-
деформированного тела, a dQ'—дифференциал этой площади.
Чтобы получить возможность выполнять интегрирование
в формуле (III.9) не по поверхности деформированного тела,
а по поверхности тела в исходном его положении, выразим
dQ' через dQ (дифференциал площади поверхности недефор-
мированного т?ла).
Рассмотрим с этой целью на поверхности, ограничивающей
тело до его деформации, элементарную прямоугольную пло-
площадку со сторонами da, db, площадь которой будет равна
dQ = dadb,
а ориентация -которой определяется направлением вектора
единичной нормали:
iw=*LX_tfb. (ШЛО)
В результате деформации указанная прямоугольная пло-
площадка превратится в элемент поверхности деформированного
тела, который будет иметь вид параллелограма со сторонами
A -\-Ea)da, (\-\-E^db, причем косинус угла между этими
сторонами будет равен
чь A11.11)
)(l+2)
где Еа и Еь — относительные удлинения в направлениях da,
db, а еаа, вьь, еаь — соответствующие компоненты деформации.
Отсюда площадь элемента поверхности, ограничивающей
деформированное тело
2Ввв)A + 2еьь) -slb.dQ = ^- dQ. A11.12)
Коэффициент ¦<?¦, равный отношению элементарных пло-
площадок после и до деформации, может быть выражен через
7 Ьак. 3804. В. Новожилов.

98 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [гл. III
компоненты деформации в системе X, Y, Z и три косинуса,
задающих направление нормали к поверхности, ограничи-
ограничивающей тело до деформации.
Для этого надо подставить в формулу
^е26 (III. 13)
вместо компонентов деформации гаа, еьь, еаЬ их выражения
через ехх> ..., еуг и косинусы углов между направлениями
X, Y, Z и da, db, n.
Тогда, после элементарных (хотя и громоздких) пре-
преобразований (с учетом формул 1.36, 1.33 и 1.59), будем
иметь:
w
cosa(/»,.y)
—* + Уху c©s (и, х) cos (и, .у) -| >
I V |
~ЬТжгС08 (я> х) cos (и, г) -j~Yj/zcos(tt> ^)cos(«, г), (Щ.14)
где
 Тжу = — 5а;г/+ 5жг82/г ~ 2?жг/?ж, (III.15)
у Tt/г = Зг/г Т 5жг?жг/
а «л:, «у, nz суть углы между нормалью к поверхности,
ограничивающей тело до деформации, и осями X, Y, Z.
Таким образом приращение работы приложенных к телу
поверхностных сил на виртуальных перемещениях ои, bv,
bw может быть записано в виде:
где dQ — площадь элемента поверхности, ограничивающей
тело до деформации, в соответствии с чем интегрирование

§ 27J ВЫВОД УРАВНЕНИЙ РАВНОВЕСИЯ 99
в выражении (III. 16) должно быть распространено по всей
этой поверхности, а не по поверхности деформированного
тела, как это требовало выражение (III.9).
То что теперь все объемные и поверхностные интегралы,
входящие в равенство (I.I.7), р-спространены в пределах
тела до (а не после) деформации, представляет неоспоримое
удобство, так как пределы интегрирования оказываются при
этом независимыми от неизвестны к величин (перемещений).
§ 27. Вывод дифференциальных уравнений равновесия
деформированного изотропного тела из принципа
возможных перемещений
Сформулированный в предыдущем параграфе принцип
позволяет получить дифференциальные уравнения, описываю-
описывающие равновесие деформированного тела. Выведем эти
ууранения, предполагая, что работа деформации определяется
формулой (III. 6), то-есть считая, что тело однородно и
изотропно и что роль диссипативных сил в его деформации
незначительна.
Тогда
ЬА = 8j J J Ф (ва, а1У а0) dxdydz=*
=/J78 [ф (а2>"»»а°)] dxd- dz> (шл7)
но
о [Ф (а2, ап аб)}= -^- Ъгхх -f -^- 5s -f ST~ К, +
где [в силу формул (III. 4)]
дФ дФ да-ч I дФ day , ^Ф дал
да0
дФ \ дФ f . . , дФ
7*

100
дФ
дФ
работа Деформации, граничные условия [гл. ш
дФ | дФ
дФ
1 2
4 xx
\ дФ , 1 ЙФ /1
i! йф , i a<
аФ адр
2 dai жг ' 2 да0 \2
2 a^i " 2'^ддо \2
Учитывая далее, что, согласно формулам A.22),
E»)
r
Z/J'
=о
i
(О={2«««.+«,j sa—I- [-2 ev*—
(IH-20)

§ 27]
ВЫВОД УРАВНЕНИЙ РАВНОВЕСИЯ
ду ) \ 2 ея* Ш*>
s/ s /1
и подставляя эти значения
находим:
101
, 8(8^) в (III. 18),
<?Ф д(Ьи) . дФ д (So) . дФ д (Ьу) .
' йож й^ ' dvy ду ' даг дг '
дФ d(lw) ¦ <?Ф
1ЙГЖ ад: ' дту
у ду

102 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
где
дФ дФ
дФ | /1
dx
дФ
—
дФ
<ЭФ , /1
^(
dz
дФ дФ (\
дФ
дФ

§ 27] ВЫВОД УРАВНЕНИЙ РАВНОВЕСИЯ 103
дФ дФ
/ 1 \ дФ . (\
-; я
дФ дФ (\
bz
причем -5—¦, ..., -т— определяются формулами (III. 19).
Если теперь обозначить через (III.23)
U — вектор с проекциями на оси X, Y, Z: ¦*— , ^— , -^— ,
v у у 7. дФ_ дФ дФ
' ' dvx' dvy ' dvz '
W— x у z. дФ дФ дФ
" > > • д^х' Охру> ^щ)г >
то формулу A11.21) можно записать следующим, более крат-
кратким, образом
8 [Ф (а„ а{, а0)] = U • grad (8a).+ V • grad (8г>
+ W-grad(8w),
где символ • означает операцию скалярного умножения двух
векторов, а символ grad означает градиент.
Подставляя этот результат в выражение (III.17), имеем:
8Л = J j J[U • grad (8«) + V • grad (Щ -f
+ W • grad (Щ] dxdydz. A11.25)

104 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
Учтем далее, что для любой скалярной функции
И ВСКТОрНОЙ фуНКЦИИ 4
ду
ду * дг ) т ^ та ад. "Г
A11.26)
На основании этого тождества можем написать
U • grad (8и) = div (U8«) — 8a div U,
V • grad (8©) = div (Vbv) — lv div V, A11.27)
W • grad (8te/) = div (W8w) — bw divW.
После чего формула A11.25) приводится к виду:
8Л = Г Г Г [div (U8a + V8© -f- W8«»)] rfxrfyrf.' —
r r rJ J J A11.28)
— J J J fS« div U + Sir div V + 8w div WJ dxdydz.
Но объемный интеграл от расхождения вектора может
быть по теореме Гаусса приведен к поверхностному интег-
интегралу. Именно
j j j [divQ] dxdydz = jJQndQ, A11.29)
где Qn — проекция вектора Q на внешнюю нормаль к по-
поверхности, ограничивающей рассматриваемый объем (см., на-
например, „Векторное исчисление" Н. Е. Кочина, стр. 144, или
„Курс теоретической механики* Я. И. Френкеля, стр. 85).
Ввиду этого формула для вариации работы A11.25) может
быть записана следующим окончательным образом,
ЬА = — f [ С[Ъи div \J-\-to div V-\-bw div VJ]dxdydz+
-f fj[Unbu + Vnbv -f- Wjw) dxdydz. A11.30)
Здесь первый интеграл взят по всему первоначальному объему
тела, а второй — по всей поверхности тела (до его деформа-

§ 27J ВЫВОД УРАВНЕНИЙ РАВНОВЕСИЯ 105
ции), причем Un, Vn, Wn суть проекции векторов U, V, W
на внешнюю нормаль к этой поверхности.
Подставим данное выражение, а также формулы (Ш.8)
и (III. 16) в равенство (III.7).
Перенеся все члены этого равенства в правую часть, будем
иметь:
/ / J{(div U + FP) Ьи + (div V + DF$ bv +
+ (div W +DF^) 5ву} dxdydz-\-
О+ (ш-31
Так как, в силу принципа возможных перемещений, это
равенство должно соблюдаться при любых значениях Ьи,
bv, bw, то отсюда следуют три уравнения, которые должны
выполняться во всех точках внутри тела
divU-f F\D=0,
divV-j-/7*D = O, A11.32)
и три равенства
//_?*/• у — — Г W — —/* (Ш.ЗЗ)
которые должны выполняться во всех точках поверхности
тела, где заданы не перемещения, а силы (в тех точках, где
заданы перемещения, как было выше оговорено, вариации
8и, bv, bw считаются равными нулю и поэтому на данных
участках поверхности тела члены, входящие во второй из

106 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. Ill
интегралов формулы (III.31), будут также равны нулю).
Учитывая, что проекции векторов U, V, W суть величины
(III.23), можем переписать уравнения (Ш.32) в следующем
виде:
д (дФ\, д (дФ\ , д (дФ\
*=о, (Щ.34)
,. дФ дФ
Или, если подставить сюда вместо -г— ...... -=г— их значе-
значения по формулам (III.22), то будем иметь:"
+ '>
дФ
1 \ аФ], к*

§ 28J СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И КОМПОНЕНТАМИ 107
1 \ дФ | A , \ дФ . ,л , ч дФ "I
¦^ / "ьа;а; \ ^ / "^ху usxz J
д
дх
дФ
Коль скоро вид входящей сюда функции Ф (а2, at, a0)
известен, то три уравнения (III.35) будут образовывать систему
с тремя неизвестными — перемещениями точек тела и, v, w,
к решению которой и сводится исследование равновесия де-
деформированного твердого тела.
§ 28. Связь между напряжениями и компонентами
деформации
Сравним уравнения (Ш.35) с уравнениями A1.43), выра-
выражающими условия равновесия того, выделенного из деформи-
деформированного тела, объемного элемента, который до деформа-
деформации являлся прямоугольным параллелепипедом с ребрами dx,
dy, dz, параллельными осям X, Y, Z.
Из сопоставления этих двух систем видно, что одна пре-
превращается в другую, если положить, что:
* дФ * дФ * дФ
ух
foxy'
дФ * дФ * 6Ф,
Таким образом для того, чтобы выведенные в этой главе
из принципа возможных перемещений дифференциальные

108 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
уравнения, описывающие равновесие деформированного тела,
были согласованными с полученными в предыдущей главе
уравнениями, выражающими условия равновесия бесконечно
малого элемента, выделенного из тела, необходимо предпо-
предположить, что между производными функции Ф (удельной ра-
работы деформации, отнесенной к единице первоначального
объема тела) по компонентам деформации и величинами о*.
имеет место связь, выражаемая формулами A11.36).
Из этих формул сразу же следует, что
A11.37)
О существовании данных равенств было уже сказано (§ 20,
глава II). Теперь они подтверждены. Подставляя в формулы
A11.36) вместо о^ их выражения через составляющие напря-
напряжений по направлениям tu i$, is [согласно формулам A1.44)],
а вместо производных функции Ф(а2, av a0) по компонен-
компонентам деформации их выражения [согласно формулам (III. 19)],
будем иметь:
• SJiJxx ^* I Ге 4
о* —
ху
а* =
хг
0* =
У*
*
0* .
zy
Sx 1 + Ех — да2
* —i °yy _^*._i_E*Cs 4-
1 2
48
дФ |^ дФ , , . ,
~ Ш1 "Г dai(«» "т" »^; "т"

§ 28]
СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И КОМПОНЕНТАМИ
109
soy
¦ о = —
гу
5* S*
Здесь ZE, JL
JL определяются через компоненты дефор-
мации формулами A1.36) и A1.37), а удлинения Eg, ?^, ?г —
формулами A.29).
Выражения (III.38) являются общей формою связи, кото-
которая должна существовать между составляющими напряже-
напряжения и компонентами деформации. При их выводе были ис-
использованы только два допущения, а именно предполагалось,
что тело изотропно и что значение диссипативных сил в про-
процессе взаимодействия частиц тела настолько мало, что ими
(по сравнению с консервативными силами) можно пренебречь.
Правые части формул (III.38) являются линейными функ-
функциями компонентов ' трех симметричных тензоров второго
ранга
(единичный тензор)
2 &xt \
A11.39)

по
па=
VIizz
*1
РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. Ш
1 -Я ! - - 1 - ! - - _ 1 е\
_1_
г 4
1
4 ^хггцг 2 zvxyt
2
г' 4
причем коэффициентами при компонентах этих тензоров яв-
дФ дФ дФ
ляются три инварианта -т— , ^— , -з— .
да^ оа^ да0
В соответствии со сделанным замечанием, формулы (III.38)
могут быть объединены следующей символической записью
где под S подразумевается симметричный тензор
¦ = Ожу,
который можно назвать тензором напряжения, обобщенным
на случай произвольной деформации. Укажем далее, что если
ввести обозначения
дФ
дФ
дФ
(Ш.42)
то формулы (III.38) приводятся к виду:
* И)» I \Tf I VIT f е^ I _ -'
. 1 2
-j 4*) ' (ш-43)

§ 28J СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И КОМПОНЕНТАМИ 111
— J {*>*„ -f ^0 [(В
[ *уу) *ху + \
|5rs+ *
Таким образом установленные выше зависимости между
напряжениями и деформациями, путем замены одних инва-
инвариантных коэффициентов другими, можно несколько видо-
видоизменять.
Существенно отметить, что при всех подобных преобра-
преобразованиях эти зависимости всегда будут сохранять структуру,
выражаемую формулой
^ЧуТо + Ч^ + ВД» A11.44)
где ^F2, fj, Wo — функции инвариантов деформации По— еди-
единичный тензор, Л1 — тензор, компоненты которого суть ли-
линейные комбинации компонентов деформации, П2—тензор,
компоненты которого суть квадратичные комбинации компо-
компонентов деформации.
Хотя соотношения (III.38) и (III.43) в достаточной сте-
степени неопределенны, поскольку в них входит неизвестная
функция Ф(аа, av a0), тем не менее они проливают неко-
некоторый свет на те общие свойства, которые присущи фор-
формулам, связывающим напряжения с деформациями.
В частности данными соотношениями вполне выясняются
вариантные (то-есть изменяющиеся при переходе от одной
системы координат к другой) элементы этой связи. Неоп-
Неопределенными остаются только три инвариантных коэффи-
дФ дФ дФ ,
циента: -т— , т— , g— , которые будут неодинаковыми для
различных материалов и для нахождения которых необхо-
необходимо проведение соответствующих опытов.
В заключение отметим, что из выражений (III. 18) и (III.36)
вытекает возможность написания формулы для приращения
работы деформации (III. 17) в виде
d dxdydz. A11.45)

112 РАВОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
Это выражение является обобщением аналогичной фор-
формулы классической теории упругости на случай деформа-
деформаций произвольной величины.
§ 29. Граничные условия
Формулы (III.33) выражают условия, которые должны
соблюдаться в тех точках поверхностей, ограничивающих
деформированное тело, в которых заданы не перемещения,
а поверхностная нагрузка.
С учетом Ш1.23) они принимают вид:
? »ео. (я,
i|cos (я, X) + J|cos (я, Y) + Ц- cos (я, Z)= f^ 011.46)
Здесь пХ, nY, nZ суть углы, образуемые осями X, К, Z
с нормалью к поверхности, ограничивающей тело до дефор-
деформации, a /j, j\, /?, суть проекции на те же оси удельной
поверхностной силы» действующей в соответствующей точке
поверхности деформированного тела.
На основании сравнения уравнений (III.34) с тремя урав-
уравнениями, получающимися после проектирования на X, Y, Z
векторного равенства A1.39), имеем:
та.
Sa; дФ Sy _ дФ Sg

§ 30] СЛУЧАЙ МАЛОЙ ДЕФОРМАЦИИ 113
где оЙ1, ?) о„„ ч, Ощ, г — проекции напряжения ащ на X, Y, Z
°»», ь °«t. т)> °»i,г, — проекции напряжении а„г на X, Y, Z
°»м е» a»t. ч> 3»з, с — проекции напряжения а„3 на A", F, Z.
Теперь формулы могут быть записаны следующим обра-
образом:
5* S*
-~- о„1( е cos (я, X) -f ^ оп„ ? cos (я, У) -f-
5* S*
•я2- вв1, cos (я, А) + -^ °«». -оcos С
^ s. (Ш.48)
5* S*
^- оП]11 cos (я, X) + -# а»„ с cos (я, F) +
причем входящие сюда проекции напряжений вП1, а11г, ап,
можно выразить [с помощью формул A1.12), (III.36)] через
компоненты деформации, что позволяет рассматривать ле-
левые части выражений (Ш.48), как функции перемещений
и, v, w.
При такой замене данные выражения будут математиче-
математической формулировкою условий, которые должны быть наложены
на перемещения в тех точках ограничивающей тело поверх-
поверхности, где и, v, w не заданы непосредственно.
§ 30. Упрощение полученных формул в случае
малой деформации
Если деформация мала, то ее компонентами можно пре-
пренебрегать в тех формулах, куда они входят наряду с членами
порядка единицы. Последнее позволяет не делать различия
(при определении напряжений) между размерами площадок
до и после деформации, что равносильно отождествлению
обобщенных напряжений, о* с истинными напряжениями a{j.
8 5ак. 3804. В. Новожилов.

114 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ {гл. ill
Соответствующее упрощение может быть введено в формулы
A11.38), A11.43) и A11.48).
Коль скоро малы по сравнению с единицею'не только
компоненты деформации, но и углы поворота, то (как было
показано во II главе) уравнения (III.35) можно упростить,
пренебрегая etj по сравнению с единицею и atj.
Дальнейшее мыслимое упрощение заключается в пренеб-
пренебрежении в уравнениях A1.35) как вц, так и о^-, после чего
они принимают вид:
эф] , э г дФ1 , а гаФ
[?] + [] + Tz [
Тх [а?] + Ту
Последнее упрощение равносильно принятию'равенств:
ЭФ _ дФ ЭФ _ ЭФ _ ЭФ ЭФ _ дф ЭФ
д&хх диа> ' деху диу ~ dvx ' дгхг дщ ди^
ЭФ ЭФ дФ ЭФ ЭФ дФ ЭФ ...
чему отвечает определение компонентов деформации форму-
формулами A.120), то-есть формулами классической теории упру-
упругости.
При этой точности рассуждений граничные'условия (III.48)
могут быть записаны в форме
ee cos (я, X) + eg, cos (я, Y) -\- efc cos (я, Z) =fb
4cos(n,X) + amcos(n, Y) + arjC cos (я, Z) = /„ A11.51)
ou cos (я, A') -f a^ cos (я, Y) -f- aK cos (я, Z) =/,.,
где оц, ... o^ суть компоненты напряжения на площадках
перпендикулярных осям X, К, Z.
Формулы (III.51) соответствуют подчинению решения гра-
граничным условиям без учета деформации тела. (Так и посту
пают, как известно, в классической теории упругости.)

§ 30] СЛУЧАЙ МАЛОЙ ДЕФОРМАЦИИ 115
Все описанные выше упрощения по своему характеру ана-
аналогичны тем, которые неоднократно рассматривались в гла-
главах I и II. Они могут быть объединены под названием „гео-
„геометрических" упрощений, так как основываются либо на
пренебрежении изменениями некоторых размеров, либо на
пренебрежении изменениями некоторых углов. Теперь нам
предстоит рассмотреть возможности упрощения соотношений
между напряжениями и компонентами деформации [то-есть
формул A11.38) или (III.43)]. Хотя данные упрощения-, как
и предыдущие, будут зависеть от величины деформаций,
однако сравнивать последние придется уже не с единицей,
а с некоторыми, характерными для каждого конкретного
материала, физическими константами.
Представим функцию Ф(а2, av aQ) в виде ряда по сте-
степеням трех параметров, от которых она зависит. Отрицатель-
Отрицательные степени в этом ряду не могут принять участия, поскольку
тогда удельная работа деформации стремилась бы к беско-
бесконечности, при бесконечно малых смещениях точек тела от
исходного их положения, что абсурдно.
Кроме того, если считать что в начальном положении
энергия деформации тела равна нулю и тело свободно от
каких-либо напряжений, то суммирование в указанном ряду
нужно начать с членов, содержащих компоненты деформации
во второй степени.
Учитывая все эти замечания, можем написать
Ф8(а8, аи а0)
ваао
A11.52)
Здесь постоянным Aj соответствуют члены, содержащие
компоненты деформации во второй степени, Bj— компоненты
деформации в третьей степени, Cj — компоненты деформации
в четвертой степени и т. д.
&*

i i6 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
Этот ряд можно рассматривать как общее выражение для
удельной работы деформации изотропного тела, свободного
в начальном своем положении от каких-либо внутренних сил.
Его сходимость зависит как от величины параметров а2> ai>
а0 (причем очевидно, что с их уменьшением она улучшается),
так и от значения коэффициентов Aj, Bp Ср Dp . .., являющихся
физическими константами.
Поэтому a priori невозможно указать, на каком члене ряд
(III.52) следует оборвать, даже если известно, что а2, av aQ
заведомо весьма малы по сравнению с единицею. Вопрос
этот должен решаться путем опытов.
§ 31. Закон Гука
Чтобы получить отправную точку для дальнейших рассуж-
рассуждений, предположим, что компоненты деформации бесконечно
малы.
Тогда, какова бы ни была сравнительная величина фи-
физических констант Aj, Bp Ср ... (все они имеют, между
работа
прочим, одинаковую размерность = -^ -, или если силы
выражать в кг, а длины в см — кг/см*), их влияние будет
побеждено бесконечною малостью деформаций, и в ряду
(III.52) можно будет сохранить только члены, содержащие
компоненты деформаций в наименьшей (то-есть второй) сте-
степени.
Таким образом для бесконечно малых деформаций выра-
выражение удельной работы упрощается до вида
Ф(а2, аи o0) = ^ + M- (Щ-53)
Подставляя этот результат в формулы (III.38), приходим
к следующим соотношениям между напряжениями и дефор-
деформациями:
"J A*S™>(Ш-54)
( _J_ • _ _ x
I \sxx T eyy)> Qyss — azy -г ~ъ '

§ 31] ЗАКОН ГУКА 117
Если ввести сюда вместо А1 и Л2 новые постоянные Е и ja,
связанные с предыдущими равенствами:
то вместо формул (III.54) будем иметь:
.а 3 Ё
—2[J. 2/ * *"" 2A
в) ° = ° =
2A+,*)
2 A + [i.)
- (Ш'56)
Таким образом при бесконечно малых удлинениях и сдви-
сдвигах (но не перемещениях и углах поворота, величина которых
предыдущими рассуждениями никак не ограничивается) суще-
существует линейная связь между напряжениями и деформациями.
Формулы (III. 56) выражают хорошо известный закон
Гука (обобщенный на случай пространственной деформации),
причем константы Е и ji суть модуль Юнга и коэффициент
Пуассона.
Из вышеизложенного следует, что для всякого материала
можно указать такую область малых деформаций, в которой
закон Гука будет приближенно справедлив. При этом, как
показывает опыт, данная область для различных материалов
будет не одинакова.
Если обратиться к наиболее интересному для техники ма-
материалу—стали, то оказывается, что для нее (глава I, § 11
и рисунок к нему) линейная связь между деформациями и на-
напряжения .ж наблюдается до удлинений порядка 10-8~5.10-3
(в зависимости от марки металла) и до сдвигов, примерно
вдвое меньших. При дальнейшем увеличении деформаций
характер зависимости между ними и напряжениями резко из-
изменяется и для достаточно точного математического ее опи-
описания в этой области в ряду (III. 52) приходится удерживать
много членов (хотя удлинения и сдвиги все еще остаются
весьма матыми по Сравнению с единицею).
Таким образом сразу, как только закон Гука теряет свою
силу, задача установления связи между напряжениями и дефэр-

118 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. Ш
мациями резко усложняется. Она усложняется, кроме того,
еще и потому, что вскоре после перехода за предел пропор-
пропорциональности существенно возрастает роль диссипативных
сил, в связи с чем только часть сообщенной телу работы,
возвращается при снятии с него нагрузки. Последнее ставит
под сомнение возможность применения в указанной выше
области деформаций формул (III. 38), поскольку их вывод
основан на предположении, что деформация вполне обратима.
§ 32. О возможности применения формул (III. 38)
к упруго-пластическим деформациям
Тем не менее не трудно показать, что все основные зависи-
зависимости теории пластичности Генки могут быть получены из фор
мул (III. 38) если ввести в них соответствующие предположения
дФ дФ
относительно характера зависимости производных -, - , -=—
и -^— от компонентов деформации. Чтобы это показать,
установим предварительно на основании данных формул связь
между двумя инвариантами тензора напряжения:
* * , * , *
с\ - Ъс\ = -2 \(?*хх — ЬуУ + (°*х - <4J +
(Ш.57)
+ (ауу - 4J + 6 (?% + е& + о',))
и инвариантами деформации а^, аи ай.
Подставив сюда <зхх, ..., ayz, согласно формулам (III. 38);
(что удобно сделать, отнеся последние формулы к главным
напряжениям и деформациям), после несложных выкладок
будем иметь:
1 * 1 / • , • , • ч дФ . 2 дФ .
3-

§ 32] ПРИМЕНЕНИЕ ФОРМУЛ 119
Опыты показывают, что при переходе от упругих дефор-
деформаций к пластическим резко изменяется только характер
второй из двух написанных зависимостей, первая же (пред-
(представляющая связь между средним значением трех главных
напряжений и инвариантами деформации) изменяется настолько
мало, что ее без особой погрешности можно принять такой
же, как и в упругой области. Но, как следует из формул
A11.56), в упругой области
?) fr?3jre«- <П1-Б9>
Отсюда, обобщая эту зависимость и на пластическую
область деформаций, можем написать:
дФ . 2 „ дФ . 1 дФ 1 Е п ,,„ д_ч
+в»-д5Г + Тв»-3^==8-Т^^Га« (IIL60)
Далее, как показывают опять-таки результаты опытов,
инвариант напряжений cl—3ct можно считать зависящим
только от аналогичной комбинации инвариантов деформации
а2 и at, то-есть от величины а\ — За^. Чтобы привести вторую
из формул (III.58) в соответствие с этим фактом, в ней
дФ „ дФ
достаточно положить -з— = 0 и считать кроме того -з—
функцией только а\ — 2>av С учетом этих двух предполо-
предположений, а также формулы (III.59), выражения (III.58) при-
принимают вид:
дФ 2
5 = Т • W G),
где
/За1), ОН-62)
wen — — —
w('>— да% •
Инвариант 5 в теории пластичности принято называть
интенсивностью касательных напряжений, а инвариант Т—ин-

120 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. III
тенсивностью деформаций сдвига. Здесь нет нужды пояснять
происхождение этих наименований, поскольку в наши цели
отнюдь не входит полное изложение теории пластичности.
Возвращаясь теперь к формулам (III.38) и подставляя в них
определенные указанным выше образом значения производ-
производных функций Ф по инвариантам деформации, будем иметь:
(Ш.63)
-j Т (Г)
Полученные формулы суть не что иное, как предложенные
Генки для упругопластических тел соотношения Между ком-
компонентами деформации и компонентами напряжения.
Таким образом данные формулы теории пластичности
заключаются в формулах (III.38), как частный случай.
Иными словами, несмотря на необратимость пластической
деформации, она может быть описана с помощью формул, вы-
выведенных исходя из явного предположения обратимости дефор-
деформации, что на первый взгляд парадоксально. Следует отметить,
однако, что использование формул A11.38) в теории пластич-
пластичности допустимо лишь, в том случае, когда процесс дефор-
деформации активен, то-есть когда на всех своих промежуточных
этапах деформация идет монотонно в сторону возрастания па-
параметра Т. При наличии в процессе деформации разгрузки
формулы (Ш.63) терают силу.
Л. М. Качанов [18J, [19J на основе термодинамического ана-
анализа активной пластической деформации доказал, что в этом
случае упруго пластическое тело должно быть практически
неотличимо от идеально упругого тела с идентичной диаграм-
диаграммой растяжения. Упомянутое исследование внесло физическую

§ 33] ВАРИАНТЫ НЕЛИНЕЙНОЙ СВЯЗИ 121
ясность в вопрос и показало, что никакого парадокса в воз-
возможности рассматривать активную пластическую деформацию
с помощью формул, выведенных для обратимых дефор-
деформаций, — по существу нет.
§ 33. О наиболее простых вариантах нелинейной связи
между напряжениями и деформациями
Предположим, что деформации настолько велики, что
закон Гука оказывается недостаточно точным. Тогда в ка-
качестве второго приближения можно удержать в ряду (III.^2)
кроме членов, содержащих компоненты деформации во второй
степени, также члены, содержащие их в третьей степени.
При этом в ряду A11.52) будет сохранено пять первых членов,
откуда ясно, что упругие свойства материала в данном случае
будут требовать для своего описания знания пяти физических
констант. Из них первые две будут константами закона Гука,
поскольку в пределе (при бесконечно малых деформациях)
этот закон должен получаться из рассматриваемого.
Подставляя выражение
ai-\-Bйa0 (Ш.64)
в формулы (III.38), будем иметь:
4у = B Л» + AJ «а + C В, -Ь В2) а\
4у = B Л» + AJ «а + C В, -Ь В2) а\ + (В2 + В3) а, —
4- Ва) ая] гуу
гу
4 = B А, 4- At) ?2 4 C 5, + В.2)У2 + (Вв -f BJ а, -
— [Л2 + (В, + В8) а2] еет + В9 [ei -f 14. 4" т 4J.
^ — ^[(в^ -f- syy) гху -f-
4-tV Vl(. (И-65)

122 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. Ill
+ В3) «2] s^ —S3[(s^ + O *xz +
~Т Y smy syz\ j >
Полученные формулы можно записать также в виде:
4 = 7^ {С1 + Pi «2)s^+ YTT2JI «2 + Ра «2 — Pi Й1 +
« + "ИA1L66)
+ Pi Й2> e^i, + Ps 1(в»ш + syy)
2 A
* _ E
"T 2 &XV еУ^ \ '
"Г *
2*
где Е, [а, р:, (За, C8 суть новые константы, введенные вместо
Ли Л2, Blt B2, и fi8 и связанные с ними равенствами, сле-
следующими из сравнения формул A11.65) с формулами A11.66).

§ 33]
ВАРИАНТЫ НЕЛИНЕЙНОЙ СВЯЗИ
123
Сопоставляя формулы (III.66) с законом Гука (III.56),
видим, что уже во втором приближении зависимости между
напряжениями и деформациями оказываются гораздо более
громоздкими, чем в первом.
Существенно отметить, что второе приближение отли-
отличается от первого лишь членами, являющимися четными функ-
функциями от компонентов деформации. При изменении знака
всех деформаций на обратный эги члены будут оставаться
неизменными.
б)
Рис. 16.
Кривая растяжения — сжатия для такого материала будет
вся лежать по одну сторону от своей касательной в начале
координат (рис. 16 а). Между тем, для большинства матерка-
лов кривые растяжения — сжатия имеют вид, показанный на
рис. 16 б из чего следует, что отклонения от закона Гука
обусловливаются обыкновенно не столько членами, содержа-
содержащими деформации в четных степенях, сколько членами, со-
содержащими их в нечетных степенях. Ввиду этого формулы
(III. 66) далеко не полно охватывают возможные варианты
кривых растяжения — сжатия.
Несмотря на это, пятиконстантная теория упругости, осно-
основанная на принятии удельной потенциальной энергии в форме
(III. 64), пользуется в настоящее время значительным вни-
вниманием и рассматривалась во многих работах. Упругий за-
закон, ей соответствующий, обычно называют законом Мурна-

124 РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [ГЛ. Ill
гана 'З^.хотя фактически впервые его предложил, и притом
много ранее, Фойгт '42'. Первая же попытка рассмотрения
связи между напряжениями и деформациями, в форме, от-
отличной от закона Гука, была сделана Бюльфингером в
работе Ы, опубликованной в трудах Российской Академии
Наук в 1729 г.
В свете сделанных выше замечаний небезынтересно наря-
наряду с пятиконстантной теорией упругости Фойгта исследовать
и такие формы нелинейной связи между напряжениями и
деформациями, в которых первые являются нечетными функ-
функциями последних.
Для самого грубого учета такой нелинейности удельную
работу деформации нужно принять в виде:
Ф (а2, av а0) = Ау а\ + Л2 аг -f Cj at -f- C2 a\ aL +
+ C8aaa0+C4fl?, A11.67)
удерживая в ряду A11.52) все члены с четными степенями
деформации (до четвертой включительно). Тогда после под-
подстановки (Ш.67) в A11.38) или A11.43) и рассуждений, по-
подобных предыдущим, будем иметь следующие выражения,
связывающие напряжения с деформациями:
Tfi
Здесь E, [a, ifi» T2> Тз> Т4 СУТЬ шесть физических кон-
констант, из коих пять последних безразмерны, а первая имеет
размерность напряжения. Эти формулы еще более громоздки,
чем формулы A11.66), и следовательно учет нелинейности
связи между напряжениями и деформациями (даже в самых
грубых приближениях) может доставить много математи-
математических неприятностей при решении конкретных задач.

§34] ЗАКЛЮЧЕНИЕ 125
Данное заключение остается в силе даже, если учесть, что
некоторые из шести физических констант, входящих в фор-
формулы (III.68), видимо могут быть пренебрежены или выраже-
выражены друг через друга (что можно установить опытным путем).
§ 34. Заключение
В этой главе было установлено, что нелинейность про-
проникает в теорию упругости по трем путям, а именно через
формулы для деформаций A.22), через уравнения равновесия
объемного элемента тела A1.43) и через формулы связи
между напряжениями и деформациями (III.38).
При этом в первых двух из перечисленных совокупностей
формул учет нелинейных членов обусловливается геометри-
геометрическими соображениями (необходимостью считаться с углами
поворота при определении изменений размеров линейных
элементов и формулировке условий равновесия объемного
элемента).
Что касается третьей совокупности формул, то в ней
нелинейные члены появляются, если деформации превосходят
по величине некоторые характерные для рассматриваемого
материала физические константы (именуемые пределами про-
пропорциональности ).
Таким образом в рассматриваемой задаче можно говорить
о нелинейностях лвух типов — геометрической и физической.
Их можно считать не связанными друг с другом, поскольку,
как неоднократно подчеркивалось еще в I главе, малость
углов поворота не влечет за собою малости удлинений и
сдвигов (и наоборот).
Отсюда в теории упругости могут встречаться задачи
следующих четырех типов:
1) линейные физически и геометрически;
2) нелинейные . физически, линейные геометрически;
3) линейные физически, нелинейные геометрически;
4) нелинейные физически и геометрически.
В задачах первого типа углы поворота будут величинами
одного порядка с удлинениями и сдвигами, а удлинения
будут менее предела пропорциональности для рассматривае-
рассматриваемого материала. Простейшим примером задач этого типа
является растяжение прямого стержня силами, вызывающими

12б РАБОТА ДЕФОРМАЦИИ, ГРАНИЧНЫЕ УСЛОВИЯ [|Л. Ill
в нем напряжения, не превосходящие предела пропорцио-
пропорциональности.
В задачах второго типа углы поворота также будут не-
несущественными при проектировании сил, действующих на
объемный элемент и при определении деформаций, однако удли-
удлинения будут превосходить предел пропорциональности, что
потребует написания зависимостей между напряжениями и
деформациями в нелинейной форме. Пример задач такого типа
можно получить из рассмотренного выше примера, осложнив
его предположением, что напряжения в стержне превосходят
предел пропорциональности.
В задачах третьего типа углы поворота будут существенно
велики (при деформациях, не выходящих за пределы пропор-
пропорциональности) .
В качестве примера на этот тип задач можно указать изгиб
тонкой стальной полосы. Известно, что полосы из хорошей
стали допускают сведение своих концов и потом выпрямляются
без следов остаточных деформаций, что свидетельствует
о том, что в них, даже при весьма больших перемещениях
и углах поворота, напряжения не выходят за предел теку-
текучести (который для стали близок к пределу пропорцио-
' нальности).
Наконец, в задачах четвертого типа деформации будут
выше предела пропорциональности, а углы поворота настолько
велики, что потребуют учета нелинейных членов как в фор-
формулах, связывающих напряжения с деформациями, так и в урав-
уравнениях равновесия элемента и выражениях для деформаций.
Пример для этого случая можно получить, осложнив предыду-
предыдущий пример предположением, что напряжения в изгибаемой
полосе превосходят предел пропорциональности.
Как уже сказано, для стали предел пропорциональности
близок к пределу текучести, так что физически нелинейные
задачи для этого материала по существу входят в компетен-
компетенцию уже не теории упругости, а теории пластичности. Поэтому
задачи второго и четвертого типа рассматриваться в дальней-
дальнейшем не будут. Не будут также рассматриваться и задачи
первого типа, поскольку они являются предметом классиче-
классической (линейной) теории упругости.
Таким образом, имея в виду применение выведенных формул
к металлам (и притом главным образом к стали) и придержи-

§ 34) заключение 127
ваясь темы „нелинейная теория упругости", мы должны
в дальнейшем сосредоточить свое внимание только на зада-
задачах третьего типа (линейных физически, нелинейных геомет-
геометрически). Иными словами, мы будем предполагать в дальней-
дальнейшем, что связь между напряжениями и деформациями со-
соответствует закону Гука (что равносильно предположению,
что. удлинения и сдвиги весьма малы по сравнению с едини-
единицею), а углы поворота настолько велики, что ими нельзя
пренебрегать ни при определении деформаций, ни при напи-
написании уравнений равновесия объемного элемента, выделен-
выделенного из деформированного тела.

ГЛАВА IV
О ПОСТАНОВКЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
В НАПРЯЖЕНИЯХ
§ 35. Еще две формы написания уравнений равновесия
объемного элемента
Возвратимся к системе A1.43) и попытаемся преобразовать
ее таким образом, чтобы коэффициенты в ней стали функциями
не параметров е^, <ojy а компонентов деформации.
Учитывая, что упомянутые параметры выражаются через
перемещения и, v, w формулами A.6), A.7) и выполняя
в системе A1.43) дифференцирование произведений, получаем
следующие три уравнения:
0+
даи *
(iv.i)
2+2+

§ 35) ДВЕ ФОРМЫ НАПИСАНИЯ УРАВНЕНИЙ 129
dw (д°*х , д°'*у . Kzs dW(Ky д°'уу . д°УЛ .
л? [-7Г + ~дТ + IF) + dj [17 + ~W + ~дТ) +
v*
Умножим первое из них на 1-(-Д, второе на ¦*¦ , третье
на ^— и затем сложим все три равенства. Результатом
указанной операции, если принять во внимание, что
Л I ди\ди , Л
dtxw ^ ^
^ ~ I,1 ~T дх) дх* + ол: <?лга"+" дх дл*
dexx Л . ^u\ d*u . dv d^o . dw d*w
dy ~~ \ ' дх) дхду i дх дхду ~i"дх дхду
дгхх / . ?и\ _?2_« _, dv д* и t dw
dz ^V ~^Тх)^Ш~i Fxdlcdz'^"d
~дТ~т~~5у~ ~1F = 2 [I/ "¦"^
будет уравнение
p ш) ^ = о,
&ак. 3804. В. Новожилов.

130 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ [ГЛ. IV
в котором
Установим тут же физический смысл полученного диф-
дифференциального соотношения. Как видно из II главы, три
уравнения системы A1.43), а следовательно, и системы (IV. 1)
выражают равенство нулю сумм проекций на оси X, Y, Z
всех сил, действующих на элемент, выделенный из дефор-
деформированного тела.
С другой стороны (согласно таблице, приведенной в § 2),
1+.
1
1
1
X
+E*
. ди
' дх ,
dv
dw
Отсюда, ясно что уравнение (IV.3) выражает равенство
нулю проекции на направление it главного вектора всех
сил, действующих на элемент деформированного тела
(рис. 14).
Соответственно Fx есть проекция на то же направле-
направление удельной объемной силы, действующей в рассматриваемой
точке.
Подобным же образом (а именно путем сложения ра-
равенств (IV. 1), после предварительного их умножения сначала
ди - , dv dw ди dv (Л , dw\
тду> г+Ту> д~у " затем на й> й, A + дг) можно вы-
вывести еще два уравнения, аналогичные (IV.3), выражающие

§ 35] ДВЕ ФОРМЫ НАПИСАНИЯ УРАВНЕНИЙ 131
равенство нулю сумм проекций ка направления 12 и 13 всех
сил, действующих на объемный элемент тела.
Эти два уравнения получаются из уравнений AV.3), (IV.4),
AV.5) путем циклической перестановки букв х, у, z и со-
соответственно и, v, w.
В итоге приходим к следующей совокупности дифферен-
дифференциальных уравнений:
„.. 0<з„„ 0а,,
0. AV.7)
' л« i Ш~)"т"8г/21 л». ~г f)v "г 7ST ,
Здесь Ly и Lz определяются по формуле (IV.4) путем цик-
циклической перестановки х, у, z.
Рассматривая уравнение (IV.7) как алгебраическую сис-
систему с тремя неизвестными (выражениями, стоящими в круглых
скобках) и решая ее, находим:
9*

132
О ПОСТАНОВКЕ ЗАДАЧ В 'НАПРЯЖЕНИЯХ
да!
[ГЛ. IV
где
1 + 2егг
= ^sld + 2«w) (I -f 2.„) - гу1 ] = ^ Т(М>
1 "л ' " ч " ' " ч—«И^'тйТм/. (IV9)
' *VJ ГJ •'**>
. = 4гт«, (iv. Ю)
.д,) е^д. егх] — -^
р-яж— —-
Причем D — известный по I главе определитель формулы
[1.94; 1.95], а ча — см. формулы A11.15). Система (IV.8),
подббно системе AV.7), имеет определенный физический смысл,
который поясним без доказательства. Именно — если система
(IV.7), как было выше указано, формулирует условие ра-
равенства нулю главного вектора всех сил, действующих на
элемент тела путем приравнивания нулю сумм Их проекций
на Направления i\, i2, is, то система (IV.8) формулирует
тоже условие путем приравнивания нулю сумм Их составляю-
составляющих по тем же направлениям.
Поскольку векторы ij, i2, i8 не ортогональны, постольку
уравнения (IV.7) и (IV.8) не тождественны, хотя констати-
констатируют один и тот же физический факт.
Таким образом мы теперь имеем три варианта написания
уравнений равновесия элемента, выделенного из деформиро-
рованного тела:
а) систему A1.43), выражающую условие равенства нулю
главного вектора всех сил, действующих на элемент тела,
путем проектирования этих сил на неподвижные оси X, Y, Z;

§ 36] УРАВНЕНИЯ ПРИ МДЛрЙ ДЕФОРМАЦИИ 133
б) систему (IV.7), выражающую то же условие, путем
проектирования этих сил на направления Jj, Ia, I,;
в) систему (IV. 8), выражающую то же условие, путем
разложения этих сил по направлениям ilt Ja, J3.
§ 36. Упрощение уравнений (IV.7), (IV.8) применительно
к малой деформации
Если удлинения и сдвиги весьма малы по сравнению с еди-
единицею, то (как было указано еще во II главе) допустимо
пренебрегать дефррмацией элемента тела при формулировке
условий его равновесия. В этом, случае важно учесть при
проектировании сил только поворот элемента.
Иначе говоря, при составлении уравнений статики можно
считать llt J2, J3 ортогональными, не делая, следовательно,
различия между проекциями и составляющими какой-либо
силы по направлениям этих единичных векторов. Из сказан-
сказанного ясно, что при малой деформации разница между систе-
системами (IV.7) и (IV.8) должна исчезать, и они должны стано-
становиться тождественными
Чтобы достигнуть этого, надо в первой системе пренебречь
еяах> вуиг ss« п0 сравнению с единицею (отбросив кроме того
члены, содержащие множителями вху, еа,, еуг), а во второй
системе надо положить:
(IV. И)
1 — 2гууж 1, gv*т—еугшО,
В итоге указанных упрощений уравнения (IV.7) и (IV.8)
превращаются в систему:
*»« д<у *и . I дгху дгуу,
1Г ' ду ' dz ~Т~аУУ\~ду дх-)~Т~
I * (text де^\. . де^а, , . dtq.

1S4 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ (ГЛ. IV
Л-" да* д°*г . / дгху
О,
~T~avy[~dy
Первое из написанных уравнений есть условие равенства
нулю суммы проекций (составляющих) на направление it,
всех сил, действующих на объемный элемент тела. Соот-
Соответственно два других уравнения выражают аналогичные
условия, но для проекций (составляющих) сил на направле-
направления i2 и i3.
Напомним, что речь идет об элементе тела, выделенном
в окрестности точки х, у, z и представляющем до деформа-
деформации прямоугольный параллелепипед с ребрами dx, dy, dz,
параллельными осям X, Y, Z.
§ 37. Еще одна форма граничных условий
В предыдущей главе (§ 29) было установлено, что в тех
точках поверхности, ограничивающей деформированное тело,
где заданы не перемещения, а силы, должны соблюдаться
равенства (III.46).
Данные равенства имеют следующий развернутый вид:
• ди\ » , ди » I да
, да « . ди *
да * , ди
^ +

§ 37] ЕЩЕ ОДНА ФОРМА ГРАНИЧНЫХ УСЛОВИЙ 135
+ [Ш °«* +11 + by)a» + 37 e« J cos ("-zj = 5T
[dw * , dw * . /, , йг»\ •  /
TZ°** + Ty °°>У +11 + Тг) °™ \ C0S
и выражают условия, что проекции на направления X, Y, Z
напряжения, действующего на поверхности, ограничивающей
тело, должны быть равны соответствующим проекциям удель-
удельной поверхностной нагрузки.
Но равенство вектора напряжения вектору удельной по-
поверхностной нагрузки может быть сформулировано также
и путем приравнивания проекций данных двух векторов на
направления lu J2, i8.
Для получения граничных условий в такой форме умножим
первое из выражений (IV. 13) на П -\--=r- \ второе на -^-,
dw
третье на -g— и сложим затем все три выражения.
В итоге (§ 35) придем к равенству:
! A + 2 е^) о* х -f еху оху + sxz а*хz] cos («, X) -f
+ [A4-2 гхх) oly + Eaw Qyy + &xz o*,| cos (л, Y) +
+ [A + 2 гхх) а*г + гху o*yz + еад <s*zz] cos (я, Z) = Av-14)
dv ,» , dw

136 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ [ГЛ. IV
Но в силу (IV.6)
*
где /х — проекция удельной поверхностной нагрузки на на-
направление ij.
Таким образом
°a»I C0S (Я>
+ [A + 2 BvJol, + •*, 4„ + в., о»] cos (л, К) 4- (IV. 16)
+ [A + 2 гхзо) о*г -f *a,y <Ь» + «„я a*J CO5 (я, Z) =
Отсюда путем циклической перестановки букв х, у, г
можно получить еще две формулы, выражающие равенство
проекций на направления i , i3 вектора напряжения на по-
поверхности, ограничивающей тело, сответствующим проекциям
удельной поверхностной нагрузки. Если удлинения и сдвиги
пренебрежимо малы по сравнению с единицею, то в формулах
вида (IV. 16) можно пренебречь всеми членами, содержащими
множителями компоненты деформации, в результате чего придам
к следующей упрощенной формулировке граничнцх условий:
<Jam COS (п, X) + <Зху COS (n, Y) -f <ta,z cos («. Z) — f* >
oy!Bcos (n,X)-{-ayyCOS (я, Y)-\-aytcos (n,Z) —fy, (IV. 17)
aZ(B cos (я, X) + ozy cos (я, F) rf оет cos (n, Z)—f».
Заслуживает быть отмеченным лишний раз тот факт, что
АЛЛ
пХ, nY, nZ суть углы, образуемые нормалью к поверх-
поверхности, ограничивающей тело в положении до деформации.
Что касается о^ — то это составляющие (проекции) напря-
напряжения по направлениям ij J2, i8, .. . , а f*x, fy, fz — проекции
на эти же направления удельной поверхностной нагрузки.

§ 38] СЛУЧА», КОГДА УГЛУ ПОЦОВОТА МАЛЫ 137
§ 38. Упрощение уравнений (IV.7), (IV.8) нрименительно
к случаю, когда утлы поворота малы
Если углы поворота малы по сравнению С единицею, пре-
превышая в то же время существенно удлинения и сдвиги, то
(как было установлено в § 22) уравнения равновесия A1.43)
могут быть приближенно заменены уравнениями A1.49). Дан-
Данному упрощению соответствует замена системы (IV. 12) си-
системою:
d<az дюу д1»,,
д<оУ , . (дшУ
КГ + V \sy —
д<»г
из которой следует, что при, пренебрежимо малых по срав-
сравнению с единицею углах поворота должны существовать
приближенные равенства:
дх
дшг
M4L%( И/Ч/ w/fv ' I*
a7^1i—17^?- (iv.ia).
'е«г ^Еж* ^Егг дшу
дг" U ^ 5"'
}у йг" ^ ~Зг* '

138 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ [ГЛ. IV
day ди>г ^ дгху ds^g ds.yz
ду дг ~ дг ду дх '
<Э<ог дах дгуе дг дгхя
-ш ~ ът «~ш + dt ~ if' <IV-2°)
д«>х ?«V^ ^^f?f _L_ ?f^f д?ЭД
17 ду~ ^ Ту i ~дх ~~ дг '
формулы (IV. 19) будут непротиворечивы только при условии,
что производные
д*ту д*а:г ^yz дгху дг^ деуг
17' ~дТ' ~дТ' ~дГ> IF"' ду ' К"-*1)
пренебрежимо малы по сравнению с производными
дх ' дг ' ду ' ду ' дх ' дг Kiy/-Zl )
(соответственно).
Противоречия не будет и в том случае, когда все (или
некоторые) из производных (IV.21') окажутся пренебгежимо
малыми вместе с соответствующими производными (IV.2P.
Кроме вышеуказанного требования необходимо еще соб-
соблюдение какого-либо одного из следующих трех соотношений
дгуг
дх '
ду ' UV.^J
^_ dJ^y
дх ^ дг '
что вытекает из (IV. 20).
Таким образом предположение, что все углы поворота малы
по сравнению с единицей, налагает определенные ограничения
на величину производных от компонентов деформации.
Формулы (IV. 19), (IV.20) устанавливают связь между
производными от компонентов деформации и производными
от компонентов поворота, имеющую место в рассматриваемом
частном случае. Из данных формул следует, что те и другие про-
производные являются, вообще говоря, величинами одинакового
порядка. Отсюда (поскольку повороты считаются значительно

§ 39] ОБОБЩЕНИЕ СООТНОШЕНИЙ СЕН-ВЕНАНА 139
превосходящими удлинения и сдвиги) можно сделать заклю-
заключение, что компоненты деформации должны быть существенно
более быстро изменяющимися функциями координат, чем
углы поворота (по крайней мере в некоторых направлениях).
Чтобы данный вывод не противоречил предположению о ма-
малости деформаций, приходится допустить, что размеры тела
в указанных выше направлениях малы, так как в этом слу-
случае нарастание деформаций, за счет большого их градиента
будет ограничиваться малостью области изменения соответ-
соответствующей координаты. Последнее остается справедливым
и при углах поворота, сравнимых с единицей.
Таким образом геометрически нелинейные задачи (то-есть
задачи, в которых удлинения и сдвиги считаются не выхо-
выходящими за пределы справедливости закона Гука, а относи-
относительные повороты волокон считаются большими по сравнению
с деформациями) могут встречаться только при исследовании
деформации таких тел, которые имеют в некоторых направ-
направлениях существенно малые размеры. Подобными телами явля-
являются тонкие стержни (тела имеющие малые размеры в плос-
плоскости их поперечного сечения), тонкие пластины и тонкие
оболочки (тела имеющие малыз размеры в направлении, пер-
перпендикулярном их срединной поверхности).
Лишь для таких тел геометрически нелинейные задачи
имеют реальное значение.
§ 39. Обобщение соотношений Сен-Венана на случай
больших поворотов и деформаций
В классической теории упругости существенную роль
играют дифференциальные соотношения, выведенные Сен-
Венаном и называемые либо условиями совместности дефор-
деформаций, либо условиями интегрируемости уравнений, связы-
связывающих перемещения с деформациями. С помощью данных
соотношений задачи теории упругости можно решать непо-
непосредственно в напряжениях, не прибегая к предварительному
определению перемещений. Аналогичные, но соответственно
более громоздкие соотношения (тождественно удовлетворяю-
удовлетворяющиеся при подстановке в них компонентов деформации,
выраженных через перемещения) могут быть установлены
и в нелинейной теории упругости.

140 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ |ГЛ. IV
Следуя обычному принципу изложения этой книги, мы
получим их сначала без каких-либо пренебрежений (то-есть
применительно к произвольной деформации) и затем упростим
применительно к случаю, когда удлинения и сдвиги малы
(но повороты какие угодно). Путь вывода искомых соотно-
соотношений весьма прост, если воспользоваться сведениями из
тензорного исчисления и, наоборот, весьма затруднителен,
если эти сведения не принимать во внимание. Поскольку
данный вывод относится скорее к области дифференциальной
геометрии, чем к теории упругости, мы проведем его в тен-
тензорной форме, рекомендую читателю, для которого он окажется
труден, пропустить приводимые ниже выкладки, ознакомиз-
шись лишь с их окончательным результатом.
В самом начале книги была допущена возможность по-
построения- декартовой системы координат X, Y, Z. Это равно-
равносильно утверждению, что рассматриваемое пространство
является эвклидовым. Но если так, то компоненты тен-
здра риадана—-Кристоффеля (тензора кривизны простран-
пространства) дрлж.#ы быть равны нулю, какой бы криволинейной систе-
системою координат в этом пространстве мы ни пользовались.
В частности они должны быть равны нулю и в системе х,
у, а, которая приняга нами для определения положения то-
точек деформированного тела.
Для' ковариантных компонентов тензора Римана — Крис-
тоффеля существуют следующие выражения (см. „Векторное
исчисление и начала тензорного исчисления" Н. Е. Кочина,
изд. 1938 г., стр. 445).
Pg* \
dx*dxv- /
(IV.23)
— суть ковариантные составляющие фундаментального
тензора криволинейной системы координат х1, л;2, л:3,
—контравариантные составляющие этого тензора,
— символы Кристоффеля, выражающиеся через ко-
ковариантные составляющие фундаментального тен-
тензора посредством формул:
1 (dgij dgik^ dgjk\ /iv 9^

§ 39] обобщение Соотношений сен-венана 141
Отметим, что (по установившемуся в тензорном исчислении
обычаю) в правой части формулы (IV.23) опущёй знак двой-
двойной суммы по индексам о и р. Применим формулу (IV.23)
к криволинейной системе координат х, у, г '(установив для
определенности соответствие x-i-x1, у-*-х*, z-i-x9). Кова-
риантные составляющие ее фундаментального тензбра будут
равны:
gmx — 1 + 2s тх, gyy = 1 -f 2eyy, gzz = 1 + 2sM,
*xy, gyai = st/^ gyz=eyz> (IV.25)
в чем можно убедиться, составив на оснбваний формул A.21)
и A.5) выражение для квадрата расстояния межАу двумя
произвольными точками деформированного тела. Что касается
контравариантных составляющих фундаментального тензора,
то они (см. цитированный курс Н. Е. Кочина, «тр. 390)
будут определятся формулами (IV.9), (IV. 10).
Подставляя (IV.9), (IV.25) и (IV.24) в (IV.23), получим все
ковариантные компоненты тензора Римана-Кристоффеля в си-
«•Ч/ t*J «NJ
стеме х, у, г.
Из них различными будут только шесть (поскольку речь
идет о пространстве трех измерений — см. курс Н. Е. Кочика,
стр. 445). Приравнивание их нулю даст искомые шесть
дифференциальных соотношений между компонентами дефор-
деформации (ибо только через них выражаются в данном случае
как ghh так и g*»).
Ниже приводятся два из этих шести дифференциальных
соотношений.
Остальные четыре могут быть получены из них путем
циклической перестановки букв х, у, г.
д?еам» . 1 д <дгху dixz д*уг\
дуд г "г" 2 дх { дг "г" ду дх)^
„л, Г ! дгхх/дгху дгхг feyz\ &ххдгхх\ ,
~g \_2 дх \ дг г ду ЫГ)~~дТ дг J "Г
J_ nini I дгуу f^M d?aiai\ l дгУУ(дг*У i деУ* *<и] ,
"г ™ [ дг V дх ЬУ)~ 2 дх \~dT~i дх ~5у~\ "Г
\дегг/дгХ!1 5*0,0,4 1 dtg-g/dtxg.dfy, dtaiy\
[~ду~\~дх ЪТ/Т'дТУ'ду- + U дТ)

142 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ fl Л. IV
fexxfexy devvdsxx] . „, Г 1 д«яя (дъХ
dy dz dx dz J^& [2 dx V dz
. дгхг деуг\ . dexxdeaz д*хх $*ха
' ду дх) ' дх ду dz ду
i~ dy \ дх ду ) дх дх
-l{-dJ + -dx—1z-){-dz- + ——dj)\' (IV'2§)
дхду ду2 дх*
dx dz )\ду dz J 4 \ dy ^
feyz _ fcxyVSl , f (д*ху_ _ ^xx\ (&hcy _
"Г dx dz ) J-i-^ \\ dx dv A dy
deVV\ i ae^ dsVV о
dx
dsyz deyy\ dixx /(texg deyz дех!>\-\
dy dz ) dy \ dy "T" ^л: ^лг jj"+"
x ^г ^ ay i I, d^r aj< ) \ dy
if if I tAja | I/* '
rf* ч dy i йлг d
Выведенные шесть дифференциальных соотношений долж-
должны оставаться в силе при любых значениях перемещений
и, v, w.

§ 40] СООТНОШЕНИЯ ДЛЯ МАЛОЙ ДЕФОРМАЦИИ 14S
Отсюда следует, что они должны удовлетворяться тожде-
тождественно при подстановке в них вместо компонентов дефор-
деформации их выражений согласно формулам A.22).
§ 40. Упрощение соотношений (IV.26) для малых
деформаций
Если удлинения и сдвиги весьма малы по сравнению
с единицею, то разница между контра- и ковариантными
составляющими тензора Римана—Кристоффеля в криволи-
криволинейной системе координат х, ,v, z будет несуществен-'
ной, происходя лишь за счет членов порядка компонентов
деформации. Чтобы устранить соответствующие члены в фор-
формулах (IV.26), надо принять упрощение, заключающееся в
формулах (IV. 10), то-есть надо отбросить в (IV.26) все чле-
члены, имеющие множителями компоненты деформации (но не
их производные!).
В итоге этого пренебрежения получатся следующие шесть
приближенных соотношений
ЯгЛм \ nv ) ~l\ fix ) Г 4 лг Т
ду"- ' дх2 дхду \ оу / > \ дх
дгхя дгЯу\л /дгхя деха!\ ,дгуг дгуу\
| ду Ыг~) \ дх дг ) \ ду дг )
deVV (de*V ?ехх\
(
ду~\&х ду) дх \ ду сх)'
дг* i ду2 дуог ' \ дг
^_ дгху deyz\2 /ёеух деуу\ /дехи ^гг\
| ~дг дх) V ду дк) \ дг~ дх)
дг \ду дг ) ду \ дг ду)'
+ дх ду) \дг ду) { дх ду )
d~f \~~дТ ~д~х) дТ \~дх дТ]'

144 о постановке задач й напРйж^йнях [гл. iv
... дг*хъ 1 д /ЬгЫу дгхг д^_даххдг„х
IV> д$ЭГ~'2&\~дГ~Т-~5у~~^5Г)~ ду дг "Г
1 dtyy /дгху ^V ^*Л , L ^« /ава:2 ,
~Т~~2~~дх~\~дТ~Т~ дх ду)~Т~~2 дх \ ду "г
2 дх \ ду ^ дг дх)
д\у 1 дцдуь дгху
д\у 1 дцдгуь ^
dxdz 2 ду\д~х"Т~ дг ду )~~ дх дг
1 d*zz (д*уг &*х* д*ху\ !
~dJ\~dT~^^ дТ)~т~1Г
д*хя d*yz\ 1 де-уу/деХу 'дгу? деХ1!\
i ду дх) 2 ду \ дг "+" дх ду )
~дх~ \ ду ЫГ) Ъ~г~ {~ду ~дх~Р
VI- д'хду~~2"дг\~ду"^~дх' Ш~)=!='дх"ду'^
_1_ (
"Г 2 дг \ ду ~Г ^г дх )~Т~ 2 дг { дх ~t~
. дгху дгх„\ |_^f« fdet/n , ^sa^ ^ea*v\
~Г~й~ ~фГ/ 2 дг~\~дх г gy ~Jfc)
d?a:a, /<Ws ^гг\ ^уу^ f^yz_ ^еги\
ду \ дг дх) дх \ дг ду)'
Само собой разумеется, что эти последние соотношения
уже не будут тождественно удовлетворяться при подстановке
в них формул (I. 22). Однако, это будет происходить лишь
за счет членов, имеющих множителями компоненты дефор-
деформации, то есть за счет членов, пренебрежимо малых по срав-
сравнению с членами формул (IV. 27). Поэтому формулы (IV. 27)
можно рассматривать как условия совместности деформаций
при малых удлинениях и сдвигах, считая их обобщением
сен-венановых соотношений на этот случай.
Наличие в (IV. 27) дополнительных членов по сравнению
с соотношениями Сен-Венана обусловливается тем, что по-
последние соотношения выводятся в предположении, что углы

§ 41] ФОРМУЛИРОВКА ЗАДАЧ ТЕОРИИ УПРУГОСТИ 145
поворота и деформации малы по сравнению с единицею и
являются величинами одинакового порядка малости, тогда
как формулы (IV. 27) заключают в себе только предполо-
предположение о малости деформаций, но не налагают никаких огра-
ограничений на углы поворота.
§ 41. О возможности формулировки задач теории
упругости в напряжениях и деформациях
Сведения, изложенные в трех первых главах этой книги,
позволяют написать дифференциальные уравнения нелинейной
теории упругости в перемещениях и поставить для данных
уравнений надлежащее число краевых условий.
Настоящая глава дает принципиальную возможность ре-
решать некоторые задачи нелинейной теории упругости и не-
непосредственно в напряжениях.
Действительно — уравнения равновесия в форме (IV. 7)
или (IV. 8), при отсутствии объемных сил, не содержат пе-
перемещений в явном виде: в них входят лишь компоненты
напряжения и компоненты деформации. Соответственно не
.входят (явно) перемещения и в граничные условия (IV. 16).
Отсюда, дополнив уравнения (IV. 7) или (IV. 8) формулами
(III. 38) и (IV. 27), мы можем решать задачи нелинейной
теории упругости без необходимости выражения деформаций
через перемещения. Тем самым задача нелинейной теории
упругости сформулирована в напряжениях и деформациях
(при условии отсутствия объемных сил и независимости
fx, fy, fz от перемещений).
Не исключена возможность, что этот второй путь ре-
решения в некоторых конкретных случаях будет более удобен,
чем первый (то-есть чем путь решения задач в перемеще-
перемещениях). Однако и независимо от этого результаты настоящей
главы представляют интерес, так как изложенные в ней
формы уравнений равновесия и граничных условий часто
оказываются удобными и при решении задач в перемещениях.
Что касается соотношений (IV. 27), то они могут быть
полезными при проверке степени точности тех или иных
упрощенных формул, обычно принимаемых при определении
деформаций в геометрически нелинейных задачах.
В связи с последним замечанием следует вспомнить, что,
как было указано (§ 38), областью применения геометри-
10 &ак. 3804. В. Новожилов.

146 О ПОСТАНОВКЕ ЗАДАЧ В НАПРЯЖЕНИЯХ [ГЛ. IV
чески нелинейной теории упругости является исследование
упругого равновесия гибких тел (тонких стержней, пластнн
и оболочек). Для всех подобных тел задача о их дефор-
деформации может быть упрощена путем некоторых вполне обо-
обоснованных пренебрежений. Так, например, при исследовании
плоского изгиба стержней, можно считать, что по высоте
профиля стержня перемещения изменяются линейно. Послед-
Последнее равносильно пренебрежению углами сдвига по сравнению
с углами поворота. Аналогичный прием может быть исполь-
использован также и в теории пластин и оболочек. Кроме перечислен-
перечисленных упрощений, отражающихся лишь на формулах для дефор-
деформаций, используются также и упрощения уравнений равнове-
равновесия, основанные на том, что при деформации гибких тел неко-
некоторые из возникающих в них напряжений всегда' оказываются
существенно малыми по сравнению с другими напряжениями.
Все упомянутые упрощения, хорошо известные по ли-
линейной теории пластин, оболочек и стержней, полностью
переносятся и в нелинейную теорию, где они являются еще
в большей мере обоснованными, поскольку разница между
углами поворота и углами сдвига в нелинейной теории ока-,
зывается еще более значительной, чем в линейной теории.
Соответственно еще более значительной оказывается разница
между большими и малыми напряжениями. Применимость
геометрически нелинейной теории упругостн к гибким телам
и вытекающие из этого указанные выше упрощения фор-
формул в значительной мере облегчают решение геометрически
нелинейных задач. В конечном счете данные упрощения сво-
сводят любую трехмерную геометрически нелинейную задачу
к двухмерной или даже одномерной. Однако, несмотря на
все эти упрощения, геометрически нелинейные задачи (ввиду
нелинейности соответствующих дифференциальных уравнений)
остаются достаточно трудными. Точное их решение — как
правило, невозможно, а приближенное — связано с весьма
громоздкими вычислениями.
Тем не менее значительное число геометрически нелиней-
нелинейных задач в настоящее время уже нашли свое решение, а
проявляемый к ним повсеместно интерес позволяет надеяться,
что в ближайшем будущем круг решенных задач будет про-
продолжать расширяться.

ГЛАВА V
ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ
§ 42. Неоднозначность решения задачи теории
упругости
Известно, что дифференциальные уравнения линеализиро-
ванной теории упругости, основывающейся на принятии за-
закона Гука и пренебрежении нелинейными членами как в фор-
формулах для компонентов деформации, так и в уравнениях
равновесия объемного элемента, имеют в каждом конкрет-
конкретном случае единственное решение. Иными словами, класси-
классическая теория упругости дает для каждого тела, при задан-
заданных для него нагрузке и условиях закрепления, единственное
положение упругого равновесия.
На самом же деле решение рассматриваемой физической
задачи не всегда однозначно. Фактически одно и то же
упругое тело при одних и тех же нагрузке и условиях за-
закрепления может иметь и несколько возможных положений
равновесия. Неправильный вывод, к которому приходит
в данном случае классическая теория упругости, объясняется
недостаточной точностью ее формул, при выводе которых
отбрасывается влияние поворотов на выражения для компо-
компонентов деформации и на уравнения равновесия. Между тем,
при исследовании неоднозначных форм равновесия упругих
тел учет этого влияния совершенно необходим.
Когда тело имеет несколько возможных положений упру-
упругого равновесия, то обычно не все они бывают устойчивы
и, следовательно, не все они являются равновероятными.
Отсюда в задачу теории упругости входит не только оты-
отыскание форм упругого равновесия, но и выяснение их устой-
устойчивости. Существенно при этом отметить, что в случае на-
10*

148 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
личия нескольких возможных форм равновесия, та форма,
которую дает классическая теория упругости, обычно
является неустойчивой. Из этого замечания ясно, что исполь-
использование классической теории упругости при расчете проч-
прочности и деформации реальных конструкций может привести
к катастрофическим последствиям, ввиду того, что иногда
в действительности конструкция будет деформироваться совер-
совершенно иначе, чем предусматривает расчет.
В настоящей главе будет изложена теория устойчивости
упругого равновесия тела произвольной формы в области
деформаций, не выходящих за пределы справедливости закона
Гука. Чтобы получить отправной пункт для дальнейших рас-
рассуждений, предположим сначала, что составляющие поверх-
поверхностных и объемных сил, действующих на тело, бесконечно
малы. Тогда (при конечной жесткости тела) перемещения
всех его точек будут также бесконечно малыми. Соответ-
Соответственно бесконечно малыми будут удлинения, сдвиги и по-
повороты. Но бесконечно малая деформация подчиняется урав-
уравнениям классической теории упругости и, следовательно
(в силу указанной выше теоремы единственности), при бес-
бесконечно малых нагрузках всякое тело будет иметь только
одну форму упругого равновесия и притом такую, какая
может быть получена из уравнений классической теории.
Примем далее, что нагрузка на тело зависит только от
одного параметра и начнем этот параметр постепенно уве-
увеличивать. В некоторых пределах данного изменения решение
будет продолжать оставаться единственным и только по
достижении параметром нагрузки некоторого определенного
значе ия (которое назовем критическим) появится возмож-
возможность еще одной, не предусматриваемой классической теорией,
формы у 'ругого равновесия.
Поскольку критической нагрузке соответствует мо-
момент наступления возможности раздвоения решения за-
задачи, постольку два положения равновесия, ей соответ-
соответствующие, будут лишь бесконечно мало отличаться
друг от друга.
Последнее обстоятельство и будет положено в даль-
дальнейшем в основу теории определения критических нагрузок.
Из вышеизложенного видно, что в случае, когда внеш-
внешняя нагрузка на тело зависит всего от одного параметра

§ 43] УРАВНЕНИЯ ДЛЯ КРИТИЧЕСКИХ НАГРУЗОК 149
условие устойчивости упругого равновесия выражается не-
неравенством:
Р < Ркр.,
причем ркр. будет функцией формы и размеров тела, его
упругих свойств, условий его закрепления и характера на-
нагрузки.
Так как во многих задачах нагрузка действительно
характеризуется всего одним параметром, рассмотренный
выше случай представляет наибольший практический интерес.
Тем не менее, встречаются и такие задачи, в которых
нагрузка зависит от двух или даже большего числа пара-
параметров (р, q, г...).
Задавшись тогда какими-либо значениями отношений
и увеличивая затем параметр р, мы придем опять к фор-
формулировке условия упругой устойчивости конструкции в виде
неравенства
Р<Ркр.
Однако в данном случае ркр будет функцией не только пе-
перечисленных ранее факторов, но и функцией отношений
ku ka Отсюда ясно, что при зависимости нагрузки на
тело от нескольких параметров, условие его упругой устой-
устойчивости будет выражаться неравенством вида
д, г..
где /—некоторая функция параметров нагрузки, а К—число,
от нагрузки не зависящее. .
§ 43. Дифференциальные уравнения для определения
критических нагрузок
Пусть нагрузка на тело равна критической. Тогда для
него будут возможны два и притом бесконечно близких по-
положения равновесия.
Перемещения, соответствующие одному из них (тому,
которое в . рассматриваемый момент теряет свою устой-

50 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
чивость), будем обозначать а0 v0 w0, а перемещения, соот-
соответствующие другому, будут:
и==ио-(-аи1, v = vQ-f- avv w = wo-\-awv (V.I)
Здесь: аи, (х, у, г), avx (лг, у, г), awl (х, у, г) суть те
дополнительные перемещения, которые нужно сообщить точ-
точкам тела, находящимся в первом (исходном) положении равно-
равновесия, чтобы перевести их во второе (новое) положение
равновесия. При этом функции «ц vu w1 будем считать
конечными, а коэффициент а бесконечно малой, независимой
от х, у, г величиной.
Выразим компоненты деформации, соответствующие вто-
второму положению равновесия, через компоненты деформации,
отвечающие исходному положению равновесия и дополни-
дополнительные перемещения. Подставляя (V.1) в A.22), находим:
гхх
где:
==8L+as«+a2C (V.2)
= гуг -f ae'yz -j- ah"y3,
(V.3)
дх ~г ду~ ~*~ дх ду т дх ду ~^~ дх ду
дщ . дщ , dua duo , дщ д^о , дщ <>Щ
~~ дх ' ду > дх ду' дх ду "+" дх ду
суть значения компонентов деформации в первом положении
равновесия;
i дих , дщдщ , dvpdut , dwQ dwj
еха> — д7~т"д7'дх"гд7дх~~1~дх дх'
' (V.4)
/ dvi , dtti . dun dui , chip d«t , dvQ dv-i , dv0 dv± p
Sa* ~Jx~>~Ту i"dxdy~~>"ду"дх"< дх ду 'г'ду"дх>
, dwodwi , dwodWi
< дх ду ~г ду дх\

§ 43] УРАВНЕНИЯ ДЛЯ КРИТИЧЕСКИХ НАГРУЗОК 151
суть параметры, зависящие как от производных uQ, vQ, w0,
так и от производных alt vit wt;
(V.5)
дх ду т~ дх ду ~~^~ дх dy
дщ дих , dvi dv\ , dw^ dwi
~ дх"ду "i ~dx dy~ ' ~d* W
суть параметры, зависящие только от производных ult vu w^
и притом содержащие лишь квадратичные члены.
Подставляя (V.2) в (III.56), то-есть в формулы, выра-
выражающие закон Гука, будем иметь:
* I ' Т 9 " ° 1 ' I 9 "
°Ш = аУУ + а°УУ + а24»' аа;г = aa» "f «а^ 4" а2а'^> (V-6)
°zz = °к + аа« + а2агг, ауг = о°г 4" аз^г -f а2а^г.
Здесь:
о о о •
Cl 2 = Ъхх -\- Ьуу + ^zf,
I » « » •
a ofj и оу выражаются через sjj и е^- подобно тому, как оу
выражаются через s/j-
Заметим, что в силу бесконечной малости йараметра а
члены формул (V.2) и (V. 6), содержащие его в квадрате,
будут величинами второго порядка малости. Учет их для
дальнейших рассуждений этого и следующего параграфов
несущественен и поэтому они могут быть отброшены. При-
Применим теперь ко второму из двух рассматриваемых поло-
положений тела выведенные во второй главе уравнения равно-

152 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ {ГЛ. V
весия объемного элемента (которые будем принимать в форме
написания A1.48), так как, допуская применимость закона
Гука, мы должны считать компоненты деформации прене-
пренебрежимо малыми по сравнению с единицею). Вводя переме-
перемещения (V.1) и напряжения (V.6) в данные уравнения и от-
отбрасывая при этом члены, содержащие множитель а в сте-
степенях выше первой, находим
3J1 (* + ехх + <*ехх) ахх -|- a (I -f ехх) <зхоо -f
+ [у (е°ху + ае'*у) — ш* — a<B* J °^ + а G e*v ~ WV а*У +
+ I Y (ехг + ^xz) + «>у + а% J ажг -f а ("г" еы + Ш2/) °а
[7 (e'xz 4
I. /Iе
«; + «ш; ] 4 + а A ^ + »») 4} + ^* = 0. (V.8)
Два других уравнения этой системы могут быть полу-
получены из написанного путем циклической перестановки ин-
индексов х, у, г.
При этом в уравнении (V.8), кроме ранее принятых обозна-
обозначений, ец, <oj суть значения вц и а^- при и = и0, v = v0,
wt=fwQ, и е'ц, щ при « = «!, v = vv iw = wx.
Поскольку перемещения и0, v0, w0, так же как и и, v, w,
соответствуют равновесному положению точек тела, по-

§ 43] УРАЧНЕНИЯ ДЛЯ КРИТИЧЕСКИХ НАГРУЗОК 153
стольку, кроме уравнений вида (V.8), должны существовать
и уравнения вида:
дх У-1 + ?хх> °хх + ( вху ~ ш«) а^ + (y е<** + шу) а**} ~Г
+ Щ, {О + е°хх) °ху + (у ^ — <°г) °да + (д <4 + <о°) <3°yxj -f
= О, (V.9)
(два других уравнения — циклической перестановкой хуг),
получающиеся при отнесении системы A1.48) к исходному
положению равновесия. Заметим, что компоненты объемной
силы F(_, Fv F^ можно считать независимыми от перемеще-
перемещений, то-есть одинаковыми как в первом, так и во втором
положениях равновесия. Это вытекает из того, что единст-
единственной объемной силой, с которой приходится считаться
в статических задачах теории упругости, является удельный
вес тела, компоненты которого на независимые от дефор-
деформации направления, будут постоянными величинами (если
не считаться с изменением объема тела при деформации).
Учитывая это замечание и вычитая затем из уравнения (V.8)
уравнение (V.9\ приходим (после возможного сокращения
на а) к следующей системе однородных дифференциальных
уравнений:
| еп j (I -j- ехх) охх -\- (у еху — <оЛ аху -\-
exz
-f- [-Jеху—пг) зХу + [ j eaz+ <ovj axz -f {-j ex
~T Sy\ е<взРхУ + ^ + e*ai) °xy + 1^2 exy
-f- [-2 exy — Щ) °yV + [j exz + a>y) ayz -f- ^ exz + <s>y) a^| -f
+ dz { exx°x» + (J + e*>x) °хг + ( вхУ "~ ш*)аУг
-f- (-j ely — <o°j с'уг -j- ^ ^ + «i,) агг -f

154 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
(два других уравнения — циклической перестановкой хуг).
Существенно отметить, что система (V.10) будет линей-
линейной относительно производных от ult vlt wl по а:, у, г.
Последнее явствует из того, что оу, ец, ау входят в (V.10)
линейно, а сами они (в силу формул A.6), A.7) и A11.54)
являются линейными функциями упомянутых производных.
Что касается системы уравнений (V.9), соответствующей
исходному положению равновесия, то она, вообще говоря,
будет нелинейной относительно производных от и0, v0, w0.
Однако, в большинстве практических задач углы пово-
поворота, отвечающие начальной форме равновесия тела, бывают
либо равными нулю, либо величинами одного порядка с удли-
удлинениями и сдвигами. Иными словами, к исходному положе-
положению равновесия обычно можно применять формулы класси-
классической теории упругости. В этом, наиболее важном по
своему практическому значению частном случае уравнения
(V.9) принимают вид:
о о о
дх * ду I" dz ' *~~ '
в о _ э
до до GG
Ху | уу I yZ I_j7 (\ t\7 I 1\
дх ~ ду ~ дг
где
¦ J32JL Oi>> °ХУ — 2 A +н.) Вху '
Решив линейную систему (V.I 1) при задаиных граничных
условиях, которые могут быть удовлетворены без учета
деформации поверхностей, ограничивающих тело, мы полу-

§ 43] УРАВНЕНИЯ ДЛЯ КРИТИЧЕСКИХ НАГРУЗОК 155
чим перемещения w0, v0, w0 и напряжения, соответствующие
исходному положению равновесия: При этом указанные ве-
величины станут известными функциями координат а:, у, г и
неопределенного пока что параметра (или параметров) внеш-
внешней нагрузки.
Вводя затем данные функции в уравнения (V.10), мы
придем к линейной, однородной дифференциальной системе
относительно uv v^, wr
Эта система (при задании для нее однородных граничных
условий, которые выяснятся несколько ниже) будет иметь
отличные от нуля решения лишь при вполне определенных
(являющихся ее характеристическими числами) значениях
параметра нагрузки. Каждому такому его значению будет
соответствовать точка разветвления решения уравнений тео-
теории упругости.
Таков путь исследования упругой устойчивости.
Заметим, что из предположения о допустимости примене-
применения к исходному положению равновесия классической теории
упругости вытекают некоторые возможности упрощения
также и уравнений (V.10). В самом деле—для перехода от
системы (V.9) к системе (V.11) нужно было пренебречь
в первой системе всеми членами, имеющими в качестве
коэффициентов e(j, <oj, что, как известно (§ 23), равносильно
пренебрежению углами поворота линейных элементов тела,
при проектировании сил, действующих яа его объемный
элемент.
Но если так, то нет основания сохранять аналогичные
члены и в системе (V.10).
Отсюда эта система может быть написана следующим
образом:
(V.13)
( •
1/ ' \ ° ' '¦ /1
/1
ду \ ахУ+е*>* °*У I ( J ехУ~ ш0 ага+( 2
2 еху — <°z ) <3уг +
. . . .Сус.1.

156 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
Рассмотрим далее выражения (V.4), записав их предва-
предварительно в виде:
1 „ , ° \ dvi , /1 • '\dw,
^ + J i+1 еш)
axy-
В соответствии с намеченной выше системою упрощений
и здесь следует пренебречь всеми членами, умноженными
на еу, atj. Тогда для параметров гц получим (вместо формул
(V.4) гораздо более простые выражения:
' ' дщ i ' __ dui . dvi
s.yy — vyy — , sxz — exz — dz^dx' * * '
r ' dwy ' ' dvi ¦ dv»!
8ггЕ=вгя>^17' S^ "~ еУ ~ ~di~ "I ~dy '
Возвращаясь теперь вновь к уравнениям (V. 13), заметим,
что в них параметры <oj пропорциональны дополнительным
углам поворота, которые получает объемный элемент тела
при переходе от первого положения равновесия во второе.
Что касается до е^, то они, как только что было установ-
установлено, пропорциональны (с тем же коэффициентом пропорци-
пропорциональности а) дополнительным компонентам деформации.
Для задач на потерю устойчивости упругого равновесия
обычно характерно превращение форм равновесия с малыми
углами поворота в формы равновесия с углами поворота,
существенно превосходящими компоненты деформации. Это
дает основание пренебречь в уравнениях (V.13) всеми чле-
членами, умноженными на ец=. г™, по сравнению с членами,

§ 44] КРАЕВЫЕ УСЛОВИЯ 15?
умноженными на <oj. Учитывая данную возможность, приво-
приводим систему (V.13) к следующему виду:
+ Ту [ °ху ~ Шг °«* "г "» **• J +
I d Г ' '°1 ' л
' Tz I °xz ~ Шг °У ' ^^ а*г J = '
^ [ ^ — <ах ажг + <»г <*хх J -+-
[ a
' ~dz~ I а^ —<0'»а» + шв°*а>1 — °»
Г ' ' • ' | ' * |
.1 °хг — «j/ aa;a; + а>х аХу -j-
+ бу [ V ~ ш» a^ + '"^ aW J +
I Й Г ' ' * I ' ° 1 П
+ gj| а»г — <Ог/Згя. +<ожагг/ j = О,
который и будем считать окончательным.
После подстановки сюда вместо о^, »j их выражений, урав-
уравнения (V.16) превратятся в систему из трех линейных одно-
однородных дифференциальных уравнений с тремя неизвестными
uv vu wv к определению характеристических чисел которой
(при заданных краевых условиях) и сводится вопрос нахож-
нахождения критических нагрузок, если исходное напряженное
состояние относится к числу задач классической теории
упругости.
§ 44. Краевые условия проблемы упругой
устойчивости
Сформулируем, воспользовавшись для этого результатами
предыдущей главы, краевые условия для системы (V.16).
Они могут быть получены путем сравнения краевых ус-
условий для первого положения равновесия с краевыми усло-
условиями для второго положения равновесия.

158 проблема упругой устойчивости (гл. v
Пусть на некоторой, части поверхности, ограничивающей
тело, заданы геометрические граничные условия, то-есть
явно заданы перемещения. На остальной части этой по-
поверхности пусть заданы компоненты внешней нагрузки fx,
fy> /г- Общий вид геометрических граничных условий мо-
может быть записан в форме:
« = ?i С*. У, «). v = ?а (•*, у, г), w = <?a (х, у, z), (V. 17)
где: <?1(х, у, г), <ра(лг, у, г), <?а(х, у, г) — заданные функции.
Эти равенства должны соблюдаться как в первом, так и
во втором положениях равновесия. Отсюда (на соответствую-
соответствующих участках поверхности, ограничивающей тело) имеем:
Вычитая верхние равенства из нижних, приходим к сле-
следующим краевым условиям для ttt, vlt wk:
Ul = 0, vL = 0, да1==0, (V.19)
которые должны соблюдаться в тех точках границ тела, где
перемещения явно заданы. * Выпишем далее для первого и
второго положений равновесия краевые условия в тех точ-
точках, где задана внешняя поверхностная нагрузка.
Для исходного положения равновесия (если учесть, что
оно считается относящимся к числу задач линейной теории
упругости) условия равенства сил на поверхности тела бу-
будут иметь вид:
е'хх cos (л, X) -J- aly cos (n, Y) -\- чхг cos (n, Z) —
= Л(«о. «о» Щ) = /1
<3ху COS (rt, X) -j- O°vy COS (Я, Y) -\- a'yg COS (rt, Z) =
—/4 («о» "о. Щ)=А>
а°Хг cos (n,X)-\- vyz cos (я, Y) -J- a^ cos (я, Z) =
* Отметим, что «i, t^. ^ в точках тела, где перемещения за-
заданы, должны подчиняться тем же условиям, какие там же нала-
налагались иа вариации перемещений. Данное обстоятельство будет
использовано в следующем §.

§ 44] краевые условий 159
где /е (и0, vc, wo)> /„ («о, t»0. да0), /t(«0, *0, w0) суть значе-
значения проекций удельной поверхности нагрузки на оси А", К, Z
в первом положении равновесия. Для второго положения
равновесия (смежного с предыдущим) аналогичные условия
напишутся следующим образом:
• o»>i,e cos (я, X) 4- <3пгл cos (я, У) -{- ап,д cos (я, Z) =
= Л ("о + аи1> vo + «¦»!. w0 + а^о),
<»„„,, cos (я, <Y) 4- о„„ч cos (я, Г) 4- <*n,,t cos (я, Z) =
о»!,; cos (я, Л^ 4^«..сcos (rt> r) + ап„с cos (я, Z) =
или, если учесть формулы A1.39), A1.42) и (V.6), а также
те упрощения, которые были приняты в предыдущем пара-
параграфе, имеем:
4 ^ Х ^ COS (яАГ) 4"
— <°'гада 4" °VV)] cos (яУ) 4" ,у j
] cos (rtZ) ^
Вычитая формулы (V.20) из формул вида (V.22), приходим
к следующей формулировке граничных условий, которые
должны быть наложены на функции ult vit ivy в тех точ-
точках поверхности тела, в которых заданы внешние силы.
(<4в <йг°ху 4- m'tPx*) C0S (nX) +
4 (°ед — "V»w + »^) cos (яК) 4"
4" ("ет — «VV + ®»О«г) COS (flZ) =
= lim ji [Д (»0 4- a «1( i?0 4.« Wl, w0 -f « Wl) _y
Два других граничных условия могут быть получены пу-
путем циклической перестановки л:, у, z.

160 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
Заметим, что если в предыдущем параграфе объемные
силы можно было считать независящими от перемещений,
то в отношении поверхностных сил такой возможности,
вообще говоря, нет. В частности, если поверхность тела
находится под действием гидростатического давления (дав-
(давления жидкости или газа), то удельная поверхностная на-
нагрузка хотя и будет при деформации сохранять свою вели-
величину, однако, ее направление будет изменяться (поскольку
гидростатическое давление всегда направлено по нормали
к поверхности, на которую оно действует). Отсюда будут
изменяться при деформации и ее компоненты _/|, Д, _Д. Та-
Таким образом, правые части формул вида (V.23) считать
равными нулю нельзя.
Для тел, поверхность коих находится под действием
гидростатического давления
Л («о» % wo) = — Р cos (я0, X),
/у («о, <>о» «о) = - Р cos (я°> !0. (V-24)
Л ("о. «о» wo) = — Р cos (я°1 z).
ц) = —pcos(n},X),
1)= —pcos (я1, К). (V.25)
Л («о + « «1. •»<) + « *>u ^о + « wt) = —pcos (я1, Z),
где р — внешнее давление, а под я° и пх подразумеваются
направления нормалей к поверхностям, ограничивающим тело
в первом и втором положениях равновесия.
На основании формул (§ 2) имеем:
COS («°, X) = -^щ- [(l + %f) COS (Я, X) +
cos (я, У) +^ cos (я,
cos (я°, У) = —1-г. [^ cos (я,
1 -г- ? L Л*

§ 44] КРАЕВЫЕ УСЛОВИЯ 161
c-s n-
cos
где я означает направление нормали к поверхности, ограни-
ограничивающей тело до деформации, а Е°п, Е1п суть относитель-
относительные удлинения в этом направлении, соответствующие пер-
первому и второму положениям равновесия.
Предположение о малости деформаций позволяет упро-
упростить эти формулы путем пренебрежения Еп, Ехп по сравне-
сравнению с единицею.
Подставив после этого (V.26) в (V.24), a (V.27)
в (V.25), получаем граничные условия задачи упругой-устой-
упругой-устойчивости для тела, нагруженного гидростатическим давлением
в виде:
(°а>а> — Wxy -f- ay4,) COS (я, X) -\- (о^ — (O/W H~
+ <VV) cos (я, Y) -\- (с4 — а)^а + ш'уо1г) cos (я, Z) = (V.28)
= - р [жcos (». V + т5"cos ("• ^ + ^cos
[ж
И &ак. 3801. В. Новожилов.

162 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
учитывая далее формулы:
й«! ' dut 1 ' '
$-!«:+«;, (v.29)
а также принимая во внимание, что в предыдущем пара-
параграфе была установлена возможность пренебрежения пара-
параметрами еу но сравнению с <oj, приходим к следующей окон-
окончательной формулировке граничных условий (V.28).
{рхх — шг а°у -\- ш'у cs°xz) cos (я, X) -f
-\-{р'ху — Щ°у)>-\- Vyiyz) cos (я, Y) -\-
+ (<»» - *'?* + «>») cos (я, Z) = (V.30)
= p[<o«cos(n, У) —<4
§ 45. Энергетический критерии определения
критических нагрузок
Указанный выше путь отыскания критических нагрузок
сводит эту задачу к определению характеристических чисел
системы линейных однородных дифференциальных уравне-
уравнений (V.16) при граничных условиях (V.19) или (V.23). Этот
путь выгоден, если ставить себе целью получение возможно
более точного решения. Однако, во многих конкретных слу-
случаях последнее оказывается недостижимым и тогда более
удобно решать проблему упругой устойчивости, исходя из
иного критерия, который может быть получен путем сле-
следующих рассуждений.
Из формулы (III.45) и закона Гука вытекает возможность
написания выражения для работы деформации упругого тела
в виде:
JJ J J (
°yysyy
Vs») dxdydz (V.31)

§ 45]
ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ
1.63
(имея в виду использование этой формулы в дальнейшем лишь
для случая малых деформаций, мы не делаем здесь различия
между обобщенными напряжениями а<у и истинными напря-
напряжениями а^-). Применим (V.31) ко второму из двух смежных
положений равновесия тела, то-есть к положению, которому
соответствуют перемещения (V.I). При этом в отличие от
предыдущих параграфов будем удерживать .не только члены
первого порядка малости (то-есть умноженные на а), но и
члены второго порядка (то-есть умноженные на о3).
Придерживаясь этой степени точности рассуждений (необ-
(необходимость которой выяснится из дальнейшего), будем иметь:
(V.32)
где
о о ¦ о о | о о
-о 1 С Г Ct о о
А = -^ J J J \^xxsx
+ "хг^х» + OyjSy») dxdydz,
Л<'> =  J J J {Зхх^х
¦
"Г
O'iO
s °
+
' о i f о
AB> = -j J J J (з'ххь'х
'O r'O,
axxsxx -\~ ayysyy "T"
о , ' о
+ "msJj, -(-
' ' i ' '
i 0 " I 0
-f- аг,е^_у -f- <3x
i ' ' i ' ' i ° " i о " I
"T" axz%xz -f- Qyzzys -f- Gxxsxx -f- QyySyy T"
0 " i 0 " i  i " 0 i
S QS \ Ъ^ ^^УУ "Т
4" °zzSzz 4" aay4v 4" а^°г + a'yzSy
, (V.33)
причем параметры е</, s^-, e^, определяются формулами (V.3),
(V.4), (V.5), а параметры а%, a^, o</ связаны с ними фор-
формулами вида (V.7).
11*

164 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
Заметим, что, на основании упомянутых формул (V.7), выра-
выражения для А$) и А№ могут быть записаны следующим более
простым образом:

dxdydz,
2i S S ayzeys)] dxdydz, (V.34)
что нетрудно проверить, если выразить в двух последних
формулах (V.33) a'tj через stj, а г% через а°у.
Воспользуемся теперь началом возможных перемещений,
причем виртуальные приращения будем давать не суммарным
перемещениям (V.1), а лишь дополнительным перемеще-
перемещениям аи,, avlt awi, то-есть будем рассматривать возмож-
возможные перемещения вида: o8«j, о8г»1} abwv При этом Ьии bvit
bwt надо будет считать равными нулю в тех точках ограни-
ограничивающей тело поверхности, где перемещения заданы.
В такой постановке начало возможных перемещений для
второго из двух рассматриваемых положений равновесия
выразится равенством:
U = а [8 (ДО) + а8 (А&)\ = а [8 (/?,) -f 8 (/?»)], (V.35)
где: о8 /?: — работа объемных сил, а8 R2 — работа поверх-
поверхностных сил на виртуальных перемещениях ab ult aivu abwv
(Вариация 8 (Л°) = 0, поскольку А0 от ии vt, w1 не зави-
зависит.)
Работа объемных сил будет равна:
<х8 /?, = a J J JVj: 8«! + Z7^! + F^wJ dxdydz,
где под F%, Fv F^ следует подразумевать значения проек-
проекций удельной объемной силы для второго положения равно-
равновесия. Однако, как было указано i§ 43), величины и напра-
направления объемных сил можно считать независимыми от де-

§ 45] ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ 165
формации, что позволяет отождествлять F$, F^, Fz в фор-
формуле (V.36) с их значениями для исходного положения
равновесия.
Что касается работы поверхностных сил, то она опре-
определится выражением:
а8#2 = a J J[/e8Ml 4-ДЧ +/$Щ] dQ,. fV.37)
где Д, fv /c суть составляющие удельной поверхностной
нагрузки во втором положении равновесия. Их нельзя отожде-
отождествлять с аналогичными составляющими для исходного поло-
положения равновесия (как уже было отмечено в предыдущем
параграфе).
Вследствие этого представим формулу (V.37) в виде:
(V.38)
где:
//[Л («о- о0> ©о)
^» (V.39)
Ит A//[(Л -/^) 8«, + (/, -/?) 8г»: + (Д -
На основании вышеизложенного формула (V.35), после
сокращения ее на бесконечно малый, но отличный от нуля
множитель а, принимает вид:
8 [Ат] + <х8 [ДB)] = 67?, + 8MI} + «8#22). (V.40)
Обратим теперь внимание на то, что
— в силу первой из формул (V.34) есть прираще-
приращение работы деформации тела, находящегося в ис-
исходном положении равновесия при сообщении
его точкам виртуальных перемещений 8и}1 8г»1;
8

166 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
8/?! — есть работа объемных сил, соответствующих ис-
исходному положению равновесия (на тех же воз-
возможных перемещениях);
ЪЯ^Р — есть работа поверхностных сил, отвечающих ис-
исходному положению равновесия (на тех же воз-
возможных перемещениях).
Отсюда (поскольку положение тела, характеризующееся
перемещениями и0, v0, w0, является равновесным его поло-
положением) имеем равенство:
которое есть не что иное, как математическая форму-
формулировка начала возможных перемещений для первого из
двух рассматриваемых положений равновесия.
Но тогда из (V.40), после сокращения на о, следует, что
8[ДB>] = 8#B2). (V.42)
Это последнее равенетво и является вариационной форму-
формулировкой проблемы упругой устойчивости. Из него путем
операций аналогичных тем, которые были использованы
в III главе, могут быть выведены дифференциальные уравне-
уравнения вида (V.10) и краевые условия для них. Соответственно
из (V.41) может быть получена система (V.9). Мы предста-
представляем читателю самостоятельно во всем этом убедиться.
Вышеизложенные рассуждения проводились при сохране-
сохранении всех встречавшихся членов за исключением тех, кото-
которые могли быть отброшены ввиду малости удлинений и сдви-
сдвигов. Но в двух предыдущих параграфах было установлено,
что в большинстве практических задач исходное напряжен-
напряженное состояние тела можно рассматривать как задачу класси-
классической теории упругости. Это позволило заменить уравне-
уравнения (V.9) системой (V. 11), а уравнения (V.10) системой
(У. 16), что равносильно принятию равенств (V.15) и пре-
пренебрежению параметрами ец по сравнению с <aj.
Но тогда во второй из формул (V.34) под &ц можно под-
подразумевать ец, введя соотвествующее изменение в формулы
вида (V.7), выражающие оу через е^-.

§ 45] ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ 167.
Кроме того, поскольку параметры е^ (формулы V.5) могут
быть представлены в виде:
" 1Г, / >, , /1 ' . Л2 , (\ > '\91
*>хх —  I {exxy -\- {-^ еху-\- tuaj -f- \-^ eX2 — wy) \>
&ху = ехх [~ еху — <oej -f еуу [^ еху -f »2J + (V.43)
поскольку (принимая во внимание допустимость указанного
выше пренебрежения е^ по сравнению с <»j) их можно опре-
определить следующими упрощенными выражениями
s'L—у [ (<4)а + (ш'г)а] > еед= — о4<4,
4 | ? ^. «« = -»Х (V.44)
Отсюда для Ж2) может быть написана приближенная
формула
где
(V.45)
4" агг (<"ж + <Uj/)a — 2 [о^Ша, (Uj, -(- 3xz <Пя<йг "Ь
-f- V шу <аг] \ dx dy dz,
b2 — exx-j~eyy-\-e'zz,
bi = exx eyy -f e^ егг -\- eyy ezz — ^{elv-\- exz -\- e'yz),

168 ПРОБЛЕМА УПРУГОЙ УСТОЙЧИВОСТИ [ГЛ. V
каковой и следует пользоваться во всех тех случаях, когда
исходное напряженное состояние может рассматриваться, как
задача классической теории упругости.
Формулировка проблемы упругой устойчивости, выра-
выражаемая равенством (V.42), позволяет использовать для реше-
решения кбнкретных задач прямые методы вариационного исчис-
исчисления. Для этого надо задаться функциями «j, vvwl в виде:
.«1П+-... (V-46)
где: a.j, fa, у независящие от л:, у, z неизвестные коэффициенты,
a uf, vi, isi)l известные функции х, у, г, равные нулю в тех
точках поверхности, ограничивающей тело, где перемещения
явно заданы. Выбор этих функций в значительной мере про-
произволен: важно только, чтобы первые из членов рядов (V.46),
то-есть' функции и1, v\ wl по виду примерно соответство-
соответствовали ожидаемому характеру решения (каковой при некотором
навыке всегда можно качественно предвидеть). Тогда осталь-
остальные члены рядов (V.46) будут носить характер поправок.
Поскольку функции и), vi, wi известны, постольку варьи-
варьирование выражений (V.46) сводится к варьированию входя-
входящих в них неопределенных коэффициентов а^, fy, у. Подставляя
(V.46) в (V.42) и требуя, чтобы это равенство выполнялось
при любых значениях 8(<fy), S (j^), 8(^), мы получим систему
из Зя-линейных однородных алгебраических уравнений (где я—
число членов, удержанных в каждом из рядов (V.46) с неиз-
неизвестными a,j, $j, у. Данная система будет иметь решение,
отличное от нуля, лишь в том случае, если определитель,
составленный из ее коэффициентов, равен нулю. Эти коэффи-
коэффициенты являются функциями, во-первых, от параметров,
характеризующих размеры тела, во-вторых, от параметров,
характеризующих его упругие вещества, и, в-третьих, от
параметра внешней нагрузки.
Последний будет, единственной неизвестной характеристи-
характеристического определителя, причем его значения, обращающие

§ 45] ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ 169
определитель в нуль, будут соответствовать (как ясно из
вышеизложенного) критическим значениям нагрузки.
Намеченный путь приближенного решения задач теории
упругой устойчивости принадлежит к числу наиболее эффек-
эффективных, поскольку во многих случаях удержание в рядах
(V.46 только их первых членов уже дает близкий к истине
результат. В то же время этот путь требует от лиц, им
пользующихся, некоторого навыка, а главное понимания фи-
физической сущности решаемой задачи, так как точность рас-
рассматриваемого метода в значительной степени зависит от
удачного интуитивного выбора основных апроксимирующих
функций и1, vl, w1.

ГЛАВА VI
О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ
§ 46. Деформация пластин
В настоящей главе будут изложены специфические упро-
упрощения, возможные при изучении деформации гибких тел.
Мы начнем при этом с исследования деформации пластин,
поскольку именно эта задача наиболее проста.
Рассмотрим тонкую пластину постоянной толщины 8, огра-
ограниченную контуром произвольного вида. Начало декартовой
г
Рис. 17.
системы координат расположим в одной из точек срединного
слоя пластины, направив ось Z перпендикулярно этому слою,
а в качестве осей X и Y приняв две любые лежащие
в его плоскости перпендикулярные прямые (рис. 17).
При построении теории деформации тонких пластин, изги-
изгибаемых поперечной нагрузкой, обычно полагают, что всякая
точка пластины остается и после деформации на том же
перпендикуляре к срединному слою и на таком же от него
расстоянии, на каких она находилась до деформации.

§ 46] ДЕФОРМАЦИЯ ПЛАСТИН 171
Данное утверждение записывается аналитически в виде
следующих трех дифференциальных уравнений:
_ / , ди\ ди , dv dv , dw Л ,dw\ _0
ди ди . Л , dv\ dv . dw Л , dw\ _ ,-,., 1Ч
dw ,
(причем равенство нулю ехг и е^ означает перпендикуляр-
перпендикулярность к срединному слою после деформации тех волокон
пластины, которые были к нему перпендикулярны до дефор-
деформации, а равенство нулю егг означает сохранение расстояния
между произвольной точкою, лежащей на одном из таких
волокон, и срединным слоем).
Попытаемся удовлетворить уравнения (VI. 1) выражениями
вида:
и = и(х, у)-{-гЬ(х,у),
*Хх,у), (VI. 2)
w = w (x, у) + гу(х, у),
где и, v, w — суть перемещения точек срединного слоя (что
становится ясно, если в (VI.2) положить г = 0).
Подставляя (VI.2) в (VI. 1), приходим к соотношениям
ди\ <ч . dv , , dw ,. , ч ~
°' (VL3)
которые позволяют выразить Ь, <J» и у через перемещения
л л л
срединного слоя и, v, w.
Рассматривая первые две из формул (VI.3) как алгебраи-
алгебраическую систему с неизвестными 9 и ф, находим:
«зз

172 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
Здесь а81, а^, а88 определяются из формул A.15) при замене
в них и, v, w через и, v, w.
Введя (VI.4) в последнее из соотношений (VI.3), будем
иметь:
А
3 — 1 (VI5)
у=
'XZ | * 2 , *2
а31"Г а32 "Г аЗЗ
но в силу таблицы II (§ 2)
где ?) = 1 -)- Д, а ??с — относительное удлинение линейного
элемента пластины, который после деформации параллелен
оси г. Замена в (VI.6) a{j на a{j, означающая замену и, v, w
на и, v, w, равносильна рассмотрению D и Е^ у срединного
слоя.
Отсюда видно, что с точностью до пренебрежения удли-
удлинениями и сдвигами по сравнению с единицей
и, следовательно (с тою же степенью точности),
i dv dw
. • dw (. , ди\ . ди dw n/I й.
, й« | dv . ди dv да dv
Подставив данные значения 0, <]» и у в (VI.2), мы по-
получим перемещения произвольной точки пластины, выражен-
выраженные через перемещения соответствующей ей точки середин-
серединного слоя и, v, w (функции только х и у).
Закон изменения перемещений по толщине пластины
оказывается при этом линейным.
Заметим, что предполагая удлинения и сдвиги пренебре-
пренебрежимо-малыми по сравнению с единицею, мы не налагали
в то же время никаких ограничений на величину поворотов.

§ 46] ДЕФОРМАЦИЯ ПЛАСТИН 173
Отсюда перемещения, определяемые формулами (VI.2), (VI.8),
могут быть названы перемещениями, соответствующими силь-
сильному изгибу пластины.
Подставляя эти значения перемещений в общие выраже-
выражения для компонентов деформации е^, еуу, е^, находим:
ехх = ехх V г жхх I г vaa»
где
да_ I 1 Г / ди \2 . / dv \2 ,
л л л л л о /\ ^
А иИ I OZf I utt G// i uXf OZf * uXSO nHJ
g i _ I __ I , __^ J . I . ^_^_ i t ____ _ _
"'^ c[y ' дх ~ й_у Элг ' й-с oly ' Эл: Э_у
dx -r dx dx -t- dx dx -t dx dx ,
^ "+" 'ду ду "*" "clj 157 "T" ~ду ~ду~'
Т" ду дх ~T
dw dX , dw дX
_аоа» , d^dj. , дхдл
x« дх ду ~гдхду~*~дх ду '
При г —0 формулы (VI.9) дают:

174 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
откуда видно, что ехх, еуу, е^ — суть удлинения и сдвиг
срединного слоя пластины.
Члены же z/.xx, гг*.уу, г*ху в формулах (VI.9) соответ-
соответствуют удлинениям и сдвигам, линейно изменяющимся по
толщине пластины, тогесть соответствуют изгибу и кручению
пластины. Наконец, в (VI.9) присутствуют и члены, содер-
содержащие г2. Их наличие говорит о том, что линейному закону
изменения перемещений по толщине пластины отвечает,
вообще говоря, нелинейное изменение по толщине дефор-
деформаций. Однако, при малых удлинениях и сдвигах поправки,
вносимые в (VI.9) членами чххг*, vyyz2, чхуг*, являются не-
незначительными, что будет показано ниже на примере.
Учитывая это, можем написать:
ехх — sxx V гглхх<
evv = *svv + z*w> (VI. 12)
еху — еху Г гжху
Параметры п.хх, *yy, *ху характеризуют кривизну деформи-
деформированного срединного слоя пластины.
Когда углы поворота элементов пластины пренебрежимо
малы по сравнению с единицею, выведенные формулы допу-
допускают существенное упрощение. Именно — в этом частном слу-
ди dv , *
чае производные -g- , ¦*- следует считать (по соображениям,
изложенным в § 14) величинами одного порядка с удлине-
удлинениями срединной поверхности ехх, гуу. Кроме того, в этом
ди dv
случае следует считать, что производные ч-, ¦*- являются
величинами одного порядка со сдвигом езд- Последнее
вытекает из того, что при слабых искривлениях пластина,
будучи в своей плоскости массивным телом, не допускает
относительных поворотов своих элементов вокруг оси г,
значительных по сравнению со сдвигами.
По перечисленным соображениям в формулах (VI. 10) можно
отбросить (имея ввиду частный случай, когда углы поворота
элементов пластины малы по сравнению с единицею) все не-
нелинейные члены, содержащие производные перемещений «иг».

§ ,47] ДЕФОРМАЦИЯ БЕСКОНЕЧНО ДЛИННОЙ ПОЛОСЫ 175
Выполняя намеченное упрощение, приходим к выражениям:
da. , 1 /dw\% db ,
v
dy * дх'
dx^ ~~ dx*'
du.dv.dw dw .... „.
<==flZ-rrr + -^'JZ> (VI. 13)
x
-a* ~ dy ' дх ~ длду "
Подстановка (VI. 13) б (VI. 12) дает формулы для дефор-
деформаций пластины, предложенные Т. Карманом. Этой степени
точности рассуждений соответствует определение перемеще-
перемещений точек пластины выражениями:
А OXSf л OW л /\тт 1 л\
и = и г -^ > v = v z~fy~ » w w- \ • )
Дальнейшее мыслимое упрощение формул (VI. 13) заклю-
заключается в пренебрежении в них всеми их нелинейными членами.
В итоге этой операции получаются формулы классической
теории пластин. Из вышеизложенного видно, что для возмож-
возможности использования последней теории необходимо, вообще
говоря, чтобы квадраты поворотов
dw dw
были пренебрежимо малы по сравнению с удлинениями и
сдвигами. Таким образом классическая теория пригодна только
для описания деформации слабо изогнутых пластин. Сильный
изгиб пластин, как уже упоминалось, описывается формулами
(VI. 10), (VI.8), (VI. 12). Формулы Кармана (VI. 13) относятся
к промежуточному случаю.
§ 47. Двухмерная деформация бесконечно длинной
полосы
Предположим, что пластина имеет вид бесконечно длинной
полосы с параллельными прямыми краями, причем деформа-
деформацию ее будем считать независящей от координаты у, прини-
принимая, кроме того, что перемещение v = 0.

176 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
Сформулированная таким образом плоская задача по сути
дела эквивалентна задаче о изгибе балки. Применительно
к ней формулы предыдущего параграфа дают:
еякв = ех*-\-г %хх + г* vxx, (VI. 15)
где
• • du , \_ [7<*м\2 , /rfffi»\2]
dx
a dw du
dx ' л dje
_ ой о m)
Так как производные — , -т- считаются величинами су-
существенно большими по сравнению с удлинением гхя, то
правая часть первой из формул (VI. 16) должна неизбежно
являться малой разностью входящих в нее членов. Отсюда
du dw
при определении зависимости между -т- и -т— можно прибли-
женно положить гхх = 0.
Тогда
(VI. 17)
откуда
1 dw
A
§,¦ (VI.18)
-<щ

§ 47]
ДЕФОРМАЦИЯ ВЕЙКОНЕЧНО ДЛИННОЙ ПОЛОСЫ
177
Подставляя эти значения ххх, чхх в последнюю из фор-
формул (VI. 15), находим:
(VI. 19)
Поскольку zxxx есть величина порядка удлинений, которые
предполагаются пренебрежимо малыми по сравнению с еди-
единицею, постольку
г "Ах
Остается выяснить смысл параметра ч.хх.
Обратимся с этой целью к рис. 18.
Рис. 18.
Декартова координата х, определяющая положение точки
на срединном слое пластины до деформации, после дефор-
деформации становится длиною дуги той цилиндрической поверх-
поверхности, в которую превращается срединный слой после де-
деформации. Отсюда ясно, что
4| = sin 6,
но тогда
dx~
ds '
(VI.21)
12 Ьак. 8804. В. Новожилов.

178 О ДЕФОРМАЦИИ ГИЁКИХ ТЕЛ [гл. VI
то-есть у~хх суть кривизна деформированного в цилиндри-
цилиндрическую поверхность срединного слоя пластины. Сопоставляя
полученный результат с (VI.20), видим, что наши выводы
вполне совпадают с обычной теорией плоской деформации
гибких, первоначально прямых стержней.
В заключение параграфа следует обратить внимание чи-
читателя на тот факт, что, принимая равенство гхх = 0 при
упрощении формул для жхх, мы тем не менее сохранили гхх
в формуле (VI. 20), поскольку первый член упомянутой
формулы может быть в некоторых случаях не менее суще-
существенным, чем второй. На первый взгляд здесь допускается
противоречие. Фактически, однако, его нет, если понимать
равенство ехх = 0 лишь как использование того обстоятель-
обстоятельства, что члены, входящие в а^, образуют малую разность
больших величин, а члены входящие в t.xx, не являются
малой разностью. Таким образом равенство ехх = 0 не сле-
следует понимать буквально. В дальнейшем, при изложении
общей теории деформации стержней, мы не раз столкнемся
о подобным приемом.
§ 48. Деформация оболочек
Теория деформации тонких оболочек может быть по-
построена по аналогии с теорией деформации пластин, поскольку
оболочки суть пластины, срединный слой которых в недефор-
мированном положении является не плоскостью, а кривой
поверхностью.
Будем определять положение точек на срединной поверх-
поверхности оболочки гауссовыми криволинейными координатами
этой поверхности «t и ос2 (то есть такими кроволинейными
координатами, линии которых являются линиями главной
кривизны срединной поверхности). Соответствующие этой
криволинейной системе коэффициенты Ляме обозначим через
А1 и А2, а главные радиусы кривизны — через Rt и R2.
Исходя из данной двухмерной ортогональной системы кри-
криволинейных координат, построим трехмерную систему. Для
этого опустим из произвольной точки М, не лежащей на
срединной поверхности, перпендикуляр на эту поверхность.
Тогда положение рассматриваемой точки в пространстве бу-

§ 84]
ДЕФОРМАЦИЯ ОБОЛОЧЕК
179
дет фиксировано тремя параметрами: координатами at и <х2
основания упомянутого перпендикуляра и его длиною г. При
этом г условимся считать
положительным, если точка
лежит со стороны центров
отрицательной кривизны
срединной поверхности (со
стороны выпуклости сре-
срединной поверхности, если
ее точки суть эллиптиче-
эллиптического типа). Если наобо-
наоборот, то г будем считать
отрицательным. Простран-
Пространственная система криволи-
криволинейных координат а1э а2, г, Рис Ш
как ясно из способа ее по-
построения, ортогональна. Ее коэффициенты Ляме будут равны:
#3=1, (VI.22)
причем Аи Л2, Rlt /?2 (являющиеся функциями только at и
аа) должны подчиняться известным из теории поверхно-
поверхностей соотношениям Гаусса — Кодацци.
= .1 dAl
Ai дац) i да, \A2 й«2 /
(VI. 23)
Подс.авляя в формулы A.122) указанные выше значения
коэффициентов Ляме и учитывая при этом соотношения
(VI.23), будем иметь:
\ да ,\дАх ,
1 / 1 ди
z
1_ дА9 . w\
AiAt dot! " i" RJ'
dw
(VI. 24)
12*

О ДЕФОРМАЦИИ ГИЁКИХ ТЕЛ [ГЛ. Vt
1 / 1 dv 1 дА,
У' 1 / 1 да 1_
^,_,«U д<*2 At/
«г
д« , 1
л», = -
Rt
Здесь и, v, w — суть перемещения произвольной точки по
направлениям линий а1 и ос2 и по нормали к срединному слою.
Введя далее коэффициенты Ляме (VI.22) в A.124), при-
ходим^к следующим выражениям для составляющих век-
вектора о) по тем же направлениям.
_' ' (VI.25)
+ Rz
Теперь формулы A.125) дают возможность написать раз-
развернутые выражения для компонентов деформации оболочки
в криволинейной системе а1г ос2, г. При этом следует учесть,
что аналогия, существующая между пластинами и оболоч-
оболочками, позволяет, при определении перемещений последних,
воспользоваться такими же упрощениями, какие были исполь-
использованы при исследовании деформации пластин (§46).
Предположение о том, что прямые, волокна, нормальные
к срединному слою оболочки до деформации, остаются
прямыми и нормальными к срединному слою и после де-

§ 48] ДЕФОРМАЦИЯ ОБОЛОЧЕК 181
формации, аналитически записывается в виде следующих
двух равенств:
ди . 1 / 1 dw и \ . 1 / 1 du ,
i I dAt , ш» \ du . 1 / 1 du
dv
— o
(VI. 26)
z \A
\ йи j_ 1 /J_йш^ v\dw_
U) dz i ~~5 U2 da, Rl) dz
1+
а предположение, что эти нормальные волокна не получают
удлинений, сводится к равенству:
Попытаемся удовлетворить систему из трех уравнений
(VI.26), (VI.27), взяв перемещения и, v, w в виде:
и = и(<х„ a3
S K, a,), (VI.28)
Здесь «, г», w суть перемещения срединной поверхно-
поверхности оболочки (что вытекает из формул (VI.28) при 2 = 0).
Подстановка (VI.28) в (VI.27), (VI.26) приводит к пяти
равенствам, два из коих будут, однако, следствием одного

182 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
из трех остальных. Поэтому независимы будут только три
равенства, а именно:
»1 + Ф"--!-A+Х)>=1. (VL29)
да 1 дА*
dv
На основании двух последних из этих трех уравнений
имеем:
& = aJL(l+z), фв??A+7), (VI.30)
Я33 а88
где в данном случае
a
3t
a33 = С1
причем
- _ 1 да , 1
еп — 7 л,-,. ~г
А
Л
Lai
л
1
1
_ 1
1
А%
1
dv
д«2
ди
i 1 дл2
' AtAi дц
1 Mi
и
1 5Л2
/Ili4a до!
7?s '
(VI.32)

§ 48] ДЕФОРМАЦИЯ ОБОЛОЧЕК 183
Подставляя (VI.30) в первое из равенств (VI.29), прихо-
приходим к следующему выражению для ^
(vi>33)
Г о31 -f- a32 -+- a33
Здесь (по соображениям, аналогичным § 46)
«It + ^ + ^l (VI-34)
«
с точностью до пренебрежения удлинениями по сравнению
с единицею.
Отсюда:
У, ~ «33 — ! = «И + «22 + е11р22 — е12Р21- (VI.35)
Вводя это значение ^ в (VI.30), находим:
& = — в18A+'аа) + вазв12. (VI.36)
Ф = — «98 ( ! + «11) + ««4 •
Формулы (VI.35), (VI.36) и (VI.28) определяют переме-
перемещения произвольной точки оболочки через перемещения
соответствующей ей точки срединной поверхности. Поскольку
выше не было сделано никаких пренебрежений, кроме тех,
которые следуют из предположения о малости удлинений и
сдвигов, постольку полученный результат действителен при
произвольных относительных поворотах оболочки, лишь бы
они были совместны с предположением о малости деформа-
деформаций. Иначе говоря, выведенные формулы относятся к случаю
сильного изгиба оболочек.
Остановимся далее на определении удлинений и сдвигов
в слое оболочки, удаленном от срединного на расстояние г.
Соответствующие компоненты деформации, после подстановки
в формулы A.125) коэффициентов Ляме (VI.22),принимают вид:
1 / 1 ди , 1 дАх \J
2 (l+ A"J LUi A«i T AiM да2 г я J "Г

184 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
1 / 1 dv , 1
77Х
1 1 Г/ 1 ди 1 dAj \a ,
2 / , г \з |_\/42 dog i4i^42 да] / i
1 ov 1 оАч "Ш \2 / 1 dw v \* х, г*
_1 д »/ I I ] I — 1 I ( VI
I dv I dAt \ , 1 / 1 ди
L ц 1 —L , . [
Ах да, AiAi да% J I , Z \Ai 0а2
U-—+
1 /1
(.,г\(г\
dt; 1 dAi
Так как — S/g^^^^/g, то для тонких оболочек можно
в написанных формулах полагать:
l_j_JL~l_|__?L;^l. (VI.38)
Используя это упрощение и подставляя затем в (VI.37) пе-
перемещения и, v, w в виде (VI.28), будем иметь:
(VI.39)
Здесь ея, sg2, e12 суть удлинения и сдвиг срединной поверх-
поверхности оболочки.
•» = ё2 2 + Va ГЙ1 + 4 + 4], (VI.40)
S12 == ^12 Г ^21 "f" ^1^91 ~Ь ^33^18 4~ ^13^23'

§ 49] О СУЩНОСТИ ДОПУЩЕНИЙ КИРХГОФА 135
а хп, y^, х12 суть параметры, характеризующие изменение
кривизны срединной поверхности, обусловленное деформацией:
^22 = A + ё2а) *аа + ё2Л1
х12 = *я A + e,i) f кя A + e9
+ *22ё
причем
1 Л.1. 1 Л Я
(VI.42)
Что касается выражений для vn, v22, v]2) то нет необхо-
необходимости их приводить, так как соответствующие члены фор-
формул (VI.39) при малых удлинениях и сдвигах всегда оказы-
оказываются несущественными (аналогично тому, как это было
в теории деформации пластин).
Изложенное выше исчерпывает теорию деформации тон-
тонких оболочек при малых деформациях и произвольных пово-
поворотах. Удерживая в полученных ф^мулах только члены
линейные относительно перемещений и их производных, мы
придем к обычной теории деформации тонких оболочек.
Соответственно из вышеприведенных формул может быть
выведена и теория деформации оболочек, аналогичная (по
своей точности) теории пластин Т. Кармана.
§ 49. О сущности допущений Кирхгофа
Выясним более подробно математический фундамент до-
допущений, которые были положены выше в основу построе-
построения теории деформации пластин и оболочек,

186 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
В связи с этим будем искать точное решение задачи о
деформации пластины, разлагая компоненты перемещения
в степенные ряды:
, . , /ди\ , 1 /д2и\ „ ,
= Hx, у, о(
, . . (dw
Если в каждом из данных рядов удержать только два
первых члена и ввести кроме того обозначения:
и(х,у,о) = и, v{x,y,o)=v, w(x,y,o) = w
то получатся формулы (VI.2).
Таким образом, можно констатировать, что допущения
Кирхгофа прежде всего утверждают достаточность сохра-
сохранения в рядах (VI.43) только двух первых членов (при
решении задачч о деформации тонкой пластины). Однако,
кроме этого, упомянутые допущения устанавливают связь между
перемещениями срединного слоя пластины и, v, w и пара-
параметрами 0, 6, ¦/_, позволяющую выразить вторые через
первые.
Чтобы выяснить природу данной связи, вспомним, что со-
согласно таблице 1 (§2),
1 ди , „ . \ 1 *dv ... . ч
cos(A- i) cos(F i)
dz у 1 -f- 2егг dz
. + 4r-W cos (Z, 1,). (VI-45)
Здесь в рассматриваемом случае i3 есть единичный вектор,
касательный к волокну пластины, которое до деформации
было прямым и перпендикулярным к срединному слою.

§ 49] О СУЩНОСТИ ДОПУЩЕНИЙ КИРХГОФА 187
Из (VI.44) и (VI.45) следует, что:
сов(Г, f9),
, fB), (VI.46)
где i3 — направление касательной к упомянутому волокну
в точке его пересечения со срединным слоем егг — удлинение
данного волокна в той же точке.
Формулы (VI.46) говорят, что если пренебречь удлине-
удлинением по сравнению с единицею, то параметры 8, ф, 1+х
могут быть отождествлены с косинусами углов, образуемых
после деформации волокном пластины, которое до дефор-
деформации было перпендикулярно срединному слою. Но в задаче
об изгибе пластины углы поворота всегда велики по сравне-
сравнению со сдвигами.
Это позволяет при определении единичного вектора i3
(тоесть при определении параметров 8, ф, у) пренебрегать
величиною тех сдвигов, которые влияют на направление
вышеуказанного вектора.
Иначе говоря, при отыскании 8, ty, у можно пользоваться
уравнениями:
ев|,дав„«0. (VI.47)
Пренебрегая далее б (VI.46) егг по сравнению с единицей,
и складывая эти три равенства (после предварительного воз-
возведения их в квадрат), будем иметь:
92.
что, как известно (§ 46), эквивалентно равенству
егг = 0. (VI. 48)
Таким образом последнее равенство может быть истолко-
истолковано как пренебрежение удлинением волокна, перпендикуляр-
перпендикулярного к срединному слою пластины, при определении его
направления после деформации,

188 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. \1
Вышеизложенные рассуждения подразделяются на два этапа.
В первом была установлена связь между основными допу-
допущениями теории пластин и разложениями перемещений в ряды
по степеням расстояния точки пластины от ее срединного
слоя. Это позволило выяснить зависимость между ft, ij>, ^
и производными от перемещений и, v, w no z. При этом
оказалось, что ft, ^, ^ характеризуют направление после
деформации волокна пластины, первоначально перпендикуляр-
перпендикулярного срединному слою.
Вторым этапом явилось пренебрежение деформациями,
влияющими на направление упомянутого волокна, по сравне-
сравнению с поворотами, что привело нас к равенствам (VI.47),
(VI.48).
В § 46 мы шли обратным путем, а именно постулировали
уравнения (VI.47), (VI.48), из чего немедленно вытекало все
остальное. Этот путь, более краток, но менее ясен, так как
написав сразу (VI.47), (VI.48), мы не получаем представле-
представления, что и по сравнению с чем в данном случае пренебре-
гается.
Будучи поняты как математически точные равенства (VI.47),
(VI.48) —абсурдны, ибо приводят, вообще говоря, к противо-
противоречиям при формулировке условий равновесия элемента пла-
пластины.
Будучи же истолкованы лишь как пренебрежение неко-
некоторыми из компонентов деформаций при определении напра-
направления орта i3, равенства (VI.47), (VI.48) становятся на свое
место, причем сразу же оказываются более ясными и те усло-
условия, при соблюдении которых этими равенствами можно поль-
пользоваться.
Разумеется, вышеизложенные рассуждения, проведенные
применительно к пластинам, могут быть полностью перене-
перенесены и на оболочки.
Из сказанного вытекают следующие выводы.
а) Гипотеза Кирхгофа в теории деформации пластин и
оболочек покоится на упрощениях типа пренебрежения удли-
удлинениями и сдвигами по сравнению с поворотами при опреде-
определении направления волокон деформированного тела.
Поскольку тонкие пластины и оболочки суть гибкие тела,
при деформации коих углы поворота обычно велики по

§ 50 деформация Стержней (первое приближение)
сравнению с удлинениями и сдвигами, принятие этой гипо-
гипотезы обычно вносит в расчет оболочек и пластин лишь
незначительную погрешность. Отсюда ясно, что упрощение
теории пластин, предложенное Кирхгофом и затем перенесен-
перенесенное Лявом на оболочки, вряд ли правильно называть (как
это обычно делают) гипотезой, ибо по существу речь идет
о чисто геометрических пренебрежениях, всегда допускаю-
допускающих оценку своей погрешности.
б) „Гипотеза" Кирхгофа не включает в себя никаких
предположений о свойствах материалов, из коих изгото-
изготовлены пластины и оболочки. Поэтому использование теории,
основанной на данной „гипотезе", с равным успехом воз-
возможно как для тел, следующих закону Гука, так и для тел,
ему не следующих. Важно только, чтобы выполнялось основ-
основное условие применимости рассматриваемых допущений,
а именно — малость соответствующих деформаций по сравне-
сравнению с углами поворота.
Отмеченное обстоятельство еще более подчеркивает неги-
негипотетический характер упрощений, принимаемых при по-
построении теории пластин и оболочек.
Кстати, когда говорят о применении „гипотезы" плоских
сечений к балкам, работающим в упруго-пластической области
деформаций, обычно считают необходимым сослаться на
опыт, который эту „гипотезу" в данном случае подтверждает.
Из вышеизложенного видно, что постановку специальных
опытов для проверки „гипотезы" плоских сечений в области
упруго-пластического изгиба следует отнести за счет недо-
недостаточно ясного понимания существа данной гипотезы.
§ ЕО. Деформация стержней (первое приближение)
Разобравшись в теории деформации тонких пластин и
оболочек, используем теперь аналогичные приемы для по-
построения теории деформации тонких стержней. Как выяснится,
эта задача несколько сложнее, чем две предыдущие, почему
и рассматривается после них.
Пусть Имеется тонкий призматический стержень произ-
произвольного поперечного сечения (рис. 20).
В центре тяжести площади одного из его торцов распо-
расположим начало системы XYZ, направив при этом ось Z вдоль

190
О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ
[ГЛ. VI
стержня, а в качестве осей X и Y взяв главные оси инерции
площади поперечного сечения стержня. *
В результате деформации
произвольная точка стержня
получит перемещения и (х, у,
г), v (х, у, z), w (х, у, г).
При этом поскольку в рассма-
рассматриваемой задаче область изме-
изменения координат дг и у су-
существенно мала по сравнению
с областью изменения коорди-
координаты г, постольку можно пред-
предположить, что, разложив пе-
перемещения в ряды по степе-
степеням х и у, мы получим ряды,
достаточно хорошо сходящие-
сходящиеся в интересующих нас пре-
пределах.
Эту мысль, ценность кото-
которой выше была показана при
рассмотрении деформации пластин и оболочек, мы положим
в основу теории деформации стержней.
Итак — запишем перемещения произвольной точки стержня
в виде:
и (х, у, z) = и (г) + *», (z) -f
(VI.49)
Рис. 20.
v (х, у, z)=v (z
(г) +
*» У>
w (х, у, z) — w (г) + хул (г) +
• Заметим, что в пределах настоящей главы мы могли бы
направлять оси и иначе, чем указано выше. Соответственно не
было бы обязательным и расположение начала декартовой системы
именно в центре тяжести площади торца стержня. Однако, по-
поскольку при рассмотрении условий равновесия объемного элемента
стержня принятое выше направление осей X н Y и положение
начала координат обладают определенными преимуществами—мы
вводим их уже в этой главе.

§ 50] ДЕФОРМАЦИЯ СТЕРЖНЕЙ (ПЕРВОЕ ПРИБЛИЖЕНИЕ) 191
Здесь
и = и(о, о, г), v=v{o, о, z),
W — w (о, о, z) (VI.50)
а / ди \ / ди \ . fdv\ (dw \
°» - \~дх) ~ VdlH' *i - [Ш)о' /л = {~дЧH '
/ди\ /ди \ / dv \ /dw \
\ ду ) \ dy /о' \ ду /о ' \ ду /q '
при х = 0
(vl52)
V дх* JoT 2 -у \ dy*J0
Из последних формул видно, что
а) и, v, w суть перемещения точек, лежащих на оси
стержня.
б) l-f-ftj, 8a, tj»i, l-j-'l'a, Xi> X2 СУТЬ величины порядка
косинусов тех углов, которые после деформации образуют
с осями X, Y, Z волокна стержня, первоначально парал-
параллельные осям X и Y (табл. 1, § 2).
Эти параметры (все или хотя бы некоторые из них)
считаются в дальнейшем существенно превосходящими уд-
удлинения и сдвиги.
в) и, v, w объединяют в себе все члены степенных рядов
для перемещений, начиная с четвертых.
Отсюда ясно, что при х = 0, у = О
— — — ди ди dv dv dw dw n,,\n cos
и =t)='W=-3- = 5— = t— = ^- = T— = 5—= 0. (VI.53)
dx dy dx dy dx dy л '
В дальнейшем и, v, w будут рассматриваться как попра-
поправочные члены формул (VI.49), весьма малые по сравнению

192 о Деформации гибких тел [гл. vi
с остальными членами этих формул. Если данными членами
пренебречь, то выражения (VI.49) напишутся следующим
образом:
(VI.54)
w = w -f- *
причем очевидно, что принятие перемещений стержня в такой
форме соответствует той степени точности рассуждений,
какая принималась выше при построении теории деформаций
пластин и оболочек.
Разница между (VI.2) и (VI.54) состоит лишь в том,
что в первом случае разложения в ряды ведутся по одной
координате, а во втором — по двум координатам, поскольку
у пластин лишь координата z меняется в узких1] преде-
пределах, тогда как у стержней этим свойством обладают две
координаты (х и у). Что касается качества удержанных
членов, то в этом отношении формулы (VI.2) и (VI.54)
вполне аналогичны, так как в обоих случаях ряды обры-
обрываются на членах, линейно зависящих от тех координат, по
которым выполняются разложения.
Но если для пластин и оболочек точность формул (VI.2)
и является вполне достаточной, то для стержней формулы
(VI.54) оказываются, вообще говоря, неприемлемыми, так
как, основываясь на них, нельзя подчинить решение суще-
существенному граничному условию. Поэтому при исследовании
деформации стержней приходится принимать перемещения
не в форме (VI.54), а в более сложном виде (VI.49), в чем
и заключается принципиальное отличие теории деформации
стержней от теории деформации оболочек и пластин. Однако,
в целях достижения большей ясности, мы начнем с того, что
предположим формулы (VI.54) достаточными. Проведя затем
все выкладки до конца, мы убедимся, что сохранили не все
необходимое для решения задачи. После этого будут введены
нужные поправки, что не составит особых затруднений, по-
поскольку читатель будет уже вполне в курсе основной канвы
рассуждений.
Принимая формулы (VI.54) и подставляя их в выражения
для компонентов деформации [то есть в формулы A.22)],

§ 50] ДЕФОРМАЦИЯ СТЕРЖНЕЙ (ПЕРВОЕ ПРИБЛИЖЕНИЕ) 193
будем иметь:
<vL55>
где
12
О +
. dv
I
du , ,л , , s dv
dz ) ^ \dz ) < \ dz
суть значения компонентов деформации на оси стержня,
являющиеся функциями только координаты г.
Величины kxx, kyy, k^y также зависят лишь от г, опре-
определяясь при этом выражениями:
dv <% I Л i dw
\ d/jX
) '
Зак. 3804. В. Новожилов.

194 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
Что касается коэффициентов vxx, vyy, чХ]/, то они будут
равны
x« dz dz i dz dz "I" dz dz '
Как уже было указано, параметры bv 02» I'd ^2 Xi> X2
все (или, по крайней мере, некоторые из них) надо считать
величинами, существенно превосходящими компоненты дефор-
деформации, поскольку в задаче о изгибе тонкого стержня все,
или хотя бы некоторые из углов поворота, велики по срав-
сравнению с удлинениями и сдвигами. Этим же свойством и по
той же причине будут обладать и -т-, — , — (таблица 1, § 2).
Отсюда вытекает, что правые части формул (VI. 56) должны
представлять собою малые разности входящих в них членов.
Тем самым, при определении девяти перечисленных выше
параметров допустимо пользоваться шестью равенствами:
*хх = "ьуу = ?зд = ^ = V = е** = 0, (VI.59)
которые, разумеется, отнюдь не следует истолковывать как
пренебрежение всеми деформациями стержня на его оси,
а нужно понимать лишь в том смысле, какой был выше
указан.
Все шесть равенств (VI.59) тождественно удовлетво-
удовлетворяются, если положить:
ftj = cos a cos p cos f — sin a sin [3 — 1, 02 = cos C sin f,
<5it = — cos a sin f , <Ji2 = cosf— 1, (VI.60)
•fa — cos a sin C cos -y -(- sin a cos [3 , X2 — s*n P s'n Ъ
¦? = — cosaeinC — sin a cos C cos f , (VI.61)
-^ = sin a sin f, ~ = cos a cos 3—,sina sin 3 cosy — 1.
az ' dz ' г 1

§ 50] ДЕФОРМАЦИЯ СТЕРЖНЕЙ (ПЕРВОЕ ПРИБЛИЖЕНИЕ) 195
Здесь а, р, f — три произвольных угла, являющиеся
функциями только z (поскольку и, v, w — функции только
этой координаты).
Нетрудно выяснить геометрический смысл формул (VI.60),
(VI.61). Преследуя эту цель, рассмотрим на оси стержня про-
произвольную точку М и три линейных элемента dx, dy, dz, из
нее исходящих (рис. 21).
В результате деформации точка М получит перемещения
и, v, w и займет положение М*, причем упомянутые линей-
Рис. 21.
ные элементы окажутся направленными по ортам I,, 12, 18.
Если углы поворота элементов стержня велики по сравнению
со сдвигами, то последними, при определении направлений
iv I2. 18, можно пренебречь. При такой точности рассужде-
рассуждений триедр It, I2, is трактуется как ортогональный, причем
параметры
, 1 о о . , i . du dv
l+»i, »a> <h> ! -ИЧ»а» Xi» X2. dl'd'z'
будут (если пренебречь удлинениями по сравнению с едини-
единицей) равны косинусам углов, образуемых направлениями ilt
13*

196
О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ
(ГЛ. VI
ia, i8, с осями X, Y, Z. Последнее ясно из формул (VI.54)
и таблиц 1 и 5 (I глава).
Но, как известно, одна система трех взаимно перпендику-
перпендикулярных направлений может быть фиксирована по отношению
к другой с помощью трех эйлеровых углов. Вводя послед-
последние в соответствии с рис. 22 и учитывая сказанное выше,
получаем формулы (VI.60); (VI.61).
Рис. 22.
Таким образом в последних формулах а, р, f суть эйле-
эйлеровы углы, определяющие направления il5 i2, i3 по отноше-
отношению к осям X, Y, Z (с точностью до углов сдвига).
Подставляя (VI.60) и (VI.61) в (VI.57) и (VI.58), полу-
получаем:
&ХХ А7 '
d-i | , , dB
' cos *-г-\- sin <x sin y yZ
dz ' ' dz
1 / , о
klv)>
(VI.62)
(VI-63)

¦ § 50] деформация Стержней (первое приближение) 197
Вводя эти значения коэффициентов v^, vyy, чху в послед-
последнюю из формул (VI.55), имеем:
+i (kly + k*y)** + **A»*.v. <VI-64)
видим, что члены, соответствующие данным коэффициентам,
могут быть отброшены, как величины порядка квадратов
удлинений и сдвигов.
С учетом этого упрощения формулы (VI.55) принимают
вид:
АЛЛ
ехх ~ sxx> гуу == syyt zxy — sxy
, и?хх
« = * + *
, и?хх I .
= *xz + * ~аг -гуЪху (VL65)
^X
4z=i+xKx + у kyy-
Здесь kxx, kyy, kxy определяются выражениями (VI.62).
dtxx dtyy dexy
Так как производные —г— , —т—, —т- обычно малы по ссав-
uZ uZ CIZ
нению с параметрами kxx, kyy, kxy, характеризующими кри-
кривизну оси стержня после деформации, то в формулах (VI.65)
члены, содержащие упомянутые производные, могут быть
пренебрежены, после чего окончательно будем иметь:
гхх = sxx> syy = svy> exy = ъху* (VI.66)
гхг = ежг -\-ykxy, еуг = syz — xkxy, егг = еж -f- xkxx-\-ykyy.
Последние формулы основываются на предположении, что
удлинения и сдвиги пренебрежимо малы по сравнению с еди-
единицею и по сравнению с углами поворота элементов стержня.
Однако, помимо этого при выводе формул (VI.66) была по-
постулирована достаточность формул (VI.54), то-есть доста-
достаточность сохранения в рядах Тейлора для перемещений
только их трех первых членов. Это утверждение не оче-
очевидно и более того — оно неправильно, в чем можно убе-

198 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
диться, применив формулы (VI.66) к частному случаю, когда
стержень не изгибается, а только скручивается, и притом
равномерно по всей длине.
При этом:
а = р = О, t=sz, (VI.67)
где т — постоянный коэффициент.
Вводя эти значения эйлеровых углов в формулы (VI.60),
(VI.61), находим
9j== — A—cost г), 92 = sini:z,
<h = — sin zz, <JJ = — A — cos -с z), (VI.68)
л л л
du dv dw
Xi = Xa =5J = -Ji — -g-z = 0-
Отсюда получаем следующие формулы для перемещений:
и =з — х A — cos х z) —у sin -с z,
v=-\-xsinxz—у (I — cost г), (VI.69)
и для деформаций
е«в^ V = —XT- (VL7°)
Последние выражения совпадают не с теорией кручения
по Сен-Венану, а со „старой" теорией кручения, которая,
как известно, несостоятельна, так как не позволяет освобо-
освободить боковую поверхность стержня от напряжений, что
в данной задаче является существенным. Отсюда ясно, что
и общие формулы (VI.66) недостаточны, причем уже по-
понятно, то они нуждаются в таком уточнении, которое по-
позволило бы получать из них, как частный случай, теорию
кручения Сен-Венана. Чипы уточнить достигнутые в этом
параграфе результаты, приходится отказаться от формул
(VI.54) и перейти к формулам (VI.49), учитывающим оста-
остаточные ены степенных рядов, объединенные в обозначе-
обозначениях: и, v, w.

§ 51] ДЕФОРМАЦИЯ СТЕРЖНЕЙ (ВТОРОЕ ПРИБЛИЖЕНИЕ) 199
§ 51. Деформация стержней (второе приближение)
Повторим предыдущие выкладки, исходя, однако, уже
не из формул (VI.54), а из формул (VI.49).
Добавочные перемещения и, v, w, которые до сих пор
не учитывались, будем считать малыми, пренебрегая членами,
содержащими их произведения или произведения их про-
производных.
Подставляя (VI.49) в формулы для компонентов дефор-
деформации A.22), получаем:
л , ди , д'о А ¦ ди , д'о
zaoao sxa> "Т "^ЗГ ' 5УУ &УУ "Т" ~ду ' ВхУ 8^ ~Г ~оу Г ~fa >
4 ++?
Здесь, как и раньше, гХЯ), .. . ., егг определяются фор-
формулами (VI.56), kxx, _kyy, kxy, v^, v^, v^ — формулами
(VI.57) и (VI.58), a a, v, w — формулами (VI.52).

200 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
Что касается новых обозначений л, Ь, ft), то они объе-
объединяют в себе следующие члены:
По соображениям, аналогичным предыдущему параграфу,
можно ввести три угла а, C, f, через которые \)v 92> Фи Фа»
Xi, Хг выразятся формулами (VI.60), а производные -т—, -р,
-з формулами (VI.61). После этого для kxx, kyy, kxy по-
получатся формулы (VI.62), а для v v v j.—формулы
(VI.63).
Отсюда вытекает возможность пренебрежения в послед-
последней из формул (VI.71) всеми членами, содержащими три по-
последних коэффициента.
Кроме того, по аналогии с предыдущим параграфом, можно
отбросить в формулах (VI.71) и члены, содержащие произ-
хх yy xy
водные —;— , —р , —=-=¦.
Мы хотим далее показать, что кроме перечисленных
выше упрощений, возможность коих была обоснована в § 50,
в формулах (VI. 71), можно пренебречь также и совокуп-
совокупностью тех членов, которые подчеркнуты.
Подставляя в выражения
dz x dz ' dz '

§ 51] ДЕФОРМАЦИЯ СТЕРЖНЕЙ (ВТОРОЕ ПРИВЛИЖЕНИе) 201
вместо 91# 82, tyu <JJ> Xi> Хй их значения, согласно формулам
(VI. 60), и заменяя далее производные ~, -J-, -^, на ос-
основании формул (VI. 62), будем иметь:
(VI. 74)
Учитывая далее (VI. 72) и (VI. 73), можем записать
(VI. 74) следующим образом:
bka;yi
Отсюда
_ to kxx —
У11уу
kxy + b xkyykxy K ' '
Так как xkxso, ykyy суть величины порядка компонентов
деформации, то
Xtttokxx — Ыг ,
(VI. 77)
Таким образом подчеркнутые члены третьей и чертвертой
из формул (VI. 71) являются величинами порядка произве-
произведений u, t>, tt) на параметры кривизны оси стержня после
деформации. Но дополнительные перемещения u, to, tt> всегда
получаются весьма малыми по сравнению с поперечными
размерами стержней. Отсюда (поскольку произведения па-
параметров кривизны оси стержня kxa!, kyy, kxy на его по-
поперечные размеры суть величины порядка компонентов
деформации) можно сделать заключение, что X и Y весьма
малы по сравнению с удлинениями и сдвигами, на основании
чего подчеркнутые члены четвертый и пятый из формул
(V*. 71) могут быть пренебрежены. Путем аналогичных рас-

202 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
суждений можно выяснить несущественность и подчеркнутых
членов последней из формул (VI. 71).
Выполняя все намеченные выше упрощения, приходим
к следующим выражениям для компонентов деформации
тонкого, первоначально призматического стержня:
" , ди_ л . дь
ехх ехх Т" JjJ" > еуу — ? ЬУ ~Т~ ~ду '
• , ди , дь
е!су—вху-Г <^ + 1*'
J*^ + ?+^. (VI- 78)
XKxy ^dz^dj'
Здесь u, b, tt) — функции всех трех координат х, у, г,
которые обладают следующими свойствами:
а) они весьма малы по сравнению с поперечными размерами
стержня, а их производные суть величины порядка компо-
компонентов деформации. В силу этого произведениями их произ-
производных друг на друга и на величины порядка компонентов
деформации можно пренебрегать;
б) при дг==О, ,у = 0:
. du ди oito дЪ (Ко ?to „
и — v — го — дх — ду = дх — ду => дх — ду — и,
что следует из (VI. 49) и (VI. 72).
Распоряжаясь дополнительными перемещениями и, Ь, Й),
можно согласовать формулы (VI. 78) с граничными усло-
условиями на боковой поверхности стержня.
§ 62. Чистое кручение
Пусть стержень подвергается равномерному кручению по
всей своей длине.
Тогда
«= Р=>w = *»=о; т=т*. (VI-79)

§ 52] ЧИСТОЕ КРУЧЕНИЕ 203
где
(VI.80)
является в данном случае постоянной величиною.
Предположим кроме того, что
V =
то-есть пренебрежем деформациями, равномерно распреде-
распределенными по площади поперечного сечения стержня.
Далее, на основании (VI. 79) и (VI. 81):
u = v = 'W=0. (VI.82)
Учитывая все это, будем иметь:
и = — д:A — cost г) — _у sin iz-\- a,
v = -f- х sin т z—у{\—zostz)-\-v, (VI.83)
дп дъ du.db
хх ~ дх ' УУ ~~ ду ' Sxv ~ ду + дх '
1 oz ' ax (VI.84)
Vе "¦" dz "¦" ду'
8гг = "ai ¦
Если теперь положить
U = b == 0, h) = т <р (д;, _у), (VI.85)
то выражения (VI.84) примут вид:
sax ==eW= Sxy e szz = °>
(VI.86)

204 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. VI
превращаясь в формулы теории кручения Сен-Венана. Таким
образом эта последняя теория заключается в общих фор-
формулах (VI.78) как частный случай.
Заметим, что б наших рассуждениях перемещения точек
скрученного стержня определяются выражениями (VI.83), а
не выражениями классической теории.
и=— yzx, v = xzx, w — xy(x, у). (VI.87)
Последние формулы могут быть получены из (VI.83),
если считать xz<^l, то-есть если считать, что углы по-
поворота при кручении пренебрежимо малы по сравнению
с единицею. Из вышеизложенного ясно, что данное ограни-
ограничение для теории Сен-Венана не является обязательным.
§ 53. Окончательные выражения для деформаций
тонкого стержня
Можно предвидеть, что при рассмотрении общего случая
деформации стержня (когда, кроме кручения он подвергается
также изгибу), формулы (VI.66) будут недостаточными, по-
поскольку они (как было показано в конце § 49) недостаточны
уже для случая чистого кручения. Можно, далее, предвидеть,
что поправки, которые нужно ввести в упомянутые формулы,
и в общем случае будут иметь такой же характер, как и
в задаче о чистом кручении. Именно — эти поправки должны
позволить устранить скручивающие стержень напряжения,
действующие на его поверхности, каковые неизбежно по-
появляются при использовании формул (VI.66) (если только
поперечное сечение стержня отлично от кругового).
Отсюда следует попытаться построить общую теорию
деформации тонких стержней, полагая (по аналогии с пре-
предыдущим параграфом) что:
(VI.88)
Тогда формулы (VI.78) принимают вид:
== гху>
^ — j kxy,
(VL89)

§ 54] заключение 205
Последние выражения действительно достаточны для рас-
рассматриваемой задачи. Отправляясь от них, можно построить
последовательную теорию деформации гибких стержней, огра-
ограниченную лишь предположением, что удлинения и сдвиги
пренебрежимо малы по сравнению с единицею. Погрешность
этой теории может быть оценена сравнением удлинений и
сдвигов с углами поворота, поскольку при выводе (VI.78)
мы систематически пренебрегали первыми по сравнению со
вторыми.
§ 64. Заключение
Обычно теория деформации гибких тел (пластин, оболо-
оболочек, стержней) строится путем постулирования некоторых
допущений, принятие каковых сразу сводит рассматриваемую
задачу к двухмерной (в случае пластин и оболочек) или одно-
одномерной (в случае стержней). Однако, при таком способе
рассуждений неизбежно утрачивается ощущение связи между
теориями' пластин, оболочек и стержней и общей теорией
упругости. Ввиду этого многие рассматривают теорию гиб-
гибких тел как своего рода гипотетическую надстройку над
общей теорией упругости, как инородное в нее вклю-
включение.
Только таким образом, вероятно, может быть объяснен
тот факт, что большинство современных курсов теории упру-
упругости обходят молчанием проблему деформации гибких тел,
столь важную по своему практическому значению. Уже
в курсе Лява были предприняты шаги по увязке „гипотез"
теории деформации гибких тел с общей теорией дефор-
деформации.
Но особенную работу в этом направлении проделал
Б. Г. Галеркин, в трудах которого классическая теория обо-
оболочек и пластин стала поистине отделом общей теории упру-
упругости.
Основная мысль, которую пропагандировал Б. Г. Галер-
Галеркин, заключалась в том, что проблемы изгиба пластин и
оболочек надо всегда рассматривать б контакте с общей тео-
теорией. Эта столь же простая, сколь и глубокая идея в зна-
значительной мере обеспечила успехи развития теории пластин
и оболочек в Советском Союзз и оказалась плодотворной
не только для толстых пластин и оболочек, но и для тонких.

206 О ДЕФОРМАЦИИ ГИБКИХ ТЕЛ [ГЛ. V
Естественно продолжить данную мысль и в сторону не-
нелинейной теории упругости, поскольку можно ожидать, что
и здесь многие результаты удается привести в систему, от-
отправляясь от общих формул. Настоящая глава и является
попыткой дать единообразный метод исследования деформа-
деформации гибких тел, исходя из общей нелинейной теории дефор-
деформаций. В нашу цель входило осветить с помощью формул
общей теории те „гипотезы", на которых основывают, обычно,
теорию деформации пластин, стержней и оболочек и рас-
рассмотреть с одной точки зрения все эти задачи, которые
обычно рассматриваются разрозненно, несмотря на их общие
черты.

БИБЛИОГРАФИЯ
1. BulfingeilG. De solfrdorum resistentia specimen. Commen-
tarii Academiae scieniarum imperialis Petropolitanea vol 4., 1729,
стр. 164.
2. Ясинский Ф. О сопротивлении продольному изгибу, 1Р02.
3. Тимошенко С. Устойчивость упругих систем, Киев 1910.
4. Бубнов И. Строительная механика корабля, 1912.
5. Галеркин Б. Стержни и пластинки. „Вестник инженеров",
No 19, 1915.
6*. Николаи Е. Об упругой линии двоякой кривизны, 1916.
7. Соколов П. О напряжениях в сжатых пластинках после по-
потери устойчивости. Труды НИСС, вып. 7, 193?.
8. Д инн и к А. Устойчивость упругих систем, ОНТИ, 1935.
9. Штаерман И., Пиковский А. Методы расчета конструк.
ций на устойчивость, Укргизместпром, 1939.
10. Зволинский Н., Риз П. Закон Гуна при конечных пере-
перемещениях. Изв. СНТ Акад. Наук СССР, 1938, стр. 17—20.
11. Панов Д. Применение метода акад. Б. Г. Галеркию для ре-
решения некоторых нелинейных задач теории упругости. „Прикл.
мат. мех/, т. Ill, вып. 2, стр. 139—141, U39.
12. Панов Д. Вторичные эффекты при кручении эллиптического
цилиндра. Труды ЦАГИ, вып. 459, 1 Ш.
13. М у ш т а р и X. Некоторое обобщение теории тонких оболочек.
Изв. Физ. мат. общества при Казанском университете, т. XI,
сер. 8, 1938.
14. Риз П. О некоторых явлениях при кручении круглого цилин-
цилиндра. Тр^ды ЦАГИ, вып. 408, 1939.
15. Зволинский Н. и Риз П. О некоторых задачах нелиней-
нелинейной теории упругости. „Прикл. мат. мех.", т. II, вып. 4,
стр. 417-4^6. 1939.

208 БИБЛИОГРАФИЯ
16. ЗволинскийН. Кручение бруса, растянутого постоянными
массовыми силами, „Прикл. мат. мех.", т. III, вып. 3. стр. 3—31,
1939.
17. Блох В. О конечных деформациях. Научн. зап. Харьк. мех.
маш. инст., т. V, стр. 3—26, 1940.
18. Качано в Л. К механике пластических средин. „Прикл. мат.
мех.«, т. 12, вып. 3, стр. 37—42, 1940.
19. К а ч а н о в Л. Упруго-пластическое состояние твердых тел.
„Прикл. мат. мех., т. V, вып. 3, стр. 431—437, 1941.
20. П а п к о в и ч П. Строительная механика корабля, ч. II, Обо-
ронгиз, 1941.
21. Новожилов В. Общая теория#устойчивости оболочек. Докл.
Акад. Наук СССР, т. XXXII, № 5, стр. 316-319, Ь41.
22. П а н о в Д. О больших прогибах круглой мембраны со слабым
гофром. „Прикл. мат. мех.", т. V, вып. 2, 1941.
23. Рух адзе А. Изгиб силой растянутого призматического стержня.
Сообщение Акад. Наук Груз. ССР, т. И, № 7, стр.609—617, 1941.
24. Горидзе А., Рухадзе А. Изгиб парой закрученного
стержня. Сообщения Акад. Наук. Груз. ССР, т. V, № 3,
стр. 253-262, 1944.
25. ФеодосьевВ. О больших прогибах и устойчивости круг-
круглой мембраны с мелкой гофрировкой. „Прикл. мат. мех.а, т. IX,
стр. 389, 1945.
26. Феодосьев В. К расчету хлопающей мембраны. „Прикл.
мат. мех.а, т. X, вып. 2, стр. 295-300, 1946.
27. Ландау Л.. ЛифшицЕ. Механика сплошных сред, 1944.
28. Л ей бе нз он Л. Курс теории упругости, Гостехиздат, 1947.
?9. ЗволинскийН., Риз П. Общее решение задачи кручения
в нелинейной теории упругости. „Прикл. мат. мех.а, т. VII,
стр. 149—154, 1943.
30. Л у р ь е А. Обобщение теоремы Кастильяно. Труды Ленингр.
Политехи, инст. № 1, 1946.
31. Блинник С, МалининН., Пономарев С, Феодосьев В.
Новые методы расчета пружин, Машгиз, 1946.
32. Крылов В. Большие перемещения в плоской задаче. „Прикл.
мат. мех.", 1946, вып. 5—6.
33. Риз П. Об упругих константах в нелинейной теории упругости.
„Прикл. мат. мех.а, т. XI, 1947.
34. Попов Е. Теория и расчет гибких упругих деталей. Изд.
ЛКВВИА, 1947.

БИБЛИОГРАФИЯ 209
35. Рухадзе А. Влияние на изгиб стержня парой изгиба от по-
поперечной силы. „Прикл. мат. мех.", т. XI, 351—356, 1947.
36. К у т и л и н Д. Теория конечных деформаций. Гостехиздат,
стр. 1-275, 1947.
37. Риз П. Теория упругости при больших деформациях, превос-
превосходящих предел пропорциональности. Докл. Акад. Наук СССР,
т. IX, № 2, 223-225, 1948.
38. Saint-Venant В„ Memoire sur Tequilibre des corps solides
dans les Iimites de leur elasticite, et sur les conditions de leur resis-
resistance, quand les deplacement eprouves par leurs points ne sont
pas tres petits. Compte rendus, vol. XXIV, 1847.
39. K[irchhoff G. Ueber die Gleichungen des Gleichgewichts
eines elastischen Korpers bei nicht unendlich kleinen Verschie-
bungen seiner Teile. Sitzgsber, der Mathnaturwiss. Klasse der K.
Ak. Wiss., IX, 1852, стр. 762.
40. К i г с h h о f f G. Ueber das Gleichgewicht und die Bewegung.
eines unendlich dunnen elastischen Stabes, Borchardts Journ.
Bd. 56, 1858.
41. Brillouin, Deformation homogenes finies, energie d'un corps
isotrope. C. R. Acad. Sci. Paris, CXII, 1891.
42. V о i g t W., Ueber eine anscheinend nothwendige Erweiterung
der Elasiizitatstheorie. Getting. Nachr., 1894, № 1, стр. 33—43.
43. Love A., A treatise on the mathematical theory of elasticity
(имеется русский перевод: А. Ляв „Математическая теория
упругости", ОНТИ, A9J5).
44. С о s s e r a t E. et F., Sur la theorie de l'elasticite. Ann. de Tou-
Toulouse, X, 1896.
45. Duhem, Recherches sur 1'elasticite, Ann. de Гecole Ijorm. Sup.ё
Зте serie, V. XXI, XXII, XXIII, A904-1906),
46. Mar со Ion go, Le formole de Saint-Venant per le deformazioni
finite. Rend, del circ. mat. di Palermo, XIX, 1905, стр. 151.
47. С r u d e 11 i. Sopra le deformationi finite. Le equazioni de Saint-
Venant. Rendic. Lincei, 2° sem., 1911, стр. 300.
48. Burgatti, Sulle deformationi finite dei corpl continui. Mem. dell
Ac. di Bologna, ser. 7a, 1 A913—1914), стр. 3.
49. A1 m a n s I E., L'ordinaria teoria deli elasticita e la teoria delle
deformationi finite., Rend. Lincei, 2° sem., 1917.
5Э. Biezeno С and Hencky H., On the general theory of
elastic stability. Proc. Acad. Sci. Amsterdam, vol. XXXI, № 6,
1928.
14 Зак. 3804. В. Новожилов.

210 БИБЛИОГРАФИЯ
51. В i е z е п о С. and Н е п с ку Н., On the general theory of elastic
stability. Proc. Acad. Sci. Amsterdam, vol. XXXII, № 4, 1929.
52. Treff tz E., Handbuch der Physik, Bd. VI. „Meehanik der elasti-
schen Кбгрег", 1928. (Имеется русский перевод под редакцией
А. Лурье: Э. Трефтц, „Математическая теория упругости*,
ОНТИ, A934.)
53. Treff tz E., Zur Theorie, der Stabilitat des elastischen Gleichge-
wichts. Zeitschr. fur angew. Math, und Mech. (Z. a. M. M.), 13,
1933, стр. 160 — 165.
54. С e r u t i G. Sopra un' estensione della teoria elastica, alia seconda
approssimazicne. Rend, reale 1st. Lombardo. II, s. 65. 1932,
стр. 997 — 1012.
55. В о n v i n с i n i D. Sulle deformazioni non infenitesime. Atti Accad.
Lincei, Rend. VI, s. 16, 1932, стр. 6'7 — 612.
56. Ariano R. L'isotropia nelle deformazioni finite. I. L'isotrcpfa in
„senso largo", II. L'isotropia in „senso ristretto". 1st. Lombardo,
Rend, II, s. 66, 1933, стр, 92 — 104 и 207 — 220.
57. Ariano R., Sulla resistenza a tensione d.lla gomma elastica e
ebonite, Politecnico, 1933.
58. S i g n о г i n i A., Sulle deformazioni finite dei sistemi a transforma-
transformation reversibili. Atti Accad, naz. Lincei, Rend. VI, s. 18, 1933,
стр. 388 —ЗУ4.
59. ;K a p p u s R., Zur Elastizitatstheorie endlicher Verschiebungen
Z. a. M. M., Bd. 19, 1939, стр. 271 — 285 и 344 — 361.
60. Bi ot M., Increase of torsional stiffness of a prismatical bar due to
axial tension. J. appl. Physics, 10, 1939, стр. 860 — 864.
61. Locate Hi P., Sopra il teorema del minimo lavoro per corpi
non perfaitamento elastici. Ferie Acad., 1939, стр. 10—18.
62. Marguerre 1С, Ober die Anwendung der energetischen Me-
thode auf Stabilitutsi.robleme. J, b. dtsch, Luftf. Forschg. 1., Flug-
werk, 1C8. стр. 433 — 443.
63. Biot M., Theory of elasticity with large displacements and ro-
rotations. Proc. 0 intern. Congr. appl. iv.ech., 1939, стр. 117—122.
64. Ariano R., La deformazicni finite. R. Scuola d'ingegn. Milano.
Atti ricerche studi, Fasc. 18, 1935
65. Seth В., Finite strain in elastic problems. Phil. Trans. Roy. Soc,
Vol. 234 A, 1935. 231 —2o4.
66. -Biezeno C, Ober die BesHmmung der „Durchschlagkrafi" einer
schwachgekru 1 mten kreisformigen Platte. Z. a. M. M., Bd. 15,
H. 1/2. 1935, стр. 10 - 22.

БИБЛИОГРАФИЯ 211
67. М о u г n a g h a n F., Finite deformation of an elastic solid. Amer.
Jounu of Math., Vol. 59, 1937, стр. 235 — 260.
68. Marguerre K.,ZurTheoriedergekrummtenPlatte grosserForman-
dcrung. Proc. 5 int. congr. for appl. Mech., 1939, стр. 93—101.
69. New ing S. and Shepherd W. Finite strain: dislocation solu-
solutions. Phil. Mag. s. 26, 1938, стр. 557 — 559.
70. Birch F., The effect of pressure upon the elastic parameters of
Ssotropic solids, according to Mournaghan's theory of finite strain.
J. appl. Phys. 9, 1938, стр. 279 — 288.
71. Shepherd W. and Seth В., Finite strain in elastic problems.
Proc. Roy. Soc. London, 156 A, 1936, стр. 171 —192.
72. Biot M., Elastizitatstheorie zweiter Ordnung mit Anwendungen.
Z. a. M. M., Vol. 20, 1940, стр. 89 — 99.
73. К arm an Th. and Shen Tsien H., The buckling of spherical
shells by external pressure. J. Aeron. Sci. 7, 1939, стр. 43 — 50.
74. LatshawE., An elastic theory for гиЬбег. J. Franklin inst. 234,
1942, стр. 63 — 73.
75. Bergeot P., On the formula for the energy of deformation in
the case of finite deformations. C. R. Acad. Sci. Paris, 218, 1944,
стр. 824 — 825.
76. С hi en W., The intrinsic theory of thin plates and shells. I. Ge-
General theory. II. Application to thin plates.III. Application to thin
shells. Quart. Appl. Math., 1944 A. стр. 297 — 327, 2. стр. 43 — 59,
3. стр. 120 — 135).
77. M о и г n a g h a n F., On the theory of tension of an elastic cylin-
cylinder. Proc. Nat. Acad. Sci. Wasch., 30, 1944, стр. 382 — 384,
78. James H. and G и t h E., Wave equations for finite elastic strains.
J. appl. Physics. 16, 1945, стр. 643 — 644.
79. Seth В., Finite strains in aelotropic elastic bodies. Bull. Calcutt,
math. Soc, 37, 1945, стр. 62 — 68.
80. Broraberg E. and Stoker J., Nonlinear theory of curved ela-
elastic sheets. Quart, appl. math., 3, 1945, стр. 246 — 265.
81. Sadowsky M., Nonlinear springs. J. Franklin inst., Dec. 1945,
стр. 469 — 476.
82. Sokolni koff I., Mathematical theory of elasticity, 1946.
83. S t e r n b e г g E., Nonlinear theory of elasticity with Smalf defor-
deformations. J. appl. mech.t 13, 1946, A 53 — 60.
БИБЛИОТЕК
ИНСТИТУТА
имени И. В. СТАЛИНА
14*

Опечат ки
Стр.
29
29
37
37
118
Строка
13 снизу
9 снизу
8 снизу'
7 снизу
11 снизу
tg28
V(*<№B —
V(exx
Напечатано
2 г — г
VV г
*ууJ+*1у™
еуу) "Г ^t/
е^г cos26
Z
B8 + Р)
sin if
•' =(t -
uyz \bsz
tg
Должно быть
-6^») sin 26 +
0
'*? + *.-*
е'уг COS 26
sin 7
По чьей
вине
Корр.
Авт.
Ред.
•
Корр.
За к- 804.

ОГИЗ СССР
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
„ГОСТЕХИЗДАТ"
Москва, Орликов пер., 3
Ленинград, Невский пр., 28
ИМЕЮТСЯ В ПРОДАЖЕ КНИГИ:
Александров В. Л., Техническая гидромеханика.
Изд. 3-е, перераб. Допущено Министерством Высшего
Образования СССР в качестве учебного пособия для выс-
высших учебных заведений, 1946. Стр. 432. Цена 9 р. 50 к.
Ананьев И. В.* Справочник по расчету собствен-
собственных колебаний упругих систем. Стр. 224.
Цена 9 р. 50 к.
Динник А. Н., У стой чивость арок. Стр. 128. Цена 5 р.
Зауэр Р., Введение в газовую динамику. Пер. с не-
немецкого. Стр. 228. Цена 7 р. 50 к.
Кочин Н. Е., Кибель И. А. и Розе Н. В., Теоретическая
гидромеханика. Т. I. Изд. 4-е, перераб. Допущено
Министерством Высшего Образования СССР в качестве
учебника для университетов. Стр. 535. Цена 16 р.
Лейбензон Л. С, Курс теории упругости. Изд. 2-е,
испр. и дополн. Допущено Министерством Высшего Обра-
Образования в качестве учебника для университета. Стр. 4о4.
Цена 12 р.
Лейбензон Л. С, Движение природных жидкостей
и газов в пористой среде. Стр. 244. Цена 8 р.
Лехницкий С.Г., Анизотропные пластинки. Стр. 35э.
Цена 14 р. 50 к.
Нейбер Г., Концентрация напряжений. Пер. с не -
мецкого под ред. проф. А. И. Лурье. Стр. 204. Цена 9 р. 75 к.
Попов С. Г., Измерение воздушных потоков.
Стр. 296. Цена 9 р.
Фнлоненко-Бородич М. М., Теория упругости. Изд. 3-е,
перераб. и значительно дополненное. Допущено Мини-
Министерством Высшего Образования СССР в качестве учеб-
учебника для высших технических учебных заведений. Стр. 300.
Цена 8 р. 50 к.
Книги продаются в книжных магазинах КОГИЗа и других
книготорговых организаций, а также высылаются наложенным
платежом без задатка. Заказы шлите по адресу:
Москва, центр, Куйбышевский.проезд, 8, МОГИЗ
„К ни га—п о ч той".
Ленинград „88", Невский пр., 28, „Дом Книги".
Отдел „Книга — почтой" Ленокогиза.

Современные
проблемы
механики
В.В. Но вож ило в
основы
НЕЛИНЕЙНОЙ
ТЕОРИИ
УПРУГОСТИ
огиз
ГОСТЕХИЗДАТ