Р.Курант, Г.Роббинс
ЧТО ТАКОЕ МАТЕМАТИКА
Книга написана крупным математиком Рихардом Курантом в соавторстве с Г.
Роббинсом. Она призвана сократить разрыв между математикой, которая
преподается в школе, и наиболее живыми и важными для естествознания и
техники разделами современной математической науки. Начиная с элементарных
понятий, читатель движется к важным областям современной науки. Книга
написана очень доступно и является классикой популярного жанра в математике.
Книга предназначена для школьников, студентов, преподавателей, а также для
всех интересующихся развитием математики и ее структурой.
Содержание
Предисловие ко второму русскому изданию 5
Предисловие к первому изданию 15
Предисловие ко второму, третьему и четвертому изданиям 17
Как пользоваться книгой 18
Что такое математика? 20
Глава I. Натуральные числа 25
Введение 25
§ 1. Операции над целыми числами 26
1. Законы арифметики. 2. Представление целых чисел с помощью
письменных знаков (нумерация). 3. Арифметические действия в
недесятичных системах счисления.
§ 2. Бесконечность системы натуральных чисел. Математическая 35
индукция
1. Принцип математической индукции. 2. Арифметическая
прогрессия. 3. Геометрическая прогрессия. 4. Сумма п первых
квадратов. *5. Одно важное неравенство. *6. Биномиальная теорема.
7. Дальнейшие замечания по поводу метода математической
индукции.
Дополнение к главе I. Теория чисел 47
Введение 47
§ 1. Простые числа 48
1. Основные факты. 2. Распределение простых чисел.
§2. Сравнения 60
1. Общие понятия. 2. Теорема Ферма. 3. Квадратические вычеты.
§ 3. Пифагоровы числа и большая теорема Ферма 69
§4. Алгоритм Евклида 72
1. Общая теория. 2. Применение к основной теореме арифметики. 3.
Функция Эйлера <р(п). Еще раз о теореме Ферма. 4. Непрерывные
дроби. Диофантовы уравнения.
Глава II. Математическая числовая система 82
Введение 82
§ 1. Рациональные числа 82
1. Рациональные числа как средство измерения. 2. Возникновение

надобности в рациональных числах внутри самой математики.
Принцип обобщения. 3. Геометрическое представление
рациональных чисел.
§ 2. Несоизмеримые отрезки. Иррациональные числа, пределы 88
1. Введение. 2. Десятичные дроби: конечные и бесконечные. 3.
Пределы. Бесконечные геометрические прогрессии. 4. Рациональные
числа и периодические десятичные дроби. 5. Общее определение
иррациональных чисел посредством стягивающихся отрезков. *6.
Иные методы определения иррациональных чисел. Дедекиндовы
сечения.
§ 3. Замечания из области аналитической геометрии 105
1. Основной принцип. 2. Уравнения прямых и кривых линий.
§4. Математический анализ бесконечного 110
1. Основные понятия. 2. Счетность множества рациональных чисел и
несчетность континуума. 3. «Кардинальные числа» Кантора. 4.
Косвенный метод доказательства. 5. Парадоксы бесконечного. 6.
Основания математики.
§ 5. Комплексные числа 124
1. Возникновение комплексных чисел. 2. Геометрическое
представление комплексных чисел. 3. Формула Муавра и корни из
единицы. *4. Основная теорема алгебры.
§ 6. Алгебраические и трансцендентные числа 139
1. Определение и вопросы существования. *2. Теорема Лиувилля и
конструирование трансцендентных чисел.
Дополнение к главе II. Алгебра множеств 144
1. Общая теория. 2. Применение к математической логике. 3. Одно
из применений к теории вероятностей.
Глава III. Геометрические построения. Алгебра числовых полей 154
Введение 154
Часть 1. Доказательства невозможности и алгебра 157
§ 1. Основные геометрические построения 157
1. Построение полей и извлечение квадратных корней. 2.
Правильные многоугольники. 3. Проблема Аполлония.
§ 2. Числа, допускающие построение, и числовые поля 165
1. Общая теория. 2. Все числа, допускающие построение, —
алгебраические.
§ 3. Неразрешимость трех классических проблем 173
1. Удвоение куба. 2. Одна теорема о кубических уравнениях. 3.
Трисекция угла. 4. Правильный семиугольник. 5. Замечания по
поводу квадратуры круга.
Часть 2. Различные методы выполнения построений 180
§ 4. Геометрические преобразования. Инверсия 180
1. Общие замечания. 2. Свойства инверсии. 3. Геометрическое
построение обратных точек. 4. Как разделить отрезок пополам и как

найти центр данного круга с помощью одного циркуля.
§ 5. Построения с помощью иных инструментов. Построения Маскерони с 187
помощью одного циркуля
1. Классическая конструкция, служащая для удвоения куба. 2.
Построения с помощью одного циркуля. 3. Черчение с помощью
различных механических приспособлений. Механические кривые.
Циклоиды. *4. Шарнирные механизмы. Инверсоры По-селье и Гарта.
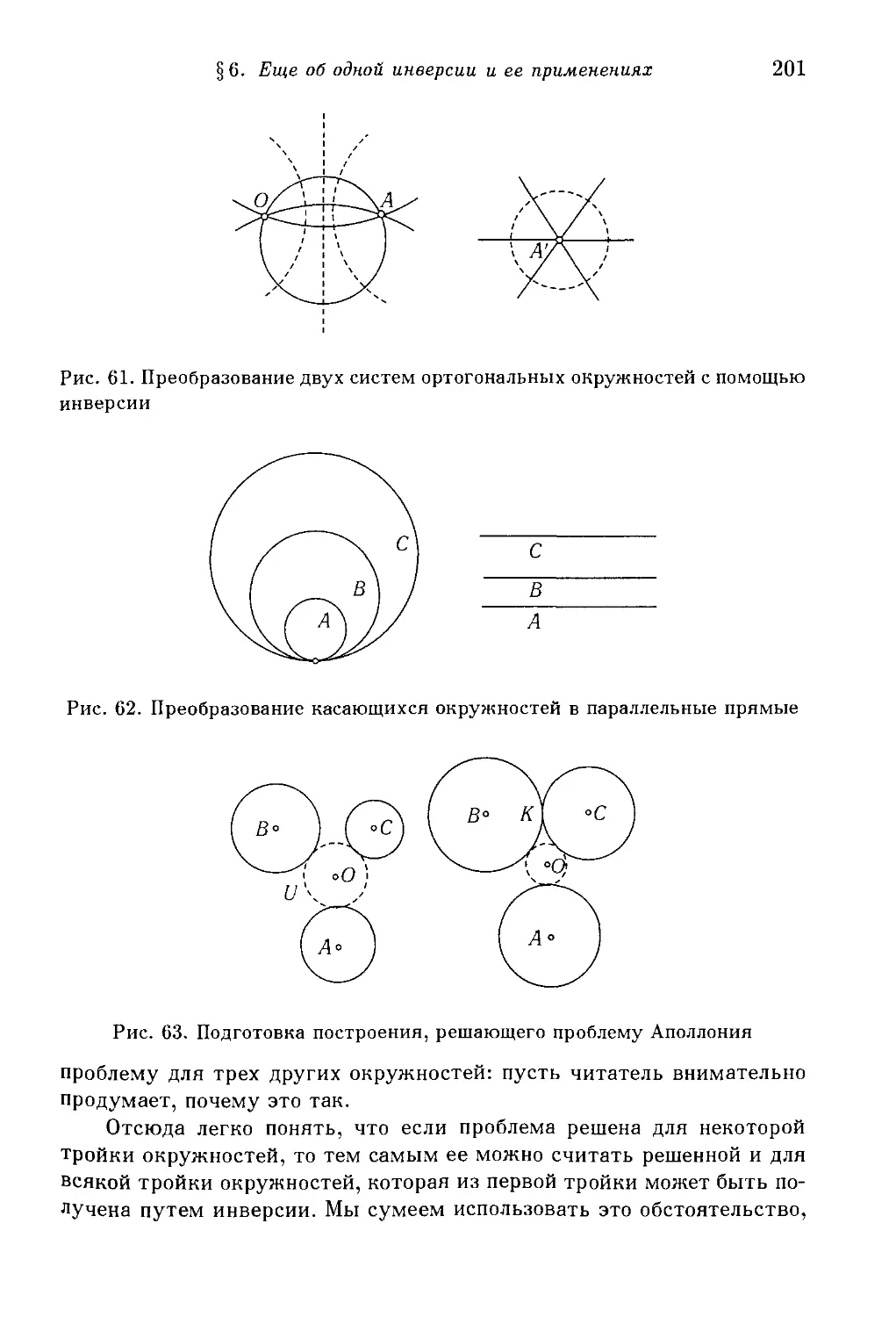
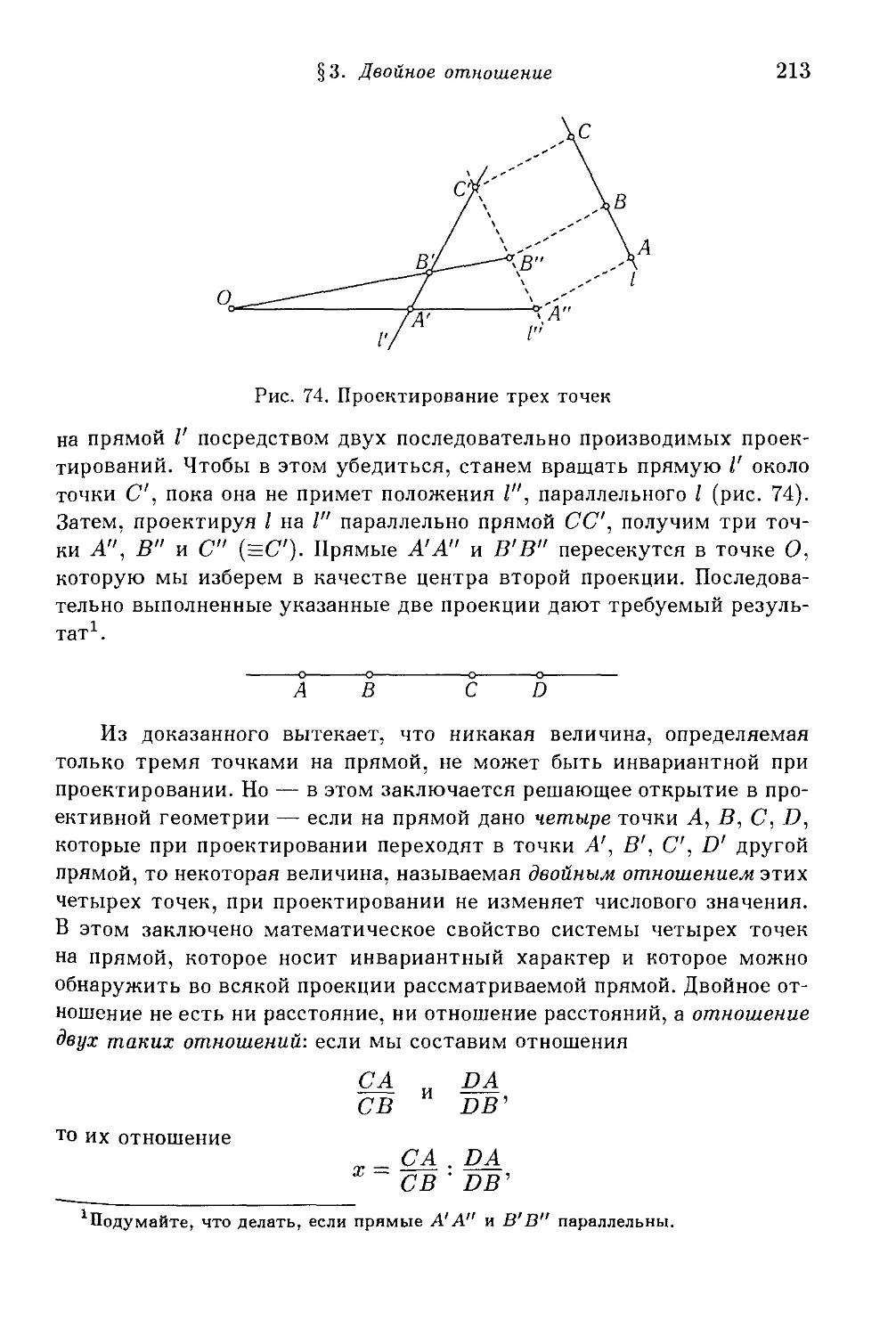
§6. Еще об одной инверсии и ее применениях 198
1. Инвариантность углов. Семейства окружностей. 2. Применение к
проблеме Аполлония. 3. Повторные отражения.
Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии 205
§ 1. Введение 205
1. Классификация геометрических свойств. Инвариантность при
преобразованиях. 2. Проективные преобразования.
§ 2. Основные понятия 208
1. Группа проективных преобразований. 2. Теорема Дезарга.
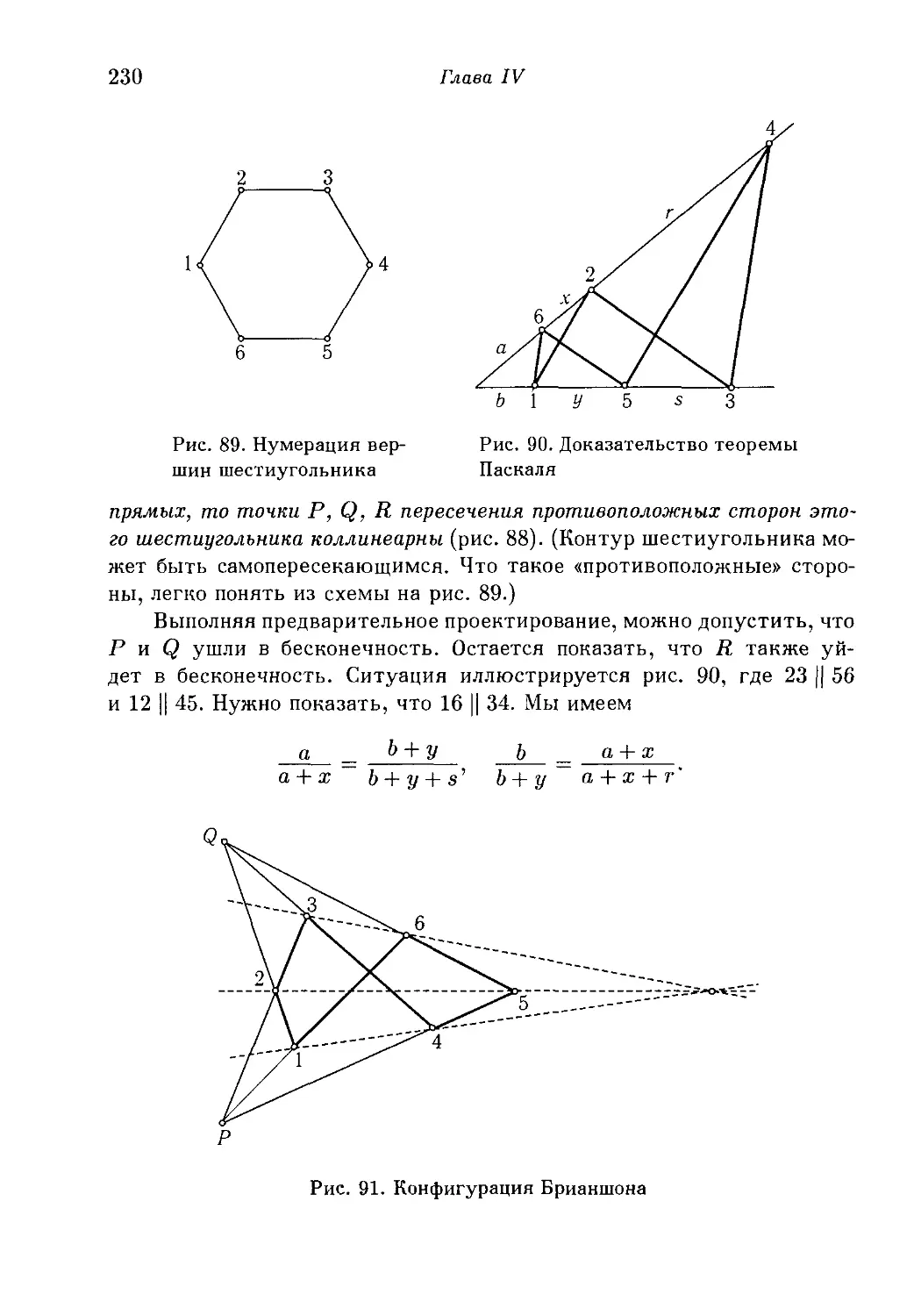
§3. Двойное отношение 212
1. Определение и доказательство инвариантности. 2. Применение к
полному четырехстороннику.
§4. Параллельность и бесконечность 220
1. «Идеальные» бесконечно удаленные точки. 2. Идеальные
элементы и проектирование. 3. Двойное отношение с бесконечно
удаленными элементами.
§ 5. Применения 226
1. Предварительные замечания. 2. Двумерное доказательство
теоремы Дезарга. 3. Теорема Паскаля. 4. Теорема Брианшона. 5.
Замечание по поводу двойственности.
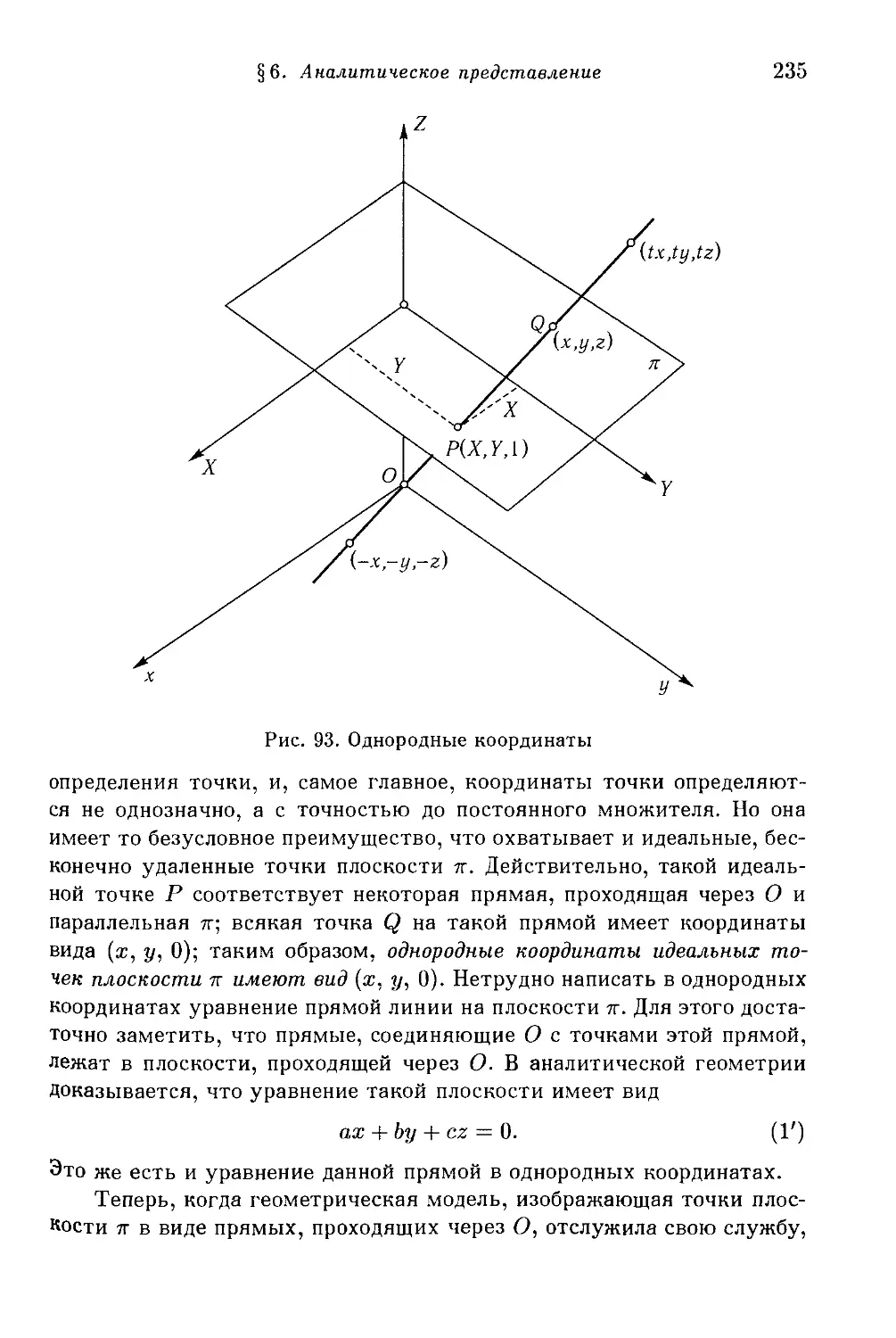
§ 6. Аналитическое представление 232
1. Вводные замечания. *2. Однородные координаты. Алгебраические
основы двойственности.
§ 7. Задачи на построения с помощью одной линейки 238
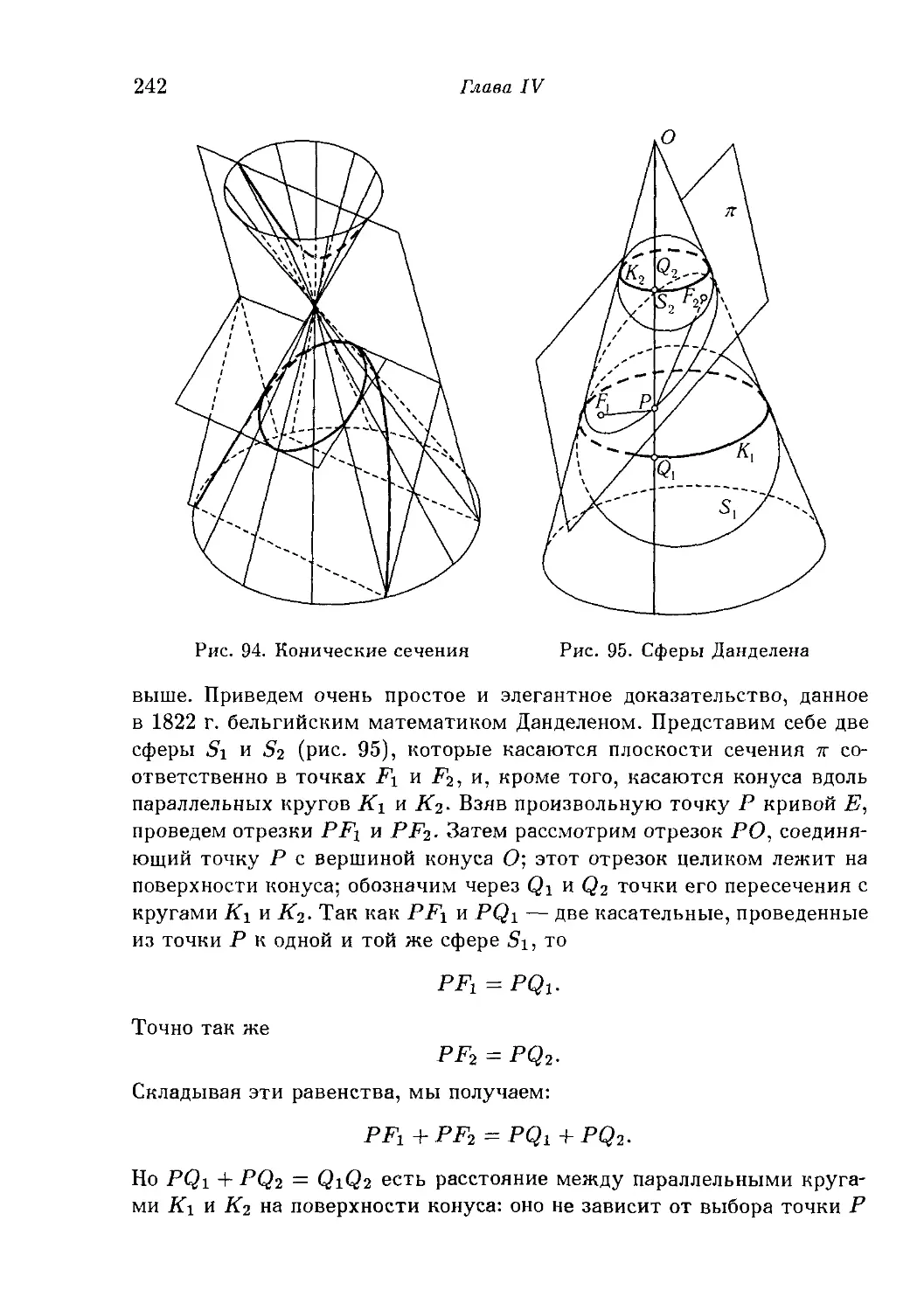
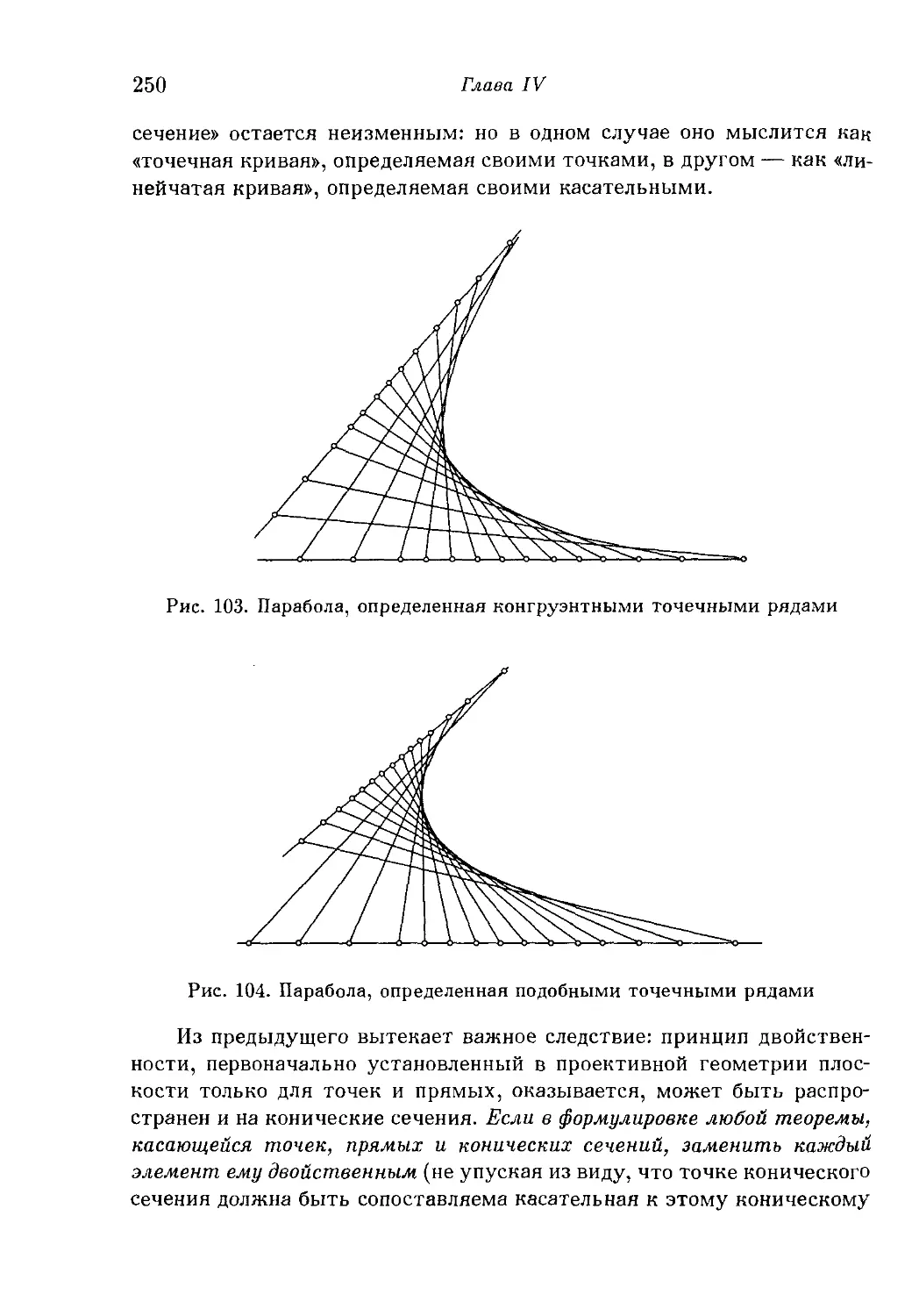
§ 8. Конические сечения и квадрики 240
1. Элементарная метрическая геометрия конических сечений. 2.
Проективные свойства конических сечений. 3. Конические сечения
как «линейчатые кривые». 4. Теоремы Паскаля и Бри-аншона для
общего случая произвольных конических сечений. 5. Гиперболоид.
§ 9. Аксиоматика и неевклидова геометрия 256
1. Аксиоматический метод. 2. Гиперболическая неевклидова
геометрия. 3. Геометрия и реальность. 4. Модель Пуанкаре. 5.
Эллиптическая, или риманова, геометрия.
Приложение. Геометрия в пространствах более чем трех измерений 270
1. Введение. 2. Аналитический подход. *3. Геометрический, или
комбинаторный, подход.
Глава V. Топология 278

Введение 278
§ 1. Формула Эйлера для многогранников 279
§ 2. Топологические свойства фигур 284
1. Топологические свойства. 2. Свойства связности.
§ 3. Другие примеры топологических теорем 287
1. Теорема Жор дана о замкнутой кривой. 2. Проблема четырех
красок. *3. Понятие размерности. *4. Теорема о неподвижной точке.
5. Узлы.
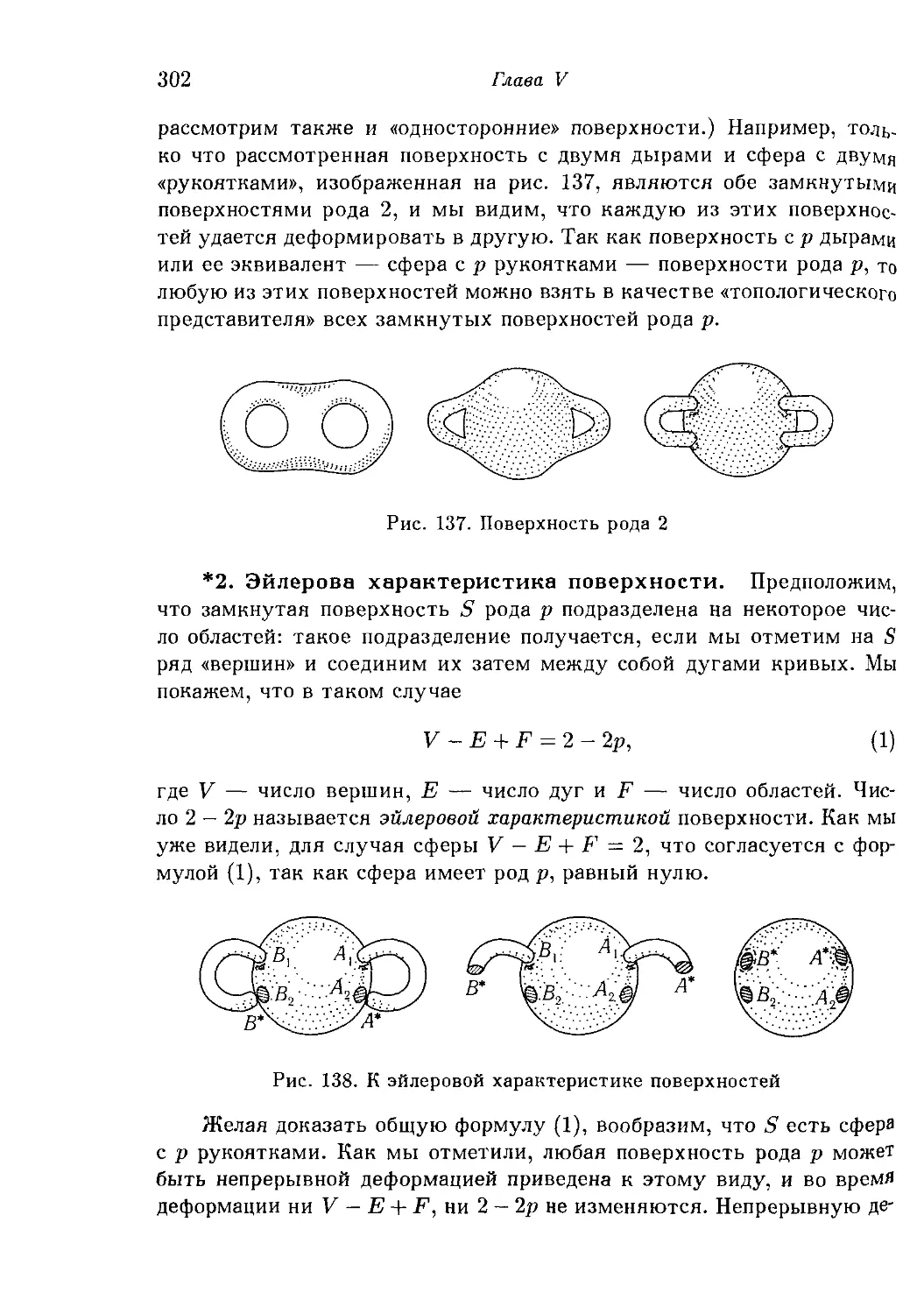
§4. Топологическая классификация поверхностей 300
1. Род поверхности. *2. Эйлерова характеристика поверхности. 3.
Односторонние поверхности.
Приложение 308
*1. Проблема пяти красок. 2. Теорема Жор дана для случая
многоугольников. *3. Основная теорема алгебры.
Глава VI. Функции и пределы 316
Введение 316
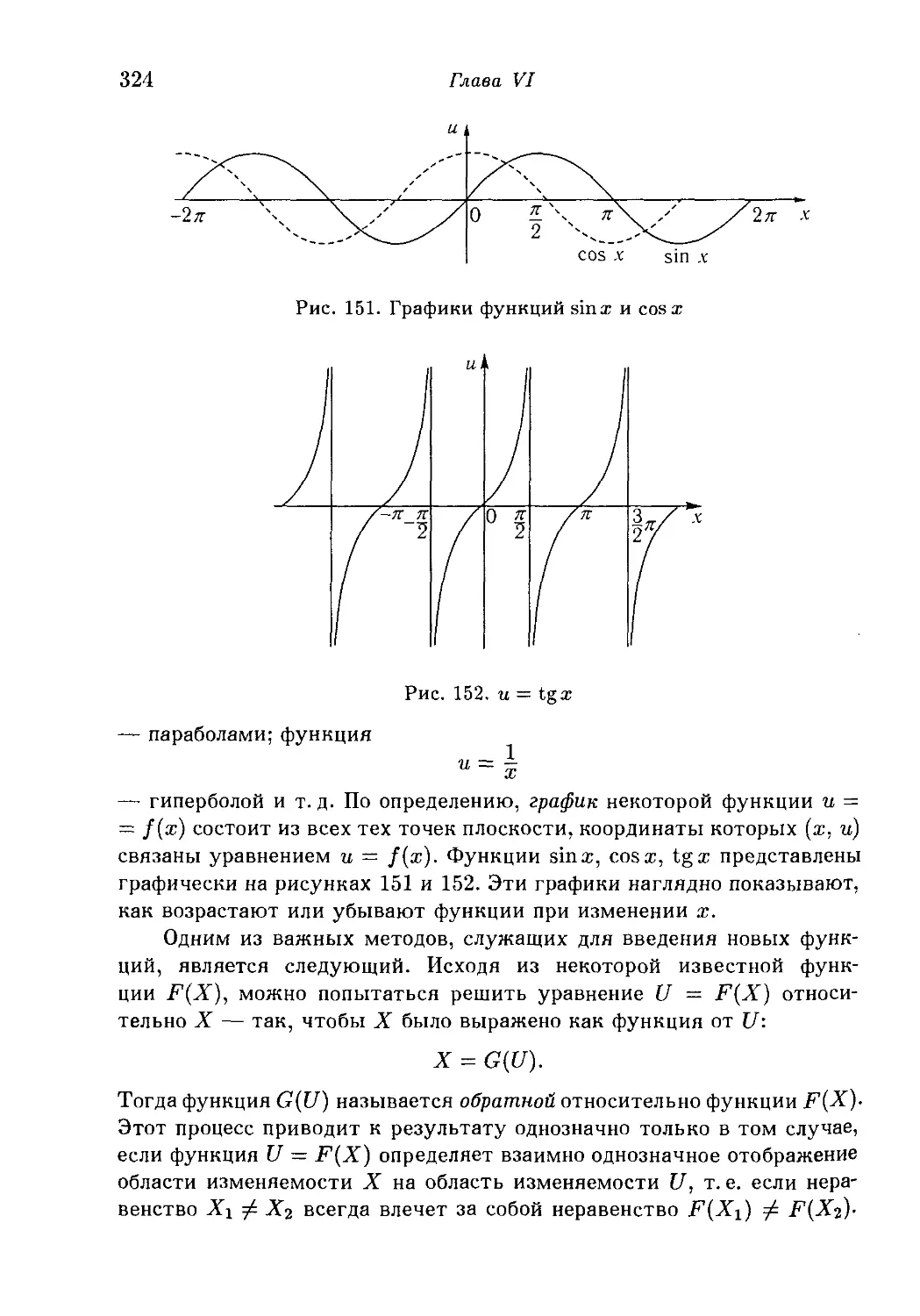
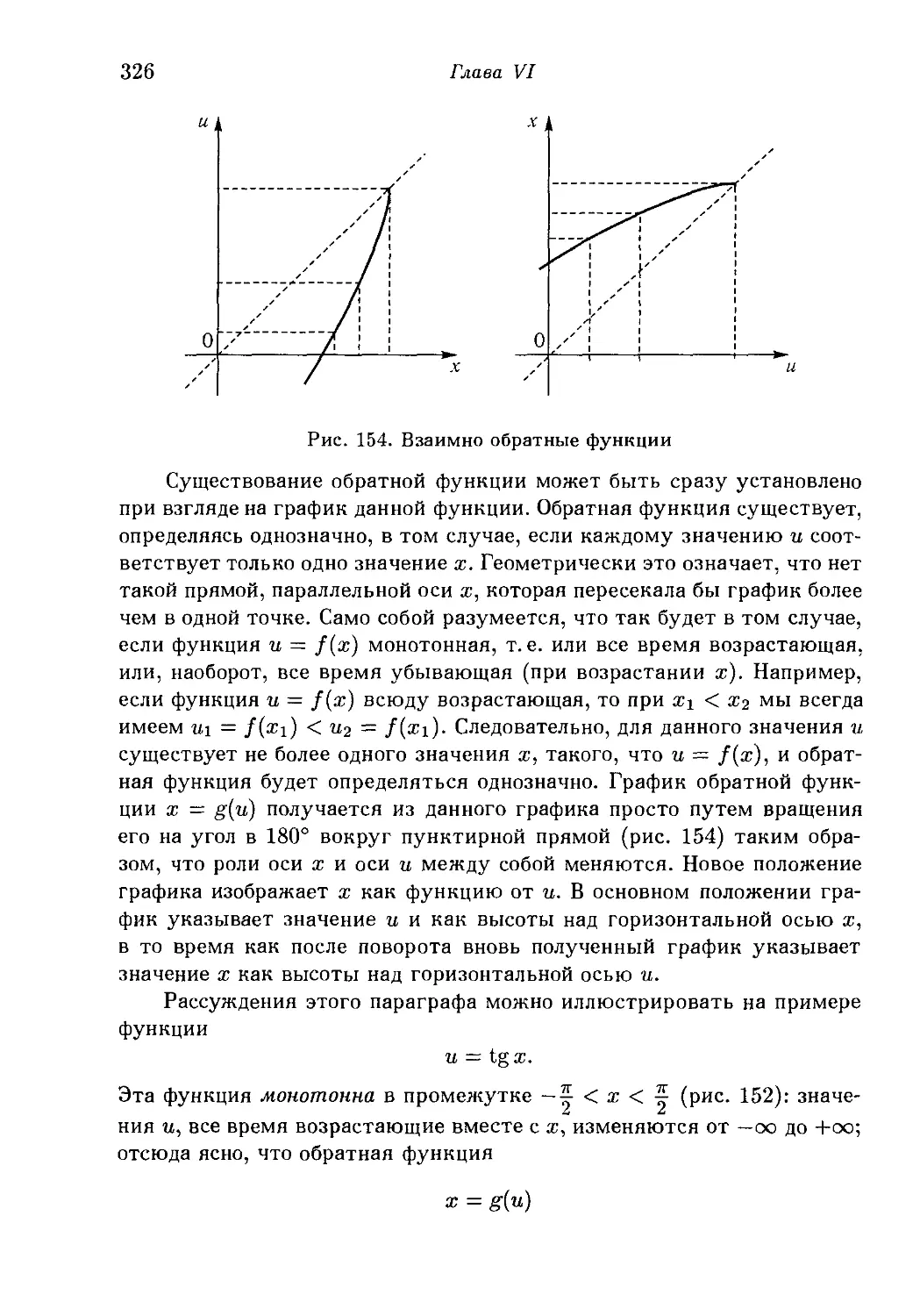
§ 1. Независимое переменное и функция 317
1. Определения и примеры. 2. Радианная мера углов. 3. График
функции. Обратные функции. 4. Сложные функции. 5.
Непрерывность. *6. Функции нескольких переменных. *7. Функции
и преобразования.
§ 2. Пределы 335
1. Предел последовательности а„. 2. Монотонные
последовательности. 3. Число Эйлера е. 4. Число п. *5. Непрерывные
дроби.
§ 3. Пределы при непрерывном приближении 351
1. Введение. Общие определения. 2. Замечания по поводу понятия
предела. 3. Предел sin(x)/«: 4. Пределы при х —»<х>.
§4. Точное определение непрерывности 358
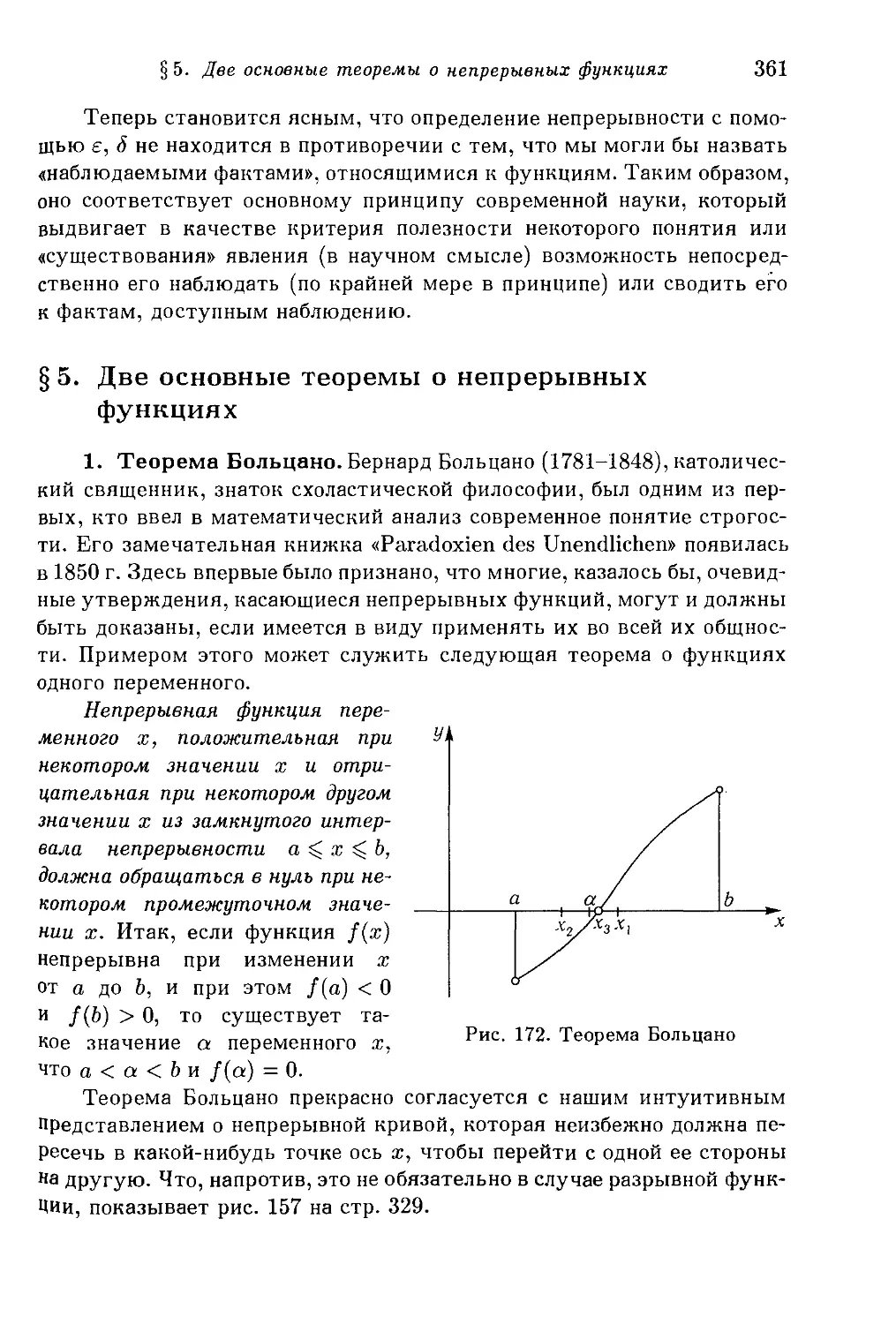
§ 5. Две основные теоремы о непрерывных функциях 361
1. Теорема Больцано. *2. Доказательство теоремы Больцано. 3.
Теорема Вейерштрасса об экстремальных значениях. *4. Теорема о
последовательностях. Компактные множества.
§ 6. Некоторые применения теоремы Больцано 366
1. Геометрические применения. *2. Применение к одной
механической проблеме.
Дополнение к главе VI. Дальнейшие примеры на пределы и 371
непрерывность
§ 1. Примеры пределов 371
1. Общие замечания. 2. Предел qn. 3. Предел ц[р . 4. Разрывные
функции как предел непрерывных. *5. Пределы при итерации.
§ 2. Пример, относящийся к непрерывности 378
Глава VII. Максимумы и минимумы 379

Введение 379
§ 1. Задачи из области элементарной геометрии 3 80
1. Треугольник наибольшей площади при двух заданных сторонах. 2.
Теорема Герона. Экстремальное свойство световых лучей. 3.
Применения к задачам о треугольниках. 4. Свойства касательных к
эллипсу и гиперболе. Соответствующие экстремальные свойства. *5.
Экстремальные расстояния точки от данной кривой.
§2. Общий принцип, которому подчинены экстремальные задачи 389
1. Принцип. 2. Примеры.
§ 3. Стационарные точки и дифференциальное исчисление 392
1. Экстремальные и стационарные точки. 2. Максимумы и
минимумы функций нескольких переменных. Седловые точки. 3.
Точки минимакса и топология. 4. Расстояние точки от поверхности.
§4. Треугольник Шварца 397
1. Доказательство, предложенное Шварцем. 2. Другое
доказательство. 3. Тупоугольные треугольники. 4. Треугольники,
образованные световыми лучами. *5. Замечания, касающиеся задач
на отражение и эргодическое движение.
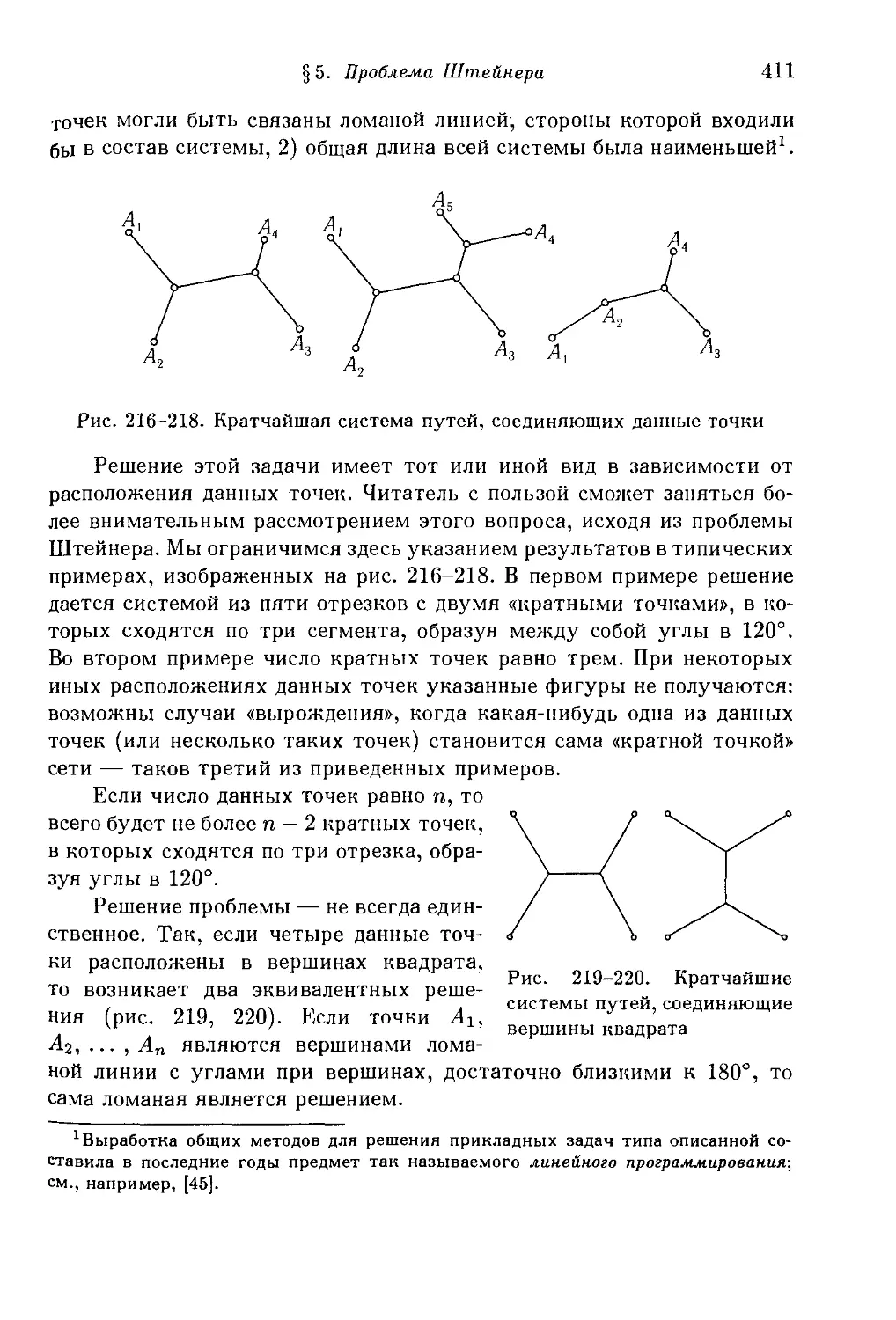
§ 5. Проблема Штейнера 405
1. Проблема и ее решение. 2. Анализ возникающих альтернатив. 3.
Дополнительная проблема. 4. Замечания и упражнения. 5.
Обобщение: проблема уличной сети.
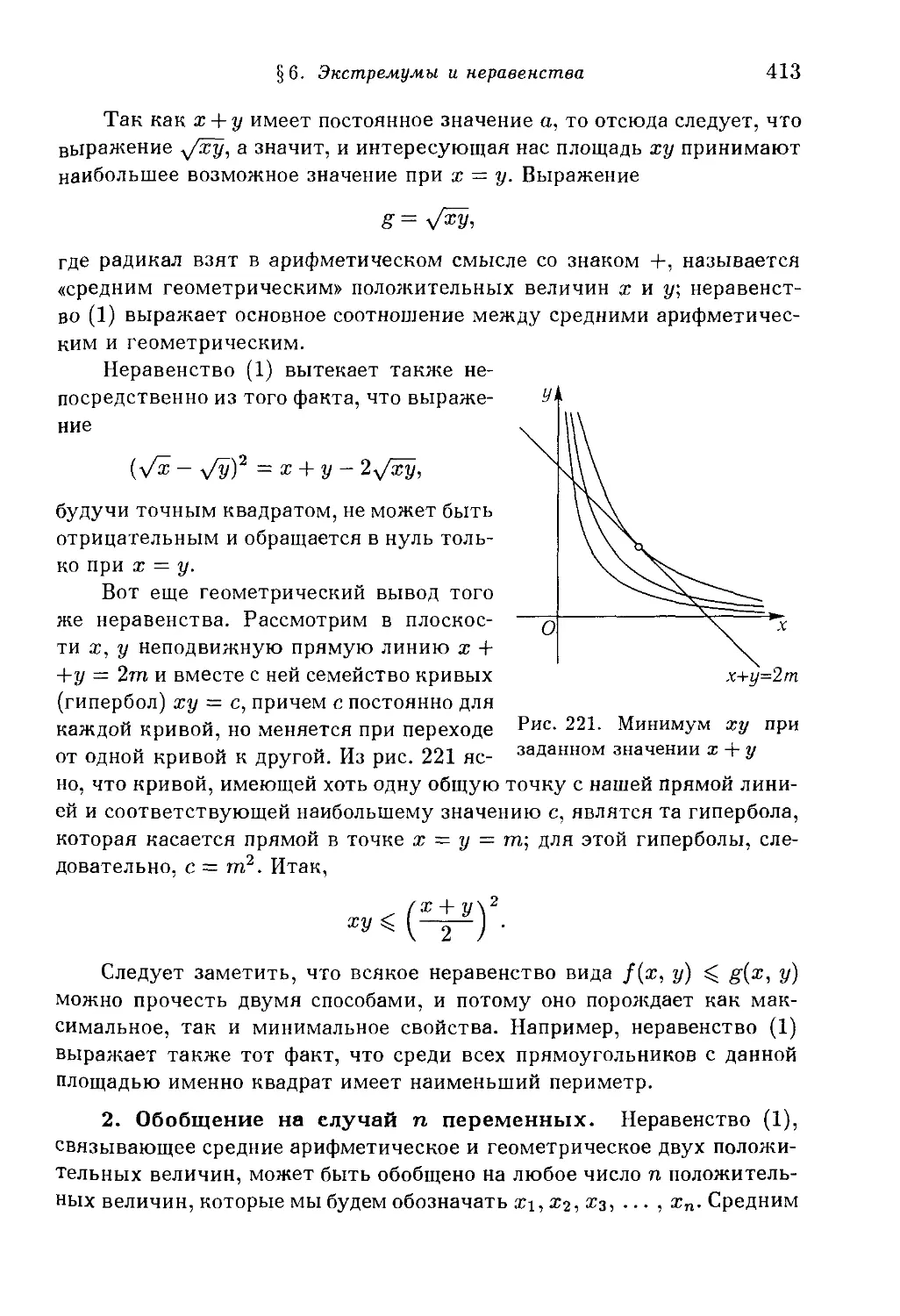
§ 6. Экстремумы и неравенства 412
1. Средние арифметическое и геометрическое двух положительных
величин. 2. Обобщение на случай п переменных. 3. Метод
наименьших квадратов.
§ 7. Существование экстремума. Принцип Дирихле 417
1. Общие замечания. 2. Примеры. 3. Экстремальные проблемы
элементарного содержания. 4. Трудности, возникающие в более
сложных случаях.
§8. Изопериметрическая проблема 425
§ 9. Экстремальные проблемы с граничными условиями. Связь между 428
проблемой Штейнера и изопериметрической проблемой
§ 10. Вариационное исчисление 432
1. Введение. 2. Вариационное исчисление. Принцип Ферма в оптике.
3. Решение задачи о брахистохроне, принадлежащее Якобу
Бернулли. 4. Геодезические линии на сфере. Минимаксы.
§ 11. Экспериментальные решения минимальных проблем. Опыты с 438
мыльными пленками
1. Введение. 2. Опыты с мыльными пленками. 3. Новые опыты,
относящиеся к проблеме Плато. 4. Экспериментальные решения
других математических проблем.
Глава VIII. Математический анализ 451
Введение 451

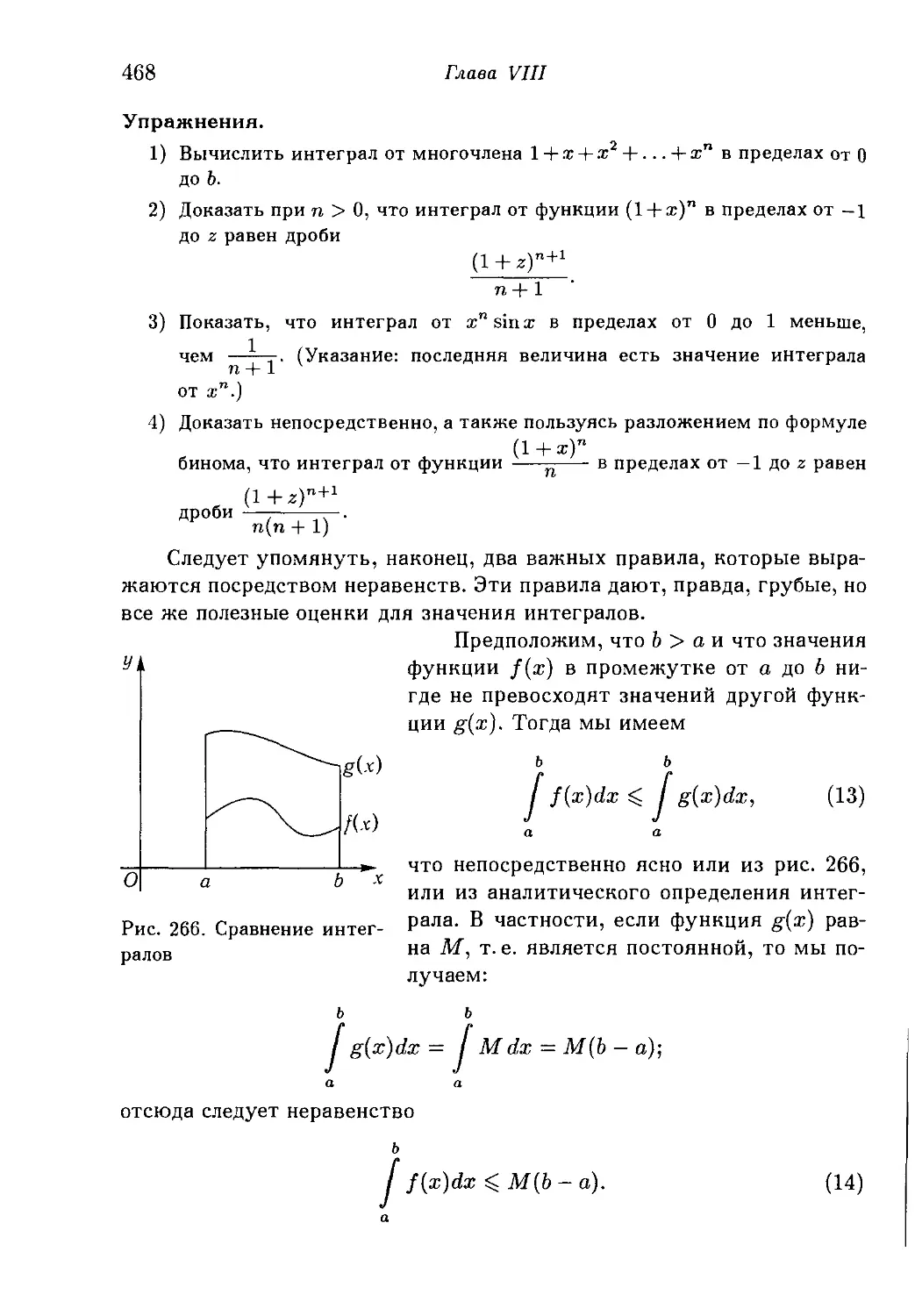
§ 1. Интеграл 452
1. Площадь как предел. 2. Интеграл. 3. Общие замечания о понятии
интеграла. Общее определение. 4. Примеры интегрирования.
Интегрирование хг. Правила «интегрального исчисления».
§ 2. Производная 469
1. Производная как наклон. 2. Производная как предел. 3. Примеры.
4. Производные от тригонометрических функций. *5.
Дифференцируемость и непрерывность. 6. Производная и скорость.
Вторая производная и ускорение. 7. Геометрический смысл второй
производной. 8. Максимумы и минимумы.
§3. Техника дифференцирования 484
§ 4. Обозначения Лейбница и «бесконечно малые» 490
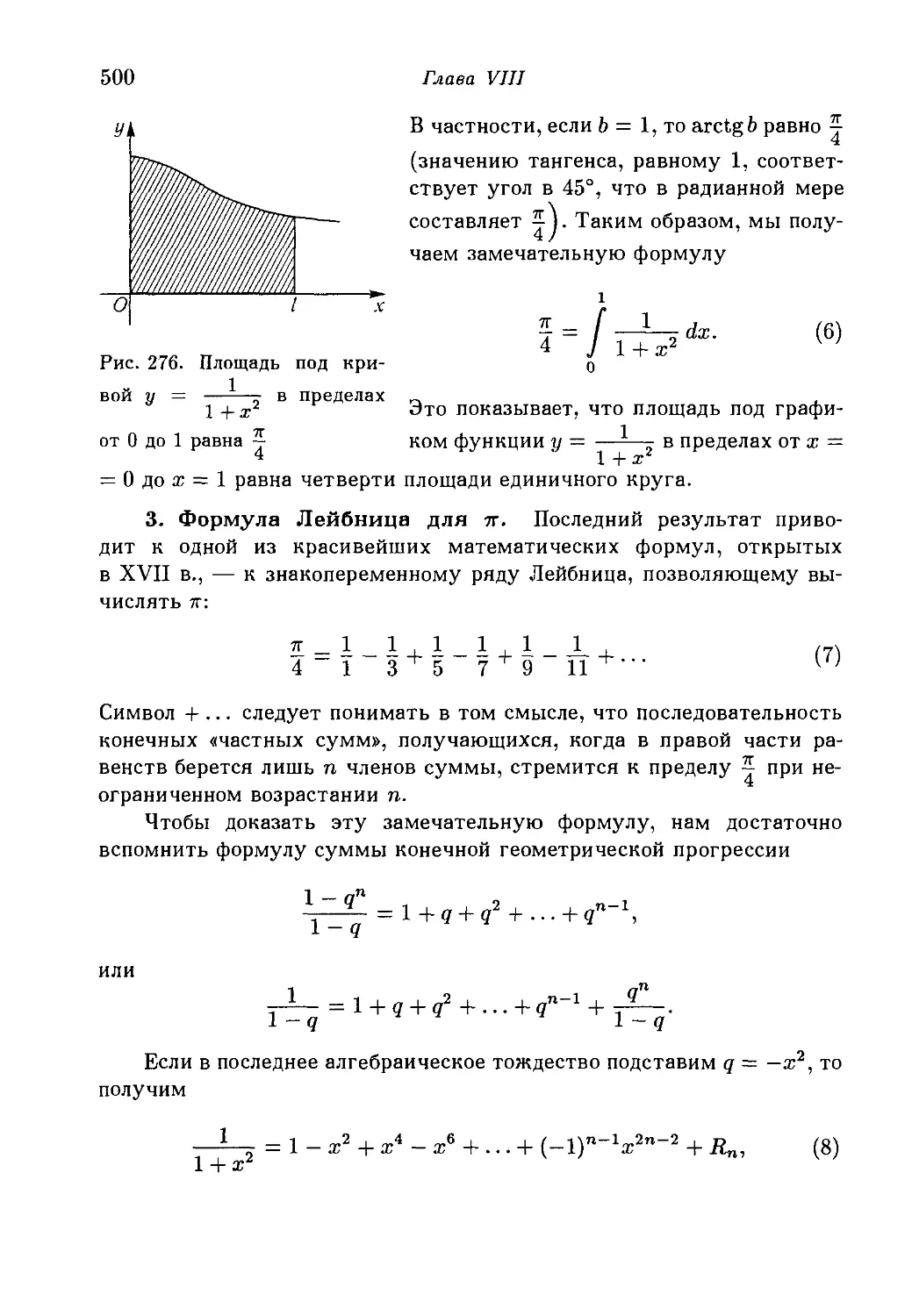
§ 5. Основная теорема анализа 494
1. Основная теорема. 2. Первые применения. Интегрирование
функций xr, cos х, sin х. Функция arctg x. 3. Формула Лейбница для к.
§6. Показательная (экспоненциальная) функция и логарифм 502
1. Определение и свойства логарифма. Эйлерово число е. 2.
Показательная (экспоненциальная) функция. 3. Формулы
дифференцирования функций е*, ах, ха 4. Явные выражения числа е
и функций е* и In х в виде пределов. 5. Бесконечный ряд для
логарифма. Вычисление логарифмов.
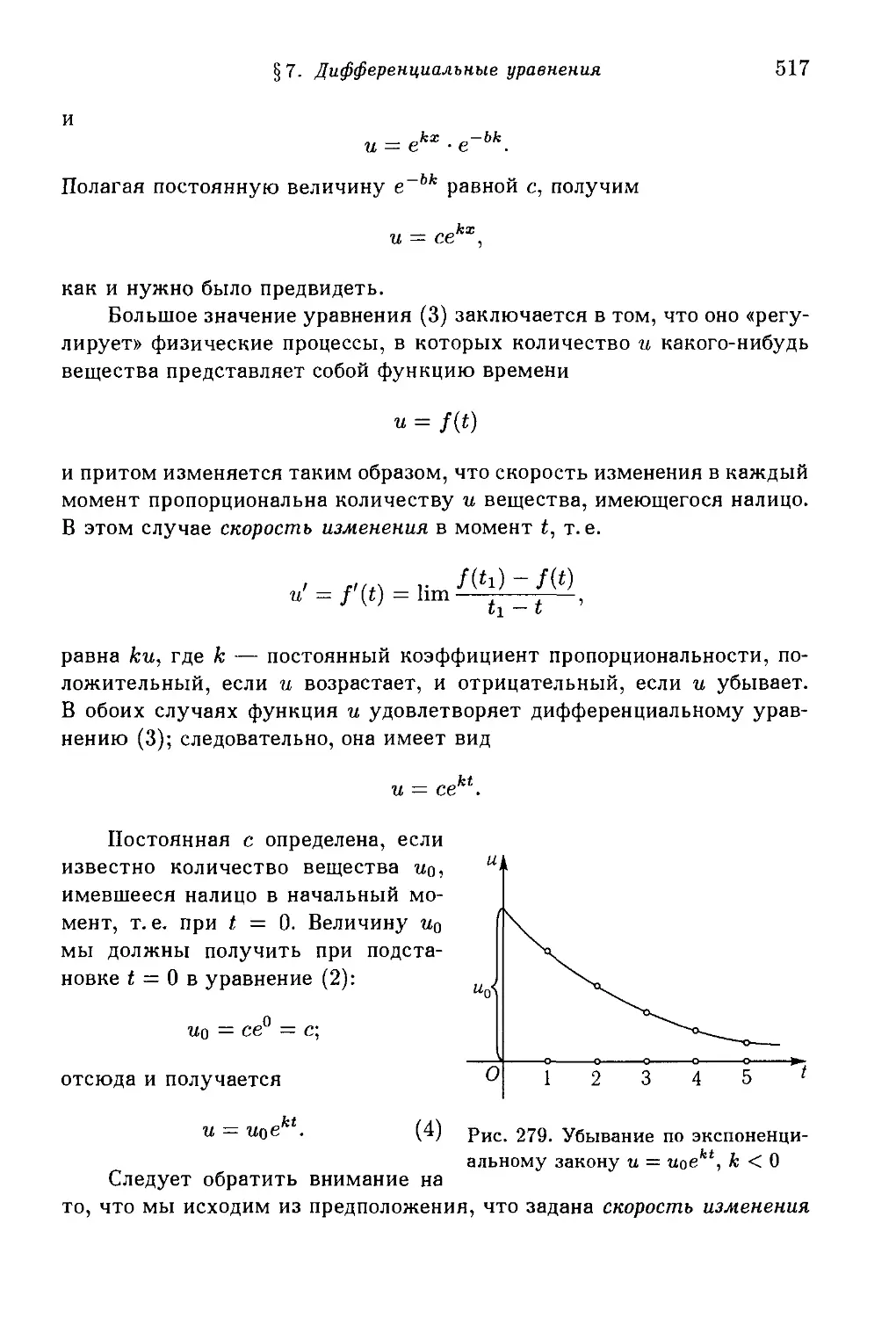
§ 7. Дифференциальные уравнения 515
1. Определения. 2. Дифференциальное уравнение экспоненциальной
функции. Радиоактивный распад. Закон роста. Сложные проценты. 3.
Другие примеры. Простейшие колебания. 4. Закон движения
Ньютона.
Дополнение к главе VIII. 524
§1. Вопросы принципиального порядка 524
1. Дифференцируемость. 2. Интеграл. 3. Другие приложения понятия
интеграла. Работа. Длина кривой.
§ 2. Порядки возрастания 532
1. Показательная функция и степени переменного х. 2. Порядок
возрастания \п(п!).
§3. Бесконечные ряды и бесконечные произведения 536
1. Бесконечные ряды функций. 2. Формула Эйлера cos х + i sin x =
eix. 3. Гармонический ряд и дзета-функция. Формула Эйлера,
выражающая sin x в виде бесконечного произведения.
§ 4. Доказательство теоремы о простых числах на основе статистического 548
метода
Приложение. Дополнительные замечания, задачи и упражнения 553
Арифметика и алгебра 553
Аналитическая геометрия 555
Геометрические построения 562
Проективная и неевклидова геометрия 563

Топология
Функции, пределы, непрерывность
Максимумы и минимумы
Дифференциальное и интегральное исчисления
Техника интегрирования
Рекомендуемая литература
Предметный указатель
564
567
568
571
573
580
584
Абсолютное значение 88
Аксиоматика 256
Аксиомы 256
Алгебра булева 151
— множеств 144
— основная теорема 136, 313
— числовых полей 154
Алгебраические уравнения 136
— числа 139
Алгоритм Евклида 72
Анализ математический 451
основная теорема 494
Аналитическая геометрия 105
и-мерная 270
Аполлония проблема 163
Аргумент комплексного числа 130
Арифметика законы 26
— основная теорема 50
Арифметические прогрессии 38
простые числа в а. п. 54
Арифметическое значение корня 325
Архимеда метод трисекции угла 178
Асимптота гиперболы 108
Асимптотически равно 57, 534
Ассоциативные законы для множеств
148
для натуральных чисел 26
для рациональных чисел 84
Бесконечно удаленная плоскость 225
прямая 222
— удаленные точки 221
элементы (в проективной
геометрии) 221
«Бесконечно малые» 490
Бесконечность 35, ПО
— ряда простых чисел 49
Предметный указатель
Бесконечные десятичные дроби 94
— непрерывные дроби 348
— произведения 546
— ряды 536
Биномиальная теорема 42
Биномиальный ряд 539
Больцано теорема 361
применения 365
Брахистохрона 433, 435
Брианшона теорема 231
Вариационное исчисление 432
Вейерштрасса теорема об
экстремальных значениях 362
Вектор 131
Вероятность 151
Взаимная непрерывность
(соответствия, отображения)
285
— однозначность (соответствия,
отображения) 111
Возрастания порядок 533
Вторая производная 481
Вычеты квадратические 67
Гармонически сопряженные пары
216
Гармонический ряд 544
Гарта инверсор 197
Геодезическая 379
Геодезические на сфере 437
Геометрическая прогрессия 39
Геометрические построения
Маскерони 188
квадратичных корней 160
правильных многоугольников
160
рациональных чисел 158

с помощью одного циркуля 188
с помощью одной линейки 192
с помощью различных
инструментов 193
теория 154
числовых полей 159
Геометрические преобразования 180
Геометрия и-мерная 270
— Римана 268
— аксиомы 259
— аналитическая 105
— гиперболическая 260
— комбинаторная 273
— метрическая 209
— неевклидова 260
— проективная 209
— синтетическая 232
— теория построения 157
— элементарная, экстремальные
задачи 379
Герона теорема 380
Гипербола свойство касательных 385
— уравнение 108
Гиперболические функции 572
Гиперболический параболид 332
Гиперболоид 254
Гипоциклоида 194
Гольдбаха проблема 58
Граничные условия в задачах на
экстремумы 428
График функции 323
Группа 208
Двенадцатеричная система 31
Движение эргодическое 403
Движения (преобразования) 181
Двоичная система 34
Двойное отношение 212
Двойственности принцип в алгебре
множеств 149
в геометрии 232
Дедекиндово сечение 104
Дезарга теорема 210
Действительные числа 94, 103
Декартовы координаты 106
Деление на нуль 86
Деление окружности, уравнение 135
Десятиугольник правильный,
построение 160
Десятичные дроби 92
Деформация 285
Дзета-функция 545
Динамика Ньютона 522
Диофантовы уравнения 80
Дирихле принцип 417
Дистрибутивные законы для
множеств 148
для натуральных чисел 26
для рациональных чисел 84
Дифференциалы 492
Дифференциальные уравнения 515
Дифференциальный символ 493
Дифференцирование 477
Дифференцируемость 524
Длина кривой 530
Доказательство: конструктивное,
косвенное, д. существования
120
Дополнение множества 149
Дроби десятичные 92
— непрерывные 79
е выражение 510
— иррациональность 346
— как основание натуральных
логарифмов 505
— как предел 345
— эйлерово число 344, 502
Евклида алгоритм 73
Единица (корень из е.) 133
Единичная окружность 129
Жордана теорема 287, 311
Зависимое переменное 319
Затухающие колебания 521
Идеальные элементы в проективной
геометрии 221
Извлечение квадратного корня (в
геометрии) 160
Измерение 82
Изопериметрические проблемы 425

Инвариантность 198
— двойного отношения 214
— углов при инверсии 198
Инверсия 181
— окружность 181
— полюс (центр) 182
Инверсоры 196
Индексы 297
Индукция математическая 35
— эмпирическая 35
Интеграл 452, 527
Интервал 88
Интуиционизм 257
Инцидентность (принадлежность)
210
Иррациональные числа как
бесконечные десятичные дроби
94
— — определяемые
последовательностями 105
определяемые сечениями 103
определяемые стягивающимися
отрезками 102
Исключенного третьего закон 121
Исчерпания метод 453
Исчисление вариационное 432
Итерации (пределы при и.) 376
Канторова теория (бесконечных)
множеств ПО
Канторово множество 291
Кардинальное число (мощность) 117
Карта регулярная 308
Касательная 469
Касательные к эллипсу и гиперболе,
свойство 383
Квадранты (координатные четверти)
106
Квадратные уравнения 124
Квадратный корень, геометрическое
построение 160
Квадратура круга 180
Квадрики 254
Классификация (топологическая)
поверхностей 300
Клейна бутылка 306
— модель 263
Коаксиальные плоскости 217
Колебания 520
Коллинеарные точки 210
Комбинаторная геометрия 273
Коммутативные законы для
множеств 148
для натуральных чисел 26
для рациональных чисел 84
Компланарные прямые 216
Комплексного переменного теория
функций 543
Комплексные числа 124
(операции с к.ч.) 125
аргумент 130
модуль 128
тригонометрическое
представление 130
Конгруэнтность 206
Конические сечения 240
как множества прямых 249
как множества точек 249
метрическое определение 240
проективное определение 245
уравнения 108
Конкурентные прямые 211
Константа (постоянная) 320
Конструктивные доказательства 121
Континуум действительных чисел 94
Континуум-гипотеза 123
Координаты обобщенные 233
— однородные 234
— прямоугольные (декартовы) 106
Корни из единицы 134
Косвенное доказательство 120
Кратность корней алгебраического
уравнения 138
Кривая длина 530
— уравнение 107
Кривизна 482
Кросс-кэп 305
Лейбница формула для тт 500
Линии уровня 332

Лиу вилля теорема 140
Логарифм натуральный 502
Логика математическая 150
Логическая сумма 147
Логическое произведение 147
Максимумы и минимумы 379, 483
Маскерони построения 188
Математическая индукция 35
— логика 150
Математический анализ 451
основная теорема 494
Мебиуса лента (лист) 304
Метрическая геометрия 209
Механические инструменты,
построения с их помощью 193
Минимакса точки 395
Мнимые числа (см. комплексные
числа) 125
Многогранники и-мерные 275
— правильные 280
— простые 280
— род 303
— эйлерова характеритика 303
Множеств алгебра 144
— эквивалентность 117
Множество ПО, 144
— дополнение 149
— компактное 366
— пустое 145
Множители простые 50
Модуль комплексного числа 128
Монотонная последовательность 341
— функция 326
Морза соотношения 396
Муавра формула 132
Наименьших квадратов метод 415
Наклон 469
Направление угла 200
Натуральные числа 25
Нахождение середины отрезка с
помощью одного циркуля 186
Неевклидова геометрия 260
Независимое переменное 319
Неподвижная точка 295
Непрерывное переменное 318
Непрерывность функции многих
переменных 333
одного переменного 328
Непрерывные дроби 79
Неравенства 412
Неразрешимость классических
проблем 173
Несоизмеримые отрезки 89
Несчетность континуума 114
и-мерная геометрия 270
Нуль 85
Ньютоновская динамика 522
Область изменения переменной 317
Обобщения принцип 86
Образ 181
Обратные операции 84
— функции 323
Объединение множеств 147
Ограниченная последовательность
342
Однозначность разложения на
множители 50
Однородные координаты 234
Односвязность 286
Односторонние поверхности 303
Окружность, уравнение 107
Опыты с мыльными пленками 439
Оси конических сечений 108
— координат 106
Основания математики 123
Основная теорема алгебры 136, 313
анализа 494
арифметики 50
Отображение (преобразование) 181
Отражение в общих экстремальных
задачах 381
— относительно одной или
нескольких прямых 181
окружностей 181
системы окружностей 204
треугольника 381
Отражение повторное 203
Отрезки вложенные 101

— стягивающиеся 101
Отрицательные числа 85
Паппа теорема 229
Парабола 241
Парадоксы Зенона 353
— бесконечного 121
Параллельность и бесконечность 220
Паскаля теорема 229, 252
— треугольник 43
Первообразные (примитивные)
функции 496
Переменное 317
— действительное 318
— зависимое 319
— комплексное 543
— независимое 319
Пересечение множеств 147
Пересчет 112
Перспектива 207
71346
Пифагоровы числа 69
Плато проблема 438
Плотность множества рациональных
чисел 88
Площадь 452
Поверхности односторонние 303
Подмножество 146
Подполе 167
Позиционная система 29
Показательная (экспоненциальная)
функция 505
дифференциальное уравнение
516
порядок возрастания 533
Поле 86
Полный четырехсторонник 219
Поля числовые алгебра 166
геометрическое построение 166
Порядок возрастания 533
— точки 314
Поселье инверсор 196
Последовательность 101, 114, 335
— монотонная 341
— ограниченная 342
— сходящаяся, расходящяяся,
колеблющаяся 342
Построения геометрические 157
— с помощью одного циркуля 188
Постулат о параллельных 260
Постулаты 256
Правильные многогранники 280
и-мерные 275
— многоугольники, построение 160
Правильный десятиугольник,
построение 160
Пределы 95, 335
— бесконечных десятичных дробей
99
— геометрических прогрессий 97
— последовательностей 337
— при итерации 376
непрерывном приближении 351
— примеры 371
Преобразования геометрические 180
— проективные 207
— топологические 285
— уравнения 333
Принцип наименьшего числа 50
Присоединение иррациональных
чисел 94
Проблема ракраски карт 289
Прогрессии арифметические 38
— геометрические 39
Проективная геометрия 209
Проективное преобразование 207
— соответствие 219
Произведение бесконечное 546
— логическое 147
Производная 469
— вторая 481
Прообраз (при отображении) 181
Простая замкнутая кривая 288
Простой многогранник 280
Простые числа 48
распределение 55, 548
Прямой линий уравнение 107
Прямые компланарные 216
— конкуррентные 210

Пустое множество 145
Пучок прямых 245
Пятиугольник правильный,
построение 190
Работа 528
Радианная мера 322
Радиоактивный распад 518
Разложение на простые множители,
единственность 50
Размерность 291
Разрешимость проблем 155
Разрыв со скачком 329
Разрывность функции 329
Разрывные функции как пределы
непрерывных 375
Распада закон 518
Расстояние 106
Расходимость последовательностей
340
— рядов 536
Расширение поля 167
Рациональные числа 82
операции 84
плотность 88
счетность 112
Рациональные операции,
геометрическое построение 157
Решето Эратосфена 52
Риманова геометрия 268
Род поверхности 300
Ряды бесконечные 536
Световые лучи 380
Связность 286
Сегмент (отрезок) 88
Семиричная система 33
Семиугольник правильный,
невозвоможность построения
178
Сечение (множества действительных
чиселI04
Символ 125
Синтетическая геометрия 232
Скорость 478
Сложение действительных чисел 105
— комплексных чисел 125
— множеств 147
— натуральных чисел 26
— рациональных чисел 84
Сложные проценты 519
— функции 327
Соответствие (отображение) между
множествами 111
Сопряженные комплексные числа
128
Составные числа 48
Сравнения 60
Среднее арифметическое 412
— геометрическое 413
Стационарные точки 392
Сумма логическая 147
— первых квадратов 40
кубов 41
Существование в математике 123
— доказательство 121
Сходимость последовательностей
340
— рядов 536
Счетность множества рациональных
чисел 112
Тейлора ряд 540
Теорема о неподвижной точке 295
пяти красках 308
четырех красках 289
Теоремы существования 48
Теория чисел 48
Топологическая классификация
поверхностей 300
Топологическое преобразование 284
Топология 278
Тор 300
— трехмерный 308
Точечный ряд 249
Точки коллинеарные 210
Трансцендентность числа тг 180
Трансцендентные числа 139
Треугольники образованные
световыми лучами 402
— экстремальные свойства 380

Тригонометрические функции 322
Трисекция угла 176
Удвоение куба 173 Узлы
299
Уличной сети проблема 410
Уоллиса формула 348, 579
Уравнение гиперболы 108
— деления окружности 135
— диофантово 80
— квадратное 124
— корни 137
— кратность корней 138
— кривой 107
— прямой 107
— эллипса 108
Уравнения движения 521
Уровня линии 332
Ускорение 481
Факториал 44
Ферма великая теорема 71
— принцип 433
— теорема 65
— числа 156
Фокус конического сечения 108
Формализм 124, 257
Функция 316
— (кривая) вогнутая, выпуклая 482,
568
— график 323
— комплексного переменного 541
— многих переменных 331
— монотонная 326
— непрерывная 329
— обратная 323
— определение 318
— первообразная 496
— сложная 327
Целые числа отрицательные 85
положительные 85
Центр окружности, построение с
помощью одного циркуля 186
Циклоиды 193
Четырехсторонник полный 219
Числа Ферма 156
— алгебраические 139
— действительные 88-91
— допускающие построение 165
— кардинальные 117
— комплексные 124
— натуральные 25
— отрицательные 85
— пифагоровы 69
— простые 48
— рациональные 82
— составные 48
— трансцендентные 139
Числовая система 82
Числовые поля 166
Шарнирные механизмы 195
Шварца проблема 397
Штейнера построения 192
— проблема 405
Эйлера функция 77
Эйлерова характеристика
поверхности 302
Эквивалентность множеств 111
Экстремальное решение задач на
минимум 428
Экстремальные задачи 379
в элементарной геометрии 379
общий принцип 389
с граничными условиями 428
— расстояния от данной кривой 386
Экстремумы и неравенства 412
Эксцентриситет (конического
сеченияI08
Эллипс свойство касательных 383
— уравнение 108
Эллиптическая геометрия 268
Эллиптические точки 269
Эпициклоида 195
Эратосфена решето 52
Эрлангенская программа 207

ПОСВЯЩАЕТСЯ
Эрнесту, Гертруде, Гансу и Леоноре Курант
Предисловие ко второму русскому изданию
Выход в свет второго русского издания нашей книги — весьма
приятное для меня событие. Я всегда с глубоким восхищением отно-
относился к замечательному вкладу в нашу науку, сделанному многими
выдающимися математиками Советского Союза. Пожалуй, в большей
степени, чем в некоторых странах Запада, русская математическая тра-
традиция сохранила идеал единства нашей науки и способствовала упроче-
упрочению роли математики в научных и технических приложениях. На меня
также производит сильнейшее впечатление активное участие, которое
принимают крупные математики Советской России в деле подъема ма-
математического образования. Я рад, что свое место в русской научно-
педагогической литературе по математике заняла и наша книга.
Настоящее издание отличается от предыдущих английских и не-
немецких изданий небольшими исправлениями и уточнениями, которыми
мы обязаны, в частности, профессору К. Л. Зигелю, Отто Нейгебауэру
и другим своим коллегам.
Нью-йоркский университет.
9 мая 1966 г. Р. Курант

Книга Р. Куранта и Г. Роббинса уже издавалась в СССР в 1947 г.
Она пользуется большим успехом у любителей математики самых раз-
различных возрастов и уровней подготовки, но давно уже стала библио-
библиографической редкостью. В серии «Математическое просвещение» она
займет свое почетное место.
Перевод, выполненный для первого издания под редакцией покой-
покойного проф. В.Л.Гончарова, был выправлен и пополнен по последним
английскому A948) и немецкому A962) изданиям. Восстановлен также
предметный указатель. Список «рекомендуемой литературы» следует
оригиналу лишь в части книг, переведенных на русский язык; редакто-
редакторы русского издания дополнили его рядом книг, имеющихся на русском
языке.
Примечания редакторов русского издания немногочисленны. Ре-
Редакторы, не желая нарушать цельный и впечатляющий стиль книги,
не стремились исправлять авторов и восполнять довольно случайный
выбор их указаний на историю вопроса и принадлежность отдельных
результатов определенным лицам.
Мы рады поблагодарить проф. Р. Куранта за любезное внимание,
оказанное им новому изданию книги на русском языке. В своем ко-
коротком обращении к русскому читателю он еще раз подчеркивает ру-
руководящую идею своей педагогической деятельности: пропаганду ор-
органического единства математики и ее неразрывной связи с естест-
естествознанием и техникой. При этом имеются в виду не нравоучения об
обязанности математиков быть полезными, а наглядная демонстрация
того, что живые источники математического творчества неотделимы
от интереса к познанию природы и задачам управления природными
явлениями.
В новом издании использованы замечания проф. К. Л. Зигеля и
проф. Отто Нейгебауэра, которым мы вместе с авторами выражаем
искреннюю признательность.
Москва. А. Н. Колмогоров
12 ноября 1966.

Предисловие к первому изданию
На протяжении двух с лишним тысячелетий обладание некоторы-
некоторыми, не слишком поверхностными, знаниями в области математики яв-
являлось необходимой составной частью интеллектуального багажа каж-
каждого образованного человека. В наши дни установленному традицией
воспитательному значению математики угрожает серьезная опасность.
К сожалению, профессиональные представители математической науки
в данном случае не свободны от ответственности. Обучение математи-
математике нередко приобретало характер стереотипных упражнений в решении
задач шаблонного содержания, что, может быть, и вело к развитию кое-
каких формальных навыков, но не призывало к глубокому проникно-
проникновению в изучаемый предмет и не способствовало развитию подлинной
свободы мысли. Научные исследования обнаруживали тенденцию в сто-
сторону чрезмерной абстракции и специализации. Приложениям и взаи-
взаимоотношениям с иными областями не уделялось достаточно внимания.
И все же эти малоблагоприятные предпосылки ни в какой мере не мо-
могут послужить оправданием для политики сдачи позиций. Напротив,
те, кто умеют понимать значение умственной культуры, не могут не
выступить — и уже выступают — на ее защиту. Преподаватели, уча-
учащиеся — все, хотя бы и не связанные со школой, образованные люди —
требуют не идти по линии наименьшего сопротивления, не складывать
оружия, а приступить к конструктивной реформе преподавания. Целью
является подлинное понимание существа математики как органическо-
органического целого и как основы научного мышления и действования.
Несколько блестящих книг биографического и исторического со-
содержания и кое-какие публицистические выступления разбудили в ши-
широких кругах, казалось бы безразличных к математике, на самом деле
никогда не угасавший к ней интерес. Но знание не может быть достиг-
достигнуто с помощью одних лишь косвенных средств. Понимание математи-
математики не приобретается только безболезненно развлекательными способа-
способами — так же, как, например, вы не сможете приобрести музыкальной
культуры путем чтения журнальных статей (как бы ярко они ни были
написаны), если не научитесь слушать внимательно и сосредоточенно.
Нельзя обойтись без действенного соприкосновения с самим содержани-
содержанием живой математической науки. С другой стороны, следовало бы избе-

16 Предисловие к первому изданию
гать всего слишком технического или искусственного, делая изложение
математики в одинаковой степени свободным от духа школьной рути-
рутины и от мертвящего догматизма, отказывающегося от мотивировок и
указания целей, — того самого догматизма, который представляет со-
собой столь неприятное препятствие для честного усилия. Нет ничего не-
невозможного в том, чтобы, начиная от элементов и следуя по прямому
пути, добраться до таких возвышенных точек, с которых можно ясно
обозреть самую сущность и движущие силы современной математики.
Настоящая книга делает такую именно попытку. Поскольку она не
предполагает иных сведений, кроме тех, которые сообщаются в хоро-
хорошем школьном курсе, ее можно было бы назвать популярной. Но она —
не уступка опасной тенденции устранить всякое напряжение мысли и
упражнение. Она предполагает известный уровень умственной зрелос-
зрелости и готовность усваивать предлагаемое рассуждение. Книга написана
для начинающих и для научных работников, для учащихся и для учите-
учителей, для философов и для инженеров; она может быть использована как
учебное пособие в учебных заведениях и в библиотеках. Может быть,
намерение обратиться к такому широкому кругу читателей является
чересчур смелым и самонадеянным. Нужно признать, что под давле-
давлением иной работы мы вынуждены были при публикации этой книги
искать компромиссы: подготовка велась многие годы, но так и не была
по-настоящему закончена. Мы будем рады критике и готовы выслушать
пожелания.
Если ответственность за план и философское содержание этой пуб-
публикации ложится на нижеподписавшегося, то воздаяние ее достоинст-
достоинствам (если таковые имеются) мне подобает разделить с Гербертом Роб-
бинсом. С самого момента присоединения к задуманной работе он от-
отдался ей с увлечением, как своей собственной, и его сотрудничество
сыграло решающую роль в окончательном придании книге ее настоя-
настоящей формы.
Я должен выразить свою глубокую благодарность за помощь мно-
многочисленным друзьям. Беседы с Нильсом Бором, Куртом Фридрихом
и Отто Нейгебауэром оказали влияние на мои позиции в вопросах фи-
философского и исторического характера. Большое количество конструк-
конструктивных критических замечаний с точки зрения педагога высказала Эд-
Эдна Крамер. Давид Гильбарг записал лекции, положенные затем в осно-
основу книги. Эрнест Курант, Норман Девидс, Чарльз де Прима, Альфред
Горн, Герберт Минтцер, Вольфганг Вазов и другие помогли в поистине
бесконечной работе по перепечатке рукописи и внесли в нее множес-
множество улучшений. Доналд Флендерс внес много ценных предложений и

Предисловие ко второму, третьему и четвертому изданиям 17
тщательно выверил рукопись к печати. Джон Кнудсен, Герта фон Гум-
пенберг, Ирвинг Риттер и Отто Нейгебауэр изготовили чертежи. Часть
упражнений для приложения в конце книги исходит от Г. Уитни. Кур-
Курсы лекций и статьи, положенные в основу книги, были осуществлены
благодаря щедрой поддержке Отдела народного образования рокфелле-
рокфеллеровского фонда. Я должен также поблагодарить издательство Waverly
Press, особенно г-на Гровера К. Орта, за чрезвычайно квалифицирован-
квалифицированную работу и издательство Oxford University Press, особенно г-на Фи-
Филипа Бодрена и г-на У. Омана, за инициативу и поддержку.
Нью-Рошель, Нью-Йорк, Р. Курант
22 августа 1941 г.
Предисловие ко второму, третьему и
четвертому изданиям
В последний год под воздействием совершающихся событий воз-
возник усиленный спрос на математическую информацию и соответству-
соответствующий инструктивный материал. Сейчас больше чем когда-либо сущест-
существует опасность выхолащивания и разочарований, если только учащиеся
(и учителя) не сумеют увидеть и схватить то, что лежит за формулами
и преобразованиями, — истинное существо и содержание математики.
Именно для тех, кто видит глубже, была написана эта книга, и отклики
на первое издание поддерживают в авторах надежду, что она принесет
пользу.
Благодарим читателей, чьи критические замечания позволили вне-
внести в новые издания многочисленные поправки и улучшения. За боль-
большую помощь в подготовке четвертого издания сердечно благодарим
г-жу Наташу Артин.
Нью-Рошель, Нью-Йорк, Р. Курант
18 марта 1943 г.
10 октября 1945 г.
28 октября 1947 г.

Как пользоваться книгой
Порядок изложения в книге — систематический, но это не значит
никоим образом, что читатель обязан читать ее подряд — страницу за
страницей, главу за главой. Главы в значительной степени независимы
одна от другой. Часто начало раздела покажется легкодоступным, но
потом дорога постепенно пойдет вверх, становясь круче в конце главы
и в дополнениях к ней. Поэтому читатель, нуждающийся скорее в общей
информации, чем в приобретении специальных знаний, поступит пра-
правильно, если удовлетворится таким отбором материала, который может
быть осуществлен по принципу избегания более детализированных рас-
рассмотрений.
Учащийся с ограниченной математической подготовкой пусть вы-
выбирает по своему вкусу. Звездочками и мелким шрифтом отмечено то,
что может быть опущено при первом чтении без серьезного ущерба для
понимания последующего. Больше того, беды не будет, если при изуче-
изучении книги читатель ограничится теми разделами или главами, которые
представляют для него наибольший интерес. Большинство упражнений
не носит чисто формального характера; более трудные отмечены звез-
звездочкой. Не надо слишком огорчаться, если вы не сумеете выполнить
некоторые из них.
Преподаватели школ найдут в главах, посвященных геометричес-
геометрическим построениям и максимумам и минимумам, материал, подходящий
для кружковых занятий или для отдельных групп учащихся.
Мы надеемся, что книга сможет послужить и учащимся разных
классов колледжей и лицам тех или иных профессий, действительно
интересующимся проблемами точного знания. Она может быть поло-
положена в основу «свободных» курсов в колледжах по основным понятиям
математики. Главы III, IV и V подходят для курса геометрии, тогда
как главы VI и VIII, вместе взятые, образуют законченное изложение
основ анализа с опорой скорее на понимание, чем на достижение техни-
технического совершенства. Они могут быть использованы в качестве ввод-
вводного текста преподавателем, который пожелал бы дополнить учебный
курс в соответствии с теми или иными специфическими потребностя-
потребностями и в особенности — обогатить его более разнообразными примерами.

Как пользоваться книгой 19
Многочисленные упражнения разбросаны по всей книге; дополнитель-
дополнительное собрание упражнений в конце могло бы, как мы полагаем, облегчить
ее использование в школьной обстановке.
Мы надеемся, что и специалист обнаружит кое-что интересное в де-
деталях и в иных элементарных рассуждениях, содержащих в себе зерно
более широких идей.

Что такое математика?
Математика содержит в себе черты волевой деятельности, умозри-
умозрительного рассуждения и стремления к эстетическому совершенству. Ее
основные и взаимно противоположные элементы — логика и интуиция,
анализ и конструкция, общность и конкретность. Как бы ни были раз-
различны точки зрения, питаемые теми или иными традициями, только
совместное действие этих полярных начал и борьба за их синтез обеспе-
обеспечивают жизненность, полезность и высокую ценность математической
науки.
Без сомнения, движение вперед в области математики обусловлено
возникновением потребностей, в большей или меньшей мере носящих
практический характер. Но раз возникшее, оно неизбежно приобрета-
приобретает внутренний размах и выходит за границы непосредственной полез-
полезности. Совершающееся таким образом превращение прикладной нау-
науки в теоретическую наблюдается в истории древности, но не в мень-
меньшей степени также и в наши дни: достаточно принять во внимание
тот вклад, который сделан в современную математику инженерами и
физиками.
Самые ранние из дошедших до нас образцов математической мыс-
мысли появились на Востоке: около двух тысячелетий до нашей эры ва-
вавилоняне собрали обширный материал, который мы склонны были бы
в настоящее время отнести к элементарной алгебре. Но как наука в со-
современном смысле слова математика возникает позднее на греческой
почве, в пятом и четвертом столетиях до нашей эры. Все усиливающе-
усиливающееся соприкосновение между Востоком и Грецией, начавшееся во вре-
времена Персидской империи и достигшее апогея в период, непосредст-
непосредственно следующий за экспедициями Александра, обеспечило для греков
возможность перенять достижения вавилонян в области математики
и астрономии. Математика не замедлила стать объектом философских
дискуссий, обычных в греческих государствах-городах. Таким обра-
образом, греческие мыслители осознали значительные трудности, связан-
связанные с основными математическими концепциями — непрерывностью,
движением, бесконечностью — и с проблемой измерения произвольных
величин данными заранее единицами. Но обнаружилась и решимость
преодолеть препятствия: возникшая в результате великолепного уси-
усилия мысли эвдоксова теория геометрического континуума представля-

Что такое математика? 21
ет собой такое достижение, которое можно поставить в один ряд только
с современной теорией иррациональных чисел.
Хотя теоретико-постулативная тенденция незыблемо остается од-
одной из самых ярких особенностей греческой математики и, как та-
таковая, оказала беспримерное влияние на дальнейшее развитие науки,
тем не менее необходимо со всей энергией указать, что практические
потребности и связь с физической реальностью участвовали никак не
в меньшей мере в создании античной математики и что изложению,
свободному от евклидовой строгости, очень часто отдавалось предпо-
предпочтение.
Не исключено, что именно слишком раннее открытие трудностей,
связанных с «несоизмеримыми» величинами, помешало грекам развить
искусство численных операций, сделавшее в предшествовавшие эпохи
значительные успехи на Востоке. Вместо этого они стали искать пу-
пути в дебрях чистой аксиоматической геометрии. Так началось одно из
странных блужданий в истории науки, и, может быть, упущены бы-
были при этом блестящие возможности. Почти на два тысячелетия вес
греческой геометрической традиции задержал неизбежную эволюцию
идеи числа и буквенного исчисления, ставшего позднее фундаментом
точных наук.
После периода медленного накопления сил — с возникновением
в XVII столетии аналитической геометрии и дифференциального и
интегрального исчислений — открылась бурная революционная фаза
в развитии математики и физики. В XVII и XVIII вв. греческий иде-
идеал аксиоматической кристаллизации и систематической дедукции по-
потускнел и утерял свое влияние, хотя античная геометрия продолжала
высоко расцениваться. Логически безупречное мышление, отправляю-
отправляющееся от отчетливых определений и «очевидных», взаимно не проти-
противоречащих аксиом, перестало импонировать новым пионерам матема-
математического знания. Предавшись подлинной оргии интуитивных догадок,
перемешивая неоспоримые заключения с бессмысленными полумисти-
полумистическими утверждениями, слепо доверяясь сверхчеловеческой силе фор-
формальных процедур, они открыли новый математический мир, полный
несметных богатств. Но мало-помалу экстатическое состояние мысли,
упоенной головокружительными успехами, уступило место духу сдер-
сдержанности и критицизма. В XIX столетии осознание необходимости кон-
консолидировать науку, особенно в связи с нуждами высшего образования,
после французской революции получившего широкое распространение,
повело к ревизии основ новой математики; в частности, внимание бы-
было направлено к дифференциальному и интегральному исчислениям и

22 Что такое математика?
к уяснению подразумеваемого анализом понятия предела. Таким обра-
образом, XIX в. не только стал эпохой новых успехов, но и был ознаменован
плодотворным возвратом к классическому идеалу точности и строгости
доказательств. В Этом отношении греческий образец был даже превзой-
превзойден. Еще один раз маятник качнулся в сторону логической безупреч-
безупречности и отвлеченности. В настоящее время мы еще, по-видимому, не
вышли из этого периода, хотя позволительно надеяться, что установив-
установившийся прискорбный разрыв между чистой математикой и ее жизнен-
жизненными приложениями сменится эрой более тесного единения. Приобре-
Приобретенный запас внутренних сил и, помимо всего прочего, чрезвычайное
упрощение, достигаемое на основе ясного понимания, позволяют се-
сегодня манипулировать математической теорией таким образом, чтобы
приложения не упускались из виду. Установить еще раз органическую
связь между чистым и прикладным знанием, здоровое равновесие меж-
между абстрактной общностью и полнокровной конкретностью — вот как
нам представляется задача математики в непосредственно обозримом
будущем.
Здесь не место входить в подробный философский или психологи-
психологический анализ математики. Хочется отметить все же некоторые момен-
моменты. Чрезмерное подчеркивание аксиоматико-дедуктивного характера
математики представляется мне весьма опасным. Конечно, начало кон-
конструктивного творчества, интуитивное начало, являющееся источни-
источником наших идей и доводов в их пользу, с трудом укладываются в прос-
простые философские формулировки; и тем не менее именно это начало есть
подлинная суть любого математического открытия, даже если оно от-
относится к самым абстрактным областям. Если целью и является четкая
дедуктивная форма, то движущая сила математики — это интуиция и
конструкции. В допущении, что математика есть не более чем система
следствий, извлекаемых из определений и постулатов, которые должны
быть только совместимы между собой, а в остальном являются про-
продуктом свободной фантазии математиков, таится серьезная угроза для
самого существования науки. Если бы это было действительно так, ма-
математика была бы занятием, недостойным мыслящего человека. Она
была бы просто игрой с определениями, правилами и силлогизмами, не
имеющей ни причины, ни цели. Представление, согласно которому че-
человеческий интеллект может творить лишенные какого бы то ни было
смысла системы постулатов, есть обман, точнее, полуправда.
Получать результаты, имеющие научную ценность, свободный ра-
разум может, только подчиняясь суровой ответственности перед приро-
природой, только следуя некоей внутренней необходимости.

Что такое математика? 23
Хотя созерцательное направление логического анализа и не пред-
представляет всей математики, оно способствовало более глубокому пони-
пониманию математических фактов и их взаимозависимости и более ясному
овладению существом математических понятий. Именно из этого на-
направления выросла современная точка зрения на математику как на
образец универсально приложимого научного метода.
Каких бы философских позиций мы ни придерживались, все задачи
научного исследования сводятся к нашему отношению к воспринимае-
воспринимаемым объектам и инструментам исследования. Конечно, восприятие са-
само по себе еще не есть ни знание, ни понимание; нужно еще согласовать
их между собой и истолковать в терминах некоторых лежащих за ними
сущностей, «вещей в себе», не являющихся предметами непосредствен-
непосредственно физического изучения, а принадлежащими к метафизической сфере.
Но для научного метода существенным является отказ от метафизичес-
метафизических умозрений и, в конечном счете, представление всех наблюдаемых
фактов в форме понятий и конструкций. Отказ от претензии понима-
понимания природы «вещей в себе», от постижения «окончательной истины», от
разгадки внутренней сущности мира, быть может, будет психологичес-
психологически тягостен для наивных энтузиастов, но на самом-то деле этот отказ
оказался в высшей степени плодотворным для развития современной
научной мысли.
Некоторым из величайших открытий физики мы обязаны смелому
следованию принципу устранения метафизики. Когда Эйнштейн попы-
попытался свести понятие «одновременных событий, происходящих в раз-
разных местах» к наблюдаемым явлениям, когда он понял, что вера в то,
что это понятие само по себе непременно должно иметь какой-то точ-
точный смысл, есть попросту метафизический предрассудок, в этом от-
открытии уже было заключено ядро его теории относительности. Когда
Нильс Бор и его ученики вдумались в тот факт, что любое физическое
наблюдение связано с взаимодействием между прибором и наблюдае-
наблюдаемым объектом, то им стало ясно, что точное одновременное определе-
определение положения и скорости частицы в том смысле, в каком это пони-
понимается в физике, невозможно. Далеко идущие следствия этого откры-
открытия, составившие современную систему квантовой механики, хорошо
известны ныне каждому физику. В девятнадцатом столетии господст-
господствовала идея, согласно которой механические силы и передвижения час-
частиц в пространстве суть вещи в себе, а электричество, свет и магнетизм
можно свести к механическим явлениям (или «объяснить» в механичес-
механических терминах), подобно тому как это было сделано с теорией теплоты.
Была выдвинута концепция гипотетической среды — так называемого

24 Что такое математика?
«эфира», — способной к не вполне понятным механическим передви-
передвижениям, представляющимся нам в качестве света или электричества.
Постепенно выяснилось, что этот эфир принципиально ненаблюдаем,
т.е. что это понятие принадлежит скорее метафизике, нежели физике.
Вначале с сожалением, а затем с облегчением идея механического объ-
объяснения световых и электрических явлений — а вместе с ней и понятие
эфира — была окончательно отброшена.
Подобная же ситуация, и даже еще более отчетливая, создалась и
в математике. В течение столетий математики рассматривали интере-
интересующие их объекты — числа, прямые и т.д. — как некие субстанции,
вещи в себе. Поскольку, однако, эти «сущности» упорно не поддавались
попыткам точного описания их природы, математики девятнадцатого
столетия стали понемногу укрепляться в мысли, что вопрос о значении
этих понятий как субстанциальных объектов в рамках математики (да
и где бы то ни было) просто не имеет смысла. Математические утверж-
утверждения, в которые входят эти термины, относятся вовсе не к физической
реальности; они лишь устанавливают взаимосвязи между математи-
математически «неопределимыми объектами» и правила оперирования с ними.
Вопрос о том, чем «на самом деле» являются точки, прямые и числа, не
может и не должна обсуждать математическая наука. Действительно
существенными и имеющими непосредственное касательство к «про-
«проверяемым» фактам являются структура и взаимосвязи между этими
объектами: что две точки определяют прямую, что из чисел по опре-
определенным правилам получаются другие числа, и т. п. Ясное осознание
необходимости отказа от представления об основных математических
понятиях как о реально существующих предметах явилось одним из
самых важных и плодотворных завоеваний современного аксиомати-
аксиоматического развития математики.
К счастью, творческая мысль забывает о догматических философ-
философских верованиях, как только привязанность к ним становится на пу-
пути конструктивных открытий. И для специалистов, и для любителей
не философия, а именно активные занятия самой математикой смогут
дать ответ на вопрос: Что такое математика?

Глава I
Натуральные числа
Введение
Число есть основа современной математики. Но что такое число?
Если мы говорим, что i + i = ]i-i = i или что (-1) • (-1) = 1, то
какой смысл вкладывается в эти утверждения? В школе мы изучаем
механизм действий с дробями и с отрицательными числами, но, чтобы
приобрести подлинное понимание того, как устроена система чисел, не-
недостаточно ограничиваться элементарными сведениями и нужно пойти
несколько дальше. Греки в древнее время в основу созданной ими мате-
математики положили геометрические концепции точки и прямой; руково-
руководящим принципом современной математики стало сведение в конечном
счете всех утверждений к утверждениям, касающимся натуральных
чисел 1, 2, 3, ... «Бог создал натуральные числа, все прочее — дело
рук человека». Этими словами Леопольд Кронекер A823-1891) опреде-
определил тот прочный фундамент, на котором может быть построено здание
математики.
Числа служат для того, чтобы считать объекты, входящие в состав
тех или иных объединений или собраний. Числа решительно никак не
связаны с индивидуальной характеристикой считаемых объектов. Так,
число «шесть» есть результат абстрагирования, производимого при рас-
рассмотрении всевозможных собраний, содержащих по шесть объектов:
оно нисколько не зависит ни от специфических свойств этих объектов,
ни от употребляемых символов (обозначений). Но абстрактный харак-
характер идеи числа становится ясным только на очень высокой ступени
интеллектуального развития. В глазах детей числа всегда остаются со-
соединенными с самими осязаемыми объектами — допустим, пальцами
или камешками; в языках народов числа также трактуются конкретно:
для обозначения предметов различных типов употребляются различ-
различные сочетания числительных слов.
Мы воспользуемся тем, что математик (как таковой) не обязан
заниматься философской проблемой перехода от собраний конкретных

26 Глава I
объектов к абстрактному понятию числа. Мы примем поэтому нату-
натуральные числа как данные вместе с двумя основными операциями, над
ними совершаемыми: сложением и умножением.
§ 1. Операции над целыми числами
1. Законы арифметики. Математическую теорию натураль-
натуральных (иначе, целых положительных) чисел называют арифметикой. Эта
теория основана на том факте, что сложение и умножение целых чи-
чисел подчинены некоторым законам. Чтобы сформулировать эти законы
во всей их общности, нельзя воспользоваться символами вроде 1, 2, 3,
относящимися к определенным, конкретным числам. Утверждение
1+2=2+1
есть только частный случай общего закона, содержание которого заклю-
заключается в том, что сумма двух чисел не зависит от порядка, в котором
мы рассматриваем эти числа. Если мы хотим выразить ту мысль, что
некоторое соотношение между целыми числами имеет место (оправды-
(оправдывается, осуществляется), каковы бы ни были участвующие числа, то бу-
будем обозначать их символически, т.е. условно, буквами а, Ь, с, .... Раз
такого рода соглашение принято, сформулировать пять основных зако-
законов арифметики — очевидно, близко знакомых читателю — не пред-
представит труда:
1) а + Ь = Ъ + а, 2) ab = Ьа, 3) а + F + с) = (а + Ь) + с,
4) а{Ьс) = (аЪ)с, 5) а(Ь + с) = ab + be.
Два первых закона — коммутативный (переместительный) закон
сложения и коммутативный закон умножения — говорят, что при сло-
сложении и при умножении можно менять порядок чисел, над которыми
совершается действие. Третий — ассоциативный (сочетательный) за-
закон сложения — говорит, что при сложении трех чисел получается один
и тот же результат независимо от того, прибавим ли мы к первому чис-
числу сумму второго и третьего или прибавим третье к сумме первого и
второго. Четвертый закон есть ассоциативный закон умножения. По-
Последний — дистрибутивный (распределительный) — закон устанавли-
устанавливает то обстоятельство, что при умножении суммы на некоторое целое
число можно умножить на это число каждое слагаемое и полученные
произведения сложить.

j 1. Операции над целыми числами
27
Рис. 1. Сложение
Эти арифметические законы со-
совсем просты и, пожалуй, могут по-
показаться очевидными. Но следует все
же заметить, что к иного рода объек-
объектам — не к целым числам — они мо-
могут оказаться и неприменимыми. На- Рис- 2- Умножение
пример, если а и b обозначают не числа, а химические вещества и ес-
если «сложение» понимается в смысле обычной речи, то легко понять,
что коммутативный закон сложения не всегда оправдывается. В самом
деле, если, скажем, к воде будем прибавлять серную кислоту, то по-
получится разбавленный раствор, тогда как прибавление воды к чистой
серной кислоте может закончиться неблагополучно для эксперимента-
экспериментатора. С помощью таких же иллюстраций можно показать, что в хи-
химической «арифметике» иногда нарушаются и ассоциативный, и дист-
дистрибутивный законы сложения. Итак, можно вообразить и такие типы
арифметических систем, в которых один или несколько законов 1)-5)
теряют силу. Такие системы, действительно, изучались современной
математикой. Основа, на которой покоятся законы 1)-5), дается кон-
конкретной моделью для абстрактного понятия целого числа. Вместо то-
того чтобы пользоваться обыкновенными знаками 1, 2, 3 и т.д., станем
обозначать число предметов в данной совокупности (например, сово-
совокупности яблок на данном дереве) системой точек в четырехугольном
«ящичке» — таким образом, чтобы каждому предмету соответствовало
по одной точке. Оперируя этими ящичками, мы сможем исследовать
законы арифметики целых чисел. Чтобы сложить два целых числа а
и Ь, мы сдвигаем вместе соответствующие ящички и затем уничтожа-
уничтожаем перегородку. Чтобы умножить а на Ь, мы выстроим точки в двух
ящичках в ряд и затем устроим новый ящичек, в котором точки будут
расположены так, что образуют а горизонтальных и Ь вертикальных
рядов. И тогда ясно видно, что правила 1)-5) выражают интуитивно-
очевидные свойства введенных операций с ящичками.
Рис. 3. Дистрибутивный закон

28 Глава I
Рис. 4. Вычитание
На основе определения сложения двух целых чисел можно теперь
дать определение неравенства. Каждое из двух эквивалентных утверж-
утверждений, именно, а < Ь («а меньше, чем Ы) и Ь > а («6 больше, чем о»),
обозначает, что ящичек Ь может быть получен из ящичка а посредством
прибавления надлежащим образом выбранного третьего ящичка с — та-
таким образом, что Ь = а + с. Если это так, то мы напишем
с = b - о,
чем и определяется операция вычитания.
Сложение и вычитание называются обратными операциями, так
как, если к числу а прибавить число d, а затем из того, что получится,
отнять d, то получится снова исходное число а:
(а + d) — d = a.
Нужно заметить, что число Ь — а было определено только при усло-
условии Ь > а. Значение символа Ь — а как отрицательного целого числа
при условии Ь < а будет рассмотрено далее (стр. 84 и след.). Часто бы-
бывает удобно пользоваться обозначением b ^ a («6 больше или равно а»)
или а $С Ь («а меньше или равно 6», «а не превосходит 6»), понимая под
этим не что иное, как отрицание того, что а > Ь. Таким образом, можно
написать 2 ^ 2 и можно также написать 3^2.
Мы можем еще несколько расширить область положительных це-
целых чисел, которые мы изображаем ящичками с точками. Введем це-
целое число нуль, изображаемое совершенно пустым ящичком; условимся
обозначать такой пустой ящичек обычным символом 0. Тогда, согласно
нашему определению сложения и умножения, каково бы ни было целое
число о, получаются соотношения
а + 0 = а, а • 0 = 0.
Действительно, а + 0 обозначает прибавление пустого ящичка к ящич-
ящичку а, а а • 0 обозначает ящичек, в котором вовсе нет вертикальных
рядов, т.е. пустой ящичек. Тогда уже вполне естественно расширить
определение вычитания, полагая
при любом а. Таковы характерные арифметические свойства нуля.

§ 1. Операции над целыми числами 29
Геометрические модели вроде ящичков с точками (сюда относится
древний абак) широко применялись при арифметических вычислениях
вплоть до конца средневековья и только мало-помалу уступили место
гораздо более совершенным символическим методам, основанным на
десятичной системе.
2. Представление целых чисел с помощью письменных
знаков (нумерация). Необходимо очень тщательно делать различие
между целым числом и тем символом (например, 5, V и т.п.), которым
пользуются для его письменного воспроизведения. В нашей десятичной
системе нуль и девять целых натуральных чисел обозначаются цифра-
цифрами 0, 1, 2, 3, ... , 9. Числа большей величины, как, скажем, «триста
семьдесят два», представляются в виде
300 + 70 + 2 = 3 • 102 + 7 • 10 + 2
и в десятичной системе записываются символом 372. Существенно
в данном случае то, что смысл каждой из цифр 3, 7, 2 зависит от ее
положения — от того, стоит ли она на месте единиц, десятков или со-
сотен. Используя «поместное значение» цифр (позиционный принцип), мы
имеем возможность изобразить любое натуральное число с помощью
всего лишь десяти цифр в их различных комбинациях. Общее правило
такого изображения даетея схемой, которая иллюстрируется примером
где а, Ь, с, d представляют собой целые числа в пределах от нуля до
девяти. Число z в этом случае сокращенно обозначается символом
abed.
Заметим, между прочим, что коэффициенты d, с, Ь, а являются не чем
иным, как остатками при последовательном делении числа z на 10. Так,
например,
372 [10
2 ,37 [10
7_3_[10_
3 0
С помощью написанного выше выражения для числа z можно изобра-
изображать только те числа, которые меньше десяти тысяч, так как числа,
большие чем десять тысяч, требуют пяти или большего числа цифр.

30 Глава I
Если z есть число, заключенное между десятью тысячами и ста тыся-
тысячами, то его можно представить в виде
z = а • 104 4- Ь ¦ 103 + с • 102 + d ¦ 10 + е
и тогда записать символически как abode. Подобное же утверждение
справедливо относительно чисел, заключенных между ста тысячами
и одним миллионом, и т.д. Чрезвычайно важно располагать способом,
позволяющим высказать результат, к которому мы приходим, во всей
его общности посредством одной-единственной формулы. Мы можем
добиться этой цели, если обозначим различные коэффициенты е, d,
с, ... одной и той же буквой а с различными значками (индексами)
ао, а\, п2, ..., и вместе с тем то обстоятельство, что степени числа 10
могут быть сколь угодно большими, выразим тем, что высшую степень
числа 10 обозначим не 103 или 104, как в предыдущих примерах, а ста-
станем писать 10™, понимая под п совершенно произвольное натуральное
число. В таком случае любое целое число z в десятичной системе может
быть представлено в виде
z = ап ¦ 10" + an-i ¦ 10" + ... + аг ¦ 10 + а0 A)
и записано посредством символа
Как и в частном, рассмотренном выше, примере, мы обнаруживаем,
что ао, ах, а%, ... , ап являются остатками при последовательном деле-
делении z на 10.
В десятичной системе число «десять» играет особую роль как «осно-
«основание» системы. Тот, кому приходится встречаться лишь с практичес-
практическими вычислениями, может не отдавать себе отчета в том, что такое
выделение числа десять не является существенным и что роль осно-
основания способно было бы играть любое целое число, большее единицы.
Например, была бы вполне возможна семиричная система с основанием
семь. В такой системе целое число представлялось бы в виде
6п-7п + 6„_1-7"-1+... + 61-7 + Ь0, B)
где коэффициенты b обозначают числа в пределах от нуля до шести,
и оно записывалось бы посредством символа

§1. Операции над целыми числами 31
Так, число «сто девять» в семиричной системе обозначалось бы симво-
символом 214, потому что
109 = 2 • 72 4- 1 • 7 + 4.
В качестве упражнения читатель может вывести общее правило
для перехода от основания 10 к любому основанию В: нужно выполнять
последовательные деления на В, начиная с данного числа z; остатки и
будут «цифрами» при записи числа в системе с основанием В. Напри-
мер, 1Q9| 7
1 2[7_
~2 0
109 (в десятичной системе)=214 (в семиричной системе).
Естественно, возникает вопрос: не был ли бы особенно желатель-
желательным выбор какого-либо специального числа в качестве основания сис-
системы счисления? Мы увидим дальше, что слишком маленькое основа-
основание должно было бы вызвать кое-какие неудобства; с другой стороны,
слишком большое основание потребовало бы заучивания многих цифр и
знания расширенной таблицы умножения. Высказывались соображения
в пользу системы с основанием 12 («двенадцатеричной»): указывалось,
что 12 делится без остатка на два, на три, на четыре и на шесть, и по-
потому вычисления, связанные с делениями и дробями, при основании 12
были бы несколько проще. Чтобы написать произвольное число в две-
двенадцатеричной системе, понадобились бы две лишние цифры — для
обозначения чисел десять и одиннадцать. Пусть а обозначало бы де-
десять и /3 одиннадцать. Тогда в двенадцатеричной системе «двенадцать»
пришлось бы написать в виде 10, «двадцать два» в виде 1а, «двадцать
три» — в виде 1/3, «сто тридцать один» в виде а/3.
Изобретение позиционной нумерации, основанной на поместном
значении цифр, приписывается шумерийцам и вавилонянам; развита
была такая нумерация индусами и имела неоценимые последствия в ис-
истории человеческой цивилизации. Более древние системы нумерации
были построены исключительно на аддитивном принципе1. Так, в рим-
римской нумерации CXVIII обозначает «сто+десять+пять+один+один+
+один». Египетская, еврейская и греческая системы были на том же
уровне. Неудобством чисто аддитивной системы является то обстоя-
обстоятельство, что с увеличением изображаемых чисел требуется неогра-
неограниченное число новых символов. Но главнейшим недостатком древних
1На самом деле элементы «позиционности» есть и в римской нумерации, во вся-
всяком случае, порядок расположения «разрядов» играет роль; так, VI = V + I, но
IV = V - I, LX = L + X, но XL - L - X и т. п.

32 Глава I
систем (вроде римской) было то, что сама процедура счета была очень
трудна: только специалисты-профессионалы могли решать даже самые
простые задачи. Совсем иначе обстоит дело с распространенной в на-
наше время индусской «позиционной» системой. В средневековой Европе
она появилась через итальянских купцов, в свою очередь заимствовав-
заимствовавших ее у мусульман. Позиционная система обладает тем чрезвычайно
выгодным свойством, что все числа, и малые и большие, могут быть
записаны с помощью небольшого числа различных символов; в деся-
десятичной системе таковыми являются «арабские цифры» 0, 1, 2, ... , 9.
Отнюдь не меньшее значение имеет и легкость счета в этой системе.
Правила действий с числами, записываемыми по позиционному прин-
принципу, могут быть резюмированы в виде таблиц сложения и умножения
и могут быть раз и навсегда выучены на память. Старинному методу
счета, которым раньше владели лишь немногие избранные, теперь обу-
обучают разве лишь в начальных школах. В истории культуры найдется
немного примеров того, чтобы научный прогресс оказал на практичес-
практическую жизнь столь глубокое, столь облегчающее влияние.
3. Арифметические действия в недесятичных системах
счисления. Исключительная роль десятка восходит к истокам циви-
цивилизации и без всякого сомнения связана со счетом по пальцам на двух
руках. Но наименования числительных в разных языках указывают и
на наличие (в былые времена) иных систем счисления, именно с ос-
основаниями двадцать и двенадцать. В английском и немецком языках
слова, обозначающие 11 и 12, построены не по десятичному принципу,
сочетающему десятки с единицами: они лингвистически независимы от
слов, обозначающих число 10. Во французском языке слова, обозначаю-
обозначающие 20 и 80, позволяют предполагать о первоначальном существовании
системы с основанием 20, используемой для тех или иных надобностей.
В датском языке слово halvfirsindstyve, обозначающее 70, буквально пе-
переводится «пол пути от трижды двадцать до четырежды двадцать».
Вавилонские астрономы пользовались системой, частично шестидеся-
теричной структуры (с основанием 60), и предполагается, что именно
в этом обстоятельстве следует искать объяснение того факта, что час
и угловой градус подразделены на 60 минут.
В недесятичных системах счисления правила арифметики, конеч-
конечно, те же самые, но таблицы сложения и умножения однозначных чисел
отличны от наших десятичных. Будучи приучены к десятичной систе-
системе и связаны наименованиями числительных в нашем языке, мы, если
попытаемся считать по иным системам, сначала испытаем известное
неудобство. Попробуем поупражняться в умножении по семиричной

§1. Операции над целыми числами 33
системе. Прежде чем приступить к этому, рекомендуется выписать две
таблички, которыми придется пользоваться.
Сложение Умножение
1
2
3
4
5
6
1
2
3
4
5
6
10
2
3
4
5
6
10
11
3
4
5
6
10
11
12
4
5
6
10
11
12
13
5
6
10
11
12
13
14
6
10
11
12
13
14
15
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
11
13
15
3
3
6
12
15
21
24
4
4
11
15
22
26
33
5
5
13
21
26
34
42
6
6
15
24
33
42
51
Станем теперь умножать 265 на 24, причем эти числа предполага-
предполагаются написанными в септимальной системе. (Если написать числа по
десятичной системе, то речь идет об умножении 145 на 18.) Начнем
с умножения 5 на 4, что дает 26, как показывает таблица умножения.
Х265
х 24
Х563
10416
Мы пишем 6 на месте единицы, затем переносим двойку в следу-
следующий разряд. Далее, находим, что 4 • 6 = 33 и что 33 + 2 = 35. Пишем
в произведении 5 и продолжаем таким же образом, пока умножение не
закончится. При сложении чисел 1456 и 5630 на месте единиц получа-
получаем 6 + 0 + 6, затем на месте семерок 5 + 3 = 11. Пишем 1 и 1 переносим
на место «сорокадевяток», где получается 1+6 + 4 = 14. Окончательный
результат: 265 • 24 = 10 416.
Для проверки проделаем то же действие в десятичной системе.
Чтобы переписать число 10 416 по десятичной системе, придется найти
степени 7 вплоть до четвертой: 72 = 49, 73 = 343, 74 = 2 401. Отсю-
Отсюда следует, что 10416 = 2 401 + 4-49+7 + 6, причем правая часть
равенства написана уже по десятичной системе. Складывая числа, мы
находим, что число 10416, написанное по септимальной системе, рав-
равно числу 2610, написанному по десятичной. Умножим теперь 145 на 18
в десятичной системе: получается как раз 2 610, и проверка «сошлась^.
Упражнения.
1) Составьте таблицы сложения и умножения в двенадцатеричной системе
и проделайте несколько примеров вроде приведенного выше.
3 — 340

34 Глава I
2) Напишите «тридцать» и «сто тридцать три» в системах с основаниями 7,
11, 12.
3) Что обозначают символы 11 111 и 21 212 в этих системах?
4) Составьте таблицы сложения и умножения для систем с основаниями 5,
11, 13.
С теоретической точки зрения система, построенная по позици-
позиционному принципу с основанием 2, выделяется в том смысле, что это
основание — наименьшее возможное. В этой двоичной (диадической,
бинарной) системе имеются лишь две цифры: 0 и 1; всякое иное чис-
число записывается как комбинация этих символов. Таблицы сложения и
умножения сводятся к двум правилам: 1 +1 = 10 и 1 • 1 = 1. Но непрак-
непрактичность такой системы достаточно очевидна: чтобы изобразить уже
небольшие числа, нужны длинные выражения. Так, число «семьдесят
девять», которое представляется в виде 1 • 26 + 0 • 25 + 0 • 24 + 1 • 23 +
4-1 • 22 + 1 • 2 + 1, записывается в двоичной системе как 1 001111.
Чтобы проиллюстрировать, насколько просто производится умно-
умножение в диадической системе, перемножим числа семь и пять, которые
записываются соответственно в виде 111 и 101. Принимая во внимание,
что в этой системе 1 + 1 = 10, мы пишем:
111
101
111
111
100011 = 25 +2 + 1,
и в итоге, как и следовало ожидать, получается тридцать пять.
Готфрид Вильгельм Лейбниц A646-1716), один из величайших
умов своего времени, расценивал двоичную систему чрезвычайно высо-
высоко. Вот что говорит по этому поводу Лаплас: «В своей бинарной арифме-
арифметике Лейбниц видел прообраз творения. Ему представлялось, что еди-
единица представляет божественное начало, а нуль — небытие, и что Выс-
Высшее Существо создает все сущее из небытия точно таким же образом,
как единица и нуль в его системе выражают все числа».
Упражнение. Исследуйте в общем виде вопрос о представлении чисел
в системе с основанием о. Чтобы называть числа в этой системе, нужны наи-
наименования для однозначных чисел 0, 1, ... , о —1 и для различных степеней а:
а, о2, о3, .... Сколько именно числительных потребуется, чтобы назвать все
числа до одной тысячи в системах с основанием о = 2, 3, 4, 5, ... , 15? Ка-
Каково должно быть основание о, чтобы число этих имен числительных было
наименьшим? (Примеры: если а = 10, то нужно десять числительных для од-
однозначных чисел. Затем еще три числительных, обозначающих 10, 100 и 1000,

§ 2. Бесконечность системы натуральных чисел 35
всего -— 13. При о = 20 нужно двадцать числительных для однозначных чисел
и еще числительные для 20 и 400; всего — 22. При о = 100 понадобится 101
числительное.)
§ 2. Бесконечность системы натуральных чисел.
Математическая индукция
1. Принцип математической индукции. Последовательность
натуральных чисел 1, 2, 3, 4, ... не имеет конца: действительно, как
только достигается некоторое число п, вслед за ним сейчас же мож-
можно написать ближайшее к нему натуральное число п + 1. Желая как-
нибудь назвать эти свойства последовательности натуральных чисел,
мы говорим, что этих чисел существует бесконечное множество. По-
Последовательность натуральных чисел представляет простейший и са-
самый естественный пример бесконечного (в математическом смысле),
играющего господствующую роль в современной математике. Не раз
в этой книге нам придется иметь дело с собраниями, или «совокуп-
«совокупностями», содержащими бесконечное множество объектов; таковы, на-
например, совокупность всех точек на прямой линии или совокупность
всех треугольников на плоскости. Но бесконечная последовательность
натуральных чисел безусловно представляет простейший пример бес-
бесконечных совокупностей.
Последовательный, шаг за шагом, переход от п к п + 1, порож-
порождающий бесконечную последовательность натуральных чисел, вместе
с тем лежит в основе одного из важнейших и типичных для матема-
математики рассуждений, именно принципа математической индукции. «Эм-
«Эмпирическая индукция», применяемая в естественных науках, исходит
из частного ряда наблюдений некоторого явления и приходит к конста-
констатации общего закона, которому подчиняется явление в его различных
формах. Степень уверенности, с которой закон, таким образом, уста-
устанавливается, зависит от числа отдельных наблюдений и выводимых
из них заключений. Часто подобного рода индуктивные рассуждения
бывают вполне убедительными; утверждение, что солнце взойдет завт-
завтра с востока, столь несомненно, сколько это вообще возможно; и все
же характер констатации в данном случае совсем иной, чем в случае
теоремы, доказываемой на основе строгого логического, т.е. математи-
математического рассуждения.
Что касается математической индукции, то она применяется иным,
отличным способом с целью установления истинности математической
теоремы в бесконечной последовательности случаев (первого, второго,
3*

36 Глава I
третьего и так далее — без всякого исключения). Обозначим через А
некоторое утверждение, относящееся к произвольному натуральному
числу п. Пусть А будет хотя бы такое утверждение: «Сумма углов в вы-
выпуклом многоугольнике с п + 2 сторонами равна 180° • п». Или еще:
обозначим через А' утверждение: «проводя п прямых на плоскости,
нельзя разбить ее больше чем на 2" частей». Чтобы доказать подобно-
подобного рода теорему для произвольного значения п, недостаточно доказать
ее отдельно для первых 10, или 100, или даже 1000 значений п. Это
как раз соответствовало бы принципу эмпирической индукции. Вмес-
Вместо того нам приходится воспользоваться строго математическим и от-
отнюдь не эмпирическим рассуждением; мы уясним себе его характер
на частных примерах доказательства предложений, которые мы обо-
обозначили через А и А'. Остановимся на предложении А. Если п = 1,
то речь идет о треугольнике, и мы знаем из элементарной геометрии,
что сумма углов такового равна 180° • 1. В случае четырехугольника,
при п = 2, мы проводим диагональ, разделяющую четырехугольник на
два треугольника, и тогда сейчас же становится ясно, что сумма уг-
углов четырехугольника равна сумме углов в двух треугольниках, имен-
именно равна 180° + 180° = 180° ¦ 2. Обращаясь к случаю пятиугольника
(п = 3), мы разбиваем его таким же образом на четырехугольник и
треугольник. Так как первый из названных многоугольников, по до-
доказанному, имеет сумму углов 180° • 2, а второй — 180° • 1, то всего
в случае пятиугольника мы получаем сумму углов 180° • 3. И теперь
нам уже становится ясно, что рассуждение может быть продолжено со-
совершенно таким же образом неограниченно. Мы докажем теорему для
случая п = 4, затем для случая п = 5, и т.д. Как и раньше, каждое сле-
следующее заключение неизбежно вытекает из предыдущего, и теорема А
оказывается установленной при произвольном значении п.
Так же обстоит дело и с предложением А'. При п = 1 оно, очевид-
очевидно, справедливо, так как всякая прямая делит плоскость на 2 части.
Проведем вторую прямую. Каждая из двух прежних частей разобьет-
разобьется в свою очередь на две части — при условии, что вторая прямая
непараллельна первой. Но, как бы то ни было, в случае п = 2 всего ока-
окажется не более 4 = 22 частей. Добавим еще третью прямую. Каждая из
уже имеющихся частей или будет разбита на две части, или останется
нетронутой. Таким образом, число вновь полученных частей не превы-
превысит 22 • 2 = 23. Считая это установленным, мы точно так же перейдем
к следующему случаю, и т. д. — без конца.
Сущность предыдущего рассуждения заключается в том, что, же-
желая установить справедливость некоторой общей теоремы А при любых

§ 2. Бесконечность системы натуральных чисел 37
значениях п, мы доказываем эту теорему последовательно для беско-
бесконечного ряда специальных случаев Ах, А2, ... Возможность этого рас-
рассуждения покоится на двух предпосылках: а) имеется общий метод до-
доказательства того, что если справедливо утверждение Аг, то следующее
по порядку утверждение Аг+\ также справедливо; б) известно, что пер-
первое утверждение А\ справедливо. В том, что эти два условия достаточ-
достаточны для того, чтобы справедливость всех утверждений А\, А2, А3, ...
была установлена, заключается некоторый логический принцип, имею-
имеющий в математике столь же фундаментальное значение, как и класси-
классические правила аристотелевой логики.
Сформулируем этот принцип следующим образом. Предположим,
что требуется установить справедливость бесконечной последователь-
последовательности математических предложений
Ах, А2, А3, ... ,
которые все, совместно взятые, образуют некоторое общее предложе-
предложение А. Допустим, что а) проведено математическое рассуждение, по-
показывающее, что если верно Аг, то верно и Аг+1, каково бы ни было
натуральное число г, и б) установлено, что Ах верно. Тогда все пред-
предложения нашей последовательности верны и, следовательно, предложе-
предложение А доказано.
Мы примем принцип индукции без колебаний (так же, как мы при-
принимаем все правила обыкновенной логики), будем его рассматривать
как основной принцип, на котором строится математическое доказа-
доказательство. В самом деле, мы можем установить справедливость каждого
утверждения А„, исходя из допущения б) о том, что Ai справедливо,
и, многократно пользуясь допущением а), последовательно установим
справедливость утверждений А2, А3, Л4,... и т.д., пока не достигнем
утверждения Ап. Принцип математической индукции вытекает, таким
образом, из того факта, что за каждым натуральным числом г следует
(непосредственно) другое натуральное число г + 1 и что, отправляясь
от натурального числа 1, можно после конечного числе таких переходов
достигнуть любого натурального числа п.
Часто принцип математической индукции применяют без явного
о том упоминания или же просто он скрывается за формулой «и так
далее». Такая скрытая форма применения принципа индукции в осо-
особенности свойственна преподаванию элементарной математики. Но при
доказательстве иных, более тонких и более глубоких теорем этим прин-
принципом неизбежно приходится пользоваться явно. Мы приведем далее

38 Глава I
некоторое число относящихся сюда простых и все же не совсем триви-
тривиальных примеров.
2. Арифметическая прогрессия. Каково бы ни было значение п,
п „ п(п + 1)
сумма l + 2 + 3 + ... + n первых п натуральных чисел равна .
Чтобы доказать эту теорему по принципу математической индукции,
мы должны для произвольного значения п установить справедливость
соотношения Ап:
1 + 2 + 3 + .. . + n=I*Ltl>. (!)
а) Если г — некоторое натуральное число и если известно, что
утверждение АТ справедливо, т. е. если известно, что
1 + 2 + 3 + .. . + г=Г±±1±,
то, прибавляя к обеим частям последнего равенства по г + 1, мы полу-
получаем:
(г + 1)(г + 2)
а это как раз и есть утверждение Ar+i.
б) Утверждение А±, очевидно, справедливо, так как 1 = ^f~- Итак,
по принципу математической индукции утверждение Ап справедливо
при любом п, что и требовалось доказать.
Обыкновенно эту теорему доказывают иным способом. Пишут
сумму 1 + 2 + 3 + ... + п в двух видах:
Sn = n + (n- 1) + ... + 2 + 1.
Складывая, мы видим, что числа, стоящие на одной вертикали, вместе
составляют п + 1, и так как вертикалей всего имеется п, то отсюда
следует, что
25„ =п(п + 1),
и остается еще разделить на 2.

§ 2. Бесконечность системы натуральных чисел 39
Из формулы A) сразу же вытекает общая формула для суммы
/п _(_ 1) первых членов любой арифметической прогрессии:
Рп = а + (а + d) + (а + 2d) 4-... + (а + nd) = (" + 1)(|° + "d)- B)
В самом деле,
Рп = (п + 1)а + A + 2 + ... + n)d = (п + 1)о +
2(n + l)a + n(n + l)d (n + l)Ba
В случае, когда а = 0, d = 1, последнее соотношение превращается
в соотношение A).
3. Геометрическая прогрессия. Таким же образом можно
рассуждать и по поводу геометрической прогрессии (в общем виде).
Мы покажем, что, каково бы ни было п,
1 _ 0»+i
Gn = a + aq + aq2 + ... + aqn = а^~- . C)
(Мы предполагаем, что q ф 1, иначе правая часть C) лишена смысла.)
Наше утверждение, несомненно, справедливо при п = 1, так как
в этом случае
= a(l + q).
~L - ' -* l-q l-q
И если мы допустим, что
S4 V L ~ Q
Gr = a + aq + ... + ag = а—=
X — i
то, как следствие, отсюда немедленно вытекает:
Gr+1 = {a + aq + ... + aqr) + aqr+1 = GT + aqr+1 =
= a
+aq = „
l-q H \-q
r+i _ qr+2 x _ gr+2
I _ qr+\ + q q
= a = = a
l-q

40 Глава I
Но это как раз и есть утверждение C) при п = г + 1. Доказательство
закончено.
В элементарных учебниках дается другое доказательство. Поло-
Положим:
Gn = а + aq + ... + aqn.
Умножая обе части на q, получим
qGn = aq + aq2 + ... + aqn+1.
Вычитая затем последнее равенство из предпоследнего, получаем далее
Gn - qGn = а - aqn+1,
а\ s~i /-« Tl-(-l\
~ q)(jn — яA — q ),
r l-9"+1
1-9
4. Сумма п первых квадратов. Следующее интересное при-
применение принципа математической индукции относится к сумме п пер-
первых квадратов. Путем проб мы устанавливаем (по крайней мере для
кое-каких небольших значений п), что
1^2-+3^- + n^n(n + 1NBn + 1), D)
и затем естественно высказать в виде догадки утверждение, что эта за-
замечательная формула справедлива при всех целых положительных зна-
значениях п. Чтобы доказать это, воспользуемся опять методом матема-
математической индукции. Заметим прежде всего, что если утверждение Ап,
которое заключается как раз в соотношении D), справедливо при п — г,
так что
9 9 9 9 Г(Г + 1)BГ + 1)
I2 + 22 + З2 + ... + г2 = -^ g '-,
то, прибавляя к обеим частям по (г + IJ, мы получаем,
r(r + l)Br
l)Br2+7r + 6) _ (r + l)(r + 2)Br
6 ~ 6

§ 2. Бесконечность системы натуральных чисел 41
а это и есть утверждение Ar+i, так как оно получается из соотноше-
соотношения D) посредством подстановки г + 1 вместо п. Чтобы закончить до-
доказательство, достаточно обратить внимание на то, что справедливо
утверждение Аг, которое сводится к равенству
2 1A
1 =
Итак, соотношение D) верно при всех значениях п.
Подобного же рода формулы можно написать для сумм третьих
и четвертых степеней, вообще для сумм вида 1к + 2к + Зк + ... + пк,
где к — произвольное целое положительное число. В качестве упраж-
упражнения читатель может доказать с помощью математической индукции
формулу
г- т I -п 1 I 1 л i
E)
Необходимо заметить в заключение, что, хотя принципа матема-
математической индукции совершенно достаточно для того, чтобы доказать
формулу E) — раз она уже написана, однако доказательство не дает ре-
решительно никаких указаний, как прийти к самой этой формуле: почему
именно нужно догадываться, что сумма п первых кубов равна выра-
Гп(п + 1)]2
жению , а не какому-нибудь иному в таком же роде, напри-
например, —^——- или —" ~ п — и т.д. Выбор велик! Тот факт, что
L о J о
доказательство теоремы заключается в применении таких-то простых
логических правил, не оказывает ни малейшего влияния на творческое
начало в математике, роль которого — делать выбор из бесконечного
множества возникающих возможностей. Вопрос о том, как возникает
гипотеза E), принадлежит к той области, в которой нет никаких общих
правил; здесь делают свое дело эксперимент, аналогия, конструктивная
индукция. Раз только правильная гипотеза сформулирована, принципа
математической индукции часто бывает достаточно, чтобы теорема бы-
была доказана. Но так как само такое доказательство никак не указывает
пути к открытию, то его лучше было бы называть проверкой.
*5. Одно важное неравенство. В следующей главе нам пона-
понадобится неравенство
A+р)">1 + пр, F)

42 Глава I
имеющее место при всякому, удовлетворяющем условию р > —1, и при
любом целом положительном значении п. (Ради общности мы предвос-
предвосхищаем здесь применение отрицательных и нецелых чисел, предпола-
предполагая, что р может быть любым числом, большим, чем —1. Доказатель-
Доказательство неравенства — одно и то же, независимо от того, каково число р.)
Мы воспользуемся и на этот раз математической индукцией.
а) Если верно, что A + р)т ^ 1 + гр, то, умножая обе части нера-
неравенства на положительное число 1 +р, мы получаем:
{l+p)r+1 ^l + rp+p + rp2.
Отбрасывая вовсе положительный член гр2, мы только усилим это не-
неравенство; итак,
1
Полученный результат показывает, что неравенство F) имеет место и
при п = г + 1. б) Совершенно очевидно, что A + рI ^ 1 + р. Таким
образом, доказательство закончено.
Ограничение, заключающееся в условии р > — 1, существенно. Ес-
Если р < — 1, то 1 +р отрицательно, и рассуждение а) отпадает, так как
при умножении обеих частей неравенства на отрицательное число знак
неравенства должен измениться. (Например, умножая обе части нера-
неравенства 3 > 2 на —1, мы получили бы —3 > —2, а это неверно.)
*6. Биномиальная теорема. Часто бывает нужно написать
в раскрытом виде выражение для га-й степени бинома (а + Ъ)п. Непо-
Непосредственное вычисление показывает, что
при п = 1 (а + бI = а + Ь,
при п - 2 (а + ЬJ - (a + b)(a + b) =
= а(а + Ь) + Ь(а + Ь) = а2 + 2ab + Ъ2,
при п = 3 (а + бK = (а +Ь)(а + ЬJ =
= а{а2 + 2ab + Ъ2) + Ъ(а2 + 2аЬ + Ь2) =
= а3 +За2Ъ + Ш2 + Ь3,
и так далее. Но какой общий закон скрывается за словами «и так далее»?
Проанализируем процесс вычисления (а + ЬJ. Так как (а + ЪJ = (а +
+ b)(a + b), то мы получили выражение для {а + бJ, умножая каждый
член выражения а + Ь на а, затем на 6 и складывая то, что получилось.
Ту же процедуру пришлось применить при вычислении (а + ЬK = (а +
+ Ъ){а + ЬJ. Так же точно вычисляются (а + ЬL, (а + ЬM и так далее

§ 2. Бесконечность системы натуральных чисел 43
до бесконечности. Выражение для (а + Ь)п мы получим, умножая вы-
выражение (а + Ъ)п~1 сначала на а, потом на Ъ, затем складывая то, что
получится. Это приводит к следующей диаграмме:
а+Ь =
/V/ч
а + 2ab
+ + Ь
/ X / X / X
(а+ЬK= а + ЪаЬ + ЗаЬ~ + Ь3
</ \ / X / X / X
(а + Ь) = а + 4а b + 6а b + Aab + b
позволяющей сразу разобраться в общем законе составления коэффи-
коэффициентов в разложении (а + Ь)п. Мы строим треугольную схему из на-
натуральных чисел, начиная с коэффициентов 1, 1 двучлена а + Ь таким
образом, что каждое число в треугольнике является суммой двух чисел,
стоящих над ним в предыдущей строке (слева и справа). Такая схема
известна под названием треугольника Паскаля.
1
1
1 7
1
6
1
5
21
1
4
15
1
3
10
35
2
6
20
1
3
10
35
1
4
15
1
5
21
1
6
1
1
7 1
Коэффициенты в разложении (а + Ь)п по убывающим степеням а и воз-
возрастающим степеням b стоят в п-й строке этой схемы.
Так, например,
(а + ЬO = а7 + 7а6Ь + 21а5Ь2 + 35а463 + 35а364 + 21а265 + lab6 + b7.
Пользуясь очень сжатыми обозначениями с применением нижних
и верхних значков (индексов), обозначим числа, стоящие в n-й строке
треугольника Паскаля следующим образом:
Gn 1 rrn s~in /~in s~in f~in -I
О - 'i ^1) ^2i °3> •" ' ^n-1-i ^п ~ 1-
Тогда общей формуле для разложения (а + Ь)п можно придать вид:
(а + Ь)п =ап+ С?ап-1Ъ + С^ап~2Ь2 + ... + C^ab71'1 + Ьп. G)

44 Глава I
Согласно закону, лежащему в основе построения треугольника Паскаля,
мы имеем соотношение
С? = С?_-11+СГ1- (8)
В качестве упражнения читатель, имеющий уже некоторый опыт
в применении математической индукции, может воспользоваться этим
принципом, а также очевидными равенствами Сд = С\ = 1, для того
чтобы доказать общую формулу
[>
1-2-3. .Л t'(n-i)!"
[При любом целом положительном значении п символ п\ (чита-
(читается «n-факториал») обозначает произведение п первых натуральных
чисел: п\ = 1 • 2 • 4 • ... • п. Удобно также в качестве определения по-
положить 0! = 1, так чтобы формула (9) оправдывалась также и при i,
равном 0 или п.]
Выводу этой раскрытой формулы для коэффициентов биномиаль-
биномиального разложения иногда дается наименование биномиальной теоремы
(см. также стр. 539).
Упражнения.
Доказать с помощью метода математической индукции следующие равен-
1)
ства:
1,1, , 1
1-2 2-3 т"' п{п + 1) п + У
on 1,2,3. , п _ о п + 2
*3) 1 + 2q + 3<j2 + ... + ид"'1 = —
.2 , , „„n-i_ --v"-rl)g + n<z"+1
A-9J
*4) A + o)(l + o2)(l + a4). ¦ ¦ A + q2 ) = —; .
1-9
Найти сумму следующих геометрических прогрессий:
5) — 1 1-... + •
¦'^1 2 /-1 i 2\2 /-t, 2\п.
6)

2. Бесконечность системы натуральны.! чисел 45
Пользуясь формулами D) и E), доказать:
2 2 , ,2 (n
*8) I2 + З2 + ... + Bга + IJ = -
•9) I3 + З3 + ... + Bга + IK = (га + 1JBга2 + 4га + 1).
10) То же самое доказать непосредственно методом математической ин-
индукции.
7. Дальнейшие замечания по поводу метода математической
индукции. Принцип математической индукции может быть слегка об-
обобщен следующим образом: «Если имеется последовательность утвержде-
утверждений As, Aa+i, As+2, ¦ ¦¦ , где s — некоторое положительное число, и если:
а) при всяком значении г ^ s справедливость Ar+i следует из справед-
справедливости АТ, и
б) известно, что As справедливо,
то все утверждения As, j4s+i5 Ai+2,... справедливы». Иначе говоря, Ап «спра-
«справедливо при любом п ^ з». То же самое рассуждение, которое привело нас
к обыкновенному принципу математической индукции, пригодно и в данном
случае, только последовательность 1, 2, 3, ... заменяется на этот раз подоб-
подобной ей последовательностью s, s + 1, s + 2, s + 3, ....
Пользуясь принципом индукции в этой форме, мы можем несколько уси-
усилить неравенство на стр. 42, исключая возможность знака равенства. Имен-
Именно: каково бы ни было р ф 0 и > — 1 и каково бы ни было целое число п ^ 2,
имеет место неравенство
A+р)п>1 + пр. A0)
Доказательство предоставляется читателю.
С принципом математической индукции тесно связан «принцип наимень-
наименьшего целого числа», утверждающий, что во всяком непустом множестве С
натуральных чисел имеется наименьшее число. Множество С может быть ко-
конечным, как, например, множество 1, 2, 3, 4, 5, или бесконечным, как, напри-
например, множество всех четных чисел 2, 4, 6, 8, 10, .... Множество называется
пустым, если оно не содержит ни одного элемента; примером пустого мно-
множества может служить множество всех кругов, одновременно являющихся
прямыми линиями, или множество натуральных чисел га, удовлетворяющих
соотношению га > п. По понятным причинам мы оговариваем в формулировке
«принципа наименьшего целого числа», что пустые множества исключаются.
Всякое непустое множество С целых чисел непременно содержит хоть одно
число, например га, и тогда наименьшее из чисел 1, 2, 3, ... , га, принадлежа-
принадлежащее множеству С, есть наименьшее целое число множества.
Нет иного способа уяснить значение этого принципа, как указав на то
обстоятельство, что он неприменим ко множествам, состоящим из нецелых

46 Глава I
чисел; например, множество положительных дробных чисел 1, —, -, -;,..¦
2 о 4
не содержит наименьшего числа.
С чисто логической точки зрения небезинтересно отметить то обстоя-
обстоятельство, что с помощью принципа наименьшего целого числа принцип мате-
математической индукции доказывается как теорема. В самом деле, пусть име-
имеется последовательность таких утверждений Ai, A2, A3, ¦ ¦. , что
а) при любом г справедливость j4r+i вытекает из справедливости Аг,
б) известно, что А\ справедливо.
Мы докажем, что предположение о том, что хоть одно из утверждений А
несправедливо, придется отбросить. Действительно, если бы хоть одно из
утверждений А было неверным, то множество всех натуральных чисел га,
для которых Ап неверно, не было бы пустым. Тогда, согласно принципу наи-
наименьшего целого числа, оно содержало бы наименьшее число р, которое вслед-
вследствие б) должно было бы быть больше чем 1. Но тогда Ар было бы неверно,
а Ар-г верно. Это противоречит условию а).
Подчеркнем еще раз, что принцип математической индукции резко
отличается от эмпирической индукции, свойственной естественным на-
наукам. Подтверждение общего закона на конечном числе случаев (как бы
это число ни было велико) никоим образом не представляет собой дока-
доказательства в математическом смысле, даже если неизвестно ни одного
исключения. При таких обстоятельствах рассматриваемое утвержде-
утверждение, или «закон», есть не что иное, как вполне разумная гипотеза, ко-
которую могут видоизменить результаты будущих экспериментов. В ма-
математике «закон» может считаться доказанным только тогда, когда он
выведен как неизбежное логическое следствие из предпосылок, призна-
признаваемых справедливыми. Существует немало примеров математических
утверждений, которые были проверены и оправдывались во всех до на-
настоящего времени рассмотренных частных случаях, но для которых
еще не было найдено общего доказательства (см. пример на стр. 58).
Можно подозревать, что теорема справедлива во всей общности, если
она подтверждается на большом числе примеров, и тогда есть основа-
основание пытаться доказать ее с помощью математической индукции. Если
попытка удается, то тем самым справедливость теоремы устанавли-
устанавливается; в противном случае вопрос о том, верна или неверна теоре-
теорема, остается открытым, и она может быть доказана или опровергнута
когда-нибудь в будущем уже иными методами.
Применяя принцип математической индукции, необходимо всегда тща-
тщательно следить за тем, чтобы условия а) и б) были действительно выполнены.
Иначе можно иной раз прийти и к абсурду. Мы предлагаем читателю раз-
разобраться в следующем софизме. Мы «докажем» сейчас, что любые два целых
положительных числа равны между собой; например, 5 = 10. Начнем с опре-

Введение 47
деления. Если а и Ь — два неравных между собой целых положительных
числа, то через тах(о, Ь) будем обозначать о или Ь — смотря по тому, какое
из чисел больше: о или Ь; если же о = Ь, то положим тах(а, Ь) — а = Ь.
Так, тахC, 5) = тахE, 3) = 5, тогда как тахD, 4) = 4. Далее, через Ап
обозначим следующее утверждение: «Если а и Ь — два таких целых положи-
положительных числа, что тах(а, Ь) = п, то а ~ Ь».
а) Предположим, что Ат верно. Пусть а и b — два таких целых положи-
положительных числа, что тах(а, Ь) = г + 1. Рассмотрим числа
а = а-1, /3 = Ь — 1;
тогда тах(а, /3) = г. В таком случае а = /3, так как Ат верно. Но отсюда
следует, что а — Ь\ значит, верно и ^4г+1-
б) Ai, очевидно, верно, так как если тах(а, Ь) — 1, то а и Ь, по предполо-
предположению — целые положительные числа, должны быть каждое в отдельности
равны 1.
Итак, по принципу математической индукции, А„ верно при любом п.
Пусть теперь а и b — два произвольных целых положительных числа;
положим тах(а, Ъ) = г. Было показано, что Ап верно при любом п; значит,
в частности, верно Аг. Следовательно, а = Ь.
Дополнение к главе I
Теория чисел
Введение
Мистические и суеверные представления, связывавшиеся первона-
первоначально с целыми числами, мало-помалу изгладились, но среди матема-
математиков интерес к числам не ослабевал никогда. Евклид (около 300 г. до
нашей эры), громкая слава которого объясняется той частью его «На-
«Начал», которая посвящена основаниям геометрии (изучаемым в школе),
по-видимому, сделал оригинальные открытия в области теории чисел,
тогда как его геометрия в значительной степени представляет собой
компиляцию ранее полученных результатов. Диофант Александрийс-
Александрийский (около 275 г. нашей эры), один из первых алгебраистов, оставил
также след в теории чисел. Пьер Ферма A601-1665), живший в Тулузе,
по специальности юрист, вместе с тем замечательнейший математик
своей эпохи, положил начало современным теоретико-числовым изыс-
изысканиям. Эйлер A707-1783), наиболее изумительный из математиков
в смысле богатства продукции, в своих исследованиях весьма часто
углублялся в область теории чисел. Сюда же следует прибавить ряд
иных имен, знаменитых в анналах математики: Лежандр, Дирихле, Ри-
ман. Гаусс A777-1855), виднейший из математиков более близкой к нам

48 Дополнение к главе I
эпохи, в равной степени отдававший себя различным отраслям матема-
математики, как передают, следующими словами определил свое отношение
к теории чисел: «Математика — царица наук, теория чисел — царица
математики».
§ 1. Простые числа
1. Основные факты. Многие утверждения в области теории
чисел, как и математики вообще, относятся не к отдельным объектам,
скажем к числу 5 или числу 32, а к целому классу объектов, имеющих
какое-то общее свойство; примерами могут служить класс всех четных
чисел
2,4,6,8,...,
или класс чисел, делящихся на 3,
3,6,9,12,...,
или класс квадратов целых чисел
1,4,9,16,...
и так далее.
В теории чисел особенно важную роль играет класс всех простых
чисел. Очень многие числа могут быть разложены на меньшие множи-
множители: 10 = 2-5,111 = 3-37,144 = 3-3-2-2-2-2 и т. п. Числа, которые таким
образом не разлагаются, носят название простых. Точнее, простым на-
называется такое целое число р, большее чем единица, которое не имеет
иных множителей, кроме единицы и самого себя. (Число а есть множи-
множитель или делитель числа Ь, или делит число 6, если существует такое
целое число с, что Ь = ас.) Числа 2, 3, 5, 7, 11, 13, 17, ... — простые,
тогда как, например, число 12 не является простым, так как 12 = 3-4.
Значение класса простых чисел заключается в том, что каждое чис-
число может быть представлено как произведение простых: если само дан-
данное число не есть простое, то его можно последовательно разлагать на
множители до тех пор, пока все множители не окажутся простыми; так,
например, 360 = 3-120 = 3-30-4 = 3-3-10-2-2 = 3-3-5-2-2-2 = 23-32-5. Чис-
Число, отличное от 0 и 1 и не являющееся простым, называется составным.
Один из первых вопросов, возникающих по поводу класса простых
чисел, заключается в том, существует ли только конечное число раз-
различных простых чисел или же класс простых чисел содержит бесконеч-
бесконечное число членов — подобно классу всех целых чисел, частью которого

§ 1. Простые числа 49
он является. Ответ таков: простых чисел существует бесконечное мно-
множество.
Данное Евклидом доказательство существования бесконечного
множества простых чисел представляет собой типический образец ма-
математического рассуждения. В основе его лежит «косвенный метод» (до-
(доказательство от противного, приведение к нелепости). Сделаем попыт-
попытку допустить, что рассматриваемое предложение неверно. Это означало
бы, что существует лишь конечное число простых чисел, хотя, может
быть, и очень много — скажем, около миллиарда; тогда допустим, что
это число, представленное в «общей» или «неопределенной» форме, бу-
будет п. Пользуясь знаками, мы можем обозначить все простые числа
через pi,P2t •¦¦ , рп- Всякое иное число тем самым — составное и долж-
должно делиться по меньшей мере на одно из простых чисел pi, P2, ... , рп.
Сейчас мы создадим противоречие, именно, построим число А, которое
будет отлично от каждого из чисел pi, P2, ¦ ¦ ¦ , рп, так как будет больше
их всех и, тем не менее, не будет делиться ни на одно из них. Вот это
число:
A =PlP2---Pn +1-
Как видно, оно равно единице плюс произведение тех чисел, которые
образуют совокупность всех простых чисел. Число А больше, чем лю-
любое из чисел р, и потому должно быть составным. Но при делении на р\
нарг и т. д. А дает всякий раз остаток 1, таким образом, А не делится ни
на одно из чисел р. Сделанное нами допущение, что существует лишь
конечное число простых чисел, приводит, таким образом, к противо-
противоречию, так что приходится заключить, что это допущение ошибочно,
а следовательно, истинным может быть только противоположное ему.
Итак, теорема доказана.
Хотя это доказательство и «косвенного» характера, все же небольшое его
видоизменение приводит, по крайней мере теоретически, к методу построе-
построения бесконечной последовательности простых чисел. Предположим, что, ис-
исходя из некоторого простого числа, скажем р\ = 2, мы уже нашли п простых
чисел рх, р2, ... , рп; заметим, далее, что число ргр2 .. .рп + 1 — или прос-
простое, или содержит множителем простое число, отличное от тех, которые уже
найдены. Так как такой множитель всегда может быть найден (хотя бы непо-
непосредственными пробами), то в обоих названных случаях мы в итоге получаем
новое простое число pn+i', продолжая таким же образом дальше, убеждаем-
убеждаемся, что последовательность простых чисел, которые мы действительно можем
построить, не имеет конца.
Упражнение. Выполнить намеченное построение, начиная с простых
Чисел pi = 2, р2 = 3; найти еще пять простых чисел.
4 — 340

50 Дополнение к главе I
Если какое-нибудь число представлено в виде произведения прос-
простых множителей, то эти множители можно, конечно, располагать в ка-
каком угодно порядке. Занимаясь разложением чисел на простые мно-
множители, мы очень скоро приходим к заключению, что с точностью до
порядка сомножителей, разложение любого числа N на простые мно-
множители обладает свойством единственности: каждое натуральное чис-
число N, большее единицы, может быть разложено на простые множители
только одним способом. Это утверждение кажется, на первый взгляд,
таким очевидным, что неспециалист склонен обыкновенно отвергать
необходимость его доказательства. Все же рассматриваемое предложе-
предложение отнюдь не тривиально; с другой стороны, его доказательство, хо-
хотя и совсем элементарного содержания, требует более или менее тон-
тонких рассуждений. Классическое доказательство этой «основной теоре-
теоремы арифметики», данное Евклидом, базируется на методе («алгоритме»)
нахождения общего наибольшего делителя двух чисел. Этот метод бу-
будет нами рассмотрен на стр. 72. Здесь же мы вместо того приведем
доказательство менее почтенной давности, которое несколько короче,
чем доказательство Евклида, и вместе с тем выглядит несколько более
«софистическим». Оно также является типическим образцом «косвенно-
«косвенного» рассуждения. Мы допустим, что существует такое число, которое
может быть разложено на простые множители двумя существенно раз-
различными способами, и это допущение приведет нас к противоречию.
Возникновение противоречия будет свидетельствовать о том, что ги-
гипотеза существования числа, допускающего два существенно различ-
различных разложения на простые множители, несостоятельна; и отсюда мы
заключим, что разложение чисел на простые множители обладает свой-
свойством единственности.
* Если существует хоть одно число, допускающее два существенно
различных разложения на простые множители, то существует непре-
непременно и наименьшее число, обладающее таким свойством (см. стр. 45)
m=p1p2...pr = qiq2---qs, A)
где через р и q обозначены простые числа. Меняя, если потребуется,
порядок этих множителей, мы можем допустить, что
Pi ^ Рг ^ • • • ^ Pr, <7i ^ Q2 ^ ¦ ¦ ¦ ^ qg.
Заметим, что р\ отлично от q^: иначе, деля равенство A) на общий про-
простой множитель, мы получили бы два существенно различных разло-
разложения на простые множители числа, которое было бы меньше, чем тп,

§1. Простые числа 51
и это противоречило бы предложению о том, что т — наименьшее
число, обладающее таким свойством. Следовательно, одно из двух:
или pi < <?i> или Qi < Pi- Пусть pi < q\. (Если бы оказалось <?i < Pi,
то в дальнейшем рассуждении достаточно было бы поменять местами
буквы р и q.) Рассмотрим целое число
т' = т- (pi<72<?3 ... qs). B)
Подставляя вместо т его два выражения, взятые из равенства A), мы
можем представить число т' в любом из двух видов:
т' = (Pip2.--Pr) - (pi<7293 ¦••<?*) = Pi (Р2---Рг- 9293 •••<?«), C)
т/ = (<7i<?2 •••<?*) - (Рк?2<7з---<?8) = (<7i -Pi)<?2<73 •••<?«• D)
Из равенства D) следует, что т' — положительное число, так как
р! < <7i; из равенства B) следует, с другой стороны, что т' меньше
чем т. Но раз так, то разложение т! на множители должно быть един-
единственным (не говоря о порядке множителей). Из равенства C) далее
видно, что pi входит множителем в т'; значит, из равенства D) можно
в таком случае заключить, что р\ входит множителем или в qi —pi, или
в 92*73 •••'7s- (Это вытекает из единственности разложения т! на прос-
простые множители; см. рассуждение в следующем абзаце.) Но последнее
невозможно, так как все q больше чем р. Поэтому рг должно входить
множителем в qi — р\, т.е. qi — p\ должно делиться на р±. Другими
словами, существует такое целое число h, что
q\-Pi=Pi-h или q1=p1(h + l).
Но это значит, что qx делится на pi, чего, однако, быть не может, так
как, по предположению, q\ — число простое. Противоречие, к которому
мы пришли, показывает несостоятельность первоначально сделанного
допущения, и этим заканчивается доказательство основной теоремы
арифметики.
Вот одно важное следствие основной теоремы.Если простое чис-
число р входит множителем в произведение аЪ, то оно непременно входит
множителем или в а, или в Ь. В самом деле, если бы р не входило
множителем ни в а, ни в Ь, то, перемножая разложения на простые
Множители чисел а и Ь, мы получили бы разложение на простые мно-
множители числа ab, не содержащее множителя р. С другой стороны, так
как предполагается, что р входит множителем в произведение аЬ, то
это значит, что существует такое целое число t, что
аЬ = pt.
4*

52 Дополнение к главе I
Поэтому, перемножая р и разложение на простые множители числа t,
мы получим разложение на простые множители числа аЪ, содержащее
множитель р. Таким образом, приходится признать, что существует
два различных разложения числа ab на простые множители, а это про-
противоречит основной теореме.
Примеры. Если установлено, что 2 652 делится на 13 и что 2 652 =
= 6 • 442, то отсюда можно сделать заключение, что 442 делится на 13.
С другой стороны, 240 делится на 6 и притом 240 = 15-16, но ни 15, ни 16
не делятся на 6. Этот пример показывает, что условие основной теоремы
относительно того, что число р — простое, является существенным.
Упражнение. Чтобы найти все делители числа а, достаточно разло-
разложить а в произведение
где все множители р — простые и различные, причем каждый из них возво-
возводится в некоторую степень. Все делители числа а имеют вид
0 — Pi Рг ¦ • • Рт 1
где показатели C — произвольные целые числа, подчиненные условиям
Докажите это утверждение. В качестве следствия установите, что число всех
делителей а (включая 1 и само а) равно произведению
Так, например,
144 = 24 • З2
имеет 5 • 3 делителей. Вот они: 1, 2, 4, 8, 16, 3, 6, 12, 24, 48, 9, 18, 36, 72, 144.
2. Распределение простых чисел. Можно составить список
всех простых чисел, не превышающих какого-то данного числа N, сле-
следующим образом. Напишем подряд все натуральные числа от 2 до N,
затем вычеркнем все числа, являющиеся кратными 2 (не считая самого
числа 2), все числа, являющиеся кратными 3 (не считая 3), и т.д. —
пока не будут вычеркнуты все составные числа. Эта процедура, из-
известная под названием «решета Эратосфена», позволит выловить все
простые числа в пределах от 2 до N. Усовершенствования этого метода
мало-помалу привели к тому, что в настоящее время составлены вполне
надежные таблицы простых чисел примерно до 10 000 000. Они предо-
предоставляют в наше распоряжение обширнейший эмпирический материал,

§1. Простые числа 53
позволяющий судить о распределении и свойствах простых чисел. Осно-
Основываясь на этих таблицах, мы можем высказать ряд в высшей степени
правдоподобных гипотез — совершенно так, как будто бы теория чисел
была экспериментальной наукой. Часто доказательство этих гипотез
оказывается необычайно затруднительным.
а) Формулы, дающие простые числа
Были сделаны попытки найти элементарные арифметические фор-
формулы, которые давали бы только простые числа, хотя бы и не требуя
того, чтобы они давали все простые числа. Ферма высказал предполо-
предположение (не выставляя его в качестве положительного утверждения), что
все числа вида
F(n) = 22" + 1
являются простыми. В самом деле при п = 1, 2, 3, 4 мы получаем
f A) = 22 + 1 = 5,
F{2) = 22' + 1 = 24 + 1 = 17,
FC) = 22' + 1 = 28 + 1 = 257,
FD) = 22" + 1 = 216 + 1 = 65 537
— только простые числа. Но в 1732 г. Эйлер разложил на множители
число 22 +1 = 641-6 700 417; таким образом, число FE) — уже не прос-
простое. Позднее среди этих «чисел Ферма» удалось обнаружить другие со-
составные числа, причем ввиду непреодолимых трудностей, с которыми
были связаны непосредственные пробы, в каждом случае были вырабо-
выработаны более глубокие теоретико-числовые методы. В настоящее время
остается неизвестным даже то, дает ли формула Ферма бесконечное
множество простых чисел.
Вот другое простое и замечательное выражение, дающее много
простых чисел:
f(n) = п2 - п + 41.
При п = 1, 2, 3, ... , 40 f(n) есть простое число; но уже при п = 41
простого числа не получается:
/D1) = 412.
Выражение
п2 - 79п + 1601
дает простые числа до п = 79 включительно; при п = 80 получается
составное число.

54 Дополнение к главе I
В итоге можно сказать, что поиски элементарных формул, даю-
дающих только простые числа, оказались тщетными. Еще менее обнадежи-
обнадеживающей следует считать задачу нахождения такой формулы, которая
давала бы только простые числа и притом все простые числа.
Ь) Простые числа в арифметических прогрессиях
Если доказательство того, что в последовательности всех нату-
натуральных чисел п = 1, 2, 3, 4,... содержится бесконечное множество
простых чисел, носит вполне элементарный характер, то следующий
шаг в сторону таких последовательностей, как, например, 1, 4, 7, 10,
13;... или 3, 7, 11, 15, 19,..., или, вообще говоря, в сторону произ-
произвольной арифметической прогрессии а, а + d, а + 2с?, ... , а + nd, ...
(где а и d не имеют общих множителей) оказался связанным с гораз-
гораздо большими трудностями. Все наблюдения только подтверждали тот
факт, что в каждой такой прогрессии содержится бесконечное число
простых чисел, как и в простейшей из них 1, 2, 3, .... Но понадоби-
понадобились величайшие усилия для того, чтобы доказать эту общую теорему.
Успех был достигнут Леженом Дирихле A805-1859), одним из ведущих
математиков прошлого столетия, который применил при доказательст-
доказательстве самые усовершенствованные средства математического анализа из
известных в то время. Его замечательные работы в этой области даже
для настоящего времени остаются непревзойденными; прошло около ста
лет, но доказательства Дирихле все еще не упрощены настолько, что-
чтобы они могли быть поняты теми, кто не овладел полностью техникой
математического анализа и теорией функций.
Мы не будем здесь пытаться привести доказательство общей тео-
теоремы Дирихле и ограничимся рассмотрением более легкой задачи: об-
обобщим Евклидово доказательство о существовании бесконечного мно-
множества простых чисел таким образом, чтобы оно охватило некоторые
специальные прогрессии, например, 4п + 3 или 6п + 5. Рассмотрим пер-
первую из этих прогрессий. Заметим прежде всего, что всякое простое
число, большее чем 2, — непременно нечетное (иначе оно делилось бы
на 2) и, следовательно, имеет вид 4п + 1 или 4п + 3 (при целом п). Далее,
произведение двух чисел вида 4п + 1 также есть число того же вида,
так как
Dа + 1)DЬ + 1) = ЫаЬ + 4а + 46 + 1 = 4Dа6 + а + Ь) + 1.
Допустим теперь, что существует лишь конечное число простых чисел
вида 4п + 3; обозначим их pi, Р2, ... , рп и рассмотрим число
N = Цр1Р2 ... рп) - 1 = 4(pi... р„ - 1) + 3.

§1. Простые числа 55
Одно из двух: или число N — простое, или оно разлагается на произве-
произведение простых чисел, среди которых, однако, не может быть ни одного
из чисел pi, P2, • • ¦ , Рп, так как эти числа делят N с остатком — 1.
Заметим дальше, что все множители, входящие в N, не могут быть
вида Ап + 15 так как само N — не этого вида, тогда как мы видели, что
произведение чисел вида 4п + 1 является числом того же вида. Итак,
хоть один из множителей, входящих в N, должен быть вида Ап + 3,
а это невозможно, так как ни одно из чисел р не входит множителем
в N, а числами р все простые числа вида Ап + 3, по предположению,
исчерпываются. Таким образом, допуская, что существует лишь конеч-
конечное число простых чисел вида An + 3, мы приходим к противоречию,
и значит, число таких чисел бесконечно.
Упражнение. Докажите соответствующую теорему для прогрес-
прогрессии 6га + 5.
с) Теорема о распределении простых чисел
В исследованиях, связанных с законом распределения простых чи-
чисел, решительный шаг был сделан тогда, когда математики отказались
от тщетных попыток найти элементарную математическую формулу,
которая давала бы все простые числа или же точное число простых
чисел, содержащихся среди п первых натуральных чисел, и сосредото-
сосредоточили вместо того внимание на распределении в среднем простых чисел
среди всех натуральных.
При всяком целом п обозначим через Ап число простых чисел сре-
среди чисел 1, 2, 3, ... , п. Если мы выделим среди первых чисел нату-
натурального ряда
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ...
те, которые являются простыми, то не представит труда подсчитать
ряд значений Ап:
Ai =0, А2 = 1, А3 = Ai = 2, А5=А6= 3,
АТ = As = А9 = А10 — 4, Ац = Аи = 5,
Ахз = Аы = А15 = А16 = 6, Air = -4i8 = 7, Ai9 = 8 и т. д.
Возьмем теперь какую-нибудь неограниченно возрастающую по-
последовательность значений п, например,
п = 10, Ю2, 103, Ю4, ... ;

56
Дополнение к главе I
тогда соответствующие значения Ап:
, А10з, А104, ...
также будут возрастать безгранично (хотя и более медленно). Действи-
Действительно, множество простых чисел, как мы уже знаем, бесконечно, и по-
потому значения Ап рано или поздно станут больше любого назначенного
числа. «Плотность» распределения простых чисел среди п первых чи-
чисел натурального ряда дается отношением -^; не представляет особого
труда с помощью таблиц простых чисел подсчитать значения -^ при
достаточно больших значениях п:
103
106
109
0,168
0,078498
0,050847478
У
ху=\
Последняя, скажем, из выписанных строчек в приведенной табличке да-
дает вероятность того, что число, случайно выхваченное из 109 первых
чисел натурального ряда, окажется простым: всего имеется 109 воз-
возможных выборов, из них А109 соответствуют простым числам.
Распределение отдельных простых
чисел отличается чрезвычайно неправиль-
неправильным характером. Но эта неправильность
«в малом» исчезает, если мы направим
внимание к распределению «в среднем»,
находящему свое выражение в измененн-
измененной
ях отношения -~ при неограниченно рас-
растущем п. Простой закон, которому подчи-
подчиняется поведение этого отношения, следу-
следует отнести к числу самых замечательных
открытий, сделанных во всей математи-
математике. Для того чтобы сформулировать тео-
теорему о распределении простых чисел, к ко-
1
Рис. 5. Площадь заштрихо-
заштрихованной области под гипербо-
гиперболой определяет Inn
торой мы теперь подходим, необходимо предварительно разъяснить,
что такое «натуральный логарифм» числа п. Для этой цели возьмем
в плоскости две взаимно перпендикулярные оси и рассмотрим геомет-
геометрическое место таких точек на плоскости, для которых произведение
расстояний х и у от двух осей равно единице. В терминах координат х

jl. Простые числа
57
и у это геометрическое место есть равносторонняя гипербола, урав-
уравнение которой имеет вид ху = 1. Мы определим In n как площадь
(рис. 5) фигуры, ограниченной гиперболой и двумя вертикальными
прямыми х — 1 и х — п. (Более детально логарифм и его свойства будут
рассмотрены в главе VIII.) Чисто случайно, в связи с изучением табли-
цы простых чисел, Гаусс заметил, что отношение -? приблизительно
равно -т-^- и что точность этого приближения, по-видимому, улучша-
улучшается при возрастании п. Насколько удовлетворительно приближение,
А Л
можно судить по отношению -^- : у-5—, значения которого при п=1000,
1000 000, 1000 000 000 показаны в следующей табличке:
п
103
106
109
Ап
п
0,168
0,078498
0,050847478
1
logn
0,145
0,072 382
0,048 254 942
Ап . l
п logn
1,159
1,084
1,053
Основываясь на такого рода эмпирической очевидности, Гаусс высказал
в качестве предположения, что отношение —2- «асимптотически рав-
. Смысл этого утверждения заключается в следующем: если
но»
In п
возьмем последовательность значений п, становящихся все больше и
больше, например,
10, 102, 103, 104,...
(как мы делали и раньше), то отношение
1
п
In
вычисляемое для этих последовательно рассматриваемых значений п,
будет становиться все более и более близким к числу 1, а именно, раз-
разность между указанным отношением и единицей будет делаться столь
малой, сколь будет назначено, лишь бы только мы рассматривали до-
достаточно большие значения п. Такого рода соотношение символически
А
выражается знаком ~: —2-
п
Ап
1
-г^— означает, что
In п п
1
In п
при воз-
возрастании п стремится к 1. Что знак ~ не может быть заменен знаком
обыкновенного равенства (=), ясно хотя бы из того факта, что Ап —
непременно целое число, тогда как
In п
не является таковым.

58 Дополнение к главе I
То обстоятельство, что распределение простых чисел хорошо опи-
описывается с помощью логарифмической функции, нельзя не признать
поистине поразительным, так как здесь вступают в тесное соприкос-
соприкосновение два математических понятия, казалось бы, не имеющие друг
к другу никакого отношения.
Хотя схватить содержание высказанного Гауссом предположения
не представляет особой трудности, однако его строгое математическое
доказательство во времена Гаусса было за пределами возможностей ма-
математической науки. Для того чтобы доказать теорему о распределении
простых чисел, говорящую лишь о самых элементарных математичес-
математических понятиях, неизбежно нужно прибегнуть к самым мощным методам
современной математики. Пришлось ждать почти сто лет, пока анализ
получил достаточное развитие для того, чтобы Адамар A896) в Пари-
Париже и Валле-Пуссен A896) в Лувэне смогли дать исчерпывающее дока-
доказательство теоремы о распределении простых чисел. Упрощения и важ-
важные дополнения были затем внесены Мангольдтом и Э. Ландау. Задолго
до Адамара значительное продвижение в этой области было сделано
Риманом A826-1866) в его знаменитой работе, намечающей основные
стратегические линии предстоящей атаки. Совсем недавно американ-
американский математик Норберт Винер сумел видоизменить доказательство
таким образом, чтобы избежать применения комплексных чисел в уз-
узловых моментах проводимых рассуждений. Но все же доказательство
теоремы о распределении простых чисел остается слишком сложным
для того, чтобы его можно было предложить начинающему. Мы вер-
вернемся к этому вопросу на стр. 548 и следующих.
d) Две еще не решенные задачи о простых числах
Если проблема распределения простых чисел («в среднем») была
разрешена удовлетворительно, то справедливость ряда других гипотез,
эмпирически совершенно несомненная, все еще не доказана.
Сюда относится прежде всего знаменитая гипотеза Гольдбаха.
Гольдбах A690-1764) сам по себе не оставил никакого следа в исто-
истории математики: он прославился только проблемой, которую предло-
предложил Эйлеру в письме, относящемся к 1742 г. Он обратил внимание на
тот факт, что ему всегда удавалось представить любое четное число
(кроме 2, которое само есть простое число) в виде суммы двух прос-
простых. Например, 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 +5, 12 = 5 + 7,
14 = 7 + 7, 16 = 13 + 3, 18 = 11 + 7, 20 = 13 + 7, ..., 48 = 29 + 19, ...,
100 = 97 + 3, и т. д.

§1. Простые числа 59
Гольдбах спрашивал у Эйлера, может ли он доказать, что такого
пода представление возможно для всякого четного числа, или же, на-
напротив, сможет указать пример, опровергающий такое предположение.
Эйлер так и не дал ответа; не дал его никто и в дальнейшем. Эмпири-
Эмпирическая очевидность гипотезы Гольдбаха, как легко проверить, вполне
убедительна. Источник же возникающих затруднений — в том, что по-
понятие простого числа определяется в терминах умножения, тогда как
сама проблема касается сложения. Вообще, находить связи между муль-
мультипликативными и аддитивными свойствами чисел очень трудно.
До недавнего времени доказательство гипотезы Гольдбаха каза-
казалось задачей совершенно неприступной. Сегодня дело обстоит уже не
так. Очень значительный успех, оказавшийся неожиданным и порази-
поразительным для всех специалистов по данному вопросу, был достигнут
в 1931 г. тогда неизвестным молодым русским математиком Шнирель-
маном A905-1938), который доказал, что всякое целое положительное
число может быть представлено в виде суммы не более чем 800 000
простых. Хотя этот результат и производит несколько комическое впе-
впечатление (по сравнению с первоначально поставленной целью доказать
гипотезу Гольдбаха), тем не менее он представлял первый шаг в долж-
должном направлении. Доказательство Шнирельмана — прямое и носит кон-
конструктивный характер, хотя и не обеспечивает практического метода
для представления произвольного целого числа в виде суммы простых.
Еще позднее русский же математик Виноградов, пользуясь методами
Гарди, Литтлвуда и их поистине великого сотрудника по работе ин-
индуса Рамануджана, сумел понизить число слагаемых в формулиров-
формулировке Шнирельмана с 800 000 до 4. Это уже гораздо ближе к решению
проблемы Гольдбаха. Но существует очень резкое различие между ре-
результатами Шнирельмана и Виноградова: более резкое, чем различие
между числами 800 000 и 4. Теорема Виноградова была им доказана
лишь для всех «достаточно больших» чисел; точнее говоря, Виногра-
Виноградов установил существование такого числа N, что всякое целое чис-
число п > N может быть представлено в виде суммы четырех простых
чисел. Метод Виноградова не позволяет никак судить о величине N;
в противоположность методу Шнирельмана он — существенно «кос-
«косвенный» и неконструктивный. По существу Виноградов доказал сле-
следующее: допуская, что существует бесконечное множество чисел, не
представимых в виде суммы четырех (или менее того) простых чи-
чисел, можно получить противоречие. Здесь перед нами прекрасный при-
пример, показывающий глубокое различие между двумя типами доказа-

60 Дополнение к главе I
тельств — прямым и косвенным (см. общее обсуждение этого вопроса
на стр. 49I.
Следующая проблема, еще более любопытная, чем проблема Гольд-
Гольдбаха, нисколько не приблизилась к своему разрешению. Было подмече-
подмечено, что простые числа нередко встречаются парами в виде р и р + 2. Та-
Таковы 3 и 5,11 и 13, 29 и 31 и т. д. Предположение о существовании беско-
бесконечного множества таких «близнецов» кажется весьма правдоподобно,
но до сих пор не удалось даже приблизиться к его доказательству.
§ 2. Сравнения
1. Общие понятия. Всякий раз, как приходится говорить о де-
делимости целых чисел на некоторое определенное целое число d, все
рассуждения становятся яснее и проще, если пользоваться отношением
сравнения, введенным Гауссом, и соответствующими обозначения.
Чтобы ввести понятие сравнения, рассмотрим остатки, получаю-
получающиеся при делении различных чисел, например, на 5. Мы получаем:
0 =0-5-
1 =0-5-
2 = 0-5-
3 =0-5-
4 =0-5-
5 =1-5-
6 = 1-5H
hO
(-1
h2
h3
h4
hO
hi
7 =1-5-
8 =1-5-
9 =1-54
10 =2-5H
11 =2-5H
12 = 2-5H
и т.д.
h2
h3
h4
hO
hi
h2
-1 = -1-5-
-2 = -1-5-
-3 = -1-5-
-4 = -1-5-
_5 = -1-5-
-6 = -2-5-
и т.д.
h4
h3
h2
hi
hO
h4
1Основной результат И.М.Виноградова A937) устанвливает существование та-
такого натурального N, что всякое нечетное п > N представимо в виде суммы трех
простых чисел:
п = Pi +Р2 + Рз, E)
из чего, разумеется, вытекает уже представимость любого натурального п > N + 2
в виде суммы четырех простых чисел. Результат Виноградова о нечетных числах
окончателен — число слагаемых C) в его формулировке уменьшить нельзя. Что же
касется четных чисел, то из представимости их в виде A) вытекала бы сразу и пред-
представимость любого четного п в виде суммы двух простых слагаемых (т. к. в этом
случае одно из слагаемых равно 2). Однако при всей правдоподобности гипотезы
о представимости в таком виде любого четного п > 3, проблема ее доказательства
чрезвычайно трудна и превышает, по-видимому, еще возможности математиков.
Неэффективный характер теоремы Виноградова устранен в 1939 г. К. Г. Борозд-
е41,9в
киным, показавшим, что в виде A) представимо любое нечетное п > С = ее ;
в 1956 г. ему же удалось снизить эту оценку до С = ее . Конечно, уменьшение кон-
константы С до разумных пределов позволило бы решить гипотезу о представимости
в виде A) нечетных п, 6 < п < С, — и тем самым любого нечетного п > 6 —
посредством прямой вычислительной проверки. (А. Н.К.)

§2. Сравнения 61
Заметим, что остатком при делении на 5 может быть только одно из
чисел 0, 1, 2, 3, 4. Говорят, что два числа а и b сравнимы по модулю 5,
если при делении на 5 они дают один и тот же остаток. Так, все чис-
числа 2, 7, 12,17, 22, ... , -3, -8, -13, -18, ... сравнимы по модулю 5, так
как при делении на 5 все они дают остаток 2. Вообще, говорят, что два
числа а и Ь сравнимы по модулю d (где d — некоторое целое число), если
при делении на d они дают один и тот же остаток; другими словами,
если существует такое целое число п (положительное, отрицательное
или нуль), что а — Ь = nd. Например, 27 и 15 сравнимы по модулю 4,
так как
27 = 6-4 + 3, 15 = 3-4 + 3.
Для отношения сравнения введено специальное обозначение — ес-
если а и Ь сравнимы по модулю d, то пишут: a = b (mod d). [Если же а не
сравнимо с b по модулю d, то пишут a^b (mod d).] Если ясно, какой
модуль имеется в виду, то приписку «mod d» опускают.
Сравнения часто встречаются в повседневной жизни. Например,
часовая стрелка указывает время по модулю 12; автомобильный счет-
счетчик отмечает пройденные расстояния по модулю 100 000 (миль или
километров).
Прежде чем перейти к более детальному рассмотрению сравнений
и их свойств, пусть читатель проверит, что следующие утверждения
в точности эквивалентны:
1. а сравнимо с b по модулю d.
2. а = b + nd, где п — целое.
3. а — b делится на d.
Введенные Гауссом обозначения для сравнений подчеркивают то
обстоятельство, что сравнения обладают многими свойствами обычных
равенств. Напомним эти свойства:
1) Всегда а = а.
2) Если а = Ь, то b = а.
3) Если а = b и b = с, то а = с.
Кроме того, если а = а' и b = b', то
4) а + Ъ = а' + Ъ'.
5) а - Ъ = а' - Ъ'.
6) аЪ = а'Ъ'.
Эти же свойства сохраняются, если соотношение равенства а = b
заменяется соотношением сравнения а = а (mod d). Именно:
1') Всегда а = a (mod d).
2') Если a = b (mod d), то b = a (mod d).
3') Если a = b (mod d), то b = с (mod d), то а = с (mod d).

62
Дополнение к главе I
(Проверьте! — это нетрудно.)
Точно так же, если а = а' (mod d) и b = b' (mod d), то
4') a + b = a' +b' (mod d).
5') a~b = a' -b' (mod d).
6') ab = a'b' (modd).
Таким образом, сравнения по одному и тому же модулю можно склады-
складывать, вычитать и умножать. В самом деле, из
а = а' + rd, b = b' + sd
вытекают:
a + b = a' + b' + (r + s)d,
a-b= a' -b' + (r - s)d,
ab = a'b' + (a's + b'r + rsd)d,
что и приводит к нужным заключениям.
-3 -2 -1
О
1
Рис. 6. Геометрическое представление целых чисел
Сравнения допускают великолепное гео-
геометрическое представление. Если хотят
дать геометрическое представление целым
числам, то обыкновенно выбирают прямо-
прямолинейный отрезок единичной длины и затем
откладывают кратные отрезки в обе сторо-
стороны. Таким образом, для каждого целого чис-
числа получается соответствующая ему точка
на прямой — числовой оси (рис. б). Но если
приходится иметь дело с числами по дан-
данному модулю d, два сравнимых числа —
поскольку речь идет о делимости на d —
рассматриваются как нечто неразличимое,
так как дают одни и те же остатки. Чтобы
изобразить все это геометрически, возьмем
окружность, разделенную на d равных час-
частей. Всякое целое число при делении на d
дает в качестве остатка одно из чисел 0, 1,
2, ... , d — 1: эти числа мы и расставим по
окружности на равных расстояниях. Каждое число сравнимо с одним из
Рис. 7. Геометрическое
представление целых чисел
по модулю 6

§2. Сравнения 63
этих чисел по модулю d и, следовательно, представляется соответству-
соответствующей точкой; два числа сравнимы, если изображаются одной и той же
точкой. Рис. 7 сделан для случая d = 6. Циферблат часов может также
служить моделью.
В качестве примера применения мультипликативного свойства
сравнений 6') определим остатки, получающиеся при делении на одно и
то же число последовательных степеней числа 10. Так как 10 = -1 + 11,
то
10 = —1 (mod 11).
Умножая многократно это сравнение само на себя, получаем дальше
102 = (-1)(-1) = 1 (mod 11),
103 = (-1) (mod 11),
104 = 1 (mod 11)
и т.д.
Отсюда можно заключить, что всякое целое число, запись по десятич-
десятичной системе которого имеет вид:
z = а0 + ai ¦ 10 + а2 ¦ Ю2 + ... + ап • 10",
дает тот же остаток при делении на 11, что и сумма его цифр, взятая
с чередующимися знаками
t = по — щ + а,2 — ¦ ¦ ¦
В самом деле, мы имеем:
z - t = ах ¦ 11 + а2(Ю2 - 1) + а3A03 + 1) + а4A04 - 1) + ...
Так как все выражения 102 — 1, 103 + 1, ... сравнимы с нулем по моду-
модулю 11, то z — t также сравнимо с нулем, и потому z при делении на 11
дает тот же остаток, что и t. В частности, число делится на 11, т. е. дает
остаток 0 при делении в том и только в том случае, если знакочереду-
знакочередующаяся сумма его цифр делится на 11. Например, число z = 3162 819
делится на 11, так как 3-1 + 6-2 + 8-1 + 9 = 22 делится на 11.
Найти таким же образом правило делимости на 3 или на 9 еще проще,
так как 10= 1 (mod 3 и 9), и потому 10™ = 1 (mod 3 и 9) при любом п.
Отсюда следует, что число z делится на 3 и на 9 в том и только в том
случае, если сумма его цифр
s = а0 + ai + а2 + • ¦. + ап
Делится соответственно на 3 и на 9.

64 Дополнение к главе I
Если в качестве модуля возьмем 7, то получим
10 = 3, 102 = 2, 103 = -1, 104 = -3, 105 = -2, 106 = 1.
Далее остатки повторяются. Таким образом, z делится на 7 в том и
только в том случае, если выражение
г = а0 + За! + 2а2 — аз — 3«4 - 2а5 + а6 + За7 + ...
делится на 7.
Упражнение. Найти подобный же признак делимости на 13.
Складывая и умножая сравнения по определенному модулю, ска-
скажем, d = 5, можно всегда обеспечить то, чтобы входящие числа не
становились слишком большими, заменяя всякий раз встречающееся
число одним из чисел
0, 1, 2, 3, 4,
а именно тем, с которым оно сравнимо. Так, вычисляя суммы и про-
произведения различных чисел по модулю 5, нужно только пользоваться
следующими таблицами сложения и умножения:
6=0
a=Q
1
2
3
4
0
1
2
3
4
a +
1
1
2
3
4
0
6
2
2
3
4
0
1
3
3
4
0
1
2
4
4
0
1
2
3
6=0
a=.O
1
2
3
4
0
0
0
0
0
ab
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
Из второй таблицы видно, что произведение ab сравнимо с нулем по
модулю 5 только в том случае, если а или 6 = 0 (mod 5). Это наводит
на мысль о существовании следующего общего закона:
7) а6 = 0 (mod d) только в том случае, если а = 0 или 6 = 0 (mod d),
что является распространением хорошо известного свойства обыкно-
обыкновенного умножения:
ab = 0 только в том случае, если а = 0 или 6 = 0.
Но закон 7) действителен только при том условии, что модуль d
есть простое число. Действительно, сравнение
ab = 0 (mod d)

§2. Сравнения 65
означает, что ab делится на d, а мы уже видели, что произведение ab
делится на простое d в том и только в том случае, если один из мно-
множителей а или b делится на d, т. е. если
а = 0 (mod d) или 6 = 0 (mod d).
С другой стороны, закон теряет силу при d составном: можно тогда
написать d = г ¦ s, где оба множителя г и s меньше, чем d, так что
r^O (modd), s^O (mod d)
и, однако,
rs = d = 0 (mod d).
Например, 2^0 (mod 6) и 3^0 (mod 6), но 2-3 = 6 = 0 (mod 6).
Упражнение. Покажите, что имеет место следующее правило сокра-
сокращения на простой множитель.
Если ab = ас и а ^ 0, то Ъ = с.
Упражнения.
1) С каким числом в пределах от 0 до 6 включительно сравнимо число
11 • 18 • 2322 -13-19 по модулю 7?
2) С каким числом в пределах от 0 до 12 включительно сравнимо число
3 • 7 • 11 • 17 • 19 • 23 • 29 • 113 по модулю 13?
3) С каким числом в пределах от 0 до 4 включительно сравнима сумма
1 + 2 + 22 + ... + 219 по модулю 5?
2. Теорема Ферма. В XVII столетии Ферма, основатель совре-
современной теории чисел, открыл чрезвычайно важную теорему. Если р —
простое число, не делящее целого числа а, то
а"-1 = 1 (mod p).
Другими словами, (р - 1)-я степень а при делении на р дает остаток 1.
Некоторые из ранее произведенных нами вычислений подтвержда-
подтверждают эту теорему: так, мы видим, что 106 = 1 (mod 7), 102 = 1 (mod 3)
и 1010 = 1 (mod 11). Таким же образом легко проверить, что
212 = 1 (mod 13) и 510 = 1 (mod 11). Для этой цели нет необходимости
на самом деле вычислять столь высокие степени данных чисел; доста-
достаточно использовать мультипликативное свойство сравнений:
24 = 16ee3 (mod 13), 52 = 3 (mod 11),
28 = 9 = -4 (mod 13), 54 = 9 =-2 (mod 11),
212 =-4-3=-12 = 1 (mod 13), 58 = 4 (mod 11),
510 = 3-4 =12 = 1 (mod 11).
5 — 340

66 Дополнение к главе I
Обращаясь к доказательству теоремы Ферма, рассмотрим числа,
кратные а:
mi = а, Ш2 = 2а, тз = За, ... , rap_i = (р — 1)а.
Никакие два из этих чисел не могут быть между собой сравнимы по
модулю р. В противном случае р должно было бы делить разность
тпГ — ms = (г — s)a, где г, s была бы пара целых чисел, подчиненных
ограничению 1 ^ г < s ^ (р — 1). Но из закона 7) следует, что этого
не может случиться: так как s — г меньше, чем р, то р не делит s — г;
с другой стороны, по предположению, р не делит и а. Таким же образом
мы убеждаемся, что ни одно из чисел га не сравнимо с нулем. Отсюда
следует, что числа rai, ГП2, ... , rap_i соответственно сравнимы с чис-
числами 1, 2, ... ,р — 1, взятыми в некоторой их перестановке. Дальше
заключаем:
m1m2...mp-1 = 1 -2-3... (р- l)ap-1 =l-2-3...(p-l) (mod p),
или же, полагая ради краткости К = 1 • 2 • 3... (р — 1),
#(ар-х -1)=0
Число К не делится на р, так как ни один из входящих в него множи-
множителей не делится на р; значит, согласно закону 7), (а*^1 - 1) должно
делиться на р, т. е.
а"'1 -1 = 0 (mod p).
Это и есть теорема Ферма.
Проверим эту теорему еще раз. Возьмем р = 23 и а = 5; тогда
получаем по модулю 23 52 = 2, 54 = 4, 58 = 16 = -7, 516 = 49 = 3, 520 = 12,
522 =24=1. Если возьмем а = 4 вместо 5, то будем иметь, опять-таки по
модулю 23, 42 = -7, 43 = -28 = -5, 44 = -20 = 3, 48 = 9, 4п = -45=1, 422 =
= 1. В примере, где было взято а = 4,р = 23 (как и во многих иных),
можно заметить, что не только (р — 1)-я степень, но и более низкая
степень а уже оказывается сравнимой с единицей. Наименьшая такая
степень — в нашем примере степень 11 — непременно есть делитель
числа р - 1 (см. ниже упражнение 3).
Упражнения.
1) С помощью подобных же вычислений проверить, что
28 = 1 (mod 17); 3s = -1 (mod 17); З14 = -1 (mod 29);
214 = -1 (mod 29); 414 = 1 (mod 29); 514 = 1 (mod 29).

§2. Сравнения 67
2) Проверить теорему Ферма, взяв р = 5, 7, 11, 17 и 23 и придавая числу а
различные значения.
3) Доказать общую теорему: Наименьшее число е, для которого
а" = 1 (mod р), должно быть делителем р — 1. [Указание: произвести
деление р — 1 на е, получая
р — 1 = ке + г,
где 0 ^ г < е, и дальше воспользоваться тем обстоятельством,
qToaP-^^EEl (modp).]
3. Квадратические вычеты. Обращаясь снова к примерам, ил-
иллюстрирующим теорему Ферма, мы можем подметить, что не только
всегда справедливо сравнение ар~1 = 1 (mod р), но (предположим, что р
есть простое число, отличное от 2, значит, — нечетное, р = 2р' + 1) при
некоторых значениях а справедливо также сравнение ар = а^р~1^2 = 1
(modj!?). Это обстоятельство вызывает ряд заслуживающих внимания
соображений. Теорему Ферма можно записать в следующем виде:
а"'1 - 1 = а2"' - 1 = (</ - 1)(ар> + 1) = 0 (mod p).
Так как произведение делится на р только в том случае, если один из
множителей делится на р, то, значит, одно из чисел ар — 1 или ар + 1
должно делиться на р; поэтому, каково бы ни было простое число р > 2
и каково бы ни было число а, не делящееся на р, непременно должно
иметь место одно из двух сравнений:
Начиная с самого возникновения современной теории чисел, мате-
математики были заинтересованы выяснением вопроса: для каких чисел а
оправдывается первое сравнение, а для каких — второе? Предположим,
что а сравнимо по модулю р с квадратом некоторого числа х,
а = х2 (modp).
Тогда а(р~^>12 =хр~г, и согласно теореме Ферма правая, а следователь-
следовательно, и левая части сравнения должны быть сравнимы с 1 по модулю р.
Такое число а (не являющееся кратным р), которое по модулю р срав-
сравнимо с квадратом некоторого числа, называется квадратическим выче-
вычетом р; напротив, число 6, не кратное р, которое не сравнимо ни с каким
квадратом по модулю р, называется квадратическим невычетом р. Мы
только что видели, что всякий квадратический вычет а числа р удов-
удовлетворяет сравнению а^'/2 = 1 (mod p). Довольно легко установить,
5*

68 Дополнение к главе I
что всякий невычет b числа р удовлетворяет сравнению ft(P-1)/2 = —1
(modp). Кроме того, мы покажем (несколько дальше), что среди чи-
чисел 1, 2, 3, ... , р— 1 имеется в точности ?-^— квадратических вычетов
р-1
и —-— невычетов.
Хотя с помощью прямых подсчетов можно было собрать нема-
немало эмпирических данных, но открыть сразу общие законы, регулиру-
регулирующие распределение квадратических вычетов, было нелегко. Первое
глубоко лежащее свойство этих вычетов было подмечено Лежандром
A752-1833); позднее Гаусс назвал его законом взаимности. Этот закон
касается взаимоотношения между двумя различными простыми чис-
числами р и q. Он заключается в следующем:
1) Предположим, что произведение ^-^— • —~ четное. Тогда q
есть вычет р в том и только в том случае, если р есть вычет q.
2) Предположим, напротив, что указанное произведение — нечет-
нечетное. Тогда ситуация резко меняется: q есть вычет р, если р есть невы-
невычет q, и наоборот.
Первое строгое доказательство закона взаимности, долгое время
остававшегося гипотезой, данное Гауссом еще в молодости, явилось од-
одним из крупных его достижений. Доказательство Гаусса никоим обра-
образом нельзя назвать простым, и в наше время провести доказательство
закона взаимности стоит известного труда, хотя количество различных
опубликованных доказательств очень велико. Истинный смысл закона
взаимности вскрылся лишь в недавнее время — в связи с новейшим
развитием алгебраической теории чисел.
В качестве примера, иллюстрирующего распределение квадрати-
квадратических вычетов, возьмем р = 7. Так как по модулю 7
02=0, 12 = 1, 22=4, 32=2, 42 = 2, 52 = 4, б2 = 1
и так как дальнейшие квадраты повторяют эту последовательность, то
квадратическими вычетами числа 7 являются числа, сравнимые с 1, 2
и 4, а невычетами — числа, сравнимые с 3, 5 и 6. В общем случае квад-
ратические вычеты р составляются из чисел, сравнимых с числами I2,
22, ... , (р — IJ. Но эти последние попарно сравнимы, так как
х2 = (р — хJ (modp) (например, 22 = 52 (mod 7)).
Действительно, (р — хJ = р2 — 2рх + х2 = х2 (mod p). Значит, поло-
половина чисел 1,2, ... , р — 1 представляет собою квадратические вычеты
числа р, а другая половина — невычеты.

§3. Пифагоровы числа и большая теорема Ферма 69
Чтобы дать иллюстрацию также и закону взаимности, поло-
положим р — 5, q = 11- Так как 11 = I2 (mod 5), то 11 есть квадратический
вычет по модулю 5, и так как, кроме того, произведение — — —
четное, то, согласно закону взаимности, 5 должно быть также квад-
ратическим вычетом по модулю 11; и в самом деле, мы видим, что
5 = 42 (mod 11). С другой стороны, положим р = 7, q = 11. Тогда про-
7-1 11-1 •• ЛЛ
изведение —ц— • —¦= нечетное, и в этом случае 11 есть вычет по
модулю 7 (так как 11 = 22 (mod 7)), а 7 — невычет по модулю 11.
Упражнения.
1) б2 = 36 = 13 (mod 23). Является ли 23 квадратическим вычетом по
модулю 13?
2) Мы видели, что х2 = (р — хJ (mod р). Покажите, что иного вида срав-
сравнений между числами I2, 22, З2, ... , (р — IJ быть не может.
§ 3. Пифагоровы числа и большая теорема Ферма
Интересный вопрос из области теории чисел связан с теоремой Пи-
Пифагора. Теорема эта, как известно, алгебраически выражается равен-
равенством
а2 + Ь2 = с2, A)
где а и Ь — длины катетов, ас — длина гипотенузы. Проблема разыска-
разыскания всех прямоугольных треугольников, стороны которых выражаются
целыми числами, таким образом, эквивалентна проблеме нахождения
всех решений (а, Ь, с) в целых числах уравнения A). Каждая тройка це-
целых чисел (а, Ь, с), удовлетворяющих этому уравнению, носит название
пифагоровой тройки.
Все пифагоровы тройки могут быть найдены довольно просто.
Пусть целые числа a, b и с образуют пифагорову тройку, т.е. связа-
связаны соотношением а2 + Ь2 = с2. Положим ради краткости ° = х, | = у.
Тогда ж и у — рациональные числа, связанные равенством х2 + у2 = 1.
Из последнего следует у2 = A — а;)A +х) или -т-^— = ~ х. Общее зна-
значение двух отношений в полученной пропорции есть число t, которое
может быть представлено как отношение двух целых чисел j*. Можно,
далее, написать: у = t(l + х) и A — х) = ty, или же
tx - у = —t, х + ty = 1.

70 Дополнение к главе I
Из полученной системы уравнений немедленно следует, что
1 - t2 2t
х =
Ъ
Подставляя | и | вместо х и у и ^ вместо ?, будем иметь:
а
с
V2
V2
-
+
ы2
Ъ
с
2uv
«2 +V2
Отсюда вытекает:
a = (v2~u2)r, b=Buv)r, c=(u2+v2)r, B)
где г — некоторый рациональный множитель пропорциональности.
Итак, если числа (а, Ь, с) образуют пифагорову тройку, то они соответ-
соответственно пропорциональны числам вида v2 — и2, 2uv, и2 + г»2. Обратно,
легко проверить, что всякие три числа (а, Ь, с), определенные равенст-
равенствами вида B), образуют пифагорову тройку, так как из равенств B)
следует
а2 = (и4-2и2ь2+У*)г2,
Ъ2 = Du2v2)r\
c2 = (u4 + 2u2v2 + v4)r\
так что а2 + Ь2 = с2.
Этот результат можно несколько упростить. Из некоторой пифаго-
пифагоровой тройки (а, Ь, с) легко выводится бесконечное множество других
пифагоровых троек (sa, sb, sc), каково бы ни было целое положитель-
положительное s. Так, из C, 4, 5) получаются F, 8, 10), (9, 12, 15) и т.д. Такие
тройки не являются существенно различными, так как соответству-
соответствуют подобным треугольникам. Мы условимся говорить о примитивной
пифагоровой тройке, если числа a, b и с не имеют общего множителя.
Можно показать, что формулы
а — v2 — и2, b = 2uv, с = и2 + v2,
где и и v — произвольные целые положительные числа (v > и), не име-
имеющие общих множителей и не являющиеся одновременно нечетными,
дают нам все примитивные пифагоровы тройки.
Упражнение. Докажите последнее утверждение.
Вот примеры примитивных пифагоровых троек:
v = 2, и = 1 : C, 4, 5), v = 4, и = 3 : G, 24, 25),
v = 3, и = 2 : E, 12, 13), v = 10, и = 7 : E1, 140, 149) и т. д.

§3. Пифагоровы числа и большая теорема Ферма 71
В связи с рассмотрением пифагоровых чисел более или менее естес-
естественно возникает вопрос о возможности следующего обобщения зада-
задачи: можно ли найти такие целые положительные числа а, Ь, с, которые
удовлетворяли бы уравнению а3 + Ь3 = с3, или уравнению а4 + Ь4 = с4
или, вообще говоря, уравнению
ап + Ьп = с", C)
где показатель п — целое число, большее 2? Ответ был дан Ферма,
который пришел к нему умозрительным путем. Ферма изучал одно со-
сочинение Диофанта, известного математика древности, занимавшегося
теорией чисел, и имел обыкновение делать примечания на полях книги.
Хотя он не затруднял себя тем, чтобы приводить тут же доказательст-
доказательства многих высказанных им теорем, но все они постепенно в дальней-
дальнейшем были доказаны — за одним весьма значительным исключением.
По поводу пифагоровых чисел Ферма сделал пометку, что уравнение C)
неразрешимо в целых числах, если п > 2, но что найденное им остро-
остроумное доказательство этой теоремы слишком длинно, чтобы его можно
было поместить на полях книги, с которой он работал.
Это утверждение Ферма в его общей форме никогда и никем впо-
впоследствии не было ни доказано, ни опровергнуто, несмотря на усилия
целого ряда крупнейших математиков. Правда, теорема была доказана
для очень многих значений п, в частности, для всех п < 619, но не для
всех возможных значений п; вместе с тем не было указано и примера,
опровергающего теорему. Хотя сама по себе теорема и не имеет очень
большого значения в математическом смысле, но попытки доказать ее
положили начало многим важнейшим исследованиям в области теории
чисел. Проблема вызвала большой интерес и в более широких кругах, —
отчасти благодаря премии размером в 100 000 марок, предназначенной
для лица, которое впервые даст решение, причем присуждение премии
было поручено Геттингенской Академии. Пока послевоенная инфляция
в Германии не свела на нет денежную ценность этой премии, ежегодно
представлялось громадное число «решений», содержащих ошибки. Да-
Даже специалисты-математики не раз бывали вводимы в заблуждение и
представляли или публиковали доказательства, которые затем отпада-
отпадали после обнаружения в них иной раз каких-нибудь поверхностных не-
недосмотров. Со времени падения курса марки ажиотаж около пробле-
проблемы Ферма несколько ослабился; и все же время от времени пресса не
перестает осведомлять нас о том, что решение найдено каким-нибудь
новоявленным «гением».

72 Дополнение к главе I
§ 4. Алгоритм Евклида
1. Общая теория. Читатель прекрасно знаком с обыкновенной
процедурой «длинного» деления одного целого числа а на другое число Ъ
и знает, что эту процедуру можно продолжать до тех пор, пока остаток
не станет меньше, чем делитель. Так, если а = 648 и b = 7, то мы
получаем частное q = 92 и остаток г = 4.
648 \7_
63 92 648 = 7 • 92 + 4.
Л8
14
По этому поводу можно сформулировать следующую общую теорему:
если а и Ь — целые числа, причем Ь отлично от нуля, то можно всегда
найти такое целое число q, что
a = b-q + r, A)
где г есть целое число, удовлетворяющее неравенству 0 ^ г < Ь.
Докажем эту теорему независимо от процедуры длинного деления. До-
Достаточно заметить, что число а или само есть кратное числа Ь, или же лежит
между двумя последовательными кратными Ь,
bq <a <b(q + l) = bq + b.
В первом случае равенство A) оправдывается, причем г — 0. Во втором слу-
случае из первого неравенства вытекает, что
а — bq — г > 0,
а из второго, что
а — bq = г < Ь,
так что число г в этом случае удовлетворяет условию 0 < г < Ь.
Из указанного обстоятельства можно вывести большое число раз-
различных важных следствий. Первое из них — это метод для нахождения
общего наибольшего делителя двух целых чисел.
Пусть а и b — два каких-то целых числа, не равных одновременно
нулю; рассмотрим совокупность всех чисел, на которые делятся и а,
и Ь. Эта совокупность, несомненно, конечная, так как, если, напри-
например, а^О, то никакое число, большее чем а, не может быть делите-
делителем а. Отсюда следует, что число общих делителей а и Ь конечно: пусть

§4. Алгоритм Евклида 73
через d обозначен наибольший из них. Число d называется общим наи-
наибольшим делителем а и Ь, и мы условимся обозначать его d = (а, Ь).
Так, если а = 8, Ь — 12, то непосредственная проверка показывает, что
/g? 12) = 4; если а = 5, b = 9, то мы точно так же получаем E, 9) = 1.
Если а ч b — достаточно большие числа, например, а = 1804, b = 328,
то попытки найти общий наибольший делитель с помощью непосред-
непосредственных проб довольно утомительны. Короткий и вполне надежный
метод вытекает из алгоритма Евклида. (Алгоритмом называют всякий
систематизированный прием вычисления.) Он основан на том обстоя-
обстоятельстве, что из соотношения вида
a = b-q+r B)
необходимо следует, что
(а, Ь) = F, г). C)
В самом деле, всякое число и, которое одновременно делит и а и 6,
а = su, b — tu,
делит также и г, так как г = а — bq = su — qtu = (s — qt)u; и обратно,
всякое число v, которое одновременно делит b и г,
b = s'v, r — t'v,
делит также и а, так как а = bq + г — s'vq + t'v = (s'q + t')v. Значит,
каждый общий делитель а и b есть вместе с тем общий делитель b и г,
и обратно. Но раз совокупность всех общих делителей а и b совпада-
совпадает с совокупностью всех общих делителей b и г, то ясно, что общий
наибольший делитель а и b должен совпадать с общим наибольшим де-
делителем b и г. А это и выражено равенством C). Мы сейчас убедимся
в полезности установленного обстоятельства.
Для этого вернемся к примеру нахождения общего наибольшего
делителя чисел 1804 и 328. Обыкновенное «длинное» деление
1804 [328
1640 5
164
приводит нас к заключению, что
1804 = 5 • 328 + 164.

74 Дополнение к главе I
Отсюда, на основании C), следует, что
A804, 328) = C28, 164).
Заметим, что задача вычисления общего наибольшего делителя
A804, 328) заменена теперь аналогичной задачей, но зависящей от
меньших чисел. Можно продолжать эту процедуру. Так как
328|164
328 2
0
то мы получаем дальше 328 = 2-164 + 0, так что C28, 164) = A64, 0) =
= 164. Значит, A804, 328) = C28, 164) = A64, 0) - 164, и общий наи-
наибольший делитель найден.
Эта самая процедура нахождения общего наибольшего делителя
двух чисел в геометрической форме описана в «Началах» Евклида. Мы
дадим ее общее описание в арифметической форме, исходя из произ-
произвольных целых чисел а и Ь, которые оба одновременно не равны нулю.
Так как сразу ясно, что (а, 0) = а, то можно допустить, что b ф0.
Последовательные деления приводят нас к цепи равенств
а = bqx +п @ < п < 6)
b = nq2+r2 @ < г2 < 7-1)
П = r2<fr+r-3 @ < г3 < г2) D)
r-2 = r3q4+r4 @ < п < г3)
Деление продолжается, пока какой-нибудь из остатков п, г2, г%,...
не обратится в нуль. Рассматривая неравенства, выписанные справа,
мы видим, что последовательно получаемые остатки образуют убыва-
убывающую последовательность положительных чисел:
b > п > г2 > гз > г4 > ... > 0. E)
Отсюда ясно, что после конечного числа делений (нужно сделать не
более b операций, но часто гораздо меньше, так как разности между со-
соседними г обыкновенно превышают единицу) должен получиться оста-
остаток 0:
Гп-2 = rn-iqn + rn, rn-x - rnqn+i + 0.

§4. Алгоритм Евклида 75
только это получилось, мы можем утверждать, что
(а, Ь) = г„;
другими словами, общий наибольший делитель (а, Ь) равен последнему
остатку в последовательности E). Это следует из многократного при-
применения равенства C) к соотношениям D); в самом деле, из этих соот-
соотношений следует:
(а, Ь) = {Ъ, П ), (Ъ, П) = (П, Г2), (Г1, Г2) = (г2, Гз),
(т-2, Г-з) = (Г3, Г4), •••, (т-„-1, Г„) = (Г„, 0) = Г„.
Упражнение. Выполните алгоритм Евклида с целью нахождения об-
общего наибольшего делителя: а) 187; 77 б) 105; 385. в) 245; 193.
Из равенств D) можно вывести одно чрезвычайно важное свойство
общего наибольшего делителя (а, Ь). Если d = (а, Ь), то можно найти
такие целые положительные или отрицательные числа к и I, что
d = ka + lb. F)
Чтобы убедиться в этом, рассмотрим последовательные остатки E).
Первое из равенств D) нам дает
П = а- дгЬ,
так что ri может быть записано в форме kia + lib (в данном случае
к\ = 1, I = — qi). Из следующего равенства получается:
r2 = b - q2ri = b — q2(kia + lib) = (-q2ki)a + A - q2h)b = k2a + l2b.
Очевидно, такое же рассуждение можно по очереди применить ко всем
остаткам гз, г±, ..., пока не придем к представлению
rn = ka + lb,
которое мы и желали получить.
В качестве примера рассмотрим алгоритм Евклида в применении
к нахождению F1,24): общий наибольший делитель есть 1, и интере-
интересующее нас представление числа 1 получается из равенств
61 = 2-24+13, 24=1-13+11, 13 = 1-11 + 2,
11 = 5-2 + 1, 2 = 2-1 + 0.

76 Дополнение к главе I
Первое из этих равенств дает
13 = 61 - 2 • 24,
второе —
11 = 24 - 13 = 24 - F1 - 2 • 24) = -61 + 3 • 24,
третье —
2 = 13 - 11 = F1 - 2 • 24) - (-61 + 3 • 24) = 2 • 61 - 5 • 24
и, наконец, четвертое —
1 = 11-5-2 = (-61 + 3 • 24) - 5B • 61 - 5 • 24) = -11 • 61 + 28 • 24.
2. Применение к основной теореме арифметики Тот факт,
что d = (а, 6) всегда может быть записано в форме d — ka + lb, позволит
нам привести доказательство основной теоремы арифметики, отличное
от того, которое было изложено на стр. 50. Сначала, в качестве леммы,
мы докажем следствие, приведенное на стр. 51, а затем уже из него
выведем некоторую теорему. Таким образом, ход мыслей будет теперь
противоположен прежнему.
Лемма. Если произведение ab делится на простое число р, то
или а, или Ь делится на р.
Предположим, что а не делится на р; тогда (а, р) = 1, так как р
имеет лишь два делителя: р и 1. В таком случае можно найти такие
целые числа к и /, что
1 = ка + 1р.
Умножая обе части равенства на Ь, получим:
b = kab + Ipb.
Так как ab делится на р, то можно написать
ab = рг,
так что
b = крг + Ipb = р(кг + lb),
и отсюда ясно, что 6 делится на р. Таким образом, мы установили, что
если ab делится на р, но а не делится, то b непременно делится на р;
значит, во всяком случае или а, или b делится на р, раз ab делится на р.
Обобщение на случай произведения трех или большего числа мно-
множителей не представляет труда. Например, если abc делится на р, то до-
достаточно дважды применить лемму, чтобы получить заключение, что

§4. Алгоритм Евклида 77
по меньшей мере один из трех множителей ab и с делится на р. В самом
деле, если р не делит ни а, ни Ь, ни с, то не делит ab и, следовательно,
не делит (аб)с = abc.
Упражнение. Обобщение этого рассуждения на случай произведения
из произвольного числа п множителей требует явного или неявного приме-
применения принципа математической индукции. Воспроизведите все детали со-
соответствующей аргументации.
Из полученного результата немедленно получается основная тео-
теорема арифметики. Предположим, что имеется два разложения целого
числа N на простые множители:
N = Р\Р2 ¦¦¦Рг = Ч\Ч2 ¦¦¦Qs-
Так как р\ делит левую часть равенства, то должно делить и правую
и, значит (см. предыдущее упражнение), должно делить один из мно-
множителей <7fc. Но <7fc — простое число; значит, р\ должно равняться <&.
Сократив равенство на общий множитель р\ = qk, обратимся к множи-
множителю р2 и установим таким же образом, что он равен некоторому qt.
Сократив на р2 = qt, переходим, далее, к множителю р3 и т. д. В конце
концов сократятся все множители р, и слева останется 1. Так как q —
целые положительные числа, то и справа не может остаться ничего,
кроме 1. Итак, числа р и числа q будут попарно равны, независимо от
порядка; значит, оба разложения тождественны.
3. Функция Эйлера <p{ri). Еще раз о теореме Ферма. Го-
Говорят, что два целых числа а и b — взаимно простые, если их общий
наибольший делитель равен 1:
(а, Ь) = 1.
Например, числа 24 и 35 — взаимно простые, но числа 12 и 18 — не
взаимно простые.
Если а и Ь — взаимно простые, то можно подобрать такие целые
числа к и I, что
ka + lb= 1.
Это следует из свойства (а, 6), отмеченного на стр. 75.
Упражнение. Докажите теорему: если произведение ab делится на г,
причем г и а — взаимно простые, то Ъ делится на г. (Указание. Если г и а —
взаимно простые, то можно найти такие целые числа к и I, что
кг + 1а = 1.

78
Дополнение к главе I
Затем умножьте обе части равенства на Ь). Эта теорема обобщает лемму на
стр. 76, так как простое число р в том и только в том случае является взаимно
простым с а, если а не делится на р.
Пусть п — произвольное целое положительное число; обозначим
через <р{п) число таких целых чисел в пределах от 1 до п, которые явля-
являются взаимно простыми с числом п. Выражение f(n), впервые введен-
введенное Эйлером, представляет собой очень важную теоретико-числовую
функцию. Легко подсчитать значения <р{п) для нескольких первых зна-
значений п:
так как
VC)
VD)
Ф)
VF)
VG)
VA0)
:2,
2,
:4,
¦2,
6,
4,
6,
= 4,
» »
1
1
1 и 2
1 и З
1, 2, 3, 4
1,5
1, 2, 3, 4, 5, 6
1, 3, 5, 7
1, 2, 4, 5, 7, 8
1, 3, 7, 9
является взаимно простой с
являются взаимно простыми с
1
2
3
4
5
6
7
8
9
10
и т.д.
Заметим, что <р(р) = р — 1, если р — простое число; в самом деле,
у числа р нет делителей, кроме 1 ир, и потому все числа 1,2, ... , р — 1
являются взаимно простыми с р. Если п — составное, причем его раз-
разложение на простые множители имеет вид
п — Pi
Рг
где числа р обозначают различные простые множители, причем каждое
из них возводится в некоторую степень, то тогда
Например, из разложения 12 = 22 • 3 следует
что легко проверить и непосредственно. Доказательство приведенной
теоремы совершенно элементарно, но мы его не приводим.

§4. Алгоритм Евклида 79
Упражнение. Пользуясь функцией Эйлера <р(п), обобщить теорему
ферма, приведенную на стр. 65. Обобщенная теорема формулируется сле-
следующим образом: если п — целое число и а — взаимно простое с п, то
а*4"' = 1 (mod n).
4. Непрерывные дроби. Диофантовы уравнения Алгоритм
Евклида, служащий для нахождения общего наибольшего делителя двух
целых чисел, сразу же приводит к очень важному методу представ-
представления отношения двух целых чисел в виде некоторой сложной дроби
особого вида.
Например, в применении к числам 840 и 611 алгоритм Евклида
дает ряд равенств
840 = 1-611 + 229, 611 = 2-229+153,
229 = 1-153 + 76, 153 = 2-76 + 1,
которые, между прочим, показывают, что (840, 611) = 1. Но из этих
равенств, с другой стороны, получаются следующие:
611 ~ ^ 611 -^ /enV
V229/
611 9, 153 9, 1
229 ^ 229 ^ (т
V153
229 _ , 76 _ 1 1
+ 153 +
1
153 + 153 + /163V
\ 76 )
153 _ о , 1
Комбинируя последние равенства, мы приходим к следующему разло-
разложению числа ||^
611
840
611~ 2+ I
l+-i-

80 Дополнение к главе I
Выражение вида
+ —1-
1 -, G)
где все числа а — целые положительные, называется непрерывной дро-
дробью. Алгоритм Евклида дает метод для представления всякого рацио-
рационального числа в виде такой непрерывной дроби.
Упражнение. Разложите в непрерывные дроби рациональные числа
2 43 169
5' 30' 70 '
* Непрерывные дроби играют важную роль в той области высшей ариф-
арифметики, которую иногда называют диофантовым анализом. Диофантово урав-
уравнение — это алгебраическое уравнение с одним или с несколькими неизвест-
неизвестными, все коэффициенты которого — целые числа, причем ставится задачао-
тыскания лишь целых его корней. Такое уравнение может или вовсе не иметь
решений, или иметь их в конечном числе, или, наконец, иметь бесконечное
множество решений. Простейшее диофантово уравнение — линейное, с двумя
неизвестными
ах + by = с, (8)
где а, Ъ, с — данные целые числа, и требуется найти целые решения х, у.
Полное решение уравнения этого типа может быть найдено посредством ал-
алгоритма Евклида.
Прежде всего этот алгоритм позволит нам определить d = (о, Ь); затем,
как мы знаем, при надлежащем выборе целых чисел к и I выполняется ра-
равенство
ак + Ы = d. (9)
Итак, уравнение (8) имеет частное решение х = к, у = I в том случае, если
с = d. Несколько общее, если с есть кратное d:
c = d-q,
то из равенства (9) мы выводим
a(kq) + b(lq) = dq = с,
так что в этом случае уравнение (8) имеет частное решение х = х" = kq,
у = у" = lq. Обратно, если уравнение (8) имеет при данном с хоть одно
решение х, у, то с должно быть кратным d = (а, Ь): действительно, d делит
и а и Ь, следовательно, должно делить с. Мы доказали, таким образом, что
уравнение (8) имеет (хоть одно) решение в том и только в том случае, если с
кратно (а, Ь).

§4. Алгоритм Евклида 81
Посмотрим теперь, как, зная одно решение х = х*, у = у* уравнения (8),
определить все прочие решения. Пусть х = х', у = у1 есть какое-либо иное
решение; тогда х = х' — х", у = у' — у* есть решение «однородного» уравнения
0. A0)
Действительно, из равенств
ах' + by' = с и ах* + by* = с
посредством вычитания получаем:
а(х'-х*) + Ь(у'-у*)=0.
Обращаясь теперь к уравнению A0), мы видим, что общее его решение имеет
вид х = -, , , у = — Та , где г — произвольное целое число. (Предостав-
(а, Ь) (а, Ь)
ляем доказательство читателю в качестве упражнения. Указание: разделите
на (а, Ъ) и воспользуйтесь упражнением на стр. 77.) Затем окончательно бу-
будем иметь общее решение уравнения (8):
х-х* + гЪ v = v*^
хх + v = v
(а, Ь) (а, Ь)
Подведем итоги. Линейное диофантово уравнение ах + by = с, где a, b
и с — целые числа, имеет целые решения в том и только в том случае, если с
кратно (а, Ь). В этом случае частное решение х = х*, у = у* может быть
найдено посредством алгоритма Евклида, а самое общее имеет вид
-г - -г* -I- rb ¦ и - ?/* га
(а, Ь) (а, Ь)
где г — произвольное целое число.
ПРИМЕРЫ. Уравнение Зх + 6у = 22 не имеет целых решений, так
как C, 6) = 3 не делит 22.
Уравнение 7х + 11у = 13 имеет частное решение х = —39, у = 26, которое
находится с помощью следующих вычислений:
11 = 1-7 + 4, 7 = 1-4 + 3, 4 = 1-3+1, G, 11) = 1,
1 = 4-3 = 4-G-4) = 2-4-7 = 2A1 - 7) - 7 = 2 • И - 3 • 7.
Отсюда следует
7-(-3) + 11-B) = 1,
7-(-39)+ 11-B6) = 13.
Остальные решения даются формулами
х = -39 + Иг, у = 26 - 7г,
где г — произвольное целое число.
Упражнение. Решите диофантовы уравнения:
а) Зх - 4у = 29; б) Их + 12у = 58; с) 153ж - 34?/ = 51.
6 — 340

Глава II
Математическая числовая система
Введение
В дальнейшем мы должны в очень значительной степени расши-
расширить понятие числа, связываемое первоначально с натуральным рядом,
для того чтобы сконструировать мощный инструмент, способный удов-
удовлетворять потребностям и практики, и теории. Исторически — в про-
процессе долгой и неуверенно протекавшей эволюции — нуль, целые от-
отрицательные числа и рациональные дроби приобрели постепенно те же
права, что и числа натурального ряда, и в наши дни правилами дей-
действий со всеми этими числами прекрасно овладевает средний ребенок
школьного возраста. Но для того чтобы обеспечить полную свободу
в алгебраических операциях, нужно идти и дальше и охватить расши-
расширенным понятием также иррациональные и комплексные числа. Хотя
эти обобщения понятия числа употреблялись уже столетия тому на-
назад и на них базируется вся современная математика, но на прочный
логический фундамент они были поставлены лишь в недавнее время.
В настоящей главе мы дадим очерк основных этапов этого развития.
§ 1. Рациональные числа
1. Рациональные числа как средство измерения. Нату-
Натуральные числа возникают как абстракция в процессе счета объектов,
образующих конечные совокупности. Но в повседневной жизни нам
приходится не только считать объекты, индивидуально отделенные
один от другого, но и измерять величины, например, такие, как длина,
площадь, вес, время. Если мы хотим обеспечить свободу операций с ре-
результатами измерения таких величин, могущих неограниченно делить-
делиться на части, нам необходимо, не ограничиваясь натуральным рядом,
расширить пределы арифметики и создать новый мир чисел. Первый
шаг заключается в том, чтобы проблему измерения свести к проблеме
счета. Мы выбираем сначала совершенно произвольно единицу изме-
измерения — фут, ярд, дюйм, фунт, грамм — смотря по случаю, и этой
единице приписываем меру 1. Затем мы считаем число таких единиц,

§1. Рациональные числа 83
входящих в измеряемую величину. Может случиться, что данный ку-
кусок свинца весит ровно 54 фунта. Но в общем случае, как мы замечаем,
процесс счета «не сходится»: данная величина не измеряется абсолютно
точно выбранной единицей, не оказывается ей кратной. Самое большее,
что мы можем сказать в этом случае, — это то, что она заключена
между двумя последовательными кратными этой единицы, допустим,
между 53 и 54 фунтами. Если так действительно происходит, то мы де-
делаем следующий шаг и вводим новые подъединицы, получающиеся от
подразделения первоначальной единицы на некоторое число п равных
частей. На обыкновенном языке эти новые подъединицы могут иметь
те или иные названия; например, фут подразделяется на 12 дюймов,
метр — на 100 сантиметров, фунт — на 16 унций, час — на 60 ми-
минут, минута — на 60 секунд и т. д. Однако в общей математической
символике подъединица, получаемая при подразделении первоначаль-
первоначальной единицы на п частей, обозначается символом —, и если рассмат-
рассматриваемая величина содержит ровно т таких подъединиц, то ее мера
тогда есть Щ. Этот символ называется дробью или отношением (иног-
(иногда пишут т : п). Последний, и самый существенный, шаг был совершен
уже осознанно, после многих столетий накопления отдельных усилий:
символ Щ был освобожден от его конкретной связи с процессом из-
измерения и самими измеряемыми величинами и стал рассматриваться
как отвлеченное число, самостоятельная сущность, уравненная в своих
правах с натуральным числом. Если тип — натуральные числа, то
символ Щ называется рациональным числом.
Употребление термина «число» (первоначально под «числами» по-
понимали только натуральные числа) применительно к новым символам
оправдывается тем обстоятельством, что сложение и умножение этих
символов подчиняются тем же законам, что и соответствующие опера-
операции над натуральными числами. Чтобы в этом убедиться, нужно сна-
сначала определить, в чем заключается сложение и умножение рациональ-
рациональных чисел, а также определить, какие рациональные числа признаются
равными между собой. Эти определения, как всем известно, таковы:
а , с _ ad + be a ? _ ас 9. — \ ас _ а /,\
Ъ d ~ bd ' b'd~bd' a~ ' be ~ bJ [>
гДе а, Ь, с, d — произвольные натуральные числа. Например:
2 4 = 2-5 + 3-4==10+12 = 22 2 4 = 2-4 8
3 5 3-5 15 15' 3'5 3-5 15'
3 , _8_ _ 2jJ: _ 2
3 ' 12 3-4 3'
6*

84 Глава II
Эти самые определения мы вынуждены принять, если имеем в виду ис-
использовать рациональные числа для измерения длин, площадей и т.п.
Но с более строгой логической точки зрения эти правила сложения и
умножения и это толкование равенства по отношению ко вновь вво-
вводимым символам устанавливаются независимо по определению, не бу-
будучи обусловлены какой-либо иной необходимостью, кроме взаимной
совместимости (непротиворечивости) и пригодности к практическим
приложениям. Исходя из определений A), можно показать, что основ-
основные законы арифметики натуральных чисел продолжают сохраняться
и в области всех рациональных чисел:
р + q = q + р (коммутативный закон
сложения),
р + (q + г) = (р + q) + г (ассоциативный закон
сложения),
pq = qp (коммутативный закон B)
умножения),
p(qr) = (pq)r (ассоциативный закон
умножения),
p(q + г) = pq + рг (дистрибутивный закон).
Так, например, доказательство коммутативного закона сложения в слу-
случае дробей ясно из следующих равенств:
а с _ ad Л- be _ cb + da _ с а
Ь d~ bd ~ db ~ d 6'
здесь первое и последнее равенства оправдываются определением сло-
сложения A), а среднее есть следствие коммутативных законов сложения
и умножения в области натуральных чисел. Читатель сможет, если по-
пожелает, проверить таким же образом четыре остальных закона.
2. Возникновение надобности в рациональных числах
внутри самой математики. Принцип обобщения. Независимо
от «практического» основания для введения рациональных чисел су-
существует основание более глубокое и носящее в известном смысле
еще более принудительный характер. Эту сторону дела мы рассмот-
рассмотрим здесь совершенно независимо от приведенной выше аргументации.
В обыкновенной арифметике натуральных чисел мы всегда можем вы-
выполнять основные прямые операции — сложение и умножение. Но об-
обратные операции — вычитание и деление — не всегда выполнимы.
Разность b — а двух натуральных чисел а и Ь есть, по определению, та-
такое натуральное число с, что а + с= Ь, т.е. это есть решение уравнения
а + х — Ъ. Но в области натуральных чисел символ Ь — а имеет смысл

§1. Рациональные числа 85
лишь при ограничении Ь > а, так как только при этом условии уравне-
уравнение а + х = Ь имеет решением натуральное число. На пути к снятию
этого ограничения серьезный шаг был сделан уже тогда, когда был вве-
введен символ 0 для обозначения а —а. Но еще более значительным успехом
было введение символов —1, —2, —3, ... и вместе с тем определения
{Ь-а) = -{а-Ь)
для случая Ь < а: после этого можно было утверждать, что и вычи-
вычитание обладает свойством неограниченной выполняемое™ в области
всех целых — положительных и отрицательных — чисел. Вводя новые
символы —1, —2, —3, ... и тем самым расширяя числовую область, мы
обязаны, конечно, определить операции со вновь вводимыми числами
таким образом, чтобы первоначальные правила арифметических опера-
операций не были нарушены. Так, например, правило
(-1) - (-1) = 1, C)
которое лежит в основе умножения отрицательных чисел, есть следст-
следствие нашего желания сохранить дистрибутивный закон a(b + c) = ab + ac.
Действительно, если бы мы, скажем, декларировали, что (—1) • ( — 1) =
= —1, то, полагая а = —1, Ь = 1, с = —1, получили бы (—1) • A — 1) =
= —1 — 1 = —2, тогда как на самом деле ( — 1) • A — 1) = ( — 1) -0 = 0.
Понадобилось немало времени, чтобы среди математиков было хо-
хорошо осознано, что «правило знаков» C) и вместе с ним все прочие
определения, относящиеся как к отрицательным числам, так и к дро-
дробям, никак не могут быть «доказаны». Они создаются, или деклари-
декларируются, нами самими с целью обеспечить свободу операций и при-
притом без нарушения основных арифметических законов. Что может —
и должно — быть доказываемо, это только то, что если эти опреде-
определения приняты, то тем самым сохранены основные законы арифмети-
арифметики: коммутативный, ассоциативный и дистрибутивный. Даже великий
Эйлер пользовался совершенно неубедительной аргументацией, желая
показать, что (—1) • (—1) «должно» равняться +1. Он говорил: «рассмат-
«рассматриваемое произведение может быть только или +1, или —1; но —1 быть
не может, так как -1 = (+1) • (-1)».
Совершенно подобно тому, как введение отрицательных целых чи-
чисел и нуля расчищает путь для неограниченной выполнимости вычита-
вычитания, введение дробных чисел устраняет арифметические препятствия,
мешающие выполнять деление. Отношение, или частное, х = ^ двух
целых чисел определяется как решение уравнения
ах = Ь D)

86 Глава II
и существует как целое число только в том случае, если а есть дели-
делитель Ь. Но если это не так (например, при а = 2, b = 3), то мы просто
вводим новый символ ^, называемый дробью и подчиненный условию,
выражающемуся равенством а ¦ ^ = Ь, так что - есть решение D)
«по определению». Изобретение дробей как новых числовых символов
обеспечивает неограниченную выполнимость деления за исключением
деления на нуль, которое исключается раз навсегда.
Выражения вроде ^ jL jj и т.п. останутся для нас символами,
лишенными смысла. Если бы мы допустили деление на 0, то из верного
равенства 0-1 = 0-2 вывели бы неверное следствие 1 = 2. Как ни как,
иногда бывает целесообразно обозначать такие выражения символом
«бесконечность», однако с условием, чтобы не делалось даже попытки
оперировать этим символом так, как будто бы он подчинялся обычным
законам арифметики.
Теперь нам ясны принципы, согласно которым сконструирована
система всех рациональных чисел — целых и дробных, положительных
и отрицательных. В этой расширенной области не только полностью
оправдываются формальные законы — ассоциативный, коммутатив-
коммутативный и дистрибутивный,— но и уравнения а + х = Ьиах = Ь всег-
всегда имеют решения х = Ь — аих= ^ с единственной оговоркой, что
в случае второго уравнения а не должно равняться нулю. Иными слова-
словами, в области рациональных чисел так называемые рациональные опе-
операции — сложение, вычитание, умножение и деление — выполнимы
неограниченно и не выводят за пределы области. Такие замкнутые чи-
числовые области называются полями. Мы повстречаемся с дальнейшими
примерами полей ниже, в этой же главе, а также в главе III.
Расширение области посредством введения новых символов, совер-
совершаемое таким образом, что законы, которые имели место в первона-
первоначальной области, сохраняются и в расширенной, есть одна из форм
характерного в математике принципа обобщения. Переход путем обоб-
обобщения от натуральных чисел к рациональным удовлетворяет одновре-
одновременно и теоретической потребности в снятии ограничений, которые
наложены на вычитание и деление, и вместе с тем — практической
потребности в числах, пригодных для фиксации результатов измере-
измерений. Именно тот факт, что рациональные числа идут навстречу сразу
теоретической и практической потребностям, придает им особую важ-
важность. Как мы видели, расширение понятия числа совершилось путем
о
введения новых абстрактных символов вроде 0, —2 или j. В наше вре-

§1. Рациональные числа 87
МЯ мы оперируем этими символами бегло и уверенно, не вдумываясь
в их природу, и трудно даже себе представить, что еще в XVII столетии
они пользовались доверием гораздо в меньшей степени, чем натураль-
натуральные числа, что ими, если и пользовались, то с известным сомнением и
трепетом. Свойственное человеческому сознанию стремление цеплять-
цепляться за «конкретное» — воплощаемое в ряде натуральных чисел — обу-
обусловливает ту медленность, с которой протекала неизбежная эволюция.
Логически безупречная арифметическая система может быть сконстру-
сконструирована не иначе, как в отвлечении от действительности.
3. Геометрическое представление рациональных чисел.
Выразительное геометрическое представление системы рациональных
чисел может быть получено следующим образом.
На некоторой прямой линии,
«числовой оси», отметим отрезок ~3j -2 -Л О I 2 3 *~
от 0 до 1 (рис. 8). Тем самым
устанавливается длина единично- Рис- 8- Числовая ось
го отрезка, которая, вообще гово-
говоря, может быть выбрана произвольно. Положительные и отрицатель-
отрицательные целые числа тогда изображаются совокупностью равноотстоящих
точек на числовой оси, именно, положительные числа отмечаются впра-
вправо, а отрицательные — влево от точки 0. Чтобы изобразить числа со
знаменателем п, разделим каждый из полученных отрезков единичной
длины на п равных частей; точки деления будут изображать дроби
со знаменателем п. Если сделаем так для значений п, соответствую-
соответствующих всем натуральным числам, то каждое рациональное число будет
изображено некоторой точкой числовой оси. Эти точки мы условимся
называть «рациональными»; вообще термины «рациональное число» и
«рациональная точка» будем употреблять как синонимы.
В главе I, § 1 было определено соотношение неравенства А < В для
натуральных чисел. На числовой оси это соотношение отражено сле-
следующим образом: если натуральное число А меньше, чем натуральное
число В, то точка А лежит левее точки В. Так как указанное геомет-
геометрическое соотношение устанавливается для любой пары рациональных
точек, то естественно пытаться обобщить арифметическое отношение
неравенства таким образом, чтобы сохранить этот геометрический по-
порядок для рассматриваемых точек. Это удается, если принять следу-
следующее определение: говорят, что рациональное число А меньше, чем
Рациональное число В (А < В), или что число В больше, чем чис-
число А (В > А), если разность В — А положительна. Отсюда следует
(при А < В), что точки (числа) между А я В — это те, которые одно-

88 Глава II
временно > А и < В. Каждая такая пара точек А и В, вместе со всеми
точками между ними, называется сегментом (или отрезком) и обо-
обозначается [А, В] (а множество одних только промежуточных точек —
интервалом (или промежутком), обозначаемым (А, В)).
Расстояние произвольной точки А от начала 0, рассматриваемое
как положительное число, называется абсолютным значением А и обо-
обозначается символом
|Л|.
Понятие «абсолютное значение» определяется следующим образом: если
А ^ 0, то |Л| = А; если А < 0, то |Л| = —А. Ясно, что если числа Аи В
имеют один и тот же знак, то справедливо равенство |Л + 5| = |А| + |.В|;
если же Аи В имеют разные знаки, то \А + В\ < |Л| + \В\.Соединяя
эти два результата вместе, мы приходим к общему неравенству
которое справедливо независимо от знаков А и В.
Факт фундаментальной важности выражается следующим предло-
предложением: рациональные точки расположены на числовой прямой всюду
плотно. Смысл этого утверждения тот, что внутри всякого интервала,
как бы он ни был мал, содержатся рациональные точки. Чтобы убе-
убедиться в справедливости высказанного утверждения, достаточно взять
число п настолько большое, что интервал @, —) будет меньше, чем дан-
данный интервал (А, В); тогда по меньшей мере одна из точек вида ^
окажется внутри данного интервала. Итак, не существует такого ин-
интервала на числовой оси (даже самого маленького, какой только можно
вообразить), внутри которого не было бы рациональных точек. Отсю-
Отсюда вытекает дальнейшее следствие: во всяком интервале содержится
бесконечное множество рациональных точек. Действительно, если бы
в некотором интервале содержалось лишь конечное число рациональ-
рациональных точек, то внутри интервала, образованного двумя соседними таки-
такими точками, рациональных точек уже не было бы, а это противоречит
тому, что только что было доказано.
§ 2. Несоизмеримые отрезки. Иррациональные
числа, пределы
1. Введение. Если мы станем сравнивать по величине два пря-
прямолинейных отрезка а и Ь, то не является исключенным, что а содер-
содержится в 6 в точности целое число раз г. В таком случае длина отрезка b

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 89
очень просто выражается через длину отрезка а: длина Ь в г раз больше,
чем длина а. Может случиться и так, что целого числа г, которое обла-
обладало бы указанным свойством, не существует; но при этом возможно,
что, разделив отрезок а на некоторое число, скажем, п равных частей
(каждая — длины Ц) и взяв целое число т таких частей, мы в точности
получим отрезок Ъ:
ъ=Щ*. а)
Если осуществляется соотношение вида A), то говорят, что два отрез-
отрезка а и 6 соизмеримы, так как они обладают некоторой «общей мерой»:
таковой является отрезок длины ^, который содержится в отрезке а
ровно п раз, а в отрезке Ь ровно т раз. Некоторый отрезок Ь соизмерим
или несоизмерим с отрезком а в зависимости от того, можно или нель-
нельзя подобрать два таких натуральных числа т и п (п ф 0), что имеет
место равенство A). Обращаясь к рис. 9, предположим, что в качестве
отрезка а избран единичный отрезок [0, 1], и рассмотрим всевозможные
отрезки, у которых один из концов совпадает с 0. Тогда из этих отрез-
отрезков те и только те будут соизмеримы с единичным отрезком, у которых
второй конец совпадает с некоторой рациональной точкой Щ.
Для практической цели изме-
измерения рациональных чисел всег- Тз -2-5 -* о^ 1 \ 2 3 *"
да совершенно достаточно. Да-
Даже с точки зрения теоретичес- Рис. 9. Рациональные точки
кой — поскольку рациональные
точки расположены всюду плотно — могло бы показаться, что все точ-
точки на числовой оси — рациональные. Если бы дело обстояло именно так,
то всякий отрезок был бы соизмерим с единичным. Но дело обстоит не
так просто, и в установлении этого обстоятельства заключается одно
из самых поразительных открытий в математике: оно было сделано
уже в древнейшие времена (в школе Пифагора). Существуют несоиз-
несоизмеримые отрезки, или иначе (если мы допустим, что каждому отрезку
соответствует некоторое число, выражающее его длину), существуют
иррациональные числа. Осознание этого факта было научным событи-
событием величайшей значимости, почти откровением. Весьма возможно, что
именно оно положило начало тому, что мы теперь считаем строгим ма-
математическим методом и рассматриваем как вклад в науку, сделанный
Древними греческими математиками. Без сомнения, это замечательное
открытие глубоко повлияло на всю математику и даже философию от
Древних времен и до наших дней.

90 Глава II
Эвдоксова теория несоизмеримых величин, изложенная в геомет-
геометрической форме в «Началах» Евклида, представляет собой тончайшее
достижение греческой математики (ее изложение обыкновенно про-
пропускается в разжиженных пересказах Евклида, предназначенных для
школьного обучения). Эта теория получила подобающую ей высокую
оценку лишь в конце XIX столетия — после того как усилиями Деде-
кинда, Кантора и Вейерштрасса была создана строгая теория иррацио-
иррациональных чисел. Мы изложим в дальнейшем эту теорию в ее современ-
современном арифметическом аспекте.
Прежде всего установим: диагональ квадрата несоизмерима с его
стороной. Предположим, что сторона квадрата избрана в качестве еди-
единицы длины, длину же диагонали обозначим через х. Тогда, согласно
теореме Пифагора, мы получаем
х2 = I2 + I2 = 2.
(Такое число х обозначают символом \/2.) Если бы х было соизмеримо
с единицей, то можно было бы найти два таких целых числа р и q,
что х = jj, и тогда мы пришли бы к равенству
P2=2q2. B)
Можно допустить, что дробь Ц несократима, иначе мы с самого начала
сократили бы ее на общий наибольший делитель чисел р и q. С правой
стороны имеется 2 в качестве множителя, и потому р2 есть четное
число, и, значит, само р — также четное, так как квадрат нечетного
числа есть нечетное число. В таком случае можно положить р = 2г.
Тогда равенство B) принимает вид
4r2 = 2g2 или 2r2 = q2.
Так как с левой стороны теперь имеется 2 в качестве множителя, зна-
значит, q2, а следовательно, и q — четное. Итак, и р и q — четные числа,
т.е. делятся на 2, а это противоречит допущению, что дробь ^ несокра-
несократима. Итак, равенство B) невозможно и ж не может быть рациональ-
рациональным числом.
Иначе этот результат можно сформулировать, утверждая, что \/2
есть число иррациональное.
Только что приведенное рассуждение показывает, что иной раз са-
самое простейшее геометрическое построение приводит к отрезку, несо-
несоизмеримому с единицей. Если такой отрезок будет отложен с помощью
циркуля на числовой оси от точки 0, то построенная таким образом

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 91
точка (конец отрезка) не совпадает ни с какой
рациональной точкой. Итак, система рациональ-
рациональных точек (хотя и всюду плотная) не покрыва-
покрывает всей числовой оси. Наивному сознанию, не-
сомненно, может показаться странным и пара-
доксальным, что везде плотное множество ра- рис 10 Построение
циональных точек не покрывает всей прямой. числа ^
Никакая наша «интуиция» не поможет нам «уви-
«увидеть» иррациональные точки или отличить их от рациональных. Нет
ничего удивительного в том, что открытие несоизмеримого потрясло
греческих математиков и мыслителей и что его существование и в на-
наши дни продолжает оказывать провоцирующее воздействие на людей,
склонных к углубленному мышлению.
Не представило бы труда конструировать столько отрезков, несо-
несоизмеримых с единицей, сколько бы мы пожелали. Концы всех таких
отрезков — при условии, что их начала совпадают с точкой 0, — об-
образуют совокупность иррациональных точек. Заметим теперь, что ру-
руководящим принципом уже при введении рациональных дробей было
желание обеспечить возможность измерения длин отрезков посредст-
посредством чисел, и тот же принцип продолжает руководить нами и тогда,
когда речь идет о несоизмеримых отрезках. Если мы требуем, чтобы
существовало взаимное соответствие между числами, с одной сторо-
стороны, и точками на прямой линии — с другой, то неизбежно приходится
ввести в рассмотрение иррациональные числа.
Подводя итоги до сих пор оказанному, мы констатируем, что ирра-
иррациональное число обозначает длину отрезка, несоизмеримого с едини-
единицей. В следующих разделах мы должны будем уточнить это несколько
смутное и всецело геометрическое определение и в результате придем
к определению, более удовлетворительному с точки зрения логической
строгости. Рассматривая этот вопрос, мы будем вначале исходить из
десятичных дробей.
Упражнения.
1) Докажите, что числа \/2, %/3, Vb, \/3 — иррациональные. (Указание:
воспользуйтесь леммой на стр. 76.)
2) Докажите, что числа \/2 + %/3 и \/2+ V2 — иррациональные. (Указание:
если бы, например, первое из этих чисел было рациональным числом г,
то, написав %/3 = r — \fi и возведя в квадрат, мы заключили бы, что \/2
есть рациональное число.)
3) Докажите, что число \/2 + %/3 + \/5 — иррациональное. Попробуйте
придумать еще подобные и более общие примеры.

92 Глава II
2. Десятичные дроби: конечные и бесконечные. Чтобы по-
покрыть числовую ось везде плотным множеством точек, нет необходи-
необходимости использовать всю совокупность рациональных чисел: достаточ-
достаточно, например, ограничиться только теми числами, которые возникают
при подразделении единичного отрезка на 10, потом на 100, 1 000 и т.д.
равных частей. Получающиеся при этом точки деления соответствуют
«десятичным дробям». Так, числу 0,12 = -±- + -^- соответствует точка,
расположенная в первом единичном интервале, во втором «подынтерва-
«подынтервале» длины 10, и именно она есть начальная точка третьего «подподын-
тервала» длины 10~2 (а~п означает Чг)- Если такого рода десятичная
дробь содержит п знаков после запятой, то она имеет вид
/ = z + а.! ¦ КГ1 + а2 ¦ 10~2 + а3 • 10 + ... + ап ¦ 10~",
где z — целое число, а коэффициенты а — цифры 0, 1, 2, ... , 9, обо-
обозначающие число десятых, сотых и т.д. Сокращенно число / записы-
записывается в десятичной системе следующим образом: z, ai аг «з • • • ап- Мы
убеждаемся непосредственно, что такого рода десятичные дроби могут
быть представлены в виде обыкновенных дробей ^ где q = 10"; так,
например, / = 1,314 = 1 + А + _1_ + _|_=Ш1. Если окажется,
что р и q имеют общий множитель, то дробь можно сократить, и тогда
знаменатель будет некоторым делителем числа 10™. С другой стороны,
несократимая дробь, у которой знаменатель не есть делитель некото-
некоторой степени 10, не может быть представлена в виде десятичной дроби
указанного типа. Например, | = ^ = 0,2; ^ = j-щ = 0,004; но | не
может быть написана как десятичная дробь с конечным числом п де-
десятичных знаков, как бы ни было велико п: в самом деле, из равенства
вида
1 _ Ъ
3 10"
следовало бы
10" = 36,
а последнее равенство невозможно, так как 3 не входит множителем ни
в какую степень числа 10.
Возьмем теперь на числовой оси какую-нибудь точку Р, которая
не соответствует никакой конечной десятичной дроби; можно, напри-
например, взять рациональную точку ^ или иррациональную точку у/2. Тог-
Тогда в процессе последовательного подразделения единичного интерва-
интервала на 10 равных частей точка Р никогда не окажется в числе точек

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 93
деления: она будет находиться внутри десятичных интервалов, дли-
длина которых будет неограниченно уменьшаться; концы этих интервалов
соответствуют конечным десятичным дробям и приближают точку Р
с какой угодно степенью точности. Рассмотрим несколько подробнее
этот процесс приближения.
Предположим, что точка Р лежит в первом единичном интервале.
Сделаем подразделение этого интервала на 10 равных частей, каждая
длины 1СР1, и предположим, что точка Р попадает, скажем, в третий из
этих интервалов. На этой стадии мы можем утверждать, что Р заклю-
заключена между десятичными дробями 0,2 и 0,3. Подразделяем снова интер-
интервал от 0,2 до 0,3 на 10 равных частей, каждая длины 10~2, и обнаружим,
что Р попадает, допустим, в четвертый из этих интервалов. Подразде-
Подразделяя его, как раньше, видим, что точка Р попадает в первый интервал
длины 10~3. Теперь можно сказать, что точка Р заключена между 0,230
и 0,231. Этот процесс может быть продолжен до бесконечности и при-
приводит к бесконечной последовательности цифр «ц. а2, аз> • •• > о,п, ...,
обладающей таким свойством: каково бы ни было п, точка Р заключена
в интервале /„, у которого начальная точка есть 0, ai a2 аз • • • an-i ап,
а конечная — 0,аха2а3 ... an-i(an + 1), причем длина /„ равна 10~".
Если станем полагать по порядку п = 1, 2, 3, 4, ..., то увидим, что
каждый из интервалов 1\, /г, /з, ... содержится в предыдущем, причем
их длины 10, 10~2, 10~3, ... неограниченно уменьшаются. Мы ска-
скажем, более кратко, что точка Р заключена в стягивающуюся последо-
последовательность десятичных интервалов. Например, если точка Р есть ^,
о
то все цифры ai, а,2, аз, ... равны 3, и Р заключена в любом интерва-
интервале /„ от 0,333... 33 до 0,333... 34, т. е. | больше чем 0,333... 33 и мень-
о
ше 0,333...34, сколько бы ни взять цифр после запятой. Мы скажем
в этих обстоятельствах, что n-значная десятичная дробь 0,333...33
«стремится к ^», когда число цифр п неограниченно возрастает. И мы
условимся писать
| = 0,333
причем точки обозначают, что десятичная дробь может быть продлена
«До бесконечности».
Иррациональная точка \/2, которая была рассмотрена в пункте 1,
также приводит к бесконечной десятичной дроби. Но закон, которо-
которому подчиняются последовательные цифры десятичного разложения, на
этот раз далеко не очевиден. Мы затрудняемся указать формулу, ко-
которая давала бы цифру, стоящую на га-м месте, хотя можно вычислить

94 Глава II
столько цифр, сколько мы пожелали бы себе заранее назначить:
12 = 1<2<22=4
A,4J = 1,96 < 2 < A,5J = 2,25
A,41J = 1,9881 < 2 < A,42J = 2,0264
A,414J = 1,999396 < 2 < A,415J = 2,002225
A,4142J = 1,99996164 < 2 < A,4143J = 2,00024449
и т.д.
В качестве общего определения мы скажем, что точка Р, которая
не может быть представлена в виде десятичной дроби с конечным чис-
числом десятичных знаков, представляется в виде бесконечной десятичной
дроби z, а,1 а,2 аз ..., если, каково бы ни было п, точка Р лежит в ин-
интервале длины 10~" с начальной точкой z, a,i а,2 а,з ... ап.
Таким образом, мы устанавливаем соответствие между всеми точ-
точками числовой оси и всеми (конечными или бесконечными) десятич-
десятичными дробями. Теперь мы попытаемся ввести предварительное опре-
определение: «число»есть конечная или бесконечная десятичная дробь. Те
бесконечные десятичные дроби, которые не представляют рациональ-
рационального числа, называются иррациональными числами. До середины XIX
столетия соображения, подобные приведенным выше, казались доста-
достаточными для объяснения того, как устроена система рациональных и
иррациональных чисел — числовой континуум. Необычайные успехи
математики, достигнутые начиная с XVII столетия, в частности, раз-
развитие аналитической геометрии и дифференциального и интегрально-
интегрального исчислений, твердо базировались именно на таком представлении
о системе чисел. Однако в период критического пересмотра принципов
и консолидации результатов стало ощущаться все более и более явст-
явственно, что понятие иррационального числа должно быть подвергнуто
более точному и глубокому анализу. Но, прежде чем перейти к очерку
современной теории числового континуума, нам придется рассмотреть
и разобрать — на более или менее интуитивной основе — одно из ма-
математических понятий капитальной значимости — понятие предела.
Упражнение. Вычислить приближенно \/2 и \/5 с ошибкой, не превы-
превышающей 10~2.
3. Пределы. Бесконечные геометрические прогрессии. Как
мы видели в предыдущем пункте, иногда случается, что некоторое ра-
рациональное число s бывает приближаемо последовательностью других
рациональных чисел sn, причем индекс п принимает последовательно

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 95
все значения 1, 2, 3, Так, например, можно взять: s = i и при-
притом «1 — 0,3, s2 = 0,33, s3 = 0,333 и т. д. Вот еще пример. Разобьем
единичный интервал на две равные части, вторую половину — снова
на две равные части, вторую из полученных двух частей — снова на
две равные части и т.д., пока наименьший из полученных таким обра-
образом интервалов не станет равным 2~~п, где п — сколь угодно большое
наперед заданное число, например, п = 100, п = 100 000 и т.д. Затем,
складывая вместе все интервалы, кроме самого последнего, мы получа-
получаем общую длину
&п= 2 + 4 + 8 + 16+--'+ 2^ C)
Легко понять, что sn отличается от 1 на ( - ) и что эта разность ста-
становится сколь угодно малой, или «стремится к нулю», при неограни-
неограниченном возрастании п. Говорить, что эта разность равна нулю, ког-
когда п равно «бесконечности», — не имеет никакого смысла. Бесконечное
в математике связывается с некоторым процессом, не имеющим конца,
и никогда не связывается с актуальной величиной. Желая описать по-
поведение sn, мы говорим, что сумма sn стремится к пределу I, когда п
стремится к бесконечности, и пишем
2 + 4 + 8 + 16' ()
причем то, что возникает справа, есть бесконечный ряд. Последнее «ра-
«равенство» не следует понимать в том смысле, что имеется в виду сло-
сложить вместе бесконечное число слагаемых: это только сокращенная за-
запись того факта, что 1 есть предел конечных сумм sn, получающийся,
когда п стремится к бесконечности (и ни в коем случае не равно бес-
бесконечности). Итак, равенство D), заканчивающееся неопределенным
символом «+...», как бы стенографирует некоторую точную мысль,
выражаемую, по неизбежности, длинным рядом слов:
«1 равна пределу (при п, стремящемся к бесконечности) выражения
*п = \ + ^ + ^ + • • • + ^г». E)
Еще более кратко и более выразительно пишут следующим образом:
я„ -> 1 при п -> оо. F)

96 Глава II
Говоря о пределах, рассмотрим еще пример. Пусть перед нами име-
имеется бесконечная последовательность различных степеней числа q:
<1, I2, I3, q4, ... ,qn, ... ¦
Если -1 < q < 1, например, q=\ или q - -f, то qn стремится к нулю
о о
при неограниченном возрастании п. При этом, если q — отрицательное
число, то знаки qn чередуются: за + следует -, и обратно; таким обра-
образом, qn стремится к нулю «с двух сторон». Так, если q = ^, то q2 = ~у
q3 = h'q4 = iij ¦¦¦'ноесли ? = ~|' T°i2 = |' I3 = ~|' 1*= п> ••••
Мы утверждаем, что предел qn, когда п стремится к бесконечности,
равен нулю, или, символически,
qn -> 0 при п -> оо, если - 1 < q < 1. G)
(Между прочим, если q > 1 или g < —1, то qn уже не стремится к нулю,
а неограниченно возрастает по абсолютному значению.)
Приведем строгое доказательство утверждения G). Мы видели на
стр. 42, что при любом целом положительном значении п и при усло-
условии р > — 1 имеет место неравенство A + р)п ^ 1 + пр. Пусть q —
о
какое-то положительное число, меньшее единицы, например, q = j-.
Тогда можно положить q = —-—, где р > 0. Отсюда следует:
-1. = A+р)п ^1+пр>пр,
или же (см. определение 4 на стр. 84)
и <Ч <рп-
Значит, qn заключено между постоянным числом 0 и числом i-i, кото-
которое стремится к нулю при неограниченном возрастании п (так как р —
постоянное). После этого ясно, что qn -> 0. Если q — отрицательное
число, то мы положим q = — у-=—, и тогда q" будет заключено между
числами — i • yi и = • ^; рассуждение заканчивается так же, как раньше.
Рассмотрим теперь геометрическую прогрессию
sn = l+q + q2 + q3 + ... + qn. (8)

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 97
(Случай g = 2 был рассмотрен выше.) Как уже было показано
(см. стр. 39), сумма sn может быть представлена в более простой и
сжатой форме. Умножая sn на q, мы получаем
qsn = q + q2 + q3 + q4 + ... + qn+l (8a)
и вычитая (8а) из (8), убеждаемся, что все члены, кроме 1 и qn+1,
взаимно уничтожаются. В результате будем иметь
или же, деля на 1 - q,
1 - qn+1 1 qn+1
sn = —
\-q 1-q 1-q'
С понятием предела мы повстречаемся, если заставим п неограниченно
возрастать. Мы видели только что, что qn+1 = q-qn стремится к нулю,
если — 1 < q < 1, и отсюда можем заключить:
sn -» при п -» оо, если - 1 < q < 1. (9)
Тот же результат можно записать, пользуясь бесконечным рядом
1 + q + q2 + q3 + ••• = 7^—, если — 1 < g < 1. A0)
1 — q
Например,
2 22 23 1
2
в полном соответствии с равенством D); подобным же образом
9 9 9 9 9 1
+ + +
ю Ю2 10» io4
10 1-^
=1
или, иначе, 0,9999... = 1. Совершенно так же конечная дробь 0,2374 и
бесконечная дробь 0,23739999... представляют одно и то же число.
В главе VI мы вернемся к общему обсуждению понятия преде-
предела, рассматривая вопрос с современной, логически более строгой точки
3Рения.
7-340

98 Глава II
Упражнения.
1) Доказать, что
1 — q + q2 — q3 + q4 — . .. = - , если \q\ < 1.
2) Каков предел последовательности ai, аг, аз, ..., где а„ = —ТТ? (Ука-
(Указание: напишите данное выражение —^— в виде 1 —— и обратите
внимание на то, что вычитаемое стремится к нулю.)
3) Каков предел П9 7 ПРИ п ~* °°' (Указание: напишите это выра-
выражение в виде
4) Предполагая q по абсолютному значению меньшим чем 1, докажите,
что 1 + 2q + 3g2 + 4g3 + ... = =—-. (Указание: воспользуйтесь ре-
результатом упражнения 3 на стр. 44.)
5) Каков предел бесконечного ряда
I_2g + 3g2-4g3 + ...?
6) Вычислить пределы выражений
l+2 + 3 + ... + n I2 + 22 + З2 + ... + п2 I3 + 23 + З3 + ... + п3
п2 п3 п4
(Указание: воспользуйтесь результатами, полученными на стр. 38-41).
4. Рациональные числа и периодические десятичные дро-
дроби. Такие рациональные числа Ц, которые не могут быть представ-
представлены в виде конечных десятичных дробей, разлагаются в бесконеч-
бесконечные десятичные дроби посредством обыкновенного приема «длинно-
«длинного» деления. На каждой ступени этого процесса возникает остаток, не
равный нулю, иначе дробь оказалась бы конечной. Различные возни-
возникающие остатки могут быть только целыми числами от 1 до q — 1,
так что имеется всего q — 1 возможностей для значений этих остат-
остатков. Это значит, что после q делений некоторый остаток к появится
во второй раз. Но тогда все следующие остатки также будут повто-
повторяться в том же порядке, в каком они уже появлялись после перво-
первого возникновения остатка к. Таким образом, десятичное разложение

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 99
всякого рационального числа обладает свойством периодичности; после
некоторого числа десятичных знаков одна и та же группа десятичных
знаков начинает повторяться бесконечное число раз. Например, i =
= 0,166666666...; | = 0,142857142857142857...; ^ = 0,09090909...;
J2JL = 0,1109090909...; U; = 0,122222222 ... и т. д. (Заметим по пово-
1100 90
ду тех рациональных чисел, которые представляются в виде конечной
десятичной дроби, что у этой конечной дроби можно вообразить после
последнего ее десятичного знака бесконечно повторяющуюся цифру 0,
и, таким образом, рассматриваемые рациональные числа не исключа-
исключаются из данной выше общей формулировки.) Из приведенных примеров
видно, что у некоторых из десятичных разложений, соответствующих
рациональным числам, периодическому «хвосту» предшествует непери-
непериодическая «голова».
Обратно, можно показать, что все периодические дроби представ-
представляют собой рациональные числа. Рассмотрим, например, бесконечную
периодическую дробь
р = 0,3322222...
Можно написать: р = ущ + 10~3 • 2A + 10 + 10~2 + ...). Выражение
в скобках есть бесконечная геометрическая прогрессия:
1 + КГ1 + КГ2 + Ю~3 + ... = —-— = Щ.
'-То
Значит,
= .33, 1П-3 о 10 _ 2970+20 __ 2990 299
Р 100 9 9-ю3 9000 900"
В общем случае доказательство строится таким же образом, но затруд-
затруднено необходимостью вводить несколько громоздкие обозначения. Рас-
Рассмотрим периодическую дробь общего вида
р = 0, а^а2а3... атЪ\Ъ2Ъ3 ... bnbib2b3... Ьп ...
Обозначим через В = 0,bib2b3 ...bn периодическую часть нашего раз-
разложения. Тогда можно написать:
р = 0, аха2а3 ...ат + 10~тВA + 10"" + 10~2п + 10~3" + ...).
7*

100 Глава II
Выражение в скобках — бесконечная геометрическая прогрессия, для
которой q = 10~n. Сумма этой прогрессии, согласно формуле A0) пре-
предыдущего пункта, равна ~^> и потому
1 Q — т. . D
р = 0, а\ аоаз .. .ат Л
Упражнения.
1) Разложить в десятичные дроби следующие рациональные числа: —,
12 12
— ,—,—, — и определить периоды разложений,
хо Хо J-I х I
* 2) Число 142 857 обладает тем свойством, что при умножении его на 2, 3,
4, 5 или 6 в нем совершаются только перестановки цифр. Объяснить
это свойство, исходя из разложения числа - в десятичную дробь.
3) Разложить числа, приведенные в упражнении 1, в бесконечные дроби
с основаниями 5, 7 и 12.
4) Разложить число — в двоичную дробь.
О
5) Напишите разложение 0,11212121.... Установить, какое число оно
представляет при основаниях 3 или 5.
5. Общее определение иррациональных чисел посредством
стягивающихся отрезков. На стр. 94 мы провизорно ввели опре-
определение: «число» есть конечная или бесконечная десятичная дробь. Мы
условились вместе с тем десятичные дроби, не представляющие ра-
рационального числа, называть иррациональными числами. На основе ре-
результатов, полученных в предыдущем пункте, мы можем теперь пред-
предложить следующую формулировку: «числовой континуум, или система
действительных чисел («действительные» числа противопоставляются
здесь «мнимым» или «комплексным», см. § 5), есть совокупность всевоз-
всевозможных бесконечных десятичных дробей». (Приписывая нули, можно,
как уже было отмечено, конечную десятичную дробь написать в виде
бесконечной, или есть другой способ: последнюю цифру дроби а заме-
заменить через а — 1 и к ней приписать бесчисленное множество девяток.
Так, мы видели, например, что 0,999... = 1. См. п. 3.)
Рациональные числа суть периодические дроби; иррациональные
числа суть непериодические дроби. Но и такое определение не представ-
представляется вполне удовлетворительным: действительно, мы видели в гла-
главе 1, что самой природой вещей десятичная система ничем особым не

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 101
уделяется из других возможных: таким же образом можно было бы
оперировать, например, двоичной системой. По этой причине являет-
является чрезвычайно желательным дать более общее определение числово-
числового континуума, независимое от специального выбора основания 10 или
любого иного. Вероятно, простейший метод для введения такого обоб-
обобщения заключается в следующем.
Рассмотрим на числовой оси
некоторую последовательность Д,
h, /з, • • • > Л»> • • • отрезков с pa- |
циональными концами; предполо- I ' "
жим, что каждый следующий от-
отH 1-
-\ Ь
-ы-
-н-
-н-
резок содержится в предыдущем
и что длина n-го отрезка /„ стре-
стремится к нулю при неограничен-
неограниченном возрастании п. Такую после-
последовательность «вложенных» друг
в друга отрезков мы будем назы-
называть последовательностью стя-
о Рис. 11. Стягивающиеся отрезки. Пре-
гивающихся отрезков. В случае ^ v v
Т делы последовательностей
десятичных отрезков длина /„
равна 10~п, но с таким же успехом она могла бы равняться, ска-
скажем, 2~п, или можно ограничиться хотя бы тем требованием, чтобы
она была меньше i. Дадим теперь следующую формулировку, которую
будем рассматривать как основной геометрический постулат: какова
бы ни была последовательность стягивающихся отрезков, существует
одна и только одна точка числовой оси, которая одновременно содер-
содержится во всех отрезках. (Совершенно ясно, что существует не более
одной такой точки, так как длины отрезков стремятся к нулю, а две
различные точки не могли бы содержаться в отрезке, длина которого
была бы меньше, чем расстояние между точками.) Эта точка, по опре-
определению, и называется действительным числом; если она не является
рациональной, то называется иррациональным числом. С помощью та-
такого определения мы устанавливаем полное соответствие между точка-
Ми и числами. Здесь не прибавлено ничего существенно нового: всего
лишь определению числа как бесконечной десятичной дроби придана
более общая форма.
Все же читателя в этом месте могут охватить известные со-
сомнения, которые следует признать вполне обоснованными. Что же на
самом деле представляет собой та «точка» на числовой оси, которая,
как мы допускаем, содержится одновременно во всех стягивающихся

102 Глава II
отрезках последовательности в случае, если она не соответствует ра-
рациональному числу? Наш ответ таков: существование на числовой оси
(рассматриваемой как геометрический образ) точки, содержащейся во
всех стягивающихся отрезках с рациональными концами, есть основ-
основной геометрический постулат. Нет надобности делать редукцию, при-
приводя его к иным математическим предложениям. Мы принимаем его,
как принимаем в математике другие аксиомы или постулаты, основы-
основываясь на его интуитивной правдоподобности и на его полезности, обна-
обнаруживающейся при построении логически последовательной системы
математических предложений. Чисто формально мы могли бы исхо-
исходить из числовой прямой, которую мыслили бы как совокупность одних
только рациональных точек, и затем определили бы иррациональную
точку как символ, обозначающий некоторую последовательность стя-
стягивающихся отрезков. Иррациональная точка полностью определяется
последовательностью стягивающихся рациональных отрезков, длины
которых стремятся к нулю. Значит, наш основной постулат на самом
деле способен служить определением. Принять такое определение, после
того как мы были приведены к последовательности стягивающихся от-
отрезков интуитивным ощущением, утверждающим «существование» ир-
иррациональной точки', — значит отбросить костыли интуиции, на кото-
которые опиралось наше рассуждение, и осознать, что все математические
свойства иррациональных точек могут быть понимаемы и представля-
представляемы как свойства последовательностей стягивающихся отрезков.
С чисто математической точки зрения в данном случае важно то
обстоятельство, что, приняв определение иррационального числа как
последовательности стягивающихся отрезков, мы приобретаем возмож-
возможность дать определения сложения, умножения и т.д., а также отно-
отношений неравенства, являющихся непосредственным обобщением соот-
соответствующих определений в поле рациональных чисел, и притом с со-
сохранением всех основных законов, действующих в поле рациональных
чисел. Так, например, чтобы определить сумму двух иррациональных
чисел а и /3, исходя из двух последовательностей стягивающихся отрез-
отрезков, определяющих числа а и /3, построим новую последовательность
стягивающихся отрезков, складывая соответственно начальные точки
и конечные точки промежутков, входящих в состав данных последова-
последовательностей. То же можно сделать с произведением а/3, разностью а — /3
и частным а//3. И можно показать, на основе этих определений, что
арифметические законы, рассмотренные в § 1 этой главы при переходе
к иррациональным числам, не нарушаются. Подробности, сюда относя-
относящиеся, мы опускаем.

§2. Несоизмеримые отрезки. Иррациональные числа, пределы 103
Проверка всех этих законов проста и производится непосредствен-
непосредственно без особых затруднений, но могла бы показаться несколько скуч-
скучноватой начинающему читателю, который, естественно, интересуется
скорее тем, что можно сделать с помощью математики, чем анализом
ее логических основ. Нередко случается, что новейшие учебники мате-
математики отталкивают читателя именно тем, что с первых же страниц
дают педантическое обоснование системы действительных чисел. Чи-
Читатель, спокойно игнорирующий эти страницы, пусть успокоит свою
совесть сознанием того факта, что вплоть до конца XIX столетия все
великие математики делали свои открытия на основе «наивной» концеп-
концепции числового континуума, доставляемой непосредственно интуицией.
Наконец, с физической точки зрения, определение иррациональ-
иррационального числа посредством последовательности стягивающихся отрезков
естественно уподобляется определению числового значения некоторой
доступной наблюдению величины — путем ряда измерений, произво-
производимых последовательно со все возрастающей точностью. Всякая опе-
операция, совершаемая, скажем, с целью определения длины некоторого
отрезка, практически осмыслена лишь в пределах некоторой возмож-
возможной погрешности, величина которой определяет точность инструмента.
Так как рациональные числа расположены на прямой всюду плотно, то
никакая физическая операция, как бы точна она ни была, не позволит
различить, является ли данная длина рациональной или же иррацио-
иррациональной. Таким образом, могло бы показаться, что в иррациональных
числах нет никакой необходимости для адекватного описания физи-
физических явлений. Но, как мы увидим в главе VI, при математическом
описании физических явлений истинное преимущество, приобретаемое
посредством привлечения иррациональных чисел, заключается в чрез-
чрезвычайном упрощении этого описания — именно благодаря свободному
использованию понятия предела, основой которого является числовой
континуум.
*6. Иные методы определения иррациональных чисел. Де-
Декиндовы сечения. Несколько иной путь для определения ир-
иррациональных чисел был избран Рихардом Дедекиндом A831-1916),
одним из самых выдающихся основоположников логического и фи-
философского анализа основ математики. Его статьи — «Stetigkeit
und irrationale Zahlen»1 A872) и «Was sind und was sollen die
Zahlen?»2 A887) — оказали глубокое влияние на исследование основ-
«Непрерывность и иррациональные числа».
«Что такое числа и чем они должны быть?»

104 Глава II
ных принципов математики. Дедекинд предпочитал общие абстрактные
концепции конкретным построениям вроде последовательностей стяги-
стягивающихся отрезков. Его процедура базируется на идее «сечения»; мы
сейчас опишем, что это такое.
Предположим, что каким-то способом удалось разбить совокуп-
совокупность всех рациональных чисел на два класса А и В таким образом,
что всякое число Ь класса В больше, чем всякое число а класса А. Вся-
Всякое разбиение такого рода называется сечением в области рациональ-
рациональных чисел. Если произведено сечение, то должна осуществиться одна
из следующих трех логически мыслимых возможностей.
1) Существует наибольший элемент а* в классе А. Такое поло-
положение вещей имеет место, например, в том случае, если к классу А
отнесены все рациональные числа ^ 1, к классу В — все рациональные
числа > 1.
2) Существует наименьший элемент Ь* в классе В. Это происхо-
происходит, например, в том случае, если к классу А отнесены все рациональ-
рациональные числа < 1, к классу В — все рациональные числа ^ 1.
3) Нет ни наибольшего элемента в классе А, ни наименьшего
в классе В. Сечение этого рода получится, например, в том случае,
если к классу А отнесены все рациональные числа, квадрат которых
меньше чем 2, а к классу В — все рациональные числа, квадрат кото-
которых больше чем 2. Классами А и В исчерпываются все рациональные
числа, так как было показано, что такого рационального числа, квадрат
которого равен 2, не существует.
Такой случай, когда в классе А есть наибольший элемент а* и вмес-
вместе с тем в классе В — наименьший элемент Ь*, логически немыслим,
а* +6*
так как тогда рациональное число —^—, заключенное как раз меж-
между а* и Ь*, было бы больше, чем наибольший элемент в А, и меньше,
чем наименьший элемент в В, и, значит, не могло бы принадлежать ни
к Л, ни к В.
В третьем случае, когда нет ни наибольшего рационального числа
в классе А, ни наименьшего в классе В, тогда, по Дедекинду, сечение
определяет, или, лучше, представляет собой, некоторое иррациональ-
иррациональное число. Не представляет труда проверить, что определение Дедекин-
да согласуется с определением, в основе которого находятся вложен-
вложенные отрезки: из всякой последовательности вложенных отрезков /i,
7г, /з) ••• мы получаем сечение, если отнесем к классу А все те ра-
рациональные числа, которые меньше, чем левый конец хотя бы одного
интервала /„, к классу В — все прочие рациональные числа.

§ 3. Замечания из области аналитической геометрии 105
В философском отношении определение иррациональных чисел по Деде-
кинду находится на более высоком уровне абстракции, так как оно не ограни-
ограничивает ни в чем того математического закона, который определяет классы А
и В. ДРУГОИ! более конкретный метод для определения континуума действи-
действительных чисел принадлежит Георгу Кантору A845-1918). На первый взгляд
резко отличный как от метода вложенных отрезков, так и от метода сечений,
0Н однако, эквивалентен любому из них в том смысле, что числовой контину-
континуум, получающийся на основе всех трех методов, обладает одними и теми же
свойствами. Идея Кантора базируется на тех обстоятельствах, что 1) действи-
действительные числа можно трактовать как бесконечные десятичные дроби, 2) бес-
бесконечные десятичные дроби можно рассматривать как пределы конечных
десятичных дробей. Чтобы не связывать себя зависимостью от десятичных
дробей, мы, следуя Кантору, принимаем, что всякая «сходящаяся» последова-
последовательность рациональных чисел ai, 02, аз, ... определяет действительное чис-
число. При этом «сходимость» понимается в том смысле, что разность (ат — ап)
между двумя членами последовательности стремится к нулю, если тип
одновременно и независимо друг от друга неограниченно возрастают. (Как
раз последовательные десятичные приближения обладают этим свойством:
любые два из них после n-го отличаются меньше чем на 10~п.) Так как одно
и то же действительное число по методу Дедекинда может быть определяемо
самыми разнообразными последовательностями рациональных чисел, то при-
приходится добавить, что две последовательности а\, п2, а,з, ¦ ¦ ¦ и Ь\, Ьг, &з,
определяют одно и то же действительное число, если разность ап — Ьп стре-
стремится к нулю при неограниченном возрастании п. Определить, идя по пути,
намеченному Дедекиндом, сложение и т. д. не представляет труда.
§3. Замечания из области аналитической
геометрии1
1. Основной принцип. Уже начиная с XVII в. числовой кон-
континуум, принимаемый как нечто само собой разумеющееся или же
подвергаемый более или менее поверхностному критическому анали-
анализу, стал основой математики, в частности, аналитической геометрии и
Дифференциального и интегрального исчислений.
Введение числового континуума дает возможность сопоставить
каждому отрезку прямой в качестве его «длины» некоторое определен-
определенное действительное число. Но можно пойти и дальше. Не только дли-
длина, но и всякий вообще геометрический объект, всякая геометрическая
операция могут найти свое место в царстве чисел. Решительный шаг
Читателю, не вполне освоившемуся с предметом этого параграфа, рекоменду-
рекомендуйся обратиться к упражнениям, которые помещены в приложении в конце книги,
СТР- 553 и дальше.

106
Глава II
Q'
У
II
О
Рис. 12. Прямоугольные
координаты точки
О
III
IV
Рис. 13. Четыре квадранта
в направлении арифметизации геометрии был сделан не позднее 1629 г.
Ферма A601-1665) и в 1637 г. Декартом A596-1650). Основная идея
аналитической геометрии заключается в использовании «координат» —
чисел, связанных (координированных) с данным геометрическим объ-
объектом и полностью этот объект характеризующих. Большинству чита-
читателей известны так называемые прямоугольные, или декартовы коор-
координаты служащие для того, чтобы фиксировать положение произволь-
произвольной точки на плоскости. Мы исходим из двух неподвижных взаимно
перпендикулярных прямых на плоскости «оси х» и «оси уь и к ним от-
относим каждую точку. Эти оси рассматриваются как ориентированные
числовые прямые, причем измерение совершается с помощью одного и
того же единичного отрезка. Каждой точке Р (рис. 12) сопоставлены две
координаты х и у. Они получаются следующим образом. Рассмотрим
ориентированный отрезок (вектор), идущий из «начала» О в точку Р,
и затем спроектируем ортогонально этот вектор на обе оси, получая
ориентированный отрезок ОР' на оси а; и такой же отрезок OQ' на
оси у. Два числа х и у, измеряющие соответственно ориентированную
длину отрезков ОР' и OQ', называются координатами точки Р. Обрат-
Обратно, если х и у — два произвольных наперед заданных числа, то соответ-
соответствующая точка Р определяется однозначно. Если числа х и у — оба по-
положительные, то Р попадает в первый квадрант координатной системы
(рис. 13); если оба — отрицательные, то в третий; если а; положительно,
а у отрицательно, то в четвертый и, наконец, если а; отрицательно, а у
положительно, то во второй.
Расстояние между точкой Pi с координатами xi, y± и точкой Рг
с координатами х2, у2 дается формулой
d2 = (x1-x2J + (y1-y2J. A)
Это немедленно следует из пифагоровой теоремы (рис. 14).

§3. Замечания из области аналитической геометрии
Ук
107
Уг
У\
0
d/
/
1
X,
Уг~У\
:2 X
О
Рис. 14. Расстояние
двумя точками
между
Рис. 15. Окружность
2. Уравнения прямых и кривых линий. Если С есть непо-
неподвижная точка с координатами х — а, у — Ь, то геометрическое место
всех точек Р, находящихся от точки С на данном расстоянии г, есть
окружность с центром С и радиусом г. Из формулы для расстояния
между двумя точками A) следует, что точки этой окружности имеют
координаты х, у, удовлетворяющие уравнению
(х-аJ + (у-ЪJ =г2.
B)
Это уравнение называется уравнением окружности, так как оно вы-
выражает полное (необходимое и достаточное) условие того, что точка Р
с координатами х, у лежит на окружности с центром С и радиусом г.
Если скобки раскрыть, уравнение принимает вид
х2 + у2 - 2ах - 2Ьу = к,
C)
где к = г2 — а2 — Ь2. Обратно, если задано уравнение вида C), причем а,
Ь и к — произвольные постоянные и сумма к + а2 + Ь2 положительна,
то с помощью алгебраической процедуры «дополнения до квадрата» мы
можем написать то же уравнение в форме
(я - аJ + (у~ ЪJ = г2,
где г2 = к + а2 + Ь2. И тогда ясно, что уравнение C) определяет окруж-
окружность радиуса г, центр которой — в точке С с координатами а, Ь.
Уравнение прямой линии еще проще по своей форме. Так, напри-
MePi уравнение оси х, имеет вид у = 0, так как координата у равна
нУлю для всех точек этой оси и ни для каких иных точек. Точно так
*е ось у имеет уравнение х — 0. Прямые, проходящие через начало и

108
Глава II
делящие пополам углы между осями, имеют уравнения х = у и х = ~у.
Легко показать, что всякая прямая линия имеет уравнение вида
ах + by = с, D)
где а,Ь,с — постоянные, характеризующие эту прямую. Как и в других
случаях, смысл уравнения D) тот, что пары действительных чисел х
и у, удовлетворяющих этому уравнению, являются координатами не-
некоторой точки на прямой, и обратно.
Может быть, читатель учил в школе,
что уравнение вида
В'
Рис. 16. Эллипс с фокусами
% + h =г E)
р я
представляет эллипс (рис. 16). Эта кри-
кривая пересекает ось а; в точках А(р, 0)
и А'(-р, 0) и ось у — в точках В@, q)
и В'@, -q). (Обозначение Р(х, у), или,
еще короче, (а;, у), вводится ради крат-
краткости и должно быть расшифровано так:
«точка Р с координатами х и у».) Ес-
Если р > q, то отрезок АА' длины 2р называется большой осью эл-
эллипса, а отрезок ВВ' длины 1q — его малой осью. Эллипс есть
геометрическое место точек Р, сумма расстояний которых от то-
точек F(y/p2 — q2, 0) и F'{—^/p2 — q2, 0) равна 2р. Читатель смо-
сможет проверить это в качестве упражнения, применяя формулу A).
Точки F и F' называются фокусами эллипса, а отношение е =
называется его эксцентриситетом. Уравнение вида
2 у2
р^~72=1'
представляет гиперболу. Эта кривая состоит из двух ветвей, пересека-
пересекающих ось а; соответственно в точках А(р, 0) и А'(— р, 0) (рис. 17). Отре-
Отрезок АА' длины 2р называется «действительной» осью гиперболы. Гипер-
Гипербола, удаляясь в бесконечность, приближается к двум прямым qx±py =
= 0, однако никогда с ними не встречается; эти прямые называются
асимптотами гиперболы. Гипербола есть геометрическое место то-
точек Р, разность расстояний которых до двух точек F{\Jp2 + q2, 0)
и F'(—y/p2 + q2, 0) по абсолютному значению равна 2р. Эти точки
в случае гиперболы тоже называются фокусами; под эксцентрисите-
F)
том гиперболы понимают отношение е =

§3. Замечания из области аналитической геометрии
109
Рис. 17. Гипербола с фокусами
Уравнение
У,
ху = 1
G)
также определяет гиперболу, но такую,
для которой асимптотами являются две
оси (рис. 18). Уравнение этой «рав-
«равносторонней» гиперболы геометрически
означает, что площадь прямоугольни-
прямоугольника OP'PQ' (см. рис. 12), связанного с
точкой Р, для всякой точки Р кривой
равна 1. Равносторонняя гипербола не-
несколько более общего вида
ху = с,
Gа)
Рис. 18. Равносторонняя ги-
гипербола. Площадь прямоуголь-
прямоугольника, определенного точкой
Р(х, у), равна 1
где с — постоянная, представляет собой частный случай гиперболы
в том же смысле, в каком окружность представляет собой частный
случай эллипса. Отличительная характеристика равносторонней гипер-
гиперболы заключается в том, что ее две асимптоты (в нашем случае — две
°си) взаимно перпендикулярны.
Во всем этом для нас самым интересным является руководящая
Идея: геометрические объекты могут полностью описываться в ариф-
арифметической или алгебраической форме. То же справедливо и относи-
относительно геометрических операций. Например, если нам требуется найти
точки пересечения двух прямых, то мы рассматриваем их два уравне-

110 Глава II
ния
ах + by = с,
а'х + Ь'у = с', 18)
и для нахождения общей точки этих двух прямых достаточно решить
систему (8); решение дает нам координаты искомой точки. Таким
же образом, точки пересечения двух произвольных кривых (скажем,
окружности х2 + у2 - 2ах - 2Ьу = к и прямой ах + by = с) находятся
посредством совместного решения их уравнений.
§ 4. Математический анализ бесконечного
1. Основные понятия. Последовательность натуральных чисел
1,2,3,...
представляет собой первый и самый важный пример бесконечного мно-
множества. Не нужно видеть ничего таинственного в том, что она — беско-
бесконечная, что у нее «нет конца»: как бы велико ни было натуральное чис-
число п, можно построить другое, за ним следующее число, еще большее —
п + 1. Но при переходе от прилагательного «бесконечный», означающего
просто-напросто «не имеющий конца», к существительному «бесконеч-
«бесконечность» никоим образом не следует привносить допущения, что «бес-
«бесконечность», обыкновенно изображаемая особым символом оо, может
быть рассматриваема как обыкновенное число. Нельзя включить сим-
символ оо в числовую систему действительных чисел, не нарушая при этом
основных законов арифметики. И тем не менее идея бесконечности про-
пронизывает всю математику, так как математические объекты изучают-
изучаются обыкновенно не как индивидуумы — каждый в отдельности, а как
члены классов или совокупностей, содержащих бесчисленное множес-
множество элементов одного и того же типа; таковы совокупности натураль-
натуральных чисел, действительных чисел или же треугольников на плоскости.
Именно по этой причине возникает необходимость в точном математи-
математическом анализе бесконечного. Современная теория множеств, создан-
созданная Георгом Кантором и его школой в конце XIX столетия, приступив
к разрешению этой задачи, достигла значительных успехов. Канторова
теория множеств глубоко проникла по многие области математики и
оказала на них огромное влияние; она стала играть особо выдающуюся
роль в исследованиях, связанных с логическим и философским обосно-
обоснованием математики. Исходным в канторовой теории является общее по-
понятие совокупности или множества. При этом имеется в виду собрание

§4. Математический анализ бесконечного 111
объектов (элементов), которое определяется некоторым правилом, поз-
позволяющим с полной определенностью судить о том, входит ли данный
объект в число элементов собрания или не входит. Примерами могут
служить множество всех натуральных чисел, множество всех периоди-
периодических десятичных дробей, множество всех действительных чисел или
множество всех прямых в трехмерном пространстве.
Для того чтобы сравнивать множества с точки зрения «количества»
содержащихся в них элементов, нужно ввести основное в этой теории
понятие «эквивалентности» множеств. Если элементы двух множеств А
и В могут быть приведены в попарное соответствие такого рода, что
каждому элементу множества А сопоставлен один и только один эле-
элемент множества В, а каждому элементу множества В сопоставлен один
и только один элемент множества А, то установленное таким образом
соответствие называется взаимно однозначным, а о самих множествах А
и В тогда говорят, что они между собой эквивалентны. Понятие экви-
эквивалентности в случае конечных множеств совпадает с обыкновенным
понятием числового равенства, так как два конечных множества в том
и только в том случае могут быть приведены во взаимно однозначное
соответствие, если содержат одно и то же число элементов. На этом и
основывается, нужно заметить, идея счета, когда мы «считаем» элемен-
элементы множества, то процесс счета как раз и заключается в установлении
взаимно однозначного соответствия между элементами множества и
числами 1, 2, ... , п.
Чтобы установить эквивалентность двух конечных множеств, иногда
нет необходимости «считать» элементы. Так, например, не считая, можно
утверждать, что конечное множество кругов единичного радиуса эквива-
эквивалентно множеству их центров.
Перенося понятие эквивалентности на бесконечные множества,
Кантор имел в виду создать «арифметику» бесконечного. Множество
действительных чисел и множество точек на прямой линии — эквива-
эквивалентны, так как после того, как выбраны начало и единичный отрезок,
данная прямая становится «числовой прямой», и каждой ее точке Р
в качестве координаты взаимно однозначно сопоставляется некоторое
совершенно определенное действительное число х:
Р<—»ж.
Четные числа образуют правильное подмножество множества всех
натуральных чисел, а все целые числа образуют правильное подмно-
подмножество множества всех рациональных чисел. (Говоря о «правильном»
Подмножестве некоторого множества S, мы имеем и виду такое мно-
множество 5', состоящее из элементов множества 5, но не из всех его эле-

112 Глава II
ментов.) Совершенно ясно, что если данное множество конечно, т. е. со-
содержит какое-то число п элементов, и не более того, то оно не мо-
может быть эквивалентно никакому своему правильному подмножеству,
так как всякое правильное его подмножество содержало бы самое боль-
большее п — 1 элементов. Но если данное множество содержит бесконечное
число элементов, то, как это ни парадоксально, оно может быть эк-
эквивалентно некоторому своему истинному подмножеству. Например,
схема
12 3 4 5 •¦¦ п •••
111 I
2 4 6 8 10 ••• 2п ¦¦¦
устанавливает взаимно однозначное соответствие между множеством
натуральных чисел и множеством всех четных целых положительных
чисел, и эти два множества оказываются эквивалентными, хотя второе
есть истинное подмножество первого. Такое противоречие с ходячей
истиной «целое больше своей части» показывает, какие сюрпризы нас
ждут в области «арифметики бесконечного».
2. Счетность множества рациональных чисел и несчет-
несчетность континуума. Одно из первых открытий Кантора в области
анализа бесконечного заключалось в том, что множество рациональ-
рациональных чисел (содержащее в качестве правильного подмножества беско-
бесконечное множество натуральных чисел и потому само бесконечное) эк-
эквивалентно множеству натуральных чисел. На первый взгляд кажется
странным, что всюду плотное множество рациональных чисел не бо-
более богато элементами, чем множество натуральных чисел, элементы
которого «рассеяны» редко и стоят на значительном расстоянии один
от другого. И в самом деле, с сохранением порядка возрастания нель-
нельзя расположить положительные рациональные числа так, как это мож-
можно сделать с натуральными: самое маленькое число а будет первым,
следующее за ним по величине b вторым и т. д.; дело в том, что ра-
рациональные числа расположены везде плотно, и потому ни для одного
из них нельзя указать «следующего по величине». Но Кантор заметил,
что если отказаться от требования «располагать по величине», то тогда
оказывается возможным расставить все рациональные числа в ряд п,
i, гз, 7*4, ..., подобный ряду натуральных чисел. Такое расположение
предметов некоторого множества в виде последовательности часто на-
называют пересчетом («нумерацией») этого множества. Множества, для
которых пересчет может быть выполнен, называются счетными или
исчислимыми. Указывая один из способов пересчета множества рацио-

§4. Математический анализ бесконечного 113
нальных чисел и устанавливая, таким образом, его счетность, Кантор
тем самым показал, что это множество эквивалентно множеству нату-
натуральных чисел, так как схема
1 2 3 4 ••• п ¦••
I t I I I
г\ г2 г3 г4 ••• гп ¦¦¦
создает взаимно однозначное соответствие между двумя множествами.
Мы опишем сейчас один из возможных способов пересчета множества
рациональных чисел.
1 2 3 4 5 6 7 ¦ • ¦
12 3 4 5 6 7
2 2 2 2 2 2 2
12 3 4 5 6 7
3 3 3 3 3 3 3 '"
12 3 4 5 6 7
4 4 4 4 4 4 4 '"
12 3 4 5 6 7
5 5 5 5 5 5 5 "'
12 3 4 5 6 7
6 6 6 6 6 6 6'"
Рис. 19. Пересчет рациональных чисел
Каждое рациональное число записывается в виде ^, где а и b —
целые числа; все эти числа могут быть расположены в такой таблице,
чтобы число у, стояло в а-тл строчке и в Ь-ы столбце. Например, 4 ста-
6 4
нет в третьей строчке и в четвертом столбце таблицы. Предположим,
что все свободные места, или «клеточки», в таблице заполнены соответ-
соответствующими числами, и затем мы проведем по таблице непрерывную
ломаную линию, которая пройдет через все клеточки. Начиная с 1, мы
сделаем сначала один шаг вправо и получим 2 в качестве второго члена
последовательности; затем по диагонали налево и вниз — получим тре-
третий член 1; следующий шаг прямо вниз даст нам четвертый член 1;
п
потом движемся по диагонали вправо и вверх через =г к 3; вправо —
к 4; по диагонали влево и вниз через ^ и ~ к ± и т. д., как показано на
рис. 19. В результате движение по ломаной линии приводит к последо-

114 Глава II
вательности рациональных чисел
19II2O43211234,
' ' 2' 3' 2' ' ' 2' 3' 4' 5' 4' 3' 2' ' "'
Если мы выбросим теперь все дроби, у которых числитель и знаме-
знаменатель имеют отличные от 1 общие делители, то останется последо-
последовательность, в которой каждое рациональное число встретится один
и в точности один раз:
1211ч4-
' ' 2' 3' ' ' 2' 3' 4' 5' ' ¦'¦
Так устанавливается, что множество всех рациональных чисел явля-
является счетным. Принимая во внимание, что рациональные числа вза-
взаимно однозначно связаны с рациональными точками числовой прямой,
можно также сказать, что множество рациональных точек на числовой
прямой счетно.
Упражнения.
1) Покажите, что множество всех целых, положительных и отрицатель-
отрицательных, чисел — счетное. Покажите, что множество всех рациональных,
положительных и отрицательных, чисел — счетное.
2) Покажите, что если S и Г — счетные множества, то множество S + T
(см. стр. 147) — также счетное. То же покажите для суммы трех, четы-
четырех и, вообще, п множеств; покажите, наконец, что множество, состав-
составленное посредством сложения счетного множества счетных множеств,
также счетное.
Раз оказалось, что множество рациональных чисел — счетное, то
могло бы возникнуть подозрение, что и всякое бесконечное множест-
множество — также счетное, и на этом, естественно, закончился бы весь анализ
бесконечного. Но это совсем не так. Тому же Кантору принадлежит от-
открытие исключительной важности: множество всех действительных
(рациональных и иррациональных) чисел — несчетное. Другими сло-
словами, совокупность всех действительных чисел совершенно иного (так
сказать более высокого) «типа бесконечности», чем совокупность одних
только целых или одних только рациональных чисел. Принадлежащее
Кантору остроумное «косвенное» доказательство этого факта стало мо-
моделью для многих иных доказательств в математике. Идея рассуждения
такова. Мы исходим из допущения, что все действительные числа уда-
удалось перенумеровать, располагая их в виде последовательности, и пос-
после этого демонстрируем число, которое никак не может быть числом

§4. Математический анализ бесконечного 115
этой последовательности. Отсюда возникает противоречие: ведь было
предположено, что все действительные числа вошли в состав последо-
последовательности, и это предположение должно быть признано ложным, ес-
если хотя бы одно число оказывается за пределами последовательности.
Таким образом обнаруживается несостоятельность утверждения, что
все действительные числа поддаются «пересчету», и ничего другого не
остается, как только признать вместе с Кантором, что множество дей-
действительных чисел несчетно.
Однако проведем это рассуждение фактически. Допусктим, что все
действительные числа, представленные в виде бесконечных десятич-
десятичных дробей, расположены в порядке последовательности, или списка:
1-е число Ni, aia2a3a4fl5 • • •
2-е число Nz, 6162636465 • • ¦
3-е число N3, C1C2C3C4C5 ...
где буквы N{ обозначают целую часть, а буквы а, 6, с,... представля-
представляют собой десятичные знаки, стоящие вправо от запятой. Мы допуска-
допускаем, что эта последовательность дробей охватывает все действительные
числа. Существенной частью доказательства является построение с по-
помощью «диагональной процедуры» такого нового числа, относительно
которого можно показать, что оно не входит в наш список.
Построим такое число. Для этого возьмем первую цифру после за-
запятой а, какую угодно, но отличную от а\, а также от 0 и 9 (последнее,
чтобы избежать затруднений, возникающих из равенств вроде следу-
следующего: 0,999... = 1,000...); затем вторую цифру 6 возьмем отличной
от 6г, а также от 0 и 9; третью цифру с — отличной от сз, и т.д.
(Для большей определенности можно условиться в следующем: мы бе-
берем а = 1, если только а± ф 1, а в случае а\ = 1 возьмем а = 2; и ана-
аналогично для всех прочих цифр 6, с, d, е, ...) Теперь рассмотрим число
z = 0, abode ...
Это новое число z наверное не входит в наш список; действительно,
оно не равно первому числу, стоящему в списке, так как от него отли-
отличается первой цифрой после запятой, оно не равно второму числу, так
как от него отличается второй цифрой после запятой, и вообще отлично
от п-го числа по списку, так как от него отличается n-й цифрой после
запятой. Итак, в нашем списке, составленном будто бы из всех дейст-
действительных чисел, нет числа z. Значит, множество всех действительных
чисел неисчислимо.
8*

116
Глава II
т
Рис. 20. Взаимно однозначное соответствие между точками согнутого интер-
интервала и точками прямой линии
Читателю может прийти в голову мысль, что несчетность контину-
континуума обусловливается неограниченной протяженностью прямой линии и
что конечный отрезок прямой будет содержать лишь счетное множес-
множество точек. Чтобы убедиться в ложности такого предположения, доста-
достаточно установить, что весь числовой континуум в целом эквивалентен
некоторому конечному интервалу, скажем, единичному интервалу от 0
до 1, за исключением конечных точек. Получить необходимое для этой
цели взаимно однозначное соответствие можно, например, сгибая ин-
интервал в точках i и | и затем проектируя так, как показано на рис. 20.
о о
Отсюда видно, что даже конечный интервал (и, конечно, отрезок) со-
содержит несчетное множество точек.
Упражнение. Показать, что любой отрезок [А, В] числовой прямой
эквивалентен любому другому отрезку [С, D] (рис. 21).
Стоит привести еще другое доказатель-
доказательство несчетности континуума, носящее, по-
пожалуй, более интуитивный характер. Доста-
Достаточно (принимая во внимание последнее до-
доказанное предложение) сосредоточить вни-
внимание на точках единичного отрезка от 0
до 1. Доказательство, впрочем, как и рань-
раньше, будет «косвенное». Предположим, что
множество всех точек названного отрезка
может быть расположено в виде последова-
последовательности
D
Рис. 21. Взаимнооднознач-
Взаимнооднозначное соответствие между
точками двух отрезков
различной длины
а2, а3, •••
A)
Покроем точку aj интервалом, длина которого пусть будет равна -^т,
точку п2 — интервалом длины -^ и т. д. Если бы все точки единичного
отрезка входили в последовательность A), то весь единичный отрезок

§4. Математический анализ бесконечного 117
оказался бы покрытым бесконечным множеством таких отрезков (мо-
(может быть, частью перекрывающихся), длины которых суть i -1^, ...
(Беды нет, если некоторые из наложенных отрезков выйдут за пределы
основного единичного отрезка.) Сумма всех длин наложенных отрезков
равна
A- + J- + J-4- = 1 1 = 1
10 102 103 1П 1 1 q"
iu 1 10 у
Итак, допущение, что последовательность A) содержит все действи-
действительные точки единичного отрезка, приводит к заключению, что весь
этот отрезок, длина которого равна 1, можно покрыть множеством про-
промежутков с общей длиной i; с интуитивной точки зрения это — не-
У
лепость. Это рассуждение мы позволим себе рассматривать как дока-
доказательство, хотя строго логически тут был бы нужен более глубокий
анализ.
Приведенное только что рассуждение, между прочим, позволяет устано-
установить одну теорему, имеющую большое значение в современной «теории ме-
меры». Заменяя упомянутые выше промежутки меньшими промежутками —
длины yfrTi где е — произвольно малое положительное число, мы убедимся,
что всякое счетное множество точек на прямой может быть покрыто мно-
множеством отрезков с общей длиной ^. Так как е произвольно мало, то и ^
У У
может быть сделано столь малым, сколь нам угодно. Пользуясь фразеоло-
фразеологией «теории меры», мы скажем, что счетное множество точек имеет меру
нуль.
Упражнение. Доказать аналогичную теорему для счетного множества
точек на плоскости, заменяя отрезки площадями квадратов.
3. «Кардинальные числа» Кантора. Резюмируем полученные
результаты. Число элементов конечного множества А не может равнять-
равняться числу элементов другого конечного множества В, если А содержит
больше элементов, чем В. Но если мы заменим понятие «множеств, име-
имеющих одно и то же конечное число элементов» более общим понятием
«эквивалентных множеств», то — в случае бесконечных множеств —
предыдущее утверждение уже не будет справедливо: множество всех
целых чисел содержит «больше» элементов, чем множество всех чет-
четных чисел, а множество всех рациональных чисел — «больше» элемен-
элементов, чем множество всех целых чисел; и, однако, как мы видели, все эти
множества эквивалентны. Можно было бы заподозрить, что все беско-
бесконечные множества между собой эквивалентны, но Кантор опроверг это

118 Глава II
предположение: существует множество — континуум действительных
чисел, — которое не эквивалентно никакому счетному множеству.
Итак, существует по меньшей мере два различных «типа бесконеч-
бесконечности»: счетная бесконечность натуральных чисел и несчетная беско-
бесконечность континуума. Если два множества А и В, конечные или бес-
бесконечные, эквивалентны, мы скажем иначе, что им соответствует од-
одно и то же кардинальное число (или мощность). В случае конечных
множеств кардинальное число сводится к обыкновенному натурально-
натуральному числу, но понятие кардинального числа носит более общий харак-
характер. Далее, если случится, что множество А эквивалентно некоторо-
некоторому подмножеству (части) множества В, но само В неэквивалентно ни
множеству А, ни какой бы то ни было его части, то говорят, следуя
Кантору, что множеству В соответствует большее кардинальное число,
чем множеству А. Это употребление термина «число» также согласует-
согласуется с обычным употреблением в случае конечных множеств. Множество
целых чисел есть подмножество множества всех действительных чи-
чисел, тогда как множество действительных чисел не эквивалентно ни
множеству целых чисел, ни какому бы то ни было его подмножеству
(оно ни счетное, ни конечное). Значит, по данному определению, кон-
континууму действительных чисел соответствует большее кардинальное
число, чем множеству натуральных чисел.
* Кантор показал фактически, как можно построить бесконечную после-
последовательность бесконечных множеств, которым соответствуют все большие
и большие кардинальные числа. Так как можно исходить из множества на-
натуральных чисел, то достаточно показать, что, каково бы ни было данное
множество А, можно построить другое множество В, у которого кардиналь-
кардинальное число будет больше чем у А. Вследствие большой общности этой теоремы
доказательство ее по неизбежности несколько абстрактно. Множество В мы
определяем как множество, элементами которого являются все возможные
подмножества множества А. Говоря о «подмножествах» А, мы в данном слу-
случае имеем в виду не только «правильные подмножества» А, но не исключаем
и самого множества А, а также «пустого» множества 0, не содержащего ника-
никаких элементов. (Так, если А состоит из трех целых чисел 1, 2, 3, то В содер-
содержит 8 различных элементов {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3} и 0.)
Каждый элемент множества В сам есть множество, состоящее из каких-то
элементов множества А. Допустим теперь, что В эквивалентно А или некото-
некоторому подмножеству А, т. е. что существует некоторое правило, приводящее
во взаимно однозначное соответствие элементы А или некоторого подмно-
подмножества А со всеми элементами В, т. е. всеми подмножествами А.
а <—> 5а, B)
где через Sa обозначено то подмножество А, которому соответствует эле-

§4. Математический анализ бесконечного 119
мент а множества А. Мы придем к противоречию, если укажем некоторый
элемент В, т. е. некоторое подмножество Т множества А, которому не мо-
ткет соответствовать никакой элемент а. Чтобы построить подмножество Г,
заметим прежде всего, что для всякою элемента х из А существуют две воз-
возможности: или множество Sx, сопоставляемое зависимостью B) элементу х,
содержит элемент х или не содержит. Мы определим Т как подмножество А,
состоящее из всех таких элементов х, что Sx не содержит х. Определен-
Определенное таким образом множество Т отличается от всякого Sa по крайней мере
элементом а, так как если Sa содержит а, то Т не содержит а, а если 5а не
содержит а, то Т содержит а. Итак, Т не включено в соответствие B). Это и
показывает, что невозможно установить взаимно однозначное соответствие
между элементами А (или некоторого подмножества А) и элементами В. Но
соотношение
устанавливает взаимно однозначное соответствие между всеми элемента-
элементами А и подмножеством В, состоящим из одноэлементных подмножеств А.
Значит, по данному выше определению, множеству В соответствует большее
кардинальное число, чем множеству А.
* Упражнение. Если множество А содержит п элементов, то опреде-
определенное выше множество В содержит 2" элементов. Если А есть множество
натуральных чисел, то В эквивалентно континууму действительных чисел,
заключенных между 0 и 1. (Указание: сопоставьте каждому подмножеству А
символ, состоящий из последовательности — конечной в первом примере,
бесконечной во втором —
а\
где ап = 1 или 0, смотря по тому, принадлежит или не принадлежит п-й
элемент А рассматриваемому подмножеству.)
Могло бы показаться легкой задачей построить множество точек, обла-
обладающее большим кардинальным числом, чем множество точек единичного
отрезка. Казалось бы, что квадрат со стороной 1, как «двумерная» фигура,
должен содержать «больше» точек, чем «одномерный» отрезок. Но, как это ни
странно, дело обстоит иначе: кардинальное число точек квадрата в точнос-
точности равно кардинальному числу точек отрезка. Для доказательства достаточ-
достаточно установить взаимно однозначное соответствие между точками квадрата
и точками отрезка. Постараемся это сделать.
Если (х, у) есть какая-нибудь точка единичного квадрата, то координа-
координаты ее х и у могут быть представлены в виде десятичных разложений
х = 0, а\ 0,2 аз at ... ,
у = О, Ь\ 6г 6з Ъь ... ,
причем пусть будет условлено (ради избежания всяких сомнений), что, на-
например, число -7 будет записываться в виде 0,25000 ..., а не в виде 0,24999 ....

120 Глава II
Названной точке квадрата (ж, у) мы сопоставим точку единичного отрезка
z = 0, ai Ъ\ а,2 Ьг аз Ьз а-4 Ъа
Очевидно, различным точкам квадрата (ж, у) и (ж', у') сопоставляются раз-
различные же точки отрезка z и z'; это и значит, что кардинальное число мно-
множества точек квадрата не превышает кардинального числа множества точек
отрезка.
(Собственно говоря, в данном случае построено взаимно однозначное
соответствие между множеством всех точек квадрата и некоторым под-
подмножеством точек отрезка: никакая точка квадрата не будет соответство-
соответствовать, например, точке отрезка 0,2140909090..., так как мы условились пи-
писать 0,25000..., а не 0,24999 .... Но можно слегка видоизменить построение
таким образом, чтобы действительно осуществлялось взаимно однозначное
соответствие между множеством всех точек квадрата и множеством всех
точек отрезка.)
Аналогичное рассуждение показывает, что кардинальное число точек ку-
куба не превышает кардинального числа точек отрезка.
Все эти результаты, казалось бы, стоят в противоречии с интуитивным
представлением о «размерности». Но нужно обратить внимание на то, что
вводимые нами соответствия не являются «непрерывными»; когда мы пере-
перемещаемся по отрезку от 0 к 1 непрерывно, соответствующие точки в квадрате
не образуют непрерывной кривой, а будут появляться в порядке совершенно
«хаотическом». Размерность множества точек зависит не только от карди-
кардинального числа точек, но и от того, как они расположены в пространстве. Мы
вернемся к этому вопросу в главе V.
4. Косвенный метод доказательства. Теория кардинальных
чисел представляет собой лишь один из аспектов общей теории мно-
множеств, созданной Кантором несмотря на наличие суровую критику со
стороны наиболее выдающихся математиков того времени. Многие из
критиков, например, Пуанкаре и Кронекер, возражали против неопре-
неопределенности общего понятия «множества» и против неконструктивного
характера рассуждений, применявшихся при определении некоторых
множеств.
Возражения против неконструктивных рассуждений относятся
к тем доказательствам, которые можно было бы назвать «существен-
«существенно косвенными». Сами по себе «косвенные» доказательства есть самый
обыкновенный элемент математического мышления: желая установить
истинность предложения А, мы вначале допускаем, что справедливо
иное предложение А', противоположное А; затем некоторая цепь рас-
рассуждений приводит нас к утверждению, противоречащему А', и тем
самым обнаруживается несостоятельность предложения А'. Тогда, на

§4. Математический анализ бесконечного 121
базе основного логического принципа «исключенного третьего», из лож-
ложности А' следует истинность А.
В разных местах этой книги читатель найдет ряд таких примеров,
для которых косвенное доказательство легко может быть превраще-
превращено в прямое, но «косвенная» форма создает преимущества краткости и
освобождает от рассмотрения подробностей, имеющих второстепенный
интерес с точки зрения поставленной ближайшей цели. Но попадаются
и такие теоремы, для которых до настоящего времени не удалось дать
иных доказательств, кроме косвенных. О некоторых из этих теорем
можно даже сказать, что, по-видимому, по самой природе теорем пря-
прямые, конструктивные их доказательства принципиально невозможны.
Сюда относится, например, теорема, приведенная на стр. 114. Не раз
бывали случаи в истории математики, когда все усилия математиков
были направлены в сторону построения («конструкции») решения тех
или иных проблем, разрешимость которых предполагалось установить,
а затем кто-нибудь приходил, если так можно выразиться, со стороны
и ликвидировал все трудности с помощью «косвенного» неконструктив-
неконструктивного рассуждения.
Когда речь идет о доказательстве существования объекта опреде-
определенного типа, то имеется существенное различие между тем, чтобы
построить осязаемый пример объекта, и тем, чтобы доказать, что из не-
несуществования объекта можно вывести противоречивые заключения.
В первом случае получается осязаемый объект, во втором — ничего,
кроме противоречия. Не так давно некоторые математики (весьма за-
заслуженные) провозгласили более или менее полное устранение из мате-
математики всех неконструктивных доказательств. Даже если бы выполне-
выполнение этой программы признать желательным, необходимо указать, что
это повлекло бы за собой в настоящую эпоху чрезвычайные усложнения,
и можно было бы даже опасаться, что в процессе совершающихся по-
потрясений подверглись бы разрушению существенные части организма
математики. Поэтому нечего удивляться, что школа «интуиционистов»,
принявшая упомянутую программу, встретила упорное сопротивление,
и что даже наиболее ортодоксальные интуиционисты не всегда в состо-
состоянии жить согласно своим убеждениям1.
5. Парадоксы бесконечного. Хотя бескомпромиссная пози-
позиция, занятая интуиционистами, с точки зрения большинства матема-
:Об интуиционизме и выросшем из него конструктивном направлении в матема-
математике и логике, на исчерпывающую характеристику которых никак не претендуют
эти строки, см., например, [25] и [27] в списке литературы в конце книги (номера
По которому всюду указываются в квадратных скобках).

122 Глава II
тиков является слишком экстремистской, волей-неволей приходится со-
согласиться, что для внешне прекрасной теории бесконечных множеств
возникла серьезная угроза, когда в пределах самой этой теории обна-
обнаружились совершенно явные логические парадоксы. Очень скоро было
замечено, что неограниченная свобода в пользовании понятием «мно-
«множество» неизбежно ведет к противоречиям. Мы приведем здесь один
из парадоксов, обнаруженный Бертраном Расселом. Вот в чем он за-
заключается.
Как правило, множества не содержат себя в качестве элемента. На-
Например, множество А всех целых чисел содержит в качестве элементов
только целые числа; так как само А не есть целое число, а есть мно-
множество целых чисел, то А себя в качестве элемента не содержит. Усло-
Условимся называть такие множества «ординарными». Но могут существо-
существовать и такие множества, которые содержат себя в качестве элемента.
Рассмотрим, например, множество S, определенное следующим обра-
образом: «S содержит в качестве элементов все множества, которые можно
определить посредством предложения, содержащего меньше двадцати
слов». Так как само множество S определяется предложением, содержа-
содержащим меньше двадцати слов, то выходит, что оно является элементом
множества S. Такие множества назовем «экстраординарными». Как бы
то ни было, большинство множеств — ординарные; попробуем не иметь
дела с дурно ведущими себя экстраординарными множествами и будем
рассматривать только множество всех ординарных множеств. Обозна-
Обозначим его буквой С. Каждый элемент С есть множество, притом орди-
ординарное множество. Но вот возникает вопрос: а само множество С —
ординарное или экстраординарное'! Несомненно, оно должно быть или
тем, или другим1. Если С — ординарное множество, то оно содержит
себя в качестве элемента, так как С определено как множество всех
ординарных множеств. Раз дело обстоит так, значит, С — экстраорди-
экстраординарное множество, так как экстраординарными, согласно определению,
названы множества, содержащие себя в качестве элемента. Получается
противоречие. Значит, С должно быть экстраординарным множеством.
Но тогда множество С содержит в качестве элемента себя, т. е. оно есть
экстраординарное множество, а это противоречит определению С как
множества всех ординарных множеств. Итак, мы видим, что уже одно
только допущение существования множества С внутренне противоре-
противоречиво.
1 Получаемое далее противоречие может быть выведено и без использования так
называемого закона исключенного третьего, подразумеваемого в утверждении этой
фразы. См., например, А. Френкель и И. Бар-Хиллел, Основания теории множеств,
пер. с англ., М., изд. «Мир», 1966, гл. I, § 2.

§4. Математический анализ бесконечного 123
6. Основания математики. Парадоксы вроде вышеприведен-
вышеприведенного побудили Рассела и других подвергнуть систематическому изуче-
изучению основания математики и логики. Конечная цель этих исследований
заключается в создании для математических рассуждений такой логи-
логической базы, относительно которой можно было бы доказать, что она
свободна от возможных противоречий, и которая вместе с тем была
бы достаточно обширной, чтобы из нее можно было путем дедукции
вывести все, что в математике признается существенным или хотя бы
многое из того. Поскольку такой самонадеянной цели достигнуть не
удавалось (а может быть, ее и нельзя достигнуть), математическая
логика как особый предмет привлекала внимание все возрастающего
числа исследователей. Многие относящиеся сюда проблемы необходи-
необходимо признать крайне трудными, хотя формулировки их вполне просты.
В качестве примера назовем гипотезу континуума, утверждающую,
что не существует множества, для которого кардинальное число боль-
больше, чем кардинальное число множества натуральных чисел, но мень-
меньше, чем кардинальное число множества действительных чисел. Из этой
гипотезы можно вывести много интересных следствий, но сама гипо-
гипотеза до наших дней не была ни доказана, ни опровергнута. Впрочем,
не так давно Курт Гёдель доказал, что если система обычных постула-
постулатов, лежащих в основе теории множеств, не содержит противоречий,
то в таком случае расширенная система постулатов, получающаяся при
добавлении континуум-гипотезы, также не содержит противоречий1.
Вопросы, рассматриваемые в математической логике, в конечном счете
упираются в один основной вопрос: что понимать под существованием
в математике? К счастью, существование самой математики не зависит
от того, найден ли удовлетворительный ответ на этот вопрос. Школа
«формалистов», во главе которой стоял великий математик Гильберт,
утверждает, что в математике «существование» означает «свободу от
Противоречия». Если принять эту точку зрения, то очередной и необ-
необходимой задачей является как раз построение системы постулатов, из
которых всю математику можно было бы вывести путем логической
Дедукции, и доказательство того, что эти постулаты не могут привес-
привести ни к какому противоречию. Недавние результаты Гёделя и других
как будто бы показывают, что такая программа, по крайней мере в той
форме, в какой она была намечена самим Гильбертом, не может быть
осуществлена. Весьма многозначительно то обстоятельство, что гиль-
гильбертова теория формализированного построения математики сущест-
11940 г. А в 1963 г. американским математиком П.Дж. Коэном доказана независи-
независимость континуум-гипотезы от принятой Гёделем системы аксиом теории множеств.

124 Глава II
венно опирается на интуитивные процедуры. Тем или иным путем,
в открытой или в скрытой форме, даже прикрытая самым безупреч-
безупречным формалистическим, логическим, аксиоматическим одеянием, кон-
конструктивная интуиция всегда остается самым жизненным элементом
в математике1.
§ 5. Комплексные числа
1. Возникновение комплексных чисел. По ряду причин воз-
возникла потребность в расширении понятия числа даже за пределы конти-
континуума действительных чисел — посредством введения так называемых
комплексных чисел. Необходимо ясно представлять себе, что все подоб-
подобного рода расширения и нововведения приходят отнюдь не в результа-
результате чьих-то индивидуальных усилий. Скорее их можно рассматривать
как итог некоторой постепенной и исполненной колебаний эволюции,
в которой не должна быть преувеличиваема роль отдельных личнос-
личностей. Одной из причин, которые обусловили появление и употребление
отрицательных и дробных чисел, было стремление к большей свободе
в формальных вычислениях. Только к концу средневековья математи-
математики стали терять ощущение беспокойства и неуверенности, с которым
они оперировали этими понятиями, тогда как ничего подобного не на-
наблюдалось в отношении таких интуитивно ясных и конкретно воспри-
воспринимаемых понятий, как понятие натурального числа.
Простейшая процедура, требующая применения комплексных чи-
чисел, есть решение квадратных уравнений. Напомним, как обстояло дело
с линейным уравнением ах = Ь, когда нужно было определить удов-
удовлетворяющее ему значение неизвестной величины х. Решение имеет
вид х = -, и введение дробных чисел как раз обусловливается требо-
требованием, чтобы всякое линейное уравнение с целыми коэффициентами
(при а ф 0) было разрешимо. Уравнения вроде
х2 = 2 A)
не имеют решения в области рациональных чисел, но имеют таковое
в расширенном поле всех действительных чисел. Но даже поле действи-
действительных чисел недостаточно обширно, чтобы в нем можно было постро-
построить полную и законченную теорию квадратных уравнений. Например,
следующее очень простое уравнение
х2 = -1 B)
'Подробнее об этих вопросах см. [24] и [25].

§5. Комплексные числа 125
не имеет действительных решений, так как квадрат действительного
числа никак не может быть отрицательным. Нам приходится или удо-
удовольствоваться тем положением, что такие простые уравнения неразре-
неразрешимы, или следовать по уже знакомому пути — расширять числовую
область и вводить новые числа, с помощью которых удастся решить
уравнение. Именно это самое и делается, когда вводят новый символ г
и принимают, в качестве определения, что г'2 = — 1. Разумеется, этот
объект — «мнимая единица» — не имеет ничего общего с числом как
орудием счета. Это — отвлеченный символ, подчиненный основному
закону г2 = —1, и ценность его зависит исключительно от того, бу-
будет ли достигнуто в результате его введения действительно полезное
расширение числовой системы.
Так как мы хотим складывать и умножать с помощью символа г
так же, как с обыкновенными числами, то естественно пользоваться
символами вроде 2г, Зг, —г, 2 + 5г, вообще, а + Ы, где а и b — дейст-
действительные числа. Раз эти символы должны подчиняться коммутатив-
коммутативному, ассоциативному и дистрибутивному законам, то должны быть
возможны, например, такие вычисления:
B + Зг) + A + 4г) = B + 1) + C + 4)г = 3 + 7г;
B + Зг) • A + 4г) = 2 + 8г + Зг + 12г2 = B - 12) + (8 + 3)г = -10 + 11г.
Руководствуясь этими соображениями, мы начинаем системати-
систематическое изложение теории комплексных чисел со следующего определе-
определения: символ вида а + Ы, где а и b — два действительных числа, носит
название комплексного числа с действительной частью а и мнимой час-
частью Ь. Операции сложения и умножения совершаются над этими чис-
числами так, как будто бы г было обыкновенное действительное число,
однако с условием заменять г2 через — 1. Точнее говоря, сложение и
умножение определяются по формулам
( (а + Ы) + (с + di) = (a + c) + (b + d)i,
\ (а + Ы)(с + di) = (ас - bd) + (ad + bc)i.
В частности, мы получаем
(о + Ы)(а - Ы) = а2 - abi + abi - b2i2 = a2 + b2. D)
Основываясь на этих определениях, легко проверить, что для комп-
комплексных чисел справедливы коммутативный, ассоциативный и дистри-
дистрибутивный законы. Далее, не только сложение и умножение, но также и
вычитание и деление, будучи применены к двум комплексным числам,

126 Глава II
приводят снова к комплексным числам того же вида а + Ы, так что
комплексные числа образуют поле (см. стр. 86):
(о + Ы) - (с + di) = (а~ с) + (b - d)i,
а + Ы __ {а + Ьг)(с - di) _ (дс+ bd\ (be- ad\ . E)
(Второе равенство теряет смысл, если c + di = 0 + (И, так как тогда
с2 + d2 = 0. Значит, и на этот раз нужно исключить деление на нуль,
т.е. на 0 + 0г). Например,
B + Зг) - A + 4г) = 1 - г,
2 + Зг _ 2 + Зг 1 - 4г _ 2 - 8г + Зг + 12 _ 14 5 ¦
1+4г ~ 1 + 4г ' 1 - 4г ~ 1 + 16 ~ 17 17*"
Поле комплексных чисел включает поле действительных чисел
в качестве «подполя», так как комплексное число а + 0г отождеств-
отождествляется с действительным числом а. Заметим, с другой стороны, что
комплексное число вида 0 + Ы = Ы называется «чисто мнимым».
Упражнения.
,, п A + 0B + 0C + 0 .
1) Представить в форме а + Ьг.
A — г)
2) Представить (~^+*~о~) в форме а + 6г.
3) Представить в форме а + Ы следующие выражения:
1 + г 1 + » 1 1 D - ЫJ
1-Г 2-i' i5' (-2 + 0A-30' B-ЗгJ'
4) Вычислить у/5 + 12г. (Указание: напишите \/5 + 12г' = x + yi, возведите
в квадрат и сравняйте действительные части и мнимые части.)
Вводя символ г, мы расширили поле действительных чисел и полу-
получили поле символов а + Ы, в котором квадратное уравнение
имеет два решения: х = i и х = —г. В самом деле, согласно опреде-
определению, i ¦ i = (—г)(—г) = г'2 = —1. Нужно сказать, что мы приобрели
гораздо больше: можно легко проверить, что теперь каждое квадратное
уравнение
ах2 + Ьх + с ~ 0 F)

J5. Комплексные числа
127
становится разрешимым. В самом деле, выполняя над равенством F)
ряд преобразований, мы получаем:
Ь _с
ах ~ о'
с
а'
(* + &)' =
b2 - iac
G)
х —
Заметим теперь, что если Ь2 —Аас ^ 0, то \/Ь2 — 4ос есть обыкновенное
действительное число и корни уравнения G) — действительные; если
же Ъ2 — 4ас < 0, то тогда 4ас — Ь2 > О, и, следовательно, \Jb2 — Аас =
= yj— Dос — Ь2) = \/4ас ~Ъ2 -i, так что уравнение G) имеет в качестве
корней мнимые числа. Так, например, уравнение
х2 - Ъх - 6 = О
имеет действительные корни х =
как уравнение
5±
5±1
= 2 или 3, тогда
имеет мнимые корни ж =
х1 - 2ж + 2 = О
2± л/4 -8 2 ±2
= 2 = 1 + i или 1
2 2
2. Геометрическое представление комплексных чисел. Уже
в XVI столетии в математических работах появляются квадратные кор-
корни из отрицательных чисел в формулах, дающих решения квадратных
уравнений. Но в те времена математики затруднились бы объяснить
точный смысл этих выражений, к которым относились почти с суевер-
суеверным трепетом. Сам термин «мнимый» до сих пор напоминает нам о том,
что эти выражения рассматривались как нечто искусственное, лишен-
лишенное реального значения. И только в начале XIX в., когда уже выясни-
выяснилась роль комплексных чисел в различных областях математики, было
Дано очень простое геометрическое истолкование комплексных чисел и
операций с ними, и этим был положен конец сомнениям в возможнос-
возможности их законного употребления. Конечно, с современной точки зрения

128
Глава II
формальные операции с комплексными числами полностью оправдыва-
оправдываются на основе формальных определений, так что геометрическое пред-
представление логически не является необходимым. Но такое представле-
представление, предложенное почти одновременно Весселем A745-1818), Арганом
A768-1822) и Гауссом, позволило рассматривать комплексные числа и
действия с ними как нечто вполне естественное с интуитивной точ-
точки зрения и, кроме того, имеющее чрезвычайно большое значение в
приложениях комплексных чисел как в самой математике, так и в ма-
математической физике.
Геометрическая интерпретация комп-
комплексных чисел заключается в том, что комп-
комплексному числу z = х + уг сопоставляет-
сопоставляется точка на плоскости с координатами х, у.
Именно действительная часть числа мыслит-
мыслится как ж-координата, а мнимая — как у-ко-
ордината. Таким образом устанавливается
взаимно однозначное соответствие между
комплексными числами и точками «число-
«числовой плоскости», подобно тому как нами было
установлено раньше (см. § 2), соответствие
между действительными числами и точка-
точками «числовой оси». Точкам на оси х в число-
числовой плоскости соответствуют действитель-
действительные числа z = х + Ог, тогда как точкам на
оси у — чисто мнимые числа z = 0 + уг.
z=x+yi
z=x-yi
Рис. 22. Геометрическое
представление комплекс-
комплексных чисел. Точка z имеет
прямоугольные координа-
координаты ж, у
Если
z — х + уг
есть какое-то комплексное число, то мы называем число
J = х — yi
сопряженным с числом z. В числовой плоскости точка ~z получается из
точки z посредством зеркального отражения относительно оси х. Если
мы условимся расстояние точки z от начала обозначать через р, то на
основании теоремы Пифагора
р2 = х2 + у2 = (х + уг){х - уг) = z • z.
Действительное число р = у/х2 + у2 называется модулем z и обознача-
обозначается
p=\z\.

§5. Комплексные числа
129
Бели z лежит на действительной оси, то модуль совпадает с абсолют-
абсолютным значением z. Комплексные числа с модулем 1 изображаются точ-
точками, лежащими на «единичном окружности» с центром в начале и ра-
радиусом 1.
Если \z\ = 0, то z = 0. Это следует из определения \z\ как рассто-
расстояния точки z от начала. Далее, модуль произведения двух комплексных
чисел равен произведению модулей
z2\ =
\z2\.
Это вытекает как следствие из более общей теоремы, которая будет
доказана на стр. 131.
Упражнения.
1) Доказать последнюю теорему, исходя непосредственно из определения
умножения двух комплексных чисел z\ = Х\ + y\i и zi = Х2 + J/2*-
2) Пользуясь тем обстоятельством, что произведение двух действитель-
действительных чисел равно нулю в том и только в том случае, если один из мно-
множителей равен нулю, доказать соответствующую теорему для комп-
комплексных чисел. (Указание: основывайтесь при доказательстве на двух
последних теоремах.)
Согласно определению сложения двух
комплексных чисел z\
= х2 + у2г, мы имеем
= х\ +;
и z2 =
z2 =
х2)
y2)i.
Таким образом, точка z\+z2 изображает-
изображается в числовой плоскости четвертой вер-
вершиной параллелограмма, у которого тре-
тремя первыми вершинами являются точки
О, z\, z2. Это простой способ построения
суммы двух комплексных чисел ведет ко
многим важным следствиям. Из него мы
Рис. 23. Сложение комплекс-
комплексных чисел по правилу парал-
параллелограмма
заключаем, что модуль суммы двух комплексных чисел не превышает
суммы модулей (ср. стр. 88)
\zi+z2\ ^ |zi| + |z2|.
Достаточно сослаться на то, что длина стороны треугольника не пре-
превышает суммы длин двух других сторон.
9-340

130 Глава II
Упражнение. В каких случаях имеет место равенство \zi +гг| = |zi|-f
Угол между положительным направлением оси х и отрезком Oz на-
называется аргументом z и обозначается буквой <р (см. рис. 22). Числа г
и ~z имеют один и тот же модуль
W = \z\,
но их аргументы противоположны по знаку:
То = —(р.
Конечно, аргумент z определяется не однозначно, так как к нему мож-
можно прибавлять или из него вычитать любой угол, кратный 360°, не
изменяя направления отрезка Oz. Итак, углы
tp, <p + 360°, <р-
<р - 360°, <р - 720°, <р - 1080°, ...
графически дают один и тот же аргумент. Так как, согласно определе-
определениям синуса и косинуса,
х = pcostp, у = ps'mtp,
то любое комплексное число z выражается через его модуль и аргумент
следующим образом:
z = х + yi = p(cos ip + i sin ф). (8)
Например,
в случае
» »
» »
» »
так что
z = i
z = l + i
z = l-i
z = -l-+
мы имеем /
» » /
» » /
- VSi » » /
э = 1,
5= \/2,
9 = 2,
If =
Ч> =
<р =
V> =
90°,
45°,
-45°,
120°,
i= I(cos90° + tsin90°),
1+г = л/2(соз45° + i sin 45°),
1 - i = \/2(cos(-45°) + isin(-45°)),
-1 + y/U = 2(cos 120° + i sinl20°).
Читатель может проверить эти утверждения посредством подстановки
числовых значений тригонометрических функций.

5 5. Комплексные числа
131
Тригонометрическим представлением (8) очень полезно восполь-
воспользоваться, чтобы уяснить себе геометрический смысл умножения двух
комплексных чисел. Если
z = p(cos <р + i sin tp)
z = p'(cos<p' + isintp'),
то
zz — pp' {(cos ip cos ip' — sintpsintp') + (costpsintp' + sin <p cos <p')i}-
Но, в силу основных теорем сложения синуса и косинуса,
cos ip cos ip' — sin tp sin tp' = cos(<? + tp'),
cos <p sin tp' + sin tp cos tp' = sin(<p + tp').
Итак,
zz' = pp'{cos(tp + tp') + i sm(tp + <p')}.
(9)
zz
В правой части последнего равенства мы
видим написанное в тригонометрической
форме комплексное число с модулем рр'
и аргументом tp + tp'. Значит, мы мо-
можем отсюда заключить, что при умноже-
умножении двух комплексных чисел их модули пе-
перемножаются, а аргументы складывают-
складываются (рис. 24). Таким образом, мы видим,
что умножение комплексных чисел как-
то связано с вращением.
Установим точнее, в чем тут дело.
Назовем направленный отрезок, идущий
из начала в точку z, вектором точки z;
тогда модуль р = \z\ есть его длина.
Пусть z — какая-нибудь точка единич-
единичной окружности, так что р' = 1. В таком
случае умножение z на z' просто поворачивает вектор z на угол tp'. Если
Же р' ф 1( То5 помимо вращения, длина вектора должна быть умножена
На р'¦ Рекомендуем читателю самостоятельно проиллюстрировать эти
факты, умножая различные комплексные числа на z\ = i (вращение
Рис. 24. Умножение комплекс-
комплексных чисел: аргументы скла-
складываются, модули перемно-
перемножаются

132 Глава II
на 90°); zi — —i (то же вращение на 90°, но в обратном направлении);
гз = 1 + г и Z4 — 1 — i.
Формула (9) в особенности представляет интерес, если z = г'-
в этом случае имеем:
z2 — р2 (cos 2ip + i sin 2ip).
Умножая снова на z, будем иметь
z3 = р3 (cos Zip + г sin Zip);
и, вообще, для любого п, повторяя операцию, получим
zn = pn(cosrnp + is'mnip). A0)
В частности, если точка z находится на единичной окружности, так
что р = 1, мы приходим к формуле, открытой французским математи-
математиком А.де Муавром A667-1754):
(cosip + isirnp)" — cosnip + i sin rup. A1)
Эта формула — одно из самых замечательных и полезных соотношений
в элементарной математике. Поясним это примером. Возьмем п = 3 и
разложим левую часть по формуле бинома
{и + vK = и3 + 3u2v + Zuv2 + v3.
Тогда получим:
cos3y? + ism Zip = cos3 Zip — 3 cos <p sin2 tp + iCcos2 tpsintp — sin3 ip).
Одно такое комплексное равенство равносильно двум равенствам, свя-
связывающим действительные числа. В самом деле, если два комплексных
числа равны, то в отдельности равны их действительные части и их
мнимые части. Итак, можно написать
cos Zip = cos3 ip — 3 cos ip sin2 ip, sin Sip = 3 cos2 ip sin ip — sin3 <p.
Пользуясь затем соотношением
cos2 tp + sin2 tp = 1,
получим окончательно:
cos Zip = cos3 ip — 3 cos tp(l — cos2 tp) = 4 cos3 tp — 3 cos tp,
sin Zip = —4 sin3 tp + Z sin tp.
Подобного рода формулы, выражающие sinrup и cos mp соответственно
через sin у? и cos tp, легко получить при каком угодно целом значении п.

5 5. Комплексные числа
133
упражнения.
1) Написать аналогичные формулы для sin4y> и cos4y>.
2) Предполагая, что точка z находится на единичном круге: z = cosy> +
+ i sin <p, показать, что — = cos ip — i sin tp.
3) Без вычислений установить, что модуль числа — равен единице.
' а — т
4) Доказать: если z\ и z2 — два комплексных числа, то аргумент z\ — zi
равен углу между положительным направлением действительной оси
и вектором, идущим от гг к zi.
5) Дан треугольник с вершинами 2j, 22, 23; установить геометрический
Z\ — Zi
смысл аргумента числа .
6) Доказать, что отношение двух комплексных чисел с одинаковым аргу-
аргументом есть действительное число.
— 21
„\ тт Zz 21 24 — Z\
7) Доказать, что если аргументы чисел и равны между
собой, то четыре точки zi, 22, 23, Z4 лежат на окружности или на прямой
линии, и обратно.
8) Доказать: четыре точки zi, 22, Z3, zi лежат на окружности или на пря-
прямой линии, если число
Z3 - Zi Z4 - 21
23 - 22 Z4 - Z2
действительное.
3. Формула Муавра и корни из
единицы. Под корнем n-й степени из
числа а мы понимаем всякое такое чис-
число Ь, что Ьп = а. В частности, число 1 име-
имеет два квадратных корня: 1 и —1, так как
I2 = (— IJ = 1. Число 1 имеет один дей-
действительный кубический корень, имен-
именно 1, тогда как оно же имеет четыре кор-
корня четвертой степени: два действитель-
действительных, 1 и —1, и два мнимых, i и —г. Эти
факты наводят на мысль, что в комплекс-
комплексной области должно существовать еще два
кубических корня из 1 (а всего кубичес- Рис. 25. Двенадцать корней
ких корней тогда будет три). С помощью двенадцатой степени из еди-
формулы Муавра мы покажем, что эта до- ничы
гадка справедлива.

134 Глава II
Мы убедимся, что в поле комплексных чисел существует ровно
п корней степени п из 1. Эти корни изображаются вершинами пра-
правильного п-уголъника, вписанного в единичный круг и имеющего точку 1
в качестве одной из вершин.
Сказанное почти ясно из рис. 25 (соответствующего случаю п = 12).
Первая вершина многоугольника есть 1. Следующая есть
так как аргумент должен равняться n-й части угла в 360°. Еще следу-
следующая вершина есть а-а = а2, так как мы получим ее, вращая вектор а
на угол ^^-. Дальше получаем вершину а и т.д.; после п шагов воз-
возвращаемся снова к вершине 1, т.е. получаем
что следует также из формулы A1), так как
(cos Щ^- + i sin ^^) = cos 360° + i sin 360° = 1 + 0 • i = 1.
Итак, а1 = а есть корень уравнения хп = 1. To же справедливо отно-
относительно следующей вершины
Мы убедимся в этом, если напишем
(а2)" = а2п = (а"J = I2 = 1,
или же воспользуемся формулой Муавра
(a2)" =cos(n-^f-}+isia(n-'?j?-') = cos 720° + г sin 720° = 1 + 0г = 1.
Точно так же мы заключаем, что все п чисел
1, а, а2, а3, ..., а"
являются корнями степени п из 1. Если будем степени увеличивать
дальше или рассмотрим отрицательные степени, то новых корней не
получим. В самом деле,
а = — = ^- = ап~г; точно так же а™ = 1, ап+1 = (ап)а = 1 • а = а

§5. Комплексные числа 135
И Т.Д., так что ранее полученные корни повторяются. Читателю пре-
предоставляем в качестве упражнения показать, что иных корней, кроме
перечисленных, рассматриваемое уравнение не имеет.
Если п — четное, то одна из вершин n-угольника попадает в точ-
точку — 1, в соответствии с общеизвестным алгебраическим фактом: —1
есть корень четной степени из 1.
Уравнение, которому удовлетворяют корни п-Ш степени из 1,
хп - 1 = 0, A3)
п-й степени, но легко понизить его степень на единицу. Воспользуемся
алгебраической формулой
(хп - 1) = (х - 1){хп~1 + хп~2 + хп~3 + ... + 1). A4)
Так как произведение двух чисел равно 0 в том и только в том случае,
если один из множителей равен нулю, то выражение A4) обращается
в нуль или при х = 1, или при условии, что удовлетворяется уравнение
ж»-1 + ж" + ж" + ... + ж + 1 =0. A5)
Этому уравнению удовлетворяют корни а, а2, ... , а™"; оно называ-
называется циклотомическим, или уравнением деления окружности. Так, на-
например, мнимые кубические корни из 1
а = cos 120° + г sin 120° =
а2 = cos 240° + г sin 240° = ~ * ~ 1^3
являются корнями уравнения
х2 + х + 1 = 0,
как читатель сможет убедиться, выполняя подстановки. Таким же об-
образом корни пятой степени из 1 (кроме самого числа 1) удовлетворяют
Уравнению
ж4+х3+ж2+х + 1 = 0. A6)
Чтобы построить правильный пятиугольник, нам приходится решить
Уравнение четвертой степени. Простое алгебраическое ухищрение —

136 Глава II
замена w = х + ^ — приводит к уравнению второй степени. Мы делим
уравнение A6) на х2 и переставляем члены:
X
( 1\2 1 1
и, принимая во внимание, что ж+ф =x+-ir + 2, получаем
w2 + w - 1 = 0.
По формуле G) пункта 1 корни этого квадратного уравнения имеют
вид:
_ -1 + %/5 _ -\-УЪ
1 2 ' 2
Итак, мнимые корни пятой степени из 1 являются корнями следующих
двух квадратных уравнений:
1 1 \ ( i~ \
х + ¦= = w± или х + п\ v 5 — 1) х + 1 =0
х 2v '
и
x+^=w2 или х2 - ^(л/б + 1)х + 1 = 0.
Читатель сможет их решить по той же формуле G).
Упражнения.
1) Найти корни 6-й степени из 1.
2) Вычислить A + г)п.
3) Вычислить все различные значения выражений
VI + г, у/7 - 4», Vi, V^l.
4) Вычислить —(г1 — г~7).
*4. Основная теорема алгебры. Не только уравнения ви-
вида ах2 + Ьх + с — 0 или хп — 1 = 0 разрешимы в поле комплексных чисел,
но можно утверждать гораздо больше: всякое алгебраическое уравнение
степени п с действительными или комплексными коэффициентами
f{x) =xn + an-ix"-1 + ап-2хп-2 + ... + п1х + а0 = 0 A7)
разрешимо в поле комплексных чисел. Для случая уравнений 3-й и 4-й
степеней эта теорема была установлена в XVI в. Тартальей, Карданом и

§5. Комплексные числа 137
другими: оказалось, что такие уравнения решаются посредством фор-
формул, подобных формуле квадратного уравнения, но значительно более
сложных. В течение почти двух столетий длилось настойчивое изуче-
изучение общего уравнения 5-й и более высоких степеней, но все усилия раз-
разрешить их теми же методами оказались напрасными. Когда молодому
Гауссу в его докторской диссертации A799) удалось впервые доказать,
что решения существуют, то это уже было крупнейшим успехом; прав-
правда, вопрос о возможности обобщить на случай степеней ^ 5 класси-
классические формулы, позволяющие находить корни с помощью рациональ-
рациональных операций и извлечения корней, оставался в то время открытым
(см. стр. 155).
Теорема Гаусса утверждает, что, каково бы ни было алгебраическое
уравнение вида A7), где п — целое положительное число, а коэффици-
коэффициенты а — действительные или даже комплексные числа, существует
по крайней мере одно такое комплексное число а = с + di, что
f{a) = 0.
Число а называется корнем уравнения A7). Доказательство этой
теоремы будет приведено в этой книге на стр. 313-315. Предположим
пока, что теорема доказана, и выведем из нее другую теорему, извест-
известную под названием основной теоремы алгебры (было бы, впрочем, пра-
правильнее назвать ее основной теоремой комплексной числовой системы):
всякий алгебраический полином степени п
f(x) = хп + an-ixn~l + ... + ахх + а0 A8)
может быть представлен в виде произведения ровно п множителей:
f(x) = (x-ai)(x-a2)-.-(x-an), A9)
где ах, ct2, ¦ ¦ • , ап — комплексные числа, корни уравнения f(x) = 0.
Так, например, полином
f(x) = ж4 - 1
Разлагается на множители следующим образом:
f(x) = (х - 1){х - г)(ж + i)(x + 1).
Что числа а являются корнями уравнения f(x) = 0, это очевидно из
самого разложения A9), так как при х = аг один из множителей f(x),
а следовательно, и сам полином f(x) обращаются в нуль.

138 Глава II
В иных случаях не все множители х — ot\, х — а2, ... полинома f(x)
степени п оказываются различными; так, в примере
f{x) = х2 - 2х + 1 = (ж - 1)(х - 1)
мы имеем только один корень, х = 1, «считаемый дважды», или «крат-
«кратности 2». Во всяком случае, полином степени п не может разлагаться
в произведение более чем п различных множителей вида х — а, и соот-
соответствующее уравнение не может иметь более п корней.
При доказательстве основной теоремы алгебры мы воспользуем-
воспользуемся — не в первый раз — алгебраическим тождеством
хк - ак = {х - аХх*-1 + ахк~2 + а2хк~г + ... + ак'2х + а*), B0)
которое при а = 1 служило нам для определения суммы геометри-
геометрической прогрессии. Предполагая теорему Гаусса доказанной, допустим,
что а = c*i есть корень уравнения A7), так что
/(ai) = a? + On-ia^1 + ап-2а^~2 + ... + а^а1 + a0 = 0.
Вычитая это выражение из f(x) и перегруппировывая члены, мы полу-
получим тождество
= (хп - О + an-xix"-1 - а7?'1) + • • • + аг(х - ai). B1)
Пользуясь теперь формулой B0), мы можем выделить множитель
х — а.\ из каждого члена и затем вынести его за скобку, причем сте-
степень многочлена, остающегося в скобках, станет уже на единицу мень-
меньше. Перегруппировывая снова члены, мы получим тождество
f(x) = (х - oti)g(x),
где g(x) — многочлен степени п - 1:
g(x) = ж" + Ъп-2хп-2 + ... + Ь1Х + Ъ0.
(Вычисление коэффициентов, обозначенных через Ь, нас здесь не инте-
интересует.) Применим дальше то же рассуждение к многочлену g(x). По
теореме Гаусса, существует корень а2 уравнения g(x) = 0, так что
g(x) = (x- a2)h(x),

§6. Алгебраические и трансцендентные числа 139
где h(x) — новый многочлен степени уже п — 2. Повторяя эти рас-
су?кдения п — 1 раз (подразумевается, конечно, применение принципа
^тематической индукции), мы, в конце концов, приходим к разложе-
разложению
/(ж) = (ж-а1)(ж-а2)...(ж-а„). B2)
Цз тождества B2) следует не только то, что комплексные числа а.\,
а2) ... , а„ суть корни уравнения A7), но и то, что иных корней урав-
уравнение A7) не имеет. Действительно, если бы число у было корнем урав-
уравнения A7), то из B2) следовало бы
/Ы = (У ~ сц)(у - а2)... (у - ап) = 0.
Но мы видели (стр. 129), что произведение комплексных чисел равно
нулю в том и только в том случае, если один из множителей равен
нулю. Итак, один из множителей у — аТ равен 0, т.е. у = аг, что и
требовалось установить.
*§ 6. Алгебраические и трансцендентные числа
1. Определение и вопросы существования. Алгебраическим
числом называется всякое число х, действительное или мнимое, удов-
удовлетворяющее некоторому алгебраическому уравнению вида
опх" + а„_1ж"~1 +... + oix + o0 = 0, (п ^ 1, апф0), A)
где числа а* — целые. Так, например, число \/2 — алгебраическое, так
как оно удовлетворяет уравнению
х2 - 2 = 0.
Таким же образом алгебраическим числом является всякий корень лю-
любого уравнения с целыми коэффициентами третьей, четвертой, пятой,
какой угодно степени, и независимо от того, выражается или не вы-
выражается он в радикалах. Понятие алгебраического числа есть естест-
естественное обобщение понятия рационального числа, которое соответствует
частному случаю п = 1.
Не всякое действительное число является алгебраическим. Это вы-
вытекает из следующей, высказанной Кантором теоремы: множество всех
Алгебраических чисел счетно. Так как множество всех действительных

140 Глава II
чисел несчетное, то обязательно должны существовать действительные
числа, не являющиеся алгебраическими.
Укажем один из методов пересчета множества алгебраических чи-
чисел. Каждому уравнению вида A) сопоставим целое положительное чис-
число
— \а„
\ао\
которое назовем ради краткости «высотой» уравнения. Для каждого
фиксированного значения п существует лишь конечное число уравне-
уравнений вида A) с высотой h. Каждое из таких уравнений имеет самое
большее п корней. Поэтому может существовать лишь конечное число
алгебраических чисел, порождаемых уравнениями с высотой h; следо-
следовательно, все алгебраические числа можно расположить в виде после-
последовательности, перечисляя сначала те из них, которые порождаются
уравнениями высоты 1, затем — высоты 2 и т. п.
Это доказательство счетности множества алгебраических чисел
устанавливает существование действительных чисел, которые не яв-
являются алгебраическими. Такие числа называют трансцендентными
(от латинского transcendere — переходить, превосходить); такое наи-
наименование им дал Эйлер, потому что они «превосходят мощность ал-
алгебраических методов».
Канторово доказательство существования трансцендентных чисел
не принадлежит к числу конструктивных. Теоретически рассуждая,
можно было бы построить трансцендентное число с помощью диаго-
диагональной процедуры, производимой над воображаемым списком деся-
десятичных разложений всех алгебраических чисел; но такая процедура
лишена всякого практического значения и не привела бы к числу, раз-
разложение которого в десятичную (или какую-нибудь иную) дробь мож-
можно было бы на самом деле написать. Наиболее интересные проблемы,
связанные с трансцендентными числами, заключаются в доказательст-
доказательстве того, что определенные, конкретные числа (сюда относятся числа тг
и е, о которых см. стр. 344-348) являются трансцендентными.
**2. Теорема Лиувилля и конструирование трансцендент-
трансцендентных чисел. Доказательство существования трансцендентных чисел
еще до Кантора было дано Ж.Лиувиллем A809-1862). Оно дает воз-
возможность на самом деле конструировать примеры таких чисел. Дока-
Доказательство Лиувилля более трудно, чем доказательство Кантора, и это
неудивительно, так как сконструировать пример, вообще говоря, слож-
сложнее, чем доказать существование. Приводя ниже доказательство Лиу-
Лиувилля, мы имеем в виду только подготовленного читателя, хотя для

§6. Алгебраические и трансцендентные числа 141
понимания доказательства совершенно достаточно знания элементар-
элементарной математики.
Как обнаружил Лиувилль, иррациональные алгебраические числа
обладают тем свойством, что они не могут быть приближены рацио-
рациональными числами с очень большой степенью точности, если только не
взять знаменатели приближающих дробей чрезвычайно большими.
Предположим, что число z удовлетворяет алгебраическому урав-
уравнению с целыми коэффициентами
/(х) = а0 +а1х + а2х2 + ... + апхп = 0 (а„ ф 0), B)
но не удовлетворяет такому же уравнению более низкой степени. Тог-
Тогда говорят, что само х есть алгебраическое число степени п. Так, на-
например, число z = \/2 есть алгебраическое число степени 2, так как
удовлетворяет уравнению х2 — 2 = 0 степени 2, но не удовлетворяет
уравнению первой степени; число z = л/2 — степени 3, так как удовле-
удовлетворяет уравнению х3 — 2 = 0, но не удовлетворяет (как мы покажем
в главе III) уравнению более низкой степени. Алгебраическое число
степени п > 1 не может быть рациональным, так как рациональное
число z = ^ удовлетворяет уравнению qx — р = 0 степени 1. Каждое
иррациональное число z может быть с какой угодно степенью точности
приближено с помощью рационального числа; это означает, что всегда
можно указать последовательность рациональных чисел
Р\_ Р2
q\' ?2 '
с неограниченно растущими знаменателями, обладающую тем свойст-
свойством, что
— -» z
Теорема Лиувилля утверждает: каково бы ни было алгебраическое
число z степени п > 1, оно не может быть приближено посредством
рационального числа ^ с точностью, лучшей чем -^Ц-; другими сло-
вами, при достаточно больших знаменателях непременно выполняется
неравенство
>-кл- C)
Мы собираемся привести доказательство этой теоремы, но раньше
Покажем, как с ее помощью можно строить трансцендентные числа.

142 Глава II
Рассмотрим число
z = a1- 1(Г1! + а2 ¦ 10~2! + а3 ¦ 1(Г3! + ... + а
+ ат+1 ¦ 10"(т+1)! + ... = 0, а1а2000аз00000000000000000а4000
где а, обозначают произвольные цифры от 1 до 9 (проще всего было
бы положить все а,- равными 1), а символ п\, как обычно (см. стр. 44),
обозначает 1 • 2 • ... • п. Характерным свойством десятичного разложе-
разложения такого числа является то, что быстро возрастающие по своей длине
группы нулей чередуются в нем с отдельными цифрами, отличными от
нуля. Обозначим через zm конечную десятичную дробь, получающую-
получающуюся, когда в разложении возьмем все члены до ат • 10~т! включительно.
Тогда получим неравенство
z-zm\ < 10-l(T(m+1)!. D)
Предположим, что z было бы алгебраическим числом степени п. Тогда,
полагая в неравенстве Лиувилля C) ^ = zm = т1, мы должны иметь
\z - z
при достаточно больших значениях т. Сопоставление последнего нера-
неравенства с неравенством D) дает
10 _ 1
откуда следует (п + 1)т\ > (т + 1)! — 1 при достаточно больших т.
Но это неверно для значений т, больших чем п (пусть читатель потру-
потрудится дать детализированное доказательство этого утверждения). Мы
пришли к противоречию. Итак, число z — трансцендентное.
Остается доказать теорему Лиувилля. Предположим, что z — ал-
алгебраическое число степени п > 1, удовлетворяющее уравнению A),
так что
f(z) = 0. E)
Пусть zm = ~- — последовательность рациональных чисел, при-
причем zm -> z. Тогда
/СО = /СО - f(z) = oi(zm - z) + a2(z2m -z2) + ... + an{z^ - zn).
Деля обе части на zm - z и пользуясь алгебраической формулой
~~- = и"'1 + un~2v + un~3v2 + ... + uvn~2 + vn~\

§6. Алгебраические и трансцендентные числа
143
получаем
Zm
=ai+ a2(zm + z) + a3(z2m + zmz + z2)
«п^Г1
')¦ F)
Так как zm стремится к z, то при достаточно больших т рациональное
число zm будет отличаться от z меньше, чем на единицу. Поэтому при
достаточно больших т можно сделать следующую грубую оценку:
+ n\an\(\z\ + l)n-1=M, G)
причем стоящее справа число М — постоянное, так как z не меняет-
меняется в процессе доказательства. Выберем теперь т настолько большим,
чтобы у дроби zm = ^- знаменатель qm был больше, чем М; тогда
\z — z
\f(zm)\
М
(8)
Ради краткости условимся дальше писать р вместо рт и q вмес-
вместо qm. В таком случае
\П*т)\ =
aoqn
апрТ
(9)
Рациональное число zm — ^ не может быть корнем уравнения f(x) = О,
так как тогда можно было бы из многочлена f(x) выделить множи-
множитель (x — zm), и, значит, z удовлетворяло бы уравнению степени, низшей
чем п. Итак, f(zm) ф 0. Но числитель в правой части равенства (9) есть
целое число и, следовательно, по абсолютному значению он по меньшей
мере равен единице. Таким образом, из сопоставления соотношений (8)
и (9) вытекает неравенство
\z - z,.
A0)
как раз и составляющее содержание указываемой теоремы.
На протяжении нескольких последних десятилетий исследования,
касающиеся возможности приближения алгебраических чисел рацио-
рациональными, были продвинуты гораздо дальше. Например, норвежский

144 Дополнение к главе II
математик А.Туэ A863-1922) установил, что в неравенстве Лиувил-
ля C) показатель п + 1 может быть заменен меньшим показате-
показателем Ц + 1. К. Л.Зигель показал, что можно взять и еще меньший (еще
меньший при больших п) показатель 2i/n.
Трансцендентные числа всегда были темой, приковывающей к се-
себе внимание математиков. Но до сравнительно недавнего времени сре-
среди чисел, которые интересны сами по себе, было известно очень не-
немного таких, трансцендентный характер которых был бы установлен.
(В главе III будет доказана трансцендентность числа тг, и отсюда бу-
будет следовать невозможность квадратуры круга с помощью линейки
и циркуля.) В своем выступлении на Парижском международном ма-
математическом конгрессе 1900 г. Давид Гильберт предложил тридцать
математических проблем, допускающих простую формулировку, неко-
некоторые — даже совсем элементарную и популярную, из которых ни одна
не только не была решена, но даже и не казалась способной быть разре-
разрешенной средствами математики той эпохи. Эти «проблемы Гильберта»
оказали сильное возбуждающее влияние на протяжении всего последу-
последующего периода развития математики. Почти все они мало-помалу были
разрешены, и во многих случаях их решение было связано с ясно выра-
выраженными успехами в смысле выработки более общих и более глубоких
методов. Одна из проблем, казавшаяся довольно безнадежной, заклю-
заключалась в доказательстве того, что число
является трансцендентным (или хотя бы иррациональным). На протя-
протяжении трех десятилетий не было даже намека на такой подход к во-
вопросу с чьей-нибудь стороны, который открывал бы надежду на успех.
Наконец, Зигель и, независимо от него, молодой русский математик
А.Гельфонд открыли новые методы для доказательства трансцендент-
трансцендентности многих чисел, имеющих значение в математике. В частности,
была установлена трансцендентность не только гильбертова числа 2^,
но и целого довольно обширного класса чисел вида аь, где а — алгеб-
алгебраическое число (ф 0 и ф 1), а Ь — иррациональное алгебраическое
число.
Дополнение к главе II
Алгебра множеств
1. Общая теория. Понятие класса, или совокупности, или мно-
множества объектов — одно из самых фундаментальных в математике.

Алгебра множеств 145
Множество определяется некоторым свойством («аттрибутом») 21, кото-
которым должен или обладать, или не обладать каждый рассматриваемый
объект; те объекты, которые обладают свойством 21, образуют множес-
множество А. Так, если мы рассматриваем целые числа и свойство 21 заключа-
заключается в том, чтобы «быть простым», то соответствующее множество А
состоит из всех простых чисел 2, 3, 5, 7,
Математическая теория множеств исходит из того, что из мно-
множеств с помощью определенных операций можно образовывать новые
множества (подобно тому как из чисел посредством операций сложе-
сложения и умножения получаются новые числа). Изучение операций над
множествами составляет предмет «алгебры множеств», которая име-
имеет много общего с обыкновенной числовой алгеброй, хотя кое в чем и
отличается от нее. Тот факт, что алгебраические методы могут быть
применены к изучению нечисловых объектов, каковы множества, ил-
иллюстрирует большую общность идей современной математики. В по-
последнее время выяснилось, что алгебра множеств бросает новый свет
на многие области математики, например, теорию меры и теорию ве-
вероятностей; она полезна также при систематизации математических
понятий и выяснении их логических связей.
В дальнейшем / будет обозначать некоторое постоянное множество
объектов, природа которых безразлична, и которое мы можем называть
универсальным множеством (или универсумом рассуждения), а А, В,
С, ... будут какие-то подмножества /. Если / есть совокупность всех
натуральных чисел, то А, скажем, может обозначать множество всех
четных чисел, В — множество всех нечетных чисел, С — множество
всех простых чисел и т.п. Если / обозначает совокупность всех точек
на плоскости, то А может быть множеством точек внутри какого-то
круга, В — множеством точек внутри другого круга и т. п. В число
«подмножеств» нам удобно включить само /, а также «пустое» множес-
множество 0, не содержащее никаких элементов. Цель, которую преследует
такое искусственное расширение, заключается в сохранении того по-
положения, что каждому свойству 21 соответствует некоторое множество
элементов из /, обладающих этим свойством. В случае, если 21 есть уни-
универсально выполняемое свойство, примером которого может служить
(если речь идет о числах) свойство удовлетворять тривиальному ра-
равенству х = х, то соответствующее подмножество / будет само /, так
как каждый элемент обладает таким свойством; с другой стороны, ес-
если 21 есть какое-то внутренне противоречивое свойство (вроде х ф х),
то соответствующее подмножество не содержит вовсе элементов, оно —
«пустое» и обозначается символом 0.
Ю — 340

146 Дополнение к главе II
Говорят, что множество А есть подмножество множества В, ко-
короче, «А входит в ??», или «В содержит А», если во множестве А нет
такого элемента, который не был бы также во множестве В. Этому
соотношению соответствует запись
АС В или В D А.
Например, множество А всех целых чисел, делящихся на 10, есть под-
подмножество множества В всех целых чисел, делящихся на 5, так как
каждое число, делящееся на 10, делится также на 5. Соотношение А С В
не исключает соотношения В С А. Если имеет место и то и другое, то
мы пишем
А = В.
Это означает, что каждый элемент А есть вместе с тем элемент В,
и обратно, так что множества А и В содержат как раз одни и те же
элементы.
Соотношение А С В между множествами во многих отношениях
напоминает соотношение a i^ b между числами. В частности, отметим
следующие свойства этого соотношения:
1)АсА.
2) Если А с В и В с А, то А = В.
3) Если А с В и В с С, то А с С.
По этой причине соотношение А С В иногда называют «отношением
порядка». Главное отличие рассматриваемого соотношения от соотно-
соотношения а ^ b между числами заключается в том, что между всякими
двумя заданными (действительными) числами аи i непременно осу-
осуществляется по меньшей мере одно из соотношений а ^ b или b ^ а,
тогда как для соотношения А С В между множествами аналогичное
утверждение неверно. Например, если А есть множество, состоящее из
чисел 1, 2, 3,
А = {1,2,3},
а В — множество, состоящее из чисел 2, 3, 4,
В = {2, 3, 4},
то не имеет места ни соотношение А С В, ни соотношение В С А.
По этой причине говорят, что подмножества А, В, С, ... множества /
являются «частично упорядоченными», тогда как действительные чис-
числа а,Ь, с, ... образуют «вполне упорядоченную» совокупность.
Заметим, между прочим, что из определения соотношения А С В
следует, что, каково бы ни было подмножество А множества /,

Алгебра множеств
147
4) 0 С Л
и
5) А С I.
Свойство 4) может показаться несколько парадоксальным, но, если
вдуматься, оно логически строго соответствует точному смыслу опре-
определения знака С. В самом деле, соотношение 0 С А нарушалось бы
только в том случае, если бы пустое множество 0 содержало элемент,
который не содержался бы в А; но так как пустое множество не содер-
содержит вовсе элементов, то этого быть не может, каково бы ни было А.
А+В
Рис. 26. Объединение и пересечение множеств
Мы определим теперь две операции над множествами, формально
обладающие многими алгебраическими свойствами сложения и умно-
умножения чисел, хотя по своему внутреннему содержанию совершенно от-
отличные от этих арифметических действий. Пусть Аи В — какие-то два
множества. Под «объединением», или «логической суммой», А и В по-
понимается множество, состоящее из тех элементов, которые содержатся
или в А, или в В (включая и те элементы, которые содержатся, и в А,
и в В). Это множество обозначается А + В.1 Под пересечением, или
«логическим произведением», А и В понимается множество, состоящее
из тех элементов, которые содержатся и в Л и в В. Это множество
обозначается АВ.2 Проиллюстрируем приведенные определения при-
примером. Возьмем опять в качестве А и В множества
Тогда
А = {1,2,3}, В = {2, 3,4}.
+ В = {1, 2, 3, 4}, АВ = {2, 3}.
Аи В.
2Или АП В.
10*

148 Дополнение к главе II
Среди важных алгебраических свойств операций А + В и АВ пе-
перечислим следующие. Читатель сможет проверить их справедливость,
исходя из определения самих операций:
6)
8)
10)
12)
14)
16)
A +
A +
A +
A{B
A +
A +
B = B + A.
(B + C) = {A
A = A.
+ C) = AB +
0 = A.
1 = 1.
+ B)-
AC.
7)
1-C. 9)
И)
13)
15)
17)
АВ = В A.
A(BC) = (AB)C.
AA = A.
A + (BC) = {A +
AI = A.
A0 = 0.
18) Соотношение А С В эквивалентно каждому из двух соотноше-
соотношений А + В = В, АВ = А.
Проверка всех этих законов — дело самой элементарной логики.
Например, правило 10) констатирует, что множество элементов, содер-
содержащихся или в А, или в А, есть как раз множество А; правило 12)
констатирует, что множество тех элементов, которые содержатся в А
и вместе с тем содержатся или в В, или в С, совпадает со множеством
элементов, которые или содержатся одновременно в А и в В, или содер-
содержатся одновременно в А и в С. Логические рассуждения, используемые
при доказательствах подобного рода правил, удобно иллюстрируются,
если мы условимся изображать множества А, В, С, ... в виде некото-
некоторых фигур на плоскости и будем очень внимательны в том отношении,
чтобы не упустить ни одной из возникающих логических возможнос-
возможностей, когда речь идет о наличии общих элементов двух множеств или,
напротив, наличии в одном множестве элементов, которые не содер-
содержатся в другом.
Читатель, несомненно, обратил внимание на то обстоятельство, что
законы 6), 7), 8), 9) и 12) внешне тождественны с хорошо знакомыми
коммутативным, ассоциативным и дистрибутивным законами обык-
обыкновенной алгебры. Отсюда следует, что все правила обыкновенной ал-
алгебры, вытекающие из этих законов, действительны также в алгебре
множеств. Напротив, законы 10), 11) и 13) не имеют своих аналогов
в обыкновенной алгебре, и они придают алгебре множеств более прос-
простую структуру. Например, формула бинома в алгебре множеств сво-
сводится к простейшему равенству
(А + В)п = (А + В) ¦ (А + В)... (А + В) = А + В,
которое следует из закона 11). Законы 14), 15) и 17) говорят о том,
что свойства множеств 0 и/по отношению к операциям объединения
и пересечения множеств весьма похожи на свойства чисел 0 и 1 по

Алгебра множеств 149
отношению к операциям числовых действий сложения и умножения.
Но закон 16) не имеет аналога в числовой алгебре.
Остается дать определение еще одной операции в алгебре множеств.
Пусть А — какое-нибудь подмножество универсального множества /.
Тогда под дополнением А в I понимается множество всех элементов /,
которые не содержатся в А. Для этого множества мы введем обозна-
обозначение А'. Так, если / есть множество всех натуральных чисел, а А —
множество всех простых чисел, то А' есть множество, состоящее из
всех составных чисел и числа 1. Операция перехода от Л к А', для ко-
которой нет аналога в обыкновенной алгебре, обладает следующими свой-
свойствами:
19) А + А' = I. 20) АА' = 0.
21) 0' = /. 22) 1 = 0.
23) А" = А.
24) Соотношение Ас В эквивалентно соотношению В' С А'.
25) {А + В)' = А'В'. 26) (АВ)' = А'+ В'.
Проверку этих свойств мы опять предоставляем читателю.
Законы 1)—26) лежат в основе алгебры множеств. Они обладают
замечательным свойством «двойственности» в следующем смысле:
Если в одном из законов 1)-26) заменить друг на друга соответ-
соответственно символы
СиЗ
0 и /
+ и ¦
(е каждом их вхождении), то в результате снова получается один из
этих же законов. Например, закон 6) переходит в закон 7), 12) — в 13),
17) — в 16) и т. д. Отсюда следует, что каждой теореме, которая мо-
может быть выведена из законов 1)—26), соответствует другая, «двойст-
«двойственная» ей теорема, получающаяся из первой посредством указанных
перестановок символов. В самом деле, так как доказательство первой
теоремы состоит из последовательного применения (на различных ста-
стадиях проводимого рассуждения) некоторых из законов 1)—26), то при-
применение на соответствующих стадиях «двойственных» законов соста-
составит доказательство «двойственной» теоремы. (По поводу подобной же
«двойственности» в геометрии см. главу IV.)
2. Применение к математической логике. Проверка зако-
законов алгебры множеств основывалась на анализе логического смысла со-
соотношения А С В и операций А + В, АВ и А'. Мы можем теперь обра-
обратить этот процесс и рассматривать законы 1)—26) как базу для «алгебры
логики». Скажем точнее: та часть логики, которая касается множеств,

150
Дополнение к главе II
или, что по существу то же, свойств рассматриваемых объектов, мо-
может быть сведена к формальной алгебраической системе, основанной на
законах 1)—26). Логическая «условная вселенная» определяет множест-
множество /; каждое свойство 21 определяет множество А, состоящее из тех
объектов в I, которые обладают этим свойством. Правила перевода
обычной логической терминологии на язык множеств ясны из следую-
следующих примеров:
А + В
АВ
А'
(А + В)', или, что то же, А'В'
{АВ)', или, что то же, А' + В'
«А или В»
«А и В»
«Не Л»
«Ни А, ни В»
«Не сразу А и В»
«Всякое А есть Вь,
или
«Если А, то В»,
или
.«Из А следует В)>
«Какое-то А есть В»
«Никакое А не есть Вч>
«Какое-то А не есть В»
«Нет никакого А»
АсВ
АВфа
АВ = 0
АВ' ф0
А = 0
В терминах алгебры множеств силлогизм «Barbara», обозначаю-
обозначающий, что «если всякое А есть В и всякое В есть С, то всякое А есть С»,
принимает простой вид:
3) Если А С В и В С С, то А с С.
Аналогично «закон противоречия», утверждающий, что «объект не
может одновременно обладать и не обладать некоторым свойством»,
записывается в виде:
20) АА' = 0,
и «закон исключенного третьего», говорящий, что «объект должен или
обладать, или не обладать некоторым свойством», записывается:
19) А + А' = 1.
Таким образом, та часть логики, которая выразима в терминах
символов С, +, • и ', может трактоваться как формальная алгебраичес-
алгебраическая система, подчиненная законам 1)-26). На основе слияния логичес-
логического анализа математики и математического анализа логики создалась
новая дисциплина — математическая логика, которая в настоящее вре-
время находится в процессе бурного развития,
С аксиоматической точки зрения заслуживает внимания тот за-
замечательный факт, что утверждения 1)-26), вместе со всеми прочими

Алгебра множеств 151
теоремами алгебры множеств, могут быть логически выведены из сле-
следующих трех равенств: А + В = В + А
27) (А + В) + С =А + {В + С),
(А' + В')' + (А' + В)' = А.
Отсюда следует, что алгебра множеств может быть построена как чис-
чисто дедуктивная теория, вроде евклидовой геометрии, на базе этих трех
положений, принимаемых в качестве аксиом. Если эти аксиомы приня-
приняты, то операция АВ и отношение А С В определяются в терминах А + В
и Л':
АВ обозначает множество (А' + В')',
А С В обозначает, что А + В = В.
Совершенно иного рода пример математической системы, в кото-
которой выполняются все формальные законы алгебры множеств, дается
системой восьми чисел 1, 2, 3, 5, 6, 10, 15, 30: здесь а + b обозначает,
по определению, общее наименьшее кратное а и b, ab — общий наи-
наибольший делитель а и Ь, а С Ь — утверждение «Ь делится на а» и а' —
число ^. Существование таких примеров повлекло за собой изучение
общих алгебраических систем, удовлетворяющих законам 27). Такие
системы называются «булевыми алгебрами» — в честь Джорджа Бу-
Буля A815-1864), английского математика и логика, книга которого «An
investigation of the laws of thought» (Исследование законов мышления)
появилась в 1854 г.
3. Одно из применений к теории вероятностей. Алгебра мно-
множеств имеет ближайшее отношение к теории вероятностей и позволяет взгля-
взглянуть на нее в новом свете. Рассмотрим простейший пример: представим себе
эксперимент с конечным числом возможных исходов, которые все мыслятся
как «равновозможные». Эксперимент может, например, заключаться в том,
что мы вытягиваем наугад карту из хорошо перетасованной полной колоды.
Если множество всех исходов эксперимента обозначим через I, a А обознача-
обозначает какое-нибудь подмножество /, то вероятность того, что исход эксперимен-
эксперимента окажется принадлежащим к подмножеству А, определяется как отношение
/ \ _ число элементов А
число элементовI'
Если условимся число элементов в каком-нибудь множестве А обозна-
обозначать через п(А), то последнему равенству можно придать вид
В нашем примере, допуская, что А есть подмножество треф, мы полу-
получим п(А) = 13, пA) = 52 и р(А) = Щ = i.

152 Дополнение к главе II
Идеи алгебры множеств обнаруживаются при вычислении вероятностей
тогда, когда приходится, зная вероятности одних множеств, вычислять ве-
вероятности других. Например, зная вероятности р{А), р(В) и р(АВ), можно
вычислить вероятность р(А + В):
¦B)=p(A)+p(B)-p(AB). B)
Доказательство не представляет труда. Мы имеем
п(А + В) = п(А) + п{В) - п(АВ),
так как элементы, содержащиеся одновременно в А и в В, т. е. элементы АВ,
считаются дважды при вычислении суммы п(А) + п(В), и, значит, нужно
вычесть п(АВ) из этой суммы, чтобы подсчет п(А + В) был произведен
правильно. Деля затем обе части равенства на пA), мы получаем соотно-
соотношение B).
Более интересная формула получается, если речь идет о трех множест-
множествах А, В, С из I. Пользуясь соотношением B), мы имеем
р(А + В + С) = р[(А + В)+С]=р(А + В} + р(С) - р[(А + В)С].
Закон A2) из предыдущего пункта дает нам: (А + В)С = АС + ВС. Отсюда
следует
р[(А + В)С)} = р(АС + ВС) = р(АС) + р{ВС) - р(АВС).
Подставляя в полученное раньше соотношение значение р[(А + В)С] и
значение р(А + В), взятое из B), мы приходим к нужной нам формуле
р(А + В + С) = р(А) + р(В) + р(С) -
-р{АВ)-р(АС)-р(ВС)+р(АВС). C)
В качестве примера рассмотрим следующий эксперимент. Три цифры 1,
2, 3 пишутся в каком попало порядке. Какова вероятность того, что по край-
крайней мере одна из цифр окажется на надлежащем (в смысле нумерации) месте?
Пусть А есть множество перестановок, в которых цифра 1 стоит на первом
месте, В — множество перестановок, в которых цифра 2 стоит на втором
месте, С — множество перестановок, в которых цифра 3 стоит на третьем
месте. Нам нужно вычислить р(А + В + С). Ясно, что
- 2 _ 1
6 ~ 3'
действительно, если какая-нибудь цифра стоит на надлежащем месте, то име-
имеются две возможности переставить остальные две цифры из общего чис-
числа 3 • 2 • 1 = 6 возможных перестановок трех цифр. Далее,
Р(АВ) = р(АС) = р(ВС) = |, р(АВС) = |,

Алгебра множеств 153
так как в каждом из этих случаев возникает только одна возможность. И тог-
тогда формула C) дает нам
P(A + B + C)=3-i-3-i + i=l-i+i= 0,6666 . . .
Л DO Z О
Упражнение. Вывести соответствующую формулу для р(А + В + С +
+ D) и применить ее к эксперименту, в котором будут участвовать 4 цифры.
Соответствующая вероятность равна ^ = 0,6250.
о
Общая формула для объединения п множеств имеет вид
+ А2 + ... + An) = 5
D)
2_^ -...±p(AiA2...An),
з
где символы ?], ?], ?], ... , X) обозначают суммирование по всем возмож-
12 3 п-1
ным комбинациям, содержащим одну, две, три, ... , (п — 1) букв из числа А\,
Аг, ••• , Ап. Эта формула может быть установлена посредством математи-
математической индукции — точно так же, как формула C) была выведена из форму-
формулы B).
Из формулы D) можно заключить, что если п цифр 1, 2, 3, ... , п напи-
написаны в каком угодно порядке, то вероятность того, что по крайней мере одна
из цифр окажется на надлежащем месте, равна
р = 1^ + + ±А E)
причем перед последним членом стоит знак + или —, смотря по тому, явля-
является ли п четным или нечетным. В частности, при п = 5 эта вероятность
равна
В главе VIII мы увидим, что, когда п стремится к бесконечности, выражение
9 -1-1 + 1- ±1
" ~ 2! 3! + 4! ' • п!
стремится к пределу -, значение которого, с пятью знаками после запятой,
равно 0,36788. Так как из формулы E) видно, что рп = 1 - 5„, то отсюда
следует, что при п —> оо
Рп -> 1 - \ = 0,63212.

Глава HI
Геометрические построения. Алгебра
числовых полей
Введение
Задачи на построение всегда всегда были одним из самых любимых
предметов геометрических занятий. С помощью только циркуля и ли-
линейки, как читатель знает из школьного курса, можно выполнить очень
много разнообразных построений: разделить пополам отрезок или угол,
провести через точку перпендикуляр к данной прямой, вписать в дан-
данный круг правильный шестиугольник и т.д. Во всех этих построениях
линейка служит только для того, чтобы проводить прямую линию, но
не для того, чтобы измерять или откладывать расстояния. Традицион-
Традиционное ограничение — пользоваться только циркулем и линейкой — восхо-
восходит к глубокой древности, хотя на практике сами греки без колебания
прибегали и к другим инструментам.
Одной из самых знаменитых, классических задач на построение яв-
является задача Аполлония (около 220 года до нашей эры): даны три круга,
требуется провести четвертый, касательный к трем данным. В част-
частности, не исключено, что один или большее число из данных кругов
«вырождаются» в точку или прямую («круг» с «нулевым» или с «беско-
«бесконечным» радиусом). Например, может идти речь о проведении круга,
касательного к двум данным прямым и проходящего через данную точ-
точку. Если такого рода специальные случаи не связаны с затруднениями,
то в общей постановке задача принадлежит к числу весьма трудных.
Из всех задач на построение задача построения (с помощью цир-
циркуля и линейки) правильного n-угольника представляет, может быть,
наибольший интерес. Для случая ряда значений п, например, при п = 3,
4, 5, 6, решение было известно уже в древности и излагается в школь-
школьной геометрии. Но в случае правильного семиугольника (п = 7) постро-
построение, как было доказано, невозможно. Вот еще три классические проб-
проблемы, решение которых разыскивалось долго и безрезультатно: разде-
разделить на три равные части данный произвольный угол, удвоить данный
куб (т.е. построить сторону куба, объем которого вдвое больше чем

Введение 155
объем куба, сторона которого задана) и выполнить «квадратуру» круга
(т.е. построить квадрат, имеющий такую же площадь, как и данный
Круг). И в этих проблемах предполагается, что, кроме циркуля и ли-
линейки, другие инструменты не применяются.
Проблемы подобного рода, не поддающиеся решению, привели к од-
одному из самых замечательных и оригинальных направлений математи-
математической мысли. После нескольких столетий безуспешных поисков мате-
математики утвердились в подозрении, что найти решение невозможно. На
очередь стал соблазнительный по своей трудности новый вопрос: как
можно доказать, что та или иная проблема не может быть разрешена'!
В области алгебры тот же вопрос возник в связи с проблемой реше-
решения уравнений 5-й и более высоких степеней. В течение XVI столетия
было установлено, что алгебраические уравнения степени 3 и 4 реша-
решаются посредством той же процедуры, что и квадратные. Эта процеду-
процедура может быть, вообще говоря, охарактеризована следующим образом:
решения, или «корни», уравнения представляются в виде выражений,
составленных из коэффициентов уравнения и содержащих операции,
из которых каждая есть или рациональная — сложение, вычитание,
умножение, деление — или же извлечение корня — квадратного, ку-
кубического или четвертой степени. Говорят короче, что алгебраическое
уравнение не выше четвертой степени «решается в радикалах» (radix
по-латыни означает «корень»). Казалось как нельзя более естественным
пытаться обобщить эту процедуру на уравнения 5-й и более высоких
степеней, пользуясь, конечно, и радикалами соответствующих степе-
степеней. Но ни одна из попыток не увенчалась успехом. В XVIII столетии
были случаи, когда даже выдающиеся математики впадали в заблуж-
заблуждение, предполагая, что решение ими найдено. Но только в начале XIX
столетия у итальянца Руффини A765-1822) и у гениального норвежско-
норвежского математика Н. Г. Абеля A802-1829) возникла поистине революцион-
революционная в то время идея — доказать невозможность решения в радикалах
общего алгебраического уравнения степени п. Нужно понимать совер-
совершенно отчетливо, что речь не идет о существовании решения алгеб-
алгебраического уравнения степени п: существование решений было строго
Доказано Гауссом в его докторской диссертации в 1799 г. Таким обра-
образом, уже не было никаких сомнений в том, что каждое алгебраическое
Уравнение действительно имеет корни, в особенности после того, как
были указаны приближенные методы для их вычисления с какой угодно
степенью точности. «Численное» решение алгебраических уравнений,
имеющее громадное значение в приложениях, прекрасно разработано.
Проблема Абеля и Руффини была поставлена совсем иначе: может ли

156 Глава III
быть найдено решение с помощью одних только рациональных операций
и операций извлечения корней? Именно, стремление добиться полной
ясности в этом вопросе послужило толчком для великолепного разви-
развития современной алгебры и теории групп, начатого работами Руффини,
Абеля и Э.Галуа A811-1832).
Доказательство невозможности некоторых геометрических по-
построений оказывается как раз в числе примеров, иллюстрирующих то
направление в алгебре, о котором только что было сказано. Именно опе-
оперируя алгебраическими понятиями, мы сможем установить в этой гла-
главе невозможность и трисекции угла, и построения правильного семи-
семиугольника, и удвоения куба с помощью одних только циркуля и линей-
линейки. (Проблема квадратуры круга значительно сложнее; см. по этому
поводу стр. 180.) Подходя ближе к интересующему нас вопросу, мы
должны будем подойти к нему с другой стороны, сосредоточиваясь не
на его отрицательной стороне — невозможности выполнения тех или
иных построений, а придавая ему положительный характер: как могут
быть полностью охарактеризованы конструктивные проблемы, допус-
допускающие решение? После того как ответ на этот вопрос будет найден,
не представит труда установить, что рассматриваемые нами проблемы
не входят в эту категорию.
В возрасте 17 лет Гаусс исследовал возможность построения пра-
правильных <ф-угольников», где р — простое число. В то время были из-
известны построения только для случаев р = 3 и р = 5. Гаусс установил,
что построения возможны в том и только в том случае, если р есть
простое «число Ферма»:
р = 22" + 1.
Первые числа Ферма суть 3, 5, 17, 257, 65 537 (см. стр. 53). Это откры-
открытие произвело на Гаусса такое впечатление, что он сразу отказался от
филологической карьеры и решил посвятить свою жизнь математике и
ее приложениям. Он и позднее смотрел на это первое из своих откры-
открытий с особенной гордостью. После смерти Гаусса в Гёттингене была
воздвигнута его бронзовая статуя, с пьедесталом в форме правильно-
правильного 17-угольника. Трудно придумать более достойную почесть.
Когда идет речь о геометрических построениях, никак не следу-
следует упускать из виду, что проблема заключается не в практическом
вычерчивании фигур с известной степенью аккуратности, а в том, мо-
может ли построение быть выполнено теоретически, предполагая, что на-
наши инструменты дают абсолютную точность. Гаусс именно и доказал
принципиальную возможность рассмотренных им построений. Его те-
теория не касается того, как выполнить построение на самом деле, какие

§ 1. Основные геометрические построения 157
следует использовать приемы, чтобы упростить процедуру или даже
уменьшить число необходимых конструктивных операций. Все это —
вопросы не столь высокого теоретического значения. С практической
точки зрения, такие построения не дают столь удовлетворительного
результата, какой может быть достигнут посредством хорошего транс-
транспортира. Вероятно, именно непониманием теоретического характера
вопроса о геометрических построениях, с одной стороны, а с другой —
упорным нежеланием считаться с прекрасно установленными научны-
научными фактами, нужно объяснять то обстоятельство, что еще продолжают
существовать нескончаемые вереницы «трисекторов» и «квадратурщи-
ков». Тем из них, которые способны понимать элементарную матема-
математику, можно порекомендовать заняться изучением этой главы.
В заключение отметим, что в известном отношении наша постанов-
постановка вопроса о геометрических построениях представляется искусствен-
искусственной. Циркуль и линейка, конечно, — простейшие из геометрических
инструментов, но требование ограничиваться именно этими инстру-
инструментами при построениях не вытекает из существа самой геометрии.
Как уже давным-давно установили греческие математики, некоторые
проблемы — скажем, удвоение куба — могут быть решены, например,
с привлечением угольника (с прямым углом); можно изобрести всякие
другие инструменты, помимо циркуля, которые позволили бы чертить
эллипсы, гиперболы и более сложные кривые: тем самым область фи-
фигур, допускающих построение, была бы значительно расширена. Одна-
Однако мы будем придерживаться прочно установившегося понимания вы-
выполнимости геометрических построений, подразумевая, что разрешено
пользоваться только циркулем и линейкой.
Часть 1
Доказательства невозможности и алгебра
§ 1. Основные геометрические построения
1. Построение полей и извлечение квадратных корней.
В порядке развития общих идей мы начнем с рассмотрения неболь-
небольшого числа классических построений. Более углубленное изучение воз-
возможности геометрических построений неизбежно связано с переводом
геометрической задачи на язык алгебры. Всякая проблема геометри-
геометрического построения может быть схематизирована следующим образом:

158
Глава HI
О
о
a+b
A
дано некоторое число отрезков, скажем, а, Ь, с, ...; требуется постро-
построить один или несколько отрезков х, у, ... Даже если на первый взгляд
проблема как будто имеет совсем иной вид, ее всегда можно перефор-
переформулировать таким образом, чтобы она включилась в указанную схе-
схему. Искомые отрезки фигурируют или в виде сторон треугольника,
который требуется построить, или в виде радиусов кругов, или как
прямоугольные координаты каких-то искомых точек (см., например,
стр. 163). Предположим для простоты, что требуется построить один
отрезок х. В таком случае геометрическое построение приводит к ре-
решению алгебраической задачи: устанавливить соотношение (в форме
уравнения) между искомой величиной х и данными величинами а, Ь,
с, ...; затем, решая это уравнение, найти формулу для величины х и,
наконец, выяснить, можно ли свести вычисление х к таким алгебра-
алгебраическим процедурам, которые соответствуют построениям, выполни-
выполнимым с помощью циркуля и линейки. Таким образом, в основе всей
рассматриваемой теории лежит принцип аналитической геометрии —
количественная характеристика геометри-
геометрических объектов, основанная на введении
континуума действительных чисел.
Заметим прежде всего, что простей-
простейшие алгебраические операции соответству-
соответствуют элементарным геометрическим постро-
построениям. Если даны два отрезка, длины ко-
которых равны а и b (измерение произво-
производится посредством «единичного» отрезка),
то очень легко построить а + b, a — Ь, га
(где г — рациональное число), ^ и аЬ.
Чтобы построить а + b (рис. 27), мы
проводим прямую линию и на ней откла-
откладываем циркулем отрезки О А = а и АВ =
= Ь. Тогда ОВ = а + Ь. Точно так же в слу-
случае а — Ь мы откладываем О А = а и АВ =
= Ь, но на этот раз откладываем Ь в сторо-
сторону, противоположную той, в которую от-
отложили а. Тогда ОВ = а — Ь. Чтобы по-
построить За, мы просто строим а + а + а;
аналогично поступаем, если нужно построить га, где г — целое чис-
число. ^ строится следующим приемом (рис. 28): на произвольной прямой
о
откладываем ОА = а и затем проводим другую прямую через точ-
В
a-b
¦A
Рис. 27. Построение а + Ь и
а-Ь
О
Рис. 28. Построение ^

jl. Основные геометрические построения
159
ку О. На этой прямой откладываем произвольный отрезок ОС = с и
строим OD = За Соединяем А и D прямой линией и проводим через
точку С прямую, параллельную AD; пусть эта прямая пересекает О А
в точке В. Треугольники ОВС и OAD подобны; значит,
ОВ
ОВ
ОА
= ^-^- = i и ОВ = ^. Таким же образом можно вообще построить ^
целое. Совершая эту операцию над отрезком ра. мы постро-
где q
им га, где г = -
какое угодно рациональное число.
О
-* а-Ь
А
^-
Рис. 29. Построение ^
о
Рис. 30. Построение ab
Чтобы построить ~ (рис. 29), откладываем О В = Ь и О Л = а на
сторонах произвольного угла с вершиной О и на стороне ОВ отклады-
откладываем отрезок OD = 1. Через ?> проводим прямую, параллельную АВ;
пусть она пересекает О А в точке С. Тогда будем иметь: ОС = ^.
Построение ab показано на рис. 30; здесь AD — прямая, проходящая
через А и параллельная ВС.
Из этих соображений вытекает, что «рациональные» алгебраические
операции — сложение, вычитание, умножение и деление, — производи-
производимые над заданными величинами, могут быть выполнены посредством
геометрических построений. Исходя из данных отрезков, измеряемых
действительными числами а, Ь, с, ..., мы можем, последовательно вы-
выполняя эти простые построения, построить любую величину, которая
через а, Ь, с, ... выражается рационально, т.е. с помощью лишь пере-
перечисленных выше четырех основных действий. Совокупность всех ве-
величин, которые таким образом могут быть получены из а, Ь, с, ...,
образует то, что называется числовым полем — множество чисел, обла-
обладающее тем свойством, что любая рациональная операция, совершен-
совершенная над двумя (или более) элементами этого множества, приводит сно-
снова к элементу этого же множества. Мы напоминаем, что совокупность

160
Глава III
всех рациональных чисел, совокупность всех действительных чисел, со-
совокупность всех комплексных чисел образуют такие поля. В рассмат-
рассматриваемом нами теперь случае говорят, что поле порождается данными
числами а, Ь, с, ...
Существенно новой операцией, выво-
выводящей нас за пределы полученного по-
поля, является извлечение квадратного кор-
корня. Если задан отрезок а, то отрезок </а
может быть построен с помощью только
циркуля и линейки. На произвольной пря-
прямой мы откладываем О А = а и АВ = 1
(рис. 31). Проводим, далее, окружность
с диаметром ОВ и из точки А восставля-
восставляем перпендикуляр к ОВ: пусть он пересе-
пересекает окружность в точке С. Угол С в треугольнике ОВС — прямой,
согласно теореме, известной из элементарной геометрии: угол, вписан-
вписанный в полуокружность, — прямой. Значит, /ОСА = /ABC, прямо-
прямоугольные треугольники О АС и CAB подобны, и, полагая АС = х, мы
получаем
п т о /—
= а, х = V а.
О
А
, 1 ,
в
Рис. 31. Построение л/а
а
х
х
1'
Рис. 32. Правильный десяти-
десятиугольник
Рис. 33. Правильный шести-
шестиугольник
2. Правильные многоугольники. Рассмотрим теперь несколь-
несколько более сложные конструктивные задачи. Начнем с построения пра-
правильного десятиугольника. Предположим, что правильный десятиуголь-
десятиугольник вписан в круг радиуса 1 (рис. 32); обозначим его сторону через х.
Так как центральный угол, под которым эта сторона х видна из центра

§ 1. Основные геометрические построения 161
круга, содержит 36°, то остальные два угла большого треугольника со-
содержат каждый по 72°, и, значит, пунктирная линия, делящая пополам
угол А, разбивает треугольник ОАВ на два равнобедренных треуголь-
треугольника с равными боковыми сторонами длины ж. Радиус круга, таким
образом, составляется из отрезков ж и 1 — ж. Так как треугольник ОАВ
подобен меньшему из двух треугольников, на которые он разбивается,
то мы получаем i = х_ . Эта пропорция приводит к квадратному
уравнению х2 + х - 1 = 0, решение которого имеет вид ж = ~ .
(Другое решение нас не интересует, так как оно соответствует отри-
отрицательному значению х.) Из полученной формулы ясно, что отрезок ж
может быть построен геометрически. Имея же отрезок ж, мы сможем
построить правильный десятиугольник, откладывая по окружности де-
десять раз хорду ж. Отсюда уже легко получить и правильный пятиуголь-
пятиугольник, соединяя вершины десятиугольника через одну.
Вместо того чтобы строить у/Ь тем методом, который указан на рис. 31,
мы можем также построить гипотенузу прямоугольного треугольника со сто-
сторонами 1 и 2. Затем придется отнять единичный отрезок и то, что получится,
разделить пополам.
Отношение —~ в рассмотренной задаче было названо «золотым»,
АИ
так как, по мнению греческих математиков, прямоугольник, стороны
которого находятся в этом отношении, эстетически особенно приятен
для глаза. Значение отношения приблизительно равно 1,62.
Из всех правильных многоугольников легче всего построить шес-
шестиугольник. Так как длина стороны такого шестиугольника, вписан-
вписанного в круг, равна радиусу круга, то сам шестиугольник строится без
затруднений, если отложим шесть раз по окружности отрезок, равный
радиусу.
Имея правильный n-угольник, можно сейчас же получить и пра-
правильный 2п-угольник, деля пополам дуги между соседними вершинами
гс-угольника. Начиная с диаметра круга (правильного вписанного «дву-
«двуугольника»), мы построим последовательно 4, 8, 16,..., 2™-угольни-
ки. Таким же образом, начиная с шестиугольника, мы получим 12, 24,
48, ... -угольники, а начиная с десятиугольника, — 20, 40, ... -угольни-
-угольники.
Если sn обозначает длину стороны правильного n-угольника, вписанного
в единичный круг (т.е. круг с радиусом 1), то сторона правильного вписан-
вписанного 2п-угольника будет иметь длину
S2n = V 2 -

162
Глава III
D
Доказывается это следующим образом (рис. 34):
пусть sn = DE = 2DC, s2n = DB и АВ = 2.
Площадь прямоугольного треугольника ABD
равна t;BD ¦ AD, или, с другой стороны, -цАВ ¦
'В CD. Так как AD = VAB2 - DB2, то, подстав-
подставляя АВ = 2, BD = S2n, CD = jrsn и сравнивая
между собой два выражения для площади, мы
получаем
Рис. 34. Удвоение числа
сторон правильного много-
многоугольника
Sn =
ИЛИ
- sln).
Остается решить квадратное уравнение относи-
относительно х = sin и ПРИ выборе корня принять во
внимание, что х должно быть меньше 2.
Из этой формулы, так как длина S^ (сторона квадрата) равна \/2, сле-
следует, что
s32 = A/2 - у 2 + у2 + \/2 и т.д.
В качестве общей формулы мы получаем (при п > 2):
S2n
= \ 2-\j2 + J2 + ... + y/2,
причем в правой части должно быть всего п — 1 радикалов. Периметр
2"-угольника, вписанного в круг радиуса 1, равен 2nS2n- Когда п стремится
к бесконечности, этот периметр в пределе переходит в длину окружности, по
определению равную 2тг:
2"в2п —> 2тг при п —> оо.
Деля на два и подставляя т вместо п — 1, мы получаем следующую формулу
для тг:
у 2 - у 2 + \/
2 + ... + \/2 —> тг (при m —»• оо).
m радикалов
Упражнение. Пользуясь тем, что 2т —> оо, доказать, как следствие,
что
У 2 - т/2 + ...
\/2->2 (при п -> оо).
п радикалов

§1. Основные геометрические построения 163
Резюмируем полученные здесь результаты таким образом: сторо-
стороны правильных, вписанных в единичный круг 2™ -угольников, 5 • 2™ -уголь-
-угольников и 3-2"-угольников вычисляются посредством рациональных опера-
операций — сложения, вычитания, умножения, деления — и операции извле-
извлечения квадратного корня; следовательно, могут быть построены с по-
помощью только циркуля и линейки.
3. Проблема Аполлония. Другая конструктивная проблема,
решающаяся весьма просто, если подойти к ней с алгебраической точки
зрения, это — знаменитая и уже упомянутая выше проблема Аполлония
о проведении окружности, касательной к трем данным окружностям.
В настоящем контексте нам не представляется необходимым искать
ее особенно элегантное решение. Нам существенно лишь установить
принципиально важное положение: проблема Аполлония решается с по-
помощью циркуля и линейки. Мы вкратце приведем соответствующее до-
доказательство; вопрос же о наиболее элегантном построении будет раз-
разобран ниже (см. стр. 200).
Пусть центры трех данных кругов имеют соответственно коорди-
координаты (жь ?/i), (x2, 2/2) и (ж3, уз), а радиусы равны ги г2 и г3. Обозна-
Обозначим координаты центра искомого круга через (ж, у), а радиус через г.
Легко написать условие касания двух окружностей, если учесть, что
расстояние между центрами должно равняться сумме или разности ра-
радиусов — смотря по тому, имеет ли место внешнее или внутреннее
касание. Записывая в алгебраической форме три условия задачи, мы
получаем три уравнения
(х-х1J + (у-у1J-(г±г1J=0, A)
(х-х2J + (у-у2J-(г±г2J=0, B)
(ж-ж3J + B/-2/зJ-(г±гзJ=0, C)
которые после преобразований принимают вид
ж2 + у2 - г2 - 2жж1 - 2yyi ± 2rri + ж2 + у\ + г\ = 0 Aа)
и т.п.
В каждом из уравнений нужно брать знак плюс или минус, в зави-
зависимости от того, каково касание — внешнее или внутреннее (рис. 35).
Все уравнения A), B), C) — второй степени относительно неизвест-
неизвестных х, у, г, но они обладают тем свойством, что члены второй степе-
степени входят в одинаковой комбинации, как видно из развернутой фор-
формы Aа). Таким образом, вычитая B) из A), мы получаем уравнение,
11*

164
Глава HI
Рис. 35. Круги Аполлония
линейное относительно ж, у, г:
ах + by + cr = d,
D)
где а = 2(ж2 — Х\) и т.д. Точно так же, вычитая C) из A), будем иметь
другое линейное уравнение
а'х + Ь'у + с'г = а".
E)
Решая уравнения D) и E) относительно неизвестных ж и у, ко-
которые, таким образом, выразятся линейно через г, и затем подстав-
подставляя в A), придем к уравнению, квадратному относительно г, каковое
может быть решено с помощью рациональных операций и извлечения
корня (см. стр. 161). Это уравнение, вообще говоря, будет иметь два ре-
решения, из которых лишь одно будет положительным. Определив г, най-
найдем дальше значения хну, подставляя г в ранее полученные формулы.
Окружность с центром ж, у и радиусом г и должна быть касательной
к трем данным кругам. Во всей процедуре решения участвуют только
рациональные операции и извлечение квадратного корня. Отсюда сле-
следует, что построение ж, у и г может быть выполнено с помощью только
циркуля и линейки.
В общем случае будет иметься 8 решений проблемы Аполлония, со-
соответственно возможным 2-2-2 = 8 комбинациям в выборе знаков +
и — в уравнениях A), B) и C); выбор же знаков надлежит делать в за-
зависимости от того, какого рода касание — внешнее или внутреннее —
желательно иметь по отношению к каждому из данных кругов. Вполне

§ 2. Числа, допускающие построение, и числовые поля 165
возможно, что наша алгебраическая процедура не приведет к дейст-
действительным значениям ж, у и г. Таков будет, например, случай, когда
все три данных круга — концентрические; тогда, очевидно, наша гео-
геометрическая задача не будет иметь ни одного решения. Следует также
предвидеть возможность и случаев «вырождения»; например, если все
три круга «вырождаются» в точки, лежащие на одной прямой, тогда
аполлониев круг тоже «вырождается» в эту самую прямую. Мы не ви-
видим необходимости рассматривать вопрос во всех подробностях: это
сделает сам читатель, если обладает некоторыми алгебраическими на-
навыками.
§ 2. Числа, допускающие построение, и числовые
поля
1. Общая теория. В предыдущем изложении мы постарались
охарактеризовать общий, так сказать, алгебраический фон геометри-
геометрических построений. Каждое геометрическое построение представляет
ряд последовательных этапов из числа следующих: 1) проведение пря-
прямой линии через две точки, 2) нахождение точки пересечения двух
прямых, 3) проведение окружности с данным центром и радиусом,
4) нахождение точки пересечения окружности с другой окружностью
или прямой линией. Элемент (точка, прямая, окружность) считается
известным или в том случае, если он задается условием задачи, или
в том случае, если он построен на предыдущей стадии задачи. Прово-
Проводя теоретический анализ задачи, мы относим всю рассматриваемую
конструкцию к некоторой координатной системе х, у (см. стр. 105).
Тогда заданные элементы изображаются в виде точек или отрезков
в плоскости ж, у. Если задан только один отрезок, его можно принять
в качестве единичного, в результате чего фиксируется точка ж = 1,
у = 0. Иногда в процессе построения возникают произвольные элемен-
элементы: проводятся произвольные прямые, строятся произвольные точки
или круги. (Пример произвольного элемента мы имеем при нахожде-
нахождении середины отрезка: мы проводим два круга с центрами в концах
отрезка и с одинаковыми, но произвольными радиусами, затем соеди-
соединяем точки их пересечения.) В подобных случаях всегда можно считать
произвольный элемент рациональным: произвольную точку можно вы-
выбрать так, чтобы у нее были рациональные координаты, произвольную
прямую ах + by + с = 0 так, чтобы у нее были рациональные коэффи-
коэффициенты а, 6, с, произвольный круг — так, чтобы рациональными были
координаты центра и радиус. Мы условимся, что, если в построении

166 Глава III
участвуют произвольные элементы, мы будем выбирать их рациональ-
рациональными: раз эти элементы в самом деле произвольны, такой выбор не
повлияет на результат построения.
Ради простоты допустим в ближайшем рассуждении, что в усло-
условии задачи задается только один элемент — отрезок длины 1. Тогда,
в соответствии с результатами § 1, мы можем построить с помощью
циркуля и линейки все числа, получающиеся из единицы посредством
рациональных операций, т.е. рациональные числа |, где г и s — целые
числа. Система рациональных чисел «замкнута» по отношению к рацио-
рациональным операциям: сумма, разность, произведение, частное (исклю-
(исключая, как всегда, деление на 0) двух рациональных чисел снова являются
рациональными числами. Всякое множество чисел, обладающее таким
свойством замкнутости по отношению к четырем рациональным опе-
операциям, мы назвали числовым полем (стр. 86).
Упражнение. Покажите, что каждое числовое поле во всяком случае
содержит все рациональные числа. (Указание. Если а есть какое-нибудь не
равное нулю число из поля F, то ? = 1 также принадлежит к F, а из 1 можно
получить все рациональные числа посредством рациональных операций.)
Отправляясь от единицы, можно построить все рациональное чи-
числовое поле и, следовательно, все рациональные точки (т. е. точки, у ко-
которых обе координаты рациональны) в плоскости ж, у. Дальше, с по-
помощью циркуля можно построить новые, иррациональные числа вроде
числа %/2, которое, как мы знаем из главы II, § 2, находится уже за
пределами рационального поля. Но построив \/2, можно еще дальше
с помощью «рациональных» построений (§ 1) получить все числа вида
а + Ъу/2, A)
где а и Ь — рациональные и, следовательно, сами допускают построе-
построение. Можно также построить и числа вида
где о, Ь, с, d — рациональные. Однако эти числа всегда можно написать
в форме A). В самом деле,
а + Ьу/2 а + ЬлД с - йлД ас - 2bd be-ad дг
c2-2d2 с2 - 2d2

§2. Числа, допускающие построение, и числовые поля 167
где р и q — рациональные. (Знаменатель с2 — 2d2 отличен от нуля, так
как из с2 — 2gP = 0 следовало бы \[2 = - что противоречит факту
а
иррациональности i/2.) Точно так же
(а + Ьу/2)(с + dy/2) = {ас + 2bd) + {be + ad) у/2 = г + s\/2,
где г и s — рациональные. Итак, все, что мы можем построить, исходя
из у/2, это — числа вида A), где а и b — произвольные рациональные
числа.
Упражнение. Напишите в форме A) числа
о; Р т р , \Р Р ) ri п 1 , )
4 1 — г q +pr
где положено
P-1 + V2, 9 = 2-\/2, г = -3 + \/2.
Как показывает предшествующее рассуждение, числа A) снова об-
образуют поле. Это поле обширнее, чем поле рациональных чисел, вклю-
включая его как часть («подполе»). Но, конечно, новое поле менее обширно,
чем поле всех действительных чисел. Обозначим через Fo поле рацио-
рациональных чисел, а через Fi — поле чисел вида A). Мы установили воз-
возможность построения каждого числа из «расширенного» поля i*\. Можно
и дальше расширять область чисел, допускающих построение, напри-
например, таким образом: выберем число из поля Fi, скажем к = 1 + у/2,
и, извлекая из него корень, получим новое допускающее построение
число
)Jl + y/2= у/к.
Это число в свою очередь порождает (§ 1) поле, состоящее из всех
чисел вида
P+q^k, B)
где р и q теперь уже — числа из поля i<\, т. е. вида а + Ьу/2, где a, b —
из Fo, т.е. рациональные.
Упражнение. Представить числа
/¦ B-
U
' 1 + у/к ' (v/JfcK - 3 ' 1 + у/Зк
в форме B).

168 Глава III
Все эти числа были построены в предположении, что первоначально был
задан только один отрезок. Если задано два отрезка, то один из них можно
принять за единичный. Предположим, что второй отрезок выражается через
первый в виде числа а. Тогда можно построить поле G, состоящее из всех
чисел вида
атат + am-ia + ... + +
bnan+bn-1a"-1 + .
где ао, ... , ат и Ьо, • • • , Ь„ — рациональные, а т и п — произвольные целые
положительные числа.
Упражнение. Считая заданными отрезки 1 и а, выполнить построения
для 1 + а + а2, , а3.
1 — а
Будем исходить теперь из более общего предположения, что мы
умеем строить все числа некоторого числового поля F. Убедимся, что
применение одной линейки не выведет нас за пределы поля F. Уравнение
прямой, проходящей через две точки с координатами oi, 6i и аг, &2 из
поля F, имеет вид (bi — Ь2)х + (п2 — a\)y + (aib2 — o,2bi) = О (см. стр. 558);
коэффициенты в этом уравнении рационально зависят от чисел из по-
поля F и, следовательно, сами принадлежат полю F. Далее, если у нас
имеются две прямые ах + Ру + у = 0 и а'х + Р'у + у' = 0 с коэффи-
коэффициентами из F, то координаты точки пересечения, получающиеся при
решении системы этих уравнений, суть
_ j/ /7 _
Х~ ар' ра" У~
ар' -ра" У~ ар -Ра1'
Так как и они тоже являются числами из F, то ясно, что применение
одной только линейки не выведет нас за пределы F.
Упражнение. Прямые х + \/2у — 1 = 0, 2х — у + \/2 = 0 имеют ко-
коэффициенты, принадлежащие полю A). Вычислить коэффициенты точки их
пересечения и проверить, что они также вида A); соединить точки A, \fi)
и (\/2, 1 —\/2) прямой линией ax+by+с = 0 и проверить, что коэффициенты а,
6, с имеют вид A). То же сделать по отношению к полю B) соответствен-
соответственно для прямых v 1 + \/2х + \/2у = 1, A + \/2)х — у = 1 — у 1 + л/2 и для
точек (ч/2, -1), A + у/2, \/l + \/2).
Но с помощью циркуля можно выбраться за пределы поля F. Для
этой цели выберем в поле F такое число к, что число \/к уже не будет
принадлежать F. Число Vk можно построить с помощью циркуля, так
же как и все числа вида
а + Ь\/к, C)

§2. Числа, допускающие построение, и числовые поля 169
где а, Ъ — произвольные числа из F. Сумма и разность двух таких
чисел а + b\/k и с + d\/k, их произведение (о + b\/k)(c + d\/k) = (ас +
,, л / . i_ л /Г a + bVk {а + Ьл/к)(с - dVk)
+ kbd) + {ad - bc)Vk и их отношение ^ v = 5-^— =
с + dVk С - kd'
— 9^——_ -|—с ~ а y/k — снова числа вида р + qs/k, где р и q при-
с — kd с — kd
надлежат F. (Знаменатель с2 — kd2 не обращается в нуль, так как с
и d одновременно не обращаются в нуль: иначе мы получили бы \[к =
— -, что противоречит допущению, что \/к не принадлежит F.) Итак,
а
множество чисел вида а + bs/k образует некоторое поле F'. Поле F'
включает поле F как «подполе» (достаточно положить Ъ = 0). Будем
называть F' «расширенным» полем.
В качестве примера рассмотрим поле F чисел вида а + Ь\/2, где
a, b — рациональные: возьмем к = \[2. Тогда числа расширенного по-
поля F' имеют вид р + q\/2, где р и q принадлежат F, р = а + Ь\/2,
q = а' + Ь'у/2, а числа а, 6, а', Ь' — рациональные. Всякое число из F'
может быть записано в этой форме, например,
1 у/2- #2 л/2- </2 уД #2
Упражнение. Пусть F есть поле p + qy2 + у/2, гдер, q — вида а + Ь\/2,
, „ 1 + \/2 + V?
а числа а, о — рациональнее. Представить — в таком же виде.
2 -3V2 + V2
Мы убедились, что, отправляясь от некоторого поля F чисел, до-
допускающих построение, и выбрав произвольное число к из этого поля,
мы можем с помощью циркуля и линейки построить число \/к, а зна-
значит, и все числа вида а + Ь\/к, где а, Ъ принадлежат F.
Покажем теперь, обратно, что, пользуясь только циркулем, мы мо-
можем получить числа только указанного вида. В самом деле, в резуль-
результате однократного применения циркуля можно сделать только одно из
двух: или найти точку пересечения окружности и прямой, или найти
точку пересечения двух окружностей (то и другое равносильно постро-
построению координат точка пересечения). Окружность с центром ?, ? и ра-
Диусом г имеет уравнение (ж — ?J + (У ~ СJ — г2> поэтому, если ?, ?,

170 Глава III
г принадлежат F, то уравнение круга, написанное в виде
х2 + у2 + 2ах + 2/Зу + у = 0,
будет иметь коэффициенты а, /3, у, принадлежащие также F. Прямая
линия
ах + by + с = 0,
соединяющая две точки с координатами F, имеет также коэффициенты
из F (см. стр. 168). Исключая у из этих двух уравнений, мы получаем
для координаты ж точки пересечения окружности и прямой квадратное
уравнение вида
Ах2 +Ву + С = 0.
с коэффициентами А, В, С из F (именно, А = а2 + Ь2, В = 2(ас + Ь2а -
- ab/3), С = с2 - 2Ъф + Ь2у). Решение дается формулой
-В± VB2^4AC
Х=2А'
каковая имеет BURp+qVk, гдер, q, к принадлежат F. Такая же формула
получается и для координаты у точки пересечения.
С другой стороны, если речь идет о двух окружностях
х2 +у2 + 2ах + 2j3y + у = 0,
х2 +у2 + 2а'х + 20 у + у' = 0,
то, вычитая одно уравнение из другого, мы получим линейное уравне-
уравнение
(а - а')х + (C- (З')у + (у - у') = 0,
которое можно решить совместно с одним из уравнений двух окруж-
окружностей.
В обоих случаях построение дает нам обе координаты одной или
двух новых точек, и эти новые величины имеют вид p + qVk, причем р,
q, к принадлежат F. В частности, \[к может сам оказаться принадле-
принадлежащим F, например, если к = 4. Но, вообще говоря, этого не будет.
Упражнение. Рассмотрим окружность с центром в начале и радиу-
радиусом 2\/2 и прямую, соединяющую точки ( ^, 0J, D\/2, \/2). Определите по-
поле F', порождаемое точками пересечения окружности и прямой. Сделайте то
же по отношению к точкам пересечения данной окружности с окружностью,
л/2
у которой радиус равен -^—, а центр есть @, 2\/2).
Подведем еще раз итоги. Отправляясь от некоторых заданных вели-
величин (отрезков или чисел), с помощью одной только линейки мы можем

§2. Числа, допускающие построение, и числовые поля 171
построить все величины из поля F, порождаемого данными величина-
величинами с помощью рациональных операций, но не выйдем за пределы этого
поля. Воспользовавшись циркулем, мы расширяем поле величин, допус-
допускающих построение, и получаем новое расширенное поле F', состоящее
из чисел вида а + b\/k, где a, b, к принадлежат F. Поле F есть подполе
поля F': всякое число из F принадлежит также F', так как в форму-
формуле а + Ъл/к можно положить Ъ = 0. (Предполагается, что \/к есть новое
число, не принадлежащее F; иначе F' совпало бы с F.) Мы убедились,
что в результате каждого геометрического построения (т.е. проведе-
проведение прямой через две известные точки; проведение окружности, име-
имеющей известный центр и известный радиус; нахождение пересечения
двух известных прямых или окружностей) или получаются величины,
принадлежащие первоначальному полю, или же, при построении квад-
квадратного корня, открывается новое, расширенное поле величин, допус-
допускающих построение.
Мы теперь в состоянии точно характеризовать совокупность всех
величин, допускающих построение с помощью только циркуля и линей-
линейки. Будем исходить из некоторого поля Fo, определяемого величинами,
входящими в условие задачи; например, это будет поле рациональных
чисел, если задан только один отрезок, выбираемый в качестве еди-
единичного. Далее, «присоединяя» к полю величину \/^о (гДе &о принад-
принадлежит Fo, но у/к~о ему не принадлежит), строим новое поле Fi чисел,
допускающих построение вида по + Ьоу/к~о, где ао, Ьо принадлежат Fo.
Еще дальше, посредством «присоединения» \/к[ (где к\ принадлежит Fi,
но \fk~l не принадлежит), получается новое поле F2 чисел вида а\ +
+Ь\\/к[, где ai и fci принадлежат F\. Повторяя эту процедуру, приходим
вообще к полю Fn после «присоединения» п квадратных корней. Допус-
Допускают построение с помощью только циркуля и линейки те и только те
числа, которые после конечного числа «присоединений» описанного выше
типа включаются в расширенное поле Fn. Число п необходимых «при-
«присоединений» не имеет особенно большого значения; но оно до некоторой
степени характеризует, насколько сложна рассматриваемая проблема.
Иллюстрируем описанную процедуру следующим примером. Нуж-
Нужно построить число
Пусть Fo — поле рациональных чисел. Полагая ко = 2, получаем по-
поле Fi, содержащее число 1 + \/2- Возьмем затем ki = 1 + \/2 и fe = 3.
Число 3 содержится уже в начальном поле Fq, а значит, и подавно в по-

172 Глава III
ле i<2, так что положить &2 = 3 вполне допустимо. Потом возьмем: кз =
= \Л + \/2 + \/3 и, наконец, /с4 = у \/Т+\/^+ \/3 + 5. Полученное
после этого поле F5 уже содержит интересующее нас число, так как \/б
в нем содержится: действительно, \/2 и \/3, а следовательно, и их про-
произведение, содержатся уже в F$, значит, и подавно — в F$.
Упражнение. Отправляясь от рационального поля, проверьте, что сто-
сторона правильного 2т-угольника (см.стр.163) допускает построение (п = т—1).
Проследите за тем, какова последовательность постепенно расширяемых по-
полей. Сделайте то же самое с числами
2. Все числа, допускающие построение, — алгебраические.
Если начальное поле Fo есть рациональное поле (порождаемое единственным
отрезком), то все числа, допускающие построение, принадлежат к числу ал-
алгебраических. (Определение алгебраических чисел было дано на стр. 139).
Именно, числа поля Fi являются корнями квадратных уравнений, числа по-
поля i<2 — корнями уравнений четвертой степени и вообще числа поля Fj, —
корнями уравнений степени 2fc с рациональными коэффициентами. Докажем
это сначала для поля i<2, причем начнем с примера. Пусть х = \/2 + уЗ + у/2.
Мы получаем (х-%/2J = 3 + \/2, х2 + 2-2\Дх - 3 + >/2, или х2 -1 = \/2Bж +
+ 1) — квадратное уравнение с коэффициентами из F\. Возведение в квадрат
приводит к уравнению
(х2 - IJ = 2Bа; + IJ
четвертой степени с рациональными коэффициентами.
В общем случае любое число поля Fi имеет вид
х =р + qy/w, D)
где р, q, w принадлежат полю Fi и, значит, имеют вид р = а
q = с + dy/s, w = е + fy/s, где a, b, с, d, e, f, s — рациональные числа. Из
равенства D) мы получаем
х2 — 2рх +р2 = q2w,
причем все коэффициенты принадлежат полю Fi, порождаемому величи-
величиной y/s. Поэтому последнее равенство можно переписать а виде
х2 + их + v = \/И(гх + t),

§3. Неразрешимость трех классических проблем 173
где коэффициенты г, s, t, и, v — рациональные. Возводя в квадрат, получим
уравнение четвертой степени
(x2+ux + vJ = s(rx + tf E)
с рациональными коэффициентами, как и требовалось.
Упражнения.
1) Построить уравнение с рациональными коэффициентами для чисел:
а) х = V 2 + \/3, Ь) х = \/2 + у/3, с) х = —=J
2) Построить таким же образом уравнение восьмой степени для чисел
a) x= V2+ J2 + V2, b)x = V2 + Jl + V3,
Чтобы закончить доказательство теоремы в общем случае, когда ж при-
принадлежит полю Fk с произвольным индексом fc, достаточно установить, как
выше, что х удовлетворяет квадратному уравнению с коэффициентами из
поля Fk-i- Затем, повторяя процедуру доказательства, убеждаемся, что х
удовлетворяет уравнению степени 22 = 4 с коэффициентами из поля Ffc-2
и т. д.
Упражнение. Закончите это общее доказательство, применяя метод
математической индукции: докажите, что х удовлетворяет уравнению сте-
степени 21 с коэффициентами из поля Fk-i, 0 < I ^ к. При I = к получается
окончательный результат.
§3. Неразрешимость трех классических проблем
1. Удвоение куба. Теперь мы уже достаточно подготовлены
к исследованию проблем древности: трисекции угла, удвоения куба
и построения правильного семиугольника. Рассмотрим прежде всего
проблему удвоения куба.
Если данный куб имеет ребро, равное единице, его объем будет ра-
равен кубической единице; требуется найти ребро ж куба, объем которого
вдвое больше. Итак, искомое ребро удовлетворяет простому кубичес-
кубическому уравнению
ж3-2 = 0. A)

174 Глава III
Наше доказательство невозможности построения числа ж с помо-
помощью только циркуля и линейки будет носить «косвенный» характер. До-
Допустим, что такое построение возможно. Тогда, согласно полученным
выше результатам, число ж должно принадлежать некоторому полю F^,
полученному так, как было объяснено раньше из рационального поля по-
посредством последовательного «присоединения» квадратных корней. Мы
сейчас убедимся в том, что такое допущение приведет к противоречию.
Мы уже знаем, что число х не может принадлежать рациональному
полю Fo, так как -\/2 есть число иррациональное (см. упражнение 1
на стр. 91). Значит, придется допустить, что оно принадлежит одному
из расширенных полей Fjj, где к — целое положительное число. Мы
имеем право допустить, что к есть наименьшее из таких целых чисел,
т.е. что ж принадлежит к Fk, но не принадлежит к Ffc_i. Это значит,
что ж имеет вид
х = р + q\fw,
где р, q и w принадлежат какому-то полю Fk-i, но *Jw ему не принад-
принадлежит. Основываясь, далее, на довольно простом алгебраическом рас-
рассуждении (подобные рассуждения приходится применять нередко), мы
убедимся, что еслир + gV'w есть решение уравнения A), то у = p — q^/w
есть также его решение. Так как х принадлежит полю F/., то ж3 и х3 — 2
тоже принадлежат F^ и, значит,
ж3 - 2 = а + b,/w, B)
где aab принадлежат F/.-1. Нетрудно подсчитать, что а = р3 + 3pq2w — 2,
Ь = ip2q + q3w. Если положим
у =р- qVw,
то сразу видно, что
у3 - 2 = а - bVw. B')
Так как мы предположили, что ж есть корень уравнения A), то
а + Ь^ = 0. C)
Но из последнего равенства следует (это основной момент рассужде-
рассуждения!), что оба числа а и Ъ равны нулю. Действительно, если бы Ъ было
отлично от нуля, то из C) получилось бы равенство л/w = —j-, это про-
противоречит допущению, что л/w не принадлежит полю F^-i. Итак, Ъ = О,
и тогда из C) следует, что а = 0. Но раз мы установили, что а — b = 0,
то уже из равенства B') немедленно вытекает, что у = р — q\fw есть ре-
решение уравнения A), так как уэ—2 = 0. Далее, у ф х, т. е. ж — у ф 0, так

§3. Неразрешимость трех классических проблем 175
как число х ~ у = 2q^/w могло бы обращаться в нуль только при q = О,
а в этом случае х = р принадлежало бы полю Ffc_i, чего мы не предпо-
предполагали.
Мы установили, что если х = р + q\/w есть корень кубического
уравнения A), то у = р — q\/w есть другой, не равный ему корень того
же уравнения. Но это немедленно приводит к противоречию: у = р —
— q\/w есть, очевидно, действительное число, так как числа р, q, \fw
действительные, уравнение же A) имеет только один действительный
корень, а два — мнимых (см. стр. 134).
Наше первоначальное допущение привело к противоречию, значит,
оно ошибочно, поэтому корень уравнения A) не может принадлежать
никакому полю Fk- Итак, удвоение куба с помощью только циркуля и
линейки невозможно.
2. Одна теорема о кубических уравнениях. Заключитель-
Заключительная часть только что приведенного алгебраического рассуждения была
приспособлена к специальному уравнению, которым мы занимались. Но
если мы хотим исследовать две другие проблемы древности, то жела-
желательно основываться на некоторой теореме общего характера. С алгеб-
алгебраической точки зрения все три проблемы связаны с решением куби-
кубического уравнения. Отлично известно, что если х\, Х2, Жз — три корня
кубического уравнения
z3 + az2 + bz + с = 0, D)
то они связаны между собой соотношением
хг + х2 + х3 = -а. 1 E)
Рассмотрим кубическое уравнение D), в котором коэффициенты а, Ь, с
пусть будут рациональными числами. Может, конечно, случиться, что
один из корней уравнения есть рациональное число: например, уравне-
уравнение ж3 — 1 = 0 имеет один корень 1 — рациональный, тогда как два дру-
других, удовлетворяющих квадратному уравнению ж2 + ж + 1 = 0,— мни-
мнимые. Но мы сейчас докажем такую общую теорему: если кубическое
1 Многочлен z3 + az2 + bz + с можно представить в виде произведения трех мно-
множителей (z-X\)(z — X2)(z-X3), где х\, Х2, хз — корни уравнения D) (см. стр. 137).
Отсюда следует тождество
z3 + az2 + bz + с = г3 - (х\ + Х2 + жз)г2 + (xix2 + х2хз + хгхз)г - х\х2хз,
и так как коэффициенты при одинаковых степенях должны быть равны между со-
собой, то
—а = xi + Х2 + хз, Ь = х\Х2 + жгжз + х\хз, с = — ж

176 Глава III
уравнение с рациональными коэффициентами не имеет рациональных
корней, то ни один из его корней не может быть построен с помощью
циркуля и линейки, исходя из рационального поля Fo.
Доказательство будем вести, как раньше, косвенным методом. До-
Допустим, что число ж, являющееся корнем уравнения D), допускает по-
построение. Тогда ж должно принадлежать некоторому полю Fjj, послед-
последнему в цепи постепенно расширяемых полей Fo, i<\, ... , Fk.
Мы, как раньше, имеем право допустить, что никакой корень урав-
уравнения D) не принадлежит полю Fk-\. (Что к не есть нуль, следует
как раз из условия теоремы: ж не может быть рациональным числом.)
Итак, ж может быть записано в виде
х = р + q\/w,
причем р, q, w принадлежат полю F^-i, но л/w не принадлежит Fk-\.
Такое же самое рассуждение, какое было проведено в предыдущем
пункте, приводит к заключению, что число
у = р
также принадлежащее Fk, является корнем уравнения D). Мы видим,
как раньше, что q ф 0; значит, х фу.
Из равенства E) мы теперь заключаем, что третий корень урав-
уравнения D) дается формулой и = —а — х — у. Но так как х + у = 2р, то,
значит,
и = —а — 2р.
Радикал y/w здесь исчез, так что оказывается, что и принадлежит по-
полю -Ffc-i. Это противоречит сделанному допущению, согласно которо-
которому к есть наименьшее целое число, такое, что некоторое поле F^ содер-
содержит корень уравнения D). Придется отвергнуть сделанное допущение,
раз оно привело к противоречию, и признать, что ни один из корней
уравнения D) не принадлежит никакому полю Fjj. Теорема доказана.
На основании этой теоремы можно утверждать, что некоторое число не
может быть построено с помощью только циркуля и линейки, как толь-
только установлено, что это число является корнем кубического уравнения
с рациональными коэффициентами, не имеющего рациональных кор-
корней. Теперь мы можем перейти к рассмотрению двух других проблем
древности; заметим, что каждая из них облекается в алгебраическую
форму не столь непосредственно, как уже рассмотренная.
3. Трисекция угла. Покажем, что трисекция угла с помощью
только циркуля и линейки в общем случае невозможна. Конечно, су-

§3. Неразрешимость трех классических проблем 177
ществуют углы, например, углы в 90° или в 180°, для которых три-
секция выполняется. Но мы должны показать, что не существует про-
процедуры построения, пригодной для всякого угла. Так как общий метод
должен был бы относиться ко всем углам, то наша цель будет достиг-
достигнута, если мы укажем хотя бы один какой-нибудь угол, для которого
трисекция невозможна. Итак, несуществование общего метода трисек-
трисекции будет установлено, если мы убедимся, что, например, угол в 60° не
может быть разделен на три равные части с помощью только циркуля
и линейки.
Алгебраический эквивалент рассматриваемой проблемы можно по-
получить разными способами; самый простой способ — считать, что
угол в задан своим косинусом: cos в = g. Тогда проблема сводится к вы-
(\
числению величины х = cos^. Интересующие нас косинусы связаны
о
между собой простой тригонометрической формулой (см. стр. 133)
cos в = 4 cos3 | -3cosf.
о о
Другими словами, проблема трисекции угла в (такого, что cos# = g)
равносильна построению корня кубического уравнения
4г3 - iz - g = 0. F)
Так как по предыдущему мы имеем право положить в = 60°, g —
= cos 60° = ~, то уравнение F) принимает вид
8z3-6z = l. G)
В силу теоремы, доказанной в предыдущем пункте, для нашей цели
достаточно показать, что это уравнение не имеет рациональных корней.
Положим v = 2z; уравнение примет еще более простой вид
v3 - 3v = 1. (8)
Если бы существовало рациональное число v = |, удовлетворяющее
этому уравнению, где г и s — целые числа без общего множителя (> 1),
то мы должны были бы иметь равенство г3 — 3s2r = s3. Отсюда следо-
следовало бы, что число s3 — г (г2 — 3s2) делится на г, и тогда получилось бы,
что г и s имеют общий множитель, если только г не равно ±1. Совер-
Совершенно так же мы заключили бы, что число г3 = s2(s + 3r) делится на s2,
а это значило бы, что г и s имеют общий множитель, если только s не
равно ±1. Но так как дробь |, по предположению, несократима, то,
значит, остается заключить, что числа г и s равны ±1, т. е. v = ±1. Но,
!2 - 340

178 Глава III
подставляя v = +1 и v = -1 в уравнение (8), мы видим, что в обоих
случаях уравнение не удовлетворяется. Итак, уравнение (8), а следо-
следовательно, и уравнение G) не имеют рациональных корней: тем самым
невозможность трисекции угла доказана.
Эта теорема доказана в предположении, что линейка рассматривается
как инструмент, служащий для проведения прямой через две данные точки,
и никак иначе. В самом деле, когда мы давали общую характеристику чисел,
которые допускают построение, имелось в виду только такое употребление
линейки. Если допустить иные приемы пользования линейкой, то совокуп-
совокупность выполненных построений чрезвычайно расширяется. Хорошим приме-
примером является следующий метод трисекции угла, указываемый в сочинениях
Архимеда.
Рис. 36. Прием трисекции угла, указанный Архимедом
Пусть дан угол х (рис. 36). Продолжим горизонтальную сторону угла
влево и затем проведем полукруг с центром О и произвольным радиусом г.
Отметим на самой линейке такие точки А и В, что АВ = г. Затем приведем
линейку в такое положение, чтобы точка А линейки была на продолженной
стороне угла, точка В на проведенном полукруге и вместе с тем линейка про-
прошла бы через точку пересечения второй стороны угла с полукругом. В этом
положении линейки Проведем по ней прямую линию, образующую с продол-
продолженной стороной данного угла угол, который обозначим через у.
Упражнение. Доказать, что у = %¦
о
4. Правильный семиугольник. Перейдем теперь к проблеме
построения стороны х правильного семиугольника, вписанного в еди-
единичный круг. Проще всего справиться с этой проблемой, если прибег-
прибегнуть к комплексным числам (см. главу II, § 5). Мы знаем, что вершины
правильного семиугольника служат корнями уравнения
z7 - 1 = 0, (9)
причем координаты х, у каждой вершины являются действительной
и мнимой частями комплексного числа z = х + гу. Один из корней

§3. Неразрешимость трех классических проблем 179
есть z = 1, а остальные удовлетворяют уравнению
^± = z6+zb + z4+z3+z2 + z + 1 = 0 A0)
(см. стр. 135). Деля на z3, получаем новое уравнение
z3 + \+z2 + \ + z + l + l = 0. A1)
Простые алгебраические преобразования приводят его к виду
[z + iK - з(* + \) + (z + |J - 2 + (z + |) +1 = 0. A2)
Положив теперь
мы приходим окончательно к уравнению третьей степени
2/3+2/2-22/-1 = О. A3)
Мы знаем, что z, корень седьмой степени из единицы, дается фор-
формулой
z = cosy + г sin у, A4)
где ip = " есть угол, под которым из центра круга видна сторо-
сторона семиугольника; кроме того, из упражнения 2 на стр. 133 следует,
что i = cos ip — i simp, так что
у — z + - = 2 cos (p.
Если мы сумеем построить у, то сумеем построить и cosy, и об-
обратно. Итак, раз будет установлено, что величина у не может быть
построена, то тем самым будет установлено, что не могут быть по-
построены ни величина cosy, ни величина z; следовательно, невозможно
будет построение семиугольника.
Таким образом, в силу теоремы пункта 2, остается показать, что
Уравнение A3) не имеет рациональных корней. Это тоже доказывается
косвенным методом. Допустим, что уравнение A3) имеет рациональ-
рациональный корень ?, где г и s — целые числа без общих множителей. В таком
случае должно удовлетворяться равенство
г3 +r2s-2rs2-s3 =0; A5)
отсюда ясно, что г3 делится на s, a, s3 — на г. Так как г и s — взаимно
простые числа, то отсюда следует, что каждое из них равно ±1. Значит,
12*

180 Глава III
и у, если только это число рациональное, должно равняться или +1,
или —1. Но подстановка в уравнение A3) показывает, что ни +1, ни -1
не являются корнями уравнения. Итак, нельзя построить величины у,
а следовательно, и стороны семиугольника.
5. Замечания по поводу квадратуры круга. Сравнительно
элементарные методы позволили нам довести до конца исследование
проблем удвоения куба, трисекции угла и построения правильного се-
семиугольника. Но проблема квадратуры круга гораздо сложнее и тре-
требует техники математического анализа. Так как круг радиуса г имеет
площадь тгг2, то проблема построения квадрата, площадь которого рав-
равна площади круга с радиусом 1, равносильна построению числа у/ж,
равного стороне искомого квадрата. Число у/ж допускает построение
в том и только в том случае, если допускает построение число ж. Исхо-
Исходя из данной нами общей характеристики чисел, допускающих постро-
построение, мы установили бы неразрешимость проблемы квадратуры круга,
если бы показали, что ж не содержится ни в каком поле Fk, возни-
возникающем из поля рациональных чисел посредством последовательных
присоединений квадратных корней. Так как все числа, принадлежащие
таким полям, являются алгебраическими, т.е. удовлетворяющими ал-
алгебраическим уравнениям с целыми коэффициентами, то неразреши-
неразрешимость квадратуры круга была бы доказана, если бы было установлено,
что число ж — не алгебраическое, а трансцендентное (см. стр. 139).
Технический аппарат, необходимый для доказательства трансцен-
трансцендентности числа ж, был создан Шарлем Эрмитом A822-1905), который
доказал вместе с тем трансцендентность числа е. Несколько усовершен-
усовершенствовав метод Эрмита, Ф. Линдеман (в 1882 г.) сумел доказать транс-
трансцендентность числа ж и тем самым окончательно исчерпал вопрос, оста-
остававшийся без ответа на протяжении тысячелетий. Доказательство Лин-
демана — вне пределов, намеченных для этой книги, хотя оно и по
плечу учащемуся, несколько знакомому с математическим анализом.
Часть 2
Различные методы выполнения построений
§ 4. Геометрические преобразования. Инверсия
1. Общие замечания. В настоящей, второй части этой главы
мы систематически рассмотрим некоторые общие принципы, которые

§4. Геометрические преобразования. Инверсия 181
могут быть приложены к конструктивным проблемам. Многие из этих
проблем обозреваются гораздо легче, если смотреть на них с общей
точки зрения «геометрических преобразований». Вместо того чтобы из-
изучать отдельное построение, мы займемся сразу целым классом проб-
проблем, связанных между собой теми или иными процедурами преобразо-
преобразований. Способность бросать яркий свет на существо вещей, присущая
идее класса геометрических преобразований, никоим образом не огра-
ограничена конструктивными проблемами, но имеет ближайшее отношение
ко всей геометрии в целом. В главах IV и V мы будем иметь случай
оценить роль геометрических преобразований в этом более широком
аспекте. Пока же мы подвергнем изучению один из частных типов пре-
преобразований — инверсию плоскости относительно окружности, пред-
представляющую собой обобщение обыкновенного зеркального отражения
относительно прямой линии.
Говоря о преобразовании (отображении) плос-
плоскости самой в себя, мы имеем в виду некоторое Р
правило, сопоставляющее каждой точке Р плос-
кости некоторую другую точку Р' той же плос-
кости. Точка Р' называется образом точки Р, точ- ;
ка Р — прообразом точки Р'. Простейший пример 4
такого преобразования — зеркальное отражение рис 37 Отражение
(осевая симметрия) плоскости относительно дан- точки относительно
ной прямой линии L: точка Р по одну сторону L прямой
имеет своим образом точку Р', расположенную по
другую сторону L таким образом, что L является перпендикуляром
к отрезку РР', восставленным из его середины. Преобразование может
оставлять некоторые точки плоскости неподвижными; в нашем приме-
примере таковы точки самой прямой L.
Дальнейшими примерами преобразований являются вращения плос-
плоскости относительно неподвижной точки О, затем параллельные перено-
переносы, перемещающие каждую точку в данном направлении на одно и то
же расстояние (эти преобразования не имеют неподвижных точек), и,
наконец, в качестве несколько более общего примера следует назвать
движения плоскости, которые можно представлять себе составленными
Из вращений и параллельных перенесений.
Но в данный момент нас интересует иной, частный класс преобра-
преобразований — именно инверсии относительно окружностей. (Иногда их на-
называют круговыми отражениями, вследствие наличия приблизительно-
приблизительного сходства с отражениями в круглых зеркалах.) Пусть в неподвижной
Плоскости задана некоторая окружность С с центром О (называемым

182 Глава III
центром (или полюсом) инверсии) и радиусом г.
Образ точки Р определяется как точка Р', лежа-
лежащая на прямой ОР по ту же сторону от О, что
и Р, и такая, что
ОР-ОР' = г2. A)
Из этого определения следует, что если Р' есть
образ Р, то и Р есть (в данном преобразова-
преобразовании) образ Р'. Это дает право называть точки Р
Рис 38 Инверсия и Р'взаимно обратными относительно окруткнос-
точки относительно ти С- Инверсия превращает внутреннюю область
окружности окружности во внешнюю, и обратно: в самом де-
деле, из неравенства ОР < г следует неравенство ОР' > г и, напротив, из
неравенства ОР > г — неравенство ОР' < г. Неподвижными точками
плоскости являются точки самой окружности С.
Правило A) не определяет никакого образа для центра О. Но ясно,
что, когда движущаяся точка Р приближается к О, ее образ Р' уходит
неограниченно далеко. По этой причине иногда говорят, что при инвер-
инверсии образом центра является бесконечно удаленная точка. Полезность
этой терминологии вытекает из того обстоятельства, что она дает нам
право утверждать, что инверсия устанавливает взаимно однозначное
соответствие между всеми точками плоскости без исключения и их
образами: каждая точка плоскости имеет один и только один образ и
сама является образом одной и только одной точки. Отметим, что это
последнее свойство принадлежит также и раньше приведенным приме-
примерам геометрических преобразований.
2. Свойства инверсии. Самое важное свойство инверсии заклю-
заключается в том, что она преобразует прямые линии и окружности в прямые
линии и окружности. Точнее, мы сейчас обнаружим, что в результате
инверсии:
a) прямая, проходящая через О, становится прямой, проходящей
через О,
b) прямая, не проходящая через О, становится окружностью, про-
проходящей через О,
c) окружность, проходящая через О, становится прямой, не прохо-
проходящей через О,
d) окружность, не проходящая через О, становится окружностью,
не проходящей через О.
Утверждение а) не требует доказательства, так как из самого опре-
определения инверсии ясно, что каждая точка на рассматриваемой прямой

}4. Геометрические преобразования. Инверсия
183
Рис. 39. Инверсия прямой
относительно окружности
имеет в качестве образа другую точку на
той же прямой, так что хотя отдельные
точки на прямой перемещаются, но пря-
прямая в целом остается неизменной.
Докажем утверждение Ь). Из О опус-
опустим перпендикуляр на данную прямую L
(рис. 39). Пусть А — основание этого пер-
перпендикуляра, А' — точка, обратная точ-
точке А. Возьмем произвольную точку Р на L
и обозначим через Р' точку, ей обратную.
Так как О А ¦ О А' = ОР ¦ ОР' = г2, то
отсюда следует, что
ОА' = ОР_
ОР' О А'
Поэтому треугольники ОР' А' и О АР подобны и, значит, угол ОР' А'
прямой. В таком случае из теорем элементарной геометрии вытекает,
что Р' лежит на окружности К с диаметром О А'; эта окружность и яв-
является, следовательно, образом прямой L. Итак, утверждение Ь) доказа-
доказано. Утверждение с) следует из того, что если образ L есть К, то образ К
есть L. Остается доказать утверждение d). Пусть К — окружность, не
проходящая через О, с центром М и радиусом к (рис. 40). Чтобы полу-
получить его образ, проведем через О прямую, пересекающую К в точках А
а В, и затем посмотрим, как изменяются образы А' и В', когда направ-
направление прямой изменяется и она пересекает К самыми разнообразными
способами. Обозначим расстояния ОА, ОВ, ОА', ОВ', ОМ через а, Ь,
а', Ь', га, и пусть t есть длина касательной к К, проведенной из точки О.
По определению инверсии мы имеем аа' = ЬЬ' = г2, а по элементарно
Рис. 40. Инверсия окружности

184 Глава III
геометрическому свойству окружности ab — t2. Если разделим первые
равенства на второе, то получим
9L - К - г! - 2
ь ~ а ~ е ~с'
где с2 зависит только от г и t и, значит, не зависит от положения
точек А и В. Теперь проведем через А' прямую, параллельную ВМ;
пусть Q есть точка ее пересечения с ОМ. Положим OQ = q, A'Q = p.
Тогда
m b k:
или же
Это означает, что при всевозможных положениях А и В точка Q на
прямой ОМ всегда будет одна и та же и что расстояние A'Q также не
будет меняться. Точно так же B'Q — р, так как ^- = ^-. Итак, обра-
образами точек А и В на К будут точки, расстояния которых от Q равны
постоянной величине р, т.е. образ К есть окружность. Утверждение d)
доказано.
3. Геометрическое построе-
построение обратных точек. Следующая
теорема будет полезна в пункте 4
этого параграфа: точка Р', обратная
данной точке Р относительно окруж-
окружности С, может быть построена гео-
геометрически с помощью одного толь-
только циркуля. Рассмотрим сначала тот
случай, когда точка Р находится вне
Рис. 41. Инверсия точки, внеш- окружности С. Радиусом ОР опишем
ней относительно окружности круговую дугу с центром Р, пересе-
пересекающую С в точках R и 5. Затем из
этих точек, как центров, опишем круговые дуги радиусом г, равным
радиусу круга С, эти дуги пересекутся в О и еще в точке Р' на пря-
прямой ОР. В равнобедренных треугольниках ORP и ORP'
/.ORP = Z.POR = /.OP'R,
так что треугольники подобны, и потому
OR „ „
OR OP"
Значит, Р' есть искомая точка Р.

§4. Геометрические преобразования. Инверсия
185
Рис. 42. Удвоение отрезка
Рис. 43. Инверсия точки, внут-
внутренней относительно окружности
Если данная точка Р лежит внутри С, то построение и доказатель-
доказательство остаются в силе, лишь бы окружность радиуса ОР с центром Р
пересекала окружность С в двух точках. Если же пересечений не по-
получается, то можно редуцировать построение к предыдущему случаю
посредством следующего простого приема.
Прежде всего заметим, что на прямой, соединяющей две данные
точки А и О, можно с помощью одного циркуля построить такую точ-
точку С, что АО = ОС. Для этого достаточно провести окружность с цент-
центром О и радиусом г = АО. Затем, начиная от точки А, отметить после-
последовательно на этой окружности такие точки Р, Q, С, что АР = PQ =
— QC = г. Тогда С есть как раз искомая точка: это ясно из того, что
треугольники АОР, OPQ, OQC — равносторонние, так что угол меж-
между О А и ОС содержит 180° и ОС = OQ = АО. Повторяя указанную
процедуру, мы имеем возможность отложить отрезок АО по прямой
сколько угодно раз. Кстати, так как длина отрезка АО равна ?-\/3 (как
читатель проверит без всякого труда), то нам удалось построить \/3,
исходя из единичного отрезка, не пользуясь линейкой.
Теперь мы можем построить точку, обратную точке Р относитель-
относительно окружности С, как бы точка Р ни была расположена внутри С.
Прежде всего на прямой ОР найдем такую точку R, что OR есть крат-
кратное ОР, и вместе с тем R лежит уже вне С:
OR = n- OP.
Для этого достаточно последовательно откладывать расстояние ОР по-
посредством циркуля, пока мы не выберемся из круга С. Затем с помо-
помощью уже известного построения найдем точку R', обратную точке R.
Тогда будем иметь
г2 = OR' ¦ OR = OR' ¦ (n • OP) = (n • OR') ¦ OP.

186
Глава III
Останется построить точку Р' по условию OP' = n-OR', и задача будет
закончена.
4. Как разделить отрезок пополам и как найти центр дан-
данного круга с помощью одного циркуля. После того как мы на-
научились находить точку, обратную данной, можно с помощью одно-
одного циркуля выполнить дальнейшие интересные построения. Например,
сейчас мы найдем середину отрезка, концы которого А и В заданы,
с помощью одного циркуля — не проводя самого отрезка. Вот решение
этой задачи. Опишем окружность радиусом АВ с центром В и на нем,
отправляясь от А, как раньше, отмерим последовательно три дуги ра-
радиусом АВ. Последняя точка С будет лежать на прямой АВ, причем
мы будем иметь: АВ = ВС. Затем опишем окружность радиуса АВ
с центром А и построим точку С", обратную точке С относительно
этой окружности. Тогда получим:
АС -АС = АВ2,
АС1 -2АВ = АВ2,
2АС = АВ.
Значит, С есть искомая середина отрезка.
Рис. 44. Нахождение середи-
середины отрезка
Рис. 45. Нахождение центра
круга
Другое построение с помощью одного циркуля, также использую-
использующее обратные точки, заключается в нахождении центра данной окруж-
окружности, когда начерчена только сама окружность, а центр не известен.
Берем произвольную точку Р на окружности и около нее, как цент-
центра, описываем круг произвольного радиуса, пересекающийся с данным
кругом в точках R и S. Из этих последних точек, как центров, опи-
описываем дуги радиусом RP = SP, пересекающиеся, кроме точки Р,

§ 5. Построения с помощью иных инструментов
187
еще в точке Q. Сравнивая то, что получилось, с рис. 41, мы видим,
что неизвестный центр Q' есть точка, обратная точке Q относительно
окружности с центром Р, и Q' может быть, как мы видели, построена
с помощью одного циркуля.
§5. Построения с помощью иных инструментов.
Построения Маскерони с помощью одного
циркуля
Рис. 46. Инструмент, служащий для удвоения куба
1. Классическая конструкция, служащая для удвоения ку-
куба. Мы рассматривали до сих пор только проблемы геометрических
построений без использования иных инструментов, кроме циркуля и
линейки. Если допускаются и другие инструменты, то, разумеется,
разнообразие возможных построений сильно увеличивается. Следую-
Следующий пример может служить образцом того, как греки решали пробле-
проблему удвоения куба. Рассмотрим (рис. 46) жесткий прямой угол MZN
и подвижной прямоугольный крест VW, PQ. Двум дополнительным
стержням RS и TU предоставлена возможность скользить, оставаясь
перпендикулярными к сторонам прямого угла. На кресте пусть выбра-
выбраны фиксированные точки Е и G, причем расстояния GB = а и BE = f
заданы. Располагая крест таким образом, чтобы точки Е и G соответ-
соответственно лежали на NZ и MZ, и перемещая стержни TU и RS, можно

188 Глава III
весь аппарат привести в такое положение, чтобы лучевые перекладины
креста BW, BQ, BV проходили через вершины A, D, Е прямоуголь-
прямоугольника ADEZ. Указанное на чертеже расположение всегда возможно при
условии / > а. Мы видим сразу, что а : х = х : у = у : /, откуда, в част-
частности, если положено / = 2а, получается х3 = 2а3. Значит, х есть ребро
куба, объем которого вдвое больше, чем объем куба с ребром а. Таким
образом поставленная задача решена.
2. Построения с помощью од-
^ ного циркуля. Если вполне естес-
естественно, что с допущением большего
разнообразия инструментов оказывает-
оказывается возможным решать более обшир-
обширное множество задач на построение, то
•Ач JfQ можно было бы предвидеть, что, напро-
напротив, при ограничениях, налагаемых на
Рис. 47. Нахождение середины инструменты, класс разрешимых задач
дуги без линейки будет суживаться. Тем более замеча-
замечательным нужно считать открытие, сде-
сделанное итальянцем Маскерони A750-1800): все геометрические постро-
построения, выполнимые с помощью циркуля и линейки, могут быть выполне-
выполнены с помощью одного только циркуля. Следует, конечно, оговорить, что
провести на самом деле прямую линию через две данные точки без
линейки невозможно, так что это основное построение не покрывается
теорией Маскерони. Вместо того приходится считать, что прямая за-
задана, если заданы две ее точки. Но с помощью одного лишь циркуля
удается найти точку пересечения двух прямых, заданных таким обра-
образом, или точку пересечения прямой с окружностью.
Вероятно, простейшим примером построения Маскерони является
удвоение данного отрезка АВ. Решение было уже дано на стр. 185. Да-
Далее, на стр. 186 мы научились делить данный отрезок пополам. Посмот-
Посмотрим теперь, как разделить пополам дугу окружности АВ с центром О.
Вот описание этого построения. Радиусом АО проводим две дуги с
центрами А и В. От точки О откладываем на этих дугах две такие
дуги ОР и OQ, что OP = OQ = АВ. Затем находим точку R пе-
пересечения дуги с центром Р и радиусом РВ и дуги с центром Q и
радиусом QA. Наконец, взяв в качестве радиуса отрезок OR, опишем
дугу с центром Р или Q до пересечения с дугой АВ — точка пере-
пересечения и является искомой средней точкой дуги АВ. Доказательство
предоставляем читателю в качестве упражнения.

§ 5. Построения с помощью иных инструментов
189
С
Рис. 48. Пересечение окружности и
прямой, не проходящей через центр
Было бы невозможно доказать
основное утверждение Маскерони,
указывая для каждого построения,
выполнимого с помощью циркуля
и линейки, как его можно выпол-
выполнить с помощью одного циркуля:
ведь возможных построений бес-
бесчисленное множество. Но мы до-
достигнем той же цели, если уста-
установим, что каждое из следующих
основных построений выполнимо с
помощью одного циркуля:
1. Провести окружность, если
заданы центр и радиус.
2. Найти точки пересечения
двух окружностей.
3. Найти точки пересечения прямой и окружности.
4. Найти точку пересечения двух прямых.
Любое геометрическое построение (в обычном смысле, с допуще-
допущением циркуля и линейки) составляется из выполнения конечной после-
последовательности этих элементарных построений. Что первые два из них
выполнимы с помощью одного циркуля, ясно непосредственно. Более
трудные построения 3 и 4 выполняются с использованием свойств ин-
инверсии, рассмотренных в предыдущем пункте.
Обратимся к построению 3: найдем точки пересечения данной
окружности С с прямой, проходящей через данные точки Aw В. Прове-
Проведем дуги с центрами А и В и радиусами, соответственно равными АО
и ВО; кроме точки О, они пересекутся в точке Р. Затем построим точ-
точку Q, обратную точке Р относительно окружности С (см. построение,
описанное на стр. 186). Наконец, проведем окружность с центром Q и
радиусом QO (она непременно пересечется с С): его точки пересече-
пересечения X и X' с окружностью С и будут искомыми. Для доказательст-
доказательства достаточно установить, что каждая из точек X и X' находится на
одинаковых расстояниях от О и Р (что касается точек А и В, то ана-
аналогичное их свойство сразу вытекает из построения). Действительно,
Достаточно сослаться на то обстоятельство, что точка, обратная точ-
точке Q, отстоит от точек X и X' на расстояние, равное радиусу окруж-
окружности С (см. стр. 184). Стоит отметить, что окружность, проходящая
через точки X, X' и О, является обратной прямой АВ в инверсии отно-
относительно круга С, так как эта окружность и прямая АВ пересекаются

190
Глава III
с С в одних и тех же точках. (При инвер-
инверсии точки основной окружности остаются
неподвижными.)
Указанное построение невыполнимо
только в том случае, если прямая АВ про-
проходит через центр С. Но тогда точки пере-
пересечения могут быть найдены посредством
Рис. 49. Пересечение окруж- построения, описанного на стр. 188, как
ности и прямой, проходящей
через центр
получающихся, когда мы проводим произ-
произвольную окружность с центром В, пересе-
пересекающуюся с С в точках В\ и 5г- Метод
проведения окружности, обратной прямой, соединяющей две данные
точки, немедленно дает и построение, решающее задачу 4. Пусть пря-
прямые даны точками А, В и А', В' (рис. 50).
Проведем произвольную окружность С
и с помощью указанного выше метода по-
построим окружности, обратные прямым АВ
и А'В'. Эти окружности пересекаются в точ-
точке О и еще в одной точке Y. Точка X, об-
обратная точке Y, и есть искомая точка пере-
пересечения: как ее построить — уже было разъ-
разъяснено выше. Что X есть искомая точка, это
ясно из того факта, что Y есть единственная
точка, обратная точке, одновременно принад-
принадлежащей обеим прямым АВ и А'В'; следова-
следовательно, точка X, обратная Y, должна лежать
одновременно и на АВ, и на А'В'.
Этими двумя построениями заканчивается доказательство эквива-
эквивалентности между построениями Маскерони, при которых разрешается
пользоваться только циркулем, и обыкновенными геометрическими по-
построениями с циркулем и линейкой.
Мы не заботились об изяществе решения отдельных проблем, нами
здесь рассмотренных, так как нашей целью было выяснить внутренний
смысл построений Маскерони. Но в качестве примера мы еще укажем
построение правильного пятиугольника; точнее говоря, речь идет о на-
нахождении каких-то пяти точек на окружности, которые могут служить
вершинами правильного вписанного пятиугольника.
Пусть А — произвольная точка на окружности К. Так как сторо-
сторона правильного вписанного шестиугольника равна радиусу круга, то не
представит труда отложить на К такие точки В, С, D, что ^
Рис. 50. Пересечение двух
прямых

j 5. Построения с помощью иных инструментов
191
=w ВС =^ CD = 60° (рис. 51). Проводим дуги с центрами А и D
радиусом, равным АС; пусть они пересекаются в точке X. Тогда, ес-
если О есть центр К, дуга с центром А и радиусом ОХ пересечет К
в точке F, являющейся серединой дуги ВС (см. стр. 188). Затем ради-
радиусом, равным радиусу К, опишем дуги с центром F, пересекающиеся
с К в точках G и Н. Пусть Y есть точка, расстояния которой от точек G
и Н равны ОХ и которая отделена от X центром О. В таком случае
отрезок AY как раз и есть сторона искомого пятиугольника. Доказа-
Доказательство предоставляется читателю в качестве упражнения. Интересно
отметить, что при построении использу-
используются только три различных радиуса.
В 1928 г. датский математик Ельм-
слев нашел в книжной лавке в Копенгагене
экземпляр книги под названием Euclides
Danicus, опубликованной в 1672 г. никому
неизвестным автором Г.Мором (G.Mohr).
По титульному листу можно было сделать
заключение, что это — просто один из ва-
вариантов евклидовых «Начал», снабженный,
может быть, редакторским комментари-
комментарием. Но при внимательном рассмотрении
оказалось, что в ней содержится полное ре-
решение проблемы Маскерони, найденное за-
задолго до Маскерони.
С
К
Рис. 51. Построение пра-
правильного пятиугольника
Упражнения.
В дальнейшем дается описание построений Мора. Проверьте их пра-
правильность. Почему можно утверждать, что они решают проблему Мас-
Маскерони?
1) К отрезку АВ длины р восставить перпендикуляр ВС. (Указание. Про-
Продолжить АВ до точки D таким образом, что АВ = BD. Провести
произвольным радиусом дуги с центрами Аи D и таким образом опре-
определить С.)
2) В плоскости даны как угодно расположенные отрезки длины р и q,
причем р > д. Построить с помощью 1) отрезок длины х = у/р2 — д2.
3) По заданному отрезку о постройте отрезок а%/2- (Указание. Обратите
внимание, что (а%/2J = (aVSJ — о2.)
4) По данным отрезкам р и q построить отрезок х = \/р2 + Я2- (Указание.
Примите во внимание, что х2 = 2р2 — (р2 — q2).) Придумайте сами
аналогичные построения.

192 Глава III
5) Пользуясь предыдущими результатами, постройте отрезки р+д и p — q,
предполагая, что отрезки длины рад заданы как-то на плоскости.
6) Проверьте и постарайтесь обосновать следующее построение середи-
середины М данного отрезка АВ длины а. На продолжении отрезка АВ най-
найдем такие точки С и ?), что С А = АВ = BD. Построим равносто-
равносторонний треугольник ECD согласно условию ЕС = ED = 1а и опреде-
определим М как пересечение окружностей с диаметрами ЕС и ED.
7) Найти прямоугольную проекцию точки А на отрезок ВС.
8) Найти х по условию х : а = р : q, где а, р и q — данные отрезки.
9) Найти х = ab, где а и b — данные отрезки.
Вдохновляясь результатами Маскерони, Якоб Штейнер A796-1863)
предпринял попытку исследования построений, выполнимых с помо-
помощью одной только линейки. Конечно, одна только линейка не выводит
за пределы данного числового поля, и потому она недостаточна для вы-
выполнения всех геометрических построений в классическом их понима-
понимании. Но тем более замечательны результаты, полученные Штейнером
при введенном им ограничении — пользоваться циркулем только один
раз. Он доказал, что все построения на плоскости, выполнимые с помо-
помощью циркуля и линейки, выполнимы также с помощью одной линейки
при условии, что задан единственный неподвижный круг вместе с цент-
центром. Эти построения подразумевают применение проективных методов
и будут описаны позднее (см. стр. 238).
* Без круга, и притом с центром, обойтись нельзя. Например, если дан
круг, но не указан его центр, то найти центр с помощью одной линейки
невозможно. Мы сейчас докажем это, ссылаясь, однако, на факт, который
будет установлен позднее (см. стр. 263): существует такое преобразование
плоскости самой в себя, что а) заданная окружность остается неподвижной,
Ь) всякая прямая линия переходит в прямую, с) центр неподвижной окруж-
окружности не остается неподвижным, а смещается. Само существование такого
преобразования свидетельствует о невозможности построить центр данной
окружности, пользуясь одной линейкой. В самом деле, какова бы ни была про-
процедура построения, она сводится к ряду отдельных этапов, заключающихся
в проведении прямых линий и нахождении их пересечений друг с другом
или с данной окружностью. Представим себе теперь, что вся фигура в це-
целом — окружность и все прямые, проведенные по линейке при выполнении
построения центра — подвергнута преобразованию, существование которого
мы здесь допустили. Тогда ясно, что фигура, полученная после преобразова-
преобразования, также удовлетворяла бы всем требованиям построения; но указываемое
этой фигурой построение приводило бы к точке, отличной от центра данной
окружности. Значит, построение, о котором идет речь, невозможно.

I 5. Построения с помощью иных инструментов
у=ах +Ьх+с
193
Рис. 52. Графическое решение кубического уравнения
3. Черчение с помощью различных механических приспо-
приспособлений. Механические кривые. Циклоиды. Изобретение раз-
различных механизмов, предназначенных для того, чтобы чертить различ-
различные кривые, помимо окружности и прямой линии, чрезвычайно расши-
расширяет область фигур, допускающих построение. Например, если имеется
инструмент, позволяющий чертить гиперболы ху = к, и другой инстру-
инструмент, вычерчивающий параболы у = ах2 + Ьх + с, то любая проблема,
приводящая к кубическому уравнению
ах3 + Ьх2 + сх = к,
A)
может быть решена конструктивно, с помощью только этих инстру-
инструментов. В самом деле, решение уравнения A) равносильно решению
системы
ху = к, у = ах2 + Ьх + с;
B)
точнее, корни уравнения A) являются ж-координатами точек пересече-
пересечения гиперболы и параболы, представляемых уравнениями B). Таким
образом, решения уравнения A) допускают построение, если разреша-
разрешается пользоваться инструментами, с помощью которых можно начер-
начертить кривые B).
13
340

194
Глава III
Рис. 53. Циклоида
Уже математикам древности были известны многие интересные
кривые, которые могут быть определены и начерчены с помощью прос-
простых механических приспособлений. Среди таких «механических» кри-
кривых особенно видное место занимают циклоиды. Птоломей (около 200
года до нашей эры), обнаруживая необычайную проницательность, су-
сумел использовать эти кривые для описания планетных движений.
Циклоида самого простого вида представляет собой траекторию
движения точки Р, фиксированной на окружности диска, катящегося
без скольжения по прямой линии. На рис.53 изображены четыре по-
положения точки Р в различные моменты времени. С внешней стороны
циклоида напоминает ряд арок, опирающихся на горизонтальную пря-
прямую.
Разновидности этой кривой получаются, если возьмем точку Р
или внутри диска (как на спице колеса), или на продолжении радиуса
за пределы диска.
Эти две кривые показаны на рис. 54.
Рис. 54. Циклоиды общего вида
Дальнейшие разновидности циклоиды возникают, когда наш диск
катится не по прямой, а по дуге окружности. Если при этом катящийся
диск с радиусом г остается все время касающимся изнутри той большой
окружности С радиуса R, по которой он катится, то траектория точки,
фиксированной на окружности диска, называется гипоциклоидой.
Когда диск прокатывается по всей окружности С ровно один раз, то
точка Р возвращается в исходное положение только в том случае, если
радиус С является кратным радиуса с. На рис.55 изображена замкну-
замкнутая гипоциклоида, соответствующая предположению R = Зг. В более

§ 5. Построения с помощью иных инструментов
195
общем случае, если R = Щ-r, то гипоциклоида замкнется после того,
как диск с прокатится по окружности С ровно п раз, и будет состоять
из т арок. Заслуживает особого упоминания случай R = 2г. Любая
точка Р на окружности диска будет описывать в этом случае один из
диаметров большой окружности С (рис. 56). Предоставляем читателю
доказать это в качестве задачи.
Рис. 55. Трехрогая гипо-
гипоциклоида
Рис. 56. Прямолинейное
движение при качении
круга по кругу двойного
радиуса
Рис. 57. Преобразование прямолинейного движения во вращательное
Еще один тип циклоид получается, когда диск с катится по окруж-
окружности С, касаясь ее все время извне. Получающиеся при этом кривые
носят название эпициклоид.
*4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
Оставим на время в стороне вопрос о циклоидах (они появятся еще раз
в этой книге — довольно неожиданно) и обратимся к иным методам
механического воспроизведения кривых линий. Мы займемся сейчас
Шарнирными механизмами.
13*

196
Рис. 58. Инверсор Поселье, преобразующий вращательное движение в прямо-
прямолинейное
Механизм этого типа представляет собой систему сочлененных
между собой твердых стержней, обладающих такой степенью свободы,
чтобы каждая его точка была способна описывать определенную кри-
кривую. Циркуль также является простейшим шарнирным механизмом, по
существу состоящим из одного стержня с закрепленным концом.
Шарнирные механизмы издавна находят себе применение как со-
составные части машин. Одним из самых знаменитых (в историческом
отношении) примеров является так называемый «параллелограмм Уат-
та». Это приспособление было изобретено Джемсом Уаттом при решении
следующей проблемы: как связать поршень с точкой махового коле-
колеса таким образом, чтобы вращение колеса сообщало поршню прямоли-
прямолинейное движение? Решение, данное Уаттом, было лишь приближенным,
и, несмотря на усилия многих первоклассных математиков, проблема
конструирования механизма, сообщающего точке в точности прямо-
прямолинейное движение, долгое время оставалась нерешенной. Было даже
сделано предположение, что такой механизм неосуществим: это было
как раз тогда, когда всякого рода «доказательства невозможности» при-
привлекли к себе всеобщее внимание. Тем большее изумление было вызва-
вызвано в кругах математиков, когда французский морской офицер Поселье
(в 1864 г.) все же изобрел несложный механизм, действительно раз-
разрешающий проблему в положительном смысле. В связи со введением
в употребление хорошо действующих смазочных веществ техническая
проблема потеряла свое значение для паровых машин.
Назначение механизма Поселье заключается в том, чтобы превра-
превращать круговое движение в прямолинейное. В основе этого механизма

i 5. Построения с помощью иных инструментов
197
D F
Рис. 59. Инверсор Гарта
лежит теория инверсии, изложенная в § 4. Как видно из чертежа 58,
механизм состоит из семи жестких стержней, два из них — длины t,
четыре — длины s и один — произвольной длины. Точки О и R за-
закреплены и расположены таким образом, что OR = PR. Весь аппарат
может быть приведен в движение, будучи подчинен указанным услови-
условиям. Мы сейчас убедимся, что, когда точка Р описывает дугу окружнос-
окружности с центром R и радиусом RP, точка Q описывает прямолинейный
отрезок. Обозначая основание перпендикуляра, опущенного из точки S
на прямую OPQ, через Т, мы замечаем, что
OP-OQ = (ОТ - РТ) ¦ (ОТ + РТ) = ОТ2 - РТ2 =
= {ОТ2 + ST2) - (RT2 + ST2) =t2 -s2.
Величина t2 — s2 — постоянная; положим t2 — s2 = г2. Так как OP-OQ =
= г2, то точки Р и Q — взаимно обратные относительно окружности
с центром О и радиусом г. В то время как Р описывает дугу окруж-
окружности, проходящей через О, Q описывает кривую, обратную этой дуге.
Но кривая, обратная окружности, проходящей через О, есть, как мы
видели, не что иное, как прямая линия. Итак, траектория точки Q есть
прямая, и инверсор Поселье чертит эту прямую без линейки.
Другой механизм, решающий ту же проблему, есть инверсор Гарта.
Он состоит всего лишь из пяти стержней, сочленение которых показано
на рис. 59. Здесь АВ = CD, ВС = AD. Через О, Р и Q обозначены
точки, соответственно зафиксированные на стержнях АВ, AD и СВ,
притом таким образом, что ^ = -^ = ^ = Щ. Точки О и S
закреплены на плоскости неподвижно, с соблюдением условия 05 =
~ PS. Больше связей нет, и механизм способен двигаться. Очевидно,

198 Глава III
прямая АС всегда параллельна прямой BD. В таком случае точки О,
Р и Q лежат на одной прямой, и прямая ОР параллельна прямой АС.
Проведем перпендикуляры АЕ и CF к прямой BD. Мы имеем
ACBD = EF-BD = {ED + ЕВ) ¦ {ED - ЕВ) = ED2 - ЕВ2.
Но ED2 + АЕ2 = AD2 и ЕВ2 + АЕ2 = АВ2. Значит, ED2 - ЕВ2 =
= AD2 - АВ2. Далее,
OP = АО = тп OQ = ОВ = п
BD АВ т + п АС АВ т + п'
Следовательно,
OP-OQ= тп , • BD ¦ АС = тп , • {AD2 - АВ2).
{т + п) {т + п)
Последняя полученная величина не изменяется при движении механиз-
механизма. Поэтому точки Р и Q являются взаимно обратными относительно
некоторого круга с центром О. При движении механизма точка Р опи-
описывает окружность с центром S, проходящую через О; значит, обратная
точка Q описывает прямую линию.
Можно построить — по крайней мере теоретически — другие шар-
шарнирные механизмы, которые будут чертить эллипсы, гиперболы и даже
любую наперед заданную алгебраическую кривую f{x, у) = 0, какова
бы ни была ее степень.
§ 6. Еще об одной инверсии и ее применениях
1. Инвариантность углов. Семейства окружностей. Хо-
Хотя круговая инверсия есть преобразование, довольно резко меняющее
внешний вид геометрических фигур, все же весьма замечательным яв-
является то обстоятельство, что вновь получаемые фигуры сохраняют
некоторые свойства первоначальных фигур. Эти свойства, не теряющи-
теряющиеся при преобразовании, называются «инвариантными». Мы уже знаем,
что при инверсии круг или прямая переходят в круг или прямую. При-
Прибавим теперь еще одно важное свойство инверсии: угол между двумя
прямыми или кривыми при инверсии не изменяется. Говоря подробнее,
это означает, что инверсия преобразовывает две пересекающиеся кри-
кривые в две другие кривые, которые пересекаются под тем же углом. Под
углом между кривыми подразумевается угол между их касательными.
Доказательство получается при рассмотрении рис. 60, где имеется
в виду частный случай пересечения в точке Р произвольной кривой С

§6. Еще об одной инверсии и ее применениях 199
A't ^
О
С
Рис. 60. Инвариантность углов при инверсии
с прямолинейным отрезком OL, проведенным из центра инверсии О.
Кривая С", обратная кривой С, пересекается с OL в точке Р', обрат-
обратной Р, так как Р', так же как и Р, лежит на OL. Покажем, что угол х0
между OL и касательной к С в точке Р по величине равен углу уо
между OL и касательной к С" в точке Р'. Для этого возьмем точку А
на кривой С вблизи Р и проведем секущую АР.
Точка, обратная А, есть А'; так как она находится на прямой О А
и на кривой С", то является их точкой пересечения. Проведем также
секущую А'Р'. По определению инверсии, г2 = ОР ¦ ОР' = О А • О А',
или же
ОР
_
О А ОР''
т.е. треугольники О АР и О А'Р' подобны. Значит, угол х равен
углу О А'Р', который мы обозначим через у. Последний шаг в нашем
Рассуждении заключается в том, чтобы заставить точку А приближать-
приближаться по кривой С к точке Р. При этом секущая АР переходит в касатель-
касательную к кривой С в точке Р, и угол х стремится к xq. В то же время А'
будет приближаться к Р' и прямая А'Р' перейдет в касательную к кри-
кривой С" в точке Р', а угол у будет стремиться к у0. Так как при всяком
Положении точки А мы имеем равенство х = у, то оно сохранится
И в пределе х0 = у0.

200 Глава III
Наше доказательство еще не закончено, так как мы рассмотрели
пока только случай пересечения кривой С с прямой, проходящей через
центр О. Но рассмотреть общий случай пересечения двух произвольных
кривых С и С* теперь уже совсем легко. Пусть эти кривые пересекают-
пересекаются в точке Р и образуют между собой угол z. Тогда прямая ОРР' делит
этот угол на два угла, из которых каждый в отдельности не изменяется
при инверсии.
Следовало бы оговорить, что, хотя инверсия не изменяет величины угла,
однако она изменяет направление его отсчета: если вообразим, что при посто-
постоянном увеличении угла хо одна сторона его неподвижна, а другая вращается
против часовой стрелки, то подвижная сторона соответствующего «обратно-
«обратного» угла вращается по часовой стрелке.
Частным следствием инвариантности углов при инверсии являет-
является то, что две ортогональные (т.е. пересекающиеся под прямым уг-
углом) окружности или прямых после инверсии сохраняют это свойство,
и если две окружности взаимно касаются («пересекаются под углом,
равным нулю»), то касаются и обратные им окружности.
Рассмотрим семейство окружностей, проходящих через центр ин-
инверсии О и еще через одну и ту же неподвижную точку плоскости А.
Мы знаем (§ 4, пункт 2), что это семейство преобразуется в семейство
прямых, проходящих через точку А', являющуюся образом А. В то же
время семейство окружностей, ортогональных первоначальному семей-
семейству, превращается в семейство окружностей, ортогональных упомяну-
упомянутому семейству прямых. (На рис. 61 ортогональные семейства изобра-
изображены пунктиром.) С внешней стороны семейство прямых, проходящих
через одну и ту же точку, мало напоминает семейство окружностей, но
эти семейства связаны теснейшим образом — с точки зрения теории
инверсии они, так сказать, вполне эквивалентны.
Вот другой пример того, к каким результатам приводит инвер-
инверсия. Пусть дано семейство окружностей, проходящих через центр ин-
инверсии и имеющих в этой точке общую касательную. После инверсии
получается семейство параллельных прямых. Действительно, так как
окружности проходят через О, то они превращаются в прямые, и так
как окружности, кроме О не имеют точек пересечения, то получаемые
прямые — параллельны.
2. Применение к проблеме Аполлония. Прекрасной иллюст-
иллюстрацией того, насколько полезна теория инверсии, является следую-
следующее простое геометрическое решение проблемы Аполлония. При ин-
инверсии относительно какого бы то ни было центра проблема Аполлония
для трех данных окружностей трансформируется в соответствующую

j6. Еще об одной инверсии и ее применениях
201
Рис. 61. Преобразование двух систем ортогональных окружностей с помощью
инверсии
Рис. 62. Преобразование касающихся окружностей в параллельные прямые
v_v
Рис. 63. Подготовка построения, решающего проблему Аполлония
проблему для трех других окружностей: пусть читатель внимательно
продумает, почему это так.
Отсюда легко понять, что если проблема решена для некоторой
тройки окружностей, то тем самым ее можно считать решенной и для
всякой тройки окружностей, которая из первой тройки может быть по-
получена путем инверсии. Мы сумеем использовать это обстоятельство,

202
Глава III
Рис. 64. Решение проблемы Аполлония
выбирая из всевозможных «эквивалентных» троек такую, для которой
проблема решается особенно просто.
Предположим для определенности, что три данных окружности
с центрами А, В, С взаимно не пересекаются и лежат каждый вне
двух других, и допустим, что речь идет о нахождении окружности U
с центром О и радиусом р, касающейся трех данных окружностей внеш-
внешним образом. Заметим, что если мы увеличим радиус всех трех данных
окружностей на одну и ту же величину d, то окружность с центром О и
радиусом р — d, очевидно, был бы решением видоизмененной таким об-
образом проблемы. Пользуясь этим обстоятельством, увеличим радиусы
данных окружностей на такую величину, чтобы две из трех окруж-
окружностей оказались взаимно касающимися в некоторой точке, которую
обозначим К (рис. 63). Затем произведем инверсию всей фигуры отно-
относительно какой-нибудь окружности с центром К. Окружности с цент-
центрами В и С станут параллельными прямыми 6 и с, а третья окруж-
окружность превратится в некоторую окружность а (рис. 64). Мы уже знаем,
что а, Ь, с, смогут быть построены
с помощью циркуля и линейки. Что
касается искомой окружности С/, то
она преобразуется в окружность и, ка-
касающуюся прямых 6, с и окружнос-
окружности а. Ее радиус г, очевидно, должен
равняться половине расстояния меж-
между прямыми бис; центр же его О'
должен совпадать с одной из точек
пересечения средней линии между Ъ
и с с окружностью, концентрической
окружности а, но имеющей радиус на г
больший. Остается применить обрат-
Рис.65. Повторное отражение ную инверсию к окружности и, и тогда
относительно прямолинейных получим искомую аполлониеву окруж-
стен ность U.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

J6. Еще об одной инверсии и ее применениях
203
-х-
Рис. 66. Правильные системы треугольных зеркал
3. Повторные отражения. Каждому из нас приходилось наблю-
наблюдать странные явления отражения, возникающие, если имеется более
одного зеркала. Если четыре стены прямоугольной комнаты представ-
представляют собой идеальные зеркала, ни в малой степени не поглощающие све-
света, то освещенная, находящаяся в этой комнате точка создает бесконеч-
бесконечное множество отражений, по одному на каждую из конгруэнтных пря-
прямоугольных комнат, возникающих из первой посредством отражений
(рис. 65). При менее правильной форме соединения зеркал, например,
при трех зеркалах, создается более сложная система отражений. Полу-
Получающейся конфигурации легко дать описание только в том случае, если
отраженные треугольники, не перекрывая друг друга взаимно, полнос-
полностью покрывают плоскость. Таким свойством обладают только прямо-
прямоугольный равнобедренный треугольник, равносторонний треугольник
Рис. 67. Повторное отражение относительно двух сферических дуг

204 Глава III
Рис. 68. Отражение относительно трех сферических зеркал
и прямоугольный треугольник, представляющий собою половину рав-
равностороннего (рис. 66).
Еще более курьезные обстоятельства возникают, если мы ста-
станем рассматривать повторные инверсии относительно пары окруж-
окружностей. Поместившись между двумя концентрическими сферически-
сферическими зеркалами, мы увидали бы бесчисленное множество концентри-
концентрических отражений. Одна последовательность отражений уходила бы
в бесконечность, другая — сосредоточивалась бы около центра. Случай
двух окружностей, расположенных одна вне другой, несколько сложнее:
окружности и их отражения последовательно отражаются одна в дру-
другой, уменьшаясь после каждого отражения и теснясь к двум предель-
предельным точкам, по одной в каждой из данных окружностей. (Эти точки
обладают свойством взаимной обратности относительно каждой из дан-
данных окружностей.) Все это показано на рис. 67. Что получится в случае
трех кругов, об этом читатель может составить впечатление, взглянув
на узор, изображенный на рис. 68.

Глава IV
Проективная геометрия. Аксиоматика.
Неевклидовы геометрии
§ 1. Введение
1. Классификация геометрических свойств. Инвариант-
Инвариантность при преобразованиях. В геометрии рассматриваются свой-
свойства фигур на плоскости и в пространстве. Эти свойства столь мно-
многочисленны и столь разнообразны, что необходим какой-то принцип
классификации для того, чтобы внести порядок в обширное собрание
накопленных знаний. Можно было бы, например, положить в основу
классификации метод, применяемый при выводе получаемых утверж-
утверждений. С этой точки зрения обыкновенно различаются «синтетические»
и «аналитические» процедуры. Синтетические доказательства сущест-
существенно связаны с классическим аксиоматическим методом, идущим от
Евклида: рассуждение строится на чисто геометрической основе, неза-
независимо от средств алгебры и концепции числового континуума, и все
теоремы выводятся формально логическим путем, исходя из некоторо-
некоторого числа начальных положений, называемых аксиомами или постулата-
постулатами. Другой метод подразумевает введение числовой координатной сис-
системы и пользуется техническим аппаратом алгебры. Этот метод про-
произвел глубокие изменения в самой математической науке, слив в одно
органическое целое геометрию, анализ и алгебру.
В этой главе, однако, нас будет интересовать не столько класси-
классификация метода, сколько классификации содержания, то есть сами по
себе утверждения теорем, а не способы их доказательства. В элемен-
элементарной геометрии плоскости легко различаются две группы теорем;
в одних идет речь о равенстве фигур, об измерении отрезков и углов,
в других — о подобии фигур, для которого существенно измерение уг-
углов, но не отрезков. Указанное различие не столь уж существенно, так
как длины отрезков и величины углов довольно тесно связаны меж-
ДУ собой и разделять их — несколько искусственно. (Изучение этой
связи составляет, главным образом, предмет тригонометрии.) Отметим
Иную сторону дела. В элементарной геометрии мы имеем дело с вели-
величинами: отрезками, углами, площадями. Две фигуры там считаются

206
Глава IV
эквивалентными, если они конгруэнтны, т. е. могут быть переведены
одна в другую посредством движения — преобразования, меняюще-
меняющего только положение фигуры, но не числовые значения величин, с ней
связанных. Возникает вопрос: является ли значение величин — и вмес-
вместе с тем конгруэнтность или подобие фигур — чем-то существенно
неизменным в геометрии? Или же имеются иные, более глубоко ле-
лежащие свойства геометрических фигур, которые сохраняются также и
при преобразованиях более общего типа, чем движения? Мы увидим,
что такие свойства существуют.
Рис. 69. Сжатие окружности
Представим себе, что на прямоугольной доске, изготовленной из
мягкого эластичного материала, нарисован круг с парой взаимно пер-
перпендикулярных диаметров (рис. 69). Если мы положим эту доску в тис-
тиски и сожмем до половины ее первоначальной ширины, то окружность
превратится в эллипс и углы между диаметрами уже не будут прямы-
прямыми. Окружность обладает тем свойством, что все точки его находятся
на одном и том же расстоянии от центра, но эллипс не обладает та-
таким свойством. Могло бы показаться, что сжатие уничтожает все гео-
геометрические свойства первоначальной конфигурации. Но и это пред-
предположение далеко от истины: например, утверждение, что центр делит
диаметры пополам, одинаково справедливо и для окружности, и для
эллипса; в данном случае мы встречаемся с таким свойством фигуры,
которое сохраняется при весьма резком изменении в размерах ее от-
отдельных элементов. Сделанные замечания наводят на мысль о возмож-
возможности классифицировать теоремы, относящиеся к той или иной гео-
геометрической фигуре, в зависимости от того, сохраняют ли они силу
или теряют ее при равномерном сжатии (или растяжении). Можно по-
поставить и более общий вопрос: исходя из некоторого данного класса
преобразований фигуры (такого рода классы, например, порождаются
совокупностью всех движений, или сжатий, или, скажем, круговых ин-

§1. Введение 207
версий и т.д.); можно поинтересоваться тем, какие свойства фигуры
остаются неизменными, когда фигура подвергается различным пре-
преобразованиям данного класса. Система теорем, утверждающих такие
свойства, составляет геометрию рассматриваемого класса преобразова-
преобразований. Идея классифиции различных отраслей геометрии в соответствии
с классами преобразований принадлежит Феликсу Клейну A849-1925);
она была высказана им в 1872 г. в его знаменитом выступлении, полу-
получившем широкую известность под именем «Эрлангенской программы».
С тех пор эта идея оказала решающее влияние на направление многих
геометрических исследований.
В главе V мы будем иметь случай установить весьма удивитель-
удивительное обстоятельство, заключающееся в том, что некоторые свойства гео-
геометрических фигур заложены настолько глубоко, что не исчезают даже
после совершенно произвольных деформаций: так, фигуры, нарисован-
нарисованные на куске резины, не потеряют кое-каких характеристических черт
при самых разнообразных и самых резких деформациях. Но в насто-
настоящей главе мы займемся теми свойствами, которые сохраняются, или
«инвариантны», при некотором специальном классе преобразований, бо-
более широком, чем весьма ограниченный класс движений, но более уз-
узком, чем самый общий класс произвольных деформаций. Мы говорим
о классе «проективных преобразований».
2. Проективные преобразования. Изучение относящихся сю-
сюда геометрических свойств было выдвинуто перед математиками в дав-
давнее время проблемами перспективы, которые изучались художниками,
в том числе Леонардо да Винчи и Альбрехтом Дюрером. Изображение,
создаваемое художником, следует рассматривать как проекцию ориги-
оригинала на плоскость картины, причем центр проекции помещается в гла-
глазе художника. При проектировании в зависимости от относительных
положений различных изображаемых объектов — длины отрезков и уг-
углы неизбежно подвергаются искажениям. И тем не менее на картине
обычно не представляет труда распознать геометрическую структуру
оригинала. Как объяснить это обстоятельство? Нельзя объяснить ина-
иначе, как указав на наличие геометрических свойств, «инвариантных от-
относительно проектирования» — свойств, сохраняющихся на картине и
делающих возможным узнавание нарисованного оригинала. Отыскание
и анализ этих свойств составляют предмет проективной геометрии.
Совершенно ясно, что в этой отрасли геометрии не содержится по-
положительных утверждений, относящихся к длинам отдельных отрезков
Или к величинам отдельных углов; не идет речь и о равенстве фигур.
Некоторые изолированные факты, касающиеся проективных свойств,

208
Глава IV
были известны уже в XVII в., а иногда, как в случае «теоремы Ме-
нелая», даже в древности. Но систематические исследования в области
проективной геометрии развернулись впервые лишь к концу XVIII сто-
столетия, когда знаменитая Ecole Polytechnique в Париже открыла новую
страницу в истории математики, в частности геометрии. Эта школа,
созданная Французской революцией, подготовила большое число офи-
офицеров, оказавших на военной службе выдающиеся услуги своей рес-
республике. В числе ее питомцев был Жан-Виктор Понселе A788-1867),
написавший свой «Трактат о проективных свойствах фигур» в 1813 г.,
будучи в плену в России.
В XIX в. под влиянием Штейнера, Штаудта, Шаля и других проек-
проективная геометрия стала одним из излюбленных предметов математи-
математических исследований. Своей популярностью она обязана отчасти при-
присущей ей особенной эстетической привлекательности, отчасти же спо-
способности проливать свет на геометрическую науку в целом, а также
глубокой внутренней связи с неевклидовой геометрией и с алгеброй.
0о
Рис. 70. Проекция из точки
§ 2. Основные понятия
1. Группа проективных преобразований. Прежде всего
определим класс, или «группу»1, проективных преобразований. Пусть
'Термин «группа» в применении к классу преобразований подразумевает, что
последовательное выполнение двух преобразований из рассматриваемого класса есть
также преобразование этого класса, и что преобразование, «обратное» по отношению
к преобразованию из рассматриваемого класса, также принадлежит этому классу.
Групповые свойства математических операций играли и продолжают играть очень
большую роль во многих областях, однако по отношению к геометрии значение
понятия «группы» в свое время, возможно, было несколько преувеличено.

J2. Основные понятия 209
Рис. 71. Параллельная проекция
в пространстве заданы две плоскости тг и тг', параллельные или непарал-
непараллельные между собой. Мы выполняем центральную проекцию тг на тг'
с данным центром О, не лежащим ни на тг, ни на тг', сопоставляя каж-
каждой точке Р плоскости тг такую точку Р' плоскости тг', что Р и Р'
лежат на одной и той же прямой, проходящей через О. Аналогично мы
выполняем подобным же образом параллельную проекцию, предполагая,
что проектирующие прямые параллельны между собой. Точно так же
определяется проекция прямой или кривой линии / в плоскости тг на
некоторую линию /' в плоскости тг', причем и в этом случае проекция
может быть центральной или параллельной.
Всякое отображение одной фигуры на другую, получающееся
посредством проектирования (центрального или параллельного) или
же посредством конечной последовательности таких проектирований,
называется проективным преобразованием1. Проективная геометрия
плоскости или прямой составляется из системы геометрических тео-
теорем, сохраняющихся при произвольных проективных преобразованиях
соответствующих фигур. Проективной геометрии противопоставляет-
противопоставляется метрическая геометрия, которая понимается как система теорем,
устанавливающих связи между величинами в рассматриваемых фигу-
фигурах, инвариантные только относительно класса движений.
Некоторые проективные свойства можно формулировать непосред-
непосредственно. Точка, разумеется, проектируется в точку. Далее, прямая ли-
линия проектируется в прямую: в самом деле, если прямая / в плоскости тг
Если две фигуры связаны только одним проектированием, то говорят обычно,
Что они перспективны. Таким образом, если сказано, что фигура F в результате
проективного преобразования переходит в фигуру F', то это значит, что или фигу-
Ры F и F1 перспективны, или же можно указать последовательность таких фигур F,
"li F2, ... , Fn, F', что любые две рядом стоящие в ней фигуры перспективны.
14 — 340

210 Глава IV
проектируется на плоскость тг', то линия пересечения V плоскости тг
с плоскостью, проходящей через О и /, — обязательно прямая1. Если
точка А и прямая I инцидентны2, то точка А' и прямая I', возникающие
из них при проективном преобразовании, также инцидентны. Другими
словами, инцидентность точки и прямой есть свойство, инвариант-
инвариантное относительно группы проективных преобразований. Из этого обсто-
обстоятельства вытекает ряд простых, но весьма важных следствий. Если
три точки (или более трех точек) коллинеарны, т. е. инцидентны с одной
и той же прямой, то их отображения также коллинеарны. Аналогично,
если в плоскости тг три прямые (или более трех прямых) конкуррентны,
т. е. инцидентны с одной и той же точкой, то их отображения — также
конкуррентные прямые. В то же время как эти простые свойства —
инцидентность, коллинеарность, конкуррентность — являются проек-
проективными свойствами (т.е. свойствами, инвариантными относительно
проективных преобразований), величины отрезков и углов, а также и
отношения этих величин, вообще говоря, изменяются при проектиро-
проектировании. Равнобедренные или равносторонние треугольники могут, на-
например, спроектироваться на треугольники с тремя различными сто-
сторонами. Отсюда следует, что хотя понятие «треугольник» принадлежит
проективной геометрии, понятие «равносторонний треугольник» ей не
принадлежит, а принадлежит только метрической геометрии.
Q R
Рис. 72. Конфигурация Дезарга на плоскости
1За исключением того случая, когда прямая ОР (или плоскость, проходящая че-
через О и I) оказывается параллельной плоскости ir. Такие исключения будут устра-
устранены в § 4.
2Точка и прямая называются инцидентными, если прямая проходит через точку
или точка лежит на прямой. Этот «нейтральный» термин подчеркивает взаимность
рассматриваемого отношения.

J2. Основные понятия
211
Рис. 73. Конфигурация Дезарга в пространстве
2. Теорема Дезарга. Одним из самых ранних открытий в об-
области проективной геометрии является замечательная теорема Дезарга
A593-1662): если на плоскости два треугольника ABC и А'В'С рас-
расположены таким образом, что прямые, соединяющие соответственные
вершины, конкуррентны, то три точки, в которых пересекаются, бу-
будучи продолжены, три соответственные стороны, — коллинеарны. Эта
теорема здесь иллюстрируется чертежом (рис. 72), но пусть читатель
проверит ее справедливость, экспериментируя на самостоятельно по-
построенных чертежах. Доказательство теоремы не является тривиаль-
тривиальным, несмотря на всю простоту чертежа, состоящего только из прямых
линий. Теорема явственно принадлежит проективной геометрии, так
как при проектировании рассматриваемый чертеж не теряет свойств,
упомянутых в теореме. В дальнейшем мы еще вернемся к этой теореме
(стр. 261). В настоящий же момент мы хотели бы привлечь внимание
читателя к тому любопытному обстоятельству, что теорема Дезарга
справедлива также и в том предположении, что рассматриваемые тре-
треугольники расположены в двух различных (непараллельных) плоскос-
плоскостях и что подобного рода «трехмерная» или «пространственная» теоре-
теорема Дезарга доказывается без малейших затруднений. По предположе-
предположению, прямые АА', ВВ' и СС пересекаются в одной и той же точке О
(рис. 73). В таком случае прямые АВ и А'В' лежат в одной плоскости
и, значит, пересекаются в некоторой точке R; пусть, таким же обра-
образом, АС и А'С пересекаются в точке Q, а ВС и В'С' — в точке Р.
Так как точки Р, Q и R находятся на продолжениях сторон треуголь-

212 Глава IV
ников ABC и А'В'С, то все они лежат в плоскости каждого из этих
треугольников и потому — на прямой пересечения этих двух плоскос-
плоскостей. Значит, Р, Q и R коллинеарны, что и требовалось доказать.
Это простое доказательство наводит на мысль, что можно было
бы попытаться доказать «двумерную» теорему Дезарга, так сказать,
с помощью перехода к пределу, постепенно сплющивая всю простран-
пространственную конструкцию таким образом, чтобы две плоскости в пределе
совпали в одну, и в этой последней, вместе с другими, оказалась и точ-
точка О. Выполнить, однако, указанный предельный переход не так прос-
просто, так как прямая пересечения PQR при совмещении плоскостей не
определяется однозначно.
Тем не менее, конфигурация, изображенная на рис. 72, может быть
истолкована как перспективное изображение пространственной конфи-
конфигурации рис. 73, и это обстоятельство можно использовать при доказа-
доказательстве «плоской» теоремы.
Есть существенное различие между теоремой Дезарга на плоскости
и в пространстве. Наше доказательство, относящееся к случаю трех изме-
измерений, опиралось только на геометрические соображения, относящиеся к ин-
инцидентности точек, прямых и плоскостей. Можно показать, что доказатель-
доказательство двумерной теоремы — при дополнительном требовании не выходить
из данной плоскости — неизбежно должно опираться на некоторые свойства
подобных фигур, принадлежащих уже не проективной, а метрической гео-
геометрии.
Теорема, обратная теореме Дезарга, утверждает, что если три точки,
в которых пересекаются соответственные стороны, коллинеарны, то пря-
прямые, соединяющие соответственные вершины, конкуррентны. Доказатель-
Доказательство этой теоремы — в случае, когда треугольники лежат в непараллельных
плоскостях, — предоставляется читателю в качестве упражнения.
§ 3. Двойное отношение
1. Определение и доказательство инвариантности. Если
длина отрезка прямой представляет собой своего рода ключ к мет-
метрической геометрии, то существует и в проективной геометрии одно
основное понятие, с помощью которого могут быть выражены все от-
отличительные проективные свойства фигур.
Предположим, что три точки А, В и С расположены на одной
прямой. Проектирование, вообще говоря, изменяет не только расстоя-
Л R
ния АВ и ВС, но и их отношение -~. В самом деле, любые три точки А,
В, С на прямой I могут быть переведены в любые три точки А', В', С

5 3. Двойное отношение
213
А"
Рис. 74. Проектирование трех точек
на прямой V посредством двух последовательно производимых проек-
проектирований. Чтобы в этом убедиться, станем вращать прямую Г около
точки С", пока она не примет положения /", параллельного / (рис. 74).
Затем, проектируя / на /" параллельно прямой СС, получим три точ-
точки А", В" и С" (=С). Прямые А'А" и В'В" пересекутся в точке О,
которую мы изберем в качестве центра второй проекции. Последова-
Последовательно выполненные указанные две проекции дают требуемый резуль-
результат1.
В
С
D
Из доказанного вытекает, что никакая величина, определяемая
только тремя точками на прямой, не может быть инвариантной при
проектировании. Но — в этом заключается решающее открытие в про-
проективной геометрии — если на прямой дано четыре точки А, В, С, D,
которые при проектировании переходят в точки А', В', С, D' другой
прямой, то некоторая величина, называемая двойным отношением этих
четырех точек, при проектировании не изменяет числового значения.
В этом заключено математическое свойство системы четырех точек
на прямой, которое носит инвариантный характер и которое можно
обнаружить во всякой проекции рассматриваемой прямой. Двойное от-
отношение не есть ни расстояние, ни отношение расстояний, а отношение
двух таких отношений: если мы составим отношения
СА
СВ
то их отношение
х =
СА
РА
DB'
DA
СВ ' DB'
1Подумайте, что делать, если прямые А'А" и В'В" параллельны.

214
Глава IV
по определению, есть двойное отношение четырех точек А, В, С, D,
взятых в указанном выше порядке.
Убедимся теперь, что двойное отношение четырех точек инвари-
инвариантно при проектировании, т.е. что если А, В, С, D и А', В', С, D' —
две четверки точек на двух прямых, и между ними установлено про-
проективное соответствие, то тогда справедливо равенство
ОА . DA = С А1 . Р'А'
СВ ' DB С В' ' D'B1'
Доказательство вполне элементарно. Вспомним, что площадь треуголь-
треугольника равна половине произведения основания на высоту и, с другой
стороны, равна половине произведения двух сторон на синус заключен-
заключенного между ними угла. Тогда получим, глядя на рис. 75:
площадь
площадь
площадь
площадь
Отсюда следует:
ОСА = ±h-CA= \OA ¦ ОС sin COA,
ОС В =lh-CB= ±ОВ ¦ ОС sinCO~B,
ОБА =\h-DA= \ОА ¦ OD si
ODB =±
¦ OD smDO~B.
ОА . DA = ОА.Ш = OA-OCsmCOA OB -OP sin DOB =
CB'DB CB DA OB-OCsinCOB OA-ODsinDOA
_ sin COA sin DOB
sin COB sinSoi'
Таким образом, двойное отношение точек А, В, С, D зависит толь-
только от углов, образованных в точке О отрезками О А, ОВ, ОС, OD. Так
как эти углы — одни и те же, каковы бы ни были четыре точки А', В',
С", D', в которые при проектировании переходят А, В, С, D, то ясно,
что двойное отношение не изменяется при проектировании.
Что двойное отношение не изменяется при параллельном проектирова-
проектировании, следует из элементарных свойств подобных треугольников. Доказатель-
Доказательство предоставляется читателю в качестве упражнения (рис. 76).
До сих пор, говоря о двойном отношении четырех точек А, В, С, D,
расположенных на прямой I, мы предполагали, что это отношение со-
составлено из положительных отрезков. Целесообразно видоизменить это
определение следующим образом. Примем одно из двух направлений

j3. Двойное отношение
О
215
С
D
Рис. 75. Инвариантность двойного отношения при центральном проектиро-
проектировании
В С
D
{ABCD)>0
Л-
Рис. 76. Инвариантность двойного
отношения при параллельном про-
проектировании
(ABCD)<0
Рис. 77. Знак двойного отно-
отношения
прямой I за положительное и условимся, что все отрезки, отсчитывае-
отсчитываемые в этом направлении, будут считаться положительными, а отрезки,
отсчитываемые в противоположном направлении, — отрицательными.
Теперь определим двойное отношение точек А, В, С, D (взятых в ука-
указанном порядке) согласно формуле
(ABCD) =
СА РА
СВ ' DB'
причем знаки чисел С А, СВ, DA, DB берутся в соответствии с указан-
указанным выше условием. Так как при изменении направления на прямой I,
принятого за положительное, меняются только знаки всех четырех от-
Резков, то значение (ABCD) не зависит от выбора направления. Легко

216 Глава IV
понять, что (ABCD) имеет отрицательный или положительный знак,
смотря по тому, разделена ли пара точек А, В парой точек С, D или не
разделена. Так как свойство «разделяться» инвариантно относительно
проектирования, то понимаемое в новом смысле (как величина, спо-
способная иметь тот или иной знак) двойное отношение (ABCD) также
инвариантно. Выберем начальную точку О на прямой / и сопоставим
каждой точке на прямой I в качестве координаты х ее расстояние от О,
взятое с надлежащим знаком; тогда, обозначая координаты A, S, С, D
соответственно через х\, х2, Жз, Х4, получим формулу
(ABCD) =
= =
С В ' DB хъ - х2 ' xi - х2 х3 - х2 Xi-xx'
Если (ABCD) = — 1, так что ~~- = — ^~, то точки С и D делят
отрезок АВ внутренне и внешне в одном и том же отношении. В этом
случае принято говорить, что С и D делят отрезок АВ гармонически,
и каждая из точек С и D считается гармонически сопряженной с другой
точкой относительно пары точек А, В. Если (ABCD) = 1, то точки С
и D (или А и В) совпадают.
Необходимо не упустить из виду, что при определении двойного
отношения (ABCD) существенную роль играет порядок, в котором бе-
берутся точки А, В, С, D. Например, если (ABCD) = Л, то двойное от-
отношение (BACD) равно i тогда как (DACB) = 1 — А, в чем читатель
убедится без труда. Четыре точки Л, 5, С, D могут быть переставлены
между собой 4-3-2-1 = 24 различными способами, и каждой перестанов-
перестановке соответствует некоторое значение двойного отношения. Некоторым
перестановкам соответствует то же числовое значение двойного отно-
отношения, что и начальной перестановке А, В, С, D; например, (ABCD) =
= (ВADC). Читателю предоставляется в качестве упражнения дока-
доказать, что при 24 возможных перестановках четырех точек получается
всего лишь шесть различных значений двойного отношения, а именно,
х 1 \ I
Л, 1 Л, ,
А' А ' 1-А' А-Г
Эти шесть величин, вообще говоря, различны, но при некоторых зна-
значениях А могут и совпадать по две, например, при значении А = —1
в случае гармонического деления.
Мы можем также определить двойные отношения четырех компла-
компланарных (т.е. лежащих в одной плоскости) и конкуррентных прямых 1,

о
§3. Двойное отношение
ABC D
217
Рис. 78. Координатное выражение для двойного отношения
2, 3, 4, как двойное отношение четырех точек пересечения этих пря-
прямых с некоторой прямой, лежащей в той же плоскости. Положение этой
пятой прямой несущественно вследствие инвариантности двойного от-
отношения при проектировании. Эквивалентным этому определению яв-
является следующее:
A234) = ±
l, 3)
l, 4)
sinB, 3) ' sinB, 4)'
где нужно взять знак плюс, если пара прямых 1, 2 не разделяется па-
парой 3, 4, и знак минус, если разделяется. (В этой формуле A, 3), на-
например, обозначает угол между прямыми 1 и 3.) Наконец, можно опре-
определить двойное отношение четырех коаксиальных плоскостей (четырех
плоскостей, пересекающихся по одной прямой, или «оси»). Если некото-
некоторая прямая пересекает плоскости в четырех точках, то двойное отноше-
отношение этих точек всегда будет иметь одно и то же значение, независимо от
выбора прямой (доказательство предлагается в качестве упражнения).
Таким образом, полученное значение
можно назвать двойным отношени-
отношением рассматриваемых четырех плос-
плоскостей. Иначе, можно назвать двой-
двойным отношением четырех коаксиаль-
коаксиальных плоскостей двойное отношение
четырех прямых, по которым они пе-
пересекаются произвольной пятой плос-
плоскостью (рис. 79).
Понятие двойного отношения че-
четырех плоскостей побуждает поста-
поставить вопрос о том, нельзя ли дать
определение проективного преобразо-
преобразования трехмерного пространства са-
самого на себя. Определение с помо-
Щью центральной проекции, очевид-
н°, не обобщается непосредственно от
Рис. 79. Двойное отношение четы-
четырех плоскостей

218
Глава IV
О'
случая двух измерений на случай трех измерений. Но можно дока-
доказать, что каждое непрерывное преобразование плоскости самой на се-
себя, взаимно однозначно переводящее точки в точки и прямые в пря-
прямые, есть проективное. Это обстоятельство наводит на мысль ввес-
ввести следующее определение для случая трех измерений: проективным
преобразованием пространства называется непрерывное взаимно одно-
однозначное преобразование, переводящее прямые линии в прямые линии.
Можно показать, что такие преобразования
оставляют значения двойных отношений не-
неизменными.
Добавим к предыдущему еще кое-какие
замечания. Пусть на прямой даны три раз-
различные точки А, В, С с координатами Х\,
х2, х3- Требуется найти четвертую точку D
таким образом, чтобы удовлетворялось ра-
равенство (ABCD) = А, где А задано. (Част-
(Частный случай, когда А = — 1 и задача заключа-
заключается в построении четвертой гармонической
точки, будет подробно рассмотрен в следу-
следующем пункте.) Вообще говоря, задача имеет
А' В' С Г)'
одно и только одно решение; действительно,
Рис. 80. Проективное со- если х — координата искомой точки D, то
ответствие между точка- уравнение
ми двух прямых
х3
х - х2
X - Xi
— А
имеет ровно одно решение. Считая х\, ж2 и Хз заданными и полагая
3 1 = к, мы придадим решению вид
ради краткости
- Х2
Например, если точки А, В, С находятся на равных расстояниях друг
от друга и имеют соответственно координаты Х\ = 0, х2 = d, хз = 2d,
то тогда к =
2d-0
= 2 и х =
2d-d 2-У
Если прямая / спроектирована из двух различных центров О' и О"
на две различные прямые V и /", то получается соответствие Р ~?± Р'
между точками прямых I и V и соответствие Р *=!¦ Р" между точка-
точками прямых / и /". Этим устанавливается соответствие Р' <=* Р" между
точками прямых V и I", и притом такое, что каждые четыре точки А',

§3. Двойное отношение 219
27'5 С", D' на V имеют то же самое двойное отношение, что и соответ-
соответствующие точки А", В", С", D" на I". Всякое взаимно однозначное со-
соответствие между точками двух прямых, обладающее этим свойством,
называется проективным соответствием, независимо от того, каким
способом это соответствие установлено.
Упражнения.
1) Доказать, что если даны две прямые вместе с проективным соответ-
соответствием, установленным между ними, то можно подвергнуть одну из
прямых такому параллельному перенесению, что заданное соответ-
соответствие будет получаться посредством простой проекции. (Указание. Сов-
Совместите какую-нибудь пару взаимно соответствующих точек на дан-
данных прямых.)
2) Пользуясь предыдущим результатом, показать, что если между точка-
точками двух прямых I и V установлено соответствие посредством конечно-
конечного числа последовательных проектирований на различные промежуточ-
промежуточные прямые, при произвольных центрах проекций, то тот же результат
может быть получен посредством всего лишь двух проектирований.
2. Применение к полному четырехстороннику. В качестве
интересного применения инвариантности двойного отношения мы дока-
докажем одну простую, но важную теорему проективной геометрии. Речь
идет о полном четырехстороннике — фигуре, образованной произволь-
произвольными четырьмя прямыми, из которых никакие три не являются кон-
куррентными, и шестью точками их пересечения. На рис. 81 названные
четыре прямые суть АЕ, BE, BI, AF. Прямые АВ, EG и IF являют-
являются диагоналями четырехсторонника. Рассмотрим одну из диагоналей,
например АВ, и отметим на ней точки С и D, где она пересекается
с двумя другими диагоналями. Тогда теорема утверждает существо-
существование равенства (ABCD) = —1; словами это выражается так: точки
пересечения одной диагонали с двумя другими делят отрезок между вер-
вершинами четырехсторонника гармонически. Для доказательства доста-
достаточно обратить внимание на то, что
х = (ABCD) = (IFHD) (проектируем из Е),
(IFHD) = (BACD) (проектируем из G),
Как нам известно,
таким образом, х = i, х2 = 1, х = ±1. Но так как С, D разделяют А, В,
То двойное отношение х отрицательно и потому оно должно быть равно
Именно —1, что мы и хотели доказать.

220 Глава IV
Рис. 81. Полный четырехсторонник
Полученное замечательное свойство полного четырехсторонника
дает нам возможность с помощью одной лишь линейки построить точ-
точку, гармонически сопряженную с точкой С относительно пары А, В
(если А, В, С коллинеарны). Нужно только, выбрав произвольную точ-
точку Е вне данной прямой, провести прямые ЕА, ЕВ, ЕС; затем, взяв
произвольно точку G на ЕС, провести прямые AD и BD, пересекаю-
пересекающие ЕВ и ЕА, скажем, в точках F и I; провести, наконец, прямую IF,
которая и пересечет исходную прямую в искомой точке D.
Задача. На плоскости задан отрезок АВ и область R, как показано на
рис. 82. Желательно продолжить прямую АВ вправо от R. Как это можно сде-
сделать с помощью одной линейки и при условии, чтобы в процессе построения
не покрывать линейкой никакой части области Л? (Указание. Выберите на
отрезке АВ две произвольные точки С и С", затем постройте сопряженные
с ними гармонические D и D' относительно пары точек А, В; при построении
воспользуйтесь четыре раза теоремой о полном четырехстороннике.)
В
Рис. 82. Проведение прямой через препятствие
§ 4. Параллельность и бесконечность
1. «Идеальные» бесконечно удаленные точки. Вниматель-
Внимательное рассмотрение изложенного в предыдущем параграфе обнаружива-

§4. Параллельность и бесконечность 221
ет, что во многих случаях приведенная аргументация теряет силу —
именно тогда, когда прямые, точка пересечения которых нужна для
построения, оказываются параллельными. Например, построение чет-
четвертой гармонической точки D становится невыполнимым, если пря-
прямая IF параллельна АВ. Геометрические рассуждения на каждом шагу
затруднены тем обстоятельством, что параллельные прямые не имеют
общей точки, и потому всякий раз, когда речь идет о пересечении пря-
прямых, приходится отдельно рассматривать и особо оговаривать случай
параллелизма. С другой стороны, если производится проектирование,
мы вынуждены различать и трактовать независимо рядом с централь-
центральной также и параллельную проекцию. Если бы из такого положения
не было выхода, то проективная геометрия, будучи вынуждена вни-
вникать в детальное исследование каждого встречающегося исключения
и особого случая, неизбежно была бы чрезвычайно усложнена. Все это
побуждает искать выхода в ином направлении, именно, на пути та-
такого обобщения основных понятий, которое устраняло бы возможные
исключения.
Тут нам поможет геометрическая интерпретация; мы видим, что
если прямая, пересекающая другую прямую, медленно вращается, при-
приближаясь к положению параллельности, то точка пересечения двух пря-
прямых неограниченно удаляется. Это дает повод к наивному утвержде-
утверждению: две прямые пересекаются «в бесконечно удаленной точке». Подоб-
Подобного рода формулировке существенно придать точный смысл с таким
расчетом, чтобы с «бесконечно удаленными», или, как иногда говорят,
с «идеальными» точками можно было проводить точные и надежные
рассуждения, как с обыкновенными точками на плоскости или в про-
пространстве. Иными словами, мы желали бы, чтобы все правила поведе-
поведения точек, прямых, плоскостей оставались в силе и для «идеальных»
геометрических элементов.
В математическом смысле существование «бесконечно удаленных
точек» обеспечено, если отчетливо и без взаимных противоречий уста-
установлены математические свойства этих вновь вводимых элементов,
т.е. их взаимоотношения с «обыкновенными» точками и между собой.
Обыкновенно система геометрических аксиом (например, в евклидо-
евклидовой геометрии) вытекает путем абстракции из наблюдений над физи-
физическими объектами: таковы следы прикосновения карандаша к бумаге
или мела к доске, натянутые нити, световые лучи, твердые стержни
и т. п. Свойства, приписываемые аксиомами математическим точкам
и прямым, представляют собой в высшей степени упрощенные и иде-
идеализированные описания поведения соответствующих им физических

222 Глава IV
«двойников». Через любые два карандашных пятнышка можно провести
не одну, а много карандашных «прямых». Если пятнышки становятся
все меньше по диаметру, то все такие «прямые» станут трудно отличи-
отличимыми одна от другой. Вот что мы, собственно говоря, имеем в виду,
высказывая в качестве геометрической аксиомы, что «через любые две
точки можно провести одну и только одну прямую»: мы при этом гово-
говорим об «абстрактных», чисто умозрительных, геометрических точках
и прямых. Геометрические точки и прямые обладают гораздо более
простыми свойствами, чем какие бы то ни было физические объекты.
Упрощение является существенным условием, позволяющим строить
геометрию как дедуктивную дисциплину.
Как уже было отмечено, обыкновенная геометрия точек и прямых
весьма осложнена тем обстоятельством, что две параллельные прямые
не имеют точки пересечения. Это побуждает нас сделать дальнейшее
упрощение в структуре геометрии, расширяя понятие геометрической
точки таким образом, чтобы устранить указанное исключение — со-
совершенно так же, как мы расширяли понятие числа с целью устранения
ограничений при вычитании и делении. В геометрии, как и в арифмети-
арифметике, мы озабочены неукоснительно сохранением в расширенной области
тех законов, какие регулировали отношения в первоначальной области.
Итак, мы уславливаемся в том, что к обыкновенным точкам вся-
всякой прямой добавляем еще одну, «идеальную», точку и будем считать
эту точку, принадлежащей одновременно всем прямым, параллельным
данной — и никаким другим. Следствием такого условия является то,
что всякая пара прямых на плоскости теперь уже пересекается в един-
единственной точке: если прямые не параллельны, то в «обыкновенной точ-
точке; если параллельны, то в им обеим принадлежащей «идеальной» точке.
По причинам интуитивного порядка эта идеальная точка на прямой на-
называется бесконечно удаленной точкой на этой прямой.
Интуитивное представление о точке, удаляющейся в бесконечность по
прямой линии, могло бы навести на мысль, что следует добавить две иде-
идеальные точки на каждой прямой — по одной для каждого направления. Если
мы добавляем только одну, то причина этому заключена в том, что мы за-
заинтересованы в сохранении закона: через каждые две точки проходит одна
и только одна прямая. Если бы прямая содержала две бесконечно удаленные
точки вместе со всеми, ей параллельными, то вышло бы, что через две такие
«точки» проходит бесконечное множество прямых.
Мы уславливаемся также в том, что к обыкновенным прямым на
плоскости добавляем еще одну «идеальную», так называемую «бесконеч-
«бесконечно удаленную» прямую, содержащую все бесконечно удаленные точки

§4. Параллельность и бесконечность 223
плоскости — и никаких других. Мы вынуждены принять именно такое
условие, если хотим сохранить первоначальный закон — «через всякие
две точки проходит одна прямая» и вновь утвержденный закон — «вся-
«всякие две прямые пересекаются в одной точке». В самом деле, возьмем две
какие-нибудь идеальные точки. Единственная прямая, которая должна
проходить через эти точки, не может быть обыкновенной прямой, так
как, по принятому условию, каждая обыкновенная прямая содержит
только одну идеальную точку. С другой стороны, эта прямая не может
содержать обыкновенных точек, так как через обыкновенную точку и
одну из идеальных точек непременно прошла бы обыкновенная прямая.
Наконец, рассматриваемая прямая непременно содержит все идеальные
точки, так как мы хотим, чтобы она имела одну общую точку со всякой
обыкновенной прямой. Итак, прямая, о которой идет речь, неизбежно
должна обладать как раз всеми теми свойствами, которыми мы наде-
наделили идеальную прямую в нашей плоскости.
Согласно принятым условиям, каждая бесконечно удаленная точка
определяется или представляется семейством параллельных прямых,
точно так же, как иррациональное число определяется последователь-
последовательностью «вложенных» рациональных отрезков. Такого рода условный
способ описывать параллелизм — с помощью терминов, первоначально
предназначенных для интуитивно отличных объектов, — единственной
своей целью имеет сделать излишним перечисление исключительных
случаев; эти последние теперь автоматически покрываются теми же
терминами (и оборотами речи), которые первоначально употреблялись
для «обыкновенных» случаев.
Резюмируем: наши условия, касающиеся бесконечно удаленных
элементов, были выбраны таким образом, чтобы законы, регулирую-
регулирующие отношение инцидентности между обыкновенными точками и пря-
прямыми, сохранялись и в расширенной области, чтобы операция нахожде-
нахождения точки пересечения двух прямых, ранее возможная только в случае
непараллельности, могла быть выполнена без ограничений. Соображе-
Соображения, которые привели нас к формальному упрощению в отношениях
инцидентности, способны показаться несколько абстрактными. Но чи-
читатель убедится на следующих страницах, что они будут вполне оправ-
оправданы результатами.
2. Идеальные элементы и проектирование. Введение бес-
бесконечно удаленных точек и бесконечно удаленной прямой на плоскос-
плоскости позволит нам гораздо более удовлетворительным образом рассмот-
рассмотреть проектирование одной плоскости на другую. Пусть плоскость тг
проектируется на плоскость тг' из центра О (рис. 83). Эта проекция

224
Глава IV
Рис. 83. Возникновение бесконечно удаленных элементов при проектирова-
проектировании
устанавливает соответствие между точками и прямыми тг и точками и
прямыми тг'. Каждой точке Л на тг соответствует единственная точка А'
на тг' со следующими исключениями: если выходящий из О проекти-
проектирующий луч параллелен плоскости тг', то он пересекает тг в точке А,
которой не соответствует никакая обыкновенная точка плоскости тг'.
Такие исключительные точки плоскости тг расположены на прямой /,
которой не соответствует никакая обыкновенная прямая плоскости тг'.
Но оговаривать эти исключения становится излишним, если мы усло-
условимся точке А сопоставлять бесконечно удаленную точку на плоскос-
плоскости тг', взятую в направлении прямой ОА, а прямой / — сопоставлять
бесконечно удаленную прямую в плоскости тг'. Аналогично, некоторую
бесконечно удаленную точку в плоскости тг мы сопоставляем каждой
точке В' на такой прямой т' в плоскости тг', через которую проходят
все лучи, выходящие из О и параллельные плоскости тт. Самой пря-
прямой т' соответствует бесконечно удаленная прямая плоскости тг. Та-
Таким образом, посредством введения в плоскости бесконечно удаленных
точек и прямой достигается то, что проекция одной плоскости на другую
устанавливает такое соответствие между точками и прямыми двух
плоскостей, которое взаимно однозначно без всяких исключений. (Так
устраняются исключения, упомянутые в сноске на стр. 213.) Далее,
легко понять, что из принятых соглашений вытекает следствие: точ-

§4. Параллельность и бесконечность 225
ка лежит на прямой, если проекция точки лежит на проекции прямой.
Отсюда видно, что все теоремы, относящиеся к коллинеарным точкам,
конкуррентным прямым и т. д. и говорящие только о точках, прямых и
отношениях инцидентности, инвариантны относительно проектирова-
проектирования в расширенном смысле. Это дает возможность оперировать с бес-
бесконечно удаленными точками плоскости тг, заменяя их соответствую-
соответствующими получающимися при проектировании обыкновенными точками
ПЛОСКОСТИ 71"'.
* Можно воспользоваться интерпретацией бесконечно удаленных
точек плоскости тг с помощью проектирования из внешней точки О на
обыкновенные точки другой плоскости тг', чтобы получить конкретную
евклидову «модель» расширенной плоскости. Для этого не будем обра-
обращать внимания на плоскость тг', а сосредоточимся на плоскости тг и пря-
прямых, проходящих через О. Каждой обыкновенной точке тг соответству-
соответствует прямая, проходящая через О, непараллельная тг; каждой бесконеч-
бесконечно удаленной точке тг — прямая, проходящая через О, параллельная тт.
Итак, совокупности всех точек тг, обыкновенных и идеальных, соответ-
соответствует совокупность прямых, проходящих через О, и это соответствие
взаимно однозначно без всяких исключений. Точки на некоторой пря-
прямой в плоскости тг переходят в прямые на плоскости, проходящей че-
через О. Точка и прямая в плоскости тг инцидентны в том и только в том
случае, если инцидентны соответствующие прямая и плоскость, прохо-
проходящие через О. Другими словами, геометрия инцидентности точек и
прямых в расширенной плоскости совершенно равносильна геометрии
инцидентности обыкновенных прямых и плоскостей, проходящих через
фиксированную точку пространства.
Положение вещей в трехмерном пространстве вполне аналогично,
хотя отпадает возможность пользоваться наглядным аппаратом проек-
проектирования. Здесь тоже мы вводим особую бесконечно удаленную точ-
точку, связанную с каждым семейством параллельных прямых. В каждой
плоскости имеется бесконечно удаленная прямая. Затем вводится но-
новый элемент — бесконечно удаленная плоскость, состоящая из всех бес-
бесконечно удаленных точек пространства и содержащая все бесконечно
удаленные прямые. С бесконечно удаленной плоскостью каждая обык-
обыкновенная плоскость пересекается по своей собственной бесконечно уда-
удаленной прямой.
3. Двойное отношение с бесконечно удаленными элемен-
элементами. Еще одно замечание следует сделать по поводу двойных отно-
отношений с бесконечно удаленными элементами. Будем обозначать симво-
символом со бесконечно удаленную точку на прямой /. Посмотрим, как опре-
15 — 340

226 Глава IV
>оо
А В С Р
Рис. 84. Двойное отношение с участием бесконечно удаленной точки
деляется символ (АВСоо), если А, В, С — три обыкновенные точки
на I. Пусть Р — некоторая точка на I; тогда (АВСоо) рассматривается
как предел (АВСР), когда Р удаляется в бесконечность по I. Но
PA
и, когда Р неограниченно удаляется, j^r стремится к 1. Отсюда выте-
вытекает определение:
(АВСоо) = %.
В частности, если (АВСоо) = 1, то С есть середина отрезка АВ: сред-
средняя точка отрезка и бесконечно удаленная точка, взятая в направле-
направлении отрезка, делят отрезок гармонически.
Упражнение. Что представляет собой двойное отношение четырех пря-
прямых h, h, h, h, если они параллельны? Что получится, в частности, с этим
двойным отношением, если в качестве Ц будет взята бесконечно удаленная
прямая?
§ 5. Применения
1. Предварительные замечания. После введения бесконечно
удаленных элементов уже нет необходимости явно оговаривать все ис-
исключительные случаи параллельности, возникающие при построениях
и доказательствах теорем. Достаточно помнить, что если точка явля-
является бесконечно удаленной, то все проходящие через нее прямые парал-
параллельны. Отпадает и необходимость делать различие между центральной
и параллельной проекциями, так как параллельная проекция есть не
что иное, как проекция из бесконечно удаленной точки. На рис. 72 точ-
точка О или прямая PQR могут оказаться бесконечно удаленными (рис. 85

227
Рис. 85. Дезаргова конфигурация с центром в бесконечности
изображает первый из упомянутых случаев); мы предоставляем чита-
читателю в качестве упражнения сформулировать в «финитных» (т. е. не
содержащих упоминания о бесконечности) терминах соответствующие
утверждения дезарговой теоремы.
Не только формулировка, но и доказательство теоремы, принад-
принадлежащей проективной геометрии, нередко упрощаются в результате
введения бесконечно удаленных элементов. Общий принцип заключа-
заключается в следующем. Условимся под «проективным классом» некоторой
геометрической фигуры F понимать класс всех фигур, в которые F
может быть переведена проективными преобразованиями. Проектив-
Проективные свойства F ничем не отличаются от проективных свойств любой
фигуры ее проективного класса, так как — по самому определению —
проективные свойства сохраняются при проектировании. Таким обра-
образом, любая проективная теорема (т. е. теорема, говорящая только о про-
проективных свойствах), которая верна для фигуры F, будет также верна
для любого «представителя» проективного класса этой фигуры, и об-
обратно. Поэтому, чтобы доказать такую теорему для F, достаточно до-
доказать ее для некоторого «представителя» проективного класса F. Мы
можем воспользоваться указанным обстоятельством и выбрать тако-
такого «представителя», для которого доказательство проще, чем для самой
фигуры F. Например, произвольные две точки А, В плоскости тг могут
быть спроектированы в бесконечность из данного центра О, если про-
проектировать на плоскость, параллельную плоскости, проходящей через
точки О, А, В; прямые, проходящие через А или через В, при этом
превратятся в семейства параллельных прямых. Именно такое предва-
предварительное преобразование мы выполним при доказательстве проектив-
проективных теорем, которыми займемся в этом параграфе.
15*

228
Глава IV
Рис. 86. Подобие треугольников, образованных параллельными прямыми
В дальнейшем нам придется воспользоваться следующим обстоя-
обстоятельством, относящимся к параллельным прямым. Пусть две прямые,
проходящие через точку О, пересекаются прямыми 1\ и /г> в точках А,
В, С, D, как показано на рис. 86. Если прямые 1± и 1^ параллельны,
то ^~ = ^^; и обратно, если выполнено последнее соотношение, то
прямые li и /г параллельны. Доказательство, вытекающее из элемен-
элементарных свойств подобных треугольников, предоставляется читателю.
Рис. 87. Доказательство теоремы Дезарга
2. Двумерное доказательство теоремы Дезарга. Докажем
теперь, не прибегая к пространственному проектированию, что если два
треугольника ABC и А'В'С расположены на плоскости так, как изоб-
изображено на рис. 72, т.е. если прямые, соединяющие соответствующие
вершины, встречаются в одной и той же точке, то точки пересечения
соответствующих сторон Р, Q, R лежат на одной прямой. Для этого
прежде всего спроектируем чертеж таким образом, чтобы точки Q и R
ушли в бесконечность. После такого проектирования прямая А'В' ста-
станет параллельна прямой АВ, а прямая А'С — прямой АС (рис. 87).
Как было отмечено в пункте 1 настоящего параграфа, чтобы доказать

§5. Применения
229
теорему Дезарга в общем случае, достаточно доказать ее только для
случая рассматриваемой здесь частной конфигурации. Именно, доста-
достаточно показать, что точка Р пересечения сторон ВС и В'С также
уйдет в бесконечность, т.е. что прямая В'С параллельна прямой ВС:
тогда точки Р, Q, R будут коллинеарны (так как все три будут лежать
на бесконечно удаленной прямой). Обратим внимание на то, что
АВ
А'В' влечет Ц = ?,
V О
AC || A'C влечет § = §•
Поэтому ^ = f) a отсюда следует ВС \\ В'С, что и требовалось дока-
доказать.
Следует отметить, что при-
приведенное доказательство теоремы
Дезарга опирается на математичес-
математическое понятие длины отрезка. Таким
образом, проективная теорема до-
доказана в данном случае метричес-
метрическими средствами. Другое заслужи-
заслуживающее внимания обстоятельство
заключается в следующем. Мы ука-
указывали раньше (стр. 218), что по-
понятию проективного преобразова-
преобразования может быть дано «внутреннее»
определение («проективное преоб-
преобразование плоскости — такое, кото-
которое оставляет инвариантными все
двойные отношения»): отсюда выте-
вытекает, что теорема Дезарга способна
быть сформулирована и доказана без выхода в пространство, т. е. без
использования трехмерных представлений и построений.
Упражнение. Доказать подобным же образом теорему, обратную дез-
арговой: если треугольники ABC и А'В'С' таковы, что Р, Q, R коллинеарны,
то прямые АА', ВВ', СС конкуррентны.
3. Теорема Паскаля. * Эта теорема формулируется так: если
вершины шестиугольника лежат поочередно на двух пересекающихся
1На стр. 252 будет рассмотрена более общая теорема этого же типа. Настоящий
частный случай связывается также с именем Паппа Александрийского (III столетие
до нашей эры).
R\
Рис. 88. Конфигурация Паскаля

230
Глава IV
Рис. 89. Нумерация вер-
вершин шестиугольника
Ъ 1 у 5 s 3
Рис. 90. Доказательство теоремы
Паскаля
прямых, то точки Р, Q, R пересечения противоположных сторон это-
этого шестиугольника коллинеарны (рис. 88). (Контур шестиугольника мо-
может быть самопересекающимся. Что такое «противоположные» сторо-
стороны, легко понять из схемы на рис. 89.)
Выполняя предварительное проектирование, можно допустить, что
Р и Q ушли в бесконечность. Остается показать, что R также уй-
уйдет в бесконечность. Ситуация иллюстрируется рис. 90, где 23 || 56
и 12 || 45. Нужно показать, что 16 || 34. Мы имеем
у
а + х
а + х b + y + s'1 b + y a + x + r'
Рис. 91. Конфигурация Брианшона

§5. Применения
231
Поэтому
так что 16
а _ а + х + г
b b + y + s'
34, что и требовалось доказать.
4. Теорема Брианшона. Эта теорема формулируется так: если
стороны шестиугольника проходят поочередно через две данные точ-
точки Р и Q, то три диагонали, соединяющие противоположные вершины
шестиугольника, конкуррентны (рис. 91).
Посредством предварительного про-
проектирования можно отправить в беско-
бесконечность точку Р и точку, в которой пе-
пересекаются две какие-нибудь диагонали,
например, 14 и 36. Полученная ситуация
изображена на рис. 92. Так как 14 || 36,
то ? = ^. Но вместе с тем % = %¦ и ^ = ?.
о У о b
Значит, | = | и поэтому 36 || 25, так что
все три диагонали параллельны и, следо-
следовательно, конкуррентны. Этого достаточ-
достаточно, чтобы считать теорему доказанной и
в общем случае.
5. Замечание по поводу двой-
двойственности. Читатель, вероятно, уже
заметил замечательное сходство тео-
теорем Паскаля A623-1662) и Брианшона
A785-1864). Это сходство особенно броса-
бросается в глаза, если обе формулировки по-
поставить рядом:
I
/ v
рч а
Q
3 у \
\ \ V
¦ч Чч \
ч^ N^ \
ь ч V
44. 5-
Рис. 92. Доказательство тео-
теоремы Врианшона
Теорема Паскаля
Если вершины шестиугольни-
шестиугольника лежат поочередно на двух
прямых, то точки пересечения
противоположных сторон кол-
линеарны.
Теорема Брианшона
Если стороны шестиугольника
проходят поочередно через две
точки, то прямые, соединяю-
соединяющие противоположные верши-
вершины, конкуррентны.
Не только теоремы Паскаля и Брианшона, но все вообще теоре-
теоремы проективной геометрии группируются попарно таким образом, что
две теоремы одной и той же пары сходны между собой и, так сказать,

232 Глава IV
идентичны по своей структуре. Это явление носит название двойствен-
двойственности. В геометрии плоскости точка и прямая представляют собой вза-
взаимно двойственные элементы. Провести прямую через точку и отме-
отметить точку на прямой — операции взаимно двойственные. Две фигуры
взаимно двойственны, если одна может быть получена из другой по-
посредством замены каждого элемента и каждой операции двойственным
элементом и двойственной операцией. Две теоремы взаимно двойст-
двойственны, если одна превращается в другую при замене каждого элемента
и каждой операции двойственным элементом и двойственной операци-
операцией. Например, теоремы Паскаля и Брианшона взаимно двойственны,
тогда как теоремой, двойственной теореме Дезарга, является теоре-
теорема, ей обратная. Явление двойственности резко отличает проективную
геометрию от элементарной (метрической), в которой никакой двой-
двойственности не наблюдается. (Например, было бы бессмысленно искать
какое-нибудь «двойственное» утверждение по отношению к тому факту,
что данный угол содержит 37° или что данный отрезок равен 2 линей-
линейным единицам. Принцип двойственности, согласно которому каждой
верной теореме проективной геометрии сопоставляется двойственная
ей, также верная теорема, во многих учебниках подчеркивается тем,
что формулировки взаимно двойственных теорем, вместе со взаимно
двойственными их доказательствами, приводятся, как мы это сдела-
сделали выше. Внутренняя причина явления двойственности будет изучена
в следующем параграфе (см. также стр. 249).
§ 6. Аналитическое представление
1. Вводные замечания. В раннем периоде развития проектив-
проективной геометрии существовала настойчиво проводимая тенденция выпол-
выполнять все построения на синтетической или, как говорилось, «чисто гео-
геометрической» основе, избегая вовсе применения чисел и алгебраичес-
алгебраических методов. Выполнение этой программы встретило на своем пути
большие затруднения, так как всегда оставались какие-то пункты, в ко-
которых алгебраические формулировки казались неизбежными. Полный
успех в построении чисто синтетической проективной геометрии был
достигнут только к концу XIX в. и только ценой значительных ослож-
осложнений. В этом отношении методы аналитической геометрии оказались
гораздо более плодотворными. Для современной математики характер-
характерна иная тенденция — положить в основу построения понятие числа,
и в геометрии эта тенденция, идущая от Ферма и Декарта, возымела
решительный триумф. Аналитическая геометрия перестала быть под-

§6. Аналитическое представление 233
собным аппаратом, играющим служебную роль в геометрических рас-
рассуждениях, и стала самостоятельной областью, в которой интуитивная
геометрическая интерпретация операций и результатов уже не явля-
является последней и окончательной целью, а принимает на себя функцию
руководящего принципа, помогающего угадывать и понимать аналити-
аналитические факты. Такое изменение значения геометрии есть последствие
постепенного развития геометрии в историческом плане — развития,
широко раздвинувшего рамки классических концепций; оно же обусло-
обусловило вместе с тем почти органическое слияние геометрии и анализа.
В аналитической геометрии под «координатами» геометрическо-
геометрического объекта понимается какая угодно совокупность чисел, позволяющая
определить этот объект однозначно. Так, точка определяется своими
прямоугольными координатами х, у или своими полярными координа-
координатами р, ¦&¦ с другой стороны, например, треугольник определяется ко-
координатами трех вершин, что в целом составляет шесть координат. Мы
знаем, что прямая линия в плоскости х, у представляет собой геометри-
геометрическое место всех точек Р{х, у) (об обозначениях см. на стр. 105), ко-
координаты которых удовлетворяют некоторому линейному уравнению
ах + Ьу + с = 0. A)
Поэтому можно три числа а, 6, с назвать «координатами» этой прямой.
Например, а = 0, 6=1, с=0 определяют прямую у = 0, т.е. ось х;
а = 1, 6 = —1, с = 0 определяют прямую х = у, которая делит пополам
угол между положительной осью х и положительной осью у. Таким
же образом следующие уравнения определяют «конические сечения»:
х2 + у2 = г2 — окружность радиуса г с центром в начале координат,
(х - аJ + (у - бJ = г2 — окружность радиуса г с центром (а, 6),
х2 У2 1
~ + ~ = 1 — эллипс и т.д.
а2 Ъ2
Более или менее наивный подход к аналитической геометрии за-
заключается в том, чтобы, отправляясь от чисто «геометрических» пред-
представлений — точка, прямая и т. д., — переводить их затем на язык чи-
чисел. Современная точка зрения противоположна. Мы отправляемся от
множества всевозможных пар чисел х, у и называем каждую такую па-
пару точкой, так как можем, если пожелаем, наглядно интерпретировать
такую пару чисел с помощью общедоступного понятия геометрической
точки. Точно так же прямая линия является геометрическим пред-
представлением или интерпретацией линейного уравнения, связывающего х
и у. Указанный перенос акцента от интуитивного понимания геомет-
геометрии к аналитическому открывает возможность, в частности, простой
и вполне строгой трактовки бесконечно удаленных точек в проектив-

234 Глава IV
ной геометрии; он же необходим для более глубокого проникновения
в эту область. Для тех читателей, которые обладают достаточной пред-
предварительной математической подготовкой, мы дадим теперь некоторый
очерк применения аналитических методов в проективной геометрии.
*2. Однородные координаты. Алгебраические основы двой-
двойственности. В обыкновенной аналитической геометрии прямоуголь-
прямоугольными координатами точки на плоскости являются снабженные знаками
расстояния точки от двух взаимно перпендикулярных осей. Но в та-
такой системе координат не находится места для бесконечно удаленных
точек расширенной проективной плоскости. Поэтому если мы хотим
пользоваться аналитическими методами в проективной геометрии, то
необходимо найти такую координатную систему, которая смогла бы
включить идеальные точки наравне с обыкновенными. Легче всего дать
описание такой координатной системы, если представить себе данную
плоскость X, Y (которую будем обозначать через тг), расположенной
в трехмерном пространстве с прямоугольными координатами х, у, z
(эти буквы обозначают снабженные знаками расстояния точки от трех
координатных плоскостей, образованных осями х, у и z). Представим
себе, что плоскость тг параллельна координатной плоскости х, у и нахо-
находится на расстоянии 1 от нее, так что трехмерные координаты точки Р
в плоскости тг будут (X, Y, 1). Принимая начало О координатной сис-
системы за центр проектирования, заметим, что всякой точке Р взаимно
однозначно соответствует некоторая прямая ОР, проходящая через
начало координат (см. стр. 111). В частности, бесконечно удаленным
точкам плоскости тг соответствуют прямые, проходящие через О и па-
параллельные тг.
Посмотрим теперь, что же представляет собой система однородных
координат для точек плоскости тг. Чтобы найти однородные координа-
координаты обыкновенной точки Р в этой плоскости, возьмем прямую ОР и
на ней выберем произвольную точку Q, отличную от О (рис. 93). Обык-
Обыкновенные трехмерные координаты х, у, z точки Q считаются однород-
однородными координатами точки Р в плоскости тг. В частности, координа-
координаты (X, У, 1) самой точки Р являются ее однородными координатами.
Но вместе с тем ее же однородными координатами явятся любые чис-
числа (tX, tY, t), где t ф 0, так как координаты всех точек прямой ОР
(кроме О) имеют как раз такой вид. (Мы исключаем точку @, 0, 0),
потому что она лежит на всех прямых, проходящих через О, и не мо-
может служить для их различения.)
Система однородных координат, конечно, представляет известное
неудобство в том отношении, что нужны три числа вместо двух для

§6. Аналитическое представление
Z
235
(tx,ty,tz)
Рис. 93. Однородные координаты
определения точки, и, самое главное, координаты точки определяют-
определяются не однозначно, а с точностью до постоянного множителя. Но она
имеет то безусловное преимущество, что охватывает и идеальные, бес-
бесконечно удаленные точки плоскости тг. Действительно, такой идеаль-
идеальной точке Р соответствует некоторая прямая, проходящая через О и
параллельная тг; всякая точка Q на такой прямой имеет координаты
вида (х, у, 0); таким образом, однородные координаты идеальных то-
точек плоскости тг имеют вид (х, у, 0). Нетрудно написать в однородных
координатах уравнение прямой линии на плоскости тг. Для этого доста-
достаточно заметить, что прямые, соединяющие О с точками этой прямой,
лежат в плоскости, проходящей через О. В аналитической геометрии
Доказывается, что уравнение такой плоскости имеет вид
ах + by + cz = 0. A;)
Это же есть и уравнение данной прямой в однородных координатах.
Теперь, когда геометрическая модель, изображающая точки плос-
плоскости тг в виде прямых, проходящих через О, отслужила свою службу,

236 Глава IV
можно ее отбросить и дать следующее, чисто аналитическое определе-
определение расширенной плоскости:
Точка есть не что иное, как тройка действительных чисел (х, у, z),
из которых не все равны нулю. Две такие тройки (х\, yi, zi)
и (х2, 2/2, Z2) определяют одну и ту же точку, если существует такое
число t ф 0, что
Х2 = tXi, 2/2 = tyx, Z-i = tZi.
Другими словами, можно, не меняя самой точки, умножать ее коор-
координаты на произвольный множитель, отличный от нуля. (Потому эти
координаты и называются однородными.) Точка (ж, у, z) — обыкновен-
обыкновенная, если z отлично от нуля, идеальная, если z равно нулю.
Прямая линия в плоскости тг состоит из всех точек (х, у, z), удов-
удовлетворяющих линейному уравнению вида
ах + by + cz = 0, A')
где а, Ь, с — постоянные числа, не все равные нулю. В частности, бес-
бесконечно удаленные точки плоскости тг удовлетворяют уравнению
z = 0; B)
согласно определению, это — также уравнение прямой, именно — бес-
бесконечно удаленной прямой плоскости тт. Так как прямая определяется
уравнением вида A'), то тройка чисел (а, Ь, с) может быть рассматри-
рассматриваема как однородные координаты прямой A'). Далее следует, что при
произвольном t ф 0 тройка чисел (ta, tb, tc) представляет собой коор-
координаты той же прямой, так как уравнение
(ta)x + (tb)y + {tc)z = 0 C)
удовлетворяется в точности теми же координатными тройками (ж, у, z),
что и уравнение A').
В этих определениях обнаруживается полная симметрия между
точкой и прямой: и та и другая определяются тройкой чисел — од-
однородными координатами (и, v, w). Условие того, что точка (х, у, z)
лежит на прямой (а, Ь, с), выражается равенством
ах + by + cz = 0,
и это же есть вместе с тем условие того, что точка с координата-
координатами (а, Ь, с) лежит на прямой с координатами (ж, у, z). Например, ариф-
арифметическое тождество
2-3 + 1-4+ (-5) -2 = 0
означает, что точка C, 4, 2) лежит на прямой B, 1, -5) и в равной
мере, что точка B, 1, —5) лежит на прямой C, 4, 2). Эта симметрия
и представляет собой основу двойственности между точкой и прямой

§6. Аналитическое представление 237
в проективной геометрии, так как всякое соотношение между точка-
точками и прямыми становится некоторым соотношением между прямыми
и точками, если только координаты будут подвергнуты надлежащей
переинтерпретации: координаты точек нужно при этом считать коор-
координатами прямых, координаты прямых — координатами точек. Все
алгебраические операции и результаты остаются теми же самыми, но,
толкуя их по-разному, мы получаем теорему, соответствующую пер-
первоначальной в смысле двойственности. Необходимо заметить, с другой
стороны, что в обыкновенной X, F-плоскости ни о какой двойствен-
двойственности не может быть речи, так как уравнение прямой в обыкновенных
координатах
аХ + ЬУ + с = О
несимметрично относительно X, У и а, Ъ, с. Только включение беско-
бесконечно удаленных элементов, точек и прямой, обеспечивает силу прин-
принципа двойственности.
Чтобы перейти от однородных координат х, у, z обыкновенной точки Р
в плоскости тг к обыкновенным прямоугольным координатам, мы просто по-
полагаем X = ^, У = ^. Тогда X, У обозначают расстояния точки Р от двух
перпендикулярных осей в плоскости тг, параллельной х- и г/-осям, как пока-
показано на рис. 93. Мы знаем, что уравнение
аХ + ЬУ + с = О
представляет прямую в плоскости тг. Полагая X = ^, Y = — и умножая на г,
мы найдем, что уравнение той же прямой в однородных координатах будет
ах + by + cz = О,
как это уже было указано на стр. 234. Так, уравнение прямой 2х — Зу + z = О
в обыкновенных прямоугольных координатах X, У примет вид 2Х — ЗУ +
+ 1 = 0. Разумеется, последнему уравнению бесконечно удаленная точка
рассматриваемой прямой с однородными координатами C, 2, 0) уже не отве-
отвечает.
Остается сказать еще одно. Нам удалось получить чисто аналитичес-
аналитическое определение точки и прямой: но что можно сказать о важном понятии
проективного преобразования? Можно установить, что проективное преоб-
преобразование, понимаемое в том смысле, как это было разъяснено на стр. 218,
задается аналитически системой линейных уравнений
' х' = а\х + b\y + ciz,
у' = а2х + Ъгу + C2Z, D)
z = азх + Ьзу + сзг,

238 Глава IV
связывающих однородные координаты х , у', z точек в плоскости ж' с од-
однородными координатами х, у, z точек в плоскости ж. С аналогичной точки
зрения можно определить проективное преобразование как такое, которое за-
задается системой уравнений вида D). Теоремы проективной геометрии тогда
становятся теоремами, говорящими о поведении числовых троек (х, у, z) при
таких преобразованиях. Например, доказательство инвариантности двойного
отношения при проективных преобразованиях превращается в легкое упраж-
упражнение из области алгебры линейных трансформаций. Не будем вникать в де-
детали этой аналитической процедуры и вернемся вместо того назад — к про-
проективной геометрии в ее более наглядном аспекте.
§ 7. Задачи на построения с помощью одной
линейки
В следующих построениях предполагается, что единственным инстру-
инструментом служит линейка.
Задачи 1-18 заимствованы из одной работы Я. Штейнера, в которой он
доказывает, что при геометрических построениях можно обойтись без цир-
циркуля, если задан фиксированный круг с центром (см. главу III, стр. 192).
Читателю рекомендуется проделать эти задачи в указанном порядке.
Четверка прямых а, Ь, с, d, проходящих через точку Р, называется гар-
гармонической, если двойное отношение (abed) равно —1. В этом случае говорят,
что с, d гармонически сопряжены с а, Ь, и обратно.
1) Доказать: если в гармонической четверке а, Ь, с, d прямая а делит
пополам угол между с и d, то прямая b перпендикулярна к прямой а.
2) Построить четвертую гармоническую к трем данным прямым, про-
проходящим через одну точку. (Указание: воспользуйтесь теоремой о полном
четырехстороннике.)
3) Построить четвертую гармоническую к трем данным точкам на од-
одной прямой.
4) Даны прямой угол и произвольный угол с общей вершиной и одной
общей стороной. Удвоить данный произвольный угол.
5) Дан угол и его биссектриса Ь. Построить перпендикуляр к b в вершине
данного угла.
6) Доказать: если проходящие через точку Р прямые h, l2, h, ... ,1п
пересекают прямую а в точках А\, А2, ... , Ап и прямую b в точках Bi,
В2, ... , Вп, то все точки пересечения пар прямых А{В^ и A^Bi (i ф к; к = 1,
2, ... , п) лежат на одной прямой.
7) Доказать: если в треугольнике ABC прямая, параллельная сторо-
стороне ВС, пересекает АВ в точке В' и АС в точке С', то прямая, соединяющая
точку А с точкой D пересечения прямых В'С и С'В, делит пополам ВС.
7а) Сформулировать и доказать теорему, обратную 7.
8) На прямой I даны три такие точки Р, Q, R, что Q есть середина
отрезка PR. Построить прямую, параллельную I и проходящую через данную
точку S.

§ 7. Задачи на построения с помощью одной линейки 239
9) Даны две параллельные прямые 1\ и h\ разделить пополам данный
отрезок АВ на прямой h.
10) Через данную точку Р провести прямую, параллельную двум дан-
данным параллельным между собой прямым 1\ и h- (Указание: используйте 7.)
11) Штейнер предлагает следующее решение задачи об удвоении дан-
данного отрезка АВ при условии, что задана прямая I, параллельная АВ: через
точку С, не лежащую ни на прямой /, ни на прямой АВ, провести прямые С А
и СВ: пусть А\ и В\ — соответственно точки их пересечения с прямой /. За-
Затем (см. 10) провести через С прямую, параллельную /; пусть D — точка ее
пересечения с ВА\. Если Е — точка пересечения АВ и DBi, то АЕ — 2- АВ.
Доказать последнее утверждение.
12) Разделить отрезок АВ на п равных частей, если задана прямая /,
параллельная АВ. (Указание: пользуясь 11, отложите сначала п раз данный
отрезок на прямой /.)
13) Дан параллелограмм ABCD. Через данную точку Р провести пря-
прямую, параллельную данной прямой /. (Указание: примените 10 к центру па-
параллелограмма и воспользуйтесь 8.)
14) Дан параллелограмм; увеличить данный отрезок в п раз. (Указание:
примените 13 и 11.)
15) Дан параллелограмм; разделить данный отрезок на п равных частей.
16) Дан неподвижный круг с центром. Провести через данную точку
прямую, параллельную данной прямой. (Указание: примените 13.)
17) Дан неподвижный круг с центром. Увеличить и уменьшить данный
отрезок в п раз. (Указание: примените 13.)
18) Дан неподвижный круг с центром. Провести через данную точку
перпендикуляр к данной прямой. (Указание: воспользуйтесь прямоугольни-
прямоугольником, вписанным в данный круг, с двумя сторонами, параллельными данной
прямой, и сводите к предшествующим задачам.)
19) Пересмотрев задачи 1-18, перечислите, какие основные задачи на
построение можно выполнить с помощью двусторонней линейки (с двумя
параллельными сторонами).
20) Две данные прямые h и b пересекаются в точке Р, находящейся
за пределами чертежа. Построить прямую, соединяющую данную точку Q
с точкой Р. (Указание: дополните заданные элементы таким образом, что-
чтобы получилась конфигурация плоскостной теоремы Дезарга, причем Р и Q
стали бы точками пересечения взаимно соответствующих сторон двух тре-
треугольников.)
21) Провести прямую через две точки, между которыми расстояние
больше, чем длина линейки. (Указание: примените 20.)
22) Прямые 1\ и 12 пересекаются в точке Р; прямые т\ и гаг — в точ-
точке Q; обе точки Р и Q — за пределами чертежа. Построить ту часть пря-
прямой PQ, которая находится в пределах чертежа. (Указание: чтобы получить
точку прямой PQ, постройте конфигурацию Дезарга таким образом, чтобы

240 Глава IV
две стороны одного треугольника лежали соответственно на /i и пц, две сто-
стороны другого — соответственно на Ь и тг).
23) Решить 20 с помощью теоремы Паскаля (стр. 229). (Указание: до-
достройте конфигурацию Паскаля, рассматривая 1\ и h как пару противопо-
противоположных сторон шестиугольника, a Q — как точку пересечения другой пары
противоположных сторон.)
* 24) Каждая из двух прямых, целиком лежащих за пределами чертежа,
задана двумя парами прямых линий, пересекающихся за пределами чертежа
в точках соответствующей прямой. Определить точку их пересечения с по-
помощью двух прямых, пересекающихся за пределами чертежа.
§ 8. Конические сечения и квадрики
1. Элементарная метрическая геометрия конических се-
сечений. До сих пор мы занимались только точками, прямыми, плос-
плоскостями и фигурами, составленными из конечного числа этих элемен-
элементов. Если бы проективная геометрия ограничивалась рассмотрением
таких «линейных» фигур, она была бы сравнительно мало интересна.
Но фактом первостепенного значения является то обстоятельство, что
проективная геометрия этим не ограничивается, а включает также об-
обширную область конических сечений и их многомерных обобщений.
Аполлониева метрическая трактовка конических сечений — эллипсов,
гипербол и парабол — была одним из выдающихся успехов античной
математики. Едва ли можно переоценить значение конических сечений
как для чистой, так и для прикладной математики (например, орбиты
планет и орбиты электронов в атоме водорода являются коническими
сечениями). Не приходится удивляться тому, что классическая, воз-
возникшая в древней Греции теория конических сечений и в наши дни
составляет необходимую часть математического образования. Но гре-
греческая геометрия никоим образом не сказала последнего слова. Через
две тысячи лет были открыты замечательные проективные свойства
конических сечений. Несмотря на простоту и изящество этих свойств,
академическая инерция до настоящего времени служит препятствием
их проникновению в школьное преподавание.
Начнем с того, что напомним метрические определения коничес-
конических течений. Таких определений несколько, и их эквивалентность дока-
доказывается в элементарной геометрии. Наиболее распространенные опре-
определения связаны с фокусами кривых. Эллипс определяется как геомет-
геометрическое место таких точек Р на плоскости, что сумма их расстоя-
расстояний тх и г2 от двух данных точек i<\ и F2, называемых фокусами, име-
имеет постоянное значение. (Если фокусы совпадают, кривая превращается

§8. Конические сечения и квадрики 241
в окружность.) Гипербола определяется как геометрическое место та-
таких точек Р на плоскости, что абсолютное значение разности г± — Гг
равно одной и той же постоянной величине. Парабола определяется как
геометрическое место точек Р, расстояние которых г от данной точ-
точки F равно расстоянию от данной прямой I.
В аналитической геометрии эти кривые представляются уравне-
уравнениями второй степени относительно прямоугольных координат х, у.
Нетрудно доказать, обратно, что всякая кривая, представляемая урав-
уравнением второго порядка
ах2 + by2 + сху + dx + еу + / = О,
есть или одно из трех названных выше конических сечений, или пря-
прямая линия, или пара прямых, или сводится к одной точке, или носит
чисто мнимый характер. Как показывается во всяком курсе аналити-
аналитической геометрии, для доказательства достаточно сделать надлежащим
образом подобранную замену координатной системы.
Указанные выше определения конических сечений — существенно
метрические, так как пользуются понятием расстояния. Но вот другое
определение, устанавливающее место конических сечений в проектив-
проективной геометрии: конические сечения суть не что иное, как проекции
круга на плоскость. Если мы станем проектировать круг С из некото-
некоторой точки О, то проектирующие прямые образуют бесконечный двой-
двойной конус, и пересечение этого конуса с плоскостью к будет проекцией
окружности С. Кривая пересечения будет эллипсом или гиперболой,
смотря по тому, пересечет ли плоскость только одну «полость» кону-
конуса или обе. Возможен и промежуточный случай параболы, если плос-
плоскость 7г параллельна одной из проектирующих прямых, проведенных
через О (рис. 94).
Проектирующий конус не обязан быть «прямым круговым» с вер-
вершиной О, расположенной вертикально над центром круга С: он может
быть и «наклонным». Но во всех случаях (как мы примем здесь, не
приводя доказательства) в пересечении конуса с плоскостью получа-
получается кривая, уравнение которой — второй степени; и обратно, всякая
кривая второго порядка может быть получена из круга посредством
проектирования. По этой именно причине кривые второго порядка ина-
иначе называются коническими сечениями.
Мы уже отметили, что если плоскость пересекает только одну «по-
«полость» прямого кругового конуса, то пересечение Е представляет собой
эллипс. Нетрудно установить, что кривая Е удовлетворяет обыкновен-
обыкновенному фокальному определению эллипса, которое было сформулировано
!б — 340

242
Глава IV
Рис. 94. Конические сечения
Рис. 95. Сферы Данделена
выше. Приведем очень простое и элегантное доказательство, данное
в 1822 г. бельгийским математиком Данделеном. Представим себе две
сферы 5i и S2 (рис. 95), которые касаются плоскости сечения к со-
соответственно в точках F\ и i7^, и, кроме того, касаются конуса вдоль
параллельных кругов К\ и К2. Взяв произвольную точку Р кривой Е,
проведем отрезки PFi и PF2. Затем рассмотрим отрезок РО, соединя-
соединяющий точку Р с вершиной конуса О; этот отрезок целиком лежит на
поверхности конуса; обозначим через Qi и Q2 точки его пересечения с
кругами Кх и К2. Так как PFi и PQx — две касательные, проведенные
из точки Р к одной и той же сфере Si, то
PFt = PQi.
Точно так же
PF2 = PQ2.
Складывая эти равенства, мы получаем:
PF1 + PF2 = PQi + PQ2.
Ho PQi + PQ2 = QiQ2 есть расстояние между параллельными круга-
кругами К\ и К2 на поверхности конуса: оно не зависит от выбора точки Р

} 8. Конические сечения и квадрики
243
на кривой Е. Отсюда следует, что, какова бы ни была точка Р на Е,
имеет место равенство
PFi + PF2 = const,
а это и есть фокальное определение эллипса. Итак, Е есть эллипс, a Fi
и F2 — его фокусы.
Упражнение. Если плоскость пересекает обе «полости» конуса, то кри-
кривая пересечения — гипербола. Доказать это утверждение, помещая по одной
сфере в каждой из «полостей» конуса.
2. Проективные свойства конических сечений. Основыва-
Основываясь на положениях, установленных в предыдущем пункте, примем те-
теперь временно следующее определение: коническое сечение есть про-
проекция окружности на плоскость. Это определение в большей степени
отвечает духу проективной геометрии, чем общепринятые фокальные
определения, так как эти последние всецело опираются на метрическое
понятие расстояния. Новое определение тоже не вполне свободно от это-
этого недостатка, поскольку «окружность» — также метрическое понятие.
Но через мгновение мы придем к чисто проективному определению
конических сечений.
Раз мы приняли, что коническое
сечение есть не что иное, как проек-
проекция окружности (другими словами, под
термином «коническое сечение» мы по-
понимаем любую кривую, принадлежа-
принадлежащую проективному классу окружнос-
окружности (см. стр. 226), то отсюда сейчас же
следует, что всякое свойство окружнос-
окружности, инвариантное относительно проек-
проективных преобразований, должно также
принадлежать любому коническому се-
сечению. Вспомним теперь следующее хо-
хорошо известное — метрическое — свой-
свойство окружности: «вписанные в окруж- Рис- 96- Двойное отношение в
ность углы, опирающиеся на одну и ту окружности
же дугу, равны между собой». На рис. 96 угол АОВ, опирающийся на
Дугу АВ, не зависит от положения точки О на окружности. Свяжем,
Дальше, указанное обстоятельство с проективным понятием двойного
отношения, вводя на окружности уже не две точки А, В, а четыре — А,
В, С, D. Четыре прямые а, Ь, с, d, соединяющие эти точки с точкой О
16*
о.
О'
в

244
Глава IV
на окружности, имеют двойное отношение (а, Ь, с, d), зависящее только
от углов, опирающихся на дуги С А, СВ, DA, DB. Соединяя А, В, С, D
с какой-нибудь другой точкой О' на окружности, получим прямые а',
Ь', с', d!. Из отмеченного ранее свойства окружности вытекает, что две
четверки прямых «конгруэнтны»1. Поэтому у них будет одно и то же
двойное отношение: (a'b'c'd') = (abed). Спроектируем окружность на
некоторое коническое сечение К: тогда на К получится четверка то-
точек, которые мы снова обозначим через А, В, С, D, две точки О и О'
и две четверки прямых а, Ь, с, dn а', Ь', с', d!. Эти две четверки прямых
уже не будут конгруэнтны, так как углы при проектировании, вообще
говоря, не сохраняются. Но так как двойное отношение при проекти-
проектировании не изменяется, то равенство (abed) = (a'b'c'd') по-прежнему
имеет место. Мы пришли, таким образом, к следующей основной те-
теореме: если четыре точки конического сечения К, например А, В, С,
D, соединены с пятой точкой О того же сечения прямыми а, Ь, с, d,
то двойное отношение (abed) зависит от положения О на кривой К
(рис. 97).
Это — замечательный результат.
Как нам уже известно, если четыре
точки А, В, С, D взяты на прямой, то
двойное отношение, составленное из
соединяющих эти точки с пятой точ-
точкой О прямых, не зависит от выбора
этой пятой точки. Это — исходное по-
положение, лежащее в основе проектив-
проективной геометрии. Теперь мы узнали,
что аналогичное утверждение спра-
Рис. 97. Двойное отношение на эл- ведливо и относительно четырех то-
липсе чек, взятых на некотором коничес-
коническом сечении К, однако с существенным ограничением: пятая точка О
уже не может свободно двигаться по всей плоскости, а может только
перемещаться по коническому сечению К.
Не представляет особого труда доказать и обратную теорему в сле-
следующей форме: если на кривой К имеются две точки О и О', облада-
обладающие тем свойством, что, какова бы ни была четверка точек А, В,
С, D на кривой К, двойные отношения, составленные из прямых, со-
D
1 Четверка прямых а, Ь, с, d считается конгруэнтной другой четверке а', Ь', с', d',
если углы между каждой парой прямых в первой четверке равны как по величине,
так и по направлению отсчета углам между соответствующими прямыми второй
четверки.

)8. Конические сечения и квадрики
245
О
единяющих эти точки с О, и из прямых, соединяющих эти точки с О',
равны между собой, то кривая К есть коническое сечение (а уж тог-
тогда, по прямой теореме, двойное отношение, составленное из прямых,
соединяющих четыре данные точки с произвольной точкой О" на К,
будет иметь одно и то же постоянное значение). Но доказательства мы
здесь приводить не будем.
Изложенные проективные свой-
свойства конических сечений наводят
на мысль об общем методе то-
точечного построения этих кривых.
Условимся под пучком прямых по-
понимать совокупность всех пря-
прямых плоскости, проходящих че-
через данную точку О. Рассмотрим
пучки прямых, проходящих через
две точки О и О', расположен-
расположенные на коническом сечении К.
Между прямыми пучка О и пря- Рис. 98. К построению проективных
мыми пучка О' можно устано- пучков прямых
вить взаимно однозначное соот-
соответствие, сопоставляя прямой а из первого пучка прямую а' из второго
всякий раз, как а и а' встречаются в некоторой точке А кривой К. Тог-
Тогда любая четверка прямых а, 6, с, d из пучка О будет иметь то же двой-
двойное отношение, что и соответствующая четверка а', Ь', с', d! из пучка О'.
Всякое взаимно однозначное соответствие между двумя пучками пря-
прямых, обладающее этим последним свойством, называется проективным
соответствием. (Это определение двойственно по отношению к опре-
определению проективного соответствия между точками на двух прямых,
см. стр. 231.) Пользуясь этим определением, можно теперь утверждать:
коническое сечение К есть геометрическое место точек пересечения
взаимно соответствующих прямых из двух пучков, находящихся в про-
проективном соответствии. Полученная теорема подводит фундамент под
следующее чисто проективное определение конических сечений: кони-
коническим сечением называется геометрическое место точек пересечения
взаимно соответствующих прямых из двух пучков, находящихся в про-
проективном соответствии1. Как ни соблазнительно проникнуть в глубь
теории конических сечений, строящейся на таком определении, однако
мы вынуждены ограничиться немногими замечаниями по этому поводу.
1Это геометрическое место, при известных обстоятельствах, может вырождаться
в прямую линию; см. рис. 98.

246
Глава IV
Рис. 99. Образование окружности и равносторонней гиперболы с помощью
проективных пучков
Пары пучков, находящихся в проективном соответствии, можно
получить следующим образом. Спроектируем все точки Р прямой ли-
линии / из двух разных центров О и О" и установим между проектиру-
проектирующими пучками взаимно однозначное соответствие, сопоставляя друг
другу те прямые, которые пересекаются на прямой I. Этого достаточно,
чтобы полученные пучки находились в проективном соответствии. За-
Затем возьмем пучок О" и перенесем его «как нечто твердое» в произволь-
произвольное положение О'. Что новый пучок О' будет находиться в проективном
соответствии с пучком О, это совершенно очевидно. Но замечательно
то, что любое проективное соответствие между двумя пучками можно
получить именно таким образом. (Это обстоятельство двойственно по
отношению к упражнению 1 на стр. 218.) Если пучки О и О' конгру-
конгруэнтны, получается окружность. Если углы между соответствующими
лучами в двух пучках равны, но отсчитываются в противоположных
направлениях, то получается равносторонняя гипербола (рис. 99).
Следует еще заметить, что указанное определение конического се-
сечения может, в частности, дать и прямую линию, как это показано
на рис. 98. В этом случае прямая 00" соответствует сама себе и все
ее точки должны быть рассматриваемы как принадлежащие искомому
геометрическому месту. Таким образом, коническое сечение вырож-
вырождается в пару прямых: это обстоятельство вполне согласуется с тем
фактом, что существуют сечения конуса, состоящие из двух прямых
(если секущая плоскость проходит через вершину конуса).

§8. Конические сечения и квадрики
247
Упражнения.
1) Вычертить эллипсы, гиперболы и параболы с помощью проектив-
проективных пучков. (Читателю настойчиво рекомендуется экспериментиро-
экспериментировать с подобного рода построениями. Это в высшей степени способ-
способствует пониманию сути дела.)
2) Дано пять точек О, О', А, В, С некоторого конического сечения К. Най-
Найти точки пересечения D произвольной прямой d пучка О с кривой К.
(Указание: через О проведите прямые О А, ОВ, ОС и назовите их а, Ь,
с. Через О' проведите прямые О'А, О'В, О'С и назовите их а', У, с'.
Проведите через О прямую d и постройте такую прямую d' пучка О',
что (abed) = (a'b'c'd'). Тогда точка пересечения dad' принадлежит
кривой К.)
3. Конические сечения как
«линейчатые кривые». Поня-
Понятие касательной к коническому
сечению принадлежит проектив-
проективной геометрии, так как касатель-
касательная к коническому сечению есть
прямая, имеющая с самой кривой
только одну общую точку, а это —
свойство, сохраняющееся при про-
проектировании. Проективные свой-
свойства касательных к коническим
сечениям основываются на следу-
следующей теореме: Двойное отноше-
отношение точек пересечения четырех
фиксированных касательных к ко-
коническому сечению с произвольной
пятой касательной не зависит от
выбора этой пятой касательной.
Доказательство этой теоремы весьма просто. Так как любое кони-
коническое сечение есть проекция окружности и так как в теореме идет
речь только о таких свойствах, которые инвариантны относительно
проектирования, то, чтобы доказать теорему в общем случае, доста-
достаточно доказать ее для частного случая окружности.
Для этого же частного случая теорема доказывается средствами
элементарной геометрии. Пусть Р, Q, R, S — четыре точки на окруж-
окружности К; a, b, c,d — касательные в этих точках; Т — еще какая-нибудь
точка на окружности, о — касательная в ней; пусть, далее, А, В, С, D —
точки пересечения касательной о с касательными о, Ъ, с, d. Если М —
Рис. 100. Окружность как совокуп-
совокупность касательных

248
Глава IV
_ 1
центр окружности, то, очевидно, Z.TMA — jrZTMP, и последнее выра-
выражение представляет угол, вписанный в К, опирающийся на дугу ТР.
Таким же образом Z.TMB представляет угол, вписанный в К и опира-
опирающийся на дугу TQ. Следовательно,
IAMB = \
PQ,
где - *--- PQ обозначает угол, вписанный в К и опирающийся на ду-
дугу PQ. Отсюда видно, что А, В, С, D проектируются из М четырьмя
прямыми, углы между которыми имеют величины, зависящие только
от положения точек Р, Q, R, S. Но тогда двойное отношение (ABCD)
зависит только от четырех касательных а, Ь, с, d, но не от касательной о.
Как раз это и нужно было установить.
Рис. 101. Свойство касательной к окружности
Рис. 102. Проективные ряды точек на двух касательных к эллипсу

§8. Конические сечения и квадрики 249
В предыдущем пункте мы имели случай убедиться, что коническое
сечение может быть построено «по точкам», если станем отмечать точ-
точки пересечения взаимно соответствующих прямых двух пучков, меж-
между которыми установлено проективное соответствие. Только что дока-
доказанная теорема дает нам возможность сформулировать двойственную
теорему. Возьмем две касательные а и а' к коническому сечению К.
Третья касательная t пусть пересекает а и а' соответственно в точ-
точках А и А'. Если t будет перемещаться вдоль кривой, то установится
соответствие
А^А'
между точками а и точками а'. Это соответствие будет проективным,
так как по доказанной теореме произвольная четверка точек на а бу-
будет непременно иметь тоже двойное отношение, что и соответствующая
четверка точек на а'. Отсюда следует, что коническое сечение К, рас-
рассматриваемое как «совокупность своих касательных», «состоит» из пря-
прямых, соединяющих взаимно соответствующие точки двух точечных ря-
рядов1 на а и на а', находящихся в проективном соответствии. Указанное
обстоятельство позволяет ввести новое определение конических сече-
сечений, рассматриваемых на этот раз как «линейчатые кривые». Сравним
это определение с прежним проективным определением конического
сечения, данным в предыдущем пункте:
I
Коническое сечение, рассмат-
рассматриваемое как совокупность то-
точек, состоит из точек пересе-
пересечения взаимно соответствую-
соответствующих прямых в двух проектив-
проективных пучках.
II
Коническое сечение, рассмат-
рассматриваемое как «совокупность
прямых», состоит из прямых,
соединяющих взаимно соответ-
соответствующие точки в двух проек-
проективных рядах.
Если мы станем считать касательную к коническому сечению в не-
некоторой его точке двойственным элементом по отношению к самой точ-
точке и условимся, кроме того, «линейчатую кривую» (образованную сово-
совокупностью касательных) на основе двойственности сопоставлять «то-
«точечной кривой» (образованной совокупностью точек), то предыдущие
формулировки будут безупречны с точки зрения принципа двойствен-
двойственности. При «переводе» одной формулировки в другую с заменой всех
Понятий соответствующими двойственными понятиями, «коническое
1 Совокупность точек на прямой называется точечным рядом. Это — понятие,
Двойственное по отношению к пучку прямых.

250 Глава IV
сечение» остается неизменным: но в одном случае оно мыслится как
«точечная кривая», определяемая своими точками, в другом — как «ли-
«линейчатая кривая», определяемая своими касательными.
Рис. 103. Парабола, определенная конгруэнтными точечными рядами
Рис. 104. Парабола, определенная подобными точечными рядами
Из предыдущего вытекает важное следствие: принцип двойствен-
двойственности, первоначально установленный в проективной геометрии плос-
плоскости только для точек и прямых, оказывается, может быть распро-
распространен и на конические сечения. Если в формулировке любой теоремы,
касающейся точек, прямых и конических сечений, заменить каждый
элемент ему двойственным (не упуская из виду, что точке конического
сечения должна быть сопоставляема касательная к этому коническому

j8. Конические сечения и квадрики
251
сечению), то в результате также получится справедливая теорема.
Пример действия этого принципа мы встретим в пункте 4 настоящего
параграфа.
Построение конических сечений, понимаемых как «линейчатые
кривые», показано на рис. 103-104. В частности, если в двух проек-
проективных точечных рядах бесконечно удаленные точки соответствуют
взаимно одна другой (так будет непременно, если точечные ряды кон-
конгруэнтны или подобныI, то коническое сечение будет параболой; спра-
справедливо и обратное утверждение.
Упражнение. Доказать обратную теорему: на двух неподвижных ка-
касательных к параболе движущаяся касательная к параболе определяет два
подобных точечных ряда.
Рис. 105. Общая конфигурация Паскаля. Показаны два случая: один для шес-
шестиугольника 1, 2, 3, 4, 5, 6, другой для шестиугольника 1, 3, 5, 2, 6, 4
4. Теоремы Паскаля и Брианшона для общего случая про-
произвольных конических сечений. Одной из лучших иллюстраций
принципа двойственности применительно к коническим сечениям яв-
является взаимоотношение между общими теоремами Паскаля и Бриан-
Брианшона. Первая из них была открыта в 1640, вторая — в 1806 г. И, од-
Что такое «конгруэнтные» и «подобные» ряды, — достаточно понятно без объяс-
объяснений.

252 Глава IV
нако, каждая из них есть непосредственное следствие другой, так как
всякая теорема, формулировка которой упоминает только конические
сечения, прямые и точки, непременно остается справедливой при из-
изменении формулировки по принципу двойственности.
Теоремы, доказанные в § 5 под теми же наименованиями, пред-
представляют собой «случаи вырождения» следующих более общих теорем.
Теорема Паскаля. Противоположные стороны шестиугольника,
вписанного в коническое сечение, пересекаются в трех коллинеарных
точках.
Теорема Брианшона. Три диагонали, соединяющие противопо-
противоположные вершины шестиугольника, описанного около конического сече-
сечения, конкуррентны.
Обе теоремы — очевидно проективного содержания. Их двойст-
двойственное взаимоотношение бросается в глаза, если сформулировать их
следующим образом:
Р.
Рис. 106. Общая конфигурация Брианшона. Показаны только два случая
Теорема Паскаля. Дано шесть точек 1, 2, 3, 4, 5, 6 на коничес-
коническом сечении. Соединим последовательные точки прямыми A, 2), B, 3),
C, 4), D, 5), E, 6), F, 1). Отметим точки пересечения прямых A, 2)
и D, 5), B, 3) и E, 6), C, 4) и F, 1). Эти три точки лежат на одной
прямой.
Теорема Брианшона. Дано шесть касательных 1, 2, 3, 4, 5, 6
к коническому сечению. Последовательные касательные пересекаются
в точках A, 2), B, 3), C, 4), D, 5), E, 6), F, 1). Проведем прямые, со-

J8. Конические сечения и квадрики
253
D
Рис. 107. Доказательство теоремы Паскаля
единяющие точки A, 2) и D, 5), B, 3) и E, 6), C, 4) и F, 1). Эти три
прямые проходят через одну точку.
Доказательства проводятся с помощью специализации такого же
рода, как и в рассмотренных раньше случаях вырождения. Докажем
теорему Паскаля. Пусть А, В, С, D, E, F — вершины шестиугольни-
шестиугольника, вписанного в коническое сечение К. Посредством проектирования
можно сделать параллельными прямые АВ и ED, FА и CD (и тог-
тогда получится конфигурация, изображенная на рис. 107; ради удобства
шестиугольник на чертеже взят самопересекающимся, хотя в этом нет
никакой необходимости.) Нам нужно теперь доказать только одно: что
прямая СВ параллельна прямой FE; другими словами, что противопо-
противоположные стороны пересекаются на бесконечно удаленной прямой. Для
доказательства рассмотрим четверку точек F, А, В, D, которая, как
мы знаем, при проектировании из любой точки К сохраняет одно и то
же двойное отношение, скажем, к. Станем проектировать из точки С
на прямую AF; получим четверку точек F, A, Y, оо, причем
к = (F, A, Y, оо) =
YF
YA
(см. стр. 225).
Станем теперь проектировать из точки Е на прямую В А; получим
Четверку точек X, А, В, оо, причем
к = (X, А, В, оо) = Ц.

254 Глава IV
Итак,
ВХ = YF
В A YA'
что как раз и обозначает, что YB || FX. Доказательство теоремы Пас-
Паскаля закончено.
Теорема Брианшона, как было указано, следует из теоремы Паска-
Паскаля по принципу двойственности. Но ее можно доказать и непосредст-
непосредственно — путем рассуждения, двойственного относительно только что
приведенного. Провести это рассуждение во всех деталях будет пре-
прекрасным упражнением для читателя.
5. Гиперболоид. В трехмерном пространстве мы встречаемся
с так называемыми квадриками (поверхностями второго порядка), ко-
которые в данном случае играют ту же роль, что «конические сечения»
(кривые второго порядка) на плоскости.
Простейшими из них являются сфера и эллипсоид. Квадрики более
разнообразны, чем конические сечения, и изучение их связано с боль-
большими трудностями. Мы рассмотрим бегло и без доказательств одну из
самых интересных поверхностей этого типа, именно связный (однопо-
лостный) гиперболоид».
Эта поверхность может быть получена следующим образом. Возь-
Возьмем в пространстве три прямые h, I2, /3, находящиеся в общем положе-
положении. Последнее означает, что никакие две из них не параллельны и все
три не являются параллельными одной и той же плоскости. Может по-
показаться удивительным, что существует бесконечное множество пря-
прямых в пространстве, из которых каждая пересекается со всеми тремя
данными прямыми.
Рис. 108. Построение прямых, пересекающих три данные прямые общего по-
положения

J8. Конические сечения и квадрики
255
Рис. 109. Гиперболоид
Убедимся в этом. Пусть тг — про-
произвольная плоскость, содержащая пря-
прямую 1\; эта плоскость пересекает пря-
прямые /г и 1з в двух точках, и прямая т,
проведенная через эти две точки, очевид-
очевидно, пересекается со всеми прямыми 1\, /г
и /з- Когда плоскость тг вращается около
прямой /i, прямая то будет изменять свое
положение, однако все время продолжая
пересекаться с тремя данными прямыми.
При движении т возникает поверхность,
неограниченно уходящая в бесконечность,
которая и называется однополостным ги-
гиперболоидом. Она содержит бесконечное
множество прямых типа т. Любые три та-
такие прямые, скажем mi, тг и гпз, также
будут находиться в общем положении, и те
прямые в пространстве, которые будут пе-
пересекаться с тремя прямыми т\, тг и тз
одновременно, также будут лежать на рас-
рассматриваемой поверхности. Отсюда следует основное свойство гипер-
гиперболоида: он составляется из двух различных семейств прямых линий;
каждые три линии одного и того же семейства находятся в общем поло-
положении и каждая прямая одного семейства пересекается со всеми пря-
прямыми другого.
Важное проективное свойство гиперболоида заключается в том,
что двойное отношение тех четырех точек, в которых данная четвер-
четверка прямых одного семейства пересекается с некоторой прямой второго
семейства, не зависит от выбора этой последней. Это утверждение вы-
вытекает из метода построения гиперболоида с помощью вращающейся
плоскости, и читатель может убедиться в его справедливости и ка-
качестве упражнения.
Отметим еще одно замечательное свойство гиперболоида: хотя он
содержит два семейства прямых линий, но существование этих пря-
прямых не препятствует изгибанию поверхности — не делает ее жесткой.
Если устроить модель гиперболоида из стержней, способных свободно
вращаться около точек взаимных пересечений, то поверхность в целом
может быть непрерывно деформируема, пробегая бесконечное множес-
множество различных состояний.

256 Глава IV
§ 9. Аксиоматика и неевклидова геометрия
1. Аксиоматический метод. Аксиоматический метод в мате-
математике берет свое начало по меньшей мере от Евклида. Было бы со-
совершенно ошибочно полагать, что античная математика развивалась
или излагалась исключительно в строго постулативной форме, свойст-
свойственной «Началам». Но впечатление, произведенное этим сочинением на
последние поколения, было столь велико, что в нем стали искать об-
образцов для всякого строгого доказательства в математике. Иной раз
даже философы (например, Спиноза — в его «Ethica, more geometrico
demonstrata») пытались излагать рассуждения в форме теорем, выво-
выводимых из определений и аксиом. В современной математике, после пе-
периода отхода от евклидовой традиции, продолжавшегося на протяже-
протяжении XVII и XVIII вв., снова обнаружилось все усиливающееся про-
проникновение аксиоматического метода в различных областях. Одним из
самых недавних продуктов подобного рода устремления мысли явилось
возникновение новой дисциплины — математической логики.
В общих чертах аксиоматическая точка зрения может быть харак-
характеризована следующим образом. Доказать теорему в некоторой дедук-
дедуктивной системе — значит установить, что эта теорема есть необходи-
необходимое логическое следствие из тех или иных ранее доказанных предложе-
предложений; последние в свою очередь должны быть доказаны и т.д. Процесс
математического обоснования сводился бы, таким образом, к невыпол-
невыполнимой задаче «бесконечного спуска», если только в каком-нибудь нельзя
было бы остановиться. Но в таком случае должно существовать некото-
некоторое число утверждений — постулатов, или аксиом, которые принима-
принимаются в качестве истинных и доказательство которых не требуется. Из
них можно пытаться вывести все другие теоремы путем чисто логи-
логической аргументации. Если все факты некоторой научной области при-
приведены в подобного рода логический порядок, а именно такой, что лю-
любой из них «выводится» из нескольких отобранных предложений (пред-
(предпочтительно, чтобы таковые были немногочисленны, просты и легко
усваивались), то тогда есть основание сказать, что область представи-
ма в «аксиоматической форме» или «допускает аксиоматизацию». Выбор
предложений-аксиом в широкой степени произволен. Однако мало поль-
пользы, если наши постулаты недостаточно просты или если их слишком
много. Далее, система постулатов должна быть совместимой (непроти-
(непротиворечивой) в том смысле, что никакие две теоремы, которые из них
могут быть выведены, не должны содержать взаимных противоречий,
и полной в том смысле, что всякая теорема, имеющая место в рассмат-

§ 9. Аксиоматика и неевклидова геометрия 257
риваемой области, из них может быть выведена. Желательно также,
чтобы система постулатов была независимой, т. е. чтобы ни один из
них не был логическим следствием остальных. Вопрос о непротиворе-
непротиворечивости и полноте системы аксиом был предметом больших дискуссий.
Различные философские взгляды на источники человеческого знания
обусловили различные, подчас несовместимые точки зрения на основа-
основания математики. Если математические понятия рассматриваются как
субстанциальные объекты в сфере «чистой интуиции», независимые от
определений и отдельных актов мыслительной деятельности человека,
тогда, конечно, в математических результатах не может быть ника-
никаких противоречий, поскольку они представляют собой объективно ис-
истинные предложения, описывающие реальный мир. Если исходить из
такой «кантианской» точки зрения, то никакой проблемы непротиво-
непротиворечивости вообще нет. Но, к сожалению, действительное содержание
математики не удается уложить в столь простые философские рам-
рамки. Представители современного математического интуиционизма не
полагаются на чистую интуицию в ее полном кантовском понимании.
Они признают счетную бесконечность в качестве законного детища ин-
интуиции, но допускают использование лишь конструктивных свойств.
Такие же фундаментальные понятия, как числовой континуум, следу-
следует, с их точки зрения, исключить из употребления, пожертвовав при
этом важными разделами существующей математики (а то, что после
этого остается, оказывается чрезвычайно сложным, причем без особой
надежды на упрощение).
Совершенно другую позицию заняли «формалисты». Они не при-
приписывают математическим понятиям никакой интуитивной реальнос-
реальности и не утверждают, что аксиомы выражают какие-то объективные
истины, относящиеся к объектам чистой интуиции; они (формалис-
(формалисты) заботятся лишь о формальной логической правильности процесса
рассуждений, базирующихся на постулатах. Позиция эта обладает без-
безусловными преимуществами по сравнению с интуиционистской, так
как она предоставляет математике полную свободу действий, нужную
как для теории, так и для приложений. Но она вместе с тем вынуждает
формалистов доказывать, что принятые ими аксиомы, выступающие
теперь в качестве продукта свободного творчества человеческого ин-
интеллекта, не могут привести к противоречию. На протяжении послед-
последних двадцати лет1 предпринимались многочисленные и напряженные
1 Написано в 1941г. О дальнейших работах в этой области, а также по поводу
всей обширной проблематики оснований математики и характеристики различных
направлений, см. [24], [25], [27].
!7 — 340

258 Глава IV
попытки поиска такого рода доказательств непротиворечивости, осо-
особенно по отношению к аксиомам арифметики и алгебры и к понятию
числового континуума. Результаты, полученные в этом направлении,
имеют исключительную важность, но задача в целом еще далеко не
выполнена1. Более того, полученные в последние годы результаты сви-
свидетельствуют о том, что такого рода попытки и не могут привести
к полному успеху — выяснилось, что для некоторых, строго опреде-
определенных и замкнутых систем понятий вообще нельзя доказать, что они
непротиворечивы и в то же время полны. Особенно замечательно то об-
обстоятельство, что все такого рода рассуждения, касающиеся проблем
обоснования, проводятся полностью конструктивными и интуитивно
убедительными методами.
Спор между интуиционистами и формалистами, особенно об-
обострившийся в связи с вопросом о парадоксах теории множеств
(см. стр. 121-122), породил массу страстных выступлений убежден-
убежденных сторонников обеих школ. Математический мир потрясали возгласы
о «кризисе основ». Но эти сигналы тревоги не воспринимались — да и не
следовало их воспринимать — слишком уж всерьез. При всем уважении
к достижениям, завоеванным в борьбе за полную ясность основ, вывод,
что эти расхождения во взглядах или же парадоксы, вызванные спокой-
спокойным и привычным использованием понятий неограниченной общности,
таят в себе серьезную угрозу для самого существования математики,
представляется совершенно необоснованным.
Совершенно независимо от каких бы то ни было философских рас-
рассмотрении и интереса к проблемам оснований аксиоматический под-
подход к предмету математики — самый естественный способ разобрать-
разобраться во всех хитросплетениях взаимосвязей между различными фактами
и выяснить закономерности логического строения объединяющих их
теорий. Не раз случалось, что такое сосредоточение внимания на фор-
формальной структуре, а не на интуитивном смысле понятий облегчает
отыскание обобщений и применений, которые легко было бы упустить
при более интуитивном подходе к делу. Но выдающиеся открытия и
подлинное понимание лишь в исключительных случаях оказывались
результатом применения чисто аксиоматических методов. Подлинный
источник развития математики — это творческая мысль, поддержива-
поддерживаемая интуицией. И если даже считать аксиоматизацию тем идеалом,
к которому стремится математика, было бы непростительной ошибкой
уверовать в то, что аксиоматика сама по себе является сутью матема-
математики. Творческая, конструктивная интуиция математика привносит
1См. предыдущее примечание.

§ 9. Аксиоматика и неевклидова геометрия 259
в математику недедуктивные и иррациональные моменты, уподобляю-
уподобляющие ее музыке или живописи.
Со времен Евклида геометрия неизменно была прототипом аксио-
аксиоматизированной дисциплины. На протяжении столетий система евкли-
евклидовых постулатов была предметом напряженного изучения. Но толь-
только сравнительно недавно стало совершенно ясно, что эти постулаты
должны быть изменены и дополнены, для того чтобы из них могла
быть выведена дедуктивно совокупность предложений элементарной
геометрии. Например, в конце прошлого столетия Паш обнаружил, что
при рассмотрении порядка расположения точек на прямой, т. е. соот-
соотношений, характеризуемых словом «между», требуется особый посту-
постулат. Паш выдвинул в качестве постулата следующее предложение: Ес-
Если прямая пересекает сторону треугольника в точке, не являющейся
вершиной, то она пересекается и еще с одной стороной треугольни-
треугольника. (Невнимательное отношение к этой детали приводит к ряду явных
парадоксов: абсурдные следствия — например, общеизвестное «доказа-
«доказательство» того, что все треугольники равнобедренные — как будто бы
строго «выводятся» из евклидовых аксиом. Этот «вывод» основывается
на неточном выполнении чертежа, причем некоторые прямые пересе-
пересекаются вне треугольника или круга, тогда как на самом деле должны
пересечься внутри.)
В своей знаменитой книге «Grundlagen der Geometrie» (первое из-
издание ее появилось в 1899 г.) Гильберт дал вполне удовлетворительно
построенную систему аксиом геометрии и вместе с тем произвел исчер-
исчерпывающий анализ их взаимной независимости, их непротиворечивости
и полноты.
Во всякую систему аксиом неизбежно входят некоторые неопреде-
неопределимые понятия, например, «точка» или «прямая» в геометрии. Их «зна-
«значение» (или связь с объектами реального мира) для математики несу-
несущественно. Эти понятия должны быть принимаемы чисто абстрактно,
и их математические свойства в пределах дедуктивной системы всеце-
всецело вытекают из тех соотношений между ними, которые утверждаются
в аксиомах. Так, в проективной геометрии естественно начать с основ-
ньы^понятий «точка» и «прямая» и отношения «инцидентности» и сфор-
сформулировать две двойственные аксиомы: «каждые две различные точки
инцидентны с одной и только одной прямой» и «каждые две различные
прямые инцидентны с одной и только одной точкой». В аксиоматичес-
аксиоматической системе проективной геометрии двойственность в формулировке
аксиом обусловливает двойственность в самом построении. Всякой те-
теореме, содержащей в своей формулировке и в доказательстве только
17*

260 Глава IV
двойственные элементы, непременно соответствует двойственная те-
теорема. В самом деле, доказательство исходной теоремы заключается
в последовательном применении некоторых аксиом, и применение в том
же порядке двойственных аксиом составит доказательство двойствен-
двойственной теоремы.
Совокупность аксиом геометрии составляет неявное определение
всех «неопределяемых» геометрических понятий: «точка», «прямая»,
«инцидентность» и т. д. Для применений геометрии важно, чтобы ос-
основные понятия и аксиомы геометрии находились в хорошем соответ-
соответствии с доступными физической проверке утверждениями, касающи-
касающимися «реальных», осязаемых предметов. Физическая реальность, стоя-
стоящая за понятием «точки», есть какой-то очень маленький объект, вроде
небольшого пятнышка, получаемого на бумаге при прикосновении ка-
карандаша, и таким же образом «прямая» представляет собой абстракцию
туго натянутой нити или светового луча. Свойства этих физических
точек и прямых, как можно установить путем проверки, более или ме-
менее соответствуют формальным аксиомам геометрии. Легко себе пред-
представить, что более точно поставленные эксперименты могут вызвать
необходимость в изменении аксиом, если мы хотим, чтобы они давали
адекватное описание физических явлений. Напротив, если бы существо-
существовало заметное отклонение формальных аксиом от физических свойств
предметов, то геометрия, построенная на этих аксиомах, представляла
бы ограниченный интерес. Таким образом, даже с точки зрения фор-
формалиста, есть нечто, что оказывает большее влияние на направления
математической мысли, нежели человеческий разум.
2. Гиперболическая неевклидова геометрия. В системе Ев-
Евклида имеется одна аксиома, относительно которой — на основе со-
сопоставления с эмпирическими данными, с привлечением туго натяну-
натянутых нитей или световых лучей — никак нельзя сказать, является ли
она «истинной». Это знаменитый постулат о параллельных, утвержда-
утверждающий, что через данную точку, расположенную вне данной прямой,
можно провести одну и только одну прямую, параллельную данной.
Своеобразной особенностью этой аксиомы является то, что содержаще-
содержащееся в ней утверждение касается свойств прямой на всем ее протяже-
протяжении, причем прямая предполагается неограниченно продолженной в обе
стороны: сказать, что две прямые параллельны, — значит утверждать,
что у них нельзя обнаружить общей точки, как бы далеко их ни про-
продолжать. Вполне очевидно, что в пределах некоторой ограниченной час-
части плоскости, как бы эта часть ни была обширна, напротив, можно
провести через данную точку множество прямых, не пересекающих-

§9. Аксиоматика и неевклидова геометрия 261
ся с данной прямой. Так как максимально возможная длина линейки,
нити, даже светового луча, изучаемого с помощью телескопа, непре-
непременно конечна, и так как внутри круга конечного радиуса существует
много прямых, проходящих через данную точку и в пределах круга не
встречающихся с данной прямой, то отсюда следует, что постулат Ев-
Евклида никогда не может быть проверен экспериментально. Все прочие
аксиомы Евклида имеют конечный характер, т.е. касаются конечных
отрезков прямых или конечных частей рассматриваемых плоских фи-
фигур. Тот факт, что аксиома параллельности не допускает эмпиричес-
эмпирической проверки, выдвигает на первый план вопрос о том, является ли
она независимой от прочих аксиом. Если бы она была неизбежным ло-
логическим следствием других аксиом, то тогда нужно было бы просто
вычеркнуть ее из списка аксиом и доказывать как теорему с помощью
иных евклидовых аксиом. Много столетий математики пытались найти
такое доказательство; этому способствовало широко распространенное
среди всех, кто занимался геометрией, смутное сознание того, что ак-
аксиома параллельности по своему характеру существенно отличается от
остальных, что ей недостает той убеждающей наглядности, которой,
казалось бы, должно было обладать всякое геометрическое предложе-
предложение, возводимое в ранг аксиомы.
Одна из первых попыток в указанном направлении была сделана
в IV столетии н. э. комментатором Евклида Проклом, который, чтобы
избежать необходимости вводить специальный постулат о параллель-
параллельных прямых, ввел определение, согласно которому прямая, параллель-
параллельная данной прямой, есть геометрическое место точек, расположенных
от нее на одном и том же заданном расстоянии. При этом Прокл упу-
упустил из виду, что таким образом трудность не устраняется, а только
перемещается, так как при его ходе мыслей остается недоказанным,
что названное геометрическое место действительно есть прямая линия.
Так как последнего Прокл доказать не мог, то именно это предложение
ему пришлось бы принять в качестве аксиомы параллельности, и ни-
ничто не было бы выиграно, так как мы можем легко установить, что обе
упомянутые аксиомы эквивалентны между собой. Саккери A667-1733),
а затем Ламберт A728-1777) делали попытки доказать аксиому парал-
параллельности косвенным путем, допуская противоположное утверждение
и выводя из него абсурдные следствия. Но выведенные ими следствия
оказались далеко не абсурдными: это были теоремы неевклидовой гео-
геометрии, получившей позднее дальнейшее развитие. Если бы названные
лица рассматривали свои результаты не как нелепости, а как утверж-
утверждения, свободные от внутренних противоречий, то никому иному, как
ИМ, принадлежала бы заслуга открытия неевклидовой геометрии.

262 Глава IV
Но в те времена любую геометрическую систему, не находящуюся
в абсолютном согласии с евклидовой, непременно стали бы рассматри-
рассматривать как очевидную нелепость. Кант, наиболее влиятельный философ
той эпохи, выразил свое отношение к вопросу, утверждая, что аксиомы
Евклида — не что иное, как неизбежные формы человеческого мыш-
мышления, чем, по его мнению, и объясняется их объективная значимость
по отношению к «реальному» пространству. Эта вера в аксиомы Евкли-
Евклида, как в незыблемые истины, существующие в сфере чистой интуи-
интуиции, была одним из главных догматов кантовой философии. И, однако,
с течением времени ни привычные навыки мышления, ни влияние фи-
философских авторитетов не смогли подавить растущего убеждения, что
неизменные неудачи в поисках доказательства аксиомы параллельнос-
параллельности имели своей причиной не столько недостаток изобретательности со
стороны геометров, сколько тот основной факт, что этот постулат на
самом деле независим от других. (Подобным же образом неудачи в ре-
решении при помощи радикалов общего уравнения пятой степени мало-
помалу привели к подозрению, позднее оправдавшееся, что такое реше-
решение невозможно.) Венгерский математик Бойаи A802-1860) и русский
математик Лобачевский A793-1856) положили конец сомнениям, по-
построивши во всех деталях геометрическую систему, в которой аксиома
параллельности была отвергнута. Когда молодой гениальный энтузи-
энтузиаст Бойаи послал свою работу «королю математики» Гауссу, от кото-
которого с нетерпением ждал поддержки, то получил в ответ уведомление,
что самим Гауссом открытие было сделано раньше, но он воздержался
в свое время от публикации результатов, опасаясь, слишком шумных
обсуждений.
Посмотрим, что же означает независимость аксиомы параллельнос-
параллельности? Эту независимость следует понимать в том смысле, что возможно
свободное от внутренних противоречий построение «геометрических»
предложений о точках, прямых и т. д., исходя из системы аксиом, в ко-
которой аксиома параллельности заменена противоположной. Такое по-
построение называется неевклидовой геометрией. Нужно было интеллек-
интеллектуальное бесстрашие Гаусса, Бойаи и Лобачевского, чтобы осознать,
что геометрия, основанная не на евклидовой системе аксиом, может
быть абсолютно непротиворечивой.
Чтобы убедиться в непротиворечивости новой геометрии, нет на-
надобности развивать во всех подробностях многочисленные теоремы не-
неевклидовой геометрии, как это делали Бойаи и Лобачевский. Мы умеем
теперь строить простые «модели» такой геометрии, удовлетворяющие
всем аксиомам Евклида, кроме аксиомы параллельности. Простейшая

§9. Аксиоматика и неевклидова геометрия 263
модель была указана Феликсом Клейном, работы которого в этой облас-
области стимулировались идеями английского геометра Кэли A821-1895).
В такой модели через данную точку, лежащую вне данной прямой, мож-
можно провести бесчисленное множество «прямых», «параллельных» данной
прямой. Подобного рода геометрия называется геометрией Бойаи-Ло-
бачевского, или «гиперболической» геометрией. (Основание для послед-
последнего наименования будет приведено на стр. 268.)
При построении модели Клейна сначала рас-
рассматриваются объекты обыкновенной евклидовой
геометрии; и затем некоторые из объектов и от-
отношений между ними переименовываются таким
образом, что для их описания оказывается при-
пригодной уже неевклидова геометрия. Эта послед-
последняя, тем самым, не в меньшей мере непротиво-
непротиворечива, чем первоначальная евклидова геометрия,
так как излагается (если посмотреть с другой точ-
точки зрения и описывать другими словами) как со- Рис- НО- Модель не-
вокупность фактов обыкновенной евклидовой гео- евклидовой плоскос-
метрии. С этой моделью можно легко освоиться, ги Клеина
привлекая кое-какие понятия из проективной геометрии.
При проективном преобразовании одной плоскости на другую или
на саму себя (можно после отображения совместить обе плоскости)
окружность, вообще говоря, переходит в некоторое коническое сече-
сечение. Но можно легко показать (доказательства мы не приводим), что
существует бесчисленное множество таких проективных преобразова-
преобразований плоскости на саму себя, при которых данный круг, вместе со все-
всеми заключенными внутри точками, переходит сам в себя. При таких
преобразованиях внутренние точки, как и точки контура, меняют, во-
вообще говоря, свои места, но внутренние точки остаются внутренними,
а точки контура остаются на контуре. (Центр круга, как легко убедить-
убедиться, можно перевести в любую наперед заданную внутреннюю точку.)
Рассмотрим совокупность всех таких преобразований. Конечно, они не
будут оставлять очертания фигур неизменными и потому не являют-
являются движениями в обычном смысле. Но мы теперь сделаем решающий
шаг и назовем их «неевклидовыми движениями» в той геометрии, кото-
которую строим. Посредством этих «движений» можно дальше определить
и «равенство»: две фигуры называются равными, если существует «не-
«неевклидово движение», переводящее одну фигуру в другую.
Перейдем теперь к описанию упомянутой выше клейновой моде-
модели гиперболической геометрии. «Плоскость» состоит только из точек,

264 Глава IV
внутренних по отношению к кругу, внешние точки просто отбрасы-
отбрасываются. Каждая внутренняя точка называется неевклидовой «точкой»,
каждая хорда круга называется неевклидовой «прямой»; «движения» и
«равенства» уже определены выше; проведение «прямой» через две «точ-
«точки» и нахождение «точки» пересечения двух «прямых» совершаются, как
в евклидовой геометрии. Легко убедиться, что новая конструкция удов-
удовлетворяет всем постулатам евклидовой геометрии, с единственным ис-
исключением — постулатом о параллельных прямых. Что этот постулат
здесь не выполняется, видно ясно из того, что через «точку», не лежа-
лежащую на «прямой», можно провести бесчисленное множество «прямых»,
не имеющих общей «точки» с данной прямой. Данная «прямая» есть ев-
евклидова хорда, тогда как в качестве второй «прямой» может быть взята
любая из хорд, проходящих через данную «точку» и не пересекающих
первой «прямой» внутри круга. Описанная простая модель совершенно
достаточна для того, чтобы покончить с основным вопросом, породив-
породившим неевклидову геометрию: она показывает, что аксиома параллель-
параллельности не «выводится» из остальных аксиом евклидовой геометрии. Дей-
Действительно, если бы она «выводилась» из них, то тогда была бы верной
теоремой и по отношению к модели Клейна, а мы видим, что это не
так.
Строго говоря, предыдущая аргументация построена на допущении, что
модель Клейна непротиворечива, т.е. что нельзя доказать вместе с некото-
некоторым утверждением также и противоположного утверждения. Но, во всяком
случае, геометрия модели Клейна непротиворечива в такой же степени, как и
обыкновенная евклидова геометрия, так как теоремы о «точках» и «прямых»
и т. д. модели Клейна представляют собой только своеобразно сформулиро-
сформулированные теоремы евклидовой геометрии. Удовлетворительного доказательства
непротиворечивости аксиом евклидовой геометрии дано не было, если не счи-
считать редукции к аналитической геометрии и в конечном счете к числовому
континууму; а непротиворечивость концепции континуума — также вопрос
открытый1.
Мы привлечем внимание читателя еще к одной детали (впрочем,
стоящей за пределами непосредственно поставленных нами задач) —
именно, к определению неевклидова «расстояния» в модели Клейна.
Это «расстояние» должно быть инвариантно относительно неевклидо-
неевклидовых «движений», так как обыкновенное движение не изменяет обык-
обыкновенного расстояния. Мы знаем, что двойное отношение есть инвари-
инвариант проективного преобразования. Естественно возникает мысль о том,
1 Подробнее об исследованиях в этой области см. упомянутую на стр. 122 книгу
А. Френкеля и И. Бар-Хиллела, содержащую также обширную библиографию.

J9. Аксиоматика и неевклидова геометрия
265
чтобы при определении «расстояния» между дву-
двумя различными точками Р и Q внутри наше-
нашего круга воспользоваться двойным отношени-
отношением (OSQP), где О и S — точки, в которых про-
продолженный в обе стороны отрезок PQ встреча-
встречается с окружностью. Это двойное отношение, в
самом деле, есть положительное число; но взять
это отношение непосредственно в качестве «рас-
«расстояния» PQ не представляется удобным. Дейст-
Действительно, в предположении, что три точки Р, Q,
R лежат на одной прямой, мы должны были бы
иметь равенство PQ + QR = PR, но, вообще говоря,
{OSQP) + (OSRQ) ф (OSPR).
Напротив, справедливо несколько иное равенство
(OSQP) ¦ (OSRQ) = (OSPR);
в самом деле,
Рис. 111. Неевклидо-
Неевклидово расстояние
A)
Свойство A) позволяет определить «расстояние» PQ как логарифм двой-
двойного отношения (а не как само двойное отношение), с таким расчетом,
чтобы обеспечить аддитивность расстояния: PQ = неевклидово «рас-
«расстояние» PQ = \og(OSQP). Это «расстояние» есть положительное чис-
число, так как при Р ф Q (OSQP) > 1.
Из основного свойства логарифма (см. стр. 502) следует, в силу A),
что PQ + QR = PR. По какому основанию брать логарифмы — несу-
несущественно, так как при изменении основания меняется лишь единица
измерения. Между прочим, если одна из точек, скажем Q, приближа-
приближается к окружности, то неевклидово расстояние PQ неограниченно воз-
возрастает. Это означает, что «прямая» нашей неевклидовой модели имеет
бесконечную неевклидову «длину», хотя в евклидовом смысле представ-
представляет собой конечный отрезок.
3. Геометрия и реальность. Модель Клейна показывает, что
гиперболическая геометрия, как формально-дедуктивное построение,
непротиворечива в такой же степени, как и классическая евклидова
геометрия. Возникает вопрос: которой же из двух геометрий следу-
следует отдать предпочтение, когда речь идет об описании геометрических

266 Глава IV
отношений, существующих в физическом мире? Как мы уже отмети-
отметили, эксперимент никоим образом не может решить, проходит ли через
данную точку только одна прямая, параллельная данной прямой, или
бесчисленное множество. Однако в евклидовой геометрии сумма углов
треугольника равна 180°, тогда как в гиперболической геометрии, как
можно показать, она меньше 180°. Гаусс предпринял опытное исследо-
исследование вопроса о том, как обстоит дело с суммой углов треугольника
с физической точки зрения: он очень тщательно измерил углы в тре-
треугольнике, образованном тремя достаточно удаленными друг от друга
горными пиками, и в пределах возможных ошибок измерений сумма
углов оказалась равной 180°. Если бы результат был заметно мень-
меньше 180°, то отсюда следовало бы, что гиперболическая геометрия лучше
подходит для описания внешнего мира. Но эксперимент не решил ни-
ничего, так как для небольших треугольников со сторонами длиной всего
в несколько миль отклонение от 180°, которое предвидит гиперболичес-
гиперболическая геометрия, могло быть столь ничтожным, что гауссовы инструмен-
инструменты его не обнаружили. Таким образом, не дав решающих результатов,
эксперимент все же показал, что евклидова и гиперболическая геомет-
геометрии, различающиеся только в очень обширных частях пространства,
для сравнительно малых фигур оказываются практически одинаково
пригодными для употребления. Поэтому, если рассматриваются только
локальные свойства пространства, то выбор между двумя геометрия-
геометриями остается делать лишь по принципу простоты. Но так как работать
с евклидовой геометрией гораздо легче, чем с гиперболической, то мы
и пользуемся именно ею, покуда рассматриваются небольшие (порядка
нескольких миллионов миль!) расстояния. Однако нет оснований ожи-
ожидать, что она, наверное, оказалась бы подходящей при описании физи-
физического мира в целом, во всех его обширных пространствах. Положение
вещей в геометрии совершенно такое же, какое существует и в физике,
где системы Ньютона и Эйнштейна дают неразличимые результаты
при малых расстояниях и скоростях, но обнаруживают расхождение,
когда рассматриваются большие величины.
Научно-революционное значение открытия неевклидовой геомет-
геометрии заключается в том, что оно разрушило представление об аксиомах
Евклида как о непоколебимой математической схеме, к которой при-
приходится приспособлять наши экспериментальные знания о физической
реальности.
4. Модель Пуанкаре. Математик волен видеть «геометрию» во
всякой непротиворечивой системе аксиом, говорящих о «точках», «пря-
«прямых» и т.д.; но его исследования только в том случае будут полезны

§9. Аксиоматика и неевклидова геометрия
267
Рис. 112. Модель неев-
неевклидовой плоскости Пу-
Пуанкаре
для физика, если система аксиом находится
в соответствии с поведением физических объ-
объектов в реальном мире. Мы хотели бы те-
теперь, с этой точки зрения, разобраться в смыс-
смысле утверждения: «Свет распространяется по
прямой линии». Если в этом утверждении со-
содержится физическое определение «прямой ли-
линии», то систему геометрических аксиом сле-
следует выбирать таким образом, чтобы полу-
получилось соответствие с поведением световых
лучей. Вообразим, следуя Пуанкаре, что мир
состоит из внутренности круга С и что во
всякой точке скорость света пропорциональна
расстоянию точки от окружности. Можно тогда доказать, что свет бу-
будет распространяться по круговым дугам, образующим прямые углы с
окружностью С. В таком мире геометрические свойства «прямых ли-
линий» (определенных как световые лучи) будут отличаться от свойств
евклидовых прямых. В частности, не будет евклидовой аксиомы па-
параллельности, так как через данную точку пройдет бесчисленное мно-
множество «прямых линий», не пересекающихся с данной «прямой линией».
Можно обнаружить, что «точки» и «прямые линии» в описываемом ми-
мире будут обладать в точности теми же свойствами, какими обладают
«точки» и «прямые» на модели Клейна. Другими словами, мы получи-
получили новую модель гиперболической геометрии. Но евклидову геометрию
также можно применять в этом мире: тогда выйдет, что световые лучи,
которые уже не будут неевклидовыми «пря-
«прямыми линиями», распространяются по кру-
кругам, перпендикулярным к окружности С. Та-
Таким образом, одна и та же физическая си-
ситуация способна быть описанной различными
геометрическими системами, если предполо-
предположить, что физические объекты (в нашем слу-
случае — световые лучи) связаны с различными
понятиями в этих системах:
Световой луч —> «прямая линия» — гипербо-
гиперболическая геометрия
Световой луч —> «окружность» — евклидова
геометрия.
Так как в евклидовой геометрии понятие прямой линии сопостав-
сопоставляется с поведением светового луча в однородной среде, то, говоря, что
Рис. 113. «Прямые линии»
в геометрии Римана

268 Глава IV
геометрия в описании мира внутри С гиперболическая, мы утвержда-
утверждали бы только то, что физические свойства световых лучей в этом мире
те же самые, что и свойства «прямых» гиперболической геометрии.
5. Эллиптическая, или риманова, геометрия. В евклидовой
геометрии, как и в гиперболической геометрии Бойаи-Лобачевского,
молчаливо допускается, что всякая прямая бесконечна (бесконечность
прямой существенно связана с отношением «быть между» и аксиома-
аксиомами порядка). Но после того как гиперболическая геометрия открыла
путь к свободному построению геометрий, естественно возник вопрос
о том, нельзя ли осуществить построение таких неевклидовых геомет-
геометрий, в которых прямые линии конечны и замкнуты. Разумеется, в та-
таких геометриях теряют силу не только постулат о параллельных, но и
аксиомы порядка. Современные исследования выяснили значение этих
геометрий для новейших физических теорий. Впервые такие геомет-
геометрии были подвергнуты рассмотрению в речи, произнесенной в 1851 г.
Риманом при вступлении его в должность приват-доцента в Геттин-
генском университете. Геометрии с замкнутыми конечными прямыми
могут быть построены без каких бы то ни было противоречий. Вооб-
Вообразим двумерный мир, состоящий из поверхности S сферы, причем
под «прямыми» условимся понимать большие круги сферы. Это был
бы самый естественный способ описывать «мир» мореплавателя: ду-
дуги больших кругов являются кратчайшими кривыми, связывающими
две точки на сфере, а это как раз и есть характеристическое свойст-
свойство прямых на плоскости. В рассматриваемом двумерном мире всякие
две «прямые» пересекаются, так что из внешней точки нельзя провести
ни одной «прямой», не пересекающейся с данной (т.е. ей параллельной).
Геометрия «прямых» в этом мире называется эллиптической геомет-
геометрией. Расстояние между двумя точками в такой геометрии измеряется
просто как длина кратчайшей дуги большого круга, проходящего через
данные точки. Углы измеряются так же, как и в евклидовой геометрии.
Самым типическим свойством эллиптической геометрии мы считаем
несуществование параллельных.
Следуя Риману, мы можем обобщить эту геометрию следующим
образом. Рассмотрим «мир», состоящий из некоторой кривой поверх-
поверхности в пространстве (не обязательно сферы) и определим «прямую
линию», проходящую через две точки, как кратчайшую кривую («геоде-
(«геодезическую»), соединяющую эти точки. Точки поверхности можно раз-
разбить на два класса: 1°. Точки, в окрестности которых поверхность по-
подобна сфере в том отношении, что она вся лежит по одну сторону от
касательной плоскости в этой точке. 2°. Точки, в окрестности кото-

j9. Аксиоматика и неевклидова геометрия
269
Рис. 114. Эллиптическая точка
Рис. 115. Гиперболическая точка
рых поверхность седлообразна — лежит по обе стороны касательной
плоскости. Точки первого класса называются эллиптическими точка-
точками поверхности — по той причине, что при небольшом параллельном
перемещении касательной плоскости она пересечет поверхность по кри-
кривой, имеющей вид эллипса; точки же второго класса носят название
гиперболических, так как при аналогичном перемещении касательной
плоскости получается пересечение с поверхностью, напоминающее ги-
гиперболу. Геометрия геодезических «прямых» в окрестности точки по-
поверхности является эллиптической или гиперболической, смотря по то-
МУ, будет ли сама точка эллиптической или гиперболической. На этой
Модели неевклидовой геометрии углы измеряются, как в обыкновенной
евклидовой геометрии.

270 Глава 4
Изложенная идея была развита Риманом дальше: он рассмотрел
геометрии пространства, аналогичные только что разобранным геомет-
геометриям поверхности. По Риману, «кривизна» пространства, меняясь от
точки к точке, определяет характер геометрии в окрестности точки.
«Прямые линии» у Римана — геодезические кривые. В эйнштейновой
общей теории относительности геометрия пространства есть риманова
геометрия; свет распространяется по геодезическим линиям, а кривиз-
кривизна пространства в каждой точке определяется в зависимости от свойств
материи в окрестности точки.
Возникнув из чисто аксиоматических изысканий, неевклидова гео-
геометрия в наши дни стала чрезвычайно полезным аппаратом, допуска-
допускающим различные применения при изучении физической реальности.
В теории относительности, в оптике, в общей теории колебаний неев-
неевклидово описание явлений описывается в ряде случаев гораздо более
адекватным физической реальности, чем евклидово.
Приложение.
Геометрия в пространствах более чем трех
измерений
1. Введение. То «реальное» пространство, которое служит сре-
средой нашего физического опыта, имеет три измерения, плоскость имеет
два измерения, прямая — одно. Наша, в обычном смысле понимаемая,
пространственная интуиция решительно ограничена тремя измерени-
измерениями — и дальше не простирается. Тем не менее во многих случаях
вполне уместно говорить о «пространствах», имеющих четыре или бо-
более измерений. В каком же смысле допустимо говорить об п-мерном
пространстве, где п > 3, и для чего могут быть полезны такие про-
пространства? Ответ можно дать, став или на аналитическую, или на
геометрическую точку зрения. Терминологию n-мерного пространст-
пространства дозволительно рассматривать только как образный язык, служащий
для выражения математических идей, находящихся вне пределов обык-
обыкновенной геометрической интуиции.
2. Аналитический подход. Мы уже имели случай обратить
внимание читателя на изменение роли аналитической геометрии, про-
происшедшее на протяжении ее развития. Точки, прямые, кривые линии
и т.д. первоначально рассматривались как чисто геометрические объ-

Приложение 271
екты, и задачей аналитической геометрии было всего-навсего, сопо-
сопоставляя им координаты или уравнения, интерпретировать и развивать
дальше геометрическую теорию алгебраическими или аналитически-
аналитическими методами. Но с течением времени постепенно начала утверждаться
противоположная точка зрения. Число х, или пара чисел х, у, пли трой-
тройка чисел х, у, z стали рассматриваться как исходные, основные объек-
объекты и эти аналитические объекты, далее, конкретизировались, или, еще
лучше сказать, «визуализировались» в виде точек на прямой, на плос-
плоскости, в пространстве. И тогда геометрический язык стал служить для
того, чтобы констатировать наличие тех или иных соотношений между
числами. При этом мы лишаем геометрические объекты их самостоя-
самостоятельного и независимого значения и говорим, что пара чисел х, у есть
точка на плоскости, совокупность всех пар х, у, удовлетворяющих ли-
линейному уравнению L(x, у) = ах + by + с = 0 (где а, Ь, с — данные
постоянные числа), есть прямая линия и т.д. Такие же определения
устанавливаются и для трехмерного пространства.
Даже в том случае, когда мы занимаемся собственно алгебраичес-
алгебраической проблемой, язык геометрии нередко представляется вполне удоб-
удобным для краткого и совершенно точного описания фактов, и геометри-
геометрическая интуиция начинает работать, подсказывая правильные алгебра-
алгебраические процедуры. Например, решая систему трех линейных уравне-
уравнений с тремя неизвестными х, у, z
L(x, у. z) = ax + by + cz + d = О,
L'{x, у. z) = a'x + b'y + c'z + d! = 0,
L"(x, y, z) = a"x + b"y + c"z + d" = 0,
мы истолковываем стоящую перед нами задачу геометрически и гово-
говорим, что в трехмерном пространстве Яз требуется найти точку пере-
пересечения трех плоскостей, заданных уравнениями L — 0, L' = 0, L" = 0.
Другой пример: рассматривая все такие числовые пары х, у, что х > 0,
мы скажем, что имеем дело с полуплоскостью, расположенной вправо
от оси у. В более общем случае совокупность числовых пар х, у, для
которых выполняется неравенство
L(x, у) = ах Л-by + с > 0,
интерпретируется как полуплоскость, лежащая по одну сторону пря-
прямой L = 0, а совокупность таких числовых троек х, у, z, что
L(x, у, z) = ах + by + cz + d > 0,
~~ Как «полупространство», определяемое плоскостью L = 0.

272 Глава 4
После этих разъяснений нам совсем легко перейти к «четырехмер-
«четырехмерному» или даже к «n-мерному» пространству. Рассмотрим четверку чи-
чисел х, у, z, t. Скажем, что такая четверка представляет собой точку,
или, еще проще, есть точка в четырехмерном пространстве Щ. Вообще,
по определению, точка n-мерного пространства Rn, есть не что иное,
как система из п действительных чисел Xi, х2, ••• , хп, записанных
в определенном порядке. Не так важно, что мы не «видим» этой точки.
Геометрический язык не перестает быть вполне понятным в случае, ес-
если идет речь об алгебраических свойствах п переменных. Дело в том,
что многие алгебраические свойства линейных уравнений и т.п. со-
совершенно не зависят от числа входящих переменных, или, как принято
говорить, от размерности пространства этих переменных. Мы назовем,
таким образом, «гиперплоскостью» совокупность всех таких точек х\,
Х2, ••• , хп в n-мерном пространстве Rn, которые удовлетворяют ли-
линейному уравнению
L(xi, х2, ... , хп) = aiXi + 0,2X2 + ... + апхп +6 = 0.
Точно так же основная алгебраическая задача решения системы п ли-
линейных уравнений с п неизвестными
' Li(xi, х2, ••• , in) = 0,
2{xi, х2, ... , хп) = 0,
Ln{xi, х2, ... , хп) - 0
истолковывается на геометрическом языке как нахождение точки пе-
пересечения п гиперплоскостей L\ = 0, L2 = 0, ... , Ln = 0.
Преимущество такого геометрического способа описывать мате-
математические факты заключаются в том, что он подчеркивает некото-
некоторые обстоятельства алгебраического порядка, которые не зависят от
числа измерений п и вместе с тем в случае п ^ 3 могут быть наглядно
интерпретированы. Во многих приложениях употребление геометри-
геометрической терминологии имеет также преимущество краткости, а вместе
с тем облегчает аналитические рассуждения, а иногда руководит ими
и направляет их в должную сторону. Теория относительности снова
может быть приведена здесь в качестве примера области, в которой
существенный успех был достигнут по той причине, что три простран-
пространственные координаты х, у, z и временная координата t «события» были
объединены в одно «пространственно-временное» четырехмерное мно-
многообразие х, у, z, t. Подчиняя, таким образом, «пространство-время»

Приложение 273
этой аналитической схеме и наделяя его, кроме того, свойствами неев-
неевклидовой геометрии, удалось описать многие весьма сложные ситуации
с замечательной простотой. Столь же полезными оказались п-мерные
пространства в механике, в статистической физике, не говоря уже о са-
самой математике.
Приведем еще кое-какие чисто математические примеры. Совокуп-
Совокупность всех кругов на плоскости образует трехмерное многообразие, так
как круг с центром х, у и радиусом t может быть изображен точкой
с координатами х, у, t. Так как радиус круга есть положительное число,
то совокупность рассматриваемых точек заполняет полупространство.
Таким же образом совокупность всех сфер в обыкновенном трехмерном
пространстве образует четырехмерное многообразие, так как каждая
сфера с центром х, у, z и радиусом t может быть представлена точкой
с координатами х, у, z, t. Куб в трехмерном пространстве с центром
в начале координат, ребрами длины 2 и гранями, параллельными коор-
координатным плоскостям, состоит из совокупности всех точек xi, Х2, Хз,
для которых |a;i| ^ 1, |a?21 ^ 1) |жз| ^ 1- Так же точно «куб» в п-мерном
пространстве Rn с центром в начале координат, «ребрами» длины 2
и «гранями», параллельными координатным плоскостям, определяет-
определяется как совокупность точек х\, х^, ¦¦-, хп, для которых одновременно
справедливы неравенства |a;i| ^ 1, |я?21 ^ 1, •••, \хп\ ^ 1- «Поверхность»
такого куба состоит из всех точек, для которых хотя бы в одном из
этих соотношений имеет место знак равенства. Поверхностные элемен-
элементы размерности п — 2 состоят из точек, для которых знак равенства
стоит по меньшей мере два раза; и т.д.
Упражнение. Дайте описание поверхности такого куба в трехмерном,
четырехмерном, n-мерном пространствах.
*3. Геометрический, или комбинаторный, подход. Хотя
аналитический подход к n-мерной геометрии чрезвычайно прост и удо-
удобен для многих приложений, все же следует упомянуть и о другом ме-
методе, носящем чисто геометрический смысл. Он основан на редукции
от n-мерных к (п — 1)-мерным данным и тем открывает возможность
определять многомерные геометрии с помощью процесса математичес-
математической индукции.
Начнем с того, что рассмотрим контур треугольника ABC в двух
Измерениях. Разрезая его в точке С и затем поворачивая стороны АС
и ВС соответственно около Аи В, мы выпрямим контур в прямолиней-
прямолинейный отрезок (рис. 116), на котором точка С будет фигурировать дваж-
Дьь Полученная одномерная фигура дает исчерпывающее представле-
представление контура двумерного треугольника. Сгибая фигуру в точках А и В
18 - 340

274 Глава 4
В
-о
А В
о о
в с
о о
Рис. 116. Определение треугольника по сторонам с сопоставленными друг
другу концами
и добившись совпадения двух точек С, мы имеем возможность вос-
восстановить треугольник. Но важно то, что сгибать вовсе и не нужно.
Достаточно условиться, что мы «идентифицируем» (т.е. не будем раз-
различать) обе точки С, несмотря на то, что эти две точки и не совпадают
в обычном смысле. Можно сделать еще следующий шаг: разрезая фи-
фигуру также и в точках А и В, мы получим три отрезка С А, АВ, ВС,
которые при желании можно опять сложить таким образом, чтобы был
восстановлен «настоящий» треугольник ABC, причем пары идентифи-
идентифицируемых точек совпадут между собой. Идея идентифицировать раз-
различные точки в данной совокупности отрезков, чтобы из них построить
многоугольный контур (в нашем случае — треугольник), практически
иногда оказывается очень полезной. Если нужно отправить в дальнее
путешествие какое-нибудь соединение из металлических балок, напри-
например, мостовую ферму, то удобнее всего упаковать сложенные вмес-
вместе, предварительно разъединенные балки, обозначив одними и теми же
знаками те концы различных балок, которые должны быть соединены
вместе. Такое собрание балок с мечеными концами совершенно экви-
эквивалентно пространственной конструкции. Предыдущее замечание при-
приводит к мысли о том, как можно «разнять» двумерный многогранник
в трехмерном пространстве, заменяя его фигурами низших измерений.
Возьмем, например, поверхность куба (рис. 117). Ее сейчас же можно
свести к системе из шести квадратов, стороны которых надлежащим
образом идентифицированы; следующий шаг будет состоять в том, что-
чтобы, заменить эту систему квадратов системой из 12 прямолинейных
отрезков с надлежащим образом идентифицированными концами.
Вообще какой угодно многогранник в трехмерном пространстве Яз
приводится таким образом или к системе плоских многоугольников,
или к системе прямолинейных отрезков.

Приложение
275
4
1
7
6
I
W
3
2
8
5
II
3
2
8
4
/Я
V/
7
6
7
3
VI
4 3;
I
V
5 6
III
lo-
3<^
3o-
-06 4»-
-o4 5<-
-o2
-об
Рис. 117. Определение куба по сопоставленным друг другу вершинам и реб-
ребрам
Упражнение. Выполнять указанную редукцию для всех правильных
многогранников (см. стр. 318).
Теперь уже ясно, что мы можем обратить ход наших рассуждений,
определяя многоугольник на плоскости с помощью системы прямоли-
прямолинейных отрезков и многогранник в пространстве R3 — с помощью сис-
системы многоугольников в i?2 или же, при условии дальнейшей редукции,
с помощью опять-таки прямолинейных отрезков. Но тогда совершенно
естественно определить «многогранник» в четырехмерном пространст-
пространстве Д4 с помощью системы многогранников в Дз, при надлежащей иден-
идентификации из двумерных граней; «многогранник» вй5 — с помощью
«многогранников» в i?4 и т. д. В конечном счете всякий «многогранник»
в Rn сводится к системе отрезков.
Останавливаться на этом вопросе дальше мы лишены возможности.
Добавим лишь несколько замечаний, не приводя доказательств. «Куб»
в R4 ограничен 8 трехмерными кубами, из которых каждый имеет
со своими «соседями» по идентифицированной двумерной грани. Та-
Такой куб имеет 16 вершин, в каждой вершине сходятся по четыре ребра;
ребер всего имеется 32. В Ri существует шесть правильных многогран-
многогранников. Кроме «куба», имеется один, ограниченный 5 правильными тет-
18*

276
Глава 4
Рис. 118. Простейшие элементы в 1, 2, 3, 4 измерениях
раэдрами. один, ограниченный 16 тетраэдрами, один, ограниченный 24
октаэдрами, один, ограниченный 120 додекаэдрами, и еще один, огра-
ограниченный 600 тетраэдрами. Доказано, что в Rn при п > 4 существует
только 3 правильных многогранника: один с п + 1 вершинами, ограни-
ограниченный п + 1 многогранниками из Rn_i, имеющими по п(п — 2)-мер-
ных граней; один с 2П вершинами, ограниченный In многогранниками
из Rn-i, имеющими по 2п — 2(п — 2)-мерных граней; и еще один с 2п
вершинами, ограниченный 2П многогранниками из Rn-i, имеющими
по п(п - 2)-мерных граней.
Упражнение. Сравнить определение «куба» из Ra, данное в пункте 2,
с определением, данным в настоящем пункте, и установить, что прежнее
«аналитическое» определение куба равносильно настоящему «комбинаторно-
«комбинаторному».
Со структурной, или «комбинаторной», точки зрения простейши-
простейшими геометрическими фигурами размерности 0, 1, 2, 3 являются соот-
соответственно точка, отрезок, треугольник, тетраэдр. Ради единообразия
символики обозначим фигуры этого типа соответственно То, Т\, Тг, Тз.
(Значки указывают на размерность.) Структура каждой из этих фигур
характеризуется тем, что каждая фигура типа Тп имеет п+ 1 вершин и
каждое подмножество из i+ 1 вершин фигуры типа Тп (г = 0, 1, ... , п)
определяет некоторую фигуру типа Tj. Например, трехмерный тетра-
тетраэдр Т3 имеет 4 вершины, 6 ребер и 4 грани.
Ясно, как будет дальше. Мы определим четырехмерный «тетра-
«тетраэдр» Т^ как множество, состоящее из 5 вершин, причем каждое подмно-
подмножество из 4 вершин порождает фигуру типа Тз, каждое подмножество
из 3 вершин — фигуру типа Тг и т.д. фигура типа Т± схематически
показана на рис. 118: мы видим, что у нее 5 вершин, 10 ребер, 10 тре-
треугольных граней и 5 тетраэдров.
Обобщение на п измерений не представляет труда. Из теории со-
соединений известно, что существует ровно CJ = — таких различ-
г!(г — г)!

Приложение 277
ных подмножеств по г объектов, которые могут быть составлены из
множества г объектов. Поэтому n-мерный «тетраэдр» содержит
Cf+1 = п + 1 вершин (фигур типа То),
<?2n+1 = гт^ггцт ребер (фигур типа Г1)'
С?+1 = треугольников (фигур типа Тг),
3!(п — 2)!
C^+i1 = 1 фигуру типа Тп.
Упражнение. Нарисовать схематически фигуру типа Ть и определить
число фигур типа Т;, в ней содержащихся (i = 0, 1, ... , 5).

Глава V
Топология
Введение
В середине XIX столетия возникло совершенно новое течение в гео-
геометрии, которому было суждено вслед за тем стать одной из глав-
главных движущих сил современной математики. Предметом новой отрас-
отрасли, называемой топологией (analysis situs), является изучение свойств
геометрических фигур, сохраняющихся даже тогда, когда эти фигуры
подвергаются самым резким, самым решительным преобразованиям,
уничтожающим все их и метрические и проективные свойства.
Одним из великих геометров этой эпохи был А.Ф.Мебиус A790-1868),
человек, научная карьера которого, по свойственному ему недостатку
самоутверждения, оказалась довольно ограниченной: он занимал мало-
маловыдающуюся должность астронома в одной из второразрядных немец-
немецких обсерваторий. В возрасте шестидесяти восьми лет он представил
Парижской Академии мемуар об «односторонних» поверхностях, содер-
содержащий кое-какие из наиболее изумительных фактов в новой отрасли
геометрии. Подобно многим другим важным научным работам, его ру-
рукопись ряд лет залежалась на полках Академии, пока обстоятельства не
сложились так, что ее опубликовал сам автор. Независимо от Мебиуса
геттингенский астроном И. Листинг A808-1882) сделал подобные же от-
открытия и, будучи побуждаем Гауссом, в 1847 г. издал небольшую книгу
«Vorstudien zur Topologie». Когда Бернгард Риман A826-1866) прибыл
в Геттинген, чтобы стать там студентом, математическая атмосфера
этого университетского города уже была насыщена острым любопыт-
любопытством по отношению к новым и странным геометрическим идеям. Ско-
Скоро он осознал, что именно в них нужно искать разгадку самых глубоких
свойств аналитических функций комплексного переменного. Поздней-
Позднейшее развитие топологии, вероятно, едва ли обязано чему-либо в такой
степени, как великолепному зданию римановой теории функций, в ко-
которой топологические концепции имеют самое фундаментальное значе-
значение.
На первых порах своеобразие методов, которыми приходилось дей-
действовать в новой области, воспрепятствовало тому, чтобы полученные
здесь результаты были изложены в традиционной дедуктивной форме,
типичной для элементарной геометрии.

§1. Формула Эйлера для многогранников 279
Происходило нечто совсем иное: так, Пуанкаре, делая смелые шаги
вперед, был вынужден широко и откровенно опираться на геометри-
геометрическую интуицию. Даже в наши дни изучающий топологию явствен-
явственно ощущает, что при слишком большой заботе о формальной безупреч-
безупречности существенно геометрическое содержание упускается из виду и
тонет в массе деталей. Впрочем, как бы то ни было, нужно рассмат-
рассматривать как особое достижение то обстоятельство, что самые недавние
работы по топологии включили эту отрасль геометрии в круг впол-
вполне строго построенных математических дисциплин, для которых ин-
интуиция была и остается источником, но не конечным критерием ис-
истины. По мере развития процесса «формализации» топологии, идущего
от Л. Э. И. Брауэра, удельный вес топологии по отношению к математи-
математике в целом непрерывно возрастал. Существенные успехи в указанном
направлении принадлежат американским математикам, в частности,
О. Веблену, Дж. У. Александеру и С.Лефшетцу.
Хотя топологию можно с полной определенностью назвать про-
продуктом последнего столетия, необходимо все же отметить, что еще и
раньше было сделано несколько открытий, которые, как вытекает из
современной систематики математических знаний, имеют ближайшее
отношение к топологии. Из них самым крупным, несомненно, являет-
является установление формулы, связывающей числа вершин, ребер и граней
простого многогранника: она была подмечена уже Декартом в 1640 г.,
позднее переоткрыта и использована Эйлером в 1752 г.; характерные
черты топологического утверждения в этой формуле стали очевидны-
очевидными гораздо позднее — после того как Пуанкаре в «формуле Эйлера» и ее
обобщениях усмотрел одну из центральных теорем топологии. Итак, по
причинам как исторического, так и внутреннего порядка мы начнем
наше знакомство с топологией именно с формулы Эйлера. Так как при
первых шагах в неизведанной области идеал безупречной строгости во-
вовсе не обязателен и даже мало желателен, то мы не поколеблемся по
временам обращаться непосредственно к интуиции читателя.
§ 1. Формула Эйлера для многогранников
Хотя в античной геометрии изучение многогранников занимало
одно из центральных мест, только Декарту и Эйлеру было суждено
открыть следующее предложение: пусть V — число вершин простого
многогранника, Е — число ребер, F — число граней: тогда непременно
V -E + F = 2. A)

280
Глава V
Рис. 119. Правильные многогранники
Под многогранником здесь подразумевается тело, поверхность кото-
которого состоит из конечного числа граней, имеющих форму многоуголь-
многоугольников. В случае правильных многогранников все многоугольники кон-
конгруэнтны и все плоские углы при вершинах равны между собой. Много-
Многогранник называется простым, если в нем нет «дыр», так что посредст-
посредством непрерывной деформации его поверхность может быть переведена
в поверхность сферы. На рис. 120 изображен простой многогранник, ко-
который не является правильным; на рис. 121 изображен многогранник,
который не является простым.
Предлагаем читателю проверить справедливость формулы Эйлера
для всех многогранников, представленных на рис. 119 и 120; но пусть
он убедится также, что для многогранника на рис. 121 эта формула
неверна.
Переходя к доказательству формулы Эйлера, вообразим, что наш
многогранник внутри пустой и что поверхность его сделана из тонкой

jl. Формула Эйлера для многогранников
281
Рис. 120. Простой многогран- Рис. 121. Непростой много-
ник V — E+F — 9 — 18+11 = 2 гранник V — Е + F = 16 —
-32+ 16 = 0
резины. Тогда, вырезав предварительно одну из граней пустого внутри
многогранника, можно оставшуюся поверхность деформировать таким
образом, что она расстелется по плоскости. Конечно, при этом и гра-
грани многогранника и углы между ребрами испытают резкие изменения.
Но «сетка», составленная из вершин и ребер на плоскости, будет содер-
содержать то же число вершин и ребер, что и первоначальный многогранник,
тогда как число граней станет на одну меньше, так как одна грань бы-
была вырезана. Мы убедимся теперь, что для полученной нами сетки на
плоскости будет справедливо равенство V — Е + F = 1; тогда, добав-
добавляя вырезанную грань, для первоначального многогранника получим
равенство V - Е + F = 2.
Прежде всего «триангулируем» плоскую сетку следующим образом.
Если в сетке имеются многоугольники с числом углов, большим трех,
то, выбрав один из них, проведем в нем какую-нибудь диагональ. В ре-
результате каждое из чисел Е и F увеличится на единицу, но значение
выражения V — Е + F от этого не изменится. Будем и дальше про-
проводить диагонали, соединяя пары точек (рис. 122), пока сетка не ока-
окажется состоящей из одних только треугольников (в чем и заключается
наша ближайшая цель). В триангулированной сетке величина V — E + F
имеет то же значение, какое имела и до триангуляции, так как прове-
проведение каждой новой диагонали этого значения не меняет. Некоторые из

282
Глава V
\ У
\
\\
\
\
\
в /
1
\
\
\
\
\
\
Рис. 122. Доказательство теоремы Эйлера
треугольников, далее, имеют ребра (проще сказать — стороны), при-
принадлежащие к «границе» триангулированной сетки. Некоторые из этих
треугольников (например, ABC) имеют лишь одно ребро на границе,
другие — по два. Возьмем один из такого рода «граничных» треуголь-
треугольников и удалим из него все то, что не принадлежит какому-нибудь
другому треугольнику. Так, в треугольнике ABC удалим ребро АС и
саму грань, оставляя вершины А, В, С и ребра АВ и ВС, но в тре-
треугольнике DEF удалим грань, два ребра DF и FE и вершину F. При
«уничтожении» треугольника ABC числа Е и F уменьшаются на 1, а У
не изменяется, так что V — E + F также не изменяется. При уничтоже-
уничтожении треугольника типа DEF V уменьшится на 1, Е на 2 и F на 1, так
что опять-таки V - Е + F не изменится. Последовательное осущест-
осуществление таких удалений граничных треугольников (причем всякий раз
меняется и сама граница) приводит, наконец, к одному-единственному
треугольнику, имеющему, очевидно, три ребра, три вершины и одну
грань. Для образуемой им совсем простой сетки V — Е + F = 3 — 3 +
+ 1 = 1. Но мы видели, что при «уничтожении» каждого треугольни-
треугольника V — Е + F не изменялось. Значит, V — Е + F должно было равняться
единице и для первоначальной плоской сетки, а также и для того мно-
многогранника с вырезанной гранью, из которого была получена плоская
сетка. Отсюда следует, что для исходного многогранника (до выреза-
вырезания грани) должно было иметь место равенство V — Е + F = 2. Этим
и заканчивается доказательство теоремы Эйлера.
С помощью теоремы Эйлера легко показать, что существует не более пя-
пяти типов правильных многогранников. Предположим, что правильный мно-
многогранник имеет F граней, из которых каждая есть правильный п-угольник,

§1. Формула Эйлера для многогранников 283
и что у каждой вершины сходится г ребер. Считая ребра один раз по граням,
другой — по вершинам, получим, во-первых,
nF = 2Е B)
(так как каждое ребро принадлежит двум граням и, следовательно, считается
дважды в произведении nF) и, во-вторых,
rV = 2Е C)
(так как каждое ребро упирается в две вершины). Тогда равенство Эйлера A)
нам дает
нам дает
или
2.Е , IE тр _ 0
-JJ- + —-S-2,
+ = + D)
п + г 2 + Е' (>
Заметим прежде всего, обращаясь к рассмотрению последнего соотношения,
что л ^ 3 и г ) 3, так как многоугольник имеет не меньше трех сторон
и в каждой вершине сходится не менее трех граней. С другой стороны, оба
числа п и г не могут быть более 3, так как в противном случае левая часть
равенства D) не превышала бы — и равенство было бы невозможно ни при
каком положительном значении Е. Итак, нам остается выяснить, какие зна-
значения может принять г, если п = 3, и какие значения может принять п,
если г = 3. Подсчитав все возникающие возможности, мы получим число
типов правильных многогранников.
При п = 3 равенство D) принимает вид
I _ I - 1
г 6 Е'
г может здесь равняться 3, 4 или 5 F или большее значение исключается,
так как — положительно.) При этих значениях п и г оказывается, что Е
Е
соответственно равно 6, 12 или 30. Так получаются многогранники: тетраэдр,
октаэдр и икосаэдр.
Таким же образом, при г = 3 равенство D) принимает вид
1-1 = 1.
п 6 Е'
из которого следует, что п = 3, 4 или 5, и соответственно, Е — 6, 12 или 30.
Получаются многогранники: тетраэдр, куб и додекаэдр.
Подставляя полученные значения п, г и Е в соотношения B) и C), мы
Установим число вершин V и число граней F соответствующих многогран-
многогранников.

284 Глава V
Рис. 123. Поверхности, топологически эквивалентные
§ 2. Топологические свойства фигур
1. Топологические свойства. Мы установили, что формула
Эйлера справедлива для случая любого простого многогранника. Но
эта формула не теряет смысла и значимости также и применитель-
применительно к иным, гораздо более общим случаям: вместо многогранников эле-
элементарной геометрии с плоскими гранями и прямыми ребрами можно
взять простые «многогранники», у которых «гранями» будут кривые по-
поверхности, а «ребрами» — кривые линии, или можно нарисовать «грани»
и «ребра» на поверхности, например, шара. Больше того, вообразим, что
поверхность многогранника или сферы сделана из тонкого слоя резины;
тогда формула Эйлера сохранится, как бы ни была деформирована рас-
рассматриваемая поверхность — путем изгибаний, сжатий, растяжений
и т.д., лишь бы резиновый слой не был порван. Действительно, форму-
формула Эйлера относится только к числу вершин, ребер и граней; длины же,
площади, двойные отношения, кривизна и т. п., как и иные понятия эле-
элементарной или проективной геометрии, в данном случае никакой роли
не играют.
Мы уже указывали, что элементарная геометрия имеет дело с ве-
величинами (расстояния, углы, площади), которые не меняют своих зна-
значений при движениях рассматриваемых фигур, тогда как проективная
геометрия занимается такими понятиями (точка, прямая, отношение
инцидентности, двойное отношение), которые сохраняются при более
широкой группе проективных преобразований. Однако и движения,
и проективные преобразования — только очень частные случаи гораздо
более общих топологических преобразований; топологическое преобразо-
преобразование одной геометрической фигуры А в другую А' определяется как
произвольное соответствие р <=^ р' между точками р фигуры А и точ-
точками р' фигуры А', обладающее следующими свойствами:
1. Взаимной однозначностью. Это значит, что каждой точке р
фигуры А сопоставлена одна и только одна точка р' фигуры А', и об-
обратно.

§ 2. Топологические свойства фигур 285
Рис. 124. Поверхности, топологически неэквивалентные
2. Взаимной непрерывностью. Это значит, что если мы возь-
возьмем две точки р, q фигуры А и станем двигать р так, чтобы расстояние
между р и q неограниченно уменьшалось, то расстояние между соот-
соответствующими точками р', q' фигуры А' также будет неограниченно
уменьшаться, и обратно.
Всякое свойство геометрической фигуры А, которое сохраняется
также и для той фигуры А', в которую А переходит при топологичес-
топологическом преобразовании, называется топологическим свойством фигуры А;
топология же — это та отрасль геометрии, которая рассматривает ис-
исключительно топологические свойства фигур. Представьте себе, что не-
некоторая фигура должна быть скопирована «от руки» совершенно мало-
малоопытным, но очень добросовестным чертежником, который невольно
искривляет прямые линии, искажает углы, расстояния и площади; тог-
тогда на сделанной им копии, хотя метрические и проективные свойства
фигуры, может быть, и не сохранятся, но топологические свойства все
же останутся в неприкосновенности.
Наиболее наглядными примерами топологических преобразований
могут служить деформации. Вообразите, что фигура вроде сферы или
треугольника сделана из тонкого слоя резины (или нарисована на тако-
таковом), и затем растягивайте и крутите резину самыми разнообразными
способами, лишь бы не рвать ее и не приводить двух различных то-
точек в состояние физического совпадения. (Приведение двух различных
точек в состояние физического совпадения нарушило бы условие 1. Раз-
Разрыв резинового слоя противоречил бы условию 2: действительно, рас-
рассматривая две точки, лежащие по разные стороны линии разрыва, мы
видим, что расстояние между ними может быть неограниченно малым,
тогда как после разрыва этого уже не будет.)
Фигура в окончательном ее положении — после указанных опе-
операций — будет находиться в топологическом соответствии с фигурой
в ее первоначальном положении. Треугольник можно деформировать
в другой треугольник, или в окружность, или в эллипс, и потому на-

286
Глава V
званные фигуры обладают совершенно одинаковыми топологическими
свойствами. Но никак нельзя деформировать круг в отрезок прямой
или поверхность сферы — в боковую поверхность цилиндра.
Но общее понятие топологического преобразования шире, чем по-
понятие деформации. Например, если фигура разрезана до деформации и
склеена по тем же линиям после деформации, то в итоге, несомненно,
получается некоторое топологическое преобразование первоначальной
фигуры, хотя это преобразование может и не быть деформацией. Так,
две кривые, изображенные на рис. 134 (стр. 300), топологически эк-
эквивалентны друг другу и эквивалентны каждая окружности, так как
их можно разрезать, распутать и снова склеить. Но предварительно не
разрезавши, невозможно одну кривую деформировать в другую.
Рис. 125. Односвязная и двусвязная
области
Рис. 126. После разреза
двусвязная область ста-
становится односвязной
Топологические свойства фигур (вроде того свойства, которое да-
дается теоремой Эйлера, или других, которые будут рассмотрены ниже)
представляют величайший интерес во многих математических иссле-
исследованиях. В известном смысле это — самые глубокие, самые основные
геометрические свойства, так как они сохраняются при самых «резких»
преобразованиях.
2. Свойства связности. В качестве следующего примера фи-
фигур, топологически неэквивалентных, рассмотрим две плоские области
на рис. 125. Первая состоит из всех точек, заключенных внутри круга;
вторая — из всех точек, расположенных между двумя концентричес-
концентрическими кругами. Любая замкнутая кривая, лежащая в области а, может
быть непрерывно деформирована или «сжата» в одну точку, не выходя
из этой области. Область, обладающая таким свойством, называется
односвязной. Что касается области Ь, то она не односвязна. Так, окруж-
окружность, концентрическая с двумя граничными окружностями и лежащая

J3. Другие примеры топологических теорем
287
между ними, не может быть сжата в точку, не выходя из области, так
как во время деформации кривая должна будет пройти через общий
центр кругов, а он не принадлежит рассматриваемой области. Область,
которая не является односвязной, называется многосвязной. Если дву-
связную область Ь разрезать вдоль одного из радиусов, как это сделано
на рис. 126, то полученная область становится односвязной.
Рис. 127. Редукция трехсвязной области
Вообще, можно построить области с двумя, тремя или большим
количеством «дыр». Область с двумя «дырами» изображена на рис. 127;
чтобы превратить ее в односвязную, нужно сделать два разреза. Если
нужно сделать п — 1 взаимно не пересекающихся разрезов от границы
к границе, чтобы превратить данную многосвязную область в одно-
связную, то говорят, что область имеет порядок связности п. Порядок
связности плоской области представляет собой важный топологический
инвариант этой области.
§ 3. Другие примеры топологических теорем
1. Теорема Жордана о замкнутой кривой. На плоскости
нарисована простая замкнутая кривая (нигде сама себя не пересека-
пересекающая). Посмотрим, какое свойство этой фигуры сохраняется неизмен-
неизменным даже в том случае, если плоскость будет подвергаться каким угод-
угодно деформациям, как будто бы она была сделана из тонкого слоя ре-
резины. Длина кривой или площадь ограниченной ею части плоскости
при деформациях не сохраняется. Но у рассматриваемой конфигурации
есть и топологическое свойство, столь простое, что может показаться

288
Глава V
тривиальным. Простая замкнутая кри-
кривая С на плоскости делит плоскость
ровно на две области, внутреннюю и
внешнюю. Точнее говоря, мы утверж-
утверждаем следующее: точки плоскости раз-
разбиваются на два класса — А (внеш-
(внешние точки) и В (внутренние точки) —
таким образом, что любая пара то-
точек, принадлежащих одному и тому
же классу, может быть связана кри-
кривой, не имеющей общих точек с С, тог-
тогда как всякая кривая, соединяющая
две какие-нибудь точки разных клас-
Рис. 128. Какие точки находятся С0В) непременно пересекается с С. Это
внутри этого многоугольника? утверждение вполне очевидно, напри-
например, для случая окружности или эл-
эллипса, но уже чуть менее очевидно для такой сложной кривой, каков
причудливой формы многоугольник, изображенный на рис. 128.
Впервые эта теорема была сформулирована Камиллом Жорданом
A838-1922) в его широко известном «Cours d'analyse», из которого це-
целое поколение математиков почерпнуло современную концепцию ма-
математической строгости. Как это ни странно, доказательство, данное
самим Жорданом, не было ни кратким, ни простым по своей идее, но
в особенности удивительно то, что, как оказалось, оно и не было вполне
исчерпывающим, и понадобились значительные усилия, чтобы воспол-
восполнить его пробелы. Первые строгие доказательства теоремы Жордана
были очень сложными и трудно воспринимались даже людьми с хоро-
хорошей математической подготовкой. Сравнительно простые доказатель-
доказательства были придуманы лишь недавно. Одно из затруднений заключается
в большой общности понятия «простой замкнутой» кривой, значитель-
значительно более широкого, чем понятие многоугольника или «гладкой» кривой:
по определению «простая замкнутая кривая» есть любая кривая, топо-
топологически эквивалентная окружности. С другой стороны, необходимо
таким терминам, как «внутри» или «вне» (столь ясным интуитивно),
дать логические определения, прежде чем строгое доказательство ста-
станет возможным. Проанализировать в их полной общности возникающие
на этой почве отношения и концепции есть теоретическая задача перво-
первостепенного значения, разрешению которой в большой степени служит
современная топология. Но, с другой стороны, следует иметь в виду
и то обстоятельство, что, занимаясь изучением конкретных явлений

§3. Другие примеры топологических теорем 289
в области геометрии, в громадном большинстве случаев мало уместно
вводить понятия, неограниченная общность которых создает излишние
затруднения. Так, возвращаясь к теореме Жордана, существенно то,
что для случая «хорошо ведущих себя» кривых — например, для мно-
многоугольников или для кривых с непрерывно меняющейся касательной
(которые только и встречаются в наиболее важных задачах) — доказа-
доказательство этой теоремы может быть проведено совсем просто. Для слу-
случая многоугольников мы укажем доказательство в дополнении к этой
главе.
2. Проблема четырех красок. Пример только что рассмотрен-
рассмотренной теоремы о кривой Жордана способен, пожалуй, навести на мысль,
что топология занимается придумыванием строгих доказательств для
таких истин, в которых не станет сомневаться ни один здравомысля-
здравомыслящий человек. Но это совсем не так: существует много вопросов топо-
топологического характера, в числе которых иные формулируются чрезвы-
чрезвычайно просто и на которые интуиция не дает удовлетворительных отве-
ответов. Примером может служить знаменитая «проблема четырех красок».
Раскрашивая географическую карту, обык-
обыкновенно стараются распределить цвета между
странами таким образом, чтобы две страны,
имеющие общую границу, были окрашены по-
разному. Было обнаружено на опыте, что лю-
любая карта, сколько бы ни было изображено на
ней стран и как бы они ни были расположены,
может быть раскрашена, с соблюдением ука-
указанного правила, не более чем четырьмя крас-
красками. Легко убедиться, что меньшее число до-
достаточным для всех случаев не является. На
рис. 129 изображен остров посреди моря, ко- Рис 129 расКрашива-
торый никак нельзя раскрасить менее чем че- ние карты
тырьмя красками, так как на нем имеется че-
четыре страны, из которых каждая соприкасается с остальными тремя.
Тот факт, что до настоящего времени не было ни разу найдено
такой карты, для раскрашивания которой потребовалось бы более че-
четырех красок, приводит к мысли о справедливости такой теоремы: при
любом данном разбиении плоскости на области, не покрывающие друг
"Руга ни полностью, ни частично, всегда возможно пометить их циф-
Ро-ми \, 2, 3, 4 таким образом, чтобы «прилежащие» области имели
Разные цифры. Под «прилежащими» областями понимаются такие, кото-
Pbie имеют целый отрезок границы общим: две области, имеющие лишь
1» - 340

290 Глава V
одну общую точку (или даже конечное число общих точек) — как, на-
например, штаты Колорадо и Аризона — не будут называться «прилежа-
«прилежащими», так как никакого смешения или неудобства не возникает, если
их раскрасить одинаково.
Есть основания полагать, что впервые проблема четырех красок
была поставлена Мебиусом в 1840 г.; позднее ее формулировали де Мор-
Морган в 1850 г. и Кэли в 1878 г. «Доказательство» ее было опубликовано
в 1879 г. Кемпе, но Хивуд (Heawood) в 1890 г. нашел ошибку в рассуж-
рассуждении Кемпе. Пересматривая доказательство Кемпе, Хивуд обнаружил,
что пяти красок всегда достаточно. (Доказательство теоремы о пяти
красках дано в приложении к этой главе.) Несмотря на усилия многих
выдающихся математиков, положение вплоть до нашего времени оста-
остается в сущности неизменным. Было доказано, что пяти красок доста-
достаточно для всех карт, и имеется предположение, что достаточно также
четырех. Но, как и в случае знаменитой теоремы Ферма (см. стр. 71),
ни доказательства этого предположения, ни противоречащего ему при-
примера приведено не было, и указанное предположение остается одной
из нерешенных «больших» математических проблем. Заметим, между
прочим, что проблема четырех красок была решена в положительном
смысле для частных случаев, когда число областей не превышает три-
тридцати восьми. Отсюда ясно, что если в общем случае теорема неверна,
то опровергающий пример должен быть не особенно простым.
В рассматриваемой проблеме четырех красок предполагается, что
карта нарисована или на плоскости, или на сфере. Эти два случая экви-
эквивалентны. В самом деле, каждая карта, заданная на сфере, может быть
перенесена па плоскость, если проделаем дырочку внутри одной из об-
областей А и затем расплющим оставшуюся часть сферы по плоскости,
как мы это делали при доказательстве теоремы Эйлера. Полученная
карта на плоскости покажет нам «остров», состоящий из всех нетрону-
нетронутых областей, и «море», состоящее из одной области А. С другой сто-
стороны, проделывая всю эту процедуру в обратном направлении, можно
любую карту на плоскости превратить в карту на сфере. Итак, вместо
карт на плоскости можно ограничиться рассмотрением карт на сфере.
Больше того, так как деформации областей и их границ существенно не
влияют на нашу проблему, то можно предположить, что граница каж-
каждой области есть простой замкнутый многоугольник, состоящий из дуг
больших кругов. Но даже таким образом «регуляризированная» пробле-
проблема не является решенной; трудности в данном случае (не в пример
теореме Жордана) зависят не от общности понятия области и кривой.

§3. Другие примеры топологических теорем 291
В связи с проблемой четырех красок стоит отметить то замечатель-
замечательное обстоятельство, что для некоторых поверхностей более сложного
типа, чем плоскость или сфера, соответствующие теоремы действи-
действительно были доказаны, так что, как это ни парадоксально, анализ более
сложных (в геометрическом отношении) поверхностей в данном случае
проводится легче, чем более простых. Например, было установлено для
случая поверхности тора, имеющей вид «бублика» (см. рисунок 123),
что всякая нарисованная на ней «карта» может быть раскрашена се-
семью красками и что, с другой стороны, на ней мыслимы такие «кар-
«карты», составленные из семи областей, что каждая область соприкасается
с остальными шестью.
*3. Понятие размерности. Понятие о «числе измерений», или о «раз-
«размерности», не представляет особых затруднений, поскольку речь идет о прос-
простых геометрических образах, каковы точки, линии, треугольники или мно-
многогранники. Отдельная точка или любое конечное множество точек имеет
размерность нуль, отрезок — размерность 1, поверхность треугольника или
сферы — размерность 2. Множество всех точек куба имеет размерность 3.
Однако при желании обобщить понятие размерности на точечные множества
более общих типов возникает необходимость в точном определении. Какую
размерность следует, например, приписать множеству Л, состоящему из всех
точек ж-оси, у которых координаты х — рациональные числа? Множество ра-
рациональных точек на re-оси везде плотно и потому, казалось бы, ему, как
и самому отрезку прямой, надлежало бы приписать размерность 1. С дру-
другой стороны, между всякими двумя рациональными точками существуют
иррациональные «дыры», как между всякими двумя точками конечного мно-
множества, и это говорит в пользу размерности 0.
Еще запутаннее обстоит дело с размерностью любопытного множест-
множества, впервые рассмотренного Кантором, построенного следующим образом. Из
единичного отрезка 0 ^ х ^ 1 удалим среднюю треть (интервал), т.е. все
1 2
точки х, удовлетворяющие неравенству - < х < -=. Оставшееся точечное
о о
Множество обозначим через С\. Множество С\ состоит из двух отрезков;
Удалим теперь из каждого отрезка его среднюю треть и то множество, кото-
которое останется, обозначим через Сг- Повторим опять эту процедуру, удаляя
среднюю треть у всех четырех отрезков; получим Сз. Дальше таким же об-
Разом получим Сч, Cs, Св, ¦ ¦ ¦ ¦ Обозначим через С множество точек, которое
останется, когда все средние трети будут удалены; т. е. С есть, другими сло-
словами, множество точек, принадлежащих одновременно всем множествам Ci,
Сг, Сз, ... В первой операции был удален интервал длины ^; во второй опе-
о
Рации — два интервала, каждый длины гит. д.; сумма длин всех удаленных
19*

292 Глава V
_J_LJ_L J_LJ_J
Рис. 130. Канторово множество
интервалов равна
1.1 + 2. J-+22.i+ -
з з2 з3
Бесконечный ряд в больших скобках есть геометрическая прогрессия, сумма
которой равна = 3; итак, сумма длин удаленных промежутков состав-
ляет 1. И все-таки далеко не все точки отрезка удалены: множество С не
пустое. Например, все точки, являющиеся концами удаленных отрезков
1 2. 1 2 7 8.
3' 3' 9' 9' 9' 9' "¦
ему принадлежат. Можно легко убедиться, что множество С состоит из всех
тех чисел х, разложения которых в бесконечную дробь по основанию 3 могут
быть написаны в форме
3 з2 З3 Зп '
где всякое ап есть 0 или 2, тогда как в аналогичном разложении для всякой
удаленной точки среди чисел а„ хоть раз встретится 1.
Какова же размерность множества С? Диагональный процесс, с помо-
помощью которого была доказана несчетность множества всех действительных
чисел, может быть видоизменен таким образом, чтобы тот же результат по-
получился и для множества С. Отсюда было бы естественно заключить, что
множеству С надлежит приписать размерность 1. С другой стороны, С не
содержит никакого, даже самого малого, промежутка, как и любое конечное
множество; это сближает С с множествами размерности 0. Таким же обра-
образом, восставив в плоскости х, у из каждой рациональной точки или из каждой
точки канторова множества перпендикуляр длины 1 к оси х (направляя его
в сторону положительных значений ?/), мы получим множества, относитель-
относительно которых может возникнуть сомнение — приписать ли ему размерность 2
или 1.

§3. Другие примеры топологических теорем 293
Впервые Пуанкаре (в 1912 г.) обратил внимание на необходимость бо-
более глубокого анализа и более точного определения размерности. Пуанкаре
заметил, что прямая или кривая имеет размерность 1, так как любые две
точки на ней можно разделить, удаляя одну единственную точку (множес-
(множество размерности 0); плоскость же имеет размерность 2 по той причине, что
для разделения двух точек на плоскости нужно удалить целую замкнутую
кривую (множество размерности 1). Это приводит к мысли о том, что поня-
понятие размерности имеет «индуктивную» природу: некоторому «пространству»
следует приписать размерность п, если две точки в нем разделяются при
удалении подмножества точек размерности п— 1 (но удаления подмножества
меньшей размерности уже не было бы достаточно). В сущности такого рода
индуктивное определение неявно содержится уже в евклидовых «Началах»,
где одномерный образ толкуется как нечто, граница чего состоит из точек;
двумерный образ — как нечто, граница чего состоит из линий; наконец, трех-
трехмерный образ — как нечто, граница чего состоит из поверхностей.
За последние годы была развита обширная теория — теория размер-
размерности. Определение размерности начинается с того, что разъясняется смысл
термина «точечное множество размерности 0». Любое конечное точечное мно-
множество обладает тем свойством, что каждая его точка может быть заключена
в сколь угодно малую область пространства, причем на границе области нет
точек множества. Это свойство принимается теперь за определение размер-
размерности 0. Условимся ради удобства говорить, что пустое множество имеет
размерность —1. В таком случае множество S имеет размерность 0, если оно
не имеет размерности —1 (т.е. если S содержит хоть одну точку) и если каж-
каждая точка S может быть заключена в произвольно малую область, граница
которой пересекает S по множеству размерности —1 (т. е. совсем не содержит
ни одной точки S). Так, например, множество рациональных точек на прямой
имеет размерность 0, так как каждая рациональная точка может быть рас-
рассматриваема как центр произвольно малого промежутка с иррациональными
концами. Канторово множество С — также размерности 0, так как, подобно
множеству рациональных точек, оно получается посредством удаления везде
плотного множества точек прямой.
Итак, мы уже определили понятия «размерность —1» и «размерность 0».
Теперь легко понять, что такое «размерность 1»: говорят, что множество S
имеет «размерность 1», если оно не есть ни размерности — 1, ни размернос-
размерности 0 и если каждая точка S может быть заключена в произвольно малую
область, граница которой пересекается с 5 по множеству размерности 0. От-
Отрезок прямой обладает этим свойством, так как границей каждого проме-
промежутка является пара точек, т. е. множество размерности 0 по предыдущему
определению. Дальше, продолжая таким же образом, мы можем последова-
последовательно определить, что такое размерность 2, размерность 3 и т.д., причем
каждое следующее определение основывается на предыдущем.
Таким образом, говорят, что множество S имеет размерность п, если
оно не имеет меньшей размерности и если каждая точка S может быть за-

294 Глава V
ключена в произвольно малую область, граница которой пересекается с 5 по
множеству размерности п — 1. Например, плоскость имеет размерность 2,
так как любая точка плоскости может быть заключена в кружок произволь-
произвольно малого радиуса, граница которой имеет размерность I.1 В обыкновен-
обыкновенном пространстве никакое множество точек не может иметь размерность,
большую чем 3, так как любая точка пространства есть центр произволь-
произвольно малой сферы, граница которой имеет размерность 2. Но в современной
математике термин «пространство» употребляется в более общем смысле; он
обозначает любую систему объектов, для которой введено понятие «рассто-
«расстояния» или «окрестности», и такого рода абстрактные «пространства» могут
иметь размерность, большую чем 3. Простым примером является декартово
п-пространство, «точки» которого суть системы из п действительных чисел,
взятых в определенном порядке:
Р — (xi, X2, ... , 1„),
Q = (Уи 2/2, ••• ,уп),
а «расстояние» между Р и Q определяется по формуле
d(P, Q) = у/{Х1 - ухУ + (х2 - У2У + ... + (хп - УпI
Можно показать, что это пространство имеет размерность п. Простран-
Пространство, которое не имеет размерности п, как бы велико ни было п, называется
пространством бесконечной размерности. Известно много примеров таких
пространств.
В теории размерности устанавливается одно чрезвычайно интересное
свойство двумерных, трехмерных и вообще n-мерных фигур. Начнем с дву-
двумерного случая. Если какая-то простая двумерная фигура подразделена на
достаточно маленькие «ячейки» (причем предполагается, что каждая ячей-
ячейка содержит свою границу), то непременно найдутся такие точки, которые
принадлежат сразу по меньшей мере трем ячейкам, какова бы ни была фор-
форма выбранных ячеек. Вместе с тем существуют такие подразделения фигуры
на ячейки, что никакая точка фигуры не принадлежит сразу больше чем
трем ячейкам. Так, если рассматриваемая двумерная фигура есть квадрат
(рис. 131), то непременно имеются точки вроде той, которая сразу принад-
принадлежит трем ячейкам 1, 2 и 3, но для указанного на рисунке подразделения
не существует точки, которая сразу принадлежала бы большему числу яче-
ячеек. Точно так же в трехмерном случае можно доказать, что если некоторая
1 Сказанное не означает, что доказательство того, что плоскость имеет размер-
размерность 2 в смысле нашего определения, уже закончено: остается доказать, что граница
круга («окружность») имеет размерность 1, и что сама плоскость не имеет размер-
размерности 0 или 1. Эти утверждения можно доказать, как аналогичные утверждения
для высших размерностей. Все предыдущие рассуждения показывают, что приве-
приведенное выше общее определение размерности не стоит в противоречии с обычным
его пониманием.

§3. Другие примеры топологических теорем 295
объемная фигура (тело) разбита на достаточно маленькие ячейки, то навер-
наверное существуют точки, принадлежащие по меньшей мере четырем ячейкам,
и вместе с тем можно выбрать такие подразделения, что никакая точка не
будет принадлежать сразу больше чем четырем ячейкам.
Все эти соображения приводят нас к следую-
следующей теореме, высказанной Лебегом и Брауэром: ес-
если п-мерная фигура подразделена на достаточно ма-
маленькие ячейки, то непременно существуют точки
этой фигуры, принадлежащие сразу по меньшей ме-
мере п + 1 ячейкам; вместе с тем возможно указать
и такие подразделения, что ни одна точка фигуры
не будет принадлежать сразу более чем п + 1 ячей-
ячейкам. Эта теорема характеризует размерность рас-
рассматриваемой фигуры: все фигуры, для которых те-
I . I
1
орема верна, являются n-мерными, все прочие име-
имеют иную размерность. По этой причине указанная 1еорема о
теорема может быть взята за определение размер- покрытии
ности (так и делают некоторые авторы).
Размерность фигуры относится к числу топологических ее свойств: ни-
никакие две фигуры различных размерностей не могут быть топологически
эквивалентными. В этом заключается замечательная теорема об «инвариант-
«инвариантности размерности»: чтобы оценить ее должным образом, стоит напомнить
другую теорему (доказанную на стр. 120), согласно которой множество точек
квадрата имеет ту же мощность, что и множество точек отрезка. Соответ-
Соответствие между точками, установленное при доказательстве этой теоремы, не
топологическое, так как требование непрерывности нарушается.
*4. Теорема о неподвижной точке. В приложениях топологии
к другим отраслям математики играют важную роль теоремы о «не-
«неподвижной точке». Типическим примером является излагаемая ниже
теорема Брауэра. Она гораздо менее «очевидна» в интуитивном смыс-
смысле, чем другие топологические теоремы.
Рассмотрим круглый диск на плоскости. Под таковым мы понима-
понимаем внутренность некоторого круга вместе с его границей (окружнос-
(окружностью). Предположим, что весь этот диск подвергается некоторому топо-
топологическому преобразованию (не обязательно взаимно однозначному),
при котором всякая точка диска остается точкой диска, хотя и меняет
свое положение. Например, представляя себе этот диск сделанным из
тонкой резины, можно его сжимать, растягивать, вращать, изгибать —
одним словом, деформировать как угодно, лишь бы его точки не вышли
за пределы первоначального положения диска. Иначе еще можно пред-
представить себе, что жидкость, налитая в стакан, приведена в движение
таким образом, что частицы, находившиеся на поверхности, остаются

296
Глава V
на ней и во время движения; тогда в каждый определенный момент
времени положение частиц на поверхности, определяет некоторое то-
топологическое преобразование или трансформацию первоначального их
распределения. Теорема Брауэра утверждает: каждое непрерывное пре-
преобразование такого рода оставляет неподвижной по крайней мере одну
точку; другими словами, существует по меньшей мере одна точка, по-
положение которой после преобразования совпадает с положением ее до
преобразования. (В примере с жидкостью неподвижные точки зависят
от избранного момента времени; в частности, если движение сводит-
сводится к простому круговому вращению, то неподвижной точкой в любой
момент является центр.) Излагаемое далее доказательство существо-
существования неподвижной точки — очень характерный пример рассуждений,
применяемых в топологии.
Рис. 133. К доказательству теоремы Броуэра
Рассмотрим наш диск до и после трансформации и допустим, что,
вопреки утверждению теоремы, ни одна точка не остается неподвиж-
неподвижной, так что любая точка диска после трансформации превращается
в некоторую другую точку диска. Каждой точке Р диска в его пер-
первоначальном положении сопоставим стрелку или «вектор трансформа-
трансформации» РР', причем Р' есть та точка, в которую переходит Р после
трансформации. Такая стрелка будет поставлена во всякой точке дис-
диска, так как всякая точка куда-то перемещается. Рассмотрим теперь все

§3. Другие примеры топологических теорем 297
точки граничной окружности вместе с соответствующими векторами
трансформации. Все эти векторы направлены внутрь круга, так как,
по предположению, ни одна точка не выходит за его пределы. Начнем с
какой-нибудь точки Р, лежащей на граничной окружности, и пойдем по
этой окружности в направлении, противоположном движению часовой
стрелки. При этом направление вектора трансформации будет изме-
изменяться, так как различным точкам границы соответствуют различно
направленные векторы. Все эти векторы можно также представить се-
себе (подвергнувши их параллельному переносу) выходящими из неко-
некоторой одной и той же точки плоскости (рис. 133). Легко понять, что,
когда мы обойдем один раз весь круг от точки Pi до точки Рг, соот-
соответствующий вектор,после ряда поворотов,вернется в первоначальное
положение. Число полных поворотов, сделанных при этом нашим век-
вектором, мы назовем индексом рассматриваемой граничной окружности;
точнее говоря, мы определим индекс как алгебраическую сумму различ-
различных изменений в угле векторов, условливаясь, что всякому частному
повороту по часовой стрелке приписывается знак минус, против часо-
часовой стрелки — знак плюс. Индекс есть итоговый результат, который
a priori равен одному из чисел 0, ±1, ±2, ±3, ..., соответствующих
итоговым поворотам на 0°, ±360°, ±720°, Мы утверждаем теперь,
что индекс граничной окружности равен единице, т.е. что итоговый
поворот вектора трансформации составляет один полный поворот в по-
положительном направлении. Прежде всего напомним еще раз, что вектор
трансформации, имеющий начало в точке граничного круга, направлен
непременно внутрь круга, а не по касательной. Если допустим, что
итоговый поворот вектора трансформации отличается от итогового по-
поворота касательного вектора (а этот последний поворот в точности
равен 360°, так как касательный вектор, очевидно, делает один полный
поворот), то разность между итоговыми поворотами касательного век-
вектора и вектора трансформации будет равна кратному 360°, но никак
не нулю. Отсюда следует, что вектор трансформации при обходе кру-
круга должен будет по крайней мере раз сделать полный поворот вокруг
касательного вектора, а так как оба вектора изменяются непрерывно,
то в некоторой точке окружности направления двух векторов совпадут.
Но это, как мы видели, невозможно.
Рассмотрим теперь окружность, концентрическую границе диска,
но с меньшим радиусом, а также соответствующие векторы трансфор-
трансформации. Для этой новой окружности индекс также непременно равен
единице. В самом деле, при переходе от граничной окружности к новой
окружности индекс должен меняться непрерывно, так как направле-

298
Глава V
ния самих векторов трансформации меняются непрерывно. Но индекс
может принимать только целые значения и потому остается равным
единице: действительно, переход от единицы к какому-нибудь другому
целому числу обязательно был бы связан со скачком, т.е. нарушением
непрерывности. (Очень характерное математическое рассуждение: ве-
величина меняется непрерывно, но может принимать только целые зна-
значения, значит, она постоянна.) Итак, мы можем найти окружность,
концентрическую граничной, притом сколь угодно малую, для кото-
которой индекс будет равен единице. Но это невозможно, так как, в силу
непрерывности преобразования, векторы трансформации в достаточно
малом круге должны весьма мало отличаться от вектора в центре кру-
круга. И потому итоговый поворот такого вектора при обходе круга может
быть сделан, скажем, меньше 10°, если только радиус круга будет до-
достаточно мал. Но отсюда следует, что индекс такого круга (обязательно
целое число) не может быть отличен от нуля. Полученное противоречие
показывает, что сделанное нами допущение об отсутствии неподвиж-
неподвижных точек преобразования должно быть отвергнуто. Таким образом,
теорема доказана.
Теорема о неподвижных точках имеет
место не только для кругового диска, но,
конечно, и для треугольника, квадрата и
всякой другой фигуры, в которую диск мо-
может быть переведен топологическим преоб-
преобразованием. В самом деле, если бы некото-
некоторая фигура А, получающаяся из кругового
диска посредством такого рода трансформа-
трансформации, могла быть преобразована сама в себя
без неподвижных точек, то тем самым бы-
было бы определено и топологическое преобра-
преобразование кругового диска самого в себя без
неподвижных точек, а это, как мы видели,
невозможно. Теорема обобщается также на
случай трехмерных фигур — сфер или кубов, но доказательство не
столь просто.
Хотя теорема Брауэра о неподвижных точках в случае круга не являет-
является вполне очевидной в интуитивном смысле, однако легко убедиться, что она
является непосредственным следствием такой, достаточно очевидной теоре-
теоремы: невозможно трансформировать непрерывно круговой диск в одну только
его граничную окружность таким образом, чтобы каждая точка этой окруж-
окружности оставалась неподвижной. Убедимся, что существование непрерывной
Рис. 132. Векторы преоб-
преобразования

§ 3. Другие примеры топологических теорем 299
трансформации диска на себя без неподвижных точек противоречит этой по-
последней теореме. Предположим, что указанного рода непрерывная трансфор-
трансформация Р —>¦ Р' существует. Тогда для всякой точки Р нашего диска проведем
вектор с началом в точке Р', проводя его через Р и заканчивая в точке Р*,
где он встретится с граничной окружностью. Тогда преобразование Р —} Р*
будет непрерывным преобразованием всего диска в граничную окружность,
оставляющим неподвижными все точки этой окружности, возможность чего
была отвергнута. Подобное рассуждение можно применить и при доказатель-
доказательстве теоремы Брауэра в трехмерном случае сферы или куба.
Легко убедиться, с другой стороны, что для некоторых фигур непрерыв-
непрерывные преобразования в себя без неподвижных точек возможны.
Например, кольцеобразная область между двумя концентрическими
кругами может быть подвергнута вращению около центра на угол, не явля-
являющийся кратным 360°, и это как раз будет непрерывным преобразованием
области в себя без неподвижных точек. Такое же преобразование можно про-
произвести над поверхностью сферы, сопоставляя всякой ее точке диаметраль-
диаметрально противоположную. Но, применяя тот же метод, что и в случае диска, не
представит труда доказать, что непрерывное преобразование сферической
поверхности, не переводящее ни одной точки в диаметрально противополож-
противоположную (например, всякая малая деформация), непременно имеет неподвижные
точки.
Теоремы о неподвижных точках вроде перечисленных выше доставля-
доставляют могущественный метод для доказательства многих «теорем существова-
существования» в разных областях математики, причем геометрический характер этих
теорем часто далеко не очевиден. Замечательным примером может служить
теорема Пуанкаре, высказанная им незадолго до смерти, в 1912 г., без доказа-
доказательства. Из этой теоремы непосредственно вытекает существование бесчис-
бесчисленного множества периодических орбит в ограниченной проблеме трех тел.
Пуанкаре не сумел обосновать своей догадки, доказательство этого замеча-
замечательного факта получил через год американский математик Г. Д. Биркгофф.
С тех пор топологические методы неоднократно и с большим успехом приме-
применялись к изучению качественного поведения динамических систем.
5. Узлы. В качестве последнего примера отметим, что труд-
трудные математические проблемы топологического характера возникают
в связи с изучением узлов. Узел образуется, когда из отрезка веревки
Делают петли, затем сквозь них пропускают концы веревки и, наконец,
Два конца соединяют вместе. Полученная, изготовленная из веревки за-
замкнутая кривая представляет собой геометрическую фигуру, сущест-
существенные свойства которой не изменяются, как бы в дальнейшем не пере-
перетягивать или не перекручивать веревку. Но как возможно было бы дать
внутреннюю характеристику, которая позволила бы различить тем или
иньщ способом «заузленные» кривые между собой и отличать их от

300 Глава V
Рис. 134. Топологически эквивалентные узлы, не переводящиеся друг в друга
«незаузленных» вроде круга? Ответ далеко не прост и еще менее прост
исчерпывающий математический анализ узлов разных типов. Затруд-
Затруднения встречаются даже при самых первых шагах в этом направлении.
Взгляните на два узла, напоминающие трилистники, изображенные на
рис. 134. Они совершенно симметричны друг другу, являются взаим-
взаимно «зеркальными отображениями», они топологически эквивалентны и
вместе с тем неконгруэнтны друг другу. Возникает проблема: можно
ли деформировать непрерывным движением один узел в другой? Ответ
отрицателен; но доказательство потребовало бы значительно большего
владения топологической техникой и больших знаний из области тео-
теории групп, чем предполагают рамки этой книги.
§ 4. Топологическая классификация поверхностей
1. Род поверхности. Многие простые, но весьма существенные
обстоятельства выясняются при изучении двумерных поверхностей.
Сравним, например, поверхность сферы с поверхностью тора. Взгля-
Взглянув на рис. 135, сразу можно обнаружить различие: на сфере, как и на
плоскости, замкнутая кривая, вроде С, разделяет поверхность на две
части; но на торе существуют и такие замкнутые кривые, например С",
которые не разделяют поверхности на две части. Если мы говорим, что
кривая С разделяет сферу на две части, то это означает, другими сло-
словами, что при разрезании поверхности сферы по кривой С эта поверх-
поверхность распадается на два не связанных между собой куска, или, еще
иначе, что можно найти две такие точки сферы, что всякая кривая на
сфере, их соединяющая, непременно пересечется с кривой С. Напро-
Напротив, если разрезать тор по кривой С", то после разреза поверхность не
распадется: любые две ее точки можно соединить кривой, не имеющей
общих точек с С". Указанное различие свидетельствует о том, что сфе-

L. Топологическая классификация поверхностей
301
Рис. 135. Разрезы на сфере и на торе
ра и тор в топологическом смысле не принадлежат одному и тому же
классу поверхностей: тор нельзя топологически преобразовать в сферу.
Рассмотрим теперь поверхность с двумя «дырами», изображенную
на рис. 136. На этой поверхности оказывается возможным провести сра-
сразу две замкнутые кривые А и В, которые не разделяют поверхности на
части. Тор, напротив, при проведении двух таких кривых непременно
разделится на части. С другой стороны, любые три замкнутые кривые
разделяют нашу поверхность с двумя дырами.
Все это подсказывает мысль
ввести понятие рода поверхности,
понимая под родом поверхности
наибольшее возможное число вза-
взаимно не пересекающихся простых
замкнутых кривых, которые мож-
можно провести на поверхности, не
разделяя ее на части. Род сфе-
сферы равен 0, род тора равен 1,
род поверхности, изображенной на
рис. 136, равен 2. Такая же поверх-
поверхность с р «дырами» имеет род р.
Род есть топологический инвариант поверхности: он не изменяется
при деформировании поверхности. Обратно, можно доказать (но мы
не приводим здесь этого доказательства), что если две замкнутые по-
поверхности имеют один и тот же род, то одну можно деформировать
в Другую; таким образом, род р = 0, 1, 2, ... замкнутой поверхности
полностью характеризует топологический класс, к которому она при-
Надлежит. (Здесь предполагается, что мы рассматриваем только обык-
обыкновенные «двусторонние» поверхности. В пункте 3 этого параграфа мы
Рис. 136. Поверхность рода 2

302
Глава V
рассмотрим также и «односторонние» поверхности.) Например, толь-
только что рассмотренная поверхность с двумя дырами и сфера с двумя
«рукоятками», изображенная на рис. 137, являются обе замкнутыми
поверхностями рода 2, и мы видим, что каждую из этих поверхнос-
поверхностей удается деформировать в другую. Так как поверхность с р дырами
или ее эквивалент — сфера с р рукоятками — поверхности рода р, то
любую из этих поверхностей можно взять в качестве «топологического
представителя» всех замкнутых поверхностей рода р.
Рис. 137. Поверхность рода 2
*2. Эйлерова характеристика поверхности. Предположим,
что замкнутая поверхность S рода р подразделена на некоторое чис-
число областей: такое подразделение получается, если мы отметим на S
ряд «вершин» и соединим их затем между собой дугами кривых. Мы
покажем, что в таком случае
где V — число вершин, Е — число дуг и F — число областей. Чис-
Число 2 — 2р называется эйлеровой характеристикой поверхности. Как мы
уже видели, для случая сферы V — Е + F = 2, что согласуется с фор-
формулой A), так как сфера имеет род р, равный нулю.
Рис. 138. К эйлеровой характеристике поверхностей
Желая доказать общую формулу A), вообразим, что 5 есть сфера
с р рукоятками. Как мы отметили, любая поверхность рода р может
быть непрерывной деформацией приведена к этому виду, и во время
деформации ни V — Е + F, ни 2 — 2р не изменяются. Непрерывную де-

§4. Топологическая классификация поверхностей 303
формацию мы выберем таким образом, чтобы замкнутые кривые Ai,
4», В\, Вг, •.., по которым рукоятки соединяются со сферой, пришлись
как раз на ДУГИ данного подразделения. (Рис. 138 иллюстрирует опи-
сьшаемую дальше процедуру в случае р = 2.)
Прорежем теперь поверхность 5 по кривым А?,, В2, ... и выпря-
выпрямим рукоятки. У каждой рукоятки появится свободный край, ограни-
ограниченный новой кривой А*, В*, ..., причем на появившемся крае будет
столько же вершин и столько же дуг, сколько их было соответственно
на А2, В2,
Число V — Е + F при прорезывании не изменится, так как новых
областей не возникнет, а число вновь возникших вершин уравновеши-
уравновешивается числом вновь возникших дуг. Затем деформируем поверхность
дальше, сплющивая торчащие рукоятки (включая их в поверхность сфе-
сферы). В итоге получается сфера с 2р отверстиями. Так как V — Е + F,
как нам известно, равно 2 для всякого подразделения полной сферы, то
для нашей сферы с 2р отверстиями мы получаем V — Е + F ~ 2 — 2р,
и это равенство, очевидно, справедливо также и для первоначальной
сферы с р рукоятками. Наше утверждение доказано.
Рис. 121 иллюстрирует применение формулы A) к поверхности S,
составленной из плоских многоугольников. Эту поверхность можно то-
топологически деформировать в поверхность тора, так что ее род р ра-
равен 1, и потому 2 — 2р = 2 — 2 = 0. Как и требуется по формуле A), мы
получаем
V - Е + F - 16 - 32 + 16 = 0.
Упражнение. Произвести какое-нибудь подразделение на поверхности
с двумя дырами, изображенной на рис. 137, и проверить, что V — E + F = —2.
3. Односторонние поверхности. У каждой из обыкновенных
поверхностей имеется по две стороны. Это относится и к замкнутым
поверхностям вроде сферы или тора, и к поверхностям, имеющим гра-
границы, каковы, например, диск или тор, из которого удален кусок по-
поверхности. Чтобы легко различать две стороны одной и той же поверх-
поверхности, их можно было бы раскрасить разными красками. Если поверх-
поверхность — замкнутая, две краски нигде не встретятся. Если поверхность
имеет граничные кривые, то разные краски встречаются по этим кри-
кривым. Предположим, что по таким поверхностям ползал бы клоп и что-
нибудь мешало бы ему пересекать граничные кривые; тогда он оста-
оставлен бы всегда на одной стороне поверхности.

304
Глава V
Рис. 139. Лист Мёбиуса: а, б, в — перекручивание и склеивание ленты; г —
ориентация «сторон»
Мебиусу принадлежит честь ошеломляющего открытия: существу-
существуют поверхности, у которых имеется только одна сторона. Простейшая
из таких поверхностей есть так называемая лента (или лист) Меби-
Мебиуса. Чтобы ее построить, нужно взять лист бумаги, имеющий форму
очень вытянутого прямоугольника, и склеить его концы после полупо-
полуповорота, как показано на рис. 139. Клоп, который будет ползти по этой
поверхности, держась все время середины «ленты», вернувшись в ис-
исходную точку, окажется в перевернутом положении (рис. 139, г). Если
кто-нибудь вздумает раскрасить «только одну» сторону поверхности
мебиусовой ленты, пусть лучше сразу погрузит ее всю в ведро с крас-
краской.
Другое замечательное свойство поверхности Мебиуса заключает-
заключается в том, что у нее только один край: вся граница состоит из одной
замкнутой кривой. Обыкновенная двусторонняя поверхность, получа-
получающаяся при склеивании концов ленты без всякого поворота, явственно
имеет две различные граничные кривые. Если эту последнюю поверх-
поверхность разрезать по центральной линии, она распадется на две поверх-
поверхности того же типа. Но если разрезать таким же образом по централь-
центральной линии ленту Мебиуса (см. рис. 139), то мы увидим, что распадения
на две части не будет. Тому, кто не упражнялся с лентой Мебиуса,

D. Топологическая классификация поверхностей
305
Трудно предсказать это обстоятельство, столь
противоречащее нашим интуитивным пред-
представлениям о том, что «должно» случиться. Но
если поверхность, полученную после описанно-
описанного выше разрезания ленты Мебиуса, снова раз-
разрезать по ее центральной линии, то у нас в ру-
руках окажутся две не связанные, но переплетен-
переплетенные между собой ленты!
Очень интересно разрезать по линиям, па-
паллельным границе и отстоящим от нее на ~.
v 2 Рис. 140. Кросс-кэп
I и т. д. ширины ленты. Поверхность Мебиуса, без сомнения, заслужи-
заслуживает упоминания и в школьном курсе.
Граница поверхности Мебиуса представляет собой
простую «незаузленную» замкнутую кривую и ее мож-
можно деформировать в окружность. Но придется допус-
допустить, что в процессе деформации поверхность будет са-
сама себя пересекать. Получающаяся при этом самопере-
самопересекающаяся односторонняя поверхность известна под А
названием «кросс-кэп» (рис. 140I. Линию пересечения
здесь следует считать дважды, один раз относя к од-
одному из пересекающихся листов поверхности, другой
раз — к другому. Кросс-кэп, как и всякую односторон-
одностороннюю поверхность, нельзя непрерывно деформировать
в двустороннюю (топологическое свойство).
Любопытно, что ленту Мебиуса можно, оказывается, так деформи-
деформировать, что ее граница будет плоской ломаной, — а именно, треугольни-
треугольником, — причем лента останется несамопересекающейся. Такая модель,
найденная д-ром Б. Туккерманом, показана на рис. 141, а; границей лен-
ленты служит треугольник ABC, ограничивающий половину диагональ-
диагонального квадратного сечения октаэдра (симметричного относительно это-
этого сечения). Сама лента состоит при этом из шести граней октаэдра
и четырех прямоугольных треугольников — четвертей вертикальных
Диагональных плоскостей октаэдра2.
Cross-cap — «перекрещивающаяся шляпа» (англ.).
Из поверхности октаэдра вырезаются грани АВР и BCQ. К оставшимся шес-
ти граням приклеиваются четыре треугольника ОАР, ОВР, OCQ и OBQ. На
Рис. 141, б приведена развертка описанной поверхности. По линии, соединяющей
точку О с точкой, помеченной двумя буквами А и С, надо сделать разрез, а потом
клеить соответствующие отрезки края развертки. Жирными отрезками обозначен
кРай ленты (периметр треугольника ABC).
Рис. 141а

306
D
D'
С"
Рис. 1416. Лента Мёбиуса с прямолинейным краем (а) и ее развертка (б)
Другой любопытный пример односто-
односторонней поверхности — так называемая
«бутылка Клейна». Это — замкнутая по-
поверхность, но она, в противоположность
известным нам замкнутым поверхностям,
не делит пространства на «внутреннюю» и
«внешнюю» части. Топологически она эк-
Рис. 142. Бутылка Клейна
Бивалентна паре кросс-кэпов со склеенными между собой граничными
кривыми.
Можно доказать, что всякая замкнутая односторонняя поверхность
рода р = 1, 2,... топологически эквивалентна сфере, из которой вы-
вынуты р дисков и заменены кросс-кэпами. Отсюда легко выводится, что
эйлерова характеристика V—E+F такой поверхности связана с родом р
соотношением
V-E + F = 2-p.
Доказательство этого предложения такое же, как и для двусторонних по-
поверхностей. Прежде всего убедимся, что эйлерова характеристика кросс-кэпа
или ленты Мебиуса равна 0. Для этого заметим, что, перерезая поперек ленту
Мебиуса, предварительно подразделенную на области, мы получим прямо-
прямоугольник, у которого будут все лишнее вершины и одна лишняя дуга, число
же областей останется то же самое, что и для ленты Мебиуса. Мы видели на
стр. 282, что для прямоугольника V — Е + F = 1. Следовательно, для лен-
ленты Мебиуса V — Е + F = 0. Предлагаем читателю в качестве упражнения
восстановить это доказательство во всех подробностях.
Изучение топологической структуры поверхностей, подобных тем,
которые только что были описаны, проводится более удобно, если вое-

л?
4. Топологическая классификация поверхностей
'А Л? * QA
307
6В АО
Цилиндр
АО- 9В АО
Ао-
.-''''Ьв
o—„-I
о'
~о
"О А
о А Ао
Лист Мебиуса Бутылка Клейна
Рис. 143. Замкнутые поверхности, Рис. 144. Определение трехмерно-
определенные посредством иденти- го тора посредством идентифика-
фикации сторон квадрата ции граней куба
Рис. 145. Другое представление трехмерного тора (разрезы показывают иден-
идентификацию)
пользоваться плоскими многоугольниками с попарно идентифициро-
идентифицированными сторонами (см гл. IV, приложение, пункт 3). Так, на схемах
рис. 143 стрелки показывают, какие из параллельных сторон и в ка-
каком направлении должны быть идентифицированы: если возможно, то
физически, если невозможно, то хотя бы мысленно, абстрактно.
Метод идентификации можно применить и для определения трех-
трехмерных замкнутых многообразий, аналогичных двумерным замкну-
замкнутым поверхностям. Например, отождествляя соответствующие точки

308 Глава V
взаимно противоположных граней куба (рис. 144), мы получаем замк-
замкнутое трехмерное многообразие, называемое трехмерным тором. Та-
Такое многообразие топологически эквивалентно пространственной об-
области, заключенной между двумя концентрическими поверхностями
тора (одна внутри другой), с идентификацией соответствующих точек
(рис. 145). Действительно, это последнее многообразие получается из
куба, если привести в «физическое» совпадение две пары «мысленно
отождествленных» взаимно противоположных граней.
Приложение
*1. Проблема пяти красок. Доказательство того, что всякая
карта на сфере может быть правильно раскрашена с помощью не более
чем пяти различных красок, основывается на формуле Эйлера. (В со-
соответствии с тем, что было сказано на стр. 288, карта считается рас-
раскрашенной правильно, если никакие две области, соприкасающиеся по
целой дуге, не окрашены одинаково.) Мы ограничимся рассмотрением
таких карт, на которых все области являются простыми замкнутыми
многоугольниками, ограниченными круговыми дугами. Не уменьшая
общности, можно допустить, что в каждой вершине сходится ровно
по три дуги; карту, удовлетворяющую такому условию, будем назы-
называть регулярной. Заменим каждую вершину, в которой встречается
более трех дуг, маленьким кружком и присоединим внутренность это-
этого кружка к одной из прилегающих областей: тогда получится новая
карта, в которой «кратные» вершины заменены обыкновенными. Новая
карта будет содержать столько же областей, сколько и старая, и она
будет регулярной. Если ее удастся правильно раскрасить, то, сжимая
потом кружок и сводя его в точку, мы получим требуемую раскраску
первоначальной карты. Таким образом, достаточно убедиться, что каж-
каждую регулярную карту на сфере можно правильно раскрасить пятью
красками.
Прежде всего докажем, что всякая регулярная карта содержит по
крайней мере один многоугольник с числом сторон, меньшим шести.
Обозначим через Fn число n-угольных областей нашей регулярной кар-
карты; тогда, обозначая через F число всех областей, получим равенство
F = Ft + F2 + F3 + F4 + ... A)
У каждой дуги — два конца; в каждой вершине сходится три дуги.
Поэтому, если Е обозначает число дуг, a V — число вершин на нашей

Приложение
309
карте, то
2Е = W. B)
Далее, так как область, ограниченная п дугами, имеет п вершин и каж-
каждая вершина принадлежит трем областям, то
2Е = W = 2F2 +3F3 + 4F4 + ... C)
До формуле Эйлера, мы имеем
V -E + F = 2, или 6V - 6Е + 6F = 12.
Из соотношения B) следует, что 6V — АЕ, так что 6F -2Е = 12. Тогда
соотношения A) и C) нам дают
6(F2 + F3
- BF2 + 3F3 + 4F4
или
М' \
() () ... = 12.
Так как хотя бы один из чле-
членов суммы слева должен быть положи-
положительным, то отсюда ясно, что четыре
числа F-i, F3, Fi и F5 не могут одновре-
одновременно равняться нулю. Но это и есть
то, что нам нужно было доказать.
Перейдем теперь к теореме о пя-
пяти красках. Пусть М — какая угодно
регулярная карта на сфере, п — число
всех ее областей. Мы знаем, что име-
имеется хоть одна область с числом сто-
сторон, меньшим шести.
Случай 1. М содержит область А
с 2, 3 или 4 сторонами (рис. 146).
В этом случае удалим дугу, отделяю-
отделяющую А от одной из прилежащих об-
областей. (Здесь необходимо следующее Рис. 146-147. К доказательству
примечание. Если у области А — че- теоремы о пяти красках
тыре стороны, то может случиться, что одна из прилежащих областей,
если ее обойти вокруг, окажется также прилежащей к А с противопо-
противоположной стороны. В этом случае, на основании теоремы Жордана, две
области, прилегающие к А с двух остальных сторон, будут различны-
различными, и мы сможем удалить одну из этих двух сторон.) Вновь полученная
Карта М' будет также регулярной, но содержащей уже только п— 1 об-
областей. Если карту М' можно правильно раскрасить пятью красками,

310 Глава V
то можно раскрасить и карту М. В самом деле, к области А приле-
прилегает самое большее четыре области карты М, и потому для А всегда
найдется пятая краска.
Случай 2. М содержит область А с пятью сторонами. Рассматри-
Рассматривая пять областей, прилегающих к А, обозначим их через В, С, D и F.
Можно всегда среди этих пяти областей найти две, которые не приле-
прилегают друг к другу: действительно, если, например, В и D прилегают
одна к другой, то отсюда вытекает, что С не прилегает ни к Е, ни к F,
так как в противном случае всякий путь, идущий из С в Е или F,
должен был бы пройти по крайней мере через одну из областей А, В
или D (рис. 147). (Ясно, что это утверждение существенно зависит от
теоремы Жордана, справедливой для плоскости и для сферы. Для тора,
напротив, все это рассуждение отпадает.) Итак, можно допустить, что,
например, С a F не прилегают друг к другу. Удалим те две стороны А,
которые отделяют А от С и F, и тогда получим новую карту М' с п — 2
областями, также регулярную. Если новую карту М' можно правильно
раскрасить пятью красками, то можно раскрасить и первоначальную
карту М. В самом деле, после восстановления удаленных сторон об-
область А будет прилегать к пяти областям, окрашенным не более чем
четырьмя красками (так как С и F окрашены одинаково), и потому
для А всегда найдется пятая краска.
Таким образом, во всех случаях всякий регулярной карте Men об-
областями можно сопоставить такую, также регулярную, карту, М',
с п — 1 или п — 2 областями, что если М' можно раскрасить пятью
красками, то М — также. Это рассуждение можно повторить для кар-
карты М" и т. д. В результате мы получим последовательность карт, в ко-
которой первым членом будет М;
М, М',М",
обладающую тем свойством, что каждая карта этой последовательнос-
последовательности может быть раскрашена пятью красками, если может быть раскра-
раскрашена следующая за ней. Но так как число областей в картах этой после-
последовательности неизменно убывает, то рано или поздно в ней найдется
карта с пятью областями (или меньшим числом). Такую карту всегда
можно раскрасить не более чем пятью красками. Возвращаясь по по-
последовательности карт, шаг за шагом, обратно, заключим отсюда, что
и сама карта М может быть раскрашена пятью красками. Этим дока-
доказательство и заканчивается.
Остается заметить, что это доказательство имеет «конструктив-
«конструктивный» характер: оно дает практически осуществимый, хотя может быть

Приложение 311
Л утомительный, метод нахождения требуемой раскраски данной кар-
карты М, составленной из п областей посредством конечного числа шагов.
2. Теорема Жордана для слу-
случая многоугольников. Теорема Жор-
Жордана утверждает, что всякая простая за-
замкнутая кривая С разделяет точки плос-
плоскости, не принадлежащие С, на такие
две области (не имеющие общих точек),
по отношению к которым сама кривая С
является общей границей. Мы докажем
здесь эту теорему для частного случая,
когда С есть замкнутый многоуголь- Рис. 148. Счет пересечений
ник Р.
Мы покажем, что точки плоскости (кроме точек, находящихся на
самом многоугольном контуре Р) разбиваются на два класса А и В,
обладающие следующими свойствами: 1) две точки одного и того же
класса могут быть соединены ломаной линией, не имеющей общих то-
точек с Р; 2) если две точки принадлежат разным классам, то любая ло-
ломаная линия, их соединяющая, имеет общие точки с Р. Один из назван-
названных классов образует «внутренность» многоугольника, другой состоит
из точек, находящихся «вне» многоугольника.
Приступая к доказательству, выберем какое-то фиксированное на-
направление в нашей плоскости, непараллельное ни одной из сторон Р.
Так как Р имеет конечное число сторон, то это всегда возможно. За-
Затем определим классы А и В следующим образом.
Точка р принадлежит классу А, если луч, проведенный через нее
в фиксированном направлении, пересекает Р в четном числе точек
@,2,4,6 и т.д.). Точка р принадлежит классу В, если луч, проведен-
проведенный из р в фиксированном направлении, пересекает Р в нечетном числе
точек A,3,5 и т.д.).
К этому нужно добавить, что если рассматриваемый луч проходит
через какую-нибудь вершину Р, то эта вершина идет в счет как точка
пересечения луча с Р или не идет, смотря по тому, расположены ли
прилежащие стороны многоугольника Р по разные стороны луча или
по одну и ту же его сторону.
Условимся говорить, что две точки р и q имеют одну и ту же
«четность», если они принадлежат одному и тому же из двух классов А
ИВ.
Заметим прежде всего, что все точки любого отрезка прямой, не
Пресекающегося с Р, имеют одну и ту же четность. Действительно,

312
Глава V
Рис. 149. К доказательству тео-
теоремы Жордана
четность точки р, движущейся по так0.
му отрезку, может измениться не ина-
иначе, как при пересечении соответству-
соответствующего луча с одной из вершин Р; но,
принимая во внимание наше соглаше-
соглашение о счете точек пересечения, легко
убедиться, что в каждом из двух воз-
возможных случаев четность все же не ме-
меняется. Из сказанного следует, что ес-
если некоторая точка pi области А со-
соединена ломаной линией с некоторой точкой р2 области В, то эта
линия непременно пересекает Р. Иначе четность всех точек ломаной
линии, в частности, точек р\ и р2, была бы одинаковой. Дальше, по-
покажем, что две точки одного и того же из двух классов А и В могут
быть соединены ломаной линией, не пересекающейся с Р. Обозначим
две данные точки через р и q. Если прямолинейный отрезок pq, со-
соединяющий р и q, не пересекается с Р, то доказывать больше нечего.
В противном случае пусть р' — первая, a q' — последняя точка пересе-
пересечения отрезка pq с многоугольником Р (рис. 149). Построим ломаную
линию, начинающуюся от точки р прямолинейным отрезком, распо-
расположенным по направлению pq, но заканчивающуюся непосредственно
перед точкой р': отсюда ломаная пойдет вдоль Р (безразлично, в каком
из двух возможных направлений) и будет так идти, пока не придет
снова на прямую pq — около точки q'. Весь вопрос в том, произойдет
ли пересечение с прямой pq на отрезке p'q' или на отрезке q'q: мы сей-
сейчас убедимся, что справедливо именно последнее, и тогда будем иметь
возможность закончить ломаную, соединяя последнюю из полученных
точек с точкой q прямолинейным отрезком, снова лежащим на отрез-
отрезке pq. Если две точки г и s расположены очень близко одна от другой,
но по разные стороны одной из сторон многоугольника Р, то они име-
имеют различную четность, так как выходящие из них (в фиксированном
направлении) лучи будут таковы, что на одном из них будет на одну
точку больше точек пересечения с Р, чем на другом. Отсюда ясно, что
четность меняется, когда, двигаясь по pq, мы проходим через точку q1-
Значит, ломаный «путь», намеченный на чертеже пунктиром, вернется
на pq между q' и q, так как р и q (следовательно, все точки на рассмат-
рассматриваемом «пути») имеют одну и ту же четность.
Таким образом, теорема Жордана для случая многоугольника дока-
доказана. «Внешними» по отношению к многоугольнику Р будут те точки,
которые принадлежат классу А: действительно, двигаясь по какому-

Приложение 313
нибудь лучу в фиксированном направлении достаточно далеко, мы, не-
несомненно, придем к точке, за которой пересечений с Р уже не будет,
все такие точки будут принадлежать классу А, так что их четность
будет 0. Тогда уже придется заключить, что точками «внутренними»
будут точки класса В. Каким бы запутанным ни был замкнутый много-
многоугольник Р, всегда очень легко узнать, расположена ли данная точка р
внутри или вне его: достаточно из р провести луч и посчитать число
его точек пересечения с Р. Если это число нечетное, значит, р «сидит»
внутри и не сможет выбраться наружу, не пересекая Р. Но если это чис-
число четное, то точка р — вне многоугольника Р (попробуйте проверить
это на рис. 128).
Вот идея другого доказательства жордановой теоремы для случая много-
многоугольников. Определим порядок точки ро относительно замкнутой кривой С
(не проходящей черезро) как число полных поворотов1, совершаемых стрел-
стрелкой (вектором), проведенным от р к ро, когда точка р делает один обход по
кривой С.
Затем пусть А есть совокупность точек ро (не на Р) четного порядка
относительно Р, а В есть совокупность точек ро (не на Р) нечетного порядка
относительно Р. В таком случае А и В, определенные указанным способом,
представляют собой соответственно области «внешнюю» и «внутреннюю» от-
относительно Р. Читатель может в качестве упражнения воспроизвести все
детали доказательства.
*3. Основная теорема алгебры. Основная теорема алгебры
утверждает, что если функция f(z) имеет вид
f(z) = zn + пп-гг"-1 + an-2zn~2 + ... + alZ + а0, A)
где п ^ 1 и о„_1, ап_2, ... , «i, оо — какие угодно комплексные числа,
то существует такое комплексное число а, что /(а) = 0. Другими сло-
словами, в поле комплексных чисел всякое алгебраическое уравнение имеет
корень. (Основываясь на этой теореме, мы на стр. 137 сделали дальней-
дальнейшее заключение: полином f(z) может быть разложен на п линейных
множителей
f(z) = {z- Qi)(z - а2) ¦ ¦ ¦ (z - а„),
гДе аь а2, ... , а„ — нули f(z).) Замечательно, что эту теорему мож-
Но доказать, исходя из соображений топологического характера, как и
Теорему Брауэра о неподвижной точке.
Это число нужно, конечно, брать в алгебраическом смысле, т.е. с учетом на-
набавления вращения.

314
Глава V
Пусть читатель вспомнит, что комплексное число есть символ ви-
вида х + уг, где хну — действительные числа, а символ г обладает свой-
свойством г2 = —1. Комплексное число х + уг изображается точкой (х, у)
в плоскости прямоугольных координат. Если мы введем в этой же плос-
плоскости полярные координаты, принимая начало координат за полюс,
а положительное направление оси х за полярную ось, то можно будет
написать
z = х + yi = r(cosO + ism в),
где г = \Jx2 + у2. Из формулы Муавра следует, что zn — rn(cos9 -f
+ isinO) (см. стр. 132). Отсюда ясно, что если комплексное число z
описывает круг радиуса г с центром в начале координат, то zn опи-
опишет ровно п раз круг с радиусом г™. Напомним еще, что\модуль z
(обозначаемый через \z\) представляет собой расстояние г от 0 и что,
если z' = х' + гу', то \z — z'\ есть расстояние между z и z'. После этих
напоминаний можно перейти к доказательству теоремы.
Г
Рис. 150. Доказательство основной теоремы алгебры
Допустим, что полином A) не имеет корней, так что при любом
комплексном z
/W/o.
При этом допущении, если z описывает некоторую замкнутую кривую
в х, у плоскости, то f(z) опишет некоторую замкнутую кривую Г, не
проходящую через начало координат (рис. 150). Можно определить по-
порядок точки О для функции f(z) относительно замкнутой кривой С как
число полных поворотов, совершаемых вектором, идущим от О к точ-
точке f(z) на кривой Г, когда z делает полный обход по кривой С. ВозьмеМ

Приложение 315
в качестве кривой С окружность с центром О и радиусом t и обо-
начим через ip{t) порядок точки О для функции f(z) относительно
окружности с ЦентР0М О и радиусом t. Очевидно. ip(Q) = 0, так как
круг радиуса 0 сводится к одной точке и кривая Г также сводится
к одной точке /@) Ф 0. Если мы докажем, что при достаточно больших
значениях t функция ip{t) равна п, то в этом уже будет заключаться
противоречие, так как, с одной стороны, порядок ip(t) должен быть не-
непрерывной функцией t (поскольку f(z) есть непрерывная функция z),
а с ДРУГ0И стороны, функция tp(t) может принимать только целые зна-
значения и потому никак не может перейти от значения 0 к значению п
непрерывно.
Нам остается доказать, что при достаточно больших значениях t
<p(t) = п.
Для этого заметим, что если радиус круга t удовлетворяет неравенст-
неравенствам
t>\ и t > \ао\ + \ах\ + ... + \an-i\,
то
\f(z) - zn\ = K-iz" + an-2zn~2 + ... + aoK
^ |on_i| • И" + |an_2| ¦ |z|"-2 + ... + |ao| =
= t [lOl + + +
+ ...+ ^
[ |а„-2| + ... + |ao|] < tn = \zn\.
Так как выражение слева есть не что иное, как расстояние между точ-
точками zn и f{z), а выражение в самой правой части неравенства —
расстояние точки zn от начала координат, то мы видим отсюда, что
отрезок, соединяющий точки zn и f(z), не пройдет через начало коор-
координат, если только z будет находиться на круге радиуса t с центром
в начале. В таком случае имеется возможность деформировать кри-
вУю, описываемую точкой f(t) в кривую, описываемую точкой zn, без
прохода через начало, смещая непрерывным движением каждую точ-
КУ f{z) к соответствующей точке zn по прямоугольному отрезку. При
этом порядок начала может принимать только целые значения и, вместе
с тем, во время деформации может меняться не иначе, как непрерыв-
Но; значит, для обеих функций f(z) и zn он одинаков, и так как для zn
он равен п, то имеет то же самое значение и для f(z). Доказательство
^Кончено.

Глава VI
Функции и пределы
Введение
Важнейшие разделы современной математики сосредоточиваются
около понятий функции и предела. В этой главе мы займемся система-
систематическим анализом этих понятий.
Такие выражение, как, например,
х2 + 2х - 3,
не имеют определенного числового значения, пока не указано значе-
значение х. Говорят, что значение этого выражения есть функция значения ж,
и пишут
х2 + 2х - 3 = f{x).
Например, если х = 2, то 22 + 2 • 2 - 3 = 5, так что /B) = 5. Та-
Таким же образом непосредственной подстановкой можно найти значе-
значение функции f(x) при любом целом, дробном, иррациональном и даже
комплексном значении х.
Число простых чисел, меньших чем п, есть функция тт(п) цело-
целого числа п. Когда задано значение числа п, то значение функции 7г(п)
определено, несмотря на то, что неизвестно никакого алгебраического
выражения для его подсчета. Площадь треугольника есть функция длин
трех его сторон; она меняется вместе с ними и делается фиксированной,
если зафиксированы длины сторон. Если плоскость подвергается про-
проективному или топологическому преобразованию, то координаты точ-
точки после преобразования зависят от первоначальных координат точки,
т.е. являются их функциями. Понятие «функция» выступает каждый
раз, как только величины связаны каким-нибудь определенным физи-
физическим соотношением. Объем газа, заключенного в цилиндр, есть функ-
функция температуры и давления, оказываемого на поршень. Замечено, что
давление атмосферы на воздушный шар есть функция высоты шара наД
уровнем моря. Целая область периодических явлений —- движение при-
приливов, колебание натянутой струны, распространение световых волн,

§ 1. Независимое переменное и функция 317
«спускаемых накаленной проволокой, — «регулируется» простыми три-
тригонометрическими функциями sin ж и cos ж.
Для самого Лейбница A646-1716), который впервые ввел термин
^функция», и для математиков XVIII в. идея функциональной зависи-
зависимости более или менее идентифицировалась с существованием простой
математической формулы, точно выражающей эту зависимость. Та-
Талая концепция оказалась слишком узкой по отношению к требованиям,
предъявленным математической физикой, и понятие «функция» вместе
с упомянутым выше понятием «предел» впоследствии длительно под-
подвергалось обобщениям и шлифовке.
В этой главе мы дадим краткий очерк того, как протекал этот
процесс.
§ 1. Независимое переменное и функция
1. Определения и примеры. Нередко приходится иметь дело
с математическими объектами, которые мы выбираем свободно, по на-
нашему собственному выбору, из некоторой совокупности (множества) S.
Избираемый объект в таких случаях носит название переменного (или
переменной), а совокупность S— области его (ее) изменения. Перемен-
Переменные принято обозначать последними буквами алфавита. Например, ес-
если буквой S обозначено множество всех целых чисел, то переменное X
из области S обозначает некоторое произвольное целое число. Говорят,
что «переменное X пробегает множество 5», подразумевая под этим,
что переменное X мы можем отождествить с любым элементом мно-
множества S. Пользоваться понятием переменного удобно, если мы хотим
высказать утверждение относительно элементов, которые можно про-
произвольно выбирать из целого множества. Например, если 5 обозначает,
как было указано, множество целых чисел, а X и Y — переменные из
области 5, то формула
X+Y=Y+X
представляет удобное символическое выражение того обстоятельства,
что сумма любых двух целых чисел не зависит от порядка слагаемых.
Частный случай этого выражен равенством
2 + 3 = 3 + 2,
в котором фигурируют постоянные числа; но, для того чтобы выра-
выразить общий закон, справедливый для всех пар чисел, нужно применить
символы, имеющие значение переменных.

318 Глава VI
Нет никакой необходимости в том, чтобы область S переменно-
переменного X была множеством чисел. Например, S может быть множеством
всех кругов на плоскости; тогда переменное X будет обозначать любой
индивидуальный круг. Или S может быть множеством всех замкну.
тых многоугольников плоскости, и тогда X — любой индивидуальный
многоугольник. Не является также необходимым, чтобы область пере-
переменного содержала бесконечное число элементов. Например, X может
обозначать любого отдельного человека из населения 5 данного города
в определенный момент времени. Или же X может обозначать любой из
возможных остатков при делении целого числа на 5; в этом последнем
случае область 5 состоит из пяти чисел: 0, 1, 2, 3, 4.
Наиболее важным оказывается случай числового переменного;
в этом случае употребляется обычно маленькая буква х — это тот
случай, когда областью изменяемости S является некоторый интер-
интервал (промежуток) а ^ х ^ Ь действительной числовой оси. В этом
случае говорят, что х есть непрерывное (или действительное) пере-
переменное в рассматриваемом интервале. Область изменения непрерыв-
непрерывного переменного может простираться и до бесконечности. Так, на-
например, S может быть множеством всех положительных действитель-
действительных чисел х > 0 или даже множеством всех действительных чисел без
всякого исключения. Аналогичным образом мы можем рассматривать
переменное X, значениями которого являются точки плоскости или
некоторой данной области плоскости, подобной внутренности прямо-
прямоугольника или круга. Так как каждая точка плоскости определяется
своими двумя координатами (х, у), взятыми относительно некоторой
фиксированной пары осей, то в этом случае часто говорят, что имеют
дело с парой действительных (непрерывных) переменных х и у.
Может случиться так, что каждому значению переменного X со-
сопоставляется некоторое определенное значение другого переменного U-
Тогда переменное U называется функцией переменного X. Способ, по-
посредством которого U связано с X, выражается символом вроде U =
= F(X) (читается «равно F от X»). Если X пробегает множество 5, то
переменное U пробегает некоторое другое множество, скажем, Т. На-
Например, если S есть множество треугольников X на плоскости, то под
функцией U = F(X) можно 'подразумевать длину периметра рассмат-
рассматриваемого треугольника X; Т будет, следовательно, множеством всех
положительных чисел. Отметим, что два различных треугольника Xi
и Хъ свободно могут иметь равные по длине периметры, так что равен-
равенство F(Xi) = F(X2) возможно и в том случае, если Х\ ф Х2. Проектив-
Проективное преобразование одной плоскости 5 в некоторую другую Т ставит

§1. Независимое переменное и функция 319
в соответствие каждой точке X плоскости 5 единственную точку U
плоскости Т согласно определенному правилу, которое можно выразить
функциональным символом U = F(X). В этом примере, в противопо-
противоположность предыдущему, мы имеем всегда неравенство F(Xi) ф F(X?),
если только Х\ Ф Х2, и мы говорим, в связи с этим, что отображение
плоскости 5 на плоскость Т — взаимно однозначное или однооднознач-
ное (см. стр. 224).
Функции непрерывного переменного часто определяются с помо-
помощью алгебраических выражений. Примерами могут служить следую-
следующие функции^-—
и = х2, и=-, и=
х
, и=.
х 1+х2
В первом и в последнем из этих выражений х может пробегать множес-
множество всех действительных чисел, в то время как во втором примере х
может пробегать множество всех действительных чисел за исключени-
исключением 0 (значение 0 исключается, так как символ ^ не есть число).
Число В(п) простых множителей числа п есть функция п, причем п
пробегает множество натуральных чисел. Вообще, любую последова-
последовательность чисел oi, a.2, «з5 ••• можно рассматривать как множество
значений некоторой функции и = F(n), причем областью изменения
независимого переменного при этом является множество натуральных
чисел. Только ради сокращения записи принято обозначать n-й член по-
последовательности символом ап, вместо того чтобы употреблять более
отчетливое функциональное обозначение F(n). Следующие выражения,
о которых говорилось в главе I:
являются функциями целого переменного п.
Пусть дано соотношение U = F(X); принято переменное X назы-
вать независимым переменным, а переменное U — зависимым, посколь-
КУ его значения зависят от выбора значения X.
Может случиться, что всем значениям переменного X соответству-
^ одно и то же значение переменного U, т. е. что множество Т состоит
Из одного единственного элемента. Мы тогда встречаемся с частным

320 Глава VI
случаем, при котором переменное U в сущности не меняется, т.е. (/
есть постоянное {постоянная или константа). Мы включим этот слу-
случай в общее понятие функции, несмотря на то, что начинающему это
может показаться странным, так как он склонен полагать, что основ-
основное в самой идее функции лежит как раз в изменении переменного V
(при изменении переменного X). Но беды не произойдет — а на самом
деле это окажется весьма полезным, — если мы постоянное будем рас-
рассматривать как частный случай переменного, «область изменяемости»
которого состоит из одного единственного элемента.
Понятие функциональной зависимости имеет исключительное зна-
значение не только в самой «чистой» математике, но также и в практи-
практических ее приложениях. Физические законы являются не чем иным,
как выражением способа, посредством которого некоторые величины
зависят от других, способных изменяться так или иначе. Так, напри-
например, высота звука, производимого колеблющейся струной, зависит от
ее длины, от ее веса и от степени ее натяжения; давление атмосферы
зависит от высоты; энергия пули зависит от ее массы и скорости. Зада-
Задача физики состоит в точном или приближенном определении природы
всех подобного рода зависимостей.
С помощью понятия функции можно дать точную в математичес-
математическом смысле характеристику движения. Если представим себе, что дви-
движущаяся частица сосредоточена в некоторой точке пространства с пря-
прямоугольными координатами х, у, z, и если переменное t измеряет вре-
время, то движение частицы полностью определено заданием координат х,
у, z как функций времени:
з = /(«), y = g(t), 2 = МО-
Примером этого может служить свободное падение частицы по верти-
вертикали под действием одной лишь силы тяжести: мы имеем в этом случае
соотношения
х = 0, у = 0, z = -\gt2,
где g обозначает ускорение силы тяжести. Если частица равномерно
вращается по единичному кругу в плоскости х, у, то движение ее ха-
характеризуется функциями
х = coswt, у = sinwt,
где и — постоянное число (так называемая угловая скорость враШ6"
ния).

§ 1. Независимое переменное и функция 321
Под математической функцией следует понимать просто закон,
управляющий взаимными зависимостями переменных величин — и не
более того. Понятие функции не подразумевает существования чего-
либо близкого к «причине и следствию» в отношениях между независи-
мой и зависимой переменными. Хотя в обыденной речи термин «функ-
«функциональная зависимость» сплошь и рядом употребляется именно в этом
последнем смысле, мы будем избегать такого рода философских интер-
интерпретаций. Так, например, закон Бойля, относящийся к газу, заключен-
заключенному в некоторую замкнутую оболочку при постоянной температуре,
утверждает, что произведение давления газа р на его объем v есть вели-
величина постоянная, равная с (последнее значение в свою очередь зависит
от температуры):
pv = с.
Это соотношение можно решить как относительно р, так и относитель-
относительно V.
Р=§ или »=|;
при этом не следует подразумевать ни того, что перемена объема есть
«причина» изменения давления, ни того, что изменение давления есть
«причина» изменения объема. Для математика существенна лишь фор-
форма соответствия (связи) между двумя переменными величинами, ко-
которые он рассматривает.
Следует заметить, что подход к понятию функции несколько отлича-
отличается у математиков и у физиков. Математики обычно подчеркивают закон
соответствия, математическую операцию, которую нужно применить к зна-
значению независимого переменного х, чтобы получить значение зависимого пе-
переменного и. В этом смысле /( ) есть символ математической операции; зна-
значение и = f(x) есть результат применения операции /( ) к числу х. С другой
стороны, физик часто более заинтересован в самой величине и, как таковой,
чем в какой-то математической процедуре, с помощью которой значение и
может быть получено из значения х. Так, например, сопротивление и воздуха
Движению предмета зависит от скорости v движения и может быть найдено
экспериментальным путем, независимо от того, известна ли явная математи-
математическая формула для вычисления и. Физика прежде всего интересует факти-
фактические сопротивление, а не специальная математическая формула f(v), если
т°лько эта формула не помогает при анализе поведения величины и. Таково
обычно отношение тех, кто применяет математику к физике или инженер-
инженерному делу. В некоторых высших разделах математического анализа, чтобы
Избежать путаницы, иногда бывает существенно различать совершенно от-
ЧеТЛиво, будет ли под символом и = f(x) подразумеваться операция /( ),
"Рименяемая к х для получения и, или же сама величина и, которая, в свою

322 Глава VI
очередь, может рассматриваться как зависимая, и совсем другим образом,
от некоторой другой переменной z. Например, площадь круга задается функ-
функцией и = f(x) = пх2, где х — радиус круга, но можно также написать: и =
2
= g(z) = т~> понимая под z длину окружности.
4тг
Пожалуй, наиболее простым типом математической функции одно-
одного независимого переменного являются многочлены (полиномы), имею-
имеющие вид
и = /(ж) = по + а±х + п2Х2 + ... + апхп,
с постоянными «коэффициентами» ао, a,i, ... , ап. За ними следуют ра-
рациональные функции, такие, как
- 1 _ 1 _ 2ж + 1
которые являются отношениями многочленов, и затем тригонометри-
тригонометрические функции cos ж, sin ж и tga; = -§^§> которые определяются лучше
всего с помощью единичного круга в плоскости ?, г): ?2 + rf = 1. Если
точка Р(?, rj) движется по этой окружности и если х есть направлен-
направленный угол, на который нужно повернуть положительную ось х, чтобы
она совпала с радиусом ОР, то cos ж и sin ж являются координатами
точки Р: cos ж = ?, sin ж = ц.
2. Радианная мера углов. Во всех практических применениях
углы измеряются с помощью единиц, полученных от деления прямого
угла на некоторое равное число частей. Если это число равно 90, то
единицей измерения является обычный «градус». Деление на 100 частей
подходило бы близко к нашей десятичной системе, но принцип измере-
измерения при этом оставался бы прежним. В теоретических же применениях
выгоднее использовать по существу совершенно другой метод опреде-
определения величины угла, а именно, так называемое радианное измерение.
Многие важные формулы, содержащие тригонометрические функции
углов, имеют в этой системе измерения более простой вид, чем при
измерении углов в градусах.
Для того чтобы найти радианную меру некоторого угла, опишем
из вершины этого угла, как из центра, круг радиуса 1.
Длину дуги s той части нашей окружности, которая расположена
между сторонами угла, назовем радианной мерой угла. Так как длина
всей окружности единичного радиуса равна 2тг, то «полный» угол в 360°
имеет радианную меру 2тг. Отсюда следует, что если через ж обозначить
радианную меру угла, а через у его величину в градусах, то ж и у

§ 1. Независимое переменное и функция 323
связаны соотношением -|- = ^-, или
тту = 180 ж.
Так, например, угол в 90° (у = 90) имеет радианной мерой х = ^тг = ?
loll l
и т. д. С другой стороны, угол в 1 радиан (угол, радианной мерой кото-
которого является х = 1) есть центральный угол, стягиваемый дугой, длина
которой равна радиусу окружности; градусная мера такого угла содер-
1 ЯП
жит у — ~5р = 57,2957 ... градусов. Для того чтобы от радианной меры
угла х перейти к его градусной мере у, нужно величину х умножить
1 ЯП
на число -^.
Радианная мера х некоторого угла равна также двойной площади А
сектора, вырезаемого этим углом в упомянутом круге единичного ра-
радиуса; в самом деле, эта площадь относится ко всей площади круга так,
как длина дуги относится к длине всей окружности: ^- = ^; итак, х =
= 2А.
Будем впредь под углом х подразумевать угол, радианная ме-
мера которого есть х. Угол, градусное измерение которого равно х, бу-
будем в дальнейшем, чтобы устранить всякую неясность, обозначать че-
через х°.
Позднее станет совершенно очевидным, насколько выгодно пользо-
пользоваться радианным измерением при разного рода аналитических опера-
операциях. Однако следует признать, что для практического употребления
оно скорее неудобно. В самом деле, так как тг — иррациональное чис-
число, то, сколько раз мы ни откладывали бы по кругу единичный угол,
т.е. угол с радианной мерой, равной 1, мы никогда не вернемся в на-
начальную точку. Обычное же измерение таково, что после откладывания
1 градуса 360 раз или 90 градусов 4 раза мы возвращаемся в исходную
точку.
3. График функции. Обратные функции. Часто характер
Функции чрезвычайно ясно выражается с помощью простого графика.
Если (х, и) — координаты на плоскости относительно двух взаимно
перпендикулярных осей, то линейные функции, а именно,
и = ах + b
изображаются прямыми линиями; квадратические функции
и = ах2 + Ьх + с

324
Глава VI
-2л
О
л_ \
2
cos .v sin .v
Рис. 151. Графики функций sina; и cos а;
°1
Рис. 152. и = tgx
параболами; функция
— гиперболой и т. д. По определению, график некоторой функции и =
= f(x) состоит из всех тех точек плоскости, координаты которых (х, и)
связаны уравнением и — f(x). Функции sina;, cos ж, tga; представлены
графически на рисунках 151 и 152. Эти графики наглядно показывают,
как возрастают или убывают функции при изменении х.
Одним из важных методов, служащих для введения новых функ-
функций, является следующий. Исходя из некоторой известной функ-
функции F(X), можно попытаться решить уравнение U = F{X) относи-
относительно X — так, чтобы X было выражено как функция от U:
X = G(U).
Тогда функция G(U) называется обратной относительно функции F(X)-
Этот процесс приводит к результату однозначно только в том случае,
если функция U = F(X) определяет взаимно однозначное отображение
области изменяемости X на область изменяемости U, т. е. если нера-
неравенство Х\ ф Хч всегда влечет за собой неравенство F(Xi) ф

§1. Независимое переменное и функция
325
О
Рис. 153. и = х3
Только при этом условии каждому значе-
значению U будет соответствовать единствен-
единственное значение X. Здесь будет кстати вспом-
вспомнить приведенный выше пример, в котором
роль независимого переменного X играл
любой треугольник на плоскости, а в ка- _
честве функции U = F(X) рассматривался
его периметр. Очевидно, что такое отобра-
отображение множества 5 треугольников на мно-
множество Г положительных чисел не является
взаимно однозначным, так как имеется бес-
бесконечное количество различных треуголь-
треугольников с одним и тем же периметром. Итак,
в этом случае соотношение U = F(X) не может служить для однознач-
однозначного определения обратной функции. С другой стороны, функция т =
= 2п, где п пробегает множество 5 всех целых чисел, а т — множест-
множество Г четных чисел, напротив, дает взаимно однозначное соответствие
между двумя множествами, и обратная функция п = Щ- будет опреде-
определена. В качестве другого примера данного однозначного отображения
приведем функцию
и = х3.
Когда х пробегает множество всех действительных чисел, и тоже про-
пробегает множество всех действительных чисел, принимая каждое значе-
значение один и только один раз. Однозначно определенная в этом примере
обратная функция имеет вид:
В случае функции
и — х
обратная функция не определена однозначно. В самом деле, в силу того,
что и = х2 = (—хJ, каждому положительному значению и соответ-
соответствуют два разных значения («прообраза») х. Но если под символом \рп,
подразумевать (как это часто и делается) положительное число, квад-
квадрат которого есть х, то обратная функция
х = \рп,
существует, если только мы условимся, что рассматривать будем лишь
положительные значения х и и.

326
Глава VI
и
0
/
/]
/ J\
7 7 i
[
/
X
X ,
0
/
(
и
Рис. 154. Взаимно обратные функции
Существование обратной функции может быть сразу установлено
при взгляде на график данной функции. Обратная функция существует,
определяясь однозначно, в том случае, если каждому значению и соот-
соответствует только одно значение х. Геометрически это означает, что нет
такой прямой, параллельной оси х, которая пересекала бы график более
чем в одной точке. Само собой разумеется, что так будет в том случае,
если функция и = f(x) монотонная, т.е. или все время возрастающая,
или, наоборот, все время убывающая (при возрастании х). Например,
если функция и = f(x) всюду возрастающая, то при х\ < Х2 мы всегда
имеем wi = f(xi) < U2 = f{xi). Следовательно, для данного значения и
существует не более одного значения х, такого, что и = f(x), и обрат-
обратная функция будет определяться однозначно. График обратной функ-
функции х = g(u) получается из данного графика просто путем вращения
его на угол в 180° вокруг пунктирной прямой (рис. 154) таким обра-
образом, что роли оси х и оси и между собой меняются. Новое положение
графика изображает х как функцию от и. В основном положении гра-
график указывает значение и и как высоты над горизонтальной осью х,
в то время как после поворота вновь полученный график указывает
значение х как высоты над горизонтальной осью и.
Рассуждения этого параграфа можно иллюстрировать на примере
функции
и — tg:c.
Эта функция монотонна в промежутке — ^ < х < ^ (рис. 152): значе-
ния и, все время возрастающие вместе с х, изменяются от —оо до +оо;
отсюда ясно, что обратная функция
х = g(u)

! 1. Независимое переменное и функция
327
х,,
О
Рис. 155. х = arctgu
определена для всех значений и. Эту функцию обозначают arctgu. Та-
Таким образом, arctg(l) = ^, поскольку tg j = 1. График arctgu изобра-
изображен на рис. 155.
4. Сложные функции. Вторым важным методом создания но-
новых функций из двух или большего числа данных является составление
сложных функций («композиция»). Так, например, функция
и = f(x) = \/l + х2
«составлена» из двух простых функций
z = g(x) = 1 + х2, и = h(z) = \fz
и может быть записана так:
и = f(x) = h(g[x})
(читается «h от g от ж»). Аналогично, функция
и = f{x) = 1
Д. — Jj
составлена из трех функций
z = g(x) = l-x2, w = h(z) = \/z, u = k(w) = —,
так что можно написать
Функция
u = f{x) = kih[gix)\).
« = /(*) = sin i
составлена из двух функций
z = g{x) = j, и = h(z) = sin.?.

328
Глава VI
Рис. 156. и = sin^
J
Функция f(x) = sin — не определена при х = О, так как при х = 0 выра-
выражение i не имеет смысла. График этой замечательной функции находится
в некоторой связи с графиком синуса. Мы знаем, что sin z = 0 при z = кп,
где к — произвольное положительное или отрицательное целое число. Кроме
того,
{1 при z = Dк + l)^,
2
-1 при
= Dfc-l)|,
где к — произвольное целое число. Отсюда имеем:
Ьг'
sin I = «
0
1
-1
при
при
при
X =
X =
X =
Dfe + 1)тг'
2
Dfc- 1)тг'
Если мы последовательно станем полагать к = 1, 2, 3, 4, ..., знаменатели этих
дробей будут возрастать неограниченно и, следовательно, значения х, при
которых функция sin — имеет значения 1, —1, 0, будут сгущаться все больше
и больше около точки х = 0. Между каждой такой точкой и началом будет
всегда бесконечное количество колебаний. График этой функции показан на
рис. 156.
5. Непрерывность. Графики уже рассмотренных функций да-
дают интуитивное представление о свойстве, называемом непрерывнос-
непрерывностью. Точное определение этого понятия мы дадим в § 4, после того
как понятие предела будет поставлено на строго логический фундамент.
Здесь же, ограничиваясь описательной формулировкой, мы скажем, что

i 1. Независимое переменное и функция
329
О
функция непрерывна, если ее график есть плавная, нигде не «прерыва-
«прерывающаяся» кривая. Чтобы уяснить себе, является ли функция и = f(x)
непрерывной в точке х = xi, заставим независимую переменную х
приближаться непрерывно справа и слева к значению xi. При этом
значения функции и = f(x) меняются, если только эта функция не
является постоянной в окрестности точки х\. Если оказывается, что
значение функции f(x) неограниченно приближается к значению f(xi)
этой функции в выбранной точке х = xi («стремится к пределу f(xi)»),
и притом независимо от того, приближается ли х
к xi с одной стороны или с другой, то тогда го-
говорят, что функция f(x) непрерывна в точке х\.
Бели это имеет место в каждой точке Х\ из неко-
некоторого интервала, то говорят, что функция непре-
непрерывна в этом интервале. Хотя каждая функция,
представляемая плавным графиком, непрерывна,
но очень легко определить и такие функции, кото-
которые не везде непрерывны. Например, функция на
рис. 157, определенная для всех значений х с по-
помощью формул
f(x) = 1 + х при х > О,
/(ж) = -1+а: при а:^0,
разрывна в точке xi = 0, в которой она имеет значение —1. Если мы
станем чертить карандашом график этой функции, нам придется в этой
точке оторвать карандаш от бумаги. Когда мы приближаемся к значе-
значению xi = 0 справа, то f(x) стремится к +1. Но значение это отличается
от значения функции в самой этой точке, именно —1.
Одно то обстоятельство, что функция f(x) стремится к —1, когда х
стремится к нулю слева, еще недостаточно для установления непрерыв-
непрерывности.
Функция f(x), определенная для всех значений х с помощью фор-
формул
S{x) =0 при х ф 0, /@) = 1,
при х\ = 0 имеет разрыв другого вида. Здесь существуют пределы и
справа, и слева, и они равны между собой, но это общее предельное
значение отлично от /@). Еще иного типа разрыв дается функцией,
график которой изображен на рис. 158,
Рис. 157.
«скачком»
Разрыв
и = f(x) = -L

330
Глава VI
Рис. 158. Разрыв с уходом в
бесконечность
в точке х = 0. Если заставим х стре-
стремиться к 0 с любой стороны, то и не-
неизменно будет стремиться к бесконеч-
бесконечности, но график функции «прерывает-
«прерывается» в этой точке, причем малым из-
изменениям независимого переменного х
в окрестности точки х = 0 могут со-
соответствовать очень большие изменения
зависимого переменного и. Строго го-
говоря, значение функции не определено
при х = 0, поскольку мы не считаем бес-
бесконечность числом, и поэтому нельзя говорить, что функция f(x) равна
бесконечности при х = 0. Итак, мы говорим только, что функция f(x)
«стремится к бесконечности», когда х приближается к нулю.
Совсем иной характер разрыва, наконец, у функции и = sin i в точ-
точке х — 0 (рис. 156).
Приведенные примеры показывают несколько различных типичес-
типических случаев, когда функция перестает быть непрерывной в некоторой
точке х = х\.
1) Может случиться, что функция станет непрерывной в точке х =
= xi после того, как надлежащим образом будет определено или будет
изменено уже определенное значение ее при х = х\. Например, функ-
функция и = § постоянно равна 1 при х ф 0; она не определена при х = 0,
поскольку ^ — лишенный смысла символ. Но если в этом примере мы
условимся считать, что значение и = 1 соответствует также и зна-
значению х = 0, то функция, таким образом «расширенная», становится
непрерывной во всех точках без исключения. Тот же результат будет
достигнут, если мы изменим значение функции при х — 0 во втором
из приведенных выше примеров и вместо /@) = 1 положим /@) = 0.
Разрывы этого рода называются устранимыми.
2) Функция стремится к различным пределам в зависимости от
того, справа или слева х приближается к х±, как на рис. 157.
3) Не существует предела ни с одной стороны, ни с другой стороны,
как на рис. 156.
4) Функция стремится к бесконечности, когда х приближается к х\
(рис. 158).
Разрывы трех последних типов называются существенными или
неустранимыми, они не могут быть устранены с помощью надлежащего
определения значения функции в одной лишь точке х — х\.

§ 1. Независимое переменное и функция
331
Упражнения.
1) Наметить графики функций
точки разрыва.
х - 1 х2 - 1
х3 ' x2+l' (х2 - 1){х2 + 1)
и найти
2) Наметить графики функций a; sin— и ж2 sin —; проверить, что непре-
непрерывность не нарушена в точке х = 0, если принять, что и = 0 при х = О
в обоих случаях.
*3) Показать, что функция arctg — имеет разрыв второго типа (скачок)
при х = 0.
Рис. 159. Полусфера
Рис. 160. Гиперболический
параболоид
*6. Функции нескольких переменных. Вернемся к система-
систематическому рассмотрению понятия функции. Если независимым пере-
переменным Р является точка плоскости с координатами ж, j/и если каждой
такой точке Р соответствует единственное число и (например, и может
быть расстоянием точки Р от начала), тогда принято писать
и = f(x, у).
Это обозначение употребляется также и в том случае, если, как это
часто бывает, две величины х и у явно указываются самими услови-
условиями задачи как независимые переменные. Например, давление и газа
есть функция объема х и температуры у; площадь и треугольника есть
Функция и — f(x, у, z) длин трех его сторон х, у, z.
Так же, как график дает геометрическое представление функции
одного переменного, можно получить и геометрическое представление
Функции и = f(x, у) двух переменных в виде поверхности в трехмер-
трехмерном пространстве с переменными х, у, и в качестве координат. Каж-
Каждой точке х, у в плоскости х, у мы сопоставляем точку пространства

332
Глава VI
Рис. 161. Поверхность вида и =
= /(*, у)
Рис. 162. Линии уровня поверхнос-
поверхности, изображенной на рис. 161
с координатами х, у и и = f(x, у). Таким образом, и = -у/l — х2 — у2
представляется поверхностью сферы с уравнением и2 + х2 + у2 = 1,
линейная функция и = ах + by + с — плоскостью, функция и = ху —
гиперболическим параболоидом и т.д.
Можно дать и другое представление функ-
функции и = f(x, у), притом не выходя за преде-
пределы плоскости х, у, именно, с помощью линий
уровня (горизонталей). Вместо того чтобы рас-
рассматривать трехмерный «ландшафт» поверх-
поверхности и = f(x, у) в трехмерном пространст-
пространстве, мы вычерчиваем, как это иногда делают на
географических картах, «линии уровня» функ-
функции, являющиеся проекциями на плоскость х,
у всех точек поверхности, находящихся на од-
одном и том же расстоянии и по вертикали от
плоскости х, у. Эти линии уровня имеют урав-
уравнения вида f(x, у) — с, где с постоянно для
каждой кривой. Так, например, функция и = х + у характеризуется
рис. 163. Линии уровня поверхности сферы представляют собой семей-
семейство концентрических окружностей. Функция и = х2+у2, которой соот-
соответствует параболоид вращения, характеризуется также окружностями
(рис. 165). Числами, отнесенными к каждой кривой, можно указывать
высоту и — с.
Функции нескольких переменных встречаются в физике при опи-
описании движения непрерывной среды или каких угодно протяженных
Рис. 163. Линии уровня
поверхности и = х + у

! 1. Независимое переменное и функция
333
Рис. 164. Параболоид
вращения
Рис. 165. Соответству-
Соответствующие линии уровня
объектов. Рассмотрим хотя бы струну, натянутую между двумя точка-
точками на оси х и затем деформированную таким образом, что частица с ко-
координатой х отодвинута на некоторое определенное расстояние перпен-
перпендикулярно к оси. Если струна будет отпущена, то она придет в движе-
движение, т.е. начнет колебаться; тогда точка (частица) струны с начальной
координатой х в момент времени t будет находиться на расстоянии и =
— f(x, t) от оси х. Движение струны будет полностью определено, если
только будет известна функция и = f(x, t).
Определение непрерывности, данное для функций одного пере-
переменного, распространяется непосредственно и на функции нескольких
переменных. Говорят, что функция и = f(x, у) непрерывна в точ-
ке х = Хх, у = ух, если значение f(x, у) всегда стремится к значе-
значению f(xx, ух), когда точка х, у приближается к точке Хх, ух по любому
направлению или любым способом.
Впрочем, имеется одно существенное различие между функциями
одного и нескольких переменных. В последнем случае понятие обратной
функции теряет смысл, так как мы не можем решить уравнение и =
— f{xi У), например, и = х + у, так, чтобы каждое из независимых
переменных х и у было бы выражено с помощью только одного пере-
переменного и. Но это различие между функциями одного и нескольких
переменных исчезает, если мы перейдем, далее, к рассмотрению пре-
преобразований или отображений.
*7. Функции и преобразования. Соответствие между точка-
точками некоторой прямой I, характеризуемыми координатой х на этой пря-
прямой, и точками некоторой другой прямой V, характеризуемыми ко-
координатой х', есть не что иное, как некоторая функция х' = f{x).
В случае взаимно однозначного соответствия имеем также и обратную

334 Глава VI
функцию х = g(x'). Простейшим примером является проективное пре-
преобразование, которое задается в самом общем случае дробной линейной
функцией вида
х> = f{x) = 9^±Л
ex + d
где а, Ь, с, d — постоянные (мы это утверждаем здесь без доказатель-
доказательства).
— dx' + Ъ
В этом примере обратная функция имеет вид х = -——.
сх — а
В случае, если устанавливается отображение плоскости тг с коор-
координатной системой х, у на другую плоскость тг' с координатной систе-
системой х', у', соотношение между точками не может быть задано одной
функцией х' = f(x); здесь приходится иметь дело с двумя функциями
двух переменных
х' = f(x, у), у' = g(x, у).
Например, проективное преобразование задается системой функций
. ах + Ьу + с , dx + еу + f
gx + Ну + fc' gx + hy + fc'
где a, b, ... , к — постоянные, а х, у и х', у', как сказано, — соответ-
соответственные координаты в двух плоскостях. Теперь идея обратного ото-
отображения снова приобретает смысл. Мы просто должны решить дан-
данную систему уравнений относительно хну, выразив их через х' и у'.
Геометрически это сводится к осуществлению обратного отображения
плоскости тг' на плоскость тг. Это отображение будет однозначно опре-
определено, если соответствие между точками обеих плоскостей взаимно
однозначное.
Преобразования плоскости, изучаемые в топологии, задаются не
простыми алгебраическими уравнениями, а произвольной системой
двух функций
х' = f(x, у), у' ~ g(x, у),
при условии, чтобы ими определялось взаимно однозначное и взаимно
непрерывное преобразование.
Упражнения.
1) Показать, что преобразование инверсии (глава III, стр. 182) в единич-
единичном круге аналитически задается уравнениями х' = х—-, у' =
х +у
У
= — -. Найти обратное преобразование. Доказать аналитически,
х +У
*

§2. Пределы 335
что путем инверсии совокупность прямых и окружностей преобразу-
преобразуется в совокупность опять-таки прямых и окружностей.
2) Доказать, что преобразованием х' = четверка точек на оси х
сх + о
переводится в четверку точек на оси х с тем же двойным отношением
(см. стр. 238).
§2. Пределы
1. Предел последовательности ап. Определение непрерыв-
непрерывности функции, как мы это уже видели в § 1, основывается на понятии
предела. До сих пор мы пользовались этим понятием в более или менее
интуитивной форме. В настоящем и в последующих разделах мы вве-
введем его более систематическим путем. Поскольку последовательности
несколько проще, чем функции непрерывного переменного, мы начнем
с изучения последовательностей.
В главе II мы имели дело с числовыми последовательностями ап
и изучали их пределы при условии, что п неограниченно увеличива-
увеличивается или «стремится» к бесконечности. Например, последовательность
с общим членом а„ = ^:
1 I I I A)
при неограниченном возрастании п имеет предел 0:
i -> 0 при п -> оо. B)
Постараемся выразить точно, что под этим подразумевается. При про-
продвижении по последовательности все дальше и дальше мы видим, что
члены становятся все меньше и меньше. После 100-го члена члены уже
меньше -^-, после 1000-го — меньше и т.д. Ни один из членов не
Равен в действительности 0. Но если мы продвинемся достаточно дале-
далеко по последовательности A), то мы можем быть уверены, что каждый
Из ее членов будет отличаться от 0 сколь угодно мало.
В этом объяснении может смущать единственно то, что смысл под-
подчеркнутых слов не вполне ясен. Что значит «достаточно далеко» и что
значит «сколь угодно мало»? Если мы сумеем придать точный смысл
этим выражениям, то этим самым будет установлен точный смысл по-
понятия предела последовательности.

336 Глава VI
Геометрическая интерпретация поможет нам разобраться в инте-
интересующем нас вопросе. Если мы изобразим члены последовательнос-
последовательности A) в виде соответствующих им точек на числовой оси, то заме-
заметим, что члены последовательности в нашем примере «накопляются»
или «сгущаются» около точки 0. Выберем на числовой оси некоторый
интервал / с центром в точке 0 и общей длиной 2е, так чтобы интер-
интервал простирался на расстояние е с каждой стороны от точки 0. Если мы
возьмем е = 10, то, конечно, все члены ап = ^ нашей последовательнос-
последовательности будут лежать внутри интервала /. Если же мы возьмем s = j^, то
несколько первых членов окажутся лежащими вне интервала /; однако
все члены, начиная с оц, а именно,
J_ J_ J_ i.
11' 12' 13' 14'"'
будут лежать внутри /. Даже при s = jjh^: лишь первая тысяча членов
последовательности не попадет внутрь интервала I, тогда как беско-
бесконечное множество членов, начиная с
O1002, Ol003i • • ¦
окажется внутри него. Ясно, что это рассуждение справедливо для лю-
любого положительного числа е: если положительное е выбрано, то, неза-
независимо от того, как оно мало, мы всегда можем подобрать настолько
большое целое число N, что
Отсюда следует, что все члены ап последовательности, для кото-
которых п ^ N, будут лежать внутри интервала /, и только конечное чис-
число членов ах, п2, ... , алг_1 может лежать вне его. Основные моменты
здесь таковы: во-первых, длина интервала / определяется произвольно
посредством выбора е. Затем может быть подобрано подходящее целое
число N. Этот процесс первоначального выбора числа е и последующе-
последующего подбора целого числа N может быть осуществлен при любом поло-
положительном ? независимо от его малости; тем самым устанавливается
точный смысл утверждения, что «все члены последовательности A) от-
отличаются от 0 сколь угодно мало, если только мы достаточно далеко
продвинемся по последовательности».
Подведем итоги: пусть е — какое-нибудь положительное число.
Тогда мы можем подобрать такое целое положительное число JV, что

§2. Пределы 337
все члены ап последовательности A), для которых п ^ N, будут ле-
лежать внутри интервала / длины 2е с центром в точке е. Таков смысл
предельного соотношения B).
Опираясь на этот пример, мы можем теперь дать точное опреде-
определение следующего общего утверждения: «Последовательность действи-
действительных чисел ai, а.2, аз, •¦¦ имеет предел а». Число а мы заключаем
внутрь некоторого интервала / числовой оси: если этот интервал мал,
то некоторые числа ап могут лежать вне этого интервала: но как толь-
только п становится достаточно большим, скажем, большим или равным
некоторому числу N, то все числа ап, для которых п ^ N, должны
лежать внутри интервала /. Конечно, может случиться, что придется
брать очень большое целое число N, если интервал I выбран очень ма-
малым; однако, как бы мал этот интервал / ни был, такое целое число N
должно существовать, раз предполагается, что последовательность име-
имеет предел.
Тот факт, что последовательность ап имеет предел а, выражается
символически следующей записью:
liman = а при п —> оо,
или просто
ап -» а при п -> оо
(«предел ап равен а», или «а„ стремится к пределу а»). Если последо-
последовательность имеет предел в указанном смысле, она называется сходя-
сходящейся. Определение сходимости последовательности ап можно сформу-
сформулировать более сжато, а именно, следующим образом:
Последовательность а\, а,2, аз, •¦¦ имеет предел а при неограни-
неограниченном возрастании п, если каждому сколь угодно малому положитель-
положительному числу г можно поставить в соответствие такое целое положи-
положительное число N (зависящее от е), что неравенство
\а-ап\<е C)
выполняется для всех значений
п^ N.
Такова общая, «абстрактная» формулировка понятия предела после-
последовательности. Немудрено, если тот, кто встречается с ней впервые, не
может сразу схватить и исчерпать ее содержание. К несчастью, авторы
некоторых руководств, стоящие на неправильной позиции, граничащей

338 Глава VI
со снобизмом, преподносят читателю это определение без тщательной
подготовки, как будто бы снизойти до разъяснений ниже достоинства
математика.
Определение предполагает своего рода дискуссию между двумя ли-
лицами Аи В. А выдвигает требование: заданная величина а должна быть
приближена числами ап так, чтобы ошибка не превышала границы е =
— Е\; В отвечает на это требование указанием, что существует такое
целое N = N\, что все члены ап, следующие за а^х, удовлетворяют
этому условию. Тогда А становится более требовательным и предлага-
предлагает новую, меньшую границу е = ?2\ В снова встречает это требование
подбором некоторого, может быть значительно большего, целого чис-
числа N = N2, обладающего аналогичным свойством, и т. д. Если В может
удовлетворить А независимо от того, какую малую границу назнача-
назначает А, то мы имеем дело с положением, которое кратко выражается
соотношением: ип —> а.
Имеется определенная психологическая трудность в том, чтобы со-
составить правильное представление о понятии предела. Наша интуиция
предполагает «динамическую» идею предела как результат процесса
«движения»: мы продвигаемся по ряду целых чисел 1, 2, 3, ... , п, ...
и при этом наблюдаем за поведением последовательности ап. Мы ждем,
что числа ап должны все меньше и меньше отличаться от числа а. Но
эта «естественная» точка зрения не поддается ясной математической
формулировке. Чтобы прийти к точному определению, надо перевер-
перевернуть порядок рассуждения: вместо того чтобы прежде всего обращать-
обращаться к независимому переменному пп, а затем уже к переменному ап,
мы должны основывать наше определение на том, что следует делать,
если мы по существу хотим проконтролировать утверждение ап —> а.
При такой постановке вопроса мы прежде всего должны выбрать произ-
произвольно малый интервал около а и затем решить: можем ли мы добиться,
чтобы ап с помощью выбора достаточно большого п в него попало. За-
Затем, вводя символы е и N для обозначения «произвольно малого интер-
интервала» и «достаточно большого п», мы приходим к точному определению
предела.
Обращаясь теперь к другому примеру, рассмотрим последователь-
последовательность
12 3 4 п
2' 3' 4' 5' ¦¦"' тг + 1' "•'
где ап = —^-г. Я утверждаю, что liman = 1. Если вы выберете интер-
вал с центром в точке 1 и возьмете е = —, то я смогу удовлетворить

§2. Пределы 339
вашему требованию C), выбрав N = 10; в самом деле,
П s 1 п - п + 1 ~ п
п + 1 п + 1 п + 1 10
при га ^ 10. Если вы усилите ваше требование, выбирая г = тт^ттт, то
я снова могу ему удовлетворить, выбирая N = 1000; и так дальше —
для любого положительного числа е, которое вы пожелаете выбрать,
независимо от его малости: действительно, мне только нужно будет
выбрать любое целое N, большее чем i. Этот процесс, заключающий-
заключающийся, во-первых, в выборе произвольно малого интервала длины 2е вокруг
числа а и, во-вторых, в доказательстве того, что все члены последова-
последовательности ап находятся на расстоянии, меньшем чем г от а, раз только
мы продвинемся достаточно далеко по последовательности, и есть не
что иное, как подробное описание того факта, что ап —> а. Если чле-
члены последовательности ai, 02, аз, ... представлены в виде бесконечных
десятичных дробей, то утверждение
liman = a
обозначает попросту то, что для любого целого положительного га пер-
первые т цифр числа ап совпадают с первыми га цифрами бесконечно-
бесконечного десятичного разложения числа а, раз только п выбрано достаточно
большим, скажем, большим некоторого значения N (зависящего от т).
Это просто соответствует выбору е в форме 10~т.
Существует другое и очень выразительное определение понятия
предела. Если liman = а и если мы заключим число а в интервал /,
то, независимо от малости интервала /, все числа ап при п, большем
некоторого целого числа N, будут лежать в интервале /, так что не
больше чем конечное число N — 1 членов из числа следующих:
а\, а2, а3, ... , aN-i
могут лежать вне интервала /. Если интервал / очень мал, то чис-
число N может быть очень большим, скажем, равным 100 или даже 1000
биллионам, и все же лишь конечное число членов последовательности
будет лежать вне интервала /, в то время как бесконечное множество
оставшихся членов попадет в интервал /. Можно условиться говорить
о членах некоторой бесконечной последовательности, что «почти все»
°ни обладают некоторым свойством, если лишь конечное число их (не-
(неважно, как оно будет велико) не обладает этим свойством. Так, напри-
Мер, «почти все» целые положительные числа больше 1000000000 000.

340 Глава VI
Используя эту терминологию, мы видим, что утверждение
liman = a
эквивалентно следующему утверждению: если I есть любой интервал
с центром в точке а, то почти все числа ап лежат в этом интервале.
Не мешает мимоходом отметить, что нет необходимости предпола-
предполагать, что все члены ап последовательности непременно имеют различ-
различные значения. В частности, совершенно допустимо, чтобы несколько из
них, или бесконечное число, или даже, наконец, все числа ап были рав-
равны предельному значению а. Например, вполне законно рассматривать
последовательность а\ = 0, аг = 0, ... , ап = 0, ..., и ее предел есть,
конечно, 0.
Как уже указано, последовательность ап с пределом а называет-
называется сходящейся. Последовательность, не имеющая предела, называется
расходящейся.
Упражнения.
Доказать:
1) Последовательность с общим числом ап = —-^— имеет предел, рав-
п + 1
ный 0. (Указание: ап = —-— меньше — и больше 0).
2) Последовательность ап = — имеет предел 0. (Указание: а„ —
п + 1
лежит между 0 и 4-)
3) Последовательность 1, 2, 3, 4, ..., а также «колеблющиеся» последова-
последовательности
1,2, 1,2,1,2,...
-1, 1,-1, 1, -1,1,... (т.е. а„ = (-1)")
и
1 i I I I i I I
lj 2' ' 3' ' 4' ' 5'"'
не имеют пределов.
Если в последовательности ап члены возрастают таким образом,
что рано или поздно становятся больше любого наперед назначенного
числа К, то принято говорить, что ап стремится к бесконечности,

§2. Пределы 341
И тогда пишут: liman = оо или ап —> оо. Например, я2 -> оо и 2" -> оо.
Эта терминология удобна, хотя и не вполне последовательна, так как
символ оо не принято рассматривать как число. Последовательность,
стремящаяся к бесконечности, считается расходящейся.
Упражнение. Докажите, что последовательность а„ = ^—^— стре-
стремится к бесконечности; аналогично в случае
п2 + 1 п3 - 1 пп
П + 1 П + 1 ' П + 1
Начинающие часто впадают в ошибку, думая, что переход к пре-
пределу при п —> оо может быть выполнен совершенно просто путем под-
подстановки п = оо в выражение общего члена ап. Например, i -> 0 пото-
потому, что gg = 0. Но символ оо не является числом, и его употребление
в выражении — незаконно. Попытка представить себе предел последо-
последовательности как «последний» член последовательности ап при п = оо
не попадает в цель и затемняет правильное понимание существа дела.
1 1—i i
a, a2 a3 а В
Рис. 166. Монотонная ограниченная поверхность
2. Монотонные последовательности. В общем определении
сходимости и предела на стр. 337 не содержится требований, так или
иначе стесняющих характер приближения сходящейся последователь-
последовательности а±, а.2, аз, .. ¦ к своему пределу а. Простейший тип приближения
осуществляется так называемыми монотонными последовательностя-
последовательностями, примером которых может служить следующая:
1 2 3 п
V 3' 4' ••' ' п + V ••'
Каждый член этой последовательности больше предыдущего. Действи-
Действительно:
пп+1 ~ WT2 - 1 > 1 а
п
Последовательность такого рода, в которой an+i > an, называется
монотонно возрастающей. Аналогично, последовательность, для кото-
которой ап > an+i, например, такая, как 1, ^, ^, ..., называется монотонно

342 Глава VI
убывающей. Последовательности этих двух типов могут приближаться
к своему пределу лишь с одной стороны: «слева» или «справа». В про-
противоположность этому существуют последовательности колеблющие-
колеблющиеся, например, —1, А —i j, ...Эта последовательность приближается
к своему пределу 0 «с обеих сторон» (см. рис. 11, стр. 102).
Монотонные последовательности обладают особенно простыми
свойствами. Такого рода последовательность может не иметь предела
и возрастать неограниченно, подобно последовательности
1, 2, 3, 4, ... ,
где ап = п, или последовательности
2,3,5,7, 11,13,... ,
для которой ап есть n-е простое число рп. В этом случае последо-
последовательность стремится к бесконечности. Но если члены монотонно
возрастающей последовательности остаются ограниченными, т.е. если
каждый член меньше некоторой верхней границы В, заранее извест-
известной, то интуитивно ясно, что последовательность должна стремиться
к некоторому определенному пределу а, не превышающему числа В.
Мы сформулируем это положение как принцип монотонных последо-
последовательностей: Монотонно возрастающая последовательность, ограни-
ограниченная сверху, сходится к некоторому пределу. (Аналогичное утверж-
утверждение имеет место относительно монотонно убывающей последователь-
последовательности, ограниченной снизу.) Замечательно то, что значение предела а
не должно быть известным заранее; теорема утверждает, что при вы-
выполнении указанных условий предел существует. Конечно, эта теоре-
теорема справедлива лишь при условии, что предварительно введены ирра-
иррациональные числа, и в противном случае не всегда бы оправдывалась:
в самом деле, в главе II мы видели, что каждое иррациональное число
(например, у/2) является пределом монотонно возрастающей и ограни-
ограниченной последовательности рациональных десятичных дробей, возни-
возникающих при обрывании некоторой бесконечной десятичной дроби на
n-й цифре.
* Хотя принцип монотонных последовательностей интуитивно вполне
очевиден и выглядит как абсолютная истина, однако не мешает, и даже весь-
весьма полезно, привести его вполне строгое доказательство в современном стиле.
Чтобы это сделать, надо показать, что этот принцип есть логический вывод
из определения действительного числа и определения предела.
Предположим, что числа <ц, ог, аз, ¦.. образуют монотонно возрастаю-
возрастающую, но ограниченную последовательность. Мы можем представить члены

§2. Пределы 343
этой последовательности как бесконечные десятичные дроби
а3 =
где А, — целые числа, а р,, q,, п и т. д. — цифры от 0 до 9. Пробежим
теперь вниз по столбцу целых чисел А\, Аг, Аз, .... Так как последователь-
последовательность ai, аг, аз, ... ограниченна, то эти целые числа не могут возрастать
бесконечно, а поскольку она монотонно возрастает, то целые числа после-
последовательности Ai, A2, A3, ... после достижения некоторого максимального
значения должны стать постоянными. Обозначим это максимальное значе-
значение символом А и предположим, что оно достигнуто в iVo-й строке. Станем
теперь пробегать второй столбец pi, qi, r\, ..., сосредоточивая свое внима-
внимание на членах No-Pt и последующих строк. Если х\ есть наибольшая из цифр,
появившаяся в этом столбце после Wo-й строки, то эта цифра будет появлять-
появляться всегда после своего первого появления, которое, предположим, произошло
в Wi-й строке, где JVi ^ No- (Если бы цифра в этом столбце уменьшилась
когда-либо впоследствии, то последовательность ао, а\, п2, ... не была бы
монотонно возрастающей.) Затем мы рассмотрим цифры рг, </2, Г2, ¦ ¦ ¦ треть-
третьего столбца. Рассуждение, подобное предыдущему, показывает, что, начиная
с некоторого целого числа N2 ^ Ni, цифры третьего столбца постоянно рав-
равны некоторому числу жг. Если мы повторим этот процесс для 4-го, 5-го, ...
столбцов, то получим цифры жз, Ж4, же, ... и соответствующие целые чис-
числа N3, Ni, N5, .... Легко убедиться, что число
есть предел последовательности ai, п2, аз, В самом деле, пусть выбра-
выбрано е ^ 10~т; тогда для всех п ^ Nm целая часть и первые т цифр после запя-
запятой в числах ап и а будут совпадать между собой, так что разность \а„ — а\
не может превышать 10~т. Так как это можно сделать для любого е, как
бы мало оно ни было, с помощью выбора достаточно большого т, то теорема
доказана.
Эту теорему можно также доказать, основываясь на любом из данных
в главе II определений действительного числа, например, взяв определение
с помощью вложенных интервалов или дедекиндовых сечений. Такие доказа-
доказательства можно найти в любом курсе анализа.
Принцип монотонных последовательностей мог бы быть применен в гла-
главе II при определении суммы и произведения двух положительных бесконеч-
иых десятичных дробей:
а = А,п\п2пз ...
Ь = 5,616263 • • •

344 Глава VI
Два таких выражения не могут быть ни сложены, ни перемножены обыч-
обычным путем, начиная с правого конца, поскольку нет никакого правого конца.
(В качестве примера читатель может попытаться сложить следующие две
бесконечные десятичные дроби: 0,333333 ... и 0,989898 ....) Но если сим-
символ х„ обозначает конечную десятичную дробь, полученную в результа-
результате сложения конечных десятичных дробей, возникающих при «обрывании»
на n-й цифре десятичных разложений а и 6, то последовательность xi, x2,
жз, ... будет монотонно возрастающей и ограниченной (границей может слу-
служить, например, число А+В + 2). Отсюда следует, что последовательность xi,
Х2, хз, ¦ ¦. имеет предел, и мы можем принять следующее определение:
а + Ъ = lima;n.
Посредством подобного же процесса можно определить и произведение аЪ.
Определения эти можно распространить и на все случаи, когда а и Ъ — какие
угодно положительные или отрицательные числа, применяя обычные правила
арифметики.
Упражнение. Доказать, что суммой двух вышеуказанных бесконеч-
бесконечных десятичных дробей является действительное число
1,323232...= Щ-.
Важность понятия предела в математике заключается в том, что
многие числа могут быть определены лишь как пределы (часто как пре-
пределы монотонно возрастающих последовательностей). Вот почему поле
рациональных чисел, в котором такие пределы могут не существовать,
слишком узко для надобностей математики.
3. Число Эйлера е. Число е заняло видное место в математи-
математике рядом с архимедовым числом тг сразу после опубликования Эйлером
в 1748 г. сочинения «Introductio in Analysin Infinitorum». Это число до-
доставит нам прекрасную иллюстрацию того, как принцип монотонных
последовательностей может служить для определения нового действи-
действительного числа. Пользуясь обычной сокращенной записью для произве-
произведения п первых целых чисел
п! = l-2-З-...-п,
рассмотрим последовательность а\, а,2, аз, ..., где

§2. Пределы 345
Члены последовательности ап монотонно возрастают, поскольку ап+х
получается из ап посредством прибавления положительного слагаемо-
слагаемого —. Кроме того, значения ап ограничены сверху
(п + 1).
о„ < В = 3. E)
В самом деле, мы имеем
1 = 11 1^11 1 _ _J_
я! 2'3'"я2'2" 2s'
отсюда вытекает, что
2 22 23 2"
1~-2
причем мы использовали формулу стр. 97 для суммы п первых чле-
членов геометрической прогрессии. Но в таком случае, в силу принципа
монотонных последовательностей, ап должно стремиться к некоторому
пределу при стремлении п к бесконечности; этот предел обозначается
буквой е. Чтобы выразить тот факт, что е = liman, мы можем запи-
записать е в виде «бесконечного ряда»
Это «тождество» с рядом точек на конце есть просто другой способ для
выражения двух следующих утверждений:
и
ап —> е при п -> оо.
Ряд F) позволяет вычислить е с любой степенью точности. Напри-
Например, сумма (с девятью цифрами) членов ряда F) до -|у включительно
равна числу
V = 2,71828183...

346 Глава VI
(Проверьте!) «Ошибка», т. е. разность между этим приближенным и ис-
истинным значением е, может быть легко оценена. Для разности е — ^
мы имеем выражение
J_ + J-+ < J_(i+-L + J_ + J_+ \ = Л L_ = JL.i
13! 14!+" 13! V 13 i32 133 V 13! 1 12 12!'
1 13
Это число так мало, что не может повлиять на девятую цифру, и пото-
потому, допуская возможную ошибку в последней цифре вышеприведенного
значения, мы получаем для е следующее приближенное равенство с во-
восемью верными цифрами:
е = 2,7182818.
* Число е иррационально. Чтобы это доказать, предположим про-
Р
тивное: допуская, что е = —, где р и q — целые числа, и затем, приходя
к противоречию, мы должны будем заключить о нелепости сделанного пред-
предположения. Поскольку мы знаем, что 2 < е < 3, е не может быть целым
числом, а потому q по меньшей мере должно быть равно 2. Умножим обе
части тождества F) на q\ = 1 • 2 • 3 ... q; получим
е ¦ q\ = р ¦ 2 • 3 ... (q - 1) = [g! + q\ + 3 • 4 ... q +
В левой части мы, очевидно, имеем целое число. В правой части слагаемое
в квадратных скобках также есть целое число. Остаток же в правой части
есть положительное число, меньшее ^, и значит, не есть целое число. В самом
деле, q ^ 2, а следовательно, члены ряда + ... не превышают соответ-
соответственно членов геометрической прогрессии - Н 1—г- +... сумма которых
3 3 3
равна — = -. Таким образом, формула G) противоречива: целое число
в левой части не может быть равно числу в правой части, так как это по-
последнее, являясь суммой целого числа и положительного числа, меньшего ^,
не есть целое число.
4. Число тт. Как известно из школьной математики, длина
окружности, радиус которой равен единице, может быть определена как
предел последовательности длин периметров правильных многоуголь-
многоугольников при бесконечном увеличении числа их сторон. Определенная та-
таким образом длина окружности обозначается символом 2тг. Точнее, ес-
если через рп обозначить длину вписанного, а через qn длину описанного

§2. Пределы
347
правильного n-угольника, то имеют мес-
место неравенства
рп < 2тг < <7„.
Более того, когда п возрастает, обе после-
последовательности рп и qn приближаются мо-
монотонно к 2тг, и на каждом этапе мы полу-
получаем все меньшую ошибку в том прибли-
приближении, которое рп и qn дают для числа 2тг.
На стр. 163 мы получили выражение
Р2г,
= 2"
Рис. 167. Приближение ок-
окружности многоугольниками
содержащее т — 1 перекрывающихся квадратных корней. Эту формулу
можно использовать для подсчета приближенного значения числа 2тг.
Упражнения.
1) Найти приближенное значение тг, даваемое числами р$, р$ и pie.
*2) НаЙТИ формулу ДЛЯ (J2m-
*3) С помощью этой формулы вычислить 54, q& и (ji6. Зная величины ргв
и gi6, установить границы, между которыми должно лежать число тг.
Что же это за число тг? Неравенство рп < 2тг < qn дает на это пол-
полный ответ при развертывании последовательности вложенных интер-
интервалов, которые стягиваются к точке 2тг. И все же этот ответ оставляет
желать еще чего-то, поскольку он ничего не говорит о природе тг как
действительного числа: является ли оно рациональным или иррацио-
иррациональным, алгебраическим или трансцендентным? Как мы уже указы-
указывали на стр. 144, число тг есть число трансцендентное, а следовательно,
и иррациональное. В противоположность доказательству для е доказа-
доказательство иррациональности тг, впервые данное Ламбертом A728-1777),
в достаточной мере трудно и здесь приведено не будет. Однако ряд
сведений о числе тг мы можем сообщить. Имея в виду, что целые числа
являются существенной основой математики, мы можем задать вопрос:
связывается ли число тг сколько-нибудь просто и непосредственно с це-
целыми числами? Десятичное разложение числа тг, хотя и вычисленное
с несколькими сотнями знаков, не обнаруживает ни малейшей законо-
закономерности. Это и не удивительно: ведь тг и число 10 не имеют между
собой ничего общего. Однако Эйлер (XVIII в.) и другие нашли изящные

348 Глава VI
выражения, связывающие число тг с целыми числами с помощью беско-
бесконечных рядов и произведений. Простейшей из таких формул является,
вероятно, следующая:
4 3 5 7 '
выражающая j как предел при возрастающем п сумм
= 1_11_ |(Л" 1
tj к) ь* IЬ 1 Л.
Эту формулу мы выведем в главе VIII. Вот другой бесконечный ряд,
который может служить для вычисления тг:
'6~ = F + 22+3T + 42+52+62+'"'
И еще одно удивительное выражение для тг было открыто анг-
английским математиком Джоном Уоллисом A616-1703). Его формула
утверждает следующее:
224466 2п 2п 1 ->! при п^оо.
В сокращенном виде она часто записывается так:
тг=22446688
2 1'3'3'5'5'7'7'9'"
(выражения, подобные стоящему в правой части, называются бесконеч-
бесконечными произведениями).
Доказательство последних двух формул можно найти в любом до-
достаточно полном курсе анализа.
*5. Непрерывные дроби. Интересные бесконечные процессы
возникают в связи с непрерывными дробями. Конечная непрерывная
дробь, такая, как
57 _о , 1
17 1 '
2+-1-
представляет собой некоторое рациональное число. На стр. 79 мы по-
показали, что каждое рациональное число может быть выражено в такой

§2. Пределы 349
форме с помощью алгоритма Евклида. Однако в случае иррациональных
чисел алгоритм не заканчивается после конечного числа операций. На-
Напротив, он ведет к последовательности все более «длинных» дробей, из
которых каждая представляет собой рациональное число. В частности,
все действительные алгебраические числа (см. стр. 139) степени 2 мо-
могут быть выражены таким образом. Рассмотрим, например, число х =
= \[2 — 1, являющееся корнем квадратного уравнения
х2 + 2х = 1, или х =
Если в правой части заменить х снова дробью - , то это дает выра-
1 + X
жение
о i 1
2 + х
а затем
*= 1
2 +
2 +
2 + х
и т.д., так что после п «шагов» получим равенство
1
X =
2 +
2+
2+
2 + х
(п «шагов»).
Если п стремится к бесконечности, мы получим «бесконечную непре-
непрерывную дробь»
ч/2=1 + Ц .
2 +
Эта замечательная формула связывает число у/2 с целыми числами го-
гораздо более удивительным образом, чем это делает десятичное разложе-
разложение -\/2, которое не обнаруживает никакой правильности в чередовании
десятичных знаков.

350 Глава VI
Для положительного корня любого квадратного уравнения вида
2 1
х = ах + 1, или х = а + —,
мы получаем разложение
х = а-\ .
а +
а+
Например, полагая а = 1, мы находим
х = ?A + л/5) = 1 +
Эти примеры являются частными случаями общей теоремы, утверж-
утверждающей, что действительные корни квадратного уравнения с целыми
коэффициентами разлагаются в периодическую непрерывную дробь, по-
подобно тому как рациональные числа разлагаются в периодические де-
десятичные дроби.
Эйлер сумел найти почти столь же простые разложения в непре-
непрерывные дроби для чисел е и тг. Приведем их без доказательств:
1 +
2 +
1+ 1
1+ 1
4+ L
1 +
1 +
6+...
1 +
2 +
3 +
4+ 4
5 +...

§ 3. Пределы при непрерывном приближении
351
7Г
4
1 +
2 +
1
I2
2 +
2 + ...
§3. Пределы при непрерывном приближении
1. Введение. Общие определения. В § 2, пункт 1, нам уда-
удалось дать точное определение утверждению: «последовательность ап
(т.е. функция ап = F(n) целого переменного п) имеет предел а при л,
стремящемся к бесконечности». Теперь мы дадим соответствующее
определение утверждению: «функция и = f(x) непрерывной перемен-
переменной х имеет предел а при стремлении х к значению х±».
В интуитивной форме понятие предела при непрерывном прибли-
приближении независимого переменного х употреблялось уже в § 1, пункт 5,
когда нужно было установить, непрерывна ли рассматриваемая функ-
функция в данной точке.
Начнем опять с частного примера. Функ-
Функция f(x) =
(х + х3)
определена для всех значе-
значений х, неравных нулю; при этом последнем зна-
значении х знаменатель уничтожается. Если мы вы-
вычертим график функции у = /(ж) для значений ж
в окрестности точки 0, то станет очевидным, что
при х, «стремящемся» к 0 с любой стороны, со-
соответствующие значения и = /(ж) «стремятся»
к пределу 1. Для того чтобы дать точное описа-
описание этого факта, найдем явную формулу разности
Рис. 168. и =
Между значением функции f(x) и постоянного числа 1:
х + х3
I —
ж + ж — ж
X
ж
X
Если мы условимся рассматривать лишь значения х, близкие к 0, но не
Равные самому нулю (для которого функция f(x) даже не определена),
Мы можем разделить числитель и знаменатель на ж и получить более
Простую формулу
f(x) -1 = х2.

352 Глава VI
Ясно, что эту разность мы можем сделать сколь угодно малой, ограни-
ограничивая изменение переменной х достаточно малой окрестностью зна-
значения х ^ 0. Так, например, при х = ±-^- имеем f(x) — 1 = -~
при х = ±jnn имеем f(x) - 1 = ; и т.д. Вообще: если е есть не-
некоторое положительное число, то, как бы мало оно ни было, разность
между f(x) и 1 будет меньше чем е, если только расстояние точки х
от точки 0 меньше числа S = \[е.
В самом деле, если |х| < л/ё, то
\f(x) - 1| = \х2\ < е.
Аналогия с нашим определением предела последовательности полная.
На стр. 337 мы дали определение: последовательность ап имеет пре-
предел а при п, стремящемся к бесконечности, если каждому положитель-
положительному числу е, как бы мало оно ни было, можно поставить в соответ-
соответствие такое целое N (зависящее от е), что неравенство
\а„ -а\ <е
выполняется для всех п, удовлетворяющих неравенству
n ^ N.
В случае функции f(x) непрерывного переменного х при х, стремящем-
стремящемся к некоторому конечному значению хг, мы просто слова «достаточно
большое п» (что характеризуется числом N) заменяем словами «доста-
«достаточно близко к Ж1» (что характеризуется числом S) и приходим к следу-
следующему определению предела при непрерывном приближении, впервые
данному Коши около 1820 г.: функция f(x) имеет предел а, когда х
стремится к значению xi, если каждому положительному числу е, как
бы мало оно ни было, можно поставить в соответствие такое поло-
положительное число 8 (зависящее от е), что
\f(x) -a\<e
для всех значений х ф Х\, удовлетворяющих неравенству
Если это имеет место, принято писать:
f(x) -> а при х -» х\.

§ 3. Пределы при непрерывном приближении 353
В случае функции f(x) = —-— мы выше показали, что эта функ-
функция f{x) имеет предел 1 при х, стремящемся к значению Х\ = 0. В этом
случае достаточно было всегда выбирать 5 — л/е.
2. Замечания по поводу понятия предела, е-й-определение
предела — результат столетних попыток и блужданий; оно кратко во-
воплощает результат неустанных усилий поставить понятие предела на
здоровую математическую основу. Важнейшие понятия анализа — про-
производная и интеграл — могут быть определены не иначе, как с помо-
помощью перехода к пределу. Но ясное понимание и строгое определение са-
самого понятия предела долгое время казались непреодолимо трудными.
При изучении движения в частности и какого бы то ни было изме-
изменения в общем случае математики XVII и XVIII столетий принимали,
как нечто достаточно наглядное и не подлежащее дальнейшему анали-
анализу, концепцию величины х, меняющейся и в своем непрерывном тече-
течении приближающейся к предельному значению Х\. Они рассматривали
другую величину и = /(ж), связанную с течением времени или иной,
похожей на время, независимой величиной х, и в своем поведении сле-
следующую за изменениями величины х. Оставалось все же проблемой:
какой точный математический смысл следует приписывать представ-
представлению о том, что f(x) «стремится» или «приближается» к определенному
значению а, когда х движется к Xi?
Однако еще со времен Зенона и его парадоксов все попытки дать
точную математическую формулировку интуитивному физическому
или метафизическому понятию непрерывного движения были без-
безуспешными. Нет затруднений в продвижении шаг за шагом по дискрет-
дискретной последовательности значений <ц, а2, аз, Но когда приходится
иметь дело с непрерывной переменной х, пробегающей целый интер-
интервал значений на числовой оси, то описание того, как х «приближается»
к заданному значению xi, затруднено тем, что принимаемые значе-
значения из интервала не могут быть указаны последовательно в порядке их
возрастания. В самом деле, точки прямой представляют везде плотное
Множество, и не существует точки, «следующей» за данной. Остается
неизбежное расхождение между интуитивной идеей и точным мате-
математическим языком, предназначенным для того, чтобы описывать ее
основные линии в научных, логических терминах. Парадоксы Зенона
Ярко обнаруживают это несоответствие.
Существенным достижением Коши является то, что он ясно осо-
осознал, что, поскольку дело касается математических понятий, всякая
СсЫлка на интуитивное представление о непрерывном движении долж-
должна быть отброшена. Как случается нередко, подлинный научный про-

354 Глава VI
гресс был осуществлен тогда, когда последовал отказ от попыток при-
прибегать к метафизическим объяснениям и было принято решение вес-
вести рассуждение, оставаясь на почве строго математических понятий,
соответствующих «наблюдаемым фактам» в физике. Если мы проана-
проанализируем логически, что надлежит понимать под «непрерывным при-
приближением», и какие существуют способы для того, чтобы в каждом
отдельном случае проверить, имеет ли место таковое, то мы вынуж-
вынуждены будем принять именно то самое определение, которое дано Коши,
и никакое иное. Это определение — статическое; оно не опирается на
интуитивную идею движения. Более того, только такое статическое
определение позволяет подвергнуть точному математическому анализу
само непрерывное движение и разрешает парадоксы Зенона, по крайней
мере в той их части, которая относится к математике.
В определении с помощью е, 8 независимое переменное не «движет-
«движется»; оно не «стремится» и не «приближается» к пределу Xi в каком бы
то ни было физическом смысле. Правда, эти обороты речи, как и сим-
символ —>, сохраняются, и вместе с тем математик вовсе не обязан отка-
отказываться от тех, в общем-то весьма полезных, интуитивных представ-
представлений, которые с ними связываются. Но когда в частном случае нужно
дать ответ на вопрос, существует предел или не существует, то прихо-
приходится прибегнуть именно к определению с помощью е, S. Спрашивать
о том, насколько удовлетворительно это определение соответствует ин-
интуитивному «динамическому» представлению о стремлении к пределу,
можно с таким же правом, как и о том, насколько удовлетворитель-
удовлетворительно аксиомы геометрии описывают то, что мы называем пространством
(в интуитивном смысле).
Обе формулировки в какой-то степени предоставляют возможность
работать воображению, и вместе с тем обе они создают адекватную
математическую основу для дальнейшего логического построения.
Как и в случае предела последовательности, ключ к правильному
пониманию определения Коши лежит в обращении «естественного» по-
порядка, в котором рассматриваются переменные. Прежде мы отмечаем
границу е для зависимого переменного, а уже потом стремимся опреде-
определить подходящую границу S для независимого переменного. Когда мы
говорим, что «/(ж) —> а при х —> х\», то лишь сокращенно высказываем
ту мысль, что этот процесс может быть выполнен для любого положи-
положительного числа е. В частности, ни одна из частей этого утверждения,
например, «ж —> х±ъ, не имеет смысла сама по себе.
Еще нужно подчеркнуть следующее. Заставляя х «стремиться»
к Xi, мы можем позволить х быть больше или меньше, чем х±, но воз-

§3. Пределы при непрерывном приближении
355
можность равенства явно исключается требованием х ф Х\\ х стремит-
стремится к xi, но никогда не принимает значения х\. Таким образом, мы мо-
можем применять наше определение к функциям, не определенным вовсе
при х = xi, но имеющим тот или иной предел при х, стремящемся к xi,
например, к функции /(х) =
X -4- Х^
, рассмотренной на стр. 351. Исклю-
Исключение значения х = х\ как раз соответствует тому факту, что, рассмат-
рассматривая последовательности ап при п -> оо (например, предел ап = ^),
мы никогда не подставляем в формулу значения п = оо.
Однако что касается функции f(x), то, когда х стремится к xi, ей
не запрещено стремиться к пределу а таким образом, что при некото-
некоторых значениях х ф Х\, осуществляется равенство f(x) — а. Например,
рассматривая функцию f(x) = |[ при х, стремящемся к 0, мы никогда
не позволяем х быть равным 0, но зато, напротив, равенство f(x) = 1
справедливо при всех х ф 0, и предел а существует и равен 1 в точном
согласии с определением.
3. Предел
Если х обозначает угол в радианном измере-
измерении, то выражение ^—^- определено для всех значений х, за исключе-
исключением значения х = 0, при котором оно принимает вид не имеющего
смысла символа ^. С помощью таблиц тригонометрических функций
читатель может подсчитать значение частного
для малых значе-
ний х. Эти таблицы обычно даются для градусного измерения углов;
мы напоминаем (см. § 1, пункт 2), что градусная мера х связана с ради-
анной мерой у следующим соотношением: х = -z^y = 0,01745т/ (с точ-
ностью до пятого десятичного знака). Из четырехзначных таблиц мы
находим следующие значения:
10°
5°
2°
1°
X
0,1745
0,0873
0,0349
0,0175
sin ж
0,1736
0,0872
0,0349
0,0175
sin ж
X
0,9948
0,9988
1,0000
1,0000
Хотя точность чисел здесь ограничивается четырьмя знаками, все
эти данные приводят к мысли, что
sinx
—> 1 при х —> 0.
A)

356
Глава VI
л/ Сейчас мы дадим строгое доказательство
этому предельному соотношению.
В силу определения тригонометричес-
тригонометрических функций с помощью единичного кру-
круга, мы имеем следующие соотношения для
В величины х, являющейся радианной ме-
мерой угла ВОС (см. рис. 169) при ограни-
ограничении 0 < х <
2"
Площадь треугольника О ВС = ^ • 1 • sin ж.
Рис. 169. Основное тригоно- Площадь кругового сектора ОВС = ^ • х.
метрическое неравенство
Площадь треугольника ОБА = ^ • 1 • tga;.
Отсюда вытекает двойное неравенство:
sin а; < х < tga:.
Деля на sin а;, получим, далее,
х ^ 1
1 <
или
cos а; <
sins
sin a;
cos х
х
< 1.
B)
Но, с другой стороны,
1 — cos х = A — cos х)
1 -f cos х _ 1 — cos2 х
1 -f COS X 1 + COS X
Так как sin a; < x, то отсюда следует, что
1 + COS X
<sin2a;.
1 — cos x < x ,
C)
или
1 — x2 < cos ж.
Совместно с неравенством B) это дает окончательно нужные нам не-
неравенства
1 - х2 < -^JP < 1. D)
Мы предполагаем, что 0 < х < Ц; однако неравенства D) справедли-
справедливы и при условии -тг < х < 0, поскольку ' = ~ Slnx = -§ijp
и (-а;J = x2.

§3. Пределы при непрерывном приближении 357
Предельное соотношение A) вытекает немедленно из неравенств D).
В самом деле, разность между sl^x и 1 меньше, чем х2, а х2 может быть
сделано меньше, чем любое число е, если только взять \х\ < S = ^/1.
Упражнения.
1) Вывести из неравенства C) предельное соотношение — —» О
при х —> 0.
Найти пределы при х —> 0 следующих функций:
0\ sin2 х п\ sina; ,\ tga; . sin а ж д\ этаж 7ч ж sin ж
х х(х — 1) х х smbx 1-cosx
8) sl"x, предполагая, что ж измеряется в градусах,
х tgж sin ж tga;
4. Пределы при х —»¦ оо. Если непрерывная переменная а; до-
достаточно велика, то функция f(x) = ^ становится произвольно малой,
или «стремится к 0». В самом деле, поведение этой функции при возрас-
возрастающем х по существу то же самое, что и поведение последовательнос-
последовательности ^ при возрастании п. Мы вводим общее определение: функция f(x)
имеет предел а при х, стремящемся к бесконечности, и записываем
это в форме
f(x) -> а при х —> оо,
если, как бы мало ни было положительное число е, можно к нему подо-
подобрать такое положительное число К (зависящее от е), что неравен-
неравенство
\f(x) -a\<e
выполняется при условии \х\ > К (сравнить с соответствующим опре-
определением на стр. 337).
В случае функции f(x) — i, для которой а = 0, достаточно вы-
выбрать К = i, в чем читатель может убедиться немедленно.
Упражнения.
1. Показать, что с точки зрения вышеприведенного определения утверж-
утверждение
/(ж) —> а при ж —> оо
эквивалентно следующему:
/(ж) -> о при - -> 0.

358 Глава VI
Доказать, что имеют место следующие предельные соотношения
при х —> оо:
2. —» 1 при х —> оо.
х — 1
3. х +х + 1 _у 1 ПрИ х -^ оо.
ж — ж — 1
4. ^|^ -> О при ж -> оо.
ж -Ь 1
5. — > 0 при ж —> оо.
2 + 1
6. fnx >¦ 0 при ж -> оо.
ж + cos ж г
7. ^"^ не имеет предела при ж -» оо.
8. Дайте определение: «/(ж) —> оо при а; —» оо». Приведите пример.
Имеется следующая разница между случаем функции /(ж) и случаем
последовательности ап. В случае последовательности п может стремиться
к бесконечности не иначе, как возрастая, тогда как в случае функции пере-
переменная ж, неограниченно возрастая, имеет право принимать как положитель-
положительные, так и отрицательные значения. Если желательно направить внимание
на поведение функции /(ж) только при больших положительных значениях,
то условие |ж| > К мы должны заменить условием ж > К; напротив, для
случая больших по абсолютной величине отрицательных значений ж вводим
условие ж < —К. Чтобы символизировать эти два способа «одностороннего»
стремления к бесконечности, мы пишем соответственно:
Ж —> +О0, Ж —> —ОО.
§ 4. Точное определение непрерывности
В § 1, пункт 5, мы ввели следующее определение непрерывности
функции: функция f(x) непрерывна в точке х = х±, если при стремле-
стремлении х к Xi величина f(x) стремится к пределу, равному f{x\). Если мы
проанализируем эту формулировку, то увидим, что она подразумевает
выполнение следующих двух требований:
a) существует предел а функции f(x) при стремлении переменной х
к пределу хх,
b) этот предел а должен быть равен f(x).
Если в определении предела на стр. 352 мы подставим вместо а
его значение f{x\), то условие непрерывности принимает следующий
вид: функция f(x) непрерывна при х = х\, если, как бы мало ни было

§ 4. Точное определение непрерывности 359
положительное число е, можно подобрать такое положительное число 5
(зависящее от е), что неравенство
\f(x)-f(x1)\<e
будет выполнено для всех х, удовлетворяющих условию
х - хг\ < 5
(ограничение х ф Х\, введенное в определении предела, здесь излишне,
поскольку неравенство |/(х) - f(x\)\ < е при х = хх удовлетворяется
автоматически).
В качестве примера постараемся установить непрерывность функ-
функции f(x) = х3, скажем, в точке х\ = 0. Мы имеем
f(Xl) = О3 = 0.
Выберем теперь маленькое положительное число е, например, е —
Мы должны показать, что, ограничивая значения х числами, достаточ-
достаточно близкими к 0, получим соответствующие значения функции f(x), от-
отличающиеся от 0 меньше, чем на -г^:, т.е. заключенные между -:
10ЛП' ounuiu 1ишш>, iiiuiihj 1000
и + . Мы сразу видим, что значения f(x) не выйдут из этих гра-
границ, если мы ограничим изменение х значениями, отличающимися от 0
меньше чем на 8 = ?1 = -^; в самом деле, если |х| < —, то |/(х)| =
= |а;3| < тттргк- Совершенно так же мы можем взять вместо е — „„
любое меньшее значение е = 10~4, 10~5 и т.д.; числа 5 = %/ё будут
удовлетворять нашему требованию, так как из неравенства \х\ < у/ё
следует неравенство |/(х)| = \х3\ < е.
Основываясь на определении непрерывности с помощью е, S, мож-
можно доказать аналогично, что все полиномы, рациональные функции и
тригонометрические функции непрерывны в любой точке, за исклю-
исключением, может быть, тех изолированных значений х, около которых
функции становятся бесконечными.
Связывая определение непрерывности с графиком функции и =
= /(х), можно придать ему следующую геометрическую форму. Выбе-
Выберем некоторое положительное число е и начертим прямые, параллель-
параллельные оси х на высоте f(xi) —ем f(xi)+e над ней. Тогда должно найтись
такое положительное число 8, что вся часть графика, лежащая внутри

360
Глава VI
и
и,
V А
1
'У1
X
Рис. 170. Функция, непрерыв-
непрерывная в точке х = х\
Рис. 171. Функция имеет раз-
разрыв в точке х = х\
вертикальной полоски шириной в 25 около х\, содержится также и в го-
горизонтальной полоске шириной в 2е около f(x\). Рис. 170 показывает
функцию, непрерывную в точке ii,bto время как рис. 171 показывает
функцию, имеющую разрыв в этой точке. В последнем случае, как бы
узка ни была вертикальная полоска около xi, она всегда будет содер-
содержать часть графика, лежащую вне горизонтальной полоски ширины 2е.
Если я утверждаю, что данная функция и = f(x) непрерывна в точ-
точке х = xi, то это значит, что я беру на себя по отношению к вам следующие
обязательства: вы можете выбрать любое положительное число е, сколь угод-
угодно малое, но определенное. Тогда я обязуюсь подыскать такое положительное
число 5, чтобы неравенство \х — х%\ < 5 влекло за собой неравенство |/(ж) —
— f(xi)\ < e. Но при этом я не обязуюсь найти такое число 5, которое подошло
бы ко всякому е, которое вы назовете потом: мой выбор 5 зависит от ваше-
вашего выбора е. Если вы можете выбрать хоть одно е, для которого я не смогу
подобрать подходящего 5, то моя игра проиграна — мое утверждение опро-
опровергнуто. Для того чтобы доказать, что я могу выполнить мое обязательство
в конкретном случае некоторой функции и = f{x), мне нужно построить
явно такую положительную функцию
S = ip(e),
определенную для всякого положительного числа е, для которой я могу до-
доказать, что из неравенства \х — х\\ < 5 следует всегда неравенство |/(ж) —
— f(xi)\ < е. В случае функции и = f(x) = х3 при х\ = 0 функцией 5 = <р(е)
была S — у^е.
Упражнения.
1) Доказать, что sin а: и cos а; — функции непрерывные.
1 .. . Гл i ,_2
2) Доказать непрерывность функций

I 5. Две основные теоремы о непрерывных функциях
361
Теперь становится ясным, что определение непрерывности с помо-
помощью е, 8 не находится в противоречии с тем, что мы могли бы назвать
«наблюдаемыми фактами», относящимися к функциям. Таким образом,
оно соответствует основному принципу современной науки, который
выдвигает в качестве критерия полезности некоторого понятия или
«существования» явления (в научном смысле) возможность непосред-
непосредственно его наблюдать (по крайней мере в принципе) или сводить его
к фактам, доступным наблюдению.
§ 5. Две основные теоремы о непрерывных
функциях
1. Теорема Болыдано. Бернард Больцано A781-1848), католичес-
католический священник, знаток схоластической философии, был одним из пер-
первых, кто ввел в математический анализ современное понятие строгос-
строгости. Его замечательная книжка «Paradoxien des Unendlichen» появилась
в 1850 г. Здесь впервые было признано, что многие, казалось бы, очевид-
очевидные утверждения, касающиеся непрерывных функций, могут и должны
быть доказаны, если имеется в виду применять их во всей их общнос-
общности. Примером этого может служить следующая теорема о функциях
одного переменного.
Непрерывная функция пере-
переменного х, положительная при
некотором значении х и отри-
отрицательная при некотором другом
значении х из замкнутого интер-
интервала непрерывности а ^ х ^ Ь,
должна обращаться в нуль при не-
некотором промежуточном значе-
значении х. Итак, если функция /(ж)
непрерывна при изменении х
от а до Ь, и при этом f(a) < 0
и f(b) > 0, то существует та-
такое значение а переменного х,
что а < а < Ь и /(а) = 0.
Теорема Больцано прекрасно согласуется с нашим интуитивным
представлением о непрерывной кривой, которая неизбежно должна пе-
пересечь в какой-нибудь точке ось х, чтобы перейти с одной ее стороны
на другую. Что, напротив, это не обязательно в случае разрывной функ-
функции, показывает рис. 157 на стр. 329.
Рис. 172. Теорема Больцано

362 Глава VI
*2. Доказательство теоремы Вольцано. Дадим строгое доказа-
доказательство этой теоремы. Если следовать Гауссу и другим великим матема-
математикам, то можно принять этот факт и без доказательства. Нашей целью яв-
является сведение этой теоремы к основным свойствам системы действитель-
действительных чисел, в частности, к постулату Дедекинда-Кантора о стягивающихся
отрезках (стр. 102). Для этого рассмотрим отрезок /, а < х < Ь, в котором
задана функция f(x), разобьем его на два средней точкой х\ = —г—. Если
в этой средней точке мы получим f(xi) = 0, то доказывать больше уже не-
нечего. Если, однако, }{х\) ф 0, то f(x\) должно быть или больше, или меньше
нуля. В обоих случаях одна из половинок отрезка I будет снова обладать тем
свойством, что знаки значений функции f(x) на его концах различны.
Обозначим этот отрезок через h. Мы повторим этот процесс, деля от-
отрезок /i пополам; тогда в середине 1\ или имеем f(x) = 0, или мы можем
выбрать такую половину /г отрезка Д, для которой опять знаки значений
функции на двух концах различны. Повторяя эту процедуру, мы, в конце
концов, или найдем после конечного числа делений точку, в которой /(ж) =
= 0, или получим последовательность стягивающихся отрезков It, h, h,
В последнем случае постулат Дедекинда-Кантора обеспечивает существова-
существование в исходном отрезке / такой точки а, которая принадлежит всем отрезкам
сразу. Мы утверждаем, что /(а) = 0, так что а и будет той точкой, сущест-
существование которой нужно доказать.
До сих пор предположение о непрерывности функции f(x) использовано
еще не было. Сейчас придется на него сослаться, заканчивая доказательство
способом от противного. Мы докажем, что /(а) = 0, допуская противополож-
противоположное и приходя затем к противоречию. Предположим, что /(а) Ф 0: пусть,
например, /(а) = 2е > 0. Так как функция f(x) непрерывна, то мы найдем
(может быть маленький) отрезок J длины 25 с центром в точке а — такой,
что значение функции f(x) во всем промежутке J отличается от /(а) меньше,
чем на е. Затем, так как f(a) = 2е, то мы можем быть уверены, что /(ж) > е
в каждой точке J, т. е. что f(x) > 0 в отрезке J. Но отрезок J фиксирован,
и если п достаточно велико, то маленький отрезок 1п должен непременно по-
попасть внутрь J, поскольку последовательность длин /„ стремится к нулю.
В этом заключается противоречие: в самом деле; из того, каким образом был
выбран промежуток /„, вытекает, что функция f(x) имеет противополож-
противоположные знаки в двух конечных точках каждого промежутка /„, так что функ-
функция f(x) принимает отрицательные значения где-то в промежутке J. Отсюда
следует нелепость предположения /(а) > 0, а также (совершенно таким же
образом) /(а) < 0; следовательно, доказано, что /(а) = 0.
3. Теорема Вейерштрасса об экстремальных значени-
значениях. Другой существенный и интуитивно ясный факт, касающий-
касающийся непрерывных функций, был сформулирован Карлом Вейерштрассом
A815-1897), который, возможно, более чем кто бы то ни было другой,

§ 5. Две основные теоремы о непрерывных функциях 363
является ответственным за современное устремление к строгости в ма-
математическом анализе. Эта теорема утверждает: если функция f(x) не-
непрерывна в интервале I, а ^ ж ^ Ь, не исключая также и конечных то-
точек интервала а иЪ, то в интервале I должна существовать по крайней
мере одна точка, в которой функция f(x) достигает своего наибольшего
значения М, и другая точка, в которой функция /(ж) достигает своего
наименьшего значения т. Говоря интуитивно, это значит, что график
непрерывной функции и = /(ж) должен иметь по крайней мере одну
наивысшую и одну наинизшую точки.
Существенно отметить, что это утверждение может быть невер-
неверным, если функция и = /(ж) перестает быть непрерывной в конечных
точках промежутка /. Например, функция /(ж) = i не имеет наи-
наибольшего значения в промежутке 0 < ж ^ 1, хотя она и непрерывна
внутри промежутка. И вместе с тем разрывная функция вовсе не обя-
обязательно достигает наибольшего и наименьшего значений, даже если
она ограниченная. Рассмотрим, например, «чрезвычайно» разрывную
функцию /(ж), определенную следующим образом:
/(ж) = ж при иррациональном х,
/(ж) = =- при рациональном ж,
в промежутке 0 ^ х ^ 1. Все значения, которые принимает эта функ-
функция, заключены между 0 и 1. Среди них имеются сколь угодно близкие
к 0 и 1: они получаются, если ж будем выбирать иррациональным и
достаточно близким к 0 или 1. Но /(ж) никогда не может быть равным
ни 0, ни 1, поскольку для рациональных х мы имеем f(x) = ^, а для
иррациональных мы имеем /(ж) = х. Итак, значения 0 и 1 ни в какой
точке не достигаются.
* Теорема Вейерштрасса может быть доказана почти таким же обра-
образом, как и теорема Больцано. Разобьем интервал / на два замкнутых по-
полуинтервала /' и /" и фиксируем наше внимание на /', как на интервале,
в котором следует искать наибольшее значение функции /(ж), если только
в интервале I" не найдется такой точки а, что f(a) больше всех значений
Функции }{х) в интервале I'; в этом последнем случае мы выберем интер-
интервал I". Тот интервал, который мы выбрали, обозначим через 1\. Поступим
Теперь с интервалом 1\ точно так же, как мы поступали с /; пусть при этом
получим интервал Ii и т.д. Этот процесс определит последовательность Л,
?г, Is, ... , In, •¦¦ вложенных интервалов, которые все содержат некоторую
точку z. Мы докажем, что значение функции в этой точке, f(z) = М, есть
Наибольшее из всех значений и функций }(х), достигаемых в исходном ин-

364 Глава VI
тервале, т.е. что не может существовать такой точки s, что f(s) > М. Пред-
Предположим, что нашлась бы точка s, удовлетворяющая условию f(s) = М +
+ 2е, где е есть некоторое (может быть, и очень маленькое) положительное
число. В силу непрерывности функции /(ж) мы можем точку z окружить
маленьким интервалом К, не захватывающим точки s, и притом таким, что
в интервале К значения функции f(x) отличаются от f(z) = М меньше чем
на е, так что в нем мы непременно будем иметь f(x) < М + е. Но при до-
достаточно больших п интервал 1п лежит внутри интервала К, а вместе с тем
интервал 1п был определен так, что ни одно значение f(x) при ж, лежащем
вне интервала 1п, не может превзойти значений функции f(x) в точках ж из
этого интервала.
Но точка s лежит вне интервала /„ и в ней f(s) > М + е, тогда как
в интервале К, а тем самым в интервале /„ мы имеем }{х) < М + е. Таким
образом, мы пришли к противоречию.
Существование по крайней мере одного наименьшего значения т может
быть доказано тем же самым методом; впрочем, оно является следствием пре-
предыдущего, так как наименьшее значение функции f(x) является наибольшим
значением функции g(x) = —f(x).
Теорема Вейерштрасса может быть доказана аналогичным образом и
для непрерывных функций от двух или большего числа переменных х, у, ...
В этом случае придется вместо замкнутых интервалов (со включением ко-
конечных точек) брать замкнутые области, например, прямоугольники в плос-
плоскости ж, у (со включением контура).
Упражнение. В каком пункте доказательств теорем Больцано и Вей-
Вейерштрасса мы воспользовались предположением, что функция /(ж) опреде-
определена и непрерывна во всем отрезке (замкнутом) а < ж ^ Ь, а не только
при а < х < Ь или а < х <Ы
Доказательства теорем Больцано в Вейерштрасса носят явно не-
неконструктивный характер. Они не предоставляют метода для «эффек-
«эффективного» нахождения положения нулевой точки или наибольшего и наи-
наименьшего значения функции с заранее назначенной степенью точности
в результате конечного числа операций. Доказано только лишь само
существование, или, вернее, абсурдность несуществования, упомяну-
упомянутых значений. Это обстоятельство представляет собой еще один важ-
важный пункт, против которого «интуиционисты» (см. стр. 121) выдвинули
свои возражения; некоторые из них даже настаивали, чтобы подобные
теоремы были вообще изгнаны из математики. Изучающий математи-
математику не должен, впрочем, принимать эти возражения более серьезно, чем
это сделало большинство критиков.
*4. Теорема о последовательностях. Компактные множес-
множества. Пусть xi, X2, жз, ... есть некоторая бесконечная последователь-

§5. Две основные теоремы о непрерывных функциях 365
ность чисел, различных или нет, содержащихся в отрезке I, а ^ х <i 6.
Последовательность может стремиться или не стремиться к пределу.
Но как бы то ни было, всегда можно извлечь из такой последователь-
последовательности, выбрасывая некоторые из ее членов, такую новую бесконечную
последовательность yi, y2, у3, ..., которая стремилась бы к пределу,
заключенному в промежутке I.
Чтобы доказать эту теорему, разделим интервал / с помощью сред-
средней точки х = а Т" на два замкнутых отрезка Г и /":
I : а ^ х ^ —2~
По крайней мере в одном из них будет находиться бесчисленное коли-
количество членов хп основной последовательности: обозначим его через Jj.
Выберем один из этих членов хП1 и обозначим его через ух. Проделаем
то же самое с промежутком Д. Так как в интервале 1\ имеется бес-
бесконечное множество членов хп, то их должно быть бесконечное мно-
множество также и по крайней мере в одной из половин /х; обозначим эту
половину через /г. На отрезке /г возьмем член хп, для которого п > п\,
и обозначим его через у2- Продолжая таким же образом, мы можем най-
найти последовательность вложенных отрезков 1Х, /2, /3, • • • и подпоследо-
подпоследовательность yi, j/2, 2/з, ••• членов основной последовательности таким
образом, что уп лежит в интервале /„, каково бы ни было п. Эта последо-
последовательность интервалов стягивается к некоторой точке у промежутка,
и ясно, что последовательность j/i, 2/2, 2/з, ••• имеет предел у, что и
требовалось доказать.
* Эти рассуждения допускают обобщение того типа, который характерен
для современной математики. Рассмотрим переменное X, пробегающее неко-
некоторое множество S, в котором каким-то образом определено понятие «рассто-
«расстояния». S может быть множеством точек на плоскости или в пространстве. Но
это не является необходимым; например, S может быть также множеством
всех треугольников на плоскости. Если X и Y являются двумя треуголь-
треугольниками с вершинами А, В, С и А', В', С" соответственно, то в качестве
«расстояния» между треугольниками можно взять, например, число
d(X, Y) = АА' + ВВ' + СС,
где А А' обозначает обычное расстояние между точками А и А' и т. д. Как
только во множестве введено понятие «расстояния», мы имеем возможность
определить понятие последовательности элементов Xi, X2, Х3, ..., стремя-
стремящейся к пределу X — также элементу множества S. Мы подразумеваем под

366 Глава VI
этим, что d(X, Хп) —> 0 при п —у оо. Теперь мы скажем, что множество 5
компактно, если из каждой последовательности Х\, -Хг, Хз, ¦¦¦ элементов
этого множества можно извлечь подпоследовательность, стремящуюся к не-
некоторому пределу X, принадлежащему множеству S. В предыдущем пункте
мы показали, что замкнутый промежуток a Sj x sC b компактен в указан-
указанном смысле. Таким образом понятие компактного множества можно считать
обобщением понятия замкнутого интервала на числовой оси. Отметим, что
числовая ось в целом некомпактна, поскольку последовательность целых чи-
чисел 1, 2, 3, 4, 5, ... не стремится ни к какому пределу и не содержит в себе
никакой подпоследовательности, которая бы стремилась к пределу. Также и
открытый интервал некомпактен, например, 0 < х < 1, не включающий ко-
конечных точек; действительно, последовательность -,—,—,... или любая ее
? о 4
подпоследовательность стремится к пределу 0, который не принадлежит, од-
однако, рассматриваемому открытому промежутку. Таким же образом можно
показать, что область плоскости, состоящая, скажем, из внутренних точек
некоторого квадрата или прямоугольника, некомпактна; но она становится
компактной после присоединения точек границы. Нетрудно также убедить-
убедиться, что множество всех треугольников с вершинами, лежащими внутри или
на окружности данного круга, компактно.
Понятие непрерывности допускает обобщение на случай, когда перемен-
переменное X пробегает любое множество S, лишь бы в этом последнем было предва-
предварительно введено понятие стремления к пределу. Говорят, что функция и =
= F(X) (где и мыслится как действительное число) непрерывна на элемен-
элементе X, если всякий раз, как последовательность элементов Х\, Х2, Х$, ...
имеет предел X, соответствующая последовательность чисел F(X\), F(X2),
-Р(-Хз), ... имеет предел F(X). (Можно дать определение и с помощью е, 5.)
Легко также убедиться, что теорема Вейерштрасса остается в силе для случая
обобщенной непрерывной функции F(X), заданной на некотором компактном
множестве:
Если и = F(X) есть непрерывная функция, определенная для всех эле-
элементов компактного множества S, то существует обязательно такой эле-
элемент S, для которого F(X) достигает своего наибольшего значения, и другой
элемент, для которого F(X) достигает своего наименьшего значения.
Доказательство не представит никакого труда для того, кто схватил об-
общий характер относящихся сюда идей; мы не пойдем дальше в этом же на-
направлении. Мы увидим в главе VIII, что теорема Вейерштрасса в ее общей
формулировке имеет особенно большое значение в теории максимумов и ми-
минимумов.
§ 6. Некоторые применения теоремы Больцано
1. Геометрические применения. С помощью простой и общей
теоремы Больцано можно доказать некоторые утверждения, на первый

§6. Некоторые применения теоремы Болъцано 367
взгляд отнюдь не представляющиеся вполне очевидными. Установим,
прежде всего, следующее: если А и В — две заданные фигуры на плос-
плоскости, то существует такая прямая в этой плоскости, которая обе
фигуры одновременно делит на равновеликие (в смысле площади) части.
Под «фигурой» здесь понимается всякая часть плоскости, ограниченная
простой замкнутой кривой.
Начнем доказательство с того, что
выберем произвольную фиксирован- (г.^-
ную точку Р в нашей плоскости и про-
проведем из нее фиксированный луч PR,
от которого будем вести отсчет углов.
Каков бы ни был луч PS, делающий
угол х с лучом PR, существует направ-
направленная прямая, параллельная PS и де-
делящая фигуру А на равновеликие части.
Действительно, возьмем одну из на-
направленных прямых, параллельных PS
и имеющих всю фигуру А по одну сто- Рис. 173. Одновременное деле-
рону: пусть эта прямая будет 1Х; станем ние пополам двух площадей
подвергать ее параллельному перенесе-
перенесению таким образом, чтобы при окончательном положении (которое на-
назовем /г) вся фигура А оказалась уже по другую ее сторону (рис. 173).
В таком случае функция, определяемая как разность площади части А,
расположенной вправо от направленной прямой, и площади части А,
расположенной влево («вправо» — «к востоку», «влево» — «к западу»,
если прямая направлена, скажем, «на север»), оказывается положитель-
положительной для положения прямой h и отрицательной для положения /2. Так
как эта функция непрерывна, то, по теореме Больцано, она обращается
в нуль при каком-то промежуточном положении прямой, которое мы
обозначим теперь через 1Х и при котором, очевидно, фигура А разбива-
разбивается пополам. Итак, каково бы ни было х @° ^ х < 360°), существует
прямая 1Х, разбивающая А пополам.
Обозначим теперь через у — /(ж) разность между площадью час-
части фигуры В справа от 1Х и площадью части В слева от 1Х. Допустим
Для определенности, что прямая Zo, параллельная PR и разбивающая А
пополам, справа имеет большую часть площади В, чем слева; тогда у
положительно при х = 0°. Пусть теперь х возрастает до 180°: тогда
прямая /180, параллельная PR и разбивающая А пополам, совпадает с /0
(но направлена в противоположную сторону, а «правая» и «левая» сторо-
стороны переместились); отсюда ясно, что значение у при х = 180° численно

368
Глава VI
то же, что и при х = 0°, но с обратным знаком, т.е. отрицательно. Так
как у есть функция х, непрерывная при 0° ^ х ^ 180° (упомянутая
разность площадей, очевидно, изменяется непрерывно при вращении
секущей прямой), то существует такое значение х = а, при котором у
обращается в нуль. Но тогда прямая 1а разбивает пополам обе фигуры А
и В одновременно. Наша теорема доказана.
Следует заметить, что мы устано-
установили всего-навсего существование пря-
прямой, обладающей заданным свойством,
но не указали определенной процеду-
процедуры для ее построения: в этом — ха-
характерная черта «чистых» математи-
математических доказательств существования.
Вот другая аналогичная проблема:
дана одна фигура А на плоскости; тре-
требуется разбить ее на четыре равнове-
равновеликие части двумя взаимно перпендику-
перпендикулярными прямыми. Чтобы доказать су-
существование решения, вернемся к тому
этапу решения предыдущей проблемы,
когда была введена прямая 1Х, но фигура В еще не была введена в рас-
рассуждение. Рассмотрим прямую /х+эсь перпендикулярную к 1Х и также
разбивающую А пополам. Если занумеруем четыре части А так, как
показано на рис. 174, то получим, очевидно,
Ах + А2 = А3 + А4
Рис. 174. Деление площади на
четыре равные части
А2 + А3 = Аг + А4.
Отсюда вычитанием получим
Ах - А3 = А3 -Ах,
т.е.
Ах = А3,
а значит,
А2 = АА.
Итак, существование решения нашей проблемы будет доказано, если
установим существование такого угла а, что для прямой /а будет удов-
удовлетворено равенство двух частей нашей фигуры
Ах(а) = А2(а),

§6. Некоторые применения теоремы Болъцано 369
так как отсюда будет вытекать равенство всех четырех частей. Рас-
Рассмотрим теперь функцию у = f(x),
f(x) = Ai(x) - А2(х),
где Ai(x) и А2(х) — части фигуры, соответствующие прямой 1Х.
При х = 0° пусть будет, например, /@) = Аг@) - А2@) > 0. Тог-
Тогда при х = 90° получится: /(90) = j4i(90) - Л2(90) = Л2@) -
_ А3@) = А2@) - Ai@) < 0. Но f(x) — непрерывная функ-
функция; значит, при каком-то значении а между 0° и 90° получится
/(а) = Ai(a) — А2(а) = 0. Тогда прямые 1а и /а+эо разбивают фигуру
на четыре равновеликие части.
Эти проблемы обобщаются на случай трех и большего числа изме-
измерений. В случае трех измерений первая проблема формулируется сле-
следующим образом: даны три пространственных тела; требуется найти
плоскость, разбивающую каждое из них пополам одновременно. Доказа-
Доказательство возможности решения также основывается на теореме Боль-
цано. В случае большего числа измерений аналогичное утверждение
также справедливо, но доказательство требует применения более тон-
тонких методов.
*2. Применение к одной механической проблеме. Мы за-
закончим эту главу рассмотрением одной, на первый взгляд трудной
механической проблемы, которая, однако, решается очень просто по-
посредством соображений, связанных с непрерывностью. (Проблема была
предложена Г. Уитни.)
Предположим, что поезд на
протяжении некоторого конечно-
конечного промежутка времени проходит
прямолинейный отрезок пути от
станции А до станции В. Вовсе
не предполагается, что движение Д g
происходит с постоянной скорос-
скоростью или с постоянным ускорени- Рис- 175- Проблема Уитни
ем. Напротив, поезд может двигаться как угодно: с ускорениями, с за-
замедлениями; не исключены даже мгновенные остановки или частично
Даже движение в обратном направлении, прежде чем в итоге поезд при-
Дет на станцию В. Но так или иначе движение поезда на протяжении
всего временного промежутка считается известным заранее; другими
словами, считается заданной функция s — f{t), где s — расстояние
поезда от станции A, a t — время, отсчитываемое от момента отправ-
отправления поезда. К полу одного из вагонов прикреплен на шарнире твердый

370 Глава VI
тяжелый стержень, который без трения может двигаться вокруг оси,
параллельной осям вагонов, вперед и назад — от пола до пола. (Мы
допускаем, что, прикоснувшись к полу, он в дальнейшем останется на
нем лежать, если ему не случится «подпрыгнуть» снова.) Вопрос заклю-
заключается в следующем: возможно ли в момент отхода поезда поместить
стержень в такое начальное положение, т. е. дать ему такой угол на-
наклона, чтобы на протяжении всего пути он не прикоснулся к полу, бу-
будучи предоставлен воздействию движения поезда и силе собственной
тяжести?
На первый взгляд может показаться совершенно невероятным, что-
чтобы при наперед определенной схеме движения поезда взаимодействие
силы тяжести и сил реакции было способно обеспечить требуемое рав-
равновесие стержня при единственном условии — надлежащем выборе на-
начального положения. Но мы сейчас установим, что такое начальное по-
положение всегда существует.
К счастью, доказательство не подразумевает точного знания зако-
законов динамики. (Исходя из этих законов, решить задачу было бы чрез-
чрезвычайно трудно.) Достаточно принять только одно допущение физичес-
физического содержания: последующее движение стержня зависит непрерывно
от его начального положения; в частности, если при данном начальном
положении стержень во время пути упадет на пол в одну из сторон, то
при всяком начальном положении, достаточно мало отличающемся от
данного, он не упадет на пол в противоположную сторону.
Обратим теперь внимание на то, что во всякий момент времени по-
положение стержня характеризуется углом а, который он делает с полом.
Углам а = 0° и а = 180° соответствуют два взаимно противоположных
горизонтальных (лежачих) положения. Обозначим через х значение уг-
угла а в начальном положении стержня. Доказательство нашего утверж-
утверждения будет косвенное, в соответствии с чисто экзистенциальным ха-
характером самой проблемы. Допустим, что всегда, т. е при любом началь-
начальном положении стержня, стержень непременно упадет или в одну, или
в другую сторону, так что а примет значение или 0°, или 180°. Опреде-
Определим тогда функцию f(x) согласно условию: /(ж) = +1 или —1, смотря
по тому, упадет ли стержень в сторону, соответствующую углу а =
= 0° или углу а = 180°. Свойства функции f(x) таковы: она задана
в интервале 0 ^ х ^ 180°, непрерывна в нем, и притом /@) = +1,
/A80) = —1. Отсюда, по теореме Больцано, следует, что при каком-то
промежуточном значении х @° < х < 180°) должно выполняться ра-
равенство f(x) = 0. А это противоречит тому, что функция f(x) может
принимать только значения +1 и —1. Значит, приходится отвергнуть

§1. Примеры пределов 371
сделанное допущение, согласно которому стержень упадет на пол во
время движения поезда при каком угодно начальном его положении.
Совершенно ясно, что приведенное доказательство носит чисто те-
теоретический характер, потому что не дает решительно никаких ука-
указаний на то, как определить искомое начальное положение стержня.
Вместе с тем, даже если бы такое положение и могло быть вычислено
теоретически с абсолютной точностью, практически оно было бы бес-
бесполезно вследствие своей неустойчивости. Так, например, в предельном
случае, если поезд неподвижен в течение всего «путешествия», решение
совершенно очевидно: х = 90°; но всякий, кто пытался уравновесить
иголку в стоячем положении на гладкой горизонтальной поверхности,
понимает, насколько это решение практически нереально. Тем не менее,
с математической точки зрения, приведенное доказательство имеет не-
неоспоримый интерес.
Упражнения.
1) С помощью теоремы на стр. 116 установите, что рассуждение может
быть обобщено на случай, когда «путешествие» продолжается бесконеч-
бесконечно долго.
2) Обобщите также на случай, когда поезд движется по произвольной кри-
кривой на плоскости, а стержень может падать в любом направлении,
т. е. стержень обладает двумя степенями свободы. (Указание: невоз-
невозможно непрерывно отобразить круговой диск на одну его окружность,
оставляя все точки окружности неподвижными — см. стр. 299.)
Дополнение к главе VI
Дальнейшие примеры на пределы
и непрерывность
§ 1. Примеры пределов
1. Общие замечания. Во многих случаях сходимость последо-
последовательности ап может быть доказана по следующей схеме. Мы рассмат-
рассматриваем две другие последовательности Ьп и с„, члены которых, вообще
говоря, имеют более простую структуру и обладают тем свойством,
что
Ьп^ап < сп A)
при всех значениях п. Тогда, если будет установлено, что последо-
последовательности Ьп и сп имеют один и тот же предел а, можно будет

372 Дополнение к главе VI
утверждать, что последовательность ап также имеет предел а. Фор-
Формальное доказательство этой теоремы мы можем предоставить чита-
читателю.
Ясно, что применение указанной схемы потребует оперирования
неравенствами. В связи с этим своевременно напомнить небольшое чис-
число элементарных правил, которым подчинены арифметические опера-
операции с неравенствами.
1. Если а > Ь, то а + О Ь + с (к обеим частям неравенства можно
прибавить одно и то же число).
2. Если а > Ь и с — положительно, то ас > Ъс (можно умножить
неравенство на положительное число).
3. Если а > Ъ, то —Ь > -а (направление неравенства меняется при
умножении на —1). Так, 2 < 3, но —3 < —2.
4. Если а и Ъ одного и того же знака, то из неравенства а < Ь
следует - > \.
а о
5. |а + ЬК Н + Щ-
2. Предел qn. Если q — число, большее чем 1, то члены по-
последовательности qn неограниченно возрастают; например, так будет
при q = 2:
q, q2, qz, ...
Такие последовательности «стремятся к бесконечности» (см. стр. 340).
В самом общем случае доказательство этого основывается на важном
неравенстве (см. стр. 42)
A + Л)" ^ l + nh^nh, B)
где h — какое угодно положительное число. Мы положим q = 1 + h,
где h > 0; тогда
qn = A + h)n > nh.
Пусть k — сколь угодно большое положительное число; в таком случае
достаточно взять п > —, чтобы получить неравенство
qn > nh> k;
значит, qn —>• ос. Если q = 1, то все члены последовательности равны 1,
и, значит, предел последовательности есть 1. Если q отрицательно, то
знаки qn чередуются, и в случае \q\ ^ 1 предела нет.
Упражнение. Дайте строгое доказательство последнему утверждению.

§1. Примеры пределов 373
На стр. 96 мы установили, что если -1 < q < 1, то qn -»• 0. Да-
Дадим здесь еще другое, очень простое доказательство. Рассмотрим слу-
случай 0 < q < 1. Тогда члены последовательности q, q2, q3, ... монотонно
убывают, оставаясь положительными. Отсюда следует (см. стр. 342),
что последовательность имеет предел: qn —> а. Умножая обе части по-
последнего соотношения на q, получим: qn+1 —\ aq.
Но qn+1 должно иметь тот же предел, что и qn, так как дело не
меняется от того, как обозначен возрастающий показатель — через п
или через п + 1. Значит, aq = а, или a(q — 1) = 0. Так как по условию,
A ~ я) Ф 0j то отсюда следует а = 0.
Если q = 0, предыдущее утверждение тривиально. Если, наконец,
-1 < q < 0, то 0 < \q\ < 1; поэтому, как только что доказано, \qn\ —
= \q\u -> 0. Но в таком случае qn -* 0 при условии \q\ < 1. Доказатель-
Доказательство закончено.
Упражнение. Доказать, что при п —> оо
/ „3 ч п
3) I —-—- ) стремится к бесконечности при х > 2, к нулю при |ж| < 2.
^4 + х '
3. Предел %/р. Последовательность чисел
ап = \/р,
т.е.
Р, у/р, \/Р, </р,---
имеет предел 1, каково бы ни было положительное число р:
%/р —> 1 при п —»• оо. C)
(Символ {/р обозначает, как всегда, положительный корень степени п.
В случае, если р отрицательно, при п четном не существует действи-
действительных корней степени п.)
Докажем соотношение C). Предположим, прежде всего, что р > 1;
тогда также у/р> 1. Мы можем положить
причем hn — положительная величина, зависящая от п. Из неравенст-
неравенства B) следует
P=(l + hn)n >nhn.

374 Дополнение к главе VI
Деление на п дает
0<Л„ < |.
Так как последовательности Ьп = 0 и с„ = ^ обе имеют предел О,
то на основании рассуждения, приведенного в пункте 1, hn также при
возрастании п имеет предел 0, и наше утверждение, таким образом,
доказано в случае р > 1. Мы встретились здесь с очень типическим
примером, когда предельное соотношение, в данном случае hn —»• О,
устанавливается посредством заключения hn между двумя границами,
пределы которых определяются более просто.
Кстати, мы получили оценку для разности hn между %/р и 1: эта
разность непременно меньше, чем ^.
Если 0 < р < 1, то *yf> < 1, и можно положить
где hn — снова положительное число, зависящее от п. Отсюда следует
Р A + К)п п/г„'
так что
0 < hn < Щ,
и, значит, hn стремится к нулю при п —> оо. И тогда, очевидно, ^/р —> 1.
«Уравнивающее» воздействие извлечения корня степени п, выража-
выражающееся в том, что результаты извлечения корней последовательно воз-
возрастающих степеней из данного положительного числа приближаются
к единице, остается в силе иногда и в том случае, если само подра-
дикальное выражение не остается постоянным. Мы проверим сейчас,
что
\/п —> 1 при п —> оо.
Небольшое ухищрение позволит нам сослаться опять на неравенст-
неравенство B). Вместо корня степени п из п возьмем корень степени п из s/n.
Полагая \J\/п = 1 + кп, где кп — положительная величина, завися-
зависящая от п, получим с помощью упомянутого неравенства, л/п = A +
+ кп)п > пкп, так что
" п ~ у/а'

§ 1. Примеры пределов 375
Значит,
К $fc = A + кпJ = 1 + 2кп + к2п<1 + ^= + ±.
Правая часть этого неравенства стремится к 1 при п —»• оо, и потому
то же самое можно сказать относительно у/п.
4. Разрывные функции как предел непрерывных. Будем
рассматривать такие последовательности а„, в которых члены ап — не
постоянные числа, а функции некоторой переменной ж, именно ап —
= fn(x)- Если только такая последовательность сходящаяся, то ее пре-
предел также есть функция ж:
/(ж) = Нт/„(ж).
Такого рода представления функции /(ж) в виде предела других функ-
функций часто бывают полезны, так как «более сложные» функции таким
образом приводятся к «более простым».
В частности, это обнаруживается при рассмотрении некоторых яв-
явных формул, определяющих функции с разрывами. Рассмотрим, на-
например, последовательность fn(x) = ^-г-. При \х\ = 1 мы полу-
1 + х п
чаем х2п = 1, fn{x) = i так что /п(ж) —»• i. С другой стороны,
при |ж| < 1 мы имеем х2п —\ 0 и /п(ж) —»• 1; наконец, при |ж| > 1
получается ж2п —»• оо и, следовательно, /п(ж) —\ 0. В итоге
Мы видим, что прерывная функция f(x) представлена как предел по-
последовательности непрерывных рациональных функций.
Другой интересный пример в таком же роде дается последователь-
последовательностью
При х = 0 все функции fn{x) обращаются в нуль, и потому /@) =
= lim/n@) = 0. При х Ф Q выражение —i—- положительно и меньше,
1 + х *

376 Дополнение к главе VI
чем 1, и потому теория геометрической прогрессии позволяет утверж-
утверждать, что /п(ж) сходится при п —» сю. Предел, т.е. сумма бесконечной
2 2
прогрессии, равен —2— = , т.е. 1+х2. Итак, /„(ж) стремится
1 ~ 9 1 1
1+х2
к функции /(ж) = 1 + ж2 при х^Оик /(ж) = 0 при ж = 0. Получается
функция /(ж) с устранимым разрывом в точке ж = 0.
*5. Пределы при итерации. Нередко приходится рассматри-
рассматривать последовательности, сконструированные таким образом, что ап+1
получается из ап посредством тех же операций, посредством каких ап
получается из an_i: эта процедура позволяет вычислить любой член по-
последовательности, если известен первый. В подобных случаях говорят
о процедуре «итерации».
Примером может служить последовательность
1,
каждый член ее получается из предыдущего посредством прибавления
единицы и затем извлечения квадратного корня. Таким образом, после-
последовательность определяется соотношениями
а\ = 1,
Найдем ее предел. Очевидно, что при п > 1 и ап > 1. Далее, последова-
последовательность наша монотонно возрастает, так как
an+i - ап = С1 + ап) - A + fln-i) =an- an-i.
Раз только ап > an-i, то значит, an+i > ап; но а,2 — а,\ — \/2 — 1 > 0,
и потому (с помощью индукции) отсюда следует, что ап+\ > ап при
всех значениях п. Мы замечаем дальше, что рассматриваемая последо-
последовательность ограниченная; в самом деле,
_ _ 1 + аа 1 +
a"+i - а^Г < ап+1 ~ i + a^T < l'
В силу принципа монотонных последовательностей отсюда вытекает
существование предела: ап -»• а, причем 1 < a < 2. Но видно ясно,
что а есть положительный корень уравнения ж2 = 1 + х: действительно,
соотношение а^+1 = 1 + ап в пределе при п —»• оо дает нам а2 = 1 + о.
Решая уравнение, мы убеждаемся, что о = —¦——.

§1. Примеры пределов 377
Отсюда, наоборот, легко сделать тот вывод, что это квадратное
уравнение можно решать приближенно, с какой угодно степенью точ-
точности, посредством итерационной процедуры.
Таким же образом, с помощью итераций, можно решать и другие
алгебраические уравнения. Например, кубическое уравнение ж3 - Зж +
+ 1 = 0 напишем в форме
х
и затем, взяв в качестве а\ произвольное число, скажем а\ = 0, опре-
определим дальше последовательность ап по формуле
при этом получим
а2 = | = 0,3333... , а3 = ^ = 0,3461... , аА = ^? = 0,3472 ....
Можно показать, что последовательность имеет предел, равный корню
данного кубического уравнения, а именно, а = 0,3473
Итерационные процессы в этом роде имеют громадное значение
в математике, так как с их помощью большей частью даются «доказа-
«доказательства существования»; они полезны и в приложениях, где доставля-
доставляют методы приближенного решения разнообразных проблем.
Упражнения на пределы.
При п —> оо:
1) Докажите, что у/п + 1 — \fn —> 0. (Указание: напишите разность в виде
2) Найдите предел \/п2 + а — s/n2 + Ъ.
3) Найдите предел л/п2 + an + b — п.
4) Найдите предел
/п + 1 + s/n
5) Докажите, что предел л/п + 1 равен 1.
6) Каков предел л/а" + 6", если а > 6 > 0?
7) Каков предел \/ап + Ьп + с", если а > b > с > 0?
8) Каков предел у/апЪп + апсп + Ьпсп, если а > b > с > О?

378 Дополнение к главе VI
1 + й ) •
A \"
1 Н 1 .
п '
§ 2. Пример, относящийся к непрерывности
Чтобы дать формальное доказательство непрерывности данной
функции, требуется проверка согласно определению, приведенному на
стр. 358. Иногда соответствующая процедура оказывается очень гро-
громоздкой, и, к счастью, мы имеем право сослаться на обстоятельство,
которое будет установлено в главе VIII, а именно: непрерывность сле-
следует из дифференцируемости. Так как дифференцируемость там же
будет установлена систематически для всех элементарных функций, то
мы (как это обычно делается) воздержимся от того, чтобы приводить
скучные доказательства непрерывности функций различных типов.
Но в качестве дальнейшей иллюстрации общего определения мы
все же рассмотрим здесь еще один пример, именно, функцию
Мы имеем право ограничить возможные изменения х конечным интер-
интервалом \х\ ^ М, где, впрочем, М как угодно велико. Написав
f(Xl)-f(x) =
¦ x{ 1 + x2
X X л
мы видим, что при \х\ ^ М, будет |xi| ^ M. Отсюда следует неравен-
неравенство
|/(xi) - f(x)\ ^ \х - a:i| • \х + xi| ^ \х - xi| • 2М.
Значит, разность в левой части станет меньше, чем наперед заданное
положительное число е, при условии, что будет
Следует отметить, что мы были слишком великодушны в этих
оценках. Читатель без труда убедится, что при больших значениях х
и х\ можно было бы удовлетвориться гораздо большими значениями S.

Глава VII
Максимумы и минимумы
Введение
Отрезок прямой линии определяет кратчайший путь между дву-
двумя его конечными точками. Дуга большого круга представляет собой
кратчайшую кривую, которой можно соединить две точки на сфере.
Среди всех замкнутых плоских кривых одной и той же длины наи-
наибольшая площадь охватывается окружностью, а среди всех замкнутых
поверхностей одной и той же площади наибольший объем охватывается
сферой.
Максимальные и минимальные свойства подобного рода были из-
известны древним греческим математикам, хотя и не всегда со строгими
их доказательствами. Одно из самых замечательных относящихся сюда
открытий приписывается Герону, александрийскому ученому I столе-
столетия нашей эры. Издавна было известно, что световой луч, выходящий
из точки Р и встречающийся с плоским зеркалом L, отражается в на-
направлении некоторой точки Q таким образом, что PR и QR образу-
образуют одинаковые углы с зеркалом. По преданию, Герон установил, что
если R' — любая точка зеркала, отличная от R, то сумма отрезков
PR' + R'Q больше, чем PR + RQ. Эта теорема (которую мы скоро до-
докажем) характеризует истинный путь светового луча PRQ между Р
и Q, как кратчайший путь от Р к Q с заходом на зеркало L — открытие,
которое можно рассматривать как зародыш теории геометрической оп-
оптики.
Нет ничего удивительного в том, что математики живейшим обра-
образом интересуются подобного рода вопросами. В повседневной жизни по-
постоянно возникают проблемы наибольшего и наименьшего, наилучшего
и наихудшего. Именно в такой форме могут быть поставлены многие
задачи, имеющие практическое значение. Например, каковы должны
быть очертания судна, для того чтобы оно испытывало при движении
в воде наименьшее сопротивление? Каково должно быть соотношение
размеров цилиндрического резервуара, чтобы при заданном расходе ма-
материала объем был наибольшим?

380 Глава VII
Возникнув в XVII столетии, общая теория экстремальных, т. е. мак-
максимальных и минимальных, значений величин выдвинула обширный
ряд принципов науки, служащих целям обобщения и систематизации.
Первые шаги, сделанные Ферма в области дифференциального исчис-
исчисления, были ускорены стремлением найти общие методы для изуче-
изучения вопросов о максимумах и минимумах. В последующем столетии
эти методы были значительно обогащены с изобретением вариационно-
вариационного исчисления. Становилось все яснее и яснее, что физические законы
природы в высшей степени удачно формулируются в терминах прин-
принципа минимальности, обеспечивающего естественный подход к более
или менее полному решению частных проблем. Одним из самых заме-
замечательных достижений современной математики является теория ста-
стационарных значений, дающая такого рода расширение понятия макси-
максимума и минимума, которое базируется одновременно на анализе и на
топологии.
Мы будем здесь рассматривать весь вопрос в целом с совершенно
элементарной точки зрения.
§ 1. Задачи из области элементарной геометрии
1. Треугольник наибольшей пло-
площади при двух заданных сторонах.
Даны два отрезка а и Ь; требуется най-
найти треугольник возможно большей пло-
площади, у которого две стороны были бы а
и Ь. Решением является прямоугольный
треугольник с катетами а и Ь. Рассмот-
Рис. 176. Максимум площади рим в самом деле какой-нибудь треуголь-
треугольника при двух дан- ник с двумя сторонами а и b (рис. 176).
ных сторонах Если h есть высота, соответствующая ос-
основанию а, то площадь треугольника А равна -^ah. Это последнее вы-
выражение, очевидно, принимает наибольшее значении при наибольшем
возможном значении h, что случится именно при h, равном Ь, т. е. тог-
тогда, когда треугольник прямоугольный. Итак, максимальная площадь
равна |аЬ.
2. Теорема Герона. Экстремальное свойство световых лу-
лучей. Дана прямая L и две точки Р и Q по одну и ту же ее сторону-
Как выбрать точку R на прямой L с таким расчетом, чтобы сумма от-
отрезков PR + RQ давала кратчайший путь от Р к Q с заходом на L1

>1. Задачи из области элементарной геометрии
381
В этом заключается проблема Герона о световом луче (точно такую же
проблему приходится решать тому, кто, желая из точки Р как можно
скорее пройти в точку Q, должен был бы по дороге подойти к L: пред-
представьте себе, что L — берег реки, и там нужно зачерпнуть ведро воды).
Чтобы получить решение, построим зеркальное отражение Р' точки Р
относительно прямой L, и тогда прямая P'Q пересекает L как раз в ис-
искомой точке R. Легко доказать, что PR + RQ меньше, чем PR' + R'Q,
где R' — любая точка на L, отличная от R. Действительно, PR = P'R
и PR' = P'R', значит, PR+RQ = P'R + RQ = P'Q и PR' + R'Q =
= P'R' + R'Q. Ho P'R' + R'Q больше, чем P'Q (так как сумма двух
сторон треугольника больше третьей стороны), т.е. PR' + R'Q больше,
чем PR + RQ, что и требовалось доказать. В дальнейшем существенно
предполагать, что Р и Q не лежат на самой прямой L.
Из рис. 177 видно, что Z3 = 12
и Z2 = Z1, так что Zl = Z3. Други-
Другими словами, точка R такова, что PR
и QR образуют одинаковые углы с L.
Отсюда следует, что световой луч, от-
отражающийся от L (а при отражении,
как показывает эксперимент, угол па-
падения равен углу отражения), дейст-
действительно обращает в минимум путь
из Р в Q с заходом на L — в согласии
с высказанным утверждением.
Задачу можно обобщить, вводя
несколько прямых L, М, Рас-
Рис. 177. Теорема Герона
смотрим, например, случай, когда имеются две прямые L, М и две
точки Р, Q, расположенные как на рис. 178, и поставим целью най-
найти кратчайший путь из Р в Q с заходом сначала на L, потом на М.
Пусть Q' — отражение Q относительно М и Q" — отражение Q' от-
относительно L. Проведем прямую PQ", пересекающую L в точке R,
и прямую RQ', пересекающую М в точке 5; тогда PR + RS + SQ
и есть искомый кратчайший путь. Доказательство подобно приведен-
приведенному выше и предоставляется читателю в качестве упражнения. Если
бы L и М были зеркалами, то световой луч из Р, приходящий после
отражения в L, потом в М в точку Q, попадал бы на L в точке Д,
а на М — в точке 5; итак, световой луч опять-таки избрал бы для себя
путь наименьшей длины.
Можно было бы также поставить задачу нахождения кратчайшего
пути из Р в Q с заходом сначала на М, потом на L. Таким должен

382
Рис. 178. Отражение в двух зеркалах
Рис. 179. Вариант предыдущей задачи
быть путь PRSQ (рис. 179), определяемый аналогично пути PRSQ,
рассмотренному раньше. Длина этого нового пути может оказаться или
большей, или меньшей, или равной длине прежнего пути.
Упражнение. Показать, что новый путь больше прежнего в том случае,
если точки Q и R лежат по одну сторону прямой PQ. В каком случае новый
и прежний пути окажутся равными?
3. Применения к задачам о треугольниках. С помощью те-
теоремы Герона можно легко решить следующие две задачи.
а) Задана заранее площадь А и одна сторона с = PQ треугольника;
среди всех такого рода треугольников требуется найти тот, для которо-
которого сумма двух других сторон а и b — наименьшая. Вместо того чтобы
задавать сторону с и площадь А треугольника, можно задать сторону с
и высоту h, опущенную на с, так как А = \hc. Таким образом, зада-
Z

§ 1. Задачи из области элементарной геометрии
383
R
ча сводится к тому, чтобы найти точку R (рис. 180), находящуюся на
расстоянии h от прямой PQ, и притом такую, что сумма сторон а + Ь
обращается в минимум. Из первого условия следует, что точка R долж-
должна быть расположена на прямой, параллельной прямой PQ и отстоящей
от нее на расстоянии h. Раз это установлено, становится ясно, что зада-
задача решается с помощью теоремы Герона в применении к тому случаю,
когда Р и Q находятся на одном и том же расстоянии от прямой L:
искомый треугольник PRQ равнобедренный.
б) В треугольнике пусть да-
даны: одна сторона с и сумма а + Ь
двух других сторон; требуется из
всех таких треугольников выбрать
тот, у которого площадь наиболь-
наибольшая. Эта задача — обратная по
отношению к задаче а). Решени-
Решением является опять-таки равнобед-
равнобедренный треугольник, для которо-
которого а = Ь. Как мы уже видели, для
такого треугольника при заданной
площади сумма а + Ь принимает
наименьшее значение; это значит, что во всяком другом треугольнике
с основанием с и той же площадью сумма а+Ь имеет большее значение.
С другой стороны, из а) ясно, что во всяком треугольнике с основани-
основанием с и площадью, большей чем площадь рассматриваемого равнобедрен-
равнобедренного треугольника, значение а + Ь также будет больше. Отсюда следует,
что всякий другой треугольник, имеющий заданные значения для а + Ь
и для с, должен иметь меньшую площадь, так что наибольшую площадь
при заданных с к а + Ь имеет именно равнобедренный треугольник.
Рис. 180. Треугольник наименьшего
периметра при данных основании и
площади
R
4. Свойства касательных к эл-
эллипсу и гиперболе. Соответствую-
Соответствующие экстремальные свойства. С те-
теоремой Герона связаны некоторые важ-
важные геометрические задачи. Мы устано-
установили, что если R — такая точка на пря-
прямой L, что PR + RQ обращается в ми-
минимум, то прямые PR и RQ образуют
одинаковые углы с L. Обозначим мини-
минимальное значение PR + RQ через 2а.
Пусть, с другой стороны, р и q обозна-
обозначают расстояния произвольной точки плоскости соответственно от то-
Рис. 181. Свойство касательной
к эллипсу

384 Глава VII
чек Р и Q; рассмотрим геометрическое место всех точек плоскости,
для которых р + q = 2а. Это геометрическое место — эллипс с фокуса-
фокусами Р и Q, проходящий через точку R на прямой L, причем прямая ?
касается этого эллипса в точке R. Действительно, если бы прямая ?
пересекала эллипс еще в какой-то точке, кроме R, то существовал бы
отрезок прямой L, лежащий внутри эллипса; для каждой точки этого
отрезка р + q было бы меньше, чем 2а: в самом деле, легко убедиться,
что p + q меньше или больше, чем 2а, смотря по тому, находится ли рас-
рассматриваемая точка внутри или вне эллипса. Но так как мы знаем, что
для точек на прямой L непременно р + q ^ 2а, то сделанное предполо-
предположение приходится отбросить. Итак, прямая L — касательная к эллипсу
в точке R. Кроме того, мы знаем, что PR и RQ образуют одинаковые
углы с L; отсюда в качестве побочного результата наших рассуждений
вытекает важная теорема: касательная к эллипсу образует равные углы
с прямыми, проведенными из фокусов в точку касания.
Следующая задача родственна
предыдущей. Дана прямая линия L
и две точки Р и Q по разные сто-
стороны L (рис. 182); требуется найти
такую точку R на L, чтобы величи-
величина \р — q\, т.е. абсолютное значение
разности расстояний точки R от Р
и Q, была как можно больше. (Мы до-
допускаем, что L не является перпен-
дикуляром, восстановленным из се-
середины отрезка PQ: иначе р — q рав-
Рис. 182. \PR - QR\ = maximum нялось бы нулю для всякой точки L,
и задача потеряла бы смысл.) При-
Приступая к решению задачи, построим зеркальное отражение точки Р
относительно L: полученная точка Р' расположена по ту же сторону L,
что и Q. Какова бы ни была точка R' на L, мы имеем: р — R'P = R'P',
q = R'Q. Так как разность двух сторон треугольника никогда не пре-
превышает третьей стороны, то, рассматривая треугольник R'QP', можно
заключить, что величина \р — q\ = \R'P' - R'Q\ меньше или равна P'Q;
и, как видно из чертежа, только при условии, что R', Р' и Q располо-
расположены на одной прямой, \р — q\ может оказаться равным P'Q. Поэтому
искомая точка R есть точка пересечения прямой L с прямой, проведен-
проведенной через Р' и Q. Как и в предыдущей задаче, не представляет труда
установить, ссылаясь на конгруэнтность треугольников RPR' и RP'R',
что углы, которые с прямой L делают отрезки RP и RQ, одинаковы.

§1. Задачи из области элементарной геометрии 385
Отсюда, как и в прежней задаче, уже
ничего не стоит получить свойство каса-
касательной к гиперболе. Принимая наиболь-
наибольшее значение разности \PR — RQ\ рав-
равным 2а, рассмотрим геометрическое мес-
место всех точек в плоскости, для которых
абсолютное значение p — q равно 2а. Это —
гипербола с фокусами Р и Q, проходящая
через точку R. Легко убедиться, что аб-
г „ Рис. 183. Свойство касатель-
солютное значение р — а меньше, чем 2а
ной к гиперболе
в области, заключенной между двумя вет-
ветвями гиперболы, и больше, чем 2а по ту сторону каждой из ветвей, по
которую лежит соответствующий фокус. Отсюда — в основном с по-
помощью такой же аргументации, как и в случае эллипса, — вытекает,
что прямая L касается гиперболы в точке R. К которой именно из вет-
ветвей прямая L является касательной, — это зависит от того, которая
из точек Р и Q ближе к L: если ближе точка Р, то касается прямой L
та ветвь, которая окружает Р; и аналогично для Q (рис. 183). Если Р
и Q находятся на равных расстояниях от прямой L, то L не касается
ни той, ни другой ветви гиперболы, а является одной из ее асимптот.
Об этом результате позволительно догадываться, исходя из того сооб-
соображения, что описанное выше построение в рассматриваемом случае
не дает никакой (конечной) точки R, так как прямая P'Q оказывается
параллельной прямой L.
Так же, как и в случае эллипса, наши рассуждения приводят к хоро-
хорошо известной теореме: касательная, проведенная в любой точке гипер-
гиперболы, делит пополам угол между отрезками, проведенными из фокусов
в точку касания.
Может показаться странным, что приходится решать задачу о ми-
минимуме, если точки Р и Q лежат по одну сторону L, тогда как, если
точки лежат по разные стороны L, мы рассматриваем задачу о мак-
максимуме. Но нетрудно прийти к заключению, что указанное различие
совершенно естественно. В первой задаче при удалении по прямой L
в бесконечность — в одну или в другую сторону — каждое из рас-
расстояний р и q, следовательно и их сумма, неограниченно возрастает.
Таким образом, было бы невозможно найти наибольшее значение p + q,
и единственной возможной является постановка задачи о минимуме.
Дело обстоит совершенно иначе во второй задаче, когда Р и Q лежат
по разные стороны L. В этом случае не будем смешивать три различ-
различные величины: разность p — q, обратную разность q — р и абсолютное

386
Глава VII
значение \р — q\; именно, для последней величины мы определяли мак-
максимум. Как обстоит дело, легче всего понять, если представить себе,
что точка R движется по прямой L, занимая различные положения ДХ)
R2, Дз, Существует такое положение R, для которого разность р- q
обращается в нуль: при этом прямая L пересекается с перпендикуля-
перпендикуляром к отрезку PQ, проведенным из его середины. Ясно, что при этом
положении точка R дает минимум для абсолютного значения \р — q\. Но
по одну сторону от этой точки р больше, чем q, по другую — меньше;
значит, величина р — q положительна по одну сторону точки и отри-
отрицательна — по другую. Следовательно, сама эта величина не имеет ни
максимума, ни минимума в точке, где \р — q\ = 0. С другой стороны,
та точка, в которой \р - q\ имеет максимум, наверное, дает экстремум
для р — q. Если р > q, то имеется максимум для р — q; если q > p, то
максимум для q — р и, значит, минимум для р — q. Имеется ли макси-
максимум или минимум для р — q, это зависит от положения двух данных
точек относительно прямой L.
В случае, если Р и Q находятся на равных расстояниях от L, реше-
решения задачи о максимуме, как мы видели, нет вовсе, так как прямая P'Q
(см. рис. 182) параллельна L. И тогда при удалении R в бесконечность
в том или в другом направлении величина \р — q\ стремится к некото-
некоторому конечному пределу. Этот предел есть не что иное, как длина s
проекции отрезка PQ на прямую L (читатель может доказать это в ка-
качестве упражнения). Величина \р — q\ при рассматриваемых обстоятель-
обстоятельствах всегда меньше, чем предел s, и максимума не существует, так
как, какова бы ни была данная точка R, всегда можно указать другую,
более удаленную, для которой \р — q\ будет больше и, однако, еще не
совсем равно s.
*5. Экстремальные рассто-
расстояния точки от данной кривой.
Начнем с того, что определим наи-
наибольшее и наименьшее расстояния
данной точки Р от точек данной
кривой С. Предположим для прос-
простоты, что С есть простая замк-
замкнутая кривая, имеющая всюду ка-
касательную (рис. 184). Понятие ка-
касательной к кривой, принимаемое
здесь на интуитивной основе, бу-
будет подвергнуто анализу в следую-
следующей главе. Ответ очень прост: если
Рис. 184. Экстремальные
ния до точек кривой
расстоя-

§1. Задачи из области элементарной геометрии 387
для некоторой точки R на С расстояние PR достигает минимума или
максимума, то прямая PR непременно перпендикулярна к касатель-
касательной к С в точке R; короче говоря, прямая PR перпендикулярна к С.
Доказательство вытекает из следующего обстоятельства: окружность
с центром Р, проходящая через R, должна быть касательной к кри-
кривой С. Действительно, если R есть точка наименьшего расстояния, то
кривая С должна целиком лежать вне круга и поэтому в точке R не
может его пересекать; если же R есть точка наибольшего расстояния,
то С должна целиком лежать внутри круга и потому опять-таки в точ-
точке R пересекать его не может. (Это следует из того очевидного факта,
что расстояние некоторой точки от Р меньше, чем RP, если эта точ-
точка — внутри круга, и больше, чем RP, если она — вне его.) Итак,
окружность и кривая касаются в точке R, и касательная у них в этой
точке — одна и та же. Остается заметить, что отрезок PR, как радиус
окружности, перпендикулярен к касательной к окружности в точке R
и, следовательно, к самой кривой С в той же точке.
В теснейшей связи с предыдущим стоит следующее предложение,
доказательство которого предоставляется читателю: диаметр замкну-
замкнутой кривой С (т.е. наибольшая из ее хорд) в своих концах обязательно
перпендикулярен к С. Аналогичное утверждение можно сформулиро-
сформулировать и доказать для трехмерного случая.
Упражнение. Доказать, что наикратчайший и наидлиннейший отрез-
отрезки, связывающие две взаимно непересекающиеся замкнутые кривые, перпен-
перпендикулярны в своих концах к самым кривым.
Можно обобщить и задачи пункта 4, касающиеся суммы и разности
расстояний. Рассмотрим вместо прямой линии L простую замкнутую
кривую С, обладающую касательной в каждой точке, и еще две точ-
точки Р и Q, не лежащие на С. Постараемся характеризовать те точки
на кривой С, для которых сумма р + Q или разность р — q принимают
экстремальные значения (причем р и q обозначают соответственно рас-
расстояния переменной точки на С от точек Р и Q). Теперь уже нельзя
применить то простое, основанное на отражении построение, с помо-
помощью которого мы решили обе задачи в случае, когда С была прямой
линией. Но мы можем воспользоваться для поставленной здесь цели
свойствами эллипса и гиперболы. Так как С на этот раз — замкну-
замкнутая кривая, а не линия, уходящая в бесконечность, то и максимум и
минимум на ней действительно реализуются: в самом деле, можно не
подвергать сомнению то обстоятельство, что величины p + q и p — q до-
достигают и наибольшего и наименьшего значений на всяком конечном
сегменте, кривой, следовательно, на замкнутой кривой (см. § 7).

388
Глава VII
Рис. 185. Максимум и мини-
минимум сумм PR + QR
Останавливаясь на случае суммы p+q,
предположим, что R — та точка на С,
в которой имеет место максимум; пусть
2а есть значение р + q в этой точке. Рас-
Рассмотрим эллипс с фокусами Р и Q — гео-
геометрическое место точек, для которых р+
+ q = 2а. Этот эллипс в точке R должен
касаться кривой С (доказательство пре-
предоставляется читателю в качестве упраж-
упражнения). Но мы видели, что отрезки PR
и QR делают одинаковые углы с эллип-
эллипсом в точке R, и так как эллипс в точке R
касается кривой С, то отрезки PR и QR
делают в той же точке также одинаковые
углы и с С Совершенно аналогичное рас-
рассуждение приводит нас к тому же результату и в случае, если в точке R
сумма р + q обращается в минимум.
Итак, мы пришли к теореме: дана замкнутая кривая С и две точ-
точки Р uQ вне ее; тогда в каждой из точек R, в которых сумма p + q при-
принимает наибольшее или наименьшее значение на кривой С, отрезки PR
и QR делают одинаковые углы с самой кривой (т. е. с ее касательной).
Если точка Р — внутри С, а точка Q — вне С, то теорема остается
справедливой для той точки, гцер+q принимает наибольшее значение,
но она теряет смысл для точки, где p + q принимает наименьшее зна-
значение, так как эллипс вырождается в отрезок прямой.
Рассуждая аналогичным об-
образом (воспользовавшись вместо
свойств эллипса свойством гипер-
гиперболы) читатель сможет доказать
следующую теорему: дана замк-
замкнутая кривая С и две точки Р
и Q — одна внутри, другая вне С;
тогда в каждой из тех точек R
на С, где разность p—q принима-
принимает наибольшее или наименьшее
значение, отрезки PR и QR дела-
делают одинаковые углы с самой кри-
кривой С. Но нужно вместе с тем от-
Рис. 186. Минимум разности PR — QR
да С — прямая, и случаем, когда С
метить, что между случаем, ког-
- замкнутая кривая, есть сущест-

§ 2. Общий принцип, которому подчинены экстремальные задачи 389
венное различие: в первом случае приходится разыскивать максимум
абсолютного значения разности, т.е. максимум \р — q\, тогда как во
втором сама разность р — q достигает и наибольшего и наименьшего
значений.
§ 2. Общий принцип, которому подчинены
экстремальные задачи
1. Принцип. Предыдущие задачи являются частными случая-
случаями некоторой общей проблемы, которую удобнее всего сформулировать
аналитически. Возвращаясь к первой из рассмотренных задач, касаю-
касающейся суммы р + q, мы видим, что она заключается в том, чтобы,
обозначив через х, у координаты точки R, через х\, у\ координаты
точки Р и через х2, yi координаты точки Q, найти экстремальные зна-
значения функции
f(x, у) =p + q,
где положено
Р = V(x~xiJ + (y-yiJ, q = V(x-x2J + {y-y2J.
Рассматриваемая функция непрерывна во всей плоскости, но точ-
точка й с координатами х, у подчинена требованию находиться на
кривой С. Эта последняя кривая, допустим, определена уравнени-
уравнением g(x, у) = 0; например, уравнением х2 + у2 — 1 =0, если С — еди-
единичная окружность.
Обратимся теперь к общей задаче: найти экстремальные значения
некоторой данной функции f(x, у), если переменные хну подчинены
условию g(x, у) = 0. Постараемся характеризовать решение этой зада-
задачи. Для этого рассмотрим семейство кривых f(x, у) = с; при этом под
«семейством» кривых понимаем совокупность всех кривых, определя-
определяемых указанным уравнением при различных значениях постоянной с
(но такое значение неизменно для всех точек каждой кривой в отдель-
отдельности). Предположим, что через каждую точку плоскости — или по
крайней мере некоторой ее части, содержащей кривую С, — проходит
одна и только одна кривая семейства /(ж, у) = с. Тогда при непре-
непрерывном увеличении с кривая /(ж, у) — с «заметает» некоторую часть
плоскости, однако при этом ни одну точку не «заметает» дважды. (При-
(Примеры такого рода семейств: х2 + у2 = с, х + у = с, х = с.) В частнос-
частности, одна кривая рассматриваемого семейства пройдет через точку Ri,

390
Глава VII
fU.y)=b
f(x,y)=
Рис. 187. Экстремумы функции на кривой
в которой /(ж, у) принимает наибольшее значение на кривой С, и дру-
другая — через точку R2, в которой f(x, у) принимает наименьшее зна-
значение на С. Пусть наибольшее значение есть о, наименьшее — Ь. По
одну сторону кривой /(ж, у) = а значение f(x, у) меньше, чем о, по
другую — больше, чем о. Так как на кривой С имеет место неравен-
неравенство /(ж, у) ^ о, то кривая С должна целиком лежать по одну и ту же
сторону кривой /(ж, у) = а; отсюда следует, что она в точке R\ каса-
касается кривой /(ж, у) = а. Точно так же кривая С касается в точке Дг
кривой f(x, у) = Ь.
Итак, доказана общая теорема: если в точке R на кривой С функ-
функция f(x, у) имеет экстремальное значение а, то кривая /(ж, у) = а
в точке R касается кривой С.
2. Примеры. Легко понять, что ранее полученные результаты
являются частным случаем этой общей теоремы. Если речь идет об эк-
экстремуме суммы p + q, то функция /(яг, у) есть p + q, а кривые f(x, у) =
= с — софокусные эллипсы с фокусами Р и Q. В согласии с общей тео-
теоремой эллипсы, проходящие через те точки кривой С, где достигается
экстремум одного или другого вида, касаются кривой С в этих точ-
точках. Если речь идет об экстремуме разности р — q, то функция f(x, у)
есть р — q, и тогда кривые /(яг, у) = с — софокусные гиперболы с фоку-
фокусами Р и Q: и в этом случае гиперболы, проходящие через точки, где
достигается экстремум, касаются кривой С.
Вот еще пример задачи того же типа. Дан отрезок прямой PQ и пря-
прямая I, его не пересекающая; требуется установить: из какой точки I
отрезок PQ виден под наибольшим углом?
Функция, максимум которой надлежит определить в этой задаче,
есть угол в, под которым из точки, движущейся по прямой I, виден

§ 2. Общий принцип, которому подчинены экстремальные задачи 391
Рис. 188. Софокусные эллипсы
Рис. 189. Софокусные гиперболы
Рис. 190. Из какой точки I отрезок PQ виден под наибольшим углом?
отрезок PQ; если R — какая угодно точка плоскости с координата-
координатами х, у, то угол, под которым отрезок PQ виден из R, есть функция
в — /(ж, у) от переменных х, у. Из элементарной геометрии известно,
что семейство кривых в = /(ж, у) = const состоит из окружностей, про-
проходящих через Р и Q, так как хорда круга видна под одним и тем же
углом из всех точек дуги окружности, расположенной по одну сторону
хорды. Из рис. 190 видно, что, вообще говоря, имеется две окружности
рассматриваемого семейства, касающиеся прямой /: их центры распо-
расположены по разные стороны отрезка PQ. Одна из точек касания дает
абсолютный максимум величины 0, тогда как другая — лишь «относи-
«относительный» максимум: это значит, что значения в в этой точке больше,
чем значения в некоторой окрестности рассматриваемой точки. Боль-
Больший из двух максимумов — абсолютный максимум, дается той точкой

392 Глава VII
касания, которая расположена в остром угле, образованном прямой /
и продолжением отрезка PQ, а меньший — той точкой касания, кото-
которая расположена в тупом угле, образованном этими прямыми. (Точка
пересечения прямой / с продолжением отрезка PQ дает минимальное
значение угла в — именно, в = 0.)
Обобщая рассмотренную задачу, мы можем заменить прямую /
какой-нибудь кривой С и искать точки R на кривой С, из которых
данный отрезок PQ, не пересекающий С, виден под наибольшим или
наименьшим углом. В этой задаче, как и в предыдущей, окружность,
проходящая через Р, Q и R, должна в точке R касаться кривой С.
§ 3. Стационарные точки и дифференциальное
исчисление
1. Экстремальные и стационарные точки. В предшествую-
предшествующих рассуждениях мы совсем не пользовались техническими приемами
дифференциального исчисления.
Трудно не признать, что наши элементарные методы являются бо-
более простыми и более прямыми, чем методы анализа. Вообще, занима-
занимаясь той или иной научной проблемой, лучше исходить из ее индиви-
индивидуальных особенностей, чем полагаться исключительно на общие ме-
методы, хотя, с другой стороны, общий принцип, уясняющий смысл при-
применяемых специальных процедур, конечно, всегда должен играть ру-
руководящую роль. Таково именно значение методов дифференциального
исчисления при рассмотрении экстремальных проблем. Наблюдаемое
в современной науке стремление к общности представляет только одну
сторону дела, так как то, что в математике является подлинно жизнен-
жизненным, без всякого сомнения обусловливается индивидуальными чертами
рассматриваемых проблем и применяемых методов.
В своем историческом развитии дифференциальное исчисление
в весьма значительной степени испытало воздействие индивидуальных
проблем, связанных с разысканием наибольших и наименьших значе-
значений величин. Связь между экстремальными проблемами и дифферен-
дифференциальным исчислением можно уяснить себе следующим образом. В гла-
главе VIII мы займемся обстоятельным изучением производной f'(x) от
функции f(x) и ее геометрического смысла. Там мы увидим, что, го-
говоря кратко, производная f'(x) есть наклон касательной к кривой у =
= /(ж) в точке (х, у). Геометрически очевидно, что в точках макси-
максимума или минимума гладкой кривой у = /(ж) касательная к кривой
непременно должна быть горизонтальной, т.е. наклон должен равнять-

§3. Стационарные точки и дифференциальное исчисление 393
У к
Рис. 191. Стационарные точки функции
ся нулю. Таким образом, мы получаем для точек экстремума усло-
условие /'(ж) = 0.
Чтобы отдать себе ясно отчет в том, что означает обращение в нуль
производной /'(ж), рассмотрим кривую, изображенную на рис. 191. Мы
видим здесь пять точек А, В, С, D, Е, в которых касательная к кри-
кривой горизонтальна; обозначим соответствующие значения /(ж) в этих
точках через о, Ь, с, d, е. Наибольшее значение /(ж) (в пределах облас-
области, изображенной на чертеже) достигается в точке D, наименьшее —
в точке А. В точке В имеется максимум — в том смысле, что во всех
точках некоторой окрестности точки В значение /(ж) меньше, чем Ь,
хотя в точках, близких к D, значение f(x) все же больше, чем Ь. По
этой причине принято говорить, что в точке В имеется относительный
максимум функции /(ж), тогда как в точке D — абсолютный макси-
максимум. Точно так же в точке С имеет место относительный минимум,
а в точке А — абсолютный минимум. Наконец, что касается точки Е,
то в ней нет ни максимума, ни минимума, хотя в ней все же осущест-
осуществляется равенство /'(ж) = 0. Отсюда следует, что обращение в нуль
производной /'(ж) есть необходимое, но никак не достаточное условие
для появления экстремума гладкой функции /(ж); другими словами,
во всякой точке, где имеется экстремум (абсолютный или относитель-
относительный), непременно имеет место равенство /'(ж) = 0, но не во всякой
точке, где f'(x) = 0, обязан быть экстремум. Те точки, в которых про-
производная /'(ж) обращается в нуль, — независимо от того, имеется ли
в них экстремум, — называются стационарными. Дальнейший анализ
приводит к более или менее сложным условиям, касающимся высших
производных функции /(ж) и полностью характеризующим максиму-
максимумы, минимумы и иные стационарные точки.

394
Глава VII
D
Рис. 192. Горный перевал
Рис. 193. Соответствующая
карта с линиями уровня
2. Максимумы и минимумы функций нескольких пере-
переменных. Седловые точки. Существуют экстремальные проблемы,
которые не могут быть выражены с помощью понятия функции /(ж)
от одной переменной. Простейшим относящимся сюда примером явля-
является проблема нахождения экстремумов функции z = /(ж, у) от двух
независимых переменных.
Мы всегда можем представлять себе функцию /(ж, у) как высоту z
поверхности над плоскостью ж, у, и эту картину будем интерпретиро-
интерпретировать, скажем, как горный ландшафт. Максимум функции /(ж, у) соот-
соответствует горной вершине, минимум — дну ямы или озера. В обоих
случаях, если только поверхность — гладкая, касательная плоскость
к поверхности обязательно горизонтальна. Но, помимо вершин гор и
самых низких точек в ямах, могут существовать и иные точки, в ко-
которых касательная плоскость горизонтальна: это — «седловые» точки,
соответствующие горным перевалам. Исследуем их более внимательно.
Предположим (рис. 192), что имеются две вершины А и В в горном
хребте и две точки С и D на различных склонах хребта; предположим,
что из С нам нужно пройти в D. Рассмотрим сначала те пути, ведущие
из С в D, которые получаются при пересечении поверхности плоскос-
плоскостями, проходящими через С и D. Каждый такой путь имеет самую вы-
высокую точку. При изменении положения секущей плоскости меняется и
путь, и можно будет найти такой путь, для которого наивысшая точка
будет в самом низком из возможных положений. Наивысшей точкой Е
на этом пути является точка горного перевала в нашем ландшафте; ее
можно назвать также седловой точкой. Ясно, что в точке Е нет ни мак-
максимума, ни минимума, так как сколь угодно близко к Е существуют
на поверхности такие точки, которые выше Е, и такие, которые ни-
ниже Е. Можно было бы в предыдущем рассуждении и не ограничиваться
рассмотрением только тех путей, которые возникают при пересечении
поверхности плоскостями, а рассматривать какие угодно пути, соеди-
соединяющие С и D. Характеристика, данная нами точке Е, от этого бы не
изменилась.

§3. Стационарные точки и дифференциальное исчисление 395
Точно так же, если бы мы пожелали от вершины А пройти к вер-
вершине В, то всякий путь, который мы могли бы выбрать, имел бы са-
самую низкую точку, рассматривая хотя бы только плоские сечения, мы
нашли бы такой путь АВ, для которого наименьшая точка была бы
расположена наиболее высоко, причем получилась бы опять прежняя
точка Е. Таким образом, эта седловая точка Е обладает свойством до-
доставлять самый высокий минимум или самый низкий максимум: здесь
имеет место «максиминимум» или «минимаксимум» — сокращенно ми-
нимакс. Касательная плоскость в точке Е горизонтальна; действитель-
действительно, так как Е — наинизшая точка пути АВ, то касательная к АВ в Е
горизонтальна, и аналогично, так как Е — наивысшая точка пути CD,
то и касательная к CD в Е горизонтальна. Поэтому касательная плос-
плоскость, обязательно проходящая через эти две касательные прямые, го-
горизонтальна. Итак, мы обнаруживаем три различных типа точек с го-
горизонтальными касательными плоскостями: точки максимума, точки
минимума и, наконец, седловые точки; соответственно существует и
три различных типа стационарных значений функции.
Другой способ представлять геометрически функцию f(x, у) за-
заключается в вычерчивании линий уровня — тех самых, которые
употребляются в картографии для обозначения высот на местности
(см. стр. 332). Линией уровня называется такая кривая в плоскости ху,
вдоль которой функция f(x, у) имеет одно и то же значение; другими
словами, линии уровня — то же, что и кривые семейства /(ж, у) = с.
Через обыкновенную точку плоскости проходит в точности одна линия
уровня; точки максимума и минимума бывают окружены замкнуты-
замкнутыми линиями уровня, в седловых точках пересекаются две (или более)
линии уровня. На рис. 193 проведены линии уровня, соответствующие
ландшафту, изображенному на рис. 192.
При этом особенно наглядным становится замечательное свойство
седловой точки Е: всякий путь, связывающий А и В и не проходя-
проходящий через Е, частично лежит в области, где f(x, у) < f{E), тогда как
путь АЕВ на рис. 192 имеет минимум как раз в точке Е. Таким же
образом мы убеждаемся, что значение /(ж, у) в точке Е представляет
собой наименьший максимум на путях, связывающих С и D.
3. Точки минимакса и топология. Существует глубокая
связь между общей теорией стационарных точек и топологическими
идеями. По этому поводу мы можем здесь дать только краткое указа-
указание и ограничимся рассмотрением одного примера.
Рассмотрим горный ландшафт на кольцеобразном острове В с дву-
двумя береговыми контурами С и С"; если обозначим, как раньше, высоту

396
Глава VII
Рис. 194. Стационарные точки в дву-
связной области
над уровнем моря через и =
= /(ж, у), причем допустим,
что /(яг, у) = 0 на контурах С
и С" и /(ж, 2/) > 0 внутри, то
на острове должен существовать
по меньшей мере один горный пе-
перевал: на рис. 194 такой перевал
находится в точке, где пересека-
пересекаются две линии уровня. Справед-
Справедливость высказанного утвержде-
утверждения становится наглядной, если
мы поставим своей задачей най-
найти такой путь, соединяющий С
и С, который не поднимался бы
на большую высоту, чем это неизбежно. Каждый путь от С к С" име-
имеет наивысшую точку, и если мы выберем такой путь, для которого
наивысшая точка оказывается самой низкой, то полученная таким об-
образом наивысшая точка и будет седловой точкой функции и = f(x, у).
(Следует оговорить представляющий исключение тривиальный случай,
когда некоторая горизонтальная плоскость касается кольцеобразного
горного хребта по замкнутой кривой.) В случае области, ограничен-
ограниченной р замкнутыми кривыми, вообще говоря, должно существовать не
менее чем р — 1 точек минимакса. Подобного же рода соотношения, как
установил Марстон Морз, имеют место и для многомерных областей,
но разнообразие топологических возможностей и типов стационарных
точек в этом случае значительно большее. Эти соотношения образуют
основу современной теории стационарных точек.
4. Расстояние точки от поверхности. Для расстояний точ-
точки Р от различных точек замкнутой кривой существуют (по меньшей
мере) два стационарных значения: минимальное и максимальное. При
переходе к трем измерениям не обнаруживается никаких новых фактов,
если мы ограничимся рассмотрением такой поверхности С, которая то-
топологически эквивалентна сфере (как, например, эллипсоид). Но если
поверхность рода 1 или более высокого, то дело обстоит иначе. Рассмот-
Рассмотрим поверхность тора С. Какова бы ни была точка Р, всегда, конечно,
существуют на торе С точки, дающие наибольшее и наименьшее рас-
расстояние от Р, причем соответствующие отрезки перпендикулярны к са-
самой поверхности. Но мы сейчас установим, что в этом случае сущест-
существуют и точки минимакса. Вообразим на торе один из «меридианных»
кругов L (рис. 195) и на этом круге L найдем точку Q, ближайшую к Р-

4. Треугольник Шварца
Р
397
Рис. 195-196. Расстояние от точки до поверхности
Затем, перемещая круг L по тору, найдем такое его положение, что-
чтобы расстояние PQ стало: а) минимальным — тогда получается точка
на С, ближайшая к Р; Ъ) максимальным — тогда получится стацио-
стационарная точка минимакса. Таким же образом мы могли бы найти на L
точку, наиболее удаленную от Р, и затем искать положение L, при
котором найденное наибольшее расстояние было бы: с) максимальным
(получится точка на С, наиболее удаленная от Р), d) минимальным.
Итак, мы получим четыре различных стационарных значения для рас-
расстояния точки тора С от точки Р.
Упражнение. Повторить то же рассуждение для иного типа L' замк-
замкнутой кривой на С, которая также не может быть стянута в точку (рис. 196).
§4. Треугольник Шварца
1. Доказательство, предложенное Шварцем. Герман Аман-
дус Шварц A843-1921), выдающийся математик, профессор Берлинс-
Берлинского университета, сделал многое для развития современной теории
функций и анализа. Он не считал ниже своего достоинства писать на
темы элементарного содержания, и одна из его работ посвящена сле-
следующей задаче: в данный остроугольный треугольник вписать другой
треугольник с минимальным периметром. (Говоря, что некоторый тре-
треугольник вписан в данный, мы подразумеваем, что на каждой из сторон
данного треугольника имеется вершина рассматриваемого треугольни-
треугольника.) Мы убедимся в дальнейшем, что существует только один искомый
треугольник: именно, его вершинами являются основания высот дан-
данного треугольника. Такой треугольник условимся называть высотным
треугольником.
Шварц доказал минимальное свойство высотного треугольника,
применяя метод отражения и основываясь на следующей теореме эле-
элементарной геометрии: в каждой из вершин Р, Q, R (рис. 197) две сторо-

398
Глава VII
Рис. 197. Высотный треугольник
в треугольнике ABC
ны высотного треугольника делают одинаковые углы со стороной данно-
данного треугольника, именно, каждый из этих углов равен углу при противо-
противоположной вершине данного треугольника. Например, углы ARQ и BRp
равны каждый углу С и т. д.
Докажем прежде всего эту теоре-
теорему. Так как углы ОРВ и ORB —
прямые, то около четырехугольни-
четырехугольника OPBR можно описать окружность.
Следовательно, ZPBO = ZPRO, так
как названные углы опираются на од-
одну и ту же дугу описанной окруж-
окружности. Но угол РВО дополнитель-
дополнительный к углу С, так как треуголь-
треугольник CBQ прямоугольный, а угол PRO
дополнительный к углу PRB. Поэ-
Поэтому ZPRB = АС. Таким же об-
образом, рассуждая по поводу четырехугольника QORA, заключаем,
что ZQRA = ZC и т.д.
Этот результат приводит к следствию, относящемуся к высотному
треугольнику: так как, например, ZAQR — ZCQP, то при отражении
относительно стороны АС данного треугольника сторона RQ направ-
направляется по стороне PQ, и обратно. Аналогично для других сторон.
Перейдем теперь к доказательству минимального свойства высот-
высотного треугольника. В треугольнике ABC рассмотрим, наряду с вы-
высотным треугольником, какой-нибудь другой вписанный треугольник,
скажем, UVW. Отразим всю фигуру сначала относительно стороны АС
треугольника ABC, затем вновь получившуюся фигуру отразим отно-
относительно стороны АВ, потом — относительно ВС, потом — относи-
относительно АС и, наконец, относительно АВ. Таким образом мы получим
всего шесть конгруэнтных треугольников, причем в каждом из них
будет заключен высотный треугольник и еще другой вписанный тре-
треугольник (рис. 198). Сторона ВС последнего треугольника параллельна
стороне ВС первого треугольника. В самом деле, при первом отраже-
отражении сторона ВС поворачивается по часовой стрелке на угол 1С, затем
опять по часовой стрелке на угол 2В; при третьем отражении — оста-
остается неизменной; при четвертом — поворачивается на угол 2С против
часовой стрелки и при пятом — на угол 2В опять против часовой стрел-
стрелки. Итого, общий угол поворота равен нулю.
Благодаря указанному выше свойству высотного треугольника
прямолинейный отрезок РР' равен удвоенному периметру треугольни-

§4. Треугольник Шварца 399
С
Рис. 198. Доказательство минимального свойства высотного треугольника,
данное Шварцем
ка PQR: действительно, РР' составляется из шести отрезков, по оче-
очереди равных первой, второй и третьей стороне PQR, причем каждая
из сторон входит дважды. Таким же образом ломаная линия, соединя-
соединяющая U и U', имеет длину, равную удвоенному периметру треуголь-
треугольника UVW. Эта ломаная не короче, чем прямолинейный отрезок С/С/'.
Что же касается прямолинейного отрезка С/С/', то он равен РР', так
как отрезок UU' параллелен РР'. Значит, ломаная линия С/С/' не коро-
короче, чем прямая РР', т.е. периметр высотного треугольника не больше,
чем периметр любого другого треугольника, вписанного в данный. Это
и нужно было доказать. Итак, установлено, что минимум существует
и что он реализуется в случае высотного треугольника. Что нет ино-
иного вписанного треугольника с тем же периметром — это, однако, не
доказано, и это мы докажем дальше.
2. Другое доказательство. Следующее решение задачи Швар-
Шварца является, вероятно, самым простым. Оно основывается на теореме,
ранее доказанной в этой главе: если точки Р и Q лежат по одну сторону
прямой L (но не на ней самой), то сумма расстояний PR + RQ, где R —
точка на L, обращается в минимум в том случае, если PR и QR делают
одинаковые углы с L. Пусть треугольник PQR, вписанный в данный
треугольник ABC, решает поставленную минимальную задачу. Тогда
точка R на стороне АВ должна быть такой, чтобы сумма PR + QR
была наименьшей, следовательно, углы ARQ и BRP должны быть рав-
равны; и точно так же ZAQR = ZCQP, ZBPR = ZCPQ. Таким образом,
Для искомого треугольника с минимальным периметром — если только
таковой существует — должно быть выполнено то же самое свойство

400
Глава VII
Q
А
R
В А
R
В
Рис. 199-200. Другое доказательство минимального свойства высотного тре-
треугольника
равенства углов, каким обладает высотный треугольник. Остается по-
показать, что при таком условии наш треугольник не может отличаться
от высотного. Кроме того, так как в теореме, на которую мы ссылались,
предполагается, что Р и Q не лежат на АВ, то доказательство не годит-
годится для случая, когда одна из точек Р, Q, R совпадает с какой-нибудь
вершиной данного треугольника (при этом периметр треугольника вы-
выродился бы в удвоенную соответствующую высоту); чтобы доказатель-
доказательство было исчерпывающим, нужно еще установить, что периметр вы-
высотного треугольника меньше любой из удвоенных высот данного тре-
треугольника.
Обращаясь сначала к первому пункту, заметим, что если вписан-
вписанный треугольник обладает указанным выше свойством равенства уг-
углов, то рассматриваемые углы при вершинах Р, Q и R соответственно
равны углам А, В и С. В самом деле, допустим, например, что ZARQ =
= ZBRP = ZC + д. Тогда, применяя теорему о сумме углов треуголь-
треугольника к треугольникам ARQ и BRP, мы видим, что углы при Q должны
равняться В — 6, а углы при Р должны равняться А — д. Но тогда сум-
сумма углов треугольника CPQ равна (А - 6) + (В - 6) + С — 180° - 28;
с другой стороны, она же равна 180°. Поэтому E = 0. Мы уже видели,
что высотный треугольник обладает отмеченным свойством. Всякий
иной вписанный треугольник, обладающий тем же свойством, имел бы
стороны, соответственно параллельные сторонам высотного треуголь-
треугольника; другими словами, он был бы ему подобен и подобно расположен.
Читатель докажет самостоятельно, что, кроме самого высотного тре-
треугольника, другого такого треугольника не существует (рис. 200).
Покажем, наконец, по-прежнему ограничиваясь случаем остро-
остроугольного треугольника, что периметр высотного треугольника мень-
меньше, чем любая удвоенная высота данного треугольника. Проведем пря-
прямые QP и QR и затем из вершины В (рис. 201) опустим перпендику-

j4. Треугольник Шварца
401
В
ляры на прямые QP, QR и PR; пусть L, М и N — основания этих
перпендикуляров. Так как отрезки QL и QM являются проекциями
высоты QB на прямые QP и QR,
то QL + QM < 2QB. Но QL +
+ QM = р, где через р обозна-
обозначен периметр высотного треуголь-
треугольника. Действительно, треугольни-
треугольники MRB и NRB равны, так
как ZMRB = ZNRB, а углы при
вершинах М и N — прямые. Зна-
Значит, RM = RN; и поэтому QM =
= QR + RN. Точно так же мы
убеждаемся, что PN = PL и, сле-
следовательно, QL = QP + PN. От-
Отсюда вытекает: QL + QM = QP +
+ PN + QR + RN = QP + PR +
+ RQ = р. Но раньше было показа- угольника
но, что 2QB > QL + QM. Итак, р
меньше, чем удвоенная высота QB. Это же рассуждение может быть
применено и к каждой из двух других высот. Таким образом, мини-
минимальное свойство высотного треугольника доказано полностью.
Между прочим, приведенное построение позволяет непосредственно вы-
вычислить р. Мы знаем, что углы PQC и RQA равны углу В, так что ZPQB =
= ZRQB = 90° — В и cos ZPQB = sin В. Отсюда следует, с помощью эле-
элементарных тригонометрических соображений, что QM = QL = QB sin В,
и Р — 2QBsinB. Таким же образом можно показать, что р = 2PAsmA =
= 2.RCsinC. Из тригонометрии известно, что RC — о sin В = 6 sin Л и т.д.,
откуда следует: р = 2о sin В sin С = 26 sin С sin Л = 2с sin Л sin В. И наконец,
вводя радиус описанного круга г и принимая во внимание, что а = 2r sin Л,
6= 2rsinB, с = 2rsinC, мы получим симметрическую формулу
р = 4r sin Л sin В sin С.
М<
Рис. 201. К доказательству мини-
минимального свойства высотного тре-
3. Тупоугольные треугольники. В обоих предшествующих
доказательствах предполагалось, что все три угла А, В, С — острые.
Если бы, скажем, угол С был тупой (рис. 202), то точки Р и Q лежали
бы вне треугольника. Поэтому, строго говоря, высотный треугольник
Уже нельзя было бы считать вписанным в данный, если только мы не
Условимся заранее называть вписанным такой треугольник, вершины
которого лежат на сторонах данного треугольника или на их продолже-
продолжениях. Как бы то ни было, высотный треугольник в расширенном смысле

402
Глава VII
--, Р
Рис. 202. Высотный треугольник в тупоугольном треугольнике
не обладает минимальным периметром, так как PR > CR, QR > CR,
и, значит, р = PR + QR + PQ > 2CR. Так как рассуждение в первой
части последнего доказательства показывает, что минимальный пери-
периметр — если только он не дается высотным треугольником — должен
быть равен одной из удвоенных высот, то отсюда легко заключить, что
в случае тупоугольного треугольника «вписанный треугольник» с наи-
наименьшим периметром есть не что иное, как высота, опущенная из вер-
вершины тупого угла, учитываемая в обоих направлениях; хотя треуголь-
треугольника в собственном смысле здесь и нет, однако можно все же указать
настоящие вписанные треугольники, периметры которых как угодно
мало отличаются от удвоенной высоты. В промежуточном случае, ког-
когда данный треугольник прямоугольный, оба решения (высотный тре-
треугольник и удвоенная высота, опущенная из прямого угла) совпадают.
Не лишен интереса вопрос о том, не обладают ли каким-нибудь эк-
экстремальным свойством высотные треугольники данных тупоугольных
треугольников. Не имея возможности подробно рассматривать этот во-
вопрос, отметим лишь, что такие высотные треугольники не обращают
в минимум сумму сторон р + q + г, но зато обеспечивают стационар-
стационарное значение типа минимакса для выражения вида р + q — г, где г —
та сторона вписанного (в расширенном смысле) треугольника, которая
соответствует тупому углу.
4. Треугольники, образованные световыми лучами. Если
допустим, что треугольник ABC изображает комнату с зеркальными
стенами, то высотный треугольник определяет единственный треуголь-
треугольный контур, который может быть образован световым лучом. Другие
замкнутые многоугольные контуры также не исключены, как показы-
показывает рис. 203, но высотный треугольник имеет три стороны.
Обобщим рассматриваемую проблему и спросим себя о возмож-
возможных «световых треугольниках» в произвольной области, ограниченной

§4. Треугольник Шварца
403
одной или несколькими гладкими кривыми; точнее говоря, нас инте-
интересуют треугольники, вершины которых лежат на заданных кривых,
а каждые две прилежащие стороны образуют равные углы с соответ-
соответствующей кривой. Мы видели в § 1, что равенство углов является не-
необходимым условием как для максимума, так и для минимума суммы
соответствующих сторон, так что, смотря по обстоятельствам, могут
возникать различные типы световых треугольников. Так, рассматри-
рассматривая внутренность единственной замкнутой гладкой кривой С, мы мо-
можем сказать, что вписанный треугольник максимального периметра
должен быть «световым треугольником», обладающим вышеописанны-
вышеописанными свойствами. Или предположим еще, что каждая из вершин треуголь-
треугольника ABC имеет право находиться на ей соответствующей одной из
трех замкнутых гладких кривых (идея Марстона Морза). Тогда свето-
световые треугольники характеризуются тем свойством, что их периметры
имеют стационарные значения. Но такого рода значение может быть
минимальным по отношению ко всем трем вершинам А, В, С; или мо-
может быть минимальным по отношению к двум каким-либо вершинам и
максимальным по отношению к третьей, или минимальным по отноше-
отношению к одной какой-нибудь из трех и максимальным относительно двух
других; или, наконец, максимальным относительно всех трех. Всего,
таким образом, существует по меньшей мере 23 = 8 типов световых
треугольников, так как по отношению к каждой из вершин, и притом
независимо, возможен максимум или минимум.
*5. Замечания, касающиеся
задач на отражение и эргодичес-
кое движение. В динамике и в оп-
оптике представляется задачей первосте-
первостепенной важности дать описание пути,
или «траектории», частицы или свето-
светового луча в пространстве на протяже-
протяжении неограниченного промежутка вре-
времени. Предполагая, что то или иное
приспособление физически принужда-
принуждает частицу или луч оставаться в неко-
некоторой ограниченной части пространст-
пространства, особенно интересно установить, за-
заполняет ли траектория в пределе эту
часть пространства повсюду с прибли-
приблизительно одинаковой «плотностью». Траектория, обладающая таким
свойством, называется эргодической. Допущение существования эрго-
Рис. 203. Замкнутый световой
путь в треугольном зеркале

404
Глава VII
дической траектории является исходной гипотезой для применения ста-
статистических методов в современных динамических и атомных теориях.
Но известно лишь очень немного ситуаций, при которых может быть
проведено строгое математическое доказательство «эргодическои гипо-
гипотезы».
Простейшие примеры отно-
относятся к случаю, когда движение
происходит на плоскости внут-
внутри замкнутой кривой С, причем
предполагается, что «стенка» С
представляет собой математичес-
математически совершенное зеркало, отража-
отражающее частицу (в остальном —
свободную) под тем же углом,
под каким она падает на стен-
стенку. Так, например, прямоуголь-
прямоугольный ящик — идеализированный
биллиардный стол с совершенным
Рис. 204-207. Четыре типа световых отражением, причем рассматри-
треугольников между тремя кругами ваемая частица играет роль бил-
лиардного шара,— обеспечивает,
вообще говоря, эргодическое движение: идеальный «биллиардный шар»
на протяжении бесконечного промежутка времени побывает в окрест-
окрестности любой наперед заданной точки, если только исключить некото-
некоторые особые начальные положения и направления движения. Мы не при-
приводим здесь доказательства, впрочем, не представляющего трудностей
принципиального порядка.
Особенно любопытно движение на эллиптическом столе с фокуса-
фокусами Fi и F2- Так как касательная к эллипсу делает одинаковые углы с от-
отрезками, проведенными из фокусов в точку касания, то каждая траек-
траектория, проходящая через один из фокусов, дает отражение, проходящее
через другой фокус, и т. д. Нетрудно усмотреть, что после п отражений,
независимо от начального положения, траектория при п, неограниченно
возрастающем, будет приближаться к большой оси FiF2- Если началь-
начальный луч не проходит через фокус, то возникают две возможности. Или
начальный луч проходит между фокусами: тогда все отраженные траек-
траектории будут проходить между фокусами, причем будут касательными
к некоторой гиперболе с теми же фокусами Fi и Fz- Или же начальный
луч не разделяет фокусов: тогда этим же свойством будут обладать все
отраженные лучи, причем все они будут касаться некоторого эллипса

§5. Проблема Штейнера 405
с теми же фокусами F\ и F2- Таким образом, движение внутри эллипса
ни при каких начальных условиях не оказывается эргодическим.
Упражнения.
1) Доказать, что если начальный луч проходит через какой-нибудь фо-
фокус эллипса, то его n-е отражение при неограниченном возрастании п
стремится к большой оси.
2) Доказать, что если начальный луч проходит между фокусами эллипса,
то этим же свойством обладают все отраженные лучи, и все они каса-
тельны к некоторой гиперболе с фокусами Fi и F2; точно так же, если
начальный луч не проходит между фокусами, то этим же свойством
обладают все отраженные лучи, и все они касательны к некоторому
эллипсу с фокусами F\ и F2.
(Указание: установите, что до отражения и после отражения в точке R
луч делает соответственно одинаковые углы с отрезками RFi и RF2,
потом докажите, что софокусные конические сечения характеризуются
отмеченным обстоятельством).
§ 5. Проблема Штейнера
1. Проблема и ее решение. Очень
простая и вместе с тем поучительная проб-
проблема была изучена в начале прошлого столе-
столетия знаменитым берлинским геометром Яко-
Якобом Штейнером. Требуется соединить три де- А°
ревни А, В, С системой дорог таким образом,
чтобы их общая протяженность была мини-
минимальной. В более точной математической фор-
формулировке: на плоскости даны три точки А, В,
С: требуется найти такую четвертую точку Р, Рис. 208. Проблема
чтобы сумма а + Ь + с (где а, Ь, с — расстоя- Штейнера: РА + РВ +
ния Р соответственно от А, В, С) обратилась + PC = минимум
в минимум. Решение проблемы таково: если в треугольнике ABC все
углы меньше 120°, то в качестве точки Р следует взять ту, из которой
все три стороны АВ, ВС, С А видны под углом в 120°; если же один
из углов треугольника ABC, например С, больше или равен 120°, то
точку Р нужно совместить с вершиной С.
Обосновать этот результат не представляет труда, если восполь-
воспользоваться решением уже рассмотренных экстремальных задач. Предпо-
Предположим, что Р есть искомая точка. Возможны две альтернативы: или
точка Р совпадает с одной из вершин А, В, С, или Р отлична от всех

406 Глава VII
трех вершин. В первом случае очевидно,
что Р должна быть вершиной именно само-
самого большого угла С в треугольнике ABC,
так как сумма С А + СВ меньше, чем
сумма каких-нибудь двух других сторон
треугольника ABC. Чтобы исчерпать во-
вопрос, остается проанализировать второй
возможный случай. Пусть К — окруж-
окружность с центром С и радиусом с. Тогда точ-
точка Р должна быть расположена на К таким
Рис. 209. К проблеме Штей- образом, что РА + РВ обращается в мини-
а мум. Если обе точки А и В вне К (как на
рис. 209), то на основании § 1, отрезки РА
и РВ должны образовывать одинаковые углы с окружностью К и, сле-
следовательно, с радиусом PC, который перпендикулярен к К. Так как
это рассуждение можно повторить относительно окружности с цент-
центром А и радиусом а, то отсюда следует, что все углы, образованные
отрезками РА, РВ, PC, равны между собой и, значит, каждый из них
равен 120°, как и было сказано выше. Наше доказательство было по-
построено на допущении, что обе точки А и В находятся вне круга К;
докажем, что иначе быть не может. Пусть хотя бы одна из точек А,
В, например А, находится внутри окружности К или на ней самой.
Тогда АС ^ с; так как, с другой стороны, при любом расположении
точек А, В, Р сумма а + Ь ^ АВ, то а + Ъ + с ^ АВ + АС. Это по-
последнее неравенство показывает, что наименьшее возможное значение
суммы а + Ь + с получилось бы, если Р совпадает с А, что противоре-
противоречит сделанному допущению, что Р отлично от А, В, С. Таким образом,
доказано, что точки А и В находятся вне круга К. Точно таким же об-
образом доказывается, что точки В, С находятся вне круга с центром А
и радиусом а, а точки А, С — вне круга с центром В и радиусом Ь.
2. Анализ возникающих альтернатив. Чтобы установить,
которая именно из двух возможностей имеет место, нам придется об-
обратиться к построению точки Р. Для нахождения точки Р, из кото-
которой две стороны треугольника, например, АС и ВС, видны под углом
в 120°, достаточно через точки А, С провести такую окружность К\,
у которой меньшая из дуг АС содержала бы 120°, и через точки В,
С провести окружность К2, обладающую таким же свойством; затем
взять точку пересечения двух дуг, содержащих по 120°, если только эти
дуги действительно пересекаются. Из точки Р, таким образом найден-

§5. Проблема Штейнера
407
Рис. 210-212. К анализу альтернатив в проблеме Штейнера
ной, сторона АВ непременно также будет видна под углом в 120°, так
как сумма трех углов с вершиной Р равна 360°.
Из рис. 210 видно, что если все три угла треугольника ABC мень-
меньше 120°, то две упомянутые дуги непременно пересекутся внутри тре-

408 Глава VII
угольника. С другой стороны, если один из углов треугольника ABC,
например С, больше, чем 120°, то дуги, о которых идет речь, не пере-
пересекутся (рис. 211). В этом случае не существует точки Р, из которой
каждая из трех сторон ABC была бы видна под углом в 120°: окруж-
окружности К\ и К2 пересекаются в точке Р', из которой стороны АС и ВС
видны под углом в 60°, и только одна сторона АВ, противолежащая
тупому углу, видна под углом в 120°.
Если один из углов треугольника больше 120°, то, как мы только
что видели, нет такой точки Р, из которой каждая из сторон видна под
углом в 120°; значит, искомая точка (в которой достигается минимум)
должна совпадать с одной из вершин (так как это, на основании § 1, —
единственная иная возможность), а именно, с вершиной тупого угла.
Если же у треугольника все углы меньше 120°, тогда, как мы ви-
видели, точку Р, из которой все стороны видны под углом в 120°, можно
построить. Но, чтобы доказательство было закончено, нужно еще дока-
доказать, что для такой точки Р сумма а + Ь + с меньше, чем для любой
из вершин треугольника (так как еще покамест неизвестно, которая
из двух альтернатив в рассматриваемом случае имеет место). Итак,
докажем, например, что а + Ь + с меньше, чем АВ + АС (рис. 212).
С этой целью продолжим отрезок ВР и спроектируем точку А на по-
полученную прямую; пусть найденная проекция есть D. Так как, очевид-
очевидно, ZAPD = 60°, то длина проекции PD равна |а. Так как BD есть
проекция АВ на прямую ВР, то значит BD < АВ. Но BD = Ь + |а;
поэтому Ъ+ ia < АВ. Совершенно таким же образом, проектируя А на
продолжение отрезка PC, мы убеждаемся, что с + ^а < АС. Склады-
Складывая два последних неравенства, получаем: а + Ь + с < АВ + АС. Итак,
искомая точка не может находиться в вершине А. Так как, аналогично,
она не может находиться также в вершинах В или С, то, следователь-
следовательно, найденная точка Р, из которой стороны видны под углом в 120°,
решает задачу.
3. Дополнительная проблема. Формальные математические
методы нередко ведут дальше поставленных заранее целей. Так, если
угол при вершине С больше 120°, то вместо точки Р (которая совпа-
совпадает на этот раз с точкой С) процедура геометрического построения
дает другую точку Р' — ту, из которой наибольшая сторона треуголь-
треугольника АВ видна под углом в 120°, а две другие стороны — под углом
в 60°. Конечно, точка Р' не дает решения рассматриваемой проблемы,

J5. Проблема Штейнера
¦ Р'
409
Рис. 213. Дополнительная проблема
но можно догадываться, что она имеет какое-то к ней отношение. Ока-
Оказывается, в самом деле, что точка Р' решает следующую проблему:
минимизировать выражение а + b — с. Доказательство, вполне анало-
аналогичное изложенному выше для случая выражения а + Ь + с и основан-
основанное на прямых результатах (§ 1, пункт 5), предоставляется в качестве
упражнения читателю. Соединяя вместе полученные выводы, мы при-
приходим к общей теореме.
Если все углы треугольника ABC меньше 120°, то сумма а + Ь + с
расстояний а, Ь, с некоторой точки от точек А, В, С (соответственно)
обращается в минимум в точке Р, из которой каждая из сторон видна
под углом в 120°, а выражение а + Ь — с обращается в минимум в вер-
вершине С; если же один из углов, скажем С, больше 120°, то а + Ь + с
минимизируется в точке С, а а + Ь — с — в точке Р', из которой две
меньшие стороны треугольника видны под углом в 60°, а большая —
под углом в 120°.
Таким образом, из двух ми-
минимальных проблем всегда одна
решается построением окружнос-
окружностей, решение другой дается од-
одной из вершин. В случае, ког-
когда ZC = 120°, оба решения обеих
проблем совпадают, так как точ-
точка, получаемая при геометричес-
геометрическом построении, оказывается вер-
вершиной С.
4. Замечания и упраж-
упражнения. Из произвольной точ-
точки Р, взятой внутри равносторон-
равностороннего треугольника UVW, опус-
опустим перпендикуляры РА, РВ,
PC на три стороны (рис. 214).
U
V
Рис. 214. Другое доказательство пра-
правильности решения Штейнера

410
Глава VII
Тогда точки А, В, С и Р образуют как раз такую фигуру, как мы
рассматривали выше. Это замечание может быть использовано при ре-
решении проблемы Штейнера: достаточно, исходя из точек А, В, С, найти
вершины равностороннего треугольника U, V, W.
Упражнения.
1) Выполнить указанное построение, основываясь на том обстоятельстве,
что сумма трех перпендикуляров, опущенных на стороны из произволь-
произвольной точки Р внутри равностороннего треугольника, постоянна, именно,
равна высоте треугольника.
2) Основываясь на аналогичном обстоятельстве в случае, когда Р нахо-
находится вне UVW, исследовать дополнительную проблему.
В трехмерном пространстве можно рассмотреть проблему, подобную
штейнеровской: по заданным четырем точкам А, В, С, D найти такую
пятую точку Р, чтобы сумма о + 6 + с + d обращалась в минимум.
* Упражнение. Исследовать эту трехмерную проблему и дополнитель-
дополнительную к ней методами § 1 или же пользуясь правильным тетраэдром.
5. Обобщение: проблема уличной
сети. В проблеме Штейнера были зада-
заданы три точки А, В, С. Было бы естест-
естественно обобщить эту проблему на случай
п заданных точек А\, А^, ... , Ап следую-
следующим образом: требуется найти в плоскос-
плоскости такую точку Р, чтобы сумма расстоя-
расстояний а,\ + а.2 + • • • + ап (где ai обозначает
расстояние PAi) обращалась в минимум.
(В случае четырех точек, расположенных
так, как показано на рис. 215, в качестве Р нужно взять точку пере-
пересечения диагоналей четырехугольника А1А2А3А4; пусть читатель про-
проверит это в качестве упражнения.) Эта обобщенная проблема, также
изученная Штейнером, не ведет к интересным результатам. В данном
случае мы имеем дело с поверхностным обобщением, подобных кото-
которому немало встречается в математической литературе. Чтобы полу-
получить действительно достойное внимания обобщение проблемы Штей-
Штейнера, приходится отказаться от поисков одной единственной точки Р-
Вместо того поставим задачей построить «уличную сеть» или «сеть до-
дорог между данными деревнями», обладающую минимальной общей дли-
длиной. Точнее, даны п точек А\,А%, ... , Ап; требуется найти такую связ-
связную систему прямолинейных отрезков, чтобы: 1) любые две из данных
Рис. 215. Минимум суммы
расстояний до четырех то-
точек

j5. Проблема Штейнера
411
точек могли быть связаны ломаной линией, стороны которой входили
бы в состав системы, 2) общая длина всей системы была наименьшей1.
Рис. 216-218. Кратчайшая система путей, соединяющих данные точки
Решение этой задачи имеет тот или иной вид в зависимости от
расположения данных точек. Читатель с пользой сможет заняться бо-
более внимательным рассмотрением этого вопроса, исходя из проблемы
Штейнера. Мы ограничимся здесь указанием результатов в типических
примерах, изображенных на рис. 216-218. В первом примере решение
дается системой из пяти отрезков с двумя «кратными точками», в ко-
которых сходятся по три сегмента, образуя между собой углы в 120°.
Во втором примере число кратных точек равно трем. При некоторых
иных расположениях данных точек указанные фигуры не получаются:
возможны случаи «вырождения», когда какая-нибудь одна из данных
точек (или несколько таких точек) становится сама «кратной точкой»
сети — таков третий из приведенных примеров.
Если число данных точек равно п, то
всего будет не более п — 2 кратных точек,
в которых сходятся по три отрезка, обра-
образуя углы в 120°.
Решение проблемы — не всегда един-
единственное. Так, если четыре данные точ-
точки расположены в вершинах квадрата,
то возникает два эквивалентных реше-
решения (рис. 219, 220). Если точки Ах,
Аг, ... , Ап являются вершинами лома-
ломаной линии с углами при вершинах, достаточно близкими к 180°, то
сама ломаная является решением.
Рис. 219-220. Кратчайшие
системы путей, соединяющие
вершины квадрата
1 Выработка общих методов для решения прикладных задач типа описанной со-
составила в последние годы предмет так называемого линейного программирования;
см., например, [45].

412 Глава VII
§ 6. Экстремумы и неравенства
Одной из характерных черт высших разделов математики является
та выдающаяся роль, которую в них играют неравенства. В сущности,
любая максимальная проблема всегда приводит к неравенству, выра-
выражающему тот факт, что рассматриваемая переменная величина не пре-
превышает некоторого максимального значения, доставляемого решением
этой проблемы. Во многих случаях получаемые таким образом неравен-
неравенства заслуживают внимания и независимо от экстремальной проблемы,
к ним приводящей. В качестве примера мы рассмотрим сейчас важное
неравенство, связывающее арифметическое и геометрическое средние.
1. Средние арифметическое и геометрическое двух поло-
положительных величин. Займемся прежде всего очень простой мак-
максимальной проблемой, с которой часто приходится встречаться и в са-
самой математике и в ее приложениях. В геометрической формулировке
проблема эта заключается в следующем: среди всех прямоугольников
с наперед заданным периметром найти тот, который имеет наиболь-
наибольшую площадь. Решением, как нетрудно догадаться, является квадрат.
Доказать это можно следующим рассуждением. Пусть заданный пери-
периметр равен 2а. Тогда сумма х + у длин двух прилежащих сторон пря-
прямоугольника х и у равна постоянной величине а, а в максимум следует
обратить произведение ху. «Среднее арифметическое» величин х и у
есть не что иное, как выражение
Введем еще величину
причем получатся соотношения
х = т + d, у = т — d;
из них вытекает, что
ху = (т + d)(m - d) = m2 - d2 = {^~LJ - d2.
Так как d2 не может быть отрицательно, а обращается в нуль только
при х = у, то мы немедленно приходим к неравенству
^, A)
причем знак равенства здесь возможен только при d = 0, т. е. при х — У-

F. Экстремумы и неравенства
413
Так как х + у имеет постоянное значение а, то отсюда следует, что
выражение ,/ху, а значит, и интересующая нас площадь ху принимают
наибольшее возможное значение при х = у. Выражение
g= у/ху,
где радикал взят в арифметическом смысле со знаком +, называется
«средним геометрическим» положительных величин х и у; неравенст-
неравенство A) выражает основное соотношение между средними арифметичес-
арифметическим и геометрическим.
Неравенство A) вытекает также не-
непосредственно из того факта, что выраже- У>~
ние
(у/х - у/уJ = х + у - 2у/ху,
будучи точным квадратом, не может быть
отрицательным и обращается в нуль толь-
только при х = у.
Вот еще геометрический вывод того
же неравенства. Рассмотрим в плоскос-
плоскости х, у неподвижную прямую линию х +
+у = 1т и вместе с ней семейство кривых
(гипербол) ху — с, причем с постоянно для
каждой кривой, но меняется при переходе
от одной кривой к другой. Из рис. 221 яс-
х+у=2т
Рис. 221. Минимум ху при
заданном значении х + у
но, что кривой, имеющей хоть одну общую точку с нашей прямой лини-
линией и соответствующей наибольшему значению с, являтся та гипербола,
которая касается прямой в точке х = у = т; для этой гиперболы, сле-
следовательно, с = т2. Итак,
, 2
Следует заметить, что всякое неравенство вида f(x, у) < g(x, у)
можно прочесть двумя способами, и потому оно порождает как мак-
максимальное, так и минимальное свойства. Например, неравенство A)
выражает также тот факт, что среди всех прямоугольников с данной
площадью именно квадрат имеет наименьший периметр.
2. Обобщение на случай п переменных. Неравенство A),
связывающее средние арифметическое и геометрическое двух положи-
положительных величин, может быть обобщено на любое число п положитель-
положительных величин, которые мы будем обозначать х\, жг, х3, ¦ ¦ ¦ , хп. Средним

414 Глава VII
арифметическим этих величин называют выражение
_
т -
п
а средним геометрическим — выражение
причем имеется в виду всегда положительное значение радикала. Об-
Общая теорема утверждает, что
g^m B)
и что равенство g — т возможно только в том случае, если все вели-
величины Xi равны между собой.
Было предложено много различных остроумных доказательств это-
этого общего результата. Простейший метод заключается в применении
того же простого рассуждения, которое мы провели в пункте 1. Пе-
Перед нами стоит проблема: разбить данное положительное число С
на п положительных слагаемых, С = х\ + х-i + ... + хп, таким
образом, чтобы произведение Р = Х\Х2-- -хп было возможно боль-
большим. Мы будем исходить из допущения, на первый взгляд очевидно-
очевидного, но мы позднее будем иметь случай его проанализировать (§ 7),
что наибольшее значение Р существует и достигается, скажем, при
значениях Х\ = а\, хч = аг,... ,хп = ап. Нам достаточно установить,
что ai = п2 = . ¦ ¦ = ап, ибо в этом случае g = т. Допустим, что это не
так: пусть, например, ах ф а^- Тогда рассмотрим значения
Х\ = з, х2 = s, х3 = а3, ¦ ¦ • , хп = а„,
где
_ ai + а2
S
S~ 2 •
Мы заменим, другими словами, прежнюю систему значений величин Х{
новой системой, которая отличается от прежней лишь тем, что зна-
значения двух первых величин Х\ и х2 сделаны равными между собой,
причем общая сумма С остается неизменной. Мы можем написать
а,\ — s + d, п2 = s — d,
где положено
, _ Qi - п2
О/ — 7Z .

§6. Экстремумы и неравенства 415
Новое произведение равно
Р' = s2 ¦ а3 ... о„,
тогда как прежнее произведение было
Р = (s + d)(s - d) ¦ <z3 .. • а„ = (s2 - d2) ¦ а3 ... а„.
Отсюда ясно, что при d ф О
Р<Р',
а это противоречит сделанному допущению, что произведение Р имеет
максимальное значение. Итак, d = 0, и тогда ai = аг- Таким же образом
доказывается, что а\ = а;, где а, обозначает любое из чисел а; отсюда
следует, что все числа а равны между собой. Мы убедились в том,
что 1) g = m, если все числа Х{ равны между собой, 2) наибольшее
значение g получается только тогда, когда все числа ж,- равны между
собой. Отсюда можно заключить, что во всех прочих случаях g < т.
Теорема доказана.
3. Метод наименьших квадратов. Среднее арифметичес-
арифметическое п чисел xi, X2, ¦ ¦ ¦ , х„ (которые здесь нет необходимости считать
обязательно положительными) обладает замечательным минимальным
свойством. Пусть и — числовое значение некоторой неизвестной вели-
величины, которое мы хотим определить насколько возможно точнее с по-
помощью какого-то измерительного инструмента. Пусть произведено для
этой цели п измерений, которые дали результаты х\, Жг, ••¦ , хп, слег-
слегка различающиеся между собой, что обусловливается неизбежными и
зависящими от разных причин измерительными ошибками. Возникает
вопрос: какое же значение следует приписать величине и в качестве за-
заслуживающего наибольшего доверия? Принято в качестве «истинного»
или «оптимального» значения выбирать среднее арифметическое
Дать подлинное обоснование указанной процедуре было бы невоз-
невозможно, не углубляясь в пространные рассуждения, относящиеся к об-
области теории вероятностей. Все же мы можем здесь отметить не-
некоторое минимальное свойство средней арифметической т, которое
До некоторой степени оправдывает ее выбор. Пусть и — какое угод-
угодно числовое значение измеряемой величины. Тогда разности и — xi,

416 Глава VII
и — Х2, ¦ ¦ ¦ , и — хп представляют собой отклонения этой величины от
результатов отдельных наблюдений. Эти отклонения могут быть час-
частью положительными, частью отрицательными, и совершенно естест-
естественно стремиться к такому оптимальному выбору и, при котором «то-
«тотальное» (в каком-то смысле) отклонение было бы возможно меньше.
Следуя Гауссу, берут обыкновенно в качестве «измерителей неточнос-
неточности» не сами отклонения, а их квадраты (и - х,J и затем выбирают
оптимальное значение и с таким расчетом, чтобы минимализировать
«тотальное» отклонение, под каковым понимают сумму квадратов от-
отдельных отклонений
(и - xif + {и- х2J + ... + {и- хпJ.
Определенное таким образом оптимальное значение и есть не что
иное, как среднее арифметическое то: в этом заключается исходное по-
положение знаменитого, созданного Гауссом, «метода наименьших квад-
квадратов». Мы постараемся возможно проще доказать подчеркнутое выше
утверждение. Если мы напишем
(и - ж,-) = (то - Xi) + (и - то),
то получим
(и - XiJ = (то - Х{J + {и - тоJ 4- 2(то - ж,-)(и - то).
Сложим, далее, все такие равенства, полагая г = 1, 2, ... , п. Последний
член при этом дает
2(и — m)(nm — Xi — ... — хп),
а это выражение по определению то равно нулю. Следовательно, мы
получаем
(и - ххJ + (и- х2J + ... + («- хпJ =
= (то - XiJ + (тп — ХъJ + ... 4- (то - хпJ + п(и - тпJ.
Отсюда уже ясно, что
(U - XiJ +(U- Х2J + . . . + (U - ХпJ ^
;> (т - хгJ + (т - х2J + ... + (т - ж„J,
причем знак равенства возможен только при и = пг. Как раз это самое
мы и собирались доказать.

§7. Существование экстремума. Принцип Дирихле 417
Общий метод наименьших квадратов принимает руководящий
принцип — минимализировать сумму квадратов — во всех более слож-
сложных случаях, когда нужно как-то согласовать между собой ряд слегка
противоречащих друг другу данных наблюдения. Так, представим се-
себе, что измерены координаты Xi, yi для п точек, которые, теоретически
говоря, должны лежать на прямой линии, и предположим, что получен-
полученные таким эмпирическим путем точки оказываются расположенными
по прямой не вполне точно. Как выбрать прямую, которая наилучшим
образом была бы «приложена» или «подогнана» к этим точкам? Руково-
Руководящий принцип приводит к следующему приему (который — необходи-
необходимо признать — мог бы быть заменен и другими процедурами, основан-
основанными на иных рассуждениях). Пусть у = ах + b есть уравнение искомой
прямой, так что наша проблема заключается в определении коэффици-
коэффициентов а и Ь. Измеренное по направлению оси у расстояние прямой от
точки Xi, yi равно yi — (aXi + b), т.е. yi — axi — b, причем имеет по-
положительный или отрицательный знак, смотря по тому, расположена
ли точка выше или ниже прямой. Тогда квадрат этого расстояния ра-
равен (yi — axi — bJ, и согласно основному принципу метода наименьших
квадратов нам достаточно подобрать а и b таким образом, чтобы вы-
выражение
(yi - ахг - ЬJ + (г/2 - ах2 - ЬJ + ... + (уп - ах„ - ЪJ
достигало наименьшего возможного значения. Мы приходим, таким об-
образом, к минимальной проблеме с двумя переменными величинами а
и Ъ. Хотя решение этой проблемы с исследованием всех подробностей
и не представляет особенной трудности, мы все же воздержимся здесь
от его рассмотрения.
§ 7. Существование экстремума. Принцип Дирихле
1. Общие замечания. В некоторых из рассмотренных нами эк-
экстремальных проблем прямо доказывалось, что решение дает наилуч-
наилучший результат из числа прочих возможных. Ярким примером является
принадлежащее Шварцу решение задачи о треугольнике: здесь сразу
видно, что никакой вписанный треугольник не может иметь меньший
периметр, чем высотный треугольник. Некоторые примеры такого же
типа связаны с явно написанными неравенствами, каково, например,
неравенство между средними арифметическим и геометрическим. Но
при решении других проблем мы шли по иному пути. Мы допускали

418 Глава VII
прежде всего, что решение уже найдено, и затем, анализируя это до-
допущение, получали заключения, иногда позволяющие дать полную ха-
характеристику решения и выполнить соответствующее его построение.
Так именно обстояло дело с проблемой Штейнера и таков же был план
второго решения проблемы Шварца. Названные два метода логически
различны. Первый метод, пожалуй, можно считать более совершенным,
так как он дает конструктивное доказательство правильности резуль-
результата. Второй метод, если судить по примеру проблемы Шварца (второе
решение), кажется более простым. Но он является не прямым, а кос-
косвенным и, самое главное, он условен по самой своей структуре, так
как предполагает существование решения. Он приводит к окончатель-
окончательному результату лишь постольку, поскольку существование решения
или постулировано, или доказано. Без этой предпосылки он показывает
всего-навсего, что если решение существует, то оно обладает такими-то
свойствами1.
Вследствие кажущейся очевидности предпосылки о существовании
решения математики вплоть до конца прошлого столетия не обращали
особенного внимания на указанное логическое обстоятельство и допус-
допускали существование решения экстремальных проблем как нечто само
собой разумеющееся. Некоторые из величайших ученых XIX в. — Га-
Гаусс, Дирихле, Риман — основывали некритически на такого рода допу-
допущении глубокие и иначе трудно доказуемые предложения в области ма-
математической физики и теории функций. Кризис наступил вскоре после
того, как Риман в 1849 г. опубликовал свою докторскую диссертацию,
посвященную основаниям теории функций комплексного переменного.
Эта сжато написанная работа, представляющая собой один из величай-
величайших подвигов математической мысли в новейшую эпоху, была до такой
степени неортодоксальной в трактовке вопроса, что многие предпочли
попросту ее игнорировать. Вейерштрасс в то время был уже знамени-
знаменитым профессором Берлинского университета и пользовался репутацией
основателя строго построенной теории функций. Вначале пораженный,
но все же исполненный сомнений, он вскоре обнаружил в работе Рима-
на логическую брешь, о восполнении которой сам автор не позаботился.
Уничтожающая критика Вейерштрасса не поколебала уверенности Ри-
мана в справедливости полученных им результатов, но долгое время
его теория не пользовалась признанием. Головокружительная научная
Логическая необходимость доказывать существование экстремума иллюстри-
иллюстрируется следующим парадоксом: 1 есть наибольшее целое число. Вот доказательство.
Пусть х есть наибольшее целое число. Если допустим, что х > 1, то отсюда следу-
следует х2 > х, что противоречит сделанному допущению. Итак, х должен быть равен 1.

§7. Существование экстремума. Принцип Дирихле 419
карьера Римана вскоре внезапно оборвалась: он умер от туберкулеза.
Все же его идеи поддерживались и дальше несколькими убежденными
и преданными учениками. Только через пятьдесят лет после появле-
появления диссертации Римана Гильберту удалось, наконец, открыть пути,
приводящие к исчерпывающему ответу на все вопросы, оставленные
в стороне и неразрешенные Риманом. Начатое Риманом и развернув-
развернувшееся во второй половине столетия развитие математических теорий,
глубоко проникающих в область физики, представляет одну из самых
блестящих страниц в истории современной науки.
Уязвимое место в работе Римана — как раз вопрос о существова-
существовании минимума. Свою теорию Риман основывает на принципе Дирихле
(так он сам его назвал по имени своего учителя: Дирихле, читая лек-
лекции в Гёттингене, пользовался этим принципом, но ни в одной из своих
работ о нем не писал). Предположим, для большей определенности, что
некоторая часть плоскости или какой-нибудь поверхности покрыта сло-
слоем станиоля и что стационарный электрический ток проходит по слою,
соединенному в двух точках с полюсами батареи. Нет сомнений, что
такой эксперимент приведет к некоторому однозначно определенному
распределению токов. Но как обстоит дело с соответствующей мате-
математической проблемой — проблемой, имеющей первостепенное значе-
значение в теории функций и в других областях? В теории электричества
рассматриваемое нами физическое явление описывается как «диффе-
«дифференциальное уравнение в частных производных с граничными услови-
условиями». Именно эта математическая проблема нас и интересует; возмож-
возможность ее решения кажется правдоподобной именно по той причине, что
мы допустили ее эквивалентность физическому явлению; но матема-
математическое доказательство этой возможности никоим образом не может
базироваться на сделанном допущении. В подходе Римана к решению
рассматриваемого им математического вопроса можно различить два
этапа. Во-первых, он показывает, что проблема эквивалентна некото-
некоторой минимальной проблеме: некоторая величина, выражающая энер-
энергию потока электричества, минимизируется некоторыми реально осу-
осуществляющимся потоком (по сравнению с иными потоками, совместны-
совместными с предписанными граничными условиями). Во-вторых, в качестве
«принципа Дирихле» он вводит постулат о том, что такого рода ми-
минимальная проблема допускает решение. Риман решительно ничего не
предпринял для того, чтобы найти хоть какое-нибудь математическое
оправдание для этого постулата, и именно в этом пункте его настигли
атаки со стороны Вейерштрасса. Не только существование минимума
само по себе не было очевидным, но, как выяснилось впоследствии, во-
27*

420 Глава VII
прос оказался чрезвычайно тонким: математика того времени еще не
была подготовлена к его решению, и только через несколько десятиле-
десятилетий напряженные усилия исследовательской мысли привели к закон-
законченным результатам.
2. Примеры. Мы проиллюстрируем возникающую трудность
двумя примерами.
1) Отметим на прямой L две точки А и В, находящиеся на рассто-
расстоянии d, и поставим задачу — отыскать ломаную линию кратчайшей
длины, которая, выходя из точки А по направлению, перпендикуляр-
перпендикулярному к L, заканчивалась бы в точке В. Так как прямолинейный отре-
отрезок АВ безусловно короче всех других путей, связывающих точки А
и В, то можно быть уверенным, что любой допустимый (удовлетворя-
(удовлетворяющий требованиям задачи) путь имеет длину, большую, чем d: в самом
деле, единственный путь, длина которого равна d, есть прямолинейный
отрезок АВ, а он не удовлетворяет требованию относительно направ-
направления в точке А, т.е. не является допустимым. Рассмотрим, с другой
стороны, допустимый путь АОВ на рис. 222. Заменяя точку О точ-
точкой О', расположенной ближе к А, мы можем получить новый допус-
допустимый путь, длина которого как угодно мало отличается от d; значит,
если существует кратчайший допустимый путь, то длина его не может
быть больше, чем d и, следовательно, должна быть в точности равна d.
Но мы видели, что единственный путь, имеющий такую длину, не явля-
является допустимым. Итак, кратчайшего допустимого пути не существует,
и задача наша не имеет решения.
А В L
Рис. 222-223. К вопросу о существовании минимума
2) Пусть С — некоторый круг, a S — точка, лежащая выше его
центра на расстоянии 1 (рис. 223). Рассмотрим множество поверхнос-
поверхностей, ограниченных окружностью С и проходящих через точку S, при-

§ 7. Существование экстремума. Принцип Дирихле 421
том лежащих «над» кругом С (в том смысле, что никакие две различные
точки этой поверхности не могут вертикально проектироваться в од-
одну и ту же точку круга С). Какая поверхность из рассматриваемого
множества обладает наименьшей площадью? Каким бы естественным
ни казался этот вопрос, положительного ответа на него дать нельзя:
допустимой поверхности с наименьшей площадью не существует. Если
бы поверхность не была подчинена условию проходить через точку S,
тогда решением задачи был бы, очевидно, плоский диск, ограничен-
ограниченный окружностью С. Обозначим площадь этого диска через А. Всякая
другая поверхность, ограниченная окружностью С, непременно имеет
площадь большую, чем А. Но можно указать допустимую поверхность,
площадь которой будет отличаться от А как угодно мало. В самом деле,
возьмем коническую поверхность высоты, равной 1 — такую «тонень-
«тоненькую», чтобы ее площадь была меньше заранее назначенного маленького
числа. Поместим эту поверхность посреди диска так, чтобы ее вершина
попала в точку S, и затем рассмотрим поверхность, образованную из
нашей конической поверхности и той части диска, которая окажется
вне основания конуса. Совершенно ясно, что построенная таким обра-
образом поверхность, только вблизи центра диска отличающаяся от самого
диска, обладает площадью, превосходящей А меньше, чем на заранее
назначенное число. Так как это последнее число может быть выбрано
сколь угодно малым, то отсюда следует, что минимум площади (если
он существует) не может отличаться от площади диска А. Но среди
поверхностей, ограниченных контуром С, только сам диск обладает
площадью А; однако диск не проходит через точку S и, значит, не яв-
является допустимой поверхностью; следовательно, решения задачи не
существует.
Мы можем избавить себя от труда приводить дальнейшие отно-
относящиеся сюда софистически утонченные примеры, указанные Вейер-
штрассом. Уже приведенные примеры достаточно убедительно показы-
показывают, что существование минимума не является тривиальным момен-
моментом в математическом доказательстве. Попробуем взглянуть на рас-
рассматриваемый вопрос с более отвлеченной точки зрения. Представим
себе некоторый определенный класс объектов, например, кривых или
поверхностей; пусть каждому объекту этого класса поставлено в соот-
соответствие — как функция этого объекта — некоторое число, например,
Длина или площадь. Если в классе содержится лишь конечное число
объектов, то среди соответствующих чисел неизбежно имеется наи-
наибольшее и наименьшее. Но если в классе содержится бесконечное мно-
множество объектов, то даже в том случае, если все соответствующие чис-

422 Глава VII
ла заключены между двумя конечными границами, среди них вовсе
не обязательно найдется наибольшее и наименьшее. На числовой оси
множество чисел изображается в виде множества точек. Предположим,
ограничившись простейшим случаем, что все числа множества поло-
положительные. Такое множество непременно имеет «нижнюю границу» —
такое число а, меньше которого в нашем множестве нет ни одного числа
и которое или само есть элемент множества, или как угодно мало от-
отличается от некоторого элемента множества. Если а само принадлежит
множеству, то оно является его наименьшим элементом; в противном
случае множество не содержит вовсе наименьшего элемента. Напри-
Например, множество чисел 1, ~, ^ ... не содержит наименьшего элемента,
так как нижняя граница 0 не принадлежит множеству. Такого рода от-
отвлеченные примеры иллюстрируют логические трудности, связанные
с проблемой существования. Математическое решение минимальной
проблемы нельзя назвать исчерпывающим, если в явной или в неявной
форме не устанавливается, что среди элементов числового множества,
рассматриваемого в связи с проблемой, существует наименьший.
3. Экстремальные проблемы элементарного содержания.
В задачах элементарного содержания бывает достаточно внимательно
проанализировать условия, чтобы уяснить, как обстоит дело с сущест-
существованием решения. В главе VI, § 5, было исследовано общее понятие
компактного множества и было установлено, что непрерывная функ-
функция, заданная на некотором множестве элементов, для каких-то эле-
элементов множества непременно достигает своих экстремальных значе-
значений, если данное множество обладает свойством компактности. В лю-
любой из вышеприведенных элементарных проблем сравниваемые между
собой числовые элементы могли быть рассматриваемы как значения
функции одной или нескольких переменных в области, которая или бы-
была компактным множеством, или — без существенного видоизменения
проблемы — могла быть сделана таковым. В таких случаях сущест-
существование максимума или минимума не подлежало сомнению. Остано-
Остановимся, в качестве примера, на проблеме Штейнера. Рассматриваемая
в ней величина есть сумма трех расстояний, и эта последняя зависит
от положения точки непрерывно. Хотя область, в которой может дви-
двигаться точка, есть вся плоскость, мы можем без ограничения общности
провести окружность большого радиуса (включающую весь рисунок)
и подчинить точку условию находиться внутри этой окружности или
на ней самой. В самом деле, если движущаяся точка будет находиться
достаточно далеко от вершин треугольника, сумма трех расстояний от

§ 7. Существование экстремума. Принцип Дирихле
423
Рис. 224. Кривые, между которы-
которыми нет ни наименьшего, ни наи-
наибольшего расстояния
сторон, наверное, превысит АВ + АС, а последняя величина принад-
принадлежит к числу подлежащих сравнению значений нашей функции. Та-
Таким образом, если существует минимум для «ограниченной» проблемы
(когда точка подчинена дополнительному ограничению), то существует
минимум и для неограниченной проблемы. С другой стороны, нетрудно
удостовериться, что множество, состоящее из точек внутри круга или
на его границе, компактно. Итак, существование минимума в случае
проблемы Штейнера доказано.
Насколько существенно свойст-
свойство компактности области, в которой
изменяется независимое переменное,
обнаруживает следующий пример.
Если заданы две замкнутые кри-
кривые С\ и Сг, то всегда можно найти
на С\ и Съ соответственно две такие
точки Р\ и Pi, что расстояние меж-
между ними минимально, и можно найти
две такие точки Qi и Q2, что расстояние между ними максимально.
Действительно, расстояние между точкой А\ на С\ и точкой А? на С?
есть непрерывная функция, заданная на компактном множестве, эле-
элементы которого — пары точек А\, А?. Напротив, если данные кри-
кривые, не будучи замкнутыми, уходят в бесконечность, проблема может
и не иметь решения. На рис. 224 изображены две такие кривые, что
ни наименьшее, ни наибольшее расстояния между соответственно при-
принадлежащими им точками не достигаются: при этом нижняя граница
расстояний равна нулю, верхняя граница бесконечна. В иных случаях
существует минимум, но не существует максимума. Так, в случае двух
ветвей гиперболы (рис. 17, стр. 108) минимальное расстояние реализу-
реализуется для вершин А и А', тогда как нельзя указать пары точек, между
которыми расстояние было бы максимальным.
Нетрудно понять, чем обусловливается различие между двумя пре-
предыдущими примерами; для этого достаточно искусственно ограничить
область изменения переменных. Возьмем произвольное положительное
число R и подчиним абсциссы точек ограничению
R. Тогда для
обеих проблем будет существовать и минимум, и максимум. Но в пер-
первом примере и минимум, и максимум достигаются на границе области,
каково бы ни было Я, и при неограниченном возрастании R соответ-
соответствующие точки удаляются в бесконечность. Напротив, во втором при-
примере минимальное расстояние достигается внутри области, и точки, его
Реализующие, остаются неподвижными, как бы ни возрастало R.

424 Глава VII
4. Трудности, возникающие в более сложных случаях.
Если вопрос о существовании экстремума не представляет серьезных
затруднений в элементарных проблемах, зависящих от одной, двух или.
вообще, конечного числа переменных, то дело обстоит совсем иначе
в случае проблемы Дирихле или даже в случае более простых проблем
такого же типа. Причина кроется или в том, что область изменения
независимого переменного оказывается некомпактной, или в том, что
рассматриваемая функция не является непрерывной. В первом примере
пункта 2 мы имеем множество путей АО'В, причем О' стремится к А.
Все такие пути, с точки зрения условия проблемы, одинаково допусти-
допустимы. Но пути АО'В в пределе переходят в прямолинейный отрезок АВ,
который сам уже не представляет собой допустимого пути. Множество
допустимых путей в этом примере подобно множеству чисел 0 < х ^ 1,
для которого не имеет места теорема Вейерштрасса об экстремальных
значениях (см. стр. 363). Точно такое же положение вещей и во вто-
втором примере: если конусы становятся все тоньше и тоньше, последова-
последовательность соответствующих поверхностей в пределе переходит в диск
с перпендикуляром, торчащим вверх и заканчивающимся точкой S. Но
этот предельный геометрический образ уже не может быть причисляем
к «допустимым» поверхностям: множество «до-
«допустимых» поверхностей и на этот раз не оказы-
оказывается компактным.
В качестве примера зависимости, не обла-
обладающей свойством непрерывности, рассмотрим
. длину кривой. Длину кривой нельзя считать
/\ / \ / \ - функцией от конечного числа числовых перемен-
V V V ных, так как кривая в целом не может быть
л Л Л Л Л характеризована конечным числом «координат»,
V V V V и зависимость длины кривой от самой кривой не
является непрерывной. Чтобы убедиться в этом,
l/\/ \/vv v V соединим две точки А и В, отстоящие одна от
другой на расстоянии d, зигзагообразной лома-
Рис. 225. Приближе- нои рп; вместе с отрезком АВ образующей п рав-
ние отрезка ломаны- носторонних треугольников. Из рис. 225 ясно
ми линиями видно, что длина Рп при любом п равна в точ-
точности 2d. Рассмотрим теперь последовательность ломаных линий Pi,
Р2, ... Отдельные зигзаги ломаной линии Рп уменьшаются по своей
высоте, в то время как число их увеличивается, и совершенно ясно, что
ломаная Рп в пределе переходит в прямолинейный отрезок АВ, в ко-
котором уже нет и следов «зигзагообразности». Но длина Рп все время

§8. Изопериметрическая проблема 425
равна 2d, каково бы ни было п, тогда как длина предельного отрез-
отрезка АВ равна всего лишь d. Длина кривой, таким образом, не зависит
«от самой кривой» непрерывно.
Все приведенные примеры подтверждают, что при исследовании
вопроса о существовании решения экстремальных проблем в более
сложных случаях следует проявлять крайнюю осмотрительность.
§ 8. Изопериметрическая проблема
Что среди всех замкнутых кривых данной длины именно окруж-
окружность охватывает наибольшую площадь — это один из «очевидных»
фактов математики, строгое доказательство которых возможно только
на основе новейших методов. Несколько остроумных способов доказа-
доказательства этой теоремы предложил Штейнер; мы рассмотрим одно из
его доказательств.
Начнем с допущения, что решение проб-
проблемы существует. Приняв это, предположим, rQ[
что это решение осуществляется некоторой q / \\ \^ р
кривой С, имеющей длину L и охватывающей
максимальную площадь. Легко доказать, что
кривая С выпуклая: это значит, что прямоли-
прямолинейный отрезок, соединяющий любые две точ-
точки С, лежит целиком внутри или на С. Если
бы кривая С не была выпуклой, то, как по-
показано на рис. 226, можно было бы указать рис. 226. К доказатель-
отрезок ОР, конечные точки которого нахо- ству решения изопери-
дились бы на С, а сам он был бы вне С. Ду- метрической проблемы
га OQ'P — отражение дуги OQP относительно ОР — образовывала
бы вместе с дугой ORP кривую длины L, охватывающую площадь,
большую, чем охватывает данная кривая С, так как включала бы до-
дополнительно площади I и II. Это противоречило бы допущению, что
при данной длине L кривая С охватывает наибольшую площадь. Итак,
кривая С должна быть выпуклой. Возьмем теперь какие-нибудь две
точки Л, В, которые делят кривую С (являющуюся решением пробле-
проблемы) на две дуги равной длины. Тогда отрезок АВ разделит область,
ограниченную кривой С, на две равновеликие области.
В самом деле, если бы площади двух областей не были равны, то
область большей площади можно было бы отразить относительно АВ
(рис. 227), и тогда получилась бы замкнутая кривая длины L, охва-
охватывающая площадь, большую чем та, которую охватывает кривая С.

426
Глава VII
кой проблемы
Отсюда следует, что любая незамкнутая
кривая, представляющая собой половину
(по длине) кривой С, является решением
следующей проблемы: найти дугу длины к
с конечными точками А, В, охватываю-
охватывающую вместе с отрезком АВ максимальную
площадь. Мы покажем теперь, что реше-
решением этой новой проблемы является полу-
полуокружность, и тогда будет ясно, что реше-
Рис. 227. К доказательству нием основной проблемы является окруж-
решения изопериметричес- Ность. Итак, пусть дуга АОВ решает новую
проблему. Достаточно убедиться в том, что
всякий вписанный угол, например, /.АОВ
(рис. 228), будет прямым: отсюда будет вытекать, что дуга АОВ —
полуокружность. Допустим, напротив, что угол АОВ не прямой. Заме-
Заменим тогда треугольник АОВ другим треугольником с теми же сторона-
сторонами АО и ОВ, но с заключенным между ними углом в 90°; тогда длина
дуги АОВ останется та же (тМ, и притом заштрихованные фигуры не
изменятся. Но площадь треугольника АОВ при этом увеличится, так
как треугольник с двумя данными сторонами имеет максимальную
площадь при условии, что заключенный между ними угол — прямой
(см. стр. 380). Итак, новая дуга АОВ (рис. 229) вместе с отрезком АВ
охватит большую площадь, чем первоначальная. Полученное противо-
противоречие приводит к заключению, что, какова бы ни была точка О на
рассматриваемой дуге АВ, угол АОВ должен быть прямым. В таком
случае доказательство можно считать законченным: кривая, решающая
изопериметрическую проблему, есть окружность.
Рис. 228. К доказатель-
доказательству решения изопери-
метрической проблемы
Рис. 229. К доказательству
решения изопериметричес-
кой проблемы

§8. Изопериметрическая проблема 427
Изопериметрическое свойство окружности может быть выражено
в форме неравенства. Если L есть длина окружности, то охватываемая
Г2
ею площадь равна ^-, и потому, какова бы ни была замкнутая кривая,
непременно оправдывается следующее изопериметрическое неравенст-
неравенство, связывающее длину кривой С и охватываемую ею площадь А:
Равенство здесь имеет место только в случае окружности.
* Как ясно из соображений, приведенных в § 7, доказательство
Штейнера имеет лишь условное значение: «Если существует кривая С
длины L, охватывающая максимальную площадь, то эта кривая —
окружность». Чтобы установить справедливость указанной предпосыл-
предпосылки, нужна существенно иная аргументация. Прежде всего установим
теорему элементарного содержания: среди всевозможных замкнутых
многоугольников Рп с четным числом сторон In и обладающих пе-
периметром заданной длины наибольшую площадь имеет правильный
2п-угольник. Доказательство строится по тому же образцу, что и приве-
приведенное выше доказательство Штейнера, со следующими изменениями.
С вопросом о существовании решения здесь трудностей не возника-
возникает: 2п-угольник, а также его периметр и площадь, зависит непрерывно
от An координат его вершин, и, не ограничивая общности, область изме-
изменения этих координат (в 4п-мерном пространстве) можно сделать ком-
компактной. Таким образом, мы можем смело начинать с утверждения, что
некоторый 2п-угольник Р есть решение рассматриваемой теперь проб-
проблемы, и затем переходить к анализу его свойств. Как и в штейнеров-
ском доказательстве, доказывается, что многоугольник Р выпуклый.
Затем убедимся, что все 2п сторон Р равны между собой. Допустим,
напротив, что две смежные стороны АВ и ВС имеют различные дли-
длины; тогда можно от многоугольника Р отрезать треугольник ABC и
заменить его равнобедренным треугольником АВ'С, в котором АВ' +
+ В'С = АВ + ВС и площадь которого больше (см. § 1). Тогда мы
получим многоугольник Р' с тем же периметром, но с большей пло-
площадью, вопреки сделанному допущению. Итак, все стороны Р долж-
должны быть равны между собой. Остается показать, что многоугольник Р
правильный: для этого достаточно убедиться, что около Р можно опи-
описать окружность. Доказательство строится дальше, как у Штейнера.
Устанавливаем прежде всего, что всякая диагональ, соединяющая про-
противоположные вершины, делит площадь на две равные части. Затем
Доказываем, что все вершины одного из многоугольников, возникаю-

428 Глава VII
щего при разрезании по диагонали, лежат на одной и той же окружнос-
окружности. Восстановить подробности намеченных доказательств (следующих
образцу Штейнера) предоставляем читателю в качестве упражнения.
Существование решения изопериметри-
ческой проблемы доказывается с помощью
предельного перехода: когда мы увеличиваем
неограниченно число сторон In многоуголь-
многоугольника Р, он в пределе переходит в окружность.
Этот же предельный переход дает, очевидно,
и само решение.
Рассуждение Штейнера непригодно для
доказательства изопериметрического свойст-
свойства сферы в трехмерном пространстве. Сам
Штейнер дал несколько иную, более слож-
сложную трактовку этой проблемы, пригодную
Рис. 230. К доказательст- для пространственного случая, но мы не при-
ву решения изоперимет- водам так тк Hg ee ocHQBe тр т_
рической проблемы
лучить доказательство существования реше-
решения. Вообще доказательство изопериметрического свойства сферы го-
гораздо труднее, чем доказательство соответствующего свойства окруж-
окружности; в достаточно полном и строгом изложении оно было дано позд-
позднее Г.А.Шварцем в работе, чтение которой довольно затруднительно.
Свойство, о котором мы говорим, выражается в виде неравенства
ЗбтгУ2 < А3,
где А — площадь замкнутой поверхости, V — охватываемый ею объем;
равенство осуществляется лишь для сферы.
*§ 9. Экстремальные проблемы с граничными
условиями. Связь между проблемой Штейнера
и изопериметрической проблемой
Решение экстремальных проблем принимает своеобразные черты,
если область значений переменного подчинена тем или иным гранич-
граничным условиям. Теорема Вейерштрасса (утверждающая, что в компакт-
компактной области непрерывная функция принимает наибольшее и наимень-
наименьшее значения) не исключает возможности того, что эти экстремальные
значения достигаются на границе области. В качестве простого, поч-
почти тривиального примера может служить функция и = х. Если х не

J9. Экстремальные проблемы с граничными условиями
429
подчинено никаким ограничениям и может изменяться от —оо до +оо,
то область В независимого переменного есть вся действительная ось;
отсюда легко понять, что функция и = х нигде не принимает ни наи-
наибольшего, ни наименьшего значения. Но если область В ограничена,
например, неравенством 0 ^ х ^ 1, то налицо имеется и наибольшее
значение 1, достигаемое на правом конце промежутка, и наименьшее
значение 0, достигаемое на левом. Но этим экстремальным значениям
не соответствует «вершина» или «впадина» графика рассматриваемой
функции. Иначе говоря, это экстремумы осуществляются относительно
не «двухсторонней» окрестности; оставаясь на концах промежутка, они
смещаются при расширении рассматриваемого промежутка. Если речь
идет о настоящей «вершине» или «впадине» кривой, то экстремальный
характер относится к полной окрестности рассматриваемой точки; не-
небольшие сдвиги границы промежутка никак не влияют на экстремум.
Такого рода экстремум сохраняется даже при свободном изменении
переменного во всей области В или по крайней мере в некоторой до-
достаточно малой окрестности точки. При самых разнообразных обсто-
обстоятельствах поучительно уяснить себе различие между «свободными»
и «граничными» экстремумами. В случае функции одной переменной
это различие, правда, стоит в тесной связи со свойствами монотоннос-
монотонности или немонотонности функции и потому не приводит к каким-нибудь
особенно интересным замечаниям. Но стоит труда остановиться не-
несколько внимательнее на условиях достижения экстремума на границе
области изменения в случае функций многих переменных.
Рис. 231-235. Изопериметрические фигуры, в пределе дающие решение проб-
проблемы Штейнера

430 Глава VII
Рассмотрим, например, проблему Шварца, касающуюся треуголь-
треугольника. Область изменяемости трех независимых переменных состоит
здесь из троек точек, лежащих соответственно на сторонах треуголь-
треугольника ABC. Решение проблемы носит альтернативный характер: или
минимум достигается при условии, что каждая из трех независимо дви-
движущихся точек Р, Q, R находится внутри соответствующей стороны
треугольника (и тогда задача решается высотным треугольником), или
же минимум достигается «на границе», когда какие-то две из точек Р,
Q, R совпадают с общим концом двух смежных сторон (и тогда мини-
минимальный «треугольник» есть не что иное, как дважды считаемая высота
данного треугольника). Характер решения — тот или иной, смотря по
тому, которая из возможностей имеет место.
В проблеме Штейнера, относящейся к трем «деревням», область из-
изменения точки Р есть вся плоскость, причем данные три точки А, В, С
могут считаться граничными. И в этом случае возникают две возмож-
возможности, дающие решение существенно различного характера: или мини-
минимум достигается внутри треугольника ABC (и тогда около точки Р
возникают три равных угла), или он достигается в одной из вершин —
граничных точек области изменения. Подобные альтернативы имеют
место и для дополнительной проблемы.
Рассмотрим, наконец, в качестве последнего примера изоперимет-
рическую проблему с добавочными граничными условиями. Мы уста-
установим при этом замечательную связь между изопериметрической проб-
проблемой и проблемой Штейнера и, помимо того, повстречаемся с простей-
простейшим примером экстремальной проблемы нового типа. В исходной изо-
изопериметрической проблеме замкнутая кривая данной длины, играющая
роль независимого переменного, может быть свободно деформируема,
как угодно отклоняясь от окружности, и любая получаемая кривая яв-
является «допустимой»; таким образом, окружность дает настоящий сво-
свободный минимум. Видоизмененная проблема содержит дополнительное
требование: допустимые кривые С должны заключать внутри себя дан-
данные точки Р, Q, R (или должны проходить через них); как и раньше,
площадь А считается заданной, и предлагается минимизировать дли-
длину L. В этом примере мы имеем «граничное» условие в настоящем смыс-
смысле слова.
Ясно, что при достаточно большом значении А три точки Р, Q, R
не оказывают на решение проблемы никакого влияния. В самом деле,
если только А больше (или равно) площади круга, описанного около тре-
треугольника PQR, решение дается просто-напросто окружностью, охва-
охватывающей эти точки. Но что получается в противном случае? Укажем

§9. Экстремальные проблемы с граничными условиями 431
только результаты, оставляя в стороне детали доказательства, впро-
впрочем, вполне элементарного. Итак, постараемся охарактеризовать реше-
решение проблемы, предполагая, что данное числовое значение А постепен-
постепенно становится меньше и, наконец, обращается в нуль. Как только А
делается меньше, чем площадь описанного круга, изопериметрическая
окружность превращается в три круговые дуги одного и того же радиу-
радиуса, образующие выпуклый треугольник с вершинами Р, Q, R (рис. 232).
Этот треугольник и дает решение проблемы; он определяется полнос-
полностью числовым значением А. При убывании А радиус дуг увеличива-
увеличивается, и дуги выпрямляются; когда А становится равным площади тре-
треугольника PQR, этот самый треугольник и дает решение. Если А ста-
становится еще меньше, то снова получаются треугольники, составленные
из круговых дуг одного и того же радиуса, но с выпуклостью, обращен-
обращенной внутрь треугольника, с вершинами — или, лучше сказать, «рож-
«рожками» — в точках Р, Q, R (рис. 233). При дальнейшем убывании А
наступит момент, когда две круговые дуги, смыкающиеся у одной из
данных точек, например R, станут касательными друг к другу. Еще
далее, треугольники указанного типа уже перестанут быть возможны-
возможными, и тогда обнаруживается новое явление: решение, как и перед тем,
дается вогнутым треугольником, составленным из круговых дуг, но
один из «рожков» R' отделяется от точки R, и решение тогда состоит
из кругового треугольника PQR' с добавлением «дважды считаемого»
(от R' к R и обратно) прямолинейного отрезка RR'. Этот отрезок ка-
касается двух круговых дуг, смыкающихся в точке R'. Когда А убывает
еще дальше, «рожки» отделяются и у прочих вершин. При достаточно
малых положительных значениях А мы будем иметь равносторонний
треугольник, составленный из трех круговых дуг одного и того же ра-
радиуса, касающихся друг друга в вершинах Р', Q', R'', с добавлением
трех «дважды считаемых» отрезков Р'Р, Q'Q, R'R (рис. 234). Наконец,
при обращении А в нуль названный треугольник обращается в точку,
и мы получаем решение проблемы Штейнера, которая, таким образом,
оказывается предельным случаем обобщенной (указанным выше спосо-
способом) изопериметрической проблемы.
Если Р, Q, R образуют тупоугольный треугольник с углом в 120°
или больше, то при стремлении А к нулю в пределе также получается
решение проблемы Штейнера, так как круговые дуги в конце концов
сливаются со сторонами тупого угла. Аналогичным образом, путем пре-
предельного перехода от изопериметрической проблемы, могут быть полу-
получены и решения обобщенной проблемы Штейнера (см. рис. 216-218 на
стр. 411).

432 Глава VII
§ 10. Вариационное исчисление
1. Введение. Изопериметрическая проблема представляет со-
собой, пожалуй, самый старый пример обширного класса важных проб-
проблем, к которым было привлечено общее внимание в 1696 г. Иоганном
Бернулли. В «Acta Eruditorum», выдающемся научном журнале той эпо-
эпохи, он поставил следующую проблему «о брахистохроне». Материальная
частица скользит без трения по некоторой кривой, соединяющей выше
расположенную точку А с ниже расположенной точкой В. Предпола-
Предполагая, что на частицу не действуют никакие силы, кроме силы тяжести,
требуется установить, какова должна быть кривая АВ, чтобы время,
нужное для спуска от А к В, было наименьшим. Легко понять, что для
спуска частицы от А к. В необходимо то или иное время в зависимости
от выбора пути. Прямолинейный отрезок никоим образом не обеспе-
обеспечивает наименьшего времени; то же приходится сказать о круговых
дугах и других элементарных кривых. Бернулли объявил, что он обла-
обладает замечательным решением поставленной задачи, которого, однако,
не хочет пока публиковать, имея в виду побудить крупнейших мате-
математиков своего времени приложить свое искусство к математическим
задачам нового типа. В частности, он вызвал на состязание своего стар-
старшего брата Якоба, с которым был тогда в резко враждебных отношени-
отношениях и открыто именовал невеждой. Своеобразие задачи о брахистохроне
вскоре действительно было оценено математическим миром. В проб-
проблемах, исследованных до того времени с помощью дифференциального
исчисления, подлежащая минимизации величина зависела от одной или
нескольких (в конечном числе) числовых переменных; в этой же за-
задаче рассматриваемая величина — время спуска — зависит от всей
кривой в целом, чем и обусловливается существенное различие; имен-
именно по указанной причине задача о брахистохроне не могла быть решена
ни методом дифференциального исчисления, ни каким-либо другим, из-
известным в те времена приемом.
Новизна поставленной проблемы (по-видимому, то обстоятельство,
что доказательство изопериметрического свойства круга представляет
собой вопрос той же природы, не было тогда еще осознано) подейство-
подействовала на современников Бернулли, в особенности, когда выяснилось, что
решением задачи является циклоида — как раз незадолго до того откры-
открытая кривая. (Напомним определение циклоиды: так называют траекто-
траекторию движения точки, находящейся на окружности, которая катится без
скольжения по прямой линии (рис. 236). Эта кривая уже раньше была
поставлена в связь с некоторыми интересными задачами механическо-

§ 10. Вариационное исчисление 433
Рис. 236. Циклоида
го содержания, в частности, с конструированием идеального маятни-
маятника. Гюйгенс установил, что если тяжелая частица (точка) совершает
(без трения, под влиянием силы тяжести) колебательное движение по
циклоиде, расположенной в вертикальной плоскости, то период колеба-
колебания не зависит от амплитуды (размаха). Напротив, на круговой дуге,
представляющей собой траекторию движения обыкновенного маятни-
маятника, такого рода независимость имеет лишь приближенный характер,
и в этом обстоятельстве усматривалась непригодность круговой дуги
при конструировании точных часов. Циклоиде было присвоено, в свя-
связи с указанным обстоятельством, наименование таутохроны, но теперь
она стала именоваться также и брахистохроной1.
2. Вариационное исчисление. Принцип Ферма в оптике.
Среди различных методов, с помощью которых решение брахистохрон-
ной проблемы было найдено братьями Бернулли и другими учеными,
мы выберем и изложим здесь один из самых ранних в историческом
смысле. Первые предложенные методы носили более или менее специ-
специальный характер, будучи более приспособлены к специфическим зада-
задачам. Но очень скоро Эйлер и Лагранж A736-1813) разработали более
общие методы для решения экстремальных проблем, в которых незави-
независимым элементом является не одна или несколько (в конечном числе)
числовых переменных, а кривая или функция в целом, или даже систе-
система кривых (функций). Новый метод решения подобного рода проблем
получил название вариационного исчисления.
Дать здесь изложение этой ветви математики в ее техническом
аспекте или же проанализировать сколько-нибудь глубоко отдельные
относящиеся сюда проблемы не представляется возможным. Вариаци-
Вариационное исчисление имеет множество применений в физических теориях.
Было замечено с давних пор, что явления природы часто следуют тем
Или иным экстремальным принципам. Как мы уже видели, Герон Алек-
Александрийский усмотрел, что отражение светового луча плоским зерка-
зеркалом хорошо описывается на основе принципа минимума. Ферма — уже
Таутохрона — от греч. таито (равно), xpovoq (время);
Брахистохрона — от греч. (ipa\vi (короткий),
28 _ -глп

434
Глава VII
в XVII столетии — сделал следующий шаг, заметив, что и закон пре-
преломления света также прекрасно выражается в терминах минимального
принципа. Отлично известно, что при переходе светового луча из одной
однородной среды в другую путь его изменяет направление. Так, све-
световой луч, идущий из точки Р (рис. 237) в верхней среде, где скорость
равна г», в точку R в нижней среде, где скорость есть w, совершит ло-
ломаный путь PQR. Снеллиус A591-1626) сформулировал найденный им
эмпирическим путем закон, согласно которому путь состоит из двух
прямолинейных отрезков PQ и QR, образующих с нормалью углы q
I
II
\a
Q
\
и а', причем -^Ш-З. = iL. с помощью дифференциального исчисления
sin a w
Ферма установил, что этот путь как раз обладает тем свойством, что
время, нужное для прохода луча из Р в R, минимально, т.е. меньше,
чем понадобилось бы при прохождении по любому иному пути. Таким
образом, спустя шестнадцать столетий геронов закон отражения света
был дополнен подобным ему и столь же важным законом преломления.
Ферма обобщил формулировку этого за-
закона, распространяя его на случай кривых
поверхностей раздела между двумя средами,
каковы, например, сферические поверхности
линз. Оказывается, что и в этом случае све-
световой луч следует пути, обладающему тем
свойством, что время, нужное для его про-
прохождения, меньше, чем понадобилось бы при
Рис.237. Преломление выборе любого другого пути. Наконец, Ферма
светового луча рассмотрел и случай произвольной оптичес-
оптической системы, в которой скорость света меняется по определенному за-
закону от точки к точке, например, так, как это происходит в атмосфере.
Он разделил непрерывную неоднородную среду на тонкие слои, в каж-
каждом из которых скорость света приблизительно постоянна, и предста-
представил себе новую, воображаемую среду, в которой скорость света дейст-
действительно постоянна в пределах каждого слоя. При таких условиях мож-
можно было применять прежний принцип при переходе от каждого слоя к
следующему. Затем, допуская, что толщина каждого слоя стремится к
нулю, он получил общий принцип геометрической оптики (известный
ныне под именем принципа Ферма): в неоднородной среде световой луч,
идущий от одной точки к другой, следует по такому пути, что время,
нужное для его прохождения, меньше, чем понадобилось бы при про-
прохождении любого иного пути. Этот принцип оказался в высшей степени
полезным не только теоретически, но и практически. В геометричес-

§ 10. Вариационное исчисление 435
ной оптике, оперируя техническим аппаратом вариационного исчисле-
исчисления, пользуются этим принципом как основным орудием при расчетах
систем линз.
Минимальные принципы стали затем господствующими и в других
областях физики. Так, было замечено, что устойчивое равновесие ме-
механической системы бывает достигнуто при таком расположении, при
котором «потенциальная энергия» минимальна. Рассмотрим, например,
свободно изгибаемую однородную цепь, подвешенную за два ее конца и
предоставленную действию силы тяжести. Тогда цепь займет именно
такое положение, при котором потенциальная энергия ее будет наи-
наименьшей. В указанном примере потенциальная энергия зависит от вы-
высоты центра тяжести относительно некоторой постоянной оси. Кривая,
образованная свободно подвешенной цепью, называется цепной линией
и по внешнему виду несколько напоминает параболу.
Не только закон равновесия, но также и законы движения подчи-
подчиняются экстремальным принципам. Отчетливые представления об этих
принципах впервые возникли у Эйлера, тогда как люди, склонные к спе-
спекулятивным размышлениям философского и мистического характера,
как, например, Мопертюи A698-1759), не были способны дать точные
математические формулировки и ограничивались смутными высказы-
высказываниями по поводу «божественного регулирования физических явлений
общими принципами наивысшего совершенства». Эйлеровы вариацион-
вариационные принципы в области физики, вновь открытые и обобщенные ир-
ирландским математиком Гамильтоном A805-1865), стали впоследствии
могущественнейшим орудием в таких областях, как механика, опти-
оптика, электродинамика, самые разнообразные технические науки. Физи-
Физические теории недавнего происхождения — теория относительности и
квантовая теория — полны примеров, обнаруживающих значение ме-
методов вариационного исчисления.
3. Решение задачи о брахистохроне, принадлежащее Яко-
Якобу Бернулли. Ранний метод, примененный к решению проблемы
о брахистохроне Якобом Бернулли, может быть изложен с применением
сравнительно скромных математических средств. Возьмем в качестве
исходного тот известный из механики факт, что материальная частица,
начинающая свой путь в точке А с нулевой скоростью и затем скользя-
скользящая вниз по произвольной кривой С, приходит в некоторую точку Р со
скоростью, пропорциональной величине \/h, где h есть отсчитываемое
по вертикали расстояние точки Р от точки А; иначе говоря, мы имеем
зависимость v = c\fh, где с — постоянный коэффициент. Подвергнем
Рассматриваемую задачу легкому видоизменению. Разобьем мыслен-
9а*

436 Глава VII
но пространство на множество горизонтальных слоев, каждый толщи-
толщиной d, и предположим на минуту, что скорость нашей частицы меня-
меняется не непрерывно, а небольшими скачками — при переходе от слоя
к слою; именно в первом слое, прилежащем непосредственно к точке А,
скорость равна cVd, во втором — c\/2d,
А наконец в п-м — c\fnd — c\fh, где h —
\ расстояние Р от А, отсчитываемое по
\ вертикали (рис. 238). При такой поста-
\ новке задачи мы имеем дело с конечным
^^^ числом переменных. В пределах каждого
--о слоя путь частицы должен быть прямо-
Р линейным. Вопрос о существовании эк-
Рис. 238. К проблеме брахисто- "ремума не возникает; решение должно
хронь, даваться ломаной линией; нужно только
определить ее углы при вершинах. Со-
Согласно минимальному принципу простого преломления, в каждой паре
соседних слоев движение от Р к R через Q таково, что при фиксирован-
фиксированных Р и R точка Q соответствует наименьшему времени пути. Отсюда
вытекает следующий «закон преломления»:
sin a sin a'
\fnd
Повторное применение этого рассуждения приводит к цепи равенств
sin a.\ sin с*2
y/d
A)
где ап обозначает угол между направлением пути в п-м слое и верти-
вертикалью.
Затем Бернулли предполагает, что толщина слоев d, неограниченно
уменьшаясь, стремится к нулю, причем ломаная траектория, решаю-
решающая приближенную проблему, в пределе переходит в искомую кривую,
решающую основную проблему. При этом предельном переходе равен-
равенства A) сохраняются, и потому Бернулли делает заключение: если а
обозначает угол, который в произвольной точке Р кривой С траекто-
траектория брахистохронного движения делает с вертикалью, a h — расстояние
от А до Р, рассчитываемое по вертикали, то выражение smQ должно
Vh
сохранять постоянное значение во всех точках Р кривой С. Легко по-
показать, что указанное свойство характеризует циклоиду.

§ 10. Вариационное исчисление 437
Бернуллиево «доказательство» представляет собой типичный при-
пример остроумного и плодотворного математического рассуждения, кото-
которое в то же время нельзя назвать безукоризненно строгим. В нем содер-
содержится несколько неявно принятых допущений, оправдание которых бы-
было бы сложнее и пространнее, чем само рассуждение. Так, с одной сто-
стороны, не доказывается само существование решения С, с другой — пос-
постулируется без достаточных математических оснований, что решение
приближенной проблемы является приближенным решением основной
проблемы. Вопрос о внутренней ценности такого рода эвристических
(наводящих) построений заслуживает внимательного рассмотрения, но
завел бы нас слишком далеко в сторону.
4. Геодезические линии на сфере.
Минимаксы. Во введении к этой главе была
упомянута проблема нахождения «геодезичес-
«геодезических линий» — кратчайших дуг, соединяющих
две данные точки на некоторой поверхности.
На сфере, как показывается в элементарной гео-
геометрии, такими линиями являются дуги боль-
больших кругов. Пусть Р и Q — две точки на сфере
(не являющиеся диаметрально противополож-
противоположными) и с — меньшая из двух дуг большого
круга, проходящего через Р и Q. Тогда возни- Рис. 239. Геодезичес-
кает вопрос: чем же является другая, большая кие линии на сфере
из двух дуг с' того же круга. Конечно, минимума расстояния между
точками Р и Q она не дает, но не дает и максимума, так как лег-
легко понять, что можно провести на сфере сколь угодно длинные дуги,
соединяющие две данные точки. Оказывается, что по отношению к рас-
рассматриваемой проблеме дуга с' представляет собой минимакс, «седло-
вую точку». Вообразим произвольную переменную точку S на сфере
и поставим задачей найти кратчайший путь от Р к Q, проходящий
через S. Конечно, минимум расстояния в такой постановке проблемы
Дается «ломаной» дугой, состоящей из двух дуг больших кругов PS
и SQ. А затем постараемся найти такое положение точки S, при кото-
котором наименьшее расстояние PSQ было бы максимальным. Тогда полу-
получаем следующее решение вопроса: точка S должна быть такова, чтобы
ломаная PSQ была более длинной дугой с' большого круга PQ. Можно
видоизменить проблему, сначала спрашивая себя о кратчайшем пути
на сфере от точки Р к точке S, проходящем через п наперед заданных
точек Si, S2, ¦ ¦ ¦ , Sn, и затем определяя точки Si, S2, ¦ ¦ ¦ , Sn таким об-
образом, чтобы минимальная длина была насколько возможно большой.

438 Глава VII
Решением такой задачи служит путь по большому кругу, проходяще-
проходящему через Р к Q, но обвивающийся вокруг сферы таким образом, чтобы
пройти через точки, диаметрально противоположные Р и Q ровно п раз.
Эта минимаксная проблема является типичным примером для об-
обширного класса вопросов из области вариационного исчисления, с пол-
полным успехом изученных в последнее время с помощью методов, пред-
предложенных Морзом и другими авторами.
§11. Экспериментальные решения минимальных
проблем. Опыты с мыльными пленками
1. Введение. Обыкновенно бывает очень трудно, а иногда даже
невозможно, решить вариационною проблему явно с помощью формул
или геометрических построений, включающих простые, известные эле-
элементы. Вместо того часто удовлетворяются одним лишь доказательст-
доказательством существования решения при тех или иных условиях и затем иссле-
исследуют его свойства. Во многих случаях, если доказательство существо-
существования оказывается более или менее затруднительным, бывает полезно
реализовать математические условия проблемы посредством соответ-
соответствующих физических приспособлений, рассматривая таким образом
математическую проблему как эквивалентную некоторой физической
задаче. Само физическое явление в таких случаях предоставляет ре-
решение математической проблемы. Само собой разумеется, что подоб-
подобного рода процедуру следует трактовать не как полноценное матема-
математическое доказательство, а только как «наводящую» (эвристическую):
в самом деле, при этом остается открытым вопрос о том, является ли
математическая интерпретация строго адекватной физическому явле-
явлению или же дает лишь несовершенное отображение реальной действи-
действительности. Иногда относящиеся сюда эксперименты, хотя бы они были
воображаемыми, бывают способны воздействовать убеждающе даже на
математиков. В прошлом столетии ряд фундаментальных теорем из об-
области теории функций был открыт Риманом на основе придумывания
простейших экспериментов, касающихся потока электричества в ме-
металлических листах.
В дальнейшем мы имеем в виду рассмотреть — на эксперименталь-
экспериментально-демонстративной основе — одну из более глубоких вариацион-
вариационных проблем. Речь идет о так называемой проблеме Плато. Плато
A801-1883), известный физик, по национальности бельгиец, занимался
интересными опытами, имеющими ближайшее отношение к этой проб-
проблеме. Сама по себе проблема гораздо старше по возрасту и относится

§ 11. Экспериментальные решения минимальных проблем 439
К эпохе возникновения вариационного исчисления. В простейшей фор-
формулировке содержание ее таково: найти поверхность наименьшей пло-
площади, ограниченную данным замкнутым пространственным контуром.
Мы рассмотрим также эксперименты, относящиеся к некоторым близ-
близким проблемам, и убедимся, что это позволит увидеть в новом свете
как некоторые из приведенных выше экстремальных проблем, так и
ряд экстремальных проблем нового типа.
2. Опыты с мыльными пленками. В математической поста-
постановке проблема Плато приводит к решению «дифференциального урав-
уравнения в частных производных» или же системы таких уравнений. Эй-
Эйлер установил, что всякая «минимальная» поверхность, решающая эту
проблему, если только не сводится к плоскости, непременно должна
быть во всех своих точках «седлообразной» и что ее средняя кривизна
всюду должна равняться нулю1. В течение последнего столетия реше-
решение было получено во множестве частных случаев, но существование
решения в общем случае было доказано лишь недавно Дж. Дугласом и
Т. Радо.
Опыты Плато непосредственно дают физические решения для са-
самых разнообразных контуров. Если замкнутый контур, сделанный из
проволоки, погрузить в жидкость со слабым поверхностным натяжени-
натяжением и затем вынуть оттуда, то увидим пленку, натянутую на контуре
в форме минимальной поверхности с наименьшей площадью. (Пред-
(Предполагается, что можно пренебречь силой тяжести и другими силами,
препятствующими стремлению пленки достигнуть устойчивого равно-
равновесия: последнее же наступает в том случае, если площадь пленки ока-
оказывается наименьшей, так как потенциальная энергия, возникающая
вследствие поверхностного натяжения, при этом условии минимальна.)
Вот хороший рецепт для получения такой жидкости: растворите 10 г
чистого сухого олеата натрия в 500 г дистиллированной воды и затем
смешайте 15 кубических единиц раствора с 11 кубическими единицами
глицерина. Пленки, получаемые из указанной смеси на каркасах из ла-
латунной проволоки, сравнительно устойчивы. Сами каркасы не должны
превышать 5-6 дюймов в диаметре.
'Средняя кривизна поверхности в точке Р определяется следующим образом. Во-
Вообразим перпендикуляр к поверхности в точке Р и все плоскости, через него про-
проходящие. Эти плоскости пересекаются с данной поверхностью по кривым, которые
в точке Р имеют, вообще говоря, различную кривизну. Рассмотрим, в частности,
кривые, обладающие наибольшей и наименьшей кривизной (соответствующие секу-
секущие плоскости, как можно доказать, перпендикулярны между собой). Полусумма
этих двух кривых и есть средняя кривизна поверхности в точке Р.

440
Глава VII
Рис. 240. На кубическом каркасе
натянуто 13 почти плоских по-
поверхностей
С помощью пленок очень лег-
легко «решить» проблему Плато: доста-
достаточно придать проволочному карка-
каркасу нужную форму. Красивые модели
поверхностей получаются на полиго-
полигональных каркасах, образованных из
последовательностей ребер правиль-
правильных многогранников. В частности,
любопытно погрузить в наш раствор
каркас куба весь целиком. Тогда по-
получается система поверхностей, пе-
пересекающих друг друга под углом
в 120°. (Если куб вынимать из рас-
раствора очень осторожно, то можно на-
насчитать тринадцать почти плоских
поверхностей.) Потом можно проты-
протыкать и уничтожать поверхности одну за другой, пока не останется толь-
только одна поверхность, ограниченная замкнутым полигональным конту-
контуром. Таким образом можно получить целый ряд прекрасных поверх-
поверхностей. Тот же опыт можно проделать и с тетраэдром.
3. Новые опыты, относящиеся к проблеме Плато. Опыты
с пленками не сводятся к демонстрации минимальной поверхности, на-
натянутой на замкнутый контур (как у Плато); диапазон их гораздо шире.
В последнее время проблема минимальных поверхностей была изучена
не только для одного ограничивающего контура, но и для системы та-
таких контуров; кроме того, было обращено внимание и на возможность
образования минимальных поверхностей более сложной топологической
структуры. Так, существуют односторонние минимальные поверхнос-
поверхности и минимальные поверхности рода, отличного от нуля. Возникающие
более общие проблемы порождают изумительное разнообразие геомет-
геометрических явлений, которые могут быть продемонстрированы с помо-
помощью мыльных пленок. Заметим в этой связи, что очень полезно прово-
проволочные каркасы делать гибкими и изучать изменение формы поверх-
поверхности пленки под влиянием непрерывной деформации каркаса. Дадим
описание некоторых опытов.
1. Если граничный контур представляет собой окружность, то по-
получается поверхность в виде кругового диска. Можно было бы ожидать,
что при непрерывной деформации контура минимальная поверхность
всегда будет сохранять тот же топологический характер. Но это не-
неверно. Если изогнуть контур так, как показано на рис. 241, то вместо

§ 11. Экспериментальные решения минимальных проблем
441
поверхности, топологически эквивалентной дис-
диску, получается односторонняя лента Мёбиуса. Об-
Обратно, можно производить деформацию, исходя
из контура, изображенного на чертеже, с натяну-
натянутой на него пленкой в виде ленты Мёбиуса. Для
осуществления непрерывной деформации следует
припаять к каркасу рукоятки (см. тот же рису-
рисунок). В процессе обратной деформации наступает
момент, когда внезапно топологический характер
пленки меняется и возникает снова поверхность
типа диска (рис. 242). Опять, обращая деформа-
деформацию, мы вернемся к поверхности Мёбиуса. За-
Замечательно, однако, то, что «мутация» дискооб-
дискообразной поверхности в поверхность типа Мёбиуса
происходит на более поздней стадии деформации,
чем при обратном процессе. Это показывает, что
существует непрерывная цепь замкнутых пространственных контуров,
для которых и поверхности типа Мёбиуса, и дискообразные поверхнос-
поверхности устойчивы, т.е. доставляют относительные минимумы. Но если по-
поверхность типа Мёбиуса обладает значительно меньшей площадью, чем
другая, то эта последняя все же слишком неустойчива, чтобы сущест-
существовать физически.
Рис. 241. Односто-
Односторонняя поверхность
(лента Мебиуса)
Рис. 242. Двусторон-
Двусторонняя поверхность
Рис. 243. Система
трех поверхностей
2. Можно натянуть минимальную поверхность на систему конту-
контуров, состоящих из двух окружностей. Вынув каркас из раствора, мы
Получаем не одну поверхность, а структуру, состоящую из трех поверх-

442 Глава VII
ностей, смыкающихся под углом в 120°; одна из них — обыкновенный
круговой диск, плоскость которого параллельна плоскостям граничных
окружностей (рис. 243). Уничтожая этот диск, мы получим, далее, клас-
классический катеноид (поверхность, образуемую вращением цепной ли-
линии, о которой шла речь на стр. 435, около прямой, перпендикулярной
к оси симметрии). При раздвигании граничных контуров наступает
момент, когда двусвязный катеноид лопается и превращается в два от-
отдельных диска. Указанный процесс, конечно, необратим.
Рис. 244-246. На каркасе натянуты три различные поверхности родов 0 и 1
Рис. 247. Односторонняя минимальная поверхность более сложной топологи-
топологической структуры, натянутая на простой замкнутый контур
3. Еще один замечательный пример доставляется каркасом, изоб-
изображенным на рис. 244-246; на этот каркас могут быть натянуты три
различные минимальные поверхности. Одна из них (рис. 244) имеет
род 1, тогда как две другие односвязны и в некотором смысле облада-
обладают свойством взаимной симметрии. Две последние поверхности имеют
одну и ту же площадь, если только контур вполне симметричен. Но

§ 11. Экспериментальные решения минимальных проблем 443
В противном случае только одна из поверхностей обеспечивает абсо-
абсолютный минимум площади, тогда как другая — только относительный
(мы предполагаем при этом, что минимум разыскивается только по от-
отношению к односвязным поверхностям). Возможность образования по-
поверхности рода 1 обусловливается тем обстоятельством, что, допуская
поверхности рода 1, можно получить поверхность меньшей площади,
чем для какой бы то ни было односвязной поверхности. При дефор-
деформации контура мы придем, если только деформация будет достаточ-
достаточно сильно выражена, к такому положению, когда указанное свойство
будет уже утеряно: тогда поверхность рода 1 потеряет свою устойчи-
устойчивость и, внезапно разрываясь, превратится в односвязную поверхность
одного из двух типов, изображенных на рис. 245 и 246. Если, с дру-
другой стороны, мы станем исходить из поверхности одного из этих двух
типов, — например, изображенного на рис. 246, то возможно дефор-
деформировать контур таким образом, что другой тип (см. рис. 245) ста-
станет гораздо более устойчивым. Следствием этого явится тот факт, что
в определенный момент произойдет внезапный переход от одного типа
к другому. Медленно обращая всю деформацию в обратном направле-
направлении, вернем контур снова к исходному положению, но уже с иной натя-
натянутой на нем минимальной поверхностью. Можно снова повторить весь
процесс в обратном направлении; таким образом, можно многократно
повторять переход от одного типа поверхности к другому. Оперируя
контуром надлежащим образом, удается также трансформировать од-
одну из односвязных поверхностей в поверхность рода 1. Для этой цели
нужно сблизить между собой те части контура, на которые натянуты
дискообразные части самой поверхности — с таким расчетом, чтобы
поверхность рода 1 стала гораздо более устойчивой. Иногда в процессе
выполнения описанной выше операции с контуром возникают проме-
промежуточные пленочные поверхности: их нужно уничтожать, чтобы полу-
получилась поверхность рода 1.
Этот пример показывает не только возможность решения пробле-
проблемы Плато различными поверхностями одного и того же топологичес-
топологического типа, но и поверхностями иного типа, причем на одном и том
же контуре; кроме того, он снова иллюстрирует прерывный переход от
одного решения к другому, в то время как граничные условия пробле-
проблемы меняются непрерывно. Нетрудно построить более сложные модели
в таком же роде и подвергнуть их экспериментальному исследованию.
Интересное явление — возникновение минимальных поверхностей,
ограниченных двумя или большим числом взаимно зацепленных замк-
замкнутых контуров. В случае двух круговых контуров получается поверх-

444 Глава VII
ность, изображенная на рис. 248. Если в этом при-
примере плоскости кругов взаимно перпендикулярны
и прямая их пересечения есть общий диаметр двух
кругов, то существуют две диаметрально противо-
противоположные формы минимальной поверхности с оди-
одинаковыми площадями. Представим себе теперь, что
два круга постепенно изменяют свое взаимное по-
положение, тогда и форма минимальной поверхности
будет меняться непрерывно, хотя при каждом по-
р „ля П ложении кругов только для одной из поверхностей
ность, натянутая осуществляется абсолютный минимум, для другой
на два зацеплен- же — только относительный. При некоторых по-
ных круга ложениях поверхность относительного минимума
вдруг разрывается и заменяется поверхностью аб-
абсолютного минимума. Обе минимальные поверхности в этом приме-
примере — одного и того же топологического типа (как и поверхности на
рис. 245 и 246).
4. Экспериментальные решения других математических
проблем. Благодаря действию поверхностного натяжения жидкая
пленка только при том условии может находиться в состоянии устой-
устойчивого равновесия, если площадь образуемой поверхности минимальна.
Это обстоятельство является неистощимым источником экспериментов
серьезной математической ценности. Если некоторые части границы
пленки могут свободно перемещаться по заданным поверхностям (на-
(например, плоскостям), то на этих частях границы пленка будет стоять
перпендикулярно к заданной поверхности.
Мы можем использовать последнее отмеченное обстоятельство для
наглядного решения проблемы Штейнера и ее обобщений (см. § 5).
Пусть две параллельно расположенные стеклянные поверхности (или
гладкие плитки) соединены тремя или большим числом перпендику-
перпендикулярно стоящих стержней. Если погрузить всю такого рода систему
в мыльный раствор, затем вынуть, то пленка образует между плоски-
плоскими поверхностями ряд вертикальных полос, связывающих между собой
стержни. Проекция этих полос на горизонтальные плоскости есть не
что иное, как решение проблемы Штейнера, рассмотренной на стр. 405.
Если две плоские поверхности не параллельны, или стержни к ним
не перпендикулярны, или сами поверхности не являются плоскими, то
кривые, по которым пленки пересекаются с поверхностями, не будучи
прямыми линиями, смогут иллюстрировать решение новых вариацион-
вариационных проблем.

jll. Экспериментальные решения минимальных проблем 445
Рис. 249. Демонстрация кратчайшей системы путей между 4 точками
Рис. 250. Кратчайшая система путей между 5 точками
Появление кривых, по которым смыкаются под углами в 120° раз-
различные минимальные поверхности, может рассматриваться как про-
пространственное обобщение явлений, связанных с проблемой Штейнера.
Это становится вполне ясным, если мы соединим, например, две точ-
точки А, В тремя различными пространственными кривыми и затем по-
погрузим полученную (жестко укрепленную) систему в мыльный рас-
раствор. Предположим для определенности, что одна из трех кривых есть
прямолинейный отрезок, две другие — взаимно конгруэнтные круго-
круговые дуги. То, что получается, изображено на рис. 251. Если плоскости
Дуг образуют между собой угол меньше 120°, мы получим решение
минимальной проблемы в виде трех поверхностей, смыкающихся под
Углами в 120°, но если станем поворачивать плоскости дуг, увеличивая
заключенный между ними угол, то это решение в результате непрерыв-
непрерывного изменения перейдет, наконец, в два плоских круговых сегмента.

446
Глава VII
Рис. 251. Три пересекающиеся
под углом в 120° поверхности,
натянутые на три проволоки,
соединяющие две точки
Рис. 252. Три ломаные линии,
соединяющие две точки
Рис. 253. Доказательство изопериметрического свойства круга
Допустим теперь, что точки А и В соединены более сложными кри-
кривыми. В качестве примера возьмем три ломаные, состоящие каждая из
трех ребер одного и того же куба и соединяющие диагонально противо-
противоположные вершины: тогда получатся три конгруэнтные минимальные
поверхности, пересекающиеся по диагонали куба. (Мы получили бы ту
же систему поверхностей из системы, изображенной на рис. 240, уни-
уничтожая пленки, прилежащие к трем надлежащим образом выбранным
ребрам.) Если станем деформировать ломаные линии, соединяющие А
и В, то линия взаимного смыкания поверхностей искривится, но углы
неизменно останутся те же — в 120° (рис. 252).

§ 11. Экспериментальные решения минимальных проблем 447
Все явления, связанные со смыканием трех минимальных поверх-
поверхностей по одной кривой, в основном одной и той же природы: они пред-
представляют собой обобщение плоской проблемы о соединении системы
п данных точек кратчайшей системой линий.
Наконец, добавим несколько слов о мыльных пузырях. Сферичес-
Сферический мыльный пузырь показывает, что среди всех замкнутых поверх-
поверхностей, охватывающих один и тот же объем (определенный запасом
заключенного в нем воздуха), именно сфера имеет наименьшую по-
поверхность. Если мы рассмотрим пузыри данного объема, стремящиеся
сократить свою поверхность, но подчиненные некоторым дополнитель-
дополнительным условиям, то убедимся, что получаться будут уже не обязательно
сферы, а, вообще говоря, поверхности постоянной средней кривизны,
частными примерами которых являются сферы и круговые цилиндры.
Предположим, например, что пузырь заключен между двумя па-
параллельными стеклами или плитками, предварительно смоченными
мыльным раствором. Прикоснувшись к одной из плоскостей, пузырь
внезапно принимает форму полусферы, если же происходит соприкосно-
соприкосновение также и с другой плоскостью, он сразу превращается в круговой
цилиндр, тем самым чрезвычайно наглядно демонстрируя изоперимет-
рическое свойство круга. Все дело, конечно, в том, что мыльная пленка
располагается перпендикулярно к ограничивающим поверхностям. По-
Помещая мыльные пузыри между двумя плоскостями, которые соединены
между собой стержнями, мы имеем возможность проиллюстрировать
проблемы, разобранные на стр. 411.
Рис. 254-255. Изопериметрические фигуры с граничными условиями
Можно еще рассмотреть, как изменяется решение изопериметри-
ческой проблемы при увеличении или уменьшении объема воздуха
внутри пузыря. При этом следует воспользоваться тоненькой трубоч-
трубочкой или соломинкой. Однако, высасывая воздух, мы не получим тех фи-

448
Глава VII
Рис. 256-257. Демонстрация изопериметрических свойств фигур с помощью
мыльных пленок
гур (см. стр. 429), которые состоят из касающихся друг друга круговых
дуг. При уменьшении объема воздуха внутри пузыря углы в треуголь-
треугольнике из круговых дуг, однако, не станут (теоретически) меньшими,
чем 120°: мы получим такие фигуры, какие изображены на рис. 254
и 255, причем при неограниченном уменьшении площади, заключенной
внутри, в пределе получатся те же три сегмента, с которыми мы встре-
встретились и раньше (рис. 235). С математической точки зрения объяснение
отмеченному различию заключается в том, что отрезок, связывающий
пузырь с каким-нибудь стержнем, начиная с момента отделения пузы-
пузыря от этого стержня, не должен считаться дважды. Соответствующие
опыты иллюстрируются рис. 256 и 257.
Упражнение. Разобрать математическую проблему, отвечающую на-
настоящим условиям: найти треугольник, составленный из круговых дуг и име-
имеющий данную площадь, по условию, чтобы сумма его периметра и трех отрез-
отрезков, соединяющих вершины с тремя данными точками, была минимальной.
Помещая мыльный пузырь внутрь кубического проволочного кар-
каркаса, в случае, если объем пузыря окажется больше, чем объем куба,
мы получим поверхности постоянной средней кривизны с квадратны-
квадратными основаниями. Высасывая воздух из пузыря через соломинку, будем
иметь целую цепь красивых структур, приводящих в конце концов к та-
такой, какая изображена на рис. 258. Явления устойчивости и переход от
одного состояния равновесия к другому порождают эксперименты, ко-
которые в математическом отношении нельзя не назвать весьма поучи-
поучительными. Таким образом, возникает наглядная иллюстрация к теории
стационарных значений; непрерывная цепь переходов от одного состоя-
состояния равновесия к другому может быть выбрана таким образом, что в ее
состав войдет состояние неустойчивого равновесия, все же являющееся
«стационарным состоянием».

§11. Экспериментальные решения минимальных проблем
449
Рис. 258. Пленки на кубическом каркасе
Рассмотрим в качестве примера кубическую структуру на рис. 240.
Мы видим здесь нарушение симметрии: в центре куба имеется верти-
вертикальная площадка, смыкающаяся с двенадцатью поверхностями, иду-
идущими от ребер куба. Но тогда, как нетрудно понять, должно сущест-
существовать еще по меньшей мере два положения равновесия: одно с верти-
вертикальной (иначе расположенной) и другое с горизонтальной площадкой
в центре. Чтобы на самом деле реализовать переход от одного поло-
положения равновесия к другому, нужно дуть через соломинку на ребра
центральной площадки: таким образом удается эту центральную пло-
площадку превратить в точку — центр куба, но полученное таким образом
состояние равновесия не будет устойчивым и немедленно же перейдет
в иное устойчивое состояние, причем центральная площадка снова воз-
возникает, хотя и повернувшись на 90°.
Подобный же эксперимент можно произвести и с мыльной пленкой,
демонстрирующей решение проблемы Штейнера для случая четырех
точек, помещенных в вершинах квадрата (рис. 219, 220).
Если бы мы пожелали получить решение только что рассмотренных
проблем как предельный случай цепи изопериметрических проблем, на-
например, если бы мы хотели получить рис. 240 из рис. 258, нужно было
бы понемногу высасывать воздух из центрального пузыря. Структура,

450 Глава VII
изображенная на рис. 258, строго симметрична, и в пределе, когда объ-
объем центрального «кубика» обращается в нуль, получается также строго
симметричная структура из 12 плоских треугольников с общей верши-
вершиной в центре. Этого в самом деле можно добиться. Но возникающее
предельное положение равновесия не является устойчивым: внезапно
оно сменяется одним из трех положений, изображенных на рис. 240.
Все явления можно наблюдать вполне отчетливо, если раствор сделать
несколько более вязким, чем было указано в нашем рецепте. Перед нами
возникает яркая картина, показывающая, что даже в проблемах из об-
области физики решение не всегда находится в непрерывной зависимости
от начальных данных: в самом деле, в предельном случае, когда объ-
объем воздуха, заключенного в «кубическом» пузыре, обращается в нуль,
решение, изображенное на рис. 240, не является предельным для це-
цепи решений, изображенных на рис. 258, возникающих для различных
объемов е, когда е стремится к нулю.

Глава VIII
Математический анализ
Введение
Было бы слишком большим упрощением представлять себе, что ма-
математический анализ «изобретен» двумя людьми: Ньютоном и Лейбни-
Лейбницем. В действительности он сложился в итоге долгой эволюции, которая
не была ни начата, ни закончена Ньютоном или Лейбницем, но в ко-
которой они оба сыграли значительную роль. Несколько математиков-
энтузиастов из разных стран Европы в XVII в. поставили своей целью
продолжение математической работы Галилея и Кеплера. Эти люди
поддерживали друг с другом тесное общение с помощью переписки и
личных встреч. Внимание их было привлечено двумя центральными
проблемами. Во-первых, проблемой касательной: определить касатель-
касательную к данной кривой — основная задача дифференциального исчис-
исчисления. Во-вторых, проблемой квадратуры: определить площадь, связан-
связанную с заданной кривой, — основная задача интегрального исчисления.
Величайшей заслугой Ньютона и Лейбница является то, что они ясно
осознали внутреннюю связь между этими двумя проблемами. И вот объ-
объединенный таким образом метод сделался в их руках мощным орудием
науки. В значительной степени успех был обусловлен поистине чудес-
чудесными символическими обозначениями, придуманными Лейбницем. За-
Заслуги этого ученого нисколько не умаляются тем, что им руководили
смутные неуловимые идеи, такие идеи, которые иной раз способны за-
заменить недостаток точного понимания в умах, предпочитающих мис-
мистицизм ясности. Ньютон, деятель точной науки в подлинном смысле
слова, был, по-видимому, главным образом вдохновляем своим учите-
учителем и предшественником по Кембриджу Барроу A630-1677), Лейбниц
же пришел к математике скорее со стороны. Блестящий знаток зако-
законов, дипломат и философ, один из самых деятельных и многосторонних
умов своего века, он изучил новейшую математику в невероятно ко-
короткое время у Гюйгенса, физика по специальности, во время своего
пребывания в Париже в дипломатической миссии. Вскоре после этого
°н опубликовал результаты, которые содержат в себе ядро современно-
современного анализа. Ньютон, открытия которого были сделаны много раньше,

452 Глава VIII
не был расположен их опубликовывать. Более того, хотя первоначаль-
первоначально многие результаты, содержащиеся в его несравненном произведении
«Principia», он нашел с помощью методов анализа, изложить их он пред-
предпочел в стиле классической геометрии; таким образом, в «Principia» поч-
почти совсем нет явных следов анализа. Лишь позднее были опубликованы
его работы о методе «флюксий». Его почитатели вступили в жестокую
схватку из-за приоритета с друзьями Лейбница. Они обвиняли послед-
последнего в плагиате, хотя трудно себе представить что-либо более естест-
естественное, чем одновременное и независимое открытие, когда атмосфера
уже насыщена элементами какой-нибудь новой теории. Последовавшие
пререкания по поводу «изобретения» анализа служат грустным приме-
примером того, как переоценивание вопросов о первенстве способно отравить
атмосферу естественного научного единения.
Настоящая глава должна быть рассматриваема как элементарное
введение, имеющее своей целью в гораздо большей степени познако-
познакомить читателя с основными концепциями, чем научить формальным
операциям. Мы будем здесь широко применять «интуитивный язык», но
при этом позаботимся, чтобы он не оказывался в противоречии с точ-
точными понятиями и научно обоснованными операциями.
§ 1. Интеграл
1. Площадь как предел. Для того чтобы вычислить площадь
плоской фигуры, мы в качестве единицы площади выбираем квадрат со
стороной, равной единице длины. Если единицей длины является сан-
сантиметр, соответствующей единицей площади будет квадратный санти-
сантиметр, т.е. квадрат, длина стороны которого равна сантиметру. С помо-
помощью этого определения весьма легко вычислить площадь прямоуголь-
прямоугольника. Если длины двух смежных сторон, измеренные в линейных еди-
единицах, представляются числами р и q, то площадь прямоугольника рав-
равна pq квадратных единиц или, короче, площадь равна произведению pq-
Это справедливо для любых р и q как рациональных, так и иррацио-
иррациональных. В случае рациональных значений р и q мы получаем этот
результат, выполняя замену р = ^, q = ^-, где та, n, т', п' — целые
' п
числа. После этого мы находим общую меру ^= = -Ц обеих сторон —
л/ пп
таким образом, что р = тп' ¦ —, q = пт' • -^. Наконец, мы разбива-
разбиваем прямоугольник на мелкие квадратики со стороной i ис площа-

§1. Интеграл 453
дью -\- Всего таких квадратиков будет пт' • тп', и общая площадь
равна пт' ¦ тп' • -^г = пт 'т™ = — • ^- = pq. Для случая рид ирра-
циональных тот же результат получится, если сначала заменим р и q
соответственно приближающими их рациональными числами рТ и qr,
а затем заставим рт и qr стремиться к р н q.
Геометрически очевидно, что площадь треугольника равна полови-
половине площади прямоугольника с тем же основанием Ь и высотой h; таким
образом, площадь треугольника выражается хорошо известной форму-
формулой ifr/i. Любая плоская область, ограниченная одной или несколькими
ломаными, может быть разбита на треугольники; таким образом, ее
площадь может быть получена как сумма площадей этих треугольни-
треугольников.
Потребность в более общем методе вычисления площадей возника-
возникает в связи с вопросом о вычислении площадей фигур, ограниченных уже
не ломаными, а кривыми. Каким образом станем мы определять, напри-
например, площадь круга или сегмента параболы? Этот капитальной важнос-
важности вопрос, с решением которого связано обоснование интегрального ис-
исчисления, рассматривался с очень давних пор; еще в III в. до нашей эры
Архимед вычислял площади подобного рода с помощью процедуры «ис-
«исчерпания». Попробуем вместе с Архимедом и великими математиками
до времен Гаусса стать на «наивную» точку зрения, согласно которой
криволинейные площади являются интуитивно данными сущностями,
так что вопрос стоит не об определении понятия площади, а о вычисле-
вычислении площади (см., однако, анализ понятия, произведенный на стр. 527).
В рассматриваемую криволинейную область впишем многоугольник,
ограниченный ломаной линией и обладающий прекрасно определенной
площадью. Выбирая новый многоугольник такого же типа, включаю-
включающий первый, мы получим лучшее приближение для площади заданной
области. Продолжая таким образом, мы постепенно «исчерпаем» всю об-
область и получим искомую площадь как предел площадей надлежащим
образом подобранной последовательности вписанных многоугольников
с возрастающим числом сторон. Так может быть вычислена площадь
круга с радиусом 1; ее числовое значение обозначается символом тт.
Эту общую схему Архимед провел до конца в случае круга и в слу-
случае параболического сегмента. В течение XVII столетия было с успехом
разобрано много других примеров. В каждом случае само вычисление
предела ставилось в зависимость от того или иного остроумного прие-
приема, специально подобранного для каждой отдельной задачи. Одним из

454
Глава VIII
У=П-«)
главных достижений анализа была замена этих специальных искусст-
искусственных процедур одним общим и мощным методом.
2. Интеграл. Первым основным понятием анализа является по-
понятие интеграла. В этой главе мы будем понимать интеграл как пло-
площадь под кривой, выраженную с помощью предела. Пусть дана непре-
непрерывная положительная функция у = f(x), например, у = х2 или у =
= 1 + cos ж; рассмотрим область, ограниченную снизу отрезком оси от
некоторой точки а до некоторой точки Ь, причем а меньше Ь, справа
и слева — перпендикулярами к ж-оси в этих точках, а сверху — кри-
кривой у = f(x). Цель наша — вычислить площадь А этой области.
Так как такая площадь не мо-
может быть, вообще говоря, разбита
на прямоугольники или треуголь-
треугольники, то непосредственно нельзя
указать точную математическую
формулу, которая была бы пригод-
пригодна для вычисления площади А. Но
мы можем находить приближенные
значения для А и, следовательно,
представить А как предел следую-
следующим образом: разделим промежу-
промежуток от х = а до х = Ъ на некоторое число маленьких частных проме-
промежутков, восставим перпендикуляры в каждой точке деления, и каждую
полоску области под кривой заменим прямоугольником, высоту которо-
которого выберем произвольно между наибольшей и наименьшей ординатами
кривой в этой полоске. Сумма S площадей этих прямоугольников даст
приближенное значение истинной площади «под» данной кривой. Точ-
Точность этого приближения тем лучше, чем больше число прямоугольни-
прямоугольников и чем меньше ширина каждой отдельной полоски. Итак, мы при-
принимаем следующее определение интересующей нас площади: если мы
построим последовательность
Рис. 259. Интеграл как площадь
Si,
A)
приближений прямоугольниками площади кривой, причем основание са-
самого широкого прямоугольника в сумме Sn стремится к 0, когда п воз-
возрастает, то последовательность A) стремится к пределу А:
Sn
B)
и этот предел А, представляющий собой площадь под данной кривой,
не зависит от того, каким именно образом выбрана последователь-

jl. Интеграл
455
ность A), раз только основания прямоугольников неограниченно умень-
уменьшаются. (Например, Sn может произойти из Sn_i путем прибавления
одной или нескольких новых точек к прежним, определяющим Sn-i>
или же выбор точек деления для Sn может совершенно не зависеть
от выбора точки для 5n_i.) Площадь А данной области, выраженную
указанным предельным переходом, мы называем, по определению, ин-
интегралом от функции f(x) в пределах от а до Ь. Вводя специальный
символ — знак интеграла, запишем это так:
А= f f(x)dx.
C)
/
Символ /, значок dx и название «интеграл» были введены Лейбницем,
чтобы намекнуть на способ получения этого предела. Чтобы объяснить
это обозначение, мы еще раз, с боль-
большими подробностями, повторим про-
цесс приближения площади Л. И в то
же время аналитическая формули-
ровка перехода к пределу позволит
отбросить стесняющие предположе-
предположения f(x) ^ОиЬ>аив конце концов
избавиться от первоначальной интуи-
интуитивной концепции интеграла как «пло-
щади под кривой» (это будет сделано
в дополнении, § 1).
Разделим промежуток от а до Ъ
Рис. 260. Приближение площади
ступенчатой фигурой
на п маленьких частных промежутков, которые только ради простоты
Ь-а
мы будем предполагать имеющими одинаковую длину
точки деления следующим образом:
-; обозначим
= а, х\ = а +
Ъ— а
x2 =
2(Ь - a)
п
п(Ь — а)
сп=а+ -Чп—- = Ь.
Введем для обозначения величины —^ разности между двумя после-
последовательными значениями х символ Ах (читается «дельта икс»):
л Ь — а
Ах= -^-x
где символ Д обозначает просто «разность». Это оперативный символ,
который нельзя рассматривать как числовой множитель. За высоту

456 Глава VIII
каждого приближающего прямоугольника мы можем принять значе-
значение у = f(x) в правой крайней точке соответствующего промежутка.
Тогда сумма площадей прямоугольников будет равна
Sn = /(хг)Ах + f(x2)Ax + ...+ f(xn)Ax, D)
или,сокращенно:
5„ =?/(**) Д*. E)
n
Символ ^ (читается «сумма по j от 1 до п») обозначает сумму всех вы-
ражений, получаемых, когда j последовательно пробегает значения 1,
2,3,..., п.
Употребление символа J3 для выражения результата суммирования
в сжатой форме можно иллюстрировать следующими примерами:
10 п
2 + 3 + 4 + ... + 10 = ^2 j, 1 + 2 + 3 + ... + n = J] j,
j=2 j=l
П П
12 + 22 + 32 + ... + п2 =J]j2, aq + aq2 + ... + aqn = ^2aqj,
a + (a 4- d) + (a 4- Id) + ¦. ¦ + (a + nd) = ]P(a + jd).
j=0
Построим теперь последовательность таких приближений Sn, в ко-
которых п возрастает неограниченно, так что число членов в каждой из
сумм E) стремится к бесконечности, в то время как каждый отдельный
член f(xj)Ax стремится к 0 вследствие присутствия множителя Ах =
= п". При возрастании п эта сумма стремится к площади А:
"г
А = Mm Y^f(xj)Ах = / f(x)dx. F)
3 = 1 a
Лейбниц символизировал этот предельный переход от приближаю-
приближающих сумм Sn к пределу А заменой знака суммирования J] через J,
а символа разности Д символом d. (Во времена Лейбница знак сумми-
суммирования 53 писался обычно в виде 5, и символ J представляет собой
просто стилизацию буквы 5.) Несмотря на то, что символика Лейбни-
Лейбница хорошо намекает на способ, каким был получен интеграл, не сле-
следует придавать слишком большого значения тому, что является лишь

§1. Интеграл 457
чисто условным приемом обозначения предела. В ранние дни анализа,
когда отчетливого понятия о пределах еще не существовало и необхо-
необходимость предельного перехода часто упускалась из виду, многие пыта-
пытались объяснить смысл интеграла, говоря, что «конечное приращение Да;
заменено бесконечно малой величиной dx, а сам интеграл есть сумма
бесконечно большого числа бесконечно малых слагаемых f(x)dx». Хотя
«бесконечно малое» имеет известную притягательность для умов, име-
имеющим склонность к философским спекуляциям, ему нет и не может
быть места в современной математике. Никакой полезной цели нельзя
достигнуть, окружая ясное понятие интеграла туманом не имеющих
смысла фраз. Но даже сам Лейбниц иногда поддавался соблазнительно-
соблазнительному воздействию своих символов: в самом деле, они работают так, как
если бы обозначали сумму «бесконечно малых» величин, с которыми
можно до некоторой степени оперировать, как с обыкновенными вели-
величинами. Даже само слово «интеграл» было создано для того, чтобы обо-
обозначить, что «все» или «полная» площадь А составлена из «бесконечно
малых» частиц f(x)dx. Как бы то ни было, прошло около сотни лет после
Ньютона и Лейбница, прежде чем было ясно осознано, что истинной ос-
основой определения интеграла является понятие предела, и ничего боль-
больше. Твердо став на эту точку зрения, мы избегнем всякой неясности,
всех трудностей и всех нелепостей, которые вызывали такое смущение
в ранний период развития анализа.
3. Общие замечания о понятии интеграла. Общее опреде-
определение. В нашем геометрическом определении интеграла как площади
мы явно предполагали, что функция f(x) во всем промежутке интегри-
интегрирования [а, Ь] неотрицательна, т.е. что никакая часть графика не лежит
под осью х. В аналитическом же определении интеграла как предела по-
последовательности сумм Sn такое предположение является излишним.
Мы просто возьмем малые количества f(xj)Ax, составим их сумму и
перейдем к пределу; эта процедура остается имеющей вполне опреде-
определенный смысл и в том случае, если некоторые или все значения f(xj)
отрицательны. Интерпретируя это геометрически с помощью площадей
(рис. 261), мы приходим к заключению, что интеграл от f(x) представ-
представляет собой алгебраическую сумму площадей, ограниченных графиком
и осью х, причем площади, лежащие под осью х, считаются отрица-
отрицательными, остальные — положительными.
Может случиться, что в тех или иных случаях мы придем к интег-
интегралам / f(x)dx, в которых b меньше, чем а, так что —^ = Ах
окажет-

458 Глава VIII
ь
J
Рис. 261. Положительные и отрицательные площади
ся отрицательным числом. Тогда в нашем аналитическом определении
члены вида f(xj)Ax будут отрицательными, если f(xj) положительно,
а Ах отрицательно, и т.д. Другими словами, величина этого интеграла
будет только знаком отличаться от величины интеграла в пределах от Ь
до а. Таким образом получаем следующее простое свойство интеграла:
ь
f(x)dx = - I f(x)dx.
Ь
Далее, нужно подчеркнуть, что значение интеграла не меняется и
в том случае, если точки деления Xj не будут выбираться равностоящи-
равностоящими, другими словами, если разности Да; = Xj+i - Xj не будут одинако-
одинаковы. Мы можем выбрать Xj произвольно, и тогда разности Ах = Xj+i-Xj
должны быть различаемы с помощью соответствующих значков. Даже
в этом предположении сумма
Sn = f{xi)Ax0 + f{x2)Ax1 + ... + /(жп)Дж„_1,
а также сумма
S'n = /(жо)Джо + f{x1)Axl + ... + /(ж„_1)Джп_1
будут стремиться к одному и тому же пределу, именно к значению
ь
интеграла / f(x)dx, если только мы позаботимся о том, чтобы с воз-
а
растанием х все разности Axj = Xj+i — Xj стремились к нулю таким
образом, чтобы наибольшая из них (при данном значении п) стремилась
к нулю, когда п неограниченно возрастает.
Окончательное определение интеграла дается с помощью формулы
ь
I
f(x)dx = lim ^ f{vj)Axj Fa)

jl. Интеграл
459
/1
v, x.
xn-\Vn
Рис. 262. Произвольность разбиения области определения функции при об-
общем определении интеграла
при п —» оо. Под знаком суммы число г>, может обозначать любую точку
в промежутке Xj ^ Vj ^ xj+i, и единственное ограничение, касающееся
способа разбиений основного промежутка, заключается в том, чтобы
наибольшая из разностей Axj = Xj+i — Xj стремилась к нулю, когда п
стремится к бесконечности.
Существование предела Fа) не требует доказательства, если мы
допустим как само собой разумеющееся понятие «площади под кри-
кривой», а также и возможность приближения этой площади с помощью
прямоугольников. И все же, как это выяснится из дальнейших рассуж-
рассуждений (стр. 527), более глубокий анализ показывает, что для того, чтобы
определение интеграла было логически совершенным, желательно и да-
даже необходимо доказать существование этого предела, независимо от
первоначального геометрического представления о площади и притом
какова бы ни была непрерывная функция f(x).
4. Примеры интегрирования. Интегрирование хг. До сих
пор наши рассуждения об интеграле были чисто теоретическими. Воз-
Возникает основной вопрос по поводу рассмотренного построения сумм Sn
по общей установленной схеме и последующего перехода к пределу: ве-
ведет ли эта процедура к каким-либо осязательным результатам в отдель-
отдельных конкретных случаях? Конечно, решение этого вопроса потребует
некоторых дополнительных рассуждений, приспособленных к тем спе-
специальным функциям f(x), от которых нужно найти интеграл.
Когда Архимед две тысячи лет тому назад вычислил площадь пара-
параболического сегмента, он выполнил то, что мы теперь называем интег-
интегрированием функции f(x) = х2, притом чрезвычайно остроумным спо-
способом; в XVII столетии предшественники Ньютона и Лейбница успеш-
успешно решили проблему интегрирования таких простых функций, как хп,
опять-таки с помощью специальных приемов. Только после рассмот-

460
Глава VIII
рения большого числа конкретных примеров был найден общий под-
подход к проблеме интегрирования на основе систематического метода,
и таким образом область разрешимых задач была сильно расширена.
В настоящей главе мы рассмотрим небольшое число отдельных кон-
конструктивных задач, принадлежащих к эпохе «праанализа», так как для
операции интегрирования, понимаемой как предельный процесс, луч-
лучшей иллюстрации не придумаешь.
а) Начнем с совершенно тривиального примера. Если у = f(x) яв-
ь
ляется константой, например, f(x) = 2, то, очевидно, интеграл / 2dx,
а
понимаемый как площадь, равен 2(Ь — а), поскольку площадь прямо-
прямоугольника равна произведению основания на высоту. Сравним этот ре-
результат с определенным интегралом. Если в формуле E) мы подста-
подставим f(xj) = 2 для всех значений j, то при любом значении п найдем,
что
п п п
sn = E f(xi)Ax = Е2Ах =2 Е Ах = 2<ь -а);
в самом деле,
п
\^ Ах — (xi — хо)
... + {хп - xn-i) = хп - х0 = Ь - а.
а
(а,а)
(Ь,Ь)
Рис. 263. Площадь тра-
трапеции
Ь) Почти так же просто проинтегриро-
проинтегрировать функцию f(x) = х. В этом примере ин-
ь
теграл
xdx
является площадью трапеции
(рис. 263), следовательно, согласно элементар-
элементарной геометрии выразится формулой
(Ь-о)
Ъ + а Ъ2-а2
Этот же результат получается и из опреде-
определения интеграла F), в чем можно убедиться
фактическим переходом к пределу без обращения к геометрическому
представлению: если мы в формуле E) положим f(x) = х, то сумма 5П
примет вид

i 1. Интеграл
461
= (na + Ax + 2Дг + ЗАх + ... + nAx)Ax =
= паАх + (АжJA + 2 + 3 + ... + п).
Применяя формулу A) для суммы арифметической прогрессии 1 +
+ 2 + 3 + ... + п, выведенную на стр. 38, мы получим
5„ = паАх + ^ '{АхJ.
И так как
Ах =
2
Ь — а
то отсюда следует
Sn = a(b — a)
\{Ъ - аJ
±{Ъ - аJ.
Пусть теперь п стремится к бесконечности; тогда переход к пределу
даст результат
m5n= [
а2)
в полном соответствии с геометрической интерпретацией интеграла
как площади.
с) Менее тривиальным является интегри- ^
рование функции f(x) = х2. Архимед употре-
употребил геометрический метод при решении экви-
эквивалентной задачи — нахождении площади сег-
сегмента параболы у = х2. Здесь мы будем дей-
действовать аналитически,базируясь на определе-
определении Fа). Чтобы упростить формальные выклад-
выкладки, в качестве «нижнего предела» интеграла а
выберем 0; тогда Ах = ~. Так как xj = j ¦ Ах
и f(xj) = j2(AxJ, то для суммы Sn мы полу-
получим выражение
О]
Рис. 264. Площадь под
параболой
5„ =
3=1
= A2 +22
п2
{АхK
{АхJ} ¦ Ах =

462 Глава VIII
Теперь можно фактически вычислить предел. Применяя формулу
I2 + 22 + ... + п2 = —
о
установленную на стр. 40, и заменяя Ах через ~, мы получим
п(п + 1)Bп + 1) ?3 ^з
= 6 ^з = "б"
Это предварительное преобразование облегчает предельный пере-
переход: при неограниченном возрастании п обратная величина i стремит-
Ь3 Ь3
ся к нулю, и потому в качестве предела получается просто ^--1-2 = ~;
следовательно, окончательный результат имеет вид
ь
/¦
о
Применяя этот результат к площади от 0 до а, получим
а
f
о
наконец, вычитание площадей дает
ь
[
J
2 , 9 -а3
x dx = __.
Упражнение. Тем же способом, употребляя формулу E) на стр. 41,
доказать, что
ь
64 4
— О
ах = ;—.
Применяя общие формулы для сумм 1к +2к + . .. + пк к-х степеней целых
чисел от 1 до п, можно было бы получить результат
Г к ,
]xdx=
bk+1 - ak+1
при любом целом положительном значении к.

§ 1. Интеграл 463
* Вместо того чтобы действовать этим путем, мы можем получить не-
несколько проще даже более общий результат, воспользовавшись сделанным
раньше замечанием о возможности вычислить интеграл и при неравностоя-
неравностоящих точках деления. Мы выведем формулу G) не только для любого целого
положительного к, но и для любого положительного или отрицательного ра-
рационального числа
к- -
где и — целое положительное, a v — целое положительное или отрицательное
число. Исключается только значение к = — 1, при котором формула G) теряет
смысл. Предположим также, что 0 < о < 6.
Чтобы получить формулу G), построим сумму Sn, выбирая точки деле-
деления хо = a, xi, X2, ... , хп = Ь в геометрической прогрессии. Положим у — =
= д, так что ^ = дп, и определим: хо = a, xi = од, хг = aq2, ... х„ = ад" = Ь.
При таком выборе значений Xj, как мы увидим, предельный переход совер-
совершается особенно просто. Поскольку f(xj) = хк = akqik и &Xj = Xj+i — Xj =
= aq^ + 1 — aqi, мы будем иметь выражение
с к/ \ . к к/ 2 \ . к 2к / 3 2\,
Ьп = о (од — о) + о д (од — од) + a q (aq — од ) + ...
+ akq("-1)k(aqn-aqn-1).
Так как каждый член содержит множители ak(aq — а), то можно написать
С! к + 1/ i\M i fc + 1 i 2(fc+l) . . (n-l)(/b+l)i
о„=о(д — 1){1 + q + q ' + ... + q^ n ).
Подставляя t вместо gfc+1, видим, что выражение в скобках является геомет-
геометрической прогрессией 1 +1 + t2 + ... + t"'1, сумма которой, как показано на
tn — 1
стр. 39, равна ———. Но
Таким образом,
Sn = (q-1){1
qk+1 -
где N = 2 г-
До сих пор п было фиксированным числом. Пусть теперь п возрастает;
определим тогда предел, к которому стремится N. При возрастании п ко-
корень y^=q стремится к 1 (см. стр. 373); поэтому и числитель, и зна-
знаменатель выражения N стремятся к нулю, что побуждает к осторожности.

464 Глава VIII
Предположим сначала, что к — целое положительное число, тогда можно осу-
осуществить деление на q — 1, и мы получим (см. стр. 135): N = qk + qk~1 +¦ ¦.+
+ 5 + 1. Если теперь п возрастает, так что q стремится к 1, а следовательно,
и q2, q3, ... , qk также стремятся к 1, то N стремится к к + 1. Но из этого
b _ o
вытекает, что Sn стремится к , что и требовалось доказать.
Упражнение. Доказать, что при любом рациональном к ф — 1 оста-
остается в силе та же самая предельная формула N —> к + 1, а следовательно,
сохраняется и результат G). Сначала дать доказательство, следуя нашему
образцу, в предположении, что к целое отрицательное. Затем, если к = ^,
положить q1/" = s, откуда следует
_ s(k + l)v _ 1 _ gU+v _j^ ^ su+v _ 1 sv __ 1
sv - 1 ~ sv - 1 ~ * - 1 : * - 1 '
Если п возрастает, так что q и s стремятся к 1, то отношения в последней
части равенства стремятся соответственно к u + v и к v, что в качестве
предела для N снова дает —-— = к + 1.
В § 5 мы увидим, каким образом с помощью мощных методов анализа
можно упростить это длинное и несколько искусственное рассуждение.
Упражнения.
1) Проверить предшествующее интегрирование ж* для случаев it = jk —-,
2, -2, 3, -3.
2) Вычислить значения интегралов:
-1 +12 -2 п
о) / xdx, b) / zdx, с) / х2 dx, d) I x3 dx, e) I xdx.
-2 -11 -1 О
3) Найти значения интегралов:
+ 1 2 +1 +1
о) / х3 dx, Ъ) I х3 cos xdx, с) / ж4 cos2 хsin5 xdx, d) I tgxdx.
-1 -2 -1 -1
(Указание: рассмотреть графики функций под знаком интеграла, при-
принять во внимание их симметрию по отношению к оси х = 0 и интер-
интерпретировать интегралы как площади).
*4) Проинтегрировать sinx и cosx в пределах от 0 до Ь, подставляя h вмес-
вместо Дх и применяя формулы со стр. 553.
5) Проинтегрировать /(х) = х и /(х) = х2 в пределах от 0 до Ь, произво-
производя раздробление на равные части и в формуле Fа) выбирая значения
_ Xj + Xj + 1

§1. Интеграл 465
*6) Пользуясь результатом G) и определением интеграла с равными зна-
значениями для Ах, доказать предельное соотношение
1к+2к + . к
(Указание: положить ^ = Ах и показать, что рассматриваемый предел
1
равен интегралу / х dx.)
о
*7) Доказать, что при п —> оо справедливо следующее предельное соотно-
соотношение:
(Указание: напишите эту сумму так, чтобы ее предел являлся некото-
некоторым интегралом.)
8) Вычислить площадь параболического сегмента, ограниченного ду-
дугой Р\Р? и хордой Р\Рг параболы у = ах2, выражая результат через
координаты точек Pi и Рг.
5. Правила «интегрального исчисления». Важной ступенью
в развитии интегрального исчисления явилось формулирование неко-
некоторых общих правил, с помощью которых более сложные задачи могут
сводиться к более простым, а тем самым могут быть решены почти
механически. Алгоритмический характер этих правил особенно ярко
подчеркивается обозначениями Лейбница. Однако слишком сосредото-
сосредоточивать внимание на механизме решения задач при изучении анализа
значило бы снижать содержание предмета и могло бы привести к пу-
пустой долбежке.
Некоторые простые правила интегрирования следуют сразу или из
определения F), или из геометрической интерпретации интегралов как
площадей.
Интеграл от суммы двух функций равен сумме интегралов от этих
двух функций. Интеграл от произведения функции на постоянное с ра-
равен произведению интеграла от функции на постоянное с. Эти два пра-
правила можно выразить одной формулой
ь ъ ь
f[cf(x) + kg(x)} dx = c I f(x)dx + k f g(x)dx. (9)

466 Глава VIII
Доказательство следует непосредственно из определения интеграла
как предела конечных сумм E), поскольку соответствующая формула
для суммы Sn, очевидно, справедлива. Это правило обобщается тотчас
же на сумму более чем двух функций.
В качестве примера применения этого правила рассмотрим поли-
полином
f(x) = а0 + ахх + а2х2 + ¦¦. + апхп,
коэффициенты которого ао, oi, ... , ап постоянны. Чтобы вычислить
интеграл от функции f(x) в пределах от а до Ь, мы будем интегрировать
почленно, согласно правилу. Применяя формулу G), мы найдем
о
/
Ь2 — a2 bn+1 - an+1
f(x)dx = ao{b -a) + ai = h ... + an ——: .
Другое правило, вытекающее со всей очевидностью как из аналитичес-
аналитического определения интеграла, так и из его геометрической интерпрета-
интерпретации, выражается формулой
Ь с с
( f(x)dx + ( f(x)dx = I f{x)dx. A0)
aba
Кроме того, ясно, что наш основной интеграл равен нулю, если Ъ рав-
равно а. Правило
ь а
f(x)dx = - J f(x)dx, A1)
а 6
приведенное на стр. 458, не стоит в противоречии с последними двумя,
поскольку оно получается из A0) при с— а.
Иногда бывает удобно использовать то обстоятельство, что значе-
значение интеграла не зависит от выбора наименования независимого пере-
переменного интегрируемой функции; например,
ь ь ь
J f{x)dx = / f(u)du = J f(t)dt и т. д.
а а а
В самом деле, простая замена наименования координат, к системе ко-
которых отнесен график функции, не меняет площади под данной кривой.
Аналогичное замечание относится к тому случаю, когда производится

§ 1. Интеграл
467
некоторая замена в самой системе коорди-
координат. Например, перенесем начало коорди-
координат на одну единицу вправо из точки О в
точку О', как показано на рис. 265, таким
образом, что х будет заменено новой коор-
координатой х' по формуле х = 1 + х'. Уравне-
Уравнение кривой у = f(x) в новой системе ко-
координат примет вид у = /A + х1) (напри-
1 1
мер, у = j = —^—7). Данная площадь А
Л. ~т~ X
под этой кривой, скажем, в пределах от х =
л . Рис. 265. Перемещение оси у
= 1 до х = о, в новой системе коорди- н щ у
нат будет площадью под кривой в пределах
от х' = 0 до х' = Ь — 1. Таким образом, будем иметь
ь ь-1
f(x)dx = I /A + x')dx'
1 о
и, написав букву и вместо буквы ж', получим
ь ь-1
рA + u)du; A2)
1 о
например,
О 0 — 1
J f(x)dx= I
-I
+и
du;
а для функции f(x) = x получим таким же образом
ь ь-1
fxkdx= f(l+u)kdu.
Аналогично,
Ь-1
jxkdx= f(l + u)k
о -1
du
и, поскольку интеграл в левой части A2с) равен
A + и)к du -
A2а)
A26)
A2с)
мы получим
A2d)

468
Глава VIII
Упражнения.
1) Вычислить интеграл от многочлена 1+х + х2+ .. . + хп в пределах от О
до Ь.
2) Доказать при п > О, что интеграл от функции A + ж)" в пределах от —1
до z равен дроби
3) Показать, что интеграл от ж" sin ж в пределах от 0 до 1 меньше,
чем j. (Указание: последняя величина есть значение интеграла
от ж".)
4) Доказать непосредственно, а также пользуясь разложением по формуле
A+ж)"
бинома, что интеграл от функции
дроби
в пределах от —1 до г равен
n(n + l)
Следует упомянуть, наконец, два важных правила, которые выра-
выражаются посредством неравенств. Эти правила дают, правда, грубые, но
все же полезные оценки для значения интегралов.
Предположим, что Ь > а и что значения
функции f(x) в промежутке от а до 6 ни-
нигде не превосходят значений другой функ-
функции g(x). Тогда мы имеем
У
о о
J f(x)dx ^ j g(x)dx, A3)
что непосредственно ясно или из рис. 266,
или из аналитического определения интег-
Рис. 266. Сравнение интег- Рала- В частности, если функция g(x) рав-
ралов на М, т. е. является постоянной, то мы по-
получаем:
о о
fg(x)dx= f
отсюда следует неравенство
ь
f(x)dx<:M{b-a).
I
A4)

§2. Производная 469
Если функция f(x) неотрицательна, то f(x) = \f(x)\. Если f(x) < 0,
то \f(x)\ > f(x). Отсюда, полагая в неравенстве A3) g(x) = \f{x)\, мы
получим полезную формулу:
ь ь
Jf(x)dx^J\f(x)\dx. A5)
а а
Но поскольку | - f{x)\ = \f(x)\, мы имеем также формулу
ь ь
-Jf(x)dx^J\f(x)\dx,
что дает, вместе с формулой A5), более сильное неравенство, а именно,
ь ь
\jf(x)dx\<:J\f(x)\dx. A6)
§ 2. Производная
1. Производная как наклон. В то время как понятие интег-
интеграла своими корнями уходит в античную древность, другое основное
понятие анализа — производная — было сформулировано только в XVII
столетии знаменитым математиком Ферма и другими. Сделанное Нью-
Ньютоном и Лейбницем открытие органической связи между этими поня-
понятиями, казалось бы столь различными, способствовало небывалому раз-
развитию математической науки.
Ферма интересовался вопросом об определении наибольших и наи-
наименьших значений функции у = f(x). При изучении графика функции
принято называть максимумом точку, расположенную выше всех дру-
других, а минимумом — точку, расположенную ниже всех других точек
в ее окрестности. На рис. 191 на стр. 393 точка В является максиму-
максимумом, точка С — минимумом. Естественно при нахождении максимума
или минимума использовать понятие касательной к кривой. Предполо-
Предположим, что график кривой нигде не образует острых углов и не обладает
другими особенностями, и что в каждой точке он имеет определенное
направление, определяемое касательной прямой. В точках максимума

470
01
Глава VIII
Ук
R
х
О
Рис. 267. Наклоны прямых
или минимума касательная к кривой у = f(x) должна быть параллель-
параллельна оси х; в противном случае кривая около этих точек или поднималась
бы, или опускалась бы. Это замечание побуждает нас заняться общим
вопросом об определении направления касательной к кривой у = f(x)
в любой точке Р этой кривой.
Чтобы характеризовать направление прямой в плоскости х, у,
обыкновенно задается ее наклон, который представляет собой тангенс
угла а между положительным направлением оси х и рассматриваемой
прямой. Если Р есть некоторая точка прямой L, продвигаемся впра-
вправо от нее до некоторой точки R, а затем вверх или вниз до точки Q,
/?О
лежащей на прямой, тогда наклон L равен tea, т.е. -=г=. Отрезок PR
гИ,
предполагается положительным, тогда как RQ — положительным или
отрицательным в зависимости от того, будет ли он направлен вверх или
вниз; таким образом, наклон дает нам подъем или падение на единицу
длины по горизонтали (при перемещении по прямой слева направо). На
рис. 267 наклон первой прямой равен %, в то время как наклон второй
прямой равен —1.
Под наклоном кривой в точке Р мы подразумеваем наклон ее ка-
касательной в этой точке. Поскольку мы расположены принять понятие
касательной как интуитивно данное, перед нами остается только зада-
задача — найти способ для вычисления наклона кривой. В настоящий мо-
момент мы станем на именно такую точку зрения: более тщательный ана-
анализ относящихся сюда проблем будет произведен в дополнении к этой
главе.
2. Производная как предел. Рассмотрение кривой у = f(x)
только в одной ее точке Р(х, у) не позволяет вычислить наклон кривой
в этой точке. Необходимо прибегнуть к предельному процессу, сход-
сходному с процессом вычисления площади. Этот предельный процесс яв-

§ 2. Производная
471
а
Рис. 268. Производная как предел
ляется основой дифференциального исчисления. Рассмотрим на данной
кривой другую точку Pi, близкую к Р, с координатами Х\, у\\ обозна-
обозначим прямую, проходящую через точки Р и Pl5 буквой ij.; эта прямая по
отношению к нашей кривой является секущей, которая мало отличается
от касательной к точке Р, если только точка Pi близка к точке Р. Обо-
Обозначим угол между осью х и прямой t\ буквой а±. Заставим теперь Х\
стремиться к х; тогда точка Pi будет двигаться по кривой к точке Р
и секущая t\ будет приближаться к некоторому предельному положе-
положению, которое и есть не что иное, как касательная t к нашей кривой
в точке х. Если буквой а обозначить угол между осью х и касатель-
касательной t, то при xi —> х будем иметь
2/1
Pi -> P,
а.
Касательная есть предел секущей, а наклон касательной есть пре-
предел наклона секущей1.
Хотя мы и не имеем явного выражения для наклона самой каса-
касательной t, зато наклон секущей ii дается формулой
наклон
2/1-2/
rp л rp
- f{x)
Xi — X
обозначая, как раньше, операцию образования разности символом Д,
мы получим
Ар = А/(ар
Дж
наклон
Ах
1Наши обозначения здесь слегка отличаются от обозначений главы VI, поскольку
там мы имели i -> ii, где х\ постоянно. Никакой путаницы от этого изменения
обозначений не произойдет.

472 Глава VIII
Наклон секущей ti есть «разностное отношение» — разность Ау зна-
значений функции, деленная на разность Ах значений независимого
переменного. Сверх того, имеем наклон t = предел наклона t\ =
v f(xi)-f{x) ,. Ay
— lim ——-—-^—^ = lim-r-^-, где пределы вычисляются при хх —> х,
т. е. при Ах = х\ — х —> 0.
Касательная t к данной кривой имеет наклон, равный пределу раз-
Д« .
костного отношения -г-2- при стремлении Ах — х\ — х к нулю.
Первоначальная функция f(x) давала значение «высоты» различ-
различных точек кривой у = f{x). Предположим теперь, что точка Р движет-
движется по кривой у = f(x). Тогда рассматриваемый наклон в точке Р будет
представлять некоторую новую функцию от х, которую мы обозначим
через f'(x) и назовем производной от функции f(x).
Предельный процесс, с помощью которого получена производная,
называется дифференцированием функции f(x). Этот процесс есть та-
такая операция, которая по определенному правилу сопоставляет данной
функции f(x) некоторую другую функцию f'(x). Подобным же образом
при определении самой функции f(x) было установлено правило, кото-
которое сопоставляло каждому значению переменного х некоторое значение
функции f{x). Итак:
/(ж) есть высота кривой у = f(x) в точке х,
f'(x) есть наклон кривой у = f(x) в точке х.
Слово «дифференцирование» объясняется тем обстоятельством,
что f'(x) есть предел разности (differentia) f(xi) — f(x), деленной на
разность Х\ — х:
f'(x)=\imfiXlJZfx{X) при Х1->х. A)
Другим часто употребляемым обозначением является
f{x) = Df(x),
где символ «D» есть первая буква слова differentia, что значит «раз-
«разность»; кроме того, для производной от функции у = f(x) существуют
еще обозначения Лейбница
&у_ dfjx)
dx dx '

j 2. Производная
473
ftx)=O
Рис. 269. Знак производной
которые мы подвергнем обсуждению в § 4, и намекающие на то,
Ди
что производная получается как предел разностного отношения -—
или
Ах
Условившись в том, что движение по кривой совершается в на-
направлении возрастающих значений х, мы можем теперь заключить:
то обстоятельство, что производная в некоторой точке положитель-
положительна, f'(x) > 0, означает подъем кривой (значения у возрастают). На-
Напротив, то обстоятельство, что производная отрицательна, f'(x) < О,
означает падение кривой (значения у убывают); наконец, если произ-
производная обращается в нуль, f'(x) = 0, то это означает горизонтальное
направление кривой для соответствующего значения х. В точках мак-
максимума и минимума наклон должен быть равен нулю (рис. 269). Таким
образом, решая уравнение
fix) = О
относительно х, мы можем найти положение максимумов и миниму-
минимумов, как это и было впервые сделано Ферма.
3. Примеры. Может показаться, что рассуждения, приведшие
к определению A), лишены всякого практического смысла. В самом де-
деле, одна проблема подменена другой: вместо того чтобы искать наклон
касательной к кривой у = f(x) в некоторой точке, мы должны вычис-
вычислять предел A), что с первого взгляда кажется одинаково трудным. Но,
как только мы откажемся от рассмотрении в общем виде и перейдем
к отдельным функциям, мы получим весьма реальные результаты.
Простейшей из функций является функция f(x) = с, где с— посто-
постоянно. График этой функции у = f(x) = с есть горизонтальная прямая,
*В русском издании в дальнейшем используются именно эти, общепринятые у нас
обозначения.

474 Глава VIII
совпадающая со всеми своими касательными; очевидно, для всех зна-
значений х имеет место соотношение
Это вытекает также и из определения A); в самом деле,
Ay _ f(xi)-f(x) с-с 0
Дж Xi — х xi — х Х\ — х
Таким образом, получаем тривиальный результат:
= 0.
f(x ) _ f(x)
lim —— !-^-i = 0 при xi -> x.
Xi — x
Вслед за этим рассмотрим простую функцию у — f(x) = x, графи-
графиком которой является биссектриса угла первого квадранта. Геометри-
Геометрически ясно, что для всех значений х
а аналитическое определение A) снова дает
f{xi)-f(x) xi-x
Х\ — X Х\ — X
/Ы - Пх)
= 1, так что
— х
= 1 при хл -> х.
Простейшим нетривиальным примером является дифференцирова-
дифференцирование функции
y = f(x)=x2,
что в сущности является нахождением наклона параболы. Это — прос-
простейший случай, на котором мы можем учиться совершать переход
к пределу, когда результат с первого взгляда не очевиден. Мы имеем
Ay f(xi)-f(x) xl-x2
Ах xi-x xi - х
Если бы мы попытались перейти к пределу непосредственно в числите-
числителе и в знаменателе, то получили бы не имеющее смысла выражение jj.
Но этого затруднения можно избежать, сократив дробь на мешающий

§ 2. Производная 475
нам множитель х\—х до перехода к пределу. (Такое сокращение законно,
так как при вычислении предела разностного отношения мы считаем,
что х\ ф х, см. стр. 352.) Таким образом мы получаем результат
х2 — х2 (х\ — х)(х\ + х)
— = — = xi + х.
Х\— X Х\ — X
После сокращения нахождение предела при х\ —> х не представляет
уже никаких трудностей. Этот предел получается путем простой «под-
«подстановки», так как разностное отношение в своем новом виде xi + х
непрерывно, а предел непрерывной функции при х\ —? х есть просто
значение этой функции при Xi = x; в нашем примере мы получаем
непосредственно х + х = 2х и, следовательно, если f(x) = х2, то
f'(x) = 2х.
Совершенно аналогично мы можем доказать, что в случае функ-
функции f(x) = х3 мы будем иметь f'(x) = Зж2. В самом деле, отношение
Ay = f(Xl)-f(x) = х3-х3
Ах х\ — х х\ — х
может быть упрощено по формуле
х\ — х3 = {х\ — х){х\ + х\х + х2);
знаменатель Ах = х\ — х сокращается, и мы получаем непрерывное
выражение
Ау о ,
Ах х
При стремлении х\ к х это выражение стремится к сумме х2 + х2 + х2;
в качестве предела получается выражение
/'(*)=3х2.
И вообще, для функции
J Vх/ — •*' >
где п — целое положительное, производная будет иметь вид
f{x)=nxn-1.
Упражнение. Доказать этот результат. (Примените алгебраическую
формулу
xi - хп = (xi - ж)(хГХ + ж" ~2х + х1~3х2 + ... + xixn~2 + ж").)

476 Глава VIII
В качестве следующего примера, позволяющего непосредственно
определить производную, рассмотрим функцию
Мы имеем
/ Л х-
^Aj/ _ 2/1-2/ _ /J_ _ 1Л 1 _
Ах ~ xi - х ~~ \х\ x)'xi~x~
Х\-х
Сократим опять дробь и тогда получим
Ay = |_
Ах xix
— выражение, опять-таки непрерывное в точке х\ = х; в качестве
предела мы, следовательно, будем иметь
/» =-Л-
Само собой разумеется, что в данном случае ни производная, ни сама
функция не определены в точке х = 0.
Упражнение. Доказать аналогичным способом, что функция f(x) =
1 9 1
= — имеет производную /'(ж) = -; функция /(ж) = -—¦ имеет производ-
х х х
ную f'(x) = ^-; функция /(ж) = A + ж)" имеет производную /'(ж) =
= пA + ж)".
Продифференцируем теперь функцию
У = f(x) = Vx.
В качестве разностного отношения мы получаем:
Ау _ 2/1-2/ _ V%i- Vх
Ах Xi — х Х\ — х
Воспользовавшись формулой х\—х = (i/жГ- у/х) (,/жГ + Vx), можно со-
сократить знаменатель с первым из множителей и получить выражение,
непрерывное в точке х\ = х,

§2. Производная 477
Переход к пределу дает
Упражнения. Доказать, что функция /(х) = — имеет производ-
ную /'(х) = ; доказать далее:
2 (-у/ж)
а) что функция /(х) = -\Ух имеет производную /'(х) = * ;
Зч/ж2
X
b) » » /(x) = Vl - x2 » » f'(x)=--
y/1 — X2
N /f \ _ nf . f1 I \ — 1
4. Производные от тригонометрических функций. Теперь
мы приступим к чрезвычайно важному вопросу — к дифференциро-
дифференцированию тригонометрических функций. Предварительно условимся, что
измерение углов будем производить исключительно в радианах.
Чтобы продифференцировать функцию у = f(x) = sin ж, поло-
положим Xi - х = h, так что х\ = х + h и /(zi) = sinsi = sin(a; + h). Вос-
Воспользовавшись тригонометрической формулой для синуса суммы двух
углов, sin(yl + В), мы получим
f(xi) = sin(a; + h) — sin x cos h + cos x sin h.
Отсюда
xi - x h h h
Если x\ стремится к х, то h стремится к 0, sin h стремится к 0, a cos h
стремится к 1.
Применяя далее результаты стр. 356, мы получим
=l и li
lim
п
Правая часть соотношения (*) стремится, следовательно, к cos ж, и мы
получаем окончательный результат: функция f(x) = sin ж имеет своей
производной функцию f'(x) — cosx или, короче,
d(s'mx)
—^— = cos ж.
ах

478 Глава VIII
dicosx)
Упражнение. Доказать, что ; = -smi.
ах
Чтобы продифференцировать функцию f(x) = tga;, мы напишем
tga; = 1^ и получим, далее,
f{x + h) - f(x) _ / sin(a: + h) _ sjnx\ 1 _
h \cos(x + h) cosx)'h
sin(:c + h) cos ж — cos(a; + h) sin ж
h cos(a; + h) cos x
sin/i 1
h cos(a; + h) cos ж
(Последнее равенство получается с помощью формулы sin(yl — В) =
= sin A cos В — cos A sin В, где А = х + h, В = х.) Если /г стремится
к 0, то S1 стремится к 1, cosfa; + h) стремится к cos ж, и отсюда мы
h
делаем заключение:
Производная функции /(ж) = tgж есть функция /'(ж) = —\—, или
cos ж
d(tgx) i
Упражнение 1. Доказать, что
dx cos2 ж
d(ctgx)
dx sin2 x
*5. Дифференцируемость и непрерывность. Необходимым
условием дифференцируемости некоторой функции является ее непре-
непрерывность. В самом деле, если существует предел дифференциального
отношения д-2- при стремлении Дж к нулю, то ясно, что приращение Ау
функции /(ж) должно становиться неограниченно малым при стремле-
стремлении Дж к нулю. Каждая дифференцируемая функция неизбежно явля-
является в то же время и непрерывной; поэтому, встречаясь в этой главе
не раз с дифференцируемыми функциями, мы воздерживаемся от того,
чтобы без особой необходимости постоянно упоминать, что они пред-
предполагаются непрерывными, или доказывать их непрерывность.
6. Производная и скорость. Вторая производная и ускоре-
ускорение. До сих пор понятие производной мы связывали с геометричес-
геометрическим представлением графика функции. Однако было бы грубой ошиб-
ошибкой ограничивать роль понятия производной одной лишь задачей об

§2. Производная 479
определении наклона касательной к данной кривой. Еще более важной,
с научной точки зрения, задачей является вычисление скорости изме-
изменения какой бы то ни было величины fit), меняющейся с течением
времени. Именно с этой стороны Ньютон и подошел к дифференциаль-
дифференциальному исчислению. В частности, Ньютон стремился проанализировать
явление скорости, рассматривая время и положение движущейся час-
частицы как переменные величины (по выражению Ньютона, «флюэнты»).
Когда некоторая частица движется вдоль оси х, то ее движение впол-
вполне определено, раз задана функция х = fit), указывающая положение
частицы х в любой момент времени t. «Равномерное движение» с посто-
постоянной скоростью b по оси х определяется линейной функцией х = a + bt,
где а есть положение частицы в начальный момент (при t = 0).
Движение частицы на плоскости описывается уже двумя функци-
функциями
х = fit), у = git),
которые определяют ее координаты как функции времени. В частности,
равномерному движению соответствуют две линейные функции
х = а + Ы, у — с + dt,
где bud — две «компоненты» постоянной скорости, а а и с — коорди-
координаты начального положения частицы (при t = 0); траекторией частицы
является прямая линия, уравнение которой
(ж - a)d - (у - с)Ь = 0
получается путем исключения t из двух стоящих выше соотношений.
Если частица движется в вертикальной плоскости х, у под дей-
действием одной лишь силы тяжести, то движение ее (это доказывается
в элементарной физике) определено двумя уравнениями
х = а + Ы, у = с + dt — -~gt2,
где а, Ь, с, d — постоянные величины, зависящие от состояния части-
частицы в начальный момент, a g — ускорение силы тяжести, равное при-
приблизительно 9,81, если время измеряется в секундах, а расстояние —
в метрах. Траектория движения, получаемая путем исключения t из
двух данных уравнений, есть парабола
ц-с | d, х 1 jx-a?

480 Глава VIII
если только Ь ф 0; в противном случае траекторией является отрезок
вертикальной оси.
Если частица вынуждена двигаться по некоторой данной кривой
(подобно тому как поезд движется по рельсам), то движение ее может
быть определено функцией s(t) (функцией времени t), равной длине ду-
дуги s, вычисляемой вдоль данной кривой от некоторой начальной точ-
точки Pq до положения частицы в точке Р в момент времени t. Например,
если речь идет о единичном круге х2 + у2 = 1, то функция s = ct
определяет на этом круге равномерное вращательное движение со ско-
скоростью с.
* Упражнение. Начертить траектории плоских движений, заданных
уравнениями: 1) х = sint, у = cosi; 2) х ~ sin2i, у — cos3i; 3) х = sin2i,
у = 2sin3?; 4) в описанном выше параболическом движении предположить
начальное положение частицы (при t = 0) в начале координат и считать b > 0,
d > 0. Найти координаты самой высокой точки траектории. Найти вре-
время t и значение х, соответствующие вторичному пересечению траектории
с осью х.
Первой целью, которую поставил себе Ньютон, было нахождение
скорости частицы, движущейся неравномерно. Рассмотрим для просто-
простоты движение частицы вдоль некоторой прямой линии, заданное функ-
функцией х — f(t). Если бы движение было равномерным, т.е. соверша-
совершалось с постоянной скоростью, то эту скорость можно было бы найти,
взяв два момента времени t и t\ и соответствующие им положения
частиц /(?) и f(ti) и составив отношение
расстояние хг - х f{h)-f(t) Л
v = скорость = время = ^—г = h_t ¦ B)
Например, если t измерено в часах, а а; в километрах, то при ti — t = 1
разность Xi — х будет число километров, пройденных за 1 час, a v —
скорость (километров в час). Говоря, что скорость есть величина по-
постоянная, имеют в виду лишь то, что разностное отношение
не изменяется при любых значениях t и t\. Но если движение неравно-
неравномерно (что имеет, например, место при свободном падении тела, ско-
скорость которого по мере падения возрастает), то отношение C) не дает
значения скорости в момент t, а представляет собой то, что принято
называть средней скоростью в промежутке времени от t до t\. Что-
Чтобы получить скорость в момент t, нужно вычислить предел средней

§2. Производная 481
скорости при стремлении t\ к t. Таким образом, вместе с Ньютоном
определим скорость так:
скорость в момент t = lim —-—7 ~— = f'(t). D)
t\ — t
Другими словами, скорость есть производная от «пройденного пути»
(координаты частицы на прямой) по времени, или «мгновенная ско-
скорость изменения» пути по отношению ко времени — в противополож-
противоположность средней скорости изменения, определяемой по формуле C).
Скорость изменения самой скорости называется ускорением. Уско-
Ускорение — это просто производная от производной; оно обычно обознача-
обозначается символом /"(?) и называется второй производной от функции /(?).
Галилей' заметил, что вертикальное расстояние х, проходимое при
свободном падении тела в течение времени t, выражается формулой
х = /(*) = \gt\ E)
где g-есть ускорение силы тяжести. Из формулы E), путем дифферен-
дифференцирования ее, можно получить скорость v тела в момент времени t; эта
скорость выражается формулой
v = f(t)=gt, F)
а ускорение а, которое постоянно, — формулой
а = f"(t) = g.
Предположим, что нужно найти скорость тела через 2 секунды пос-
после начала падения. Найдем сначала среднюю скорость за промежуток
времени от t — 2 до t = 2,1:
о#*BД) — «? 4 Q05 • 0 41
= ol = ' (метров в секунду).
2 1 _2= ol
Подставляя же в формулу F) значение t — 2, мы найдем, что значе-
значение мгновенной скорости в конце второй секунды равно 19,62 (метров
в секунду).
Упражнение. Какова средняя скорость тела за промежуток времени
от t = 2 до t = 2,01, от t = 2 до t - 2,001?
При движении точки на плоскости две производные f'{t) и gf{t)
двух функций х = /(?) и у = g(t) определяют компоненты скорости.
При движении вдоль заданной кривой скорость нужно определить как
производную от функции s = f(t), где s — длина дуги.

482
Глава VIII
У i.
О
f"(x)>0
О
Рис. 270-271. Вогнутость кривой
7. Геометрический смысл второй производной. Вторая
производная /"(ж) имеет также важное значение в анализе и в геомет-
геометрии; в самом деле, представляя собой скорость изменения наклона /'(ж)
кривой у = /(ж), вторая производная дает указание на то, как изогну-
изогнута кривая. Если в некотором промежутке вторая производная больше
нуля, то скорость изменения наклона /'(ж) положительна. Положитель-
Положительный знак скорости изменения некоторой функции указывает на то, что
эта функция возрастает с возрастанием аргумента ж. Следовательно,
неравенство f"(x) > 0 указывает на то, что наклон /'(ж) есть возрас-
возрастающая функция ж, и, значит, при увеличении ж кривая становится
более крутой там, где наклон ее положителен, и более пологой там, где
наклон отрицателен. Условимся говорить, что в этом случае кривая во-
вогнута (рис. 270). Аналогично, если /"(ж) < 0, то будем говорить, что
кривая у = /(ж) выпукла (рис. 271).
Парабола у = /(ж) = ж2 всюду вогнута, так как ее вторая произ-
производная (f"(x) = 2) всегда положительна. Кривая у = /(ж) = ж3 вогнута
при ж > 0 и выпукла при ж < 0 (рис. 153); это видно по ее второй
производной /"(ж) = 6ж, в чем читатель может легко убедиться сам.
Между прочим, при ж = 0 имеем f'{x) = Зж2 = 0 (но нет ни минимума,
ни максимума!), а также и /"(ж) — 0 при ж = 0. Эта точка называ-
называется точкой перегиба. В точках, которые так называются, касательная
(в данном случае ось ж) пересекает кривую.
Если буква s обозначает длину дуги кривой, а буква а — угол
наклона, то функция а = h(s) есть функция переменного s. При пере-
передвижении точки по кривой функция а = h(s) будет меняться. Скорость
этого изменения h'(s) принято называть кривизной кривой в точке, для
которой длина дуги равна s. Без доказательства отметим, что кривиз-
кривизна к может быть выражена с помощью первой и второй производных
от функции у = /(ж), определяющей кривую, согласно следующей фор-

§2. Производная 483
муле:
8. Максимумы и минимумы. Чтобы найти наибольшие и
наименьшие значения заданной функции /(ж), мы прежде всего должны
составить ее производную f'(x), найти затем те значения ж, при кото-
которых эта производная обращается в нуль, и, наконец, исследовать, в ка-
каких точках из числа найденных функция имеет максимум и в каких —
минимум. Последний из этих вопросов может быть решен с помощью
второй производной /"(ж), знак которой указывает на выпуклость или
вогнутость графика кривой; если же вторая производная обращается
в нуль, то обыкновенно это указывает на то, что мы имеем дело с точ-
точкой перегиба, и тогда экстремума нет. Принимая во внимание знаки
первой и второй производных, можно не только найти экстремумы
функции, но и определить вид ее графика. Указанный способ позволяет
нам выделить те значения х, при которых функция имеет экстремум;
для того чтобы найти соответствующие значения самой функции у =
= /(ж), нужно сделать подстановку найденных значений х в выраже-
выражение /(ж).
В качестве примера рассмотрим многочлен:
/(ж) = 2ж3 - 9а;2 + 12ж + 1;
его производные выражаются формулами:
/'(ж) = 6ж2 - 18ж + 12, /"(ж) = 12ж - 18.
Квадратное уравнение /'(ж) = 0 имеет корни Xi — 1, Жг = 2, и в этих
точках значения второй производной равны f'{x\) = — 6 < 0, j"{x-i) =
= 6 > 0.
Следовательно, функция /(ж) имеет максимум j{x\) — 6 и мини-
минимум /(ж2) = 5.
Упражнения.
1) Наметить график рассмотренной функции.
2) Исследовать и наметить график функции /(ж) = (х2 — 1)(ж2 — 4).
3) Найти минимум функций —j—, х + ^-, рх+ ^, считая значения р и q
положительными. Имеют ли максимум эти функции?
4) Найти максимум и минимум функций sinx и sin(x2).

484 Глава VIII
§ 3. Техника дифференцирования
До сих пор наши усилия были направлены на то, чтобы продиф-
продифференцировать целый ряд отдельных функций, причем мы предвари-
предварительно придавали надлежащий вид разностному отношению. Важным
шагом вперед в работах Ньютона, Лейбница и их последователей была
замена этих разрозненных индивидуальных приемов мощными общими
методами. С помощью этих методов можно почти автоматически диф-
дифференцировать любую функцию из числа тех, с которыми обыкновенно
приходится иметь дело в математике; нужно только запастись неболь-
небольшим числом простых правил и уметь их применять. Совокупность этих
приемов приобрела характер вычислительного «алгоритма».
Мы не можем вникать в подробности этой техники. Укажем только
немногие наиболее простые правила.
a) Дифференцирование суммы. Если а и b — постоянные, и функ-
функция к(х) задана формулой
к(х) = af(x) + bg(x),
то, как это легко докажет сам читатель, справедливо следующее:
к'(х) = af(x) + bg'(x).
Аналогичное правило имеет место при любом числе слагаемых.
b) Дифференцирование произведения. Производная произведения
.Р(х) = f(x)g(x)
выражается формулой
р'(х) = f(x)g'(x) + f'(x)g(x).
Это легко доказывается следующим приемом: прибавим и отнимем
от р(х + К) - р(х) одно и то же выражение, а именно f(x + h)g(x):
р(х + h) - р(х) = f(x + h)g(x + h)- f{x)g(x) =
= f(x + h)g{x + h)- f(x + h)g(x) + f{x + h)g{x) - f(x)g(x).
Объединяя первые два и последние два члена, мы получим
p(x + h)-p(x) _ tt , u^g(x + h)-g{x) | f J(x + h) -f{x)
^ -J(x + h) ^ +g(x) ^ .
Заставим теперь h стремиться к нулю; поскольку /(ж + К) при этом
стремится к fix), наше утверждение доказывается немедленно.

§ 3. Техника дифференцирования 485
Упражнение. Пользуясь этим правилом, доказать, что производная
функции р(х) = хп есть р'(х) = па;™. (Указание: примите во внимание,
что х" = х ¦ х"~2, и примените математическую индукцию.)
С помощью правил а) и Ь) можно дифференцировать любой поли-
полином
/(ж) = а0 + агх + ... + апхп,
его производная равна выражению
/'(ж) = d + 2а2х + За3х2 + ... + папхп~1.
В качество одного из применений можно доказать биномиальную те-
теорему (см. стр. 44). Согласно этой теореме степень бинома A + х)"
разлагается в полином следующего вида:
/(ж) = A + ж)" = 1 + ахх + а2х2 + а3х3 + ... + апхп, A)
где коэффициент а^ дается формулой
n(n-l)...(n-fc+l)
ak = ?j • B)
Мы уже видели (упражнение на стр. 476), что дифференцирование
левой части формулы A) дает пA + ж)™. На основании предыдущего
пункта
пA + ж)п-1 = аг + 2а2х + За3ж2 4-... 4- папхп~1. C)
Если теперь в этой формуле положить х = 0, то получим п = а\, что
соответствует формуле B) при к = 1. Снова продифференцируем фор-
формулу C) и тогда будем иметь:
п(п - 1)A 4- х)п~2 = 1а2 Л- 3 • 2а3х + ... + п{п - 1)апхп~2.
Подстановка в эту формулу нуля вместо ж дает п(п — 1) = 2аг, в соот-
соответствии с формулой B) при к — 2.
Упражнение. Доказать формулу B) при к = 3 и при любом к (с помо-
помощью математической индукции).
с) Дифференцирование частного. Если
q(x) = —-,

486 Глава VIII
то
я'(х) = rvr:
Доказательство предоставляется в виде упражнения читателю. Очевид-
Очевидно, нужно предполагать, что g(x) ф 0.
Упражнение. С помощью последнего правила вывести производные
от tgx и ctgx, зная производные от sin ж и cos ж. Доказать, что производными
от sec ж = „„с„ и csca; = — являются соответственно -2—г— и
cos а;
sin а;
Мы умеем теперь дифференцировать любую функцию, являющу-
являющуюся отношением двух многочленов. Например,
f(r\ - 1~х
J\x) — 1 _|_ х
имеет производную
w,_4 -{1+х)-{1-х) 2
^1 -г J'y ^l -r XJ
Упражнение. Продифференцировать функцию
предполагая тп целым положительным. Результат:
// / \ —ГП — 1
(х) = -тпх
d) Дифференцирование обратных функций. Если функции
у = /(ж) и х = g{y)
взаимно обратные (например, у = х2 и х = ^/у, то производная одной из
них является обратной величиной по отношению к производной другой.
Именно,
Это утверждение легко доказать, если обратиться ко взаимно об-
ратным разностным отношениям -~- и =~; это видно ясно также
из геометрической интерпретации обратных функций, приведенной на
стр. 326, если отнести наклон касательной к оси у, а не к оси х.

§ 3. Техника дифференцирования 487
В качестве примера продифференцируем функцию
y = f(x)= ^ = х1'т,
обратную по отношению к функции х = ут (см. также более полное
рассуждение, относящееся к случаю т = ^, на стр. 476). Поскольку
функция ж = ут имеет своей производной выражение тут~1, то мы
имеем
f(r) - Х - * . -L - 1 т.~т
откуда, делая подстановки у = ж1/™ и j/~m = ж, получим
*'(х) - J_2.i/(™-i)
В качестве следующего примера продифференцируем обратную
тригонометрическую функцию (см. стр. 326)
у = arctga; (что равносильно х = tgy).
Для того чтобы обеспечить однозначное определение функции у,
предположим, что переменная у, обозначающая меру угла в радианах,
ограничена промежутком -|тг < у < |тг.
1 ^CM.
1
COS2 I
стр
/
. 4K
sin2
i), ЧТО -
у + cos2
cos2 у
dy
У
1-
cos
btg2
V
У -
и
: 1
так
+ x
как
2
то можно заключить, что
d(arctgx) 1
dx I 4- х2'
Таким же точно путем читатель сможет вывести следующие формулы:
d(arcctgx) i
dx = ~ 1 + х2'
d(arcsin x)

488
Глава VIII
Рис. 272. у = sin
i/=sin0c2)
Рис. 273. у = sin(x2)
Наконец, мы приходим к следующему важному правилу:
е) Дифференцирование сложных функций. Сложные функции состав-
составляются из двух (или нескольких) простых (см. стр. 327). Например,
функция г = sin^x составлена из функций z = siny и у = ^/х; функ-
функция z = л/х + ч/ж** составлена из функций z = у + у5 и у = л/х; функ-
функция г = sin(x2) — из функций z = siny и у ~ ж2; функция z = sin i —
из функций z = siny и у = ^.
Если из двух данных функций
z = g(y) и у = f{x)
вторую подставить в первую, то получается сложная функция
z = к(х) = g[f(x)}.
Докажем справедливость формулы
k'(x)=g>(y)f(x).
С этой целью составим разностное отношение
D)
-к{х)
-X
zi-z
yi-у
-ж'
где г/1 = f(x\) и z\ = g(yi) = k(xi); при стремлении х\ к х левая
часть стремится к к'(х), а два множителя в правой части стремятся
соответственно к g'(y) и к /'(ж), чем и доказывается формула D).
В этом доказательстве было необходимо условие yi — у ф 0. В са-
самом деле, мы делили на Дг/ = у\ — у; поэтому нужно было считать
исключенными те значения х\, при которых ух - у = 0. Однако форму-
формула D) остается в силе даже в том случае, если Дг/ равно нулю в про-
промежутке, окружающем точку х. При этом предположении у остается

§ 3. Техника дифференцирования 489
постоянным, так что /'(ж) = 0; с другой стороны, и k(x) = g(y) оста-
остается постоянным относительно х (поскольку у не меняется при изме-
изменении х) и, следовательно, к'[х) = 0; итак, формула D) справедлива
также и в рассматриваемом случае.
Читатель должен проверить следующие примеры:
к(х) = sin \/х, к'(х) = (cos \fx) • ——,
2\Jx
к(х) = s/x -
>w™ > 2y/x'
k{x) = sin(a;2), k'(x) = cos(x2) • 2x,
KyXJ — Sill ~? К \X J — СОЬI ~ j * ~ j
^ ' X
k'{x) = ~1 • 2x = ~x
Упражнение. Сопоставляя результаты стр. 484 и стр. 487, доказать,
что функция
f(x) = V^7
имеет производную
f(x) = ii"""-1'
Теперь можно уже отметить, что все наши формулы, касающиеся
степеней х, могут быть объединены в одну общую:
При любом положительном или отрицательном рациональном г
функция
имеет производную
f'(x) = rxr-1.
Упражнения.
1) Произвести дифференцирования в упражнениях на стр. 477, пользуясь
только что выведенными правилами.
2) Продифференцировать следующие функции: xsina;, slnnx, (ж3 — Зж2 —
1+х
— х + IK, l+sin2a;, ж2 sin—, arcsin(cosnz), tg , arctg -z ,

490 Глава VIII
3) Найти вторые производные от некоторых из вышеприведенных функ-
функций и от следующих функций:
ж, arctgx, sin2 ж, tga;.
4) Продифференцировать функцию
U = С1^/(Ж - XlJ +Vl + C2\j{x ~ X2J +yi
и доказать минимальные свойства отраженного и преломленного луча,
установленные в главе VII, стр. 380. Предполагается, что отражение и
преломление происходят в точке на оси х и что данные начальная и
конечная точки заданы координатами (xi, уг) и (жг, j/г).
(Примечание: производная от этой функции обращается в нуль только
в одной точке, и поскольку в этой точке неизбежно имеется минимум,
а не максимум, нет необходимости исследовать вторую производную.)
Дальнейшие задачи на максимум и минимум.
5) Найти экстремумы следующих функций, наметить их графики, опре-
определить промежутки возрастания, убывания, выпуклости и вогнутости:
3 1 Ж2 2
X ОЖ ~\~ Ji. ~, т, COS Ж.
1 + х2 1 + ж4
6) Изучить максимумы и минимумы функции ж3 + Зож + 1 в зависимости
от значения параметра а.
7) Которая из точек гиперболы 2у2 —ж2 = 2 — самая близкая к точке ж = 0,
» = 3?
8) Из всех прямоугольников данной площади найти прямоугольник с са-
самой короткой диагональю.
9) Вписать прямоугольник наибольшей площади в эллипс
о Ь
10) Из всех круговых цилиндров данного объема найти цилиндр с наимень-
наименьшей поверхностью.
§ 4. Обозначения Лейбница и «бесконечно малые»
Ньютон и Лейбниц умели находить интегралы и производные как
пределы. Но самые основания анализа были долго окружены таинст-
таинственностью вследствие нежелания признать за понятием предела ис-
исключительного права быть источником новых методов. Ни Ньютон,

§4. Обозначения Лейбница и «бесконечно малые» 491
ни Лейбниц не смогли занять ту отчетливую позицию, которая нам
кажется простой и естественной теперь, когда понятие предела полнос-
полностью выяснено. Их пример господствовал больше столетия, в течение
которого сущность дела была затемнена бесплодными рассуждениями
о «бесконечно малых величинах», о «дифференциалах», о «последнем от-
отношении» и т. д. Неохота, с которой эти понятия были, в конце концов,
отвергнуты, глубоко коренилась в философских концепциях того вре-
времени и в самой природе человеческого мышления. Казалось, что можно
рассуждать так: конечно, интеграл и производную можно вычислить
как пределы. Но все же, в конце концов, чем же являются эти объек-
объекты «в себе», независимо от того специфического способа их описания,
каким является предельный переход? Ведь интуитивные понятия —
такие, как площадь или наклон кривой, — имеют как будто бы абсо-
абсолютный смысл «в себе», и нет надобности в привлечении каких-либо
вспомогательных вписанных многоугольников или секущих и их пре-
пределов. Без сомнения, желание сформулировать адекватные определения
площади или наклона кривой как «вещей в себе» вполне оправдано с пси-
психологической точки зрения. Но при зрелых установках, которые так
часто расчищали путь к подлинному прогрессу мысли, приходится от-
отбросить это желание и в предельном переходе видеть их единственное
приемлемое в научном смысле определение. В XVII в. не было интел-
интеллектуальных традиций, которые допускали бы такой радикализм.
Попытка Лейбница «объяснить» производную стоит в непосредст-
непосредственной и безупречной связи с введенным им обозначением для разност-
разностного отношения функции /(ж)
Ay = f(xi)-f(x)
Ах хг-х
Предел этого отношения, т. е. производную (которую мы, следуя обы-
обычаю, введенному впоследствии Лагранжем, обозначили через f'(x)),
Лейбниц записывает с помощью символа
dx'
заменяя, таким образом, символ разности «дифференциальным симво-
символом» d. Никаких трудностей и никакой таинственности не возникает
при условии ясного понимания того, что этот символ является всего
лишь указанием на необходимость осуществить предельный переход
при Ах —> О, что влечет за собой Ау —> 0. До перехода к пределу

492 Глава VIII
Ay
в разностном отношении -г-2- нужно сократить числитель и знамена-
знаменатель на Дж или суметь преобразовать это отношение так, чтобы пе-
переход к пределу совершался безболезненно. Это и является в каждом
отдельном случае узловым пунктом процесса дифференцирования. Ес-
Если бы мы попробовали перейти к пределу без таких предварительных
А у г»
сокращений, то получили бы не имеющее смысла выражение -^~- = Н
что не принесло бы нам никакой пользы. Таинственность и неясность
наступают только в том случае, если мы, по примеру Лейбница или
многих его последователей, стали бы говорить нечто подобное следую-
следующему: «Дж не стремится к нулю. Напротив, «последнее значение» Дх
не есть нуль, а является «бесконечно малой величиной», «дифференци-
«дифференциалом)}, обозначаемым символом dx; аналогично Ду имеет «последнее»
бесконечно малое значение dy. Настоящее отношение этих бесконеч-
бесконечно малых дифференциалов есть опять обыкновенное число /'(ж) = ~».
(XX
Поэтому Лейбниц и называл производную «дифференциальным отноше-
отношением». Такие бесконечно малые величины рассматривались как некие
новые числа, хотя и отличные от нуля, но меньшие любого положитель-
положительного числа из системы действительных чисел.
Считалось, что такие понятия доступны лишь немногим избран-
избранным, обладающим настоящим математическим чутьем, и что анализ
поэтому, по существу, очень труден, так как не всякий обладает этим
чутьем или может его развить. Интеграл, аналогичным образом, рас-
рассматривался как сумма «бесконечно большого числа бесконечно малых
слагаемых», а именно вида f{x)dx. Существовало представление, буд-
будто такая сумма есть интеграл или площадь, в то время как вычисле-
вычисление ее значения как предела последовательности конечных сумм обык-
обыкновенных слагаемых J(xj)Axj рассматривалось как некий придаток.
Теперь мы попросту отбрасываем желание «непосредственного» объяс-
объяснения и определяем интеграл как предел последовательности конечных
сумм. Этим путем все трудности устраняются, и все, что ценно в ана-
анализе, приобретает твердую основу.
Несмотря на все сказанное выше, в дальнейшем употребление обо-
обозначений Лейбница: -~ — для производной и / f(x)dx — для интег-
интеграла, не только сохранилось, но и оказалось чрезвычайно полезным.
Против такого употребления нечего возразить, если не упускается из
виду, что символ d есть только символ перехода к пределу. Преиму-
Преимущество обозначений Лейбница состоит в том, что с пределами отноше-
отношений или сумм можно в какой-то мере оперировать так, «как если бы»

§4. Обозначения Лейбница и «бесконечно малые» 493
они были в самом деле отношениями или суммами. Подсказывающая
сила этой символики всегда вводила в соблазн приписывать этим сим-
символам некоторый совершенно нематематический смысл. Если не подда-
поддаваться этому соблазну, то обозначения Лейбница являются по меньшей
мере превосходным сокращением более громоздких явных выражений,
содержащих предельный переход; по существу же они совершенно не-
необходимы в более развитых частях теории.
Например, правило d) (стр. 486) дифференцирования функции х —
= g(y), обратной по отношению к функции у = /(ж), заключалось в ра-
равенстве g'{y)f'{x) = 1. В обозначениях Лейбница оно выглядит следую-
следующим образом: — f- = 1, т. е. так, «как если бы» можно было сокращать
ау ах
на дифференциалы подобно тому, как это делается с обыкновенными
дробями. Аналогично запись в дифференциальной форме выведенного
на стр. 488 правила е) дифференцирования сложной функции z = k(x),
где
имеет вид
dz. _ dz_ dy
dx dy dx
Кроме того, обозначения Лейбница обладают еще и тем преиму-
преимуществом, что они указывают явно на самые величины х, у, z в большей
степени, чем на их функциональные взаимоотношения. Последние вы-
выражают процедуру или совокупность операций, с помощью которых из
одной величины х получается другая у; например, функция у = /(ж) =
= х2 определяет величину у, равную квадрату величины х. Именно
сама операция, в данном случае возвышение в квадрат, есть предмет
внимания математики. Физики же или инженеры в первую очередь ин-
интересуются самими величинами. Поэтому акцентирование самих вели-
величин в обозначениях Лейбница имеет особенную привлекательность для
лиц, занимающихся прикладной математикой.
Присоединим еще одно замечание. В то время как «дифференциалы»
в качестве бесконечно малых величин из математического обихода из-
изгнаны теперь окончательно, и не без позора, само слово «дифференциал»
прокралось обратно через заднюю дверь, правда, на этот раз для того,
чтобы обозначить безукоризненно законное и полезное понятие. Теперь
оно обозначает просто разность Дж, когда Да; мало по сравнению с дру-
другими рассматриваемыми величинами. Но здесь мы не можем вступить
в обсуждение роли, которую это понятие играет в приближенных вы-
вычислениях. Не можем мы также рассматривать другие математические

494
Глава VIII
объекты, законно именуемые «дифференциалами» и в некоторых слу-
случаях показавшие себя весьма полезными в анализе и его приложениях
к геометрии.
§ 5. Основная теорема анализа
1. Основная теорема. Понятие об интегрировании, и в неко-
некоторой мере о дифференцировании, было хорошо развито раньше работ
Ньютона и Лейбница. Но было совершенно необходимо сделать одно
очень простое открытие, для того чтобы дать толчок к огромной эволю-
эволюции вновь созданного математического анализа. Два как будто бы вза-
взаимно не соприкасающихся предельных процесса, употребляемые один
для дифференцирования, другой для интегрирования функций, оказа-
оказались тесно связанными между собой. В самом деле, они являются вза-
взаимно обратными операциями, подобно таким операциям, как сложение
и вычитание, умножение и деление. Дифференциальное и интегральное
исчисления представляют собой нечто единое.
Великое достижение Ньютона и Лейбница заключается в том, что
они впервые ясно осознали и использовали эту основную теорему ана-
анализа. Без сомнения, их открытие лежало на прямом пути естественного
научного развития, и нисколько не удивительно, что различные лица
пришли независимо и почти одновременно к ясному пониманию ука-
указанного выше обстоятельства.
Для того чтобы точно сформулировать
основную теорему, рассмотрим интеграл от
функции у = /(ж) в пределах от постоянного
числа а до числа х, которое будем считать
переменным. Чтобы не смешивать верхнего
предела интегрирования х с переменной, фи-
гурирующей под знаком интеграла, запишем
интеграл в следующем виде (см. стр. 459):
Рис. 274. Интеграл как
функция верхнего предела
X
F(x) = J f(u)du,
A)
демонстрируя таким образом наше намерение изучать интеграл как
функцию F{x) своего верхнего предела (рис. 274). Эта функция F(x)
есть площадь под кривой у = f(u) от точки и = а до точки и = х.
Иногда интеграл F{x) с переменным верхним пределом называют «не-
«неопределенным интегралом».

§ 5. Основная теорема анализа
495
Основная теорема анализа читается следующим образом:
Производная неопределенного интеграла A) по его верхнему преде-
пределу х равна значению функции f(u) в точке и — х:
F'(x) = f{x).
Другими словами, процесс интегрирования, ведущий от функции /(ж)
к функции F(x), «уничтожается» обратным ему процессом дифферен-
дифференцирования, применяемым к функции F{x).
На интуитивной основе доказатель-
доказательство этого предложения не представляет У>-
труда. Оно базируется на интерпретации
интеграла F(x) как площади, и было бы
затемнено, если бы мы попытались пред-
представлять функцию F(x) в виде графика
и истолковывать производную F'(x) как О
соответствующий наклон. Оставляя в сто-
стороне установленную ранее геометричес- ^ис- ^75. К доказательству
кую интерпретацию производной, мы со- основной теоремы
храним геометрическое толкование интеграла F(x) как площади, а диф-
дифференцировать функцию F(x) станем аналитическим методом. Раз-
Разность
F(Xl)-F(x)
есть просто площадь под кривой tj = f(u) между пределами и = Х\
и и — х (рис. 275), и нетрудно понять, что числовое значение этой
площади заключено между числами (xi — х)т и (xi — х)М:
- х)т
- F(x) < (an - х)М,
где М и т являются (соответственно наибольшим и наименьшим зна-
значениями функции /(и) в промежутке от и = х до и = Х\. Действитель-
Действительно, эти произведения дают площади двух прямоугольников, из которых
один содержит рассматриваемую криволинейную область, а другой со-
содержится в ней.
Отсюда следует:
т
F(xi) - F(x)
- х
Предположим, что функция /(к) непрерывна, так что при стрем-
стремлении Х\ к х обе величины М ит стремятся к значению функции /(к)

496 Глава VIII
в точке и = х, т.е. к значению /(х). В таком случае можно считать
доказанным, что
РЦ^1 = т. B)
Интуитивный смысл этого результата заключается в том, что при воз-
возрастании скорость изменения площади под кривой у = /(ж) равна вы-
высоте кривой в точке ж.
В некоторых руководствах содержание этой основной теоремы за-
затемняется вследствие неудачно выбранной терминологии. Именно, мно-
многие авторы сначала вводят понятие производной, а затем определяют
«неопределенный интеграл» просто как результат операции, обратной
по отношению к дифференцированию: они говорят, что функция G(x)
есть неопределенный интеграл от функции /(ж), если
G'(x) = f(x).
Таким образом, этот способ изложения непосредственно связывает диф-
дифференцирование со словом «интеграл». Только позднее вводится поня-
понятие «определенный интеграл», трактуемое как площадь или как пре-
предел последовательности сумм, причем недостаточно подчеркивается,
что слово «интеграл» обозначает теперь нечто совершенно другое, чем
прежде. И вот оказывается, что самое главное, что содержится в тео-
теории, приобретается лишь украдкой — через заднюю дверь, и учащий-
учащийся встречается с серьезными затруднениями в своих усилиях понять
существо дела. Мы предпочитаем функции G(x), для которых G'(x) —
= /(ж), называть не «неопределенными интегралами», а первообразными
функциями от функции f(x). Тогда основная теорема может быть сфор-
сформулирована следующим образом:
Функция F(x), являющаяся интегралом от функции f(x) при по-
постоянном нижнем и переменном верхнем пределе х, есть одна из пер-
первообразных функций от функции /(ж).
Мы говорим «одна из» первообразных функций по той причине, что
если G(x) является первообразной функцией от /(ж), то непосредствен-
непосредственно ясно, что и любая функция вида #(ж) = G{x) + с (с — произвольная
постоянная) есть также первообразная, так как Н'(х) = G'(x). Обрат-
Обратное утверждение также справедливо. Две первообразные функции G{x)
и Н(х) могут отличаться одна от другой не иначе, как постоянным
слагаемым. Действительно, разность U(x) = G(x) — Н(х) имеет в ка-
качестве производной С/'(ж) = G'(x)-H'(x) =/(ж)-/(ж) = 0, т.е. эта раз-
разность постоянна, так как очевидно, что если график функции в каждой

§5. Основная теорема анализа 497
своей точке горизонтален, то сама функция, представляемая графиком,
непременно должна быть постоянной.
Это ведет к очень важному правилу вычисления интеграла в пре-
пределах от а до Ь — в предположении, что нам известна какая-либо пер-
первообразная функция G{x) от функции /(ж). Согласно нашей основной
теореме, функция
х
F{x) = [ f(u)du
есть также первообразная функция от функции /(ж). Значит, F(x) =
= G(x)+c, где с — постоянная. Значение этой постоянной определится,
если мы примем во внимание, что F(a) = / f(u)du = 0. Отсюда
сле-
следует: 0 = G(a) + с, так что с = — G(a). Тогда определенный интеграл
в пределах от а до ж тождественно удовлетворяет равенству
F(x) = / f{u)du = G{x) - G{a);
a
замена х через b приводит к формуле
f(u)du = G(b) - G(a), C)
/¦
независимо от того, какая именно из первообразных функций была
«пущена в ход». Другими словами: чтобы вычислить определенный ин-
ь
теграл I f(x)dx, достаточно найти такую функцию G(x), для кото-
а
рой G'{x) = f(x), и затем составить разность G(b) — G(a).
2. Первые применения. Интегрирование функций xr, cos x,
sin ж. Функция arctga;. Здесь невозможно дать исчерпывающее
представление о роли основной теоремы, и мы ограничимся тем, что
приведем несколько выразительных примеров. В задачах, встречаю-
встречающихся в механике и физике или в самой математике, очень часто
приходится подсчитывать числовое значение некоторого определен-
определенного интеграла. Прямая попытка найти интеграл как предел может

498 Глава VIII
быть непреодолимо трудной. С другой же стороны, как мы это ви-
видели в § 3, любое дифференцирование выполняется сравнительно лег-
легко, и без труда возможно накопить очень большое количество формул
дифференцирования. Каждая такая формула G'(x) = f(x), обратно, мо-
может быть рассматриваема как формула, определяющая первообразную
функцию G(x) от функции /(ж).
Формула C) позволяет использовать известную первообразную
функцию для вычисления интеграла от функции /(х) в некотором дан-
данном промежутке.
Если мы, например, хотим найти интегралы от степеней ж2, ж3,
или в общем виде, хп, то самое простое — это действовать, как ука-
указано в § 1. По формуле дифференцирования степени производная от хп
равна пхп~1, так что производная от функции
есть функция
«." + !
В таком случае функция ——- является первообразной функцией
по отношению к функции /(ж) = ж™, а следовательно, мы немедленно
получаем формулу
о
/
ж" dx = G(b) - G(a) = " .
Это рассуждение несравненно проще громоздкой процедуры непосред-
непосредственного вычисления интеграла как предела суммы.
Как более общий случай, мы нашли в § 3, что при любом рациональ-
рациональном s как положительном, так и отрицательном, производная функ-
функции ж8 равна sx"~1, а потому при s = г + 1 функция
имеет производную f(x) = G'(x) = xr (мы предполагаем, что г ф — 1,
х
т.е. что s ф 0). Итак, функция х есть первообразная функция, или

§5. Основная теорема анализа 499
«неопределенный интеграл» от хг, и мы получаем (при положительных а
и Ь и при г ф — 1) формулу
ь
В формуле D) приходится предполагать, что стоящая под интегралом
функция хт определена и непрерывна в промежутке интегрирования, так что
нужно исключить точку х = О, если г < 0. Вот потому мы и вынуждены
допустить, что в этом случае о и b положительны.
Если положим G{x) = — cosx, то получим G'(x) = sinx, и отсюда
возникает соотношение
а
sin х dx = — (cos a — cos 0) = 1 — cos a.
о
а
/
Аналогично, если G{x) = sinx, то G'(x) = cosa;, и, значит,
cos x dx = sin a — sin 0 = sin a.
/<
Особенно интересный результат получается из формулы диффе-
дифференцирования функции arctgx:
d(arctgx) i
dx 1 + x2'
Раз функция arctgx есть первообразная по отношению к функ-
функции —=^-г-, то на основании формулы C) можно написать
1 + х
ь
arctg Ь — arctg 0 = г dx.
J l + xz
о
Но arctg 0 = 0 (нулевому значению тангенса соответствует нулевое
значение угла). Итак, мы имеем
ь
arctg Ь = / dx. E)
J 1 + х

Глава VIII
В частности, если Ь = 1, то arctgb равно j
(значению тангенса, равному 1, соответ-
соответствует угол в 45°, что в радианной мере
составляет j). Таким образом, мы полу-
получаем замечательную формулу
О
Рис. 276. Площадь под кри-
1
вой у = в пределах
1 + х
от 0 до 1 равна —
2L= /_J,
4 J 1 + :
dx.
F)
Это показывает, что площадь под графи-
графиком функции у = —-—- в пределах от х =
1 +г
= 0 до х = 1 равна четверти площади единичного круга.
3. Формула Лейбница для тт. Последний результат приво-
приводит к одной из красивейших математических формул, открытых
в XVII в., — к знакопеременному ряду Лейбница, позволяющему вы-
вычислять 7г:
9 11
G)
Символ + ... следует понимать в том смысле, что последовательность
конечных «частных сумм», получающихся, когда в правой части ра-
равенств берется лишь п членов суммы, стремится к пределу — при не-
неограниченном возрастании п.
Чтобы доказать эту замечательную формулу, нам достаточно
вспомнить формулу суммы конечной геометрической прогрессии
l-gn
i-q
„П-1
или
1-q ~ ' H ' ч ч ^ 1-g-
Если в последнее алгебраическое тождество подставим g = — х2, то
получим
1
= 1-х2+х4-х6
(8)

§5. Основная теорема анализа 501
где «остаточный член» Rn выражается формулой
„2п
n = (-1)
п X
1+Х
,2'
Равенство (8) можно проинтегрировать в пределах от 0 до 1. Следуя
правилу а) из § 3, мы должны взять в правой части сумму интегралов
от отдельных слагаемых. На основании D) мы знаем, что
о
L77
771 -J
т
откуда, в частности, получим / х dx = г-, а следовательно,
J т + 1
о
1
0>Х 1 1,1 1 , , / л\п—1 1
3^5 7^"-^v X! 2п-1
i
/r2n
—-—- dx. Согласно формуле E), левая часть форму-
1 + х
о
лы (9) равна ~. Разность между j и частной суммой
+ +
5п = 13 + 5"-+ 2п-1
равна ? — 5„ = Тп. Остается доказать, что Т„ стремится к нулю при
возрастании п. Мы имеем неравенство
Вспомнив формулу A3) § 1, устанавливающую неравенство
ь ь
/ f(x)dx ^ / g{x)dx при /(ж) ^ g(x) и а < Ъ,

502 Глава VIII
мы видим, что
1 1
/о /*
™Ап I о
1 + X J
о о
Правая часть в этом неравенстве, согласно формуле D), равна ;
поэтому \Т„\ < . Окончательно имеем неравенство
1
" 2п + У
Так как стремится к нулю, то это и показывает, что 5„ стремит-
стремится к j при возрастании п. Таким образом, формула Лейбница доказана.
§ 6. Показательная (экспоненциальная) функция
и логарифм
Концепции анализа предоставляют возможность построить гораздо
более полную теорию логарифма и показательной функции, чем это де-
делает та элементарная процедура, которая лежит в основе обычного пре-
преподавания в школе. Там обычно отправляются от целых степеней а™ по-
положительного числа а, а затем определяют корень а1/ = л/а, получая,
таким образом, значения аг при любом рациональном показателе г =
— щ. Затем значение степени ах при иррациональном х определяется
так, что ах должна быть непрерывной функцией от х, — деликатный
вопрос, обыкновенно опускаемый в элементарном изложении. Наконец,
логарифмом числа у при основании а называется функция, обратная по
отношению к показательной функции у = ах.
В последующем изложении теории этих функций, построенном на
основах анализа, ход мыслей — противоположный. Мы начнем с лога-
логарифма, а затем придем к показательной функции.
1. Определение и свойства логарифма. Эйлерово чис-
число е. Определим логарифм, или, точнее говоря, «натуральный лога-
логарифм» F(x) = In а; (его связь с обычным десятичным логарифмом бу-
будет установлена в пункте 2), как площадь под кривой у — ^ в пределах
от и = 1 до и = х, или, что сводится к тому же, как следующий интег-
интеграл:
X
F(x)=lnx= f \du A)

§6. Показательная (экспоненциальная) функция и логарифм 503
(см. рис. 5, стр. 56). Здесь переменная ж может быть любым положи-
положительным числом. Нуль исключается потому, что при стремлении и к ну-
нулю функция, стоящая под интегралом, становится бесконечной.
Естественно заняться изучением функции F(x). Мы знаем, что
первообразная функция по отношению к любой степени хп представля-
п + 1
ет собой функцию того же типа, так как равна ; исключительной
является степень п = —1. В этом последнем случае знаменатель п + 1
превратился бы в нуль, и формула D) стр. 499 потеряла бы смысл. Та-
Таким образом, можно ожидать, что изучение интеграла от функции ^
или ^ приведет к новому (и интересному) типу функции.
Хотя мы и принимаем формулу A) за определение функции In ж,
однако мы не «знаем» самой функции, пока не установим ее свойств и не
найдем способов находить ее числовые значения. Нужно заметить, что
для современных методов в анализе очень характерно то, что мы от-
отправляемся от общих понятий — таких, как площадь или интеграл, и на
основе этих понятий, далее, устанавливаем определения, подобные A);
затем выводим свойства определяемых объектов и лишь в конце кон-
концов, приходим к явным выражениям, позволяющим вычислять их чи-
числовые значения.
Первое важное свойство функции In ж непосредственно следует из
основной теоремы § 5. Согласно этой теореме справедливо равенство
F'(x) = i. B)
Из формулы B) следует, что производная F(x) всегда положительна,
а это указывает, очевидно, на то, что функция In ж монотонно возрас-
возрастает при возрастании х.
Главное свойство логарифма выражается формулой
\na + \nb = ln(ab). C)
Значение этой формулы в практических применениях логарифмов
к числовым выкладкам хорошо известно. Формулу C) можно было бы
получить интуитивно, воспользовавшись площадями, определяющими
три величины, а именно: In a, In Ь и \n(ab). Но мы предпочтем развер-
развернуть доказательство, типичное для анализа: наряду с функцией F(x) =
= In ж, рассмотрим другую функцию
к(х) — 1п(аж) = Inw = F(w),
полагая w = /(ж) = ах, где а — произвольная положительная посто-
постоянная. Функцию к(х) можно легко продифференцировать с помощью

504 Глава VIII
правила е) из § 3: к'(х) = F'(w) • f'(x). Вследствие формулы B) и по-
поскольку f'{x) = а, это выражение принимает вид
к'(т) = а = а = *
*¦ ' w ах х'
Итак, функция к(х) имеет ту же производную, что и функция F(x);
раз так, то, согласно сказанному на стр. 496, мы имеем тождество
Щах) ~ к{х) = F{x) + с,
где с есть постоянная, не зависящая от значения переменной х. Кон-
Константа с определяется с помощью простой подстановки х = 1 в послед-
последнем равенстве. Из определения A) следует, что
F(l) =lnl = 0
(так как интеграл, взятый в качестве определения, при значении х = 1
имеет равные верхний и нижний пределы). Теперь мы можем написать
к{\) = 1п(а • 1) = In а = In 1 + с = с,
т.е. с = In а, а потому при любом х справедливо тождество
ln(ax) = In a + In ж. (За)
Полагая х = Ь, мы получим, наконец, искомую формулу C).
В частности, при а = х мы найдем последовательно, что и далее
D)
— nlnx.
Из равенств D) можно заключить, что при неограниченном возраста-
возрастании х значения функции In а; также возрастают неограниченно. Доста-
Достаточно заметить, например, что
lnB") = nln2,
причем правая часть, очевидно, неограниченно возрастает вместе с п,
и вспомнить, что было установлено свойство монотонного возрастания
функции In ж. Далее, мы имеем

§6. Показательная (экспоненциальная) функция и логарифм 505
так что
| E)
Наконец, справедливо равенство
1пхг = г In ж F)
при любом рациональном показателе г — Щ. В самом деле, полагая
хТ = и, мы получаем
m
п In и = In ип = In х п '" = In zm = minx,
откуда следует
'п = Щ \пх.
Поскольку In а; есть монотонная и непрерывная функция от х, при-
принимающая значение 0 при х = 1 и стремящаяся к бесконечности при
неограниченном возрастании х, должно существовать некоторое чис-
число х, большее чем единица, и такое, что для него будет иметь место ра-
равенство In а; = 1. Следуя Эйлеру, обозначим это число буквой е. (Тож-
(Тождественность этого определения с определением, данным на стр. 345,
будет доказана позднее.) Итак, число е определено уравнением
1пе = 1. G)
Мы ввели число е, опираясь на свойство непрерывных функций, обес-
обеспечивающее существование корня этого уравнения. Теперь мы продол-
продолжим наше изыскание, чтобы как следствие получить явные формулы,
позволяющие вычислить е с какой угодно точностью.
2. Показательная (экспоненциальная) функция. Сумми-
Суммируя наши предыдущее результаты, мы можем сказать, что функция
F(x) = \пх равна нулю при х = 1; монотонно возрастает до бесконеч-
бесконечности при х —> оо (но при этом график имеет убывающий наклон, рав-
равный величине ^); при значениях х, меньших единицы, выражается при
помощи функции — 1п^, так что In ж стремится к отрицательной бес-
бесконечности при х —> 0.
Монотонный характер возрастания функции у = In ж позволяет рас-
рассматривать обратную ей функцию
х = Е(у),

506
Глава VIII
О
= \пх
Рис. 277. у = \пх
х=Е(у)
О\
Рис. 278. х = Е{у)
график которой (рис. 278) получается обычным путем из графика функ-
функции у — In а; (рис. 277); эта обратная функция определена при всех зна-
значениях у от —оо до +оо. При у —> — оо функция Е(у) стремится к нулю;
при у -> оо, с другой стороны, Е(у) —> оо. Рассматриваемая функция Е
обладает следующим основным свойством:
Е{а)-Е{Ь) = Е(а
(8)
при любой паре значений а и Ъ. Последнее тождество есть просто ви-
видоизменение формулы C), выражающей свойство логарифма. Действи-
Действительно, если мы придадим формуле C) вид Inх + In z = \n(xz) и затем
положим
Е(а) = х, Е{Ъ) = z (т.е. а = lnx, b = lnz),
то будем иметь
а отсюда вытекает
ln(xz) = In x + In z = a + b,
E(a + b) = xz = E(a) ¦ E(b),
что и требовалось доказать.
Так как, по определению, lne = 1, то имеет место соотношение
присоединяя к этому формулу (8), получим равенство е2 = ЕA)-ЕA) =
= ЕB) и т.д. Вообще
Е(п) = е"

§6. Показательная (экспоненциальная) функция и логарифм 507
при любом целом п. Аналогично можно получить е(~) = е1/", так что
v
полагая затем ^ = г, заключаем, что
Е(г) = ег
при любом рациональном г. Поэтому вполне естественно определить
иррациональную степень числа е по формуле
еу = Е(у),
справедливой при любом действительном у, поскольку функция Е не-
непрерывна при всех значениях у и тождественна с функцией еу при
рациональных значениях у. Формулу (8), выражающую основное свой-
свойство функции Е или по общепринятой терминологии экспоненциальной
(показательной) функции, теперь можно выразить при помощи равен-
равенства
которое тем самым установлено для произвольных рациональных или
иррациональных значений а м Ь.
Во всех этих рассуждениях мы относили логарифм и показатель-
показательную функцию к числу е как к «основанию», точнее, к «натуральному
основанию» логарифмов. Перейти от основания е к некоторому другому
положительному основанию не представляет труда. Начнем с рассмот-
рассмотрения натурального логарифма
а = \па
(что равносильно а = еа = е1па). Показательную функцию ах мы ста-
станем определять посредством следующего сложного выражения:
z = ax = еах = ех1аа. A0)
Например,
Юж = еж1п1°.
Назовем функцию, обратную по отношению к функции ах, логарифмом
при основании а; нетрудно понять, что натуральный логарифм от z есть

508 Глава VIII
произведение х на а: другими словами, логарифм числа z при основа-
основании а получается путем деления натурального логарифма числа z на
постоянный натуральный логарифм числа о. Если а = 10, то это число
(с четырьмя значащими цифрами) выражается следующим образом:
In 10 и 2,303.
3. Формулы дифференцирования функций ех, ах, Xs. Так
как показательную функцию мы определили как обратную по отноше-
отношению к функции у = In ж, то из правила дифференцирования обратных
функций (§ 3) вытекает, что
} (y), т.е.
-
Тх х
Е'(у) = Е{у).
Производная от «натуральной» показательной функции тождественно
равна самой функции. Это есть истинный источник всех свойств пока-
показательной функции и основная причина ее роли во всех приложениях,
как это станет видно в последующих разделах. Используя дифферен-
дифференциальные обозначения, мы можем записать формулу A1) в следующем
виде:
4~ех = ех. (Па)
ах
В более общем случае, дифференцируя сложную функцию
f(x)=ea*
с помощью правила, данного в § 3, мы получим равенство
f{x) = аеах = af(x).
Таким образом, полагая а = In а, мы найдем, что функция
f{x) = а*
имеет производную
fix) =axlna.
Переходя теперь к рассмотрению степенной функции
f(x) = х"

§6. Показательная (экспоненциальная) функция и логарифм 509
при любом действительном показателе s и при положительном пере-
переменном х, мы можем определить ее по формуле
Xs = eslnx.
Снова применяя правило дифференцирования сложной функции к слу-
случаю, когда f(x) = esz, z = In ж, мы найдем производную
f(x)=se" -1=
так что
f(x) = sx*-\
в полном соответствии с прежним правилом дифференцирования сте-
степенной функции при рациональном показателе s.
4. Явные выражения числа е и функций ех и In а; в виде
пределов. Для того чтобы найти явные формулы, выражающие эти
функции, мы используем формулы дифференцирования показательной
и логарифмической функции. Так как производная функции In ж рав-
равна ^, то, в силу определения производной, мы получаем соотношение
1 .. In хл — In х
- — hm при xi -> х.
х х\ — х
Положим яг1 = х + h и допустим, что h стремится к нулю, пробегая
последовательность h = ^ ^, j, ... , ^, ...; тогда, применяя правила
действий с логарифмами, мы получим
Если вместо i мы подставим z и перейдем к пределу, то написанное
выше соотношение примет вид
z = limln Il + ^J при п —)• оо.
Или, в терминах показательной функции,
при п->оо. A2)

510 Глава VIII
Мы получили общеизвестную формулу, определяющую показательную
функцию просто как предел. В частности, при z = 1 эта формула дает
A \™
1 + —J при п -> оо, A3)
а при z = — 1 получается
i=limfl-^j при га-> оо. A3а)
Эти выражения сразу ведут к разложениям в бесконечные ряды. По
биномиальной теореме можно написать
г га(га - 1) r2 rafra - 1)(га - 2) гз ~п
= 1 + пп+ 2! ~tf+ 3! rf n*'
или
Позволительно догадываться и нетрудно полностью доказать (подроб-
(подробности мы здесь пропускаем), что можно перейти к пределу при п —> оо
путем замены в каждом члене величины i на 0. Это дает хорошо
известный бесконечный ряд, который служит для вычисления функ-
функи, в частности, при х = 1 ряд, сходящийся к пределу е:
е = 1 + + + \ +
чем устанавливается идентичность е с тем числом, определение кото-
которого дано на стр. 345. При х = — 1 получается ряд
i = l_l + i-i4.
е 2! 3! 4! 5! '
который дает превосходное приближение уже при очень малом числе
членов, так как ошибка, которую мы совершаем, обрывая ряд на га-м
члене, меньше величины (га + 1)-го члена.

§6. Показательная (экспоненциальная) функция и логарифм 511
Пользуясь формулой дифференцирования показательной функции,
можно получить интересное выражение для логарифма. Имеет место
соотношение
Ph _ 1 ph „О
1 • С. X I • С. С. -1
am —-— = hm = 1,
/о ti ло h
так как указанный предел есть не что иное, как значение производной
от функции еу при у = 0, а таковое равно 1. Подставим в эту формулу
вместо h значение ^, где z — произвольное число, а п пусть пробегает
последовательность целых положительных чисел. Тогда мы получим
или
п( \[ё* -
при п —> со. Вводя обозначение z = In ж, или ez = x, можно окончатель-
окончательно написать
lnx = limn( \fx — 1) при п —> ос. A5)
Поскольку sfx —> 1 при п -> ос (см. стр. 373), формула A5) представля-
представляет логарифм в виде произведения двух множителей, из которых первый
стремится к бесконечности, а второй — к нулю.
Примеры и упражнения
Введение показательной и логарифмической функций доставляет воз-
возможность оперировать с функциями достаточно обширного класса и откры-
открывает доступ ко многим приложениям.
Продифференцировать: 1) хAпх — 1), 2) 1пAпа;), 3) 1п(ж + л/1 + ж2),
4) 1п(ж + л/1 — ж2), 5) е~х , 6) ее (сложная функция ег, где z = ех), 7) хх
(Указание: хх = ех1пх), 8) lntgx, 9) lnsinx; lncosx, 10) -^—.
In ж
Найти максимумы и минимумы функций: 11) хе~х, 12) х2е~х, 13) хе~ах.
* 14) Найти геометрическое место максимумов кривой у = хе~ах при
переменном параметре а.
15) Показать, что все последовательные производные от функции е~х
имеют вид произведения множителя е на многочлены от х последователь-
последовательно возрастающих степеней.
1
* 16) Показать, что производные n-го порядка от функции е г7 имеют
_ 1 1
вид произведения множителей е г7 • —— на многочлен степени In — 2.
х3п
* 17) Логарифмическое дифференцирование. Дифференцирование произ-
произведений может быть иногда упрощено путем применения основного свойства

512 Глава VIII
логарифма. Действительно, имея дело с произведением
Р(*) = /l (*)/2 (*).../»(*),
можно написать
, d(lnf2(x)) | |
dx
da; da; dx dx '
и дальше, с помощью формулы дифференцирования сложных функций, от-
отсюда следует
Ах1 = Ш + 1М+ /п(*)
() А() Ы) ' /()'
Воспользоваться этим при дифференцировании примеров
а) х(х + \){х + 2) + ... + (ж + п), Ь) хе~а*2.
5. Бесконечный ряд для логарифма. Вычисление логариф-
логарифмов. Числовые значения логарифмов вычисляются отнюдь не с по-
помощью формулы A5). Гораздо лучше приспособлено для этой цели
совершенно иное, более полезное, явное выражение, имеющее, кроме
того, большое теоретическое значение. С помощью метода, применен-
примененного на стр. 499 при вычислении тг, мы получим это выражение, опи-
опираясь на определение логарифма по формуле A). Но здесь необходим
один предварительный шаг: вместо функции In ж рассмотрим функ-
функцию у = 1пA + ж), составленную из функций у = In z и z — 1+х. Имеем:
dx dz dx z 1 + ж'
Итак, функция у = ln(l + ж) является первообразной по отноше-
отношению к функции т-^—, и мы заключаем, согласно основной теореме,
1 -(- X
что интеграл от функции -т-=— в пределах от 0 до ж равен выраже-
выражению 1пA + ж) - lnl = 1пA + ж); или, в символической записи,
х
- *) = I Лт. du A6)
(Эту формулу можно было бы, конечно, получить и интуитивно из гео-
геометрической интерпретации логарифма как площади. Сравните с рас-
рассуждением на стр. 503.)

§6. Показательная (экспоненциальная) функция и логарифм 513
В формулу A6) подставим вместо A+w) сумму геометрической
прогрессии, как мы это делали на стр. 499, а именно
из осторожности мы предпочитаем оперировать не с бесконечным ря-
рядом, а с конечной суммой и остаточным членом, который равен
#„ = (-1)
1+и'
Подставив эту сумму в формулу A6), можно применить правило по-
почленного интегрирования конечной суммы. Интеграл от степени и"
в пределах от 0 до ж равен ——-; таким образом, мы получим немед-
S ~т~ X
где остаточный член Т„ выражается интегралом
Покажем теперь, что Т„ стремится к нулю при возрастании п, предва-
предварительно условившись, что переменное х может быть лишь больше —1
и не превышать +1, т.е., другими словами, что выполнено неравенство
-1 < х < 1
(заметим, что х = +1 включается, в то время как х = —1 не включа-
включается). Согласно нашему предположению в промежутке интегрирования
переменное и больше, чем некоторое число —а, которое может быть
близко к —1, но во всяком случае больше, чем —1, так что —1 < —а < и.
Отсюда следует 0 < 1 —а < 1+w. Поэтому при условии, что и заключено
в промежутке от 0 до х, имеет место неравенство
<lu
1-а'
и, следовательно,

514 Глава VIII
или
Поскольку число 1 — а является постоянным, мы видим, что выраже-
выражение, стоящее справа, а следовательно, и стоящее слева \Тп\, при возрас-
возрастании п стремится к нулю; значит, из неравенства
г^^ A7)
вытекает, что при — 1 < х ^ 1 справедливо равенство
ln(l + a:) = *-y + y-^ + -.- A8)
Подставляя, в частности, z = 1, получаем любопытную формулу
1-| + ±-± + ... A9)
Эта формула по своей структуре похожа на выведенную раньше фор-
формулу, представляющую в виде ряда число j.
Ряд A8) не имеет большого практического значения для вычисле-
вычисления логарифмов, потому что область изменения величины 1 + х огра-
ограничена промежутком от 0 до 2, а также по той причине, что сходи-
сходимость ряда очень медленная: пришлось бы брать много членов, чтобы
получить сколько-нибудь точный результат. При помощи следующего
приема мы получим выражение, практически более удобное. Вместо х
в формулу A8) подставим — х:
1пA - х) = -х - f - ^ - 3? _ ... B0)
Вычитая, далее, формулу B0) из формулы A8) и применяя преобразо-
преобразование In а — In Ь = In a + In =¦ = In у, мы получим:
о о
Этот ряд сходится быстрее, и, кроме того, левая часть формулы может
теперь выразить логарифм любого положительного числа z, так как

§7. Дифференциальные уравнения 515
1 + х
уравнение ——— = z имеет при любом положительном z решение х, за-
заключенное между -1 и +1. Например, если нам нужно вычислить 1пЗ,
то мы положим х — i и тогда получим
1пЗ = In
2
9 1
Взяв всего лишь 6 членов, вплоть до члена —=-jy = , мы находим
значение
1пЗ = 1,0986
с пятью значащими цифрами.
§ 7. Дифференциальные уравнения
1. Определения. Главенствующая роль, которую показатель-
показательные и тригонометрические функции играют в математическом анали-
анализе и его применениях к задачам физики, основывается на том, что эти
функции являются решениями простейших «дифференциальных урав-
уравнений».
Дифференциальным уравнением относительно неизвестной функ-
функции и = f(x) с производной и' = f'(x) (обозначение и' очень удачно
сокращает обозначение f'(x), поскольку величина и и ее формальная за-
зависимость от х как функции f(x) не нуждаются в особенном подчерки-
подчеркивании) называется уравнение, содержащее функцию и, производную и'
и, может быть, независимое переменное х, как, например,
и = и + sin(xu)
или
и' + Зи = х2.
В более общем случае дифференциальное уравнение может содержать
вторую производную и" = f"{x) или производные более высокого по-
порядка, как, например, уравнение
и" + 2и' - Зи = 0.
Во всех подобных случаях задачей является нахождение функ-
функции и = f{x), удовлетворяющей данному уравнению.

516 Глава VIII
Решение дифференциальных уравнений есть широкое обобщение
задачи интегрирования, понимаемой как нахождение первообразной
функции по заданной функции g(x): последнее сводится к решению
простейшего дифференциального уравнения
и' = g(x).
Например, решениями дифференциального уравнения
х3
являются функции и = Цг- + с, где с — произвольное постоянное.
о
2. Дифференциальное уравнение экспоненциальной функ-
функции. Радиоактивный распад. Закон роста. Сложные проценты.
Показательная функция и = ех является решением дифференциального
уравнения
и' = и, A)
так как производная от показательной функции равна самой показа-
показательной функции. И вообще функция и = сех, где с — произвольное
постоянное, есть решение уравнения A). Аналогично функция
и = секх, B)
где с и к — две какие-нибудь постоянные, есть решение дифференци-
дифференциального уравнения
и' = ки. C)
Обратно, всякая функция и = f(x), удовлетворяющая уравнению C),
имеет вид B). В самом деле, пусть функции х = h(u) и и = f(x) вза-
взаимно обратные; в таком случае, следуя правилам дифференцирования
обратной функции, найдем
h' = — = —
и' ки
Функцией, первообразной по отношению к найденной производной ^-,
является функция Щ^; итак, х = h(u) = -—^ + Ь, где b — некоторое
постоянное. Отсюда
In и = кх — Ьк

j 7. Дифференциальные уравнения
517
и = екх ¦ е~ьк.
Полагая постоянную величину е Ьк
и = се
равной с, получим
кх
как и нужно было предвидеть.
Большое значение уравнения C) заключается в том, что оно «регу-
«регулирует» физические процессы, в которых количество и какого-нибудь
вещества представляет собой функцию времени
и = f(t)
и притом изменяется таким образом, что скорость изменения в каждый
момент пропорциональна количеству и вещества, имеющегося налицо.
В этом случае скорость изменения в момент t, т.е.
и' = f(t) = lim
/(*!)-/(*)
равна ku, где к — постоянный коэффициент пропорциональности, по-
положительный, если и возрастает, и отрицательный, если и убывает.
В обоих случаях функция и удовлетворяет дифференциальному урав-
уравнению C); следовательно, она имеет вид
и = cekt.
Постоянная с определена, если
известно количество вещества uq,
имевшееся налицо в начальный мо-
момент, т. е. при t = 0. Величину %
мы должны получить при подста-
подстановке t = 0 в уравнение B): и
Uc\ —— CG —— С*
отсюда и получается
и = ще . D) Рис. 279. Убывание по экспоненци-
экспоненциальному закону и = uoekt, к < 0
Следует обратить внимание на
то, что мы исходим из предположения, что задана скорость изменения

518 Глава VIII
величины и, и выводим закон D), который позволяет вычислить фак-
фактическое количество вещества и в любой момент времени t. Эта зада-
задача как раз противоположна задаче нахождения производной от какой-
нибудь функции.
Типичным примером явления указанного типа можно считать рас-
распад некоторого радиоактивного вещества. Пусть и = /(?) есть коли-
количество вещества в момент времени t; если принять гипотезу, что каж-
каждая индивидуальная частица вещества имеет некоторую определенную
вероятность распада и что эта вероятность не зависит от присутствия
других частиц, то скорость, с которой количество и будет распадаться
в данный момент времени t, будет пропорциональна общему количест-
количеству вещества и, имеющемуся налицо. Таким образом, функция и должна
удовлетворять уравнению C) при отрицательной постоянной к, которая
измеряет быстроту процесса распада; итак, вид функции следующий:
и — щеи.
Отсюда вытекает, что в равные, определенные, промежутки времени
подвергается распаду определенная, одна и та же, доля вещества, имею-
имеющегося налицо; действительно, если щ есть количество вещества, име-
имеющегося в момент времени ti, а «2 — в некоторый последующий мо-
момент времени t2, то
«2 _ p _ к
и последнее выражение зависит только от разности ti — t\. Вычис-
Вычислим, например, сколько времени потребуется для того, чтобы в про-
процессе распада осталась ровно половина вещества: нам нужно опреде-
определить з = <2 — h из уравнения
U2 _ 1 _ ке
ui ~ 2 '
и мы получаем
ks = Шт, s = -г—. E)
Напротив, зная s, можно определить к:

§7. Дифференциальные уравнения 519
Для каждого радиоактивного вещества значение s носит название «пе-
«периода полураспада». Число s или некоторое аналогичное (например, та-
такое, как значение г, при котором ~ = -Ш^) может быть найдено экс-
экспериментальным путем. Для радия «период полураспада» равен прибли-
приблизительно 1550 годам и, следовательно,
ч
ч
fc=1550=-°'0000447-
Отсюда мы находим, что
Примером закона, близкого к рассмотренному только что закону
показательной функции, может служить явление так называемых слож-
сложных процентов. Пусть некоторый капитал «о (долларов) отдан в рост из
расчета 3% (сложных) в год. По истечении одного года капитал станет
равным
щ = и0 A + 0,03) ;
по истечении двух лет он будет
«2 = wi(l + 0,03) = uo(l + 0,03J;
наконец, по истечении t лет он выразится числом
и*=«оA+0,03)*. F)
Теперь, если начисление процентов происходило бы не один раз в год,
а один раз в месяц, или, вообще, один раз в n-ю часть года, то по
истечении t лет наращенный капитал выразился бы формулой
Если предположить, что число п очень велико, так что проценты при-
считываются ежедневно или даже ежечасно, то, воображая, что п стре-
стремится к бесконечности, мы заметим, что величина, стоящая в скобках,
стремится к е0>03 согласно сказанному в § 6, и в пределе капитал по
истечении t лет выразится формулой
«ое0'03', G)

520 Глава VIII
что соответствует процессу непрерывного присчитывания сложных
процентов. Можно также вычислить время s, нужное для того, чтобы
удвоить основной капитал, отданный в рост по 3 сложных непрерывно
начисляемых процента. Мы имеем ^\ = 2, откуда s = -Ц^1п2 =
= 23,10. Итак, капитал удвоился бы по истечении приблизительно 23
лет.
Вместо того чтобы шаг за шагом проделывать описанную выше
процедуру и затем переходить к пределу, мы могли бы получить форму-
формулу G), просто сказав, что скорость и' возрастания капитала и пропор-
пропорциональна этому капиталу, с коэффициентом пропорциональности к =
= 0,03, согласно дифференциальному уравнению
и' = ки, где к = 0,03.
Тогда формула G) вытекала бы непосредственно из общей формулы D).
3. Другие примеры. Простейшие колебания. Показатель-
Показательная функция встречается часто в более сложных комбинациях. Напри-
Например, функция
и = е~к*\ (8)
где к — положительная константа, является решением дифференциаль-
дифференциального уравнения
и' = — 2кхи.
Функция (8) играет большую роль в теории вероятностей и в статис-
статистике, выражая, как говорят, «нормальный» закон распределения.
Тригонометрические функции и = cost и v = sint также удовле-
удовлетворяют простому дифференциальному уравнению. Прежде всего об-
обратим внимание на соотношения
и' = - sin t = —v, v' = cos t = и,
образующие «систему двух дифференциальных уравнений с двумя не-
неизвестными функциями». Дифференцируя вторично, мы находим
и" — —v' = —и, v" = и' = —v;
таким образом, обе функции и и v временного переменного t могут рас-
рассматриваться как решение одного и того же дифференциального урав-
уравнения
z" + z = 0. (9)

{7. Дифференциальные уравнения
521
О
-1 +
2/г t
z=s'm2t z = sm3t
Рис. 280. Гармонические колебания
Это — очень простое дифференциальное уравнение «второго порядка»,
т.е. уравнение, содержащее вторую производную от функции z. Оно,
или, лучше сказать, его обобщение, содержащее положительную посто-
постоянную к2,
z" + k2z = 0 A0)
(решениями которого являются функции z = coskt и z = sinkt), посто-
постоянно встречается при изучении теории колебаний, и потому «синусо-
«синусоидальные» кривые и = sinkt и и = coskt (рис. 280) в высшей степени
интересуют всех, кто занимается конструкцией механизмов, соверша-
совершающих или порождающих колебательные движения.
Следует заметить, что дифференциальное уравнение A0) представ-
представляет «идеальный» случай, когда трение или сопротивление предполага-
предполагаются отсутствующими.
В дифференциальном уравнении колебательного движения сопро-
сопротивление выражается лишним членом, а именно rz\ так что уравнение
имеет вид
rz'
k2z = 0;
(П)
его решениями являются «затухающие» колебания, выражающиеся ма-
математически с помощью формулы
rt
2 cos u>t
или
что графически представлено на рис. 281. (В качестве упражнения чи-
читатель пусть проверит правильность этих решений путем дифферен-
дифференцирования.) Затухающие колебания того же самого типа, что и обык-
обыкновенные синусоиды или косинусоиды, но с течением времени их раз-
размах уменьшается вследствие присутствия показательного множителя,

522
Глава VIII
Рис. 281. Затухающее колебание
убывающего более или менее быстро, в зависимости от величины ко-
коэффициента трения г.
4. Закон движения Ньютона. Хотя более подробный анализ
подобных явлений нами не предусмотрен, мы все же хотим включить
их в общую схему, на основе которой Ньютон произвел подлинную
революцию в механике и физике.
Рассмотрим вместе с Ньютоном движение некоторой частицы,
имеющей массу т; обозначим ее пространственные координаты, яв-
являющиеся функциями времени t, через x(t), y(t), z(t); таким обра-
образом, компоненты ускорения равны вторым производным x"(t), y"(t),
z"(t). В истории науки фактом решающего значения оказалось осозна-
осознание Ньютоном того, что величины тпх", my", mz" могут быть рас-
рассматриваемы как компоненты силы, действующей на частицу. С пер-
первого взгляда может показаться, что в этой формулировке содержится
всего лишь формальное определение понятия «силы». Но большой успех
Ньютона заключается в том, что он первый привел это определение
в соответствие с действительными явлениями природы: дело обстоит
так, как будто бы сама природа предоставляла силовое «поле», которое
мы можем считать известным, тогда как нам ничего не известно зара-

§ 7. Дифференциальные уравнения 523
нее об интересующем нас движении частицы в этом поле. Величайший
триумф Ньютона в динамике — оправдание им законов Кеплера о дви-
движении планет — ясно показывает полную гармонию между его матема-
математическими концепциями и явлениями природы. Прежде всего Ньютон
предположил, что сила тяготения обратно пропорциональна квадрату
расстояния. Если мы допустим, что Солнце находится в начале коорди-
координатной системы, и примем величины х, у, z за координаты данной пла-
планеты, то компоненты силы по направлениям трех координатных осей
будут равны соответственно
_ь.-^- -к-У- -к -?-
iT>J *»«* <р°
где к есть постоянная тяготения, не зависящая от времени, а г =
= л/х2 + у2 + z2 есть расстояние от Солнца до планеты. Эти выражения
определяют силовое поле независимо от движения в нем частицы. Из-
Известные нам данные, характеризующие это поле, нужно связать с об-
общим ньютоновым законом движения (т. е. связать кинематические и
динамические элементы); приравнивая два различных выражения век-
вектора, мы получим систему трех дифференциальных уравнений
и — кх
тх =
ту" =
{x2+y2 + z2fl2'
-ky
(ж2 + 2/2+_г2K/2'
// - kz
mz =
(x2 +y2 + ,
с тремя неизвестными функциями x(t), y(t), z(t). Эту систему можно
решить, и тогда обнаружится, что в полном согласии с кеплеровскими
эмпирическими наблюдениями орбита планеты есть коническое сече-
сечение с Солнцем в одном из фокусов; что площади, описываемые в рав-
равные промежутки времени радиусом-вектором, проведенным от Солнца
к планете, равны между собой и что квадраты периодов полного об-
обращения двух планет вокруг Солнца пропорциональны кубам их рас-
расстояний от Солнца. Доказательство этих утверждений мы вынуждены
опустить.
Задача о колебательном движении предоставляет более элементар-
элементарную иллюстрацию метода Ньютона. Предположим, что мы имеем час-
частицу, движущуюся по прямой линии, по оси х, и связанную с началом

524 Дополнение к главе VIII
\
координат силой упругости, что можно, например, осуществить с по-
помощью пружины или резинки.
Если частица выведена из положения равновесия (в начале коорди-
координат) и помещена в некоторую точку с координатой х, то сила потянет ее
назад. Мы предположим, что эта сила пропорциональна растяжению х;
так как она направлена к началу координат, то представится в виде
—к2х, где — к2 — отрицательный множитель пропорциональности, вы-
выражающий силу упругости пружины или резинки.
Мы предположим, далее, что налицо имеется трение, замедляющее
движение, и что это трение пропорционально скорости х' частицы с ко-
коэффициентом пропорциональности, равным -г. Тогда результирующая
сила в любой момент времени выразится через —к2х — гх', и, пользуясь
общим принципом Ньютона, мы приходим к уравнению тх" = —к2х —
— гх', или
тх" + гх' + к2х = 0.
А это — не что иное, как рассмотренное выше дифференциальное урав-
уравнение A1) затухающих колебаний. Предыдущий простой пример имеет
большое значение, так как многие колебания механических или элек-
электрических систем могут быть математически записаны с помощью
именно этого дифференциального уравнения. Здесь мы имеем типич-
типичный пример того, как отвлеченная математическая формулировка од-
одним ударом обнажает внутреннюю структуру многих, казалось бы, со-
совершенно различных и не связанных между собой отдельных явлений.
Подобного рода абстрагирование от частного характера данного явле-
явления и переход к общему закону, регулирующему обширный класс яв-
явлений, есть характерная черта математической трактовки физических
проблем.
Дополнение к главе VIII
§ 1. Вопросы принципиального порядка
1. Дифференцируемоеть. Понятие производной от некоторой
функции у = f(x) мы связывали с интуитивным представлением о ка-
касательной к графику этой функции. Но так как общая концепция функ-
функции чрезвычайно широка, то в интересах логической законченности не-
необходимо уничтожить эту зависимость от геометрической интуиции.
В самом деле, мы ведь не гарантированы от того, что интуитивные
свойства, бросающиеся в глаза при рассмотрении простых кривых, по-
подобных кругу или эллипсу, не исчезнут для графиков более сложных

§1. Вопросы принципиального порядка
525
Ук
О
Рис. 282. у = х + \х\
Рис. 283. у = \х
О
Рис. 284. у = х
функций. Рассмотрим, например, функцию, изображенную на рис. 282,
график которой имеет угловую точку.
Эта функция определяется уравнением у = х + \х\, где символом \х\
обозначается абсолютная величина х; иными словами,
у = х + х = 2х
у = х — х — 0
при х ^ О,
при х < 0.
Другим примером такого рода может служить функция у =
функция у =
а также
\х\ + (х — 1) + |х—1|. Графики этих функций в некоторых
точках перестают иметь определенную касательную, т. е. определенное
направление; это значит, что функция в соответствующих точках х не
имеет производной.
Упражнения.
1) Построить (т. е. записать с помощью конкретных аналитических вы-
выражений) функцию /(ж), график которой есть половина правильного
шестиугольника.
2) Где расположены угловые точки графика
Каковы точки разрыва производной /'(ж)?
В качестве простого примера недифференцируемости уже иного
типа приведем функцию
V = f(x) =xsini,
получаемую посредством умножения функции sin — (см. стр. 328) на
множитель х; положим, по определению, что f(x) = 0 при х — 0. Эта

526
Дополнение к главе VIII
у.-
функция, график которой для положи-
положительных значений переменного х изоб-
изображен на рис. 285, непрерывна в каждой
точке. График осциллирует бесконечно
часто в окрестности точки х = 0, при-
причем «волны» становятся бесконечно ма-
малыми, если мы приближаемся к нулю.
Наклон этих волн дается формулой
J \x) - smx ~ x cos x
(пусть читатель проверит это в ка-
качестве упражнения): при стремлении х
к нулю этот наклон осциллирует меж-
между все возрастающими положительной
и отрицательной границами. Мы мо-
можем сделать попытку найти производ-
производную в точке х = 0, переходя к пределу
при h —> 0 в разностном отношении
Рис. 285. у =
ДО +/О-ДО)
/isin i
h . 1
h h
Но при h -> 0 это разностное отношение осциллирует между -1 и +1
и не стремится ни к какому пределу, следовательно, функция не может
быть продифференцирована в точке х = 0.
Эти примеры указывают на трудности, внутренне присущие само-
самому вопросу. Вейерштрасс удивительно ярко иллюстрировал положение
вещей, построив непрерывную функцию, график которой не имеет про-
производной ни в одной точке. В то время как дифференцируемость влечет
за собой непрерывность, непрерывность, как показывает этот пример,
отнюдь не влечет за собой дифференцируемости; в самом деле, функция
Вейерштрасса всюду непрерывна, а вместе с тем нигде не дифферен-
дифференцируема. На практике трудности такого рода не встретятся. Обычно
встречающиеся кривые являются «гладкими» (за исключением разве
только отдельных изолированных точек), т.е. дифференцирование не
только возможно, но даже сама производная является непрерывной. Что
же в таком случае может нам помешать просто сделать оговорку, что
никакие «патологические» явления не будут фигурировать и задачах,
подлежащих нашему рассмотрению? Именно так и поступают в ана-
анализе те, кому приходится иметь дело только с дифференцируемыми

§1. Вопросы принципиального порядка 527
функциями. В главе VIII мы провели дифференцирование обширного
класса функции и тем самым доказали их дифференцируемость.
Поскольку дифференцируемость функции не есть логическая не-
неизбежность, она — с математической точки зрения — должна быть
или постулирована или доказана. В таком случае само понятие о ка-
касательной или о направлении кривой (первоначальный источник идеи
производной) ставится в зависимость от чисто аналитического опреде-
определения производной: если функция у = f(x) дифференцируема, т. е. если
f(x + h)-f(x) „
разностное отношение имеет единственный предел / ух)
при стремлении h к нулю с обеих сторон, то принято говорить, что со-
соответствующая кривая имеет касательную с наклоном f'(x). Таким
образом, наивная позиция Ферма, Лейбница и Ньютона в современном
анализе вывернута наоборот — в интересах логической стройности.
Упражнения.
1) Показать, что непрерывная функция, определенная формулой f(x) =
= ж2 sin — и добавочным условием /@) = 0, дифференцируема в точ-
точке х = 0.
2) Показать, что функция arctg j разрывна при х = 0, что функция
a; arctg — непрерывна в этой точке, но не имеет в ней производной,
и что функция х2 arctg ^ дифференцируема при х = 0. (В двух послед-
последних примерах следует положить значение функций при х = 0 равным
нулю.)
2. Интеграл. Совершенно подобным является положение с ин-
интегралом от непрерывной функции f(x). Вместо того чтобы «площадь
под кривой» принимать как величину, объективно существующую и ко-
которую a posteriori можно выразить с помощью предела последователь-
последовательности конечных сумм, этот предел в анализе принимают в качестве
определения интеграла. Эта концепция интеграла образует первичную
основу, из которой затем выводится понятие площади. Мы вынуждены
стать на эту точку зрения вследствие сознания того, что геометри-
геометрическая интуиция обладает известной расплывчатостью, когда она при-
применяется к таким общим аналитическим понятиям, как непрерывная
функция. Мы начнем с построения суммы

528 Дополнение к главе VIII
где Хо = a, Xi, ... , хп = b — точки деления промежутка интегриро-
интегрирования, Axj = Xj — Xj-i — приращение переменной х, или длина j-ro
частного промежутка, a Vj — произвольное значение переменного х
в этом частном промежутке, т.е. Xj-i sC Vj ^ Xj (мы можем взять,
например, Vj = Xj или Vj = Xj-\.)
Далее, мы образуем последовательность подобных сумм, в кото-
которых число п частных промежутков возрастает, причем длина мини-
минимального частного промежутка стремится к нулю. Тогда справедливо
следующее основное положение: сумма Sn, составленная для данной
непрерывной функции /(ж), стремится к некоторому определенному
пределу А, не зависящему от способа разбиения промежутка интегри-
интегрирования и от выбора точек Vj. По определению, этот предел есть ин-
-jn
теграл А = f(x)dx. Конечно, существование этого предела должно
о
быть аналитически доказано, если мы не хотим ссылаться на инту-
интуитивное геометрическое представление площади. Это доказательство
приводится в каждом руководстве анализа, учитывающем требования
математической строгости.
Сравнение дифференцирования и интегрирования приводит нас
к следующему противопоставлению. Свойство дифференцируемости,
несомненно, налагает ограничительное условие на класс всех непрерыв-
непрерывных функций; вместе с тем фактическое выполнение операции диффе-
дифференцирования сводится на практике к процедурам, основанным лишь
на нескольких простых правилах. В противоположность этому, каждая
непрерывная функция без исключения интегрируема, так как обладает
интегралом между любыми двумя данными пределами. Однако прямое
вычисление интегралов, понимаемых как пределы сумм, даже в случае
самых простых функций, вообще говоря, дело очень трудное. Но тут-то
и оказывается, что основная теорема анализа со многих случаях стано-
становится решающим орудием при осуществлении интегрирования. И все
же для большей части функций, в том числе даже для некоторых совер-
совершенно элементарных, интегрирование не дает простых явных выраже-
выражений, и числовые выкладки для интегралов требуют более продвинутых
методов.
3. Другие приложения понятия интеграла. Работа. Длина
кривой. Оторвав аналитическое представление интеграла от его пер-
первоначальной геометрической интерпретации, мы встречаемся с целым
рядом других, не менее важных интерпретаций и приложений этого
основного понятия. Например, в механике интеграл может быть ин-

§1. Вопросы принципиального порядка 529
терпретирован как выражение работы. Достаточно будет разъяснить
это на следующем простом примере. Предположим, что некоторая мас-
масса движется по оси х под влиянием силы, направленной вдоль этой
оси. Будем считать, что вся масса сосредоточена в одной точке с ко-
координатой х и что сила задана как функция этой точки f(x), причем
знак функции /(ж) указывает на направление силы. Если сила посто-
постоянна и передвигает массу из точки а в точку 6, то работа, произведен-
произведенная ею, равна произведению величины силы / на пройденный массой
путь: F — a)f. Но если сила меняется вместе с изменением х, то при-
придется определять общую произведенную работу с помощью предельно-
предельного процесса (подобно тому, как мы прежде определяли скорость). Для
этой цели мы разобьем промежуток от а до Ь, как и прежде, на мелкие
частные промежутки точками Хо = a, Xi, X2, ¦ ¦ • , хп = 6; затем пред-
предположим, что в каждом частном промежутке сила остается постоянной
и равной, скажем, величине f(xv), истинному значению силы в конеч-
конечной точке, и вычислим работу, соответствующую такой «ступенчатой»
силе,
п
Если мы теперь, как раньше, станем уменьшать промежутки деления,
заставляя п неограниченно расти, мы увидим, что сумма будет стре-
стремиться к интегралу
ъ
f(x)dx.
Таким образом, работа, совершаемая непрерывно меняющейся силой,
определена с помощью интеграла.
В частности, рассмотрим массу т, связанную с началом коорди-
координат х = 0 упругой пружиной. Сила f(x), согласно рассуждению на
стр. 524, будет пропорциональна х,
f(x) = -k2x,
где к2 — положительная постоянная. Тогда работа, совершенная этой
силой при перемещении массы т из начала координат в точку 6, выра-
выразится интегралом
/<-
ЯА ЪЛП

530
Дополнение к главе VIII
Рис. 286. К
длины дуги
определению
а работа, которую мы сами должны затра-
затратить при растяжении пружины до точки 6,
равна +fc2^-.
Другое приложение общего понятия ин-
интеграла — это вычисление длины дуги кри-
кривой. Предположим, что рассматриваемая
часть кривой представлена функцией у =
= f(x), производная которой /'(ж) = ~-
(XX
также непрерывная функция. Для того что-
бы определить длину, мы будем действо-
действовать точно так, как если бы нам надо было измерить длину кривой для
практических целей при помощи линейки с делениями. Впишем в ду-
дугу АВ ломаную линию с п маленькими сторонами, измерим общую
длину (периметр) Ln этой ломаной и станем рассматривать эту длину
как некоторое приближение; заставим п возрастать, а наибольшую из
сторон ломаной — стремиться к нулю; тогда мы получим в качестве
длины дуги АВ следующий предел:
L = limLn.
(В главе VI этим же способом была получена длина окружности как пре-
предел периметра вписанного правильного n-угольника.) Можно доказать,
что для достаточно гладких кривых этот предел существует и не зави-
зависит от того, каким образом выбирается последовательность вписанных
ломаных. Те кривые, для которых это имеет место, называются спрям-
спрямляемыми. Всякая «порядочная» кривая, встречающаяся в теории или ее
приложениях, оказывается спрямляемой, и мы не станем углубляться
в исследование «патологических» случаев. Достаточно будет показать,
что дуга АВ для функции у = f(x) с непрерывной производной f'(x)
имеет длину L в указанном смысле и что длина L может быть выражена
с помощью интеграла.
С этой целью обозначим абсциссы точек А и В соответственно
через а и Ь, затем разобьем промежуток от а до Ь, как и прежде, точка-
точками а — хо, xi, X2, ••• , хп — Ь с разностями Axj = Xj — Xj-\ и рассмот-
рассмотрим ломаную линию с вершинами (xj, yj = f(xj)), расположенными
над точками деления. Длина одной из сторон ломаной выразится фор-
формулой

§ 1. Вопросы принципиального порядка 531
Отсюда для общей длины ломаной линии получается выражение
Если заставить теперь п стремиться к бесконечности, то разностное
отношение -г—- будет стремиться к производной -j- = /'(ж), и мы по-
ZA Xj &Х
лучим для длины L интегральное выражение
ь
^ B)
Не вдаваясь в дальнейшие подробности этих теоретических рас-
рассуждений, мы сделаем два дополнительных замечания. Во-первых, если
точку В считать подвижной точкой на данной кривой с абсциссой х,
то L = L(x) становится функцией переменного ж, и, согласно основной
теореме, мы имеем формулу
L'(x) = g = v/l + №)]2,
которую часто приходится применять. Во-вторых, хотя формула B)
и дает «общее» решение задачи нахождения длины дуги, все же она
редко позволяет найти явное выражение этой длины в отдельных част-
частных случаях. В самом деле, чтобы получить числовое значение длины
дуги, мы должны подставить данную функцию f(x), или, точнее, f'{x),
в формулу B) и тогда осуществить фактическое интегрирование полу-
полученного выражения. Но здесь возникают, вообще говоря, непреодоли-
непреодолимые трудности, если мы ограничим себя областью элементарных функ-
функций, рассмотренных в этой книге. Укажем небольшое число случаев,
для которых интегрирование возможно. Функция
у = f(x) = \Л - х2
имеет графиком единичный круг; для нее мы получаем
следовательно, длина дуги окружности выражается интегралом
ь
arcsin b — arcsin a.
Г dx =
J s/l-x2

532 Дополнение к главе VIII
Для случая параболы у = х2 мы имеем /'(ж) = 2х, а длина дуги от х = О
до х = b равна
ь
/ v 1 + 4ж2 dx.
а
Для кривой у = In sin ж мы имеем f'(x) — ctga;, и длина дуги выража-
выражается интегралом
/ \Л + ctg2 xdx.
Мы удовольствуемся лишь простым написанием этих интеграль-
интегральных выражений. Их можно было бы вычислить, применяя несколько
более развитую технику интегрирования, чем та, которая имеется в на-
нашем распоряжении, но мы не пойдем дальше в этом направлении.
§ 2. Порядки возрастания
1. Показательная функция и степени переменного х.
В математике мы постоянно встречаемся с последовательностями чи-
чисел ап, которые имеют бесконечный предел. Часто бывает нужно срав-
сравнить такую последовательность с другой последовательностью, напри-
например, чисел Ьп, тоже стремящихся к бесконечности, но, может быть,
«быстрее», чем последовательность чисел ап. Уточним это понятие: мы
скажем, что Ьп стремится к бесконечности быстрее чем ап, или Ьп
имеет более высокий порядок возрастания, чем ап, если отношение -^-
о„
(в котором как числитель, так и знаменатель стремятся к бесконеч-
бесконечности) стремится к нулю при возрастании п. Например, последователь-
последовательность Ьп = п2 стремится к бесконечности быстрее, чем последователь-
последовательность ап = п, а эта последовательность в свою очередь быстрее, чем
последовательность сп = у/п, так как
Ьп п2 п пп п у/п
Ясно, что ns стремится к бесконечности быстрее, чем пТ при s > г > О,
Если отношение -^- стремится к некоторой конечной постоянной с,
отличной от нуля, то мы говорим, что обе последовательности ап и Ьп

§2. Порядки возрастания 533
стремятся к бесконечности с одинаковой скоростью или что они имеют
одинаковый порядок возрастания. Так, например, ап = п2 и Ьп — 2п2 + п
имеют один и тот же порядок возрастания, потому что
On = П2 = 1 ^ 1
2п2 + п о,1 2"
п
Могла бы возникнуть мысль, что возрастание любой последова-
последовательности ап с бесконечным пределом может быть «измерено» с помо-
помощью степеней п" так же, как любой отрезок может быть измерен с по-
помощью линейки с делениями. Стоило бы только для этого найти подхо-
подходящую степень п" с тем же порядком возрастания, что и ап, т. е. такую,
что отношение ^ стремится к некоторой конечной, отличной от нуля
ft
постоянной. Но совершенно замечательным является то обстоятельст-
обстоятельство, что осуществить это отнюдь не всегда возможно — хотя бы потому,
что показательная функция ап при а > 1 (например, еп) стремится
к бесконечности быстрее, чем какая бы то ни было степень п", как бы
велик ни был показатель s; с другой стороны, функция Inn стремит-
стремится к бесконечности медленнее, чем какая бы то ни было степень ns,
как бы мал ни был положительный показатель s. Другими словами, мы
имеем соотношения
^Г -> 0 B)
при п —> оо. Заметим, что показатель степени s — не обязательно целое
число; он может быть любым фиксированным положительным числом.
Для того чтобы доказать соотношение A), мы упростим наше
утверждение тем, что извлечем из соотношения A) корень степени s;
ясно, что вместе с корнем стремится к нулю и подкоренное выражение.
Итак, нам остается только доказать, что
5
» О
ап/я
при возрастании п. Пусть Ь — а1/8; так как, по предположению, а боль-
больше единицы, то и b и \/b = б1/2 также больше 1. Можно написать
б1/2 = 1 + 9,
где q положительно. Теперь, в силу неравенства F) на стр. 42,
б"/2 = A + q)n > 1 + nq > nq,

534 Дополнение к главе VIII
так что
и, следовательно,
ап/в =ЬП
n n
an/s n2g:
Так как выражение справа стремится к нулю при п —> оо, доказатель-
доказательство закончено.
Нужно заметить, что соотношение
остается в силе, когда х стремится к бесконечности любым способом,
пробегая последовательность Х\, Х2, ¦ ¦ •, которая может и не совпадать
с последовательностью 1, 2, 3, ... целых положительных чисел. В самом
деле, при п — 1 ^ х ^ п мы имеем
Это замечание можно использовать для доказательства соотноше-
соотношения B). Если положить х = Inn и е8 = а, так что п8 = (ев)х, то дробь
в левой части B) примет вид
х
а*'
и мы приходим к выражению, имеющемуся в соотношении C)
при 8 = 1.
Упражнения.
1) Доказать, что при х —> оо функция In In ж стремится к бесконечности
медленнее, чем In ж.
2) Производная от функции -^— равна разности j. Доказать,
ш ж ш ж (In ж)
что при возрастании х производная «асимптотически равна» первому
члену, -—, т. е. что отношение упомянутых величин при ж —> оо стре-
стремится к 1.
2. Порядок возрастания 1п(п!). Во многих приложениях, на-
например, в теории вероятностей, важно знать порядок возрастания или
«асимптотическое поведение» выражения п! при очень больших значе-
значениях п. Займемся здесь изучением логарифма от п!, т. е. выражения
Р„ =

j2. Порядки возрастания
535
/12
п-\ п п+\
Рис. 287. Оценка 1п(п!)
Мы покажем, что в качестве «асимптотического значения» выраже-
выражения Рп может служить произведение n In п, т. е. что
nlnn
при п —> оо.
Проведем доказательство так, как это обыкновенно делается, ког-
когда нужно сравнить сумму с интегралом. На рис. 287 сумма Рп равна
сумме площадей прямоугольников, верхние стороны которых обозна-
обозначены сплошными линиями и общая площадь которых не превосходит
площади
71+1
\nxdx - (га + 1Iп(га + 1) - (п + 1) + 1
в пределах от 1 до п + 1 под логарифмической кривой [см. стр. 577,
упражнение (а)]. Но в то же самое время сумма Рп равна сумме площа-
площадей прямоугольников, верхние стороны которых обозначены пункти-
пунктиром и общая площадь которых превосходит площадь под той же кривой
в пределах от 1 до п,
/ In a; «fa; = п In п — п + 1.
1
Отсюда мы имеем
п In п - п + 1 < Рп < (п + 1) 1п(га + 1) - п;
разделив неравенство на nlnn, получим
1п(п + 1) 1
1-
Inn nlnn nlnn
In n In n
Inn + ln(l + 1/n)
Inn
Inn'

536 Дополнение к главе VIII
Очевидно, и верхняя и нижняя границы, между которыми заключено
Р
отношение ——, стремятся к единице, и таким образом наше утверж-
птп
дение доказано.
Упражнение. Доказать, что упомянутые выше границы соответствен-
соответственно больше чем 1 — ^ и меньше чем 1 + ^.
§ 3. Бесконечные ряды и бесконечные произведения
1. Бесконечные ряды функций. Мы не раз уже имели случай
указать, что, выражая величину s в виде «суммы бесконечного ряда»
s = bi + b2 + b3 + .-., A)
мы не утверждаем ничего иного, кроме того, что s есть предел при
возрастающем п последовательности конечных «частных сумм»
«1, «2, S3, ¦¦¦ ,
где
sn = b1+b2 + bz + ... + bn. B)
Таким образом, равенство A) равносильно предельному соотношению
limsn = s при п -^ сю, C)
где sn определено с помощью B). Если предел C) существует, то мы
говорим, что ряд A) сходится к значению я; напротив, если предел C)
не существует, то мы говорим, что этот ряд расходится.
Например, ряд
сходится к значению j, а ряд
сходится к значению In 2; но, напротив, ряд
1-1 + 1-1 + ...

§3. Бесконечные ряды и бесконечные произведения 537
расходится, так как частные суммы здесь равны поочередно то 1, то 0;
а ряд
1 + 1 + 1 + 1 + ...
расходится по той причине, что частные суммы стремятся к бесконеч-
бесконечности.
Нам приходилось уже встречаться с рядами, у которых общий член
есть функция переменной ж, имеющая вид
h = ах1,
причем Cj не зависит от ж. Такие ряды называются степенными, для
них частными суммами являются многочлены
sn = с0 + cix + с2ж2 + ... + с„жп;
прибавление постоянного члена cq потребует лишь несущественного из-
изменения обозначений в формуле B).
Разложение функции /(ж) в степенной ряд
f(x) = со + Сгх + с2ж2 + ...
есть, таким образом, один из способов представить функцию f(x) при-
приближенно с помощью простейших функций — полиномов. Подводя ито-
итоги предыдущим результатам и несколько дополняя их, составим сле-
следующий список уже известных нам разложений в степенные ряды:
г. = 1-х + х2-х3 + ... (справедливо при -1 < х < +1), D)
arctgx = х — — + \— ... (справедливо при - 1 ^ х ^ +1), E)
о о
2 3
1пA + х) = х- Цг- + Щ- - ... (справедливо при -1<ж^+1), F)
ilnfi^ =x+ 2- + %- + ... (справедливо при -1< ж <+1). G)
и X Ж о О
Г2 „3 „4
ex-l + x+^ + ^- + j^... (справедливо при всех ж). (8)
Сюда же мы присоединим еще два важных разложения
sinx = х — ^г + ^j - ... (справедливо при всех ж), (9)
cosx = l — ^j- + ^j--... (справедливо при всехх). A0)

538 Дополнение к главе VIII
Доказательство этих разложений может быть построено как прос-
простое следствие из соотношений (см. стр. 499)
X X
а) / sin и du = 1 — cos x, b) cosudu = sinx.
о о
Мы отправляемся от следующего очевидного неравенства:
cos ж ^ 1.
Интегрируя от 0 до х, где х есть некоторое фиксированное положитель-
положительное число, мы находим по формуле A3), стр. 468:
sin a; ^ х;
интегрируя это еще раз, получим
ж2
1 — cosa; ^ -^-,
что равносильно
ж2
cosa; ^ 1 —=-.
Проинтегрировав последнее неравенство, найдем
х3 х3
sin х ^ х - ;р-5 = ж - —.
Продолжая таким же способом до бесконечности, мы получаем две се-
серии неравенств:
sin ж ^ х, cos ж ^ 1,
х3 х2
sina;^a;-—, cosa; ^ 1 - —,
х3 х5 г2 г4
;Ж~3!~+5Г cosa;^l-- + -,
Установим теперь, что при неограниченном возрастании п имеет место
соотношение 2Ц- —> 0.

§3. Бесконечные ряды и бесконечные произведения 539
Для того чтобы это доказать, выберем некоторое фиксированное
число т, такое, что ^ < i, и введем обозначение с = 2Ц-. Любое
"' 2 ml
целое п > т представим в виде суммы п = т + г, тогда
О ^ ж _ ж ж ж ^ fl
n! ~ m + 1 m + 2"-m + r Ы
так как из того, что п -» оо, следует, что г -> оо, то с • (| J -» 0.
Отсюда и вытекает, что справедливы тождества
_ х3 х5 х7
-x--^- + _-_ + ...
Поскольку члены этих рядов, меняя поочередно знаки, убывают по ве-
величине (по крайней мере, при \х\ ^ 1), то ошибки, совершаемые при
обрывании каждого из рядов на некотором члене, не превышают по аб-
абсолютной величине первого из отброшенных членов.
Эти ряды можно использовать при составлении таблиц.
Пример. Чему равен sinl0? 1° равен в радианном измерении числу j^-;
loll
следовательно,
sin _*L = _J[__ If JLV 4-
180 180 6V180/
Если ограничиться выписанными двумя членами, то совершаемая при
этом ошибка не будет превышать числа т^7т(т?тг) , которое меньше,
lzU \1ои/
чем 0,000 000 000 02. Итак, sin Г и 0,017 452 4064, с 10 десятичными знаками.
Наконец, упомянем без доказательства о «биномиальном ряде»
A + х)а = 1 + ах + С%х2 + С$х3 + ... , A1)
где С* — «биномиальный коэффициент»
Если а = п есть целое положительное число, то С^ = 1, и в формуле A1)
все коэффициенты С" при s > n обращаются в нуль, так что мы прос-
просто получаем конечную формулу обыкновенной биномиальной теоремы.
Одно из крупных открытий Ньютона, сделанных им в начале его дея-
деятельности, заключалось в том, что он обобщил биномиальную теорему
на случай всех возможных значений показателя а как положительных,
так и отрицательных, как рациональных, так и иррациональных. Ес-
Если а не есть целое положительное число, то правая часть формулы A1)
дает бесконечный ряд, сходящийся к значению, равному левой части,

540 Дополнение к главе VIII
при — 1 < х < +1. Если же \х\ > 1, то ряд A1) расходится, и знак
равенства теряет всякий смысл.
В частности, подставляя в формулу A1) значение а — |, мы найдем
разложение
^=1 + 1*-^ + ^»-1^ + ... A2)
Подобно другим математикам XVIII в., Ньютон не дал настоящего
доказательства своей формулы. Удовлетворительный анализ сходимос-
сходимости и пределы, в которых разложение оказывается справедливым, не
были установлены для подобных рядов вплоть до XIX в.
ции
Упражнение. Написать степенные ряды, в которые разлагаются функ-
1
Разложения D)—A1) являются частными случаями общей формулы
Брука Тейлора A685-1731), дающей разложение функции f(x) в степен-
степенной ряд вида
/(ж) = с0 + ах + с2х2 + с3х3 + ... A3)
Подмечая закон, выражающий коэффициенты этого ряда Cj с помощью
функции f(x) и ее производных, можно утверждать справедливость
этого разложения для очень обширного класса функций.
Здесь невозможно привести строгое доказательство формулы Тей-
Тейлора; невозможно также точно сформулировать условия, при которых
она справедлива. Но следующие общедоступные соображения прольют
некоторый свет на относящиеся сюда взаимоотношения и существен-
существенные факты.
Допустим предварительно, что разложение A3) возможно. Далее
предположим, что функция f(x) дифференцируема, что ее производ-
производная f'(x) дифференцируема, и так далее, так что существует бесконеч-
бесконечная последовательность производных
Наконец будем дифференцировать бесконечный степенной ряд почлен-
почленно точно так, как если бы это был конечный многочлен, не озабочива-
озабочиваясь вопросом о законности такой процедуры. После всех этих допуще-
допущений можно определить коэффициенты сп, зная поведение функции f(x)

§3. Бесконечные ряды и бесконечные произведения 541
в окрестности точки х = 0. Прежде всего, подставляя в формулу A3)
х = 0, мы находим
со = /@),
так как все члены ряда, содержащие переменное х, исчезают.
Дифференцируя тождество A3), мы получаем
f'(x) = Cl+ 2с2х + Зс3х2 + ... + пспхп-1 +...; A3')
снова подставляя значение х = 0, но на этот раз в формулу A3'), мы
находим
сх = /'@).
Дифференцируя A3'), мы получаем
f"(x) = 2с2 + 2 • Зс3х + ... + (п - 1)п • спхп-2 + ...; A3")
подставляя затем в полученную формулу A3") х = 0, мы видим, что
2!с2 = /"@).
Аналогично, продифференцировав A3") и затем подставив х = 0, полу-
получаем
3!с3 = /'"@)
и, продолжая дальше таким же образом, мы найдем общую формулу
для коэффициента сп:
где /'"'@) представляет собой значение n-й производной от функ-
функции f{x) при х = 0. В результате получим ряд Тейлора
f(x) = /@) + z/'@) + ^/"@) + ^/'"@) + ... A4)
Пусть читатель в качестве упражнения проверит, что в примерах
D)—A1) коэффициенты степенных рядов составлены как раз по этому
закону.
2. Формула Эйлера cos ж + г sin а; = ег3!. Одним из самых по-
поразительных достижений Эйлера, полученных им на основе его форма-
формалистических манипуляций, является тесная внутренняя связь, сущест-
существующая в области комплексного переменного между функциями синус
и косинус, с одной стороны, и показательной функцией — с другой.

542 Дополнение к главе VIII
Нужно заранее указать, что ни «доказательство» Эйлера, ни следую-
следующие далее доводы ни в какой мере не носят строгого характера; это —
типичные для XVIII в. примеры формальных буквенных переделок, на-
насыщенные доверием к силе математического символизма.
Начнем с тождества Муавра, доказанного в главе II:
(cos тир + i sin тир) = (cos y> + i sin ip)n.
Подставка ip = — приводит нас к соотношению
It x\n
cos ж + г sin ж = I cos щ + lsmn ) ¦
Если х зафиксировано, то cos ^ будет мало отличаться от cos 0 = 1 при
неограниченном возрастании п; кроме того, так как -
1
(см. стр. 355), то мы заключаем, что sin ^ асимптотически равен ^. По-
Поэтому можно считать более или менее естественным такой предельный
переход
I гх\п
cos ж + г sin ж = hml 1 + — ) при п -> оо.
Преобразовывая правую часть этого равенства согласно формуле
(стр. 510)
ez = lim(l + ^J при п ->• сю,
мы получим соотношение
cosx + isinx = е'х. A5)
Это и есть результат, полученный Эйлером.
Мы можем вывести эту самую формулу и другим, тоже формалис-
формалистическим путем — из разложения функции ег,
вместо z подставляя ix, где х — действительное число. Если мы вспом-
вспомним, что последовательными степенями числа г являются числа i, — 1,

§3. Бесконечные ряды и бесконечные произведения 543
—г, +1 и т.д., периодически, то, собирая действительные и мнимые
части, мы получим
V 3! + 5! 7!+"V'
2! + 4! 6!+"
заменяя, далее, ряды в правой части их суммами cos.t и sin ж, мы снова
получаем формулу Эйлера.
Такое рассуждение отнюдь не является настоящим доказательст-
доказательством соотношения A5). Против нашего второго «вывода» можно возра-
возразить, что разложение в ряд для функции е" было проведено в предпо-
предположении, что z — действительное число; поэтому подстановка z = ix
должна быть оправдана дополнительными соображениями. Точно так же
полноценность первого рассуждения уничтожается тем, что формула
ez = limf 1 + щJ при п -» оо
была раньше выведена только для действительных значений z.
Чтобы формула Эйлера из области чистого формализма перешла
в область строгих математических истин, потребовалось развитие те-
теории функций комплексного переменного — одного из величайших до-
достижений XIX в. Многие другие глубокие проблемы стимулировали это
далеко идущее развитие. Мы видели, например, что промежутки схо-
сходимости разложений различных функций в степенные ряды различны.
Почему некоторые разложения сходятся всюду, т.е. для всех значе-
значений х, в то время как другие теряют смысл при \х\ > 1?
Рассмотрим, например, геометрическую прогрессию D), приведен-
приведенную на стр. 537, которая сходится при \х\ < 1. Левая часть этого ра-
равенства вполне осмысленна при х = 1, именно, равна = i; в то
же время ряд в правой части ведет себя очень странно: он принимает
вид 1-1 + 1-1 + ....
Этот последний ряд не является сходящимся, поскольку его част-
частные суммы колеблются между 1 и 0. Это свидетельствует о том, что
функция может порождать расходящийся ряд даже в том случае, если
сама она не обнаруживает какой-либо иррегулярности. Правда, функ-
функция -т-7— становится бесконечной при х = — 1. И так как легко до-
1 + х
казать, что сходимость степенного ряда в точке х = а > 0 влечет за
собой сходимость в промежутке —а < х < а, то мы могли бы, пожа-
пожалуй, усмотреть «объяснение» странного поведения нашего разложения
в разрывности функции zr-=— при х = —1. Однако рассмотрим теперь
1 + х

544 Дополнение к главе VIII
функцию —^-г-; она может быть разложена в ряд
1 + х
1 +X2
как мы убеждаемся, подставляя х2 вместо х в формулу D). Полученный
ряд тоже сходится при \х\ < 1; вместе с тем при х = 1 он снова приводит
к ряду 1-1 + 1-1 + ..., а при \х\ > 1 он резко расходится, и однако
же сама функция всюду ведет себя безупречно.
Оказывается, что полное объяснение этим явлениям возможно
лишь тогда, когда функции изучаются в области комплексных значе-
значений переменного х, охватывающей как действительные, так и мнимые
его значения. Например, ряд для функции т должен расходиться
1 + х
при х = г, так как знаменатель дроби при этом значении переменно-
переменного равен нулю. Отсюда следует, что ряд должен расходиться при всех
таких значениях х, что \х\ > \г\ = 1, поскольку можно доказать, что
сходимость его для одного такого значения х повлекла бы за собой его
сходимость при х = г. Таким образом, вопрос о сходимости рядов, ко-
которым полностью пренебрегали в период возникновения анализа, стал
одним из главных факторов создания теории функций комплексного
переменного.
3. Гармонический ряд и дзета-функция. Формула Эйлера,
выражающая sin а; в виде бесконечного произведения. Ряды,
члены которых являются простыми комбинациями целых чисел, осо-
особенно интересны. В качестве примера рассмотрим «гармонический ряд»
отличающийся от известного нам ряда, сумма которого равна In 2, толь-
только знаками членов, стоящих на четных местах.
Поставить вопрос, сходится ли этот ряд, все равно, что спросить
себя, стремится ли к конечному пределу последовательность чисел
«ъ s2, s3, ... ,
где

§3. Бесконечные ряды и бесконечные произведения 545
Несмотря на то, что по мере продвижения по ряду A6) члены его
приближаются к 0, легко увидеть, что ряд этот не сходится. Дейст-
Действительно, взяв достаточное количество членов, мы можем превысить
любое положительное число; таким образом, sn возрастает беспредель-
беспредельно, и, значит, ряд A6) «расходится к бесконечности». Чтобы в этом
убедиться, заметим, что
и вообще
= 1 + f- A8)
Таким образом, например, частные суммы «2т превышают 100, если
только т ^ 200.
Если гармонический ряд расходится, то, с другой стороны, можно
доказать, что ряд
1 + + + + ^ +
сходится при всяком значении s, большем чем 1, и сумма его, рас-
рассматриваемая как функция переменного s, есть так называемая дзета-
функция:
( ^ ^ ^ ^) при п->оо. B0)
Эта функция, очевидно, определена только при s > 1.
Существует важное соотношение между дзета-функцией и просты-
простыми числами, которое мы выведем, исходя из свойств геометрической
прогрессии. Пусть р есть какое-нибудь простое число; тогда при s Jj 1
так
ЧТО
ОЛ{\
1
Р3
0
<
!
Р
р"
1
<
]
1—1
L

546 Дополнение к главе VIII
Перемножим такого рода равенства, написанные для всех простых
чисел р = 2, 3, 5, 7, ... (не задаваясь вопросом о законности такой
операции). В левой части мы получим «бесконечное произведение»
= lim —^~г~ ¦ ¦ ¦ —±—г- при п -> оо;
1
1
1
р!
1
1
1
Рп
в это же время в правой части мы получаем ряд
в силу того обстоятельства, что каждое целое число, большее чем 1, мо-
может быть единственным образом представлено как произведение сте-
степеней различных простых чисел. Итак, нам удалось выразить дзета-
функцию в виде произведения
Если бы существовало только конечное число простых чисел, ска-
скажем, pi, p2, рз, ••• , рг, то произведение в правой части формулы B1)
было бы обыкновенным конечным произведением и имело бы поэтому
конечное значение даже при s = 1. Однако мы видели, что дзета-ряд
при s = 1
расходится, стремясь к бесконечности. Это рассуждение, которое лег-
легко превратить в строгое доказательство, показывает, что существует
бесконечное множество простых чисел. Конечно, это доказательство го-
гораздо запутаннее и искусственнее, чем данное Евклидом (см. стр. 49).
Но оно столь же привлекательно, как трудный подъем на вершину горы,
которая могла бы быть достигнута с другой стороны по комфортабель-
комфортабельной дороге.
С помощью бесконечных произведений, подобных тому, которое
дается формулой B1), функции иногда выражаются так же удобно, как
и с помощью бесконечных рядов.
Другое бесконечное произведение, открытие которого представля-
представляет собой еще одно из достижений Эйлера, относится к тригонометри-
тригонометрической функции sin ж. Чтобы понять найденную Эйлером формулу, мы

§3. Бесконечные ряды и бесконечные произведения 547
начнем со следующего замечания относительно многочленов. Если
f(x) = а0 + ахх + ... + апхп
есть многочлен степени п и имеет п различных нулей х\, ... , хп, то,
как известно из алгебры, функция f(x) может быть разложена на ли-
линейные множители
f(x) = ап{х - хг)... (х - хп)
(см. стр. 137). Вынося за скобку произведение X\Xi.. .хп, мы можем
написать
где С — постоянная, равная а0, что легко установить, положив х = 0.
Далее возникает вопрос: возможно ли аналогичное разложение уже не
для полиномов, а для более сложных функций /(ж)? (В общем случае
ответ не может быть утвердительным, в чем легко убедиться на при-
примере показательной функции, которая вовсе не имеет нулей, посколь-
поскольку ех ф 0 при любых значениях х.) Эйлер открыл, что для функции
синус такое разложение возможно. Чтобы написать формулу в ее прос-
простейшем виде, мы рассмотрим не sin ж, a siiiTra:. Последняя функция име-
имеет нулями точки х = 0, ±1, ±2, ±3,..., так как smnn = 0 при всех
целых щ иных же нулей она не имеет никаких. Формула Эйлера уста-
устанавливает соотношение
Стоящее справа бесконечное произведение сходится при всех значени-
значениях ж и является одной из красивейших формул математики. При х = |
формула дает
1_\
Если мы напишем
sinf = х = 111"
1 = Bп-1)Bп
2п-2п
то после небольших преобразований получим произведение Уоллиса
2 1 ' 3 ' 3 ' 5 ' 5 7-7'9'"'
упомянутое на стр. 348.

548 Дополнение к главе VIII
За доказательствами всех этих соотношений мы вынуждены на-
направить читателя к руководствам по анализу (см. также стр. 578).
*§4. Доказательство теоремы о простых числах
на основе статистического метода
Применяя математические методы к изучению явлений природы,
обычно удовлетворяются такими рассуждениями, в ходе которых цепь
строгих логических доводов прерывается более или менее правдоподоб-
правдоподобными допущениями. И даже в чистой математике можно подчас встре-
встретить рассуждение, которое хотя и не обеспечивает строгого доказатель-
доказательства, но все же, несмотря на это, подсказывает правильное решение и
дает направление, в котором можно искать это строгое доказательство.
Именно таков характер решения задачи о брахистохроне, данного
Якобом Бернулли (см. стр. 435), а также очень многих других проблем
раннего периода развития анализа.
Пользуясь процедурой, типичной для прикладной математики
и в особенности для статистической механики, мы приведем сейчас
одно рассуждение, которое сделает по меньшей мере правдоподобной
справедливость знаменитого гауссова закона о распределении простых
чисел. (Упомянутая процедура была подсказана одному из авторов спе-
специалистом по экспериментальной физике Густавом Герцем.) Эта теоре-
теорема, рассмотренная с эмпирической точки зрения в дополнениях к гла-
главе I, утверждает, что число А(п) простых чисел, не превышающих п,
асимптотически равно -——:
Inn
А(п)
Под этим подразумевается то, что отношение А(п) стремится к пределу
—— при стремлении п к бесконечности.
Inn
Допустим прежде всего, что существует математический закон
распределения простых чисел, обладающий следующим свойством: при
больших значениях п определенная выше функция А(п) приблизитель-
п
но равна интегралу / W(x)dx, где W(x) можно назвать функцией, из-
2
меряющей «плотность» простых чисел. (В качестве нижнего предела
интеграла мы выбрали число 2, так как при х < 2 имеем, очевид-
очевидно, А(х) = 0.) Более точно, пусть х — растущая величина и Ах —

может
§4. Доказательство теоремы о простых числах 549
другая растущая величина, но такая, что порядок возрастания х боль-
больше порядка возрастания Ах. (Например, можно принять, что Ах = л/х.)
Сделаем, далее, гипотезу, что распределение простых чисел настолько
равномерно, что число простых чисел в промежутке от х до х + Ах
приближенно равно выражению вида W(x)Ax, и даже более того, что
71
функция W(x) изменяется так плавно, что интеграл / W(x)dx
2
быть заменен соответствующей интегральной «ступенчатой» суммой,
не изменяя своего асимптотического значения. После этих предвари-
предварительных замечаний мы подготовлены для того, чтобы начать наше рас-
рассуждение.
Мы уже доказали ранее (стр. 535), что при больших целых числах
выражение 1п(п!) асимптотически равно произведению nlnn:
ln(n!) ~ n\nn.
Мы дадим сейчас другую асимптотическую формулу для 1п(п!), вы-
выражающуюся через простые числа, а затем сравним оба выражения.
Сосчитаем, сколько раз произвольное простое число р, меньшее, чем п,
входит множителем в целое число р\ = 1 • 2 • 3... п. Обозначим симво-
символом [а]р наибольшее целое число к, такое, что а делится нарк. Из того,
что разложение любого целого числа на простые числа единственно,
вытекает зависимость [ab]p = [а]р + [Ь]р при любых целых а и Ь. Отсюда
следует
[п\]р = [1]р + [2}р + Щр + ... + [п]р.
В последовательности 1,2,3, ... , п члены, делящиеся на рк, имеют
внцрк, 2рк, Зрк, ...; их число Nk при больших п приближенно равно —-.
Р
Из этих членов число Мк таких, которые делятся на рк, но не де-
делятся на более высокие степени р, равно разности Nk — Nk+i- Следова-
Следовательно, имеем
[nl]p = М1+2М2+Ш3 + ...=
= (N! - N2) + 2{N2 - N3) + 3{N3 ~N4) + ...=
V p p P~l
(Само собой разумеется, что эти равенства только приближенные.)
Отсюда следует, что при больших п число п\ приближенно вы-
выражается произведением всех выражений вида рп1(р~^> с ограничени-

550 Дополнение к главе VIII
ем р < п. Таким образом, мы получили формулу
р<п
Сравнивая полученное выражение с нашей прежней асимптотической
формулой для 1п(п!), мы находим:
У2 A)
/~/ p-l v I
р<х
(вместо п подставлено х).
Следующим — и решающим — шагом является нахождение асимп-
асимптотического выражения для правой части соотношения A). Если х
очень велико, можно промежуток от 2 до ж = п разделить на
большое число г достаточно больших частных промежутков точка-
точками 2 = ?i, &,--- ) ?r> ?r+i = x с соответственными прираще-
приращениями Д?л- = ?j+i - ?j. В каждом частном промежутке могут нахо-
находиться простые числа, и каждое простое число j-ro частного проме-
промежутка приближенно равно числу ?_,-. В силу нашего предположения
о функции W{x), в j-м частном промежутке содержится приблизитель-
приблизительно W(?j)A?j простых чисел; следовательно, сумма в правой части со-
соотношения A) приближенно равна выражению
Заменив эту конечную сумму интегралом, к которому она приближа-
приближается, мы получим формулу
B)
Отсюда мы теперь определим неизвестную функцию W(x). Если мы
заменим значок ~ знаком обыкновенного равенства и продифферен-
продифференцируем обе части по х, то, в силу основной теоремы анализа, можно
написать
, W{x)=*=±. C)
— 1 хтх

§4. Доказательство теоремы о простых числах 551
В самом начале нашего рассуждения мы предположили, что А(х)
асимптотически равно интегралу
х
fw(x)dx.
2
Итак, А(х) приближенно равно интегралу
х- 1
J ж In ж
2
dx. D)
Для того чтобы вычислить этот интеграл, заметим, что функция f(x) =
= -^— имеет следующую производную:
та;
J ' '~ In я; (In жJ'
При больших значениях ж два выражения
_1 L_ и Л L_
In ж (In жJ In ж ж In ж
асимптотически равны, так как вторые члены в обоих выражениях мно-
много меньше первых. Следовательно, интеграл D) будет асимптотически
равен интегралу
X
f'(x)dX = f(x) - /B) = ^ - -?-r
так как две сравниваемые нами функции мало отличаются на всем про-
п
межутке интегрирования. При больших значениях х членом -г=— как
in ii
постоянным можно пренебречь, и тогда мы приходим к окончательно-
окончательному результату
v
Это и есть теорема о простых числах.
Мы не можем претендовать на то, чтобы предыдущее рассуждение
рассматривалось как математическое доказательство, а не как индук-
индукция. Однако более глубокий анализ приводит к следующему заключе-
заключению. Нетрудно оправдать каждый, с такою смелостью сделанный нами

552 Дополнение к главе VIII
шаг, в частности, доказать справедливость асимптотической формулы
суммы и интеграла, стоящих соответственно в правых частях соот-
соотношений A) и B), и, наконец, обосновать шаг, ведущий от соотноше-
соотношения B) к соотношению C). Гораздо труднее доказать существование
гладкой функции «плотности» W(x), которое мы постулировали в самом
начале. Но раз это принято, то оценка самой функции VF(:e) является
делом сравнительно простым; таким образом, в задаче о распределе-
распределении простых чисел наиболее трудным представляется доказательство
существования «плотности» W(x).

Приложение
Дополнительные замечания, задачи
и упражнения
Многие из следующих задач предназначены для более или менее
подготовленного читателя. Они имеют в виду не столько развитие ру-
рутинной техники операций, сколько находчивости и инициативы.
Арифметика и алгебра
1. Откуда мы знаем, что, как говорится на стр. 92, никакая сте-
степень 10 не делится на 3? (см. стр. 63).
2. Докажите, что принцип наименьшего целого числа вытекает как
следствие из принципа математической индукции (см. стр. 35).
3. Применяя биномиальную теорему к разложению A + 1)п, дока-
докажите, что Q + С? + С2" + ... + Q = 2".
* 4. Задумайте какое-нибудь число z = abc..., составьте сумму
его цифр а + Ь + с + . ¦., вычтите ее из z, вычеркните одну цифру из
остатка и обозначьте через w сумму оставшихся цифр. Нельзя ли найти
правило для того, чтобы определить вычеркнутую цифру, зная только
значение wl (Будет не вполне определенный случай, если w = 0.) Как
и многое другое из того, что связано со сравнениями, этот пример при-
пригоден в качестве «развлекательной задачи с угадыванием».
5. Арифметической прогрессией первого порядка называется такая
последовательность чисел a, a + d, a + 2d, a+3d, ..., что разность между
следующим членом и предыдущим постоянна. Арифметическая про-
прогрессия второго порядка есть такая числовая последовательность ai,
а2, аз, ¦ ¦ ¦ 1 что разности a,i+i — ai образуют арифметическую прогрес-
прогрессию первого порядка. Вообще арифметической прогрессией порядка к
называют последовательность, обладающую тем свойством, что раз-
разности рядом стоящих членов образуют арифметическую прогрессию
(к — 1)-го порядка. Проверить, что квадраты натуральных чисел обра-
образуют арифметическую прогрессию 2-го порядка, и затем установить,

554 Приложение
по математической индукции, что к-е степени натуральных чисел об-
образуют арифметическую прогрессию порядка к. Доказать, что всякая
последовательность чисел ап, где о„ = Со + С\П + С2П2 + ... + СкПк
и все с — постоянные, есть арифметическая прогрессия порядка к.
* Доказать обратное утверждение для случая к = 2, к = 3, для
любого к.
6. Доказать, что суммы п первых членов арифметической прогрес-
прогрессии порядка к образуют арифметическую прогрессию (к + 1)-го поряд-
порядка.
7. Сколько делителей у числа 10 296? (см. стр. 52).
8. Пользуясь алгебраической формулой
(а2 + Ь2)(с2 + d2) = (ас - bdJ + (ad + beJ,
докажите с помощью индукции, что любое целое число г = а\а2 ...ап
может быть представлено как сумма двух квадратов, если каждый из
множителей а обладает тем же свойством. Проверьте это на примерах
г =160, г =1600, г = 1300, г = 625,
принимая во внимание, что
2 = 12 + 12, 5 = 12 + 22, 8 = 22+22 и т. д.
Если возможно, найдите два различных представления этих чисел как
суммы двух квадратов.
9. Воспользуйтесь результатом предыдущего упражнения для того,
чтобы по заданным пифагоровым тройкам чисел строить новые.
10. Составьте правила делимости (подобные приведенным на
стр. 63) для систем счисления с основаниями 7, 11, 12.
11. Докажите: неравенство г > s между двумя положительными
рациональными числами г = ^ и s = -. равносильно неравенству ас —
о а
- bd > 0.
12. Докажите: если г и s — положительные числа, причем г < s, то
г < Цг^ < s и < 2rs < (r + sJ.
(hi)'
13. Предполагая, что z — какое угодно комплексное число, дока-
докажите с помощью индукции, что zn + ~ может быть представлено как
полином степени п относительно w = z + j (см. cjp. 135).

Дополнительные замечания, задачи и упражнения 555
* 14. Если положим ради краткости E(ip) = cos ip + г sin уз, то по-
получим [E(ip)]m = E(mip). Воспользовавшись этой формулой, а также
формулой для суммы геометрической прогрессии (на стр. 40; эта фор-
формула сохраняется и для комплексных величин), докажите, что
<р ( \\
cos ¦»¦ - cosl п + 2 )V
sin ip + sin 2ip + sin 2>ip + ... + sin nip = ,
|
2 sin |
й + cos ip + cos 2ip + cos 3ip + ... + cos nip —
2sin|
15. Что получится из формулы упражнения 3 на стр. 44, если под-
подставить q = E(ip)?
Аналитическая геометрия
Внимательное выполнение следующих упражнений, сопровождае-
сопровождаемое чертежами и числовыми примерами, даст возможность овладеть
элементами аналитической геометрии. Определения и простейшие фак-
факты из тригонометрии предполагаются известными.
Во многих случаях целесообразно представлять себе прямые или
отрезки направленными от одной точки к другой. Под направленной
прямой PQ (или направленным отрезком PQ) мы будем понимать пря-
прямую (или отрезок), направленную от Р к Q. Если разъяснения отсут-
отсутствуют, то предполагается, что направленная прямая / имеет безраз-
безразлично какое, но вполне определенное направление; только в случае на-
направленной оси х неизменно принимается, что она направлена от нача-
начала О к любой ее точке с положительной координатой х, и аналогично
для оси у. О направленных прямых (или отрезках) мы будем говорить,
что они параллельны, в том и только в том случае, если они направ-
направлены одинаково. Направление направленного отрезка на направленной
прямой может быть фиксировано знаком + или —, присоединяемым
к расстоянию между конечными точками отрезка, смотря по тому, сов-
совпадает или не совпадает направление отрезка с направлением прямой.
Целесообразно понятие «отрезок PQ» обобщить и на тот случай, когда
точки Р и Q совпадают; таким «отрезкам» приписывается длина нуль
и не приписывается никакого направления.

556 Приложение
16. Докажите: если Pi(xi, 2/1) и Р2(х2, у2) — какие-нибудь две точ-
точки, то координаты середины отрезка Р\Р2 — Ро(хо, 2/о) определяются
формулами Хо = ^—^—-, 2/о = ^-s—-• Установите более общее поло-
жение: если точки Р\ и Р2 различны, то та точка Pq на направленной
прямой Р\Р2, для которой отношение направленных отрезков * ° рав-
но к, имеет координаты
х0 = A - к)хг + кх2, 2/о = A - к)ух + ку2.
(Указание: примите во внимание свойство пропорциональности отрез-
отрезков при пересечении сторон угла параллельными прямыми.)
Таким образом, все точки на прямой PiP2 имеют координаты ви-
вида х = Ai^i + А2ж2, 2/ = Ai2/i + А22/2, причем Ai + А2 = 1. При Хх = 1
и А2 = О получаются соответственно точки Pi и Р2. Отрицательным
значениям Ai соответствуют точки по ту сторону Р2, отрицательным
значениям А2 — точки по ту сторону Pi, т.е. точки, лежащие на пря-
прямой Р1Р2 вне отрезка PiP2.
17. Охарактеризовать подобным же образом положение точки на
прямой в зависимости от числовых значений к.
В такой же мере существенно использовать положительные и от-
отрицательные числа для обозначения направленных вращений. По опре-
определению, в качестве положительного направления вращения избирает-
избирается то, которое направленную ось х переводит в ось у после поворота
на 90°. При обыкновенном расположении осей (когда ось х направлена
вправо, а ось у — вверх) положительное вращение направлено против
часовой стрелки. Мы определим теперь угол от направленной прямой 1\
к направленной прямой 12 как угол, на который нужно повернуть пря-
прямую li, чтобы она стала параллельной прямой Z2. Разумеется, этот угол
определен лишь с точностью до величин, кратных 360°. Так, угол меж-
между осью х и осью у равен 90° или —270° и т.д. Вместо «угол от /i до Z2»
мы будем говорить короче: «угол между 1Х и /2», учитывая, конечно,
что «угол между /i и 12 и «угол между 12 и 1\)> различаются знаком.
18. Пусть а обозначает угол между направленной осью х и направ-
направленной прямой I. Пусть Pi, Р2 — две точки на I и d — направленное
расстояние от Pi до Р2. Тогда покажите, что
2:2—2:1 • 2/2 - 2/1 / ч . / ч
cos а = , sma= —, (х2 — xi)sma = (у2 — ух) cosa.
Если прямая I не перпендикулярна к оси х, то наклон I определяется
формулой
. 2/2-yi
т = tea = —.
6 2:2-2:1 _

Дополнительные замечания, задачи и упражнения 557
Значение т не зависит от того, как направлена прямая I, так как tga =
= tg(a + 180°), или, что равносильно,
2/1 - 2/2 2/2 - 2/1
xi -х2 х2 - xi
19. Докажите: наклон прямой равен нулю, положителен или отри-
отрицателен, смотря по тому, пойдет ли прямая, параллельная данной и про-
проходящая через начало, по оси х или через первый и третий квадранты,
или через второй и четвертый квадранты.
Мы условимся различать две «стороны» направленной прямой —
положительную и отрицательную (менее удобно было бы говорить о по-
положительной и отрицательной полуплоскостях). Пусть Р — какая-
нибудь точка, не лежащая на прямой /, и Q — основание перпенди-
перпендикуляра к /, проведенного через Р. Тогда Р лежит с положительной или
с отрицательной стороны /, смотря по тому, будет ли угол между I
и направленной прямой QP равен 90° или -90°.
Затем мы определим уравнение направленной прямой /. Через на-
начало О проведем прямую т, перпендикулярную к /, и направим ее так,
чтобы угол между т и I был равен 90°. Обозначим через /3 угол меж-
между направленной осью х и прямой т. Тогда а ~ 90° +/3, sine* = cos/3,
cos a = — sin/3. Пусть R(xi, y\) есть точка пересечения / и т. Обозна-
Обозначим через d направленное расстояние OR на направленной прямой т.
20. Показать, что d положительно в том и только в том случае, если
начало О находится с отрицательной стороны /.
Мы имеем хх — dcos/З, у\ = dsin/З (см. упражнение 18). Отсюда
следует (х — х\) sin а = (у — у\) cos a или
(х - d cos j3) cos /3 = - (у — d sin /3) sin /3,
что приводит окончательно к уравнению
xcos/3 + ?/sin/3 — d — 0.
Это — нормальная форма уравнения прямой I. Следует заметить, что
это уравнение не зависит от направления прямой I, так как изменение
ее направления повлекло бы за собой изменение знаков у всех членов
в левой части, причем уравнение осталось бы тем же самым.
Умножая нормальное уравнение на произвольный множитель, мы
получаем общую форму уравнения прямой линии
ах + by + с = 0.

558
Приложение
Чтобы получить, обратно, из этой общей формы геометрически содер-
содержательную нормальную форму, придется умножить обе части урав-
уравнения на такой множитель, чтобы коэффициенты при х и у свелись
к величинам вида cos/З и sin/З, квадраты которых в сумме составля-
1
ют 1. Таким множителем является
нормальную форму
Ь
он придает уравнению
= 0;
здесь мы имеем
а
= cos/3,
= sin/З, --
= d.
21. Доказать, что: а) кроме
1
не существует
иных множителей, приводящих общее уравнение к нормальной форме;
b) выбор того или иного множителя фиксирует направление прямой;
c) после того как выбор того или иного множителя сделан, можно ска-
сказать, что начало О находится с положительной или с отрицательной
стороны прямой или находится на самой прямой, смотря по тому, бу-
будет ли d отрицательным, положительным или нулем.
22. Доказать непосредственно, что прямая с наклоном т, проходя-
проходящая через данную точку Ро(хо, уо), представляется уравнением
у - 2/о = гп(х - х0), или у = тх + (уо - тх0).
Доказать, что прямая, проходящая через две данные точки Pi(xi, j/i)
и Рг(ж2, 2/2), имеет уравнение
B/2 - 2/1)(ж - xi) = (Х2 - хг){у - ух).
Условимся: координата х точки пересечения прямой с осью х назы-
называется «отрезком на оси ж»; аналогично относительно «отрезка на оси уь.
23. Докажите, что, деля общее уравнение, полученное в упражне-
упражнении 20, на надлежащим образом подобранное число, получим уравнение
прямой «в отрезках на осях»
х у
—h — = 1
а о
причем а и Ь — отрезки, которые прямая образует соответственно на
оси х и оси у. Могут ли быть исключительныехлучаи?

Дополнительные замечания, задачи и упражнения 559
24. Покажите, что в результате подобной же процедуры уравнение
всякой прямой, не параллельной оси у, может быть «решено относи-
относительно у»:
у = тх + Ъ.
(Если же прямая параллельна оси ?/, то ее уравнению можно придать
вид х = а.)
25. Предположим, что ах + Ьу+с = 0 и а'х+Ь'у+с' = О — уравнения
двух данных прямых / и /'; пусть т и т' — соответственно их наклоны.
Докажите, что / и Г параллельны или перпендикулярны, смотря потому,
будет ли: а) т = т' или тгп' = —1, Ь) аЬ' — а'Ь = 0 или аа! + ЬЬ' = 0.
(Обратите внимание, что формулировка Ь) пригодна и для того случая,
когда у прямой «нет никакого наклона», т. е. она параллельна оси у.)
26. Установите, что уравнение прямой, проходящей через точ-
точку Ро(хо, уо) и параллельной данной прямой / с уравнением ах + by +
+ с = 0, имеет вид ах + by = ахо + Ьуо. Установите, что если условие
параллельности заменить условием перпендикулярности, то соответ-
соответствующее уравнение примет вид bx — ay = bxo ~ ауо- (Интересно заме-
заметить, что если уравнение / написано в нормальной форме, то в такой
же форме получается и новое уравнение.)
27. Пусть уравнения xcosfi + г/sin/3 - d ~ 0 и ах + by + с = 0
представляют в нормальной форме и в общей форме одну и ту же пря-
прямую /. Докажите, что направленное расстояние h от I до некоторой
точки Q(u, v) дается формулой
h = и cos /3 + v sin j3 — d,
или же
, аи + bv + с
п = -
и что h — положительное или отрицательное число, смотря по тому,
лежит ли Q с положительной или с отрицательной стороны, направ-
направленной прямой I (причем направление / фиксируется или углом /3, или
выбором знака при \Ja2 + &2). (Указание: напишите в нормальной форме
уравнение прямой т, проходящей через Q и параллельной т, и затем
определите расстояние между / и т.)
28. Предположим, что 1(х, у) = 0 есть сокращенная запись уравне-
уравнения ах + by + с = 0 некоторой прямой I; аналогично — для 1'(х, у) = 0.
Пусть Л, и А' — постоянные числа, причем А + А' = 1. Докажите, что
если прямые / и V пересекаются в точке Pq(xq, y0), то всякая прямая,

560 Приложение
проходящая через Ро, имеет уравнение вида
М(х,у)+Х'1'(х,у) = 0,
и обратно; и что всякая такая прямая однозначно определяется выбором
пары значений А и А'. (Указание: в том и только в том случае Ро лежит
на I, если 1(хо, уо) = ахо + Ьуо + с = 0). Что представляет уравнение
в случае, если / и /' параллельны? (Заметьте, что в условии А + А' = 1
нет никакой необходимости: оно служит только для того, чтобы каж-
каждой прямой, проходящей через Ро, соответствовало одно определенное
уравнение.)
29. Воспользуйтесь результатами предыдущего уравнения для то-
того, чтобы написать уравнение прямой, проходящей через точку пере-
пересечения Ро прямых I и /' и еще через другую точку Р\{х\, у\), не на-
находя при этом координат Ро- (Указание: определите А и А' из условий
M(xi, г/i) + \'l'(xi, yi) = 0, А + А' = 1.) Сделайте проверку, определяя
координаты Ро (см. стр. 370) и устанавливая затем, что Ро лежит на
прямой, уравнение которой вы нашли).
30. Докажите, что уравнения биссектрис углов, образованных пе-
пересекающимися прямыми / и /', имеют вид
Va'2 + Ъ'21(х, у) = ±л/а2 +ЪЧ'(х, у).
(Указание: см. упражнение 27.) Что представляют эти уравнения, если
прямые / и V параллельны?
31. Двумя способами выведите уравнение прямой, проходящей че-
через середину отрезка Р1Р2 и к нему перпендикулярной: а) Напиши-
Напишите уравнение Р1Р2; найдите координаты середины Ро отрезка Р1Р2;
напишите уравнение прямой, проходящей через Ро и перпендикуляр-
перпендикулярной к Р\Рг- Ь) Выразите в виде уравнения то условие, что расстояние
(стр. 106) между Pj и какой-нибудь точкой Р(х, у) искомой прямой
равно расстоянию между Pi и Р; возведите обе части равенства в квад-
квадрат и сделайте упрощения.
32. Двумя способами выведите уравнение окружности, проходящей
через три точки Pi, Pj, P3, не лежащие на одной прямой: а) Напиши-
Напишите уравнение перпендикуляров, проведенных к отрезкам Р1Р2 и Р2Р3
через их середины; найдите координаты центра как точки пересечения
этих перпендикуляров, определите радиус как расстояние между цент-
центром и Pi. b) Искомое уравнение должно иметь вид х2+ у2— 2ах — 2Ъу = к
(см. стр. 107). Так как каждая из данных точек лежит на окружности,

Дополнительные замечания, задачи и упражнения 561
то мы должны иметь
х\+у\- 2ахх - 2Ьух = к,
- 2Ьу2 = к,
так как точки лежат на кривой в том и только в том случае, если ее
координаты удовлетворяют уравнению кривой. Затем решите систему
относительно а, Ь, к.
33. Напишем уравнение эллипса с большей осью 2р, малой осью 2q
и с фокусами F(—e, 0) и F'(e, 0), причем е2 = р2 — q2. Воспользуемся
расстояниями гиг' произвольной точки Р(х, у) кривой от F и F'. По
определению эллипса г + г' = 2р. С помощью формулы для расстояния
между точками (стр. 106) установите, что
г'2 - г2 = (х + еJ - (х - еJ = Аех.
Так как
г'2 - г2 = (г' + г)(г' - г) = 2р{г' - г),
то отсюда выведите соотношение г' — г — -|^. Решая последнее уравне-
уравнение совместно с уравнением г + г' = 2р, вы получите важные формулы
г = -^х + р, г' = ^х + р.
Так как (опять по формуле расстояния) г2 = (х — еJ + у2, то можно бу-
будет приравнять полученное выражение для
полученному раньше, и тогда будем иметь
( ) у
дет приравнять полученное выражение для г2 выражению (— ~х + рJ,
Раскройте скобки, соберите члены, подставьте р2 — q2 вместо е2 и сде-
сделайте упрощения. Приведите окончательно к виду
Сделайте аналогичные вычисления для гиперболы, определяя ее как
геометрическое место точек Р, для которых абсолютное значение раз-
разности г — г' равно данному числу 2р. Но в этом случае е2 = р2 + q2.

562 Приложение
34. Парабола определяется как геометрическое место точек, рас-
расстояние которых от данной прямой (директрисы) равно расстоянию от
данной точки (фокуса). Выбрав в качестве директрисы прямую х = —а,
а в качестве фокуса точку F(a, 0), покажите, что уравнение параболы
может быть написано в виде
у2 = Аах.
Геометрические построения
35. Докажите невозможность построения с помощью только цир-
циркуля и линейки чисел -\/3, -\/4, \/5. Доказать, что построение числа ^/а
возможно только в том случае, если а есть куб рационального числа
(см. стр. 173 и далее).
36. Найти стороны правильных 3-2™-угольников и 5-2™-угольников.
Дать характеристику последовательно вводимых полей расширения.
37. Доказать невозможность трисекции с помощью только циркуля
и линейки углов в 120° или 30°. (Указание для случая угла в 30°: мы
приходим к уравнению 4z3 — 3z = cos 30° = -^VS- Введя новую пере-
менную и = z\/S, вы получите уравнение, с которым рассуждайте так
же, как на стр. 177.)
38. Доказать невозможность построения правильного 9-угольника.
39. Установить, что инверсия точки Р(х, у) в точку Р'(х', у') от-
относительно окружности с центром в начале координат и радиусом г
дается формулами:
i _ хт , _ уг
аг + у аг + у*
Решите эти уравнения относительно х и у.
* 40. Основываясь на упражнении 39, установить аналитически,
что при инверсии окружности и прямые переходят в окружности и
прямые. Проверьте, в частности, свойства a)-d) со стр. 182, а также
преобразования, указанные на рис. 61.
41. Что станет с двумя семействами прямых х = const и у = const,
параллельных координатным осям, при инверсии относительно единич-
единичной окружности с центром в начале? Дайте ответ без помощи аналити-
аналитической геометрии и с помощью аналитической геометрии.
42. Выполните построение Аполлония в простых случаях по ваше-
вашему собственному выбору. Попробуйте найти решение в аналитической
форме, как было указано на стр. 163.

Дополнительные замечания, задачи и упражнения 563
Проективная и неевклидова геометрия
43. Найти все значения двойного отношения А четырех гармоничес-
гармонических точек, если эти точки подвергаются всевозможным перестановкам.
(Ответ: А = -1, 2, ±.)
44. При каких расположениях четырех точек какие-нибудь два из
шести значений двойного отношения на стр. 216 совпадают между со-
собой? (Ответ: только при А = —1 или А = 1; имеется только одно мнимое
значение А, при котором А = -: ему соответствует «эквигармони-
ческое» двойное отношение.)
45. Удостоверьтесь, что равенство двойного отношения (ABCD)
единице означает совпадение точек С и D.
46. Докажите утверждения, касающиеся двойного отношения плос-
плоскостей, приведенные на стр. 217.
47. Докажите: если точки Р и Р' взаимно обратны относительно
окружности и диаметр АВ коллинеарен с точками Р и Р', то четверка
точек А, В, Р, Р' гармоническая. (Указание: воспользуйтесь форму-
формулой B) на стр. 218; предположите, что данная окружность единичная
и что АВ — ось координат.)
48. Найдите координату четвертой гармонической точки относи-
относительно данных точек Р1; Р^, Рз- Что случится, если Р3 станет прибли-
приближаться к середине отрезка РгРг1- (См. стр. 225.)
* 49. Попробуйте развить теорию конических сечений, исходя из
сфер Данделена. В частности, докажите, что все они, за исключением
окружностей, являются геометрическим местом точек, для которых
расстояния от данной точки и от данной прямой находятся в посто-
постоянном отношении к. При к > 1 получается гипербола, при к = 1 —
парабола, при к < 1 — эллипс. Прямая / получается как пересечение
плоскости конического сечения с плоскостью того круга, по которому
сфера Данделена соприкасается с конусом. (Именно по той причине, что
круг приходится особо оговаривать как предельный случай, не совсем
удобно принимать указанное свойство в качестве определения коничес-
конических сечений, что, впрочем, делается довольно часто.)
50. Обсудите следующее положение: «коническое сечение, рассмат-
рассматриваемое одновременно как множество точек и как множество каса-
касательных прямых, само себе двойственно» (см. стр. 249).
* 51. Попробуйте доказать теорему Дезарга, выполняя предельный
переход от пространственной конфигурации, изображенной на рис. 73
(см. стр. 211).
36*

564 Приложение
* 52. Сколько можно провести в пространстве прямых, пересе-
пересекающихся с данными четырьмя прямыми? Как их можно характери-
характеризовать? (Указание: через три данные прямые проведите гиперболоид,
см. стр. 255.)
* 53. Возьмем в качестве круга Пуанкаре единичный круг в комп-
комплексной плоскости. Пусть Zi и Z2 — какие-то две точки внутри этого
круга, a u>i и и>2 — точки пересечения с окружностью «прямой линии»,
проходящей через Z\ и z-r- Тогда двойное отношение ——— : ———,
Z\ — Wi Z2 — W2
в соответствии с упражнением 8 на стр. 133, имеет действительное
значение; докажите это. По определению, его логарифм есть гипербо-
гиперболическое расстояние между z\ и z^-
* 54. С помощью инверсии преобразуйте круг Пуанкаре в верх-
верхнюю полуплоскость. Исследуйте эту полуплоскость как модель Пуан-
Пуанкаре и непосредственно, исходя из преобразования инверсии.
Топология
55. Проверьте формулу Эйлера на пяти правильных многогранни-
многогранниках и на других многогранниках. Сделайте схемы соответствующих
разверток.
56. При доказательстве формулы Эйлера (стр. 279) нам приходится,
путем последовательного выполнения двух основных операций, редуци-
редуцировать произвольную сетку треугольников к сетке, состоящей только
из одного треугольника, и тогда получаем V — Е + F = 3 — 3 + 1 = 1.
Почему мы можем быть уверены, что в конечном результате не ока-
окажется двух треугольников без общих вершин, и тогда было бы V — Е +
+ F = 6 — 6 + 2 = 2? (Указание: можно с самого начала исходить из
предположения, что сетка треугольников связная, т. е. что по ребрам
(сторонам) можно пройти от любой вершины к любой. Докажите, что
это свойство не теряется при выполнении каждой из основных опера-
операций.)
57. Мы допустили при редукции сетки треугольников только две
основные операции. Но не могло ли бы случиться на какой-то стадии
редукции, что у нас окажется треугольник, имеющий только одну об-
общую вершину с прочими треугольниками сетки? (Постройте пример.)
В таком случае потребовалась бы еще третья операция: удаление двух
вершин, трех ребер и одной грани. Как это отразилось бы на доказа-
доказательстве?
58. Можно ли вокруг палки обернуть три раза широкую резиновую
ленту так, чтобы она всюду лежала плотно, т. е. не делала бы складок?
(Конечно, лента должна где-то сама себя пересекать.)

Дополнительные замечания, задачи и упражнения 565
59. Установите, что после удаления центральной точки круговой
диск допускает непрерывное преобразование в самого себя без непо-
неподвижных точек.
* 60. Преобразование, переводящее каждую точку диска на еди-
единицу в определенном, одном и том же, направлении, очевидно, не об-
обладает неподвижными точками. Конечно, это не есть преобразование
в себя, так как некоторые точки диска после преобразования окажутся
вне диска. Почему в этом случае рассуждение, приведенное на стр. 295
(основанное на преобразовании Р -> Р*), уже не годится?
61. Допустим, что внутренняя сторона тора выкрашена в белую
краску, а внешняя — в черную. Можно ли, сделав маленькую дыроч-
дырочку в поверхности, деформировав ее и затем запечатав дырочку опять,
вывернуть тор «наизнанку» — так, чтобы внутренняя сторона была
черная, а внешняя — белая?
* 62. Установите, что в трехмерном пространстве не существует
«проблемы четырех красок»: каково бы ни было число п, всегда можно
п тел расположить так, чтобы каждое из них имело общую поверхность
с каждым.
* 63. На торе или на плоскости с граничной идентификацией
(рис. 143) сделайте карту из семи областей, из которых каждая имела
бы общую границу с каждой (см. стр. 291).
64. Четырехмерный тетраэдр, изображенный на рис. 118, состоит
из пяти точек а, Ь, с, d, e, причем каждая связана отрезком с каж-
каждой. Даже если бы было позволено искривлять эти отрезки, всю фи-
фигуру нельзя было бы уместить в плоскости таким образом, чтобы со-
соединяющие линии не пересекались. Другая конфигурация, содержащая
девять соединяющих линий, которые нельзя провести без пересечения,
составляется из шести точек а, Ь, с, а', Ь', с', причем каждая из то-
точек а, Ь, с должна быть соединена с каждой из точек а', Ь', с'. Про-
Проверьте эти утверждения экспериментально и затем попробуйте найти
доказательство, основанное на теореме Жордана. (Доказано, что любая
конфигурация точек и линий, которую нельзя уместить в плоскости без
пересечений, непременно содержит как часть одну из двух указанных
здесь конфигураций.)
65. Рассмотрите конфигурацию, составленную из 6 ребер трехмер-
трехмерного тетраэдра с добавлением отрезка, связывающего середины двух
противоположных ребер. (Два ребра тетраэдра считаются противопо-
противоположными, если у них нет общей вершины.) Установите, что эта конфи-
конфигурация эквивалентна одной из описанных в предыдущем упражнении.
* 66. Пусть р, q, r обозначают три горизонтальные черты в бук-

566 Приложение
ве Е. Эта буква после перемещения дает другое Е с горизонтальными
чертами р', д', г'. Можно ли связать р с р', q с q', г с г' линиями, которые
не пересекались бы взаимно и не пересекали бы ни одного из двух Е?
67. Если мы обходим вокруг квадрата, то меняем направление че-
четыре раза, всякий раз на 90°, а всего — на Д = 360°. Если обходим
вокруг треугольника, то, как известно из элементарной геометрии,
и в этом случае общее изменение направления составляет Д = 360°.
Докажите, что в случае любого простого замкнутого многоугольни-
многоугольника С получается Д = 360°. (Указание: разбейте внутренность С на тре-
треугольники, затем удаляйте граничные отрезки, как на стр. 282. Обозна-
Обозначим последовательно образующиеся границы через В\, В2, Вз, • ¦ • , Вп.
Тогда В\ — С, а Вп есть треугольник. Предполагая, что изменение Дг-
соответствует границе В{, докажите, что Д, = Д,-_х.)
* 68. Пусть С — простой замкнутый контур, обладающий во всех
точках касательным вектором с непрерывно меняющимся направлени-
направлением, и пусть Д есть общее изменение направления при обходе конту-
контура. Докажите, что и в этом случае Д = 360°. (Указание: пусть р0,
Pi) P2) ¦•• ) Рп, Ро — точки на контуре С, разбивающие С на ма-
маленькие, почти прямолинейные отрезки. Пусть контур С составлен из
прямолинейных отрезков poPi, PiP2> ••• , Pi-iPi и из первоначальных
дуг PiPi+i, ... , р„ро- Тогда Со = С, а С„ есть многоугольник. До-
Докажите, что Д^ = Д»+1, и воспользуйтесь результатом предыдущего
упражнения.) Справедливо ли это утверждение для гипоциклоиды, из-
изображенной на рис. 55?
69. Покажите, что если на диаграмме бутылки Клейна (см. стр. 306)
все четыре стрелки направить одинаково (по часовой стрелке), то полу-
получится поверхность, эквивалентная сфере, у которой односвязный кусок
поверхности заменен кросс-кэпом. (Эта поверхность топологически эк-
эквивалентна также расширенной проективной плоскости.)
70. Бутылка Клейна, изображенная на рис. 142, может быть раз-
разрезана плоскостью на две симметрически расположенные части. Пока-
Покажите, что каждая из этих частей есть лента Мебиуса.
* 71. В ленте Мебиуса (см. рис. 139) отождествляются два конца
каждого поперечного отрезка. Убедитесь, что результат топологически
эквивалентен бутылке Клейна.
Все возможные пары точек на прямолинейном отрезке, взятых
в определенном порядке (две точки могут и совпадать), образуют квад-
квадрат в следующем смысле. Если точки фиксируются их расстояниями х,
у от одного из концов А, то пара чисел (х, у) может быть рассматрива-
рассматриваема как прямоугольные координаты некоторой точки квадрата.

Дополнительные замечания, задачи и упражнения 567
Все возможные пары точек на прямолинейном отрезке, взятых не-
независимо от порядка (т. е. пара (х, у) и пара (у, х) рассматриваются как
одинаковые), образуют поверхность S, топологически эквивалентную
квадрату. Чтобы убедиться в этом, будем считать первой ту точку, ко-
которая ближе к концу А, если х ф у. Тогда S состоит из всех пар (х, у),
где или х < у или х — у. В плоскости прямоугольных координат полу-
получается треугольник с вершинами @, 0), @, 1), A, 1).
* 72. Какая поверхность получается из множества пар точек, взя-
взятых в определенном порядке: первая — на прямолинейном отрезке, вто-
вторая — на окружности? (Ответ: цилиндр).
73. Какая поверхность получается из множества пар точек, взятых
в определенном порядке, причем обе точки берутся на окружности?
(Ответ: Тор).
* 74. Какая поверхность получается из множества пар точек, взя-
взятых независимо от порядка на окружности? (Ответ: Лента Мебиуса).
75. Вот правила игры с монетами (одинаковых размеров) на боль-
большом круглом столе. А и В кладут монеты на стол по очереди. Монеты
не должны касаться друг друга; их можно класть на столе как угодно,
лишь бы они не перекрывались и не выступали за край стола. Раз мо-
монета положена, двигать ее уже нельзя. Рано или поздно стол покроется
монетами таким образом, что для новой монеты места уже не найдется.
Выигрывает тот, кто положит монету последним. Докажите, что, как
бы ни играл В, если только А начинает игру, он может быть уверен
в выигрыше — лишь бы играл правильно.
76. Убедитесь, что в случае, если стол в предыдущем упражнении
имеет форму, показанную на рис. 125Ь, то В всегда имеет возможность
выиграть.
Функции, пределы, непрерывность
77. Разложить в непрерывную дробь отношение ОВ : АВ со
стр. 161.
78. Докажите, что последовательность ао ~ у/2, ап+\ = у/2 + у/а^
монотонно возрастает, ограничена числом В = 2 и, значит, имеет пре-
предел. Докажите, что этот предел не может быть отличен от 2 (см. стр. 341
и 375).
* 79. Попробуйте доказать посредством рассуждений, подобных
тем, какие были приведены на стр. 366 и далее, что, какова бы ни была
гладкая замкнутая кривая, всегда можно начертить квадрат, стороны
которого будут касаться кривой.

568 Приложение
80. Функция и = /(ж) называется вогнутой, если середина отрез-
отрезка, соединяющего две любые точки соответствующего графика, лежит
выше самого графика. Например, функция и = ех вогнутая (рис. 278),
тогда как функция и = log ж (рис. 277) — вогнутая.
Докажите, что функция и — f(x) вогнута в том и только в том
случае, если
f() + f{) r(Xi+X2,
причем равенство допускается только при Х\ = ж2.
* 81. Докажите, что в случае вогнутой функции оправдывается и
более общее неравенство
Ax/(xi) + А2/(ж2) > /(AiZi + А2ж2),
где Ai, А2 — две постоянные, подчиненные ограничениям Ai + А2 = 1,
Ai ^ 0, А2 ^ 0. Это равносильно утверждению, что ни одна из точек от-
отрезка, соединяющего две произвольные точки графика, не лежит ниже
кривой.
82. Пользуясь условием упражнения 80, доказать, что функции и —
= у/1 + х2 и и = 2 (при х > 0) — вогнутые, т. е. что при положитель-
положительных значениях
X2j ' Xx+Xi'
83. Докажите то же для и = х2, и = х11 при х > 0; для и — sin ж
при 7Г ^ х ^ 2тг; для м = tgx при 0 ^ х < ^ и для и = -\/1 - а;2
при \х\ ^ 1.
Максимумы и минимумы
84. Найдите кратчайший путь от точки Р к точке Q на рис. 178,
если требуется подойти по очереди п раз к каждой из двух данных
прямых (см. стр. 382).
85. Найдите кратчайший путь от точки Р к точке Q внутри ост-
остроугольного треугольника, если требуется подойти к каждой стороне
в данном порядке (см. стр. 382).
86. Наметьте линии уровня и удостоверьтесь в существовании по
меньшей мере двух седловых точек на поверхности, расположенной над

Дополнительные замечания, задачи и упражнения 569
трехсвязной областью, границы которой находятся на одном и том же
уровне (см. стр. 395). И здесь нужно сделать исключение для того слу-
случая, когда касательная плоскость к поверхности горизонтальна вдоль
некоторой кривой.
87. Исходя из двух произвольных положительных рациональных
чисел по, bo, одну за другой построить пары an+i = \/anbn, 6n+i =
= о (an + bn). Доказать, что они образуют последовательность вложен-
ных интервалов. (Предел этой последовательности при п —> ос есть так
называемое арифметико-геометрическое среднее чисел а$, bo, игравшее
большую роль в ранних исследованиях Гаусса.)
88. Найти длину всего графика на рис. 219 и сравнить с суммой
длин двух диагоналей квадрата.
* 89. Исследовать, при каких условиях, наложенных на точки А\,
Аъ, Аз, А^, получается схема рис. 216 и при каких — схема рис. 218.
* 90. Найти такие расположения пяти точек, для которых сущест-
существовали бы различные минимальные системы путей, удовлетворяющие
угловым условиям. Некоторые из этих систем будут соответствовать
относительным минимум (см. стр. 393).
91. Докажите неравенство Шварца
+ ... + anbnf sC (а\ + ... + a2n){b\ + ... + Ъ2П),
справедливое для каких угодно а,- и Ь^, докажите, что знак равенст-
равенства возможен только при условии пропорциональности между числа-
числами ai и bi. (Указание: обобщите алгебраическую формулу, приведенную
в упражнении 8.)
* 92. Исходя из п положительных чисел х\, ... , хп, мы строим
выражения Sk, определяемые формулами
...Хк + ¦¦¦
причем в числителе стоит сумма всевозможных произведений, состав-
составленных из всех сочетаний п чисел по к. Докажите, что
и что знак равенства возможен только в случае равенства всех чисел
93. При п = 3 эти неравенства сводятся к следующим:
а + Ь + с
3^3
Какие отсюда вытекают экстремальные свойства куба?
?

570 Приложение
* 94. Найти дугу кривой минимальной длины, соединяющую две
точки А, В и вместе с прямолинейным отрезком АВ ограничивающую
наперед заданную площадь. (Ответ: Дуга должна быть круговая.)
* 95. Даны два отрезка АВ и А'В'. Найти дуги кривых, соединя-
соединяющие А с В н А' с В', ограничивающие вместе с отрезками данную
площадь и обладающие наименьшей суммой длин. (Ответ: Дуги должны
быть круговыми, с одинаковыми радиусами.)
* 96. Тот же вопрос — при каком угодно числе отрезков АВ, А'В1
и т.д.
* 97. Даны две прямые, пересекающиеся в точке О. Найти на каж-
каждой из них по точке А и В и затем соединить эти точки кривой линией
таким образом, чтобы при заданной площади, ограниченной кривой и
обеими прямыми, длина дуги была минимальной. (Ответ: Дуга должна
быть круговой и перпендикулярной к обеим прямым.)
* 98. Тот же вопрос со следующим видоизменением: обратить
в минимум требуется не длину кривой АВ, а весь периметр фигуры,
т. е. сумму дуги АВ и отрезков О А и ОВ. (Ответ: Дуга — по-прежнему
круговая, но выпячивается наружу, касаясь отрезков в их концах.)
* 99. Обобщите эту проблему на случай нескольких угловых сек-
секторов.
* 100. Установите, что «почти плоские» поверхности на рис. 240 не
являются в точности плоскими, кроме стабилизирующей поверхности
в центре куба. (Замечание: определить эти поверхности аналитически
представляет заманчивую, еще не решенную проблему. То же относит-
относится и к поверхностям на рис. 251. Что касается рис. 258, то здесь в самом
деле имеется 12 симметрических плоскостей, образующих по диагона-
диагоналям углы в 120°.)
Некоторые дополнительные предложения по поводу опытов с мыль-
мыльными пленками. Сделайте опыты, указанные на рис. 256 и 257, при чис-
числе стержней, большем трех. Изучите, что происходит в предельных слу-
случаях, когда объем воздуха становится все меньше. Экспериментируйте
с непараллельными плоскостями и другими поверхностями. Раздувайте
центральный кубик на рис. 258, пока он не наполнит весь большой куб
и не выпятится за пределы граней; потом выдувайте из него воздух,
пытаясь обратить процесс.
* 101. Найти два равнобедренных треугольника с данной суммой
периметров и с минимальной суммой площадей. (Ответ: Треугольники
должны быть конгруэнтны. Воспользуйтесь методами дифференциаль-
дифференциального исчисления.)
* 102. Найти два треугольника с данной суммой периметров и мак-

Дополнительные замечания, задачи и упражнения 571
симальной суммой площадей. (Ответ: Один треугольник вырождается
в точку, другой должен быть равносторонним.)
* 103. Найти два треугольника с данной суммой площадей и мини-
минимальной суммой периметров.
* 104. Найти два равносторонних треугольника с данной суммой
площадей и максимальной суммой периметров.
Дифференциальное и интегральное исчисления
— /х+1
105. Составьте производные от функций yl -f x, vl + ж2, '
ж-1'
исходя непосредственно из определения, затем преобразовывая раз-
разностное отношение таким образом, чтобы не представило труда вы-
вычислить предел при х —> х\ (см. стр. 474-477).
106. Докажите, что функция у = е~х1х~ с дополнительным услови-
условием у = 0 при х = 0 имеет производные всех порядков, равные нулю,
в точке х = 0.
107. Установите, что функция упражнения 106 не разлагается в ряд
Тейлора в точке х = 0 (см. стр. 540).
108. Найти точки перегиба (f"(x) = 0) кривых
у = е~х и у = хе~х .
109. Покажите, что если f"(x) — полином с п различными корня-
корнями Xi, X2, • ¦ . , Хп, ТО
f С-тЛ
J V**'/
* 110. Исходя из определения интеграла как предела суммы, дока-
доказать, что при п -» оо
„/1,1, I 1 ^ ) *
W2 + 2 222+"
22+n2+" n2+nV 4-
* 111. Таким же образом доказать, что
112. Нарисуйте рис. 276 на клетчатой бумаге в крупном масштабе
и затем, подсчитывая маленькие квадратики, попадающие в заштрихо-
заштрихованную область, найдите приближенное значение тт.

572 Приложение
113. Воспользуйтесь формулой G) на стр. 499, чтобы вычислить тг
с погрешностью, не превышающей 0,01.
114. Докажите, что е = —1 (см. стр. 542).
115. Данная замкнутая кривая увеличивается, расширяясь в отно-
отношении 1 : х. Пусть L(x) и А(х) обозначают длину расширенной кривой
и ограниченную ею площадь. Покажите, что —— -> 0 при х -> оо и что
А(х)
даже —-—г —> 0 при х —> оо, если к > \. Проверьте это для окружности,
А{х)к 1
квадрата и * эллипса. (Площадь более высокого порядка возрастания,
чем длина кривой. См. стр. 532 и дальше.)
116. Показательная функция часто встречается в следующих ком-
комбинациях:
и = shx = hex - е~х), v = chx = \{ех + е~х),
ад = th ж = ,
х х
называемых соответственно гиперболическим синусом, гиперболическим
косинусом и гиперболическим тангенсом. Эти функции обладают многи-
многими свойствами, напоминающими свойства тригонометрических функ-
функций. Они связаны с гиперболой и2 — v2 = 1 так же, как тригонометри-
тригонометрические функции и — cos х и v = sin х связаны с окружностью и2 + v2 = 1.
Читателю предлагается проверить следующие формулы и сопоставить
их с тригонометрическими формулами:
d(shx) d(shx) , d(thx) i
= chx =shx -
dx ' dx ' dx ch2
sh(x + x1) — shx • char' + chx • shx',
ch(x + ж') = chx • char' + shx • shx'.
Обратные функции таковы:
x = Arshu =
x = Archi> =
x — Arthiu —
In (и +
ln(«-
2Ы1
л/и2 +
1),
T)
\w\<
(О
l),

Дополнительные замечания, задачи и упражнения 573
Их производные имеют вид
d(Arshu) i d(Archw) \
117. Уясните себе аналогию между гиперболическими и тригоно-
тригонометрическими функциями на основе формулы Эйлера.
* 118. Выведите простые формулы для сумм
sh х + sh 2х + ... + sh nx
tj + ch x + ch 2x + ... + ch nx
аналогично формулам, выведенным в упражнении 14 в случае тригоно-
тригонометрических функций.
Техника интегрирования
Теорема, доказанная на стр. 496, сводит проблему интегрирования
функции f(x) в пределах от а до & к нахождению функции G(x), перво-
первообразной по отношению к функции f(x). Интеграл тогда просто равен
разности G(b) — G{a).
Для таких первообразных функций (определяемых с точностью до
постоянного слагаемого) употребительно наименование «неопределен-
«неопределенный интеграл» и чрезвычайно удобное обозначение
G(x) = J f(x)dx,
без обозначения пределов интегрирования. (Это обозначение может не-
несколько дезориентировать начинающего: см. замечания на стр. 496.)
Из каждой формулы дифференцирования легко получить, путем
ее обращения, некоторую формулу неопределенного интегрирования.
К этой, несколько эмпирической, процедуре мы здесь добавим два важ-
важных правила, которые по существу представляют собой не что иное, как
обращение правил дифференцирования сложной функции и произведе-
произведения двух функций. В их интегральной форме их называют правилами

574 Приложение
интегрирования посредством подстановки и интегрирования «по час-
частям».
А) Первое правило вытекает из формулы дифференцирования
сложной функции
Н(и) = G(x),
где функции
х = ф(и) и и — <р(х)
предполагаются взаимно однозначно связанными в рассматриваемой
области.
В таком случае мы имеем
Я'(«) = G\x)rl/{u).
Полагая
G'(x) = /(я),
мы можем написать
G{x) = I f(x)dx
и также
С(х)ф'(и) = f(x)i>'(u),
а это вследствие предыдущей формулы для Н'(и) равносильно
Я(и) = f f[ip(u)]ip'{u)du.
Итак, принимая во внимание, что Н(и) = G(x), мы получаем
\}iP'{u)du. (I)
Будучи записано в обозначениях Лейбница (см. стр. 490), это пра-
правило принимает практически очень удобный вид
f(x)dx = I f(x)
оказывается, что мы не сделаем ошибки, если символ dx заменим сим-
символом ^р- du так, как будто бы dx и du были числами, а 4^ — их отно-
du du
шением.
Проиллюстрируем полезность формулы (I) несколькими примера-
примерами.

Дополнительные замечания, задачи и упражнения 575
a) J = / —— du. Станем читать формулу (I) справа налево, по-
полагая в ней х = \пи = ф(и). Тогда получим ip'(u) = i, f(x) = -, так
что
или
du
J и]
= lnlnu.
f, In и
Результат можно проверить посредством дифференцирования; мы
получаем
и In и du
Ъ) J = f ctgudu = f C?SM du. Полагая x = sinw = ib(u), мы имеем
откуда следует
или
/ ctg и du = In sin u.
И этот результат проверяется дифференцированием.
c) Допустим, что задан интеграл более общего вида
/ф'(и)
ф(и)
положив х = ф{и), f(x) = х, мы найдем
J = J -— =1пж = 1пг/)(м).
d) J = / sin ж cos a; dx. Полагаем sin ж = «, cos ж = ^. Тогда
Udx X~ J U U" 2 - 2Sm X'
e) J = J -i—i du. Полагаем In и = ж, — = —. Тогда

576 Приложение
В следующих примерах мы используем формулу (I), считая ее сле-
слева направо.
{) J = J ^~ Полагаем у/х = и. Тогда х = и2 и ~ = 2м. Поэтому
J = / \-2udu = 2u- 2y/x.
g) С помощью подстановки х = аи, где а — постоянная, получаем
J a2 + x*~J du a2 1 + n2 U~/ al + U2~« C8a'
h) J = f \/l - ж2 ds. Полагаем ж = cos и, =^ = -sin и. В таком
случае
J=- I sin2 udu = -
Принимая во внимание, что
sin 2u = 2 sin и cos « = 2 cos u v 1 — cos2 u,
приходим к формуле
J = — 77 arccos ж + тгжу 1 — ж2.
Вычислите следующие интегралы и проверьте результаты посред-
посредством дифференцирования:
/я
и du 124. / dx.
u2-u+l J x2 + 2ax + b'
120. / ue du. 125. j t2 \Jl + i3 dt.
t i i
_dt.
t2
121 f du 126 f t + 1
' J мAпм)"- - У y/TZTi
122. / o Sx. dx. 127. fj^—dt.
J 3 + 4ж J l-(
123. / „ da: . 128. [cosntsintdt
J x2 + x + 1 У
129. Докажите, что
"¦x _ A Arth — / йа- =
(Сравните с примерами g), h).)
Arsh^.

Дополнительные замечания, задачи и упражнения 577
В) Правило дифференцирования произведения (стр. 484)
(р(х) ¦ q(x))' = р(х) ¦ q'(x) +p'(x) ¦ q(x)
в интегральной форме записывается следующим образом:
р{х) ¦ q{x) = / р(х) ¦ q'{x)dx + / р'(х) ¦ q(x)dx,
или же
/ Р(х) ' q'{x)dx = p(x)q(x) - / р'(х) ¦ q{x)dx. (II)
В этой форме оно называется правилом интегрирования по частям. Это
правило бывает полезно в тех случаях, когда функция, стоящая под ин-
интегралом, имеет Buap(x)q'(x), причем неопределенный интеграл q(x) от
функции q'{x) известен. Формула (II) сводит проблему неопределенного
интегрирования функции p(x)q'(x) к проблеме интегрирования функ-
функции p'(x)q(x), что часто оказывается более простым.
a) J = flnxdx. Положим р(х) = In ж, q'(x) = 1, так что q(x) = х.
Тогда формула (II) нам дает
/ In х dx — х In x — I — dx = x In x — x.
b) J = f xlnxdx. Положим p(x) = In ж, q'{x) = x. Тогда
с) J = f xs'mxdx. На этот раз положим р(х) = x, q(x) = —cosж и
получим
/ ж sin ж dx = —х cos ж + sin ж.
Вычислите по частям следующие интегралы:
130. fxexdx. 131. fx2cosxdx.
(Указание: примените (II) дважды.)
132. f xa\nxdx{a^ -I). 133. f x2ex dx.
(Указание: воспользуйтесь упражнением 130.)

578 Приложение
Интегрируя по частям J sinm x dx, мы получаем замечательную
формулу для числа тг в виде бесконечного произведения. Напишем
функцию sinm х в виде sin ж-sina: и проинтегрируем по частям в пре-
пределах от 0 до ~. Тогда получим
Я-/2 Я-/2
/ sin xdx = (m — 1) / sinm 2 ж cos3 ж dx =
о
Ж/2
/" /"
— \IIL X) f Dili t*' (X»t/ T^ W/t i. I I Oil
J J
О
или же
тг/2 тг/2
/" sinm х dx = 52^1 /" Si
о о
(так как первый член в правой части (II), pq, обращается в нуль при х =
= 0 и х = тг/2). Применяя повторно последнюю формулу, найдем следу-
тг/2
= / si
о
ющие значения интегралов 1т = / sinm ж йж (формулы различаются
в зависимости от четности п):
j _ 2п- 1 2п-3 1 тг
2п ~ 2п ' 2п - 2 ""' 2 ' 2 '
Т - 2п 2"~'2 2
2n+1 2n + l n-l "¦ 3'
Так как 0 < sin ж < 1 при 0 < х < тг/2, то sin2" х > sin2" х > sin2n+1 x
и, следовательно,
/2n-i > hn > hn+i, (см. стр. 469)
или
^ ^ i
7 ^ 7 ^ i-
-*2n+l J2n+1
Подставляя в эти неравенства вычисленные значения интегралов, мы
получаем
2п + 1 1 ¦ 3 • 3 • 5 • 5 • 7 • • • Bп - 1)Bп - 1)Bп + 1)Bп +
> "
2п > 2-2-4-4-6--- Bп)Bп) 2
2 > '

Дополнительные замечания, задачи и упражнения 579
Остается положить п —> оо; тогда, убедившись, что средняя часть нера-
неравенства стремится к 1, мы получаем следующее, принадлежащее Уол-
лису, представление для числа тг/2:
тг 2-2-4-4-6-6---2п-2п---
2 1 • 3 • 3 • 5 • 5 • 7 ... Bп - 1)Bп - 1) • Bп + 1) •
24"(п!L
= lira при п —> оо.
[Bп)!]2Bп + 1)
37*

Рекомендуемая литература
Общие ссылки
[1] Ф. Клейн. Элементарная математика с точки зрения высшей. Пер.
с нем., М.-Л., Гостехиздат. 1934.
[2] Г. Радемахер и О. Теплиц. Числа и фигуры. Пер. с нем., М., изд.
«Наука», 1966.
[3] Г. Штейнгауз. Математический калейдоскоп. Пер. с польск., М.-Л.,
Гостехиздат, 1949.
[4] Е.Б.Дынкин и В.А.Успенский. Математические беседы. М.-Л.,
Гостехиздат, 1952.
[5] Г. Вилейтнер. История математики от Декарта до середины XIX
столетия. М., изд. «Наука», 1966.
[6] Ф. Клейн. Лекции о развитии математики в XIX столетии. Пер.
с нем., М.-Л., Гостехиздат, 1937.
[7] Историко-математические исследования. Вып. I-XVII, М., Гостех-
издат-Физматгиз — изд. «Наука», 1950-1965.
[8] Математика в СССР за 40 лет. М., Физматгиз, 1959, т. I.
Глава 1
[9] Л.Генкин. О математической индукции. Пер. с англ., М., Физмат-
Физматгиз, 1959.
[10] И. В. Арнольд. Теоретическая арифметика. М., Учпедгиз, 1939.
[11] Г. Н. Берман. Число и наука о нем. М., Физматгиз, 1960.
[12] А. О. Гельфонд. Решение уравнении в целых числах. М.-Л., Гостех-
Гостехиздат, 1952.
[13] А. О. Гельфонд. Трансцендентные и алгебраические числа. М., Физ-
Физматгиз, 1952.

Рекомендуемая литература 581
Глава II
[14] Б.Л.Ван дер Варден. Современная алгебра. Пер. с нем., М.-Л.,
ОНТИ, 1934.
[15] И.М.Гельфанд. Лекции по линейной алгебре. М.-Л., Гостехиздат,
1948.
[16] А.Г.Курош. Высшая алгебра. М., изд. «Наука», 1966.
[17] И.В.Проскуряков. Числа и многочлены. М., изд. «Просвещение»,
1965.
[18] А.Г.Курош. Теория групп. М., изд. «Наука», 1966.
[19] Н. Н. Лузин. Теория функции действительного переменного. М., Уч-
Учпедгиз, 1948.
[20] П. С. Александров. Введение в общую теорию множеств и функции.
М.-Л., Гостехиздат, 1948.
[21] Н.Я.Виленкин. Рассказы о множествах. М., изд. «Наука», 1966.
[22] И.С.Градштейн. Прямая и обратная теорема. М.-Л., Физматгиз,
1961.
[23] А. Тарский. Введение в логику и методологию дедуктивных наук.
Пер. с англ. М., ИЛ, 1948.
[24] П.С.Новиков. Элементы математической логики. М., Физматгиз,
1959.
[25] С.К.Клини. Введение в метаматематику. Пер. с англ., М., ИЛ,
1957. ч. I.
[26] Д. Гильберт и В. Аккерман. Введение в теоретическую логику. Пер.
с нем., М., ИЛ, 1947.
[27] А. А. Марков. Конструктивное направление {в математике и логи-
логике). «Философская энциклопедия», т. 3, М., 1964.
Глава III
[28] Л. А.Люстерник. Выпуклые тела. М.-Л., Гостехиздат, 1936.

582 Рекомендуемая литература
[29] А. Д. Александров. Выпуклые многогранники. М.-Л., Физматгиз,
1950.
[30] Б.И.Аргунов и М.Б.Балк. Построения с помощью циркуля и ли-
линейки. М., Физматгиз, 1958.
[31] М.Б.Балк. Геометрические приложения понятия о центре тяжес-
тяжести. М., Физматгиз, 1959.
[32] В. Г. Болтянский. Равновеликие и равносоставленные фигуры. М.,
Физматгиз, 1956.
Глава IV
[33] Д.Гильберт. Основания геометрии. Пер. с нем., М.-Л., Гостехиздат,
1948.
[34] Ж.Адамар. Неевклидова геометрия. Пер. с франц., М.-Л., Гостех-
Гостехиздат, 1951.
[35] О. Л. Вольберг. Основные идеи проективной геометрии. М.-Л.,
ОНТИ, 1935.
[36] В. Ф. Каган. Лобачевский. М.-Л., изд. АН СССР, 1948.
Глава V
[37] В.Г.Болтянский и В.А.Ефремович. Очерк основных идей тополо-
топологии. Сб. «Математическое просвещение», М., Физматгиз, вып. 2
A957), 3 A958) 4 A959) и 6 A961).
[38] Д.Гильберт и С.Кон-Фоссен. Наглядная геометрия. Пер. с нем., М.,
Физматгиз, 1951.
[39] П. С. Александров. Комбинаторная топология. М.-Л., Гостехиздат,
1947.
[40] Г. Зейферт и В. Трельфалль. Топология, пер. с нем., М., Гостехиздат,
1938.
Главы VI-VIII
[41] В.Г.Болтянский. Что такое дифференцирование. М., Физматгиз,
1960.

Рекомендуемая литература 583
[42] И. Б. Абельсон. Максимум и минимум. М.-Л., ОНТИ, 1935.
[43] Р. Курант. Дифференциальное и интегральное исчисление. Пер. с
нем., М.-Л., Гостехиздат, 1931.
[44] Г. М.Фихтенгольц. Курс дифференциального и интегрального исчис-
исчисления. М., изд. «Наука», 1966.
[45] А. С. Солодовников. Введение в линейную алгебру и линейное про-
программирование. М., изд. «Просвещение», 1966.

Предметный указатель
Абсолютное значение 88
Аксиоматика 256
Аксиомы 256
Алгебра булева 151
— множеств 144
— основная теорема 136, 313
— числовых полей 154
Алгебраические уравнения 136
— числа 139
Алгоритм Евклида 72
Анализ математический 451
основная теорема 494
Аналитическая геометрия 105
п-мерная 270
Аполлония проблема 163
Аргумент комплексного числа 130
Арифметика законы 26
— основная теорема 50
Арифметические прогрессии 38
простые числа в а. п. 54
Арифметическое значение корня
325
Архимеда метод трисекции угла
178
Асимптота гиперболы 108
Асимптотически равно 57, 534
Ассоциативные законы для мно-
множеств 148
для натуральных чисел 26
для рациональных чисел 84
Бесконечно удаленная плоскость
225
прямая 222
— удаленные точки 221
элементы (в проективной
геометрии) 221
«Бесконечно малые» 490
Бесконечность 35, 110
— ряда простых чисел 49
Бесконечные десятичные дроби 94
— непрерывные дроби 348
— произведения 546
— ряды 536
Биномиальная теорема 42
Биномиальный ряд 539
Больцано теорема 361
применения 365
Брахистохрона 433, 435
Брианшона теорема 231
Вариационное исчисление 432
Вейерштрасса теорема об экстре-
экстремальных значениях 362
Вектор 131
Вероятность 151
Взаимная непрерывность (соот-
(соответствия, отображения) 285
— однозначность (соответствия,
отображения) 111
Возрастания порядок 533
Вторая производная 481
Вычеты квадратические 67
Гармонически сопряженные пары
216
Гармонический ряд 544
Гарта инверсор 197

Предметный указатель
585
Геодезическая 379
Геодезические на сфере 437
Геометрическая прогрессия 39
Геометрические построения Мас-
керони 188
квадратичных корней 160
правильных многоугольни-
многоугольников 160
рациональных чисел 158
с помощью одного циркуля
188
с помощью одной линейки
192
с помощью различных ин-
инструментов 193
теория 154
числовых полей 159
Геометрические преобразования
180
Геометрия и-мерная 270
— Римана 268
— аксиомы 259
— аналитическая 105
— гиперболическая 260
— комбинаторная 273
— метрическая 209
— неевклидова 260
— проективная 209
— синтетическая 232
— теория построения 157
— элементарная, экстремальные
задачи 379
Герона теорема 380
Гипербола свойство касательных
385
— уравнение 108
Гиперболические функции 572
Гиперболический параболид 332
Гиперболоид 254
Гипоциклоида 194
Гольдбаха проблема 58
Граничные условия в задачах на
экстремумы 428
График функции 323
Группа 208
Двенадцатеричная система 31
Движение эргодическое 403
Движения (преобразования) 181
Двоичная система 34
Двойное отношение 212
Двойственности принцип в алгеб-
алгебре множеств 149
в геометрии 232
Дедекиндово сечение 104
Дезарга теорема 210
Действительные числа 94, 103
Декартовы координаты 106
Деление на нуль 86
Деление окружности, уравнение
135
Десятиугольник правильный, по-
построение 160
Десятичные дроби 92
Деформация 285
Дзета-функция 545
Динамика Ньютона 522
Диофантовы уравнения 80
Дирихле принцип 417
Дистрибутивные законы для мно-
множеств 148
для натуральных чисел 26
для рациональных чисел 84
Дифференциалы 492
Дифференциальные уравнения 515
Дифференциальный символ 493
Дифференцирование 477
Дифференцируемость 524
Длина кривой 530

586
Предметный указатель
Доказательство: конструктивное,
косвенное, д. существования
120
Дополнение множества 149
Дроби десятичные 92
— непрерывные 79
е выражение 510
—- иррациональность 346
— как основание натуральных ло-
логарифмов 505
— как предел 345
— эйлерово число 344, 502
Евклида алгоритм 73
Единица (корень из е.) 133
Единичная окружность 129
Жор дана теорема 287, 311
Зависимое переменное 319
Затухающие колебания 521
Идеальные элементы в проектив-
проективной геометрии 221
Извлечение квадратного корня (в
геометрии) 160
Измерение 82
Изопериметрические проблемы
425
Инвариантность 198
— двойного отношения 214
— углов при инверсии 198
Инверсия 181
— окружность 181
— полюс (центр) 182
Инверсоры 196
Индексы 297
Индукция математическая 35
— эмпирическая 35
Интеграл 452, 527
Интервал 88
Интуиционизм 257
Инцидентность (принадлежность)
210
Иррациональные числа как беско-
бесконечные десятичные дроби 94
определяемые последова-
последовательностями 105
определяемые сечениями 103
определяемые стягивающи-
стягивающимися отрезками 102
Исключенного третьего закон 121
Исчерпания метод 453
Исчисление вариационное 432
Итерации (пределы при и.) 376
Канторова теория (бесконечных)
множеств 110
Канторово множество 291
Кардинальное число (мощность)
117
Карта регулярная 308
Касательная 469
Касательные к эллипсу и гипербо-
гиперболе, свойство 383
Квадранты (координатные четвер-
четверти) 106
Квадратные уравнения 124
Квадратный корень, геометричес-
геометрическое построение 160
Квадратура круга 180
Квадрики 254
Классификация (топологическая)
поверхностей 300
Клейна бутылка 306
— модель 263
Коаксиальные плоскости 217
Колебания 520
Коллинеарные точки 210
Комбинаторная геометрия 273

Предметный указатель
587
Коммутативные законы для мно-
множеств 148
для натуральных чисел 26
для рациональных чисел 84
Компланарные прямые 216
Комплексного переменного теория
функций 543
Комплексные числа 124
(операции с к.ч.) 125
аргумент 130
модуль 128
тригонометрическое пред-
представление 130
Конгруэнтность 206
Конические сечения 240
как множества прямых 249
как множества точек 249
метрическое определение
240
проективное определение
245
уравнения 108
Конкуррентные прямые 211
Константа (постоянная) 320
Конструктивные доказательства
121
Континуум действительных чисел
94
Континуум-гипотеза 123
Координаты обобщенные 233
— однородные 234
— прямоугольные (декартовы)
106
Корни из единицы 134
Косвенное доказательство 120
Кратность корней алгебраическо-
алгебраического уравнения 138
Кривая длина 530
— уравнение 107
Кривизна 482
Кросс-кэп 305
Лейбница формула для 7Г 500
Линии уровня 332
Лиувилля теорема 140
Логарифм натуральный 502
Логика математическая 150
Логическая сумма 147
Логическое произведение 147
Максимумы и минимумы 379, 483
Маскерони построения 188
Математическая индукция 35
— логика 150
Математический анализ 451
основная теорема 494
Мебиуса лента (лист) 304
Метрическая геометрия 209
Механические инструменты, по-
построения с их помощью 193
Минимакса точки 395
Мнимые числа (см. комплексные
числаI25
Многогранники п-мерные 275
— правильные 280
— простые 280
— род 303
— эйлерова характеритика 303
Множеств алгебра 144
— эквивалентность 117
Множество 110, 144
— дополнение 149
— компактное 366
— пустое 145
Множители простые 50
Модуль комплексного числа 128
Монотонная последовательность
341
— функция 326
Морза соотношения 396
Муавра формула 132

588
Предметный указатель
Наименьших квадратов метод 415
Наклон 469
Направление угла 200
Натуральные числа 25
Нахождение середины отрезка с
помощью одного циркуля 186
Неевклидова геометрия 260
Независимое переменное 319
Неподвижная точка 295
Непрерывное переменное 318
Непрерывность функции многих
переменных 333
одного переменного 328
Непрерывные дроби 79
Неравенства 412
Неразрешимость классических
проблем 173
Несоизмеримые отрезки 89
Несчетность континуума 114
n-мерная геометрия 270
Нуль 85
Ньютоновская динамика 522
Область изменения переменной
317
Обобщения принцип 86
Образ 181
Обратные операции 84
— функции 323
Объединение множеств 147
Ограниченная последовательность
342
Однозначность разложения на
множители 50
Однородные координаты 234
Односвязность 286
Односторонние поверхности 303
Окружность, уравнение 107
Опыты с мыльными пленками 439
Оси конических сечений 108
— координат 106
Основания математики 123
Основная теорема алгебры 136, 313
анализа 494
арифметики 50
Отображение (преобразование)
181
Отражение в общих экстремаль-
экстремальных задачах 381
— относительно одной или не-
нескольких прямых 181
окружностей 181
системы окружностей 204
треугольника 381
Отражение повторное 203
Отрезки вложенные 101
— стягивающиеся 101
Отрицательные числа 85
Паппа теорема 229
Парабола 241
Парадоксы Зенона 353
— бесконечного 121
Параллельность и бесконечность
220
Паскаля теорема 229, 252
— треугольник 43
Первообразные (примитивные)
функции 496
Переменное 317
— действительное 318
— зависимое 319
— комплексное 543
— независимое 319
Пересечение множеств 147
Пересчет 112
Перспектива 207
7г 346
Пифагоровы числа 69
Плато проблема 438

Предметный указатель
589
Плотность множества рациональ-
рациональных чисел 88
Площадь 452
Поверхности односторонние 303
Подмножество 146
Подполе 167
Позиционная система 29
Показательная (экспоненциаль-
(экспоненциальная) функция 505
дифференциальное уравне-
уравнение 516
порядок возрастания 533
Поле 86
Полный четырехсторонник 219
Поля числовые алгебра 166
геометрическое построение
166
Порядок возрастания 533
— точки 314
Поселье инверсор 196
Последовательность 101, 114, 335
— монотонная 341
— ограниченная 342
— сходящаяся, расходящяяся, ко-
колеблющаяся 342
Построения геометрические 157
— с помощью одного циркуля 188
Постулат о параллельных 260
Постулаты 256
Правильные многогранники 280
п-мерные 275
— многоугольники, построение
160
Правильный десятиугольник, по-
построение 160
Пределы 95, 335
— бесконечных десятичных дро-
дробей 99
— геометрических прогрессий 97
— последовательностей 337
— при итерации 376
непрерывном приближении
351
— примеры 371
Преобразования геометрические
180
— проективные 207
— топологические 285
— уравнения 333
Принцип наименьшего числа 50
Присоединение иррациональных
чисел 94
Проблема ракраски карт 289
Прогрессии арифметические 38
— геометрические 39
Проективная геометрия 209
Проективное преобразование 207
— соответствие 219
Произведение бесконечное 546
— логическое 147
Производная 469
— вторая 481
Прообраз (при отображении) 181
Простая замкнутая кривая 288
Простой многогранник 280
Простые числа 48
распределение 55, 548
Прямой линий уравнение 107
Прямые компланарные 216
— конкуррентные 210
Пустое множество 145
Пучок прямых 245
Пятиугольник правильный, по-
построение 190
Работа 528
Радианная мера 322
Радиоактивный распад 518
Разложение на простые множите-
множители, единственность 50

590
Предметный указатель
Размерность 291
Разрешимость проблем 155
Разрыв со скачком 329
Разрывность функции 329
Разрывные функции как пределы
непрерывных 375
Распада закон 518
Расстояние 106
Расходимость последовательнос-
последовательностей 340
— рядов 536
Расширение поля 167
Рациональные числа 82
операции 84
плотность 88
счетность 112
Рациональные операции, геомет-
геометрическое построение 157
Решето Эратосфена 52
Риманова геометрия 268
Род поверхности 300
Ряды бесконечные 536
Световые лучи 380
Связность 286
Сегмент (отрезок) 88
Семиричная система 33
Семиугольник правильный, невоз-
воможность построения 178
Сечение (множества действитель-
действительных чисел) 104
Символ 125
Синтетическая геометрия 232
Скорость 478
Сложение действительных чисел
105
— комплексных чисел 125
— множеств 147
— натуральных чисел 26
— рациональных чисел 84
Сложные проценты 519
— функции 327
Соответствие (отображение) меж-
между множествами 111
Сопряженные комплексные числа
128
Составные числа 48
Сравнения 60
Среднее арифметическое 412
— геометрическое 413
Стационарные точки 392
Сумма логическая 147
— первых квадратов 40
кубов 41
Существование в математике 123
— доказательство 121
Сходимость последовательностей
340
— рядов 536
Счетность множества рациональ-
рациональных чисел 112
Тейлора ряд 540
Теорема о неподвижной точке 295
пяти красках 308
четырех красках 289
Теоремы существования 48
Теория чисел 48
Топологическая классификация
поверхностей 300
Топологическое преобразование
284
Топология 278
Тор 300
— трехмерный 308
Точечный ряд 249
Точки коллинеарные 210
Трансцендентность числа тг 180
Трансцендентные числа 139

Предметный указатель
591
Треугольники образованные све-
световыми лучами 402
— экстремальные свойства 380
Тригонометрические функции 322
Трисекция угла 176
Удвоение куба 173
Узлы 299
Уличной сети проблема 410
Уоллиса формула 348, 579
Уравнение гиперболы 108
— деления окружности 135
— диофантово 80
— квадратное 124
— корни 137
— кратность корней 138
— кривой 107
— прямой 107
— эллипса 108
Уравнения движения 521
Уровня линии 332
Ускорение 481
Факториал 44
Ферма великая теорема 71
— принцип 433
— теорема 65
— числа 156
Фокус конического сечения 108
Формализм 124,257
Функция 316
— (кривая) вогнутая, выпуклая
482, 568
— график 323
— комплексного переменного 541
— многих переменных 331
— монотонная 326
— непрерывная 329
— обратная 323
— определение 318
— первообразная 496
— сложная 327
Целые числа отрицательные 85
положительные 85
Центр окружности, построение с
помощью одного циркуля 186
Циклоиды 193
Четырехсторонник полный 219
Числа Ферма 156
— алгебраические 139
— действительные 88-91
— допускающие построение 165
— кардинальные 117
— комплексные 124
— натуральные 25
— отрицательные 85
— пифагоровы 69
— простые 48
— рациональные 82
— составные 48
— трансцендентные 139
Числовая система 82
Числовые поля 166
Шарнирные механизмы 195
Шварца проблема 397
Штейнера построения 192
— проблема 405
Эйлера функция 77
Эйлерова характеристика поверх-
поверхности 302
Эквивалентность множеств 111
Экстремальное решение задач на
минимум 428
Экстремальные задачи 379
в элементарной геометрии
379
общий принцип 389

592
Предметный указатель
с граничными условиями
428
— расстояния от данной кривой
386
Экстремумы и неравенства 412
Эксцентриситет (конического се-
сечения) 108
Эллипс свойство касательных 383
— уравнение 108
Эллиптическая геометрия 268
Эллиптические точки 269
Эпициклоида 195
Эратосфена решето 52
Эрлангенская программа 207
Курант Рихард, Роббинс Герберт
ЧТО ТАКОЕ МАТЕМАТИКА?
Элементарный очерк идей и методов
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Компьютерный набор и верстка С. В. Высоцкий
Корректор М. А. Ложкина
Подписано к печати 09.01.01. Формат 60 х 841/16.
Печать офсетная. Усл.печ.л. 34,41. Уч. изд. л. 35,26.
Гарнитура Computer Modern Roman. Бумага офсетная №1.
Тираж 1500 экз. Заказ № 340.
Научно-издательский центр «Регулярная и хаотическая динамика»
426057, г. Ижевск, ул. Пастухова, 13.
Лицензия на издательскую деятельность ЛУ №084 от 03.04.00.
http://rcd.ru E-mail: borisov@uni.udm.ru
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов в ГИПП «Вятка».
610033, г. Киров, ул. Московская, 122.